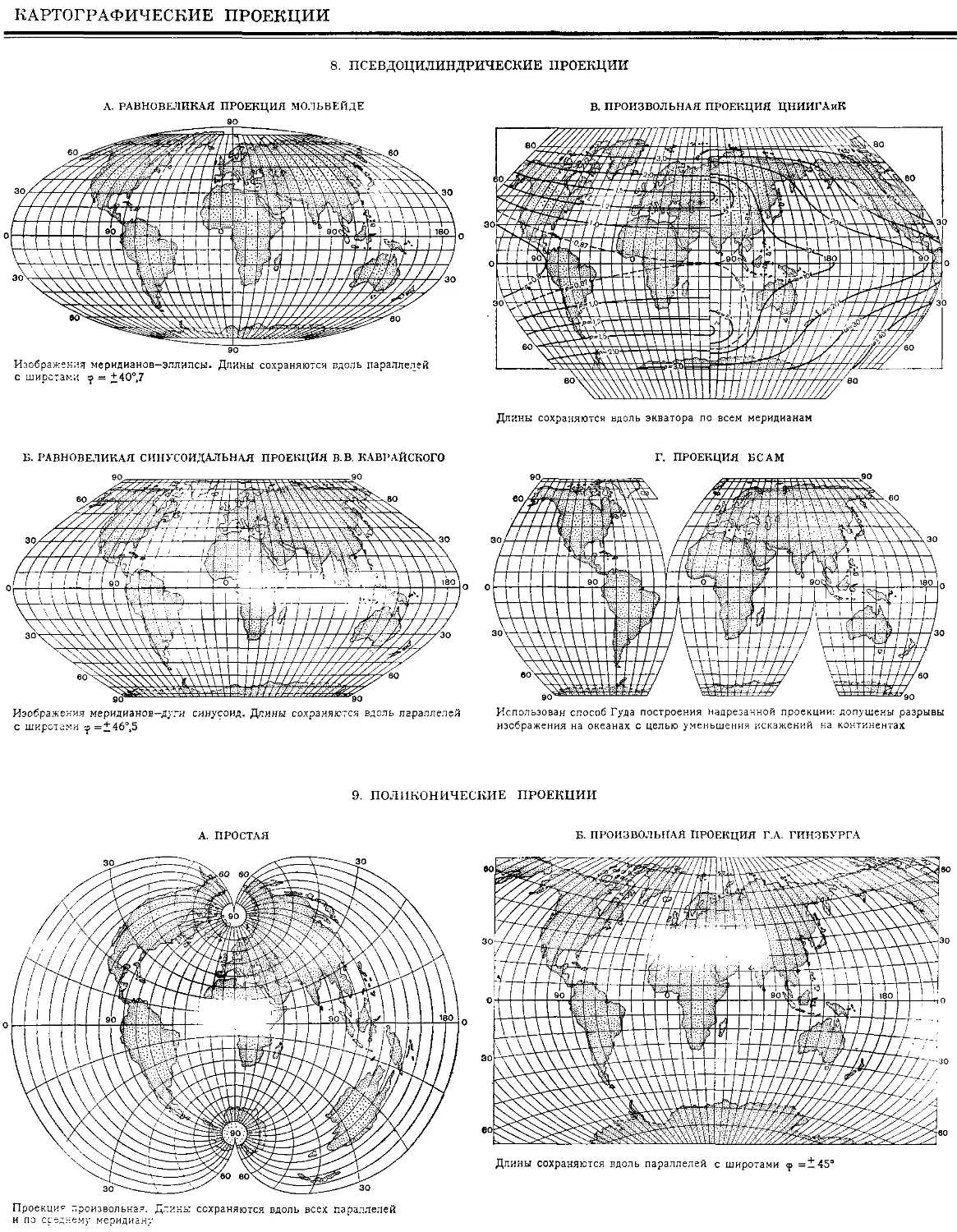
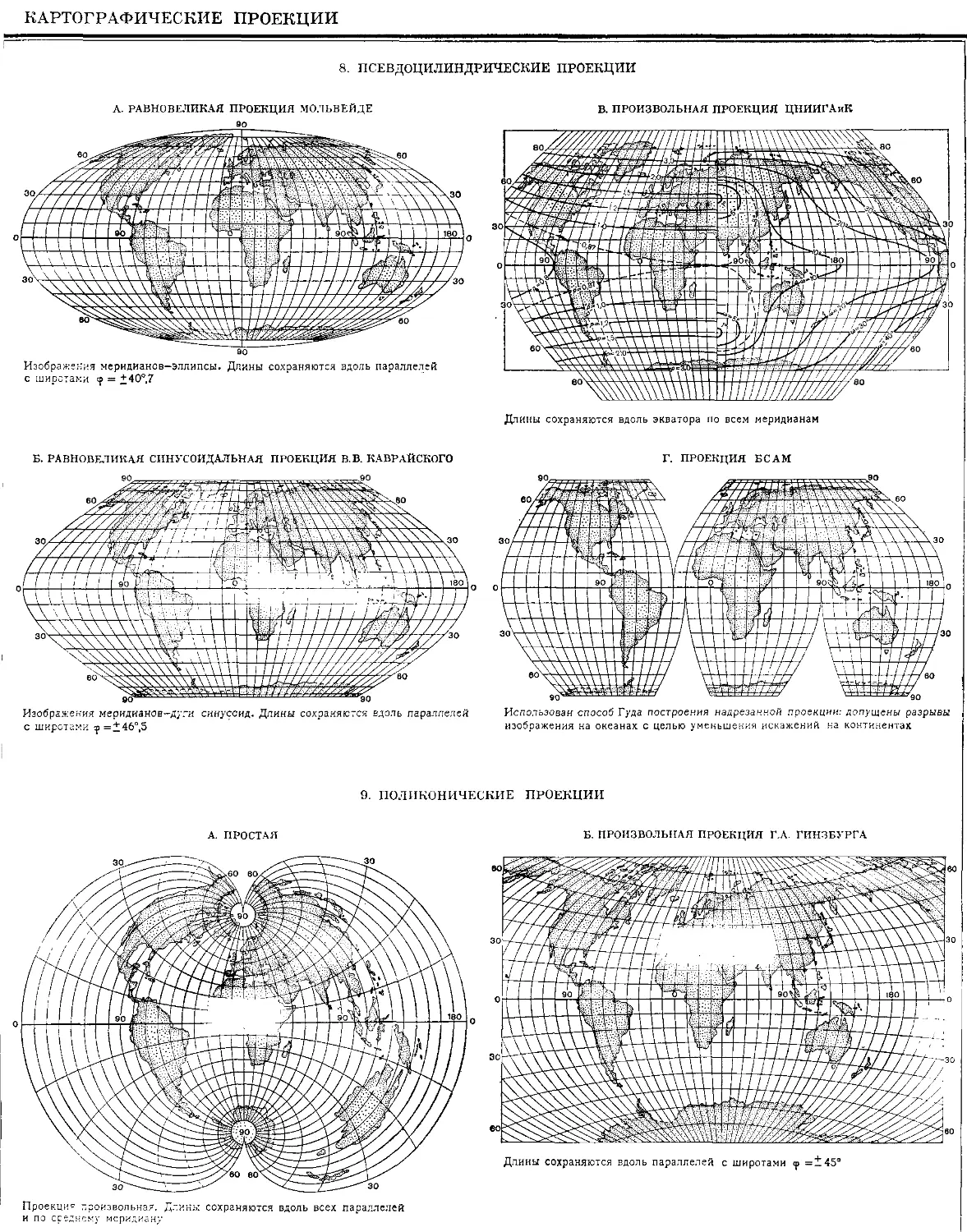
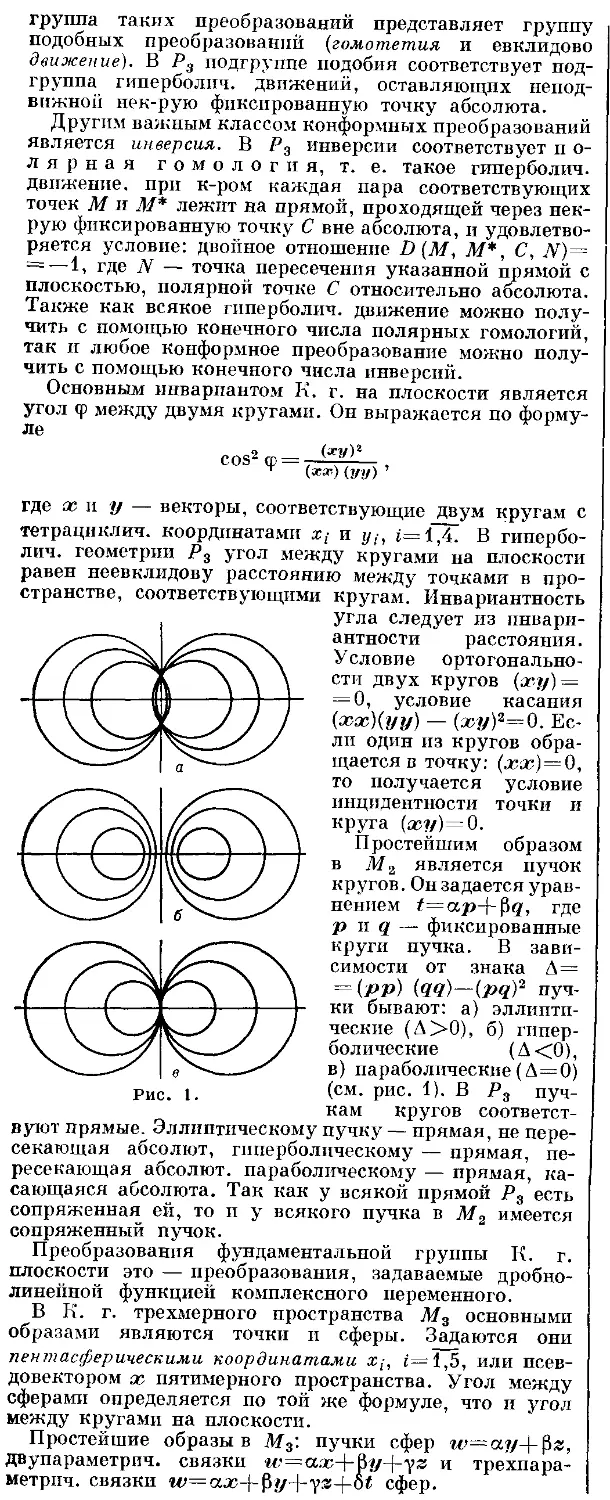
Текст
Д'АЛАМБЕРА ОПЕРАТОР, волновой опера-
оператор, даламбертиа н,— дифференциальный опе-
оператор 2-го порядка, имеющий в декартовых координа-
координатах вид
где Д — оператор Лапласа, с — постоянная. Д. о.
в сферич. координатах:
~ &Г у'^) '"Wine ев lvsin ° вёу "Г"
в цилиндрич. координатах:
_1_ а / ди\ , 1 вги , в2и 1 Э2ц ,
чар/)гр
в общих криволинейных координатах:
e
ви
?mvII,
из коэффициентов метрич. тензора g .
Назван по имени Ж. Д'Аламбера (J. D'Alembert,
1747), к-рый рассматривал его простейший вид при
решении одномерного волнового уравнения.
А. Б. Иванов.
Д'АЛАМБЕРА ПРИЗНАК сходимости ряда:
если для числового ряда
существует такое число q, 0<^<l, что начиная с
нек-рого номера выполняется неравенство
lun+ll < q
\ип\
то данный ряд абсолютно сходится; если же начиная
с нек-рого номера
то ряд расходится. В частности, если существует
предел
то рассматриваемый ряд абсолютно сходится, а если
П->- 00 I п I
то он расходится. Напр., ряд
абсолютно сходится для всех комплексных z, так как
lim
1)!
= 0,
п\
а ряд ?,in=1nizn расходится при всех z^=0, так как
Если
то ряд может как сходиться, так и расходиться: ряды
1 ri" 1
удовлетворяют этому условию, причем первый ряд
сходится, а второй расходится.
Установлен Ж. Д'Аламбером (J. D'Alembert, 1768).
Л. Д. Кудрявцев.
Д'АЛАМБЕРА ПРИНЦИП — один из основных прин-
принципов динамики несвободных механич. систем; он со-
содержит общий метод, с помощью к-рого уравнения
движения любой механич. системы можно вывести в
виде уравнений равновесия сил (и в этом смысле Д. п.
сводит динамику к статике), а также определить ре-
реакции связей. Принцип сформулирован Ж. Д'Алам-
Д'Аламбером [1] в виде правила для определения движений
(под к-рыми понимаются векторы скоростей) несколь-
нескольких тел, действующих одно на другое при помощи
нитей или жестких стержней: движения, передава-
передаваемые телам, раскладывают каждое на два движения —
на движение, фактически воспринятое телами, и на
нек-рое другое, причем эти два движения должны
быть таковыми, что если телам будет передано лишь
первое движение, то тела могут совершать это движение,
не мешая одно другому, если же телам передано лишь
второе движение, то тела будут оставаться в покое.
Д. п. был успешно применен Ж. Д'Аламбером и
другими учеными при решении ряда задач. Однако
разложение движений, требуемое принципом, и оп-
определение тех сил, к-рые должны уничтожаться, пред-
представляют трудную задачу. Это побудило Ж. Лагранжа
[2] предложить иную формулировку Д. п., основанную
на установлении равновесия между силами и вызван-
вызванными ими движениями, но направленными противо-
противоположно, к-рая близка к современной. Если обозначить
через Fv и Rv заданную активную силу и реакцию
связей, действующие на движущуюся с ускорением wv
материальную точку с массой тх , то, согласно Д. п.,
Fv-~-Rv—mvwv = 0, v = l, 2, ..., (*)
т. е. в каждый момент времени заданная активная
сила и реакция связей, приложенные к движущейся
материальной точке, уравновешиваются силой инер-
инерции — mv wv точки. Или, если разложить силу Fv на
две составляющие силы:
Fv = mvwv -[- Pv,
то равенства (*) примут вид:
Pv + i?v==0, v = l, 2,
т. е. в каждый момент времени «потерянная сила»
Pv —F\ —mv wv уравновешивается силой реакции свя-
связей (см. [3]).
Лит.: [1] D'A 1 е m b е г t J., Traitg de dynamique, P.,
1743 (рус. пер.: Даламбер Ж., Динамика, М.—Л., 1950);
[2] L a g г a n g e J., Mecanique analytique, P., 1788 (рус. пер.:
Л а г р а н ж Ж., Аналитическая механика, т. 1, 2 изд., М.—Л.,
1950); [3] С у с л о в Г. К., Теоретическая механика, 3 изд.,
М.—Л., 1946. В. В. Румянцев.
Д'АЛАМБЕРА УРАВНЕНИЕ — дифференциальное
уравнение вида
у=х<р (г/)+/(!/'),
где ф и / — дифференцируемые функции; впервые
исследовалось Ж. Д'Аламбером (J. D'Alembert, 1748).
Известно также под назв. уравнения Лагранжа.
БСи-2.
Д'АЛАМБЕРА ФОРМУЛА — формула, выражающая
решение задачи Коши для волнового уравнения с
одной пространственной переменной. Пусть заданные
функции ц>(х), ty(x) принадлежат соответственно про-
пространствам С2( — оо, +оо) и С1( — оо, +oo), a f(t, .г)
непрерывна вместе с первой производной по ж в полу-
полуплоскости {t^O, —оо <.г<-!-оо }. Тогда классич. ре-
решение u(t, х) в {2>0, —оо<.г<оо} Коши задачи
u(t,x) _ =ф(г), ou ^х) | _ =г|)(ж), B)
выражается Д. ф.:
j (Ч + oi ^ I
+ тт- \ . гЬ (?) rfc т—г- Гф (о: 4-я О -4-Ф (х — at)],
la jx — at ^ чо/ ^ ' 2 L • v ' / i т \ /j
Если функции ф(ж)и1|;(ж) заданы и удовлетворяют ука-
указанным условиям гладкости на интервале{\х—хо\<СаТ),
a /(f, x) — в треугольнике
QT ={ | х — х0 | < а (Г —«), ^5гО},
то Д. ф. дает единственное решение задачи A), B) в
<2 *„• Требования на заданные функции могут быть
ослаблены, если интересоваться решениями в нек-ром
обобщенном смысле. Напр., из Д. ф. следует, что при
/, интегрируемой по любому треугольнику Q т, ло-
х0
кально интегрируемой т|) и непрерывной ф можно опреде-
определить слабое решение задачи Коши A),B) как рав-
равномерный (в любом Q Ха) предел классич. решений (с
гладкими данными) и оно также выражается Д. ф.
Формула названа по имени Ж. Д'Аламбера (J. D'Alem-
bert, 1747).
Лит.: [1] В л а д и м и р о в В. С, Уравнения математи-
математической физики, 2 изд., М., 1971; [2] Тихонова. Н., С а-
м а р с к и и А. А., Уравнения математической физики, 3 изд.,
М., 1966. А.И.Гущин.
Д'АЛАМБЕРА — ЛАГРАНЖА ПРИНЦИП — один из
основных, наиболее общих дифференциальных вариа-
вариационных принципов классической механики, выражаю-
выражающий необходимое и достаточное условие соответствия
заданным активным силам действительного движения
системы материальных точек, стесненной идеальными
связями. В Д.— Л. п. сравниваются положения си-
системы в ее действительном движении с бесконечно близ-
близкими положениями, допускаемыми связями в рас-
рассматриваемый момент времени.
Согласно Д.— Л. п. в действительном движении си-
системы сумма элементарных работ заданных активных
сил и сил инерции на любых возможных перемещениях
меньше или равна нулю:
в любой момент времени. Знак = имеет место для об-
обратимых возможных перемещений, знак <: для необра-
необратимых возможных перемещений Srv ; Fv — заданные
активные силы, mv н wv — массы и З'скоренпя точек.
Уравнение (*) — общее уравнение динамики систем
с идеальными связями; в нем содержатся все уравне-
уравнения и законы движения, благодаря чему можно ска-
сказать, что вся динамика сводится к одной общей фор-
формуле (*).
Принцип установлен Ж. Лагранжем [1] путем обоб-
обобщения возможных перемещений принципа с помощью
Д'Аламбера принципа. Из формулы (*) для систем,
стесненных удерживающими связями, Ж. Лагранж
вывел общие свойства п законы движения тел, а также
уравнения движения и применил пх к решению ряда
задач динамики, включая задачи движения несжима-
несжимаемых, сжимаемых и упругих жидкостей, объединив
тем самым «динамику и гидродинамику как ветви
единого принципа и как выводы из единой общей
формулы».
Лит.: [1] LagrangeJ., Mecanique analytique, P., 1788
(рус пер.: Лагранж Ж., Аналитическая механика, т. 1,
2 изд., М.—Л., 1950). В. В. Румянцев.
Д'АЛАМБЕРА — ЭЙЛЕРА УСЛОВИЯ — см. Ко-
ши — Римана условия.
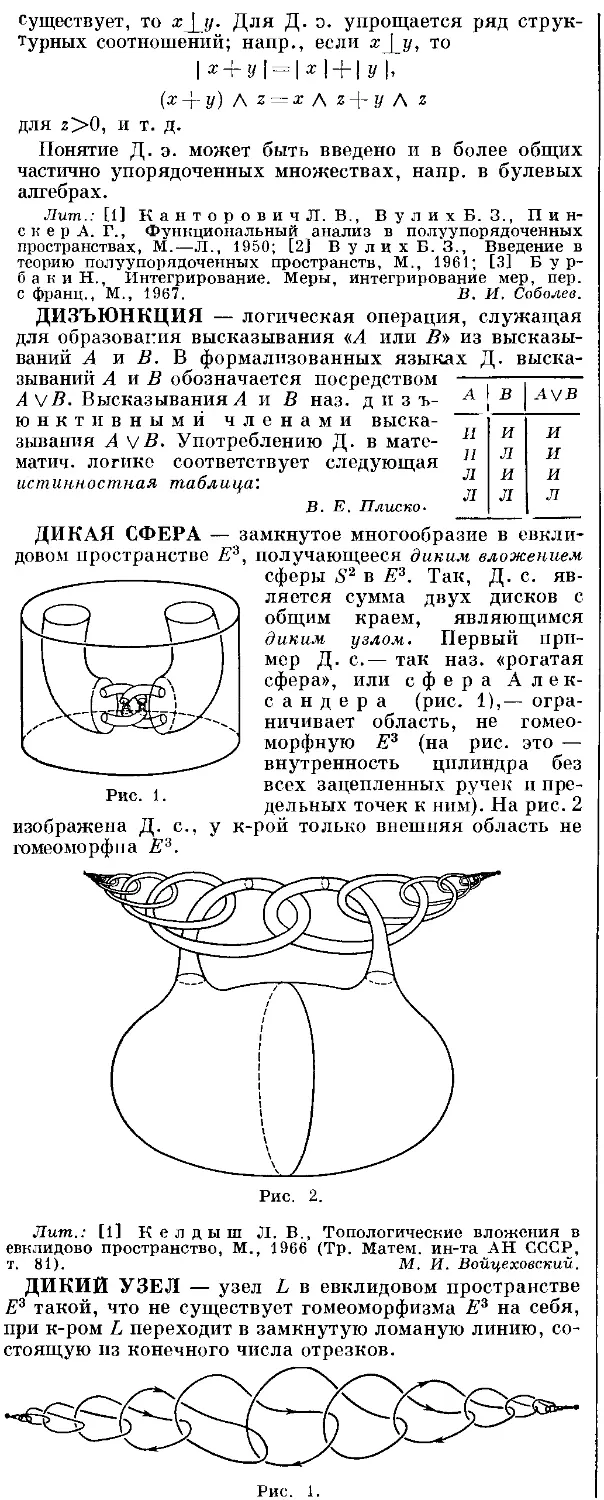
ДАНДЕЛЕНА ШАРЫ — сферы, участвующие в гео-
метрич. построении, к-рое связывает планиметрия,
определение эллипса, гиперболы или параболы со
стереометрич. определением.
Пусть, напр., в круговой ко-
конус вписаны две сферы (их и
называют шарами Д а н-
делена), к-рые касаются
поверхности конуса по окруж-
окружности с и с' (см. рис.) п неко-
некоторой плоскости л в точках F
п F'. Если взять на линии
пересечения конуса и плоско-
плоскости л произвольную точку М
и провести через нее образую-
образующую SM, к-рая пересекается
с окружностями сие' в точ-
точках Г и 7", то при переме-
перемещении точки М, точки Т и
Т' будут перемещаться по ок-
окружностям cue' с сохра-
сохранением расстояния ТТ', т. е.
линия пересечения — эллипс.
Для случая гиперболы Д. ш.
находятся в разных полостях.
Предложены Ж. Данделеном (G. Dandelin) в 1822.
Лит.: [1] Моденов П. С, Аналитическая геометрия,
М., 1969. А. Б. Иванов.
ДАНЖУА ИНТЕГРАЛ — 1) Данжуа узкий
(специальный) интеграл — обобщение по-
понятия интеграла Лебега. Функция f(x) наз. интегриру-
интегрируемой в смысле узкого (специального, D*) интеграла
Данжуа на [а, 6], если существует такая непрерывная
функция F(x) на [а, Ь], что F'(x) = f(x) почти всюду,
п каково бы ни было совершенное множество Р, су-
существует порция Р, на к-рой F (х) абсолютно непрерыв-
непрерывна и
J^j ш (F\ (а„, р,,)) < оо,
где {(а„, Р,,)} — совокупность смежных интервалов
к порции Р, (i>(F; (а, Р)) — колебание F{x) на (а, Р);
при этом
Такое обобщение интеграла Лебега ввел Л. Данжуа
[1]; он показал, что этот интеграл восстанавливает
функцию по ое точной конечной производной. Интеграл
D* эквивалентен Перрона интегралу.
2) Данжуа широкий (общий) инте-
интеграл — обобщение понятия узкого Д. и. Функция
f(x) наз. интегрируемой в смысле широкого (общего, D)
интеграла Данжуа на [а, Ь], если существует такая
непрерывная функция F(x) на [а, Ъ], что ее аппрокси-
аппроксимативная производная почти всюду равна f(x) и каково
бы ни было совершенное множество Р, существует
порция Р, на к-рой F(x) абсолютно непрерывна; при
этом
(D) \baf(x)dx = F{b)-F (а).
Введен независимо и почти одновременно А. Данжуа
[2] и А. Я. Хинчиным [3], [4]. Интеграл D восстанав-
восстанавливает непрерывную функцию по ее точной конечной
аппроксимативной производной.
3) Тотализация (T2s)g представляет собой
конструктивно определенный интеграл для решения
задачи построения такого обобщения интеграла Лебега,
к-рое позволило бы всякий всюду сходящийся триго-
нометрич. ряд рассматривать в качестве ряда Фурье
(по этому интегралу). Введена А. Данжуа [5].
4) Тотализация (T2S) отличается от тотали-
зации (T2sH тем, что при определении тотализации
(Г25)о обычный предел заменен на аппроксимативный.
Для тотализации (T2S) А. Данжуа [5] дал и дескрип-
дескриптивное определение.
О взаимосвязях тотализации (T2S)o и (Tzs) с другими
интегралами см. [6].
Лит.: [1] Den Joy А., «С. г. Acad. sci.», 1912, t. 154, p.
859—62, 1075 — 78; [2] его же, там же, 191В, t. 162, р. 377 —
80- [3] Khintchine А., там же, 1916, t. 162, р. 287—91;
[4J X и н ч и н А. Я,, «Матем. сб.», 1918, т. 30, с. 543—57; [5]
D e n ] о у A., Lecons sur le calcul des coefficients d'une serie
trigonometrique, pt 1—4, P., 1941—49; [6] Виноградова
И. А., С к в о р ц о в В. А., в кн.: Итоги науки. Математиче-
Математический анализ. 1970, М., 1971, с. 65—107; [7] Сакс С, Теория
интеграла, пер. с англ., М., 1949. Т. Я. Лукашенко
ДАНЖУА ТЕОРЕМА о производных чис-
числах: производные числа каждой конечной функции
F (х) почти в каждой точке х удовлетворяют одному
из следующих соотношений:
F+(x) = 7- (х) = +оо, F_+ (x) = F_~ (x)=— оо;
F+ (x) = F- (х) Ф оо, F+(x) = — oo, F~ (x) = + oo,
F+ (х) =~F- (х) ф oo, J+ (*) = + oo, F_~ (х)=— оо;
~F+ (x) = F_+ (x)=~F- (x)—_F- (x) ф оо.
Доказана для непрерывных функций А. Данжуа [1].
Обобщением утверждения Данжуа является теорема
[2]: для почти каждого х контингенция графика F(x)
в точке (х, F(x)) является одной из следующих фигур:
плоскость, полуплоскость (с невертикальной граничной
прямой), прямая (невертикальная).
Лит : Ш D e n ] о у A., «J. math, pures et appl.», 1915,
Ser. 7, t. 1, p. 105—240; [2] Сакс С, Теория интеграла, пер.
с англ., М., 1949. Т.П.Лукашенко.
ДАНЖУА — ЛУЗИНА ТЕОРЕМА об абсолютно схо-
сходящихся тригонометрич. рядах: если тригонометрия,
ряд
а ^—^ ^°
-f т > a,,cos nx-^bnsinnx A)
*—'n=l
сходится на множестве положительной меры Лебега,
то ряд, составленный из абсолютных величин его
коэффициентов
сходится и, следовательно, исходный ряд A) сходится
абсолютно и равномерно на всей числовой оси. Свой-
Свойство положительности меры множества сходимости
ряда A), будучи, согласно Д.— Л. т., достаточным для
сходимости ряда B), не является, однако, необходимым.
Существуют, напр., совершенные множества меры
нуль, из сходимости на к-рых ряда A) следует сходи-
сходимость ряда B).
Теорема установлена независимо А. Данжуа [1]
и Н. Н. Лузиным [2]; имеются различные ее обоб-
обобщения (см. [3]).
Лит.: [1] Den] о у А., «С. г. Acad. sci.», 1912, t. 155,
p. 135 — 6; [2] Лузин Н. Н., «Матем. сб.», 1912, т. 28,
о. 461 — 72; [3] В а р и Н. К., Тригонометрические ряды, М.,
1961. Л. Д. Кудрявцев, Е.М. Никишин.
ДАНИЕЛЯ ИНТЕГРАЛ — расширение понятия ин-
интеграла, предложенное П. Даниелем [1]. Схема по-
построения этого интеграла наз. схемой Д а н и е л я,
представляет собой продолжение на более широкий
класс функций интеграла, определенного первона-
первоначально для нек-рой совокупности функций, называемых
элементарными функциями. При сохранении способа
продолжения изменение объема исходной совокуп-
совокупности элементарных функций приводит к разным рас-
расширениям понятия интеграла. В этой схеме аксиома-
аксиоматизируется понятие элементарного интеграла, в от-
отличие от схемы Лебега (см. Лебега интеграл), аксио-
аксиоматизирующей понятие меры.
Пусть X — произвольное множество и Lo — неко-
некоторая совокупность определенных на X действительных
ограниченных функций; эти функции наз. элемен-
элементарным и. Предполагается, что Lo — векторная
решетка, т. е. из /, g?L0 и a, C?R /+P?Z
=>sup(f, g) и mf(/, g)?La.
Пусть на Lo определен функционал /(/), принимающий
действительные значения и такой, что
/ (а/ — $g) = а/ (/) -f- p/ {g) (дистрибутивность);
f (х) 5з 0 => / (/) Зз 0 (неотрицательность);
если fn(x)\O для любого х, то / (/„)^-0 (непрерывность
относительно монотонной сходимости).
Такой функционал наз. интегралом от эле-
элементарных функций, или элементар-
элементарным интегралом. Множество МаХ наз. м н о-
ж е с т в о м меры нуль, если для любого 8>0
найдется такая неубывающая последовательность
{gn}c:L0, что sup gn{x)^xM(x), где %м(х) ~ характе-
ристич. функция множества М:
sup / (gn) < е.
Функция f(x), определенная на X, принадле-
принадлежит классу L+, если существует такая последо-
последовательность {fn}czL0, что fn(x)\f(x) почти всюду и
7(/„)<с<+оо. Число
наз. интегралом от /. Интеграл / (/) не зависит
от выбора аппроксимирующей последовательности {/„}.
Классом L наз. совокупность функций /, оп-
определенных на X и представимых в виде /=/i—/2,
где /lt f2?L +. Функции класса L наз. суммиру-
суммируемым и, а число
i{1)=i(h)-iA2)
— интегралом Даниеля от функции/.
Класс L с точностью до множества меры нуль яв-
является векторной решеткой конечных функций, замк-
замкнутой относительно сходимости почти всюду с огра-
ограниченными интегралами, и Д. и. от суммируемых
функций обладает свойствами дистрибутивности, не-
неотрицательности, непрерывности (относительно схо-
сходимости почти всюду), мажорированной суммируемой
функцией (теорема Лебега о переходе к пределу под
знаком интеграла), а также рядом других естественных
свойств интеграла.
В том случае, когда Х=[а, Ь] и Lo есть совокуп-
совокупность ступенчатых функций
f(x) = ch а,-<ж < Ъ;, U?=iK'. Ь;)=[а, Ь), 6/ = а; + 1,
Д. и. совпадает с интегралом Лебега от функций,
суммируемых на [а, Ь]. Схема Даниеля применима
для построения интеграла от функций со значениями
в а-полной решетке.
Лит.: [1] D a n i е 1 1 P., «Ann. Math.», 1917, v. 19, p. 279—
94; [2] Шилов Г. Е., Г у р е в и ч Б. Л., Интеграл, мера
и производная, 2 изд., М., 1967; [3] Л ю ми с Л., Введение
в абстрактный гармонический анализ, пер. с англ., М., 1956.
В. И. Соболев.
ДАНТОВО ПРОСТРАНСТВО — один из типов топо-
логич. пространств. Пусть X — топологич. простран-
пространство, У — его подпространство, т и X — бесконечные
кардиналы. Пространство У наз. т-монолитным в X,
если для каждого 4сУ такого, что card/1 -<т замы-
замыкание U] в X является бикомпактом веса <;т. Про-
Пространство X т-подавляет подпространство У, если из
Х^т, AdY и card/1 «гехрЯ следует, что существует
А'сХ, для к-рого [Л']зЛ и car<L4'<А. Пространство
X наз. дантовым, если для каждого бесконечного
кардинала т существует всюду плотное в X подпро-
подпространство У, к-рое одновременно т-монолитно в себе
и т-подавляется пространством X. Класс Д. п. содер-
содержит класс диадических бикомпактов. Б. А. Ефимов.
ДАРБУ ВЕКТОР — направляющий вектор 6 мгно-
мгновенной оси вращения, вокруг к-рой сопровождающий
триэдр кривой L поворачивается при равномерном
движении точки М по кривой L. Д. в. лежит в спрям-
спрямляющей плоскости кривой L и выражается через еди-
единичные векторы главной нормали п и касательной t
к кривой L:
6= V т2 — a2 (t cos 0 + n sin 0),
где т и а — кривизна и кручение L, 0 — угол между
Д. в. и касательной к L. С помощью вектора Дарбу
Френе формулы могут быть записаны в виде:
i=[6, t], n = [6, n], 6= [6, 6],
где ft — бинормаль L.
Применительно к сопровождающему триэдру про-
пространственной кривой Д. в. в его геометрич. значении
впервые указан Г. Дарбу [1].
Лит.: [1] D a r b о и х G., Lecons sur la theorie generale des
surfaces..., pt 1, P., 1887—96, livre 1, ch. 1, p. 1 — 18; [2] К a-
г а н В. Ф., Основы теории поверхностей в тензорном изложе-
изложении, ч. 1, М.— Л., 1947. Е.В.Шикин.
ДАРБУ ИНВАРИАНТЫ СЕТИ — выражения h ж к.
ди ' ' dv '
составленные из коэффициентов уравнения Лапласа
д2в ае , , ее , а , .
Уравнению (*) удовлетворяет каждая из однородных
координат точки х, описывающей сопряженную сеть
из линий иивна двумерной поверхности проективного
re-мерного пространства («^=3). Г. Дарбу [1] показал,
что Д. и. с. h и к не меняют своего значения при изме-
изменении нормирования координат точки х. Накладывая
то или иное условие на Д. и. с, получают частные
виды сопряженных сетей.
Лит.: [UDarbouxG., Lecons sur la theorie generale des
surfaces..., pt 2, P., 1889, [2] T z i t z e i с a G., Geometrie dif-.
ferentielle projective des reseaux, P.—Bucarest, 1924; [3] Ф и-
н и к о в С. П., Теория конгруэнции, М.—Л., 1950.
В. Т. Базылев.
ДАРБУ КВАДРИКА — поверхность 2-го порядка,
имеющая с поверхностью S трехмерного проективного
пространства Р3 касание 2-го порядка в точке х, и у
к-рой линия пересечения с поверхностью S имеет точку
х особой точкой специального типа. Из множества
квадрик, имеющих с поверхностью S касание 2-го
порядка в точке х, можно выделить такие квадрики,
у к-рых линия пересечения с, ппврруппгтью .9 имеет
точку х особой точкой с тремя совпадающими каса-
касательными. На поверхности S существуют три направ-
направления (направления Дарбу) для этих трех
совпавших касательных. В точке х ?S существует
однопараметрич. семейство Д.к.— пучок Дарбу.
Обобщение пучка Дарбу — пучок гиперквадрик, со-
соприкасающихся в точке х с гиперповерхностью Sn
проективного пространства Pn + i- Гиперповерхность Sn
(неразвертывающаяся) вырождается в гиперквадрику
тогда и только тогда, когда равен нулю обобщенный
Дарбу тензор гиперповерхности (см. [2]).
Лит.: [1] Ф и н и к о в С. П., Проективно-дифференциаль-
ная геометрия, М.—Л., 1937; [2] Л а п т е в Г. Ф., «Тр. Моск.
матем. об-ва», 1953, т. 2, с. 275—382. В. Т. Базылее.
ДАРБУ ПОВЕРХНОСТИ — поверхности, ассоцииро-
ассоциированные с бесконечно малым изгибанием одной из них;
открыты Г. Дарбу [1]. Д. п. образуют «венок» из 12
поверхностей с радиус-векторами хг, ..., же, »1( ...,
S6i удовлетворяющими уравнениям
Лв/=[ж/-1, da;], »,-—ж,- + 1 = [г/ + 1,ж,-],
* = 1, ..., 6,
При 3TOMS,+1 и ж,- находятсяв Петерсона соответствии,
S/ + i и Ж1_г — в полярном соответствии, я,- и сс,- + 1 яв-
являются полостями конгруэнции W. Аналогичный «ве-
«венок» образуется парами изометричных поверхностей
эллиптич. пространства.
Лит.: [1] DarbouxG., Lecons sur la theorie generate
des surfaces..., pt 4, P., 1896, 3 ed., 1946; [2] Ш улик ов ский
В. И., Классическая дифференциальная геометрия в тензорном
изложении, М., 1963. М. И. Войцеховский.
ДАРБУ СУММА — сумма специального вида. Пусть
действительная функция f(x) определена и ограничена
на отрезке [а, Ь], т= {я,-}[=о — его разбиение:
а = х0 < хх < .. . < xi -1 < х,- < . .. < xk = Ь,
Axi = xi--xi-1, /»,¦= inf f (х), М(= sup / (х),
Суммы
sx =
i = l, 2, ..., к.
т: Ах; и Ьх = > ж i Ax;
наз. соответственно нижней и верхней ин-
интегральной Д. с. Для любых двух разбиений т и т'
отрезка [а, Ь] справедливо
неравенство sx <5T', т. е.
любая нижняя Д. с. мень-
меньше верхней. Если
— интегральная сумма Ри-
мана, то
s х= inf ат,
\
a j
«*)/
с, х
5Т = sup о% ¦
5' 5ft
Геометрич. смысл нижней и верхней Д. с. заключается
в том, что они равны площадям ступенчатых фигур,
состоящих из прямоугольников с основаниями длины
Ах; и высотами соответственно т,- и Mj (см. рис.). Эти
фигуры в случае, когда f(x)^0, аппроксимируют из-
изнутри и извне криволинейную трапецию, образованную
графиком функции f(x), осью абсцисс и отрезками пря-
прямых х=а и х=Ъ (которые могут вырождаться в точки).
Величины
/^ = supsx я /* = infi\ A)
наз. соответственно нижним и верхним ин-
интегралом Дарбу. Они являются пределами
нижних и верхних Д. с:
/* = lim sT , /* = lim Sx ,
6x-*o ex-*o
где
бх = max Kx;
t=i. 2, ..., h
— мелкость разбиения x. Условие
/• = /• B)
является необходимым и достаточным для того, чтобы
функция f(x) была интегрируема по Риману на отрезке
[а, Ъ]. При этом в случае выполнения условия B)
значение нижнего и верхнего интегралов Дарбу совпа-
совпадает с интегралом Римана
Условие B) с помощью Д. с. может быть сформулиро-
сформулировано в следующей эквивалентной форме: для любого
8>0 существует такое разбиение х, что
Условие
lim (S-c— sT)=0
6х->-0
также является необходимым и достаточным для интег-:
рируемости по Риману функции на отрезке [а, Ь].
При этом
где со,-(/) — колебание функции f(x) на отрезке
[*,-_!, Xi], i = l, 2, ...,k.
Понятие нижних и верхних Д. с. обобщается на
случай функций многих переменных, измеримых в
смысле нек-рой положительной меры ц. Пусть Е —
измеримое (напр., по Жордану или по Лебегу) множе-
множество re-мерного пространства га=1, 2, ..., х={?,-}^1—
разбиение множества Е, т. е. система таких измеримых
множеств Е , что
U Li Е; = Е, C)
=0 при i^i. D)
Пусть функция / ограничена на множестве Е,
ш,-= inf / (х), М[= sup / (ее), i = l, 2, . .., к. E)
х е Е . х е Е (.
Суммы
ft ^ F)
также наз. нижней и, соответственно, верхней Д. с.
Нижний 1% и верхний /* интегралы определяются по
формулам A). В случае меры Жордана их равенство
является необходимым и достаточным условием инте-
интегрируемости функции по Риману, причем их общее
значение совпадает с интегралом Римана. В случае
же меры Лебега для ограниченных измеримых по
Лебегу функций всегда
/« = /* =
Вообще, если ц — полная а-аддитивная мера, оп-
определенная на а-алгебре <Е>ц= {Е}, f — ограниченная
ц-измеримая на Е действительная функция, т= {Ej }\=i —
разбиение множества Е ?<Вц на ц-измерпмые множества
Ei, удовлетворяющие условиям C), D), Д. с. sx и Sx
определяются по формулам E) — F), а интегралы I*
и /* — по формулам A), в к-рых везде под jj, понимают
рассматриваемую меру, то
/* = /* =
Обобщением Д. с. для неограниченных ^-измеримых
функций /, определенных на множествах Е?Ч?щ, яв-
являются ряды (если они абсолютно сходятся)
G)
где т= {Е;\1°=1 — разбиение множества .Е?@ц (это
разбиение состоит, вообще говоря, из бесконечного
числа (д,-измеримых множеств ?,-, удовлетворяющих
условию D) и, конечно, таких, что \jT<=iEi=E), a го,- и М,-
определяются по формулам E), при этом в формулах
G) (как и выше в формулах F)) считается, что оо-0=
= 0-оо = 0. Если снова определить /* и /* по A), по-
понимая теперь s% и Sx в смысле G), то /*=/*, причем
в случае, когда величина / = /*=/* является конечной,
функция / интегрируема по мере ц и I=\j(x)d\i.
Названы по имени Г. Дарбу [1]. ^
Лит.: [1] D а г b о и х 6., «Ann. sci. Ecole Norm, super.»,
1875, ser. 2, t. 4, p. 57—112; [2] И л ь и н В. А., П о з н я к
Э. Г., Основы математического анализа, 3 изд., т. 1—2. М.,
1971—73; [3] К у д р я в ц е в Л. Д., Математический анализ,
2 изд., т. 1—2, М., 1973; [4] Никольский СМ., Курс
математического анализа, 2 изд., т. 1—2, М., 1975.
Л. Д. Кудрявцев.
ДАРБУ ТЕНЗОР — симметрический тензор третьей
валентности
fl . h . ba.VKv+bf$vKa.+byaK$
«aPv = Софу 4К '
где Ьар — коэффициенты второй квадратичной формы
поверхности, К — гауссова кривизна, а 6ару и Ка —
их ковариантные производные. К этому тензору в
специальных координатах впервые пришел Г. Дарбу [1].
С Д. т. связана кубическая дифференциальная форма:
dua diP duy = baPv dua dJ1 duy —
Эта форма, отнесенная к кривой на поверхности, наз.
инвариантом Дарбу. На поверхности по-
постоянной отрицательной кривизны инвариант Дарбу
совпадает с дифференциальным параметром на любой
ее кривой. Кривая, в каждой точке к-рой инвариант
Дарбу равен нулю, наз. линией Дарбу. На
нелинейчатой поверхности отрицательной кривизны
существует одно действительное семейство линий Дар-
Дарбу. На поверхности положительной кривизны сущест-
существуют три действительных семейства линий Дарбу.
Поверхность, в каждой точке к-рой Д. т. определен и
тождественно равен нулю, наз. поверхностью
Дарбу. Поверхности Дарбу являются поверхно-
поверхностями 2-го порядка, не развертывающимися на пло-
плоскость.
Лит.: [1] D a rb о и х G., «Bull. sci. math.», 1880, ser. 2,
t. 4, p. 348—84; [2] К а г а н В. Ф., Основы теории поверх-
поверхностей в тензорном изложении, ч. 2, М.—Л., 1948, стр. 210—3:5.
Е. В. Шикин.
ДАРБУ ТЕОРЕМА: если функция в каждой точке
некоторого промежутка оси действительных чисел име-
имеет конечную производную, то, принимая два каких-ли-
каких-либо значения на этом промежутке, производная при-
принимает на нем и любое промежуточное.
Л. Д. Кудрявцев.
ДАРБУ ТРЕХГРАННИК, Дарбу триэд р,—
трехгранник, связанный с точкой поверхности и оп-
определяемый тройкой векторов, составленной из оита
нормали п к поверхности и двух взаимно ортогональных
ортов г1 и г2, касательных к поверхности
дг дг »'! Х'"->
ri = an; r* = -fv'' n== l-.x/.i •
Свойства поверхности отражаются в законах пере-
перемещения Д. т., когда его вершина описывает поверх-
поверхность. Систематич. применение Д. т. к изучению по-
поверхностей привело Г. Дарбу [1J к подвижного репера
методу.
Лит.: [1] DarbouxG., Lemons sur la theorie generale
des surfaces..., pt. 1, P., 1887. А. Б. Иванов.
ДАРБУ УРАВНЕНИЕ — 1) Д. у.—обыкновенное
дифференциальное уравнение
dy_ _P (х, у) + yR (х, у)
dx Q {х, у) +1ЙA, !/)'
где Р, Q, R — целые многочлены относительно х и у.
Это уравнение впервые исследовал Г. Дарбу [1]. Част-
Частный случай Д. у.— Якоби уравнение. Пусть п — выс-
высшая степень многочленов Р, Q, R; если Д. у. имеет s
известных частных алгебраических решений, то при
s^—re(re+l)+2 его общее решение отыскивается без
квадратур, а при s= — n (н+1)+1 можно найти ин-
интегрирующий множитель (см. [2]). Если Р п Q — одно-
однородные функции степени т, a R — однородная функция
степени к, то при к=т — 1 Д. у. является однородным
дифференциальным уравнением, а при к=^=т — 1 под-
подстановкой y—zx Д. у. приводится к Бернулли урав-
уравнению.
Лит.: [1] DarbouxG., «Bull. sci. math.», 1878, t. 2,
p. 66—96; [2] А й н с Э. Л. Обыкновенные дифференциальные
уравнения, пер. с англ., Хар., 1939. Н.Х.Розов.
2) Д- У-—гиперболическое уравнение
ип Аи М?' х) ut = 0 t^O
где А, (г, х) — неотрицательная, непрерывно диффе-
дифференцируемая функция, х= (х1, х.2, . . ., хп). Для решений
Д. у., как и для решений волнового уравнения, спра-
справедлива следующая теорема единственности. Если
какое-нибудь дважды непрерывно дифференцируемое
решение и(х, t) Д. у. обращается вместе со своей про-
производной по t в нуль на основании, лежащем в пло-
плоскости t = 0, характеристич. конуса, то оно равно нулю
внутри всей области, ограниченной этим конусом.
Характеристич. конус имеет тот же вид, что и для
волнового уравнения.
При k(t, х) = п—1 > 0 решением Д. у., удовлетворя-
удовлетворяющим начальным условиям
и (t, х) |( = о = ф(а0,
с дважды непрерывно дифференцируемой функцией
ф (х), является функция
\x-y\=t
где F(z) — гамма-функция. Это решение Д. у. и ре-
решение v(x, t) волнового уравнения, удовлетворяющее
условиям
v(t,x)\t = 0--4i(x), vt(t, *)|t = 0 = 0,
связаны соотношением
Д. у. названо по имени Г. Дарбу (G. Darboux).
Лит.: [1] ИонФ., Плоские волны и сферические сред-
средние в применении к дифференциальным уравнениям с частны-
частными производными, пер. с англ., М., ]958. А. К. Гущин.
ДАРВИНА — ФАУЛЕРА МЕТОД — метод вывода
канонического и большого канонич. распределений из
микроканонического (см. Гиббса распределение). Для
этого рассматривается ансамбль одинаковых статистич.
систем, образующий в целом замкнутую систему, и
характеризующая его функция распределения сумми-
суммируется по микроскопия, состояниям всех систем ан-
ансамбля, кроме одной. Предполагается, что число систем
в ансамбле стремится к бесконечности (при большом,
но фиксированном числе частиц в каждой из систем
ансамбля), что позволяет при расчете применять метод
перевала. Использование указанной процедуры для
установления ряда общих особенностей статистич. си-
систем и расчета конкретных их характеристик приводит
к тем же результатам, что и метод, основанный на
канонич. распределениях Гиббса. Метод разработан
Ч. Дарвиным (Ch. Darwin) и Р. Фаулером (R. Fowler)
в 1923.
Лит.: [1] Ф а у л е р Р., Г у г г е н г е й м Э., Статисти-
Статистическая термодинамика, пер. с англ., М., 1949; [2] X у а н г К.,
Статистическая механика, пер. с англ., М., 1966.
И. А. Квасников.
ДВЕРНОЕ ПРОСТРАНСТВО — топологическое прост-
пространство, в к-ром любое подмножество либо открыто,
либо замкнуто. А. А. Мальцев.
ДВИЖЕНИЕ — преобразование пространства, со-
сохраняющее геометрия, свойства фигур (размеры, форму
и др.). Понятие Д. сформировалось путем абстрак-
абстракции реальных перемещений твердых тел в евклидовом
пространстве. Д. принимается иногда в качестве ос-
основного понятия при аксиоматическом построении гео-
геометрии.
Д. евклидова пространства — преоб-
преобразование пространства, сохраняющее расстояние меж-
между точками. Д. наз. собственным (Д.первого
рода) или несобственным (Д. второго
рода) в зависимости от того, сохраняет оно или не
сохраняет ориентацию пространства.
На плоскости собственные Д. выражаются аналити-
аналитически в прямоугольной системе координат (х, у) при
помощи следующих формул
х ~ х cos ф — у sin ф -\- а,
!/ = х sin ф-J- у cos ф + 6,
показывающих, что совокупность всех собственных Д.
на плоскости зависит от трех параметров а, Ь, ф. Первые
два параметра характеризуют параллельный перенос
плоскости на вектор (а, Ь), а параметр ф — вращение
(поворот) плоскости вокруг начала координат. Соб-
Собственное Д. представляет собой произведение (ком-
(композицию) вращения вокруг начала на угол ф и парал-
параллельного переноса на вектор (а, 6). Всякое собствен-
собственное Д. может быть представлено либо как паралле-
параллельный перенос, либо как вращение вокруг некоторой
точки.
Несобственные Д. выражаются при помощи формул
х = .rcos ф+ у sin ф + а,
у = х sin ф — у cos ф + 6,
показывающих, что несобственное Д. есть произведе-
произведение собственного Д. на преобразование симметрии
относительно нек-рой прямой. Всякое несобственное Д.
представляет собой произведение параллельного пере-
переноса вдоль нек-рого направления и симметрии отно-
относительно прямой, имеющей то же направление.
В пространстве собственное Д. есть или вращение
вокруг оси, или параллельный перенос, или может быть
представлено в виде произведения вращения вокруг оси
и параллельного переноса в направлении этой оси
(винтовое Д.). Несобственное Д. есть либо симметрия
относительно плоскости, либо может быть представ-
лено в виде произведения симметрии относительно
плоскости на вращение вокруг оси, перпендикулярной
к этой плоскости, либо — в виде произведения сим-
симметрии относительно плоскости на перенос в направ-
направлении вектора, параллельного этой плоскости.
В прямоугольной системе координат (х, у, z) в про-
пространстве Д. выражается аналитически при помощи
формул
х = аг1х -•- «12г/ -(- a13z 4- а,
~у = а21х + а2.,у -L a23z ->- b,
где элементы матрицы ||я,у|! удовлетворяют следующим
условиям ортогональности
{brs=i при r=s, 8rs=0 при r=?s). Д. является соб-
собственным или несобственным в зависимости от того,
равняется ли определитель этой матрицы 1 или —1.
См. Ортогональное преобразование.
Аналогично в случае n-мерных евклидовых про-
пространств Д. выражается аналитически в прямоугольных
координатах при помощи ортогональной матрицы
||
alralS Л-
Д. риманова пространства — взаимно од-
однозначное непрерывно дифференцируемое отображение
класса Cs, .0=2, при к-ром сохраняются длины соот-
соответствующих линий. Линейный элемент пространства
ds- = gaf, (х1, х2, ..., х") с1хас1х$,
где по индексам a, P производится суммирование,
инвариантен относительно Д. Аналитически Д. опре-
определяется формулами, выражающими координаты пре-
преобразованной точки М (?') через координаты исходной
точки М (х1) при помощи функций f'(x) класса Cs:
~ха=}а (х1, ж2, . .., х»), (*)
а=1, 2, . .., п.
Условие инвариантности линейного элемента означает,
что
2 ")g(x1 2 х")
Важное значение имеет понятие Д. в римановых про-
пространствах общей теории относительности: в сильных
асимметрических гравитационных полях твердые тела
могут иметь лишь весьма ограниченные движения.
Возможны также случаи, когда они не будут вовсе
допускать никаких Д. В последней ситуации при
любом преобразовании пространства метрика не ос-
остается инвариантной. Другими словами, любое пере-
перемещение сопровождается деформацией тела.
Д. пространства а 6 ф и н н о й связ-
связности — взаимно однозначное непрерывно диффе-
дифференцируемое отображение класса С*, s^s2, при к-ром
всякое поле параллельных векторов вдоль любой глад-
гладкой линии переходит в поле параллельных векторов
преобразованной кривой. При Д. объект аффинной
связности Гру (х) переходит в себя. Обратно, всякое
отображение (*), переводящее объект аффинной связ-
связности в себя, есть Д.
Д. составляют группу преобразований (см. Дви-
Движений группа). Они являются простейшими преобра-
преобразованиями пространства.
Лит.: [I] Е г о р о в II. П., Лекции по аксиоматике Вейля
и неевклидовым геометриям, Рязань, 1973; [2] его же, Дви-
жения в пространствах аффинной связности, Казань, 1965; [3]
БазыпевВ.Т., ДуничевК.И., Иваницкая
В. П., Геометрия, т. 1, М., 1974. Я. Л. Егоров.
ДВИЖЕНИЙ ГРУППА — непрерывная группа пре-
преобразований пространства, элементами к-рой являются
движения этого пространства, а групповой операцией —
последовательное выполнение в указанном порядке
двух движений. В широком смысле, любая группа не-
непрерывных преобразований пространства может быть
сделана Д. г. этого пространства. А именно, введение
для заданной группы понятия равенства фигур при-
приводит к нек-рой новой геометрии, в к-рой эта группа
служит Д. г. (см. Эрлангенская программа).
Д. г. наз. транзитивной Д. г., если для
любых двух точек пространства можно указать в дан-
данной группе движение, к-рое переводит одну точку в
другую, и и н т р а н з и т и в н о й Д. г., если су-
существуют пары точек, для к-рых такого движения ука-
указать нельзя.
Пространство, в к-ром можно ввести заданную Д. г.,
наз. пространством, допускающим эту
Д. г. Если Д. г. пространства имеет максимальный
порядок, то она наз. полной Д. г. Напр., полная
транзитивная Д. г. re-мерного евклидова пространства
есть группа порядка ге(ге+1)/2, т. о. группа, зависящая
от n(n-\-i)l2 параметров. В частном случае евклидовой
плоскости в качестве параметров полной Д. г. можно
взять координаты точки, в к-рую переходит начало
координат, и угол поворота, т. е. эта Д. г.— трех-
параметричоская. Д. г. G евклидовой плоскости есть
некоммутативная разрешимая группа. Ее подгруппа
вращений Н коммутативна и интранзптивна, а под-
подгруппа N параллельных переносов коммутативна и
транзитнвна и является нормальным делителем Д. г.
Пересечение этих двух подгрупп — единица Д. г.
Факторгруппа GIN изоморфна Н, коммутант Д. г. G
содержится в N. В качестве параметров полной Д. г.
трехмерного евклидова пространства можно взять
координаты точки О {а, Ь, с), в к-рую переходит начало,
и эйлеровы углы, т. е. эта Д. г.— шестипараметрпческая.
Исследования по Д. г. в обобщенных дифференци-
ально-геометрич. пространствах ведутся одновременно
по нескольким направлениям, важнейшими из к-рых
являются следующие.
1) Направление теоретико-группового характера [3].
Это — построение в пространстве, в к-ром действует
группа преобразований, инвариантной метрики пли
связности.
2) Изучение Д. г. в заданных пространствах, т. е.
групп, к-рые допускает пространство с заданной мет-
метрикой пли связностью (см. [1], [2]).
3) Направление, пограничное с первыми двумя и со-
состоящее в изучении лакун и лакунарных пространств,
т. е. либо построение пространств, допускающих пол-
полную Д. г. заданного порядка, либо доказательство
несуществования пространств определенного типа, до-
допускающих ту или иную заданную Д. г.
Напр., «-мерное аффинное пространство допуска-
допускает Д. г. максимального порядка г=п2+ге. Поряд-
Порядки Д. г. других пространств аффинной связности при-
принадлежат отрезку натурального ряда [1, пг-\-п\, но не
каждое число из этого отрезка может быть порядком
полной Д. г.
Интервалы наибольшей длины, составленные из
чисел, не являющихся порядками полных Д. г., наз.
лакунами, а дополнения к ним до указанного
отрезка натурального ряда — отрезками кон-
конденсации. Пространство наз. пространст-
пространством fc-й лакунарности, если порядок его
полной Д. г. принадлежит отрезку конденсации, имею-
имеющему номер к. Основная проблема состоит в распреде-
распределении лакун и отрезков конденсации возможных по-
рядков полных Д. г., определении для последних
самих Д. г. и соответствующих им лакунарных про-
пространств. Этот вопрос тесно связан с исследованием
степеней подвижности твердых тел.
Полную Д. г. порядка п(п-\-1)/2 допускает лишь
риманово пространство постоянной кривизны. Во вся-
всяком другом случае Д. г. пространства имеет меньшее
число параметров. Многообразие аффинной связности
допускает полную Д. г. (порядка ге(ге+1)) тогда и
только тогда, когда связность симметрична, а кривизна
равна нулю; при этом Д. г. является общей линейной
группой.
Лит.: [1] Е г о р о в И. П., в кн.: Итоги науки. Алгебра.
Топология. Геометрия. 1965, М., 1967, с. 375—428; [2] его
ж е, Движения в пространствах аффинной связности, Казань,
1965; [3] Р а ш е в с к и й П. К., Риманова геометрия и тен-
тензорный анализ, 3 изд., М., 1967. И. П. Егоров.
ДВОЕТОЧИЕ — топологич. пространство F, состоя-
состоящее из двух точек. Если в F открыты оба одноточеч-
одноточечных подмножества (и тогда оба замкнуты), то F наз.
простым двоеточием. Если в F открыто
лишь одно из двух одноточечных подмножеств, то F
наз. связным двоеточием. Наконец, если
в F открыты лишь пустое подмножество и все F, то
F называется слипшимся двоеточием.
Последнее пространство, в отличие от очень важных
при всей их простоте первых двух, применений не на-
находит.
Лит.: [1] Александров П. С, Введение в теорию
множеств и общую топологию, М., 1977. А. А. Мальцев.
ДВОИЧНАЯ ЕДИНИЦА в теории инфор-
информации — то же, что бит.
ДВОИЧНАЯ СИСТЕМА СЧИСЛЕНИЯ — позицион-
позиционная система счисления с основанием, равным двум.
Арифметич. операции в ней выполняются особенно
просто, так как в этой системе счисления нетривиаль-
нетривиальные действия с однозначными числами сводятся к
следующим двум: 1 + 1 = 10, 1-1=1. в. И. Нечаев.
ДВОИЧНЫЙ ДИСКОНТИНУУМ — топологическое
произведение простых двоеточий — дискретных про-
пространств, состоящих из двух точек.
ДВОЙНАЯ ПЛОСКОСТЬ — алгебраическая поверх-
поверхность, представляющая собой двумерный аналог ги-
гиперэллиптической кривой. Неособая алгебраическая
проективная поверхность X над алгебраически замк-
замкнутым полем к наз. двойной плоскостью,
если ее поле рациональных функций к (X) является
квадратичным расширением поля рациональных функ-
функций от двух переменных. Если характеристика поля
отлична от 2 (в дальнейшем это условие предпола-
предполагается выполненным), то каждая Д. п. бирационально
изоморфна аффинной поверхности, задаваемой в трех-
трехмерном аффинном пространстве уравнением
y) = 0.
Иногда именно поверхности такого типа наз. Д. п.
Для каждой Д. п. X существует морфизм / в проек-
проективную плоскость Р2(к), разлагающийся в композицию
бирациоаального морфизма
ф: Х^Х'
на некоторую нормальную поверхность X' и конеч-
конечного морфизма степени два
Кривая ветвления W морфизма ф' наз. кривой
ветвления Д. п. (и определяется, вообще го-
говоря, не однозначно по X). Кривая ветвления Д. п.
играет основную роль в их изучении. Напр., по ней
вычисляются численные инварианты Д. п. Если W
неприводима, то иррегулярность Д. п. X равна нулю.
Если степень W (всегда четная) равна 2к и все особен-
особенности W только двойные обыкновенные или каспидаль-
ные (см. Особая точка алгебраической кривой), то
арифметич. род ра(Х) и эйлерова характеристика
X (X) (топологическая или Z-адическая) вычисляются
по формулам:
В общем случае существует бирациональный морфизм
F—^-P2 (k) такой, что проекция на F нормализации X рас-
расслоенного произведения X и Fнад Р2 (А) на F является
конечным накрытием степени 2 с неособой (быть может,
приводимой) кривой ветвления W. В этом случае
имеют место формулы:
Ра {л) — Ра (А)— * 4 8~~ '
Для любой кривой W четной степени на проективной
плоскости всегда существует Д. п., имеющая W в ка-
качестве своей кривой ветвления. Выбор подходящей
кривой W позволяет во многих случаях решать задачу
построения алгебраич. поверхности с заданными инва-
инвариантами (см. [1], [3]).
Классификация Д. п. проводится отдельно в каждом
классе алгебраич. поверхностей. Описаны [5] рацио-
рациональные и линейчатые Д. п.; перечислены [3] Д. п.,
являющиеся эллиптическими поверхностями или КЗ-
поверхностями. Рассмотрено (см. [3], [4]) много приме-
примеров Д. п. основного типа.
Лит.: [1] Итоги науки. Алгебра. Топология. Геометрия,
т. 12, М., 1974, с. 77—170; [2] Zariski О., Algebraic surfa-
surfaces, В., 1971- [3] Enriques F., Le superficie algebriche,
Bologna, 1949; [4] Campedelli L., «Atti Accad. naz.
Lincei Rend.», ser. 6, 1932, y. 15, p. 203—8, 358—62, 536—42;
[5] J u n g H. W. E., «J. reine und angew. Math.», 1942, Bd
184, №4, S. 199—237. И. В. Долгачев.
ДВОЙНАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ — последова-
последовательность нек-рых элементов, занумерованных двумя
индексами:
атп, т=1, 2, . .., ге=1, 2, ...
Д. гг. по сравнению с обычными последовательно-
последовательностями (т. е. такими, у к-рых нумерация производит-
производится одним индексом) имеют ряд специфич. особенно-
особенностей: существует, напр., несколько определении пре-
пределов Д. п., не эквивалентных между собой.
Понятие двойной числовой последо-
последовательности тесно связано с понятием двойного
числового ряда
у к-рого как его члены, так и частичные суммы
составляют Д. п. При этом для всякой двойной чис-
числовой последовательности существует ряд, для к-рого
она является последовательностью его частичных
Сумм. См. также Двойной ряд. Л. Д. Кудрявцев.
ДВОЙНАЯ ТОЧКА — один из видов особых точек
кривой F(x, !/)=0, в к-рой первые частные производ-
производные равны нулю и по крайней мере одна из вторых
частных производных функции F(x, у) не равна нулю.
При исследовании строения кривой вблизи Д. т. рас-
рассматривают знак выражения
Если Д>0, то Д. т. наз. изолированной точ-
точкой; напр., у кривой
г/2
начало координат есть изолированная Д. т. (см. рис. 1).
Если Д<0, то Д. т. наз. узловой, или точкой
самопересечения; напр., у кривой
а2J—4Л2—ai=0
начало координат есть узловая точка (см. рис. 2).
Если А=0, то Д. т. кривой является либо изолирован-
У у ной, либо характери-
i i ^_^^ ^^_^^ зуется тем, что раз-
\ f f Г ^У^- ^ х личные ветви кривой
/ 0 \ Ч^__^й\^__-/ имеют в этой точке об-
щую касательную: на-
Рис. 1. Рис. 2. пример, а) точка
возврата 1-г о
рода — ветви кривой расположены по разные сто-
стороны от общей касательной и по одну сторону от
общей нормали (см., напр., рис. 3; у2—х3=0); б) т о ч-
УУ
\
Рис. 3.
Рис. 4.
Рис. 5.
ка возврата 2-г о рода — ветви кривой рас-
расположены по одну сторону от общей касательной и
по одну сторону от общей нормали (см., напр.,
рис. 4; (у—л-2J—?5=0); в) точка самопри-
самоприкосновения — ветви кривой соприкасаются (см.,
Напр., рис. 5; lJ2~Xi=0). А. В. Иванов.
ДВОЙНОГО ОТРИЦАНИЯ ЗАКОН — логический
принцип, согласно к-рому «если неверно, что неверно А,
то верно А». Д. о. з. наз. также законом снятия
двойного отрицания. В формализованном
языке логики высказывании Д. о. з. выражается фор-
формулой ~\ ~|рЗр и в таком виде (или в виде соответст-
соответствующей аксиом схемы) фигурирует обычно в перечне
логич. аксиом формальных теорий. В традиционной
содержательной математике Д. о. з. служит логич.
основанием для проведения так наз. доказа-
доказательств от противного в непротиворечи-
непротиворечивых теориях по следующей схеме: из предположения,
что суждение А данной математич. теории неверно,
выводится противоречие в этой теории, затем на ос-
основании непротиворечивости теории делается вывод,
что неверно «не А», и тогда по Д. о. з. заключают,
что верно А. В рамках конструктивных рассмотрений,
когда действует требование алгоритмич. эффективности
обоснования математич. суждений, Д. о. з. оказы-
оказывается, вообще говоря, неприемлемым. Типичным тому
примером служит всякое доказательство от противного
суждения А, имеющего вид «при всяком х существует у
такой, что верно В(х, у)», когда последний шаг, со-
состоящий в применении Д. о. з., оказывается невоз-
невозможным из-за того, что конструктивное понимание
суждения требует для его обоснования построения
алгоритма, к-рый по каждому х давал бы конструкцию у
такого, что верно В(х, у). Между тем рассуждение с
применением Д. о. з. не приводит к построению какого
бы то ни было алгоритма; более того, искомого в этом
случае алгоритма может вообще не существовать (см.
также Конструктивного подбора принцип).
Д. о. з. тесно связан с исключенного третьего за-
законом, в определенном смысле он даже эквивалентен
последнему. Так, в интуиционистском исчислении
высказываний каждый из этих двух законов выводим
из другого.
Лит.: [1] К лини С. К., Введение в метаматематику,
пер. с англ., М., 1957. Ф. А. Кабаков.
ДВОЙНОГО СЛОЯ ПОТЕНЦИАЛ — выражение вида
^(h(rXy))ii(y)dSy, A)
где Г — граница произвольной ограниченной ^-мерной
области gczE-N, N~^2, ny — внешняя по отношению
к области g нормаль к границе Г в точке у, и. (г/) — плот-
плотность потенциала — функция, заданная на Г, h (rXy) —
фундаментальное решение уравнения Лапласа
( * r2-N дг ¦> 2
r
a>N=2(V~ji)N/r(N/2) — площадь поверхности единич-
ной (Лг—1)-мерной сферы, rxy=y ^f=l(xi—Уд2 — рас-
расстояние между точками х и y?EN. Граница Г принад-
принадлежит классу О1- *¦>; она является поверхностью или
дугой Ляпунова.
Выражение A) может быть истолковано как потен-
потенциал, создаваемый диполями, помещенными на Г,
направление к-рых в каждой точке у ? Г совпадает с
направлением внешней нормали пу, а интенсивность
равна ц(у).
Если и.(г/)?С@)(Г), то и(х) определено для всех
х ? EN (в частности и для х ? Г) и обладает следую-
следующими свойствами.
1) Всюду в EN\Y функция и(х) имеет производные
всех порядков (^С10о)) и удовлетворяет уравнению
Лапласа, причем производные по координатам точки х
можно вычислять дифференцированием под знаком
интеграла.
2) При переходе через границу Г функция и(х) ис-
испытывает разрыв. Пусть х0 — произвольная точка на
Г, и+ (х0) и и~ (х0) — предельные значения изнутри
и извне, тогда и± (х0) существуют и равны
и± (*0) = ± ^+ С JL (h (г )) ц (у) dsy,
Л у
C)
причем интеграл в формуле C) как функция х0 ? Г
принадлежит С<°. «> при любом 0<а<1, кроме того,
функция, равная и в g и и+ на Г, непрерывна в g+T,
а функция, равная и в EN—(g+Г) и и~ на Г, непре-
непрерывна в EN—g.
3) Если плотность (д.(г/)?С@- а) и а<:^, то и(х),
продолженная так же, как в 2) на g+Г или EN—g,
принадлежит классу С@-°" в g+Г или в EN—g.
4) Если а>1—X, a xx и хг — две точки, принадле-
принадлежащие нормали, выходящей из точки х0, симметрич-
симметричные относительно точки х0, то
дп дП
В частности, если существует одна из производных
ди+ (хоIдп, ди~ (хоIдп, то существует и другая и
ди+ (хо)/дп=ди- (хо)/дп. Это свойство справедливо так-
также, если и.(г/)€С<0>(Г), а Г^С*2».
Перечисленные выше свойства обобщаются во многих
направлениях. Плотность ц(х) может принадлежать
ЬР(Т), />>1. Тогда u(x)?Lp(g+T), u(x)?C^> вне Г
и удовлетворяет уравнению Лапласа, формулы C)
и D) имеют место для почти всех 1,^Ги интеграл в C)
принадлежит Lp{T).
Изучены также свойства Д. с. п., понимаемых как
интегралы по произвольной мере v, определенной на Г:
здесь также и(х)?С-°°1 вне Г и удовлетворяет урав-
уравнению Лапласа, формулы C) и D) имеют место для
почти всех хо?Т по мере Лебега v(x) с заменой ц(х0)
на производную моры v'(х0). В определении A) фунда-
фундаментальное решение уравнения Лапласа может быть
заменено на произвольную функцию Леви для общего
эллиптич. оператора 2-го порядка с переменными коэф-
коэффициентами, a dldnv — на производную по конормалн.
При этом остаются' справедливыми свойства, перечис-
перечисленные выше (см. [2]).
Д. с. п. играет важную роль в решении краевых
задач для эллиптич. уравнений. Представление иско-
искомого решения (первой) краевой задачи в виде Д. с. п.
с неизвестной плотностью и, (у) и использование свой-
свойства 2) приводит к интегральному Фредголъма уравне-
уравнению второго рода на Г для определения функции и. (у)
(см. [1], [2]).
При решении краевых задач для параболнч. урав-
уравнений используется понятие теплового потен-
потенциала двойного слоя, т.е. интеграл вида
v (х, *) = ^ rfT (j г JL (G (х, t; у, т)) а (у, т) dy<
где G(x, t; у, т) — фундаментальное решение урав-
уравнения теплопроводности в iV-мерном пространстве:
G(x, t; у, т) =
о(у, т) — плотность потенциала. Функция v(x, t)
и ее обобщение на случай произвольного параболич.
уравнения 2-го порядка обладают свойствами, анало-
аналогичными указанным выше для и(х) (см. [3], [4], [5]).
Лит.: [1] ГюнтерН. М., Теория потенциала и ее при-
применение к основным задачам математической физики, М.,1953;
[2] МирандаК., Уравнения с частными производными
эллиптического типа, пер. с итал., М., 1957; [3] Тихонов
А. Н., С а м а р с к и й А. А., Уравнения математической фи-
физики, 3 изд., М., 1966; [4] С мир но в В. И., Курс высшей
математики, 5 изд., т. 4, М., 1958; [5] Фридман А., Урав-
Уравнения с частными производными параболического типа, пер.
с англ., М., 1968. II. А. Шиишарев.
ДВОЙНОЕ ОТНОШЕНИЕ, сложное (или а н-
г а р м о н.и ческое) отношение, четырех то-
точек M-l, М2, М3, МА на прямой — число, обозначае-
обозначаемое символом {M1M2M3Mi) и равное
м,м3 . M,Mt
м3м2 : м4м2-
При этом отношение М1М3/М3М2 считается положи-
положительным, если направления отрезков МгМ3 и М3М2
совпадают, и — отрицательным при различных на-
направлениях. Д. о. зависит от порядка нумерации то-
точек, к-рый может отличаться от порядка следования
точек на прямой. Наряду с Д. о. четырех точек, рас-
рассматривается Д. о. четырех прямых т1, 7;?,, т3, тпц,
проходящих через точку. Это отношение обозначается
символом (m1m2m3mi). Оно равно
sin (m,m3) . sin (т,то4)
sin (m3m2) ' sin (тп,тпг) '
причем угол (т,ту) между прямыми т,- и ту рассмат-
рассматривается со знаком.
Если точки Mi, М2, М3, Mt лежат на прямых т1,
т2, т3, mi, то
(М хМгМ3М^ = (m1m2msm4).
Если точки Mi, M2, М3, М4 и М[, М'ъ, М'3, М'\ получены
пересечением одной четверки прямых nij, m2, m3, mi,
то (M1,M2M!iMi)= (MiM'2M3Mi).
Д. о. является инвариантом проективных преобра-
преобразований. Д. о., равное —1, наз. гармониче-
гармоническим отношением (см. Гармоническая четверка
точек). э. Г. Позняк.
ДВОЙНОЙ ИНТЕГРАЛ — см. Кратный интеграл.
ДВОЙНОЙ МОДУЛЬ — 1) То же, что бимодулъ.
2) Пара подгрупп Н и F группы G, участвующая в раз-
разложении группы G на двойные смежные классы, т. е.
в разбиении G на непересекающиеся подмножества
вида HxF, где х — элемент из G. Подмножество HxF
наз. смежным классом группы G по
Д. м. (//, F), или двойным смежным клас-
классом группы Gno модулю (Н, F). Напр.,
разложение группы порядка 24 на двойные смежные
классы по модулю (//, F), где Н и F — ее силовские 2-
и 3-подгруппы, состоит из одного смежного класса
по Д. м. (//, F). Любой двойной смежный класс HxF
состоит из \H:H[\xFx~1\ смежных классов группы G
по подгруппе F и одновременно из \F:Ff\x~1Hx\ смеж-
смежных классов группы G по подгруппе Н, где |f/:F|
означает индекс подгруппы V в группе U.
Лит.: [1] ХоллМ., Теория групп, пер. с англ., М.,
1962. В. Д. Мазуров.
ДВОЙНОЙ ПРЕДЕЛ —1) Д. п. последователь-
последовательности, предел двойной последова-
последовательности {хтп}, т, 7г=1, 2, . . .,— число а,
определяемое следующим образом: для любого 8>0
существует такое Лге, что для всех m>Ne и n>JVe
выполняется неравенство
\хт„ — а\ <е.
Обозначение:
а= lim xmn.
т, п -*- х
Если для любого 8>0 существует такое NE , что для
всех m>yVg иге>Л?"е выполняется неравенство |жт„|>8,
то последовательность хтп имеет своим пределом бес-
бесконечность:
lim гот„=оо.
т, п ->- х
Аналогично определяются бесконечные пределы
lim zmn= + °° и lim zmrI = — со.
т, п —»- х т, п -*- х
Д. п. последовательности является частным случаем
Д. п. функции по множеству, а именно в случае, когда
это множество состоит из точек плоскости с целочис-
целочисленными координатами т и п. Поэтому между Д. п.
последовательности и ее повторными пределами су-
существует та же связь, что и в общем случае.
2) Д. п. ф у н к ц и и — предел функции двух перемен-
переменных, определяемый следующим образом. Пусть функ-
функция f(x, у) определена на множестве Е, расположенном
в плоскости XOY, а (х0, у0) — его предельная точка.
Число А наз. Д. п. функции f(x, у) в точке (х0, уа),
или при (х, у)^-(х0, !/0), если для любого 8>0 сущест-
существует такое 6>0, что для всех точек (х, у)?Е, коор-
координаты к-рых удовлетворяют неравенствам
0<\х-х0\<8, 0<\у-у0\<8,
выполняется неравенство
\1(х, у)-А\<г.
В этом случае пишут
lim / (х, у) = А.
(х, у) ->¦ (х„, у0)
Используя понятие предела последовательности, оп-
определение Д. п. функции можно сформулировать сле-
следующим образом:
А = lim / (x, у),
(х, ;/) ->¦ (х0, у„)
если для любой последовательности
(*п> Уп) —*-(я0, Уо). (*о. У о) Ф (хп, Уп) € Е, п = 1, 2, ...,
выполняется условие
lim /(*„, у„) = А.
П -*¦ со
Аналогично формулируются определения Д. п. функ-
функции при стремлении аргумента к бесконечности, а
также определения бесконечных Д. п. функции.
Существует связь между Д. п. функции и повторным
пределом функции в точке (х0, у0) пли в оо: пусть хй
и у0 — предельные точки (конечные пли бесконечные)
для числовых множеств X и Y, Е = XxY. Если суще-
существует конечный или бесконечный Д. п. функции
lim / (х, у)
(X, у) ->- (*„, (/„)
и при любом у ? Y существует конечный предел
Ф (у) = lim / (x, у),
х ->• х0
то существует и повторный предел
lim lim / (х, у)= lim <p (у),
У ->¦ Уа X -* х„ У-+ Уо
и он равен Д. п. функции.
Используя понятие окрестности, определению Д. п.
функции можно придать следующий вид: пусть а —
предельная точка (х0, у0) множества Е или символ оо,
причем в последнем случае множество Е неограничено,
А — число или один из символов оо, -j-oo, —оо, тогда
А = lim / (x, у),
(х, у) ->¦ (лг0, у„)
если для любой окрестности ОА точки или символа А
существует такая окрестность Оа числа или символа а,
что для всех (х, у)?Е[)Оа, (х, у)=?а, выполняется
условие f(x, у)^Ол- В этом виде определение Д. п.
функции переносится на случай, когда функция / оп-
определена на произведении топологпч. пространств X
и У, х?Х, y?Y, а значения f(x, у) также принадле-
принадлежат нек-рому ТОПОЛОГИЧ. Пространству. Л. Д. Кудрявцев.
ДВОЙНОЙ РЯД — ряд
A)
члены итп, то, ге=1, 2, . . ., к-рого образуют двойную
числовую последовательность. Конечные суммы
наз. частичными суммами Д. р. A), или
прямоугольными частичными сум-
суммами. Они также образуют двойную последователь-
последовательность. Если у этой последовательности {Smn} суще-
существует конечный двойной предел
S = lim Smn, 0,
т, п ->• оо \"!
т<7 ряд A) наз. сходящимся, а число S — его
су м м о й:
Если конечного предела B) не существует, то ряд A)
наз. расходящимся. На Д. р. переносятся
многие свойства обычных (однократных) рядов. Напр.,
если Д. р.
сходятся, то при любых числах к и jx Д. р.
, „=1
также сходится и
Если Д. р. сходится, то
lim
(необходимое условие сходимости ряда A)). Для того
чтобы Д. р. A) сходился, необходимо и достаточно,
чтобы для любого е>0 существовало такое число Л"е.
что
если только т >7Ve , n >7Ve , а к и I — любые неотрица-
неотрицательные целые. Если все члены ряда A) неотрица-
неотрицательны, то последовательность его частичных сумм Smn
всегда имеет конечный или бесконечный предел, причем
lim S,nn— sup Smn.
m, n —*- -f я rn, n— 1, 2, . . .
Д. р. обладают свойствами, обусловленными нали-
наличием у его членов двух индексов, к-рые являются
специфнч. особенностью Д. р. Если сходится Д. г.
A) и для всех п=1, 2, ... сходятся ряды
то повторный ряд
также сходится и его сумма равна сумме данного
ряда.
Д. р. наз. абсолютно сходящимся, если
сходится ряд
Если Д. р. абсолютно сходится, то он и просто схо-
сходится; более того, сходится любой ряд, полученный
перестановкой членов данного Д. р. При этом сум-
сумма любого такого ряда совпадает с суммой исходного
ряда.
На Д. р., члены к-рых являются функциями, пере-
переносятся многие понятия и свойства, присущие обыч-
обычным функциональным рядам, напр., понятно равно-
равномерной сходимости, критерий Коши равномерной
сходимости ряда, признак Вейерштрасса равномерной
сходимости. Вместе с тем, далеко не все теоремы об
однократных рядах непосредственно переносятся на
Д. р. Так, прямой аналог Абеля теоремы для степенных
рядов
не справедлив для двойных степенных рядов, т. е. ря-
рядов вида
2" СтпХтУ"- C)
Существуют, напр., Д. р. C), к-рые сходятся только
в двух точках плоскости: ряд C) с коэффициентами
соп = с „о = — ci п = — сп\ = п]-.
и = 1, 2, ..., стп = 0, 7га=э:2, reSs2,
сходится только в двух точках @, 0) и A, 1).
Кроме определения B) для Д. р. A) существуют
другие определения его сходимости и суммы, связан-
связанные также с наличием у его членов двух индексов.
Напр., пусть
(Sр наз. треугольной частичной сум-
суммой Д. р. A)), то Д. р. A) наз. сходящимся, если
последовательность {Sр} сходится; ее предел
S= lim S
р -». оо
наз. треугольной суммой ряда A).
Если положить
(Sr наз. круговой частичной суммой),
то Д. р. A) наз. сходящимся, если функция Sr пара-
параметра г имеет предел при г—*-+°°> этот предел
S = lim Sn
наз. круговой суммой ряда A).
Если через Щ обозначить произвольное конечное
множество пар индексов (т, п) и положить
то число S наз. суммой ряда A), если для любого
е>0 существует такое конечное множество ЭДе пар
индексов (то, п), что для любого 9in>?fJe выполняется
неравенство [S— 59,| <8. Если такое число S сущест-
существует, то ряд A) наз. сходящимся.
Всо эти определения сходимости Д. р. A) не экви-
эквивалентны между собой. Однако, если члены Д. р. не-
неотрицательны, то из сходимости в одном из указанных
смыслов следует сходимость во всех остальных, причем
все значения сумм Д. р. A) в этом случае совпадают.
Имеются и другие определения сходимости Д. р. Для
Д. р. существуют различные методы суммирования.
Понятие Д. р. обобщается на случай, когда его
члены являются не числами, а, напр., элементами ли-
линейного нормированного пространства.
Лит,: [1] Pringsheim A., «Miinehener Sitzungsber.
der Math.», 1897, Bd 27, S. 101—53; [2] его же, «Math. Ann.»
1900, Bd 53, S. 289—321; [3] его же, Vorlesungen uber Zah-
lenlehre, Bd 2, Lpz.— В., 1923; [4] В г о m w i e h T. J., Theo-
Theory of infinite series, 2 ed., L., 1926; [5] С а л е х о в Г. С, Вы-
Вычисление рядов, М., 1955; [В] Уиттекер Э.-Т., В а т с о н
Д.-Н., Куре современного анализа, пер. с англ., 2 изд., т. 1,
М., 1963. Л. Д. Кудрявцев.
ДВОЙНЫЕ И ДУАЛЬНЫЕ ЧИСЛА — гиперкомп-
гиперкомплексные числа вида а-{-Ье, где а и 6 — действительные
числа, и для двойных чисел е-=~\-\, а для дуальных
чисел е2=0. Сложение Д. и д. ч. определяется фор-
формулой
Умножение двойных чисел производится по формуле
(a] + V)(a2+V)= Ka2+6i62)
а дуальных чисел — по формуле
Комплексные числа, двойные числа и дуальные
числа наз. также комплексными числами
гиперболического, эллиптического
и параболического типов соответствен-
соответственно. Иногда при помощи этих чисел изображают дви-
движения трехмерных пространств Лобачевского, Римана
и Евклида (см., напр., Винтовое исчисление).
Как двойные, так и дуальные числа образуют дву-
двумерные (с базой 1 и е) ассоциативно-коммутативные
алгебры над полем действительных чисел. В отличие
от поля комплексных чисел эти алгебры содержат
делители нуля, причем в алгебре двойных чисел все
делители нуля имеют вид а^-ае. Алгебра двойных чисел
может быть разложена в прямую сумму двух полей
действительных чисел. С этим свойством связано еще
одно название двойных чисел — расщепляемые
комплексные числа. Встречается и другое
наименование двойных чисел — паракомплекс-
ные числа. Алгебра дуальных чисел рассматри-
рассматривается не только над полем R действительных чисел,
но и над произвольным полем или коммутативным
кольцом. Пусть Л — коммутативное кольцо с единицей
и М есть Л-модуль. Прямая сумма Л-модулей AQ)M
относительно умножения
(а, т)(а', т')—{аа', ат'~\-а'т)
является коммутативной Л-алгеброй и обозначается
1а(М). Она наз. алгеброй дуальных чи-
чисел относительно модуля М. Л-модуль
М отождествляется с идеалом алгебры I д(М), служа-
служащим ядром пополняющего гомоморфизма
в:1А(М)-*А ((а, т) _* а).
При этом квадрат ЛЯ данного идеала равен нулю, а
Iд(МIМс^А. Если Л — регулярное кольцо, то верно
и обратное: если В есть Л-алгебра и М — идеал в В
такой, что М2=0 и BIMczlA, то В~1 д(М), где М рас-
рассматривается как Л-модуль (см. [4J).
При М=А алгебра /д(М) (обозначаемая в этом
случае /д) изоморфна факторалгебре алгебры много-
многочленов А(Т) по идеалу Т2. Многие свойства Л-модуля
М можно переформулировать как свойства алгебры
Iд(М), что позволяет сводить многие вопросы об Л-
модулях к соответствующим вопросам в теории колец
(см. [2]).
Если В — произвольная Л-алгебра, ф: В-^-А — го-
гомоморфизм и д: В-^-М — дифференцирование В со
значением в Л-модуле М, рассматриваемом как В-
модуль относительно гомоморфизма ф, то отображе-
отображение д :В-*-1д(М) F—>-(фF), д(Ь))) является гомоморфиз-
гомоморфизмом Л-алгебры. Обратно, для любого гомоморфизма
Л-алгебр / ',В-^-1 д(М) композиция e'of:B-^-M, где
е': / д(М)—>-М — проекция Л на М, является Л-диффе-
Л-дифференцированием В со значением в М, рассматриваемом
как В-модуль относительно гомоморфизма ео/ :В—>-Л.
Это свойство Д. и д. ч. используется для определения
касательного пространства к произвольному функ-
функтору на категории схем [1], [3].
Лит.: [1] М а м ф о р д Д., Лекции о кривых на алгебраи-
алгебраической поверхности, пер. с англ., М., 1968; [2] Possum R.,
Trivial extensions of abelian categories, В., 1975; [3] S e h ё m a s
en groupes, I, В., 1970; [4] L i с h t e n b a u m S., S с h 1 e s-
singer M., «Trans. Amer. Math. Soc», 1967, v. 128, №1,
p. 41 — 70. И. В. Долгачев.
ДВОЙСТВЕННАЯ КАТЕГОРИЯ, дуальная
категория, к категории С — категория С с те-
теми же объектами, что ж С ж с множествами морфизмов
НотСо(Л, В) = Нотс(В, Л) («обращение стрелок»).
Композиция морфизмов и с v в категории С° опреде-
определяется как композиция v с и в С. Понятия и утверж-
утверждения, относящиеся к категории С, заменяются двой-
двойственными понятиями и утверждениями в С°. Так,
понятие эпиморфизма двойственно понятию мономор-
мономорфизма, понятие проективного объекта — понятию инъ-
ективного объекта, прямое произведение — прямой
сумме и т. д. Контравариантный функтор на С стано-
становится ковариантным на С°.
Иногда двойственная категория имеет
непосредственную реализацию: так, категория дискрет-
дискретных абелевых групп эквивалентна Д. к. к категории
компактных абелевых групп (Понтрягина двойствен-
двойственность) , а категория афинных схем эквивалентна Д. к.
к категории коммутативных колец с единицей.
В. И. Данилов.
ДВОЙСТВЕННОСТИ ПРИНЦИП — 1) Д. п. в ма-
математической логике — теорема о взаи-
взаимозаменяемости в определенном смысле логич. операций
в формулах формальных логических и логико-пред-
метных языков. Пусть А — формула языка логики
высказываний или логики предикатов, не содержащая
знака импликации id: формула А* наз. двойствен-
двойственной формуле А, если она может быть получена из А
заменой в А каждого вхождения символов &, V, V, Е
двойственными им операциями, т. е. соответственно
символами V, &, 3, V. Д. п. гласит, что если А^>В
истинно, то истинно В*^)А*. В частности, если фор-
формулы А и В эквивалентны, то эквивалентны и двойст-
двойственные им формулы А* и В*. Д. п. справедлив для
классич. систем, при этом эквивалентность и истин-
истинность формул в его формулировке могут пониматься
как в терминах интерпретаций, так и в смысле выво-
выводимости в соответствующем классич. исчислении. При
конструктивном понимании формул Д. п. перестает
действовать. Так, напр.. в языке логики высказываний
импликация "~\А8с~\В^> ~\ (А VВ) конструктивно верна
н даже выводима в Рейтинга формальной системе,
однако обратная импликация двойственных формул
~] (А&В)^~\А V ~\В конструктивно неверна (напр.,
нереализуема по К лини — Роузу).
С Д. и. тесно связана следующая теорема: если
F*(At, ..., Ап) — формула, двойственная пропози-
пропозициональной пли предикатной формуле F(AX, ..., А„),
построенной без употребления импликации из элемен-
элементарных высказывании Аг, . . ., Ап, то формула ~]F(A1,
..., Ап) эквивалентна формуле F*(~\Ai, ..., ~\Ап)
в классич. исчислении высказываний пли предикатов,
соответственно.
Лит.: [1] НозиковП.С, Элементы математической
логики, М., 1959; [2] К лини С. К., Введение в метамате-
метаматематику, пер. с англ., М., 1957. Ф. А. Набоков.
2) Д. п. в геометрии — принцип, формулиру-
формулируемый в нек-рых разделах геометрии и заключающийся
в том. что, заменяя в любом верном предложении все
входящие в него понятия на двойственные им, полу-
получают верное (двойственное первому) предложение.
Справедливость Д. п. в проективной геометрии вы-
вытекает из того, что каждой аксиоме проективной гео-
геометрии соответствует двойственное предложение, яв-
являющееся либо аксиомой, либо теоремой.
В проективной геометрии на плоскости двойствен-
двойственными являются понятия:
точка прямая
точка, инцидентная прямой прямая, инцидентная точке
алгебраическая линия по- алгебраический пучок прямых
рядка п класса п
касательная прямая к ли- характеристическая точка пуч-
нии ка
Если считать отношением инцидентности между точкой
и линией второго порядка принадлежность точки
линии второго порядка, а отношением инцидентности
прямой с линией второго порядка — касание прямой
к линии второго порядка, то понятием, двойственным
линии второго порядка, является линия второго по-
порядка. Примером пары двойственных утверждений
могут служить Брианшона теорема и Паскаля теорема.
В проективной геометрии в пространстве двойственны
понятия точки и плоскости; понятие прямой само себе
двойственно.
Д. п. имеет место и в эллиптич. геометрии, где, кроме
понятий проективной геометрии, двойственными явля-
являются понятия отрезка и угла. Так. напр., в эллиптич.
геометрии справедливы следующие два двойственных
утверждения:
два треугольника равны, ее- два треугольника равны, ес-
если три стороны одного соот- ли три угла одного еоответ-
ветственно равны трем сторо- ственно равны трем углам
нам другого другого
Лит.: [1] Ефимов Н. В., Высшая геометрия, 5 изд.,
М., 1971. А. С. Пархоменко.
3) Д. п. в проективной геометрии
состоит в том, что любой теореме относительно под-
подпространств Sa, Sf), . . . проективного пространства
П„ их пересечений и сумм соответствует
теорема относительно подпространств Sn-a-1, •$*„_;,_!,
... их сумм и пересечений. Д. п. определяется двой-
двойственным характером аксиом проективной геометрии
и вытекающих из них теорем. Для проективного про-
пространства Пп(Х) над телом К Д. п. справедлив тогда
и только тогда, когда К допускает инверсный
автоморфизм. В общем случае имеет место
двойственность между проективными пространствами
П„(Х) и П„(Л'*), тела К и А'* к-рых инверсно изо-
изоморфны: таковы, напр., левое и правое проективные
пространства Р1п(К) и Ргп(К) над К (см. Проективная
алгебра, Корреляция), причем соответствие между
ними, т.е. соответствие между S^ и 5„_^_! опреде-
определяется выбором пары координатных систем в П„(К)
и П„(К*). Д. п. можно обосновать также с помощью
дуальных отображений линейных пространств Qn + i(K)
над телом, к-рые используются для интерпретации
ПрОеКТНВНЫХ Пространств. М. И. Вопцеховскип.
4) Д. п. в частично упорядоченных
множествах: если верна какая-либо теорема о
частично упорядоченных множествах, сформулирован-
сформулированная в общелогич. терминах и терминах порядка, то
верна и двойственная ей теорема. Для получения тео-
теоремы, двойственной к данной, все высказывания и
понятия, относящиеся к порядку, заменяются на
двойственные (т. е. все знаки порядка <: заменяются
на Js, н обратно), а общелогич. термины остаются без
изменений. Из справедливости нек-рого утверждения
для конкретного частично упорядоченного множества
(или для конкретного класса частично упорядоченных
множеств) еще не вытекает справедливость двойствен-
двойственного утверждения для этого множества. Так, частично
упорядоченное множество может иметь наименьший
элемент, но не иметь наибольшего, оно может удов-
удовлетворять условию минимальности, но не удовлетво-
удовлетворять условию максимальности. Справедливость Д. п.
вытекает из того, что отношение, обратное к частич-
частичному порядку, само является частичным порядком.
Иногда под Д. п. понимают именно это утверждение.
Т. С. Фофанова.
ДВОЙСТВЕННОСТЬ — 1) Д. в алгебраиче-
алгебраической геометрии — двойственность между раз-
различными пространствами когомологии на алгебраич.
многообразиях.
Когомологии когерентных пуч-
пучков. Пусть X — неособое проективное алгебраич.
многообразие размерности п над алгебраически замк-
замкнутым полем к, а X — локально свободный пучок на X.
Теорема двойственности Серра ут-
утверждает, что конечномерные линейные векторные
пространства когомологии Н' (X, X) и НП~'(Х,
двойственны друг другу. Здесь a>x=Q'x — пучок рост-
ростков регулярных дифференциальных форм n-й степени
на X, a X=Hom(X,Qx)— двойственный к X локально
свободный пучок. В случае, когда X=Qx{D) — обра-
обратимый пучок, соответствующий дивизору В на X, эта
теорема устанавливает равенство
где К — канопич. дивизор на X. При ге = 1 эквива-
эквивалентное атому равенство было найдено еще в 19 в.
Существует обобщение теоремы Серра на случай кого-
когомологии произвольных когерентных пучков на полных
алгебраич. многообразных (см. [1], [4]). В частности,
когда многообразие X есть подмногообразие Коэна —
Маколея (напр., локально полное пересечение) кораз-
коразмерности d в неособом проективном многообразии У,
имеет место Д. между А-пространством Н'(Х, <f) и про-
пространством глобальных Ext'oB
где ^ — когерентный пучок на X, w_y=Ext qyFx> wk)
(дуализирующий пучок Гротенди-
к a), a n=dim.X. При этом пучок ш^ является обра-
обратимым в том и только в том случае, когда X есть схе-
схема Горенштейна (см. Горенштейна кольцо).
Этальные к о г о м о л о г и и. Пусть X — пол-
полное связное неособое алгебрапч. многообразие раз-
размерности d над алгебраически замкнутым полем к,
п — целое число, взаимно простое с характеристикой
поля к, gF — локально свободный (в этальной топологии)
пучок ?/-модулей на X, yin — пучок корней п-А
степени из единицы. Существует невырожденное спа-
спаривание z/nZ-модулей [6]:
IP (X, „Я X Ны~'1 (X, Нот ($", у.®* )) -*Z, «Z-
Более общая теорема Д. относится к гладким, но не-
необязательно полным многообразиям [5]. Существует
невырожденное спаривание Z/nZ-модулей
Я\ (X, f) X Я**-' (X, Нот (Fj fl®d )) _Z,,?Z,
где слева стоят когомологии с компактными носите-
носителями. Если поле к есть алгебраич. замыкание поля к',
X=X'®h.k и 3r=§r'(g)h,k, то группа Галуа Gal (А/А')
действует на Н'(Х, $~) и предыдущее спаривание есть
спаривание Gal (&/&')-модулей.
Аналогом первой из приведенных теорем Д. для
Z-адических когомологии является теорема двой-
двойственности Пуанкаре: существует невы-
невырожденное спаривание 2,-модулой
где 'Zi[d\ — пучок Тейта, неканонлческн изоморфный
пучку Z? (см. l-адические когомологии). Отсюда следует
изоморфизм С}гпространств
Н'{Х, Qi)sHom(ff2d-'(X, Qi)(d), Z;)
и, в частности, равенство чисел Бетти
Ъ;(Х; 1) = ЬЫ_:(Х; I).
Так же, как и в случае когомологии когерентных пуч-
пучков, имеется обобщение предыдущих результатов на
относительный случай собственного морфизма схем,
формулируемый на языке производных категорий [6].
Другие теории когомологии. Ана-
Аналоги теоремы Пуанкаре имеют место для теории кри-
кристальных когомологии [7], когомологии де Рама над
полем нулевой характеристики [8]. В теоретико-
числовых приложениях важную роль играют когомо-
когомологии пучков на плоской топологии Гротендика чис-
числовых схем. В отдельных частных случаях для таких
когомологий также имеются теоремы Д. [9].
Лит.: [1] ГротендикА., в сб.: Международный мате-
математический конгресс в Эдинбурге, М., 19E2, с. 118—37; [2]
Итоги науки и техники. Алгебра. Топология. Геометрия, т. 10,
М., 1972, с. 47 — 112; [3] С ер р Ж.-П., в сб. переводов: Рас-
Расслоенные пространства и их приложения, М., 1858, 372—450:
[4] Н а г t s h о г n e R., Residues and duality, В., 1966; [5]
Theorie des topos et cohomologie etale des schemas, t. 3, В., 1973;
Lli] V e г d i e r J. L., в кн.: Proceedings of a Conference on
Local Fields, В., 1967, S. 184—98; [7] Berthelot P.,
Cohomologie cristalline des schemas de caracteristique p >0, В.,
1974; L8] HartshorneR., Ample subvarieties of algebraic
varieties, В., 1970; [9] M a z u г В., «Amer. J. Math.», 1970,
v. 92, p. 343—61; [10] A 1 t m a n А., К 1 e i m a n S., Intro-
Introduction to Grothendieck duality theory, В., 1970.
И. В. Далгачев.
2) Д. в алгебраической топологии —
положение, когда значения одних топологич. инвари-
инвариантов определяют значения других. Д. в алгебраич.
топологии выражается: в Д. (в смысле теории харак-
характеров) между группами гомологии и когомологии одной
и той же размерности при двойственных группах
коэффициентов; в изоморфизме между группами гомо-
гомологии и когомологии дополнительных размерностей
многообразия {Пуанкаре двойственность); в изомор-
изоморфизме между группами гомологии и когомологии вза-
взаимно дополнительных множеств пространства (Алек-
сандера двойственность); во взаимозаменяемости в
определенных ситуациях гомотопических и когомото-
пических, а также гомологич. и когомологич. групп,
к-рая без дополнительных ограничений на размерность
пространства имеет место не для обычных, а для S-
гомотопич. и .S-когомотопич. групп (см. S-двойствен-
ность).
Д. между гомологиями и кого мол о-
гиями состоит в следующем. Пусть {НГ(Х, А),
/*! д} — произвольная гомологии теория над нак-рой
допустимой категорией пар пространств и их отобра-
отображений, т. е. система, удовлетворяющая Стинрода —
Эйленберга аксиомам теории гомологии с дискретной
или компактной абелевой группой НГ(Х. А). Тогда
система {ffr(X, A), /*, б}, где НГ(Х, А) — группа
характеров группы НГ(Х, А), а /* и б — гомоАгор-
физмы, сопряженные соответственно гомоморфизмам
/я и д, удовлетворяет аксиомам Стинрода — Эйленберга
теории гомологии и стало быть представляет собой
теорию когомологии над той же категорией с ком-
компактной или, соответственно, дискретной группой
НГ(Х, А). Подобным же образом для каждой теории
когомологии может быть построена двойственная тео-
теория гомологии. Следовательно, теории гомологии и
когомологии составляют двойственные пары;
при этом, преобразование одной теории в другую, с
точностью до естественных эквивалентностей, яв-
является инволюцией. Для любой теоремы теории го-
гомологии, т. е. теоремы относительно системы {НГ(Х, А),
/, д}, существует двойственное утверждение относи-
относительно системы {НГ(Х, А), /*, б}, т. е. теорема теории
когомологии, и наоборот. При переходе к двойствен-
двойственному утверждению группы заменяются их группами
характеров, гомоморфизмы меняют направление, под-
подгруппы заменяются факторгруппами, и наоборот. При-
Примерами могут служить сами аксиомы Стинрода — Эй-
Эйленберга. В случае конкретных категорий или теорий
построение этой Д. осуществляется, напр., следующим
образом. Пусть К={Р} (конечный) комплекс. За
произведение /--мерной цепи сг комплекса К над ди-
дискретной или компактной группой X коэффициентов
и r-мерной коцепи в-г комплекса К над группой X*
коэффициентов, двойственной X в смысле теории ха-
характеров, принимается число mod 1
(с,, O-)=2f€ Ксг(Псг (П-
Это произведение определяет умножение класса го-
гомологии с классом когомологии и превращает г-мерные
группы гомологии и когомологии в группы характеров
одна другой. На бесконечных комплексах имеются
группы двух видов — проекционные и спектровые.
Спектровые группы гомологии явля-
являются пределами прямых спектров групп гомологии
замкнутых подкомплексов, упорядоченных по возра-
возрастанию, а проекционные группы гомо-
гомологии — гомологич. группами пределов прямых
спектров из групп цепей указанных подкомплексов.
Группы когомологии получаются аналогично, как
пределы соответствующих обратных спектров. При
дискретной группе коэффициентов обе гомологич.
группы совпадают и дают группу гомологии конечных
циклов, а при компактной группе совпадают когомо-
когомологич. группы и дают группу когомологии бесконечных
коциклов. Д. в случае конечных комплексов порож-
дает Д. проекционных групп между собой и спектровых
групп между собой, а эти последние Д. (посредством
сингулярных комплексов, нервов покрытий и т. п.) —
Д. r-мерной проекционной (соответственно спектровой)
группы гомологии Hr(R, X) пространства R над
дискретной или компактной группой X коэффициентов
в какой-либо теории (сингулярных гомологии, Алек-
Александрова — Чеха гомологии и когомологий, Въеториса
гомологии и т. п.) с r-мерной проекционной (соответ-
(соответственно спектровой) группой когомологий Hr(R, X*)
в той же теории над группой X*, двойственной X (см.
[1], [3], [6], [9]):
IIr (R, X) | Hr (R, X*) при X | X*.
Соотношения между инвариантами, выражающими
связности дополнительных размерностей многообра-
многообразия, были установлены в первой же работе по алге-
браич. топологии — в статье А. Пуанкаре (Н. Poincare,
1895), где было показано, что для n-мерного ориенти-
ориентируемого многообразия его р-мерное и (п — р)-мерное
числа Бетти равны друг другу, равно как и ^-мерный
и (п — р — 1)-мерный коэффициенты кручения. Эта
теорема была усилена О. Вебленом (О. Veblen, 1923),
сформулировавшим ее для баз гомологии, а примене-
применение групп когомологий придало ей форму, полнее вы-
выражающую содержание этой Д. Для получения этой
формы следует поставить в соответствие каждой г-мер-
ной цепи сг, заданной на какой-либо триангуляции
К гомологического re-мерного ориентированного мно-
многообразия М" и принимающей значения из дискретной
или компактной группы X коэффициентов (п — р)-
морную коцепь сп~Р клеточного комплекса К* из ба-
барицентрических звозд К, принимающую на какой-либо
звезде то значение, которое с„ имеет на соответст-
соответствующем этой звезде симплексе. Указанное соответствие,
в силу совпадения групп комплексов К и К*, опреде-
определяет изоморфизм групп гомологии и когомологий
дополнительных размерностей многообразия Мп:
НГ(М", Х)~Пп~г (М«, X).
При этом X может быть и модулем, а в случае неори-
ентируемого многообразия теорема верна по модулю 2.
Замена группы Hn~r(Mn, X) двойственной ей группой
Нп-г(М", X*) приводит к Д. [1]:
Hr(M", X)\Hn~r(Mn, X*), при Х\Х*,
представляющей интерес еще и тем, что при ней про-
произведением оказывается индекс пересечения циклов,
произвольно выбранных из перемножаемых классов
(см. [1], [11], [12], [13], [15], [16]).
Большой этап, вначале теоретико-множественный, по
отысканию топологич. свойств множества, к-рые оп-
определялись бы топологич. свойствами его дополнения,
завершился теоремой, полученной Дж. Александером
(]. Alexander, 1922) и утверждающей, что г-мерное
число Бетти mod 2 полиэдра, лежащего в ге-мерной
сфере, равно (п — г — 1)-мерному числу Бетти mod 2
дополнения (см. Александера двойственность).
В свою очередь, эта теорема положила начало ряду
исследований, в сильной мере повлиявших на развитие
всей алгебраич. топологии. Исследования велись в
направлении обобщения классов пространств (пло-
(плоскость, евклидовы пространства, сферы и многообразия
любых размерностей, локально компактные простран-
пространства и т. д.), их подмножеств (полиэдры, замкнутые
подмножества, произвольные подмножества) и областей
коэффициентов (целые числа по модулю 2, группа целых
чисел, поле рациональных чисел, другие конкретные
группы и поля, произвольная абелева группа, тополо-
топологич., в основном компактные, абелевы группы и т. п.),
для к-рых имеет место двойственность Александера,
а также усиления тех соотношений, к-рые связывают
инварианты взаимно дополнительных множеств (ра-
(равенство чисел Бетти, изоморфизм групп, Д. тополо-
топологических групп, естественные и связывающие гомомор-
гомоморфизмы и т. п.). Ряд полученных результатов может
быть представлен в виде диаграммы (см. [1] [3], [4],
[5], [6], [7], [8], [9], [И]):
Нг(А.Х) I //„¦Г.|F.Х*)
нг(а,х*)\^ //"""¦' (е.х)'
где X — дискретная или компактная группа коэффи-
коэффициентов, Х*\Х, А и В—взаимно дополнительные мно-
множества re-мерного сферич. многообразия Мп, ИГ(А, X)
и НГ(А, X*) — r-мерные группы гомологии и кого-
мологии (с компактными носителями) Александрова —
Чеха множества А над X и соответственно X*, а #„_,._!
(В, X*) и Нп~г-1(В, X) суть (п — г — 1)-мерные спект-
ровые группы гомологии и когомологии Александ-
Александрова — Чеха множества В над X* и соответственно
над X. Указанные в диаграмме соотношения, получен-
полученные различными автогами и различными способами,
согласованы в том смысле, что соответствующие при
изоморфизмах элементы представляют собой один и
тот же характер остальных групп при вертикальных
и горизонтальных Д, Таким образом, они являются
различными формами одной и той же теоремы
двойственности. Верхняя двойственность есть
Д. зацепления, т. о. при ней произведением элементов
является зацепления коэффициент циклов, произ-
произвольно выбранных из перемножаемых классов или,
в случае компактной группы X*, определяется по не-
непрерывности зацеплением циклов. В приведенной
диаграмме группы первого столбца могут быть заме-
заменены (г+1)-мерными группами гомологии и когомо-
когомологии Стинрода с компактными носителями, а группы
второго столбца — (и — г — 1)-мерными проекцион-
проекционными группами гомологии и когомологии Александ-
Александрова — Чеха; тогда, в случае компактного А изомор-
изоморфизм главной диагонали дает теорему двойственности
Стинрода в ее первоначальном виде, если когомологич.
группу множества В заменить, но теореме Пуанкаре,
(г -L 1)-мерной группой гомологии бесконечных циклов.
Если группа X компактна, то диаграммы изоморфны;
если, кроме того, и множество А компактно, то двой-
двойственность верхней строки диаграммы представляет
собой теорему, полученную Л. С. Понтрягиным в
1934 ([1], см. Понтрягина двойственность), О даль-
дальнейших обобщениях и направлениях см. [10], [14],
[15], [16].
Важным видом двойственности Александера, касаю-
касающимся связывающего гомоморфизма и аксиомы точ-
точности, является изоморфизм между группами гомоло-
гомологии, а также между группами когомологии соседних
размерностей. Эти изоморфизмы, установленные
П. С. Александровым и А. Н. Колмогоровым, утверж-
утверждают, что r-мерная группа гомологии (соответственно
когомологии) замкнутого множества А нормального
локально бикомпактного пространства R, ацикличного
в размерностях г и r~\-i, над компактной (соответствен-
(соответственно дискретной) группой X изоморфна (г+1)-мерной
группе гомологии (соответственно когомологии) до-
полнения: ^ (Л> х) ^ я^ (/?4^ х)
НГ(А, Х)~НГ + 1(В\А, X).
Из этих изоморфизмов выводится теорема Понтрягина.
П. С. Александров [2] получил эти изоморфизмы из об-
общих соотношений Д., связывающих группы гомологии и
когомологии взаимно дополнительных множеств и
пространства, а также ядра, образы и факторгруппы
этих групп при их естественных гомоморфизмах вло-
жения п высечения. Эти соотношения несут также
много другой важной информации о расположении мно-
множеств в пространстве. П. С. Александров [2] полу-
получил их с помощью спектровых групп гомологии и
когоыологий относительно так называемых особых под-
подкомплексов нервов, состоящих из симплексов, за-
замыкания вершнн которых некомпактны. А. Н. Колмо-
Колмогоров доказал вышеуказанные изоморфизмы Д. по-
посредством так называемых функциональных групп
гомологии и когомологий (см. Колмогорова двойствен-
двойственность). Указанные выше и другие Д. (напр., Лефшеца
двойственность) связаны между собой различными со-
соотношениями. Они могут быть рассмотрены и как
следствия нек-рой общей Д., в к-рой участвуют так на-
называемые внешние группы множества, являющиеся
прямым пределом групп когомологий окрестностей
этого множества, упорядоченных по вложению (см. [3],
[4], [5], [6], [7], [12], [13]). Связи между различными
Д. приобретают новый вид при их рассмотрении с
помощью пучков теории.
Лит.: L1J П о н т р я г и н Л. С, «Успехи матем. наук»,
1947, т. 2, в. 2, с. 21—44; [2] А л е к с а н д р о в П. С, «Изв.
АН СССР. Сер. матем.», 1942, т. 6, с. 227—82; [3] его же,
«Матем. сб.», 1947, т. 21, № 2, с. 161 — 232; [4] его ж е, «Тр.
Матем. ин-та АН СССР», 1955, т. 48, с. 1 — 108; 1959, т. 54, с. 1 —
136; [5] Чогошвили Г. С, «Докл. АН СССР», 1946
т. 51, .V° 2, с. 87—90; L6] его же, «Успехи матем. наук»,
196В, т. 21, в. 4, с. 23—34; [7] KaplanS., «Trans. Amer.
Math. Soc», 1947, v. 62, p. 248 — 71; [8] СитниковК А.,
«Матем. сб.», 1954, т. 34, с. 3 — 54; 1955, т. 37, с. 385 — 434; 1959,
т. 48, с. 213 — 26; [9] Берикашвили Н. А., «Тр. Тбил.
матем. ин-та», 1957, т. 24, с. 409 — 84; [10] Б а л а д з е Д. С,
там же. 1972, т. 41, с. 41—83; [11] BourginD., Modern
Algebraic Topology, N. Y.—L., 1963; [12] СпеньерЭ.,
Алгебраическая топология, пер. с англ., М., 1971; [13] Swit-
zer R. M., Algebraic Topology Homotopy and Homology,
В. —Heid.—N. Y., 1975; [14] С к л я р е н к о Е. Г., «Изв. АН
СССР. Сер. матем.», 1971, т. 35, № 4, с. 831 — 43; [15] В о г е 1
А., М о о г е J. С, «Miehig. Math. J.», 1960, v. 7, p. 137—60;
[16] В re don G. E., Sheaf Theory, N. Y., [1967].
Г. С. Чогошвили.
3) Д. в теории аналитических про-
пространств — двойственность между различными век-
торньвш топологнч. пространствами когомолопш комп-
комплексных пространств. Имеются три типа теорем Д.,
соответствующие двойственностям Пуанкаре, Лефшеца
и Александера — Понтрягина в топологии, но отно-
относящиеся к пространствам когомологий //J^(X, JF) ком-
комплексного пространства X со значениями в когерентном
аналитич. пучке ^f и носителями в семействе Ф или
их факторпространствам (см. Когомологий со значениями
в пучке).
Первому типу принадлежит теорема д в о й-
с т в е нности Серра [1]. Пусть X — комплекс-
комплексное многообразие размерности п со счетной базой, Q —
пучок голоморфных дифференциальных форм степени п,
а. §~ — локально свободный аналитич. пучок на X.
Для каждого целого р, О ¦<;?<:«, определено билинейное
отображение
Нр (X, f) X //?"" (X, Horn (f, й)) — С, (*)
которое можно записать как композицию U -умно-
-умножения
НР(Х, $") хН?~р(Х, Нот (Г, й)) — Я?(Х\ Q)
(с означает семейство компактных носителей) и линей-
линейной формы s на Н"(Х, Q), называемой следом и имеющей
вид
*(ш) = (—1)»
где w — форма типа (п, п) с компактным носителем,
отвечающая классу w в силу теоремы Дольбо (см.
Дифференциальная форма). Теорема двойственности
Серра утверждает, что если наделить пространства
Когомологий канонической локально выпуклой топо-
логией (см. Когерентный аналитический пучок), то
отображение (*) непрерывно по первому аргументу и,
при условии отделимости пространства ДР + 1(Х, JF),
устанавливает изоморфизм векторных пространств:
(^р(л, ,7))'s*//?-"(*, Hom(f, Q)).
Пучки §~ и Нот (<jF, й) можно поменять ролями, по-
поскольку операция Нот (•, Q) на локально свободных
пучках инволютивна.
В частности, если многообразно X компактно, К
канонический, а Д — любой дивизор на X, то из тео-
теоремы Серра вытекает равенство размерностей про-
пространств Н"(Х, Qx{D)) и IIn~p(X, (ox(K—D)), к-рое
часто используется при вычислениях с когомологиями.
Известна аналогичная теорема Д. для неособых про-
проективных алгебраич. многообразий над произвольным
полем (см. Двойственность в алгебраич. геометрии).
В случае, когда $~ — произвольный когерентный
аналитнч. пучок на многообразии X, имеет место ес-
естественная топологич. Д. между отделимыми простран-
пространствами, ассоциированными с векторными топологич.
пространствами Н^,(Х, f~) и Ех1^Гр(Х; f, й), где Ф —
семейство замкнутых носителей, Ч' — семейство ком-
компактных носителей или наоборот, а через Ext"jTp(X; JF)
обозначены производные функтора Ногпцг(Х; JF\ •)•
При этом пространство Нф(Х, Iff) отделимо одновре-
одновременно с Ext\\rp+i(X; J", Q) (см. [2], [3]). Для ком-
компактного X отсюда следует изоморфизм конечномерных
пространств
(//" (X, $"))' ss Ext»-P(X; J", Q).
Если X — многообразие Штейна, то получается топо-
топологич. Д. между П°(Х, аГ) и Ext"(X; If, Q) и между
Н"с.(Х, <Г) и Ext"~P(X; Г, й)-
Имеется также обобщение этих результатов на случай
комплексных пространств с особенностями [4] и на
относительный случай [5], аналогичное соответствую-
соответствующим теоремам Д. в алгебраич. геометрии.
Аналогом теоремы Лефшеца является следующая
теорема Д. [3]: пусть X — комплексное многообразие
со счетной базой размерности п, К — штейнов компакт
в X. Для любого когерентного аналитич. пучка $ на X
и любого целого р^О пространство Extn~P(K; ,f~, Й)
имеет топологию типа DFS (сильно сопряженное к
пространству Фреше — Шварца), а его сопряженное
пространство алгебраически изоморфно НРк(Х, JF).
Другая теорема того же типа [6]: в тех же предположе-
предположениях, если YczX открыто, то пространство Нру(Х, ,f~)
имеет топологию типа QFS (факторпространства Фре-
Фреше — Шварца), Ext?~p(Y; §~, Q) имеет топологию
типа QDFS (факторпространства типа DFS), а ассо-
ассоциированные с ними отделимые пространства нахо-
находятся в топологич. Д. Пространство Нру(Х, |?~) отде-
отделимо одновременно с Ext?~p+1(l'; |Г, й).
Третий тип теорем Д. представлен следующей тео-
теоремой [8]: для любого открытого подмножества YdX=
= C/>1 — сильное сопряженное к пространству
Г (У, 6*/Г(Х, бх)) изоморфно T(X\Y, (ox)- Эта
теорема допускает следующее обобщение [7]: пусть
X — re-мерное комплексное многообразие, счетное на
бесконечности, YdX открыто, JF — когерентный
аналитич. пучок на X, р^О — целое число. Рассмат-
Рассматриваются канонич. отображения векторных топологич.
пространств
а:Л"(Х, $r)-+Hp(Y, J"),
«Г, й) — Ext?-" (X\Y; $", Q).
Для того чтобы отделимое пространство, ассоциирован-
ассоциированное с СокегC, было изоморфно сильному сопряженному
к Сокег а, необходимо и достаточно, чтобы Кег у было
замкнуто. (Известен пример, когда Кег у не замкнуто.)
В частности, если пучок <f" локально свободен и
II" (X, <F)=Up + 1(X, <F)=0,
то отделимые пространства, ассоциированные с Нр (Y, Iff)
и Hc~p~1(X\Y, Horn (f, Q)), находятся в Д.
Лит.: [1] Serre J.-P., «Comm. math, helv.», 1955, t. 29,
p. 9—26; [2] Mai grange В., Seminaire Bourbaki, 1962/63,
p. 246; [3] В a n 1 с a C., S t a n a s i 1 a O., Metode algebriee
In teoria globala a spatiilor complexe, Bucuresti, 1974; [4] R a-
ra i s J. P., R u g e t G., «Publ. IHES», 1970, t. 38, p. 77 — 91:
Ы и x ж e, «Invent, math.», 1974, Bd 26, Л1 2, S. 89 —131-; [6]
Головин В. Д., «Функциональный анализ», 1971, т. 5,
№4, с. 66; [7] его же, «Матем. заметки», 1973, т. 13, №4,
с. 561; [8] GrothendieckA., «J. reine und angew. Math.»,
1953, Bd 122, Лв 1, S. 35. В. П. Паламовов.
4) Д. в т е о р и и аналитических функ-
функций.
а) Преобразование Бореля. Э. Борелю
(Е. Borel, 1895) принадлежит идея преобразования
каждого ряда впда:
в ряд
и обратно, при условии
Hm Via,, | =a < -[¦ со.
n ->- x
Так устанавливается отношение Д. между функциями,
аналитическими в окрестности бесконечно удаленной
точки |z|>a и целыми функциями экспоненциального
типа ст. На этом пути, напр., получается теорема
П о й а: пусть к (<р) — опорная функция выпуклой
оболочки множества особенностей функции a(z) (при
аналитическом продолжении на полуплоскость вида
Re{ze~i4>)>c, а
й(ф)= hm ——
— индикатор роста целой функции А (г); тогда
к(ц>)=к(—ф), a s^q>s^2n.
В силу этого отношения двойственности задача анали-
тич. продолжения функции a(z) в круг [z| <<т эквива-
эквивалентна изучению роста соответствующей целой функции
A (z) по различным направлениям.
б) Д. в пространствах аналитич.
ф у н к ц и й. Пусть G — открытое множество расши-
расширенной комплексной плоскости С и A (G) — простран-
пространство всех аналитических в G функций с топологией,
задаваемой системой норм
/>„(/)= max |/(z)|, / g A (G),
где {Кп\ — возрастающая система компактных мно-
множеств, содержащихся в G и исчерпывающих G; таким
образом, сходимость /„—»-/ в A (G) означает равномерную
сходимость /n(z)—>-/(z) на всех компактных подмноже-
подмножествах G. Пусть oo?G, A0(G) — подпространство A(G),
для функций к-рого /(оо) = 0, и F — компактное под-
подмножество С. Рассматривается система fj^ всех откры-
открытых множеств G^)F и множество функций |J pA(G).
GeQ
Две функции /j (z) и /2 (z) из этого множества считаются
эквивалентными, если совпадают их сужения на нек-рое
множество G?QF. Введенное отношение эквивалент-
ности разбивает всю рассматриваемую совокупность
на классы /. Каждый класс наз. локально ана-
аналитической на F функцией, и совокуп-
совокупность таких функций обозначается A (F). Класс A (F)
естественным образом превращается в линейное про-
пространство, и в нем вводится топология индуктивного
продела последовательности нормированных прост-
пространств Вп. Последние строятся следующим образом.
Пусть {Gn} — убывающая последовательность мно-
множеств из QF такая, что Gn + 1dGn и VG?QF
Эло:л->по => GncG.
Тогда Вп — пространство ограниченных в Gn аналитич.
функций с нормой
||/||= max |/(z)|.
гЕС»
Простейший факт оД. пространств анали-
аналитических функций состоит в следующем.
Пусть G — открытое множество и (для определенности)
°°?G, a F=C\G. Двойственным (сопряженным) к
пространству A0(G) (в смысле теории линейных топо-
логич. пространств) является пространство A(F). Эта
Д. устанавливается следующим образом: если Л(/) —
непрерывный линейный функционал над A0(G), то
существует единственный элемент g^A(F) такой, что
где у — некоторый (сложный) контур, идущий в Си
охватывающий F, a g?g (A(f) не зависит от g{z)?g).
Пространства А (Е) могут быть определены для произ-
произвольных множеств Е<^С, а не только .для рассмотрен-
рассмотренных здесь случаев, когда E=G — открытое множество
и Е= F— компакт. Дальнейшие обобщения: рас-
рассмотрение множеств на римановых поверхностях,
пространств функций многих комплексных переменных,
пространств векторнозначных аналитич. функции (со
значениями в линейных топология, пространствах).
Развитие теории Д. пространств аналитич. функций,
с одной стороны, стимулировалось развитием общей
теории Д. линейных топологич. пространств, а с дру-
другой стороны, само стимулировало развитие общей
теории выявлением глубоких конкретных закономерно-
закономерностей. Применения Д. пространств аналитич. функций
многообразны: вопросы интерполяции и аппрокси-
аппроксимации (см. ниже), аналитическое продолжение, разде-
разделение и устранение множеств особенностей, интеграль-
интегральные представления различных классов функций.
в) Д. между теоремами полноты и
единственности. Полнота системы элементов
{/„} какого-либо локально выпуклого пространства X
имеет место в том и только том случае, когда для про-
произвольного линейного непрерывного в X функционала
Л из Л(/п) = 0, п=1, 2, ..., следует Л^О. Этот факт
приводит к установлению связи между проблемами
полноты в пространствах аналитич. функций и разного
рода теоремами единственности для аналитич. функ-
функций. С функционалом Л связывается (ср. п. 1) нек-рая
аналитич. функция F(z). Условие Л(/„) = 0, ге=1, 2, . . .,
приводит к равенству нулю F(z) в нек-рых точках или
к равенству нулю коэффициентов F(z). Теоремы един-
единственности позволяют заключить, что F{z)=0, а затем
и что функционал Л=0. Для пространств аналитич.
функций в круге был сформулирован следующий
принцип двойственности проблем един-
единственности и полноты. Пусть Ад и Ар — соответственно
пространства функций, аналитических в кругах: \z\ <Д
и |?|<.Р, где 0<Л, Р<оо и F(z, ?) — функция, ана-
аналитическая в бицилиндре: \z\ <Я, |'|</*. Пусть L
и Л — линейные функционалы, определенные в Ag
и АР, и пусть Q(Z.A% и QczAp — подмножества функ-
функций, представимых соответственно в виде AF(z, Z,)
и LF{z, ?). Последовательность функций AnF(z, ?)
г S
будет полной в Q тогда и только тогда, когда для каж-
каждой cp(?)?Q из Л„ф=0, и=0, 1, 2, .. ., следует: ф(?)=Ю.
В частности, когда R = P=°o и F(z, ?,) = ezZ, оба мно-
множества б и Q совпадают с совокупностью всех целых
функций экспоненциального типа.
г) Д. в экстремальных задачах тео-
теории ф у н к ц и й. Известно, что задачи наилучшего
приближения в нормированных пространствах двой-
двойственно связаны с нек-рыми линейными экстремаль-
экстремальными задачами. Так, если Е — подпространство в
нормированной пространстве X и ш — произвольный
элемент X, то
sup |Z(u>)|= inf[|u>-*||, A)
Х ?
где E-L — а н н у л я т о р Е, т. е. совокупность ли-
линейных функционалов I, обращающихся в нуль на
элементах Е. Соотношение A), устанавливаемое на
основании теоремы Хана — Банаха, оказалось впо-
впоследствии частным случаем двойственных связей эк-
экстремальных задач математич. программирования.
Пусть G есть n-связная область, граница dG к-рой со-
состоит из спрямляемых контуров, В1 — класс аналити-
аналитических в G функций /(z), |/(z)|«:l, E1 — класс анали-
аналитических в G функций, представимых интегралом Коши
через свои граничные значения, ш(?) — какая-либо
интегрируемая функция на dG. Имеет место равенство:
sup I \ /(Е)ш (?)<*?
f6;gi I JdG
= inf Lr|w(E)-q>(?)ll«ie|. B)
ф g ?» J OG
Слева в этом соотношении стоит линейная экстремаль-
экстремальная задача для ограниченных функций (напр., при
о" ¦/> иг получают задачу о sup|/'(zo)| —
Zni(L Z)- fBi
задачу о «лемме Шварца» — в многосвязной области);
справа — задача наилучшего приближения произволь-
произвольной функции ш(С) на dG граничными значениями ана-
литич. функций в интегральной метрике. Соотношение
B) служит отправным пунктом для проникновения в
каждую из двух экстремальных задач, содержащихся
в ном: с его помощью устанавливаются характеристич.
свойства экстремальных функций /* (z) ? В1 п^хр* (z) ? Е1,
исследуется вопрос об их единственности-и т. д. Функ-
Функция /* (z) оказывается наделенной важными геометрич.
свойствами: в задаче о лемме Шварца она отображает
G на гс-листный круг; в других задачах с ш(?), анали-
аналитической на dG, функция /* (z) отображает G на пС^п-
листный круг (см. [2] — [4]).
Лит.: [1] МаркушевичА. И., Избранные главы тео-
теории аналитических функций, М., 1976; [2] Итоги науки. Мате-
Математический анализ. 1964, М., 1966, с. 76 —164; [3] Итоги науки.
Математический анализ. 1967, М., 1969, с. 75 — 132; [4] Итоги
науки. Математический анализ. 1963, М., 1965, с. 5—80; [5]
Исследования по современным проблемам теории функций
комплексного переменного, М., 1960, с. 77—95.
А. 11. Марпушевич, С. Я. Хавиисон.
5) Д. в теории топологических век-
векторных пространств — тройка {F, G, /},
в к-рой F, G — векторные пространства над полем К,
f — билинейный функционал (форма) в FXG, облада-
обладающий свойством отделимости: если f(x, y) = 0
для каждого у, ;/?G, то х=0; если f(x, j/)=0 для
каждого х, x?F, то y=Q. Говорят также, что форма /
осуществляет Д., а пространства F, G находятся в Д.,
или образуют дуальную пару; если / фиксиро-
фиксирована, то пишут f(x, ;/)= (х, у). Важнейшим примером
является естественная двойствен-
двойственность: F= (F, т) — локально выпуклое топологи-
топологическое векторное пространство с топологией т, G=
= (F, %)' —сопряженное пространство всех линейных
т-непрерывных функционалов в F и (х, х') = х' (х) при
x?F, x' ?G; свойство отделимости для этой формы
(. , .) вытекает, напр., из локальной выпуклости топо-
топологии т (теорема о достаточном числе функционалов —
следствие теоремы Хана — Банаха). Теория Д. изучает
в основном способы построения объектов в F или G,
дуальных (двойственных) заданным относительно фор-
формы (. , .); соответствия между свойствами взаимно ду-
дуальных объектов; топологии, порождаемые Д. Основ-
Основным инструментом этого изучения является аппарат
поляр (при K=R или С полярой множества А,
AcF наз. множество
Д. порождает различные локально выпуклые топо-
топологии на F (и равным образом на G); такие, напр., как
слабая топология o(F, G) (порожденная
заданной Д.), задаваемая семейством полунорм | (•, г/)|,
у ? G, это — слабейшая топология, при к-рой все ото-
отображения (•, у) непрерывны; топология Макки
\i(F, G) с базой окрестностей нуля, образованной
полярами А° абсолютно выпуклых a(G, /^-компактных
подмножеств А в G; сильная топология
т* (F, G), база к-рой образована полярами А0 ограни-
ограниченных подмножеств Л в (G, a(G, F)). Для любого A, AaF
множество А00 является выпуклой a(F, С)-замкнутой
оболочкой множества Ли {Q} (теорема о бипо-
л я р е). Пространство G совпадает с (F, a(F, G))'
(основная теорема теории Д., показы-
показывающая, что любую Д. можно интерпретировать как
естественную). Пространство (/", a(F', F)) наз. сла-
слабым сопряженным с F.
Пусть F — локально выпуклое пространство над R
или С. Для ограниченности множества A, AcF, необхо-
необходимо и достаточно каждое из условий: а) А ограниченно
в слабой топологии; б) А0 — поглощающее множество.
Если А — окрестность, то i1 является a(F', /^-ком-
/^-компактом. Метризуемое пространство F полно в том и толь-
только в том случае, когда замкнутость множества A, AcF',
в топологии а(/<", F) равносильна замкнутости в той же
топологии всех пересечений А |~| U°, где U — окрест-
окрестность нуля в F (теорема Крейна — Шмуль-
я н а). Если F — полное сепарабельное пространство
и / — линейный функционал в F', то /? (/<", a(F', F))'
.тогда и только тогда, когда из условия lim xn=Q в
тополЪгии a(F', F) следует Пт/(ж„)=0 (теорема
\ п
Гроте ад и к а-). Подмножество А полного про-
пространства F относительно a(F, /^-компактно, если оно
относительно a(F, /^-секвенциально компактно (т е о-
рема Эберлейна). Выпуклое подмножество А
пространства Фреше над R a(F, /")-компактно тогда
и только тогда, когда для любого /, f?F', существует
а, а?А такое, что sup/=/(a) (теорема Д ж е й м-
А
с а). Для того чтобы (F, т)' = С, необходимо и доста-
достаточно условие: топология т не слабее топологии e(F, G)
и не сильное топологии |j(F, G) (теорема Мак-
Макки — Арене а, дающая важное в приложениях
описание топологий, сохраняющих Д.). Каждое из
следующих условий на пространство (F, т) достаточно
для совпадения т с топологией Макки: a) F — бочечное
пространство, б) F — борнологичоское пространство (в
частности, метризуемое). Сильная топология т* (F, G),
вообще говоря, не сохраняет Д.; если X — G локально
выпукло и X' = F, то пространство Х*= (X', т* (X', X))
наз. сильным сопряженным с X, и в
случае, когда т*(Х', X) сохраняет Д. (т. е. Х*' = Х),
пространство X наз. полурефлексивным
(X — рефлексивное пространство, если Х** = Х).
Если Н —подпространство F, то {Н, G/H0} и {F/H,
Н0}—дуальные пары относительно естественных фак-
факторизации формы (-, ¦). Если задано семейство Д. {Fa,
Gu, (•, •)<*}, то Д. произведения пространств F=HaF<x
и подпространства G=I7aGa всех финитных семейств
из Пава осуществляет форма
где
Подобным же образом описывается Д. индуктивного и
проективного пределов lim mdFa, lim prFa- Наличие
a a
в пространствах F, Fa топологий, сохраняющих Д.,
позволяет истолковать эти утверждения как описание
естественных Д. для YlaFa (тихоновская топология),
Fill (фактортопология), Н (индуцированная тополо-
топология), lim ind Fa и lim prFa, соответственно. В случае
а
нормированного пространства F естественный изомор-
изоморфизм Н* и F*1H° является изометрией:
||/|#[| = dist(/, Я»), / ? F*.
Использование Д. в конкретных задачах линейного
анализа пропорционально той роли, какую играют в
этих задачах линейные (непрерывные) функционалы.
Особенно заметными (если не определяющими) яв-
являются идеи теории Д. в следующих разделах анализа:
в исследовании линейно топологических (метрических)
свойств локально выпуклых пространств и, в част-
частности, описании естественной Д. для данного про-
пространства [1] — [3], [5], в теории обобщенных функций [4],
в теории экстремальных задач [6] — [7], в спектральной
и структурной теории линейных операторов [1], [2] в
теоремах полноты и единственности в теории аналити-
аналитических функций, в теории аналитических функциона-
функционалов Фантапье [8], см. также Двойственность в тео-
теории аналитических функций.
Лит.: [1] Б у р б а к и Н., Топологические векторные
пространства, пер. с франц., М., 1959; 12] РобертсонА. П.,
Робертеон В.-Дж., Топологические векторные пространст-
пространства, пер. с англ., М., 1967; 13] Шефер X., Топологические
векторные пространства, пер. с англ., М., 1971; [4] Д а н ф о р ц
Н., ШварцДж., Линейные операторы, пер. с англ., т. 1,
М., 1962, т. 2, М., 1966; 1.5] Д э й М. М., Нормированные ли-
линейные пространства, пер. с англ., М., 1961; [б] Иоффе
А. д., Тихомирове. М., Теория экстремальных задач,
М., 1974; t7] РокафелларР., Выпуклый анализ, пер.
с англ., М., 1973; [8] X а вин В. П., Итоги науки. Мате-
Математический анализ. 1964, М., 1966, с. 76 — 164; [9] X а в и н-
соп С. Я., «Успехи матем. наук», 1963, т. 18, в. 2, с. 25—98;
[10] D i es t e 1 J., Geometry of Banach spaces-selected topics,
В.—N.Y., 1975. H. К. Никольский.
6) Д. в экстремальных задачах и
выпуклом анализе — особенность выпук-
выпуклых множеств, выпуклых функций и выпуклых экст-
экстремальных задач, состоящая в возможности задавать
их двояким образом — в основном и сопряженном про-
пространствах. Замкнутые выпуклые множества в локально
выпуклом топологпч. векторном пространстве допус-
допускают двойственное описание: они совпадают с пересе-
пересечением замкнутых полупространств, их содержащих.
Это позволяет связать с каждым выпуклым множест-
множеством А в векторном пространстве X двойственный объект
в сопряженном пространстве — его поляру А°=
= {х*?Х* : (х*, я)<1, х?А]. Замкнутые выпуклые
функции (т. е. функции с выпуклыми и замкнутыми над-
графиками) в локально выпуклом топология, вектор-
векторном пространстве также допускают двойственное опи-
сание: они являются поточечными верхними гранями
аффинных функций, их не превосходящих. Такая Д.
позволяет связать с каждой выпуклой функцией
/ : X —>- R двойственный объект — сопряженную функ-
функцию, заданную на сопряженном пространстве X* и оп-
определяемую формулой
/*(**)= sup «х*, x> — f(x)).
хеХ
Поточечные верхние грани линейных функций в локаль-
локально выпуклом топологич. векторном пространстве суть
выпуклые замкнутые однородные функции, и в этом
факте заложена Д. между выпуклыми множествами и
выпуклыми однородными функциями. В основании опи-
описанных Д. лежат теоремы Хана — Банаха о продол-
продолжении линейных функционалов и теоремы отделимости
выпуклых множеств.
Сущность двойственного задания выпуклых множеств
н выпуклых функций находит свое отражение в инволю-
тивности оператора полярности А°°=А и сопряжения
/** = /, имеющей место для выпуклых замкнутых мно-
множеств, содержащих нуль, и выпуклых замкнутых функ-
функций, всюду больших — оо. Последний результат, каса-
касающийся функций (наз. теоремой Фенхеля —
Мор о), порождает многочисленные теоремы Д. для
экстремальных задач линейного и выпуклого про-
программирования. Примером пары двойственных задач
являются следующие две задачи линейного програм-
программирования
I. (с, х)—>-inf; II. (Ь, у)—>sup A)
Здесь
x, с ? R", (с, х) =2" cixi> У'
Для пары двойственных задач линейного программи-
программирования имеет место следующая альтернатива: либо
значения задач конечны и равны и в обеих задачах
существует решение, либо в одной из задач множество
допустимых значений пусто или значение задачи бес-
бесконечно.
Обычный прием построения двойственной задачи
состоит в следующем. Задача минимизации
/ (х) —> inf, ifX, B)
где X — линейное пространство, f : X —*- R, включает-
включается в класс подобных ей задач, зависящих от параметра:
F (х, у) —Hni, х ? X,
где Y — некоторое другое линейное пространство,
F: ХХУ->1Т, F(x, 0)=f{x) (функцию F наз. воз-
возмущением /). Обычно F предполагается выпуклой.
Двойственной к задаче по отношению к дан-
данному возмущению наз. задача
- F* @, у*) —> sup, у* ? Y*, B*)
где F* — функция, двойственная (сопряженная) с
F в смысле Лежандра — Юнга — Фенхеля. Для про-
простейших задач выпуклого программирования типа
i = l п,г^, C)
где X — линейное пространство, fi:X—*-R— вы-
выпуклые функции на X, В — выпуклое множество в X
(частными случаями C) являются задачи линейного
программирования), обычно применяются следующие
стандартные возмущения, зависящие от параметров
V 6 К^. У=(Уи •••. Ут), fo(x)^ inf, fi(x)*?yi, 1=1, ...,
т, х?В. Теоремы двойственности для
общих классов задач выпуклого программирования ут-
утверждают, что при нек-рых допущениях на возмуще-
возмущение F значения задач B) и B*) совпадают, и более того,
решение одной из задач является множителем Лагран-
жа для другой.
Лит.: [1J М i n k о w s к i H., Geometric der Zahlen, Lpz.—
В., J910- [2] e г о же, Gesammelto Abhandlung-en, Bd i—2,
Lpz.—В., 1911; [3] Fen che 1 W., «Canad. J. Math.», 1949,
v. 1, p. 73—77; [4] P о к а ф е л л а р Р., Выпуклый анализ,
пер. с англ., М., 1973; [5] Е k e I a n d I., T e m a n R., Convex
Analysis and Variational Problem, N. Y., 1976; [6] Иоффе
А. Д., Т и x о м и р о в В. М., Теория экстремальных задач,
М., 1974. В. М. Тихомиров.
7) Д. конечных абелевых групп —
классический прототип общей Понтрягина двойствен-
двойственности и различных более поздних ее модификаций. От-
Относится к свойствам изоморфного соответствия между
конечной абелсвой группой А и группой А = Нот (А, к*)
ее характеров со значениями в мультипликативной
группе к* алгебраически замкнутого поля к характери-
характеристики, не делящей порядок группы А (см. Характеров
группа). Естественное отображение / : А —>- А, опре-
определенное правилом
/
для всех а?А, %^А, также является изоморфизмом,
причем для любой подгруппы Вс^А имеет место равен-
равенство i(B)= (В1-)-1, где
В1 = {% € А | % (Ь) = 1 для всех Ъ ? В) э= AJB.
Соответствие В —»- В^- устанавливает двойственность
между решетками подгрупп групп А и А. Это соответ-
соответствие взаимно однозначно п обладает свойствами
Х=ВХ- Г) С1, (BflC)J-
Лит.: [1] ПонтрягинЛ. С, Непрерывные группы,
3 изд М., 1973, гл. 6; [2] HuppertB., tndliche Gruppen I
В., 1967, S. 688 — 96. А. И. Ностритш.
S-ДВОЙСТВЕННОСТЬ, стационарная
двойственность, Спеньера двойст-
двойственность, — двойственность в теории гомотошш,
имеющая место (при отсутствии ограничений на раз-
размерность пространств) для аналогов обычных гомо-
топич. и когомотопнч. групп в надстроечной катего-
категории — для Л'-гомотопич. и ^-когомотоипч. групп или
стационарных групп гомотопий н когомотошш, обра-
образующих экстраординарные (обобщенные) теории гомо-
гомологии и когомологий. Надстроечной кате-
горне й, пли 5-к а т е г о р н е й, паз. категория,
объектами к-рой являются топологич. пространства X,
а морфизмами — классы {/} S-t омотопных
отображений / р-кратной надстройки SPX1
в SpXr,, причем / и g : S4X1 -t- S1X2 считаются Л"-го-
мотопными, если существует такое K>max(/?, q), что
надстройки Sr~Pfn Sr~Lig гомотопны в обычном смысле.
Множество {Xi, X,} таких классов, наз. S-o т о б р а-
ж е н и я м и, составляет абелеву группу (относитель-
(относительно так наз. колейного сложения, см. [1], [2], [4], [5]).
Группа {-?,, Х2} есть предел прямого спектра мно-
множеств [SkXx, SkX2] обычных гомотопич. классов с
надстроечными отображениями в качестве проекций,
являющегося при достаточно больших к спектром групп
с гомоморфизмами. Имеет место изоморфизм S : {Xl7
Х2}—> {SXX, SX2}, при к-ром соответствующие друг
другу элементы представляются одним и тем же отобра-
отображением SPXt —>- SPX2, p^l. Полиэдром, п-
двойственным'к полиэдру X сферы Sn, наз.
произвольный полиэдр D пХ в S", являющийся S-pfi-
формационным ретрактом дополнения S"\X, т. е. если
морфизм, соответствующий вложению DnXdSn- .У,
есть Л'-эквивалентность. Полиэдр DпХ существует для
каждого X, н можно рассматривать X как DnX.
Для любых полиэдров Хг, Х.2 и любых «-двойствен-
«-двойственных им полиэдров DnXx и DnX2 существует единствен-
единственное отображение
Dn:{Xx, X2)~^{DnX2, DnXx),
удовлетворяющее следующим условиям:
а) Оно является инволютивным контравариантцым
функторнальным изоморфизмом, т. е. Dn есть такой
гомоморфизм, что если
i : ХхаХ2 и i' : DnDX
то
то
Dn({f2}-{h})=Dn{f1).Dn{ft);
если 9 — элемент из {Хх, Х2} или из {ВпХ„, DnX1},
то DnDnQ=e.
б) Оно удовлетворяет соотношениям
SDn=Dn + 1 и Dn + 1S=Dn,
где SDnXi н DnXi рассматриваются как полиэдры,
(п+1)-Двойственные к полиэдрам Х{ и, соответствен-
соответственно, SXj, i—i, 2; это значит, что оно не зависит от п и
стационарно относительно надстройки.
в) Оно удовлетворяет равенству
D^ = (Dne)*Dna,
где
Q,:lIf,(X1)-*Hp(Xt)
(DnQ)*:Il'>-P-^(DnX1) _ Hn-r-i (DnX2)
— гомоморфиЗлМЫ указанных групп гомологии и когомо-
логии, индуцированные б'-отображениями в^{Х1г Хг]
и Dn 0, а
Da : Н/>(Х!)^Лп-Р-1 (DnXi), i=l, 2,
есть изоморфизм, к-рый получается из изоморфизма
Александера двойственности заменой множества Sn\X{
его ^-деформационным ретрактом D,,X;.
Построение Dn опирается на представление данного
отображения как композиции вложения и 5-деформа-
цноннон ретракции.
5-г ом ото п и ческой группой 1 р(Х) про-
пространства X наз. группа {Sp, X}, а 5-к о г о м о т о-
п п ческой группой ТР(Х) пространства X —
группа {X, Sp}. Как и в обычной теории гомотошш,
определяются гомоморфизмы
Рассмотрение сфер S? и S"~p~ как п-двойственных
приводит к изоморфизму
и к коммутативной диаграмме
2Р(Х) ^ >Нр(Х)
Таким образом, изоморфизм Du связывает 5-гомо-
топич. и ^-когомотопич. группы подобно тому, как
изоморфизм двойственности Александера Da свянывает
группы гомологии и когомологли. Какая-либо двойст-
двойственность в S-категории приводит к двойственности в
случае обычных гомотопич. классов, если на прост-
пространство наложить требования, из к-рых следует налп-
чие взаимно однозначного соответствия множества
указанных классов с множеством 5-гомотопических
классов.
Примерами двойственных предложений в этой теории
являются теорема Гуревича об изоморфизме и теорема
классификации Хопфа. Dn переводит одну из этих тео-
теорем в другую, что означает замену б'-гомотопич. групп
5-когомотопическпмп, групп гомологии — группами ко-
гомологии, отображения фр— отображениями ср"-/*-1,
наименьшей размерности с нетривиальной гомологич.
группой — наивысшей размерностью с нетривиальной
группой когомологни, и наоборот. В обычной теории
гомотопии для определения и-когомотопнч. группы тре-
требуется, чтобы размерность пространства не превышала
In—2 (пли, более общо, чтобы пространство было
Bв—1)-косвязным. гс>1), что нарушает полную общ-
общность двойственности.
Теория обобщается в различных направлениях: напр.,
рассматриваются пространства, имеющие 5-гомотопи-
ческий тип полиэдров, относительный случай, теория
с носителями и др. (см. [3], [5], [6], [7]). Она послужила
одним из источников стационарной гомотопической
теории [8].
Лит.: Ш С п а н ь е р Э. Г., «Математика», 1959, т. 3, Л"» 1,
с. 17—2j; [2] SpanierE.H., W h i t e h e a d J. Н. С,
«Mathematics», 1955, v. 2, J\i 3, p. 56—80; [3] их же, «Ann.
Math.», 1958, v. 67, Л"» 2, p. 203 — 38; [4] Barratt M. G.,
«Proc. Lond. Math. Soc», 1955, v. 5, p. 71 — 106, 285 — 329; [5]
СпаньерЭ. Г., Уайтхед Д ж. Г., «Математика», 1959,
т. 3, М 1, с. 27 — 56; [6] Э к м а н Б., X и л т о н П., там же,
1960, т. 4, Л» 3, с. 3—27; [7] С п а н ь е р Э., Алгебраическая
топология, пер. с англ., М., 1971; [8] Уайтхед Д ж., Но-
Новейшие достижения в теории гомотопии, пер. с англ., М., 1974.
Г. С. Чогошвили.
ДВОЙСТВЕННЫЕ ФУНКЦИИ — дополнительные по
Юнгу функции, т. е. строго выпуклые функции, связан-
связанные Лежандра преобразованием.
ДВОЙСТВЕННЫЙ БАЗИС, дуальный базис,
к базису {«1, . . ., еп } модуля Е относительно формы / —
такой базис {сх, . . ., сп} модуля Е, что
/(<7, ct)=i, f(eh c,-)=0,
I ф и 1 < h /< п,
где Е — свободный АГ-модуль над коммутативным коль-
кольцом К с единицей, а / — неособая билинейная форма
на Е.
Пусть Е* — модуль, сопряженный к Е, &{е\, .. ., «„}—
базис Е*, сопряженный к исходному базису Е : е/(е,) =
= 1, е\ (е,-) = 0, гф\. Тогда каждой билинейной форме /
на Е отвечают отображения ф^, -ф^ : Е —>- Е*, опреде-
определяемые равенствами
<pf(x)(y)=f(x, у), yf(x){y) = f(y, х).
Если форма / неособая, то каждое из отображений фу,
г|)/ является изоморфизмом, и обратно. При этом двой-
двойственный к {<?], ..., еп} базис {сг, . . ., сп) характеризу-
характеризуется тем свойством, что
tf(c;) = 4 (г = 1, ..., п).
Е. Н. Hi/зъмин.
ДВОЯКОКРУГОВАЯ ОБЛАСТЬ — область D дву-
двумерного комплексного пространства С2, обладающая
свойством: существует такая точка (alt a2), что вместе
с каждой точкой (zj, z\) области D принадлежат все
точки (zj, z2) с координатами
Zj=\a/ + (zj — a/)e П,
0<фу<2я, / = 1, 2.
Точка (а±, а2) наз. центром Д. о. Если Д. о.
содержит свой центр, то она наз. п о л н о й Д. о.,
в противном случае — неполной Д. о. Примеры
полной Д. о.— шар пли бикруг, неполной — декарто-
во произведение круговых колец. Аналогично опреде-
определяется и л-круговая область, или область Рейнхардта.
Л/. Ширинбеков.
ДВОЯКОПЕРИОДИЧЕСКАЯ ФУНКЦИЯ — одно-
однозначная аналитич. функция f(z), имеющая только изоли-
изолированные особенности на всей конечной плоскости комп-
комплексного переменного z и такая, что существуют два
числа Pl, р2, отношение к-рых не является действитель-
действительным числом и к-рые являются периодами /(z), т. е.
Pl, р2 таковы, что имеет место тождество
f(z+Pl)=f(z+Pi) = f(z).
(Если отношение Pl/p2 действительно и рационально,
то /(z) — однопериодич. функция; если оно — иррацио-
иррационально, то /(z-)s=const.) Все числа вида тр1-{-пр2, где
т, п — целые, также являются периодами f(z). Все
периоды данной Д. ф. образуют дискретную абелеву
группу по сложению, наз. группой периодов
(или модулем периодов), базис к-рой (б а-
зис периодов) состоит из двух примитивных
периодов 2щ, 2ш3, \та.(щ1в>3)Ф0. Все остальные пе-
периоды этой Д. ф. представимы в виде 2т,оI + 2п(о3,
где т., п — целые. Не существует аналитич. функций
одного комплексного переменного, кроме констант,
имеющих более двух примитивных периодов.
Точки вида 2тсо1+2иоK, где т, п — целые, образуют
решетку периодов, разбивающую всю плос-
плоскость г на параллелограммы периодов.
Точки (числа) z\, z2, для к-рых
наз. конгруэнтными (сравнимыми по
модулю периодов). В конгруэнтных точках
Д. ф. /(z) принимает одно и то же значение, поэтому
достаточно изучить поведение /(z) в к.-л. основном
параллелограмме периодов. Обычно в.
качестве такоиого принимается множество точек
{z=zo+2f1cu1+2«3co3; 0«1<1, 0<г3<1},
т. е. параллелограмм с вершинами
О, ZO
Не существует отличной от константы Д. ф., регуляр-
регулярной во всем основном параллелограмме периодов. Меро-
морфные Д. ф. наз. эллиптическими функциями. Обоб-
Обобщение понятия эллиптич. функций на случай функций
/(zlt z2, .. ., zn) от 7?^1 комплексных переменных носит
название абелевых функций.
Лит.: [1] Маркушевич А. И., Теория аналитических
функций, т. 2, 2 изд., М., 1968, гл. 7; [2] Г у р в и ц А., К у-
рант Р., Теория функций, пер. с нем., М., 1968, ч. 2; [31
УиттекерЭ. Т., ВатсонДж. Н., Курс современного
анализа, пер. с англ., 2 изд., ч. 2, М., 1963, гл. 20; [4] Ахи е-
з е р Н. И., Элементы теории эллиптических функций, 2 изд.,
М., 1970. Е. Д. Соломеицев.
ДВУГРАННЫЙ УГОЛ — фигура в пространстве, об-
образованная двумя полуплоскостями, исходящими из
одной прямой, а также часть пространства, ограничен-
ограниченная этими полуплоскостями. Полуплоскости наз. гра-
гранями Д. у., а их общая прямая — ребром. Д. у.
измеряется л и н е й н ы м у г л о м, т. е. углом между
двумя перпендикулярами к ребру, выходящими из
одной точки и лежащими в разных гранях, или, иначе,
углом, образованным пересечением Д. у. плоскостью,
перпендикулярной к ребру. псэ.
ДВУЖИДКОСТНАЯ МОДЕЛЬ ПЛАЗМЫ — гидроди-
гидродинамическая модель, в к-рой плазма рассматривается
как совокупность двух «жидкостей» (электронной и
ионной), движущихся одна сквозь другую. Электрич.
сопротивление плазмы рассматривается как результат
взаимного трения этих жидкостей.
Система уравнений движения в предположении, что
на электроны действует только электронное давление
ре, а на ионы — лишь ионное давление р/, имеет вид
dmV / , \ ур
__?=_e^jB_i[rexe]J—-^-Дп,(Ге-Г,). A)
-^rL = Ze(i? + 4-[F,-Xff]J-7j-i-flfie(F,-Fe). B)
Взаимодействие элект(оаов и ионов учтено посредст-
посредством силы трения, пропорциональной произведению раз-
разности скоростей на концентрацию тормозящих частиц.
Величина R наз. коэффициентом взаимного трения, или
коэффициентом диффузионного сопротивления. Учиты-
Учитывая условие квазинейтральности плазмы (ne=zn;=n),
уравнение движения Д. м. п. приводится к виду
где
n-MV-J
¦у __. i i
Мп . + тпп
l e
— средняя массовая скорооть, p = p;Jrpe — суммар-
суммарное давление, a j=e(ZiijZt—neZe) — ионный ток. Если
т/М-^1, то »',-«Г, Ve^V—j/ne.
Уравнения A), B) могут быть использованы для по-
получения обобщенного закона Ома, связывающего плот-
плотность тока у с другими величинами. Если можно пре-
пренебречь членами вида (Vy)V (а также при тМ^Л)
обобщенный закон Ома записывается в виде:
где x=ihei —так наз. время передачи импульса,
•ve!- — эффективная частота передачи импульса, оп-
определяемая выражением:
Лит.: [1] Франк-КаменецкийД. А., Лекции по
физике плазмы, 2 изд., М., 1968; [2] Куликовский
А. Г., Любимов Г. А., Магнитная гидродинамика, М.,
19в2. В. А. Дородницын.
ДВУЗНАЧНАЯ ЛОГИКА — то же, что алгебра ло-
логики.
ДВУМЕРНАЯ КЛЕТКА — топологический образ
диска. ^-- -^- Чериавский.
ДВУМЕРНОЕ КОЛЬЦО в т опо л о гии — топологи-
топологический образ замкнутой части плоскости, заключенной
между несовпадающими концентрическими окружно-
окружностями. Д. к. есть ориентируемое двумерное многообра-
многообразие рода нуль с двумя компонентами края.
А. В. Чернаеский.
ДВУМЕРНОЕ МНОГООБРАЗИЕ — топологическое
пространство, каждая точка к-рого обладает окрест-
окрестностью, гомеоморфной плоскости или полуплоскости.
Д. м. — наиболее наглядный класс многообразий: к
ним относятся сфера, круг, лист Мёбиуса, проектив-
проективная плоскость, бутылка Клейна п др.
Точки, имеющие лишь такие окрестности, к-рые го-
меоморфны полуплоскости (если они есть), образуют
край многообразия.
Важнейший класс Д. м. состав-
составляют замкнутые ориен-
ориентируемые Д. м., или з а м-
кнутые поверхности.
Простейшая из них — сфера S2 —
поверхность рода 0. Поверхность
рода g получается из S2 удалени-
удалением 2g- пар непересекающихся ди-
дисков и отождествлением с каж-
каждой парой граничных окружно-
окружностей границ изогнутого цилиндра
Рис 1. (рис. 1). Этот процесс наз. п р и-
Рис. 3.
клеиванием ручек, а замкнутая поверхность
рода g — сферой с g ручками (рис. 2).
Более широкий класс Д. м. составляют компакт-
компактные ориентируемые Д.м., или поверхно-
поверхности с краем, получаемые из к.-л. замкнутой поверх-
поверхности удалением внутренних точек конечного числа не-
непересекающихся дисков. Их границы образуют край
возникающего Д. м.
Родом этого Д. м. счи-
считается род исходной
поверхности (рис. 3).
Д. м. рода 0 — диск или
диск с дырами.
В другой класс Д. м.
входят компактные
неориентир у е-
м ы е Д. м. Они так-
также могут быть замкну-
замкнутыми и с краем. Про-
Простейшее среди них —
Мёбиуса лист (рис. 4).
Он не может быть
ориентирован, т. е.
на нем нельзя выбрать одновременно для каждой
точкп направления вращения вокруг нее так, чтобы эти
направления переходили друг в друга непрерывно.
Другой пример — проективная плоскость RP-; лю-
любая окрестность каждой проективной прямот! на RP2 со-
содержит лист Мёбиуса и поэтому R.P2 также неориентп-
руема. В общем случае компактные неориентпруемые
Д. м. получаются из замкнутых поверхностей удале-
удалением внутренних точек непересекающихся дисков и за-
заклейкой их (не обязательно
каждого) листами Мёбиуса (на
рис, 5 лист Мёбиуса представ-
представлен в виде скрещенной крыш-
крышки, т. е. с самопересечением
по отрезку). Проективная пло-
плоскость RP2 получается из сфе-
сферы заменой одного диска на
лист Мёбиуса. Если заменить
листами Мёбиуса два диска,
то получится Клейна поверх-
поверхность (рис. 6), ее удобно изображать также как сферу с
неориентируемой ручкой. Вообще, приклейку двух
листов Мёбиуса можно заменить приклейкой одной не-
неориентируемой ручки, и наоборот. С другой стороны,
если обвести один конец обычной ручки по средней ли-
Рис. 4.
Рии
шш листа Мёбиуса, то эта ручка станет неориентируе-
неориентируемой (рис. 7). Таким образом, в неориентируемом Д. м.
любую ручку можно заменить на два листа Мёбиуса,
и наоборот.
Сферами с ручками или с листами Мёбиуса и, воз-
возможно, с удаленными дисками исчерпываются все ком-
компактные связные (состоящие из одного куска) Д. м.
Некомпактные Д. м., напр, плоскость R2, полуплос-
полуплоскость Ri и вообще любое открытое подмножество любо-
го компактного Д. м., могут быть очень сложно устрое-
устроены. Напр., если на R2 взять бесконечное число дисков,
уходящих на бесконечность, и заменить их на ручки или
листы Мёбиуса, то получится Д. м., к-рое не является
открытым подмножеством никакого компактного Д. м.
(рис. 8). Некомпактные Д. м. без края наз. открыты-
м и.
Одним из подходов к изучению Д. м. является ком-
комбинаторный подход, при к-ром Д. м. рассматривается
состоящим из выпуклых много-
многоугольников (граней), примы-
примыкающих друг к другу по общим
ребрам. Особенно важны три-
триангуляции Д. м., где гранями
являются треугольники. Если
два Д. м. триангулированы,
то их триангуляции наз. ком-
комбинаторно эквива-
эквивалентными, когда они име-
имеют изоморфные подразделе-
подразделения, между элементами которых можно установить
взаимно однозначное соответствие, сохраняющее при-
примыкание соответствующих граней. Из произвольных
двумерных комплексов триангулированные Д. м. выде-
выделяются тем, что к каждому ребру примыкают одна
(для ребер на краю) или две грани и вокруг каждой вер-
вершины триангуляции грани образуют один цикл (звезду)
Рис. 7.
/г\ АЛ Уел
Рис. 8.
последовательно примыкающих друг к другу граней
(рис. 9). Цикл замкнут, если вершина не лежит на краю
(а), и незамкнут, если она лежит там (Ь). Компактность
Д. м. равносильна конечности числа граней любой три-
триангуляции, а связность — возможности соединить лю-
любые две вершины цепочкой ребер. В связном Д. м. лю-
любые две грани соединимы цепочкой граней, в к-рой две
соседние имеют общее ребро. Неориентируемость рав-
равносильна существованию такой цепочки, к-рая содер-
содержит в себе лист Мёбиуса.
С помощью триангуляции удобно вводить инвари-
инварианты, т. е. характеристики, одинаковые у комбина-
комбинаторно эквивалентных Д. м. Важнейшим инвариантом
является эйлерова характеристи-
характеристика %(М), равная для данной три-
триангуляции числу В—Р-\-Г, где
В, Р, Г —числа вершин, ребер и
граней триангуляции соответст-
соответственно. 7 не меняется при подраз-
подразделениях, и поэтому если % (М-^ф
ф%(М2), то М1 и М2 комбина-
комбинаторно неэквивалентны. Для сфе-
сферы с g ручками 5с(М) = 2—2g, в
частности для сферы она рав-
равна 2, для тора 0, для проектив-
проективной плоскости 1, для бутылки Клейна 0, для сферы с к
листами Мёбиуса 2—к. Если из Д. м. выбросить внут-
внутренности к дисков, то %(М) уменьшится на к. Сопостав-
Сопоставляя компактному связному Д. м. три числа
(е, X, к},
Рис. 9.
где e==tl в зависимости от ориентируемости, %=%(М),
а к — число компонент края, получаем тем самым пол-
полное описание Д. м. с точностью до комбинаторной экви-
эквивалентности, поскольку эти тройки чисел различны для
описанных выше Д. м. (сфер с ручками, сфер с листами
Мёбиуса и, возможно, еще с дырами), и в то же время
любое компактное связное Д. м. комбинаторно эквива-
эквивалентно одному из этих Д. м. (см. [1], [3]). Для открытых
Д. м. классификация также проведена, но она здесь
гораздо сложнее, так как имеется несчетно много раз-
различных поверхностей [5].
Для чисто топологич. изучения Д. м. основную роль
играет Жордана теорема. Пусть С — кривая без самопе-
самопересечений, соединяющая две точки края многообразия
М или замкнутая; она называется сечением М¦
ь
Рис. 10.
Сечение С не разбивает М, если любые две точки М со-
соединимы дугой, не пересекающей С. Максимальное чис-
число сечений, к-рые вместе не разбивают М, увеличенное
на единицу, наз. числом связности М. Так,
согласно теореме Жордана, сфера и диск односвязны.
Связность замкнутой поверхности рода g равна 2g+l =
= 3 — /. Для такой поверхности имеется набор из 2g се-
сечений, к-рые все выходят из одной точки и разбиваются
на пары так, что каждая пара осуществляет разрез од-
одной ручки. Такой набор наз. каноническим
разрезом М: в результате разрезания по всем
сечениям М превращается в диск. Аналогично имеются
канонич. разрезы неориентируе-
мых Д. м. (по средним линиям
листов Мёбиуса). Для Д. м. с кра-
краем нужно провести еще сечения
из базисной точки к каждой ком-
компоненте края. Обратно, Д. м. воз-
возникает из диска, край к-рого раз-
разбит на сегменты, склеиванием этих
сегментов попарно между собой.
Если склеивание осуществляет-
осуществляется по схеме рис. 10, то полу-
получается ориентируемое Д. м., если
по схеме рис. 11, то—неориентируемоо. (Сегмент х
надо склеить с сегментом х' так, чтобы совпали направ-
направления стрелок.) Край возникает, если имеется несколь-
несколько сегментов, по к-рым не производится склейки.
Теорема Жордана позволяет также дать топологич.
характеризацию Д. м. В частности, сфера есть единст-
единственный локально связный континуум, содержащий топе-
логич. образ окружности, разбиваемый каждым об-
образом окружности и не разбиваемый никакой парой то-
точек. Вообще, Д. м. выделяются в классе локально связ-
связных континуумов тем, что они не разбиваются никакой
парой точек и разбиваются достаточно малой окруж-
окружностью (теорема У а й л д е р а, 1949).
Поскольку у гомеоморфных Д. м. любые две триан-
триангуляции комбинаторно эквивалентны, комбинаторная
классификация Д. м. имеет чисто топологич. смысл.
Хотя набором е, -/, к компактные Д. м. характеризуются
однозначно, для изучения свойств Д. м. имеют значе-
значение и другие топологич. инварианты. В первую оче-
очередь это — одномерных гомологии группа //г (Л/) и
фундаментальная группа лг (М). Для замкнутой по-
поверхности рода g Hx (Л/) равна прямой сумме 2g эк-
экземпляров группы Z целых чисел. В качестве образую-
образующих обычно берутся g пар окружностей канонич. раз-
разреза. Для неориентируемого замкнутого Д. м. с чис-
числом связности s Н1(М) есть сумма s—1 экземпляров
группы % и одного экземпляра группы ZJ2. За обра-
образующие берутся сечения канонич. разреза (за вычетом
одного) и еще дезориентирующий путь (после разреза
по которому Д. м. становится ориентируемым). Для
ях (М) непредставление удобнее всего получается с по-
помощью канонического разреза: его сечения берутся за
образующие, а соотношение получается при обходе
края диска, возникшего после разреза. В ориентируе-
ориентируемом случае получается копредставленне
\аъ 6Х; ..., ag, bg; a-fi^b^1 ... Ogbgu^bg1 = l},
а в неориентируемом
a\a\
Имеет значение тот факт, что универсальным накры-
накрытием любого связного Д. м. без края (кроме s2 и RP2)
является плоскость R2, а соответствующая монодромии
группа реализуется движениями евклидовой плоскости
или плоскости Лобачевского. Напр., тор получается
отождествлением всех точек плоскости, отличающихся
друг от друга на т i\-f-nr2, где ь\ и v2— два данных век-
вектора, а т и п — целые числа. Для применений важны
также и накрытия с ветвлением. Пусть отображение
/ : Afj —t- M2, где Мг и М2 — замкнутые и триангули-
триангулированные Д. м., линейно отображают каждую грань Мг
на некоторую грань М2, причем для каждого ребра I
в Мх примыкающие к нему две грани отображаются на
разные грани, примыкающие к ребру /(/) в М2. Для
каждой точки аг^Д/j, отличной от вершин, найдется
в jl/, окрестность, к-рую / переводит взаимно одно-
однозначно на окрестность точки f(x) в М2. Если для вер-
вершины v из Mj обойти в цпклпч. порядке примыкающие
к ней грани, то соответствующие грани в М, обойдут
в цпклич. порядке вершину f(v) в М2 целое число к раз.
Если к=1, то v — обыкновенная точка, если
же fc>l, то v — точка ветвления, а к —
кратность ветвления в точке v. Если
i~x(w) для w?M2 не содержит точек ветвления, то w
также наз. обыкновенной. Поскольку прообразы близ-
близких обыкновенных точек из Л/„ состоят из равного чис-
числа точек, по соображениям непрерывности получается,
что это число — одно и то же для всех обыкновенных
точек. Оно наз. числом листов накрытия.
Это число d равно для ориентируемого Д. м. степени
отображения f (в случае неориентируемости его сле-
следует привести по модулю два). Если f~1{w) содержит
точки ветвления с кратностямн A-j, ..., А-,, то f~l(w)
содержит на ^(к- — 1) меньше точек, чем обыкновен-
обыкновенная точка (здесь суммирование по всем точкам ветвле-
ветвления в Mt). Поскольку число вершинВ(МХ) HaJ^A,-—1)
меньше d-B(M2), а для числа ребер и граней: />(М1) =
= d-P(M2) и i'(M1\ = d-r(M.z), то
x(M1) = d.%(M2)-^\(ki- 1).
Это — формула Римана — Гурвица.
С точки зрения дифференциальной геометрии Д. м.
рассматриваются как гладкие многообразия, к-рые
снабжаются дополнительными структурами (напр., мет-
рикой, связностью и т. д.) или рассматриваются вло-
вложенными (с возможными самопересечениями) в евкли-
евклидовы пространства. Гладкое Д. м. можно триангули-
триангулировать так, что ребра будут гладкими дугами, а все
углы отличны от нуля (теорема Керне а, 1934).
Оказывается, что при этом диффеоморфным Д. м. отве-
отвечают комбинаторно эквивалентные триангуляции, и
обратно. Таким образом, классификация Д. м. сохра-
сохраняет силу и для гладких Д. м. Примером теоремы, свя-
связывающей топологич. характеристики Д. м. с его диф-
ференциально-геометрич. свойствами, является тео-
теорема Гаусса — Бонне [3]: интеграл от кри-
кривизны замкнутой поверхности (точнее, от гауссовой
кривизны, определяемой нек-рой римановой связностью,
к-рую всегда можно определить на гладком Д. м.)
равен 2пу_ (М). Этот факт, а также его интерпретация
с помощью так наз. гауссова отображения (в частности,
сферического отображения) в многообразие Грассмана,
если рассматриваемое многообразие погружено в евк-
евклидово пространство, находит обобщение в теории ха-
характеристических классов. Другая теорема, также по-
послужившая одним из истоков этой теории: сумма индек-
индексов особых точек любого векторного поля на замкну-
замкнутой поверхности равна %(М).
Важную роль Д. м. играют в теории функций комп-
комплексного переменного. Здесь Д. м. наделяются комп-
комплексными структурами, т. е. локальными параметриза-
параметризациями окрестностей точек, связанными между собой
аналптич. функциями, и наз. римановыми поверхностя-
поверхностями [4]. Они обязательно ориентируемы. Замкнутые ри-
мановы поверхности являются геометрич. моделями ком-
комплексных алгебраических кривых. Комплексное строение
на Д. м. не определяется однозначно его диффереициаль-
но-топологич. строением: напр., на поверхности рода g
комплексные структуры образуют континуум размер-
размерности 6g—6 (теорема Тейхмюллера, 1940).
К определению Д. м. иногда добавляются требования,
чтобы оно как топологич. пространство было хаусдор-
фовым или имело счетную базу (последнее, в частности,
необходимо для триангулируемости Д. м.: существуют
хаусдорфовы нетриангулируемые Д. м., см. Прюфера
поверхность).
Лит.: [1] Александров П. С, Ефремо-
Ефремович В- А., Очерк основных понятий топологии, М.—Л.,
1936; [2] Гильберт Д., Кон-Фоссен С, Нагляд-
Наглядная геометрия, пер. с нем., 2 изд., М.—Л., 1951; [3J Б а-
кельма» И. Я., В е р н е р А. Л., Кантор Б. Е., Вве-
Введение в дифференциальную геометрию «в целом», М., 1973; [4]
Спрингер Дж., Введение в теорию римановых поверх-
поверхностей, пер. с англ., М., 1960; [5] С т о и л о в С, Лекции о то-
топологических принципах теории аналитических функций, пер.
с франц., М., 1964. А. Б. Чернавский.
ДВУМЕРНОЕ МНОГООБРАЗИЕ ОГРАНИЧЕННОЙ
КРИВИЗНЫ — метрическое пространство, являющее-
являющееся двумерным многообразием с внутренней метрикой,
для к-рого определены аналоги таких понятий двумер-
двумерной римановой геометрии, как длина и интегральная
кривизна кривой, площадь и интегральная гауссова
кривизна множества.
Частным случаем Д. м. о. к. являются двумерные ри-
мановы пространства и поверхности многогранников
в трехмерном евклидовом пространстве. В общем слу-
случае класс Д. м. о. к. может рассматриваться как замы-
замыкание класса двумерных римановых многообразий отно-
относительно надлежащих предельных переходов.
Пусть М — двумерное риманово многообразие,
К(х) — гауссова кривизна М в точке х; о(Е) — пло-
площадь множества ЕаМ\ для EczAI кривизна:
со (E)=
абсолютная кривизна:
S L •к {х)'da
=S
положительная часть кривизны множества Е:
co+ (E)=\\ K+ (x) da (i),
где К+ (х)=тах {О, K(x)}. Если хну— две точки ри-
манова пространства М, то р(х, у) — нижняя грань
длин кривых на М, соединяющих точки х и //. Функ-
Функция р является внутренней метрикой. Она наз. е с-
т е с т в е н н о й метрикой риманова простран-
пространства М.
Пусть М — произвольное двумерное многообразие
с метрикой р. Говорят, что метрика р — р н м а н о-
в а, если многообразие М, наделенное метрикой р, изо-
метрично нек-рому двумерному риманову пространст-
пространству, снабженному его естественной метрикой.
Двумерное многообразие М с внутренней метрикой р
есть Д. м. о. к., если выполнено следующее условие.
Существует последовательность римановых метрик р„,
п=1, 2, . . ., определенных на многообразии М, такая,
что для всякого компактного множества АсМ будет
Рп —>- Р равномерно (т. е. функции рп{х, у) сходятся к
функции р(х, у) равномерно на множестве АХ А) и
последовательность |ы„|(^4), ге=1, 2, .... ограничена,
где | ю„ | — абсолютная кривизна римановой метрики р„.
Д. м. о. к. может быть определено аксиоматически.
В части достаточности условия данного здесь опре-
определения Д. м. о. к. могут быть ослаблены. Именно, дву-
двумерное многообразие М с внутренней метрикой р будет
Д. м. о. к., если для всякой его точки можно указать
окрестности U и Г, где VcU и последовательность рп-
мановых метрик р„, л = 1, 2, . . ., определенных на U
таким образом, что р„ -*- р равномерно на Т", п после-
последовательность {w.-1-rO*)} ограничена.
Для всякого Д.м. о. к. определены вполне аддитив-
аддитивные функции множества о(Е) и со(?) — площадь и,
соответственно, кривизна множества. В отличие от
рнманова случая, а(Е) может и не быть абсолютно не-
непрерывна от.носительно о(Е). В Д. м. о. к. определено
понятие поворота кривой — аналог понятия интеграль-
интегральной геодезич. кривизны кривой.
Всякая выпуклая поверхность в трехмерном евкли-
евклидовом пространстве есть Д. м. о. к. В этом случае кри-
кривизна множества всегда неотрицательна.
Д. м. о. к. допускают особенности типа конич. точек
р (для таких точек ш({р}) отлично от нуля), ребер, гра-
границы основания цилиндра и т. д.
Лит.: [1] Александров А. Д., 3 а л г а л л е р В. А.,
Двумерные многообразия ограниченной кривизны, Ы.—Л.,
1962; [2] Двумерные многообразия ограниченной кривизны,
ч. 2, М.—Л., 1965 (Тр. Матем. ин-та АН СССР, т. 76).
Ю. Г. Рсшстняк.
ДВУМЕРНЫЙ УЗЕЛ — класс изотопных вложений
двумерной сферы S- в четырехмерную S*. Чисто тополо-
гич. теория не развита, ибо еще не выяснено A978) со-
соотношение чистой и кусочно линейной топологии в
размерности 4. Обычно накладывается условие локаль-
локальной плоскостности. Метод изучения — рассмотрение
сечений S2 пучком параллельных трехмерных плоскос-
плоскостей. Основным является вопрос о том, будет ли узел
тривиален, если его группа nt (Sl\S2) изоморфна %.
Известно, что в этом случае дополнение 54\6 имеет
гомотопич. тип S1.
3 - л е н т о й в S1 наз. образ D3 такой иммерсии
ф : А3 —> 54, где А3 — трехмерный диск, что ф1ад3 —
вложение; самопересечения ф состоят из конечного чис-
числа попарно непересекающихся двумерных дисков
Di, . . ., Dn\ прообраз ф'(/>,-) каждого диска D; явля-
является объединением двух таких дисков Di и D"i, что
D'i[\D'i — 0, ?>,'c;int Д3, dD'l = D'if\d^. Образ края
(9А3 является двумерным узлом в Я4. Так получаемые
узлы наз. ленточными узлами. Это — один
из наиболее изученных классов Д. у. Всякий ленточ-
ный Д. у. является границей нек-рого трехмерного
подмногообразия сферы S4, гомеоморфного либо диску
Л3, либо связной сумме нек-рого числа E1х5г)\Д->.
Ленточный Д. у. тривиален тогда и только тогда, когда
фундаментальная группа его дополнения изоморфна Z-
Группа G тогда и только тогда является группой нек-
рого ленточного Д. у. в S1, когда она имеет к о п р е д-
с т а в л е н и е В и р т и н г е р а, т. е. копредстав-
ление |хх, . .., хп : гь .. ., тт\, где каждое соотношение
имеет вид ж,= co/^.-ryCof,1/, в к-ром число соотношений
на единицу меньше числа образующих в G![G, G]=Z.
Класс групп всех Д. у. полностью не описан. Из-
Известно, что этот класс шире класса групп fc-мерных
узлов в Sk + 2, к 5^3. Последний класс полностью оха-
охарактеризован (см. Многомерный узел). Свойства групп
Д. у., к-рыми, вообще говоря, не обладают группы
трехмерных узлов в S'J, таковы:
dim Я2 (G\ Q)^dimH1(C, Q),
где G' = [G, G] — коммутант; на конечной группе Т=
= Tors(G'/G") существует такая невырожденная сим-
симметричная форма L : Г(Я)Г —>- Q/Z, что для любых
m?G, х. у?Т имеет место L(x, y) = L(j.r, ry), где
т : Т -*- Т — автоморфизм, индуцированный сопряже-
сопряжением в группе G на элемент т.
Задача вычисления n2(Si\S2) решена лишь для
частных типов Д. у., напр, полученных конструкцией
Артина, ленточных и расслоенных.
А В Чернавский, М. IU. Фарбер.
ДВУПОЛОСТНЫП ГИПЕРБОЛОИД — см. Гипер-
Гиперболоид.
ДВУСТОРОННЕЕ БОРЕЛЕВСКОЕ МНОЖЕСТВО
класса а. — борелевское подмножество метриче-
метрического или (более широко) совершенно нормального
топо-логич. пространства, являющееся одновременно
множеством аддитивного класса а и мультипликативно-
мультипликативного класса а, т. е. принадлежащее одновременно клас-
классам Fa и Ga. Д. б. м. класса 0 — открыто замкнутые
множества. Д. б. м. класса 1 — множества типов Fa
и Ga одновременно. Любое борелевское множество клас-
класса а. есть Д. б. м. класса р при всяком E>а. Д. б. м.
класса а образуют поле множеств.
Лит.: [1] К у р а т о в с к и й К., Топология, т. 1, пер.
М. Я. Антоновского, Ы., 1906; [21 Хаусдорф Ф., Теория
множеств, пер. с нем.. М.—Л., 1937. А. Г. Елъкин.
ДВУСТОРОННЯЯ ОЦЕНКА — совокупность оценок
некоторой величины а сверху и снизу. Оценкой
сверху наз. неравенство вида a^iA^, оценкой
снизу — неравенство противоположного смысла
а^А0. Величины Ао, Аг. с помощью к-рых оценивается
величина а, как правило, имеют или более простой вид
или значительно легче вычисляются чем а.
Пример ы. 1) Пусть т, М — соответственно наи-
наименьшее и наибольшее значения функции / х) на отрез-
С Р
ке [а, [5]; тогда для интеграла \ f(x)dx справедлива
J (X
Д. о.:
тф — a)<fP f (x)dx<M(§ — a),
J &.
где
f(x)dx, А1 = Мф — а).
2) Д. о. констант Лебега Ln при всех п = 0, 1,2, ...:
0,9897 ... <Ln—-1-1пBп-И)<1.
3) Д. о. собственных значений. Пусть поставлена за-
задача на собственные значения линейного самосопряжен-
самосопряженного оператора Т : Ти=Хи в гильбертовом пространстве
Н. Строится следующий итерационный процесс: 7n/,;J.) =
=/„, где /0^=0. В силу самосопряженности оператора
Т скалярные произведения (/„,, /&) зависят лишь от
суммы индексов т+к. Числа ап= (/„, fn)=(fm, fn-m)
на:!, постоянными Шварца, а числа ц.п + 1=
= ап/ап + 1 — частными Рэлея — Шварца.
Если оператор Т положительный, то \хп образуют моно-
монотонную невозрастающую сходящуюся последователь-
последовательность.
Если Яо — собственное значение оператора Г, в<Я0<
<й, e<fi2fc<6, и на интервале (а, Ь) нет других точек
спектра оператора Т, то
(теорема Темпля [3]). При определенных усло-
условиях частные Рэлея — Шварца сходятся к нек-рому
собственному значению оператора Т.
Численные методы получения Д. о. (двусторонних
приближений) наз. двусторонними мето-
методами [4]. Рассмотренный выше способ построения
частных Рэлея — Шварца является примером двусто-
двустороннего метода. Нек-рые двусторонние методы осно-
основаны на использовании пары приближенных формул,
имеющих остаточные члены противоположных знаков.
Пусть, напр., функция f(x), заданная в точках (узлах
интерполяции) хо<х, < . ..О„, интерполируется мно-
многочленом Лагранжа Ь0(х) с узлами х0, х^, .. ., #n-i>
?, (х) — интерполяционный многочлен Лагранжа с
узлами хл, х2, .... х„. Тогда для остаточных членов спра-
справедливы соотношения:
Яо (x)=f (x)-L0 (x)= >in)JU) (x—x0) (х—х1)...(х—хп^),
Я, (x) = f (x)—Lx (х)=Ц7Г- (x~x1)(x—xSi)...(x-xn),
где |0, li^[^0, xn]. Если производная /(п) (х) не меняет
знака на отрезке [х0, х„], то Ro(x) H Rx(x) имеют раз-
разные знаки. Справедлива Д. о.:
min(Lg(x), JL1
Наиболее разработаны двусторонние методы реше-
решения обыкновенных дифференциальных уравнений
[5] - [9].
Двусторонние методы дают возможность указать
границы области, в к-рой заведомо лежит решение за-
задачи. При этом приходится согласиться с усложнением
алгоритма. Более того, чтобы обеспечить двусторон-
ность в реальных вычислениях (при наличии ошибок
округлений), приходится еще более усложнять алго-
алгоритм. Двусторонние методы применяются в основном
в тех случаях, когда необходимо иметь гарантирован-
гарантированную оценку погрешности.
Лит.: [1] Г а л к и н П. В., «Тр. Матем. ин-та АН СССР»,
1971, т. 109, с. 3—5; [2] К о л л а т ц Л., Задачи на собственные
значения с техническими приложениями, пер. с нем., М., 19U8;
[3] его ж е, Функциональный анализ и вычислительная ма-
математика, пер. с нем., М., 1969; [4] Б а х в а л о в Н. С, Чис-
Численные методы, 2 изд., М. 1975; [5] В о л к о в Б. А., «Тр.
Матем. ин-та АН СССР», 1971, т. 112, с. 141—51; [6] Ремез
Е. Я., «Зап. природниго-техн^чного в]ддшу» АН УССР, 1931,
№ 1, с. 1 — 38; [7] Г о р б у н о в А. Д., Ш а х о в Ю. А., «Ж.
вычисл. матем. и матем. физ.», 1963, т. 3, № 2, 239—53; 1964,
т. 6, № 3, 426 — 33; [8] Д е в я т к о В. И., там же, 1963, т. 3,
Л» 2, 254—65; [9] С а л и х о в Н. П., там же, 1962, т. 2, Л» 4,
515 — 28. В. В. Поспелов.
ДВУСТОРОННЯЯ ПОВЕРХНОСТЬ — см. Односто-
Односторонние и двусторонние поверхности.
ДВУУГОЛЬНИК сферический — фигура, об-
образованная двумя полуокружностями больших кру-
кругов сферы, исходящими из диаметрально противопо-
противоположных точек. См. Сферическая геометрия.
ДВУХ КОНСТАНТ ТЕОРЕМА — пусть D — конечно-
связная жорданова область на плоскости комплексного
переменного z, w(z) — регулярная аналитич. функция
в D, удовлетворяющая неравенству |u>(z)|<M, при-
чем на нек-рой дуге а. границы dD выполняется соот-
соотношение
lim sup | w (z) | sg: m < M, z ? D, t, ? a;
тогда в каждой точке z множества
{z ? D; О < X<co(z; a, ?>) < 1},
где co(z; a, ?)) — гармоническая мера дуги a относитель-
относительно D в точке z, выполняется неравенство
Если для нек-рого z (удовлетворяющего условию
co(z; a, />) = Х) достигается равенство, то оно сохраня-
сохраняется и для всех z?D и всех X, 0<:Х<1, а функция w(z)
в этом случае имеет вид
где a — действительное число, q>(z) — аналитич. функ-
функция в D, для к-рой Reep(z)=co(z; a, D) (см. [1], [2]).
Д. к. т. дает количественное выражение граничного
свойства единственности аналитич. функций и имеет
важные применения в теории функций [3]. Адамара
теорема о трех кругах получается из нее как частный
случай. О возможных аналогах Д. к. т. для гармонич.
функций в пространстве см. [4], [5].
Лит.: [1] N е v а п 1 i n n а F. imd R., «Acta Soc scient.
fennica», 1!>22, Bd 50, № 5; [2J Ostrowski A., «Jahresber.
Dtsch. Math. Ver.», 1923, Bd 32, H. 9 — 12; [3J H e в а н л и н-
на Р., Однозначные аналитические функции, пер. с нем.,
М.—Л., 1941; U] Мергелян С. Н., «Успехи матеы. на-
наук», 1956, т. 11, в. 5, с. 3 — 26; [5] Соломенцев Е. Д.,
«Докл. АН Арм. ССР», 1966, т. 42, JMs а, 274 —7S,
Е. Д. Соломенцев.
ДВУХ ТЕЛ ЗАДАЧА — задача о движении в трех-
трехмерном евклидовом пространстве Е3 двух материаль-
материальных точек Pi и Р2 с массами т1 и тг под действием нью-
ньютонова притяжения. Д. т. з. является частным случаем
задачи п тел, к-рая описывается системой обыкновен-
обыкновенных дифференциальных уравнений порядка Cm и имеет
10 независимых интегралов: 6 — движения центра
инерции, 3 — площадей и 1 — энергии (см. [1]).
Д. т. з. имеет, кроме того, еще три интеграла Лапласа
(из них один независим от предыдущих) и является
полностью интегрируемой (см. [2]).
Интегрирование Д. т. з. удобнее производить в спе-
специальных системах координат, использующих указан-
указанные интегралы. Если начало декартовых координат
х, у, z поместить в точку Рх (при этом используются все
6 интегралов движения центра инерции) и ось z напра-
направить по вектору, составленному из интегралов пло-
площадей (при этом используются два интеграла площадей),
то движение точки Р2 происходит в плоскости z=0 и
удовлетворяет системе
х = —дат-3, г/ = —дуг, A)
где т= У^2-Ьу2, |x=/(m1+m2), / — гравитационная
постоянная. Система A) имеет 4 интеграла:
ху — ух = с (площадей),
— (х2-\-У2)—(^г-1 = Л (энергии),
су — дхг~1 = ?11 и cxJr\iyr~1 = —Х2 (Лапласа),
связанных соотношением
При этом
*к+Х+ B)
т. е. орбиты точки Рг суть конич. сечения с параметром
р = с2/|д,, большой полуосью а= — u/B/i), эксцентриси-
эксцентриситетом е=|д,~1 \^l-\-2hc2, долготой перицентра ы
(X1 = jxe cos ы, \2 = }ie sin w)
и с фокусом в начале координат. Положение точки Р2
на орбите определяют истинной аномалией v, отсчиты-
отсчитываемой от направления на перицентр; тогда B) дает
r=pl(\.-\-e cos v). Если сфО, то возможны три типа ор-
орбит
(I) при А<0 это — эллипсы, тогда
t — т = ]/*а3 (и — е sin и),
(II) при h>0 это — гиперболы, тогда
t — т= Y~—а3 (е sh м — и),
(III) при А=0 это — параболы, тогда
Здесь т — момент прохождения через перицентр, и —
эксцентрическая аномалия. Если с=0, то движение
происходит по прямой линии. Д. т. з. описывает не-
невозмущенное коплерово движение планеты относитель-
относительно Солнца либо спутника относительно планеты и т. п.
Лит.: [1] 3 и г е л ь К. Л., Лекции по небесной механике,
пер. с нем., М., 1959; [2] А б а л а к и н В. К. (и д р.), Спра-
Справочник по небесной механике и астродинамике, М., 1971.
А. Д. Брюно.
ДВУХТОЧЕЧНЫЙ ТЕНЗОР — тензор Т, зависящий
от пар точек х. х многообразия X, т. е. тензорное поле
Т(х, х'), определенное на произведении XXX. Напр.,
Д. т. являются ковариантные производные мировой
функции Q(x, x') и вообще произвольного двухточечно-
двухточечного инварианта. Свойства Д. т., в частности пределы
совпадения Т и ого производных при х' —>- х, напр.
[7>]= lim ViVj-T (x, z'),
х' ->¦ х
используются в вариационном исчислении и теории
относительности.
Лит.: [1] С и н г Д ж.-Л., Общая теория относительности,
пер. с англ., М., 1963. М. И. Войцеховский.
ДВУЧЛЕННОЕ СРАВНЕНИЕ — алгебраическое
сравнение вида
i" = a (mod m), A)
где а, т — взаимно простые целые числа, а и^2 — нату-
натуральное число. Если сравнение A) разрешимо, то а наз.
вычетом степени п по модулю т. В противном случае в
наз. невычетом степени га по модулю т.
Вопрос о разрешимости Д. с. по составному модулю т
сводится к изучению аналогичного вопроса для случая
простого модуля р (см. Сравнение). Для простого мо-
модуля имеется критерий разрешимости, доказанный
Л. Эйлером (L. Euler): для разрешимости сравнения
г"за (mod p)
необходимо, чтобы выполнялось условие
Р-1
а б ееее 1 (mod p),
где б — наибольший общий делитель чисел п и р—1;
при выполнении этого условия данное сравнение имеет
ровно б решений.
Из критерия Эйлера непосредственно следует, что
среди чисел 1,2,.. ., р — 1 имеется в точности (р — 1)/б
вычетов и (б — 1)(р — 1)/б невычетов степени п по моду-
модулю р.
Значительно сложнее обратная задача: найти все мо-
модули р, по к-рым заданное число а является вычетом
(или невычетом) степени п^2. Л. Эйлером установлено,
что разрешимость или неразрешимость сравнения ж2=
=a(mod p) зависит от того, принадлежит или нет прос-
простой модуль р некоторым арифметич. прогрессиям. Пол-
Полное доказательство этого результата впервые получил
К. Гаусс (С. Gauss, 1801; см. [4], а таюке Гаусса закон
взаимности, Квадратичный закон взаимности). Более
того, К. Гаусс заметил, что полное решение указанной
задачи при п^З возможно только в нек-ром расширении
кольца целых рациональных чисел. Так, для установле-
установления закона взаимности для биквадратичных вычетов
он вынужден был расширить кольцо целых рациональ-
рациональных чисел до кольца целых комплексных чисел Z[i].
Разрешимость или неразрешимость биквадратичного
сравнения z45=cu(mod р) в кольце Z[i] при заданном
со?Z[i] зависит от того, каков вычет числа р по
нек-рому постоянному модулю D кольца Z[i].
Новый этап в изучении Д. с. и их применений к дру-
другим задачам теории чисел был начат работами И. М.
Виноградова, к-рый в 1914 доказал, что количество R
квадратичных вычетов по простому модулю р среди
чисел 1,2, . . .,(?, (?«:р — 1, выражается формулой
где |6|<1. Аналогичный результат был впоследствии
получен И. М. Виноградовым и для более общей зада-
задачи о числе решений сравнения
хп = у (mod p), n За 2,
когда у пробегает неполную систему вычетов 1 <!/<:(?..
Лит.: 11] ВенковБ. А., Элементарная теория чисел,
М.—Л., 1937; [2] Виноградов И. М., Основы теории
чисел, 8 изд., М., 1972; [3J его же, Иабр. труды, М.,
1952; [4] Г а у с с К. Ф., Труды по теории чисел, [пер.1„
М., 1959. С. А. Степанов.
ДВУЧЛЕННОЕ УРАВНЕНИЕ — алгебраическое урав-
уравнение вида ахп-\-Ъ—И, где а и Ь—комплексные числа,
и аЬфО. Д. у. имеют п различных комплексных корней.
v \ —
У \ а
ехР
Корни Д. у. на комплексной плоскости расположены на
окружности радиуса 1у/Г\Ь1а\ с центром в начале коор-
координат в вершинах правильного вписанного /г-угольника.
А. И. Галочпин.
ДЕБАЕВСКАЯ ДЛИНА, дебаевский ради-
радиус,— расстояние, на к-рое распространяется действие
электрического поля отдельного заряда в нейтральной
среде, состоящей из положительно и отрицательно за-
заряженных частиц (плазма, электролиты). Вне сферы
радиуса Д. д. электрич. поле заряда экранируется в.
результате поляризации окружающей среды.
Д. д. определяется формулой:
где еу, Nj, Tj — заряд, плотность и температура частиц,
сорта /, к — постоянная Больцмана. Суммирование
идет по всем сортам частиц, при этом должно выполнять-
выполняться условие нейтральности: ^jejNf—O. Важным пара-
параметром среды является число частиц в сфере радиуса
Д- Д-:
Оно характеризует отношение средней кинетич. энер-
энергии частиц к средней энергии их кулоновского взаимо-
взаимодействия:
/
Для электролитов это число мало: пд~10-4; для плазмы,
находящейся в самых различных физич. условиях,—
велико. Это позволяет использовать методы кинетич.
теории для описания плазмы.
Понятие Д. д. введено П. Дебаем (P. Debye) в связи
С изучением явлений электролиза. Д. Л. Костомаров.
ДЕВИАТОР — тензор напряжений (или деформаций)
с равным нулю первым инвариантом, т. е. с равной
нулю суммой членов главной диагонали матрицы тен-
тензора. См. Деформаций тензор, Напряжений тензор.
ДЕВЯТИ ТОЧЕК ОКРУЖНОСТЬ, окружность
Эйлер а,— окружность, на к-рой расположены сере-
середины сторон треугольника, основания его высот и се-
середины отрезков, соединяющих
ортоцентр треугольника с верши-
вершинами. Ее радиус равен половине
радиуса окружности, описанной
около треугольника. Д. т. о.
треугольника касается вписанной
в него окружности и трех вне-
вписанных окружностей. Пусть
Н — ортоцентр неравносторон-
неравностороннего треугольника, Т — центр
тяжести, О — центр описанной ок-
окружности, Е — центр Д. т. о. Точки Н, Т, О, Е ле-
лежат на одной прямой (прямая Эйлера), при-
причем Е — середина отрезка НО и пара точек Н, Т
гармонически разделяет пару точек О, Е.
Лит.: [1] 3 е т е л ь С. И., Новая геометрия треугольни-
треугольника, 2 изд., М., 1962; [2] П е р е п е л к и н Д. И., Курс элемен-
элементарной геометрии, ч. 1, М.—Л., 1948. В. Т. Впзылев.
ДЕДЕКИНДА ДЗЕТА-ФУНКЦИЯ — см. Дзета-
функция в теории чисел.
ДЕДЕКИНДА ПРИЗНАК сходимости ряда:
РЯД in=ia"'<n' гДе ап п Ьп — комплексные числа, схо-
сходится, если ряд ^„=1(а„—an+i) абсолютно сходится,
ап —>- 0 и частичные суммы ряда zln=1bn ограничены.
Л. Д. Кудрявцев.
ДЕДЕКИНДА ТЕОРЕМА о непрерывности
числовой прямой: для всякого сечения А\В
множества действительных чисел (см. Дедекиндово се-
сечение) существует действительное число а, являющееся
либо наибольшим в классе А, либо наименьшим в клас-
классе В. Это утверждение наз. также принципом
(или аксиомой) Дедекинда непрерыв-
непрерывности числовой прямой (см. Действитель-
Действительное число). Число ос является верхней гранью множест-
множества А и нижней гранью множества В. Л- Д. Кудрявцев.
ДЕДЕКИНДОВА РЕШЕТКА, дедекиндова
структура, модулярная решетка
(структур а),— решетка, в к-рой справедлив м о-
дулярный закон, т. е. в<:с влечет (а-\-Ь)с=
= а-'^Ьс для всякого Ь. Высказанное требование равно-
равносильно справедливости тождества (вс+6)с=ас+6с.
Примерами Д. р. служат решетки подпространств ли-
линейного пространства, нормальных делителей (но не
подгрупп) группы, идеалов кольца и др. Решетка, имею-
имеющая композиционный ряд, является Д. р. тогда и только
тогда, когда на ней существует функция раз-
размерности d, т. е. такая целочисленная функция,
что d(x-\-y)-\-d(xy) = d(x)-\-d(y) и что из простоты интер-
интервала [а, Ъ] вытекает rf(b) = d(a)+l. Если u;=ai1)... 0^ =
= ai\ .. alm2, каждый из элементов а\ ) не представим в
виде произведения отличных от него элементов и
то т,1=т2 и для всякого а\ найдется такой элемент
af, что
(см. [3], [6]). Ненулевые элементы ах, .. ., ап из Д. р. с ну-
нулем 0 называются независимыми, если (+
. . . + a,-_1+e,- + i+ ... +я„)а,-=О для всех г. Это опре-
определение позволяет обобщить многие свойства линейно
независимых систем векторов (см. [3], [5], [6]). Если
Oj, . . ., ап независимы, то их сумма обозначается как
ai© • •-Сг^п- Теорема О р е: если Д. р. имеет ком-
композиционный ряд и
причем каждый из элементов а,- не представляется в
виде суммы двух независимых элементов, то ml=m2
и для всякого а'/' найдется такой элемент af\ что
1=411 ©... © <*!-! 6 «Г © «JVi ©... е <
(см. [3], [6]). В случае полных Д. р., подчиненных
нек-рым дополнительным требованиям, теоремы о неза-
независимых элементах и прямых разложениях можно рас-
распространить на бесконечные множества (см. [4], [5]).
Исследовались Д. р. с дополнениями, то есть
Д. р. с 0 н 1, для каждого элемента х к-рых существует
хотя бы один такой элемент у (наз. дополнением
элемента х), что х-\-у=1, ху=0. Д. р. с дополне-
дополнениями, обладающая композиционным рядом, изоморф-
изоморфна Д. р. всех подпространств конечномерного линейного
пространства над нек-рым телом. Полная Д. p. L с до-
дополнениями изоморфна Д. р. всех подпространств ли-
линейного пространства (не обязательно конечномерного)
над нек-рым телом тогда и только тогда, когда: а) если
O^a^L, то найдется атом р<:я; б) если р — атом и
p<:sup^l, где A^L, то p<:sup F для нек-рого конечного
множества F—A ; в) если р, q — атомы, то найдется атом
г<гр+д, причем гфр, q; г) существует не менее трех
независимых атомов. Условие г) можно заменить требо-
требованием справедливости Дезарга предложения (см. [2]).
Дальнейшее обобщение этого результата, приводящее
к регулярным кольцам (см. [7], [5]), смыкается с тео-
теорией алгебр Неймана. Для Д. р. с композиционным ря-
рядом наличие дополнений равносильно представимости
единицы в виде суммы атомов.
Д. р. названы в честь Р. Дедекннда, к-рый первым
сформулировал модулярный закон и установил ряд его
следствий [1].
Лит.: [1] Dedekind R., Gesammelle mathematische
Werke, Bd 2, Braunschweig, 1931, S. 236—71; [2J Бэр Р.,
Линейная алгебра и проективная геометрия, пер. с англ., М.,
1955; 13] Б и р к г о ф Г., Теория структур, пер. с англ., М ,
1952; [4] Курош А. Г., Теория групп, 3 изд., М., 1967;
[5] Скорняков Л. А., Дедекиндовы структуры с допол-
дополнениями и регулярные кольца, М., 1961; [6] его же, Элемен-
Элементы теории структур, М., 1970; [7] Neumann J. von,
Continuous geometry, N. Y., I960. Л. А. Скориякэв.
ДЕДЕКИНДОВО КОЛЬЦО — ассоциативное комму-
коммутативное кольцо R с единицей, не содержащее делителей
нуля (т. е. коммутативная область целостности), в
к-ром каждый собственный идеал представим в виде
произведения простых идеалов (идеал Р кольца Я наз.
простым, если факторкольцо R/P не содержит де-
делителей нуля). Свое название эти кольца получили по
имени Р. Дедекинда (R. Dedekind), к-рый в числе пер-
первых изучал такие кольца в 70-х гг. 19 в.
Каждая область главных идеалов является Д. к.
Если R есть Д. к., L — конечное алгебраич. расширение
его поля частных, то целое замыкание R'
кольца йв!(т.е. совокупность элементов из L, яв-
являющихся корнями уравнений вида хп-\-а1хп-1-]- . .. 4-
+ а„=0, a[?R) снова будет Д. к. В частности, дедо-
киндовыми являются кольцо целых алгебраич. чисел
и максимальные порядки полей алгебраич. чисел, т. е.
целые замыкания кольца целых чисел в конечных ал-
алгебраич. расширениях поля рациональных чисел.
В Д. к. Л каждый собственный идеал обладает единст-
единственным представлением в виде произведения простых
идеалов. Эта теорема возникла из задачи о разложении
элементов на простые множители в максимальных по-
рядках полей алгебраич. чисел. Такое разложение,
вообще говоря, не единственно.
Кольцо Д дедекиндово тогда и только тогда, когда
полугруппа дробных идеалов этого кольца является
группой. Каждый дробный идеал Д. к. Л обладает един-
единственным представлением в виде произведения степе-
степеней (положительных или отрицательных) простых идеа-
идеалов кольца R. Д. к. обладает следующей характери-
зацией: коммутативная область целостности является
Д. к. тогда и только тогда, когда R есть нётерово коль-
кольцо, каждый собственный простой идеал кольца R макси-
максимален и R целозамкнуто, т. е. совпадает со своим целым
замыканием в поле частных. Другими словами, Д. к.
есть нётерово нормальное кольцо размерности один по
Круллю. Для Д. к. R выполняется так наз. «кита й-
ская теорема об остатка х»: для данного
конечного набора идеалов /,• и элементов х; кольца R,
i=l, 2, ..., п, система сравнений issx,-(mod /,-) имеет
решение х ? R тогда и только тогда, когда x^Xj (mod/?--f-
+//) для Ьф]. Д. к. R можно охарактеризовать также
как Крулля, кольцо размерности один. Каждое Д. к. яв-
является регулярным коммутативным кольцом и все его
локализации по максимальным идеалам есть дискрет-
дискретного нормирования кольцо. Полугруппа ненулевых идеа-
идеалов Д. к. Л изоморфна полугруппе Р дивизоров этого
кольца.
Лит.: [1] ЗарисскийО., Самюэль П., Коммута-
Коммутативная алгебра, пер. с англ., т. 1, М., 1963' [2] К у р о ш А. Г.,
Лекции по общей алгебре, 2 изд., М., 1973; [3] Б о Р е в и ч 3. И.,
Шафаревич И.Р., Теория чисел, М., 2 изд., 1972; [4] Бур-
Саки Н., Коммутативная алгебра, пер. с франц., М., 1971.
Л. А. Бокуть.
ДЕДЕКИНДОВО СЕЧЕНИЕ, с е ч е н и е,—разбие-
е,—разбиение множества действительных (или только одних
рациональных) чисел R на два такие непустые множест-
множества Л и В, в сумме дающие R, что для каждого а?А и
Ь?В выполняется неравенство а<6. Д. с. обозначается
символом А\В. Множество А наз. нижним, а множест-
множество В — верхним классом сечения А\В. Д. с. множества
рациональных чисел применяются для построения тео-
теории действительных чисел. В терминах Д. с. действи-
действительных чисел формулируется понятие непрерывности
ЧИСЛОВОЙ прямой. Л. Д. Кудрявцев.
ДЕДУКЦИИ ТЕОРЕМА— общее название ряда тео-
теорем, позволяющих устанавливать доказуемость импли-
импликации AzdB в случае, когда дан логический вывод фор-
формулы В из формулы А. В простейшем случае класси-
классического, интуиционистского и т. п. исчислений выска-
высказываний Д. т. утверждает: если Г, А\—В (из допущений
Г. А выводимо В), то
Г ;- (А гз В) (*)
(Г может быть пусто). При наличии кванторов аналогич-
аналогичное утверждение неверно:
А (я-)!— \/хА (х),
но не
\—А (х) ZD Ух А (х).
Одна из формулировок Д. т. для традиционных ис-
исчислений предикатов (классического, интуиционистско-
интуиционистского п т. п.): если Г, А\—В, то
где V^4 означает результат приписывания V -кванто-
-кванторов (см. Кеантор) по всем свободным переменным
формулы А. В частности, если А — замкнутая форму-
формула, Д. т. принимает форму (*). Эта формулировка Д. т.
дает возможность сводить поиск вывода в аксиоматич.
теориях к попеку вывода в исчислении предикатов:
формула В выводима из аксиом Аъ ...,Ап тогда и
только тогда, когда в исчислении предикатов выводима
формула
А (А (An ZDB)...).
Похожим образом формулируется Д. т. для логик,
где имеются связки, «похожие» на кванторы. Так,
для модальных логик Si и S5 Д. т. имеет вид: если
Г, А\-В, то
г
Более тонкие формулы Д. т. получаются, если вво-
вводить V-кванторы не по всем свободным переменным, а
лишь по тем, к-рые связываются кванторами в процес-
процессе вывода. Говорят, что переменная у варьирует-
варьируется для формулы А в данном выводе,
если у входит свободно в А и в рассматриваемом выводе
имеется применение правила введения V в заключение
импликации (или введения з в посылку), при к-ром
вводится квантор по г/, причем посылка этого приме-
применения зависит в данном выводе от А. Теперь Д. т. для
традиционных исчислений предикатов уточняется
так: если Г, А\—В, то
где у1, . . . , уп — полный список переменных, к-рые
варьируются для А в данном выводе. В частности, если
никакая свободная переменная из А не варьируется, то
Д. т. принимает форму (*). При формулировке соответ-
соответствующего уточнения Д. т. для модальных логик сле-
следует считать, что варьирование происходит в прави-
правилах введения ? в заключение импликации и (у — в по-
посылку.
При установлении Д. т. для исчислений релеван-
релевантной импликации (т.е. для систем, согласо-
согласованных с истолкованием A ZDB как «5 выводимо с су-
существенным использованием допущения А») прихо-
приходится либо модифицировать само понятие вывода, либо
считать, что варьирование происходит при всяком ис-
использовании «постороннего» допущения; напр., при пере-
переходе от пары А, Г]—С, Г\—Ь к A, T\—(C&D) варьирует-
варьируется формула А, т. к. она не входит во второй член пары.
Если А не варьируется в данном выводе, то Д. т. при-
принимает форму (*), а если А варьируется, то Д. т. при-
принимает вид: если А, Г]—В, то
где t — константа «истина» (или конъюнкция формул
(р^Зр) для всех пропозициональных переменных р,
выходящих в А, Г, В).
Лит.: [1] К л и н и С. К., Введение в метаматематику, пер. с
англ., М., 1957; [2] К а р р и X. Б., Основания математиче-
математической логики, пер. с англ., М., 1969. Г. Е. Минц.
ДЕЗАРГА ПРЕДЛОЖЕНИЕ, теорема Дезар-
г а: если соответствующие стороны двух треугольни-
треугольников ABC и А'В'С пересекаются в точках Р, Q, Л, ле-
лежащих на одной прямой, то
прямые, соединяющие соот-
соответствующие вершины, пере-
пересекаются в одной точке; об-
обратно: если прямые, соединя-
соединяющие соответствующие вер-
вершины треугольников ABC
и А'В'С, сходятся в одной
точке, то соответствующие **
стороны этих треугольников
пересекаются в точках, ле-
лежащих на одной прямой. Об-
Обратное утверждение для треугольников, лежащих в
одной плоскости, двойственно прямому по талону
принципу двойственности. В обоих
случаях точки и прямые составляют конфигура-
конфигурацию Дезарга (конфигурацию 103), расположен-
расположенную в нек-ром двумерном или трехмерном проектив-
проективном пространстве.
Если оба треугольника принадлежат одной проектив-
проективной плоскости, то Д. п. нельзя доказать лишь на основе
аксиом инцидентности плоскости (см. Недезаргова
геометрия), однако оно справедливо на любой проек-
проективной плоскости, к-рую можно вложить в проектив-
проективное пространство большей размерности. Пространствен-
Пространственный случай Д. п. следует из аксиом инцидентности
пространства.
Выполнение Д. п. необходимо и достаточно для пост-
построения проективной алгебры точек проек-
проективной прямой и введения синтетическим пу-
путем проективных координат. Д. п. установлено Ж. Де-
Заргом [1]. м. И. Войцеховский.
В теоретико-структурных терминах (см. Решетка)
Д. п. может быть сформулировано в виде тождества
(см. [4])
(y+u)-{-(x + u) (y + z)] (z + yX
+ z).
Л. А. Скорняков.
Лит.: [1] Bosse A., Maniere universelle de m-r Desar-
gues, pour pratiquer la perspective par petit-pied comme le geo-
metral, P., 1648; [2] Гильберт Д., Основания геометрии,
пер. с нем., М.—Л., 1948; [3] Е ф и м о в Н. В., Высшая гео-
геометрия, 5 изд., М., 1971; [4] Б и р к г о ф Г., Теория струк-
структур, пер. с англ., М., 1952.
ДЕЗАРГОВА ГЕОМЕТРИЯ, геометрия де-
заргова пространства, — геодезических гео-
геометрия, в к-рой роль геодезических играют обыкновен-
обыкновенные прямые. Точнее, дезарговым простран-
пространством R наз. G-пространство, допускающее такое
топологич. отображение в проективное пространство
Р", что каждая геодезическая Я отображается в прямую
Р".
Для того чтобы R было дезарговым пространством,
необходимо и достаточно, чтобы:
1) геодезическая, проходящая через две различные
точки, была единственна;
2) при dim Д = 2 выполнялось Дезарга предложение,
и обратное ему, если только существуют все пересече-
пересечения, имеющиеся там;
3) при dim Д>2 любые три точки R лежали в одной
плоскости.
При этом R, отображенное в Р", либо покрывает
все Рп, и в этом случае геодезические R являются
окружностями одной и той же длины, либо R не со-
содержит ни одной точки нек-рой гиперплоскости и может
рассматриваться как открытая выпуклая область аф-
аффинного пространства.
В римановом случае единственными Д. г. являются
евклидова, гиперболич. и эллиптич. геометрии, т.е.
из дезаргова характера пространства следуют весьма
сильные свойства подвижности (теорема Бельт-
р а м и). Это — пример поразительной теоремы рима-
новой геометрии, не имеющей аналога в более общих
пространствах. При достаточно сильных условиях диф-
ференцируемости был дан метод построения Д. г.,
однако окончательное и общее решение этой, так наз.
4-й проблемы Гильберта о метризации проективного
пространства или его выпуклых подобластей без какого-
то ни было предположения регулярности, дал А. В. По-
горелов [2]. Другой пример Д. г., ценный для изуче-
изучения пространств неположительной кривизны, достав-
доставляет Гильберта геометрия.
Важным примером неримановых Д. г. является Мин-
ковского геометрия, к-рую можно рассматривать как
прототип всех неримановых геометрий (в т. ч. финсле-
ровой геометрии).
Лит.: [1] Б у з е ы а н Г., Геометрия геодезических, пер.
с англ., М., 1962; [2] П о г о р е л о в А. В., Четвертая проб-
проблема Гильберта, М., 1974. М. И. Войцеховский.
ДЕЗОРИЕНТИРУЮЩИЙ ПУТЬ — замкнутый
путь в многообразии, обладающий тем свойством, что
при его обходе локальная ориентация меняет знак (ом.
Ориентация многообразия). Д. п. имеется только в не-
ориентируемом многообразии М, причем однозначно
определен гомоморфизм фундаментальной группы лхМ
на 2г с ЯДРОМ> состоящим иа классов петель, не являю-
являющихся Д. П. А. В. Че-рнаеский.
ДЕЙСТВИЕ — функционал, выражаемый определен-
определенным интегралом от функции, стационарные значения
к-рого определяют действительное движение механич.
системы под действием заданных активных сил в клас-
классе кинематически возможных движений, удовлетворяю-
удовлетворяющих определенным условиям, между нек-рыми двумя
конечными положениями Ро и Р1 в пространстве.
Различают Д. по Гамильтону, Лагранжу и Якоби,
фигурирующие в соответствующих принципах стацио-
стационарного действия.
Д. по Гамильтону:
определено в классе кинематически возможных дви-
движений голономной системы, для к-рых начальное и
конечное положения системы и время движения между
ними одинаковы с таковыми для действительного дви-
движения.
Д. по Лагранжу:
V 2Tdt,
Д. по Якоби:
определены в классе кинематически возможных дви-
движений голономной консервативной системы, для к-рых
начальное и конечное положения системы и постоянная
энергия k одинаковы с таковыми для действительного
движения. Здесь Т — кинетич. энергия системы, при-
причем для консервативной системы
г=— 7. j 1ai;9l9h
где qi — обобщенные лагранжевы координаты, U (q)
силовая функция активных сил.
Подробнее см. Вариационные принципы классической
механики, а также Гамильтона — Остроградского прин-
принцип, Лагранжа принцип, Якоби принцип.
В. В. РУМЯНЦС:.,
ДЕЙСТВИЕ ГРУППЫ на многообразии —
наиболее изученный случай общего понятия действия
группы на пространстве. Топологич. группа G дей-
действует на пространстве X, если каждому
g?G поставлен в соответствие гомеоморфизм ф^. про-
пространства X (на себя), удовлетворяющий условиям:
1) Ф^-фл = ф^л; 2) для единицы e?G отображение фе
есть тождественный гомеоморфизм; 3) отображение ф:
GXX—>- X, ф(#, x) = (fg(x) непрерывно. В случае, когда
X и G обладают дополнительными структурами, осо-
особый интерес представляют Д. г. G, учитывающие эти
структуры; напр., если X — дифференцируемое мно-
многообразие, G — группа Ли, то отображение ф обычно
предполагается дифференцируемым.
Множество {<?gD))g?G наз- орбитой (траек-
(траекторией) точки ха ? X относительно группы G;
пространство орбит обозначается X/G и
наз. также факторпространством про-
пространства Хпо группе G. Важным при-
примером является случай, когда X есть группа Ли, а
Q — ее подгруппа; тогда X/G есть соответствующее
однородное пространство. Классические примеры:
сферы Sn~1 = 0(n)l0(n — 1), Грассмана многообразия
О(п)/О(т)ХО(п—т), Штифелямногообразия 0(пI0(т).
Здесь пространство орбит есть многообразие. Обычно
же это не так, если действие группы не является свобод-
свободным, напр., если множество Х° неподвижных точек
непусто. При этом под свободным дейст-
действием группы понимается действие, при к-ром
из gx=x, х?Х, g?G следует g=e. В противополож-
противоположность этому, Ха будет многообразием, если X — диффе-
дифференцируемое многообразие, а действие группы G диф-
дифференцируемо; это утверждение верно и для когомо-
логич. многообразий над %р для G=%p (теорема
Смита).
Если G — некомпактная группа, то пространство
X/G, вообще говоря, неотделимо, и поэтому интерес
представляет индивидуальное изучение траекторий
и их взаимного расположения. Классическим является
пример группы G=R действительных чисел, действую-
действующей дифференцируемым образом на дифференцируемом
многообразии X. Изучение таких динамич. систем,
эквивалентных заданию систем обыкновенных диффе-
дифференциальных уравнений в локальных координатах,
проводится в основном аналитич. методами.
В случае компактной группы G существует предполо-
предположение, что если X — многообразие, а каждое g?G, g^e
действует на X нетривиально (т. е. не является действием
по закону (g, х) —>- х), то G есть группа Ли (см. [8]).
Поэтому интерес к случаю действия компактной группы
концентрируется вокруг действия группы Ли.
Пусть G — компактная группа Ли, X — компакт-
компактное когомологич. многообразие. Типичными являются
следующие результаты. В X существует конечное число
типов орбит, окрестности орбиты устроены как прямое
произведение (теорема о срез е), имеют место
представляющие интерес связи между когомологич.
строением пространств X, X/G, Ха.
Если G — компактная группа Ли, X — дифферен-
дифференцируемое многообразие, а действие
(f-.GXX ->- X
дифференцируемо, то естественным является отношение
эквивалентности: (X, (f)-(X', ц>') <( > найдутся такие
(X". ф"), что граница дХ" имеет вид dX"=X\JX' и что
<l"\X = <p, ф"|Х' = ф'. В случае свободного действия
группы G классы эквивалентности находятся во взаим-
взаимно однозначном соответствии с бордизмами Q%(Bq)
классифицирующего пространства Ва.
Результаты последних лет (сер. 70-х гг.) концентри-
концентрируются в основном вокруг: 1) определения типов ор-
орбит при различных дополнительных предположениях
о группе G и многообразии X (см., напр., [6]), 2) класси-
классификации Д. г., 3) отыскания связей между глобальными
инвариантами многообразия X и локальными свойст-
свойствами Д. г. G в окрестности неподвижных точек Х°.
В решении этих вопросов важную роль играют мето-
методы современной дифференциальной топологии (напр.,
перестройки), аналог /v-теории для векторных G-pac-
слоений — iirj-теорпя [1], теории бордизмов и ко-
оордизмов [3], аналитич. метод исследования Д. г. G,
основанный на изучении псевдодифференциальных опе-
операторов в G-расслоеннях (см. [2], [7]).
Лит.: []] А т ь я М., Лекции по К-теории, пер. с англ.,
М., 1967; [21 А т ь я М., Зингер И., «Успехи матем. на-
наук», 1969, т. 24, № 1, с. 127—82; [3] Б у х ш т а б е р В. М., М и-
щенкоА.С, Новикове. П., «Успехи матем. наук» ,1971,
т. 26, в. 2, с. 131 — 54; [4] К о н н е р П., Ф л о й д Э Гладкие
периодические отображения, пер, с англ.. М., 1969; [5] В г е-
don G., Introduction to Compact Transfoimation Groups, N. Y.,
1972; [fi] W u Y i H s i a n g, Cohomology Theory of TopoloRi-
cal Transformation Groups, N. Y., 1975; [7] Z a g i e r don В.,
Equivariant Pontrjagin Classes and Applications to orbit Spaces,
1972; [8] Proceedings of the Conference in Transformation Gro-
Groups, N. Y. — Hdih. —L., 1968; [9] Proceedings of the Second
Conference on Compact Transfoimation Groups, В.—Hdlb,—N. Y.,
1972. А. В. Зарелуа.
ДЕЙСТВИТЕЛЬНАЯ ФУНКЦИЯ — функция, у крой
как множество ее определения, так и множество ее
значений являются нек-рымн подмножествами множе-
множества лействительных чисел. Л Д Кудрявцев
ДЕЙСТВИТЕЛЬНОЕ АЛГЕБРАИЧЕСКОЕ МНОГО-
МНОГООБРАЗИЕ — множество A = X(R) действительных то-
точек алгебраич. многообразия X, определенного над
полем R. действительных чисел. Д. а. м. наз. н е о с о-
б ы м, если X — неособое алгебраич. многообразие.
В этом случае А является гладким многообразием, а его
размерность dim А равна размерности комплексного
многообразия СА = Х(С), называемого к о м п л е к-
спфи нацией многообразия А.
Наиболее изучены неособые регулярные полные пе-
пересечения, т. е. многообразия X в проективном про-
пространстве R/"?, являющиеся неособыми регулярными
пересечениями гиперповерхностей p,(z)=0,l <:i«:s, где
Pl(z) — однородный действительный многочлен от q пе-
переменных степени пц. В этом случае матрица
ар,-
имеет ранг s в каждой точке z?CA; dim A = n=q—s.
Пусть В обозначает Д. а. м., определяемое усечен-
усеченной системой
/>,(z)=0, l-<i<:s—1, р (z)=ps(z) и m—ms.
Примеры регулярных полных пересечений:
1) Плоская действительная алгебраич. кривая; при
этом q=2, s=l, СВ=СР2, B=RP2.
2) Действительная алгебраич. гиперповерхность;
при этом s=l, CB=CP1, B=RP1. В частности, при
q=S получается действительная алгебраич. поверх-
поверхность.
3) Действительная алгебраическая пространствен-
пространственная кривая; при этом g = 3, s=2. Поверхность В зада-
задается уравнением p1(z)=0, а кривая А высекается на
В поверхностью p2(z)=0.
Плоская действительная алгебраич. кривая А по-
порядка т1 состоит в плоскости RP2 из конечного числа
компонент, диффеоморфных окружности. При тх чет-
четном все они вложены в RP2 двусторонне, а при т1 не-
нечетном одна компонента вложена односторонне, а
остальные — двусторонне. Двусторонне вложенная
компонента кривой А иаз. овалом кривой А.
Овал, лежащий внутри нечетного числа других овалов
кривой А, наз. нечетным, остальные овалы наз.
четными.
Число компонент плоской действительной алгебраич.
кривой порядка т1 не превосходит -^- (т1—l)(mx—2)-f-l
(теорема Г а р н а к а), [1]. Для каждого т^ су-
существует плоская действительная алгебрапч. кривая с
этим наибольшим числом компонент — М-к р и в а я
(о способах построения М-кривых см. [1], [2], [3], об
обобщении этих результатов на пространственные кри-
кривые см. [2]).
Д. Гильберт (D. Hilbert) в 1900 поставил задачу
изучения топологии Д. а.м., а также вложений Д. а. м.
в RPq и одного Д. а. м. в другое Д. а. м. A6-я пробле-
проблема Гильберта). Он указал также трудные част-
частные задачи: изучить взаимное расположение овалов
кривой 6-го порядка, топологию и вложение в RP3 дей-
действительной алгебраич. поверхности 4-го порядка. Эти
частные задачи решены (см. [12], [13]).
Для плоской действительной алгебраич. кривой А
четного порядка т1 выполняется точное неравенство
Ct" 6to) + 1
где Р — число четных овалов кривой А, а N — число
ее нечетных овалов (теорема Петровского).
Если mi нечетно, то аналогичное неравенство выполне-
выполнено для A \JL, где L — прямая в общем положении [4].
При обобщении этих результатов на случай действи-
действительной алгебраич. гиперповерхности четного порядка
роль разности Р—N играет эйлерова характеристика
у(В + ), где В+ — {z?B\p(z)^0}, если же q нечетно, то
роль Р—jV играет %(А). Так, для действительной ал-
гсбранч. гиперповерхности А четного порядка mj
где s(q; mx) — число членов многочлена
степень которых не превосходит V2(<j'm1—2q—т{)\ при
нечетном q и любом rox
\X(A)l<i(m1-l)<J-2s(q; ro^ + l
(см. [5]). Для действительной алгебраической простран-
пространственной кривой (в RP3) при четном т1 выполняется не-
неравенство
I X (в ) 1< m + mm + m
(в случае m3 = 2 эта оценка точная) (см. [6]). Имеются
обобщения теорем Петровского на произвольные Д. а. м.
(см. [10]).
Для плоской действительной алгебраич. Л/-кривой чет-
четного порядка т1 выполняется сравнение
(см. [8], [9], [13]). При доказательстве этого сравнения
(см. [8], [9]) были применены для изучения Д. а. м. ме-
методы дифференциальной топологии, в форме стимули-
стимулирующей дальнейшие исследования. Пусть плоская
действительная алгебраич. кривая А имеет четный поря-
порядок т=2к, знак перед р (z) выбран так, что В+ ориен-
ориентируемо, аР + , Ро, Р _ обозначают соответственно число
овалов кривой А, ограничивающих внешним образом
компоненту множества В+ с положительной, нулевой
и отрицательной эйлеровыми характеристиками. Ана-
Аналогично, N+, NB, N - — числа таких же нечетных ова-
овалов для 5_={z^5|p(z)<0}. Тогда (см. [8], [13])
Р- SsiV—|-fc(A —1),
где
Для произвольного Д. а. м. в g-мерном проективном
пространстве выполнено неравенство
dimtf* (A; Z2)< dim Я. (С А; Хг),
где Н*{А; 22)=2Д",-(Л, 22) — пространство гомоло-
гомологии многообразия А с коэффициентами в Z2 (CM- [9])-
Это неравенство является обобщением теоремы Гарна-
ка. Если
dim Н, (СА; Жг) — diva. Н^ (А, Za) = 2t
(t всегда целое), то А наз. (М—^-многообразием. При
f=0 А есть Л/-многообразие.
Доказаны следующие сравнения:
А) Для Af-многообразия А при четном п
где о(СА) — сигнатура многообразия СА (см. [9]).
B) Для (Af—1)-многообразия А при четном п
%(А)^а(СА) ±2 mod 16
(см. обзор [13]).
C) В случае регулярного полного пересечения, если п
четно, А есть (М—1)-многообразие и гомоморфизм вклю-
вклюнулевой, то
d ... ms ^ 2 mod 4
2 mod 16, при d = 2mod8,
В этом же случае, если п четно, А есть (М—2)-мвого-
образие и г, — нулевой, то
при d з= 0 mod 8, х (А) = ± о (СЛ) mod 16,
при d = 2 mod 8, % (Л) see — а (СЛ) + 4 mod 16,
или х D) == ± а (СЛ) mod 16,
при d — 2mod8, х (А) = — а (СЛ) — 4 mod 16,
или х (Л) see ^ а (СЛ) mod 16
(см. [11]).
В частности, для действительной алгебраич. поверх-
поверхности Л порядка mi
Aiva. H^ (С A; ~Zsi)=-m\ — 4mJJ,-6mi,
если А есть Af-поверхность, то
X (Л) ess— (im1 — ml) mod 16;
если А есть (М—1)-поверхность, то
Х(Л)ЕЕ=±Dт1 — ml) ± 2 mod 16;
если Л есть (М—1)-поверхность и стягивается в RP3
в точку, то т!=2 mod 4 и
2 mod 16 при miss 2 mod 8,
—2 mod 16 при 111^ = —2 mod 8.
Если А есть (М—2)-поверхность и стягивается в RP3
в точку, то
1 0 mod 16, при mx ess 0 mod 8,
Х(Л)е=-| 0,4 mod 16, при /Их es 2 mod 8,
\ 0, —4 mod 16, при т1 == —2 mod 8.
Доказаны также нек-рые сравнения при нечетном п (см.
[9], [13]). В частности, для плоской действительной ал-
алгебраич. кривой Л, являющейся (М—1)-крквой четного
порядка т.г:
P—N=(mS) ± lmod8.
Имеются некоторые результаты о Д. а. м. с особенно-
особенностями (см. обзор [13]). Интересный подход к изучению
Д. а. м. предложен в [14].
Лит.: [1] На mack A., «Math. Ann.». 1876, Bd 10,
S. 189—99; [2] HilbertD., там же, 1891, Bd 38, S. 115—
38; [3] e г о ж e, «Arch. Math. Phys.» C), 1901, Bd 1, S. 213—37;
[4] Петровский И. Г., «Ann. Math.», 1938, v. 39, At 1.
p. 189—209; [5] Олейник О. А., П е т р о в с к и й И. Г.,
«Изв. АН СССР. Сер. матем.», 1949, т. 13, с. 389—402; [6] Оле й-
н и к О. А., «Матем. сб.», 1951, т. 29, с. 133—56: [7] Проблемы
Гильберта, М., 1969; [8] Арнольд В. И., «Функциональный
анализ», 1971, т. 5, № 3, с. 1—9; [9] Р о х л и н В. А., там гне,
1972, т. 6, № 4, с. 58—64; 1973, т. 7, № 2, с. 91—92; [10] X а Р-
ламов В. М., «Функциональный анализ», 1974; т. 8, №2,
с. 50 — 56; 1975, т. 9, Ni 3, с. 93—94; [11] его же, там же,
1975, т. 9, J* 2, с. 51—60; [12] его же, там же, 1976, т. 10,
JVi 4, с. 55—68; [13] Гудков Д. А., «Успехи матем. наук»,
1974, т. 29, в. 4, с. 3—79; [14] С у л л и в а н Д., Геометри-
Геометрическая топология, пер. с англ., М., 1975. Д. А. Гудков.
ДЕЙСТВИТЕЛЬНОЕ ЧИСЛО, вещественное
число, — положительное число, отрицательное чис-
число или нуль. Понятие Д. ч. возникло путем расширения
понятия рационального числа. Необходимость этого рас-
расширения обусловлена как практическим использовани-
использованием математики при выражении значения любой величи-
величины с помощью вполне определенного числа, так и
внутренним развитием самой математики, в частности
стремлением расширить область применимости ряда опе-
операций над числами (извлечение корня, вычисление ло-
логарифмов, решение уравнений и т. п.). К общему поня-
понятию Д. ч. подошли еще древнегреческие математики в
своей теории несоизмеримых отрезков, однако как са-
самостоятельное понятие оно было сформулировано впер-
впервые лишь в 17 в. И. Ньютоном (I. Newton) в «Arithmetica
Universales»: «Число есть не столько совокупность не-
нескольких единиц, сколько отвлеченное отношение ка-
какой-нибудь величины к другой, однородной с ней приня-
принятой за единицу». Строгие теории Д. ч. были построены
в конце 19 в. Г. Кантором (G. Cantor), P. Дедекиндом
(R. Dedekind) и К. Вейерштрассом (К. Weierstrass).
Действительные числа образуют со-
совокупность элементов, обладающую следующими свой-
свойствами.
I. Свойство упорядоченности. Для
любых двух чисел а и Ъ определено соотношение поряд-
порядка, т. е. два любых Д. ч. а и 6 удовлетворяют одному и
только одному из следующих соотношений: а<6, а=Ь
или а>6; при этом, если а<6 и 6<с, то а<Сс (транзи-
(транзитивность упорядоченности).
П. Свойство операции сложения.
Для любой упорядоченной пары чисел а и Ъ определено
такое единственное число, наз. их с у м м о й и обозна-
обозначаемое через а-\-Ь, что выполняются следующие свойст-
свойства." IIj) а+6=Ь-Ьа (коммутативность); П2) а+(Ь+с) =
= (<z-j-b)-f-e Для любых чисел а, Ь и с (ассоциативность);
П3) существует такое число, наз. нулем и обозна-
обозначаемое 0, что а+0=а для любого числа а; П4) для лю-
любого числа а существует такое число, наз. п р о т и-
воположным а и обозначаемое через —а, что
а+(—а) = 0; П5) если а<.Ь, то а+с<&-|-с для любого
числа с. Нуль единствен, и для каждого числа единст-
единственно противоположное ему число. Для любой упоря-
упорядоченной пары чисел а и Ь число а+(— Ь) наз. раз-
разностью чисел а и 6 и обозначается а—Ъ.
III. Свойство операции умножения.
Для любой упорядоченной пары чисел а и Ь определено
такое единственное число, наз. их произведени-
произведением и обозначаемое через ab, что: IIIj) ab=ba (комму-
(коммутативность); 1П2) а(Ьс)= (ab)c для любых чисел а, Ъ и с
(ассоциативность); Ш3) существует такое число, наз.
единицей и обозначаемое через 1, что ai~a для
любого числа а; Ш4) для любого числа а, не равного
нулю, существует такое число, наз. обратным
данному и обозначаемое через 1/а, что аA/а)=1; Ш5)
если а<6 и с>0, то асСЬс. Эти свойства гарантируют
единственность единицы и единственность обратного
каждому элементу. Для любой упорядоченной пары
чисел а и Ь, ЬфО, число a(ilb) наз. частным от де-
деления а на Ъ и обозначается alb.
Число 1 + 1 обозначается 2, число 2+1 обозначает-
обозначается 3 и т. д. Эти числа 1, 2, 3... наз. натуральными
числами. Числа, большие нуля, наз. положи-
положительными, а числа, меньшие нуля,— отрица-
отрицательными. Числа 0, —i, —2, . .. наз. целыми
числами (считается, что +а = а). Числа вида т/п,
где т — целое, а га — натуральное, наз. рациональ-
рациональными числами. Они включают в себя все целые
числа. Д. ч., появляющиеся рациональными, наз. и р-
рациональными.
IV. С в о й с т в о дистрибутивности ум-
умножения относительно сложения.
Для любой тройки чисел а, Ь и с (a-{-b)c=ac^rbc.
Совокупность элементов, удовлетворяющих всем пе-
перечисленным свойствам, образует линейно упорядочен-
упорядоченное поле. Д. ч. обладают еще двумя важными свойст-
свойствами.
V. А р х и м е д о в о свойство. Каково бы ни
было число а, существует такое целое число п. что я>а.
Совокупность элементов, удовлетворяющих свойствам
I — V, образует упорядоченное архимедово поле. Та-
Таковым является не только совокупность Д. ч., но и мно-
множество рациональных чисел.
Существенным свойством Д. ч. является свойство их
непрерывности, к-рым рациональные числа не обла-
обладают.
VI. Свойство непрерывности. Для
всякой системы вложенных отрезков
{[<*«, bn\}, a.n<an + i< ¦ ¦ ¦ <ъп + \<ъп, п = 1, 2, ... ,
существует хотя бы одно число, к-рое принадлежит
всем отрезкам данной системы. Это свойство наз. так-
также принципом вложенных отрезков
Кантора. Если длины Ъп—ап вложенных отрез-
отрезков стремятся к нулю при га-*- <х>, то существует един-
единственная точка, принадлежащая всем этим отрезкам.
Из перечисленных свойств Д. ч. следуют многие
другие; так, из свойств I — V можно получить, что
1>0, правила действий с рациональными дробями, пра-
правила знаков при умножении и делении Д. ч.. свойства
абсолютной величины Д. ч., правила преобразования
равенств и неравенств и т. п. Свойства I — VI полно-
полностью описывают свойства множества Д. ч. и только их,
иначе говоря, если эти свойства назвать аксиомами, то
окажется, что Д. ч. — совокупность элементов, удов-
удовлетворяющая аксиомам I — VI. Это означает, что ак-
аксиомы I — VI определяют множество Д. ч. с точностью
до изоморфизма: если имеются две совокупности X и У,
удовлетворяющие свойствам I — VI, то всегда сущест-
существует изоморфное относительно упорядоченности и опе-
операций сложения и умножения отображение X на У, т. г.
указанное отображение, обозначим его через х —>- у
(здесь ?/?У является элементом, соответствующим
элементу х?Х), взаимно однозначно отображает X на
У так, что если
х2, х1?Х, х2?Х и х1
г/i < г/г,
Отсюда следует, что множество Д. ч. (в отличие, напр.,
от множества рациональных чисел) невозможно расши-
расширить с сохранением свойств I — V, т. е. не существует
множества, в к-ром было бы введено соотношение по-
порядка, операции сложения и умножения, удовлетво-
удовлетворяющие свойствам I — V, и к-рое содержало бы подмно-
подмножество, изоморфное множеству Д. ч., и не совпадало
бы с ним. Д. ч. существенно больше, чем рациональ-
рациональных чисел, именно рациональные числа составляют
счетное подмножество множества Д. ч., которое само не-
несчетно.
Как рациональные, так и иррациональные числа об-
обладают свойством плотности во множестве всех Д. ч.:
каковы бы ни были два Д. ч. а и 6, а<6, найдутся такое
рациональное г, что а <;¦<&, и такое иррациональное \,
что а<1<&.
Со свойством непрерывности Д. ч. тесно связано свой-
свойство их полноты, состоящее в том, что всякая
фундаментальная последовательность Д. ч. является
сходящейся. Следует отметить, что множество одних
только рациональных чисел уже не обладает свойством
полноты: в нем существуют фундаментальные после-
последовательности, не сходящиеся ни к какому рацио-
рациональному числу. Свойство непрерывности множества
Д. ч. (их полнота) связано с их применением для
измерения тех или иных непрерывных величин, на-
например для измерения длин геометрических отрезков:
если выбрать отрезок единичной длины, то в силу
непрерывности множества Д. ч. каждому отрезку со-
сопоставляется определенное положительное Д. ч.— его
длина. Образно говоря, непрерывность множества
Д. ч. означает, что в не_м нет «пустых мест». Из
непрерывности множества Д. ч. следует, что из вся-
всякого положительного числа можно извлечь корень га-и
степени (п — натуральное число) и что всякое поло-
положительное число имеет логарифм по любому основа-
основанию а>0, аф1.
Свойство непрерывности Д. ч. можно сформулиро-
сформулировать иначе.
VI'. Всякое ограниченное сверху множество имеет
точную верхнюю грань (см. Верхняя и нижняя грани).
Можно использовать также понятие сечения А [В
в области Д. ч. (см. Дедекиндово сечение). Говорят, что
сечение А\В производится числом а, если а<:а<:6 для
всех aQA, b?B (при этом либо а?Л, либо а?В).
Всякое число'производит сечение.
Свойство непрерывности, наз. непрерывно-
непрерывностью Д. ч. по Дедекпнду, состоит в спра-
справедливости обратного утверждения.
VI". Всякое сечение Д. ч. производится нск-рым чис-
числом. Такое число единственно и является либо наи-
наибольшим в нижнем классе, либо наименьшим в верх-
верхнем.
Каждое из утверждений VI, VI' и VI" равносильно
каждому из остальных в том смысле, что из каждого
из них, принятого за аксиому (и остальных свойств
I—V), вытекают два других. Более того, как из свойства
VI', так и из свойства VI" (и свойств I — IV) вытекает
не только VI, но и архимедово свойство V. Определе-
Определение Д. ч. как совокупности элементов, обладающих
свойствами I—VI, является аксиоматич. построением
теории Д. ч. Существует несколько методов построения
этой теории на основе рациональных чисел.
Первая такая теория была построена Р. Дедекиндом
на основе понятия сечения R\\R2 в области ра-
рациональных чисел. Если для данного сечения R\\R%
рациональных чисел в 7?j есть наибольшее рациональ-
рациональное число пли в i?2 наименьшее, то говорят, что сече-
сечение iJili?, производится этим числом. Всякое рацио-
рациональное число производит сеченне. Сечение, у к-рого
в нижнем классе нет наибольшего, а в верхнем нет наи-
наименьшего, наз. иррациональным числом.
Рациональные и иррациональные числа наз. дейст-
действительными числами, при этом для едино-
единообразия рациональные числа рассматриваются как се-
сечения, к-рые они производят.
Пусть z=i?1|i?2 и a' = i?i|i?2- Д- ч. х наз. меньшим
Д. ч. х' (или, что то же самое, х' наз. большим х), если
R1dRi, i?1=^=i?2. Обычным образом вводятся понятия
положительных, отрицательных Д. ч. (см. выше) и аб-
абсолютной величины \х\ Д. ч. х. Суммой Д. ч. х и х' наз.
такое число х+ж', что для всех rt^Ri, r'i?Rx, r2?i?2,
Г2 (;Дз выполняются неравенства
Произведением положительных Д. ч. х и х' наз. такое
число хх', что для всех положительных гх, г[, г2, г'2 вы-
выполняются неравенства rxr'x<.xx' *ir2r'i. Для произволь-
произвольных Д. ч. х и х', не равных нулю, их произведение оп-
ределяотся как Д. ч., абсолютная величина к-рого равна
|я||а:'| и к-рое положительно, если х и х' одного знака,
и отрицательно, если х и х' разных знаков. Наконец,
для любого Д. ч. х полагается Qx=xQ=Q.
Сумма и произведение Д. ч. всегда существуют, един-
единственны и вся совокупность таким образом определен-
определенных Д. ч. с введенным в них отношением порядка и
операциями сложения и умножения обладает свойст-
свойствами I — VI.
Другая теория была построена Г. Кантором с по-
помощью понятия фундаментальной после-
последовательности рациональных чисел, т. е.
такой последовательности {г,,} рациональных чисел,
что для любого рационального числа е>0 существует
такой номер пе , что для всех п^пв и т>гае выполняет-
выполняется неравенство \гп—гт\ <е. Последовательность {г„}
рациональных чисел наз. нульпоследова-
тельностью, если для любого рационального
е>0 найдется такой номер пе , что для всех ?г>иЁ
справедливо неравенство |т-„|<8. Две фундаментальные
последовательности рациональных чисел {гп} и {г'п }
наз. эквивалентным и, если последователь-
последовательность {гп—гп} является нульпоследовательностью.
Это определение эквивалентности обладает свойствами
рефлексивности, симметричности и транзитивности, и
потому все множество фундаментальных последователь-
последовательностей рациональных чисел распадается на классы
эквивалентности. Совокупность всех этих классов
эквивалентности и наз. в этом случае множеством
действительных чисел. В силу этого оп-
определения, всякое Д. ч. представляет собой класс экви-
эквивалентности фундаментальных последовательностей ра-
рациональных чисел. Каждая из этих последовательно-
последовательностей наз. представителем данного Д. ч. Фундаменталь-
Фундаментальная последовательность рациональных чисел {г„}
наз. положительной (соответственно о т-
р и ц а т о л ь н о й), если существует такое рацио-
рациональное число г>0, что все члены этой последователь-
последовательности, начиная с нек-рого, больше, чем г (соответствен-
(соответственно, меньше, чем г). Всякая фундаментальная последо-
последовательность рациональных чисел является либо нуль-
последовательностью, либо положительной, либо от-
отрицательной. Если фундаментальная последователь-
последовательность рациональных чисел положительна (отрицатель-
(отрицательна), то и любая ей эквивалентная фундаментальная
последовательность рациональных чисел также поло-
положительна (отрицательна). Д. ч. наз. положитель-
положительным (отрицательны м), если какой-то, а, сле-
следовательно, и любой его представитель положителен
(отрицателен). Д. ч. наз. нулем, если нок-рый, а
следовательно, и любой его представитель является
нульпоследовательностью. Каждое Д. ч. либо поло-
положительно, либо отрицательно, либо нуль. Для того,
чтобы сложить или умножить два Д. ч. х и х', надо сло-
сложить, соответственно умножить, два любых их пред-
представителя {гп}?х, {гп }?х', тогда получатся снова фун-
фундаментальные последовательности рациональных чи-
чисел {rn-j-r'n} и {rnr'n}. Классы эквивалентности, пред-
представителями к-рых они являются, и наз. в этом случае
суммой х-\-х' и произведением хх' дан-
данных чисел. Эти операции определены однозначно, т. е.
не зависят от выбора представителей данных чисел.
Вычитание и деление Д. ч. определяются как действия,
обратные сложению и умножению. Если для двух Д. ч.
х ж у имеется х—г/>0, то Д. ч. х наз. большим Д. ч. у.
Таким образом определенная совокупность Д. ч. с
указанным соотношением порядка и операциями сло-
сложения и умножения снова удовлетворяет свойствам
I -VI.
Еще одна теория Д. ч. была построена К. Вейерштрас-
сом на основе бесконечных десятичных дробей. В этой
теории действительным числом наз. вся-
всякая бесконечная десятичная дробь со знаком плюс или
минус:
± ао> «i сс2 .. . а„ . ..,
где Oq — неотрицательное целое число (целые числа счи-
считаются известными), а а„, га=1, 2, ...,— одна из цифр О,
1, 2, .. ., 9. При этом бесконечная десятичная дробь
с периодом из 9:
а0, ахосг . .. ап (9), а„ Ф 9,
считается равной бесконечной десятичной дроби
а0, аха2 . . . ап_х (?*„ + !) 000 ... О ...
(в случае га=0 равной бесконечной десятичной дроби
(ao+i), 000 ... 0...). Эта дробь записывается также как
конечная десятичная дробь
a0,
и говорится, что она имеет п значащих цифр после
запятой. Бесконечная десятичная дробь, не имею-
имеющая периода (9), наз. допустимой бесконечной десятич-
десятичной дробью. Очевидно, что всякое Д. ч. уже единст-
единственным образом записывается в виде допустимой бес-
бесконечной десятичной дроби. Если Д. ч. х записывается
с помощью допустимой бесконечной десятичной дробью
со знаком плюс (минус) и среди цифр а„ имеется хоть
одна отличная от нуля, то х наз. положитель-
положительным (отрицательным) Д. ч. и пишется ж>0
(ж<0), а если все сс„=О, п=0, 1, 2, ..., то — н у-
л е м: х~0. Для числа
число a0, ax a2 ... an.. . наз. его абсолютной
величиной и обозначается \х\, а число, у к-рого
знак плюс (соответственно минус) заменен на минус
(на плюс), наз. противоположным данному и
обозначается —х. Если
— допустимая бесконечная десятичная дробь, то
число
соответственно число
хп = a0, a, a2 ... ап +10- «,
наз. нижним, соответственно верхним, десятичным
приближением порядка п числа х. Пусть х и у — два
положительных числа, записанных с помощью допу-
допустимых бесконечных десятичных дробей
По определению, полагают х<у, если либо ао<Ро,
либо существует такой номер п0, гао=0, 1, ..., что
а*=Рь А=0, 1, ..., пв, а а„0+1<риA+1. Каждое отрица-
отрицательное число и нуль считаются меньше всякого поло-
положительного числа. Если х и у оба отрицательны и
lj/|<|x|, то полагают, что х<Су.
Последовательность целых чисел п^, ft=l, 2, ...,
наз. стабилизирующейся к числу го, если существует
такой номер к0, что nk=m при всех к^к0. Последова-
Последовательность бесконечных десятичных дробей
*(*> = «$*>, ai*>aj*> . . . а{*' ...
наз. стабилизирующейся к числу
х = а0, ах a2 .. . ап . . .,
если i-й столбец бесконечной матрицы ||a; ||, i — номер
столбца, к — строчки, стабилизируется для любого
i=0, 1, 2 к числу а,-. Если _>0 и j/>0, то конечные де-
десятичные дроби
,J_n
имеют п значащих цифр после запятой и образуют по-
последовательности, стабилизирующиеся к нек-рым чис-
числам. Эти числа и наз. соответственно суммой х-\-у,
разностью х—у, произведением ху и
X
частным — Д. ч. х иг/. Эти определения распростра-
распространяются на Д. ч. произвольных знаков. Напр., если х<Л
и г/<:0, то х-\-у= — (Mt|i/I), если жиг/ разных знаков,
то ж4-г/=— ||_|—\у\\, где выбирается знак, одинаковый
со знаком того из чисел х или у, абсолютная величина
к-рого наибольшая. Для любых чисел х и у полагают
х—г/=х+(—у) (в случае ж>0, г/>0 это определение
совпадает с выше сформулированным) и т. д. Совокуп-
Совокупность допустимых бесконечных десятичных дробей с
таким образом определенными соотношениями поряд-
порядка, операциями сложения, вычитания, умножения и де-
деления удовлетворяет аксиомам I—VI.
При построении теории Д. ч. можно пользоваться не
только десятичной системой счисления, но и другими:
двоичной, троичной и т. д. Существенно, что ни при
одном из приведенных выше построений теории Д. ч.
(аксиоматическом, с помощью сечений рациональных
чисел, на базе фундаментальных последовательностей
рациональных чисел или на основе бесконечных деся-
десятичных дробей) не доказывается существование (непро-
(непротиворечивость) множества Д. ч. С этой точки зрения все
эти методы равноправны.
Геометрически множество Д. ч. изображается направ-
направленной (ориентированной) прямой, а отдельные чис-
числа — точками этой прямой. Поэтому совокупность
Д. ч. часто наз. числовой прямой, а отдель-
отдельные числа — точками. Имея в виду такое изображение
Д. ч., иногда вместо а меньше Ъ (соответственно Ъ боль-
больше а) говорят, что число а лежит левее числа Ь (соот-
(соответственно, что Ь лежит правее а). Между точками гео-
геометрической (евклидовой) прямой, упорядоченными по
их положению, и элементами числовой прямой сущест-
существует взаимно однозначное соответствие, сохраняющее
порядок. Это обстоятельство и является оправданием
изображения множества Д. ч. в виде прямой.
Лит.: [1] D e d e k i n d R., Stetig-keit imd irrationale Zah-
len, Braunschweig, 1872 (рус. пер.— Д е д е к и н д Р., Непрерыв-
Непрерывность и иррациональные числа, 3 изд., Одесса, 1914); [2] D а п-
t s с h е г V., Vorlesung-en uber die Weierstrass'sche Theorie der
irrationalen Zahlen, Lpz., 1908; [3] С a n t о г G., «Math. Ann.»,
1872, Bd 5, S. 123_30; [4] Немыцкий В. В., С л у д-
ская М. И., Черкасов А. Н., Курс математического
анализа, 3 изд., т. 1, М., 1957; [5] Ильин В. А., II о з-
н я к 9. Г., Основы математического анализа, т. 1, 3 изд., М.,
1971; [6] К у д р я в ц е в Л. Д., Математический анализ, 2 изд.,
т. 1, М., 1973; [7] Никольский С. М., Курс мате-
математического анализа, т. 1, М., 1973; [8] Фихтенгольц
Г. М., Курс дифференциального и интегрального исчисления,
7 изд., т. 2, М., 1969; [9] Б у р б а к и Н., Общая топология.
Топологические группы. Числа и связанные с ними группы и
пространства, пер. с франц., М., 1969, гл. 4. Л. Д. Кудрявцев,
ДЕКАРТА ТЕОРЕМА, правило знаков
Декарт а,— теорема, утверждающая, что число
положительных корней многочлена с действительными
коэффициентами равно или на четное число меньше
числа перемен знаков в ряду его коэффициентов (при-
(причем каждый корень считается столько раз, какова его
кратность) и нулевые коэффициенты при подсчете числа
перемен знаков не учитываются. Если известно, что
все корни данного многочлена действительны (как, на-
например, для характеристич. многочлена симметрич.
матрицы), то Д. т. дает точное число корней. Рассма-
Рассматривая многочлен /(—х) можно с помощью этой же
теоремы найти число отрицательных корней f(x).
Лит.: [1] К у р о ш А. Г., Курс высшей алгебры, 11 изд.,
М., 1975. И. В. Проскуряков.
ДЕКАРТОВ КВАДРАТ, коуниверсальный
к в' а д р а т (в категории) — диаграмма
рл
——^ S
Здесь А' \В — расслоенное произведение объектов
S
А и В, ассоциированное со схемой
А
I*
а Ра и Рв~~ канонические проекции. Диаграмма
В
Р
является Д. к. тогда и только тогда, когда она коммута-
коммутативна и для всякой пары морфизмов \i:V—*~A , v : V-+-B
такой, что au = Pv, существует единственный морфизм
X : V—>-Р, удовлетворяющий условиям |л=6А., \=уХ.
Лит.: [1] Б у к у р И., Деляну А., Введение в теорию
категорий и функторов, пер. с англ., М., 1972. О. А. Иванова.
ДЕКАРТОВ ЛИСТ — плоская алгебраич. кривая
3-го порядка, уравнение к-рой в декартовых прямо-
прямоугольных координатах имеет вид: .г3+г/3—Заху=0,
параметрические уравнения
3at 3a<2
где t — тангенс угла между радиус-вектором кривой и
осью Ох. Д. л. симметричен относительно биссек-
биссектрисы у=ж(см. рис.). В точках с координатами ( ^/<Г~
а \/i) и \п (/4 , а \/ 2 ) касательные параллельны
координатным осям. Начало координат — узловая
точка с касательными, по
к-рым проходят оси коорди-
координат. Асимптота: у=—х—а.
Площадь между кривой и
асимптотой: 5 = 3/2а2. Площадь
петли: 5=3/2а2. Д. л. назван
по имени Р. Декарта (R. Des-
Descartes), впервые его рассмот-
рассмотревшего в 1638.
Лит.: [1] С а в е л о в А. А.,
Плоские кривые, М., 1960; [2]
Смого ржевский А. С, Столова Е. С, Справочник
по теории шюских кривых третьего порядка, М., 1961.
Д. Д. Соколов.
ДЕКАРТОВ ОВАЛ — плоская кривая, расстояния
г1 и г, каждой точки Р к-рой до двух фиксированных
точек F1 n F.2 (фокусов) связаны
неоднородным линейным уравне-
уравнением
Д. о. можно определить при по-
помощи однородного линейного
уравнения
где г3 — расстояние до третьего
фокуса F3, лежащего на прямой
F1F2- Д. о. в общем случае состоит из двух замкнутых
линий, одна из к-рых объемлет другую (см. рис.).
В прямоугольных декартовых координатах уравне-
уравнение Д. о. имеет вид:
где d — длина отрезка FtF2. При го=1 и a>d Д. о.
представляет собой эллипс, при т= — 1 и a<d— ги-
гиперболу и, если m.= a/d,— Паскаля улитку. Впервые
Д. о. исследован Р. Декартом (R. Descartes) в связи
с задачами оптики (см. [1]).
Лит.: [1] Декарт Р., Геометрия, пер. [сфранц. и латин.],
М.—л., 1938; [2] С а в е л о в А. А., Плоские кривые, М.,
1960. Е. В. Шикин.
ДЕКАРТОВА ПРЯМОУГОЛЬНАЯ СИСТЕМА КООР-
КООРДИНАТ ортонормированная — прямолиней-
прямолинейная система координат в евклидовом пространстве.
Д. п. с. к. на плоскости задается двумя взаимно
перпендикулярными прямыми — осями коорди-
координат, на каждой из к-рых выбрано положительное
направление и задан отрезок единичной длины. Точка
пересечения осей координат (О) наз. началом
координат. Одна из осей (Ох) координат наз.
осью абсцисс, другая — осью ординат
(Оу). Оси координат делят плоскость на четыре равные
области — четверти, или квадранты.
Прямоугольными декартовыми
координатами точки М наз. упорядоченная
пара чисел (х, у), первое из к-рых (абсцисса)
равно величине ортогональной проекции направленного
отрезка ОМ на ось абсцисс, второе (ордината) —
величине ортогональной проекции направленного от-
отрезка ОМ на ось ординат.
Д. п. с. к. в трехмерном пространстве задается
аналогично случаю плоскости: осью абсцисс, осью
ординат, осью аппликат и началом координат
О. Плоскости, проходящие через оси координат, наз.
координатными плоскостями. Они делят
пространство на 8 областей — октантов.
Иногда пользуются косоугольной (общей)
декартовой системой координат, к-рая отлича-
отличается от Д. п. с. к. тем, что углы между осями коорди-
координат не обязательно прямые.
Д. п. с. к. названа по имени Р. Декарта (R. Descar-
Descartes), к-рый ввел метод прямолинейных координат
(см. [1]).
Лит.: [1] Декарт Р., Геометрия, пер. [с франц. и ла-
латин.], М.—Л., 1938. А. В. Иванов.
ДЕКАРТОВО ПРОИЗВЕДЕНИЕ — то же, что полное
прямое произведение.
ДЕКАРТОВО РАЗЛОЖЕНИЕ (в топологии) — разло-
разложение пространства в топологич. произведение. Важна
задача о нетривиальных Д. р. кубов I" и евклидовых
пространств R". Напр., если пространство М получено
из Rm, 3<:то<га, отождествлением точек дуги lczRm,
для к-рой ях (Rm\!)=^=l (см. Дикое вложение), то JWxR =
= R"I + 1 и MxM=R2m. Любое гладкое компактное
стягиваемое многообразие Мт есть сомножитель /",
и>то. Любой сомножитель /", л<:4, есть 1т, т<_п.
Лит.: [1] Итоги науки. Алгебра. Топология. Геометрия.
1965, М., 1967, с. 227, 243. А. В. Чернавский.
ДЕКАРТОВЫ КООРДИНАТЫ — способ определения
положения точек на плоскости их расстояниями до двух
фиксированных перпендикулярных прямых — осей.
Это понятие усматривается уже у Архимеда и Апполо-
гия Пергского более двух тысяч лет назад и даже у
древних египтян. Впервые эта идея была системати-
систематически развита П. Ферма (P. Fermat) и Р. Декартом
(R. Descartes); в их формулировках расстояния могли
быть только положительными числами или нулем.
Мысль о том, что одно или оба эти расстояния можно
считать также и отрицательными, принадлежит И. Нью-
Ньютону (I. Newton). Г. Лейбниц (G. Leibniz) первым
назвал эти расстояния «координатами». См..Декартова
прямоугольная система координат. М. И. Войцеховский.
ДЕКОДИРОВАНИЕ — см. Кодирование и декоди-
декодирование.
ДЕЛЁЖ (в теории игр) — удовлетворяющее условиям
рациональности распределение в кооперативной игре
общего выигрыша всех игроков между отдельными игро-
игроками. Формально, если игра с множеством игроков
/={1, .., га} задана характеристической функцией
v(J), то Д. есть такой вектор х= (х1г. . ., хп), что
^,i=1Xi~v(J); x^v(i), t—l,..., га. г. н. Дюбин.
ДЕЛЕНИЕ — действие, обратное к умножению;
заключается в нахождении такого х, что Ъх=а или xb = a
при заданных а и Ъ. Результат Д. х ыаз. частным,
или отношениемаи Ь; при этом а наз. дели-
делимым, а Ь — делителем. Для обозначения Д.
употребляются знаки двоеточия (а : 6), горизонталь-
горизонтальной или косой черты (-^- или alb).
В поле рациональных чисел Д. возможно всегда,
кроме деления на нуль, при этом результат Д. опре-
определен однозначно. В кольце целых чисел Д. не всегда
возможно. Напр., 10 делится на 5, но не делится на 3.
Если при Д. (в поле рациональных чисел) целого числа
а на целое число Ъ в частном получается целое число,
то говорят, что а делится нацело (или без ос-
остатка) на Ь, и записывают это следующим образом: Ь\а.
Д. комплексных чисел производится по формуле
а + Ы (ac + bd) + (bc-ad) i
c + di c* + d* '
а Д. комплексных чисел, записанных в тригонометрич.
форме,— по формуле
г (cos а.+ i sin a)
Деление с остатком — это, по существу,
совершенно особая операция, отличная от Д. в опреде-
определенном выше смысле. Если а и ЬфО — целые числа,
то операция Д. с остатком числа а на число Ъ состоит в
определении таких целых чисел х и у, что
а=Ьх+у, где 0«i/<|6|.
При этом а наз. делимым, Ъ — делителем, х—
частным, а у — остатком. Эта операция всегда
осуществима и однозначна. Если г/ = 0, то говорят, что
а делится на Ъ без остатка. В этом случае частное по-
получается то же самое, что и частное при обычном Д.
Аналогично определяется Д. с остатком для много-
многочленов с коэффициентами из некоторого поля. Она
состоит в нахождении по двум заданным многочленам
А(х) и В (х) многочленов Q{x) и R(x), удовлетворяю-
удовлетворяющих условиям
A(x)=B(x)Q(x)+R(x)
и степень R(x) меньше степени Q(x). Эта операция так-
также всегда осуществима и однозначна. Если Я(х)^0,
то говорят, что многочлен А (х) делится на многочлен
В(х) без остатка. С. А. Степанов.
ДЕЛЕНИЯ КРУГА МНОГОЧЛЕН, круговей
многочлен,— многочлен, имеющий вид
где ф? — первообразные корни степени п из единицы и
произведение берется по всем числам к, взаимно простым
с га и взятым из ряда 1,2,..., п. Степень многочлена
Фи(х) — число натуральных чисел, меньших, чем га, и
взаимно простых с га. Д. к. м. удовлетворяют соотно-
соотношению
где произведение берется по всем положительным дели-
делителям d числа п, включая и само п. Это соотношение
позволяет рекурсивно вычислять многочлены Ф„(х)
путем деления многочлена х" — 1 на произведение
всех Ф,*(х), d<re, d\n. При этом коэффициенты много-
многочлена оказываются лежащими в исходном простом
поле Р,ав случае поля рациональных чисел — целыми
числами. Так,
(Di (*) = * —1, Ф2(х) = х + 1, Ф3(х) = х2 + х + 1.
Если п=р — простое и поле Р имеет характеристику О,
то
Для многочлена Ф«(х) можно указать явное выраже-
выражение через Мёбиуса^ функцию \i(k):
Напр.,
) = (х12 —1)(х6 —l)-
Над полем рациональных чисел все многочлены Ф„(х)
неприводимы, но над коночными простыми полями эти
многочлены могут быть приводимы. Так, над полем вы-
вычетов по модулю 11 имеет место соотношение:
Ф12 (х)=х4 —х2 + 1 = (х2 + 5х^1) (х2 — Ъх— 1).
Уравнение Ф„ (х)=0, дающее все первообразные
корни л-й степени из единицы, наз. уравнением
деления круга (окружности). Решение
этого уравнения в тригонометрич. форме имеет вид:
2йя . . . 2Лл 2/гяг/п
rft = cos—+isin —= e
где дробь kin несократима, т. с. inn взаимно просты.
Решение в радикалах уравнения деления круга тесно
связано с задачей построения правильного л-угольника
или с эквивалентной ей задачей деления окружности
на п равных частей, а именно, задача деления окруж-
окружности на п частей решается с помощью циркуля и ли-
линейки тогда и только тогда, когда уравнение Ф„(ж)=0
решается в квадратных радикалах. Последнее, как до-
доказал К. Гаусс (С. Gauss, 1801), имеет место в том и
только в том случае, когда
2т . . ps,
где т — целое неотрицательное число и рх, /?2,...,
ps — попарно различные простые числа, представимые
2ft
в виде 2 +1 с целым неотрицательным к.
Лит.: [1] Ван дер ВарденБ. Л., Алгебра, пер. с
нем., М., 1976; [2] G у ш к е в и ч А. К., Основы высшей ал-
алгебры, 4 изд., М.—Л., 1941. И. В. Проскуряков,
ДЕЛЕНИЯ КРУГА ПОЛЕ — то же, что круговое
поле.
2>-ДЕЛИМАЯ ГРУППА, группа Барсот-
т и — Тейта,— обобщение понятия коммутативной
формальной группы. Гомоморфизм, индуцируемый умно-
умножением на простое число р, является эпиморфизмом
для р-Д. г.
Пусть S — схема, р — простое число; р-ц. е л и м о в
группой высоты h наз. индуктивная система
G=(Gn, in) коммутативных конечных групповых схем
Gn порядка p"h такая, что последовательности
n r 1" г Ф" г
U >¦ 1гл * Ьп+1 >¦ Un + 1
являются точными (здесь <ря — гомоморфизм умножения
на рп). Морфизм />-Д. г. ость морфизм индуктивных
систем. р-Д. г. наз. связной (соответственно эта-
л ь н о й), если все Gn — связные (этальные) групповые
схемы. Связная р-Д. г. над иолом характеристики р
есть коммутативная формальная группа (рассматри-
(рассматриваемая как индуктивный предел ядер ср„ — умножения
на />"), для к-рой умножение на р является изогениец
[6]. Этот факт обобщается на случай произвольной
базисной схемы S, на к-рой гомоморфизм, индуцируе-
индуцируемый умножением на р, локально нильпотентон [4].
Категория этальных р-Д- г. эквивалентна категории
/>-адических представлений фундаментальной группы
схемы S. Каждая р-Д. г. G над артшювой схемой S
содержит максимальную связную подгруппу G0, на-
называемую связной компонентой едини-
ц ы, фактор по к-рой является этальной р-Д. г. Раз-
Размерность алгебры Ли для любой (?°)„ наз. размер-
размерностью р-Д- г. G.
Пусть А — абелево многообразие над полем к раз-
размерности d, А (га) — ядро гомоморфизма умножения
на р" в A, in : А (га)—>-Л (ге+1) — естественное вло-
вложение. Индуктивная система А(оо)-—(А(п), in) явля-
является р-Д. г. высоты 2d. Ее связная компонента еди-
единицы Л(оо)° совпадает с формальным пополнением А
вдоль единичного сечения, а высота А (оо)° представляет
важный инвариант абелевой схемы.
Пусть G=(G,2, in) — р-Д. г. высоты h, Gn — двой-
двойственные по Картье конечные групповые схемы, in '.
: Gn—>-Gn + 1 — отображение, двойственное к отображе-
отображению умножения на р : G,,+ l-^-Gn. Система ?=(<?„,
in) является р-Д. г. высоты h и наз. двойствен-
двойственной к р-Д. г. G. Сумма размерностей G и G равна h.
Как и для формальных групп, для р-Д. г. вводится
понятие модуля Дьедонне, играющее важную роль в
теории деформации р-Д. г. (см. [2], [3], [4]).
В случае, когда S есть спектр разнохарактеристичес-
кого кольца дискретного нормирования А с полем вы-
вычетов характеристики р, структура р-Д. г. тесно свя-
связана со структурой пополнения алгебраич. замыкания
поля частных К кольца А , рассматриваемого как модуль
над группой Галуа поля К (см. [6]).
Лит.: [1] Barsottil., в кн.: Coloque sur la theorie
des groupes algebriques tenu a Bruxelles, P., 1962, p. 77—85;
[2] Grothendieck А., в кн.: Actes du Congres internatio-
international des mathematiciens. 1970, t. 1, P., 1971, p. 431—36; [3]
MazurB., Messing W., Universal Extensions and one
Dimensional Crystalline Cohomology, В., 1974; [4] Messing W.,
The Srystals Associated to Barsotti — Tate Groups: with Applica-
Applications to Abelian Schemas, В., 1972; [5] Serre J.-P., «Sem.
Bourbaki», expose 318, 1966—67, N. Y., 1968; [6] Тейт Д т.,
«Математика», 1969, т. 13, Ns 2, с. 3—25. И. В. Долгачев.
ДЕЛИМОСТИ ПРИЗНАК на натуральное
числом — условие, к-рому удовлетворяет натураль-
натуральное число А в том и только в том случае, если оно делит-
делится на d. Желательно, чтобы это условие можно было
легко проверить и чтобы эта проверка была не сложнее
непосредственного деления числа А на d.
Если разность чисел А и В делится на d, то число А
делится на d тогда и только тогда, когда число В де-
делится на d. На этом свойстве основан вывод многих
Д. п. Пусть запись числа А в десятичной системе счис-
счисления имеет вид:
А = (ап . . . a2aia0I0 = а0 + Юа^ + 102а2 + . . .
тогда
А=ао-'Г1ОАи где Л1 = а1 + Юа2+ .
А =я0 + 10а1 + 100Л2, где Л2=а2+1Оа3+ . .. +10"-2а„;
где
Из этих равенств сразу получаются Д. п. на делители
чисел 10, 100, 1000,... В частности, для того чтобы
число А делилось на2, необходимо и достаточно,
чтобы его последняя цифра, т. е. число а0, делилось
на 2; для того чтобы число Л долилось на 4
(н а 8), необходимо и достаточно, чтобы число, изобра-
изображаемое двумя (соответственно тремя) последними циф-
цифрами числа А, т. е. число ao-|-10ai, делилось на 4
(соответственно ао-\-\Оа1-}-ЮОа2 делилось на 8). Так
как разность (а^-Юа^ — (ао+2%) кратна 4, то Д. п.
на 4 можно дать и в такой форме: число А делится на 4
тогда и только тогда, когда число ао-)-2а1 делится на 4.
Каждый Д. п. на число d позволяет сопоставить
с числом А . если оно не слишком мало, нек-рое неотрица-
тельное целое число, меньшее А, к-рое делится на d
в том и только в том случае, когда само число А де-
делится на d. Другими словами, каждый Д. п. на число d
определяется нек-рой функцией /, принимающей целые
значения и удовлетворяющей условиям: \f{A)\<.A
для каждого натурального А, начиная с некоторого;
f(A) делится на d тогда и только тогда, когда число А
делится на d. Любая целозначная функция, удовлет-
удовлетворяющая перечисленным условиям, наз. функци-
функцией делимости на число d; множество всех
таких функций обозначается Q(d). Ясно, что
Поскольку
A -
h (A) = aQ-i-ax+ . . . +an?Q (9) С Q C).
Итак, число А д е л и т с я н а 3 (н а 9) тогда и только
тогда, когда сумма цифр этого числа делится на 3 (соот-
(соответственно на 9). Аналогично,
+ 11 (Л1_Л2+...+(-1)«-2Л„_1).
Следовательно,
fg(A) = al) — a1+... + (-l)nan€ Q (И).
Используя представления чисел в системе счисления
с основанием 10*, где к=2, 3,..., можно найти Д. п.
на делители чисел вида 10*+1. Так, при к—2 получа-
получаются следующие функции делимости на 11 и 101:
/8 (Л) =
Поскольку 103+1 = 7-11-13, получается объединенный
Д. п. на числа 7, 11, 13: чтобы узнать, делится ли
данное число на какое-нибудь из чисел 7, 11 или 13,
достаточно разбить цифры этого числа на грани, начи-
начиная справа, по три в каждой, а затем соединить попе-
попеременно знаками+и — числа, образованные этими
гранями. Полученное число делится на 7, Пили
13 тогда и только тогда, когда данное число делится
соответственно на 7, 11 или 13. Таким образом,
/в (А) =
A3).
Если целые числа с и d взаимно просты, то число
Ас делится на d тогда и только тогда, когда число
А делится на d. Это соображение также часто исполь-
используется при построении Д. п. Пусть d — какой-нибудь
делитель разности 10с — 1, тогда числа cud взаимно
просты, и из равенства
следует, что число А делится на d в том и только в том
случае, если число А-^-{-сай делится на d. Напр., при
d=19, с=2 разность 10с—1 делится на 19. Поэтому
Чтобы узнать, делится ли число на 19, можно последо-
последовательно применять этот признак. Пусть d — какой-
нибудь делитель суммы 10с+1. Из равенства
следует, что число А делится на d тогда и только тогда,
когда число Аг — са0 делится на d. Так, при с= 11 число
10c-f-l делится на 37. Поэтому
fu(A) = A1-Ha0^QC7).
Соответствующий Д. п. можно сформулировать так:
чтобы узнать, делится ли число А на 37 или нет, доста-
достаточно вычеркнуть последнюю цифру числа А и из числа,
образуемого невычеркнутыми цифрами, вычесть произ-
произведение 11 на число, изображаемое вычеркнутой
цифрой. Число Лделитсяна37в том и только в
том случае, если полученное число делится на 37. По-
Подобным образом можно вывести Д. п. и на делители
чисел вида 10*c:tl.
Лит.: [1] Воробьев Н. Н., Признаки делимости,
2 изд., М., 1974. В. И. Нечаев.
ДЕЛИМОСТЬ в кольце —• обобщение понятия
делимости целых чисел нацело (см. Деление).
Элемент а кольца А делится на другой элемент
&?А, если существует такой с?А, что а=Ъс. При этом
говорят также, что J делит а, на наз. кратным
элемента 6, а Ь — делителем элемента а. Для
обозначения Д. а на 6 употребляют символ Ъ\а.
В любом ассоциативно-коммутативном кольце
имеют место следующие свойства Д.:
если Ь | а и с\Ь, то с \ а;
если Ь | а, с Ф О, то сЪ \ са\
если с | а и с | Ь, то с | (а ± Ь).
Последние два свойства равносильны тому, что мшг
жество элементов, делящихся на Ь, образует идеал ЬА
кольца А (главный идеал, порожденный элементом Ъ),
к-рый содержит 6, если А — кольцо с единицей.
В области целостности элементы а и Ь делятся друг
на друга одновременно (а\Ъ и Ь\а) тогда и только тогда,
когда они ассоциированы, т. е. а=е,6, где е —
обратимый элемент. Два ассоциированных элемента
порождают один и тот же главный идеал. Делители
единицы совпадают, по определению, с обратимыми
элементами. Простым элементом в кольце
наз. ненулевой элемент, не имеющий собственных
делителей, кроме делителей единицы. В кольце целых
чисел такие элементы наз. простыми числами, в кольце
многочленов — неприводимыми многочленами. Кольца,
в к-рых подобно кольцу целых чисел или кольцу много-
многочленов имеет место однозначное разложение на простые
множители (с точностью до делителей единицы и поряд-
порядка следования), наз. факториалъными кольцами. В та-
таком кольце для всякой конечной совокупности эле-
элементов существуют наибольший общий делитель и наи-
наименьшее общее кратное, оба определенные однозначно
с точностью до делителей единицы.
Лит.: [1] К u m m е г Е., «J. reine und angew. Math.»,
1847, Bd 35, S. 319—26; [2] Виноградов И. М., Основы
теории чисел, 8 изд., М., 1972; [3] Б о р о в и ч 3. И., Ш а ф а-
ревич И. Р., Теория чисел, 2 изд., М., 1972.
О. А. Иванова, С. А. Степанов.
ДЕЛИТЕЛЕЙ ПРОБЛЕМЫ — проблемы теории чи-
чисел, касающиеся асимптотич. поведения сумматорных
функций
(где т(га) — число делителей п, а т^(п), /с>2,— число
представлений п в виде произведения к натуральных
чисел), а также модификаций этих функций.
Проблема делителей Дирихле —
проблема наилучшей оценки остаточного члена Л (х)
в асимптотич. формуле
"V. т (ra)^zlnx-j-BC — 1I +Да:,
где С — Эйлера постоянная. Асимптотика суммы
впервые рассмотрена П. Дирихле (P. Dirichlet) в 1849.
Он исходил из того, что данная сумма равна числу точек
(м, v) с целыми положительными координатами под
гиперболой uv=x, и доказал, что
D (x) = xlnx + BC — \)х-\-О(У~х).
Эта формула наз. формулой Дирихле чис-
числа делителей.
Д. п. явилась одной из тех моделей, на к-рых разви-
развивались методы оценок числа целых точек в разного рода
расширяющихся областях. Пусть В — нижняя грань
чисел а в соотношении А(х)<^ха. Согласно П. Дирихле,
В<1/2. Г. Ф. Вороной доказал, что G^'/з. Далее после-
последовательно были получены оценки
Истинный порядок величины Л(х) (к 1978) неизвестен.
Существует гипотеза, что
" 1п2х.
С другой стороны, X. Харди (Н. Hardy) доказал, что
В1/4 или, точнее,
lim ^ < 0 <
х _>. 0 (х In х) In In х
x ->¦ 0 (x In x) ' In In x
Кроме того, известна формула
(A — постоянная), показывающая справедливость «в
среднем» гипотезы о порядке Д(х).
Обобщенная проблема делите-
делителей — проблема наилучшего асимптотич. выражения
при х—>-оо суммы
в частности, при к=2
Обобщенная Д. п. тесно связана с поведением дзета-
функции Римана ?(s) в критич. полосе значений s.
Именно, для нецелого х>0, е>1 имеет место формула
< г с + i со , ~s
Здесь подинтегральная функция имеет в точке s=l по-
полюс порядка к с вычетом вида хР^(\пх), где Р^—много-
Р^—многочлен степени к—1.
Пусть
и пусть Yft<Y<l, где уи — нижняя грань чисел ff,
для к-рых
Тогда справедливы формула
j ("t + iT xs
^fc (x) — 2iii ^m \ S (s) ~J~ '
и обратная формула М е л л и н а:
где интеграл существует в смысле среднего квадратич-
квадратичного для l
Оценки остаточного члена Д*(х) в формуле Dь(х)
еще далеки (к 1978) от ожидаемых. Пусть ад — наи-
наименьшее из чисел а, для к-рых
при любом е>0. Известны оценки:
Kfe</?Ti для к^Л-
Имеются уточнения этих оценок для частных значе-
значений к:
Последний результат оценки сверху а^ получен в
[3] на основе развития идей Виноградова метода: дока-
доказано существование такой абсолютной постоянной с>0,
что
= 2, 3,...
Эта оценка есть следствие оценки ?,($) в критич. полосе:
для ]/.,<га<:1, U|^2 существует такая постоянная
й>1, что
n(l~o)S *
С другой стороны, X. Харди (G. Hardy) доказал, что
Относительно величины Д/;(х) существует гипотеза:
ft-l
при всех /г>2. Однако для ее обоснования недостаточно
даже решения Линделе'фа гипотезы:
?(а-)-«)<М1е
при любых е>0, a>V2.
Дальнейшее обобщение Д. п. [4]: равномерно относи-
относительно целых fcjs2, m>l при 1
где
Проблема делителей в арифмети-
арифметических прогрессиях —проблема равномер-
равномерных относительно х, d, 0<.l<.d, (I, d)=l, оценок сумм
Эти суммы изучались на основе аналитич. методов
теории //-функции и важны для многих проблем
теории чисел (см. [7]). В простейшем случае (т=1)
для них получены аспмптотич. выражения:
при к=2 для d<.x'!'3 (см. [5]),
при к—4 для d<.x''' (см. [6]),
при /с>4 для d<x2 к/\пс х [см. [8]).
При любом т>1 и к—2 найден (см. [9]) истинный поря-
порядок роста (X) Для d^x1~a, 0<a<1/2:
В общем случае доказано [10|, что
2, 1/2
где Akm>(x\ d) — ожидаемый главный член роста,
М — положительная сколь угодно большая постоянная,
е>0 — любое число.
Последнее неравенство, в частности, показывает,
что суммы Окт) (х; d, I) при любых целых &>2, m^l
«в среднем» имеют один и тот же главный член роста для
всех примитивных арифметич. прогрессий разности
Лит.: [1] Т и т ч м а р ш Е. К., Теория дзета-функции Ри-
мана, пер. с англ., 1953; 12] X у а Л о - г е н, Метод тригоно-
тригонометрических сумм и его применения в теории чисел, пер. с нем.,
М., 1964; 13] Карацуба А. А., «Тр. Матем. ин-та АН СССР»,
1971, т. 112. с. 241 — 55; Г4] М а р д ж а н и ш в и л и К. К.,
«Докл. АН СССР», 1939, •¦¦. 22, с. 391—93; [5] Но о ley С,
«Proc. London Math. Soc », ser. 3, 1957, v. 7, № 27, p. 396—413;
16] ЛинникЮ. В., «Матем. сб.», 1961, т. 53, № 1, с. 3—38;
17] его ж е, Дисперсионный метод в бинарных аддитивных
задачах, Л., 1961; L8] Лаврик А. Ф., «Изв. АН СССР.
Сер. матем.», 1966, т. 30, № 2, с. 433—48; [9] Виноградов
А И Л Ю В У 1957, 12
Н
Сер. ма., 6, , , . ; ] рд
А. И., Л и н н и к Ю. В., «Успехи матем. наук», 1957, т. 12,
в. 4, с. 277—80; [10] Виноградов А. И., «Изв. АН СССР.
Сер. матем.», 1965, т. 29, JSS 4, с. 903—34. А. Ф. Лаврик.
ДЕЛИТЕЛЕЙ ЧИСЛО — функция натурального ар-
аргумента га, равная количеству натуральных делителей
числа га. Эта арифметич. функция обозначается т(га),
либо d(n). Известна формула:
где
— канонич. разложение п на простые сомножители.
Для простых р т(/>)=2, но существует бесконечная
последовательность га, для к-рых
(>
т(л) > 2 1п1п", е>0.
Однако всегда
т(га) — мультипликативная арифметическая функция;
т(га) равно числу точек с натуральными координатами
на гиперболе ху=п. Для среднего значения т(га) имеется
асимптотич. формула Дирихле (см. Делителей пробле-
проблемы). Обобщением функции т(га) является функция
Т(,(га) — число решений уравнения n=x1xi... х^ в
натуральных числах хи х2,.., х^.
Лит.: [1] Виноградов И. М., Основы теории чисел,
8 изд., М., 1972. Н. И. Климов.
ДЕЛИТЕЛЬ целогочисла а — целое число
Ъ, делящее без остатка число а. Другими словами, Д.
целого числа а — это такое целое число Ь, для к-рого
справедливо равенство a—be при нек-ром целом с.
Делителем многочлена А (х) наз. много-
многочлен В(х), делящий без остатка А (х) (см. Деление).
Более общо, в произвольном кольце А делителем
элемента а?А наз. такой элемент Ь?А, что а=Ьс
ДЛЯ НОК-рого с?А. с. А. Степанов.
ДЕЛИТЕЛЬ ЕДИНИЦЫ — элемент а кольца (ком-
(коммутативного с единицей 1), для к-рого существует о б-
ратный, т. е. такой элемент 6, что а6=1. В теории
алгебраических чисел и алгебраических функпий Д. е.
наз. также единицами. О. А. Иванова
ДЕЛИТЕЛЬ НУЛЯ в кольце или полу-
полугруппе с нулем — ненулевой элемент, произ-
произведение к-рого на некоторый ненулевой элемент равно
нулю. Элемент а наз. левым (соответственно пр а-
в ы м) Д. н., если а6=0 (соответственно Ьа=0) хотя
бы ДЛЯ ОДНОГО ЬфО. о. А. Иванова.
ДЕЛЬТА АМПЛИТУДЫ — одна из трех основных
Якоби эллиптических функций. Обозначается
dn и = dn (и, к)=А am и.
Д. а. следующим образом выражается через сигма-
функщш Вейерштрасса, тета-функции Якоби или при
помощи ряда
= 1— A-2 ~~ к2 D + A-2)|f — к2 A64-44/г2 + &4) ^f— ••¦ .
где &—модуль Д. a., 0<Л:<1; v=u/2a>, 2w=
= я#5 @). При &=0, 1 соответственно
anii = l, dn м = -г—.
' ch u
См. также Вейерштрасса эллиптические функции, Эл-
Эллиптические функции.
Лит.: [1] Г у р в и ц А., К у р а н т Р., Теория функций,
пер. с нем., М., 1968, ч. 2, гл. 3. Е. Д. Соломенцев.
ДЕЛЬТА-ФУНКЦИИ МЕТОД — метод нахождения
Грина функции линейных дифференциальных уравне-
уравнений математнч. физики (т. е. метод определения функ-
функции влияния точечного источника) с помощью дельта-
функции 8(.г). Функция Грина G(x, x') линейного диф-
дифференциального оператора L(x) определяется из урав-
уравнения
L{x)G(x, х')=—Ь(х—х'),
как G(x, х')=—L-1(x)f>(x—х'), т. е. выражает влияние
точечного источника, расположенного в точке х' на
значение возмущения в точке х. Наиболее просто вид
обратного оператора Л-1(х) определяется в часто
встречающемся случае, когда L(x) является дифферен-
дифференциальным оператором с постоянными (не зависящими
от х) коэффициентами. Решение неоднородного линей-
линейного дифференциального уравнения общего вида для
возмущения <р(х) с источником р(х):
L(x)q>(x)=—p(x),
с помощью функции Грина G(x, x') записывается в
виде свертки:
ф(ж)=\ G(x, x')p(x')dx',
тде интегрирование производится по всей области, в
к-рой действует источник р(ж).
Лит.: [1] Иваненко Д., Соколов А., Класси-
Классическая теория поля, М.—Л., 1951. В. Д. Нупин.
ДЕЛЬТА-ФУНКЦИЯ, о-ф у н к ц и я, б-ф у н к-
ция Дирака, б(х),— функция, позволяющая за-
записать пространственную плотность физич. величины
(масса, заряд, интенсивность источника тепла, сила и
т. п.), сосредоточенной или приложенной в точке а
пространства Rn. Напр., плотность точечной массы т,
находящейся в точке а, записывается с помощью
Д.-ф. в виде тё(х—а). Д.-ф. может быть определена фор-
формальным соотношением
\ 6(x-a)f(x)dx =
для любой непрерывной функции f(x). Аналогично
можно определить производные 8(*'(ж) для Д.-ф.:
[ б* (х — a)f (x) dx = (— l)*/(*)(a)
для класса функций f(x), непрерывных в Д„ со своими
производными /(*'(х)до порядка к включительно. Часто
используемые формальные операторные соотношения,
выражающие свойства Д.-ф.:
б (— х) = б (х); 6{сх) = \с\~18(х), с = const;
х6(х)=0; 6(х) + х6' (ж) = 0
и т. п., следует понимать в смысле данных выше опре-
определений, т. е. эти соотношения приобретают смысл
лишь после интегрирования их с достаточно гладкими
функциями. Таким образом, Д.-ф. не является обычной
функцией в смысле классич. теории1 функций и опре-
определяется в теории обобщенных функций как сингуляр-
сингулярная обобщенная функция, т. е. как непрерывный ли-
линейный функционал в пространстве бесконечно диффе-
дифференцируемых финитных функций f(x), который сопо-
сопоставляет f(x) ее значение в нуле: (б, /)=/@).
В. Д. Кукин.
ДЕМИКВАДРИКА — линейная система оо' прямо-
прямолинейных образующих какой-либо квадрики.
ДЕМУЛЕНА ПОВЕРХНОСТЬ — поверхность, обла-
обладающая сопряженной сетью линий, касательные к
к-рым образуют две конгруэнции W,— так наз. особой
сопряженной системой. Д. п. и только они допускают
проективное изгибание. Введена А. Демуленом [1].
Лит.: [1] DemoiilinA., «С. г. Acad. sci.», 1911, t. 153,
p. 590 — 93, 705—07, 797—99, 927 — 29. M. И. Войцеховский.
ДЕМУЛЕНА ТЕОРЕМА: геликоид имеет бесконечное
число (а именно оо2) систем сопряженных сетей линий,
сохраняющихся в непрерывном изгибании этой по-
поверхности — ее главных оснований (см. Изгибание
на главном основании). Установлена А. Демуленом
[1]. При этом оказывается, что указанные главные ос-
основания являются Фосса сетями. Обратное утверждение
(теорема Финикова): единственная поверх-
поверхность с бесконечным числом главных оснований есть
прямой геликоид (см. [2]).
Лит.: [1] DemoulinA., «С. г. Acad. sci.», 1901, t. 133,
p. 986—90; [2] Фи ни ков С. П., Изгибание на главном
основании и связанные с ним геометрические задачи, М.—Л.,
1937. М. И. Войцеховский.
ДЕМУЛЕНА ЧЕТЫРЕХУГОЛЬНИК — четырех-
четырехугольник, образованный двумя парами llt l\ и 12, 1%
прямолинейных образующих соприкасающейся квад-
квадрики Ли в гиперболич. точке М поверхности трехмер-
трехмерного (проективного) пространства. Прямые 1г, 1^, 12,
4 наз. прямыми Демулена, они параллельны
ребрам МХМ3 и МгМ3 соответственно канонического
тетраэдра Т(М, Ми М2, М3), ассоциированного с
квадрикой Ли и называемого тетраэдром Де-
Демулена. Д. ч. невырожден тогда и только тогда,
когда невырождена 3-я Фубини форма. Рассмотрен
А. Демуленом [1].
Лит.: [1] Demoulin А., «С. г. Acad. sci.», 1908, t.
147. p. 493—96. M. И. Войцеховский.
ДЕНА ЛЕММА: пусть в трехмерном многообразии
М расположена двумерная клетка D с самопересече-
самопересечениями, имеющая границей простую замкнутую поли-
полигональную кривую С без особых точек; тогда сущест-
существует двумерная клетка ?*0 с границей С, кусочно линей-
линейно вложенная в М. Д. л. приведена в [1], однако дока-
доказательство ее содержало пробелы; полное обоснование
дано в [2]. С Д. л. связан результат, наз. теоремой
о петле: пусть М — компактное трехмерное много-
многообразие и N — одна из компонент его края; если ядро
гомоморфизма щ (N) -nix(M) нетривиально, то су-
существует простая петля на N, к-рая не гомотопна
нулю на TV и гомотопна нулю в М. Теорема о петле
и Д. л. обычно применяются совместно. Они могут
быть объединены в следующую теорему: если М —
трехмерное многообразие с краем Лг и ядро гомомор-
гомоморфизма включения лг (N) ~* nt (M) нетривиально, то
в М существует кусочно линейно вложенный двумер-
двумерный диск D, край к-рого лежит на N и не стягиваем
яа N. К этим теоремам примыкает теорема о
сфере, являющаяся вместе с Д. л. и теоремой о
петле одним из основных средств топологии трехмер-
трехмерных многообразий: если М — ориентируемое трех-
трехмерное многообразие с л2 (М)=?0, то в М существует
полмногообразие 2, гомеоморфное двумерной сфере,
к-рое не гомотопно нулю в М.
Эти результаты имеют многочисленные применения
в топологии трехмерных многообразий и, в частности,
в теории узлов. Так, если К — узел, то n1(S3\K) изо-
изоморфно 1i тогда и только тогда, когда К — тривиаль-
тривиальный узел. Для «-компонентного зацепления L в S3
следующие условия равносильны: 1) л2 (S3\L)^0;
2) щ (S3\L) есть свободное произведение двух нетри-
нетривиальных групп; 3) в 53\Л существует такое подмно-
подмногообразие JV, гомеоморфное двумерной сфере, что обе
компоненты 53\iV содержат точки из Л. В частности,
если L — узел (т. е. ге=1), то я2 (S3\L) = 0 (теорема
об асферичности узлов).
Лит.: [1] Dehn M., «Math. Ann.», 1910, Bd 69, S. 137—
168; [2] Папакирьякопулос С. Д., «Математика»,
1958, т. 2, К 4, с. 23 — 47; [3] МассиУ., Столлингс
Д ж., Алгебраическая топология. Введение, пер. с англ., М.,
1977. М. II. Войцеховский, М. Ш. Фарбер.
ДЕНДРИТ — локально связный континуум, не со-
содержащий простых замкнутых кривых. Континуум,
каждая точка к-рого имеет окрестность, являющуюся
Д., наз. локальным дендритом.
А. А. Мальцев.
ДЕНОТАТ данного имени — объект, обозначе-
обозначением к-рого является это имя. в. Е. Плиско.
ДЕ НУ МЕР АНТ — число D (n; alt a2 , ат) раз-
разбиений целого числа п на части, равные аг, а2,. . .,
ат, т. е. число решений в целых неотрицательных
числах уравнения
Производящая функция для Д. имеет вид:
D (t; oj, а2, . . ., ат) = 2-°(п; аъ «г- • ¦ ¦. ат) <" =
= 1/A— «а')A — *аг) ... (i — t"m) .
Наиболее просто Д. вычисляется по рекуррент-
рекуррентному соотношению Эйлера:
D (п; 1, 2, .... k)—D{n — k; 1, 2, ..., к) =
= ?> (п; 1, 2, ..., А —1).
Формулы в явном виде для нек-рых Д. могут быть по-
получены из следующей теоремы: если а является наи-
наименьшим общим кратным чисел аг, а2,. . ., ат, то Д.
D (an + b; аъ а2, . . ., ат),
6 = 0, 1, ..., а —1,
оказывается многочленом степени т—1 относительно п-
Лит.: [1] Р и о р д а н Д ж., Введение в комбинаторный
анализ, пер. с англ., М., 1963. В. Е. Тараканов.
ДЕ РАМА КОГОМОЛОГИИ — см. Рама когомологии.
ДЕ РАМА КРУЧЕНИЕ — см. Рама кручение.
ДЕ РАМА ТЕОРЕМА — см. Рама теорема.
ДЕРЕВО в теории графов — связный не-
неориентированный граф G, не содержащий циклов. Д.
не имеет кратных ребер и петель. Являясь простейшими
связными графами, Д. служат хорошими моделями
для рассмотрения различных вопросов теории графов.
Любое Д. с л вершинами содержит п—1 ребер. Число
различных Д., к-рые можно построить на п нумеро-
нумерованных вершинах, равно п"~2. Д. с одной выделен-
выделенной вершиной наз. корневым дерево si.
Перечисляющий ряд
для числа Тп неизоморфных корневых Д. с п вершина-
вершинами удовлетворяет функциональному уравнению
Перечисляющий ряд
для числа tn неизоморфных Д. с п вершинами можно
представить с помощью перечисляющего ряда для кор-
корневых Д.:
Функциональные уравнения для Т (х) и t(x) позволяют
вычислять значения Тп и tn для конкретных значений
п (см., напр., [1]).
Доказано, что при п—<-оо
tn~C а"/;г6/2,
где С--=0,534948..., а=2,95576. .. (см. [2]). Задачи
перечисления Д. определенного вида возникают, напр.,
в химии при изучении изомеров.
Д. можно достаточно просто кодировать наборами
из нулей и единиц. Рассмотрим, напр., к.-л. правильную
(без пересечения ребер) укладку Д. D на плоскости (см.
Графа укладка). Начиная с к.-л. вершины, будем дви-
двигаться по ребрам Д. D, сворачивая в каждой вершине
на ближайшее справа ребро и поворачивая назад в
концевых вершинах Д. Проходя по нек-рому ребру,
записываем 0 при движении по ребру в первый раз и 1 при
движении по ребру второй раз (в обратном направле-
направлении). Если m — число ребер Д. D, то через 2т шагов
мы вернемся в исходную вершину, пройдя по каждому
ребру дважды. Полученная при этом последовательность
из 0 и 1 (код Д.) длины 2т позволяет однозначно вос-
восстанавливать не только само Д. D, но и его укладку на
плоскости. Произвольному Д. соответствуют несколько
кодов. Из этого способа кодирования вытекает оценка:
4
„„
Д. G с п вершинами однозначно восстанавливается
(с точностью до изоморфизма) по набору всех его (п — 1)-
вершинных подграфов G—v, получаемых из G удале-
удалением каждой из его вершин v.
Любое Д. однозначно определяется также расстоя-
расстояниями (длиной наименьшей цепи) между его концевыми
(степени 1) вершинами.
Остовное дерево (остов) — это подграф
данного графа, содержащий все его вершины и являю-
являющийся Д. Число остовных Д. произвольного связного
графа G без петель и кратных ребер можно вычислить
следующим образом. Пусть М — матрица, полученная
из матрицы смежности графа G изменением знаков всех
элементов на противоположный и заменой г-го элемента
главной диагонали степенью вершины v;. Тогда алгеб-
раич. дополнения всех элементов главной диагонали
матрицы М равны между собой и их общее значение
есть число остовов графа G. Остовные Д. используются,
напр., для нахождения независимых циклов в электрич.
схеме.
Важное значение для приложений имеет задача на-
нахождения в связном графе, ребрам к-рого приписаны
веса, остовного Д. с наименьшей суммой весов ребер.
Такая задача возникает, напр., при проектировании
коммуникационных сетей. Известен алгоритм для реше-
решения этой задачи о кратчайшем связы-
связывающем дереве (см. [3]). Д., растущим (или
выходящим) из вершины v0, наз. ориентированный
граф, к-рый является (без учета ориентации) корневым
Д. с корнем v0 и в к-ром для любой вершины v1 (един-
(единственная) цепь, соединяющая v0 с vx, является ориенти-
ориентированным путем из i>0 в t>x. Такие Д. используются,
напр., для описания детерминированных функций, для
представления информации в информационно-поиско-
информационно-поисковых системах и т. д.
Обобщением понятия «Д.» является понятие «леса»;
лес — это граф без циклов (не обязательно связный).
Лит.: [1] X а Р а р и Ф., Теория графов, пер. с англ.,
М., 1973 (лит.); [2] OtterR., «Ann. Math.», 1948, v. 49,
№ 3, p. 583—99; [3] Прим Р. К., «Кибернетический сбор-
сборник», 1961, в. 2, с. 95 —107. В. Б. Алексеев.
ДЕСКРИПТИВНАЯ ТЕОРИЯ МНОЖЕСТВ — раздел
теории множеств, изучающий внутреннее строение
множеств в зависимости от тех операций, при помощи
к-рых эти множества могут быть построены из мно-
множеств сравнительно простой природы (напр., замкну-
замкнутых или открытых подмножеств данного евклидова,
метрич. или топологич. пространства). К указанным
операциям относятся объединение, пересечение, взятие
дополнения, проектирование и т. д. Д. т. м. зароди-
зародилась в начале 20 в. в трудах Э. Бореля (Е. Borel),
Р. Бэра (R. Baire) н А. Лебега (Н. Lebesgue) в
связи с проблемой измеримости множеств. Множества,
измеримые по Борелю, получили название борелевских
множеств, или В-множесгв. С другой стороны, Р. Бэр
дал классификацию функций, названных впоследствии
бэровскими функциями, и доказал ряд теорем об этих
функциях (см. Бэра классы, Бэра теорема). А. Лебег
доказал, что В-множества тождественны Лебега мно-
множествам бэровских функций, дал первую классифика-
классификацию В-множеств и доказал непустоту каждого ее класса.
Изучение В-множеств стало важной задачей Д. т. м.,
причем в первую очередь надлежало выяснить вопрос о
мощности В-множеств. После введения Лебега меры
оказалось, что класс измеримых множеств значительно
шире класса В-множеств, и возник вопрос об отыскании
средств установления измеримости того или иного мно-
множества. Решение этого вопроса в каждом конкретном
случае связано, как правило, с выяснением того про-
процесса, при помощи к-рого это множество может быть
построено, т. е. его дескриптивной структуры. Так оп-
определился еще один важный круг задач Д. т. м.— оты-
отыскание возможно более широкого класса (сохраняю-
(сохраняющих измеримость) операций над множествами и иссле-
исследование свойств результатов этих операций. Решение
этих вопросов, возникших в работах французских ма-
математиков, было дано преимущественно русскими
математиками — Н. Н. Лузиным и его школой.
Один из наиболее важных вопросов — вопрос о
мощности В-множеств — был решен П. С. Александ-
Александровым [1] в 1916, построившим для этого А-операцию.
Им было показано, что посредством Л-операции, от-
отправляясь от интервалов, можно построить любое В-
множество и что всякое несчетное множество, полу-
полученное путем Л-операции (и называемое Л-м н о ж е-
с т в о м), содержит совершенное множество и, значит,
имеет мощность континуума. Этот результат был неза-
независимо получен Ф. Хаусдорфом (F. Hausdorff).
М. Я. Суслин [2] показал, что существует Л-множест-
во, не являющееся борелевским. Он же ввел и название
Д-множества, равно как и Л-операции (в честь П. С. Але-
Александрова). Л-множества наз. также сусли неки-
некими множествами или, реже, аналитичес-
аналитическими множествами. Для того чтобы Л-мно-
жество было В-множеством, необходимо и достаточно,
чтобы: 1) дополнение к нему снова было Л-множеством
(Суслина критерий); 2) оно являлось результатом
Л-операции с непересекающимися слагаемыми {Лузина
критерий). Все Л-множества измеримы и обладают
Бэра свойством. Были найдены следующие новые
способы получения Л-множеств, эквивалентные А-
операции: Л-множества суть проекции В-множеств
(и даже Сб); Л-множества суть непрерывные образы
пространства / иррациональных чисел; и, значит, А-
множества суть непрерывные образы В-множеств [3].
В то же время, непрерывный взаимно однозначный (и
даже счетно кратный [4]) образ В-множества есть В-
множество и всякое несчетное iJ-множество есть объ-
объединение не более чем счетного множества и непрерыв-
непрерывного взаимно однозначного образа пространства /
(см. [3]). Наконец, Н. Н. Лузиным был найден еще
один важный способ задания Л-множеств при помощи
введенной им операции решета (см. Лузина решето).
Трансфиннтные индексы решета и конституанты стали
мощным орудием исследования свойств А -множеств и
их дополнений — СА-множеств.
При исследовании проблемы о мощности СА-ияо-
жеств Н. Н. Лузин вводит проективные множества.
Каждый класс а проективных множеств содержит мно-
множества, не принадлежащие классам <а (см. [3], [5]).
Важным инструментом при доказательстве этой и дру-
других теорем о непустоте тех или иных классов множеств
является понятие универсального множества (см. [3], [б],
[5]). Изучение проективных множеств даже второго клас-
класса наталкивается на непреодолимые трудности. Так, не
решен полностью вопрос об измеримости множеств
B?2), их мощности и о наличии у них свойства Бэра.
Важные результаты в этом направлении получены
П. С. Новиковым [4]: существует несчетное С А -мно-
-множество, относительно к-рого непротиворечиво предпо-
предположение, что оно не содержит совершенного подмно-
подмножества; существует множество (В2), относительно к-рого
непротиворечиво утверждение, что оно неизмеримо.
Введение П. С. Александровым [7] Г-операции,
дополнительной к ^.-операции, явилось первым шагом
в направлении построенной А. Н. Колмогоровым
[8] и Ф. Хаусдорфом [9] общей теории теоретико-
множественных операций; однако основной класс опе-
операций составляют положительные теоретико-множе-
теоретико-множественные операции, или бх-операции. Для каждой
бз-операции Ф была определена дополнительная бе-
операция Фс и дана формула
к-рая может рассматриваться как определение Фс.
Было введено также понятие нормальной бз-операции
(для любого семейства М множеств Ф (Ф (М))=Ф (М),
см. [8]). Л-операция и Г-операция являются взаимно
дополнительными нормальными бя-операциями. То же
самое справедливо относительно операций счетного объ-
объединения и счетного пересечения. Одной из ключевых
теорем общей теории операций над множествами, ле-
лежащими в топологич. пространствах, является тео-
теорема Колмогорова о дополнениях:
если пространство содержит дисконтинуум, М — систе-
система всех замкнутых подмножеств этого пространства и
Ф — произвольная теоретико-множественная операция,
то дополнение хотя бы одного множества семейства
Ф (М) ему не принадлежит (см. [8|, [5], [9]). Применение
к данному семейству М множеств попеременно 6s-onepa-
ции Ф и Фс позволяет построить возрастающую транс-
трансфинитную последовательность классов М0=М, М1,...,
Ма,..., a<W], относительно к-рой верна теорема
Колмогорова о непустоте классов:
если Ф есть нормальная es-операция более мощная,
чем операции счетного объединения (или счетного перс-
сечения), а М есть семейство всех замкнутых подмно-
подмножеств метрич. пространства, содержащего дисконти-
дисконтинуум, то все классы Ма, а<Щ, порождаемые опера-
цией Ф из семейства М, попарно различны. При этом
б«-операция Ф считается более мощной, чем 6s-onepa-
ция г|з, если Ф (М) z=yty(M) для любого семейства М
множеств (см. [8], [5]). Если Ф= иГ (или Di°), то
классы Ма, <х<ю17 порожденные операцией Ф из
семейства М, представляют собой классы 5-множеств,
порожденных семейством М (классификация
X а у с д о р ф а). Аналогичным образом ^-операция
порождает из семейства М борелевеких множеств клас-
классы Ма, a<W!, С-множеств (Лузина множеств). Каж-
Каждое С-множество измеримо и обладает свойством Бэра.
Все С-множества входят в класс (В2), но не исчерпыва-
исчерпывают его.
Исключительно важную роль в Д. т. м. играет
введенное Н. Н. Лузиным понятие отделимости [4].
Первый принцип отделимости: всякие
два непересекающиеся ^-множества отделимы (В).
Второй принцип отделимости: если
Е и Р — два ^.-множества (или СЛ-множества), то
множества Е\Р и Р\Е отделимы (СА). Существуют
два СА -множества, неотделимые (В). Проблема отде-
отделимости проективных множеств второго класса была
решена П. С. Новиковым [4J; при этом принципы от-
отделимости оказались обращенными: они получаются
из соответствующих теорем для проективных множеств
первого класса заменой (^4) на (СА2), (СА) на (А2) и
(В) на (В2). Проблема отделимости в классе С-множеств
была также решена П. С. Новиковым [4] (см. также
[3]). Им же введено обобщение понятия отделимости
множеств — понятие одновременной или кратной отде-
отделимости множеств, равно как и основной инструмент
при доказательстве теорем кратной отделимости —
принцип сравнения индексов [4].
Важная глава в развитии Д. т. м. связана с реше-
решением проблемы униформизации. Множество Р унифор-
мизует множество EczXXY, если PczE и если Р имеет
ту же, что и Е, проекцию на X и проектируется на X
взаимно однозначно. Всякое В-множество униформи-
зуется С А -множеством. Процесс эффективного выбора
точки [4] в непустом СЛ-множестве позволил полу-
получить более сильный результат: всякое С А -множество
униформизуется СА -множеством. Всякое Л-множество
униформизуетея множеством типа Араб [3] (см. также
[10]). Существует А -множество в евклидовой плоскости,
не униформизуемое ни А -множеством, ни С А -множе-
-множеством (см., напр., [11], с. 57). В вопросе о том, в каких
случаях Д-множество может быть униформизовано В-
множеством, наиболее общий результат имеет вид:
всякое плоское В-множество, пересекающееся с пря-
прямыми х= const по множествам типа Fo , униформизуется
В-множеством. Проблема униформизации возникла при
решении проблемы о неявных В-функциях (см. [3]).
При этом возникли и другие задачи: о природе проек-
проекций В-множеств, о расщеплении множеств, о накрытии
множеств, о природе множества всех тех точек проек-
проекции данного В-множества Е, нрообразы к-рых (в пере-
пересечении с Е) обладают нек-рым фиксированным свой-
свойством. Представление о второй и третьей задачах дают
следующие теоремы [3]: ^-множество, имеющее счетно-
кратную проекцию, является объединением счетного
числа униформных В-множеств, причем, каковы бы ни
были два таких множества, одно из них лежит под
другим (теорема о расщеплении JB - м н о-
ж е с т в а); всякое А -множество, имеющее счетнократ-
ную проекцию, содержится в нек-ром В-множестве,
обладающем этим свойством (теорема о накры-
накрытии ^.-множества).
Помимо классификаций В-множеств, принадлежа-
принадлежащих А. Лебегу и Ф. Хаусдорфу, существует класси-
классификация Лузина — Балле Пуссена.
В этой классификации в"; качестве инструмента для ис-
исследования строения множеств данного класса Ка,
а<(в1, выбраны множества, предегавимые в виде
пересечения и не представимые в виде объединения
счетного числа множеств классов <а; эти множества
наз. элементами класса а. Всякое множество
класса Ка есть объединение счетного числа попарно
непересекающихся элементов классов <sa. Каждый
класс Ка разбивается на подклассы Ка, fS<u>i, причем
в каждом классе существуют подклассы со сколь угодно
большими номерами p<Oj. Поскольку каждое мно-
множество класса а строится из элементов, то возник вопрос
об исследовании строения самих элементов, в частно-
частности о существовании в каждом классе Ка такого основ-
основного топологич. типа элементов, названных кано-
каноническими, чтобы каждый элемент класса а мог
быть представлен в виде объединения счетного числа
канонич. элементов классов <:а (все рассматривается
в пространстве / иррациональных чисел). В первом
классе имеются канонич. элементы двух типов — одно-
одноточечное множество и топологич. образ канторова
совершенного множества. Во втором классе [12] каж-
каждый элемент есть объединение канонич. элемента клас-
класса 2, каковым является множество, гомеоморфное про-
пространству /, и множества класса <:1. Были найдены и
канонич. элементы третьего класса: ими оказались
элементы третьего класса, построенные Р. Бэром,
к-рые являются каноническими (см. [3]). Проблема
существования канонич. элементов высших классов,
оказавшаяся исключительно трудной, была решена
Л. В. Келдыш [13], установившей существование
канонич. элементов в каждом классе a<Wi и выяснив-
выяснившей их строение. Каждый элемент класса сс>2 яв-
является объединением одного канонич. элемента класса а
и не более чем счетного числа множеств классов <«.
Еще одна грудная задача из этого круга связана с по-
построением арифметич. примеров В-множеств низших
классов. Такой пример для класса 3 построен Р. Бэ-
Бэром (см. [3]). Арифметич. примеры элементов всех ко-
конечных классов даны Л. В. Келдыш [13] (см. также
[3]), указавшей на принципиальную возможность
построения таких примеров для классов cc^sco0.
Важную роль в Д. т. м. играет Лаврентьева теорема
о продолжении гомеоморфизма (см. [9]): пусть X и У
полные метрич. пространства, AczX, BczY и f:Ali^B
есть гомеоморфизм; тогда существует продолжение
отображения / до гомеоморфизма двух Сё-множеств,
лежащих в этих пространствах. Из этой теоремы легко
следует теорема о топологической ин-
инвариантности (см. [9]): пусть 23 — система
замкнутых множеств и Ф — такая бх-операцпя, что
пересечение Ф ($23)-множества (т. е. множества семей-
семейства Ф B3) с <?б -множеством есть снова Ф (ЗЗ)-множество;
тогда каждое Ф B3) -множество, лежащее в полном
метрич. пространстве, является Ф (ЗЗ)-множеством в лю-
любом метрич. пространстве, в к-ром оно топологически
содержится. Система 23 в этой теореме может быть заме-
заменена системой 31 открытых множеств. Таким образом,
Ф (ЗЗ)-множества, гдеФ удовлетворяет указанному выше
условию, лежащие в полных метрич. пространствах,
являются абсолютными Ф (ЗЗ)-множествами, и то же
самое верно для Ф B()-множеств (при этом имеется
в виду абсолютность в классе метрич. пространств).
Для ряда частных случаев, напр. С А -множеств [7]
(Ф есть Г-операция), этот результат был установлен
без применения теоремы Лаврентьева. Всякое полное
метрич. пространство есть абсолютное Ge ¦ Всякое (ме-
тризуемое) абсолютное бб гомеоморфно нек-рому пол-
полному метрич. пространству (теорема Алек-
Александрова — Хаусдорфа, см. [9]).
Справедлива следующая теорема Александ-
Александрова — Урысона [12] о топологич. характери-
характеристике пространства иррациональных чисел: каждое
нульмерное мегрич. пространство X со счетной базой,
не имеющее ни одной точки локальной компактности и
являющееся абсолютным Сб, гомеоморфно простран-
пространству /. А так как / есть абсолютное Gg и обладает всеми
остальными свойствами пространства X, то перечислен-
перечисленные в теореме свойства пространства X полностью
характеризуют пространство / с топологич. точки зре-
зрения. Эта характеризация позволила доказать следую-
следующий результат [14]: каждое метрич. пространство, яв-
являющееся непрерывным образом пространства / (и,
значит, абсолютным А -множеством), есть также фак-
факторный образ пространства /. К этому кругу резуль-
результатов принадлежат также следующие: непустое сепара-
бельное метрич. пространство есть непрерывный от-
открытый образ пространства / тогда и только тогда,
когда оно есть абсолютное G6 (см. [15]); здесь «открытый»
можно заменить на «замкнутый». Обобщением непрерыв-
непрерывного отображения является понятие ^-измеримого ото-
отображения, или В-функции, в частности, В-измеримого
отображения класса а; обобщениями гомеоморфизма
являются понятия обобщенного гомеоморфизма класса
(а, Р) и В-изоморфизма. Об этих отображениях см. [6].
При формулировке результатов, как правило, не ука-
указывался тот класс пространств, для к-рого они справед-
справедливы. Это объясняется том, что большинство классич.
результатов было получено для подмножеств простран-
пространства /, но почти все они (исключения всегда оговарива-
оговаривались) справедливы при замене / любым сепарабельным
абсолютным Сё (в частности, полным метрич. простран-
пространством со счетной базой). Дальнейшее развитие Д. т. м.
проходило по линии обобщения классич. результатов
для случая: 1) полных метрич. пространств (не обяза-
обязательно сепарабельных); 2) совершенно нормальных
топологич. пространств, в частности, бикомпактов;
3) общих топологич. пространств. Даже в первом
случае обобщение классич. теории связано с серьез-
серьезными трудностями, а часто и вовсе не имеет места.
Обобщение теории В-множеств и Л-множеств для этого
случая рассмотрено А. Стоуном [16].
Класс совершенно нормальных пространств есть
класс, за пределами к-рого уже не имеет места тот
немаловажный факт, что система В-множеств (соот-
(соответственно А -множеств), порожденных замкнутыми
множествами данного пространства, совпадает с систе-
системой В-множеств (соответственно ^-множеств), порож-
порожденных открытыми множествами этого пространства.
Справедлива важная теорема о непустоте классов [11]:
во всяком несчетном совершенно нормальном биком-
бикомпакте для каждого класса а<со1 существует В-мно-
жество класса а, не являющееся В-множеством
класса <а.
Проблема униформизации стала частным случаем
общей проблемы о сечении многозначного отображения
(см. Сечение отображения).
Современная разработка Д. т. м. в общих топологич.
пространствах (третий случай) имеет связь с потреб-
потребностями других областей математики (напр., с теорией
потенциала). Подробнее см. [17] (имеется обширная
библиография).
Идеи и методы Д. т. м. оказали большое влияние на
развитие целого ряда областей математики: анали-
анализа, теории функций, топологии, математической логи-
логики и др.
Лит.: [1] А л е к с а н д р о в П. С, «С.г. Acad. sci.», 1916,
t. 162, p. 323—25; [2] С у с л и н М. Я., там те, 1917, t. 164,
р. 88—90; [3] Л узин Н. Н., Собр. соч., т. 2,М., 1958; [4] Л я-
п у н о в А. А., «Тр. матем. ин-та АН СССР», 1973, т. 133, с.11—22;
[5] О чан Ю.С, «Успехи матем. наук», 1955, т. 10, в. 3, с. 71—128;
[6]Куратовский К., Топология, т. 1,М., 1966; [7] А л е к-
сандров П. C.,«Fimdam.inath.», 1924, t. 5, p. 160—65; [8] Кол-
Колмогоров А. Н., «Матем. сб.», 1928, т. 35, № 3—4, с. 415—22;
[9]ХаусдорфФ.. Теория множеств, пер. с нем., М.—Л., 1937;
[10]АрсенинВ. Я., Ляпунов А. А., «Успехи матем. наук»,
1950, т. 5, в. 5, с. 45—108; [11] Пономарев В. И., «Докл.
АН СССР», 1966, т. 170, № 3, с.520—23; [12] Алек сандровП.С,
У р ы с о н П. С, «Math. Ann.», 1927, Bd 98, S. 89 — Юв (рус. пер.
в кн.: УрысонП. С, Труды по топологии и другим областям
математики, т. 2, М.—Л., 1951, с. 973—92); [13] Келдыш Л.В.,
«Тр. матем. ин-та АН СССР», 1945, т. 17, с. 1 — 76; [14] М i с h a e 1
В., S t о п е А. Н., «Pacif. J. Math.», 1969, v. 28, JVs 3,р. 629—33;
[15] А р х а н г е л ь с к и й А. В., «Тр. Моск. матем. об-ва»,196В,
т 15, с. 181—223; [16] S t о п е А. Н., «General Topology and
its Application», 1972, v. 2, p. 249—70; [17] F г о 1 i k Z., ..Cze-
..Czechoslovak Mathematical Journal», 1970, v. 20, p. 406—67.
А. Г. Елькии, В. II. Пономарев.
ДЕСЯТИЧНАЯ ДРОБЬ — дробь (арифметическая),
знаменателем к-рой является целая степень числа 10.
Для Д. д. принята запись
akak-i ¦ ¦ ¦ aiao> Ъфъ .. . bh A)
где 0<а,-, 6у<10 — целые числа, причем, если кфО,
то и afi ф0.
Под A) понимается число, равное
Напр.,
A = 0,3; i^A = 35,24; ^ = 0,015.
Цифры, стоящие после запятой, наз. десятичными зна-
знаками. Если Д. д. не содержит целой части, т. е. меньше
единицы по абсолютной величине, то перед занятой
ставится нуль.
Бесконечной десятичной дробью
наз. бесконечный ряд чисел вида:
я„, ЬтЪ^...Ъп..., B)
где а0 — целое число, а каждое из чисел 6у (/=1, 2, ...)
принимает одно из значений 0, 1, 2..., 9. Любое
действительное число а является суммой некоторого
такого ряда, т. е.
Частные суммы ряда B) — конечные Д. д. а0, Ьх. .. Ьп,
являются приближенными значениями числа а с не-
недостатком, а числа
«о, ьх... ьп - -L
— приближенными значениями с избытком. Если су-
существуют такие целые числа п и т, что для всех i>re
имеют место равенства
то бесконечная Д. д. наз. периодической. Вся-
Всякую конечную Д. д. можно рассматривать как беско-
бесконечную периодическую с 6, = 0 для г>«. Если a — рацио-
рациональное число, то соответствующая ему дробь B) будет
периодической. Для иррационального числа а дробь
B) периодической быть не Может. С. А. Степанов.
ДЕСЯТИЧНАЯ СИСТЕМА СЧИСЛЕНИЯ — пози-
позиционная система счисления с основанием, равным 10.
Современная Д. с. с. возникла на основе нумерации,
зародившейся около 5 в. н. э. в Индии. Система полу-
получила название арабской, т. к. в Европе с ней впервые
познакомились по латинским переводам с арабского.
Запись числа в Д. с. с. компактна и удобна для про-
производства арифметич. операций. Очевидные преиму-
преимущества Д. с. с. в сравнении с алфавитными системами
или римской системой счисления содействовали е&
повсеместному распространению. В. И. Нечаев.
ДЕСЯТИЧНОЕ ПРИБЛИЖЕНИЕ действитель-
действительного числа — приближенное изображение дей-
действительного числа конечной десятичной дробью.
Всякое действительное число а может быть записано в
виде бесконечной десятичной дроби:
а = ± а0, аха2 . . . ап ...,
где а0 — неотрицательное число, ап — одна из цифр
0, 1, 2..., 9, ге=1, 2,. . .. Если исключить из рассмот-
рассмотрения бесконечные периодические десятичные дроби с
периодами, состоящими только из одних девяток, то
всякое действительное число будет записываться в
виде бесконечной десятичной дроби однозначным об-
образом. Пусть выбрана такая запись чисел и 0
тогда конечная десятичная дробь
(соответственно а„=а0, аха^. . . ам+10~п) наз. н и ж-
н и м (соответственно верхним) десятичным
приближением порядка п числа а. Если
а<0 и а'=—а, то нижнее а„ и верхнее ап Д. п. порядка
п числа а определяются равенствами
о_„ = — а'п, ап = —и/п.
Для Д. п. действительного числа выполняются сле-
следующие соотношения:
ап ^ап+1 <я<й„ + 1<ап,
Из них следует, что
lim (an±bn)=a±b, lim anbn = ab,
П -*¦ 00 Л ->- GO
а если ЪфО, то lim an/bn=a/b, при этом вместо ниж-
нижних
них Д. п. можно брать верхние.
Д. п. используются на практике для приближенных
вычислений. В качестве приближенных значений сумм
а-\-Ъ, разностей а—Ь, произведений аЬ и частных alb
берутся, соответственно, ап-\-Ьп, ап—Ь„, (anbn)n и
(ап/Ьп)п. В результате указанных действий над конеч-
конечными десятичными дробями ап и Ь„, имеющими не
более га значащих цифр после занятой, получаются
снова десятичные дроби с не более чем п значащими
цифрами после запятой. С помощью этих дробей иско-
искомый результат можно получить с любой степенью точ-
точности. Л. Д. Кудрявцев.
ДЕТЕРМИНАНТ — то же, что определитель.
ДЕТЕРМИНАНТНОЕ МНОГООБРАЗИЕ — множество
матриц Dt(d, n) порядка dXn и ранга меньше t, снаб-
снабженное структурой алгебранч. многообразия. Пусть
Jt{d, n) — идеал кольца многочленов
L 1 < / <
с коэффициентами в поле к, порожденный минорами
порядка t матрицы порядка dXn, составленной из пере-
переменных Tij (детерминантный идеал). Мно-
Множество нулей идеала Jf (d, n) в аффинном пространстве
Adn=Spec(k[{Tij)]) наз. детерминантным мно-
многообразием и обозначается Df{d, n). Для любой
коммутативной А-алгебры к' множество А'-точек Д. м.
Dj(d, n) естественным образом отождествляется с мно-
множеством матриц порядка d X п и ранга <г с коэффициен-
коэффициентами в к'.
Частные случаи Д. м.: Dd (d, d) есть гиперповерх-
гиперповерхность в А , задаваемая обращением в нуль определи-
определителя квадратной матрицы порядка d, составленной из
независимых переменных (детерминантная
гиперповерхность); Dz(d, n) есть аффинный
конус для образа вложения Сегре
pd-ly/pn-l j. pdn-l
произведения проективных пространств [2].
Д. м. обладают следующими свойствами: Df(d, n)
неприводимо, приведено (т. е. идеал Jf(d, n) прост),
является многообразием Коэна — Маколея (см. Кота—
Маколея кольцо), нормально, и размерность D^(d, n)
равна (t—i)(n+d—i) (см. [1], [2]). При *=1 или d=n
(и только в этих случаях) Df (d, га) является схемой
Горенштейна (см. Горенштейна кольцо) [5]. Д. м. тесно
связаны с подмногообразиями Шуберта грассманова
многообразия (см. Шуберта многообразие).
Лит.: [1] Н о с h s t е г М., Е a g о n J., «Amer. J. Math.»,
1971, v. 93, ЛЬ 4, р. 1020—58; [2] KleimanS., Landol-
f i J., «Compositio math.», 1971, v. 23, p. 407—34; [3] L a k s о v
D., «Сотр. math.». 1975, v. 30, p. 273 — 92- [4] MusiliC.
«J. Indian Math. Soc», 1974, v. 38, p. 131—45; [5] S v a n e s T.
¦«Advances Math.», 1974, v. 14, p. 369—453. 11. В. Долгачев.
ДЕФЕКТ, дефектное число операто-
оператора,— размерность dim Di дефектного подпространства
линейного оператора. Иногда, в более широком смысле,
дефектом линейного многообразия
гильбертова пространства наз. размерность ортогональ-
ортогонального дополнения этого многообразия. в. И. Соболев.
ДЕФЕКТ треугольника — недостаток до двух
прямых углов суммы внутренних углов треугольника
на плоскости Лобачевского. Д. треугольника пропор-
пропорционален площади треугольника. Максимальное зна-
значение Д. треугольника равно двум прямым углам, когда
все вершины треугольника являются бесконечно уда-
удаленными точками. А. Б. Иванов.
ДЕФЕКТНОЕ ЗНАЧЕНИЕ мероморфной
функции / — комплексное число а (конечное или
бесконечное), дефект к-рого (см. ниже) 6 (а, /) положи-
положителен. Функция / определена в круге |г|<Д«:оо комп-
комплексной плоскости С. Дефект значения а:
где Т(г, /) — характеристическая функ-
функция Неванлинны, отражающая рост / при
г->-Я, и
N (г, a,f)= У [n(t, а) — п (О, a)] din t + n @, a) In г
— считающая функция; здесь n(t, a) — число решений
уравнения f(z)=a в круге |z|<:i (с учетом кратностей).
Если Т(г)^>-оо при г—>-/?, то 0<8(а, /)<:1 для всех
а?С U {°° }• Если f(z)=?a ни для какого z, то 8(а, /) = 1
и а есть Д. з.; это равенство возможно и в более общем
случае (напр., /(z) = zeJ, R=oo и а=0).
Если
(или /^const мероморфна во всей плоскости), то
У* ё(а,/)<2 (соотношение дефектов), и чи-
ело Д. з. для такой / не более чем счетно. В осталь-
остальном множество Д. з. может быть произвольным; напр.,
для любых последовательностей {av}czC и {Sv}c:R + ,
^ SV<1, найдется целая функция / такая, что
6(av, /)=SV для всех v и других Д. з. у / нет. Ограни-
Ограничения на рост / влекут за собой ограничения на Д. з.
и их дефекты. Напр., мероморфная функция нулевого
порядка или целая функция порядка <V2 не могут
иметь более одного Д. з.
Число
(/ мероморфна в С) наз. дефектом в смысле
Валирона. Множество чисел а, для к-рых
Д(а, /)>0, может иметь мощность континуума, но все-
всегда имеет нулевую логарифмич. емкость.
См. также Исключительное значение, Распределения
значений теория.
Лит.: [1] Неванлинна Р., Однозначные аналитиче-
аналитические функции, пер. с нем., М.—Л., 1941; [2] X е й м а н У.,
Мероморфные функции, пер. с англ., М., 1966; [3] Гольд-
бергА. А., Островский И. В Распределение значе-
значений мероморфных функций, М., 1970. Е. М. Чирка.
ДЕФЕКТНОЕ ПОДПРОСТРАНСТВО операто-
оператора — ортогональное дополнение D \ области значений
Тк = {у=(А—XI)x, x?DA] оператора А\=А— XI, где
А — линейный оператор, определенный на линейном
многообразии D д гильбертова пространства Н, а Я —
регулярное значение (регулярная точка) оператора А.
При этом под регулярным значением
оператора А понимается такое значение парамет-
параметра %, при к-ром уравнение (А—Х1)х=у имеет единст-
единственное решение для любого j/, а оператор (А—Х1)~1
ограничен, т. е. резольвента оператора А ограничена.
При изменении ЯД. п. Di меняется, но его размер-
ность остается одна и та же для всех X, принадлежа-
принадлежащих связной компоненте открытого множества всех
регулярных значений оператора А.
Если А — симметрич. оператор с плотной областью
определения Dд, то его связными компонентами ре-
регулярности будут верхняя и нижняя полуплоскости.
В этом случае D\= {x?Da* , А*х=7-.х), а дефектные
числа « + = dim?*,- н n_=dim ?*_,-, где А*— сопряжен-
сопряженный оператор, наз. (положительным и отрицательным)
индексами дефекта оператора А,
Кроме того,
т. е. D а* есть прямая сумма D д, Dг-и D _/. Таким обра-
образом, если п + = «_ = 0, то оператор А является самосо-
самосопряженным; в противном случае Д. п. симметрич. опе-
оператора характеризуют степень его отклонения от само-
самосопряженного оператора.
Д. п. играют важную роль в построении расширений
симметрич. оператора до максимального оператора
или до самосопряженного (гипермаксимального) опе-
оператора.
Лит.: [1] ЛюстерникЛ. А., СоболевВ.И., Эле-
Элементы функционального анализа, 2 изд., М., 1965; [2] Ахи-
е з е р Н. И., Г л а з м а н И. М., Теория линейных операто-
операторов в гильбертовом пространстве, 2 изд., М., 1966; |3] Д а н-
фордН., ШварцДж,, Линейные операторы, пер. с
англ., ч. 1 — 2, М., 1962 — 66; [4] Рисе Ф., Секефальви-
Н а д ь Б., Лекции по функциональному анализу, пер. сфранц.,
М., 1954. В. И. Соболев.
ДЕФИНИЗИРУЮЩИЙ ОПЕРАТОР для после-
последовательности х= {?./>} — оператор М в про-
пространстве последовательностей, имеющий вид
и переводящий последовательность х в нек-рую пози-
позитивную последовательность.
Н. К. Никольский, Б. С. Павлов.
ДЕФИНИТНОЕ ЯДРО, определенное яд-
ядро,— ядро К(Р, Q) линейного интегрального Фред-
гольма оператора, удовлетворяющее соотношению
где Р, Q — точки евклидова пространства, ф — про-
произвольная суммируемая с квадратом функция, ф —
комплексно сопряженная функция. В зависимости от
знака неравенства ядро наз. соответственно неотри-
неотрицательным (или, иногда, неотрицатель-
неотрицательно определенным) или неположитель-
неположительным (соответственно неположительно оп-
определенны м).
Иногда неотрицательным (неположительным) наз.
(непрерывное) ядро, удовлетворяющее в области ин-
интегрирования неравенству К(Р, <?)^0(sS0).
А. Б. Бапушинский.
ДЕФОРМАЦИЙ ТЕНЗОР — тензор, определяющий
положение точек тела после деформации по отношению
к их положению до деформации. Д. т. представляет
собой симметричный тензор второго ранга
Эй, ди. ди, ди,
где х; — декартовы прямоугольные координаты точки
тела до деформации, и; — координаты вектора пере-
перемещения и. В теории пластичности Д. т. разлагают на
два составляющих тензора:
Uik = Щи + u"ik.
Тензор uik описывает объемную деформацию и паз.
сферическим тензором деформации:
Тензор u'ik описывает только изменение формы и сумма
его диагональных элементов равна нулю:
k
Тензор u'ik наз- девиатором тензора д з -
формации.
В случае малой деформации пренебрегают величина-
величинами 2-го порядка и Д. т. (*) определяется выражением:
да- 9и
uik = -r
В сферич. координатах г, 9, ф Д. т. (*) имеет вид:
дг ' ""99 ~~ г 99 ' дг '
(Р г sin 9 Оф 'г ^ ' г '
_ ¦ ¦ -¦• - - ' ¦ Ufl
1
ае «.ф ^ь »j -rrsjn9 йф
~ дг г г г дН '
1 Э'У , а"ф "ф
""фг —rsin9 Зф -г Sr r •
В цилиндрич. координатах г, ф, z Д. т. (.,.) имеет вид:
_диг 1 Эиф _Э^г
1 9иг 9иф Sttr 9ttz
*^2 г 9ф ' 92 ' г' 9г ' <3г '
2 - бцФ "ф 1 ^^
r(P Or г * г 9ф
Лит.; [1] Ландау Л. Д., Л и ф ш и ц Е. М., Теория
упругости, 3 изд., М., 1965; [2] Физический энциклопедический
словарь, т. 1, М., 1960, с. 553.
ДЕФОРМАЦИОННЫЙ РЕТРАКТ топологиче-
топологического пространства X — подмножество
AczX, обладающее тем свойством, что существует гомо-
топия тождественного отображения пространства X
в нек-рое отображение X—>-А, при к-рой все точки мно-
множества А остаются неподвижными. Если при гомотошш
точки из Х\Л перемещаются по Х\Л, то А наз. с т р о-
г им деформационным ретрактом. Д. р.
пространства X имеет одинаковый с X гомотопический
тип. См. также Ретракт. Е. Г. Скляренпо.
ДЕФОРМАЦИЯ — 1) Д. аналитической
структуры — семейство аналитич. пространств
(или связанных с ними аналитич. объектов), зависящее
от параметров. Теория Д. возникла из задачи классифи-
классификации всевозможных попарно не изолюрфных комплекс-
комплексных структур на данном вещественном дифференцируе-
дифференцируемом многообразии. Основная идея, восходящая к Б.
Риману (В. Riemaim), состояла здесь в том, чтобы
ввести аналптич. структуру на множестве всех таких
структур. Уточнением этой идеи являются следующие
понятия. Аналитическим семейством
комплексных многообразий, параметризованным ком-
комплексным пространством S, наз. любое гладкое
(т. е. локально устроенное как проекция прямого про-
произведения с гладким слоем) аналнтнч. отображение
л : X-vS. Если S связно, то все слои Xs, s?S, отобра-
отображения я диффеоморфны фиксированному слою Хо,
где о QS, и могут рассматриваться как семейство ком-
комплексных структур на Хо, аналитически зависящее ог
параметра s?S. Если семейство X содержит в качестве
слоев все комплексные многообразия, диффеоморфные
Ха, причем все слои попарно не изоморфны, то S наз.
пространством модулей вещественного
многообразия Хо. Можно определить также простран-
пространство модулей для многообразий, принадлежащих опре-
определенному классу. Проблема построения пространства
модулей (или проблема модулей) была реше-
решена вначале для компактных римановых поверхностей
{см. Римановых поверхностей конформные классы).
Результаты такого рода, хотя и неполные, получены
и для компактных многообразий комплексной размер-
размерности 2 (см. Аналитическая поверхность).
Для многообразий больших размерностей исследо-
исследование проблемы модулей встречает значительные труд-
трудности. В связи с этим К. Кодаира и Д. Спенсер [6],
[7], [8] предприняли локальное изучение проблемы
модулей, заложив тем самым основы теории Д. комплек-
комплексных многообразий и аналитич. расслоений. А н а л и-
тической деформацией комплексного мно-
многообразия Хо наз. аналитич. семейство я : X—>-S, при-
причем S — комплексное пространство с отмеченной точ-
точкой о, слой над к-рой совпадает с Хо. Деформация Х=
=ХОХ5 наз. тривиальной. Д. я : X—>-S многообразия
Хо наз. изоморфной Д. я : X—*-S, если существует
аналитич. изоморфизм ф : Х—>-Х, тождественный на
Хо и такой, что яоф=я. Если я : X—*-S — аналитич.
Д., то всякое аналитич. отображение / : S'—>-S, где
о' — пространство с отмеченной точкой о' и f(o')=o,
определяет при помощи замены базы Д. XXsS'—*-S' —
обратный образ данной Д. при отображении /.
Деформация я : X-+-S наз. локально полной
(в точке о), если любая аналитич. Д. л': X'—>-?' многооб-
многообразия Хо изоморфна в нек-рой окрестности отмеченной
точки ее обратному образу при нек-ром локальном
аналитич. отображении / : S'-^-S. Если при этом dfo'
определено однозначно, то Д. наз. версальной в точке
о, а если однозначно определен росток отображения
/,— то универсальной. Важную роль в теории
играет линейное отображение To(S)—*-Hx(Xo, в), где
Q=&X — пучок ростков голоморфных векторных по-
полей на Хо, к-рое сопоставляется аналитич. Д. и наз.
соответствующей инфинитезимальной де-
деформацией.
Основная теорема локальной теории Д., доказанная
М. Кураниси [9], утверждает, что для каждого ком-
компактного комплексного многообразия Хо существует
версальная в точке о Д., параметризованная (не обя-
обязательно гладким) аналитич. подпространством S в
окрестности нуля пространства Нг(Х0, в). При этом
S — слой в точке о нек-рого локального аналитич.
отображения у : Н1(ХО, @)-+Н2(Хо, 0), имеющего
вид Y(l)=tl' !]+•••. гДе [.1 ~ операция в градуиро-
градуированной алгебре Ли Н* (Хо, 0), индуцированная скоб-
скобкой Ли в пучке 0, а точки означают члены порядка
^s3. Если НХ(ХО, 6) = 0, то многообразие Хо является
жестким, т. е. любая его Д. локально тривиальна
(теорема жесткости Фрелихера — Нейен-
хёйса). Если Н2(Х, в) = 0, то 5 — окрестность нуля в
НХ(ХО, в). Касательное пространство T0(S) всегда
совпадает с Я1(ХО, в). Д. является полной в точке Q
тогда и только тогда, когда соответствующая инфини-
тезимальная Д. сюръективна, а версальность равно-
равносильна биективности инфипитезимальной Д. Если
dim//0(Xs, Qxs)< s€^> постоянна в окрестности нуля,
то деформация Кураниси является универсальной.
Локальная теория Д. компактных комплексных мно-
многообразий обобщается на случай компактных комплек-
комплексных пространств. При этом вместо гладкости отобра-
отображения я : X—*-S и компактности слоя требуют, чтобы л
было плоским и собственным отображением. Здесь
также можно доказать существование версальнон в точ-
точке о Д. (см. [3], [5], [11]).
Изучаются также Д. ростков аналитич. пространств
(пли, что равносильно, аналитич. алгебр). Справед-
Справедлива теорема о существовании версальной Д. для
изолированной особой точки комплексного простран-
пространства [4].
Наряду с теорией Д. комплексных пространств суще-
существуют теории Д. различных «аналитических объектов»—
аналитич. расслоений, подпространств, отображений,
классов когомологий, аналигич. пространств с до-
дополнительной структурой (напр., с поляризацией) н
др. Основные определения и проблематика этих теорий
аналогичны описанным выше. Результаты, полученные
для главных аналитич. расслоений, также аналогичны
перечисленным выше. В частности, для любого главного
аналитического расслоения Е с компактной базой X
и комплексной группой Ли G в качестве структурной
группы существует версальная в точке о Д. расслое-
расслоения Е, параметризованная аналитич. подпространст-
подпространством в окрестности нуля пространства Нг(Х, Qaue),
где CAd? — пучок ростков голоморфных сечений век-
векторного расслоения над X, ассоциированного с Е при
помощи присоединенного представления [1]. Если X —
компактная риманова поверхность, a G — редуктивнан
алгебраич. группа, то можно построить пространство
модулей для стабильных главных аналитич. расслое-
расслоений. В теории Д. подпространств, напротив, получены:
весьма общие результаты глобального характера. А
именно, если X — произвольное комплексное прост-
пространство ограниченной размерности, то построено [2J
плоское аналитич. семейство компактных аналитич.
подпространств в X (т. е. аналитич. подпространство
YdXxS, где S — комплексное пространство и проек-
проекция У—*-S есть собственное плоское отображение),
являющееся универсальной (в глобальном смысле)
Д. для любого компактного аналитич. подпростран-
подпространства в X. В частности, S является пространством моду-
модулей для рассматриваемой задачи. Аналогичная проб-
проблема модулей решена в относительном случае, а также
для компактных аналитич. циклов заданного комплекс-
комплексного пространства. Из решения проблемы модулей для
компактных подпространств следует решение проблемы
модулей и для аналитич. отображений заданного ком-
компактного комплексного пространства в другое заданное
комплексное пространство.
Существуют попытки унификации упомянутых выше
теорий Д. С каждой из этих теорий можно связать
контравариантный функтор D из категории аналитич.
пространств (или ростков аналитич. пространств) в
категорию множеств. Напр., в теории локальных Д.
комплексного пространства Хо множество D (S) со-
состоит из классов локально изоморфных Д. простран-
пространства Хо, параметризованных ростком аналитич. прост-
пространства S. Если фиксировать S п элемент S?D(S),
то возникает морфизм функторов Мог (., S)-^D. Сюръ-
ективность этого морфизма (пара E, б) наз. в этом
случае полной) соответствует свойству полноты
Д. б, а биективность — свойству ее универсальности.
Проблема модулей связана, таким образом, с вопросом
о представимости функтора D. В связи с этим было пред-
предпринято изучение ковариантных функторов из кате-
категории артиновых колец в категорию множеств, удов-
удовлетворяющих нек-рым естественным условиям [12],
Существование полной пары доказывается, однако,
лишь в категории формальных алгебр, что соответст-
соответствует существованию формальной полной Д. (см. Де-
Деформация алгебраического многообразия).
Обобщением теории Д. комплексных структур на
многообразии является теория Д. псевдогрупповы.г
структур, в к-рой рассматриваются семейства псевдо-
псевдогрупповых структур, гладко зависящие от параметра,
принимающего значения в вещественном аналитпч.
пространстве. В частности, для псевдогрупповой струк-
структуры на компактном гладком многообразии, соответ-
соответствующей эллиптич. транзитивной псевдогруппе пре-
преобразований, доказано существование версального ро-
ростка деформации [10].
Лит.: [1] Д он и н И. ф., «Матем. сб.», 1974, т. 94, М« 3,
с. 430— 4 3; [2] DouadyA., «Ann. Inst. Fourier», 1906, t. IB,
p. 1—!M; [3] его же, «Ann. sci. Ecole norm, sup.», 1974,
т. 7, .\» 4, p. 569—602; [4] GrauertH., «Invent, math.»,
1972, Bd 15, №3, S. 171—98: [5] его же, там же, 1974,
Bd 25, №2, S. 107—42- [6] KodairaK. Spencer
D. C, «Arm, Math.», 1958, v. 67, № 2, p. 328 — 401; [7] их же,
там же, 1998, v. 67, № 3, p. 403—66; [8] и х ж е, там же, 1960,
v. 71, № 1, p. 43—76; [9] К и г a n i s h i M., в кн.: Proceedings
of the Conference on Complex Analysis, Minneapolis. 1964, N. Y.—
В., 1965, p. 142—54; L10] Moolgavkar S. H., «Trans.
Amer, Math. Soc», 1975, v. 212, Xt 485, p. 173—97; [И] Пал а-
мод OB В. П., «Успехи матем. наук», 1976, т. 31, № 3, с. 129—
194; [12] Шлезингер М., «Математика», 1971, т. 15, JV5 4,
с. 115—29. А. Л. Онищик, Д. А. Пономарев.
2) Д. алгебраического многообра-
многообразия — включение алгебраич. многообразия в семей-
семейство алгебраич. многообразий. Теория Д. алгебраич.
многообразий и схем представляет собой алгебраич.
аналог теории Д. аналитич. структур. Ее основными
вопросами являются следующие:
Существование подъема. Дана схема
Хо над полем к, схема S, точка so?S с полем вычетов
k(so) = k. Существует лп плоская 5-схема X, для к-рой
слой XStt над точкой s0 изоморфен Хо? E-схема X наз.
деформацией, или подъемом, схемы Хо
над S).
Проблема универсальности. Су-
Существует ли версальная (соответственно уни-
универсальная) Д. схемы Хо, т. е. такая Д. М над
схемой Хо, что для любой другой Д. X—*-S найдется
(соответственно единственный) морфизм S—>-М, для
которого X=MXS?
м
Каждая Д. X—^S схемы Хо с помощью операции
формального пополнения вдоль слоя Х^а определяет
формальную деформацию х над попол-
пополнением локального кольца Cs, s<, схемы S в точке s0,
т. е. плоскую формальную схему над (j$, sQ c топология,
пространством Хо. Формальные аналоги перечислен-
перечисленных выше вопросов формулируются следующим об-
образом:
Существование формальной Д. Дано
полное локальное кольцо Л с полем вычетов к. Суще-
Существует ли плоская формальная схема над Л с тополо-
топологическим пространством Хо?
Существование формальной схемы
модулей. Существует ли формальная вер-
версальная (соответственно универсальная)
Д., т. е. плоская формальная схема р : х—>-C над
полным локальным кольцом Q с полем вычетов к та-
такая, что для любой формальной Д. х'—>-SpecA имеется
(соответственно единственный) гомоморфизм колец
б—>-Л, для которого х'^=х®(ЗЛ?
Универсальная формальная Д. гладкого многообра-
многообразия представляет собой алгебраич. аналог локального
пространства модулей в теории Д. аналитич. структур.
Если ,S=Speci?, где R — локальное артиново (соот-
(соответственно полное) кольцо с полем вычетов к, то Д.
Хо над S наз. инфинитезимальной (соответ-
(соответственно эффективной формально й). В
случае, когда R — полное локальное кольцо характе-
характеристики нуль (напр., кольцо Ватта векторов), эффек-
эффективная формальная Д. Хо наз. подъемом Хо в
характеристику нуль.
Если .Yo — гладкая А-схема и Н3(Х„, Тув) = 0, где
Тх„ — касательный пучок на Хо, то для любого арти-
ова (соответственно полного) локального кольца су-
ествует инфинитезимальная (соответственно формаль-
ная) Д. Хо. При этом, если Н1(Х0, Гу„) = 0, то такая
Д. единственна с точностью до изоморфизма (см. [4]).
Аналогичные утверждения для необязательно гладких
схем даются в терминах кокасательного комплекса
(см. [5], [6]). Вопрос о существовании эффективной
формальной Д. изучается с помощью рассмотрения
функтора Dya из категории С\ артиновых локальных
колец с полем вычетов к в категорию множеств, к-рый
сопоставляет каждому объекту R из С& множество всех
пнфинитезимальных Д. Хо над R. Универсальная фор-
формальная Д. Хо существует в том и только в том случае,
когда функтор является пропредетавимым функтором.
При этом пропредставляющий объект — полное локаль-
локальное кольцо М^-о с полем вычетов к — наз. ф о р-
м а л ь н о й схемой модулей к-схемы Хо. Форма-
Формальная версальная Д. р : х—>-М^-0 существует, если Хо соб-
собственна над к или Хо есть аффинная схема конечного
типа над к с изолированными особыми точками (см.
[2], [6]). Версальная формальная Д. является универ-
универсальной, если для любого сюръективного гомоморфизма
R'—*-Я локальных артиновых колец и Д. X'—>-R' из
Dxo(R') естественное отображение групп автоморфиз-
автоморфизмов
(X' | Хо) —>- AutR (X'R- ® R | А'„)
является сюръективным. Это условие выполняется,
напр., если Ха — гладкая схема и Н°{Х0, Туо) — О.
При этом, если Я2(Х0, Туо) = 0, то формальная схема
модулей Мх0 является полным регулярным локальным
кольцом, изоморфным кольцу Ш*!,. • •, tm]] формаль-
формальных степенных рядов от m переменных. Число m равно
в этом случае dim^H1 (Хо, Ту0) и наз. числом ло-
локальных модулей схемы Хо. В общем случае
dijnkH1(X0, Ty0) равна размерности касательного
пространства к Муа и Му0, т. е. размерности dim^m/m?,
где m — максимальный идеал соответствующего ло-
локального кольца, а
W(X0, TXo)-dim MXo<idimkHHXo, TXt).
Наличие нильпотентных элементов в формальной схеме
модулей представляет довольно частое явление.
Если версальная (соответственно универсальная)
формальная Д. х—>-Л/>-0 алгебраизуема, т. е.
существует плоская схема над Мх0, формальное по-
пополнение которой вдоль замкнутого слоя изоморфно
х, то соответствующая алгебраизация наз. локаль-
локальной версальной (соответственно универ-
универсальной) Д. А-схемы Хо. Если Хо проективна и
#a(X0,7V0)=0 ,то алгебраизация существует. Напр., для
полной гладкой кривой рода g>l существует локаль-
локальная универсальная Д. над кольцом к [Ui,. . ., *зг-з]Ь
В общем случае, для каждой поляризации а многооб-
многообразия Хд существует максимальная замкнутая под-
подсхема в формальной схеме модулей Му0, аС^у, та-
такая, что р~1(Му„, а) алгебраизуема. Коразмерность
Л/.у0, а в Муп не превышает (Ит^Я2(Х0, 6у). Напр.,
если Хо — алгебраическая КЗ-поверхность, Мх„ ре-
регулярна размерности 20, а для любой поляризации а
подсхема Му0 а регулярна размерности 19.
Теорема Артина об аппроксимации применяется для
алгебраизащш формальной схемы модулей. Существует
схема S конечного типа над к и точка so?? с полем
вычетов к такая, что пополнение ^5, so—Mxe> и сУЩе~
ствует Д. Хо над S, индуцирующая версальную ло-
локальную Д. 7' : *—>-j1^av Схема S определена однознач-
однозначно с точностью до локального изоморфизма в этальной
топологии [1]. Относительно Д. особых многообразий и
особых точек см. Особая точка алгебраического много-
многообразия. Относительно Д. групповых схем см. Груп-
Групповая схема.
Лит.: [1] АртинМ., «Математика», 1970, т. 14, №4,
с. 3—47; [2] Итоги науки и техники. Алгебра. Топология.
Геометрия, т. 12, М., 1974, с. 77—170; 13] Шлезингер М.,
«Математика», 1971, т. 15, № 4, с. 115—29; [4] Revetements
dtales et groupe fonciaraental (SGA 1), B.— Hdlb.—N. Y,, 1971;
[5] Rim D. S., в кн.: Groupes de monodromie en geometric
algebrique (SGA71), В.—Hdlb.—N. Y., 1972, p. 32—132; [6]
MumfordD.,B кн.: Z a r i s k i O., Algebraic surfaces, 2 ed.,
В. —Hdlb.—N. Y., 1971, p. 118 — 28. И. В. Долгачев.
3) Д. алгебры — семейство алгебр, зависящее
от параметров. Всевозможные билинейные операции
или алгебры Щ в пространстве V над полем к образуют
векторное пространство A(V). Два элемента этого про-
пространства представляют изоморфные алгебры тогда н
только тогда, когда они лежат на одной орбите линей-
линейной группы GL(F), естественным образом действующей
вА(У). Теория Д. алгебр позволяет исследовать ло-
локальное строение фактормножества A(V)/GL(V), т. е.
множества классов изоморфных алгебр в пространстве
F, прямое описание к-рого связано с большими труд-
трудностями. Если выделен нек-рый класс алгебр К^А (F),
то можно рассматривать Д. алгебр из класса К, не вы-
выводящие за пределы этого класса. В частности, рас-
рассматриваются Д. ассоциативных, ассоциативно-комму-
ассоциативно-коммутативных алгебр и алгебр Ли, образующие классы
K=Ass(V), iC=Gomm(F), K= Lie(F), соответственно,
инвариантные относительно действия группы GL(F).
Если dimF=n, то эти классы являются алгебраич. мно-
многообразиями в «3-мерном пространстве A(V).
Теория Д. алгебр в конечномерном пространстве F
над полем k=R и С действительных или комплек-
комплексных чисел во многом аналогична теории деформаций
аналитич. структур. Каждая конечномерная алгебра 31
над k=R или С обладает полной Д., параметризован-
параметризованной ростком аналитич. подпространства в нуле про-
пространства #2(,ЗГ, F) [если Я3(Щ, F)=0, то это под-
подпространство совпадает с Н2E1, V)]. Из этого основного
результата непосредственно следует теорема же-
жесткости: если Н*{%, F) = 0, то алгебра Щ является
жесткойв К, т. е. орбита элемента 31 относительно
GL(F) открыта в К. Напр., жесткими в классе алгебр
Ли являются полупростые алгебры Ли, а также их
подалгебры Бореля. Утверждение, обратное к теореме
жесткости, неверно. Аналогичные утверждения спра-
справедливы для конечномерных алгебр над произвольным
алгебраически замкнутым полем к. Например, если
Я2(С, F)=0, то орбита алгебры Щ в К открыта по За-
рискому.
Аналогично может быть развита теория Д. гомомор-
гомоморфизмов одной конечномерной алгебры в другую. На
самом деле, описанные выше теории включаются в об-
общую схему, использующую аппарат градуированных
алгебр Ли. Сходные результаты получены также для
Д. подалгебр.
Наряду с указанной выше теорией существует теория
формальных Д. алгебр и их гомоморфизмов над произ-
произвольным полем к. Формальной Д. алгебры,
заданной в векторном пространстве V над к, наз. алгеб-
алгебра на пространстве V(g)k((t)) над полем k((t)) формаль-
формальных степенных рядов над к с операцией о, к-рая пол-
полностью определяется условием
ао6 = а6 + 2^ фг- (а, Ь) t', a, b?V,
где q>i?A(V). Требуя, чтобы Д. принадлежала данно-
данному классу алгебр, можно говорить о формальных
Д. ассоциативных, ассоциативно-коммутативных, лие-
лиевых и других алгебр.
Две формальные Д. алгебры Щ с умножениями X
и о соответственно наз. эквивалентными, если
существует линейный автоморфизм Ф пространства
V(/)k((t)) со свойством
где ф,- : V—+ V— линейное отображение такое, что
ао6 = ф-1 (Ф (а) X Ф(*)).
Д., эквивалентная алгебре 91 с исходным умножением,
наз. тривиальной. Алгебра, не имеющая нетри-
нетривиальных формальных Д. в данном классе алгебр, наз.
формально жесткой в этом классе. Напр.,
свободная алгебра в классе всех алгебр будет формально
жесткой. В классах Ass(F), Comm(F), Lie(F) доста-
достаточным условием формальной жесткости алгебры 91
является равенство #2(9I, V) = 0. В классе Ass(V') это
условие является также и необходимым [3].
В случаях k=R или С формальные Д. алгебр служат
аппаратом для изучения аналитич. Д.
Важной областью приложений п источником приме-
примеров Д. алгебр является теоретич. физика, где, в част-
частности, возник следующий класс Д. алгебр (см. [4],
[5]). Стягиванием конечномерной алгебры 91
над k=R или С наз. непрерывная кривая Щ, 0<:i<:l,
в пространстве А (V) такая, что 2lf = 91 при 0-<t<l-
Алгебра 9Ij, полученная из 91 в результате стягивания,
наз. предельной и может не быть изоморфной
алгебре Ш. Напр., любую алгебру можно стянуть в
алгебру с нулевым умножением; любую полупростую
алгебру Ли можно стянуть в неабелеву неполупростую.
Лит.: [1] N iienhuisA., Richardson R.W.Jr,, «Bull,
Amer. Math. Soc», 1966, v. 72, № 1, p. 1—29, 1967, v. 73, Л» 1,
p. 175—79; [2] G e r s t e n h a b e г М., «Ann. Math.», 1964,
v. 79, p. 59 —103; [3] К n u d s о n D., «Trans. Amer. Math.
Soc», 1969, v. HO, p. 55—70; [4] InoniE., W i g n e r E. P.,
«Proc. Nat. Acad. Sci. USA», 1953, v. 39, ЛЙ 6, p. 510—24; [5]
HermannR., Lie groups for physicists, N. Y.— Amtterd.,
1966. А. А. Бояркин, А. В. Михалев, А. Л. Онищик.
4) Д. подмножества А пространства
X — гомотопия:
для к-рой D (а, 0) = а при а?А. Если, болео того,
множество D(AXI) принадлежит нек-рому подпро-
подпространству X' пространства X, то D наз. Д. Л в X',
а А наз. деформируемым в X' в пространстве X. Про-
Пространство X наз. деформируемым в подпространство X',
если оно деформируемо по себе в X'. В частности, X
стягиваемо тогда и только тогда, когда оно деформируе-
деформируемо в одну из своих точек. Пространство X деформируе-
деформируемо в подпространство X' тогда и только тогда, когда
для вложения i : X'—>Х существует правое гомотопи-
чески обратное отображение г : X—*-Х', т. е. i»r — 1.
Понятие Д. всего пространства по себе на подпрост-
подпространство родственно понятию слабой ретракции.
М. И. Войцеховский.
ДЕЦИЛЬ — значение х, при котором непрерывная
строго монотонная функция распределения Р(х) при-
принимает для /=1, 2,. . ., 9 значения, равные //10. Когда
Д. существуют, они дают хорошее представление о
форме кривой распределения. Расстояние между девя-
девятой и первой Д. наз. интердец ильной широ-
т о й, она дает представление о рассеянии распределе-
распределения. Д.— частный случай квантили, я. м. Халфина.
ДЖЕКОБСОНА КОЛЬЦО — коммутативное кольцо
с единицей, любой простой идеал к-рого является пере-
пересечением максимальных идеалов, его содержащих, т. е.
кольцо, любое целостное факторкольцо к-рого имеет
нулевой Джекобсона радикал. Напр., любое артиново
кольцо, кольцо целых чисел (вообще, любое дедекиндо-
во кольцо, не являющееся полулокальным) или абсо-
абсолютно плоское кольцо являются Д. к. Напротив, ло-
локальное не артиново кольцо не будет Д. к.
Если А есть Д. к., а В — целая Л-алгебра или А-
алгебра конечного типа, то В есть Д. к.; в частности,
факторкольцо Д. к. есть Д. к. Кольцо многочленов от
конечного числа переменных над полем К является
Д. к.; в случае бесконечного числа переменных ответ
зависит от соотношения числа переменных и мощности
поля К. Кольцо А является Д. к., когда пространство
максимальных идеалов кольца А квазигомеоморфно
спектру Spec (Л); это определение приводит к понятию
схемы Джекобсона.
Лит.: [1] Бур баки Н., Коммутативная алгебра, пер.
с франц., М., 1971. В. И. Данилов.
ДЖЕКОБСОНА РАДИКАЛ кольца А — идеал
J(A) ассоциативного кольца А, удовлетворяющий сле-
следующим двум условиям: 1) J (А) — наибольший ква-
квазирегулярный идеал в А (кольцо R наз. квазирегу-
квазирегулярным, если для любого его элемента а разрешимо
уравнение а-\-х+ах=0); 2) в факторкольце Л=Л//(Л)
нет квазирегулярных идеалов, кроме нулевого. Д. р.
был введен и детально исследован Н. Джекобсоном
(N. Jacobson) в 1945 (см. [1]).
Д. р. всегда существует и может быть охарактеризо-
охарактеризован весьма многими способами: J (А) есть пересечение
ядер всех неприводимых представлений кольца А,
пересечение всех модулярных максимальных правых
идеалов, пересечение всех модулярных максимальных
левых идеалов; он содержит все квазирегулярные одно-
односторонние идеалы, все односторонние нильидеалы и
т. д. Если /— идеал А, то J(I)=If]J(A), если Ап—
кольцо всех матриц порядка п над А, то
J(An) = (J{A))n.
Если на ассоциативном кольце А ввести композицию °:
а о Ь = а-\-Ь-\-аЪ,
то в полугруппе <Л, о> радикал J (А) относительно
композиции о будет подгруппой.
Над квазирегулярным (т. е. совпадающим со своим
Д. р.) ассоциативным кольцом не существует ненуле-
ненулевых неприводимых конечно порожденных модулей;
однако простые ассоциативные квазирегулярные кольца
существуют. Для того чтобы в ассоциативном кольце А
Д. р. был равен нулю, необходимо и достаточно, чтобы А
было подпрямой суммой примитивных колец.
Лит.: [1] Джекобсон Н., Строение колец, пер. с
англ., М., 1961. К. А. Жевлаков.
ДЖЕКСОНА НЕРАВЕНСТВО — неравенство, дающее
оценку скорости убывания наилучшего приближения
функции тригонометрич. полиномами или алгебраич.
многочленами в зависимости от ее дифференциально-
разностных свойств. Пусть f(x) — непрерывная на всей
оси 2я-периодич. функция, En(f) — наилучшее равно-
равномерное приближение f(x) тригонометрич. полиномами
Тп(х) порядка п, т. е.
Еп (/) = 'n' max | / (х) — Тп (х) |,
И
со (/; б) = max |/(*i)— / ('2) I
— модуль непрерывности функции f(x). Д. Джексон
[1] показал, что
Д„(/)<Ссо(/; -1) (*)
(С — абсолютная константа), а если f(x) имеет г-ю
непрерывную производную f{r){x), r^l, то
С,
где постоянная Сг зависит только от г. В случае
со(/; i) <Kta, 0 < а < 1,
неравенство (*) было независимо получено С. Н. Берн-
штейном [3].
Если f (x) непрерывна или г раз непрерывно дифферен-
дифференцируема на отрезке [а, Ь], г=1,2..., и En(f\ а, Ъ) —
наилучшее равномерное приближение функции f(x)
на [а, Ь\ алгебраич. многочленами степени п, то для
имеет место соотношение (jl)(x) = f(x))
где постоянная А г зависит только от г.
Д. н. известны также как теоремы Джексо-
н а, или прямые теоремы теории приближения функций.
Они обобщались в различных направлениях: прибли-
приближение в интегральной метрике, приближение целыми
функциями конечной степени, оценка приближения
через модуль гладкости к-то порядка, функции многих
переменных. В ряде случаев в Д. н. найдены точные
значения констант.
Лит.: [1] JacksonD., Cber die Genauigkeit der Annahe-
rung stetiger Funktionen durch ganze rationale Funktionen, Dis-
Dissertation, G6tt., 1911; [2] Никольский С. М., Прибли-
Приближение функций многих переменных и теоремы вложения, М.,
1969; [3] Бернштейн С. Н., «Сооб. Харьк. матем. об-
общества», сер. 2, 1912, т. 13, с. 49—194; [4] Корнейчук
Н. П., Экстремальные задачи теории приближения, М., 1976.
Н. П. Корнейчук, В. П. Моторный.
ДЖЕКСОНА СИНГУЛЯРНЫЙ ИНТЕГРАЛ, Джек-
Джексона оператор,— интеграл вида
УЯя1 (x + u)Kn(u)du,
в к-ром выражение
. пи
3 /slnT
[
называют ядром Джексона; впервые был при-
применен Д. Джексоном [1] для оценки наилучших приб-
приближений функции f(x) через ее модуль непрерывности
со I /, — I или через модуль непрерывности ее производ-
производной порядка /с^1. Д. с. и.— положительный опера-
оператор, являющийся тригонометрич. полиномом порядка
In—2, его ядро Кп (и) представляется в форме
Кп (и) = A + pf-2 cos t + .. . +р1Щ cos Bn-2) t,
где А=-? и p?"~2 =1—tj^-, re=l, 2,.... Имеет место
оценка
\Un(f, лг)-/(
Лит.: [1] JacksonD., The theory of approximation,
N. Y 1930' [2] H а т а н с о н И. П., Конструктивная теория
функций, М., 1949, с. 116—22. А. В. Ефимов.
ДЖЕКСОНА ТЕОРЕМ-а — теорема теории приближе-
приближения функций, дающая оценку сверху для наилучшего
приближения функции многочленами (или периоди-
периодической функции тригонометрич. полиномами). Д. т.
дает возможность исследовать свойства наилучших
приближений в зависимости от дифференциальных
свойств функции. См. Джексона неравенство.
В. И. Бердышее.
ДЖЕНКИНСА ТЕОРЕМА, общая теорема
о коэффициентах,— теорема теории однолист-
однолистных конформных отображений семейств областей на
римановой поверхности, содержащая неравенство для
коэффициентов отображающих функций, а также усло-
условия на функции, для к-рых это неравенство обращается
в равенство. Д. т. является точным выражением и
развитием (высказанного без доказательства) прин-
принципа Тейхмюллера (см. [1], с. 83), согласно
к-рому решение нек-рого класса экстремальных проб-
проблем для однолистных функций определяется квадра-
квадратичными дифференциалами соответствующего вида. По-
Получена Дж. Дженкинсом A954, см. [1] — [4]).
У с л о в и я Д. т. Пусть Si — конечная ориенти-
ориентированная риманова поверхность, Q(z)dz-— положитель-
положительный квадратичный дифференциал на $1, имеющий хотя
бы один полюс порядка ^2, н пусть Ри. . ., Рг — все
полюсы порядка 2, а Ргл.ъ,..., Рр — все полюсы по-
порядка >2. Пусть открытое всюду плотное на ill множе-
множество Д представляет собой дополнение к объединению
конечного числа замыканий траекторий и замыканий
дуг траекторий, причем Р;? Д, ?=1,..., р. Пусть
функция fo(P) отображает Д конформно и однолистно в
У{ и пусть существует гомотопня
отображения f<,(P) в тождественное отображение ft(P)^=
=/\ оставляющая неподвижными все полюсы из Д
и удовлетворяющая условию ft(P)?=R для каждого
полюса R?ffl, i?[0, 1], и всякой точки РфЯ. Пусть
Zj=Zj(P) — такой локальный параметр для полюса
Pj, что zj(Pj)=oo, /=1,..., p. Пусть, при /=1,..., р
в окрестности полюса Pj,
( аЛ/'z Г 2-j-6oлее высокие степени zj ~1, если j^r;
Q(zj)—\ . Г т .-4 „х ... m.-s-4"l
I a'J) I Zj J + V $ zj J ' если ; > r;
/а'/'г^-т-неположительные степени zj, если у^ г;
0 ^ J' I zj-\- ^ аг''^2Г5' если /' > r,
где rtj — целая часть числа ?;>(m/—3). Пусть
d(Py)= Hm (Argz,-[/,(/>)]
и пусть d(Pj)=O для всех />г, для которых Ру- лежит
на границе полосообразной области относительно
Q(z)dz2. Пусть, наконец,
( 0, если ту нечетно;
i al-i)(-~mj — lVe(n')'| , если mj четно.
Утверждение Д. т. При этих условиях
Re {2^-t аФ 1п аФ + 2j=r+ iaU)TJ
где 1па(/'=1п|а(Я|— id(Pj), /<r.
Д. т. для случая равенства. Если в (*)
имеет место знак равенства, то: а) в каждой области
Д/СД отображение /0 является изометрией в ^-метри-
^-метрике |d^| = |B(z)|I/2|dz!, каждая траектория Q(z)dz2 в Д
переходит в траекторию, и множество /0(А) всюду плот-
плотно в #$; б) для того чтобы /0 было тождественным отоб-
отображением в нек-poii области Д/СГ Д. достаточно, чтобы вы-
выполнялось одно из следующих дополнительных ус-
условий:
1) в Дг имеется такой полюс />,-, _/>г, порядка ту,
что «s" = 0 для s<min{ny-J-l, mj—3};
2) в Д; имеется полюс Pj, для к-рого /<:г и о'^=1;
3) в А[ имеется точка траектории, оканчивающейся
в простом полюсе.
Если в (*) имеет место равенство и если \а^\Ф\
при нек-ром /<:г, то 5? конформно эквивалентно сфере,
а Q(z)dz2 не имеет нулей и простых полюсов, и г=р = 2.
Если, к тому же, Д есть область, то отображение /0
конформно эквивалентно линейному преобразованию,
неподвижными точками к-рого служат образы обоих
полюсов.
Экстремальной метрики метод, лежащий в основе
доказательства Д. т., был с надлежащими модифика-
циями использован Дж. Дженкннсом также для полу-
получения ряда других результатов, в частности так наз.
специальной теоремы о коэффициен-
коэффициентах (см. [4]). Дополнение и развитие Д. т. см. в [5].
Лит.: [1] Дженкинс Дж., Однолистные функции и
конформные отображения, пер. с англ., М., L'Jtj'2; [2J J е п-
kins J. A., «Trans. Ашег. Math. Soc», 1960, v. 95. Л» 3, p. 387—
407; t3] его же, «Bull. Ашег. Math. Soc», 1962. v. «8, Ai 1,
p. 1 — 9; [4] его же, «111. J. Math.», 1964, v. S,Ml,p. 80-
99; [5] T а м р а з о в П. М., «Матем. сб.», 1967, т. 72, J4« 1,
с. 59—71. 11, М. Тамразов.
ДЖЕТ — см. Струя.
ДЖИНИ СРЕДНЯЯ РАЗНОСТЬ — величина, харак-
характеризующая разброс значений случайной величины
X. Введена К. Джини (С. Gini, 1912). Д. с. р. опреде-
определяется по формуле
Д =
где F(-) — функция распределения случайной вели-
величины. Рассматривают также коэффициент рас-
рассеяния Джини
2цГ '
где [X — математич. ожидание случайной величины X.
Лит.: HI К е н д а л л М., СтъюартА., Теория рас-
распределений, пер. с англ., М., I960. К. П. Латышев.
ДЖОЙН — см. Соединение.
ДЗЕТА-ФУНКЦИЯ, ?-ф у н к ц и я, — 1) Д.-ф. в
теории чисел — класс аналитич. функции ком-
комплексного переменного, состоящий из ?-функции Рима-
Римана, ее обобщений и аналогов. Д.-ф. и их обобщения в
виде L-функций (см. Дирихле L-функции) лежат в ос-
основе современной аналитич. теории чисел. Кроме
^-функции Римана выделяются обобщенная Д.-ф. t,(s, a),
дзета-функция Дедекинда, конгруэнц Д.-ф. и др.
Дзета-функция Римана определяется
рядом Дирихле
У i.\ _ Т1Я 1
абсолютно и равномерно сходящимся в любой конечной
области комплексной ^-плоскости, для к-рой oQSsl-f-6,
б>0. При сг>1 справедливо представление в виде-
произведения Эйлера
где р пробегает все простые числа.
Тождественность ряда A) и произведения B) пред-
представляет собой одно из основных свойств функции
?(s). Оно позволяет получить многочисленные соотно-
соотношения, связывающие ? (s) с важнейшими теоретико-
числовыми функциями. Так, при а>1
Л (п)
где п(х) — число простых чисел <:х, А(п) — Манголь-
дта функция, \i(n) — Мёбиуса функция, т(п) — число
делителей числа п, v(n) — число простых делителей
числа л, к(п) — Лиувилля функция. Отсюда та исклю-
исключительная роль, к-рую играет ? (s) в теории чисел.
Как функция действительного переменного, ? (s) была
введена в 1737 Л. Эйлером (L. Euler, см. [1]), к-рый
указал и ее разложение в произведение 12). Затем эта
функция рассматривалась П. Дирихле (P. Dirichlet)
и, особенно успешно. П. Л. Чебышевьш (см. [2]) в
связи с изучением закона распределения простых чисел.
Однако наиболее глубокие свойства функции ? (s)
были обпаружены позднее, когда ее стали рассматри-
рассматривать как функцию комплексного переменного. Первым
это сделал в 1876 Б. Риман (В. Шеглапп, см. [3]),
к-рый показал следующее.
a) l, (s) допускает аналитич. продолжение на всю
комплексную s-плоскость в виде
/ ч 1
jj ч~ , ~ / &(x)dx, C)
где Г (со) — гамма-функция,
0) 'C(s) является регулярной функцией для всех
значений s, кроме s=l, где она имеет простой полюс с
вычетом, равным 1, н удовлетворяет функциональному
уравнению
A — s). D)
Это уравнение наз. функциональным урав-
уравнением Р и м а н а. Для функции
введенной Б. Риманом для исследования Д.-ф. п назы-
называемой к с и - ф у н к ц и е н Р и м а н а, это уравне-
уравнение принимает вид
а если положить
то оно принимает вид
E(t) = S(-t).
Последняя функция Е замечательна тем, что она явля-
является четной целой функцией, действительной для дей-
действительных t, и ее нули на действительной оси соот-
соответствуют нулям функции ?(s) на прямой ст=1/2.
в) Поскольку $(s)=7fcO для <т>1, то в силу D) в полу-
полуплоскости а>0 эта функция имеет лишь простые нули
в точках s=2v, v=l, 2.. . . Эти нули наз. т р и в и-
а л ь н ы м и нулями Д.-ф. ?(s). Далее t,(s)^O
для 0<s<l. Таким образом, все нетривиаль-
нетривиальные нули Д.-ф. ?(s) являются комплексными числа-
числами, обладают свойством симметрии относительно дейст-
действительной оси г=0 и относительно вертикали <т=1/2
и лежат в полосе 0<<о"<:1, к-рая наз. критичес-
критической полосой.
Б. Риман высказал также следующие гипотезы.
1. Число ЛГ(Т) нулей функции ? (s) в прямоугольнике
0<а-<1, 0</<Г, выражается формулой
= -~T In Г-г 1+.^2л Т + О (In Г).
2. Пусть р пробегает нетривиальные нули l.(s)- Тогда
2 2
ряд 2М~2 сходится, а ряд 2'р! расходится.
3. Функция ? (s) представима в виде
4. Пусть
Тогда при
^) = Н*-2рН*Р+$Г(^ТП^-1п2' E)
где \\х — интегральный логарифм,
Ги + ic „z
Не»=\ . —dz, w = u-Liv. v 5g 0.
J -=C +IV 2 ' . ! < •>•
5. Все нетривиальные нули Д.-ф. ?(s) лежат на пря-
прямой о=1/2.
После Б. Рнмана проблема значений и, в частности,
нулей Д.-ф. приобрела широкую известность и ей посвя-
посвящено большое число исследований. Гипотезы Римана 2
и 3 были доказаны Ж. Адамаром (J. Hadamard, 1893),
причем оказалось, что в гипотезе 3 а=1'2, 6 = 1
i с1
i с1
-f-—1пя — 1——, где С — Эйлера постоянная; гипотезы 1
и 4 доказаны X. Мангольдтом (Н. Mangoldt, 1894),
к-рый, кроме того, получил, для простых чисел, сле-
следующий важный аналог формулы 5. Если
<F^ = 2< A <")' Т° (*)=у [^ (*-fO) + Y (*-0)Ь
то при
где р={5-Ну пробегает нетривиальные нули Z(s), a
символ 2ржР/р означает предел суммы 2м<У x<>^}
при Т—>-оо. Эта формула, как п формула E), показывает,
что проблема распределения простых чисел в нату-
натуральном ряду тесно связана с расположением нетриви-
нетривиальных нулей функции t(s).
Последняя гипотеза 5 не доказана и не опроверг-
опровергнута. Это — знаменитая Римана гипотеза о нулях
Д.-Ф-
Функция ? (s) однозначно определяется своим функ-
функциональным уравнением. Точнее (см. [4]), любая
функция, представимая обыкновенным рядом Дирихле
и удовлетворяющая уравнению D), при довольно широ-
широких условиях относительно ее регулярности, совпадает
с Z (s) с точностью до постоянного множителя.
При
и постоянном /t>0 для 0<а<1, х>/г, y>h, 2nxy=\t\
имеет место приближенное функцио-
функциональное уравнение
?(> ? + WS +
-f O(x~a) + O(\ t I1''-7y0'1), F)
полученное X. Харди (H. Hardy) и Дж. Литлвудом
(J. Littlewood) в 1920 (см. [4]). Это уравнение играет
значительную роль в современной теории Д.-ф. и ее
приложениях. Существуют общие методы получения
такого рода результатов не только для класса Д.-ф.,
но и вообще функции Дирихле, обладающих функцио-
функциональным уравнением риманова типа C). Наиболее
совершенный из них указан в [5]; в случае J (s) он приво-
приводит, при любом т с |argx| <я/2, к соотношению
г> с- f If
\ — , яп2т
-1 «I"*
где F(z, х) — неполная гамма-функция; при
получается приближенное уравнение F); при т=1 это
соотношение совпадает с исходной формулой C).
Главной проблемой в теории Д.-ф. является проблема
расположения ее нетривиальных нулей и вообще зна-
значений в области 1/2<:о<:1. К числу основных направ-
направлений в исследованиях Д.-ф. относятся: определение
возможно более широкой области слева от прямой <т=1,
где t,(s)=?O; проблема порядка и средних значений Д.-ф.
в критич. полосе; оценки числа нулей Д.-ф. на прямой
а—1/2 и вне этой прямой и т. д.
Первый нетривиальный результат о границе нулей
Д.-ф. был получен Ш. Ж. Балле Пуссеном (Ch. J. La Val-
lee-Poussin) в 1896; он показал, что существует такая
постоянная А >0, что
?(«) ^0 при ossl-—-^—;- с а=э1. G)
1па(| t | + 2)
Дальнейшие продвижения в этом направлении связаны
с приближенным уравнением F) и развитием методов
оценок тригонометрич. сумм.
Самый мощный метод оценок такого рода принадле-
принадлежит И. М. Виноградову (см. Виноградова метод).
Последняя (к 1978) граница области, свободной от
нулей Д--ф., получена И. М. Виноградовым в 1958
(см. [7]). Она имеет вид G) с а>2/3. Для простых чисел
ей соответствует формула
Существует определенная связь между ростом модуля
функции ?, (s) и отсутствием нулей в окрестности прямой
о=1. Так, результат G) с а>2/3 является следствием
оценок
?A + ") = О(Ь2/3М), гаТй) = ОAп2/3|г|)' |<|>2-
С другой стороны, известно (см. [4]), что
т с р с
t —У СО t —*¦ СО
и, если верна гипотеза Римана, то эти пределы, со-
соответственно, не больше, чем 2ес и^ес.
я2
Порядок дзета-функции в крити-
критической полосе есть число т](а), означающее
нижнюю границу таких чисел v, что t,(a-\-it)=O(\t\v).
При сг>1, т)(сг)=О, а при сг<0 имеет место -ц(а)=^—а.
Точные значения функции т)(о") для 0<:о-<1 неизвестны.
Простейшее предположение — Линделёфа гипотеза —
состоит в том, что
Ц(°)~—2, ° ПРИ а^Т и Tl(a)==0 при а > —¦.
Это эквивалентно утверждению, что
-i-+i.')=O(| i|e) для любого б > 0. (8)
При o>V2 справедлива оценка ?(a+^)(|)
Последняя известная (к 1978) оценка ?(s) на прямой
а=1/2 (см. [4]) далека от ожидаемой оценки (8); она
имеет вид
fe -5"
Проблема среднего значения
дзета-функции состоит в определении
свойств функции
при Т—уоо для любого заданного а и fc=l, 2, ... Ре-
Результаты имеют приложения при изучении проблемы
нулей Д.-ф. и непосредственно в теории чисел.
Доказано, что (см. [4])
При a>V2 (см. [4])
^ -^ $ \ 1С
=К Bа),
В случаях &>2 известно только, что при а>1 т
где Тд(л) — число представлений « в виде 4 целых
положительных сомножителей, и что асимптотич. соот-
соотношение
для 0">V2 является эквивалентом гипотезы Линделёфа.
Важное место в теории Д.-ф. занимает проблема
оценки функции N(a, T), означающей число нулей
P-j-jy функции ?(s) при р>сг, 0<Су<-Т. В основе совре-
современных оценок N(o, T) лежат теоремы о выпуклости
средних значений аналитич. функций, применяемые
к функции
Если для нек-рого X=X(a, T),
при Г-^-с» равномерно для а^а, где Z(a) — положи-
положительная невозрастающая функция с ограниченной про-
производной, а т^О — постоянная, то
N(o, Г)=
равномерно для o*;ssa-|-1/ln 71.
Известно также, что если при
то равномерно для 1/2-<а<:1,
N (а, Г) = О(Г2<1+2'-)а-стIп5Г).
Эти два предложения позволили получить (см. [4])
следующие плотностные теоремы о ну-
нулях дзета-функции:
равномерно для о^1/2
N (а, Т) = О (Гз <1-от B-<J) In» Г),
N (а, Т) = О [Т 4 \° 2
с привлечением иных соображений в [8] получена
плотностная теорема:
N(o, Г)=
если справедлива гипотеза Линделёфа, то
Л'(ст, Т) = О(Т2 <
О нулях дзета-функции на прямой
о=112. По гипотезе Римана, все нетривиальные нули
Д.-ф. лежат на прямой а=1/2. Тот факт, что на этой
прямой Д.-ф. имеет бесконечно много нулей, впервые
был доказан X. Харди в 1914 (см. [4]) на основе фор-
формулы Р а м а н у д ж а н а
ее —
cosxtdt = 4y ]_e2 — e - 6 (е~2х)
Последний результат принадлежит А. Сельбергу
(A. Selberg, ¦ 1942; см. [4]): число N0(T) нулей g(s),
имеющих вид 1/2^rit, удовлетворяет неравенству
N0(T) > AT In Т, А >0.
Это означает, что число нулей Д.-ф. на прямой а=1/2
имеет тот же порядок роста, что и число всех ее нетри-
нетривиальных нулей:
jV (T)~±T\nT.
Относительно нулей Д.-ф. на этой прямой известны и
другого рода результаты. Приближенное функцио-
функциональное уравнение позволяет фактически вычислить
(с нек-рой степенью точности) значения ближайших
к действительной оси нулей ?(s). На основе этого ме-
метода на ЭВМ вычислены нули ?(s) в прямоугольнике
0«х«1, 0<гг<1,6-106. Их число равно 3,5-Ю6, и
все они лежат на прямой а=1/2. Ординаты первых
шести нулей с точностью до второго десятичного знака
равны 14,13; 21,02; 25,01; 30,42; 32,93; 37,58.
Вообще, расстояние между соседними нулями Z,(s)
оценивается теоремой Литлвуда A924): для
любого достаточно большого Т функция ?(s) имеет
такой нуль Р+гу, что
\у — Т\ < Л/lnlnlnT.
Обобщенная дзета-функция опреде-
определяется для 0<а<1 рядом
При а= 1 она обращается в дзета-функцию Римана.
Аналитическое продолжение на всю плоскость осущест-
осуществляется формулой
где интеграл берется по контуру L, представляющему
собой путь из бесконечности по верхнему краю разреза
положительной действительной оси до нек-рого фикси-
фиксированного 0<г<2я, затем вдоль окружности радиуса г
против часовой стрелки и снова в бесконечность по
нижнему краю разреза. Функция ?(s, о) регулярна
всюду, кроме точки s=l, где она имеет простой полюс
с вычетом, равным 1. Она играет важную роль в теории
i-функций Дирихле (см. [9], [10]).
Дзета-функция Дедекинда — аналог
дзета-функции Римана для полей алгебраич. чисел,
введенный Р. Дедеюшдом (см. [11]).
Пусть К — поле алгебраических чисел степени
ге=г1-|-2г2>1, где г1— число действительных, г2— чи-
число пар комплексно сопряженных полей в к; пусть да-
далее А — дискриминант, h — число классов дивизоров,
R—регулятор поля к, g — число содержащихся в к
корней из 1.
Дзета-функция Дедекннда Zk(s) поля к определяется
рядом 4
где 31 пробегает все целые отличные от нуля дивизоры
поля к, iV3t — норма дивизора Щ.- Этот ряд абсолютно
и равномерно сходится при a^l + б, б>0, определяя
аналитич. функцию, регулярную в полуплоскости
<х>1.
При а>1 будет
где f{m) — число целых дивизоров поля к с нормой т,
f (т)<:тп(т), т„(то) — число представлений т в виде п
натуральных сомножителей.
При а>1 имеет место тождество Эйлера
где 55 пробегает все простые дивизоры поля к.
Основные свойства дзета-функции
Дедекинда (см. [11]).
1) Sft(s) регулярна на всей комплексной плоскости,
кроме точки s=l, где она имеет простой полюс с вы-
вычетом
2) ?ft(s) удовлетворяет функциональному уравнению
где
3) При r=r1-\-r2—1>0 в точке s=0 функция (
имеет нуль порядка г; ?*@)=^0 при г=0; в точках
s——2v, v=l, 2, ..., дзета-функция Дедекинда ?д.(«)
имеет нули порядка r-j-1, в точках s=—2v—1 при
г2>0 — нули порядка г2, а при г2 = 0 не равна нулю.
Это — тривиальные нули функции ?,k(s).
4) Все остальные нули функции ^(s) лежат в критич.
полосе 0-<а<:1.
Основная гипотеза состоит в том, что все нетриви-
нетривиальные нули функции ?ь(«) находятся на прямой
<х=1/2. Установлено, что tk(s) не имеет нулей на пря-
прямой а=1. Более того, существует абсолютная положи-
положительная постоянная А и зависящая от параметров
поля к постоянная к, обладающие тем свойством, что
?ft(,);?0 При ОЭ»1-;П^-1Г, \t\>X.
Вообще, в случае фиксированных параметров поля к
для ?й (s) имеют место многие результаты, аналогичные
результатам для дзета-функции Римана. Однако в об-
общем случае теория дзета-функции Дедекинда сложнее,
поскольку она включает в себя и теорию Дирихле
L-функций. Так, неизвестно A978), имеют ли дзета-
функции Дедекинда действительные нули между 0 и 1.
Точная зависимость между дзета-функцией Дедекинда
и L-рядами рационального поля имеет следующий вид.
Пусть к*— минимальное поле Галуа, к-рому принад-
принадлежит к, Q — группа Галуа поля к*, h — число клас-
классов группы Q, %i— простые характеры группы Q,
1<г«А. Тогда
U{s) = ^(s)J\h.^2LCi(s; %i, к*),
где ?(s) — дзета-функция Римана, L суть L-ряды Ар-
тина, c,= c,(fc) — целые положительные числа, к-рые
определяются свойствами относительной группы Галуа
поля к*. В частности, если к — круговое расширение,
то к* = к, h=(f(n), c, = l, и L-ряды Артина становятся
обычными Л-рядами Дирихле.
Наряду с дзета-функцией Дедекинда ?ft(s) рассмат-
рассматриваются и t,k(s; Hj) — дзета-функции Де-
декинда класса дивизоров Hj поля к.
Эти функции определяются теми же рядами, что и
t,k(s)i Ho только 21 пробегает не все. а лишь целые
дивизоры, к-рые принадлежат заданному классу Н/.
Функции tt{s; Ну) обладают сво1ствами, близкими
свойствам tk(s). Справедлива формула
Дзета-функции Дедекинда лежат в основе современ-
современной аналитич. теории дивизоров полей алгебрапч.
чисел. Здесь они играют такую же роль, какую играет
дзета-функция Римана в теории чисел рационального
поля.
Аналогом дзета-функции Дедекинда для полей
алгебраич. функций от одного переменного с конечным
полем констант является конгруэнц дзета-
функция, или дзет а-ф ункция Артин а—
Шмидта (см. ниже Дзета-функция в алгебраиче-
алгебраической геометрии).
Лит.: Ш Эйлер Л., Введение в анализ бесконечно ма-
малых, 2 изд., т. 1, пер. с латин., М., 1961; [2] Чебышев
П.Л.,Избр. математические труды. М.—Л.. 1946; [3] РиманБ.,
Соч., пер. с нем., М.—Л., 1948; [4] Т и т ч м а р ш Е. К., Тео-
Теория дзета-функции Римана, пер. с англ., М., 1953; [5] Лав-
р и к А. Ф., «Изв. АН СССР. Сер. матем.», 1968, т. 32, ЛД 1,
с. 134—85; [6] В и н о г р а д о в И. М., Метод тригонометри-
тригонометрических сумм в теории чисел, М., 1971; [7] е г о ж е, «Изв.
АН СССР. Сер. матем.», 1958, т. 22, с. 161—64; [8] М о н т-
г о м е р и X. Л., «Математика», 1970, т. 14, № 5, с. 133—40; [9]
П р а х а р К., Распределение простых чисел, пер. с нем., М.,
1967; [10] Чудаков Н. Г., Введение в теорию L-функций
Дирихле, М.—Л., 1947; [11] Н е с k e E., Mathematische Werke,
Gott., 1959. А. Ф. Лаврик.
2) Д.-ф. в алгебраической геомет-
геометрии — аналитическая функция комплексного пере-
переменного s, описывающая арифметику алгебраич. много-
многообразий над конечными полями и схем конечного типа
над Spec %. Если X — такая схема, X — множест-
множество ее замкнутых точек, a У (х) — число элементов
поля вычетов к (х) точки х?Х, то Д.-ф. Zx(s) задается
эйлеровым произведением
Это произведение абсолютно сходится при Re s>dim X,
допускает мероморфное продолжение в полуплоскости
Re s>dim X—— и имеет полюс в точке s=dim X
(см. [10]). В случае если X = Spec %, то ?,x(s)
есть дзета-функция Рпмана, а если X конечна над
Spec 2, то tx(s) есть дзета-функция Дедекинда чис-
числового поля.
Наиболее изучена ситуация, когда X является
алгебраич. многообразием, определенным над конеч-
конечным полем Fg. В этом случае
.V (х) = gdeg х,
где deg х — степень поля к (х) над полем Fg
и вместо функции t,x(s) обычно рассматривают функцию
Zx(t) такую, что
Если vn — число рациональных точек многообразия X
в поле F п, то оказывается (см. [14]), что
Такие Д.-ф. были введены впервые для случая ал-
алгебраич. кривых (по аналогии с полями алгебрапч.
чисел) в 1924 Э. Артином [1], к-рый заметил, что они
являются рациональными функциями от t и для них
в нек-рых случаях верен аналог гипотезы Римана о ну-
нулях. Этот аналог получил название гипотезы
А р т и н а. Для кривых рода 1 она была доказана
X. Хассе (Н. Hasse) в 1933 (в случае рода 0 ситуация
тривиальна), а для кривых произвольного рода —
А. Вейлем (A. Weil) в 1940 при помощи результатов
теории абелевых многообразий, созданной им в значи-
значительной мере для этой цели (см. [2], [14]).
А. Вейль [2] рассмотрел Д.-ф. произвольных алге-
алгебраич. многообразий и высказал гипотезы, обобщающие
результаты, полученные к тому времени для кривых.
Его исследования основаны на следующем замечании —
множество точек многообразия X, рациональных над
Fqa, является множеством неподвижных точек я-й степе-
степени Фробениуса эндоморфизма этого многообразия. Пер-
Первая гипотеза Вей л я состоит в том, что в ка-
категории алгебраич. многообразий над конечными поля-
полями существует теория когомологий, удовлетворяющая
всем формальным свойствам, необходимым для получе-
получения Лефшеца формулы. Если {Н'(Х)} — группы кого-
мологпп такой теории, то из формулы Лефшеца следует,
что
где n=dim X, a Pj(t) — характеристич. многочлены
отображений, индуцированных эндоморфизмом Фробе-
Фробениуса на Вейля когомологиях Н'(Х). В частности, функ-
функция Zx(t) рациональна.
Вторая гипотеза Вейля состоит в том,
что функция ?хМ должна удовлетворять функциональ-
функциональному уравнению, имеющему в случае гладкого проек-
проективного многообразия X вид
где х — эйлерова характеристика. равная
2 (—l)'dim. Hl(X). (Эта гипотеза является формальным
следствием существования теории когомологий.) Раци-
Рациональность ^-функции для любых X доказана Б. Двор-
ком [6] методом, не использующим когомологий. Теория
когомологий, предсказанная А. Вейлем, была создана
А. Гротендиком (A. Grothendieck) в 1958 (см. Вейля ко-
когомологий, Топологизированная категория, l-адические ко-
когомологий). А. Гротендик вместе с М. Артином (М. Artin)
доказал обе гипотезы Вейля для гладких проективных
многообразий, причем многочлены Рi(t) имели, вообще
говоря, целые Z-адические коэффициенты, зависящие от
выбора простого I, положенного в основу теории. Пред-
Предполагается, что на самом деле коэффициенты являются
целыми числами, не зависящими от I и вообще от выбора
теории когомо'логий. Это высказывание обычно наз.
третьей гипотезой Вейля, Наконец, по-
последняя — четвертая гипотеза Вейля от-
относится к нулям а,- многочленов P,{t), рассматриваемым
как целые алгебраич. числа (гипотеза Р и м а н а):
Все эти гипотезы доказаны П. Делинем [4].
Основные применения гипотез Вейля в теории чисел
относятся к изучению сравнений. Уже в случае кривых
из теоремы Вейля вытекала наилучшая оценка для ра-
рациональной тригонометрич. суммы от одной переменной
(см. [14]). Эти оценки были обобщены на суммы от любо-
любого числа переменных. Другим важным приложением
этой теории являются оценки коэффициентов Фурье
модулярных форм (проблема Рамануджана — Петер-
сона, см. [4], [15]).
Приведенные результаты являются на самом деле ча-
частными случаями гораздо более общих теорем, относя-
относящихся к произвольным L-функциям, к-рые связаны с
представлениями групп Галуа накрытий многообразия
X или, более общо, с нек-рым 2-аднческим пучком на X
(см. [5], [10]). Эти функции служат на произвольных
схемах аналогом известных в теории алгебраич. чисел
//-функций.
Пусть теперь X — схема конечного типа над Spec 2
такая, что ее общий слой X@ZQ является непустым ал-
гебраич. многообразием над полем рациональных чисел
Q. Существует предположение, что Д.-ф. ?,x(s) имеют
мероморфные продолжения на всю s-плоскость и удов-
удовлетворяют функциональному уравнению. Гипотетич.
вид этого уравнения предложен в [11]. Доказать эту
гипотезу удалось пока A978) лишь в очень специальных
случаях (рациональные поверхности, алгебранч. кри-
кривые, униформизуемые модулярными функциями, абеле-
вы многообразия с комплексным умножением, см. [15]).
Что касается аналога гипотезы Римана, то он в этой си-
ситуации даже не сформулирован.
Новый круг идей в изучении Д.-ф. принесли работы
Дж. Берча (J. Birch), П. Суиннертон-Дайера [12] и Дж.
Тейта [13]. Чтобы сформулировать принадлежащие им
гипотезы, следует заметить, что функция t,x(s) являет-
является произведением Д.-ф. t,x (s) слоев Хр отображения
X->-Spec %. Для последних, являющихся многообра-
многообразиями над конечными полями, имеется, согласно пер-
первой гипотезе Вейля, разложение на многочлены. По-
После перемножения этих разложений получается ана-
аналогичное представление для Д.-ф.
Гипотеза Берча и Суиннертон-Дайера предполагает, что
порядок нуля функции ?x'(s) в точке s=dim X—1 равен
рангу группы рациональных точек многообразия Пика-
ра Pic X (конечному, в силу теоремы Морделла —
Вейля). Эта гипотеза, тем самым, предполагает справед-
справедливость гипотезы о мероморфном продолжении Д.-ф.
В первоначальной форме гипотеза Берча и Суиннер-
Суиннертон-Дайера была высказана для эллиптич. кривых над
полем Q в результате изучения обширных таблиц для
кривых с комплексным умножением [12]. В дальнейшем
было высказано предположение о значении коэффициен-
коэффициента при соответствующей степени переменной s в разло-
разложении функции Z,x\s) в окрестности точки s=dim X — 1.
Предполагается, что он равен
[Ш] | det(a,-. a/ I
[Pic Xtors] [Pic- Jftorsj •
где [Ш] — предполагаемый конечным порядок группы
Шафаревича — Тейта локально тривиальных главных
однородных пространств многообразия Pic X, |det(aj,
я,-)| — определитель билинейной формы на группе ра-
рациональных точек многообразия Pic X, получающийся
из высоты точки, [Pic XtOrsl и [Pic'^torsl — порядки
подгрупп кручения в группе рациональных точек на
Pic X и двойственном абелевом многообразии. Это вы-
выражение обобщает хорошо известное в теории алгебра-
ич. чисел выражение для вычета дзета-функции Деде-
кинда в точке s=l. Одной из трудностей на пути к дока-
доказательству гипотезы Берча и Суиннертон-Дайера яв-
является тот факт, что группа Ш полностью не вычислена
A978) ни для одной кривой. Доказан аналог этой гипо-
гипотезы для кривых, определенных над полем функций, од-
однако и в этом случае пришлось предположить конеч-
конечность Врауэра группы, играющей здесь роль группы III
(см. [5]).
Дж. Тейт [13], изучая действие группы Галуа на ал-
алгебранч. циклы многообразий, выдвинул гипотезы о по-
полюсах функций ?,x\s) при четных значениях г, а именно,
что функция ?,XL){S) 11Меет в точке s= г-fl полюс порядка,
равного рангу группы алгебраич. циклов коразмерно-
коразмерности I. Это утверждение тесно связано с гипотезой Тейта
об алгебраич. циклах. По поводу имеющихся подходов
к доказательству этих гипотез, а также различных аргу-
аргументов в их пользу см. [5], [7], [12], [13], [17].
Независимо от описываемого здесь понятия Д.-ф.
в теории алгебраич. групп и автоморфных функций воз-
возникли и изучались Д.-ф., являющиеся преобразования-
преобразованиями Меллина модулярных форм. В 1967 А. Вейль заме-
заметил, что из общих гипотез о функции c'x^s) для эллип-
тич. кривой X над Q вытекает, что кривая X униформи-
зуется модулярными функциями, а функция ?$'($) есгь
преобразование Меллина модулярной формы, отвечаю-
отвечающей дифференциалу рода 1 на X. Это замечание привело
к предположению о том, что функции tjp(s) любой схе-
схемы X являются преобразованиями Меллина подходя-
подходящих модулярных форм. Основные результаты в этом
направлении были получены Э. Жаке и Р. Ленглендсом
(см. [7], [9]). В частности, они построили широкий класс
рядов Дирихле, удовлетворяющих нек-рому функцио-
функциональному уравнению и разлагающихся в эйлерово про-
произведение, к-рые можно представить в виде преобразова-
преобразования Меллина модулярных форм на группе GLB). Вы-
Выполнимость условий их теоремы непосредственно свя-
связана с приведенными выше гипотезами об общих свой-
свойствах Д.-ф. Пока их удается проверить лишь для кри-
кривых, определенных над полем функций.
Начиная с 1970 под влиянием работ о р-адических
Д.-ф. полей алгебраич. чисел (см. [14]) возникает ана-
аналогичный подход и к Д.-ф. схем, главным образом эллип-
тич. кривых. Имеющиеся здесь проблемы, во многом,
похожие на рассмотренные выше, отражены в [9]. Д.-ф.
эллиптич. кривой над Q тесно связана с одномерной,
формальной группой кривой и они полностью друг дру-
друга определяют [16].
Лит.: [1] А г t i n E., «Math. Z.», 1924, Bd 19, S. 153—246;
[2] Weil A., Sur les courbes algebriques et les varietes qui
s'en deduisent, P., 1948; [3] e г о ж е, «Bull. Amer. Math. Soc»,
-- --- -- --- "n ~eligne P., «Publ. Math.
sen deduisent, P., 1948; 13J e г о ж с
1949, v. 55, Jsli 5, p. 497—508; [4] D ^ ...... .
IHES», 1974, t. 43, p. 273—307; [5] Dix exposes sur la cohomolo-
gie des schemas, Amst.—P., 1968; [6] D w о г к В., в кн.: Pro-
Proceedings of the International Congress of Mathematicians,
Djursholm, 1963, p. 247—59; [7] Жаке Э., Ленглендс
P., Автоморфные формы на GL B), пер. с англ., М., 1973; [81
М а н и н Ю. И., «Успехи матем. наук», 1971, т. 26, в. В, с.
7—71; [9] Modular functions of one variable, В., 1973; [10}
С е р р Ж.-П., «Успехи матем. наук», 1965, т. 20, J* 6, с. 19—26;
[11] его же, «Математика», 1971, т. 15, Л! 1, с. 3—13; [12]
Свиннертон-Дайер П., «Математика», 1969, т. 13,
ЛГ« 5, с. 3—25; [13] Т э й т Д., «Успехи матем. наук», 1965, т.20,
Л» 6, с. 27—40: [14] Ш а ф а р е в и ч И. Р., Дзета-функция,
М., 1969; [15] ШимураГ., Введение в арифметическую
теорию автоморфных функций, пер. с англ., М., 1973; [161
X о н д а Т., «Математика», 1969, т. 13, Ы 6, с. 3—17; [17] Итоги
науки. Алгебра. Топология. Геометрия. 1970, М., 1971, с. 111—51.
А. Н. Паршин.
ДИАГОНАЛИЗИРУЕМАЯ АЛГЕБРАИЧЕСКАЯ
ГРУППА — аффинная алгебраич. группа G, изоморф-
изоморфная замкнутой подгруппе алгебраического тора. Таким
образом, G изоморфна замкнутой подгруппе мультипли-
мультипликативной группы всех диагональных матриц нек-рого
фиксированного порядка. Если G определена над полем к
и указанный изоморфизм определен над к, то Д. а. г.
G наз. разложимой (или расщепимой) над к.
Всякая замкнутая подгруппа Я в Д. а. г. G, а также
образ G при любом рациональном гомоморфизме ф яв-
являются Д. а. г. Если к тому же группа G определена и
разложима над полем к, а ф определен над к, то и Н и
ф(б) определены и разложимы над к.
Д. а. г. G разложима над к тогда и только тогда, когда
каждый элемент из группы G всех ее рациональных ха-
характеров является рациональным над к. В случае, если
в G нет неединичных рациональных над к элементов,
Д. а. г. G наз. анизотропной над к. Всякая
Д. а. г. G, определенная над полем к, разложима над
нек-рым конечным сопарабельным расширением поля к.
Д. а. г. G связна тогда и только тогда, когда она яв-
является алгебраич. тором. Связность G эквивалентна
также отсутствию кручения в группе G. Для произволь-
произвольной Д. а. г. G, определенной над к, группа Gявляется
конечно порожденной абелевой группой, не имеющей
р-кручения, где р — характеристика поля к.
Произвольная определенная и разложимая над полем
к Д. а. г. G является прямым произведением конечной
абелевой группы и алгебраич. тора, определенного и
разложимого над к. В любой связной определенной над
полем к Д. а. г. G имеется наибольший анизотропный
подтор Ga и наибольший разложимый над к подтор G^,
для которых G=GaGd и GaHCrf — конечное множество.
Если Д. а. г. G определена над полем к и Г — группа
Галуа сепарабельного замыкания поля к, то G снабжает-
снабжается непрерывным действием группы Г. Если при этом
ф: G-+H — рациональный гомоморфизм двух Д. а. г., при-
причем G, Н и ф определены над полем к, то ипдуцирован-
ный ф гомоморфизм ф: Я—>-G является Г-эквнвариант-
ным (т. е. является гомоморфизмом Г-модулей). Возни-
Возникающий таким образом контравариантный функтор из
категории дпагонализируемых /с-групп и их А-морфиз-
мов в категорию конечно порожденных абелевых групп
без р-кручения с непрерывным действием группы Г и их
Г-эквивариантиых гомоморфизмов оказывается эквива-
эквивалентностью указанных категорий.
Лит.: [1] Бор ель А., Линейные алгебраические груп-
группы, пер с англ., М., 1972; [2] О п о Т. «Ann Math.», 1961,
Л'. 74, Л» 1, р. 101 — 39. В. Л. Попов.
ДИАГОНАЛЬ —отрезок прямой,соединяющий две вер-
вершины многоугольника (многогранника), не лежащие на
одной стороне (на одной грани). Если число вершин мно-
многоугольника равно п, то число его Д. равно п(п—3)/2.
Е. В. Шикин.
ДИАГОНАЛЬНАЯ ГРУППА — группа невырожден-
невырожденных диагональных матриц. Группа матриц, сопряжен-
сопряженная с Д. г., наз. диагонализируемой ли-
линейной группой.
Лит.: [1] КаргаполовМ. И., МерзляковЮ. И.,
Основы теории групп, 2 изд., М., 1977. Ю. И. Мерзляков.
ДИАГОНАЛЬНАЯ МАТРИЦА — квадратная матри-
матрица, у к-рой все элементы, кроме, быть может, элементов
главной диагонали, равны нулю. о. А. Иванова.
ДИАГОНАЛЬНАЯ ПОДГРУППА — подгруппа де-
1:артовой степени данной группы G, состоящая из всех
элементов с одинаковыми компонентами. Напр., Д. п.
произведения GXG — это группа пар (g, g), g?G.
Ю. И. Мерзляков
ДИАГОНАЛЬНАЯ ЦЕПНАЯ ДРОБЬ — цепная дробь
у к-рой последовательности {ап}п=о и {Ьп}?1=1 должны
удовлетворять следующим условиям:
1) числа ап и Ьп целые; |6„| = 1; я„^1, если ra^l; ащ^
^s2, если 0<ш<оо;
2) &„+яп>1 для всех п; если ш=оо, то 6,,-f а„>2 для
бесконечного множества п;
3) Qn<Qn + i Для всех п\
4) все подходящие дроби цепной дроби суть все не-
несократимые дроби -д- такие, что \r—^-\ <^i и В>0, где
г — значение цепной дроби.
Для каждого действительного числа г существует од-
одна и только одна Д. ц. д., значение к-рой равно г; эта
дробь периодична, если г — квадратическая иррацио-
иррациональность, в. И Нечаев
ДИАГОНАЛЬНО КЛЕТОЧНЫЙ ОПЕРАТОР отно-
относительно данного ортогонального разложения Н=
=ift>1©^' гильбертова пространства Н — линейный
оператор А в Н, оставляющий инвариантными каждое
из подпространств Hk, k~^\. Спектр оператора А есть
замыкание объединения спектров «клеток» A\H^=Af,^
kl ||/4||=sup \\A i;\\. Д. к. о. в итипоком смысле — это
оператор А умножения на функцию к в прямом
грале гильбертовых пространств
пнт&
При этом k(t) — линейный оператор, действующий в
пространстве H(t). Каждый оператор, перестановочный
с нормальным оператором, есть Д. к. о. относительно
спектрального разложения этого оператора. См. также
Диагональный оператор.
Лит.: ll] H а й м а р к М. А., Нормированные кольца,
2 изд М 1908 § 41. Н. К. Никольский, Б. С. Павлов.
ДИАГОНАЛЬНОЕ КОЛЬЦО замкнутого симметрич-
симметричного кольца R ограниченных линейных операторов
гильбертова пространства Н — коммутативное банахо-
банахово симметричное кольцо Е операторов в Н такое, что
(R\JE)' = E. Д. к. используется для разложения кольца
операторов на неприводимые.
Лит.: [1] Н а й ы а р к М. А., Нормированные кольца,
2 изд., М., 1968. М. И. Войцеховский.
ДИАГОНАЛЬНОЕ ПРОИЗВЕДЕНИЕ ОТОБРАЖЕ-
ОТОБРАЖЕНИЙ /а : Х->-Га, а?%, — отображение / : Z-v^=
= n{Ya, <x?2I}, определяемое равенством f(x)=
— {fa(x)}?Y. Д. п. о. /а удовлетворяет для любого а
соотношению/а = яа/, где яа обозначает проектирование
произведения Уна сомножитель Ya. Диагональное про-
произведение непрерывных отображений непрерывно. Семей-
Семейство отображений fa: X—>Ya наз. расчленяющим,
если для любой точки х ? X и всякой ее окрестности Ох
существует такой индекс а и такое открытое подмноже-
подмножество UaCZYa, что x^f^Ua^Ox. Если {fa: X-+Ya} —
расчленяющее семейство отображений и / есть Д. п. о.
fa, то/ является вложением пространства X в произве-
произведение яУ<х, т. е. / : X—>fX — гомеоморфизм. Д. п. о.
было применено А. Н. Тихоновым для вложения вполне
регулярного пространства веса т в куб Iх. в в Федорчук
ДИАГОНАЛЬНЫЙ ОПЕРАТОР — оператор D, оп-
определенный на линейной оболочке базиса {e^}k^i B нор-
нормированном (или только локально выпуклом) простран-
пространстве X равенствами Deft=X^ei!, /с^1,Я/, — комплексные
числа. Если D — непрерывный оператор, то
sup | Xk \ < + оо;
k > 1
если X — банахово пространство, то это условие в том
и только в том случае равносильно непрерывности
D, когда {«ft}ft>i — безусловный базис в X. Если
{e'<}fe>l — ортонормированный базис в гильбертовом
пространстве Н, то D — нормальный оператор, причем
||.D||=sup |Я,й1, а спектр D совпадает с замыканием мно-
жества {Х^. к=1, 2, . . .}. Нормальный и вполне непре-
непрерывный оператор Л' является Д. о. в базисе своих собст-
собственных векторов; сужение (даже нормального) Д. о.
на его инвариантное подпространство не обязательно,
вообще говоря, будет Д. о.; любой нормальный опера-
оператор N в сепарабельном пространстве // при любом е>0
может быть представлен в виде ЛГ=Д + С, где D — Д. о.,
С — вполне непрерывный оператор и ||С||<е.
Д. о. в широком смысле слова — это оператор D ум-
умножения на комплексную функцию к в прямом интегра-
интеграле гильбертовых пространств
QH (t) d\i (t),
т. е.
(Df) (t) = k(t)f (t), t?M;
См. Диагонально клеточный оператор.
Лит.: [1] Singerl., Bases in Banach spaces, v. I, B.,
1970; [2] Wermor J., «Proc. Amer. Math. Soc», 1952, v. 3,
JMi 2, p. 270—77; [3] В erg I. D., «Trans. Amer. Math. Soc»,
1971, v. 160, p. 365—71. H. К. Никольский, Б. С. Павлов.
ДИАГОНАЛЬНЫЙ ПРОЦЕСС — метод построения
по последовательности, состоящей из последовательно-
последовательностей
а*=(«ги ai2, ais, •••). i = l, 2, 3, ...
последовательности a=(a1, a2, a3, . . .), где ац^ац для
любых i=l, 2, 3, ... , либо o,-=a,-,- для всех t. Д. п. в
первой форме в 1874 применил Г. Кантор (см. [1]) при
доказательстве несчетности множества действительных
чисел из отрезка [0, 1], поэтому его часто наз. к а н т о-
р о в ы м Д. п. Вторая форма Д. п. применяется в тео-
теории функций действительного и комплексного перемен-
переменного для выделения из ограниченного на множестве Е
семейства функций последовательности функций, схо-
сходящейся на счетном подмножестве из Е.
Д. п. перенумерации ставит в соответствие кратной
последовательности {а^}, i== 1,2,3,...; k=l, 2, 3, . .. ,
последовательность Оц, а12, я21; . . . ; а/ц, я^-1,2' • • • »
ak-iu + ь • • ¦ > aik\ ¦ ¦ ¦ и применяется, напр., для доказа-
доказательства счетности счетного множества счетных мно-
множеств (см. [2]).
Лит.: [1] CantorG., Gesammelte Abhandlungen, В.,
1932 («J. reine und angew. Math.», 1874, Bd 77, S. 258—62);
[2] Колмогорова. Н., Фомин С. В., Элементы тео-
Fiih функций и функционального анализа, 4 изд., М., 1976;
3] Петер Р., Рекурсивные функции, пер. с нем., М., 1954,
§§ 11, 19; [4] К л и н и С. К., Математическая логика, пер. с
англ., М., 1973, §§ 33, 34; [5] Ш ё н ф и л д Д ж. Р., Матема-
Математическая логика, пер. с англ , М., 1975, §§ 6.8, 7.5—7.9, 9.2—
9.4. Ю. Н. Субботин.
ДИАГРАММА в категории С — отображение
D ориентированного графа Г с множеством вершин /
и о множеством дуг U в категорию С, при котором
D (I) cz Ob F), D (U) а Мог F),
причем D(u)?Hom(D(i), D(j)), если дуга u?U имеет
начало г и конец /. Иногда под диаграммой в С понимает-
понимается образ отображения D, что позволяет использовать
наглядное изображение диаграммы.
Пусть <р=(и1, ... , ип) — ориентированная цепь гра-
графа Г с началом I и концом /, т. е. непустая конечная по-
последовательность дуг, в к-рой началом каждой дуги
служит конец предыдущей; и пусть D (ф): D(i)->-D(i)
означает композицию морфизмов:
D(un)o. ..оЩщ).
Диаграмма D называется коммутативной,
если?)(ф)=1)(ф') всякий раз, как фиф', являются ори-
ориентированными цепями с одним и тем же началом и
концом.
Наиболее часто встречаемые виды Д.— это после-
последовательности, треугольные диаг-
диаграммы и квадратные диаграммы. Для
определения последовательности за опре-
определяющий граф берется граф вида
и1 "п-Т
Соответствующая Д. изображается следующим образом;
I 2 *~ • • • *- &п-\ *~Ап *
здесь Ak=D (i/j) — объекты категории С, a fk=lD (u^) —
морфизмы этой категории.
Треугольная Д. в категории С соответствует
графу
'2
и изображается:
Коммутативность этой Д. означает, что /3—Л!
Квадратная Д. соответствует графу
и изображается:
Коммутативность этой Д. означает, что /2°/i=/3/4-
Класс Д. с одним и тем же графом Г образует катего-
категорию. За морфизм диаграммы D в диаграмму D' прини-
принимается семейство морфизмов v,- : D (г)—*-.D'(i), где i про-
пробегает множество вершин графа Г, что для любой дуги
и с началом i и концом / выполняется условие D'(u)^vi=
— Vj°D(u). В частности, можно говорить об и з о м о р ф-
н ы х Д. Любую категорию можно представить как
категорию диаграмм с нек-рым графом. Иногда граф Г
наз. схемой диаграмм в С.
Лит.: [1] Гротендик А., О некоторых вопросах гомо-
гомологической алгебры, пер. с франц., М., 1961. И. В. Долгачев.
ДИАДА — аффинор в гильбертовом пространстве-
хМа, х)Ь,
где а, Ь — некоторые постоянные векторы, (•, •) — ска-
скалярное произведение. Значение Д. состоит в том, что,
напр., в n-мерном пространстве всякий аффинор А пред-
представляется в виде суммы не более чем п Д.:
(в произвольном гильбертовом пространстве подобное
разложение имеет место для частных классов линейных
операторов, напр. для самосопряженных операторов,
причем а; и Ь' образуют биортогоналъную систему).
В 19 в. делались попытки положить понятие Д. в основу
теории аффиноров — так называемое «диадное исчис-
исчисление», в настоящее время термин Д. малоупотреби-
малоупотребителен.
Лит.: [1] Д у б н о в Я. С, Основы векторного исчисления,
4 изд., ч. 1,2, М.—Л., 1950—52; [2] Л а г а л л и М., Векторное
исчисление, пер. с нем., М.—Л., 1936; [3] Ч е п м е н С, К а у-
лингТ., Математическая теория неоднородных газов, пер.
с англ., М., 1960. М. И. Войцеховский.
ДИАДИЧЕСКИЙ БИКОМПАКТ — бикомпакт, яв-
являющийся непрерывным образом обобщенного канторо-
канторова дисконтинуума. Д. б. были введены П. С. Александ-
Александровым в связи с естественной попыткой обобщить на
произвольные бикомпакты теорему о том, чтр каждый
компакт является непрерывным образом канторова мно-
множества. Класс Д. б.— наименьший класс бикомпактов,
содержащий все метрич. компакты и замкнутый отно-
относительно тихоновского произведения и непрерывного
отображения. Свойства Д. б. Всякая бикомпакт-
бикомпактная топологич. группа диадична. Д. б. удовлетворяет
Суслина условию и, более того, всякое регулярное карди-
кардинальное число Ittjs^fo является калибром Д. б. (см. Ка-
либр пространства!. Отсюда вытекает существование
недиадич. бикомпактов. Таковы, напр., все бикомпакты
Александрова несчетной мощности (бикомпактифика-
ция одной точкой бесконечных дискретных пространств).
В Д. б. всякое канонич. замкнутое множество и всякое
замкнутое множество типа вь являются Д. б. Всякая
неизолированная точка Д. б. есть х-точка. Более того,
если характер точки х?Х равен т^#0, то в X содер-
содержится бикомпакт Александрова мощности ш, вершина
к-рого совпадает с т. Вес бесконечного Д. б. равен верх-
верхней грани характеров его точек, а я-вес Д. б. равен его
весу. Всякий экстремально несвязный Д. б. состоит из
конечного множества точек. Существуют разнообразные
критерии метризуемости Д. б. В частности, Д. б. X
метризуем, если выполнено одно из следующих усло-
условий: X удовлетворяет первой аксиоме счетности; X яв-
является непрерывным образом упорядоченного биком-
бикомпакта; X наследственно нормален; X наследственно ди-
адичен; X является пространством Фреше — Урысона;
X наследственно сепарабелен; X является факторпрост-
ранством метрич. пространства.
Лит.: [1] EngelkingR., An Outline of General Topo-
Topology, Amst., 1968; [2] К е л л и Д ж. Л., Общая топология,
пер. с англ., М., 1968: [3] Е ф и м о в Б. А., «Тр. Моек, матем.
о-ва», 1965, т. 14, с. 211 — 47.
А. В. Архангельский, Б. А. Ефимов.
ДИАДИЧЕСКОЕ ПРОСТРАНСТВО — тихоновское
пространство, для к-рого существует бикомпактное рас-
расширение, являющееся диадическим бикомпактом.
Класс Д. п. содержит все сепарабельные метрич. про-
пространства и замкнут относительно тихоновских произ-
произведений. На Д. п. переносится ряд свойств диадич. би-
бикомпактов. Напр., всякая псевдокомпактная группа ди-
адична, но существуют недиадические финально ком-
компактные группы. Д. п. удовлетворяет С целина условию,
но не всякое регулярное кардинальное число n^^fo
является калибром Д. п. В Д. п. диадично всякое кано-
канонич. замкнутое множество, но не всякое замкнутое G&.
Д. п., удовлетворяющее первой аксиоме счетности, мет-
ризуемо, но существуют неметризуемые наследственно
нормальные Д. п., наследственно сепарабельные Д. п.
Лит.: [1] ПономаревВ. И., «Fundam. math.», 1963,
t. 52, ,N5 3, p. 351—54: 1.2] E ф и м о в Б. А., «Докл. АН СССР»,
1963, т. 151, JV» 5, с. 1021—4. Б. А. Ефимов.
ДИАМЕТР — 1) Д. линии второго поряд-
порядка — прямая, проходящая через середины параллель-
параллельных хорд. Д. наз. сопряженным относительно
хорд (а также направлений корд), к-рые он делит попо-
пополам. Д. центральных линий второго порядка пересе-
пересекаются в центре линии; у нецентральных линий второго
порядка Д. параллельны или совпадают. Д. эллипса и
гиперболы — прямые, проходящие через их центр, Д.
параболы — ось параболы и прямые, параллельные
оси.
2) Д. множества в метрич. пространстве —
точная верхняя грань расстояний между парами точек
множества. А. Б. Иванов.
ДИВЕРГЕНЦИЯ, р а с х о ж д е и и е, векторного
поля а(х) в точке (.г1. . . . , х") — скалярная величина
5w ¦'<•>¦
где а'(х) — компоненты вектора а(х).
Д. обозначается div a{x) или в виде скалярного про-
произведения (у, а) Гамильтона оператора у= ( —- , . . . ,
—- ) на вектор а(х).
Если векторное поле а (х) есть поле скоростей устано-
установившегося течения несжимаемой жидкости, то div а (х)
совпадает с интенсивностью источников (div а >0) или
стоков (div«<0) в точке х.
Интеграл
i div (pa) dx,
где р — плотность жидкости, вычисленный для «-мер-
«-мерной области Е, равен количеству жидкости, «расходя-
«расходящейся» в единицу времени из Е. Это количество (см.
Остроградского формула) совпадает с величиной
где \=(N1, ... , Nn) — единичный вектор внешней
нормали к дЕ, ds — элемент площади дЕ. Д. div «(ж)
является производной по объему потока поля а (х) через
замкнутую поверхность:
[(N, a) ds при Е -+ х.
Таким образом, Д. носит инвариантный относительно
выбора системы координат характер.
В криволинейных координатах у={ух, ¦ ¦ ¦ , Уп), yi=
j() 1
где
а */(y) — орт. касающийся i-ii координатно11 линии в
точке у:
. . 1 ду
S(y) W^
Д. тензорного поля
а (х) = I а У ' ' .Р (х), 1 sg: ia , /p «S П \
типа (р, q), заданного в области «-мерного аффинного
пространства связности, определяется с помощью абсо-
абсолютных (ковариантных) производных компонент а (х)
с последующей сверткой и является тензором типа (р—1.
q) с компонентами
В тензорном анализе и дифференциальной геомет-
геометрии Д. называется также дифференциальный опера-
оператор, действующий в пространстве дифференциальных
форм л связанный с оператором внешнего дифференци-
дифференцирования.
Лит.: [1] К о ч и н Н. Е., Векторное исчисление и начала
тензорного исчисления, 9 изд., М., 1965; L2] Р а ш е в с к и ii
П. К., Риманова геометрия и тензорный анализ, 3 изд., М.,
1967. Л. П. Купцов.
ДИВИЗОР — обобщение понятия делителя элемента
коммутативного кольца. Впервые (под назв. «идеальный
делитель») это понятие возникло в работах Э. Куммера
[1] об арифметике круговых полой.
Теория Д. для коммутативного кольца А с единицей
без делителей нуля состоит в построении гомоморфизма
ф из мультипликативной полугруппы А * ненулевых
элементов А в нек-рую полугруппу Do с однозначным
разложением на множители, элементы к-рой наз. (ц е-
л ы ми) дивизорами кольца А. Теория Д. поз-
позволяет свести ряд вопросов, связанных с разложением
на простые множители в кольце А, где это разложение
может быть неоднозначно, к рассмотрению разложение
на простые множители в Do. Образ (p(a)?D0 элемента
а?А* обозначается (а) и наз. главным дивизо-
р о м алемента а. Говорят, что а?А* делится на Д.
a?D0, если а делит (а) в До-
Точнее, пусть Do — свободная абелева полугруппа с
единицей, свободные образующие к-рой наз. просты-
простыми дивизорами, и пусть задан гомоморфизм
ф: A*—>-Do. Гомоморфизм ср определяет теорию Д. коль-
кольца А, если он удовлетворяет следующим условиям.
1) Для о, &?А* элемент а делит Ъ в кольце А тогда
и только тогда, когда (а) делит F) в Do.
2) Для любого u?D0
{О, а?А\й делит (а)}
является идеалом кольца А.
3) Если а, а'??>0 и для любого а?А* (а) делится
на а тогда и только тогда, когда (а) делится на а', то
а=а'.
Этими условиями гомоморфизм ф, если он существу-
существует, определяется однозначно с точностью до изоморфиз-
изоморфизма. Ядро кег ф совпадает с группой единиц кольца А.
Элементы из Do наз. положительными Д.
кольца А. Пусть К — поле частных кольца А и DZ3D0—
свободная абелева группа, порожденная множеством
простых Д. Тогда для любого с?К*, К* = К\0, можно
определить главный дивизор (c)?D. Если с=
= a/b, где а, Ь?А*, то (с) = (а)/F). Элементы группы D
наз. дробными дивизорами (или просто
дивизорами) кольца А (или поля К). Каждый Д.
a?D может быть записан в виде
где pi — простые Д. Либо (в аддитивной записи):
Если a? А'* н (а) = 2ге,ф,-, то отображение a—>-Zn,- являет-
является дискретным нормированием на поле К, наз. суще-
существенным нормированием поля К. Гомо-
Гомоморфизм ср продолжается до гомоморфизма г|з: K*^>-D,
где г|;(с)— (с), содержащегося в точной последователь-
последовательности
1 —+ U (А) —>- К* -^ D ^ C(A) —el.
Здесь U(А) — группа единиц кольца А, а группа С(А)
наз. группой классов дивизоров коль-
кольца А (или поля К). Два Д., принадлежащие одному
смежному классу по подгруппе главных Д., наз. экви-
эквивалентными (в алгебраической геометрии, где
рассматривается целый ряд других эквивалентностей
для Д., эта эквивалентность называется лине й-
н о й).
Теория Д. существует для всякого дедекиндова коль-
кольца, в частности, для колец целых элементов в полях ал-
алгебраич. чисел, причем в этом случае элементы Do нахо-
находятся во взаимно однозначном соответствии с ненулевы-
ненулевыми идеалами кольца А (Д. а при этом соответствует
идеал всех элементов А, делящихся на а). По этой
причине в дедекиндовых кольцах группу Д. наз. также
группой идеалов, а группу классов Д.—
группой классов идеалов.
Группа классов Д. поля алгебраич. чисел конечна, и с
вычислением ее порядка (числа классов) и структуры
связаны многие задачи алгебраической теории чисел
(см. [2)).
Более общо, теория Д. существует для Крулля колец
(см. [11]). В этом случае роль Do играет полугруппа ди-
визориальных идеалов кольца, а роль D играет группа
дробных дивизориальных идеалов.
Обобщением понятия дробного дивизориального иде-
идеала коммутативного кольца на случай алгебраич. много-
многообразия или аналитич. пространства служит понятие
дивизора Вейля. Так называется целочислен-
целочисленная формальная конечная линейная комбинация 2 nwW
неприводимых замкнутых подпространств W в X кораз-
коразмерности 1. Дивизор Вейля наз. положительным, или
эффективным, если все rc^JsO. Все дивизоры Вейля об-
образуют группу Z'(X) (группа дивизоров В е й-
л я). В случае, когда X — гладкое алгебраич. многооб-
многообразие, понятие дивизора Вейля совпадает с понятием ал-
алгебраического цикла коразмерности 1.
Если А — нётерово кольцо Крулля, то каждый про-
простой дивизориальный идеал |) в/( определяет подпро-
подпространство F(p) коразмерности 1 в схеме X=Spec(^), a
каждый Д. а = !р™', ... , ркк может быть отождествлен
тем самым с дивизором Вейля 2;г,7(^).
Пусть X — нормальная схема, а / — мероморфная
функция на X. Каноническим образом определяется
главный дивизор Вейля:
Здесь поесть значение дискретного нормирования коль-
кольца Ox, w общей точки подмногообразия W на пред-
представителе / в Ох, №• Если
где nu7>0, а в^,<0, то дивизор Вейля (/H=2nJ'VF наз.
дивизором нулей, a 2,nwW — дивизором
полюсов функции /. Множество главных ди-
дивизоров Вейля является подгруппой Z),(X) группы
Z1(X). Факторгруппа Z1(X)IZlp(X) обозначается С(Х) я
наз. группой классов дивизоров схемы X.
Если X=Spec А, где А — нётерово кольцо Крулля, то
С(Х) совпадает с группой классов Д. кольца А.
Пусть К — поле алгебраич. функций. Д. поля К наз.
иногда формальные конечные целочисленные комбина-
комбинации дискретных нормирований ранга 1 поля К. Если К
есть поле алгебраич. функций от одной переменной, то
каждый такой Д. может быть отождествлен с дивизором
Вейля его полной неособой модели.
Пусть X — регулярная схема или комплексное мно-
многообразие и D = ~LnwW — дивизор Вейля. Для любой
точки х?Х существует такая открытая окрестность U,
что ограничение D на U
является главным Д. (fn) для нек-рой мероморфной
функции fy на U. Функция /у определена однозначно с
точностью до обратимой функции на U и наз. локальным
уравнением Д. D в окрестности U, а соответствие t/-^-/y
определяет сечение пучка MxlQx- Вообще, диви-
дивизором Картье на окольцованном пространстве
(X, fix) называется глобальное сечение пучка M*xlQ*X
(пучка ростков дивизоров). Здесь Мх обозначает пучок
ростков мероморфных (или рациональных) функций на
X, т. е. пучок, сопоставляющий каждому открытому
UdX полное кольцо частных кольца Г([/, Qx), а М*х
и Q*x — пучки обратимых элементов в Мх и Qx соот-
соответственно. Дивизор Картье можно задавать набором
локальных уравнений
/,• 6 г (г/,-, м\),
где {V(} — открытое покрытие X, причем на G,П U/
функция fjfj должна быть сечением пучка Qx- В част-
частности, мероморфная функция / определяет Д. div(/)
наз. главным. Множество х?М таких, что (fi
%Q*X,x, наз. носителем дивизора. Дивизо-
Дивизоры Картье образуют абелеву группу Div(X), а главные
Д.— ее подгруппу Div;(X). Каждый Д. D?Div(X) оп-
определяет обратимый пучок Qx(D)> содержащийся в
Mx '¦ если D представлен локальными уравнениями /,¦ на
покрытии {{/,}, то
Сопоставление D\-*Qx(D) является гомоморфизмом
группы Div(X) в Ликара группу Pic(X) = ff1(X, Q*x).
Этот гомоморфизм включается в точную последователь-
последовательность
Г (X, М*х) —+ Div (X) ~+ Pic (X) —> Я1 (X, М*х) ,
получающуюся из точной последовательности пучков
о — 6х — мх -^ мх1вх — о.
Таким образом, ker 6=Div;(X). Если D—D' есть глав-
главный Д., то D и D' наз. линейно эквивалент-
эквивалентными. Если X — квазипроективное алгебраич. мно-
многообразие или комплексное пространство Штейна, то го-
гомоморфизм б: Div (X)—>-Pic(X) сюръективен и индуци-
индуцирует изоморфизм группы классов линейно эквивалент-
эквивалентных Д. Div (X)/Divt(X) на группу Пикара Pic(X).
Если X — комплексное пространство, то вопрос о
том, когда данный Д. является главным, есть вторая
Кузена проблема. Напр., на комплексном пространстве
Штейна (X, Q) группа классов Д. тривиальна тогда н
только тогда, когда Н\Х, 2) = 0.
Д. D наз. эффективным (или положи-
положительны м), если QxdQx(D). В этом случае Qx(—D)
является пучком идеалов в Qx\ носитель Д. D со струк-
структурным пучком QXIQX(—D) образует подпространство
в X, обозначаемое также D.
Для нормальной нётеровой схемы или нормального
аналитич. пространства X имеется естественный гомо-
гомоморфизм
eye: Div(X)-^Zl(X),
переводящий ?> ? Div (X) B^\nwW, где nw~vw(f), f —
локальное уравнение D в окрестности W, a v^ — соот-
соответствующее W дискретное нормирование (см. [3]). Го-
Гомоморфизм сус инъективен и переводит эффективные Д.
в эффективные; сус биективен тогда и только тогда, ког-
когда X локально факторнально (напр., когда X — неосо-
неособая схема или аналитич. многообразие). В случае, когда
сус биективен, дивизоры Вейля и Картье отождеств-
отождествляются.
Пусть / : Х'—уХ — морфизм схем, плоский в кораз-
коразмерности 1. Тогда для любого дивизора Картье или Вей-
Вейля D на X определен его обратный образ f*(D). При
этом cyc(/*(Z>)) = /*(cyc(Z>)). Отображение D^>-f*(D) яв-
является гомоморфизмом групп, переводит главные Д. в
главные и тем самым определяет гомоморфизм групп
/*:Pic(X)—^Pic(X')
(соответственно /* : С (X)—>-С (X')).
Если X' — открытое множество в X, дополнение к
к-рому имеет коразмерность ^2 и / — вложение X' в
X, то /*: С(Х)^С(Х') — изоморфизм, а / : Pic(X)->
-^¦ТЧс(Х') является изоморфизмом при условии, что схе-
схема X локально факториальна.
Пусть X — гладкое проективное многообразие над С
Каждый Д. D на X определяет класс гомологии
двойственный по Пуанкаре к [D] класс когомологий сов-
совпадает с Чжэня классом сг@хФ))?Н2{Х, %) обратимо-
обратимого пучка Qx(D). Так на Div(X) возникает гомологич.
эквивалентность. Имеется теория пересечения Д. (см.
[7]), приводящая к понятию численной эквивалентно-
эквивалентности, тесно связанной с понятием алгебраич. эквивалент-
эквивалентности Д. (см. Алгебраический цикл). Группа
Pjc° (X) =.Diva (X)/Div, (X),
где Diva(X) обозначает группу Д., алгебраически экви-
эквивалентных нулю, естественным образом снабжается
структурой абелева многообразия (Пикара многообра-
многообразие; если X — кривая, то оно также наз. Якоби многооб-
многообразием кривой X). Группа Div (X)/Diva(X), наз. груп-
группой Нерона — Север и, имеет конечное число
образующих. Последние два факта верны и для алгеб-
раич. многообразий над произвольным полем.
Если X — одномерное комплексное многообразие
(риманова поверхность), то Д. на X можно понимать
как конечные линейные комбинации
где k;?Z, Xi?X. Число ~^к[ наз. степенью Д. D.
Для компактной римановой поверхности X рода g груп-
группа классов Д. степени 0 есть ^-мерное абелево многооб-
многообразие и совпадает с многообразием Пикара (или с много-
многообразием Якоби). Если / — мероморфная функция на
X, то главный Д.
div(/) = 2; "W —2; nJyJ'
где xj — нули, yj — полюсы функции /, а го,-, rij — их
кратности. Тогда 2mi=S 'V'Т-е- главнЬ1И Д- имеет
степень 0. Д. D степени 0 на X является главным тогда
и только тогда, когда существует такая сингулярная
одномерная цепь С, что
Г
Г ш0
для всех голоморфных форм и степени 1 на X (т е о р е-
м а Абеля). См. также Абелев дифференциал.
Лит.: [1] KummerE.E., «J. reine und angevv. Math.»,
1847, Bd 35, S. 327—67; [2] Б о p e в и ч 3. И., Ill а ф а р е-
в и ч И. Р., Теория чисел, 2 изд., М., 1972; [3] В е й л ь А.,
Введение в теорию кэлеровых многообразий, пер. с франц.,
М., 1961; [4] С artier P., «Bull. Soc. math. France», 1958,
t. 86, p. 177—251; [5] G г о t h e n d i e с k A., «Publ. Math.
IHES», 1967, № 32, ch. 4, pt. 4; [6] МамфордД., Лекции
о кривых на алгебраической поверхности, пер. с англ., М.,
1968; [7] ШафаревичИ. Р., Основы алгебраической гео-
геометрии, М., 1972; [8] Я1 е в а л л е К., Введение в теорию ал-
алгебраических функций от одной переменной, пер. с англ., М.,
1959; [9] Г а н н и н г Р., Р о с с и X., Аналитические функ-
функции многих комплексных переменных, пер. с англ., М., 1969;
[10] Ч ж э н ь Ш э н- ш э н ь, Комплексные многообразия,
пер. с англ., М., 1961; [11] Б у р б а к и Н., Коммутативная
алгебра, пер. с франц., М., 1971; [12] Спрингер Дж.,
Введение в теорию римановых поверхностей, пер. с англ., М.,
1960. В. И. Данилов, Л. В. Кузьмин, А. Л. Оиищик.
ДИВИЗОРИАЛЬНЫЙ ИДЕАЛ — дробный идеал а
целостного коммутативного кольца А такой, что а =
= А : (А : а) (здесь А : а обозначает множество эле-
элементов х из поля частных кольца А, для к-рых хааА).
Иногда Д. и. наз. дивизором кольца. Для любого
дробного идеала а идеал а = А : (А : а) дивпзори-
ален. Множество D (А) Д. и. кольца А является реше-
точно упорядоченным коммутативным моноидом (полу-
(полугруппой), если произведением двух Д. и. а и Ь считать
а-Ь, а положительными (или эффективными)
считать целые Д. и. udA. Моноид D (А) является
группой тогда и только тогда, когда кольцо А вполне
целозамкнуто; при этом обратным к дивизору а будет
А : а.
Обычно Д. и. рассматривают в кольце Крулля (напр.,
в нётеровом целозамкнутом кольце); в этом случае про-
простые идеалы высоты 1 дивизориальны и образуют базис
абелевой группы дивизоров D(A). Этот результат, по
существу, был установлен Э. Артином (Е. Artin) и
Б. Л. Ван дер Варденом (В. L. Van der Waerden) (см.
[1]) в их теории квазиравенства идеалов (идеалы а и О
к в а з и р а в н ы, если а=Ь) и завершил одну из
центральных тем алгебры того времени — изучение раз-
разложения идеалов.
Главные дробные идеалы, а также обратимые дробные
идеалы являются дивизориальными и образуют соот-
соответственно подгруппы F(A) и J(А) в D(A). Фактор-
группы D(A)lF(A) = C(A) и J(A)/F(A) = Pic(A) наз.
соответственно классов дивизоров группой и Пикара груп-
группой кольца А.
Лит.: [1] Ван дер Варден Б. Л., Алгебра, пер. с
рем., М., 1976; [2] Б у р б а к и Н., Коммутативная алгебра,
пер. с франц., М., 1971. В. И. Данилов.
ДИЕЗНАЯ НОРМА в пространстве r-м е р-
ных полиэдральных цепей СГ(Е") —
наибольшая из полунорм | -Г, удовлетворяющих для
любой клетки аг объема \аг\ неравенствам:
I о" Г < | о'|,
r+i
где Tvar — клетка, полученная сдвигом на вектор v
длины \v\.
Если Л = 2а,а(, то Д. н. \А\* выражается так:
|* = inf {2Ji"in;f'"ii +1s atTviar
ная норма цепи С
аА |* = | а | | А |# ,
где \С\Р— бемольная норма цепи С.
Имеет место:
\А |Й=о ФФ А=0,
если r=0, то |Л|" = |Лг .
Пополнение пространства Сг(Еп) является сепара-
бельным банаховым пространством С*(?"), элементы
к-рого наз. r-мерными диезными цепями. Для
любой r-мерной полиэдральной цепи А и любого векто-
вектора v имеет место
\Т А — А |# < JLAiJJLL
где TVA — цепь, полученная сдвигом А на вектор v
длины \v\. Бемольная цепь конечной массы
является диезной цепью; вообще любую бемольную
цепь можно рассматривать и как диезную цепь в таком
смысле: если A = lim'7 А,-, где А ,• — полиэдральные цепи,
и \рА = lim* A,-, где \р — линейное биективное отображе-
отображение пространства С^г(Еп) в пррстранство С*(Еп), и грС^
плотно в С* при Д. н.
Дать корректное определение границы дА диезной,
цепи невозможно (см. [1], с. 242, пример (с)); г-мерная
диезная коцепь Х=ХА есть элемент простран-
пространства С*г(Еп), сопряженного к С*(Еп), она является
бемольной коцепью, причем
I х|<|х ^<| х|Я,
где |Х| — комасса X, а диезная конорма |Х|* оп-
определяется аналогично бемольной норме |Хг . Когра-
Кограница dX диезной коцепи не обязана быть диезной ([1],
с. 241, пример (а)), однако
Константа Липшица^^Х) коцепи X опре-
определяется следующим образом:
где А — полиэдральные цепи. Для диезных коцепей ота
верхняя грань конечна и
(r + 1) j? (X)<\X\*.
Любая бемольная коцепь с конечной константой Лип-
Липшица является диезной, причем
и, кроме того,
Аналогичные понятия вводятся для r-мерных поли-
полиэдральных цепей в открытых подмножествах RczE".
См. также Диезная форма.
Диезная норма в пространстве аддитивных
функций у, значениями к-рых являются г - в е к т о-
р ы,— наибольшая из полунорм | -Г, удовлетворяющих
условиям:
М'<1?1> гДе 1 "V1 — полная вариация у;
где Tvy(Q) = yT-V{Q) — сдвиг функции у на вектор
v длины | v\:
T-v(Q) = {q-v, q € QCIE"};
для каждой точки р и любого 8 существует г\ >0 такое,
что Ivl'^elvl» если носитель sp tydUr](p) и у(Еп) = 0.
Д. н. IyI" имеет представление
|*=sup \ a>dy,
где со — r-мерные диезные формы, для к-рых [or*1 <:1.
Лит. см. при статье Бемольная норма.
М. И. Войцеховский.
ДИЕЗНАЯ ФОРМА — r-мерная дифференциальная
форма (о в открытом подмножестве RdEn такая, что ко-
конечны комасса |со]0 икомассовая константа
Липшица
гдер, q?R и \р—q\ — длина вектора р—q. Диезной
нормой формы со наз. число
|<о|* = sup {|ю|о, (r + 1) jfo (со)}.
Теорема Уитни. Каждой r-мерной диез-
диезной коцепи X в R соответствует единственная
r-мерная Д. ф. а>х, для которой
для всех r-мерных ориентированных симплексов аг;
(Ох(р) определяется формулой
Ха-
ЫХ (Р) = lim ~j—т~ >
i
где ах, а2, .. .— последовательность расположенных в
одной и той же плоскости симплексов, содержащих точ-
КУ Р> диаметры к-рых —>-0. Это соответствие является
взаимно однозначным линейным отображением прост-
пространства коцепей C*r(R) в пространство Q"r Д. ф.,
причем:
\=\Х\, т. е. комассе X;
, т. е. константе Липшица X;
= |.ДГ|'' , т. е. диезной норме X;
* является банаховым пространством.
В частности, нульмерным диезным коцепям соответст-
соответствуют диезные функции — ограниченные функ-
функции, удовлетворяющие условию Липшица.
Пространство C*(R) r-мерных диезных цепей А ко-
конечной .пассы \А\ с диезной нормой \АI* изоморфно про-
пространству rf(En) аддитивных функций множества, зна-
значениями к-рых являются г-векторыу, наделенному
диезной нормой |yl ; это соответствие определяется
формулой:
для любой коцепи X, где и>х есть r-мерная Д. ф., соот-
соответствующая коцепи X, и имеет место:
Чд(Еп)= {А}, т. е. ковектору цепи А,
\А\ = \уА\, т. е. полной вариации уд,
1Тл'*—1-41 *, т. е. диезной норме цепи А.
Таким образом, (*) является обобщением обычного
интеграла Лебега — Стилтьеса. В частности, для А тог-
тогда и только тогда существует измеримая по Лебегу сум-
суммируемая функция а(р), ассоциированная с А (см. Бе-
Бемольная форма), то есть
Х-A =
для любой коцепи X, если уА абсолютно непрерывна.
Если (Ад — регулярная форма, X — диез-
диезная коцепь, то существует форма «,^у=й«у и имеет ме-
место формула Стокса
\ cov= \ dm.
J да Л Jo
Аналогично обобщаются и другие результаты, установ-
установленные для регулярных форм.
Лит. см. при статье Бемольная форма.
М. И. Войцеховский.
ДИЗЪЮНКТИВНАЯ НОРМАЛЬНАЯ ФОРМА —
пропозициональная формула, имеющая вид
где каждое C,-y(i=l, ... , п; /=1, ... , т,-) есть либо
переменная, либо отрицание переменной. Д. н. ф. (*)
выполнима тогда и только тогда, когда при нек-ром i
среди Сц, . .., С{т. не встречаются одновременно фор-
формулы вида р и ~~\р, где р — переменная. Для всякой
пропозициональной формулы А можно построить экви-
эквивалентную ей Д. н. ф. В, содержащую те же перемен-
переменные, что и А . Такая формула В наз. Д. н. ф. формулы А.
ДИЗЪЮНКТНАЯ СУММА тополог и че cViTx
пространств Ха, а.?А,— пространство Y=
= UaeAYa, где каждое Ya есть копия Ха, и Ya,(]Ya,=
= 0 при ахфа^ а топология на Y определяется усло-
условием, что множество U открыто в Y тогда и только тогда,
когда открыто его пересечение с каждым Yа- Иначе
говоря, каждое Ya открыто и замкнуто в Y.
А. А. Мальцев.
ДИЗЪЮНКТНОЕ ДОПОЛНЕНИЕ множества
А —множество Ad= {х?Х; х_\_А } всех элементов х
векторной решетки (векторной структуры) X, дизъюнкт-
дизъюнктных множеству ЛсХ (см. Дизъюнктные элементы).
AcAdd=(Ad)d; кроме того, если X — векторная услов-
условно полная решетка, то Add является наименьшей ком-
поьеатой пространства X, содержащей А.
В. И. Соболев
ДИЗЪЮНКТНОЕ СЕМЕЙСТВО МНОЖЕСТВ — се-
семейство, состоящее из попарно не иересскающихся мно-
множеств. Б. А. Ефимов.
ДИЗЪЮНКТНЫЕ ПРЕДСТАВЛЕНИЯ — унитарные
представления лг, я2 нек-рой группы или, соответствен-
соответственно, симметричные представления нек-рой алгебры с
инволюцией, удовлетворяющие следующим экви-
эквивалентным условиям: 1) единственный ограниченный
линейный оператор из пространства представления пг
в пространство представления л2 равен нулю; 2) любые
ненулевые подпредставления представлений л1 и я2 не
эквивалентны. Понятие Д. п. плодотворно при изуче-
изучении факторпредставлений; в частности, представление я
является факторпредставлением тогда и только тогда,
когда л нельзя представить в виде прямой суммы двух
ненул-евых Д. п. Любые два факторпредставления либо
дизъюнктны, либо одно из них эквивалентно подпред-
ставлению другого (и в последнем случае представления
квазиэквивалентны). Понятие Д. п. играет важную
роль в разложении представлений в прямой интеграл:
если я — представление в сепарабельном гильбертовом
пространстве Н, 21 — Неймана алгебра в Я, порож-
порожденная операторами представления, Z — центр Ш,
— разложение пространства Н в прямой интеграл гиль-
гильбертовых пространств, соответствующее разложению
и если при этом алгебра Z соответствует алгебре диаго-
нализуемых операторов, то лA) является факторпред-
факторпредставлением для почти всех I, и представления пA) по-
попарно дизъюнктны для почти всех I. Существует про-
простая связь между дизъюнктностью представлений сепа-
рабельной локально компактной группы (соответственно
сепарабельной алгебры с инволюцией) и взаимной син-
сингулярностью представителей канонических классов
мер на квазиспектре группы (алгебры), соответствую-
соответствующих этим представлениям.
Лит.: [1] Диксмье Ж., С*-алгебры и их представле-
представления, пер. с франц., М., 1974. А. И. Штерн.
ДИЗЪЮНКТНЫЕ ЭЛЕМЕНТЫ, независимые
элементы, —элементы х ? X и у ? X векторной решет-
решетки X, обладающие тем свойством, что
где
|z| = x V ( — x),
что равносильно
|z| = sup(z, —х).
Соответственно,
что равносильно
H = inf(z, у).
Символы Л и V являются, соответственно, дизъюнкцией
и конъюнкцией. Множества АаХ и ВаХ наз. дизъ-
дизъюнктными, если дизъюнктна любая пара элемен-
элементов х?А, у?В. Элемент х?Х наз. дизъюнктным
множеству АаХ, если дизъюнктны множества
{х} и А. Дизъюнктная пара элементов обозначается
х_\_у или xdy, а дизъюнктная пара множеств — соот-
соответственно А_|_В или AdB.
Пример Д. э.: положительная х + = х\/0 и отри-
отрицательная #_==(—х)\/0 части элемента х.
Если элементы х;, i=l, 2, ... , п попарно дизъ-
дизъюнктны, то они линейно независимы; если А и В —
Д. э., то порождаемые ими линейные многообразия
тоже дизъюнктны; если ха_[_у, а?2(, причем
sup ха=х
существует, то xj_y. Для Д. о. упрощается ряд струк-
структурных соотношений; напр., если х\_у, то
(х -j- у) Л z = ж Л г + у Л г
для 2>0, и т. д.
Понятие Д. э. может быть введено и в более общих
частично упорядоченных множествах, напр, в булевых
алгебрах.
Лит.: [1] К а н т о р о в и ч Л. В., В у л и х Б. 3., П и н-
скерА. Г., Функциональный анализ в полуупорядоченных
пространствах, М.—л., 1950; [2] В у лих Б. 3., Введение в
теорию полуупорядоченных пространств, М., 1961; [3] Б у р-
бакиН., Интегрирование. Меры, интегрирование мер, пер.
с франц., М., 1967. В. И. Соболев.
ДИЗЪЮНКЦИЯ — логическая операция, служащая
для образовагия высказывания «Л или 2?» из высказы-
высказываний А. и В. В формализованных языках Д. выска-
высказываний А и В обозначается посредством
А \/В. Высказывания Л и В наз. дизъ-
дизъюнктивными членами выска-
высказывания А \/В. Употреблению Д. в мате-
матич. логике соответствует следующая
истинностная таблица:
В. Е. ПлиспО'
ДИКАЯ СФЕРА — замкнутое многообразие в евкли-
евклидовом пространстве Е3, получающееся диким вложением
____ сферы S2 в Е3. Так, Д. с. яв-
является сумма двух дисков с
общим краем, являющимся
диким узлом. Первый при-
пример Д. с.— так наз. «рогатая
сфера», или сфера Алек-
Алекса н д е р а (рис. 1),— огра-
ограничивает область, не гомео-
морфную Е3 (на рис. это —
•^ внутренность цилиндра без
всех зацепленных ручек и пре-
предельных точек к ним). На рис. 2
у к-рой только внешняя область не
А
И
11
Л
л
в
И
л
И
л
AVB
И
И
И
л
Рис. 1.
изображена Д. с.
гомеоморфпа Е3.
Рис
Лит.: [1] Келдыш Л. В., Топологические вложения в
евклидово пространство, М., 1966 (Тр. Матем. ин-та АН СССР,
т. 81). М. И. Войцеховский.
ДИКИЙ УЗЕЛ — узел L в евклидовом пространстве
Е3 такой, что не существует гомеоморфизма Е3 на себя,
при к-ром L переходит в замкнутую ломаную линию, со-
состоящую из конечного числа отрезков.
Рис. 1.
Так, дикими являются узлы, содержащие так наз.
дуги Фокса — Артина — некоторые простые
дуги, полученные диким вложением в Е3. Напр., для
дуги L1 (рис. 1) фундаментальная группа n1(E3\L) не-
Рис. 2.
тривиальна, для дуги Ьг (рис. 2) группа лг(Е3\Ь)
тривиальна, но само E3\L не гомеоморфно дополне-
дополнению в Е3 к точке.
Лит. см. при ст. Дикая сфера. М. И. Войцеховский.
ДИКОЕ ВЛОЖЕНИЕ топологического пространства
X в топологическое пространство Y — вложение, к-рое
топологически не эквивалентно вложению из нек-рого
класса выделенных вложений, наз. правильными,
или ручными, вложениями. Наиболее упо-
употребительными являются следующие случаи; в каче-
качестве Y в них берется n-мерное евклидово пространст-
пространство R".
1) Пусть М есть /с-мерное топологич. многообразие.
Топологич. вложение g : М—»-R" наз. диким, если
не существует гомеоморфизма R" на себя, переводящего
g(M) в локально плоское подмногообразие R".
2) Пусть Р есть /с-мерный полиэдр. Топологич. вло-
вложение g : P->R" наз. дики м, если не существует
гомеоморфизма R" на себя, переводящего g(P) в поли-
полиэдр (т. е. в тело нек-рой триангуляции) R".
3) Пусть К есть /с-мерное локально компактное про-
пространство. Топологич. вложение g : K-+R" наз. д и-
к и м, если не существует гомеоморфизма R" на себя,
переводящего g (К) в подмножество А-мерного Менгера
компакта Мп.
Если размерность h<.n—3 и п^5, то введенные свой-
свойства во всех трех случаях характеризуются локально го-
мотопич. свойством: вложение является диким тогда и
только тогда, когда g(X) не удовлетворяет свойству
1—ULC (см. Топология вложений). Положение вещей
для коразмерностей п—/с=1 и 2 значительно сложнее:
вопрос решен здесь для многообразий коразмерности
1 при п>6 и не решен полностью для вложений кораз-
коразмерности 2 как для многообразий, так и для полиэд-
полиэдров. Все сказанное имеет смысл и тогда, когда в каче-
качестве Y берется n-мерное многообразие, топологическое
ИЛИ КуСОЧНО ЛИНеЙНОе. М. А. Штанъко.
ДИКСОНА ГРУППА — группа экспоненциальных
автоморфизмов классической простой алгебры Ли типа
G2 над конечным полем F. Если порядок F равен q, то
порядок Д. г. равен q6(q2—1)(?6—1). При д>2 Д. г. яв-
является простой группой. Д. г. были открыты Л. Дик-
Диксоном [1]. После этого в течение 50 лет не было найдено
ни одной новой конечной простой группы, пока в 1955
К. Шевалле (С. Chevalley) не указал общий способ полу-
получения простых групп как групп автоморфизмов простых
алгебр Ли (см. [2]). Метод Шевалле позволяет получить,
в частности, и Д. г. (см. [3]).
Лит.: [1] DicksonL. E., «Math. Ann.», 1905, Bd 60,
S. 137—50; [2] Шевалле К., «Математика», 1958, т. 2,
№ 1, с. 3—53; [3] Картер Р., там же, 1966, т. 10, № 5, с.
3—47. В. Д. Мазуров.
ДИКСОНА ИНВАРИАНТ — конструкция, исполь-
используемая при изучении квадратичных форм над полями
характеристики 2, позволяющая, в частности, вводить
аналоги специальной ортогональной группы над такими
полями. А именно, Д. и. есть элемент D (и) произволь-
иого поля к характеристики 2, сопоставляемый всякому
подобию и четномерного векторного пространства Е над
к относительно симметрической билинейной формы /,
ассоциированной с невырожденной квадратичной фор-
формой Q на Е. Д. и. введен Л. Диксоном [1].
В силу условия на характеристику поля форма / яв-
является знакопеременной, ив Е существует базис elt . . .,
e2s, для к-рого
/(«1. ej) = i(es + h e*+/) = 0,
/(ем es+j) = б/у
при l<:i<:s, 1</<:s (см. Витта разложение). Пусть
/(«(*), u(ij)) = a(u)f(x, у)
для любых векторов х и у из Е, и пусть для каждого
и (е')=2/=!а ое/+2/=1ъ <ve*+j'
Тогда элемент из к вида
Я И = 2,- ¦ <<? (е<-) а'7с<7 ¦+ 0 (es + i) bijdij + bjjc,-j)
наз. инвариантом Диксона подобия и
относительно базиса elt . .. , e2S. Для того чтобы и было
подобием относительно Q с коэффициентом подобия а(и)
[т. е. <2(и(ж)) = а(«)(?(а;) для любого вектора х?Е], не-
необходимо и достаточно, чтобы D (и) = 0 или D (и) = а(и).
Подобия и относительно Q, для к-рых Z>(u) = O, наз.
прямыми подобиями. Прямые подобия об-
образуют в группе всех подобий относительно Q нормаль-
нормальный делитель индекса 2.
Если Q1 — форма, определяемая равенством Qi(x)=
~Q(u(x)) для любого вектора х?Е, а А(<?) и A((?i) —
псевдодискриминанты этих форм относи-
относительно базиса е1, .. ., e2s, т. е.
<?i ('"i) <?i (eJ + i)+ • . . +<?i (es)
то
Лит.: [1] DicksonL. E., Linear Groups..., Lpz., 1901;
12J БурбакиН., Алгебра. Модули, кольца, формы, пер.
с франц., М., 1966; [3] Дьедонне Ж., Геометрия классиче-
классических групп, пер. с франц., М., 1974. В. Л. Попов.
ДИЛАТАЦИЯ — устаревший термин для обозначе-
обозначения специальных бирациональных преобразований, на-
называемых теперь моноио'алъными преобразованиями.
В. А. Исковспих.
ДИНАМИКА — раздел механики, в к-ром изучается
движение материальных тел, происходящее под дейст-
действием приложенных к ним сил, вызывающих или изме-
изменяющих это движение,— так называемых ускоря-
ускоряющих сил.
Основы Д. заложены в нач. 17 в. Г. Галилеем (G. Ga-
Galilei), к-рый первый рассмотрел движение тел под дей-
действием силы тяжести и установил закон инерции. Ос-
Основные принципы Д. были четко сформулированы
И. Ньютоном (I. Newton) в виде трех основных законов
механики и следствий из них. Дальнейшее развитие и
совершенствование законов Д. содержится в трудах
Л. Эйлера (L. Euler), Ж. Д'Аламбера (J. D'Alembert),
Ж. Лагранжа (J. Lagrange), где были даны общие мето-
методы составления уравнений Д. Начало аналитич. мето-
методам исследования уравнений Д. положили Ж. Лагранж,
У. Гамильтон (W. Hamilton) и К. Якоби (С. Jacobi).
Позднейшим развитием этих методов занимались К. Га-
Гаусс (С. Gauss), M. В. Остроградский, А. Пуанкаре
(Н. Poincare), С. А. Чаплыгин, Н. Г. Четаев и др.
Д., основывающаяся на принципах Г. Галилея и
И. Ньютона, наз. классической или ньютоновской Д.,
в отличие от направлений, исходящих из иных прин-
принципов (квантовая механика, релятивистская Д. и др.).
Классич. Д. состоит из совокупности математич. выво-
выводов и заключений, являющихся следствиями основных
законов Галилея и Ньютона. В ней аксиоматически вво-
вводятся понятия неподвижного пространства (абсолютной
неподвижной системы отсчета или инерциальной систе-
системы отсчета) и абсолютного времени, одинакового для
всех точек пространства. Абсолютному пространству
приписываются геометрич. свойства евклидова прост-
пространства. Законы Ньютона формулируются по отноше-
отношению к абсолютному пространству и абсолютному вре-
времени. Они остаются справедливыми по отношению к
инерциальным системам отсчета. Заключения о движе-
движении материальных тел Д. получает с помощью построе-
построения моделей (материальной точки, абсолютно твердого
тела, континуума п др.).
По характеру решаемых задач Д. может быть разде-
разделена на Д. материальной точки и Д. системы материаль-
материальных точек. Понятие материальной точки является ос-
основным понятием классической Д. Материальной точ-
точкой наз. такое тело, геометрич. размерами к-рого мож-
можно пренебрегать при изучении его движения, но к-рое
обладает конечной массой. Первый и второй законы
Ньютона формулируются в Д. только для одной мате-
материальной точки. Кроме материальной точки в Д. рас-
рассматривают еще модель абсолютно твердого тела, рас-
расстояния между точками к-рого не изменяются во время
движения. Эти основные модели Д. позволяют успеш-
успешно решать ряд конкретных задач о движении реаль-
реальных тел.
В Д. системы материальных точек рассматриваются
движения таких тел, к-рые находятся во взаимосвязи
друг с другом. Д. системы включает в себя Д. твердого
тела, Д. систем с переменной массой, Д. упругого и
пластически деформируемого тела, Д. жидкости и газа
И ?р-
Характер движения материальной системы определя-
определяется действующими на нее силами (активными силами),
а также связями, наложенными на точки системы, дей-
действие к-рых может быть заменено действием сил реак-
реакций связи (пассивными силами). Действующие на сис-
систему материальных точек силы являются результатом
взаимодействия отдельных материальных точек, как
входящих, так и не входящих в рассматриваемую сис-
систему. В соответствии с этим различают силы внутрен-
внутренние и внешние. Силы могут быть представлены как
функции положений материальных точек, их скоростей
и времени.
В Д. решаются две основные задачи: 1) определение
силы, производящей данное движение материальной
точки или системы; 2) определение движения матери-
материальной точки или системы, происходящее под действием
заданных сил. Задачи Д. решаются при помощи диффе-
дифференциальных уравнений движения. Для одной матери-
материальной точки эти уравнения выражают второй закон
Ньютона и могут быть записаны в виде
где г — радиус-вектор материальной точки в рассмат-
рассматриваемой системе отсчета, cPrldt*— ее ускорение, V —
действующая на точку активная сила, N — сила реак-
реакций связи. Для определения закона движения матери-
материальной точки нужно найти значение г для каждого мо-
момента времени. Задача интегрирования уравнений Д.
решается с помощью общих теорем Д. (теорем об изме-
изменении количества движения, момента количества дви-
движения и живых сил). Эти теоремы обусловливают важ-
важные физич. зависимости между основными динамич. ха-
рактеристиками движения и взаимодействия матери-
материальных тел; в ряде случаев они значительно упрощают
процесс интегрирования уравнений Д. Кроме того, об-
общие теоремы дают возможность изучать отдельные сто-
стороны рассматриваемого движения. Общие теоремы для
системы материальных точек могут быть получены не-
непосредственным обобщением общих теорем для одной
материальной точки. При выводе из Д'Аламбера —
Лагранжа принципа они становятся более совершенны-
совершенными п не содержат реакций связи, а устанавливают непо-
непосредственную зависимость между динамич. величинами,
характеризующими движение системы, и действующими
на систему активными силами. Наиболее распростра-
распространенными являются системы с голономными идеальными
связями. Движение таких систем полностью описывает-
описывается Лагранжа уравнениями 2-го рода, получающимися
из принципа Д'Аламбера — Лагранжа. Эти уравнения
наиболее удобны при исследовании движения системы
материальных точек. Для материальных систем с него-
лономными идеальными связями наиболее общими урав-
уравнениями движения, не содержащими реакций связей, яв-
являются Аппеля уравнения.
Изучением свойств уравнений движения механич.
систем, обусловленных специфич. формой этих уравне-
уравнений, занимается аналитич. Д. Она рассматривает об-
общие принципы Д., вывод из этих принципов дифферен-
дифференциальных уравнений движения и методов их интегри-
интегрирования. Методы аналитич. Д. широко применяются
как для решения различных задач Д., так и в различных
областях физики. Большое значение для исследования
свойств движения механич. систем получили канониче-
канонические Гамильтона уравнения, к-рые дают возможность
сформулировать ряд эффективных методов решения за-
задач Д.
Помимо установления общих методов составления и
интегрирования уравнений движения материальных
тел, движущихся под действием ускоряющих сил, в Д.
рассматривается ряд специальных задач: Д. твердого
тела, Д. гироскопич. систем, теория колебаний меха-
механич. систем, теория устойчивости движения, теория
удара и др.
Лит.: [1] Г а л и л е й Г., Соч., т. 1 — Беседы и математи-
математические доказательства, касающиеся двух новых отраслей науки,
относящихся к механике и местному движению..., пер. с итал.,
М.—Л., 1934; [2] е г о же, Диалог о двух главнейших систе-
системах мира, птолемеевой и коперниковой, пер. с итал., М.—Л.,
1948; [3] Н ь ю т о н И., Математические начала натуральной
философии, пер. с латин., в кн.: К р ы л о в А. Н., Собр. тру-
трудов, т. 7, М.—Л., 1936; [4] Эйлер Л., Основы динамики точ-
точки, пер. с латин., М.—Л., 1938; [5] Д' А л а м б е р Ж., Дина-
Динамика, пер. с франц., М.—Л., 1950; [6] Л а г р а н ж Ж., Ана-
Аналитическая механика, пер. с франц., т. 1—2, М.—Л., 1950;
[7] Я к о б и К., Лекции по динамике, пер. с нем., М.—Л.,
1936; [8] Г а м и л ь т о н У., Об общем методе в динамике ...,
пер. с англ., в кн.: Вариационные принципы механики, М.,
1959; [9] Г е р ц Г., Принципы механики, изложенные в новой
связи, пер. с нем., М., 1959; [10] Остроградский М. В.,
Лекции по аналитической механике, в кн.: Остроград-
скийМ. В., Полн. собр. трудов, т. 2, К., 1961; [11] Жуков-
с к и й Н. Е., Теоретическая механика, 2 изд., М.—Л., 1952; [12]
ЧаплыгинС. А., Курсы лекций по теоретической механи-
механике, Собр. соч., т. 4, М.—Л., 1949; [13] Ч е т а е в Н. Г., Устой-
Устойчивость движения.—Работы по аналитической механике, М.,
1962. Е. Н. Беревкин.
ДИНАМИКА СОРБЦИИ — процесс поглощения ад-
сорбата (паров, газов или растворенного вещества)
твердым телом, сопровождающийся адсорбцией и аб-
абсорбцией, т. е. соответственно поверхностным и объем-
объемным поглощением. Д. с. определяется скоростями ад-
адсорбции, внешней и внутренней диффузией адсорбата,
и описывается системой дифференциальных уравнений
диффузионного переноса вещества с учетом кинетики
адсорбции. В большинстве случаев процесс сорбции
происходит в неизотермических условиях — при выде-
выделении теплоты адсорбции и при капиллярной конденса-
конденсации —так что процессы переноса массы вещества (диф-
(диффузия) сопровождаются переносом тепла (теплообме-
ном), т. е. описываются системой дифференциальных
уравнений массо- и теплопереноса. Если адсорбентом
является смесь газов и паров или смесь растворен-
растворенных веществ, то молекулярный перенос массы вещест-
вещества и тепла описывается системой уравнений Онсагера
(см. |2]).
В случае бинарной смеси система дифференциальных
уравнении тепло- и массопереноса, решение к-рой, при
соответствующих краевых условиях, определяет Д. с,
имеет вид
[ 4] /i(Pio, T) A)
cpp~ = div(XvT) + div(DpQ*vpiu) +
+ (К-К) /1 + (сЯ1 + сЯ2) ,\VT, B)
гДе Pio — относительная плотность компоненты «1»,
Pio=rPi/p; P=pi+p2i D — коэффициент диффузии, Т —
температура, т — время, ср — удельная изобарная теп-
теплоемкость, к — коэффициент теплопроводности, Q* —
изотермич. теплота переноса, кт — термодиффузионная
постоянная, h — удельная энтальпия, j1 — диффузи-
диффузионный поток массы компоненты «1», d/dx — полная или
субстанциональная производная, равная
(где v — скорость движения центра тяжести потока ад-
сорбата), /jfpxoi T) — мощность источника массы веще-
вещества, обусловленная кинетикой адсорбции и фазовыми
превращениями, к-рые в общем случае являются функ-
функциями концентрации р10 и температуры Т.
Скорость v движения потока адсорбата получается из
решений Навъе — Стокса уравнений. Краевые условия
определяются характером и физич. механизмом взаимо-
взаимодействия поверхности твердого тела с окружающей сре-
средой (адсорбатом). При этом скорость массообмена опре-
определяется внешней диффузией адсорбата к поверхности
тела и кинетикой адсорбции. Обычно рассматривают
два крайних случая:
1) массообмен определяется диффузией;
2) концентрация на поверхности тела зависит только
от скорости адсорбции.
Для случая сорбции пара капиллярнопористыми те-
телами получены решения системы дифференциальных
уравнений A), B) применительно к телам простейшей
формы (см. [1]).
Процесс десорбции водяного пара пористыми телами
составляет часть процесса сушки. Д. с. в этом случае
рассчитывается приближенно по следующим уравнени-
уравнениям массо- и теплообмена
где duldi — скорость десорбции, г — удельная теп-
теплота сорбции, р0 — плотность сухого тела, q(r) — удель-
удельный поток тепла на поверхности тела, Rv — гидравлич.
радиус тела, и — среднее влагосодержание (относи-
(относительная концентрация) тела, ир — равновесное влаго-
влагосодержание, х — относительный коэффициент сушки,
N — скорость сушки в первом периоде — периоде по-
постоянной скорости, Rb — число Ребиндера.
Лит.: [1] Л ы к о в А. В., М и х а й л о в Ю. А., Теория
тепло- и массопереноса, М.—Л., 1963; [2] Де Гроот С,
М а з у р П., Неравновесная термодинамика, пер. с англ., М.,
1964; "[3] Лыков А. В., Теория сушки, 2 изд., М., 1968;
[4] Франк-КаменецкийД. А., Диффузия и тепло-
теплопередача в химической кинематике, 2 изд., М., 1967; 15] Т и-
хоновА. Н., Самарский А. А., Уравнения математи-
математической физики, 3 изд., М., 1966. А. В. Лыков.
ДИНАМИЧЕСКАЯ ИГРА — разновидность позици-
позиционных игр, характеризующаяся тем, что в такой игре
игроки управляют «движением точки» в пространстве
состояний X. Пусть /= {i} — множество игроков. Каж-
Каждой точке х?Х соответствует множество Si1" эле-
элементарных стратегий игрока i?/ в этой
точке и тем самым — множество 5и)=ТТ,-5;д:) эле-
элементарных ситуаций в х. На X заданы п е-
рвходные функции распределения
F(xk\x1,sW,...,xk-1,slx*-l)),xi€X,*lx') g 5<*1> ,
представляющие собой закон движения управляемой
точки, известный каждому из игроков. Функция F при
фиксированном х^ измерима по всем остальным аргу-
аргументам. Последовательность Р чередующихся состояний
и элементарных ситуаций хх, s<Xl\ . .. , хк, sixk\ . ..
наз. партией общей Д. и.; она определяется ин-
индуктивно по следующей схеме: пусть уже определен
отрезок партии (дебют) хх, s(x'\ . . . , x^-i №>2), и
каждый игрок i выбирает свою элементарную стратегию
J-xk-i> ?S\xk-i> , так что складывается элементарная
ситуация s^fc-i' ; тогда игра переходит случайно, в со-
соответствии с распределением F( -\xly s{Xl>, ... , z^-i,
s'xfc-i' ), в состояние х^. На каждой партии Р определен
выигрыш hj(P) игрока i. Если множество всех партий
обозначить 5р, то Д. и. задается системой
Г = </, X,{s)?)iti,x<iX, F, {hh (Р)}и,1Ре^>.
Обычно в Д. и. считается, что к очередному моменту вы-
выбора элементарной стратегии игроки знают предшест-
предшествующий дебют. В этом случае чистая стратегия s,- игро-
игрока i есть набор функций s'x\x1, s(*i>, . .. , s^k-i* , х),
ставящих в соответствие заканчивающемуся в х дебюту
элементарную стратегию slx)?ScX). Рассматривались
также Д. и., в к-рых игрокам известен не весь пред-
предшествующий дебют, напр, игры с «запаздыванием ин-
информации».
Для того чтобы игра была определена, необходимо,
чтобы каждая ситуация s= {s;} индуцировала вероят-
вероятностную меру \is на множестве всех партий и чтобы для
каждого i существовало математич. ожидание ?hj(P)
по мере \is. Это математич. ожидание и представляет со-
собой выигрыш игрока i в ситуации s.
Функции ki(P), вообще говоря, произвольны; однако
более других изучались Д. и. либо стерминаль-
ным выигрышем (игра заканчивается, как толь-
только хь оказывается в терминальном множе-
множестве ХтаХ и hi(P) = hi(xit), где х^ — последнее со-
состояние в игре), либо синтегральным выиг-
выигрышем {hi(P)='^=1hi(xk, s(xP ).
Д. и. могут рассматриваться как игровой вариант за-
задачи оптимального управления с дискретным време-
временем, к каковой они и сводятся, если число игроков рав-
равно одному. Если в Д. и. XdR", дискретное время заме-
заменяется на непрерывное, а случайные факторы устраня-
устраняются, то получают дифференциальную игру, к-рая, та-
таким образом, может рассматриваться как разновид-
разновидность Д. и.
Частными классами Д. и. являются стохастические
игры, рекурсивные игры и игры на выживание.
Лит.: [1] В о р о б ь е в Н. Н., «Успехи матем. наук»,
1970, т. 25, в. 2, с. 81 — 140. В. К. Доманский.
ДИНАМИЧЕСКАЯ СИСТЕМА — в первоначальном
значении термина механич. система с конечным числом
степеней свободы. Состояние такой системы обычно ха-
характеризуется ее расположением (конфигурацией) и
скоростью изменения последнего, а закон движения
указывает, с какой скоростью изменяется состояние
системы.
В простейших случаях состояние можно охарактери-
охарактеризовать посредством величин w1, . . . , wm, к-рые могут
принимать произвольные (действительные) значения,
причем двум различным наборам величин шх, . .., wm и
и wi, . .. , wm отвечают различные состояния, и обрат-
обратно, а близость всех w, к ц>,- означает близость соответст-
соответствующих состояний системы. Закон движения тогда за-
записывается в виде автономной системы обыкновенных
дифференциальных уравнений:
u>i^ti(u>u ¦¦¦,">„), i = l, ..., го. A)
Рассматривая значения w1, . .. , wm как координаты
точки w в m-мерном пространстве, можно геометрически
представить соответствующее состояние Д. с. посредст-
посредством этой точки w. Последнюю наз. фазовой (иногда
также изображающей, или представляю-
представляющей) точкой, а пространство — фазовым
пространством системы. (Прилагательное «фа-
«фазовый* связано с тем, что в прошлом состояния системы
нередко называли ее фазами.) Изменение состояния со
временем изображается как движение фазовой точки по
нек-рой линии (так наз. фазовой траектории;
часто, впрочем, ее наз. просто траекторией) в фазовом
пространстве. В последнем определено векторное поле,
сопоставляющее каждой точке w выходящий из нее век-
вектор f(w) с компонентами
(fx(wu ..., wm), ..., fm(wu ..., wm)). B)
Дифференциальные уравнения A), к-рые с помощью
введенных обозначений можно сокращенно записать в
виде
ш = /Н, C)
означают, что в каждый момент времени векторная ско-
скорость движения фазовой точки (или, как часто говорят,
вектор фазовой скорости; не путать с
употреблением того же термина в оптике и вообще при
рассмотрении различных волновых процессов) равна
вектору f(w), исходящему из той точки w фазового про-
пространства, где в данный момент находится движущаяся
фазовая точка. В этом состоит так наз. кинематиче-
кинематическая интерпретация системы дифференци-
дифференциальных уравнений A).
Напр., состояние частицы без внутренних степеней
свободы (как говорят в механике, материальной точ-
точки), движущейся в потенциальном поле с потенциалом
U(x1,xi,x3),характеризуется ее положением х=(х1, х2,х3)
и скоростью х; вместо последней можно использовать
импульс р=тх, где т — масса частицы. Закон движе-
движения можно записать в виде
*="^' P=-graiU(x). D)
Формулы D) представляют собой сокращенную запись
системы шести обыкновенных дифференциальных урав-
уравнений 1-го порядка. Фазовым пространством здесь слу-
служит 6-мерное евклидово пространство, шесть компо-
компонент вектора фазовой скорости суть компоненты обыч-
обычной скорости и силы, а проекция фазовой траектории на
пространство х, (параллельно пространству импульсов)
есть траектория частицы в обычном смысле слова.
В ряде случаев оказывается, что невозможно устано-
установить такое соответствие между всеми состояниями Д. с.
и точками евклидова пространства, к-рое обладало бы
желаемыми свойствами, однако такое соответствие мож-
можно установить локально, т. е. для состояний, к-рые до-
достаточно близки друг к другу. Сохраняя термин «фазо-
«фазовое пространство» для совокупности всех состояний
Д. с, можно сказать, что в общем случае фазовое про-
пространство является не евклидовым пространством, а
нек-рым дифференцируемым многообразием W'n. Л о-
кально, т. е. в любой карте (локальной системе коорди-
координат) многообразия Wm, движение Д. с. описывается
системой дифференциальных уравнений вида A). Гло-
Глобальное же (т. о. пригодное для всех состояний Д. с.)
и инвариантное (т. е. не зависящее от выбора карты)
описание движения дается уравнением C), в к-ром /
является заданным на Wm векторным полем, сопостав-
сопоставляющим каждой точке w вектор f(w), лежащий в каса-
касательном пространстве к многообразию в этой точке;
уравнение C) означает, что в процессе движения фазо-
фазовая точка, совпадающая в данный момент времени с
точкой w? Wm, имеет в этот момент скорость f(w). В ло-
локальных координатах вектор f(w) представляется по-
посредством своих компонент B), и C) сводится к A).
Даже во многих случаях, когда фазовое пространство
является евклидовым, часть движений рассматриваемой
Д. с. может описываться посредством векторного поля
на нек-ром инвариантном многообра-
многообразии W, т.е. подмногообразии фазового пространст-
пространства, обладающем тем свойством, что траектория, прохо-
проходящая через к.-н. точку w?W, целиком лежит в W.
Так, уже в предыдущем примере, если ограничиться
движениями с определенным значением энергии Е, ну-
нужно рассматривать систему D) не во всем 6-мерном
евклидовом пространстве переменных (х, р), а на его
5-мерном подмногообразии, выделяемом уравнением
где р2—р\-\-р\-\-р\. Инвариантность этого многообра-
многообразия отражает тот факт, что при движении частицы в
потенциальном поле ее энергия сохраняется, т. е.
p2l2m-\- U (х) является первым интегралом системы D)
(так наз. интеграл энергии). Много аналогич-
аналогичных примеров связано с циклическими координатами.
Примером Д. с. с неевклидовым фазовым пространст-
пространством является твердое тело с неподвижной точкой О.
Если ввести две ортогональные системы координат с на-
началом в О — одну неподвижную, а другую жестко свя-
связанную с телом, то очевидно, что положение твердого
тела будет характеризоваться расположением второй
системы координат относительно первой, т. е. ортого-
ортогональной матрицей 3-го порядка с определителем 1 (или
к.-н. эквивалентным способом, см. Эйлеровы углы, Кэ-
ли — Клейна параметры). Поэтому совокупность все-
всевозможных положений данной механич. системы (или,
как говорят, ее конфигурационное прост-
пространство) есть специальная ортогональная группа
3-го порядка SO C). Фазовым же пространством We яв-
является касательное расслоение группы SO C), ибо ско-
скорость изменения положения характеризуется касатель-
касательным вектором к SO C). В качестве локальных координат
в SO C) (выбор таковых автоматически определяет и
нек-рые локальные координаты в И76) обычно принима-
принимают углы Эйлера; тогда уравнения движения записыва-
записываются как Эйлера уравнения (движения твердого тела).
Изложенная выше кинематич. интерпретация авто-
автономной системы обыкновенных дифференциальных
уравнений A) [или картина движения фазовых точек в
фазовом многообразии согласно уравнению C)] никак
не связана с тем, описывают ли эти уравнения к.-л.
механич. систему. Поэтому термин «Д. с.» стал приме-
применяться в более широком смысле, означая произвольную
физич. (скажем, радиотехнич.) систему, описываемую
дифференциальными уравнениями вида A) или C), а
затем — и просто систему дифференциальных уравне-
уравнений такого вида, безотносительно к ее происхождению.
Среди всех Д. с. в этом расширенном смысле слова Д. с.
механики выделяются нек-рыми специфич. свойствами;
большинство из них относится к специальному классу
гамилътоновых систем. (Однако в механике рассмат-
рассматриваются и системы, не входящие в этот класс,— тако-
во, напр., большинство неголономных систем. В то же
время гамильтоновы системы встречаются и в ряде во-
вопросов физики.)
В этом смысле понятие Д. с. эквивалентно понятию
автономной системы дифференциальных уравнений вида
A) или C). Однако практически о Д. с. говорят тогда,
когда речь идет о качественной картине поведения всех
траекторий во всем фазовом пространстве (глобальная
теория) или по крайней мере в нек-рой его части (ло-
(локальная теория); в теории Д. с. особенно большое вни-
внимание уделяется поведению фазовых траектории при
неограниченном возрастании времени. Из отдельных же
траекторий в теории Д. с. интересуются обычно теми,
свойства к-рых могут в значительной степени влиять на
качественную картину, хотя бы локальную. Сюда от-
относятся равновесия положения (или особые точки), пери-
периодические траектории (см. также Предельный цикл),
сепаратрисы.
Для системы двух уравнений вида A) (т=2) кинема-
тич. интерпретация дает весьма наглядный и эффектив-
эффективный способ исследования, поскольку векторное поле
f(w) и фазовые траектории могут быть практически изо-
изображены на фазовой плоскости. Уже в случае трех
уравнений (т=3) пришлось бы производить соответст-
соответствующие построения в 3-мерном пространстве, что до-
довольно затруднительно, а при то>3 подобные практич.
возможности вообще отпадают. Поэтому при mj>=3 (а в
ряде случаев и при т=2) роль кинематич. интерпрета-
интерпретации состоит в использовании при исследовании диффе-
дифференциальных уравнений геометрич. понятий, методов и
языка, в той или иной степени обобщающих привычные
из повседневной жизни геометрич. представления.
Уже сравнительно слабые предположения о вектор-
векторном поле f(w) (напр., его дифференцируемость) гаранти-
гарантируют то, что для каждой точки ш0 ? Wm существует ров-
ровно одно решение w(t) уравнения C), имеющее w0 своим
начальным значением: ш@) = ш0. Физически это соот-
соответствует тому, что при заданном законе движения C)
состояние системы в любой момент времени полностью
определяется ее начальным состоянием. Вообще говс-
ря, это решение может быть определено не для всех t,
а лишь на нек-ром отрезке времени. В глобальной тео-
теории Д. с. делается дополнительное предположение, что
при любом начальном значении соответствующее реше-
решение определено при всех t, тогда как в локальных во-
вопросах обычно нецелесообразно делать к.-л. предполо-
предположения о дальнейшем поведении тех траекторий, к-рые
покидают рассматриваемую область фазового простран-
пространства.
При выполнении указанного предположения, если
каждому шо? Wm сопоставить то состояние, куда перей-
перейдет за время t фазовая точка, движущаяся согласно C)
и вышедшая при t=0 из w0, то получится нек-рое ото-
отображение Sf фазового пространства Wm в себя:
Stwa — w (t),
где w(t) — решение C) и w@)=w0. Отображения Sf
образуют непрерывную однопараметрич. группу диффе-
диффеоморфизмов фазового многообразия W" [групповое
свойство SfSs=St + s является следствием автономности
системы C)]. В порядке иллюстрации в литературе не-
нередко проводят аналогию с известным из повседневной
жизни и ранее всего изученным в науке примером, где
возникает подобное семейство преобразований прост-
пространства,— стационарным течением жидкости или газа:
за время t частица жидкости перетекает из точки ц;0 в
Sfiv0. (Впрочем, эта аналогия довольно поверхностна,
ибо воображаемая «фазовая жидкость», «текущая» в фа-
фазовом пространстве, отличается от реальных сплошных
сред отсутствием взаимодействия между соседними час-
частицами.) В связи с этим в качестве синонима термина
«Д. с.» употребляется термин поток.
В физич. литературе принято говорить об а н с а м б-
ле динамических систем. Это означает,
что каждому из возможных состояний данной физич.
¦системы (т. е. каждой точке фазового пространства)
мысленно сопоставляется нек-рая физич. система, опи-
описываемая уравнением C) и находящаяся в этом состоя-
состоянии; полученную совокупность однотипных систем (ни-
(никак не взаимодействующих друг с другом), различаю-
различающихся только состояниями, к-рыми они обладают в дан-
данный момент, и называют «ансамблем». На этом языке
преобразованиям Sf фазового пространства соответству-
соответствует эволюция «ансамбля», заключающаяся в изменении
состояния входящих в него систем.
При разработке глобальных аспектов теории Д. с.
понятие Д. с. подверглось дальнейшему обобщению.
В наиболее широком смысле под динамической
системой понимают произвольное действие
труппы (или даже полугруппы) G на нек-ром мно-
множестве W, именуемом фазовым пространством. Это зна-
значит, что для любого g?G определено отображение
Sg- W-+W, причем Sg^Sg^Sg^^, и если е — единица
СГто Sе — тождественное преобразование (т. е. Se{w) = w
для всех w). Совокупность точек Sg(w0), где w0 фикси-
фиксировано, a g пробегает G, наз. траекторией (или
орбитой), проходящей через точку w0, или, короче,
траекторией этой точки. Группа G обычно считается
топологической группой, фазовое пространство — топо-
топологическим пространством, или пространством с мерой,
а отображение
GxW—>W, (g, w)—+Sg(w) E)
предполагается, соответственно, непрерывным или из-
измеримым, причем в последнем случае обычно предпо-
предполагается, что отображения Sg сохраняют меру (т. е.
прообраз измеримого подмножества фазового простран-
пространства измерим и имеет ту же меру). Соответствующие на-
направления в теории Д. с. наз. топологической динамикой
(см. [0], [И)) и эргодической теорией (см.. [4], |5], [7],
[12]). Если G—группа Ли, W — гладкое многообразие,
а отображение E) гладкое, то говорят о гладкой
динамической системе.
Впрочем, во всех трех направлениях основными яв-
являются случаи, когда G — либо группа R действитель-
действительных чисел, и тогда Д. с. наз. потоком (хотя иногда этот
термин употребляют как синоним термина «Д. с.» в
наиболее общем его значении), либо G — группа % це-
целых чисел (вариант: аддитивная полугруппа неотрица-
неотрицательных целых чисел), и тогда для таких Д. с. был пред-
предложен термин каскад (говорят также о динами-
динамической системе с дискретным време-
н е м, но этот термин может означать также и только то,
что в G берется дискретная топология). Гладкий поток,
для к-рого отображение E) — класса С2, определяется
гладким векторным полем
— при изменении t точка w=St(w0) движется согласно
C). В случае каскада отображения Sn получаются ите-
итерированием преобразования Sx и обратного к нему (ва-
(вариант: итерированием одного только отображения St);
для гладкого каскада все Sh суть диффеоморфизмы (ва-
(вариант: непрерывно дифференцируемые отображения).
Среди названных трех направлений в теории Д. с. то-
пологич. динамика имеет ярко выраженный теоретико-
множественный характер, а ее роль вначале была как
бы вспомогательной. Дело в том, что обсуждение ряда
понятий (неблуждающая точка, предельное множество
траекторий, минимальное множество, почти периодич-
периодичность, дистальность, устойчивость по Лагранжу, устой-
устойчивость по Пуассону и др.) и связей между ними, важ-
важных для трактовки более конкретных объектов —
гладких Д. с,— целесообразно провести в более аб-
страктной обстановке, отвлекаясь от задания Д. с. при
помощи диффеоморфизма или уравнения C). Это и де-
делается в топологич. динамике. Позднее она получила
значительное развитие, главным образом, в направле-
направлении изучения нек-рых минимальных множеств и их
расширений (см. [13] — [15]; а также Дисталъная ди-
динамическая система).
Зарождение эргодич. теории связано с классич. (до-
квантовой) статистич. физикой. При обосновании по-
последней возник вопрос, можно ли, не решая гамильто-
нову систему дифференциальных уравнений, к-рая опи-
описывает движение частиц, образующих рассматриваемое
макроскопич. тело, и даже не зная начальные значения
для ее решения (что означало бы задание мгновенных
положений и скоростей всех этих частиц), указать свой-
свойства статистич. характера, проявляющиеся в поведении
при i-^-oo всех или почти всех ее фазовых траекторий.
Напр., существует ли при почти всех w предел перемен-
переменного среднего
lim 4 [Т g(Stw)dt, F)
7"->оо l J о
где g(w) есть функция, заданная на фазовом простран-
пространстве, и зависит ли этот предел от ш? Приведенное выше
определение Д. с, принятое в эргодич. теории, являет-
является результатом абстрагирования от конкретного проис-
происхождения систем статистич. физики, в частности от их
гамильтоновой структуры; от последней удерживается
лишь одно из ее следствий — сохранение меры при пре-
преобразованиях St- В данном случае такое абстрагирова-
абстрагирование служит не только для логич. анализа понятий, но и
приводит к значительному увеличению общности тео-
теории, позволяя включить в нее разнообразный материал,
связанный с теорией вероятностей, функциональным
анализом, теорией чисел, топологич. алгеброй. Наличие
связей с рядом разделов математики делает содержание
эргодич. теории достаточно богатым, чтобы обеспечить
ее успешное развитие в качестве самостоятельной науч-
научной дисциплины. Наряду с изучением статистики реше-
решений при t—voo, включающим как доказательство сущест-
существования предела F) при почти всех w и вывод условий,
необходимых при его независимости от w, так и ряд
других свойств (например, перемешивание), большую
роль в эргодической теории играет проблема изомор-
изоморфизма Д- с., исследование которой привело к постро-
построению ряда инвариантов Д. с. и выделению некоторых
классов Д. с. с интересными свойствами.
Теория гладких Д. с. (см. [7], [8], [10]) в значительной
степени сливается с качественной теорией дифферен-
дифференциальных уравнений, в особенности когда речь идет о
конкретно заданной системе A) или когда (независимо
от способа задания изучаемой Д. с.) существенно ис-
используются соображения, относящиеся к выписанным
в более или менее явном виде дифференциальным урав-
уравнениям. Гладкие Д. с. исследуются и локально, и гло-
глобально. К числу локальных свойств относятся: исследо-
исследование положений равновесия и других упомянутых вы-
выше специальных типов траекторий для потоков и их ана-
аналогов для каскадов, квазипериодических движений и ин-
инвариантных многообразий для тех и других, а также и
нек-рых классов инвариантных множеств. Исследова-
Исследование этих объектов включает в себя их обнаружение и ло-
локализацию, а также изучение в их окрестности поведе-
поведения других траекторий Д. с. При исследовании непо-
неподвижных точек каскадов, положений равновесия и пе-
риодич. решений потоков применяются как аналитиче-
аналитические, так и топологич. методы (см. [2], [3], [9]); для дру-
других объектов — только аналитические. Многие из этих
методов связаны со следующей постановкой вопроса
(или в равной степени применимы при ней): что проис-
происходит с потоком или каскадом, имеющим определенные
свойства (локальные или глобальные) при малом изме-
изменении определяющего его векторного поля или диффео-
морфизма? К такому подходу примыкают также и нек-
рые из результатов и понятий глобальной теории, в
особенности связанные со стремлением выделить такие
свойства или классы Д. с, к-рые были бы в нек-ром
смысле «типичными» (см., напр., Грубая система). Дру-
Другие результаты глобального характера относятся к оп-
определенным классам Д. с, зачастую возникшим из
смежных дисциплин.
В специальном случае потоков на двумерных поверх-
поверхностях можно получить более или менее удовлетвори-
удовлетворительную информацию о могущих здесь представиться
различных вариантах поведения фазовых траекторий;
это особенно относится к системам A) с т=2 (два урав-
уравнения) (теория Пуанкаре — Бендиксона, см. [1] — [3],
[9]) и потокам без неподвижных точек на торе (см. [2],
[9], [10]). Однако при этом остается открытым вопрос,
как именно ведут себя траектории той или иной кон-
конкретной системы. Большое число работ посвящено ис-
исследованию последнего вопроса для различных классов
уравнений. Особое положение потоков на двумерных
поверхностях связано с тем, что в этом случае траекто-
траектория локально разбивает фазовое пространство. Поэтому
естественное многомерное обобщение соответствующей
теории относится не к Д. с, а к слоениям коразмерно-
коразмерности 1.
Лит.: [1] НемыцкийВ. В., Степанов В. В.,
Качественная теория дифференциальных уравнений, 2 изд.,
М.—Л., 1949; [2] КоддингтонЭ. А., Левинсон Н.,
Теория обыкновенных дифференциальных уравнений, пер. с
англ., М., 1958, гл. 13—17; [3] Л е ф ш е ц С, Геометрическая
теория дифференциальных уравнений, пер. с англ., М., 1961;
[4] X а л м о ш П. Р., Лекции по эргодической теории, пер.
с англ., М., 1959; [5] «Успехи матем. наук», 1967, т. 22, в. 5,
с. 3—172: [6] G о t t s ch a 1 k W. H., HedlundG. A.,
Topological dynamics, Providence, 1955; [7] А г n о 1 d Y. I.,
A v e z A., Problemes ergodiques de la mecanique classique, P.,
1967; L8J Смей л С, «Успехи матем. наук», 1970, т. 25, в. 1,
с. ИЗ—85; 19] ХартманФ., Обыкновенные дифференци-
дифференциальные уравнения, пер. с англ., М., 1970; [10] Н и т е ц к и 3.,
Введение в дифференциальную динамику, пер. с англ., М., 1975;
[11] С и б и р с к и й К. С., Введение в топологическую дина-
динамику, Киш., 1970; [12J Синай Я. Г., Введение в эргодиче-
скую теорию, Ер., 197 3; [13] Бронштейн И. У., Расши-
Расширения минимальных групп преобразований, Киш., 1975; [14]
Ellis R., Lectures on topological dynamics, N.Y., 1969; [15]
Veech W. A., «Bull. Amer. Math. Soc», 1977, v. 83, .V» 5,
p. 775 — 830. Д. В. Аносов.
ДИНАМИЧЕСКИЕ ЗАДАЧИ ТЕОРИИ УПРУГО-
УПРУГОСТИ — круг вопросов теории упругости, относящихся
к изучению распространения колебаний или состояния
установившихся колебаний в упругих средах. В про-
простейшем н наиболее важном для приложений случае
линейной теории однородных изотропных упругих тел
Д. з. т. у. сводятся к разысканию решений уравне-
уравнения Ламе:
цДм(г, *) + (^+И) 8rad divu(x, t) + F(x, t) =
9!u(x, *) ...
= P or ' W
удовлетворяющих в нек-рой области заданным началь-
начальным и граничным условиям, здесь и(х, 2)=("i, > из) —
вектор смещения в точке х^е=(х1, х2, х3) в момент t,
F(x, t) — объемные силы, X, ji — Ламе постоянные,
р — плотность.
Как уравнение гиперболич. типа уравнение A) допу-
допускает действительные характеристич. поверхности ш(х1,
х2, х3; г)=0, вдоль к-рых производные решения, вооб-
вообще говоря, выше 1-го порядка терпят разрывы (слабый
разрыв). Поверхность разрыва распространяется в про-
пространстве со скоростью
_ 8ш Г/во \2 /аи N2 . /8сй \2-|-1/2
V-~hTl{dxJ ' UxJ + \дх,) J
разделяя в каждый момент времени два решения. Урав-
Уравнение этой поверхности получается из условия невоз-
невозможности однозначного определения в ее точках всех
производных, исходя из знания первых производных и
пользуясь уравнением A). Из уравнения поверхности
разрыва:
[" 3 д 2 Э2
следует существование двух скоростей перемещения
этой поверхности
Эти скорости являются скоростями перемещения двух
видов деформации в линейном упругом изотропном теле:
а — скорость распространения продольных возмуще-
возмущений, Ь — поперечных возмущений. Можно также пока-
показать, что в нек-рых случаях вдоль границ раздела могут
распространяться поверхностные волны, имеющие свои
характерные скорости распространения (волны Рэлея
на свободной поверхности, волны Стоунли на границе
упругих сред).
Изучаются случаи, когда вдоль характеристик тор-
пят разрывы первые производные смещения (с и л ь-
н ы й разрыв). Если скачки вдоль характеристик
терпит лишь нормальная составляющая вектора grad и,
а касательные составляющие этого вектора и сами сме-
смещения остаются непрерывными, разрыв наз. правиль-
правильным сильным разрывом. В этом случае на по-
поверхности характеристик соблюдаются условия кинема-
тич. и динамич. совместности, играющие большую роль
при решении динамич. задач методом характеристик.
Явление динамич. деформаций упругого тела услож-
усложняется, если тело имеет конечную границу. Каждая
точка границы, как только ее коснется любой из фрон-
фронтов распространяющихся возмущений, к-рые сами яв-
являются сложными, изменяющимися во времени образо-
образованиями, начинает генерировать, по крайней мере, два
типа новых деформаций.
Важными частными случаями уравнения A) являют-
являются случаи, когда поле не зависит от времени (статика)
и, когда поле зависит от времени по закону
и(х, t) = Re [и(г)е-»ь>'],
где и(х) — комплексный вектор (амплитуда колебаний),
не зависящий от времени, со — частота установившихся
колебаний. В последнем случае уравнение A) приводит-
приводится к эллиптич. системе уравнений относительно ампли-
амплитуды
uAu(:e) + (A + u.)graddiv и (z) + со2и (я) = F (х), у
F (x, i) = Re [F (х) е-"о<]. |
Если область D, в к-рой исследуется распространение
колебаний, занимает все бесконечное пространство Е3,
для уравнения A) корректна задача Коши с начальны-
начальными условиями:
Основную роль играют специальные решения урав-
уравнения A), представляющие смещения бесконечного уп-
упругого пространства под влиянием силы, сосредоточен-
сосредоточенной в единственной точке ^=B°, х®, х°) и равной по ве-
величине б(t) (где 6(t) — дельта-функция Дирака) (ф у н-
да ментальные решения).
Если сила действует в направлении оси х^, k=i, 2, 3,
то составляющие смещения uf' (x, t)=Tkj, к, /=1, 2, 3
имеют следующие значения:
— j- е (Уь) + У a e(vJ — Y6 е(
дг дг \ 6 <У
)
где
Г 1, c^O, , \ 1, fc = /,
eW={o. c<0. ^=U, **/¦
Матрица фундаментальных решений Г (л:—ж0, <) =
= 11Гйу(г—л:0, t)\\ размера 3X3, представляет симметрич-
симметричный тензор; решение задачи Коши для уравнения A)
выражается формулой Вольтерра:
Г (*<>_*, to)<p«»(x)dx +
f < «'о
+ Г Г(*0-х, *0)<рЧ> (*)<** +
J л < а/о
Г'' Г Г(жо — х, t —10) F (x, t)dxdt. C)
JO Jr< а (/¦„-/)
Для однородной системы A'), Г^.- принимает следую-
следующий вид:
,2 _ рсо2 ,2 _ рсо2 D)
Кроме задачи Коши для уравнения A) корректны
смешанные задачи, к-рые приходится рассматривать,
когда область D имеет границу S в конечной части про-
пространства. При этом существенную роль играют гранич-
граничные условия на S, к-рые должны быть удовлетворены
вместе с условиями B).
Основными считаются следующие типы граничных за-
задач: первая — заданы смещения, вторая — заданы на-
напряжения, третья — задана линейная комбинация сме-
смещений и напряжений, четвертая — заданы нормальная
составляющая смещения и касательные составляющие
напряжения, пятая — заданы касательные составляю-
составляющие смещения и нормальная составляющая напряже-
напряжения, шестая — на одной части S заданы смещения и на
дополнении — напряжения.
В отличие от задачи Коши, к-рая формулой C) ре-
решается до конца в общем виде, решения смешанных за-
задач были получены только в частных случаях. Важней-
Важнейшими являются: решения в замкнутом виде первой и
второй основных смешанных задач для полуплоскости
и полупространства, полученные методом комплексных
волн и развитием метода характеристик; решения для
волнового уравнения в случае шара, полученные мето-
методом функционально-инвариантных интегралов; реше-
решения нек-рых задач теории упругости развитием этого же
метода, решения ряда задач дифракции. В общем слу-
случае получить решения в замкнутом виде не удается;
если, однако, от этого требования отказаться, весьма
общие результаты устанавливаются методами теории по-
потенциалов и теории сингулярных интегральных урав-
уравнений.
С помощью фундаментальных решений D), по анало-
аналогии с теорией гармонич. потенциалов, вводятся понятия
эластопотенциалов простого и двойного слоев и объем-
объемных масс, к-рые позволяют выразить регулярные реше-
решения уравнения A') формулой:
8 (х) и (х) = ^ GТ (х — у))* и (у) dyS~
Г(Ж-^) Ти (У) dvs—\D Г (х~у) F (v) dy'
где Т — оператор напряжения, * — знак транспони-
транспонирования матрицы, е(х)=1, если x?D, и е(х) = 0, если
х§р. Первые пять граничных условий, указанных вы-
выше, позволяют записать с помощью потенциалов соот-
соответствующие задачи в виде двумерных сингулярных
интегральных уравнений на замкнутой поверхности S.
Доказана разрешимость всех задач для произвольной
частоты колебаний со в случае внешней области и суще-
существование дискретного действительного неотрицатель-
неотрицательного спектра собственных частот для внутренних за-
задач. Решения выражаются рядами Фурье по нек-рой
полной системе векторов, к-рые строятся с помощью
D), и коэффициенты Фурье определяются явно.
Пусть на границе S в области D задано смещение
u\s=f(y), Si — произвольная гладкая замкнутая по-
поверхность, окружающая 5 и не имеющая с ней общих
точек, и {г*}Г — счетное множество точек на Si, рас-
распределенное всюду плотно. Через Г'(ж — х0), i—l, 2, 3,
обозначены столбцы матрицы Г(х—х°). Доказывается,
что совокупность векторов {Г'(х'г—у)}Г, s=l, 2, 3;
y?S линейно независима и полна в L2(S).
Элементы этой совокупности пронумерованы следую-
следующим образом:
где [и] — наибольшая целая часть числа п, и введена
ортонормированная совокупность
k v^ S
где aks — известные числа. Тогда решение задачи во
всякой внутренней точке выражается равномерно сходя-
сходящимся рядом:
где
Конечный отрезок ряда может служить для вычисления
приближенных значений решения.
Результаты, установленные для уравнения A'), по-
позволяют получить решения смешанных задач для урав-
уравнения A) с помощью преобразования Лапласа.
При исследовании решений уравнения Ламе для сло-
слоистых сред рассматривают распространение отдельных
волн или интерференцию всех образующихся волн. При
первом подходе используется конечность скорости рас-
распространения упругих волн и последовательно изуча-
изучаются распространение волн внутри слоев и процессы
отражения и преломления на границах. Для построения
интерференционных решений уравнения Ламе краевые
условия на границах должны удовлетворяться совмест-
совместно, что приводит к алгебраич. системе уравнений. Для
определения собственных процессов в слоистой системе
необходимо найти корни определителя этой системы,
при этом нахождение корней может быть сведено к оп-
определению собственных значений нек-рых операторов.
Собственные числа (корни) могут быть как действитель-
действительными, так и комплексными в зависимости от характера
оператора. Действительным собственным числам соот-
соответствуют интерференционные волны Рэлея и Лява,
распространяющиеся вдоль слоя без экспоненциально-
экспоненциального затухания. Расчет различных характеристик этих
волн в случае кусочно непрерывной скорости проводит-
проводится с помощью ЭВМ. Результаты этих вычислений ис-
используются для построения теоретич. сейсмограмм.
Затухающие интерференционные волны связаны с
комплексными собственными числами несамосопряжен-
несамосопряженных операторов. Оба вида интерференционных волп
рассматриваются в сейсмике для объяснения наблюдае-
наблюдаемых на практике сейсмич. волн.
Для решения ряда задач о колебаниях однородной
среды применялся метод функционально-инвариантных
решений. В частности, исследовано волновое поле, по-
порожденное точечным источником, в двух упругих полу-
полупространствах с плоской границей раздела; из точных
решений получены асимптотич. формулы, описывающие
волновое поле в прифронтовых зонах.
В теории упругих волн большое значение имеет гео-
метрич. приближение, применяемое как в стационар-
стационарном, так и в нестационарном вариантах. Вектор смеще-
смещения и ищется в виде ряда:
и (М, t) = 2"=0 и/ (М) if (t -т (Л/)), fj = f,-i, G)
где fj — в нестационарном случае функции, имеющие
особенность в нуле, в стационарном случае
— las
И отличие от скалярного случая, возможны два типа
рядов вида G), формально удовлетворяющих уравнени-
уравнениям теории упругости. Случай продольных волн, когда
iF, uo||vt,
где а — скорость продольных волн, и случай попереч-
поперечных волн, когда
где b — скорость поперечных волн.
Векторы Uj удовлетворяют рекуррентным соотноше-
соотношениям. Решения многих физически интересных задач
допускают разложения вида G), и «волны» такого вида
можно отражать и преломлять, в результате опять по-
получаются «волны», представимые рядами вида G).
Геометрооптич. методы приложимы и в случае по-
поверхностных волн. Наложением продольной и попереч-
поперечной волн вида G) с комплексными эйконалами можно
удовлетворить краевым условиям отсутствия напряже-
напряжений на поверхности. Такого рода построения приводят
к широкому классу поверхностных волн, частным слу-
случаем к-рых являются волны Рэлея.
Геометрооптич. теорию можно также развить для по-
поверхностных волн иного типа: для волн, аналогичных
волнам Лява, и для так наз. волн, удерживаемых по-
поверхностью. Аналог волн Лява, о к-рых идет речь,—
это стационарные высокочастотные волны, фазовая
скорость к-рых близка к скорости поперечных волн, а
направление вектора смещения в первом приближении
по частоте перпендикулярно нормали к поверхности и
направлению распространения волны. Волны, удержи-
удерживаемые поверхностью, тоже имеют поверхностную ско-
скорость, близкую к скорости поперечных волн. Однако их
поляризация другая — вектор смещений лежит в пло-
плоскости, образованной нормалью к поверхности и на-
направлением распространения волны.
Лит.: [1] Франк Ф., М и з е с Р., Дифференциальные
и интегральные уравнения математической физики, пер. с нем.,
ч. 2, Л.—М., 1937, гл. 12; [2] О г у р ц о в К. И., Петра-
ш с н ь Г. И., «Уч. зап. ЛГУ. Сер. матем. наук», 1951, № 149,
в. 24, с. 3—249; [3] Б а б и ч В. М. ид р., Линейные уравне-
уравнения математической физики, М., 1964, гл. 1, 2; [4] Л а д ы-
шенскаяО. А., Смешанная задача для гиперболического
уравнения, М., 1953; [5] И л ь и н В. А., «Успехи матем. наук»,
1960, т. 15, в. 2, с. 97 — 154; [6] К у п р а д з е В. Д. и др.,
Трехмерные задачи математической теории упругости и термо-
термоупругости, М., 1976; [7] П е т р а ш е н ь Г. И., «Уч. зап.
ЛГУ», 1956, №208, в. 30, с. 5—57; L8] Алексеев А. С,
Бабич В. М., ГельчинскийБ. Я., в кн.: Вопросы ди-
динамической теории распространения сейсмических волн, сб. 5,
Л., 1961, с. 3—24; [9] БабичВ. М., «Докл. АН СССР»,
1961, т. 137, J* 6, с. 1263—66; [10] БабичВ. М., Мо.щ т-
к о в И. А., «Изв. АН СССР. Физика Земли», 1966, JVi 6, с. 34 —
38; [11] Мухина И. В., Молотков И. А., там же,
1967, №4, с. 3—8; [12] 3 в о л и н с к и й Н. В., «Изв. АН
СССР. Сер. геофил.». 1957, № 10, с. 1201—18; 1958, .4» 1, с. 3—
16; № 2, с. 1U5—74; [13] Итоги науки и техники. Механика
твердых дефор. -;>усмых тел, т. 10, М., 1977, с. 5—62.
В. Д. Купрадзе, В. М. Бабич, И. А. Молотков.
ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ — pa.s-
дел математики, посвященный теории и методам реше-
решения многошаговых задач оптимального управления.
В Д. п. для управляемых процессов среди всевозмож-
всевозможных управлений ищется то, к-рое доставляет экстре-
экстремальное (наименьшее или наибольшее) значение целе-
целевой функции — нек-рой числовой характеристики про-
процесса. Под многошаговостью понимают либо
многоступенчатую структуру процесса, либо что управ-
управление разбивается на ряд последовательных этапов (ша-
гсв), соответствующих, как правило, различным момен-
моментам времени. В ряде задач многошаговость проистекает
из существа процесса (напр., в задаче определения оп-
оптимальных размеров ступеней многоступенчатой раке-
ракеты или при нахождении наиболее экономичного режима
полета самолетов), но она может вводиться искусствен-
искусственно для того, чтобы обеспечить возможность применения
метода Д. п. Таким образом, в названии Д. п. под про-
программированием понимают принятие решений, плани-
планирование, а слово динамическое указывает на существен-
существенную роль времени и порядка выполнения операций в
рассматриваемых процессах и методах.
Методы Д. п. являются составной частью методов, ис-
используемых в исследовании операций, и применяются
в задачах оптимального планирования (напр., в зада-
задачах об оптимальных распределениях ресурсов, в теории
управления запасами, в задачах замены оборудования
и т. д.) и при решении многих технических проблем
(напр., в задачах управления последовательными хими-
химическими процессами, в задачах оптимального проекти-
проектирования прокладки дорог и др.).
Проиллюстрируем основную идею. Пусть процесс уп-
управления нек-рой системой X состоит из т шагов (эта-
(этапов); на г-м шаге управление у; переводит систему из
состояния 2,-_1( достигнутого в результате (;—1)-го
шага, в новое состояние х,-. Этот процесс перехода осу-
осуществляет заданная функция f,(x, у), и новое состояние
определяется значениями х/_!, у;:
г/ = /|(*1-1. Уд-
Таким образом, управления У\, у2, . . . , ут переводят
систему из начального состояния х0 ? Хо в конечное —
хт?.Хт, где Хо и Хт — совокупности допустимых на-
начальных и конечных состояний системы X. Опишем одну
из возможных постановок экстремальной задачи. На-
Начальное состояние х0 задано. Требуется выбрать управ-
управления у1, у2, ... , ут таким образом, чтобы система X
перешла в допустимое конечное состояние и при этом
заданная целевая функция F(x0, уг, xt, у2, ... , ут, хт)
достигла максимального значения F*, т. е.
F*= max F (х0, уг, хи у2, ..., ут, хт).
Уг. Уг, ¦ ¦ ; Ут
Важной особенностью метода Д. п. является то, что
он применим лишь для аддитивной целевой функции.
В рассмотренном примере это означает, что
^=2™=1ф,(*/-1, уд-
Кроме того, в методе Д. п. требуется, чтобы задача ха-
характеризовалась отсутствием «последействия»: решения
(управления), принимаемые на шаге, оказывают влия-
влияние только на состояние x-t системы в момент i. Другими
словами, процессы, описываемые функциями вида
*!=/( (*l-l. У1, Xi-2, У1-1, ...,У1, Х0),
не рассматриваются. Оба упомянутых ограничитель-
ограничительных условия можно ослабить, но только за счет сущест-
существенного усложнения метода.
Для решения задач Д. п. обычные методы математи-
математического анализа либо вообще неприменимы, либо при-
приводят к огромному числу вычислений. В основе метода
Д. п. лежит принцип оптимальности,
сформулированный Р. Беллманом (R. Bellman): пред-
предположим, что осуществляя управление дискретной сис-
системой X, мы уже выбрали некоторые управления ди-
дискретной системой у1, у2, ... , mtn тем самым траек-
траекторию состояний х0, xlt . . . , хъ, и хотим завершить
процесс, т. е. выбрать y/t+i, yk + г, ¦ • ¦ > Ут (а значит и
:tfc+1, Zfc + 2, ..., хт)\ тогда, если завершающая часть
процесса не будет оптимальной в смысле достижения
максимума функции
то и весь процесс не будет оптимальным.
Пользуясь принципом оптимальности, легко полу-
получить основное функциональное соотношение. Опреде-
Определим последовательность функций переменной х:
(i.(i)=0, to*-х (я) = max [фд. (x, y)-\-<»k(fk(x,y))\,
v
k=l, 2, ... , т. Здесь максимум берется по всем уп-
управлениям, допустимым на шаге к. Соотношение, опре-
определяющее зависимость ш^_! от ш^, принято называть
Беллмана уравнением. Смысл функций ш^_1(ж) нагля-
нагляден: если система на шаге к—1 оказалась в состоянии х,
то ш^_1(ж) есть максимально возможное значение функ-
функции F. Одновременно с построением функций W?_i(;r)
находятся условные оптимальные уп-
управления Ук(х) на каждом шаге (т. е. значения
оптимального управления при всевозможных предполо-
предположениях о состоянии х системы на шаге к—1). Оконча-
Окончательно оптимальные управления находятся последова-
последовательным вычислением величин
u>o(zo) = F*< Hi, х\, !/2, ¦¦., Ут, хт-
Из сказанного очевидна следующая особенность мето-
метода Д. п.— с его помощью решается не одна конкретная
задача при определенном х0, а сразу все подобные одно-
однотипные задачи при любом начальном состоянии. По-
Поскольку численная реализация метода Д. п. весьма
сложна, т. к. требует большого объема памяти ЭВМ, то
его целесообразно применять в тех случаях, когда не-
необходимо многократно решать типовые задачи (скажем,
определение оптимального режима полета самолета при
меняющихся погодных условиях). Несмотря на то, что
задача Д. п. формулируется для дискретных процес-
процессов, в ряде случаев метод Д. п. с успехом применяется
для решения динамических задач с непрерывными па-
параметрами.
Д. п. дало новый подход ко многим задачам вариаци-
вариационного исчисления.
Важным разделом Д. п. являются стохастиче-
стохастические задачи Д. п.— задачи, в к-рых на состоя-
состояние системы и на целевую функцию влияют случайные
факторы. К таким задачам относятся, напр., задачи оп-
оптимального регулирования запасов с учетом возможно-
возможностей случайного пополнения запасов. Здесь наиболее
естественной областью применения Д. п. являются
управляемые марковские процессы.
Метод Д. п. был предложен Р. Беллманом. Строгое
обоснование метода Д. п. было получено в результате
работ Л. С. Понтрягина и его учеников по математиче-
математической теории управляемых процессов (см. Оптимального
управления математическая теория).
Хотя метод Д. п. существенно упрощает исходные
задачи, однако явное его применение, как правило,
весьма громоздко. Для преодоления этих трудностей
разрабатываются приближенные методы Д. п.
Лит.: [1] БеллманР., Динамическое программирова-
программирование, пер. с англ., М., 1960; [2] Болтянский В. Г., Ма-
Математические методы оптимального управления, М., 1966; [3]
X е д л и Д ж., Нелинейное и динамическое программирова-
программирование, пер. с англ., М., 1967; [4] X е д л и Д ж., У а й т и н Т.,
Анализ систем управления запасами, пер. с англ., М., 1969;
[5]ХовардР.А., Динамическое программирование и марков-
марковские процессы, пер. с англ., М., 1964.
С. А. Ашманов, В. Г. Карманов.
ДИНИ ПРИЗНАК: если 2я-периодическая интегри-
интегрируемая на отрезке [0, 2л] функция f(x) в точке х0 удов-
удовлетворяет условию
J* ±\f (*„ + *) + f(xo-z)-2S\dx< oo
при фиксированном числе S, — оо<5<+оо, и каком-
либо 6>0, то ряд Фурье функции f(x) в точке ха сходит-
сходится к числу S. Д. п. доказан У. Дини [1]. Его утвержде-
утверждение окончательно в следующем смысле. Если jj,(f)>0 —•
такая непрерывная функция, что функция \i(t)lt не
интегрируема в окрестности точки 2=0, то можно найти
непрерывную функцию /(*), ряд Фурье к-рой расходит-
расходится в точке t=0, причем
для малых t.
Лит.: [1] D i n i U., Serie di Fourier e altre rappresentazioni
analitiche delle funzione di una variable reale, Pisa, 1880; [2]
Зигмунд А., Тригонометрические ряды, пер. с англ., т. 1,
М., 1965. Б. II. Голубое.
ДИНИ ТЕОРЕМА о равномерной сходимо-
сходимости ряда: если функции ип(х). «=1,2, ... , непре-
непрерывны и неотрицательны на отрезке [а, Ь\ и сумма
ряда\^°=1 ип(х) является непрерывной на этом отрез-
отрезке функцией, то указанный ряд сходится на [а, Ь]
равномерно. Д. т. обобщается на случай, когда обла-
областью определения функций ип(х) является произволь-
произвольный компакт. Л. Д. Кудрявцев.
ДИНИ — ЛИПШИЦА ПРИЗНАК: если непрерывная
2л-периодич. функция f(x) удовлетворяет условию
lim <о(б,/)ln-4- = 0,
где ш(б, /) — модуль непрерывности функции j(x), то
ее ряд Фурье равномерно сходится к ней на всей число-
числовой оси. Д.— Л. п. доказан У. Дини |1], а в частном
случае, когда ш(б, f)=O(8a), 6—»--f-0, при каком-либо
0<а<:1, он установлен Р. Липшицем [2], Утверждение
Д.— Л. п. окончательно в следующем смысле. Если
шF) — произвольный модуль непрерывности, удовле-
удовлетворяющий условию
Tim о) F) ln-i- >0,
6 -* +0
то существует непрерывная 2я-периодич. функция /0(я),
ряд Фурье которой расходится в некоторой точке, а мо-
модуль непрерывности ш (б, /0) удовлетворяет условию
ш(б, /о)=0(шF)).
Лит.: [1] р i n i U., Sopra la serie di Fourier, Pisa, 1872;
[2] LipschitzB., «J. reine und angew. Math., 1864, Bd
63, .N} 2, S. 296—308; [3] LebesgueH., «Bull. Soc. math.
France» 1910, t. 38, p. 184—210; [4] Никольский С. М.,
«Докл. АН СССР», 1950, т. 73, JV» 3, с. 457—60; [5] Б а р и Н. К.,
Тригонометрические ряды, М., 1961. Б. И. Голубое.
ДИНОСТРАТА КВАДРАТРИСА — трансцендентная
плоская кривая, уравнение к-рой в декартовых прямо-
прямоугольных координатах имеет вид:
пх '
ctg
В полярных координатах:
о (л - 2ф)
" Я COS ф '
У Д. к. бесконечное число ветвей (рис.), пересекающих
ось абсцисс в точках х= — а, =t3a, —5a, ... и имеющих
асимптоты х=±2а, ^zia, =t6a, .... Точки пересече-
пересечения с прямой у=2а/л — точки перегиба.
у
Г
Открытие Д. к. приписывают Гиппию из Элиды D20
до н. э.). Возможность графич. решения задачи о квад-
квадратуре круга при помощи квадратрисы показал Дпно-
страт B-я пол. 4 в. до н. э.).
Лит.: [1] С а в е л о в А. А., Плоские кривые, М., 1960.
Д. Д. Соколов.
ДИОФАНТОВ АНАЛИЗ — см. Диофантова геомет-
геометрия.
ДИОФАНТОВ ПРЕДИКАТ — всякий предикат $>,
определенный на множестве упорядоченных наборов из
п целых (или целых неотрицательных, или целых поло-
положительных) чисел, для к-рого можно указать многочлен
Р(аг, . .. , ап, zl, . . . , z?) с целыми коэффициентами
такой, что набор (аг, . . . , а„) удовлетворяет предикату
У тогда и только тогда, когда диофантово уравнение
Р (di, • • ., ап, zt zft)=0
разрешимо относительно zx, . . . , z^. Область истинно-
истинности Д. п. является диофантовым множеством. Класс
Д. п. совпадает с классом перечислимых предикатов
(см. Диофантовых уравнений проблема разрешимости).
Ю. В. Матиясевич.
ДИОФАНТОВА ГЕОМЕТРИЯ, диофантов ана-
л и з,— область математики, посвященная изучению
целочисленных и рациональных решений систем алгеб-
алгебраич. уравнений, или, иначе, изучению диофантовых
уравнений, методами алгебраич. геометрии. Появление
во 2-й пол. 19 в. теории алгебраич. чисел сделало ес-
естественным изучение диофантовых уравнений с коэффи-
коэффициентами из произвольного поля алгебраич. чисел, при-
причем решения ищутся или в этом поле, или же в его коль-
кольце целых элементов. Параллельно с теорией алгебраич.
чисел развивалась и теория алгебраических функций.
Глубокая аналогия между ними, подчеркивавшаяся
Д. Гильбертом (D. Hilbert) и особенно Л. Кронекером
(L. Kronecker), привела к единообразному построению
различных арифметич. теорий для этих двух типов по-
полей (см. [3]), называемых обычно глобальными
полями. Особенно отчетливо эта аналогия просту-
проступает в том случае, когда в качестве алгебраич. функций
рассматриваются функции одного переменного и с ко-
конечным полем констант. Хорошей иллюстрацией тому
служат такие понятия как дивизоры, ветвление и такие
результаты как теория полей классов. Проникновение
этой точки зрения в теорию диофантовых уравнений
произошло позднее, и систематич. рассмотрение дио-
диофантовых уравнений не только с числовыми, но и с
функциональными коэффициентами началось только в
50-х гг. 20 в. Решающее влияние оказало на это разви-
развитие алгебраич. геометрии. Одновременное рассмотрение
числовых и функциональных полей, выступающих как
две равноправные стороны одного и того же предмета,
не только приводит к красоте и законченности резуль-
результатов, но и взаимно обогащает оба аспекта (см. [3]).
В алгебраич. геометрии неинвариантное понятие сис-
системы уравнений заменяется понятием алгебраического
многообразия над заданным полем AT, а место решений
занимают рациональные точки со значениями в поле К
или его конечном расширении. Поэтому можно сказать,
что основная задача диофантовой гео-
геометрии состоит в изучении множества Х(К) рацио-
рациональных точек алгебраич. многообразия X, определен-
определенного над полем К указанного выше вида. Целочислен-
ные решения диофантовых уравнений также имеют гео-
метрич. смысл.
При изучении рациональных (или целых) точек на
алгебраич. многообразиях прежде всего возникает во-
вопрос о существовании хотя бы одной такой точки. Д е-
сятая проблема Гильберта сформули-
сформулирована как задача нахождения общего метода, позво-
позволяющего решать этот вопрос для любого алгебраич.
многообразия. После появления точного понятия алго-
алгоритма и доказательства алгоритмич. неразрешимости
целого ряда задач стало ясно, что проблема Гильберта
может иметь и отрицательное решение (см. Диофанто-
Диофантовых уравнений проблема разрешимости), и наиболее ин-
интересным является вопрос о том, для каких классов дио-
диофантовых уравнений такой алгоритм существует. Из-
Известно несколько общих подходов к этой задаче. Наибо-
Наиболее естественным с алгебраич. точки зрения является
так наз. принцип Хассе. Он состоит в рассмот-
рассмотрении наряду с исходным полем К его пополнений Kv
по всевозможным нормированиям. Поскольку X(K)CZ
CZX(KV), то необходимым условием существования К-
рациональной точки является непустота множестн
X{KV) для всех v. Значение принципа Хассе состоит
в том, что он сводит вопрос о существовании точки к
аналогичному вопросу над локальным полем. Послед-
Последняя задача существенно проще — для нее известен ал-
алгоритм, а в частном важном случае, когда многообразие
X проективно и неособо, Гензеля лемма и ее обобщения
позволяют произвести дальнейшую редукцию и свести
все к изучению рациональных точек над конечным по-
полем, где задача решается или последовательным пере-
перебором, или более совершенными средствами (см. Алгеб-
Алгебраических многообразий арифметика; см. также [2],
[12]). Последнее существенное обстоятельство, связан-
связанное с принципом Хассе, состоит в том, что для всех v,
кроме конечного числа, множества X(KV) непусты, так
что число условий всегда конечно, и они могут быть эф-
эффективно проверены (см. [2]). Но уже для кривых 3-й
степени принцип Хассе неприменим. Так, кривая 3.г!-|-
+4г/3=5 имеет точки во всех полях р-адических чисел и в
поле действительных чисел, но не имеет рациональной
точки (см. [2], [7]). Этот пример послужил отправным
пунктом для создания теории, описывающей «отклоне-
«отклонение» от принципа Хассе в классе главных однородных
пространств абелевых многообразий (см. [7], [10]). Это
отклонение описывается в терминах специальной груп-
группы III, сопоставляемой каждому абелеву многообразию
(группа Тейта — Шафаревича). Основную трудность
теории составляет отсутствие способов вычисления
группы Ш, к-рая (к 1978) не вычислена ни для одного
многообразия. Эта теория распространена и на другие
классы алгебраич. многообразий (см. [11]).
Другое эвристическое соображение, используемое при
изучении диофантовых уравнений, состоит в том, что-
если число переменных, входящих в систему уравнений,
велико по сравнению со степенью, то система, как пра-
правило, имеет решение. Однако доказать это в тех или
иных случаях бывает очень трудно. Единственный об-
общий подход к задачам такого типа принадлежит анали-
тич. теории чисел и основан на применении оценок три-
тригонометрии, сумм (см. Тригонометрических сумм метод,
Виноградова метод; см. также [4]). Первоначально этот
метод применялся к уравнениям довольно частного вида
(напр., к Варинга проблеме). Но в дальнейшем с его
помощью было доказано, что если F — форма нечетной
степени d от п переменных и с рациональными коэффи-
коэффициентами, то при п, достаточно большом по сравнению с
d, проективная гиперповерхность ^=0 имеет рацио-
рациональную точку (см. [2]). Имеется гипотеза Артина, ут-
утверждающая, что этот результат справедлив уже при
n>d2 (см. [2], [10]). Она доказана (к 1978) только для
квадратичных форм. Аналогичные вопросы можно ста-
вить и для других полей. В частности, о результатах,
полученных для локальных полей, см. Алгебраических
многообразий арифметика; см. также [5]. Центральной
проблемой Д. г. является изучение структуры множест-
множества рациональных или целых точек и прежде всего выяс-
выяснение вопроса о том, конечно оно или нет. В этой по-
последней задаче основное эвристическое предположение
состоит в том, что если степень системы намного больше
числа переменных, то система имеет, как правило, ко-
конечное число решений (см. [10]). В отличие от рассмот-
рассмотренной выше задачи о разрешимости, никаких общих
результатов (к 1978) в этом направлении нет. Наи-
Наибольшее число исследований посвящено случаю алгеб-
раич. кривых. Оказалось, что строение множества ра-
рациональных точек Х(К) кривой X, определенной над
нолем К, сильно зависит от ее рода g. Если g=0, то
либо множество Х(К) пусто, либо кривая X бирацио-
нально эквивалентна над полем К проективной прямой.
Последнее означает, что множество Х(К) бесконечно, и
существует параметризация его рациональными функ-
функциями нек-рой переменной со значениями из поля К
(см. [7], [13], [1]). Кривые рода g=l с непустым множе-
множеством Х(К) рассматривались в 1901 А. Пуанкаре (Н. Ро-
incare), к-рый показал, что они бирационально эквива-
эквивалентны плоским кубич. кривым, и ввел на множестве
Х(К) структуру абелевой группы (см. Эллиптическая
кривая; см. также [1], [7]). Гипотеза Пуанка-
Пуанкаре о том, что при K=Q группа имеет конечное число
образующих, доказана К. Морделлом (К. Mordell, 1922)
(см. [15]). Это было обобщено А. Вейлем (A. Weil, 1928)
на произвольные поля алгебраических чисел и А.
Нероном (A. Neron, 1952) на любые глобальные поля
<см. [8]).
Группу X(К) можно представить в виде прямой сум-
суммы свободной группы ранга г и конечной группы поряд-
порядка п. Вопрос о том, ограничены ли эти числа на множест-
множестве всех эллиптич. кривых над данным полем К, при-
привлекал внимание начиная с 30-х гг. (см. [7]). Ограничен-
Ограниченность кручения п доказана в 1971. В функциональном
случае существуют кривые сколь угодно большого ран-
ранга (см. [12]). В числовом случае ответ (к 1978) неизве-
неизвестен.
Наконец, в случае кривой рода g>i имеется гипо-
гипотеза Морделла о конечности числа рациональ-
рациональных точек (высказанная для K:=Q; точную формули-
формулировку см. в [9]). В функциональном случае эта гипотеза
доказана Ю. И. Маниным в 1963 (см. [12]). Если же
основное поле — числовое, то гипотеза доказана для
модулярных кривых. Все имеющиеся результаты
дают конечность числа точек в не слишком больших рас-
расширениях основного поля (см. [12]).
Гораздо большие успехи достигнуты в изучении це-
целых точек. Здесь имеется весьма общий метод диофанто-
диофантовых приближений, предложенный в 1909 А. Туэ (A. Thue)
(см. [6], [8], [9], [13]). Он основан на следующем. Пусть
F(x, 1/)=ТС,-(г—ащ) —форма с рациональными коэф-
коэффициентами и пусть имеется целочисленное решение
{х0, !/„) уравнения F(x, y)=c, сфО. Тогда для нек-рого i
< —— , Ь = const.
Если а — алгебраич. число степени гс>3, то неравенст-
неравенство |а—plq\ <l/gE имеет конечное число решений в целых
р и q при е>гс/2+1. Отсюда следует конечность числа
целых точек на кривых вида F(x, y) = c. С тех пор каж-
каждое продвижение в проблеме диофантовых приближений
алгебраич. чисел давало соответствующие результаты
для целых точек. Так была доказана в 1929 К. Зигелем
(С. Siegel) теорема о конечности числа целых точек на
любой кривой рода g>0. О дальнейших обобщениях
этой теоремы на случай целых точек в произвольных
глобальных полях см. также [9].
Основным технич. средством, используемым в дока-
доказательстве этих и других теорем конечности в Д. г.,
является высота (см. Высота в диофантовой геометрии).
Среди алгебраич. многообразий размерности >1 наи-
наиболее изучены абелевы многообразия, представляющие
собой многомерный аналог эллиптических кривых.
Обобщая теорему Морделла, А. Вейль перенес ее ут-
утверждение о конечности числа образующих группы ра-
рациональных точек на абелевы многообразия любой раз-
размерности (теорема Морделла — Вейля). В 60-х гг. по-
появилась гипотеза Берча и Суиннертон-Дайера, связы-
связывающая ранг этой группы с порядком полюса дзета-
функции многообразия X в точке dim X (см. [7], [12]).
Несмотря на многочисленные аргументы в пользу этой
гипотезы, никаких подходов к ее доказательству
(к 1978) пока нет. Нет никакого продвижения (к 1978) и в
гипотезах конечности для рациональных точек замкну-
замкнутых подмногообразий и целых точек аффинных откры-
открытых подмножеств абелевых многообразий (см. [9], [10]).
Другой класс алгебраич. многообразий, для изуче-
изучения к-рого имеются общие методы и подходы, состоит
из многообразий вида
F (хъ ...,хп) = с, сфО,
где F — форма, разложимая в нек-ром расширении
основного поля на линейные множители. Для изучения
целых точек на таких многообразиях имеются два ме-
метода. Первый — это отмеченный выше метод диофан-
диофантовых приближений, созданный А. Туэ именно для
уравнений такого вида, но с двумя переменными. Толь-
Только в 1970 этот метод получил новое развитие: при по-
помощи теоремы Шмидта о совместных приближениях
было доказано, что число целых точек на многообразии
(*) всегда конечно, если выполняется нек-рое легко
проверяемое условие на форму F (его необходимость
была известна ранее, см. [2]). Совсем другой метод, ос-
основанный на рассмотрении уравнения (*) в области
целых р-адических чисел, был предложен в 1935 Т.
Сколемом (см. [13]). Этим методом была доказана тео-
теорема конечности для уравнения (*) для небольших зна-
значений п или т (см. [2]).
Интенсивно исследуется еще один класс алгебраич.
многообразий — рациональные и близкие к ним много-
многообразия, являющиеся аналогом кривых рода 0. Полу-
Получены многочисленные результаты об их классификации
и о строении множества рациональных точек (см. [12]).
В отличие от рассмотренных выше примеров, здесь все
обстоит сложнее, и никаких общих теорем типа
теорем Шмидта, Зигеля или Морделла — Вейля не
найдено (к 1978).
Отличительной чертой почти всех отмеченных выше
результатов является то, что они, раскрывая качест-
качественную картину множества рациональных или целых
точек, не дают никаких количественных оценок, с
помощью к-рых можно явно описать это множество.
Получение подобных результатов, или, как говорят,
эффект и визация качественных те-
теорем, принадлежит к труднейшим задачам Д. г. и
вообще теории чисел. Для случая теоремы Туэ такая
эффективизация, полученная А. Бейкером (A. Baker)
в 1968, состоит в явных оценках высот целых точек в
зависимости от коэффициентов уравнения кривой (см.
Диофантовых приближений проблемы эффективизации).
Затем такая оценка была получена для широкого клас-
класса гиперэллиптич. кривых и, в частности, всех кривых
рода 1 (см. [12]). Это дает для таких кривых алгоритм,
позволяющий найти все целые точки, и тем самым вы-
выяснить, есть ли такая точка вообще. Как уже было от-
отмечено, для любого диофантова уравнения такого ал-
алгоритма не существует.
Другим чрезвычайно интересным подходом к коли-
количественному описанию множества целых точек явля-
ется развитие кругового метода Харди — Литлвуда.
Распространение этого подхода на абелевы многообра-
многообразия привело к появлению гипотез Берча иСуиннертон-
Дайера (см. [15]), использование к-рых привело к
построению алгоритма, дающего эффективизацию те-
теоремы Морделла — Вейля. Есть все основания пола-
полагать, что дальнейшее развитие этого метода, а также ус-
установление его связи с теорией высоты будет иметь
большое значение для решения основных проблем ди-
офантовой геометрии.
Лит.: [1] Б а ш м а к о в а И. Г., Диофант и диофантовы
уравнения, М., 1972; [2] Б о р е в и ч 3. И., Шафаревич
И. Р., Теория чисел, 2 изд., М., 1972; [3] В е и л ь А., «Мате-
«Математика», 1958, т. 2, № 4, с. 49—58; [4] Виноградов И. М.,
Метод тригонометрических сумм в теории чисел, М., 1971; [5J
GreenbergM., Lectures on forms in many variables, N. Y.—
Amst., 1969; [6] Дэвенлорт Г., Высшая арифметика, пер.
с англ., М., 1965; [7] КасселсД ж., «Математика», 1068,
т. 12, № 1, с. 113—60; № 2, с. 1 — 48; [8] К о k s m a J. Р.,
Diopliantische Approximationen, В., 1936; [9] LangS., Dio-
phantine geometry, N. Y.—L., 1962; [10] ЛенгС, «Математи-
«Математика», 1961, т. 5, Л» 6, с. 3—12; [И] М а н и н Ю. И., Кубические
формы, М., 1972; [12] Итоги науки. Алгебра. Топология. Гео-
Геометрия. 1970, М., 1971, с. 111—51; [13] SkolemTh., Dio-
phantische Gleichungen, В., 1938; [14] Swinnerton-Dy-
erH. P. P., в кн.: Proceedings of Symposia in Pure Mathema-
Mathematics, v. 20. 1969. Number theory institute, Providence, 1971,
p. 1—52; [15] Алгебраическая теория чисел, пер с англ., М.,
1969, гл. XII. А. Я. Паршин.
ДИОФАНТОВО МНОЖЕСТВО — множество Щ1, со-
состоящее из упорядоченных наборов из п целых (целых
неотрицательных, целых положительных) чисел, для
к-рого можно указать диофантово уравнение
Р К, . • •, а„, xlt ..., z,) = 0, (*)
зависящее от п параметров аг, . . ., ап, допустимыми
значениями к-рых являются целые (соответственно
целые неотрицательные или целые положительные)
числа, и разрешимое относительно хх, . . ., xt тогда и
только тогда, когда (alt . . . , а„)?Щ1. Здесь несуще-
несущественно, понимается ли под разрешимостью существо-
существование решения в целых, целых неотрицательных или
целых положительных числах, поскольку уравнение
(*) разрешимо в целых (целых неотрицательных, це-
целых положительных) числах тогда и только тогда,
когда уравнение
Р («1, •••, ап, У! — ги .... yt —Zi) = 0
разрешимо в целых положительных числах (соответст-
(соответственно тогда и только тогда, когда уравнение
Р(аи ..., а„
разрешимо в целых неотрицательных числах, или соот-
соответственно тогда и только тогда, когда уравнение
Р{ах, .... ап, pl + qi + rl-jr sj, . .., pi -\-q\ +r? -f-s/ ) = 0
разрешимо в целых числах, ибо по теореме Лагранжа
каждое целое неотрицательное число представимо в
виде суммы четырех квадратов).
Для любого Д. м. можно указать соответствующее
уравнение (*), в к-ром степень многочлена Р не больше
4 (это достигается ценой увеличения числа неизвест-
неизвестных). Для каждого Д. м. целых неотрицательных чи-
чисел, помимо уравнения общего вида (*), можно ука-
указать уравнение вида Р (хи ..., xi) — ai, иными слова-
словами, каждое Д. м. целых неотрицательных чисел яв-
является множеством всех неотрицательных значений,
принимаемых некоторым многочленом с целочислен-
целочисленными коэффициентами при произвольных значениях
переменных. В качестве Р всегда можно взять многочлен
степени не выше 5, если допустимыми значениями пе-
переменных являются целые неотрицательные или целые
положительные числа, и многочлен степени не выше 6,
если переменные принимают произвольные целочислен-
целочисленные значения.
Класс Д. м. замкнут относительно операций пере-
перестановки и отождествления аргументов, объединения,
пересечения, прямого произведения и проектирования
(проекцией множества Щ}, состоящего из
упорядоченных наборов из п чисел, наз. множество
{<а1? ..., а„_1>:3б [<ai, ¦¦¦, a«-i, &>?Ш1]}), а также
относительно операции, ставящей множеству 9Л в соот-
соответствие множество
«аь ..., а„_1( 6>:Vc[e<6=><a1, . . ., а„_ь с> ?9Л]}.
Класс Д. м. совпадает с классом перечислимых мно-
множеств (см. Диофантовых уравнений проблема разреши-
разрешимости), и все результаты о перечислимых множествах
переносятся на Д. м. В частности, из теоремы о суще-
существовании универсального перечислимого множества
следует, что существует такое число I, что для каждого
п существует многочлен Un(a1, . . ., ап, т, х1, . . ., xt)
с целочисленными коэффициентами, универсальный в
следующем смысле: для каждого диофантова (перечис-
(перечислимого) множества Ш1, состоящего из упорядоченных
наборов из п чисел, можно указать такое значение пара-
параметра т (номер множества 9Л), что уравнение
U„(ах, ..., ап, т, хъ ..., xt) = 0
разрешимо относительно х±, . . ., хг тогда и только тогда,
когда («!, . . ., а„)?Щ}. Существуют многочлены, уни-
универсальные в других смыслах (см., напр., [1]).
Диофантовыми являются многие интересные с тео-
теоретико-числовой точки зрения множества, напр, мно-
множество всех простых чисел, множество всех совершен-
совершенных чисел, множество всех тех п, для к-рых разреши-
разрешимо уравнение Ферма
хп 4- уп — zn.
Доказательство теоремы о том, что перечислимые мно-
множества диофантовы, является эффективным, т. е. для
стандартно заданного перечислимого множества мож-
можно явно указать соответствующее диофантово уравне-
уравнение. Этот универсальный метод, не использующий спе-
специфики рассматриваемых множеств, приводит к до-
довольно громоздким многочленам, однако для нек-рых
конкретных множеств удается найти их сравнительно
простые диофантовы представления, опираясь, кроме
перечислимости, на другие свойства этих множеств.
Можно рассматривать и называть диофантовыми
множества, представимые как множества всех тех упо-
упорядоченных наборов из п элементов нек-рого кольца К,
для к-рых в этом кольце разрешимо относительно
хг, . . ., Х[ уравнение вида (*), где Р — многочлен либо
с целочисленными коэффициентами, либо с коэффици-
коэффициентами из К.
Лит.: [1] Матиясевич Ю. В., «Успехи матем. наук»,
1972, т. 27, в. 5, с. 185—222. Ю. В. Матиясевич.
ДИОФАНТОВЫ ПРИБЛИЖЕНИЯ — раздел теории
чисел, в к-ром изучаются приближения нуля значениями
функций от конечного числа целочисленных аргумен-
аргументов. Первоначальные задачи Д. п. касались рациональ-
рациональных приближений к действительным числам, но разви-
развитие теории привело к задачам, в к-рых некоторым дей-
действительным функциям необходимо придать «малые»
значения при целочисленных значениях аргументов.
В силу этого Д. п. тесно связаны с решением нера-
неравенств в целых числах — диофантовых неравенств, а
также с решением уравнений в целых числах (см. Дио-
Диофантовы уравнения).
Если рассматриваемая (аппроксимирующая) функ-
функция
F=--F(xu ..., хп)
линейна относительно целочисленных аргументов
х±, . . ., хп, то Д. п. с функцией F наз. линейными,
в противном случае — нелинейными. Если F —
однородный многочлен от х1, . . ., хп, то Д. п. с функ-
функцией F наз. однородными, а если F — неодно-
неоднородный многочлен, то — не однородными. Иног-
да рассматривается одновременно несколько функций F,
имеющих хотя бы один общий целочисленный аргумент.
В этом случае Д. п. наз. совместными. Совмест-
Совместные Д. п. могут быть линейными или нелинейными, од-
однородными или неоднородными в указанном выше
смысле.
Численные значения F могут считаться близкими
к нулю не обязательно при
\F(xlt ..., хп)\ < е
с некоторым е>0, но и при
O^F (хъ . .,, хп) < е
(односторонние приближения). Функции F могут за-
зависеть от параметров, непрерывно меняющихся в не-
некоторой области,— это параметрич. Д. п. Наконец,
область определения и область значений аппроксими-
аппроксимирующих функций могут быть не только подмножест-
подмножествами евклидова пространства, а существенно иных то-
пологич. пространств (см. ниже Д. п. в поле р-адиче-
скнх чисел и Д. п. в поле степенных рядов).
Наиболее старая («простейшая») задача Д. п. — при-
приближения нуля линейной формой ах—у, где а>0 —
фиксированное действительное число, х, у — перемен-
переменные целые (линейные однородные Д. п.), т. е. задача
о рациональных приближениях к а. Для специальных
а(а= У2, |/2, я) эта задача рассматривалась еще в
древности (Архимед, Диофант, Евклид), а ее тесная
связь с теорией цепных дробей была вполне выяснена
Л. Эйлером (L. Euler) и Ж. Лагранжем (J. Lagran-
ge). В частности, если хг>0, yt>0 таковы, что
I axl—y1\ = i [ \
где минимум берется по всем целым х в к.-л. интервале
0<х<?Х и но всем целым у, то дробь yJ/x1 является
подходящей дробью разложения а в цепную дробь.
Если неполные частные разложения а в цепную дробь
ограничены, то существует С=С(а)>0 с условием
х\ах—у\>С для всех целых х>0, у>0. Это верно,
напр., для квадратичных иррациональностей а, так как
тогда разложение в цепную дробь периодично. С другой
стороны, при любом иррациональном а неравенство
х\ах—у\ <1/ У 5 имеет бесконечное число целых ре-
решений ж>0, г/>0, а если а=(]Аб—1)/2, то постоянную
il У'Ъ нельзя заменить меньшим числом. Исследование
А. А. Маркова о минимумах неопределенных бинарных
квадратичных форм позволило продолжить последнее
утверждение: если а не эквивалентно (в смысле теории
цепных дробей) (У Ъ—1)/2, то неравенство х\ах—у\ <
<2~3'2 имеет бесконечное число решений; постоянная
2~3'3 не может быть улучшена, если а эквивалентно У2;
если ос не эквивалентно ни (У5—1)/2, ни ]/2, то не-
неравенство х{ах—у\ <5 B21)~''2 имеет бесконечное чис-
число решений, п т. д. (см. [1]). Постоянные 5~''2, 2~3/г,
5B21)~^2, . . . монотонно убывают и имеют предел 1/3.
Приближения нуля линейным неоднородным много-
многочленом cu+ff+P (ai Р — действительные числа, ж, у —
переменные целые) — простейший пример линейных
неоднородных диофантовых приближений. П. Л. Чебы-
шев доказал, что при любом иррациональном а н лю-
любом р неравенство x\ax-\-yJr§\ <2 имеет бесконечное
число решений в целых ж>0, у. Постоянная 2 здесь но
является наилучшей: Г. Мпнковскнй (Н. Minkowski)
доказал, что если $фаа-\-Ь (а, Ь — целые), то 2 можно
заменить на Yii чт0 является наилучшей постоянной.
Это утверждение есть следствие доказанного самим
Г. Минковским простейшего случая гипотезы о произ-
произведении неоднородных линейных форм (см. Минков-
ского гипотеза).
Более сложные задачи общей теории Д. п. касаются
аппроксимирующих функций от большего числа цело-
целочисленных аргументов (см, Дирихле теорема, Минков-
ского теорема, Кронекера теорема). Удобно ввести функ-
функцию ||a||=min |a—ra|, где минимум берется по всем
целым п (расстояние от а до ближайшего целого).
Напр., вместо рассмотренных выше линейных много-
многочленов ах—у и аг-j-y+P можно брать \\Гмх\\ и Цаж+РИ
для целых х>0. Из теоремы Дирихле следует, что для
любых действительных а1, . . ., ап существует бесконеч-
бесконечное число решений системы неравенств
х1'птах(\]а1х]], ..., ;|а„*]|) < 1
в целых ж>0. Единицу можно заменить меньшим числом
(напр., га/(га+1)), но ни для какого и>2 наилучшая
постоянная неизвестна. Она не может быть сколь угод-
угодно малым числом, как показывает пример 1, alt . . ., ап,
являющийся базисом действительного алгебраич. поля
(см. [1]). Если 1, ccj, . . ., <хп линейно независимы над
полем рациональных чисел, то при любых рх, . . .,
Р„ и любом е>0 существует бесконечное число реше-
решений системы неравенств
maxflla^-j-Px;], ..., ||а„г+рп||) < е
в целых ?>0 (теорема Кронекера). Сущест-
Существенная особенность этой теоремы о совместных неод-
неоднородных Д. п. состоит в том, что в принципе невоз-
невозможно (без специальной информации об однородных
приближениях к сц, . . ., ап) указать скорость убы-
убывания е при возрастании х: для того чтобы линейные
формы а^1х-\-у1, . . ., апх~\-у„ «хорошо» аппроксими-
аппроксимировали любые числа plt . . ., р„, необходимо и достаточ-
достаточно, чтобы эти формы не могли «хорошо» аппроксими-
аппроксимировать специальный набор чисел Pi=0, . . ., Р,,=0.
Различные на первый взгляд задачи Д. п. иногда
оказываются тесно связанными. Напр., принцип
переноса Хинчина (см. [1]) связывает разре-
разрешимость неравенства
X = max | х; | ф О W
1 <^ t <; /г
в целых числах xlt . . .7 хп с разрешимостью системы
max QI И1х Ц, ...
в целых ж>0, и обратно: если А,х и fi, соответственно
точные верхние грани тех Я>0 и [г>0, для к-рых A)
и B) имеют бесконечное число решений, то
В частности, равенства Я,1 = 0 и (г1 = О равносильны
(тогда а1? . . ., а„ соответствуют «наихудшей» аппрок-
аппроксимации, так как A) при Я,—0 и B) при [г = О имеют
бесконечное число pemeHHii какими бы ни были аг, . . .,
аи). Подобные связи существуют между однородной
и неоднородной задачами (см. [1], [5]) и не только в
случае линейных Д. п. Если, напр., аь . . ., а„ тако-
таковы, что при любом е>0 для всех целых ,г>0
||ох*И ... |]<*„*,]> С^-1, C)
где Ci~>Q зависит только от аг, . . ., а„ и е, то каковы
бы ни были действительные числа plt . . ., рл, при лю-
любом ej>0 система неравенств
имеет целое решение х с условием 0О<:Х, если
>Х0(ах, . . ., а„, ех). Более того, неравенство C) обе-
обеспечивает «сильную» равномерную расиределенность
дробных долей ({(Xj, g},..., {а„д}), гдед=1, 2, . . ., Q;
число этих дробей, попадающих в систему интервалов
/ХХ. . .XI„, каждый из к-рых лежит внутри единич-
единичного интервала, равно |/j|. . ¦\In\Q-\-O{QEl), |/| —'•
длина интервала /, е2>0 — произвольно. Выполне-
Выполнение неравенства C) для всех целых ж>0 равносильно
выполнению неравенства
для всех целых хг, . . ., хпФ@) при любом е3>0,
где С2>0 зависит только от а,, . . ., а„ и е3.
Доказательство разрешимости или неразрешимости
диофантовых неравенств, параметры к-рых определены
арифметич. или аналитич. условиями, часто является
весьма сложной задачей. Так, задача о приближениях
алгебраич. чисел рациональными, систематически изу-
изучаемая со времени доказательства неравенства Лиу-
вилля A844) (см. Лиувилля число), до сих пор не полу-
получила полного решения (см. Туэ — Зигеля — Рота тео-
теорема, Диофантовых приближений проблемы эффекти-
визации). Доказано [11], что для алгебраич. чисел
ccj,. . ., а„, вместе с 1 линейно независимых над полем
рациональных чисел, выполняются неравенства C), D)
при любых 8>0, е3>0. Из этого следует, что система
неравенств A) при любом Я>0 и система неравенств
B) при любом [х>0 имеют лишь конечное число реше-
решений. Существует тесная связь между подобными теоре-
теоремами о Д. п. к алгебраич. числам и представлением
целых чисел неполными разложимыми формами. В ча-
частности, задача о границах для решений х, у диофан-
това уравнения Туэ f(x, у) = Л при фиксированной
целочисленной неприводимой бинарной форме f(x, у)
не менее чем 3-й степени и переменном целом А рав-
равносильна изучению рациональных приближений к
корню а многочлена f(x, 1). Таким путем А. Туэ (А.
Time) доказал конечность числа решений уравнения
f(x,y) = A, предварительно получив нетривиальную
оценку рациональных приближений к а. Этот подход,
обобщенный и развитый К. Зигслем (С. Siegel), привел
его к теореме о конечности числа целых точек на ал-
алгебраич. кривых рода больше нуля (см. Диофантова
геометрия). В. Шмидт [11] использовал подобные идеи
для полного решения задачи о представлении чисел
разложимыми формами, основываясь на своих ашгрок-
спмационных теоремах. В нек-рых случаях связи между
теорией Д. п. и теорией диофантовых уравнений не
столь непосредственны, хотя законы аппроксимации
чисел могут играть главную роль в доказательствах
существования решений, асимптотики числа решений
п т. п. (задачи типа Варинга проблемы и метод Харди —
Литлвуда — Виноградова).
Д. п. к специальным числам, заданным как значе-
значения трансцендентных функций в рациональных или ал-
алгебраич. точках, изучаются методами теории тран-
трансцендентных чисел. Как правило, доказательство ирра-
иррациональности или трансцендентности к.-л. числа позво-
позволяет дать оценку аппроксимации его рациональными
или алгебраич. числами. Для трансцендентного а ве-
величину wn(a, /7) = min \P(a)\, где минимум берется
по всем ненулевым целочисленным многочленам сте-
степени не более п и высоты не более Н, наз. мерой
трансцендентности числа а. Оценка
снизу величины wn(a, H), главным образом при фик-
фиксированном п и переменном Я, составляет содержание
многих теорем теории трансцендентных чисел (см.
[12]). Напр., К. Малер ([7], [12]) доказал, что
In (n+1)
— п —
wn (е, Н)> Н 1п1пН ,
где С3>0 — абсолютная постоянная, Н>Н0(п). Дру-
Другим методом А. Бейкер [3] доказал D) для раз-
различных не равных нулю рациональных степеней е с
e3=C4(ln In х)~ч\ где
= l, 2, ..., п; С4 > О
зависит только от п, а1( . . ., а„. Так как величина
wn(a, H) будет «малой» лишь тогда, когда хотя бы
одно алгебраич. число степени не более п и высоты не
более // «близко» к а, то существует связь между оцен-
оценкой величины wn(a, It) и оценкой аппроксимации а
алгебраич. числами степени не более п. Пусть w*n(o., //) =
= min | а—х\, где минимум берется по всем алгебраич.
числам у, степени не более п п высоты не более Н, и пусть
-In те (а, Я)
A ^
« -In и* (а, Я)
Э. Вирзинг [13] нашел соотношения между величинами
wn(a, Н) и w* (a, H) (а — действительное)
(а) + 1 «• (а)
В частности, если wn(a) = n, то w"n(a) = n, и так как
wn(a)^n для всех трансцендентных а, то (
^(и+1)/2. Из последнего следует, что для всякого
трансцендентного а существует бесконечное число ал-
алгебраич. х степени не более п, удовлетворяющих не-
неравенству
\а-у.\ < ft-<«+3)/2 + es
где /ги — высота х, 84>0 — произвольно. Э. Вирзинг
высказал предположение, что w*n(a)^n для всех тран-
трансцендентных а и всех п=1, 2, .... Кроме очевидного
случая и=1 эта гипотеза доказана для п=2 (см. [4]).
Известно также, что для почти всех (в смысле меры
Лебега) действительных а верны равенства
wn(a) =wn(a) = ге, и —1, 2, ...
(см. [2], Метрическая теория чисел, Диофантовых
приближений метрическая теория).
Изучение диофантовых уравнений методами р-ади-
ческого анализа стимулировало развитие теории Д. п.
в поле р-адических чисел Qр, к-рая строится во многом
параллельно теории Д. п. в поле действительных чисел,
но с учетом неархимедовой топологии поля Qp. Напр.,
пусть со=^0 — р-адическое число. Рассматривая при-
приближения нуля (в р-адической метрике) значениями
целочисленной линейной формы сож+г/, приходят к
рациональным приближениям ш, к-рые, подобно слу-
случаю действительных чисел, тесно связаны с разложе-
разложением со в цепную (р-адическую) дробь [10]. Справед-
Справедливы аналоги теорем Дирихле, Кронекера, Минков-
ского и т. п., метрич. теорем, теорем о приближениях
алгебраич. числами п т. д. [2], [6], [8]. Диофантовы не-
неравенства в Qр можно интерпретировать как сравнения
по «высокой» степени р, что дает иногда возможность
получать чисто арифметич теоремы аналитич. методом.
Глубокое развитие Д. п. в поле Qp и его конечных рас-
расширениях позволяет использовать метод Туэ — Зпгеля —
Рота для доказательства теорем об арифметич. струк-
структуре чисел, представимых бинарными формами, об
оценке дробных долей степеней рациональных чисел
и т. п. (см. [10]).
Так как разложение функций в непрерывные дроби
осуществляется аналогично разложению чисел в цеп-
цепные дроби, то естественно возникает дальнейшая ана-
аналогия: приближение функций рациональными функ-
функциями в метрике поля степенных рядов. Этот подход
имеет далекое развитие и приводит к теории Д. п. в
поле степенных рядов. Пусть К —• произвольное ал-
алгебраич. поле, К[х] — кольцо многочленов от х над
К, К (х-1) — поле степенных рядов вида
i = — т, —
( 0 если
В поле К (х-1) вводится неархимедово нормирование
/ 1т, если со фО, a_m?i0,
( 0, е
где Z>1 — произвольное фиксированное число. Поле
Kix-1) с нормированием |ш[ становится метрич. про-
пространством. Изучение «диофантовых» приближений
осуществляется по обычной схеме, где К[х] играет
роль кольца целых чисел: рассматриваются аппроксими-
аппроксимирующие функции со значениями в К (х-1) от конечного
числа переменных со значениями в К[х], а близость
к нулю оценивается с помощью введенного нормиро-
нормирования. Есть определенное сходство получаемых таким
путем результатов со случаем Д. п. в поле действитель-
действительных чисел, но если К{х~х) заменить полем К{х) рядов
вида
а,?К, i = —т, —т-\-\, ...,
то результаты будут аналогичны приближениям в поле
/?-адических чисел (см. [2], [9]).
Д. п. в поле степенных рядов в несколько более
конкретной форме (специализации К, явная оценка
точности приближения и т. п.) составляют основу
нек-рых аналитич. методов теории трансцендентных
чисел.
В развитии теории Д. п. выделяются три подхода:
глобальный, метрический и индивидуальный. При гло-
глобальном подходе изучаются общие законы аппроксима-
аппроксимации, справедливые для всех чисел или для всех за
«редким» исключением. Сюда относятся теорема Ди-
Дирихле об однородных приближениях, теорема Кроне-
кера о неоднородных приближениях, общие теоремы о
приближении чисел алгебраическими, классификации
чисел по аппроксимационным свойствам и т. п. Соот-
Соответственно применяемые методы носят «глобальный»
характер (непрерывные дроби, применения теоремы
Минковского и методы геометрии чисел и т. п.). Ме-
Метрич. подход требует описания аппроксимационных
свойств чисел на основе понятий теории меры (см.
Диофантовых приближений метрическая теория, Ме-
Метрическая теория чисел). Получаемые результаты
касаются не всех, а почти всех (в смысле определенной
меры) чисел из рассматриваемых множеств или описы-
описываются с помощью нек-рой метрич. характеристики
(размерность Хаусдорфа, емкость и т. п.). Применяе-
Применяемые методы тесно связаны с теорией меры, теорией ве-
вероятностей и смежными дисциплинами. Индивидуаль-
Индивидуальный подход касается аппроксимационных свойств
специальных чисел (алгебраич. числа, е, я, In 2 и
т. п.) или требует построения чисел с определенными
аппроксимационными свойствами (числа Лиувилля,
Г-числа Малера и т. п.). Методы решения таких задач
специфичны и часто создаются специально для анализа
конкретной задачи.
Лит.: [1] К а с с е л с Д ж. В. С, Введение в теорию
диофантовых приближений, пер. с англ., М., 1961; [ 2] С п р и н-
дж у к В. Г., Проблема Малера в метрической теории чисел,
Минск, 1967; [3] Baker A., «Canad. J. Math.», 1965, v. 17,
p. 616—26; [4] DavenportH., SchmidtW., «Acta
Arithm.», 1967, v. 13, p. 169 — 76; [5] К о k s m a J. F., Dio-
phantische Approximationen, В., 1936; [6] LutzE., Sur ]es
approximations diophantiermes lineaires p-adiques, P., 1955; [7]
MahlerK., «Math. Z.», 1930, Bd 31, S. 729—32- [8] его
ж e, «Jahresber. DMY», 1934, Bd 44, S. 250—55; [9] его же,
«Ann. Math.», 1941, v. 42, p. 488—522; [10] его же, Lectures
on Diophantine approximations Is. 1.], pt 1, 1961; [11]
SchmidtW., «L'enseignment Math. Revue intern., ser. 2»,
1971, v. 17, №3—4, p. 187—253; [12] Schneider TL,
Einfiihrung in die transzendenten Zahlen, В., 1957; [13] Wir-
s i n g E., «J. reine und angew. Math.», 1961, Bd 206, M 1—2,
S. 67 — 77. В. Г. Спринджук.
ДИОФАНТОВЫ ПРОБЛЕМЫ АДДИТИВНОГО
ТИПА — диофантовы уравнения, для к-рых ставится
задача нахождения целочисленных решений и к-рые
могут одновременно рассматриваться как аддитивные
проблемы, т. е. как задачи о разбиении целого числа п
(произвольного или подчиненного дополнительным ус-
условиям) на слагаемые заданного типа. К Д. п. а. т.
можно отнести, напр., решение в целых числах сле-
следующих уравнений:
п = х2-\-у2 (см. Гауссово число),
п = х*-\- y2jrzi-\-l2 (см. Лагранжа теорема о сумме
четырех квадратов),
п = х" -j- уг -)- z2 (см. Целая точка),
а также Варинга проблему и др. Д. п. а. т. можно трак-
трактовать и как задачу нахождения пересечения арифме-
тич. сумм множеств. Напр., множество М целочислен-
целочисленных решений уравнения x2Jt~iy2 = z2 представляется
в виде М=А [\В, где
Лит.: El] В и н о г р а д о в И. М., Особые варианты мето-
метода тригонометрических сумм, М., 1976; [2] Г е л ь ф о н д А. О.,
Л и н н и к Ю. В., Элементарные методы в аналитической тео-
теории чисел, М., 1962; [3] О s t m a n n H. H., Additive Zahlen-
theorie, Bd 1, В., 1956. Б. М. Бредихин.
ДИОФАНТОВЫ УРАВНЕНИЯ — алгебраич. урав-
уравнения или системы алгебраич. уравнений с рациональ-
рациональными коэффициентами, решения к-рых отыскиваются
в целых или рациональных числах. Обычно предпола-
предполагается, что Д. у. имеют число неизвестных, превосхо-
превосходящее число уравнений, в связи с чем они наз. также
неопределенными уравнениями. По-
Понятие Д. у. в современной математике часто относят
также к алгебраич. уравнениям, решения к-рых оты-
отыскиваются среди целых алгебранч. чисел какого-либо
алгебраич. расширения поля рациональных чисел Q,
среди р-адических чисел и т. п.
Исследование Д. у. относится к области погранич-
пограничной между теорией чисел и алгебраич. геометрией (см.
Диофантоеа геометрия).
Решение уравнений в целых числах является одной
из древнейших математич. задач. Уже в начале 2-го
тысячелетия до н. э. вавилоняне умели решать системы
таких уравнений с двумя неизвестными. Наибольшего
расцвета эта область математики достигла в Древней
Греции. Основным источником для нас является «Ариф-
«Арифметика» Диофанта (вероятно, 3 в. н. э.), содержащая
различные типы уравнений и систем. В ней Диофант
(по его имени — название «Д. у.») предвосхищает ряд
методов исследования уравнений 2-й и 3-й степеней,
развившихся только в 19 в. (см. [1]). Создание древне-
древнегреческими учеными теории рациональных чисел при-
привело к рассмотрению рациональных решений неопре-
неопределенных уравнений. Эта точка зрения последователь-
последовательно проводится в книге Диофанта. Хотя сочинение Ди-
Диофанта содержит лишь решения конкретных Д. у.,
однако есть основания считать, что он владел некото-
некоторыми общими приемами.
Исследование Д. у. обычно связано с большими труд-
трудностями. Более того, можно явно указать многочлен
с целыми коэффициентами такой, что не существует
алгоритма, позволяющего по любому целому х узна-
узнавать, разрешимо ли уравнение
относительно уг, ¦ ¦ ., у (см. Диофантоеых уравнений
проблема разрешимости). Примеры таких многочленов
можно выписать явно. Для них невозможно дать ис-
исчерпывающего описания решений (если принимать
Чёрча тезис).
Простейшее Д. у.
ax+by=l,
где а и Ь — целые взаимно простые числа, имеет бес-
бесконечно много решений (если х0 и у0— решение, то
числа х-=хо-\-Ьп, г/=г/0—an, где п — любое целое,
тоже будут решениями). Другим примером Д. у. явля-
является
Целые положительные решения этого уравнения пред-
представляют длины катетов х, у и гипотенузы z прямо-
прямоугольных треугольников с целочисленными длинами
сторон и наз. пифагоровыми числами. Все
тройки взаимно простых пифагоровых чисел можно
получить по формулам:
х= т2—re2, y=2mn, z=m2-{-n2,
где тип — целые взаимно простые числа (та>ге>0).
Диофант в соч. «Арифметика» занимался разысканием
рациональных (не обязательно целых) решений спе-
специальных видов Д. у. Общая теория решения Д. у.
1-й степени была создана в 17 в. К. Г. Баше (С. G.
Bachet); о решении систем Д. у. 1-й степени подробнее
см. в статье Линейное уравнение. К началу 19 в. трудами
П. Ферма (P. Fermat), Дж. Валлиса (J. Wallis), Л. Эй-
Эйлера (L. Euler), Ж. Лагранжа (J. Lagrange) и К. Га-
Гаусса (С. Gauss) в основном было исследовано Д. у. вида
axi+bxy+cy'i^-dx+ey+f=O,
где а, Ъ, с, d, е, / — целые числа, т. е. общее неодно-
неоднородное уравнение 2-й степени с двумя неизвестными.
С помощью цепных дробей Ж. Лагранж исследовал об-
общее неоднородное Д. у. 2-й степени с двумя неизвест-
неизвестными. К. Гаусс построил общую теорию квадратичных
форм, являющуюся основой решения нек-рых типов
Д- У-
В исследованиях Д. у. выше 2-й степени с двумя не-
неизвестными серьезные успехи достигнуты лишь в 20 в.
А. Туэ (A. Thue) установил, что Д. у.
-1г/+ . . . +а„г/« ---с,
где п^З, а0, %, . . ., ап, с — целые, а многочлен
(Zoi"-)-^"-1-}-. . .+а„ неприводим в поло рациональных
чисел, не может иметь бесконечного числа цел-ых реше-
решений. Однако метод Туэ не дает возможности вычислять
ни границы решений, ни число решений. А. Бейкером
(A. Baker) получены эффективные теоремы о границах
решений нек-рых таких уравнений. Б. Н. Делоне соз-
создал другой метод исследования, охватывающий более
узкий класс Д. у., но позволяющий определять гра-
границы числа решений. В частности, его методом пол-
полностью решается Д. у. вида
Существует много направлений теории Д. у. Так,
известной задачей теории Д. у. является проблема
Ферма — гипотеза об отсутствии при п!>3 нетривиаль-
нетривиальных решений Д. у.
xnJl-yn = zn. A)
Исследование целых решений уравнения A) является
естественным обобщением задачи о пифагоровых трой-
тройках. Положительное решение проблемы Ферма для
ге=4 получено Л. Эйлером. Благодаря этому резуль-
результату проблема Ферма сводится к доказательству от-
отсутствия ненулевых целых решений уравнения A)
при нечетном простом п. Полное исследование решений
уравнения A) не завершено A978). Трудности, возни-
возникающие при его решении, связаны с отсутствием един-
единственности разложения на простые множители в коль-
кольце целых алгебраич. чисел. Теория дивизоров в коль-
кольцах целых алгебраич. чисел дает возможность устано-
установить справедливость теоремы Ферма для многих клас-
классов простых показателей п.
Арифметика колец целых алгебраич. чисел исполь-
используется также в ряде других задач Д. у. Так, напр., ее
методами подробно исследованы уравнения вида
N(a1x1+...+anxn) = m, B)
где N(a) — норма алгебраич. числа а, и отыскиваются
целые рациональные числа х1, х2, . . ., хп, удовлетво-
удовлетворяющие уравнению B). К уравнениям этого класса
относится, в частности, Пелля уравнение хг—йу1 = \.
В зависимости от значений а,, . . ., а„, входящих в B),
эти уравнения делятся на два типа. К первому типу —
так наз. полных форм — относятся те уравнения,
у к-рых среди а,- найдется т линейно независи-
независимых чисел над полем рациональных чисел Q, где
m=[Q (Oj, . . ., an):Q] — степень поля алгебраич. чисел
Q (а,, . . ., а„) над Q. К неполным формам отно-
относятся формы, у к-рых максимальное число линейно неза-
независимых а,- меньше т. Случай полных форм проще и в
основном его исследование доведено до конца. Можно,
напр., для всякой полной формы описать все ее реше-
решения (см. [2], гл. 2).
Второй тип — так наз. неполных форм, сложнее и
теория его далека от завершенности A978). При изу-
изучении таких уравнений применяются диофантовы при-
приближения. К уравнениям этого типа относится уравне-
уравнение
где F(x, у) — неприводимый однородный многочлен
степени п!>3. Это уравнение может быть записано в виде
где а,— все корни многочлена F{z, l) = 0. Существо-
Существование бесконечной последовательности целых решений
уравнения C) привело бы к соотношениям вида
v? D)
для какого-либо ау. Без ограничения общности можно
считать, что j/y—>-оо. Поэтому при достаточно большом
i неравенство D) будет противоречить Туэ — Зигеля —
Рота теореме, откуда следует, что уравнение F(x, ;/) =
= С, где F — неприводимая форма степени, большей
или равной 3, не может иметь бесконечного числа ре-
решений.
Уравнения вида B) представляют собой достаточно
узкий класс среди всех Д. у. Напр., несмотря на про-
простой вид, уравнения
N E)
не входят в этот класс. Исследование решений второго
из приведенных уравнений относится к сравнительно
хорошо изученному разделу Д. у.— представлению
чисел квадратичными формами. Теорема Л а г-
р а н ж а утверждает разрешимость уравнения F)
при всяком натуральном N. Суммой трех квадратов
представляется любое натуральное число, отличное от
чисел вида4а(8/с—1), где а и к — целые неотрицатель-
неотрицательные (теорема Гаусса). Известны критерии
существования рациональных или целых решений
уравнений вида
где F(x1, х2, . . ., х„) — квадратичная форма с целыми
коэффициентами. Так, теорема М и н к о в с к о-
го — X ассе утверждает, что уравнение
2,va,y^y = 6,
где an и Ь рациональны, допускает рациональное ре-
шсние тогда и только тогда, когда оно разрешимо в
действительных числах, а также в р-адических числах
для каждого простого числа р.
Представление чисел произвольными формами 3-й
степени и формами более высоких степеней изучено
меньше из-за возникающих здесь часто принципиаль-
принципиальных трудностей. Одним из основных методов исследо-
исследования представления чисел формами высших степеней
является тригонометрических сумм метод. Этот метод
состоит в явной записи через интеграл Фурье числа
решений уравнения, затем с помощью кругового метода
осуществляется, в сущности, выражение числа решений
уравнения через число решений соответствующих срав-
сравнений. Метод тригонометрических сумм меньше, чем
другие методы, зависит от алгебраической специфики
уравнения.
Существует большое число конкретных Д. у., ре-
решаемых элементарными методами (см. [5]).
Лит.: [1] Виноградов И. М., Основы теории чисел,
8 изд., М., 1972: [2] Б о р е в и ч 3. И., Ш а ф а р е в и ч И. Р..
Теория чисел, 2 изд., М., 1972; 13] D i с k s о n L. E., History
of the theory of numbers, v. 1, N. Y., 1934; [4] Б а ш м а к о в а
И. Г., Диофант и диофантовы уравнения, М., 1972; [5] С е р-
пинскийВ., О решении уравнений в целых числах, пер.
с польск,, М., 1961. С. М. Воронин.
ДИОФАНТОВЫХ ПРИБЛИЖЕНИЙ МЕТРИЧЕСКАЯ
ТЕОРИЯ — раздел теории чисел, изучающий метрич.
свойства чисел, обладающих определенными свойст-
свойствами аппроксимации (см. Диофантовы приближения,
Метрическая теория чисел). Одной из первых теорем
Д. п. м. т. является теорема Хинина (см.
[1], [2]), в современной форме утверждающая (см. [3]):
пусть ср(д)>0 — монотонно убывающая функция, оп-
определенная для целых д>0. Тогда неравенства ||ад||<
<Сф(</) для почти всех действительных а имеют беско-
бесконечное число решений в целых д>0, если расходится
ряд
и имеют лишь конечное число решений, если этот ряд
сходится (здесь и в дальнейшем \\x\\ есть расстояние от
х до ближайшего целого, т. е.
||:r||=min \x—a\,
где min берется по всем целым а; выражение «почти
все» относится к мере Лебега в соответствующем прост-
пространстве). Эта теорема характеризует точность прибли-
приближения почти всех действительных чисел рациональны-
рациональными дробями. Напр., для почти всех а существует беско-
бесконечное число рациональных приближений alq, удов-
удовлетворяющих неравенству
в то время как неравенство
а
ч
<q-2(lnq)
-1 ¦
при любом е>0 имеет бесконечное число решений лишь
для множества чисел а нулевой меры.
Обобщение этой теоремы на случай совместных при-
приближений (см. [3]): система неравенств
max (| а1(/1|, ..., \\anq\\) < ф (q) B)
имеет конечное или бесконечное число решений для
почти всех (ах, . . ., а„)?Д" в зависимости от того,
сходится или расходится ряд
23"=1 ф" (<?)• C)
Более далекие обобщения относятся к системам не-
неравенств от многих целочисленных переменных (см.
И).
Характерной особенностью теоремы Хинчина и раз-
различных ее обобщений является то, что свойство «схо-
«сходимости — расходимости» рядов типа A), C) разгра-
разграничивает те случаи, когда соответствующий порядок
аппроксимации имеет место для множества чисел ну-
нулевой меры или для почти всех чисел. Это своего рода
закон «нуля — единицы» Д. п. м. т. Еще одной осо-
особенностью указанных обобщений является то, что ут-
утверждаемое в них метрич. свойство чисел относится
к мере, определенной во всем пространстве, к-рому при-
принадлежат числа, участвующие в аппроксимации, а мера
пространства определяется как произведение мер в
координатных пространствах. Напр., в случае систе-
системы B) речь идет о приближении п «независимых» чи-
чисел и о мере Лебега в R"=RXRX. . . X R (п раз).
В связи с этим рассмотренная часть Д. п. м. т. стала наз.
Д. п. м. т. независимых величин. Эта
часть Д. п. м. т. разработана достаточно хорошо, хотя
остается ряд нерешеных (к 1978) вопросов. Одним из
них является вопрос о том, какие условия нужно на-
наложить на последовательность измеримых множеств
А (?)> ?=li 2, . . ., интервала [0,1], чтобы сходимость
или расходимость ряда 5j<7^ (?)' соответствовала ко-
конечному или бесконечному числу выполнений условия
aq^A (q) mod 1 для почти всех а. Аналогичная задача
возникает в случае системы чисел (сад, a2q, • • • , <xnq)
(см. [4]).
Д. п. м. т. зависимых величин, возникшая позднее,
сразу выдвинула ряд глубоких и своеобразных проблем
(см. [5]). Первая из них происходила из теории транс-
трансцендентных чисел (гипотеза Малера) и ка-
касалась совместных рациональных приближений к сис-
системе чисел t, i2, . . ., tn для почти всех t при любом
фиксированном натуральном п. Один из последних ре-
результатов, полученных в этом направлении, состоит
в следующем: пусть ср(д)>0 — монотонно убывающая
функция, для к-рой ряд
сходится. Тогда система неравенств
max (| *9||, ||t2e||, •••, ||*п<?1|) < ?1/лФи (?)
для почти всех t имеет лишь конечное число решений в
целых <?>0 (см. [7]).
Эта теорема утверждает определенное свойство аппро-
аппроксимации рациональными числами почти всех точек
кривой TczR". Можно рассматривать более общие мно-
многообразия в R" и получать подобные результаты.
Если почти все (в смысле меры на Г) точки (ах, . . ., ап)
многообразия Г таковы, что система B) с ср (q) = q~ 1^п~е
имеет конечное число решений в целых §>0 при лю-
любом е>0, то Г наз. экстремальным, т. е. почти
все точки допускают лишь наихудшую совместную ап-
аппроксимацию рациональными числами. Известна т е-
орема Шмидта: если Г — кривая в R2, имеющая
почти во всех своих точках отличную от нуля кривизну,
то она экстремальна [8].
Тригонометрических сумм метод (см. также Вино-
Виноградова метод) позволяет обнаружить свойство экс-
экстремальности у многообразий Г весьма широкого клас-
класса в R", но при условии, что топологическая размер-
размерность dim Г^ге/2. Если же dim Г<ге/2, то экстремаль-
экстремальное многообразие не может быть слишком общим, и его
структура должна указываться достаточно определен-
определенно [9].
Лит.: [1] Хин чин А. Я., «Math. Z.», 1926, Bd 24, S.
706—14; [2] его же, Цепные дроби, 4 изд., М., 1978; [3]
КасселсДж., Введение в теорию диофантовых приближе-
приближений, пер. с англ., М., 1961; [4] Cassels J. W. S., «Ргос.
Cambridge Philos. Soc», 1950, v. 46, № 2, p. 209—18; [5]
СпринджукВ. Г., Проблема Малера в метрической тео-
теории чисел, Минск, 1967; [6] его же, в кн.: Международный
конгресс математиков в Ницце. 1970, М., 1972, с. 301—06; [7]
В:'а k e r A., «Proc. Roy. Soc», Ser. A, 1966, v. 292, Ms 1428,
p. 92—104; [8] S с h m i d t W., «Monatsh. Math.», 1964, Bd
68, MS 2, S. 154—66; [9] С п р и н д ж у к В. Г., «Тр. Матем.
ин-та АН СССР», 1972, т. 128, в. 2, с, 212—28; [10] его же,
в сб.; Актуальные проблемы аналитической теории чисел,
Минск, 1974, с. 178 — 98. В. Г. Спринджук.
ДИОФАНТОВЫХ ПРИБЛИЖЕНИЙ ПРОБЛЕМЫ
ЭФФЕКТИВИЗАЦИИ — получение эффективных ре-
решений задач диофантовых приближений, для к-рых
известно решение, полученное неэффективными мето-
методами, т. е. методами, не допускающими принципиаль-
принципиальной возможности численного выражения результата.
Таковы, например, теоремы А. Туэ (A. Thue), К. Зи-
геля (С. Siegel), К. Рота (К. Roth), В. Шмидта
(W. Schmidt), их обобщения, аналоги и следствия
(см. Туэ — Зигеля — Рота теорема, Диофантовы при-
приближения). Неэффективность этих теорем объясняется
логич. структурой метода, основанного на предполо-
предположении о существовании объектов, не определяемых
конструктивно. Так, в случае рациональных прибли-
приближений к алгебраич. числам граница для знаменателей
«хороших» приближений, устанавливаемая в процессе
рассуждений, зависит от одного из этих «хороших»
приближений, существование к-рого не доказывается.
Эффективное решение задачи часто представляет
большие трудности. Лишь недавно удалось получить
эффективное усиление неравенства Лиувилля (см.
Лиувилля число). Метод доказательства существенно
отличается от метода Туэ — Зигеля — Рота и связан
с привлечением эффективных методов теории трансцен-
трансцендентных чисел (см. Линейная форма от логарифмов
алгебраич. чисел). Наилучший известный результат
A978) имеет вид
\ах — у\ > сх-п+1+ь,
где а — алгебраич. число степени ге^З, ж>0, у — це-
целые рациональные, с>0 и б>0 определяются в явном
виде через а (см. [3]). Это неравенство далеко от своего
неэффективного аналога: вместо показателя — ге+1+6
неэффективные методы дают —1—е с любым е>0, но
с неизвестной функцией с от а и е. Доказательство эф-
эффективного неравенства
\а,х—у\ > Сл--*<п»
с функцией ц>(п), растущей, напр., как пЕ , представляет
большой интерес в связи с нахождением границ реше-
решений диофантова уравнения
/(*, у) = 0,
где многочлен f(x, у) определяет кривую рода ^1 (ко-
(конечность числа решений доказана в 1929 К. Злгслем,
использовавшим неэффективные оценки, см. Диофан-
Диофантова геометрия).
Несмотря на то, что эффективные оценки получаются
значительно хуже неэффективных, знание их зависи-
зависимости от параметров задачи позволяет устанавливать
новые результаты, недоступные неэффективным мето-
методам. Так, эффективные оценки линейных форм от ло-
логарифмов алгебраических чисел позволили Туэ най-
найти оценки решений многих диофантовых уравнений, в
частности уравнения Туэ и уравнений, задающих кри-
кривые рода 1, а также дать еще одно решение проблемы
десятого дискриминанта, установить границу для ди-
дискриминантов двухклассных мнимых квадратичных по-
полей, оценить снизу наибольший простой делитель
значений бинарной формы степени ^3 и величину
свободного от квадратов ядра целочисленного много-
многочлена (см. [2]).
Лит.: [1] С п р и н д ж у к В. Г., «Изв. АН СССР. Сер.
матем.», 1971, т. 35, Mi 5, с. 991 — 1007; 1972, т. 36, MS 4, с. 712—
741; [2] его же, в сб.; Актуальные проблемы аналитической
теории чисел, Минск, 1974, с. 178—98; [3] Ф е л ь д м а н Н. И.,
там же, с. 244—68; [4] е г о же, «Изв. АН СССР. Сер. матем.»,
1971, т. 35, Ms 5, с. 973—90; [5] Baker A., «Phil. Trans.
Royal Soc. London», Ser. A., 1968, v. 263, p. 173—91, 193—208;
[6] его же, в кн.: Actes du Congres International des Ma-
thematiciens. 1970, t. 1, P., 1971, p. 19—26. В. Г. Спринджук.
ДИОФАНТОВЫХ УРАВНЕНИЙ ПРОБЛЕМА РАЗРЕ-
РАЗРЕШИМОСТИ — проблема отыскания алгоритма для рас-
распознавания по любому диофантову уравнению, имеем
ли оно решение.
Существенным в постановке проблемы является тре-
требование найти универсальный метод, к-рый должен быть
пригоден для любого уравнения (все известные спосо-
способы для распознавания наличия решений у диофантовых
уравнений применимы лишь к уравнениям из отдель-
отдельных более или менее широких классов). Такой метод
позволял бы решать и системы диофантовых уравне-
уравнений, ибо система Рх=0, . . ., Р&=0 эквивалентна урав-
уравнению
Задача нахождения такого универсального метода
для распознавания наличия решений в целых числах
была поставлена Д. Гильбертом (D. Hilbert, см. [1]).
В начале 50-х гг. 20 в. появились первые работы,
нацеленные на доказательство невозможности алгорит-
алгоритма, требуемого в Д. у. п. р. В это время была высказана
гипотеза (гипотеза Дейвиса, см. [2]) о том, что
каждое перечислимое множество является диофантовым
множеством. Поскольку известны примеры перечис-
перечислимых, но алгоритмически неразрешимых множеств,
то из справедливости этой гипотезы немедленно сле-
следует отрицательное решение Д. у. п. р.
В 1961 было доказано (см. [3]) более слабое утвержде-
утверждение: каждое перечислимое множество является п о-
казательпо-диофантовым множе-
множеством, т. е. для каждого перечислимого множества
ЗД1 существуют такие выражения К и /,, построенные
из натуральных чисел и переменных a, zx, . . ., zn с
помощью сложения, умножения и возведения в сте-
степень, что а ?!Ш тогда и только тогда, когда показатель-
показательно-диофантово уравнение K=L разрешимо относитель-
относительно zb . . ., zn. После этого для доказательства гипоте-
гипотезы Дейвиса осталось указать способ, позволяющий пре-
преобразовать произвольное показатольно-диофантово
уравнение в нек-рое диофантово уравнение, имеющее
или не имеющее решения одновременно с ним. Было до-
доказано [4], что такое преобразование возможно, если
существует диофантово уравнение
G(u, v, Z], . . ., Zft) = 0,
обладающее следующими двумя свойствами: 1) в лю-
любом решении этого уравнения и<«"; 2) для любого к
существует решение, в к-ром v>uk (про такое уравне-
уравнение говорят, что оно имеет экспоненциальный
рос т). Пример диофантова уравнения, имеющего
экспоненциальный рост, к-рый впервые был построен
в [5], завершил доказательство гипотезы о диофанто-
вости поречислимых множеств (полностью доказатель-
доказательство гипотезы Дейвиса изложено в [6], [7]). Обратное
утверждение о перечислимости диофантовых множеств
доказывается легко. Таким образом, класс перечисли-
перечислимых множеств совпадает с классом дпофантовых мно-
множеств.
Из этого результата следует возможность указать
конкретный многочлен W(a, zl5 . . ., zn) с целыми коэф-
коэффициентами такой, что не существует алгоритма, по-
позволяющего по значению параметра а узнавать, раз-
разрешимо ли уравнение W(a, zx, . . ., zn) = 0 относительно
zlt . . ., zn, и, тем более, не существует требуемого в
Д. у. п. р. алгоритма для распознавания наличия ре-
решений у произвольного диофантова уравнения.
Вопрос о существовании алгоритма, позволяющего
распознавать разрешимость диофантовых уравнений в
рациональных числах, эквивалентен вопросу о сущест-
существовании алгоритма, позволяющего распознавать разре-
разрешимость однородных диофантовых уравнений в целых
числах. Эта важная проблема пока A978) остается от-
открытой и малоисследованной.
Лит.: [1] Гильберт Д., в кн.: Проблемы Гильберта,
М., 1969, с. 11—64; [2] Д э в и с М., «Математика», 1964, т. 8,
№5, с. 15—22; [3] ДэвисМ., ПутнамХ., Робин-
Робинсон Д ж., там же, с. 69—79; [4] Робинсон Д ж., там же,
с. 3—14; [5] М а т и я с е в и ч Ю. В., «Докл. АН СССР»,
1970, т. 191, №2, с. 279—82; [6] его же, «Успехи матем.
наук», 1972, т. 27, в. 5, с. 185—222; [7] М а н и н Ю. И., в сб.:
Итоги науки и техники. Современные проблемы математики,
1973, т. 1, с. 5—37; [8] Davis M., МатиясевичЮ. В.,
Robinson J., «Proc. Symp. Pure Math.», 1976, v. 28,
p. 323—75. Ю. В. Матиясевич.
ДИРАКА ДЕЛЬТА-ФУНКЦИЯ — см. Дельта-функ-
Дельта-функция.
ДИРАКА МАТРИЦЫ — четыре эрмитовы матрицы
ak, k=i, 2, 3, и р размера 4x4, удовлетворяющие
условиям
где Е — единичная матрица размера 4X4. Вместо ма-
матриц a/t, р используются также эрмитовы матрицы
•у*=—iP«ft, fc=l, 2, 3, и антиэрмитова матрица Y°=?p,
удовлетворяющие условиям
=-2*,*?, х, а,=о, 1, 2, з,
гДе ?оо=—gkk~^-, gK}"=z0 при кф-'К, что позволяет за-
записать Дирака уравнение в форме, ковариантной отно-
относительно группы преобразований Лоренца. Матрицы
^ki M Т" определены с точностью до произвольного
унитарного преобразования и представление этих ма-
матриц может быть выбрано различными способами.
Напр.,
/1 0\ , / 0 o
1 * '
где a^— двухрядные Паули матрицы, а 1 и 0 — двух-
двухрядные единичная и нулевая матрицы соответственно.
С помощью Д. м. можно факторизовать Клейна— Гор-
Гордона уравнение:
(? —
-<^и=о ' дхк \
где ? — оператор Д'Аламбера.
Д. м. введены П. Дираком (P. Dirac) в 1928 при вы-
выводе уравнения Дирака. в. Д. Пукин.
ДИРАКА СПИНОР — четырехкомпонентная ком-
комплексная функция в четырехмерном пространстве-
времени, удовлетворяющая Дирака уравнению. В спи-
норном анализе Д. с. определяется как биспинор 1-го
ранга, реализующий неприводимое линейное пред-
представление общей группы Лоренца на R4 с псевдоевкли-
псевдоевклидовой метрикой
х=(х°, х\ х2, х3).
Дирака матрицы, входящие в уравнение Дирака,
определены с точностью до произвольного унитарного
преобразования, поэтому Д. с. определен с точностью до
того же унитарного преобразования. Это свойство поз-
позволяет выбирать наиболее удобное из физических сооб-
соображений представление матриц Дирака и, соответст-
соответственно, Д. С. В. Д. Кукин.
ДИРАКА УРАВНЕНИЕ — релятивистское волновое
уравнение, играющее фундаментальную роль в реляти-
релятивистской квантовой механике и квантовой теории поля.
Д. у. применяется для описания частиц со спином 1/2
(в единицах К), то есть электронов, нейтрино, мюонов,
протонов, нейтронов и др., а также позитронов и всех
др. античастиц и гипотетических субчастиц— кварков.
Д. у. является основой теории частиц полуцелого спина
(V2i 3/27 5/г и т- Д-)> то есть фермиопов, к-рые подчини-
ются Ферми статистике. Напр., обобщением Д. у.
для частиц спина 3/2 является Рарита — Швингера
уравнение.
Д. у. есть система четырех линейных однородных диф-
дифференциальных уравнений с частными производными
1-го порядка с постоянными комплексными коэффици-
коэффициентами, инвариантная относительно общей группы пре-
преобразований Лоренца:
дха
= 0, 1, 2, 3,
где \i=mcl%, т — масса покоя, ха = х°, х1, х2,
с псевдоевклидовой метрикой (х, y) = r\apdxady$, a
—10 0 0
0 10 0
0 0 10
0 0 0 1
— метрический тензор пространства Минковского с
сигнатурой +2; ^ — Дирака спинор (биспинор):
Фз
Y<*=y°, Y1, Y2' У3— Дирака матрицы.
При преобразованиях переменных из общей группы
Лоренца — Пуанкаре x'a=L(xa) (см. [2]) биспинор яр
преобразуется по формуле г|/ (x')=S (L)ty(x), где S (L) —
неособенная комплексная матрица размерности 4x4.
5-матрицы образуют специальное двузначное представ-
представление группы L. Д. у. относительно новых переменных
г|/ (х'а) не изменяет своего вида (релятивистская инва-
инвариантность):
Случай ц.= 0 дает уравнение Вейля, опи-
описывающее нейтрино. При этом Д. у. разбивается на два
независимых уравнения для спинорных функций
(спиноров Ван дер Вардена) ф=(г|)!, г|>2)
и у, = (фз1 ty<i)- Каждое из них будет не инвариантным
относительно отражений (теория с несохранением чет-
четности).
Любое решение Д. у. удовлетворяет Клейна — Гордо-
Гордона уравнению, описывающему бесспиновые скалярные
частицы
=о, 1, г, з,
но не всякое решение этого уравнения удовлетворяет
Д. у., к-рое получается факторизацией уравнения
Клейна — Гордона.
Из Д. у. следует факт наличия у электрона собст-
собственного механического спинового момента Л/2. Д. у.
полностью описывает движение атомных электронов в
поле ядра и в других электромагнитных полях, а также
взаимодействие электрона с известными элементар-
элементарными частицами.
Любое релятивистски инвариантное уравнение можно
представить в форме Д. у.:
J
r-и-о,
где Га— обобщение уа. Для уравнения Клейна — Гор-
Гордона функция гр имеет 5 компонент, а Га— 4 пятиряд-
ные матрицы, удовлетворяющие соотношениям
(Дуффина — Кеммера матриц ы).
Подобно тому как взаимодействие фермионов с элек-
электромагнитным полем учитывается в Д. у. заменой про-
производной д1дха на компенсирующую производную
д/Ъха—iAa(Aa—4-потенциал электромагнитного поля),
учет взаимодействия фермионов с гравитационным полем
в соответствии с общей теорией относительности при-
приводит к обобщению Д. у. на риманово пространство
введением соответствующей компенсирующей (кова-
риантной) производной (см. [3]):
где Са— спинорные коэффициенты связности, опреде-
определенные сначала с помощью тетрадного формализма,
удовлетворяющие соотношениям
Г«р —символы Кристоффеля. Общорелятивистское обоб-
обобщение Д. у. необходимо при исследовании гравитаци-
гравитационного коллапса, при описании предсказываемого эф-
эффекта рождения частиц в сильных гравитационных по-
полях и др.
В пространстве с кручением в Д. у. возникает не-
нелинейный добавок кубического типа (см. [4]) и оно
переходит в нелинейное уравнение
гдеу=гу5, l2=3nGh/c3, G — гравитационная постоянная.
Уравнение установлено П. Дираком (P. Dirac, 1928).
Лит.: [1] Д и р а к П. А. М., Принципы квантовой механи-
механики, пер. с англ., М., 1960; [2] Б о г о л ю б о в Н. Н., Ш и р-
ковД. В., Введение в теорию квантованных полей, 2 изд.,
М., 1976; [3] Новейшие проблемы гравитации, пер. с англ.,
М., 1961; [4] Р о д и ч е в В. И., «Ж. эксперим. и теор. физ.»,
1969, т. 40. В. Г. Кречет.
ДИРЕКТРИСА — прямая, лежащая в плоскости
конического сечения (эллипса, гиперболы или параболы)
и обладающая тем свойством, что отношение расстоя-
расстояния от любой точки кривой до фокуса кривой к расстоя-
расстоянию от той же точки до этой прямой есть величина по-
постоянная, равная эксцентриситету. е В Шикин
ДИРИХЛЕ ВАРИАЦИОННАЯ ЗАДАЧА — задача
отыскания минимума Дирихле интеграла
при заданных граничных условиях «laG=<p, где функ-
функция (р задана на границе 0G re-мерной области G. Ре-
Решение этой задачи является и решением первой краевой
задачи для уравнения Лапласа:
Д« = 0, и 9G = <P-
Д. в. з.— первая задача на минимизацию функцио-
функционала, к к-рой было сведено решение краевой задачи для
дифференциального уравнения с частными производ-
производными.
Д. в. з. естественно рассматривать в классе функций,
имеющих первые обобщенные производные, суммируе-
суммируемые с квадратом. В случае ограниченной области это
множество функций совпадает с Соболева пространст-
пространством Wl(G), и потому обладает свойством полноты в
соответствующей метрике. Кроме того, каждая функ-
функция этого пространства имеет на 0G граничные значе-
значения в смысле сходимости почти всюду, к-рые в случае
достаточной гладкости границы совпадают с граничны-
граничными значениями в смысле сходимости в среднем или в
смысле предела граничных значений непрерывных в
замкнутой области функций, аппроксимирующих в
метрике пространства W\(G) заданную функцию. Если
G — ограниченная область и если существует хоть одна
функция и, для к-рой \D (и)\ <оо и u\QQ=tf (такие функ-
функции наз. допустимыми), то решение и0 Д. в. з.
существует и единственно. Это решение щ является
гармонической в G функцией (см. Дирихле принцип).
Если граница dG области G гладкая, то для того чтобы
класс допустимых функций был не пуст, необходимо и
достаточно, чтобы (p?2?y»CG). Решение и0 Д. в. з. мо-
может быть найдено прямым вариационным методом. Эти
результаты обобщаются как на случай квадратичных
эллиптич. функционалов, содержащих производные
высших порядков, так и на случай неограниченных
областей.
Лит.: [1] Курант Р., Гильберт Д., Методы мате-
математической физики, пер. с нем., т. 2, 2 изд., М.— Л., 1951; [2]
Соболеве. Л., Некоторые применения функционального
анализа к математической физике, Новосиб., 1962; [3] Н и-
кольскийС. М., «Матем. сб.», 1954, т. 35, № 2, с. 247—66;
[4] К у д р я в ц е в Л. Д., «Тр. Матем. ин-та АН СССР»,
1959, т. 55, с. 1 —181. Л. Д. Кудрявцев.
ДИРИХЛЕ ЗАДАЧА — задача отыскания регуляр-
регулярной в области D гармонич. функции и, к-рая на гра-
границе Г области D еовпадает с наперед заданной непре-
непрерывной функцией ф. Задачу отыскания регулярного в
области решения эллиптич. уравнения 2-го порядка,
принимающего наперед заданные значения на границе
области, также наз. Д. з., или первой краевой зада-
задачей. Вопросы, связанные с этой задачей, рассматрива-
рассматривались еще К. Гауссом (С. Gauss, 1840), а затем П. Ди-
Дирихле [1].
Для областей D с достаточно гладкой границей Г
решение и(х) Д. з. можно представить интегральной
формулой
где dG(x, хо)/дпо— производная по направлению вну-
внутренней нормали в точке хо?Т Грина функции G{x, ж0),
характеризуемой следующими свойствами:
1) G (х, xo) = Sn1r2-"-iry{x, xB) при в
G(x, zo)=^ln— + y(x, x0) при и = 2,
где г=\х—хо\ — расстояние между точками х и х0, sn—
площадь единичной сферы в R", у(х, х0) — регуляр-
регулярная в D гармонич. функция как относительно коорди-
координат х, так и относительно координат х0;
2) G(x, xo)=O, когда xo?D, х?Г.
Для шара, полупространства и нек-рых других про-
простейших областей функция Грина строится явно и фор-
формула A) дает эффективное решение Д. з. Получаемые
при этом для шара и полупространства формулы носят
название Пуассона формул.
Д. з. является одной из основных проблем потенциала
теории. Она служила и служит как бы пробным кам-
камнем для разрабатываемых новых методов, к-рые затем,
в той или иной мере, становятся достоянием общей тео-
теории уравнений с частными производными.
Для исследования Д. з. применяются следующие мэ-
тоды.
Вариационный метод основан на том, что среди всех
функций и, заданных в D и принимающих наперед за-
заданные значения на Г, минимизирует Дирихле инте-
интеграл
— гармоническая функция. Для D (и) строится специ-
специальная минимизирующая последовательность и доказы-
доказывается сходимость этой последовательности. Поскольку
от искомого решения и Д. з. требуется, чтобы сущест-
вовал интеграл D(u), то вариационный метод применим
лишь для таких функций ф, к-рые являются следами
на Г функций F, заданных в D, и таких, что D(F)
существует и ограничен.
В методе потенциалов решение Д. з. ищется в виде
потенциала двойного слоя с неизвестной плотностью,
определенной на Г. При помощи формул скачка отно-
относительно этой плотности получается интегральное урав-
уравнение Фредгольма, из к-рого следует существование
решения Д. з. с учетом того, что единственность этого
решения следует из принципа максимума. Предполага-
Предполагается, что Г?Л а> to,
В альтернирующем методе Шварца рассматриваются
две области Dt и D2 с непустым пересечением ?>0 такие,
что для ?>! и D2 в отдельности известен способ решения
Д. з. Затем строится процесс, позволяющий найти ре-
решение Д. з. для области D—D^D^. Границы Г\ и
Г2 областей й, и JJ предполагаются кусочно глад-
гладкими, причем во всех точках пересечения Тг с Г2 как
Г\, так и Г, являются гладкими и пересекаются под
ненулевым углом. Строятся последовательности регу-
регулярных в областях />! и Z>2 гармония, функций, удов-
удовлетворяющих специальным граничным условиям. За-
Затем доказывается, что эти последовательности рав-
равномерно сходятся и в Do их пределы совпадают. Пре-
Предельная гармоннч. функция регулярна в D и является
искомым решением Д. з. Метод Шварца можно приме-
применять для объединения или пересечения любого конеч-
конечного числа областей.
Метод выметания в той форме, в к-рой он первона-
первоначально был введен А. Пуанкаре (Ы. Poincare, 1890),
применяется к таким областям, к-рые допускают исчер-
исчерпание счетным множеством шаров. Исходным в этом
методе является построение ньютонова потенциала,
принимающего на границе Г заданные значения ф, а
задача затем сводится к замене этого потенциала по-
потенциалом масс, расположенных на Г, без изменения
значений <р на Г, т. е. к выметанию масс. При помощи
формулы Пуассона такой процесс выметания для шара
D легко осуществить в явном виде. Счетное число вы-
выметаний из шаров, объединение к-рых исчерпывает
область D общего вида, приводит к нек-рому потенциа-
потенциалу масс, расположенных на границе Г, к-рый и дает
решение Д. з.
Близким к методу выметания является Перрона ме-
метод (пли метод верхних и нижних функций), примени-
применимый к областям D весьма общего вида. В этом методе
строятся последовательности верхних (супергармони-
(супергармонических) и нижних (субгармонических) функций, общим
пределом к-рых является искомое решение Д. з. Для
того чтобы :)то решение принимало заданное значение
в точке Q?T, необходимо и достаточно существование
локального барьера u>q. Функция co<j непрерывна, су-
супергармонична в пересечении ДП2 B —шар с
центром в точке Q); (uq>0 всюду в ?>Л2, кроме точки
Q, где она обращается в нуль.
Точки Г, для к-рых существует локальный барьер,
наз. регулярными точками. Если Г состоит только из
регулярных точек, то полученное решение Д. з. не-
непрерывно в D н принимает заданные значения на Г.
Однако на Г могут существовать и иррегулярные точки.
Напр., в R- иррегулярными являются изолированные
точки Г, а в R3 иррегулярной будет вершина достаточ-
достаточно тонкого острия, входящего внутрь D. Наличие ирре-
иррегулярных точек приводит к тому, что Д. з. не является
разрешимой для всех непрерывных на Г функций ф,
либо же решение является неустойчивым по отношению
к изменению граничных данных (см. [6]).
Обобщенное решение Д. з., введенное Н. Винером
(N. Wiener, 1924), удовлетворяет условиям: а) оно
применимо для любых областей; б) оно приводит к
классич. решению Д. з., если таковое существует.
Пусть область D — предел монотонно возрастающей
последовательности регулярных областей {Dn} такой,
что DncDn+1dD, и любой компакт KdD содержится в
D„ при п~>п(К). Обобщенное решение Д. з. и получается
как предел последовательности {ип} решений Д. з. для
областей Dn и непрерывно продолженной граничной
функции ф внутрь D. Решение и не зависит ни от вы-
выбора исчерпывающей последовательности {Dn}, ни от
способа непрерывного продолжения ф внутрь D-
Имеется трактовка обобщенного решения Д. з. на
основе метода Перрона. Пусть #ф — нижняя огибаю-
огибающая семейства всех верхних супергармонич. функций
v, удовлетворяющих на Г условию
liminf v (
Для любых области D и функции ф имеет место не-
неравенство Нф-^Лу. В случае равенства Нц, = Н =-и
эта функция и является гармонической. Она наз. обоб-
обобщенным решением Д. з., а граничная функция ф — раз-
разрешимой. Любая непрерывная функция ф разрешима,
поведение же обобщенного решения и в точке ха ? Г
определяется регулярностью или иррегулярностью ха.
Для обобщенного по Винеру решения Д. з. справед-
справедливо интегральное представление в виде форму-
формулы Балле Пуссена
(|o) , B)
являющейся обобщением формулы A). Здесь dw(x, E) —
гармонич. мера множества ?сГ в точке х0 (см. [5]).
Отсюда возникает возможность рассмотрения обоб-
обобщенной Д. з. для произвольных граничных функций ф,
при этом можно требовать удовлетворения граничного
условия лишь в нок-рой ослабленной форме. Напр.,
если D — область R2 с достаточно гладкой границей Г,
а граничная функция ф имеет только точки разрыва
1-го рода, то можно требовать удовлетворения гранич-
граничного условия лишь в точках непрерывности ф, для обес-
обеспечения единственности решения в точках разрыва
требуется ограниченность решения. В постановке
Н. Н. Лузина обобщенная Д. з. ставится для произволь-
произвольной измеримой и конечной почти всюду на Г граничной
функции ф. Граничное условие может состоять в том,
чтобы граничные значения решения по нормали к Г
существовали и совпадали с ф почти всюду на Г.
Для общего эллиптич. уравнения 2-го порядка
Д. з. фредгольмова. При этом ищется регулярное в об-
области решение, принимающее на границе наперед
заданные значения. Приведенные выше методы иссле-
исследования Д. з. для гармонич. функций обобщаются и на
уравнение C).
Для равномерно эллиптич. систем Д. з. может ока-
оказаться не только нефредгольмовой, но даже иметь бес-
бесконечно много линейно независимых решений (см. [8]).
Д. з. рассматривается и для нек-рых неэллиптич.
уравнений или вырождающихся уравнений. В этил
случаях Д. з. иногда оказывается некорректной.
Лит.: Ш D i г i с h I e t P. G. L., «Abh. der Koniglich.
Preus. Acad. der Wiss.», 1850, S, 99—116; [2] M и р а н д а К.,
Уравнения с частными производными эллиптического типа,
пер. с итал., М., 1957; [3] К у р а н т Р., Принцип Дирихле,
конформные отображения и минимальные поверхности, пер. с
англ., М., 1953; Ш его же, Уравнения с частными производ-
производными, пер. с англ., М., 1964; [5] Брело М., Основы класси-
классической теории потенциала, пер. с франц., М., 1984; [8] К е л-
дыш М. В., «Успехи матем. наук», 1941, в. 8, с. 171—292;
[7] его же, «Докл. АН СССР», 1951, т. 77, с. 181—83; [8]
Б ицадзеА. В., Краевые задачи для эллиптических уравне-
уравнений второго порядка, М., 1966. А. Янушаускас.
ДИРИХЛЕ ИНТЕГРАЛ — функционал, связанный
с решением Дирихле задачи для уравнения Лапласа
вариационным методам. Пусть Q — ограниченная об-
область в Rn с границей Г класса С1, х=(х±, . . ., х„), а
функция u(x)?W\{Q) (см. Соболева пространство).
Д. п. для функции и(х) наз. выражение
dx.
D [и] = \ У | —— I
Для некоторой заданной на Г функции ф(ж) рассматри-
рассматривается множество яф функций из w\(Q), к-рые удовлет-
удовлетворяют граничному условию и1х6г = Ф- Если множество
Яф не пусто, то существует единственная функция
ио(х)?-Л(р, для которой
D [uo]= inf D [и],
иеяф
и эта функция является гармонической в области Й.
Верно и обратное утверждение: если гармонич. функ-
функция щ (х) принадлежит множеству Лф, то на ней дости-
достигается inf D[u]. Таким образом, ио(х) является обоб-
обобщенным из w\ (Q) решением задачи Дирихле для урав-
уравнения Лапласа. Однако не для всякой функции ф
можно найти такую функцию ио(х). Существуют даже
непрерывные на Г функции, для к-рых множество я
пусто, т. е. в пространстве W\ (Q) не существует ни
олной функции и(х), удовлетворяющей условию
«|жбГ = ф. Классич. решение задачи Дирихле для урав-
уравнения Лапласа с такой граничной функцией ф не может
иметь конечного Д. и. и не является обобщенным ре-
решением из пространства W^(Q).
Лит.: [1] М и х а й л о в В. П., Дифференциальные "урав-
"уравнения в частных производных, М., 1976. А. К. Гущин.
ДИРИХЛЕ ПРИЗНАК сходимости число-
числовых рядов: если последовательность действитель-
действительных чисел dn монотонно стремится к нулю, а последова-
последовательность частичных сумм ряда ^п=1Ьп ограничена
(члены этого ряда могут быть комплексными), то ряд
2n=i^n*n СХ°ДИТСЯ- Установлен П. Дирихле [1].
Лит.: [1] DirichletP., «J. de math.», B) 1862, t. 7,
p 253—55. Л. Д. Кудрявцев.
ДИРИХЛЕ ПРИНЦИП — метод решения краевых
задач для эллиптич. уравнений с частными производ-
производными сведением их к вариационным задачам отыскания
минимумов нек-рых функционалов в определенных клас-
классах функций. В узком смысле Д. п. означает решение
1-й краевой задачи
в области G с границей 0G для уравнения Лапласа
Ди = 0 B)
сведением ее к отысканию минимума Дирихле интеграла
¦?-)'*?, и = и(хъ ...,*„)
в классе функций, удовлетворяющих условию
D(u)<+оо C)
и условию A) (см. Дирихле вариационная задача).
Д. п. возник и получил широкое распространение
в нач. 19 в. Он применялся как с чисто теоретическими
целями для доказательства существования и един-
единственности решений краевых задач, так и при решении
практически важных задач. Наиболее четкая и полная
формулировка Д. п. для класса функций непрерывных
.вместе со своими частными производными, по-видимому,
была дана в лекциях П. Дирихле (P. Dirichlot), опуб-
опубликованных в 1876 одним из его учеников. Доказатель-
Доказательства, данные Дирихле, были неполны, в частности, у
него даже не ставился вопрос о необходимости доказа-
доказательства существования минимума рассматриваемого
функционала в классе допустимых функций, т. е.
функций, удовлетворяющих условиям A) и C). В кон-
конце 60-х гг. 19 в. Д. п. был подвергнут критике К. Вей-
ерштрассом (К. Weierstrass), показавшим на примере,
что дифференциальная краевая задача -A), B) при нек-
некрой граничной непрерывной функции ф может иметь
решение, а соответствующая вариационная задача —
нет, за счет того, что в этом случае интеграл Дирихле
для решения задачи A), B) обращается в бесконечность.
Обосновать Д. п. в предположении, что существует
хоть одна допустимая функция, удалось лишь Д. Гиль-
Гильберту (D. Hilbert) на рубеже 19 и 20 вв. Дальнейшее
существенное развитие Д. п. содержится в работах
С. Л. Соболева, показавшего, что всякая функция,
определенная на га-мерной области и имеющая в ней
обобщенные частные производные достаточно высокого
порядка, принадлежащие пространству Lp, p^l, при-
принимает на всяком достаточно гладком /«-мерном мно-
многообразии, 0s?m<n, естественные устойчивые гранич-
граничные значения. Это позволило С. Л. Соболеву сформули-
сформулировать и обосновать Д. п. для полигармонич. уравне-
уравнения, причем и в случае, когда граница области состоя-
состояла из многообразий различной размерности.
Возникновение Д. п. явилось существенным этапом в
развитии теории краевых задач уравнений с частными
производными, так как оно означало создание прин-
принципиально новой точки зрения на эту теорию. Д. п. и
его всевозможные модификации, основанные, в конце
концов, на сведении рассматриваемой задачи к той или
иной вариационной задаче, получили широкое распро-
распространение как в различных разделах самой математики,
так и в ее приложениях. Это связано с тем, что этот
метод позволяет как доказывать общие теоремы о ре-
решениях уравнений, так и получать их конкретные ре-
решения в виде пределов так наз. минимизирующих
последовательностей (т. е. последовательностей допусти-
допустимых функций, значения минимизирующего функциона-
функционала на к-рых стремятся к его минимуму), при этом чис-
численные методы, основанные на построении минимизи-
минимизирующих последовательностей, удобны для отыскания
приближенных решений на ЭВМ. л. д. Кудрявцев.
ДИРИХЛЕ ПРИНЦИП «я щ и к о в» — утверждение,
согласно к-рому в любой совокупности из п множеств,
содержащих в общей сложности более п элементов,
есть хотя бы одно множество, содержащее но менее
двух элементов. Наиболее популярная форма Д. п.:
если в п «ящиках» лежит п-f-l «предмет», то хотя бы
в одном из «ящиков» лежит не меньше двух «предме-
«предметов». Д. п. часто применяется в теории диофантовых
приближений и в теории трансцендентных чисел для
доказательства разрешимости в целых числах систем
линейных неравенств (см. Дирихле теорема в теории
диофантовых приближений). В г Сприпджук.
ДИРИХЛЕ РАЗРЫВНЫЙ МНОЖИТЕЛЬ — интег-
грал
( л/2 при В < а,
(*=° sin ax Q , I ,/ о
\ —-— cos рх dx = ¦! л/4 при р = а,
V 0 при р > а,
являющийся разрывной функцией от параметров а>0 и
В>0. П. Дирихле использовал его в своих исследова-
исследованиях о притяжении эллипсоидов (см. [1]). Д. р. м.
встречался ранее у Ж. Фурье (J. Fourier), С. Пуассона
(S. Poisson) и А. Лежандра (A. Legendre).
Лит.: [1] DirichletP., Werke, Bd Г, В., 1889; [2]
Фихтенгольц Г. М., Курс дифференциального и инте-
интегрального исчисления, т. 2, 7 изд., М., 1969, т. 3, 5 изд., М.,
1970. Т. П. Лукашенко.
ДИРИХЛЕ РАСПРЕДЕЛЕНИЕ — распределение ве-
вероятностей в симплексе
ft=2, 3, . . ., определяемое плотностью вероятности
/ ч СС*ГГ x"i' ' если^ь •••. xk)€sh
р(хъ ...,хк) = \ аа« = 1
1 0 , если {хи .. ., хк) О. Sk,
^ г-
причем Vj>0, . . ., V/;>0 и
где Г(-) — гамма-функция. Частный случай Д. р.—
бета-распределение — возникает при к=2. Д. р. иг-
играет важную роль в теории порядковых статистик.
Напр., если Хх, . . ., Хп— независимые случайные
величины, подчиняющиеся равномерному распределе-
распределению на отрезке [0, 1], и ХA><. . .<Х(П) — соответ-
соответствующий вариационный ряд, то совместное распреде-
распределение к разностей вида
(предполагается, что 1<т1<го2<. . .<.ть-т) подчиня-
подчиняется Д. р., причем v1=m1, v2=m2 — тх, . . ., v/!_1=
Лит.: [1] У и л к с С, Математическая статистика, пер.
с англ., М., 1967, с. 192—96. Л. Я. Большее.
ДИРИХЛЕ РЯД — функциональный ряд вида
2Г=1 V~V' A)
где ап—'комплексные коэффициенты; Хп, 0<|Я„||оо,—
показатели Д. p., s=a-}-it— комплексное переменное.
При Я,„=1п п получается так наз. обыкновенный
ряд Дирихле
Soo ап
Ряд
представляет для а>1 дзета-функцию Римана. Ряды
где х(га) — функция, наз. Дирихле характером, изу-
изучались П. Дирихле (см. Дирихле L-функция). Ряды A)
с произвольными показателями Хп наз. общими
рядами Дирихле.
Общие ряды Дирихле с положи-
положительными показателями. Пусть сначала
Хп— положительные числа. Имеет место аналог Абеля
теоремы для степенных рядов: если ряд A) сходится в
точке so=ao-\~ito, то он сходится в полуплоскости а><т0,
причем внутри любого угла |arg(s—«0)|<ф0<я/2 схо-
сходится равномерно. Открытая область сходимости ря-
ряда есть нек-рая полуплоскость о>с. Число с наз.
абсциссой сходимости Д. р., прямая
а=с — прямой сходимости Д-р., полупло-
полуплоскость о^>с — полуплоскостью сходи-
сходимости Д-р. Наряду с полуплоскостью сходимости
рассматривается полуплоскость абсолют-
абсолютной сходимости Д. р.: а>а — открытая
область, в к-рой ряд сходится абсолютно (при этом а —
абсцисса абсолютной сходимости). Абсциссы сходи-
сходимости и абсолютной сходимости, вообще говоря, раз-
различны; всегда
—c<rf, где d= lim -lUZL,
причем имеются Д. р., для к-рых a—c=d. В случае
d=0 для вычисления абсциссы сходимости (абсциссы
абсолютной сходимости) имеется формула
In I а„ I
а = с = lim —LJU. ,
представляющая собой аналог формулы Коши — Ада-
мара. Случай d>0 сложнее: если величина
положительна, то с=C; если |3<0 и ряд A) в точке s=0
расходится, то с=0; если р<0 и ряд A) в точке s=0
сходится, то
c= lim —r— In
n ~*-oo n
Сумма ряда F(s) в полуплоскости сходимости есть ана-
литич. функция. При а—>--(-оо функция F(o) ведет себя
асимптотически как первый член ряда: ахе~ 1° (если
агФО). Если сумма ряда равна нулю, то и все коэффи-
коэффициенты ряда равны нулю. Максимальная полуплоскость
a>/i, в к-рой F(s) является аналитич. функцией, наз.
полуплоскостью голоморфности функ-
функции F{s), прямая a = h наз. прямой голоморф-
голоморфности. Справедливо неравенство i<c, причем воз-
возможны случаи, когда Л<с. Пусть q — нижняя грань
таких чисел C, что в полуплоскости а>|3 функция
F(s) по модулю ограничена (д<:а). Имеет место формула
а„= lim ^ \p + t F (s) e " ds, n — l, 2, ...; p > q,
из к-рой вытекают неравенства
|а„|< _[')(|, М(а)= sup \F(a-{-it)\,
представляющие собой аналог неравенств Коши для
коэффициентов степенного ряда.
Сумма Д. р. не может быть произвольной функцией,
аналитической в какой-либо полуплоскости a>h:
она, напр., должна стремиться к нулю при а—>--{-оо.
Однако имеет место следующий факт: какова бы ни
была функция (p(s), аналитическая в полуплоскости
ct>/i, найдется такой Д. р. A), что его сумма F(s) будет
отличаться от (p(s) на целую функцию.
Если последовательность показателей имеет плот-
плотность
т= lim т— < оо,
то разность между абсциссой сходимости (абсциссы схо-
сходимости и абсолютной сходимости совпадают) и абс-
абсциссой голоморфности не превосходит величины
Л2 '
б = lim ji- I
п->- со Лв
!¦'(*„>
причем имеются ряды, для к-рых эта разность равна 6.
Величина б может быть любой из [0, оо]; в частности,
если Я,„ + 1— Я„^д>0, п=1, 2, . . ., то 6 = 0. Прямая
голоморфности обладает тем свойством, что на ней в
любом отрезке длины 2ят у суммы ряда имеется хотя
бы одна особенность.
Если Д. р. A) сходится во всей плоскости, то его
сумма F(s) есть целая функция. Пусть
lim !2Л < со;
i?-n орядком целой функции F(s) (по-
(порядком по Ритту) наз. величина
-j^- Ь in м (ст)
СТ-*-оо -ст
Через коэффициенты ряда она выражается по формуле
1 — In I а„ I
Можно также ввести понятие Д-т ипа функции
F(s). Если
lim т-= т < оо
п —>-со п
и если в горизонтальной полосе ширины, большей 2ят,
функция F(s) по модулю ограничена, то F(s)=O (ана-
(аналог Лиуеилля теоремы).
Ряды Дирихле с комплексными по-
показателями. У Д. р.
F(,) = 2;= .«„Г*"»' B)
с комплексными показателями 0<|Я,г| <|Я,2| <:. . ., от-
открытая область абсолютной сходимости выпукла. Если
hm — = 0,
П->-00 ЛП
то открытые области сходимости и абсолютной сходи-
сходимости совпадают. Сумма F(s) ряда B) в области сходи-
сходимости есть аналитич. функция. Область регулярности
функции F(s), вообще говоря, шире области сходимости
Д. р. B). При условии
lim ^- = 0
область регулярности выпукла.
Пусть
lim " = т < оо,
L(X)—какая-нибудь целая, функция экспоненци-
экспоненциального типа, к-рая в точках Я,г, п^1, имеет простые
нули, y(t) — функция, ассоциированная по Борелю
с L(X) (см. Бореля преобразование), D — наименьшее
выпуклое замкнутое множество, содержащее все осо-
особенности функции y{t), и
r
Тогда функции tyn{t) регулярны вне />,я|)„(оо)=0, и они
обладают свойством биортогональности * системе {е п }:
где С — замкнутый контур, охватывающий D. В том
случае, когда г|)„(() непрерывны вплоть до границы об-
области D, в качестве С можно взять границу 3D. Произ-
Произвольной функции F(s), аналитической в D (открытой
части области D) и непрерывной в D, отнесем ряд
Для данной конечной выпуклой области D можно по-
построить такую целую функцию L(X) с простыми нуля-
ми Х1г Я,2, . . ., что для любой функции F(s), аналитиче-
аналитической в D и непрерывной в D, ряд C) равномерно схо-
сходится внутри D и сходится к F(s). Для функции <p(s),
аналитической в D (не обязательно непрерывной в D),
можно найти целую функцию нулевого экспоненциаль-
экспоненциального типа
и функцию F(s), аналитическую в D и непрерывную в
D, такие, что
Ф («) = М (D) F (») = 2Г=ОС«ЯП) (s>-
Тогда
Представление произвольных аналитич. функций
Д. р. в области D установлено также в случаях, когда
D — вся плоскость или D — выпуклая бесконечная
многоугольная область (ограниченная конечным числом
прямолинейных отрезков).
Лит.: [1] Л е о н т ь е в А. Ф., Ряды экспонент, М., 1976;
[2] Мандельбройт С, Ряды Дирихле, принципы и ме-
методы, пер. с англ., М., 1973. А. Ф. Леонтьев.
ДИРИХЛЕ РЯД для аналитической поч-
почти периодической функции — ряд вида
/ (») ~ 2„ АпеЛп\1А»< = 2„ АпеАп\ а <т< р, (*)
представляющий собой все ряды Фурье аналитической
регулярной почти периодической в полосе (а, C),
— оо<а<Р<+оо, функции /(s)=/(T+it) на конти-
континуальной совокупности прямых R(s) = r (см. Почти
периодическая функция аналитическая).
Двум различным почти периодическим в одной и
той же полосе функциям соответствуют два различных
Д. р. В случае 2я-периодич. функции ряд (*) переходит
в ряд Лорана. Числа Ап и А„ наз., соответственно,
коэффициентами и показателями
Дирихле. В отличие от классического Д. р. мно-
множество действительных показателей А„ в (*) может
иметь конечные предельные точки, и, даже, быть всюду
плотным. Если все показатели Дирихле имеют один и
тот же знак, напр., если /(s) — почти периодич. функ-
функция в полосе (а, Р) и в (*) Л„<0, то /(s) — почти пе-
периодич. функция в полосе (а, +оо), и lim /(s) = 0 рав-
%-*+ оо
номерно по t. Аналогичная теорема имеет место для
положительных показателей Дирихле (см. [2]). Если
}{s) — почти периодич. функция в полосе [а, |3] и
неопределенный интеграл функции f(s) в полосе [а, р]
ограничен, то ряды
2jAn<oAne ' ZAn>0Ane
являются рядами Дирихле двух функций /j (s) и /2(s),
почти периодических в любой полосе [ах, +оо), at>a,
соответственно (—оо, рх], рг<р.
Лит.: [1] Бор Г., Почти периодические функции, пер
с нем., М.—Л., 1934; [2] Левитан Б. М., Почти периодиче-
периодические функции, М., 1953. Е. А. Бредихина.
ДИРИХЛЕ ТЕОРЕМА — 1) Д. т. в теории д и о-
фантовых приближений: для любого дей-
действительного числа а и натурального Q существуют
целые а и q, удовлетворяющие условию
\aq — a\<Q~\ 0
Дирихле принцип «ящиков» позволяет доказать и более
общую теорему: для любых действительных чисел
аг, . . ., ап и натурального (?>1 существуют такие це-
це0
max (| сад — Oil \anq—an\) < 0-V«. 0 <
Лит.: [1] К а с с е л с Д ж. В. С, Введение в теорию
диофантовых приближений, пер. с англ., М., 1961.
В. И. Берник.
2) Д. т. о единицах — теорема, описываю-
описывающая структуру мультипликативной группы единиц
в порядках полей алгебраич. чисел; получена П. Г. Л.
Дирихле (см. [1]).
Каждое поле алгебраич. чисел К степени п над полем
рациональных чисел Q имеет п различных изоморфиз-
изоморфизмов в поле комплексных чисел С. Если при изомор-
изоморфизме а : А'—»-С образ поля содержится в поле действи-
действительных чисел, то этот изоморфизм наз. вещест-
вещественным; в противном случае он наз. комплексным.
Наряду с каждым комплексным изоморфизмом а име-
имеется сопряженный к нему комплексный изоморфизм
а : К—>-С, определяемый равенством и(а)-=а(а), а?К.
Таким образом число п можно представить в виде
>i = s-|-2i, где s — число вещественных, a 2i — число
комплексных изоморфизмов поля К в поло С.
Теорема Дирихле: в произвольном поряд-
порядке А поля алгебраич. чисел К степени n = s-\~2t суще-
существует r=s-\-t—1 единиц Ej, . . ., гг таких, что всякая
единица е?Л однозначно представима в виде произ-
произведения
где s1, . . ., sr — пелые числа, а ? — некоторый корень
из 1, содержащийся в А. Единицы Ej, . . ., ег, существо-
существование к-рых устанавливается Д. т. наз. основны-
основными единицами порядка А. В частности,
основные единицы максимального порядка D поля К,
совпадающего с кольцом всех целых чисел поля К,
наз. обычно основными единицами поля
алгебраических чисел К.
Лит.: [1] D i г i с h I e t P. G. L., Werke, Bd 1, В., 1889;
[2] Б о р е в и ч 3. И., Ш а ф а р е в и ч И. Р., Теория чисел,
2 изд., М., 1972. С. А. Степанов.
3) Д. т. о простых числах в арифме-
арифметической прогрессии: каждая арифметич.
прогрессия, первый член и разность которой — нату-
натуральные взаимно простые числа, содержит бесконечное
число простых чисел. Фактически П. Дирихле доказал
(см. [1]), что при любых фиксированных натуральных
взаимно простых числах I, k
где суммирование ведется по всем простым числам р
с условием p=Z (mod к), а ф(А) — функция Эйлера. Это
соотношение можно интерпретировать как закон рав-
равномерного распределения простых чисел по классам
вычетов l(mod к), поскольку
lim у _L:ln_!- = l,
s^l+O ?upps «-1
где суммирование ведется по всем простым числам.
Пусть х~>\ — целое, я(х; I, к) — число простых р<:л
с условием p=l(mod к), где 0<Z<&, Ink — взаимно
просты. Тогда
с х с1ц)
л(х; I, k)^±L^.
где оценка остаточного члена равномерна по всем
&<:Aп х)А при любом фиксированном А >0, с=с(.4)>
>0 — величина, зависящая только от А (неэффективно).
Это современная форма Д. т., непосредственно показы-
показывающая характер распределения простых чисел р=
sil (mod к) в натуральном ряде чисел. Существует
предположение (расширенная гипотеза
Р и м а н а), что при фиксированных взаимно простых
I и к и любых целых
Sx du
„ _ ^
где е>0 — произвольно, а О — величина, зависящая от
к и е.
Лит.: [1] Д и р и х л е П. Г. Л., Лекции по теории чисел,
пер. с нем., М.—Л., 1936; [2] Прах ар К., Распределение
простых чисел, пер. с нем., М,, 1967; [3] К а р а ц у б а А. А.,
Основы аналитической теории чисел, М., 1975.
В. Г. Спринджук.
4) Д. т. о рядах Фурье: если функция f(x)
периода 2л кусочно монотонна на отрезке [ — л, л] и
имеет на нем не более, чем конечное число точек раз-
разрыва, т. е. выполнены так называемые условия
Д и р и х л е, то ее тригонометрич. ряд Фурье сходится
к f(x) в каждой точке непрерывности и к [/(ж+0)+
-rf(x—0)J/2 в каждой точке разрыва. Доказана впервые
П. Дирихле [1]. На функции ограниченной вариации
Д. т. обобщил К. Жордан [3].
Лит.: [1] D i r i с h I e t P. G. L., «J. Math.», 1829, Bd 4,
S. 157—69; [2] его же, Werke, Bd 1, В., 1889; [3] Jordan
С, «С. г. Acad. sci.», 1881, t. 92, Xi 5, p. 228 — 30; [4] Бари
H. К., Тригонометрические ряды, М., 1961; [5] Зигмунд
А., Тригонометрические ряды, пер. с англ., 2 изд., М., 1965.
Т. П. Лукашенко.
ДИРИХЛЕ ФОРМУЛА числа делителей —
асимптотическая формула
где т(п) — число делителей п, С — Эйлера постоянная.
Д. ф. получил П. Дирихле (P. Dirichlet) в 1849, заме-
заметив, что указанная сумма равна числу точек (х, у) с
целыми положительными координатами в области, ог-
ограниченной гиперболой y=Nlx и осями координат,
т. е. равна
где [а] — целая часть а.
Лит.: [1] Титчмарш Е., Теория дзета-функции Рима-
на, пер. с англ., М., 1953. А. Ф. Лаврик
ДИРИХЛЕ ФУНКЦИЯ — функция, равная единице
в рациональных точках и нулю в иррациональных точ-
точках. Д. ф. задается формулой:
/ (х) = lim lim (cos mliraJ";
m —*-co n -^-oo
она принадлежит второму Бэра классу. Д. ф. не инте-
интегрируема по Риману на любом отрезке, но, будучи почти
всюду равной нулю, интегрируема по Лебегу.
Лит.: [1] Н а т а н с о н И. П., Теория функций вещест-
вещественной переменной, 3 изд., М., 1974. Л. Д. Кудрявцев.
ДИРИХЛЕ Х-ФУНКЦИЯ, Дирихле t-p я д,
L-p яд, — функция комплексного переменного s=
=-o-\-it, определяемая для всех Дирихле характеров
¦/ mod d рядом
М-,х) = У" х-^- A)
Д. L-ф. mod d как функции действительного перемен-
переменного s введены в 1837 П. Дирихле (P. Dirichlet, см.
[1]) в связи с доказательством бесконечности простых
чисел в арифметич. прогрессии dm-\-l, разность d и
первый член I к-рой взаимно простые числа. Они пред-
представляют собой естественное обобщение — дзета-
функции Римана ? (s) на арифметич. прогрессии и слу-
служат мощным средством исследований в аналитич. тео-
теории чисел (см. [2] — [4]).
Ряды A), наз. Дирихле рядами, абсолютно и рав-
равномерно сходятся в любой конечной области комплек-
комплексной s — плоскости, для к-рой 0^1 -\-у, у>0. Если ^ -
неглавный характер, то
^<uX(n)u-s-^du. B)
В силу ограниченности суммы под знаком интеграла
эта формула осуществляет аналитическое продол-
продолжение L(s, %) как регулярной функции в полуплос-
полуплоскость а>0.
Для любого X mod d справедливо представление
L(s, x) в виде произведения Эйлера по простым чис-
числам р:
1
Отсюда, если Y=Xn— главный характер mod d, то при
L(s, Xo) = ?M.
а для
Поэтому свойства L (s, Xo) на всеи комплексной пло-
плоскости в основном определяются свойствами ? («).
В частности, функция L (s, Xo) регулярна для всех s,
кроме s=l, где она имеет простой полюс с вычетом
d-:cp(d), ср — функция Эйлера. Если же х=И=Хо и X* —
примитивный характер, к-рый индуцирует характер
X mod d, то
JI^^) D)
Тем самым в главном Д. L-ф. с характерами%ФХа
сводятся к таковым для примитивных характеров. Это
свойство Д. ? = ф. играет существенную роль, так как
многие результаты, касающиеся L(s, у), имеют простой
вид лишь для примитивных характеров. В случае при-
примитивного характера х mod d аналитич. продолжение
на всю плоскость и функциональное уравнение функ-
функции L (s, x) получаются прямым обобщением метода
Римана для ?(s). Результат, если положить
S + 6
/„ „Л А_1-Х(-1>
имеет вид _
g(l-s,X) = e(XM(«.X). E)
где Г — гамма-функция, e(x)=i6d'/2/x{%), |e(x)|=l,
х(х) — Гаусса сумма, % — характер, комплексно со-
сопряженный с Х- Это равенство наз. функциональ-
функциональным уравнением функции L(s, у).
Из него и формул B) и D) следует, что функции L(s, %),
t (s, х) являются целыми функциями для всех %ФХо-
Причем, при а«:0 L{s, х) = 0 лишь в точках s=—2v—б,
v=0, I, 2, . . ., ив точках s, где произведение из D)
обращается в нуль; эти точки наз. тривиальными
нулями L(s, x)- Остальные нули L(s,y) наз.
нетривиальными нулями. Для а>1 функ-
функция L(s, %)Ф0; Ш. Н\. Балле Пуссен (Ch. J. Vallee-
Poussin) показал, что L(i-\-it, %)фО; так что все не-
нетривиальные нули Д. L-ф. лежат в области 0<а<1,
к-рая наз. критической полосой.
Распределение нетривиальных нулей, вообще зна-
значений L (s, X) в критпч. полосе, является важнейшей
проблемой теории Д. L-ф., имеющей фундаментальное
значение для теории чисел.
То, что каждая из функций L (s, %) имеет бесконечно
много нетривиальных нулей и что законы распределения
простых чисел в арифметич. прогрессиях находятся в
прямой зависимости от расположения этих нулей, по-
показывают соответствующие аналоги формул Римана.
Именно, пусть N(T, x) — число нулей функции L(s, у)
с примитивным х mod d в прямоугольнике 0<сг<1
\t\<T, 7>2. Тогда
Пусть Л(п) — функция Мангольдта, l<Z<d, (I, d)=i,
Тогда по свойству ортогональности характеров
где суммирование производится по всем характерам
% mod d, и для ^-примитивного характера %, а=1—б:
~ llm j toil ~V — alnx>
где p—fi-\-iy пробегает нетривиальные нули L(s, %),
L' — производная L no s.
Практически более полезны приближенные формулы
для я|)(.г; а): для произвольного %ф%0, 2<?.Т<?.х,
a для х=хо
У (x;Xo)=2jn<xA ('<)-'< О (In* In d). (8)
Последняя функция вносит в сумму F) величину, пред-
представляющую главный член.
Существует гипотеза, наз. расширенной ги-
гипотезой Р и м а и а, о том, что все нетривиальные
нули Д. L-ф. лежат на прямой 0=1/2. Если эта гипотеза
справедлива, то для d-s?.x
и многие другие важные проблемы теории чисел полу-
получили бы свое окончательное решение. Однако вопросы,
касающиеся расположения нетривиальных нулойД. L-ф.
исключительно трудны и в настоящее время A978) в
этом отношении известно сравнительно немного, при-
причем для комплексных характеров получены более силь-
сильные результаты, чем для действительных.
Обобщением метода, указанного в 1899 Ш. Ж. Балле
Пуссеном для функции Z(s), получена граница нетри-
нетривиальных нулей L(s,x): Для комплексного характера
X mod d существует абсолютная постоянная С такая,
что L (s, x) не имеет нулей в области
0 > 1 — C/lnd(| t |-i-2);
если же у_ — действительный неглавный характер mod d.
то L (s, x) может иметь в этой области самое большое
один простой действительный (?=0) нуль, к-рый наз.
исключительным нулем L{s, %). Для ис-
исключительного нуля Р, из формул числа классов квад-
квадратичных полей, выведено неравенство
Р<1 — C/d1''2 h\2d.
Последняя известная граница для Р указана в 1935
К. Зигелем (С. Siegel): при любом е>0 существует по-
положительное число С (г) такое, что
. Эта оценка имеет однако существенный недостаток, она
является неэффективной в том смысле, что по заданному
е нельзя оценить численное значение постоянной С (г).
Таким же недостатком страдают и теоретико-числовые
результаты, вывод к-рых опирается на оценку Зигеля.
Вследствие указанных границ для нетривиальных
нулей Д. L-ф. и формул F) — (8) справедлив асимпто-
тич. закон распределения простых чисел в виде:
"Ф (х; d. 1) = -?п\ + О (*ехр[—С, /"hTiJ),
где Сг— абсолютная постоянная для d<:(ln хI—V при
нек-ром фиксировании у>0 и Cl = C1(N) ¦—«неэффек-
¦—«неэффективная» постоянная для d<(ln d)N при любом фикси-
фиксированном N~>\ — у.
Эти результаты являются лучшими в проблеме
равномерного распределения простых чисел в арифме-
тич. прогрессиях растущей разности d. Для фиксирован-
фиксированных значений d известно несколько больше. В таком
случае теория Д. L-ф. при 1фО во многом аналогична
теории дзета-функции Римана (см. [5]) и последняя
граница нулей L(s, %), полученная по Виноградова ме-
методу оценки тригонометрич. сумм, имеет вид:
для© > 1— С/1пг/3(| * |-(-2)ln1/3ln(|<|-j-2),
где С — положительная постоянная, зависящая от й.
Этой границе нетривиальных нулей Д. L-ф. фикси-
фиксированного mod d отвечает лучший A977) остаточный
член в асимптотич. формуле для г|)(ж; d, l) в виде:
< х ехр [—С 1п3/5 х | In1/5 In x].
Все формулы относительно асимптотики функции
ty(x; d, I) имеют аналоги для функции п(х; d, I) —
числа простых чисел р<.х, p^sl (mod d), с главным чле-
членом П xly(d) вместо x/(f(d)n остаточным членом, мень-
меньшим на множитель In x.
К числу основных направлений исследований в со-
современной теории Д. L-ф. относятся также исследования
плотности распределения нетривиальных нулей Д. L-ф.,
содержание к-рых составляют оценки величин:
N(a,T,x), 2XmoddiV(a, T,X),
где N(o, T, %) обозначает число нулей L(s, %) в пря-
прямоугольнике 0<а<сг<1, |(|<Т, х* — примитивный
характер mod d.
Лит.: [1] Дирихле П. Г. Л., Лекции по теории чисел,
пер. с нем., М.—Л., 1936; [2] Дэвенпорт Г., Мультипли-
Мультипликативная теория чисел, пер. с англ., М., 1971; [3] Прахар
К., Распределение простых чисел, пер. с нем., М., 1967; [4]
Чудаков Н. Г., Введение в теории JL-функций Дирихле,
М.—Л., 1947; [5] W а 1 f i s z A., Weylsche Exponentialsummen
in der neueren Zahlentheorie, В., 1963; [6] M о н т г о м е р и Г.,
Мультипликативная теория чисел, пер. с англ., 1974; [7] Л а в-
р и к А. Ф., «Матем. заметки», 1975, т. 17, в. 5, с. 809 —17.
А. Ф. Лаврик.
ДИРИХЛЕ ХАРАКТЕР (mod k) — функция %(п) =
— Х(п; к) на множестве целых чисел, удовлетворяю-
удовлетворяющая условиям."
()^0
Иными словами, Д. х. (mod к) — это арифметич. функ-
функции, к-рые не равны тождественно нулю, вполне муль-
мультипликативны и периодичны с периодом к.
Понятие Д. х. ввел П. Дирихле (P. Dirichlet, см.
[1]) в связи с изучением закона распределения простых
чисел в арифметич. прогрессиях. Он же разработал
основы теории Д. х. (см. [2] — [8]), исходя из прямого
конструктивного построения их.
Пусть
— канонич. разложение к, п — целое взаимно простое
с к, (п, А)=1; С—Со=1, если а=0 или а=1; С=2,
С0=2а~'\ если сс>2; С1 = ф(р1а'). • • -, Сг=ф(р<Х''), где
Ф —функция Эйлера. Пусть, далее, у, у0, у1, . . ., уг ¦—
система индексов числа n no mod к, т. е. система наи-
Меньших неотрицательных целых чисел, удовлетворя-
удовлетворяющих сравнениям
и=(—l)Vo(mod2a), n = g]> (modpp), ;=l,...,r,
где gj—наименьший первообразный корень по mod р ./ ;
е, е0, е1( . . ., ег — система каких-либо корней из 1 со-
соответственно порядков С, Со, Си . . ., Сг. Функция
v(n)=/e1>eo#ei1-erVr. если (п. *) = 1>
I 0, если (п, к)'ф1,
определенная на множестве всех натуральных чисел,
наз. характером Дирихле (mod к). Пере-
Перебирая все возможные значения е, е0, ех, . . ., ег полу-
получают
различных функций / — Д. х. mod к. Характер с
8—8A=8!=. . . = ег= 1 наз. главным характе-
р о м; он обозначается %0:
< 1, если (п, к) = 1,
Хо(п) = |О) есди ^ к)ф^
Для любых натуральных чисел п, I и к:
x(n)x(')=x(»i);
у.(п)=хA), если n=?(mod к);
Х(п, к) = Х(п; 2а)Х(п, р^)...%(п; р?г);
если х(п) — Д- х. (mod к), то комплексно сопряженная
функция х(п) — также Д. х. (mod к);
Наименьшее из чисел v, удовлетворяющее равенству
Xv (n) = %Q{n) наз. степенью Д. х. Для v=l су-
существует один такой характер %0. Если v=2, то % (п)
может принимать лишь значения 0; =tl; такие Д. х. наз.
действительными, или кв адратичными.
Если VJ&3, до Д. х. наз. комплексным. %(п) наз.
четным или нечетным соответственно тому,
будет х (—1)=1 или х (—1)= — 1- Главные свойства
сумм Д. х. выражаются формулами
У ()[У{к)' если х =
х(п)[
mod k к \ о, если % Ф Хо1
\ 4>(к), если Z = l (mod А),
х{'~\ о, если I ф\ (mod к),
где в 1-й формуле ге пробегает полную систему вычетов
(mod к), а % во 2-й формуле — все <р(к) характеров
(mod к).
При (/, к)=1 справедлива формула
у (п) у (I) = I *> если п = ( )'
ft X 0, если n^Z (mod /c),
наз. свойством ортогональности Д. х.
Она является одной из основных формул Д. х., при-
применяемых в разного рода исследованиях арифметич.
прогрессий: /cv+Z, v=0, I, 2, .... В теории и прило-
приложениях Д. х. важны также понятия ведущего модуля
характера и примитивного характера. Пусть х (и! к) —
произвольный неглавный характер (mod к). Если для
значений п, удовлетворяющих условию (п, &)=1, число
к является наименьшим периодом % (п; к), то к наз.
ведущим, или основным, модулем ха-
характера Xt а сам характер х — примитивным,
или первообразным, характером (mod к).
В противном случае существуют единственные число
делящее к, к^<Ск и примитивный характер
fcj) такие, что
(п; kj), если (п, к) = 1,
О, если (п, к)ф\.
В этом случае % (n; &) наз. н е п р и м и т и в н ы м,
или производным, характером
X(modd) и говорят, что %i индуцирует %. Тем самым
многие вопросы о характерах сводятся к таковым для
примитивных характеров.
Характер % {п\ к) является примитивным тогда и
только тогда, когда для любого d, делящего к, d<.k,
существует а с условиями:
a=l (modd), %(a; к) ф 0; 1.
В аналитич. теории широко используются суммы
Гаусса, определяемые для %(modk) равенством
Для примитивного характера % mod к
При этом справедливо разложение % (п) в виде:
Y М = —i=- V * х"( e27linmi'k.
т(Х) Z-im=1
Одной из основных проблем в теории Д. х. является
проблема оценки сумм Д. х. Y_(m°dA),
Имеет место оценка Виноградова:
S (N; M)<4 /Flnfc.
Установлено [7], что
S(N; M)<4k(r+1^/4r2(N — М^-^/'Чп к, г = 1,2, ...,
к — простое число. При M=i, N~k/2 существует
(см. [8]) бесконечная последовательность чисел к,
являющихся модулями примитивного действительного
характера у_, для к-рой
| S (N; М) | ~ 2-^ Vklnlnk,
у — Эйлера постоянная. Это асимптотич. равенство
показывает, что предыдущие оценки, вообще говоря,
существенно усилить нельзя. Однако существует г и-
потеза Виноградова, согласно к-рой для
любого е>0, lAf
\S (N; M) \<^ke (N — MI/2.
Доказательство этой гипотезы позволило бы решить ряд
крупных проблем теории чисел.
Теория Д. х. лежит в основе теории Дирихле L-функ-
ций и является частным случаем общей теории харак-
характеров абелевых групп.
Лит.: [1] Дирихле П. Г. Л., Лекции по теории чисел,
пер. с нем., М.— Л., 1936; [2] Виноградов И. М., Избр.
тр,, М., 1952; [3] Карацуба А. А., Основы аналитической
теории чисел, М., 1975; [4] Прах ар К., Распределение
простых чисел, пер. с нем., М., 1967; [5J Ч у д а к о в Н. Г.,
Введение в теорию L-функций Дирихле, М., 1947; [6] Д э в е н-
порт Г., Мультипликативная теория чисел, пер. с англ.,
М., 1971; t7] BurgessD. А., «Тр. Матем. ин-та», 1973,
т. 132, с. 203—205; [8] Л а в р и к А. Ф., «Изв. АН СССР.
Сер. матем.», 1971, т. 35, № 6, с. 1189—207. А. Ф. Даврик.
ДИРИХЛЕ ЯДРО — выражение
sin
U—
П. Дирихле [1] доказал, что частная сумма Sn(x) ряда
Фурье функции f(x) выражается через Д. я.:
2 -^ft=i
= ±[Л f(t)Dn(t-x)dt;
интеграл справа наз. сингулярным интегра-
интегралом Дирихле.
По аналогии с Д. я. (см. [3]) выражение
х (
cos—--cos ( n+
sin kx = 2V
наз. сопряженным ядром Дирихле. Част-
Частная сумма ряда, сопряженного к ряду Фурье функ-
функции / (х), выражается через сопряженное Д. я.:
bfecosfer — a.flsinkx =
f(t)Dn(t-x)dt.
-л
Лит.: [1] Dirichlet P., «J. fur Math.», 1829, Bd 4,
S. 157—69: [2] его же, Werke, Bd 1, В., 1889; [3] T a li-
liber A., «Monatsh. Math.», 1891, Bd 2, S. 79—118; [4] Бари
H. К., Тригонометрические ряды, М., 1961; [5] 3 и г м у н д А.,
Тригонометрические ряды, т. 1—2, пер. с англ., М., 1965.
Г. Л. Лукашенко.
ДИСК в топологии — поверхность, гомеоморф-
ная кругу, т. е. ориентируемое двумерное многообразие
рода 0 с одной компонентой края. Локально связный
континуум без локально разбивающих точек в точности
тогда гомеоморфен Д., когда любая окружность вне
нек-рой точки этого континуума разбивает его и имеется
окружность, к-рая его не разбивает. а. в. Чернавский.
ДИСКРЕПАНС последовательности точек <в=
= (ж1, . . ., ждО из единичного s-мерного куба Ks=
= {ж : 0<:xv <l,v = l, s} — норма функционала
4,(a,a) = v-^jp, A)
вычисленная в той или иной метрике. Здесь v и N (V) со-
соответственно объем области V= {х : 0<zv <av <1,
v=l,s} и число точек последовательности и, принадле-
принадлежащих области V. Если рассматривается распределение
точек последовательности и по областям вида F=
= {ж : 0«av <xv <PV <1, v=l, s}, то в A) принято
вместо <р(«, со) писать <р(а, Р, со).
Наиболее употребительны нормы функционала A):
DN (w) = sup | ф (а, р, ш) |,
«6KJ; Р«К5
D*n (ш) = sup | ф (а, <й)|,
/ С1 Г1]/ \- j
jV'C0' Р'~ \ ) о'" J о '^ ' ' ' ai'">>
Последовательность точек m=(iKj, . . ., агдг, . . .) из
единичного s-мерного куба Ks равномерно распределена
тогда и только тогда, когда (см. l IJ):
lim DN(co)=0.
Для любой бесконечной последовательности одномер-
одномерных точек и= {хп : 0<:ж„<:1, я=1, оо } справедлива
теорема (см. [3]):
Urn NDN (<в) = оо.
Какова бы ни была последовательность <а= {хп : О <:
-<.г„<:1, ге=1, оо} можно указать последовательность
Nlt . . ., Nk . . . такую, что при N=N\ (см. [4]):
NDN (<й) 5s Сх УШЖ
Окончательный результат для бесконечных последова-
последовательностей одномерных точек состоит в том, что при
N=Nk (см. [5]):
NDN (со) =з= C2 In N.
Исследовался Д. различных конкретных последова-
последовательностей (см. [6] — [8]) и получены оценки сверху
NDN (со, Ьг) < С3 (s) ln^1 N,
XDA' (со) < С4 (s) \ns N,
соответственно для конечных и бесконечных последова-
последовательностей; и оценки снизу (см. [4]): для любой последо-
последовательности из N точек имеет место неравенство
XDA, (со, Ьг)^Сь (s) ln<s+1)/2iV;
какова бы ни была бесконечная последовательность
ш= {•/:„ : •кп^К$, п=1, оо } можно указать последова-
последовательность номеров Л\, . . . , Nk, . . . , таких, что при
N=Nk:
NDN (и, i2)SsC6 (s) Ins/2JV.
При этом
Лит.: [1] W е у 1 Н., «Math. Ann.», 1916, Bd 77, S. 313 — 52;
[2] Van d e г С о г р и t J. G., «Proc. Koninkl. ned. akad.
wet. A», 1935, dl 38, № 8, p. 813 — 21; Ко 10, p. 1058 — 66; [3]
Van Aordenne-Ehrenfert Т., «Indagat. math,»,
1949, dl 11, p. 264—69; Ц] R о t h K. F,, «Mathematika», 1954
v 1, p. 73—79; [5] Schmidt W. M., «Acta arithm.», 1972
t. 21, p. 45—50; 16] Hal ton J. H., «Numer. Math.», 1960,
Bd 2, Л» 2, S. 84—90; [7] Соболь И. М., «Ж. вычисл. ма-
тем. и матем. физ.», 1967, т. 7, Ni 4, с. 784—802; 18] Кор о-
б о в Н. М., Теорикочисловые методы в приближенном анализе,
М., 1963; [9]Kuipers L., Niederreiter H., Uniform
distribution of sequences, N. Y., 1974. В. М. Соловое.
ДИСКРЕТНАЯ ГРУППА преобразований —
группа Г гомеоморфизмов хаусдорфова топологич. про-
пространства X, удовлетворяющая следующему условию:
для любых точек х, у?Х найдутся такие их окрестно-
окрестности U, V соответственно, что множество
{y?T\y(U)[\r Ф 0}
конечно. Стабилизатор
точки х?Х относительно Д. г. преобразований конечен,
а орбита любой точки х?Х дискретна. В случае, когда
X — метрическое пространство и преобразования из Г
являются изометриями, этих двух условий достаточно
для того, чтобы группа Г была Д. г. преобразований.
Примеры. 1) Группа параллельных переносов
действительной плоскости R.2 на всевозможные целочис-
целочисленные векторы:
(х, у)—у(х^-п, у + т), где (i, j) f R!; n, roB.
2) Пусть X — верхняя комплексная полуплоскость
С+ = {г g C|Imz >0},
рассматриваемая в обычной хаусдорфовой топологии, а
Г — группа дробно-линейных преобразований вида
az + b
cz + d '
где а, Ь, с, d — целые числа и ad—6с=1 (м о д у-
лярная группа Клейна).
3) Любая конечная группа Г гомеоморфизмов хаус-
хаусдорфова топологич. пространства X. Если X отделимо,
то Г будет собственно разрывной группой преобразова-
преобразований (пример неприводимого алгебраич. многообразия с
топологией Зариского показывает, что условие отдели-
отделимости X является существенным).
4) Скольжений группа произвольного регулярного
накрытия р : X-+Y, где X— связное и локально линей-
линейно связное, a Y— хаусдорфово топологич. пространст-
пространство, является Д. г. преобразований действующей
свободно (т. е. Гх={1} для любой х^Х), причем
само накрытие р совпадает с отображением фактори-
факторизации по этой группе. Обратно, если Г — свободно дей-
действующая Д. г. преобразований связного топологич.
пространства X, то факторпространство XIТ хаусдор-
хаусдорфово и отображение факторизации р: Х—>-Х/Г — регу-
регулярное накрытие пространства Х/Г с группой
скольжения Г. В частности, в силу теоремы унифор-
мизации Пуанкаре — Кёбе, всякая риманова поверх-
поверхность, за несколькими тривиальными исключениями,
может быть получена факторизацией верхней комп-
комплексной полуплоскости С+ по свободно действующей
Д. г. дробно-линейных преобразований с действитель-
действительными коэффициентами (так наз. фуксовой группе).
5) В теории модулей римановых поверхностей (и, бо-
более общо, модулей комплексных многообразий того или
иного типа) Д. г. преобразований появляются как мо-
модулярные группы. Простейшая из этих групп рассмотре-
рассмотрена в примере 2.
6) К числу Д. г. преобразований относятся кристал-
кристаллографические группы. Весьма широкий класс Д. г. пре-
преобразований, включающий фуксовы и кристаллогра-
фич. группы, составляют дискретные подгруппы топо-
топологич. групп (в частности, групп Ли), рассматриваемые
как группы преобразований однородных пространств.
Замкнутое подмножество D топологич. пространства
X с Д. г. Г преобразований наз. фундаменталь-
фундаментальной областью группы Г, если оно является
замыканием открытого подмножества и если множества
y(D), где у?Г, не имеют попарно общих внутренних
точек и образуют локально конечное покрытие прост-
пространства X. Так, напр., для группы параллельных пере-
переносов из примера 1 в качестве фундаментальной обла-
области можно взять квадрат
или, более общо, любой параллелограмм с вершинами
в целых точках, не имеющий целых точек внутри и на
сторонах, а для модулярной группы Клейна (пример
2)) — так наз. модулярную фигуру
D=\z ? С+ — -i-
Фундаментальная область может быть построена во
многих случаях. Напр., если X — полное риманово
многообразие, Г — Д. г. преобразований пространства
X, состоящая из изометрий этого пространства, и
х0 ? X — какая-либо точка, для к-рой стабилизатор ГХо
тривиален, то в качестве фундаментальной области мо-
может быть взята область Дирихле
D ~ {х € X | d (х, х0) < d (x, у (х0)) для всех нетожде-
ственпых преобразований у ? Г}.
(Здесь через d (x, у) обозначено расстояние между точ-
точками х и у из X.) Если X — односвязное полное про-
пространство постоянной кривизны, т. е. сфера, евклидово
пространство или пространство Лобачевского, то об-
область Дирихле является выпуклым многогранником.
Построение фундаментальной области и исследование
ее свойств доставляют важную информацию о Д. г.
преобразований. Так, факторпространство Х/Т полу-
получается из фундаментальной области путем «склеивания»
нек-рых граничных точек. Напр., для группы парал-
параллельных переносов (пример 1)) факторпространство по-
получается из квадрата (*) склеиванием противополож-
противоположных сторон и гомеоморфно двумерному тору. Понятие
фундаментальной области лежит в основе к о м б и н а-
торно-геометрического метода в те-
теории Д. г. преобразований, восходящего
к работам А. Пуанкаре по фуксовым [1] и клейновым
[2] группам. Этот метод позволяет, с одной стороны, вы-
выяснить строение Д. г. преобразований как абстрактной
группы (т. е. найти ее образующие и определяющие со-
соотношения) и, с другой стороны, доказать дискретность
и найти фундаментальную область группы преобразова-
преобразований с данными образующими. Суть этого метода состоит
в следующем. Пусть Г — Д. г. изометрий п-мерного
односвязного полного пространства X постоянной кри-
кривизны и Ф — выпуклый многогранник, являющийся ее
фундаментальной областью. Тогда группа Г порож-
порождается множеством
М = {у ? Г \6Ит(Ф[]у(Ф)) = п — 1}.
При этом в качестве определяющих соотношений могут
быть взяты всевозможные соотношения следующих двух
типов: YiY2=l, где ух, у2?М и YiYa- • -Yft=1' г«е Yi>
у2, ... , ук?М,
dim (ФП Yi (Ф) Л TiT2 (Ф) П • ¦ • П Т1Т2... Yfc-1 (Ф)) = « — 2.
Y/Yi4r#l при i=l,2,... , к—1 и YiY2- • -Y^1 ПРИ
1<к (см. [7], [3], [6]). Обратно, пусть Ф — выпуклый
многогранник в n-мерном односвязном полном простран-
пространстве X постоянной кривизны (не исключается вырож-
вырожденный случай, когда некоторые двугранные углы мно-
многогранника Ф равны я), и для каждой (п—1)-мерной
грани F многогранника Ф задана изометрия ур прост-
пространства X такая, что Ф[\уг(Ф)=Р. И пусть: A) для
каждой (п—1)-мерной грани F многогранника Ф сущест-
существует такая грань F',что УрУр,= ^\ B) для каждой (п—2)-
мерной грани Е многогранника Ф существует такая по-
последовательность Flt F2, . .. , Fk его (п — 1)-мерных
граней, что УР,УРг-•-Урк=^>
и многогранники Ф, ур (Ф), ^^^ р^р/
у (Ф) не имеют попарно общих внутренних точек.
Тогда группа изометрий пространства X, порожденная
преобразованиями у дискретна и многогранник Ф
является ее фундаментальной областью. Это вытекает
из более общего результата А. Д. Александрова [4] о
заполнении пространства выпуклыми многогранника-
многогранниками (см. также [8]). Следующее описание свободно дей-
действующих фуксовых групп с компактным факторпрост-
ранством, принадлежащее А. Пуанкаре (Н. Poincare),
служит примером сказанного выше. При этом считается,
что верхняя комплекс-
комплексная полуплоскость
С + наделена стандарт-
стандартным образом геомет-
геометрией Лобачевского
модель Пуан-
Пуанкаре плоскости Ло-
Лобачевского). Фунда-
Фундаментальная область
любой из фуксовых
групп рассматривае-
рассматриваемого типа может быть выбрана в виде выпуклого
ограниченного 4^-угольника Ф, обладающего свойст-
свойствами: а) сумма его внутренних углов равна 2я; б) если
при фиксированном направлении обхода границы дФ
многоугольника Ф обозначить его стороны через b1, b2,
di, d2, b3, 64, d3, di; . . . , b2g-!, b*g, d2(?-i, d2g, то дли-
длина bj равна длине d; при всех i=l, 2, . .. , 2g. На ри-
рисунке изображена такая область Дирихле для g=3.
Если при этом обозначить через у;, i=l, ... , 2g, изо-
метрию плоскости С + , сохраняющую ориентацию и
переводящую с изменением направления 6,- в d; при j
четном и d[ в 6,- при i нечетном (считается, что стороны
Ф имеют направления, индуцированные выбранным на-
направлением обхода дФ), то набор {ylt у2, . . . , y2g} яв-
является системой образующих группы Г. Единственное
соотношение между этими образующими имеет вид
Обратно, если Ф — произвольный выпуклый ограничен-
ограниченный многоугольник, удовлетворяющий условиям а) и б),
то группа Г, порожденная изометриями уг, у2, . . . , y2g,
есть свободно действующая фуксова группа, причем
Ф — ее фундаментальная область, а комплексное мно-
многообразие С + /Г является компактной рнмановой по-
поверхностью рода g.
Когомологич. теория Д. г. преобразований состоит
в изучении связи между когомологиями пространства
X, пространства Х/Т и группы Г. В частности (пример
4)) есаи Г — Д. г. преобразований, являющаяся груп-
группой скольжений регулярного накрытия р : А"—>-А7Г,
где X — ациклическое тонологич. пространст-
пространство (т. е. Н„(Х) = 0 при п>1 и Н0(Х) = Ж), то сингуляр-
сингулярные когомологии пространства Х/Т и когомологии Г
как абстрактной группы с коэффициентами в абелевой
группе А (с тривиальной Г-модульной структурой) свя-
связаны некоторыми изоморфизмами
Нп(Х/Т, A)ssHn (Т, А), и = 0, 1, ...,
естественными по А (см. [10]). В общем случае связь
между упомянутыми выше группами когомологии вы-
выражается при помощи некоторых спектральных после-
последовательностей (см. [9], [10]).
См. также Автоморфная форма, Автоморфная функ-
функция, Арифметическая группа.
Лит.: [1] Пуанкаре А., Избр. тр., т. 3, М., 1974,
с. 9—62; [2] Р о i n с а г ё Н., «Ada math.», 1883, t. 3, p. 49—
92; [3] G e r s t e n h a b e r M., «Proc. Amer. Math. Soc»,
1953; v. 4, p. 745—50; [4] Александров А. Д., «Вестник
ЛГУ», 1954, K2, с. 34—43; [5] Coxeter H. S. М., М о-
s e r W. O.J., Generators and relations for discrete groups, B.—•
Hdlb.—N. Y., 1972; [6] В ей ль А., «Математика», 1963,
т. 7, N° 1, с. 3—12; [7] Macbeath A.M., «Ann. Math.»,
1964, у. 79, p. 473—88; [8] Abels H., Geometrische Erzeugung
von diskontinuierlichen Gruppen, Mlmster, 1966; [9] Г р о т е н-
д и к А., О некоторых вопросах гомологической алгебры, пер. с
франц., М., 1961; [10] М а к л е й н С, Гомология, пер, с англ.,
М., 1966; [11] Lehner J., Discontinuous groups and automor-
phic functions, Providence, 1964; [12] Cepp Ж. -П., «Матема-
«Математика», 1971, т. 15, № 5, с. 3—6. Э. В. Винберг, В. Л. Попов
ДИСКРЕТНАЯ МЕРА — мера, сосредоточенная на
не более чем счетном множестве. Точнее, пусть Я и
ц — меры (вообще говоря, знакопеременные), опреде-
определенные на одном полукольце множеств (со своим ст-коль-
цом измеримых множеств). Мера Я наз. дискрет-
дискретной мерой относительно меры ц, если X сосредо-
сосредоточена на не более чем счетном ц-меры нуль множест-
множестве, всякое одноточечное подмножество к-рого Я-изме-
римо. Так, напр., дискретная мера Лебега — Стилтьеса
линейных множеств Я равна на полуинтервалах прира-
приращению нек-рой функции скачков, имеющей ограничен-
ограниченную вариацию, когда X ограничена, и неубывающей,
когда X положительна.
Лит.: [1] К о л м о г о р о в А. Н., Ф о м и н С. В., Эле-
Элементы теории функций и функционального анализа, 4 изд
М., 1976. А. П. Терехин
ДИСКРЕТНАЯ ПОДГРУППА — подгруппа Г топо-
логич. группы G (в частности, подгруппа группы Ли),
являющаяся дискретным подмножеством топологич.
пространства G. В локально компактных топологич.
группах (в частности, в группах Ли) выделяют решет-
решетки — Д- п., для к-рых факторпространство Г\С имеет
конечный объем в смысле меры, индуцированной лево-
инвариантной Хаара мерой на группе G. К числу реше-
решеток относятся равномерные Д. п., для к-рых
факторпространство F\G компактно.
Если К — компактная подгруппа локально компакт-
компактной топологич. группы G, то подгруппа TdG дискретна
тогда и только тогда, когда она является дискретной
группой преобразований пространства X=G/K (в смыс-
смысле действия, индуцированного естественным действием
группы G на X). При этом Г является решеткой (соот-
(соответственно равномерной Д. п.) тогда и только тогда,
когда факторпространство Г\Х имеет конечный объем
в смысле меры, индуцированной G-инвариантной мерой
на X (соответственно компактно). Это дает возможность
использовать при изучении Д. п. групп Ли геометрич.
методы.
Одна из основных задач теории Д. п. групп Ли —
классификация таких подгрупп с точностью до соизме-
соизмеримости. Подгруппы 1\, Г2 группы G наз. соизме-
соизмеримыми, если Г, П Г2 имеет конечный индекс как
в Т1, так и в Г2. Если одна из соизмеримых подгрупп
локально компактной топологич. группы является
Д. п. (соответственно решеткой, равномерной Д. п.),
то и другая обладает этим свойством.
До середины 20 в. рассматривались в основном от-
отдельные классы Д. п. групп Ли, обязанные своим про-
происхождением арифметике, теории функций и физике.
Исторически первая нетривиальная Д. п.— подгруппа
SL2(Z) группы SL2(R), названная впоследствии моду-
модулярной группой Клейна — фактически рассматривалась
Ж. Лагранжем (J. Lagrange) и К. Гауссом (С. Gauss) в
их исследованиях по арифметике квадратичных форм
от двух переменных. Ее естественным обобщением яв-
является подгруппа SLnB) группы SLn(R). Исследование
этой группы как дискретной группы преобразований
пространства положительно определенных квадратич-
квадратичных форм от п переменных составило предмет теории
приведения, разработанной А. Н. Коркиным, Е. И. Зо-
Золотаревым,. Ш. Эрмитом (Ch. Hermite), Г. Минковским
(Н. Minkowski) и др. во 2-й пол. 19 — начале 20 вв. Ряд
арифметически определяемых Д. п. классич. групп Ли:
группы единиц квадратичных форм с рациональными
коэффициентами, группы единиц простых алгебр над
Q, группу целочисленных симплетич. матриц — иссле-
исследовал в 40-х гг. 20 в. К. Зигель (С. Siegel). Он, в част-
частности, доказал, что все эти группы являются решет-
решетками в соответствующих группах Ли.
В теории функций комплексного переменного интег-
интегрирование алгебраич. функций и, более общо, решение
дифференциальных уравнений с алгебраич. коэффициен-
коэффициентами привело к рассмотрению нек-рых специальных
функций (названных впоследствии автоморфными функ-
функциями), инвариантных относительно различных ди-
дискретных групп, состоящих из преобразований вида
SL2(R). A)
Некоторые возникающие таким образом Д. п. группы
SL2(R) были рассмотрены примерно в середине 19 в. в
работах Ш. Эрмита, Р. Дедекинда (R. Dedekind) и
И. Л. Фукса (I. L. Fuchs). Среди них была и группа
SL2(Z) (но представленная другим образом, чем у
Ж. Лагранжа и К. Гаусса). Обширный класс таких
групп, в том числе группа SL2(Z) и нек-рые соизмеримые
с ней подгруппы группы SL2(R), был изучен Ф. Клей-
Клейном (F. Klein). Почти одновременно, в 1881—82 А. Пу-
Пуанкаре (Н. Poincare) дал геометрич. описание всех ди-
дискретных групп, состоящих из преобразований вида A).
Эти группы были им названы фуксовыми группами.
В 1-й половине 20 в. рассматривались отдельные
классы автоморфных функций многих переменных. Эти
функции были связаны с некоторыми арифметически оп-
определяемыми Д. п. групп (SL2(R.))* (модулярные функ-
функции Гильберта), Sp2n (R) (модулярные функции Зигеля)
и других полупростых групп Ли.
В кристаллографии начиная с конца 19 в. рассмат-
рассматривались группы симметрии кристаллич. структур,
являющиеся не чем иным, как равномерными Д. п.
группы движений трехмерного евклидова пространства.
Эти и подобные им группы движений n-мерного евкли-
евклидова пространства — так наа. кристаллографические
группы — были изучены с алгебраич. точки зрения
Л. Бибербахом (L. Bieberbach) в 1911. Он доказал, в
частности, теорему о том, что всякая кристаллографич.
группа содержит равномерную Д. п. группы параллель-
параллельных переносов.
Все эти исследования послужили исходным материа-
материалом для общей теории Д. п. групп Ли, основы к-рой
были заложены в 50—60-е гг. 20 в.
Построена исчерпывающая теория Д. п. нильпотент-
ных групп Ли [9]. Ее основные утверждения: 1) Если
Н — ушшотентная алгебраич. группа, определенная
над Q, то группа Н„ ее целых точек является равномер-
ной Д. п. в группе HR ее действительных точек. (При
этом #R — односвязная нильпотентная группа Ли.)
2) Всякая равномерная Д. п. Г односвязной нильпо-
тентной группы Ли G арифметична в том смысле,
что существуют унипотентная алгебраич. группа Н,
определенная над Q, и изоморфизм ср: Hr-^-G такие, что
подгруппа Г соизмерима с <р(Н ). 3) Если 1\, Г2 —
равномерные Д. п. односвязных нильпотентных групп
Ли Glt G2 соответственно, то всякий изоморфизм Г1—>-Г2
однозначно продолжается до изоморфизма G1-+G2.
4) Абстрактная группа Г вкладывается в виде равно-
равномерной Д. п. в односвязную нильпотентную группу Ли
тогда и только тогда, когда Г — конечно порожденная
нильпотентная группа без кручения.
Д. п. разрешимых групп Ли изучены достаточно хо-
хорошо, но результаты здесь не отличаются таким со-
совершенством, как для нильпотентных групп. Всякая
решетка в разрешимой группе Ли является равномер-
равномерной Д. п. Если Г — решетка в односвязной разрешимой
группе Ли G, то группа G допускает точное матричное
представление, при к-ром элементы группы Г представ-
представляются целочисленными матрицами [13]. Это утверж-
утверждение можно рассматривать как обобщение теоремы 2)
Мальцева. Аналогом теоремы 4) является следующее
утверждение. Всякая решетка в односвязной разреши-
разрешимой группе Ли есть строго полициклическая группа; и
обратно, всякая строго полициклич. группа обладает
подгруппой конечного индекса, изоморфной решетке
в односвязной разрешимой группе Ли.
Наиболее тонкие результаты теории Д. п. групп Ли
относятся к Д. п. неразрешимых и, в частности, полу-
полупростых групп Ли. В [4] доказана следующая теорема,
включающая в себя в виде частных случаев теорему 1)
Мальцева, Дирихле теорему о единицах поля алгебра-
алгебраич. чисел и упомянутые выше результаты Зигеля о
нек-рых арифметич. Д. п. полупростых групп Ли. Пусть
Н — линейная алгебраич. группа, определенная над
Q. Для того чтобы подгруппа Н_ была решеткой в НR,
необходимо и достаточно, чтобы группа Н не допускала
рациональных гомоморфизмов на группу С*, опреде-
определенных над Q (это условие, в частности, выполняется,
если группа Н полупроста или унипотентна). Для того
чтобы подгруппа Н' была равномерной Д. п. в #R>
необходимо и достаточно, сверх этого, чтобы все уни-
потентные элементы группы Hq лежали в Uq, где U —
ушшотентный радикал группы Н.
Аналогом теоремы 2) для Д. п. полупростых групп
Ли является следующая теорема арифметичности [11].
Пусть Г — решетка в связной полупростой группе Ли
G, не имеющей компактных множителей, и пусть (для
удобства формулировки) центр группы G тривиален.
Пусть, кроме того, решетка Г неприводима в том смыс-
смысле, что группа G не может быть разложена нетривиаль-
нетривиальным образом в прямое произведение G1X G2 так, чтобы
Г была соизмерима с подгруппой вида FjXFj, где
F1czG1, FaczG2. Тогда, если вещественный ранг группы
G больше единицы, подгруппа Г арифметична в том
смысле, что существуют полупростая алгебраич. груп-
группа Н, определенная над Q, и гомоморфизм ф: Н^—>G
(где if^ — связная компонента единицы группы #R)
такие, что ядро гомоморфизма ф компактно и подгруппа
Г соизмерима с ш(Я„). Предположение о том, что веще-
ственный ранг группы G больше единицы, существенно.
Известно, что теорема неверна для группы PSL2(R)
(группы движений плоскости Лобачевского), к-рая вооб-
вообще играет особую роль в теории Д. п. групп Ли, а так-
также [6], [8] для групп движений пространств Лобачев-
Лобачевского размерностей 3, 4 и 5.
Аналогом теоремы 3) для Д. п. полупростых групп
Ли является следующая сильная теорема же-
жесткости. Пусть Гх, Г2 — неприводимые решетки
в связных полупростых группах Ли G1? G2, не имеющих
компактных множителей, и пусть центры групп G1, G2
тривиальны. Тогда если группы Glt G2 не изоморфны
PSL2(R.), то всякий изоморфизм 1\—>-Г2 однозначно про-
продолжается до изоморфизма G1-^~G2 (см. [10], [14]). Исто-
Исторически доказательству этой теоремы предшествовало
доказательство слабой теоремы жесткости [5] о продол-
продолжении изоморфизмов, достаточно близких к тождествен-
тождественному (в случае, когда Gy — G^). Из слабой теоремы жест-
жесткости вытекает, в частности, существование базиса, в
к-ром элементы Д. п. записываются алгебраич. числа-
числами. Это обстоятельство сыграло важную роль в разви-
развитии теории Д. п. полупростых групп Ли.
О Д. п. группы'РБЦ(К) см. Фуксова группа.
Из других общих теорем о Д. п. полупростых групп
Ли следует отметить теорему плотности Б о-
реля и теорему максимальности Вана.
Пусть Г — решетка в связной полупростой группе Ли,
не имеющей компактных множителей. Тогда Г плотна в
G в топологии Зариского [3] и содержится лишь в ко-
конечном числе решеток в группе G [17].
Описание решеток в произвольных группах Ли в из-
известной степени сводится к описанию решеток в полу-
полупростых группах Ли благодаря теоремам, аналогичным
упомянутой выше теореме Бибербаха о кристаллогра-
фич. группах. Говорят, что нормальная подгруппа N
группы Ли G обладает свойством Биберба-
х а, если для любой решетки Г в группе G подгруппа
NT замкнута (и тогда автоматически N Г) Г — решетка
в N, а Г/jVnr — решетка в GIN). Теорема Бибербаха
состоит в том, что в группе движений евклидова про-
пространства подгруппа параллельных переносов обладает
свойством Бибербаха. Существует обобщение этой тео-
теоремы на группы Ли, являющиеся расширением одно-
связной нильпотентной группы Ли при помощи ком-
компактной [1]. Другая теорема такого типа заключается в
следующем. Пусть G — связная группа Ли, R — ее ра-
радикал, S — максимальная связная полупростая под-
подгруппа, С — максимальная связная компактная нор-
нормальная подгруппа группы S; тогда подгруппа RC об-
обладает свойством Бибербаха в G [2]. Известно также,
что свойством Бибербаха обладают нильпотентный ра-
радикал связной разрешимой группы Ли [12] и коммутант
односвязной нильпотентной группы Ли [9].
Топологич. методами (см. Дискретная группа преоб-
преобразований) доказывается, что всякая равномерная Д. п.
связной группы Ли является конечно представимой
группой [5]. В действительности всякая решетка в
связной группе Ли конечно представима [17], [18].
Лит.: [1J Auslander L., «Amer. J. Math.», 1961, v. 83,
p. 276—80; [2] его же, там же, 1963, v. 85, p. 145—50; [3]
В о г е 1 A., «Ann. Math.», 1960, v. 72, p. 179—88; [4]Б о р е л ь
А., Хариш-Чандра, «Математика», 1964, т. 8, № 2,
с. 19—71; [5] В е й л ь А., там же, 1963, т. 7, Л5 1, с. 3—41; [6]
ВинбергЭ. Б., «Матем. сб », 1967, т. 72, Л« 3. с 471—88:
[7] Garland H., Raghunathan M. S., «Ann.
Math.», 1970, v. 92, p. 279—326; [8] M а к а р о в В. С, «Докл.
АН СССР», 1966, т. 167, № 1, с. 30 — 33' [9] Мальцев А. И.,
«Изв. АН СССР. Сер. матем.», 1949, т. 13, № 1, с. 9—32; [10]
МаргулисГ. А., «Успехи матем. наук», 1974, т. 29, № 1,
с. 49—98; [11] MargulisG. A., Discrete groups of motions
of manifolds of non-positive curvature, в кн.: Congres Internati-
International des Mathematiques, Vancouver, 1974; [12] M о s t о w G. D.,
«Ann. Math.», 1954, v. 60, p. 1—27; [13] его же, «Amer.
J. Math.», 1970, v. 92, p. 1—32; [14] его же, Strong rigidity
of locally symmetric spaces, N.Y., 1973; [15] РагунатанМ.,
Дискретные подгруппы групп Ли, пер. с англ., М., 1977; [1В]
СельбергА., «Математика», 1962, т. 6, № 3, с. 3—15; [17]
WangH.-C., «Amer. J. Math.», 1967, v. 89, p. 124—32; [18]
его же, в кв.: Symmetric Spaces, N. Y., 1972, p. 459—87.
9. В. Винберг.
ДИСКРЕТНАЯ СЕРИЯ представлений — се-
семейство непрерывных неприводимых унитарных пред-
представлений локально компактной группы G, эквива-
эквивалентных представлениям регулярного представления
этой группы. Если группа G унимодулярна, то непре-
непрерывное неприводимое унитарное представление я груп-
группы G тогда и только тогда принадлежит Д. с, когда
матричные элементы представления я лежат в L2(G).
В этом случае существует такое положительное число
ёъ, называемое формальной размерностью
представления я, что соотношения
$с (я (г) 6, л) («(г) Г, л') <**=•*? F, 6')(лГ?); A)
(n(g)l, ф(л(8I', r]') = d^(l, r\')(n(g)l', Ti) B)
выполняются для всех векторов |, т), |', т)' из простран-
пространства #„ представления я. Если я1; л2 — два неэквива-
неэквивалентных представления группы G в пространствах НХН2,
соответственно, принадлежащие Д. с, то для любых
5 e^ 1 б^ выполняются соотношения
\ (Jii (g) ?iT)i) (я2 (g) S2TI2) ^ = 0, C)
•> о
(ni(g)li, J]i) *{n2(g)l2, r\2)=0. D)
Соотношения A)—D) являются обобщениями соотноше-
соотношений ортогональности для матричных элементов пред-
представлений компактных топологич. групп (см. Представ-
Представления компактных групп); группа G компактна тогда
и только тогда, когда все непрерывные неприводимые
унитарные представления группы G принадлежат Д. с,
и если G компактна и мера Хаара dg удовлетворяет ус-
условию \ dg=i, то число d^ совпадает с размерностью
J G
представления я. Односвязные нильпотентные веще-
вещественные группы Ли и комплексные полупростые
группы Ли не имеют Д. с.
Класс эквивалентности представления я, входящего
в Д. с, является замкнутой точкой в дуальном прост-
пространстве G группы G, и мера Планшереля этой точки сов-
совпадает с формальной размерностью dK; если при этом
нек-рый ненулевой матричный элемент представления я
суммируем, то представление я является открытой точ-
точкой в носителе регулярного представления группы G,
но открытые точки в G могут не соответствовать пред-
представлениям Д. с. Свойства представлений Д. с. частич-
частично распространяются на случай неунимодулярных ло-
локально компактных групп.
Лит.: [1] Д и к с м ь е Ж., С *-алгебры и их представле-
представления, пер. с фанц., М., 1974; [2] Harish-Ghandra,
«Acta Math.», 1965, v. 113, p. 241—318' 1966 v. 116, p. 1—111;
[3] SchmidW., «Ann. Math.», 1976, v. 103, p. 375—94;
[4] Kleppner A., L i p s m a n R., «Ann. sci. Ecole norm,
sup.», 1972, t. 5, p. 459 — 516; 1973, t. 6, p. 103—32.
A. II. Штерн.
ДИСКРЕТНАЯ ТОПОЛОГИЯ на множестве
X — топология, в к-рой любое множество открыто (и
потому любое множество замкнуто). Д. т. в решетке
всех топологий на данном множестве есть наибольший
элемент. Иногда термин «Д. т.» понимается несколько
шире: топология, в к-рой пересечения любого числа от-
открытых множеств открыты. Для ^-пространств оба
определения совпадают. В этом понимании теория ди-
дискретных пространств эквивалентна теории частично
упорядоченных множеств.
Лит.: [1] А л е к с а н д р о в П. С, «Матем. сб.», 1937,
т. 2 с 501—20. А. А. Мальцев.
ДИСКРЕТНОГО НОРМИРОВАНИЯ КОЛЬЦО, д и с-
кретно нормированное кольц о,— коль-
кольцо с дискретным нормированием, т. е. область целост-
целостности с единицей, в к-рой существует такой элемент я,
что любой ненулевой идеал порождается нек-рой сте-
степенью элемента я; такой элемент наз. у н и ф о р м и-
з и р у ю щ и м и определен с точностью до умножения
на обратимый элемент. Каждый ненулевой элемент
Д. н. к. единственным способом записывается в виде
нли, где и — обратимый элемент, а п^О — целое. При-
Примерами Д. н. к. являются кольцо g. целых р-адических
чисел, кольцо /с [[У]] формальных степенных рядов от
одной переменной Т над полем к, кольцо Bumma векто-
векторов W(k) для совершенного поля к.
Д. н. к. может быть определено также как: локальное
кольцо главных идеалов; локальное дедекиндово коль-
кольцо; локальное одномерное кольцо Крулля; локальное
нётерово кольцо с главным максимальным идеалом; нё-
терово кольцо нормирования; кольцо нормирования
с группой значений %.
Пополнение (в естественной топологии локального
кольца) Д. н. к. снова есть Д. н. к. Дискретно норми-
нормированное кольцо компактно тогда и только тогда, когда
оно полно, а его'поле вычетов конечно; любое такое
кольцо либо изоморфно к [[Г]], где к — конечное поле,
либо является конечным расширением Ър.
Если АаВ — локальный гомоморфизм Д. н. к. с
унпформизнрующими я и П, то я=мП<?, где и — обра-
обратимый элемент в В. Целое число e=e(BlA) наз. индек-
индексом ветвления расширения Лс?, а
[#/ПЛ:Л,лЛ]=/ (В/А)
наз. степенью вычетов. Такая ситуация воз-
возникает, когда рассматривают целое замыкание В кольца
дискретного нормирования А с полем частных К в ко-
конечном расширении L поля К. В этом случае В есть по-
полулокальное кольцо главных идеалов, и если щ, . . . ,
X\s — его максимальные идеалы, то B, = BJt являются
Д. н. к. Если предположить, что L — сепарабельное
расширение К степени п, то верна формула
2*<=1 e(Bi/A)f(Bt/A) = n.
Если L/K есть расширение Галуа, то все е(В;/А) и все
j(BjlA) равны между собой, и n~sef. Если же Л —
полное Д. н. к., то уже само В будет Д. н. к., и
e(B/A)f(B/A)=n. В этих предположениях расширение
icB (а также L над К) наз. неразветвленным
расширением, если е(В/Л)=1, а поле В1\\ сепа-
рабельно над А/т; слабо разветвленным, ес-
если е (В/А) взаимно просто с характеристикой поля
А/т, а В/п сепарабельно над А/т; вполне раз-
разветвленным, если 1 (B/A) = i.
Теория модулей над Д. н. к. имеет большое сходство
с теорией абелевых групп (см. [3]). Любой модуль ко-
конечного типа есть прямая сумма циклич. модулей; мо-
модуль без кручения является плоским модулем; любой
проективный модуль или подмодуль свободного модуля
свободен. Однако прямое произведение бесконечного
числа свободных модулей не свободно. Модуль без кру-
кручения счетного ранга над полным Д. н. к. является пря-
прямой суммой модулей ранга 1.
Лит.: [1] Б у р б а к и Н., Коммутативная алгебра, пер.
с франц., М., 1971' [2] Алгебраическая теория чисел, пер. с ¦
англ., М., 1969; [3] KaplanskyJ, «Trans. Amer. Math.
Soc», 1952, v. 72, p. 327 — 40. ' В. И. Данилов.
ДИСКРЕТНОЕ НОРМИРОВАНИЕ — нормирование
тела, группа значений к-рого изоморфна группе целых
чисел 2. В этом случае кольцо нормирования является
дискретного нормирования кольцом. Иногда Д. н., точ-
точнее Д. н. в ы с о т ы (или р а н г а) г, наз. нормирова-
нормирование, имеющее группой значений r-ю прямую степень
группы % с лексикографич. порядком. в. И. Данилов.
ДИСКРЕТНОЕ ПРОГРАММИРОВАНИЕ — область
математики, занимающаяся исследованием и решением
экстремальных задач на конечных множествах. Пусть
М= {аг, а2, . .. , а„} и / — числовая функция, опреде-
определенная на элементах множества М. Требуется найти
элемент а,?М, на к-ром достигается абсолютный мини-
минимум (или' абсолютный максимум) / на М. Сокращенно
такие задачи записываются:
/ (х) —)- extr
хчМ
/ (х)—^min или / (х)—*тах\ .
Х?М «J» )
Из указанного класса задач Д. п. исследует только
нетривиальные задачи, выделяемые следующими до-
дополнительными условиями.
1. Число п=|Л/1 должно быть достаточно большим
настолько, чтобы задача не решалась непосредственным
просмотром значений /(а,) вручную или на ЭВМ. Так,
в задаче коммивояжера, к-рая является типичной зада-
задачей Д. п., число вариантов Q при обходе т пунктов
равно
. . — / т—1
(т — 1)! ~ cV-,
В задачах минимизации булевых функций (см. Булевых
функций минимизация, Булевых функций метрическая
теория) \М\>22".
2. Задача не должна быть регулярной. Задача наз.
регулярной, если: а) для каждого а/ ? М определе-
определена непустая окрестность S (а,-, М), и |5(а,-, М)\<ф,М\;
б) локальный экстремум /, т. е. точка а; такая, что
/(a,)=extr f(x), x?S(ai, M), определяется при по-
помощи простого алгоритма, в) локальный экстремум сов-
совпадает хотя бы с одним глобальным.
Таким образом, Д. п. рассматривает задачи, имею-
имеющие, вообще говоря, несколько локальных экстрему-
экстремумов. В типичных случаях число локальных экстремумов
весьма велико. Напр., в задачах целочисленного линей-
линейного программирования, с булевыми переменными, в
к-рых функционал и ограничения зависят от перемен-
переменных xlt . . . , Xfr, число элементов в М не больше 2*, а
число локальных экстремумов может быть равным
2k
const--t=l (см. [2]). Трудность решения задач Д. п. и
V k
определяется наличием большого числа локальных
экстремумов. Универсальных эффективных методов ре-
решения задач Д. п. не создано A978). Как показывают
исследования по минимизации булевых функций — хо-
хорошо исследованной модельной задаче Д. и. (см. также
Алгоритм локальный), создание таких методов, по-види-
по-видимому, невозможно. Методы, в достаточной степени уни-
универсальные, такие, как метод ветвей и гра-
границ (см. [1]) и его различные модификации, являются
методами направленного перебора. Они эффективно
применяются для решения специализированных задач
Д. п. Однако для каждого из таких методов существуют
обширные классы задач, для к-рых методы направлен-
направленного перебора мало отличаются по сложности от мето-
методов полного перебора. Другой источник математич.
трудностей в задачах Д. п. состоит в том, что множество
М, на к-ром ищется экстремум /, часто задается в не-
неявной форме. Так, в задачах целочисленного линейного
программирования множество М определяется как со-
вокупность целочисленных решений системы линейных
неравенств. При таком и более сложных способах зада-
задания М нетривиальной становится не только задача пол-
полного перечисления М, но и указания хотя бы одного
элемента из М. В силу изложенного, основные резуль-
результаты Д. п. получены при решении и исследовании более
узких классов задач. К таким классам относятся транс-
транспортная задача, задача о коммивояжере и нескольких
коммивояжерах, линейное целочисленное программи-
программирование, задача о расписаниях (см. Расписаний тео-
теория), экстремальные задачи на графах (см. Графов тео-
теория), задачи минимального представления булевых
функций и функций А-значной логики и т. д.
Другое направление в теории дискретных экстре-
экстремальных задач состоит в развитии приближенных ме-
методов, обычно применяемых при решении практич. за-
задач большой размерности. Принципиально эти методы
не отличаются от соответствующих методов поиска экст-
экстремумов непрерывных функций и функционалов. В Д. п.
используются аналоги алгоритмов локальной оптимиза-
оптимизации, алгоритмов спуска, случайного поиска и т. п. (см.
обзор приближенных методов решения задач Д. п. в [3]).
Интересным как с теоретич. точки зрения, так и в ре-
решении прикладных задач является статистиче-
статистический подход к задачам Д. п. Пусть совокупность
задач {Z} можно представить в виде {Z}= (Jn=i {z}m
где | {Z},|>| {Z}j\ при (>/ и | {Z}n\->-°o при /ц-оо. Го-
Говорят, что подмножество
{Z'}=U*=l{Z'}n. {Z'}nc:{Z}n,
составляет почти все задачи Z, если
Для различных классов задач Д. п. имеет место сле-
следующий факт: существует (а часто и эффективно описы-
описывается) совокупность {Z' } почти всех задач {Z}, для
к-рых нахождение экстремума или хорошего приближе-
приближения к экстремуму возможно в классе простых алгорит-
алгоритмов. Это было замечено впервые при решении задач син-
синтеза оптимальных управляющих систем, напр, в мини-
минимизации булевых функций в классе дизъюнктивных
нормальных форм, см. Булевых функций нормальные
формы, а также [4]. Напр., задача выделения экстре-
экстремальных конъюнкций, входящих хотя бы в одну мини-
минимальную дизъюнктивную нормальную форму булевой
функции f(xx, ... , хп), неразрешима в классе локаль-
локальных алгоритмов при k 4<const -2", где к — индекс
локального алгоритма, I — величина памяти. В то же
время задача выделения элементарных конъюнкций,
входящих хотя бы в одну «почти минимальную» дизъ-
дизъюнктивную нормальную форму для почти всех булевых
функций, разрешима в классе локальных алгоритмов
ирпк=2, 1=1 (см. [5]). Столь же значительное сокраще-
сокращение трудоемкости при переходе к почти всем задачам
получается для экстремальных задач на графах, в за-
задаче о построении оптимальных покрытий и т. д.
Лит.: [1] КорбутА. А., ФинкельштейнЮ.Ю.,
Дискретное программирование, М., 1969; [2] Коробков
В. К., «Проблемы кибернетики», 1965, в. 14, с. 297—99; [3]
Финн ельштейнЮ. Ю., Приближенные методы и при-
прикладные задачи дискретного программирования, М., 1976; [4]
Дискретная математика и математические вопросы кибернетики,
т. 1, М., 1974; [о] Журавлев Ю. И., «Дискретный анализ»,
1964, № 3, с. 41—77. Ю. И. Журавлев.
ДИСКРЕТНОЕ ПРОСТРАНСТВО — пространство, на-
наделенное дискретной топологией. с М Сирота
ДИСКРЕТНОЕ ПРОСТРАНСТВО-ВРЕМЯ — одна из
гипотез возможной структуры пространства в микро-
микромире, характеризуемая представлением об элементар-
элементарных попарно несвязных компонентах пространства,
точки к-рых не разделяются наблюдаемыми величина-
величинами. Приемлемой формализацией Д. п.-в. могут быть
топологические пространства Y, в к-рых связной ком-
компонентой точки y?Y является ее замыкание у, а в от-
отделимых У — сама эта точка (вполне несвязные про-
пространства). Примерами Y являются дискретное топо-
топологическое пространство, рациональная прямая, ана-
литич. многообразия и группы Ли над полями с уль-
ультраметрическими абсолютными значениями.
Первоначально гипотеза Д. п.-в. разрабатывалась
в варианте конечного вполне несвязного пространства,
в моделях конечных геометрий на полях Галуа, а в тео-
теории поля впервые (в варианте кубического решетча-
решетчатого пространства) в работах В. А. Амбарцумяна и
Д. Д. Иваненко A930). В квантовой теории гипотеза
Д. п.-в. возникла в моделях, в к-рых координатное
(импульсное и др.) пространство как спектр С*-алгебры
соответствующих операторов является вполне несвяз-
несвязным (как, напр., спектр С*-алгебры вероятностных
мер). Серьезное обоснование она находит в концепции
«фундаментальных длин», возникающих в нелинейных
обобщениях электродинамики, мезодинамики и спи-
норного уравнения Дирака, в которых константы само-
самодействия полей имеют размерность длины, и в квантовой
теории поля в связи с необходимостью введения все-
всевозможных обрезающих факторов. На базе этой кон-
концепции, а затем нелокальных моделей, сформировалось
представление о минимальных областях пространст-
пространства, в к-рых, по-видимому, уже невозможно принятое
в квантовой теории описание микрообъектов через их
взаимодействие с макроприбором, следствием чего
является неприменимость пространственно-временного
континуума для параметризации пространственно-эво-
пространственно-эволюционных отношений в этих областях (например, га-
мпльтонова формализма — в нелокальных теориях) и
неразделимость их точек наблюдаемыми величинами
(в пространствах Y это можно представить как наличие
неотделимой равномерной структуры). Гипотеза Д. п.-в.
получает свое развитие в концепции нелинейного ва-
вакуума, согласно которой в экстремальных условиях
внутри частиц, а возможно в астрофизических и космо-
космологических сингулярностях, пространственные харак-
характеристики могут выступать как динамические характе-
характеристики физической системы и в моделях к-рого эле-
элементы пространства наделяются некоммутативной би-
бинарной операцией.
Лит.: [1] Соколов А., Иваненко Д., Квантовая
теория поля, М.—Л., 1952; [2] В я л ь ц е в А. Н., Дискрет-
Дискретное пространство-время, М., 1965; [3] Б л о х и н ц е в Д. И.,
Пространство и время в микромире, М., 1970; L4] Марков
М. А., О природе материи, М., 1976; [5] FinkelsteinD.,
«Phys. Rev.», 1974, v. 9, №8, p. 2219. Г. А. Сарданашвили.
ДИСКРЕТНОЕ РАСПРЕДЕЛЕНИЕ — распределение
вероятностей, сосредоточенное на конечном или счет-
счетном множестве точек выборочного пространства Q. Точ-
Точнее, пусть а»!, со2, ... — выборочные точки и
Pi = p(v>i), i = i, 2, ..., A)
суть нек-рые числа, удовлетворяющие условиям
Р,-Зг<>, 2,-Р/ = 1- B)
Соотношения A) и B) полностью определяют Д. р. в
пространстве Q, так как вероятностная мера любого
множества Ad Q определяется равенством
В соответствии с этим распределение случайной вели-
величины Х(а) наз. дискретным, если с вероятностью 1
она принимает конечное или счетное число различных
значений х; ¦ с вероятностями р,-=Р{о> : Х((й)=х,}.
Для Д. р. на прямой функция распределения F(x) =
= V1 pi имеет скачки в точках х,-, равные
-<iJ{i : xi < x)yl " у
Pi—F(x[-\-0) — F(x[), и постоянна в интервалах
[xj, x;+1). Наиболее распространены следующие Д. р.:
биномиальное распределение, геометрическое распреде-
распределение, гипергеометрическое распределение, отрицатель-
отрицательное биномиальное распределение, полиномиальное рас-
распределение, Пуассона распределение. А. В. Прохоров.
ДИСКРЕТНОЕ СЕМЕЙСТВО МНОЖЕСТВ — семей-
семейство подмножеств А топологич. пространства такое, что
каждая точка пространства имеет окрестность, к-рая
пересекает самое большее один элемент семейства А.
В. А. Ефимов.
ДИСКРЕТНЫЕ СИСТЕМЫ в статистиче-
статистической механике — системы, микроскопич. со-
состояния к-рых определяются заданием состояний в каж-
каждом из узлов фиксированной пространственной решет-
решетки. С точки зрения приложений — это модели твердого
тела, в к-рых одно из микроскопич. движений, связан-
связанное с изменением состояний в узлах решетки, выделено
и считается независимым от других. Одна из наиболее
простых Д. с.— модель Изинга A925) — характери-
характеризуется гамильтонианом
где i=ri — координаты узлов решетки, a,-=±i.
Эта модель используется для исследования сплавов
типа замещения, магнетиков, решетчатого газа и др.
Для Д. с. такого типа характерно наличие в них при
температуре ниже Х-точки дальнего поряд-
порядка — общей регулярности в направлении спинов а,-
магнетиков или регулярности в чередовании атомов
различного сорта в бинарных сплавах, к-рая при повы-
повышении температуры пропадает в точке 0я (точке Х-пере-
хода) с характерным выбросом теплоемкости cv, в то
время как ближний порядок — корреляция
отдельного узла с окружающими его узлами — такого
резкого изменения не претерпевает. Качественное опи-
описание явлений упорядочения укладывается в теорию
типа теории молекулярного поля. Несмотря на матема-
тич. простоту модели, точное решение в общем виде по-
получено только для одномерной модели и для плоской
ферромагнитной решетки (/(г, /)>0) с взаимодействием
только ближайших соседей и в случае h=0. Одномерная
модель фазового перехода не претерпевает, а двухмер-
двухмерная имеет особенность теплоемкости логарифмич. типа
(принципиально в случае N—voo). Для общего случая
разработаны приближенные методы в области низких
и высоких температур.
Из других моделей распространена модель магне-
магнетиков Гейзенберга, гамильтониан к-рой отличен от га-
гамильтониана модели Изинга тем, что числа а; заменены
на erf, а произведение а,-Оу — на (а,-, оу), где а; — спи-
спиновые Паули матрицы.
Целый класс Д. с. с определенным типом взаимодей-
взаимодействия узлов решетки допускает асимптотически точное
при N—voo рассмотрение с помощью метода аппроксими-
аппроксимирующих гамильтонианов [3].
Лит.: [1] ХуангК., Статистическая механика, пер. с
англ., М., 1966; [2] 3 а й м а н Д ж., Принципы теории твер-
твердого тела, пер. с англ., М., 1966; [3] Боголюбовы. Н.
(мл.), Метод исследования модельных гамильтонианов, М., 1974.
И. А. Квасников.
ДИСКРЕТНЫЙ АНАЛИЗ — область математики, за-
занимающаяся изучением свойств структур финитного (ко-
(конечного) характера, к-рые возникают как в самой ма-
математике, так и в области ее приложений. К числу таких
конечных структур могут быть отнесены, напр., конеч-
конечные группы, конечные графы, а также нек-рые матема-
тич. модели преобразователей дискретной информации,
такие как автоматы конечные, Тьюринга машины и др.
Иногда допускают расширение предмета Д. а. до произ-
произвольных дискретных структур и приходят к дискрет-
дискретной математике, отождествляя последнюю с
Д. а. К числу таких структур могут быть отнесены неко-
торые алгебраич. системы, бесконечные графы, нек-рые
виды вычислительных сред (напр., однородные струк-
структуры) и т. п. В качестве синонима понятий Д. а. и ди-
дискретной математики иногда употребляется термин к о-
нечная математика. Ниже Д. а. понимается в
широком смысле, включающем дискретную математику.
В отличие от Д. а. классич. математика в основном
занимается изучением свойств объектов непрерывного
характера. Использование классической или дискрет-
дискретной математики как аппаратов исследования связано с
тем, какие задачи ставит перед собой исследователь, и, в
связи с этим, какую модель изучаемого явления он рас-
рассматривает — дискретную или непрерывную. Само де-
деление математики на классическую и дискретную в зна-
значительной мере условно, поскольку, с одной стороны,
происходит активная циркуляция идей и методов между
ними, а с другой — часто возникает необходимость ис-
исследования моделей, обладающих одновременно как ди-
дискретными, так и непрерывными свойствами. Кроме
того, в математике существуют подразделы, использую-
использующие средства дискретной математики для изучения не-
непрерывных моделей, и, наоборот, часто средства и по-
постановки задач классич. анализа используются при ис-
исследовании дискретных структур. Это указывает на из-
известное слияние рассматриваемых областей.
Д. а. представляет собой важное направление в мате-
математике, имеющее характерные для него предмет иссле-
исследования, методы и задачи, специфика к-рых обуслов-
обусловлена, ъ первую очередь, необходимостью отказа в Д. а.
от основополагающих понятий классич. математики —
предела и непрерывности — и (в связи с этим) тем, что
для многих задач Д. а. сильные средства классич. мате-
математики оказываются, как правило, мало приемлемыми.
Наряду с выделением Д. а. путем указания его предме-
предмета, методов и задач можно также охарактеризовать Д. а.
посредством перечисления подразделов, составляющих
его. К ним, в первую очеред-ь, относятся комбинатор-
комбинаторный анализ, графов теория, теория кодирования и деко-
декодирования, теория функциональных систем и нек-рые
другие. Часто под термином «Д. а.» (в предположении,
что его предмет исчерпывается конечными структурами)
понимается именно совокупность перечисленных дисци-
дисциплин. За счет расширения понимания его круга вопросов
возможно и более широкое толкование Д. а. С этой
точки зрения, к Д. а. могут быть отнесены также как
целые разделы математики, напр, математич. логика, так
и части таких разделов, как теория чисел, алгебра, вы-
вычислительная математика, теория вероятностей и не-
некоторые другие, в к-рых изучаемый объект носит дис-
дискретный характер.
Элементы Д. а. возникли в глубокой древности и, раз-
развиваясь параллельно с другими разделами математики,
в значительной мере являлись их составной частью. Ти-
Типичными для того периода были задачи, связанные со
свойствами целых чисел, приведшие затем к созданию
теории чисел. Позже, в основном в связи с игровыми за-
задачами, появились элементы комбинаторного анализа и
дискретной теории вероятностей, а в связи с общими
проблемами теории чисел, алгебры и геометрии воз-
возникли важнейшие понятия алгебры такие, как группа,
поле, кольцо и др., определившие развитие и содержа-
содержание алгебры на много лет вперед и имевшие по существу
дискретную природу. Стремление к строгости матема-
математич. рассуждений и анализ рабочего инструмента мате-
математики — логики — привели к выделению еще одного
важного раздела математики — математич. логики. Од-
Однако наибольшего развития Д. а. достиг в связи с появ-
появлением кибернетики и ее теоретич. части — математич.
кибернетики. Математич. кибернетика, непосредствен-
непосредственно изучающая с позиций математики самые разнообраз-
разнообразные проблемы, к-рые ставит перед кибернетикой прак-
тика, является важным поставщиком идей и задач для
Д. а., вызывая в нем целые новые направления. Так,
прикладные вопросы, требующие большой числовой
обработки, стимулировали появление сильных числен-
численных методов решения задач, оформившихся затем в
вычислительную математику, а анализ понятий вычис-
вычислимости и алгоритма привел к появлению важного
раздела математич. логики — алгоритмов теории. Рас-
Растущий поток информации и связанные с ним задачи
хранения, обработки и передачи информации привели к
возникновению теории кодирования; экономич. задачи,
задачи электротехники, равно как и внутренние зада-
задачи математики, потребовали разработки теории графов;
задачи конструирования и описания работы сложных
управляющих систем привели к теории функциональных
систем и т. д. В то же время математич. кибернетика
использует результаты Д. а. при решении своих задач.
Наряду с отмеченными, Д. а. обладает рядом и дру-
других особенностей. Так, вместе с задачами типа сущест-
существования, имеющими общематематич. характер, важное
место в Д. а. занимают задачи, связанные с алгоритмич.
разрешимостью и построением конкретных решающих
алгоритмов, что характерно именно для Д. а. Особен-
Особенностью Д. а. является и то, что он по существу первым
столкнулся с необходимостью глубокого исследования
так наз. дискретных многоэкстремальных задач, часто
возникающих в математич. кибернетике. Соответствую-
Соответствующие методы классич. математики для поиска экстрему-
экстремумов, существенно использующие гладкость функций,
в этих случаях оказываются мало эффективными. Ти-
Типичными задачами такого рода в Д. а. являются, напр.,
задачи об отыскании в нек-ром смысле оптимальных
стратегий в шахматной партии при ограниченном числе
ходов, а также важный вопрос математич. кибернетики
о построении минимальных дизъюнктивных нормаль-
нормальных форм для булевых функций, т. е. так наз. проблема
булевых функций минимизации. Особенностью Д. а.,
связанной уже с задачами для конечных структур, яв-
является и то, что для многих из этих задач, как правило,
существует алгоритм решения, в то время как в клас-
классич. математике полное решение задачи часто возможно
лишь при весьма жестких ограничениях. Примером та-
такого алгоритма может служить алгоритм просмотра
всех возможных вариантов, т. е. алгоритм типа «полно-
«полного перебора». К числу задач указанного вида можно от-
отнести, напр., упомянутые задачи о стратегиях в шах-
шахматной партии, о минимизации булевых функций и др.
Вместе с тем решения типа «полного перебора» очень
трудоемки и практически мало приемлемы, в связи с чем
возникает ряд новых задач, связанных с условиями,
ограничивающими перебор и приводящими к сведению
индивидуальных задач, характеризующихся конкрет-
конкретными значениями параметров, к массовой проблеме, ха-
характеризующейся бесконечным множеством значений
параметров; возникают задачи наложения ограничений
на средства решения, естественных для этого класса
задач, и др. Постановка такого рода вопросов и раз-
разработка методик осуществляется на конкретных моде-
моделях, доставляемых различными разделами математики,
напр, на моделях минимизации булевых функций и син-
синтеза управляющих систем из математич. кибернетики.
Лит.: [1] Я б л о н с к и й С. В., Обзор некоторых резуль-
результатов в области дискретной математики, «Информационные ма-
материалы», 1970, 5, с. 5 —15; 12] КемениДж., С не л л
Дж., ТомпсонДж., Введение в конечную математику,
пер. с англ., 2 изд., М., 1965. См. сб. «Проблемы кибернетики»
и «Дискретный анализ», ж. «Кибернетика». В. Б. Кудрявцев.
ДИСКРИМИНАНТ — 1) Д. многочлена
f(x) = agxn-\-a1 xn~1Jr. . .-\-ап, с а0Ф0, корни к-рого рав-
равны а15 а2, ... , а„,— произведение
Д. равен нулю тогда и только тогда, когда многочлен
имеет кратные корни. Д. симметричен относительно кор-
корней многочлена и поэтому может быть выражен через
его коэффициенты.
Д. квадратного трехчлена ах2-\~Ьх-{~с равен б2—4яе;
Д. многочлена x3-{~px-{~q (корни к-рого вычисляются по
Кардано формуле) равен —27д2—4р3. Если/(ж) — много-
многочлен над полем характеристики 0, то
где R(f, /') — результант многочлена f(x) и его произ-
производной f (х). Производной многочлена
f(x)=a(sxn-\-a1x"-1-{-.. .-\~ап с коэффициентами из лю-
любого поля наз. многочлен па0л;'г-1+(и—1)а1ж'г-2+. ..+
Лит.: [1] К у р о ш А. Г., Курс высшей алгебры, 11 изд.,
М., 1975. И. В. Проскуряков.
2) Д.полуторалинейной формы /в ба-
базисе (v)= {vlt . .. , vn} — элемент из кольца А, рав-
равный
Df (vu ..., vn) = det
'„, Vi). . .f {Vn, Vn) I
где (v) — фиксированный базис конечномерного сво-
свободного Л-модуля Е над коммутативным кольцом А с
единицей, снабженным автоморфизмом а. Есяи (ш)=
= {»!, ... , wn) — другой базис в Е, а
Сц. . .С1п
С=
сп\ • • ¦ спп
— матрица перехода от (v) к (w), то
Df(wlt ...,wn) = (AetC)(detCfD/(vu ...,vn).
Если кольцо А не имеет делителей нуля, то для невы-
невырожденности / необходимо и достаточно, чтобы
Df(vi, ..., оп)ф0.
Если vi, ... , vn — произвольный набор п элементов
из Е, то элемент Df(v±, ... , vn) кольца А , определяемый
формулой (*), наз. дискриминантом / отно-
относительно системы vi, ... , vn. Пусть А без
делителей нуля и / — невырожденная полуторалиней-
ная форма. Тогда для того, чтобы система элементов
vi, ... , vn из Е была свободной, необходимо и достаточ-
достаточно, чтобы Df(vi, . . . , и„)=?0. При этом i;1( . .. , vn будет
базисом в Е тогда и только тогда, когда Df(vu ... , vn) и
Dj{u-y, . . ., ип) ассоциировании в А для некоторого ба-
зиоа «1, . . . , ип в А.
Лит.; [1] Бурбаки Н., Алгебра. Модули, кольца,
формы, пер. с франц., М., 1966; [2] Дьедонне Ж., Геомет-
Геометрия классических групп, пер. с франц., М., 1974.
В. Л. Попов.
3) Д.системы элементов поля — одна из
важных конструкций в теории расширений полей.
Пусть К — конечное расширение поля к степени п.
Отображение КХ К в к:
(х, у)^Тг(ху),
где х, у?К, а Тг а — след элемента а,?К, является
симметрической билинейной формой на поле К, рас-
рассматриваемом как линейное пространство над /с. Д. этой
билинейной формы (см. Дискриминант полуторалинеп-
ной формы) относительно системы элементов w1, ... ,
wm из К наз. дискриминантом системы
и>1, .. . , wm и обозначается D(w!, ... , wm). В частно-
частности, если указанная система есть базис К над /с, то ее
Д. наз. дискриминантом базиса ЛГнад
к. Д. двух базисов отличаются множителем, являющим-
являющимся квадратом нек-рого ненулевого элемента поля к. Д.
всякого базиса К над к не равен нулю тогда и только
тогда, когда расширение К/к сепарабельно. Если fx(t) —
многочлен степени т, являющийся минимальным много-
членом элемента х из сепарабельного расширения К/к,
то D A, х, хг, ..., хт) совпадает с Д. многочлена fx(t).
Приведенные определения могут быть перенесены так-
также на случай произвольной конечномерной ассоциа-
ассоциативной алгебры над полем (см. ниже п. 4).
В случае сепарабельного расширения К/к Д. базиса
wlt ... , wn может быть вычислен по формуле
D(Wl, ..., wn) = (det (a,- (w,-))J,
где Oj, . . . , а„ — все различные вложения К в фикси-
фиксированное алгебраич. замыкание поля к, оставляющие
неподвижным к.
Пусть k~Q — поле рациональных чисел, К — поле
алгебраич. чисел и М — некоторый модуль ранга п в К.
Тогда для любых двух базисов модуля М значения Д.
совпадают и это общее значение Д. наз. дискрими-
дискриминантом модуля М. Если М совпадает с коль-
кольцом целых чисел поля К, то Д. модуля М наз. просто
дискриминантом поля К и обозначается
D/;. Число Die является важной характеристикой поля
К. Напр., если К допускает s вещественных и 2i комп-
комплексных вложений в поле комплексных чисел С, то
r,S + t „tf
lim (Н)Е*(!)
где Zi;(q) — дзета-функция Дедекинда, h — число клас-
классов дивизоров, R — регулятор гголя К и т — число
корней из единицы в поле К. Имеется оценка
которая показывает, что \im\Djt\ = oo. Для квадратич-
ного поля-О( ~\/~d), где d — свободное от квадратов целое
рациональное число, dj=i, имеют место формулы:
Dft=d, если d = l (mod 4),
Dk = id, если d = 2 или 3 (mod 4).
Для кругового поля if=Q(e), где е — примитивный ко-
корень /э^-й степени из единицы
(знак минус берется при рг=4 пли pss3(mod4), a
плюс — в остальных случаях).
Указанное определение Д. модуля в поле алгебраич.
чисел может быть обобщено на тот случай, когда к —
поле частных дедекиндова кольца А, а К — конечное
сепарабельное расширение поля к степени п. Пусть В —
целое замыкание кольца А в К и Ь — произвольный
дробный идеал кольца В. Тогда д и с к р и м и н а н-
т о м идеала b наз. А -модуль D(b), порожденный
всеми Д. вида D(w-l, ... , ш„), где {wly ... , wn) про-
пробегает всевозможные базисы поля К над к, лежащие в
b. D (Ь) оказывается дробным идеалом кольца А, причем
имеет место равенство D (b)=N(bJD (В), где N(Ь) —
норма идеала Ь. Д. D (В) совпадает с нормой дифферен-
дифференты кольца В над А.
Лит.: [1] Б о р е в и ч 3. И., Ш а ф а р е в и ч И. Р., Тео-
Теория чисел, 2 изд., М., 1972; [2J JI е н г С., Алгебраические чис-
числа, пер. с англ., М., 1966; [3] 3 а р и с с к и й О., С а м го-
эль П., Коммутативная алгебра, пер. с англ., т. 1, М., 1963: •
[4] Джекобсон Н., Теория колец, пер. с англ., М., 1947.
В. Л. Попов.
4) Д. алгебры — Д. симметричной билинейной
формы (х, у)ь=Т(ху), где х, у—элементы конечномер-
конечномерной ассоциативной алгебры А над полем F, а Т(а) —
главный след элемента а?_А, определяемый следую-
следующим образом. Пусть е1, . . ., е„ — к.-л. базис алгебры
А, Ф = Р(?>1, ... , |„) — чисто трансцендентное расши-
расширение поля F с помощью алгебраически независимых
элементов |lt . .. , |п, Аф = А^@Ф — соответствую-
соответствующее скалярное расширение алгебры А, тогда элемент
ж=^1е1+. . .-j-| „е„? А ф наз. общим эле мен-
том алгебры А, а минимальный многочлен (над
Ф) элемента х — минимальным многочле-
многочленом алгебры А. Пусть
g(t; ?) = f-TO1(?)«>--1+...4-(-lKm,.(?)
— минимальный многочлен алгебры А', коэффициенты
то,-(?) оказываются на самом деле многочленами из F [|lt
. . . , ?„]. Если а=а1е1-1г. . .Jra.en(rXi^_F) — произволь-
произвольный элемент из А, то тх(ах, .... а.п)= Т(а) наз. глав-
главным следом элемента a, mr(ax, . . . , а„) =
= Лт(а) — главной н о р м о й, а многочлен g(t\ alt
... , а.п) — главным многочленом. Коэффи-
Коэффициенты главного многочлена для данного элемента а ? А
не зависят от выбора базиса, поэтому упомянутая выше
билинейная форма (х, у) на А определена инвариантно,
в то время как ее Д. определен с точностью до мульти-
мультипликативного множителя, являющегося квадратом не-
ненулевого элемента из F. Алгебра А сепарабельна (см.
Сепарабелъная алгебра) тогда и только тогда, когда ее
Д. отличен от нуля.
Лит.: [1] Джекобсон Н., теория колец, пер. с. англ.,
М., 1947. Е. Н. Кузьмин.
ДИСКРИМИНАНТНАЯ КРИВАЯ обыкновенного диф-
дифференциального уравнения 1-го порядка F(x, у, г/')=0
— множество точек (х, у) плоскости, координаты ко-
которых удовлетворяют уравнению <f{x, у) = 0, получаю-
получающемуся исключением ;/ из соотношений F—0 и F'y—0
или исключением х из соотношений G=0 и GX' = 0, где
G (у, х, x')=F(x, у, 1/х') (в предположении, что F',,,
существует). Если Д. к. для уравнения F—0 — непу-
непустое множество и не вырождается в отдельные точки,
то она (или каждая ее ветвь) может:
1) являться решением уравнения Р=0, в каждой точ-
XI
Т7
/н-
Рис. 1.
Рис. 2.
ке которого нарушается единственность,— в таком слу-
случае Д. к. есть огибающая семейства интегральных кри-
кривых (напр., г/=1 и у=—1 для уравнения у'2-гу2—1 — 0,
рис. 1; !/=-0 для уравнения
у'3—у'1 "О, рис. 2); 2) яп-
ляться решением уравнения
Р=0, в каждой точке к-ро-
го имеет место единственность
(напр., у = 0 для уравнения
;/'2—i/^О, рис. 3); 3) не яв-
являться решением уравнения
F—0, в таком случае Д. к.
есть множество либо точек воз-
возврата интегральных кривых
(например, х-—0 для уравнения у'2—ж=0, рис. 4),
либо точек прикосновения различных интегральны:.
с'
' 0
>-
р
X
-><
f
/
Ч *
РИС. 4.
Рис. 5.
кривых (например, х=0 для уравнения у'2—х2=0,
рис. 5).
Рассматривается также уравнение F=0 в комплекс-
комплексной области, когда F — многочлен от у' (см., напр.,
[2]. гл. II).
Лит.: [1] С а неоне Д ж., Обыкновенные дифференци-
дифференциальные уравнения, пер. с итал., т. 2, М., 1954; [2] Голубев
В. В., Лекции по аналитической теории дифференциальных
уравнений, 2 изд., М.—Л., 1950. Н. X. Розов.
ДИСКРИМИНАНТНАЯ ФУНКЦИЯ — статистика,
служащая для построения правила различения в зада-
задачах дискриминантного анализа с двумя распределения-
распределениями. Задача различения (дискриминации) для двух рас-
распределений состоит в следующем. Пусть наблюденный
объект с вектором измерений х=(хх, . . ., хр) принадле-
принадлежит одной из совокупностей я,-, г=1, 2, причем неиз-
неизвестно какой. Требуется построить правило, согласно
к-рому по значению наблюденного вектора х объект от-
относят к л,- (правило различения). Построение такого
правила основывается на разбиении выборочного про-
пространства вектора х на такие области Д/, г=1, 2, чтобы
при попадании х в R,- было разумно (с точки зрения вы-
выбранного принципа оптимальности решения) отнести х
к я,-. Если правило дискриминации основывается на
разбиении: R1= {х : Т(х)<а}, R2= {x : T(x)^sb), где а
и 6 — константы, а<6, то статистику Т(х) наз. Д. ф.,
а область, где ai?.T(x)<ib,— зоной сомнения.
Особую роль, из-за простоты применений, играют ли-
линейные Д. ф. В частном случае, когда распределения
нормальны и имеют одинаковые матрицы ковариаций,
Д. ф. оказывается линейной при разумных требованиях
оптимальности к указанному правилу. В задачах ди-
дискриминантного анализа со многими распределениями
при бейесовском подходе (см. Бейесоеский подход к ста-
статистическим задачам) вводится понятие дискриминант-
дискриминантного информанта. Н. Ы. Митрофанова, А. П. Хусу.
ДИСКРИМИНАНТНЫЙ АНАЛИЗ — раздел мате-
матич. статистики, содержанием к-рого является раз-
разработка и исследование статистич. методов решения сле-
следующей задачи различения (дискримина-
(дискриминации): основываясь на результатах наблюдений, опреде-
определить, какой из нескольких возможных совокупностей
принадлежит объект, случайно извлеченный из одной
из них. На практике задача различения возникает,
напр., в тех случаях, когда наблюдение признака, пол-
полностью определяющего принадлежность объекта к той
или иной совокупности, невозможно или требует чрез-
чрезмерных затрат средств или времени; в случаях, когда
информация о таком признаке утеряна, и ее нужно вос-
восстановить, а также, когда речь идет о предсказании бу-
будущих событий на основе имеющихся данных. Ситуации
первого типа встречаются в медицинской практике,
напр, при установлении диагноза по комплексу неспе-
неспецифических проявлений заболевания. Пример ситуа-
ситуации второго типа — определение пола давно умершего
человека по останкам, найденным при археологич.
раскопках. Ситуация третьего типа возникает, напр.,
при статнетич. прогнозе отдаленных результатов лече-
лечения. Методом Д. а. является многомерный статистиче-
статистический анализ, служащий для количественного выраже-
выражения и обработки имеющейся информации в соответствии
с выбранным критерием оптимальности решения.
В общем виде задача различения ставится следующим
образом. Пусть результатом наблюдения над случай-
случайным объектом является реализация р-мерного случай-
случайного вектора х' = (х1, ... , хр) (штрих означает транспо-
транспонирование) значений р признаков объекта. Требуется
установить правило, согласно к-рому по значению век-
вектора х объект относят к одной из возможных совокуп-
совокупностей я,-, i= 1, ... , к. Построение правила диск-
дискриминации состоит в том, что все выборочное про-
пространство R значений вектора х разбивается на области
Ri, 1=1, ... , к, так что при попадании х в Л,- объект
относят к совокупности я,-. Выбор правила дискри-
дискриминации среди всех возможных производится в соот-
соответствии с установленным принципом оптимальности
на основе априорной информации о совокупностях я,- и
вероятностях д,- извлечения объекта из я,-. При этом
учитывается размер убытка от неправильной дискри-
дискриминации. Априорная информация о совокупностях я,-
может состоять в том, что известны функции распреде-
распределения вектора признаков объекта в каждой из этих со-
совокупностей, она может быть представлена также и в ви-
виде выборок из каждой из этих совокупностей, при этом
априорные вероятности q,- совокупностей могут быть
либо известны, либо нет. Очевидно, чем полнее исходная
информация, тем точнее могут быть рекомендации.
Пусть рассматривается случай двух совокупностей
щ и я2 в ситуации, когда имеется полная исходная ин-
информация: известны функции распределения вектора
признаков в каждой из совокупностей и априорные ве-
вероятности (бейесовский подход). Пусть Р±(х) и Р2(х) —
функции распределения вектора признаков соответст-
соответственно в Я! и я2, Pi(x) и р2(х) — плотности распределе-
распределения, a C(i\i), i, j—l, 2,— убыток вследствие отнесения
объекта из /-й совокупности к г-н. Тогда вероятности
неправильной дискриминации объектов нз лг и я2 соот-
соответственно равны:
pl(x)dx, jPA|2; R) = ^Rpt (x) dx
(символом P(i\i; R) обозначена вероятность приписы-
приписывания объекта из яу к совокупности я,-при использова-
использовании правила R), а математич. ожидание потерь, связан-
связанных с неверной дискриминацией, равно
СB|1)ЯB|1; R)qi+C(i\2)P(\\2; R)q2.
Естественным в рассматриваемой ситуации принципом
оптимальности является принцип минимизации этой
величины, к-рый приводит в этом случае к следующему
разбиению пространства выборок [1]:
„ .Pi (x) С A | 2) дг \
П1'р2 (ж) — С B | 1)д, • I
п .Р. (X) СA | 2)g2 j ^ >
2
2 | 1)д, • I
1 | 2)g2 j
2 | 1) д, • )
(.х) ^ С (
Если выполнены условия
р.(х)_ СA 1 2)д, I
pTW- С B 11)9,
то такое разбиение единственно с точностью до множе-
множества нулевой вероятности. К аналогичному правилу
различения в рассмотренном случае можно прийти и
другими путями, напр, с помощью Неймана — Пирсона
леммы из теории проверки статистич. гипотез.
При выбранном критерии оптимальности о качестве
правила различения судят по величине математич.
ожидания потерь, и из двух правил лучшим считается
то, к-рое приводит к меньшему значению этой величины.
Если в задаче различения априорные вероятности q-t
неизвестны, то естественно искать решение в классе
допустимых правил, выбирая среди них правило, ми-
минимизирующее максимум по всем </,¦ математич. ожида-
ожидания потерь (такое правило наз. минимаксны ы),
Математич. ожидания потерь при условии, что наблю-
наблюдения производились соответственно над объектами из
щ или я2, равны
СB|1)РB|1; Л)=гA, R), СA\2)РA\2; Л) = гB, R).
Справедливо утверждение (см. [1]): если выполнены
условия
то класс бейесовских методов является минимальным
полным классом. Минимаксное правило R* из этого
класса получается при значении qlt для к-рого выпол-
выполнено условие PB|l; R*)=PA\2; Ft*). В важном случае,
когда P-l и Р2 — многомерные нормальные распределе-
распределения с векторами средних цA) и ц<2> и общей ковариаци-
ковариационной матрицей 2, правило дискриминации A) прини-
принимает вид: _ 1
2 )
I B)
где й=24Ц||-!- Если СA|2)=СB|1) и ?a=9l, то In А:=0
^¦^^"НИ0")'^^1'-^1')- C)
Если априорные вероятности неизвестны, то можно вы-
выбрать In k=c, напр, из условия минимальности ошибки
неверной дискриминации или из условия обращения в
нуль математич. ожидания потерь от неверной дискри-
дискриминации. Вообще говоря, выбор критерия оптимально-
оптимальности, как правило, определяется характером самой за-
задачи. Выражение в левой части C) наз. дискриминант-
дискриминантной функцией данной задачи; ее можно толковать как
поверхность в выборочном пространстве, разделяющую
совокупности Л]Ня2. В приведенном примере дискрими-
нантная функция линейна, т. е. такая поверхность есть
гиперплоскость. Если в приведенном примере матрицы
ковариации неодинаковы, то дискриминантная функция
будет квадратичной функцией от х. В целях упроще-
упрощения вычислений найден минимальный полный класс ли-
линейных процедур различения для этого случая (см. [3]).
С точки зрения применений Д. а. наиболее важной яв-
является ситуация, когда исходная информация о рас-
распределениях представлена выборками из них. В этом
случае задача дискриминации ставится следующим об-
образом. Пусть xi\ х"\ . .. , хп. — выборка из совокуп-
совокупности я,-, (=1, ... , к; 3;/"= (хI\ • . • , ж/'}) — вектор
признаков /-го объекта выборки из i-й совокупности, и
произведено дополнительное наблюдение х' = (х1, ... ,
Хр) над объектом, принадлежащим одной из совокупно-
совокупностей щ. Требуется построить правиле приписывания
наблюдения х к одной из этих совокупностей. Первый
подход к решению этой задачи в случае двух совокуп-
совокупностей принадлежит Р. А. Фишеру — основоположнику
Д. а. [4]. Используя в задаче различения вместо вектора
признаков, характеризующих объект, их линейную
комбинацию — гиперплоскость, в нек-ром смысле наи-
наилучшим образом разделяющую совокупность выбороч-
выборочных точек,— он пришел к дискриминантной функции C).
Наиболее изученным является случай, когда извест-
известно, что распределения векторов признаков в каждой
совокупности нормальны, но нет информации о пара-
параметрах этих распределений. Здесь самым естествен-
естественным является подход, состоящий в замене неизвестных
параметров распределений в дискриминантной функции
C) их наилучшими оценками (см. [5], [6]). Как и в слу-
случае известных распределений, правило дискриминации
можно основывать на отношении правдоподобия (см.
[7], [8]).
Подавляющая часть результатов Д. а. получена в
предположении нормальности распределений. Изуча-
Изучаются вопросы применимости оптимальных в нормаль-
нормальном случае методов в ситуациях, где предположение о
нормальности носит лишь приближенный характер [9].
В этих работах задачи Д. а. рассматриваются в рамках
общей теории решающих функций и изучаются свойст-
свойства правил дискриминации по отношению к так наз.
принципу (^-оптимальности, естественным образом ох-
охватывающему как бейесовский, так и минимаксный под-
подходы. Именно, пусть R (?, б) — вероятность ошибки
при применении правила дискриминации <5, когда век-
вектор априорных вероятностей есть |. Пусть известно, что
?€<?! гДе Q — некоторое множество в пространстве век-
векторов |. Правило б* наз. ^-оптимальным, если
supi? (?, 6*)= inf supR (I, 6) = R0, D)
i?Q 6e?>leQ
где D — множество всех возможных правил дискрими-
дискриминации. Пусть известен функциональный вид Р;(х, Я,),
зависящих от параметра распределений вектора при-
признаков в каждой из совокупностей, г=1, 2, но параметр
Я неизвестен и оценивается по выборке. Тогда если
Р; (х, Я,) таковы, что существует ^-оптимальное
правило б*(Я1; Я2) дискриминации для распределений
Р;(х, Я,), i=l, 2, когда значение параметра \=(к1, Я2)
известно, и {Я ' } — сильно состоятельная оценка
параметра Я/ по выборке объема п;, то при нек-рых до-
дополнительных условиях последовательность правил
{б*(Я'1', Я!,™2')} при «j, и2—>-оо является асимптотиче-
асимптотически (>-оптимальной, то есть с вероятностью 1
lim supi?(g, б*(Я(), Я<Л2>)) = Д0, E)
где риск R в левой части E) может быть вычислен как
при истинном значении параметров, так и при замене
истинных значений их оценками Я. ' . Если потребо-
потребовать лишь состоятельности оценки, то имеет место не-
несколько более слабое утверждение.
Непараметрич. методы дискриминации, не требую-
требующие знаний о точном функциональном виде распределе-
распределений и позволяющие решать задачи дискриминации на
основе малой априорной информации о совокупностях,
являются особо ценными для практических применений
[2], [10].
В задачах Д. а. приходится иметь дело со случай-
случайными наблюдениями как над количественными, так и
над качественными признаками (возможен и смешанный
случай). Между этими случаями нет принципиальной
разницы. Если признаки качественные, то вводится
понятие многомерного состояния объекта и рассматри-
рассматривается распределение по нему. От природы наблюдений
зависит способ оценки функции распределений вектора
признаков. В соответствующих ситуациях снова приме-
применимы бейесовский и минимаксный подходы и можно
строить процедуру различения, основываясь на отно-
отношении правдоподобия. Иногда целесообразно перехо-
переходить от количественных величин к качественным путем
разбиения функции частот, и наоборот, от качественных
к количественным, вводя фиктивные переменные, пре-
преобразующие качественную информацию в количествен-
количественную. При этом, разумеется, нужно исследовать вопрос
о том, но происходит ли существенного ухудшения ка-
качества правила.
Выше рассматривались задачи Д. а. при фиксирован-
фиксированной размерности пространства значений вектора при-
признаков. Однако практич. ситуации чаще всего таковы,
что выбор размерности осуществляется исследователем.
На первый взгляд кажется, что добавление каждого
нового признака в дискриминантной функции по край-
крайней мере не ухудшит ее качества. Однако многие фак-
факторы могут при этом вести к потере эффективности раз-
различения (достаточно вспомнить, что вместо истинных
значений параметров распределений часто используют-
используются их оценки). К тому же увеличение числа признаков
ведет к быстрому возрастанию трудностей счета. Имеет-
ся много рекомендаций для выбора признаков, диктуе-
диктуемых часто здравым смыслом. Теоретически наиболее
обоснованным методом выбора признаков является ме-
метод, основанный на вычислении расстояния Махалано-
биса между двумя распределениями [11]. Особый инте-
интерес представляют последовательные методы выбора
признаков.
Долгое время задачи отнесения объекта к одной из
нескольких возможных совокупностей носили общее
название задач классификации. Здесь приведена терми-
терминология Кендалла [21, разделившего все задачи, свя-
связанные с выбором одной из нескольких равноправных
возможностей на три класса. Он назвал задачи рассмат-
рассматриваемого здесь вида задачами различения (дискрими-
(дискриминации), оставив термин «классификация» для задач раз-
разбиения данной выборки или всей совокупности на груп-
группы, по возможности однородные. Если в задачах разли-
различения существование групп оговорено в условиях, то
здесь это — предмет исследования. Выше были рас-
рассмотрены задачи различения, когда исследуемый объект
есть результат случайного выбора из нек-рого конечно-
конечномерного распределения. Возможна более общая ситуа-
ситуация, когда исследуемый объект представляет собой ре-
реализацию нек-рого случайного процесса с непрерывным
временем.
Д. а. тесно связан также с теорией распознавания об-
образов.
Лит.: [1] Андерсон Т., Введение в многомерный ста-
статистический анализ, пер. с англ., М., 1963; 12] Kendall
М. G., Stuart A., The advanced theory of statistics, v. 3,
L., 1966; [3] A n d e г s о n T. W., В a h a d u r R. R., «Ann.
Math. Statistics», 1962, v. 33, Л» 2, p. 420 — 31; [4] F i s с h e r
R. A., «Ann. Eugenics», 1936, v. 7, Л° 11, p. 179—188; [5] W a 1 d
A., «Ann. Math. Statistics», 1944, v. 15, № 2, p. 145—62; [6]
JohnS., «Sankhya», 1960, v. 22, pt. 3—4, p. 301 — 16; [7]
WelchB. L., «Biometrika», 1939, v. 31, pt. 1—2, p. 218 —
220; [8] G u p t a S. D., «Ann. Math. Statistics», 1965, v. 36,
•NS 4, p. 1174—84; [9] BunkeO., «Z. Wahrscheinlichkeitsthe-
or. und verw. Geb.», 1967, Bd 7, JVi 2, S. 131—46; [10] R у z i n
J. van, «Sankhya», ser. A, 1966, v. 28, pt. 2 — 3, p. 261 — 70; [11]
Kudo A., «Memoirs of the Faculty of Science. Kyushu Univ.»
ser. A, 1963, v. 17, .N5 1, p, 63 — 75; [12] У р б а х В. Ю., в сб.:
Статистические методы классификации, в. 1, М., 1969, с. 79—
173 (лит.). Н. М. Митрофанова, А. П. Хусу.
ДИСКРИМИНАНТНЫЙ ИНФОРМАНТ — термин
дискриминантного анализа, означающий величину,
служашую для построения правила приписывания объ-
объекта с измерениями х=(х1, ... , хр), извлеченного из
смеси к совокупностей с плотностями распределений
Pi{x), ...,pk(x) п априорными вероятностями qt, . ..,
qti, к одной из этих совокупностей. При этом i-n Д. и.
объекта с измерениями х определяется как
(х) ru-i- ... ~qkPk (х) rki\, i=A, ...,к,
где г;; — убыток, обусловленный отнесением объекта
из г-го распределения к /-му. Правило, состоящее в от-
отнесении объекта к распределению с наибольшим значе-
значением Д. и., имеет минимальное математпч. ожидание
потерь. В частности, если все к распределений нормаль-
нормальны и имеют одинаковые матрицы ковараций, то все
Д. и. линейны. Тогда в случае fc = 2 разность S1— S2
есть линейная дискриминантная функция Фишера.
Лит.: [1] Р а о С. Р., Линейные статистические методы и
их применения, пер. с англ., М., 1968.
Н. М. Митрофанова, А. П. Хусу
ДИСКРИМИНАНТНЫЙ ТЕНЗОР — кососимметриче-
ский тензор е,,,...,,¦ в я-мерном аффинном простран-
пространстве, (единственный) коэффициент внешней я-формы,
или монома максимального порядка.
ДИСПЕРСИИ ТОЧКА — точка топологич. простран-
пространства, в дополнении к к-рой нет неодноточечных связных
Множеств. А. А. Мальцев
ДИСПЕРСИОННОЕ ОТНОШЕНИЕ — см. Диспер-
Дисперсионный анализ.
ДИСПЕРСИОННОЕ СООТНОШЕНИЕ — соотношение,
связывающее нек-рые величины, характеризующие рас-
рассеяние частиц, с величинами, характеризующими их по-
глощение. Более точно, Д. с.— это соотношение, свя-
связывающее эрмитову часть амплитуды рассеяния (в бо-
более общем случае — Грина функции) с определенного
рода интегралами от ее антиэрмнтовой части. Пусть
функция /(<) абсолютно интегрируема на оси и удовлет-
удовлетворяет условию причинности f(t) = O, г<0. Тогда ее
преобразование Фурье — Лапласа
/"(?)=$/@
есть голоморфная функция в верхней полуплоскости
</>0, а действительная и мнимая части граничного зна-
значения f(p) удовлетворяют Д. с.
При описании реальных физнч. процессов Д. с. типа
(*) усложняются, так как функция /(?) может расти иа
оо как многочлен (в этом случае получают Д. с. с в ы-
ч и т а н и я м и), граничное значение f(p) может быть
обобщенной функцией медленного роста, а число пере-
переменных — больше одного (многомерные Д. с.).
Лит.: [1] Б о г о л ю б о в Н. Н., Медведев Б. В.,
Поливанов!. К., Вопросы теории дисперсионных соог-
ношений, М., 1958; [2J Владимиров В. С, Обобщен-
Обобщенные функции в математической физике, М., 1976.
В. С. Владимиров.
ДИСПЕРСИОННОЕ УРАВНЕНИЕ — уравнение, свя-
связывающее частоту колебаний со и волновой вектор к
плоской волны, зависящей от времени и координат по
закону
exp {i (a>t— кг)}.
Д. у. выводится из уравнений, описывающих рассмат-
рассматриваемый процесс, и определяет дисперсию волн (см.,
напр., случай элоктродннамич. процессов в [1], [2]).
В зависимости от характера задачи оно может быть ис-
использовано для определения частот колебаний по вол-
волновому вектору со„= <»„(/>;) или величин волновых век-
векторов по их направлению и частоте колебаний.
Первый случай тесно связан с решением задачи Коши
и исследованием устойчивости положения равновесия,
соответствующего тривиальному решению уравнений
рассматриваемого волнового процесса. С помощью раз-
разложения начальных условий в интеграл Фурье решение
задачи Коши может быть записано в виде суперпозиции
плоских волн с частотами ьуп(к). Если при нек-ром дей-
действительном /.: среди этих частот имеется хотя бы одна
с отрицательной мнимой частью, то это означает сущест-
существование ограниченных начальных возмущений, к-рым
соответствуют экспоненциально нарастающие решения,
т. е. неустойчивость.
Второй случай решения Д. у. связан с задачами воз-
возбуждения монохроматич. колебаний внешними источ-
источниками, гармонически зависящими от времени.
Лит.: [1] Ландау Л. Д., ЛившицЕ. М., Электро-
Электродинамика сплошных сред, М., 1957; [2] С и л и н В. П., Р у-
х а д з е А. А., Электромагнитные свойства плазмы и плазмо-
подобных сред, М., 1961. Д. П. Костомаров.
ДИСПЕРСИОННЫЙ АНАЛИЗ в м а т е м а т и ч е-
ской статистике — статистический метод,
предназначенный для выявления влияния отдельных
факторов на результат эксперимента, а также для по-
последующего планирования аналогичных эксперимен-
экспериментов. Первоначально Д. а. был предложен Р. Фишером
[1] для обработки результатов агрономич. опытов по вы-
выявлению условий, при к-рых испытываемый сорт сель-
сельскохозяйственной культуры дает максимальный уро-
урожай. Современные приложения Д. а. охватывают ши-
широкий круг задач экономики, социологии, биологии и
техники и трактуются обычно в терминах статистич.
теории выявления систематич. различий между резуль-
результатами непосредственных измерений, выполненных при
тех или иных меняющихся условиях.
Если значения неизвестных постоянных а1; . . . , а/
могут быть измерены с помощью различных методов или
измерительных средств М1, ..., Mj, и в каждом случае
систематич. ошибка 6,у может, вообще говоря, зависеть
как от выбранного метода Mj, так и от неизвестного из-
измеряемого значения а,-, то результаты таких измерений
представляют собой суммы вида
К,
где К — количество независимых измерений неизвест-
неизвестной величины а,- методом Mj, a y;jk — случайная ошиб-
ошибка А:-го измерения величины а,- методом Mj (предпола-
(предполагается, что все yijk — независимые одинаково распре-
распределенные случайные величины, имеющие нулевое мате-
матич. ожидание: Ег/.у;;=О). Такая линейная модель
наз. двухфакторной схемой Д-а.; пер-
первый фактор — истинное значение измеряемой величины,
второй — метод измерения, причем в данном случае
для каждой возможной комбинации значений первого и
второго факторов осуществляется одинаковое количе-
количество К независимых измерений (это допущение для це-
целей Д. а. не является существенным и введено здесь
лишь ради простоты изложения).
Примером подобной ситуации могут служить спор-
спортивные соревнования / спортсменов, мастерство к-рых
оценивается / судьями, причем каждый участник сорев-
соревнований выступает К раз (имеет К «попыток»). В этом
случае а,- — истинное значение показателя мастерства
спортсмена с номером i, b,j — систематич. ошибка,
вносимая в оценку мастерства г-го спортсмена судьей с
номером /, x;jk — оценка, выставленная ;-м судьей г-му
спортсмену после выполнений последним к-й попытки,
a yijk — соответствующая случайная погрешность. По-
Подобная схема типична для так наз. субъективной экс-
экспертизы качества нескольких объектов, осуществляемой
группой независимых экспертов. Другой пример —
статистпч. исследование урожайности сельскохозяйст-
сельскохозяйственной культуры в зависимости от одного из / сортов
почвы и / методов ее обработки, причем для каждого
сорта i почвы и каждого метода обработки с номером /
осуществляется к независимых экспериментов (в этом
примере Ъ;j — истинное значение урожайности для г-го
сорта почвы при ;'-м способе обработки, х; ,-j. — соответ-
соответствующая экспериментально наблюдаемая урожайность
в А:-м опыте, a yiiu — се случайная ошибка, возникаю-
возникающая из-за тех или иных случайных причин; что же ка-
касается величин а/, то в агрономич. опытах их разумно
считать равными нулю).
Положим Cij = aj-{-bjj-, и пусть с,-*, c^j и с^ъ — ре-
результаты осреднений c/j по соответствующим индексам,
т. е.
— J- V —-1V
С'* ~ J ZujC'i' C*J ~~ I Z-4C'J'
— J_ V —-L
e« ~~ и Z-4j го' - i
Пусть, кроме того, а=с*%, Р/=с,-*—с**, Y/ = c*/—с** и
б,у=с/у—с,-,—с*у+с**. Идея Д. а. основана на очевид-
очевидном тождестве
Если символом (cjj) обозначить вектор размерности //,
получаемый из матрицы ||с,71| порядка IX J с помощью
какого-либо заранее фиксированного способа упорядо-
упорядочивания ее элементов, то A) можно записать в виде ра-
равенства
где все векторы имеют размерность //, причем а,7=а,
Р,у=Р,-, Y,y=Yy- Так как четыре вектора в правой части
B) ортогональны, то а,7=ос — наилучшее приближение
функции c,-j- от аргументов i л / постоянной величиной
[в смысле минимальности суммы квадратов отклонений
2,-(с/у—осJ]- В том же смысле а,у+Р,у=а-|-р,- — наи-
наилучшее приближение е,-у функцией, зависящей лишь от
i, ot/y+Y,y=ot+Yy — наилучшее приближение с,-у функ-
функцией, зависящей лишь от /, а а,-у+Р,-у+у,у=а+Р,+у/—
наилучшее приближение c;j суммой функций, из к-рых
одна (напр., сс+Р/) зависит лишь от i, а другая — лишь
от /. Этот факт, установленный Р. Фишером (см. [1])
в 1918, позднее послужил основой теории квадратичных
приближений функций.
В примере, связанном со спортивными соревнования-
соревнованиями, функция б,,- выражает «взаимодействие» г-го спорт-
спортсмена и /-го судьи (положительное значение 6,-у означает
«подсуживание», т. е. систематич. завышение /-м судьей
оценки мастерства i-го спортсмена, а отрицательное зна-
значение 6,-у означает «засуживание», т. о. систематич. сни-
снижение оценки). Равенство всех б,-у- нулю — необходи-
необходимое требование, к-рое надлежит предъявлять к работе
группы экспертов. В случае же агрономич. опытов такое
равенство рассматривается как гипотеза, подлежащая
проверке по результатам экспериментов, поскольку ос-
основная цель здесь — отыскание таких значений i и /,
при к-рых функция A) достигает максимального значе-
значения. Если эта гипотеза верна, то
max с,-у = а + max р,- -)- max уу,
и значит, выявление наилучших «почвы» и «обработки»
может быть осуществлено раздельно, что приводит к
существенному сокращению числа экспериментов (напр.,
можно при каком-либо одном способе обработки ис-
испытать все / сортов «почвы» и определить наилучший
сорт, а затем на этом сорте опробовать все / спосо-
способов «обработки» и найти наилучший способ; общее ко-
количество экспериментов с повторениями будет равно
(/+/) К). Если же гипотеза {все 6/у=0} неверна, то
для определения max с,-,- необходим описанный выше
«полный план», требующий при К повторениях IJК
экспериментов.
В ситуации спортивных соревнований функция у,-у=
= У/ может трактоваться как систематич. ошибка, до-
допускаемая /-м судьей по отношению ко всем спортсме-
спортсменам. В конечном счете уу — характеристика «строгости»
или «либеральности» /-го судьи. В идеале хотелось
бы, чтобы все уу были нулевыми, но в реальных услови-
условиях приходится мириться с наличием ненулевых значе-
значений уу и учитывать это обстоятельство при подведении
итогов экспертизы (напр., за основу сравнения мастер-
мастерства спортсменов можно принять не последовательно-
последовательности истинных значений a+Pi+yy, ..., a+P/+Yy> а
лишь результаты упорядочиваний этих чисел по их ве-
личипе, поскольку при всех /= 1, ... , / такие упорядо-
упорядочивания будут одинаковыми). Наконец, сумма двух ос-
оставшихся функций a,-y-|-P,-y=a+p,. зависит лишь от i
и поэтому может быть использована для характериза-
ции мастерства г-го спортсмена. Однако здесь нужно
помнить, что а-ЬР/=а/-|-&,-я,=И=а,-. Поэтому упорядочива-
упорядочивание всех спортсменов по значениям a+Р/ (или по сс+
+ Р/ + уу при каждом фиксированном /) может не совпа-
совпадать с упорядочиванием по значениям а,-. При практи-
практической обработке экспертных оценок этим обстоя-
обстоятельством приходится пренебрегать, так как упомяну-
упомянутый полный план экспериментов не позволяет оценивать
отдельно а,- и bj%. Таким образом, число a+P,-=a,—\-b,-#
характеризует не только мастерство t-го спортсмена, но
и в той или иной мере отношение экспертов к этому мас-
мастерству. Поэтому, напр., результаты субъективных экс-
экспертных оценок, осуществленных в разное время (в
частности, на нескольких Олимпийских играх), едва
ли можно считать сопоставимыми. В случае же агроно-
агрономич. опытов подобные трудности не возникают, по-
поскольку все а,-=0 и значит, ос+Р/=6,*.
Истинные значения функций а, Р/, у у и 6,-у неизвестны
и выражаются в терминах неизвестных функций с,-у.
Поэтому первый этап Д. а. заключается в отыскании
статистич. оценок для с/у по результатам наблюдений
xiji,. Несмещенная и имеющая минимальную дисперсию
линейная оценка для c/j выражается формулой
Так как а, Р/, у у и 6,-у — линейные функции от элемен-
элементов матрицы \kjjW, то несмещенные линейные оценки
для этих функций, имеющие минимальную дисперсию,
получаются в результате замены аргументов cjj соот-
соответствующими оценками, c/j, т. е.
О /у = л: /у* ^1 ** ^г-у'.-е I" ^.-s» >
причем случайные векторы (а/у), (Р,у), (у/у) п (б/у), оп-
определенные так же, как введенные выше (а,-у), (р,у),
(у,у) и (б/у), обладают свойством ортогональности, и
значит, они представляют собой некоррелированные
случайные векторы (иными словами, любые две компо-
компоненты, принадлежащие разным векторам, имеют нуле-
нулевой коэффициент корреляции). Кроме того, любая раз-
разность вида
х ijk **•//*¦== xijk cij
некоррелирована с любой из компонент этих четырех
векторов. Рассмотрим пять совокупностей случайных
величин {г/уft}, {xi]k—xijm}, {p,}, {у,} и {б/у}. Так как
xijk—xij* = yijb—Vij*, Pi -- Pi + (г/1**—г/***).
У/= У/+(!/„/,,—г/«.*),
то дисперсии эмпирич. распределений, соответствую-
соответствующих указанным совокупностям, выражаются формула-
формулаU0"-lJKjL*ijk \xUk — xij*> - -¦ 1JK
Sl = T 2-ч P2 = T -Z-i,- t
¦^ = 77 Х,7^ = /7 X/yfS'V+ B/G* — УЫ*—У*;* + г/***)]2-
Эти эмпирич. дисперсии представляют собой суммы
квадратов случайных величин, любые две из к-рых не-
коррелпрованы, если только они принадлежат разным
суммам; при этом относительно всех yiju справедливо
тождество
s*=s\ + s\ + sl+s\,
объясняющее происхождение термина «Д. а.».
Пусть /, /, К^:2 и пусть
2
So
К С2 2 IJK С2 2 IJK С2
2 IJK С2
: S2 = J_l ,
в таком случае
где a? — дисперсия случайных ошибок j/,yft.
На основе этих формул и строится второй этап Д. а.,
посвященный выявлению влияния первого и второго
факторов на результаты эксперимента (в агрономич.
опытах первый фактор — сорт «почвы», второй — спо-
способ «обработки»). Напр., если требуется проверить ги-
гипотезу отсутствия «взаимодействия» факторов, к-рая
выражается равенством ^. б|/=0, то разумно вычис-
вычислить дисперсионное отношение si/so— F3.
Если это отношение значимо отличается от единицы, то
проверяемая гипотеза отвергается. Точно так же для
проверки гипотезы 2j Y/=0 полезно отношение sl/sl=F2,
к-рое надлежит также сравнить с единицей; если при
этом известно, что 2j- -6f/= 0, то вместо Fz целесообразно
сравнить с единицей отношение
(ijk-1-j- о 4 »
(Z-l) (J -I) sg
Аналогичным образом можно построить статистику, по-
позволяющую дать заключение о справедливости или лож-
ложности гипотезы ^).3/==0.
Точный смысл понятия значимого отличия указан-
указанных отношений от единицы может быть определен лишь
с учетом закона распределения случайных ошибок ;/,yft.
В Д. а. наиболее обстоятельно изучена ситуация, в
к-рой все у,-,¦/; распределены нормально. В этом случае
(а,-/). @//)» (у i/), F,7) — независимые случайные векто-
векторы, a so, si, s'i, S3 — независимые случайные величины,
причем отношения
подчиняются нецентральным распределениям хи-квад-
рат с fm степенями свободы и параметрами нецентраль-
нецентральности кт, т=0, 1, 2, 3, где
Яо = 0, Xi = JK 2,- Р?/а3, Я2 = IK 2/ у)-'о2
Если параметр ноцентральности равен нулю, то нецент-
нецентральное распределение хи-квадрат совпадает с обычным
распределением хи-квадрат. Поэтому в случае справед-
справедливости гипотезы Я3=0 отношение s<i/so=F3 подчиняется
/'-распределению (распределению дисперсионного от-
отношения) с параметрами /3 и /0. Пусть х — такое число,
для к-рого вероятность события {F3>z} равна задан-
заданному значению е, называемому уровнем значи-
значимости (таблицы функции х=х(е; /3, /0) имеются в
большинстве пособий по математич. статистике). Кри-
Критерием для проверки гипотезы Я3=0 служит правило,
согласно к-рому эта гипотеза отвергается, если наблю-
наблюдаемое значение F3 превышает х\ в противном случае
гипотеза считается не противоречащей результатам на-
наблюдений. Аналогичным образом конструируются кри-
критерии, основанные на статистиках F2 и F±.
Дальнейшие этапы Д. а. существенно зависят не
только от реального содержания конкретной задачи, но
также и от результатов статистич. проверки гипотез на
втором этапе. Напр., в условиях агрономич. опытов
справедливость гипотезы Я3=0, как указано выше, по-
позволяет более экономно спланировать аналогичные
дальнейшие эксперименты (если помимо гипотезы Я3 = 0
справедлива также и гипотеза Я2=0, то это означает, что
урожайность зависит лишь от сорта «почвы», и поэтому
в дальнейших опытах можно воспользоваться схемой
однофакторного Д. а.); если же гипотеза Я,3=0 отвер-
отвергается, то разумно проверить, нет ли в данной задаче
неучтенного третьего фактора? Если сорта «почвы» и
способы ее «обработки» варьировались не в одном и том
же месте, а в различных географич. зонах, то таким
фактором могут быть климатич. или географич. усло-
условия, и «обработка» наблюдений потребует применения
трехфакторного Д. а.
В случае экспертных оценок статистически подтверж-
подтвержденная справедливость гипотезы Я31=0 дает основание
для упорядочивания сравниваемых объектов (напр.,
спортсменов) по значениям величин а+Р/, г=1, ... , /.
Если же гипотеза Я3=0 отвергается (в задаче о спортив-
спортивных соревнованиях это означает статистич. обнаруже-
обнаружение «взаимодействия» нек-рых спортсменов и судей),
то естественно попытаться перевычислить все резуль-
результаты заново, предварительно исключив из рассмотрения
x[jk с такими парами индексов (г, /), для к-рых абсо-
абсолютные значения статистич. оценок 6,7 превышают
нек-рый заранее установленный допустимый уровень. Это
означает, что из матрицы ||л:,у* || вычеркиваются нек-рые
элементы, и значит, план Д. а. становится неполным.
Модели современного Д. а. охватывают широкий круг
реальных экспериментальных схем (напр., схемы не-
неполных планов, со случайно или неслучайно отобран-
отобранными элементами хц%). Соответствующие этим схемам
статистич. выводы во многих случаях находятся в ста-
стадии разработки. В частности, еще (к 1978) далеки от
окончательного решения те задачи, в к-рых результаты
наблюдений Xijk=ci/~\~yi/k не являются одинаково рас-
распределенными случайными величинами; еще более труд-
трудная задача возникает в случае зависимости величин
хць- Неизвестно решение проблемы выбора факторов
(даже в линейном случае). Суть этой проблемы заклю-
заключается в следующем: пусть с=с(и, v) — непрерывная
функция и пусть u=u(z, w) и u—v(z, w) — какие-либо
линейные функции от переменных z и w. Фиксируя зна-
значения zlt . .., Z[ и wl, . .., wj, можно при каждом за-
заданном выборе линейных функций и и и определить сц
формулой
С1}=С [u(z;, Wj), V(Z{, Wj)}
и построить Д. а. этих величин по результатам соответ-
соответствующих наблюдений x;j^. Проблема заключается в
отыскании таких линейных функций и и ь; к-рым соответ-
соответствует минимальное значение суммы квадратов ^. .6'ij ,
где
{предполагается, что функция с(и, и) неизвестна). В тер-
терминах Д. а. эта проблема сводится к статистич. оты-
отысканию таких факторов z=z(u, v) и w=w(u, v), к-рым
соответствует «наименьшее взаимодействие».
Лит.: [1] Fisher R. A., Statistical methods for research
workers, Edinburgh, 1925; [2] Шеффе Г., Дисперсионный
анализ, пер. с англ., М., 1963; [3] X а л ь д А., Математическая
статистика с техническими приложениями, пер. с англ., М.,
1956; [4] С н е д е к о р Д ж. У., Статистические методы в при-
применении к исследованиям в сельском хозяйстве и биологии, пер.
с англ., М., 1961. Л. Н Большее.
ДИСПЕРСИОННЫЙ МЕТОД в теории чисел—
метод для решения нек-рых бинарных уравнений (би-
(бинарных аддитивных проблем) вида
ос+Р=и, A)
где аир принадлежат к достаточно густым и хорошо
распределенным в арифметич. прогрессиях последова-
последовательностям натуральных чисел.
Д. м., разработанный Ю. В. Линником в 1958—61 и
поэтому называемый также дисперсионным ме-
методом Линника, соединяет в себе элементар-
элементарные теоретико-вероятностные понятия (в частности,
понятие дисперсии и неравенства типа Чебышева) с
аналитич. и алгебраич. идеями И. М. Виноградова и
А. Вейля (A. Weil). Сущность Д. м. состоит в следую-
следующем (см. также Аддитивная теория чисел).
Уравнение A) сводится к уравнениям вида
vZ)'+P=«; B)
здесь v, D' независимо пробегают нек-рые значения из
прямоугольной области v?(v), D' (z(D), где (v) и (D) —
некоторые интервалы; при этом числа v — простые, а
на D' могут быть наложены различные дополнительные
условия. Пусть через F обозначено число решений этого
уравнения.
Пусть теперь имеется уравнение
при произвольном D?(D), и через А (я, D) обозначено
число его решений, найденных из каких-либо эвристи-
эвристических соображений. Тогда (гипотетически) число ожи-
ожидаемых решений уравнения B) записывается в виде
Оценка разности F—S=V имеет вид
^ = 5 B 1 —Л (и, ?>')). C)
Применение неравенства Коши приводит к неравенству
F2<Z>0F\ D)
где Do — длина интервала (D), а
У' = У] (У, \—A(n,D')Y E)
есть дисперсия числа решений уравнения B).
Если распространить суммирование в E) на все D ?
?z(D), то будут сняты все дополнительные условия, на-
наложенные на D' в B). В то же время величина дисперсии
может только возрасти. Поэтому
KjUv
Суммы 2-l, 22и23в нек-рых случаях удается вычис-
вычислить асимптотически. Главную трудность представляет
вычисление 2t — основной суммы Д. м. Асимптотич.
расчет суммы Хх осуществляется при помощи Вино-
Виноградова метода по подсчету для нек-рых функций коли-
количества их дробных частей, попадающих в заданный сег-
сегмент, а также с использованием новейших оценок три-
гонометрич. сумм, полученных средствами алгебраич.
геометрии. Асимптотика для сумм 22 и 23 находится пу-
путем элементарного суммирования. Если, в результате,
дисперсия оказывается не слишком большой, то из C)
и D) получается асимптотика для числа решений урав-
уравнения B).
Объединение числа решений всех уравнений вида B)
приводит к асимптотич. формуле для числа решений
уравнения A).
Рассмотренная схема Д. м. применима и для решения
уравнений вида
а—р=г,
где I — заданное целое число, отличное от нуля.
При помощи этого метода 10. В. Линником и др. (см.
[3]) был решен ряд классических бинарных аддитивных
проблем, к-рые до создания Д. м. могли быть решены
только на основе эвристических или гипотетических
соображений. К числу таких проблем относятся:
аддитивная проблема делителей (<х=х1, х.2 . . . х^,
к= const, Р = л";/); Титчмарша проблема делителей
(а~р — простое, $=ху); Харди — Литлвуда проблема
(а=р — простое, P=j;2+z/2).
При помощи Д. м. решены также нек-рые аналоги
и обобщения этих проблем, в частности найдена аспмп-
тотика для числа решений общего уравнения
Хард и — Литлвуда:
где р — простое, а <р(?, т|) — заданная примитивная
положительно определенная квадратичная форма. До-
Доказано существование бесконечного множества про-
простых чисел вида
где 1фО — любое фиксированное целое число.
Область применения Д. м. пересекается с областью
применения метода большого решета Ю. В. Линника.
Лит.: [1] ЛинникЮ. В., Дисперсионный метод в би-
бинарных аддитивных задачах, Л., 1961; [2] Приложение 1 в кн.:
П р а х а р К., Распределение простых чисел, пер. с нем., М.,
1967' [3] Бредихин Б.М., «Успехи матем. наук», 1965,
т. 20, в. 2, с. 89 — 130; [4] Бредихин Б. М., Л и н-
ник Ю. В., в сб.: Актуальные проблемы аналитической
теории чисел, Минск, 1974, с. 5—22. Б. М. Бредихин.
ДИСПЕРСИЯ в теории вероятностей—
мера DX отклонения случайной величины X от ее
математич. ожидания ЕХ, определяемая равенством:
DX = E(X — EXJ. A)
Свойства Д.:
если с — действительное число, то
D (cX) = c2DX,
в частности D(—X)=D(X).
Когда говорят о Д. случайной величины А', всегда
предполагают, что существует математич. ожидание
ЕХ; при этом Д. DX может существовать (т. е. быть
конечной) или не существовать (т. е. быть бесконеч-
бесконечной). В современной теории вероятностей математич.
ожидание случайной величины определяется через
интеграл Лебега по пространству элементарных собы-
событий. Однако важную роль играют формулы, выража-
выражающие математич. ожидание различных функций от
случайной величины X через распределение этой
случайной величины на множестве действительных
чисел (см. Математическое ожидание). Для Д. DX
эти формулы имеют вид:
для дискретной случайной величины X, принимающей
не более чем счетное число различных значений а,-
с вероятностями р, = Р{Х=а,};
6)DX=f°° (x — EXJ p (x)dx
для случайной величины X, имеющей плотность рас-
распределения вероятностей р(х);
в) DX = [ х (х — ЕXJ dF (x)
в общем случае, где F(x) — функция распределения
случайной величины X и интеграл понимается в смысле
Лебега — Стилтьеса или Римана — Стилтьеса.
Д. не является единственной мыслимой мерой от-
отклонения случайной величины от ее математич. ожи-
ожидания. Возможны другие меры отклонения, устроенные
по тому же принципу, напр. Е|А"—ЕХ|, Е(Х— ЕХL
и т. д., а также меры отклонения, основанные на кван-
квантилях. Особая важность Д. объясняется главным
образом тон ролью, к-рую играет это понятие для
предельных теорем. Грубо говоря, оказывается, что
если знать математич. ожидание и Д. суммы большого
числа случайных величин, то можно полностью оп-
определить закон распределения этой суммы: он ока-
оказывается нормальным (приблизительно) с соответст-
соответствующими параметрами (см. Нормальное распределение).
Таким образом, важнейшие свойства Д. связаны с
выражением для Д. D(X1-!r.. .-\-Хп) суммы случайных
величин Хх, . .., Х„:
D(X1+... + Xn) = 2"= , 0Х( + 2 2( < , cov (X,; Xj),
где
обозначает ковариацию случайных величин Х( и X/.
Если случайные величины Х1} . . ., Хп попарно неза-
независимы, то cov(X,-, Xj) = 0. Поэтому для попарно не-
независимых случайных величин
B)
Обратное утверждение неверно: из B) не следует
независимость. Однако, как правило, применение
формулы B) базируется на независимости случайных
величин. Строго говоря, для справедливости B) до-
достаточно лишь, чтобы cov(X,-, X/)~0, т. е. чтобы слу-
случайные величины X-l, ..., Хп были попарно некорре-
лированы.
Применения понятия Д. развиваются по следующим
двум направлениям. Во-первых, применения в области
предельных теорем теории вероятностей. Если после-
последовательность случайных величин Хх, Х2, ..., Хп,. . .
обладает тем свойством, что DXn—vO при «-*-оо, то
, для любого е>0 при п—*-оо
Р{\Хп-ЕХп\ > е}-+0
(см. Чебышева неравенство), т. е. практически при
больших п случайная величина Х„ совпадает с неслу-
неслучайной величиной ЕХп. Развитие этих соображений
приводит к доказательству закона больших чисел (см.
Больших чисел закон), к доказательству состоятель-
состоятельности оценок (см. Состоятельная оценка) в математич.
статистике, а также к иным применениям, в к-рых
устанавливается сходимость по вероятности случайных
величин. Другое применение в области предельных
теорем связано с понятием нормировки. Нормировка
случайной величины X производится путем вычитания
математич. ожидания и деления на среднее квадра-
квадратичное отклонение УоХ, иными словами, рассматри-
рассматривается величина Y= (X — EX)/ YdX. Нормировка по-
последовательности случайных величин обычно необхо-
необходима для получения сходящейся последовательности
законов распределения, в частности сходимости к
нормальному закону с параметрами 0 и 1. Во-вторых,
применение понятия Д. в математич. статистике при
обработке выборок. Если смотреть на случайную ве-
величину как на реализацию случайного эксперимента,
то произвольное изменение шкалы отсчета приведет
к преобразованию случайной величины X в величину
Y=aX-~-a, где а — любое действительное число, а —
положительное число. Поэтому часто имеет смысл
рассматривать не один теоретич. закон распределения
F(х) случайной величины X, а тип законов, т. е. се-
семейство законов распределения вида
сящих по крайней мере от двух параметров а и а.
Если ЕХ = 0, DX=1, то ЕУ= a, DY= а2. Поэтому пара-
параметры теоретич. закона имеют следующий смысл а=ЕУ
и о= У^ЭУ. Отсюда вытекает способ определения этих
параметров по выборке.
Лит.: [1] Г н с д е н к о Б. В., Курс теории вероятностей,
5 изд., М., 1969; [2] Ф е л л е р В., Введение в теорию вероят-
вероятностей и ее приложения, пер. с англ., т. 1—2, М., 1964—67;
[3] К р а м е р Г., Математические методы статистики, пер.
с англ., 2 изд., М., 1975. В. Н. Тутубалин.
ДИСПЕРСНОЕ ПРОСТРАНСТВО, наследствен-
наследственно несвязное пространство,— тополо-
топологическое пространство, не содержащее неодноточечных
СВЯЗНЫХ множеств. А- А- Мальцев.
ДИССИПАТИВНАЯ СИСТЕМА, С-система,
предельно ограниченная систем а,—
система обыкновенных дифференциальных уравнений
x = f(t, x), х? R",
с непрерывной правой частью, решения x(t; %, х0)
к-рой удовлетворяют свойству единственности и бес-
бесконечной продолжимости вправо и для к-рой сущест-
существует такое число р>0, что для любого решения
x(t; t0, х0) найдется такой момент T(t0, xo)^to, что
\\x(t\ t0, г0) || < р при всех t 2э Т (t0, x0).
Иными словами, каждое решение рано или поздно
погружается в фиксированный шар ||ж||<р. Важным
частным случаем Д. с. являются так наз. системы
с конвергенцией, у которых все решения
x(t; @, хд) определены при i0«:f<oo и, кроме того, су-
существует единственное определенное и ограниченное
на всей оси решение, и оно асимптотически устойчиво
в целом. Такие системы изучены наиболее полно (см.,
напр., [1]).
Лит.: [1] П л и с с В. А., Нелокальные проблемы теории
колебаний, М.—Л., 1964; [2] Демидович Б. П., Лекции
по математической теории устойчивости, М., 1987.
К. С. Сибирский.
ДИССИПАТИВНАЯ ФУНКЦИЯ, функция
рассеяния,— функция, вводимая для учета влия-
влияния сил вязкого трения на движение механич. системы.
Д. ф. характеризует степень убывания механич. энер-
энергии этой системы; вводится также вообще для учета
перехода энергии упорядоченного движения в энергию
неупорядоченного движения (в конечном счете — в
тепловую).
Для изотропной среды Д. ф., отнесенная к единице
объема, имеет вид:
где dvjdxb — компоненты тензора скоростей дефор-
деформаций, ц и t] — коэффициенты вязкости, характеризу-
характеризующие соответственно вязкость при сдвиге и вязкость
при объемном расширении.
Уравнение изменения энтропии в вязкой среде имеет
вид:
где S — удельная энтропия, р — плотность жидко-
жидкости, Т — ее температура.
Д. ф. характеризует силы вязкого трения при дви-
движении сплошной среды. Уравнение движения вязкой
среды имеет вид:
V dt dxk r dxk '
где a,-ft •— компоненты тензора напряжений,
— компоненты «вязкого» тензора напряжений, причем
Д. ф. используется: для учета влияния сопротив-
сопротивлений на малые колебания системы около ее положения
равновесия; исследования затухания колебаний в уп-
упругой среде; учета тепловых потерь при затухании
колебаний электрич. тока в системе контуров и др.
Лит.: [1] Ландау Л. Д., Лифшиц Е. М., Меха-
Механика сплошных сред, 2 изд., М., 1954, ч. 1, § 16.
В. А. Дородницын.
ДИССИПАТИВНЫЙ ОПЕРАТОР — линейный опера-
оператор А с областью определения В д, плотной в гильбер-
гильбертовом пространстве //, и такой, что
Im (Ах, х)^?0 при х ? DА.
Иногда это требование заменяется условием
Re(Ax, ж)<:0 при х^Вд, т. е. диссипативность А в этом
смысле эквивалентна диссипативности оператора (—iA).
Д. о. наз. максимальным, если он не имеет
собственных диссипативных расширений. Д. о. всегда
допускает замыкание, к-рое также будет Д. о., в част-
частности максимальный Д. о.— замкнутый оператор. Вся-
Всякий Д. о. допускает расширение до максимального.
Для Д. о. все точки Я с 1тЯ<0 есть точки регулярного
типа, при этом
\\Ах — Хх\\ > |1тЯ |||а:[], х ? ВА.
Д. о. является максимальным тогда и только тогда,
когда при всех Я с Im Я<0 имеет место (А—К1)Вд=Н.
Эквивалентное условие максимальности Д. о. А —•
его замкнутость и выполнение условия
1т(А*у, г/)<0, у ? ВА*.
Если А(, — максимальный симметрический оператор,
то либо Ао, либо (—А0) является максимальным Д. о.
Для произвольного симметрич. оператора Ао можно
рассматривать диссипативные и, в частности, макси-
максимальные диссипативныо расширения; задача их опи-
описания эквивалентна задаче описания всех максималь-
максимальных диссипативных расширений консервативного опе-
оператора B0~iA0: Re(BQx, z)=0, х?Вд.
Д. о. тесно связаны со сжатиями и с так наз. а к-
кретивными операторами, т.е. такими
операторами А, для к-рых iA есть Д. о. В частности,
аккретивный оператор А максимален тогда и только
тогда, когда (—А) является порождающим оператором
(генератором) непрерывной однопараметрич. полу-
полугруппы сжатий {Ts}s> в //. С помощью преобразо-
преобразований Кэли "~"
где А — максимальный аккретивный оператор, а Т —
сжатие, не имеющее Я= 1 собственным значением,
строится функциональное исчисление и, в частности,
теория дробных степеней максимальных Д. о.
Для ограниченных линейных операторов А опреде-
определение Д. о. эквивалентно требованию Лу>0, где
Лу = 2-^(у1*—А) — мнимая компонента оператора А.
Для вполне непрерывного Д. о. в сепарабельном гиль-
гильбертовом пространстве Н с ядерной мнимой компонен-
компонентой Aj имеются многочисленные критерии (т. е. не-
необходимые и достаточные условия) полноты системы
их корневых векторов. Напр.,
2-_ lmkj (A) = Sp Aj,
где kj(A) — все собственные значения оператора А, /'=
= 1, ..., v(yl)<oo, a Sp^ly—след оператора Aj (кри-
(критерий Лившица);
Шп п+(р'А*>=0 „ли Km
где Ад= — (А-\-А*) — действительная компонента опе-
оператора А, а п± — количество характеристич. чисел
оператора Ar в отрезках [0, р] и [—р, 0] (критерий
Крейна). Система Ьр/} собственных век-
векторов, отвечающих различным собственным числам
Я;, /=1, 2, ... Д. о., образует базис своей замкнутой
линейной оболочки, эквивалентный ортонормирован-
ному, если
„ х im kj im kh
Понятие Д. о. введено и для нелинейных и даже
многозначных операторов А. Такой оператор в гиль-
гильбертовом пространстве наз. Д. о., если для любых
двух его значений выполнено неравенство
Т\о(Ах1—Ах2, х1—ж2)<:0.
Это понятие лежит в основе теории однопараметриче-
ских нелинейных сжимающих полугрупп и связанных
с ними дифференциальных уравнений. Другое обоб-
обобщение понятия Д. о. относится к операторам, дей-
действующим в банаховых пространствах с так называе-
называемым полувнутренним произведением. Наконец, имеет-
имеется обобщение, связанное с операторами, действую-
действующими в гильбертовом пространстве с индефинитной
метрикой.
Лит.:[1]Секефальви-НадьБ., Фояш Ч., Гар-
Гармонический анализ операторов в гильбертовом пространстве,
пер. с франц., М., 1970; [2] К р е й н С. Г., Линейные диффе-
дифференциальные уравнения в банаховом пространстве, М., 1967;
[3] Лившиц М. С, «Матем. сб.», 1954, т. 34, Х5 1, с. 145 —
99; [4] Ф и л л и п с Р. С, «Математика», 1962, т. б, JV» 4, с. 11 — 70;
[5] Crandall М Р а г у A., «J. Fund. Analys.», 1969,
v 3, p. 376—418; [6] Lamer G., Phillips R., «Pacific
j' Math» 1961, v. 11, p. 679 — 98. И. С. Иохвидов.
ДИСТАЛЬНАЯ ДИНАМИЧЕСКАЯ СИСТЕМА — та-
такая динамическая система {Ti} с метрич. фазовым
пространством X, что для любых точек хфу нижняя
грань расстояний
Если в нск-рой динамич. системе какая-либо пара
точек хфу обладает последним свойством, то говорят,
что эта пара точек дистальна; таким образом,
Д. д. с.— это динамич. система, для к-рой все пары
точек хфу дистальны.
Приведенное определение годится для «общих» ди-
динамич. систем, когда «время» t пробегает произвольную
группу G. Содержательные результаты получаются,
если G локально компактна (основными являются
«классические» случаи каскада или потока, т. е. когда
G= % или G= R, но рассуждения при этом почти не
упрощаются), а X компактно. Особый интерес при
этом представляет тот случай, когда X является ми-
минимальным множеством (общий случай в известном
смысле сводится к этому, а именно, при указанных
ограничениях на G и X замыкание каждой траектории
оказывается минимальным множеством). Важнейший
пример Д. д. с.— система, возникающая в замыкании
почти периодич. траектории какой-нибудь динамич.
системы. Другой пример — нильпотоки (см. [1]). Как
и в этих примерах, строение Д. д. с. с минимальным X
при указанных условиях допускает довольно детальное
описание алгебраич. характера (см. [2]; изложение
теории Д. д. с. и их обобщений и библиографию см.
в [3]).
Лит.: [1] Ауслендер Л., Грин Л., Хан Ф.,
Потоки на однородных пространствах, пер. с англ., М., 1966;
[2] Furstenberg H., «Amer. J. Math.», 1963, v. 85, № 3,
p. 477 — 515; [3] Бронштейн И. У., Расширения мини-
минимальных групп преобразований, Киш., 1975. Д. В. Анисов.
ДИСТРИБУТИВНАЯ КВАЗИГРУППА — квазигруп-
квазигруппа, в к-рой выполняются левый и правый дистрибу-
дистрибутивные законы: x-yz=xy-xz, yz-x=yx-zx. Эти два за-
закона в квазигруппах не зависят друг от друга (сущест-
(существуют леводистрибутивные квазигруппы, не являющиеся
праводистрибутивными, [1]). Примером Д. к. служит
множество Q рациональных чисел с операцией (х-\-у)/2.
Всякая идемпотентная медиальная
квазигруппа (т. е. квазигруппа Q, в к-рой
выполняются соотношения х2=х и ху¦ uv=xu-yv для
всех х, у, и, v?Q) дистрибутивна. В общем случае
всякая Д. к. Q(-) изотопна коммутативной My фанг
лупе [3]. Парастрофы (квазигруппы относи-
относительно обратных операций, см. Квазигруппа) Д. к.
тоже дистрибутивны и изотопны той же коммутативной
лупе Муфанг. Если четыре элемента а, Ъ, с, d в Д. к.
связаны медиальным законом: ab-cd=ac-bd,
то они порождают медиальную подквазигруппу. В част-
частности, всякие три элемента Д. к. порождают медиаль-
медиальную подквазигруппу. В Д. к. трансляции являются
автоморфизмами, поэтому в определенном смысле Д. к.
однородна: ни один элемент, ни одна подквазигруппа
не выделяются. Группа, порожденная х всеми правыми
трансляциями Д. к., разрешима [4].
Лит.: [1] Stein Sh., «Publ. Math. Debrecen», 1959,v. 6,
,N» 1—2, p. 10—14; [2] Б е л о У с о в В. Д., «Матем. сб.», 1960,
т. 50, ЛЬ 3, с. 267 — 98; [3] его ж е, Основы теории квази-
квазигрупп и луп, М., 1967; [4] Fischer В., «Math. Z.» 1964,
Bd 83, Ns 4, S. 267 — 303 В. Д. Белоусов.
ДИСТРИБУТИВНАЯ РЕШЕТКА, дистрибу-
дистрибутивная структур а,— решетка, в к-рой спра-
справедливо тождество
(a-\-b)c=ac-\-bc,
равносильное как
аЬ+с=(а+с)(Ь+с),
так и
(а+Ь)(а+с)(Ъ+с) = аЪ+ас+Ьс.
Д. р. характеризуются тем, что все их выпуклые под-
решетки служат смежными классами конгруэнции.
Всякая Д. р. изоморфна решетке подмножеств (но не
обязательно всех) нек-рого множества. Важнейшим
частным случаем Д. р. являются булевы алгебры.
В Д. р. для любого коночного множества / выпол-
выполняются равенства
а также
где J (i) — конечные множества, а Ф — множество
всех однозначных функций ф, ставящих в соответствие
элементу i из / элемент q>(i) из J(i). В полной Д. р.
указанные равенства имеют смысл и в случае беско-
бесконечных множеств / и J(i). Однако справедливы они
не всегда. Полные Д. р. (см. Полная решетка), удов-
удовлетворяющие последним двум тождествам для любых
множеств / и J(i), наз. вполне дистрибу-
дистрибутивными.
Лит.: [1] Биркгоф Г., Теория структур, пер. с англ.,
М., 1952; [2] Скорняков Л. А., Элементы теории струк-
структур, М., 1970; [3] G г a t z е г G., Lattice theory. First concepts
and distributive lattices, S. F., 1971. Л. А. Скорняков.
ДИСТРИБУТИВНОСТЬ, дистрибутивности
закон, распределительность, некоторой
операции относительно другой — свойство пары би-
бинарных алгебраических операций, выражающееся одним
из тождеств:
Д1. (yxyz) X * (у ф Z) = (**!/)© (X * Z),
Д2. (VXyz) A0!,)*! = (х * z) © (у * z),
где ©, * — символы бинарных операций, а х, у, z —
предметные переменные. Если в множестве А опре-
делены две конкретные оинарные операции ж-j-j/, х>у,
т. е. заданы два отображения
-J-: АхА—>¦ А, а: АхА—>А,
то, интерпретируя символы ф, * как знаки операций
+ , о в А, соответственно, можно говорить об истин-
истинности или ложности в А каждой из формул Д1, Д2.
Если при этом обе формулы Д1, Д2 истинны в А, то
операция о наз. дистрибутивной относи-
относительно Операции + В А. Д. М. Смирнов.
ДИФРАКЦИИ МАТЕМАТИЧЕСКАЯ ТЕОРИЯ —
раздел математич. физики, в к-ром изучаются задачи,
возникающие при математич. описании волновых яв-
явлений. Такое определение Д. м. т. включает и гео-
метрич. оптику, к-рую. однако, по традиции считают
самостоятельным разделом математич. физики. Ос-
Основные уравнения с частными производными, описы-
описывающие волновые процессы,— это Максвелла уравнения,
уравнения динамических задач теории упругости, вол-
волновое уравнение (к-рое в случае двух пространственных
переменных описывает колебания мембраны, а в случае
трех пространственных переменных — распростране-
распространение звука), уравнения гидродинамики и ряд других.
Постановка задач Д. м. т. может быть
рассмотрена на примере волнового уравнения; задачи
для других уравнений, описывающих волновые про-
процессы, ставятся аналогично.
Нестационарные задачи дифрак-
дифракции — это, по существу, смешанные задачи, т. е.
задачи с начальными и краевыми условиями для вол-
волнового уравнения
1 MJ = F(M,t) A)
—TrrUu — MJ = F(M,t)
с* (М) " \ ' >
в области @<i<-r°°)X Q, где Q — область на пло-
плоскости или в трехмерном пространство; при этом
{7
dt
B)
яа границе S области Q в простейших случаях
U] =Ф(М, t) пли — =Y (M, t); M ?S, t > 0. C)
S Oil s
Здесь F, Uo, U-,, Ф, ty — заданные функции. Иногда
коуффициент с(М) на нек-рых поверхностях (в трех-
трехмерном случае) или линиях (в плоском случае) имеет
скачки; тогда для U должны быть заданы еще и «ус-
«условия сопряжения», связывающие значения функции
U и ее производных по разные стороны поверхности,
на к-рой с (М) имеет скачок. Корректность постановки
задач такого рода доказывается при помощи априорных
оценок искомого решения в различных нормах с ис-
использованием соображении компактности. Тонкие во-
вопросы описания сингулярности решений, поведения
решений при t—коо, разработки практически приме-
применимых алгоритмов численного решения еще далеки
от своего окончательного решения.
Стационарные задачи дифракции.
Важную роль в Д. м. т. играют решения, гармонически
зависящие от времени, т. е. решения уравнения A),
имеющие вид
U (M, t)=e-iatu(M), со = const. D)
Параметр со соответствует частоте колебаний. Функции
F(M, t), Ф(М, t) и ^{М, t) [см. формулы A) и CI
тоже должны гармонически зависеть от времени:
F (M, t)=f (М)е~ш;
Ф (М. t)=q> (М)е~ш;
Уравнение A) и краевые условия C) дают
^Тй)" = -/ W' М € й- E)
ЛГ) или |^^ = г1)(М). F)
Для ограниченной области Q большое значение имеет
задача на отыскание нетривиальных решений урав-
уравнения E) при /=0 в случае однородных краевых ус-
условий ф(М) = 0 или т\>{М) = 0. Это — так наз. задача
нахождения собственных функций. Однако основной
интерес в Д. и. т. представляет решение уравнений
E) в случае краевых условий F) при неограниченной
области Q. При этом условий E) и F) уже недостаточно
для определения функции и: нужно задать еще «ус-
«условия на бесконечности».
Наиболее часто задача дифракции ставится физи-
физически следующим образом: предполагается, что ре-
решение и уравнения E) задается в виде суммы uj-\-us
двух функций, где и,- — известная функция («падаю-
(«падающая волна»), a us — «отраженная» или возникшая
в результате дифракции волна. Волна us не должна
содержать в себе волн, идущих из бесконечности. Это
физич. условие и приводит к вышеуказанным условиям
на бесконечности. Соответствующие условия для слу-
случая, когда Q есть внешность ограниченной области,
со>0, с(М) вне сферы достаточно большого радиуса
есть константа, a f(M) — финитная функция, наз.
условиями излучения (см. Излучения ус-
условия). Задача E), F), при выполнении условий из-
излучения, поставлена корректно, что доказывается
путем сведения задачи к интегральным уравнениям
или с помощью априорных оценок. Имеются также
способы отбора единственного решения задачи E), F)
с помощью принципа предельной амплитуды п прин-
принципа предельного поглощения. В случае, когда Q —
внешность ограниченной области,— оба эти принципа
выделяют те же решения, что и условия излучения.
Сколько-нибудь общей теории задач для уравнения
Гельмгольца в случае неограниченных областей не
создано. Во всех практически важных случаях реше-
решения, представляющие физич. интерес, могут быть вы-
выделены при помощи принципа предельного поглоще-
поглощения.
В случае c(M)=const представление решений задач
Дирихле (ц| =<p(Af)) и Неймана (j^A =г|) j может
быть получено в виде потенциалов соответственно
двойного и простого слоев:
ikr
p(N)L—dS.
Для искомой плотности (x(JV) получается интегральное
уравнение Фредгольма 2-го рода. При проведении
соответствующего доказательства разрешимости задач
Дирихле и Неймана приходится преодолевать трудно-
трудности, вполне аналогичные классич. трудности, возника-
возникающей при исследовании методами теории потенциа-
потенциала внешней задачи Дирихле для уравнения Лапласа.
Методы решения задач Д. м. т. Боль-
Большое значение в задачах Д. м. т. имеет соотношение
между длиной волны и характерными размерами тела,
в окрестности к-рого изучается волновой процесс.
Если длина волны велика (соответственно мала) по
сравнению с характерными размерами тела, то говорят
о дифракции длинных (соответственно к о-
р о т к и х) волн. В случае дифракции длинных
волн величина со в уравнении E) может рассматри-
ваться как малый параметр. Это позволяет применять
в длинноволновом случае различные варианты теории
возмущений. В качестве первого приближения можно
взять решение уравнения Лапласа. Кроме того, в
длинноволновом случае для решения задач Д. м. т.
применимы обычные численные методы математич.
физики, напр., вариационный метод, численное реше-
решение интегральных уравнений теории потенциала. Для
областей частного вида задачи Д. м. т. могут быть
решены в явном виде, т. е. их решение представимо
в виде рядов или интегралов, содержащих специальные
функции. Наиболее важными приемами, позволяющими
сделать это, являются метод разделения переменных,
или Фурье метод, и Винера — Хопфа метод.
«Доведение до числа» явных решений задач Д. м. т.
удавалось ранее лишь в длинноволновом случае (чем
меньше длина волны, тем хуже сходятся ряды и ин-
интегралы). С развитием вычислительной техники стали
поддаваться расчету многие задачи и в области,
когда длина волны сравнима с характерными разме-
размерами неоднородности. Наиболее эффективными здесь
являются методы сведений задач дифракции к инте-
интегральным и интегродиффоренциальным уравнениям и
различные варианты проекционных методов.
Асимптотические методы Д. м. т. При
малой длине волны численное решение дифракционной
задачи весьма затруднительно, даже с использованием
ЭВМ. Здесь на первый план выступают асимптотич.
методы, к-рые представляют интерес еще и тем, что
позволяют делать нек-рые общие заключения о рас-
рассматриваемой задаче. Под асимптотическими
методами Д. м. т. понимаются нек-рые приемы
нахождения приближенного выражения для искомых
функций. Приемы эти базируются на физнч. сообра-
соображениях и формальных преобразованиях, чаще всего
строго не обоснованных. Одним из первых приемов,
позволяющих находить в виде нек-рой квадратуры
приближенные решения коротковолновых задач ди-
дифракции, был Кирхгофа метод, широко применяю-
применяющийся и теперь при решении прикладных задач. Не
менее важное значение имеет лучевой метод, породив-
породивший целую серию приемов, позволяющих находить
асимптотику многих дифракционных задач. Построения
лучевого метода, как правило, бывает нетрудно про-
провести, если соответствующее поле лучей регулярно.
Если же оно имеет какие-либо особенности, то возни-
возникает ситуация, характерная для пограничного слоя
теории: везде, кроме нек-рой весьма малой окрест-
окрестности тех точек, где поле лучей теряет регулярность,
асимптотика решений известна. Нужно найтн ее только
в этой малой области, т. е. в пограничном слое. Соот-
Соответствующий аналог методики пограничного слоя по-
получил название параболического уравнения метода.
Он часто используется как для численного решения
задач Д. м. т., так и для вывода асимптотич. формул.
Важные асимптотич. формулы для решения задач
Д. м. т. могут быть получены в тех случаях, когда
известно явное выражение для решения. Это явное
решение по хорошо разработанной уже методике (так
наз. метод Ватсона) преобразуют в контурный
интеграл, асимптотика к-рого ищется либо примене-
применением перевала метода, либо теоремы о вычетах. Пред-
Представляет интерес тот факт, что полученные на этом
пути асимптотич. выражения иногда могут быть ис-
использованы как образец («эталон»), при помощи к-рого
можно «угадывать» вид асимптотич. разложения в
дифракционных задачах, явное решение к-рых неиз-
неизвестно. Именно такие построения характерны для
«метода эталонных задач», к-рый является дальнейшим
развитием метода параболич. уравнения.
Лит.: [1] Б а б и ч В. М., Б у л д ы р е в В. С, Асимпто-
Асимптотические методы в задачах дифракции коротких волн, М.,
1972; [2] В а й н ш т е й н Л. А., Теория дифракции и метод
факторизации, М., 1966; [3] Н и к о л ь с к и й В. В., Вариа-
Вариационные методы для решения внутренних задач электродинами-
электродинамики, М., 19С7; [4] К у п р а д з е В. Д., Граничные задачи тео-
теории колебаний и интегральные уравнения, М.—Л., 1950; [5]
КупрадзеВ.Д. и др., Трехмерные задачи математиче-
математической теории упругости, 2 изд., М., 1976; [6] Фридлендер
Ф., Звуковые импульсы, пер. с англ., М., 1962; [7] X ё н л X.,
МауэА., ВестпфальК., Теория дифракции, пер. с
нем., М., 1964; [8] С в е ш н и к о в А. Г., в кн.: International
congress of mathematicians, Vancouver, 1974, p. 29—30.
В. М. Бабич.
ДИФФЕОМОРФИЗМ, дифференцируемый
гомеоморфизм, гладкий гомсомор-
ф и з м,— взаимно однозначное и непрерывно диффе-
дифференцируемое отображение /: M-^-N дифференцируемого
многообразия М (напр., области в евклидовом про-
пространстве) в дифференцируемое многообразие Лг, обрат-
обратное к к-рому тоже является непрерывно дифференци-
дифференцируемым. Если /(M) = W, то говорят, что М и N д и ф-
феоморфны. С точки зрения дифференциальной
топологии, диффеоморфные многообразия имеют одина-
одинаковые свойства, и она интересуется классификацией
многообразии с точностью до Д. (последняя не совпа-
совпадает с более грубой классификацией с точностью до
гомеоморфизма, исключая случаи малых размерностей).
Хотя сам термин «Д.» был введен сравнительно
недавно, фактически многочисленные преобразования
и замены переменных, давно используемые в мате-
математике, являются Д., а многие семейства преобразо-
преобразований — группами Д. В частности, это относится к Д.,
сохраняющим ту или иную дополнительную структуру
на многообразии (напр., контактную, симплектическую,
конформную или комплексную). Исторически такие Д.
в ряде случаев получили особые названия (в указанных
примерах — контактные преобразования и канониче-
канонические отображения, конформные отображения и биго-
ломорфные отображения), вместо к-рых в последнее
время G0-е гг. 20 в.) нередко употребляют термин «Д.»
с добавлением прилагательного, характеризующего
сохраняемую структуру (напр., «спмплектический Д.»
вместо «канонического преобразования»).
Изучались и топологические (точнее, гомотопиче-
гомотопические) свойства группы DiffM всех Д. многообразия М
на себя, в к-рой надлежащим образом введена топо-
топология. Они могут быть неожиданно сложными (см.,
напр., [1], где имеются также обзор и библиография).
Этот вопрос связан с рядом важных задач гомотопич.
топологии (напр., с гомотопич. группами сфер). В прин-
принципе знание свойств DiffM помогло бы в решении этих
задач, однако в настоящее время A978) ситуация
является скорее обратной: продвижение в изучении
DiffM связано как раз с использованием того, что уже
известно об этих задачах, или, в лучшем случае, осу-
осуществляется параллельно с их решением и при помощи
тех же методов. Относительно алгебраич. свойств группы
Д. класса С (случай г= оо не исключается) замкну-
замкнутого /г-мерного многообразия доказано, что при гфп-j-i
ее связная компонента единицы является простой
группой, т. о. не имеет нетривиальных нормальных
делителей (см. [2], [3]; при г=л+1 ситуация не выяс-
выяснена). Для незамкнутого тг-мерного многообразия М
доказана простота группы всех тех Д. / класса С
[гфп--\), к-рые можно соединить с тождественным
отображением 1д; посредством непрерывного семей-
семейства Д. /(@«:?<:1, /о=1дь /i —/)> не сдвигающего точек
вне нек-рого компакта (зависящего от этого семейства).
Лит.: [1] AntonelliP. L., BurgheleaD., Kahn
P. J., «Topology», 1972. v. 11, Ns 1, p. 1 — 49; [2] Tliurs-
ton W., «Bull. Amer. Math. Sec», 1974, v. 80, ЛГ» 2, p. 304 —
307; [3] Mather J. N.. «Comment, math, hclf.», 1974, v. 49,
.45 4, p. 512 — 28; 1975, v. 50, Xs 1, p. 33 — 40. Д. В. Аносов.
J'-ДИФФЕОМОРФИЗМ — диффеоморфизм, порож-
порождающий У-систему.
ДИФФЕРЕНЦИАЛ — главная линейная часть при-
приращения функции.
1) Действительная функция y = f(x) действительного
переменного наз. дифференцируемой в точке
х, если она определена в нек-рой окрестности этой
точки и если существует такое число А, что прира-
приращение
Ay=f(x+Ax)-f(x)
(при условии, что точка х~\- Ах лежит в упомянутой
окрестности) может быть представлено в виде
Ау=А Ax-tol,
где а/Лж—<-0 при Аж-И). При этом А Ах обозначается
через dy И наз. дифференциалом функции
f(x) в точке х. Д. dy при фиксированном х пропорцио-
пропорционален Ах, т. е. является линейной ф у и к ц и е й
от- Ах. Дополнительный член а при Дж-^-0 явля-
является, в силу определения, бесконечно малой более вы-
высокого порядка по сравнению с Ах (и по сравнению
с dy, если А фО). Именно в этом смысле Д. и наз. глав-
главной частью приращения функции.
Для функции, дифференцируемой в точке х, Ау-^~О
при Дж-^-0, т. е. функция, дифференцируемая в не-
некоторой точке, непрерывна в ней. Функция f(x) диф-
дифференцируема в точке х в том н только в том случае,
если она имеет в этой точке конечную производную
/'(*)= lim -g = A;
при этом
dy = f (x)Ax.
Существуют непрерывные, но не дифференцируемые
функции.
Кроме обозначения dy используется обозначение
df(x); тогда предыдущее равенство принимает вид
df(x)==f (х)Ах.
Приращение аргумента Ах обозначается также через
dx и наз. дифференциалом независи-
независимого переменного. Поэтому можно писать
dy=f (x)dx.
Отсюда /' {x) = dy!dx, т. е. производная равна отно-
отношению Д. dy и dx. Если Л = 0, то Ay/dy—*-i при Дж-^0,
т. е. Ау и dy при Дж-^-0 являются в случае АфО эк-
эквивалентными бесконечно малыми; этим, равно как
и простой структурой Д. (линейностью по Ах), часто
пользуются в приближенных вычислениях, полагая
Ay^dy при малых Ах. Если хотят, напр., вычислить
f(x-\-Ax), зная /(ж) (Ах мало), то полагают
Конечно, такое рассуждение имеет ценность, если
можно оценить соответствующую погрешность.
Геометричес к ое
истолкование Д.
Уравнение касательной к
графику функции y=f(x)
в точке М (х„, у0) имеет
вид y—yo = f (xo)(x—х0). Ес-
Если положить х=х0^- Ах, то
У—i/o=/' (хо)Ах. Правая
часть есть значение Д. функ-
функции f(x) в точке х0, отвечаю-
отвечающее рассматриваемому зна-
значению Ах. Таким образом,
Д. совпадает с соответствую-
соответствующим приращением ординаты
касательной к кривой y=f{x) (см. отрезок NT на рис. 1).
При этом а= Ау—dy, т.е. значение |а| совпадает с
длиной отрезка TS.
2) Определение дифференцируемое™ и Д. естест-
естественным образом обобщается на действительные функ-
функции от п действительных переменных. Напр., в случае
п=2 действительная функция z=f(x, у) наз. диффе-
дифференцируемой в точке (х, у) по совокупности перемен-
переменных х и у, если она определена в нек-рой окрестности
этой точки и ее полное приращение
Az=f(x+Ax, y-{-Ay)—f(x, у)
может быть представлено в виде
Az-=A Ах+ВАу+а,
где А и В — некоторые числа, а/р—>-0 при р—*-0, р=
= У Ахг-г Ау2; предполагается, что точка (х-\- Ах, у-\- Ау)
принадлежит упомянутой окрестности (см. рис. 2).
При этом вводится обозначение
dz=df(x, у) = ААхцгВАу
и dz наз. полным дифференциалом, или
просто дифференциалом, функции f(x, у)
в точке (х, у) (иногда с добавлени- ^. ^
ем: «по совокупности переменных х / ц+Ьх^у+Ьу!
и у»). Для фиксированной точки (х,у) / VT ' \
Д. dz есть линейная функция { Р \fx y) J
от Ах и Ау; разность а= Az—dz есть t ' /
бесконечно малая более высокого \ /
порядка по сравнению с р. В этом *ч^ ^,''
смысле dz есть главная линей- Ри^, 2
ная часть приращения Дг.
Если f(x, у) дифференцируема в точке (х, у), то она
непрерывна в этой точке и имеет в ней конечные част-
частные производные
fx(x, y) = A, f'y(x, y)=B.
Таким образом
dz = df(x, y) = f'x(x, y)Ax-\-f'y(x, у) Ay.
Приращения Ах и Ау независимых переменных, как
и в случае одного переменного, обозначаются dx и dy.
По этой причине можно написать
dz = df(x, y) = f'x(x, у) dx-\-fy(x, y)dy.
Существование конечных частных производных, во-
вообще говоря, не влечет дифференцируемости функции
(даже если предполагать заранее ее непрерывность)—•
здесь нарушается аналогия с функциями одного пере-
переменного.
Если функция f(x, у) имеет в точке (х, у) частную
производную по х, то произведение fx(x, y)dx наз. ее
частным дифференциалом по х; анало-
аналогично, f'y(x, y)dy есть частный Д. по у. Если функция
дифференцируема, то ее пол-
flx,y)- ный Д. равен сумме част-
частных Д. Геометриче-
Геометрически полный Д. df(xQ, т/0)
есть приращение апплика-
аппликаты касательной плоскости к
поверхности z=f(x, у) в точ-
точке (ж0, у0, zo), где zo=f(xo, y0)
(см. рис. 3).
Достаточный приз-
признак дифференцируемо-
дифференцируемому' сти функции: если в некс-
Рис. з. торой окрестности точки
(жо> У а) функция f(x, у) име-
имеет частную производную f'x , непрерывную в точке
(х0, у0), и, кроме того, имеет в точке (х0, у0) частную про-
производную fy, то f(x, у) дифференцируема в этой точке.
Если функция f(x, у) дифференцируема в каждой
точке открытой области D, то в любой точке этой области
dz=--A(x, y)dx+B{x, y)dy,
причем А (х, y) = fx(x, у), В(х, y)=f'y(x, у). Если при
этом существуют непрерывные в D частные производ-
производные Ау и В'х, то всюду
А'у^В'х.
Это показывает, в частности, что не всякое выражение
А (х, y)dx+B(x, y)dy
с непрерывными А и В (в области D) является в этой
области полным Д. нек-рой функции двух переменных.
В этом состоит еще одно нарушение аналогии с функ-
функциями одного переменного, где любое выражение
A (x)dx с непрерывной в нек-ро.м промежутке функцией
А (.г) служит Д. для нек-рой функции.
Выражение Adx^-Bdy является полным Д. нек-рой
функции z=f(x, у), в односвязной открытой области D,
если Л (ж, у) и В (х, у) непрерывны в этой области и
удовлетворяют условию А' = В'Х и при этом а) А'( и В'х
непрерывны или б) А (х, у) и В (х, у) дифференцируемы
по совокупности переменных х и у всюду в D (см.
[7], [8]).
О Д. действительных функций одного или несколь-
нескольких действительных переменных и о Д. высших поряд-
порядков см. также Дифференциальное исчисление.
3) Пусть функция f(x) определена на нек-ром мно-
множестве Е действительных чисел, х — предельная точка
этого множества, х?Е, x^-AxQE, Ay=A Дж+а, где
а/Дж-ч>-0 при Дж—>-0; тогда функция f(x) наз. диффе-
дифференцируемой по множеству Е в точке
х, a dy=A Ax наз. ее дифференциалом по
множеству Е в точке х. Это есть обобщение Д.
действительной функции одного действительного пе-
переменного. Разновидностями этого обобщения являют-
являются Д. в концах промежутка, на котором определена
функция, и аппроксимативный Д. (см. Аппроксиматив-
Аппроксимативная дифференцируемоетъ).
Подобным же образом вводится Д. по множе-
множеству для действительных функций многих дей-
действительных переменных.
4) Все эти определения дифференцируемости и Д.
почти без изменений распространяются соответственно
на комплексные функции одного или нескольких
действительных переменных, на действительные и
комплексные вектор-функции одного или нескольких
действительных переменных, на комплексные функции
и вектор-функции одного или нескольких комплексных
переменных. В функциональном анализе они распро-
распространяются на функции точки абстрактного простран-
пространства. Можно говорить о дифференцируемости и Д.
функции множества по отношению к нек-рой мере.
Лит.: [1] Т о л с т о в Г. П., Элементы математического
анализа, 2 изд., т. 1—2, М., 1974; [2] ФихтенгольцГ. М.,
Курс дифференциального и интегрального исчисления, 7 изд.,
т. 1, М., 1969; [3] К у д р я в ц е в Л. Д., Математический ана-
анализ, 2 изд., т. 1, М., 1973; [4] Никольский С. М., Курс
математического анализа, 2 изд., т. 1, М., 1975; [5] Р у д и н У.,
Основы математического анализа, пер. с англ., М., 1966; [6]
Колмогорова. Н., Ф о м и н С. В., Элементы теории
функций и функционального анализа, 4 изд., М., 1976; L7]
ТолстовГ. П., О криволинейном и повторном интеграле,
М,—Л., 1950 (Тр. Матем. ин-та АН СССР, т. 35); [8] его ж е,
«Успехи матем. наук», 1948, т. 3, в. 5, с. 167 — 70.
Г. П. Толстое.
ДИФФЕРЕНЦИАЛ НА РИМАНОВОЙ ПОВЕРХНО-
ПОВЕРХНОСТИ — дифференциальная форма на римановой по-
поверхности S, инвариантная относительно конформного
преобразования локального униформизирующего
параметра z=x-\-iy. Чаще всего встречаются дифферен-
дифференциалы (д.) первого порядка — это диффе-
дифференциальные формы размерности 1, линейные относи-
относительно дифференциалов каждой из переменных (х, у),
вида
<u=pdx-\-qdy=p(x, y)dxJrq(x, y)dy,
n — rdx-\-sdy,
инвариантные относительно замены параметра, с до-
достаточно гладкими коэффициентами р, д, . . .; д. ну-
нулевого порядка — это достаточно гладкие ком-
комплексные функции f=f(x, у), g=g(x, у), ..., инвари-
инвариантные относительно замены параметра, т. е. функции
точки Pf5; д. второго порядка имеют вид
Q = Adxdy=A (х, y)dxdy, U.=Bdxdy.
Все д. на римановых поверхностях порядков &>2
тождественно равны 0.
Сложение д. на римановых поверхностях одного и
того же порядка определяется естественным путем:
f+g, w+ji= {p + r)dx+ (q+s)dy, Й + П= (A+B)dxdy,
оно коммутативно и ассоциативно. Внешнее ум-
умножение д. на римановых поверхностях дистри-
дистрибутивно относительно сложения, обозначается знаком
Л и определяется правилами:
/ Л g = fg; / Л со = (fp) dx + (fg) dy,
dx Л dx = dy Л dy = 0, dy Л dx = — dx Л dy = — dx dy;
отсюда
<BAJt^(ps— qr)dxdy, яЛсо =—соЛя; /ЛЙ = (fA)dxdy.
Вообще, при внешнем умножении д. порядка к на
д. порядка I при к-{-1<.2 получается д. порядка к-\-1,
а при /с + />2 — тождественный нуль. Линейный опе-
оператор дифференцирования d= -^dx-{--g— dy переводит
д. порядка к в д. порядка й+1:
,, а/ , , э/ ,
=^.— ^ dxdy, dfi=0.
Кроме того,
d(fg)=fdg+gdf,
d(fa>)= {df)a+f(d(o)=-(o(df)+f(d(o)
и всегда dd=O. Для д. на римановых поверхностях
важен также линейный оператор звездного
сопряжения
*<в = — qdx-i-pdy.
При этом
* (/ЛО)) = /л(* со), <вл(*я) = ял(* (й) = (рг-\- qs) dx dy,
сол(*со) = (р2 + д2) dxdy, *d = — -^dx + -^dy,
* (df) = (* d) /, (* d) со = * dco = — d * со.
Оператор звездного сопряжения не совпадает с опе-
оператором комплексного сопряжения. Последний обо-
обозначается чертой: если f=g-\-ih, то f=g—ih, (o=pdx-\-
¦\-qdy, Q=Adxdy; далее, dco=dco, *co=*co. Оператор
Лапласа &=d*d определен на д. нулевого порядка:
Дифференциал со наз. точным, если существует
функция / на S такая, что всюду a>=df, если a=*df,
то со наз. коточным; д. со наз. замкнутым,
если dco=0 на S, если d*a>=0, то со — козам к-
н у т ы й д. Из точности вытекает замкнутость, но
обратное неверно. Пусть clt с2, . ..— циклы на S.
Интегралы \ со, \ со, ..., называемые п е р и о-
дами дифференциалам, определяются обыч-
обычным образом при помощи локальных униформизирую-
щих. Если сх и с2 гомологичны на S и со — замкнутый
д., то \ (о= \ со, т. е. периоды замкнутого д.
•J С\ •) Сг
зависят только от класса гомологии. Все периоды точ-
точного д. равны нулю. Обратно, замкнутый д. является
точным тогда и только тогда, когда все его периоды
равны 0.
Функция /?С2 наз. гармонической на S,
если Д/=0. Дифференциал со^С1 наз. гармони-
гармоническим дифференциалом на S, если со
замкнут п козамкнут, dco=d*co=0. Гармонич. д. со
является полным дифференциалом гармонич. функции
в окрестности каждой точки P0?S. Если действитель-
действительные функции и, v^C1 на S связаны соотношением
dv=*du, то они суть сопряженные гармонич. функции,
удовлетворяющие условиям Коши — Римана. Следо-
Следовательно, функция f=uJ^iv?iC1 является регу-
регулярной аналитической, или голоморф-
голоморфной, на S, если *d/= — idf. Дифференциал со?Сх
наз. регулярным аналитическим, или
голоморфным, дифференциалом на S,
если dco=O и *со= — tсо. Голоморфный д. о> является
полным дифференциалом голоморфной функции в
окрестности каждой точки Ро ? S. Голоморфный д. со
представим локально в виде w=fdz, где dz= d,r+ idy,
a f — голоморфная функция от z.
Классы эквивалентности измеримых комплексных диф-
дифференциалов на римановой поверхности, для к-рых ин-
интеграл^ \ о>Л (*со) конечен, образуют гильбертово про-
пространство L2(S) с обычным сложением, умножением
на комплексные скаляры и скалярным произведением
(со, л)=\\ сод (*л). Каждый д. со класса L2(S) Г) C3(S)
единственным образом представим в виде суммы со=
= <x>fl-rdf-{-*dg, где /, g?C2(S) и coft — гармонический
д. на римановой поверхности.
Рассмотренные выше гармонические и голоморфные
функции или д. класса С1 на S наз. регулярными
на S. Пусть в проколотой окрестности U точки P0?S
определен д. 9, к-рый, напр., гармоничен в U. Тогда
говорят, что гармонич. д. со имеет особенность
9 в Ро, если разность со—9 является регулярным гар-
гармонич. д.
Аналогичные определения применяются для гармо-
гармонич. и аналитич. функций, аналитпч. д. и т. п. В част-
частности, в случае аналитического д. a=fdz
обычно предполагается, что функция / либо регулярная
аналитическая в окрестности каждой точки P0?S,
либо имеет на S лишь изолированные особые точки
однозначного характера. Аналитич. д. со, имеющий
на S только особенности в виде полюсов
наз. мероморфным дифференциалом;
при этом а-пф0, п — порядок полюса, при п=1 полюс
наз. простым, <г_!— вычет д. со в полюсе Ро. Меро-
морфные д. на компактной римановой поверхности S
наз. абелевыми дифференциалами. Гармонич. функции
на S или на нек-рой области DczS, имеющие заданные
особенности, иногда наз. абелевыми потен-
потенциалам и.
Интегрирование абелевых д. приводит к абелевым
интегралам, исчерпывающим в сущности все инте-
интегралы от алгебраич. функций. При изучении аналитич.
д. на произвольной, вообще говоря, некомпактной
римановой поверхности S естественное требование со-
сохранения основных черт классич. теории д. на ком-
компактных рпмановых поверхностях приводит к необ-
необходимости наложить на рассматриваемые регулярные
д. дополнительные конформно инвариантные ограни-
ограничения, наиболее употребительным из к-рых является
условие интегрируемости, напр., аналитич. д. <i)=fdz
с квадратом, т. е. условие конечности интеграла Ди-
Дирихле:
И|/ \2dxdy < -J-oo.
S
В теории д. на римановых поверхностях основное
значение имеет проблема существования гармонич.
и аналитич. д. с заданными особенностями на произ-
произвольной римановой поверхности 5. С этим вопросом
непосредственно связана проблема глобальной унифор-
мизации римановых поверхностей, т. к. построение
глобальной униформизирующей требует именно умения
строить д. с заданными особенностями.
Ниже приведены основные результаты по проблеме
существования.
Если на 5 существует цикл с, не гомологичный нулю,
то на S существует всюду регулярный гармонич. д.
со с периодом \ со^О и всюду регулярный аналптич.
д. со+?*со. Эти д. не являются точными, и поэтому
при их интегрировании нельзя получить однозначных
на S гармонич. или аналитич. функций. На компактной
римановой поверхности S всякий гармонический И
точный д. тождественно равен нулю. Напротив, на
некомпактных римановых поверхностях существуют
отличные от тождественного нуля всюду регулярные
точные гармонические и голоморфные д.
Пусть Ро — любая фиксированная точка произволь-
произвольной римановой поверхности S, п — любое натуральное
число. Тогда существуют: точный гармонич. д. с осо-
особенностью d(ilzn) в Ро; точный действительный гар-
гармонич. д. с особенностью Re d(i/z") или Imd(l/z") в
Ро; гармонич. функция с особенностью l/zB в Ро; ана-
аналитич. д. с особенностью d(ilzn) в Ро, у к-рого дей-
действительная часть есть точный д.
Пусть Ро и Р[ - любые различные точки S. Тогда
существуют: гармонич. или аналитич. д. на S с особен-
особенностями —dzlz в Ро и dzlz в Рг; действительная гар-
гармонич. функция на 5 с особенностями —ln|z| в Рй и
1пЫ в Pi.
Пусть Ро, Ри .. ., Р„ — любые попарно различные
точки на S и с0, clt . . ., сп— любые отличные от нуля
комплексные числа такие, что со-)-с1+- • .-\-сп=0. Су-
Существует гармонический или аналитический д. на S,
всюду регулярный, кроме Ро, Рг, . . ., Р„, а в точках
Рj имеющий простые полюсы соответственно с вычетами
с', 1 = 0, 1, ..., п.
Для жордановых областей DdS, т. е.
таких областей, граница к-рых 6D состоит из п непере-
непересекающихся жордановых кривых с1г с2, . . ., с„, воз-
возможно также решение Дирихле задачи.
Наиболее законченной является теория д. для ком-
компактных римановых поверхностей 5. Пусть род S
равен g. Векторное пространство fe регулярных гар-
гармонич. д. со над полем комплексных чисел имеет раз-
размерность 2g. Если a1b1a2b2. . .agbg — циклы канонич.
базиса гомологии S, то в качестве канонич. базиса д. §
можно выбрать д. со/, ?=1, 2, . . ., g, с периодом 1 вдоль
а/, а вдоль ау, ]ф1, и вдоль всех 6,- — с периодом 0;
далее, cOg. + /, ?=1, 2, . . ., g, имеют период 1 вдоль 6/,
а вдоль bj, ]ф1, и вдоль всех а,- — период 0. Любой
гармонич. д. со представляется в виде линейной ком-
комбинации
где А; — так наз. А -периоды со вдоль циклов a,-, a Bi
суть Л-периоды со вдоль циклов Ь[.
Голоморфные д. на компактной римановой поверх-
поверхности наз. абелевымп дифференциала-
дифференциалами первого рода. Размерность векторного
пространства голоморфных д. равна g.
Все введенные выше д. на римановой поверхности
можно выразить через переменные z и z, напр.:
/ = /(z, z), CO — pdz-\-qdz =p (z, z) dz^-q (z, z) dz,
Q = AdzAdz = A(z, z) dz л dz
и т. д. В отличие от комплексных многообразий выс-
высших размерностей, на римановых поверхностях не-
нетривиальны только внешние дифференциальные формы
типов @, 0), A, 0), {0, 1) и A, 1), имеющие соответст-
соответственно вид /, pdz, qdz, Adz Adz. При этом аналитич. д.
зависят только от z:
/=/(z), со=р (z)dz.
Применяются также нелинейные дифференциальные
формы вида p(z, z)dzmdzn, где т и п — целые числа.
Они также наз. дифференциалами типа (т, п), или
размерности (т, п). При этом д. типа @, 0)
наз. функциями, типа A, 0) — линейным и
дифференциалами, типа (—1, 0) — обрат-
обратными дифференциалами, типа B, 0) —
квадратичными дифференциалами.
Наибольшие применения получили квадратичные диф-
дифференциалы. См. также Глобалы1ая структура траек-
траекторий, Локальная структура траекторий, Риманоеа
поверхность, Униформизация.
Лит.: [1] Спрингер Д т., Введение в теорию римано-
римановых поверхностей, пер. с англ., М., I960; [2] Н е в а н л и н-
н а Р., Униформизация, пер. с нем., М., 1955; [3] Ш и ф ф е р
М., Спенсер Д. К., Функционалы на конечных римановых
поверхностях, пер. с англ., М., 1957; L4] В е h n k e H., S о ю-
merF., Theorie der analytischen Funktionen einer komplexen
veranderlichen, В., 1955. E. Д. Соломенцев.
ДИФФЕРЕНЦИАЛОВ МОДУЛЬ, модуль к э-
леровых дифференциалов,— алгебраиче-
алгебраический аналог понятия дифференциала функции. Пусть
А — коммутативное кольцо, рассматриваемое как ал-
алгебра над своим подкольцом В. Д. м. 5-алгебры А
определяется как фактормодуль Од/В свободного А-
модуля с базисом (dx)xiA по подмодулю, порожден-
порожденному элементами вида
d(x-fy)—dx—dy, d(xy)—xdy—ydx, db,
где x, y?A, b?B. Канонич. гомоморфизм Л-модулей
d: A—>-Q\/b является Л-дифференцированием кольца
А (см. Дифференцирование кольца) со значением в
А -модуле Й^'д, обладающим следующим свойством уни-
универсальности: для любого Л-дифференцирования д:
А—уМ со значением в А -модуле М существует однознач-
однозначно определенных"! гомоморфизм А -модулей д : Q^,B-+M
такой, что dod=d. Соответствие д—*-д определяет изо-
изоморфизм А-модулей
Tierв (А, М)^ЯогаД(п\/в, М) .
В частности, модуль дифференцирований кольца А
в себя изоморфен двойственному А -модулю к модулю
«А/В-
Если А(х)вА рассматривать как Л-алгебру относи-
относительно гомоморфизма
А~>А®ВА (а-+а®1)
и / — идеал, порожденный элементами вида
GBI — 1 (g)a,
то А -модуль Q\/B изоморфен А -модулю III2.
Д. м. Q1 обладает следующими свойствами:
1) Если S — мультипликативно замкнутое множе-
множество в А и Т= S П В, то существует канонич. изоморфизм
локализации
2) Если q~: А-^~А' — гомоморфизм 5-алгебр, то оп-
определена каноническая точная последовательность А'-
модулей:
3) Если / — идеал кольца А ц А' = А/1, то сущест-
существует каноническая точная последовательность Л'-мо-
Л'-модулей:
где гомоморфизм d' индуцирован дифференцированием
4) Поле К является сепарабельным расширением
поля k конечной степени трансцендентпостщ п в том
и только в том случае, когда существует изоморфизм
if-пространств Q^^&sK".
5) Если А=В [7*!, ..., Тп] — алгебра многочленов,
то QA в свободный Л-модуль с базисом dT1, . . ., dT n.
6) Алгебра Л конечного типа над совершенным
полем к Является регулярным кольцом тогда и только
тогда, когда Л-модуль йд,,й проективен.
7) В свойстве 2) Л-алгебра Л' конечного типа яв-
является гладкой над Л тогда и только тогда, когда
гомоморфизм а ннъективен, а Д. м. пА,,^ проективен
и его ранг равен относительной размерности А' над Л.
Внешняя степень aQa/B Д. м. Qa/b наз. м о д у-
лем дифференциальных ?-ф о р м Л-ал-
гебры Л и обозначается Q\,B.
Свойство 1) позволяет для любого морфизма схем
X—»-У определить пучок относительных
(или кэлеровых) дифференциалов &x/Y
и их внешние степени пгХ/,у-
Лит.: [1] Ш а ф а р е в и ч II. Р., Основы алгебраической
геометрии, М., 1972; 12] Grothendieck A., Revetements
Stales et groupe fondamentale, В. —Hdlb.—N. Y., 1971; [3J его
же, «Publ. math. IHES», 1964, Л! 20; [4] Kahler E.,
Algebra und Differentialrechmmg, В., 1958. И. В. Долгачев.
ДИФФЕРЕНЦИАЛЬНАЯ АЛГЕБРА — алгебра Л
над полем (кольцом) К, являющаяся дифференциаль-
дифференциальным кольцом; при этом каждое дифференцирование д
должно коммутировать с умножениями на элементы
из К, т. е. д(ах)==ад(х), где а?А', х?А.
О. А. Иванова.
ДИФФЕРЕНЦИАЛЬНАЯ АЛГЕБРА — раздел ал-
алгебры, изучающий объекты, в к-рых, наряду с опера-
операциями сложения и умножения, имеются операции диф-
дифференцирования: дифференциальные кольца, диффе-
дифференциальные модули, дифференциальные поля, диф-
дифференциальные алгебраич. многообразия.
Один из основных объектов Д. а.— алгебра диф-
дифференциальных полиномов(jp{Уj, . . ., У,,}, являющаяся
аналогом кольца многочленов в коммутативной ал-
алгебре (см. Расширение дифференциального поля). Каж-
Каждой системе дифференциальных уравнений
F\ = 0, . F/i = 0
ставится в соответствие совершенный дифференциаль-
дифференциальный идеал {/"], . .., /''*:}, порожденный этой системой
в алгебре дифференциальных полиномов. Теорема
Р н т т а — Рауденбаха о базисе утверждает,
что таким образом получаются все совершенные диф-
дифференциальные идеалы (дифференциальный идеал /
наз. совершенным, если из а" ?1 для нек-рого
n>0 следует, что а?1), т. е. в любом из них можно
выбрать конечное число дифференциальных полиномов
таких, что совершенный дифференциальный идеал,
порожденный этими полиномами, совпадает с данным. В
отличие от теоремы Гильберта о базисе в кольце много-
многочленов, в теореме Ритта — Рауденбаха существенна
совершенность идеалов, т. е. дифференциальный идеал
(даже совершенный) может не являться конечно по-
порожденным дифференциальным модулем.
Совершенному дифференциальному идеалу ставится
в соответствие дифференциальное алгебраич. много-
многообразие — множество точек в аффинном пространстве
над нек-рым универсальным расширением поля коэф-
коэффициентов, аннулирующих любой полином из данного
идеала. Имеет место аналог теоремы Гильберта о нулях.
Пусть F1, . . ., Fр — конечная система дифференци-
дифференциальных полиномов и пусть G — дифференциальный
полином, обращающийся в нуль во всех решениях
данной системы. Тогда некоторая степень полинома G
является линейной комбинацией полиномов F и их
производных разного порядка с коэффициентами из
алгебры дифференциальных полиномов. В частности,
если система /\, . . ., Fр не имеет нулей, то нек-рая
линейная комбинация полиномов F и их производных
разного порядка равна единице.
Совершенный дифференциальный идеал допускает
представление в виде пересечения конечного числа
простых дифференциальных идеалов. Этому представ-
представлению соответствует разложение многообразия на
конечное число неприводимых компонент. Для простых
дифференциальных идеалов вводится понятие общего
нуля и его размерности, как и в алгебраич. геометрии.
Для неприводимого замкнутого множества V в диф-
дифференциальном аффинном пространстве, т. е. в аффин-
аффинном пространстве над универсальным расширением U
поля коэффициентов, определяется дифференциальный
размерностный полином
K>V= > a
где т — количество дифференцирований в поле F.
Коэффициент ат наз. дифференциальной
размерностью множества V, степень полинома
T=deg coy — дифференциальным типом
множества V, а коэффициент а% — его типичной
дифференциальной размерностью. Полином coy яв-
является бирациональным инвариантом, но не является
дифференциальным бирациональным инвариантом. Та-
Таковыми будут am(V), r(V) и aX{V)(V). Нахождение
дифференциальных бирациональных инвариантов пред-
представляет значительный интерес. Другая проблема —
оценить возможные значения полученных инвариантов.
Пусть 2 — подмножество в §r{Y1, . . ., У,,}. Если эле-
элементы из 2 имеют ограниченный порядок, то диффе-
дифференциальные размерностные полиномы компонент {2 }
подчинены некоторым ограничениям. В частности,
если для каждого Y j порядок относительно Yj любого
элемента из 2 не превосходит еу, то для любой компо-
компоненты многообразия {2 } из условия ат(р)=О следует,
что ат_!(р)<:2еу. В общем случае имеется гипо-
гипотеза, что
Если множество Serf {Ylt ..., Yn} состоит из п диф-
дифференциальных полиномов Flf ..., Fn, то выдвигаются
еще две гипотезы. Пусть
где я пробегает симметрии, группу S„. Первая гипо-
гипотеза утверждает, что для любой компоненты р много-
многообразия {/"j, . . ., Fn}ii3 а,л(р) = О следует, что am_x(^)^:
¦</г. Это предположение доказано в нек-рых частных
случаях. Вторая гипотеза состоит в том, что для любой
компоненты р многообразия {Flt . . ., F„} из <гст(р) =
= aw_1(p) = O следует, что сор = 0.
Одной из сложных проблем, исследуемых Д. а.,
является проблема разложения дифференциально ал-
гебраич. многообразия на неприводимые компоненты.
Даже если система 2 состоит из одного неприводимого
дифференциального полинома ст, то соответствующее
многообразие состоит, в общем случае, из нескольких
компонент, одна из к-рых содержит все неособые
решения уравнения ст— О (хотя может содержать и
особые решения), а все остальные компоненты состоят
из решений, обращающих в 0 любую сепаранту
дифференциального полинома ст. Случай гиперповерх-
гиперповерхности (система 2 из одного уравнения) особенно важен,
т. к. всякое дифференциально алгебраич. многооб-
многообразие над обыкновенным дифференциальным полем
дифференциально бирационально изоморфно гиперпо-
гиперповерхности.
Поскольку всякий простой дифференциальный идеал
полностью определяется своим характеристич. множе-
множеством, проблему разложения дифференциально алге-
алгебраического многообразия {р} можно разделить на
две: 1) найти конечное множество 3( авторедуцирован-
авторедуцированных подмножеств в §~{Ylt . . ., У,,}, каждое из к-рых
является характеристич. множеством простого диффе-
дифференциального идеала, содержащего Ф, такое, что %
включает в себя характеристич. множество каждой
компоненты {Ф}; 2) для данного авторедуцированного
множества в йГ{Уц • ¦ ., Y„} определить, является ли
оно характеристич. множеством какой-нибудь компо-
компоненты {Ф }.
Решение проблемы 2) в общем случае не известно
A978), но в важном специальном случае, когда Ф со-
состоит из одного дифференциального полинома, полное
решение дается двумя теоремами Ритта: теоремой о
компонентах и теоремой о низких степенях (см. ниже).
Задача нахождения компонент многообразия {ф}
может быть также редуцирована к проблеме 1) и сле-
следующей проблеме: 3) для данных характеристич.
множеств А и В простых дифференциальных идеалов
р и С| соответственно определить, имеет ли место
включение Ipcq.
Проблема 3) также далека от решения. В частном
случае, когда А состоит из одного неприводимого диф-
дифференциального полинома А и q является дифферен-
дифференциальным идеалом [ylt . .., У„], это — задача о том,
лежит ли точка @, . . ., 0) в общем решении диффе-
дифференциального уравнения А=0.
Проблема 1) решена для конечного множества
OcrJFfyi, • • •> Yп} «в принципе»: при помощи индуктив-
индуктивной процедуры (теория исключения для систем алгебраи-
алгебраических дифференциальных уравнений) она сводится к
некоторым «более легким» задачам о многочленах от ко-
конечного числа неизвестных над JF, т. е. задача об алге-
алгебраических дифференциальных уравнениях сводится
к задаче об алгебраич. уравнениях.
Теорема о компонентах утверждает, что особые ком-
компоненты являются в свою очередь общими компонен-
компонентами других дифференциальных полиномов, точнее:
пусть JP—дифференциальное поле и F—ненулевой диф-
дифференциальный полином в |Г{Уъ •¦-,Yn). Если р—ка-
р—какая-либо компонента идеала {F} кольца JF{^i, ..., У п},
то существует неприводимый дифференциальный поли-
полином 5€JF0'i> ••¦¦> Yn) такой, что р=ру(В)—общая
компонента многообразия {В}.
Теорема о низких степенях дает
критерий для определения того, является ли общая
компонента неприводимого дифференциального поли-
полинома A ^§r{Y1, . . ., У„} компонентой для {F}. Точнее,
пусть F, A^:gr{Y1, . .., У,,}, порядки F и А относи-
относительно У„ равны т и I соответственно, А/ есть /-я
производная от А и S — сепаранта для А. Сущест-
Существуют г^О н г>0 такие, что
где pj^O, ikj^O, никакие два множества i1}-, . . .,
im-i,j не совпадают, порядок cj относительно Yn не
превосходит I и cj не делится на А. Если найдено такое
разложение, то теорема о низких степенях гласит:
общая компонента многообразия {А } является компо-
компонентой многообразия {F} тогда и только тогда, когда
выписанное разложение содержит член с^АРк, сво-
свободный от производных А, и степень к-рого ниже
степени любого другого слагаемого в выписанном
разложении, рассматриваемом как полином от А, Аг,
..., Ат_1(в ненулевой характеристике это условие не
является ни необходилшм, ни достаточным).
Другое направление исследований в Д. а. пред-
представляет вопрос о расширении специализации. Пусть
(%, ..., т)„) и (?!, . . ., ?„) — точки в U", где U — уни-
универсальное расширение дифференциального поля Цр.
Точка (?ь . . ., ?„) наз. дифференциальной
специализацией точки (т]1? . . ., т]„) над JF
(что обозначается (тI? . . ., Т]п)—»-(?i, ..., ?,п)), если лю-
любой дифференциальный полином, обращающийся в
нуль в (т)!, . . ., т]„), обращается в нуль и в (?i, • ¦ •, Sn)-
Если {т}1? ..., !!„)-)-(?!, ..., gn) и 1</с<тг, то очевидно,
что (т]!, ..., Tit)->-(?i, ..., g/). Говорят, что первая
специализация является расширением второй.
Пусть даны (т)ь . . ., т),,) и к и пусть ??JF{У1, . . ., Y„}
таков, что ^(т]!, . . ., т]„)^=0. Доказано, что существует
ненулевой дифференциальный полином 50?,fF{У1, . - .,
У^}, удовлетворяющий условию ^0A1!, . . ., г\к)ф0,
и такой, что любая дифференциальная специализация
(г\и . . ., T)ft)->-(Si, •• ., t*), для которой 50(gl7 . . ., t,t)?=0,
может быть расширена до дифференциальной специа-
специализации (т)!, . .., т)„)->-(?!, . .., ?«), где В(^, ..., ?п)ф0.
Однако, в отличие от ситуации в алгебраич. геомет-
геометрии, дифференциальная специализация (t^, . . ., т|^)—>•
W
(Si, • • -I Sa) не всегда может быть расширена до диффе-
дифференциальной специализации (ци ..., T]n)-^-(J1, . . ., ?„)
даже если элементы St + i, ••¦, Sn будут принимать
значение оо. Таким образом возникает задача: най-
найти критерий, когда дифференциальная специализа-
специализация (т)!, .. ., T]ft)—»-(?i, • •-i Sft) может быть расширена
до дифференциальной специализации (лх, ..., г]„)—>-
(Ei, -.., р-
Частный случаи этой проблемы встречается в про-
проблеме неопределенных форм. Пусть полиномы F,
GQgr{Y1, ..., У,,} взаимно простые, вфО, и F и G
обращаются в нуль в точке @, ..., 0). Проблема со-
состоит в том, чтобы отношению FlG приписать значение
в точке @, . . ., 0). Пусть элементы tlf . . ., tn? U диф-
дифференциально алгебраически независимы над %f и
u = F{t^ ..., tn)IG(tu ..., tn).
Естественно сказать, что FlG допускает значение а
в точке @, .. ., 0), если (tu ..., tn, u)->-@, ..., 0, а).
W
Таким образом проблема сводится к нахождению рас-
расширений (*!, ..., ?„)->-@, ..., 0) до (tlf ..., tn, и). Это
эквивалентно определению элементов a?U таких, что
(О, . . ., О, а) является нулем общей компоненты диф-
дифференциального полинома Yn + 1G— F?$~{Yl7 . . .,Yn + 1].
Дж. Рнтт (J. Ritt) предположил, что а либо опреде-
определено однозначно (возможно, равно то), либо полно-
полностью произвольно; он доказал это предположение для
обыкновенных дифференциальных полей при п=1,
ordG?G)=l. Изучаются свойства конкретных диффе-
дифференциальных идеалов в кольце tf{Ylt . . ., Y,,}. Для
бесконечной последовательности 2Ь . . ., 2^, ... про-
простых дифференциальных идеалов в JF{Ti, . . ., Y п),
где каждый 2 ,• — собственный делитель идеала 2,- + 1,
пересечение всех 2 ,• является простым дифференци-
дифференциальным идеалом и размерность соответствующего мно-
многообразия Щ1 больше размерности многообразия Щ[,
соответствующего 2/ для любого i.
Из других результатов о дифференциально алге-
бранч. многообразиях следует отметить аналог теоремы
Люрота: если (М расширение дифференциального ноля
JF, к-рое содержится в <f~<м>, то & содержит элемент v
такой, что (f"<f>=0'.
Однако теория дифференциально алгебраич. кривых
(многообразий дифференциальной размерности 1) на-
находится в начальной стадии развития; даже для таких
инвариантов, как род кривой в алгебраич. геометрии,
дифференциально алгебраич. аналоги не найдены.
Значительный интерес представляет теория пересече-
пересечений дифференциально алгебраич. многообразий. Для
них неверно утверждение, что пересечение двух не-
неприводимых многообразий размерности р и q в «-мер-
«-мерном аффинном пространстве имеет размерность не
менее р-\-д—п. Однако дифференциально алгебраич.
многообразия, кроме размерности, характеризуются
также порядком относительно выбранного базиса диф-
дифференциальной трансцендентности. Для порядка пере-
пересечения многообразий относительно специальным об-
образом выбираемого базиса получены нек-рые оценки
сверху. В аналитическом случае доказана следующая
теорема о пересечении компонент одного дифференци-
дифференциального полинома: если F — дифференциальный по-
полином от неизвестных Уь . . ., Y„, то нуль полинома F,
содержащийся более чем в одной компоненте F, анну-
аннулирует dFldYjj для i=l, ..., п и любого /. Понятия
дифференциально алгебраич. многообразия можно обоб-
обобщить (уже не предполагая его аффинным). В частности,
можно ввести понятия дифференциально однородных
полиномов и проективных дифференциально алгебраич.
многообразий.
Для дифференциального поля F не существует диф-
дифференциально алгебраич. замыкания, не существует
дифференциально алгебраич. замкнутых полей. За-
Заменой их, в нек-ром смысле, являются так наз. «стес-
«стесненные» расширения.
Одним из направлений в Д. а. является теория Га-
луа дифференциальных полей. Для дифференциального
поля JF строится универсальное дифференциальное
расширение U и рассматривается множество диффе-
дифференциальных изоморфизмов конечно порожденного
дифференциально алгебраич. расширения © поля $
в U, тождественных на §~. Если & является сильно
нормальным расширением ^", то на множестве G диф-
дифференциальных изоморфизмов & в U можно ввести
структуру алгебраич. группы над полем констант К
поля U. Частным случаем сильно нормальных расши-
расширений являются расширения Пикара — Вессио, по-
получающиеся присоединением к полю JF решений ли-
линейного однородного дифференциального уравнения с
коэффициентами в поле JF. Группа Галуа расширения
Пикара — Вессио является алгебраической матричной
группой. Связь между промежуточными полями и
подгруппами группы G описывается следующей тео-
теоремой.
Пусть ® — сильно нормальное расширение диффе-
дифференциального поля Iff с полем констант С. а) Если gr1 —
дифференциальное поле такое, что ^сг^СГ®, то ©
сильно нормально над <f~i, группа Галуа G(l>VjFi)
является С-подгруппой в G(®l^) и поле инвариантов
G((SV) У § б) G
дру (^) р
группы G((SVjFi) в (У совпадает с §г1. б) Если Gx яв-
является С-подгруппой группы G(@/(fr) и jpj обозначает
множество инвариантов группы Gx в (S), то <f", — диф-
дифференциальное поле, d'crlFiC:© и G(®/§r1) = G1.
Нормальным делителям Gx группы G((SV/'1) соот-
соответствуют при этом сильно нормальные расширения
|Гх поля JF, и наоборот. Для связных разрешимых
групп решена обратная задача Галуа, т. е. вопрос о
существовании у поля <f" сильно нормального расши-
расширения ©, группа Галуа к-рого G@>Vpf) изоморфна
заданной группе. Эта задача сведена к оценке размер-
размерности нек-рого векторного пространства над полем
констант С поля |Р и ранга некоторой абелевой груп-
группы. Имеются результаты по теории Галуа бесконеч-
бесконечных расширений. Смежными с теорией Галуа вопро-
вопросами занимается теория интегрирования в конечном
виде.
Разрабатывается теория дифференциальных алге-
браич. групп, существенно отличающаяся от своего
алгебраич. аналога. В частности, дифференциальное
кольцо всюду определенных дифференциальных ра-
рациональных функций на аффинном дифференциальном
алгебраич. множестве не является дифференциальным
координатным кольцом, и в общем случае не конечно
порождено как дифференциальная алгебра.
Среди результатов о приближении дифференциально
алгебраич. функций рациональными может быть от-
отмечен аналог теоремы Лиувилля о приближении ал-
алгебраич. чисел рациональными. Однако доказатель-
доказательство аналога теоремы Туэ — Зигеля — Рота остается
A978) проблемой.
Развивается теория колец с высшими дифференци-
дифференцированиями. При изучении объектов ненулевой харак-
характеристики высшие дифференцирования представляют
более сильное средство. Если характеристика диффе-
дифференциального кольца А равна р, то р-л степень любого
элемента является константой, в то время как для
колец с высшими дифференцированиями это не так.
Для колец с высшими дифференцированиями полу-
получены аналоги многих перечисленных выше резуль-
результатов, касающихся как теории пересечения идеалов,
так и теории Галуа.
Лит.: [1] К а п л а н с к и й И., Введение в дифференци-
дифференциальную алгебру, пер. с англ., М., 1959; [2] R i t t J. F., Dif-
Differential algebra, N. Y., 1950; [3] Kolchin E. R., Diffe-
Differential algebra and algebraic groups, N. Y.—L., 1973; [4] его
ж е, Some problems in differential algebra, в сб.: Тр. междуна-
международного конгресса математиков. Москва 1966, М., 1968.
А. В. Михалев, Е. В. Панкратьев.
ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ — раздел
геометрии, в к-ром изучаются геометрич. образы, в
первую очередь кривые и поверхности, методами ма-
тематич. анализа. Обычно в Д. г. изучаются свойства
кривых п поверхностей в малом, т. е. свойства сколь
угодно малых их кусков. Кроме того, в Д. г. изуча-
изучаются свойства семейств линий и поверхностей (см.,
напр.. Конгруэнция, Сеть).
Д. г. возникла и развивалась в тесной связи с ма-
тематич. анализом, к-рый сам в значительной степени
пырос из задач геометрии. Многие геометрич. понятия
предшествовали соответствующим понятиям анализа.
Так. напр., понятие касательной предшествовало по-
понятию производной, понятие площади и объема —
понятию интеграла.
Возникновение Д. г. относится к 18 в. и связано с
именами Л. Эйлера (L. Euler) и Г. Монжа (G. Monge).
Перпое сводное сочинение по теории поверхностей
написано Г. Монжем (Приложение анализа к геомег-
рии, 1795). В 1827 К. Гаусс (С. Gauss) опубликовал
работу «Общее исследование о кривых поверхностях»,
в к-рой заложил основы теории поверхностей в ее
современном виде. С тех пор Д. г. перестала быть
только приложением анализа и заняла самостоятельное
место в математике.
Открытие в 1826 Н. И. Лобачевским неевклидовой
геометрии сыграло огромную роль в развитии всей
геометрии, в том числе и Д. г. Фактически Н. И. Ло-
Лобачевским было отвергнуто априорное представление
о пространстве, господствовавшее ранее в математике
и философии. Он открыл, что возможны пространства,
отличные от евклидова. Эта идея Н. И. Лобачевского
нашла отражение в различных математнч. исследова-
исследованиях. Так, в 1854 Б. Риман (В. Riemann) своей лек-
лекцией «О гипотезах, лежащих в основаниях геометрии»
заложил основы риманоеой геометрии, к-рая в при-
применении к многомерным многообразиям находится в
таком же отношении к геометрии n-мерного простран-
пространства, как внутренняя геометрия поверхности к евкли-
евклидовой геометрии на плоскости.
Теоретико-групповая точка зрения Ф. Клейна
(F. Klein), изложенная в его «Эрлангенскои программе»
A872), т. е.: геометрия — учение об инвариантах
групп преобразований, в применении к Д. г. была
развита Э. Картаном (Е. Cartan), к-рый построил
теорию пространств проективной связности и аффинной
связности.
В России школу Д. г. создали Ф. Миндинг и К. М.
Петерсон. Их исследования посвящены в значитель-
значительной степени вопросам изгибания поверхностей, т. е.
таким непрерывным деформациям поверхностей, при
которых внутренняя геометрия все время остается
неизменной. Эти исследования были продолжены в
работах многих русских и советских геометров.
Теория кривых. В теории кривых обычно
рассматривают так наз. регулярные кри-
в ы е. Это — кривые, допускающие локальное задание
уравнениями вида
x=x(t), y=y(t), z=z(t), (V
где x(t), y(t), z(i) — достаточно регулярные функции
параметра t. В зависимости от свойств дифференци-
руемости функций x(t), y(t), z(t), задающих кривую,
говорят о степени регулярности
кривой. Кривая допускает бес-
численное множество различных
способов параметрпч. задания
уравнениями вида A). Среди
них особое значение имеют так
наз. естественная пара- Рис.
метризация, когда парамет-
параметром служит длина дуги кривой, отсчитываемая от нек-рой
фиксированной точки. Точка кривой наз. обыкно-
обыкновенной, если при подходящем выборе прямоуголь-
прямоугольной декартовой системы координат х, у, z она допу-
допускает в окрестности этой точки задание уравнениями
вида
у = у(х), z=z(x),
где у(х) и z(x) — дифференцируемые функции. В про-
противном случае точка наз. особой (см. Особая точка).
В Д. г. основное изучение кривой относится к окрест-
окрестности обыкновенной точки. Для того чтобы точка
кривой, заданной общим уравнением A), была обык-
обыкновенной, достаточно, чтобы в этой точке было
Ряд основных понятий теории кривых вводится с
помощью понятия соприкосновения мно-
множеств, к-рое состоит в следующем. Пусть М и т —
два множества с общей точкой О. Говорят, что множе-
ство М имеет с т в точке (^соприкосновение
порядка <х^1, если
| ХО \а ~~*
при Х—>-0, где б(Х) — расстояние точки X множества
М от т. Если в качестве М взять кривую, а в каче-
качестве т прямую, проходящую через точку О кривой,
то при txjjsl условие соприкосновения определяет
касательную к кривой в точке О (рис. 1). Гладкая
(дифференцируемая) кривая в каждой точке имеет
определенную касательную. Направление касатель-
касательной в точке <0 кривой, задаваемой уравнениями A),
совпадает с направлением вектора [х (t0), у'(to), z (S0)J-
В Д. г. выводятся уравнения касательной для раз-
различных способов аналитич. задания кривой. В част-
частности, для кривой, задаваемой уравнениями A), урав-
уравнения касательной в точке, отвечающей значению
параметра t0, будут
Х-х„ __ У-j/o __ Z-Zp
хо Уо zo
где индекс 0 указывает на значение функций х, у, z
и их производных в точке t0. Если взять в качестве т
плоскость, проходящую через точку О кривой М,
то условие соприкосновения при а^2 определяет
соприкасающуюся плоскость
кривой (рис. 2). Дважды
дифференцируемая кривая
в каждой точке имеет
соприкасающуюся плос-
плоскость. Она либо единствен-
единственная, либо любая плоскость,
проходящая через касатель-
касательную кривой, является со-
соприкасающейся .
М\ ^<У Рис- 2- При движении вдоль кри-
кривой ее касательная вра-
вращается. Скорость этого вращения при равномерном,
с единичной скоростью, движении вдоль кривой наз.
кривизной кривой. В случае параметрич. задания кри-
кривой уравнениями A) кривизна кривой определяется
по формуле
, | г' (() X r"(t) |
1Ь\ — ,
I /•' (О |3/2
где r(t) — вектор-функция с координатами x(t), y(t),
z(t). Прямые и только прямые имеют всюду равную
нулю кривизну. Дважды дифференцируемая кривая
в каждой точке, где кривизна отлична от пуля, имеет
единственную соприкасающуюся плоскость. При дви-
движении вдоль кривой в окрестности такой точки сопри-
соприкасающаяся плоскость вращается, причем касательная
кривой является мгновенной осью этого вращения.
Скорость вращения соприкасающейся плоскости при
равномерном, с единичной скоростью, движении вдоль
кривой наз. кручением кривой. В зависимости от на-
направления вращения определяется знак кручения.
Трижды дифференцируемая кривая в каждой точке с
отличной от нуля кривизной имеет определенное кру-
кручение. В случае параметрич. задания кривой уравне-
уравнениями A) кручение кривой определяется по формуле
*"- |г'Хг-|« •
Плоская кривая в каждой точке имеет кручение, рав-
равное нулю. Обратно, кривая с тождественно равным
нулю кручением — плоская.
Прямая, перпендикулярная касательной, проходя-
проходящая через точку касания, наз. нормалью к кривой.
Нормаль, лежащую в соприкасающейся плоскости,
наз. главной нормалью, а нормаль, перпендикулярную
соприкасающейся плоскости, наз. бинормалью. Фигура,
составленная из касательной, главной нормали и би-
бинормали, а также из трех плоскостей, попарно содер-
содержащих эти прямые, наз. естественным трехгранником
(трехгранником Френе). Если ребра естественного трех-
трехгранника в данной точке кривой принять за оси пря-
прямоугольной декартовой системы координат, то урав-
уравнение кривой в естественной параметризации имеет в
окрестности этой точки вид
* = »+..., j/ = iLs24-..., Z=-^s3+...,
где ()[ и ij — кривизна и кручение кривой в указан-
указанной точке. На рис. 3 изображены проекции кривой на
У
Рис. 3.
грани естественного трехгранника вблизи точки с
отличными от нуля кривизной и кручением.
Единичные векторы т, v, ft касательной, главной
нормали и бинормали кривой при движении вдоль
кривой изменяются. При соответствующем выборе
направления этих векторов из определения кривизны
и кручения получаются формулы
т' —М, P'=A-2v, v'=— кЛх~ кф, B)
где штрихом обозначено дифференцирование по дуге
кривой. Формулы B) наз. Френе формулами. Кривая
с отличной от нуля кривизной определяется с точностью
до положения в пространстве заданием ее кривизны
и кручения в функции дуги s кривой. В связи с этим
систему уравнений
наз. натуральными i/раенениями кривой.
Важный класс кривых представляют плоские
кривые, т. е. кривые, лежащие в плоскости. Для
плоских кривых можно различать направление враще-
вращения касательной при движении вдоль кривой, поэтому
кривизне можно приписывать знак в зависимости от
направления этого вращения. Кривизна плоской кри-
кривой, задаваемой уравнениями x=x(t), y = y(t), опре-
определяется по формуле
к=±
у х'-х'у'
Знак -f- или — берется по соглашению, но сохраняется
вдоль всей кривой. Для кривых вводится важное
понятие соприкасающейся окружности. Это — окруж-
0
ность, имеющая с
кривой соприкосно-
соприкосновение порядка aJ2s2
(рис. 4). Она сущест-
существует в каждой точке
дважды дифференци-
дифференцируемой кривой с от-
отличной от нуля кри-
кривизной. Центр со-
соприкасающейся ок- Рис. 4. Рис. 5.
ружности наз. цент-
центром кривизны, а радиус — радиу-
радиусом кривизны. Радиус кривизны является ве-
величиной, обратной кривизне. Геометрич. место центров
кривизны кривой наз. эволютой. Кривая, ортогонально
пересекающая касательные кривой, наз. эвольвентой
(рие. 5). Для эвольвенты данной кривой эволютой
является сама кривая.
Кривая у наз. огибающей семейства кривых у«>
зависящих от параметра а, если она в каждой своей
точке касается хотя бы одной кривой семейства и каж-
каждым своим отрезком касается бесконечного множества
этих кривых.
Теория поверхностей и ее обоб-
обобщения. В теории поверхностей обычно рассматри-
рассматриваются регулярные поверхности. Это —
поверхности, допускающие локальное задание урав-
уравнениями вида
х=х(и, v), У=у{и, v), z=z(u, v), C)
где х(и, v), у (и, v), z(u, v) — регулярные функции
параметров и, v. В зависимости от степени регуляр-
регулярности функций, входящих в уравнения поверхности,
говорят о степени регулярности поверхности. Поверх-
Поверхность допускает бесчисленное множество способов
параметрич. задания уравнениями вида C). Точка
поверхности наз. обыкновенной, если в ее
окрестности при подходящем выборе системы коорди-
координат х, у, z поверхность допускает задание вида
z=~z(x, у),
где z(x, у) — гладкая функция. В противном случае
точка поверхности наз. особой. В Д. г. основное
изучение поверхности ведется в окрестности обыкно-
обыкновенных точек. Для того чтобы точка (uQ, v0) поверх-
поверхности, задаваемой уравнениями C), была обыкновен-
обыкновенной, достаточно, чтобы, в этой точке ранг матрицы
( хчУч2ч \ был равен двум. Когда поверхность зада-
ется уравнениями вида C), это условие обычно пред-
предполагается выполненным и специально не оговари-
оговаривается. Уравнения C) при фиксированном и или v
задают кривые, лежащие на поверхности. Эти кривые
наз. координатными линиями на по-
поверхности. Параметры и, v наз. координатами на
поверхности или гауссовыми криволинейными коор-
координатами.
Через понятие соприкосновения определяется каса-
касательная плоскость к поверхности. Это — плоскость,
проходящая через точку поверхности и имеющая в
этой точке с поверхностью соприкосновение порядка
a S= 1 ¦ Гладкая (дифференцируемая) поверхность имеет
в каждой точке единственную касательную плоскость.
Касательная плоскость поверхности, задаваемой урав-
уравнениями C), при условии D) в точке (и0, v0) опреде-
определяется уравнением
— х° Y—y° Z — zO
0 0 0
хи Уи zu
= 0,
где индекс 0 указывает на значение функций х(и, v),
у (и, v), z(u, v) и их производных в точке (ы0, i;0). Пря-
Прямая, проходящая через точку поверхности перпенди-
перпендикулярно касательной плоскости в этой точке, наз.
нормалью к поверхности. Если r(u, v) — вектор с коор-
координатами х(и, v), y(u,v), z(u, v), то
raxrv
имеет направление нормали поверхности.
Для поверхностей вводится важное понятие сопри-
соприкасающегося параболоида. Это — параболоид, для к-рого
нормаль к поверхности в данной точке является его
осью и к-рый имеет соприкосновение порядка а^>2
с поверхностью в этой точке. В каждой точке дважды
дифференцируемой поверхности существует единствен-
единственный соприкасающийся параболоид, к-рый может вы-
вырождаться в параболич. цилиндр или плоскость. Если
поверхность отнести к прямоугольным декартовым
координатам, приняв данную точку поверхности за
начало координат, а касательную плоскость в ней за
плоскость ху, то уравнение поверхности в окрестности
точки касания будет
z=f(x, у),
а уравнение соприкасающегося параболоида в этой
точке
* U^ + V
(производные функции / берутся в точке касания).
В зависимости от вида соприкасающегося параболоида
точки поверхности подразделяются на эллиптические
точки, гиперболические точки, параболические точки и
уплощения точки. Значение соприкасающегося пара-
параболоида состоит в том, что он воспроизводит форму
поверхности с точностью до бесконечно малых 2-го
порядка (касательная плоскость воспроизводит ее
форму с точностью до бесконечно малых 1-го порядка).
С помощью соприкасающегося параболоида вводится
понятие сопряженных направлений на поверхности.
Именно два направления на поверхности в данной
точке наз. сопряженными, если содержащие
их прямые сопряжены относительно соприкасающе-
соприкасающегося параболоида в этой точке. Ортогональные сопря-
сопряженные направления наз. главными. В данной
точке поверхности, как правило, два главных направ-
направления. Исключение составляют точки уплощения и
специальные эллиптич. точки (округления точки), в
к-рых каждое направление главное. Линия, у к-рой
в каждой точке направление является главным, наз.
кривизны линией. В точках поверхности, не являю-
являющихся эллиптическими, существуют самосопряженные
направления. Они наз. асимптотическими направле-
направлениями. Линия на поверхности, направление к-рой в
каждой точке асимптотическое, наз. асимптотической
линией.
Подобно тому, как для семейства кривых на пло-
плоскости, вводится понятие огибающей семейства поверх-
поверхностей. При этом семейство поверхностей может быть
однопараметрическим или двухпараметрическим. В тео-
теории поверхностей особое значение имеет огибающая
однопараметрич. семейства плоскостей.
В теории поверхностей важную роль играют две диф-
дифференциальные квадратичные формы поверхности, свя-
связанные с поверхностью. Если через г (и, v) обозначить
вектор точки на поверхности, а через п(и, v) единич-
единичный вектор нормали к поверхности, то эти квадратич-
квадратичные формы записываются в виде
I = dr2, II = — drdn.
Коэффициенты первой и второй квадратичных форм
обычно обозначаются Е, 2F, G и L, 2M, N соответст-
соответственно. Первая из этих форм дает расстояние на по-
поверхности между точкой (и, v) н бесконечно близкой
точкой (u-\-du, v-\-dv):
ds= Y~E du2 + IF du d-d -j- G dv2.
Длина кривой, задаваемой на поверхности уравне-
уравнениями u=u(t), v=v(t), вычисляется при помощи пер-
первой квадратичной формы
L=\to у Ей'2 + 2Fu'v' + Gi/ dt.
Первая квадратичная форма поверхности определяет
углы между кривыми на поверхности. В частности, для
угла ©между координатными линиями it=const, v= const
в точке их пересечения имеет место формула
R
cos ф = —_=г- .
V EG
Отсюда видно, что координатная сеть на поверхности
ортогональна, если F=0. Площадь поверхности также
определяется первой квадратичной формой и для
области Q на поверхности вычисляется по формуле
S = f С YEG — F*du dv.
Вторая квадратичная форма характеризует искрив-
искривленность поверхности в пространстве. Именно, отно-
отношение второй квадратичной формы к первой
. L du" + 2Mdu dv + Ndv2
E du2 + IF dudv + Gdc2
представляет собой кривизну плоского сечения, нор-
нормального к поверхности, проведенного в направлении
du : dv (см. Нормальная кривизна поверхности). Суще-
Существует простая связь между кривизной кривой, лежа-
лежащей на поверхности, и кривизной нормального сечения
поверхности, проведенного через касательную кривой
(Менъе теорема). Экстремальные значения нормальной
кривизны поверхности в данной точке наз. главными
кривизнами. Они достигаются по главным направле-
направлениям. Нормальная кривизна поверхности в произ-
произвольном направлении выражается через главные кри-
кривизны и углы, к-рые это направление образует с глав-
ны.чн (Эйлера формула). Главные кривизны kY и к2
определяются из уравнения
Ek — L Fk~M
Fk — M Gk — N
Их полусумма называется средней кривизной поверх-
поверхности. Важный класс поверхностей составляют поверх-
поверхности нулевой средней кривизны — так называемые
минимальные поверхности. Они отличаются тем, что
достаточно малый кусок такой поверхности имеет
наименьшую площадь среди поверхностей с тон же
границей. Произведение К=кукъ главных кривизн
наз. гауссовой кривизной поверхности
„_ LN-M*
Л ~ EG-F2 '
Из этой формулы видно, что гауссова кривизна по-
поверхности выражается через коэффициенты первой и
второй квадратичных форм. Однако гауссову кривизну
можно выразить через коэффициенты только первой
формы и их производные (Гаусса теорема).
Две поверхности, между к-рыми может быть уста-
установлен гомеоморфизм, сохраняющий длины кривых,
наз. изометричными поверхностями.
Коэффициенты первой и второй квадратичных форм
независимы. Одно из соотношений между этими
коэффициентами дает теорема Гаусса. Существуют еще
два соотношения, открытые К. М. Петерсоном и Д. Ко-
дацди (D. Codazzi) (см. Петерсона — Кодацци урав-
уравнения). Эти три соотношения составляют полную си-
систему независимых соотношений между коэффициен-
коэффициентами первой и второй квадратичных форм поверхности.
Согласно Бонне теореме, если для двух дифференци-
дифференциальных квадратичных форм, из к-рых первая положи-
положительно определенная, выполнены соотношения Гаусса,
Петерсона, Кодацци, то существует, и притом един-
единственная, с точностью до положения в пространстве,
поверхность, имеющая эти формы первой и соответ-
соответственно второй квадратичными формами.
Раздел теории поверхностей, в к-ром изучаются свой-
свойства фигур на поверхности, зависящие только от
измерения длин кривых на поверхности, наз. внутрен-
внутренней геометрией поверхностей. Так как длины кривых
определяются первой квадратичной формой, то речь
идет о таких свойствах, к-рые связаны только с первой
квадратичной формой. В частности, объектами внут-
внутренней геометрии поверхностей являются длины кри-
кривых, углы между кривыми, площадь и гауссова кри-
кривизна. Важным понятием внутренней геометрии по-
поверхности является понятие геодезической линии. Так
называется линия, к-рая на достаточно малом уча-
участке является кратчайшей среди всех кривых на повер-
поверхности, соединяющих ее концы. Следующее важное поня-
понятие внутренней геометрии поверхности — понятие гео-
геодезической кривизны кривой. Гаусса — Бонне теорема
связывает интеграл от гауссовой кривизны поверх-
поверхности по площади, интеграл от геодезич. кривизны
края по его длине и эйлерову характеристику.
Внутренняя геометрия поверхности может быть по-
построена как геометрия двумерного метрич. многооб-
многообразия, в к-ром расстояние между бесконечно близкими
точками (и, v) и (u-\-du, v-\-dv) определяется с помощью
заданной дифференциальной формы ds2. При таком
подходе к внутренней геометрии поверхности она до-
допускает естественное обобщение, при к-ром заданное
многообразие имеет любую размерность п, а метрика
задается дифференциальной положительно определен-
определенной квадратичной формой п переменных ds2 = gaaduadufi.
Дальнейшее обобщение состоит в отказе от положи-
положительной определенности формы ds2. Это приводит к
теории пространств общей теории относительности, в
частности к Минковского пространствам. Если, на-
наконец, отказаться и от квадратичной формы линейного
элемента ds2, а рассматривать общую положительную
однородную форму первой степени от dua, то получим
Финслерово пространство. Еще более далеким обоб-
обобщением внутренней геометрии поверхности является
геометрия пространств со связностью данной группы,
в частности геометрия пространств с аффинной связ-
связностью, проективной связностью и конформной связ-
связностью.
Лит.: [1] В i anclil L., Lezioni di geometria differenziale,
t. 1—2, 3 ed., Bologna, 1927—30; 12] DarbouxG., Lemons
sur la theorie generale des surfaces et les applicatons geomelriques
du calcul infinitesimal, p. 1—4, 2 <5d., P., 1894 — 1925; [3]
Стройк Д. Д ж., Очерк истории дифференциальной геомет-
геометрии до XX столетия, пер. с англ., М.—Л., 1941; [4] Р а ш с в-
скийП. К., Курс дифференциальной геометрии, 4 изд., М.,
1956; [5] П о г о р е л о в А. В., Дифференциальная геомет-
геометрия, 5 изд., М., 1969; [6] Б л я ш к е В., Введение в дифферен-
дифференциальную геометрию, пер. с нем., М., 1957; [7] его же, Диф-
Дифференциальная геометрия и геометрические основы теории от-
относительности Эйнштейна, пер. с нем., т. 1, М.—Л., 1935; [81
СтернбергС, Лекции по дифференциальной геометрии,
пер. с англ., М., 1970; [9] К а г а н В. Ф., Основы теории по-
поверхностей в тензорном изложении, ч. 1—2, М.—Л., 1947—48;
[10] ШуликовскийВ. И., Классическая дифференци-
дифференциальная геометрия в тензорном изложении, М., 1963; til] С х о у-
т е н И. А., Стройк Д. Д ж., Введение в новые методы диф-
дифференциальной геометрии, пер. с англ., т. 1—2, М.—Л., 1939 —
1948; [12] Фиников С. П., Проективяо-дифференциальная
геометрия, М.—Л 1937; [13] его же, Теория конгруэнции,
М.—Л., 1950; [14] Ш и р о к о в П. А., III и р о к о в А. П.,
Аффинная дифференциальная геометрия, М., 1959; [15] Нор-
денА. П., Пространства аффинной связности, М.—Л., 1950.
А. В. Погорелое,
ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ МНОГООБ-
МНОГООБРАЗИЙ — раздел дифференциальной геометрии, изу-
изучающий различные инфинитезималъные структуры
на многообразии и их связи со структурой многооб-
многообразия и его топологией.
К середине 19 в. в результате возникновения неев-
неевклидовой геометрии Лобачевского, многомерной гео-
геометрии Грассмана, а также развития проективной гео-
геометрии и геометрии в комплексной области стало ясно,
что привычная евклидова геометрия не является един-
единственно возможной, и в математике с пользой можно-
развивать другие неевклидовы геометрии, независимо
от их отношения к геометрии физического пространства.
В 1854 Б. Риман (В. Riemann) в лекции «О гипотезах,
лежащих в основании геометрии» предложил новую,
весьма плодотворную концепцию «многообразия» (см.
Риманово пространство). Тем самым он положил на-
начало римановой геометрии, являющейся важнейшей
и наиболее разработанной частью Д. г. м. Концепция
Римана не только позволила единообразно описать
широкий класс геометрий (включая евклидову геомет-
т
ф
1
рию и неевклидову геометрию Лобачевского), но и
дала математич. аппарат, в рамках к-рого разнообраз-
разнообразные задачи матоматпч. физики и анализа, связанные
с дифференциальными уравнениями, получили геомет-
геометрич. трактовку, что позволило применять для их
решения различные геометрич. и топологнч. сообра-
соображения, открыв новые возможности для применения
геометрии к анализу. Именно в рамках римановой
геометрии А. Эйнштейну (A. Einstein) удалось реали-
реализовать идеи о физич. пространстве как о континууме,
свойства к-рого определяются распределением мате-
материи. Римановым пространством наз. дифференцируемое
многообразие М, у к-рого в каждом касательном про-
пространстве ТрМ задана евклидова метрика gp (т. е.
положительно определенное скалярное произведение),
гладко зависящая от точки р?М. Наличие в каса-
касательном пространстве ТрМ риманова пространства М
скалярного произведения позволяет по формулам
евклидовой геометрии определить угол между инфи-
нитезимальными кривыми (т. е. векторами из ТрМ),
длину инфинитезимальной кривой, а также объем
А-мерного параллелепипеда в Т/УМ, а затем, с помощью
интегрирования, длину гладкой кривой на ? и объем
А-мерного подмногообразия в М. Это, в свою очередь,
позволяет рассматривать в рамках римановой геомет-
геометрии различные вариационные задачи и, в частности,
определить в римановом пространстве понятие геоде-
геодезической (или геодезической линии) как кривой экс-
экстремальной длины н минимальной поверхности, как
подмногообразия экстремального объема.
Изучение геодезических риманова пространства пред-
представляет собой одну из основных задач современной
(глобальной) римановой геометрии. Важность ее для
приложений определяется тем, что разнообразные
динамич. системы физики интерпретируются как рав-
равномерное движение по геодезическим того или иного
псевдориманова пространства. К таким системам от-
относятся, напр., движения пробных тел (см. Геодезиче-
Геодезических гипотеза) в общей теории относительности, рас-
распространение света в неоднородной среде в прибли-
приближении геометрической оптики, различные системы
классической механики. Было обнаружено, что нек-рые
важные уравнения с частными производными (урав-
(уравнение движения идеальной жидкости и уравнение Эйн-
Эйнштейна общей теории относительности) интерпрети-
интерпретируются как уравнения геодезических для нек-рых бес-
бесконечномерных римановых пространств, называемых
также гильбертовыми многообразиями (см. [5], [12]).
Эти открытия стимулировали развитие геометрии бес-
бесконечномерных многообразий — глобальный анализ.
Уравнения геодезических удается полностью про-
проинтегрировать только в редких случаях. В связи с
этим важную роль приобретают геометрич. и топологич.
методы качественного исследования поведения геоде-
геодезических. Важнейшим среди них является созданная
М. Морсом (М. Morse) вариационная теория геодези-
геодезических (см. Морса теория).
Обобщение теории Морса на псевдоримановы про-
пространства привело к доказательству теорем сингуляр-
сингулярности, утверждающих, что в рамках общей теории
относительности физическое пространство-время, как
правило, должно обладать сингулярностью (неполным)/
геодезическими). Физически сингулярности интер-
интерпретируются, напр., как «черные дыры» (см. [7]).
Поведение геодезических риманова пространства в
значительной степени определяется его кривизны тен-
тензором — тензором Римана — геометрическим объектом,
характеризующим отклонение риманова пространства
от евклидова. Подобно гауссовой кривизне поверх-
поверхности, обобщением к-рой он является, тензор кривизны
риманова пространства М в точке х определяет свой-
свойства пространства М в окрестности точки х. Более
того, тензор кривизны несет богатую информацию о
глобальных свойствах рнманова пространства и о его
топологии, напр, о фундаментальной группе, о Бетти
числах и о характеристических классах. Изучение
связи между локальными свойствами тензора кри-
кривизны п глобальными свойствами риманова прост-
пространства составляет одну из главных задач современной
глобальной римановой геометрии.
Любое подмногообразие N риманова пространства М
наследует от М структуру риманова пространства.
Изучение подмногообразий риманова пространства,
а также выяснение вопроса о реализации данного ри-
риманова пространства N в виде подмногообразия дан-
данного риманова пространства М составляют основное
содержание геометрии подмногообразий (см. также
Изометрическое погружение).
Важным направлением исследования рпмановых про-
пространств, начатым работами С. Ли (S. Lie) п В. Кил-
линга (W. Killing), является изучение его группы
движений (т. е. преобразований, сохраняющих длины
кривых), к-рая всегда есть группа Ли. Многие рима-
новы пространства М обладают достаточно богатой
группой движений, причем наличие такой группы ока-
оказывается очень полезным при изучении целого ряда
геометрия, вопросов. Наличие транзитивной группы
движений G позволяет свести изучение геометрии и
топологии пространства М к вопросам теории групп
Ли (см. Однородное пространство).
Описание (связной) группы G движений риманова
пространства (М, g) сводится к описанию алгебры Ли
инфинитезимальных движений (или, иначе, Киллинга
векторов), определяемых как поля скоростей однопа-
раметрич. подгрупп группы G. Важную роль играют
качественные геометрич. методы изучения киллин-
говых полей и выяснение связи между киллинговыми
полями и геометрич. свойствами пространства, прежде
всего свойствами его тензора кривизны. Так, напр.,
доказывается, что в компактном римановом простран-
пространстве с отрицательной кривизной Риччи не существует
киллинговых полей; интегральная кривая киллингова
поля, проходящая через точку экстремума его длины,
является геодезической [16]; поведение киллингова
поля X вблизи его неподвижных точек (точек, где Х=0)
определяет важный топологич. инвариант риманова
пространства — его Понтрягина числа [19].
Особый интерес представляют римановы простран-
пространства, обладающие достаточно большой группой дви-
движений. Как обнаружил еще в 1868 Г. Гельмгольц
(Н. Helmlioltz) и строго доказал С. Ли, n-мерное ри-
маново пространство М, обладающее для данного п
максимальной (в смысле размерности) группой движе-
движений является постоянной кривизны пространством
(а именно, евклидовым пространством Е", простран-
пространством Лобачевского Ап или сферич. пространством
Римана S"). Наиболее близкими к пространствам
постоянной кривизны по своим свойствам являются
симметрические пространства, т. е. римановы про-
пространства, в к-рых геодезич. симметрия относительно
произвольной точки является движением. Эти про-
пространства всегда имеют транзитивную группу движений
и допускают классификацию с помощью теории полу-
полупростых алгебр Ли (см. [8]).
Важную роль в дифференциальной геометрии иг-
играет понятие ковариантной производной уХТ тензор-
тензорного поля Т на М по направлению вектора Х?ТрМ,
к-рое ввел Г. Риччи (G. Ricci), развивший на основе
этого понятия «абсолютное дифференциальное исчис-
исчисление» (см. Тенз-эрный анализ). Аппарат ковариантного
дифференцирования оказался удобным для получения
инвариантов геометрических объектов. Так, найден-
найденная Э. Кристоффелем (Е. Christoffel) и Р. Липшицем
(R. Liepschitz) полная система инвариантов римановой
метрики состоит из тензора кривизны и его последо-
последовательных ковариантных производных.
Понятие ковариантной производной позволяет ка-
нонич. образом определить в римановом пространстве
ряд дифференциальных операторов, свойства к-рых тес-
тесно связаны с геометрией пространства. Важнейшими из
них являются оператор Бельтрами—Лапласа Д, введен-
введенный Э.Бельтрами (Е. Boltrami) и совпадающий для евкли-
евклидова пространства с Лапласа оператором. Широкий
класс линейных уравнений с частными производными
2-го порядка получает интерпретацию в рамках псевдо-
римановыхпространств как уравнений, соответствующих
оператору Бельтрами — Лапласа. Это позволяет ис-
использовать риманову геометрию для изучения урав-
уравнений. Первый пример такого подхода (для уравнений
теплопроводности) был дан Б. Риманом [1]. К настоя-
настоящему времени получены результаты, устанавливающие
связь между свойствами оператора Бельтрами — Лап-
Лапласа риманова пространства, в частности его спектром,
и геометрией пространства — его кривизной, числом
замкнутых геодезических и т. п. (см. [19]).
Геометрическую интерпретацию понятия ковариант-
ковариантной производной дал Т. Леви-Чивита (Т. Levi-Civita).
Он показал, что в римановом пространстве можно ка-
каноническим образом определить параллельный пере-
перенос касательных векторов (тензоров) вдоль кривых, а
оператор ковариантной производной Риччи является
оператором инфинитезимального параллельного пе-
переноса (см. Леви-Чивита связность).
В 1926 Э. Картан (Е. Cartan) ввел понятие голоно-
нии группа, как группы Гр линейных преобразований
касательного пространства ТрМ риманова пространства
М, порожденной операторами %у параллельного об-
обноса вдоль всевозможных петель у. Оказалось, что
группа голономии тесно связана с тензором кривизны
пространства и для односвязного аналитич. простран-
пространства полностью определяется тензором кривизны в
точке и всеми его ковариантными производными, — с
другой стороны, она содержит нек-рую информацию о
геометрии и топологии пространства. Так, зная группу
голономии, можно найти все параллельные поля, а
также решить вопрос о возможности разложения
риманова пространства в прямое произведение двух
других римановых пространств. По группе голономии
симметрич. пространства можно восстановить само
пространство и описать его группу движений.
В 1919 Г. Вейль (Н. Weyl), развивая идею парал-
параллельного переноса Т. Левн-Чивита и обобщая риманову
концепцию пространства, рассмотрел пространство
линейной связности — многообразие, в к-ром задан
закон параллельного переноса касательных векторов
вдоль кривых. В пространстве линейной связности
определяются понятия геодезической, тензора кривизны,
группы голономии. Риманово пространство является
частным случаем пространства линейной связности, для
к-рого группа голономии содержится в ортогональной
группе. Если группа голономии содержится в линейной
группе гомотетий R*-SO(«), то связность наз. кон-
конформно й. В этом случае на многообразии возни-
возникает конформная структура.
Развитие идей Г. Вейля привело к созданию совре-
современной теории связности, изучающей связность (т. е.
закон параллельного перенесения слоев вдоль кривых
на базе) в данном расслоении. В рамках теории связ-
ностей развивается, в частности, теория характеристич.
классов [И], [14]. Важную роль играет понятие связ-
связности в современной физике. Различные физич. поля
(в частности, электромагнитное и гравитационное)
могут быть интерпретированы как поля кривизны
связности в том или ином расслоении в рамках теории
Янга — Миллса. Наличие связности в любом физич.
расслоении, т. о. расслоении, сечениями к-рого явля-
ются физU4. поля, вытекает из физич. возможности срав-
сравнения характеристик поля в разных точках про-
пространства — времени.
Другим обобщением риманова пространства явля-
является финслерово пространство, определяемое как мно-
многообразие с финслеровой метрикой. Примером такой
метрики является лагранжиан механич. системы. Финс-
леровы многообразия естественным образом появ-
появляются также и в оптике.
Новый групповой подход к обоснованию геометрии,
известный под названием «эрлангенской программы»,
был предложен Ф. Клейном (F. Klein) в 1872. В ка-
качестве основного объекта изучения геометрии Ф. Клейн
предложил рассматривать G-пространство — множе-
множество М вместе с заданной группой G его преобразо-
преобразований.
Основной задачей геометрии по Клейну является
изучение инвариантов группы преобразований (см. Эр-
лангенская программа). Несмотря на то, что подход
Ф. Клейна оказался слишком узким — многие важные
римановы пространства обладают тривиальной группой
движений,— этот подход сыграл важную роль в раз-
развитии Д. г. м. Он привлек внимание к важному клас-
классу — однородным пространствам (т. е. G-простран-
ствам с транзитивной группой G), изучение геометрии
к-рых сводится в рамках эрлангенской программы к
вопросам теории групп Ли, и способствовал дальней-
дальнейшему обобщению концепции Римана. Это обобщение
состояло в рассмотрении геометрии других (неримано-
вых) инфинитезимальных структур на многообразии,
задаваемых полем тех или иных геометрич. величин.
Многие из этих структур впервые появились как инва-
инварианты группы движений того или иного однородного
пространства.
Примерами неримановых инфинитезимальных гео-
геометрич. структур являются абсолютный параллелизм
(поле реперов), конформная связность, проективная
связность, линейная связность, распределение (или,
более общо, флаговая структура), почти комплексная
структура, почти симплектическая структура, поле
аффиноров и т. п. Геометрия этих структур развива-
развивается по аналогии с римановой геометрией. Ее основ-
основными вопросами являются следующие: 1) Построение
по данной геометрической структуре других (произ-
(производных от нее) структур и, в частности, инвариантов.
Иными словами, построение функторов из категории
геометрич. структур данного типа в другие категории.
2) Изучение группы автоморфизмов геометрич. струк-
структуры, изучение геометрич. структур с достаточно
большой группой автоморфизмов, описание структур
данного типа с максимальной группой автоморфизмов,
классификация структур данного типа на однородных
пространствах. 3) Проблема эквивалентности, т. е.
нахождение необходимых и достаточных условий для
того, чтобы две геометрич. структуры были эквива-
эквивалентны. 4) Изучение связи между топологией и струк-
структурой гладкого многообразия, с одной стороны, и свой-
свойствами заданной на нем геометрич. структуры — с
другой. 5) Изучение отображений многообразий с гео-
геометрич. структурами, в частности изучение расслоений
и подмногообразий.
Наиболее важным классом геометрических структур
являются транзитивные структуры или G-структуры (см.
[10]). Все перечисленные выше примеры структур
(кроме поля аффиноров) являются G-структурами.
Общая теория G-структур основана на двух фунда-
фундаментальных идеях Э. Картана: понятии продолжения
и понятии структурной функции. В частности, для
римановой метрики эти понятия приводят к параллель-
параллельному перенесению Леви-Чивиты и тензору кривизны.
Теория G-структур конечного типа развивается во
многом аналогично римановой геометрии. В геометрия
G-структур бесконечного типа наиболее изученные
вопросы относятся к случаю локально плоских (ин-
(интегрируемых) структур. Важнейшими из них являются
комплексная структура (см. Аналитическое многооб-
многообразие) и симплектическая структура, лежащая в ос-
основе гамильтоновой механики.
Э. Картан, развивая геометрич. методы решения
систем уравнений с частными производными (систем
Пфаффа), создал теорию внешних дифференциальных
форм, оказавшую исключительно большое влияние на
развитие дифференциальной геометрии. Оператор внеш-
внешнего дифференцирования d оказался полезным для
выражения условия интегрируемости систем урав-
уравнений с частными производными. Так, напр., необхо-
необходимым и достаточным условием полной интегрируемо-
интегрируемости систем уравнений Пфаффа щ =. . .==@^=0 является
замкнутость идеала /, порожденного линейными диф-
дифференциальными формами (Oj, . .., a>k относительно
d(dJczJ) (Фробениуса теорема). Теория дифференци-
дифференциальных форм была успешно применена Э. Картаном
для решения разнообразных задач дифференциальной
геометрии и теории групп Ли подвижного репера ме-
методом. Теория интегрирования устанавливает связь
между исчислением дифференциальных форм и гомо-
логиями многообразия (см. Рама когомологии, Диффе-
Дифференциальная форма).
В римановом пространстве оператор внешнего диф-
дифференцирования d выражается через оператор кова-
риантного дифференцирования V- Более того, теория
Ходжа устанавливает глубокую связь между опера-
оператором d и оператором Бельтрами — Лапласа А, дей-
действующим в пространстве дифференциальных форм,
к-рый можно выразить через оператор V- Теорема
Ходжа утверждает, что пространство когомологии
компактного многообразия изоморфно пространству
гармонических (т. е. аннулируемых оператором Д)
дифференциальных форм (см. Гармоническая форма).
Это и ряд других утверждении теории Ходжа дает
информацию о строении кольца когомологии Н*М
риманова пространства, обладающего нетривиальными
параллельными дифференциальными формами (см. Па-
Параллельное поле) и, тем самым, имеющего нестандартную
группу голономии T=^SO (п), О(п). Примерами таких
пространств являются кэлеровы многообразия и симме-
симметрические пространства.
Важным направлением исследований современной
дифференциальной геометрии является изучение ес-
естественных расслоений над произвольным многооб-
многообразием М (касательных и кокасательных расслоений
порядка к, тензорных расслоений, расслоений реперов
порядка к, расслоений струй и др.) и выявление имею-
имеющихся там естественных (т. е. инвариантных относи-
относительно диффеоморфизмов многообразия М) геометри-
геометрических структур. Примерами таких структур являются
канонические симплектическая структура в кокаса-
тельном расслоении Т* М и контактная структура в
расслоении /ЦЛ/, R) 1-струп функций на М, играю-
играющие важную роль в теории дифференциальных урав-
уравнений с частными производными 1-го порядка и в га-
гамильтоновой механике, а также оператор внешнего
дифференцирования в расслоении Л* (М) внешних
дифференциальных форм на М.
Успешно развивается алгебраич. подход к диффе-
дифференциальной геометрии. В качестве исходного понятия
рассматривается не многообразие М, а коммутативное
кольцо F (кольцо функций на многообразии), а само
многообразие М определяется в терминах кольца F
как пространство максимальных идеалов (см. Схема).
Векторные поля на М определяются как дифференци-
дифференцирования кольца (см. Дифференциальный оператор
модуля). Такой подход позволяет обобщить различные
результаты дифференциальной геометрии и упростить
их доказательство, применить идеи дифференциальной
геометрии к другим математич. теориям (напр., теории
колец и модулей) и, наоборот, использовать различные
алгебраич. результаты в дифференциальной геометрии
(см. [17]).
Лит.: [1] РиманБ., Избранные произведения, пер. с
нем., М.—Л., 1948; [2] К ар тан Э., Геометрия римановых
пространств, пер. с франц., М.—Л., 1936; [3] К а г а н В. Ф.,
Очерки по геометрии, М., 1963, с. 437—519; [4] Рашевский
П. К., Риманова геометрия и тензорный анализ, 3 изд., М.,
1967; [5] А р н о л ь д В. И., Математические методы класси-
классической механики, М., 1974; [6] Э й з е н х а р д Л. П., Рима-
Риманова геометрия, пер. с англ., М., 1948; [7] X о к и н г С, Э л-
л и с Д ж., Крупномасштабная структура пространства — вре-
времени, пер. с англ., М., 1977; [8] X е л г а с о н С, Дифферен-
Дифференциальная геометрия и симметрические пространства, пер. с
англ., М., 1964; [9] Б и ш о п Р.-Л., Криттенден Р.-Д ж.,
Геометрия многообразий, пер. с англ., М., 1967; [10] Стерн-
бергС, Лекции по дифференциальной геометрии, пер. с
англ., М., 1970; [11] Шварц Дж,, Дифференциальная гео-
геометрия и топология, пер. с англ., М., 1970; [12] Л е н г С, Вве-
Введение в теорию дифференцируемых многообразий, пер. с англ.,
М., 1967; [13] 3 у л а я к е П., ВинтгенП., Дифференциаль-
Дифференциальная геометрия и расслоения, пер. снем., М., 1975; [14] У э л л с
Р., Дифференциальное исчисление на комплексных многообра-
многообразиях, пер. с англ., М., 1976; [15] Lichnerowicz A., Geo-
metrie des groupes de transformations, P., 1958; [16] К о b a y-
ashiS., Nomizu K., Foundations of differential geometry,
v. 1—2, N. Y., 1963—69; [17] Виноградов А.М., К р а-
сильщикИ. С, Л ы ч а г и н В. В., Применения нелиней-
нелинейных дифференциальных уравнений, М., 1977; [181 Чжень
С. С, «Успехи матем. наук», 1973, т. 33, в. 3, с. 15 — 111; [19]
Молчанове. А., там же, 1975, т. 30, в. 1, с. 3—59.
Д. В. Алексеевский.
ДИФФЕРЕНЦИАЛЬНАЯ ГРУППА — абелева груп-
группа С, в к-рой задан такой эндоморфизм d: С—уС, что
сР=О. Этот эндоморфизм наз. дифференциалом.
Элементы Д. г. наз. цепями, элементы ядра Ker d —
циклами, элементы образа \т d — грани-
граница М И. А. В. Михалев.
ДИФФЕРЕНЦИАЛЬНАЯ ОКРЕСТНОСТЬ 2 k-т о
порядка многообразия М класса СР,
p~^k-\-i,— локальная карта k-го итерированного ка-
касательного расслоения Т1г(М). А.Б.Иванов.
ДИФФЕРЕНЦИАЛЬНАЯ ТОПОЛОГИЯ — раздел то-
топологии, изучающий топологич. проблемы теории
дифференцируемых многообразий и дифференцируемых
отображений, в частности диффеоморфизмов, погруже-
погружений и расслоений. Попытки последовательного по-
построения топологии на базе многообразий, отображений
и дифференциальных форм предпринимались еще А. Пу-
Пуанкаре (Н. Poincare) в конце 19 в., но в то время
полная реализация этой программы оказалась невоз-
невозможной. Систематическое построение Д. т. удалось
осуществить лишь в 30-х гг. 20 в. благодаря усилиям
ряда крупных математиков.
В Д. т. были выработаны важные общематематич.
понятия — такие, как расслоенные пространства и свя-
связанные с ними дифференциально-геометрич. и тополо-
топологич. понятия: связности, G-структуры, характеристич.
классы, а также оснащенные многообразия. Большое
значение в развитии Д. т. имела теория (ко)бордизмов,
получившая ряд приложений в алгебраич. и аналитич.
геометрии (теорема Римана — Роха), теории эллиптич.
операторов (теорема об индексе), а также в самой
топологии. В 50-х гг. были открыты различные глад-
гладкие структуры на сферах, затем была найдена класси-
классификация многообразий гомотопического типа сферы и
доказана обобщенная гипотеза Пуанкаре, решена зада-
задача нахождения полной системы инвариантов всех
односвязных многообразий (размерности не менее 5)
относительно диффеоморфизмов. В 60-х гг. методами
Д. т. был решен ряд основных топологич. проблем:
установлена топологическая инвариантность характе-
характеристич. классов действительных многообразий, за-
затем выяснено взаимоотношение между категориями
дифференцируемых, кусочно линейных и тополо-
топологических многообразий, были обобщены на неодно-
связные многообразия (правда, недостаточно эффек-
эффективно) методы классификации гладких многообразий,
возникла алгебраич. А'-теория и эрмитова А-теория.
Для неодносвязных многообразий были открыты глу-
глубокие связи между характеристич. классами и эрмито-
эрмитовыми формами над фундаментальной группой многооб-
многообразия и ее гомологиями. В дальнейшем в проблеме
гомотопич. инвариантности классов и теории эрмито-
эрмитовых форм над коцепями с инволюцией были получены
глубокие результаты методами функционального ана-
анализа и алгебраич. методами. Важное значение име-
имеют методы, связанные с задачей классификации погру-
погружений одного многообразия в другое и ее различных
обобщений.
Особым направлением Д. т., пограничным с вариа-
вариационным исчислением, является глобальная теория
экстремалей различных функционалов на многооб-
многообразиях геодезических, к-рая оказала большое влияние
на развитие самой топологии, позволив дать класси-
классификацию векторных расслоений и в дальнейшем создать
метод исследования топологич. инвариантов, именуе-
именуемый А"-теорией. Многомерные глобальные задачи вариа-
вариационного исчисления на многообразиях оказались
более трудными, рассматривалась в основном проблема
минимальных поверхностей, как экстремалей функцио-
функционала типа Дирихле. Ряд принципиально новых то-
топологических проблем многомерного вариационного
исчисления возник в 70-х гг. из теории элементарных
частиц.
Другим особым направлением Д. т., пограничным с
дифференциальной геометрией и теорией динамич.
систем, является теория слоений (вполне интегриру-
интегрируемых локально систем Пфаффа). Так, было установ-
установлено существование замкнутого слоя у любого дву-
двумерного гладкого слоения на многих трехмерных
многообразиях (напр., сфере). Ряд результатов каче-
качественной теории слоений был направлен на выяснение
вопроса о существовании на многообразиях важного
класса гиперболических динамич. систем. В даль-
дальнейшем возникло другое — дифференциально-геомет-
рич. направление теории слоений, где был построен
своеобразный аналог теории характеристич. классов
для слоений, основанный на теории гомологии алгебр
Лп векторных полей.
Значительным успехом методов Д. т. является теория
«типичных» особенностей отображений и функций.
Методы Д. т. нашли применение в классических за-
задачах алгебраической геометрии; ранее результаты
этой области (в частности, теоремы об овалах алге-
алгебраич. кривых) стояли изолированно, в стороне от
основного развития топологии и геометрии. Развитие
Д. т. вызвало к жизни ряд новых проблем и методов
в алгебре — напр., так наз. стабильная алгебра, метод
формальных групп и др., а также в теории диффе-
дифференциальных уравнений с частными производными и
динамич. систем, функциональном анализе и геометрии.
В 70-х гг. резко усилился интерес современных об-
областей физики к методам Д. т., связанный с увеличе-
увеличением роли так называемых калибровочных полей (связ-
ностей в расслоениях с базой пространство — время)
в теории элементарных частиц, сложной топологией
решений в теории жидких кристаллов, теории фазо-
фазовых переходов, в частности в низкотемпературном жид-
жидком гелии.
Лит.: [1] П о н т р я г и н Л. С, Гладкие многообразия и
их применения в теории гомотопий, 2 изд., М., 1976; L2] W h i t-
ney H., «Ann. Math.», 1936, v. 37, p. 645—80; [3] T о м Р.,
в сб.: Расслоенные пространства и их приложения, М., 1958,
с. 293—351; [4] Н о в и к о в С. П., «Изв. АН СССР. Сер. матем.»
1964, т. 28, Л*« 2, с. 365—474; [5] Милнор Д ж., «Успехи
матем. наук», 1965, т. 20, в. 6, с. 41—54; [6] С м е й л С, там же,
1964, т. 19, в. 1, с. 125«-38; [7] М и л н о р Д ж., У о л л е с А.,
Дифференциальная топология- Начальный курс, пер. с англ.,
М., 1972; Г8] Munkres J., Elementary differential to-
topology, N. Y., 1963; [9] Милнор Д ж.. Теорема об Л-кобор-
дизме, пер. с англ., М., 19G9; [10] Р о х л и н В. А., Ф у к с Д. В.,
Начальный курс топологии. Геометрические главы, М., 1977;
[11] Рурк К., Сандерсон Б., Введение в кусочно
линейную топологию, пер. с англ.,М., 1974; [12] Wall С,
Surgery on compact manifolds, N. Y.— L., 1970; [13] В г о w-
der W., Surgery on simply connected-manifolds, N. Y., 1972;
Il4] К о н н е р Л., Ф л о й д Э., Гладкие периодические отоб-
отображения, пер. с англ., М., 1909; [15] С т о н г Р., Заметки по
теории кобордизмов, пер. с англ., М., 1973; [16] Новиков
С. П., «Тр. Моск. матем. об-ва», 1965, т. 14, с. 248—78; [17]
Целочисленные потоки и минимальные поверхности, пер. с
англ. и итал., М., 1973; [18] Мищенко А. С, «Успехи ма-
матем. наук», 1976, т. 31, в. 2, с. 69—134; [19] Гладкие динами-
динамические системы, пер. с англ., М., 1977. С. П. Новиков.
ДИФФЕРЕНЦИАЛЬНАЯ ФОРМА — 1) Д. ф. сте-
степени р, р-форма на дифференциру-
дифференцируемом многообразии М — р раз ковариант-
ное тензорное поле на М. Ее можно интерпретировать
также как р-линейное (над алгеброй F(M) гладких
вещественных функций на М) отображение S?(M)P^>-
-^-F(M), где SC{M) есть F(M)-yiopym> гладких век-
векторных полей на М. Формы степени 1 наз. также
пфаффовыми формами. Примером такой
формы является дифференциал df гладкой функции
/ на М, определяемый следующим образом: (df)(X),
X?&(М), есть производная X/функции / по направ-
направлению поля X. Римановы метрики на многообразии М
служат примерами симметрических Д. ф. степени 2.
Часто, однако, термин «Д. ф.» относят к кососим-
метрическим, или внешним Д. ф., имеющим наи-
наибольшее число приложений.
Если (ж1, . . ., х") — локальная система координат
в области UczM, то формы dx1, . . ., dxn составляют
базис в кокасательном пространстве ТХ(М)*, x?U.
Поэтому (см. Внешняя алгебра) любая внешняя р-
форма а записывается в U в виде
а=У. я, , dxil Л ... Л dxP, A)
¦"'i lp ' ••' р
где а/, ,- — функции в U. В частности,
Пусть ЕР=ЕР(М) — пространство всех внешних р~
форм класса С°°, причем Е°(М) = F(M). Внешнее ум-
умножение алР превращает Е* (M) = 'Syn Ер(М)(щв
n = dim M) в ассоциативную градуированную алгебру
над F(M), удовлетворяющую условию градуированной
коммутативности
аЛ^НЛрла. а € Ер, р ? ЕЧ. B)
Гладкое отображение многообразий f:M-*-N порож-
порождает гомоморфизм /* : E*(N)-*-E* (M) алгебр над R.
Понятие дифференциала функции обобщается сле-
следующим образом. Для всякого р^О существует един-
единственное линейное отображение d : Ep-*-Ep + l (внеш-
(внешний дифференциал), совпадающее при р = 0
с введенным выше дифференциалом и обладающее
свойствами:
d(a Л P) = da Л Р + (—1)р а. Л d$,
a € ?/J. P € Еч, d(da)=Q.
Внешний дифференциал формы а, записанной в ло-
локальных координатах в виде A), выражается формулой
<*а = 2, ,- dail ... i Л Лх'1 Л ... Л dxP.
Его бескоординатная запись:
где Х1У . . ., Хр + 1^^"(М). Оператор взятия Ли про-
производной Lx, X?J%"(M), на Д. ф. связан с внешним
дифференциалом соотношением
Lx=d о ix-\- ixod,
где \,х : Ер-+Ер~х — оператор внутреннего ум-
умх
ножения на I:
Оператор d превращает Е* (М) в коцепной комплекс
(комплекс де Рама). Коциклы этого ком-
комплекса наз. замкнутыми формами, когра-
кограницы .— точными формами. Согласно де Рама
теореме, алгебра когомологий
комплекса де Рама изоморфна алгебре Н* (М, R) ве-
вещественных когомологий многообразия М. В част-
частности, Hp{Rn)=0 при р>0 (лемма Пуанкаре).
С теоремой де Рама тесно связана другая опера-
операция — интегрирование Д. ф. Пусть D — ограничен-
ограниченная область в Rp, s — гладкое отображение Rp—>M,
определенное в окрестности замыкания D. Если
а?Ер(М), то s*a=adx1A .. ./\dxp, где а — гладкая
функция в fl". Интеграл ф о р м ы а по поверх-
поверхности s определяется формулой
a(xi> •••. xp)dxl ... dxp.
Если D имеет кусочно гладкую границу, то справед-
справедлива формула
Jjda=Sd506' a€?/?~1(Af), C)
где \ а. определяется как сумма интегралов формы а
по гладким кускам границы, снабженных естествен-
естественными параметризациями. Частными случаями этой
формулы являются классич. формулы Ньютона —
Лейбница, Грина, Гаусса — Остроградского, Стокса
(см. также Стокса теорема). В силу формулы C)
каждая замкнутая р-форма а определяет р-мерный
сингулярный коцикл, значение к-рого на симплексе s
равно \ а. Это соответствие как раз и реализует
изоморфизм из теоремы де Рама.
Формула C) была опубликована в 1899 А. Пуанкаре
(см. [2]), к-рый рассматривал внешние формы как
подинтегральные выражения для образования инте-
интегральных инвариантов. Одновременно Э. Картан (см.
[3]) дал близкое к современному определение внешних
форм и внешнего дифференциала (вначале на пфаффо-
пфаффовых формах), подчеркнув связь своей конструкции с
внешней алгеброй.
Наряду с определенными выше скалярными внеш-
внешними формами можно рассматривать внешние Д. ф.
со значениями в векторном пространстве V над R.
Если V является алгеброй, то в пространстве Е{М, V)
форм со значениями в V определено естественное ум-
умножение (обобщение внешнего умножения). Если при
этом алгебра V ассоциативна, то и Е{М, V) ассоциа-
ассоциативна; если V коммутативна, то Е(М, V) градуиро-
ванно-коммутативна (формула B)); если V — алгебра
Ли, то Е(М, V) — градуированная алгебра Ли. Часто
рассматривается также следующее, еще более общее
понятие. Пусть F — гладкое векторное расслоенное
пространство с базой М. Если сопоставить каждой
точке х?М кососимметрическую р-линейную функцию
иа ТХ(М) со значениями в слое Fx расслоения F, то
получится так наз. F-значная р-форма. F-знач-
ную р-форму можно интерпретировать также как р-
линейное (над F{M)) отображение модуля ??(М)Р в
модуль гладких сечений расслоения F. Пространство
таких форм обозначается EP{F). Если F задано ло-
локально постоянными функциями перехода или, что
то же, в F задана плоская связность, то можно кор-
корректно определить комплекс де Рама и обобщить тео-
теорему де Рама на этот случай.
Формы со значениями в касательном расслоении
Т(М) наз. также векторными Д. ф.; векторные
р-формы можно отождествить с р раз ковариантными
и 1 раз контравариантными тензорными полями на М,
кососимметричными по ковариантным индексам. С по-
помощью векторных Д. ф. описываются дифференци-
дифференцирования алгебры внешних форм Е(М) [4]. Векторные
формы (а также их обобщение — струйные формы)
находят применение в теории деформаций комплексных
и других дифферендиально-геометрич. структур на
многообразиях.
Аналоги Д. ф. можно построить также в симшгаци-
альной теории. Одна из таких конструкций, восходя-
восходящая к X. Уитни [5], может быть использована для
вычисления рациональных когомологий симплициаль-
ного комплекса X. Кусочно линейной фор-
формой (или PL-ф о р м о й) на if наз. согласованный
набор Д. ф., заданных на симплексах комплекса К
и имеющих в качестве коэффициентов при записи в
барицентрич. координатах многочлены с рациональ-
рациональными коэффициентами. PL-формы на К образуют гра-
дуированно-коммутативную дифференциальную алгеб-
РУ Epl(K) над О. Интегрирование форм определяет
изоморфизм алгебры когомологий этой алгебры на
алгебру И* (\K\,Q), где \К\ —полиэдр, отвечающий
комплексу К. Алгебра Epi(K) полностью определяет
также рациональный гомотопич. тип (в частности,
ранги гомотопич. групп) пространства \К\. Анало-
Аналогично алгебра Е* (М) на дифференцируемом многооб-
многообразии М определяет его вещественный гомотопич.
тип [9].
Исчисление внешних форм на комплексном аналитич.
многообразии имеет ряд особенностей [6]. В этой си-
ситуации обычно рассматриваются пространства Ер(М, С)
комплекснозначных форм или пространства Ep(F),
где F — голоморфное векторное расслоение на М. Имеет
место разложение
ЕР (М, С) = у Er,s
где Er's(M)—пространство форм типа (г, s)
форм а, локально представимых в виде
2 ,„..., i , /, / A..AAA.A ,
где (г1, . . ., z") — локальная аналитич. система коор-
координат на М. Аналогично
Далее, d=d'-\-d", где
d:Er,s (M) —^ Er+\ s (M), d":Er, s (M) —* ?'Vf+1 (M,.
При этом d'2—d=0, так что d' и d" определяют ко-
цепные комплексы. Наиболее известен комплекс опе-
оператора d" (комплекс Дольбо), когомологий
к-рого обозначаются через Hr's(M). сГ'-коциклы типа
(р, 0) суть голоморфные р-формы (см. Голоморфная
форма). Для d" справедлива следующая лемма
Гротендика: если а — форма типа (г, s) с s>0
в окрестности нуля пространства С" и d"a=0, то в
меньшей окрестности нуля существует такая форма $
типа (г, s— 1), что а=сГр. Комплекс Дольбо можно
определить также и для F-значных форм, где F — го-
ломорфное векторное расслоение. Это приводит к
пространствам когомологий Hr's (F). Из леммы Гро-
тендика вытекает следующий изоморфизм:
Hr,s(F)~Hs(M, Qr (F)),
где Qr(F) — пучок ростков голоморфных F-значных
г-форм (теорема Д о л ь б о). В частности,
Hr,s(M) = Hs(M, Qr (M)),
где Qr (M) — пучок ростков голоморфных г-форм
на М. Существует спектральная последовательность с
первым членом 2 r sHr's (M), сходящаяся к Н*(М,С).
Эйлерова характеристика Х(М) компактного комплекс-
комплексного многообразия М выражается через когомологий
Дольбо по формуле
t (М) = 2r s (—i)r+s dim И', s (M).
Д. ф. являются важной составной частью аппарата
дифференциальной геометрии (см. [7], [8]). Они си-
систематически используются также в топологии, теории
дифференциальных уравнений, механике, теории ком-
комплексных многообразий и функций многих комплекс-
комплексных переменных. Обобщением Д. ф., аналогичным
обобщенным функциям, являются потоки. Алгебраич.
аналог теории Д. ф. (см. Дифференциалов модуль)
позволяет определить дифференциальные формы на
алгебраических многообразиях и на аналитических
пространствах (см. Дифференциальное исчисление на
аналитических пространствах). См. также Рама ко-
когомологий, Дифференциал на римановой поверхности,
Гармоническая форма, Голоморфная форма, Лапласа
оператор.
Лит.: [1] д е Рам Ж., Дифференцируемые многообразия,
пер. с франц. М., 1956; [2] Р о i n с а г ё Н., Les methodes nou-
velles de la mecanique celeste, t. 3, P., 1899; [3] С а г t a n E.,
(Euvres completes, pt. 2, t. 1, p. 303—96; [4] F г б 1 i с h e r A.,
N i j e n h u i s A., «Proc. Koninkl. ned. akad. wet.», Ser. A,
1956, v. 59, № 3, p. 338—59; [5] У итни Х., Геометрическая
теория интегрирования, пер. с англ., М., 1960; [6] У э л л с Р.,
Дифференциальное исчисление на комплексных многообразиях,
пер. с англ., М., 1976; [7]Стернберг С, Лекции по диффе-
дифференциальной геометрии, пер. с англ., М., 1970; [8] К а р т а н А.,
Дифференциальное исчисление. Дифференциальные формы, пер.
с франц., М., 1971; [9]Гриффитс Ф. [и др.], «Успехи ма-
тем. наук», 1977, т. 32, в. 3, с. 119—52. А. Л. Онищип.
2) Д. ф. на алгебраическом много-
многообразии — аналог понятия дифференциальной фор-
формы на дифференцируемом многообразии. Пусть X —
неприводимое алгебраич. многообразие размерности d
над алгебраически замкнутым полем к, К — его поле
рациональных функций. Дифференциальной
формой степени г на .X" наз. элемент .ff-прост-
.ff-пространств а
где QK ,h — дифференциалов модуль поля К над полем к.
Если хг, ..., ocd — сепарабельный базис трансцендент-
трансцендентности расширения К/к, то каждая Д. ф. co^Q^X)
записывается в виде
ш:=2ач...<•/**,л •¦• A(bv
где а,-,, . .. ,• ?К- Д- ф. w наз. регулярной на
открытом множестве UczX, если со при-
принадлежит подмодулю Qk\U~l/h пространства Qr(X),
рассматриваемого как модуль над кольцом k[U] регу-
регулярных функций на подмножестве U. Д. ф. со наз.
регулярной, если любая точка х ? X имеет
такую окрестность U, что со регулярна на U. Регу-
Регулярные Д. ф. на X образуют модуль над к[Х], обозна-
обозначаемый Qr[JV]. Его элементы отождествляются с сече-
сечениями пучка Q^y/& на многообразии X. В окрестности
любой точки х?Х регулярная Д. ф. co?QrIx] запи-
записывается в виде
т=2а(, ...<//(, Л ¦¦• Adf'r'
где функции ai i ,/,-,,..., /{ регулярны в точке х.
Если X — полное многообразие, то пространства
S3r[JV] конечномерны, а в случае, когда X неособое,
размерность pg(X) = dim/iQ'i[X] наз. геометри-
геометрическим родом многообразия X. В слу-
случае, когда X — полное многообразие над полем ком-
комплексных чисел, пространство Q'TX] совпадает с про-
пространством голоморфных Д. ф. степени г на соответ-
соответствующем аналитич. пространстве Хап.
Пусть X —нормальное многообразие и ay^Qd[X];
для любой точки x^X^i коразмерности 1 Д. ф. со
может быть записана в виде
ы = а dt л dt1 л ... Л d^_j, (*)
где а принадлежит полю частных Кх локального кольца
6х, х-1 t — образующая его максимального идеала,
*!,'..., t^-i—сепарабельный базис трансцендентности
над к поля вычетов кольца Qxr x- Значение нормирова-
нормирования на элементе а, определяемое кольцом Qx, x, не за~
висит от выбора представления со в виде (*) и обозна-
обозначается vx(co). Дивизор
определен и наз. дивизором дифференци-
дифференциальной формы со. Д. ф. со регулярна тогда и
только тогда, когда ее дивизор D^sO, т.е. vx(co)^O
для всех x^JVA). Дивизоры любых двух Д. ф. экви-
эквивалентны, более того, дивизоры всех Д. ф. на данном
алгебраич. многообразии образуют класс дивизоров
относительно линейной эквивалентности. Этот класс
наз. каноническим классом много-
многообразия X ш обозначается через К х- Для неосо-
неособого многообразия X класс Кх совпадает с первым
классом Чженя обратимого пучка Й^д, в частности
для любого ? х
Для любого доминантного рационального отобра-
отображения алгебраич. многообразий f:X'-+X определен
канонич. гомоморфизм
При этом, если X и X' — неособые, а X — полное, то /*
переводит регулярные Д. ф. в регулярные. В част-
частности, если неособые полные многообразия X и X'
бирационально изоморфны, то векторные пространства
Qr[X] и Q'l.X"] изоморфны над полем к.
Для любого г>1 элементы г-й симметрич. степени
S'(Qr(X)) АГ-пространства Qr(X) наз. г-к р а т н ы м и
дифференциальными формами сте-
степени г на X. Каждую такую Д. ф. можно рассмат-
рассматривать как рациональное сечение пучка 5'(Q^,ft).
Регулярные сечения
со?Г(Х, Si(QrXfk))
наз. регулярными г-к ратными диффе-
дифференциальными формами степени г
на X. Для неособого полного многообразия X раз-
размерность
d)
наз. i-родом многообразия!. Для бирацио-
бирационально изоморфных многообразий их i-роды совпадают.
Лит.: [1] Ш а ф а р е в и ч И. Р., Основы алгебраической
геометрии, М., 1972; [2] Бальдассарри М., Алгебраичес-
Алгебраические многообразия, пер. с англ., М., 1961. И. В. Долгачев.
ДИФФЕРЕНЦИАЛЬНАЯ ЭНТРОПИЯ — формаль-
формальный аналог понятия энтропии для случайных величин,
имеющих плотность распределения. Д. э. А(?) случай-
случайной величины ?, определенной на нек-ром вероятност-
вероятностном пространстве (Q, 9t, P), принимающей значения в
га-мерном евклидовом пространстве R." и имеющей
плотность распределения р(х), x?Rn, дается формулой
R» Р (X) l0g P {Х) ЛХ
(здесь OlogO считается равным 0). Таким образом, Д. э.
совпадает с энтропией меры Р(-) относительно меры
Лебега Х( •), где Р(-) — распределение ?.
Понятие Д. э. оказывается полезным при вычис-
вычислении различных теоретико-информационных харак-
характеристик, в первую очередь информации количества
/E, г\) случайных векторов \ и т). В случае, когда
h (I), h(r\) и h(l, ц) (Д. э. пары (I, т))) конечны,
справедлива формула:
J(l, ti)==—Л(Б
Среди свойств Д. э. можно отметить следующие два:
1) в отличие от обычной энтропии, Д. э. не ковари-
антна относительно изменения системы координат
и может принимать отрицательные значения; 2) пусть
<р(?) — дискретизация с шагом Ах n-мерной случай-
случайной величины ?, обладающей плотностью, тогда для эн-
энтропии Л((р(й,)) справедлива формула
при Дх^^О. Таким образом, H((f(x))^>.-\-oo при Ах—>-0,
главный член асимптотики 7У(срE)) зависит от размер-
размерности пространства значений ?, Д. э. задает следующий
по порядку член асимптотич. разложения, не завися-
зависящий от Ах, причем это первый член, в к-ром прояв-
проявляется зависимость от конкретного вида распреде-
распределения |.
Лит.: [1] Гельфанд И. М., Колмогоров А. Н.,
Я г л о м А. М., в кн.: Тр. 3-го Всесоюзного математического
съезда, т. 3, М., 1958, с. 300—320; Щ В 6 п у i A., Wahrschein-
lichkeitsrechnung, В., 1962. Р. Л. Добрушин, В. В. Прелое.
ДИФФЕРЕНЦИАЛЬНО-ГЕОМЕТРИЧЕСКАЯ СТРУК-
СТРУКТУРА — одно из основных понятий современной
дифференциальной геометрии, включающее конкретные
изучаемые в ней структуры. Д.-г. с. определяется для
данного дифференцируемого многообразия М" как
дифференцируемое сечение в расслоенном пространстве
(Хр, jD/r, Мп) с базой Мп, ассоциированном с нек-рым
главным расслоением (X, р, Мп), или, в другой терми-
терминологии, как дифференцируемое поле нек-рого гео-
метрич. объекта на М". Здесь F является нек-рым диф-
дифференцируемым ©-пространством, где (Si — струк-
структурная группа Ли главного расслоения (X, р, Мп),
или, в другой терминологии, пространством представ-
представления группы Ли (Й.
Если (X, р, Мп) — главное расслоение реперов в
касательных к Мп пространствах, G — нек-рая замкну-
замкнутая подгруппа в ®=GL(n, R), a F — однородное про-
пространство (sj/G, то соответствующая Д.-г. с. на Мп наз.
G-c т р у к т у р о й, или инфинитезимальной
структурой 1-г о порядка. Напр., если
G состоит из всех таких линейных преобразований (эле-
(элементов из GL(n, R)), к-рые оставляют инвариантным
m-мсрное пространство в R.", то соответствующая G-
структура определяет на Мп распределение т-мерных
подпространств. Если G является ортогональной груп-
группой 0(п, R) — подгруппой элементов из GL(n, R),
сохраняющих скалярное произведение в R™, то G-
структура есть риманова метрика на Мп, т. е. поле
положительно определенного симметрич. тензора g,j.
Аналогично, частными случаями G-структуры на TVf"
являются почти комплексная и комплексная структуры.
Обобщением ff-структуры является инфините-
зимальная структура r-т о порядка,
г>1 (или G-структура высшего порядка); здесь (X, р,
Мп) является главным расслоением реперов г-го
порядка на Мп, a G — замкнутой подгруппой его
структурной группы Dn.
Важными частными случаями Д.-г. с. являются связ-
связности. Напр., связность в главном расслоении полу-
получается, если в роли Мп выступает пространство Р
нек-рого главного расслоения (Р, р, В), а G-структурой
на Р является такое распределение m-мерных, т= dim.P—
—dim5, подпространств, дополнительных к касательным
пространствам слоев, к-рое инвариантно относительно
действия в Р структурной группы расслоения. Связ-
Связности на многообразии Мп являются частными слу-
случаями Д.-г. с. на М", но более общими, чем G-струк-
туры на М". Напр., аффинная связность
на Мп, к-рую можно определить полем объекта связ-
связности Tij(x), получается как Д.-г. с. на Мп, при
к-рой (X, р, Мп) является главным расслоением репе-
реперов 2-го порядка, © — его структурной группой D"n ,
а пространство F представления группы Dn — про-
пространством R.3" с координатами Г,-,-, где представление
определяется формулами
здесь
Ai =
j_ A =
Эх'"/о' l'i' V Эх'' dxl
— координаты элемента группы D\, и Л('Л('=б{.
В случае проективной связности на Мп
имеют дело с нек-рым представлением группы Dn
в пространстве (R3<n+1)> а в случае связностей высшего
порядка — с представлениями группы Dn. При таком
подходе теория Д.-г. с. имеет самый тесный контакт
с геометрических объектов теорией.
Лит.: [ОВагнер В.В., [Дополнение], в кн.: В ебпен О.,
Уайтхед Дж., Основания дифференциальной геометрии, пер.
с англ., М., 1949, с. 135—223; [2] Л а п т е в Г. Ф., «Тр. Моск.
матем. об-ва», 1953, т. 2, с. 275—382; [3] X ь ю з м о л л е р Д.,
Расслоенные пространства, пер. с англ., М., 1970; [4J С т е р н-
берг С, Лекции по дифференциальной геометрии, пер. с
англ., М., 1970 Ю. Г. Лумисте.
ДИФФЕРЕНЦИАЛЬНОЕ ВКЛЮЧЕНИЕ, м н о г о-
значное дифференциальное уравне-
уравнение, дифференциальное уравнение
с многозначной правой часть ю,— со-
соие, дифференц
многозначной
отношение
где x=x(i) — неизвестная вектор-функция на нек-ром
интервале, F(t, х) — множество в и-мерном простран-
пространстве, зависящее от числа t и вектора х= {х1у . .., хп).
Решением Д. в. A) обычно называется абсолютно не-
непрерывная вектор-функция x(t), почти всюду на рас-
рассматриваемом интервале изменения t удовлетворяющая
соотношению
В частности, если множество F(t, x) состоит из одной
точки, то Д. в. превращается в обыкновенное диффе-
дифференциальное уравнение dxldt=F(t, x). Уравнения вида
Dx(t)?F(t, x(t)), где Dx(t) — контингенция [1],
в широком классе случаев равносильны Д. в.
К Д. в. приводят, напр., задача о функциях, удовле-
удовлетворяющих дифференциальному уравнению с заданной
точностью
дифференциальные неравенства
х
дифференциальные уравнения с разрывной правой
частью (см. [1], [2]); задачи теории оптимального уп-
управления (см. [3], [4]). В задачах управления обычно
рассматривается уравнение
где x=x(t) — искомая вектор-функция, a u=u(t) —
управление, т. е. вектор-функция, к-рую можно выби-
выбирать произвольно среди всех допустимых уп-
управлений (таких, что u(t)?U при каждом t,
где U — заданное множество, могущее зависеть от t
ii от x=x(t)). Множество решений уравнения B) при
всевозможных допустимых управлениях м=м(() удов-
.ютворяет Д. в. A), где F(t, х) — множество всех зна-
значений функции / (t, х, и), когда и п-робегает множе-
множество U.
В теории Д. в. обычно предполагается, что при лю-
любых t, х из рассматриваемой области G множество
F(t, х) есть непустое замкнутое ограниченное множе-
множество «-мерного пространства. Если множество F(t, x)
всегда выпукло, при каждом t оно является полу-
полунепрерывной сверху функцией от х (т. е.
для любых t, х и любого в>0 при всех достаточно
малых \х'—х\ множество F(t, x') содержится в е-
окрестности множества F(t, х)), а при каждом х— изме-
измеримой функцией от t (т. е. для любого х и любого шара
В в гс-мерном пространстве множество значений t, при
к-рых множество F(t, х)Г\В непусто, является изме-
измеримым по Лебегу), и если F(t, x) всегда содержится
в шаре |ж|<:т(/), где функция m(t) интегрируема по
Лебегу, то при любых начальных условиях x(to)-=xo,
Coi ^0N^' решение Д. в. существует (см. [5]) и инте-
интегральная воронка, состоящая из таких решений, обла-
обладает обычными свойствами [5]. От требования выпук-
выпуклости множества F(t, x) можно отказаться, если оно
непрерывно зависит от х. При этом существование
решения сохраняется [6J, а свойства интегральных во-
воронок — нет.
Обзор работ по теоремам существования решений
для Д. в. и связи Д. в. с задачами управления см.
в [7]. Для Д. в. рассматривается понятие устойчивости
[8]; изучаются существование ограниченных и нерио-
дич. решений и другие свойства Д. в. [9].
Лит.: [1] Барбашин Б. А., Алимов Ю. И., «Изв.
вузов. Математика», 1962, Х° 1, с. 3—13; [21 Филиппов
А. Ф., «Матем. сб.», 1960, т. 51, Л5 1, с. 99 — 128; [3J W a z e w s-
ki Т., «Bull. Acad. Polon. Sci., ser. math.», 1961, t. 9, №3,
p. 151 — 55; [4] Филиппов А. Ф., «Вестн. МГУ. Сер. ма-
матем.», 1959, MS 2, с. 25 — 32; [5] D a v у J. L., «Bull. Austral.
Math. Soc», 1972, v. 6, № 3, p. 379—98; [б] О 1 с с h С, «Boll
Uniono mat. ital.», 1975, t. 11, №3, p. 189—97; [7] Благо-
датских В. И., Summer School on ord. dif. eq, «Difford 74»
(Czechosl.), 1974, p. 29—67; [8] R о x i n E., «J. Dif. Equat.»
1965, v. 1, № 2, p. 115 — 50; [9] П о в о л о ц к и й А. И., Г а н-
г о Е. А., «Уч. зап. Ленпнгр. гос. пед. ин-та», 1970, т. 464,
ч. 1, с. 235 — 42. А. Ф. Филиппов
ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ — раздел
математики, в к-ром изучаются понятия производной
и дифференциала и способы их применения к исследо-
исследованию функций. Развитие Д. и. тесно связано с раз-
развитием интегрального исчисления. Неразрывно и их
содержание. Вместе они составляют основу математич.
анализа, имеющего чрезвычайное значение для ес-
естествознания и техники. Основной предпосылкой для
создания Д. и. явилось введение в математику пере-
переменных величин (Р. Декарт, R. Descartes). В общих
чертах построение дифференциального и интегрального
исчислений было завершено в трудах И. Ньютона
(I. Newton) и Г. Лейбница (G. Leibniz) к концу 17 в.,
однако вопросы обоснования с помощью понятия пре-
дела были разработаны О. Коши (A. Couchy) лишь
в начале 19 в. Создание дифференциального и инте-
интегрального исчисления явилось началом периода бур-
бурного развития математики и связанных с ней приклад-
прикладных наук. Под Д. и. обычно понимают классич. Д. и.,
в к-ром рассматриваются действительные функции
одного или нескольких действительных переменных,
хотя в современном толковании может идти речь и о
Д. и. в абстрактных пространствах. Д. и. основано на
понятиях действительного числа, функции, предела и
непрерывности — важнейших понятий математики,
сформировавшихся и получивших современное содер-
содержание в процессе развития математич. анализа и ра-
работы над его обоснованием. Центральные понятия
Д. и.— производная и дифференциал — и разработан-
разработанный в Д. и. аппарат, связанный с ними, доставляют
средства для исследований функций, локально сходных
с линейной функцией или многочленом, а именно такие
функции в первую очередь интересны для приложений.
Производная. Пусть функция y = f(x) опре-
определена в нек-рой окрестности точки хй, КхфО есть
приращение аргумента, Ay=f(xo-\-Ax)—/(.г0) — соот-
соответствующее приращение функции. Если существует
(конечный или бесконечный) предел
lim $?,
то он наз. производной функции f(x) в точке х0
н обозначается / (*„), —j—, у , ух, j^- Итак, по
определению,
I- lim ?2 =
Ax -+ О ДЖ Д*
lim
¦ о
(х„ + Ax)- / (х„)
Дх
Операция вычисления производной наз. диффе-
дифференцированием. Если /' (х0) — конечна, функ-
функция f(x) наз. дифференцируемой в точке
х0. Функция, дифференцируемая в каждой точке
нек-рого промежутка, наз.
дпффер е н ци р у е-
м о й в промежутке.
Геометрпчес ко е
истолкование про-
производной. Пусть С —
плоская кривая, заданная
в прямоугольной системе ко-
координат уравнением у—}(х),
где /(ж) определена и непре-
непрерывна в нек-ром интервале,
М (х0, у0) — фиксированная
точка на С, Р (х, у) —
произвольная точка кри-
кривой С, МР — секущая (см.
рис. 1). Прямая МТ наз.
касательной к кривой
С в точке М, если угол ф между секущей МР и этой
прямой стремится к нулю, когда х—>-ж0 (иными сло-
словами, когда точка Р?С произвольным образом стре-
стремится к точке М). Если упомянутая касательная
существует, то она — единственна. Если положить
х^=х„+Ах, Ay=f(xo+Ax)— f(x0), то для угла Р между
МР и положительным направлением оси Ох будет
иметь место равенство tgP=-^ (см. рис. 1). Кривая С
имеет в точке М касательную в том и только в том слу-
случае, если существует lim -^-, т. е. существует
/' (х0). При этом для угла а между касательной и по-
положительным направлением оси Ох справедливо
равенство tga=/' (x0). В случае конечной производной
/' (х0) касательная образует с Ох острый угол, т. е.
х = хо + Ах
Рис. 1.
— — <а<-у; в случае f'(xa)=oo касательная образует
с Ох прямой угол (см. рис. 2). Таким образом, произ-
производная непрерывной функции f(x) в точке х0 совпадает
с угловым коэффици-
коэффициентом tga касатель-
касательной к кривой, задан-
заданной уравнением у=
Д)Г —f(x), в ее точке с абс-
абсциссой х0.
Механичес кое
истолков а ние
производной.
Пусть точка М дви-
движется прямолинейно
по закону s=f(t). За
время At точка М
х сместится на As=
= f(t+At)-f(t). От-
Отношение As/At пред-
представляет собой сред-
среднюю скорость иСр точки за время At. При неравномер-
неравномерном движении уср не постоянна. Мгновенной
скоростью в момент t наз. предел средней ско-
скорости при Д?—>-0, т. е. v=f'(t) (в предположении, что
эта производная существует).
Такпм образом, понятие производной доставляет
общее решение задачи о построении касательной к
плоской кривой и задачи о вычислении скорости пря-
прямолинейного движения. Эти две задачи явились основ-
основными предпосылками в формировании понятия произ-
производной.
Функция, имеющая в точке х0 конечную производную,
непрерывна в этой точке. В случае бесконечной произ-
производной этого может не быть. Непрерывная функция мо-
может не иметь ни конечной, ни бесконечной производ-
производной. Существуют непрерывные функции, не имеющие
производной ни в одной точке области определения.
Для производных основных элементарных функций
справедливы следующие формулы (в любой точке
области определения; исключения оговариваются):
1) если / (х) = C = const, то f (х) = С" = 0;
2) если f(x) = x, то f (х)=1\
3) (ха)' = аха~1, cc = const (x ф 0, если а<1);
4) (ах)' = ах In a, o = const>0, а Ф i, в частности,
(ех)' =ех:
5) (log0z)'=-
ж In a
а = const > 0, а ф 1,
6) (sin х)' = cos x;
7) (cos >)' = — sin x;
8> ^ХУ
9) (ctg*)' = --
10) (arcsinz)' = :
1
sin2 x '
1
11) (arccos*)'= ——
V [—x*
12) (arctgz)'= -j^r- ;
13) (arcctgz)' = j-^- ;
1q) (СП. 3Cj z= Sll 3C'^
16) (tha)'= ¦¦1 ;
17) (Ci\ix)'=--±- .
. хф ±1;
, x ф ±i;
Имеют место также следующие правила дифферен-
дифференцирования;
1) Если функции и(х) и v(x) дифференцируемы в
точке х0, то функции
си (где с = const), и ± v, uv, u/v (v ф 0)
также дифференцируемы в этой точке, причем
(си)' ~си',
(и ± и)' — и' ± v',
(uv)' = u'v-\-uv',
u'v — vv'
2) Теорема о производной сложной
функции: если функция y=f(u) дифференцируема
в точке и0, а функция (р(х) дифференцируема в точке г0,
причем ко=ср(жо), то сложная функция у=1(ц>{х))
дифференцируема в точке х0 и yx=f (мо)ф' (ха) или, в
dii du du
другой записи, -г=-г з~-
1 J dx du dx
3) Теорем а о производной обратной
функции: если y=f(x) и x=g(y) — две взаимно
обратные возрастающие (или убывающие) функции,
заданные на нек-рых интервалах, и существует конеч-
конечная производная ]'(хо)фО, то в точке yo=f(xo) сущест-
существует конечная производная g' (j/0)= тг,—\, или, в дру-
1
roii записи, ¦^-=d~- Эта теорема допускает обобще-
dx
ние: если, при выполнении прочих условий, /' (zo) =
-0(f (ж0)=оо), то g' (уо)= °° (соответственно g' (уо)=О).
Односторонние производные. Если
в точке х0 существует предел
Ау_
Ах '
lim
Да:-* 0
Ах > 0
то он наз. правой производной функции
y=f(x) в точке х0 (в этом случае нет необходимости
требовать, чтобы функция была определена всюду в
нек-рой окрестности точки хд; достаточно потребовать
этого лишь для х~^х0). Аналогично определяется
левая производная — как предел
Ах _
Ах
Функция f(x) имеет производную в точке х0 в том и
только в том случае, если в этой точке существуют
равные между собой правая и левая производные. Для
непрерывной функции су-
существование в точке правой
(соответственно левой) про-
производной равносильно су-
существованию в соответствую-
соответствующей точке ее графика пра-
правой (соответственно левой)
односторонней полукаса-
полукасательной с угловым коэффи-
коэффициентом, равным значению
этой односторонней произ-
производной. Точки, в к-рых полукасательные не образу-
образуют одну прямую, называются угловыми точка-
м и (см. рис. 3).
Производные высших порядков.
Пусть функция y=f(x) имеет конечную производную
y'=f (x) в каждой точке нек-рого интервала; эта про-
производная наз. также первой производной,
или производной первого порядка,
к-рая, будучи функцией от х, может, в свою очередь,
иметь производную y"=f"(x), называемую второй
производной, или производной вто-
второго порядка, функции f(x), и т. д. Вообще
и-я производная, или производная по-
порядка га, определяется по индукции равенством
ylrl)= (у*"')', в предположении, что г/"-1» определена
на нек-ром интервале. При этом, наряду с г/п), исполь-
зуются также обозначения /(я) (х), —-—! , а для ге=2, 3
ещеу",1"(х), y"',f"(x).
Вторая производная имеет механич. истолкование:
это есть ускорение w=-rr2=f"(t) в момент I точки,
движущейся прямолинейно по закону s=/(().
Дифференциал. Пусть функция y=f(x) оп-
делена в нек-рой окрестности точки х и существует
такое число А, что приращение Ау может быть пред-
представлено в виде Ау=А Ах-\-ы, где со/Дяг—>-0 при Ах—И).
Член А Ах в этой сумме обычно обозначается символом
dy, или df(x), и наз. дифференциалом функ-
функции f(x) (по переменному х) в точке х. Дифференциал
есть главная линейная часть приращения функции
(геометрически изображается отрезком LT на рис. 1,
где МТ — касательная к кривой y=f(x) в рассматри-
рассматриваемой точке (х0, г/о))-
Функция y—f(x) имеет в точке х дифференциал в
том и только в том случае, если она имеет в этой точке
конечную производную
/'(*)= Hm %=A.
Ах — О дж
Функция, для к-рой существует дифференциал, наз.
дифференцируемой в рассматриваемой точ-
точке. Таким образом, дифференцируем ость
функции означает одновременно и существование
дифференциала, и существование конечной производ-
производной. При этом dy=df(x)=f (x)Ax. Для независимого
переменного х полагают dx= Ax и поэтому можно
писать dy=f (x)dx, т. е. производная равна отношению
дифференциалов:
См. также Дифференциал.
Формулы и правила вычисления для производных
приводят к соответствующим формулам и правилам
вычисления для дифференциалов. В частности, спра-
справедлива теорема о дифференциале слож-
сложно й функции: если функция г/=/(м) дифференци-
дифференцируема в точке м0, а функция <f>(x) дифференцируема в
точке х0, причем uo=(f(xo), то сложная функции г/=
=/(ф(ж)) дифференцируема в точке х0 и dy=f (uo)du,
где du=q>' (xo)dx. Дифференциал сложной функции
имеет точно такой же вид, как если бы переменное и
было независимым. Это свойство наз. инвариант-
инвариантностью формы дифференциала. Од-
Однако, если и — независимое переменное, du—Аи есть
произвольное приращение, а если и — функция, то
du есть дифференциал этой функции, вообще говоря,
не совпадающий с ее приращением.
Дифференциалы высших порядков.
Дифференциал dy наз. также первым диффе-
дифференциалом, или дифференциалом пер-
первого порядка. Пусть y=f(x) имеет дифференциал
dy=f (x)dx в каждой точке нек-рого интервала. Здесь
dx= Ax — некоторое число, не зависящее от х, и по-
поэтому можно считать dx= const. При этом dy оказы-
оказывается функцией только от я и, в свою очередь, может
иметь дифференциал, к-рый наз. вторым диффе-
дифференциалом, или дифференциалом вто-
второго порядка функции f(x), и т. д. Вообще, ге-й
дифференциал, или дифференциал п-т о
порядка, определяется по индукции равенством
d"y=d(d"-1y) в предположении, что дифференциал
dn~1y определен в нек-ром интервале и что значение dx
одно и то же на всех шагах. Свойство инвариантности
для d2y, d3y, . .., вообще говоря, не имеет места (ис-
(исключение составляет г/=/(м), где и — линейная функ-
функция).
Повторный дифференциал от dy имеет
вид
6(dy)=f"(x)dx8x
и вторым дифференциалом является значение 8(dy)
при dx=8x.
Основные теоремы и приложения
Д. и. К основным теоремам Д. и. для функций одного
переменного обычно относят Ролля теорему, Лагранжа
теорему (о конечном приращении), Коши теорему и
Тейлора формулу. Эти теоремы лежат в основе наиболее
важных приложений Д. и. к исследованию свойств
функций — таких, как возрастание и убывание функ-
функции, выпуклость и вогнутость графика, к отысканию
экстремумов, перегиба точек, асимптот графика. Д. и.
позволяет вычислять пределы функций во многих
случаях, когда простейшие теоремы о пределах не
позволяют сделать этого (см. Неопределенностей рас-
раскрытие). Д. и. находит широкие приложения во мно-
многих разделах математики, в частности в геометрии.
Д. и. функций многих переменных.
Для простоты рассматривается случай функций двух
переменных (за нек-рым исключением), хотя все по-
понятия легко распространяются на случай трех и боль-
большего числа переменных. Пусть функция г=/(ж, у)
задана в нек-рой окрестности точки (х0, у0) и пусть за-
зафиксировано значение #=г/о- Тогда f(x, y0) есть функ-
функция только от х. Если она имеет в х0 производную
по х, то эта производная наз. частной произ-
производной функции f(x, у) по х в точке (х0, у0) и обо-
значается fax,, г/о), й/ (х? у'\ д?, zx, g. Итак, по
определению,
/* (*о. У о) = lira -^ЕГ = lim * <*°+Аж- *>>-' <*-«»> ,
где Axz=f{xa+Ax, yo)—f(xo, y0) — частное при-
приращение функции по х (dz/дх в общем случае
нельзя рассматривать как дробь; д/дх есть символ
операции).
Аналогично определяется частная произ-
производная по у.
f'y(x0, »„) = Вт ?-= lim /<«..* +a»)-/ex.,,,,,)
у Ay ->- О Лу Ду -* О ЛУ '
где Д„2 — частное приращение функции по у. Другие
обозначения: а **"' Уо\ ~, z'y, ~. Частные производ-
производные вычисляются по правилам дифференцирования
функций одного переменного (при вычислении
z'x нужно считать у= const, а при вычислении z'y —
считать х= const).
Частными дифференциалами функ-
функции z=f(x, у) в точке (х0, у0) наз. (соответственно)
выражения
dx2 = f'x (жо. у о) dx; dyz = f'y (*o, г/о) dy
(где, как и в случае одного переменного, dx= Ax, dy=
= Ay означают приращения независимых переменных).
Первые частные производные —=
= f'x(x, у) и ^=}'у(х, у), или частные произ-
водные первого порядка, являясь функ-
функциями от х и у, могут в свою очередь иметь частные
производные по х и у, к-рые называются, по отноше-
отношению к функции z=f(x, у), частными произ-
производными второго порядка, или вто-
вторыми частными производными. При
этом полагают
дх \ дх ) дх2 ' ду \ дх ) вхву '
дг \ дгг д ( дг \ д'г
дх \ ду / дудх ' ду \ ду
Вместо дгг1дхг употребляют также обозначения
» - дЧ (х, у) 04 ¦¦
2Z J
вместо д2г/дхду — обозначения
" дЧ (х, у) дЧ
i I хг \xi У),
< У)
*У дхду ' дхду ' Тху
и т. д. Подобным образом вводятся частные произ-
производные третьего порядка и выше, и соответствующая
символика: дпг1дхп — функция z дифференцируется п
раз по х; d"z/dxPdyi, где n=p-\-q,— функция z диффе-
дифференцируется р раз по х и q раз по у. Частные произ-
подные второго и высших порядков, являющиеся
результатом дифференцирования по разным переменным,
наз. смешанными частными производ-
производными.
Каждой частной производной отвечает нек-рый
частный дифференциал, получаемый ум-
умножением ее на дифференциалы независимых перемен-
переменных, взятые в степенях, равных числу дифференциро-
дифференцирований по соответствующему переменному. Так полу-
получаются п-е частные дифференциалы, или
частные дифференциалы ге-г о п о р я д-
к а:
d"z , d"z , р , а
dx", -dxFdy4-
дх" дхР дуЧ
Справедлива следующая важная теорема о сме-
смешанных производных: если в нек-рой ок-
окрестности точки (х0, у0) функция z=f(x, у) имеет сме-
смешанные частные производные fXy(x, у) и f"yK(x, у) и
эти производные непрерывны в точке (х0, у0), то
f'xy (xoi !/o)=fyx(xo, y0)-
Функция z=/(j, у) наз. дифференцируемой
в точке (х„, у0) по совокупности переменных х и у, если
она определена в нек-рой окрестности этой точки и ее
лолное приращение
y0)
может быть представлено в виде
Az=A Ax-{-BAy-\- со,
где А и В — некоторые числа, ш/р—»-0 при р=
= уГ( ДжJ+(Д[/J->0 (при условии, что точка (хо+ Ах,
уя-\-Ау) принадлежит упомянутой окрестности). При
этом выражение
dz=df(x0, yo) = AAx+BAy
паз. полным дифференциалом (первого
порядка) функции f(x, у) в точке (х0, у0); это есть
главная линейная часть приращения. Функция, диф-
дифференцируемая в точке, непрерывна в этой точке (об-
(обратное не всегда верно!). Более того, дифференциру-
емость влечет существование конечных частных про-
производных
Д
А
1'х («о. г/о) = J|mo -~ = A, f'y (*0, уо)= дМто -^ -В.
Таким образом, для функции, дифференцируемой в
(*<» г/о).
или
= df(x0, yo) =
Ax + fy (*o, У о) ДУ.
>о, г/о) <?г/.
f(x.y)
Рис.
если, подобно случаю одного переменного, положить
для независимых переменных dx= Ax, dy=Ay.
Существование конечных ттастных производных в
общем случае не влечет ее дифференцируемости (здесь
нарушается аналогия
с функциями одного
переменного). Доста-
Достаточный признак диф-
ференц ируемости
функции двух пере-
переменных: если в
нек-рой окрестности
точки (ха, уа) функция
f(x, у) имеет конеч-
конечные частные произ-
производные f'x{x, у) и
f'y(x, у), непрерывные
в точке (х0, у0), то /
дифференцируема в
этой точке. Геомет-
Геометрически полный диф-
дифференциал df(x0, y0) есть приращение аппликаты
касательной плоскости к поверхности z=f(x,y) в точ-
точке (х„, 1/0, z0), где zo = / (х0, у0) (см. рис. 4).
Полные дифференциалы высших
порядков, подобно случаю функций одного пере-
переменного, вводятся по индукции равенством
d"z = d (dn~1 z)
в предположении, что дифференциал dn~^z определеп
в нек-рой окрестности рассматриваемой точки и что
приращения аргументов их, dy берутся одни и те же
на всех шагах. Аналогично определяются и повторные
дифференциалы.
Производные и дифференциалы
сложных функций. Пусть w=f(u1, . .., ит) —
функция т переменных, дифференцируемая в каждой
точке открытой области D m-мерного евклидова про-
пространства Rm, и пусть т функций м1=ф1(з:1, . . ., х„),
..., um=(fm(x1, ..., хп) — от п переменных заданы в
открытой области G re-мерного евклидова пространства
Rn. Пусть, наконец, точка (мх, . . ., ит), соответствую-
соответствующая точке (хи . .., xn)?G, не выходит из области D.
Тогда справедливы следующие теоремы:
1) Если функции фг, ..., фт имеют конечные частны*'
производные по хх,
(
, фт
р хп, то сложная функция ю=
=f(u1, .. ., ит) от хх, . .., хп также имеет конечные
частные производные по хх, ..., хп и
dw __ а/ ей, . of дип
диу
дх,
дх
df За,
ди1 дх~
ди„
ди_
2) Если функции ф!, ..., фт дифференцируемы
по совокупности переменных х±, ..., хп в точке
(хх ,. .., #„)?<?, то и сложная функция w^f(uly ..., ит)
дифференцируема в этой точке и
12 п
где dux, . .., dum — дифференциалы функций ult ...,
ит. Таким образом, свойство инвариантности первого
дифференциала имеет место и для функций нескольких
переменных. Для дифференциалов второго и высших
порядков это свойство, вообще говоря, нарушается.
Д. и. применяется к изучению свойств функций
многих переменных: к отысканию экстремумов, к ис-
исследованию функций, задаваемых одним или несколь-
несколькими неявными уравнениями, к теории поверхностей
н т. д. Одним из главных инструментов при этом яв-
является Тейлора формула.
Понятия производной и дифференциала и их про-
простейшие свойства, связанные с арифметич. действиями
над функциями и суперпозицией функций, включая
свойство инвариантности первого дифференциала,
почти без изменений распространяются на комплексные
функции одного или нескольких действительных пере-
переменных, на действительные и комплексные вектор-
функции одного или нескольких действительных пере-
переменных, на комплексные функции и вектор-функции
одного или нескольких комплексных переменных.
В функциональном анализе понятия производной и
дифференциала распространяются на функции точки
абстрактного пространства.
Лит.: История дифференциального и ин-
интегрального исчисления — [1] История матема-
математики с древнейших времен до начала XIX столетия, т. 1—3,
М., 1970—72; [2] Рыбников К. А., История математики,
т. 1—2,М., 1960—63; [3] В и л е й т н е р Г., История математики
от Декарта до середины XIX столетия, пер. с нем., 2 изд., М.,
1966; [4] С т р о й к Д. Я., Краткий курс истории математики,
пер. с нем., 2 изд., М., 1969; [5] Б у р б а к и Н., Очерки по
истории математики, пер. с франц., М., 1963; [6] С a n t о г М.,
Vorlesungen uber Geschichte der Mathematik, 2 Aufl., Bd 1—4,
Lpz., 1900—08.
Работы основоположников и классиков
дифференциального и интегрального ис-
исчисления — [7] Ньютон И., Математические работы,
пер. с латин., М.— Л., 1937; [8] Лейбниц Г., Избранные
отрывки из математических сочинений, пер. с латин., «Успехи
матем. наук», 1948, т. 3, в. 1; [9] Л'О п и т а л ь Г. Ф. де, Ана-
Анализ бесконечно малых, пер. с франц., М.— Л., 1935; 110] Э й-
л е р Л., Введение в анализ бесконечных, пер. с латин., 2 изд.,
т. 1, М., 1961- [11] его же, Дифференциальное исчисление,
пер. с латин., М.—Л., 1949; [12] К о ш и О. Л., Краткое изло-
изложение уроков о дифференциальном и интегральном исчислении,
пер. с франц., СПБ, 1831; [13] его же, Алгебраический ана-
анализ, пер. с франц., Лейпциг. 1864.
Учебники и учебные пособия по диффе-
дифференциальному и интегральному исчисле-
исчислению— [14] Гурса Э., Курс математического анализа,
пер. с франц., 3 изд., т. 1, М.—Л., 1936; [15] Ла Балле
Пуссен Ш. Ж. де, Курс анализа бесконечно малых, пер.
с франц., т. 1, Л.—М., 1933; [16] Курант Р., Курс диф-
дифференциального и интегрального исчисления, пер. с нем. и англ.,
4 изд., т. 1.М., 1967; [17] Р у д и н Р., Основы математического
анализа, пер. с англ., М., 1966; [18] Ильин В. А., П о з-
няк Э. Г., Основы математического анализа, т. 1, 3 изд., М.,
1971; т. 2, 1973; [19] К у д р я в ц е в Л. Д., Математический
анализ, 2 изд., М., 1973; [20] Никольский С. М., Курс ма-
математического анализа, 2 изд., М., 1975; [21] Толстов Г. П.,
Элементы математического анализа, т. 1—2, 2изд.,М., 1974; [22]
С ми р н о в В. И., Курс высшей математики, 22 изд., т. 1, М.,
1967; [23] Фихтенгольц Г. М., Курс дифференциально-
дифференциального и интегрального исчисления, 7 изд., М., 1969; [24] X и н ч и н
А. Я., Восемь лекций по математическому анализу, 3 изд.,
М,— Л., 1948. Г. П. Толстов.
ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ на ана-
аналитических пространствах — обобще-
обобщение классич. исчисления дифференциальных форм и
дифференциальных операторов на случай аналитич.
пространств. Об исчислении дифференциальных форм
на комплексных многообразиях см. Дифференциальная
форма. Пусть (X, Qx) — аналитич. пространство над
полем к, А — диагональ в XXX, J — пучок идеалов,
определяющий Д и порожденный всеми ростками вида
n\f—n\f, где / — произвольный росток из Qx, я/:
ХХХ-+-Х — проекция на ?-й сомножитель.
Аналитич. пучок щ (///2)=йх наз. пучком ана-
аналитических дифференциальных форм
первой степени на X. Если / — росток ана-
аналитич. функции на X, то росток к^—яг/ принадлежит
/ и определяет элемент df пучка Qx, n1(J/J2), называ-
емый дифференциалом ростка /. Тем
самым определяется гомоморфизм пучков векторных
пространств d : 0д-*-Йх- Если Х = к", то их — сео6од-
ный пучок, порожденный dx1, . . ., dxm где^, . .., хп—
координаты в к". Если X — аналитич. подпрост-
подпространство в к", определяемое пучком идеалов /, то
С каждым аналитич. отображением / : X-+Y можно
связать пучок относительных диффе-
дифференциалов Их- Это — аналитич. пучок &х/у >
индуцирующий Qx на каждом слое Xs(s?Y) отобра-
отображения /; он определяется из точной последовательности
/* Q^ —* Qx —> QXjy —> 0.
Пучок вх=Нот^ (Q^, Qx) наз. пучком рост-
ростков аналитических векторных по-
полей на X. Если X — многообразие, то Их и ©х —
локально свободные пучки, естественно изоморфные
пучкам ростков аналитич. сечений кокасательного и
касательного расслоений над X соответственно.
Аналитич. пучки QPx= Л Их наз. пучками ана-
6х
литических внешних дифференци-
дифференциальных форм степени р на X (при /с=С
их наз. также голоморфными формами). Для всякого
р^О определяется гомоморфизм пучков векторных
пространств dP: Q'x-^-Qx^1, совпадающий при р=0
с введенным выше и удовлетворяющий условию df + 1dP=
= 0. Комплекс пучков (Q*x, d) наз. комплексом
д е Рама пространства X. Если X — многообразие
и /с=С или R, то комплекс де Рама является точным
комплексом пучков. Если X многообразие Штейна или
вещественное аналитич. многообразие, то когомологии
комплекса сечений Г (Их), часто также называемого
комплексом де Рама, изоморфны НР(Х, к).
Если X имеет особые точки, то комплекс де Рама
не обязан быть точным. В случае, когда к=С, доста-
достаточным условием точности комплекса де Рама в точке
х?Х является наличие у х комплексно аналитически
стягиваемой окрестности. Гипергомологии комплекса
Г (Их) при /с= С содержат когомологии пространства X
с коэффициентами в С в качестве прямого слагаемого
и совпадают с ними, если X гладко. Сечения пучка ву
наз. аналитическими (а при к=С также
голоморфными) векторными полями
на X. Поле Z?T(X, &x) определяет для любого от-
открытого UczX дифференцирование алгебры аналитич.
функций Г(U, Qx)t действующее по формуле ср—>-Zq>=
= Z(d(f). Если А:=С или R, то Z задает локальную
однопараметрич. группу expt Z автоморфизмов про-
пространства X. Если при этом X компактно, то группа
expt Z определима глобально.
Пространство Г(Х, в^), снабженное скобкой Ли,
является алгеброй Ли над к. Если X — компактное
комплексное пространство, то Т(Х, вх) — алгебра Ли
группы Aut X.
Дифференциальные операторы на аналитич. прост-
пространстве (X, Qx) определяются аналогично дифферен-
дифференциальным операторам модуля. Если F, G — аналитич.
пучки на X, то линейным дифференциаль-
дифференциальным оператором порядка <i, действую-
действующим из F в G, наз. гомоморфизм пучков векторных
пространств F—t-G, продолжающийся до аналитич. го-
гомоморфизма F@n1(Qxxx/Il + 1)—>-G- Если X гладко, a F
и G локально свободны, то это определение приводит
к обычному понятию дифференциального оператора на
векторном расслоении [3], [4].
Ростки линейных дифференциальных операторов
F-+G образуют аналитич. пучок Diil(F, G) с фильт-
фильтрацией
Diffo (F, G) с Diff1 (F, С) с ... С DifF (F, G) с=...,
где DiHl(F, G) —пучок ростков операторов порядка
<С1. В частности, Diff@, Q) — фильтрованный пучок
ассоциативных алгебр над к относительно композиции
отображений. Имеем
Diff»(^, G)ssHobiq(F, G),
Diff1 F, 6)/Diffo (Q, Q) a= вх.
Изучение пучка Diff(Q, 6) проведено (в негладком
случае) лишь для нек-рых специальных типов особых
точек. В частности, в случае неприводимого одномер-
одномерного комплексного пространства X доказано, что
пучок алгебр Diff@, Q) и соответствующий пучок
градуированных алгебр допускают конечные системы
образующих [5].
Лит.: [1] М а 1 g г a n g е В., «Enseign. math.», 1988, ser. 2,
t. 14, № 1, p. 1—20; [2] К о u p W., «Math. Ann.», 1965, Bd 160,
№ 1, S. 72—92; [3] Шварц Л.. Комплексные многообразия.
Эллиптические уравнения с частными производными, пер. с нем.,
М., 1904; [4] У э л л с Р., Дифференциальное исчисление на
комплексных многообразиях, пер. с англ., М., 1976; [5] В 1 о о m
Т h., «Rice Univ. Stud.», 1973, v. 59, JVB 2, p. 13—19; 1б] В е r-
E e г R., |u. a.], Differentialrechnung in der anaytilschen Geome-
Geometric, В.— Hdlb.—N. Y., 1967; [I] F i sc he г G., Complex ana-
analytic geometry, В.— Hdlb.— N. Y., 1976. Д. А. Пономарев.
ДИФФЕРЕНЦИАЛЬНОЕ КОЛЬЦО — кольцо, в
к-ром отмечено одно или несколько дифференциро-
дифференцирований (см. Дифференцирование кольца). Если d(a) = 0
для всех этих дифференцирований, то а наз. кон-
константой. Л А Скорняков.
ДИФФЕРЕНЦИАЛЬНОЕ НЕРАВЕНСТВО — пера
венство, связывающее аргумент, неизвестную функцию
и ее производные, напр.,
y'(x)>f(x, у(х)), A)
где у(х) — неизвестная функция аргумента х. Основ-
Основная проблема теории Д. н.— по заданному Д. н. и
дополнительным (начальным или граничным) усло-
условиям описать совокупность всех его решений.
Большую группу составляют Д. н., получающиеся
из дифференциальных уравнений хорошо изученных
классов заменой знака равенства на знак неравенства,
что равносильно добавлению к одной из частей урав-
уравнения заранее не уточняемой функции определенного
знака. Представляет интерес сравнение решений таких
Д. н. с решениями соответствующих дифференциальных
уравнеиий. Так, для любого решения Д. н. A) спра-
справедливы оценки |1]:
у (х) < z (х) при з-1<г< ,г0,
у (х) > z (х) при х0 < х^х2,
где
г' = / (х, z), z {хо) = у (х0),
на любом интервале [xt, x2] существования обоих
решений. Это простое утверждение широко применя-
применяется для оценок решений дифференциальных уравне-
уравнений (путем перехода к соответствующему Д. н. с легко
указываемым частным решением), области продолжи-
продолжимости решений, разности между двумя решениями,
для вывода условий единственности решения и т. д.
Справедливо аналогичное утверждение [2] и для Д. н.
(неравенство Чаплыгина)
y(m4 а1(х)у(«'-1>-{-...+ат(х) у > f (х).
Здесь оценки типа B) для решений, удовлетворяющих
при х==х0 одинаковым начальным условиям, таранти-
руются лишь на интервале, определяемом коэффици-
коэффициентами alt . . ., ат: напр., для Д. н. y"-\-y~>f(x) это
интервал [х0—я, хо-\-л].
Для системы Д. н.
у\ (х) > fi (*> Уи ¦• •. Уп) (i = i, ..., п)
было указано [3], что если каждая функция /,¦ не убы-
убывает по аргументам yjDj=?i), то имеет место оценка
У! (х) > z; (х) при ха < х^х2; i = l, ..., п,
подобная B). Развитие этих рассмотрений приводит
к теории Д. н. в пространствах с конусом.
Разновидностью Д. н. является требование знакопо-
стоянства полной производной от заданной функции:
d „ , , dF . dF ' , | dF ' n
^F(x,yly ..., yn)^- + — yl+... + — yn<0,
применяемое в теории устойчивости.
Представителем другой группы является Д. н.
max | у\ — U (х, уи ..., у„)|<е (о)
1=1. ..., П
(е>0 задано), исследованное впервые в связи с общей
концепцией о приближенном описании реальной задачи
дифференциальными уравнениями [4]. Здесь интересно
описание интегральной воронки, т. е. со-
совокупности всех точек всех решений, удовлетворяющих
заданным начальным условиям, в частности поведение
воронки при ?_>-оо. Естественным обобщением Д. н. C)
является дифференциальное уравнение в континген-
циях, к-рое задается с помощью поля конусов, обоб-
обобщающего понятие поля направлений.
Для Д. н. изучалась и теория краевых задач. Д. н.
O (Д — оператор Лапласа) определяет суб-
субгармонические функции, Д. н. ^— Дм<0
определяет субпараболические функции.
Рассматривались и более общего вида Д. н. (обеих
упомянутых выше групп) с частными производными
для дифференциальных операторов различных типов.
Лит.: Ill P e t г о v i ts с h M., «Math. Ann.», 1901, Bd 54,
№ 3, S. 417—36; [2] Чаплыгин С. А., Основания нового
способа приближенного интегрирования дифференциальных
уравнений, М., 1919; [3] Waiewski Т., «Ann. Soc. polon.
math.», 1950, t. 23, p. 112—66; [4] Bohl P., «J. reine und angew.
Math.», 1914, Bd 144, S. 284—313; [5] Haar А., в кн.: «АИ
del Congresso Internazionale del Mathematici. Bologna». 1928,
t. 3, Bologna, 1930, p. 5—10; [6] WalterW., Differential-
und Integral-Ungleichungen und ihre Anwendung bei Abschat-
zungs- und Eindeutigkeitsproblemen, В., 1964; [7] S z a-
rski J., Differential inequalities, Wars., 196.5; [8] Laki-
hmikantham V., Leeta S., Differential and integral
inequalities, v. 1—2, N. Y., 1969. А. Д. Мышпыс.
ДИФФЕРЕНЦИАЛЬНОЕ ПОЛЕ — дифференциаль-
дифференциальное кольцо, являющееся полем. Множество констант
Д. п. является подполем, оно наз. полем кон-
констант. Л. А. Скорняков
ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ АБСТРАКТ-
АБСТРАКТНОЕ — дифференциальное уравнение в том или ином
абстрактном пространстве (гильбертовом, банаховом
и т. п.) или дифференциальное уравнение с оператор-
операторными коэффициентами. Классическим и наиболее часто
встречающимся Д. у. а. является уравнение
Lu = ?-Au = f, A)
где неизвестная функция м= и (t) принадлежит нек-рому
функциональному пространству X, 0<.t*?T<ioo, и
А:Х—*-Х — оператор (как правило — линейный), дей-
действующий в этом пространстве. Если оператор А ог-
ограничен и постоянен (не зависит от t), то формула
дает единственное решение уравнения A), удовлетво-
удовлетворяющее условию м@)=мо. Для переменного A(t)
оператор е('-тМ заменяется эволюционным оператором
u(t, т). В случае неограниченного оператора А решения
задачи Коши м@)=и0 могут: не существовать при
нек-рых м0, быть не единственными, обрываться при
t<CT. Исчерпывающее изучение однородного (/=0)
уравнения A) с постоянным оператором дается теорией
полугрупп, а вопросы существования и единственности
решаются в терминах свойств резольвенты А (см.
[1], [5]). Этот же метод применим и для переменного
оператора при условиях его гладкой зависимости от t
(см. [5]). Другим методом изучения уравнения A),
дающим, как правило, более грубые результаты, но
применимым к более широким классам уравнений (в
некоторых случаях — даже к нелинейным), является
использование энергетич. неравенств: [|и||<:с||?и|1, по-
получаемых также за счет тех или иных предположений
относительно А. Для гильбертова пространства X
постулируются, как правило, различные свойства
положительности скалярного произведения (Аи, и)
(см. [2]). Все сказанное в значительной степени рас-
распространяется и на более общее Д. у. а.
d'u . , du
+ A
рассматриваемое при условиях и@)=и0, ut(O) = u1.
Зачастую, изучение уравнения B) тем или иным при-
приемом (сведением к системе уравнений 1-го порядка,
заменой и-— \ v(x)dx, расщеплением левой части на
произведение двух операторов 1-го порядка и т. п.)
сводится к изучению уравнения A). Основным источ-
источником интереса к Д. у. а. является возможность све-
сведения к уравнениям вида A) или B) так наз. смешан-
смешанных задач в цилиндрич. областях для классических
параболич. и гиперболич. уравнений 2-го порядка:
функция u(t, х1, . . ., хп) рассматривается как функция t
со значениями в соответствующем пространстве функ-
функций от х, а дифференцирования по х, вместе с гранич-
граничными условиями на боковых поверхностях цилиндра
(образующие к-рого параллельны оси t), порождают
операторы А, Аи- Уравнения A), B), в к-рых постули-
постулируемые свойства операторов А, А ь совпадают с полу-
получающимися в описанной выше ситуации, наз. абстракт-
абстрактными параболическими или гиперболическими. Реже
рассматриваются абстрактные эллиптич. операторы.
Часто формулируются в терминах полугрупп и
уравнения A) задачи в теории рассеяния [3], рассмат-
рассматривающей интервал —оо<г<-}-оо. Сведение задач для
дифференциальных уравнений с частными производ-
производными к задачам для Д. у. а. A) и B) оказывается
весьма удобным при разработке нриближенных (напр.,
разностных [4]) методов решения и при рассмотрении
асимптотич. методов («малый» и «большой» параметры).
Общие Д. у. а. с оператором
и граничными условиями на обоих концах интервала
(О, Т) при неограниченных операторах А ^ поддаются
содержательному изучению лишь при весьма специ-
специальных предположениях относительно А/.. Для огра-
ограниченных A /j соответствующее обобщение теории обык-
обыкновенных дифференциальных уравнений не вызывает
затруднений.
Лит.: [1] X и л л е Э., Ф и л л и п с Р., Функциональный
анализ и полугруппы, пер. с англ., [2изд.1, М_. 1962; L2] L i-
onsJ., Equations differentielles operatiounelles et problemes aux
limites, В., 1961; L3J Л а к с П.,Филлипс Р., Теория рас-
рассеяния, пер. с англ., М., 1971; [4] С а м а р с к и й А. А., Вве-
Введение в теорию разностных схем, М., 1971; [5j К р е й н С. Г.,
Линейные уравнения в банаховом пространстве, М., 1971.
А. А. Лезии.
ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ В ПОЛНЫХ
ДИФФЕРЕНЦИАЛАХ — обыкновенное дифференци-
дифференциальное уравнение
F (х, у, у', ..., у<»>) = 0, A)
левая часть к-рого может быть записана в виде полной
производной:
^Ф(х, у, у', ..., j/(«-1)) = 0.
Другими словами, уравнение A) является Д. у. в п. д.,
если существует такая дифференцируемая функция
Ф{х, м0, щ, . .., «„_!>, что
F (х, и0, «!,..., и„) = ф^+М1ф'ио+„2ф'и1+. . .+и„Ф^_1
тождественно по всем аргументам. Решение уравнения
re-го порядка в полных дифференциалах сводится к
решению уравнения (?г—1)-го порядка
Ф (х, у, у', ..., у<-"-1>)^=С, C = const.
Пусть F(x, ий, Mt, . . ., и„) есть п раз непрерывно
дифференцируемая функция, а Ф (х, и0, щ, . .., и,,--^—
функция, имеющая непрерывные частные производ-
производные до 2-го порядка включительно. Пусть
U (v1)
" un-v
Для того чтобы уравнение A) было Д. у. в п. д., до-
достаточно, чтобы функции Av^\ v=0, I, . . ., га, не за-
зависели от м„ и AnF=O (см. [1]). В частности, м„ может
входить в /' только линейно.
Уравнение 1-го порядка
М(х, y) + N(x, y)y'=O, B)
где функции М, N, My, N'x определены и непрерывны
в открытой односвязной области D плоскости (х, у) и
M2Jj-N*>0 в D, будет Д. у. в п. д. в том и только
в том случае, когда
М'у(х, y)^N'x(x, у) в D.
Общее решение уравнения B) в полных дифференциа-
дифференциалах имеет вид ф (х, у) = 0, где
Ф (х. У) =\{*'У) М (х, у) dx + N(x, у) dy
и интеграл берется по любой спрямляемой кривой,
лежащей в области D и соединяющей произвольную
фиксированную точку (х0, ya)Q.D с точкой (х, у) (см.
[2]). Уравнение B) (в общем случае уравнение A),
линейное по у{п)) может быть приведено (при нек-рых
предположениях) к Д. у. в п. д. умножением на ин-
интегрирующий множитель.
Лит.: [1] Камке Э,, Справочник по обыкновенным диф-
дифференциальным уравнениям, пер. с нем., 5 изд., М., 1978; [2]
Ё р у г и н Н. П., Книга для чтения по общему курсу дифферен-
дифференциальных уравнений, 2 изд., Минск, 1972. Н. X. Розов.
ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ ОБЫКНО-
ОБЫКНОВЕННОЕ — уравнение, в к-ром неизвестной является
функция от одного независимого переменного, причем
в это уравнение входят не только сама неизвестная
функция, но и ее производные различных порядков.
Термин «дифференциальные уравнения» был пред-
предложен Г. Лейбницем (G. Leibniz, 1676). Первые ис-
исследования Д. у. о. были проведены в конце 17 в. в
связи с изучением проблем механики и нек-рых гео-
метрич. задач.
Д. у. о. имеют большое прикладное значение, яв-
являясь мощным орудием исследования многих задач
естествознания и техники: они широко используются
в механике, астрономии, физике, во многих задачах
химии, биологии. Это объясняется тем, что весьма
часто объективные законы, к-рым подчиняются те
или иные явления (процессы), записываются в форме
Д. у. о., а сами эти уравнения, таким образом, яв-
являются средством для количественного выражения
этих законов. Напр., законы механики Ньютона по-
позволяют механич. задачу описания движения системы
материальных точек или твердого тела свести к мате-
матич. задаче нахождения решений Д. у. о. Расчет
радиотехнич. схем и вычисление траекторий спутников,
исследование устойчивости самолета в полете и выяс-
выяснение течения химич. реакций — все это производится
путем изучения и решения Д. у. о. Наиболее важные
и интересные технич. приложения Д. у. о. находят
в колебаний теории и в автоматического управления
теории. В свою очередь прикладные вопросы служат
источником новых постановок задач в теории Д. у. о.;
именно так возникла, напр., оптимального управления
математическая теория.
В дальнейшем независимое переменное будет обо-
обозначаться через t, неизвестные функции — через х, у, z
и др., а производные этих функций по t — через х, х,
. . ., х{п) и т. д.
Простейшее Д. у. о. встречается уже в анализе:
нахождение первообразной для данной непрерывной
функции /(() является по существу задачей об опре-
определении такой неизвестной функции x=x(t), к-рая
удовлетворяет уравнению
i = f(t). A)
Для доказательства разрешимости этого уравнения
необходимо было построить специальный аппарат —
теорию интеграла Римана.
Естественным обобщением уравнения A) является
Д. у. о. 1-го порядка, разрешенное относительно про-
производной:
x = f(t,x), B)
где f(t, х) — известная функция, определенная в нек-рой
области D плоскости t, x. Многие практич. задачи сво-
сводятся к задаче решения (или, как часто говорят, ин-
интегрирования) этого уравнения. Р е ш е н и е м Д. у. о.
B) наз. функция x=x(t), определенная и дифференци-
дифференцируемая на нек-ром интервале / и удовлетворяющая
условиям:
(?D ?I
Решение Д. у. о. B) геометрически можно изобразить
на плоскости t, x в виде кривой с уравнением x=x(t),
t?I. Эта кривая наз. интегральной кривой, в каждой
своей точке она имеет касательную и целиком лежит
в области D. Геометрич. интерпретацию самого урав-
уравнения B) дает поле направлений в области
D, к-рое получается, если через каждую точку (t, x)?D
провести отрезок Ц х малой длины с угловым коэффи-
коэффициентом f(t, x). Любая интегральная кривая x=x(t)
в каждой своей точке (t, x(t)) касается отрезка lt,X(t)-
Ответ на вопрос о том, когда уравнение B) имеет
решение, дает теорема существования:
если /(*, x)^C(D) (т. е. непрерывна в D), то через
любую точку (t0, xo)?D проходит по крайней мере одна
непрерывно дифференцируемая интегральная кривая
уравнения B), и каждая из этих кривых может быть
продолжена в обе стороны вплоть до границы любой
замкнутой подобласти, целиком лежащей в D и содер-
содержащей точку (t0, x0). Другими словами, для всякой
точки (f0, xq)?D найдется хотя бы одно непродолжа-
емое решение x=x(t), t?I, такое, что x(t)?Cx(I)
(т.е. непрерывна в / вместе с производной x(t)),
x(to)=xo C)
и x(t) стремится к границе области D, когда t стре-
стремится к правому или левому концам интервала /.
Важнейшим теоретич. вопросом является выяснение
того, какие предположения о правой части Д. у. о.
надо сделать и какие дополнительные условия можно
присоединить к уравнению, чтобы выделить одно един-
единственное его решение. Справедлива следующая тео-
теорема существования и единствен-
единственности: если f(t, x)?C(D) и удовлетворяет в D Лип'
шица условию по х, a (t0, xo)?D, то уравнение B)
имеет единственное непродолжаемое решение, удовле-
удовлетворяющее условию C). В частности, если два решения
x=x1(t), t^/j, и x=x2(t), t?I2, такого уравнения
B) совпадают хотя бы для одного значения t=t0, т. е.
(
Геометрич. содержание этой теоремы заключается в
том, что вся область D покрыта интегральными кри-
кривыми уравнения B), к-рые нигде не пересекаются
между собой. Единственность решений имеет место
и при нек-рых более слабых предположениях отно-
относительно функции f(t, x) (см., напр., [6]).
Соотношение C) наз. начальным условием. Числа t0
и х0 наз. начальными значениями для решения урав-
уравнения B), а точка (t0, х0) — начальной точкой
соответствующей интегральной кривой. Задача оты-
отыскания решения этого уравнения, удовлетворяющего
начальному условию C) (или, как еще говорят, имею-
имеющего начальные значения t0, х0), наз. Коши задачей,
или начальной задачей. Сформулированная только что
теорема дает достаточные условия однозначной разре-
разрешимости задачи Коши B), C).
Часто прикладные вопросы приводят к системам
Д. у. о., в к-рые входят несколько неизвестных функ-
функций от одного и того же независимого переменного и их
производные. Естественным обобщением уравнения B)
является нормальная форма системы диф-
дифференциальных уравнений re-го порядка:
x'=f'(t, х1, х2, ..., хп), г = 1, ..., и, D)
где х1, х2, ..., хп — неизвестные функции от перемен-
переменного t, а /', i=l, 2, ..., п, суть заданные функции от
п-\~\ переменных. Полагая
ас = (х1, ..., х"),
f(t, ж) = (/!('. а?), ..., f"(t, ас)),
можно переписать систему D) в векторной форме:
x=f(t,x). E)
Решением системы D) или векторного урав-
уравнения E) является вектор-функция
ao = oa(t) = (x^(t), ...,x"(t)), t?I. F)
Каждое решение можно представлять себе в (п-\~ 1 ^мер-
^мерном пространстве t, х1, х2, ..., х" в виде интегральной
кривой — графика вектор-функции F).
Задача Коши для уравнения E) состоит в отыскании
решения, удовлетворяющего начальным условиям
zi(t0) = 4, •••. x"(to) = 4,
или
ae(to) = xo. G)
Решение задачи Коши E), G) удобно записывать в виде
x = ac(t, t0, аз0), t?l. (8)
Теорема существования и единственности для урав-
уравнения E) формулируется так же, как и для уравне-
уравнения B).
Весьма общие системы Д. у. о. (разрешенные отно-
относительно старших производных всех неизвестных функ-
ций) сводятся к нормальным системам. Важным част-
частным классом систем E) являются линейные системы
Д. у. о. гс-го порядка:
где A (t) — матрица типа геХгс.
Большое значение в приложениях и в теории Д. у. о.
имеют автономные системы Д. у. о.:
ж=/(ж), (9)
т. е. нормальные системы, правая часть к-рых явно
не зависит от переменного t. В этом случае уравнение
F) удобно рассматривать как параметрич. представ-
представление кривой, сопоставляя решению фазовую траекто-
траекторию в «-мерном фазовом пространстве х1, х2, ..., хп.
Если x,= x(t) есть решение системы (9), то ей удовле-
удовлетворяет также функция 05 = ж(?-}-с), где с — произволь-
произвольная постоянная.
Другим обобщением уравнения B) является Д. у. о.
n-го порядка, разрешенное относительно старшей
производной:
?M = f(t, У, У J/1»-1»). (Ю)
Важный частный класс таких уравнений — линейные
Д. у. о.:
Уравнение A0) сводится к нормальной системе и-го
порядка, если ввести новые неизвестные функции пере-
переменного t по формулам
Если, напр., уравнение A0) описывает динамику
нек-рого объекта и нужно исследовать движение
этого объекта, начинающееся в определенный момент
t=t0 из определенного начального состояния, то к
уравнению A0) добавляются дополнительные условия:
yih) = Vo, V(h) = y\, .... J/("-1)('o) = J/(o">- (H)
Задача отыскания такой п раз дифференцируемой
функции y~y(t), t?I, к-рая обращает уравнение A0)
в тождество при всех 1^/ н удовлетворяет начальным
условиям A1), наз. задачей Кош и.
Теорема существования и един-
единственности: если
/(«, иъ щ, ...,
и удовлетворяет условию Липшица по иг, м2, ..., ип, а
(f0, j/o, Vo, •¦•- И'
то задача Коши A0), A1) имеет единственное решение.
Задача Коши далеко не исчерпывает тех задач, к-рые
изучаются для уравнений A0) высших порядков [как
и систем E)]. Конкретные физич. и технич. проблемы
часто приводят не к начальным условиям, а к допол-
дополнительным условиям иного вида (так наз. краевым
условия м), когда значения искомой функции y(t)
и ее производных (или соотношения между ними)
задаются для нескольких различных значений неза-
независимого переменного. Напр., в задаче о брахистохроне
требуется проинтегрировать уравнение
при краевых условиях у(а)=А, у(Ъ)=В; отыскание
2я-периодич. решения для Дуффинга уравнения сво-
сводится к выделению такого его решения, к-рое удов-
удовлетворяет условиям периодичности: у@)=г/Bя), у@)=
= уBп)\ при изучении обтекания пластинки ламинар-
ламинарным потоком встречается задача:
"у + УУ = О, у @) = у @) = 0, у (t) —> 2 при i —> оо .
Задача отыскания для Д. у. о. высшего порядка или
системы Д. у. о. решения, удовлетворяющего условиям,
отличным от начальных условий A1), наз. краевой за-
задачей. Теоретич. анализ существования и единственно-
единственности решения краевой задачи имеет существенное значе-
значение для прикладной проблемы, приводящей к этой кра-
краевой задаче, поскольку он показывает взаимную согла-
согласованность допущений, принятых при математич. описа-
описании проблемы, и известную полноту этого описания.
Одной из важных краевых задач является Штурма —
Лиувилля задача. Краевые задачи для линейных урав-
уравнений и систем тесно связаны с задачами о собственных
значениях и собственных функциях, а также со спект-
спектральным анализом обыкновенных дифференциальных
операторов.
Главной задачей теории Д. у. о. является изучение
решений таких уравнений. Однако вопрос о том, что
значит изучить решения Д. у. о., в разное время
понимали по-разному. Первоначально стремились осу-
осуществить интегрирование уравнений в квадратурах,
т. е. получить замкнутую формулу, дающую (в явной,
неявной или параметрич. форме) выражение зависи-
зависимости того или иного решения от t через элементарные
функции и интегралы от них. Такие формулы, если
они найдены, оказывают существенную помощь в
вычислениях и при исследовании свойств решений.
Особый интерес представляет описание всей совокуп-
совокупности решений данного уравнения. При весьма общих
предположениях уравнению E) удовлетворяет семей-
семейство вектор-функций, зависящее от п произвольных
независимых параметров. Если уравнение этого се-
семейства имеет вид
ж = ф (t, съ с2, ..., с„),
то функция ф наз. общим решением урав-
уравнения E).
Однако в середине 19 в. были указаны первые при-
примеры Д. у. о., к-рые нельзя проинтегрировать в квад-
квадратурах. Оказалось, что решение в замкнутой форме
удается найти лишь для небольшого числа классов
уравнений (см., напр., Бернулли уравнение, Диффе-
Дифференциальное уравнение в полных дифференциалах, Ли-
Линейное дифференциальное уравнение с постоянными
коэффициентами). Не выражающиеся в квадратурах
решения отдельных, наиболее важных и часто встре-
встречающихся уравнений (напр., Бесселя уравнение} стали
изучать подробно, ввели для них специальные обо-
обозначения, исследовали их свойства и составили таб-
таблицы значений. Так появились многие специальные
функции.
В связи с потребностями практики постоянно ра»г
рабатывались и способы приближенного интегриро-
интегрирования Д. у. о., напр, последовательных приближений
метод, Адамса метод и др. Были предложены также
разнообразные приемы графич. и механич. интегри-
интегрирования этих уравнений. Математика располагает
богатым набором численных методов решения многих
задач для Д. у. о. (см. Дифференциальное уравнение
обыкновенное; приближенные методы ре-
решения). Эти методы представляют собой удобные
алгоритмы вычислений с эффективными оценками
точности, а современная вычислительная техника дает
возможность экономно и быстро довести решение каж-
каждой такой задачи до числового результата.
Однако численные методы для конкретного урав-
уравнения дают лишь конечное число частных решений
на конечном отрезке изменения независимого пере-
менного. Они не могут ответить на вопросы о том,
каково асимптотическое поведение решений, есть ли
у данного уравнения периодическое решение имеет
ли это уравнение колеблющееся решение. Между тем
во многих прикладных задачах важно установить
характер решения на бесконечном промежутке изме-
изменения независимого переменного, изучить полную
картину интегральных кривых. В связи с этим центр
тяжести в теории Д. у. о. был перенесен на исследо-
исследование общих закономерностей поведения решений
Д. у. о., разработку методов, к-рые позволяли бы
получать представление о глобальных свойствах реше-
решений по самому дифференциальному уравнению, без
его интегрирования.
Все это составило предмет качественной теории
дифференциальных уравнений, возникшей в конце
19 в. и интенсивно развивающейся.
Принципиальное значение имеет выяснение того,
является ли задача Коши для Д. у. о. корректно по-
поставленной задачей. Поскольку в конкретных задачах
начальные значения не могут быть указаны абсолютно
точно, то важно выяснить, когда малые изменения
начальных значений влекут за собой также малые
изменения решений. Справедлива теорема о непре-
непрерывной зависимости решений от на-
начальных значений: пусть (8) есть решение
уравнения E), где f(t, ac)^C(D) и удовлетворяет ус-
условию Липшица по as; тогда для любого е>0 и любого
замкнутого Jdl, to?J, найдется такое б>0, что ре-
решение »¦((, @, яг'ч) этого уравнения, где \яео—хо\<.6,
определено на / и при всех t?J
| ж U, t0, ж*0 )—ж (t, t0, х0) | < е. A2)
Другими словами, если задаться определенным зам-
замкнутым отрезком изменения независимого перемен-
переменного, то при достаточно малом изменении начальных
значений решение мало изменится на всем выбранном
промежутке. Этот результат может быть обобщен
в сторону получения условий, обеспечивающих диф-
ференцируемостъ решений Д. у. о. по начальным зна-
значениям.
Однако сформулированная теорема не исчерпывает
актуальную для приложений проблему, поскольку в
ней речь идет лишь о замкнутом отрезке изменения
независимого переменного. Между тем часто (напр.,
в теории управления движением) рассматривается
решение задачи Коши E), G), определенное при всех
t^t0, и необходимо выяснить устойчивость этого
решения по отношению к малым возмущениям началь-
начальных значений на всем бесконечном промежутке t^t0,
т. е. получить условия, обеспечивающие справедли-
справедливость неравенства A2) при всех t^t0. Именно к этой
задаче сводится исследование устойчивости положения
равновесия или стационарного режима конкретной
системы. Решение, мало изменяющееся на бесконеч-
бесконечном промежутке [t0, оо) при достаточно малых откло-
отклонениях начальных значений, называется устойчи-
устойчивым по Ляпунову (см. Устойчивость по Ля-
Ляпунову).
При выводе Д. у. о., описывающего реальный про-
процесс, всегда приходится чем-то пренебрегать, что-то
идеализировать. Иначе говоря, Д. у. о. описывают
процесс приближенно. Напр., изучение работы лампо-
пого генератора приводит к Ван дер Поля уравнению
при нек-рых предположениях, к-рые не вполне точно
соответствуют действительному положению вещей. Да-
Далее, на ход процесса часто оказывают влияние возму-
возмущающие факторы, учесть к-рые при составлении урав-
уравнений практически невозможно; известно лишь, что их
влияние «мало». Поэтому важно выяснить, как меня-
меняется решение при малых изменениях самой системы
уравнений, т. е. при переходе от уравнения E) к во з-
мущенному уравнению
O5=/(t, X)+S(t, Ж),
учитывающему малые поправочные члены. Оказывает-
Оказывается, что на замкнутом отрезке изменения незави-
независимого переменного (при тех же предположениях, что
и в теореме о непрерывной зависимости решений от
начальных значений) решение мало меняется, если
возмущение R(t, ас) достаточно мало. Если это свойство
имеет место на бесконечном промежутке t^t0, то ре-
решение наз. устойчивым при постоянно
действующих возмущениях.
Исследование устойчивости по Ляпунову, устой-
устойчивости при постоянно действующих возмущениях и их
модификаций составляют предмет важнейшего раздела
качественной теории — устойчивости теории. Для
практики в первую очередь представляют интерес такие
системы Д. у. о., решения к-рых мало изменяются
при всех малых изменениях этих уравнений; такие
системы наз. грубыми системами.
Другой важной задачей качественной теории яв-
является получение схемы поведения семейства решений
во всей области определения уравнения. Примени-
Применительно к автономной системе (9) речь идет о построении
фазовой картины, т. е. о качественном опи-
описании в целом всей совокупности фазовых траекторий
в фазовом пространстве. Такая геометрич. картина дает
полное представление о характере всех движений,
к-рые могут происходить в рассматриваемой системе.
Для этого существенно прежде всего выяснить пове-
поведение траекторий в окрестности положений равнове-
равновесия, отыскать сепаратрисы и предельные циклы. Особо
актуальной задачей является нахождение устойчивых
предельных циклов, ибо им соответствуют автоколе-
автоколебания в реальных системах.
Любой реальный объект характеризуется различ-
различными параметрами, к-рые часто входят в виде нек-рых
величин (е1, е2, ..., е*)=е в правую часть системы
Д. у. о., описывающей поведение объекта:
bo=f(t, ж, г). A3)
Значения этих параметров не могут быть известны
абсолютно точно, и потому важно выяснить условия,
обеспечивающие устойчивость решений уравнения A3)
по отношению к малым возмущениям параметра е.
Если задаться определенным замкнутым отрезком
изменения независимого переменного, то при естест-
естественных предположениях о правой части уравнения A3)
имеет место непрерывная (и даже дифференцируемая)
зависимость решений от параметров.
Выяснение зависимости решений от параметра имеет
прямое отношение к вопросу о том, насколько хороша
идеализация, приводящая к математич. модели пове-
поведения объекта — системе Д. у. о. Одним из типичных
примеров идеализации является пренебрежение малым
параметром. Если учет этого малого параметра при-
приводит к системе A3), то непрерывная зависимость
решений от параметра позволяет при изучении пове-
поведения объекта на конечном отрезке времени безболез-
безболезненно пренебречь этим параметром, т. е. в первом при-
приближении рассматривать более простую систему
i=/(t, ж, 0).
Этот результат лежит в основе имеющих широкие
приложения малого параметра метода, Крылова —
Боголюбова метода усреднения и других асимптотиче-
асимптотических методов решения Д. у. о. Однако исследование
ряда явлений приводит к системе дифференциальных
уравнений с малым параметром при производных:
ex = f(t, х, у), y = g(t, х, у).
Здесь уже нельзя, вообще говоря, принимать е=0,
даже если пытаться составить грубое представление
о явлении на конечном отрезке времени.
В теории Д. у. о. рассматриваются нек-рые плодо-
плодотворные и важные обобщения перечисленных выше за-
задач. Прежде всего, можно расширить класс функций,
в к-ром ищется решение задачи Коши B), C): опре-
определить решение в классе абсолютно непрерывных
функций и доказать существование таких решений.
Особый интерес для приложений представляет опре-
определение решения уравнения B) в случае, когда функ-
функция f(t, х) разрывна или многозначна по х. Наиболее
общей в этом направлении является задача о решении
дифференциального включения.
Рассматривается и более общее, чем A0), неразре-
неразрешенное относительно старшей производной Д. у. о.
71-го порядка
F (t, у, у, . ..,у<«-1>, y<»>)=0;
исследования этого уравнения тесно связаны с тео-
теорией неявных функций.
Уравнение B) связывает производную решения в
точке t со значением решения в этой же точке: x(t) =
=f(t, x(t)). Но нек-рые прикладные задачи (напр.,
требующие учета эффекта запаздывания исполнитель-
исполнительного устройства) приводят к дифференциальным урав-
уравнениям с запаздывающим аргументом:
x(t)=f(t, x(t~T));
здесь производная решения в точке t связывается со
значением решения в точке t—т. Изучению таких
уравнении, а также более общих дифференциальных
уравнений с отклоняющимся аргументом посвящен
специальный раздел теории Д. у. о.
Изучение фазового пространства автономной си-
системы (9) позволяет подойти к еще одному обобщению
Д. у. о. Траекторию этой системы, проходящую через
точку ж0, будем записывать в виде as=x(t, ж0). Если то-
точке ха поставить в соответствие точку х(t, ж0), то по-
получится преобразование фазового пространства, завися-
зависящее от параметра (, к-рое определяет движение в фа-
фазовом пространстве. Свойства этих движений исследу-
исследуются в теории динамич. систем. Такие движения можно
рассматривать не только в евклидовом пространстве,
но и на многообразиях, изучая, напр., дифференциаль-
дифференциальные уравнения на торе.
Выше речь шла о Д. у. о. в поле действительных
чисел [напр., отыскивалась действительная функция
x(t) действительного переменного t, удовлетворяющая
уравнению B)]. Однако нек-рые вопросы теории таких
уравнений удобнее изучать с привлечением комплекс-
комплексных чисел. Естественным дальнейшим обобщением
является изучение Д. у. о. в поле комплексных чисел.
Так, можно рассмотреть уравнение
dw , , ,
— = f(z, w),
где f(z, w) — аналитич. функция своих переменных,
и поставить задачу о нахождении аналитич. функции
w(z) комплексного переменного z, к-рая удовлетворяла
бы этому уравнению. Исследование таких уравнений,
уравнений высших порядков и систем составляет пред-
предмет аналитической теории дифференциальных урав-
уравнений; в частности, она содержит важные для прило-
приложений к математич. физике результаты, касающиеся
линейных дифференциальных уравнений второго по-
порядка.
Можно также рассматривать уравнение
¦?=/(*.*). а*)
считая, что ж принадлежит бесконечномерному бана-
банахову пространству В, t — действительное или комплекс-
комплексное независимое переменное, a f(t, ж) — оператор,
отображающий произведение (— оо, +oo)Xi? в В.
В виде уравнения A4) можно трактовать, напр., си-
системы Д. у. о. бесконечного порядка (см. Дифферен-
Дифференциальные уравнения системы бесконечного порядка).
Уравнения вида A4) изучает теория дифференциальных
уравнений абстрактных, лежащая на стыке Д. у. о.
и функционального анализа. В частности, большой
интерес представляют линейные дифференциальные
уравнения
с ограниченными или неограниченными операторами;
в форме такого уравнения удается записать нек-рые
классы дифференциальных уравнений с частными про-
производными.
Лит.: [1] К а м к е Э., Справочник по обыкновенным диф-
дифференциальным уравнениям, пер. с нем., 5 изд., М., 1976; 1^1
Коддингтон Э. А., Л е в и н с о н Н., Теория обыкновен-
обыкновенных дифференциальных уравнений, пер. с англ., М., 1958; [3}
Л е ф ш е ц С, Геометрическая теория дифференциальных урав-
уравнений, пер. с англ., М., 1961; [4] П е т р о в с к и й И. Г.,
Лекции по теории обыкновенных дифференциальных уравнений,
6 изд., М., 1970; [5] П о н т р я г и н Л. С, Обыкновенные диф-
дифференциальные уравнения, 3 изд., М., 1970; [6] Сан со не
Д ж., Обыкновенные дифференциальные уравнения, пер. с
итал., т. 1—2, М., 1953—54; [7] X а р т м а н Ф., Обыкновенные
дифференциальные уравнения, пер. с англ., М., 1970.
Е. Ф. Мищенко*
ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ ОБЫКНО-
ОБЫКНОВЕННОЕ; приближенные методы реше-
решения — методы получения аналитич. выражений (фор-
(формул), либо численных значений, приближающих с
той или иной степенью точности искомое частное
решение дифференциального уравнения (д. у.) или
системы для одного или нескольких значений аргу-
аргумента. Важность приближенных методов решения д. у.
обусловливается тем, что точные решения в виде ана-
аналитич. выражений получаются лишь для немногих
типов д. у.
Одним из старейших методов приближенного реше-
решения обыкновенных д. у. является метод разложения
в ряд Тейлора. Согласно этому методу решение урав-
уравнения
y'=f(x, у)
с начальным условием
У{хо) = Уо
приближается отрезком ряда Тейлора
Производные y*~k)(xQ) выражаются через f(x, у) и ее
частные производные:
y'=f(x, у), y" = f'x(x, y) + f'y(x, у) у',
»"'=/«(*. v)+*t"xy (*. у) v' + t"yy (x> у) y'2+f'y (*. у) у"
и т. д. Погрешность метода пропорциональна (х—ха)п + 1.
При больших значениях х—хй погрешность медленно
стремится к нулю при п—>-оо, а если значение х—хй,
превосходит значение радиуса сходимости ряда Тей-
Тейлора, то погрешность вообще не стремится к нулю
при п—>-оо. Это обстоятельство, а также необходимость
вычисления большого числа частных производных
резко ограничивают область применения метода. Обычно
метод разложения в ряд Тейлора, так же как и методы
разложения в ряды более общего вида, применяют для
нахождения приближенного решения в виде аналитич.
выражения. К методам, применяемым для этой же цели,
относятся Чаплыгина метод, использующий диффе-
дифференциальные неравенства, и последовательных прибли-
жений метод. Эти методы применяются в основном в
теоретич. исследованиях и редко используются для
получения численных решений д. у. в практич. рас-
расчетах.
В приложениях часто используются асимптотич.
методы приближенного решения Д. у., основанные на
выделении в решаемом уравнении главных членов и
членов, малых по сравнению с главными. Примером
может служить малого параметра метод для урав-
уравнения у'=/(ж, г/; ц). Асимптотич. методы использу-
используются как для получения аналитич. выражений, при-
приближающих решение, так и для исследований каче-
качественного поведения решений.
Наиболее распространенными методами численного
решения д. у. являются методы, в к-рых решение
ищется в виде таблицы приближенных значений иско-
искомой функции у(х) длн ряда значений аргумента х
из отрезка ,го<.г<жо+Х. Напр., пусть ищется решение
уравнения у =f{x, у) с начальным условием у(хо)=уо
жа отрезке хо^.х^.хо-\-Х в предположении, что решение
вычисляется для значений аргумента
xp = x0 + ph, р = 0, 1, ..., N, h = X/N;
значения хр наз. узлами, а величина h — ш а-
т о м; через у р обозначено значение приближенного
решения в узле хр.
Один из простейших численных методов — Эйлера
метод основан на приближенном вычислении в тож-
тождестве
х +i
Р f(x, y)dx,
ХР
квадратуру по формуле прямоугольников:
yP+i = yP-^hf (хР, уР)-
Погрешность метода Эйлера пропорциональна h2.
Приближая интеграл
p + if(x,y)dx A)
более точными квадратурными формулами, можно по-
получить более точные численные методы. Напр., если
воспользоваться для приближения A) формулой тра-
трапеций, то
У У + (/ (х y)+f(x y ))
Обычно это уравнение неразрешимо относительно р
Для его решения можно воспользоваться итерацион-
итерационными методами, взяв в качестве начального прибли-
приближения значение yp + i, полученное по методу Эйлера.
Одна итерация приводит к следующим формулам:
Ур+1 = УР + — (к1 (ХР, УР) + к2(хР, УР)),
где
kl (Xp, Vp)=f {Xp, Ур)
и
Ма> yP)::=f(xp + h> yP + hki{xp, yp)).
Эти формулы имеют погрешность порядка h3. Они от-
относятся к семейству Рунге — Кутта методов. Один
из наиболее распространенных методов этого семейства
имеет порядок погрешности Л5. Методы Рунге — Кутта
наз. одношаговыми, так как для вычисления ур + 1 до-
достаточно знать лишь ур — значения приближенного
решения на предыдущем шаге. Это обстоятельство
позволяет применять формулы метода Рунге — Кутта
для неравноотстоящих узлов, то есть в случае, когда
разность хр + 1—Хр непостоянна. При выборе шага ин-
интегрирования полезно иметь в распоряжении нек-рую
характеристику погрешности метода на шаге. Для
оценки погрешности на шаге часто используется прием,
называемый экстраполяцией по Ричард-
Ричардсону: Ур + 2 вычисляется дважды — при помощи
двух шагов h и одного шага 2й; полученные значения
обозначаются через Уа12 и У{р\г соответственно; по-
погрешность на шаге
| B) _ A) I
^р+2 Ур+2|
гр+2
где s+1 — порядок гр + 2 по h (для метода Эйлера «=1,
для формулы трапеций s=2 и т. д.)- Другой способ
оценки погрешности на шаге состоит в получении фор-
формул метода Рунге — Кутта с контрольным членом,
к-рый с точностью до малых более высокого порядка
приближает главный член погрешности метода на шаге.
Разработаны так наз. неявные одношаговые методы,
к-рые оказались весьма эффективными для нек-рых
классов задач.
Помимо семейства одношаговых методов для числен-
численного решения д. у. используются также и многошаговые
методы (или конечноразностные). В этих методах для
определения г/л + i требуются не только ур, но и зна-
значения ур-i в нек-рых нескольких предыдущих узлах.
Формулы fe-шаговых методов имеют вид:
где а_,-, &_,¦ — постоянные, а0ф0. Если &0=0, соот-
соответствующий метод наз. экстраполяционным,
или явным; если Ь0ф0,— интерполяцион-
интерполяционным, или неявным, методом. Частным случаем
многошаговых методов являются методы типа Адамса
(см. Адамса метод):
Ур-УР-1= h^kq = ob-gf (xP-g, Ур-g)-
Обычно вычисления ведут по паре /г-шаговых формул,
одна из к-рых явная, а другая неявная. Такие пары
формул наз. методами прогноза и кор-
коррекции. В качестве примера формул прогноза и
коррекции можно привести формулы Хеммин-
—107/ (х,-!, г^.^+ЮЭ/ (Хр_2, yp_2)~25f (xD_3, yp_3))t
* 707 , * **.
Ур + 1— Ур+1 ~т50 \Ур~Ур >'
** IVp-i+Vp-t ft
УР+1 з 1-72 B5/(*,,+!, ур+1) +
+ 91/ (Хр, yp)+^f(xp-1, yp-i)+9f(xp_2, yp_2)).
** |^ 43 . • **
Ур + i— Ур+i + 750 (Ур + 1~Ур+1>>
имеющие на шаге погрешность порядка h . При счете
по формулам Хемминга сначала вычисляется «про-
«прогноз» j/D+i, затем — «поправка» yp + i, затем — «кор-
рекция» yp+i и, наконец,— приближенное решение
Ур + i-
В небесной механике широко используются формулы
Штермера (см. Штермера метод), особенно удобные
для уравнений вида
y"=f(x, у);
они имеют вид:
(явная формула Штермера) и
Д!!//,_1 = й2/ (хр, ур)+ Y^q=1 С-д-Лд + Ч(*р-д, Ур-д)
(неявная формула Штермера). В фор-
формулах Штермера
Д*(/) — конечная разность порядка q.
Применение многошаговых методов возможно лишь
в случае, если известны значения решения в к первых
узлах. Для нахождения этих значений обычно поль-
пользуются одношаговыми методами, погрешность к-рых
пропорциональна соответствующей степени h.
Иногда для вычисления ур-д используется несколько
предшествующих значений yp-q, как в многошаговых
методах, но в то же время на каждом шаге производится
несколько вычислений правой части, как в методах
Рунге — Кутта.
Решение краевых задач для обыкновенных д. у.
обычно сводится к решению нескольких задач с началь-
начальными условиями. Простейшим методом такого рода
является стрельбы метод, применяемый как к линей-
линейным, так и к нелинейным краевым задачам. Пусть,
напр., требуется решить краевую задачу для одного
уравнения 2-го порядка:
>/"=/(¦?, у, у'), у(О) = а, уA)=Ъ.
Полагая у'@) = с, можно решить задачу с начальным
условием
V"=f(x, У, У'), у(О)=а, у'(О) = е, B)
на отрезке 0<:ar<:i и вычислить значение уA, с). Из
условия y(l, co)—b определяется с0. Тогда решение
краевой задачи будет совпадать с решением задачи с
начальными условиями г/(О) = а, у' @) = с0. Корень с0
уравнения уA, с)=Ъ обычно ищется каким-либо при-
приближенным методом и его нахождение связано с мно-
многократным решением задачи с начальными условиями
B). Метод стрельбы часто неустойчив к вычислительной
погрешности.
Для линейных краевых задач часто применяют
прогонки метод, при к-ром решение краевой задачи
для уравнения 2-го порядка сводится к решению
трех задач с начальным условием для уравнений 1-го
порядка. Напр., пусть решается краевая задача
y"=p(x)y+f, y'(O)=aoy@)+bo, y'{l) = a1y{l)+b1.
Подбираются функции а (х) и Ъ(х) такие, что у'(х)=
= а(х)у(х)+Ъ(х) при всех О«гж«г. Эти функции могут
быть получены как решения задач с начальными усло-
условиями
а'(х)+а*(х)=р(х), а(О)=ао
b'(x)+a(x)b(x)=f(x), 6@)=Ь0.
Решение этих задач наз. прямой прогонкой.
В результате прямой прогонки получаются два условия
для определения уA) и у'(I)'.
Из этих условий находится y(l)=yi, после чего решение
у (к) исходной краевой задачи получается как решение
задачи с начальным условием
у' (х) = а(х)у(х)+Ъ(х), уA) = У1
на отрезке 0<Г2т«:? ¦— так наз. обратная про-
прогонка. Методы стрельбы и прогонки применимы для
решения краевых задач в случае систем д. у. В вы-
числительной практике широко используются разност-
разностные аналоги этих методов.
Для решения нелинейных краевых задач, кроме
метода стрельбы, используют методы линеаризации в
сочетании с методом прогонки. Наиболее распростра-
распространенным методом этого класса является Ньютона метод.
При решении краевых задач применяются также и
различные вариационные методы: Ритца метод. Галер-
кина метод и др. Вариационные методы сводят решение-
краевых задач к минимизации нек-рого функционала;
приближение к решению ищется в задаваемом виде
у {x) — g (аъ ..., ап, х);
параметры ах, . . ., ап определяются из условия мини-
минимума функционала.
Большинство численных методов решения обыкно-
обыкновенных д. у. реализовано в виде библиотечных про-
программ ЭВМ.
Кроме аналитических и численных методов для
приближенного решения обыкновенных д. у. применя-
применяются графич. методы, напр, метод изоклин, связанный
с построением поля направлений, определяемого д. у.
Применяются также аналоговые вычислительные ма-
машины и другие моделирующие устройства.
Лит.: [1] Б а х в а л о в Н. С, Численные методы, М., 1973;
[2] Б е р е з и н И. С, Ж и д к о в Н. П., Методы вычислений,
т. 2, 2 изд., М., 1962; [3] М и х л и н С. Г., С м о л и ц к и й
X. Л., Приближенные методы решения дифференциальных и
интегральных уравнений, М., 1965; [4] Моисеев Н. Н.,
Численные методы в теории оптимальных систем, М., 1971; [51
Милн В. Э., Численное решение дифференциальных урав-
уравнений, пер. с англ., М., 1955; [6] К о л л а т ц Л., Численные
методы решения дифференциальных уравнений, пер. с нем.,
М., 1953; [7] X е м м и н г Р. В., Численные методы..., пер. с
англ., 2 изд., М., 1972; [8] Годунов С. К., Рябенький
В. С, Разностные схемы. Введение в теорию, М., 1973; [91
КоллатцЛ., Задачи на собственные значения..., пер. с нем.,
М., 1968. С. С, Гайсарян.
ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ С ЗАПАЗ-
ЗАПАЗДЫВАЮЩИМ АРГУМЕНТОМ — дифференциальное-
уравнение с отклоняющимся аргументом запаздываю-
запаздывающего типа, т. е. уравнение, в к-ром старшая произ-
производная от искомой функции при каком-либо значении
аргумента определяется через саму эту функцию и
младшие производные, взятые при меньших либо рав-
равных значениях аргумента. Эти уравнения и их системы,
если аргументом служит время, описывают процессы
с последействием, скорость к-рых в любой момент
определяется их состоянием не только в тот же момент
(как для обыкновенных дифференциальных уравнений),
но и в предшествующие моменты. Такая ситуация
возникает, в частности, в системах автоматич. управ-
управления (см. Автоматического управления теория) при
наличии запаздывания в органе регулирования.
А. Д. Мышкис.
ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ С ОТКЛО-
ОТКЛОНЯЮЩИМСЯ АРГУМЕНТОМ — дифференциальное
уравнение, связывающее аргумент, искомую функцию
и ее производные, взятые, вообще говоря, при различ-
различных значениях этого аргумента. Примеры:
x'(t)=ax(t-i), A)
х'(t)=ax(kt), B)
где постоянные а, х, к заданы; т в уравнении A) и t—kt
в уравнении B) — отклонения аргумента. Встре-
Встречаются и более сложные Д. у. с о. а., включающие
большее число отклонений аргумента, могущих пред-
представлять собой заданные функции (в частности, если
они постоянны, то уравнение часто наз. дифферен-
дифференциал ь н о-р азностным) или даже зависеть от
искомого решения. Эпизодически рассматривались та.к-
же Д. у. с о. а., в к-рых искомая функция зависит
более чем от одного аргумента. Д. у. с о. а. впервые-
появились в связи с формальным решением уравнений
с частными производными и затем неоднократно рас-
сматривались как сами по себе, так и в связи с зада-
задачами геометрии, а позднее — в связи с различными
приложениями, прежде всего к теории автоматич.
управления. Построение систематич. теории Д. у. с о. а.
было начато в 1949.
Определение Д. у. с о. а. допускает любые супер-
суперпозиции искомого решения [типа x(x(t))] и интегралы
от него, поэтому формально класс Д. у. с о. а. вклю-
включает в себя все уравнения математич. анализа. Все
же обычно, говоря о Д. у. с о. а., имеют в виду тот
или иной естественный класс дифференциальных урав-
уравнений, в к-рых введено отклонение аргумента, допу-
допускающее построение содержательной теории. При этом
ряд свойств Д. у. с о. а. имеет непосредственную ана-
аналогию со свойствами обычных дифференциальных
уравнений, тогда как иные свойства являются прин-
принципиально новыми.
Уравнение (или система уравнений)
x^(t) = f(t; x^)(t~xx), ..., x(ms)(t-rs)) C)
{для системы х и / — векторы), где все Ту^О, наз.
уравнением (системой) запаздыва-
запаздывающего, нейтрального или опережа-
опережающего типа, если max,my<п, =ге, >ге, соответ-
соответственно. Для уравнений иных видов такая классифи-
классификация проводится на основе преобразования к виду C)
с помощью замены t-*-%(t), % — возрастающая функ-
функция; напр., уравнение A) запаздывающего типа при
т^О и опережающего (замена t—>-?+т) — при т<0.
Если отклонения ту зависят от t, то уравнение C)
может менять тип; напр., уравнение B) для k<.i за-
запаздывающего типа при t^O и опережающего — при
*<:0. Если ту зависят от искомого решения, то урав-
уравнение C) может иметь различный тип для различных
«го решений. Наиболее подробно разработана теория
Д. у. с о. а. запаздывающего типа, менее — нейтраль-
нейтрального типа и почти не изучена теория уравнений опере-
опережающего типа.
Один из простейших классов Д. у. с о. а. следующий:
x'(t) = f(t, x(t), x(t-r)), T>0. D)
Для этого класса Д. у. с о. а. ставится основная
начальная задача: заданы начальная точка
t0, начальная функция гр(f), t0—T«r?<:?0, и значение
ж(го+О); под решением задачи для уравнения D)
понимается функция x(t), t>t0, обращающая урав-
уравнение D) в тождество, причем при <>@, t—x<.t0 в
правую часть вместо х(t—т) надо подставлять ср((—т).
Для решения поставленной задачи можно применить
метод шагов: при fo<t<:fo+T решают начальную
задачу для уравнения D), в к-ром вместо x(t—т) под-
подставлено ф(*—т); при io+T<f<fo+2T будет to<.t—т<
<<о+т, т. е. x(t—т) уже построено, и т. д.; таким
образом, на каждом шаге приходится решать задачу
Коши для уравнения без отклонения аргумента. Если
функции / и ф непрерывны и ж(го+О) = ф(<о), то решение
задачи существует на нек-ром интервале ?0<i<:f0+/j
и может быть продолжено обычным образом, а если
функция f(t, х, у) удовлетворяет по х условию Лип-
Липшица, то это решение единственно и непрерывно за-
зависит от /, ф, т. Если при этом функция / достаточно
гладкая, то х' (I) непрерывна при t>t0, x"(t) непрерывна
при t>«0+T и т. д. (свойство сглажива-
сглаживания). ,
Аналогично ставится начальная задача и строится
решение для систем уравнений вида D) и для урав-
уравнений высших порядков. В случае нескольких запаз-
запаздываний за шаг принимают наименьшее из них. Если
т=т@> то ф(<) должна быть задана на всем началь-
начальном множестве значений t—x(t)^.t0, i>i0.
Наличие у т(() нулей препятствует применению метода
шагов, однако с помощью простых аппроксимационных
или итерационных методов можно доказать теорему
о разрешимости начальной задачи, аналогичную при-
приведенной выше. Численные методы ее решения в прин-
принципе те же, что для т=0. Если заданные функции раз-
разрывны или х(го+О)^=ф(t0), то понятие решения должно
быть естественно обобщено.
Решение сформулированной начальной задачи стро-
строится только в направлении возрастания t. Другая ее
особенность состоит в том, что многообразие решений
при произвольной ф(?), вообще говоря, бесконечно-
бесконечномерное. (Исключением служат уравнения без
предыстории, для к-рых to*?t—т(/)<:/ при t^t0;
напр., уравнение B) при 0</с<1, to=O.) Это сущест-
существенно отличает теорию Д. у. с о. а. от теории урав-
уравнений без отклонения аргумента.
В уравнении D) запаздывание сосредоточен-
сосредоточенное. Рассматриваются также уравнения с распре-
распределенным запаздыванием, правая часть к-рых
включает интегралы
x(t-\-s)r(t, s)ds=V x(s)r1(t,s) ds
(это — интегро-дифференциальные уравнения типа
Вольтерра) или, комбинированный случай,
dsr (tf s)
и т. п. Наиболее общим видом Д. у. с о. а. запазды-
запаздывающего типа 1-го порядка служит дифференциально-
функциональное уравнение типа Вольтерра
х' (t) = F [х (t + s); t], — T<s<0,
где правая часть при каждом ?>?0 представляет собой
функционал. И для таких уравнений начальная задача
разрешима.
Для Д. у. с о. а. нейтрального типа, напр.
x'(t) = f(t, x(t), ar(t-Ti), x'(t—x2)), т1( T2>0,
постановка и свойства начальной задачи аналогичны
указанным выше, однако свойство сглаживания от-
отсутствует; кроме того, возможны осложнения, если
переменное запаздывание т2@ имеет нули. Начальная
задача для Д. у. с о. а. опережающего типа является
некорректной.
Лучше других изучены линейные автономные (т. с.
с постоянными коэффициентами и постоянными от-
отклонениями аргумента) Д. у. с о. а. Уравнение (без
подобных членов)
т (my) It т Л 1"\\
(все а/ФО) имеет частные решения х=еР(, где р удов-
удовлетворяет характеристическому уравнению
р (р) = />»—]? ajpmi e~ %JP = 0. F)
Здесь Р(р) — квазиполином; /с-кратному корню урав-
уравнения F) отвечают решения еР*, ..., tk~1ePt уравнения
E). Если хотя бы одно Т/фО, то уравнение F) имеет
бесконечное число корней plt p2, ... Чтобы уравнение
E) имело запаздывающий (нейтральный) тип, необхо-
необходимо и достаточно условие
Re pr ». — оо I — со < lim Re pr < оо
В этих случаях каждое решение уравнения E) разла-
разлагается в ряд по указанным частным решениям, а при
решении начальной задачи для уравнения E) и соот-
соответствующего неоднородного уравнения можно поль-
пользоваться обычными методами операционного исчисле-
исчисления. Аналогичными свойствами обладают системы урав-
уравнений и уравнения с распределенным запаздыванием.
Обычные определения устойчивости решения непо-
непосредственно распространяются на Д. у. с о. а. запаз-
запаздывающего и нейтрального типов. Для асимптотич.
устойчивости решений уравнения E) необходимо и
достаточно условие:
sup Re pr < 0.
г
При выполнении этого условия асимптотически устой-
устойчиво и нулевое решение нелинейных автономных
уравнений, для к-рых E) служит линейным прибли-
приближением.
Метод функций Ляпунова на исследование устой-
устойчивости Д. у. с о. а. распространил Н. Н. Красовский
[5].0нпредложилпользоватьсяфункционалами F[^(s); t]
в С[—т, 0] X [0, оо); полную производную такого
функционала «вдоль решения» заданного уравнения
вида D) можно вычислить в силу этого уравнения, и
она представляет собой функционал того же типа, т. е.
?v[x(t + s); A = F,[.t(H-s); t].
Аналог теоремы Ляпунова об устойчивости: если
/ (t, 0, 0) = 0; (уА > 0) inf V [*|; (s); Ц > 0;
НФП >Л. t>t0
V[q(s); t0] _+ 0; ^<0,
11*11-0
то тривиальное решение уравнения D) устойчиво.
Основные теоремы об устойчивости, выраженные в
таких терминах, допускают обращение.
Ряд результатов получен для периодических Д. у.
с о. а. Так, если
f( + T, х, y) = f(t, .г, у), Т >0,
то неподвижные точки оператора
(t0—T<s<t0; x(t) — решение уравнения D) при на-
начальной функции ф; к — натуральное) определяют
йГ-периодич. решения уравнения D). Этот и другие
аналогичные факты дают возможность применить к
отысканию периодич. решений и к выяснению их
устойчивости методы теории нелинейных операторов.
Для линейных однородных Г-периодич. Д. у. с о. а.
запаздывающего типа доказана возможность аппрок-
аппроксимации каждого решения с любой степенью точности
по шкале экспонент линейной комбинацией решений
вида
**А* a(t), a(t + T)^a (t); k = 0, 1, ..., kr.
Из других направлений исследования Д. у. с о. а.
выделяются: детальное изучение асимптотических и
осцилляционных свойств уравнений
ж'(*)= ± М (t)x (t — x(t)), M(fMsO,
и аналогичных уравнении 2-го порядка; получение
асимптотич. выражений для решений систем с малыми
отклонениями аргумента Или с малой нелинейностью;
распространение на Д. у. с о. а. асимптотич. методов
Крылова — Боголюбова (см. Крылова — Боголюбова
метод усреднения); распространение на Д. у. с о. а.
теории оптимального управления Л. С. Понтрягина (см.
Оптимального управления математическая теория); ис-
исследование краевых задач; исследование эволюционных
уравнений с частными производными и запаздыванием
во времени; исследование стохастич. Д. у. с о. а. (см.
Стохастическое дифференциальное уравнение) и т. д.
Лит.: [1] Э л ь с г о л ь ц Л. Э., Н о р к и н С. Б., Введе-
Введение в теорию дифференциальных уравнений с отклоняющимся
аргументом, М., 1971; 12] 11 и н н и Э., Обыкновенные дифферен-
дифференциально-разностные уравнения, пер. с англ., М., 1961; [3J Б е лл-
ман Р., Кук К. Л., Дифференциально-разностные урав-
нения, пер. с англ., М., 1967; [4] М ы ш к и с А. Д.. Линейные
дифференциальные уравнения с запаздывающим аргументом,
2 изд., М., 1972; [5]Красовский Н. Н., Некоторые задачи
теории устойчивости движения, М., 1959; [6] Н о р к и н С. Б,,
Дифференциальные уравнения второго порядка с запаздываю-
запаздывающим аргументом, М., 1965; [7] Р у б а н и к В. П., Колебания
квазилинейных систем с запаздыванием, М., 1969; [8] О g u г-
toreli M. N., Time-Lag control systems, N. Y.— L., 1966; [9]
Hal an а у A., Differential equations, N.Y.—L., 1966; [10]
Hale J. K., Functional differential equations, N. Y., 1971.
А. Д. Мышкис.
ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ С ЧАСТНЫ-
ЧАСТНЫМИ ПРОИЗВОДНЫМИ — уравнение вида
F(x, ..., Pii . ,v ...)=0, A)
где F — заданная действительная функция точки
ж= {х1, . . ., хп) области D евклидова пространства Еп,
j>2 и действительных переменных
''
xi
дх'< ... dxin
1 п
(и(х) — неизвестная функция) с неотрицательными
целочисленными индексами ilt . . ., in, 2—i ij~—k,k — Q,
..., m, m~^l, по крайней мере одна из производных
функции F отлична от нуля; натуральное число т
наз. порядком уравнения A).
Определенная в области D задания уравнения A)
функция и(х), непрерывная вместе со своими част-
частными производными, входящими в это уравнение и
обращающая его в тождество, наз. регулярным
решением. Наряду с регулярными решениями в
теории Д. у. с ч. п. важное значение имеют решения,
перестающие быть регулярными вблизи изолированных
точек или многообразий особого вида: к ним относятся,
в частности, элементарные (фундамен-
(фундаментальные) решения. Они позволяют строить
широкие классы регулярных решений (так наз. потен-
потенциалов) и устанавливать их структурные и качест-
качественные свойства.
В предположении непрерывности частных произ-
производных 1-го порядка функции F относительно пере-
переменных
Pi / i 7 i I = т >
в теории уравнений вида A) фундаментальную роль
играет форма порядка т:
к 1Л1. ...» Л,,) — Л г ^-i ... Л \?)
относительно действительных параметров %и . .., Хп,
к-рая наз. характеристической формой,
соответствующей уравнению A).
Когда F — линейная функция переменных р,\ ... / ,
уравнение A) наз. линейным. Линейное уравнение
с частными производными 2-го порядка можно записать
в виде:
где A if, Bj, Cnf — заданные в области D действитель-
действительные функции точки х. Уравнение C) наз. однород-
однородным, если /(ж) = 0 для всех x?D. В случае урав-
уравнения C) форма B) является квадратичной:
с коэффициентами А ,¦/, зависящими только от точки
x'^D. В каждой точке x?D квадратичная форма Q
при помощи неособого аффинного преобразования
переменных Я,-=Я/(|Ь . .., ?„), i=l, ..., га, может
быть приведена к канонич. виду
где коэффициенты ос/, z=l, . . ., п, принимают значения
1, —1, 0, причем число отрицательных коэффициен-
коэффициентов (индекс инерции)и число нулевых коэф-
коэффициентов (дефект формы) являются аффин-
аффинными инвариантами. Когда все а, = 1 или все ос/= — 1,
т. е. когда форма Q соответственно положительно или
отрицательно определена (дефинитна), уравнение C)
наз. эллиптическим в точке x?D. Если один
из коэффициентов ос/ отрицателен, а все остальные
положительны (или наоборот), то уравнение C) наз.
гиперболическим в точке х. В случае,
когда /, \.<X<ji— 1, коэффициентов а,-положительны,
а остальные п — 1 отрицательны, уравнение C) наз.
ультрагиперболическим. Если же хотя
бы один из этих коэффициентов (но не все) равен нулю,
то уравнение C) наз. параболическимв точке
х. Говорят, что в области D своего задания уравнение
C) является уравнением эллиптического, гиперболи-
гиперболического или параболического типа, если оно соот-
соответственно эллиптично, гиперболично или параболично
в каждой точке этой области. Эллиптическое в области
D уравнение C) наз. равномерно эллипти-
эллиптическим, если существуют действительные числа к0
и кх одинакового знака такие, что
2,=г
для всех X?D. Когда в разных частях области D
уравнение C) принадлежит к различным типам, то
говорят, что оно является уравнением смешанно-
г о типа в этой области.
Лапласа уравнение
¦г-л п д2и „
теплопроводности уравнение
учп-1 д'ц ди .
2-1»= 1 ~~дх\ в*^~
и волновое уравнение
являются типичными примерами линейных эллиптич.,
параболич. и гиперболич. уравнений 2-го порядка
соответственно (подробнее см. Линейное гиперболиче-
гиперболическое уравнение и система, Линейное параболическое
уравнение и система, Линейное эллиптическое уравне-
уравнение и система).
Трикоми уравнение
Х21х\ + 1х\ = °
относится к уравнениям смешанного типа в любой
области плоскости переменных хх, х2, пересечение
к-рой с осью х2 = 0 не пусто (подробнее см. Смешанного
типа уравнение с частными производными).
В случае линейного уравнения с частными произ-
производными порядка т
1 п
где Lx — линейный дифференциальный оператор с
частными производными порядка ниже т, форма B)
имеет вид
к (кг, ...,К) = 2 а ^.. .*„<*) ^ • • • *»"• E)
Если при фиксированном значении x?D можно найти
такое аффинное преобразование Я./=Я.,-(ц,1, ..., ц„),
i=l, . . ., га, в результате к-рого полученная из E)
форма содержит лишь I, 0<Z<n, переменных и., то
говорят, что уравнение D) в точке х параболи-
параболически вырождается. При отсутствии пара-
болич. вырождения и если конич. многообразие
k(\lt ...,к„) = 0 F)
не имеет действительных точек, кроме Х1=0, ..., Х„=0>
то уравнение D) в точке х наз. эллиптическим-
Уравнение D) наз. гиперболическим в точке
х, если в пространстве переменных Хг, . . ., Хп сущест-
существует прямая б такая, что если принять ее за коорди-
координатную прямую в новых переменных j^, . . ., |х„, полу-
полученных аффинным преобразованием А.1? . . ., кп, то
относительно координаты, изменяющейся вдоль б,
преобразованное уравнение F) имеет ровно т дей-
действительных корней (простых или кратных) при любом
выборе остальных координат ц.
Аналогичным образом по характеру формы B)
происходит классификация по типам уравнения A)
и в нелинейном случае. Поскольку в этом случае коэф-
коэффициенты формы B) зависят, наряду с точкой х, от
искомого решения и от его производных, классифи-
классификация по типам имеет смысл лишь для этого решения.
См. также Нелинейное уравнение с частными произ-
производными.
Когда F представляет собой TV-мерный вектор F=
= (Fi, . . ., Fw) с компонентами
1
зависящими от
Pi i = (/'(
, ,...), i = l, 2, ..., Л',
' * п
и от Af-мерных векторов
М \ дки
дх 1. . . дх "
1 п
векторное равенство A) наз. системой диффе-
дифференциальных уравнений с частными
производными относительно неизвестных функ-
функций «lt ...,идгили относительно неизвестного вектора
ц= (ии . . ., им). Максимальный порядок производных
от искомых функций, входящих в данное уравнение
системы, наз. порядком этой системы (уравне-
(уравнения). Когда M—N и порядок каждого уравнения
системы A) равен т, определитель
«—1 il 9F;
где
dF,-
, I, ; = 1, ..., N,
— квадратная матрица, представляет собой форму
порядка Nm относительно действительных скалярных
параметров ки ..., Хп и наз. характеристиче-
характеристическим детерминантом системы A). Клас-
Классификация по типам системы A) происходит по харак-
характеру формы G) точно так же, как при рассмотрении
одного уравнения порядка т. Фигурирующие в левой
части уравнения A) величины могут быть комплекс-
ными. Комплексное Д. у. с ч. п. очевидным образом
заменяется системой Д. у. с ч. п.
Д. у. с ч. п. может вовсе не иметь решения. Однако
встречающиеся в приложениях Д. у. с ч. п., как пра-
правило, имеют целые семейства решений. При выводе
этих уравнений из общих законов, к-рым подчинены
изучаемые явления природы, естественно возникают
дополнительные условия, налагаемые на искомые
решения. Центральное место в теории Д. у. с ч. п.
занимают задачи отыскания именно таких регулярных
решений, к-рые удовлетворяют этим условиям. Ус-
Условия задач, к-рым должно удовлетворять искомое
решение, существенно зависят от типа рассматрива-
рассматриваемого уравнения.
Для эллиптич. уравнений обычно рассматриваются
так наз. краевые задачи, к-рые, напр., в случае урав-
уравнения 2-го порядка в основном охватываются следую-
следующей постановкой: ищется регулярное в области D
решение и(х) уравнения A), удовлетворяющее условию
f I х, и, ...,—, г, .
ех^...вхп«
Н[ х, t,u(t), ..., —d'u(t) . , ... )dst = O, (8)
M'l1 ¦ ¦ ¦ К"
где S — граница области D, / и Н — заданные дей-
действительные функции, dsf — элемент площади поверх-
поверхности S, а под
<. i ' ^/= 1 V —'•
вх1К..вхп"
при x?S понимаются пределы соответствующих про-
производных функции и(х), когда точка х изнутри области
D стремится к S.
В такой общей постановке задача (8) далека от
своего сколько-нибудь полного решения. Сравни-
Сравнительно хорошо исследованы такие частные случаи
этой задачи, какими являются так наз. первая и вторая
краевые задачи (см. Дирихле задача и Неймана задача)
для линейных уравнений, удовлетворяющих условию
равномерной эллиптичности.
В отличие от краевых задач для эллиптич. уравне-
уравнений, в к-рых носителем данных является вся граница
области, где ищется решение, для широких классов
уравнений гиперболич. и параболич. типов носите-
носителями дополнительных данных могут служить опреде-
определенным образом ориентированные незамкнутые по-
поверхности пространства Е", причем от них сущест-
существенно зависит область определения искомого решения.
К таким задачам относятся, напр., Коши задача с на-
начальными данными, характеристическая задача Коши.
Особо ставятся краевые задачи для уравнений сме-
смешанного типа. В теории Д. у. с ч. п. значительное
внимание уделяется обширному классу смешанных
задач. См. Смешанная задача для гиперболического
уравнения и системы, Смешанная и краевая задачи
для параболического уравнения и системы.
Задача считается в классич. смысле корректно (пра-
(правильно) поставленной, если она имеет и притом един-
единственное устойчивое решение. Задачи, не удовлетво-
удовлетворяющие этим требованиям, до недавнего времени счи-
считались лишенными смысла. Начиная с 40-х гг. 20 в.
широта диапазона математнч. проблем физики, меха-
механики и техники заставила расширить не только поня-
понятие корректности постановок задач для Д. у. с ч. п.,
но и понятие самого решения. Были введены так наз.
обобщенные решения. Наряду с вопросами существо-
существования и единственности точных решений тех или иных
задач для Д. у. с ч. п. в приложениях значительную
важность приобрели понятия в определенном смысле
приближенных решений и фактическое построение
таких решений.
Исторически одним из первых методов, позволяющих
строить решения ряда задач для важных классов Д. у.
с ч. п., является метод разделения пере-
переменных, или Фурье метод, к к-рому тесно примыка-
примыкает метод интегральных преобразований (см. Фурье инте-
интеграл). От применения этого метода берет свое начало
спектральная теория дифференциальных операторов.
Сравнительно позже был создан параметр икса метод,
на основе к-рого построен потенциалов метод. Этот
метод позволяет привлекать к исследованию краевых
задач для эллиптич. уравнений аппарат интегральных
уравнений. Далеко идущим развитием метода пара-
метрикса являются методы теории функций комплекс-
комплексного переменного, успешно применяющиеся при ис-
исследовании эллиптич. уравнений с двумя независимыми
переменными. См. Дифференциальное уравнение с част-
частными производными; методы комплексного переменного.
Когда изучаемое Д. у. с ч. п. представляет собой
уравнение Эйлера для многомерной задачи вариаци-
вариационного исчисления, часто пользуются вариационным
методом. Вариационный метод весьма удобен в тех
случаях, когда уравнение Эйлера является уравне-
уравнением эллиптич. типа. См. также Дифференциальное
уравнение с частными производными; вариационные
методы решения.
Начиная с ЗО-х гг. 20 в. при исследовании Д. у. с
ч. п. широко используются методы функционального
анализа, среди к-рых центральное место занимают
Шаудера метод и его дальнейшее развитие — метод
априорных оценок. Эти методы позволяют сравни-
сравнительно легко установить существование слабых реше-
решений и сильных решений как для линейных, так и для
нек-рых классов нелинейных Д. у. с ч. п. См. Диф-
Дифференциальное уравнение с частными производными;
функциональные методы решения.
Среди методов, успешно приводящих к цели при
построении приближенных решений Д. у. с ч. п.,
чаще всего применяются методы конечных разностей
исчисления. См. также Гиперболического типа урав-
уравнение, численные методы решения; Параболического
типа уравнение, численные методы решения; Эллип-
Эллиптического типа уравнение, численные методы решения.
Лит.: [1] Б е р с Л., Джон Ф., Ш е х т е р М., Уравне-
Уравнения с частными производными, пер. с англ., М., 1966; [2] Б н-
цадзе А. В., Уравнения математической физики, М., 1976;
[3] В л а д и м и р о в В. С, Уравнения математической физики,
2 изд., М., 1971; [4] К у р а н т Р., Уравнения с частными про-
производными, пер. с англ., М., 1964; [5] Т и х о н о в А. Н.,
С а м.а р с к и й А. А., Уравнения математической физики,
4 изд., М., 1972. А. В. Бицавзе.
ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ С ЧАСТНЫ-
ЧАСТНЫМИ ПРОИЗВОДНЫМИ; вариационные ме-
методы решения — методы решения краевых за-
задач для Д. у. с ч. п. при помощи сведения этих задач
(когда это возможно) к соответствующим образом
подобранным вариационным задачам (т. е. к задачам
на отыскание минимума или максимума нек-рого функ-
функционала) и решения последних.
Вариационные методы широко применяются как в
теоретич. исследованиях (для доказательства теорем
существования, единственности и устойчивости реше-
решений, при исследовании дифференциальных свойств
решений, в спектральной теории, при изучении раз-
разнообразных вопросов оптимизации и т. д.), так и в
вопросах, связанных с нахождением приближенных
решений уравнений. Приближенные решения вариа-
вариационных задач можно находить при помощи решения
конечных систем алгебраич. уравнений, при этом
алгоритмы нахождения приближенных решений ва-
вариационных задач часто оказываются проще и удобнее,
чем имеющиеся алгоритмы решения соответствующих
задач для Д. у. с ч. п.
Вариационный метод исследования краевых задач
возник в сер. 19 в. в виде так наз. Дирихле принципа
отыскания в области G гармония, функции, принимаю-
принимающей на границе dG области G данное значение Ц>(х),
x?dG, как функции, дающей в рассматриваемом классе
функций минимум интегралу Дирихле. Первоначально
принцип Дирихле применялся лишь в теории линейных
эллиптич. уравнений 2-го порядка (впоследствии и
более высоких порядков), а затем и в теории уравнений
других типов, причем не только линейных, но и не-
нелинейных. Разработке вариационных методов были
посвящены работы Б. Римана (В. Riemann), К. Вей-
ерштрасса (К. Weierstrass), Д. Гильберта (D. Hilbert).
Большую роль в развитии вариационных методов, в
частности в вопросе их обоснования, сыграли вложения
теоремы и их обобщения.
Одним из простых и типичных примеров использо-
использования вариационных методов является решение Ди-
Дирихле задачи для эллиптического самосопряженного
уравнения 2-го порядка
Аи^-си=О, A)
где с=
C)
{G — область конечномерного евклидова пространства,
dG — ее граница, ср — заданная на dG функция), и
существует постоянная я>0 такая, что для всех точек
x^G и всех чисел |l7 g2, ..., \п выполняется нера-
неравенство (условие эллиптичности)
В этом случае вариационный метод решения задачи
A) — B) состоит в отыскании функции и(х), для к-рой
функционал
/=1 ; dxi дх/
(уравнение A) является Эйлера уравнением для функ-
функционала К (и)) принимает наименьшее значение в
классе допустимых функций, т. е. таких функций и(х),
для к-рых А"(и)<+оо, и выполняется граничное ус-
условие B). Вариационный метод применим только
тогда, когда класс допустимых функций не пуст.
Условия, к-рым должна удовлетворять заданная на
границе функция ср для того, чтобы класс допустимых
функций был не пуст, даются теоремами вложения.
Функция и(х), для к-рой функционал К (и) принимает
наименьшее значение в классе допустимых функций,
является обобщенным решением задачи A) — B) (см.
Дифференциальное уравнение с частными производными;
функциональные методы решения) и, напр., в класси-
классическом случае непрерывной дифференцируемости коэф-
коэффициентов aij(x) оператора C) — обычным решением
этой задачи.
Другим типичным примером использования вариа-
вариационных методов является их применение к отысканию
собственных значений и собственных функций опе-
оператора C).
Функция, дающая минимум нек-рому функционалу,
может быть получена как предел так наз. минимизи-
минимизирующей последовательности, т. е. последовательности
функций, значения функционала на членах к-рой стре-
стремятся к указанному минимуму. Для построения мини-
минимизирующих последовательностей и установления ско-
скорости их сходимости разработаны специальные методы
(напр., Ритца метод).
Лит.: [1] Курант Р., Уравнения с частными производ-
производными, пер. с англ., М., 1964; [2] е г о же, Принцип Дирихле,
конформные отображения и минимальные поверхности, пер. с
англ., М., 1953; [3] С о б о л е в С. Л., Некоторые применения
функционального анализа в математической физике, Новосиб.,
1962; [4] С м и р н о в В. И., Курс высшей математики, т. 3—5,
М., 1958—59; [5] Михл ин С. Г., Вариационные методы в мате-
математической физике, 2 изд., М., 1970; [6] Ладыженская О. А.,
УральцеваН. Н., Линейные и квазилинейные уравнения
эллиптического типа, 2 изд., М., 1973; [7] М и х а й л о в В. П.,
Дифференциальные уравнения в частных производных, М., 1976.
Л. Д. Кудрявцев.
ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ С ЧАСТНЫ-
ЧАСТНЫМИ ПРОИЗВОДНЫМИ; задача с данными
на характеристиках — задача, состоящая
в решении дифференциального уравнения или системы
уравнений с частными производными по заданным
условиям на характеристических многообразиях. Ос-
Основными задачами такого типа являются характери-
характеристическая задача Копш и Гурса задача.
В случае характеристич. задачи Коши, когда на-
начальное многообразие является характеристич. в каж-
каждой точке, начальные данные не могут быть заданы
произвольным образом. Они должны удовлетворять
определенным условиям, к-рые диктуются дифференци-
дифференциальным уравнением. Поэтому характеристич. задача
Коши, вообще говоря, не является корректно постав-
поставленной, если на класс искомых решений и на заданные
функции не наложены дополнительные условия (осо-
(особенно вдоль многообразия, не касательного к началь-
начальному). Напр., для теплопроводности уравнения
Щ ¦= ихх
характеристич. задача Коши
и [<=0=--ф (?)
корректна в классе функций, растущих на бесконеч-
бесконечности не быстрее ехр(сг2); если же показатель 2 при х
заменить на 2+е, то единственности уже не будет.
Существует широкий класс уравнений, для к-рых
характеристич. задача Коши корректна.
Если начальное многообразие S одновременно яв-
является многообразием вырождения типа или порядка
уравнения, то характеристич. задача может оказаться
правильно поставленной. Напр., для уравнения
ихх — г/Я1«уг/ = О, у > 0, 0 < т = const < 1,
с достаточно гладкими начальными данными на любом
интервале S характеристики г/=0 задача разрешима
и притом единственным образом.
К задачам с данными на характеристиках относятся
задачи с неполными и видоизмененными начальными
данными, к-рые возникают в теории вырождающихся
гиперболич. и параболич. уравнений и систем. Эти
задачи для уравнений вида
ихх~ ymuby4-aux + buy^rcu = 0, у > 0, т > 0,
ставятся следующим образом. Требуется отыскать
решение и(х,у) уравнения, удовлетворяющее видо-
видоизмененным начальным данным
lim ф (х, у)и = х(х), lim г|) (х, y)uy = v(x),
где аО<|3, ф, т, г|) и v — заданные функции, или
неполным начальным данным, т. е. одному из этих
условий.
Лит.: [1] Бицадзе А. В., Уравнения смешанного типа,
М., 1959; [2] К у р а н т Р., Уравнения с частными производны-
производными, пер. с англ., М., 1964; [3] Т и х о н о в А. Н., «Матем. сб.»,
1935, т. 4а, с. 199—216; [4] X е р м а н д е р Л., Линейные диф-
дифференциальные операторы с частными производными, пер. с
англ., М., 1965; [5] е г о же, «Математика», 1968, т. 12, № 2,
с. 88 —109. А. М. Нахушев.
ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ С ЧАСТНЫ-
ЧАСТНЫМИ ПРОИЗВОДНЫМИ; задача с косой (на-
(наклонной) производной — линейная крае»
вая задача для эллиптич. уравнений 2-го порядка.
Пусть D — область действительного евклидова про-
пространства с декартовыми координатами xlt х2, .. ., хп,
граница dD к-рой представляет собой (п—1)-мерную
гиперповерхность Ляпунова. Пусть в области D задано
линейное дифференциальное уравнение 2-го порядка
с действительными коэффициентами а/у, Ь,-, с, F, удов-
удовлетворяющими условию Гёльдера в D\JdD, и, кроме
того, в D соблюдено условие равномерной эллиптич-
эллиптичности уравнения. Пусть l—(lt, l2, . .., /„) — заданный
на dD непрерывный действительный вектор, к-рый
нигде не обращается в нуль. Задача с косой производ-
производной состоит в следующем: найти регулярное в области
D решение и(х) уравнения A), непрерывное в D\JdD,
для к-рого в каждой точке y?dD существует предел
lim [I (у) gradxu]=\(u),
xeD
совпадающий с заданной непрерывной на dD функцией
Ну)-
М«) =/(!/), V&D. B)
В краевом условии B) без ограничения общности
можно считать, что I — единичный вектор. Неймана
задача является частным случаем задачи с косой про-
производной, когда левая часть в краевом условии B)
совпадает с производной от искомого решения по
конормали v:
Если соблюдены условия
с (.«•)«) C)
inf (N1) > 0, D)
!/€dD
где N — внешняя нормаль 0D в точке у, то соответ-
соответствующая задаче A), B) однородная краевая задача
<?(и) = 0, Х(и)=О, E)
в силу принципов Хопфа и Зарембы — Жиро (см.,
напр., [1]), не может иметь решения, отличного от
постоянной. В частности, когда в условии C) по край-
крайней мере в одной точке выполняется строгое неравен-
неравенство, задача A), B) не может иметь более одного ре-
решения. При исследовании вопроса о существовании
решений задачи A), B) обычно пользуются методом
интегральных уравнений, априорными оценками или
методами конечных разностей исчисления.
Выполнение условия D) гарантирует фредголь-
мовость задачи A), B), то есть: а) размерность
у.у пространства решении однородной задачи E) ко-
конечна; б) если И!=0, то задача A), B) всегда разре-
разрешима и притом однозначно; если Х!>0, то существует
пространство линейных функционалов, обращение в
нуль к-рых над F и / является условием, необходимым
и достаточным для существования решений задачи A),
B); причем размерность этого пространства также
равна Xj. Фредгольмовость задачи A), B) может на-
нарушиться лишь тогда, когда множество М точек //,
для к-рых (Nl)=O, не пусто. В частности, при ?г=2
в предположении, что
2,2. /= 1 v'vv=div grad м {х)
(а это не ограничивает общность), задача A), B) реду-
редуцируется к эквивалентному сингулярному интеграль-
интегральному уравнению с ядром Кошп, откуда следует н ё-
теровость задачи, то есть: а) размерность щ
пространства решений однородной задачи E) конечна;
б) размерность х2 пространства линейных функцио-
функционалов, обращение в нуль к-рых над F и / является
условием, необходимым и достаточным для разреши-
разрешимости задачи A), B), также конечна; в) разность х1—
—х2=х (индекс задачи A), B)) дается формулой
где 2лр — приращение arg(^ — il.2) при однократном
обходе контура dD области D в положительном на-
направлении. В рассматриваемом случае задача A), B)
будет фредгольмовой лишь при р =—1. Число р ха-
характеризует вращение векторного поля
(ij, Z2). Когда A) представляет собой равномерно эл-
липтич. систему, т. е. когда F и и являются т. компо-
компонентными векторами, а а,у, Ь; и с — квадратными
матрицами порядка т, причем матрицы a;j удовле-
удовлетворяют условию
при определении оператора X(и) в краевом условии B)
задачи с косой производной под 1г, 12, . .., 1п следует
понимать квадратные матрицы порядка то, а под / —
вектор с т компонентами.
Нётеровость задачи с косой производной имеет место
для широких классов равномерно эллиптич. систем
и операторов Х{и). Так, напр., когда и = 2 и а,у=0, 1Ф),
ац=Е, где Е — единичная (диагональная) матрица,
выполнение условия det(Zx+И%)фО всюду на dD га-
гарантирует нётеровость задачи A), B). При соблюдении
этого условия индекс задачи A), B) вычисляется по
формуле х = 2(р-\-т), где 2яр — приращение arg det(l —
— il.2) при однократном обходе контура dD области D
в положительном направлении.
С 60-х гг. 20 в. ведется интенсивное исследование
задачи с косой производной при и^З (см. [1]).
Лит.: [1] Б и ц а д з е А. В., Краевые задачи для эллип-
эллиптических уравнений второго порядка, М., 1966; [2J В е к у а
И. Н., Обобщенные аналитические функции, М., 1959; [3] М у-
с х е л и ш в и л и Н. И., Сингулярные интегральные уравне-
уравнения, 3 изд., М., 1968; [4] Bouligand G., Giraud G.,
Delens P., Le probleme de la derivee oblique en thcorie du
potentiel, P., 1935. А. В. Бицадве.
ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ С ЧАСТНЫ-
ЧАСТНЫМИ ПРОИЗВОДНЫМИ; задача с разрывн ы-
м и коэффициентами — задача для Д. у. с
ч. п., в к-рой коэффициенты дифференциальных опе-
операторов испытывают разрывы 1-го рода (или скачки)
при переходе через нек-рые поверхности и на этих
поверхностях заданы условия сопряжения.
Задача с разрывными коэффициентами в случае эл-
эллиптич. операторов 2-го порядка (задача транс-
трансмисс и и) состоит в следующем. В произвольной
ограниченной открытой Л'-мерной области g с грани-
границей Г задана (Лг — 1)-мерная поверхность 1\, разби-
разбивающая область g на подобласти g1 и g2; в области
(g-j-Г) ставится задача:
L,n--/,(.r) в g,, J = 1,2,
где
LlU "-= Z(. /= iа" ('г) ё^- ^Xf = i *' {x) "9^7+c {x)u
— определенный в области gt линейный дифференци-
дифференциальный оператор эллиптич. типа;
[и] |Г1^«|Х_Г1_О —
ди,
дч
х-
до.
где dldvi — производная по конормали, равная
\* a'/j1 cos (n, Xj) —— ,
77 — внешняя нормаль к Г1у а символы Гх—0 и 1\+0
означают, что берутся предельные значения соответ-
соответственно с внутренней и с внешней сторон поверхности
Г1 по отношению к области g1? ft, ф, г|), % — заданные
функции.
Здесь для простоты считается, что имеется лишь
одна поверхность разрыва коэффициентов — поверх-
поверхность 1\.
Задача (*) является математич. описанием стацио-
стационарных физич. процессов, происходящих в области,
составленной из различных сред, напр, рассеяния
электромагнитной волны на каком-либо препятствии
или распространения тепла в слоистой среде.
У задачи (*) существует классич. решение при ус-
условиях, к-рые в случае отсутствия разрыва у коэф-
коэффициентов и при ф—1|з=0 переходят в Жиро условия
разрешимости задачи Дирихле (см. [3], [4], [5]). Для
задачи (*) изучались: обобщенные из W-z решения (см.
[1], [2]); задача на собственные значения и оценки
собственных функций для самосопряженных операторов
L/ (см. [6], [8]); случаи вырождения в связи с марков-
марковскими процессами (см. [9], [10]); случаи с квазилиней-
квазилинейными операторами Li (см. [13]). Для задачи (*) могут
быть установлены оценки Шаудера (см. [6], [7]); раз-
разработаны численные методы ее решения [11], [12].
Построена теория разрешимости задач с разрывными
коэффициентами для эллиптич. уравнений и систем
порядка 2т (см. [18], [19], [20]).
Задача с разрывными коэффициентами для парабо-
лич. и гиперболич. операторов 2-го порядка столь же
подробно изучена (см. [2], [9], [14], [15], [16], [17]).
Лит.: [1] Ладыженская О. А., «Докл. АН СССР»,
1954, т. 96, .\Ь 3, с. 433 — 36; [2] О л е й н и к О. А., «Изв. АН
СССР. Сер. матем.», 1961, т. 25, Л1 1, с. 3—20; [3] И л ь и н В. А.,
Ши шмар ев И. А., «Сиб. матем. ж.», 1961, т. 2, JMo 1
с. 46—58; [4] И л ь и н В. А., «Докл. АН СССР», 1961, т. 137,
№ 1, с. 28—30; [5] Ладыженская О, А., у р а л ь ц е в а
Н И., Линейные и квазилинейные уравнения эллиптического
типа, М., 1964; [6] Ш и ш м а р е в И. А., «Докл. АН СССР»,
1961, т. 137, № 1, с. 45—47; [7] Ван Тун, «Ж. вычисл. матем
и матем. физ.», 1964, т. 4, № 3, с. 577—80; [8] И л ь и н В. А
«Докл. АН СССР», 1961, т. 137, № 2, с. 272—75; [9] Г и р с а-
н о в И. В., «Докл. АН СССР», 1960, т. 135, Mi 6, с. 1311 — 13-
[10] Ф р е й д л и н М. И., «Докл. АН СССР», 1962, т. 144, № з,
с. 501—04; [11] Самарский А. А., в кн.: Тр. 4-го Всесо-
Всесоюзного матем. съезда. Ленинград, 1961, т. 2, Л., 1964; [12] его
ж е, «Ж .вычисл. матем. и матем. физ.», 1961, т. 1, Л» 3, с. 441 —
460; [13] Б о р с у к М. В.,«Докл. АН СССР», 1967, т. 177, Л|« 5,
с. 991—94; [14] Камынин л. П., в кн.: Материалы к совме-
совместному советско-американскому симпозиуму по уравнениям с
частными производными, Новосиб., 1963, с. 3 — 6; [15] Камы-
Камынин Л. И., Масленникова В. Н., «Сиб. матем. ж »
1961, т. 2, Mi 3, с. 384—99; [16] II л ь и н В. А., «Докл. АН СССР»'
1962, т. 142, ,М5 1, с. 21 — 4; [17] Егоров Ю. В., «Докл
АН СССР», 1960, т. 134, Л1 3, с. 514 — 17; [18] S с h е с h t e r Ж.,
«Ann. Scuola norm, super. Pisa. Sci. fis. e mat.», 1960, v. 14
p. 207—36; [19] Ройтберг Я. А., Шертель З. Г
«Докл. АН СССР», 1963, т. 148, ЛЬ 5, с. 1034 — 37; [20] их же]
«Успехи матем. наук», 1967, т. 22, в. 5, с. 181—82.
И. А. Шишмарев.
ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ С ЧАСТНЫ-
ЧАСТНЫМИ ПРОИЗВОДНЫМИ; задача с разрывны-
разрывными начальными (краевыми) условия-
условиями — задача для Д. у. с ч. п., в к-рой функции,
задающие (начальные) краевые условия, не являются
непрерывными.
Пусть, например, для гиперболического уравнения
второго порядка
^=«2^-/, о<*<1, t>t0,
поставлена смешанная задача с начальными условиями:
и краевыми условиями
"]=с=о = "Фх. »|ж=1=^;
в этом смысле разрывы начальных функций ср0 и срх
влекут за собой разрывы и и du/dt вдоль характеристи-
характеристических лучей х—a?=const и x-\-at=const, причем мера
разрыва
% = и(с ± at + O, t) — u(c±at — 0, t),
или
Х = щ{с ± ai + 0, t) — ut (с ± at—0, t),
где eg[0, 1] —точка разрыва функций ф0 или <р1?
удовлетворяет вдоль характеристического луча урав-
уравнению
т. е. x = const. Аналогичные результаты справедливы
для гиперболических уравнений 2-го порядка с пере-
переменными коэффициентами:
В этом случае разрывы начальных функций и краевых
условий также влекут за собой разрывы и и du/dt
вдоль характеристических лучей, определяемых из
системы уравнений
~ = 2^ , аа И ^/' 2,-, j=iai'{)
мера разрыва / удовлетворяет уравнению:
где функция ф(ж) определяет характеристическую по-
поверхность в виде уравнения (р(х)=С.
Для уравнения эллиптического типа разрывы кра-
краевых условий внутрь области D не распространяются,
т. к. в этом случае характеристические лучи комплекс-
комплексны. Для таких уравнений эллиптического типа изучен
вопрос о существовании и единственности решения и
об удовлетворении решения граничным условиям. Так,
для эллиптических уравнений 2-го порядка в произ-
произвольной области
j—ttj\ J dXjdXj A^i= 1 ox i
и\до=У' пли |г + k W " \dD = ¦*
доказано, что если граничная функция г|)^ W'J* (dD)
для первой краевой задачи и if^L2(9D) для второй
краевой задачи, то существует обобщенное решение
из W\(D), к-рое удовлетворяет граничному условию
в среднем, т. е. \\и—"фЛ^^р у->-0, где поверхности
дТ)п аппроксимируют поверхность dD. В случае пара-
параболических уравнений (также как и для эллиптических
уравнений) разрывы внутрь области D не распростра-
распространяются, если разрывны начальные данные или краевые
условия. Для этих задач изучены также вопросы о
существовании и единственности обобщенного решения
граничному условию.
Лит.: [1]Т и х о н о в А. Н.. С а м а р с к и й А. А., Урав-
Уравнения математической физики, 4 изд.,М., 1972; [2] В л а д и м и-
р о в B.C., Уравнения математической физики, М., 1976; [3]
Бицадзе А. В., Уравнения математической физики, М.,
1976; [4] К у р а н т Р., У. авнения с частными производными,
пер. с англ., М., 1964; [5] Вере Л., Д ж о н Ф., Ш е х-
т е р М., Уравнения с частными производными, пер. с англ., М.,
1966; [6] Ладыженская О. А., Уральцева Н. Н.,
Линейные и квазилинейные уравнения эллиптического типа.
2 изд., М., 1973; [7] Л а д ы ж е н с к а я О. А., С о л о н н и-
к о в В. А.,Уральцева Н. Н., Линейные и квазилинейные
уравнения параболического типа, М., 1967; 18] Ф р и д м а н А.,
Уравнения с частными производными параболического типа,
пер. с англ., М., 1968; [9] М и р а н д а К., Уравнения с част-
частными производными эллиптического типа, пер. с итал., М., 1957;
[10] А г м о н С, Д У г л и с А., Ниренберг Л., Оценки
решений эллиптических уравнений вблизи границы ...,
пер. с англ., М., 1962. Е. И.Моисеев.
ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ С ЧАСТНЫ-
ЧАСТНЫМИ ПРОИЗВОДНЫМИ; задача со свобод-
свободными границами — задача, в к-рой требуется
найти решение системы Д. у. с ч.
п. с соответствующими начальны-
начальными и граничными условиями
д .S в области, граница к-рой частич-
частично или полностью неизвестна и
подлежит определению. К такого
^_ типа задачам приводят многие
0 х проблемы фильтрации, диффузии,
теплопроводности и др. разделов
механики сплошных сред. Так, напр., задача Гель-
мгольца — Кирхгофа о симметричном струй-
струйном обтекании равнобочного клина с углом раствора
2<хя неограниченным потоком идеальной жидкости за-
заключается в отыскании компонент скорости и=и(х, у),
v=v(x, у), являющихся решением системы уравнений
Коши — Римана:
ди j^ dv „ ди ду „
дх '¦ ду ' ду дх у
и удовлетворяющих на известной границе условиям
(см. рис.):
Неизвестная граница BS является линией тока, и на
ней задано дополнительное условие
u2jrvi = v]e, Птм = (.'те, г= у Ж2 _|_ уг
(ва рис. приведена верхняя половина течения у~^0,
при !/<0 течение симметрично).
При изучении плоских задач со свободными грани-
границами большую роль играют методы теории функций
комплексного переменного.
См. также Стефана задача.
Лит.: [1] Монахов В. Н., Краевые задачи со свободными
границами для эллиптических систем, Новосиб., 1977; [2]
Кружков С. Н.,«Прикл матем. и механ.», 1967,т. 31, в. 6,
с. 1009—20; [3J Шишкин Г. И., «Докл. АН СССР», 1971,
т. 197, Mi 6, 1276 — 79. Ф. П. Васильев.
ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ С ЧАСТНЫ-
ЧАСТНЫМИ ПРОИЗВОДНЫМИ; метод уравнений
Фишера — Рисе а, метод Пикон е,— метод
решения краевых задач для Д. у. с ч. п., основанный
ва применении формулы Грина и приводящий к си-
системе интегральных уравнений (Фишера — Рисса) для
нек-рого подходящим образом подобранного неизвест-
неизвестного вектора. Метод дает возможность находить чис-
численные значения решений, но может быть применен и
для доказательства теорем существования.
Пусть L* и L — сопряженные линейные эллипти-
эллиптические операторы 2-го порядка в пространстве точек
(xlt x2, . .., хп) с действительными коэффициентами
? с,
D — конечная область, ограниченная замкнутой по-
поверхностью S. Пусть в классе функций, допускающих
интегральные представления по формулам Грина,
ищется решение и(х) задачи Дирихле:
, lim u(x)=<p(y).
S
Пусть, далее, v(x) — произвольная функция из того
же класса. Применение формулы Грина к и(х) и v(x)
приводит к соотношению
Г
С1)
Df(*)» (*) dx,
где
COS пх; О; —
да
ik
v — внутренняя конормаль. Пусть U= (щ, и2) —двух-
компонентный вектор, составляющие к-рого — дейст-
действительные функции с суммируемым квадратом, при-
причем первая составляющая определена в D, а вторая —
на S. Пусть L2(D, S) — множество этих векторов;
норма вводится через скалярное произведение U и V
из L2(D, S):
Пусть {vk} — множество, выбранное так, что совокуп-
совокупность двухкомпонентных векторов
Vk = (—L*rk(x), vk(y)), x?D,
полна в гильбертовом пространстве L2(D, S). Тогда,
обозначив через U = (и1, и2) вектор с первой составля-
составляющей их(х), равной и(х'), и второй составляющей
и2(у), совпадающей с ди/д\\ можно записать A) в виде
системы интегральных уравнений
Фишера — Рисе а:
Если совокупность {Ffc} ортонормирована и выпол-
выполняются условия Рисса — Фишера теоремы, то система
B) определит в L2(D, S) коэффициенты Фурье с& век-
вектора U=(ul, и?) относительно полной системы базис-
базисных векторов {i'k}- Если известно, что решение рас-
рассматриваемой задачи существует и единственно, то
ряд Фурье 2fcCfcFfc сходится в среднем к искомому
решению и только к нему. В противном случае выбор
функций {vii} связан с необходимостью дополнитель-
дополнительного исследования. Так, если допускаются собствен-
собственные решения ио(х) (нарушена единственность), сово-
совокупность {t'fe} должна удовлетворять равенствам
где ?г0= (ио(х), dujdx). Если в качестве
последовательность одночленов xrilx'X2.. .xam с целыми
1 - т
неотрицательными показателями аг, а2, ..., ат, то
значения и(х) и ди/д\, найденные из B), вместе с за-
заданным на S значением и(х), удовлетворяют функцио-
функциональным соотношениям Грина:
(x)krnu(x) =^["Ы (J
A(y)w(y, .r)) -w(y,X)^jdy-^Dfw(y, x)dy,
x?D,
д (x) = { '
где кт — отличная от нуля постоянная, зависящая от
т, и w(y, x) — фундаментальное решение уравнения
L*v=0. В этом случае все решения системы уравнений
Фишера — Рисса B) и только они являются реше-
решениями рассматриваемой краевой задачи. Центральным
пунктом этого метода является построение подходящим
образом выбранной совокупности функций {vn}, удов-
удовлетворяющих условию L*vn=0 либо нек-рым усло-
условиям полноты [4].
Этот способ не требует задания явного выражения
фундаментального решения, но если последнее извест-
известно, то, в силу того, что совокупность {w(y, х^)}, где
ж(*> — счетная бесконечная последовательность про-
произвольных точек, не принадлежащих D\]S, линейно
независима и полна в L2(S) [4], можно значительно
упростить вычисления; эта теорема позволяет также
распространить метод уравнений Фишера — Рисса на
задачи с косыми производными (см. Дифференциальное
уравнение с частными производными; задача с косой
производной) и другие типы уравнений.
Лит.: [1] Pi cone M., «Atti Accad. sci. Torino. CI. sci.
fis., mat. e natur.», 1940, v. 75, p. 413—26; [2] Amerio L.,
«Amer. J. Math.», 1947, v. 69, № 3, p. 447—89; [3] F i с h e r a G.,
«Ann. Scuola norm, super. Pisa. Sci. fis. e mat.», 1950, t. 4,
fasc. 1—2, p. 35—99; [4] К у п р а д з е В. Д., «Успехи матем.
наук», 1967, т. 22, в. 2, с. 59—107; [5] М и р а н д а К., Урав-
Уравнения с частными производными эллиптического типа, пер. с
итал., М., 1957. В. Д. Купрадзе.
ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ С ЧАСТНЫ-
ЧАСТНЫМИ ПРОИЗВОДНЫМИ; методы комплекс-
комплексного переменного — методы решения эл-
эллиптических Д. у. с ч. п., в к-рых используется пред-
представление решений через аналитич. функции комплекс-
комплексного переменного.
Теория аналитич. функций
w(z)=u(x, у)+ги(х, у)
комплексного переменного z=x-{-iy представляет собой
теорию двух действительных функций и(х, у) и v(x, у),
удовлетворяющих системе уравнений Коши — Римана:
их—vy=0, Uy-^vx=Q, к-рая по существу эквивалентна
уравнению Лапласа
Начиная с 30-х гг. 20 в. методы аналитич. функций
интенсивно стали проникать в общую теорию уравне-
уравнений эллиптич. типа. Это привело к созданию нового
раздела анализа, существенно расширяющего рамки
классич. теории аналитич. функций и ее применений.
В этой области фундаментальную роль играют раз-
различные формулы представления всех решений весьма
широкого класса эллиптич. уравнений через аналитич.
функции одного комплексного переменного. Для ли-
линейных уравнений эти представления осуществляются
с помощью нек-рых линейных операторов, выражаю-
выражающихся посредством коэффициентов. Эти формулы дают
возможность распространить свойства аналитич. функ-
функций на решения уравнений эллиптич. типа, причем,
в ряде случаев в дословной формулировке сохраняются
такие важные свойства, как теорема единственности,
принцип аргумента, теорема Лиувилля и др. В естест-
естественной форме обобщаются ряды Тейлора и Лорана,
интегральная формула Коши, принцип компактности,
принцип аналитич. продолжения и др.
Формулы комплексного представления позволяют
строить разнообразные семейства частных решений
уравнения, обладающие теми или иными заданными
свойствами. Напр., можно строить различные классы
так наз. элементарных решений, имеющих точечные
особенности, к-рые используются для получения раз-
различных интегральных формул, а также так наз. полные
системы частных решений; последние обладают тем
свойством, что при помощи их линейных комбинаций
можно приближать любые решения. Формулы ком-
комплексного представления позволяют также редуци-
редуцировать широкий круг граничных задач к эквивалент-
эквивалентным краевым задачам для аналитич. функций, а также
строить эквивалентные задаче интегральные уравнения
(типа Фредгольма или сингулярные). Этот метод по-
зволяет исследовать краевые задачи нефредгольмового
типа, получить условие нормальной разрешимости и
явную формулу индекса. См. Краевая задача; методы
комплексного переменного.
Эллиптические уравнения с аналитическими коэффи-
коэффициентами. Пусть дано уравнение 2-го порядка эллип-
тич. типа
Ди + «(*. У)^ + Ъ(х, у)^г + с(х, у)и = О, A)
где а, Ъ и с — аналитич. функции действительных
переменных х, у в нек-рой области плоскости z~x-\-iy.
Аналитическое продолжение коэффициентов в об-
область независимых комплексных переменных z=x-\-iy,
? = х — iy приводит уравнение A) к виду:
~ + A(z, Q*L + B(z, C)-g- + C(*, Q« = 0. B)
Односвязная область Do наз. основной обла-
областью уравнения A), если А, В и С — аналитич.
функции двух независимых переменных в цилиндрич',
области (Do, Do), где Do обозначает зеркальное изоб«
ражение Do относительно действительной оси.
Если D<z.DQ — односвязная область, то все регуляр-
регулярные в области D решения уравнения A) выражаются
по формуле
и(х, !/) = Re|G(z, z0; z, z~)(D(z) —
j C)
где Ф (z) — произвольная голоморфная функция в
области D, 2If zo?D — произвольные фиксированные
точки; аналитич. функция G(z, ?, t, т) четырех незави-
независимых комплексных аргументов в цилиндрич. области
(Do. Do, Do, Do) наз. функцией Римана уравне-
уравнения A). Она является решением интегрального урав-
уравнения типа Вольтерра:
G (z, I, t, т) - ^ А (г, т)) G (z, т), t, т) dr\ —
а, 5)С(Е, 5, (, x)dt +
С (I, ч) G (I, л, t, т) dri= 1. D)
Осуществляемое формулой C) соответствие между
семейством решений {и) уравнения A) и семейством
голоморфных функций {Ф} взаимно однозначно, если
зафиксировать значения мнимой части ф в фиксиро-
фиксированной точке z1 области D. При z1=zo=O имеет место
формула обращения:
, -{А— и (О, 0)G@, 0, 2, 0).
Уравнение D) можно решить методом последователь-
последовательных приближений. Таким путем можно найти прибли-
приближенные выражения для функции Римана.
В случае многосвязной области D формула C) дает,
вообще говоря, многозначные решения. Чтобы полу-
получить в этом случае все однозначные решения уравнения
A), в качестве Ф в C) надо брать многозначные функции
определенного вида.
Пусть D — двухсвязная область (DczZH), D' — огра-
ограниченный континуум, дополняющий D до односвязной
области. Тогда все однозначные в области D решения
уравнения A) даются формулой
и(х, i/) = Re<G(z, 20, z, г) Ф (z) —
Ф(*)Я(*. 70, z,7)dt}, E)
где zx?D, zo^D' —фиксированные точки, Ф (z) —
многозначная аналитич. функция вида
z, F0)d«] In (z-z0).
Здесь a — произвольная действительная постоянная,
Ф0(г) — произвольная голоморфная функция в обла-
области D, L — любая простая замкнутая кусочно гладкая
кривая, лежащая в D и окружающая D'. Функции
Н и Н* выражаются по формулам
H(t, х, z, ?) = -A_G(i, т, 2, l)-B(t, i)G(t, x, z, ?),
Я* (t, x, 2, ?) =-§; G (t, т, z, l) — A (t, x) G (i, t, z, ?)•
Комплексные представления вида C) распространяются
также и на системы уравнений, записываемых в век-
векторной форме в виде A), где и — вектор с компонен-
компонентами щ, . .., м„, а, Ь, с — квадратичные матрицы по-
порядка га, элементы которых — аналитич. функции
переменных х, у.
В той области, где уравнение A) имеет хотя бы одно
положительное решение ио>О, подстановкой и=иар
его можно привести к виду
(такое решение всегда существует в малой окрестности
любой фиксированной точки, а также в любой области,
где с<0). В этом случае уравнение A) эквивалентно
системе уравнений, к-рая представляет собой частный
случай обобщенной системы Коши — Римана вида
ux — Vy-\- ви + bv = O, Uy -f- vx -\- cu -\- dv = 0. F)
Вводя в рассмотрение комплексную функцию w=u-\-iv,
эту систему можно записать в виде
0—w-\- А B) w-\- В (z) ш = 0, 23_ = <5Л4-id,,. G)
Если коэффициенты А и В — аналитич. функции
комплексных аргументов z и ? B=.z+ij/, ?=а:—tj/)
в нек-рой цилиндрич. области (Do, Do), где Do — одно-
связная область, то решение уравнения F) в односвяз-
ной области DczZ)o выражается формулой
W (z) = ехр ( [Z A B, x) d% ) X
J ^0
ft(*,l,t)<b(t)dt\, (8)
в к-рой Г] и Г2 — аналитич. функции своих аргумен-
аргументов, выражающиеся через А и В; они строятся по
методу последовательных приближений, Ф — произ-
произвольная аналитич. функция переменного z.
В случае, когда А и В — целые функции перемен-
переменных х и у, представление (8) имеет место для любой
односвязной области плоскости z без ограничений
на поведение коэффициентов А и 3 вблизи беско-
бесконечности.
Пусть дано эллиптич. уравнение вида
«'*>
=0, (9)
где а^р\ — аналитич. функции х, у. Если Do — основ-
основная область уравнения (9), то всякое регулярное
решение этого уравнения в односвязной области DcD0,
выражается формулой
и (х, 2/) = Re JG (z, Го, z, 7) ф0 (z) —
где Фо, ..., Ф„_!—произвольные голоморфные в
области D функции
Здесь G — комплексная функция Римана уравнения
(9), к-рая аналитически зависит от комплексных ар-
аргументов (t, т, 2, ?) в цилиндрич. области (Do, Z)o, Do, Do).
При выполнении условий
формула A0) осуществляет взаимно однозначное соот-
соответствие между семейством решений {и} уравнения (9)
и семейством голоморфных функций {(Фо, . . •, Ф„_1>}.
Если D — многосвязная область, то формула A0)
дает, вообще говоря, многозначные решения. Но,
как и в случае уравнения 2-го порядка, можно видо-
видоизменить эту формулу так, чтобы она давала все одно-
однозначные решения уравнения (9) и в многосвязной
области. Формула A0) распространяется также на
систему уравнений вида (9), где и — вектор, а коэф-
коэффициенты — матрицы.
Для ряда уравнений математич. физики функция
Римана выражается в явной форме при помощи эле-
элементарных или специальных функций.
В случае уравнения колебаний мембраны
= 0, X = const,
G(z, I, t, T) = J0(XV(z — t)(t, — T;)),
где Jo — функция Бесселя нулевого порядка; в ка-
качестве основной области можно взять всю комплекс-
комплексную плоскость. Случай Х=0 дает уравнение Лапласа
Дм=0; тогда G=1 и формула C) принимает вид
«=Re[O>(z)].
Для уравнения сферич, функций
Ди-|-ге (ге + 1) A + ж2 + г/2)-2 м = 0, re = const,
t r)-
гДе P'n — функция Лежандра первого рода; в каче-
качестве основной области можно взять любую односвязную
область Do, для к-рой выполняется условие: если
z€-Do. Z(zD0, то zZr?=i (напр., круг |г|<1). Для урав-
уравнения Эйлера — Дарбу
Дм+г/ (^¦uxJra'uy) = 0. а, а'= const,
G(z, I, t, т) = (т— 2)-3' (S —1)-&(?— z)P+P' X
' >" '' (z-x)it-t)
где 2ft = a' + ia, 2ft' = a' — ia, F — гипергеометрич. ряд;
в качестве основной области можно взять полупло-
полуплоскости !/>0 или !/<0.
Для уравнения
G<z Г t т)
(n-l)! (n-l)l
и имеет место формула Гурса
Метод комплексных представлений решений приме-
применим также к нек-рому классу нелинейных уравнений.
Пусть, напр., дано известное в дифференциальной гео-
геометрии уравнение Гаусса
Ам = — 2keu,
где к(х, у) — заданная функция. Если va(z) — какое-
либо частное решение этого уравнения, то его же ре-
решениями являются функции вида
мB)-МФB)]|Ф'(г)|2,
где Ф (z) — произвольная аналитич. функция. Если к=
= const, то уо=4A— kzz)~2 и все решения уравнения
Гаусса выражаются формулой:
и(х, !/) = 4|Ф'B)|2A4-й|Ф(г)|2)-2.
Если fc<0, то надо предполагать, что |O(z)l<—к~1.
Эллиптические уравнения с неаналитическими коэф-
коэффициентами. Пусть дана обобщенная система уравнений
Копти — Римана G) с коэффициентами А и В, задан-
заданными на всей плоскости Е комплексного переменного z
и принадлежащими классу LPi2(E), т. е.
A(z), B
р > 2, |2|<1.
Если коэффициенты заданы в ограниченной области S
и принадлежат классу Lp(S), _p>2, то они будут удов-
удовлетворять предыдущим условиям при продолжении
их вне S нулем. При этих предположениях уравнение
^7), вообще говоря, не имеет решения в классическом
¦смысле. Поэтому рассматриваются так наз. обобщен-
обобщенные решения: функция u?(z)^Z,!E) наз. решением урав-
вения G) в области S, если она обладает производной
ъ смысле С. Л. Соболева д-W^L1(S) и удовлетворяет
уравнению почти везде в S-
Теория функций, удовлетворяющих уравнению G),
представляет собой далеко идущее обобщение классич.
¦теории аналитич. функций (А=В=0) и сохраняет
существенные черты последней. Поэтому решения
уравнения вида G) наз. обобщенными аналитическими,
функциями.
Всякое решение уравнения G) (в S) удовлетворяет
интегральному уравнению
»в<»^)^дл=о, (И)
где ? = Ц-8Т), Ф (г) — голоморфная функция в S.
Если (b?Lq(S), ?>~Г7, Р>2, то уравнение A1)
имеет единственное решение, к-рое выражается фор-
формулой вида
ш (г)=Ф {г) + J Js Г г (z, I) Ф (О
Г2 (z, E) Ф (?) dl dx\. A2)
о
Резольвенты Tt и Г2 зависят от коэффициентов урав-
уравнения G) и строятся при помощи процесса последо-
последовательных приближений.
Формула A2) дает общее (линейное) представление
решений уравнения G) через аналитич. функции Ф (z).
<Эна. в частности, позволяет построить так наз. основные
ядра
Qx(z, t)=Xj(z, t)+iX2(z, t),Q2(z,t)=X1(z, t) — iX2(z, t),
где t — некоторая фиксированная точка, a Xt и Х2 —
решения интегрального уравнения A1), соответст-
соответствующие функциям
, = (t-*)-1.
Эти ядра позволяют написать обобщенную
формулу К о ш и:
2Яг Jc
fw (z), z?S,
= \~w(z), z?dS, A3)
0, z (? 5 .
При Л=В=0 она обращается в классич. формулу
Коши. При помощи формулы A3) на обобщенные ана-
аналитич. функции распространяются многие из тех
свойств аналитич. функций, к-рые доказываются обыч-
обычно с помощью формулы Коши. В частности, можно
обобщить классич. теоремы об аналитич. продолжении,
построить теорию обобщенных интегралов типа Коши,
получить представления обобщенных аналитич. функ-
функций в виде контурных интегралов с действительной
плотностью и др.
Основными ядрами сопряженного уравнения
г * * * '
являются функции
Если w и ш* удовлетворяют в S уравнениям G) и A4),
соответственно, и непрерывны в S, то имеет место
тождество (аналог классической теоремы Коши):
Re[i ?asw(z)u;,(z)dz]=0.
Если w(z) — решение уравнения G) в области S, то
существует такая аналитическая в S функция Ф(г),
что имеет место равенство
w (z) — ц> (z) e , A0}
где
и принадлежит классу Са(Е), а=р/(р—2), причем
co(z)-^-0, если г—»-оо.
Эта формула, в частности, позволяет распространить
на решения уравнений вида G) основные теоремы
классич. теории аналитич. функций: теорему единст-
единственности, теорему Лиувилля, принцип аргумента,
принцип компактности и др. Формула A5) допускает
обращение: задавая аналитич. функцию Ф, можно
найти функцию w(z), удовлетворяющую нелинейному
интегральному уравнению A5).
Пусть Ф (z) — аналитическая в области S функция,
к-рая может иметь любые особенности, и * — фикси-
фиксированная точка. Тогда существует решение w(z) урав-
уравнения G) такое, что функция шо=ш/Ф непрерывно
продолжима на всю плоскость Е, принадлежит классу
Са(Е), а= (р—2)/р, не обращается в нуль нигде на
плоскости Е и ш0 (*)—!• Функция ш0 удовлетворяет
интегральному уравнению
к-рое имеет единственное решение, а функция ш=Ф (z)w0
удовлетворяет нелинейному интегральному уравнению
) = Ф W ехР {^ $ U ^Щ^
A8)
из к-рого при i-^-oo получается представление A5).
Проблема приведения эллиптич. уравнепия 2-го
порядка общего вида
а26 + с —+ d- + ,- + /(M)=0 A9)
к виду A) эквивалентна задаче редукции к канонич.
виду положительной квадратичной формы
adx2-^2bdxdy+cdy2, a>0, Д=ас—62>0.
Последняя проблема эквивалентна отысканию гомео-
гомеоморфизмов уравнения Бельтрами
д-w—q (z) dzw = 0, w=u-'riv, B0)
где
q (z) = (a- Y"K- ib) {а + yrA + ib)~1, \q(z)\ < 1.
Если A9) — равномерно эллиптич. уравнение
(Д 5= Ао = const > 0), то \q (z) | s? g0 = const < 1.
При изучении уравнения Бельтрами основным во-
вопросом является построение нек-рого его гомеоморфиз-
гомеоморфизма для данной области S; если co(z) — гомеоморфизм
уравнения Бельтрами, реализующий топологич. ото-
отображение области S на область a>(S), то всякое другое
его решение в S имеет вид
ШB) = Ф[ШB)], B1)
где Ф — произвольная аналитич. функция в области
(o(S).
Если q(z) — измерима, ^(г)=0 вне S и \q(z)\ <gro<l,
то уравнение Бельтрами B0) имеет решение вида
где р удовлетворяет сингулярному интегральному
уравнению (интеграл понимается в смысле главного
значения по Коши):
J^^f^IL = ?B). B3)
Это уравнение имеет единственное решение в нек-ром
классе Lp(E), p>2; его можно получить методом по-
последовательных приближений. Функция B2) принад-
принадлежит классу Са(Е), а=р/(р—2), реализует топо-
топологич. отображение плоскости на себя, причем ю(оо) =
= оо, z~1w{z)-^l при z->-oo. Если q^Ca(E), 0<сс<1,
т>0, то w(z)€C%+1(E).
Равномерно эллиптич. система 1-го порядка общего
вида в комплексной записи имеет вид
d-w — fjfi (z) dzw — q2 (z) д-w -f iis-f Bw = 0,
г z ' B4)
С помощью гомеоморфизма нек-рого уравнения вида B0)
ее можно привести к виду G).
Всякое решение уравнения B4) в нек-рой ограни-
ограниченной области S при условии, что A, B?Lp(S), p>2,
представлено в виде
B5)
где w(z) — некоторый гомеоморфизм уравнения Бельт-
Бельтрами B0) с коэффициентом
q (z) = qi (z) + q2 (z) -gi_ t
Ф((в) — аналитич. функция в области <u(S), функция
ф(г)€Cа(?'), а= (р—2)/р голоморфна вне S и исчезает
на бесконечности. Представление B5) имеет место и
тогда, когда коэффициенты левой части уравнения B4)
зависят от w и ее производных любого порядка, лишь
бы на рассматриваемых решениях выполнялись ука-
указанные выше условия. Как и A5), формула B5) допу-
допускает обращение.
Формула B5) позволяет перенести целый ряд свойств
классич. теории аналитич. функций на решения урав-
уравнения B4); теорему единственности, принцип аргу-
аргумента, принцип максимума и др.
Общее квазиконформное отображение Q является
решением нек-рой равномерно эллиптич. системы вида
B4) (при Л=.В=0). Справедливо и обратное утверж-
утверждение. Поэтому указанные выше результаты позволяют
решить чисто аналитич. путем основные проблемы
квазиконформных отображений.
Системы уравнений 1-го порядка эллиптич. типа с
In, ге>1, неизвестными функциями двух независимых
переменных, при нек-рых естественных ограничениях,,
приводятся к канонич. виду:
д-w—Q (z)dzw+Aw±Bw = 0, B6)
где w — искомый вектор с п комплексно значными
компонентами, Q, А, В — квадратные матрицы по-
порядка п. Теория уравнений вида B6) имеет много
сходства со случаем п=1, но она имеет и свои особен-
особенности.
Лит.: [1] В е к у а И. Н., Новые методы решения эллипти-
эллиптических уравнений, М.— Л., 1948; [2J е г о же, Обобщенные
аналитические функции, М., 1959; [3] е г о те, «Матем. сб.»,
1952, т. 31, № 2, с. 217—314; [4] Б е р г м а н С, Интегральные
операторы в теории линейных уравнений с частными производ-
производными, пер. с англ., М., 1964; [51 В е г s L., Theory of pseudo-
analytic functions, N. Y., 1953; [6] Б о я р с к и й Б. В., «Докл.
АН СССР», 1958, т. 122, № 4, с. 543—46; [7] е г о те, там же,
1959, т. 124, № 1, с. 15—18; [8] С а г 1 е m a n Т., «С. г. Acad.
sci», 1933, t. 197, p. 471; [9] Б и ц а д з е А. В., Краевые задачи
для эллиптических уравнений второго порядка, М., 1966; [10}
X а л и л о в 3. И., «Изв. АН СССР. Сер. матем.», 1947, т. 11,
с. 345—62; [11] С о и г a n t R., H i I b e r t D., Methods of
mathematical physics, v. 2, 2 ed., N. Y.— L., 1962.
II. H. Benya.
ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ С ЧАСТНЫ-
ЧАСТНЫМИ ПРОИЗВОДНЫМИ; функциональные ме-
методы решения — методы, основанные на рас-
рассмотрении левой части уравнения как оператора, дей-
действующего в функциональном пространстве, определен-
определенном соответствующим образом. Наибольшее развитие
функциональные методы получили в применении к
линейным уравнениям с частными производными. В этом
случае функциональные методы условно могут быть раз-
разбиты на две группы: а) относящиеся к спектральной
теории дифференциальных операторов и б) использу-
используемые при выяснении общего характера разрешимости
уравнений, краевых задач и свойств решений. Внутри
группы б) удобно, в свою очередь, выделить, с одной
стороны, методы, опирающиеся лишь на общие теоремы
функционального анализа (теории операторов), а с
другой — методы, существенно использующие технику
преобразования Фурье. Для первых характерно не-
непосредственное рассмотрение краевых задач для общих
уравнений с переменными коэффициентами; для вторых
отправной точкой является изучение дифференциаль-
дифференциального оператора с постоянными коэффициентами, част»
безотносительно к краевым условиям, а переход к
переменным коэффициентам (когда это возможно)
осуществляется при помощи соответствующей «теории:
возмущений». Получаемые в обоих направлениях
результаты дополняют друг друга.
Функциональные методы возникли при использо-
использовании связи между задачей минимизации функционала
в классе действительных функций и(х, у), удовлетво-
ряющих на границе S области V (для простоты — дву-
двумерной) условию
«|s = 0, B)
и задачей решения уравнения Пуассона
-Ди=/ C)
в V [являющегося уравнением Эйлера для A)] при
тех же краевых условиях B). Если / не является глад-
гладкой (напр., f^H{V) — гильбертову пространству функ-
функций с суммируемым в V квадратом), то минимум для
A) достигается на функциях, не имеющих, вообще
говоря, вторых производных, входящих в уравнение
C), т. е. эти функции цают лишь обобщенное решение
задачи C), B). Для исчерпывающего описания воз-
возникающей ситуации (см. [1], [2]) вводится гильбертово
пространство W1, получаемое пополнением линейного
многообразия гладких функций, удовлетворяющих B),
в норме, порождаемой скалярным произведением
/ ди dv i ди dv \ ,.,
Тогда под решением задачи C), B) понимается элемент
и?цп такой, что для любого элемента v^W1 выпол-
выполняется равенство
{и, v}=(f, v), D)
где круглые скобки означают скалярное произведение
в H{V). Минимум для A) при любой f^H также до-
достигается в W1 и дает решение задачи C), B) в смысле
D), являющееся единственным. Всякое классическое
(имеющее вторые производные) решение задачи C),
B) удовлетворяет равенству D) при любой допустимой
•функции v и, значит, является обобщенным. Отсюда,
в частности, следует определение, с помощью обоб-
обобщенного решения, нек-рого расширения классич. опе-
оператора — А, заданного первоначально на гладких
функциях, удовлетворяющих условию B). Вопрос «при
каких условиях на / и границу S обобщенное решение
будет классическим?» значительно более сложен (это —
вопрос о так наз. дифференциальных свойствах обоб-
обобщенного решения).
В рассмотренной схеме существование обобщенного
решения следовало из существования в W1 элемента,
реализующего минимум функционала A). В даль-
дальнейшем было замечено, что теорема существования
может быть получена непосредственно из определения
¦D) при помощи так наз. теоремы Рисса об общем виде
линейного ограниченного функционала (см. [1]). По-
Последующее развитие теории идет в нескольких направ-
направлениях. Приведенные построения немедленно обоб-
обобщаются на случай, когда —А заменяется на общий
самосопряженный положительный эллиптич. оператор
порядка 2т с переменными коэффициентами. При этом,
¦естественно, в скалярное произведение будут входить
производные порядка т. Свойство полной непрерыв-
непрерывности обратного оператора позволяет установить ха-
характер спектра соответствующих задач и установить
¦справедливость для них Фредголъма альтернативы.
Можно получить теорему существования решения и в
случае, когда в уравнении присутствует подчиненный
главной эллиптич. части кососимметрич. оператор
¦(напр., вместе с —А имеются члены а(х, у) ¦— -\-
•\-Ъ(х, у)-^), т. е. и при отсутствии связи с вариаци-
вариационными задачами [3].
Обобщения иного характера возникают из замечания
о сохранении теоремы существования и единственности
•обобщенного решения задачи C), B) и в том случае,
-когда/ — произвольный ограниченный линейный функ-
ционал над W1. Пространство всех таких функцио-
функционалов может быть получено пополнением // по новой
норме
|/, W-*\ = sup ' «• w)' . E)
Получаемое пространство W~l оказывается сущест-
существенно шире //. Напр., в одномерном случае (V — ин-
интервал (—1, 1)) последовательность функций
2T
О, \х\ > е, е = 1, 2~\ 2~\ ...,
сходится в W-1, но расходится в Н. Продол этой по-
последовательности не является функцией в обычном
смысле, т. е. пространство W~x содержит обобщенные
функции. В то же время неравенство
|</, ш>|<|/, W-1\\w, \Уг\
(скобки ( , ) обозначают действие функционала / на
элемент w^W1) обеспечивает справедливость теоремы
существования и единственности в случае /? W~l. Этот
результат интересен еще и в том отношении, что теперь
оператор —Д устанавливает изоморфизм между про-
пространствами W1 и W'1. При f?H и гладкой S обоб-
обобщенное решение задачи C), B) не только принадлежит
W1, но всегда имеет и вторые обобщенные производные
(и?1У2), причем
\и, W"-\<c\f, H\.
При ге=2 (п — размерность V) пространство W~2 (фуш;
ционалов над W2) содержит б-функцию, т. е. функцио-
функционал, определяемый равенством F^-0, u)=u(xa). Су-
Существует принадлежащее пространству Н обобщенное
решение уравнения
— Л"л-о = <5*о
такое, что для и-обобщенного решения задачи C), B)
верна формула
(— Дм, vXo) = <м, — ДуХо> =- <и, бХо> =- и (хв),
или
Это составляет абстрактную теорему существования
функции Грина задачи C), B). Соответствующие пост-
построения осуществимы и в пространстве произвольного
числа измерений для общих эллиптич. операторов [4].
Следующим (после эллиптич. операторов) объектом,
к к-рому успешно были применены общие функцио-
функциональные методы, явились уравнения с выделенным
переменным — «временем», непосредственно обобща-
обобщающие классические параболич. и гиперболич. урав-
уравнения математпч. физики. Здесь основные результаты
условно могут быть разбиты на 3 группы: относящиеся
к операторным уравнениям с 1-й и 2-й производной
по времени [5], к симметричным положительным си-
системам с частными производными 1-го порядка [3],
[6] и к задаче Копти для гиперболич. уравнения произ-
произвольного порядка. Первая группа результатов изла-
излагается обычно либо в контексте обыкновенных диффе-
дифференциальных уравнений в банаховом пространстве и
теории полугрупп операторов, либо, вместе со второй
и третьей группами, в рамках так наз. техники энер-
гетич. неравенств. Последняя, в общих чертах, за-
заключается в следующем. Для гладких решений урав-
уравнения со временем, записанного в операторной форме
Lu=U F)
подчиненных соответствующим начальным и краевым
условиям, устанавливается неравенство вида
\и, H^^Lu, Н2\, G)
где Нг, Н2 — соответствующим образом определенные
функциональные пространства. Для простоты их счи-
считают гильбертовыми. Напр., для и?С2, удовлетво-
удовлетворяющих в единичном квадрате V уравнению
И УСЛОВИЯМ
1=0
г и и, U U
dt2 Ox- ~~ J
-щ
= 0,
умножением на du/dt, интегрированием по V и эле-
элементарными преобразованиями можно получить нера-
неравенство вида
(являющееся математич. выражением нек-рого закона
сохранения, откуда и термин «энергетическое неравен-
неравенство»), соответствующее неравенству G) при надлежа-
надлежащем определении норм в Ни Н2. Определив обобщенное
решение уравнения F) как элемент и?//ь для к-рого
существует последовательность гладких функций и,-,
удовлетворяющих описанным краевым условиям, та-
такая, что и;—уи в Нх и Liii—t~f в Н2, одновременно по-
получают определение оператора L: Н1—>-Н2 (снова яв-
являющегося расширением классического), для к-рого
существует ограниченный обратный оператор, что
эквивалентно теореме единственности обобщенного ре-
решения. Следующим шагом исследоваЕшя уравнения F)
является доказательство существования такого реше-
решения при любой допустимой правой части f?H2. Так
как область изменения RL оператора L является
замкнутым подпространством в Н2, доказательство
единственности эквивалентно доказательству пустоты
ортогонального дополнения к R^: из равенства
(Lu, vJ = () для любого и?11/. (9)
(скалярное произведение в Л2) следует v=0. Равен-
Равенство (9), с точки зрения теории операторов, означает,
что y?lti и L*?>=0, т. е. требуемый результат не-
немедленно следовал бы из теоремы о единственности
решения уравнения L*v=g. Однако доказательство
такой теоремы требует специальных построений, часто
весьма сложных, поскольку для L* (определенного
с точки зрения классич. анализа с помощью нек-рого
интегрального тождества) наличие неравенства, ана-
аналогичного G) (так же, как и наличие для v последова-
последовательности сходящихся к ней гладких функций, удов-
удовлетворяющих нужным граничным условиям), отнюдь
не очевидно. Возникающие трудности являются отра-
отражением несамосопряженности задач со «временем».
При исследовании гиперболич. уравнений 2-го и выс-
высшего порядков использование (9) для доказательства
равенства v=Q проводится обычно следующим образом:
подбирается оператор Р* такой, что P*v(^Wi и
(LP*v, vJ5-c\v, Я2|2. A0)
Если заметить еще, что получение G) основано обычно
на рассмотрении выражения вида (Lu, QuJ, где Q —
оператор, подобранный так, что
(Lu, QuJ^c\u, Hx\2,
и записать теперь A0) в виде
(L*v, P*vI ^sc\v, #2 |2,
то можно считать, что исследование F) основывается
на этой паре неравенств (называемых иногда дуаль-
дуальными). Сказанное относится главным образом к ги-
перболич. уравнениям. Параболич. уравнения допу-
скают трактовку, более близкую к эллиптич, случаю.
Преобразование Фурье позволяет провести, в из-
известном смысле, исчерпывающее изучение задачи Коши
для уравнений с постоянными коэффициентами [10].
Кроме того, преобразование Фурье, вместе с так наз.
«замораживанием коэффициентов» (т. е. заменой опе-
оператора с переменными коэффициентами оператором с
постоянными коэффициентами, равными значениям
соответствующих коэффициентов в нек-рой фиксиро-
фиксированной точке), часто используется для получения энер-
гетич. неравенств при использовании схем рассмотрен-
рассмотренного выше типа, а также играет важную роль в ло-
локальной характеризации операторов и краевых условий
при исследовании краевых задач для эллиптич. урав-
уравнений [10]. Дальнейшее развитие этих идей привело
к введению и изучению псевдодифференциальных опе-
операторов. Кроме того, с помощью преобразования Фурье
было установлено, что для дифференциальной опе-
операции L с постоянными коэффициентами, рассматри-
рассматриваемой в компактной области V евклидова простран-
пространства на функциях m?C°°(F), т. е. равных нулю на
границе вместе со всеми производными, всегда имеет
место неравенство
\и, H(V)\<c\Lu, H(V)\. (И)
Взяв для L замыкание L в // (V) (областью определения
для L считают С°° (F)) и определив L как сопряженный
к L (в II(V)), получают, что Д~ = //(К). Наличие
неравенства A1) для решений уравнения F), обеспе-
обеспечивающее единственность решения, автоматически вле-
влечет и разрешимость при любой правой части уравнения
L*v=g, содержащего сопряженный оператор. Ис-
Используя теорему Банаха, можно заключить, что су-
существует оператор L, LcL(Z.L (т„ е. L является рас-
расширением мипимальпого оператора L и сужением
максимального L), такой, что R-.=H{V), причем су-
существует ограниченный (в Н) обратный оператор
Z/-1 (см. [10]). Можно считать, что L соответствует
нек-рой краевой задаче (определяется нек-рой системой
условий, «сосредоточенной» на границе и находящейся
«между» тождественно нулевыми условиями и полным
отсутствием условий). О характере условий, опреде-
определяющих оператор L, в общем случае известно мало.
Использование преобразования Фурье лежит также
в основе исследования широкого круга вопросов теории
дифференциальных операторов, связанных с изучением
структуры фундаментального решения и так наз.
локальных свойств решений уравнений (в отличие от
исследования свойств решений краевых задач). Сюда
относятся теорема о существовании фундаментального
решения для общего оператора с постоянными коэф-
коэффициентами, теорема о локальной (в окрестности дан-
данной точки) разрешимости уравнения с правой частью
и о характере гладкости этого решения (см. [9], [11]).
В связи с тем, что в случае переменных (комплексных)
коэффициентов локальная разрешимость неоднород-
неоднородного уравнения F) не всегда имеет место (для урав-
уравнения
. ди , ди о , | . * ди {
имеется такая /^С°°, что не существует решения, даже
в классе обобщенных функций, ни в каком открытом
непустом подмножестве Л3, см. [9]), исследуются усло-
условия, обеспечивающие локальную разрешимость.
Использование функциональных методов весьма пло-
плодотворно и при изучении нелинейных уравнений с
частными производными. Это прежде всего относится
к вариационным методам (если вместо функционала A)
рассматривать более общий, то связанное с ним уравне-
уравнение Эйлера оказывается нелинейным) (см. [12]), различ-
различным вариантам метода неподвижной точки (см. Шаудера
метод), к методу продолжения по параметру (см. [3],
[13]), и другим, применяемым главным образом к эллип-
тич. и параболич. уравнениям. Метод энергетич. нера-
неравенств успешно используется при изучении квази-
квазилинейных гиперболич. уравнений.
• Лит.: [1J С о б о л с в С. Л., Некоторые применения функ-
функционального анализа в математической физике, Новосиб.,
1962; 12] Курант Р., Гильберт Д., Методы математи-
математической физики, пер. с нем., 3 изд., т. 1—2, М.— Л., 1951; [3]
Б е р с Л., Джон Ф., Ш е х т е р М., Уравнения с частными
производными, пер. с англ., М., 1906; [4] L i о n s J., Equations
diffcrcntielles operationelles et problemes aux limites, В., 19С1;
L5J X и л л е Э., Ф и л л и п с Р., Функциональный анализ и
полугруппы, пер. с англ., 2 изд., М., 1962; [0] Н а г у м о М.,
Лекции по современной теории дифференциальных уравнений в
частных производных, пер. с япон., М.,1Э67; [7J Г о р д и н г Л.,
Задачи Коши для гиперболических уравнений, пер. с англ., М.,
1961; [8J Гельфанд И. М., Шилов Г. Е., Некоторые
вопросы теории дифференциальных уравнений, М., 1958; [9]
Хёрмандер Л., Линейные дифференциальные операторы
с частными производными, пер. с англ., М., 1965; [10] его же,
К теории общих дифференциальных операторов в частных про-
производных, пер. с англ., М., 1959; [И] Трев Ж., Лекции по
линейным уравнениям в частных производных с постоянными
коэффициентами, пер. с англ., М., 1965; L12] Ладыженская
О. А., Уральцева Н. Н., Линейные и квазилинейные
уравнения эллиптического типа, М., 1964; [13] Миранда К.,
Уравнения с частными производными эллиптического типа,
пер. с итал., М., 1957. А. А. Дезин.
ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ С ЧАСТНЫ-
ЧАСТНЫМИ ПРОИЗВОДНЫМИ ВТОРОГО ПОРЯДКА — урав-
уравнение, к-рое содержит хотя бы одну производную 2-го
порядка от неизвестной функции и(х) и не содержит
производных более высокого порядка. Напр., линей-
линейное уравнение 2-го порядка имеет вид
Zn , . S2u (ж) хтг ди (х)
+ с (я) и (ж)+ /(*)= 0, A)
где точка х= (хг, х2, ..., хп) принадлежит нек-рой
области Qczi?n, в к-рой определены действительно-
действительнозначные функции aij(x), bi(x), c(x), и в каждой точке
x?Q хотя бы один из коэффициентов a;j(x) отличен
от нуля. Для любой точки х0 ? Q существует такое
неособое преобразование независимых переменных 5;=
= ?(#), что уравнение A) в новых координатах ?= (Si.
|2, . . ., 1„) примет вид
V" * its 92ц(%) I У" ь* lt\ ди A) |
+ c»ffi) «(|)-i-/*ffi)= 0, B)
где коэффициенты а*ц{.\) в точке |0=g(a:0) равны нулю
при Хф], и равны =tl или 0 при i= j. Уравнение B)
наз. канонич. видом уравнения A) в точке х0.
Число к положительных и число I отрицательных
в точке §о коэффициентов ац(^) в уравнении B) за-
зависит только от коэффициентов a;j(x) уравнения A).
Это обстоятельство позволяет классифицировать диф-
дифференциальные уравнения A) следующим образом.
Если fe=n или 1=п, то уравнение A) наз.. эллип-
эллиптическим в точке ха\ если к=п—1, а 1=1, или
к=1, a Z=n — 1, то — гиперболическим; если
к-\-1=п и 1<&<п —1, то — ультрагипербо-
ультрагиперболическим. Уравнение наз. параболическим
вши роком смысле в точке х0, если хотя бы
один из коэффициентов я;;(§) равен нулю в точке
|0=|(х0), к~\-1<Сп; уравнение наз. параболиче-
параболическим в точке х0, если только один из коэффициентов
а*с(%) равен нулю в точке 10 (пусть aii(|o) = O), а все
остальные коэффициенты аи(|) одного знака и коэф-
коэффициент Г
В случае двух независимых переменных (п = 2) тип
уравнения удобнее определять с помощью функции
Так, уравнение A) является эллиптическим в точке х0,
если Д (¦?•(,)>(); гиперболическим, если Д(ж0)<0, и
параболическим в широком смысле, если Д(го) = О.
Уравнение наз. эллиптическим, гиперболическим и
т. д. в области, если оно эллиптично, соответственно,
гиперболично и т. д. в каждой точке этой области. Так,
напр., уравнение Трикоми yuxx-\-u,jy=0 эллиптично
при у>0, гиперболично при г/<0 и параболично в
широком смысле при г/=0.
Преобразование переменных |=§(ж), к-рое приводит
уравнение A) к канонич. виду в точке х0, зависит
от этой точки. В случае трех и более независимых
переменных, вообще говоря, не существует неособого
преобразования, приводящего уравнение A) к канонич.
виду одновременно во всех точках нек-рой окрестности
точки х0, т. е. к виду
В случае же двух независимых переменных (я = 2)
такое приведение уравнения A) к канонич. виду воз-
возможно при нек-рых условиях на коэффициенты aij(x);
напр., если функции a.jj(x) непрерывно дифференци-
дифференцируемы до 2-го порядка включительно и уравнение A)
одного типа в нек-рой окрестности точки х0.
Пусть
Ф (х, и, uXl, ..., их , uXlXl, их,Хг, ..., и \ = 0 C)
\ п п п/
— нелинейное уравнение 2-го порядка, где цх-=Эц^
' uxi '
xjx.= l)x.ox > и пусть в каждой точке из области
определения действительнозначной функции Ф сущест-
ОФ
вуют производные j^u и выполнено условие
х(х.
ЭФ \2
)°
Для классификации нелинейных уравнений вида C)
фиксируют некоторое решение и* (х) этого уравнения
и рассматривают линейное уравнение
> . . a<y(-c) ахах =0 №
с коэффициентами
, . дФ
xixj u = u* (x)
Уравнение (З) для данного решения и* (х) наз. эл-
эллиптическим, гиперболическим и т. д. в точке х0 (или
в области), если эллиптично, гиперболично и т. д. в
этой точке (соответственно в области) уравнение D).
К решению дифференциальных уравнений 2-го по-
порядка сводится весьма широкий класс физических
задач. См., напр., Волновое уравнение, Телеграфное
уравнение, Теплопроводности уравнение, Лапласа урав-
уравнение, Пуассона уравнение, Гелъмголъца уравнение,
Трикоми уравнение. А к рущин.
ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ С ЧАСТНЫ-
ЧАСТНЫМИ ПРОИЗВОДНЫМИ ПЕРВОГО ПОРЯДКА — урав-
уравнение, связывающее искомую функцию л(х), ее первые
производные Diu=ux, j=l, . .., re, и независимые
переменные z= (zlt . . ., xn). Всякая система диффе-
дифференциальных уравнений с частными производными
может быть приведена к нек-рой системе Д. у. с ч.п.п.п.
Для этого достаточно ввести в качестве новых искомых
функций все частные производные от каждой функции
и; (.г) до порядка I/ — 1 включительно, если хотя бы
одна производная порядка I; входит в к.-л. уравнение
рассматриваемой системы. При этом систему следует
пополнить новыми уравнениями, выражающими ра-
равенство различных смешанных производных. Напр.,
уравнение
F (х, у, и, их, Uy, ихх, их1., Ицц) —О
после введения вспомогательных искомых функций
v=ux, w=Uy приводится к следующей системе урав-
уравнении 1-го порядка:
F (х, у, и, v, w, vx, Vy, Wy) = 0,
ux — v = 0,
uy — ш = 0,
i'y-wx = 0
(последние три уравнения не независимы).
Одно Д. у. с ч. п. п. п. с одпоп искомой функцией
задается соотношением:
F(x, и, р) = 0, A)
W р=(ри р2, ..., pn)=(D1u, D2u, ..., Dnu). Всякое
решение и=и(х) уравнения A) при определенных
требованиях определяет нек-рую поверхность (инте-
(интегральную поверхность) в пространстве
Еп + 1 переменных (хг, . . ., хп, и), причем р; являются
компонентами вектора нормали к этой поверхности.
Поэтому уравнение A) задает связь между составляю-
составляющими pi вектора нормали к интегральной поверх-
поверхности и в каждой точке (х, и) определяет (га—1)-пара-
метрич. семейство касательных к интегральной поверх-
поверхности плоскостей [или несколько таких семейств,
соответствующих различным решениям уравнения A)
относительно р]. Огибающая этого семейства плоско-
плоскостей наз. конусом М о н ж а [в данной точке (х, и)],
а направления его образующих — характери-
характеристическими направлениями. В каждой
точке (х, и) эти направления определяются уравнениями
dxt dx2 dxn du ,,,,
~F ~F ~---~F — ^r,n „ ' <>
Pi Pi P ^ P "-P
П j^^i ^ ' P '
где p= (plt p2, . .., pn) — любой вектор, удовлетворя-
удовлетворяющий уравнению A). Кривая с непрерывно изменяю-
изменяющейся касательной, имеющая в каждой своей точке
характеристич. направление, наз. кривой М о н ж а,
пли фокальной кривой. Фокальная кривая
является интегральной кривой системы B) при произ-
произвольно заданном непрерывно дифференцируемом век-
векторе р = р(х, и) таком, что F(x, и, р) = 0.
Поскольку каждой точке фокальной кривой сопо-
сопоставлен вектор р, определяющий направление пло-
плоскости, касательной к кривой в этой точке, то фокаль-
фокальная кривая задается одновременно со своими касатель-
касательными плоскостями и наз. поэтому фокальной
полосой. Если а — параметр на фокальной кри-
кривой, то уравнение
ди V* г<
системы B) наз. уравнением (или условием)
полосы.
Если фокальная кривая принадлежит интегральной
поверхности и=и(х) уравнения A) и в каждой ее
точке выполнены равенства p;=Dju(x), то она наз.
характеристической кривой (биха-
(бихарактеристикой)^ соответствующая фокальная
полоса — характеристической поло-
с о й. Характеристич. полоса определяется системой
уравнений:
dxi du dp(
()
к-рая наз. характеристической систе-
системой уравнения A). Функция F(x, и, р) является
интегралом системы уравнений C), поэтому условие
F=0 выполнено на всей характеристич. кривой, если
оно выполнено в к.-л. ее точке. Интегральная поверх-
поверхность уравнения A), касаясь в каждой своей точке
конуса Монжа, является огибающей семейства конусов
Мошка и тем самым — огибающей семейства харак-
характеристич. полос. Последнее означает, что интегральная
поверхность состоит из характеристич. кривых, так
что ее нахождение сводится к интегрированию харак-
характеристич. системы C). Фокальные кривые, но сводя-
сводящиеся к характеристическим (если они существуют),
являются огибающими последних на интегральной
поверхности и=и(х). Их проекции на пространство
(ж1? х2, . . ., хп) состоят из точек сингулярности решения
и{х).
Уравнение A) наз. квазилинейным, если
F (х, и, р) — 2"= х U (¦*, и) Pi + jn+1(x, и).
Уравнения B) в этом случае имеют вид:
dxi du ,4
/,-(x,u) /„+l(x'u)
и не содержат р; конус Монжа вырождается в прямую
(ось М о н ж а), и все фокальные кривые являются
характеристическими.
Задача Коши для уравнения A) состоит в
нахождении интегральной поверхности, проходящей
через заданное (п — 1)-мерноо (начальное) многооб-
многообразие:
*, = *•? (Як ...,K-ih и=и»(Хъ ..., >.„_,). E)
Эта интегральная поверхность состоит из характери-
характеристич. кривых, проведенных через точки начального
многообразия. В случае квазилинейного уравнения
последние получаются интегрированием характеристич.
системы D) с начальными условиями E). В общем
случае для построения характеристич. кривых условия
E) нужно дополнить заданием начальных значений
Pi=p1(ki, ..., Xn^j), к-рые определяются из урав-
уравнений:
получающихся дифференцированием условий E), и
уравнения
F (хй, и0, р<>)=0. G)
Ввиду нелинейности, уравнения F) и G) определяют
Pi(K) и, соответственно, решение задачи Коши A),
E), вообще говоря, неоднозначно. Пусть
л7 = Х,-(а, Л,, ..., Я„_!), u=U(a, Яг, ..., Я„_!) (8)
— уравнения характерпстич. кривых, проходящих
через точки начального многообразия. Если начальное
многообразие E) не является характеристическим (см.
Характеристическое многообразие), то эти уравне-
уравнения — параметрические уравнения искомой интеграль-
интегральной поверхности, они определяют решение и=и(х)
задачи Коши, если эта поверхность однозначно проек-
проектируется на пространство независимых переменных
(x1 xn). В случаях, когда уравнения (8) опреде-
определяют поверхность, но представимую, однако, уравне-
уравнением и=и(ж), т. е. не проектирующуюся однозначно
на пространство (xlt . . ., хп), вводят понятие обобщен-
обобщенного решения задачи Коши A), E).
Решение нелинейного уравнения A), по существу,
сводится к решению системы квазилинейных уравнений
с одинаковой главной частью:
получающейся дифференцированием уравнения A).
Примеры. (D1»J+ (?>2иJ=1; характеристич. по-
полосы задаются уравнениями:
О 0 / 0\2 г / 0\2 л
Pi = Pi, P2 = P-z, \Pi) -\-\Pi) =1-
~ -f- «тг^ = 0; характеристич. система C) имеет вид
дх ди dt х—х0
— = -jj- = -j-, уравнения характеристик: —р = и0,
u=uQ, решение задачи Коши с начальным условием
и(х, 0)=м°(ж) задается параметрич. уравнениями
Полным интегралом уравнения A) наз.
решение
и=ф(х, а) (9)
уравнения A), существенно зависящее от п параметров
в,, а2, . . ., ап. Решение вида (9) есть полный интеграл,
если ранг матрицы
Фа, Флг.а, ••• Ч>Хпп
Фа Флг в • • • Флг
/г /г
равен ге (в нек-рой -области изменения переменных).
Путем образования огибающих из полного интеграла
строятся решения уравнения A), зависящие от произ-
произвольных функций.
Если из и-параметрич. семейства поверхностей (9)
выделить (п—&)-параметрич. семейство, предполагая
параметры а связанными к соотношениями ш((а)=0,
t=l, 2, . . ., к, то огибающая этого семейства зависит
от к произвольных функций п—к переменных; соот-
соответствующие решения, зависящие от произвольных
функций, наз. общими интегралами. Оги-
Огибающая и-параметрич. семейства (9) (если она суще-
существует) не содержит никакого произвола и дает осо-
особый интеграл, к-рый может быть также найден
исключением р из соотношений F=Fp=0.
Многообразие касания поверхности семейства (9)
с огибающей ятого семейства является характеристич.
многообразием к измерений. В частности, при к=1
это многообразие является характеристич. кривой.
На этом основан способ построения общего решения
характеристич. системы уравнений C) по полному
интегралу уравнения A) (метод Я к о б и), часто
применяемый при интегрировании канонич. урав-
уравнений.
Переопределенные системы Д. у. с
ч. п. п. п.— это системы уравнений вида A), в к-рых
число независимых уравнений' больше числа искомых
функций. Такие системы, вообще говоря, противоре-
чивы, и выделение классов непротиворечивых (совмест-
(совместных) систем составляет предмет теории совместности
дифференциальных уравнений с частными производ-
производными.
Пусть имеется переопределенная система
^•(*, />)^2"=1//;М;>/ = 0, 1 = 1, ...,m, (Ю)
для одной искомой функции и(х). Пусть все уравнения
системы A0) независимы, так что т<:га. Эта система
наз. замкнутой, если все уравнения вида
/^" Of- df
({ , } — скобки Пуассона) являются следствиями ис-
исходных уравнений, и незамкнутой — в против-
противном случае. Незамкнутую систему с помощью присо-
присоединения независимых уравнений вида A1) можно рас-
расширить до замкнутой. При т=п замкнутая система
имеет только тривиальное решение, а при т<га коли-
количество ее независимых решений равно п — т.
Лит.: [1] G о и г s a t E., Lesons sur HntcSgration des equa-
equations aux derivees partielles du premier ordre, 2 ed., P., 1921;
[2] Carat, heodory C., Variationsreclmung und partielle
Differentialgleichungen erster Ordnung, Lpz.— В., 1935; [3]
Гюнтер Н. М., Интегрирование уравнений первого порядка
в частных производных, Л.— М., 1934; [4] Курант Р.,
Уравнения с частными производными, пер. с англ., М., 1964; [5]
Петровский И. Г., Лекции по теории обыкновенных диф-
дифференциальных уравнений, 6 изд., М., 1970; [6] е г о те, Лек-
Лекции об уравнениях с частными производными, Зизд.,М., 1961;
[7] К а р т а н Э., Внешние дифференциальные системы и их
геометрические приложения, пер. с франц., 1962; [8] Р а ш е в-
с к и й П. К., Геометрическая теория уравнений с частными про-
производными, М.— Л., 1947; [9] Фиников СП., Метод внеш-
внешних форм Картана в дифференциальной геометрии, М.— Л.,
1948; [10] Яненко Н. Н., Р о ж д е с т в е н с и и й Б. Л.,
Системы квазилинейных уравнений и их приложения к газовой
динамике, М., 1968. Н. Н. Кузнецов, Б. Л. Рождественский.
ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ С ЧАСТНЫ-
ЧАСТНЫМИ ПРОИЗВОДНЫМИ С ОСОБЕННОСТЯМИ В КО-
КОЭФФИЦИЕНТАХ — уравнение с частными производ-
производными, коэффициенты и свободный член к-рого на не-
некоторых многообразиях из замыкания области их
задания имеют разрывы первого рода или обращаются
в бесконечность.
Типичными уравнениями такого типа являются, на-
например, уравнение Лаврентьева — Б и-
ц а д з е
и уравнение Эйлера — Пуассона —
Дарбу
иху+тЬ;их—-у^иу = 0> Р и р'= const
где Д — оператор Лапласа по переменным хг, . . ., хп.
К уравнениям с особенностями в коэффициентах
относятся многие вырожденные уравнения с частными
производными.
Центральное место в теории дифференциальных
уравнений с особенностями в коэффициентах занимает
исследование разрешимости начальных краевых и
смешанных задач в их классической и обобщенной
постановках, а также поиск новых корректно постав-
поставленных задач. Сравнительно полно исследованы кра-
краевые задачи для линейных эллиптич., гиперболич. и
параболич. уравнений 2-го порядка со слабыми особен-
особенностями в коэффициентах, к-рые, как правило, сумми-
суммируемы со степенью, большей размерности области их
задания. В случае, когда коэффициенты этих уравне-
уравнений претерпевают лишь разрывы первого рода на
нек-рых достаточно гладких поверхностях, лежащих
внутри области задания, создана весьма полная теория
основных краевых задач. См. Дифференциальное урав-
уравнение с частными производными; задача с разрывными
коэффициентами, а также [3], [5], [6].
Лит.: [1] Б и ц а Д з с А. В., Уравнения смешанного типа,
М., 1959; [2] В е к у а И. Н., Обобщенные аналитические функ-
функции, М., 1959; [3] Л а д ы ж е н с к а я О. А., Уральцева
Н. Н., Линейные и квазилинейные уравнения эллиптического
типа, М., 1964; [4J М и р а н д а К., Уравнения с частными про-
производными эллиптического типа, пер. с итал., М., 1957" IЬ]
Олейник О. А., «Докл. АН СССР», 1959, т. 124, N, 8,
с. 1219—22; [6] С а м а р с к и й А. А., «Докл. АН СССР»,
1958, т. 121, Лв 2, с. 225 — 28. А. М. Нахушев.
ДИФФЕРЕНЦИАЛЬНО-РАЗНОСТНОЕ УРАВНЕ-
УРАВНЕНИЕ — см. Разностное уравнение.
ДИФФЕРЕНЦИАЛЬ Н О-Ф УНКЦИОНАЛЬНОЕ
УРАВНЕНИЕ — уравнение, связывающее аргумент,
а также искомую функцию и ее производные, взятые,
вообще говорл, от функционально преобразованного
аргумента; при этом выражение функционального
преобразования может включать искомую функцию,
в результате чего в уравнении могут встречаться комби-
комбинации вида у'(у(х)) и т. п. Понятия Д.-ф. у. и диффе-
дифференциального уравнения с отклоняющимся аргументом
часто отождествляются.
Лит.: [1] Камке Э., Справочник по обыкновенным диф-
дифференциальным уравнениям, пер. с нем., 5 изд., М., 1976.
А. Д. Мышкис.
ДИФФЕРЕНЦИАЛЬНЫЕ ИГРЫ — раздел матема-
тич. теории управления (см. Автоматического управ-
управления теория), в к-ром изучается управление в кон-
конфликтных ситуациях. Теория Д. и. иримыкает также к
общей игр теории. Первые работы по теории Д. и.
появились в сер. 50-х гг. 20 в.
Постановка задач теории дифференциальных игр.
Различают Д. и. двух игроков и нескольких игроков.
Основные результаты получены для задач с двумя
игроками. Содержательное описание этих задач укла-
укладывается в следующую схему. Имеется динамическая
система, в к-рой часть управляющих воздействий под-
подчинена игроку I, а другая часть — игроку II. При
постановке задачи, стоящей перед игроком I или II,
предполагается, что выбор управлений этого игрока,
гарантирующий ему достижение определенной цели
при любом неизвестном заранее управлении против-
противника, может опираться лишь на нек-рую информацию
о текущих состояниях системы. В теории Д. и. рас-
рассматриваются также задачи управления в условиях
неопределенности, когда помехи, действующие на
систему, трактуются как управления противника.
Напр., постановка задачи игрока I описывается сле-
следующим образом. Обычно предполагается, что движе-
движение управляемой системы задается дифференциальным
уравнением
x = f (t, x, и, v), A)
где х — фазовый вектор системы, и и v — управляю-
управляющие векторы игроков I и II соответственно. Определен
класс стратегий 41 игрока I, и для каждой
стратегии U^il определен пучок движений X(U),
к-рый порожден этой стратегией в паре со всевозмож-
всевозможными управлениями противника и выходит из началь-
начального состояния системы A). Эти понятия выбираются
так, чтобы они соответствовали заданным ограниче-
ограничениям на управления игроков и характеру информации
о текущих состояниях системы, предоставленной иг-
игроку I. На движениях x(t), t^it0, системы A) задан
функционал у(х( •)) (п л а т а игр ы), значение к-рого
игрок I стремится минимизировать (иногда функцио-
функционал у зависит также от реализаций u(t), v(t), t^t0,
управлений игроков). Учитывая самую неблагоприят-
неблагоприятную реализацию движения x(-)?X(U), выбор к-рой
в этой задаче предоставляется противнику, качество
стратегий U ?11 оценивается величиной
Задача игрока I состоит в определении стратегии
U0?1l, на к-рой достигается минимум функционала
^1 (эта задача наз. задачей степени). Иногда
рассматривается так наз. задача качества,
в к-рой требуется определить условия существования
стратегии UC?4L, удовлетворяющей неравенству
Xj(t/C)<:c, где с — нек-рое заданное число.
Аналогичным образом формулируются задачи игрока
II, к-рый максимизирует плату игры. Стратегии иг-
игрока II F?9TJ оцениваются величиной
Задача степени здесь состоит в выборе стратегии
Vf>?<J/;>, максимизирующей значение функционала и2,
а задача качества — в определении условий, при
к-рых x2(Vc)^c для нек-рой стратегии VC?^/'J.
Если в задачах игроков I и II классы стратегий
11 и '"Т'3 таковы, что для всякой пары (U, V)?cy3
можно определить хотя бы одно движение
порожденное этой парой, то говорят, что эти две задачи
составляют дифференциальную игру, оп-
определенную на классе стратегий 1lX'J/^>. Если в
Д. и. выполняется равенство
inf sup y(a(.)) =
и (,яс x(-)eX(U)
= sup inf y(-r(-))=co.
V<J/3 x(-)e x (V)
то величина с0 наз. ценой дифференциаль-
дифференциальной игры.
Типичным примером Д. и. является игра пре-
преследования — уклонения. В этой игре х=
= (xi, ¦ ¦ ., Ji; + i)= {'Л, ¦ ¦., уь Zi, . . ., z,), где у и z —
фазовые векторы преследователя и преследуемого
соответственно, движение к-рых описывается уравне-
уравнениями
y=g (t, У, и), z = h(t, z, v).
Наиболее часто рассматривается случай, когда выбор
управлений стеснен ограничениями вида
и?Р, v?Q, B)
где Р и Q — некоторые компакты. Платой в этой игре
является время до встречи, т. е.
Y (*(.)) = Г (*(•)) =
гДе {у)т и U}m — векторы, составленные из первых
т компонент векторов у и z. Таким образом, сближение
точек {y(t)}m и {z(()}mHa заданное расстояние е трак-
трактуется как встреча объектов. В случае, когда игроки
располагают информацией о текущей позиции
и г р ы ((, x(t)), т. е. в позиционной игре преследования-
уклонения, существует цена игры.
Формализации дифференциальных игр. Для матема-
тич. формализации Д. и. необходимы строгие опреде-
определения перечисленных выше понятий. Основное внима-
внимание в теории Д. и. было уделено задачам, в к-рых
игрокам известна позиция игры, а управления удов-
удовлетворяют ограничениям B). В этом случае естественно
было определить стратегии игроков как функции
и=и((, х), v~v(t, х) со значениями в компактах Р и Q
соответственно. Оказалось, однако, что при таком
подходе нередки случаи, когда приходится рассмат-
рассматривать разрывные стратегии, а порожденные ими дви-
движения нельзя определить известными в теории диффе-
ренциальных уравнений понятиями. Трудности, воз-
возникшие сначала на этом пути, привели к созданию
иных постановок Д. и. Ниже рассмотрены такие фор-
формализации, где не используются позиционные стра-
стратегии. Затем дана формализация позиционных Д. и.,
к-рая охватывает разрывные позиционные стратегии
и базируется на специальном определении движений.
Среди сложившихся направлений в теории Д. и.
прежде всего следует отметить цикл исследований
(см., напр., [2] — [4]), восходящих к работе У. Фле-
Флеминга [1]. Здесь рассматривается аппроксимация Д. и.
многошаговыми играми, где игроки последовательно
(по шагам) выбирают свои управления на заданных
промежутках времени \t;, ti + 1), i=0, 1, . . ., N. Причем
обычно выделяется игрок, выбирающий каждый раз
свое управление первым и сообщающий этот выбор
противнику. В зависимости от того, минимизирует
или максимизирует этот игрок плату игры, различают
мажорантную и минорантную мно-
многошаговые игры. Применение этого подхода
сводится к доказательству теорем существования цены
Д. и., определенной здесь как общее значение, к к-рому
сходятся цены мажорантной и минорантной игр при
измельчении разбиений [t;, i, + 1), i = 0, 1, . . ., N (уве-
(увеличении числа шагов). Однако построение позицион-
позиционных стратегий, не зависящих от дискретизации вре-
времени, при таком подходе, как правило, не рассмат-
рассматривается.
Л. С. Понтрягин предложил постановку игровых
задач управления (см., напр., [5] — [8]), где допуска-
допускается информационная дискриминация
противника, т.е. при постановке задачи игрока I
(или II) предполагается, что кроме реализовавшейся
позиции игры (t, x(t)) этому игроку известно управ-
управление противника v(t) (соответственно и(т)), к-рое
будет выбрано на промежутке [t, t+6] F>0 — малое
число). При таком подходе достигается удобное опи-
описание игрового процесса, что позволяет построить
строгую математич. теорию для широкого круга задач
конфликтного управления. Однако введение инфор-
информационной дискриминации дает одному из игроков I
информационное превосходство над противником и
вместе с тем накладывает ограничения на поведение
противника, в частности не позволяет ему формировать
управление по принципу обратной связи
v[t] = v(t, x(t))
(соответственно u[t]=u(t, x(l))). При переходе к содер-
содержательной трактовке результатов, полученных в ус-
условиях дискриминации противника, вместо инфор-
информации об управлении противника, к-рое будет выбрано
им на промежутке [t, i+6), можно использовать ин-
информацию об управлении, реализованном на проме-
промежутке [t—б, t). Такую замену нетрудно обосновать
для систем, где
f(t, х, и, v)=f1(t, х, и)+/2(г, х, v).
Содержательное использование глубоких теоретич.
результатов, полученных в условиях дискриминации
противника, достигается при рассмотрении позицион-
позиционных Д. и. (см. ниже описание процедуры управления
с поводырем).
Формализация позиционных Д. и. разрабо-
разработана Н. Н. Красовским и его сотрудниками (см., напр.,
[9J). Здесь рассматриваются позиционные стратегии U
и V — функции u=u(t, x) и v=v(t, x), значения к-рых
содержатся в компактах Р и Q соответственно. Отно-
Относительно этих функций не предполагается к.-л. ус-
условий непрерывности. Движения x(t, t0, х0, U)(t^t0,
x(t^) = xa), порожденные стратегией U^u(t, .r) игрока I,
определяются как равномерные на любом отрезке
[to,T] пределы последовательностей аппроксимацион-
ных движений xk{t), A-=l, 2, . . ., абсолютно непрерыв-
непрерывных функций, удовлетворяющих уравнению
xk(t) = f(t, xk(t), uk[t], vk[t]), (i)
где v^t] ?Q(t^t0) — произвольные измеримые функ-
функции,
Uk[t\ = u(«{*>, Xk(tf% *;*><*< 4?i, t=o,i, ...
причем
sup (f|+'i —tift)) —>- 0 при к —>¦ oo.
i
Аналогичным образом вводятся движения ж((, i0, з:0, F),
t^t0, x(to)=xo. При таком определении стратегий и
движений справедливо следующее положение.
Альтернатива 1. Пусть для любых векторов
(t, зг)^К"+1 и s?R" справедливо равенство
rnin maxs'/((, а1, и, у) = max min s'f (t, x, и, г), D)
иеР veQ vuQuiP
где s'/ — скалярное произведение векторов s и /.
Тогда, каковы бы ни были замкнутые множества
Mcc;R" + 1 и NccRn + 1, начальная позиция (f0, x0) и
момент i5^?0' всегда либо существует стратегия ГУ*
такая, что для любого движения x(t) = x(t, t0, х0, U*)
точка (t, x(t)) попадет на Мс к моменту t=b, оставаясь
в Nc вплоть до ее встречи с Мс; либо существует стра-
стратегия F*, к-рая для любого движения x{t) = x(t, t0, x0, V*)
гарантирует или уклонение точки (t, x(t)) от по-
попадания на Мс при Ц^Ь^ё-Ь, или нарушение фазового
ограничения (t, x(t))?Nc раньше, чем точка (t, x(i))
попадет на Мс.
К решению такой игры сближения-уклонения сво-
сводится исследование многих типов Д. и., для к-рых
из альтернативы 1 следует существование цены игры.
При постановке позиционных Д. и. возможны и другие
определения стратегий и движений. Напр., при рас-
рассмотрении разрывных стратегий иногда удобно либо
заменять разрывную правую часть дифференциального
уравнения неоднозначной и использовать аппарат тео-
теории дифференциальных уравнений в контингенциях,
либо аппроксимировать разрывные стратегии непре-
непрерывными (см., напр., [10]). Однако такие подходы могут
оказаться неудачными. Известны примеры, в к-рых
оптимальное решение Д. и., полученное в рамках опи-
описанной здесь формализации, не удается достичь и даже
аппроксимировать в рамках других формализации,
опирающихся на уравнения в контингенциях или не-
непрерывные стратегии.
Если условие D) нарушается, то различают поста-
постановку Д. и. в классе стратегий одного и контрстратегий
другого игроков, к-рой отвечает детерминированное
решение Д. и., и постановку Д. и. в классе смешанных
стратегий обоих игроков, содержание к-рой раскры-
раскрывается при аппроксимации смешанных стратегий со-
соответствующими стохастическими процедурами управ-
управления. Контрстратегии Uv, Va отождеств-
отождествляются с функциями «=w(t, х, v)?P, v=v(t, х, u)?Q,
борелевскими по переменным v, и соответственно.
Движения x(t, t0, х0, Uv), f^st0, x(to) = xo, определяются
как пределы аппрокспмацпонных движений x^t) C),
где
ик \t] = и (ti"\ xk (t{*>), vk [t]), t'k> < t < *{*>ь 1 = 0, 1,... .
Аналогично определяются движения x(t, t0, x0, Vu).
Смешанные стратегии U, V отождествля-
отождествляются с функциями u,= u,(i, x), v=v(t, x), значениями
к-рых являются вероятностные меры, заданные на ком-
компактах Р, Q соответственно. Движения x(t, t0, xQ, U),
x(to)=xo, определяются как пределы аппрокси-
мационных движений x^t), t^t0, удовлетворяющих
уравнению
р \ q f (i'
где
vj[i] — некоторая слабо измеримая функция. Анало-
Аналогичным образом вводятся движения x(t, t0, x0, V).
Для Д. и. сближения-уклонения всегда справедлива
альтернатива 2 (альтернатива 3), фор-
формулировка к-рой получается пз формулировки альтер-
альтернативы 1 заменой стратегии одного из игроков на со-
соответствующую контрстратегию (соответственно, за-
заменой стратегий U* и F* смешанными стратегиями {/„
и Т„). Для Д. и., сводящихся к игре сближения-
уклонения и рассматриваемых в классе позиционных
стратегий одного из игроков и контрстратегий против-
противника (в классе смешанных стратегий {[/} и {V}), уста-
устанавливается существование цены Д. и., причем здесь
не предполагается условие D). Решения Д. и. в ука-
указанных классах стратегий могут оказаться неустой-
чт'"мми по отношению к информационным помехам.
Для стабилизации этих решений вводится проце-
процедура управления с поводырем (см.
[91). Здесь наряду с реальной системой рассматри-
рассматривается эталонная система — поводырь, движение к-рой
моделируется в вычислительной машине и известно с
любой требуемой точностью. Управление игрока в
реальной системе и движение поводыря формируются
так, чтобы движения исходной и моделируемой систем
взаимно отслеживались, причем поводырь сохраняется
на нек-ром мосту, соединяющем начальную позицию
с целевым множеством. Такая процедура управления
оказывается устойчивой к ошибкам измерения и по-
помехам, действующим на систему. При моделировании
движения поводыря можно использовать конструкции,
допускающие дискриминацию противника.
Методы теории дифференциальных игр. Один из
методов решения Д. и. был предложен Р. Айзексом [11].
Этот подход примыкает к методу динамического про-
программирования и основан на интегрировании специ-
специального уравнения с частными производными, решение
к-рого определяет цену игры co(t, x) как функцию ис-
исходной позиции игры. Оптимальные стратегии игрока I
(или II) выбираются здесь так, чтобы обеспечить не-
невозрастание (неубывание) цены игры вдоль порожден-
порожденных ими движений системы. Однако нередки случаи, >
когда цена игры является разрывной функцией пози-
позиции игры, поэтому применение данного подхода тре-
требует специального анализа решений вблизи поверх-
поверхностей разрыва функции co(t, x) или ее частных произ-
производных. Полное исследование сингулярностей и обо-
обоснование этого метода оказываются весьма сложными
и их удается осуществить лишь в немногих примерах.
Наиболее полно изучены линейные Д. и., т. е.
случай, когда
/(*, х, и, v) = A{t)x+B{t)u+C(t)v,
где А, В, С — непрерывные матрицы соответствующих
размерностей. Для линейных задач преследования и
уклонения Н. Н. Красовский сформулировал пра-
правило экстремального прицелива-
прицеливания (см., напр., [12]), к-рое позволило решить эти
задачи (без дискриминации противника) при условии
регулярности и, в частности, в случае однотипных
объектов. Элементы этого решения описываются сле-
следующим образом. Пусть W(t№, d, G) — множество про-
программного поглощения, т.е. совокупность
точек x%?Rn, для к-рых для всякого управления
существует управление и (t)^P,t^^.t^e&, та-
такое, что пара этих управлений переводит систему из
состояния х(¦<*) = х* на множество GaR" в момент
времени ?=#. Вводится функция
eo(i, х, #) = inf {e:z?W(t, ¦&, Ms )},
где Ме — евклидова е-окрестность целевого мно-
множества М. В области Г]Э,= {(t, x) : eo(t, x, 0)>0} вели-
величина 6o(i, х, iD) определяется соотношением
eo(t, х,Ь, ) = maxx(Z, t, x, Ъ), ZgR", \\l\\^i, E)
где для функции х известно простое выражение через
опорные функции множеств Р, Q и выпуклого мно-
множества М (см. [12]). При условии выпуклости функ-
функции х по переменной I (сильное условие регулярности)
в области Г^ максимум в E) достигается на единствен-
единственном векторе lo(t, x, д), к-рый выбирается в качестве
краевого условия в принципе максимума, определяю-
определяющем выбор экстремального управления и0. Построен-
Построенная таким образом стратегия U0~u0(t, x) обеспечивает
встречу с множеством М к моменту ?=# из любой по-
позиции (t0, х0), где eo(to, ха-> 0)=0. [Указанные построения
опираются лишь на информацию о позиции игры и
эффективно реализуются на ЭВМ.1 Решение задачи
сближения с помощью программной конструкции
можно получить и при ослабленных условиях регуляр-
регулярности.
Исследование линейных задач преследования при
различных предположениях регулярности проводилось
Е. Ф. Мищенко, Л. С. Понтрягиным, Б. Н. Пшеничным
(см., напр., [13], [14], в частности, описано [13] решение
линейной задачи преследования при так наз. условиях
локальной выпуклости, при к-рых имеет место указан-
указанное выше сильное условие регулярности).
Одним из наиболее удобных способов решения игро-
игровых задач управления является прямой метод.
В тех задачах, где возможно применение этого метода,
управление игрока выбирается так, чтобы при любом
противодействии противника осуществлялось отслежи-
отслеживание нек-рого вспомогательного процесса, приводящее
к успешному окончанию игры. В случае однотипных
объектов (С=—В, (>=Я,Р, Я,<:1) и при условии дискри-
дискриминации противника прямой метод решения задачи
преследования назначает выбор управления игрока I
в виде суммы двух слагаемых, одно из к-рых копирует
управление противника, а другое совпадает с решением
программной задачи на быстродействие перевода си-
системы
х = А (t)z-\-B (t)w, w? A— \)Р,
на целевое множество М. Впервые прямой метод был
описан Л. С. Понтрягиным [5] для линейной задачи
преследования. Позднее были указаны условия, при
к-рых прямой метод дает оптимальный результат [15].
Затем прямой метод был развит для решения нелиней-
нелинейных задач и для задач с интегральными ограниче-
ограничениями (см., напр., [16], [17]). Во всех этих исследова-
исследованиях прямой метод использовался при условии ди-
дискриминации противника; он был развит также и для
решения позиционных игр (см., напр., [9]).
Задача об убегании. В этой задаче тре-
требуется определить условия, при к-рых преследуемый
объект может обеспечить уклонение от встречи с пре-
преследователем при всех t~^ta. Исследование этого воп-
вопроса было начато Л. С. Понтрягиным и Е. Ф. Ми-
Мищенко (см. [7], [8]), к-рые указали условия разреши-
разрешимости линейной задачи об убегании и получили оценку
гарантируемого расстояния между преследующей и
преследуемой точками. Подход, предложенный ими,
был обобщен затем для исследования других случаев
задачи об убегании.
Предложенное Л. С. Понтрягиным [6] понятие
альтернированного интеграла позво-
позволило описать структуру множества начальных пози-
позиций, из к-рых возможно окончание линейной игры пре-
преследования в заданный момент времени ?=#. Альтер-
Альтернированный интеграл определяется как предел рекур-
рекуррентной процедуры, в к-рой исходное множество Ао
совпадает с целевым множеством JlfcR", а каждое
последующее множество Л, + 1 определяется по преды-
предыдущему операцией программного поглощения, т. е.
Ai + 1=W(Ti + 1, т,-, At), где t/ + i=t,— Д. т0=0, Д>0 —
шаг рекуррентной процедуры. Б. Н. Пшеничный [18]
при исследовании структуры Д. и. преследования в
качестве элементарной операции также использовал
программное поглощение, где в отличие от предыдущего
случая требовалось лишь, чтобы продолжительность
перехода из точек х?А,- + 1 на А; не превосходила
числа Д, но, вообще говоря, не равнялась этому числу.
Такая рекуррентная процедура позволила в общем
случае нелинейной системы описать структуру множе-
множества позиций, из к-рых игру преследования можно
окончить к заданному моменту времени.
Была также предложена экстремальная
конструкция для решения позиционных Д. и.
(см., напр., [9]). Этот подход используется как для
решения конкретных примеров, так и при доказа-
доказательстве общих положений, в частности альтернатив
1—3, указанных выше. Напр., при решении задачи
сближения с McczR" + 1 в классе стратегий U-i-u(t, x)
при условии D), согласно экстремальной конструкции, в
пространстве позиций выделяется множество W,,c:Rn + 1,
образующее мост, к-рый соединяет начальную по-
позицию с целевым множеством Мс и лежит целиком во
множестве Nс. Мост обладает так иаз. свойством
и - с т а б и л ь н о с т и, т. е. для любых (tt, я*)? Wu,
v* ? Q и **> '* существует решение х (t) уравнения в кон-
тингенциях
*(**) = **.
для к-рого либо (t*, x(t*))?Wu, либо (т., х(т))?Мс
при нек-ром xgU*, t*]. Вводится экстремаль-
экстремальная к мосту Wu стратегия ?7<(?>-Mi<e>(i, x), оп-
определяемая соотношением
min max (ж — w)' f (t, x, и, v) =
uePvsQ
= max (x — w)' f (t, x, u{e) (t, x), v),
oeQ
где w — вектор, для к-рого (t, w) — точка множества Wa,
ближайшая к позиции (t, x). Экстремальная стратегия
удерживает движения на мосту Wu и тем самым до-
доставляет решение задачи о сближении.
В этой конструкции основным моментом является
определение подходящих стабильных мостов, после
чего построение экстремальных стратегий не достав-
доставляет больших трудностей. Использование известных
рекуррентных процедур для определения таких мостов
ограничивается значительными трудностями вычисли-
вычислительного характера, поэтому важным является иссле-
исследование эффективных способов построения стабильных
мостов. Один из таких способов доставляет прямой
метод. Другой способ — построение стабильпых мостов
в форме множеств регулярного программного погло-
поглощения. В нелинейном случае программное поглощение
определяется с помощью специальных программных
управлений-мер (см., напр., [9]). В регулярных слу-
случаях программного поглощения решение задач кон-
конфликтного управления можно довести до алгоритмов,
реализуемых на ЭВМ.
Основные направления исследований дифференциаль-
дифференциальных игр. Изложенные выше результаты относились
в основном к Д. и., в к-рых движение описывается
обыкновенным дифференциальным уравнением A), где
управляющие векторы удовлетворяют ограничениям B).
Аналогичные результаты получены для игровых задач
управления, в к-рых движение описывается дифферен-
дифференциальными уравнениями с отклоняющимся аргумен-
аргументом, а также для задач с интегральными ограничениями
на управления игроков (см., напр., [17]).
Для исследования структуры Д. и. представляет
интерес изучение задач конфликтного управления, где
движение задается обобщенной динамич. системой (см.,
напр., [19], [20]). Рассмотрено решение Д. и. в классе
квазистратегий, к-рые формируют управление игрока
по реализовавшемуся управлению противника; пред-
предложены также итерационные процедуры для опреде-
определения функции цены и стабильных мостов (см., напр.,
[21]). '
Кроме Д. и. с двумя игроками, рассматриваются
также Д. и. N лиц. Постановка Д. и. N лиц обычно
предполагает, что каждый из игроков, распоряжаю-
распоряжающийся выбором своего управления, стремится мини-
минимизировать нек-рый функционал, определенный на
траекториях управляемой системы. При этом допус-
допускается использование ими лишь информации о текущих
позициях игры. Задача заключается, напр., в опреде-
определении условий, при к-рых в таких играх имеется точка
равновесия по Нэшу в заданном классе стратегий иг-
игроков.
Важный раздел теории Д. и. составляют игровые
задачи управления с неполной ин-
информацией. В этих задачах предполагается, что
неполнота информации заключается либо в незнании
части компонент фазового вектора x(t), либо в изме-
измерении текущей позиции игры с нек-рым запаздыва-
запаздыванием, либо в неточном измерении положения фазовой
точки x(t), причем возможен случай, когда для погреш-
погрешности измерения указаны лишь допустимая область, и
случай, когда задано нек-рое статистич. описание этой
погрешности.
Лит.: [1] Fleming W. H., «Contributions to the theory
of games», 1957, v. 3, p. 407—12; [2] V а г a i у a P., L i n
Jiguan G., «SIAM J. Contr.», 1969, v. 7, № 1, p. 141—57;
[3] П е т р о в Н. Н., «Докл. АН СССР», 1970, т. 190, №6,
с. 1289—91; [4] Friedman A., «J. Different, equat.», 1970,
v 7, Я« 1, р. 111 — 25; [5] П о н т р я г и н Л. С. «Докл. АН
СССР», 1967, т. 174, М- 6, с. 1278—80; [6] е г о ж е, там же,
т. 175, № 4, с. 764—66; [7] его же, «Тр. Матом, ин-та АН
СССР», 1971, т. 112, с. 30 — 63; [8] Понтрягин Л. С,
Мищенко Е. Ф., «Дифференц. уравнения», 1971, т. 7, Л6 3,
с. 436—45; [9]Красовский Н. Н., Субботин А. II.,
Позиционные дифференциальные игры, М., 1974; [10] Кротов
В. Ф., Гурман В. И., Методы и задачи оптимального управ-
управления, М., 1973; [11] А й з е к с Р., Дифференциальные игры,
пер. с англ., М., 1967; [12] Красовский Н.Н., Игровые
задачи о встрече движений, М., 1970; 113] Мищенко Е. Ф.,
Понтрягин Л. С, «Докл. АН СССР», 1967, т. 174, JMi 1,
с. 27—29; [14] Пшеничный Б. Н., «Кибернетика», 1967,
.№ 6 с 54—64; [15] Гусятников П. Б., Никольский
М. С, «Докл. АН СССР», 1969, т. 184, N, 3, с. 518—21; [16]
Ч и к р и й А. А., сб. «Теория оптимальных решений. Тр. се-
семинара», в 3, К. 1969, с. 17—25; [17] Никольский М. С,
«Дифференц. уравнения», 1972, т. 8, № 6, с. 964—71; [18] Пше-
Пшеничный Б. Н., «Докл. АН СССР», 1969, т. 184, J4» 2. с. 285 —
871 [19] Nardzewski С. R., «Adv. in game theory. Ann.
of Math. Studies», 1964, p. 113—26; [20] R о х i n E.,«J. Optimiz.
theory and appl.», 1969, v. 3, №3, p. 153—63; [21] Чей-
ц о в А. Г., «Матем. сб.», 1976, т. 99, № 3, с. 394—420.
М. С. Ниполъспий, А. И, Субботин.
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ: систе-
система бесконечного порядка — бесконечная
совокупность дифференциальных уравнений
¦^L=-.ft(t, *„ ...), 1 = 1, 2 A)
содержащая бесконечное множество неизвестных функ-
функций xu(t), k=i, 2, . . ., и их производные. Решением
такой системы наз. множество функций {xk{t)}, обра-
обращающих все уравнения системы в тождества.
Система A) наз. счетной, в отлично от н е-
счетной системы
-5г = /а(*. .... *а. •••). B)
где а пробегает нек-рое несчетное множество значений.
Система вида B) содержит в себе несчетное множество
функций {xa(t}}, подлежащих определению, и их про-
производные. Рассматриваются также Д. у., содержащие
бесконечное множество неизвестных функций двух и
более аргументов и их частные производные.
Начало развитию теории систем Д. у. вида A) по-
положила работа А. Н. Тихонова [1]. Основным ее ре-
результатом является доказательство теоремы сущест-
существования решения системы A) в предположении, что ее
правые части определены при произвольных значениях
хг, х2, ... @<:?—to^a), непрерывны по отношению к
хи х2, . . . при фиксированном значении t, измеримы
по t при фиксированных xlt х2, . . . и ограничены
некоторыми суммируемыми на сегменте [(„, го+а2]
функциями М ,•((), i=l, 2, ... При дополнительных пред-
предположениях о выполнении обобщенных условий Лип-
Липшица
|/n(t, a-i, .4, ...)—fn(t,x'[,xl, .
и о сходимости и равномерной ограниченности рядов
доказана теорема единственности решения xt(t), г=1,
2, . . ., системы A) при заданных начальных условиях
такого, что ряд
сходится.
Дальнейшее развитие теория счетных систем полу-
получила в направлении исследований условий ограничен-
ограниченности решений (см. [2]), аналитической зависимости от
параметра, устойчивости по Ляпунову и других свойств
решений (см. [2]). Особенно глубоко изучены линейные
и квазилинейные счетные системы дифференциальных
уравнений.
К изучению систем бесконечного порядка плодотвор-
плодотворно применяются операторные методы. Так, например,
вместо системы A) рассматривается операторное урав-
уравнение
-|г=/(*.*). C)
где x(t) — бесконечномерный вектор нек-рого банахова
пространства В, f(t, x) — бесконечномерная вектор-
функция со значениями в том же пространстве, произ-
производная рассматривается в смысле Фреше. В частности,
для уравнения C) были получены следующие резуль-
результаты (см. [3]).
Если f(t, x) — ограниченный оператор, то из выпол-
выполнения локальной теоремы существования и отрицатель-
отрицательности генерального показателя (см. [3]) следует не-
неограниченная продолжимость решений с достаточно
близкими к нулю начальными значениями.
Если
f(t,x)^Ax
(где А — бесконечномерная постоянная матрица) —
ограниченный оператор, то в гильбертовом простран-
пространстве ограниченность всех решений при —со <t<co имеет
место тогда и только тогда, когда оператор А подобен
косоэрмитову. В этом же случае найдено явное выра-
жение решения задачи Коши с начальными условия-
условиями x(to) = xo в виде
x(t) = eA(t-'^x0,
где eAi— операторная экспонента.
Если
где А имеет прежнее значение, a f(t)— непрерыв-
непрерывная Г-периодическая вектор-функция, то существует
единственное периодическое решение, когда спектр
о(А) оператора А не содержит точек мнимой оси
2knilT, Ar=O, itl, rt2, . ..
Для случая
f(t, x) = Ax-\-F{t, x)
найдены условия устойчивости но Ляпунову в нуле
в виде требования
\\F(t, x)\\<g\\xl i>0, |ЫКр,
при достаточно малом д>0 и расположении спектра
оператора А в левой открытой полуплоскости.
Лит.: [1] Тихонов А. Н. «Матем. сб.», 1934, т 41 в
4, с. 551—60; [2] В а л е е в К. Г., Ж а у т ы к о в О. А., Бе-
Бесконечные системы дифференциальных уравнений, А.-А., 1974;
[3] Д а л е ц к и й Ю. Л., К р е й н М. Г., Устойчивость реше-
решений дифференциальных уравнений в банаховом пространстве
М., 1970. II. П. Макаров
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ НА ТОРЕ,
потоки на тор е,— класс динамических систем.
Примером может служить поток, порожденный груп-
групповыми сдвигами тора (как Ли группы) на элементы
к.-л. однопараметрич. подгруппы тора. В терминах
«угловых», или «циклических», координат на торе,
отсчитываемых по модулю 1 (их можно рассматривать
как обычные координаты в евклидовом пространстве R",
из к-рого тор Тп получается как факторгруппа по цело-
целочисленной решетке Z"), этот поток описывается так: за
время t точка x=(xlt . . ., хп) переходит в точку
Т*х:^х+г<о, A)
где со=(соь . . ., <»„) — набор так наз. базисных
частот. Все траектории этого потока являются
квазипериодическими функциями времени; их свойства
определяются арифметич. свойствами базисных частот.
Так, траектории периодичны, если все <о,- кратны
одному и тому же числу. В другом крайнем случае,
когда со,- линейно независимы над % (т. е. никакая
нетривиальная линейная комбинация ^/с,со,- с целыми
ki не равна нулю), каждая траектория всюду плотно
заполняет тор (говорят об иррациональной
обмотке тора), а поток эргодичен (по отноше-
отношению к Хаара мере на Т"; мера Хаара естественным об-
образом получается из меры Лебега в R" при фактори-
факторизации по г?" и сохраняется при сдвигах Т1) и даже
строго эргодичен; его спектр дискретен.
Подобные потоки часто возникают в различных воп-
вопросах. Напр., для интегрируемых гамилътпоновых си-
систем «типичные» финитные (т. е. остающиеся в конеч-
конечной области фазового пространства) движения приводят
как раз к ним (соответствующие торы суть многообра-
многообразия уровня системы первых интегралов, см. [8]). Обычно
такие инвариантные торы с иррациональными обмот-
обмотками имеются также и у гамильтоновых систем, доста-
достаточно близких к интегрируемым (этот вопрос тесно
связан с малыми знаменателями).
Для двумерного тора Т2 А. Пуанкаре (Н. Poincare,
[1]), А. Данжуа [2] (см. также [3]) и X. Кнезером ([4],
модифицированное изложение см. в [5], [6]) полностью
выяснены возможные типы качественного поведения
траекторий потоков без положений равновесия. (Из всех
замкнутых поверхностей только на торе и Клейна
поверхности возможны такие потоки, причем изучение
потоков на последней в основном сводится к изучению
потоков на торе, являющемся ее двулистной накрываю-
накрывающей поверхностью). Об этих потоках известно следую-
следующее. Если на поверхности имеется двусвязная область
(«кольцо Кнезера»,) к-рая ограничена двумя замкну-
замкнутыми траекториями и внутри к-рой траектории сви-
свиваются с одной из них и навиваются на другую в проти-
противоположном направлении (см. рис.), то качественное
поведение траекторий на поверхности напоминает по-
поведение траектории в ограниченной области на плос-
плоскости. В частности, все непериодич. траектории в обе
стороны по времени стремятся к пе-
периодическим. Более интересен слу-
случай (возможный лишь на торе), когда
колец Кнезера нет; это эквивалент-
эквивалентно существованию замкнутой транс-
версали L (т. е. замкнутой кривой,
нигде не касающейся векторного по-
поля), к-рую каждая траектория пере-
пересекает бесконечное число раз. На L
определено отображение последования
S — гомеоморфизм, переводящий точку x?L в первую
по времени точку пересечения проходящей через х
положительной полутраектории с L. Характеристикой
каскада {Sn } на L служит число вращения Пуанкаре о.
(см., например, [3]. Оно отчасти зависит от конкрет-
конкретного выбора L; совершенно инвариантной характери-
характеристикой исходного потока является асимптотический
цикл [14]). Согласно теореме Д а н ж у а, если
S — класса С2 (что гарантировано при соответствую-
щей гладкости трансверсали и исходного потока на
торе) и а иррационально, то S топологически сопря-
сопряжен с поворотом окружности на угол 2яа, т. е. на L
можно так ввести циклич. координату х, что S пред-
представится в виде х—>-х-\-а mod 1. (Если S — класса С1,
то это не обязательно так, см. [2].) Тогда разбиение
тора на траектории с точностью до гомеоморфизма
является таким же, как и в случае A) (однако это не
относится к скорости движения по ним). Гладкость за-
замены координат, гарантируемая теоремой Данжуа, за-
зависит (помимо гладкости S) от арифметических свойств
числа вращения а. При почти всех а из SaC", и2э:3,
следует, что замена координат принадлежит классу
С"~2 [9], но для чисел вращения, очень быстро при-
приближающихся рациональными числами, замена коор-
координат, вообще говоря, не гладкая, даже если преобра-
преобразование S аналитическое (см. [7]).
Если исходный поток на Т2 имеет интегральный ин-
инвариант, то колец Кнезера быть не может, a S (неза-
(независимо от рациональности или иррациональности а)
гладко сопряжено с поворотом окружности; таким об-
образом, при отсутствии положений равновесия на торе
существуют циклич. координаты х, ;/ того же класса
гладкости, что и сам поток, в к-рых последний прини-
принимает вид:
*'=/(*. у), y = af(x, у), /(.г, у)>0 B)
(здесь а — число вращения, отвечающее замкнутой
трансверсали а;= const). При достаточной гладкости /
и надлежащих свойствах а поток B) можно привести
к A) (с п=2 и ш=A, а)) посредством нек-рого диф-
диффеоморфизма, в общем же случае это не всегда возмож-
возможно, и даже эргодические свойства потока B) могут от-
отличаться от свойств потоков A) (возможен непрерыв-
непрерывный спектр, хотя перемешивание в гладком случае
невозможно). См. [10] (опущенные доказательства вос-
восстановлены в [11], [12]) и [13].
Лит.: [1] Пуанкаре А., О кривых, определяемых диф-
диференциальными уравнениями, пер. с франц., М.—Л., 1947-
[2] D enj о у A., «J. math, pures et appl.», sei\ 9, 1932, t. 11, Nj 4
p. 333 — 75; [3] Крддингтон Э. А., Л ев и неон Н.',
Теория обыкновенных дифференциальных уравнений, пер. с
англ., М., 1958; [4] Kncscr H., <<Math. Ann.», 1924, Bd 91,
ф
[2
JV° 1 — 2, S 135—54; [5] R e i n h a r t B. L., «Araer. J. Math.»,
1959, v 81, № 3, p. 617 — 31; [6] A e p p 1 у А., М а г к u s L.,
«Araer J. Math.», 1963, v. 85, № 4, p. 633 — 54; [7] A p н о л ь д
В. И., «Изв. АН СССР. Сер. матем.», 1961, т. 25, № 1, с. 21—86;
[В] его же, «Сиб матем. ж.», 1963, т. 4, К« 2, с. 471—74;
[9] Herman M. R., «С. г. Acad. sci.», 1976, t. 283, №8,
p. 579 — 82; LlO] Колмогоров А. Н.,«Докл. АН СССР»,
1953 т. 93, №5, с. 763—66; [11] Stcrnberg S., «Amer.
J. Math.», 1957, v. 79, Mt 2, p. 397 —402; [12] Шк л о в е р М. Д.,
«Изв ВУЗов. Математика», 19С7, №10, с. 113—24; [13] К о-
чергин А. В., «Докл. АН СССР», 1972, т. 205, J\fi 3, с.
515—18; [14] Schwartz man S., «Ann. Math.», 1957, v. 66,
№ 2, p. 270 — 84. Д. В. Аносов.
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ С МАЛЫМ
ПАРАМЕТРОМ ПРИ ПРОИЗВОДНЫХ — система вида
ц %- = F{z, у, t), -% = f(z, у, t), A)
где z и у суть, соответственно, М- и m-мерные векторы,
|i>0 — малый параметр. Полагая в A) формально
|i=0, получим так наз. вырожденную си-
систему
o = F(z, ;/, t), -|f = M*. У' *)• B)
Пусть решение x(t, и.) системы A) (х означает гиг/
в совокупности) определяется нек-рыми дополнитель-
дополнительными условиями. При выяснении возможности исполь-
использования уравнений B) для построения асимптотиче-
асимптотического при малых [х приближения к x(t, и.) возникают
трудности, связанные с тем, что система B) более низ-
низкого порядка, чем A), и поэтому ее решение не может
удовлетворить всем условиям, поставленным для A).
Априори не ясно, какие из дополнительных условий,
поставленных для A), следует оставить для определе-
определения решения B), а какие — отбросить. Кроме того,
уравнение F(z, у, () —0 имеет относительно z, вообще
говоря, несколько корней, и снова априори не ясно,
какой из этих корней нужно выбрать при решении
системы B), чтобы получить правильное приближение.
Эти моменты отличают постановку задачи об асимп-
асимптотике решения системы A) от регулярного
случая, когда [х входит не в качестве множителя при
производных, а в правые части и притом регулярно.
Первые работы, относящиеся к системе вида A),
были посвящены начальной задаче
z|« = o=z°' У /*=о = У°- C)
В наиболее законченной форме результат был дан
А. Н. Тихоновым [1]. В общих чертах он состоит в сле-
следующем. Пусть уравнение F(z, у, 0 = 0 определяет
в пек-рой замкнутой ограниченной области D несколько
изолированных корней
2=ф((г/, t).
Введем так называемую присоединенную
систему
-^ = F(z, у*, *•), D)
в к-рой у* и t* рассматриваются как параметры. Возь-
Возьмем один из корней z=q>,- и обозначим его z=<p(i/, t).
Корень г=ф(г/, t) наз. устойчивым в D, если
для каждой точки (у*, t*)^D соответствующая точка
покоя z=q>(y*, t*) присоединенной системы D) яв-
является асимптотически устойчивой. Областью
влияния устойчивого корня z=q>(i/, t)
наз. множество точек (z*, у*, t*) "таких, что решение
системы D), определяемое начальным условием z|T=o=
= z*, стремится к <р(у*, t*) при т->со. Оказывается,
что если z=<p(j/, t) — устойчивый корень, а точка
(z°, у", 0), являющаяся начальной для рассматривае-
рассматриваемого решения x(t, \x.) начальной задачи C), принадле-
принадлежит его области влияния, то это решение при [х—v0
стремится к решению вырожденной системы B), причем
в качестве решения первого уравнения в B) берется
2=ф(;/, t), а в качестве начального условия — усло-
условие C) для у (условие C) для z отбрасывается). Другими
слешами,
lim y(t, (x) = J/o(<). 0«i«7\ E)
lim z(t, ц) = 2о(О = ф(г/о(О. *)> 0<i<7\ F)
ц->0
где уо(г) находится из системы
¦If = /(Ф(у, 0> у- О G)
при начальном условии уо\ r_0= i/°; Г связано с разме-
размерами области /). Таким образом, в отличие от регу-
регулярного случая близость при малых ^ решения x(t, |.i)
системы A) к решению системы, в к-рой положено
ц=0, т. е. системы B), имеет место только при спе-
специальных условиях.
Предельный переход F) не является равномерным
в связи с тем, что, вообще говоря, z°=^cp(i/°, 0). Иными
словами, в связи с «потерей» начальных условий для z,
и в окрестности t=Q имеется (правда, бесконечно су-
сужающаяся при ц->0) область, где z(t, ц.) и zo{t)
не близки. Это явление получило название явления
пограничного слоя (название заимствовано из гидроди-
гидродинамики).
Понятие устойчивости корня z=<p(y, t) играет боль-
большую роль при исследовании системы A). Различным
критериям устойчивости точки покоя по Ляпунову
(см. Устойчивость по Ляпунову) соответствуют раз-
различные критерии устойчивости корня z=<p(i/, t). Наи-
Наиболее употребителен критерий первого
приближения, состоящий в требовании, чтобы
собственные значения а матрицы
dz \г = <$(у, t) ( '
удовлетворяли неравенству Re a<0 в D. Если Re a>0,
то для задачи A), C) имеет место результат, аналогич-
аналогичный описанному выше, но для ?<0. Если матрица (8)
имеет собственные значения с действительными час-
частями разных знаков, т. е.
Бе А,- < 0, i = l, .. ., к, Re А,- > 0, i = k + i, ..., М, (9)
то решение начальной задачи A), C), вообще говоря,
предела при и->0 не имеет. Однако если для A) поста-
поставить не начальную, а краевую задачу, причем при
(=0 задать к компонент вектора z (компоненты будем
обозначать нижними индексами), а при t=T задать
М—к компонент вектора z (значение у можно задавать
как при ?=0, так и при t=T):
¦° " - - * «. - i -° -• и i л м, A0)
A1)
то для решения x(t, |х) задачи A), A0), A1) при вы-
полнешш нек-рых условий (аналогичных требованию
принадлежности начальной точки области влияния
устойчивого корня в случае начальной задачи) будет
справедлив предельный переход E), F), где yo(t) опре-
определяется по-прежнему системой G). При этом пре-
предельный переход F) справедлив для 0<?<7", и погра-
пограничный слой появляется как в окрестности ?=0, так
и в окрестности t=T, поскольку при j.i=0 происхо-
происходит «потеря» дополнительных условий A0), задан-
заданных и при ?=0, и при t=T. Случай (9) получил на-
название условно устойчивого случая
(см. [2]).
После того как был установлен предельный переход
E), F), исследование задачи A), C) развивалось в на-
направлении построения асимптотич. разложения ее
решения. В регулярном случае решение начальной
задачи представляется степенным рядом по ц
..., A2)
к-рый при условии достаточной гладкостл правых час-
частей является асимптотич. рядом. В случае A), благо-
благодаря наличию пограничного слоя, асимптотич. разло-
разложение решения носит более сложный характер, а
именно: к степенному разложению типа A2) следует
добавить еще так наз. пограничный ряд
x(t, (Х) = :ГО (О+ Ц*1 (*)+•••
Члены T\ix(tl\i.) наз. пограничными чле-
членам и. Они играют роль вблизи t=Q, а далее быстро
убывают по закону exp(at/[i), где а>0. (Подробное
описание алгоритма построения асимптотич. разложе-
разложения решения задачи A), C) дано в [2]; там же доказано,
что остаточный член асимптотич. разложения A3) при
достаточной гладкости правых частей A) имеет поря-
порядок О(ц" + 1) равномерно относительно t?[0, T].) По-
Подобного же рода асимптотич. разложение имеет место
для решения задачи A), A0), (И). Отличие заклю-
заключается в том, что в этом случае к степенному разложе-
разложению типа A2) добавляются уже два пограничных ряда
в связи с наличием пограничного слоя в окрестности
и *=0, и t=T.
Асимптотич. представление A3) (при наличии устой-
устойчивого корня) или аналогичное ему представление
с двумя пограничными слоями (при наличии условно
устойчивого корня) дает возможность доказать су-
существование и получить асимптотику решения задач
с более сложными дополнительными условиями, чем
C) шш A0), A1) (см. [2]):
Я(*@), х(Т)) = 0. A4)
Во всех описанных выше задачах в построении функ-
функции, к к-рой при ц,—>-0 стремится рассматриваемое ре-
решение, участвовал один корень z—<f(y, t) уравнения
F(z, у, t) = Q. Однако при наличии нескольких корней
уравнения F(z, у, t) = 0 часто наблюдается явление
перехода (или срыва), когда решение урав-
уравнения A), удовлетворяющее нек-рым дополнительным
(вообще говоря, краевым) условиям, имеет в качестве
предельной кривую (вообще говоря, разрывную), со-
состоящую из нескольких кусков, каждый из к-рых на
соответствующем участке определяется вырожденной
системой B), причем в качестве решения уравнения
F(z, у, t) = 0 выбирается надлежащим образом один
из корней z=<p,-{y, t). При переходе от участка к участку
корень, вообще говоря, меняется. Границы участков
наз. точками срыва. В окрестности каждой
точки срыва возникает пограничный слой, называемый
внутренним пограничным слоем.
Причины срыва весьма разнообразны. В одних случаях
асимптотика решения с точками срыва может быть
описана разложением типа A3) (см. [2]), в других —
носит более сложный характер (см., напр., [3], [4]).
Существует много работ, посвященных отдельным
весьма разнообразным задачам, напр., таким, как иссле-
исследование случаев обращения Re X в нуль, исследование
A) на бесконечном промежутке, изучение решения на-
начальной задачи с сингулярными по ц начальными
значениями z, изучение A) в абстрактной форме и др.
(см. обзор [4]). Большое количество исследований по-
посвящено линейным уравнениям типа A). Для линейных
уравнений одной из характерных задач является за-
задача исследования асимптотики собственных значений
и собственных функций (см., напр., [5]), построение
асимптотики фундаментальной системы решений в це-
лом. Исследование последнего вопроса сильно затруд-
затрудняется, если в системе имеются так наз. точки пово-
поворота (подробный обзор этого рода проблем см. в [4]).
Ряд результатов, полученных для дифференциальных
уравнений типа A), был перенесен на интегро-диффе-
ренциальные уравнения с малым параметром при про-
производных (см., напр., [6]). Имеется также значительный
круг работ, посвященных уравнениям с частными про-
производными, содержащими при старшей производной
малый параметр (см., напр., [5], [7]). Совершенно ана-
аналогичные аспмптотич. закономерности наблюдаются для
дифференциально-разностных уравнений в случае ма-
малого отклонения аргумента (см. [4]).
Дифференциальные уравнения вида A), а также дру-
другие, сходные с ними в отношении асимптотич. поведения
решений, получили, в отличие от регулярного случая,
название сингулярно возмущенных
уравнен и й. Для исследования сингулярно воз-
возмущенных систем с успехом применяется метод усред-
усреднения Крылова — Боголюбова, к-рый особенно эффек-
эффективен при исследовании колебательных процессов и ре-
резонансных явлений; был предложен также так наз.
метод подъема, или метод регуляри-
регуляризации (см. [8]). Сингулярно возмущенные уравнения
встречаются в самых различных областях физики и
техники: в теории нелинейных колебаний, гидродина-
гидродинамике, небесной механике, квантовой механике, кине-
кинетике и др.
Лит.: [1] Тихонов А. Н., «Матем. сб.», 1952, т. 31,
КЗ, с. 575—86; [2] Васильева А. Б., Бутузов
В. Ф., Асимптотические разложения решений сингулярно воз-
возмущенных уравнений, М., 1973; [3] М и щ е н к о Е. Ф., Ро-
Розов Н. X., Дифференциальные уравнения е малым параметром
и релаксационные колебания, М., 1975; [41 Б у т у з о в В. Ф.,
Васильева А. Б., Федорюк М. В., в кн.: Итоги
науки. Математический анализ. 1907, М., 1969, с. 5—75; [5]
В и ш и к М. И., Л ю с т е р н и к Л. А., «Успехи матем.
наук», 1957, т. 12, в. 5, с. 3—122; 1900, т. 15, в. 3, с. 3—80;
[6] И м а н а л и е в М. И., Асимптотические методы в теории
сингулярно-возмущенных интегро-дифференциальных систем,
Фр., 1972; [7] Треногий В. А., «Успехи матем. наук»,
1970, т. 25, в. 4, с. 123 — 56; [8] Ломов С. А., Теория воз-
возмущений сингулярных краевых задач, А.-А., 1976.
А. Б. Васильева,
ДИФФЕРЕНЦИАЛЬНЫЙ БИНОМ — выражение
вида
хт(а-~Ьх")р dx,
где а и Ь — действительные, а т, п и р — рациональ-
рациональные числа. Неопределенный интеграл от Д. б.
[ х™ («| bx"f dx
в случае, когда хоть одно из чисел р, (т+1)/ге
и (m+l)/n+p целое, сводится к интегралу от рацио-
рациональных функций. Во всех остальных случаях, как
это было показано П. Л. Чебышевым A853). интеграл
от Д. б. не выражается через элементарные функции.
Л. Д. Кудрявцев.
ДИФФЕРЕНЦИАЛЬНЫЙ ИНВАРИАНТ — выраже-
выражение, составленное из одной или нескольких функций,
их частных производных по независимым переменным
различных порядков, а иногда и дифференциалов этих
переменных, инвариантных относительно того или
иного преобразования.
Пусть в дифференцируемом многообразии Хп, эле-
элементом к-рого является точка (и1, и2, . . ., и"), задан
геометрический объект Q (см. Геометрических объектов
теория). Геометрич. объект со того же многообразия
наз. дифференциальным инвариантом
порядка г относительно объекта Q, если его коор-
координаты Ыд, A — \,2,...,N, являются функциями коор-
координат Qa, а=1, 2, . .., М, объекта Q и их частных
производных по координатам и', г=1, 2, . . ., п, до
порядка г:
и обладают следующим свойством инвариантности от-
относительно нок-рого преобразования координат.
Именно, при замене координат
и'— и' (и1', и2', .. ., и"')
новые координаты со^ объекта со выражаются через
новые координаты п'д объекта Q и их частные производ-
производные по новым координатам — теми же самыми функ-
функциями /д:
Пусть, напр., Q — объект линейной аффинной связ-
связности (без кручения). Объект со (тензор кривизны):
есть тензорный Д. и. порядка 1 относительно Кристо-
ффеля символов Г[/.
Пусть в Хп задана группа (псевдогруппа) G точеч-
точечных преобразований
и' =fl (и1, п2, .. ., п») A)
и Mh — подмногообразие Хп размерности h:
w' = cp<(«\ t\ ..., t"), B)
параметры к-рого подвергаются преобразованиям бес-
бесконечной группы С„:
Геометрическим дифференциальным
инвариантом порядка г многообразия Mh отно-
относительно группы (псевдогруппы) G наз. функцию
координат и' точки М^ и их частных производных до
порядка г по параметрам Vх'.
обладающую свойством инвариантности относительно
преобразований A) и B). Именно, если в C) заменить
и' по формулам A), а частные производные от и{ по
ta — их выражениями через частные производные от
и' по Vх", то получается та же функция F от и' и их
производных ио ta :
аи' дгп1
l * ¦ '
Если координаты и1' однородны, то функция F должна
быть также инвариантна относительно преобразований
u*'=k (t1, ..., t") и', X Ф 0.
В определении геометрич. Д. и. функцию F можно
заменить геометрич. объектом. Если этот объект —
ковариантный (контравариантный) вектор, то его наз.
ковариантом (контравар и анто м).
Если инвариантно обращение в нуль нек-рого
объекта, то его наз. относительным диффе-
дифференциальным инвариантом.
Лит.: [1] Thomas T. Y., The differential invariants of
generalized spaces, Carab., 1934; [2] W e i t z e n b б с h R.,
Jnvarianten-theorie, Groningen 1923. В. И. Шуликовский.
ДИФФЕРЕНЦИАЛЬНЫЙ КОМИТАНТ — дифферен-
дифференцируемое отображение q> тензорного пучка Т на много-
многообразии М в тензорный пучок Т' на том же многооб-
многообразии такое, что если р': Т-+М и р' : Т'—*-М — проек-
проекции пучков Т и Т' на М, то
Компоненты тензора 7" = ф(Г) в локальной карте §
на М зависят от | только через посредство компонент
тензора Т.
В частности, когда Т' сводится к пучку относитель-
относительных скаляров веса g, Д. к. является дифференциаль-
дифференциальным инвариантом веса g. м. и. Войцеховспий.
ДИФФЕРЕНЦИАЛЬНЫЙ ОПЕРАТОР — обобщение
оператора дифференцирования. Д. о. (вообще говоря,
не непрерывный, не ограниченный и не линейный) —
оператор, определенный нек-рым дифференциальным
выражением и действующий в пространствах (вообще
говоря, векторнозначных) функций (или сечений диф-
дифференцируемых расслоений) на дифференцируемых
многообразиях, или в пространствах, сопряженных
к пространствам этого типа. Дифференциаль-
Дифференциальное выражен и е — это такое отображение к мно-
множества О в пространстве сечений расслоения | с ба-
базой М в пространство сечений расслоения т] с той же
базой, что для любой точки р?М и любых сечений
/. S € Д из совпадений их А--струй в точке р следует
совпадение kf и g в топ же точке; наименьшее из
чисел к, удовлетворяющих этому условию для всех
р?М, наз. порядком дифференциаль-
дифференциального выражения и порядком Д-о.,
определенного этим выражением.
На многообразии М без края Д. о. часто является
расширением оператора, естественно определяемого
фиксированным дифференциальным выражением на
нек-ром (открытом в подходящей топологии) множестве
бесконечно (или достаточно много раз) дифференци-
дифференцируемых сечений данного векторного расслоения | с
базой М и, таким образом, допускает естественное обоб-
обобщение на случай пучков ростков сечений дифференци-
дифференцируемых расслоений. На многообразии М с краем дМ
Д. о. L часто определяется как расширение аналогично-
аналогичного оператора, естественно определенного дифференци-
дифференциальным выражением на множестве тех дифференцируе-
дифференцируемых функций (или сечений расслоения), ограничения
к-рых на дМ лежат в ядре нек-рого Д. о. I на дМ (или
удовлетворяет каким-либо др. условиям, определяемым
теми или иными требованиями к области значений опе-
оператора I на ограничениях функций из области опреде-
определения оператора L, напр., неравенствами); Д. о. I наз.
определяющим граничные условия
для Д. о. L. Линейные Д. о. в пространствах, сопря-
сопряженных к пространствам функций (или сечений), опре-
определяются как операторы, сопряженные к Д. о. ука-
указанного выше вида в этих простраЕштвах.
Примеры. 1) Пусть F — действительная функ-
функция к+2 переменных х, у0, уг, . . ., ук, определенная
в нек-ром прямоугольнике Д=/Х/0Х/1Х . . .Х/д; диф-
дифференциальное выражение
^ de* / du dku
Du=^f \^x, и, -5F, ••.,—?¦
(где функция F обычно удовлетворяет нек-рым усло-
условиям регулярности — измеримости, непрерывности,
дифференцируемое™ ц т. п.) определяет Д. о. D на
многообразии Д, область определения которого Q со-
состоит из всех функций и?С*(Д), удовлетворяющих
условию и("(з;)^// для 1=0, 1, . . ., к; если F непре-
непрерывна, то D может рассматриваться как оператор
в С (I) с областью определения Q; Д. о. D наз. общим
обыкновенным Д. о. Если F зависит от у^,
то порядок D равен к. Д. о. D наз. квазилиней-
квазилинейным, если F линейно зависит от у^\ линейным,
если F линейно зависит от у0, уи . . ., yk; линей-
линейным с постоянными коэффициен-
коэффициентам и, если F не завист от х и D является линейным
Д. о. Остальные Д. о. наз. нелинейными. Ква-
Квазилинейный Д. о. при нек-рых условиях регулярности
функции F может быть расширен до Д. о. из одного
Соболева пространства в другое.
2) Пусть х=(хх, . . ., xN) пробегает область Q в RN,
F=F(x, и, D{n)(u)) — дифференциальное выражение
определяемое действительной функцией F на произве
дении области 0 на нек-рый открытый прямоуголь-
прямоугольник со, здесь ВШ)(и) — набор частных производных
f)al + ... + aN
вида Dau=—— ¦, где «!+...+ адг <п, а функ-
(Ох'У*ч ..(dx/v)ajV
ция F (как и в 1) удовлетворяет нек-рым условиям ре-
регулярности. Определенный этим выражением Д. о.
на пространстве достаточно дифференцируемых функ-
функций на QX со наз. общим Д. о. с частными
производными. Аналогично 1) определяются
нелинейные, квазилинейные и линейные Д. о. с част-
частными производными и порядок Д. о.; Д. о. наз. э л-
липтическим, гиперболическим или
параболическим, если он определяется диф-
дифференциальным выражением соответствующего типа.
Иногда рассматриваются функции F, зависящие от
производных всех порядков (напр., в виде формальной
линейной комбинации их); таким дифференциальным
выражениям, не определяющим Д. о. в обычном смысле,
тем не менее могут быть сопоставлены нек-рые опера-
операторы (напр., в пространствах ростков аналитич. функ-
функций), наз. Д. о. бесконечного порядка.
3) Предыдущие примеры могут быть перенесены на
случай комплексного поля, локально компактного
вполне несвязного поля и (по крайней мере в случае
линейных Д. о.) даже в более общую ситуацию, см.
Дифференциальная алгебра.
4) Системы дифференциальных выражений опреде-
определяют Д. о. в пространствах вектор-функций. Напр.,
Д. о. Коши—Римана, определенный дифференциаль-
ным выражением {^ — j^, gj+arb преобразует
пространство пар гармонических функций на плос-
плоскости в себя.
В определении Д. о. и его обобщений (кроме обычных
производных) часто используются не только обобщен-
обобщенные производные (естественно возникающие при рас-
рассмотрении расширений Д. о., заданных на дифферен-
дифференцируемых функциях) и слабые производные (связан-
(связанные с переходом к сопряженному оператору), но и
производные дробного и отрицательного порядков.
Более того, само дифференцирование заменяется пре-
преобразованием Фурье (или другим интегральным пре-
преобразованием), применяемым к области определения и
значения такого обобщенного Д. о. (см. Псевдодифферен-
циалъный оператор) так, чтобы получить возможно
более простое представление соответствующей Д. о.
функции F и достичь разумной общности постановки
задач и хороших свойств рассматриваемых объектов,
а также построить функциональное или операционное
исчисление (продолжающее соответствие между опера-
оператором дифференцирования и оператором умножения на
независимую переменную, осуществляемое преобразо-
преобразованием Фурье).
Такие вопросы теории дифференциальных уравне-
уравнений, как существование, единственность, регулярность,
непрерывная зависимость решений от начальных дан-
данных или правой части, явный вид решения дифферен-
дифференциального уравнения, определенного данным диффе-
дифференциальным выражением, естественно интерпрети-
интерпретируются в терминах теории операторов как задачи Д. о.,
определенного данным дифференциальным выражением
в подходящих функциональных пространствах, а
именно — как задачи о ядре, образе, изучении струк-
структуры области определения данного Д. о. L или его
расширения, непрерывности обратного оператора к дан-
данному Д. о. и явного построения этого обратного one-
ратора. Вопросы аппроксимации решений и построе-
построения приближенных решений дифференциальных урав-
уравнений также находят естественное обобщение и усо-
усовершенствование в задачах о соответствующих Д. о.,
а именно — о подборе таких естественных топологий
в области определения и области значений, чтобы опе-
оператор L (при условии единственности решений) осу-
осуществлял гомеоморфизм области определения и об-
области значении в этих топологиях (эта теория связана
с теорией интерполяции и шкал функциональных прост-
пространств, особенно в случаях линейных и квазилиней-
квазилинейных Д. о.), или в подборе Д. о., близких к данному
в том или ином смысле (что позволяет, используя раз-
различные топологии в множестве Д. о., обосновывать
методы аппроксимации уравнений, в том числе метод
регуляризации, метод штрафа и нек-рые итерационные
методы регуляризации). Теория Д. о. позволяет при-
применить классич. методы теории операторов, напр,
теорию вполне непрерывных операторов, и метод
сжатых отображений в различных теоремах сущест-
существования и единственности решений дифференциальных
уравнений, в теории бифуркации решений н в нели-
нелинейных задачах о собственных значениях. Часто ока-
оказывается возможным использовать наличие в функ-
функциональных пространствах, где определен Д. о., естест-
естественной структуры порядка (в частности, применить
теорию монотонных операторов), использовать методы
линейного анализа (теорию двойственности, теорию
выпуклых множеств, теорию сопряженных операторов,
теорию диссипативных операторов), вариационные ме-
методы и теорию экстремальных задач, а также наличие
нек-рых дополнительных структур в области определе-
пия области значений (напр., комплексной, симпле-
ктической и т. д.) для выяснения структуры области
значений и ядра Д. о., т. е. получения информации о
классе решений соответствующих уравнений. Ряд за-
задач, связанных с дифференциальными выражениями,
приводит к необходимости изучения дифференциальных
неравенств, естественно связанных с многозначными
Д. о.
Таким образом, теория Д. о. позволяет разрешить
ряд трудностей классич. теории дифференциальных
Уравнений. Использование различных расширений
обычных Д. о. приводит к понятию обобщенного ре-
решения соответствующего дифференциального урав-
уравнения (к-рое в ряде случаев, связапных, напр., с эл-
липтич. задачами, оказывается необходимо классиче-
классическим), а использование линейной структуры позволяет
вводить понятие слабых решений дифференциальных
уравнений. При выборе подходящего расширения Д. о.,
определенного дифференциальным выражением, важ-
важную роль играют связанные с конкретным видом по-
последнего априорные оценки для решений, к-рые по-
позволяют указать такие функциональные пространства,
Что в этих пространствах Д. о. непрерывен или огра-
ограничен.
Но теория Д. о. дает возможность поставить и ре-
решить и ряд принципиально новых задач по сравнению
с классич. задачами теории дифференциальных урав-
уравнений. Так, для нелинейных операторов представляют
интерес изучение структуры множества его непод-
неподвижных точек и действие оператора в их окрестности,
а также классификация этих особых точек и вопрос об
устойчивости типа особой точки при возмущении дан-
данного Д. о.; для линейных Д. о., кроме указанных выше
задач, представляют интерес задачи об описании и изу-
изучении спектра Д. о., построения его резольвенты, вы-
вычислений индекса, описание структуры инвариантных
подпространств данного Д. о., построение связанного
с данным Д. о. гармонич. анализа (в частности, разло-
разложения по собственным функциям, что требует предва-
предварительного изучения вопросов полноты системы собст-
венных и присоединенных функций), изучения линей-
линейных и нелинейных возмущений данного Д. о. Эти за-
задачи представляют особый интерес для эллиптич. Д. о.,
порожденных симметричными дифференциальными вы-
выражениями, в связи с теорией самосопряженных опе-
операторов в гильбертовом пространстве (в частности, со
спектральной теоремой для таких операторов и тео-
теорией расширений симметрич. операторов). Теория
ряда задач гиперболических и параболических (не обя-
обязательно линейных) Д. о. связана с теорией групп и
полугрупп преобразований локально выпуклых прост-
пространств.
Пожалуй, наиболее исследованный (помимо линей-
линейных) класс Д. о., к тому же имеющий широкое прак-
тич. применение, — Д. о., не изменяющиеся вообще
или меняющиеся по вполне определенному закону при
действии на область их определения и соответствующим
образом на дифференциальное выражение нек-рых
преобразований, составляющих группу G (или полу-
полугруппу). Таковы, напр., инвариантные дифференциаль-
дифференциальные операторы, тесно связапные с представлениями
группы G; ковариантная производная или, более общо,
пульверизация — Д. о. на пространствах дифферен-
дифференцируемых тензорных полей (здесь G группа всех диф-
ферморфизмов), длинный ряд операторов теоретич.
физики и т. п. Функционально-геометрич. методы
полезны и при исследовании Д. о. с так наз. скрытой
симметрией (см., напр., Кортевега — дс-Фриза урав-
уравнение).
Теория Д. о., являющаяся составной частью общей
теории операторов, играет в последнее время все более
значительную роль не только в теории дифферен-
дифференциальных уравнений, но и вообще в современном ана-
анализе, причем не только как важный конкретный пример
неограниченных операторов (это в особенности ка-
касается теории линейных Д. о.), но и как аппарат пред-
представления и средство изучения объектов различной
природы: так, напр., любая обобщенная функция
(и даже гиперфункция) получается действием нек-рого
обобщенного Д. о. на непрерывную функцию. Нако-
Наконец, непрерывно возрастает роль и влияние теории
Д. о. в других разделах математики — напр., одно из
решений так наз. проблемы индекса (см. Индекса фор-
формулы) связывает топологич. характеристики многооб-
многообразия с наличием на нем определенного класса Д. о.,
что позволяет сделать заключение о свойствах эллиптпч.
комплексов на этом многообразии.
Лит.: [1] Курант Р., Уравнения с частными производ-
производными, пер. с англ., М., 1964; [2] Н а й м а р к М. А., Линейные
дифференциальные операторы, 2 изд., М., 1969; [3] X ё р м а н-
д е р Л., Линейные дифференциальные операторы с частными
производными, пер. о англ., М., 1965; [4 ] Б у р б а к и Н.,
Дифференцируемые и аналитические многообразия. Сводка
результатов, пер. с франц., М., 1975; [5] Канторович
Л. В., А к и л о в Г. П.. Функциональный анализ, 2 изд.,
М., 1977; [6] П а л е Р., Семинар по теореме Атьи—Зингера
об индексе, пер. с англ., М., 1970; [7] Рейссиг Р.,
С а н с о н е Г., К о н т и Р., Качественная теория нелиней-
нелинейных дифференциальных уравнений, пер. с нем., М., 1974; [8]
Фиников СП., Метод внешних форм Картана в дифферен-
дифференциальной геометрии, М.— Л.. 1948; [9] С к р ы п н и к И. В.,
Нелинейные эллиптические уравнения высшего порядка, К.,
1973; [10] Г е л ь ф а н д И. М., М и н л о с Р. А., Ш а п и р о
3. Я., Представления группы вращений и группы Лоренца,
их применения, М., 1958; [11] С х о у т е н Я.-А., Тензорный
анализ для физиков, пер. с англ., М., 1965; [12] Лионе Ж.
П., Некоторые методы решения нелинейных краевых задач,
пер. с франц., М., 1972; [13] Рождественский Б. Л.,
Яненко Н. Н., Системы квазилинейных уравнений и и\
приложения к газовой динамике, М., 1908.
М. И. Войцсховский, А. И. Штерн.
ДИФФЕРЕНЦИАЛЬНЫЙ ОПЕРАТОР модуля —
отображение модулей над коммутативным кольцом,
являющееся аналогом понятия дифференциального
оператора. Пусть R — коммутативное кольцо, S —
подкольцо кольца R, N и М — два Л-модуля. Гомо-
Гомоморфизм 5-модулей D: N^>-M наз. дифферен-
циальным оператором порядка
(т — неотрицательное целое), если для любого xQR
отображение Dx: TV—>-M, определяемое формулой
Dx(n) = D (xn)—xD {п),
является Д. о. порядка <:т—1. При этом Д. о. по-
порядка 0 наз. гомоморфизм Д-модулей N—уЛ1. Мно-
Множество всех таких Д. о. образует подмодуль Diffs'GV, M)
Д-модуля всех гомоморфизмов S-модулей HonisGV, M).
В частности,
Dili s(N, М) ~ Нот;? (TV, M),
а фактормодуль
Diff s (TV, Л/)/Difi s (Лг, М)
изоморфен модулю б'-дифференцирований Оег5(Д, M)
кольца Д со значениями в М. Объединение Diff$ (M)
возрастающего семейства подмодулей
Diff s(M, M) d Diff s{M, M)d ...
является фильтрованным ассоциативным кольцом отно-
относительно операции композиции отображений. Это
кольцо наз. кольцом дифференциаль-
дифференциальных операторов Д-модуля М над подкольцом
S, а соответствующее градуированное кольцо
Symbs(M)= ф(. > „ Symb^ (M),
где
Symb's(Af)=Difft(>/, Д/)/Difffe G1/, М),
наз. кольцом символов. Образ Д. о. D ?
?Diffs (М, М) в кольце SymbsGV/) наз. символом
Д. о.
Если R является алгеброй над полем рациональных
чисел и модуль дифференциалов Q^/s ироективен, то
существует изоморфизм 5-алгебры Diff5(i?) и оберты-
обертывающей алгебры алгебры Ли ^-дифференцирований
Dersfi?, R). В этом случае кольцо Symbsti?) изоморфно
симметрич. алгебре Д-модуля Der(R, R).
Напр., пусть R = k[T] — кольцо многочленов над
полем к; отображения д/дТ': R—*-R, определяемые
формулой
(ТП=
ОТ'
являются Д. о. кольца R над к порядка г. Кольцо Д. о.
Difffc(.ff) — свободный модуль над Д с базой д/дТ°,
д/дТ1, ..., д/дТ'. Умножение задается формулой
. ., =, i+A
вт
В частности,
д
1
от1 J дтп
(формула Тейлора), что в случае, когда
характеристика поля к равна 0, дает
Если SpecG?) является аффинной групповой S-
схемой, то можно рассматривать также инвариантные
Д. о. кольца R (см. [2]).
Лит.: [1] В и н о г р а д о в А. М., Красильщиков
Н. С, «Успехи матем. наук», 1975, т. 30, в. 1, с. 173—98;
[2] Grothendieck A., Elements dc geometrie algebrique,
P., 1967, ch. 4- [3] D e m a z u г e M., Gabriel P., Grou-
pes algebriques, t 1, P.—Amst., 1970; [4] B] ork J.-E., «Invent.
Math.», 1972, v. 17, № 1, p. 07 — 78. И. В. Долгачев.
ДИФФЕРЕНЦИАЛЬНЫЙ ПАРАМЕТР, д и ф ф е-
р е н ц н а т о р,— совместный дифференциальный ин-
инвариант одной или нескольких функций и метрич.
тензора g,y римановой геометрии.
Д. п. 1-го порядка (первый Д. п.) функ-
функции V есть квадрат ее градиента:
Смешанный Д. п. 1-го порядка функций V и W
есть скалярное произведение градиентов этих функций
В трехмерном евклидовом пространстве в декартовой
прямоугольной системе координат эти Д. п. выра-
выражаются формулами:
Д. п. 2-го порядка (второй Д. п.) функ-
функции есть дивергенция ее градиента:
А2 (V) = ^^V
где g — определитель матрицы ||g,-y ||. В трехмерном
евклидовом пространстве в декартовой прямоугольной
системе координат второй Д. п. выражается формулой
Первоначально Д. п. были введены Г. Ламе [1]
в евклидовой геометрии. Обобщение этого понятия для
римановой геометрии принадлежит Э. Бельтрами [2].
Поэтому Д. п. иногда паз. д и ф ф е р е и и и а л ь и ы-
м и параметрами Ламе, или д и ф ф е р е н-
ц и а л ь и ы м и параметрами Бельтрами.
Лит.: [1] L a m & G., Lecons sur les coordonnees curvilignes
et leurs diycrses applications, P., 1859; [2] В e 1 t г a m i E.,
Ricerche di analisi applicata alia geometria, «G. mat. Battag-
lini», 1864, v. 2, 1865, v. 3; [3] К а г а н В. Ф., Основы те-
теории поверхностей в тензорном изложении, ч. 1—2, М.— Л.,
1947—48; [4] Ш у л и к о в с к и й В. И., Классическая диффе-
дифференциальная геометрия в тензорном изложении, М., 1963.
В. 11. Шуяиковский.
ДИФФЕРЕНЦИРОВАНИЕ — операция, к-рая отно-
относит функции ее производную или дифференциал. При
этом речь может идти о производной или дифференциале
в точке или на нек-ром множестве, о частных произ-
производных, о производной по направлению, о частных и
полных дифференциалах, а сами функции могут быть
не только числовыми, но и функциями более общей
природы. Г. П. Толстое.
ДИФФЕРЕНЦИРОВАНИЕ кольца — отображе-
отображение д кольца R в себя, являющееся эндоморфизмом
аддитивной группы кольца R и удовлетворяющее со-
соотношению
Пусть М — левый Д-модуль. Дифференциро-
Дифференцированием кольца R со значениями в М
наз. гомоморфизм соответствующих аддитивных групп,
удовлетворяющий условию
для всех х, у из R. Для любого элемента с из центра С
кольца R отображение х-^-сд(х), где д — дифференци-
дифференцирование, является Д. Сумма двух дифференцирований
также является Д. Это определяет па множестве всех
Д. кольца R со значениями в М структуру С-модуля,
обозначаемого Der(R, M). Если S подкольцо в R,
то Д. д такое, что <9(s) = 0 для всех s?S наз. 5-днф-
ференцированием. Множество всех S-дифференциро-
S-дифференцирований образует подмодуль в Der(R, M), обозначаемый
Ders (R, М). Операция
[д, д'\ = д°д' — д'од
определяет в 5-модуле Ders (Я, М) структуру 5-ал-
гебры Ли. Если ци Я->-М — гомоморфизм Л-модулей,
то для любого d?Dev(R, R) композиция
?D(i? M
(, )
Пусть R — кольцо полиномов A[Tt, ..., Тп] с коэф-
коэффициентами в коммутативном кольце А. Отображение
является Л-дифференцированием кольца R, а Д-модуль
Der^fi?, R) — свободным модулем с базисом д/дТг,
..., д/дТп.
Для любого элемента а ассоциативного (соответст-
(соответственно лиева) кольца R отображение х-+ах—ха (соот-
(соответственно х—>-ах) будет Д. кольца R, наз. внут-
внутренним дифференцированием. Д., не
являющееся внутренним, наз. внешним.
Если R — подкольцо кольца R' и d?Der(R, R),
то говорят, что 3?Dcr(i?', R') продолжает д, когда
ограничение д на R совпадает с д. В случае, когда
Л — коммутативное целостное кольцо, a R'— его поле
частных, а также в случаях, когда R'— сепарабельное
алгебраич. расширение поля R или R — алгебра Ли
над полем к, a R'— ее обертывающая алгебра, сущест-
существует единственное продолжение любого Д. д : R—>-Д
на R'.
Имеется тесная связь между Д. и изоморфизмами
колец. Напр., если д — нильпотентное Д.,
т. е. <9" = 0, и R — алгебра над полем характеристики
нуль, то отображение
является автоморфизмом /с-алгебры R. Если R — ло-
локальное коммутативное кольцо с максимальным идеа-
идеалом т, то имеет место биекция между множеством Д.
Бег(Д, Rim) и множеством автоморфизмов кольца
Д/tft2, индуцирующих тождественный автоморфизм поля
вычетов Rim. Д. несепарабельных расширений полей
играют роль элементов группы Галуа сепарабельных
расширений в теории Галуа таких расширений [4].
Лит.: [1] Бур баки Н., Алгебра. Многочлены и поля.
Упорядоченные группы, пер. с франц., М., 1965; [2] Д ж е-
к о б с о н Н., Теория колец, пер. с англ., М., 1947; [3] Л е н г
С, Алгебра, пер. с англ., М., 1968; [4) М о г d e s о n J., V i-
п о g r a Q е В., Structure of arbitrary purely inseparable exten-
extension fields, В., 1970. И. В Долгачев
ДИФФЕРЕНЦИРОВАНИЕ В СИЛУ СИСТЕМЫ —
оператор, к-рый определяется следующим образом.
Пусть
—автономная система, .r^R", /=(/1? . .., /„) и fj : G—y
—>-Л — гладкие отображения, где G — область в R".
Пусть дано гладкое отображение ф : G^-R. Произ-
Производная 8^ф в силу системы (*) функции ф
в точке x°?G определяется выражением
(е/Ф)хо = ?«=1 Щ)/,.(*o)sJL (ф {х {t, ,o})) ,/=fei
где x(t, х°) — решение системы (*) такое, что x(t°, х°)=
=х°. Свойства оператора 6^: 1) линейность по ф,
2) в/(ф1ф2)=ф19/<р2+фав/ф1. Функция (8/ф)(ж) совпа-
совпадает с производной ф по векторному полю /.
Лит.: [1] П о н т р я г и н Л. С, Обыкновенные дифферен-
дифференциальные уравнения, 3 изд., М., 1970. М. В Федорюк.
ДИФФЕРЕНЦИРОВАНИЕ ОТОБРАЖЕНИЯ — на-
нахождение дифференциала или, иначе, главной линейной
части отображения. Нахождение дифференциала, т. е.
аппроксимация отображения в окрестности нек-рой
точки линейными отображениями, является важнейшей
операцией дифференциального исчисления. Дифферен-
циальное исчисление наиболее разработано в топологич.
линейных пространствах.
Пусть X и Y—линейные топологич. пространства.
Пусть отображение / определено на открытом мно-
множестве V пространства X и принимает значения в про-
пространстве Y. Если разность /(го+/г)—f(x0), где xo?V
и xo-\-h?V, может быть аппроксимирована линейной
относительно приращения k функцией 1Хо : X —>- Y,
то / наз. дифференцируемым отобра-
отображением в точке х0. При этом аппроксимирующая
линейная функция 1Хв наз. производной или
дифференциалом отображения в точке
х0 и обозначается символом f'(x0) или df(x0). Отобра-
Отображения, имеющие в данной точке одинаковые произ-
производные, наз. касательными отображе-
отображениям и друг к другу в этой точке. Значение аппрок-
аппроксимирующей функции на элементе h ? X (обозначаемое
символом f'(x0) h или dhf(x0)) наз. дифференциа-
дифференциалом отображения / в точке х0 при
приращении h.
В зависимости от того, что понимается под аппрокси-
аппроксимацией приращения f(xo-\-h)—f{x0) линейным по h
выражением, приходят к различпым понятиям диффе-
ренцируемости и производной. Все важнейшие суще-
существующие определения см. и [1], [2].
Пусть F — совокупность всех отображений из X в У
и т — нек-рая топология или псевдотопология в F.
Отображение r? F является малым в нуле, если
кривая
rt: r(tx)lt,
понимаемая как отображение
прямой—оо<«<оо в F, непрерывна в нуле в псевдо-
псевдотопологии т. Далее, отображение f?F дифферен-
дифференцируемо в точке х0, если существует такое
линейное (непрерывное) отображение 1Ха, что отобра-
отображение
г : h^f(xo+h)-f(xo)-lXo(h)
является малым в нуле. В зависимости от выбора т в
F получаются различные определения производных.
Напр., в случае, если в качестве топологии т выби-
выбирается топология поточечной сходимости, получается
дифференцируемость по Гато (см.
Гато производная). В случае, если X и Y — банаховы
пространства, а топология в F ость топология равно-
равномерной сходимости на ограниченных множествах в X,
приходят к дифференцируемости по
ф р е ш е (см. Фреше производная).
Если X = Rn, a Y=Rm,To производная f'(x0) диффе-
дифференцируемого отображения f(x) = (f1 (x), ..., fm(x)), где
х=(х1, ..., хп), задается Якоби матрицей \\<ifi(xo)ldxj\\
и является непрерывным линейным отображением
из R" в Rm.
Производные отображений обладают многими свой-
свойствами производных функций одного переменного.
Напр., для них в самых широких предположениях име-
имеет место свойство линейности:
(а/)'(а*,) = «/'(*„):
во многих случаях для них верна формула
дифференцирования сложной функции; для отображе-
отображений в локально выпуклые пространства справедливо
обобщение теоремы Лагранжа о среднем значении.
Понятие дифференцируемого отображения распрост-
распространяется на случай, когда X и Y — гладкие диффе-
дифференцируемые многообразия, как конечномерные, так
и бесконечномерные [4], [5], [6]. Дифференцируемые
отображения бесконечномерных пространств и их
производные были определены впервые В. Вольтерра
(V. Volterra, 1887), М. Фреше (М. Frechet, 1911),
Р. Гато (R. Gateau, 1913). Подробнее об истории раз-
развития понятия производной в многомерных про-
пространствах см. [2].
Лит.: ШФрёлихер А., Б у х е р В., Дифференциаль-
Дифференциальное исчисление в векторных пространствах без нормы, пер.
с англ., М., 1970; [2] А в е р б у х В. И., С м о л я н о в О. Г.,
«Успехи матем. наук», 196", т. 22, в. 6, с. 201—60; 1968, т. 23,
в. 4, с. 67—116; [3] Дьедонне Ж., Основы современного
анализа, пер. с англ., М., 1964; [4] Л е н г С, Введение в теорию
дифференцируемых многообразий, пер. с англ., М., 1967; [51
Бурбаки Н., Дифференцируемые и аналитические много-
многообразия. Сводка результатов, пер. с франц., М., 1975; [6] Спи-
вак М., Математический анализ на многообразиях, пер. с
англ., М., 1968.
О. Г. Смоляное, В. И. Соболев, В. М. Тихомиров.
ДИФФЕРЕНЦИРОВАНИЕ ПО СЕТИ — специальное
понятие дифференцирования функций множеств if (Я).
Сеть N — совокупность разбиений {А)} основного
пространства X с мерой ц, при этом
/i Ф h, i = l, 2, 3, . . .,
и для каждого Ax-+l найдется содержащее его мно-
множество Аг- . Все А) измеримы и их совокупность в оп-
определенном смысле (см. [1]) аппроксимирует все изме-
измеримые множества. Множества А) при фиксированном i
наз. множествами г-го ранга. Для каждой точки х0
и любого п имеется одно и только одно множество
Ап(х0) п-то ранга, содержащее точку х0.
Производной функции ty(E) по дан-
данной сети jV в точке ха наз. выражение
если этот предел существует. Можно также определить
понятие производных чисел по сети Лг.
Простейшим примером Д. по с. служит дифференци-
дифференцирование приращения функции одного действительного
переменного по двоично-рациональным интервалам
вида (jj > 3-jr~\-
Производная по сети для каждой счетно аддитивной
функции ty(E) существует почти всюду и совпадает
с плотностью абсолютно непрерывной составляющей
функции ty(E). В и-мерном пространстве обычно рас-
рассматривается Д. по с. полуоткрытых сегментов, диа-
диаметр к-рых стремится к нулю с ростом ранга (см. [2]).
Понятие сети и дифференцирования по ней может
быть обобщено на случай абстрактных пространств
без меры (см. [3]).
Лит.: [1] Ш и л о в Г. Е., Гуревич Б. л., Интеграл,
мера и производная, 2 изд., М., 1967; [2] Сакс С, Теория
интеграла, пер. с англ., М., 1949; [3] К е п у о n H., Mor-
Morse А. Р., Web derivatives, N. Y., 1973 («Mem. Amer. Math.
Soc», .V> 132). В. А. Скворцов.
ДИФФЕРЕНЦИРОВАНИЕ ЧИСЛЕННОЕ — нахож-
нахождение производной функции численными методами.
Д. ч. используется в случаях, когда методы дифферен-
дифференциального исчисления неприменимы (функция задана
таблично), или их применение вызывает значительные
трудности (функция имеет сложное аналитическое вы-
выражение).
Пусть на отрезке [а, Ъ] определена функция и=и(х)
и заданы узловые точки х/, a=Xj<?2<. . .<х„=Ь.
Совокупность точек (ж,-, м,-=м(х,-)), г=1, ..., п, наз.
таблицей. Результатом Д. ч. таблицы является функция
щ(х), в каком-либо смысле приближающая k-ю про-
изводную ft— функции на нек-ром множестве An
точек х. Применение Д. ч. целесообразно, когда полу-
получение функции и„(х) для каждого х?Х* требует не-
ней Об
фу () д ? ру
значительной затраты вычислительных средств. Обычно
используются линейные методы Д. ч., где результат
Д. ч. записывается в виде
=2"= 1в'а*
<н{х) — функции, определенные на X*. Наиболее рас-
распространенный метод получения формул A) состоит
в следующем: строят функцию
интерполирующую и(х), и полагают
ft / ч _ й*"л (ж) _ ^ " dkai(х)
У, "'
Точность алгоритмов, основанных на интерполяцион-
интерполяционных формулах Лагранжа, Ньютона и др., существен-
существенным образом определяется выбором способа интерполя-
интерполяции и может быть иногда весьма низкой даже для доста-
достаточно гладких функций и=и(х) и при большом числе
узловых точек (см. [1]). От этого недостатка часто сво-
свободны алгоритмы Д. ч., использующие сплайн-интер-
сплайн-интерполяцию (см. [2]). Если требуется вычисление прибли-
приближенных значений производной только в узловых точ-
точках х;, то формула A) принимает вид
и un{xj) полностью определяется заданием для данного к
матрицы коэффициентов ац. Формулы типа B) наз.
разностными формулами Д. ч. Коэффициенты а*/ этих
формул определяют из условия наивысшего порядка
малости по ft,,= max|.?, + 1—х;\ разности
И
dku(x\ n
Формулы B), как правило, весьма просты и удобны
на практике. Напр., при h=hn=(x2—x1) = (x3— ж2) =
= ... = (ж„—xn-i) они имеют вид:
du
—dx— = Th
dzu (x Л и. —2и,+ и.
. L^! _i±i
dx* ~~ ft'
Алгоритмы Д. ч. часто применяются к таким таблицам,
в к-рых значения и(х;) заданы (или получены) неточно.
В этом случае требуется их предварительное сглажл-
вание, так как непосредственное применение Д. ч.
может привести к большим погрешностям в результа-
результатах (см. [3]).
Лит.: [1] Б е р е з и н И. С, Ж и д к о в Н. П., Методы
вычислений, 3 изд., т. 1, М., 1966; [2] А л ь б е р г Д ж., Ни ль-
с о н Э., У о л ш Д ж., Теория сплайнов и ее приложения,
пер. с англ., М., 1972; [3] М о р о з о в В. А., в кн.: Вычисли-
Вычислительные методы и программирование, в. 14, М., 1970, с. 46—62.
В. А. Морозов.
ДИФФЕРЕНЦИРУЕМАЯ ФУНКЦИЯ — функция,
имеющая дифференциал.
ДИФФЕРЕНЦИРУЕМОЕ МНОГООБРАЗИЕ — ло-
локально евклидово пространство, наделенное диффе-
дифференциальной структурой.
Пусть X — хаусдорфово топологич. пространство.
Если для каждой точки х ? X найдется ее окрестность U,
гомеоморфная открытому множеству пространства R",
то X наз. локально евклидовым про-
прост ранством, или топологическим много-
многообразием размерности га. Пара (U, ф), где ф —
указанный гомеоморфизм, называется локальной
картой X в точке х. Таким образом, каждой
точке соответствует набор га действительных чисел
(ж1, ..., х"), называемых координатами ж в кар-
те (U, Ф).
Семейство карт {(Ua, ф«)}, сх?Л, наз. и-мерным
С'-атласом @<?.к<.оо, а) многообразия X, если: а) со-
совокупность всех Ua покрывает X, Х= [Jag а^а, б) для
любых а, $?А таких, что UaГ\и$Ф0, отображение
принадлежит дифференцируемости классу Ck; ф? яв-
является дифференцируемым отображением с отличным
от нуля якобианом и наз. преобразованием координат
точки х из карты (Ua, Фа) в карту (U^, фр ).
Два С*-атласа наз. эквивалентными, если
их объединение снова является С*-атласом. Совокуп-
Совокупность С*-атласов разбивается на классы эквивалент-
эквивалентности, к-рые наз. Ск- структурами, при
1 <:fe«:oo — дифференциальными (или
гладкими) структурами, при к= а —
аналитическими структурами. Топо-
логич. многообразие X, наделенное С*-структурой,
называется Ск-м ногообразием, или д и ф-
ференцируемым многообразием
класса Ск.
Понятие дифференциальной структуры можно ввести
для произвольного множества X, заменив гомеомор-
гомеоморфизмы фа биективными отображениями на открытые
множества R"; при этом топология С*-многообразия
описывается как топология объединения, построенная
по любому атласу соответствующей структуры. В этом
случае n-мерные многообразия обладают очевидной
га-мерной С°-структуроп.
Задачи аналитич. и алгебраич. геометрии приводят
к необходимости рассматривать в определении диффе-
дифференциальной структуры вместо пространства R" более
общие пространства С" или даже Кп, где К —
полное недискретное нормированное поле. Так, в слу-
случае К = С соответствующая Сй-структура, k^i,
непременно оказывается О-структурой, она наз.
комплексно аналитической, или просто
комплексной, а соответствующее Д. м.— ко м-
плексным многообразием. При этом на
любом таком многообразии есть и естественная дейст-
действительная Са-структура.
На любом Са-многообразии есть согласованная с ней
С°°-структура, и на С*-многообразии, 0<fe<:°o, —
С-структура, если 0<:/•«:&-. Обратно, любое пара-
компактное С-многообразие, г^1, можно наделить
Са-структурой, совместимой с заданной, причем эта
структура (с точностью до изоморфизма, см. ниже)
единственна. Может, однако, случиться, что С-много-
образие нельзя снабдить С^-структурой (т. е. существу-
существуют несглажиеаемые многообразия), а если это удает-
удается, то такая структура неединственна. Например,
число 8(?г) С^-неизоморфных С°°-структур на «-мер-
«-мерной сфере таково:
га | 1 2 I 3 4 151 6 7 [8 i 9 I 10 11 I 12
6(га) | 1 | 1 | 1 | ? | 1 | 1 | 28 | 2 | 8 | 6 | 992 | 1
Пусть / : X -v Y—непрерывное отображение С-
многообразий X, Y; оно наз. С*- морфизмом (или
Ск- отображением, А<г, или отображе-
отображением класса Ск) Д. м., если для любой пары
карт (Ua, фа) на X и (Fp , ifp) на У такой, что/(?/а)сг7р1
отображение
1\х °/°Ф|3~ * ^ Фа (^а ) ^ V V
принадлежит классу С*. Биективное отображение / та-
такое, что оно и /-1 суть Сп-отображения, наз. С"- и з о-
м орфизмом (или диффеоморфизмом)
класса С. В этом случае X и У и определяющие их
С-структуры наз. С"-изоморфными.
Подпространство У «-мерного (^-многообразия X
наз. С1'- подмногообразием размерности т
в X, если для всякой точки y?Y существуют ее окрест-
окрестность VciY и карта (U, ф) С*-структуры X такие, что
VdU и ф индуцирует гомеоморфизм V на пересечение
y(U[\Y) с (замкнутым) подпространством R^cR";
другими словами, существует карта с координатами
х1, . . ., ж" такая, что Uf]Y определяется соотноше-
соотношениями ?OT+1= . . . = Z« = 0.
Отображение / : X -> У наз. С* ¦ в j о ж е в и е м,
если /(X) есть С*-подмногообразие в У, а X —>- /(X) —
СЛ'-диффсоморфизм. Всякое «-мерное С*-многообра-
зие допускает вложение в R2» + 1 и даже в R.2".
Более того, множество таких вложений является
всюду плотным в пространстве отображений Ск(Х,
R2n + 1) относительно компактно-открытой топологии.
Тем самым, рассмотрение Д. м. как подмногообра-
подмногообразий евклидова пространства дает один из способов
изложения их теории, на этом пути устанавливают-
устанавливаются, напр., указанные выше теоремы о Са-струк-
турах.
В топологии Д. м., иначе наз. дифференциальной то-
топологией,— две основные проблемы. Первая — задача
классификации Д. м. Существуют три основных клас-
класса Д. м.— замкнутые, компактные многообразия с кра-
краем и открытые. Важными инвариантами, различаю-
различающими Д. м., являются гомотопический тип и касатель-
касательное расслоение, в частности характеристические клас-
классы. С их помощью проведена классификация гладких
структур для односвязных многообразий данного гомо-
топич. типа. С помощью другого инварианта — класса
бордизма Д. м.— решена обобщенная Пуанкаре гипо-
гипотеза, изучены неподвижные точки при действии группы
на многообразии и т. д. При этом потребовалось вве-
введение дифференциальных структур на многообразиях
с краем и аппарата сглаживания. Наконец, полезными
здесь оказываются методы алгебраич. топологии, по-
поскольку, напр., установлена триангулируемость про-
произвольного С'-многообразия.
Вторая — задача классификации отоб-
отображений Д. м. Прежде всего здесь выделяются
классы иммерсий, или погружений, обобщающих вло-
вложения; их классификация сведена к гомотопич. задаче
в отличие от вложений, полная классификация к-рых
не получена A978) (см. Топология вложений), и субмер-
сий, или расслоений, одного Д. м. в (на) другое. Важ-
Важную роль, в частности, в вопросах устойчивости (ста-
(стабильности) и в исследовании типичных особенностей
отображений играет понятие трансверсальности ото-
отображения вдоль подмногообразия. Существование транс-
версальных отображений обеспечивается теоремами ти-
типа Сарда теоремы. Все это, а также задачи дифференци-
дифференциальной динамики, изучающей строение различных групп
диффеоморфизмов, в частности интегральных траекто-
траекторий и особых точек векторных полей на Д. м. (динамичен
ских систем), и различные отношения эквивалентности:
изотопия, топологическая и С*-сонряженность и т. п.,—-
диктует необходимость рассмотрения, наряду с конечно-
конечномерными пространствами R", произвольных банаховых
(или гильбертовых) пространств и определения соот-
соответствующих дифференциальных структур. При этом
требуется выполнение разумных в отношении прило-
приложений дополнительных условий, напр. Д. м. отде-
лимо тогда и только тогда, когда преобразования
координат имеют замкнутый график. Получающиеся
наделением такой структурой, вообще говоря, беско-
бесконечномерные многообразия, соответственно именуемые
банаховыми (или гильбертовыми) мно-
многообразиями, типичным примером к-рых служат
многообразия отображений конечномерных Д. м., ока-
оказываются полезным средством исследования и геомет-
рич. интерпретацией задач аппроксимации отображений
(как в указанной выше теореме вложения), анализа
петель пространства — надлежащей области для по-
построения теории Морса и т. д.
Д. м. являются естественной базой для построения
дифференциальной геометрии. Там на Д. м. вводятся
дополнительные инфинитезимальные структуры — ори-
ориентации, метрика, связность и т. д., и изучаются те свой-
свойства, связанные с этими объектами, к-рые инвариант-
инвариантны относительно группы диффеоморфизмов, сохраня-
сохраняющих дополнительную структуру. С другой стороны,
использование той или иной структуры позволяет ис-
исследовать строение самого Д. м. Простейший при-
пример — выражение характеристич. классов через кри-
шгану Д. м., наделенного линейной связностью.
Лит.: [1] П о н т р я г и н Л. С, Гладкие многообразия и
их применения в теории гомотопий, 2 изд., М., 1976; [2] Бур-
баки Н., Дифференцируемые и аналитические многообразия.
Сводка результатов, пер. с франц., М., 1975; [3] д е Рам Ж.,
Дифференцируемые многообразия, пер. с франц., М., 1956;
Ш Л е н г С, Введение в теорию дифференцируемых многооб-
многообразий, пер. с англ., М., 1967; [5] Рохлин В. А., Фукс
Д. Б.. Начальный курс топологии. Геометрические главы, М.,
1977; [6] У и т н и X., Геометрическая теория интегрирования,
пер. с англ., М., 1960; [7] II о с т н и к о в М. М., Введение в
теорию Морса, М., 1971; [8] Нарасимхан Р., Анализ на
действительных и комплексных многообразиях, пер. с англ..
М., 1971; [9] Уэллс Р., Дифференциальное исчисление на
комплексных многообразиях, пер. с англ., М., 1976; [10] Г о-
лубицкий М., Гийемин В., -Устойчивые отображения
и их особенности, пер. с англ., М., 1977; [11] Б р е к е р Т.,
Ландер Л., Дифференцируемые ростки и катастрофы, пер.
с англ., М., 1977; [12] Н и т е ц к и 3., Введение в диффе-
дифференциальную динамику, пер. с англ., М., 1975; [13]
Стернберг С, Лекции по дифференциальной геометрии,
пер. с англ., М., 1970; [14] Г о д б и й о н К., Дифференци-
Дифференциальная геометрия и аналитическая механика, пер. с франц.,
М., 1973; [15] 3 у л а н к е Р., В и н тг е н П., Дифференци-
Дифференциальная геометрия и расслоения, пер. с нем., М., 1975.
См. также лит. при статье Дифференциальная топология.
М. И. Войцеховский.
ДИФФЕРЕНЦИРУЕМОСТИ КЛАСС, гладкости
класс С*, 0<А<оо,а—понятие, характеризующее
дифференцируемые отображения (в частности, функции).
Класс С0 состоит из всех непрерывных функций, класс
С* — из функций, имеющих непрерывные производные
всех порядков, не превосходящих к (в частности, С°° —
из функций с непрерывными производными всех по-
порядков), класс Са — из всех действительных аналити-
аналитических функций. м. И. Войцеховский.
ДИФФЕРЕНЦИРУЕМОСТЬ РЕШЕНИЙ диффе-
дифференциальных уравнений — свойство реше-
решений дифференциальных уравнений, состоящее в суще-
существовании у решений определенного числа непрерывных
производных по независимому переменному t и пара-
параметру (х, входящему в уравнение. В теории дифферен-
дифференциальных уравнений вопрос ставится так: какими
свойствами должна обладать правая часть уравнения,
чтобы решение имело столько-то непрерывных произ-
производных по t и (х? Вопрос о Д. р. наиболее системати-
систематически исследован для обыкновенных дифференциаль-
дифференциальных уравнений.
Пусть имеется уравнение вида (х может быть также
и вектором):
¦?=/(*, *,(!), A)
где [1 — параметр (тоже, вообще говоря, вектор),
и пусть x(t, (x) — его решение, определяемое началь-
начальным условием
x\t=t=xo- B)
Пусть рассматривается сначала Д. р. по (. В случае
непрерывности /по !iiib нек-рой области справедлива
теорема существования непрерывного решения задачи
A) — B), и тогда из тождества, получаемого после
подстановки x(t, u.) в A), последует также существо-
существование непрерывной производной х\. Наличие п непре-
непрерывных производных / по t и х обеспечивает существо-
существование и+1 непрерывных производных от решения
по (; х\п) можно найти (выразить через x(t, jx)),последо-
jx)),последовательным дифференцированием тождества, получае-
получаемого в результате подстановки x(t, jx) в A).
В ряде вопросов, напр, для построения асимптотики
решения по параметру [х, необходимо исследовать
производные по [1 от x(t, jx). Для определенности рас-
рассмотрим задачу о существовании производных по fi
при (х=0. Когда f(t, х, jx) непрерывна и обладает не-
непрерывными частными производными по х и jx в нек-рой
области, то % = % существует и определяется из так
наз. уравнения в вариациях (линейного
относительно т],), получаемого из A), если обе части
продифференцировать по |х и положить |х = 0:
^ =/i(t, r(t, 0), О)тц -rf'vit, x(t, 0), 0), C)
и при помощи начального условия
в случае, если х0 от jx не зависит; если же xg=x0(ii),
то T)ilf = fo=«0@).
Производная r\k от x(t, ц) по jx порядка к (при усло-
условии, что / обладает непрерывными частными произ-
производными до к-то порядка) определяется из уравнения
в вариациях порядка к, к-рое отличается от C) только
неоднородностью, зависящей от t, x(t, 0), %, . . ,,
г]^-!. При наличии А+1 непрерывных производных от
x(t, (x) по (х можно воспользоваться формулой Тей-
Тейлора в качестве асимптотич. формулы для x(t, ц)
по (х:
x(t, \i) = x(t, 0) + Н.гц@+---+И*т1* (i) + O(nA + 1). E)
Это имеет важное значение, так как x(t, 0) и т|,- нахо-
находятся из более простых уравнений, чем A).
В случае аналитич. зависимости правой части от
своих аргументов решение является аналитич. функ-
функцией параметра (х (см., напр., [2]).
Вопрос о Д. р. по [I сохраняет смысл также в ряде
случаев, когда правая часть не является регулярно
зависящей от (х. Один из таких случаев имеет место,
когда (х входит множителем при производных:
н- dt . . . \t-t0 о. Fj
-^- = f(y< xi f), x\t = t0 =xo-
Если F) переписать в виде A), т. е. разрешить относи-
относительно производных, то в правой части при (х —у 0
появляется особенность типа полюса. Оказывается,
что и в этом случае при наличии Дг-f-l непрерывных
производных от правых частей п при нек-рых специаль-
специальных условиях, так наз. условиях устойчи-
устойчивости, справедливо разложение E), где iq,-— пре-
предельные значения производных по jx от решения F)
при ii —у 0, определяемые из уравнений в ва-
вариациях, строящихся по тому же правилу: нужно
продифференцировать F) по jx и положить (х=0. Но
при этом в отличие от регулярного случая система
уравнений в вариациях будет более низкого порядка,
чем F), и начальные значения для щ, несмотря на то,
что у0, х0 от (х не зависят, уже не будут нулевыми,
а будут равны нек-рым, вообще говоря, отличным от
нуля, постоянным, получаемым по определенному
правилу [3].
Лит.: [1] П е т р о в с к и й И. Г., Лекции по теории обык-
обыкновенных дифференциальных уравнений, 6 изд., М., 1970; [2]
Тихонов А. Н., «Матем. сб.», 1948, т. 22, Лг° 2, с. 193—
204; ГЗ] В а с и л ь е в а А. Б., Б у т у з о в В. Ф., Асимптоти-
Асимптотические разложения решений сингулярно возмущенных уравнений,
М., 1973. А. Б. Васильева.
ДИФФЕРЕНЦИРУЕМЫЙ ВЕКТОР в простран-
пространстве V представления Т группы Ли
G — вектор % ? V, для к-рого отображение
является бесконечно дифференцируемой (класса С°°)
вектор-функцией на G со значениями в V- Для диффе-
ренцируемости вектор-функции / : G —*¦ V необходимо
(а в случае локально выпуклого квазиполного прост-
пространства V и достаточно), чтобы были дифференцируемы
все скалярные функции вида F°f, где F — линейный
непрерывный функционал на V (см. [1]). Теорема
Гельфанда — Горд и нг а: если Т — непре-
непрерывное представление группы Ли G в банаховом прост-
пространстве V, то множество V°° дифференцируемых векто-
векторов плотно в V. Для однопараметрич. групп эта тео-
теорема доказана в [2], на общий случай доказательство
перенесено в [3]. Обобщение этого результата на ши-
широкий класс представлений в локально выпуклых
пространствах получено в [4], см. также [5].
Наличие дифференцируемых векторов в пространстве
представления группы Ли позволяет построить пред-
представление соответствующей алгебры Ли и тем самым
связать теорию представлений групп Ли с теорией
представлений алгебр Ли (см. [6] § 10).
Лит.: [1] Grothendieck A., Espaces vectoriels to-
polopiques, Sao Paulo, 1954; [2] Г е л ь ф а н д И. М., «Докл.
АН СССР», 1939, т. 25, с. 711—16; [3] GJrding L., «Proc.
Nat. Acad. Sci. USA», 1947, v. 33, p. 331—32; [4]M о о г е R. Т.,
Measurable, continuos and smooth vectors for semigroups and group
representations, Providence, 1968; [5] Ж е л о б е н к о Д. П.,
«Вестн. МГУ. Сер. матем.», 1965, т. 1, с. 3—10; [6] Кириллов
А. А., Элементы теории представлений, 2 изд., М., 1978.
А. А. Кириллов.
ДИФФУЗИИ УРАВНЕНИЕ — дифференциальное
уравнение с частными производными 2-го порядка,
описывающее процесс диффузии, т. е. процесс вырав-
выравнивания концентрации в среде с неравномерным рас-
распределением вещества. Д. у. имеет вид
Lu = c -|i —div(?>gradM) = 0, A)
где с — коэффициент пористости, D — коэффициент
диффузии, и(х, t) — концентрация вещества в точке х
среды в момент времени t. Вывод Д. у. проводится
путем подсчета баланса массы вещества с использо-
использованием закона диффузии Нернста. При этом подразу-
подразумевается, что в рассматриваемой области отсутствуют
источники вещества и диффузия во внешнюю среду.
Такое Д. у. наз. однородным Д. у. Если в рас-
рассматриваемой области имеются источники вещества
с объемной плотностью распределения F (x, t), то про-
процесс диффузии описывается неоднородным
Д. у. с правой частью F(x, t). Учет распада или раз-
размножения вещества со скоростью, пропорциональной
наличной концентрации, приводит к члену ±"Кди1дх
в правой части Д. у.
Д. у. есть уравнение параболического типа. Для
выделения единственного решения ставятся начальное
и краевые условия. Начальное условие для
Д. у. состоит в задании концентрации ио(х) вещества
в начальный момент
и(х,0)=щ(х). B)
Если при этом вещество заполняет все пространство,
то получают задачу Коши A), B). Если же диффунди-
рующее вещество заполняет объем V, ограниченный
боковой поверхностью 5, то, наряду с начальным усло-
условием B), на S задается граничное условие.
Основными являются следующие три линейных
граничных условия для Д- У-
1) На S задана концентрация в(х, t) вещества; тогда
и(х, t)=Q(x, t)
есть граничное условие I рода.
2) Задана плотность потока q(x, t) вещества, входя-
входящего в V через S; тогда
где п — внутренняя нормаль к поверхности S, есть
граничное условие II рода (если S не-
непроницаема, то q(x, f)=0).
3) S полупроницаема и диффузия во внешнюю среду
с заданной концентрацией Q(x, t) через S происходит
по линейному закону; тогда
ди (х, t) , , , ч г. , ., ч ~- а
\-jr±=—h{u{x, t) — Q(x, t)), x?S,
есть граничное условие III рода.
Возможны и другие, в том числе и нелинейные гра-
граничные условия на S, а также условия, содержащие
производные более высокого порядка, чем входящие
в Д. у. Являясь частным случаем дифференциального
уравнения, описывающего физич. процессы выравни-
выравнивания, Д. у. аналогично теплопроводности уравнению,
Навье — Стокса уравнению для ламинарного потока
несжимаемой жидкости, уравнению чистой электропро-
электропроводности и т. д.
Лит.: [1] Т и х о н о в А. Н., Самарский А. А., Урав-
Уравнения математической физики, Зизд., М., 1966. Л. И. Камынин.
ДИФФУЗИОННОЕ ПРИБЛИЖЕНИЕ — метод ре-
решения кинетич. уравнения переноса нейтронов (или
других частиц, квантов). Д. п. основано на представ-
представлении плотности потока нейтронов (неизвестной функ-
функции координат точки наблюдения, компонент век-
вектора скорости и времени) в виде двух первых членов
разложения по сферическим функциям, зависящим от
угловых координат вектора скорости нейтронов. В од-
носкоростной стационарной задаче это приводит к диф-
диффузии уравнению.
Д. п. применимо вдали от источников, границ облас-
областей с различными свойствами и дает решения, совпа-
совпадающие по форме с асимптотич. частью решений урав-
уравнения переноса. Об усовершенствованиях Д. п. см.
Диффузионные методы.
Лит.: [1] Глесстон С, Эдлунд М., Основы теории
ядерных реакторов, пер. с англ., М., 1954; [2] Марчун Г. И.,
Методы расчета ядерных реакторов, М., 1961. В. А. Чуяпов.
ДИФФУЗИОННЫЕ МЕТОДЫ — методы решения ки-
кинетич. уравнения переноса нейтронов (или других
частиц), модифицирующие уравнения диффузионного
приближения. Поскольку диффузионное приближение
дает правильную форму асимптотич. решения уравне-
уравнения переноса (вдали от источников и границ раздела
сред с различными свойствами), то его усовершенство-
усовершенствования заключаются в правильном выборе констант
(напр., коэффициента диффузии) и разумной поста-
постановке граничных условий с вакуумом и между облас-
областями с различными физич. характеристиками.
Усовершенствованный Д. м. использует в односко-
ростной задаче трансцендентное уравнение для беско-
бесконечной среды,
Аг th ft .
р —ft—=1,
чтобы определить коэффициент диффузии
где р — отношение сечения рассеяния к полному се-
сечению, к — корень характеристического уравнения.
На границах сред в экстраполированных точках
ставятся граничные условия, полученные из точного
решения задачи для двух сред с постоянным полным
сечением (равенство логарифмич. производных и ска-
скачок асимптотич. плотности).
Другой путь улучшения диффузионного приближе-
приближения — использование /^-приближения метода сферич.
гармоник (см. Сферических гармоник метод). Обычное
диффузионное приближение исходит из /^-приближе-
ния метода сферич. гармоник. Переход к /^-прибли-
/^-приближению приводит к уравнению диффузии с исправлен-
исправленными параметрами и улучшенными граничными усло-
условиями, причем плотность нейтронов на границе терпит
разрыв.
Кроме того, возможно применение решения уравне-
уравнения диффузии для ускорения сходимости последова-
последовательных приближений кинетич. уравнения переноса
с использованием в следующей итерации приближен-
приближенного решения кинетич. уравнения для вычисления
поправок к коэффициенту диффузии.
Возможно также, в рамках одной задачи, такое
сопряжение диффузионного решения с точным реше-
решением, при к-ром диффузионное приближение исполь-
используется вдали от областей, занятых поглотителями,
источниками и т. п., а в этих областях решается точное
уравнение переноса.
Лит.: [1] Романов Ю. А., в кн.: Исследования критиче-
критических параметров реакторных систем, М., 1960, с. 3—26; 12]
Теория и методы расчета ядерных реакторов, М., 1962; [3] Вы-
Вычислительные методы в теории переноса, М., 1969. В. А. Чуяное.
ДИФФУЗИОННЫЙ ПРОЦЕСС — непрерывный
марковский процесс X=X(t) с переходной плотностью
p(s, х, t, у), удовлетворяющей следующим условиям:
существуют функции a(t, х) и o2(t, х), называемые соотт
ветственно коэффициентами сноса и
диффузии, такие, что для любого е>0
A)
(у — лг) /> (t, x, t-\-At, у) dy=
x I <r fi
= a(i, x)-{
= a2(«, ж)+о(Д«)
(причем обычно предполагается, что эти предельные
соотношения выполняются равномерно по t в каждом
конечном интервале to^.t<^.t1 и по х, —оо<х<°°).
Важнейшим представителем этого класса процессов
является процесс броуновского движения, впервые рас-
рассмотренный как математич. модель процессов диффузии
(отсюда и название «Д. п.»).
Если переходная плотность р (s, x, t, у) непрерывна
по s и х вместе со своими производными -- p(s, x, t, у)
и yi p(s> xi I-* y)i т0 она является фундаментальным
решением дифференциального уравнения
-gj- /> ^, х, i, у) — —a (S, х) —^ р (S, х, I, у) —
к-рое наз. обратным уравнением Кол-
Колмогорова.
В однородном случае, когда коэффициенты сноса
a(t, х)=а(х) и диффузии а2((, х)=а2(х) не зависят
от времени t, обратное уравнение Колмогорова для
соответствующей переходной плотности р (s, х, t, у)~
=p(t—s, х, у) имеет вид:
¦Jjt-Pit, х, y) = a(x)±p(t, x, y)^-j^(x)^;p(t,x,y).
Если переходная плотность р (s, x, t, у) имеет непре-
непрерывную по t и у производную ^ р (s, х, t, у) такую, что
функции ~[a(t, y)p(s, x, t, у)} Пщ-, [a2(i, y)p(s, x, t, у)]
непрерывны по у, то она является фундаментальным
решением дифференциального уравнения
-§Г Р (s- ж> *' У) = —|г [а V' у) р (s' х' *' yN +
к-рое наз. уравнением Фоккера — План-
к а, или прямым уравнением Колмо-
Колмогорова. Дифференциальные уравнения B) и C)
для плотности вероятности являются основой аналитич.
методов изучения Д. п. Существует и другой, чисто
«вероятностный», подход к Д. п., основанный на пред-
представлении процесса X(t) как решения стохасти-
стохастического дифференциального урав-
уравнения Ито
dX(t) = a{t, X(t))dt + o(t, X(t))dY(t),
X(t) = X(tls)+\t a(*,X(*))d*+V a (s, X (*)) dY (s),
J 'o J to
где Y(t) — стандартный процесс броуновского дви-
движения. Грубо говоря, при таком подходе считают
X(t) связанным с нек-рым процессом броуновского
движения Y(t) таким образом, что при условии X(t) = x
за последующее время At приращение AX(t)=
= X(t+At)—X(t) есть
АХ (t) ~ a (t, x)At~\-a (t, x) AY (t).
Если понимать это асимптотич. соотношение в том
смысле, что
Е {АХ @-(а (*, х) \t + o(t, x) AY (<)) \X(t) = x} = o (At),
B{AX (t)-(a(t, x)\t + o(t, x) AY (t))* \ X (t) = x} =
= o (At),
где o(At) — величины того же типа, что и в равенст-
равенствах A), то рассматриваемый процесс X (t) будет диф-
диффузионным и в смысле этого определения.
Многомерным Д. п. обычно наз. непрерывный
марковский процесс X(t)= {Xx(t), . . ., Хп(()}в /г-мерном
векторном пространстве Е", переходная плотность
p(s, х, t. у) к-рого удовлетворяет следующим условиям:
для любого е>0
\\у-х\>гР {tyX
Jly-x
~„ г1<гЛУкк) Р(, , + , y)dy =
i у — x i -^j. e
= ak(t, x)At + o(At),
*. У) dV =
x\<e (УкХк) iyjxj)P(^ ¦
= 2bkJ(t, x)At + o(At),
k,j = l,...,n, X-=(xlt ..., Xn), !/=(!/!, ...,У„).
Вектор a— {at(t, x), .. ., an(t, x)} характеризует локаль-
локальный снос процесса i(t), матрица о2= \\2bt.j(t, x)\\,
к, i=l, ..., и, характеризует среднеквадратичное от-
отклонение случайного процесса |(г) от исходного поло-
положения х за малый промежуток времени от t до t^ At.
При нек-рых дополнительных ограничениях пере-
переходная плотность p(s, х, t, у) многомерного Д. п.
удовлетворяет обратному и прямому дифференциаль-
дифференциальным уравнениям Колмогорова:
Многомерный Д. п. X(t) может быть описан также
при помощи стохастических дифферен-
дифференциальных уравнений И то:
dXk (t)=ak (t, X («)) dt ~- ?"=i akJ (t, X (t)) dYj (t),
где Y^i), ..., Уn(t) — взаимно независимые процессы
броуновского движения, а
°/={ai/(«. г), . . ., anf(t, г)}, /^1, .. ., п,
суть собственные векторы матрицы oz=\\2bkj(t, x)\\-
Лит.: [1] Г и х м а н И. И., Скороход А. В., Введение
в теорию случайных процессов, М., 1965; [2] и х же, Стоха-
Стохастические дифференциальные уравнения, К., 1968.
Ю. А. Розанов.
ДИХОТОМИЯ — свойство линейной системы обык-
обыкновенных дифференциальных уравнений
х = А (*) х, х?Еп, 1^0,
с ограниченными непрерывными коэффициентами об-
обладать такими положительными постоянными К, L,
а, Р, что существует разложение Еп— Ет-\-Еп~т, для
к-рого
* @) ??» =ф || х (t) ||<* |] х (т) || ехр [- а (*-т)],
х @) ??«-OT => || ж (*)|| < L || х (т) || ехр [— р (т- 0],
(экспоненциальная Д.; при а=р=0 —
обыкновенная Д.)- Наличие экспоненциаль-
экспоненциальной Д. эквивалентно тому, что неоднородная система
х = A (t) x-\-f (t)
при любой ограниченной непрерывной функции /((),
?^0, имеет хотя бы одно ограниченное на [0, оо) ре-
Б1ение (см. [1]). Теория Д. (см. [2]) перенесена на урав-
уравнения в банаховых пространствах, используется также
для изучения потоков и каскадов на гладких много-
многообразиях [4].
Лит.: [1] Р err о п О., «Math. Z.», 1930, Bd 32, JVS 5, S. 703—
728; [2] M а с с е р а Х.-Л., Ш е ф ф е р Х.-Х., Линейные диффе-
дифференциальные уравнения и функциональные пространства, пер.
с англ., М., 1970; [3] Д а л е ц к и й Ю. Л., К р е й н М. Г.,
Устойчивость решений дифференциальных уравнений в банахо-
банаховом пространстве, М., 1970; [4] Аносов Д. В., «Тр. матем.
ин-та АН СССР», 1967, т. 90. Р. А. Прохорова.
ДИЭДРА ГРУППА, диэдральная групп а,—
группа, изоморфная группе вращений диэдра, т. е.
правильной удвоенной пирамиды. Если в основании
пирамиды лежит n-угольник, то соответствующая Д. г.
имеет порядок In и порождается двумя вращениями
<р и ij) порядков п и 2, соответственно, с определяющим
отношением фг|зфг|з=1. Иногда под Д. г. подразумевают
только Д. г. порядка 8. Два различных элемента по-
порядка 2 в любой конечной группе порождают Д. г.
Лит.: [1] X о л л М., Теория групп, пер. с англ., М., 1962.
В. Д. Мазуров.
ДЛИНА — числовая характеристика протяженности
линий в метрич. пространстве. Д. отрезка пря-
прямой — расстояние между его концами, измеренное
каким-либо отрезком, принятым за единицу Д.
Длина ломаной — сумма Д. ее звеньев. Д.
простой дуги — точная верхняя грань длин
ломаных, вписанных в эту дугу. Всякая непрерывная
кривая имеет Д.— конечную или бесконечную. Если
ее Д. конечна, то кривая наз. спрямляемой.
Д. плоской кривой, заданной в прямоуголь-
прямоугольных координатах уравнением ;/=/(ж), a<?z^b (f(x)
имеет непрерывную производную f'(x)), выражается
интегралом
Если кривая задана в параметрич. форме
x = x(t), y=--y(t), «!<<<i2,
то Д. кривой равна
V[r' (t)]2-\-[y' (t)]*dt.
Д. спрямляемой кривой не зависит от параметризации.
Д. пространственной кривой, заданной
в параметрич. форме x=x{t), y=y(t), z=z(t),
выражается формулой
'" J^V (*)]* + [?'(*)]"+[*'С)]2 dt;
в случае га-мерного пространства
Пусть у — непрерывно дифференцируемая кривая,
заданная функциями u=u(t), v=v(t), на непрерывно
дифференцируемой поверхности r=r(u, v). Тогда длина
дуги кривой от точки, соответствующей значению пара-
параметра t= t0, равна
где / — первая квадратичная форма поверхности.
Д. непрерывно дифференцируемой кривой, заданной
функциями x' = x'(t), t!<:f<:f2, в римановом пространстве
с метрич. тензором glk, равна
dx* ,,
А. Б. Иванов.
ДЛИНА частично упорядоченного
множества — наибольшая из длин цепей этого
множества. Существуют бесконечные множества ко-
конечной ДЛИНЫ. Т. С. Фофанова.
ДЛИНЫ И ПЛОЩАДИ ПРИНЦИП — принцип, вы-
выражающий зависимость между длинами кривых, при-
принадлежащих нек-рому специальному семейству, и пло-
площадью, покрываемой этим семейством кривых.
Пусть w=f(z) — регулярная в открытом множестве
G функция. Пусть п (w) — число корней уравнения
f(z) = w, лежащих в G; 1(р) — суммарная длина кри-
кривых в G, на к-рых |/(z)|=p; А — площадь G и
р(р) = ~-^0Л n(peie)dQ, p>0;
тогда Д. и п. п. выражается неравенством (см. [2]):
Д. и п. п. получил широкое применение в теории функ-
функций комплексного переменного (см. [1] — [4]).
Д. и п. п. используется, напр., при изучении свойств
функций, регулярных в круге |z|<l. В частности,
с помощью Д. и п. п. доказывается следующая теорема
(см. [2]): если функция w—f(z)—a9Jraiz-\-..., цд=
= max |av|, регулярна в \z\ <1 и имеет в нем не более
q нулей, из которых не более h лежит в U|<V2, то
С ^2 dn „, 1 ...
где
h1 (z)|, 0 < г
i
I Z | = Г
Л (?) — константа, зависящая от q.
Д. и п. п. и различные его обобщения (напр., д л и-
ны и объема принцип) применяются и в слу-
случае гс-мерных пространств к квазиконформным ото-
отображениям, а также к отображениям с ограниченным
Дирихле интегралом (см. [4] — [7]).
При выводе Д. и п. п. существенным образом ис-
используется неравенство Буняковского. Дальнейшее
рассмотрение связи между длинами кривых и пло-
площадью, покрываемой ими, привело к важному методу
изучения однолистных конформных и квазиконформ-
квазиконформных отображений — экстремальной метрики методу
(см., напр., [8]). В конце 20-х — начале 30-х гг. ме-
метод экстремальной метрики в менее совершенной форме
(метод полос) успешно применялся для исследования
свойств указанных выше отображений односвязных и
многосвязных областей.
Лит.: [1] A h 1 1 о г s L. W., «Acta Soc. scicnt. fennica», 1930,
A. 1, Л' 9; [2] X e й м а н В. К., Многолистные функции, пер.
с англ., М., 1960; [3] Н е в а н л и и н а Р., Однозначные
аналитические функции, пер, с нем., М,—Л., 1941; [4] С у в о-
роз Г. Д., Семейства плоских топологических отображений,
Новосиб., 1965; [5] К р е й н е с М. А., «Матем. сб.», 1941, т. 9,
№ 3, с. 713—19; [6] Овчинников И. С, «Метрические
вопросы теории функций и отображений», 1971, в.З, с. 98 —115;
[7J L е 1 о n g-F errand J., Representation eonforme et trans-
transformations a integral de Dirichlet bornees, P., 1955; [8] Д ж е н-
кинс Д ж., Однолистные функции и конформные отображе-
отображения, пер. с англ., М., 1962. И. П. Митюк.
ДОВЕРИТЕЛЬНАЯ ВЕРОЯТНОСТЬ — см. Довери-
Доверительное оценивание.
ДОВЕРИТЕЛЬНАЯ ГРАНИЦА — см. Доверитель-
Доверительное оценивание.
ДОВЕРИТЕЛЬНОЕ МНОЖЕСТВО — см. Довери-
Доверительное оценивание.
ДОВЕРИТЕЛЬНОЕ ОЦЕНИВАНИЕ — метод мате-
матич. статистики, предназначенный для построения
множества приближенных значений неизвестных пара-
параметров вероятностных распределений.
Пусть X — случайный вектор, принимающий зна-
значения на множестве ?Р в евклидовом пространстве,
причем распределение вероятностей этого вектора при-
принадлежит параметрпч. семейству распределений, за-
заданному плотностями р(х\0), х???, 6? в, относи-
относительно нск-рой меры \х,{х). Предполагается, что истин-
истинное значение параметрич. точки 0, соответствующей
результату наблюдений X, неизвестно. Суть Д. о.
заключается в построении такого множества С(Х),
зависящего от X, к-рое содержит значение заданной
функции и (8), соответствующее неизвестному истин-
истинному значению параметрич. точки 8.
Пусть U — множество значений функции к (9),
6?6, и пусть С(х), х???,— какая-либо совокупность
множеств, принадлежащих U при всех х из ?Р, причем
предполагается, что для произвольного элемента и ? U
и любого значения 0?в определена вероятность собы-
события {С(Х)^и). Эта вероятность выражается интегра-
интегралом
и наз. вероятностью накрытия множест-
множеством С(Х) значения и при заданном значении 8.
Если истинное значение 8 неизвестно, то множество
С(X) (из совокупности множеств С(х), х???), соот-
соответствующее результату наблюдений X, наз. д о в е -
рительным множеством, или интер-
интервальной оценкой, для неизвестного истинного значения
функции и@). В качестве вероятностной характери-
характеристики интервальной оценки С(Х), построенной по
указанному правилу, используется доверитель-
доверительная вероятность РГ(Э), выражающаяся в тер-
терминах вероятности накрытия равенством
рсф) = рс[и{щ, в], е^е.
Иными словами, РГ(Э) — вероятность накрытия мно-
множеством С (X) значения заданной функции u(Q), соот-
соответствующего неизвестной истинной параметрич. точ-
ко 9.
В тех случаях, когда доверительная вероятность
Рс@) от 8 не зависит, интервальную оценку С(X) наз.
подобной пространству выборок. Это
название обусловлено аналогией формул
Рс (е) = Р {б1 (X)Э и @) | 9} = const
В более общей ситуации Рг@) зависит от неизвест-
неизвестного 0, и поэтому в практич. работе принято характе-
характеризовать качество интервальной оценки коэффи-
коэффициентом доверия
где нижняя грань вычисляется на множестве 0 (иногда
коэффициент доверия наз. доверительным
уровне м).
Оптимизация Д. о. определяется теми требованиями,
к-рые предъявляются к интервальным оценкам. Напр.,
если цель заключается в построении доверительных
множеств, подобных пространству выборок и имеющих
заданный коэффициент доверия со @,5<:со<1), то
первое требование выражается тождеством
Рс [и F), 0] =со, 9?в.
При этом естественно искать такие интервальные оцен-
оценки, к-рые накрывают истинное значение иF) с вероят-
вероятностью, не меньшей вероятности накрытия любого
произвольного значения u?U. Иными словами, второе
требование, называемое требованием несмещен-
несмещенности, выражается неравенством
Рс(и, G)<co, и?<7
В этих условиях «наилучшей» разумно считать ту ин-
интервальную оценку С, к-рая с меньшей вероятностью
накрывает любое значение и, отличное от истинного
и@). Отсюда возникает третье требование «наиболь-
«наибольшей селективности»: для всякого другого доверитель-
доверительного множества С", отличного от С п удовлетворяющего
условию
должно выполняться неравенство
Рс(и,Щ<Рс,(и,в), u?U,
Задача отыскания интервальных оценок С, удовлет-
удовлетворяющих указанным трем требованиям, эквивалентна
задаче построения несмещенных, наиболее мощных
статистич. критериев, подобных пространству выборок
и имеющих уровень значимости 1 — со.
Вопросы существования решения такой задачи и его
конструктивного описания составляют основу общей
теории статистич. проверки гипотез.
Наиболее часто применяется Д. о. в ситуации, когда
и(8) — скалярная функция. Пусть Xlf ..., Хп, га^2,
— независимые случайные величины, подчиняющиеся
одному и тому же нормальному распределению с неиз-
неизвестными параметрами EX,- = 8t и DX, = 82, причем
требуется построить интервальную оценку для и(8)=91.
Пусть
Поскольку случайная величина Т= У"п(Х — 9t)/s под-
подчиняется Стъюдента распределению с п— 1 степенями
свободы и это распределение не зависит от неизвест-
неизвестных параметров 8Х и 92 (|9Х| <°о, 92>0), то при любом
положительном t вероятность события
{Х — tsl У~п < 9t < Т+ tsl Y~n)
зависит лишь от t. Если указанный интервал принять
за интервальную оценку С для 9lt то ему будет соот-
соответствовать доверительная вероятность
РсФъ е2) = р{т< О,
не зависящая от 9=@1? 92). Такую интервальную
оценку наз. доверительным интерва-
интервалом, а ее концевые точки — доверительными
границами, или доверительными
пределами, причем в данном случае доверитель-
доверительный интервал представляет собой интервальную оценку,
подобную пространству выборок. В приведенном при-
примере интервальная оценка является несмещенной и
наиболее селективной.
Лит.: [1] У и л к с С, Математическая статистика, пер.
с англ., М., 1967; [2] Шметтерер Л., Введение в матема-
математическую статистику, пер. с нем., М., 1976; [3] Л е м а н Э.,
Проверка статистических гипотез, пер. с англ., М., 1964; [4]
Большее Л, Н., «Теория вероят. и ее примен.», 1965,
т. 10, в. 1, с. 187—92. Ю. В. Линник, Н. М. Халфина.
ДОВЕРИТЕЛЬНЫЙ ИНТЕРВАЛ — см. Довери-
Доверительное оценивание.
ДОВЕРИТЕЛЬНЫЙ УРОВЕНЬ — см. Доверитель-
Доверительное оценивание.
ДОДЕКАЭДР — один из пяти ти-
типов правильных многогранников.
Д. имеет 12 граней (пятиуголь-
(пятиугольных), 30 ребер, 20 вершин (в каж-
каждой вершине сходятся 3 ребра). Ес-
Если а — длина ребра Д., то его
объем
v = °-j- A5 + 7 У~Ь) х 7,6631а3.
БСЭ-5.
ДОДЕКАЭДРА ПРОСТРАНСТВО — первый пример
Пуанкаре пространства. Построен А. Пуанкаре
(Н. Poincare) в 1904. Получается отождествлением
противоположных граней додекаэдра после поворота
их друг относительно друга на угол я/5. Д. п. есть
многообразие рода 2, имеющее Зейферта расслоение,
и представляет собой единственное известное прост-
пространство Пуанкаре с конечной фундаментальной груп-
группой. Д. п. является пространством орбит свободного
действия бинарной группы икосаэдра на трехмерной
сфере.
Лит.: [1] 3 е й ф е р т Г., Трельфалль В., Топология,
пер. с нем., М.—Л., 1938. А. В Чернавский
ДОКАЗАТЕЛЬСТВ ТЕОРИЯ — раздел математич. ло-
логики, посвященный исследованию понятия доказа-
доказательства в математике, приложениям этого понятия
в различных разделах науки и техники.
Доказательство в широком смысле этого
слова есть способ обоснования истинности того или
иного суждения. Степень убедительности доказатель-
доказательства решающим образом зависит от средств, используе-
используемых для обоснования истинности. Напр., в точных
науках выработаны определенные условия, при вы-
выполнении к-рых сообщаемый экспериментальный факт
может считаться доказанным (необходима устойчивая
воспроизводимость эксперимента, отчетливое описание
методики эксперимента, его точности, применяемого
оборудования и т. n.i. В математике, для к-рой ха-
рактерен аксиоматический метод исследования, сред-
средства доказательства достаточно четко определились
уже на раннем этапе ее развития. Доказательство фи-
фигурирует в математике как последовательное выведе-
выведение одних суждений из других, причем способы этого
выведения допускают точный анализ.
Истоки Д. т. можно проследить со времен античности
(дедуктивный метод рассуждения в элементарной гео-
геометрии, силлогистика Аристотеля и др.), но современ-
современный этап ее развития начинается в конце 19 в.— па-
чале 20 в. под влиянием работ Г. Фреге (G. Frege),
Б. Рассела (В. Russell) и А. Уайтхеда (A. Whitehead),
Э. Цермело (Е. Zermelo) и, в особенности, Д. Гильберта
(D. Hilbert). В это время в теории множеств Г. Кантора
(G. Cantor) были обнаружены антиномии, поставив-
поставившие под сомнение достоверность даже простейших
рассуждений с произвольными множествами. Л. Бра-
уэр (L. Brouwer) подверг весьма серьезной критике
нек-рые классич. способы доказательства существо-
существования объектов в математике и предложил радикаль-
радикальную перестройку математики в духе интуиционизма.
Вопросы оснований математики приобрели особую ак-
актуальность. Д. Гильберт предложил выделить часть
практич. математики, так наз. финитную ма-
математику, не вызывающую возражений как с точки
зрения появления антиномий, так и с точки зрения
интуиционистской критики. В рамках финитной мате-
математики к рассмотрению допускаются лишь конструк-
конструктивные объекты, напр, натуральные числа, и лишь
такие способы рассуждений, к-рые согласуются с аб-
абстракцией потенциальной осуществимости и не при-
привлекают абстракции актуальной бесконечности. В част-
частности, ограничивается использование закона исключен-
исключенного третьего. В финитной математике никаких анти-
антиномий не обнаружено и нет оснований их ожидать.
С философской точки зрения способы рассуждения
в финитной математике значительно более удовлет-
удовлетворительным образом отражают конструктивные про-
процессы реальной действительности, чем в общей теоре-
теоретико-множественной математике. Идея Д. Гильберта
состояла в том, чтобы обосновать все основные разделы
классич. математики, оставаясь на твердой почве
финитной математики. С этой целью Д. Гильберт пред-
предложил метод формализации, являющийся
одним из основных методов Д. т.
В общих чертах метод формализации состоит в сле-
следующем: формулируется логико-математич. язык (пред-
(предметный язык) L, в терминах к-рого суждения данной
математич. теории Т записываются в виде формул.
Далее описывается нек-рый класс А формул L, назы-
называемых аксиомами теории, и описываются вывода пра-
правила, с помощью к-рых можно переходить от одних
формул к другим. Для аксиом и правил вывода упот-
употребляется общий термин — постулаты. Заданием
постулатов определяется формальная теория (в другой
терминологии — исчисление) Т*. Формулы, получае-
получаемые из аксиом формальной теории по ее правилам
вывода, наз. выводимыми, или доказуе-
доказуемым и, в данной теории. Сам процесс вывода может
быть при этом оформлен в виде дерева вывода (см.
Вывода дерево). Исчисление Т* представляет особен-
особенный интерес по отношению к содержательной мате-
математич. теории Т, если аксиомы Т* являются записями
истинных суждений Т, а правила вывода ведут от ис-
истинных суждений к истинным. В этом случае Т* можно
рассматривать как уточненный фрагмент теории Т,
а понятие вывода в Т* можно рассматривать как уточ-
уточнение неформальной идеи доказательства в теории Т,
по крайней мере в рамках, формализованных исчисле-
исчислением Т*. Таким образом, при построении исчисле-
исчисления Т* нужно предварительно уметь определять, ка-
какие постулаты считать пригодными с точки зрения тео-
рин Т. Это, однако, не означает, что необходимо уже
иметь развитую семантику теории Т: здесь можно ис-
использовать практич. навыки, включать в число посту-
постулатов наиболее часто употребляющиеся или наиболее
интересные в теоретич. отношении факты и т. п. Точ-
Точный характер описания выводов исчисления Т* по-
позволяет применять для их исследования математич.
методы и таким образом судить о содержании и свой-
свойствах теории Т.
В Д. т. выработаны стандартные приемы формализа-
формализации содержательных математич. теорий. Аксиомы и
правила вывода исчислений обычно делятся на логиче-
логические и прикладные. Логич. постулаты служат для по-
получения высказываний, истинных независимо от фор-
формализуемой теории уже в силу своей формы. Такие
постулаты определяют логику формальной теории и
оформляются в виде высказываний исчисления или пре-
предикатов исчисления (см. также Логические исчисления,
Математическая логика. Интуиционизм, Конструк-
Конструктивная логика, Строгой импликации исчисление). При-
Прикладные постулаты служат для описания истин, отно-
относящихся к особенностям данной математич. теории.
Напр., в аксиоматич. теории множеств — это выбора
аксиома, в элементарной арифметике — схема аксиом
индукции Сем. Математическая индукция), в интуи-
интуиционистском анализе — бар-индукция.
Гильбертову программу обоснования математики
можно описать следующим образом. Можно надеяться,
что всякую, даже весьма сложную и абстрактную мате-
математич. теорию Т (такую, напр., как теория множеств),
можно в ее существенных частях формализовать в виде
исчисления Т*, причем формулировка самого исчисле-
исчисления требует лишь финитной математики. Далее, ана-
анализируя выводы Т* чисто финитными средствами,
можно пытаться установить непротиворечивость Т* и,
следовательно, установить отсутствие антиномий в Т,
по крайней мере в той ее части, к-рая отражена в по-
постулатах Т*. Для обычных методов формализации
отсюда непосредственно следует, что нек-рые простей-
простейшие суждения (в терминологии Гильберта — реаль-
реальные суждения) выводимы в Т*, только если
они истинны в финитном смысле. Первоначально на-
надежда состояла в том, что в виде исчисления, формули-
формулируемого финитным образом, удастся описать практи-
практически всю классич. математику, а затем финитно же
доказать ее непротиворечивость. Невыполнимость этой
программы в целом была установлена в 1931 К. Гёде-
лем (К. Godel), к-рый показал, что при нек-рых естест-
естественных предположениях непротиворечивость исчисле-
исчисления Т* невозможно доказать даже мощными средст-
средствами, формализуемыми в Т*. Тем не менее исследова-
исследование различных формальных исчислений остается важ-
важнейшим методом в основаниях математики. Во-первых,
представляет интерес построение исчислений, отражаю-
отражающих существенные разделы современной математики и
построенных в расчете на непротиворечивость, даже
если непротиворечивость таких исчислений и нельзя
доказать в настоящее время убедительным для всех
математиков способом. Примером такого рода исчисле-
исчисления является система теории множеств Цермело —
Френкеля, в к-рой могут быть выведены практически
все результаты, полученные в современной теоретико-
множественной математике. Доказательства невыво-
невыводимости в этой теории ряда фундаментальных гипотез,
полученные в предположении непротиворечивости
теории (см. Аксиоматическая теория множеств, Вы-
нуждепия метод), свидетельствуют о независимости
этих гипотез от применяемых в математике теоретико-
множественных принципов. Это, в свою очередь, можно
рассматривать как подтверждение той точки зрения,
что существующих представлений недостаточно для
доказательства или опровержения рассматриваемых
гипотез. Именно в этом смысле П. Коэн (P. Cohen)
установил независимость континуум-гипотезы Г. Кан-
Кантора.
Во-вторых, широко изучается класс исчислений,
непротиворечивость к-рых можно установить финит-
финитными средствами. Так, К. Гёдель в 1932 предложил
погружающую операцию, перерабаты-
перерабатывающую формулы, доказуемые в классическом ариф-
метич. исчислении, в формулы, доказуемые в интуи-
интуиционистском арифметич. исчислении. Если последнее
считать непротиворечивым (напр., в силу его естест-
естественной финитной интерпретации), то отсюда следует
непротиворечивость и классического арифметич. ис-
исчисления.
Наконец, перспективным является исследование
средств более широких, чем традиционный финитизм
Д. Гильберта, но в то же время достаточно удовлетво-
удовлетворительных с нек-рой точки зрения. Так, оставаясь
в рамках потенциальной осуществимости, можно ис-
использовать так наз. общие индуктивные определения.
Это позволяет применять полуформальные теории,
в к-рых некоторые из правил вывода имеют бесконечное
(но конструктивно порожденное) множество посылок,
и перенести в финитную математику многие семанти-
семантические результаты. К этому направлению относятся
результаты П. С. Новикова A943), установившего
непротиворечивость классич. арифметики с использо-
использованием эффективных функционалов конечного типа,
К. Спектора (С. Spector, 1961), доказавшего непротиво-
непротиворечивость классич. анализа с помощью расширения
естественных интуиционистских средств доказательства
на интуиционистские эффективные функционалы конеч-
конечного типа, А. А. Маркова A971) по конструктивно!
семантике, использующие общие индуктивные опреде-
определения. Кроме того, ряд важных проблем, относящихся
к исчислениям, можно рассматривать и вне связи
с основаниями математики. Сюда относятся вопросы
о полноте и разрешимости формальных теорий, вопрос
о независимости нек-рых утверждений от данной фор-
формальной теории и др. В такой ситуации нет необходи-
необходимости ограничиваться в рассуждениях определенными
средствами и можно развивать Д. т. как обычную ма-
тематич. теорию, пользуясь любыми математич. сред-
средствами доказательства, убедительными для исследо-
исследователя.
Инструментом для исследования исчислений, а также
часто и мотивировкой для самого введения ряда исчис-
исчислений служит точно определенная семантика для
формул рассматриваемого языка, т. е. точное определе-
определение смысла суждений, выразимых в данном языке.
Напр., для классич. исчисления высказываний такая
семантика хорошо известна: в этом исчислении выво-
выводимы тавтологии и только они. В общем случае, чтобы
показать, что нек-рая формула А не выводится в рас-
рассматриваемом исчислении Т*, достаточно построить
семантику для формул языка этой теории таким образом,
чтобы все формулы, выводимые в Т*, были истинны
в этой семантике, в то время как А не истинна. Семан-
Семантика может быть классической, интуиционистской или
иного типа в зависимости от того, с какими логич.
постулатами она согласована. В исследовании классич.
исчислений с успехом применяются неклассич. семан-
семантики, напр, отношение вынуждения П. Коэна при
естественном уточнении задает интуиционистскую се-
семантику. В другом известном варианте теории П. Коэна
используются многозначные семантики — модели с ис-
истинностными значениями в полной булевой алгебре.
С другой стороны, семантики типа Крипке моделей,
определенные классическим теоретико-множествен-
теоретико-множественным способом, позволяют выяснить многие свойства
модальных и нестандартных логик (включая интуици-
интуиционистскую логику).
Алгебраич. методы получили широкое развитие в
Д. т. в виде моделей теории. Алгебраич. система, со-
сопоставляющая каждому начальному символу языка
нек-рый алгебраич. объект, естественно определяет
нек-рую классич. семантику языка. Алгебраич. си-
система паз. моделью формальной теории
Т*, если все формулы, выводимые в Т*, истинны в
семантике, порожденной алгебраич. системой. К. Гё-
дель я 1931 показал, что всякое непротиворечивое
исчисление (с классич. логикой) имеет модель. Не-
Несколько позже А. И. Мальцев независимо от результата
К. Гёделя установил, что если каждый конечный фраг-
фрагмент исчисления имеет модель, то и все исчисление в
целом имеет модель (так наз. теорема о ком-
компактности логики первого поряд-
порядка). Эти две теоремы легли в основу целого направ-
направления в математич. логике.
Рассмотрение нестандартных моделей арифметики
позволило установить неаксиоматизируемость понятия
натурального ряда в рамках теорий 1-го порядка, до-
доказать независимость принципа математич. индукции
от других аксиом арифметич. исчисления. Относитель-
Относительность понятия мощности множества в классич. мате-
математике выявилась при изучении счетных моделей для
формальных теорий, стандартная интерпретация к-рых
предполагает лишь заведомо несчетные модели (так
наз. парадокс Сколема). Многие синтакенч. результаты
были получены вначале из теоретико-модельных сооб-
соображений. В терминах конструкций теории моделей
можно дать простые критерии для многих понятий,
интересных с точки зрения Д. т. Так, критерий Скотта
гласит, что класс К алгебраич. систем данного языка
тогда и только тогда является аксиоматизируемым,
когда он замкнут относительно ультрапроизведепий,
изоморфизмов и взятия элементарных подсистем.
Формальная теория наз. разрешимой, если
существует алгоритм, позволяющий по произвольной
формуле А выяснять, выводима ли А в этой теории
или нет. Известно, что всякая формальная теория,
содержащая нек-рый фрагмент теории рекурсивных
функций, необходимо неразрешима. Отсюда следует
неразрешимость элементарной арифметики, системы
Цермело — Френкеля и многих других теорий. В Д. т.
разработаны тонкие методы интерпретации одних
теорий в других; с помощью таких интерпретаций
можно установить неразрешимость и ряда очень про-
простых исчислений, в к-рых не интерпретируются непо-
непосредственно рекурсивные вычисления. Примерами мо-
могут служить элементарная теория групп, теория двух
отношений эквивалентности, элементарная теория ча-
частичного порядка. С другой стороны, имеются примеры
интересных разрешимых теорий, таких, как элементар-
элементарная геометрия, элементарная теория действительных
чисел, теория множеств натуральных чисел с един-
единственной операцией следования. Разрешимость теорий
доказывается теоретико-модельными и ыштаксич. ме-
методами. Синтаксические методы часто дают более про-
простые разрешающие алгоритмы. Так, например, для
элементарной теории р-адичеекпх чисел разрешимость
была установлена сначала теоретш-.о-моделышми ме-
методами. Позднее был найден примитивно-рекурсивный
алгоритм распознавания выводимости для этой теории
с помощью нек-рой модификации синтаксич. метода
элиминации кванторов. Существенной является оценка
сложности алгоритмов разрешения теорий. Как пра-
правило, для разрешимых теорий имеется примитивно-
рекурсивный разрешающий алгоритм, и проблема со-
состоит в том, чтобы указать более точные границы слож-
сложности. Перспективным направлением исследований
является изучение разрешимости естественных фраг-
фрагментов известных формальных теорий. В этом отно-
отношении особенно подробно изучено классич. исчисление
предикатов, где эффективно описаны все разрешимые
и неразрешимые классы формул, заданные в терминах
расположения кванторов в формуле и вида предикат-
предикатных символов, встречающихся в формуле. Описан ряд
разрешимых фрагментов арифметич. исчисления, эле-
элементарной теории множеств.
Внимание исследователей привлекают и методы оцен-
оценки сложности выводов. Сюда относятся такие проблемы,
как отыскание сравнительно коротких формул, необ-
необходимо имеющих сложные доказательства, или формул,
из к-рых уже сравнительно несложно можно получить
большое количество результатов. Такие формулы
можно рассматривать как выражающие в нек-ром
смысле «глубокие» факты теории. Рассматриваются
естественные меры сложности вывода: длина доказа-
доказательства; время, требуемое для поиска вывода; слож-
сложность формул, фигурирующих в выводе, и др. В этой
области методы Д. т. смыкаются с методами теоретич.
кибернетики.
Лит.: [1] Клини С. К., Математическая логика, пер.
с англ., М., 1973; [2] Френкель А., Бар-Хил л ел И.,
Основания теории множеств, пер. с англ., М., 1966; [3] Е р ш о в
10. Л. и др., «Успехи матем. наук», 1965, т. 20, в. 4, с. 37 —108.
А. Г. Драгалин.
ДОКАЗАТЕЛЬСТВО — рассуждение по определенным
правилам, обосновывающее какое-либо предложение
(утверждение, теорему); основанием Д. служат исход-
исходные утверждения (аксиомы). Конкретное Д. не обяза-
обязательно начинается с аксиом, оно может опираться на
ранее доказанные предложения. Всякое Д.— относи-
относительно, поскольку базируется на нек-рых недоказыва-
емых положениях. Правила, по к-рым ведутся рас-
рассуждения, а также методы Д. изучает логика. См.
Доказательств теория. А. С. К/зичев.
ДОМИНАНТА топологического прост-
пространства X — любое топологич. пространство, для
К-рого X служит ретрактом. А. В. Чернавский.
ДОМИНИРОВАНИЕ — 1) Какое-либо из возможных
соотношений порядка для дифференциальных операто-
операторов, формулируемое в терминах характеристического
многочлена Р(?,). Напр., если
я а 1
Р(а)A)=
то Р(D) сильнее Q(D), когда для любого %?Rn
Q (DIP (I) < const.
Существуют и другие определения Д. (см. [1], с. 99, 103).
Лит.: [1] Хёрмандер Л., Линейные дифференциаль-
дифференциальные операторы с частными производными, пер. с англ., М., 1965.
А. А. Дезин.
2) Д. в теории игр — отношение, выражающее
превосходство одного объекта (стратегии, дележа)
над другим. Д. стратегий: стратегия s игрока i доми-
доминирует (строго доминирует) ого стра-
стратегию t, если его выигрыш в каждой ситуации, содер-
содержащей s, не меньше (соответственно больше), чем его
выигрыш в ситуации, состоящей из тех же стратегий
остальных игроков и стратегии t. Д. дележей (в коопе-
кооперативных играх): дележ х доминирует дележ у
(обозначение х^у), если существует такая непустая
коалиция PdN, что
2,-еР *«¦<»(*)
и Х[ >;/,- для i?P (v — характеристическая функция
Игры). И. Н. Врублееспая.
3) Д. в теории потенциала — отношение
порядка v{^v2 между функциями, в частности потен-
потенциалами определенных классов, т. е. выполнение
неравенства v1(x)^v2(x) для всех х в общей области
определения v1 и v2. В различных принципах
доминирования отношение v^v2 устанавли-
устанавливается как следствие выполнения неравенства ь\ (х)^
^v.2(x) на нек-рых собственных подмножествах об-
области определения. Простейший принцип доми-
доминирования Картана: пусть v=v(x) — неот-
неотрицательная супергармоническая функция (см. Суб-
Субгармоническая функция) на евклидовом пространстве
R", п>3, и Ufi= U\x,{x) —ньютонов потенциал меры
ii>0 конечной энергии (см. Энергия мер). Тогда, если
'iix)^iUa(x) на нек-ром множестве ЛсК" таком, что
||(СЛ)=0, то имеет место Д. v^U^. См. также Потен-
Потенциала теория абстрактная.
Лит.: []] Брело М., Основы классической теории потен-
потенциала, пер. с франц., М., 1984; [2] его же, О топологиях
и границах в теории потенциала, пер. с англ., М., 1974.
Е. Д. Соломенцев.
ДОПЛЕРА ЭФФЕКТ — изменение воспринимаемой
частоты колебаний в зависимости от скорости движения
источника колебаний и наблюдателя относительно
друг друга. При сближении источника и наблюдателя
частота повышается, при удалении — понижается. Д. э.
возникает при распространении волн любой природы:
акустических, упругих, электромагнитных.
Пусть х/ и х', где /=0, 1, 2, 3, x°—t, x°=t — время,
являются ннерциальными системами отсчета источника
электромагнитных волн в вакууме и наблюдателя.
II пусть фазовый множитель плоской волны имеет
вид ехр(гсоуж-') в первой и соответственно ехр(гсоу.с-')
во второй системах отсчета. Д. э. выражается форму-
формулой, связывающей временные компоненты (частоты)
ш0 и со0 четырехмерных волновых векторов {coy} и {соу}:
соо = со0
' 1 cos ф
Здесь г; — относительная скорость источника и на-
наблюдателя, ф — угол между скоростью v и линией
наблюдения, измеренный в системе наблюдателя, с —
скорость света в вакууме.
Д. э. назван по имени К. Доплера (Ch. Doppler),
к-рый впервые обосновал этот эффект в 1842.
Лит.: [1] Ландау Л. Д., Лифшиц Е. М., Теория
поля, о изд., М., 1907, гл. 6; [2] Ф р и ш С. Э., Т и м о р с в а
А. В., Курс общей физики, 10 изд., М., 1962, т. 1, гл. 12.
В. М. Бабич, М. М. Попов.
ДОПОЛНЕНИЕ — операция, к-рая ставит в соответ-
соответствие подмножеству М данного множества X другое
подмножество NczX так, что если известны М и .V,
то тем или иным способом может быть восстановлено
множество X. В зависимости от того, какой структурой
наделено множество X, получаются различные опре-
определения Д. и разные способы восстановления X по
М и N.
В общей теории множеств дополнением под-
подмножества (или дополнительным под-
подмножеством) до множества X наз. подмножество
Сх М (или СМ, а также Х\М), состоящее из всех
элементов в х?Х, не принадлежащих М; одним из
важных его свойств является принцип двойственности:
Пусть X наделено структурой линейного простран-
пространства и L —подпространство X. Подпространство NczX
наз. прямым алгебраическим допол-
дополнением (или короче алгебраич. дополнением) под-
подпространства X, если \fx?X однозначно представим
в виде x=y-\-z, y?L, z?N. Это эквивалентно усло-
условиям: X=L-f-N; Lf\N={0}. Алгебраич. Д. любого
подпространства X всегда существует, но определяется
неоднозначно.
Пусть (X, т) — линейное топологич. пространство
и .Y — прямая алгебраич. сумма X=L-j-iV своих
подпространств L и N, рассматриваемых как линейное
топологич. пространство с индуцированной топологией.
Если x=y-\-z, y^L, z?N, то взаимно однозначное
отображение (х, у)—*-х-\-у декартова произведения LXN
на X, непрерывное в силу линейности топологии т,
вообще, не взаимно непрерывно. Если же это отобра-
отображение есть гомеоморфизм, т. с. если X является топо-
топологич. прямой суммой пространств L и N, то подпро-
подпространство Лг наз. прямым топологическим
дополнением подпространства L, к-рое наз.
в этом случае дополняемым. В произвольном линейном
топологич. пространстве не всякое подпространство,
даже конечномерное, дополняемо. Имеют место сле-
следующие необходимые и достаточные условия дополня-
дополняемости: существует непрерывный проектор Р простран-
пространства X на подпространство L; подпространство L топо-
топологически изоморфно X/N, где N — алгебраическое
Д. L. Из утих критериев вытекают следующие доста-
достаточные условия дополняемости: L замкнуто и имеет
конечную коразмерность; X — локально выпукло, L —
конечномерно, N — замкнуто и др.
Специальным случаем топологич. Д. является орто-
ортогональное Д. подпространства L гильбертова простран-
пространства //. Это — множество
являющееся замкнутым подпространством пространства
Н. Важнейшим для теории гильбертовых пространств
является тот факт, что всякое замкнутое подпростран-
подпространство L гильбертова пространства имеет ортогональное
Д. и H=LC^Li-.
Пусть, наконец, X — условно полная векторная
решетка (Л'-пространство). Дизъюнктным до-
дополнением множества МаХ называется
совокупность элементов вида
являющаяся линейным подпространством X. Если
М — линейное подпространство, то в общем случае
ХфМ-\-М*, но если М компонента (по другой терми-
терминологии полоса, замкнутый идеал), т. е. линейное
подпространство такое, что: из х?М и |г/|<;|ж| следует
у^М; М чамкнуто относительно операций перехода
к точным верхним и нижним границам, то Х^М-тМа
(для любого М множество М^есть компонента; Mdd—
•~ (Md)d есть наименьшая компонента, содержащая
множество МсХ).
Лит.: [1] Б у р б а к и Н., Теория множеств, пер. с франц.,
М., 1965; [2] е г о же, Топологические векторные пространства,
пер. с франц., М., 1959; [3] Б и р к г о ф Г., Теория структур,
пер. с англ., М., 1952; [4] Робертсон А.,Робертсон
В., Топологические векторные пространства, пер. с англ., М.,
1967; [5] Ш е ф е р X., Топологические векторные пространства,
пер. с англ., М., 1971; [6] В у л и х Б. 3., Введение в теорию
полуупорядоченных пространств, М., 1961. В. И. Соболев.
ДОПОЛНИТЕЛЬНАЯ СЕРИЯ представле-
представлений — семейство неприводимых непрерывных уни-
унитарных представлений локально компактной группы
G, ненулевые матричные элементы к-рых не могут быть
аппроксимированы конечными линейными комбина-
комбинациями матричных элементов регулярного представ-
представления группы G в топологии равномерной сходимости
на компактах в G. Д. с. группы G непуста в том и
только в том случае, если G не аменабельна, т. е. если
на пространстве L°°(G) но существует нетривиального
левоинвариантного среднего (см. [2]). Связная группа
Ли G тогда и только тогда имеет непустую Д. с, когда
полупростая факторгруппа группы G по максималь-
максимальному связному разрешимому нормальному делителю
группы G некомпактна (см. Леей — Мальцева разло-
разложение). Д. с. впервые обнаружена для комплексных
классич. групп [1]. Д. с. полностью описана (к 1978)
лишь для нек-рых локально компактных групп. Нек-
рые задачи теории чисел (см., напр., [5]) равносильны
задачам теории представлений, связанных с Д. с.
групп аделей линейных алгебраич. групп.
Лит.: [1] Гельфанд И. М., Н а и м а Р к М. А..
Унитарные представления классических групп, М., 1950; [2]
Г р и н л и ф Ф., Инвариантные средние на топологических груп-
группах и их приложения, пер, с англ., М., 1973; [3] Н а й м а р к
М. А., Линейные представления группы Лоренца, М., 1958;
14] К о с т а н т Б., «Математика», 1970, т. 14, As 2, с. 102 — 16;
[5] Petersson H., «Math. Ann.», 1937/1938, Bd 115, S.
23 — 67. ¦ ' А. И. Штерн.
ДОПУСТИМОЕ ПРАВИЛО — вывода правило, до-
добавление к-рого в исчисление не меняет объема выво-
выводимых в этом исчислении слов. Введение в исчисление
Д. п. является мощным и часто применяемым средством
сокращения выводов, во многих случаях полезно для
совершенствования алгоритмов установления выводи-
выводимости. Одним из важнейших результатов математич.
логики является теорема о допустимости правила се-
сечения (см. Генцена формальная система). См. Выво-
Выводимое правило, Производное правило. с Ю Маслое
ДОСТАТОЧНАЯ СТАТИСТИКА для семейства рас-
распределений вероятностей {Pq ; 0 ? в} или для пара-
параметра 9?в — статистика (векторная случайная вели-
величина) такая, что для любого события А существует
вариант условной вероятности Pq (А\Х=х), не зави-
зависящий от 6. Это эквивалентно требованию, что условное
распределение любой другой статистики Y при ус-
условии Х=х не зависит от 6.
Знание Д. с. X дает исчерпывающий материал для
статистич. выводов о параметре 9, поскольку любые
дополнительные статистич. данные ничего не добав-
добавляют к той информации о параметре, к-рая содержится
и распределении X. Математич. выражением этого
свойства является один из результатов теории стати-
статистич. решений, утверждающий, что множество решаю-
решающих правил, основанных на Д. с, образует сущест-
существенно полный класс. Переход от исходного семейства
распределений к семейству распределений Д. с. наз.
редукцией статистической задачи.
Смысл редукции заключается в уменьшении (часто
весьма значительном) размерности пространства на-
наблюдений.
Практический способ нахождения Д. с. основан на
следующей теореме факторизации. Пусть семейство
{Рв } доминировано cr-конечной мерой ц. и пусть ре =
= dPQ:'d\i —плотность распределения Ре относительно
меры jx. Статистика X достаточна для семейства {Pq }
в том и только в том случае, когда
где gg , h — неотрицательные измеримые функции (h
не зависит от 9). Для дискретных распределений в ка-
качестве ц, можно взять «считающую» меру: в этом случае
/>g(w) в соотношении (:¦=) имеет смысл вероятности
элементарного события {со}.
Пусть, напр., Хх, . . ., Хп — последовательность
независимых случайных величин, принимающих зна-
значение 1 с неизвестной вероятностью v и значение О
с вероятностью 1—v (схема Бернулли). Тогда
> х- п- > х-
=nf"=1v*'<1-v)I"Jr/=v A~v) •
Равенство (*) выполняется, если положить
Таким образом, эмпирическая частота
является Д. с. для неизвестной вероятности v в схеме
Бернулли.
Пусть Х1, ..., Хп — последовательность независи-
независимых нормально распределенных величин с неизвест-
неизвестными средним значением ц и дисперсией сг2. Совмест-
Совместная плотность распределения Xlt .. ., Хп по мере
Лебега дается выражением
зависящим от xlt . .., г„ только через величины
.i-J(=l " ^.1 = 1 х< •
Поэтому векторная статистика
является Д. с. для двумерного параметра 6= (|х, сг2).
Д. с. здесь будет и совокупность выборочного среднего
и выборочной дисперсии
поскольку величины
могут быть выражены через (г и с2.
Для одного и того же семейства распределений может
существовать много Д. с. В частности, тривиальной
Д. с. является совокупность всех наблюдений [в рас-
рассмотренных выше примерах (Хь . .., Хп)]. Однако
основной интерес представляют статистики, позволя-
позволяющие осуществить действительную редукцию статис-
тич. задачи. Д. с. наз. минимальной, или н е-
обходимой, если она есть функция от любой
другой Д. с. Необходимая Д. с. осуществляет макси-
максимально возможную редукцию статистич. задачи. В рас-
рассмотренных примерах найденные Д. с. являются не-
необходимыми.
Важное применение понятия достаточности — метод
улучшения несмещенных оценок, основанный на т е о-
реме Рао — Блэкуэлла — Колмогоро-
в а: если X — Д. с. для семейства {Ре }, Хг — произ-
произвольная статистика, принимающая значения в вектор-
векторном пространстве Rd, то для действительной непрерыв-
непрерывной выпуклой функции g на Rd
Eeg(xt-Ee(xx))s,Eeg(Х1-Ев(ij)), ege,
где Zx=Ee (Xi\X) — условное математич. ожидание
статистики Хг относительно X (к-рое фактически не
зависит от 9 в силу достаточности X). В качестве
функции потерь g здесь часто берется положительно
определенная квадратичная форма на Rd.
Статистика X наз. полной, если равенство
Ее/(Х)=0, 6?в, влечет f(X) = O почти наверное от-
относительно Pq , 9? в. Одно из следствий теоремы
Рао — Блэкуэлла — Колмогорова утверждает, что ес-
если существует полная Д. с. X, то она является равно-
равномерно по 9 наилучшей несмещенной оценкой своего
математич. ожидания <?(9)=Ее X. Подобная ситуация
имеет место в приведенных примерах. Так, эмпириче-
эмпирическая частота v является равномерно наилучшей не-
смещенной оценкой вероятности v в схеме Бернулли,
а выборочные среднее ц, и дисперсия о — равномерно
наилучшие несмещенные оценки параметров нормаль-
нормального распределения ц и сг2.
В теоретическом плане иногда удобнее иметь дело не
с Д. с, а с достаточными cr-алгебрами. Если {Pq ;
8?<Э} — семейство распределений на вероятностном
пространстве (Q, ,Jf), то cr-подалгебра <3id,A наз.
достаточной для {Pq }, если для любого события
А^./1 существует вариант условной вероятности
Pq (А\&1), не зависящий от 9. Статистика X достаточна
тогда и только тогда, когда достаточна порождаемая
ею а-подалгебра Л=Х-1C}).
Лит.: [1] Н а 1 m о s P. R., S a v a g e L. I., «Ann. Math.
Statistics», 1949, v. 20, p. 225—41; [2] Колмогоров А. Н.,
«Изв. АН СССР. Сер. матем.», 1950, т. 14, Л. 4, с. 303—26; [3]
Рао С. Р., Линейные статистические методы и их применения,
пер. с англ., М., 1968. А. С. Холево.
ДОСТАТОЧНОЕ МНОЖЕСТВО ФУНКЦИОНАЛОВ,
тотальное множество функциона-
функционалов,— множество Г непрерывных линейных функцио-
функционалов f(X), определенных на линейном топологич.
пространстве X и обладающих тем свойством, что не
существует элемента х?Х, хфО, на к-ром равенство
f(x) = Q выполнялось бы для всех /?Г. Каждое ло-
локально выпуклое пространство обладает Д. м. ф.
М. II. Кадец^
ДОСТИЖИМАЯ ГРАНИЧНАЯ ТОЧКА — совокуп-
совокупность точки границы области и класса эквивалентных
путей, ведущих изнутри области в эту точку. Пусть
% — точка границы dG области G на плоскости комплекс-
комплексного переменного z и пусть существует путь с урав-
уравнением z—z(t), где функция z(t) определена и непре-
непрерывна на нек-ром отрезке [а, р1], z(t)?G при а<?<р\
z(P) = ?. Тогда говорят, что этот путь ведет в точку |
(изнутри G) и определяет Д. г. т., изображаемую точ-
точкой |. Два пути, ведущие в ?, наз. эквивалентными (или
определяющими одну и ту же Д. г. т.), если сущест-
существует третий путь, также ведущий в ? изнутри G и имею-
имеющий с каждым из рассматриваемых двух путей непу-
непустые пересечения внутри G в любой близости от ?.
Совокупность точки | ? dG и класса эквивалентных
путей, ведущих в | изнутри G, наз. Д. г. т. области G.
Не всякая точка |?3(? изображает Д. г. т.; с другой
стороны, одна и та же точка ??3G может изображать
несколько, и даже бесконечное множество, различных
Д. г. т.
Д. г. т. является единственной точкой граничного
элемента 1-го рода; (многоточечный) граничный эле-
элемент 2-го рода содержит ровно одну Д. г. т., а гранич-
граничные элементы 3-го и 4-го родов не содержат Д. г. т.
Каждая точка границы жордановой области является
Д. г. т.
Лит.: [1] М а р к у ш е в и ч А. И., Теория аналитических
функций, 2 изд., т. 2, М., 1968; [2] К о л л и н г в у д Э., Л о-
ватер А., Теория предельных множеств, пер. с англ., М,
1971, гл. 9. Е. П. Долженко.
ДОСТИЖИМАЯ ДУГА ГРАНИЦЫ области
Сна плоскости z — жорданова дуга, входящая
в состав границы области G и одновременно входящая
в состав границы нек-рой жордановой области gaG.
Каждая точка Д. д. г. является достижимой (изнутри
g) граничной точкой области G (см. Достижимая гра-
граничная точка). Конформное отображение односвязной
области G на единичный круг ?):|z|<l непрерывно
продолжимо на неконцевые точки Д. д. г. до гомеомор-
гомеоморфизма открытой Д. д. г. на нек-рую открытую дугу
окружности |г| = 1. Е. П. Долженко
ДОСТИЖИМАЯ ПОДГРУППА — подгруппа Н,
к-рую можно включить в конечный нормальный ряд
группы G, т. е. ряд
в к-ром каждая подгруппа Я,- инвариантна в Я, + 1
Свойство подгруппы быть Д. п. транзитивно. Пересече-
Пересечение Д. п. есть Д. п. Подгруппа, порожденная двумя
Д. п., может не быть Д. п. Группа G, у к-рой каждая
подгруппа является Д. п., удовлетворяет нормали-
заторному условию, т. е. всякая подгруппа
отлична от своего нормализатора и, следовательно,
локально нильпотентна.
Лит.: [1] К у р о ш А. Г., Теория групп, 3 изд., М., 1967.
В. М. Нопытов.
ДОСТИЖИМОЕ ПРОСТРАНСТВО, 7\-п рострап-
с т в о,— топологич. пространство X, в к-ром замы-
замыкание любого одноточечного множества совпадает с
ним самим. Это условие равносильно тому, что пе-
пересечение всех окрестностей точки х?Х совпадает
с х или что каковы бы ни были две различные точки
х<у?Х, существуют их окрестности Ux и Uy такие,
что ихфу и Uy%x, т. е. выполняется отделимости
аксиома Т±.
Достижимость, т. е. выполнение 7\,— наследствен-
наследственное свойство: всякое подпространство Д. п. есть Д. п.,
и топология, мажорирующая топологию Д. п., яв-
является достижимой топологией. Всякое отделимое про-
пространство (Г2-пространство) является Д. п., обратное
неверно: существуют ^-пространства, не являющиеся
^-пространствами, таково, напр., бесконечное мно-
множество р1, наделенное топологией, в к-рои открытыми
считаются те множества, дополнения к к-рьш конечны.
М. И. Вопцехоескип.
ДОСТОВЕРНОЕ СОБЫТИЕ — событие, которое ап-
априори должно обязательно произойти. Точнее, если
Q={co}— пространство элементарных исходов, то со-
событие А, наступающее вместе с любым из элементарных
исходов со, наз. Д. с. и, очевидно, должно совпадать
со всем пространством Q. Поэтому естественно припи-
приписать Д. с. вероятность, равную 1:
Р (А) = мера {ш : ы?А} = Р (Q) = l.
Дополнительным к А является невозможное событие.
А. В. Прохоров.
ДОСТОВЕРНОСТЬ — априорное убеждение в осу-
осуществимости нек-рого явления, исключающее всякое
сомнение. Д. характеризует реализуемость нек-рого со-
события, отмечая его наивысшим значением вероятно-
вероятности. В теории вероятностей понятие Д. связано с
достоверными событиями и с событиями, происходя-
происходящими с вероятностью 1. На практике говорят о Д.
уже тогда, когда вероятность нек-рого события доста-
достаточно близка к 1. а. в. Прохоров.
ДОУПОРЯДОЧИВАЕМАЯ ГРУППА — группа, вся-
всякий частичный порядок в к-рой может быть продолжен
до линейного (см. Упорядочиваемая группа). Д. г. наз.
также О*-г р у п п а м и. Существует следующий кри-
критерий доупорядочиваемости группы. Пусть S (g) —
минимальная инвариантная подполугруппа группы G,
содержащая элемент g. Группа G доупорядочиваема
тогда и только тогда, когда для всякого g^e подполу-
подполугруппа S (g) не содержит единицы группы G и для любых
х> y^S(g) пересечение S(x)[)S(y) не пусто.
Д. г. являются все нильпотентные группы без кру-
кручения и все упорядочиваемые двуступенно разрешимые
группы. Свободные группы ранга большего 2 и свобод-
свободные разрешимые группы класса разрешимости большего
2 дают примеры упорядочиваемых групп, к-рые не
доупорядочиваемы. Для Д. г. справедлива локальная
теорема (см. Мальцева локальные теоремы), т. е. если
все конечно порожденные подгруппы группы G доупо-
доупорядочиваемы, то и G — Д. г. Однако подгруппа Д. г.
не обязана быть Д. г. Если факторгруппа Д. г. упоря-
упорядочиваема, то она есть Д. г. Имеются упорядочива-
упорядочиваемые, но недоупорядочиваемые группы, факторгруппа
по центру к-рых есть Д. г. Класс Д. г. замкнут отно-
сительно прямых произведении, но не замкнут отно-
относительно полных прямых произведений и, следова-
следовательно, неаксиоматизируем (см. Аксиоматизируемый
класс). Сплетение Д. г. не всегда доупорядочиваемо.
Подгруппа Н группы G наз. Г-доупорядочи-
в а е м о й, если всякий максимальный частичный
порядок группы G индуцирует на Н линейный порядок.
Лит.: [1] К о к о р и н А. И., К о п ы т о в В. М., Линейно
упорядоченные группы, М., 1972; [2] Ф у к с Л., Частично упо-
упорядоченные алгебраические системы, пер. с англ., М., 1965.
А. И. h'ompuH, В. М. Копытов.
ДРЕВОВИДНОЕ МНОГООБРАЗИЕ — гладкое нечет-
номерное многообразие специального вида, являющее-
являющееся краем четномериого многообразия, строящегося из
расслоений над сферами с помощью склеек по схеме,
задаваемой нек-рым графом (деревом).
Пусть pi\E\n-*~Si, i=l, 2, ...— расслоение над
n-сферами со слоем n-шар D" и структурной группой
SOn и пусть В? — замкнутый стандартный п-шар
в п-сфере Sf\ тогда
где D" — слой расслоения />,-. Пусть
— гомеоморфизм, осуществляющий склейку двух рас-
расслоений р;, pj п переводящий каждый n-шар ВпХх
из BfxD" в некоторый шар yXDn из BjXD] (склейка
меняет сомножители прямого произведения BnXD").
Результатом склейки двух расслоений р/, pj является
2п-мерное многообразие ??™UV. Ер, к-рое превра-
превращается в гладкое многообразие с помощью операции
«сглаживания углов».
Расслоения Ё}п рассматриваются как «строительные
блоки», из к-рых с помощью попарных склеек резуль-
результирующее гладкое многообразие строится следующим
образом. Пусть Т — одномерный конечный комплекс
(граф). Каждой вершине графа Т сопоставляется блок
Е\п, выбираются в Sf непересекающиеся n-шары Bf.
в количестве /с=1, 2, . . ., равном индексу ветвления
соответствующей вершины, и производится склейка
по схеме, указанной графом Т. Полученное таким об-
образом многообразие с краем обозначается (опуская
зависимость от выбора расслоений Efn) через W2n(T).
В случае, если Т есть дерево, то есть граф без циклов,
то край dWitl(T)~M-n~1 наз. древовидным
многообразием.
Если Т — дерево, то W2n(T) имеет гомотопич. тип
букета и-сфер в количестве, равным числу вершин
дерева Т.
Д. м. M2n-1=dW2n(T) является целочисленной го-
мологич. B?г—1)-сферой тогда и только тогда, когда
определитель матрицы целочисленной билинейной
(—1)"-формы пересечений, определенной на решетке
n-морных гомологии Hn(W2n, Z), равен =tl. Если это
условие выполнено, то многообразие W2n(T) наз.
п л го м б и н г о м.
Если Т — произвольный граф и п>2, то W2n(T)
тогда и только тогда односвязно, когда Т — дерево.
Если Т — дерево и и^З, то dW2n(T) односвязно; если
W2" — плюмбинг, то край dW2n является гомотопич.
сферой, п :з; 3.
Если плюмбпнг Wik — параллелизуем, то на глав-
главной диагонали матрицы пересечений 2&-мерных циклов
стоят четные числа; в этом случае сигнатура матрицы
пересечений делится на 8. Плюмбинг Wik тогда и
только тогда параллелизуем, когда все расслоения
над S2k, использованные при построении Wik, явля-
ются стабильно тривиальными; напр., если все рас-
расслоения, используемые при построении И74*, являются
касательными расслоениями на диски над 2&-мерными
сферами, то плюмбинг Wik параллелизуем. Плюмбинг
W^k + 2 ТОГда и только тогда параллелизуем, когда
каждое расслоение Е\ +2, используемое в качестве
блоков при построении плюмбинга Wik + i, принадле-
принадлежит к одному из двух типов: оно либо тривиально,
либо является трубчатой окрестностью диагонали в
произведении S'lk + 1X S2k + 1, то есть касательным
расслоением на диски над 52* + 1. Если плюмбинг
Wik + 2 параллелизуем, то его матрица пересечений
приводится к симплектическому виду, состоящему из
блоков 11-1 oil, расположенных вдоль главной диа-
диагонали.
Среди плюмбингов особо выделяются многооб-
многообразия Милнора размерности Ак, fc>l и м н о-
гообразия Кервера размерности 4А+2, к^О.
Многообразия Милнора строятся следующим образом:
в качестве блоков берутся несколько экземпляров
трубчатой окрестности Eik диагонали в произведении
S2kXS2k; в качестве графа Т берется граф следующего
вида:
о 1 / с в 7 При этих условиях много-
многого .—.—Z—f—. . образце Wik(T) реализует
I квадратичную форму 8-го
порядка, у которой на глав-
главной диагонали стоят двойки, а сигнатура равна 8.
Для построения многообразий Кервера К4к + 2 бе-
берутся два экземпляра блока, получающегося как
трубчатая окрестность Eik + 2 диагонали в произведении
52* + 1Х S2k + 1. Склеиваются они так, что матрица
пересечений имеет вид |[_?Jil.
Край многообразия Милнора дМ4к (сферы М и л-
н о р а) всегда недиффеоморфен стандартной сфере
Sik~1-, относительно многообразий Кервера этот во-
вопрос до конца не решен A978). Если 2к-\-1ф2'— 1, то
край многообразия Кервера dKik + i (сферы К ер-
вера) всегда нетривиален, если же 2fc+l = 2' — 1,
то для 1 <:?<:& получится стандартная сфера Sik + 1,
для остальных i решение неизвестно (см. Кервера
инвариант).
Многообразия Кервера Kik + 2 размерности 2, 6, 14
представляют собой произведения сфер S'lk + 1X S2k + 1,
к = 0, 1, 3, с выкинутой открытой клеткой, а все другие
многообразия Корвера не гомеоморфны произведениям
сфер с выкинутой клеткой.
В топологии многообразий часто используются PL-
многообразия Mik и Kik, полученные добавлением
конуса над краем, соответственно, многообразий Мил-
Милнора Mik и многообразий Кервера Kik^'2, а также
два 4-мерных гладких многообразия — одно из них
Wi(T) (Т не обязательно дерево) является параллелн-
зуемым односвязным многообразием, край к-рого диф-
фооморфен 3-сфере, а сигнатура равна 16. Такое
многообразие P4=Wi(T) наз. многообразием
(или п л ю м б и п г о к) Рохлина. В известных
примерах многообразий Роилина минимальное значе-
значение двумерного числа Бетти равно 22. Другое много-
многообразие есть W*{T), где Г — граф, указанный выше, в
качестве блока берется трубчатая окрестность диаго-
диагонали в произведении S2XS2. Край получающегося
многообразия Qi=W4:(T) есть ноодносвязное додекаэдра
пространство.
Трехмерные Д. м. M3=dWi(T) принадлежат к так
называемым многообразиям Зей|ерта. Но всякое 3-
мерное многообразие является Д. м., и для Д. м. спра-
справедлива гипотеза Пуанкаре. В частности, 3-мерные
линзовые пространства получаются от склейки только
двух блоков.
Лит.: [1] К е г v a i r e M., «Comment, math, helv.», 1960,
v. 34, p. 257—70; [2] К е г v a i r e M., Milnor J., «Ann.
Math.», 1963, v. 77, JV° 3, p. 504—37; [3] M и л н о р Д ж., «Успе-
«Успехи матем. наук», 1965, т. 20, в. 6, с. 41—54; [4] Н i r-
г е b г и с h F., Neumann W. D. К о h S. S., Differenti-
eble manifolds and quadratic forms, N. Y., 1971; [5] В г о w-
der W., Surgery on simply-conuected manifolds, В., 1972.
M. А. Штанъко.
ДРЕЙФОВЫЕ УРАВНЕНИЯ — приближенные урав-
уравнения движения заряженной частицы в электрическом
и магнитном полях, полученные с помощью усреднения
по быстрому вращению частицы под действием магнит-
магнитного поля. Д. у. справедливы в том случае, когда маг-
магнитное поло В медленно меняется в пространстве и во
времени, а электрич. поле Е мало по сравнению с
магнитным:
^?~е, -?-|v*l~e. §~г. A)
Здесь е — малый параметр, а>р=еВ/тс — л а р м о-
ровская частота, р^— v^/\ coB| — ларморов-
ский радиус, v — величина скорости частицы,
v , — составляющая скорости в направлении, перпен-
перпендикулярном магнитному полю. Д. у. получаются из
полных уравнений движения разложением по степеням
е при помощи метода усреднения [1]. Они имеют сле-
следующий вид:
d^ ~V "\v o\
? (*)<>. D)
-> .->¦->¦ mcV
У ?[ЕВ] +
Система B) — D), называемая дрейфовой си-
систем о й, записана относительно вспомогательных
усредненных переменных Я, V^, V,, , связанных с
исходными переменными г, v определенными соотно-
соотношениями. Дрейфовая скорость Гдр в уравнении B)
описывает медленное движение по усредненной тра-
траектории в направлении, перпендикулярном магнит-
магнитному полю:
7др. - ev, Vav,B-^0.
Уравнения C), D) имеют второй порядок точности
по е и определяют величины V^ и Уц с точностью до
членов первого порядка в течение промежутка вре-
времени t, содержащего много ларморовских периодов
t—1/е]<ид |. Уравнение B) имеет первый порядок точ-
точности по е.
Величина \y=VjjB, к-рая представляет собой ин-
интеграл дрейфовой системы B) — D),
является приближенным интегралом истинного дви-
движения. Она наз. адиабатическим инвари-
инвариантом. В статическом случае, когда rot E = 0 и Е=
= —уф, уравнение C) допускает интеграл энергии
— т ( Vх + V ||) -j- еф = const
для усредненного движения.
Возможно обобщение дрейфовой системы на реляти-
релятивистский случай (см. [2], [3]).
Лит.: [1] Боголюбов Н. Н., Митропольский
Ю. А., Асимптотические методы в теории нелинейных колеба-
колебаний, 3 изд., М., 1963; [2] С и в у х и н Д. В., в кн.: Вопросы
теории плазмы, в. 1, М., 1963, с. 7—97; [3] М о р о з о в А. И.,
Соловьев Л. С, там же, в. 2, М., 1963, с. 177—261.
Д. П. Костомаров.
ДРОБНАЯ ДОЛЯ ЧИСЛА — функция, определенная
для всех действительных чисел х и равная разности
между х и целой частью (антье) [х] числа х. Дробная
доля числа х обычно обозначается знаком {х}. Напр.,
{1,03}=0,03; {-1,25}=0,75; {я}= {3,14.. .}=0,14...
С А, Степанов.
ДРОБНАЯ КОНГРУЭНЦИЯ — конгруэнция т)/В
факторсистемы А/в, определяемая формулой
где Т] — некоторая конгруэнция алгебраической систе-
системы А, содержащая данную конгруэнцию 9, и [а]е =
= {х?А\хва}. Факторсистема (A/Q)/(r\/Q) изоморфна
системе А/г\. д. м. Смирнов.
ДРОБНАЯ СТЕПЕНЬ линейного операто-
оператора А в комплексном банаховом про-
пространстве Е — функция /(А) от этого оператора
такая, что f(z) = za. Если оператор А ограничен, и
спектр его не содержит и не окружает нуля, то А а
определяется Коши интегралом по контуру, окружаю-
окружающему спектр Л и не содержащему внутри себя нуль.
Если А неограничен, то контур приходится брать бес-
бесконечным, и возникают вопросы об условиях сходи-
сходимости интеграла. Если А имеет плотную в Е область
определения D (А) и при А,<0 имеет резольвенту
Я (А., Л)=(Л— XI)-1
с оценкой
|| Д (-s, 4)||<Jl/(l + s)-i, s>0, A)
-a = ~'\iTk-aR(k, A)dk,
где Г состоит из сторон угла, строящегося по М. Опе-
Операторы А ~а ограничены и А~ах—^х при любом х?Е
и а —>¦ 0. Положительные степени определяются так:
Аа = (А-а)~1; они уже являются неограниченными.
При любых действительных а и Р выполнено основ-
основное свойство степеней
для х?П(Ау) и у=тах{а, р4, а+р4}. При 0<а<1
D«)Р4«Р При любых а<р<у и ж?.О(Л7)
|| А*х || ^ С (а, р, у) |) Ла^ ||v-« || АЬ: \\У~а
(неравенство моментов). Полугруппа сте-
степеней А~а допускает расширение до полугруппы A~z>
аналитической в правой полуплоскости.
Ряд приведенных свойств Д. с. обобщается на слу-
случай, когда А не имеет ограниченного обратного и
справедлива оценка \\R (—s, A)\\^Ms~1, s>0. При
условии A) и при 0<а<1
Если оператор В — производящий оператор сжимаю-
сжимающей полугруппы U(t), то
Из условия A) не вытекает, что —А является произ-
производящим оператором сильно непрерывной полугруппы,
но оператор —Аа при а^г/2 является производящим
оператором аналитич. полугруппы.
Оператор В подчинен оператору А, если
D(B)ZDD{A) и ||Вх||<с|иг||, x?D(A). Если В подчи-
подчинен А и резольвенты обоих операторов обладают свой-
свойством A), то Ва подчинен лРпри 0<а<Р<:1.
Если А — положительный самосопряженный опе-
оператор в гильбертовом пространстве, то его Д. с. оп-
определяется через спектральное разложение
Аа =
В неравенстве моментов для такого оператора констан-
константа с(а, Р, у)=1. Пусть А и В — два самосопряженных
положительных оператора, действующие в гильбер-
гильбертовых пространствах Н и Н1 соответственно. Если
Т — такой ограниченный линейный оператор из Н
в #! с нормой М, что TD(A)cD(B) и ЦВТх\\<:М1 \\Ах\],
x?D(A), то TD(Aa)cD{B«t) и
\\Ва Тх || sj Л/1"*;!/? || 4й* [|, 0 s? а s? 1
(неравенство Хайнца). В частности, при
Н^=Н1 и Т=1 из подчиненности В оператору А сле-
следует подчиненность Ва оператору Аа при 0-<а<:1.
Д. с. операторов применяются при исследовании не-
нелинейных уравнений. Они детально изучены для
операторов, порожденных эллиптпч. праевьши за-
задачами.
Лит.: [1] Функциональный анализ. [Справочная математи-
математическая библиотека], 2 изд., М., 1972; [2] К р е й н С. Г., Ли-
Линейные дифференциальные уравнения в банаховом пространстве,
М., 1967; [3] Си ли Р., «Математика», 1968, т. 12, N I,
с. 96 — 112. С. Г. Крейн.
ДРОБНОЕ ИНТЕГРИРОВАНИЕ И ДИФФЕРЕНЦИ-
ДИФФЕРЕНЦИРОВАНИЕ — распространение операций интегрирова-
интегрирования и дифференцирования на случай дробных порядков.
Пусть f(x) интегрируема на отрезке [а, Ъ], Iif(x) —
интеграл от / по [а, х], a I%f(x) — интеграл от Ia-if(x)
по [а, х], а = 2, 3, ... . Имеет место соотношение
где Г(а)= (а—1)! — гамма-функция. Правая часть в A)
имеет смысл при всех а>0. Соотношение A) определяет
дробный интеграл (или интеграл Ри-
мана — Лиувилля) порядка а от / с началом в
точке а. Оператор 1% при комплексных значениях
параметра z изучался Б. Риманом (В. Riemann, 1847).
Оператор /а линеен и обладает полугрупповым свой-
свойством:
Операция, обратная дробному интегрированию, но-
носит название дробного дифференцирования: если Iaf=
= F, то / есть дробная производная поряд-
порядка а от F. При 0<а<1 имеет место формула
М а р ш о:
( F(x)-F(x-t)\
{
Понятие Д. и. и д. впервые ввел Ж. Лиувилль (J. Li-
ouville, 1832), в частности он рассмотрел оператор
fit)
(при соответствующих ограничениях на функцию /;
см. [1], где приведены также оценки оператора /«в
Lp).
Для интегрируемой 2я-периодической функции f(x)
с нулевым средним значением по периоду удобно (см.
[2]) определение, предложенное Г. Вейлем (Н. Weyl,
1917): если
/ (г\
то н н т е г р а л В е й л я fa(x) порядка а>0 функции
/ определяется формулой
производная /Р порядка Р>0 определяется при этом
равенством
где п — наименьшее целое, большее р (отметим, что
fa(x) совпадает с Iaf(x)).
Перечисленные определения получили дальнейшее
развитие в рамках теории обобщенных функций. Для
периодических обобщенных функций
операция дробного интегрирования Iaf=fa выполнима
по формуле B) для любых действительных а (при
отрицательных a Iaf совпадает с дробной производной
порядка а) и обладает групповым свойством по пара-
параметру а.
В n-мерном пространстве X аналогом оператора
дробного интегрирования является риссов по-
потенциал (или интеграл типа потен-
потенциала)
(т)
Обратная к На операция наз. риссовой произ-
производной порядка а.
Лит.: [1] X а р Д и Г. Г., Литтльвуд Д. Е., П о-
лиа Г., Неравенства, пер. с англ., М., 1948; [2] Зиг-
Зигмунд А., Тригонометрические ряды, пер. с англ., т. 1, М.,
1965; [3] X и л л е Э., Ф и л л и п с Р., Функциональный ана-
анализ и полугруппы, пер. с англ., 2 изд., М., 1962; [4] Д ж р 6 а-
ш я н М. М., Интегральные преобразования и представления
функций в комплексной области, М., 1966. П. И. Лизоркин.
ДРОБНО-ЛИНЕЙНАЯ ФУНКЦИЯ — функция вида
' = ?(*)=:
где z= (z1, ..., zn) — комплексные или действительные
переменные, а;-, Ъ, cj, d — комплексные или действи-
действительные коэффициенты, 1^1 + .. .+ |с„| + |й|>0. Если
1 сх| ==. . .= |с„|=0, то Д.-л. ф. является целой линейной
функцией; если ранг матрицы А = || *' ' ' c"d II равен
единице, то L(z) — постоянная. Собственно Д.-л. ф.
получается, если Icjl-f- • • -+к„1 >0 и ранг А равен
двум; ниже эти условия предполагаются выполнен-
выполненными.
В случае га=1 и действительных %=a, c1=c, zx — z
график Д.-л. ф. есть равнобочная гипербола с асимп-
асимптотами z=—die и w=a/c. В случае ге=2 и действитель-
действительных ах, а2, Ь, С], с2, d, zlt z2 график Д.-л. ф. есть гипер-
болпч. параболоид.
В случае ге=1 Д.-л. ф. L(z) есть аналитич. функция
комплексного переменного z всюду в расширенной
комплексной плоскости С, за исключением точки
z=—d/c, в к-рой L(z) имеет простой полюс. При п>1
Д.-л. ф. L (z) есть мероморфная функция в простран-
пространстве С" комплексных переменных z= (zlt . .., zn),
имеющая полярным множеством множество
См. также Дробно-линейное отображение.
Е. П. Долженко, Е. Д. Соломенцее
ДРОБНО-ЛИНЕЙНОЕ ОТОБРАЖЕНИЕ, дробно-
линейное преобразование,— отображе-
вне комплексного пространства Си—>-Си, осуществля-
осуществляемое дробно-линейными функциями.
В случае комплексной плоскости СХ=С — это от-
отличное от константы отображение вида
т / \ UZ -f Ь ,1-.
z -,w = L(z) = —[, A)
где ad—ЪсфО; часто применяется унимодуляр-
ная нормировка ad—bc=i. Всякое Д.-л. о.
доопределяется соответствиями оо—>-а/с и —die—>-оо
до взаимно однозначного отображения расширенной
плоскости С на себя. Простейшими среди Д.-л. о.
являются линейные: z—>-ш=аг+Ь, получающиеся при
с=0. Всякое нелинейное Д.-л. о. представимо в виде
суперпозиции двух линейных отображений и отобра-
отображения Lo: z—*-w=i/z. Свойства Д.-л. о. Lo становятся
наглядными на Римана сфере, так как при стереогра-
фич. проекции ему соответствует поворот сферы на
180° вокруг диаметра, проходящего через образы
точек rfclgC.
Основные свойства. Д--л. о. отображает
взаимно однозначно и конформно С на себя. Круго-
Круговое свойство: при Д.-л. о. любая окружность
на С (т. е. окружность на С или прямая, пополненная
точкой оо) переходит в окружность на С. Инвари-
Инвариантность отношения симметрии двух
точек: пара точек z, z*, симметричных относительно
какой-либо окружности на С, при Д.-л. о. переходит
в пару точек w, w*, симметричных относительно образа
этой окружности. Двойное отношение четырех точек
на С инвариантно относительно Д.-л. о., т. е. если
точки ?1; ?2, !3> ?4 ПРИ Д-"л- °- переходят соответст-
соответственно В ?х, ?2> ?з. ^4. Т0
Для любых заданных_троек ?ь ?2, |3 и ?1? g2, t,3, попарно
различных точек на С, существует и притом только одно
Д.-л. о., переводящее соответственно |^—>-^, &=1, 2, 3.
Это Д.-л. о. можно найти из уравнения B), подстав-
подставляя в него z и w соответственно вместо ?4 и ^.Груп-
^.Групповое свойство: совокупность всех Д.-л. о. об-
образует некоммутативную группу относительно суперпо-
суперпозиции (L1L2)(z) = L1(L2(z)) с единицей E(z) = z. Свой-
Свойство универсальности: всякий конформный
автоморфизм С есть Д.-л. о., и, таким образом, группа
всех Д.-л. о. совпадает с группой Aut С всех конформ-
конформных автоморфизмов С.
Все конформные автоморфизмы единичного круга
S={zgC; |z|<l} образуют подгруппу Aut В группы
Aut С, состоящую из Д.-л. о. вида:
1 -CXZ
Im6 = 0.
Так же обстоит дело с конформными автоморфизмами
верхней полуплоскости {z?C; Im z>0}, имеющими вид:
z—^Ш=^ТЗ> Im(a, Ь, с, d) = 0, ad — be > 0.
Все конформные гомеоморфизмы верхней полуплоско-
полуплоскости на единичный круг имеют вид:
z—*ш = е'6-^, Imp>0, Im6 = 0.
2-Р
Исключив тождественное Д.-л. о. E(z), можно ска-
сказать, что Д.-л. о. имеет не более двух различных не-
неподвижных точек Ij, g2 на С. В случае двух различных
неподвижных точек ?>1Ф%2 семейство окружностей 2,
проходящих через ?х и \2, переводится Д.-л. о. A)
само в себя. При этом семейство 2' всех окружностей,
ортогональных к окружностям 2, также переходит
само в себя. Здесь возможны в свою очередь три
случая.
1) Каждая окружность 2 переходит сама в себя;
такое Д.-л. о. наз. гиперболическим, и он»
представимо в нормальной форме:
где м н о ж и т е л ь Д.-л. о. jx>0, ]i=?i, оо. Унимо-
дулярное Д.-л. о. A) является гиперболическим тогда
и только тогда, когда a+d?R и |а+й|>2.
2) Каждая окружность 2' переходит сама в себя;
такое Д.-л. о. наз. эллиптическим ив нор-
нормальной форме C) характеризуется множителем jx
таким, что |(i,| = l, цф\. Унимодулярное Д.-л. о. A)
является эллиптическим тогда и только тогда, когда
+d?R |+|2
?, +|
3) Ни одна из окружностей семейств 2 и 2' не пере-
переходит сама в себя; такое Д--л. о. называется лок-
локсодромическим ив нормальной форме C) ха-
характеризуется множителем (г ? С, | |х| Ф1, таким, что либо
Im \1фО, либо (г<0. Унимодулярное Д.-л. о. A) явля-
является локсодромическим тогда и только тогда, когда
+?CR
Если же две неподвижные точки сливаются в одну
?х, то Д.-л. о. наз. параболическим. Семей-
Семейство 2 состоит при этом из всех окружностей, имеющих
в |х общую касательную; каждая окружность 2 пере-
переходит сама в себя. Нормальная форма параболич.
Д.-л. о. имеет вид либо
^ a€C, афО,
при |х ф оо, либо
w = z-\-a, a?C, арО,
при gx=oo. Унимодулярное Д.-л. о. A) является
параболическим тогда и только тогда, когда a+d==t2.
Благодаря перечисленным богатым элементарным
свойствам, Д.-л. о. находят самое широкое применение
во всех разделах теории функций комплексного пере-
переменного и в различных прикладных дисциплинах. В ча-
частности, Д.-л. о. позволяют построить модель Лоба-
Лобачевского геометрии.
Среди подгрупп общей группы всех Д.-л. о. наиболее
важны, с точки зрения их применений для аналитич.
теории дифференциальных уравнений, теории автоморф-
ных функций и других вопросов анализа, дискретные
группы Г Д.-л. о. Элементарные дискретные группы
Д.-л. о.— это конечные группы; они изоморфны либо
циклическим группам вращений сферы Римана, либо
группам вращений правильных многогранников. Диск-
Дискретные группы Д.-л. о. Г, имеющие инвариантную
окружность у на С, общую для всех преобразований Г,
причем внутренность у при всех преобразованиях Г
переходит сама в себя, наз. фуксовыми группами. Лок-
содромич. Д.-л. о. не может быть фуксовым. Истори-
Исторически первым примером фуксовой группы была моду-
модулярная группа, возникшая в теории эллиптич. функций
(см. также Модулярная функция). Модулярная группа
состоит из всех унимодулярных Д.-л. о. A), у к-рых
коэффициенты а, Ь, с, d — целые действительные чис-
числа; действительная ось инвариантна относительно
модулярных Д.-л. о. Более сложны и менее изучены
неэлементарные группы Д.-л. о., не являющиеся фук-
фуксовыми,— клейноеы группы.
Д.-л. о. комплексного пространства С", re^l, наз.
невырожденное отображение
z = (z±, ..., zn) —>m=(it,1 . . .,wn) = (L1(z), . . ,,Ln(z))r
осуществляемое дробно-линейными функциями
aifeZl+... + Vn + b k = i
Наиболее важны тс Д.-л. о. С", к-рые продолжаются
в какую-либо компактификацию С™. Так, в простран-
пространство теории функций С™ продолжаются все линейные
преобразования, переставляющие координаты, а также
Д.-л. о. вида
z — izi, ..., zn)—>-w=(L1(z1), ..., Ln(zn)),
где Li,(zi;) — Д.- л. о. вида A) на плоскости z^. Порож-
Порождаемая перечисленными отображениями группа Д.-л. о.
совпадает с группой Aut С™ всех биголоморфных авто-
автоморфизмов компактификации С™. Соответствующая
подгруппа Aut U" с
исчерпывает все автоморфизмы единичного поликруга
цп— {Z?C™; |zy|<l, /==1, .. ., п}. В проективное
замыкание СР™ пространства С™ продолжаются Д.-л. о.,
у к-рых
в однородных координатах это продолжение имеет вид
Этими отображениями исчерпывается группа AutCP™
всех бнголоморфных автоморфизмов СР™. Автоморфиз-
Автоморфизмы единичного шара Вп= {z?C™ ; |z|<l} образуют
подгруппу Aut/?™ группы AutCP™, состоящую из всех
Д.-л. о. вида D), у к-рых коэффициенты подчинены
известным дополнительным условиям (см. [2], ч. 2).
Лит.: [1] II р и в а л о в И. И., Введение в теорию функций
комплексного переменного, 11 изд., М., 1967; [2] III а б а т Б. В.,
Введение в комплексный анализ, 2 изд., ч. 1—2, М., 1976; L3]
Стой лов С, Теория функций комплексного переменного,
пер. с рум., т. 1, М., 1962; [4] Форд Л. Р., Автоморфные
функции, пер. с англ., М.— Л., 1936.
Е. II. Долженко, Е. Д. Соломенцев, Е. М. Чирка.
ДРОБНО-РАЦИОНАЛЬНАЯ ФУНКЦИЯ — см.
Рациональная функция.
ДРОБНЫЙ ИДЕАЛ — подмножество Q поля част-
частных К коммутативной области целостности Л, имеющее
вид Q~a-lI, где a?R, афО, I — идеал кольца R.
В других терминах Q есть Л-подмодуль поля К, все
элементы к-рого допускают общий знаменатель, т. е.
существует алемент a?R, афО, такой, что ax?R для
всех x?Q- Д. и. образуют относительно умножения
полугруппу 5t с единицей R. Для дедекиндовых колец
и только для них эта полугруппа является группой.
Обратимые элементы полугруппы 31 наз. обрати-
обратимыми идеалами. Каждый обратимый идеал
имеет конечный базис над R.
Лит.: [1] 3 а р и с с к и й О., Самюэль П., Коммута-
Коммутативная алгебра, пер. с англ., т. 1, М., 1963; [2] Бур ба-
баки Н., Коммутативная алгебра, пер. с франц., М., 1971.
Л. А. Бокуть.
ДРОБНЫХ ШАГОВ МЕТОД — метод построения эко-
экономичных (в смысле числа операций) устойчивых раз-
разностных схем для решения дифференциальных урав-
уравнений математич. физики.
При увеличении размерности задачи число операций
для получения численного решения растет как вслед-
вследствие роста числа точек, так и вследствие логич. труд-
трудностей составления программы расчета. Для системы
дифференциальных уравнений
ди Т ...
Lu (!)
где L = L(g-) — дифференциальный оператор, и=
= и(х, t), x= (xj, .. ., хп), абсолютно устойчивые неяв-
неявные схемы простой аппроксимации
п + 1 п
B)
становятся неэффективными в случае мпогомерных за-
задач. В одних случаях требуется использовать слишком
мелкий шаг но времени, в других нахогкдение каждого
un + i требует const •Лга<т) операций, где N— число точек
на одно измерение, т — число пространственных из-
измерений, а а(т) сильно растет с увеличением т.
Для получения экономичных устойчивых разност-
разностных схем предложены методы, основанные на следую-
следующих идеях:
1) расщепления разностных схем;
2) приближенной факторизации;
3) расщепления (слабой аппроксимации) дифферен-
дифференциальных уравнений.
В случае уравнения A) соответствующие разност-
разностные схемы имеют вид (для простоты взяты два дробных
шага и рассматривается периодич. задача Коши):
схема расщепления:
I + V2 n
JiJf+v
схема приближенной факторизации:
(Я — тЛц) (Е — тЛ12) W+1=(E + xQ) и", D)
схема слабой аппроксимации:
¦|^=(aiL1 + a,i,)« = L«, L = Lt + L1, E)
-i (t, т)==2, a2 (t, т) = 0 при t? [nx, ( n-\ — j x\ ,
,, (t, x)^0, a2(t, т)---2 при t
В случае схем C) и D) обращение оператора Е—xAt
заменяется обращением оператора (Е—тЛ11)(?'—тЛ12),
т. е. последовательным обращением операторов Е—
— тЛп, Е—тЛ12, вообще говоря, более простой струк-
структуры.
Трактовка E) позволяет рассматривать схему рас-
расщепления
как простую аппроксимацию уравнения E), слабо ап-
аппроксимирующего уравнение A).
Таким образом, в основе этих методов лежит пред-
представление сложных операторов через простейшие, при
этом интегрирование исходного уравнения сводится
к интегрированию уравнений более простой структуры,
а методы дробных шагов обязаны удовлетворять усло-
условиям аппроксимации и устойчивости только в оконча-
окончательном итоге (при записи их в «целых» шагах). Мето-
Методом расщепления решаются многие сложные задачи
математич. физики.
Большое развитие получили схемы расщепления
повышенного порядка точности. К одной из модифика-
модификаций метода расщепления принадлежит метод «частиц
в ячейках»: здесь расщепление производится по фи-
физическим процессам и не связано с понижением раз-
размерности операторов.
Лит.: [1] Я н е н к о Н. Н., Метод дробных шагов решения
многомерных задач математической физики, Новосиб., 1967;
[2] С а м а р с к и й А. А., Введение в теорию разностных схем,
М.. 1971. Н. Н. Яненко.
ДРОБОВОЙ ЭФФЕКТ — математическое описание
флуктуации напряжений на выходе линейной системы,
на входе к-рой действуют случайные возмущения,
возникающие в случайные моменты времени. Если
W(t, т) — выходная реакция системы в момент вре-
времени t на единичный импульс, приложенный в момент
времени т<:?, то Д. э. может быть описан случайным
процессом
X(*) = 2{ft:Tfe<i} OLkW(t, Tfe),
где . . . <т_1<т0<т1<. . . <Tft<. . .— моменты поступ-
поступления импульсов, а а/. — случайные величины, харак-
характеризующие величину интенсивностей импульсов. В ча-
частном случае, когда W(t, t)—W(t—x), W(s) = 0, s<0,
величины а/, суть независимые одинаково распределен-
распределенные случайные величины с конечной дисперсией, а
. . .<t_1<!Tq<Ti <!. . . образуют щ/ассоновский поток
событий с параметром X, процесс X (t) является стацио-
стационарным в узком смысле процессом с
EX (t) = "AEa1 \ W (s) ds,
DX (t) — ЯЕст.1 { °° W2 (s) ds.
Лит.: fl] Л о н и н г Д ж. X., Бонин Р. Г., Случай-
Случайные процессы в задачах автоматического управления, пер. с
англ., М., 1958. А. Н. Ширяев.
ДРОБЬ арифметическая — число, состоя-
состоящее из одной или из нескольких равных частей (долей)
единицы. Д. изображается символом -2- (или alb), где
а и Ъ — целые числа. Числитель а Д. -2- пока-
показывает число взятых долей единицы, разделенной на
столько долей, какова величина знаменателя Ъ.
Д. можно рассматривать также, как частное от деления
а на Ъ.
Д. -2- но меняется, если ее числитель и знаменатель
умножить на одно и то же отличное от нуля целое
число. Благодаря этому любые две Д. -2- и -2- можно
привести к общему знаменателю, т. е. заменить -2- и —¦
на равные им Д., имеющие один и тот же знаменатель.
Кроме того, Д. можно сокращать, поделив ее числитель
и знаменатель на одно и то же число, вследствие чего,
всякую Д. можно представить в виде несократимой,
т. е. такой, у к-рой числитель и знаменатель не имеют
общих множителей.
Сумма и разность Д. -2- и -?- с одинаковыми знаме-
знаменателями определяются по правилу:
а . с а±с
Т ± ~ъ~ ~ ~ь~~ ¦
Чтобы сложить или вычесть Д. с разными знаменате-
знаменателями, надо предварительно привести их к общему зна-
знаменателю. Обычно в качестве общего знаменателя дро-
дробей -~ и — берется наименьшее общее кратное чисел Ь
и d. Умножение и деление Д. производятся по прави-
правилам:
а с A-е п с (i-d
b d b-d ' b ' d Ъ с
Д. — наз. правильной, если ее числитель
меньше знаменателя, и неправильной — в про-
противном случае. Д. наз. десятичной, если ее
знаменатель является степенью числа 10 (см. Десятич-
Десятичная дробь).
Формальное определение дробей.
Д. могут быть определены как упорядоченные пары
целых чисел (а, Ь), где Ъ ФО, для к-рых задано отно-
отношение эквивалентности (отношение равенства Д.),
а именно, считается, что (а, Ь)= (с, d), если ad=bc.
Кроме того, во множестве Д. определены операции
сложения, вычитания, умножения и деления, подчи-
подчиненные следующим правилам:
(а, 6)± (с, d)=(ad±bc, bd),
(а, Ъ)-(с, d)=(ac, bd),
(а, Ъ) : (с, d)^= (ad, be)
(таким образом, деление определено только в том
случае, когда сфО).
Подобное определение Д. удобно для обобщений и
принято в современной алгебре (см. Частных кольцо).
ДРУЖЕСТВЕННЫЕ ЧИСЛА — пара натуральных
чисел, каждое из к-рых равно сумме собственных де-
делителей другого, т. е. делителей, отличных от самого
числа. Определение Д. ч. имеется уже в «Началах»
Евклида, а также в трудах Платона. Древним грекам
была известна одна пара Д. ч.: 220 и 284; суммы их
делителей соответственно равны
1 + 2+4+5+10+11 + 20+22+44+55+110=284
1 + 2+4+71 + 142 = 220.
Л. Эйлер (L. Euler) отыскал около 60 пар Д. ч.
Несколько сот Д. ч. удалось найти с использованием
ЭВМ. Неизвестно, однако, существует ли пара Д. ч.,
одно из которых четное, а другое нечетное.
А. И. Галочкин.
ДУАЛЬНАЯ АЛГЕБРА — топологическая алгебра,
в к-рой для любого замкнутого левого (соответственно
правого) идеала / левый аннулятор правого (соответ-
(соответственно правый аннулятор левого) аннулятора идеала
/ совпадает с /. Наибольший интерес представляют
вопросы реализации Д. а. в виде алгебр операторов и
установление связей между свойствами аннулятор-
ности и дуальности топологич. алгебр различных клас-
классов^ частности комплексных банаховых алгебр с ин-
инволюцией, в том числе гильбертовых алгебр и С*-
алгебр.
С*-алгебра вполне непрерывных линейных операто-
операторов в гильбертовом пространстве и гильбертова алгеб-
алгебра операторов Гильберта — Шмидта в гильбертовом про-
пространстве — Д. а. Всякая дуальная банахова алгебра,
являющаяся С*-алгеброй, изоморфна пополнению ал-
алгебраической прямой суммы алгебр вполне непрерыв-
непрерывных операторов в нек-рых гильбертовых пространствах.
Всякая полная гильбертова алгебра дуальна; она изо-
изоморфна прямой ортогональной сумме гильбертовых
алгебр операторов Гильберта — Шмидта в нек-рых
гильбертовых пространствах. Всякая полупростая Д. а.
с непрерывным квазиобратным — пополнение прямой
суммы всех своих минимальных замкнутых двусторон-
двусторонних идеалов, к-рые являются топологически простыми
Д. а.; топологически простая Д. а. А может быть реа-
реализована как алгебра непрерывных линейных опера-
операторов в нек-ром топологическом векторном простран-
пространстве Е, содержащая множество К(Е) конечномерных
непрерывных линейных операторов в Е; если А —
банахова алгебра, то образ А при этой реализации
содержится в равномерном замыкании F(E) алгебры
К(Е). С другой стороны, существует рефлексивное
банахово пространство Е такое, что (топологически
простая, аннуляторная) банахова алгебра F(E) не
является дуальной.
Лит.: [1] На им ар к М. А., Нормированные кольца,
2 изд., М., 1968; [2] D a v i e A. M., «Bull. London Math. Soc»,
1973, v. 5, № 1, p. 79—80. А. И. Штерн.
ДУАЛЬНАЯ ПАРА — пара (Е, Е') векторных про-
пространств над одним и тем же полем вместе с невырож-
невырожденной билинейной формой (х, х') на ЕХЕ'. См. Двой-
Двойственность в теории топологических векторных про-
пространств. М. И. Войцеховский.
ДУБЛЕТ — упорядоченная пара гиперплоскостей
n-мерного аффинного пространства. Задание Д. равно-
равносильно заданию ковариантного вектора. В центроаф-
финной геометрии Д. определяется единственной ги-
гиперплоскостью — краем Д. М. И. Войцеховский.
ДУБЛЬ РИМАНОВОЙ ПОВЕРХНОСТИ — двулист-
двулистная накрывающая поверхность W конечной римановой
поверхности R. Каждой внутренней точке p?R ста-
ставится в соответствие пара точек р и р Д. р. п. W;
иными словами, над р расположены две сопряженные
точки Д. р. п. р и р. Каждой точке q края R ставится
в соответствие одна точка q?W. При этом над каждой
окрестностью внутренней точки p?R расположены
две непересекающиеся окрестности точек р, p?W.
Если z — локальная униформизмруюшая в окрестности
внутренней точки p^R, то она же будет локальной
униформизирующей в VF-окрестности одной из двух
сопряженных точек W, лежащих над р, скажем в W-
окрестности точки р ? W; тогда в VF-окрестности со-
сопряженной точки р униформизирующей является ком-
комплексно сопряженная z переменной z. Если z — ло-
локальная униформизирующая в точке q края R, то уни-
униформизирующей в лежащей над ней точке q?W яв-
является переменная, равная z на одном листе W и z —
на другом.
Для случая компактной ориентируемой римановой
поверхности R Д. р. п. W состоит просто из двух
компактных ориентируемых римановых поверхностей,
и поэтому в этом случае его рассмотрение интереса не
представляет. Во всех остальных случаях Д. р. п. W —
компактная ориентируемая риманова поверхность,
что и позволяет упростить исследование нек-рых
вопросов теории функций на R путем сведения их к
исследованию функций на W- Род W равен g-\-m—1,
где g — род R, т — число компонентов края Л, пред-
предполагаемых невырожденными. Например, дублем одно-
связной плоской области является сфера, а дуб-
дублем m-связпой плоской области — сфера с т—1 руч-
ручками.
Аналитические дифференциалы на римановой по-
поверхности R среди аналитич. дифференциалов на Д. р. п.
W характеризуются тем, что они принимают сопряжен-
сопряженные значения в сопряженных точках W и действи-
действительных значениях в точках q?W, лежащих над
точками края R.
Лит.: [1] Щ и ф ф е р М., Спенсер Д. К., Функционалы
на конечных римановых поверхностях, пер. с англ., М., 1957;
[2] Р i с а г d E., Traite" d'analyse, t. 2, P., 1893.
E. Д. Соломенцев.
ДУГА, простая дуга, жорданова
дуг а,— часть кривой, заключенная между двумя
ее точками (и не содержащая кратных точек). Д. на
плоскости определяют, задавая координаты ее точек
как непрерывные функции x=q>(t), y=ty(t) некоторо-
некоторого параметра t, а-<г<:6; при этом предполагают,
что различным значениям t соответствуют различные
точки.
ДУГА БЕЗ КОНТАКТА — гладкая кривая без само-
самопересечений на фазовой плоскости двумерной автоном-
автономной системы дифференциальных уравнений
х = Р(х, у), y = Q(x, у), (*)
обладающая тем свойством, что в каждой точке этой
кривой вектор фазовой скорости системы (см. Фазовой
скорости вектор) определен, отличен от нуля и не
является касательным вектором к кривой. Это понятие
было введено А. Пуанкаре (Н. Poincare, [1]); оно ши-
широко используется в качественной теории дифференци-
дифференциальных уравнений (см. [2]). Через любую обыкновен-
обыкновенную точку произвольной траектории системы (*)
можно провести, напр., отрезок без контак-
т а достаточно малой длины. Д. б. к. характеризуется
тем, что все траектории системы (*), пересекающие эту
кривую, пересекают ее в одном направлении. Если
производная в силу системы (*) (см. Дифференциро-
Дифференцирование в силу системы) в каждой точке гладкой кривой
не обращается в нуль, то эта кривая есть Д. б. к.
Замкнутая Д. б. к. наз. циклом без кон-
контакта.
Лит.: ШПуанкаре А., О кривых, определяемых диф-
дифференциальными уравнениями, пер. с франц., М.— Л., 1947; [2J
Л е ф ш е ц С, Геометрическая теория дифференциальных урав-
уравнений, пер. с англ., М., 1961. Н. X. Розов.
ДУГЛАСА ЗАДАЧА — см. Плато задача.
ДУФФИНГА УРАВНЕНИЕ — обыкновенное диффе-
дифференциальное уравнение 2-го порядка
х"-\-kx'-\-<а\х-^ ах3 = F cos coi, (*)
где /с>0, со0, a, F, со — постоянные. Это уравнение
представляет собой важный пример системы (с одной
степенью свободы) с нелинейной восстанавливающей
силой f(x)= — (Oo.z—ах3 и затуханием, совершающей
вынужденные колебания при гармоническом внешнем
воздействии F(()=Fcos(Oi. При а>0 говорят о жесткой
упругой силе, а при а<0 — о мягкой. Впервые ис-
исследование решений уравнения (*) предпринял Г. Дуф-
финг (G. Duffing, [1]).
Решения Д. у. в замкнутой форме получить не уда-
удается. Доказано, что оно имеет большое число разно-
разнообразных периодич. решений. В уравнении (*) возможны
гармония, колебания x=Acoswt с амплитудой А =А (со),
к-рая является функцией частоты (амплитудная кри-
кривая); для нок-рых значений частоты со могут иметь
место несколько видов колебаний, отличающихся по
амплитуде. При определенных условиях в Д. у. воз-
возникают субгармонич. колебания с частотами со/л, где
п — целое число. Для изучения решений уравнения
(*) часто применяются методы малого параметра.
Лит.: [1] Duffing G., Erzwungene Schwingunsen bei
veranderlicher Eigenfrequenz und ihre technische Bedeulung.
Braunschweig, 1918; [2] С т о к е р Д., Нелинейные колебания в
механических и электрических системах, пер. с англ., 2 изд.,
М., 1953; [3] X а я с и Т., Нелинейные колебания в физических
системах, пер. с англ., М., 1968. Н. X. Розов.
ДУЭЛЬ — игра с выбором момента времени, описы-
описывающая конфликт следующего типа. Два противника
могут стрелять друг в друга в течение нек-рого отрезка
времени, располагая при этом оружием, имеющим
ограниченное количество боеприпасов. Стратегиями
игроков являются выборы моментов стрельбы. Функция
выигрыша определяется как математич. ожидание
нек-рой заданной случайной величины, принимающей
конечное число значений, соответствующих возможным
исходам Д. В зависимости от информации о действиях
противника Д. делятся на шумные и бесшумные (ти-
(тихие). Напр., если каждый из противников имеет по
одному выстрелу, к-рые они могут произвести в ин-
интервале [О, 1], функции меткости (т. е. вероятности
попадания игроков I и II) соответственно равны р(х)
и q(y), и если игрок I получает 1, когда он убивает II,
теряет 1, когда гибнет сам, и выигрыш равен 0 в ос-
остальных случаях, то функции выигрыша К (х, у) в
шумной и бесшумной Д. равны:
шумная Д.
P(x) — (i—p(x)) sup q(y), x < у,
У > *
К(х, у)^< p(x) — q(x), х = У,
— ?Ы + A— 9 (У)) sup p(x), х>у;
\ х> У
бесшумная Д.
К(х, у)=\ p(x) — q(x), .т=у,
I ?W+(l-?(!l))fW, *> У-
Рассматриваются Д., в к-рых противники располагают
несколькими выстрелами или же могут расходовать
имеющиеся ресурсы непрерывно.
Лит.: [1] Кар лин С, Математические методы в теории
игр, программировании и экономике, пер. с англ., М., 19В4.
Е. Б. Яновская.
ДЬЁДОННЕ МОДУЛЬ — модуль М над кольцом
Витта векторов W(k), где к — совершенное поле харак-
характеристики р>0, снабженный двумя эндоморфизмами
Рм и Vmi удовлетворяющими следующим соотношениям:
FM (VM () = VM (FM (m)) = pm.
Здесь m?M, @= (a0, . . ., an, ...)?W(k), co(/"= (a,
..., an, ...)¦ Эквивалентное определение состоит в
том, что М есть левый модуль над кольцом D ^ (к о л ь-
ц о м Д ь ё д о н н е), порожденным W(k) и двумя
переменными F и V связанными соотношениями
/Чв = ш<я> F, a>V=V<x>iP\
FV=VF = p, a?W (k).
Для любого целого п>0 существует изоморфизм
n ~ End* (Wntt),
где D kV" — левый идеал, порожденный V", a Wnk—
усеченная /с-схема Витта. Д. м. играют важную роль
в классификации унипотентных коммутативных алге-
алгебраических групп (см. [1]). Д. м. наз. также левые
модули над пополнением D ь кольца D & относительно
топологии, порождаемой степенями двустороннего идеа-
идеала (F, V) кольца Dk-
Лит.: [1] D i e u d о n n ё J., «Amer. J. Math.», 1957, v. 79,
№ 2, p. 331—88; [2]Demazure M., Gabriel P., Groupes
algebriques, t.l, P.— Amst., 1970; [3] M а н и н Ю. И., «Успехи
чатем наук», 1963, т. 18, в. 6, с. 3—90. И. В. Долгачев.
ДЮАМЕЛЯ ИНТЕГРАЛ — представление решения
Коши задачи или смешанной задачи с однородными
граничными условиями для неоднородного линейного
уравнения с частными производными через решение со-
соответствующей задачи для однородного уравнения.
Пусть для уравнения
Э'цэ(/; X) + L[u(t, x)]=f(t, x); t>0,x?Rn, A)
где L — линейный дифференциальный оператор с не-
независящими от t коэффициентами, содержащий произ-
производные по ( не выше 1-го порядка, поставлена задача
Коши с начальными условиями:
И пусть достаточно гладкая функция v(t, x; т), ,
т:==0, х ? Rn, является при t>x решением однородного
уравнения
d2v%^x) + L[v(t, х- т)]=0,
удовлетворяющим при t=i начальным условиям:
Тогда решение задачи Коши A), B) выражается Д. и.:
Сформулированное утверждение носит название п р и н-
ципа Дюамеляи является аналогом метода ва-
вариации постоянных.
Аналогичное построение можно провести и в случае
задачи Коши с однородным начальным условием для
уравнения
du(tmx) + M [и (t, х)] =/ (t, х); t > 0; i?Rn,
где М — линейный дифференциальный оператор с не-
независящими от ( коэффициентами, содержащий про-
производные только по переменным х.
Решение задачи Коши с однородными начальными
условиями для неоднородного уравнения теплопровод-
теплопроводности выражается Д. и.
п i х — \ I2
[4n(f-x)fT е "<'-*> /(т,
а для волнового уравнения в случае я=1
Д. и. наз. по имени Ж. Дюамеля (J. Duhamel).
Лит.: [1] Т и х о н о в А. Н., Самарский А. А., Урав-
Уравнения математической физики, 3 изд., М., 1966; [2] Й о н Ф.,
Плоские волны и сферические средние в применении к дифферен-
дифференциальным уравнениям с частными производными, пер. с англ.,
М,, 1958. А. К. Гущин.
ДЮБУА-РЕЙМОНА ЛЕММА, Дю-Буа-
Реймонда лемма: если N (х) — непрерывная
функция на отрезке [х^ х2] и если для всех дифферен-
дифференцируемых функций г) (ж), обращающихся в нуль при
х=х1, х=х2, справедливо соотношение:
[Х'г\' (х) N (х) dx = 0,
то A'(-r) = const на отрезке \хи х2]; сформулирована
П. Дюбуа-Реймоном [1].
Д.-Р. л. применяется в вариационном исчислении
для вывода Эйлера уравнения в интегральной форме
и при этом позволяет не предполагать заранее, что
экстремум функционала достигается на дважды диф-
дифференцируемой кривой — достаточно предположения
о непрерывной дифференцируемое™.
Лит.: ll] D u Bois-Reymond P., «Math. Ann.»,
1879, Bd 15, S. 313; [2] Лаврентьев М. А., Л ю с т е р-
н и к Л. А., Курс вариационного исчисления, 2 изд., М.— Л.,
1950 И. Б. Вапнярский.
ДЮБУА-РЕЙМОНА ПРИЗНАК сходимости ря-
ряда: ряд ^] ап^>т гДе ап и Ьп—комплексные числа, схо-
сходится, если рядУ Ь„ сходится, а ряд У1. (ап—ап + 1)
абсолютно сходится. Установлен П. Дюбуа-Реймоном
(P. Du Bois Reymoild). Л Д Кудрявцев.
ДЮБУА-РЕЙМОНА ТЕОРЕМА о единствен-
единственности разложения функции в ряд:
если сумма всюду сходящегося тригонометрия, ряда
интегрируема по Риману, то этот ряд является ее рядом
Фурье; доказана П. Дюбуа-Реймоном [1]. Важный част-
частный случай сходимости тригонометрия, ряда к нулю
несколько ранее рассмотрел Г. Кантор [2].
Д.-Р. т. обобщалась в различных направлениях.
Для интеграла Лебега с условием ограниченности
суммы аналогичную теорему доказал А. Лебег (Н. Le-
besgue), без этого условия — Ш. Ж. Балле Пуссен
(Ch. J. de la Vallee-Poussin) (см. [З], с. 200, 789). Име-
Имеются аналоги этой теоремы для интегралов Данжуа
(см. [5]).
Другое направление обобщений заключается в ос-
ослаблении условия сходимости всюду. У. Юнг (W. Young)
доказал, что можно пренебрегать счетным множеством
(см. [3], с. 792), Д. Е. Меньшов показал, что нельзя
пренебрегать любым множеством меры нуль (см. Мень-
Меньшова пример нуль-ряда пли [3], с. 804). О дальнейших
работах в этом направлении см. [3], [4]. Еще одно на-
направление обобщений получается при замене требо-
требования сходимости требованием суммируемости. Впер-
Впервые этим стал заниматься М. Рисе (М. Riesz, [4]).
Лит.: [l]Du Bois-Reymond P., «Abh. Akad. Wiss.
Math.-Phys. Kl.», 1876, Bd 12, Tl 1, S 117—06; [2] Cantor
G., «Math. Ann.», 1872, Bd 5, S. 123 — 32; [3] Б а р и Н. К.,
Тригонометрические ряды, М., 1961; [4] Зигмунд А.,
Тригонометрические ряды, т. 1—2, пер. с англ., М., 1965; [5]
Виноградова И. А., Скворцов В. А., в сб.; Итоги
науки. Математический анализ. 1970, М., 1971, с. 65—107.
Т. П. Лукашенко.
ДЮПЕНА ИНДИКАТРИСА, индикатриса
кривизны,— плоская кривая, к-рая дает нагляд-
наглядное представление об искривленности поверхности
в данной ее точке. Д. и. лежит в плоскости, касательной
к поверхности S в точке Р, и яв-
является совокупностью концов от-
отрезков, отложенных от точки Р
в направлении I в касательной
плоскости и имеющих длину,
равную l/y\Ki\, где \Kt\ — аб-
абсолютная величина нормальной
кривизны поверхности S в точке
Р в направлении I. Пусть v—
=r(u, v) — параметрич. уравнение
поверхности S в окрестности точки Р. Введем декар-
тову систему координат на плоскости, касательной к S
в точке Р, принимая точку Р за начало координат,
векторы га и rv за базисные векторы этой координатной
системы. Тогда уравнение Д. и. имеет вид
\Lx2-\-2Mxy+Nif\ = i,
где х ш у — координаты точки Д. и., a i, M и N —
коэффициенты второй квадратичной формы поверхно-
поверхности S, вычисленные в точке Р. Д. и. представляет со-
собой: а) эллипс, если Р — эллиптическая точка (окруж-
(окружность, если Р — округления точка); б) пару сопряжен-
сопряженных гипербол, если Р — гиперболическая точка; в) пару
параллельных прямых, если Р — параболическая точка.
Д. и. названа по имени Ш. Дюпена (Ch. Dupin), впер-
впервые приментшшего эту кривую к исследованию поверх-
поверхностей A813).
Лит.: [1] К а г а н В.Ф., Основы теории поверхностей в тен-
тензорном изложении, ч. 2, М.— Л., 1948. Е. В. Шикин.
ДЮПЕНА ТЕОРЕМА: если даны три семейства
поверхностей, образующих триортогоналъную систему,
то линия пересечения каждых двух поверхностей раз-
различных семейств будет линией кривизны для каждой
из этих поверхностей. Напр.. софокусные центральные
поверхности 2-го порядка пересекаются по линиям
кривизны. Д. т. названа по имени Ш. Дюпона, к-рому
принадлежит ее первое доказательство [1].
Лит.: [1] Dupin Ch., Devcloppements de geometrie, P.,
1813; [2] К а г а н В. Ф., Основы теории поверхностей в тензор-
тензорном изложении, ч. 1, М.— Л., 1947. Е. В. Шикин.
ДЮПЕНА ЦИКЛИДА — поверхность, оба семейства
линий кривизны к-рой состоят из окружностей, так что
она является частным случаем каналовой поверхности.
Обе полости эволюты Д. ц. вырождаются в кривые 1\
п Г2, являющиеся фокальными кривыми 2-го порядка.
Различают Д. ц. трех типов.
1) Эволюты — эллипс и гипербола, радиус-вектор
соответствующей Д. ц.:
^ Vb sin и Ub sh v Va cos и + Vc ch у
x ~~ u + v ' y ~~ u + v ' z ~~ WTv '
где
U=ccosu-'-d, F= — ac\\v—d, d=const.
2) Эволюты — фокальные параболы, радиус-вектор:
_ Vи _ Uv _ V (:1и2-р2)-и Bv"-p")
X~U + V' 1J~U+V' Z~" Up (U + V) '
где
тг 2u2 +- p^q -c7 2r2- P2~(/3
U= uP > F= 7p—L' 9 = const.
3) Эволюты — окружность и прямая, соответствую-
соответствующая Д. ц.— тор.
Д. ц. являются алгебраическими поверхностями 4-го
порядка в случаях 1) и 3) и 3-го порядка — в случае
2).
Лит.: [1] Dupin С п., Developpements de Keometrie,
Р , 1813; [2] Клейн Ф., Высшая геометрия, пер. с нем
М.— Л., 1939. И. X. Сабитов.
е, число е, — обозначение предела, к к-рому
/ 1 \п
стремится выражение ( 1-j ) при неограниченном
возрастании га:
е= lim fl+ — У = 2,718281 828459045. ..;
П -* к, \ П /
служит основанием натуральных логарифмов; е —
трансцендентное число, что впервые доказано в 1873
Ш. Эрмитом (Ch. Hermite). Иногда число е малообос-
малообоснованно называют неперовым числом.
С. А. Степанов.
ЕВКЛИДА АЛГОРИТМ — способ нахождения на-
наибольшего общего делителя двух целых чисел, двух
многочленов (и вообще, двух элементов евклидова
кольца) или общей меры двух отрезков. Описан в гео-
метрич. форме в «Началах» Евклида C в. до н. э.).
Для случая положительных целых чисел а^Ь этот
способ состоит в следующем. Деление с остатком числа
а на число Ь всегда приводит к результату а=?г6+61,
где частное п — целое положительное число, а остаток
Ъх либо 0, либо положительное число, меньшее 6,
СЪ. Производится последовательное деление:
где все п,- — положительные целые числа и 0<:&,-<&,- + 1,
до тех пор, пока не получится остаток, равный 0. Ряд
равенств (*) закончится так:
Последний положительный остаток bk в этом процессе
и является наибольшим общим делителем чисел а и 6.
Е. а. для многочленов или отрезков аналогичны Е. а.
для целых чисел. В случае несоизмеримых отрезков
применение Е. а. приводит к бесконечному процессу.
БСЭ-з.
ЕВКЛИДА ТЕОРЕМА о простых числах:
множество простых чисел является бесконечным («На-
(«Начала» Евклида, книга IX. теорема 20). Более точную
количественную информацию о множестве простых
чисел в натуральном ряде содержит Чебышева теорема
о простых числах и асимптотич. закон распределения
простых чисел. С. М. Вороний.
ЕВКЛИДОВА ГЕОМЕТРИЯ — геометрия простран-
пространства, описываемого системой аксиом, первое система-
систематическое (но не достаточно строгое) изложение к-рой
было дано в «Началах» Евклида. Обычно пространство
Е. г. описывается как совокупность объектов трех
родов, называемых «точками», «прямыми», «плоско-
«плоскостями»; отношениями между ними: принадлежности,
порядка («лежать между»), конгруэнтности (или по-
понятием движения); непрерывностью. Особое место в
аксиоматике Е. г. занимает аксиома о параллельных
(пятый постулат). Первая достаточно строгая ак-
аксиоматика Е. г. была предложена Д. Гильбертом
(D. Hilbcrt, см. Гильберта система аксиом). Существуют
модификации системы аксиом Гильберта и другие ва-
рианты аксиоматики Е. г. Напр., в векторно-точечной
аксиоматике за одно из основных понятий принято
понятие вектора; в основу аксиоматики Е. г. может
быть положено отношение симметрии (см. [5]).
Лит.: [1] Гильберт Д,, Основания геометрии, пер. с
нем., М.— Л., 1948; [2] К а г а н В. Ф., Основания геометрии,
ч. 1, М.— Л., 1949; [3] П о г о р е л о в А. В., Основания гео-
геометрии, 3 изд., М., 1968; [4] Энциклопедия элементарной ма-
математики, кн. 4, Геометрия, М., 1963; L5] Б а х м а н Ф., По-
Построение геометрии на основе понятия симметрии, пер. с нем.,
М., 1969. А. Б. Иванов,
ЕВКЛИДОВА СВЯЗНОСТЬ — дифференцпалыю-гео-
метрическая структура на евклидовом векторном рас-
расслоении, обобщающая Леви-Чиеита связность и ри-
манову связность в римановой геометрии. Гладкое век-
векторное расслоение наз. евклидовым, если каж-
каждый его слой обладает структурой евклидова вектор-
векторного пространства со скалярным произведением ( , },
так что для любых гладких сечений X и Y функция
(X, Y) является гладкой функцией на базе. Линейная
связность в евклидовом векторном расслоении наз.
евклидовой связностью, если при про-
произвольном параллельном перенесении любых двух век-
векторов их скалярное произведение остается постоянным.
Это равносильно тому, что метрич. тензор, определяю-
определяющий скалярное произведение { , ) в каждом слое,
ковариантно постоянен. Е. с. в касательном векторном
расслоении риманова пространства является римановой
связностью. Иногда термин «Е. с.» применяется только
в этом смысле, и тогда «римапова связность» означает
связность Леви-Чивита. ю. Г. Лумисте.
ЕВКЛИДОВО КОЛЬЦО — область целостности с
единицей такая, что всякому ее элементу а, отличному
от нуля, поставлено в соответствие неотрицательное
целое число п(а), причем выполняется следующее
требование: для любых двух элементов а, Ь, если 6=И=0,
можно так подобрать элементы q и г, что
a=bq+r,
причем или г=0, или n(r)<n(b).
Всякое Е. к. является главных идеалов кольцом и,
следовательно, факториалъным кольцом, однако, су-
существуют кольца главных идеалов, не являющиеся
евклидовыми. К числу Е. к. принадлежат кольцо
целых чисел (роль п(а) в нем играет абсолютная вели-
величина \а\), а также кольцо многочленов от одного пере-
переменного над полем (и(а) — степень многочлена). Во
всяком Е. к. для разыскания наибольшего общего
делителя двух элементов можно применять Евклида
алгоритм.
Лит.: [1] К урош А. Г., Лекции по общей алгебре,
2 изд., М., 1973. О. А. Иванова.
ЕВКЛИДОВО ПОЛЕ — упорядоченное поле, в к-ром
каждый положительный элемент является квадратом.
Напр., поле R действительных чисел — Е. п. Поло
Q рациональных чисел не является Е. п. в. л. Попов.
ЕВКЛИДОВО ПРОСТРАНСТВО — пространство,
свойства к-рого описываются аксиомами евклидовой
геометрии. В более общем смысле Е. п.— конечномер-
конечномерное действительное векторное пространство Rn со
скалярным произведением (х, у), х, y?Rn, к-рое в над-
надлежащим образом выбранных координатах (декарто-
(декартовых)
ж = (л:1, ..., х„) и !/ = (!/], ..., уп)
выражается формулой
1
Е. Д. Соломенцев.
ЕГОРОВА СИСТЕМА поверхностей — триор-
тогональная система 2, состоящая из потенциальных
поверхностей; названа по имени Д. Ф. Егорова, под-
подробно рассмотревшего (под названием потенциальных
систем) в 1901 (см. [1]) общую теорию и многочислен-
многочисленные примеры систем указанного впда. Е. с. 2 может
быть определена как система, допускающая (однопара-
метрическую) группу преобразований, переводящих 2
саму в себя таким образом, что нормали в соответст-
соответственных точках 2 остаются параллельными. Механи-
Механическим истолкованием этой группы служит перено-
переносящее поверхности Е. с. стационарное течение жид-
жидкости, имеющее потенциал скоростей.
Пусть
и''(х, V, z] = const, S = l, 2, 3,
— уравнения поверхностей, образующих Е. с. 2, Н; —
коэффициенты Ламе, фигурирующие в выражении
квадрата линейного элемента пространства в криволи-
криволинейных координатах {и'}:
Pi — расстояние начала координат от трех касатель-
касательных плоскостей 2, Д,^—главные радиусы кривизны
поверхности u'=const, соответствующие элементу дуги
Hkduk, P;ft=—HjjRik — величины, через к-рые вы-
выражаются линейные элементы do; сферич. изображений
поверхностей:
(<*а,-J = Р?й (du*)* + tfi (duty, 1фкф1.
Функции Р{ и Н/ удовлетворяют одной и той же си-
системе уравнений:
d
Решения этих уравнений определяют еще две Е. с.
2j и 2_х того же сферич. изображения, для к-рых
Продолжение этого преобразования в ту и другую
стороны дает ряд Е. с. (р я д Егорова)
..., 2_2, *j —1, 2, 2Х, 22, ...
одного сферич. изображения, из к-рых каждая следую-
следующая 2 k+i получается из предыдущей 2^ с помощью
формул:
D(ft + 1) Tr(k)
г I — Jlj .
И вообще, изыскание сферич. изображения Е. с. 2
приводится к изысканию потенциальной системы на
сфере: любую такую систему можно приЕять за сферич.
изображение одного из трех семейств, составляющих 2.
Е. с. 2 характеризуется тем, что
»г_ да
ди1
где ш — некоторая функция, имеющая смысл потен-
потенциала скоростей соответствующего течения, т. е. м'=
= const — потенциальные поверхности. При этом, для
любой потенциальной поверхности S определяется
Е. с. 2, в состав к-рой входит S. Касательная к линии
пересечения какой-либо поверхности <о= const с по-
поверхностью u' = const в любой точке параллельна лучу
V, соединяющему центры геодезич. кривизн линий
кривизны поверхности и'=const; во всякой точке
пространства три луча Р-, I2, I3 параллельны одной и
той же плоскости — касательной плоскости поверх-
поверхности ш= const, а соприкасающиеся плоскости коор-
динатных линий проходят через одну прямую. Вели-
Величины Р,Л и Лik для Е. с. удовлетворяют соотношениям:
(симметричность р,^ так?ке необходима и достаточна
для того, чтобы триортогональная система была Е. с).
Лит.: [1] Е г о р о в Д. Ф., Работы по дифференциальной
геометрии, М., 1970. М. И. Войцеховский.
ЕГОРОВА ТЕОРЕМА о связи между понятиями
сходимости почти всюду и равномерной сходимости
последовательности функций: пусть и. есть сг-аддитив-
ная мера, определенная на сг-алгебре ©ц, ??2ц и по-
последовательность ^-измеримых почти везде конечных
функций fk(x), х?Е, к={, 2, . . ., сходится почти всюду
к функции }{х)\ тогда для любого е>0 существует такое
измеримое множество ЕъсЕ, что ji (Е\Ее)<Се, и на
множестве Ее последовательность f it(x) сходится к
функции f(x) равномерно. В случае, когда jx — мера
Лебега на прямой, это утверждение доказано Д. Ф. Его-
Егоровым [1].
Е. т. допускает различные обобщенные формулиров-
формулировки, расширяющие ее возможности. Пусть, напр.,
fk(x) — последовательность измеримых отображений
локально компактного пространства X в метризуемое
пространство Y, причем предел
lim fk(x)=l(x)
к -*¦ оо
существует локально почти всюду на X по Радона мере
(х^О. Тогда функция /: X—>-Y измерима по мере (х
и для любых компакта КаХ и числа g>0 найдется
компакт КхаК такой, что \и(КГ\ К1)<е, а сужения fk
на Кх непрерывны и равномерно сходятся на Кг к /.
Заключения Е. т. могут не выполняться, если Y не
метризуемо.
Лит.: [1] Егоров Д. Ф., «С.г. Acad. sci», 1911, t. 152,
p. 244—6; [2] Колмогоров А. Н., Фомин С. В.,
Элементы теории функций и функционального анализа, 4 изд.,
М., 1976. Л. Д. Кудрявцев.
ЕДИНИЦА —1) Наименьшее из натуральных чисел:1.
При умножении любого числа на 1 получается то же
самое число.
2) Элемент е множества М наз. левой (правой)
единицей по отношению к бинарной алгебраиче-
алгебраической операции *, определенной на множестве М, если
для любого элемента а^М выполняется равенство
Если существуют хотя бы одна левая Е. и хотя бы одна
правая Е., то они совпадают и других Е. нет. Если на
множестве М определено несколько бинарных операций
(напр., сложение и умножение в кольце), то Е. наз.
только Е. по отношению к одной из этих операций,
обычно по отношению к умножению. Е. по отношению
к сложению наз. тогда нулем.
3) Единицей решетки (структуры) наз. ее
наибольший элемент, т. е. Е. относительно операции
объединения.
4) Единицей, или делителем единицы,
области целостности К наз. всякий ее обратимый эле-
элемент, т. е. такой элемент е, для к-рого существует
обратный е и ее~1=1. Все Е. области целостности
образуют группу по умножению. Эта же терминология
иногда сохраняется и при переходе к полю частных
кольца К (т. е. единицами поля частных
наз. Е. самого кольца К). Напр., Е. поля алгебраич.
чисел к наз. единицы кольца целых алгебраич. чисел
поля к, р-адическими Е. наз. единицы кольца целых
р-адических чисел и т. д.
5) Единичный морфизм объекта в категории иногда
наз. просто единицей. о. А. Ивпнпва.
ЕДИНИЧНОЕ ПРЕДСТАВЛЕНИЕ — одномерное
представление группы G, сопоставляющее любому
элементу из группы G число 1. Е. п. иногда наз. также
тривиальным представлением. Е. п.
группы G в векторном пространстве Е наз. представ-
представление группы G, сопоставляющее любому элементу из
группы G единичный оператор в пространстве Е.
А. И. Штерн.
ЕДИНСТВЕННОСТИ МНОЖЕСТВО, U - м н о ж е-
с т в о,— множество ?cz[O, 2я] такое, что тригономет-
рич. ряд, сходящийся к нулю во всякой точке @, 2л]\.Е,
есть ряд нулей. Множество, не являющееся ^-множе-
^-множеством, наз. множеством неединственно-
неединственности, или Л/-множеством. Эти понятия связаны с
проблемой единственности представления функции схо-
сходящимся к ней тригонометрия, рядом всюду, за ис-
исключением, быть может, заданного множества Е.
Г. Кантор (G. Kantor, 1872) показал, что конечное (а
также пустое) множество является Е. м., и распро-
распространение этого результата на бесконечные множества
привело его к созданию множеств теории.
Множества положительной меры Лебега всегда яв-
являются Л/-множествами. Всякое счетное множество
есть ^/-множество. Существуют совершенные множества
меры нуль, к-рые являются как М-множествами
(Д. Е. Меньшов, 1916), так и ^/-множествами (Н. К. Ба-
Бари, 1921); напр., канторово множество с постоянным
рациональным отношением 9 является ^/-множеством
тогда и только тогда, когда 1/9 есть целое число, т. е.
свойство числового множества быть U- или Af-множе-
ством зависит от арифметич. природы составляющих
его чисел. Существуют, однако, такие множества
Ес[0, 2я] (так наз. ?'(е)-множества) полной меры, что
каждый тригонометрич. ряд, сходящийся к нулю в
каждой точке [0, 2я]\?' и имеющий коэффициенты
вида О(гп), где гп 10, есть ряд нулей.
Понятия U- и if-множества обобщаются и на ряды
Фурье — Стнлтьеса.
Лит.: [1] Бари Н. К., Тригонометрические ряды, М., 1961;
[2] 3 и г м у н д А., Тригонометрические ряды, т. 1— 2, пер. с
англ., [2 изд.], М., 1965; [3] Б а р и Н. К., «Успехи матем.
наук», 1949, т. 4, в. 3, с. 3—68. В. Ф. Емельянов.
ЕДИНСТВЕННОСТИ СВОЙСТВА аналитичес-
аналитических функций — свойства аналитич. функций,
состоящие в том, что они вполне определяются своими
значениями на нек-рых подмножествах точек их об-
области определения или границы этой области, в связи
с чем различают внутренние Е. с. и граничные Е. с.
Внутренние свойства единственности. Пусть D —
некоторая область плоскости С = С* комплексного
переменного z. Классическая внутренняя тео-
теорема единственности для голоморфных,
т. е. однозначных аналитич., функций в D утверждает:
если голоморфные в D функции /(z) и g(z) совпадают
на нек-ром множестве EczD, имеющем хотя бы одну
предельную точку в С, то /(z)s=g(z) всюду в D. Иначе
говоря, если голоморфная в D функция /(z) принимает
нулевые значения на множестве EczD, имеющем хотя
бы одну предельную точку в D, то /(z)=0. Доказатель-
Доказательство этого внутреннего Е. с. аналитич. функций пока-
показывает, что оно, в сущности, является Е. с. степенных
рядов по одному комплексному переменному z. E. с.
полностью сохраняется и для мероморфных в D функ-
функций /(z) и g(z), если рассматривать полюсы /(z) и g(z)
как точки, в к-рых функции принимают значение оо.
В частности, если две аналитич. функции /(z) и g(z)
совпадают на сколь угодно малой окрестности нек-рой
точки или на сколь угодно малой дуге нек-рой непре-
непрерывной кривой, то f(z)=g(z). Другое следствие: множе-
множество А-т о ч е к аналитич. функции /(z), т. е. таких
точек z, в к-рых f(z)=A, не может иметь предельных
точек внутри области определения D, если только
f()^A
Полные аналитические функции F(z), G(z) в смысле
Вейерштрасса, вообще говоря, мпогозначные, обладают
следующим внутренним Е. с: пусть f(z) и g(z) — одно-
однозначные элементы, или ветви полных аналитич. функ-
функций F(z) и G(z), определенные соответственно в обла-
областях D1 и D2, D1r\D2=i?=0. Тогда, если f(z) и g(z) сов-
совпадают на нек-ром множестве точек Ec:D1f\D2l имею-
имеющем хотя бы одну предельную точку zo?D1f\D2, то
функции F(z) и G(z) имеют одну и ту же область суще-
существования и всюду совпадают как полные аналитич.
функции.
На случай аналитич. функций f(z) многих комплекс-
комплексных переменных z= (zt, z2, ..., zn), ге>1, Е. с. в при-
приведенных формулировках не переносится. Напр., ана-
аналитич. функция f(z) = z1z2 не равна тождественно нулю,
но обращается в нуль на комплексно (п — 1)-мерных
аналитич. плоскостях гг = 0 и z2 = 0. Для таких функций
имеют место следующие Е. с:
1) Если /(z) — аналитич. функция в области D ком-
комплексного пространства С", обращающаяся в нуль во
всех точках нек-рого непустого открытого подмноже-
подмножества C'oD. то /(z)=0 в D.
2) Если /(z) — аналитич. функция в области DczC",
обращающаяся в нуль в нек-рой точке z°?.D вместе со
всеми частными производными ^f ^
k=k1+k.2+...+kn; k.-=0, 1, 2, ... ; /=1, 2, ..., n,
то /(z)=0 в D.
3) Если /(z) — аналитич. функция в области DdC",
обращающаяся в нуль в действительной окрестности
U$ точки z"=x°-\-iy°?D, т.е. на множестве U$= {z=
= x-\-iy?Cn; \x—xu\<r, у=у0}, то /(z)=0 в D.
Различие во внутренних Е. с. для случаев п = 1 и
п>1 обусловлено различием в поведении кратных сте-
степенных рядов по сравнению со степенными рядами по
одному переменному.
Граничные свойства единственности. Сформулирован-
Сформулированная выше внутренняя теорема единственности аналитич.
функций /(z) одного комплексного переменного допу-
допускает ряд обобщений на тот случай, когда нули f(z)
лежат не внутри области аналитичности D, а на ее
границе Г. Так, напр., если Г содержит жорданову
дугу о", причем всюду на сг существуют и равны нулю
граничные значения f(z) изнутри области D, то /(z)=0
в D. Наиболее общие и глубокие граничные теоремы
единственности получены Н. Н. Лузиным и И. И. При-
Приваловым в 1925. Пусть D — область плоскости z,
ограниченная спрямляемой кривой Г, и /(z) — меро-
морфная в D функция. Пусть ?0 — точка Г, в к-рой
существует касательная к Г; таким свойством обладают
почти все точки спрямляемой кривой. Говорят, что
функция /(z) имеет в точке ?0 угловое гранич-
граничное значение А, если / (z) стремится к А, когда
точка z стремится к ?0, оставаясь внутри пересечения
области D с внутренностью любого угла раствора мень-
меньше я с вершиной ?„ и нормалью к Г в ?0 в качестве
биссектрисы.
Справедлива граничная теорема един-
единственности Лузина — Привалова в
случае угловых граничных значе-
н и й: если мероморфная в области D, ограниченной
спрямляемой кривой Г, функция /(z) принимает угло-
угловые граничные значения нуль на множестве ?сГ
положительной лебеговой меры, то /(z)=0. Вообще
говоря, мероморфная функция .ножет и не иметь гра-
граничных значений на Г, но для довольно широких
классов мероморфных функций, напр. для функций
ограниченного вида, установлено существование угло-
угловых граничных значений почти всюду на Г.
Наряду с этим имеются примеры ограниченных ана-
аналитич. функций в единичном круге D, стремящихся к
нулю во всех смыслах на заданном множестве Е точек
единичной окружности Г меры нуль. Кроме того,
Н. Н. Лузин и И. И. Привалов построили примеры
аналитических в единичном круге D функций, имеющих
нулевые радиальные граничные значе-
н и я, т. е. стремящихся к нулю по радиусам, всюду на
нек-ром множестве ЕаТ полной меры 2я. Оказалось,
что в вопросах единственности весьма важно также
понятие категории множества по Бэру. Именно, спра-
справедлива граничная теорема единствен-
единственности Лузина — Привалова в случае
радиальных граничных значений:
если мероморфная в единичном круге D функция /(z)
имеет радиальные граничные значения нуль на множе-
множестве Е, расположенном на дуге а единичной окруж-
окружности Г, метрически плотном и второй категории по
Бэру на о", то /(z)=0. (Множество Е наз. метриче-
метрически плотным на а, если каждая порция ? на с
имеет положительную меру.)
См. также Граничные свойства аналитических функ-
функций, Предельное множество.
Исследование граничных Е. с. аналитич. функций
многих комплексных переменных еще (к 1978) не до-
достигло такой степени полноты, как для функций одного
переменного (см. [5], [6]).
Лит.: Ш М а р к у ш е в и ч А. И., Теория аналитических
функций, 2 изд., т. 1, М., 1967, гл. 3; [2] Ш а б а т Б. В., Вве-
Введение в комплексный анализ, М., 1969, ч. 1, гл. 2, ч. 2, гл. 1 и
ел.; [3] Привалов И. И., Граничные свойства аналитиче-
аналитических функций, 2 изд., М.—Л., 1950; [-4] К о л л и н г в у д Э.,
Ловатер А., Теория предельных множеств, пер. с англ.,
М., 1971; 15] Ру дин У., Теория функций в поликруге, пер.
с англ., М., 1974; [6] X е и к и н Г. М., Чирка Е. М., в кн.:
Итоги науки и техники. Современные проблемы математики,
т 4, М., 1975, с. 13—142. Е. Д. Соломенцев.
ЕДИНЫЕ ТЕОРИИ ПОЛЯ — собирательное назва-
название для попыток представить все или нек-рые (чаще
всего — гравитационное и электромагнитное) физич.
поля в виде проявлений одного фундаментального поля
подобно тому, как электрическое и магнитное поля —
проявления электромагнитного поля. Е. т. п. условно
можно разбить на два типа: в первом фундаментальным
полем является поле нек-рого геометрического объекта
в пространстве событий (напр., различные варианты
Е. т. п. А. Эйнштейна [1], геометродинамика); во вто-
втором — фундаментальное поле не имеет геометрич.
природы (напр., нелинейные сшшорные теории поля
[3], [4]). В нек-рых Е. т. п. удается получить удачные
оценки основных физич. констант.
Лит.: [1] Эйнштейн А., Собр. научных трудов, т. 2,
М., 1966; [2] У и л е р Д ж. А., Гравитация, нейтрино и Все-
Вселенная, пер. с англ., М,, 1962; [3]Гейзенберг В., Введе-
Введение в единую полевую теорию элементарных частиц, пер. с
англ., М., 1968; [4] Нелинейная квантовая теория поля. Сб.
статей, М., 1959. Д. Д. Соколов.
ЕМКОСТНЫЙ ПОТЕНЦИАЛ, равновесный
потенциал,— см. Емкость, Робела задача.
Е. Д. Соломенцев.
ЕМКОСТЬ множества — функция множества,
возникшая в потенциала теории как аналог физич.
понятия электростатич. емкости.
Пусть S и S* — две гладкие замкнутые гиперповерх-
гиперповерхности в евклидовом пространстве R", п^З, причем S*
олватывает S. Такую систему наз. конденсат о-
Р о м (S, S*). Пусть и(х) — гармонич. функция в
'-бласти D между S и S*, принимающая значения 1
на S и 0 на S*. Емкостью конденсатора
C{S, S*) наз. число
С \
I grad и (x) |2 dm, A)
где сгп=2яп/-/Г(п/2) — площадь единичной сферы в
R", ди/дп — производная по направлению внешней
нормали к любой промежуточной гиперповерхности
S', лежащей между S и S* и охватывающей S, do —
элемент площади S', dot — элемент объема. Иначе Е.
конденсатора C(S, S*) можно определить как нижнюю
грань интегралов
| grad v (x) |2 dut
(n-2)O
в классе всех непрерывно дифференцируемых в D
функций v(x), к-рые на S и S* принимают значения,
соответственно, 1 и 0. Если гиперповерхность S* =
= 5@, R) есть сфера достаточно большого радиуса Л
с центром в начале координат, то, переходя в A) к
пределу при Я—>-оо, получают емкость компак-
компакта^, ограниченного гиперповерхностью S, называ-
называемую также гармонической емкостью К,
или ньютоновой емкостью К:
С (#)= lim С (S, S @, Л)),
R ->¦ 00
при этом 0-<С(.йГ)<оо. Е. С(К) есть аналог электро-
статнч. Е. уединенного проводника К.
В случае плоскости R2 конденсатор (L, L*)
есть система двух гладких замкнутых непересекающих-
непересекающихся простых кривых L и L*, причем L* охватывает L.
Пусть и(х) — гармонич. функция в области D между
L и L*, принимающая значения 1 на I и 0 на L*. Е м-
костью конденсатора C(L, L*) наз. число
с ^ L*) = - к \ v д-^гds = к
где ds — элемент длины дуги линии L', лежащей между
L и L* и охватывающей L. Пусть кривая L*~S@, R)
есть окружность достаточно большого радиуса R с
центром в начале, тогда предельный переход при Л-^-оо
в формуле
дает винеровскую емкость, или посто-
постоянную Р о бен а, компакта К, ограниченного
линией L; винеровская Е. может принимать любые
значения, —оо <W(AT)<oo. Чаще используется лога-
логарифмическая емкость, называемая также
гармонической или конформной:
C(K) = e~W^= lim Re C(L, К@,Л))> B)
R -* x
к-рая изменяется в пределах 0<:С(А')<оо.
Е. компакта К, ограниченного гиперповерхностью
S, при п^З можно определить и несколько иначе.
Пусть vK(x) — емкости ы и, или равновес-
равновесный, потенциал этого компакта, т. е. гармони-
гармоническая всюду вне К, регулярная на бесконечности
функция, принимающая на S значение 1. Тогда
C)
где D' — внешность S. Формула C) показывает, что
Е. С(К) есть совокупная положительная мера (лE1),
распределенная на S и такая, что ньютонов потенциал
простого слоя, порождаемый этой мерой, в точности
совпадает с емкостным потенциалом v^(x), т. е.
Мора (л наз. емкостной, или равновесной,
м е р о й.
В классе всех положительных борелевских мер %
на К таких, что Х(К) = \х (S) = C(K), емкостная мера ц.
дает минимум интегралу энергии
хК \х-у ,"-
Иначе говоря, Е. С (К) можно определить формулой
C(K)=l/mf E(X), где нижняя грань берется в классе
всех положительных мер X, сосредоточенных на К
и нормированных условием Х(К)=1.
При п = 2, вследствие особого поведения логарифмич.
потенциала на бесконечности, вышеуказанное построе-
построение емкостного потенциала возможно только для кон-
конденсатора, напр, для (L, S@, Л)) при помощи Грина
функции G(x, у) для внутренности D" окружности
S@, R) в виде '
ик(х; S@, R))=\ G(x, y)dy,(y), x
C(L, 5@, R))=
тде емкостный потенциал ик (х; S@, R)) совпадает в D
с ранее введенной для конденсатора (L, S@, R)) гар-
ыонич. функцией и(х). Е., определяемая по формулам
E), иногда наз. г р и н о в о й емкостью; эта
конструкция возможна при любом п^2. Формула
W(K)=l/ini E(K) ,X(K) — i, при п=2 дает впнеровскую
Е. компакта К, так как интеграл энергии
теперь не всегда положителен.
Емкость произвольного компакта
i'cR", я^З. можно определить при помощи описан-
описанного свойства минимума энергии:
где интегралы Е (}.) вычисляются по формуле D). При
п = 2 такой путь приводит к определению в и н е р о в-
ской емкости произвольного ком-
компакта:
где энергия Е(X) вычисляется по формуле F). Переход
к логарифмич. Е. осуществляется по формуле С(К)=
Равносильный способ состоит в построении емкост-
емкостного потенциала vK (x) для произвольного компакта К.
При »^3 его можно определить как наибольший: из
потенциалов U}. (х) положительных мер К, сосредото-
сосредоточенных на К и таких, что t/'я (.?)¦< 1. Порождающая
ик (х) мера ц является емкостной, \i(K) = C(K). При
п = 2 построение емкостного потенциала, как и выше,
ведется для конденсатора (К, 5@, /?)) при помощи
функции Грина для круга D". Е. компакта С (К) по-
получается далее предельным переходом, как в фор-
формуле B).
Если v/( (ж) = 0, то С(АГ) = О. При п=2 равенства
С(ЛТ)=О и W(K} = -\-oo равносильны. Компакты нуле-
нулевой Е. играют в теории потенциала ту же роль, что и
множества меры нуль в теории интегрирования. Напр.,
равенство vK (x) = l на К имеет место всюду, за возмож-
возможным исключением множества точек, принадлежащего
нек-рому компакту нулевой Е. Потенциал любой
положительной меры, сосредоточенной на компакте К
нулевой Е., неограничен. Более того, для любого ком-
компакта К нулевой Е. существует сосредоточенная на К
положительная мера v такая, что Uv (х)=-\-оо при
х?К и Uv(x)<-\-oo при хфК, т.е. любой компакт
нулевой Е. является полярным множеством.
Свойства емкостных потенциалов
и емкостей компактов: 1) отображения
K-^-vK (x) и К-*-С(К) возрастающие, т. е. из включения
K1czK2 вытекает, что всюду v (x)<v (x), Cf-ft^)^
<iC(K2); 2) эти отображения непрерывны справа, т. е.
для любого фиксированного x?Rn и любого е>0
существует открытое множество со такое, что если ком-
компакт К' подчинен условиям КаК'сш, то всюду
vK,(x)-vK (х)<е, С(К') — С(К)<е; 3) vK(x) и С (К),
как функции К, с и л ь н о субаддитивны, т. е.
vKt U Кг W -'-"К, п Кг (х) < % (X) + VK2 (*),
С (Ki U Кг) + С (Ki Г\К2)^С (Кг) + С (К2).
Если G — открытое множество, лежащее в шаре
В = В@, R), то, по определению, Е. C{G) = C(B) —
— C\B\G). Для произвольного множества Е внут-
внутренняя ~Е._С(Е) определяется как верхняя грань
С (E) = sup C(K) по всем компактам КсЕ. Внеш-
Внешняя Е. С(Е) определяется как нижняя грань С(Е) —
= infC (G) по всем открытым множествам GzdE. Множе-
Множество Е наз. С-и змеримым, если С(Е) = С(Е) —
= С(Е). Все борелевские и даже аналитич. множества
в R" являются С-нзмеримыми. Таким образом, Е. С (Е)
представляет собой функцию множества, инвариантную
относительно движений, но не являющуюся, однако,
аддитивной. Особенно важна характеристика множе-
множества Е, даваемая условием, что его Е. С (Е) равна нулю.
Во многих вопросах теории потенциала множествами
нулевой Е. в определенном смысле можно пренебрегать.
Так, напр., справедливо следующее усиление
принципа максимума. Пусть w(x) — огра-
ограниченная сверху субгармонич. функция в области
GdR", я^З, °°фр; пусть неравенство lim sup w(x)<?.M
х-+у
имеет место для всех точек у ? dG, за возможным ис-
исключением множества Е, С(Е)--0, оо&Е. Тогда всюду
в G имеем w(x)^.M, причем знак равенства хотя бы
в одной точке возможен только в случае w(x)=M.
Понятие Е. обобщается в различных направлениях.
Исходя из понятия емкостного потенциала и емкостной
меры или энергии, теорию Е. строят для неньютоновых
потенциалов таких, как бесселевы потенциалы, нелиней-
нелинейные потенциалы, Рисса потенциалы и др. Эти постро-
построения позволяют, в частности, варьировать понятие мно-
множества нулевой Е. применительно к различным проб-
проблемам математич. физики и анализа (см. [6]).
По Г. Шоке (G. Choquet), E. компактов К в абстракт-
абстрактном отделимом тонологич. пространстве X определя-
определяется аксиоматически как числовая функция множе-
множества К-+С(К), удовлетворяющая аксиомам возра
стания, непрерывности справа и сильной субаддитив-
субаддитивности. Несколько иной подход к теории Е. в абстракт-
абстрактных пространствах X получается в рамках общей ак-
аксиоматики потенциала теории абстрактной или теории
гармонических пространств. В абстрактной теории Е.
основной является теорема Шоке, утверждаю-
утверждающая, что С-измеримыми являются К-& н а л и т и ч е-
с к и е множества, т. е. непрерывные образы
множеств типа Коб из нек-рого компактного простран-
пространства.
Вообще, в различных задачах теории функций, свя-
связанных главным образом с аппроксимацией в опреде-
определенных классах функций, весьма полезным оказалось
введение своих специфич. понятий Е. Так, напр.,
большое значение в вопросах приближения аналитич.
функциями имеет понятие аналитической емкости.
Пусть К — компакт на комплексной плоскости z,
f(z) — аналитич. функция вне К, |/(z)|<l, /(oo)=0;
аналитической Е. у(К) наз. число
у (К) = sup
где L' — контур, охватывающий К, и верхняя грань
берется по всем f(z), удовлетворяющим выписанным
условиям.
Лит.: [1] Л а н д к о ф Н. С, Основы современной теории
потенциала, М., 1966; [2] Брело М., Основы классической
теории потенциала, пер. с франц., М., 1964; [3] Полна Г.,
С ё г е Г., Изопериметрические неравенства в математической
физике, [пер. с англ.], М., 1962; [4] В г е 1 о t M., Ledures on
potential theory, Bombay, 1960; [5] Деллэшери К., Ем-
Емкости и случайные процессы, пер. с франц., М., 1975; [6]
К а р л е с о н Л., Избранные проблемы теории исключитель-
исключительных множеств, пер. с англ., М., 1971; [7] В и т у ш к и н А. Г.,
в кн.: Итоги науки и техники. Современные проблемы матема-
математики, т. 4, М., 1975, с. 5 —12. Е. Д. Со.гомснцев.
ЕРМАКОВА ПРИЗНАК сходимости число-
числовых рядов с положительными чле-
членам и: пусть f(x) — положительная убывающая при
x^i функция. Если при указанных х для Х<1 выпол-
выполняется неравенство
exf(ex) ,
/w ~~- '
то ряд
сходится; если выполняется неравенство
exf(ex) ,
/ <*) — '
то ряд расходится. В частности, если существует продел
( х\
Л < i
lim
1
то ряд сходится (расходится). Установлен В. П. Ер-
Ермаковым [1].
Лит.: [1] Е р м а к о в В. ГГ., Новый признак сходимости
и расходимости бесконечных знакопостоянных рядов, К., 1872.
Л. Д. Кудрявцев.
ЕСТЕСТВЕННО УПОРЯДОЧЕННЫЙ ГРУППОИД —
частично упорядоченный группоид Н, в к-ром все эле-
элементы положительны (т. е. a<ab и Ь<.аЪ для любых
а, Ъ?Н) и больший из двух элементов всегда делится
(и справа и слева) на меньший, т. е. из а<СЬ следует
ах=уа=Ь для некоторых х, у^Н, Положительный
конус любой частично упорядоченной группы являет-
является естественно упорядоченной полугруппой.
О. А. Иванова.
ЕСТЕСТВЕННЫЙ ЛОГИЧЕСКИЙ ВЫВОД — фор-
формальный вывод, по возможности приближенный к со-
содержательному рассуждению, привычному для мате-
матика и логика. Критерии естественности и качества
вывода не уточняются полностью, но обычно имеются
в виду выводы, осуществляемые по общеупотребитель-
общеупотребительным правилам логических переходов, компактные (в
частности, не содержащие излишних применений пра-
правил вывода), «склеенные» (повторяющиеся участки
выводов должны устраняться, напр., при помощи
вычленения вспомогательных лемм) и др.
Первоначально формализации логических и мате-
матич. теорий не преследовали целей естественности
(см. Логические исчисления); решающее продвижение
в атом направлении составило исчисление натуральных
выводов (см. Генцена формальная система), имити-
имитирующее форму обычных математич. умозаключений и
позволяющее вводить и использовать допущения при-
привычным образом. Довольно естественно выглядят и
приемы обращения с допущениями в секвенциальных
исчислениях, к-рые обладают дополнительным пре-
преимуществом — под форму льности свойством и поэтому
лежат в основе дальнейших продвижений в проблеме
построения Е. л. в.
Для автоматизации поиска Е. л. в. были предложены
[2] вспомогательные секвенциальные исчисления, об-
обладающие свойством подформульности, но запрещаю-
запрещающие переход допущений в сукцедент (см. Секвенция).
По выводу в таком исчислении легче строить Е. л. в.
На этой основе была разработана методика поиска
Е. л. в., включающая учет «родственностей» (т. е.
равных подформул в составе испытуемых формул) для
сокращения выводов и их «склеивания», «прополку»
излишних формул и применений правил, возможность
варьирования тактик установления выводимости и
др. В рамках логических средств классического вы-
высказываний исчисления эта методика была доведена до
машинного алгорифма (программа находила Е. л. в.
данного утверждения из данного списка гипотез и
записывала этот вывод в виде логико-математич.
текста на русском языке). К проблеме поиска Е. л. в.
примыкают задачи корректирования гипотез и усиле-
усиления теорем (речь идет о методах, позволяющих вводить
в заданную формулу небольшие исправления так,
чтобы она стала теоремой пли превратилась в более
сильную теорему, и об исследовании критериев качества
таких исправлений).
Разработки в области Е. л. в. в основном посвящены
классич. логикам, но возникшие методы носят более
общий характер.
Лит.: [I] Математическая теория логического вывода, сб.
переводов, М., 1967; [2] Ш а н и н Н. А. и др., Алгорифм ма-
машинного поиска естественного логического вывода в исчислении
высказываний, М.— Л., 1965; [3] Prawiiz D., Natural
deduction, Stockh., 1965. С. Ю. Мослов.
ЖАНЕ ТЕОРЕМА: во всяком аналитическом рима-
ноеом многообразии размерности п с отмеченной точкой
существует окрестность этой точки, допускающая
изометрическое аналитич. вложение в евклидово про-
пространство Es", где размерность sn=re(re+l)/2. Ж. т.
сохраняет силу при замене пространства Es" произ-
произвольным аналитическим римановым многообразием
размерности sn с отмеченной точкой (в к-рую должна
переходить отмеченная точка вкладываемого много-
многообразия). Ж. т. справедлива в случае псевдоримановых
многообразий при условиях
где ге+ и ге_ = ге—п+—размерности положительной
и отрицательной частей метрического тензора на по-
погружаемом многообразии, д+ и q~=q—q + —соот-
—соответствующие размерности объемлющего многообразия
(см. |3]). Ж. т.— первая общая теорема вложения в
римановой геометрии (см. Изометрическое погружение).
Ж. т. впервые была высказана как гипотеза Л. Шлеф-
ли [1], доказана М. Жане [2].
Лит.: [1] Schlafli L., «Ann. mat. pura ed appl.», 1873,
ser. 2, t. 5, p. 178—93; [2] J a n e t M., «Ann. polon. math.»,
1926, t. 5, s. 38—43; [3] Ф р и д м а н А., в сб.: Гравитация и
топология, М., 1966, с. 182—88. А. Б. Иванов.
ЖЕГАЛКИНА АЛГЕБРА — специальная алгебра
А=(А, Q), где
Л={0, 1}, п={х-у, х+у(то&2),0, 1 },
х-у — операция умножения. Интерес представляет
клон F действия Q на А. Каждая операция из F пред-
представляется в виде полинома по mod 2, к-рый наз. п о-
линомом Жегалкина по имени И. И. Же-
галкина, начавшего изучение этого клона [1]. Им
было показано, что всякая конечноместная операция
на А содержится в F. Таким образом, изучение свойств
клона F включает в себя, в частности, изучение всех
алгебр А=(А, Q' > при произвольном Я'.
Лит.: [1] Ж е г а л к и н И. И., «Матем. сб.», 1927, т. 34,
Ni 1, с. 9—28; [2] Кон П., Универсальная алгебра, пер. с
англ., М., 1968; [3] Яблонский С. В., ГавриловГ. П.,
Кудрявцев В- ?•¦» Функции алгебры логики и классы
Поста, М., 1966. В. Б. Кудрявцев.
ЖЕЗЛ — плоская трансцендентная кривая, уравне-
уравнение к-рой в полярных координатах имеет вид:
р = а/' Y Ч>-
Каждому значению ср соответствуют два значения р —
положительное и отрицательное. Кривая состоит из
двух ветвей, каждая из к-рых
асимптотически приближается к
полюсу (см. рис.). Прямая ср = О,
ф = я при р= — °о является асимп-
асимптотой, (V2, а/2) и (—V2,
—я у 2) — точки перегиба. Ж. относится к так наз.
алгебраич. спиралям.
Лит.: [1] С а в е л о в А. А., Плоские кривые, М., 1960.
Д. Д. Соколов.
ЖЕЛОБ — двусвязная поверхность S типа кольца,
содержащая внутри себя плоскую замкнутую кривую
L, плоскость Р к-рой во всех точках L касается S.
Вдоль L гауссова кривизна К Ж. S обращается в нуль.
Если при этом L разделяет Ж. S на две части, на каж-
дой из к-рых К знакопостоянна, то соответствующие
части S наз. положительным и отрицательным полуже-
полужелобами. Примером Ж. является узкая полоска тора
вдоль одной из его замкнутых параболических парал-
параллелей.
Ж. занимает промежуточное положение между объ-
объектами геометрии «в целом» и геометрии «в малом»,
так как он, заключая в себе определенную замкнутую
кривую L, не может быть сколь угодно малым, и в то
же время размеры его в трансверсальных к L направ-
направлениях могут быть сколь угодно малыми. Интерес
к изучению Ж. вызывается тем, что достаточно узкая
полоска поверхностей знакопеременной кривизны вдоль
замкнутой параболич. линии часто представляет собой
Ж., и поэтому знание свойств Ж. при различных де-
деформациях позволяет иногда получать информацию о
соответствующих свойствах всей поверхности «в целом».
Наиболее подробно исследованы так наз. плоский
Ж. (для к-рого кривая L является выпуклой, а сам
Ж. S располагается по одну сторону от Р, имея с Р
касание 1-го порядка) и Ж. вращения (когда L яв-
является параллелью поверхности вращения). Для ана-
литич. плоских Ж. доказана их жесткость относительно
аналитических бесконечно малых изгибаний 2-го по-
порядка, а для Ж. вращения изучение их бесконечно
малых изгибаний 1-го и 2-го порядков распространено
до класса регулярности С1 [3]. С точки зрения диффе-
дифференциальных уравнений исследование Ж. сводится к
изучению уравнений смешанного типа.
Лит.: [1] Ефимов Н. В., «Успехи матем. наук», т. 3,
в. 2, 1948, с. 47—158; [2] К о н-Ф о с с е н С. Э., Некоторые
вопросы дифференциальной геометрии в целом, М., 1959; [3]
Сабитов И. X., «Матем. сб.», 1975, т. 98, № 1, с. 113—29;
1976, т. 99, № 1, с. 49 — 57. И. X. Сабитов.
ЖЕРГОННА ТОЧКА—
точка пересечения пря-
прямых, соединяющих вер-
вершины треугольника с
точками касания вписан-
вписанной окружности с про-
противоположными этим вер-
вершинам сторонами. Назва-
Названа по имени Ж. Жергонна
(J. Gergonne, 19 в.). а. Б. Иванов.
ЖЕСТКАЯ ДИФФЕРЕНЦИАЛЬНАЯ СИСТЕМА —
система обыкновенных дифференциальных уравнений,
при численном решении к-рой явными методами типа
Рунге — Кутта или Адамса, несмотря на медленное
изменение искомых переменных, шаг интегрирования
обязан оставаться малым. Попытки уменьшить время
вычисления решения Ж. д. с. за счет увеличения шага
интегрирования приводят к резкому возрастанию
погрешности (взрыв погрешности).
Автономная система обыкновенных дифференциаль-
дифференциальных уравнений
GCR", A)
наз. /К. д. с, если для любых начальных значений
z(O) = z°?G на заданном отрезке [О, Т], принадлежащем
интервалу существования решения A), выполнены
условия:
а) максимальный модуль собственных значений мат-
матрицы Якоби (спектральный радиус) ограничен вдоль
решения z(t):
0
' 8/ (z)
dz
dt (z)
\дК (f + т, t)
дх
< 00,
б) существуют такие числа тп, N, v, что при
справедливо неравенство
дук (t+x, t)\
8xv
N J 1
здесь
K(t+x, t)=X(t+x)X-!((),
X (!) — фундаментальная матрица уравнения в ва-
вариациях для системы A),
тп — длина пограничного слоя. К Ж. д. с. отно-
относятся все системы вида A), для к-рых условия а) и б)
выполняются совместно после масштабирования ком-
компонент вектора z(t) на каждом решении.
Неавтономная нормальная система обыкновенных
дифференциальных уравнений порядка m наз. Ж. д. с,
если жесткой является равносильная ей автономная
система порядка т+1. Примером жесткого неавтоном-
неавтономного уравнения может служить скалярное уравнение:
^=?[2(*)-Ф (*)] + *??!, Z(O) = Z», B)
СР, ОгСг<оэ, — заданная функция. Другой при-
пример Ж. д. с.— линейная однородная система
*??L=Az(t), z(O) = z«, C)
с постоянной (шХ т)-матрицей А, имеющей различные
собственные значения, разделенные на две группы:
max Re k; < а, аЗэО,
i
\ т.
у,[ D)
Условие а) для системы C) очевидно выполняется.
Норма
]дК (t + x, ¦
дт
= \\АеЛт
¦ограничена сверху величиной CjPeaT при т>тп=С2/Л,
где Cj, С2 — некоторые постоянные. При C1^>eaT<^.L,
N=L/ (C1fieaT) выполняется условие б). Вектор d2z(t)/dt2
при t^.xn ограничен сверху:
d"z (t) ;
dt'
- || дК (i, 0)
! i'l dt
Поэтому для вектора dz(t)ldt при г^тп можно построить
интерполяционный алгобраич. многочлен нулевой сте-
степени с равномерно распределенными узлами и выбрать
шаг интерполяции в виде Н=С3/С1$еаТ, где С3 — не-
некоторая постоянная (см. [1]), зависящая от заданной
погрешности. С другой стороны, использование метода
ломаных Эйлера для системы C) требует ограничения
сверху на шаг интегрирования на всем отрезке решения
системы (см. [1]):
\l-\-hXt\ < 1, h < —max " "' <-^-, i — s+i, . . .,m. E)
i | Л,- |- -L
При этом составляющие приближенного решения си-
системы C) методом ломаных Эйлера, соответствующие
первой группе собственных значений D), будут пред-
представлены с достаточной точностью (см. [1]):
<^ NCs/2 < Hjh.
Ограничение вида E) на шаг интегрирования харак-
характерно для экстраполяционных методов типа Рунге —
Кутта и Адамса. Отношение Hlh, к-рое может рас-
рассматриваться как качественная мера жесткости си-
системы C), достигает во многих случаях величин по-
порядка 104—1010. Математич. описание динамич. про-
процессов и явлений в физике, химии, биологии, технике
и экономике, связанное с учетом все большего числа
факторов, повышающих порядок дифференциальных
систем, приводит к увеличению жесткости. Ж. д. с.
требуют специальных методов решения.
В некоторых случаях исходную систему A) можно
преобразовать, используя теорию и асимптотич. ме-
методы для дифференциальных уравнений с малым пара-
параметром при старшей производной, поведение решения
к-рых в пограничном слое описывается экспоненциально
затухающими функциями (см. [2]). Однако Ж. д. с.
обычно трудно привести к подобному виду, и, кроме
того, после асимптотич. преобразования жесткость
не всегда существенно уменьшается. Поэтому для ре-
решения систем общего вида используются численные
методы, основным свойством к-рых является обеспече-
обеспечение подавления быстро затухающих составляющих
решения системы A) вне пограничного слоя при ве-
величине применяемого шага интегрирования, близкой
к величине шага алгебраич. интерполяции.
Для решения Ж. д. с. целесообразно использование
неявных методов (см. [9], [17]). Для построения неявных
схем можно использовать способ неопределенных ко-
коэффициентов на основе формулы Тейлора, записанной
в виде:
dx, F)
JO Р'-
dtv
:(t)
dtP+i
где n — целое положительное число, Н~>0, nH=tn.
Напр., такие методы описаны в [9]:
г=1, яо=1, ai=—1 —неявный метод ломаных;
3 1
г=2, ао = —, аг=—2, а2= ——неявный метод 2-й
степени;
о И о 3 1
г=6, ао=—, «!=—6, а2 = -2", а3= g неявный
метод 3-й степени;
, 25 , о 4 1
г—4, а0——i а1 4, а2 = о, а3=——, а4= неяв-
неявный метод 4-й степени.
Под степенью метода понимается наиболь-
наибольшая степень Нк в разложении G) по степеням Н,
множитель при к-рой совпадает с соответствующим
множителем в F).
Применение неявного метода ломаных к системе C)
приводит к разностным уравнениям
п + 1 = Уп, yo = z°. (8)
Пусть система C) асимптотически устойчива по Ля-
Ляпунову. Тогда матрица \\Е—НА II — неособенная при
любом Н. При использовании формулы Лагранжа —
Сильвестра решение (8) представляется в виде
Для неявного метода ломаных (8) условие асимптотич.
устойчивости
1
1 - НК;
< 1
выполняется при любом Н, и в (9), с ростом п состав-
составляющие решения, соответствующие второй группа
собственных значений D), будут быстро убывать по
модулю. Величина Н ограничивается только усло-
условиями требуемой точности приближенных решений.
Стремление повысить степень линейных многошаговых
методов вступает в определенное противоречие с их
устойчивостью (см. [11]).
r-Шаговый метод
наз. А -устойчивым, если все решения A0) стре-
стремятся к нулю при п—>-оо с фиксированным положитель-
положительным Н в случае применения A0) к скалярному урав-
уравнению
dz ,.,.
где q — комплексная постоянная с отрицательной
действительной частью. Явный r-шаговый метод не
может быть А -устойчивым. Степень линейного много-
многошагового Л-устойчивого метода не может превышать
двух. Наименьшая константа ошибки С5=1/,2 полу-
получается для неявного метода трапеций (см. [11]):
Уп + 1 = Уп + -^[1(Уп + 1) + 1(Уп)]- A2)
Требование А (а)-устойчивости накладывает менее
жесткие ограничения на методы в отличие от А -устой-
-устойчивости. r-Шаговый метод A0) при фиксированном
#>0 наз. А (а) -устойчивым, если все решения
A0) стремятся к нулю при ге—>-оо в случае применения
A0) к уравнению A1), q — комплексная постоянная,
к-рая принадлежит множеству
sa^-{z?C ||arg(-z)| < a, z^0},
С — комплексная плоскость. Явный r-шаговый метод
не может быть А (О)-устойчпвым. Существует только
один А (О)-устойчивый r-шаговый метод со степенью
равной г+1 — метод A2). Для всех а?[0, -^-) суще-
существуют А (а)-устойчивые методы со степенью, равной г
при г=3, 4 (см. [13]).
Следующее ослабление требований Л-устойчивости
содержится в так наз. определении Гира (см.
[14]): метод A0) наз. жестко устойчивым,
если все решения A0) стремятся к нулю при п—>-оо
в случае применения A0) к уравнению A1). Hq — ком-
комплексная постоянная, принадлежащая множеству
R1\JR2' где
| Re Яд < — a},
причем для Hq ^ R1 обеспечивается заданная точность.
Методы G) жестко устойчивы и, следовательно,
А (а)-устойчивы. Для них а<:0,7.
Можно построить согласно F) неявные аналоги яв-
явных методов Рунге — Кутта любой степени, обладаю-
обладающие ^-устойчивостью и жесткой устойчивостью. Напр.,
метод 2-й степени
Уп + 1 = Уп + Н1 (yn + x—^rf(yn+x)) . A3)
Применение метода A3) к системе C) приводит к раз-
разностным уравнениям
которые доказывают его Л-устойчивость. Для метода
З-ii степени:
Уп + 1^У„+т(К1-г^Кг + К3), A4)
аналогично получаются разностные уравнения:
Так же строятся А -устойчивые и жестко устойчивые
методы более высоких степеней. Методы A3) и A4)
и методы, опубликованные в [5], принципиально отли-
отличаются от так наз. неявных методов Рунге — Кутта
(см. [16]), не получивших распространения из-за
большой вычислительной трудоемкости. Применение
неявных методов требует большей вычислительной
работы на одном шаге, чем применение явных методов,
но это оправдывается в Ж. д. с. за счет резкого уве-
увеличения шага интегрирования. При решении задачи
C) необходимо обращать матрицу или решать систему
линейных уравнений. Здесь может возникнуть проблема
плохой обусловленности, так как число обусловлен-
обусловленности матрицы НЕ—НА II увеличивается с увеличением
//. В общем случае A) на каждом шаге интегрирования
необходимо решать нелинейную систему уравнений
относительно вектора yn + i- Обычно при этом поль-
пользуются модифицированным методом Ньютона с на-
начальным условием, вычисленным по любой экстраполя-
ционной формуле, использующей вектор ;/„. Метод
экстраполирования при этом наз. предиктором,
а неявный метод — корректором. Метод про-
простой итерации в Ж. д. с. неприменим из-за больших
значений LII. Поскольку в неявных схемах приме-
применяется метод Ньютона для решения уравнений F(yn + 1)=
= 0 и, следовательно, необходимо вычислить матрицу
Якоби системы A), то иногда включают эту матрицу
непосредственно в формулы методов, к-рые при реше-
решении линейных систем также обладают свойством А-
устойчивости (см. [12], [15]). Для решения Ж. д. с.
широко применяется процедура Г и р а (метод
Г и р а) с автоматич. контролем погрешности на шаге
и изменением по этому критерию как степени методов,
так и шага интегрирования [14]. В процедуре Гира в
качестве корректора используются и методы G) (см. [9]).
Другой подход к созданию методов интегрирования
жестких систем уравнений связан с учетом в формулах
методов решений соответствующих линейных систем
(см. [4] — [8], [10]). В первых работах этого направ-
направления рассмотрены жесткие системы уравнений с из-
известными собственными значениями матрицы df(z)/dz,
по к-рым строились матричные коэффициенты методов.
В связи с трудностью решения проблемы собственных
значений это направление длительное время не разви-
развивалось. В [6], [7], [8] предложены способы построения
матричных коэффициентов без решения проблемы
собственных значений для матрицы df(z)!dz системы
A). Методы этого направления можно строить на основе
равенства (см. [7]):
Ф (*„+,)?
ХФ(«.+ т)^
где ср^и+тО^С1, 0<:т<:Я\— неособенная (тХт)-мат-
рица, С — матрица, не зависящая от т.
Различный выбор матриц cp(tn+T) и С приводит к
разностным уравнениям, соответствующим тем или
иным методам численного интегрирования, если пре-
пренебречь правой частью в A5). При С=0 получаются
явные методы, а при СфО — неявные. Пусть cp(fn+T) =
= Е. Тогда неявный метод ломаных G) соответствует
С=—НЕ; метод трапеций A2) С=—^-Е; явный метод
ломаных С=0. При q>(tn-\-T) = eAx, где А — постоянная
(тХ т)-матрица, получается обобщенный метод лома-
ломаных (см. [7]):
У (*» + i) = У (tn) + J" eAx dx 1 (у ((„)). A6)
Формула A6) переходит в явный метод ломаных при
А=0. Метод A6) дает точное решение системы урав-
уравнений
для дискретных значений tn=nH. Если известна мат-
матрица
Ф(А, К) = [heAxdt,
то использование к раз рекуррентной формулы
Ф(А, 29 + 11г) = Ф(А, 24h) [2Е+АФ(А, 2«h)] A8)
приводит к матрице
Ф(А,
применяемой в A6). В качестве начального приближе-
приближения для A8) при достаточно малом hi?l/\\A II целесо-
целесообразно употреблять приближенную формулу:
или, если собственные значения матрицы действитель-
действительные, то
J0 — jL,ty=O (v+l)! ° К '
Формула A9) дает соответствие по устойчивости в
смысле Ляпунова решений системы дифференциальных
A7) и разностных A6) уравнений в случае комплексных
собственных значений А с малой действительной ча-
частью. Если область существования решений GcG
является замкнутой, выпуклой по z, и приближенные
решения принадлежат той же области, то погрешность
метода A6) удовлетворяет разностному уравнению
(см. [7]):
где zn=zn—у„, a zn=z(tn), yn=y(tn) — решения A) и
A6) соответственно. Пусть \\у || =тах|г/,-|—норма вектора
г
(норма матриц подчинена принятой норме вектора)
ц в области G:
¦dp— A
По матрице А с действительными элементами вычис-
вычисляется число
/? = тах
Тогда справедлива оценка
Л = 0, || ев+х || < A + МО II 8„ || + ^-
0<,11<-Я=а, ||ев
R н
Л, Цвв+г11<«я*1в
0< Л<щ. I]en+I|j<g2>t-H||en||+ ''*'
Если 0<а=—Л^^!, погрешность е„ можно оцени-
оценивать, считая Л = 0. В оценках возможны другие нормы
векторов, соответствующие им нормы матриц и лога-
рифмич. нормы (см. [3]). Приведенные оценки показы-
показывают, что при решении системы A) шаг интегрирования
Н можно использовать значительно большим, чем в
классич. методах. Матрицу А следует выбирать близ-
близкой по всем элементам к матрице Якоби системы A).
В пограничном слое, когда переменные изменяются
быстро, грубо оценивая цг, ц2, I, R по приближенному
решению, можно менять матрицу А, добиваясь необ-
необходимой точности. Так как за пограничным слоем
переменные системы A) меняются медленно, на прак-
практике часто оказывается достаточно одной матрицы А,
чтобы вычислить все решение при Тп-гй^Г. Проверку
точности можно производить по правилу Рунге (см.
[1]).
С целью увеличения точности на основе метода A6)
в [7] предложен класс системных методов численного
интегрирования. Для методов этого класса выполня-
выполняются требования: 1) системный метод s-й степени должен
быть точным при интегрировании алгебраич. много-
многочленов степени s—1 при Л=0; 2) системный метод
любой степени должен быть точным при решении
уравнений A7).
Одношаговый метод 2-й степени имеет вид:
Н/2 Ах
[2f(yn+ \"'
X
Там же построены явный одношаговый метод 3-й сте-
степени и многошаговые системные методы. Даны асимп-
тотич. оценки их погрешностей. При .4=0 эти методы
переходят в формулы типа Рунге — Кутта или Адамса.
При аппроксимации интегралов от е^т дробно рацио-
рациональными матричными полиномами от А с учетом не-
неособенности соответствующих матриц системные методы
переходят в явную форму соответствующих неявных
методов, получающихся после итераций по методу
Ньютона. Неявным системным методом 1-й степени
является метод
"eAxdr[f(yn + 1)-f(yn)~A(yn + 1-yn)]. B1)
Он получается из A5), если выбрать
Ах п I
Уравнения B1) получаются способом приведения диф-
дифференциальных уравнений к интегральным (см. [8]).
Интеграл от еАх в методе B1) вычисляется по форму-
формулам A8) с начальным условием B0). Исследован способ
коррекции этого интеграла по ходу решения (см. [8]).
Лит.: [l] Б а х в а л о в Н. С, Численные методы, 2 изд.,
М., 1975; [2] В а с и л ь е в а А. Б., «Матем. сб.», 1960, т. 50,
в. 1, с. 43—58; [3] Б ы л о в Б. Ф. и др., Теория показателей
Ляпунова..., М., 1966; [4] Г а в у р и н М. К., в сб.: Методы
вычислений, 1963, в. I, с. 45 — 51; [5] Р а к и т с к и й Ю В.,
«Докл. АН СССР», 1970, т. 193, ЛГ» 1, с. 40—42; [6] е г о же,
там же, 1972, т. 207, № 4, с. 793—95; [7] е г о же, «Тр. Ленингр.
политехи, ин-та», 1973, № 332, с. 88 — 97; 18] Павлов Б. В.,
Повзнер А. Я., «Ж. вычисл. матем. и матем. физ.», 1973, т.
13, А1» 4, с. 1056—59; [9]Curtiss С. F., HirschfelderJ. О.,
«Ргос. Nat. Acad. Sci. USA», 1952, v. 38, p. 235—43; [10] M a h
R. S. H., Michaelson S., Sargent R. W, «Chem.
Engng- Sci.», 1962, v. 17, p. 619 — 39; [11] D a h 1 q u i s t G.,
«Nord. tidskr. Informationsbehandling», 1963, b. 3, s. 27—43;
[12] Rosenbrock H. H., «Comput. J.», 1963, v. 5, p. 329—
30; [13] Widlund О. В., «Nord. tidskr. Informationsbehand-
Informationsbehandling», 1967, b. 7, s. 65—70; [14] G e a r С W., в кн.: Information
Processing 68, v. 1, Amst., 1969, p. 187—93; [15] Lambert
J. D., S i g u r d s s о n S. Т., «SIAM J.Numer Anal.», 1972,
v. 9, p. 715—33; [16] L a m b e r t J. D., Computational methods
in ordinary differential equations, N.Y., 1973; [17] Stiff diffe-
differential systems, [The IBM research simposia series], N.Y.— L.,
1974. Ю. В. Ракитский.
ЖЕСТКОЕ АНАЛИТИЧЕСКОЕ ПРОСТРАНСТВО —
вариант понятия аналитич. пространства, относящийся
к случаю, когда основное поле К является полным
неархимедово нормированным полем.
Аналитич. функции р-адического переменного рас-
рассматривались еще в конце 19 в. в теории алгебраич.
чисел, однако соответствующий глобальный объект —
Ж. а. п. — был введен Дж. Тейтом (J. Tate) лишь в на-
начале 60-х гг. 20 в. (см. [1]). Этой конструкции пред-
предшествовало более прямолинейное построение по об-
образцу теории комплексно аналитич. многообразий.
Главный недостаток последнего подхода связан с тем,
что обычное локальное определение аналитич. функции,
как разлагающейся в степенной ряд в окрестности
каждой точки, неудобно в силу полной несвязности
основного поля К. Определенных таким образом ана-
аналитич. функций оказывалось «слишком много» (а ана-
аналитич. многообразий, соответственно, «слишком мало»).
Напр., всякое компактное аналитич. многообразие
над К является объединением конечного множества
замкнутых шаров (см. [3], с. 168). Конструкция Тей-
та начинается с выбора локальных объектов — а ф-
финоидных пространств, аналогичных аффинным
многообразиям в алгебраич. геометрии. Пусть Тп —
алгебра степенных рядов от п переменных !ь . . ., tn
над К, сходящихся в полидиске |(j|<1, . . ., |tn|<l.
Факторалгебры алгебры Тп наз. аффиноидными
алгебрами. Эти алгебры нётеровы и в них имеется
естественная банахова топология, в к-рой все идеалы
замкнуты, а гомоморфизмы непрерывны. Оказывается,
что любой максимальный идеал такой алгебры имеет
конечную коразмерность и пространство МахА мак-
максимальных идеалов состоит, с точностью до сопряже-
сопряжения, из геометрич. точек, определенных над конечными
расширениями поля К. В частности, МахГ„ есть по-
полидиск единичного радиуса, а вообще, для произволь-
произвольного А пространство МахЛ представляет собой анали-
аналитическое подмножество в полидиске. Гомоморфизмы
ф: Л—>-5 определяют морфизмы ф*: МахВ->-МахЛ,
так что аффиноидные пространства образуют кате-
категорию.
Жесткостью на топологич. пространстве X
наз. набор Т, Covf/, Qx, где Т есть семейство открытых
множеств из X, называемых допустимыми,
Covf/ для каждого U?T — семейства покрытий мно-
множества U допустимыми множествами (допусти-
(допустимые покрытия), a Qx~ предпучок колец на Т.
Для допустимых покрытий требуется выполнимость
естественных аксиом, в частности допустимые покры-
тия можно измельчать, а предпучок Qx должен быть
пучком относительно всех допустимых покрытий до-
допустимых множеств. Морфизмы пространств с жест-
жесткостью, а также понятие индуцированной на подпро-
подпространстве жесткости определяются по аналогии с
такими же понятиями для окольцованных пространств.
Каждое аффиноидное пространство можно наделить
канонической жесткостью, сохраняющейся при любых
морфизмах. Жесткое аналитическое
пространство есть, по определению, топологич.
пространство с жесткостью, на к-ром существует до-
допустимое покрытие X={JX; такое, что каждое X, с
индуцированной жесткостью изоморфно аффиноидному
пространству, наделенному канонич. жесткостью.
Для Ж. а. п. получен ряд результатов, аналогичных
известным теоремам теории комплексных пространств.
Так, имеют место аналоги теорем А и В Картана (см.
Картана теорема [4]). Точнее, когерентные пучки
(З^-модулей на аффиноидных пространствах однозначно
определяются модулем своих сечений, а их когомологии
в размерностях J&1 обращаются в нуль. Верен также
аналог теоремы Грауэрта о когерентности прямого
образа когерентного пучка при собственном отобра-
отображении (однако определение собственного отображения
здесь сильно отличается от обычного). Построен р-ади-
ческий аналог униформизации алгебраических кривых
и абелевых многообразий (см. [5]). Обнаружена связь
между понятием Ж. а. п. и понятием формальной схемы
в алгебраич. геометрии (см. [5]).
Лит.: [1] Тэйт Дж., «Математика», 1969, т. 13, ЛГ« 3,
с. 3—37; [2] Б у р б а к и Н., Дифференцируемые и аналити-
аналитические многообразия. Сводка результатов, пер. с франц., М..
1975; [3] С е р р Ж.-П., Алгебры Ли и группы Ли, пер. с англ.
и франц., М., 1969; [4] У з е л ь К., «Математика», 1969, т. 13.
№ 3, с. 38 — 49; [5] Итоги науки и техники. Современные проо-
лемы математики, т. 3, М., 1974, с. о—92. А. Н. Паршин.
ЖЕСТКОСТЬ — свойство подмногообразия М в ри-
мановом пространстве V, заключающееся в том, что
любая его изометрич. вариация (бесконечно малое
изгибание) является тривиальной, т. е. соответствую-
соответствующее поле скоростей z на М индуцируется полем
Киллинга вектора ?, на М: z=?oi, где V. М—>-F — изо-
изометрическое погружение М в V. Вопрос о Ж. подмно-
подмногообразий — по существу вопрос о единственности
решения системы дифференциальных уравнений, яв-
являющихся линеаризацией основной системы уравнений
теории поверхностей — почти не исследован в случае,
когда dim M>2 и dim V>3, однако и в простейшей
ситуации (dim M=dim V—1 = 2) более или менее за-
законченную теорию удается построить лишь для по-
поверхностей положительной кривизны, расположенных
в пространствах постоянной кривизны (см. Векуа ме-
метод). О Ж. поверхностей неположительной и перемен-
переменной кривизны известны лишь отдельные результаты,
причем на Ж. поверхности, помимо ее пространствен-
пространственной формы, оказывает влияние степень регулярности
рассматриваемых деформаций.
Как правило, незамкнутая поверхность нежесткая,
однако: 1) построены примеры поверхностей с уплощения
точкой т, любая окрестность к-рой является жесткой
или допускает бесконечно малые изгибания ограничен-
ограниченной регулярности; 2) существуют жесткие незамкнутые
выпуклые поверхности с полной кривизной, равной 4я,
окаймленные плоскими параболич. кривыми (части
поверхностей типа Т).
На Ж. поверхности влияет то, насколько ограничена
подвижность края поверхности или линий внутри ее;
так, напр., 1) сферич. сегмент S, скользящий по пло-
плоскости, будет жестким или нет в зависимости от того,
меньше или больше S полусферы; 2) кусок гиперболич.
параболоида с двумя пересекающимися неподвижными
образующими — жесткий; 3) кусок плоскости с за-
закрепленным краем — нежесткий.
Замкнутые поверхности изучены с точки зрения Ж.
более детально; так, напр., 1) замкнутая выпуклая
поверхность — жесткая (см. Бляшке — Вейля формула,
а также [2]); 2) в то же время есть и нежесткие замкну-
замкнутые поверхности вращения знакопеременной кривизны;
3) тор — жесткий; 4) замкнутый цилиндроид жесткий
тогда и только тогда, когда площадь среднего сечения
где Si и S2 — площади верхнего и нижнего основа-
оснований; 5) метрич. произведение к двумерных сфер яв-
является жестким в евклидовом пространстве Eak и
нежестким в E'ik + l, i>0.
Так определенное понятие Ж. иногда наз. Ж. 1-го
порядка, вводится также Ж. 2-го и высших порядков.
Понятие Ж. переносится на нерегулярные поверхности,
напр, многогранники, однако и там основные резуль-
результаты касаются лишь выпуклых многогранников (см.
Коши теорема о многогранниках), и на поверхности
в римановом пространстве, напр, замкнутые поверх-
поверхности любого рода с положительной внешней кривиз-
кривизной — жесткие.
Лит.: [ll Ефимов Н. В., «Успехи матем. наук», 1948,
т. 3, № 2, с. 47 — 158; [2] Погорелой А. В., Внешняя
геометрия выпуклых поверхностей, М., 1969; [3] К о н - Ф о о-
сен С. Э., Некоторые вопросы дифференциальной геометрии
в целом, М., 1959; [4] В е к у а И. Н., Обобщенные аналитиче-
аналитические функции, М., 1959; [5] А л е к с а н д р о в А. Д., Выпук-
Выпуклые многогранники, М.—Л., 1950; [6] Ф о м е н к о В. Т.,
«Матем. заметки», 1974, т. 16, в. 3, с. 441—45.
М. И. Войцехоеский.
ЖИРО УСЛОВИЯ — условия разрешимости в клас-
сич. смысле основных краевых задач для линейного
эллиптич. уравнения 2-го порядка. Пусть в ограничен-
ограниченной iV-мерной (А^2) области D с границей Г задано
эллиптич. уравнение
Требуется найти функцию и(х), к-рая: 1) принадлежит
классу CB>(D)[) C<0)(Z> + r); 2) удовлетворяет в области
D уравнению (*); 3) на границе Г удовлетворяет усло-
условию и(г) = ср(ж) (-первая краевая задача, или задача
Дирихле), или условию
2ам± + Их)и(х) = у(х)
(вторая краевая задача, или задача Неймана), или
условию
д ()
(третья краевая задача). Здесь v — направление ко-
нормали, его направляющие косинусы равны
cos (v, */) = |У* аи (х) cos (в, хЛ,
п — внешняя нормаль к границе Г, I — произвольное
направление, для к-рого cos(/, rc)^8>0 для всех х?Т,
знак + показывает, что берется предельное значение
изнутри области D.
Жиро условия разрешимости указанных кра-
краевых задач состоят в следующем. Если коэффициенты
a,j(x), b,(x), с(х) оператора L принадлежат в области
(jD + Г) классу С<0>м.>, правая часть уравнения f(x)?
?С<°,и> (.О)П<?<">(?>+Г), краевое условие ср(г)^С<°)(Г)
и Р (ж) ? С@) (Г) (для второй и третьей краевых задач),
cos(l, xi)?C(°,^>(Г) (для третьей краевой задачи), а
граница Г области D принадлежит классу Аа^\ то
для первой, второй и третьей краевых задач справед-
лива альтернатива Фредгольма, т. е.
либо соответствующая однородная задача имеет только
тривиальное решение и тогда неоднородная задача
имеет единственное решение при любых / и ф, либо
однородная задача имеет р, 0<р<оо, линейно неза-
независимых решений м1? . . ., ир и тогда неоднородная
задача разрешима лишь в случае, если р определенных
линейных функционалов от / и ф обращаются в нуль,
причем при выполнении этого последнего условия
неоднородная задача имеет бесконечно много решений,
и если «0—одно из этих решений, то общее решение пред-
ставимо в виде мо+2^ c'ui-> где ci — произвольные
постоянные. В случае, когда коэффициенты оператора L
являются более гладкими (a/y?CB-W, &,?СA-^>),
так что можно рассматривать сопряженный оператор
L*, требование обращения в нуль линейных функцио-
функционалов от / и ср сводится к ортогональности / и (р ко всем
р линейно независимым решениям однородной сопря-
сопряженной задачи. Ж. у. получены Ж. Жиро [1] — [3].
Лит.: ll] G i г а u d G.. «С г. Acad. sci.», 1936, t. 202,
p. 380—82; [2] e г о же, «Bull. soc. math. Prance», 1932, t. 56,
p. 248—72, 281—312, 316—52; [3] e г о же, «J. math, pures et
appl.», 1939, t. 18, p. Ill—43; [4] M и р а н д а К., Уравнения
с частными производными эллиптического типа, пер. с итал., М.,
1957. И. А. Шишмарев.
ЖОРДАНА КРИВАЯ — гомеоморфный образ окруж-
окружности. Назв. по имени К. Жордана (С. Jordan), пред-
предложившего это определение. См. также Линия.
ЖОРДАНА ЛЕММА: пусть /(г) — регулярная ана-
литич. функция комплексного переменного z при
UI>c^0, Im z>0, за исключением дискретного мно-
множества особых точек. Если существует последователь-
последовательность полуокружностей
такая, что максимум M(/?n)=max|/(z)| на полуок-
полуокружности y(Rn) стремится к нулю, когда п—>-оо; то
С
J
e'«/(z)dz=0,
V(Hn)
где а — любое положительное число. Ж. л. позволяет
применять вычеты не только при условии z/(z)—»-0,
но уже при равномерном стремлении f(z)-+-0 на последо-
последовательности полуокружностей в верхней или нижней
полуплоскости для вычисления, напр., интегралов вида
\ / (х) cos ax dx, \ / (х) sin ax dx.
Получена К. Жорданом [1].
Лит.: tl] Jordan С, Cours d'analyse, t. 2, 2 ed , Р
1894, p. 285—86; [2] Ш а б а т Б. В., Введение в комплексный
анализ, 2 изд., М., 1976; [3] У и т т е к е р Э. Т., В а т с о н
Д.-Н., Курс современного анализа, пер. с англ., 2 изд., ч 1,
М., 1963, гл. 6. Е. Д. Соломенцев.
ЖОРДАНА МЕРА параллелепипеда
Д = {а,-<*,¦<&,•; а,- < Ь{, i = i,2,...,n) (*)
в R" объем mA= JT" F,-—а,) этого параллелепипеда.
Для ограниченного множества EczR" определяются:
внешняя мера Жордана
к тА/, U * Д/ГЗ Я, /с = 1,2, ...
и внутренняя мера Жордана
m,-?' = sup2_ таДу, Е 3 Ду,
где Ду попарно не пересекаются (здесь Д; — парал-
параллелепипеды вида (*)). Множество Е паз. измери-
измеримым по Жордану (квадрируемым при и=2,
кубируемым при и^З), если meE=miE или, что рав-
равносильно,
теЕ Л- те (Д чч Е) = тА,
где Лз-Е. В этом случае Ж. м. равна тЕ=теЕ=т,Е.
Ограниченное множество EczR" измеримо по Жордану
тогда и только тогда, когда его граница имеет Ж. м.
нуль (или, что равносильно, когда его граница имеет
Лебега меру нуль).
Приведенное понятие меры ввели Дж. Пеано [1]
и К. Жордан [2]. Внешняя Ж. м. одна п та же для Е
и Е (замыкания множества Е) и равна Бореля мере Е.
Измеримые по Жордану множества образуют кольцо
множеств, на к-ром Ж. м. конечно аддитивная функ-
функция. См. также Квадрируемость.
Лит.: [1] Peano G., Applicazioni geometriche del calcolo
infinitesimale, Torino, 1887; [2] Jordan C, «J. math, pures
etappl.», 1892, t. 8, p. 69—99; [3] H и к о л ь с к и й СМ., Курс
математического анализа, т. 2, М., 1973; [4] Колмогоров
А. Н., Фомин СВ., Элементы теории функций и функци-
функционального анализа, 4 изд., М., 1976. А. П. Терехин.
ЖОРДАНА ПРИЗНАК сходимости рядов
Фурье: если 2л-периодическая функция / (х) имеет
ограниченную вариацию на отрезке [а, Ъ], то ее ряд
Фурье сходится в каждой точке х? (а, Ь) к числу
у[/(ж+0)+/(^~0)]; если при этом функция f(x)
непрерывна на отрезке [а, Ь], то ее ряд Фурье схо-
сходится к ней равномерно на всяком отрезке [а'. Ь'],
строго внутреннем к [а, Ь]. Ж. п. установлен К. Жор-
даном [1]; он обобщает Дирихле теорему о сходимости
рядов Фурье кусочно монотонных функций.
Лит.: [1] Jordan С. «С г. Acad. sci.», 1881, t. 92,
p. 228—30; [2] Б а р и Н. К., Тригонометрические ряды, М.,
1961, с. 121. Б. И. Гелубов
ЖОРДАНА РАЗЛОЖЕНИЕ — 1) Ж. р. функции
ограниченной вариации — представление
функции / в виде
f=h-h,
где /i и /2 — монотонно возрастающие функции. Ж. р.
наз. также представление обобщенной меры, или заряда
ц(?) измеримого множества Е в виде разности мер
где хотя бы одна из мер |х+ или ц~ конечна. Установ-
Установлено К. /Корданом.
Лит.: ll] Jordan С, Cours d'analyse, t. 1, P., 1893; [2]
Халмош П., Теория меры, пер. с англ., М., 1953; [3]
Натансон И. П., Теория функций вещественной перемен-
переменной, 3 изд., М., 1974. М. И. Войцеховский.
2) Ж. р. эндоморфизма ? конечномер-
конечномерного векторного пространства — пред-
представление этого эндоморфизма в виде суммы полупро-
полупростого и нильпотентного эндоморфизмов, коммутирую-
коммутирующих между собой: g=gs+gn- Эндоморфизмы gs и gn
наз. соответственно полупростой и нильпо-
тентной компонентами Ж. р. эндоморфиз-
эндоморфизма g. Такое представление наз. а ддитивным Ж. р.
(Полупростой эндоморфизм — эндомор-
эндоморфизм, обладающий при нек-ром расширении основного
поля базисом из собственных векторов, н и л ь п о-
тентный — равный в некоторой степени нулю.)
Если в нек-ром базисе пространства матрица На,-у II
эндоморфизма g является жордановой матрицей, а t—
такой эндоморфизм, что в том же базисе его матрица
имеет вид llb,y II, где 6,-у = 0 при всех 1ф] и Ъц=ац для
всех г, то
g= t+ (g- t)
будет Ж. р. эндоморфизма g с gs= in gn=g— t.
Ж. р. существует и единственно для любого эндо-
эндоморфизма g векторного пространства V над алгебраи-
алгебраически замкнутым полем К. Более того, gs==P(g) и
gn=Q(g) для некоторых многочленов Р и Q над полем К
(зависящих от g) с нулевыми свободными членами.
Если W инвариантное относительно g подпространство
в V, то W инвариантно относительно gs и gn, причем
g \w =
является Ж. р. для g\yy (здесь \w обозначает сужение
эндоморфизма на подпространство W). Если к — под-
подполе в А* н g рационально над к (относительно неко-
некоторой /с-структуры на V), то gs и gn но будут, вообще
говоря, рациональными над к; можно лишь утверж-
утверждать, что gs и gtl рациональны над нолем кР~°°, где
р — характеристическая экспонента поля к (при р = 1
кР~°° совпадает с А, а при р >1 это—множество всех
элементов из К, чисто несепарабельных над к).
Если g — автоморфизм пространства V, то gs —
также автоморфизм V и
где gu = {vJrg~s1gn, ly — тождественный автоморфизм
пространства V. Автоморфизм gu является у н и п о-
т е н т н ы ы, т. е. все его собственные значения равны
единице. Всякое представление автоморфизма g в
виде произведения коммутирующих полупростого и
унипотентного автоморфизмов совпадает с описанным
представлением g=gsga~gugs- Это представление наз.
мультипликативным Ж. р. автомор-
автоморфизма g, a gs и gn — полупростой и унипотентной
компонентой автоморфизма g. Если g рационален над
к, то gs и gu рациональны над кР~°°- Если W — ин-
инвариантное относительно g подпространство в Г, то
W инвариантно относительно gs и ga, a
g \w — Ss \wgu \w
— мультипликативное Ж. р. автоморфизма g\ <$/.
Понятие Ж. р. может быть обобщено на локально
конечные эндоморфизмы бесконечномерного векторного
пространства V, т. е. такие эндоморфизмы g, что V
порождается конечномерными ^-инвариантными под-
подпространствами. Для g имеют место существование и
единственность представления в виде суммы gs~{~gni
а в случае автоморфизма — в виде произведения gsgu,
коммутирующих локально конечных полупростого и
нильпотентного эндоморфизмов (соответственно по-
полупростого и унипотентного автоморфизмов), т. е.
таких эндоморфизмов, что любое конечномерное ^-инва-
^-инвариантное подпространство W в V инвариантно относи-
относительно gs и gn (соответственно gs и ga) и g\w —
= gs\w+gn\w (соответственно g\w=gs\wgu\ w есть
Ж. р. для g\w).
Указанное распространение понятия Ж. р. на ло-
локально конечные эндоморфизмы позволяет ввести
определение Ж. р. в алгебраич. группах и алгебраич.
алгебрах Ли. Пусть G — аффинная алгебраич. группа
над К, g — ее алгебра Ли, р — представление G в
группу автоморфизмов алгебры K[G] регулярных функ-
функций на G, определенное правыми сдвигами, и dp — его
дифференциал. Для любых g из G и X из % эндомор-
эндоморфизмы р(^) и dp(X) векторного пространства K[G\
являются локально конечными, поэтому можно гово-
говорить об их Ж. р.:
р (в) = р (g)s P (е)и
Один из важных результатов теории алгебраич. групп
состоит в том, что указанные Ж. р. реализуются с
помощью элементов из G и g соответственно. Точнее,
существуют однозначно определенные элементы gs,
gu?G и Xs, Xn^ такие, что
g = gsgu = gugs, A)
X = Xs + Xn, [Xs, 2Г„]=0, B)
и
dp (Xs) = (dp (X))s, dp (Xn) = (dp (X))n.
Разложение A) наз. Ж. р. в алгебраической
группе G, а разложение B) — Ж. р. в а л г е-
бра и ческой алгебре Ли '§. Если G опре-
определена над подполем к поля К и элемент g?G (соот-
(соответственно Х?$) рационален над к, то gs, gu (соот-
(соответственно Xs, Xn) рациональны над кР~°°. Более
того, если G реализована как замкнутая подгруппа
полной линейной группы GL(V) автоморфизмов не-
некоторого конечномерного векторного пространства V
[и, следовательно, <§ реализуется как подалгебра в
алгебре Ли группы GL(V)), то Ж. р. A) для элемента
g?G совпадает с введенным выше мультипликативным
Ж. р. для g, а разложение B) для X?g — с аддитив-
аддитивным Ж. р. для X (рассматриваемых как эндоморфизмы
пространства V). Если ср: G1—>-G2 — рациональный го-
гомоморфизм аффинных алгебраич. групп и с/ср: gj—*-g2 —
соответствующий гомоморфизм их алгебр Ли, то
<f(gs)=4>(g)s, V(gu) = <P(g)m
для любых g?lt G^i
Понятие Ж. р. в алгебраич. группах и алгебрах Ли
позволяет ввести определение полупростого, унипо-
тентного (соответственно нилыютентного) элементов
в произвольной аффинной алгебраич. группе (соот-
(соответственно алгебраич. алгебре Ли). Элемент g?G
наз. полупростым, если g=gs- и у н и п о-
т е н т н ы м, если g=gu', элемент Х?$ наз. полу-
полупростым, если Х = Х$, и н и л ь п о т с н т н ы м,
если Х= Хп. Пусть G определена над к, тогда
является /с-замкнутым подмножеством в G, а
S« = {* € <§\Х = Хп)
— /с-замкнутым подмножеством в %. В общем случае
не является замкнутым множеством, но если G ком-
коммутативна, то Gs и Gu являются замкнутыми подгруп-
подгруппами и G=GSXGU. Множества G, и б„ в произвольной
аффинной алгебраич. группе инвариантны относитель-
относительно внутренних автоморфизмов, и изучение разбиения
этих множеств на классы сопряженных элементов
составляет предмет специальных исследований [3].
Лит.: [1] Б о р е л ь А., Линейные алгебраические группы,
пер. с англ., М., 1972; Г2] Kolchin E. R., «Ann. Math.»,
1948, v. 49, p. 1—42; [3] Семинар по алгебраическим группам,
пер. е англ., М., 1973. В. Л. Попов.
ЖОРДАНА ТЕОРЕМА: плоская простая замкнутая
кривая Г разбивает плоскость R2 на две связные ком-
компоненты и является их общей границей. Установлена
К. Жорданом [11. Вместе с примыкающим к ной утверж-
утверждением: простая дуга не разбивает плоскость, это —
старейшая теорема теоретико-множественной тополо-
топологии.
Из двух компонент одна (внутренность Г) — огра-
ограниченная; характеризуется тем, что порядок любой
точки, ей принадлежащей, относительно Г равен
— 1; другая (внешность Г) — неограниченная, и по-
порядок ее точек относительно Г равен нулю. Для любой
точки х ограниченной компоненты А и любой точки
хо 6 Г существует простая дуга с концами х0 и х, все
точки к-рой, отличные от х0, содержатся в А (тео-
(теорема Шёнфлиса).
Ж. т. обобщается по размерности: любое (Л/—1)-
мерное подмногообразие в RjV, гомеоморфное сфере,
разбивает пространство на две компоненты и является
их общей границей; при N=3 это доказано А. Лебегом
(Н. Lebesgue), в общем случае — Л. Брауэром (L. Brou-
wer), отчего ЛТ-мерная Ж. т. иногда наз. Ж о р д а н а —
Брауэра теоремой.
Лит.: [1] Jordan С, Cours d'analyse, t. I, P., 1893;
[2] Балл е-П у с с е н Ш. Ж. д е, Курс анализа бесконеч-
бесконечно малых, пер. с франц., т. 2, Л.— М., 1933; [3] А л е к с а н-
дров П. С, Комбинаторная топология, М.— Л., 1947; [41
Дьедонне Ж., Основы современного анализа, пер. с англ.,
М., 1964; [5] Г у р е в и ч В В о л м э н Г., Теория размерно-
размерности, пер. с англ., М., 1948; [6] Ф и л и п п о в А. Ф., «Успехи
матем. наук», 1950, т. 5, в. 5, с. 173—76. М. И. Войцеховский.
ЖОРДАНА — ГЁЛЬДЕРА ТЕОРЕМА: если группа
обладает композиционными рядами, то любые два ее
композиционных ряда изоморфны. К. Жордан [1],
[2] и О. Гёльдер [3], занимаясь вопросом о разреши-
разрешимости уравнений в радикалах (см. Галуа теория),
исследовали группы подстановок. Для этих групп
К. Жордан ввел понятие композиционного и главного
рядов и доказал, что индексы двух одноименных рядов
{т. е. индексы подгруппы G; в С(+1), с точностью до
расположения, одинаковы. Иными словами, было дока-
доказано совпадение последовательностей порядков фак-
факторов двух композиционных (главных) рядов с точ-
точностью до расположения. О. Гёльдер доказал изомор-
изоморфизм соответствующих факторов. О. Шрейером [4]
было доказано еще более общее утверждение: любые
два нормальных ряда произвольной группы обладают
изоморфными уплотнениями (теорема Шрейе-
р а). Ж.— Г. т. была доказана также для групп с
произвольной областью операторов (Э. Нётер, Е. No-
other, В. Крулль, W. Krull), откуда, в частности,
вытекали аналогичные теоремы для характеристиче-
характеристических и вполне характеристич. рядов.
В дальнейшем обобщения Ж.— Г. т. пошли по сле-
следующим направлениям. 1) Были получены обобщения
теорем Шрейера и Жордана — Гёльдера для беско-
бесконечных нормальных систем и, в частности, вполне
упорядоченных нормальных и композиционных рядов,
а также доказано, что все возрастающие нормальные
ряды группы с простыми факторами изоморфны (эти
ряды могут и не быть композиционными) (см. [5]).
2) Ж.— Г. т. была перенесена на ряды идеалов колец
и других алгебраич. образований. Эти направления
объединились рядом результатов для Я-групп (муль-
тиоператорных групп), й-алгебр и для универсальных
алгебр с одноэлементной подалгеброй и перестановоч-
перестановочными конгруэнциями (см. [5] — [8]). 3) Рассматрива-
Рассматривались различные способы обобщения Ж.— Г. т. на языке
теории решеток и частично упорядоченных множеств.
Получено обобщение теоремы Шрейера для цепочек
элементов дедекиндовых решеток. В ряде работ для
определения нормального ряда элементов решетки вво-
вводилось дополнительное отношение нормальности или
операция умножения (см. [5], [6], [9] — [11]). 4) Были
получены обобщения Ж.— Г. т. и теоремы Шрейера
для нормальных категорий (см. [8]).
Лит.: [1] J о г d a n С, «С. г. Acad. sci.», 1869, t. 68, p. 257;
[2] e г о же, Traite des substitutions et des equations algebriques,
P., 1870 B ed., 1957); [3] H б 1 d e г О., «Math. Ann.», 1889,
Bd 34, S. 26—56; [4] S с h г e i e г О., «Abh. Math. Semin.
Univ. Hamburg», 1928, Bd 6, № 3—4, S. 300—02; ЫКурош
А. Г., Теория групп, 3 изд., М., 1967; [6] Б и р к г о ф Г.,
Теория структур, пер. с англ., М., 1952; [7] К о н П., Универ-
Универсальная алгебра, пер. с англ., М., 1968; [8] Ц а л е н к о М. Ш.,
Шульгейфер Е. Г., Основы теории категорий, М., 1974;
[9] Итоги науки. Алгебра. 1964, М., 1966, с. 237—74; [10] Итоги
науки. Алгебра. Топология. Геометрия. 1966, М., 1968, с. 109—
136; 1968, М., 1970, с. 101 — 54; [11] Фофанова Т. С, в сб.;
Упорядоченные множества и решетки, в. 3, Саратов, 1974,
с. 99 —108. И. В. Стеллецкий.
ЖОРДАНОВА ДУГА, простая дуг а,— топо-
топологическое пространство, гомеоморфное отрезку [0, 1]
ЧИСЛОВОЙ прямой. А. А. Мальцев
ЖОРДАНОВА МАТРИЦА — квадратная блочно-диа-
гональная матрица J над полем к, имеющая вид
/ =
о
где Jm(X) — квадратная матрица порядка т вида
X 1
X 1
Jm(X) =
X 1
к
Матрица Jm(X) называется жордановой
клеткой порядка то с собственным числом X.
Каждая клетка определяется элементарным делите-
делителем (см. [5]).
Для произвольной квадратной матрицы А над ал-
алгебраически замкнутым полем к всегда существует
такая квадратная невырожденная матрица С над к,
что С-1АС является Ж. м. (иначе говоря, Л подобна
над к некоторой Ж. м.). Это утверждение справедливо
и при более слабых ограничениях на поле к', для того
чтобы матрица А была подобна над к нек-рой Ж. м.,
необходимо и достаточно, чтобы поле к содержало все
корни минимального многочлена матрицы А. Мат-
Матрица С~1АС, указанная выше, наз. жордановой
формой (или жордановой нормальной
формой) матрицы А. Такая нормальная форма
рассматривалась одним из первых К. Жорданом [1]
(см. также историч. очерк к гл. VI и VII книги [2]).
Жорданова форма матрицы определена не однознач-
однозначно, а с точностью до порядка жордаиовых клеток.
Точнее, две Ж. м. подобны над к в том и только в том
случае, когда они составлены из одних и тех же жор-
дановых клеток и отличаются друг от друга лишь
расположением этих клеток на главной диагонали.
Количество Ст (X) жордановых клеток порядка т с
собственным числом X в жордановой форме матрицы А
определяется формулой
Ст (X) ^
(А —ХЕ)'*-1 —
-.. гк (А—ХЕ)П
(А —\Е)>"
где Е — единичная матрица того же порядка п, что
и А , гк В — ранг матрицы В, а гк (А—ХЕ)°, по опре-
определению, равен п.
Помимо жордановой нормальной формы, имеется и
ряд других типов нормальных форм матрицы. К их
рассмотрению прибегают, напр., когда хотят исклю-
исключить неоднозначность приведения к жордановой форме
или когда основное поле не содержит всех корней
минимального многочлена матрицы (см. [2] — [5]).
С точки зрения теории инвариантов Ж. м.— это
канонич. представители в орбитах присоединенного
представления для полной линейной группы. Нахож-
Нахождение аналогичных представителей для произвольной
редуктивной алгебраич. группы является пока A978)
нерешенной до конца задачей (см. [6], [7]).
Лит.: [1] Jordan С, Traite des substitutions et des equa-
equations algebriques, P., 1870, p. 114—25; [2] Б у р б а к и Н., Ал-
Алгебра. Модули, кольца, формы, пер. с франц., М., 1966; [3]
Гантмахер Ф. Р., Теория матриц, 2 изд., М., 1966;
[i] Л е н г С, Алгебра, пер. с англ., М., !968; [5] М а л ь-
цев А. И., Основы линейной алгебры, 4 изд., М., 1975; [6]
Семинар по алгебраическим группам. Сб. статей, пер. с англ.,
М., 1973; [7] Steinberg R., в кн.: Тр. Международного
конгресса математиков. Москва. 1966, М., 1968, с. 277—83.
В. Л. Попов.
ЖОРДАНОВА НОРМАЛЬНАЯ ФОРМА матриц ы—
см. Жорданова матрица.
ЖУКОВСКОГО ТЕОРЕМА — одна из основных тео-
теорем гидромеханики несжимаемой идеальной жидкости,
полученная Н. Е. Жуковским в 1906 методами теории
функций комплексного переменного: подъемная сила
крыла (на единицу длины крыла), обтекаемого устано-
установившимся плоскопараллельным потоком жидкости (га-
за), ортогональна к скорости потока на бесконечности
и по величине равна произведению этой скорости на
циркуляцию скорости и на плотность жидкости. При
применении Ж. т. следует иметь в виду, что величина
циркуляции скорости однозначно определяется из
условия Жуковского конечности скорости
жидкости у задней острой кромки крыла (см. рис. 2
И ЛИТ. , В СТ. Жуковского функция). Е. Д. Соломенцев.
ЖУКОВСКОГО ФУНКЦИЯ — рациональная функ-
функция комплексного переменного z:
,. 1 /_\ 1 / _ i 1
Важна своими применениями в гидромеханике, откры-
открытыми Н. Е. Жуковским (см. [1], [2]) в основном для
построения it изучения профиля Жуковского
(крыла Жуковского). Пусть в плоскости z
заданы окружность К, проходящая через точки z==tl
(рис. 1), и окружность К', касающаяся К извне в точке
z=l, с центром а и радиусом р. При отображении
w=K(z) образом окружности К' является нек-рая
замкнутая кривая V с острием в
точке и>= 1, касающаяся в отой точ-
точке дуги окружности L (образа К)
Рис. 1.
Рис. 2.
и изображенная на рис. 2,— это и есть профиль Жу-
Жуковского. Функция w—X(pt-\-a) отображает внешность
единичного круга плоскости t на внешность L'. Для
получения профилей Жуковского более общего вида
и расположения применяется обобщенная Ж. ф.
(см. [3], [4], [5]):
w =JL (а — Ъ) z + 4"
) — . а > Ъ > 0.
Лит.: [1] Ж у к о в с к и й Н. Е., Гидродинамика, Собр.
соч., М.—Л., т. 2, 1949; [2] его же, Теоретические основы
воздухоплавания, Собр. соч., т. 6, 1950; [3] М а р к у ш е в и ч
А. И., Теория аналитических функций, 2 изд., т. 1 — 2, М.,
1967—E8; [4] Седов Л. И., Плоские задачи гидродинамики
и аэродинамики, 2 изд., М., 1966; [5] К о ч и н Н. Е., К и б е л ь
И. А., Розе Н. В., Теоретическая гидромеханика, ч. 1, 6 изд.,
М., 1963. Е. Д. Соломенцев.
ЖУРДЕНА ПРИНЦИП — дифференциальный вариа-
вариационный принцип механики, установленный Ф. Жур-
деном [1] и выделяющий действительные движения
системы из класса кинематически возможных движений,
удовлетворяющих условиям наложенных на систему
идеальных связей и условиям постоянства положений
точек системы для рассматриваемого момента времени.
Согласно Ж. п., для действительного движения системы,
стесненной идеальными двусторонними (удерживаю-
(удерживающими) связями, сумма элементарных работ активных
сил и сил инерции на любых вариациях кинематически
возможных скоростей равна нулю в любой момент
времени. См. также Вариационные принципы класси-
классической механики.
Лит.: [1] J о и г d а i n Р. Е. В., «Quart. J. Pure and Appl.
Math.», 1908, v. 39, p. 375—84. В. В. Румянцев.
ЖЮЛИА ТЕОРЕМА: если а — изолированная су-
существенно особая точка аналитич. функции /(z) ком-
комплексного переменного z, то существует по крайней
мере один выходящий из а луч 5= {z; arg(z—а)=90}
такой, что в любом угле
F={z; | arg (z —а) —90 | < г], г > О,
симметричном относительно этого луча, функция /(z)
принимает каждое конечное значение, за исключением,
быть может, одного, в бесконечной последовательности
точек {zk)czV, сходящейся к а. Этот результат Г. Жю-
лиа (см. [1]) дополняет большую Пикара теорему
о поведении аналитич. функции в окрестности су-
существенно особой точки.
Фигурирующие в Ж. т. лучи наз. лучами Ж го-
голи а. Так, для функции f(z) = ez и а= оо лучами Жюлиа
являются положительная и отрицательная части мни-
мнимой оси. В связи с Ж. т. для мероморфной, напр, в
единичном круге D= {z; |z|<l}, функции w=f(z)
хорда S с конечной точкой еге° на окружности lz| = l
наз. отрезком, или хордой, Жюлиа, если
в любом открытом угле V с вершиной е'9°, содержащем S,
функция w=j(z) принимает все значения на римановой
сфере w, за исключением, быть может, двух. Точка
е " наз. точкой Жюлиа для /(z), если любая
хорда S с концом е ° является хордой Жюлиа для f(z).
Существуют мероморфные функции ограниченного вида,
для к-рых каждая точка окружности |z| = l является
точкой Жюлиа.
См. также Асимптотическое значение, Иеерсена тео-
теорема, Предельное множество.
Лит.: [1] Julia G., Lemons sur les fonctions uniformes S
point singulier essentiel isole, P., 1924; [2] Маркушевич
А. И., Теория аналитических функций, 2 изд., т. 2, М., 1968,
гл. 8. Е. Д. Соломенцев.
зависящий от параметров интеграл —
интеграл вида
J (У) = \ f {х, у) dx,
в к-ром точка х= (xlt х2, . . ., х„) пробегает пространство
R" (в случае, если эта точка пробегает только нек-рую
область D в пространстве Rn, то функцию f(x, у) можно
считать равной нулю при x?Rn*\D), а точка у= (ylt
уг, ..., ут), образующая совокупность параметров
yi, у2, . .., ут, изменяется в пределах нек-рой области G
пространства Rm.
Основные вопросы теории таких интегралов — это
выяснение условий непрерывности и дифференцируе-
мости функции /(у) по параметрам ух, у2, . . ., ут. Менее
стеснительные условия непрерывности и дифференци-
руемости J(y) получают при понимании интеграла в
смысле Лебега. Справедливы следующие утверждения.
1) Если функция f(x, у) для почти всех x?Rn непре-
непрерывна по у в области Gcz.Rm и если существует интег-
интегрируемая в R" функция g(x) такая, что для каждого
y?G и для почти всех x?Rn справедливо неравенство
lf(x, y)\^ig(x), то интеграл J(y) является непрерывной
функцией у в области G.
2) Если функция f(x, t), определенная при x?Rn,
t?(a, b), для почти всех ;r?R" и каждого t? (я, Ь)
имеет производную ~ (х, t), к-рая для почти каждого
г-R" является непрерывной функцией ( на интервале
(а, Ь), и если существует интегрируемая в R." функция
g(x) такая, что для каждого t? (а, Ь) и для почти всех
x?Rn справедливо неравенство l-jj(x, f)l<?(a:)I то
из существования при нек-ром to?(a, Ь) интеграла
г, tQ) dx
следует дифференцируемость по t на интервале (а, Ъ)
функции
(х, t) dx
и возможность вычисления производной /' (t) диффе-
дифференцированием под знаком интеграла:
Г (t) = \ -|f (x, t) dx.
Из 1) — 2) получают ряд более простых утвержде-
утверждений о непрерывности и дифференцируемостп интегра-
интегралов по параметрам, относящихся к трактовке интег-
интеграла в смысле Римана и более частным случаям (см.
[2] - [4]).
Несобственные интегралы, зави-
зависящие от параметров. Для простейшего
несобственного интеграла 1-го рода
вводят понятие равномерной сходимости по параметру
t на нек-ром сегменте c<:;<:d. Этот интеграл наз. рав-
номерно сходящимся по t на сегменте [с, d], если для
любого е>0 найдется А (е)>0 такое, что
)д/(*. *)**
< 8
для всех R^A (e).
Справедливы следующие утверждения:
а) Если функция f(x, t) непрерывна в полуполосе
[я<ж<оо, c<r(<d] и интеграл (*) сходится равно-
равномерно по t на сегменте [с, d], то функция J(t) не-
непрерывна на сегменте c^t^d.
б) Если f(x, t) и производная -j (x, t) непрерывны
в полуполосе [а<ж<оо, c<sgt«:d], интеграл A) сходится
для нек-рого f?[c, d], а интеграл
df
(x l)d
сходится равномерно относительно t на сегменте [с, d],
то функция J(t) дифференцируема на сегменте [с, d]
и ее производная может быть найдена по формуле
Аналогичные утверждения справедливы и для не-
несобственного интеграла 2-го рода.
Лит.: [1] Владимиров В. С, Уравнения математи-
математической физики, 2 изд., М., 1971; [2] И л ь и н В. А., П о-
з н я к Э. Г., Основы математического анализа, ч. 2,М., 1973;
[3] Кудрявцев Л. Д., Математический анализ, т. 2,
М., 1970; [4] Никольский С. М., Курс математического
анализа, т. 2,М., 1973; [5] Тихонова. Н., Самарский
А. А., Уравнения математической физики, 4 изд., М., 1972.
В. А. Ильин.
ЗАМЕНА БАЗЫ — теоретико-категорная конструк-
конструкция, частными случаями которой являются понятие
индуцированного расслоения в топологии, а также
понятие расширения кольца скаляров в теории мо-
модулей.
Пусть С — категория с расслоенными произведе-
произведениями и g: S'-+S — морфизм этой категории. 3. б.
при помощи морфизма g есть функтор из категории
5-объектов (т. е. из категории морфизмов /: X—>-S,
где X — объект из С) в категорию ^'-объектов, сопо-
сопоставляющий 5-объекту /: X-+-S S'-объект /': X'—>-S',
где X' = XXsS', а морфизм /' есть проекция на второй
сомножитель. Морфизм g при этом наз. м о р ф и з-
мом замены базы. Говорят также, что объект
X' получен 3. б. из объекта X.
Частным случаем понятия 3. б. является понятие слоя
морфизма /: X-+S схемы S. А именно, слой мор-
морфизма /над точкой s?S есть схема
т. е. схема, получаемая из X 3. б. при помощи ес-
естественного морфизма s—>-S. Аналогично определяется
геометрический слой Xs, он получается
3. б. npi' ломощи морфизма Spec К—>S, связанного с
точкой S, где К — алгебраически замкнутое поле.
Многие свойства 5-схемы X сохраняются при 3. б.
Обратная задача — восстановление свойств схемы X
по свойствам схемы, полученной из X 3. б., рассмат-
рассматривается в теории спуска (см. также [3]).
Пусть морфизм /': X'—+S' получен 3. б. при помощи
g: S'^-S из морфизма /: X-vS, т. е. задан декартов
квадрат
Х'-^-Х
''I 1'
S' ~^S
g
И пусть F — пучок множеств на X. Тогда существует
естественное отображение пучков -vp: g*f*{F)—>f'*g'*(P).
Если F — пучок абелевых групп, то для каждого д^О
существует естественный гомоморфизм пучков
%¦ g* (Л«/. (*")) -* я*;'. (gl* (/¦)).
При этом г|> и гр? также наз. морфизмами за-
замены базы. Принято говорить, что справедлива
теорема о замене базы, если гр или, соот-
соответственно, г|>? являются изоморфизмами. Иначе говоря,
теорема о 3. б. это — утверждение о согласованности
(коммутировании) функторов Rift с функтором за-
замены базы. В частности, если g есть вложение точки
s?S, то теорема о 3. б. означает существование ес-
естественного изоморфизма: (Л9/, (F))x S^. Hi (Xx, F | Хх)
между слоем q-то прямого образа пучка F и ^-мерной
группой когомологий слоя морфизма /. Теорема о 3. б.
справедлива в следующих ситуациях: 1) / — собствен-
собственное отображение паракомпактных топологич. про-
пространств, S — локально компактное пространство [1];
2) / — отделимый квазикомпактный морфизм схем, g —
плоский морфизм, F — квазикогерентный пучок Ох~
модулей (теорему о сравнении когомологий обычных
и формальных схем (см. [2]) также мощно интерпрети-
интерпретировать как теорему о 3. б.); 3) / — собственный мор-
морфизм схем, F — пучок кручения в этальной топологии.
Некоторые другие случаи, в к-рых справедлива тео-
теорема о 3. б., рассмотрены в [3].
Лит.: ШГодеман Р., Алгебраическая топология и те-
теория пучков, пер. с франц., М., 1961; [2] Grot hen d i -
eck A., Dieudonne J., Elements de geometrie algebrique,
P., 1961, (Publ. math. IHES, № 11); [3] Theorie des topos et
conomolof?ie etale des schemas, В., 1973. В. И. Данилов.
ЗАМКНУТАЯ ГЕОДЕЗИЧЕСКАЯ — замкнутая глад-
гладкая кривая на римановом многообразии М, к-рая яв-
является геодезической линией. Более общее понятие —
геодезическая петля, т. е. геодезическая
y(t) (a<:(<:6), проходящая при t==a и t=b через одну
и ту же точку р; рассматриваемая как замкнутая
линия, она может иметь «излом» в точке р. Геодезич.
петля является 3. г. только в том случае, когда такого
излома нет, т. е. когда y{t) при t=a и при t==b имеет
одну и ту же касательную. Замкнутые траектории
геодезического потока в пространстве ТМ касательных
векторов к М проектируются в 3. г. при естественной
проекции ТМ^г-М. Кривая, получающаяся, когда
одна и та же 3. г. обходится несколько раз, наз. к р а т-
н о й 3. г. Если 3. г. не является кратной, то она
наз. простой 3. г.
Определение 3. г. и геодезич. петли дословно пере-
переносится на тот случай, когда М снабжено финслеровой
метрикой или аффинной связностью. Если же М —
метрич. пространство (в этом случае геодезич. линия
определяется как локально кратчайшая линия), то
определение геодезпч. петли сохраняется дословно,
тогда как определение 3. г. нужно несколько изме-
изменить, поскольку нельзя говорить о гладкости или
изломе. Геодезич. петля y(t) (a<f<b), где y(a) = y(b)=p
и у не постоянна ни на каком отрезке, будет 3. г.,
если при достаточно малом е>0 линия
— fy(b~s),
Т t y(a + s), 0<s<e,
(состоящая из двух дуг линии у: первая дуга соединяет
у{Ь—г) с у(Ь)=р, вторая соединяет р=у(а) с у(а-\-е))
является кратчайшей линией между своими концами
у(Ъ—е) и у(а+е).
Исследования 3. г. проводились главным образом
для 3. г. на замкнутых римановых многообразиях;
имеется также ряд результатов для финслеровых
многообразий; нек-рые результаты получены и в более
общем случае метрич. пространств с нек-рыми специ-
специальными свойствами (так наз. G-пространства Бузе-
Буземана, см. Геодезических геометрия) [1]. Эти исследо-
исследования были начаты Ж. Адамаром [2], А. Пуанкаре
(Н. Poincare [3]) и Дж. Биркгофом [4].
Ж. Адамар положил начало исследованиям геодезия,
линий (не обязательно замкнутых) на многообразиях
отрицательной кривизны. Основные современные ре-
результаты относятся к случаю замкнутых многообразий
М, кривизна к-рых отрицательна по всем двумерным
направлениям во всех точках. Относительно 3. г. на
таком М доказано, что замкнутые траектории геодезич.
потока всюду плотны в ТМ (см. [5]) (аналогичное
явление наблюдается и в ряде примеров с положитель-
положительной кривизной, но не всегда F]); имеется оценка роста
числа 3. г., длина к-рых не превосходит I, с увеличе-
увеличением I (см. [7]). Ж. Адамар аппроксимировал длинные
отрезки незамкнутых геодезических с помощью 3. г.,
что можно считать началом символической дина-
динамики.
К Ж. Адамару восходит также теорема, дающая
нек-рую информацию о 3. г. на замкнутом многообра-
многообразии М (уже без каких-либо предположений о кривизне)
в терминах свойств фундамен талъной группы лг (М). Ори-
Ориентированная замкнутая кривая у определяет некото-
некоторый класс сопряженных элементов [у] группы щ (М)\
все такие кривые, отвечающие одному классу, получа-
получаются друг из друга посредством свободной сомотопии.
Оказывается, что для каждого класса К сопряженных
элементов щ (М), кроме класса, состоящего из единицы
этой группы, среди всех замкнутых кривых у с [у] — К
существуют кратчайшие, л они являются 3. г. Эта
теорема (справедливая не только для римановых или
финслеровых метрик, но и в общем случае G-npo-
странств Буземана) является простейшим и исторически
первым результатом вариационного исчисления «
целом. Однако возникновение последнего как само-
самостоятельного направления связано с более сложным
применением вариационных методов к исследованию
3. г. на многообразиях, гомеоморфных сфере, для
к-рых (как и вообще для односвязных многообразий)
предыдущая теорема бессодержательна.
Вопрос о 3. г. на таких многообразиях поставил
А. Пуанкаре (точнее, у него речь шла об о в а л о и д е,
т. е. двумерной замкнутой выпуклой поверхности).
Он предположил, что в «общем» случае на овалоиде
имеются три 3. г. без самопересечений, причем две из
них устойчивы в линейном приближении,. а одна не-
неустойчива. Такая связь вопроса о существовании 3. г.
и оценке их числа с вопросом об их свойствах устой-
устойчивости составляет существенную особенность эври-
эвристических рассуждений А. Пуанкаре, связанных пре-
преимущественно с теорией динамич. систем. Эти рассуж-
рассуждения могут быть проведены вполне строго, однако
только для метрик, достаточно близких к «стандартной»
(обычной метрике на сфере #2-f-i/a+z2=l в евклидовом
пространстве, см. [8]). Для метрик, далеких от стан-
стандартной, предполагавшиеся А. Пуанкаре свойства
устойчивости 3. г. могут не иметь места [9].
Открытие вариационного подхода к вопросу о 3. г.
на односвязных многообразиях принадлежит Дж. Бирк-
гофу [4]. Он доказал, что на многообразии, гомеоморф-
ном сфере, существует хотя бы одна 3. г.; в частности,
предположение о существовании на двумерной сфере
трех 3. г. без самопересечений было доказано Л. А. Лю-
стерником и Л. Г. Шнирельманом (см. [10]).
Имеются работы о свойствах 3. г. для «типичных»
римановых (или финслеровых) метрик (т. е. образую-
образующих множество второй категории в пространстве всех
метрик данного класса гладкости) (см. [11] — [13]).
Стандартная метрика на сфере обладает тем свой-
свойством, что все ее геодезические замкнуты и имеют
одинаковую длину; на сфере имеются и другие метрики
с тем же свойством [14]. Исследовался также вопрос о
топологич. свойствах многообразия и о метрике на нем,
если последняя обладает указанным свойством или
каким-нибудь вариантом такового.
Подробное изложение теории 3. г. см. в [15].
Лит.: [1] Буземан Г., Геометрия геодезических, пер.
с англ., М., 1962; [2] Н a d a m a r d J., «J. math pure appl.»,
1898, t. 4, p. 27—75; [3] П у а н к а р е А., Избр. труды, М.,
1972, т. 2, с. 735—74; L4] В i r k h о f f G. D., «Trans Amer.
Math. Soc», 1917, v. 18, p. 199 — 300; [5] А н о с о в Д. В.,
Геодезические потоки на замкнутых римановых многообразиях
отрицательной кривизны М., 1967; 1б] We in stei n А., «С. г.
Acad. sci.», 1970, t. 271, А504; [7] С и н а й Я. Г., «Изв. АН СССР.
Сер. матем.», 1966, т. 30, в. 6, с. 1275—96; [8] Г р ю н-
таль А. И., «Успехи матем. наук», 1977, т. 32, в. 4, с. 244—45; [9]
его же, там же, в. 5, с. 166; [10] Л ю с т е р н и к Л. А.,
Ш н и р е л ь м а н Л. Г., там же, 1947, т. 2, в. 1, с. 166 —
217; [11] Abraham R.,b кн.: «Global Analysis, N. Y., 1970
(Proc. Symp. Pure Math., v. 14), p. 1—3; [12] К 1 i n g e n-
berg W., Та kens P., «Math. Ann.», 1972, Bd 197, № 4, S.
323—34; [131 Klingenberg W., «J. differential geometry»,
1976, v. 11, p. 299—308; [14] ZollO., «Math. Ann.», 1903,
Bd 57, S. 108—33; [15] Klingenberg W., Lectures on
closed geodesies, Grundlehren der mathematischen Wissenschaf-
ten, № 230, В.—Hdlb.—N. Y., 1978. Д. В. Аносов.
ЗАМКНУТАЯ КАТЕГОРИЯ — категория с дополни-
дополнительной структурой, позволяющей использовать внут-
внутренний Hom-функтор как сопряженный справа функтор
к абстрактному тензорному произведению.
Категория ЗД} наз. замкнутой, если в ней задан
бифунктор ®:?ШХЩ1—*-9Л (см. Функтор), выделен
объект /, заданы естественные изоморфизмы
Яавс'- (A®B)®C->-A(g)(B(g)C) (ассоциативность),
\л: /®Л—уА (левая единица),
9А- А®1—*А (правая единица),
КАВ- -4 ®5->-5®Л (коммутативность)
и выполнены следующие условия: 1) естественные изо-
изоморфизмы а, X, р, у. когерентны; 2) каждый функтор
нАВ(Х)^нт(А®х, я)-.дл-^<г,
где <5 — категория множеств, представим. Представ-
Представляющие объекты обычно обозначаются Нотж(Л, В),
и их можно рассматривать как значения на объектах
бифунктора Нот!М: Ш}*ХШ?->-Ш1 (внутренний Hom-
функтор). Если бифунктор ® совпадает с произведе-
произведением, а объект / является правым нулем (терминальным
объектом) категории ЗД}, то Ш наз. декартово
замкнутой.
Декартово замкнутыми являются: категории мно-
множеств, категория малых категорий, категория пучков
множеств над топологич. пространством; замкнутыми —
категория модулей над коммутативным кольцом с
единицей, категория действительных (или комплекс-
комплексных) банаховых пространств и линейных отображений
с нормой, не превосходящей единицы.
Лит.: [1] Бунге М., «Математика», 1972, т. 16, MS 2,
с. 11—46; [2] Toposes, Algebraic Geometry and Logic, В.— Hdlb.—
N Y 1972- [3] D u b u с Е., Kan extensions in enriched category
theory B,— Hdlb.— N.Y., 1970. М.Ш. Цаленко.
ЗАМКНУТАЯ ПОДСХЕМА — подсхема схемы X,
задаваемая квазикогерентным пучком идеалов / струк-
структурного пучка ($х следующим образом: топологич.
пространство подсхемы V(J) является носителем фак-
торпучка Qx/J, а структурный пучок — ограничением
QxlJ на свой носитель. Морфизм. схем /: У—»-Х наз.
замкнутым вложением, если / осуществ-
осуществляет изоморфизм Y с нек-рой 3. п. в X; замкнутое
вложение является мономорфизмом в категории схем.
Для любого замкнутого подмножества YdX сущест-
существует минимальная 3. п. в X с пространством Y — так
наз. приведенная 3. п. с пространством Y,
Если Y — подсхема X, то наименьшая 3. п. Y' в X,
содержащая Y, наз. (схемным) замыканием
П О Д С X е М Ы Y В X. В. И. Данилов.
ЗАМКНУТАЯ СИСТЕМА элементов, зам-
замкнутая система функций,— система эле-
элементов ф„ некоторого линейного нормированного про-
пространства Н такая, что любой элемент /?// можно
сколь угодно точно приблизить в метрике пространства
Н конечной линейной комбинацией элементов из этой
системы, т. е. для всякого е>0 найдутся такие числа
с0, сг, . .., сп, что выполняется неравенство
. е. A)
Напр., система степеней [хп }, га=0, 1, 2, . .., замкнута
в пространстве Lo[a, b, djx(x)] функций, суммируемых
в степени p^szl на конечном отрезке [а, Ь\ с интеграль-
интегральным весом ц(х), причем неравенство A) в этом случае
имеет вид
¦) < еР, B)
где Q,,(x) — многочлен степени га. Обычно рассмат-
рассматривается случай, когда {(рп} —ортонормированная
последовательность элементов в гильбертовом про-
пространстве Н. Тогда условие замкнутости A) эквива-
эквивалентно выполнению для всех элементов f^H равенств
2
Г=оа'"
где {ап } — коэффициенты Фурье элемента / по системе
{ф„}. В случае тригонометрич. системы функций
условие C) наз. равенством Парсеваля;
оно имеет вид
/*()*ff2<+b>
Это равенство рассматривали М. Парсеваль (М. Раг-
seval, 1806), III. Балле Пуссен (Ch. La Vallee Poussin,
1890), А. Гурвиц (A. Hurwitz, 1901—03); строгое его
доказательство дал (в случае, когда f(x) ограничена)
А. М. Ляпунов A896).
Общий случай условия замкнутости C) впервые
подробно исследовал В. А. Стеклов A898) в связи с
решением нек-рых задач математич. физики. Введя
термин «замкнутость», В. А. Стеклов рассмотрел с
этой точки зрения различные конкретные системы
ортогональных функций, и в частности фундаментальные
решения уравнения Штурма — Лиувилля (см. Штур-
Штурма — Лиувилля задача). Поэтому равенство C) часто
наз. условием замкнутости Парсе-
Парсеваля — Стеклов а.
Понятие замкнутости широко применяется в теории
ортогональных многочленов. Если отрезок ортогональ-
ортогональности конечен, то система ортогональных многочленов
замкнута при любом весе. В случае бесконечного ин-
интервала ортогональности В. А. Стеклов установил
ряд условий на весовую функцию, достаточных для
замкнутости соответствующей системы ортогональных
многочленов; в частности, он доказал замкнутость
систем многочленов Эрмита и Лагерра. Одно из доста-
достаточных условий Стеклова в случае интервала (а, сю)
заключается в том, что существует такая последова-
последовательность положительных чисел {ап }, для к-рой выпол-
выполняются соотношения
lim а„=оо, lim —!L- = 0,
где h (x) — дифференциальны й вес на
интервале (а, оо) (т. е. d\i (x) = h(x)dx). Для всего
интервала (—оо, -|-оо) достаточное условие состоит в
том, чтобы дифференциальный вес h {х) был почти
всюду положителен и удовлетворял неравенству
h (х) sg с ехр (— а | х |), а > 0, ig (—оо, оо).
Это условие в нек-ром смысле близко к необходимому,
ибо, как показал еще В. А. Стеклов, система много-
многочленов незамкнута в случае весовой функции вида
А(х) = охр(-|х|Р), $ = ¦%—, 1я = 1,2, ....
Полное решение вопроса об условиях замкнутости
системы многочленов в пространстве L2[a, b, d^i(x)]
в случае бесконечного интервала дал М. Рис (М. Riesz,
1922^. Он доказал, что для замкнутости системы много-
многочленов в L2 [а, Ъ, d\k (x)\ необходимо и достаточно,
чтобы либо соответствующая моментов проблема была
определенной, либо в случае неопределенности функция
ц (х) была так наз. jV-экстремальным решением про-
проблемы моментов.
С понятием замкнутости тесно связано понятно
полноты системы функций, к-рое заключается в том,
что из равенства нулю линейного ограниченного функ-
функционала / на всех элементах системы {ф„} следует
условие /=0. В гильбертовом пространстве эти два
понятия эквивалентны. Полнота системы {(рп(х)} в
пространстве Lp эквивалентна замкнутости этой же
системы в Lq, где р^1, g^l и Ь—=1.
В комплексной области подробно изучены аналоги
неравенств типа A) или B) для систем многочленов и
более общих систем функций (см. Ортогональные мно-
многочлены в комплексной области).
Лит.: fl] К а ч м а ж С, Ш т е й н г а у з Г., Теория орто-
ортогональных рядов, пер. с нем., М., 1958; [2] Геронимус Я. Л.,
Теория ортогональных многочленов. Обзор достижений отече-
отечественной математики, М.— Л., 1950; [3] С е г ё Г., Ортогональ-
Ортогональные многочлены, пер. сангл., М., 1962; [4] Стеклов В. А.,
«Зап. Акад. наук» (физ.-матем. сер.), 1911, т. 30, .MS 4,
с. 1—86; 1914, т. 33, № 8, с. 1—59; [5] е г о ж е, Основные за-
задачи математической физики, ч. 1 — 2, П., 1922—23; [6] R i-
е s •/. М.. в кн.: Acta lltterarum ас Scientiarum regial Universitatis
Hunsaricac. Sec. scient. mathemat., 1922—1923, kot. 1, old.
209 — 25; L7] H e w i t t E.,«Amer. Math. Monthly», 1954, v. 61, p.
249 —ГH. П. К. Суетин.
ЗАМКНУТАЯ ФОРМУЛА — см. Арифметика фор-
формальная.
ЗАМКНУТОЕ МНОГООБРАЗИЕ — компактное мно-
многообразие без края. Например, совокупность всех кра-
краевых точек ^-мерного компактного многообразия есть
(к — 1)-мерное 3. м.
ЗАМКНУТОЕ МНОЖЕСТВО в топологиче-
топологическом пространстве — множество, содержащее
все свои предельные точки. Таким образом, все точки
дополнения к 3. м.— внутренние, и потому 3. м. можно
определить как дополнение к открытому. Понятие 3. м.
лежит в основе определения топологич. пространства
как непустого множества X с заданной системой мно-
множеств (называемых замкнутыми), удовлетворяющей
аксиомам: все X и пустое множество ф замкнуты;
пересечение любого числа 3. м. замкнуто; объединение
конечного числа 3. м. замкнуто.
Лит.: [1] К у р а т о в с к и й К., Топология, [пер. с англ.],
т. 1, М., 1966. А. А. Мальцев.
ЗАМКНУТОЕ ОТОБРАЖЕНИЕ — отображение одно-
то топологич. пространства на другое, при к-ром образ
всякого замкнутого множества есть замкнутое множе-
множество. Класс непрерывных 3. о. играет важную роль
в общей топологии и ее приложениях. Непрерывные
замкнутые бикомпактные отображения наз. совер-
совершенными. Непрерывное отображение /: Х_»-У,
/(Х)=У ^-пространств замкнуто тогда и только тогда,
когда разбиение {f~ly: y?Y} непрерывно в смысле
Александрова (непрерывно сверху) или когда для каж-
дого открытого в X множества U множество /*Е/=
= {г/?У, /~1!/czbr} открыто в U. Последнее свойство
лежит в основе определения полунепрерыв-
полунепрерывных сверху многозначных отображений. Т. о.,
/ замкнуто тогда и только тогда, когда обратное (мно-
(многозначное) отображение непрерывно сверху. Каждое
непрерывное отображение бикомпакта на хаусдорфово
пространство — 3. о. Каждое непрерывное 3. о. Тх-
пространств факторно; обратное неверно. Ортогональ-
Ортогональное проектирование плоскости на прямую непрерывно
и открыто, но не замкнуто. Также не всякое непре-
непрерывное 3. о. открыто. Если /: X—»-У непрерывно и
замкнуто, аХиУ вполне регулярны, то /-1г/ =[/~1г/]рХ
для любой точки y?Y (здесь рх — Стоуна — Чеха
бикомпактное расширение, а /: РХ—»-РУ — непрерывное
продолжение отображения на расширения Стоуна —
Чеха пространств X и У); в классе нормальных про-
пространств справедливо и обратное. Для непрерывных
З.о. при переходе к образу сохраняются следующие
топологич. свойства: нормальность; коллективная нор-
нормальность; совершенная нормальность; паракомпакт-
паракомпактность; слабая паракомпактность. Полная регулярность
и сильная паракомпактность могут для непрерывных
замкнутых и даже совершенных отображений не со-
сохраняться. При переходе к прообразу для непрерывных
3. о. перечисленные выше свойства могут не сохра-
сохраняться. Это объясняется тем, что для непрерывного
3. о. прообразы точек могут быть небикомпактными,
хотя во многих случаях непрерывные 3. о. мало от-
отличаются от совершенных. Если / — непрерывное
3. о. метрич. пространства X на пространство У с
первой аксиомой счетности, то Y метризуемо, а граница
полного прообраза f-1y бикомпактна для любого y?Y,
Если / — непрерывное 3. о. метрич. пространства X
на ^-пространство Y, то множество всех точек y?Y,
при к-рых /-1;/ небикомпактно, а-дискретно.
Лит.: [1] Архангельский А. В. «Успехи матем
наук», 1966, т. 21, в. 4, с. 133—84; [2] Архангельский
А. В., П о н о м а р е в В. И., Основы общей топологии в зада-
задачах и упражнениях, М., 1974; [3] Engelking R., Outline
of General Topology, Amst., 1968. В. И. Ломолюрев
«¦-ЗАМКНУТОЕ ПРОСТРАНСТВО, абсолютно
замкнутое пространство,— хаусдорфово
пространство, к-рое при любом топологич. вложении
в какое бы то ни было хаусдорфово пространство У
является в У замкнутым множеством. #-3. п. харак-
характеризуются тем, что из каждого их открытого покрытия
можно выделить конечную подсистему, замыкания эле-
элементов к-рой покрывают это пространство. Регулярное
Н-3. п.—бикомпакт. Если каждое замкнутое под-
подпространство пространства //-замкнуто, то само про-
пространство — бикомпакт. Разработана теория Я-за-
мкнутых расширений хаусдорфовых пространств.
Лит.: [1] Александров П. С, Урысон П. С,
Мемуар о компактных топологических пространствах, 3 изд.,
М., 1971; [2] Илиадис С. Д., Фомин С. В., «Успехи
матем. наук», 1966, т. 21, в. 4, с. 47—76; [3] М а л ы х и н В. И.,
Пономарев В. И., в кн.: Итоги науки и техники. Алгебра.
Топология. Геометрия, т. 13, с. 149—230. В. И. Пономарев.
ЗАМКНУТЫЙ ГРАФИК, теорема о за-
замкнутом графике: пусть X и У — полные
линейные метрические пространства с метриками, ин-
инвариантными относительно сдвига, т. е. р (х, у) =
= р (х-\-а, у-\-а), х, г/, а ? X (соответственно для У) и
А—линейный оператор из X в У. Если график
Gr А ={(х, Ах) | х ? X} этого оператора есть замкну-
замкнутое подмножество декартова произведения XxY, то
оператор А непрерывен. Теорема о 3. г. допускает
ряд обобщений, напр.: линейное отображение с за-
замкнутым графиком отделимого бочечного пространст-
пространства в совершенно полное пространство непрерывно. К
теореме о 3. г. тесно примыкают теорема об открытом
отображении и теорема Банаха о гомеоморфизме.
Лит.: [1] Рудин У., Функциональный анализ, пер. с
англ., М., 1975; [2] Робертсон А.-П., Робертсон
В.-Дж., Топологические векторные пространства, пер. с англ.,
М., 1967. В. И Соболев,
ЗАМКНУТЫЙ ОПЕРАТОР —оператор A: D A-+Y
такой, что из xn?D д, хп-^-х и Ахп—+у следует x?Dд
и Ах=у (здесь X, Y — банаховы пространства над
одним и тем же полем скаляров и D даХ — область
определения оператора А). Понятие 3. о. распростра-
распространяется и на операторы, действующие в отделимых
линейных топологич. пространствах, только вместо
последовательностей {хп} надо рассматривать произ-
произвольные направления (сети) {х. }. Если 6гЛ — график
оператора А, то А замкнут тогда и только тогда, когда
Gr.4 есть замкнутое подмножество декартова произве-
произведения XXY. Это свойство часто принимается за оп-
определение 3. о.
Понятие 3. о. есть обобщение понятия оператора,
определенного и непрерывного на замкнутом подмно-
подмножестве банахова пространства. Примером замкнутого,
но не непрерывного оператора является оператор
А = -гг, определенный на множество С-\а, Ъ\ непре-
непрерывно дифференцируемых функций пространства С[а, Ъ].
Замкнутыми, но не непрерывными являются многие
операторы математич. физики.
Оператор А допускает замыкание (т. е.— замыкаем),
если существует замкнутое расширение этого опера-
оператора. Для того чтобы оператор был замыкаем, необ-
необходимо и достаточно, чтобы из хп, x'n?Dд,
lim ^„ = lim x'n, limiin=j, limAxn=y'
следовало у=у'. Наименьшее замкнутое расширение
оператора наз. его замыканием. Симметриче-
Симметрический оператор в гильбертовом пространстве с плотной
областью определения всегда допускает замыкание.
Линейный ограниченный оператор А: X—»-У замкнут.
Обратно, если А определен на всем X и замкнут, то
он ограничен. Если А замкнут \\ А~х существует, то А -1
также замкнут. ТсГк как А: X—*-Х замкнут тогда и
только тогда, когда А— XI замкнут, то А замкнут,
если резольвента Rx (А)— (А—Я,/) существует и
ограничена хотя бы для одного значения параметра
Я?С
Если D , всюду плотно в X и, следовательно, одно-
однозначно определен сопряженный оператор A*: Da*—^Х*,
Da*czY*, то А* — 3. о. Если, кроме того, Da* = Y
и X, Y рефлексивны, то Л — замыкаемый оператор и
А** является замыканием А-
3. о. А с помощью введения новой нормы в области
его определения можно сделать ограниченным. Пусть
I] * iio = II * !, A'J-|i -4-r!i У-
Тогда flj с новой нормой будет банаховым простран-
пространством и А, как оператор из (D^H-llo) в Y, будет огра-
ограниченным.
Лит.: [1] И о с и д а К., Функциональный анализ, пер.
с англ., М., 1967; [2] К а т о Т., Теория возмущений линейных
операторов, пер. с англ., М., 1972. В. И. Соболев.
ЗАМКНУТЫХ КЛАССОВ СИСТЕМА — система клас-
классов функций, замкнутых относительно операций рас-
рассматриваемой функциональной системы. Важнейшими
примерами 3. к. с. являются системы подалгебр ал-
алгебры логики, конечнозначных логик, автоматных
отображений, алгебр рекурсивных функций и нек-рые
другие. В. Б. Кудрявцев.
ЗАМЫКАНИЕ ВЫЧИСЛИТЕЛЬНОГО АЛГОРИТ-
АЛГОРИТМА — система уравнений
Lzu = f2, O^z^Z, A)
предельная при h—>-0, z(m, h)-*-z для системы частично
разрешенных уравнений
h fhm, т = 0, 1, .... М, B)
описывающих последовательные этапы вычислитель-
вычислительного алгоритма решения уравнения
Lhuh = jh C)
(напр., сеточного уравнения, тогда h — шаг сетки),
аппроксимирующего при /t_>-0 уравнение
Lu=f. D)
При этом LQ=Lh, /о=/Л, Ьм— тождественный опе-
оператор, /м= (Lfl)~1fh=uh, т. е. на М-ш этапе алгоритма
получается окончательное решение аппроксимирую-
аппроксимирующего уравнения C). Функция z(m, h) предполагается
возрастающей вместе с т (напр., линейной возрастаю-
возрастающей) и удовлетворяющей граничным условиям z@,
h) = 0, z(M, h) = Z. He исключается возможность 71/=оо;
в этом случае Ь„, /„, z(oo, h) понимаются как пре-
пределы переменных Lm, fin, z(m, h) при m->-oo. Случай
M= оо соответствует итерационным методам решения
уравнения C).
Если операторы Lz в уравнении A) ограничены
равномерно по z, то говорят, что алгоритм B) имеет
регулярное замыкание. Хотя множества
алгоритмов с регулярным замыканием и реально
устойчивых алгоритмов не совпадают, построение
3. в. а. часто помогает при исследовании устойчивости
алгоритма к различным возмущениям, в частности к
вычислительной погрешности (см. [3], [4]).
Понятие 3. в. а. введено в [1]. Там же получено и
исследовано замыкание алгоритма последовательного
исключения неизвестных решения сеточного уравне-
уравнения, аппроксимирующего уравнение D), где Lu=u—А к,
А — интегральный оператор Фредгольма.
Построение 3. в. а. и обратная операция — построе-
построение по непрерывному процессу дискретного алгоритма,
имеющего этот процесс своим замыканием,— бывают
полезными при конструировании новых методов реше-
решения задач. В частности, большое число итерационных
методов имеет своими замыканиями устанавливающиеся
процессы. Напр., методу простой итерации решения
сеточного уравнения Лапласа соответствует процесс
установления щ= Аи, трехслойному итерационному
методу — процесс установления и^+агг/=Дгг (см. [5]).
Лит.: [1] С о б о л е в С. Л., «Изв. АН СССР. Сер. матем.»,
1956, т. 20, № 4, с. 413 — 36; [2] Б а б у ш к а И., П р а г е р
М., В и т а с е к Э., «Ж. вычисл. матем. и матем. физ.», 1964,
т. 4, JV« 2, с. 351—53; [3] Б а х в а л о в Н. С, Вычислительные
методы решения обыкновенных дифференциальных уравнений,
К., 1970; [4] е г о же, Численные методы, 2 изд., М., 1975;
[5] С а у л ь е в В. К., Интегрирование уравнений параболиче-
параболического типа методом сеток, М., 1960; [6] Ш а п к и н А. Ф.,
«Ж. вычисл. матем. и матем, физ.», 1967, т. 7, № 2, с. 411 —16.
А. Ф. Шапкин.
ЗАМЫКАНИЕ МНОЖЕСТВА в топологиче-
топологическом пространстве — пересечение всех замк-
замкнутых множеств, содержащих данное множество.
А А. Мальцев.
ЗАМЫКАНИЯ ОТНОШЕНИЕ в частично упо-
упорядоченном множестве М — однозначное
отображение множества М в себя, сопоставляющее
каждому элементу а?М некоторый элемент а?М,
наз. замыканием элемента а, и удовлетворяющее
следующим аксиомам: 1) а^а; 2) если а«:Ь, то а<:Ь;
3) а=а. Элемент а наз. замкнутым, если он сов-
совпадает со своим замыканием. 3. о, в множестве М од-
однозначно определяется заданием системы всех замк-
замкнутых элементов. 3. о. может быть введено, в част-
частности, в системе всех подмножеств произвольного
множества М, частично упорядоченной по теоретико-
множественному включению. В этом случае также
принято говорить, что 3. о. задано в самом множестве М.
Во всяком множестве М можно задать 3. о., беря
в качестве системы замкнутых подмножеств любую
систему подмножеств, содержащую как само М, так
и пересечение любой своей подсистемы. Два частично
упорядоченных множества с 3. о. наз. изоморфными,
если существует такой изоморфизм этих частично упо-
упорядоченных множеств, при к-ром образы и прообразы
замкнутых элементов замкнуты. Важную роль в мате-
математике играют З.о. на множестве всех подмножеств М,
обладающие следующим дополнительным свойст-
свойством: замыкание объединения двух подмножеств мно-
множества М равно объединению замыканий этих под-
подмножеств. Такое 3. о. наз. топологией в мно-
множестве М.
Лит.: [ll Кон П., Универсальная алгебра, пер. с англ.,
М. 1968' [2] К у р о ш А. Г., Лекции по общей алгебре, М.,
1962. ' О. А. Иванова.
ЗАМЫКАНИЯ УСЛОВИЕ — условие в тканей гео-
метрии, при выполнении к-рого из некоторых пнциден-
ций точек и линии
S
хг
У >
h
и
\
\
\
\
ч
\
\
ткани вытекает но-
новая инциденция. При-
Примером 3. у. может
служить условие
':з а м ык а ния
Т о м с е н а (см.
г2 рис. а): первое и
х< Х2 второе семейства ли-
линий ткани изобра-
изображены параллельными прямы-
прямыми, третье — кривыми линия-
линиями; 3. у. означает, что из
принадлежности А и В и С и D
линиям третьего семейства
следует принадлежность та-
такой же линии точек Е и F.
Если х, у и г — параметры,
определяющие линии трех се-
семейств, то 3. у. можно при-
придать абстрактную форму си-
системы условных тождеств, ес-
если рассматривать z как результат «умножения» х и у.
z=xy,
, \
>3 '
"л
¦*|—"
\
\
\
ч
ч
ч
ч
\
ч
хг
Если z=xy рассматривать как квазигрупповую опе-
операцию, то условие замыкания Томсена равносильно
изотопности квазигруппы абелевой группе.
На рис. б ж в изображены условие замыка-
замыкания Рейдемейстера и условие ш е-
ст и уголь ноет и (все три условия равносильны
для плоской три-ткани даже без предположения диф-
ференцируемости). В абстрактной форме они ведут к
разным классам квазигрупп и луп, в многомерной
геометрии тканей — к разным классам тканей.
К 3. у. относятся также некоторые предложения
проективной геометрии (например, теоремы Дезарга
и Паппа).
Лит ¦ [1] Бляшке В., Введение в геометрию тканей,
пер. с нем., М., 1959; [2] Б е л о у с о в В.Д.,Рыжков В. В.,
в сб ¦ Итоги науки и техники. Алгебра. Топология. Геометрия,
т. 10, М., 1972, с. 159—88; [3] Б е л о у с о в В. Д., Алгебраиче-
Алгебраические' сети и квазигруппы, Киш., 1971. В. В. Рыжков.
ЗАОСТРЕНИЯ ТОЧКА — то же, что возврата точка.
ЗАПАЗДЫВАЮЩИХ ПОТЕНЦИАЛОВ МЕТОД,
принцип Дюамеля,— метод отыскания реше-
решения однородной задачи Коши для неоднородного ли-
линейного дифференциального уравнения или системы
с частными производными по известному решению
однородного уравнения или системы.
Пусть дано уравнение
Lu = f(x, t), u=u(x, <), x = (xi, ..., хп), A)
dth
где L — произвольный линейный дифференциальный
оператор, к-рый не содержит производных по t выше
n — 1 порядка. Частное решение и(х, t) уравнения A)
при ?>0 ищется в виде Дюамеля интеграла
и(х, t)=V (f(x, t; x)dt, B)
J 0
где ф является (регулярным или обобщенным) реше-
решением однородного уравнения
Если
) при к = 0, 1, . . ., т — 2,
' (х, т) при к = т — 1,
то функция B), полученная с помощью суперпозиции
импульсов ф, будет решением задачи Коши
"ё" ^о^0' *=0' *• ¦•¦' т~1' C)
для неоднородного уравнения A).
В случае обыкновенных дифференциальных уравне-
уравнений и систем 3. п. м. известен под названием метода
вариации постоянных, или метода им-
импульсов. Этот метод для линейных обыкновенных
дифференциальных уравнений порядка т:
заключается в том, что если щA), u2(t), . . ., um(t)—
какая-либо фундаментальная система решений урав-
уравнения Zu=O, то решение u(t) неоднородного уравнения
D) отыскивается в виде
Функции cJ=dcJldt, /=1, ..., т, однозначно опреде-
определяются как решения системы алгебраич. уравнений
(t) dkUj-l'dtk = O, k-=0, i, ..., т — 2.
_
с отличным от нуля детерминантом Вроньского.
Если f(t)=O при t<cO, то решение Uf(t) однородной
задачи Коши C) для уравнения D) принято наз. нор-
нормальной реакцией на внешнюю нагрузку f(i). Функция
uj(t) представима в виде свертки или интеграла Дюа-
Дюамеля
Гоф {t~x) f (т)
где l(f(t)=Q при t>0 и
0 при k = 0, I, ..., т — 2,
t =0 I 1 при k=m — 1.
dtf
Пусть f(x, t), x= (хг, ..., xn),— функция, имеющая
непрерывные частные производные до порядка (ге+1)/2
в случае нечетного п и («+2)/2 — в случае четного п,
a Mr[f(x, t)] —среднее значение / на сфере \у—х\ — г
с центром в точке х и радиуса г. Зависящая от неотри-
неотрицательного параметра т<:< функция
является решением волнового уравнения
? V ЕЕЕЕ Vit ДУ = 0,
удовлетворяющим начальным условиям
v(x, 0; r)=0, vt(x, 0; т) = /(г, т).
Интеграл Дюамеля
и (.г, t)--=^v(x, t — x; T)rfx E)
представляет собой решение однородной задачи Коши:
н(.г, 0) = 0, щ(х, 0) = 0 для уравнения Q ц=/(ж, ?)•
При л=2 и гс=3 из E) получаются выражения
¦"•¦>-sj:*s .<."?
(?/'pf"P>dy' »=(l'l. »». »3), F)
*Jl J p < t
ГДР (l=\x—y\.
Если же п=1, то
u(x, t) — — \ dx [x + ~x f (y, x) dy, y = y\.
- jo J x-t+x
Интеграл F) наз. запаздывающим потен-
потенциалом с плотностью /.
3. п. м. (метод вариации параметров) особенно прост
и полезен, когда он применяется к линейным системам
дифференциальных уравнений 1-го порядка вида
] Ahix^Bu = f(x, t), G)
где и=и(х, t) — вектор с к компонентами, А' и В —
ладанные матрицы размера кХк, а / — заданный век-
вектор.
Пусть вектор ф=ф(:г, t; т), зависящий от параметра
т</, есть решение задачи Коши
Ф (х, т; т) = / (х, т)
для однородной системы S(f=O. Тогда вектор
и (х, t) =
является решением неоднородной системы G) с на-
начальным условием
и(х, 0) = 0. (9)
Функция ц>(х, t; т), соответствующая неоднородному
уравнению теплопроводности
щ — а Ди = / (х, t), a = const > 0, A0)
имеет вид
\х-у\г
ф (х, t; т) — \ „ [Ana (t — т)] ~ "/2 е 4а ('~т* / (у, х) dy,
A1)
где Л" — евклидово пространство. Решение u (x, t)
уравнения A0) с начальным условием (9) задается
интегралом Дюамеля C), где под знаком интеграла
стоит функция A1).
3. п. м. используется и при исследовании смешанных
задач для уравнений с частными производными пара-
болич. и гиперболич. типов, позволяя общую задачу
редуцировать к задачам со специальными начальными
и граничными функциями.
Напр., пусть в области Q= {(x, t)\a<x<$, 0<t<T}
задано уравнение с частными производными
где В, b, e=const, B<.0,
{ ^0 = const при а«?;г*сО,
А = <
\ 0 при 0<?sg;p,
ao = const > 0 при
ax = const при
к-рое гиперболично при х<0 и параболично при х>0.
Если <f(x, t) — непрерывно дифференцируемое при
х=0 решение смешанной задачи
Ф (х, 0) = 0, а < х <: р, щ(х, 0) = 0, а < х < 0,
к (а, t) = l, фх (Р, *)=0, 0 < * < Т,
для уравнения A2) в области Q, то, согласно 3. п. м.,
интеграл Дюамеля
и(х, 0--й-5'0Ф(«, <-т)/(т)Л^Г/ A3)
с непрерывно дифференцируемой плотностью f(t) будет
решением смешанной задачи
и (х, 0)=0, а<ж<р, Mt (ж, 0) = 0, а < .г < 0,
и (а, *) = /(*), М*(Р> 0=0, 0 < i < Г,
для уравнения A2) в области Q.
Интеграл Дюамеля A3) по существу есть формула
представления линейного оператора Т, к-рый преоб-
преобразует ваданную граничную функцию f(i) в решение
и(х, t). Интегральная формула Дюамеля имеет место
не только для оператора Т из A3), но и для всех ли-
линейных операторов Т, удовлетворяющих следующим
условиям.
1) Оператор Т определен для всех функций f(t),
равных нулю при i<0, и преобразует / в функцию
Tf=u(xl7 . . ., хп, t), также равную нулю при t<CO.
2) Т j? / [9 (t, т)] dx= J? Tf [6 (t, т)] dx,
где Q(t, x) — некоторая функция t и параметра х.
3) Если /@)=0 и f(t) дифференцируема, то
dt Ч — 1 at ¦
4) Если Tf(t) = (p(t), то для всех х>0
Лит.: [1] Бицадзе А. В., Уравнения математической
физики, М., 1976; [2] Б е р с Л., Джон Ф., Ш е х т е р М.,
Уравнения с частными производными, пер. с англ., М., 1966;
[3] Владимиров B.C., Уравнения математической физики,
3 изд., М., 197В; [4] К у р а н т Р., Уравнения с частными про-
производными, пер. с англ., М., 1964; [5] П о н т р я г и н Л. С,
Обыкновенные дифференциальные уравнения, 3 изд., М., 1970;
[6] Т и х о н о в А. Н., С а м а р с к и й А. А., Уравнения ма-
математической физики, 4 изд., М., 1972. А. М. Нахушев.
ЗАПОЛНЕННОЕ ПРОСТРАНСТВО — топологическое
пространство X такое, что каждое отображение g: A-+X
любого замкнутого подмножества А произвольного
нормального пространства Y может быть распростра-
распространено на все пространство Y. Прямое произведение и
ретракт 3. п. являются 3. п. В частности, 3. п. яв-
являются единичный интервал /, n-мерный куб 1п и
гильбертов куб I®. Любые два отображения бинор-
бинормального пространства в 3. п. гомотопны, а бинор-
бинормальное 3. п. стягиваемо к точке. м.и. Вопцеховский.
ЗАПЯТАЯ — термин, относящийся к представлению
действительного числа дробью, к способу представления
действительных чисел в цифровой вычислительной
машине.
Пусть выбрана система счисления с основанием q,
и пусть для действительного числа х имеет место раз-
разложение
где а/, — целые числа, заключенные в пределах от 0
до q—1. В представлении числа х g-ичной дробью
х=(апа„_1 ... а^р, a_ia_2...) B)
3. (так наз. д-жчн&я запятая) разделяет коэффициенты
разложения A), относящиеся соответственно к неот-
неотрицательным и отрицательным степеням д.
По способу представления действительных чисел
цифровые вычислительные машины делятся на машины
с фиксированной 3. и машины с плавающей 3.
Арифметика с фиксированной запятой
предполагает, что все числа имеют модуль, меньший 1.
Для хранения коэффициентов a_lt сс_2 . .. отводится
фиксированное число разрядов. Если при выполнении
арифметич. операции над числами с фиксированной 3.
результат имеет модуль, больший 1, то выполнение
программы прерывается, и выдается сигнал перепол-
переполнения. Чтобы избежать этого, программист заранее
должен предусмотреть возможность переполнения
и предупредить его соответствующим масштабированием.
К числу машин с фиксированной 3. относится, напр.,
«Сетунь», работающая в троичной системе счисления.
Трудности программирования для арифметики с фик-
фиксированной 3. объясняют тот факт, что большинство
современных ЭВМ используют арифметику с плаваю-
плавающей 3. Число с плавающей запятой имеет вид
при этом р наз. порядком, а (c^cxj- . .ап) — ман-
мантиссой числа х. Для хранения порядка и ман-
мантиссы числа с плавающей 3. обычно отводится фик-
фиксированное число разрядов (определяемое длиной
машинного слова), что вызывает ограничения на
величину порядка такого числа. Число с плавающей
3., у к-рого ахф0, наз. нормализованным
числом. Обычно результаты арифметич. операций
в машине с плавающей 3. автоматически нормализу-
нормализуются суммирующим устройством машины.
X. Д. Икрпмое.
ЗАРИСКОГО КАСАТЕЛЬНОЕ ПРОСТРАНСТВО к
алгебраическому многообразию или
схеме X в точке х — векторное пространство над
полем вычетов к (х) точки х, двойственное к простран-
пространству ifflx/0Jl?, где Ш\х — максимальный идеал локаль-
локального кольца Ох,х точки х на X. Если ХаА\ и задается
системой уравнений
где Fa^klX1, ..., Х„], то 3. к. п. в рациональной
точке х= (х1, ..., хп) задается системой линейных
уравнений
Многообразие X неособо в рациональной точке х
тогда и тодько тогда, когда размерность 3. к. п. к X
в х равна размерности X. Для рациональной точки
г^ХЗ. к. п. двойственно к пространству Qg<h@k(x) —
слою в точке х кокасательного пучка fljf/ft- Неприво-
Неприводимое многообразие X над совершенным полем к гладко
тогда и только тогда, когда пучок ?2^/й локально
свободен. Векторное расслоение Тх= ^(^x/ft)> ассо-
ассоциированное с пучком fijf/?, наз. касательным
расслоением X над к; оно функториально свя-
связано с X. Его пучок сечений называется каса-
касательным пучком к X. 3. к. п. рассмотрено
О. Зариским [1].
Лит.: [l] Z а г i s к i О., «Trans. Amer. Math. Soc», 1947,
v. 62, p. 1—52; [2] S a m u e 1 P., Methodes d'algebre abstraite
en geometrie algebrique, 2 ed., В.— Hdlb.— N.Y., 1967; [3]
ГДафаревич И. Р., Основы алгебраической геометрии, М.,
1972, с. 107. В. И. Данилов.
ЗАРИСКОГО ТЕОРЕМА о связности: пусть /:
X—+-Y — собственный сюръективный морфизм непри-
неприводимых многообразий и пусть ноле рациональных
функций к (Y) сепарабельно алгебраически замкнуто
в к(Х), a y?Y — нормальная точка, тогда f~1(y)
связно (и более того, геометрически связно) (см. [2]).
Эта теорема обосновывает классический принцип
вырождения: если общий цикл алгебраич. системы
циклов является многообразием (т. е. геометрически
неприводим), то любая специализация этого цикла
связна.
Частным случаем 3. т. о связности является так
наз. основная теорема Зариского, или
теорема Зариского о бирациональ-
ных соответствиях: бирациональный мор-
физм алгебраич. многообразий j'-X—>-У является от-
открытым вложением в окрестности нормальной точки
г/?У, если f~1(y) — конечное множество (см. [1]).
В частности, бирацноналъный морфизм нормальных
многообразий, биективный на точках, является изо-
изоморфизмом. Другая формулировка этой теоремы: пусть
f:X—>-Y — квазиконечный отделимый морфизм схем,
а У — квазикомпактная квазиотделимая схема, тогда
существует разложение f=uog, где и — конечный мор-
морфизм, а в — открытое вложение [3].
Лит.: [1] Zariski О., «Trans. Amer. Math. Soc», 1943,
v. 53, Ki 3, p. 490—542; [2] e г о же, «Mem. Amer. Math, Soc»,
1951, J\r» 5, p. 1—90- [3] G ro t h e n d i e с k A., «Publ. Math.
IHES», 1961, AS 11; 1967, № 32. В. И. Данилов.
ЗАРИСКОГО ТОПОЛОГИЯ на аффинном
пространстве — топология, множество замк-
замкнутых подмножеств к-рой совпадает с множеством
алгебраич. подмногообразий данного аффинного про-
пространства Ап. Если X — аффинное алгебраич. много-
многообразие (см. Аффинное алгебраическое множество) в Ап,
то индуцированная на X топология также наз. 3. т.
Аналогично определяется 3. т. аффинной схемы Spec A
кольца А (она наз. иногда спектральной то-
топологией) — замкнутыми считаются множества ви-
вида
V(I) = {p?SvecA, pr>/},
где / — идеал кольца А.
3. т. впервые была рассмотрена О. Зариским [1]
как топология в множестве нормирований поля ал-
алгебраич. функций. Хотя 3. т. в общем случае не яв-
является отделимой топологией, на нее переносятся
многие конструкции алгебраич. топологии [2]. Аффин-
Аффинная схема, снабженная 3. т., квазикомпактна.
Топологию, к-рая естественно определена на произ-
произвольной схеме, также наз. 3. т., чтобы отличать ее от
этальной топологии или, если многообразие X опре-
определено над полем С, то — от топологии аналитич.
пространства на множестве комплекснозначных точек
Х(С).
Лит.: [1] Zariski О., «Bull. Amer. Math. Soc», 1944,
v. 50, № 10, p. 683—91; [2] С е р р Ж. П., в сб.: Расслоенные
пространства и их приложения, пер. с франц. ,М.. 1958, с. 372—
450. В. И.Данилов.
ЗАРЯД, обобщенная мера,— действитель-
действительная а-аддитивная функция множества, определен-
определенная на а-алгебре, борелевских подмножеств области
GcR" и конечная на компактах KaG. Разность двух
мер является 3.; обратно, таким способом получаются
все 3.: для любого 3. v существует разложение G на
два непересекающихся множества G+ и G~ таких,
что v(e)^0 приесгС" и v(e)<:0 при eaG~. Меры v + =
= v(ef]G+) и v~ = v(e[)G~) не зависят от выбора G +
и G" и наз. положительной и отрица-
отрицательной вариациями 3. v, а мера |v| =
=v ++v~ — полной вариацией 3. v. Имеет
место разложение Хана — Жордана: v=
=v + _j_v-) B силу к-рого свойства 3. могут быть выра-
выражены в терминах теории меры.
Лит.: [1] Л а н д к о ф Н. С, Основы современной теории
потенциала, М., 1966; [2] X а л м о ш П., Теория меры, пер. с
англ., М., 1953. М. И. Войцеховский.
ЗАУЗЛЕННАЯ СФЕРА — нетривиальный двумер-
двумерный узел в 4-мерном евклидовом пространстве ?"*, сфера
S2, к-рую нельзя получить вращением в ?4 (заузленной)
дуги к, расположенной в полупространстве ?+вокруг
ограничивающей это полупространство плоскости. Для
3. с. фундаментальная группа я(Е4\52) не является
группой узла.
Лит.: [1] К р о у э л л Р., Ф о к с Р., Введение в теорию
узлов, пер. с англ., М., 1967. М. И. Войцеховский.
ЗАЦЕПЛЕНИЯ КОЭФФИЦИЕНТ — целое или дроб-
дробное число, сопоставляемое двум непересекающимся
циклам zh~x и zn~k в многообразии М размерности п,
классы гомологии к-рых принадлежат подгруппам
кручения в целочисленных гомологиях Iffc-i(M, Z)
и lIn-k(M, Z) соответственно. Простейшим примером
является 3. к. двух непересекающихся замкнутых
спрямляемых кривых Llt L2 пространства R3, выража-
выражаемый так наз. интегралом Гаусса:
(х,-х,, dx,, йхг)
I
l*i-** IV
(здесь x1 и x2 — радиус-векторы Ьг и L2).
Понятие 3. к. обобщается на случай замкнутых
ориентированных многообразий Mk~x и М"~к, распо-
расположенных в пространстве R": 3. к. равен степени
отображения % ориентированного прямого произве-
произведения М'-'ХМ"-' в сферу >S"-1c:R", где %(х, у),
х^Мк~1, у^Мп~к, есть точка пересечения с Sn ~1 луча,
отложенного параллельно вектору (х, у) от начала
координат. 3. к. равен пересечения индексу любой
А-мернойцепи С*, дляк-ройбС*=си*-1, с циклом zn~k,
деленному на а. Это число не зависит от выбора пленки
С*. Если поменять ролями циклы z*-1 и zn~k, то 3. к.
умножится (в ориентируемом случае) на (—1 )*(«-*>.
Если заменить любой из циклов на гомологичный
ему в дополнении к другому, то 3. к. не изменится.
Этот факт является основой при интерпретации Алек-
сандера двойственности с помощью зацеплений. При
замене одного из циклов на любой гомологичный с ним
3. к. изменяется на целое число, благодаря чему опре-
определено спаривание подгрупп кручения в Нь-\{М, %)
и Hn-k(M, Z) со значениями в факторгруппе Q/Z,
где Q — рациональные числа. Это спаривание уста-
устанавливает между ними Понтрягина двойственность.
В частности, для подгруппы кручения в Нт(М, Z)
в случае га=2т+1 этим задается невырожденная
квадратичная форма самозацеплений со значениями в
0/Z. к-рая является гомотопич. инвариантом много-
многообразия. Напр., с ее помощью впервые были обнаружены
асимметричные многообразия, а именно, нек-рые лин-
линзовые многообразия.
3. к. рассматриваются также в случае других об-
областей коэффициентов, напр., если на многообразии
действует свободно группа я, то группы гомологии
являются групповыми модулями, и значение 3. к.
определено в соответствующим образом локализован-
локализованном групповом кольце.
Лит.: ШЗейферт Г., Трельфалль В., Тополо-
Топология, пер. с нем., М.—Л., 1938; [2] П о н т р я г и н Л. С,
Гладкие многообразия и их применения в теории гомотопий,
2 изд., М., 1976. А. В. Чернавский.
ЗВЕЗДА ЭЛЕМЕНТА ФУНКЦИИ, звезда Мит-
т а *-Л е ф ф л е р а,— звездообразная область, в к-рую
данный элемент
аналитич. функции может быть аналитически продол-
продолжен по лучам, выходящим из его центра а. 3. э. ф.
состоит из тех точек комплексной плоскости z, к-рые
можно достичь, аналитически продолжая элемент f(z)
в виде степенного ряда вдоль всевозможных лучей,
исходящих из центра элемента а. Если при продолже-
нии элемента вдоль данного луча z=a+'"eI(P, 0<r<+oo,
нельзя достичь произвольной точки этого луча, то на
луче найдется точка цфа такая, что продолжение
возможно до любой точки интервала [a, zr), но далее
неосуществимо. Если продолжение возможно в любую
точку луча, то полагают z1=oo. Совокупность точек,
принадлежащих всем интервалам [a, zx) представляет
собой (односвязную) звездообразную область отно-
относительно точки а — это и есть 3. э. ф. Sj. В резуль-
результате аналитич. продолжения в S f получают регулярную
аналитич. функцию /(z), являющуюся однозначной
ветвью в Sf полной аналитич. функции, порождаемой
данным элементом.
Все точки границы dSf 3. э. ф. являются достижи-
достижимыми граничными точками. В вопросах аналитического
продолжения (см. также Адамара теорема) различают
также угловые, доступные и хорошо доступные точки
границы dS f. Точка zx ? dS f наз. угловой точкой
границы 3. э. ф., если она имеет наименьший
модуль |zjj среди всех точек dS f с тем же аргументом
arg zx. Точка z1 ? dS f наз. доступной точкой
границы 3. э. ф., если существует полукруг V(zr)
такой, что f(z) регулярна всюду внутри F(zj) и в точках
его диаметра, отличных от z1. Точка z1^dS/ наз. хо-
хорошо доступной (или хорошо дости-
достижимой) точкой границы 3. э. ф., если
существует угол F(zx) с вершиной zl раствора больше я
и такой, что /(z) регулярна в области (F^)!") (U—гг1 <
<б)} при достаточно малом 6>0.
. Г. Миттаг-Леффлер [1] показал, что регулярную
функцию f(z) в ее звезде Sj можно представить в виде
равномерно сходящегося внутри S/ ряда многочленов
Формула (*) наз. М и т т а г-Л еффлера разло-
разложением в звезде. Здесь степени многочленов
кп и коэффициенты с'оп>, с^л>, . . ., с^', га=0, 1, .... не
зависят от вида /(z) и могут быть вычислены раз на-
навсегда. Такое вычисление было проделано П. Пенлеве
(P. Painleve; см. [2], [3]).
Лит.: [l]Mittag-Leffler G., «Acta math.», 1900,
V. 23, p. 43 — 62; 1901, v. 24, p. 183 — 204, 205—44; 1902 v. 26,
p. 353—93; 1905, v. 29, p. 101 — 82; [2] M a p к у ш е в и ч А. И.,
Теория аналитических функций, 2 изд., т. 2, М., 1968, гл. 8;
[3] Borel E., Lemons sur les fonctions de variables reelles et
les deVeloppements en series de polynomes, P., 1928.
E. Д. Соломенцев.
ЗВЕЗДНОЕ ТЕЛО с центром в точке О —
открытое множество <3 «-мерного евклидова простран-
пространства R", обладающее свойством лучистости
(относительно О): если a?S, где @— замыкание 2,
то и весь отрезок [О, а) (здесь О?[О, а), аф[О, а)) лежит
в <2. Иногда к 3. т. причисляют и точки его границы.
3. т. 2 с центром в О можно охарактеризовать следую-
следующим образом: О есть внутренняя точка 2>; каждый луч,
выходящий из О, или целиком лежит в 2>, или содержит
такую точку а, что отрезок луча [О, а) лежит внутри S,
а отрезок луча (а, +°°) лежит вне ®. Это определение
эквивалентно первому, с точностью до точек на гра-
границе 2- 3. т. есть частный случай звездного
множества с центром в О — множества, облада-
обладающего свойством: обобщенной лучистости
относительно О: если а ?@, то и весь отрезок [О, а]
лежит в 2. Частным случаем 3. т. является выпуклое
тело.
Каждому 3. т. 2 с центром в начале координат О
можно взаимно однозначно сопоставить лучевую функ-
функцию F(x) = F&(x) так, что 2 есть множество точек
x?Rn с условием F(x)<i.
Это сопоставление задается формулой
i > О
При этом 3. т. (g> ограничено тогда и только тогда,
когда F(x) — положительная лучевая функция, и
выпукло тогда и только тогда, когда F(x) — выпуклая
лучевая функция.
Лит.: [1] Кассе л с Д ж. В. С, Введение в геометрию
чисел, пер. с англ., М., 1965. А. В. Малышев.
ЗВЕЗДНОЙ АСТРОНОМИИ МАТЕМАТИЧЕСКИЕ
ЗАДАЧИ —• задачи, возникающие при исследовании
общих закономерностей строения, состава, динамики
и эволюции звездных систем.
Основным типом уравнений, решаемых в задачах
звездной статистики, являются уравнения, связываю-
связывающие функции распределения видимых и истинных
характеристик объектов. Это, как правило, интеграль-
интегральные уравнения для искомых функций распределения
истинных характеристик. Напр., важное для исследо-
исследования строения Галактики уравнение Шварц-
ш и л ь д а:
A (m) = co f" Д (r)<p(M)dr, A)
в к-ром неизвестной в данном телесном угле ю яв-
является функция распределения звезд по расстояниям
Л (г), а функция распределения звезд по видимым
звездным величинам А (т) и по абсолютным звездным
величинам ср(М) известна по наблюдениям (М=
= т — 5 lg г+5). Уравнение A) имеет точное решение
в характеристич. функциях. Трудность задачи состоит
в том, что А (т) известна лишь до нек-рой, предельной
для телескопов, видимой звезДной величины т.
Другим примером является уравнение типа Абеля:
связывающее наблюдаемую поверхностную звездную
плотность (здесь и далее под звездной плотностью
подразумевается плотность распределения звезд как
объектов) F(r) сферически симметричного скопления
звезд или галактик, имеющего радиус Л, с простран-
пространственной плотностью /(р).
Примером двумерного интегрального уравнения яв-
является уравнение, связывающее функции распределе-
распределения видимых конфигурации (р(?, т)) и истинных кон-
конфигураций /(ж, ;/) тройных звезд
\ \ k(*—i, </, л) / (ж- у)
где
оно получается в предположении, что все ориентации
плоскости истинных конфигураций тройных звезд рав-
равновероятны; | и т) (соответственно х и у) суть коорди-
координаты третьего компонента тройной звезды, если
(О, 0) — координаты первого и @, 1) — второго компо-
компонентов.
Для звездной кинематики характерно решение из-
избыточных систем условных уравнений, получаемых
для отдельных звезд или для отдельных площадок неба.
Примеры: 1) Система для определения эквато-
экваториальных компонентов X, Y, Z локальной скоро-
скорости Солнца по наблюденным собственным движениям
звезд \ia п цб , их расстояниям г и экваториальным
координатам а и б:
X sin а — У cos а = 4,74г(ха cos б,
X cos а sin б + У sin а sin б — Z cos б = 4,74гц.6
и лучевым скоростям звезд vr:
X cos a cos б + Y sin а cos б + Z sin б = — vr.
2) Система
Л г sin 2 (I— la) = vr,
А г cos 2 (I —10) + Вг = 4,74ц,
для определения коэффициентов Оорта Л
и Л характеризующих угловую скорость ю(Л) вра-
вращения Галактики в районе Солнца:
А= — -i-До»' (Ло), Л = Л—ю(Л„)
и долготы галактич. центра ?0 (J — галактич. долготы
звезд, находящихся вблизи галактич. экватора).
Основным уравнением звездной динамики является
уравнение Больцмана
1 Эх Эй г ду dv "Т" 8z 8w^ ^ at У(>г' ' '
где г|; — фазовая плотность, Ф — потенциал звездной
системы. Так как звездная система самогравитирую-
щая, уравнение B) должно решаться совместно с
уравнением Пуассона
При рассмотрении только регулярных сил (создава-
(создаваемых всей системой в целом) звездной системы правая
часть B) равна нулю; при учете также и иррегулярных
сил (возникающих при сближении звезд системы)
нужно учитывать интеграл столкновений. Исследо-
Исследование уравнений B) и C) показывает, что в сферич.
системах имеются два, а во вращающихся системах —
три интеграла движения.
В гидродинамическом приближении рассматриваются
гидродинамич. уравнения, получаемые из уравнения B).
В теории иррегулярных сил звездных систем изме-
изменение скорости звезды часто рассматривается как
непрерывный случайный процесс и решается уравнение
Фоккера — Планка
^-= Р divj, (fv) + q\jvF,
где F(x, у, t)dv — вероятность того, что звезда в мо-
момент t имеет скорость v в промежутке [у, y-\-dy], если
в начальный момент ее скорость была равна х. Здесь
Р и q соответственно коэффициенты динамич. трения
и диффузии, определяемые характеристиками звездного
поля.
Более точное приближение дает рассмотрение изме-
изменения скорости звезды в рамках чисто разрывного
случайного процесса. После нахождения плотности
переходной вероятности Р(х, у) и плотности вероят-
вероятности скачка р (х) решение уравнения Колмогорова
ЭУ (х, у, t)
Ш
lp(z)P(z, y)dzF(x, z, t) D)
определяет функцию F(x, г/, t). Ввиду наличия крити-
критической скорости в звездных системах уравнение D)
рассматривается также с поглощающим экраном.
При исследовании устойчивости звездных систем в
уравнении Больцмана для равновесной системы рас-
рассматривают вариации фазовой плотности и потенциала.
Это приводит к уравнениям, схожим с уравнениями,
используемыми в физике при исследовании плазменных
неустойчивостей. Существенной особенностью для звезд-
звездных систем при решении этих уравнений является
самогравитация и неаддитивность энергии.
При изучении распределения плотности р(а) во
внешних галактиках решается интегральное уравнение
а'р (о) da
в к-ром v(R) — наблюдаемая круговая скорость вра-
вращения галактики, е — эксцентриситет ее меридиан-
меридианного сечения.
Лит.: [1] П а р е н а г о П. П., Курс звездной астрономии,
3 изд., М., 1954; [2] 3 о н н В,, Рудницкий К., Звездная
астрономия, пер. с польск., М., 1959; [3] Огородников
К. Ф., Динамика звездных систем, М., 1958. Т. А. Агепян.
ЗВЕЗДООБРАЗНАЯ ОБЛАСТЬ, звездная об-
область, относительно фиксированной точки О — об-
область D комплексного пространства С", и>1, такая,
что отрезок, соединяющий любую точку области D
с точкой О, целиком принадлежит этой области.
Односвязная открытая риманова поверхность D
над плоскостью w наз. р-листно звездооб-
звездообразной относительно фиксированной точки a?D
(р — натуральное число), если имеется р точек D
над и>=а (с учетом кратности) и если для любой точки
Q?D существует путь T?D из Q в одну из точек над
w=a такой, что проекция Г на плоскость w есть от-
отрезок, соединяющий проекцию Q с «г=а.
Пусть В — двусвязная область плоскости w, Ег
н Е2 — дополнительные континуумы, оо ?Е2, а —
фиксированная точка из Е1, 1\ и Г2 — граничные ком-
компоненты В. Тогда область В наз. 3. о. относительно
точки а, если либо звездообразна относительно точки а
каждая из односвязных областей, содержащих точку а
и ограниченных соответственно кривыми 1\ и Г2, либо
Г\ состоит из отрезков, выходящих из точки а, а об-
область Ei\J В звездообразна относительно точки а.
Лит.: [1] Г о л у з и н Г. М., Геометрическая теория функ-
функций комплексного переменного, 2 изд., М., 1966; [2] Н u m m e 1
J. A., «J. d'Analyse math.», 1967, v. 18, p. 133—60.
ЗВЕЗДООБРАЗНАЯ ФУНКЦИЯ, однолистная
звездообразная функци я,— функция w=
=/(z), регулярная и однолистная в круге |z|<l,
/@) = 0, и такая, что она отображает |z|<l на звездо-
звездообразную область, относительно точки w—0. Для того,
чтобы функция /(z), f{z)=?O в 0<|z| <1, /@) = 0, /' @)^0,
регулярная в круге |z| <1, была в нем 3. ф., необхо-
необходимо п достаточно, чтобы она удовлетворяла условию:
|*|<1-
Все 3. ф. в |z|<l, нормированные условиями /@) = 0,
/'@)=1, образуют класс S*, для к-рого имеет место
параметрическое представление интегралом Стилтьеса
= zexp
[-2
где (x(i) — неубывающая функция на [—я, л],
ц(я) — ц(—я)=1.
Для класса S* решена коэффициентов проблема, най-
найдены точные оценки для |/(z)|, \f (z)|, arg /(z), arg /' (z)
(под аргументом функции понимается ветвь, обращаю-
обращающаяся в Нуль при z=0), причем экстремальными функ-
функциями этих оценок являются функции/(z) = z/(l—el®zf,
где 0 вещественно. Класс S* функций /(z) связан с
классом функций <p(z), ф@)=0, ф'@)=1, регулярных
и однолистных в |z|<l, отображающих |z[<l на вы-
выпуклую область, по формуле: ztp'(z)=/(z).
3. ф., удовлетворяющая условию
a, |z|<l, а< 1,
наз. 3. ф. порядкаав круге \z\ <1.
Рассматривались также однолистные 3. ф. в кольце
(см. [1] с. 586—87), р-листные 3. ф. и слабо 3. ф. в
круге (см. [2], [4]), е-локально звездные функции (см.
[1] с. 584), функции, звездообразные в направлении
действительной оси (см. [3]). Относительно 3. ф. многих
комплексных переменных см. [5].
Лит.: [1] Г о л у з и н Г. М., Геометрическая теория функ-
функций комплексного переменного, 2 изд., М., 1966; [2] Н u m m e 1
J. A., «J. (ГAnalyse math.», 1967, v. 18, p. 133 — 60; [3] П о-
bertson M. S.,«Amer. J. Math.», 1936, v. 58, № 3, p. 465—72;
[4] G о о d m a n A. W., «Bull. Amer. Math. Soc», 1968, v. 74,
№ 6, p. 1035—50; [5] Б а в р и н И. И., Классы голоморфных
функций многих комплексных переменных и экстремальные во-
вопросы для этих классов функций, М., 1976 Е. Г. Голузина.
ЗВЕЗДООБРАЗНОСТИ ГРАНИЦА, точный ра-
радиус звездообразност и,— точная верхняя
граница Ru радиусов кругов |z|-<r, где U — некоторый
класс функций u>=/(z) = z+. .. , регулярных и одно-
однолистных в круге \z\ <1, а круги \z\ <r при отображении
круга \z |<1 каждой функцией класса U отображаются
на звездообразные области относительно точки w=0-
Всякое число г из интервала 0<г<Л„ наз. р а д и у
сом звездообразност и класса U.
Для нахождения 3. г. обычно используется следую-
следующий критерий звездообразност и: круг
\z\ <r при отображении w=f(z) тогда и только тогда
переходит в звездообразную область, когда на |z| = r
или, что то же,
3. г. Д3 класса S всех функций вида /(z) = z+...,
регулярных и однолистных в круге \z\ <1, равна th-^-=
= 0,65 ....
Лит.: [1] Г о л у з и н Г. М., Геометрическая теория функ-
ций комплексного переменного, 2 изд., М., 1966.
Е. Г. Голузипа.
ЗЕЙДЕЛЯ МЕТОД — итерационный метод решения
системы линейных алгебраич. уравнений Ах=Ъ. Ре-
Решение системы .г* находится как предел последователь-
последовательности
вычисляемой по правилу
1- «,-,- 1-1+ ац ац
J=l, 2, ..., п,
где aij— элементы матрицы А, 6/ — компоненты век-
вектора Ь\ диагональные элементы матрицы А предпо-
предполагаются отличными от пуля. Вычисления (*) отлича-
отличаются от простой итерации метода лишь тем, что на
к-и шаге при вычислении г-й компоненты учитываются
вычисленные к-е приближения первых (i—1) ком-
компонент.
В матричной записи 3. м. представляется следую-
следующим образом. Если А = В-\-С, где
ап 0 ... 0
й21 а2г • • ¦ О
''-т
С =
0 а12 а13 ¦ ¦ ¦ ат
0 0 а23 ... а2я
0 О U ... 0
то соотношение (*) соответствует матричному соотно-
соотношению x{k)——В-1Сх{к~1)-{-В~1Ь. 3. м. равносилен ме-
методу простой итерации, примененному к системе х=
= —В-1Сх^-В~1Ь, эквивалентной исходной. Для схо-
сходимости 3. м. необходимо и достаточно, чтобы все
собственные значения матрицы В~1С по модулю были
меньше 1. Иначе, чтобы все корни уравнения det(C+
-}-В"а) = 0 были по модулю меньше 1.
На практике более удобны следующие достаточные
условия сходимости 3. м. 1) Пусть при всех i,l<:i<n,
2i=fc'a';'<"?'a"'' ?<"^" Тогда 3. м. сходится и для
скорости сходимости имеет место оценка:
1'-**)), 11*11!= max \xi\.
1 < i < n
2) Пусть А — эрмитова положительно определенная
матрица. Тогда 3. м. сходится.
3. м. относится к классу релаксации методов, наибо-
наиболее употребительным из к-рых является сверхрелак-
сации метод.
Известны модификации 3. м., использующие пред-
предварительное преобразование исходной системы в эк-
эквивалентную ей систему i=3fz+/ (см. [4]).
Метод предложен Л. Зейделем в [1].
Лит.: [1] S e i d е 1 L., «Abhandl. Bayer. Akad. Wiss.
Math.-naturwiss. Kl.», 1874, Bd 11, № 3, S. 81 — 108; [2] Бах-
Бахвалов H. С, Численные методы, 2 изд., М., 1975; [3] Б е-
резин И. С, Жидков Н. П., Методы вычислений 3 изд.,
т. 1, М., 1966; [4] Ф а д д е е в Д. К., Ф а д д е е в а В. Н.(
Вычислительные методы линейной алгебры, 2 изд., М.— Л.,
1963. Г. Д. Ним.
ЗЕЙФЕРТА МАТРИЦА — матрица, сопоставляемая
узлам и зацеплениям для алгебраич. изучения их
топологич. свойств. Названа в честь Г. Зейферта [1],
применившего эту конструкцию для получения алге-
Сраич. инвариантов одномерных узлов в S3. Пусть
L= (S" + 2, ln) есть n-мерное m-компонентное зацепление,
т. е. пара, состоящая из ориентированной сферы Sn+2
и ее дифференцируемого или кусочно линейного ори-
ориентированного подмногообразия 1п, гомеоморфного не-
несвязной сумме т экземпляров сферы S". Существует
компактное (п+1)-мерное ориентируемое подмного-
подмногообразие V сферы Sn + 2 такое, что с? F=Z, оно наз. мно-
многообразием Зейферта зацепления L. Ори-
Ориентация многообразия Зейферта V определяется ори-
ориентацией его края dV=l, и, поскольку ориентация
сферы S" + 2 фиксирована, нормальное расслоение к V
в Sn + 2 оказывается ориентированным, так что можно
говорить о поле положительных нормалей к V. Пусть
i + :V-+Y малый сдвиг вдоль этого поля, где У — до-
дополнение открытой трубчатой окрестности V в Sn + 2.
Если n=2q—1 — нечетное число, то определено спа-
спаривание
к-рое сопоставляет элементу z1@z2 коэффициент за-
зацепления класса zy^HqV и класса i + xz2?HqY. Спа-
Спаривание 0 наз. спариванием Зейферта
зацепления L. Если z1 или z2 имеет конечный порядок,
то 8(z!B)z2)=0. Имеет место формула
0 (Zl (g) z2) + (-1)? 6 (z2 (g) Zl) = Zl • z2,
где справа — индекс пересечения классов гг и z2 на V.
Пусть ег, ..., еь— базис свободной части группы
IlqV. Целочисленная (кХА)-матрица А = ||0(е,-B)еу)||наз.
матрицей Зейферта зацепления L. 3. м.
всякого Bд—1)-мерного узла обладает следующим
свойством: матрица А-\-( —1I А' унимодулярна, а
если д=2, то сигнатура матрицы Л+Л' делится на 16
(А'— матрица, транспонированная к А). Всякая
целочисленная квадратная матрица А является 3. м.
нек-рого Bq—1)-мерного узла, если q^2 и матрица
^4+( — \)ЧА' унимодулярна.
Сама по себе 3. м. не является инвариантом зацеп-
зацепления L; это связано с неоднозначностью построения
многообразия Зейферта V и выбора базиса е±, ..., е^.
Матрицы вида
А
а
0
0
0 0
1 0
А
0
Р
0
0
0
1
0
где а — вектор-строка, а р — вектор-столбец, наз.
элементарными расширениями квад-
квадратной матрицы А, а матрица А наз. элементар-
элементарной редукцией своих элементарных расшире-
расширений. Две квадратные матрицы наз. 5-э квивалент-
н ы м и, если одну можно получить из другой последо-
последовательностью элементарных редукций, элементарных
расширений и унимодулярных конгруэнции (т. е.
преобразований вида А-^-Р'АР, где Р — унимодуляр-
ная матрица). Для многомерных узлов (т=1) и для
одномерных зацеплений (ге=1) класс 5-эквивалент -
ности 3. м. является инвариантом типа зацепления L.
В случае, когда L — узел, 3. м. А полностью опреде-
определяет % [t, г-а]-модуль HqX, где X — бесконечное цик-
циклическое накрывающее дополнения узла. Полиноми-
Полиноминальная матрица tA-{-( —1LА' является матрицей
Александера (см. Александера инварианты) модуля
HqX. 3. м. определяет также <jr-MePHble гомологии и
коэффициенты зацепления в цнклич. накрытиях сферы
SSQ + 1, разветвленных над зацеплением.
Лит.: [1] S e i f е г t H.,«Math. Ann.», 1934, Bd 110, S. 571—
592; [2] К р о у э л л Р., Фокс Р., Введение в теорию узлов,
пер. с англ., М., 1967; [3] Levine J., «Ann. Math.», 19НК,
v. 84, p. 537—54; [4] e г о же, «Comment, math, helv.», 1970,
v. 45, p. 185 — 98. M. Ш. Фарбер.
ЗЕЙФЕРТА МНОГООБРАЗИЕ — многообразие, име-
имеющее Зейферта расслоение. а. В. Чернавский.
ЗЕЙФЕРТА РАССЛОЕНИЕ — класс расслоений трех-
трехмерных многообразий на окружности; определенX. Зей-
фертом [1]. Каждый слой 3. р. имеет в многообразии
М3 окрестность со стандартным расслоением на окруж-
окружности, к-рое возникает из произведения D2X[0, 1]
диска на отрезок при склейке каждой точки (х, 0) с
точкой (g(x), 1), где g — поворот D2 на угол 2лу/ц
(ц и v — взаимно простые целые числа, 0<:v<jj,).
Образы отрезков хХ[0, 1] в полученном полтштории Р
составляют слои: каждый слой, кроме центрального,
состоит из ц отрезков; центральный слой наз. о с о-
б ы м, если v>0. Инварианты (ц, v) обычно заменяются
инвариантами Зейферта (а, |3), где а=|х,
a P определяется из условий
0<Р<а, рЧ>^1 moda.
Геометрич. смысл аир состоит в следующем: если в
расслоении, индуцированном на крае Р, взять меридиан
m (кривая, стягиваемая в Р) и параллель I (пересе-
(пересекающую m трансверсально один раз), а также любой
слой / и секущую g (все четыре кривые простые и замк-
замкнутые), то при надлежащей ориентации
m=ag+P/, Z=—vg—ц/.
причем pv—ац=1.
Первая задача относительно 3. р. состоит в их клас-
классификации с точностью до послойного гомеоморфизма.
Оказывается [1], что если М3 имеет 3. р., то существует
отображение я: М3-+В2, где В2 — двумерное много-
многообразие, и слоями служат л~*(х), х?В2. Имеется
шесть типов 3. р.: типы О1 и О2, в к-рых В2 ориенти-
ориентируемо и Мя ориентируемо в случае Ох и неориенти-
руемо в случае О2, причем род В2 в этом случае не
меньше единицы, и типы и,-, i=l, 2, 3, 4. для к-рых
В2 неориентируемо. В случае щ обнос слоя вдоль
пути в В2 не меняет ориентацию слоя, в случае м2
имеется система образующих, обнос вдоль к-рых ме-
меняет ориентацию, в случае п3 не меняет ориентацию
только одна из образующих, а в случае ni — только
две из образующих, причем род В2 не меньше двух
для п3 и не меньше трех для ni. Многообразие М3
ориентируемо только для типа п2. Каждому 3. р. от-
относится система инвариантов
{6; (в, р); К, р\); ... ; (ar, pV)},
так что с точностью до послойного гомеоморфизма
имеется одно и только одно 3. р. с таким набором.
Здесь в=О,- или п;, р — род Вг, (а,-, Р/) — инварианты
Зейферта для особых слоев расслоения, число к-рых
равно г, причем р,-«:а/2 в случаях г=О2, щ_, п3, ni, и,
наконец, Ь — целое число, если г=О1 или п2 и вычет
mod2 в остальных случаях, при этом Ь=0, если а, = 2
хотя бы для одного слоя. Геометрич. смысл Ъ: на крае
окрестности каждого особого слоя выбирается сечение,
и вся их совокупность продолжается до сечения во
всем дополнении к особым слоям. Это возможно сде-
сделать вплоть до одного неособого слоя, к к-рому край
продолжаемого сечения подойдет, накручиваясь на
него со степенью 6. При изменении ориентации М3
в случаях Ох и п2 число Ъ меняется на ~Ъ—г, а р,- —
на а,—Р/.
Вторая задача относительно 3. р. заключается в
установлении того, что на замкнутом многообразии
,1/3 может существовать не более одного такого рас-
глоения с точностью до послойных гомеоморфизмов.
Это доказано для так наз. больших 3. р., к-рые
являются пространствами типа К (я, 1), т. е. гомотопич.
тип к-рых определен фундаментальной группой. Фун-
Фундаментальную группу пх (М3) многообразия, снабжен-
снабженного 3. р., удобно описывать с помощью специальной
системы образующих: сечений gj на краях окрестностей
особых слоев, элементов а,-, 6,- (или и;, если В2 неори-
ентируемо), образы к-рых в щ (В2) являются канонич.
образующими, h — неособый слой. При этом определяю-
определяющие соотношения в случаях Ох и О2 следующие:
a;hai 1 = fe ', b[hbi =hl, g/hg,- =h, gjlh-> = i,
gi ¦ ¦ ¦ gr K, h] ¦¦¦ [ap, bp]=hb,
а в случаях nf.
gi ... grvl ... i>l = hb,
где Ei= —1 в зависимости от того, обращается ли ори-
ориентация слоя при обносе вдоль соответствующей обра-
образующей щ (В2). К многообразиям с малыми 3. р.
относятся: для типа Ох все расслоения с
{-2; (Оь 0); B, 1); B, 1); B, 1); B, 1)};
для типа О2 только расслоения с р=1, г=0; для типов
п-у и п2 расслоения с р = 1, г<:1; р=^2, г=0; для типа
п3 расслоения с р = 2, г=0. Все 3. р. типа ni большие.
Малые 3. р. все перечислены, их имеется 10 типов
(см. [3]).
Свободные действия конечных групп на трехмерной
сфере коммутируют с естественным действием на ней
группы SO B), и поэтому пространства орбит этих
действий оказываются 3. р. с конечными фундамен-
фундаментальными группами. Это — единственные известные
A977) примеры М3 с конечной щ(М3). Нек-рые из
3. р. встречаются как границы сферич. окрестностей
изолированных особых точек алгебраич. поверхностей,
инвариантных относительно действия мультипликатив-
мультипликативной группы комплексных чисел. Именно, это 3. р.
типа: {Ъ; (Ои р)\ (ах, р\), ..., (аг, рг)} при Ъ+г>0.
Идентификация этих многообразий позволяет по-
построить явное разрешение особенностей с учетом дей-
действия С* (а также дать полное описание изолированных
особенностей поверхностей в С3, допускающих действие
С*). 3. р. имеются также на локально плоских римано-
вых многообразиях, полученных при факторизации
евклидова пространства по свободному действию диск-
ретной группы движений (имеется 6 ориентированных
и 4 неориентируемых многообразия, все из к-рых,
кроме одного, являются различными расслоениями
над окружностью со слоем тор или поверхность Клейна).
В топологии трехмерных многообразий 3. р. важны,
напр., для идентификации многообразий, фундамен-
фундаментальные группы к-рых имеют центр [4]. Имеются
также обобщения 3. р. на другие классы расслоений
с особыми слоями.
Лит.: [llSeifert Н., «Acta Math.», 1933, Bd 60, S. 147 —
238; [2] Н о 1 m a n n H., «Math. Ann.», 1964, Bd 157, S. 138—66;
[3] Orlik P., Seifert manifolds, В.— Hdlb.—N. Y. 1972;
[4] Hemp el J., 3-manifolds, N.Y., 1976. А. В. Чернавский.
ЗЕНОНА ПАРАДОКС — одна из антиномий.
ЗИГЕЛЯ МЕТОД — метод исследования арифметич.
свойств значений в алгебраич. точках ^-функций, удов-
удовлетворяющих линейным дифференциальным уравне-
уравнениям с коэффициентами из C(z); был предложен К. Зи-
гелем [1].
Целая функция
наз. Е-ф у н к ц и е й, если все коэффициенты сп при-
принадлежат нек-рому алгебраич. полю конечной степени,
причем для каждого е>0 максимум модулей, сопря-
сопряженных с сп, есть О(пгп) и существует последователь-
последовательность целых рациональных чисел qn=O(nSn) таких,
что д„с/г есть целое алгебраич. число для А=0,.1, ..., п.
Таковы, напр., ez, sin z, функция Весселя /0(z>-
Пусть [а, 0]=1, а [а, и]=(а+п—1) [а, л—1], л=1,
2, ... Если %,..., аг и &!,..., Ът — рациональные
числа, ЪкФ — 1, —2, ... и т.—Z=i>0, то функция
является ^-функцией; она удовлетворяет линейному
дифференциальному уравнению порядка т с коэффи-
коэффициентами из C(z).
Основной результат К. Зигеля относится к значе-
значениям функции
^~ ' I
К G\ = > I —
"-\У> Х< п! (Я+1) (Я + п) " V 2
где Jx (z) — функция Весселя. Если X — рациональное
число, % jzdz—, —1, —-^-, —2, ..., то при любом алге-
браическом а=^=0 числа Къ (а) и К\ (а) алгебраически
независимы над Q.
В 1949 К. Зигель придал своему методу общую форму,
однако условия, к-рым должны были удовлетворять
?-функции f1{z), ..., fm(z) для того, чтобы можно
было утверждать, что их значения алгебраически не-
независимы, оказались очень трудно проверяемыми.
И это не позволило установить какие-либо новые
конкретные результаты.
Дальнейшее развитие и обобщение 3. м. получил
в работах А. Б. Шидловского (см. [2] — [3]): пусть
совокупность Я-функций /i(z), ...,fm(z) является ре-
решением системы дифференциальных уравнений
и алгебраич. число а отлично от нуля и особых точек
системы A); тогда, для того чтобы т чисел f1(oc), . . .,
/от(а) были алгебраически независимы над полем <Qr
необходимо и достаточно, чтобы функции /j{z), ......
fm(z) были алгебраически независимы над С (г.). Из
этой теоремы, в частности, следует трансцендентность
всех чисел /д(а), если /i(z), ..., fm(z) алгебраически
независимы, а также трансцендентность отличных от
нуля и полюсов системы A) Л-точек функций /^(z)
при алгебраическом А; она позволила получить много-
многочисленные результаты, относящиеся к конкретным Е-
функциям, доказать алгебраич. независимость значений
^-функций, удовлетворяющих линейным однородным
и неоднородным дифференциальным уравнениям поряд-
порядка большего двух. Напр., для функции
удовлетворяющей линейному дифференциальному урав-
уравнению порядка к с коэффициентами из C(z), справед-
справедливо следующее утверждение: при любом алгебраиче-
алгебраическом афО, г(г+1)/2 чисел ц'к (а), 1=0, 1, ..., к—1,
/с = 1, 2, ..., г алгебраически независимы над Q.
При тех же условиях максимальное количество ал-
алгебраически независимых над Q чисел среди fl(<x), ...,
/и (а) равно максимальному количеству алгебраически
независимых над C(z) функций среди ДB), ..., /m(z).
Если f1(z), ...,fi(z) — алгебраически независимые над
С (z) Ё-функции, удовлетворяющие системе A), то для
всех, кроме конечного числа, точек а числа fi(a), ...,
fi(a) алгебраически независимы над Q. В каждом
конкретном случае исключительные точки могут быть
определены.
Этими теоремами решаются, по существу, все задачи
общего характера о трансцендентности и алгебраич.
независимости значений ?-функций в алгебраических
точках.
3. м. позволяет оценивать меру алгебраич. незави-
независимости чисел Л(а), ..., /m(a), придав тем самым ре-
результатам количественную форму. Если функции
/i(z), ..., /m(z) алгебраически независимы, то (Df/^a),
..., /„, (а); п, Н)>СН~у"т, где С>0 не зависит от Н,
а v>0 зависит только от т и степени алгебраич. числа а.
Лит.: [1] S 1 е g е 1 С. L., «Abhandl. Dtsch. Akad. Wiss. Phys.
Math. Kl.», 1929, № 1, p. 1 — 41- [2] Ш и д л о в с к и й А. Б.,
«Изв. АН СССР. Сер. матем.», 1959, т. 23, № 1, с. 35 — 66; [3] е г о
ж о, там же, 1962, т. 26, JM» 6, с. 877—910; [4] его же, «Тр.
Матем. ин-та АН СССР», 1973, т. 132, с. 169—202; [5]
Lang S., «Mathem.», 1962, v. 9, с. 157—61; [6] Фельдман
Н. И., Ш и д л о в с к и й А. Б.», «Успехи матем. наук», 1967,
т. 22, в. 3, с. 1 — 81. Ю. В. Нестереино.
ЗИГЕЛЯ ОБЛАСТЬ — неограниченная область в
(п-\- ?п)-мерном комплексном аффинном пространстве
имеющая вид
D (V, F) = {(z, w)?C"XCm | Imz — F (w, w)?V),
где V — открытый выпуклый конус в пространстве R",
a F: CmxCm—>-С™— отображение, являющееся V-
эрмитовой формой, а именно, F линейно по
первому аргументу, F(w', w)=F(w, w'), F(w, w) ? V
(V — замыкание V), F(w, u/) = 0 только при w=0.
В случае, когда то=0 (и, стало быть, F=0) область
7) (Г, F) наз. 3. о. первого рода и обозначается просто
D (Г); в случае, когда тфО, область D (V, F) наз. 3. о.
второго рода.
Простейшим примером 3. о. (первого рода) является
верхняя полуплоскость одного комплексного перемен-
переменного. В работе К. Зигеля [1] в связи с исследованием
абелепых многообразий была рассмотрена область IIр
в пространстве комплексных симметричных матриц
порядка р, образованная матрицами, мнимая часть
к-рых положительно определена. Эта область, наз.
теперь верхней полуплоскостью Зи-
Зигеля (и при р=1 совпадающая с обычной верхней
полуплоскостью), является 3. о. первого рода, ассо-
ассоциированной с конусом положительно определенных
симметричных матриц порядка р. Общее понятие 3. о.
возникло в связи с изучением автоморфных функций
многих комплексных переменных (см. [5]). Впослед-
Впоследствии это понятие стало центральным в теории одно-
однородных ограниченных областей.
Всякая 3. о. аналитически изоморфна ограниченной
области. Напр., при и=1 3. о. изоморфна комплексному
шару
{zgC'« + 1||zi|2 + |z2|2+...+|zOT + 1|2< 1}.
Всякая однородная ограниченная область изоморфна
3. о., однородной относительно аффинных преобразо-
преобразований. Две 3. о. аналитически изоморфны тогда и
только тогда, когда они переводятся одна в другую
аффинным преобразованием (см. [3]).
Лит.: [1]S i e g е 1 С. L.,«Math. Ann.», 1939, Bd 116, S. 617—
57; [2] 3 и г е л ь К., Автоморфные функции нескольких ком-
комплексных переменных, пер. с англ., М., 1954; [3] К a u p W.,
Matsushima Y., Ochiai Т., «Amer. J. Math,», 1970.
v. 92, p. 475—98; [4] Murakami S., On Automorphisms of
Siegel Domains, B.— Hdlb.— N.Y., 1972; [5] Итоги науки.
Матем. анализ. 1963, М., 1965, с. 81 — 124. Э. Б. Винберг.
ЗИГЕЛЯ ТЕОРЕМА — 1) 3. т. о ^-функциях
Дирихле: для любого в>0 существует с=с(е)>0
такое, что для всякого неглавного действительного
Дирихле характера % модуля к выполняется
Установлена К. Зигелем [1]. Эквивалентное утверж-
утверждение относится к действительным нулям Л-функций;
для любого е>0 существует сх=сх (в) такое, что L (z, %)r-
ФО при z>l—С]/А;Е для всякого неглавного действи-
действительного характера Дирихле %. Константы с(е) и сг(г)
не эффективны в том смысле, что ни при одном е<: .
нет способа оценивать их снизу. В силу этого приме-
применения 3. т. носят неконструктивный характер. Напр.,
если h(—D) есть число классов дивизоров квадратич-
квадратичного поля дискриминанта —D, то из 3. т. следует, чти
с неэффективной константой с2(в) при в<1/3. Анало-
Аналогично, оценка, равномерная при 1<А<1плл;, (к, 1)=1,
где я (х, к, I) — число простых чисел вида кп+l, мень-
меньших х, содержит неэффективную константу с3.
Лит.: [1] S i e g е 1 С. L., «Acta arithmetica», 1935, v. 1,
p. 83—86; [2] Д э в е н и о р т Г., Мультипликативная теория
чисел, пер.с англ., М., 1971; [3] К а р а ц у б а А. А., Основы
аналитической теории чисел, М., 1975, гл. IX. С. М. Воронин.
2) 3. т. о целых точках — теорема о конеч-
конечности числа решений в целых числах одного класса
диофантовых уравнений. В своей простейшей форме
эта теорема утверждает, что если F (х, у) — многочлен
с целыми коэффициентами, определяющий неприводи-
неприводимую кривую F=0 рода g>0, то уравнение F(х, у) = 0
имеет конечное число решений в целых числах. Этот
результат (в более общем виде для целых алгебраич.
чисел) был получен в 1929 К. Зигелем [1] с помощью
теории диофантовых приближений и теории абелевых
многообразий. Он явился завершением начатого в
1908 А. Туэ (A. Time, см. [2], [3]) направления в теории
диофантовых уравнений. В дальнейшем эта теорема
была обобщена на случай произвольных аффинных
кривых рода g>0, определенных над подкольцами
конечного типа глобальных полей (см. [5*]). В част-
частности, приведенное выше уравнение F (х, г/) = 0 имеет
конечное число решений в числах вида
где т, т1, . . ., ms^W1, a pt, . .., ps — фиксированные
простые числа. До недавнего времени доказательства
этих теорем имели существенный недостаток — ут-
утверждая лишь конечность числа решений, они не да-
давали никакой границы для их величины (см. Высота
в диофантовой геометрии), так что не имелось никакого
алгоритма для построения решений в явном виде.
Первый результат в этом направлении был получен
А. Бейкером (A. Baker, 1967). Эффективные доказа-
доказательства 3. т. получены для различных классов дио-
фантовых уравнений, однако в общем случае вопрос
остается A978) открытым (см. [4]). Другой важной
задачей является обобщение 3. т. на многообразия
размерности больше 1.
Лит.: [1] S i e g е 1 С. L., «Abhandl. Dtsch, Akad. Wiss.
f'liys. Math. Kl.», 1929, № 1, S. 41 — 69; [2] Г е л ь ф о н д А. О.,
Решение уравнений в целых числах, 2 изд., М., 1956; [3] Д э-
венпорт Г., Высшая арифметика, пер. с англ., М., 1965;
[4] Проблемы теории диофантовых приближений, пер. с англ.,
М.. 1974; [5] Lang S., Diophantine Geometry, N. Y.—L.,
1962. A. H. Паршин.
ЗИГМУНДА КЛАСС функций — класс ZM не-
непрерывных 2я-периодических функций f(x), для к-рых
существует такая постоянная М>0, что при всех х
и fe>0 имеет место неравенство
\f (x + h)-2f (x)+f (x-h)\<Mh.
" lace 2д[ введен А. Зигмундом [1]. В терминах класса
2д[ получает окончательное решение задача Джексона —
ъернштейна о прямых и обратных теоремах теории
приближения функций. Напр., имеет место следующее
утверждение: для того чтобы непрерывная 2я-перио-
дическая функция f(x) входила в 3. к. при некотором
Л/>0, необходимо п достаточно, чтобы ее наилучшее
приближение En(f) тригонометрич. полиномами по-
порядка не выше п удовлетворяло неравенству
где А >0 — постоянная. Для модуля непрерывности
ш (б, /) любой функции / (х) ? .Zjh имеет место оценка
•(«Й<в1п
причем постоянная Af/21n( 1^2+1) на всем 3. к. Zj^
не может быть улучшена [3].
Лит.: [1] Zygmund A., «Duke Math. J.», 1945, v. 12,
К 1, p. 47—76; [2] Никольский С. М., Приближение
функций многих переменных и теоремы вложения, М., 1969;
[3] Е ф и м о в А. В., «Изв. АН СССР. Сер. матем.», 1957, т. 21,
,\'о 2, с. 283—8. А. В. Ефимов
ЗМЕЕВИДНЫЙ КОНТИНУУМ — континуум, допус-
допускающий для любого в>0 открытое покрытие, нерв
к-рого — конечный линейный комплекс. Иначе говоря,
для любого е>0 3. к. должен покрываться конечной
системой Gn, га=1, 2, . .., р, открытых множеств такой,
что все Gn имеют диаметр меньше в, и Gi^Gj-Фф тогда
и только тогда, когда |?—/| = 1 (такие системы наз.
е-ц е п я м и). Всякий 3. к. неприводим (см. Неприво-
Неприводимый континуум) между любой парой своих точек.
Всякий подконтинуум 3. к. змеевиден. Два наслед-
наследственно неразложимых 3. к. (см. Неразложимый кон-
континуум), содержащих более одной точки, гомеоморфны
и называются псевдодугами. Каждый 3. к.
топологически содержится в плоскости. Всякий одно-
однородный 3. к. есть псевдодуга. Каждый 3. к. есть не-
непрерывный образ псевдодуги и предел обратного спект-
спектра из дуг.
Лит.: [1] К у р а т о в с к и й К., Топология [пер. с англ.],
т. 2, М.. 1969. А. А. Мальцев.
ЗНАКИ МАТЕМАТИЧЕСКИЕ — условные обозна-
обозначения, предназначенные для записи математич. поня-
понятий и выкладок. Напр., понятие «квадратный корень
из числа, равного отношению длины окружности к ее
диаметру» обозначается кратко Vn, а предложение
«отношение длины окружности к ее диаметру больше,
чем три и десять семьдесят первых, и меньше, чем
три и одна седьмая» записывается в виде:
Развитие математической символики было тесно
связано с общим развитием понятий и методов мате-
математики.
Первыми 3. м. были знаки для изображения чисел —
цифры, возникновение которых, по-видимому, пред-
предшествовало введению письменности. Наиболее древние
системы нумерации (системы счисления) — вавилонская
и египетская — возникли еще за З1/^ тысячелетия до
н. э.
Первые 3. м. для произвольных величин появились
много позднее (начиная с 5—4 вв. до н. э.) в Греции.
Произвольные величины (площади, объемы, углы)
изображались в виде отрезков, а произведение двух
произвольных величин — в виде прямоугольника, по-
построенного на соответствующих отрезках. В «Началах»
Евклида C в. до н. э.) величины обозначаются двумя
буквами — начальной и конечной буквами соответст-
соответствующего отрезка, а иногда и одной. У Архимеда C в.
до н. э.) последний способ обозначения становится
обычным. Подобное обозначение содержало в себе
возможности развития буквенного исчисления. Однако
в классической античной математике над буквами ни-
никаких операций не производилось, а буквенного ис-
исчисления создано не было.
Начатки буквенного обозначения и исчисления воз-
возникают в позднеэллинистич. эпоху в результате ос-
освобождения алгебры от геометрич. формы. Диофант
(вероятно, 3 в.) обозначал неизвестную (х) и ее степени
следующими знаками:
X
S'.
я2
85
X3
х5
ж4
38"
я5
8х°
л6
тех"
F"°—от греч. термина ботацц, обозначавшего квад-
квадрат неизвестной, хи— от греч. иирод — куб). Справа
от неизвестной или ее степеней Диофант писал коэф-
коэффициенты, напр. Зхъ обозначалось 6ии7 (где у=3).
При сложении Диофант приписывал слагаемые друг
к другу, при вычитании употреблял специальный
знак/1\; равенство Диофант обозначал буквой t (от греч.
icroc; — равный). Напр., уравнение
{х*+8х)— Eх2+1) = х
у Диофанта записалось бы так:
(здесь a=l, ti=8, e=5, a [i°a означает, что единица a
не имеет множителя в виде степени неизвестного).
Несколько веков спустя индийцы, разрабатывавшие
числовую алгебру, ввели различные 3. м. для не-
нескольких неизвестных (сокращения наименований цве-
цветов, обозначавших неизвестные), квадрата, квадратного
корня, вычитаемого числа. Так, уравнение
в записи Брахмагупты G в.) имело бы вид:
йа ва 3 йа 10 ру 8
йа ва 1 йа 0 ру 1
(йа — от йават — тават — неизвестное, ва — от вар-
га — квадратное число, ру — от рупа — монета ру-
рупия — свободный член, точка над числом означает
вычитаемое число).
Создание современной алгебраич. символики отно-
относится к 14—17 вв.; оно определялось успехами практич.
арифметики и учения об уравнениях. В различных
странах стихийно появляются 3. м. для нек-рых дей-
ствий и для степеней неизвестной величины. Проходят
многие десятилетия и даже века, прежде чем выраба-
вырабатывается тот или иной удобный для исчисления символ.
Так, в конце 15 в. Н. Шюке (N. Chuquet) и Л. Пачоли
(L. Pacioli) употребляли знаки сложения и вычитания
р и m (от лат. plus и minus), немецкие математики
ввели современные + (вероятно, сокращение лат. et)
и — . Еще в 17 в. можно насчитать около десятка 3. м.
для действия умножения:
?,*;„,,,; J ;•; х.
Поучительна история знака радикала. Вслед за
Леонардо Пизанским (Leonardo Pisano, 1220) многие
обозначали (вплоть до 17 в.) квадратный корень знаком
R, (от лат. radix — корень). Н. Шюке обозначал квад-
квадратный, кубический и т. д. корни знаками R,2, R,3
и т. д. В немецкой рукописи ок. 1480 квадратный ко-
корень обозначался точкой перед числом, кубич. корень—
тремя точками, а корень четвертой степени — двумя
точками. У К. Рудольфа (Ch. Rudolff, 1525) корень
уже обозначался у. Для обозначения корней высших
степеней различные ученые то пишут этот знак не-
несколько раз подряд, то ставят после него букву — со-
сокращение наименования показателя, то — соответст-
соответствующую цифру в кружке или с круглой или квадратной
скобкой, чтобы отделить ее от подрадикального числа
[горизонтальную черту над подрадикальным выраже-
выражением ввел Р. Декарт (R. Descartes), 1637], и лишь в
начале 18 в. входит в обиход запись показателя корня
вверху над отверстием знака радикала, встречающаяся
ранее у А. Жирара (A. Girard, 1629). Таким образом,
эволюция знака радикала длилась почти пятьсот лет.
Весьма различны были 3. м. неизвестной и ее степе-
степеней. В 16 и начале 17 вв. конкурировало более десяти
обозначений для одного только квадрата неизвестной,
напр, се (от census — лат. термин, служивший пере-
переводом греч. Suvanig), Q (от quadratum), У, —, А B),
1~, А", аа, а2 и т. д. Так, уравнение
г>+5г= 12
имело бы у Дж. Кардано (G. Cardano, 1545) вид:
I. cubus p. у. positionibus xquantur 12
(cubus — куб, positio — неизвестная, oequantur — рав-
равно); r
у М. Штифеля (М. Stifel, 1544):
у Р. Бомбелли (R. Bombelli, 1572):
1 ^ р. ^ ^ egua/e a t 2
A — кУб неизвестной, i, — неизвестная; eguale a —
равно);
у Ф. Виета (F. Viete, 1591):
IС ¦+¦ / N, aequatur j г
(С — cubus — куб, N — numerus — число);
у Т. Гарриота (Т. Harriot, 1631):
ааа -+- %.а _____ : ,г
В 16 и начале 17 вв. входят в употребление знаки
равенства и скобки: квадратные (Р. Бомбелли, 1550),
круглые (Н. Тарталья, N. Tartaglia, 1556), фигурные
(Ф. Виет, 1593).
Значительным шагом вперед в развитии математич.
символики явилось введение Ф. Виетом A591) 3. м.
для произвольных постоянных величин в виде пропис-
прописных согласных букв латинского алфавита В, D, что
дало ему возможность впервые записывать алгебраич.
уравнения с произвольными коэффициентами и опери-
оперировать с ними. Неизвестные Ф. Виет обозначал глас-
ными прописными буквами А, Е, ... . Напр., запись
Ф. Виета
A cubus -+- В piano in A j, aequatur Dsolido
[cubus — куб, planus — плоский, т. е. В — двумер-
двумерная величина; solidus — телесный (трехмерный), раз-
размерность отмечалась для того, чтобы все члены были
однородны] в наших символах выглядит так:
Ф. Виет явился творцом алгебраич. формул. Р. Де-
Декарт A637) придал знакам алгебры современный вид,
обозначая неизвестные последними буквами латинского
алфавита х, у, z, а произвольные данные величины —
начальными буквами а, Ъ, с. Ему же принадлежит
нынешнее обозначение степени. Обозначения Р. Де-
Декарта обладали большим преимуществом по сравнению
со всеми предыдущими. Поэтому они скоро получили
всеобщее признание.
Дальнейшее развитие 3. м. было тесно связано с
созданием анализа бесконечно малых, для разработки
символики к-рого основа была уже в большой мере
подготовлена в алгебре. И. Ньютон (I. Newton) в своем
методе флюксий и флюент A666 и следующие годы)
ввел знаки для последовательных флюксий (произ-
(производных) величины х в виде х, х, х и для бесконечно
малого приращения о. Несколько ранее Дж. Валлис
(J. Wallis, 1655) предложил знак бесконечности оо.
Создателем современной символики дифференциального
и интегрального исчислений является Г. Лейбниц
(G. Leibniz). Ему, в частности, принадлежат упо-
употребляемые ныне 3. м. дифференциалов dx, d2x, dsx
и интеграла
\ydx.
Следует подчеркнуть принципиальное преимущество
знака интеграла, данного Г. Лейбницем, перед предло-
предложенным И. Ньютоном знаком 'х. В знаке Г. Лейбница
\ ydx, отражающем самый процесс построения инте-
интегральной суммы, явно указана и интегрируемая функ-
функция и переменная интегрирования. Благодаря этому
знак \ ydx годится и для записи формул замены пе-
переменных и легко может быть использован для записи
кратных и криволинейных интегралов. Знак И. Нью-
Ньютона ' х таких возможностей непосредственно не пред~
ставляет. Аналогично обстоит дело с лейбницевыми
знаками дифференциалов и ньютоновыми знаками
флюксий и бесконечно малого приращения.
Огромная заслуга в создании символики современной
математики принадлежит Л. Эйлеру (L. Euler). Он
ввел в общее употребление первый знак переменной
операции, именно знак функции f(x) (от лат. functio —
функция, 1734). Несколько ранее знак срж был применен
И. Бернулли (J. Bernoulli, 1718). После работ
Л. Эйлера знаки для многих индивидуальных функций,
напр, тригонометрических, приобрели стандартный
характер. Л. Эйлеру же принадлежат обозначения
постоянных е (основание натуральных логарифмов,
1736), я (вероятно, от греч. iiEpicpEpEia — окружность,
периферия, 1736), мнимой единицы i = V~—i (от франц.
imaginaire — мнимый, 1777, опубликовано в 1794),
к-рые стали общеупотребительными.
В 19 в. роль символики еще более возрастает и,
наряду с созданием новых 3. м., математики стремятся
к стандартизации основных символов. Некоторые
широко употребительные ныне 3. м. появляются лишь
в это время: знак абсолютной величины \х\ (К. Вейер-
штрасс, К. Weierstrass, 1841), вектора г (О. Коши,
A. Cauchy, 1853), определителя ?|ь2г| (А- Кэли, A. Cay-
ley, 1841) и др. Многие теории, возникшие в 19 в.,
напр, тензорное исчисление, не могли быть развиты
без подходящей символики. Характерно при этом
увеличение удельного веса 3. м. для отношений,
напр., сравнимости =не (К. Гаусс, С. Gauss, 1801),
принадлежности ?, изоморфизма S?, эквивалентности
с/з и т. д. Знаки переменных отношений появляются
с развитием математпч. логики, особенно широко
применяющей 3. м.
С точки зрения математической логики, среди 3. м.
ложно наметить следующие основные группы: А)
знаки объектов, Б) знаки операций, В) знаки отно-
отношений. Например, знаки 1, 2, 3, 4 изображают
числа, т. о. объекты, изучаемые арифметикой. Знак
операции сложения -)- сам по себе не изображает ни-
никакого объекта; он получает предметное содержание j
лишь тогда, когда указано, какие числа складываются:
запись 1+3 изображает число 4. Знак > (больше)
есть знак отношения между числами. Знак отношения
получает вполне определенное содержание, когда ука-
указано, между какими объектами отношение рассматри-
рассматривается. К указанным трем основным группам 3. м.
примыкает еще четвертая: Г) вспомогательные знаки,
устанавливающие порядок сочетания основных зна-
знаков. Достаточное представление о таких знаках дают
скобки, указывающие порядок производства ариф-
метпч. действий.
Знаки каждой из трех групп А), Б) и В) бывают
двух родов: 1) индивидуальные знаки вполне опреде-
определенных объектов, операций и отношений, 2) общие
знаки «переменных», или «неизвестных», объектов, опе-
операций и отношений. Примерами знаков первого рода
могут служить (см. также таблицу на кол. 462, 463):
Аг) Обозначения натуральных чисел 1, 2, 3, 4, 5, 6, 7,
8, 9; трансцендентных чисел е и я; мнимой единицы
i= У— 1 и т. п.
Bi) Знаки арифметич. действий + , —, •, X, : ; из-
извлечения корня Р/, дифференцирования -т-, оператора
Лапласа
Сюда же относятся знаки индивидуальных функций
sin, tg, log и т. п.
Bj) Знаки равенства и неравенства =, >, <, Ф,
знаки параллельности || и перпендикулярности _[_
и т. п.
Знаки второго рода изображают произвольные объ-
объекты, операции и отношения определенного класса
или объекты, операции и отношения, подчиненные к.-л.
заранее оговоренным условиям. Напр., при записи
тождества
{а+Ъ)(а—6) = а2—б2
буквы а и Ь обозначают произвольные числа; при
изучении функциональной зависимости
буквы х ж у изображают произвольные числа, связан-
связанные заданным отношением; при решении уравнения
з: обозначает любое число, удовлетворяющее данному
уравнению (в результате решения этого уравнения
мы узнаем, что этому условию соответствуют лишь два
возможных значения +1 и —1).
С логич. точки зрения вполне законно все такого
рода общие знаки наз. знаками переменных,
как это принято в математич. логике («область изме-
Даты возникновения некоторых
математических знаков
Знак
3 н а
со
е
я
г
<, }, к
П(а)
ж, у, z
г
3 н я
+
—
X
а2,а3,...,а"
Log |
log J
sin
cos
tg
arc. sin
Sh
Ch
dx,ddx,...,
rftv H3 V
C[*Jt , U Л , . . .
d
f'(x),y' J'x
Ax
в
"sF
J* /(x)dx
V
П
j
1 ж [
lim \
lim \
lim
Значение
Кто ввел
к и индивидуальных операц
бесконечность
основание натураль-
натуральных логарифмов
отношение длины ок-
окружности к диа-
диаметру
корень квадратный
из —1
единичные векторы,
орты
угол параллельно-
параллельности
Дж. Валлис
(J. Wallis)
Л. Эйлер
(L. Euler)
У. Джонс
(W. Jones)
Л. Эйлер
(L. Euler)
Л. Эйлер
(L. Euler)
У. Гамильтон
(W. Hamilton)
Н. II. Лобачев-
Лобачевский
Знаки переменных объектов
неизвестные или пе-
переменные величины
вектор
к и индивидуал
сложение i
вычитание;
умножение
умножение
деление
степени
корни
логарифм
синус t
косинус /
тангенс
арксинус
гиперболический Л
синус 1,
гиперболический j
косинус )
дифференциал
интеграл
производная
производная
разность, прираще-
приращение
частная производная
определенный интег-
интеграл
сумма
произведение
факториал
модуль
предел
Р. Декарт
(R. Descartes)
0. Коши
(A. Caucfiy)
Когда
введен
ий
1655
1736
1706
1736
1777
(в печати
1794)
1853
1835
1637
1853
ьных операций
немецкие
математики
У. Оутред
(W. Oughtred)
Г. Лейбниц
(G. Leibniz)
Г. Лейбниц
(G. Leibniz)
Р. Декарт
(R. Descartes)
И. Ньютон
(I. Newton)
К, Рудольф
(К. Rudolf)
А. Жирар
(A. Girard)
И. Кеплер
(J. Kepler)
Б. Кавальери
(В. Cavalieil)
Л. Эйлер
(L. Euler)
Л. Эйлер
(L. Euler)
Ж Лагранж
(J. Lagrange)
В. Риккати
(V. Riccati)
Г. Лейбниц
(G. Leibniz)
Г. Лейбниц
(G. Leibniz)
Г. Лейбниц
(G. Leibniz)
Ж. Лагранж
(J. Lagrange)
Л. Эйлер
(L. Euler)
А. Лежандр
(A. Legendre)
Ж. Фурье
(J. Fourier)
Л. Эйлер
(L. Euler)
К. Гаусс
(С. Gauss)
К. Крамп
(Ch. Kramp)
К. Вейерштрасс
(К. Weierstrass),
С. Люилье
(S. L'Huillier)
У. Гамильтон
(W. Hamilton),
многие матема-
математики
конец
15 в.
1631
1698
1684
1637
1676
1525
1629
1624
1632
1748
1753
1772
1757
1675
(в печати
1684)
1675
(в печати
1686)
1675
1770,
1779
1755
1786
1819—
22
1755
1812
1808
1841
1786
1853
начало
20 в.
Продолжение
Знак
Значение
Кто ввел
Когда
введен
I
Г
В
д
V
ф.Г
дзета-функция
гамма-функция
бета-функция
дельта (оператор Ла-
Лапласа)
набла (оператор Га-
Гамильтона)
Б. Риман
(В. Riemann)
А. Лежандр
(A. Legendre)
Ж. Бине
(J. Binet)
Р. Мёрфи
(R. Murphy)
У. Гамильтон
(W. Hamilton)
Знаки переменных операций
И. Бернулли
функция (J. Bernoulli)
Л. Эйлер
(L. Euler)
1857
1808
1839
1833
1853
1718
1734
3 н а
=
>
<
II
X
к и индивидуал
равенство
больше 1
меньше 1
сравнимость
параллельность
перпендикулярность
Ы1Ы)
р
(R.
Т.
(Т.
к
(С
У
(W.
п.
(Р.
отношений
Рекорд
Recorde)
Гарриот
Harriot)
. Гаусс
. Gauss)
Оутред
Oughtred)
Зригон
Herigone)
1557
1631
1801
1С77
(в по-
поем ертном
издании)
1634
нения» переменного может оказаться состоящей из
одного единственного объекта или даже «пустой»,
напр., в случае уравнений, не имеющих решения).
Дальнейшими примерами такого рода знаков могут
служить:
А2) Обозначения точек, прямых, плоскостей и более
сложных геометрич. фигур буквами в геометрии.
Б2) Обозначения /, F, ф для функций и обозначения
операторного исчисления, когда одной буквой L обо-
обозначают, напр., произвольный оператор вида:
2у , . „ d«v
X' - dxti
Обозначения для «переменных отношений» менее
распространены; они находят применение лишь в
математич. логике и в сравнительно абстрактных, по
преимуществу аксиоматических, математич. исследо-
исследованиях.
Лит.: [1] С а ] о г i F., A history of mathematical notations,
V. 1 — 2, Chi., 1928—29.
ЗНАКОВ КРИТЕРИЙ — непараметрический крите-
критерий для проверки гипотезы Ло, согласно к-рой случай-
случайная величина \i подчиняется биноминальному распре-
распределению с параметрами (га; р = 0,5). Если гипотеза Но
справедлива, то
где
Го
В(й, Ь) — бета-функция. Согласно 3. к. с уровнем
значимости а, 0<а<0,5, гипотезу Нь следует отверг-
отвергнуть, если
i{i, n—\ }
где т=т(а, п) — критическое значение 3. к., яв-
являющееся целочисленным решением неравенств
с' ( [
3. к. можно применять для проверки гипотезы Но,
согласно к-рой неизвестное непрерывное распределение
независимых одинаково распределенных случайных
величин Хх, ..., Хп является симметричным относи-
относительно нуля, т. с. для любого действительного числа х
выполняется равенство
?{Xt <-?.} = ? {X; >х].
В этом случае 3. к. основан на статистике
[ если °
о (К,), о (х) = {
v w \ 0, если х < О,
к-рая при справедливости гипотезы Но подчиняется
биномиальному закону с параметрами (п; /? = 0,5).
Аналогично, 3. к. используется для проверки гипо-
гипотезы Ло, согласно к-рой медиана неизвестного непре-
непрерывного распределения, к-рому подчиняются незави-
независимые случайные величины Х1, ..., Хп, имеет значение
?0, для чего нужно перейти к случайным величинам
YXH YX1
iHo* •••> Yn=Xn—10.
Лит.: L1J Б о л ь ш е в Л. Н., Смирнов Н. В., Таблицы
математической статистики, [2 изд.], М., 1968; [2] Л е м а н Э..
Проверка статистических гипотез, пер. с англ., М., 196ч; 13}
Ван дер Варден Б. Л., Математическая статистика,
пер. с нем., М., 1960; [4] С м и р н о в Н. В., Дунин-Вар-
ковский И. В., Курс теории вероятностей и математической
статистики для технических приложений, 3 изд., М., 19ti9.
М. С. Никулин.
ЗНАКОПЕРЕМЕННАЯ ГРУППА ге-й степени —
подгруппа Ап симметрической группы Sn, состоящая
из всех четных подстановок. А п является инвариантной
подгруппой индекса 2 и порядка и!/2 группы Sn. Под-
Подстановки из А п, рассматриваемые как подстановки
индексов переменных х1у ..., хп, не изменяют значения
так наз. знакопеременного многочлена П (х/—xj),
откуда и происходит назв. «3. г.». Группа Ат может
быть определена и для бесконечной мощности т, как
подгруппа симметрич. группы Sm бесконечной мощ-
мощности т, состоящая из всех четных подстановок. При
и>3 группа Sn будет (п—2)-кратно транзитивной.
При любом п, конечном или бесконечном, исключая
и=4, эта группа проста, что играет важную роль в
теории разрешимости алгебраич. уравнений в ради-
радикалах.
Лит.: [1] Холл М., Теория групп, пер. с англ., М., 1962.
П. Н. Вильяме.
ЗНАКОЧЕРЕДУЮЩИЙСЯ РЯД, знакопере-
знакопеременный ряд,— бесконечный ряд, члены к-рого
попеременно положительны и отрицательны:
—-Ь«з—-г • ¦ • +(—I)"'1 м„+ .. ., uk > 0.
Если члены 3. р. монотонно убывают (ип + 1<.ип) и
стремятся к нулю (lim ып=0), то ряд сходится (т е о-
рема Лейбница). Остаток сходящегося 3. р.
имеет знак своего первого члена п меньше его по аб-
абсолютной величине. Простейшие примеры сходящихся
3. р.:
4
—С II"-
2п-1
Сумма первого из этих рядов есть 1п2, а второго л/4.
В. И. Битюцков.
ЗНАМЕНАТЕЛЬ арифметической дроби
— — целое число Ь, показывающее (знаменующее)
размеры долей единицы, из к-рых составлена дробь.
or г А
3. алгебраической дроби -g- наз. выраже-
выражение В (СМ. Дробь). С. А. Степанов.
ЗНАЧАЩАЯ ЦИФРА — термин, относящийся к при-
приближенному заданию действительного числа. Пусть
в системе счисления с основанием q для действитель-
действительного числа х получено приближенное представление
g-ичной дробью
х та х*=(ап .. .ai<x0, a_ia_2 . • • a—m).
Пусть при этом as — первая ненулевая цифра, считая
слева. Тогда и все последующие цифры наз. знача-
значащими цифрами приближенного числа х*.
3. ц. at наз. верной, если абсолютная погреш-
погрешность Л (ж*) числа х*, то есть величина \х—х*\, удов-
удовлетворяет неравенству
А (**) < 4" qt-
Обычно при приближенном задании числа х имеет
смысл указывать только верные 3. ц. х. Д. Икрамов.
ЗНАЧИМОСТИ КРИТЕРИИ — один из основных ме-
методов статистич. проверки гипотез, применяемый для
проверки соответствия результатов наблюдений х1,
..., хп, трактуемых как реализации случайных величин
X-i, ..., Хп, нек-рой гипотезе Но о вероятностном
распределении этих случайных величин. 3. к. отвер-
отвергает либо принимает гипотезу Но в зависимости от
наблюденного значения нек-рой статистики Т=Т(Х1,
..., Хп), конкретизация к-рой зависит от постановки
задачи. При применении 3. к., вообще говоря, не
предполагается наличие какой-либо конкурирующей
гипотезы Нх, к-рую принимают в случае отклонения
#0, но если Ht задана, то, согласно общей теории
статистич. проверки гипотез, именно конкурирующая
гипотеза Нх определяет выбор статистики Т в соот-
соответствии с принципом максимизации мощности кри-
критерия.
Обычно 3. к. применяют следующим образом. Вы-
Выбрав статистику критерия Т(Хг, ..., Хп), по ее рас-
распределению при гипотезе Ло и по заранее выбранному
уровню значимости а, 0<а<0,5, определяют критиче-
критическое значение критерия ta такое, что ?{T^ta\H0} = a..
Согласно 3. к. с уровнем а гипотезу Но отвергают,
если Т(хг, . . ., xn)^ta- Если Т(хх, ..., xn)<ta, то
считают, что гипотеза Йо не противоречит результатам
наблюдений хг, . . ., хп, по крайней мере, до тех пор,
пока новые результаты наблюдений не заставят экс-
экспериментатора принять другую точку зрения.
Пример. Если за первый час работы счетчик за-
зарегистрировал 150 импульсов пуассоновского процесса,
а за второй — 117 импульсов, то спрашивается, можно
ли считать, что интенсивность поступления импульсов
в единицу времени была постоянной (гипотеза //0)?
Если гипотеза Но верна, то наблюденные значения
150 п 117 можно трактовать как реализации двух
независимых случайных величин Хг и Х2, подчиняю-
подчиняющихся одному и тому же закону Пуассона с параметром
а, значение к-рого нам неизвестно. Поскольку при
гипотезе На случайные величины
приближенно подчиняются нормальному распределе-
распределению с параметрами @,1), то статистика
распределена приближенно по закону yv3 с одной сте-
степенью свободы, т. е.
По таблицам //-распределения находят критическое
значение xi@,05)==3,841, соответствующее заданному
уровню значимости а=0,05, т. е.
Р{Х^=* 3,841} =0,05.
Далее, по наблюденным значениям Хх=150 и Х2=117
вычисляют значение X2 статистики критерия:
[— j/~4-117+ l]2 = 4,087.
Поскольку Z2 = 4,085>xi@,05)^3,841, то гипотеза
Ho о сохранении интенсивности отвергается по 3. к.
типа у2 с уровнем значимости а—0,05.
Лит.: [1] Крамер Г., Математические методы статисти-
статистики, пер. с англ., 2 изд., М., 1975; [2] Л е м а н Э., Проверка ста-
статистических гипотез, пер. с англ., М., 1964; [3] Смирнов
Н. В., Дунин-Барковский И. В., Курс теории ве-
вероятностей и математической статистики для технических при-
приложений, 3 изд., М., 1969; [4] Д е в я т о в Б. И., «Теория веро-
ятн. и ее иримен.», 1969, т. 14, Ла 1, с. 175—78.
М. С. Никулин.
ЗНАЧИМОСТИ УРОВЕНЬ статистического
критерия — вероятность ошибочно отвергнуть ос-
основную проверяемую гипотезу, когда она верна. В тео-
теории статистич. проверки гипотез 3. у. наз. вероят-
вероятностью ошибки первого рода. Понятие «3. у.» возникло
в связи с задачей проверки согласованности теории с
опытными данными. Если, напр., в результате на-
наблюдений регистрируются значения п случайных ве-
величин Хг, . . ., Хп и если требуется по этим данным
проверить гипотезу Н, согласно к-рон совместное
распределение величин Хг, . . . , Xп обладает пек-рым
определенным свойством, то соответствующий стати-
стнч. критерий конструируется с помощью подходящим
образом подобранной функции Y=/(Xi, ..., Хп);
эта функция обычно принимает малые значения, когда
гипотеза Н верна, и большие значения, когда // ложна.
В частности, если Xlt ..., Хп — результаты незави-
независимых измерений некоторой известной постоянной а
и гипотеза Н представляет собой предположение об
отсутствии в результатах измерений систематич. оши-
ошибок, то для проверки Н разумно в качестве Y выбрать
Bт—пJ, где то — количество тех результатов изме-
измерений X,-, к-рые превышают истинное значение а.
Наблюдаемое в опыте большое значение Y можно рас-
рассматривать как значимое статистич. опровержение
пшотетич. согласия между результатами наблюдений
и проверяемой гипотезой. Соответствующий крите-
критерий значимости представляет собой правило,
согласно к-рому значимыми считаются значения Y,
превосходящие заданное критич. значение у. В свою
очередь выбор величины у определяется заданным
3. у., к-рый в случае справедливости гипотезы Н сов-
совпадает с вероятностью события {У>!/}.
При выборе 3. у. следует учитывать ущерб, неиз-
неизбежно возникающий при использовании любого кри-
критерия значимости. Так, напр., если 3. у. чрезмерно<
велик, то основной ущерб будет происходить от оши-
ошибочного отклонения правильной гипотезы; если же
3. у. мал, то ущерб будет, как правило, возникать от
ошибочного принятия гипотезы, когда она ложна.
Практически при обычных статистич. расчетах в ка-
качестве 3. у. выбирают вероятность в пределах от 0,01
до 0,1. Значения 3. у., меньшие, чем 0,01, исполь-
используются, напр., при статистич. выявлении токсичных
медицинских препаратов, а также в других особых
случаях, когда первостепенное значение приобретает
гарантия от ошибочного отклонения проверяемой ги-
гипотезы. См. также Доверительное оценивание.
Лит.: Крамер Г., Математические методы статистики,,
пер. с англ., 2 изд., М., 1975. Л. Н. Большее.
ЗОЛОТОЕ СЕЧЕНИЕ, гармоническое де-
деление, деление в крайнем и среднем
отношении,— деление отрезка а, при к-ром боль-
большая часть х является средней пропорциональной между
всем отрезком а и меньшей его частью а—х, то есть
а:х = х:(а— х). (*)
Для нахождения х получается квадратное уравнение
ж2+а.-— а2=0,
решение к-рого дает
x = \{V -1) ^ 0,62а.
Условие (*) можно переписать и так
х {, . х \ . а
7 11+tJ=1 или * = -•
1+—-,
1+ ...,
т. е. х получают в виде непрерывной дроби, подходящие
дроби к-рой будут:
1 1 2 35 813
Т' I' Т ' Т • 8" ' Гз ' П и т" д' '
где 1, 1, 2, 3, 5, 8, 13, 21 и т. д.— так наз. Фибоначчи
числа-.
Геометрически 3. с. отрезка АВ (см. рис.) строится
так: в точке В восстанавливают перпендикуляр к АВ,
откладывают на нем отрезок ВЕ—-^-АВ, соединяют
А и Е, откладывают ED = EB и, наконец, AC=AD,
тогда
АВ : АС=АС : СВ.
3. с. было известно еще в древности. В дошедшей
до нас античной литературе 3. с. впервые встречает-
встречается в «Началах» Евклида C в.
до н. э.).
Термин «3. с.» ввел Леонардо
да Винчи (Leonardo da Vinci)
в (кон. 15 — нач. 16 вв.). Прин-
Принципы 3. с. или близкие ему про-
" а ' порциональные отношения легли
в основу композиционного пост-
построения многих произведений мирового искусства (глав-
(главным образом произведений архитектуры античности
и Возрождения).
ЗОММЕРФЕЛЬДА ИНТЕГРАЛ — интегральное пред-
представление интегралом по контуру цилиндрических функ-
функций: Ганкеля функции 1-го рода
где С1 — кривая, пробегаемая от —т] + гоо до г]— гоо,
функции Ганкеля 2-го рода
где C2 — кривая, пробегаемая от ц — гоо до 2л—т] + гоо,
0«п]<я;
Бесселя функции 1-го рода
где С3 — кривая, пробегаемая от —т]+гоо до 2л—г|+
+ г°°, 0<:т]«:оо. Представление справедливо в обла-
области —ri<arg г<л—т]. 3. и. назван по имени А. Зом-
мерфельда (Sommerfeld А., см. [1]).
Лит.: [USommeTfeU A., «Math. Ann.», 1896, Bd 47,
S. 317—74; [2] Я н к е Е., 3 м д е Ф., Лёш Ф., Специальные
функции. Формулы, графики, таблицы, пер. с нем., 2 изд.,
М., 1968; [3] В а т с о н Г. Н., Теория бесселевых функций,
пер. с англ., ч. 1., М., 1949. А. Б. Иванов.
ЗОММЕРФЕЛЬДА УСЛОВИЯ ИЗЛУЧЕНИЯ —см.
Излучения условия.
ЗОНАЛЬНЫЕ СФЕРИЧЕСКИЕ ФУНКЦИИ — см.
Сферические функции.
ЗОНОЭДРЫ — многогранники, представимые как век-
векторная сумма конечного числа отрезков. 3. в и-мерном
пространстве наз. также зонотопами. 3.— вы-
выпуклый многогранник, причем сам 3. и его грани всех
размерностей имеют центры симметрии. Наличие цент-
центров симметрии у двумерных граней выпуклого много-
многогранника достаточно, чтобы он был 3. Всякий 3.
есть проекция куба достаточно высокой размерности.
В классе центрально симметричных выпуклых тел осо-
особую роль играют зоноиды — тела, предельные для
3.; они допускают специфическое интегральное предста-
представление опорной функции и являются конечномерными
сечениями сферы в банаховом пространстве L1.
Лит.: [1] В о 1 к е г Е., «Trans. Amer. Math. Soc», 1969,
v. 145. p. 323-45; [2] Weil W., «Math. Z.», 1976, Bd 148,
№ 1, S. 71—84. В. А. Залгаллеу.
ИВАСАВЫ РАЗЛОЖЕНИЕ — однозначное представ-
представление любого элемента g некомпактной связной полу-
полупростой вещественной группы Ли G в виде произведения
g = Kan элементов к, а, п аналитич. подгрупп К, А, N
группы G соответственно, где подгруппы К, А, N оп-
определяются следующим образом. Пусть 3=f+9l
Картана разложение алгебры Ли g группы G; пусть
О — максимальное в ty коммутативное подпростран-
подпространство пространства §р, 9J — такая нильпотентная под-
подалгебра Ли в д, что комплексификация алгебры 9?
является линейной оболочкой корневых векторов
нек-рой системы положительных корней относительно
комплексификации нек-рой максимальной коммута-
коммутативной подалгебры Ли в алгебре Ли д, содержащей а.
Разложение алгебры Ли в прямую сумму подалгебр f,
й и ЭД наз. разложением Ивасавы [1]
полупростой вещественной алгебры Ли д. Группы
К, А и N определяются как аналитич. подгруппы груп-
группы G, отвечающие подалгебрам Ли {, п, Ш соот-
соответственно. Группы К, А и N замкнуты; группы А и N
одно связны; группа К содержит центр группы G, и
образ группы К в присоединенном представлении груп-
группы G является максимальной компактной подгруппой
в присоединенной группе группы G. Отображение
(k, a, n)-+kan является аналитич. диффеоморфизмом
многообразия KXAXN на группу Ли G. И. р. играет
существенную роль в теории представлений полупро-
полупростых групп Ли. И. р. может быть определено также
для связной полупростой алгебраич. группы над
р-адическим полем (или, более общо, для группы
/i-адического типа) (см. [4, 5]).
Лит.: [1] Iwasawa К., «Ann. Math.», 1949, v. 50,
p. 507—58; [2] Найма р к М. А., Теория представлений
групп, М., 1976; [3] X е л г а с о н С, Дифференциальная гео-
геометрия и симметрические пространства, пер. с англ., М., 1964;
[4] В г u h a t F., «Publ. Math. IHES», 1964, t. 23, p. 46—74;
[5] I w a h о г i N., Matsumoto H., там же, 1965, t. 25,
p.5 —48. А. С. Феденко, А. И. Штерн.
ИВЕРСЕНА ТЕОРЕМА: если а — изолированная
существенно особая точка аналитич. функции f(z)
комплексного переменного z, то каждое исключительное
аначение а. в смысле Пикара является асимптотическим
значением для /(z) в точке а. Напр., значения аа = 0
и а2=оо исключительные и асимптотические для функ-
функции /(г)=ег в существенно особой точке а=оо. Этот
результат Ф. Иверсена [1] дополняет большую Пикара
теорему о поведении аналитич. функции в окрестности
существенно особой точки.
Лит.: [1] I verse n F., Recherches sur les fonctions in-
inverses des lonctions meromorphes, Hels., 1914; [2] К о л л и н г-
вуд Э., Ловатер А., Теория предельных множеств, пер.
с англ., М., 1971, гл. 1. Е. Д. Соломенцев.
ИГР ТЕОРИЯ — теория математических моделей
принятия оптимальных решений в условиях кон-
конфликтов.
Формальное определение игры. Под конфлик-
конфликтом понимают явление, применительно к к-рому
ложно говорить, кто и как в этом явлении участвует,
какие у него могут быть исходы и кто и как в этих
исходах заинтересован. Поэтому для формального
задания конфликта необходимо указать: 1) множество
Л'а участвующих в нем действующих начал (называ-
(называемых коалициями действи я), 2) семейство
множеств j стратегий каждой из коалиций
действия, 3) множество ситуаций J, —П^6Ж ?„
4) множество У(ц заинтересованных начал (называемых
коалициями интересов) и 5) семейства
бинарных отношений ?— на jXr {К?$и), выражаю-
К
щих предпочтения между ситуациями для коалиций
интересов. Система
наз. и г р о й.
Содержание И. т. состоит в установлении связей
между компонентами каждой игры и «оптимальными»
ее исходами, и прежде всего: в уточнении самого по-
понятия оптимальности, в доказательстве существования
оптимальных исходов и в их фактич. определении. Раз-
Развитие И. т. приводит к вопросам изучения взаимосвязей
между различными играми, что выражается в разра-
разработке разного рода исчислений игр, и к рассмотрению
классов, пространств, категорий игр.
Классификация игр. Игры, в к-рых совсем нет коа-
коалиций интересов или же имеется лишь одна такая коа-
коалиция, являются предметами изучения чисто дескрип-
дескриптивных или же традиционных оптимизационных теорий.
Игры в собственном смысле слова имеют не менее двух
коалиций интересов.
Обычно в И. т. как коалиции действия, так и коали-
коалиции интересов принято атомизировать и считать как
те, так и другие подмножествами нек-рого множества /,
элементы к-рого наз. игроками. Вначале множе-
множество игроков в игре принималось конечным, но позднее
A970-е гг.) начали изучаться игры и с бесконечными
и притом неатомическими множествами игроков.
Для игр с одной коалицией действия множество
всех ситуаций можно принять за множество стратегий
этой единственной коалиции действия и далее о стра-
стратегиях не упоминать. Поэтому такие игры наз. н е-
стратегическими. В отличие от них, все
остальные игры, с двумя или более коалициями дей-
действия, наз. стратегическими.
Весьма широкий класс нестратегич. игр может быть
получен следующим образом. Пусть / — множество
игроков, и iXu=2/. Каждому игроку i?I ставится в
соответствие координатная прямая Е1, принимаемая
за шкалу его полезностей, а каждой коалиции инте-
интересов К^!\\ц — произведение E^=UiuKEl. Наконец,
вводятся множества v(K)cEK для каждого АГ^ЙуИ
множество НсЕ1 (элементы к-рого наз. дележами)
и по определению принимается, что для дележей х,
у?Е! имеет место х^у («дележ х доминирует дележ у
К
по коалиции К») тогда и только тогда, когда х, у ? (и(К)Х
Х?ГК)Г|Я и ж,>!/,- для всех i?K. Такие игры наз.
играми без побочных платежей. Они
описывают положение, при к-ром каждая коалиция
интересов К может форсированно обеспечить для своих
членов в качестве выигрышей компоненты любого
вектора из v(K), а общие соображения целесообраз-
целесообразности делают нерациональным выбор дележей вне Я.
Обычно множества и (К) подчиняются нек-рым естест-
естественным условиям: 1) и(К) является непустым замкну-
замкнутым и выпуклым множеством, 2) если Xk?v(K) и
Уъх^хъ (неравенство векторов понимается покомпонент-
покомпонентно), то yk(zv{K) («кто способен на большее, способен и на
меньшее»), 3) если К[]Ь=ф, то v(K\]L)ZDv(K)Xv(L)
(коалиции К и L вместе могут добиться не меньше-
меньшего, чем порознь), 4) Н состоит из всех таких векторов
х?Е1, что для каждого из них найдется вектор
y(zv(I), для к-рого ifSix (таким образом, v(I) состо-
состоит из всех таких векторов выигрышей х, что / мо-
может дать своим членам не менее чем х; II состоит
из таких векторов х, что / может дать своим членам
ровно х). В частности, если
где v(K) — некоторое действительное число, а
то получится классическая кооперативная игра. В этом
случае определение v(K) означает возможность коа-
коалиции К уверенно добиться суммарного выигрыша
v(K) и произвольно перераспределить его между
своими членами. Определение И означает, что общая
распределяемая в игре сумма есть v(I) (распределять
меньшую сумму невыгодно; большей же просто нет!),
а каждый игрок i будет соглашаться лишь на долю
xi, не меньшую, чем та сумма v(i), к-рую он может
уверенно получить самостоятельно.
Основной класс стратегич. игр составляют бескоа-
бескоалиционные игры, в к-рых множество игроков / совпа-
совпадает с множествами коалиций действия Jfg и коалиций
интересов Жц. Каждый игрок i?I имеет в своем рас-
распоряжении множество стратегий у,,-, в качестве множе-
множества всех ситуаций принимается декартово произве-
произведение J=nisrj/, а отношение предпочтения ?— описы-
г
вается функцией выигрыша Н,: г.—v-E', при-
причем х'$~-х" тогда и только тогда, когда Hj(x')>Hi{x").
г
Таким образом, бескоалиционная игра может быть
описана в виде тройки Г=</, {ц}ш, {H,}ieI>.
Если все множества стратегий j,- конечны, то и бескоа-
бескоалиционная игра Г наз. конечной. Конечные
бескоалиционные игры с двумя игроками (/={1,11})
наз. биматричными играми.
Если /={1, II} и #,(z)=— Hn(x) для всех х?%,
то игра Г наз. антагонистической игрой. Всякая ан-
тагонистич. игра может быть задана в виде тройки
($, Й, Н), где 5 и 0 — множества стратегий, соответ-
соответственно, игроков I и II, а // — функция выигрыша
игрока I. Конечные антагонистич. игры наз. матрич-
матричными играми.
Если в антагонистич. игре s=t1= [0, 1], то всякая
ситуация в такой игре описывается точкой из квадрата
[О, 1]Х[0, 1]; такие игры наз. играми на единичном
квадрате.
Пусть / — множество игроков, xi(i^I) — множе-
множества их стратегий; X — множество, элементы к-рого
наз. позициям и; Т — множество, элементы к-рого
„TXI
имеют смысл моментов времени; /:?—>2 -, т.е. f
ставит в соответствие каждой ситуации определяемой
игры отношение, заданное на Т со значениями в X;
всякий /-образ ситуации наз. партией (множество
всех партий обозначается через Щ и, наконец, /г,-: ^—>-/?'.
Система
Г=<', {*,•}«=/.Г, X, U 5P. {hi)UIy
наз. общей позиционной игрой. В ко-
конечном счете в такой игре выигрыш каждого игрока
вполне определяется складывающейся ситуацией, т. е.
выбором стратегий всеми игроками. Поэтому такие
игры относятся к числу бескоалиционных игр.
Пусть в общей позиционной игре Г компонента X
является конечномерным евклидовым пространством,
Т — множеством действительных чисел, а ср: JX X X T—t
—>-Х. Пусть рассматриваются ситуации x?g, для кото-
которых система дифференциальных уравнений
¦|f = <р(ж, ж, t), ос?Х, t?T
(равенство понимается как векторное) имеет при дан-
данных начальных условиях единственное решение. Тогда
каждая ситуация определяет некоторую партию, к-рая
в данном случае наз. траекторией. Так опреде-
определенная игра наз. дифференциальной игрой.
К числу общих позиционных игр относятся также
позиционные игры И динамические игры (в том числе
стохастические игры, рекурсивные игры, а также игры
на выживание).
Основные результаты теории игр. Основная пробле-
проблематика в И. т. связана с принципами оптимальности,
которые, во-первых, должны в достаточной мере отра-
отражать содержательные представления об оптимальности,
а во-вторых, должны быть реализуемыми на достаточно
широких и естественно очерченных классах игр. Эти
два требования, предъявляемые к принципам опти-
оптимальности, в известной мере противоречат друг другу,
и поэтому для многих содержательно естественных
классов игр И. т. еще не выработала соответствующих
принципов оптимальности. Вместе с тем известны классы
игр, обслуживаемые с равным успехом несколькими
различными принципами оптимальности. Поэтому кон-
конструирование и анализ принципов оптимальности
являются существенной составной частью И. т. Каждый
принцип оптимальности реализуется (не обязательно
однозначно) в виде множества ситуаций-оптимумов.
Это множество (к-рое может оказаться пустым) наз.
решением.
Логической основой каждого решения являются
нек-рые черты обычного экстремума, сформулирован-
сформулированные применительно к одновременной экстремизации
нескольких функций. Поэтому, помимо стремления к
наибольшим (в арифметическом смысле) значениям
выигрышей, решения игр могут выражать нек-рые
характеристики устойчивости и симметрии, а также
различные комбинации того п другого.
Так, среди черт оптимальности в нестратегич. играх
можно назвать недоминируем ость, т.е. со-
соглашение считать оптимальными те и только те ситуа-
ситуации ж, для к-рых ни при какой ситуации у и коалиции
интересов К не может быть х'г-у (множество опти-
к
мальных в этом смысле ситуаций наз. с-я д р о м игры).
Другой принцип оптимальности состоит в сочетании
внутренней и внешней устойчивости; это означает,
что множество ситуаций R объявляется решением,
если при х, y?R и К^ЦИцвс может быть х^у, а по
. К
всякому x(fR найдутся такие z?R и К?Яц, что z?—я
К
(такое R наз. решением игры по Ней-
Нейману — Моргенштерну). Можно формализо-
формализовать угрозы, предъявляемые одними коалициями дру-
другим, а также ответные контругрозы, и объявить устой-
устойчивой всякую ситуацию, в к-рой каждая угроза может
парироваться контругрозой. Множество всех устой-
устойчивых в этом смысле ситуаций наз. k-я д р о м игры.
Представляет также интерес понимание оптимальности
как своеобразной «справедливости», задаваемой нек-рой
системой аксиом. Для кооперативных игр сформули-
сформулирована такая аксиоматика, приводящая к единствен-
единственному дележу (ситуации), называемому Шепли вектором.
В стратегич. играх основой принципа оптимальности
является идея равновесия. При этом оптимальными
объявляются такие ситуации, отклонения от к-рых
любым игроком не приводят к увеличению его выиг-
выигрыша. Один и тот же принцип оптимальности, формули-
формулируемый для различных по объему классов игр, может
приобретать различное содержательное выражение.
Так, описанный принцип равновесия в случае антаго-
нистич. игр превращается в минимакса принцип.
Формулы и алгоритмы, позволяющие находить реше-
решения игр, также можно отнести к числу принципов оп-
оптимальности (с узкой областью применимости). Напр.,
в матричной игре с диагональной матрицей выигрышей
принципом оптимальности можно считать выбор игро-
игроками стратегий с вероятностями, обратно пропорцио-
пропорциональными соответствующим диагональным элементам
матрицы. Реализуемость принципа оптимальности для
нек-рого класса игр состоит в существовании для
всех игр этого класса соответствующих (непустых)
множеств оптимумов. Их отсутствие в первоначально
заданных ситуациях может преодолеваться путем рас-
расширения множеств стратегий (и тем самым — множеств
конструируемых из них ситуаций). Для бескоалицион-
бескоалиционных игр плодотворно используются смешанные (ран-
(рандомизированные) стратегии.
Большинство доказательств теорем существования
решений в И. т. носит неэффективный характер (мно-
(многие из них опираются на теоремы о неподвижной точке)
и не содержат алгоритмов нахождения решений. По-
Поэтому в И. т. важны частные аналитические и численные
методы нахождения решений. При этом вопрос о фак-
фактическом нахождении решений игр нередко оказы-
оказывается очень сложным, и ответ на него удается найти
лишь для весьма узких классов игр.
В разработке исчислений игр можно выделить не-
несколько направлений. Изучаются возможности нахож-
нахождения и описания (хотя бы частичного) решений одной
игры на основе решений другой игры, в том или ином
смысле более просто устроенной. Элементарными при-
примерами таких редукций могут служить естественное
отбрасывание доминируемых стратегий игроков в бес-
бескоалиционных играх, симметризация таких игр, а
также аппроксимации бесконечных игр конечными.
Редукционным процессом можно считать также пред-
предложенное Дж. Нейманом (J. Neumann) построение
кооперативной модели бескоалиционной игры. Извест-
Известны и обратные результаты, указывающие на принци-
принципиальную несводимость решений игр того или иного
класса к решению игр более узкого класса. Напр.,
можно указать бескоалиционные игры трех лиц, реше-
решение к-рых связано с выполнением иррациональных
операций, в то время как решение биматричных игр
всегда осуществимо при помощи рациональных опера-
операций.
фиксация одних компонент в играх нек-рого класса
(напр., множества игроков и множеств их стратегий
в условиях класса всех бескоалиционных игр) и раз-
различение игр по остальным компонентам (в данном при-
примере — по функциям выигрыша игроков) приводит
к рассмотрению пространств игр, к-рое осуществляется
средствами функционального анализа и топологии.
Введение на таких пространствах игр вероятностной
меры приводит к стохастич. играм.
Связи теории игр с другими разделами математики.
И. т. тесно связана с различными разделами матема-
математики. Как общая теория множеств с несколькими би-
бинарными отношениями, она близка алгебре. В И. т.
используется весьма разнообразный математич. ап-
аппарат, а большое число вполне традиционных мате-
математич. задач допускает теоретико-игровые обобщения.
Оптимальные поведения в стратегич. играх обычно
оказываются рандомизированными, поэтому теоретико-
вероятностные понятия настолько естественно входят
в И. т. и употребляются в ней, что одно время даже
было принято считать И. т. частью теории вероятностей.
Математич. модели исследования операций (являю-
(являющиеся моделями принятия оптимальных решений)
естественно распределяются по трем уровням: детер-
детерминированному, стохастическому и неопределенному —¦
в зависимости от степени информированности принима-
принимающих решения субъектов. Принятие решения в ус-
условиях неопределенности можно интерпретировать как
конфликт принимающего решение субъекта против
«природы» и тем самым — как игру. По существу к иг-
играм относятся и все многокритериальные задачи.
Поэтому И. т. в ее методологии, основах и в практич.
ориентированности можно считать разделом исследо-
исследования операций.
И. т. является одной из составных частей математич.
аппарата кибернетики. В динамич. играх стратегии
выступают как функции «информационных состояний»
игроков, причем в ходе игры игроки могут приобретать
или утрачивать информацию. Это обусловливает связь
И. т. с информации теорией.
Приложения теории игр. Помимо разнообразных-
связей внутри математики, И. т. имеет многочисленные
приложения вне ее. Они касаются главным образом
тех отраслей знаний и видов практич. деятельности,
к-рые непосредственно имеют дело с конфликтами:
военного дела, капиталистич. экономики (в частности,
И. т. применяется в вопросах борьбы фирм за рынки,
в явлениях олигополии, в планировании рекламных ком-
компаний, при формировании цен на конкурентных рынках,
в биржевой игре и т. д.), права и т. п. С позиций
И. т. можно рассматривать и различные явления в усло-
условиях плановой экономики (напр., вопросы централиза-
централизации и децентрализации управления производством, пре-
преодоление ведомственных противоречий, оптимальное
планирование по нескольким показателям, планиро-
планирование в условиях неопределенности, порождаемой,
напр., технич. прогрессом, и т. д.).
Исторический очерк. Зарождение И. т. как мате-
математич. дисциплины можно отнести к тому же письму
Б. Паскаля (В. Pascal) к П. Ферма (P. Fermat) от 29
июля 1654, к-рое принято считать началом математич.
теории вероятностей. В дальнейшем отдельные ид:и,
к-рые можно отнести к теоретико-игровым, высказыва-
высказывались Вальдегравом (Waldegrave, 1712; нахождение
оптимальных смешанных стратегий в игре «проходящий
туз>>\ Д. Бернулли (D. Bernoulli, 1732; анализ «пе-
«петербургской игры»), П. Лапласом (P. Laplace, 1814;
рассмотрение принципов оптимальности) и Ж. Берт-
Бертраном (J. Bertrand, 1888; теоретико-игровой подход к
игре в бакара). Ряд по существу теоретико-игровых
утверждений был в эквивалентной форме рассмотрен
в других разделах математики: в теории наилучших
приближений (П. Л. Чебышев), в геометрии выпуклых
многогранников [Г. Минковский (Н. Minkowski)],
в теории линейных неравенств [Э. Штимке (Е. Stiemke)].
В 1911 Э. Цермело (Е. Zennelo) описал теоретико-
игровой подход к шахматной игре; в 1921 Э. Борель
(Е. Borel) начал систематич. изучение матричных
игр, доказав для нек-рых случаев существование оп-
оптимальных смешанных стратегий. В 1928 вышла в свет
рабвта Дж. Неймана «К теории стратегических игр»,
содержащая основные идеи современной И. т. Эти
идеи были детально разработаны Дж. Нейманом и
О. Моргеиштерном (О. Morgenstern, [1]). С тех пор
И. т. вошла в число разделов современной математики.
Лит.: [1] Нейман Дж.,Моргенштерн О.,
Теория игр и экономическое поведение, пер. с англ., М., 1970;
[2] Л ь ю с Р., Р а й ф а X., Игры и решения, пер. с англ.,
М., 1961: [31 К а р л и н С, Математические методы в теории
игр, программировании и экономике, пер. с англ., М., 1964;
[4] Воробьев Н. Н., «Успехи матем. наук», 1970, т. 15,
в. 2, с. 80—140; [5] Оуэн Г., Теория игр., пер. с англ., М.,
1971; [6] П а р т х а с а р а т х и Т., Рагха'ван Т., Не-
Некоторые вопросы теории игр двух лиц, пер. с англ., М., 1974;
[7] Воробьев Н. Н., Теория игр. Лекции для экономистов-
кибернетиков, Л., 1974; L8] его же, Entwicklung der Spiel-
theorie, В., 1975; [9] Теория игр. Аннотированный указатель
публикаций по 1968 г., Л., 1U76; [10] Журнал «International Jour-
Journal of Game Theory», Vienna (выходит с 1971). H. H. Воробьев.
ИГРА НА ВЫЖИВАНИЕ — антагонистическая ди-
намическая игра с терминальным выигрышем, прини-
принимающим лишь значения 0 и 1. Таким образом, терми-
терминальное множество Хт разбивается на два подмноже-
подмножества Хт+ и Хт~, при этом, если игра попадает в
состояние х?Хт+, то выигрывает игрок I, а если в
состояние х?Хт~, то выигрывает игрок II. В случае,
если игра никогда не заканчивается, игрок I выигры-
выигрывает, а игрок II проигрывает нек-рое число /г„?[0, 1].
Если hn = 0, то имеем дело с И. на в. игрока II, а если
Ам=1, то — с И. на в. игрока I.
Исторически понятие И. на в. восходит к классиче-
классической задаче «о разорении игрока». Прямым обобщением
этой задачи является игра, в к-рой на каждом шаге
разыгрывается одна и та же матричная подигра, а
изменения состояний выражаются в изменениях капи-
капиталов участников (см. [1]). Игрок I выигрывает, если
разоряется противник (т. е. капитал противника ста-
становится отрицательным), и проигрывает, если разо-
разоряется сам. Такая игра обладает значением, не зави-
зависящим от hoo, и оба игрока имеют стационарные е-оп-
тимальные стратегии, если все элементы матрицы по-
повторяемой подигры отличны от нуля. В этом случае
игра почти наверное заканчивается за конечное число
шагов. Другой вариант И. на в. (с многокомпонент-
многокомпонентными капиталами) представляют так наз. «игры на
истощение» (см. [2]). Дифференциальные
И. на в. могут рассматриваться как обобщение описан-
описанных игр на случай непрерывного времени.
Лит.: [1] Milnor J., S h а р 1 е у L. S., в кн.: Contri-
Contributions to the theory of games, v. 3, N. Y., 1957, p. 15—45; [2]
В 1 а с k w e 1 1 D., «Naval Res. Logist. Quart.», 1954, v. 1, p.
210—16; [3] Романовский И. В., «Теория вероят. и ее
примен.», 1961, т. 6, Л» 4, с. 426 — 29. В. К. Доманский.
ИГРА НА ГРАФЕ — обобщение позиционной игры
на случай, когда граф позиций не древовидный, а
произвольный. Частным случаем И. на г. является
игра Ним — антагонистическая игра с полной
информацией, в к-рой для каждой окончательной
позиции указано, выигрывает или проигрывает по-
последний ходивший игрок. В простейшем варианте игра
Ним состоит в следующем: имеется несколько кучек
фишек, и игроки поочередно удаляют не менее одной
фишки, причем каждый раз удаляемые фишки должны
быть мяты из одной кучки. Игрок, удаливший послед-
последнюю фишку, выигрывает партию. Решение игры Ним
состоит в описании для каждого игрока множества
выигрышных позиций, т. е. таких позиций,
начиная с к-рых данный игрок может выиграть при
любой стратегии противника. Множество выигрышных
позиций совпадает с множеством нулей функции
Г р а н д и (функция g, сопоставляющая каждой вер-
вершине к графа Г такое неотрицательное целое число
g(k), что
g(k) = min{n; n ф g (i), i?r(fc)}).
Оно обладает свойствами внутренней и внешней устой-
устойчивости и в этом отношении аналогично понятию Н-М-
решения в кооперативных играх.
Лит.: [1] Б е р ж К., Общая теория игр нескольких лиц,
пер. с франц., М., 1961; [2] В out on С. L., «Ann. Math.»,
ser. 2, 1902, v. 3, Л*. 1, p. 35 — 9. A. H. Ляпунов.
ИГРА НА ЕДИНИЧНОМ КВАДРАТЕ — антаго-
антагонистическая игра, в к-рой множеством чистых стратегий
игроков I и II является сегмент [0, 1]. При надлежащей
нормировке к И. на е. к. может быть сведена любая
антагонистич. игра с континуальными множествами
стратегий у обоих игроков. И. на е. к. задаются функ-
функцией выигрыша К(х, у), определенной на единичном
квадрате. Смешанными стратегиями игроков являются
функции распределения на единичном интервале.
Если функция выигрыша ограничена и измерима по
обеим переменным, то выигрыш игрока I, в условиях
применения игроками I и II смешанных стратегий
F и G соответственно, равен, по определению,
K(F, G)=$J$Jtf(*. y)dF(x)dG{y).
Если функция К(х, у) непрерывна по обеим перемен-
переменным, то
max min К (F, G) = min max К (F, G) = v,
F G G F
т. е. для такой игры реализуем минимакса принцип
и существуют обозначенное через v значение игры и
оптимальные стратегии у обоих игроков. В дальнейшем
теоремы о существовании значения игры (теоремы о
минимаксах) были доказаны при более слабых пред-
предположениях относительно функции выигрыша. Из
общих теорем о минимаксах следует, напр., существо-
существование игры для И. на е. к. с ограниченной функцией
выигрыша, полунепрерывной сверху по х или снизу
по у. Доказаны теоремы существования значения игры
для нек-рых специальных классов разрывных функций
выигрыша (напр., для игр с выбором момента времени).
Однако не все И. на е. к. обладают значением игры.
Так, для функции К(х, у), равной
(— \, х < у Ф I и х = 1, у Ф i;
К (х, у)=\ О, х = у-
У 1, у < х ф 1 и у = i, х Ф i;
имеют место равенства
supinf К (F, G) = — 1, infsupA'(F, G) = l.
F G G F
Для И. на е. к. с непрерывной функцией выигрыша
выйснена структура множества игр с единственным
решением. Именно, множество непрерывных функций
от двух переменных, для к-рых соответствующая
И. на е. к. имеет единственное решение, оптимальные
стратегии обоих игроков непрерывны и их носителями
(см. Носитель меры) являются нигде не плотные совер-
совершенные замкнутые множества лебеговой меры нуль,
содержит всюду плотное подмножество типа Ge ¦
Общих методов решения И. на е. к. не существует.
Тем не менее для нек-рых классов И. на е. к. можно
либо найти решение аналитически (таковы, напр.,
игры с выбором момента времени, игры с функцией
выигрыша, зависящей только от разности стратегий
игроков и обладающие оптимальными выравнивающими
стратегиями), либо доказать для таких игр сущест-
существование оптимальных стратегий с конечным носителем
(таковы, напр., выпуклые игры, вырожденные игры,
колоколообразные игры) и тем самым получить возмож-
возможность свести задачу нахождения решения И. на е. к.
к решению нек-рой матричной игры. Для решения
игр с непрерывной функцией выигрыша можно приме-
применять приближенные методы.
Лит.: [1] К а р л и н С, Математические методы в теории
игр, программировании, экономике, пер. с англ., М., 1964.
ИГРА С ВЫБОРОМ МОМЕНТА ВРЕМЕНИ—
бескоалиционная игра, в к-рой стратегиями игроков
являются моменты совершения ими нек-рых действий,
выбираемые из нек-рого фиксированного интервала,
а функция выигрыша игроков непрерывна на множе-
множестве ситуаций (за исключением тех ситуаций, в к-рых
среди выбранных игроками моментов имеются совпада-
совпадающие) и монотонно возрастает в областях непрерыв-
непрерывности по стратегиям соответствующего игрока. Наи-
Наиболее изученным классом И. с в. м. в. являются анта-
антагонистические игры, в к-рых каждый игрок выбирает
один момент времени, т. е. игры на единичном квадрате.
функции выигрыша к-рых имеют разрыв на диагонали
квадрата, возрастают по первой переменной и убывают
по второй. В таких играх существуют значение игры
и оптимальные стратегии у обоих игроков. При нек-рых
дополнительных предположениях решение таких игр
сводится к решению интегральных уравнений. Другим
классом И. с в. м. в. являются дуэли — антагонистич.
игры, в к-рых действия игроков направлены на уни-
уничтожение противника, так что в дуэли возможны четыре
различных исхода. Для дуэлей существуют аналитич.
методы нахождения оптимальных (или е-оптимальных)
стратегий игроков. Теория дуэлей имеет как военное,
так и экономич. приложения (конкурентная борьба
ла рынки, рекламная кампания и т. п.).
Лит.: [1] К а р л и н С, Математические методы в теории
игр, программировании, экономике, пер. с англ., М., 1964.
Е. Б. Яновская.
ИГРА С ИЕРАРХИЧЕСКОЙ СТРУКТУРОЙ — мо-
модель конфликтной ситуации при фиксированной по-
последовательности ходов и обмена информацией участ-
участников. Основным объектом исследования в теории
И. с и. с. является задача об отыскании наибольшего
гарантированного результата и оптимальной стратегии
выделенного игрока. Пусть игроки I, II стремятся к уве-
увеличению, соответственно, функций выигрыша Д (х1ч х2)
и 12{хх, х2), непрерывных на произведении ком-
компактов Хг, Х2\ х1^Х1, х2?Х2. В зависимости от ха-
характера информации и порядка ходов могут быть сфор-
сформулированы следующие различные игры.
Игра Гх. Игрок I выбирает хх ? Х± и сообщает
свой выбор игроку II. Пусть
Р (хх) = {х21 /2 (хи х2) = max /2 (хи у)}
уех2
— множество оптимальных выборов игрока II. Тогда
наибольший гарантированный результат игрока I
равен
Gt— sup min /j (хг, х2).
Игра Г2. Игрок I рассчитывает иметь и дейст-
действительно будет иметь информацию о выборах игрока II;
сообщает свою стратегию — функцию х1^х1(х2), где
х1^Х1 — множество всех отображений из Х2 в Хг,
игроку П. Наибольший гарантированный результат
игрока I равен
G2= sup inf /iOej, x2),
Xt? Xi Х2еРг(Хх)
где множество оптимальных выборов игрока II есть
Р2 (*!> = {Х2 | /2 (Х~и Х2) = Slip /„ (Xt (у), !/) —б (*!)},
у?Х2
6(ii)>0, при этом 6(xj)=0 тогда и только тогда, когда
достигается max /2 (хх {у), у).
уеХг
Игра Г3. Игрок I рассчитывает иметь и действи-
действительно будет иметь информацию о выборах игрока II
вида х2=х2(х1), где х2?Х2 —множество всех ото-
отображений из Х1 в Х2\ сообщает игроку II свою стра-
стратегию х1=х1(х2), где x^^X-l — множество всех ото-
отображений из Х2 в Х1. Наибольший гарантированный
результат игрока I равен
G3= sup_ inf _ /л (хи х2),
хх 6 Xi х2 б Р3 (х,)
где
Рз(х1) = {хг \f2(xi, хг)= sup/a^j (у), у) —
6C^M30, при этом 8(х1) = 0 тогда и только тогда, когда
достигается max /2 (х1(у), у).
у2
Соотношение между результатами в этих играх
определяет для игрока I значимость информации о
действиях игрока II: G1<G3<<?2. Пользуясь указанной
схемой в построении стратегий игроков, можно форму-
формулировать игры с произвольной глубиной рекурсии.
Имеет место утверждение: в играх Г2т, т>1, наиболь-
наибольший гарантированный результат игрока I равен G2;
в играх Г2т + ь Л1>1, наибольший гарантированный
результат равен G3. Задача отыскания Gx относится к
классу задач на максимин со связанными ограниче-
ограничениями.
Развиты методы решения игры 1\, использующие
штрафные функции, необходимые условия оптималь-
оптимальности, приближение исходной игры игрой с однознач-
однозначными ответами игрока II. Полностью решены частные
классы игр: с близкими интересами, биматричные,
билинейные и др. Задача отыскания Gt некорректна
относительно изменения функции f2(x1, x2) в равномер-
равномерной метрике и множеств Хг, Х2 в метрике Хаусдорфа.
Предложен общий метод регуляризации решения игры
Гх; регуляризация задачи по функции выигрыша иг-
игрока II осуществляется за счет введения искусственной
неточности определения max f2(xlt х2). Отыскание
величины G2 сводится к решению ряда задач матема-
математического программирования.
Пусть для любого е>0 определены функции, мно-
множества и величины:
/2 (xi (%г), х2)= min /2 (жь х2),
х, е X,
1-2= max f 2 (xi {Х2)> жг) = max min i2(x1, x2),
х2 € Х2 х2 е х2 хх е Xi
/iW
sup fx (xi, x2), если D ф 0,
—oo, если D = 0,
х\)^К-ъ, {xf, xfl g D ф 0,
M= inf sup 1\{x-l, x2),
? X
a?2) ! /2 (a?i. X2) > L2},
fi(xie(x2), x2)^iz sup fx(xu x2) — e.
В указанных условиях G2=max[A", M] и стратегия
xf(x2),
хг (х2)
если х2 = х%, К > М.
в остальных случаях
гарантирует игроку I при достаточно малых е полу-
получение max[Af, M]—е. Как видно из определения, опти-
оптимальная стратегия состоит из нескольких ветвей, по-
последняя играет роль стратегии наказания.
Если L2<f2(x1, x2) и у функции {г(хи х2) нет локаль-
локальных максимумов со значением Ьг на XtXX2, то К^М
и оптимальная стратегия имеет простой вид:
если ж2 =
И
е
х-1-
(x2), если хг
Аналогичным образом может быть найдено решение
игры Г3, оно также сводится к решению ряда задач
математич. программирования.
При введении в И. с и. с. побочных платежей со сто-
стороны игрока I, как функций от выборов игрока II,
выражение для наибольшего гарантированного ре-
результата игрока I значительно упрощается. В игре Г2,
где
«>i = /i(-ri> xs) — z. w2 = f2(x1, x2)-\-z,
Xi(zXx, x2?X2, 0<z<z°, и игрок I выбирает стратегии
х1(х2), z(x2\, отыскание G2 сводится к решению задачи
математич. программирования
G2= maxminl/x^i, х2); f1(x1, x2)-^rf2(x1. x2)—L2],
Вообще применение сколь угодно малых побочных
платежей z(x2) в И. с и. с. позволяет игроку I реали-
реализовать наибольший гарантированный результат, рас-
рассчитанный на благожелательность партнера.
Сформулированные игры допускают обобщение на
случай постепенного получения и использования ин-
информации в динамике. В случае, когда состояние иг-
игроков описывается дифференциальными или разност-
разностными уравнениями, возникает обширный класс задач,
связанный с разнообразием форм информированности
игроков о состоянии и течении как физич. процесса,
так и процесса принятия решения. Рассмотрены обоб-
обобщения игр Fj и Г2 на случай запрещенных ситуаций,
т. е. при наличии совместных ограничений на выборы
игроков.
Приведенные формулировки относятся к случаю
полной информированности игрока I о функции вы-
выигрыша и множестве его выборов. Если игроку I из-
известно, что непрерывная функция выигрыша игрока II
удовлетворяет неравенствам
fi (Xi, Х2) г? /2 (хи Х2) si ft Aц Х2)
при известных непрерывных функциях fz(xi, x2), /2 (хг,
х2), то его наибольший гарантированный результат в
игре Г2 определяется из условия максимизации функ-
функции от одной переменной.
Более общий вариант неполной информированности
игрока I об интересах игрока II состоит в следующем:
игроку I известна функция /2(zi, x2, а), а?А, и из-
известно, что при нек-ром (неизвестном) значении сс=сср
истинная функция 12(хг, x2) = f2(x1, x2, а0). При такой
информированности решение игры Г2 для конечных
множеств А сводится к максимизации функции не-
нескольких переменных; при бесконечных множествах А
задача еще более сложна. Наличие неопределенных
факторов в постановке игры 1\ не приводит к прин-
принципиальному усложнению задачи, поскольку этот
случай сводится к игре без неопределенностей. Для
игры Г2 при неопределенности рассмотрен ряд задач,
когда понятие стратегии игроков расширено за счет
предложения игрока I игроку II сообщить свой крите-
критерий эффективности, т. е. нек-рое а?А, так чтобы
окончательный выбор х1 мог быть сделан по получении
информации о х2 и критерия эффективности игрока II.
Если в этом случае игрок II осторожен, т. е. придер-
придерживается принципа наибольшего гарантированного
результата, а игрок I сообщает ему параметризованную
стратегию xia(x2,a), a?A, то можно показать, что
наибольший гарантированный результат игрока I
равен G2=inf Gia, где ?2а — наибольший гарантиро-
ванный результат игрока I в игре Г2 при данном ?
Аналогичный результат без предположения об осто-
осторожности игрока II имеет место, когда игроку I из-
известно параметрич. семейство множеств Х2(а), а?А,
одно из к-рых совпадает с истинным.
Близка к рассмотренным задача, об отыскании наи-
наибольшего гарантированного результата игрока I в
игре Г2 при наличии в функциях выигрышей игроков
параметра а, характеризующего природную неопреде-
неопределенность, когда игрок II при своем выборе информиро-
информирован о конкретной величине а, а игрок I не информиро-
информирован.
В случае, когда игра Г2 при неопределенности по-
повторяется, информированность игрока I об интересах
и возможностях игрока II может быть повышена за
счет информации, содержащейся в откликах игрока II
на действия игрока I. Построены соответствующие
процедуры, позволяющие игроку I, начиная с нек-рой
партии, получать результат, сколь угодно близкий к
результату, гарантированному ему при полной ин-
информированности. Такие же результаты получены и в
игре 1\ с неопределенностями. Если моменты полу-
получения игроком I информации о неопределенном факторе
а не фиксированы, то игрок I может получить в осталь-
остальных повторениях результат, сколь угодно близкий к
гарантированному ему в условиях полной информи-
информированности, при более слабых предположениях от-
относительно функций выигрышей участников. Кроме
того, в игре Гх аналогичный результат игрок I может
получить, наблюдая только за значениями собственной
функции выигрыша.
Формулировки рассматриваемых игр естественно
переносятся на случай многих лиц, взаимодействия
к-рых в смысле приоритета действий и передачи инфор-
информации имеют иерархическую структуру. При анализе
этих игр необходимо оговаривать также правила взаи-
взаимодействий игроков одного уровня. Так, при рас-
рассмотрении игры трех лиц, где функции выигрышей
игроков имеют вид
Wl = fl(xl, Х2, хз), U>2 = f2(Xl> Х2> Хз), И;3 = /з(;г1. Ж2> Х3^
lei 2^2t ^зё^з» Для отыскания наибольшего
гарантированного результата выделенного игрока I,
обладающего приоритетом в действиях, необходимо
конкретизировать его информацию о поведении иг-
игроков II и III. Если игроки II и III образуют известную
игроку I жесткую коалицию, т. е. формулируют коа-
коалиционный критерий и сообща определяют свои вы-
выборы, то для игрока I данный случай эквивалентен
рассмотренным ранее играм двух лиц. Обозримые
результаты получаются также в случае, когда игроки
II и III либо находятся в известной игроку I коалиции,
либо действуют индивидуально, если таким образом
могут получить результат больший, чем дает коалиция:
при этом каждый из игроков II и III не имеет самостоя-
самостоятельной информации о ходе другого и порядок п.\
ходов задается игроком I. Подробно проанализированы
игры, имеющие «веерную» структуру: выделенный
игрок (управляющий центр) По и п игроков на сле-
следующем уровне иерархии (производители продукции)
стремятся к увеличению функций выигрыша fo(xo, х)
и /,-(жо! х;), г=1, . . ., п, соответственно, где жо= {х„, ...,
х1} — выбор По, хо?Хо, х10?Х10, х={хх, ..., хп] — со-
совокупный выбор игроков на нижнем уровне иерархии,
причем они действуют независимо, и каждый игрок
номера i распоряжается выбором х/^Х,-. Все множеств»
полагаются компактными, а функции непрерывными.
Игрок По рассчитывает на информацию (и будет ее
иметь) о выборах х/?Х; и сообщает каждому игроку
i соответствующую стратегию функцию х1о=х1о(х;),
определенную на X,- со значениями из Хо. Для И. с и. с.
п лиц получены выражения наибольшего гарантиро-
гарантированного результата выделенного игрока при различных
расширениях его класса стратегий за счет передачи
игрокам нижнего уровня информации о действиях
партнеров, а также введения элементов блефа. Как
и в играх двух лиц, возможность побочного платежа
со стороны выделенного игрока значительно упрощает
отыскание его гарантированного результата.
При помощи И. с и. с. получают естественную интер-
интерпретацию различные механизмы централизованного
управления активными экономия, подсистемами. Иг-
Игра Г, описывает процесс централизованного управления
при помощи цен; игра Г2 моделирует политику штрафов
и поощрений при стимулировании производства; игрой
Г3 моделируется процесс распределения ресурсов
как функций от производственных способов исполь-
использования данных ресурсов.
Лит.: [1J Герме й е р Ю. Б., Игры е непротивополож-
непротивоположными интересами, М., 1972. И. А. Ватель, Ф. 11. Ерешко.
ИГРОВАЯ СИТУАЦИЯ, с и т у а ц и я,— результат
выбора всеми коалициями действия (см. Игр теория)
своих стратегий с учетом всех связей между стратегия-
стратегиями различных коалиций действия. Множество всех
ситуаций можно понимать как подмножество декартова
произведения Т1КеКаХк, где Хк — множество всех
стратегий коалиции действия К, Ь\э — множество всех
Коалиций деЙСТВИЯ. А. С. Михайлова.
ИГРОК — индивидуальное действующее и заинтере-
заинтересованное начало в игре (см. Игр теория).
ИДЕАЛ — специального рода подобъект в иек-рой
алгебраич. структуре. Понятие И. возникло первона-
первоначально в теории колец. Название И. ведет свое про-
происхождение от идеальных чисел.
Для алгебры, кольца или полугруппы А идеал/
есть подалгебра, подкольцо или полугруппа, замк-
замкнутая относительно умножения на элементы из А.
При этом И. / наз. левым (соответственно пра-
в ы м), если он замкнут относительно умножения слева
(соответственно справа) на элементы из А, т.е.
А1 = 1 (соответственно 1А = 1),
где
{
IA = J Ьа
.
И., являющийся одновременно левым и правым (т. е.
выдерживающий любые умножения на элементы из А),
наз. двусторонним. В коммутативном случае
все эти три понятия совпадают. Любому утверждению
о левых И. отвечает двойственное утверждение о пра-
правых И. (далее формулировки будут приводиться только
в «левом случае»).
Двусторонние И. в кольцах и алгебрах играют ту
же роль, что и нормальные делители в группах. Для
всякого гомоморфизма /: А—+В ядром Кег/ (т. е.
множеством элементов, отображающихся / в 0) служит
И., и обратно, всякий И.— ядро нек-рого гомомор-
гомоморфизма. Более того, И. / однозначно определяет кон-
конгруэнцию к в А, нулевым классом к-рой он является,
и, следовательно, однозначно (с точностью до изомор-
изоморфизма) определяет образ Af гомоморфизма /, ядром
к-рого он служит: Af изоморфно факторкольцу (фа-
кторалгебре) А/у., обозначаемому также All. Ана-
Аналогичными свойствами относительно гомоморфизмов
обладают И. мультиоператорных групп. В мультиопе-
раторной Q-группе А И. определяется как нормальный
делитель ее аддитивной группы, удовлетворяющий
условию: для всякой га-арной операции со, любых эле-
элементов Ь?1 и tfj, а2, . . ., ап?А при всяком i=l, 2,
. . ., п должно иметь место включение—(alt a2. . .ana>)-f-
-\-at . . . a,-_j(b-f- <7,)я, + 1. . . яло>?/ (для колец и
алгебр это понятие индуцирует понятие двусторон-
двустороннего И.).
Двусторонние И. полугрупп, напротив, не дают опи-
описания всех гомоморфных образов данной полугруппы.
Если задан гомоморфизм / полугруппы А на полугруп-
полугруппу В, то только в случае, когда В — полугруппа с ну-
нулем, с гомоморфизмом / естественно связан двусторон-
двусторонний И. /~1@), к-рый, однако, не обязан определять
однозначно /. Тем не менее, если / — И. в Л, то среди
факторполугрупп полугруппы А, имеющих в качестве
элемента класс /, существует максимальная фактор-
полугруппа А/1 (наз. идеальным фактором).
Элементами этой полугруппы будут элементы множест-
множества А\1 и сам И. /, к-рын будет нулем в All.
Для любого подмножества ХаА можно определить
идеал Iх, порожденный X, как пересечение
всех И., содержащих множество X. Множество X
наз. базисом идеала I х- Разные базисы могут
порождать один и тот же И. Идеал, порожденный одним
элементом, наз. главным.
Пересечение, а в случае полугрупп и объединение
левых (двусторонних) И. снова будет левым (двусторон-
(двусторонним) И. Для колец и алгебр теоретико-множественное
объединение И. не обязано быть И. Пусть /х, /2—
левые или двусторонние И. в кольце (алгебре) А. С у м-
м о й идеалов 1г и 12 наз. И. 1^1%— {а+Ы а (¦;/],
Ь?/2}, он является минимальным И. в А, содержащим
/х и /2. Относительно операций пересечения и взятия
суммы все (левые или двусторонние) И. кольца (или
алгебры) образуют решетку. Многие классы колец и
алгебр определяются условиями на их И. или решетку
И. (см. Главных идеалов кольцо, Артиново кольцо,
Нётерово кольцо).
И. мультипликативной полугруппы кольца может и
не быть И. кольца. Полугруппа А является группой
тогда и только тогда, когда А не содержит (как ле-
левых, так и правых) И., отличных от самой А. Таким
образом, обилие И. в полугруппе характеризует от-
отчасти степень отличия данной полугруппы от группы.
Для fc-алгебры А (алгебры над полем к) И. кольца А
может, вообще говоря, не быть И. алгебры А. Напр.,
если А есть fc-алгебра с нулевым умножением, то мно-
множество всех И. кольца А совпадает с множеством всех
подгрупп аддитивной группы А, а множество всех И.
алгебры А совпадает с множеством всех подпространств
векторного fc-пространства А. Однако в случае, когда
А — алгебра с единицей, оба эти понятия И. совпада-
совпадают. Поэтому многие результаты одинаково формулиру-
формулируются как для колец, так и для алгебр.
Кольцо, не имеющее двусторонних И., наз. про-
простым. Кольцо без собственных односторонних И. яв-
является телом. Левые И. кольца А можно определить
также, как подмодули левого Л-модуля А. Нек-рые
свойства колец не меняются при замене левых И. на
правые. Напр., Джекобсона радикал, определенный с
помощью левых И., совпадает с радикалом Джекоб-
Джекобсона, определенным с помощью правых И. С другой
стороны, нётерово слева кольцо может не быть нётеро-
вым справа.
Изучение И. коммутативных колец — важная часть
коммутативной алгебры. С любым коммутативным коль-
кольцом с единицей связано топологич. пространство Spec A,
точками к-рого являются все простые И. кольца А,
отличные от А. При этом существует взаимно одно-
однозначное соответствие между всеми И. кольца А и всеми
замкнутыми подмножествами пространства Spec A.
В коммутативной алгебре встречается понятие И.
поля, точнее И. поля относительно кольца. При этом
кольцо А коммутативно, с единицей и без делителей ну-
нуля, а поле Q — поле частных кольца А. Идеалом
поля Q наз. ненулевое подмножество IczQ, явля-
являющееся подгруппой аддитивной группы поля Q, вы-
выдерживающее умножения на элементы из А (т. е. для
любых а?А, b?I, ab?I) и такое, что существует эле-
элемент q?Q, для к-рого qlczA. И. наз. целым, если
он содержится в Л (и тогда он служит обычным И.
кольца А), в противном случае / наз. дробным идеалом.
Идеалом решетки наз. непустое подмно-
подмножество / элементов решетки, удовлетворяющее услови-
условиям: 1) если а, Ь?1, то а-\-Ь^1; 2) если с«:«?/, то
rG^- Дуальный идеал (или фильтр) ре-
решетки определяется двойственным образом (а, ?>?/=$>
=>яЬ?/, c^sa?J=?>c?J). И. решетки, упорядоченные
включением, сами образуют решетку. Максимальный
элемент в множестве всех собственных И. решетки наз.
максимальным идеалом. Если / — гомо-
гомоморфизм решетки в частично упорядоченное множество
с нулем, то полный прообраз нуля является И. Он
наз. ядерным идеалом гомоморфизма /. И.
S решетки L наз. стандартным, если для любых
a, b?L, s?S неравенство a<.b-\-s влечет a=x-\-t, где
ж<:6 и t?S. Всякий стандартный И. является ядерным.
Ядерный И. решетки с относительными дополнениями
(см. Решетка с дополнениями) является стандартным.
И. / наз. простым, если из ab?I следует, что а?1 или
Ь?1. Каждое из следующих условий эквивалентно
простоте для И. / решетки L: а) дополнение Ь\1 яв-
является фильтром; б) / — полный прообраз нуля при
нек-ром гомоморфизме решетки L на двухэлементную ре-
решетку. В дистрибутивной решетке каждый максималь-
максимальный И. прост.
Не вполне согласовано с предыдущим определение
И. в частично упорядоченном мно-
множестве. А именно, вместо условия 1) требуется вы-
выполнение более сильного условия: для всякого подмно-
подмножества элементов, лежащих в И., их объединение,
если оно существует в этом частично упорядоченном
множестве, также лежит в /.
Идеалом объекта А категории с нулевыми
морфизмами наз. подобъект (U, (х) объекта А такой, что
(x=kera для нек-рого морфизма a : А—>-В. Этот И.
можно отождествить с совокупностью всех мономор-
мономорфизмов, являющихся ядрами нек-рого морфизма (см.
также Нормальный мономорфизм). Двойственным обра-
образом определяется коидеал объекта категории. Понятие
И. для Q-групп является частным случаем понятия И.
объекта категории.
Левым идеалом категории Я наз.
класс морфизмов Д, содержащий вместе со всяким
своим морфизмом <р все произведения сс<р, где а?.Н,
если они определены в категории Я. Двойственным об-
образом определяется правый идеал катего-
категории. Двусторонний идеал — класс мор-
морфизмов, являющийся как левым, так и правым И.
Лит.: [1] Б о р е в и ч 3. И., Ш а ф а р е в и ч И. Р.,
Теория чисел, 2 изд., М., 1972; [21 Б у р б а к и Н., Коммута-
Коммутативная алгебра, пер. с франц., М., 1971; L3J Ван-дер-
Вар д е н Б. Л., Алгебра, пер. с нем., М., 1976; [4] К л и ф-
форд А., Престон Г., Алгебраическая теория полу-
полугрупп, пер. с англ., т. 1—2, М., 1972; L5J Курош А. Г.,
Лекции по общей алгебре, 2 изд., М., 1973; [6] Л я п и н Е. С,
Полугруппы, М., 1960; [7J Скорняков Л. А., Элементы
теории структур, М., 1970; 18] Ц а л е н к о М. Ш.,< Ш у л ь-
гейфер Е. Г., Основы теории категорий, М., 1974.
Л. В. Кузьмин, Т. С. Фофанова, М. Ш. Цаленко.
Т-ИДЕАЛ свободной ассоциативной
алгебры — вполне характеристич. идеал этой ал-
алгебры, т. е. идеал, инвариантный относительно всех
эндоморфизмов. Совокупность полиномиальных тож-
тождеств произвольной ассоциативной алгебры над полем
F образует Т-И. в счетно порожденной свободной ал-
алгебре F [X], Х= {хг, ..., ж/г ,...}. Поэтому существует
взаимно однозначное соответствие между Т-И. алгебры
F [X] и многообразиями ассоциативных алгебр над
полем F- Если поле F имеет характеристику 0, то для
любого Т-И. T^F [X] существует такое натуральное
число 7г=л(Г), что элементами Т являются нек-рые
степени элементов Мn(F) и только они, где Mn(F) —
идеал тождеств алгебры квадратных матриц Fп порядка
п над F. В этом случае Т-И. можно определить также
как (односторонний) идеал, замкнутый относительно
всех дифференцирований свободной алгебры. Фактор-
алгебра F [Х]1Т является Р1-алгеброй, совокупность
полиномиальных тождеств к-рой совпадает с Т. Она
наз. относительно свободной алгеб-
алгеброй Т-И. тождеств Т (и является свободной алгеброй
многообразия алгебр, определяемого тождествами из Т).
Алгебра F [Х]/Т не имеет делителей нуля тогда и только
тогда, когда T=Mn(F) для некоторого натурального
числа п. Всякий Т-И. Т свободной ассоциативной алгеб-
алгебры является примарным идеалом.
Т-И. свободной ассоциативной алгебры с бесконеч-
бесконечным множеством порождающих над полем нулевой ха-
характеристики образуют свободную полугруппу отно-
относительно операции умножения идеалов. В этом случае
Т-И. можно определить как идеалы, инвариантные от-
относительно всех автоморфизмов свободной алгебры.
Вопрос о том, обладает ли всякий Т-И. алгебры F [X]
конечным числом образующих как вполне характери-
стич. идеал (проблема Шпехта), открыт
A977). См. также Колец многообразие.
По аналогии с ассоциативным случаем Т-И. можно
определить в неассоциативных алгебрах (лиевых, аль-
альтернативных и др.).
Лит.: Ll] Procesi С, Rings with polynomial identities,
N.Y., 1973; [2] Джекобсон Н., Строение колец, пер.
с англ., М., 1961; [3] Херстейн И., Некоммутативные
кольца, пер. с англ., М., 1972; [4] Amitsur S., «J. London.
Math. Soc», 1955, v. 30, p. 470—75; [5] S p e с h t W., «Math.
Z.», 1950, Bd 52, S. 557—89; [6] Bergman G., L e w i n J.,
«J. London. Math. Soc», 1975, ser. 2, v. 11, J* 1, p. 21—31.
В. Н. Латышев.
ИДЕАЛЬНАЯ ТОЧКА, несобственная точ-
точка, бесконечно удаленная точк а,—
точка, к-рой пополняется плоскость для описания не-
некоторых геометрич. соотношений и систем. Напр., ин-
инверсия является взаимно однозначным отображением ев-
евклидовой плоскости, пополненной И. т.; пополнение
аффинной плоскости идеальными точками приводит к
понятию проективной плоскости. См. также Бесконечно
удаленные элементы. а. Б. Иванов.
ИДЕАЛЬНОЕ ЧИСЛО — элемент полугруппы D
дивизоров кольца А целых чисел нек-рого поля алге-
браич. чисел. Полугруппа D — коммутативная сво-
свободная полугруппа с единицей; ее свободные образую-
образующие наз. простыми идеальными числа-
м и. В современной терминологии И. ч. наз. цел ы-
м и дивизорами кольца А. Они допускают ес-
естественное отождествление с идеалами кольца А.
И. ч. были введены в связи с отсутствием однознач-
однозначности разложения на простые множители в кольцах
целых алгебраич. чисел. Для каждого а?А разложе-
разложение соответствующего дивизора <р(а) в произведение
простых И. ч. можно рассматривать как нек-рую замену
однозначности разложения на простые множители в
случае, когда такое разложение в кольце А неодно-
неоднозначно.
Напр., кольцо А всех целых чисел поля Q ty~^§\
состоит из всех чисел вида а-\-Ь У—5 с целыми а и
Ь. В этом кольце число 6 допускает два различных раз-
разложения на множители:
6 = 2 ¦ 3 = A — У:=Ъ) A — У:=Ъ),
причем числа 2, 3, 1—У—5 и 1+ У—5 —простые
попарно неассоциированные элементы кольца А; та-
таким образом, разложение на простые множители в А
неоднозначно. Однако в полугруппе D элементы <рB),
<рC), фA+]^—5), <рA— У— 5) не будут простыми, а
именно: <pB)=pi, <pC) = }Jp3, cp(l— V~ZIb) = \IV2,
фA+ У — 5)=ргр3, гДе Pi> Ра. Рз— простые И. ч. в
D. Таким образом, два разложения числа 6 на простые
множители в кольце А продолжаются до одного и того
же разложения <pF)=pip2p3 в D.
Понятие И. ч. было введено Э. Куммером (Е. Kummer)
в связи с исследованием арифметики круговых полей
(см. [1] — [2]). Пусть K=Q(^) — поле деления круга
на р частей и -4=Z(?) — кольцо целых чисел поля К.
И. ч. для кольца А определялись как произведение
простых И. ч., а эти последние — как «идеальные»
простые делители простых натуральных чисел. Для по-
построения всех простых И. ч., делящих заданное простое
натуральное q, использовалась Куммера теорема.
Пользуясь тем, что А имеет степенной базис 1, ?,
?2, . . .,Е?~г над %, Э. Куммер рассматривал разло-
разложение кругового многочлена F р(Х) в кольце z/qW, [X].
И. ч., делящими число д, объявлялись элементы, на-
находящиеся во взаимно однозначном соответствии с не-
неприводимыми множителями Fр(Х) в %lq% \Х\ (не-
(несколько другого подхода требовал случай p = q)- Спе-
Специальный метод применялся для определения показа-
показателя степени, с к-рым данное простое И. ч. входит в
данное а?А. Аналогичный метод он разработал для
создания теории делимости в полях вида Q(?, у т),
где m?Q(?).
Перенесение теории И. ч. на случай произвольного
поля алгебраических чисел принадлежит в основном
Л. Кронекеру (L. Кгопескег) и Р. Дедекинду (R. Dede-
kind). Уже в их работах наметилось разделение теории
И. ч. на теорию дивизоров (подход Л. Кронекера) и
теорию идеалов. Р. Дедекинд каждому И. ч. взаимно
однозначно сопоставлял идеал кольца А, к-рый оп-
определялся им как подмножество в А, состоящее из О
и всех таких а, что а делится на это И. ч. При этом,
если аь . . ., а„— образующие идеала /, то соответ-
соответствующее / И. ч. является наибольшим общим делите-
делителем И. ч. <р(ах), . . ., ф(а„).
Впоследствии понятие идеала было распространено
на случай произвольного кольца А ; кольца, для к-рых
понятия идеала и дивизора совпадают, наз. теперь де-
декиндовыми.
Лит.: [1] Kummer E., «J. reine und angew. Math.»,
1847, Bd 35, S. 319—26, 327—67; [2J его же, «J. math, pure.?
etappl.», 1851, t. 16, p. 377—498; [3] Edward Harold M.,
«Arch. Hist. Exact. Sci.»>, 1975, v. 14, № 3, p. 219—36; 1.4] Бур-
баки H., Коммутативная алгебра, пер. с франц., М., 1971;
[5] ого же, Очерки по истории математики, пер. с франц.,
М., 1963. Л. В. Кузьмин.
ИДЕАЛЬНЫЙ РЯД полугруппы S — такая
последовательность подполугрупп
что Л/ есть (двусторонний) идеал в А, + 1, ?=1, 2, . . . ,
т—1. Подполугруппа Аг и факторполугруппы Риса
Ai + j/Ai (см. Полугруппа) наз. факторами ряда(*).
Два И. р. наз. изоморфными, если между их
факторами можно установить взаимно однозначное соот-
соответствие, при к-ром соответствующие факторы изоморф-
изоморфны. И. р.
наз. уплотнением ряда (*), если каждое А ,•
совпадает с некоторым В у. И. р. наз. композици-
композиционным рядом, если он не обладает отличными от
него самого уплотнениями. Для любых двух И. р. по-
полугруппы существуют изоморфные уплотнения; в ча-
частности, в полугруппе, обладающей композиционным
рядом, все такие ряды изоморфны (аналоги теорем
Шрейера и Жордана — Гёльдера о нормальных рядах
групп, см. [1], [2]). И. р. наз. главным рядом,
если его члены суть идеалы всей полугруппы и он не
обладает отличными от него уплотнениями, состоящими
из идеалов полугруппы. Если полугруппа обладает
композиционным рядом, то она имеет и главный ряд;
обратное неверно. В полугруппе S с главным рядом
факторы его изоморфны главным факторам S.
Как и для нормальных рядов групп, приведенные
понятия (и их свойства) естественным образом обоб-
обобщаются на случай бесконечных систем вложенных
подполугрупп. В частности, возрастающий
И. р. полугруппы S — это вполне упорядоченная по-
последовательность
At С.С Аас:Аа+1 С. • .С А$ = S,
где на предельных местах стоят объединения предыду-
предыдущих членов, и А а есть идеал в Aa+i для любого а<р.
Лит.: [1] Курош А. Г., Теория групп, 3 изд., М.,
1967; [2] Клиффорд А., Престон Г., Алгебраическая
теория полугрупп, пер. с англ., т. 1, М., 1972. Л. Я. Шеврин.
ИДЕЛЬ — обратимый элемент кольца аделей. Сово-
Совокупность всех И. образует по умножению группу,
наз. группой и д е л е й. Элементами группы И.
поля рациональных чисел являются последовательно-
последовательности вида
а = (а„, а2, . . ., ар, . . .),
где а„— ненулевое действительное число, ар— отлич-
отличное от нуля р-адическое число, р=2, 3, 5, 7, ... и
\ар\р=\ при всех р, кроме конечного числа (здесь
\х\р—р-адическая норма). Последовательность И.
АП) I (П) <Л) (Л) \
а = (а,*, , а2 , .. ., ас , . ..)
считается сходящейся к И. а, если она сходится к а
покомпонентно и если существует такое N, что
при n>N Up1ap")|/,= 1 для всех р. Группа И. с такой
топологией является локально компактной топологич.
группой. Аналогично строится группа И. произволь-
произвольного числового поля.
Мультипликативная группа поля рациональных чи-
чисел изоморфно вкладывается в группу И. этого поля.
Именно, каждому рациональному числу гфО сопо-
сопоставляется последовательность
(г, г, . . ., г, . . .),
являющаяся И. Такой И. наз. главным. Подгруппа
главных И. дискретна в группе всех И.
Понятия аделей и И. были введены К. Шевалле
(С. Chevalley) в 1936 для целей алгебраич. теории чи-
чисел. Новый язык показал свою плодотворность при
изучении арифметич. аспектов теории алгебраич. групп.
Для этих целей А. Вейль (A. Weil) обобщил определе-
определения аделей и И. на случай любой линейной алгебра-
алгебраической группы, определенной над числовым полем.
Лит.: [1] Вейль А., Основы теории чисел, пер. с англ.,
М., 1972; [2] Алгебраическая теория чисел, пер. с англ., М.,
1969. В. Л. Попов.
ИДЕМПОТЕНТ, пдемпогентный эле-
м е н т,— элемент е кольца, полугруппы или группои-
группоида, равный своему квадрату: е2=е. Говорят, что И. е
содержит И. / (обозначается e^f), если ef=e=fe.
Для ассоциативных колец и полугрупп отношение ^г
является отношением частичного порядка в множестве Е
идемпотентных элементов и наз. естественным
частичным порядком на множестве Е.
Два И. и и и кольца наз. ортогональными,
если uv=0=vu. С каждым И. кольца (а также с каж-
каждой системой ортогональных И.) связано так наз. пир-
совское разложение кольца. Для n-арной алгебраич.
операции со И. наз. такой элемент е, что (е. . .е)ц) — е.
п
ИДЕМПОТЕНТОВ ПОЛУГРУППА, и д е м"па-
м"патентная полугруппа, — полугруппа, каж-
каждый элемент к-рой есть идемпотент. И. п. наз. также
связкой (это согласуется с понятием связки полу-
полугрупп: И. п. есть связка одноэлементных полугрупп).
Коммутативная И. п. наз. полуструктурой,
или полурешеткой; этот термин согласуется с
его употреблением в теории частично упорядоченных
множеств: если коммутативную И. п. S рассмотреть
относительно естественного частичного порядка, то
ah будет наибольшей нижней гранью элементов a, b?S.
Всякая полурешетка есть подпрямое произведение
двухэлементных полурешеток. Полугруппа S наз.
сингулярной, если S удовлетворяет одному из
тождеств ху=х, ху=у; в первом случае S наз. лево-
сингулярной, или полугруппой ле-
левых нулей, во втором — п р а в о с и и г у л я р-
н о и, или полугруппой правых нулей.
Полугруппа наз. прямоугольной, если она
удовлетворяет тождеству хух=х (этот термин исполь-
используется иногда и в более широком смысле, см. [1]).
xyz-xzyz
хух^ух
xyz=yxz
I I Следующие условия для
j --.^ __„— [ полугруппы S эквива-
^ "" лентны: 1) S прямоуголь-
прямоугольна, 2) S есть идеально
простая И. п. (см. Про-
Простая полугруппа), 3) S
есть вполне простая по-
полугруппа идемпотентов,
4) S изоморфна прямому
произведению ?ХД,где
L — левосингулярная, а
R — правосингулярная
полугруппы. Всякая И.
п. является клиффордовой полугруппой и разлагается
в полурешетку (см. Связка полугрупп) прямоугольных
полугрупп. Это разложение служит исходным пунк-
пунктом при изучении многих свойств И. п. Любая И. п.
локально конечна.
И. п. изучались с разных точек зрения, в том числе
с точки зрения теории многообразий. Решетка всех
подмногообразий многообразия Sg всех И. п. полностью
описана в [4] — [6]; она счетна и дистрибутивна, каждое
подмногообразие ее может быть задано внутри УЗ одним
тождеством. Диаграмму этой решетки см. на рис.;
там же указаны тождества, задающие в 5Р многообразия
из нескольких нижних «этажей».
Лит.: Ll] Клиффорд А., Престон Г., Алгебраиче-
Алгебраическая теория полугрупп, пер. с англ., т. 1—2, М., 1972; [2]
McLean D.,«Amer. Math. Monthly», 1954, v. 61, №2,p. 110 — 13;
[3] Kimura N., «Pacif. J. Math.», 1958, v. 8, p. 257—75;
[4] Бирюков А. П., «Алгебра и логика», 1970, т. 9, JMi 3,
с. 255—73; [5] Gerhard J. «J. Algebra», 1970, v. 15, № 2,
p. 195—224; [6] Fennemore С h., «Math. Nachr.», 1971,
Bd 48, № 1 — 6, S. 237—62. Л. Н. Шеврин.
ИЕНСЕНА НЕРАВЕНСТВО в простейшей
дискретной форме:
Kf (*„),
A)
где / (х) — выпуклая (см. Выпуклая функция) на нек-ром
множестве С функция, х;?С, Х/>0, 1—1,2, . . ., п,
Равенство достигается тогда и только тогда, когда
либо ;г1=з:2=. . ¦=:хп, либо f(x) — линейная функция.
Интегральное И. н. для выпуклой функции
fix):
f ( Jd К (I) x (t) dt
где x(D)cC, X(«)>0 при
Я, @ / (x (t)) dt,
B)
Равенство достигается тогда и только тогда, когда либо
z(?) = const на D, либо f(x) линейна на x(D). Если
f(x) — вогнутая функция, знаки неравенств A) и B)
меняются на противоположные. Неравенство A) уста-
установлено О. Гёльдером [1], неравенство B)— И. Иенсе-
ном [2].
При соответствующем подборе выпуклой функции
f(x) и весов к,- или весовой функции k(t) неравенства
A) и B) переходят в конкретные неравенства, среди
которых большинство классич. неравенств. Например,
если в A) положить /(ж)=—In x, ж>0, то получается
неравенство между взвешенными средним арифметиче-
арифметическим и средним геометрическим:
x 1х2 V
¦¦¦+ К*
C)
приА,1=А,2=. . . = Я„=1/п неравенство C) принимает вид
У . xns^ (х1 + х2-\- . . .-^ хп)/п.
Лит.: [1] Holder О., «Gtitt. Nachr.», 1889, S. 38—47;
t2] Jensen J. L., «Acta math.», 1906, v. 30, p. 175—93;
[3] Харди Г., Литтльвуд Д., Полна Г., Неравен-
Неравенства, пер. с англ., М., 1948, с. 90—91, 182—83. Е. К. Годунова.
ИЕНСЕНА ФОРМУЛА — соотношение, связываю-
связывающее значения мероморфной функции внутри круга с ее
граничными значениями на окружности и с ее нулями и
полюсами. Пусть /(z) — мероморфная функция в круге
|z|sgi?; яц, |яц| <Л, и bv,|bv | <Д,— соответственно все
нули и полюсы f(z), причем каждый нуль или полюс
считается столько раз, какова его кратность или поря-
порядок. Если /@)^=0, то справедлива И. ф.:
In | / @) | = -±-$ \П In
в к-рой суммы распространены на все нули и полюсы
f(z) внутри круга \z\ <Я; формула A) получена И. Иен-
сеном [1]. Небольшое видоизменение позволяет приспо-
приспособить формулу A) и для случая /@)=0.
Справедлива и более общая формула, названная
Р. Неванлинной формулой Пуассона —
Иенсена и дающая значения In |/(z)| в любой точке
z=re'e, отличной от нулей и полюсов:
+?,
In
R (z-b
(z-bv)
.In
R2 -a,,z
P(z
Rlz - ,
ti.
B)
Формулу B) можно рассматривать как обобщение Пу-
Пуассона интеграла для круга. Точно так же, обобщая
Шварца интеграл для круга, получают формулу
Шварца — Иенсена:
R*-bvz
Д2-а
r< R.
Возможно также построение формул типа A) — C) для
полуплоскости и других областей. Формулы A) — C)
играют важную роль в распределения значений теории.
Широкое обобщение формул A) — C) получено М. М.
Джрбашяном в его теории классов мероморфных функ-
функций (см. [3]). Ему удалось получить целое семейство
таких формул, зависящее от нек-рого непрерывного
параметра а, —1<а<+°°, связанного с интегро-
дифференциальным оператором Da, причем, напр.,
формула C) оказывается частным случаем при а=0.
Формулы A) и B) обобщаются для субгармонич.
функций (см. [4]) и(х) в шаре \х\ <:Д евклидова про-
пространства R", ге;з=2, следующим образом:
а(Д)
ц( )
\x-y\n
G(x, у) dp (у),
где a(R) — площадь сферы \y\ = R в R», G(x, у) —
Грина функция для шара |г/|<Я с полюсом в точке х,
(I — положительная мера, ассоциированная с субгар-
монич. функцией и(х). Первое слагаемое в формуле
D) — наименьшая гармоническая мажоранта функции
в (я) в шаре \х\ <:_/?, выраженная в виде интеграла Пу-
Пуассона от граничных значений; второе слагаемое — по-
потенциал Грина, в частных случаях вырождающийся в
логарифмы модуля Бляшке произведений, фигурирую-
фигурирующие в формуле B). Формула B) получается из D) с
учетом того, что In \f(z)\ для мероморфной функции
/(z) есть разность двух субгармонических функций;
для функций последнего типа формула D) также при-
применима .
Пусть теперь / (z) — голоморфная функция многих
комплексных переменных z= (zlt . . . , zn), re^l, в
замкнутом поликруге
7/« = {z; |2/|<Ду, / = 1, ..., п}.
Большое значение имеет также легко выводимое из
свойств плюрисубгармонических функций неравен-
неравенство Иенсена, в случае ге=1 непосредственно
вытекающее из формулы B):
где
— ядро Пуассона для поликруга U", т„(ф) — норми-
нормированная мера Хаара на остове
T" = {z; \zf\ = RJt j = l, ..., п), mn(T«) = i
(см. [5], [6]). Неравенство E) и нек-рые многомерные
аналоги формулы B) находят применения в современ-
современной многомерной теории распределения значений
(см. [7]).
Лит.: [1] Jensen J. L., «Acta math.», 1899, v. 22.
p. 359—64; 12] Неванлинна Р., Однозначные аналити-
аналитические функции, пер. с нем., М.— Л., 1941; [3] Д ж р 6 а-
шян М. М., Интегральные преобразования и представления
функций в комплексной области, М., 1966; [4] Привалов
И. И., Субгармонические функции, М.— Л., 1937; 15] Вла-
Владимиров В. С, Методы теории функций многих комплекс-
комплексных переменных, М., 1964; [6] Г а н н и н г Р., Р о с с и X.,
Аналитические функции многих комплексных переменных,
пер. с англ., М., 1969; [7] Гриффите Ф., Кинг Д ж.,
Теория Неванлинны и голоморфные отображения алгебраи-
алгебраических многообразий, пер. с англ., М., 1976.
Е. Д. Соломенцев.
ИЕРАРХИЯ — классификация тех или иных мате-
матич. объектов в соответствии с их сложностью.
Первые И. были построены в дескриптивной теории
множеств (см. [3]). В этих И. переход к более сложному
классу множеств осуществляется путем применения
теоретико-множественных и топологич. операций к эле-
элементам более простых классов. Важнейшие И. дескрип-
дескриптивной теории множеств определяются следующим обра-
образом. Если Т — некоторое семейство подмножеств мно-
множества X, то через СТ обозначается семейство всех
дополнений в X к элементам из Т, через То — семейство
всех счетных объединений элементов из Т, через Те, —
семейство всех счетных пересечений элементов из Т. Для
фиксированного топологического пространства X через /''
обозначается семейство всех замкнутых подмножеств
пространства X, через G — семейство всех открытых
подмножеств пространства X. По трансфинитной
индукции определяется последовательность F, Fa, Fa6,
Fa6a, ¦ ¦ ¦, классы, стоящие в ней на местах, отвечающих
предельным ординалам, получаются в результате при-
применения операции б к объединению всех предшествую-
предшествующих классов. Аналогично, с заменой всюду операций ст
и б на операции б и ст, соответственно, определяется
последовательность классов G, G& , Gua, Сбаб, ....
При этом G=CF, Ge = С Fan т. д. Построенные последо-
вательности образуют борелевскую И. под-
подмножеств пространства X. Объединение всех классов
этой И. наз. классом борелевских подмножеств про-
пространства X и обозначается В. Если Т — некоторое
семейство подмножеств топологич. пространства X,
то через РТ обозначается семейство всех образов эле-
элементов семейства Т при непрерывных отображениях X
в X. Классы В, РВ, СРВ, РСРВ и т. д. образуют про-
проективную И. подмножеств пространства X. При
этом аналитические множества (А-множества) состав-
составляют класс РВ, дополнения к ним (СА-множества) —
класс СРВ и т. д.
В математич. логике рассматриваются И. множеств
и отношений, задаваемых формулами логич. языков
(см. [1], [2], [5]). Важнейшими примерами таких И.
являются И., основанные на представлении отношения
Р(хи . . ., xk) в виде
Р (хи ..., xk) ФФ <?j!/i.. .QnVnR (хи ¦•-, a-fc, !/i. •• ¦. Уп)-
(*)
Здесь xi, . . ., х/;, г/х, . . ., уп— переменные, одни из
к-рых пробегают множество натуральных чисел (число~
вые переменные), другие — множество всех подмно-
подмножеств натуральных чисел (множественные переменные);
QiDi, ¦ . ., Qnyn— последовательность кванторов, в к-рой
кванторы всеобщности и существования чередуются,
т. е. из любых двух соседних кванторов один является
квантором всеобщности, а другой — квантором суще-
существования; R(x1, . . ., х^ У\, ¦ ¦ ¦, уп) — произволь-
произвольное рекурсивное отношение с числовыми и множест-
множественными переменными. Класс 2° (соответственно П")
состоит из всех отношений Р (х1, . . ., xk), представимых
в виде (*), где переменные у1, . . ., ;/„— числовые и
символ (?]— это 3 (соответственно V). Классы 2" и
П", п = 0, 1, ... образуют арифметическую
иерархию К лини — Мостовского (см.
Клини — Мостовского классификация). Объединение
всех этих классов наз. классом арифметич. отношений.
Классы ^n-i (соответственно njj_!), ге>1, состоятизот-
ношений Р{х1, . . ., xk), представимых в виде (*), где
все переменные ух, . . ., уп-\ — множественные,
переменная уп — числовая и символ Qx— это
3 (соответственно V). Через 2J и I1J обозначается
класс арифметич. отношений. Классы 2^, ГЦ, д=0,
1, . . ., образуют аналитическую иерар-
иерархию Клини. Продолжением иерархии Клини —
Мостовского можно считать гиперарифметич. И. мно-
множеств из класса A^SJfinjfcM. [2], [5]).
Различные И. могут рассматриваться единым обра-
образом с точки зрения определимости в логич. языках.
В частности, начальные классы борелевской И. можно
задать аналогично классам иерархии Клини — Мостов-
Мостовского, аналитич. И. аналогична проективной. При этом
ряд утверждений, касающихся строения классов И.,
получает общую формулировку, а часто, и сходное
доказательство (см. [1]). Примером такого утверждения
является принцип редукции, состоящий в следующем.
Пусть U — класс некоторой И., X и Y — его элементы,
тогда существуют такие X' и У из U, что Х'^Х, Y'~Y,
X[)Y==X' UУ" и Х'(]У' = ф. Этот принцип выполня-
выполняется, в частности, когда U совпадает с ГЦ, 2? или СРВ,
РСРВ. В моделей теории также строятся И. классов
моделей по виду формул, задающих эти классы; име-
имеются аналогии между этими И. и упомянутыми выше
(см. [1]).
Построение И. рекурсивных функций осуществляется
в теории алгоритмов. Один из общих методов построе-
построения таких И. основан на задании рекурсивных функций
с помощью нек-рых исходных функций и операций
(подстановки, примитивной рекурсии и др.). Переход
к более сложному классу некоторой И. может осуществ-
осуществляться, напр., в результате добавления к предыдущему
классу элемента нек-рой фиксированной последователь-
последовательности рекурсивных функций и замыкания полученного
множества относительно операций подстановки и огра-
ограниченной рекурсии. Для получения более сложного
класса, наряду с замыканием относительно каких-либо
операций (как в предыдущем примере), используется
однократное применение, напр., операции примитивной
рекурсии к элементам более простого класса (см. [4]).
Другой метод построения И. рекурсивных функций ос-
основан на их классификации по сложности вычислений
(см. [4]). Рассмотрение характеристич. функций мно-
множеств позволяет строить И. разрешимых множеств,
исходя из И. рекурсивных функций.
Лит.: [1] Аддисон Д ж., Математическая логика и ее
применения, пер. с англ., М., 1965, с. 23—36; [2] Н i n m a n Р.,
Recursion-theoretic hierarhies, В., 1976; [3] К у р а т о в-
с к и й К., Жостовский А., Теория множеств, пер. с
англ., М., 1970; [41 Проблемы математической логики, сб. пере-
переводов, М., 1970; [5] Роджерс X., Теория рекурсивных
функций и эффективная вычислимость, пер. с англ., М., 1972.
ИЗБЫТОК ТРЕУГОЛЬНИКА, с ф е р и ч с сТи°й
избыток, эксцес с,— разность между суммой
углов сферич. треугольника и двумя прямыми углами.
И. т. пропорционален площади сферич. треугольника.
А. Б, Иванов.
ИЗБЫТОЧНОСТЬ — мера возможного увеличения
скорости передачи информации за счет использования
статистич. зависимостей между компонентами сообще-
сообщения, вырабатываемого источником сообщений. И. ста-
стационарного источника сообщений с дискретным вре-
временем, вырабатывающего сообщение ?=(. . ., ?-ц ?0>
5i, . • .), образованное стационарным случайным про-
процессом
lk,k=. .. -1,0, 1, ... ,
где \ь принимает значения из нек-рого конечного мно-
множества X с числом элементов N, определяется раз-
разностью
здесь Н(U) — скорость создания сообщений данным
источником U (см. Сообщений скорость создания),
a ^rrax=l°g N — максимально возможная скорость
создания сообщений источником с дискретным временем,
компоненты к-рого принимают N различных значений.
Лит. см. [4], [5] при ст. Капал связи.
Р. Л. Добрушин, В. В. Прелое.
ИЗВИВАНИЕ КРИВОЙ, собственный по-
поворот криво й,— часть вариации поворота кри-
кривой на нерегулярной поверхности, не вызванная сос-
сосредоточением интегральной кривизны поверхности на
множестве точек кривой. Для простой дуги ? И. к. равно
(о>+а; — й)/2, где о>, Ст(— вариации правого и левого
поворотов L, a Q — вариация кривизны L как множест-
множества. Кривые с нулевым извиванием наз. квазигеодези-
квазигеодезическими линиями.
Лит.: П] Александров А. Д., Стрель-
Стрельцов В. В., «Тр. матем. ин-та АН СССР», 1965, т. 76, с. 67—80.
Ю. Д. Бурого.
ИЗГИБАНИЕ — изометрическая деформация под-
подмногообразия М в римановом пространстве V, т. е.
деформация, при к-рой длины кривых на М не изме-
изменяются. Задача об И. поверхностей ведет свое начало
от К. Гаусса (С. Gauss) и принадлежит к числу основ-
основных проблем дифференциальной геометрии.
Помимо общего случая, было достаточно широко иссле-
исследовано И. поверхности с сохранением нек-рой внешнс-
геометрич. характеристики; при этом обычно оказы-
оказывалось, что лишь поверхности определенного класса
допускают такого рода И. Сюда относятся, напр.:
1) поверхности, изгибающиеся с сохранением средней
кривизны (поверхности постоянной средней кривизны
и, в частности, минимальные поверхности, нек-рые
поверхности, наложимые на поверхность вращения);
2) поверхности, изгибающиеся с сохранением одного
семейства асимптотич. линий (этот класс составляют
линейчатые поверхности); 3) поверхности, допускаю-
допускающие изгибание на главном основании, и т. д.
По своему характеру задачу об И. поверхности в
евклидовом пространстве условно можно разделить
на и з г и б а н и е в м а л о м, т. е. И. какой-нибудь
достаточно малой окрестности Up нек-рой точки Р
поверхности, и и з г и б а н и е в ц е л о м, т. е. И.
произвольного заранее заданного куска поверхности
или полной поверхности. Как правило, любая поверх-
поверхность допускает И. в малом; однако если Р является
точкой уплощения, то при нек-рых условиях и при
сильных предположениях регулярности допускаемых
деформаций Up оказывается неизгибаемой даже в ма-
малом.
Первыми утверждениями, касающимися И. в целом,
были теорема Э. Либмана (Е. Liebmann) о неизгибаемости
сферы, а также результат Д. Гильберта (D. Hilbert): мак-
максимум изгиба куска сферы достигается на границе.
Дальнейшими исследованиями установлено, что любая
замкнутая выпуклая поверхность неизгибаема в клас-
классе выпуклых поверхностей без всяких дополнительных
условий регулярности. Найдены также теоремы типа
принципа максимума, относящиеся к И. произволь-
произвольного куска выпуклой поверхности класса С3, из к-рых
следует неизгибаемость замкнутой выпуклой поверх-
поверхности. Однако доказано, что, напр., сфера в классе С1
допускает изгибания того же класса.
Относительно И. замкнутых поверхностей положи-
положительного рода установлены лишь частные результаты;
так, напр., поверхности типа Т (тора), т. е. поверхно-
поверхности, состоящие из конечного числа областей с кусочно
гладкими границами, в каждой из к-рых гауссова кри-
кривизна К не меняет знака и обращается в нуль только
на границе, причем полная кривизна всех областей с
К~>0 равна 4я,— неизгибаемы при нек-рых дополни-
дополнительных условиях (аналитичность, отсутствие двух
замкнутых асимптотических), в частности, обыкновен-
обыкновенный тор неизгибаем.
Полные незамкнутые поверхности, как правило, из-
изгибаемы. Полная выпуклая поверхность S неизгибае-
неизгибаема, если { \KdS = 2n, и допускает И., если [ \ KdS<2n;
произвол допускаемых ею И. определяется И. ее пре-
предельного конуса. Нек-рые классы полных поверхностей
отрицательной кривизны также допускают И., таковы,
напр., минимальные поверхности, в частности катеноид
изгибания в геликоид.
Исследования И. незамкнутых поверхностей с гра-
границей также относятся главным образом к поверхностям
знакопостоянной гауссовой кривизны, причем деталь-
детально рассмотрен случай, когда И. определяется единст-
единственным образом различного рода граничными условия-
условиями. Так, напр., при любом И. выпуклой поверхности F
хотя бы одна точка ее края dF изменяет свое расстоя-
расстояние от нек-рой фиксированной точки О, из к-рой F
видна изнутри и к-рая расположена вне выпуклой обо-
оболочки (так что F неизгибаема, если расстояние любой
точки края dF от О неизменно); аналогично, при любом
И. выпуклой поверхности F, однозначно проектирую-
проектирующейся на плоскость я и ограниченной плоским конту-
контуром, хотя бы одна точка края dF изменяет свое расстоя-
расстояние от я (так что F не допускает изгибаний скольже-
скольжения— таких И., при к-рых точки края движутся па-
параллельно нек-рой плоскости я); при И. поверхности
этого типа хотя бы в одной точке кривизна х края dF
меняется, причем число перемен знака разности кри-
кривизн краев поверхности F и ее изгибания F' не менее
четырех (так что если кривизна края не изменяется, то
/неизгибаема). Что касается поверхностей отрицатель-
отрицательной кривизны, то достаточно широкий класс их И. по-
получается при решении задачи Коши для уравнений
Гаусса и Петерсона — Кодацци, так, напр., И. куска
поверхности с Я<0, ограниченного отрезками а0, ах
геодезических и двумя отрезками Ьо, Ъ1 их ортогональ-
ортогональных траекторий однозначно определяется И. края Ъй.
Относительно И. поверхностей знакопеременной кри-
впзны ряд результатов получен лишь для поверхностей
вращения.
Для изучения И. поверхностей применяются методы
теории уравнений с частным производными, напр.,
эллиптич. типа, к-рыми описываются И. поверхностей
положительной гауссовой кривизны, а также И. поверх-
поверхностей с сохранением средней кривизны; кроме того,
для выпуклых поверхностей особую роль играют ме-
методы прямых предельных переходов от многогранни-
многогранников (см. Склеивания метод) в комбинации с теоремами
о регулярности поверхности, имеющей регулярную
метрику. При достаточной близости выпуклой поверх-
поверхности F:=F0 к ее изгибанию F± исследование И. сво-
сводится с помощью Кон-Фоссена преобразования к ана-
аналогичным задачам теории бесконечно малых изгибаний
так наз. серединной поверхности
/"«/,= (М-*i)/2.
Лит.. [1] Каган В. Ф,, Основы теории поверхностей,
ч. Ч. М.— Л., 1948; [2] Ш у л и к о в с к и й В. И., Классиче-
Классическая дифференциальная геометрия, М., 1963; [3] Ефимов
Н. В., Качественные вопросы деформаций поверхностей «в ма-
малом», «Тр. матем. ин-та АН СССР», 1949 т. 30; [4] е г о же,
«Успехи матем. наук», 1948, т. 3, в. 2, с. 47—158; [5] П о г о-
релов А. В., Изгибание выпуклых поверхностей, М.— Л.,
1951; [6] Бляшке В., Дифференциальная геометрия, пер.
с нем., т. 1, М.— Л., 1935; [7J К о н - Ф о с с е н С. Э., Неко-
Некоторые вопросы дифференциальной геометрии в целом, М.,
1959. М. И. Войцеховский.
ИЗГИБАНИЕ НА ГЛАВНОМ ОСНОВАНИИ — из-
изгибание Ft поверхности F=F0, при к-ром направления
экстремального изгиба остаются неиз-
неизменными. Сеть, образованная линиями, имеющими на-
направление экстремального изгиба, является сопря-
сопряженной на каждой из поверхностей Ff и наз. глав-
главным основанием изгибания. Напр., ге-
геликоид имеет бесконечное число главных оснований;
вращения поверхности и каналовые поверхности до-
допускают И. на г. о., одно из семейств к-рого состоит из
геодезич. линий (см. также Фосса поверхности). За-
Задача исследования И. на г. о. была поставлена К. М. Пе-
терсоном [1] в 1866; он же установил, что если нек-рая
поверхность F изометрично преобразована в две дру-
другие поверхности /¦" и F" так, что направления экстре-
экстремального изгиба (и, следовательно, основание изгиба-
изгибания) F в F' совпадают с направлениями экстремального
изгиба F в F", то существует изгибание Ft поверхности
F, включающее F' и F"', с теми же направлениями эк-
экстремального изгиба; другими словами, если нек-рая
сопряженная сеть на F служит основанием двух раз-
различных ее изгибаний F' и F", то она является главным
основанием изгибания.
Если известны поверхности F, F', F", то все осталь-
остальные поверхности Ff, получаемые при изгибании F на
главном основании, определяются теоремой: пусть х —
нормальная кривизна F в направлении одного из двух
семейств главного основания сг в произвольной точке
M?F. a х', х", y-t— нормальные кривизны поверхно-
поверхностей F' , F" и Ff в соответствующих точках и направле-
направлениях, тогда двойное отношение <=(х2,х'2,х. щ) сохра-
сохраняет постоянную величину для всех положений М на F.
Поверхность, допускающая И. на г. о., может быть
охарактеризована только сферическим изображением
главного основания: уравнения, описывающие И. на
г. о., преобразуются так, что содержат только коэффи-
коэффициенты линейного элемента сферич. изображения по-
1 2
верхности и получают вид: —li— ^с12=2Г12Г12 (урав-
(уравнения Коссера), где Г}2, Г?2— символы Кри-
стоффеля третьей квадратичной формы поверхности, а
дифференцирование ведется вдоль координатных линий
и, v, составляющих главное основание изгибания.
Сферич. изображение главного основания изгибания
совпадает со сферич. изображением асимптотич. линий
Бианки поверхности, к-рая является вращений инди-
индикатрисой (или присоединенной поверхностью) беско-
бесконечно малого изгибания F, соответствующего И. на г. о.,
а также с изображением в смысле Клиффорда асимптотич.
линий нек-рой поверхности в эллиптич. пространстве
(являющейся поворотов диаграммой И. на г. о. по-
поверхности F).
Не все поверхности обладают главным основанием,
т. е. поверхности, допускающие И. на г. о., образуют
специальный класс поверхностей [4]. Обобщением
И. на г. о. является изгибание на кинема-
кинематическом основании, к-рое определяется
тем, что коэффициенты второй квадратичной формы b,y
удовлетворяют уравнению Ь^А^ = с, где А'/—неко-
А'/—некоторый невырожденный тензор, с — функция, завися-
зависящая от метрики gij поверхности F и ее производных.
Лит.: [1] П е т е р с о н К. М., «Матем. сб.», 1866, т. 1,
с. 391—438; [2] Каган В. Ф., Основы теории поверхностей,
ч. 2, М.— Л., 1948; [3] Фиников С. П., Изгибание на
главном основании и связанные с ним геометрические задачи,
М.—Л., 1937; [4] Лузин Н. Н., «Изв. АН СССР. Отдел.
техн. наук», 1939, Л» 2, с. 81 — 106; № 7, с. 115—32; Л» 10,
с. 65—84. М. И. Войцеховский.
ИЗЛОМА ТОЧКА, у г л о- п
вая точка,— особая точ-
точка плоской кривой, обладаю-
обладающая тем свойством, что в ней 0
прекращаются две ветви кри- ~~
вой, причем каждая из них
имеет в этой точке (односторон-
(одностороннюю) касательную, отличную
от другой. Напр., у кривой
( И. т. — начало координат (см. рис.).
В И. т. правая и левая производные не совпадают.
А. Б. Иванов.
ИЗЛУЧЕНИЯ УСЛОВИЯ — условия на бесконеч-
бесконечности единственности решения внешних краевых задач
для уравнений эллиптич. типа, являющихся матема-
тич. моделью установившихся колебаний различной
физич. природы. Физнч. смысл И. у. заключается в вы-
выделении решения краевой задачи, описывающей рас-
расходящиеся волны, источники (действительные или фик-
фиктивные) к-рых находятся в ограниченной области (см.
[1]). Решения уравнения установившихся колебаний,
описывающие волны, источники к-рых находятся на
бесконечности (напр., плоская волна), не удовлетво-
удовлетворяют И. у.
Впервые аналитич. форма И. у. для уравнения
Гельмгольца
Au + k2u= — f A)
была предложена А. Зоммерфельдом [2]. Если A) соот-
соответствует задаче об установившихся колебаниях при
временной зависимости e~iat, то соответствующие И. у.,
получившие название условий излучения Зоммерфель-
да, в случае пространства трех измерений имеют вид
—«, B)
в случае двух измерений условия излучения Зоммер-
фельда имеют вид
Первое условие в B) и C), как показано в [3], явля-
является следствием второго и требования удовлетворения
уравнению A).
Условия B), C) могут быть ослаблены. В частности,
условия B) в ряде случаев могут быть заменены нело-
нелокальным интегральным условием
lim С
R -> ж J г=Я
Условия B) — D) в тех случаях, когда граница внеш-
внешней области имеет бесконечно удаленные точки, не
являются универсальными в том смысле, что они не
всегда определяют класс функций, в к-ром соответст-
соответствующая краевая задача однозначно разрешима. Напр.,
• в слое между двумя параллельными плоскостями, на
к-рых ставятся однородные граничные условия Дирих-
Дирихле или Неймана, не существует классич. решения
уравнения A) с локальной правой частью, удовлетво-
удовлетворяющего условиям излучения Зоммерфельда B) или D)
(см. [4]). Для разрешимости задачи эти условия долж-
должны быть заменены на так наз. парциальные И. у.
(см. [4]).
В отличие от условий B) — D), парциальные И. у.
можно формулировать уже не в виде асимптотич. выра-
выражений, а в виде точных соотношений, к-рым должны
удовлетворять компоненты разложения решения по
нек-рой системе базисных функций. Соответствующая
система базисных функций вводится различным образом
в зависимости от специфики исходной краевой задачи.
Так, в случае краевой задачи для уравнения A) с
локальной правой частью в бесконечном цилиндре с
осью z при однородных граничных условиях Дирихле
или Неймана на боковой поверхности цилиндра парци-
парциальные И. у. могут быть записаны в виде
JS dz
С ?1.
JS dz
z<z,
г<г,
E)
vnda,
где S — поперечное сечение цилиндра, vn— нормиро-
нормированные собственные функции краевой задачи для урав-
уравнения Лапласа в S:
— О в случае условий Дирихле, i ,ft>
OS > ^D^
вп
= 0 в случае условий Неймана,
7п=^2—Я.п, Im уп^0 и носитель правой части лежит в
области, ограниченной сечениями zx, z2.
Поскольку аналитич. вид И. у. B) — E) различен,
то естественно возникает проблема формулировки об-
общего принципа излучения, не зависящего от вида той
неограниченной области, в к-рой ищется решение зада-
задачи об установившихся колебаниях. Возможны два раз-
различных подхода к решению данной проблемы. В [5]
сформулирован так наз. принцип предельной
амплитуд ы, согласно к-рому решение уравнения
установившихся колебаний однозначно определяется
требованием, чтобы зто решение являлось пределом
при i—>-оо амплитуды решения задачи Коши с нулевыми
начальными условиями для волнового уравнения с пе-
периодической правой частью, и дано обоснование прин-
принципа предельной амплитуды для задачи об установив-
установившихся колебаниях во всем неограниченном простран-
пространстве. Обобщение принципа предельной амплитуды на
внешние задачи для достаточно общего класса дифферен-
дифференциальных операторов при нек-рых дополнительных
условиях на внутреннюю границу неограниченной
области см., напр., в [6].
Другой подход при формулировке общего принципа
излучения, носящий название принципа предельного
поглощения, заключается в том, что решение внешней
краевой задачи об установившихся колебаниях в среде
без поглощения ищется как предел ограниченного ре-
решения соответствующей краевой задачи в среде, обла-
обладающей поглощением, при стремлении последнего к
нулю. Впервые этот метод был использован при реше-
решении конкретной задачи дифракции электромагнитных
волн на бесконечно длинной проволоке (см. [7]). Име-
Имеются обобщения принципа предельного поглощения,
как условия единственности решения внешних крае-
краевых задач для общих эллиптич. операторов и для до-
достаточно широкого класса внутренних границ неогра-
неограниченной области (см., напр., [8]).
Принципы предельной амплитуды и предельного по-
поглощения широко используются при исследовании об-
общих свойств решений внешних краевых задач, однако,
поскольку они так же, как и условия излучения Зоммер-
фельда B) — D), имеют асимптотич. характер, их ис-
использование при численном решении внешних крае-
краевых задач оказывается в ряде случаев недостаточно
эффективным. В этих случаях обычно применяются
парциальные И. у., к-рые в сочетании с проекци-
проекционными методами дали возможность провести полное
численное исследование большого числа практически
важных задач (см., напр., [9]).
Лит.: [1] Смирнов В. И., Курс высшей математики,
т. 4,ч. 1, 6 изд., 1974; [2] Sommerfeld A., «Jahresber.
Dtsch. Math.—Ver.», 1912, Bd 21, S. 309—53; [3] Векуа
И. Н., «Тр. Тбил. матем. ин-та АН Груз. ССР», 1943, т. 12,
с. 105—74; [4] Свешников А. Г., «Докл. АН СССР»,
1950, т. 73, №5, с. 917—920; [5] Тихонов А. Н„ Са-
Самарский А. А., «Ж. эксперимент, и теоретич. физики»,
1948, т. 18, № 2, с. 243 — 48; [6] Лаке П. Д., Ф и л л и п с
Р. С Теория рассеяния, пер. с англ., М., 1971; [7J И г н а-
т о в с к и й В. С, «Ann. phys.», 1905, Bd 18, № 13, S. 495—
522; № 15, S. 1078; [8] Эйдус Д. М., «Успехи матем. наук»,
1969, т. 24, в. 3, с. 91 — 156; [9] Свешников А. Г., Проб-
Проблемы математической физики и примыкающие к ним вопросы вы-
вычислительной математики и дифференциальных уравнений,
М., 1977. А. Г. Свешников.
ИЗМЕЛЬЧЕНИЕ, измельчающееся се-
семейство множест в,— множество F в тополо-
гич. пространстве X такое, что для любой точки х?Х
и любой ее окрестности Ох найдется у ? F, обладающее
свойством: объединение всех элементов семейства у,
содержащих х и наз. звездой St7(^) точки х
относительно семейства у, содержится в Ох.
Важны И. открытых покрытий. Они играют сущест-
существенную роль в теории размерности, в теории биком-
бикомпактных расширений, теории равномерных пространств,
теории непрерывных отображений, метризационной
проблематике. Измельчаемость множества открытых
покрытий означает, говоря неформальным языком, что
это множество покрытий своими элементами сколь
угодно точно аппроксимирует данное пространство
вблизи каждой точки. Часто требование измельчаемо-
сти соединяется с ограничениями, обеспечивающими
определенные соотношения между покрытиями семей-
семейства — типа вписанности, звездной вписанности или
направленности. Так, на этом пути получается опре-
определение равномерной структуры, совместимой с данной
топологией. В связи с теорией паракомпактных про-
пространств рассматриваются И. локально конечных по-
покрытий, а в теории бикомпактных пространств — И.
конечных открытых покрытий. В теории размерности
особое значение имеют направленные отношением впи-
вписанности И. открытых покрытий данной кратности.
И. замкнутых покрытий, на к-рые не наложено зара-
заранее ограничений типа локальной конечности, не пред-
представляют интереса, напр, покрытие любого ^-про-
^-пространства всеми его одноточечными подмножествами
образует И., к-рое не несет никакой информации о то-
топологии пространства.
Важную роль играют счетные И. открытых покрытий,
записываемые часто при произвольной нумерации их
элементов натуральными числами в виде измельчаю-
щнхся последовательностей. Такие И. выдвинулись на
первый план в проблеме метризации пространств, на-
наличие их является необходимым признаком метризуе-
метризуемости. Этот признак не достаточен в классе всех вполне
регулярных пространств, но добавление паракомпакт-
паракомпактности (также являющейся следствием метризуемости)
уже делает его таковым. Точнее, ^-пространство ме-
трпзуемо в том и только том случае, если оно коллек-
коллективно нормально и обладает счетным И. В частности,
бикомпакт со счетным И. метризуем. Существует ли
без дополнительных аксиоматич. предположений не-
мегризуемое нормальное пространство со счетным И.,
неизвестно A978), однако известно, что существование
такого пространства совместимо с аксиоматикой Цер-
мело — Френкеля, хотя и «наивного» примера до сих
пор не построено.
Класс пространств со счетным И. сам по себе облада-
обладает хорошими свойствами. Он замкнут относительно опе-
операций перехода к произвольному подпространству и
счетного перемножения, устойчив относительно совер-
совершенных отображений в сторону образа. Однако целый
ряд закономерностей, действующих в классе метризуе-
иых пространств, для пространств со счетным И. нару-
нарушается. Так, сепарабельное пространство со счетным
II. уже не обязано иметь счетной базы. Пространство со
счетными И. паракомпактно в том и только в том слу-
случае, если оно метризуемо. Не будучи, вообще говоря,
метризуемыми, пространства со счетными И. допуска-
допускают обобщенную метризацию посредством симметрик,
удовлетворяющих условию Кощи. Имеется также удоб-
удобная характеристика пространств со счетным И., как
образов метрич. пространств при непрерывных откры-
открытых отображениях, подчиненных требованию: прообраз
каждой точки лежит на положительном расстоянии от
дополнения к прообразу любой ее окрестности.
Лит.: til Архангельский А. В., Понома-
Пономарев В. И., Основы общей топологии в задачах и упражне-
упражнениях, М., 1974. А. В. Архангельский.
ИЗМЕРИМАЯ ФУНКЦИЯ — 1) В первоначальном
понимании И. ф.— функция f(x) действительного пере-
переменного, обладающая тем свойством, что для любого а
множество Еа точек х, для к-рых /(ж)<Ся есть измеримое
множество (по Лебегу). И. ф. на отрезке [х1, х2] может
быть сделана непрерывной на [хг, х2] путем изменения
ее значений на множестве сколь угодно малой меры;
это — так наз. С-свойство И. ф. (Н. Н. Лузин, 1913).
2) И. ф. на пространстве X определяется относительно
выбранной системы измеримых множеств А в X. Если А
есть а-кольцо, то действительная функция /, заданная
на пространстве X, наз. измеримой функци-
е й, если
А
для любого действительного а, где
Еа = {х: х?Х, }(х) < а),
Rf={x: i?X, f(x) ?0}.
Это определение равносильно следующему: действи-
действительная функция / измерима, если
для любого борелевского В. В случае, когда А есть
а-алгебра, функция / является измеримой, если измери-
измеримы множества Еа (или {х : х?Х, f(x)?B}). Класс И. ф.
замкнут относительно арифметических и структурных
операций, т. е., если /„, ге=1, 2, ... измеримы, то
/i+/2. /1/2, niaxf/j^/a), minf/i, /2), я/, где а действитель-
действительно, измеримы; lim /„, lim /„ тоже измеримы. Комплекс-
Комплексная функция измерима, если измеримы ее действи-
действительная и мнимая части. Обобщением понятия И. ф.
является понятие измеримого отображения одного из-
измеримого пространства в другое.
Лит.: [1] X а л м о ш П., Теория меры, пер. с англ.,М.,
1953; [2] Д а н ф о р д Н., Шварц Д ж. Т., Линейные опе-
операторы, пер. с англ., т. 1, М., 1962; [3] Колмогорова. Н.,
Фомин С. В., Элементы теории функций и функционального
анализа, 4 изд., М., 1976. В. В. Сазонов.
ИЗМЕРИМОЕ МНОЖЕСТВО — подмножество из-
измеримого пространства (X, А), принадлежащее
А-кольцу или а-кольцу его подмножеств. Понятие
возникло и развивалось в процессе решения и обоб-
обобщения проблемы измерения площадей (длин, объемов)
различных множеств, т. е. проблемы продолжения
площади (длины, объема) как аддитивной функции
многоугольников (отрезков, многогранников) на более
широкую систему множеств. И. м. определялось как
множество той системы, на к-рую осуществлено про-
продолжение; последнее называлось мерой. Так были
определены Жордана мера, Бореля мера и Лебега
мера с множествами, измеримыми соответственно по
Жордану, Борелю и Лебегу. Решение задачи продол-
продолжения произвольной фиксированной меры в Rn при-
привело к Радона мере (мере Лебега — Стилтьеса) и мно-
множествам, измеримым по данной мере Радона (Лебега—
Стилтьеса). И. м., связанные с мерой, определенной
в абстрактном множестве,— это множества, на к-рых
определена рассматриваемая мера.
Лит.: [1] Колмогоров А. Н., Фомин С. В.,
Элементы теории функций и функционального анализа, 4 изд.,
М., 1976. " А. П. Терехин.
ИЗМЕРИМОЕ ОТОБРАЖЕНИЕ — отображение / из-
измеримого пространства (Хь ,Л\) в измеримое простран-
пространство (Х2, А2) такое, что
В случае, когда ,Л\ есть ст-алгебра, а (Х2, ./?2) — дей-
действительная прямая с ст-алгеброй А2 борелевских
множеств, понятие И. о. сводится к понятию измери-
измеримой функции (однако, когда А\ есть лишь ст-кольцо,
определение измеримой функции обычно видоизменя-
видоизменяется в связи с нуждами теории интегрирования). Су-
Суперпозиция И. о. измерима. Если Ai, Аг — кольца,
и f~1(B)^Ai для любого В из нек-рого класса мно-
множеств В^Ач. такого, что кольцо, им порожденное,
совпадает с А%, то / измеримо. Аналогичное утвержде-
утверждение верно и для случая а-колец, алгебр и о-алгебр.
Если (Хг, Ai), (X2, .//2) — топологич. пространства с
ст-алгебрами борелевских множеств, то всякое непре-
непрерывное отображение Х1 в Х2 измеримо. Пусть X — то-
топологич. пространство, А есть а-алгебра его борелев-
борелевских подмножеств и \х —конечная неотрицательная ре-
регулярная мера на А (регулярность означает, что
ji(A) = sup iix(F) : FdA, F замкнуто}). Пусть, далее,
S — сепарабельное метрич. пространство, 55 есть а-ал-
а-алгебра его борелевских подмножеств и / — измеримое-
отображение (X, А) и (Y, °Л). Тогда для любого е>0
найдется замкнутое подмножество FdX такое, что
li(X\F)<e и / непрерывно на F (теорема Лу-
Лузин а).
Лит.: [1] X а л м о ш П., Теория меры, пер. с англ., М.,
1953; [2] Неве Ж. Математические основы теории вероят-
вероятностей, пер. с франц., М., 1969; L3] Б у р б а к и Н., Интегри-
Интегрирование. Меры, интегрирование мер, пер. с франц., М., 1967;
[4] Данфорд Н., Шварц Дж., Линейные операторы.
Общая теория, пер. с англ., М., 1962. В. В. Сазонов.
ИЗМЕРИМОЕ ПРОСТРАНСТВО (X, А) — мно-
множество X с выделенным кольцом или ст-кольцом .Л (в
частности, алгеброй или а-алгеброй) его подмножеств.
Примеры: R"c кольцом измеримых по /Кордану
(см. Жордана мера) множеств, R" с а-кольцом множеств
конечной Лебега мерой, топологич. пространство Е с
ст-алгеброй борелевских множеств.
Лит.: [1] Халмош П., Теория меры, пер. с англ., М.„
1953. В. В. Сазонов.
ИЗМЕРИМОЕ РАЗБИЕНИЕ пространства
с мерой (М, fi) — разбиение | этого пространства
на непересекающиеся подмножества (именуемые эле-
элементами разбиения), к-рое можно получить как раз-
биение на множества уровня нек-рой измеримой функ-
функции (с числовыми значениями) на М. Это определение
можно переформулировать в терминах «внутренних»
свойств разбиения (см. [1]). В соответствии с общей
тенденцией пренебрегать в вопросах теории меры мно-
множествами меры нуль часто под И. р. понимают разбие-
разбиение, измеримое по mod 0, т. е. эквивалентное по mod О
нек-рому И. р. (два разбиения |, т) пространства с ме-
мерой М эквивалентны по mod 0, если существует такое
множество N меры 0, что разбиения пространства M\N,
•состоящие из пересечений с M\N элементов разбиений
| и т], совпадают).
Хотя приведенное определение имеет смысл для лю-
любого пространства с мерой, фактический, р. рассмат-
рассматривают почти исключительно для Лебега пространства
(и иногда для пространств, в какой-то степени обла-
обладающих свойствами последних, напр, для пространств
с совершенной мерой, см. [2], [3]), так как именно в
этих пространствах И. р. обладают рядом «хороших»
свойств. Так, в этом случае существует система ус-
условных мер (или, как говорили раньше [1], канониче-
каноническая система мер), принадлежащая И. р. Это есть си-
система мер ji(-|C) на элементах С разбиения ^позволя-
^позволяющая представить интегрирование по \х в виде повторно-
повторного интегрирования: сначала на элементах С осуществля-
осуществляется интегрирование по соответствующим мерам \х( АС),
а затем полученный результат, к-рый можно рассма-
рассматривать как функцию на факторпространстве М/%,
надо проинтегрировать по имеющейся в последнем
¦естественной мере [ле (М1\, по определению, имеет свои-
своими точками элементы разбиения ?, а своими измеримы-
измеримыми подмножествами — те, прообразы к-рых при ес-
естественной проекции я : M—*-Ml% измеримы; мера
\it(A)=\i(n-1(A))). Интерпретируя (М, fi) как про-
пространство элементарных событий в теории вероятно-
вероятностей, можно сказать, что система условных мер явля-
является нек-рым «усовершенствованием» условной веро-
вероятности, тесно связанным со спецификой пространства
Лебега: для произвольных пространств элементарных
событий условную вероятность, вообще говоря, нель-
нельзя интерпретировать с помощью набора каких-то мер
на элементах каких-то разбиений.
Неизмеримые (и неизмеримые по mod 0) разбиения
отнюдь не всегда являются «патологическими» объек-
объектами, как неизмеримые множества или функции.
Напр., разбиение фазового пространства эргодической
динамич. системы на ее траектории может иметь вполне
«классическое» происхождение; просто его свойства
отличны от свойств И. р.
Лит.: [1] Рохлин В. А., «Матем. сб.», 1949, т. 25,
№ 1, с. 107—50: [2] Г н е д е н к о Б. В., К о л м о г о-
р о в А. Н., Предельные распределения для сумм независимых
случайных величин, М.— Л., 1949; [3] Сазонов В. В.,
«Изв. АН СССР. Сер. матем.», 1962, т. 26, № 3, с. 391 — 414.
Д. В. Аносов.
ИЗМЕРИМЫЙ ПОТОК в пространстве с
мерой (М, ц) — семейство {Т*} (t пробегает со-
совокупность действительных чисел R) автоморфизмов
этого пространства такое, что: 1) T1(Ts(x))= Tt + S(x)
для всех t, s?R, x?M; 2) отображение MXR-yM,
переводящее (х, t) в Tfx, измеримо (мера в MXR вво-
вводится как прямое произведение меры ц в М и меры
-Лебега в R). «Автоморфизмы» здесь понимаются в стро-
строгом смысле слова (а не по mod 0), т. е. Тг должны быть
биекцпями М-*-М, переводящими измеримое множе-
множество в измеримое множество той же меры. При исполь-
использовании автоморфизмов по mod 0 оказывается целе-
целесообразным заменить условие 2) условием иного ха-
характера, что приводит к понятию непрерывного потока.
И. п. изучаются в эргодической теории. д в. Аносов.
ИЗОБРАЖЕНИИ МЕТОД, отображений ме-
метод,— метод теории потенциала для решения некото-
некоторых краевых (граничных) задач для дифференциальных
уравнений с частными производными в области D,
при к-ром выполнение краевых (граничных) условий
на границе дО=Г достигается путем соответствующего
подбора нек-рых дополнительных источников ноля,
расположенных вне D и называемых источника-
источниками-изображениями.
Наибольшее развитие И. м. получил в электростатике.
Пусть, напр., требуется решить Дирихле задачу для
Пуассона уравнения Аи=—2лр(л:, у) в полуплоскости
?)={(а;, у); !/>0, —ОО<Ж<+Оо} С ЗвДвННОЙ Нв ГрЭ-
нице Г= {(х, у): у = 0, —oo<z<-f с»} функцией ty(x),
т. е. требуется найти потенциал электрич. зарядов
плотности р(х, у), расположенных в D, при условии, что
на Г поддерживается потенциал ty(x). Известно, что
для решения этой задачи достаточно знать Грина функ-
функцию G(x, у; х0, у0), представляющую собой потенциал
единичного точечного заряда в точке (х0, yo)^D, когда
граница Г заземлена, т. е. G(x, 0; х0, Уо) = О- При этом
решение и(х, у) исходной задачи выражается через
G(x, у; х0, у0) следующим образом:
и(х, y)=
<U
Потенциал точечного заряда при отсутствии границ
записывается в виде фундаментального решения Лап-
Лапласа уравнения 1пA/ \"(х—zoJ-f- (у—у0J)- Добавляя
отрицательный единичный заряд-изображение в точке
(х0, — у0) и составляя сумму потенциалов этих двух за-
зарядов, получают искомую функцию Грина:
G(x, у; х0, уо) =
= ln j in 1 -. B)
1 (х- ха)" + (и -Уо)* У(х-х„J + (у + уо>*
В случае полосы D= {(х, у): 0<!/<Ь, —с»<а;<+оо},
отражая единичный заряд (х0, yo)(^D от прямых г/=0
и г/=Ь, получают бесконечную последовательность
зарядов-изображений —1, —1, +1, +1> •••> распо-
расположенных, соответственно, в точках (х0,— у0), (х0,
'2й—г/0), (х0, —2Ь+г/0), (х0, 2&+г/0), ... . Функция
Грина в этом случае будет выражаться в виде бесконеч-
бесконечного ряда потенциалов точечных зарядов.
Для области D в виде круга D= {(р, ф): 0«:р<а,
0<ф<2я} изображением единичного заряда в точке
(Ро> фо) будет отрицательный единичный заряд, рас-
расположенный в точке (а2/р0, ф0), являющейся отображе-
отображением точки (р0, ф0) при помощи инверсии относительно
окружности р=а.
Возможны и другие конфигурации границ, состав-
составленных из прямых и окружностей, когда решение дос-
достигается построением соответствующей последова-
последовательности зарядов-изображений.
При решении задачи Дирихле для уравнения Пуас-
Пуассона Ди=—Апр(х, у, z) в полупространстве
D={(x, у, z): z>0, — oo-Cr, y<+oc),
отражая единичный заряд (х0, у0, zo)?D от плоскости
z=0, вместо B) получают формулу
G (х, у, z; х0, у0, zo) =
1 1
V(X-X0)- + (У-У„У* + (Z-ZOJ У(Х-Х0)г+ (у-!/0J+ B+20J -
В случае шара D= {{г, 9, ф): 0<г<я, 0<9<л,
0<ф<2я} следует применить Кельвина преобразование,
и изображением единичного заряда в точке (г0, Во, фо)?
?D будет заряд величины —я/г0, расположенный в
точке (а2/г0, Во, ф0), являющейся отображением точки
(г0, Во, ф0) при помощи инверсии относительно сферы
т-а. Отсюда получается, что если известно решение
уравнения Пуассона Аи=—4яр(г, В, ф) в нек-рой об-
области D, то функция v(r, 6, (f) = (a/r)u(a2/r, 9, ф)
дает решение уравнения Пуассона Дг;=—4 яр' (г, 6, ф)
с плотностью р' (г, 9, ф)=(а/гMр(а2/г, В, ф) в области!)',
являющейся отображением D при инверсии относи-
относительно сферы г=а. В такой форме И. м. иногда наз.
методом инверсии. При применении метода
инверсии необходимо обращать внимание на то, что
краевые (граничные) условия, вообще говоря, также
преобразуются.
Для более сложных пространственных областей,
граница к-рых состоит из нескольких плоскостей или
сфер, возможно также применение бесконечных после-
нательностей зарядов-изображений. В комбинации
с предельными переходами, когда один или несколько
1кючников удаляются в бесконечность, И. м. допускает
решение и более сложных задач таких, напр., как оты-
отыскание потенциала электростатич. поля в случае про-
проводящего шара, помещенного в однородном на беско-
бесконечности поле.
В случае уравнения Гельмгольца Аи-{-к*и=0 И. м.
применим только для областей, ограниченных прямыми,
пли для пространственных областей, ограниченных
плоскостями, с использованием соответствующих фун-
фундаментальных решений /Уд1'(Ар), Л102) (Ар) или eikrlr,
e'ikrlr.
Лит.: [1] Гринберг Г. А., Избр. вопросы математи-
математической теории электрических и магнитных явлений, М.— Л.
1948: Г2] Смайт В., Электростатика и электродинамика
пер. с англ., М., 1954; 13] К о ч и н Н. Е., К и б е л ь И. А.
Розе Н. В., Теоретическая гидромеханика, т. 1, М.— Л.
1963. Е. Д. Соломенцев
ИЗОГЕНИЯ — эпиморфизм групповых схем с ко-
конечным ядром. Морфизм групповых схем / : G—+G'
над базисной схемой S наз. и з о г е н и е й, если /
сюръективен и его ядро Кег(/) есть плоская конечная
групповая 5-схема.
В дальнейшем предполагается, что S есть спектр
поля А характеристики р>0. Пусть G групповая схема
конечного типа над к и Л ее конечная групповая подсхе-
подсхема. Тогда фактор G\H существует, а естественное ото-
отображение G-+G\H является И. Обратно, если / : G-+G'
— И. групповых схем конечного типа и Д"=Кег(/), то
G'—G\H. Для любой И. / : G-yG' связных коммута-
коммутативных групповых схем конечного типа существует
И. g '¦ G'—*-G такая, что композиция gof совпадает с
гомоморфизмом uq умножения на п групповой схемы G.
Композиция И. является И. Две групповые схемы G и
G' наз. и з о г е н н ы м и, если существует И. / : G-+G'.
Изогения / : G-+-G' наз. сепарабельной, если
Кег(/) является этальной групповой схемой над к.
Последнее эквивалентно тому, что / есть конечное
этальное накрытие. Примером сепарабельной И. служит
гомоморфизм iiq, где (ге, р)=1. Если к — конечное
поле, то каждая сепарабельная И. связных коммута-
коммутативных групповых схем конечного типа / : G->G' про-
пропускается через И. rj: G-+-G, где р = F—id0, a F —
Фробениуса эндоморфизм. Примером несепарабельной
И. является гомоморфизм умножения на п=рг абелева
многообразия А.
Локализация аддитивной категории А {к) абелевых
многообразий над полем к относительно И. определяет
абелеву категорию М(к), ее объекты наз. а б е л е в ы-
jiii многообразиями с точностью до
и з о г е н и и. Каждый такой объект можно отожде-
отождествить с абелевым многообразием А, а морфизмами
А—>-А' в М(к) служат элементы векторного простран-
пространства над полем рациональных чисел ИотА{к)(А, A)'(g)Q.
г
И. / : А^>-А определяет изоморфизм соответствую-
соответствующих объектов в М(к). Категория М(к) полупроста:
каждый ее объект изоморфен произведению неразло-
жимых объектов. В случае, когда к — конечное поле,
имеется полное описание категории М(к) (см. [4]).
Понятие И. определяется также и для формальных
групп. М орфизм / : G-*~G' формальных групп над полем
к наз. И., если его образ в факторкатегории Ф (к) ка-
категории формальных групп над к относительно под-
подкатегории артиновых формальных групп является
изоморфизмом. И. групповых схем определяет И. со-
соответствующих формальных пополнений. Имеется опи-
описание категории Ф (к) формальных групп с точностью
до И. (см. [1], [5]).
Лит.: [1] Манин Ю. И., «Успехи матем. наук», 1963,
т. 18, в. 6, с. 3—90; [2] М а м ф о р д Д., Абелевы многообра-
многообразия, пер. с англ., М., 1971; [3] Серр Ж., Алгебраические
группы и поля классов, пер. с франц.,М., 1968; [4] Т е й т Д ж.,
«Математика», 1970, т. 14, в. 6, с. 129—37; [5] D i e u d о n n ё J.,
«Comment, math, helv.», 1954, t. 28, № 1, p. 87—118.
И. В. Долгачев.
ИЗОГОНАЛЬНАЯ ТРАЕКТОРИЯ — плоская линия,
пересекающая кривые заданного на плоскости одно-
параметрич. семейства под одним и тем же углом. Если
F(x,y,y')=0 A)
— дифференциальное уравнение заданного семейства
кривых, то И. т., пересекающая кривые этого семейст-
семейства под углом а, где 0<а<л, афп/2, удовлетворяет
одному из двух уравнений:
FJx, г, *'~*а )=Q, р(х, z, *'+,tga ) =0.
V ' ' 1 + z'tgct/ ' \ ' 1-z'tga/
В частности, уравнению
f(x, z, --p-)=0 B)
удовлетворяет ортогональная траекто-
траектория, т. е. плоская линия, образующая в каждой своей
точке прямой угол с проходящей через эту же точку
кривой семейства A). Ортогональные траектории для
заданного семейства A) образуют однопараметрич. се-
семейство плоских кривых — общий интеграл уравнения
B). Напр., если рассмотреть семейство силовых линий
плоского электростатич. поля, то семейство ортогональ-
ортогональных траекторий будет представлять собой эквипотен-
эквипотенциальные линии.
Лит.: [1] Степанов В. В., Курс дифференциальных
уравнений, 9 изд., М., 1966. Я. X. Розов.
ИЗОГОНЫ И ИЗОЭДРЫ — выпуклые трехмерные
многогранники, все многогранные углы к-рых равны
(изогон ы), или равны все грани (и з о э д р ы);
причем группа поворотов (с отражениями) изогона (изо-
эдра) вокруг центра тяжести переводит любую его
вершину (грань) в любую другую его вершину (грань).
Каждому изогону соответствует дуальный нзоэдр, и
обратно. Если выпуклый многогранник является и
изогоном и изоэдром, то он правильный многогран-
многогранник. Комбинаторно разных изогонов имеется 13 специ-
специальных и две бесконечные серии, которые могут быть
реализованы как полуправильные многогранники.
В. А. Залгаллер.
ИЗОКЛИНА обыкновенного дифференциального урав-
уравнения 1-го порядка
y' = f(x, У) (*)
— множество точек плоскости х, у, в к-рых наклон
направлений поля, определяемого уравнением (*), один
и тот же. Если к — произвольное действительное число,
то /с-изоклина уравнения (*) есть множество
{(x,y)\f(x,y) = k)
(в общем случае — кривая); в каждой ее точке (ориен-
(ориентированный) угол между осью х и касательной к про-
проходящему через эту точку решению уравнения (*)
равен arctg к. Напр., 0-изоклина определяется урав-
уравнением / (х, г/) = 0 и включает в себя те и только те
точки плоскости х, у, в к-рых решения уравнения (*)
пмсют горизонтальную касательную, й-изоклина урав-
уравнения (*) является одновременно решением этого урав-
уравнения тогда и только тогда, когда она представляет
собой прямую с угловым коэффициентом к.
Приближенное качественное представление о картине
поведения интегральных кривых уравнения (*) можно
составить, если построить И. данного уравнения для
достаточно частого набора значений параметра к и
отметить на каждой И. соответствующий наклон ин-
интегральных кривых (метод изоклин). Полезно
также построить оо-изоклину, определяемую уравне-
уравнением 1//(ж, у)=0; в точках оо-изоклины интегральные
кривые уравнения (*) имеют вертикальную касатель-
касательную. Точки (локального) экстремума решений урав-
уравнения (*) могут лежать только на 0-изоклине, а точки
перегиба решений — только на линии
~te ' Н*. у> ~ду— ~и-
Для уравнения 1-го порядка, не разрешенного от-
относительно производной
F{x, у,у') = 0,
fc-изоклина определяется как множество
{(х, y)\F(x, y,k)=O}.
В случае автономной системы 2-го порядка
x = i (х, у), y = g (х, у)
совокупность точек фазовой плоскости, в к-рых век-
векторы фазовой скорости коллинеарны, есть И. уравнения
dy_ g (х, у)
dx ~ f (ж, у) '
Лит.: [1] Степанов В. В., Курс дифференциальных
уравнений, 9 изд., М., 1966. Я. X. Розов.
ИЗОЛИРОВАННАЯ ОСОБАЯ ТОЧКА для эле-
элемента аналитической функции /(z) —
точка а комплексной плоскости z, относительно к-рой
выполняются условия: 1) этот элемент функции /(z) не
допускает аналитического продолжения по какому-либо
пути в точку я; 2) существует такое число R >0, что в
проколотой окрестности U= {z?C : 0<|z—a\ <Л } точки
а аналитич. продолжение элемента /(z) возможно по
любому пути.
Если при аналитич. продолжении /(z) вдоль замкну-
замкнутого пути, расположенного в U и окружающего а,
напр, вдоль окружности \z—я| = р, 0<р<Я, получается
новый элемент, отличный от исходного, то а наз. вет-
ветвления точкой, или И. о. т. многозначного
характера. В противном случае элемент f(z)
определяет однозначную аналитич. функцию в U и а
наз. И. о. т. однозначного характера.
В проколотой окрестности U И. о. т. я однозначного
характера функция f(z) разлагается в Лорана ряд:
с правильной частью Д (z)=^,^=ocft(-z—a)k и главной
частью /2 (z) = ^ft = _cccfe(z—a)k- Поведение аналитич.
функции f(z) в проколотой окрестности 1/И.о. т. од-
однозначного характера определяется в основном глав-
главной частью ряда Лорана. Если все коэффициенты глав-
главной части равны нулю, то, полагая f(a) = c0, получим
однозначную аналитич. функцию в полной окрестно-
окрестности а. Этот случай фактического отсутствия особенно-
особенности характеризуется также тем, что /(z) ограничена в
проколотой окрестности U, или тем, что существует
конечный предел lim f(z) = c0, z?U.
Если среди коэффициентов главной части имеется
лишь конечное число отличных от нуля и наимень-
наименьший номер среди них имеет c_m^t0, то а есть полюс по-
рядка т. Полюс а характеризуется также тем, что
lim /(z) = oo, z?U.
Наконец, если среди коэффициентов главной части
имеется бесконечное множество отличных от нуля, то
а — существенно особая точка. В этом случае не суще-
существует конечного или бесконечного предела
lim /(z), z?U.
г -» а
Для бесконечно удаленной И. о. т. я—оо элемента
/(z) проколотая окрестность имеет вид U= {z?C : r<
<|z|<oo}, а ряд Лорана —
Здесь правильная часть/1(z) = ^Jft__aj с^к, а главная
часть /2B)=2/ьЛсАг*- С этими условиями описанные
выше классификация и признаки типов И. о. т. без
дальнейших изменений переносятся на случай я=оо
(см. также Вычет). Следует отметить, что элементы раз-
различных ветвей полной аналитической функции f(z) в
одной и той же точке а ? С могут иметь особенности со-
совершенно различных типов.
Голоморфные функции /(z) многих комплексных пе-
переменных, z= (zb z2, . . ., г„), при п^2 не могут иметь
И. о. т. При и^2 особые точки составляют бесконечные
множества особенностей.
Лит.: [1] Маркушевич А. И., Теория аналитических
функций, 2 изд., т. 1, м., 1967; [2] Ш а б а т Б. В., Введение
в комплексный анализ 2 изд М. 1976. Е. Д. Соломенцев.
ИЗОЛИРОВАННАЯ ПОДГРУППА — подгруппа А
группы G такая, что из gn?A, g"^l, следует g?A;
другими словами, если уравнение хп = а (гдо1=^а?Л)
разрешимо в G, то его решение принадлежит А. Под-
Подгруппа А наз. сильно изолированной,
если из а?А следует, что централизатор элемента а
во всей группе лежит в подгруппе Л. Изолятором
множества М элементов группы наз. минималь-
минимальная И. п., содержащая М.
В if-группах (т. е. группах с однозначным извлече-
извлечением корня) понятие И. п. соответствует понятию сер-
вантной подгруппы абелевой группы. Пересече-
Пересечение изолированных подгрупп в 7?-группе — И. п.
Нормальный делитель Н Д-группы G изолирован тогда
и только тогда, когда факторгруппа GlH является груп-
группой без кручения. Центр Я-группы изолирован.
В отличие от общей теории групп, в теории упоря-
упорядоченных групп И. п. называют иногда выпуклые, под-
подгруппы. О. А. Иванова.
ИЗОЛИРОВАННАЯ ТОЧКА подпространства А то-
топологического пространства X — такая точка а?А,
что пересечение нек-рой ее окрестности с А состоит
ИЗ единственной ТОЧКИ а. А. А. Мальцев.
ИЗОЛЬ — рекурсивной эквивалентности тип изо-
изолированного (т. е. конечного или иммунного) множества
натуральных чисел. Множество всех И. континуальной
является полукольцом относительно операций сложе-
сложения и умножения, определяемых для произвольных
типов рекурсивной эквивалентности. Это полукольцо
наз. арифметикой И. Последняя обладает рядом свойств
арифметики натуральных чисел, в частности в ней вы-
выполнены все универсальные хорновские формулы, эле-
элементарные подформулы к-рых представляют собой
равенство так наз. комбинаторных функций. Примером
такой формулы является закон сокращения: X+Z=
= Y~Z=?>X = Y. И. рассматриваются как рекурсивные
аналоги мощностей конечных поДедекин-
ду множеств, т. е. множеств, не равномощных
никакому своему собственному подмножеству.
А. Л. Семенов,
ИЗОМЕТРИЧЕСКИЙ ОПЕРАТОР — отображение
U метрич. пространства (X, рх) в метрич. пространство
(Y, ру) такое, что
длялюбых а1!, х2?Х. Если X и У — действительные
пшенные нормированные пространства, U(X)=Y и
{/@)=0, то U — линейный оператор.
II. о. U отображает X на U(X) взаимно однозначно,
так что существует обратный оператор U~x, также явля-
являющийся И. о. Оператор, сопряженный с линейным И. о.,
действующим из одного линейного нормированного
пространства в другое, также будет изометрическим.
Линейный И. о., отображающий X на все Y, наз. у н и-
тарным оператором. Условием унитарности
линейного оператора, действующего в гильбертовом
пространстве //, является равенство U*=U~1. Спектр
унитарного оператора расположен на единичной
окружности, и имеет место представление
где {Erf} — соответствующее разложение единицы.
И. о., определенный на подпространстве гильбертова
пространства со значениями в таком же пространстве,
может быть продолжен до унитарного, если ортого-
ортогональные дополнения области его определения и обла-
области его значений имеют одинаковую размерность.
Каждому симметрич. оператору А с областью опре-
определения D^dH соответствует И. о.
наз. преобразованием Кэли оператора А.
Если А — самосопряженный оператор, то оператор UА
унитарен.
Операторы А и В с общей областью определения
D наз. метрически равными, если В = UA,
где U — И. о., то есть если ||Ла:||=||4а:|| для всех x?D.
Такие операторы обладают рядом общих свойств. Для
любого ограниченного линейного оператора А, дей-
действующего в гильбертовом пространстве, существует
один и только один положительный метрически равный
ему оператор, определяемый равенством В= У^А*А.
Лит,: [1] А х и е з е р Н. И., Глазман И. М., Тео-
Теория линейных операторов в гильбертовом пространстве, 2 изд.,
М., 1966; [2] П л е с н е р А. И., Спектральная теория линей-
линейных операторов, М., 1965; [3] М a z u r S., U 1 a m S., «С.г.
Acad. sci.», 1932, t. 194, p. 946 — 48. В. И. Соболев.
ИЗОМЕТРИЧЕСКОЕ ОТОБРАЖЕНИЕ — отображе-
отображение / метрического пространства А в метрич. пространст-
пространство В, сохраняющее расстояние между точками: если
х,у?А и j(x), f(y)?B, то
РА (х, У)=Рв (/ (х), f (У))-
И. о. является инъективным отображением специально-
специального вида, а именно — погружением. Если f(A)~B,
т. е. биективное И. о. наз. и з о м е т р и е й А на В,
а про Аи В говорят, что они находятся в изометри-
изометрическом соответствии, или изометричны друг
другу. Изометричные пространства гомеоморфны. Если,
кроме того, В совпадает с 4, то И. о. наз. и з о м е-
трическим преобразованием, а также
движением пространства 4.
Если метрич. пространства 40 и А1 являются подмно-
подмножествами нек-рого топологич. пространства М и су-
существует деформация Ff : A-+-B такая, что при каждом
/ отображение Ft является И. о. 40 на At, то {4^}наз.
изометрической деформацией, или
изгибанием, 40 в 4Х.
И. о. метрич. линейных пространств является ли-
линейным отображением; оно осуществляется (а также
И называется) изометрическим оператором.
М. И. Войцеховский.
ИЗОМЕТРИЧЕСКОЕ ПОГРУЖЕНИЕ — погружение
^-мерного метрич. многообразия Мк в «-мерное риманово
пространство V, п^к, в виде Л-мерной поверхности
Ф, при к-ром расстояние между любыми двумя точками
на Мк совпадает с расстоянием между их образами, из-
измеренным по поверхности Ф в пространстве V. Это
определение можно обобщить, если риманово простран-
пространство заменить более общим метрич. пространством.
Частным случаем И. п. является изометриче-
изометрическое вложение — взаимно однозначное погру-
погружение.
Основными вопросами теории И. п. являются: 1) про-
проблема возможности И. п. данного многообразия в дан-
данное пространство; 2) в случае существования И. п.—
проблема его единственности. Эти проблемы рассма-
рассматриваются при различных условиях на многообразие
и его изометрпч. образ — гладкости, регулярности,
аналитичности, выпуклости и т. д. При каждом из пе-
перечисленных условий конкретизация основных вопро-
вопросов теории И. п. производится в следующих аспектах:
а) вопрос глобального И. п. Мк в V"; б) вопрос локаль-
локального И. п. Мк в V" (отыскание И. п. в V" достаточно
малой окрестности отмеченной точки v(^Mk); в) в ло-
локальном и глобальном случаях отыскание минимально-
минимального р такого, что Мк погружаемо в евклидово простран-
пространство Ек+Р размерности к-\-р (число р наз. классом
погружения многообразия Мк); г) вопросы изги-
изгибания И. п.
С аналитич. точки зрения задача нахождения И. п.
Мк в V равносильна решению системы нелинейных
уравнений с частными производными. Для И. п. в Еп
эта система имеет вид:
где x={xa(us)} — искомое И. п., gij—метрический
тензор многообразия Мк в локальных координатах
и1, . . ., ик. При решении этой системы в глобальном
случае используются так наз. свободные отображения х
в Е" (см. Нэша теорема о неявной функции). В локаль-
локальных аналитич. задачах место теоремы о неявной функ-
функции занимает Коши — Ковалевской теорема. Роль сво-
свободного отображения и теоремы о неявной функции
сохраняется и в общем случае для погружений класса
С, s«:r<:оо, г=а, в римановы и псевдоримановы про-
пространства. И. п. класса С1 используют иные методы,
основанные на деформации погружения, позволяющей
менять погружения и следить за изменением метрики.
При исследованиях И. п. в Еп используется также сис-
система уравнений Гаусса — Петерсона — Кодацци.
Глобальные изометрические по-
погружения. Всякое компактное риманово многооб-
многообразие Мк класса СгC<:г<оо) допускает изометрич.
вложение класса С в любой шар пространства Еп, где
ге<:C/с2+11А;)/2; если Мк некомпактно, то оно допу-
допускает вложение класса С в любую часть пространства
Еп, где 3«г«оо и ге<(ЗЛ2+11А;) (Л+1)/2 (см. [6]).
Размерность пространства Еп снижается в случаях
г= оо и г=а: всякое риманово многообразие Мк (ком-
(компактное или нет, с краем или без края) класса С°°(Са)
допускает изометрич. вложение класса С°°(Са) в Е",
где n<ik{k+i)/2+3k+5.
Для /с-мерного гиперболич. пространства (&>2)
получено в явном виде изометрич. вложение класса
С°° в ?6*-5, а для А-мерного эллиптич. пространства
(к>2) — изометрич. вложение класса С" в Е", п=
= &(И-3)/2.
В перечисленных результатах гладкость поверхности
Ф не выше, чем гладкость погружаемой метрики. Этот
факт не является случайным: именно, всякая /с-мер-
ная (a<:fc<re—1) поверхность Ф класса Сг-а,г^2,
0«зс<1, в Еп является И. п. класса С-а нек-рого
рнманова многообразия Мк класса С-а (см. [8]).
Нижняя граница для размерности пространства Еп,
в к-рое можно осуществить И. п. риманова многообра-
многообразия, дается теоремой: пусть компактное риманово мно-
многообразие Мк класса С4 обладает следующим свойством:
в каждой точке Мк существует g-плоскость такая, что
в ней все кривизны по всем двумерным направлениям
неположительны; тогда Мк не допускает И. п. класса
С4 в любое Еп с л</с+?—1; если условие, наложенное
на кривизну многообразия Мк, распространяется на од-
одну точку и q=n, то существует И. п. класса С4 в Е-к~2-
Так, напр., плоский й-мерный тор не допускает И. п.
класса С4 в Е2к~1; если к — степень двойки, то действи-
действительное проективное пространство RPk, снабженное
метрикой со всюду положительной скалярной кри-
кривизной, в частности /с-мерное эллиптич. пространство,
не допускает изометрич. вложения класса С2 в Е'2к.
Результаты, относящиеся к И. п. класса С1, резко
отличаются от предыдущих. Они формулируются в
следующем виде: если компактное риманово многооб-
многообразие Мк класса С0 (с границей или без нее) допу-
допускает погружение класса С1 в Еп при га^А+1, то оно
также допускает И. п. класса С1 в Е"; если некомпакт-
некомпактное риманово многообразие Мк класса С" допускает
короткое погружение (т. е. не удлиняю-
удлиняющее в каждой точке линейный элемент) класса С1 в
Е", га^А+1, не пересекающее свое предельное множе-
множество, то оно допускает также И. п. класса С1 в Е" (см.
[7]) (здесь предельное множество погружения многооб-
многообразия Мк в Е" есть совокупность точек х пространства
Еп, для каждой из к-рых в Мк существует расходящаяся
последовательность, образ к-рой сходится в Еп к х).
В частности, любое компактное риманово многообразие
Мк класса С0 (с границей или без нее) допускает И. п.
класса С1 в Е2к; любое некомпактное риманово многооб-
многообразие класса С° допускает И. п. класса С1 в Е2к + 1.
Если И. п. (изометрич. вложения) класса С1 риманова
многообразия Мк в Е" с ге>& можно соединить корот-
короткой регулярной гомотопией (короткой диффеотопией),
то их можно соединить изгибанием, составленным из
И. п. (изометрич. вложений) класса С1. В частности, в
компактном случае И. п. (изометрич. вложения) клас-
класса С1 тогда и только тогда можно соединить изгибанием,
составленным из И. п. (изометрич. вложений) класса
С1, когда они регулярно гомотопны (диффеотопны).
Локальные изометрические по-
погружения. В 1873 Л. Шлефли (L. Schlafli) вы-
высказал гипотезу, согласно к-рой всякое риманово мно-
многообразие размерности к допускает локальное И. п. в
евклидово пространство Еп, где n=k(k-{-i)/2. Эта ги-
гипотеза доказана лишь для аналитич. многообразий
(см. Жане теорема); более того, во всяком римановом
многообразии Мк класса С с отмеченной точкой суще-
существует окрестность отмеченной точки, допускающая изо-
изометрич. вложение класса С в Еп, п=к(к-{-1)/2. В ри-
римановом пространстве Мк класса С°° с отмеченной точ-
точкой существует окрестность отмеченной точки, допу-
допускающая изометрич. вложение класса С°° в Еп, где
n=fc(i+l)/2+/c (см. [7]). С другой стороны, у всякого
риманова многообразия класса С" с отмеченной точкой
существует окрестность ее, допускающая изометрич.
вложение класса С1 в Ек + 1.
Несколько иное направление составляет отыскание
условий, при к-рых данное многообразие М имеет
И. п. в Е", где ге</с(А+1)/2. Это связано с тем, что не
всякое риманово многообразие Мк допускает И. п. в
Еп: при г>А:2(&-}-1)/2 — *, г—1</<оо, множество
римановых метрик, локально индуцируемых на глад-
гладком многообразии Мк с отмеченной точкой локальными
вложениями класса С в Е", ?г<к(к-{-1)/2, нигде не
плотно во множестве всех римановых метрик класса
С1 на Mk, снабженном обычной С'-топологией; при
г=2 и 2«:Z<:oo утверждение остается верным, если п
и к связаны неравенством re<C-^-{fc(fc-(-l)/2-(-fc-(-l}.
При решении задачи об определении класса (см.
выше) И. п. многообразия минимальное р, найденное
в локальной постановке, оценивает снизу значение р
и для глобального И. п. Однако точное значение наи-
наименьшего р, при к-ром любое многообразие Мк, /с>2,
класса С, 2<:г<:оо допускает И. п. класса С в Ек+Р,
неизвестно. Имеются нек-рые частные приемы вычисле-
вычисления класса И. п. данного риманова многообразия Мк
в пространство Еп. Так, р=0 в том и только в том слу-
случае, если тензор кривизны многообразия Мк тождест-
тождественно равен нулю. Существует алгебраич. критерий,
позволяющий установить, будет ли класс И. п. данного
многообразия равен 1, и основанный на том факте, что
для метрик класса 1 при нек-рых дополнительных ус-
условиях уравнения Петерсона — Кодацци являются
следствием уравнений Гаусса [11]. В частности, метрики
постоянной положительной кривизны имеют класс 1 и
реализуются при /с>3 в виде гиперсфер евклидова про-
пространства. Но если Риччи кривизна для Mk равна нулю,
то рф\.
Почти все изложенные результаты обобщаются на
И. п. одного риманова пространства в другое. Так,
напр., обстоит дело с погружениями класса С1, с локаль-
локальными И. п., с достаточно гладкими И. п. /с-мерных мно-
многообразий в V большой размерности, со связями между
порядками гладкости поверхности и ее метрики и т. д.
Задачи И. п. переносятся на псевдоримановы много-
многообразия. В этом случае кроме размерностей к и п
учитываются размерности к+ и к- = к—к + положитель-
положительной и отрицательной части метрич. тензора на погру-
погружаемом многообразии Мк и соответствующие размер-
размерности п+ и п_ = ге—п+ объемлющего пространства V.
Так, теорема Жане сохраняется в псевдоримановом
случае при п~^к(к-{-1)/2, п + ~^к+, п^^к-.
Изометрические погружения дву-
двумерных многообразий. Многие задачи это-
этого типа получили законченное решение в том смысле,
что пространство, в к-ром строится погружение, имеет
минимальную размерность. Здесь разработаны спе-
специальные методы решения, основанные на общей теории
нелинейных дифференциальных уравнений с частны-
частными производными и топологогеометрич. соображениях.
Вейля проблема, поставленная в 1916, гласит: до-
допускает ли двумерное риманово многообразие М2 И. п.
в Е3, если оно гомеоморфно сфере и имеет положитель-
положительную гауссову кривизну? Полное решение проблемы
Вейля, обобщенной в том смысле, что речь идет об
И. п. М2 в трехмерное риманово пространство Vs, дано
А. В. Погореловым [3]: пусть У3 — полное трехмерное
риманово пространство, М\— замкнутое гомеоморф-
ное сфере риманово многообразие с гауссовой кривиз-
кривизной, всюду большей нек-рой постоянной к0 (большей,
меньшей или равной нулю); тогда, если кривизна про-
пространства всюду меньше к0, то м\. допускает И. п. в
виде регулярной поверхности Ф. Это погружение мож-
можно осуществить так, чтобы данный двумерный элемент а
многообразия Мк (точка и пучок направлений в ней)
совпал бы с данным изометричным а двумерным эле-
элементом а' в пространстве V3, и поверхность располага-
располагалась бы по заданную сторону от площадки элемента ее'.
Если метрика пространства V3 и многообразия М'+ при-
принадлежат классу С, г^гЗ, то поверхность Ф принадле-
принадлежит по крайней мере классу Cr~1-V, 0<v<l. Поверх-
Поверхность двумерным элементом определяется однозначно.
Любые два И. п. класса С, г>3, г=а, в V3 можно
соединить изгибанием, составленным из И. п. того же
класса.
С совершенно иной точки зрения проблема Вейля
исследована А. Д. Александровым, к-рый построил те-
теорию (нерегулярных) двумерных многообразий с выпук-
выпуклой метрикой [4] (такие многообразия можно опреде-
определить путем предельного перехода от регулярных мно-
многообразий с положительной гауссовой кривизной)
и наметил следующий план решения проблемы Вейля:
1) обобщить постановку проблемы, беря в качестве Мг
многообразие с произвольной, вообще говоря, нерегу-
нерегулярной выпуклой метрикой; 2) затем установить ре-
регулярность И. п. в зависимости от регулярности мет-
метрики Мг. Осуществление (им же) первой части этого
плана привело к исчерпывающему результату: всякое
гомеоморфное сфере многообразие с выпуклой метрикой
допускает И. п. в Е3 в виде замкнутой выпуклой
поверхности. Реализация второй части плана про-
проведена А. В. Погореловым в [3], где полностью ре-
решен вопрос о регулярности выпуклой поверхности с
регулярной метрикой: если выпуклая поверхность
Фей3 имеет метрику класса С*.а, к^2, 0<а<1, и по-
положительную гауссову кривизну, то Ф принадлежит
классу Ck'a. Если метрика поверхности Ф — аналити-
аналитическая, то и поверхность Ф — аналитическая. Сходные
теоремы имеют место для выпуклых поверхностей в
пространстве постоянной кривизны. При определенных
условиях существуют И. п. двумерных римановых мно-
многообразий положительной гауссовой кривизны, гомео-
морфных плоскости или кругу. Наряду с этим по-
построены примеры аналитич. метрик положительной
кривизны, заданных в круге и не допускающих И. п.
класса С2 в Е3.
Теорема Гильберта о непогружаемости класса С2 в
Е3 плоскости Лобачевского естественно привела к во-
вопросу, погружаются ли в Е3 какие-либо полные дву-
двумерные метрики с кривизной, ограниченной сверху отри-
отрицательной константой (так наз. метрики типа Л)?
Решение этой проблемы дано Н. В. Ефимовым [14]:
если Ф — полная поверхность класса С2 в Е3 с гаус-
гауссовой кривизной К(х), то sup K{x)^sO, так что, в част-
ности, метрики типа Л не допускают И. п. в Е3.
В связи с этой теоремой представляет интерес вопрос
о том, какие части метрик типа Л (т. е. области
двумерного многообразия, на к-ром задается дву-
двумерная метрика) могут быть погружены в Е3. Опре-
Определенный ответ на этот вопрос получен в [15]. Пусть
в бесконечной полосе
Па={0<я«?а, — оо<г/<+оо}
плоскости Е2 с декартовыми координатами х, у задана
форма ds2=dx2-\-B2(x, у) dy2, причем функция В?СГ-1,
г^З, и обладает следующими свойствами: а) она сама,
все ее производные до r-го порядка, а также константы
Липшица по у для производных по ;/ от производных
(г— 1)-го порядка ограничены в Па; б) inf ?>0; в) га-
гауссова кривизна К—— BxxlB^—f}2=const<0. Тогда
форма ds2 порождает на многообразии с краем Па ри-
манову структуру класса С-1, и полученное риманово
многообразие допускает И. п. класса СгД, г>3, в Е3.
В частности, существует И. п. любого геодезич. круга с
произвольной (регулярной) метрикой отрицательной
кривизны. Имеется ряд теорем об И. п. в Е3 некомпакт-
некомпактных частей метрик отрицательной кривизны [5]. Даны
также оценки размеров области, на к-рую однозначно
проектируется поверхность отрицательной (и отделен-
отделенной от нуля) кривизны.
Так как метрики типа Л в целом в Е3 не погружаются,
то ставится вопрос об И. п. этих метрик в евклидовы
пространства больших размерностей. В этом направле-
направлении имеются лишь частные результаты; так, напр.,
существует изометрич. вложение класса С°° плоскости
Лобачевского в Е6 и И. п. в Еъ; дан пример регулярной
метрики типа Л, допускающей И. п. в Е4\ неизвестно,
однако, допускает ли плоскость Лобачевского И. п..
класса С, г>2, в Е4.
Вопрос И. п. в Е3 метрик знакопеременной кривизны
остается открытым даже в случае локальной проблемы.
Так, напр., построен [16] пример двумерного риманова
многообразия класса С2'1, не допускающего локального
И. п. класса С2.1 в Е3. Вместе с тем задача о реализации
аналитич. метрик знакопеременной кривизны решается
следующей теоремой [17]: пусть в прямоугольнике-
Пдй={0<ж<а, 0<!/<6} плоскости Е2 задана метрика
ds2=dx2-\-B2 (х, у) dy2 и пусть В (х, у) — аналитич.
функция в нек-ром открытом прямоугольнике, содер-
содержащем Пд ь; тогда аналитическое риманово многообра-
многообразие с краем, порожденное на ПаЬ заданной метрикой,
допускает аналитич. И. п. в Е3. Имеется ряд результа-
результатов, касающихся И. п. регулярных метрик знакопере-
знакопеременной кривизны в евклидово пространство более высо-
высокой (но близкой к трем) размерности. Так, если М2 —
полное риманово многообразие класса С3-а, гомеоморф-
ное плоскости, то любая его компактная часть допу-
допускает И. п. класса С'1-а в Е4; гомеоморфное тору риманово
многообразие также допускает И. п. в Е4. Всякое ком-
компактное двумерное риманово многообразие класса
С°°{Са) допускает И. п. (и даже вложение) класса С°° (Са)
в Е10, а если оно не имеет замкнутых компонент, то
— в Е9. Двумерная сфера с произвольной римановой ме-
метрикой класса С°° допускает И. п. класса С°° в Е~, а
поверхность Клейна и лист Мёбиуса — И. п. в Е*.
Если отказаться от регулярности погружения, то-
всякая двумерная риманова метрика класса С, г^О.
допускает И. п. класса С1 в Е3. Однако при этом будут
нарушены обычные связи между внутренней и внешней,
геометрией поверхности, реализующей метрику. По-
Построено локальное И. п. метрики двумерной сферы в
виде локально невыпуклой поверхности в Е3 класса
С-а при любом а<1/13 и аналогичное И. п. в целом при
а<1/25- С другой стороны, если поверхность Ф принад-
принадлежит классу С1-а, а>2/з> то поверхность Ф, имеющая
знакопостоянную внутреннюю кривизну, будет иметь
ограниченную внешнюю кривизну. В частности, если
внутренняя кривизна Ф положительна, то Ф будет
локально выпуклой поверхностью, и если сверх
того метрика поверхности регулярна, то регулярна
и сама поверхность. Таким образом, нижняя грань
значений а, при к-рых сохраняются связи между
внутренней и внешней геометрией поверхности Ф
класса С1-а со знакопостоянной внутренней кривизной,
принадлежит отрезку [Vis» 2/зЬ Наконец, все ориенти-
ориентируемые многообразия ограниченной внешней кривиз-
кривизны, не имеющие точек с кривизной 2я, допускают
изометрич. вложения в Е3 в виде дифференцируемых по-
поверхностей. При исследовании нерегулярных И. п. изу-
изучались также кусочно линейные И. п. кусочно линей-
линейных метрик: так, всякая развертка, гомеоморфная зам-
замкнутой области на ориентируемой замкнутой поверх-
поверхности, может быть изометрич. вложена в Е3 в виде-
многогранника.
Лит.: [11 Ефимов Н. В., в кн.: Тр. 4 Всесоюзного ма-
математического съезда, т. 1, Л., 1963, с. 86—99; [2] Б а к е л ь-
м а н И. Я., В е р н е р А. Л., Кантор Б. Е., Введение-
в дифференциальную геометрию «в целом», М., 1973; [31 Поте-
Потере лов А. В., Внешняя геометрия выпуклых поверхностей,
М., 1969; [4] Александров А. Д., Внутренняя геомет-
геометрия выпуклых поверхностей, М.— Л., 1948: [5] П о з н я к
Э. Г., Ш и к и н Е. В., в сб.: Итоги науки и техники. Алгебра.
Топология. Геометрия, т. 12, М., 1974, с. 171 — 207; [6] Нош
Д т., «Успехи матем. наук», 1971, т. 36, в. 4, с. 173—216;
17] Г р о м о в М. Л., Рохлин В. А., там же, 1970, т. 25,
в. 5, с. 3—62; 18] С а б и т о в И. X., Ш е ф с л ь С. 3., «Сиб.
матем. щ.», 1976, т. 17, № 4, с. 918—25; [9] Otsuki Т., «J.
Math. Soc. Japan», 1954, v. 6, p. 221—34; [10] Нэш Дж.,
«Математика», 1957, т. 1, Л» 2, с. 3—16; [11] Розенсон
Н. А., «Изв. АН СССР. Сер. Матем.», 1943, т. 7, с. 253—84;
[12] Friedman A., «J. Math., Mech.», 1961, v. 10, р*
625—49; [13] С а б и т о в И. X., «Сиб. матем. ж.», 1976, т. 17.,
№ i, с. 907—15; [14] Ефимов Н. В., «Матем. сб.», 190-4, т.
64, Ка 2, с. 286 — 320; Но] II о з н я к Э. Г., «Укр. грчме-р.
сб.», 1966, в. 3, с. 78—92; [16] П о г о р е л о в А. В. «;.(ir.i.
АН СССР», 1971, т. 198, ,Х. 1, с. 42 — 43; [17] П о з н я к О. Г.,
«Успехи матем. наук», 1973, т. 28, в. 4, с. 47—76; [18] Б у р а-
г о Ю. Д., 3 а л г а л л е р В. А., «Вестн. Ленингр. ун-та.
Сер. матем., механ. и астрон.», 1960, т. 7, ;N5 2, с. НС — 80.
ИЗОМЕТРИЧНЫЕ ПОВЕРХНОСТИ — поверхности 'в
евклидовом или римановом пространстве такие, что
между ними можно установить взаимно однозначное
точечное соответствие, при к-ром каждая спрямляемая
кривая одной из поверхностей имеет своим образом тоже
спрямляемую кривую н той же длины. Другими сло-
словами, И. п. характеризуются (попарным) изометрич. со-
соответствием — нзометрией (см. Изометрическое ото-
отображение) относительно внутренних метрик, индуциро-
индуцированных на них метрикой объемлющего пространства.
Важнейший пример И. п.— совокупность поверхно-
поверхностей, полученных изгибанием данной поверхности.
Если изометрия поверхностей влечет их равенство,
точтее, если для любой поверхности F из нек-рого
класса К, изометричной поверхности Fo, пространствен-
пространственные расстояния между соответствующими по изометрии
точками F и Fo равны, то Fo наз. однозначно
определенной, или для Fo имеет место одназнач-
ная определенность (внутренней метрикой) в классе К.
Понятие И. п. обобщается на более общие категории
метрич. пространств и их подмножеств.
М. 11. Войцеховский.
ИЗОМОРФИЗМ — соответствие (отношение) между
объектами или системами объектов, выражающее в неко-
некотором смысле тождество их строения. И. в произвольной
категории есть обратимый морфизм, т. е. морфизм ср,
для к-рого существует такой морфизм ср-^что произ-
произведение ф-1ф=фф~1=е — единичный морфизм.
Понятие И. возникло в математике применительно
к конкретным алгебраич. системам (прежде всего к
группам) и было естественным образом распространено
на более широкий класс математич. структур. Классич.
примером изоморфных, «одинаково устроенных» сис-
систем могут служить множество R всех действительных
чисел с определенной на нем операцией сложения и
множество Р положительных действительных чисел с
заданной на нем операцией умножения.
Пусть А ж А' произвольные однотипные алгебраиче-
алгебраические системы, записанные в сигнатуре
с функциональными символами Ft, i?I и предикатными
символами Р;, /?/:
А = <А; {Fr.
А' = <А'; {Fr.
Изоморфизмом, или изоморфным отображением,
системы А на систему А' наз. взаимно однозначное отоб-
отображение ф множества А на множество А', обладающее
свойствами:
i>y-(ai. ¦¦-. amj)€>P/(<P(ai), ¦¦•, ф (ату)
для всех элементов а1г а2, . . . из А и всех i?, /?
Таким образом, во всякой категории алгебраич. систем
И. есть гомоморфизм, являющийся биекцией. И. алге-
алгебраич. системы на себя наз. автоморфизмом.
Отношение И. обладает свойствами рефлексивности,
симметричности и транзитивности, т. е. является от-
отношением эквивалентности, разбивающим любое мно-
множество, на к-ром оно определено, на непересекающиеся
классы эквивалентности — классы попарно изоморф-
изоморфных систем. Класс алгебраич. систем, содержащий вме-
вместе со всякой системой все ей изоморфные, наз. а б-
•страктным классом.
О. А. Иванова, Д. М. Смирнов.
ИЗОМОРФИЗМА ПРОБЛЕМА — задача отыскания
алгоритма, позволяющего по любой паре эффективно
заданных алгебраических систем из данного класса
установить, изоморфны они или нет. Частная И. п.
для фиксированной алгебраич. системы А состоит в
отыскании алгоритма, распознающего по эффективному
заданию алгебранч. системы из рассматриваемого клас-
класса, изоморфна она системе А или нет. Положительное
решение (частной) И. и. состоит в указании искомого
алгоритма (И. п. разрешима), отрицательное — в дока-
доказательстве того, что искомого алгоритма нет (И. п. не-
неразрешима). Обычно И. п. ставится для алгебр, зада-
задаваемых образующими и определяющими соотношениями.
Для многих важных классов алгебр И. п. неразреши-
неразрешима. Доказана неразрешимость частной И. п. для про-
произвольной конечно определенной полугруппы в клас-
классе всех конечно определенных полугрупп [2] и частной
И. п. для произвольной конечно определенной группы
в классе всех конечно определенных групп [1]. В классе
всех групп из многообразия ?г-ступенно разрешимых
групп, задаваемых в этом многообразии конечным чис-
числом образующих и определяющих соотношений, при
п^7 И. п. также неразрешима [3].
И. п. разрешима в классе всех конечных конечно оп-
определенных алгебр фиксированной сигнатуры, в классе
абелевых групп.
Открытыми остаются пока (к 1978) И. п. для ниль-
потентных групп ступени 2, групп с одним определяю-
определяющим соотношением. И. п. для групп связана с алго-
ритмич. проблемами топологии.
Лит.: [1] Ад ян С. И., «Тр. Моск. матем. об-ва», 1957,
т. 6, с. 231 — 98; [2] Марков А. А., Теория алгорифмов,
М.—Л., 1954 (Тр. матем. ин-та АН СССР, т. 42); [3] Кир-
кинский А. С, Ремесленников В. Н., «Матем.
заметки», 1975, т. 18, JnB 3, с. 437 — 43. А. Л. Семенов.
ИЗООПТИЧЕСКАЯ КРИВАЯ — плоская кривая,
представляющая собой траекторию вершины данного
угла у, к-рый перемещается в плоскости так, что сто-
стороны его при любом положении угла касаются задан-
заданной кривой. Если Y=jt/2, то И. к. наз. ортоопти-
ческой кривой. Напр., ортооптич. кривая эл-
эллипса — окружность.
Лит.: [1] С а в е л о в А. А., Плоские кривые, М., 1960.
Д. Д. Соколов.
ИЗОПЕРИМЕТРИЧЕСКАЯ ЗАДАЧА — одна из ос-
основных задач классического вариационного исчисления.
И. з. состоит в минимизации функционала:
Jo (у) = \г*/о (я, У, y')dx
при ограничениях вида
i = 1, . . ., m,
и нек-рых краевых условиях.
И. з. приводится к Лагранжа задаче при помощи вве-
введения новых переменных z,-, удовлетворяющих диффе-
дифференциальным уравнениям
и граничным условиям
z/(*i) = 0, z,-(za)=c/, i = l, ..., т.
Необходимые условия оптимальности И. з. имеют тот же
вид, что и для простейшей задачи вариационного ис-
исчисления относительно Лагранжа функции:
L(x, у, у', Я0) ..., A,ffl) = 27=о *•'/'" (*> у' у")ш
Название «И. з.» происходит от следующей класси-
классической задачи: среди всех замкнутых линий на плоскос-
плоскости с заданным периметром найти линию, к-рая ограни-
ограничивает наибольшую площадь.
Лит.: [1] Б л и с с Г. А., Лекции по вариационному ис-
числению, пер. с англ., М., 1950; [2] Цлаф Л. Я., Вариа-
Вариационное исчисление и интегральные уравнения, 2 изд., М., 1970;
[3] Лаврентьев М. А., Люстерник Л. А., Курс
вариационного исчисления, 2 изд., М.— Л., 1950.
И. Б. Вапнярский.
ИЗОПЕРИМЕТРИЧЕСКОЕ НЕРАВЕНСТВО (в гео-
геометрии и физике) — общий термин для обозначения не-
неравенства 4jxF<:.F2 между площадью V и периметром F
плоской области, для разнообразных его обобщений и
для других неравенств между геометрич. характеристи-
характеристиками фигур, множеств, многообразий. К И. н. относят
также оценки величин фнзич. происхождения (мо-
(моменты инерции, жесткость кручения упругой балки,
основная частота мембраны, электростатич. емкость
и др.) через геометрич. характеристики. Точное И. н.
эквивалентно решению нек-рой экстремальной задачи.
И. н. могут связывать как две, так и большее число ве-
величин.
О наиболее известном И. н.— классическом, его ана-
аналогах в пространствах Минковского Мп, Лобачев-
Лобачевского Ln, сферическом S" и его уточнениях см. статью
Изопериметрическое неравенство классическое.
Обширная сводка И. н. между элементами простей-
простейших фигур — главным образом многоугольников —
имеется в [1]. Такие И. н. наз. геометрически-
геометрическими неравенствами.
Элементарные И. н. между такими параметрами мно-
множеств в Л", как объем V, диаметр D, радиус R наимень-
наименьшего описанного шара и т. п., см. в [2], [3]. Среди них:
неравенство Юнга:
неравенство Гей л а:
где I — длина ребра наименьшего описанного правиль-
правильного симплекса; неравенство Бибербаха:
еравенство Лумиса — Уитни:
где V'i— Аг-мерный объем проекции множества на г-ю
из Х=Сп попарно различных fc-мерных координатных
плоскостей для декартовых координат. Первые три
неравенства допускают обобщения на пространства
М", Ln, S" (см. [4], [5]). В неравенстве Бибербаха диа-
диаметр может быть заменен средней шириной (см. [5]).
В связи с задачами размещения и покрытия рассмат-
рассматривались И. п., специфичные для многогранников,
с привлечением числа или суммы длин ребер и т. п.
(см. [6]).
Для выпуклых тел многие И. н. (в том числе класси-
классическое И. н. и серия неравенств между интегралами
от снмметрич. функций главных кривизн) являются
частными случаями неравенств между смешанными объе-
объемами (см. Смешанных объемов теория, Минковского
неравенство).
Использование И- н., как оценок одних параметров
фигур через другие, вышло за рамки геометрии. При
этом в математич. физике, теории функций комплексно-
комплексного переменного, функциональном анализе, теории
приближений функций, вариационном исчислении обо-
обогатился сам класс И. н. Заметно усложняются И. н.
в римановой геометрии.
В математич. физике И. н. возникли (сначала в виде
предположений) в работах А. Сен-Венана (A. Saint-
Venant, 1856):
2лР < F2,
где Р — жесткость кручения призматической упругой
балки; Рэлея (Rayleigh, 1877):
где Л — основная частота мембраны, ; — первый по-
положительный корень бесселевой функции J0(x); в ра-
работах А. Пуанкаре (Н. Poincare, 1903):
где с — электростатич. емкость тела. V в этих неравен-
неравенствах, соответственно, площадь сечения балки, площадь
мембраны, объем тела. Многочисленные результаты та-
такого рода подытожены в [7] и [8]. Нек-рые оценки для
первого собственного числа Л оператора Лапласа на
замкнутых римановых многообразиях имеются в [9].
В функциональном анализе в терминах И. н. (связы-
(связывающих меры и емкости) были даны (см. [10], [11])
условия ограниченности и компактности операторов
вложения (см. Вложения теоремы) для пространств
Соболева.
Например, оценка
где (х — неотрицательная мера, q~^2, ?г>2, справедли-
справедлива для всех и?С<Г (R") в том и только в том случае,
когда для всех компактов edRn выполняется И. н.:
[V-Iq (e) <q cap (е).
Здесь cap (•) — емкость Винера (см. Емкость мно-
множества).
И. н. для объема и площади применяются при доказа-
доказательстве априорных оценок решений линейных и ква-
квазилинейных эллиптич. уравнений (см. [12], [26]).
Специфич. И. н. возникают для выпуклых тел про-
пространства Минковского в связи с теорией приближения
функций (см. Самопериметр, Поперечник).
В теории конформных и квазиконформных отобра-
отображений применение И. н. является обычным приемом.
Примером конформно-инвариантного И. н. служит
приводимое ниже неравенство D).
И. н., включающие среднюю кривизну подмногообра-
подмногообразия, в частности для минимальных поверхностей, игра-
играют важную роль при решении Плато задачи.
В римановой геометрии неоднородных пространств
обобщения классического И. н. детально изучены толъ-
ко в двумерном случае. Пусть М — односвязное ком-
компактное двумерное многообразие с краем и положи-
положительная часть ш+ интегральной кривизны М меньше,
чем 2я.
Тогда (см. [13]):
2 Bя — со + ) V^F*. A)
И. п. A) справедливо и для более общих, чем римановы,
двумерных многообразий ограниченной кривизны. Ра-
Равенство в A) достигается на нерегулярном объекте —
области, изометричной боковой поверхности прямого
кругового конуса с полным углом 2я—со+ вокруг вер-
вершины. С помощью A) устанавливаются оценки длины
кривой, умещающейся в области, в зависимости от F,
со+ и собственного поворота (извивания кривой). В ча-
частности, для геодезической длины L
L ( 1 + cos-jj- @+ ) s^ F при со+ <л,
//sin-^-W" s^ F при я<со+ < 2я.
И. н. A) является частным случаем оценки
Ss0, B)
где а — любое действительное число, /_ — эйлерова ха-
рактеристика компактной области с краем, ш + =
= \ {К—a)+dV, а К — гауссова кривизна. К И. н. B)
примыкают оценки для площади ^-окрестности границы
области и для наибольшего удаления точек области от
границы (см. [14]). Если поверхность М является глад-
гладким подмногообразием в R3, то оценки A), B) дополня-
дополняются И. н., включающими внешние характеристики
поверхности. Для замкнутых поверхностей из инте-
интегральных тождеств (см. [15]) следует точное И. н.
где д — радиус шара в R3 , содержащего М. Сходные
неравенства (не точные) получены и для поверхностей
с краем (см. [16]). В частности, для односвязной седло-
вой поверхности в R" с границей длины F:
_L > е = const > 0.
Упомянутые неравенства остаются справедливыми и
для общих (нерегулярных) поверхностей в R", га^2,
если вместо ы+ ввести в рассмотрение внешнюю поло-
положительную кривизну — меру в множестве локально
опорных плоскостей (см. [16]).
Для n-мерного риманова пространства V" И. н.,
как правило, связаны с односторонними ограничениями
на секционную кривизну или кривизну Риччи. Про-
Простейшей является оценка объема V(t) шара радиуса t
в V" через объем v(t, К) шара того же радиуса в полном
односвязном пространстве постоянной кривизны К:
V(t)<.v(t, К), C)
где (п—1) К есть минимальное значение кривизны
Риччи в V"; если К>0, то предполагается, что *<л/ У К
(см. [17]). Аналогичное И. н. справедливо для трубчатой
i-окрестности р-мерного подмногообразия в V", 0<:р<п;
в таком И. н. (вместо кривизны Риччи) участвуют ми-
минимум секционных кривизн V" и максимум нормальных
кривизн подмногообразия (см. [18]).
Если верхняя грань К секционных кривизн отрица-
отрицательна, то объем V замкнутого многообразия оценива-
оценивается снизу через К (см. [19]). Для области М в полном
односвязном V" при этом имеет место линейное И. н.
где F есть (п—1)-мерная площадь границы М, а также
И. н.
V~ =S с (и) F,
точное значение с(п) неизвестно.
В пространствах неотрицательной кривизны для
выпуклых областей М получен ряд оценок, обобщаю-
обобщающих И. н. для выпуклых тел в R" (см. [20], [21]). Так,
где г — наибольшее удаление точек М до границы.
Если в М нижняя грань секционных кривизн К>0,
то г Ук<Сл и левое неравенство уточняется:
sin»-1 t]/~Kdt<,V.
Справедлива оценка rH^F, где Н — интегральная
средняя кривизна. Для трехмерного случая верно
И. н.:
где х — эйлерова характеристика границы М, a Q
интегральная скалярная кривизна М.
В классическом И. н. площадь оценивается сверху.
Для замкнутых неодносвязных поверхностей площадь
может быть оценена снизу через длину Я кратчайшей
негомотопной нулю петли
J4)
Точное значение С {%) известно лишь для тора (= 13/2)
и проективной плоскости (=2/л). Неравенство D) яв-
является следствием И. н. (см. [22]):
К^С-\х) D')
для экстремальной длины Хе семейства негомотопных ну-
нулю петель.
Вопрос об аналогичных неравенствах для V" при
п>2 обсуждается в [22]. Если М — топологический
n-мерный куб с внутренней метрикой g, то его п-объем
где gi— расстояние в метрике g между г-й парой про-
противоположных (га—1)-мерных rpaHeii. Подробнее см.
[24], [25].
В теории минимальных и родственных им поверх-
поверхностей получен ряд И. н., к-рые справедливы не только
для гладких ^-мерных подмногообразий в R", п^к^2,
но и для более общих ^-мерных «пленок»: подмногообра-
подмногообразий с особенностями, потоков и др. Так, в [26], [27]
установлено неравенство
) (jF-f #)*<'<*-D , E)
где F — (к—1)-площадь границы, а Н — интеграл от
модуля средней кривизны h пленки. Если /с=2, то
при условии а=2—max|/i[diam 7lf>0 выполняется сле-
следующее И. н.:
К И. н. E) по методам доказательств и применениям
примыкают оценки снизу для объема V(t) пересечения
/fc-пленки М с шаром радиуса t с центром р?М. Так, для
минимальной поверхности М функция t~kV(t) возра-
возрастает при всех t<d(x, дМ). Нек-рые обобщения для
минимальных пленок в V" (и для пленок при условии
|й|<: const) см. [27], [28].
Лит.: [1] Bottema О., Geometric inequalities, Gronin-
gen, 1969; [2] X а д в и г е р Г., Лекции об объеме, площади
поверхности и изопериметрии, пер. с нем., М., 1966; [3] В о li-
line sen Т., Pen che I W., Theorie der konvexen Korper,
В., 1934; [4] Данцер Л., Грюнбаум Б., К ли В.,
Теорема Хелли и ее применения, пер. с англ., М., 1968; [5]
Мельников М. С, «Успехи матем. наук», 1963, т. 18,
в. 4, с. 165—70; [6] Тот Л. Ф., Расположения на плоскости,
на сфере и в пространстве, пер. с нем., М., 1958; [7] Полна Г.,
С е г е Г., Изопериметрические неравенства в математической
физике, [пер. с англ.], М., 1962; [8] Payne L. E., «Siam
Rev.», 1967, v. 9, №3, p. 453—88; [9] Berger M., G a n-
d u с h о n P., M a z e t E., Le spectre d'une variety riemanni-
enne, В., 1971; [10] Мазья В. Г., в кн.: Проблемы матема-
математического анализа, в. 3, Л., 1972, с. 33—68; [11] его же,
в кн.: Теоремы вложения и их приложения, М., 1970, с. 142—59;
[12] его же, «Тр. Моск. матем. об-ва», 1969, т. 20, с. 137—72;
[13] Александров А. Д., Стрельцов В. В., «Тр.
матем. ин-та АН СССР», 1965, т. 76, с. 67—80; [14] Б у р а г о
Ю. Д., «Сиб. матем. ж.», 1973, т. 14, № 3, с. 666—68; [15] S h a-
hin J. К., «Ргос. Amer. Math. Soc», 1968, v. 19, № 3, p.
609—13; [16] Бураго Ю. Д., Неравенства изопериметрн-
ческого типа в теории поверхностей ограниченной внешней
кривизны, Л., 1968; [17] Бишоп Р. Л., К р и т т е н-
д е н Р. д ж., Геометрия многообразий, пер. с англ., М., 1967;
[18] Cheeger I. H., «Amer. J. Math.», 1970, v. 92, №1,
p. 61—74; [19] Маргулис Г. А., в кн.: VI Всесоюзная
топологическая конференция. Тезисы, Тб., 1972; [20] Дек-
стер Б. В., «Матем. сб.», 1972, т. 88, JnB 1, с. 61—87; [21]
Волков Ю. А., Декстер Б. В., «Матем. сб.», 1970,
т. 83, в. 4, с. 616—38; [22] Berger M., «Ann. sci. Ecole norm,
super», ser. 4, 1972, t. 5, JMi 1. p. 1—44; [23] его же, там же,
1972, т. 5, № 2, р. 241—60; [24] Derrick W. R., «J. Math,
and Mech.», 1968, v. 18, .№ 5, p. 453—72; [25] A 1 m g r e n F.,
«Proc. Amer. Math. Soc», 1964, v. 15, K« 2, p. 285; [26]
Michal J., Simon L., «Commims Pure and Appl. Math.»,
1973, v. 26, JVC. 3, p. 361 — 79; [27] A 1 1 a r d W., «Ann. Math.»,
1972, v. 9-5, p. 417—91; [28] Фоменко А. Т., «Изв. АН
СССР. Сер. матем.», 1972, т. 36, Лв 5, с. 1049 — 79.Ю. Д. Бураго.
ИЗОПЕРИМЕТРИЧЕСКОЕ НЕРАВЕНСТВО КЛАС-
КЛАССИЧЕСКОЕ — неравенство между объемом V области
в евклидовом пространстве R", п>2, и (п—1)-мерноп
площадью F, ограничивающей область гиперповерхно-
гиперповерхности:
где vn— объем единичного n-мерного шара. Равенство
в II. н. к. имеет место только для шара. И. н. к. дает
решение изопериметрической задачи. Для п=2, 3 И. н. к.
известно с глубокой древности. Строгое доказательство
П. н. к. для п=2 дано Ф. Эдлером (F. Edler) в 1882,
дляге=3 — Г. Шварцем (Н. Schwarz) в 1890 п для
i.n'X ге^2 — Л. А. Люстерником в 1935 и Э. Шмид-
Шмидтом (Е. Schmidt) в 1939 (см. [1], [2]. [3]).
В двумерном случае есть много доказательств
И. н. к. (см. [4]), при п >2 известно лишь два подхода.
Первый — метод симметризации, предложенный Я.
Штейнером (J. Steiner). Э. Шмидт, используя этот ме-
метод, получил аналоги И. н. к. (и неравенства Брунна —
Минковского) для сферического и гиперболического
«-мерных пространств (см. [5]). Второй подход состоит в
сведении И. н. к. к Брунна — Минковского неравенству
(см. Брунна — Минковского теорема) и использовании
метода пропорционального деления объемов. При та-
таком подходе естественно возникает более общее нера-
неравенство
nnV"-\A) V(B) ?s:Fn (А, В) (*)
для объемов V(A), V(B) двух множеств и площади
F{A, В) по Минковскому множества А по отношению к
В. Неравенство (*) допускает интерпретацию как
И. н. к. в пространстве Минковского; равенство при
фиксированном «шаре» Минковского В достигается,
вообще говоря, не для единственного тела А, причем
эти тела отличны от «шара» (см. [6]).
Имеется ряд обобщений И. н. к., при к-рых рассмат-
рассматриваются не области с кусочно гладкой границей, а
более широкие классы множеств, причем площадь гра-
границы понимается в обобщенном смысле (площадь Мин-
копского, площадь по Лебегу, периметр множества по
Каччопполи — Де Джорджи, масса потока, см. [7],
[8]). И. н. к. остается справедливым во всех этих слу-
случаях, а также для гиперповерхностей с самопересече-
самопересечениями и соответствующего им ориентированного объема
(см. [9]). Эти обобщения получаются из И. н. к. пре-
предельным переходом при различных вариантах понятия
сходимости.
Дляизопериметрич. разности Fn—nnvnVn~1, как и для
изопериметрич. отношения Fn\n~n, известны оценки,
усиливающие И. н. к. (см. [2]). Часть таких оценок по-
получена для множеств специального вида, в первую оче-
очередь для выпуклых множеств и многогранников (см.
[10]). Напр., Боннезена неравенство для плоских фигур:
F* — inV^(F — 4ягJ,
где г — радиус наибольшего вписанного круга, и его
обобщение (см. [11]) для выпуклых тел в R":
рпцп-i) (Л> ?)_„«/<«-!) V (A
Здесь 9= max {ЦХВ можно поместить в А }. Относитель-
Относительная изопериметрич. разность выпуклых тел
F"(A, B) — n"V"-1(A)V(B)
может служить мерой их негомотетичности (см. [12]).
Это используется, напр., при доказательстве теоремы
устойчивости в проблеме Минковского (см. [13]).
Об обобщениях И. н. к. на пространства переменной
кривизны и родственных им неравенствах см. ст.
Изопериметрическое неравенство.
Лит.: [1] Крыжановский Д. А., Изопериметрьг,
3 изд., М., 1959; [2] Хадвигср Г., Лекции об объеме,
площади поверхности и изопериметрии, пер. с нем., М., 1966: [3]
Л ю ст ер н и к Л. А., «Успехи матем. наук», 1936, в. 2, с. 47—54;
[4] Бляшке В., Введение в дифференциальную геометрию,
пер. с нем., М., 1957; [5J Schmidt E., «Math. Nachr.»,
1948, Bd 1, S. 81 — 157; [6] Busemmann H. «Amer. J.
Math.», 1949, v. 71, p. 743 — G2; [7] De Giorgl E., «Atti
Accad. naz. Lincei. Mem. Cl. sci fis., mat. e natur. Ser. 8», 1958,
M 5, № 2, p. 33 — 44; [8] Ф е д е р е р Г., Ф л е м и н г У. X., в
сб.: Целочисленные потоки и минимальные поверхности, М.,
1973, с. 9—90; [9] R a d о Т., «Trans. Amer. Math. Soc», 1947,
v. 61, jVi 3,p. 530—55; [10] Тот Л. Ф., Расположения на пло-
плоскости, на сферой в пространстве, пер. с нем., М 1958; [11] Ди-
Дискант В. И., «Докл. АН СССР», 1973, т. 213, Xs 3, с. 519 —
21; [12] его же, «Сиб. матем. журнал», 1972, т. 13, № 4, с.
767 — 72; [13] Волков Ю. А., «Вестн. Ленигр. ун-та. Сер.
матем. и астроном.», 1963, в. 1, с. 33—43. Ю.Д. FJypmo.
ИЗОТЕРМИЧЕСКАЯ ПОВЕРХНОСТЬ — поверх-
поверхность, линии кривизны к-рой образуют изотермическую
сеть. Напр., И. п. являются квадрики, вращения по-
поверхности, поверхности постоянной средней кривизны
и, в частности, минимальные поверхности. Инвариант-
Инвариантный признак И. п.— градиентность чебышевского век-
вектора сети линий кривизны. Для каждой И. п. определя-
определяется с точностью до гомотетии другая И. п., находящая-
находящаяся с первой в конформном Петерсона. соответствии.
Инверсия пространства сохраняет класс И. п.
И. X. Сабитов.
ИЗОТЕРМИЧЕСКАЯ СЕТЬ — ортогональная сеть на
поверхности F2 евклидова пространства, малые че-
четырехугольники к-рой, образованные двумя парами ли-
линий из различных семейств, с точностью до бесконечно
малых 1-го порядка являются квадратами. Линии И. с.
суть линии уровня двух сопряженных гармонич. функ-
функций. В параметрах И. с. линейный элемент поверхности
имеет вид:
где X=h(u, v). И. с.— частный случай ромбической
сети. На поверхности вращения меридианы и парал-
параллели образуют И. с, асимптотическая сеть на мини-
минимальной поверхности — И. с. в. Т. Вазылев.
ИЗОТЕРМИЧЕСКИЕ КООРДИНАТЫ — координаты
двумерного риманова пространства, в к-рых квадрат
линейного элемента имеет вид:
И. к. задают конформное отображение двумерного
риманова многообразия на евклидову плоскость. И. к.
всегда можно ввести в компактной области регулярного
двумерного многообразия. В И. к. гауссова кривизна
может быть вычислена по формуле:
,_ A In Я
?. '
где А — оператор Лапласа.
И. к. рассматриваются и в двумерных псевдоримано-
вых пространствах; квадрат линейного элемента имеет
при этом вид:
Часто используются естественно связанные с И. к.
координаты (х, v, в к-рых квадрат линейного элемента
имеет вид:
ds2=X(\i, v) dfidy.
В этом случае линии |л=const и v=const — изотропные
геодезические, в связи с чем система координат ц, v
наз. изотропной. Изотропные координаты на-
находят широкое применение в общей теории относитель-
относительности, д. д. Соколов.
ИЗОТОННОЕ ОТОБРАЖЕНИЕ — однозначное ото-
отображение ф частично упорядоченного множества А в
частично упорядоченное множество В, сохраняющее
порядок. И. о. играют роль гомоморфизмов частично
упорядоченных множеств (рассматриваемых как ал-
алгебраические системы с одним отношением). И. о. наз.
также монотонными отображениями.
О. А, Иванова.
ИЗОТОПИЯ — отношение на классе всех группоидов,
определенных на одном и том же множестве G. А имен-
именно, два группоида на G наз. изотопными, если
существуют такие подстановки р, а и т множества G,
что для любых a, b?G
aob= (ap-bo) т,
где • и о обозначают операции в этих группоидах.
Отношение И. является отношением эквивалентности
для бинарных операций на множестве G. Изоморфизм
двух бинарных операций, заданных на одном и том же
множестве — частный случай И. (при р— а=т-1). И.
наз. главной, если т является тождественной под-
подстановкой. Всякий изотоп группоида изоморфен его
главному изотопу. Всякий группоид, изотопный квази-
квазигруппе, сам будет квазигруппой. Всякая квазигруппа
изотопна нек-рой лупе (теорема Алберта).
Если лупа (в частности, группа) изотопна нек-рой груп-
группе, то они изоморфны. Если группоид с единицей изо-
изотопен полугруппе, то они изоморфны, т. е. оба являются
полугруппами с единицей.
Лит.: [1] К у р о ш А. Г., Общая алгебра, М., 1974.
ИЗОТОПИЯ — гомотопия топологич. пространства
X по топологич. пространству Y : ff : X^t-Y (здесь
и всюду далее t?[0,l] = /), в к-рой при любом t отобра-
отображение ff является гомеоморфизмом X на нек-рое
подмножество Y. Эквивалентно, И.— послойное не-
непрерывное отображение / : XXI—>YXI такое, что /
гомеоморфно переводит слой X X t на подмножество
слоя YXt. И. Ft : Y^-Y, при к-рой Ff(Y)=Y для лю-
любого t, наз. изотопией пространства Y.
Накрывающей (или объемлющей)
изотопией для II. ff.X—yY наз. И. пространства
Ff-. Y^>-Y такая, что Fi\x =//. Два вложения /0, f1 : X—у
—yY пространства X в пространство Y паз. изотоп-
изотопным и, если существует накрывающая И. Ft : Y-+-Y,
для к-рой F0=id, Fi(fo(X))=fi(X). Пространства X, Y
наз. п з о т о п и ч е с к и эквивалентными,
если существуют вложения / : X—yY и g : У—>-Х такие,
что композиции gof : X—уХ и fog : Y^yY изотопны тож-
тождественному отображению. Изотопически эквивалент-
эквивалентные пространства наз. также (по аналогии с гомотопич.
типом) пространствами одного и того же изотопи-
изотопического типа. Если пространства гомеоморфны,
то они нзотопически эквивалентны, однако есть него-
меоморфные пространства одного изотопич. типа, напр.
n-мерный шар и такой же шар с приклеенным к его
поверхности (своим концом) отрезком. Любой гомото-
гомотопич. инвариант является нзотопич. инвариантом, но
существуют изотопич. инварианты, напр, размерность,
не являющиеся гомотопическими.
Основным вопросом в теории И. является задача
продолжения изотопии, т. е. вопрос о су-
существовании И. Ff, накрывающей данную И. /(. Этот
вопрос, равно как и общая задача нахождения полной
системы изотопич. инвариантов для вложений, чаще
всего рассматривается в категории топологич. много-
многообразий и ее подкатегориях кусочно линейных и диф-
дифференцируемых многообразий.
Топологич. И. ft многообразия Mk по многообразию
Мп, к^п, продолжается до накрывающей И. Ff :
Мп—^-Мп тогда и только тогда, когда соответствующее
прослойное вложение f(MkX[a, b])dMnXI является
локально плоским, здесь [а, Ь] — подотрезок интер-
интервала @, 1). Если п—кф2 и пф4, то И./( накрывается
И. Ft при условии, что вложение ft(Mk) a Mk являет-
является локально плоским для любого t? [0,1]. В коразмер-
коразмерности 2 это неверно (пример — «затягивание узелка»
на окружности в Е3), и потому для существования на-
накрывающей И. необходимы дополнительные гомотопич.
предположения. Достаточно близкие локально плос-
плоские вложения при п—кф2 изотопны.
Теорема о продолжении кусочно линейной И. в об-
общем случае формулируется аналогично (при естествен-
естественном условии, что соответствующее послойное вложение
является локально плоским в кусочно линейном смы-
смысле). Если п—к^З, то кусочно линейная И. продолжа-
продолжается всегда, так как в этих коразмерностях кусочно ли-
линейное вложение является локально плоским в кусоч-
кусочно линейном смысле. Для п—к=2 или 1 необходимо
дополнительное предположение, что вложения ft(Mk)c
dM" являются в кусочно линейном смысле локально
плоскими, поскольку в этих коразмерностях кусочно
линейное вложение может не быть локально плоским
даже в топологич. смысле, напр, конус над узлом.
Дифференцируемая И. всегда продолжается до диф-
дифференцируемой накрывающей И.
Задача нахождения полной системы изотопич.инва-
изотопич.инвариантов расположения многообразий Мк в Мп решена
только в небольшом числе частных случаев. Так. вся-
всякое локально плоское (в топологич. смысле) вложение
сфер SkdSn при п—А^З или при п—&=1, п=И=4, изо-
изотопно стандартному, а если п—к=2, пфк, то локально
плоская сфера Sn~2 в Sn тогда и только тогда изотопна
стандартной, когда дополнение Sn\Sn~2 имеет гомото-
гомотопич. тип окружности (теоремы Столлпнгса
и Б р а у н а). В коразмерности 2 могут существовать
неизотопные узлы. Точно так же формулируется тео-
теорема Зимана — Столлингса о кусочно ли-
линейной И. (незаузленности) кусочно линейных сфер.
Инвариант кусочно линейной И. является более тон-
тонким по сравнению с топологич. И. Так, вопрос о то-
топологич. изотопности произвольного гомеоморфизма
сферы Sn тождественному решен в положительном смы-
смысле для гс=^=4, при этом же ограничении доказана изотоп-
ность любых двух гомеоморфизмов сферы S" на себя,
сохраняющих ориентацию. В кусочно линейной ситуации
эти утверждения получаются элементарными метода-
методами без всяких ограничений. Достаточно близкие го-
гомеоморфизмы топологич. многообразия на себя изо-
изотопны, однако существуют как угодно близкие кусочно
линейно неизотопные кусочно линейные гомеомор-
гомеоморфизмы кусочно линейных многообразий, напр, «-мер-
«-мерных торов при п^гб.
В отличие от топологического и кусочно линейного
случая далеко не всегда два диффеоморфизма п-мерной
сферы на себя дифференцируемо изотопны. Изотопич.
классы дифференцируемых вложений сфер S1' в S"
подробно изучены для любого к*<п. Если к^п—3, то
существует нек-рое топологич. пространство Сд, д=
= п—к такое, что гомотопич. группы ль(Сд) находятся
во взаимно однозначном соответствии с классами вло-
вложений Sk в S"; при этом л^(Сс1) = 0 для k<!2q—3, а
n-zq-v{Cq) есть Z или 22 в зависимости от того, является
ли q четным или нечетным числом. Таким образом,
Ar-мерная стандартная сфера Sk, вложенная в S", мо-
может при &<:;?—3 заузливаться в дифференцируемом
смысле, т. е. существуют такие вложения SkaSn, к-рые
дифференцируемо не изотопны стандартному. Эти узлы
наз. узлами X е ф л и г е р а. Если к==п—2, то
дифференцируемые узлы S"~2 с S" могут заузливаться
в топологич. смысле, однако их намного больше, чем
топологических или кусочно линейных; когда п не-
нечетно, имеется их полная классификация. Если к = п—1,
пф4, то любое дифференцируемое вложение S" с S"
дифференцируемо изотопно стандартному вложению.
Тот факт, что существуют диффеоморфизмы сферы S"
на себя, неизотопные тождественному, приводит к су-
существованию нетривиальных дифференциальных струк-
структур на сферах размерности п+1. Хотя всякий гомео-
морфизм сферы Sn, пфА, на себя аппроксимируется
диффеоморфизмом, не всегда близкие диффеоморфизмы
сферы дифференцируемо изотопнь-, т. е. диффеоморфизм
сферы на себя можно как угодно малым возмущением
превратить в непзотопньга ему.
Лит.: [1] Келдыш Л. В., Топологические вложения
•евклидово пространство, М., 1966 (Тр. Матем. ин-та АН СССР,
! 81); [2] Р у р к К., Сандерсон Б., Введение в кусочно
линейную топологию, пер. с англ., М., 1974; [3] Новиков
С. П., «Изв. АН СССР. Сер. матем.», 1965, т. 29, К° 1, с. 71—96;
14] Ч е р н а в с к и й А. В., «Матем. сб.», 1969, т. 79, Л» 3,
с. 31O—56; [5] Rushing Т., Topological Embedding,
X.Y. — L., 1972; [6] К i г b у R., Siebenmann L., Foun-
dational essays on topological manifolds smootings and triangu-
lations, N.Y., 1977. " M. А. Штпнъко.
ИЗОТРОПИИ ГРУППА — множество Gx таких эле-
элементов заданной группы G, действующей на нек-ром
множестве М как группа преобразований, к-рые остав-
оставляют неподвижной точку х. Это множество оказывается
подгруппой в С и наз. группой изотропии
точки х. В этом же смысле употребляются термины:
стационарная подгруппа, стабили-
стабилизатор, G - ц е н т р а л и з а т о р. Если М являет-
является топологич. хаусдорфовым пространством и G — то-
пологич. группой, непрерывно действующей на М, то
Gx есть замкнутая подгруппа. Если при этом М и G
локально компактны, G имеет счетную базу и действует
на М транзитивно, то существует естественный гомео-
гомеоморфизм между пространством М и топологич. фактор-
чпостранством GlH, где Н — одна из И. г.; с ней изо-
изоморфны все Gx, х?М.
Пусть М — гладкое многообразие и С — группа Ли,
,ладко действующая на М. Тогда И. г. Gx точки х^М
индуцирует нек-рую группу линейных преобразований
касательного векторного пространства ТХ(М); эта
последняя группа наз. линейной группой
изотропии в точке х. При переходе к касатель-
касательным пространствам высшего порядка в точке х полу-
получаются естественные представления И. г. в структурных
группах соответствующих касательных расслоений
высшего порядка; они наз. группами изотро-
изотропии высшего порядка (см. также Изо-
Изотропии представление).
Лит.: [1] Понтрягин Л. С, Непрерывные группы,
3 изд., М., 1973; [2] X е л г а с о н С, Дифференциальная гео-
геометрия и симметрические пространства, пер. с англ., М., 1964;
13] Зуланке Р., Винтген П., Дифференциальная
геометрия и расслоения, пер. с нем., М., 1975.
Ю. Г. Лумисте.
ИЗОТРОПИИ ПРЕДСТАВЛЕНИЕ — естественное ли-
линейное представление изотропии группы в касательном
пространстве к многообразию. Если G — группа диф-
дифференцируемых преобразований многообразия М и
Gx— соответствующая группа изотропии в точке х?М,
то И. п. Isx: Gx^yGL (ТХМ) сопоставляет каждому h ?Gx
дифференциал lsx(h)=dhx преобразования h в точке х.
Образ И. п. lsx(Gx) наз. линейной группой
изотропии в точке х. В случае, когда G — группа
Ли со счетной базой, гладко и транзитивно действующая
на М, касательное пространство ТХМ естественно ото-
отождествляется с пространством Q,lct,x, где flZDCj*— ал-
гобры Ли групп G^>GX. И. п. ^отождествляется при
им с представлением Gx—>-GL(q/qx), к-рое пндуци-
"тся ограничением присоединенного представления
лиг, группы G на Gx.
Если однородное пространство М редуктивно,
т. е. 3=Д*-г-та, где m — подпространство, инвариант-
инвариантное относительно Ado(Gx), то ТХМ отождествляется с т,
a Is,;—с представлением h—>-(Ado/i)|m (см. [3]). В этом слу-
случае И. п. является точным, если G действует эффективно.
И. п. и линейная группа изотропии играют важную
роль при изучении инвариантных объектов на однород-
однородных пространствах. Инвариантные тензорные поля на
однородном пространстве М находятся во взаимно
однозначном соответствии с тензорами в пространстве
ТХМ, инвариантными относительно И. п. В частности,
М обладает римановой инвариантной метрикой тогда
и только тогда, когда в ТХМ существует евклидова ме-
метрика, инвариантная относительно линейной группы
изотропии. Существование на однородном пространство
М положительной инвариантной меры равносильно
условию |det Л| = 1 для всех A ?Isx(Gx). Однородное
пространство ориентируемо тогда и только тогда, когда
det A >0 (A ? Isx(Gx)). Инвариантные линейные связ-
связности на М находятся во взаимно однозначном соот-
соответствии с линейными отображениями Л : $—*-$[(ТхМ),
обладающими следующими свойствами:
Л ((AdA) X) = Is, (А) Л (X) Is.v. (Д) (h?Gx).
Обобщением понятия И. п. является понятие И. п.
порядка г. Это гомоморфизм h-*-jx h группы Gx
в группу Lr(ТХМ) обратимых r-струй диффеоморфиз-
моз пространства ТХМ, переводящих в себя нуль. Это
понятие применяется при изучении инвариантных объ-
объектов высших порядков.
Лит.: [1] 3 у л а н к е Р., В и н т г е н П., Дифферен-
Дифференциальная геометрия и расслоения, пер. с нем., М., 1975; [2]
Хелгасон С., Дифференциальная геометрия и симметри-
симметрические пространства, пер. с англ., М., 1964; 13] Р а ш е в с к и й
П. К., в кн.: Тр. семинара по векторному и тензорному анализу
с их приложениями к геометрии, механике и физике, в. 9, М.—
Л.,1952, с. 49 — 74; [4] К а р т а н Э., Геометрия групп Ли и
симметрические пространства, пер. с франц., М., 1949.
А. Л. Онищип.
ИЗОТРОПНАЯ КОНГРУЭНЦИЯ — конгруэнция С
неопределенными главными поверхностями.
ИЗОТРОПНЫЙ ВЕКТОР — вектор, ортогональный
сам себе. Пусть Е — векторное пространство над полем
действительных или комплексных чисел, Ф — невы-
невырожденная билинейная форма с сигнатурой (р, д),
рФО, q?=0 на ?Х?. Изотропным вектором
наз. ненулевой вектор х?Е, для к-рого Ф(х, ж) = 0.
Иногда говорят, что И. в. имеет нулевую длину (или
норму). Множество всех И. в. наз. изотропным
конусом. Подпространство VcE наз. изотропным,
если существует ненулевой вектор z? V, ортогональный
V (т. е. сужение формы Ф на VX V вырождено: Т'П V^-ф
=^{0}). Векторное подпространство V наз. вполне
изотропным, если все его векторы суть И. в.
В релятивистской интерпретации Вселенной про-
пространство-время локально рассматривается как четы-
четырехмерное векторное пространство с формой сигнатуры
C, 1), траектории фотонов — как изотропные прямые,
а изотропный конус наз. световым конусом.
А. Б. Иванов.
ИКОСАЭДР — один из пяти пра-
правильных многогранников. И. имеет
20 граней (треугольных), 30 ребер,
12 вершин (в каждой вершине схо-
сходятся 5 ребер). Если а — длина ре-
ребра И., то его объем
V = ^a3C+ уП5~) s 2,1817a3.
ИКОСАЭДРА ПРОСТРАНСТВО —
трехмерное пространство, являю-
являющееся пространством орбит действия
бинарной группы икосаэдра на трехмерной сфере.
Открыто А. Пуанкаре как пример гомологпч. сферы
рода 2 при рассмотрении Хегора диаграмм. II. п. яв-
является разветвленным р-листным накрытием S3 с вет-
ветвлением вдоль торичоского узла типа (q, r), где
р, q, r любая перестановка чисел 2, 3, 5. Аналити-
Аналитически И. п. может быть задано как пересечение поверх-
поверхности
в С2 с единичной сферой. Наконец, И. п. может быть
отождествлено с додекаэдра пространством.
А. В. Чернавскуй.
ИММЕРСИЯ — то же, что погружение.
ИММУННОЕ МНОЖЕСТВО — бесконечное множе-
множество натуральных чисел, не содержащее бесконечных
рекурсивно перечислимых подмножеств. В частности,
само И. м. не является рекурсивно перечислимым.
И. м. по своей насыщенности рекурсивно перечислимы-
перечислимыми подмножествами в известном смысле противополож-
противоположны продуктивным множествам. Рекурсивно перечис-
лимыо множества с иммунными дополнениями наз.
простыми и образуют один из важных классов
нерекурсивных рекурсивно перечислимых множеств.
Типы рекурсивной эквивалентности иммунных и ко-
конечных множеств, называемые и з о л я м и, представ-
представляют интерес с точки зрения рекурсивного аналога
теории кардинальных чисел. В рекурсивной теории
множеств и ее приложениях используются также некото-
некоторые специальные подклассы класса И. м., особенно
гнпериммунные (г и п е р и м м у н н ы м наз. мно-
множество натуральных чпеел, последовательность эле-
элементов к-рого, расположенных в порядке возрастания,
не мажорируется никакой общерекуренвной функцией;
рекурсивно перечнелпмое множество с гипериммун-
гипериммунным дополнением наз. гиперпростым).
Лит.: [1] Роджерс X., Теория рекурсивных функций
и эффективная вычислимость, пер. с англ., М., 1972.
ИМПЛИКАТИВНАЯ НОРМАЛЬНАЯ ФОРМА™—
пропозициональная форма вида
с1=>(С2=>...(сп=>±)...),
где все С;, i = 1, . . . , н, имеют вид
каждое С,-у. 2=1, . . ., п; /=1, . . ., т,-, есть либо пере-
переменная, либо отрицание переменной, и _[_ есть логич.
символ, обозначающий ложь. Для всякой пропозици-
пропозициональной формулы А можно построить классически
эквивалентную ей И. н. ф. В, содержащую те же пе-
переменные, что и А . Такая формула В наз. И. н. ф. фор-
формулы А.
Лит.: 11] Ч ё р ч А., Введение в математическую логику,
пер. с англ., т. 1, М., 1960. С. И. Соболев.
ИМПЛИКАТИВНОЕ ПРОПОЗИЦИОНАЛЬНОЕ ИС-
ИСЧИСЛЕНИЕ — пропозициональное исчисление, ис-
использующее единственную исходную связку 7D (им-
(импликацию). Примерами И. п. и. являются полное
(или классическое) И. п. и., задаваемое аксио-
аксиомами
p=>(q=> р), ((р => q) ZD ({q => г) ZD (p ZD г))),
((р => q) ¦=> р) ZD р
и правилами вывода: модус поненс и подстановка, а
также позитивное Й. п. и., задаваемое аксио-
аксиомами
p=>(q=> p), (P=>(q=> г)) 3 ((/> 3 q) 3 (р 3 г))
и теми же правилами вывода. Всякая имплика-
т и в н а я ф о р м у л а, т. е. формула, содержащая
только связку з, выводима в полном (или позитивном)
И. п. и. тогда и только тогда, когда она выводима в
классическом (соответственно интуиционистском) про-
пропозициональном исчислении. Для любого конечного
множества V переменных среди импликативных фор-
формул с переменными из V существует лишь конечное
число попарно не эквивалентных в позитивном И. п. и.
(см. [3]). Существуют конечно аксиоматизируемые
И. п. и. с неразрешимой проблемой выводимости
(см. [4])
Лит.: Ш Чёрч А., Введение в математическую логику,
пер. с англ. т. 1, М., I960: [2] Lukasiewicz J., Т а г-
ski А., «С. г. Soc. Sci. Lettres Varsovie, Cl. Ill», 1930,
v. 23, p. 30—50; [3] Diego A., Sur les algebres de Hilbert,
P., 1966; 14] Gladstone M. D., «Trans. Amer. Math. Soc»,
1965, v. 118, p. 192 — 210. С. К. Соболев.
ИМПЛИКАЦИЯ — логическая операция, соответ-
соответствующая образованию высказывания «если А , то В» из
высказываний А к В. В формализованных языках И.
чаще всего обозначается символами 23, —*-, =5>. Выска-
Высказывание А наз. посылкой высказывания AZ2B,
а высказывание В — его заключением. Точный
смысл высказывания A DB различен при классическом,
конструктивном и других подходах к построению се-
семантики языка. В языках с классич. семантикой упот-
употребление II. согласовано с истинностной таблицей:
А
И
И
Л
л
в
и
л
и
л
А Э В
И
л
и
и
Так понимаемая И. наз. материальной и .м-
п л и к а ц и е й. в. д. плиско.
ИМПРИМИТИВНАЯ ГРУППА — группа G взаим-
взаимно однозначных отображений на себя (подстановок)
нек-рого множества S, для к-рой существует разбиение
множества S в объединение непересекающихся под-
подмножеств Sj, . . ., Sm, m^2, обладающее следующими
свойствами: число элементов хотя бы в одном из S/ боль-
больше единицы; для любой подстановки g^Gu любого но-
номера г, 1 ¦<(¦<»!, существует такой номер ;, 1</<:т,
что f> отображает 5,- на ?,.
Набор подмножеств 5,,'..., ?,„ наз. системой
импримитивности, а сами подмножества S,—
областями импримитивности группы
G. Не импримитивная группа подстановок наз. при-
примитивной.
Примером И. г. может служить нетривиальная ин-
транзитивная группа G подстановок множества S (см.
Транзитивная группа): в качестве системы имприми-
импримитивности можно взять набор всех орбит (областей тран-
транзитивности) G на S. Транзитивная группа подстановок
G множества S примитивна тогда и только тогда, когда
для какого-либо (а, значит, и для любого) элемента
y?S множество подстановок из G, оставляющих у на
месте, является максимальной подгруппой в G.
Понятие И. г. подстановок имеет аналог для групп
линейных преобразований векторных пространств.
Именно, линейное представление р группы G наз. и м-
примитивным, если существует разложение про-
пространства V представления р в прямую сумму собствен-
собственных подпространств \\, . . ., Vт, обладающее следую-
следующим свойством: для любого элемента g(^G и любого
номера г", 1<г<:т, найдется такой номер /, 1<:/<:7?i, что
р (г) (Уд ¦-=-- Vj.
Набор подпространств 1\, . . ., Vт наз. системой
импримитивности представления р. Если V не
обладает разложением указанного типа, то представ-
представление р наз. примитивны м. Импримитивное пред-
представление р наз. транзитивным имприми-
т и в н ы м, если для любой пары подпространств V; и
Vj из системы импримитивности существует такой эле-
элемент g? G, что р (g) (F/)= V/. Группа р (G) линейных пре-
преобразований пространства V и G-модуль V, определяе-
определяемый представлением р, также наз. импримитивными
(примитивными), если представление р является импри-
митивным (примитивным).
Примеры. Представление р симметрич. группы
Sn в я-мерном векторном пространстве над полем /с,
переставляющее элементы базиса е15 . . ., еп, является
транзитивным импримитивным; одномерные подпро-
подпространства {kely . . ., ке„] образуют для р систему им-
импримитивности. Транзитивным импримитивным явля-
является также регулярное представление конечной группы
G над полем к; набор одномерных подпространств kg,
где g пробегает всю G, образует систему импримитив-
импримитивности. Более общо, любое мономиальное представление
конечной группы является импримитивным. Представ-
Представление циклич. группы порядка то^З поворотами дей-
действительной плоскости на углы, кратные 2л/т, при-
примитивно.
Понятие пмпримитивного представления тесно свя-
связано с понятием индицированного представления.
А именно, пусть р — импрп.митивное конечномерное пред-
представление конечной группы G с системой импримитив-
импримитивности {\\, . ¦ ., Vn). Множество {V1, . . ., Vn} разби-
разбивается в объединение орбит относительно действия груп-
группы С. определенного представлением р. Пусть {Vjx, . . .,
V;s) — полный набор представителей различных орбит
этого действия,
цт— представление группы Нт в V;n, определенное
сужением представления р на Нт, и рт— представление
группы G, индуцированное ц>т. Тогда р эквивалентно
прямой сумме представлений р1; . . ., р^. Обратно,
пусть Нг, . . ., IIs— какой-либо набор подгрупп груп-
группы G, фт — представление группы Нт в конечномерном
векторном пространстве Wrn, т=1, . . ., s, и рт—
представление группы G, индуцированное фт. Пусть
также {gmjY™ — система представителей левых смеж-
смежных классов группы G по Нт. Тогда прямая сумма пред-
представлений р1? . . ., ps импримитивна, a p(gmyl) (Wm),
/=1, . . ., гт, т=1, . . ., s, является системой импри-
импримитивности (здесь Wm канонически отождествляется
с подпространством в V).
Лит.: Ill Холл М., Теория групп, пер. с англ., М., 1962;
[2] К э р т и с Ч., Р а й н е р И., Теория представлений
конечных групп и ассоциативных алгебр, пер. с англ., М., 1969.
Н. Н. Вильяме, В. Л. Попов.
ИМЯ — языковое выражение, служащее для обо-
обозначения определенного объекта. Объект, обозначаемый
данным И., наз. денотатом. В математике широко
используются И. для конкретных математических объ-
объектов, напр, е, л — для известных трансцендентных чи-
чисел, sin — для функции синус, 0 — для пустого мно-
множества и т. д. Из таких простейших И. могут быть обра-
образованы составные имена, к-рые называют
объект, используя И. других объектов. Напр., sin л
есть другое И. числа 0. Имя не только называет дено-
денотат, но и выражает определенный смысл. Так, выраже-
выражения
lim ?/ п и sin-g-
п -> х
суть И. числа 1, однако смысл их различен. Смыслом
И. однозначно определяется его денотат. Если в со-
составном И. нек-рое входящее в него И. заменить на
И., имеющее тот же денотат, то денотат составного
И. не изменится. Если в составном И. нек-рое входя-
входящее в него И. заменить на его синоним (т. е. И.,
имеющее тот же смысл), то смысл составного И. не изме-
изменится.
Наряду с И. в математике употребляются выражения,
содержащие переменные и превращающиеся в И. после
подстановки вместо переменных И. объектов из области
значений переменных. Такие выражения наз. имен-
именными формами. Выражения ех, \ ——dt, где
х — переменная для действительных чисел, являются
примерами именных форм.
Лит.: [1] Чёрч А., Введение в математическую
логику, пер. с англ., т. 1, М., I960. В.Е.Плиско.
ИНВАРИАНТ — отображение ф рассматриваемой со-
совокупности М математич. объектов, снабженной фик-
фиксированным отношением эквивалентности р, в дру-
гую совокупность N математич. объектов, постоянное
на классах эквивалентности М по р (точнее: И. от-
отношения эквивалентности р на М). Если X — объект
из М, то весьма часто говорят, что <р(М) — И. объекта
X. Концепция И. является одной из важнейших в
математике, поскольку изучение И. непосредственно
связано с задачами классификации объектов того или
иного типа. По существу, целью всякой математич.
классификации является построение нек-рой полной
системы И. (по возможности, наиболее простой), то
есть такой системы, к-рая разделяет любые два не-
неэквивалентных объекта из рассматриваемой совокуп-
совокупности.
Простейшим примером И. могут служить так наз. И.
действительных плоских линий второго порядка. А имен-
именно, пусть М — множество всех таких линий, ар —
отношение эквивалентности на М, определенное пра-
правилом: Г?Л/ эквивалентна Г'?Л/ тогда и только тог-
тогда, когда Г' получается из Г движением (т. е. изоме-
трией) плоскости. Если Ax2-Jr2Bxy-\-Cy2Jr2Dx-\-2EyJr
-{-F=0 — уравнение линии Г?Л/ в какой-либо де-
декартовой системе координат, то числа а(Г)=А-\-С,
ABD
б(Г)= № и Д(Г) =
ВСЕ
DEF
не зависят от выбора сие-
темы координат (хотя само уравнение линии Г — за-
зависит). Если две линии Г и Г' ?Л/ эквивалентны, то
а(ГНа(Г), 6(Г)=6(Г) и А(Г)=Д (Г'). Иначе говоря,
отображения а, б и А множества М в множество N
всех действительных чисел являются И. отношения эк-
эквивалентности р — эти отображения и называют И.
действительных плоских линий второго порядка. Зна-
Значения этих И. на конкретной линии позволяют опреде-
определить тип этой линии (эллипс, гипербола, парабола,
пара прямых, мнимая кривая).
Другой классич. пример — двойное отношение упо-
упорядоченного набора четырех точек, лежащих на одной
прямой в действительном проективном пространстве.
Двойное отношение не изменится, если подвергнуть
эти точки проективному преобразованию всего про-
пространства. В этом примере: М — это множество упо-
упорядоченных четверок точек проективного пространст-
пространства, лежащих на одной прямой; отношение эквивалент-
эквивалентности р на М определяется по правилу: наборы F
и F'?М эквивалентны тогда и только тогда, когда F
переводится в F' проективным преобразованием про-
пространства; N — множество действительных чисел. Взя-
Взятие двойного отношения определяет отображение М в N,
являющееся И. отношения р; именно в этом смысле
говорят, что двойное отношение — И. четырех точек
(относительно проективной группы).
Сопоставление квадратичной форме от п переменных ее
ранга также доставляет пример И.: ранг не меняется
при замене формы на эквивалентную (коротко: ранг
есть И. квадратичной формы). Более того, если формы
рассматриваются над полем комплексных чисел, то
ранг составляет полную систему И. форм от п перемен-
переменных — две формы эквивалентны тогда и только тогда,
когда их ранги равны. Если же рассматривать формы
над полем действительных чисел, то появляется еще
один И.— сигнатура формы; ранг и сигнатура сое
тавляют полную систему И. В этих примерах М — мно-
множество квадратичных форм от п переменных, р — отно-
отношение эквивалентности, определенное невырожденны-
невырожденными линейными преобразованиями переменных, N — мно-
множество целых чисел.
Общая черта, объединяющая эти (и многие другие)
примеры, состоит в том, что отношение эквивалент-
эквивалентности р определяется с помощью нек-рой группы G
преобразований множества М (т. е. X и Y?M
р-эквивалентны тогда и только тогда, когда Y--=g(X)
для нек-рого g(zG); И., возникающие в таких слу-
чаях, наз. И. группы G. В первом примере — это пре-
преобразования М, индуцированные группой изометрий
плоскости, во втором — проективной группой, в треть-
третьем — полной линейной группой невырожденных пре-
преобразований переменных. Эти примеры иллюстрируют
общую концепцию, выдвинутую Ф. Клейном (F. Klein)
(так наз. эрлангенская программа), со-
согласно к-рой всякая группа преобразований может
служить группой «преобразований систем координат»
(автоморфизмов) в некоторой геометрии; величины,
определяемые объектами этой геометрии и не меняю-
меняющиеся при «смене координат» (инварианты), описыва-
описывают внутренние свойства рассматриваемой геометрии
и дают «структурную» классификацию ее теорем. Так,
напр., задача проективной геометрии — нахождение
И. (и соотношений между ними) для проективной груп-
группы, евклидовой геометрии — для группы движений
(изометрий) евклидова пространства и т. д. На этом
пути возникла классическая инвариантов теория, в
к-рой рассматриваются лишь И. специального вида
(полиномиальные или рациональные И. для групп ли-
линейных преобразований или, шире, числовые функции,
постоянные на орбитах нек-рой группы).
Однако общее понятие И. является более широким
и не может быть ограничено рамками И. групп преоб-
преобразований, поскольку не всегда отношение эквивалент-
эквивалентности р на рассматриваемом множестве М матема-
тич. объектов определено действием группы. Примеры
И. такого типа можно указать во многих областях ма-
математики. В алгебраич. и гомотопич. топологии каждо-
каждому топологнч. пространству сопоставляют его гомото-
гомотопич. группы, а также группы сингулярных гомологии
(с коэффициентами в нек-рой группе); эти группы явля-
являются И. относительно гомотопич. эквивалентности
пространств. В алгебраич. геометрии рассматривается
отношение бирациональной эквивалентности алгебра-
алгебраич. многообразий; размерность многообразия и, если
ограничиться рассмотрением гладких полных многооб-
многообразий, арифметич. род дают примеры И. этого отноше-
отношения эквивалентности. В дифференциальной топологии
многообразия рассматриваются с точностью до диф-
диффеоморфизма; классы Штифеля — Уитни многообра-
многообразия являются И. относительно этого отношения эквива-
эквивалентности. В классической дифференциальной геоме-
геометрии рассматривается полная кривизна поверхности;
она является И. изгибания. В теории абелевых групп
рассматриваются так наз. И. конечно порожденных
групп — ранг и порядки примарных компонент; они
составляют полный набор И. для множества таких
групп, рассматриваемых с точностью до изоморфизма.
В. Л. Попов.
Arf-ИНВАРИАНТ, инвариант Арф а,— ин-
инвариант квадратичной формы по модулю 2, заданной на
целочисленной решетке, снабженной билинейной ко-
сосимметрич. формой. Пусть П — целочисленная ре-
решетка размерности &=2т иг|з(х, ;/) — форма, для к-рой
лр(х, у) =—ty(y, x). Имеются базисы вида {еь /,,...,
ет, fm], наз. симплектическими, в к-рых матрица формы
г|з (х, у) приводится к блочнодиагональному виду: по
диагонали стоят блоки _iJ| ' т' е'
а в других местах — нули.
Пусть на П задано отображение
ifo : П-^Й2,
для к-рого
Уо(х, у)=%(^)+Ч:о(у)+Ч> (^, У) mod 2
— «квадратичная форма по модулю 2». Выражение
и наз. инвариантом Арфа [1 ]. Если это
выражение равно нулю, то существует симплектпческий
базис, на всех элементах к-рого форма г|з0 равна
нулю, если же это выражение равно единице, то суще-
существует симплектический базис, на всех элементах
к-рого, кроме е1 и Д, форма равна нулю, в то время
как
Лит.: [1] А г f С, «J. reinc und angew. Math.», 1941, Bd 183,
S. 148 — 67. А. В. Чернявский.
ИНВАРИАНТНАЯ МЕРА — 1) И. м. в измеримом
пространстве (X, ф) относительно измеримого преобра-
преобразования Т этого пространства — такая мера ц на SB,
что ц(А)—-и. (Т~1А) для всех А ?$8. Обычно подразу-
подразумевается, что мера конечная (т. е. ц.(Х)<оо) или по
крайней мере а-конечная (т. е. X можно представить
в виде счетного объединения [jXn, где (х(Х„)<°о- В наи-
наиболее важном случае, когда Т — биекция и отображе-
отображение 7'~1тоже измеримо (тогда говорят, что Т обратимо,
имея в виду обратимость в классе измеримых преобразо-
преобразований), инвариантность меры ц. эквивалентна тому, что
ц(А)=и. (ТА) для всех А ?33. Наконец, II. м. для се-
семейства (измеримых) преобразований — полугруппы,
группы, потока и т. д.— называется мера, инвариант-
инвариантная относительно всех преобразований из этого семей-
семейства. Понятие И. м. играет важную роль в теории ди-
намич. систем и эргодич. теории. В последней рассма-
рассматриваются различные свойства динамич. систем в про-
пространстве с мерой (X, SB, i-i), имеющих ц своей И. м.
Если динамич. система имеет несколько И. м., напр, ц
и v, то ее свойства как системы в (X, 5>3, и.) (свойства
по отношению к И. м. jx) могут отличаться от ее же
свойств как системы в (X, $}, v) (свойств по отноше-
отношению к v). Когда у фиксированной динамич. системы
рассматриваются разные И. м., то о свойствах системы
относительно И. м. ц, часто говорят короче как о свой-
свойствах меры jx (напр., «эргодичность jx» означает эрго-
эргодичность данной системы как системы в (А*, ф, |х), т. е.
отсутствие инвариантных множеств
с
Исторически первые примеры И. м. связаны с диффе-
дифференциальными свойствами преобразований, образующих
потоки нек-рых специальных типов на гладких многооб-
многообразиях (см. Гамилътонова система, Интегральный ин-
инвариант). В терминах (локальных) координат хх, . . .,
хп эти меры (л представляются в виде d[i = pdx1 . . . dxn,
причем имеются явные выражения для плотности
р=р(ж1, . . ., хп). В примерах алгебранч. происхожде-
происхождения (групповые сдвиги и т. д.) И. м. часто является мера
Хаара или мера, получающаяся из нее с помощью ка-
какой-нибудь естественной конструкции.
В топологич. динамике Н. Н. Боголюбовым и Н. М.
Крыловым ([1], см. также [2], [3]) доказано существо-
существование конечных эргодпч. И. м. для непрерывных по-
потоков и каскадов на метрнч. компакте X (возможны
нек-рые обобщения [4], [5], [6]). Неэргодические ко-
конечные И. м. являются, в нек-ром смысле, линейными
комбинациями эргодпческих; носители конечных И. м.
определенным образом связаны с поведением траекто-
траекторий в X (все эти И. м. сосредоточены на так наз. ми-
минимальном центре притяжения [3]). Не приходится
рассчитывать на более подробные утверждения о свой-
свойствах И. м. в общем случае — они могут быть совсем
различными. Так, в одном случае эргодич. И. м. может
быть сосредоточена в одной точке, в другом — быть
положительной для всех открытых подмножеств X
и обладать свойствами «квазислучайного» характера
(перемешивание, положительная энтропия и т. д.),
описание и исследование к-рых относится к эргодич.
теории (тогда как обращение к последней в предыду-
щем случае было бы бессодержательным). Поэтому име-
имеется ряд исследований о существовании И. м. с теми
или иными интересными свойствами у динамич. систем
того или иного специального типа.
Наконец, возможна чисто метрич. постановка во-
вопроса об И. м. Пусть динамич. система имеет квази-
квазиинвариантную меру (х; существует ли у нее И. м. V,
эквивалентная jx? (Обсуждение этой постановки воп-
вопроса см. в [7]. О другой постановке см. [8]). Ответ в
общем случае отрицательный, даже если требовать
только 0-конечности v, а (X, Ф, и.) — Лебега простран-
пространство [9]. Известны различные варианты необходимых и
достаточных условий существования конечной И. м.;
наиболее удачными представляются условия Хаджана
И Какутани [10], [8]. Д. В. Аносов.
2) И. м. в теории вероятностей определяется отно-
относительно переходной вероятности. Пусть (X, Л) — из-
измеримое пространство, где Л есть о-алгебра, и Р(х, А),
х?Х, А ?Л — переходная вероятность (т. е. Р(х,-),
есть вероятностная мора на Л при каждом х?Х и
Р(-, А) — измерима относительно Л при каждом
А?А)- Счетно-аддитивная мера ц на (X, Л) наз. ин-
инвариантной относительно Р, если
Р (х, А)ц(с1х), ЧА?Л-
Если Т — измеримое отображение (X, Л) в себя, то
мера ц инвариантна относительно Т тогда и только
тогда, когда она инвариантна относительно переходной
вероятности Р(х, А)=%Пх) (А), где %у(А)=1 при у?А и
%v(A)=0 при У^А. В. В. Сазонов.
Лит.: [1] Боголюбов Н. Н., Избр. труды, т. 1, К., 1969,
с. 411—463; 12] О к с т о б и Д ш.. «Успехи матем. наук»,
1953, т. 8, в. 3, с. 75—97; [3] Н е м ы ц к и й В. В., Степ а-
н о в В. В., Качественная теория дифференциальных уравне-
уравнений, 2 изд., М.— Л., 1949; [4J Боголюбов Н. Н., Избр.
труды, т. 1, К., 1969, с. 561 — 69; [5] Фомин С. В., «Матем.
сб.», 1943, т. 12, JSB 1, с. 99 — 108; [6] его же, «Язв. АН
СССР. Сер. матем.», 1950, т. 14, № 3, с. 261—74; [7] X а л-
мош П. Р., Лекции по эргодической теории, пер. с англ., М.,
1959; [8] В л а д и м и р о в Д. А., Булевы алгебры, М., 1969;
[9] Ornstein D. S., «Bull. Amer. Math. Soc», 1960, v. 66,
X. 4 p. 297—300; [10] Hayian A., Kakutani Sh.,
«Trans. Amer. Math. Soc», 1964, v. 110, p. 136—51; [11] Неве
Ж., Математические основы теории вероятностей, пер. с франц.,
М., 1969; 112] Д а н ф о р д Н., Шварц Д ж., Линейные
операторы. Общая теория, пер. с англ., М., 1962; [13] И о с и-
да К., Функциональный анализ, пер. с англ., М., 1967.
ИНВАРИАНТНАЯ МЕТРИКА — риманова метрика
m на многообразии М, не изменяющаяся при всех пре-
преобразованиях из данной группы Ли G преобразований.
Сама группа G при этом наз. группой движе-
движений (и з о м е т р и й) метрики m (или рпманова про-
пространства (М, тп)).
Группа Ли G преобразований многообразия М, дей-
действующая на М совершенно (т. е. так, что отображение
GXM—>MXM, (g, x)-+(gx, x) является собственным),
обладает инвариантной метрикой. Обратно, группа всех
движений любой римановой метрики (а также любая ее
замкнутая подгруппа) является совершенной группой
Ли преобразований. В этом случае стабилизатор
любой точки х?М — компактная подгруппа в G.
Если сама группа G компактна, то G-инвариантную
метрику т0 на М можно построить, усреднив произ-
произвольную метрику m на М по группе G:
где интеграл берется по мере Хаара.
В случае, когда группа G транзитивна, многообразие
М отождествляется с пространством смежных классов
GIH группы G по стабилизатору H=GX фиксированной
точки хо?М, и для существования С-инвариантной
метрики на М необходимо и достаточно, чтобы линей-
ная группа изотропии (см. Изотропии представление)
имела компактное замыкание в GL(TX (M)) (в част-
частности, достаточно, чтобы Н была компактна). В этом
случае пространство G/II редуктивно, т. с. алгебра Ли
@ группы G допускает разложение © = Jp + ЗУ}, где ,Cj —
подалгебра, отвечающая Л, QJ1 — подпространство, ин-
инвариантное относительно AdH, где Ad — присоединен-
присоединенное представление группы G. Если отождествить т
с Тх (М), то любая G-инвариантная метрика m на М
получается из нек-рой АсШ-инвариантной евклидовой
метрики ( ,) на ОЛ следующим образом:
mx(X, Y) = <g~1X, g-iY>, X, Y?TXM,
где g?G — такой элемент, что g.ro=a:.
Тензорные поля, связанные с G-инвариантной метри-
метрикой (тензор кривизны, его коварнантные производные
и т. п.), суть G-инвариантные поля. В случае однород-
однородного пространства M=G/7/ их значение в точке ха
выражается через операторы Номидзу
Lx(^End(?Q\), задаваемые формулой
где X*— поле скоростей однопараметрич. группы пре-
преобразований exp tX, v — оператор ковариантного диф-
дифференцирования римановой связности, а Ж — оператор
производной Ли. В частности, для оператора кривизны
Riem (X, Y) и для секционной кривизны К (X, Y) по
направлению, задаваемому ортонормальным базисом
X, У?0Л, справедливы следующие формулы:
Riem(X, Y) = [LX, LY]-L[X^ y],
К (X, У) == —<Riem (X, Y) X, Y> =
=<LXY, LXY>-<[X, Y)m, [X, Y]a>-<[Y, [Y, X]]m, X>-
— <Ljl, LyYy,
где Zm— проекция Z?® на 2Л вдоль §.
Операторы Номидзу выражаются в терминах алгеб-
алгебры Ли @ и метрики ( ,) формулой
2<LXY, Z> =
= <[Х, Y]m, Z>-<X, [Y, Z]m>-<Y, [X, Z]rn>,
где Х?<Ъ, У, Z?0Jb Из определения операторов Но-
Номидзу следует, что их действие на G-пнвариантные поля
отличается только знаком от действия ковариантной
производной в точке х0. Если риманово пространство
(G/H, т) не содержит плоских сомножителей в разло-
разложении де Рама, то линейная алгебра Ли, порожденная
операторами Номидзу Lx, X?(9>, совпадает с алгеброй
голономии пространства (GIH, т) в точке х0.
Описание геодезических инвариантной метрики на
однородном пространстве можно дать следующим обра-
образом. Пусть сначала M=G — группа Ли, действующая
на себе при помощи левых сдвигов. Пусть yt— геодези-
геодезическая левоинвариантной метрики т на группе Ли G
и Xt=yT1yt — соответствующая ей кривая в алгебре
Ли (У (годограф скорост и). Кривая Xt
удовлетворяет уравнению годографа
где ad* X — оператор, сопряженный оператору при-
присоединенного представления adX. Геодезическая yt
восстанавливается по своему годографу скорости xt
из дифференциального уравнения yf=ytXt (линейного,
если группа G линейна) или из функциональных соот-
соотношений
<XU (Ad y(t))Y> = const, Y?®,
задающих первые интегралы этого уравнения. Таким
образом, описание геодезических метрики т сводится
к интегрированию уравнения годографа, к-рое иногда
удается полностью проинтегрировать. Напр., в случае,
когда метрика т инвариантна и относительно правых
сдвигов, геодезические, проходящие через точку е,
«уть однопараметрич. подгруппы группы G. Такая
метрика существует на любой компактной группе Ли.
В случае произвольного однородного пространства
M=GlII инвариантную метрику т на G можно «под-
«поднять» до такой левоинвариантной метрики т на G,
что естественное расслоение G-+GIH риманова простран-
пространства (G, т) над римановым пространством (GlII, т) яв-
является римановым расслоением, т. е. при проектирова-
проектировании длина касательных векторов, ортогональных к
слою, не меняется. Для этого достаточно продолжить
метрику < ,} на всю алгебру C, полагая
<?, ШЬ = 0 и <Х, Y>= —TrLxLy(X, Y??>),
и разнести ее левыми сдвигами до метрики т на G.
Геодезические риманова пространства {G/H, т) явля-
являются проекциями ортогональных к слоям геодезиче-
геодезических риманова пространства (G, т).
Поскольку функция Х-^(Х, X) на ® всегда явля-
является первым интегралом уравнения годографа (и н-
тегралом энергии), соответствующее урав-
яению векторное поле на @ касается сфер (X, Х)~
= const. Это влечет за собой полноту уравнения годо-
годографа, а тем самым и полноту любой инвариантной ри-
мановой метрики на однородном пространстве. Для
псевдоримановых метрик свойство полноты, вообще
говоря, уже не имеет места. Однако любая инвариант-
инвариантная псевдориманова метрика на компактном однород-
однородном пространстве полна.
См. также Симметрическое пространство.
Лит.: [1] Хелгасон С, Дифференциальная геометрия
и симметрические пространства, пер. с англ., М., 1964; [2J Пет-
Петров А. 3., Новые методы в общей теории относительности,
М., 1966; [3] Kobayashi S., Nomizu К., Foundation
of differential geometry, v. 2, N.Y., 1969; [4] Kobayashi S.,
Transformation groups in differential geometry, B.—Hdlb.—N.Y.,
1972; [51 Wolf J. A., Spaces of constant curvature, N. Y.,
1967; [6] Liehnerowicz A., Geometrie des groupes de
1972; [51 Wolf j. A., Spaces of constant curvature, N. Y
1967; [6] Liehnerowicz A., Geometrie des groupes d
transformations, P., 1958. Д. В. Алексеевский.
ИНВАРИАНТНАЯ ПОДГРУППА — то же, что
нормальный делитель, т. е. подгруппа Н группы G,
переходящая в себя при любом внутреннем автоморфиз-
автоморфизме группы G.
ИНВАРИАНТНАЯ СТАТИСТИКА — статистика,
принимающая постоянные значения на орбитах, по-
порожденных группой взаимно однозначных измеримых
преобразований выборочного пространства. Таким об-
образом, если (?, 33) — выборочное пространство, G~
= {g} — группа взаимно однозначных 33-измеримых
преобразований ЭЁ на себя, a t(x) — И. с, то t(gx)~
= t(x) для всех я^ЭЁи^С И. с. играют важную роль
при построении инвариантных критериев.
Лит.: [1] Л е м а н Э,, Проверка статистических гипотез,
пер. с англ., М., 1964; [2] 3 а к с Ш., Теория статистических
выводов, пер. с англ., М., 1975; [3] Климов Г. П., Инвари-
Инвариантные выводы в статистике, М., 1973. М.С. Никулин.
ИНВАРИАНТНОЕ ИНТЕГРИРОВАНИЕ на груп-
группе — интегрирование функций на топологич. группе,
обладающее нек-рым определенным свойством инвари-
инвариантности относительно групповых операций. А именно,
пусть G — локально компактная топологич. группа,
C0(G) — векторное пространство всех непрерывных
•финитных (с компактными носителями) комплексно-
значных функций на G, / — интеграл на C0(G), т. е.
линейный положительный G/^0 при /^0) функционал
на Са (G). Интеграл / наз. левоинвариантным
(правоинвариантным), если / (gf) —If (со-
(соответственно / (fg)=--If) для всех g?G, f(zC0(G); здесь
{gf)(*)=t(g-1*h (fg) (*) = / (*ff - 4 •
Интеграл / наз. двусторонне инвариант-
н ы м, если он одновременно лево- и правоинвариантен.
Отображение /—>-/, где //=//, J(x)=f(x~1), определяет
взаимно однозначное соответствие между классами ле-
воинвариантных и правоинвариантных интегралов в
Со (G). Если 1=1, то интеграл / наз. инверсионно
инвариантным.
На всякой локально компактной группе G сущест-
существует ненулевой левоинвариантный интеграл, единст-
единственный с точностью до числового множителя (теоре-
(теорема Хаара — Неймана — Вей л я). Этот ин-
интеграл наз. левым интегралом Хаара.
Имеет место равенство
где g?G, f(zC0(G), а Л — непрерывный гомоморфизм
группы G в мультипликативную группу положитель-
положительных действительных чисел (положительный
характер). При этом 7/=/(//А). Характер А
наз. модулем группы G. Если A(g)=l, то группа
G наз. ун и модулярной. В этом случае /
является двусторонне инвариантным интегралом.
В частности, унимодулярпа всякая компактная груп-
группа (причем Л<оо,/=1/) и всякая дискретная группа
(причем If=^gf(g), f?C0(G)).
Согласно теореме Рисе а, всякий интеграл на
Со (G) является интегралом Лебега по нек-рой борелев-
ской мере ц, определяемой однозначно в классе регуляр-
регулярных борелевских мер, конечных на каждом компакт-
компактном подмножестве KczG. Лево- (право-) инвариантная
мера (х, отвечающая левому (правому) интегралу Хаара
в C0(G), наз. левой (правой) Хаара мерой на G.
Пусть Н — замкнутая подгруппа в G, Ао— модуль
группы Н. Если Ао продолжается до непрерывного по-
положительного характера группы G, то на левом одно-
однородном пространстве X = G/H существует относи-
относительно инвариантный интеграл /,
т. е. положительный функционал на пространстве С0(Х)
непрерывных финитных функций на X, удовлетворяю-
удовлетворяющий тождеству
для всех g?G, f?C0(X)\ здесь
Ш) (x)=f(g-1x), 8(g)=A0(g)/A(g),
А — модуль группы G. Этот интеграл определяется
по правилу //=/(8/), где I — левый интеграл Хаара
на G, 7 — функция на G такая, что
A0— левый интеграл Хаара на Н, а фя— сужение
функции q> на подгруппу Л). Это определение корректно,
поскольку /->/ является отображением Со (G) на С0(Х) и
Jf=O при /=0. С И. и. тесно связано понятие инва-
инвариантного среднего.
Лит.: [1] Бурбаки Н., Интегрирование. Векторное
интегрирование. Мера Хаара. Свертка и представления, пер.
с франц., М., 1970; [2] В е й л ь А., Интегрирование в тополо-
топологических группах и его применения, пер. с франц., М., 1950;
[3] Л ю м и с Л., Введение в абстрактный гармонический ана-
анализ, пер. с англ., М., 1956; [4] X ь ю и т т Э., Росс К.,
Абстрактный гармонический анализ, т. 1, пер. с англ., М.,
1976. Д. П. Желобенко.
ИНВАРИАНТНОЕ МНОЖЕСТВО фазового
пространства R динамической сис-
системы f(p,t) — множество М, заполненное целыми
траекториями, т. е. множество, удовлетворяющее ус-
условию
/ {М, t) = M, t?R,
где f(M, t) — образ множества М при преобразовании
группы f(p, t), соответствующем данному t.
Как множество метрич. пространства Л И. м. М
может иметь определенную топологии, структуру:
быть, напр., топологическим или гладким многообра-
многообразием, поверхностью, замкнутой жордановой кривой,
отдельной точкой. Об II. м. М говорят тогда как об
инвариантном многообразии, инва-
инвариантной поверхности, инвариант-
инвариантной криво й или инвариантной точке.
Инвариантную точку наз. обычно точкой покоя
дннамич. системы, поскольку для этой точки движение
сводится к покою: /(р, t) --p для всех значений t.
Замкнутая инвариантная кривая, не содержащая то-
точек покоя динамич. системы, всегда образована тра-
траекторией периодич. движения, т. е. движения, удов-
удовлетворяющего условию
/(р, t+T)=f(p, t)
для всех ifRn нек-рого Т>0 и наз. в силу этого пер и-
одической траекторией. Примерами ин-
инвариантных многообразий могут служить сфера, тор,
диск; инвариантных поверхностей — конус, лист Мё-
Мёбиуса, сфера с ручками; инвариантных множеств —
множество всех точек покоя, множества П^и Ар всех,
соответственно, ш- и сс-предельных точек движения
f(p, t), а также множество всех блуждающих W или
неблуждающих R\W точек.
Инвариантная точка динамич. системы на плоскости
L
dt
У), 1ТГ =
У)
A)
по характеру поведения траектории в ее окрестности
принадлежит к одному из 4 типов: узел, фокус, седло,
центр (см. рис.). Узел и фокус бывают асимптотически
устойчивыми или неустойчивыми, седловина — неус-
неустойчива, центр — устойчив. Индекс Пуанкаре узла,
центра и фокуса равен -j-1, седла —1.
В случае, когда матрица Якоби
df(x,y)\
J (х, у) =
вх ву
'Ах, У) 8g(x, у) J
а.х
правой части системы A) в точке покоя х=х0, у=у0
имеет собственные значения Хг, Я2 с ненулевой действи-
действительной частью, инвариантная точка является: узлом,
если значения Я,х, Я2 действительны и одного знака;
седлом, если значения "кл, Я2 действительны и разных
знаков; фокусом, если значения Х1; Я2 комплексно со-
сопряженные.
Во всех этих случаях тип особой точки системы A)
такой же, как у линейной системы, получаемой из A)
разложением ее правой части в ряд Тейлора в точке
х=х0, у — Уо, т. е. как тип точки a;j = O, t/1=0 системы
матрица (" bd) к-рой равна /(ж0, у0). Между траекто-
траекториями системы A) в окрестности особой точки рассма-
рассматриваемых типов и траекториями системы B) существует
более глубокая, чем отмечено выше, связь. Именно,
всякий раз, когда в окрестности инвариантной точки
х=хо~0, 7/=^7/0= 0 функции / и g голоморфны и матри-
матрица J(х0, у0) имеет, ненулевые действительные части
собственных значении, существует непрерывно диффе-
ренцируемая в нек-рой окрестности U точки х=0,
у = 0 замена переменных
x1^x + F1(x. у), y1 = y+F1(x, у),
; (О, 0) dF,- @, 0)
Fi(«, 0)=4^^
приводящая систему уравнений A) к системе B).
Если значения Хг, Я2 мнимые, то инвариантная точка
х0, уа может быть либо фокусом, либо центром. Вопрос
выяснения типа особой точки в этом случае представля-
представляет собой отдельную и трудную проблему — проблему
центра и фокуса — и требует для отличения центра от
фокуса привлечения более тонких критериев (см. [1],
[7]). Аналогичные трудности возникают при определе-
определении типа особой точки и в случае, когда матрица / (х0, у0)
вырождена.
Лит.: [1] -Н е м ы ц к и й В, В., Степанов В. В.,
Качественная теория дифференциальных уравнений, 2 изд.,
М.— Л., 1949; [2] Б и р к г о ф Д ж., Динамические системы,
пер. с англ., М.— Л., 1941; [3] Степанов В. В., Курс
дифференциальных уравнений, 8 изд., М., 1959; 14] X а р т-
ман Ф., Обыкновенные дифференциальные уравнения, пер.
с англ,, М., 1970; [5] М а л к и н И. Г., Теория устойчивости
движения, 2 изд., М., 19IH); [6] Ляпунов А. М., Собр. соч.,
т. 2, М.—Л., 1956; [7] Сибирский К. С, Алгебраиче-
Алгебраические инварианты дифференциальных уравнений и матриц, Киш.,
1976. А. М. Самойленко.
ИНВАРИАНТНОЕ ПОДМНОЖЕСТВО группы
G — подмножество Н группы G, содержащее вместе с
каждым своим элементом h все сопряженные с h в G
элементы, т. е. все элементы вида g hg. Инвар и-
антная подполугруппа — подполугруппа,
являющаяся одновременно инвариантным подмноже-
подмножеством. О. А. Иванова.
ИНВАРИАНТНОЕ ПОДПРОСТРАНСТВО, дону с
тимое подпространство, векторного про-
пространства V относительно данного множества М линей-
линейных отображений пространства V в себя — подпро-
подпространство U, удовлетворяющее условию ug с U для
всех u(^U, g?M (иначе М-п нвариантное, М-
допустимое подпространство).
Ю. И. Мерзляков.
ИНВАРИАНТНОЕ ПОДПРОСТРАНСТВО представ-
представления я группы (алгебры, кольца, полугруппы) X
в векторном пространстве (соответственно в топологич.
векторном пространстве) Е — векторное (соответст-
(соответственно замкнутое векторное) подпространство FczE
такое, что для любого ^F» любого х?Х выполняется
соотношение: n(x)^,(^F. Если Р — проектор в Е на F,
то F тогда и только тогда является И. п. представления
л, когда Рп(х)Р = л(х)Р для всех х?Х. Подпространст-
Подпространства {0} и ? являются IT. п. для любого представления в
пространстве Е; они наз. тривиальными И. п.;
остальные И. п. (если они есть) наз. нетривиальными.
См. также Сужение представления, Вполне приводимое
множество, Неприводимое представление. А.И.Штерн.
ИНВАРИАНТНОЕ СРЕДНЕЕ на группе или полу-
полугруппе G, точнее, инвариантное среднее на пространстве
X функций на G,— непрерывный линейный функционал
т на замкнутом подпространстве X пространства В (G)
всех ограниченных комплекснозначных функций на G,
снабженном равномерной нормой, содержащем посто-
постоянные функции и инвариантном относительно опера-
операций комплексного сопряжения, причем т и X удовле-
удовлетворяют следующим условиям: 1) пространство X ин-
инвариантно относительно левого сдвига, т. е. если f?X,
то и xf? X, Tjs,exf(t)=f(xt) для всех ж, t?G, /? А'; 2) т —
среднее на X, т. е. т(/) = то(/) для всех f?X и inf {f{x) }<:
<:т (/) <:sup {/ (х)} для всех действительнозначных / ? X;
3) m(xf)=m(f) для всех /fin всех x(^G. В этом случае
И. с. т наз. лево инвариантным сред-
н и м; аналогично определяется п р а в о и н в а р и-
антное среднее и двустороннее И. с. на G.
Если на X=B(G) существует двустороннее И. с,
то группа G нал. а м е н а б е л ь н о и. Аменабель-
Аменабельность группы G связана с существованием инвариант-
инвариантных мер относительно нек-рых групп преобразований,
связанных с G (см. [1]). Если G — локально компактная
топологии, группа, то на пространствах почти периодич.
функций и слабо почти периодич. функций на G суще-
существует нетривиальное левое И. с. С другой стороны,
следующие условия эквивалентны: 1) существует левое
И. с. на пространстве X = L°°(G); 2) существует левое
И. с. на пространстве X = CB{G) ограниченных непре-
непрерывных комплексных функций на G; 3) существует
левое И. с. на пространстве X=UCB(G) двусторонне
непрерывных ограниченных комплексных функций;
4) существует двустороннее И. с. на одном из прост-
пространств L°°(G), CB(G), UCB(G); 5) группа G не имеет до-
дополнительной серии представлений; 6) носитель регу-
регулярного представления группы G совпадает с дуальным
пространством этой группы; 7) единичная функция на
группе G может быть на любом компакте KaG равно-
равномерно аппроксимирована конечными линейными ком-
комбинациями матричных элементов регулярного пред-
представления группы О; 8) если jx — левая мера Хаара на
G, v — такая ограниченная комплексная регулярная
борелевская мера на G, что
для всех финитных непрерывных функций / на G, то
\ ; 9) для нек-рого <?>1, q?=°° любого е>0 и лю-
\
«) G
бого компакта KaG существует неотрицательная функ-
функция q>?LQ(G), ||ф||„=1, удовлетворяющая условию
IU-ф—ф!!<7<8 Для всех Х?.К\ Ю) предыдущее условие
выполняется для всех g>l, q^=°°; 11) для любого е>0
и любого компакта KczG существует такое борелевское
множество UaG, что 0<yi(U)<oo и (х-1 (U) jx (xUAU)<
<в для всех х?К; 12) любое непрерывное действие
группы G на компактном выпуклом множестве в ло-
локально выпуклом пространстве непрерывными аффин-
аффинными преобразованиями имеет неподвижную точку.
Локально компактная группа, удовлетворяющая любо-
любому из равносильных условий 1) — 12), наз. а м е-
набельной. Непрерывные образы амонабель-
ных групп, замкнутые подгруппы аменабельных групп,
расширения аменабельных групп с помощью амена-
аменабельных, индуктивные пределы аменабельных групп —
аменабельны. Равномерно ограниченное представление
аменабельной группы в гильбертовом пространстве
эквивалентно унитарному представлению в том же
пространстве. Нек-рые из перечисленных результатов
могут быть распространены на случай общих тополо-
гпч. групп, допускающих И. с. на пространстве огра-
ограниченных непрерывных комплексных функций. Теория
И. с. и аменабельных групп имеет существенные при-
приложения в теории динамич. систем, яргодич. теории,
теории алгебр Неймана и в абстрактном гармонич. ана-
анализе.
Лит.: [1] von Neumann J., «Pundam, math,», 1929,
v. 13, p. 73 —116; [2] Г р и n л и ф Ф., Инвариантные средние
на топологических группах и их приложения, пер. с англ., М.
1973; [3] Дик емье Ж., С*-алгебры и их представления,
пер. с франц., ИГ., 1974. А. И. Штерн.
ИНВАРИАНТНОСТИ ПРИНЦИП: пусть Хг,Х2,...~
независимые одинаково распределенные действитель-
действительные случайные величины с нулевым математич. ожи-
ожиданием и дисперсией а2; пусть построена случайная
ломаная
Yn()^{Slntl + ([nt])
а I n
где Sm = ?i=1Xi\ если / — непрерывная действительная
функция на пространстве С [0, 1] непрерывных функ-
ций на [О, 1] с равномерной нормой (или хотя бы непре-
непрерывная всюду за исключением множества винеровской
меры нуль), то f(Yn) по распределению сходится к
f(W), где W — винеровская случайная функция. Та-
Таким образом, предельное распределение для f(Yn) не
зависит от каких-либо специальных свойств величин
Хи Х2, . . .
Типичная схема использования И. п. состоит в отыс-
отыскании предельного распределения для f(Yn) путем
нахождения предельного распределения для f(Y'n),
где Yп — такая же, как Y п, случайная ломаная, по-
построенная по нек-рой другой специальным образом
подобранной последовательности х[, Хг, . . . Напр.,
если
f(x)= sup x (t),
О < < < 1
то / непрерывна на С, и так как
—— max Ьт
о ' п 1 < т < п
по распределению сходится к sup W(t). Для нахожде-
t
ния распределения sup W(t) используется последова-
последовательность {х'п} : Р{х'п=1} = Р{Х'п——1}=1/2, ив
результате вычислений получается
Р {sup l'F(i)<a} = -i/Al_ [a e-u'/2du, a^sO.
t У ft J 0
Лит.: [1] D о n s k e r M., «Mem, Amer. Math. Soc», 1951,
v. 6, p. 1—12; [2] Прохоров 10. В., «Теория вероятн. и
ее примен.», 1956, т. 1, № 2, с. 177—238; [3] Б и л л и н г с л и
П., Сходимость вероятностных мер, пер. с англ., М., 1977.
В. В. Сазонов.
ИНВАРИАНТНОСТЬ СТАТИСТИЧЕСКОЙ ПРОЦЕ-
ПРОЦЕДУРЫ — эквивариантность (см. ниже) какого-либо
решающего правила в статистич. задаче, постановка
к-рой допускает группу G симметрии, относительно этой
группы G. Понятие И. с. п. возникает в первую оче-
очередь в так наз. параметрич. задачах математич. ста-
статистики, когда имеется априорная информация; рас-
распределение вероятностей Р (dtst) исходов со наблюдений
принадлежит известному семейству {Рв , 8 ? 6 }. Го-
Говорят, что статистич. проблема решения Э-э к в и-
вариантна относительно группы G измеримых
преобразований g измеримого пространства (й, BQ)
исходов, если выполнены условия: 1) существует гомо-
гомоморфизм / группы G на нек-рую группу G преобразова-
преобразований пространства в параметров
со свойством
2) существует гомоморфизм k группы G на нек-рую
группу G измеримых преобразований измеримого про-
пространства (D, Вр) решений d,
со свойством
Mi(fl), g(d)) = L(Q, d),
где L@, d) — функция потерь; 3) вся дополнительная
априорная информация о возможных значениях па-
параметра (априорная плотность р (9), разбиение на аль-
альтернативы 0 = 0^ . . . U®.? и т. п.) G-инвариантна
или G-эквивариантна. При этих условиях решающее
правило б : a->6((o)^D, безразлично детерминирован-
ное пли рандомизированное, наз. инвариантной
(точнее G-э к в и вариантной) процедурой,
если
Риск
rfi (9) - Ео L (9, о (ш))
эквивариантной решающей процедуры б является
G-пнвариантом, в частности он не зависит от 9, если
группа G действует на 0 транзитнвно.
Как правило, в параметрич. задачах не существует
гарантированно наилучшей решающей процедуры,
к-рая минимизировала бы риск при каждом значении
параметра в?в. В частности, процедура может при-
приводить к очень малым значениям риска для нек-рых
8 за счет ухудшения качества при других априори
столь же возможных значениях параметра. Эквивари-
антность в какой-то степени обеспечивает беспри-
беспристрастность подхода. Когда группа G достаточно бога-
богата, существует оптимальная инвариантная процедура
с равномерно наименьшим среди инвариантных проце-
процедур риском.
Инвариантные процедуры широко применяются в
проверке гипотез (см. также Инвариантный крите-
критерий) и в оценивании параметра закона распределения.
Так, в задаче оценки неизвестного вектора средних
для семейства го-мерных нормальных законов
с единичной матрицей ковариаций и гауссовой функ-
функцией потерь 2/Су — аА~ оптимальной эквивариантной
оценкой будет обычное выборочное среднее
Группой G здесь служит произведение группы S ^ пе-
перенумерации наблюдений и группы Ort (m) движений
евклидова пространства Rm; <3=<3=Ort (m). При т^гЗ
в задаче существуют неэквивариаптные оценки, при-
приводящие к меньшему, чем у as*, риску при всех а, од-
однако область существенной «сверхэффективности» ока-
оказывается незначительной и безгранично уменьшается с
ростом объема N выборки. Возможность сверхэффок-
тивных процедур связана с некомпактностью G.
Эквивариантные статнетнч. процедуры возникают
также в ряде непараметрич. задач статистики, когда
априорное семейство распределений Р исходов сущест-
существенно бесконечномерно, а также при построении дове-
доверительных множеств для параметра G распределения
при наличии мешающих параметров.
Лит.: [1] Л е м а н Э., Проверка статистических гипотез,
пер. с англ., М., 196-4. Н. Н. Ченцов.
инвариантный дифференциальный опе-
оператор — оператор, не меняющий своего вида при
тех или иных преобразованиях пространства, в к-ром
он определен. Напр., если ?,{^-\— оператор с част-
частными производными, записанный в некоторой системе
координат (*!, . . ., хп), a xk=<pk(y), у=(уи . . ., у„) —
некоторое преобразование координат, порождающее
соответствующее отображение ср* в множестве функций
и(х) (каждой функции и(х) сопоставляется естествен-
естественным образом функция Ф*"(г/)), и
причем оператор L в правой части этого равенства вы-
выражается через д/дуктак же, как оператор L через dldxi,
в левой, то говорят, что L инвариантен относительно
преобразования q> (или L перестановочен с оператором
преобразования ф*). Наиболее важен случай, когда
И. д. о. инвариантен относительно нек-рой совокуп-
совокупности преобразований, образующей группу. Опредоле-
ние И. д. о. существенно усложняется при рассмотре-
рассмотрении систем функций, преобразующихся по нек-рому
представлению этой группы преобразований. И. д. о.,
связанные с группой Лоренца и ортогональной груп-
группой (волновой оператор, операторы Клейна — Гордона,
Лапласа и др.) играют важнейшую роль в ыатематнч.
физике. В анализе на дифференцируемых многообразиях
широко используются оператор внешнего дифферен-
дифференцирования d, инвариантный относительно диффеомор-
диффеоморфизмов, и метрически сопряженный с ним оператор б,
инвариантный относительно гладких преобразований,
сохраняющих метрический тензор. В теории групп
Ли весьма важны так наз. лево- или правоинвариант-
ные операторы относительно соответствующих сдвигов
на группе.
Лит.: 1] Петровский И. Г., Лекции об "уравнениях с
частными производными, 3 изд., М., 1961; [2] Наймарк М, А.,
Линейные представления группы Лоренца, М., 1958; [3] Де
Рам Ж., Дифференцируемые многообразия, пер. с франц.,
М., 1956; [4] X е л г а с о н С, Дифференциальная геометрия
и симметрические пространства, пер. с англ., М., 1964.
ИНВАРИАНТНЫЙ КРИТЕРИЙ — статистический
критерий, построенный на инвариантной статистике.
Пусть A, $8, Рв , Э?в) — выборочное пространство
и пусть проверяется гипотеза Йо : 6^в0сгв против
альтернативы Н1 : 9?0] = в\во, причем гипотеза //„
инвариантна относительно группы G= {g} взаимно од-
однозначных 23-измеримых преобразований пространства
SB на себя, т. о.
п0о = 0о и g&1 = Q1 для любого
где g—элемент индуцированной группы G={g} вза-
взаимно однозначных преобразований вероятностных мер
P - определяемых для всех 9?0 и g?G по
S
формуле P-S (B)=Pe(g-1B), B?$i. Так как гипоте-
гипотеза Ло инвариантна относительно группы G, то пред-
представляется естественным для проверки гипотезы //0
использовать критерий, построенный на инвариан-
инвариантной статистике относительно этой же группы G. Такой
критерий называется И. к., причем класс всех И. к,
совпадает с классом критериев, построенных на мак-
максимальном инварианте. В теории И. к. важную роль
играет теорема Хан та — Стейна: если гипо-
гипотеза Но инвариантна относительно группы G, то в классе
И. к., построенных для проверки гипотезы По, суще-
существует максиминный критерий. И. к. является част-
частным случаем инвариантной статистической процеду-
процедуры (см. Инвариантность статистической процедуры).
Лит.: [1] Ломан Э., Проверка статистических гипотез,
пер. с англ., М., 1964; 12] Шметтерер Л., Введение в ма-
математическую статистику, пер. с нем., М., 1976; [3] Hall W.,
Wijsman R., С h о s h 1., «Ann. Math, Statistics», 1965, v,
36, p. 575; [4] Климов Г. П., Инвариантные выводы в ста-
статистике, М,, 1973; [Г>] 3 а к с III., Теория статистических вы-
выводов, пер. с англ., М., 1975. М. С. Никулин.
ИНВАРИАНТНЫЙ ОБЪЕКТ на однородном про-
пространстве — поле геометрич. величин на однородном
пространстве M=GlH группы Ли G, не меняющееся
при всех преобразованиях из G. Более строгое опреде-
определение И. о. состоит в следующем. Пусть
я: E-+M=GlH
— локально тривиальное однородное расслоение над
однородным пространством M=GIH группы Ли G.
Сечение расслоения я наз. И. о. (типа я) на М, если
оно инвариантно относительно действия LE группы
G в пространстве Г (Е) сечений этого расслоения. Мно-
Множество И. о. типа я находится в естественном взаимно
однозначном соответствии с множеством //-инвариант-
ных элементов слоя рассматриваемого расслоения над
точкой т^М, соответствующей смежному классу еН.
Важнейший и наиболее изученный частный случай:
я есть векторное расслоение. Тогда Н действует в слое
над точкой т линейно, и И. о. типа я находятся во взэ-
имно однозначном соответствии с //-инвариантными
векторами этого слоя, что сводит их классификацию к
классич. задаче теории инвариантов. Для тензорных
расслоений (ассоциированных с касательным расслое-
расслоением) задача классификации И. о. сводится к нахожде-
нахождению инвариантов линейной группы изотропии.
И. о. часто возникают в следующем контексте.
Пусть s — поле геометрия, величин (геометрия, объект)
на гладком многообразии М, a Aut (s) — его группа
симметрии, т. е. множество таких диффеоморфизмов q>
многообразия М, ято q>*s=s, где ф*— индуцированное
ф преобразование s. И пусть группа Aut (s) содержит
транзитивную на М подгруппу G, являющуюся груп-
группой Ли. Тогда М отождествляется с однородным про-
пространством GIH, где Н — стационарная подгруппа про-
произвольной точки т?М, а объект s становится И. о. на
однородном пространстве G/ff. Классич. примерами
И. о. являются инвариантные риманова метрика, ком-
комплексная структура, симплектич. структура, кон-
контактная структура, обыкновенное дифференциальное
уравнение (в частности, пульверизация и связность),
дифференциальный оператор. Широкий класс И. о. до-
допускает единообразное описание в рамках теории
G-структур.
И. о. появляются естественным образом в различ-
различных областях математики и физики. Напр., линейное
дифференциальное уравнение с постоянными коэффи-
коэффициентами есть И. о. на евклидовом пространстве, рас-
рассматриваемом как однородное пространство векторной
группы. Эйлерово движение твердого тела происходит
по геодезическим левоинвариантнои римановои метрики
на группе SOC). Однородность пространства Ньютона
и пространства-времени Минковского вместе с принци-
принципом относительности Галилея приводят к разнообраз-
разнообразным И. о. в ньютоновской и релятивистской физике,
причем требование инвариантности часто позволяет
почти однозначно определить рассматриваемый объект
(уравнение, лангранжиан и т. п.) (см. [9]). Изучение
свойств И. о. обычно легко сводится к тем или иным
вопросам линейной алгебры (часто допускающим пол-
полное решение). Это определяет важную роль И. о. как
простых модельных примеров, проясняющих общую
ситуацию. Часто И. о. устроены проще, чем произволь-
произвольные объекты данного типа. Напр., в отличие от произ-
произвольных римановых метрик, любая инвариантная ри-
риманова метрика на однородном пространстве полна
(так же как и любая инвариантная псевдориманова ме-
метрика на компактном однородном пространстве), а лю-
любая ее самопересекающаяся геодезическая замкнута.
Вопросы классификации И.о. продвинуты в основном
для небольшого числа классических тензорных И. о.
Наиболее полные результаты получены для однородных
пространств компактных групп Ли.
Большой интерес с различных точек зрения пред-
представляет изучение И. о. на неоднородных G-простран-
ствах, т. е. геометрич. объектов, инвариантных отно-
относительно данной нетранзитивной группы Ли G преоб-
преобразований многообразия М. В случае компактной груп-
группы G для построения И. о. здесь часто используется
метод усреднения по группе (пример — теорема о су-
существовании G-инвариантной римановои метрики). Дру-
Другой более тонкий метод (применимый для более широ-
широкого класса групп Ли преобразований — так наз. со-
совершенных групп преобразований) основан на сущест-
существовании слайса (среза), наличие к-рого означает «почти
локальную тривиальность» расслоения многообразия М
на орбиты группы G.
Важным обобщением понятия И. о. является поня-
понятие ковариантного объекта: пусть на слоях Fm рас-
расслоения я задана дополнительная структура tm, гладко
зависящая от точки т?М (например, структура вектор-
векторного пространства) и Am=Aut(tm) — группа автомор-
физмов структуры tm слоя Fm. Множество сечений
к : m-^Sm?Am расслоения г|з: А={)тШАт-*-М об-
образует нек-рую группу автоморфизмов расслоения я,
называемую калибровочной группой.
Пусть К — некоторая ео подгруппа. Сечение s рассло-
расслоения я наз. /v-ковариантным объектом типа я на
M=GlH, если (L^s) (m)-^=kg(m) s (то) Vg?G, т?М,
где g—ykg— некоторый гомоморфизм G—>-ЛГ. Важнейший
частный случай получается, если я: E-*-M = GlH —
векторное расслоение, К — группа положительных
функций на М, рассматриваемая как группа автомор-
автоморфизмов расслоения я, ке=к(т) е, где к?К, т=я(е),
е?Е. В этом случае АТ-ковариантный объект наз. также
конформно инвариантным объек-
объектом, а определяемое им сечение соответствующего про-
проективного расслоения является И. о.
Лит.: [1] Kobayashi S., Nomizu К., Foundations
of differential geometry, v. 2, N.Y., 1969; [2] L i с h n e r o-
w i с z A., Geometrie des groupes de transformations, P., 1958;
[3] Wolf J. A., Spaces of constant curvature, N.Y., 1967;
[41 Kobayashi S., Transformation groups in differential-
geometry, В. —Hdlb. — N.Y., 1972; [5] X e л г а с о н С, Диф-
Дифференциальная геометрия и симметрические пространства, пер.
с англ., М., 1964; [б] К о м р а к о в Б. П., Дифференциально-
геометрические структуры и однородные пространства, ч. 1,
Минск, 1977; [7] Итоги науки. Алгебра. Топология. 19C2, М.,
1963; [8] Итоги науки. Алгебра. Топология, Геометрия. 1965,
М., 1967; [9]Levy-LeblondJ. M., «Commun. Math. Ph.»,
1969, v. 12, № 1, p. 64—79. Д. В. Алексеееспий.
ИНВАРИАНТОВ ТЕОРИЯ в классическом
определении — алгебраическая теория (иногда
называемая также алгебраической И. т.),
изучающая алгебраич. выражения (многочлены, ра-
рациональные функции или их совокупности), изменяю-
изменяющиеся определенным образом при невырожденных ли-
линейных заменах переменных. При этом, вообще говоря,
рассматривается не полная линейная группа (т. е. не
все множество невырожденных линейных замен пере-
переменных), а нек-рая ее подгруппа (напр., ортогональная,
симплектическая и др.). И. т. возникла под влиянием
ряда задач теории чисел, алгебры и геометрии. Еще К.
Гаусс (С. Gauss), занимаясь теорией бинарных квадра-
квадратичных форм, поставил задачу изучения многочленов
от коэффициентов формы ах*-\-2Ьху-\-су2, не меняю-
меняющихся при преобразовании этих коэффициентов, опреде-
определяемом подстановкой вида ж-э-аж+р1?/, у-*-ух-\-Ьу,
где аб — Py=1 и а, р\ у, б — целые. С другой стороны,
в проективной геометрии при внутренней характериза-
ции конфигураций и связей появляются алгебраич.
выражения от проективных координат, не меняющиеся
при проективной коллинеации. Предшествующей сту-
ступенью И. т. являлось также учение о детерминантах.
Арифметич. к алгебраич. вопросами, так или иначе
связанными с И. т., занимались К. Якоби (К. Jacobi),
Ф. Эйзенштейн (F. Eisenstein), Ш. Эрмит (Ch. Hermite).
Собственно И. т. как математич. дисциплина сложилась
к сер. 19 в. Этот период характеризуется интересом к
формально-алгебраич. проблемам и их приложениям к
геометрии. Понятия группы, инварианта и основные
задачи теории формулируются к этому времени точным
образом, и постепенно становится ясно, что факты клас-
сич. и проективной геометрии есть просто выражение
тождеств (сизигий) между инвариантами или ковариан-
тами соответствующей группы преобразований. Пер-
Первой работой по И. т. следует, видимо, считать «Мемуар
о гипердетерминантах» А. Кэли (A. Cayley, 1846). Все
обычные термины И. т.— инвариант, ковариант, ко-
комитант, дискриминант и т. д.— были введены Дж. Силь-
Сильвестром (J. Sylvester).
Одним из первых объектов изучения И. т. были так
наз. инварианты форм. Рассматривается фор-
форма степени г от и переменных с неопределенными коэффи-
коэффициентами:
после линейной замены переменных
где CLij— действительные или комплексные числа,
она преобразуется в форму
I (Х1, ¦ ¦ ¦¦> хп) = 2j^ ^ ^_ _raii, ..., lnxi ¦¦¦ хп'
так что указанное линейное преобразование перемен-
переменных определяет нек-рое преобразование коэффициентов
формы:
a»i in ""*" а*и . . ., in-
Многочлен q> (..., ait . . ., in, . . .) от коэффициентов
формы f(x1, . . ., хп) наз. (относительным) ин-
инвариантом формы, если при всех невырожден-
невырожденных линейных заменах переменных выполнено соот-
соотношение
ф("- а'и, . ... iB> •¦¦) =|а//!*ф(.-.. «.', <„. •••)-
где |а,-у| — определитель линейного преобразования, а
g — константа (в е с). Если ?=0, инвариант наз. а б-
с о л ю т н ы м. Так, простейшим примером инвариан-
инварианта является дискриминант D=b2—ас бинарной квадра-
квадратичной (ге=г=2) формы/(ж, y) = ax2Jr2bxy-\-cy2, или дис-
дискриминант Д=ЗЬ2с2 + 6 abed—4b3d—4ас3—а2й2 тернар-
тернарной (п=2, г=3) формы/(ж, y)=ax3+3bx2y + 3cxy2+dy3.
Если задана не одна, а несколько форм от одних и тех
же переменных, то можно рассматривать многочлены
ф от коэффициентов всех этих форм, преобразующиеся
указанным выше способом при линейной замене пере-
переменных,— так получается понятие совместного
инварианта системы форм. Напр., опре-
определитель \а[/\ есть совместный инвариант системы и ли-
линейных форм fi(xx, ..., х„) = ^•_ j aijx/, I < i <га-
Аналогичным образом может быть определен ковариант
и, более общим образом,— комитант.
Классич. постановка основной задачи И. т.— фак-
фактически вычислить инварианты, а также дать полное
их описание (то же для ковариантов). С этой целью были
разработаны всевозможные формальные процессы, поз-
позволяющие строить инварианты (поляризация, рести-
реституция, тождество Капелли, Q-процесс Кэли и т. п.).
Кульминацией этой деятельности является создание
так наз. символич. метода в И. т.— некоторого фор-
формального способа вычислять все инварианты степени
не выше заданной (см. [3], [6], [11]).
Развившаяся к 30-м гг. 20 в. глобальная теория по-
полупростых групп и их представлений позволила дать
следующую наиболее общую постановку основной задачи
классич. И. т. [6]. Задана произвольная группа С и ее
конечномерное линейное представление р в линейном
пространстве V над полем к. Если xt, . . .,хп— коор-
координаты в V (в каком-либо базисе), то каждый элемент
g?G определяет линейную замену переменных хг, . . .,
хп; производя эту замену переменных в произвольном
многочлене ц>(х1г . . ., х„), получают новый многочлен,
так что g индуцирует нек-рое преобразование (автомор-
(автоморфизм) кольца всех многочленов к [хг, . . ., хп\ от пере-
переменных х1, . . ., хп над полем к. Многочлен ц>(хг1 . . .,
хп), не меняющийся при всех таких преобразованиях (т.е.
когда g пробегает всю G), называется инвариан-
инвариантом представления р группы G. Все
инварианты образуют fc-алгебру, и цель И. т.— описа-
описание этой алгебры. Так, инварианты форм — это ин-
инварианты полной линейной группы относительно ее
представления в пространстве симметрич. тензоров фик-
фиксированного ранга основного (или сопряженного) про-
пространства (коэффициенты исходной формы / и есть ком-
компоненты этого тензора), рассмотрение ковариантов сво-
сводится к изучению алгебры инвариантов для представле-
представления в пространстве тензоров смешанной валентности.
В такой постановке задача описания инвариантов есть
частный случай следующей общей задачи теории ли-
линейных представлений: разложить пространство тен-
тензоров заданной валентности на неприводимые инвари-
инвариантные подпространства относительно заданной груп-
группы линейных преобразований основного линейного
пространства (отыскание инвариантов может быть све-
сведено к выделению одномерных инвариантных подпро-
подпространств).
Уже на первых этапах развития И. т. было обнару-
обнаружено следующее обстоятельство, позволившее обозреть
всю систему инвариантов в целом: во всех разобранных
случаях удавалось выделить конечное число базис-
базисных инвариантов q>l7 . . ., ц>т, т. е. таких
инвариантов, что всякий другой инвариант q> заданно-
заданного представления может быть выражен в виде много-
многочлена от них: ф=^(ф1, . . ., ф,л). Иначе говоря, алге-
алгебра инвариантов оказывалась конечно порожденной.
Выяснилось также, что эти базисные инварианты, вооб-
вообще говоря, не являются независимыми (т. е. алгебра ин-
инвариантов не является свободной алгеброй):могут су-
существовать нетривиальные многочлены Р (tlt . . ., tm),
называемые соотношениями, или сизиги-
сизигиями, к-рые после подстановки ?,- = q>/, l<is^/n,
тождественно обращаются в нуль. В самом множеств©
соотношений можно снова указать конечное число ба-
базисных соотношений, алгебраич. следствиями к-рых
являются все остальные (соотношения образуют идеал
в кольце многочленов от переменных tt, . . ., tm и
базисные соотношения — его образующие). В свою
очередь, базисные соотношения сами, вообще говоря,
не независимы — так могут быть определены вторы©
сизигии и т. д. Построенная цепь сизигий всегда оказы-
оказывалась конечной. Напр., если G — симметрическая
группа всех перестановок координат х1, . . ., хп, то
алгебра инвариантов есть алгебра всех симметрических
многочленов от i,, . . ., ж„; элементарные симметрич.
многочлены являются базисными инвариантами, к-ры©
алгебраически независимы (в этом случае сизигий нет).
Эти факты привели к формулировке двух основных
проблем в классич. И. т.:
1. Доказать конечную порожденность алгебры инва-
инвариантов заданного представления заданной группы
(первая основная теорема И. т.) и определить систему
базисных инвариантов.
2. Доказать существование конечного базиса сизи-
сизигий (вторая основная теорема И. т.) и найти его.
Первая основная теорема И. т. для инвариантов
формы произвольной степени от произвольного конеч-
конечного числа неизвестных была доказана Д. Гильбертом
(D. Hilbert) [1] (см. также Гильберта теорема об ин-
инвариантах). Им же доказано, что вторая основная
теорема И. т. справедлива во всех случаях, когда
справедлива первая основная теорема И. т., а также,
что в этом случае цепь сигизий всегда конечна. Д. Гиль-
Гильберт получил доказательства основных теорем клас-
классич. И. т. на базе доказанных им (специально с этой
целью) общих абстрактных алгебраич. утверждений,
составивших позднее фундамент современной комму-
коммутативной алгебры (Гильберта теорема о базисе, Гиль-
Гильберта теорема о сизигиях, Гильберта теорема о кор-
корнях). Первоначальное доказательство первой основ-
основной теоремы И. т. было неконструктивным и не давало
оценки сверху на степени базисных инвариантов, однако
позднее такие оценки были получены [2] (см. также [11]).
Указанные выше формальные вычислительные методы
И. т. позволяют, по крайней мере, в принципе, найти с
использованием этих оценок все базисные инварианты.
В 30-х гг. 20 в. Г. Вейль (Н. Weyl), развивая идею
Д. Гильберта и А. Гурвица (A. Hurvitz, см. [14]), до-
доказал первую основную теорему И. т. для конечномер-
конечномерных представлений любых компактных групп Ли и для
конечномерных представлений любых комплексных
полупростых групп Ли [6]. Книга [6], подводящая итог
развития классич. И. т., содержит описание базисных
инвариантов и сизигий для представлении классиче-
классических групп, а также нек-рых других групп. Одним из
важных приложений методов И. т. явилось описание
чисел Бетти классических компактных групп Ли.
Доказательство второй основной теоремы И. т. вскры-
вскрыло общую алгебраич. природу этой теоремы (она явля-
является следствием теоремы Гильберта о базисе). Пытаясь
выяснить, справедливо ли это же в отношении первой
основной теоремы И. т.. Д. Гильберт сформулировал
следующую проблему A4-я проблема Гиль-
Гильберта): пусть А- — поло, А = к [ж,, . . ., хп] — алгеб-
алгебра многочленов над к от переменных х1, . . ., хп и
L — произвольное подполе поля частных алгебры А,
содержащее А-; будет ли алгебра A [\L конечно порожде-
порождена над к? Из положительного ответа на этот вопрос вы-
вытекала бы справедливость первой основной теоремы
И. т. для любых групп. Отрицательное решение 14-й
проблемы Гильберта было получено в [9], где приведен
пример представления коммутативной унипотентной
группы, для к-рого алгебра инвариантов не имеет ко-
конечного числа образующих. В 50-х гг. 20 в. получен
ряд результатов об инвариантах коночных групп, в осо-
особенности групп, порожденных отражениями (см. Отра-
Отражений группа, Копстера группа). Было доказано [13],
{14], что конечные линейные комплексные группы, по-
порожденные унитарными отражениями, могут быть оха-
охарактеризованы как конечные линейные группы, алгеб-
алгебра инвариантов к-рых не имеет сизигий.
Новый этап развития И. т. связан с расширением
круга задач и геометрич. приложений этой теории. Со-
Современная П. т. (или геометрическая И. т.)
стала частью общей теории алгебраич. групп преобра-
преобразовании; ее фундаментом является теория алгебраич.
групп, построенная в 50-х гг. 20 в., а языком — язык ал-
алгебраич. геометрии. В отличие от классич. 11. т., основ-
основным объектом к-рой являлось кольцо многочленов от п
переменных над полем к вместе с группой автоморфиз-
автоморфизмов, индуцированных линейными заменами перемен-
переменных, современная .И. т. рассматривает произвольную
конечно порожденную ^-алгебру Л и алгебраич. груп-
группу G ее ^-автоморфизмов. Вместо линейного простран-
пространства V и представления р рассматривается произволь-
произвольное аффинное алгебраич. многообразие X и алгебраич.
группа G его алгебраич. преобразований (автоморфиз-
(автоморфизмов), так что Я — это кольцо регулярных функций на
X, а действие G на R индуцировано действием G на X.
Элементы из R, неподвижные относительно G, есть
инварианты; все их множество образует ^-алгебру RG.
Обобщаются и другие понятия классич. И. т., напр,
комитант — это регулярное отображение одного та-
такого многообразия в другое, коммутирующее с дей-
действием группы; если Д" конечно порождена, то гово-
говорят, что выполнена первая основная теорема И. т.
Устанавливается, что R0 будет конечно порождена,
если G — геометрически редуктивная группа (см.
Мамфорда гипотеза). Во многих важных случаях,
напр, в приложении к проблеме модулей, G является
именно такой группой. Если IXй конечно порождена, то
существует аффинное алгебраич. многообразие W,
для к-рого Ra является алгеброй регулярных функций;
включение R°czR индуцирует морфизм я : X—t-W.
Если G геометрически редуктивна, то многообразие W
классифицирует замкнутые орбиты G в W: отображение
я сюръективно, и в каждом его слое лежит ровно одна
замкнутая орбита. Необходимое условие существования
фактормногообразия X по G — замкнутость всех ор-
орбит — оказывается в этом случае и достаточным, и
этим фактормногообразием оказывается W. Отсюда
видна роль Ra в решении геометрич. проблем классифи-
кации и построении фактормногообразий; вместе с тем
изучение Ra (к-рое было конечной целью классич.
И. т.) есть лишь начальный этап решения этих геоме-
трич. проблем, ибо значение Ra не даот, вообще говоря,
полной информации об орбитах G в X и потому должно
сочетаться с рассмотрением незамкнутых орбит, их за-
замыканий и стабилизаторов (так наз. орбитальных
разложений). Более того, изучение действий ал-
гебраич. групп на аффинных алгебраич. многообразиях
есть лишь «локальная часть» общей теории алгебраич.
групп преобразований (так же, как теория аффинных
многообразий — «локальная часть» общей теории ал-
гебранч. многообразий).
В общем случае рассматривается алгебраическое
(регулярное) действие G на произвольном алгебраич.
многообразии X (склеенном из аффинных кусков), так
что, напр., решение задачи о построении фактормно-
гообразия X (или подходящего открытого подмноже-
подмножества в X) по действию G сводится к рассмотрению
G-инвариантного аффинного покрытия X и примене-
применению указанной выше конструкции к каждому элементу
этого покрытия с последующей «склейкой» полученных
аффинных фактормногообразий. Для успешного приме-
применения этой процедуры следует, вообще говоря, заме-
заменить X на пек-рое его инвариантное открытое подмно-
подмножество (само X может и не допускать инвариантного
аффинного покрытия).
В настоящее время исследования по теории алгебраич.
групп преобразований ведутся в различных направле-
направлениях, из к-рых можно выделить следующие. Получе-
Получение информации о свойствах общего положения точек
многообразия X, на к-ром регулярно действует алгеб-
алгебраич. группа G. Описание орбитальных разложений
различных конкретных действий (в основном, линей-
линейных представлений). Теоремы стратификации общих
пространств преобразований на более простые, стан-
стандартные пространства, Теоремы о фактормногообра-
зиях, пространствах орбит, сечениях, квазисечениях
и «слайсах»; многообразия неподвижных точек. Теоремы
об эквиварнантных вложениях. Критерии аффинности
и квазиаффинности орбит (см. Мацусимы критерий).
Структура замыканий орбит различных специальных
видов, теория квазиодиородных многообразий (т. е.
многообразий с плотной орбитой), действия с три-
тривиальной алгеброй инвариантов. Алгебраич. свойства
колец инвариантов, алгебро-геометрич. свойства про-
пространств преобразований и фактормногообразий. Связь
с теорией особенностей [16]. Проблема рациональности
полей инвариантов, связь с теорией алгебранч. торов и
алгебраич. теорией чисел [17].
Лит.: [1] Hilbert D., «Math. Ann.», 1890, Bd 36
S. 473—534; [2] его же, там же, 1893, Bd 42, S. 313—73;
[3] Weitzcnbock R., Invarianten-Theorie, Groningen
1923; [4] Hurvitz A., «Gott. Nachr.», 1897, S. 71—90; [sj
Клейн Ф,, Лекции о развитии математики в XIX столетии,
пер. с нем,, ч. 1, М.— Л., 1937; l6j Г у р е в и ч Г. Б., Основы
теории алгебраических инвариантов, М,— Л., 1948; [7] Вейль
Г., Классические группы, их инварианты и представления, пер
с англ., М., 1947; [8] Проблемы Гильберта, М., 1969; L9] N а-
i> a t a M., в кн.: Procledings of the International Congress of
Mathematics (Edinburgh, 1958), Camb., 1960, p. 459—62; Qo]
с г о ж е, «Amer. J. Math,», 1959, v. 81, p. 766—72; hi]
M u in г о r d D., Geometric Invariant Theory, B.—Hdlb,—
N. Y., 1965; [12] Дьедонне Ж., К e p p о л Д ж., М а м-
ф о р д Д., Геометрическая теория инвариантов, пер. с англ
М., 1974; [13] Fogarty S., Invariant theory, N.Y.—Amst '
1969; [14] С he valley С, «Amcr. J. Math.», 1955, v. 77
p. 778-82- [15] ChephardG. CTodd J. A., «Canad
j. Math.», 1954, v. 6, p. 274—304; 116] «Proc. Symp. Pure
Math.», 1975, v. 29, p. 633—42; [17] Воскресен-
c к и ii В. Б., «Успехи матем. наук», 1972, т. 28, в. 4, с
77 — 102 В.Л.Попов.
ИНВЕРСИЯ — преобразование, переводящее каж-
каждую точку А плоскости в такую точку А', лежащую на
луче ОА, что ОА' -ОА = к, где к — некоторое постоян-
постоянное действительное число. Точка О наз. центром,
или полюсом И., к — степенью, или к о э ф-
флциентом И. Если й=а2, то точки окружности
5 с центром О и радиусом а переходят при И. сами в
юбя; внешние по отношению к S точки переходят во
внутренние, а внутренние — во внешние (иногда И.
наз. симметрией относительно ок-
окру ж н о с т и). Центр И. не имеет образа. И. с отри-
отрицательной степенью к равносильна И. с тем центром О и
положительной степенью |А|, сопровождаемой симме-
симметрией относительно точки О. Иногда И. с положитель-
положительной степенью наз. гиперболической И., а с
отрицательной степенью — эллиптической И.,
или а н т и н н в е р с и е й. Прямая, проходящая
через центр И., переходит при И. сама в себя. Прямая,
но проходящая через центр П., переходит в окружность,
проходящую через центр И. Окружность, проходящая
через центр П., переходит в прямую, не проходящую
через центр И. Окружность, не проходящая через
центр И., переходит в окружность, не проходящую через
центр И. В декартовых прямоугольных координатах И.
может быть задана формулами:
х> ^ hx ,/ hV
или в плоскости комплексного переменного: z=klz.
И. является антиконформным преобразованием, т. е.
сохраняет углы между линиями и меняет ориентацию.
Аналогично определяется И. в пространстве.
Иногда И. определяется как отображение плоскости,
сопоставляющее каждой точке А, отличной от центра
заданной связки окружностей, точку А' пересечения
окружностей связки, проходящих через точку А.
Лит.: [1] Энциклопедия элементарной математики, кн. 4,
Геометрия, М., 1963; L2] Ш а б а т Б. В., Введение в комплек-
комплексный анализ, М., 1969. А. Б. Иванов.
ИНВЕРСИЯ в комбинаторике, беспоря-
беспорядок, — перестановка из п элементов, в к-рой элемент
j не может занимать г-ю позицию, г=1, 2, . . ., п. За-
Задача подсчета числа Dn инверсий известна как «зада-
«задача о встречах». Справедлива следующая формула:
И.— частный случай перестановок, удовлетворяющих
заданным ограничениям на позиции переставляемых
элементов. Напр., известная задача «о супружеских
парах» состоит в подсчете числа перестановок Un, про-
противоречивых двум перестановкам: A, 2, . . ., п) и
(в, 1,2,.. ., п—1). (Две перестановки из п элементов
противоречивы, если г-й элемент, i=l, 2, . . ., п,
занимает в них разные позиции.) Числа Un вычисля-
вычисляются по формуле:
Т7 v^n in
Через О„и Un подсчитывается число L(r, n) латинских
прямоугольников размера гХп при г=2, 3, а именно
LB, n) = n\Dn,
L C, n) = n\2jk = Q t^k) Dn-kDkUn_
2jk = Q ^k) 2k.
Лит.: [l] P а й з е р Г. Д ж., Комбинаторная математика,
пер. с англ., М., 1966; [2] Риордан Д ж., Введение в ком-
комбинаторный анализ, пер. с англ., М., 1963. В. М. Михеев.
ИНВЕРСНАЯ ПОЛУГРУППА — полугруппа, в крой
для любого элемента а существует единственный ин-
инверсный к нему элемент а~г (см. Регулярный элемент).
Свойство полугруппы S быть инверсной эквивалентно
каждому из следующих: S регулярная полугруппа и лю-
любые два ее идемпотента перестановочны (таким обра-
образом, множество всех идемпотентов И. п. есть по-
полурешетка, см. Идемпотентов полугруппа); каждый
левый и каждый правый главные идеалы полугруппы S
имеют единственный порождающий идемпотент. Вся-
Всякая группа будет И. п., группы и только они являют-
являются И. п. с единственным идемпотентом. Важную роле>
при изучении И. п. играет следующее отношение е с-
тественного частичного порядка <:
на произвольной И. п. S : а<:й тогда и только тогда,
когда ab-^^aa-1 (a, b?S). На полурешетке идемпо-
тентов И. п. оно совпадает с естественным частичным
порядком этой полурешетки (см. Идемпотент). Полу-
Полурешетка инверсных полугрупп (см. Связка полугрупп)
будет И. п. Сдвиговая оболочка И. п. (см. Сдвиги полу-
полугрупп) также будет И. п. [7]. Всякая конгруэнция на
И. п. определяется своими классами, содержащими
идемпотенты.
Пусть Jx — множество всех взаимно однозначных
частичных преобразований множества X (включая и
«пустое преобразование» — отображение пустого мно-
множества на себя). Относительно операции суперпозиции
множество Jx является И. п., к-рая наз. симметри-
симметрической И. п. на множестве X. Принципиальное
значение имеет следующая теорема Вагнера —
Престона: произвольная И. п. S изоморфно вло-
жима в симметрическую И. п. J$.
Теория И. п. представляет собой один из важных и
глубоко разработанных разделов теории полугрупп.
Изучены представления И. п. взаимно однозначными
частичными преобразованиями и матрицами над полем
(см. [1]). Исследуются конгруэнции на И. п. Изучаются
И. п. с условиями конечности. Выделен целый ряд важ-
важных специальных типов И. п. Накладываемые при этом
ограничения по большей части либо носят характер
простоты в нек-ром смысле (напр., бипростота, см.
Простая полугруппа), либо относятся к полурешетке
идемпотентов Е, либо являются комбинациями усло-
условий обоих типов. Ограничения на Е могут касаться аб-
абстрактных свойств Е как полурешетки (например, Е —
цепь специального вида), либо тех или иных относи-
относительных свойств Е в полугруппе, в частности поведе-
поведения Е относительно нек-рых конгруэнции. На любой
И. п. 5 существует наименьшая конгруэнция а с тем
свойством, что Sla есть группа (наименьшая
групповая конгруэнция), причем
а={(а, Ь)\ае = Ье для некоторого е?Е}.
И. п. наз. собственной, если Е составляет
ст-класс. На любой И. п. S существует наибольшая кон-
конгруэнция (х, разделяющая идемпотенты, причем
jt = {(a, b) | a~1ea = b~1eb для любого е?Е}
и ft содержится в отношении ffl (см. Грина отношения
эквивалентности); И. п. наз. фундаменталь-
фундаментальной, если |х совпадает с отношением равенства. Для
упомянутых типов И. п. получено немало структурных
теорем. При этом во многих случаях описание И. п. осу-
осуществляется «по модулю групп»: группы выступают в
качестве блоков различных конструкций, в к-рых уча-
участвуют также полурешетки, гомоморфизмы групп и
т. п. Таковы, напр., типичные описания клиффор-
довых И. п. (см. Клиффордова полугруппа) и вполне
О-простых И. п. (см. Брандта полугруппа).
И. п. можно рассматривать и как универсальные
алгебры с двумя операциями: бинарной — умножени-
умножением и унарной — взятием инверсного элемента. Получе-
Получена классификация м о н о г е н н ы х (т. е. порожден-
порожденных одним элементом) И. п. как таких алгебр [6], [9].
Относительно указанных операций класс всех И. п. яв-
является многообразием; он может быть задан, напр.,
следующей системой тождеств [8]:
(xy)z = x(yz), (х~1)-1 = х, хх~1х = х,
Лит.: [1] Клиффорд А., Престон Г., Алгебраи-
Алгебраическая теория полугрупп, пер. с англ., т. 1—2, М., 1972; L2]
Ляпин Е. С, Полугруппы, М., 1960; [3] Курош А. Г.,
Общая алгебра. Лекции 1969—1970 учебного года, М., 1974;
[4] Вагнер В. В., «Докл. АН СССР», 1952, т. 84, №6,
с. 1119—22; [5] Preston G., «J. Lond. Math. Soc», 1954,
v. 29, Ns 4, p. 396—403; [6] Г л у с к и н Л. М., «Матем. сб.»,
1957, т. 41, №1, с. 23—36; [7] Понизовский И. С,
«Успехи матем. наук», 1965, т. 20, М 6, с. 147—48; [8] Теория
полугрупп и ее приложения, в. 1, Саратов, 1965, с. 286—324;
[9] Ершова Т. И., «Матем. зап. Уральского ун-та», 1971,
т. 8, Nt 1, с. 30—33; [10] Mann W. D., в кн.: Semigroups,
N.Y.—L., 1969, р. 107—23; [11] О'С а г г о 1 L., «J. Algebra»,
1976, v. 42, р. 26—40. Л. Н. Шеврин.
ИНВОЛЮТИВНОЕ РАСПРЕДЕЛЕНИЕ — геометри-
геометрическая интерпретация вполне интегрируемой диффе-
дифференциальной системы на и-мерном дифференцируемом
многообразии Мп класса С*, к^З. р-м е р н ы м рас-
распределением (или дифференциальной
системой размерности р) класса С, 1 <:
на Мп наз. функция, относящая каждой точке
р-мерное линейное подпространство D (х)
касательного пространства Тх(Мп), так что х имеет
окрестность U ср такими С-векторными полями Х1У . . .
. . ., Хр на ней, что векторы Хг(у), . . ., Хр(у) обра-
образуют базис пространства D (у) для каждой точки y?U.
Распределение D наз. инволютивным, если для
всех точек y?U
Это же условие формулируется и в терминах диф-
дифференциальных форм. Распределение!) характеризуется
тем, что
D (У) = {Х?Ту (М«):ш« (у) (Х) = 0), р < а<гс,
где wP + 1, . . ., со" суть 1-формы класса С, линейно
независимые в каждой точке x?U, т. е. D локально
эквивалентно системе дифференциальных уравнений
ша=0. Тогда D является И. р., если на U существуют
1-формы со? такие, что
т. е. внешние дифференциалы du>a принадлежат иде-
идеалу, порожденному формами о)Р.
Распределение D класса С на Мп инволютивно тогда
и только тогда, когда оно (как дифференциальная сис-
система) есть интегрируемая система (теорема Фро-
б е н и у с а).
Лит.: [1] Шевалле К., Теория групп Ли, т. 1, пер.
с англ., М., 1948; [2] Нарасимхан Р., Анализ на дейст-
действительных и комплексных многообразиях, пер. с англ., М.,
1971. Ю. Г. Пумисте.
ИНВОЛЮЦИОННАЯ СИСТЕМА — система диффе-
дифференциальных уравнений с частными производными 1-го
порядка
Ft(x, и, р)=0, ls?is?m, A)
где х= (xlt . . ., х„), и=и(хх, . . ., xn),p = (Pl, . . ., р„) =
= (-^- , . . ., -~ ) , для к-рой все Япоби скобки равны
уахг oxn j
нулю
[F;, Fj]=O, 1<I, j<m, B)
тождественно по (х, и, р). Равенства B) наз. усло-
условиями разрешимости.
Для квазилинейных систем это определение несколько
видоизменяется. Пусть все функции —--, 1<г<:т,
opk
l<fc<n, не зависят от р=(рг, ¦ ¦ ., рп). Тогда этим
свойством обладают и функции
dF,. дЖ,-
[Fi, FA—Fi—J- -i-Fj-jr-!- .
L " J' ' ди ¦ J ди
В классе квазилинейных уравнений условие инволю-
ционностп системы определяется равенствами
OF- dFt
[F F]F F 0 К
Когда F; не зависят от и, это определение совпадает с
предыдущим. Иногда последнее определение инволю-
ционности распространяют на все системы вида A).
Если система A) линейна, однородна и записана
в виде
Р{ (и) = 0, 1< i<ro,
где Р{ — линейные дифференциальные операторы 1-го
порядка, то ее инволюционность можно определить как
условие коммутируемости PjPj=PjPi для всех 1<{,
Всякая И. с. является полной системой. Обратно,
если A) полная система и имеет нормальную форму,
т. е. 1<т<л и
Ft(x, и, p) = Pi — fi(x, и, рт + 1, ..., рп), ls
то она инволюционна. Это позволяет привести полную
систему к И. с, если т<л, и ее можно разрешить не-
неособым преобразованием относительно нек-рых т
переменных р=(рг, . • ., рп)-
Если система A) не зависит от и, т=п, определитель
I а*\-
¦—- ^=0 иPi=pi(x) разрешены из уравнений Fj (x,p)=
=0,1 <:?<:«, то инволюционность этой системы означает,
что выражение
является полным дифференциалом. На этом основано
применение метода Якоби [2] решения И. с, не зави-
зависящих от и и состоящих из т функционально неза-
независимых уравнений, тп<и. В соответствии с этим ме-
методом исходную, систему расширяют до И. с. из п
уравнений с вышеуказанными свойствами. Расширение
идет в несколько этапов, каждая последующая систе-
система получается из предыдущей добавлением ее незави-
независимых первых интегралов в инволюции. Этот метод
допускает применение и для системы уравнений, за-
зависящей от и (см. [3]).
Лит.: [1] Caratheodory С, Variationsrechnung und
partielle Differentialgleichungen erster Ordnung, 2 Aufl., Lpz.,
1956; [2] J а с о b i C, «J. reine und angew. Math.», 1862,
Bd 60, S. 1—181; [3] Goursat E., Lemons sur l'mtegration
des equations aux derivees partielles du premier ordre, P., 1891;
[4] Г ю н т e p H. M., Интегрирование уравнений первого по-
порядка в частных производных, Л.— М., 1934; [5] Камке 3.,
Справочник по дифференциальным уравнениям в частных про-
производных первого порядка, пер. с нем., М., 1966.
А. П. Солдат**
ИНВОЛЮЦИЯ — 1) Эндоморфизм второго порядка
т. е. отображение объекта на себя, квадрат к-рого явл;
ется единичным морфизмом (см. также Категория
инволюцией). Иногда инволюцией наз. также п е ри о
дическое отображение, т. е. морфизм
нек-рая ненулевая степень к-рого является единичным
морфизмом. Минимальная из таких степеней наз. п с-
р и о д о м И.
Часто под И. группы понимают ее элементы второго
порядка.
И. в алгебре Е над полем действительных или ком-
комплексных чисел — отображение х-^-х* алгебры Е на
себя, удовлетворяющее следующим аксиомам ин-
инволюции: 1) х** = х для всех х?Е; 2) (х-\-у)* =
= х*-\-у* для всех х, у?Е; 3) (Кх)* = Хх* для всех х?Е
и всех чисел X из соответствующего поля; 4) (ху)* =
= у*х* для всех х, у?Е. Алгебра Е над полем комплек-
комплексных чисел, снабженная И., наз. симметричной
алгеброй.
Лит.: [I] Коннер П., Ф л о й д Э., Гладкие периоднчс-
кие отображения, пер. с англ., М., 1969.
2) И. в проективной геометрии — проек
тивное преобразование, квадрат к-рого есть тождест-
тождественное преобразование. Не тождественная И. действи-
действительной проективной прямой имеет только две непод-
неподвижные точки (гиперболическая И.) либо не
имеет неподвижных точек (эллиптическая И.).
Если А я Б — неподвижные точки гиперболической
И., то соответствующие друг другу точки М и М' гар-
гармонически разделяют пару А, В. На проективной пло-
плоскости всякая И. есть гиперболическая гомология.
Лит.: [1] Ефимов Н. В., Высшая геометрия, 6 изд., М.,
1977.
3)И. на алгебраическом многооб-
многообразии — автоморфизм конечного порядка ал-
гебраич. многообразия. Если X — неособое проектив-
проективное алгебраич. многообразие над алгебраически зам-
замкнутым полем к и g — И. многообразия X, то фактор-
многообразие Х\ [g} по действию циклич. группы {g}
является проективным многообразием и наз. обра-
образом инволюции g. Множество неподвижных
точек F(g) инволюции g образует неособое подмно-
подмногообразие в X. В случае, когда F(g) имеет в каждой
своей точке коразмерность, равную 1, образ инволюции
g является неособым многообразием. Численные ин-
инварианты неособой модели X многообразия Х\ {g} могут
быть вычислены с помощью Лефшеца формулы.
Лит.: [1] А т ь я М., Зингер И., «Успехи матем. наук»,
1969, т. 24, в. 1, с. 127—82; [2] Итоги науки. Алгебра. Тополо-
Топология. Геометрия, т. 12, М., 1975, с. 77—170; [3] G о d e a u x L.,
Theorie des involutions cycliques appartenant к une surface al-
gebrique et applications, Roma, [1963].
ИНДЕКС числа а по модулю т — показатель
у в сравнении a^gV (mod то), где а и т взаимно просты,
а g — некоторый фиксированный первообразный корень
по модулю т. И. числа а по модулю то обозначается
через 7=ind^ а или, более кратко, y=ind а. Первооб-
Первообразные корни существуют только для модулей вида
т=2, 4, ра, 2ра, где р>2 — простое число, и следова-
следовательно, только для таких модулей определено поня-
понятие И.
Если g — первообразный корень по модулю т и у
пробегает значения 0, 1, . . ., ф(то)—1, где <р(т) —
Эйлера функция, то gt пробегает приведенную систему
вычетов по модулю т. Следовательно, каждому числу
а, взаимно простому с то, соответствует единственный
индекс у такой, что 0<:у«:ф(т)—1. Любой другой ин-
индексу' числа а удовлетворяет сравнению у' ^у mod ф(т).
Поэтому И. числа а образуют класс вычетов по модулю
ф(т).
Понятие И. аналогично понятию логарифма и И. об-
обладает рядом свойств логарифма, а именно:
ind (ab) = ind a 4- ind b (mod ф (т)),
ind (a") ^ n ind a (mod ф (т)),
ind —¦ she ind a — ind Ъ (mod ф (т)),
где alb означает корень сравнения
fczEEE<z(mod m).
Если m=2apf1 . . . pfs— каноническое разложение
произвольного натурального числа то и gx, . . ., gs —
первообразные корни по модулям pf1, . . ., pfs соот-
соответственно, то для всякого а, взаимно простого с т,
существуют целые числа у, у0, у1, . . ., ys такие , что
a = (_ l)V5Vo(mod 2«),
а ^ gj'(mod р^),
Указанная система у, у0, у1? . . ., ys наз. систе-
системой индексов числа апо модулю то.
Каждому числу а, взаимно простому с т, соответствует
единственная система индексов у, у0, yt, . . ., ys такая,
что
где Ci=(f(pfi), г=1, 2, . . ., s, а с и с0 определены сле-
следующим образом:
с = 1, с0 = 1 при а = 0 или а = 1,
с = 2, со = 2«-2 при а^э2.
Всякая другая система у', у'о, у[, . . ., у'3 И. числа а
удовлетворяет сравнениям
у' = у (mod с), ye = Yo (mod c0),
7i = 7i (modcx), -^ = ys (mod с*).
Понятие системы И. числа а по модулю т удобно
для явного построения характеров мультиплика-
мультипликативной группы приведенных классов вычетов по мо-
модулю т.
Лит.: [1] Виноградов И. М., Основы теории чисел,
8 изд., М., 1972. С. А. Степанов.
ИНДЕКС ОПЕРАТОРА — разность размерностей
дефектных подпространств линейного оператора
А : Lo-^-L1— его ядра Кег А = А~1@) и его коядра
Coker A = L1lA(L0), если эти пространства конечно-
конечномерны. И. о. является гомотопич. инвариантом, ха-
характеризующим разрешимость уравнения Ах=Ъ.
ИНДЕКСА ФОРМУЛЫ — соотношения между ана-
литич. и топологич. инвариантами операторов нек-рого
класса. Именно, И. ф. устанавливают связь между ана-
литич. индексом линейного оператора
D :
'l0, Lx— топологич. векторные пространства), опреде-
определяемым формулой
га (D) = dim Ker D — dim Coker D ?Z
и измеряющим таким образом «разность» между дефект-
дефектными подпространствами D : его ядром Ker D = D~1@)
и его коядром Coker D = LjD (Lo), и топологич. ин-
индексом — нек-рой топологич. характеристикой опера-
оператора D и пространств Lo, Lx. Для общего эллиптическо-
эллиптического дифференциального оператора на замкнутом много-
многообразии задача нахождения И. ф. поставлена в кон-
конце 50-х гг. 20 в. [1] и решена в 1963 (см. [2]). хотя част-
частные виды И. ф. были известны и ранее: такова, напр.,
Гаусса—Бонне теорема и ее многомерные варианты.
В дальнейшем был получен ряд обобщений И. ф. на
объекты более сложной природы; в этих случаях вме-
вместо индекса — целого числа — могут фигурировать
произвольные комплексные числа и даже функции.
Элементарные формулы индекса.
1) Пусть М — дифференцируемая граница ограничен-
ограниченной области QczRn + 1, А — эллиптический псевдодпф-
ференциальный оператор, отображающий пространство
С°°(М, С) дифференцируемых комплекснозначных
вектор-функций на М со значениями в Ср в себя.
Пусть В (М) —многообразие касательных векторов к
М длины <:1, ориентированное посредством 2п-формы
(dx^dl,) Л... Л (dx"Adln),
где х1, . . ., х" — локальные координаты на М,
|х, . . ., \п — соответствующие координаты в касатель-
касательном пространстве, S (М) — ориентированная граница
В (М), образованная единичными касательными век-
векторами. В силу эллиптичности А его символ а является
невырожденной (рХр)-матричной функцией на S(M).
Оказывается, что для индекса оператора А имеет место
формула [7]:
Bяг)" Bn-l)! J
Tr(
S(M)
где (a~1da)A2"~1— внешняя степень матричной диф-
дифференциальной формы a~2da, а через Тг обозначен
след (рХр)-матричной формы. В частности, если р<ге
или если А — дифференциальный оператор на нечет-
номерном многообразии, i'o ind Л = 0 (для псевдодиф-
псевдодифференциального оператора последнее, вообще говоря,
неверно).
2) Пусть А — эллиптический дифференциальный
оператор вида (здесь а — мультииндекс)
в пространстве C°°(Q), By, . . ., Вт/9 — краевые диф-
дифференциальные операторы из C°°(Q) в С°°(М) вида
Набор операторов {A, By, . . ., Вт,2} задает эллипти-
эллиптическую краевую задачу, если не вырождается на S(М)
¦функция ?—)-гу^(|). Здесь гуд — коэффициенты поли-
полиномов
являющихся остатками от деления Я-полиномов Ьу(|, Я)
на Я-полином а+ (g, Я), где
a <z + определяется из разложения а=а + а~, где
? |, v — единичные касательный вектор и вну-
внутренняя нормаль к М соответственно; а+ (соответствен-
(соответственно а~) — Я-полином, не имеющий нулей в верхней
(соответственно, нижней) Я-полуплоскости. Индексом
описанной краевой задачи наз. индекс соответствующего
ей линейного оператора 31 изС'°°(Й)в C°°(Q)X C°°(M)m/2 ,
переводящего m?C"(Q) в набор {Аи, Вуи]^, . . .,
?т/2и\м}- Оказывается, что индекс эллиптической
краевой задачи совпадает с индексом эллиптического
псевдодифференциального оператора на М, символом
к-рого служит матрица г=(г,-^). В частности, индекс
задачи Дирихле |Л, 1, -^ , . . ., (^j j равен
нулю. Имеются общие И. ф. для граничных задач [16],
[17].
Формулы Атьи — Зингера. Пусть С°° (|) и
С°°(т|) — пространства бесконечно дифференцируемых
сечений векторных расслоений \ и ц над дифференцируе-
дифференцируемым замкнутым ?г-мерным многообразием М, D — (псев-
додифференциальнып) эллиптич. оператор, действую-
действующий из С°°(|) в С°°(г|). Топологич. индекс цф) опера-
оператора D определяется следующим образом. Вследствие
эллиптичности символ o(D) оператора D определяет
изоморфизм поднятий векторных расслоений на5(М):
где я : S{M)^>-M — расслоение единичных сфер кока-
сательного расслоения Т*М многообразия М. Пусть
В (М) — пространство расслоения единичных шаров
в Т*М, это — 2«-мерное многообразие с краем S(M).
Склейкой двух экземпляров В+(М) и В~ (М) многооб-
многообразия В (М) по их общей границе получается замкну-
замкнутое 2ге-мерное многообразие 2 (М) = В+ [)S{M)S~, над
Jt-рым строится векторное расслоение
тде л± : В- (М)^-М, a a(D) использовано для отожде-
отождествления | и т| вдоль S(M). Это векторное расслоение
V(a) несет всю топологич. информацию, нужную для
определения топологич. индекса. Именно:
it (D) = {chF (а) -4сГ (М)} [2 (И)], B)
где ch V(a) — когомологический Чжэня характер рас-
расслоения ^(сг^ $~ (М) — когомологический Тодда класс
комплексифицированного кокасательного расслоения
Т*М® RC, п^ ¦ 2 (М)-+М, п*?~(М)=?~(Ъ (М)), и спра-
справа стоит значение 2п-мерной компоненты элемента
ch V(a)-n^^r (M) на фундаментальном цикле мно-
многообразия [S (М)]. Таким образом, отображение
V(o(D))-+i-t(D) определяет гомоморфизм К(Х (Af))-»-Z,
тривиальный на образе К(М), здесь К(Х) — Гротен-
дика группа, порожденная комплексными векторными
расслоениями над X.
Теорема об индексе Атьи — Зинге-
ia(D) = it(D). C)
Формула B) допускает ряд модификаций. Вводится
следующим образом зависящий от символа a(D) ра-
рациональный класс когомологип ch [a(D)]: тройке
{я* (|), я* (т|), a(D)} сопоставляется различающий эле-
элемент, к-рый можно рассматривать как первое препят-
препятствие к распространению изоморфизма а на все В (М),
[a (D)\ ?K (В (M)/S (М)) = К(ТМ),
где ТМ — касательное расслоение, к-рое (с помощью
римановой метрики на М) можно отождествить с Т*М,
К (ВIS) — относительная группа Гротендика вектор-
векторных расслоений над B/S, и следовательно — характер
Чжэня [a(D)] : ch [a(D)]?H* (B/S; Q). Теперь форму-
формула для топологич. индекса D принимает вид:
ц (D) = (- 1)" {ch [a (D)} -п*$-(М)} [ТМ], D)
где л : ТМ-+М, п*<$~(М)=?Г(ТМ).
Тома изоморфизм
<р„:Я* (B/S) = Н* (ТМ) ->¦ Н* (М)
позволяет записать D) в виде
it(D) = (— l)»(» + D/2 {Фз,сп[а (D)]. $-(М)} [М] E)
(в D) и E) справа по-прежнему, как и в B), значения
соответствующих элементов на фундаментальных цик-
циклах.)
В терминах Я-теории топологич. индекс выражается
следующим образом. Пусть i : М-^-Е — дифференцируе-
дифференцируемое вложение М в евклидово пространство, W — труб-
трубчатая окрестность М в Е, к-рую можно рассматривать
как действительное векторное расслоение над М, при-
причем TW изоморфно (над R) л* (VF(g)RC) — комплек-
сификации расслоения W, поднятой на ТМ проек-
проекцией л : ТМ-^М. Композиция изоморфизма Тома
ф : K(TM)->-K(TW) с естественным гомоморфизмом
K(TW)-+K(TE), индуцированным вложением W-v?,
определяет гомоморфизм г, : K(TM)—>-K(TW). Пусть
E: К(ТЕ)—у~^_—изоморфизм периодичности Ботта. Тогда
гомоморфизм (Зо;, : К(ТМ)^.~%_ не зависит от вложения,
и
Примеры. 3) Пусть М — замкнутое ориентиро-
ориентированное риманово многообразие, %k=Ak(T*M) (>?) С —
расслоение комплексных дифференциальных Л-форм
над М,
d:C°° (|*) -* С" (?* + *), d*:C°° (g* + 1) -*• С" (?*)
— оператор внешнего дифференцирования и его сопря-
сопряженный, соответственно. Оператор
где ?е=фД2^, ia=(Bpl2p+1> эллиптичен, для него
справедлива И. ф. C), причем топологич. индекс равен
эйлеровой характеристике % (М) (Ходжа — де Ра-
на теорема). При dim M=2 получается теорема
Гаусса — Бонне.
4) Пусть %± — собственные (±)-пространства ин-
инволюции I(а)=1Р '^-х) + **а, <*??/>, где * есть оператор
двойственности, определяемой метрикой на М, dim M=
=2к. Сужение оператора й-{-й* до оператора из С°°(|+)
в С°°(%~), называемое сигнатурным оператором 6^,—
эллиптический оператор, для него справедлива И. ф.
C), причем аналитич. индекс равен сигнатуре многооб-
многообразия М, а топологич. индекс равен L-роду (теоре-
(теорема X и р ц е б р у х а).
5) Пусть т| — голоморфное векторное расслоение
над компактным комплексным многообразием М, |°'? —
расслоение дифференциальных форм типа @, q),
4\®V'4 — расслоение форм типа @, q) с коэффициентами
в г], ?0'9 — С-модуль гладких сечений этого расслое-
расслоения. Пусть d:Z,a'ct^Z,a'ct + 1— оператор Коши — Рима-
на — Дольбо, д*— его сопряженный, t,e = (r)pV'2pi
t?=Qpt?'iP + 1. Тогда оператор 1+д* : tf-^-t,0 является
эллиптическим, и для него справедливо C), причем
аналптич. индекс равен эйлеровой характеристике М
с коэффициентами в пучке ростков голоморфных се-
сечений расслоения т), а топологический индекс —
{ch т| х?Г(М)} [М], где ch т) — характер Чжэня рас-
расслоения 1-), аГ(М) — класс Тодда касательного расслое-
расслоения к М (теорема Римана — Роха — X и р-
це б р у х а).
Эллиптические комплексы. В более
общей ситуации, естественно возникающей, напр., в
дифференциальной геометрии, вместо одного оператора
D рассматривается комплекс (псевдодифференциальных)
операторов
А:0 -> С" (?о) — С" (Si) — ¦¦¦ —^ С°° (Ы - О,
где |у — дифференцируемые векторные расслоения над
замкнутым многообразием М, DJ + 1Dj=0. Симво-
Символом комплекса А наз. соответствующая после-
последовательность главных символов
а (А):0 + я*' (?„) Д я* (У ^ ... -^1 л* (lN) -+ О,
где л* (?у) — поднятие расслоений ^у на S(M) с по-
помощью проекции я : Т*М-+М. Комплекс А наз. эл-
эллиптическим, если его символ является ациклическим
комплексом, т. е. точен всюду вне нулевого сечения.
Аналитическим индексом комплек-
комплекса А наз. его эйлерова характеристика:
где HJ(А) — группы когомологий комплекса А. Дву-
Двумя важными примерами эллиптич. комплексов являются
комплекс де Рама и его комплексный аналог — ком-
комплекс Дольбо. Проблема вычисления %(А) через класс
комплекса а (А) в К(ТМ) может быть сведена к вы-
вычислению индекса для одного оператора [3].
Если компактная группа G действует на А (и ком-
коммутирует с действием Dj, т. е. А есть G-комплекс), то
Hi (A) будут G-модулями, и %(А) определяется как
эледгент кольца характеров группы G. Это — функция
из C°°(G). Оказывается при этом, что теорема об ин-
индексе может рассматриваться как обобщение Лефшеца
теоремы о неподвижных точках, поскольку топологич.
индекс в точке g?G может быть выражен через индекс
сужения символа на подмножество М&сМ неподвиж-
неподвижных точек отображения, задаваемого элементом g.
Пусть G — топологическая циклическая группа, т. е.
в G существует элемент g, степени к-рого плотны в
G, NS. — нормальное расслоение к MS в М, и [а(Л)]?
^ Kq(ТМ) — класс символа А. Пусть ?*[а(Л)] (g) ^
?KG{TMS) и X_1(iV«0RC (g) — ограничение на MS
его и класса, порожденного стандартным комплексом
внешних степеней расслоения я* (N?(g)RC) соответ-
соответственно (здесь i: М?^>~М, я : ТМ?—*-М&). Тогда число
Лефшеца L(g, А), равное 2 (—1)/ Jv{g\H J (А)),
задается формулой:
где ind : X GTilf^')^)C^C — естественное расширение
топологич. индекса Л'(ГМ8) —«-]?. Когомологический
вариант этой формулы:
indoA(g)=/ ChiVg;^(^ п'ЯЧШп Ш ]¦ F)
1 chX_1(jV?®RC)(g) f
Без условия компактности G, но в предположении,
что М? — нульмерное подмногообразие и действие G
является невырожденным (т. е. график g трансверсален
диагонали в МХМ), имеет место аналогичная формула.
Она может быть выражена таким образом. Если Р?МЯ,
то dg(P) оставляет на месте ТМ\р, a g индуцирует в
слое |у|/> линейное преобразование lj{g, Р), и
indG A (g) = 2Р 6 ме S/-1)У Тг '/ <*• P)/det(l -dg (P))-
Возможно, наконец, ослабление условия эллиптично-
эллиптичности G-комплекса А рассмотрением так наз. транс-
версально эллиптических ком-
комплексов; в этом случае индекс оказывается обоб-
обобщенной функцией на группе G(cm. [8]). В частности,
если G — конечна, то трансверсальная эллиптич-
эллиптичность эквивалентна эллиптичности, так что применимы
прежние формулы. Если M=GlH — однородное про-
пространство, то все комплексы операторов трансверсально
эллиптичны, и здесь И. ф. по существу совпадает о
Фробениуса формулой взаимности для индуцированных
представлений группы G.
Нефредгольмовы операторы. В этом
случае также иногда удается дать другое определение
аналитич. индекса н получить соответствующие И. ф.
Примеры: 6) Пусть D — равномерно эллиптич. опе-
оператор на R" с почти периодич. коэффициентами. Ана-
Аналитич. индекс ia(D) вводится с помощью относитель-
относительной размерности в II^-факторе (см. Неймана алгебра)
и является действительным числом (см. [11]). Имеет ме-
место формула, аналогичная A), но вместо интеграла по
R" в ней используется среднее значение почти перио-
периодич. функции.
7) Пусть на многообразии М свободно действует
дискретная группа Г и факторпространство М=М1Т
компактно; пусть g, rj — векторные расслоения над
М и Г действует на них согласованно с ее действием
на М. Для эллиптич. оператора D : С°°B;)—<-С°°(г|) на М,
перестановочного с действием Г, аналитич. индекс оп-
определяется формулой
1аф)=ТггР,-ТггР2, G)
где .Р], Р2— ортогональные проекторы на Кот D и на
Ker D* в L2(M, dfx), d\i — любая Г-инвариантная глад-
гладкая плотность на М, а ТггР для оператора Р, переста-
перестановочного с Г и имеющего гладкое ядро Р(х, у), опре-
определяется формулой
Тгг Р = [ tr P (х, у) d\i
(здесь Мо— любая фундаментальная область группы Г
на М, tr — след матрицы). Оказывается, что ia(D)=
= ia(D), где D — оператор на М, символ к-рого a(D)
индуцирует a(D) при поднятии на М с помощью кано-
нической проекции л : М—^-М [12J. Таким образом И. ф.
для оператора D может быть получена из И. ф. для
оператора D на компактном многообразии М. Этот ре-
результат позволяет обнаруживать нетривиальность про-
пространств, в к-рых реализуются представления дискрет-
дискретных серий [13].
8) Если коэффициенты равномерно эллиптического
оператора D на R" образуют однородное измеримое
случайное поле, то можно ввести аналитич. индекс
ia(D), являющийся случайной величиной (в эргоди-
ческом случае — действительным числом), определяемой
по формуле G) с заменой ТттР на ТгР, где ТтР стро-
строится по ядру Р (х, у) оператора Р через среднее значе-
значение по х : Tr P=Mx{tr Р(х, х)}. Этот пример — обоб-
обобщение (.г 6) и для него имеет место [14] аналогичная
И. ф.
Если дано семейство эллиптических
операторов, параметризованное точками у ком-
компактного пространства Y, то определен его аналитич.
индекс ia(D)?K(Y) (см. [15]). Топологич. индекс it(D)
строится аналогично формуле F) (все построения де-
делаются «послойно» над Y) и имеет место теорема об
индексе.
Лит.: [1] Гельфанд И. М., «Успехи матем. наук»,
1960, т. 15, в. 3, с. 121 — 32; [2] А т ь я М. Ф., Зингер И. М.,
«Математика», 1966, т. 10, N° 3, с. 29—38; [3] их же, «Успехи
матем, наук», 1968, т. 23, в. 5, с. 99 — 142; [4] А т ь я М. Ф.,
С е г а л Г. Б., там же, в. 6, с. 135—49; [5] А т ь я М. Ф.,
Зингер И. М., там же, 1969, т. 24, в. 1, с. 127—82; [6] и х
ж е, там же, 1972, т. 27, в. 4, с. 161—88; [7] Федосов Б. В.,
«Тр. Моск. матем. об-ва», 1974, т. 30, с. 159—241; [8] A t i-
у a h . М., Elliptic operators and compact groups, В.—Hdlb.—
N.Y., 1974; [9] Пале Р., Семинар по теореме Атьи — Зин-
Зингера об индексе, пер, с англ., М., 1970; [10] Атья М. Ф.,
Б о т т Р., П а т о д и В. К., «Математика», 1973, т. 17,
Л» 6, с. 3—48; [11] Coburn L., Моуег R., Singer
I. M., «Acta Math.», 1973, v. 130, № 3—4, p. 279—307; [12]
Atiyah M. F., «Asterisque», 1976, v. 32—33, p. 43—72;
[13] Atiyah M. Г., Sclimid W., «Inventiones math.»,
1977, v. 42, p. 1—62; [14] Федосов Б. В., Шубин М. А.,
«Докл. АН СССР», 1977, т. 236, № 4, с. 812—5; [15] АтьяМ. Ф.,
Лекции по К-теории, пер. с англ., М., 1967; [16] Boutet de
Monvel L., «Acta math.», 1971, v. 126, №1—2, p. 11 — 51;
[17] Федосов Б. В., «Матем. сб.», 1974, т. 93, №1, с.
62—89; т. 95, .\в 4, с. 525 — 50; 1976, т. 101, № 3, с. 380 — 401.
М. И. Войцеховский, М. А. Шубин.
ИНДЕФИНИТНАЯ МЕТРИКА — термин, использу-
используемый в теории пространств с индефинитной метрикой
для обозначения (в зависимости от типа пространства)
либо билинейной формы, либо полуторалинейной фор-
формы, либо (нелинейного) функционала нек-рой степени
однородности, заданного в рассматриваемом простран-
пространстве. И. м. не является метрикой (т. е. расстоянием),
а эпитет «индефинитная» означает, что либо рассматри-
рассматриваемая полуторалинейная форма не является положи-
положительно определенной, либо рассматриваемый функцио-
функционал не является степенью нормы в пространстве. Раз-
Различные типы И. м. носят название G-метрики, /-метри-
/-метрики, /-метрики (см. Гильбертово пространство с ин-
индефинитной метрикой, Понтрягина пространство).
А. И. Штерн.
ИНДИВИДНАЯ КОНСТАНТА, предметная
констант а,— символ формального языка, слу-
служащий для обозначения нек-рого выделенного, фик-
фиксированного элемента (индивида) в структурах, описы-
описываемых этим языком. Всякую И. к. можно рассматри-
рассматривать как 0-местную функциональную константу.
Напр., язык теории полей содержит две И. к.: 0 и 1,
а язык проективной геометрии совсем не содержит И. к.
С. К. Соболев.
ИНДИВИДНАЯ ПЕРЕМЕННАЯ, предметная
переменная, — символ формального языка, слу-
служащий для обозначения произвольного элемента (инди-
(индивида) в структурах, описываемых этим языком. Вся-
Всякий формальный язык содержит один или несколько
сортов И. п., причем переменных каждого сорта — бес-
бесконечное множество. Напр., язык теории векторного
пространства содержит два сорта И. п.: для векторов и
для скаляров, а язык арифметики — один сорт: для
неотрицательных целых чисел. с. к. Соболев.
ИНДИВИДУАЛЬНАЯ ЭРГОДИЧЕСКАЯ ТЕОРЕ-
ТЕОРЕМА — другое название Биркгофа эргодической теоремы
И ее обобщений. Д- В. Аносов.
ИНДУКТИВНАЯ РАЗМЕРНОСТЬ, большая Ind X
и малая Ind X— размерностные инварианты топо-
топологического пространства X, определяемые параллель-
параллельно с помощью понятия перегородки между двумя мно-
множествами следующим образом по индукции. Для пустого
пространства Х~ф полагается Ind0 = ind 0 =—l.B
предположении, что уже известны те пространства X, для
к-рых Ind X < п, где п — неотрицательное целое число,
для пространства X считается Ind X < п +1, если для
любых двух дизъюнктных замкнутых множеств А и В
в X имеется перегородка С между ними, для к-рой
Ind С < п. При этом замкнутое множество С наз. пе-
перегородкой между множествами Л и В в прост-
пространстве X, если открытое множество Х\С есть сумма
двух открытых дизъюнктных множеств Нд и Нд, со-
содержащих, соответственно, А ж В. Это определение
переходит в определение малой И. p. indJf, если счи-
считать одно из множеств А ж В состоящим из одной лишь
точки, а другое — произвольным замкнутым множест-
множеством, не содержащим эту точку.
Большая И. р. была определена для достаточно ши-
широкого класса (метрических) пространств Л. Брауэром
[1]. Малая И. р. определена независимо П. С. Урынсо-
ном [2] и К. Менгером [3].
Исследование И. р. и вообще размерностных инва-
инвариантов содержательно лишь в предположении, что
пространство X удовлетворяет достаточно сильным от-
отделимости аксиомам, в основном аксиоме нормальности.
Лит.: [1] Brouwer L. E. J., «J. reine imd angew.
Math.», 1913. Bd 142, S. 146—52; [21 Урысон П. С,
«С. г. Acad. sci.», 1922, t. 175, p. 440—42; [3] MengerK.,
«Monatsh. Math, und Phys.», 1923, Bd 13, S. 148—60; [4]
Александров П. С, Пасынков Б. А., Введение в
теорию размерности, М., 1973. В. И. Зайцев.
ИНДУКТИВНОЕ ОПРЕДЕЛЕНИЕ — определение
какого-либо понятия А (п), зависящего от неотрица-
неотрицательного целого параметра п, протекающее по следую-
следующей схеме: а) задается значение А @); б) задается пра-
правило получения значения А (га+1) по и и по значению
А (п). Типичным И. о. является определение функ-
функции и!: а) 0! = 1; б) (га+1)!=п! (га+1). Более общим
Й. о. является определение по трансфинитной индук-
индукции, с помощью к-рого вводится какое-либо понятие
А (а), зависящее от ординального (трансфинитного)
числа а. Такое определение осуществляется заданием
нек-рого правила, позволяющего получать значение
А (а) по известным значениям А (Р) для всех C<<х.
Напр., сумма у+а ординалов у и а определяется так:
для сс>0.
Другим расширением понятия И. о. является так
наз. обобщенное И.о., к-рым задается класс
каких-либо объектов. Оно протекает по следующей
схеме: 1) задаются нек-рые (исходные) объекты опре-
определяемого класса; 2) задаются нек-рые правила, поз-
позволяющие из уже определенных объектов получать
другие объекты определяемого класса; 3) объектами
определяемого класса являются только те, к-рые полу-
получены согласно пп. 1) и 2) этого определения (этот
пункт всегда подразумевается и поэтому часто опус-
опускается). Примером обобщенного И. о. является опре-
определение понятия теоремы для данной аксиоматич. си-
системы S: всякая аксиома системы S является теоремой;
если посылки какого-нибудь правила вывода системы
S — теоремы, то заключение этого правила вывода так-
также является теоремой.
Чтобы доказать, что любой объект из класса, заданно-
заданного нек-рым обобщенным И. о., напр, всякая теорема
какой-нибудь аксиоматич. системы S, обладает
нек-рым свойством Р, достаточно показать следующее:
всякая аксиома системы S обладает свойством Р; если
посылки какого-нибудь правила вывода обладают свой-
свойством Р, то заключение этого правила вывода также
'«'ладает свойством Р. Доказательства такого рода наз.
доказательствами индукцией по опре-
определению соответствующего понятия (в данном примере—
теоремы) или по построению соответствующего объек-
объекта, в зависимости от контекста.
Лит. .¦ [1J Шенфилд Д ж., Математическая логика, пер.
с англ., М., 1975; [2] Куратовский К., Мост о в-
скнй А., Теория множеств, пер. с англ., М., 1970.
С. К. Соболев.
ИНДУКТИВНЫЙ ПРЕДЕЛ — конструкция, края
впервые появилась в теории множеств, а затем стала
широко использоваться в алгебре, топологии и других
областях математики. Важный частный случай И. п.—
это И. п. направленного семейства однотипных мате-
математических структур. Пусть С — направленное по
возрастанию предупорядоченное множество, т. е. в С
задано рефлексивное и транзитивное отношение-Зи для
любых элементов ос, р ? С найдется такой элемент
у?С, что oc^y и р"-<у. И пусть каждому а? С сопостав-
сопоставлена некоторая структура Аа (для определенности
можно считать, что Аа — группы) и при а—^E заданы
гомоморфизмы фар : А а-^-А р , удовлетворяющие двум
условиям: (paa = iAa Для любого а?С и фарфр?=фа7
для любых а-^Р-^7 из С. На множестве A=\JaiCAa
вводится отношение эквивалентности ~: элемент х?Аа
эквивалентен элементу у?Ао, если x(Pay=y(Pg,y Для
некоторого у. Фактормножество А=А1~ можно снаб-
снабдить структурой группы: если х?Аа, у?А$ и а-^у,
Р~,7> т0 произведением классов эквивалентности с
представителями х и у считается класс эквивалент-
эквивалентности с представителем (-мра7Нг/фр7). Построенная
группа А наз. И. п. семейства групп Аа.
Для каждого я?С существует естественный гомомор-
гомоморфизм сра '.А^—^-А, который элементу х?Аа сопостав-
сопоставляет его класс эквивалентности. Группа А, вместе с
гомоморфизмами <ра, обладает следующим универсаль-
универсальным свойством: для любой системы гомоморфизмов
% :Аа-»В, agC, для которой Ц>а=Уа$р при а-^р,
существует такой единственный гомоморфизм i|) : А—>В,
что г))а=:фа'Ф для любого а?С.
Обобщением данной конструкции И. п. является
индуктивный предел (прямой пре-
предел, копредел) функтора. Объект А категории
It наз. индуктивным пределом ковари-
антного функтора F:3} -^Я, если:
1. существуют такие морфизмы фд : F(?))—>-Л, где
DgOb-2?, что F(a.)(fD =(fD для любого морфизма
а : D-+Dx из X;
2. для любого семейства морфизмов i|)d : F(D)-+B,
где/) ?ОЬЗ), для к-рого F(a)\pD =1|зд при любом a : Д->
-kDx из 35, существует такой единственный морфизм
7 : А-уВ, что -фс(;=Фо7' Д?ОЬ?.
И. п. обозначается (А, фо)=Нт F или A = \im F
или Л = Нт F(D). И. п. контравариантного функтора
F : X —>-Я определяется как индуктивный предел кова-
рпантного функтора F* из двойственной к 2) категории
Я}* в категорию SX-
Всякое предупорядоченное множество С можно
рассматривать как категорию, объектами к-рой являют-
являются элементы множества С, а морфизмами — всевозмож-
всевозможные пары (а, |$), где а, р" ?С и a—i$ с очевидным зако-
законом композиции. В произвольной категории 5? семей-
семейство объектов Аа, а?С, и морфизмов фар : Ла—>-Лр,
где а—^р, можно рассматривать как образ функтора
F:C-+$t, если Фаа = 1 и фаРФр?=Фа1, при а-$Р-$у.
Если Я — категория множеств (групп, топологич.
пространств и т. п.), то И. п. функтора F : C—>-St
совпадает с приведенной выше конструкцией индуктив-
индуктивного предела.
Если 2) — малая дискретная категория, то И. п.
любого функтора F из 2) в произвольную категорию
Я есть копроизведение объектов F(D), Z)?3). В част-
частности, если категория 3) пуста, то И. п. есть левый
нуль, или инициальный объект категории ,ft. Коядра
пар морфизмов любой категории й являются И. п.
функторов со значениями в Ш, к-рые определены на
категории с двумя объектами ХпУи четырьмя морфиз-
мами 1у, 1у и а, Р : X^>-Y.
Всякий ковариантный функтор F из произвольной
малой категории b в категорию Я обладает И. п.
тогда и только тогда, когда Я — категория с копроиз-
ведениями и коядрами пар морфизмов.
Лит.: [1] Александров П. С, Топологические тео-
теоремы двойственности, ч. 1, JVT., 1955 (Тр. Матем. ин-та АН СССР,
т. 48); [2] Б у к у р И., Деляну А., Введение в теорию кате-
категорий и функторов, пер. с англ., М., 1972; [2] Цаленко
М. III., Шульгейфер Е. Г., Основы теории категорий,
М., 1974. М. Ш. Цаленко.
ИНДУКЦИИ АКСИОМА — утверждение о справед-
справедливости для всех х нек-рого предиката Р (х), определен-
определенного на множестве всех неотрицательных целых чисел,
если выполняются следующие условия: 1) справедливо
Р@), 2) для любого х, если верно Р(х), то верно
и Р(х-\-1). И. а. записывается в виде
Р @) & у* (Р (х) 3 Р (х + 1)) 3 ухР (х).
В применениях И. а. Р(х) наз. индукционным
предикатом, или индукционным пред-
предложением, а х — индукционной пере-
переменной, или переменной, по к-рой производится
индукция (в тех случаях, когда Р (х) содержит, креме
х, и другие параметры). При этом проверка выполнен-
выполненности условия 1) наз. базисом индукции,
а проверка условия 2) — индукционным ша-
шагом. Допущение внутри 2) справедливости Р(х),
из к-рого затем выводится Р(х-\-1), наз. индуктив-
индуктивным предположением.
Принципом (математической) ин-
индукции в содержательной математике наз. схема
всех И. а. для всевозможных предикатов Р(х). В систе-
системе FA арифметики формальной схема индукции со-
состоит лишь из тех И. а., к-рые соответствуют вырази-
выразимым в FA предикатам (таких предикатов счетное мно-
множество). Этим обстоятельством, т. е. невозможностью
выразить в FA индукцию в полном объеме, объясняется
неполнота системы FA (см. Гёделя теорема о неполноте).
Иногда вместо И. а. рассматривается аксиома: пусть
Р (х) — некоторое свойство неотрицательных целых
чисел; если для любого х из допущения, что Р (у) верно
для всех у, меньших х, следует, что верно и Р(х), то
Р(х) справедливо для всех х, т. е.
ух ((уу <х)Р (у)=>Р (х)) з ухР (х).
Эта аксиома носит название полной, или воз-
возвратной, И. а. Принцип полной индукции эквива-
эквивалентен принципу обычной индукции. См. также Транс-
Трансфинитная индукция.
Лит.: [1] К ли ни С. К., Введение в метаматематику, пер.
с англ., М., 1957. С. К. Соболев.
ИНДУЦИРОВАННОЕ ПРЕДСТАВЛЕНИЕ — пред-
представление л локально компактной группы G, индуци-
индуцированное представлением р ее замкнутой подгруппы Н,
точнее, представление я группы G в нек-ром простран-
пространстве Е функций / на группе G, принимающих значения
в пространстве V представления р и удовлетворяющих
условию f(hg) = p(h)f(g) для всех g?G, h?H, причем
[n(g1)f](g)=f(gg1) для всех f?E, g, gx?G. И. п. it
обычно обозначается Indp, Up, hUp , hU%. Операция
построения И. п. является простейшим и важнейшим
приемом построения представлений более сложных
групп, исходя из представлений более простых групп, и
для широких классов групп полное описание неприво-
неприводимых представлений может быть дано в терминах
И. п. или их обобщений.
Если G — конечная группа, то индуцирующее пред-
представление р предполагается конечномерным, а в каче-
качестве пространства V рассматривается пространство
всех функций / на группе G, принимающих значения в
V и удовлетворяющих условию f(hg)=p(h)f(g). Пред-
Представление ie)UPo, где р — единичное представление
единичной подгруппы {е}, есть правое регулярное пред-
представление группы G; представление qUpq эквивалентно
представлению р. Представление ниЪ эквивалентно
представлению ст в пространстве W всех функций на
однородном пространстве X=G\H со значениями в V,
определенному формулой вида [a(g)f](x)=a(g, х) f(xg),
причем функция а определяется следующим образом:
если s : Х—>-G — некоторое отображение, удовлетво-
удовлетворяющее условию s(x)?x для всех х?Х, то a(g, x) =
= р(А), где s(x)g=hs{xg) для всех х?Х, g?G. Функ-
Функция а является одномерным коциклом группы G с
коэффициентами в группе функций на X со значения-
значениями в обратимых операторах в V. Если рх эквивалент-
эквивалентно представлению р2, то Ind p1 эквивалентно Ind p2;
представление Ind(p0a) эквивалентно представлению
Ind р ф Ind ст. Если К, Н — подгруппы группы G,
КаН, ир — представление группы К, то представ-
представление группы G, индуцированное представлением ^Ufj
группы Н, эквивалентно представлению KUpa (теоре-
(теорема о сквозном индуцировании). Если
я, р — представления группы Си ее подгруппы Н со-
соответственно, то пространства сплетающих операторов
Нот (я, hUq) и Нот(я|яр) изоморфны, где я|я — су-
сужение представления я на подгруппу Н (теорема
двойственности Фробениуса); в ча-
частности, если я и р неприводимы, то я входит в UP с
той же кратностью, с к-рой р входит в п\ц. Характер
%л И. п. я= Up группы G определяется формулой:
где %р—характер представления р группы Н, продол-
продолженный нулем на всю группу С, а б пробегает набор
представителей правых смежных классов группы G
по подгруппе Н. Пусть Н, К — подгруппы группы
G, р — представление группы Я, Gg=Kr\g~1Hg для
всех g ? G и п8 — представление группы К, индуциро-
индуцированное представлением р*' группы Gg, определяемым
формулой ps(x)—p(gxg~1), x?Gg; тогда представление
nS однозначно определяется двойным классом HgK,
содержащим элемент g, и сужение И. п. ци% на под-
подгруппу К эквивалентно прямой сумме представлений
п?, где сумма берется по множеству представителей все-
всевозможных двойных классов HgK, g?G (теорема
об ограничении И. п. на подгруппу).
Эта теорема может быть применена, в частности, к раз-
разложению тензорного произведения И. п. Пространство
операторов, сплетающих данные И. п., допускает яв-
явное описание. Представление я группы G тогда и толь-
только тогда эквивалентно И. п. вида hUpg для нек-рых
Н и р, когда существует такое отображение Р множе-
множества подмножеств пространства H\G в множество про-
проекторов в пространстве Е представления я, что 1) Р @) =
=0, P(If\G)=l; 2) если М, NdH\G и Mf)N=(f>, то
P(M{]N)=P{M)+P{N); 3) P(Mf]N)=P(M)P(N) для
всех М, NczH\G; 4) P(Mg)=n~1(g)P(M)n(g) для всех
MdH\G, g?G (такое отображение Р наз. с и с т е-
мой импримитивности для представления я
с базой H\G. И. п. конечной группы может быть непо-
непосредственно описано в терминах модулей над групповой
алгеброй, а также может быть определено в категорных
терминах. Конечная группа наз. м о н о м и а л ь-
н о й, если любое ее неприводимое представление
индуцировано одномерным представлением пек-рой
подгруппы. Всякая мономиальная группа разрешима;
всякая нильпотентная группа мономиальна.
Определение И. п. локально компактной группы 6'
существенно зависит от выбора пространства Е; напр..
в качестве Е часто рассматривается пространство всех
непрерывных функций на G, удовлетворяющих условию
f(hg) = p(h)f(g), или (если G — группа Ли) пространство
всех дифференцируемых функций на G, удовлетворяю-
удовлетворяющих тому же условию. С другой стороны, пусть р —
непрерывное унитарное представление замкнутой под-
подгруппы HdG в гильбертовом пространстве V, пусть s—
измеримое отображение локально компактного простран-
пространства X=H\G в G, удовлетворяющее условию s(x)?x
для всех х?Х; пусть До, Ки— модули групп (см.
Хаара мера) G и Н соответственно н vs — такая
G-квазиинвариантная мера на X, что
dvs (xg)/dvs (x) = Аи (A*, S) Д-» (ТА S),
где s(x)g=hx' gs(xg) для всех х?Х, g?G; пусть L2(G.
Н, р) — гильбертово пространство измеримых вектор-
функций F на группе G со значениями в V, удовлетво-
удовлетворяющих условию
F (kg) = [Дя (А)/До (A)] V2. р (A) F (g)
для всех h?H, g?G и таких, что интеграл
сходится; непрерывное унитарное представление я
группы С в L2(G, H, р), определенное формулой
ln(gl)F](g)=F(gei)
для всех g, gi ?G, F ?L2(G, H, p), наз. унитарным
индуцированным представлением
локально компактной группы G. Большая часть резуль-
результатов об И. п. конечных групп допускает обобщение на
случай унитарных И. п. локально компактных групп,
в том числе свойства представлений Ind(p1@p2)H
Ind(p1®p2), связь И. п. с коциклами на группе G,
теоремы о сквозном индуцировании и об ограничении
И. п. на подгруппу, формула для характера И. п.,
критерий индуцированности представления, свойства
мономиальных групп и теорема двойственности фро-
бениуса допускают более или менее непосредственное
обобщение на случай унитарных И. п. И. п. локально
компактной группы G связаны с представлениями нек
рых обобщенных групповых алгебр этой группы. Если
G — группа Ли, то понятие И. п. группы G допускает
различные обобщения, в том числе понятие голоморф-
голоморфно И. п., пространство к-рого Е является простран-
пространством функций на G, аналитических по нек-рым пере-
переменным, и понятие представления в когомологиях
векторных расслоений над однородными пространствами
группы G (представления в нулевых когомологиях
суть И. п.). Понятие И. п. и его обобщения играют
плодотворную роль в теории представлений; в частно-
частности, в терминах унитарных И. п. описываются пред-
представления расширений групп; основная серия непрерыв-
непрерывных унитарных представлений связной действительной
полупростой группы Ли G образована И. п., а именно—
индуцированными конечномерными унитарными пред-
представлениями борелевской подгруппы группы G; ди-
дискретная серия представлений линейной действительной
полупростой группы Ли реализуется в когомологиях
нек-рых векторных расслоений над однородными про-
странствами этой группы; неприводимые непрерывные
унитарные представления разрешимых связных групп
Ли типа I описаны в терминах голоморфно И. п. [7].
Операция И. п. допускает обобщение на случай неуни-
неунитарных представлений локально компактных групп,
а также топологич. групп, не являющихся локально
компактными. Изучен [6] аналог И. п. для С*-алгебр.
Лит.: [1] Кириллов А. А., Элементы теории пред-
представлений, М., 1972; [2] Наймарк М. А., Теория пред-
представлений групп, М., 1976; [3] Серр Ж.-П., Линейные
представления конечных групп, пер. с франц., М., 1970; [4]
Макки Г. Дж., «Математика», 1962, т. 6, №6, с. 57—103;
Ы Schmid W., «Ann. of Math.», 1976, v. 103, p. 375—94;
16] Rieffel M., «Advances in Math.», 1974, v. 13, №2, p.
176—257; [7] Auslander L., Konstant В., «Invent,
math.», 1971, v. 14, № 4, p. 255 — 354; L8] В ерши к А. М.,
Гельфанд И. М., Граев М. И. «Успехи матем. наук»,
1975, т. 30, в. 6, с. 3—50; [9] М е н с к и й М. Б., Истод инду-
индуцированных представлений. Пространство — время и концеп-
концепция частиц, М., 1976. А. И. Штерн.
ИНДУЦИРОВАННОЕ РАССЛОЕНИЕ — расслоение
/* (я): X' ->-В', индуцированное отображением / : В'—^-В
и расслоением л : Х-+В, где X' — подпространство
прямого произведения В'XI, состоящее из пар (V, х),
для которых /(Ь')=я(ж), a /* (я) — отображение, опре-
определяемое соответствием (Ь', х)-+Ъ'. Отображение
F: /* (X)—*-Х И. р. в исходное расслоение, определенное
формулой F(b', x)=x, является морфизмом расслое-
расслоений, накрывающим /. Для каждой точки Ь'?В огра-
ограничения
являются гомеоморфизмами. Кроме того, для любого
расслоения ц : Y-*-B' и морфизма Н : ц-^-л, накрываю-
накрывающего /, существует один и только один В'-морфизм
К : г]—>-/* (я), удовлетворяющий соотношениям FK=H,
f* (л)К=ц, так что имеет место коммутативная диа-
диаграмма:
Расслоения, индуцирован-
индуцированные изоморфными расслое-
расслоениями, изоморфны, расслое-
расслоение, индуцированное по-
постоянным отображением,
изоморфно тривиальному.
Для любого сечения s
расслоения it отображение
а : B'^-f* (x), определенное
формулой а(Ъ')= (b',sf(b')),
является сечением И. р. /* (я) и удовлетворяет соот-
соотношению Fa=sf. Напр., отображение л : Х-+В инду-
индуцирует расслоение я2 с пространством я* (х) и базой
X — квадрат расслоения я, оно обладает единственным
сечением s(x)= (x, х).
Лит.: [1] Годбийон К., Дифференциальная геомет-
геометрия и аналитическая механика, пер. с франц., М., 1973; [2]
С т и н р о д Н., Топология косых произведений, пер. с англ.,
М., 1953; [3] Хьюзмоллер Д., Расслоенные пространства,
пер. с англ., М., 1970. М. И. Войцехоеский.
ИНЕРТНОЕ ПРОСТОЕ ЧИСЛО в расширении
K/Q — такое простое число р, для к-рого главный идеал,
порожденный р, остается простым в K/Q, где К —
конечное расширение поля рациональных чисел Q;
другими словами, идеал (р) прост в В, где В — кольцо
целых чисел поля К. В этом случае говорят также,
что р остается инертным в расширении
K/Q. Аналогично, говорят, что простой идеал Я деде-
киндова кольца А остается инертным при
расширении К Ik, где к — поле частных кольца А и К —
некоторое конечное расширение к, если идеал JtB,
где В — целое замыкание кольца А в К, прост.
Если К/к — расширение Галуа с группой Галуа
G, то для любого идеала Я кольца ВаК определена
подгруппа У и в группе б„ разложения идеала Я, наз.
подгруппой инерции (см. Критический иде-
идеал). Расширение Кхя/К й — это максимальное промежу-
точное подрасширение в К/к, в к-ром идеал Rf\K ос-
остается инертным.
В циклических расширениях полей алгебраич. чи-
чисел всегда существует бесконечно много инертных про-
простых идеалов.
Лит.: Ш Л енг С, Алгебраические числа, пер. с англ..
М., 1966; [2] В ей ль Г., Алгебраическая теория чисел, пер.
с англ., М., 1947; [3] Алгебраическая теория чисел, пер. с англ.,
М., 1969. Л. В. Кузьмин.
ИНЕРЦИАЛЬНАЯ СИСТЕМА ОТСЧЕТА — система
отсчета в классической механике и в специальной теории
относительности, в к-рой справедлив первый закон
Ньютона. Понятие И. с. о.— абстракция, однако в
весьма широком классе физич. явлений (в их круг не
входит описание сильных гравитационных полей) су-
существуют системы отсчета с высокой точностью, близкие
к И. с. о. В том случае, когда в целом И. с. о. не су-
существует (напр., в общей теории относительности), в
каждой точке можно построить такую систему отсчета,
к-рая в малой окрестности этой точки является приб-
приближенно инерциальной. В случае общей теории отно-
относительности такие системы отсчета наз. локально-
галилеевыми системами отсчета.
Существование локально галилеевой системы отсчета
означает то, что касательное пространство в данной
точке аппроксимирует искривленное пространство-
время.
Всякая система отсчета, к-рая движется относитель-
относительно И. с. о. прямолинейно и равномерно, является
И. с. о. Различные И. с. о. в классич. механике свя-
связаны преобразованиями из неоднородной группы Га-
Галилея преобразований; в специальной теории относи-
относительности — преобразованиями из группы Пуанкаре
(см. Лоренца преобразование). Законы классич. механи-
механики и законы специальной теории относительности ин-
инвариантны относительно, соответственно, неоднородной
группы Галилея и группы Пуанкаре (см. Относитель-
Относительности принцип). Следствием принципов относитель-
относительности являются различные законы сохранения (энер-
(энергии, импульса, момента импульса), к-рые имеют место
лишь в И. с. о. В специальной теории относительности
И. с. о. обычно задаются галилеевой системой коорди-
координат, в классической механике — декартовой системой
координат.
Лит.: [1] Фок В. А., Теория пространства, времени и
тяготения, 2 изд., М., 1971. Д. Д. Соколов.
ИНЕРЦИИ ЗАКОН квадратичных форм —
теорема, утверждающая, что при любом способе приве-
приведения квадратичной формы
с действительными коэффициентами к сумме квадратов
посредством линейной замены переменных
(хъ ..., zs) = (yi, ..., ys) Q<
где Q — невырожденная матрица с действительными
коэффициентами, число р (соответственно п) таких
индексов i, что Ь/>0 (соответственно Ь,<0), остается
неизменным. В этой классич. форме И. з. установлен
Дж. Дж. Сильвестром (J. J. Sylvester). Это утвержде-
утверждение иногда называют также теоремой Силь-
Сильвестра.
В современной форме И. з.— это следующее утверж-
утверждение о свойствах симметрических билинейных форм
над упорядоченными полями. Пусть Е — конечномерное
векторное пространство над упорядоченным полем к,
снабженное невырожденной симметрич. билинейной
формой /. Тогда существует такое целое число 0
что для любого ортогонального относительно / базиса
ег, . . ., es в Е среди s элементов
/ (<?,-, <?,-), i — i, ..., s,
имеется в точности р положительных и в точности п-=
= s—р отрицательных. Пара (р, п) наз. сигнату-
сигнатурой билинейной формы /, а число п — ее индек-
индексом инерции. Две эквивалентные формы имеют
одинаковую сигнатуру. Если к — евклидово поле, то ра-
равенство сигнатур является достаточным условием
для эквивалентности билинейных форм. Если индекс
инерции п=0, форма наз. положительно оп-
определенной, а при р=0 — отрицательно
определенной. Эти случаи характеризуются
тем, что f(x, ж)>0 (соответственно f(x, ж)<0) для лю-
любого ненулевого вектора х?Е. Из И. з. вытекает, что
Е есть ортогональная относительно / прямая сумма
подпространств
Е = Е+(Р,Е-,
таких, что сужение / на Е+ является положительно
определенной, а сужение / на Е~ — отрицательно опре-
определенной билинейной формой и
dim .Е1 + = р, dimE_ = n
(так что размерности пространств Е+ и Е- не зави-
зависят от способа разложения).
Иногда сигнатурой формы / наз. разность
Если формы fug определяют один и тот же элемент
кольца Витта W(k) поля к, то a(f)=a(g). Более того,
o-{/i©/2)=o(/i)+CT(/2), о-(/1®/2)=ст(/1)ст(/2) для любых
невырожденных форм /х и /2, и ст(<1>)=1, так что
отображение /—>-а(/) определяет гомоморфизм кольца
W(k) в кольцо целых чисел ~%_. Если к — евклидово
поле, то этот гомоморфизм является изоморфизмом.
И. з. обобщается на случай эрмитовой билинейной
формы над максимальным упорядоченным полем к,
над квадратичным расширением к или над телом ква-
кватернионов над к (см. [1], [4]).
Лит.: [1] Бур баки Н., Алгебра. Модули, кольца,
¦ формы, пер. с франц., М., 1966; [2] Лен г С, Алгебра, пер.
с англ., М., 1968; [3] Ар тин Э., Геометрическая алгебра,
пер. с англ., М., 1969; [4] М i 1 п о г J., Husemoller D.,
Symmetric bilinear forms, В. — Hdlb.— N.Y., 1973. В. Л. Попов.
ИНИЦИАЛЬНОЕ МНОЖЕСТВО континуума
К — совокупность таких точек, в к-рых К — гладкий
континуум. А. А. Мальцев.
ИНТЕГРАЛ — одно из центральных понятий мате-
матич. анализа и всей математики, возникновение к-рого
«вязано с двумя задачами: о восстановлении функции
по ее производной (напр., с задачей об отыскании за-
закона движения материальной точки вдоль прямой по
известной скорости этой точки); о вычислении площади,
заключенной между графиком функции f(x) на отрезке
а^сх^Ъ и осью абсцисс (к этой же задаче приводит
вычисление работы, произведенной силой за промежу-
промежуток времени я<;г<;6, и другие вопросы).
Указанные две задачи приводят к двум видам И.:
неопределенному и определенному. Изучение свойств и
вычисление этих связанных между собой видов И. со-
составляет задачу интегрального исчисления.
В ходе развития математики и под влиянием потреб-
потребностей естествознания и техники понятия неопределен-
неопределенного и определенного И. подвергались ряду обобщений
и изменений.
Неопределенный интеграл. Первообразной
функции f(x) одного переменного х на интервале
а<х<Ь наз. любая функция F(x), производная к-рой
для любого х из этого интервала равна f(x). Очевидно,
что если F(x) является первообразной функции f(x)
на интервале а<Сх<.Ь, то и функция Fl(x)=F(x)-\-C,
где С — любая постоянная, также является первооб-
первообразной f(x) на этом интервале. Верно и обратное: любые
две первообразные одной и той же функции f(x) на
интервале а<ж<6 могут отличаться лишь на постоян-
постоянную. Следовательно, если F(x) — одна из первообраз-
первообразных f(x) на интервале а<х<Ъ, то любая первообразная
f(x) на этом интервале имеет вид F(x)-\-C, где С — по-
постоянная. Совокупность всех первообразных функции
f (х) на интервале <z<z<6 наз. неопределенным
интегралом функции f(x) (на этом интервале) и
обозначается символом
/ (х) dx.
Согласно основной теореме интегрального исчисле-
исчисления, для каждой непрерывной на интервале а<х<Ь
функции f(x) существует на этом интервале первообраз-
первообразная и, следовательно, неопределенный И.
Определенный интеграл. Понятие определенного И.
вводится либо как предел интегральных сумм (см.
Коитх интеграл, Римана интеграл, Лебега интеграл,
Колмогорова интеграл, Стилтъеса интеграл), либо в
случае, когда заданная функция f(x) определена на
нек-ром отрезке [а, Ь] и имеет на нем первообразную F,
как разность ее значений на концах рассматриваемого
отрезка F(b) — F(a). Определенный И. от функции f(x)
на отрезке [а, Ь] обозначают \ f(x)dx. Определение
И. как предела интегральных сумм в случае непрерыв-
непрерывных функций было сформулировано О. Коши (А. Саи-
chy) в 1823. Случай произвольных функций был изучен
Б. Риманом (В. Riemann, 1853). Существенное продви-
продвижение в теории определенного И. принадлежит Г. Дарбу
(G. Darboux, 1879), к-рый ввел в рассмотрение наряду
с интегральной суммой Римана верхнюю и нижнюю
суммы (см. Дарбу сумма). Необходимое и достаточное
условие интегрируемости по Риману разрывных функ-
функций в законченной форме установил A902) А. Лебег
(Н. Lebesgue).
Между определенным И. от непрерывной на отрезке
[а, Ь] функции f(x) и неопределенным И. (или первооб-
первообразной) этой функции существует следующая связь:
1) если F(x) — любая первообразная функции f(x), то
справедлива формула Ньютона — Лейбница
ja
2) для любого х из отрезка [а, Ь] неопределенный И.
непрерывной функции f(x) записывается в виде
где С — произвольная постоянная. В частности, опре-
определенный И. с переменным верхним пределом
t A)
представляет собой первообразную функцию f(x).
Для введения определенного И. от функции f(x) по
отрезку [а, Ь] в смысле Лебега разбивают множество
значений у на частичные отрезки точками ...<i/_2<
<у_1<!/0<!/1<1/2<... и обозначают через М,- множест-
множество всех значений х из отрезка [а, Ь], для к-рых ;/,_!<
</(ж)<г/,-, а через \i(M,¦) — меру множества М,- в смыс-
смысле Лебега. Интегральную сумму Лебе-
г а функции f(x) на отрезке [а, Ь] определяют равенст-
равенством
~ B)
где т),- — любое число из отрезка гц-^^.щц
Функцию / (х) наз. интегрируемой в смыс-
смысле Лебега на отрезке [а, Ь], если существуюi
предел ее интегральных сумм B) при стремлении к
нулюмаксимальной из разностей щ—г//_17 т. е. если
существует такое число /, что для любого в>0 найдется
6>и такое, что при единственном условии тах(у/—
—;/i-_i)<6 справедливо неравенство |а—/|<е. При этом
указанный предел / наз. определенным ин-
интегралом Лебега от функции / (х) по отрезку
к ь].
Вместо отрезка [я, Ь] можно рассматривать про-
произвольное множество, измеримое относительно неко-
некоторой неотрицательной полной счетно аддитивной меры.
Возможно и другое введение интеграла Лебега, когда
этот И. первоначально определяют на множестве так
наз. простых функций (т. е. измеримых функ-
цгт. принимающих не более счетного множества зна-
значений),а затем с помощью операции предельного пере-
перехода вводят для произвольной функции, представляю-
Щ1н собой предел равномерно сходящейся последова-
последовательности простых функций (см. Лебега интеграл).
Каждая интегрируемая в смысле Римана функция яв-
является интегрируемой и в смысле Лебега. Обратное не-
неверно, ибо существуют разрывные на множестве поло-
положительной меры и вместе с тем интегрируемые в смысле
Лебега функции (напр., функция Дирихле).
Для интегрируемости по Лебегу ограниченной функ-
функции необходимо и достаточно, чтобы эта функция при-
принадлежала классу измеримых функций. Функции, встре-
встречающиеся в математич. анализе, как правило, измери-
измеримы. Это означает, что интеграл Лебега обладает общ-
общностью, исчерпывающей потребности анализа.
Интеграл Лебега охватывает и все случаи абсолютно
сходящихся несобственных интегралов.
Общность, достигнутая определением И. в смысле
Лебега, весьма существенна во многих вопросах совре-
современного математич. анализа (теория обобщенных функ-
функций, определение обобщенных решений дифференциаль-
дифференциальных уравнений, изоморфизм гильбертовых пространств
Ь,г и 12, эквивалентный так наз. теореме Рисса — Фи-
Фишера в теории тригонометрических или произвольных
ортогональных рядов,— все эти теории оказались
возможными только при понимании И. в смысле Лебега).
Первообразную в смысле Лебега естественно опреде-
определить с помощью равенства A), в к-ром И. понимается
в смысле Лебега. При таком понимании соотношение
F'(x)=f(x) будет справедливо всюду, кроме, может
быть, множества, имеющего меру, равную нулю.
Другие обобщения понятия интеграла. В 1894
Т. Стилтьесом (Т. Stieltjes) было дано другое важное
для приложений обобщение интеграла Римана (полу-
(получившее название интеграла Стилтьеса), в к-ром рас-
рассматривается интегрируемость одной функции f(x),
определенной на некотором отрезке [а, Ь], относитель-
относительно другой функции, определенной на том же отрезке.
Интеграл Стилтьеса функции f(x) относи-
относительно функции U (х) обозначают символом
{x)dU(x). C)
Если V (х) имеет ограниченную и интегрируемую в
смысле Римана производную U' (х), то интеграл Стил-
Стилтьеса сводится к интегралу Римана по формуле
в частности при и(ж)=.т-|-С интеграл Стилтьеса C)
является интегралом Римана \ f(x)dx.
Однако для приложений интересен случай, когда
интегрирующая функция U (х) не имеет производной.
Примером может служить рассмотрение в качестве
U(x) спектральной меры при изучении спектральных
разложений.
Криволинейный интеграл
вдоль кривой Г, определяемой уравнениями a-=cp(
!/=i|)(?), a^.t*g.b, представляет собой частный случай
интеграла Стилтьеса, так как может быть записан в виде
[ф@, Ч> С)] *Р (О-
Дальнейшим обобщением понятия И. послужило
интегрирование по произвольному множеству в прост-
пространстве любого числа измерений. В самом общем случае
удобно рассматривать И. как функцию от того множе-
множества М, по к-рому производится интегрирование (см.
Функции множеств) вида
F (М) =
=\ f(x)dU(x),
где U — также некоторая функция множества М (в
частном случае его мера), а точка принадлежит множе-
множеству М, по к-рому идет интегрирование. Частными слу-
случаями такого рассмотрения являются кратные интегра-
интегралы и поверхностные интегралы.
Другим обобщением понятия И. является понятие
несобственного интеграла.
В 1912 А. Данжуа (A. Denjoy) ввел понятие И. (см.
Данжуа интеграл), применимое ко всякой функции
i(x), являющейся производной нек-рой функции F(x).
Это позволило привести конструктивное определение
И. к такой степени общности, при к-рой оно целиком
отвечает задаче разыскания неопределенного И., пони-
понимаемого в смысле первообразной.
Лит.: [1] И л ь и н В. А., П о а н я к Э. Г., Основы ма-
математического анализа, ч. 1—2, М., 1971—73; [2] Колмо-
Колмогоров А. Н., Ф о м и н С. В., Элементы теории функций и
Функционального анализа, 4 изд., М., 1976; [3] Кудряв-
Кудрявцев Л. Д., Математический анализ, т. 1—2, 2 изд., М., 1973;
[4] Никольский С. М., Курс математического анализа,
т. 1—2, 2 изд., 1975; [5] Смирнов В. И., Курс высшей ма-
математики, т. 5, М., 1959; [б] Лебег А., Интегрирование и
отыскание примитивных функций, пер. с франц., М.—Л.,
1934. В. А. Ильин.
Л-ИНТЕГРАЛ — одно из обобщений интеграла Ле-
Лебега, данное Е. Титчмаршем [1] для интегрирования
функций, сопряженных к суммируемым. Измеримую
функцию /(х) наз. Л-интегрируемойна[а, 6],
если
и существует предел
It (*I,
где
f(x), \f(x)\*zn
О , \f(x)\>n.
Число / наз. Л-интегралом и обозначают
/ (a-) dx.
Лит.: [1] Titchmarsh E. G., «Proc. London Math.
Soc», 1929, № 29, с. 49—80; [2] Виноградова И. А.,
Скворцов В. А., в кн.: Итоги науки. Математический
анализ. 1970, М., 1971, с. 65—107. И. А. Виноградова.
ИНТЕГРАЛ ВЕРОЯТНОСТИ, интеграл оши-
ошибок,— функция
erf (*)=—Lr [xe-t2dt, |я| < оо.
/я JO
В теории вероятностей используется не И. в., а функ-
функция нормального распределения:
— так наз. интеграл вероятности Г а у с-
с а. Для случайной величины X, имеющей нормальное
распределение с математич. ожиданием 0 и дисперсией
ст2, вероятность неравен-
неравенства |Х|<? равна
eri(t/Y~2). Для действи-
действительного х И. в. прини-
принимает действительные зна-
значения, в частности
erf(O) = O, lim егГ(ж) = 1.
График И. в. и его про-
'¦ |-5 х изводной см. на рис. Рас-
Рассматриваемый и как функция комплексного перемен-
переменного z, И. в. erf(z) есть целая функция от z.
Асимптотич. представление при больших z, Rez>0:
2
1,0
0,5
n
у
У
/
ч
/
/
s
s
s
s
er
f(xh-
6
4,
4-
1
V00 ( 1)frl-3-..-Bft-l) 1 \
—erf (z)
В окрестности z=0 И. в. представляется в виде ряда
1! 3 ^ • " • ^ftl B
С Френеля интегралами C(z) и 5(z) И. в. связан соот-
соотношениями:
l + i t / 1 -г \ п , . . .„ , ,
-s- erf ( —— z ) = С (г) + г5 (z),
Производная И. в.:
[erf (z)]'=—е-*2.
l' я
Иногда используются следующие обозначения:
в (х) = Я (*) = Ф (j) = erf (x),
Етй (х) = — i XA eri (ix) = \X et2dt,
Л JO
и -pip { т I — ij 11 X —
Лит.: [1] Б е й т м е н Г., Э р д е й и А., Высшие транс-
трансцендентные функции. Функции Бесселя, функции параболиче-
параболического цилиндра, ортогональные многочлены, пер. с англ., 2 изд.,
М., 1974; [2] Янке Е., Змде Ф., Лёш Ф., Специальные
функции. Формулы, графики, таблицы, пер. с нем., 2 изд., М.,
1968; [3] К р а т ц е р А., Франц В., Трансцендентные фун-
функции, пер. с нем., М., 1963; Ш Лебедев Н. Н., Специаль-
Специальные функции и их приложения, 2 изд., М., 1963. А. Б. Иванов.
ИНТЕГРАЛ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕ-
УРАВНЕНИЯ — решение дифференциального уравнения.
И. д. у. наз. преимущественно соотношение вида
Ф(х, ?/)=0, определяющее решение у обыкновенного
дифференциального уравнения
F(x, у, у', ..., уМ)=0 A)
как неявную функцию независимой переменной х.
В этом случае говорят также о частном интег-
интеграле в противоположность общему интегра-
л У уравнения A), т. е. соотношению
Ф(х, у, Съ ..., Сп) = 0, B)
из к-рого при соответствующем выборе постоянных
С1,..., Сп получается любая интегральная кривая урав-
уравнения A), проходящая в рассматриваемой области G
плоскости (х, у). Если из соотношения B) и из и соот-
ношений, получающихся из него последовательным
дифференцированием по х (причем у рассматривается
как функция х), исключить произвольные постоянные
Сх, ..., Сп, то в результате приходят к уравнению A).
Возникающее в процессе интегрирования уравнения
A) соотношение вида
Ф(х, у, у', ..., j/Cft), d, ..., Cn_ft) = 0, C)
содержащее производные до к-то порядка,
и п—к произвольных постоянных, иногда наз. про-
промежуточным интегралом уравнения A).
Знание промежуточного интеграла C) сводит решение
уравнения A) порядка п к решению уравнения C)
порядка к. Если соотношение C) содержит лишь одну
произвольную постоянную, т. е. к=п—1, то оно наз.
первым интегралом уравнения A). Это урав-
уравнение имеет ровно п независимых первых интегралов;
знание п таких интегралов позволяет получить общее
решение уравнения A) путем исключения из них вели-
величин у',. . ., i/"-1*.
Если рассматривается система обыкновенных диффе-
дифференциальных уравнений
d^l = fl(t, *!, ..., хп), г = 1, ..., п, D)
то под ее общим интегралом имеют в виду совокупность
соотношений
Ф,-(«, хъ ..., х„) = С;, г = 1, ..., п, E)
где С,- — произвольные постоянные, в неявном виде
описывающую все решения системы D) в нек-рой облас-
области G пространства (t, xlt..., хп). Каждое из соотношений
E) в отдельности наз. первым интегралом системы D).
Чаще под первым интегралом системы
D) понимают функцию u(t, x1,..., хп), обладающую
тем свойством, что она принимает постоянное значение
вдоль любого решения системы D) в области С. Система
D) имеет ровно п независимых первых интегралов,
знание к-рых дает возможность найти общее решение
без интегрирования системы; знание к независимых пер-
первых интегралов позволяет свести решение системы D)
порядка п к решению системы порядка п—к. Гладкая
функция u(t,x1,. . ., хп) является первым интегралом
системы D) с гладкой правой частью тогда и только
тогда, когда она удовлетворяет уравнению
Аналогичная терминология иногда употребляется в
теории дифференциальных уравнений с частными про-
производными 1-го порядка. Так, под И. д. у.
F ( X, у, Z, -т- , -ТГ- ) =0, F)
или под его частным интегралом, понимают
решение этого уравнения (интегральную поверхность).
Полным интегралом уравнения F) наз.
семейство решений Ф(х, у, z, а, Ь) = 0, зависящее от
двух произвольных постоянных. Общий интег-
интеграл уравнения F) — соотношение, содержащее одну
произвольную функцию и при каждом выборе этой
функции дающее решение уравнения.
Лит.: [1] Степанов В. В., Курс дифференциальных
уравнений, 8 изд., М., 1959. Н. X. Розов.
ИНТЕГРАЛ ПО ТРАЕКТОРИЯМ, континуаль-
континуальный интеграл, функциональный
и н т е г р а л,— интеграл, областью интегрирования
к-рого служит то или иное функциональное простран-
пространство. Чаще всего И. по т. определяется как обычный
интеграл Лебега от функционала, заданного на прост-
пространстве функций (возможно, обобщенных) по нек-рой
мере (быть может, комплексной) в этом пространстве.
В тех случаях, когда лебеговская конструкция интегра-
интеграла оказывается неприменимой, рассматриваются и
другие способы континуального интегрирования. Напр.,
вместо мер используются предмеры (или квазимеры),
т. е. аддитивные функции множества, определенные
на алгебре всех цилиндрич. подмножеств функциональ-
функционального пространства и такие, что их сужения на любую
о-подалгебру цилиндрич. множеств с фиксированным
носителем являются уже мерами. Иногда И. по т. опре-
определяется как предел при п->оо n-кратных интегралов
(вычисляемых по мере Лебега в R"), возникающих при
подходящей аппроксимации пространства функций
(области интегрирования) ?г-мерным пространством, а
интегрируемого функционала — функцией от п пере-
переменных. Эти и другие определения И. по т. применимы
каждое к своему специальному классу функционалов,
причем в тех случаях, когда эти определения пригод-
пригодны одновременно, они могут, вообще говоря, приводить
к различным значениям интеграла. Наконец, И. по т.,
встречающиеся в литературе по физике, подчас вообще
не имеют точного смысла, а рассматриваются как фор-
формальные выражения, с к-рыми оперируют как с обыч-
обычными интегралами (замена переменных, мажорирование,
дифференцирование по параметру, предельный переход
и т. д.), часто, однако, получая при этом серьезные
и эвристически ценные результаты.
И. по т., появившиеся первоначально в теории слу-
случайных процессов, позднее были использованы для
представления группы
а также полугруппы операторов
ехр{—tH), t > 0,
где if — Штурма — Лиувилля оператор в пространстве
R" (оператор энергии для системы квантовых частиц).
Подобные представления были получены затем для
более широкого класса операторов Н (всякое такое
представление обычно наз. формулой Фейнмана —
Каца) и явились удобным средством для изучения
свойств этих операторов (оценка границ спектра,
асимптотика собственных значений, свойства рассея-
рассеяния и т. д. [3]).
Среди применений И. по т. в математич. физике
(основанных главным образом на формуле Фейнмана —
Каца) наиболее глубоким оказалось их использование в
проблемах квантовой статистич. физики [4] и квантовой
теории поля [5], [6]. С И. по т. связано отчасти и раз-
развитие общих вопросов теории меры и интегрирования в
бесконечномерных пространствах [7], [8].
Лит.: [1] Ф е й н м а н Р., X и б с А., Квантовая меха-
механика и интегралы по траекториям, пер. с англ., М., 1968; [2]
Kan M., Вероятность и смежные вопросы в физике, пер. с
англ., М., 1965; F3] Гельфанд И. М., Яг лом А. М.,
«Успехи матем. наук», 1956, т. 11, № 1, с. 77—114; [4] Gen i-
bre J., Statistical mechanics and quantum field theory, N.Y.,
1971; [5] Боголюбов H. H., Ill и р к о в Д. В., Введе-
Введение в теорию квантованных полей, М., 1957; [6] Саймон Б.,
Модель Р(фJ евклидовой квантовой теории поля, пер. с англ.,
М., 1976; [7] С м о л я н о в О. Г., Ф о м и н СВ., «Успехи
матем. наук», 1976, т. 31, Л!> 4, с. 3—56; [8] S с h w a r t г L.,
Radon measures on arbitrary topological spaces and cylindrical
measures, L., 1973. P. А. Минлос.
ИНТЕГРАЛЫ В ИНВОЛЮЦИИ — решения диффе-
дифференциальных уравнений, Якоби скобки к-рых равны
нулю. Функция G(x, и, р) 2ге+1 переменных х= (х±,. . .,
1„), и, р = (р1,. . ., рп) есть первый интеграл уравнения
с частными производными первого порядка
F (х, и, р)=0, A)
и=и(хи ..., хп), Pi = -g^r , 1<г<ге,
если она постоянна вдоль каждой характеристики
этого уравнения. Два первые интеграла G,(x, и, р),
i= 1,2, находятся в инволюции, если их скобка Якоби
тождественно равна нулю по (х, и, р):
[Gu C2] = 0. B)
Вообще, две функции Gt, G2 находятся в инволюции,
если выполнено условие B). Любой первый интеграл G
уравнения A) находится в инволюции с F; последняя
функция сама является первым интегралом.
Эти определения распространяются и на системы
уравнений
F; (.г, и, р) = 0, 1 < i < m. C)
При этом первый интеграл этой системы G(x, и, р)
можно рассматривать как решение системы линейных
уравнений
[Fh G]=0, l<i<m, D)
с неизвестной функцией G.
Если C) является инволюционной системой, то D) —
полная система. Она инволюционна, если функции
F( в C) не зависят от и.
Лит.: [1] Гюнтер Н. М., Интегрирование уравнений
первого порядка в частных производных, Л.— М., 1934; [2]
Камке Э., Справочник по дифференциальным уравнениям
в частных производных первого порядка, пер. с нем., М., 1966.
А. П. Солдатов.
ИНТЕГРАЛЬНАЯ ВОРОНКА точки P(t0, x0) для
дифференциального уравнения dxldt=f(t, x) — мно-
множество всех точек, лежащих на интегральных кривых,
проходящих через точку Р [под уравнением можно
понимать систему уравнений в векторной записи с х=
= {х±,..., хп)]. Если через точку Р проходит только одна
интегральная кривая, то И. в. состоит из одной этой
кривой. В случае я=1, т. е. когда х — скаляр, И. в.
состоит из точек (t, x), для к-рых x,(t)<x<gx* (t), где
х* (t) и х„. (t) — верхнее и нижнее решения, т. е. наи-
наибольшее и наименьшее из решений, проходящих через
точку Р.
Если функция f(t, x) непрерывна (или удовлетворяет
условиям теоремы существования Каратеодори), то
И. в.— замкнутое множество. Если при этом все реше-
решения, проходящие через точку Р, существуют на отрезке
a<j<:6, то отрезок воронки (часть И. в., определяемая
неравенствами a<:t<:6) и сечение И. в. любой плоско-
плоскостью t=t1?[a, b] являются связными компактами.
Любую точку на границе И. в. можно соединить с точ-
точкой Р куском интегральной кривой, лежащим на гра-
границе И. в. Если последовательность точек Р^, &=1, 2,
..., сходится к точке Р, то отрезки воронок точек Р^
сходятся к отрезку воронки точки Р в том смысле,
что для любого е>0 они содержатся при k>k1(e) в
е-окрестности отрезка воронки точки Р. Аналогичными
свойствами обладают И. в. для дифференциальных вклю-
включений
x?F(t, x)
при определенных предположениях о множестве F(t, x).
Лит.:[1] Катке Е., «Acta math.», 1932, v. 58, p. 57—85;
[2] Бокштейн М. Ф., «Уч. зап. МГУ, сер. матем.», 1939,
в. 15, с. 3—72; [3] Р u g h С. С, «J. Dif. Equat.», 1975, v. 19,
№ 2, p. 270—95. А. Ф. Филиппов.
ИНТЕГРАЛЬНАЯ ГЕОМЕТРИЯ — теория инвари-
инвариантных (относительно непрерывных групп отображений
пространства на себя) мер на множествах, состоящих из
подмногообразий пространства (напр., прямых, плос-
плоскостей, геодезических, выпуклых поверхностей и т. п.
многообразий, сохраняющих свой тип при рассматри-
рассматриваемых преобразованиях). И. г. строится для различ-
различных пространств, прежде всего для евклидовых, проек-
проективных, однородных.
И. г. занимается введением инвариантных мер, их
связями и геометрич. применениями. Возникла в связи
с уточнением постановки задач о геометрич. вероятно-
вероятностях.
Для введения инвариантной меры предварительно
ищут такую функцию от координат точки в пространст-
пространстве, интеграл от к-рой по некоторой области пространст-
пространства не изменялся бы после непрерывного преобразования
координат пространства, составляющих определен-
определенную группу Ли. Это требует отыскания интегрального
инварианта заданной группы Ли. Последний находится
как решение системы дифференциальных уравнений в
частных производных
V" -^[gfc (*)*»] = О, А = 1, ...,г, A)
где F(x) ¦— искомый интегральный инвариант, х —
точка n-мерного пространства, 1^ — коэффициент ин-
финитезимального преобразования группы, г — коли-
количество параметров преобразования. Важное значение
в И. г. имеют измеримые группы Ли, т. е. такие груп-
группы, к-рые допускают существование одного и только
одного (с точностью до постоянного множителя) ин-
инварианта. Последними, в частности, являются простые
транзитивные группы.
Следующая задача И. г. состоит в установлении меры
множества многообразий, которые сохраняют свой тип
после нек-рой группы непрерывных преобразований.
Мера устанавливается равной интегралу
\ | F (а1, . . ., а4) | da1 Л . . . л da.4, B)
J а
где Аа — множество точек в пространстве параметров
группы Ли, F — интегральный инвариант группы, оп-
определяемый уравнением A), или плотность меры. Под-
интегральное выражение в B) наз. также элемен-
элементарной мерой множества многообразий. Опреде-
Определенный выбор этой меры полностью устанавливает
соответствие с основной задачей учения о геометрич.
вероятностях. Фактически под геометрич. вероятно-
вероятностью множества многообразий со свойством А1 пони-
понимается относительная доля этого множества, рассмат-
рассматриваемого как подмножество многообразий множества
многообразий, имеющих более общее свойство А. За-
Задача сводится к установлению мер множества многооб-
многообразий со свойством А, подмножества со свойством Аг и
их отношения. Последнее и есть геометрич. вероятность.
В случае однородного многомерного пространства
мера множества многообразий (напр., точек, прямых,
гиперплоскостей, пар гиперплоскостей, гиперсфер, ги-
гиперповерхностей 2-го порядка) однозначно (с точностью
до постоянного множителя) определяется интегралом
} х dH = 1®1, «2, •-., юл], C)
где {со,} суть относительные компоненты (i= 1, ..., h) за-
заданной транзитивной группы Ли G2. Линейные комби-
комбинации с постоянными
Внешняя охватывающая кривая^,—^ коэффициентами этих от-
относительных компонент
представляют собой ле-
левые части уравнений си-
системы Пфаффа, соответст-
соответствующей рассматриваемо-
рассматриваемому множеству многообра-
многообразий. Мера C) наз. к и-
нематической
> мерой в однородном
Перекрестно охватывающая кривая просРтранстве с заданной
Рис. 1. в нем группой преобра-
преобразований. Она представ-
представляет собой обобщение так наз. кинематичес-
кинематической меры Пуанкаре. (Далее все меры указы-
указываются с точностью до постоянного множителя.)
II. г. на евклидовой плоскости Е- обыч-
обычно рассматривает лишь одно непрерывное преобразо-
вание — группу движений (без отражений). Для мно-
множества точек интегральный инвариант — единица, для
множества прямых — тоже единица, если в качестве
параметров прямых выбраны параметры ее нормаль-
нормального уравнения р и ф. Длина произвольной кривой
равна -у- \ ndpdtp, где п — число пересечений прямых с
кривой, а интегрирование ведется по множеству пря-
прямых, пересекающих кривую. Мера множества прямых,
пересекающих две выпуклые фигуры (овалы), равна
разности длин перекрестно охватывающей овалы кривой
и внешней охватывающей кривой (см. рис. 1). Мера
множества прямых, разделяющих два овала, равна дли-
длине перекрестно охватывающей кривой без суммы длин
контуров овалов. Мера множества пар точек определя-
определяется как
\ I h — h \dp Л d(p Л dti A dt2,
где р, <р — параметры нормального уравнения прямой,
проходящей через точки, a t] и 1, суть расстояния по
этой прямой от точек до точки пересечения прямой и
перпендикуляра к прямой, проведенного из начала
координат (см. рис. 2). Мера множества пар прямых
равна
\ | sin (аг— а2) | dx Л dy Л dax Л da2,
где х ж у — координаты точки пересечения пары пря-
прямых, а ах и а2 — углы, к-рые составляют эти пряные с
Рис. 2.
*0
Рис. 3.
одной из координатных осей (см. рис. 3). Мера множе-
множества пар кривых, пересекающих овал, равна половине
квадрата длины кривой, ограничивающей овал, без
площади овала, умноженной на я (ф о р м у л а К р о ф-
т о н а). Применение кинематич. меры к множеству
конгруэнтных овалов, пересекающих заданный овал,
позволяет получить одно из изопериметрич. неравенств,
а именно классическое Боннезена неравенство. Если
r"l h — t1\dpAdq>Adt1Adt2,
где а — длина хорды овала Н, G — множество пересе-
пересекающих овал прямых, г — расстояние между двумя
точками внутренней области овала, то
что позволяет просто определить среднее расстояние
между двумя точками внутри овала. Кинематич. мера
множества фигур есть мера множества фигур, конгру-
конгруэнтных данной. Она равна
f dx A dy а Ар,
где X — множество точек фигуры, х, у — координаты
ее фиксированной точки, <р — угол, определяющий по-
поворот фигуры. Кинематич. мера может трактоваться
как мера множества подвижных систем координат.
Если неподвижную систему координат сделать подвиж-
подвижной, а подвижную — неподвижной, то для одного и того
же множества преобразований кинематич. мера оста-
нется неизменной (симметричность кинематич. меры).
Если с каждым элементом множества конгруэнтных
фигур связать иную подвижную систему, то кинематич.
мера также сохраняется. Мера множества конгруэнт-
конгруэнтных конечных дуг произвольной кривой, пересекающих
заданную дугу нек-рой кривой, равна учетверенному
произведению длин дуг (формула Пуанка-
р е). Количество отрезков прямой данной длины I,
пересекающих овал, равно 2nFe+2ZL0, где Fo и Lo —
площадь овала и длина ограничивающей его кривой.
Если заменить овал незамкнутой кривой, то ^0=0, и
число пересечений будет равно 2lL0. Мера множеств
овалов, пересекающих данный овал, равна 2n(F0-\-F)-\-
+L0L, где F0,F суть соответствующие площади, a Lo и
L — длины кривых, ограничивающих овалы.
И. г. в евклидовом пространстве Е3
строится по аналогии с И. г. в Е2. Для множеств точек
интегральный инвариант также равен единице. Если
множество прямых задано множеством их уравнений в
двух проектирующих плоскостях:
x=kz-{-a, y=/jz+b,
ю интегральный инвариант для совокупности парал-
параллельного переноса и поворота осей равен (/с2+/г2+1)~2-
В частности, мера множеств прямых, пересекающих вы-
выпуклую замкнутую поверхность (поверхность овалоида),
равна половине поверхности овалоида.
Введение по аналогии с Е2 меры множества пар точек
позволяет вычислить среднее значение 4-й степени
длин хорд овалоида, к-рое равно iZVlnS, где V и S —
его объем и поверхность. Для пар пересекающихся пря-
прямых, заданных уравнениями в двух проектирующих
плоскостях:
x=kiZ-\-a—Ajc; y=h1z-\-b—кгс
и
x=k2z~\-a—Л2с; !/=/j2z-|-&—/i2c,
где а, бис — координаты точек пересечения прямых,
она равна
Меры множества пересечений двух заданных подвижных
овалоидов относятся как их объемы. Для плоскости,
заданной уравнением в отрезках, интегральный инва-
инвариант равен
(а-2 + 6-2 + е-2)-2,
где а, Ь, с — длины отрезков. Мера множества плос-
плоскостей, пересекающих поверхность площади S, равна
n2S/2, а среднее значение длин кривых, по к-рым ова-
лоид пересекается множеством плоскостей, равно
л?2/2Ж, где Н — интегральная средняя кривизна.
Для пар плоскостей интегральный инвариант равен
произведению интегральных инвариантов множеств
плоскостей. Кинематич. мера в Е3 равна произведению
меры множества по-различному ориентированных
плоскостей и элементарной кинематич. меры в ориен-
ориентирующей плоскости. Интегральный инвариант для
вращений пространственной фигуры, имеющей одну
неподвижную точку, равен
., , 7—1 7—1 7-
1+h+h+h,
где ?,=a,-tg(q)/2), а a,-, i= 1,2,3, суть направляющие ко-
косинусы оси вращения, <р — угол поворота вокруг этой
оси. Мера множеств тел, имеющих общую точку и отли-
отличающихся поворотом в пространство, равна я2.
И. г. на поверхности строится введением
меры множества геодезических как интеграла от внеш-
внешней дифференциальной формы поверхности по всему
множеству. Таким образом, внешняя дифференциаль-
дифференциальная форма есть плотность множества геодезических,
так как она инвариантна относительно выбора системы
криволинейных координат на поверхности и относи-
относительно выбора параметра, определяющего положение
точки на геодезической. В геодезических полярных
координатах плотность имеет вид
dG = {д ( Y~g (p, 6))/dp) [dO dp],
в частности для сферы dG= cosp[d0dp], а для псевдосфе-
псевдосферы dG=chp[dOdp]. Для множества геодезических, пере-
пересекающих гладкую или кусочно гладкую кривую, плот-
плотность равна dG=|sin<p[[d(pds], где ф — угол пересече-
пересечения, s — длина кривой. Плотность кинематич. меры
(кинематич. плотность) равна dK=[dPdV]. где dP —
элемент площади поверхности, V — угол между геоде-
геодезической и полярным радиусом. Многие результаты
И. г. на Е2 обобщаются на случай однородной поверх-
поверхности. Плотность меры множества представляет собой
кинематич. плотность, что позволяет получить обобще-
обобщение формулы Пуанкаре для Е2. Меры множества
пар геодезических и пар точек строятся так же, как
для Е2.
На основе так наз. полиметрическо й гео-
геометрии П. К. Рашевского (см. [4]) результаты
И. г. на произвольной однородной поверхности обоб-
обобщаются на более широкий класс поверхностей. Обоб-
Обобщение производится путем использования биметрич.
системы Рашевского. Сначала двумя способами вводится
мера в двупараметрич. множестве кривых плоскости.
Затем все выводы, справедливые в случае плоскости"
(рассматриваемой как множество линейных элементов),
обобщаются на случай линий постоянной геодезич..
кривизны произвольной поверхности.
И. г. на проективной плоскости i32.
Для полной группы проективных преобразований на.
Р2:
х, _g,a: + bij/+Ci . , =агх+Ъгу + с, .„
а3х + 63у+1 ' У а,х + Ь3у+1 ' * '
интегральный инвариант существует лишь для совокуп-
совокупности трех точек и равен кубу обратной величины
площади треугольника, вершинами к-рого являются
эти точки. Для пар точек и группы аффинных унимоду-
лярных преобразований
х'= а1х-\-Ь1у-\-с1, у'= а2хЛ-Ь2у-\-с2, a1b2— а2й1 = 1E)
интегральный инвариант равен единице, а для группы
аффинных преобразований интегральный инвариант
множества пар точек равен (х1у2—^2.'/i)~2> гДе xii У1 п
я2, У2 суть координаты точек.
Множество прямых проективной плоскости неизме-
неизмеримо, но для пар точка — прямая и полной группы
проективных преобразований D) интегральный инва-
инвариант равен (х0а+у0&+1)-3, где х0, у0 суть коорди-
координаты точки, а прямая задается уравнением ом;+Рг/+
+ 1 = 0. Множество параллелограммов, заданных урав-
уравнениями
}..-..,
Vi(«i^+PiJ/) + 1=0
причем а:Р2—a2pi=^=0, имеет плотность меры
для группы аффинных преобразований
х' = а1ж+61г/+с1, у' = а2х-{-Ь2у-\-с2, й\Ъ2 — а2Ь1^фй. F)
Для множества окружностей на Р2, заданных уравне-
уравнемаксимальной группой преобразований является груп-
группа преобразований подобия
х=ах'
Плотность меры для нее равна (у—а2—(З2)". На ее
основе вычисляется мера множеств окружностей (цент-
(центры к-рых находятся в нек-рой области), пересекаю-
пересекающихся с заданной кривой. Мера множества окружностей
на Р2 равна кинематич. мере совокупности групп транс-
трансляции и гомотетии.
Множество конич. сечений (инвариант Д=^=0) имеет
в качестве максимальной группы инвариантности про-
проективную группу:
причем det|a,y 1=^=0, г, /=1, 2, 3. Плотность меры для него
равна А~2. Для множества гипербол максимальная
группа инвариантности есть аффинная группа F).
Плотность меры их множества равна а~1А~2|/^62—ас,
где а, Ь, с суть коэффициенты общего уравнения гипер-
гиперболы. Аналогично измерима максимальная группа ин-
инвариантности эллипсов, а для парабол она неизмерима.
Для парабол измеримы лишь ее подгруппы: группы
унимодулярных аффинных п центроаффинных преобра-
преобразований. Элементарная кинематич. мера группы проек-
проективных преобразований D) равна Д~3, где А — опре-
определитель преобразования.
Множество прямых центроаффинной плоскости из-
измеримо. Плотность меры их множества равна р~3,
где р — свободный член нормального уравнения пря-
прямой. Кинематич. мера группы преобразований E) не
центроаффинной плоскости равна а^1. Если Д=Д(<р)
есть ширина овала, то Д~2 есть его плотность меры для
аффинного унимодулярного преобразования.
И. г. в проективном пространстве
Р3. Группа движений в проективном пространстве Р3
€ прямоугольной декартовой системой координат яв-
является измеримой лишь для совокупности четырех то-
точек, и плотность меры равна при этом Д~4, где А есть
объем тетраэдра, вершинами к-рого являются эти точ-
точки. Для совокупностей двух и трех точек измерима
лишь группа аффинных унимодулярных преобразова-
преобразований. Плотность ее меры равна единице. Для трех точек
также измерима группа центроаффинных преобразований
(при условии, что точки не лежат на одной прямой).
Множество прямых в Р3 имеет в качестве максимальной
группы инвариантности полную группу движений, но
она для них неизмерима (измерима лишь нек-рая ее
подгруппа). Измерима полная группа преобразований
для пар прямых. Множество плоскостей относительно
полной группы преобразований в Р3 не допускает меры;
для множества плоскостей Измерима лишь ее подгруппа
ортогональных преобразований. Пары плоскостей до-
допускают меру для группы центроаффинных унимодуляр-
унимодулярных преобразований. Параллелепипеды допускают ме-
меру частной группы аффинных преобразований, множест-
множество пар плоскость — точка допускает мору полной
группы преобразований в Р3. Множество сфер в Р3 до-
допускает меру группы преобразований подобия, причем
плотность меры равна i?~4, где R — радиус сферы.
Множество поверхностей 2-го порядка допускает меру
полной группы преобразований в Р3, причем плотность
меры равна Д~5, где А есть инвариант поверхности.
Множество окружностей в Р3 допускает меру группы
преобразований подобия, причем плотность меры рав-
равна /?~4, где R — радиус окружности. Кинематич. мера
в Р3 полной группы преобразований равна Д~4, где Д
есть ее определитель. Плотность меры множества точек
в центроаффинном унимодулярном пространстве трех
измерений равна единице. Измеримо и множество плос-
плоскостей в этом пространстве с плотностью р ~4, где р
•есть параметр нормального уравнения плоскости.
И. г. на поверхности постоянной
кривизны V2. Семейству кривых в V2 с постоянной
положительной кривизной соответствует максималь-
максимальная группа инвариантности G3 (х). Семейства специаль-
специального вида (трех-, двух- и однопараметрические) допу-
допускают плотности меры максимальной группы инвари-
инвариантности (инфинитезимальных преобразований группы
Gt(x)), а в случае одного параметра — группы G1(x).
То же справедливо для V2 с отрицательной постоянной
кривизной. Трехпараметрич. кривые специального вида
допускают плотность меры максимальной группы
инвариантности преобразований GJ~(x), равную едини-
единице. Меры существуют у группы и в случае специальных
видов двух- и однопараметрич. семейств. В обоих слу-
случаях условие допущения семейством кривых Fg (x) ме-
меры максимальной группы инвариантности G2 (x) состоит
в пространственной транзитивности (измеримости) при-
присоединенной группы Н2(а.).
Обобщение И. г. Вышеприведенное изложение
относится к традиционному пониманию содержания
И. г. как теории инвариантной меры множества гео-
метрич. объектов в различных пространствах, в основ-
основном в однородных. При понимании И. г. как теории
преобразования функций, заданных на множестве од-
одних геометрич. объектов в нек-ром пространстве, в
функции, заданные на множестве иных геометрич.
объектов того же пространства, в качестве основной ста-
ставится задача, обратная интегрированию нек-рой функ-
функции точек пространства по нек-рому геометрич. объек-
объекту этого же пространства. Напр., если вводится интег-
интегральное преобразование функции / (х) в n-мерном аффин-
аффинном пространстве (преобразование Радона) как интегри-
интегрирование ее по гиперплоскости, то в качестве обратной
ставится задача восстановления / (х) по ее интегралам
по гиперплоскостям, т. е. задача нахождения обрат-
обратного преобразования Радона. Аналогично ставятся
и решаются задачи о восстановлении функции на линей-
линейчатых поверхностях 2-го порядка в 4-мерном комплекс-
комплексном пространстве, когда известны ее интегралы по
прямым, составляющим эту поверхность, а также о
восстановлении функции по ее интегралам, взятым
по орисферам в действительном и мнимом пространст-
пространствах Лобачевского.
Лит.: [1] Бляшке В., «Успехи матем. наук», 1938,
в. 5, с. 97—149; [2] С а н т а л о Л. А., Введение в интеграль-
интегральную геометрию, пер. с англ., М,, 1956; [3] Гельфанд И. М.,
Граев М. И., В и л е н к и н Н. Я., Интегральная гео-
геометрия и связанные с ней вопросы теории представлений, М.,
1962; [4] Р а ш е в с к и й П. К., Полиметрическая геометрия,
в кн.; Тр. семинара по векторному и тензорному анализу, в. 5
М.— Л., 1941, с. 21 — 147; [5] S t о k a M. I., Geometric integ-
integrals, Вис, 1967; [6] Итоги науки. Алгебра. Топология. Геомет-
Геометрия. 1968, М., 1970, с. 157—91. С. Ф. Шушурин
ИНТЕГРАЛЬНАЯ КРИВАЯ — график решения
у=у(х) нормальной системы
»' = /(*, у), 2/?R",
обыкновенных дифференциальных уравнений. Напр.,
И. к. уравнения
суть окружности ?2+у2— с2, где с — произвольная
постоянная. Часто И. к. отождествляют с решением.
Геометрич. смысл И. к. скалярного уравнения
y'=f(x, у) (*)
состоит в следующем. Уравнение (*) определяет на
плоскости поле н а п р а в л е н и й, т. е. поле от-
отрезков, тангенс угла наклона к-рых к оси Ох в каждой
точке (х, у) равен f(x, у). Тогда И. к. уравнения (*)
суть кривые, к-рые в каждой точке имеют касательную,
совпадающую с отрезком поля направлений в этой точ-
точке. И. к. уравнения (*) заполняют всю область, в к-рой
функция f(x, у) удовлетворяет условиям, обеспечи-
обеспечивающим существование ц единственность решения за-
задачи Коши, нигде не пересекаясь и не касаясь друг
друга.
,'1ит.: [1] Петровский И. Г., Лекции по теории
обыкновенных дифференциальных уравнений, 6 изд., М., 1970.
Н. Н. Ладис.
ИНТЕГРАЛЬНАЯ ПОВЕРХНОСТЬ — поверхность в
(/)-г1)-мерном пространстве, заданная уравнением и=
-tp(x1,..., хп), где функция и=ц>(х1,. . ., хп) является
решением дифференциального уравнения С . частными
производными. Напр., рассмотрим линейное однородное
уравнение 1-го порядка
ди
UU, I . -y (Jib s\
(*)
,;д1.'сь и — искомая, а Хи. .., Хп — заданные функции
от аргументов хХ1. . ., хп. Пусть в нек-рой области G
и-мерного пространства функции Xlt. . ., Хп непре-
непрерывно дифференцируемы и не обращаются одновремен-
одновременно в нуль, а функции ф! (xj,. ..,ж„),..., cpn_i(xb..., хп)
являются функционально независимыми первыми ин-
интегралами в области G системы обыкновенных дифферен-
дифференциальных уравнений в симметрии, форме
Тогда уравнение всякой И. п. уравнения (*) в области
G можно представить в виде
где Ф — непрерывно дифференцируемая функция.
Для Пфаффа уравнения
Р(х, у, z)dxJrQ(x, у, z)dy+R{x, у, z)dz— 0,
вполне интегрируемого в нек-рой области G трехмер-
трехмерного пространства и не имеющего в G особых точек,
через каждую точку области G проходит И. п. Эти И. п.
нигде не пересекаются и не касаются друг друга.
Лит.: [1] Степанов В. В., Курс дифференциальных
уравнений, 8 изд., М., 1959. н. Н. Ладис.
ИНТЕГРАЛЬНАЯ ПОКАЗАТЕЛЬНАЯ ФУНК-
ФУНКЦИЯ — специальная функция, определяемая для дей-
действительного хфО равенством
J -co t J -
,-t
dt.
График И. п. ф. см. на рис.
Ш
ft
1
/ ¦ , 1 /
/
E
И
r
-t
I
4
1
r
i
i
!
|
H
X
При ж>0 подинтеграль-
ная функция имеет беско-
бесконечный разрыв в точке х-=0
и И. п. ф. понимается в смыс-
смысле главного значения этого
интеграла:
= lim
E-, + 0
Графики функций y=Ei(—x),
j/ = Ei* (x), iy = Li (x).
')¦
И. п. ф. представляется в
виде рядов
) = C4-ln(—ж) +
хк
Я ft
x > 0,
B)
где C=0,5772. . .— Эйлера постоянная.
Имеет место асимптотическое представление:
Еi (— х) « ( * :г ~т~2 "Г? т~ ¦ • ¦ , х —v-I- оэ.
Как функция комплексного переменного z, И. п. ф.
есть однозначная аналитич. функция в плоскости z с
разрезом вдоль положительной действительной полуоси
@<argz<2n); значение ln(—z) выбирается при этом
так, чтобы —я<1т!п(—г)<я. Поведение Ei (z) вблизи
разреза- описывается предельными соотношениями:
lim Ei (z + ir\) = Ei (z) — гя,
Асимптотич. представление в области 0<argz<2n
И. п. ф. связана с интегральным логарифмом \i(x) соот-
соотношениями:
Ei(z)=li(e*), у < О,
Ei(lna:) = li(z), г < 1,
с интегральным, синусом Si (ж) и интегральным косину-
косинусом Ci (я) соотношениями:
Ei(± iz)=.Ci (я) ± iSi(z) T-f-, г > °-
Формула дифференцирования:
Иногда используются обозначения
Ei+ (z) = Ei (z + Ю), Ei- (z) = Ei (z — Ю),
Ei* (z) = ET(zj = Ei (z) + яг.
Лит.: [1] Бейтмен Г., Эрдейи А., Высшие транс-
трансцендентные функции. Функции Бесселя, функции параболиче-
параболического цилиндра, ортогональные многочлены, пер. с англ., 2 изд.,
М., 1974; [2] Я н к е Е., Э м д е Ф., Л ё ш Ф., Специальные
функции. Формулы, графики, таблицы, пер. с нем., 2 изд., М.,
1968; 13] К р а т ц е р А., Франц В., Трансцендентные
функции, пер. с нем., М., 1963; L4] Лебедев Н. Н., Спе-
Специальные функции и их приложения, 2 изд., М., 1963.
А. Б. Иванов.
ИНТЕГРАЛЬНАЯ СУММА — см. Интеграл, Ин-
Интегральное исчисление.
ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ — раздел матема-
математики, в к-ром изучаются понятия интеграла, его свой-
свойства и методы вычислений. И. и. непрерывно связано с
дифференциальным исчислением и составляет вместе с
ним основу матсматич. анализа. Истоки И. и. относятся
к античному периоду развития математики и связаны с
исчерпывания методом, разработанным математиками
Древней Греции. Этот метод возник при решении задач
на вычисление площадей плоских фигур и поверхно-
поверхностей, объемов тел, нек-рых задач статики и гидродина-
гидродинамики. Он основан на аппроксимации рассматриваемых
объектов ступенчатыми фигурами или телами, состав-
составленными из простейших фигур или пространственных
тел (прямоугольников, параллелепипедов, цилиндров и
т. п.). В этом смысле метод исчерпывания можно рас-
рассматривать как античный интегральнып метод. Наиболь-
Наибольшее развитие метод исчерпывания в древнюю эпоху
получил в работах Евдокса D в. до н. э.) и особенно
Архимеда C в. до н. э.). Дальнейшее его применение и
совершенствование связано с именами многих ученых
15 — 17 вв.
Основные понятия и теория интегрального и диффе-
дифференциального исчислений, прежде всего связь опера-
операций дифференцирования и интегрирования, а также
их применения к решению прикладных задач, были
разработаны в трудах И. Ньютона (I. Newton) и Г. Лей-
Лейбница (G. Leibniz) в конце 17 в. Их исследования яви-
явились началом интенсивного развития математич. ана-
анализа. Существенную роль в его создании в 18 в. сыграли
работы Л. Эйлера (L. Euler), Я. и И. Бернулли (Jacob,
Johann Bernoulli), Ж. Лагранжа (J. Lagrange). В 19 в. в
связи с появлением понятия предела И. и. приобрело
логически завершенную форму [работы О. Коши (А. Саи-
chy), Б. Римана (В. Riemann) и др.]. Разработка тео-
теории и методов И. и. происходила в конце 19 в. и в
20 в. одновременно с исследованиями по теории меры,
играющей существенную роль в И. и.
С помощью И. и. стало возможным решать единым
методом многие теоретич. и прикладные задачи, как
новые, к-рые ранее не поддавались решению, так и
старые, требовавшие прежде специальных искусствен-
искусственных приемов. Основными понятиями И. и. являются
два тесно связанных понятия интеграла: неопределен-
неопределенного и определенного.
Неопределенный интеграл от данной
действительной функции на нек-ром промежутке оп-
определяется как совокупность всех ее первообразных
на этом промежутке, т. е. функций, производные к-рых
совпадают с заданной функцией. Неопределенный
интеграл от функции / (х) обозначается через \f(x)dx.
Если F(x) — какая-либо первообразная функция f(x),
то любая другая ее первообразная имеет вид F(x)-\-C,
где С — произвольная постоянная, поэтому пишут
Операция нахождения неопределенного интеграла наз.
интегрированием. Интегрирование является
операцией, обратной к операции дифференцирования:
С F' (x) dx = F (ж) + С, d С / (x) dx = f (x) dx.
Операция интегрирования линейна: если на нек-ром
промежутке существуют неопределенные интегралы
\ ft (x) dx и С /2 (х) dx,
то для любых действительных чисел Хг и Х2 на том же
промежутке существует интеграл
-¦) +Я.2/2 W] ^х = Я,! \ /х (.г) da: +Я.2 \ /2 (ж) da:.
Для неопределенных интегралов справедлива форму-
формула интегрирования по частям: если функции и(х) и
v(х) дифференцируемы на нек-ром промежутке и ин-
интеграл \ vdu существует, то существует и интеграл
\ udv, причем имеет место равенство
\ udv = uv — \ vdu.
Справедлива формула замены перемен-
переменного: если для функций f(x) и x=tf(t), определенных
на нек-рых промежутках, имеет смысл сложная функ-
функция f[(p(t)], функция (f(t) дифференцируема и сущест-
существует интеграл \ f(x)dx, то существует и интеграл
(см. Интегрирование подстановкой).
Всякая непрерывная на нек-ром промежутке функ-
функция имеет на нем первообразную и, следовательно,
для нее существует неопределенный интеграл. Задача
фактического нахождения неопределенного интеграла от
конкретно заданной функции осложняется тем, что
неопределенный интеграл от элементарной функции
не является, вообще говоря, элементарной функцией.
Известны многие классы функций, для к-рых оказывает-
оказывается возможным выразить их неопределенные интегралы
через элементарные функции. Простейшими примерами
этого являются интегралы, к-рые получаются из табли-
таблицы производных основных элементарных функций (см.
Дифференциальное исчисление):
2) \Щ- =
axdx = - \-С, а > 1, а у= 1, в
частности
п
4) \sina;d^ = — cos x4- С;
5) \ cos х dx = sin x -j- С;
7)
8) С shxdx = chx-\-C;
9) f ch.r dx = shx-Jt-C;
13)
d.T
14) f --т==-= arc sin — + C = — arc cos-|-+ C,
|*|<|a|;
dx
15) С = In | *+ J/V ± a2 | + С (когда под
J 1- x2 ± о2
предполагается, что
корнем стоит х2 — а2,
Если знаменатель подинтегральной функции обра-
обращается в нуль в нек-рой точке, то написанные формулы
справедливы лишь для тех промежутков, в к-рых не
происходит обращения в нуль указанного знаменателя
(см. формулы 1, 2, 6, 7, И, 13, 15).
Неопределенный интеграл от рациональной функции
на всяком промежутке, на к-ром знаменатель не обра-
обращается в нуль, является суперпозицией рациональных
функций, арктангенсов и натуральных логарифмов.
Нахождение алгебраич. части неопределенного инте-
интеграла от рациональной функции может быть осуществ-
осуществлено Остроградского методом. К интегрированию ра-
рациональных функций с помощью подстановок сводятся,
напр., интегралы вида
cx + d
где ги r2,..., rm — рациональные числа, интегралы
вида
[ R (х, У ах2 4- Ъх -L- с) dx
(см. Эйлера подстановки), нек-рые случаи интегралов
от дифференциальных биномов, интегралы вида
\ R (sin х, cos .r) dx, \ R (sh x, ch x) dx
(здесь везде R(y\, у%,..., у„) — рациональные функ-
функции), интегралы
[ еа* cos $х dx, [ ea* sin $x dx,
\ хп cos a.r dx, \ xn sin а.г da;,
\ хп arcsin х dx, \ xn arccos x dx,
\ хп arctg х dx, \ x" arcctg x dx, я = 0, 1, 2, ...
и мн. др. Вместе с тем, напр., интегралы
sin* 1
dx
„ = 1,2,...
не выражаются через элементарные функции.
Определенным интегралом
\bf(x)dx
от функции f(x), заданной на отрезке [я, Ь], наз. предел
интегральных сумм определенного вида (см. Коши
интеграл, Римана интеграл, Лебега интеграл, Колмо-
Колмогорова интеграл, Стилтъеса интеграл и т. д.). Если
этот предел существует, функцию f (х) наз. интегри-
интегрируемо й соответственно по Коши, по Риману, по
Лебегу и т. д.
Геометрич. смысл интеграла связан с понятием пло-
площади: если функция f(x)^0 непрерывна на отрезке
[а, Ь], то значение интеграла
равно площади криволинейной трапеции, образованной
графиком функции i(x), т. е. множеством, граница
к-рого состоит из графика функции f(x), a<:#«:fc, от-
отрезка [а, Ь] и двух отрезков прямых х=а и х=Ь, к-рые
иогут вырождаться в точки. К задаче вычисления пре-
предела интегральных сумм, т. е. нахождению определен-
определенного интеграла, сводится вычисление многих встре-
встречающихся на практике величин: площадей фигур и
поверхностей, объемов тел, работы силы, координат
центра тяжести, значений моментов инерции различ-
различных тел и т. п.
Определенный интеграл обладает свойством линей-
линейности: если функции /х (х) и /2 (х) интегрируемы на от-
отрезке [а, Ь], то для произвольных действительных чи-
чисел Х1 и Х2 функция
^¦i/i (x)-\~h2f2 (х)
также интегрируема на отрезке и
Интегрируемость функции на отрезке обладает свой-
свойством монотонности: если функция / (х) интегрируема
на отрезке [а, Ь] и [с, d]d[a, b], то функция f(x) ин-
интегрируема и на отрезке [с, d]. Справедливо свойство
аддитивности интеграла относительно отрезков, по
к-рым происходит интегрирование: если а<с<6 и
функция f(x) интегрируема на отрезках [а, с] и [с, Ь],
то она интегрируема и на отрезке [а, Ъ], причем
(х) dx^J (х) dx+[bcf {т) dx.
Если функции f(x) и g(x) интегрируемы, то их произве-
произведение также интегрируемо. Если f(x)^g(x) на [а, Ъ\, то
Если функция f(x) интегрируема на [а, Ь], то ее абсо-
абсолютная величина \f(x)\ также интегрируема на [а, Ь] и
| $
По определению полагают
" f (x) dx = 0 и V f (x)dx = — \Ь f (x) dx, a < Ъ.
Для определенных интегралов справедливы теоремы о
среднем. Напр., если f(x) и g(x) интегрируемы на отрез-
отрезке [а, Ь], m«/(z)<Af, х?[а, Ь] и функция g(х) не
меняет знака на отрезке [а, Ь], т. е. либо неотрица-
неотрицательна, либо неположительна на этом отрезке, то
существует такое число m<:|a<:Af, что
При дополнительном предположении непрерывности
на отрезке [а, Ъ\ функции / (х) на интервале (а, Ь) су-
существует такая точка |, что
\a (x)dx.
В частности, если g(x)s^\, то
Интегралы с переменным верхним
пределом. Если функция f(x) интегрируема по
Риману на отрезке [а, 6], то функция
*» = J*/(t)dt, a.
непрерывна на этом отрезке. Если, кроме того, функция
f(x) непрерывна в точке х0, то функция F(х) дифферен-
дифференцируема в этой точке и F' (xo)=f{xo). Иначе говоря, в
точках непрерывности функции справедлива формула
Следовательно, для всякой интегрируемой по Риману
на отрезке [а, Ь] функции эта формула справедлива
во всех точках, кроме, быть может, множества точек,
имеющих меру Лебега, равную нулю, ибо если функция
интегрируема по Риману на некотором отрезке, то мно-
множество ее точек разрыва имеет меру нуль. Таким обра-
образом, если функция j (х) непрерывна на отрезке [а, Ь],
то функция
является ее первообразной на этом отрезке. Эта теорема
показывает, что операция дифференцирования являет-
является обратной к взятию определенного интеграла с пе-
переменным верхним пределом, тем самым устанавливая
связь между определенным и неопределенным инте-
интегралами:
Геометрич. смысл этой свйзи состоит в том, что задача о
нахождении касательной к кривой и вычисление пло-
площадей плоских фигур являются в указанном смысле
взаимно обратными.
Для любой первообразной F(x) непрерывной функции
f(x) на отрезке [а, Ь] имеет место формула Нью-
Ньютона — Лейбница:
Она показывает, что определенный интеграл по некото-
некоторому отрезку от непрерывной функции равен разности
значений на концах этого отрезка любой из ее первооб-
первообразных. Эту формулу иногда принимают за определение
определенного интеграла. В этом случае доказывается,
что введенный таким образом интеграл \ / (х) dx яв-
ляется пределом соответствующих сумм.
Для определенных интегралов справедливо правило
замены переменного и формула интегрирования по
частям. Пусть, напр., функция /(х) непрерывна на инте-
интервале (а, 6) и функция ф(г) непрерывна вместе со своей
производной ф' (t) на интервале (а, Р), причем интер-
интервал (а, Р) отображается с помощью функции фD) в ин-
интервал (а, Ъ): a<(f(t)<b при a<i<p и, следовательно,
на (a, P) имеет смысл суперпозиция /[ф(?)]. Тогда, если
ao€(a, P), Ро€(а, Р)> то имеет место формула
замены переменного
Формула интегрирования по частям:
\ и (х) di' (х) = и (х) v (х) — \ v (x) du (x),
Ja к ' у ' v ' v ' х=а Jo
где функции и(х) и v(x) имеют на отрезке [а, Ь] интегри-
интегрируемые производные.
Формула Ньютона — Лейбница сводит вычисление оп-
определенного интеграла к отысканию значений его пер-
первообразной. Поскольку задача отыскания первообраз-
первообразной является сама по себе сложной, то большое значе-
значение имеют другие методы нахождения определенных
интегралов, среди к-рых прежде всего следует отметить
метод вычетов и метод дифференцирования и интегри-
интегрирования по параметру зависящих от параметров
интегралов. Разрабатываются также численные ме-
методы приближенного вычисления интегралов.
Обобщение понятия интеграла на случай неограни-
неограниченных функций и случай неограниченного промежутка
приводит к понятию несобственного интеграла, к-рый
определяется при помощи еще одного дополнительного
предельного перехода.
Понятия неопределенного и определенного интегра-
интегралов переносятся на комплекснозначные функции.
Представление любой регулярной функции комплекс-
комплексного переменного в виде Коши интеграла по контуру
сыграло важную роль в развитии теории аналитич.
функций.
Обобщение понятия определенного интеграла от
функции одного переменного на случай функций многих
переменных приводит к понятию кратного интеграла.
Для неограниченных множеств и неограниченных
функций многих переменных, также как и в одномер-
одномерном случае, вводится понятие несобственного интеграла.
Расширение практич. использования И. и. обуслови-
обусловило введение понятий криволинейного интеграла — ин-
интеграла по кривой, поверхностного интеграла — ин-
интеграла по поверхности и вообще — интеграла по
многообразиям, сводимых в нек-ром смысле к опреде-
определенному интегралу (криволинейный интеграл — к
интегралу по отрезку, поверхностный — к интегралу
по области (плоской), интеграл по «-мерному многооб-
разию — к интегралу по п-мерной области). Интегралы
по многообразиям, в частности криволинейные и по-
поверхностные, играют важную роль в И. и. функций
многих переменных; с их помощью можно установить
связь между интегрированием по области и ее границе
или, в общем случае, по многообразию и его краю. Эта
связь устанавливается Стокса формулой (см. также
Остроградского формула, Грина формулы), являющей-
являющейся обобщением на многомерный случай формулы Нью-
Ньютона — Лейбница.
Кратные, криволинейные и поверхностные интегралы
находят непосредственное применение в математич.
физике, з частности в теории поля. Кратные интегралы
и связанные с ними понятия широко используются
при решении конкретных прикладных задач. Длячис
ленного вычисления кратных интегралов разработана
теория кубатурных формул.
Теория и методы И. и. числовых функций конечного
числа переменных переносятся и на более общие объек-
объекты. Напр., теория интегрирования функций, значения
к-рых принадлежат линейным нормированным простран-
пространствам, функции, заданных на топологич. группах.
обобщенных функций и функций бесконечного числа
переменных (континуальный интеграл). Наконец, но-
новое направление II. и. связано также с появлением и
развитием конструктивной математики.
И. и. применяется во многих разделах математики
(в теории дифференциальных и интегральных уравне-
уравнений, в теории вероятностей и математич. статистике,
в теории оптимальных процессов и др.), и в ее прило-
приложениях.
Лит.: см. [1] — [24] при статье Дифференциальное исчисле-
исчисление, а также дополнение к разделу «Работы основоположников
и классиков...»: 125] Архимед, Сочинения, М., 1962;
[28] Кеплер Ы., Новая стереометрия винных бочек, [пер.
слатин.], М.— Л., 1934; [27] Кавальери Б., Геометрия...,
[пер. с латин.], М,— Л., 1940; [28] Эйлер Л., Интегральное
исчисление, пер. с латин., т. 1—3, М., 1956—58.
Л. Д. Кудрявцев.
ИНТЕГРАЛЬНОЕ МНОГООБРАЗИЕ — множество
Sf точек фазового пространства (?, ж-пространства)
системы
-sr= х (t, х), Н
заполненное интегральными кривыми этой системы, оп-
определенными для всех t ? R, и являющееся многооб-
многообразием в t, ^-пространстве. Размерность сечения S\
плоскостью ?= const наз. обычно размерностью И. м.
Sf. При определении И. м. требование быть много-
многообразием заменяют иногда требованием аналитической
представимости множества Sf уравнением
x=f(t, С)
с функцией /, определенной для всех t из R и i —
= (Сг,. .., Ст) из нек-рой области D и обладающей опре-
определенной гладкостью по t, С при t, C?RxD. И. м.
наз. тогда то-м е р н ы м и той гладкости, какова глад-
гладкость функции /.
Примеры: интегральная кривая периодич. реше-
решения системы (*), т. е. периодическая интегральная
кривая; семейство интегральных кривых системы
(*), образованное семейством квазипериодич. решений
системы (*), заполняющих при i=0 m-мерный тор ^-про-
^-пространства — m-мерное тороидальное интегральное
многообразие, и т. д.
Наиболее изученными И. м. являются торои-
тороидальные многообразия, т. е. множества
Sf, являющиеся торами при любом фиксированном
t?R. Эти многообразия широко встречаются в систе-
системах вида (*), описывающих колебательные процессы.
Лит.: [1] Боголюбов Н. Н., О некоторых статисти-
статистических методах в математической физике, Львов, 1945; [2] Бо-
Боголюбов Н. Н., Митропольский Ю. А., в кн.:
Тр. Международного симпозиума по нелинейным колебаниям,
т. 1.К., 1963, с. 93—154; [3] их же, в кн.: Тр. 4 Всесоюзшго
математического съезда, т. 2, Л., 1964, с. 432—37; [4] Боголю-
Боголюбов Н. Н., Митропольский Ю. А., Самой-
ленко А. М., Метод ускоренной сходимости в нелинейной
механике, К., 1969; [5| Митропольский Ю. А.,
Проблемы асимптотической теории нестационарных колебаний,
М., 1964; L6J М и т т> о п о л ь с к и й Ю. А.. Лыкова О. Б.,
интегральные многообразия в нелинейной механике, М., 1973.
Л. М. Самойленпо.
ИНТЕГРАЛЬНОЕ ПРЕДСТАВЛЕНИЕ АНАЛИТИ-
АНАЛИТИЧЕСКОЙ ФУНКЦИИ — представление аналитич. фун-
функции в виде интеграла, зависящего от параметра.
И. п. а. ф. возникли на ранних стадиях развития тео-
теории функций и математич. анализа вообще как удобный
аппарат для обозримого представления аналитич.
решении дифференциальных уравнений, для исследова-
исследования асимптотики этих решений и их аналитич. продол-
продолжения. Несколько позже И. п. а. ф. нашли применения
Ш решения граничных задач теории аналитических
функций и сингулярных интегральных уравнений,
исследования внутренних и граничных свойств аналити-
аналитических функций различных классов, а также для реше-
решения других, самых разнообразных вопросов матема-
тпч. анализа. В процессе развития теории функций
изучение свойств отдельных, наиболее важных, типов
И.п. а. ф. обособлялось в виде самостоятельных глав
теории функций (см., напр., Коши интеграл, Пуассона
интеграл, Шварца интеграл).
Обширный класс И. п. а. ф., используемых для полу-
получения и исследования аналтттич. решений дифферен-
,сальных уравнений, описывается общей формулой:
*(Z, ?)i>(?)d?, A)
где K(z, Z) — ядро интегрального представления,
v(t) — плотность н L — контур (или система контуров)
в совмещенной плоскости комплексных переменных
z, ?. Целесообразное и, по возможности, наиболее
простое решение трех взаимосвязанных вопросов о вы-
выборе ядра К, плотности v и контура L для пррдставле-
!пя данной функции /(z) (или данного класса функций)
является определяющим с точки зрения успешного
применения метода И. п. а. ф. При этом свойства
представления A), в первую очередь, существенно за-
зависят от того, является ли ядро K(z, ?) целой функцией
комплексных переменных z, ?, или же ядро K(z, Q
сингулярное, т. о. имеет те или иные особенности.
Вообще говоря, ядро И. п. а. ф. не обязательно явля-
является аналптич. функцией переменных z, ? — аналитич-
аналитичность функции / (г) может обеспечиваться за счет специ-
фнч. свойств плотности. Формула A) как формула
простого однократного интегрирования также, вообще
говоря, не обязательна — имеются типы И. п. а. ф., в
к-рых используются повторные интегралы.
Общая схема получения интегральных представлений
специальных функций f(z), являющихся решениями
нек-рого обыкновенного дифференциального уравнения
iy/Kz) = 0, сводится в основном к следующему. За
счет целесообразного выбора, чаще всего несингуляр-
несингулярного, ядра К должна оказаться осуществимой следую-
следующая переброска действия оператора 4^:
K{z, %)\[v\ (t)dl^P[v, К], B)
т. е. ядро должно, в первую очередь, удовлетворять
по возможности простому уравнению с частными про-
производными %г[К] = Ш^[К], допускающему последую-
последующее интегрирование по частям с целью восстановления
первоначального вида ядра под интегралом и переброс-
переброску действия получающегося при этом сопряженного
оператора -О^ на плотность v. Получив формулу вида
B), подбирают достаточно простую плотность v, удов-
удовлетворяющую сопряженному уравнению &-Ы(?) = О,
и контур L, обеспечивающий обращение в нуль обин-
тегрированного члена P[v, К]. При этом необходимо
иметь в виду, что выбор контура L определяет частное
решение исходного уравнения ?z [/] (z) = 0. Наибольшее
применение находят ядра:
К (z, Z,) = e& или К (z, ?) = e'z?,
K(z, g) = zS и K(z, ?) = B-?)a,
иногда называемые соответственно ядром Лап-
Лапласа — Фурье, ядром Меллина и ядром
Эйлера. Различные замены переменных приводят к
видоизмененным формам ядер. В описанном виде полу-
получение И. п. а. ф. самым тесным образом связано с мето-
методом интегральных преобразований.
Таким путем, напр., получается известное интеграль-
интегральное представление функций Бесселя:
где контур L имеет вид восьмерки, охватывающей точки
— 1 и -|-1. Представление C) характерно, с одной сто-
стороны, том, что его плотность у(?)=(?2—1)р~ '2 гораздо
проще, чем представляемые трансцендентные функции
Jp(z), а с другой стороны — тем, что оно позволяет
довольно просто обозреть свойства функций Jp(z) и,
в частности, изучить их асимптотику.
Целесообразное изменение контура L позволяет
осуществить аналитич. продолжение, т. е., иными
словами, позволяет получить И. п. а. ф., пригодное во
всей ее области существования. Напр., интеграл
Эйлера второго рода:
Г (г) = р tz-ie-tdt, Rcz>0,
представляет гамма-функцию Г (z) при Rez>0, а если
выбрать контур интегрирования Ьг в виде петли
(рис. 1), то получается интегральное представление
пригодное для всех z, кроме точек z=— 1, —2, ..., в
к-рых Г (z) имеет простые полюсы. Аналогично, анали-
Рис. 1. Рис. 2.
тич. продолжение интеграла Э й л е р а пер-
первого рода:
В (z, w)= [ Х tz-i A — t) w~1dt, Res>0, Reu?>0,
выражающего бета-функцию В (z, w) при Rcz>0,
Rety>0, осуществляется путем перехода к контуру
интегрирования в виде двойной петли L2 (рис. 2).
Изучались интегральные представления специальных
функций (см. [1], [2]); интегральные представления
весьма обширных классов функций в связи с интеграль-
интегральными преобразованиями [7].
Универсальный характер в теории аналитич. функ-
функций имеют сингулярное ядро Кош и
и соответствующее И. п. а. ф.— Коши интеграл:
* \z>— 2Л!
Это И. п. а. ф. выражает значения однозначной анали-
тич. функции /(z) в области D, ограниченной простым
замкнутым контуром L (или системой таких контуров),
напр., в случае, когда функция /(z) непрерывна в замк-
замкнутой области D=D (]L; в дополнительной области CD,
оо ? CD, интеграл из правой части D) тождественно
обращается в нуль. Фундаментальная роль представ-
представления D) в теории аналитич. функций обусловливается
тем. что интеграл Когаи есть свертка /(г) с фундамен-
фундаментальным решением 1/2ягг оператора Коши — Римана
9 _ 1 / 3 , . 9
поэтому из представления D) получаются все основные
свойства аналитич. функций. С точки зрения общих
свойств И. п. а. ф. интеграл Коши выделяется особенно
простой структурой ядра и тем, что плотность v{?)=
=/E) совпадает со значениями представляемой функции
на контуре L. Это последнее свойство остается в силе,
если под интегралом D) заменить ядро Коши 1/2ягE—z)
на любую однозначную аналитическую по z в замкнутой
области D функцию K(z, ?,), имеющую в точке z=?
простой полюс с вычетом 1. Среди таких функций
K(z, ?) ядро Коши наиболее простое, но указанная
свобода выбора ядра в интеграле Кошп часто исполь-
используется при решении граничных задач.
Совпадение плотности v(t,) с граничными значениями
/(?) аналитич. функции /(z) в сущности есть лишь форма
выражения свойства аналитичности. При использовании
интегрального представления D) с априори произвольно
заданной плотностью i>(?) получается интеграл типа
Коши, в к-ром связь плотности с граничными значе-
значениями выражается гораздо сложнее через сингулярный
интеграл по контуру L.
В граничных задачах теории аналитич. функций
для решения сингулярных .интегральных уравнений
роль интегралов типа Коши и их модификаций исклю-
исключительно важна (см. [5], [6]).
При исследовании внутренних и граничных свойств
аналитич. функций различных классов применяются
более общие И. п. а. ф., чем A), в виде зависящих от
параметра интегралов
по борелевской граничной мере |^, вообще го-
говоря комплексной, сосредоточенной на ограничиваю-
ограничивающем область D контуре L и выражающейся при помощи
той или иной процедуры через представляемую функцию
Напр., все функции /(z), регулярные в единичном
круге D={z;|z|<l} и имеющие положительную дей-
действительную часть, Ref(z)>0, характеризуются пред-
представимостью по формуле Герглотца:
идея к-рой по существу восходит к Шварца интегралу.
Здесь (х — произвольная положительная мера, сосре-
сосредоточенная на окружности L= {?; | ?| = 1}. В теории
однолистных функций находят существенные примене-
применения и другие весьма разнообразные И. п. а. ф. вида E),
известные также под названиями параметрических
представлений, или структурных формул.
Так, для класса типично вещественных
функций /(z) = z+c2z2+. . . в круге D= {z; |z|<l}
(т. е. таких, что Im f(x)=0 при —1<ж<1 и Im /(z)x
Xlmz>0 при Imz=^=O) характерно представление
где \i — произвольная положительная мера, сосредото-
сосредоточенная на окружности L= {?; |?| = 1} и нормированная
условием ||ц,||= \ d\i,(Q=l. Часто применяются также
модификации представления E) в виде
(z)=q> >$*(*. 5) <*!*(»}.
/(z)=
где ф : С—>-С — некоторая особо подбираемая, по воз-
возможности простая, функция, напр. <p(z) = exp z.
Исходя из пон1шания меры \i как функциона-
функционала, И. п. а. ф. E) можно истолковать как значение
{(xj, K(z, Z)} функционала ц на ядре К (г, ?). Следова-
Следовательно, развитием метода И. п. а. ф. является ана-
литич. представление обобщенных функций V в виде
значения V на ядре K(z, ?):
V(z)= (VZ, tf(*. 5)>. F)
При этом в дополнении носителя обобщенной функции
F функция V(z) является аналитической [ядро К (z&)
предполагается аналитическим по z при z=f=Z\. Пред-
Представления вида F) находят важные применения в мате-
матич. физике (см. [10], [11]).
В теории аналнтич. функций/ (г) нескольких комплекс-
комплексных переменных z=(z1,..., zn), п>1, И. п. а. ф. про-
простейшего вида выражаются общей формулой:
/ (z) = J i> (?) <о (z, E), G)
где v(?) — плотность, так или иначе связанная с /(г),
ш (z, ?) — дифференциальная форма по переменным
?= (Si,- • -, ?,,), T=(ti,---, Zn), коэффициенты к-р_ой
зависят от параметров z=(z!,..., г„), z=(z1,..., zn),
причем интегрирование производится по всей границе
дЪ области определения D функции /(г) или по нек-рой
ее части. Употребляются и представления в виде ли-
линейной комбинации интегралов типа G). Напр., функ-
функция /(z), голоморфная в поликруговой области D =
=JD1X .. .XDn и непрерывная в замыкании D, всюду в
D представима в виде интеграла Коши:
где дифференциальная форма ш имеет особенно простой
вид
а интегрирование производится по остову Г=дВ1Х...
. . .XdDn области D (см. Бергмана—Вейля представле-
представление, Лере формула, Бохнера—Мартинелли представле-
представление, а также [8], [9]).
Как и в случае одного комплексного переменного,
дальнейшим развитием И. п. а. ф. G) являются пред-
представления вида:
f(z) = {Vl, K(z, Ш
выражающие аналитич. функцию f(z) в нек-рой обла-
области в виде значения функционала V на ядре K(z, Q
или на форме-ядре a>(z, Z,). При этом V интерпретиру-
интерпретируется, соответственно, как обобщенная функция на
определенном пространстве функций или как поток
на определенном пространстве дифференциальных форм.
Лит.: [1] Смирнов В. И., Курс высшей математики,
т. 3, ч. 2,6 изд., М., 1956; [2] Кр атцер А., Франц В., Транс-
Трансцендентные функции, пер. с нем., М., 1963; [3] Привалов
И. И., Граничные свойства аналитических функций, 2 изд.,
М.— Л., 1950; [4] Голузин Г. М., Геометрическая тео-
теория функций комплексного переменного, 2 изд., М., 1966;
Ij] M у с х е л и ш в и л и Н. И., Сингулярные интегральные
уравнения, 3 изд., М., 1968; [6] Г а х о в Ф. Д., Краевые за-
задачи, 3 изд., М., 1976; [71 Джрбашян М. М., Интеграль-
Интегральные преобразования и представления функций в комплексной
области, М., 1966; [8] Владимиров В. С, Методы теории
функций многих комплексных переменных, М., 1964; [9] Ш а-
г>ат Б. В., Введение в комплексный анализ, 2 изд., М., 1976;
[10] Бремерман Г., Распределения, комплексные пере-
переменные и преобразования Фурье, пер. с англ., М., 1968; [11]
Владимиров В. С, Обобщенные функции в математиче-
математической физике, М., 1976. Е. Д. Соломенцев.
ИНТЕГРАЛЬНОЕ ПРЕОБРАЗОВАНИЕ — функцио-
функциональное преобразование вида
F{x)=\ K(x, t)f(t)dt, A)
где С — конечный или бесконечный контур в комп-
комплексной плоскости, К(х, t) — ядро И. п. Наиболее
часто рассматриваются И. п., для которых К(х, г)=
sK(xt) и С — действительная ось или ее часть (а, Ь).
Если —оо <а, Ь<оо, то И. п. наз. конечным
II. п. Формулы, позволяющие восстановить функцию
/(() по известной F(x), наз. формулами обра-
обращения И. п.
При меры И. п. Преобразование Б о х-
н е р а:
[Tf] (г)=2пг1-"/» 5"/л/я-1 Bягр) pn/4(p)dp,
где Jv (х) — функция Бесселя 1-го рода порядка v,
р — расстояние в R™. Формула обращения: /= T2f.
Равенство Парсеваля:
J J I2 г* -1 dr = J* |/ (р) р p*-idp.
Преобразование Вебера:
F (и,а) = [Х cv(tu,au) tf (t) dt, a< t < oo,
где cv(a, P)=/v(a)F(P)-Fv(a)/v(P), Jv(x), Yv(x) -
функции Бесселя 1-го и 2-го рода. Формула обращения:
Sec с,, (xu.au)
—;—2 5- mF (u,a) du.
При a^O преобразование Вебера переходит в п р е о б-
разование Ганке л я:
oYxtJv(xt)f(t)dt, 0<г<оо.
При v= — 1/ъ это преобразование сводится к синус-
н косинус-преобразованиям Фурье. Формула обраще-
обращения: если /?Z-i@, oo), f(t) имеет ограниченную вариа-
вариацию в окрестности точки ?0>0 и v^ — ]/2, то
v (tux)F(x)dx.
Равенство Парсеваля: если v^ —1/2, F(х) и G(x) —
преобразования Ганкеля функций f(t) и g(t), причем
G?M0 )
f()g()
Другие формы преобразования Ганкеля:
[ °° /v (xt) tf (t) dt, \ °° /v B V^il) / («) d«.
Jo «Jo
Преобразование Вейерштрасса:
/(x) =f ехр[(^г)/4]/@^<
У 4я J — со
является частным случаем свертки преобразования.
Цепные преобразования. Пусть
1i + i(*) = \1 fi(t) Ki(xt) dt, i = l, 2, ..., га,
причем fn + i(x)=f1(x). Такая последовательность И. п.
наз. цепочкой И. п. При я=2 цепные И. п. часто наз.
преобразованиями Фурье.
Кратные (многомерные) И. п.— преоб-
преобразования вида A), где t, x?Rn, С — некоторая об-
область и-мерного комплексного евклидова пространства.
И. п. обобщенных функций могут быть построены
следующими основными способами:
1) Строится пространство основных функций U,
содержащее ядро К(х, t) рассматриваемого И. п. Т.
Преобразование Tf для любой обобщенной функции
f(t)?U' определяется как значение функционала /
на основной функции К(х, t) формулой
T[f(t)](x) = <f, К(х, <)>.
2) Строится пространство основных функций U, на
к-ром определено классическое И. п. Т, отобража-
отображающее U на нек-рое пространство основных функций
V. И. п. Т'/ обобщенной функции /?F' вводится ра-
равенством
<T'f, ф> = </
3) Рассматриваемое И. п. выражается через другое
И. п., к-рое определено для обобщенных функций.
См. также ст. Ватсона преобразование, Гаусса пре-
преобразование, Гегенбауэра преобразование, Конторовича—
Лебедева преобразование, Мейера преобразование, Меле-
ра — Фока преобразование, Меллина преобразование,
Свертки преобразование, Стилтъеса преобразование,
Уиттекера преобразование, Фурье преобразование, Харди
преобразование, Эйлера преобразование, Эрмита преоб-
преобразование, Якоби преобразование.
Лит.: [1] Диткин В. А., П р у д н и к о в А. П.,
в сб.: «Итоги науки. Математический анализ. 1966», М., 1967,
с. 7—82; [2] Брычков Ю. А., Прудников А. П.,
Интегральные преобразования обобщенных функций, М., 1977;
[3] Владимиров В. С, Обобщенные функции в матема-
математической физике, М., 1976. Ю. А. Брычков. А. П. Прудников.
ИНТЕГРАЛЬНОЕ УРАВНЕНИЕ — уравнение, со-
содержащее искомую функцию под знаком интеграла.
И. у. делятся на два основных класса: линейные И. у.
и нелинейные И. у.
Линейные И. у. имеют вид
K(x, *)<p(s)ds = f(z), x?D, A)
где А, К, / — заданные функции, из которых А наз.
коэффициентом, К — ядром, / — сво-
свободным членом (или правой частью)
И. у., D — ограниченная или неограниченная область
евклидова пространства одного или многих измерений,
х, s — точки этого пространства, ds — элемент объема,
ф — искомая функция. Требуется определить ф так,
чтобы уравнение A) удовлетворялось для всех (или
почти всех, если интеграл рассматривается в смысле
Лебега) х из D. Если в A) А, К — матрицы, /, ф —
вектор-функции, тогда A) наз. системой линейных И. у.
Если /=0, то И. у. наз. однородным, в противном
случае — неоднородным.
В зависимости от коэффициента А различают три ти-
типа линейных И. у. Если А (х) = 0 для всех x^D, то A)
наз. уравнением 1-го рода; если А (х)Ф0 для
всех x?D — уравнением 2-го рода; если
А (х) обращается в нуль на некотором подмножестве об-
области D — уравнением 3-г о рода.
В дальнейшем, для простоты изложения, рассматри-
рассматриваются И. у. в одномерном случае, когда D — конеч-
конечный отрезок [а, Ь]. В этом случае линейные И. у.
1-го и 2-го рода можно представить соответственно в
виде:
К (х s) ф (s) ds = / (.т) x ^ f я 61 B)
ф (#) —A, \ К (j;t s) ф (s) ds = f (x), .r ^ [a, &]; C)
постоянное число X наз. параметром И. у.
При исследовании задач математич. физики особенно
часто встречаются уравнения 2-го рода. Если ядро К
фредгольмово, т. е. интегральный оператор в уравне-
уравнениях B), C) вполне непрерывен, то И. у. B), C) наз.
уравнениями Фредгольма 1-го и 2-го
рода соответственно. Важным примером уравнения
Фредгольма является уравнение, в к-ром ядро К удов-
удовлетворяет условию
' \К (х, s) \2dxds < оо, D)
а правая часть / и искомая функция ф — интегрируемые
с квадратом функции.
Уравнение
гъ 1-
(х s)w(s)ds = Q x(-\a 61 E)
наз. однородным И. у., соответствующим
неоднородному И. у. C). Аналогично определяется
однородное И. у., соответствующее уравнению B).
Однородное И. у. всегда имеет решение ф=0, к-рое наз.
нулевым (или т р и в и а л ь н ы м) р е ш е н и е м.
Значение параметра X, при к-ром И. у. E) имеет нену-
ненулевое решение ф, наз. характеристическим
(или фундаментальным) значением
(ч и с л ом) ядра К пли И. у. E), а ненулевое решение
ф — собственной (или фундаменталь-
фундаментально й) ф у н к ц и е й ядра К или И. у. E), принад-
принадлежащей (или соответствующей) данно-
данному характеристнч. значению X. Если X не есть харак-
характеристич. число, тогда его наз. правильным
(или регулярным) значением (числом).
Комплексное ядро К наз. эрмитовым, если
К (х, s) =- К (s, x), F)
где черта означает переход' к комплексно сопряжен-
сопряженному значению. В случае вещественного ядра равенство
F) принимает вид К(х, s)=K(s, x). Такое ядро наз.
симметричным.
Фредгольмово ядро может не иметь характеристич.
числа (напр., в случае ядра Вольтерра, см. ниже).
Если ядро симметрично и не равно нулю почти всюду,
тогда оно имеет, по крайней мере, одно характеристич.
число и все характеристнч. числа вещественны.
Если ядро К обращается в нуль при s~>x (так наз.
ядро Вольтерра), то уравнения B) и C) прини-
принимают вид:
\"аК(х, s)<p(s)ds = f(x), a^s^x^b, G)
г, s) ф (s) ds — f (x), a=s;ssS;a:^;6. (8)
Эти уравнения наз. Волътерра уравнениями 1-го и 2-го
рода соответственно.
Частные примеры И. у. начали появляться в 1-й
пол. 19 в. И. у. стали объектом особого внимания
математиков после того, как удалось свести решение
Дирихле задачи для уравнения Лапласа к исследованию
линейного И. у. 2-го рода. Построение общей теории
линейных И. у. было начато в конце 19 в. Основополож-
Основоположниками этой теории считаются В. Вольтерра (V. Vol-
terra, 1896), Э. Фредгольм (Е. Fredholm, 1903 [5]),
Д. Гильберт (D. Hilbert, 1912 [6]) и Э. Шмидт (Е. Schmidt,
1907 [7]). Еще до исследований этих ученых для
построения решения И. у. был предложен метод после-
последовательных приближений. Этот метод применялся сна-
сначала для решения нелинейных И. у. типа Вольторра
(по современной терминологии) в связи с исследования-
исследованиями обыкновенных дифференциальных уравнений в ра-
работах Ж. Лиувилля (J. Liouville, 1838), Л. Фукса
(L. Fuchs, 1870), Дж. Пеано (G. Реапо, 1888) и др., а
К. Нейманом (С. Neumann, 1877) — для построения
решения линейного И. у. 2-го рода. Общую форму ме-
методу последовательных приближений придал Э. Пикар
(Е. Picard, 1893).
При изучении уравнения колеблющейся мембраны
A. Пуанкаре (Н. Poincare, 1896) пришел к идее введения
переменного численного параметра X в уравнении C).
Тогда же им была высказана гипотеза, что (аналогично
случаю уравнения колеблющейся мембраны) решение
И. у. C) является мероморфиой функцией от X. Эту
гипотезу доказал Э. Фредгольм A900—03). Работам
Э. Фредгольма предшествовали исследования В. Воль-
терра A896 — 97), к-рый изучил И. у. вида G), (8).
Он доказал, что если ядро и правая часть уравнения
непрерывны, то (8) имеет при любом конечном значении
X одно и только одно непрерывное решение, к-рое можно
построить по методу последовательных приближений.
Уравнение C) изучалось Э. Фредгольмом в предполо-
предположении, что его ядро, а также правая часть и искомое
решение — непрерывные функции соответственно на
квадрате [а, Ь])<[а, Ь] и на сегменте [а, Ь]. Следуя
B. Вольтерра, Э. Фредгольм заменил интеграл в C)
интегральной суммой и рассмотрел интегральное урав-
уравнение C) как предельный случай конечной системы
линейных алгебраич. уравнений (см. Фредгольма урав-
уравнение). С помощью формального перехода к пределу
Э. Фредгольм получил формулу, дающую решение
уравнения C); доказал, что построенная формула яв-
является решением уравнения C) за исключением конеч-
конечного или счетного множества значений параметра X,
и доказал теоремы об условиях разрешимости уравне-
уравнения C). Построенную теорию уравнения C) Э. Фред-
Фредгольм распространил на случай системы И. у., а также
на случаи ядра со слабой особенностью (см. Интеграль-
Интегральный оператор). Решение системы приводится к решению
одного уравнения, ядро к-рого имеет линии разрыва,
параллельные осям координат.
Д. Гильберт показал A904), что теоремы Фредголь-
Фредгольма можно доказать путем строгого обоснования процес-
процесса предельного перехода, и построил общую теорию
линейных И. у. на базе теории линейных и билинейных
форм с бесконечным числом переменных. Э. Шмидт [7]
придал более простую и несколько более общую форму
исследованиям Д. Гильберта. Он построил теорию
линейных И. у. с действительным симметричным ядром
независимо от теории Фредгольма, представив ядро в
виде суммы вырожденного и «малого» ядра. Значитель-
Значительное ослабление ограничений, налагаемых в теории
И. у. 2-го рода вещественным симметричным ядром на
заданные и искомые элементы уравнения, было достиг-
достигнуто Т. Карлеманом (Т. Carleman). Им же был распро-
распространен (см. [8]) метод Фредгольма на случай, когда ядро
И. у. C) удовлетворяет условию D). В работах Ф. Рисса
(Riesz, 1918) и Ю. Шаудера (J. Schauder, 1930) теоремы
Фредгольма были обобщены для нек-рого класса ли-
линейных операторных уравнений в банаховых простран-
пространствах.
Основным методом исследования И. у. 1-го рода яв-
является так наз. регуляризации метод.
И. у. 3-го рода явились предметом специальных ис-
исследований Г. Бейтмана (Н. Bateman, 1907), Э. Пика-
ра (Е. Picard. 1910), Дж. Фубини (G. Fubini, 1912),
Ш. Платрпе (Ch. Platrier, 1912).
Если линейное И. у. не является уравнением Фред-
Фредгольма, то его наз. сингулярным (или особым)
уравнением. Общая теория Гильберта квадра-
квадратичных форм с бесконечным числом переменных дает
возможность и в этом случае получить ряд важных
результатов. Для нек-рых конкретных классов сингу-
сингулярных И. у. разработаны специальные способы их
решения, учитывающие характерные свойства этих
уравнений. Так, напр., для сингулярных И. у. и И. у.
типа свертки, вообще говоря, неверна теорема Фред-
гольма о том, что два транспонированных однородных
И. у. имеют одинаковое число линейно независимых
решений.
Параллельно с линейными И. у. изучались и нели-
нелинейные И. у., когда неизвестная функция может вхо-
входить в уравнение в степени п, и>1, как это, напр.,
имеет место в уравнении
ф (х)—Х [ЬК (х, s) «p« (s) ds = f (х), x? [а, Ь].
Она может входить и более общим образом, как, напр.
в уравнении
(см. Гаммерштейна уравнение, Нелинейное интеграль-
интегральное уравнение).
Лит.: [1] П р и в а л о в И. И., Интегральные уравнения,
¦1 изд., М.— Л., 1937; [2] М и х л и н С. Г., Лекции по линей-
линейным интегральным уравнениям, М., 1959; [3] Т р и к о м и Ф.,
Интегральные уравнения, пер. с англ., М., 1960; [4] Смир-
Смирнов В. И. Курс высшей математики, т. 4, ч. 1, 6 изд., М.,
1974; [51 F г е d h о 1 m I., «Acta Math.», 1903, v. 27, p. 365—
390; [6] H i 1 b e r t D., Grundziige einer allgemeinen Theorie
der linearen Integralgleichungen, Lpz. — В., 1912 B Aufl., Lpz.,
1924); [7] Schmidt E., «Math. Ann.», 1907, Bd 63, S. 433—
47(i; Bd 64, S. 161 — 74; 1908, Bd 65, S. 370 — 99; [8] Carle-
man Т., «Math. Z.», 1921, Bd 9, S. 196 — 217. Б. В. Хведелидзе.
ИНТЕГРАЛЬНОЕ УРАВНЕНИЕ; численные
методы решения,— методы нахождения при-
приближенных решений И. у.
Требуется найти решение ф (х) одномерного уравнения
Фредгольма 2-го рода
(х, s)<p(s)ds + f(z), A)
где f(x) непрерывна на [а, Ь], К — числовой пара-
параметр, К(х, s) непрерывна на а<?х, s<ib.
Пусть X не является собственйым значением ядра
К(х, s). Тогда уравнение A) имеет единственное реше-
решение <f(x), непрерывное на [а, Ъ]. При этих условиях
можно указать следующие способы получения прибли-
приближенного решения.
Первый способ. Пусть а и Ь — конечные
числа. Интеграл в A) заменяют интегральной суммой
по сетке {s,}, /=0, 1, 2,..., п, а переменной х при-
придают значения х1, х2,. . ., хп. Получается система
линейных алгебраич. уравнений относительно фу
где Aij=^i— ХС,К (х;, Xj), Cj — коэффициенты квадра-
квадратурной формулы, по к-рой интеграл в A) заменен ин-
интегральной суммой. Система B) при достаточно больших
п НМ1Ч-1 с,;|гиственное решение {фу}. В качестве прибли-
приближенного решения уравнения A) можно брать функцию
Ф„(*) = /()+* 2
J — 1
так как при п—*- оо и А„ = тах {|^,- + i — х; |} —э-0 по-
i
следовательность функций ф„(г) равномерно сходится
на [а, Ь] к искомому решению уравнения A). См. [1]
[2], [3J, [4].
При замене интеграла по квадратурной формуле на-
надо иметь в виду, что чем более точная квадратурная
формула используется, тем большую гладкость ядра
и решения (а следовательно, и f (х)) надо требовать.
В случае, когда промежуток интегрирования (а, Ъ)
бесконечный, его заменяют конечным промежутком
(аг, bt), пользуясь априорной информацией о поведении
искомого решения ф(я) при больших значениях \х\.
Полученное уравнение решают приближенно описан-
описанным способом; либо заменой переменной интегрирова-
интегрирования сводят промежуток интегрирования к конечному;
либо применяют квадратурные формулы для бесконеч-
бесконечного промежутка.
Второй с п о с о б. В уравнении A) ядро К(х, s)
заменяют аппроксимирующим его вырожденным ядром
в к-ром функции {at-(x)} линейно пезависимы. Полу-
Получающееся при этом уравнение
Ф (.г) = X J* 2"= ! ai М Ъ[ (s) ф (*) ds + / (х) C)
имеет решение ф(я) вида
в к-ром постоянные
подлежат определению. Подставляя функцию <р(х) в
уравнение C) и сравнивая коэффициенты при функ-
функциях а;(х), получают систему линейных алгебраич.
уравнений для С; вида
1 ^^ ^ „ г* о . • л 9 n
I Л / ; , СХг у С- j — Р[, I — 1, ь, . . . , /?,
где
я/ (s)b;(s)ds, Р,- =
Определив С,- из этой системы и подставив их в D),
получают функцию ц>(х), к-рая и принимается за при-
приближенное решение уравнения A), так как при доста-
достаточно хорошей аппроксимации ядра К(х, s) вырожден-
вырожденным ядром решение уравнения C) произвольно мало
отличается от искомого решения <р(х) на любом отрезке
[ai,&i] С! (а, Ь), а если (а, Ь) — конечный промен,уток,
то—и на отрезке [а, Ь] (см. [1], [4]).
Третий способ. В качестве приближенных
решений берутся функции ц>п(х), получаемые методом
итераций по формулам
K(x, s)(fn(s)ds + f(x), n = 0, 1, 2, ...,
Фо(я)—/(ж), так как последовательность {ф„(^)} рав-
равномерно сходится к искомому решению при п—>-оо, если
\%\<ИМ{Ъ—а), M=suy\K(x, s)\. Сходимость {<рп(х)}
X, S
к точному решению имеет место и для ядер с интегри-
интегрируемой особенностью (см. [1]). Оценки погрешностей
этих методов содержатся в [1] — [7]. В [8] рассматри-
рассматривается вопрос о минимальном число арифметич. опера-
операций, необходимых для того, чтобы получить приближен-
приближенное значение интеграла с заданной точностью. Реше-
Решение этой задачи эквивалентно отысканию величины
минимальной погрешности приближенного решения за-
задачи при заданном числе арифметич. операций.
Для решения интегральных уравнений Фредгольма
1-го рода требуется применять специальные методы,
так как эти задачи являются некорректно поставленны-
поставленными. Если в уравнении A) X совпадает с одним из соб-
собственных значений ядра К(х, s), то в этих условиях
задача нахождения решения уравнения A) является не-
некорректно поставленной и требует применения специ-
специальных методов (см. Некорректные задачи).
Нелинейные И. у. 2-го рода приближенно решают
обычно методом итераций (см. [3]).
Для получения приближенных решений как линей-
линейных, так и нелинейных И. у. применяют также Галер-
кина метод.
Аналогичные методы можно применять и для полу-
получения приближенных решений многомерных интеграль-
пых уравнений Фредгольма 2-го рода. Однако числен-
численная реализация их сложнее. О кубатурных формулах
приближенного вычисления кратных интегралов и
оценках их погрешностей см. [5] — [10]. В [10] рас-
рассмотрен метод Монте-Карло приближенного вычисле-
вычисления кратных интегралов.
Лит.: [1] Петровский И. Г., Лекции по теории ин-
интегральных уравнений, 3 изд., М., 1965; [2] Бахвалов
Н. С, Численные методы, 2 изд., М., 1975; [3] Березин
И. С, Жидков Н. П., Методы вычислений, 3 изд., т. 1,
1966; [4] Канторович Л. В., Крылов В. И., При-
Приближенные методы высшего анализа, 5 изд., М.— Л., 1962;
[5] М ы с о в с к и х И. П., «Сиб. матем. ж.», 1964, т. 5, X» 3,
с. 721—23; [6] его же «Ж. вычисл. матем. и матем. физ.»,
1972, т. 12, № 2; [7] е г о ж е, там же, 1975, т. 15, Mi 6; [8]
Емельянов К. В., Ильин А. М., «Ж. вычисл. матем. и
матем. физ.», 1967, т. 7, № 4, с. 905 — 10; [9] С о б о л е в С. Л.,
Введение в теорию кубатурных формул, М., 1974; [10] С о-
б о л ь И. М., Многомерные кубатурные формулы и функции
Хаара, М., 1969. В. Я. Арсенин.
ИНТЕГРАЛЬНОЕ УРАВНЕНИЕ С СИММЕТРИЧ-
СИММЕТРИЧНЫМ ЯДРОМ — интегральное уравнение (н. у.) с сим-
симметричным действительным ядром:
К(х, s)=K (s, х).
Теория линейных и. у. с симметричным и действи-
действительным ядром была впервые построена Д. Гильбертом
(D. Hilbert, 1904) привлечением теории симметричных
квадратичных форм с помощью перехода от конечного
числа переменных к бесконечному. Затем Э. Шмидт
(Е. Schmidt, 1907) предложил более элементарный
метод обоснования результатов Д. Гильберта. Поэтому
теорию И. у. с с. я. часто наз. также теорией Гильберта—
Шмидта. Значительное ослабление ограничений, нала-
налагаемых в этой теории на заданные и искомые элементы
уравнения, было достигнуто Т. Карлеманом (Т. Carle-
man) (см. ниже).
Пусть имеется и. у. 2-го рода с действительным сим-
симметричным ядром:
(х, s)y(s)ds = f(x), х?[а,Ъ]. A)
При построении теории И. у. с с. я. достаточно пред-
предполагать, что симметричное ядро К измеримо на квад-
квадрате [a, b]X[a, b]
С* [Ьа\К (х, s)\*dxds < оо, B)
а свободный член / и искомая функция ф — интегри-
интегрируемые с квадратом функции на отрезке [а, Ь] (инте-
(интегралы понимаются в смысле Лебега).
Газработка теории И. у. с с. я. начинается с изуче-
изучения ряда общих свойств собственных чисел п собствен-
собственных функций однородного симметричного и. у.:
K(x, s)y{s)ds = O, х? [а, Ь]. C)
А именно, доказывается, что: уравнение C) обладает
по крайней мере одним собственным числом (когда К
почти всюду не равно нулю); собственные функции,
принадлежащие различным собственным числам,—
ортогональны; собственные числа — действительны;
ввиду действительности ядра без ограничения общности
можно предполагать, что собственные функции действи-
действительны; на любом конечном сегменте значений парамет-
параметра "к может находиться лишь конечное множество соб-
собственных чисел.
Множество всех собственных чисел уравнения C)
наз. спектром этого уравнения. Спектр — непустое
конечное или счетное множество чисел {(Xj, ц2, . . .,
..., |i,,,...}; каждому числу \х,п спектра соответствует
конечное множество линейно независимых собственных
функций. Собственные числа и собственные функции
можно расположить в виде последовательностей:
A.J, Я2, ..., Кт, ... \
так, что абсолютные величины собственных чисел не
убывают \Хк\ <|A,ft+il; каждое собственное число по-
повторяется столько раз, сколько собственных функций
ему соответствует. Поэтому каждому числу %и в D)
соответствует лишь одна собственная функция. Можно
считать, что система функций {ф^} ортонормирована.
Последовательности D) наз. системой собственных чи-
чисел и собственных функций симметричного ядра К
или уравнения C). Нахождение этой системы равно-
равносильно полному решению однородного симметричного
и. у. C).
Ряд Фурье ядра К (х, s), рассматриваемого как функ-
функция от s относительно ортонормированной системы
{(}, будет
Так составленный ряд из системы собственных чисел
и собственных функций симметричного ядра К наз.
билинейным рядом ядра К или билинейным разложе-
разложением ядра К по его собственным функциям. Этот ряд
сходится в среднем к ядру К, т. е.
lim \Ь\Ь\К(Х, 8)-У" X*2 ф*(*)фА (
Если же билинейный ряд E) сходится равномерно,
g)=y- ,
В частности, это последнее равенство всегда имеет
место, если ядро обладает лишь конечным множеством
собственных чисел. В этом случае ядро К является вы-
вырожденным. Имеет место и обратное утверждение:
вырожденное симметричное ядро имеет конечное множе-
множество собственных чисел (и, следовательно, конечное
множество собственных функций). Билинейный ряд не-
непрерывного на квадрате [а, Ь] X [а, Ь] ядра К с положи-
положительными собственными числами сходится равномерно.
Зная систему D) собственных чисел и собственных
функций, можно построить решение неоднородного
уравнения A). Имеют место следующие теоремы.
Если % не является собственным числом ядра К,
то симметричное и. у. A) имеет единственное решение
ф, выражаемое формулой
Ф (х) = 1 (х) + К 22 *= г ^гг Ф* (*), F)
где А,? — собственные числа, fk — коэффициенты Фурье
функции / относительно ортонормированной системы
{фт} собственных функций ядра, т. е.
/*=$*/(«)ф* (•)<*«, * = 1, 2, ...
Пусть Х=Х± — собственное число ядра К; тогда сим-
симметричное и. у. A) разрешимо лишь в случае, если
удовлетворяются условия
*/()*(*)<**=0, * = 1, 2, ...,«/,
/*=$*/
где ф1т..., ф9 — собственные функции, принадлежа-
принадлежащие собственному числу К1. При соблюдении этих усло-
условий все решения уравнения A) выражаются формулой
Ф (*) = /(*) +
где с1,..., Сд — произвольные постоянные.
Если ядро К имеет бесконечное множество собствен-
собственных чисел и, следовательно, в правых частях формул F).
G) стоят бесконечные ряды, то они сходятся в среднем.
Если от ядра К дополнительно потребовать, что оно
удовлетворяет условию
^ | К (х, s) |2 ds s? const, x?[a, Ь],
то упомянутые ряды будут сходиться абсолютно и рав-
равномерно.
Формулы F) и G) наз. формулами Шмид-
т а. Большая часть теории И. у. с с. я. легко распро-
распространяется и на комплекснозначные функции. В этом
случае аналогом действительного симметричного ядра
является эрмитово ядро: К (х, s) = K (s, x).
Если известна система D) собственных чисел и соб-
собственных функций симметричного ядра К, то можно
легко исследовать симметричное уравнение Фредголь-
ма 1-го рода
К(х, s) <p(s)ds = f (x), х?[а,Ь]. (8)
Пусть, как и выше, симметричное ядро К уравнения
(8) — интегрируемая с квадратом функция на квадрате
[а, Ь]Х[а, Ь], а правая часть / и искомое решение ф —
такие же функции на сегменте [а, Ь]. Симметричное
ядро наз. полным, если система его собственных функ-
функций {фт} полна (замкнута).
Теорема Пи кар а. Пусть К(х, s) — полное
ядро. Тогда для разрешимости уравнения (8) необхо-
необходимо и достаточно, чтобы ряд
где /k — коэффициенты Фурье функции /, сходился.
При выполнении этого условия решение (единственное)
представимо в виде
Ф [X) = /|.
причем последний ряд сходится в среднем.
Т. Карлеман [5] построит теорию при менее ограни-
ограничительных условиях на симметричное ядро К, чем у
Д. Гильберта и Э. Шмидта. Эти условия следующие:
1) \ К~(х, s)ds существует в смысле Лебега и
Jo
Г Ь
lim V [К (у, s) — К (х, s)]2 ds = O
у -+ х J °
для любого хфх(, где {х,} — некоторая последователь-
последовательность точек, к-рая может иметь конечное число предель-
предельных точек; 2) может существовать конечное множество
точек s1,. . ., sn? {х[}, в окрестности к-рых функция
К2 (х, s) ds
не интегрируема, но она интегрируема на множестве
Ае , оставшемся после удаления из сегмента [а, Ъ]
интервалов (s/—е, s,-f-e), t=l,..., п, где е — произ-
произвольное достаточно малое положительное число.
Пусть Кг (х, s) — функция, к-рая равна нулю на
множестве точек {(х, s)} таких, что \х—s,-| <:e, \s—s,-] <:
<е , ?=1,..., п, а вне этого множества в квадрате
[a, b]X[a, b] совпадает с ядром К уравнения A). Идея
метода Карлемана заключается в следующем: взамен
уравнения A) рассматривается линейное интегральное
уравнение второго рода с ядром Кг ¦ Изучив спектр и
решения этого уравнения, затем с помощью перехода к
пределу при е—>-0 исследуется спектр и решения урав-
уравнения A).
Лит.: Ll] Hilbert D., Grundziige einer allgemeinen Theo-
rie der linearen Integralgleichungen, Lpz.— В., 1912 B Aufl.,
1924); [2] Schmidt E., «Math. Ann.», 1907, Bd 63, S.
433—76; Bd 64, S. 161—74; 1908, Bd 65, S. 370—99; [3] В и а р-
д а Г., Интегральные уравнения, пер. с нем., М.— Л., 1933;
[4] М и х л и н С. Г., Лекции по линейным интегральным урав-
уравнениям, М., 1959; [5] С а г 1 е m a n Т., Sur les equations inte-
grales singulieres a noyau reel et symetrlque, Uppsala, 1923.
В. В. Хведеливзе,
ИНТЕГРАЛЬНОЕ УРАВНЕНИЕ ТИПА СВЕРТКИ —
интегральное уравнение, содержащее искомую функцию
под знаком интегрального преобразования свертки (см.
Интегральный оператор). Особенностью И. у. т. с,
является то, что ядра таких уравнений зависят от
разности аргументов. Простейший пример — уравнение
^ A(t —T)9(T)dT = /(t), — oo<«<oo, A)
где к и / — заданные функции, а ф — искомая функция.
Пусть к и f?Lj (— оо, оо) и решение ищется в том же
классе. Для разрешимости уравнения A) необходимо и
достаточно выполнение условия
1 — К (к) фО, -оо < Я< оо, B)
где К — преобразование Фурье функции к. При выпол-
выполнении условия B) уравнение A) в классе L1 имеет
единственное решение, представимое формулой
где k^L1(—оо, оо) однозначно определяется с помо-
помощью своего преобразования Фурье
Уравнения типа свертки на полупрямой (Винера
Хопфа уравнение)
<oo, D)
возникает при исследовании различных вопросов как
теоретического, так и прикладного характера (см. [1],
14]).
Пусть правая часть/и искомая функция <f?Lp (О, оо),
1<:р<:оо, а ядро k?L1(—оо, оо) и
а (Я)=1 — К (К) Ф 0, — оо < Я < оо. E)
Функцию а (Я) наз. символом уравнения
D). Индексом уравнения D) называется число
Еслих = 0,функции К+, К-, определенные из равенств:
являются преобразованиями Фурье, соответственно,
функций к + ,к- €j?i(—оо,оо) таких, что k+{t) =
= к- (—1) = 0 при /<0. При указанных выше условиях
уравнение D) имеет единственное решение, которое
представляется формулой
ф (t) = f (t) + f °° г (t, x) ф (т) dx, (8)
где
r(t,x) = k, (t — x) +A_(t — x)-
Если х<0, то все решения уравнения D) даются
формулой
1
+ S" г0 (t, т) [/ (т) + 2*1', ^*-^Т] dx, (9)
где С? — произвольные постоянные,
/•о (t, т) = *40) (t-x) + Л(_ц (*-т) +
-T)d*. (Ю)
а функции к'+}, fe'i* ?/-i(—00,00) однозначно определя-
определяются с помощью своих преобразований Фурье:
1 + А11' (X) = [l +Л-(_0) (л)] (К+ if (Х- i)-\
A1)
Однородное уравнение, соответствующее D), имеет
при я:<0 ровно \х\ линейно независимых решений
ф!,. . ., Ф|Н1, являющихся абсолютно непрерывными
функциями на любом конечном интервале, причем эти
решения можно подобрать так, что ф;, + 1(^) = ф^(|;),
фл(О) = О при fc=l,..., |х| — 1 и ф|-х|@)=г=0.
Если я:>0, то уравнение разрешимо лишь при соб-
соблюдении условий:
х
/mib.-ma< = 0, / = 1, ...,х, A2)
О ^
где i)),, . .., \р-л — система линейно независимых решений
транспонированного к D) однородного уравнения
При соблюдении этих условий решение (единственное)
дается формулой
где
П (*. т) = #' (*-т) -f- й(_0) (t-т)
а преобразование Фурье A*(i" (Я) и К+' (X) функций
A-™'(t) и A-+)(i)^L1(—00, 00) определяется равенством
11 равенствами A1). Для уравнения D) справедливы
теоремы Нётера (см. Сингулярное интегральное урав-
уравнение).
Первые значительные результаты по теории урав-
уравнений D) были получены в [11J, где указан эффективный
метод (так нац. метод Випера — X о п ф а)
решения однородного уравнения, соответствующего
D1, в предположении, что ядро и искомое решение
удовлетворяют условиям: при некоторых 0<<х<а и
Основным моментом в методе Винера—Хопфа являет-
является идея факторизации функции h (К), голо-
голоморфной в полосе ]1тЯ|<я, то есть идея о возможности
ее представления в виде произведения h-{\)h+(k),
где й_, й+ — некоторые голоморфные функции соот-
соответственно в полуплоскостях 1тЯ<в и 1тХ> — а, удов-
удовлетворяющие нек-рым дополнительным требованиям.
Эти результаты были развиты и дополнены (см. [4]).
Разработан метод сведения уравнения D) к граничной
задаче линейного сопряжения. Этим путем уравнение
D) было решено в следующих предположениях: к?Ьг 2
(—оо, со), K?Lij>a{~- 00, 00), 0<се<1: К(к)=
0(ШР), Р>0, при |Я|->оо и 1 — К(\)ФО, —оо<
Кроме того, была выяснена роль числа ind[l — K(k)]
в решении уравнения D). В предшествующих рабо-
работах аналогичную роль играло число нулей аналитич.
функции 1 — К (К) в некоторой полосе (см. [3]).
Условие E) является не только достаточным, но и не-
необходимым для того, чтобы в случае уравнения D)
были справедливы теоремы Нётера. Приведенные реше-
решения уравнения D) упрощаются в ряде практически важ-
важных частных случаев. Установлена асимптотика реше-
решения для специальных правых частей (см. [4]).
Уравнение D) изучено п в случае, когда к (? L1 (—оо,
оо) и преобразование Фурье К(Х) ядра k(t) имеет
разрывы 1-го рода (см. [5]) или же является почти перио-
периодической функцией (см. [2]). В этих случаях условие
E) оказывается недостаточным для того, чтобы были
справедливы теоремы Нётера.
Справедливость большинства перечисленных выше
результатов установлена также для систем уравнений
типа D), но, в отличие от одного уравнения, системы
И. у. т. с. в общем случае не решаются явно в квадра-
квадратурах (см. [6]).
К И. у. т. с. относятся также парные уравне-
уравнения (или дуальные уравнения)
A5)
* < О,
и транспонированное к ним так наз. И. у. т. с. с д в у ми
ядрами:
— [° k2 (t — х) <р(т) с?т = /(«), — оо < t < оо. A6)
J - со
Уравнения A5) решены явно в квадратурах в [3],
а уравнение A6) — в [10].
И. у. т. с. на конечном промежутке
оо, A7)
где k?Lt(—Т, Т), является Фредголъма уравнением
(см. [7], [9]).
И. у. т. с, символ к-рых обращается в нуль в конеч-
конечном числе точек и порядки нулей — целые числа, под-
поддаются явному решению в квадратурах (см. [8], [12]).
Лит.: [1] Нобп Б., Применение метода Винера —
Хопфа, пер. с англ., М., 1962; [2] Г о х б е р г И. Ц., Фельд-
Фельдман И. А., Уравнения в свертках и проекционные методы их
решения, М., 1971- [3] Рапопорт И. М., «Докл. АН СССР»,
1948, т. 59, J* 8, с. 1403—06; «Сб. тр. ин-та матем. АН УССР>>,
1949, № 12, с. 102—17; [4] К рейн М. Г., «Успехи матем.
наук», 1958, т. 13, в. 5, с. 3—120; [5] Дудучава Р. В.,
«Math. Nachr.», 1975, Bd 65, Л* 1, S. 59—82; [6] Гохберг
И. Ц., К р е й н М. Г., «Успехи матем. наук», 1957, т. 12,
в. 2, с. 44 — 118; [7] Ганин М. П., «Изв. ВУЗов. Матема-
Математика», 1963, №2, с. 31—43; [8] Г ах о в Ф. Д., С м а г и-
н а В. И., «Изв. АН СССР. Сер. матем.», 1962, т. 26, N 3,
с. 361—90; [9] С и м о н е н к о И. В., «Изв. ВУЗов. Матема-
Математика», 1959, М2, с. 213—26; [10] Черский Ю. И., «Уч.
зап. Казанск. ун-та», 1953, т. 113, кн. 10,с. 43—56; [ll]Wie-
п е г N., Н о р f E., «Sitz. Akad. Wiss. Berlin», 1931, S. 696—
706; [12] Prossdorf S., Einige Klassen singularer Glei-
chungen. В., 1974. P. В. Дудучава, Б. В. Хведелидзе.
ИНТЕГРАЛЬНОЙ РАЗДЕЛЕННОСТИ УСЛОВИЕ -
условие на линейную систему дифференциальных урав-
уравнений
(где A (t) — непрерывное отображение R +
R"), причем sup |Ц (i)||<+oo), состоящее в следующем:
teR +
система имеет решения xj(t), i=l, 2,..., п, удовлетво-
удовлетворяющие при нек-рых а>0, t?>0 неравенствам
*t{t) \-\xt (Т) |-1 3, <*ев"-Т>.| *,-_! @ |.| *,-_! (Т) |-1
для всех i = 2,..., n и всех ^^
Множество систем, удовлетворяющих И. р. у., явля-
является внутренностью множества точек непрерывности
всех Ляпунова характеристических показателей в про-
пространстве систем
x^A(t)x, sup || A (t) || <+ оо
лге R +
с метрикой
р(А (*), Я(*))= sup ||Л (*)-Д(ОЦ.
I € R +
Лит.: [1] И з о 6 о в Н. А., в кн.: Итоги науки и техни-
техники. Математический анализ, т. 12, М., 1974, с. 71 —146.
В. М. Миллионщиков.
ИНТЕГРАЛЬНЫЙ АВТОМОРФИЗМ — то же, что
специальный автоморфизм, построенный по автомор-
автоморфизму Т пространства с мерой (X, и,) и функции /
(заданной на этом пространстве и принимающей поло-
положительные целочисленные значения). Термин «И. а.»
принят главным образом в иностранной литературе.
ИНТЕГРАЛЬНЫЙ ГИПЕРБОЛИЧЕСКИЙ КОСИ-
КОСИНУС — специальная функция, определяемая для дей-
действительного х равенством
Chi (.г) = С + 1пх~[* с1и~\ dt -= Ci (ix) ~ i JL ,
где C=0,5772. . .— Эйлера постоянная, Ci (.г) — ин-
интегральный косинус. И. г. к. представляется в виде
ряда
Иногда используют обозначение chi(z).
Лит. см. при ст. Интегральный косинус. А. Б. Иванов.
ИНТЕГРАЛЬНЫЙ ГИПЕРБОЛИЧЕСКИЙ СИНУС —
специальная функция, определяемая для действитель-
действительного х равенством
где Si (ж) — интегральный синус. И.-г. с. представляется
в виде ряда
Х^ Х^
Shi (*)=*4-ш Л. _+....
И. г. с. и интегральный гиперболический косинус Chi (ж)
связаны соотношением:
Chi (x) — Shi (x) = Li e*,
где Li — интегральный логарифм.
Иногда используют обозначение shi(.r).
Лит. см. при ст. Интегральный косинус. А. В. Иванов.
ИНТЕГРАЛЬНЫЙ ИНВАРИАНТ степени к
(порядка к) гладкой динамической сис-
системы — а) абсолютный И. и.: внешняя диф-
дифференциальная форма <р степени к, переходящая в себя
под действием преобразований, образующих эту си-
систему; б) о т н о с и т е л ь н ы й И. и.: внешняя диф-
дифференциальная форма <р степени к, внешний дифферен-
дифференциал к-рой является абсолютным И. и. (имеющим уже
степень &+1).
Обычно речь идет об И. и. для потока {?(}, опреде-
определяемого системой обыкновенных дифференциальных
уравнений x=f(x), где / — гладкое векторное поле,
заданное в нек-рой области евклидова пространства
(или многообразия); в терминах координат (локальных
координат в случае многообразия) эта система имеет вид
X, — Ji\J-i, ¦ ¦ ¦ , ¦' п), I — 1> • • • , П. {I)
Важный пример И. и.— форма объема q>=p(x)dx} л. . .
/\dxn [где р(х) — положительная локально интегрируе-
интегрируемая (часто даже непрерывная или гладкая) функция
координат]. При гладкой р эта форма является абсолют-
абсолютным И. и. системы A), если
В этом случае поток имеет инвариантную меру и.(Л) =
= \ ф, к-рая в терминах (локальных) координат
задается своей плотностью р (х) (последнюю, допуская
нек-рую вольность речи, тоже часто наз. И. и.).
Гамилътонова система с (обобщенными) импульсами
и координатами р/, п;, г=1,. . ., т, имеет относительный
И. п.
и абсолютный И. и.
&=I,dpi Adq/.
Этот факт можно положить в основу определения
гамилыоновых систем и использовать при развертыва-
развертывании их теории, ибо многие специфич. особенности по-
последней непосредственно связаны с этими И. и. (см.[4],
[5]). Внешние степени ю* (в том числе и форма объема
&'") являются абсолютными, а произведения г|злю/г —
относительными И. и. любой гамильтоновой системы,
поэтому их наз. универсальными И. и. га-
мильтоновых систем. С точностью до множителя все
универсальные И. и. гамильтоновых систем сводятся к
указанным (см. [4], [7]).
Если система A) имеет абсолютный И. и. ф степени к,
то для любой fe-мерной гладкой цепи с (напр., гладкого
й-мерного многообразия)
сф = $э <с)ф- B)
Если же система A) имеет относительный И. и., то B),
вообще говоря, имеет место лишь тогда, когда цепь
является границей цепи размерности /с+1. Иногда
относительный И. и. определяют несколько более
сильным требованием, чтобы B) выполнялось для всех
циклов с. Первоначально И. и. были определены
А. Пуанкаре (см. [1], [2]) именно как интегралы ука-
указанного выше типа, остающиеся инвариантными, когда
область интегрирования движется под действием по-
потока.
Все сказанное легко распространяется на неавтоном-
неавтономные системы x—f(x, t). Более существенной является
модификация понятия И. и., предложенная Э. Картаном
(Ё. Cartan, [3]) и связанная с переходом (даже в авто-
автономном случае) к расширенному фазовому пространству
(к обычным фазовым переменным добавляется время),
в к-ром интегральные кривые рассматриваемой системы
дифференциальных уравнений образуют нек-рое семей-
семейство линий (конгруэнцию). Э. Картан требует, чтобы
интеграл формы ф по цепи с (или по циклу, если речь
идет об относительном И. и.) оставался неизменным,
когда каждую точку (х, t)?c сдвигают вдоль интег-
интегральной кривой, проходящей через эту точку; при этом
различные точки можно сдвигать по-разному, лишь бы
это было гладкой деформацией цикла с. (Напр., в новом
смысле относительным И. и. гамильтоновой системы
является не -ф, а весьма полезный интеграль-
интегральный инвариант Пуанкаре — Карта-
н a Lpjdqi—Ildt, где // — гамильтониан, см. [3] — [5].)
Родственное определение дано в [6].
Лит.:Ш Poincare H., «Acta math.», 1890, t. 13, p.
1—270; [2] Пуанкаре А., Избр. тр., пер. с франц., т. 2,
М., 1972: [3] Картан Э., Интегральные ипнарианты, пер.
с франц., М.— Л., 1940; [4] Г а н т м а х е р Ф. Р., Лекции по
аналитической механике, М., 1960; [5] А р н о л ь д В. И.,
Математические методы классической механики, М., 1974; [6]
Годбийон К., Дифференциальная геометрия и аналитиче-
аналитическая механика, пер. с франц., М., 1973; [7] Hwa-Chung
Lee, «Proc. Hoy. Soc. Edinbourgh», ser. A, 1947, v. 62, p.
237—46. Д. В. Амосов,
ИНТЕГРАЛЬНЫЙ КОСИНУС —специальная функ-
функция, определяемая для действительного z>0 равенст-
равенством:
cos / ,. р | 1 Г х 1— cos 2 7,
t J 0 t J
где С=0,5772. ..— Эйлера постоянная. График И. к.
см. на рис. Некоторые интегралы, содержащие Ci(z):
i @ si (t)dt = ~ In 2,
где si(i) — интегральный синус.
При малых х
Асимптотич. представление при больших х:
(-1)* Bft)!
И. к. представляется в виде ряда
•¦¦^\ I Bft)!2ft ^
Как функция комплексного переменного z, Ci(z), опре-
определяемая рядом (*),— однозначная аналитическая
функция в плоскости z с разрезом вдоль отрица-
отрица(*)
0,2
0,1
тельной действитель-
действительной полуоси (—л<
<argz<it); значение
lnz выбирается так,
чтобы — Jt<Imlnz<jt.
OKI ]/[ 1111 | | 1 rhKUlLJ I 11 LLU41 tH Поведение Ci(z) вбли-
вблизи разреза описыва-
_q,ii | I I I | I I | I I j | I | 1 I I I I I I i I I I I | ется предельными со-
соотношениями:
noi м 11 11 п 11 i i i 11 i i i i i и i lim Ci (x ± it]) =
' 0 1 2 3 4. 5 6_^7 Tl-eO
= Ci (| z |) ± ni,
x < 0, T) > 0.
И. к. связан с интегральной показательной функцией
Ei (z) соотношениел!
1
f
t
/
t
/
t
ш
<tifr\)
С
(
X
)
О 1 2 3 4. 5 6 .7
.Т.
Графики функций i/ = ci (ж) и
(a;).
Иногда используется обозначение ci (x)=(
См. также sici-спиралъ.
Лит.: [1] Б е й т м е н Г., Э р д е й и А., Высшие транс-
трансцендентные функции. Функции Бесселя, функции параболиче-
параболического цилиндра, ортогональные многочлены, пер. с англ., 2 изд.,
М., 1S74; 12] Янке К., Эмде Ф., Лёш Ф., Специальные
функции. Формулы, графики, таблицы, пер. с нем., 2 изд., М.,
1908; [3] К р а т ц е р А., Ф р а н ц В. Трансцендентные
функции, пер. с нем., М., 1963; [4] Лебедев Н. Н., Специ-
Специальные функции и их приложения, 2 изд., М., 1963.
ИНТЕГРАЛЬНЫЙ ЛОГАРИФМ — специальная
функция, определяемая для действительного х, хф\.,
равенством
И 1т\—[х dt ¦
11 W — J 0 In t '
при z>l подынтегральная функция имеет в точке г=1
бесконечный разрыв и И. л. понимается в смысле глав-
главного значения:
= lim
IJo
Г ж dt \
График И. л. см. па рис. при ст. Интегральная пока-
показательная функция. При малых х:
1> (х) - х
к > ~ 1пA/зс)
И. л. представляется в виде ряда
г. s ft -г -А 1
где С=0,5772...— дилера постоянная.
Как функция комплексного переменного z:
li(z) = C-fln(— lnzJ + X,", Щ?-
есть однозначная аналитич. функция в плоскости ком-
комплексного переменного z с разрезами вдоль действи-
действительной оси от —оо до 0 и от 1 до т°° (мнимые части
логарифмов берутся при этом в пределах от —л до я).
Поведение li (z) вблизи разреза A, +°°) описывается
соотношениями:
lim li (х ± Щ) = Н (.г) =F яг', х > 1, г| > 0.
И. л. связан с интегральной показательной функцией
Ei (x) соотношениями:
li (x) = Ei (In x), x < 1; Ei (,г) = Н (ех), х < 0.
Для действительного z>0 иногда используется обозна-
обозначение:
т __ ( И (?) = Ei (In х) при 0 < х < 1,
(li (.r) -|- ni = Ei* (In ж) при х > 1.
Лит. см. при ст. Интегральный косинус. А. Б. Иванов.
ИНТЕГРАЛЬНЫЙ ОБЪЕКТ кате г ори и-
объект U категории Я, для к-рого основной функтор
HU(X) = H<X(U, X) является вложением категории до
в категорию непустых множеств. Другими словами,
объект U интегральный, если для каждого объекта
А?ОЬЦ множество HS(U, А) не пусто и для любых
двух морфизмов а, E : А-+В, а.ф§, существует такой
морфиям у : U-+A, что уа,Фу$. В категории непустых
множеств каждый объект является интегральным. В пол-
полной подкатегории непустых алгебр нек-рого многообра-
многообразия универсальных алгебр каждая свободная алгебра —
И. о. В любой абелевой категории объект U является
интегральным тогда и только тогда, когда он образу-
образующий. Если в категории каждая пара морфизмов с об-
общими началом и концом имеет ядро, то образующий объ-
объект является Интегральным. М. Ш. Цаленко.
ИНТЕГРАЛЬНЫЙ ОПЕРАТОР — отображение
х—*-Ах, когда закон соответствия А задается с помощью
интеграла. И. о. наз. иногда интегральным
преобразованием. Так, напр., для интег-
интегрального оператора "Урысона (см. Урысона уравнение):
ф—>-Лф закон соответствия А определяется интегралом
(или оператор ц>—>Aq> порождается интегралом)
Лф (?) = \ Р (t, х, ф (т)) dx, t?D, A)
причем D — заданное измеримое множество конечной
меры Лебега в конечномерном пространстве: P(t, т, и),
t, x?D, —оо<и<оо — заданная измеримая функция.
Предполагается, что функции Р и ф удовлетворяют
условиям, обеспечивающим существование интеграла в
A) в смысле Лебега. Если функция P(t, т, и) нелиней-
нелинейна относительно и, то A) является примером н е л и-
нейногоИ. о. Если же P(t, т, u)=K(t, x) и, тогда
A) принимает вид
Оператор, порождаемый интегралом B), или просто
оператор B), наз. линейным И. о., а функция
К — ядром И. о.
Ядро К наз. ядром Фредгольма, если опера-
оператор B), соответствующий ядру К, действует вполне
непрерывно из заданного функционального простран-
пространства Е в нек-рое другое функциональное пространство
Ег. В этом случае сам оператор B) наз. интеграль-
интегральным оператором Фредгольма из Е
в Ех.
Линейные И. о. часто рассматриваются в функцио-
функциональных пространствах: С (D) — непрерывных на огра-
ограниченном замкнутом множестве D функций и Lp(D) —
суммируемых на D со степенью р функций. В этом слу-
случае оператор B)—оператор Фредгольма в С(D) (т. е. из
C(D) в C(D)), если К непрерывно H&DXD (такое ядро
наз. непрерывным). Он является оператором
Фредгольма в L2(D) (из L2(D) в L2 (?>)), если ядро К
измеримо на DXZ) и
\D\D\K(t,r)\*dtdT< оо. C)
Такое ядро наз. Ь2-я д р о м.
Сопряженный оператор к оператору B)
в комплексном функциональном пространстве L2(D) с
ядром, удовлетворяющим условию C), есть И. о.
ЛГ(Т. t)<f(x)dx, t?D, D)
где черта означает переход к комплексно сопряжен-
сопряженному значению. Если ядро К эрмитово (симметрично)
(то есть К (т, ?)=.К(?, т)), то соответствующий оператор
Фредгольма B) совпадает со своим сопряженным D).
Операторы, обладающие этим свойством, наз. само-
самосопряженными. Оператор Фредгольма с сим-
симметричным ядром наз. интегральным опера-
оператором Гильберта — Шмидта.
Пусть \t—т] обозначает расстояние между точками t
и т n-мерного евклидова пространства, B(t, X) — огра-
ограниченная измеримая функция на D X D, тогда ядро вида
наз. ядром типа п о т е н ц и а л а, а И. о. B) с
таким ядром — И. о. т и п а потенциала; ядро
E) наз. также полярным ядром, или ядром
со слабой особенностью, а соответствую-
соответствующий оператор B) — И. о. с о слабой особенно-
особенностью.
Если функция В (t, т) непрерывна на DXD, то И. о.
со слабой особенностью вполне непрерывен в простран-
пространстве C(D), а если B(t, x) — измеримая ограниченная
функция на DXD, то он вполне непрерывен в простран-
пространстве L2(D).
Если ядро К н m-мерное множество D таковы, что
интеграл B) не существует в смысле Лебега, но суще-
существует в смысле главного значения по Коши, то он наз.
m-м ерным сингулярным интегра-
л о м. Оператор, к-рый им порождается, наз. m-м е р-
н ы м сингулярным И. о., или о д н о м е р-
н ы м (при т=1) и многомерным (при т>1)
сингулярным И. о.
Если линия D лежит на плоскости комплексного пе-
переменного t, то равенство
где интеграл понимается в смысле главного значения
по Коши, порождает непрерывный И. о. ф_»-Лф в про-
пространстве функций, удовлетворяющих условию Гёль-
дера, если D — простая замкнутая гладкая линия; и в
пространстве Lp(D), 1<р<оо, если D — ляпуновская
линия. Оператор F) наз. сингулярным опера-
оператором Коши.
Пусть на действительной оси заданы две изме-
измеримые по Лебегу функции ф и g. Если для почти всех
/?] — oo, oo[ существует интеграл
S!jq>eoiu(T-*)idT,
то можно определить функцию
t)y(i)d%, G)
которая наз. сверткой# и ср. Если зафиксировать
функцию g, то интеграл G) определяет оператор
ТФ(*) = 0у*ф)(О. (8)
который наз. И. о. (или интегральным пре-
преобразованием) свертки с ядром g. Если
g€Lr(— оо, оо), 1<р, д, г<оо и у — ±=±_ 1, то
оператор (8) непрерывен из i?( — оо, оо) в Lp( — оо, оо).
При соответствующих предположениях И. о. свертки
применяется как на полупрямой, так и на конечном
отрезке.
Кроме указанных выше И. о., исследованы конкрет-
конкретные классы II. о., напр, интегральные преобразования
Фурье, Лапласа, Бесселя, Меллина, Гильберта и др.
Лит.: [1] Смирнов В. И., Курс высшей математики,
т. 5, М., 1959; [2] Интегральные уравнения, М., 19E8 (Спра-
(Справочная матем. б-ка); [3] Красносельский М. А. и д р.,
Интегральные операторы в пространствах суммируемых функ-
функций, М., 1966; [4] Д и т к и н В. А., Прудников А. П.,
Интегральные преобразования и операционное исчисление,
М., 1961 (Справочная матем. б-ка); [5] Мусхелишвили
Н. И., Сингулярные интегральные уравнения..., 3 изд.,
М., 1968; [6] Ми х лин С. Г., Многомерные сингулярные
интегралы и интегральные уравнения, II., 1962; [7] Т и т ч-
м а р ш Э. Ч., Введение в теорию интегралов Фурье, пер.
с англ., М.— Л., 1948; 18] Эдварде Р., Функциональный
анализ. Теория и приложения, пер. с англ., М., 1969.
В. В. Хведслидзе.
ИНТЕГРАЛЬНЫЙ СИНУС — специальная функ-
функция, определяемая для действительного х>0 равен-
равенством
„. , , Сх sin t ,, л Г и sin t ,.
Sl(*) = io —^T-J* —dt-
График И. с. см. на рис. при ст. Интегральный косинус.
Иногда используют обозначение
• / \ Г ^ sin i ,. n- / \ л:
SI (х)-=—]х -у- dt = Si (.r) ^ .
Частные значения:
Si@)=0, Si(oo) = ^, si(oo)=0.
Основные соотношения:
Si (—x) = — Si (x); si (x) + si (—х)= — л;
si* (t) <« = ¦!-; [™ e-ptsi (qt)dt = -±-arctgf;
" sin t si (i) dt = — -j-; jj ^ Ci (t) si (i) dt = — In 2,
где Ci (t) — интегральный косинус. При малых х:
Si (x) и о-.
Асимптотич. представление при больших .г:
где
И. с. представляется в виде ряда
Как функция комплексного переменного z, Si(z), опре-
определяемая формулой (*),— целая функция z во всей
плоскости z.
И. с. связан с интегральной показательной функцией
Ei (z) соотношением:
si (z)=-~ [Ei (iz)—Ei (—iz)].
См. также sici-спираль.
Лит. см. при ст. Интегральный косинус. А. В. Иванов-
ИНТЕГРАЛЬНЫХ ПРЕОБРАЗОВАНИЙ МЕТОД —
способ решения линейных дифференциальных уравне-
уравнений при заданных краевых или начальных условиях,
состоящий в переходе от данного уравнения к уравне-
уравнению для интегрального преобразования искомой функ-
функции. Последнее уравнение может оказаться более про-
простым. Пусть, напр., требуется найти решение уравне-
уравнения
на конечном или бесконечном интервале (а, р") с крае-
краевыми условиями и (а)=иа, и($) = и„. Если ядро K(s, x)
интегрального преобразования
u(s)=[?>K(s, x)u(x)dx
J ОС
удовлетворяет соотношению
d2 (а,К) d(a,K) „ „_, , , „
dx* их
B)
тде K(s) — функция s, то после умножения уравнения
A) на К (s, x) и интегрирования по частям в пределах
{а, Р) получится уравнение
Выражая из него u(s) и применяя формулу обращения
интегрального преобразования, можно найти и(х).
Аналогично И. п. м. применяется для дифференциаль-
дифференциальных уравнений с частными производными.
Таким образом, процесс решения дифференциаль-
дифференциального уравнения этим методом состоит из следующих
этапов.
1) Выбор подходящего интегрального преобразова-
преобразования.
2) Умножение уравнения и граничных условий на
ядро этого интегрального преобразования и интегри-
интегрирование в подходящих пределах по переменной, по
к-рой проводится интегральное преобразование.
3) При интегрировании в 2) используются соответ-
соответствующие граничные (или начальные) условия для вы-
вычисления членов, возникающих от пределов интегри-
интегрирования.
4) Решается полученное вспомогательное уравнение и
находится интегральное преобразование искомой функ-
функции.
5) По формуле обращения определяется искомая
функция.
Лит.: [1] Т р а и т е р К. Д ж., Интегральные преобразо-
преобразования в математической физике, пер. с англ., М., 1956; [2J К у-
рант Р., Гильберт Д., Методы математической физики,
пер. с нем., М.— Л., 1951. Ю. А. Брычков, А. П. Прудников.
ИНТЕГРАЛЬНЫХ СООТНОШЕНИИ МЕТОД, м е-
т о д поло с,— метод решения систем дифференци-
дифференциальных уравнений с частными производными, основан-
основанный на приближенном сведении уравнений с частными
производными к системам обыкновенных дифферен-
дифференциальных уравнепий. Применим к уравнениям различ-
различных типов. Предложен А. А. Дородниципым [1] как
развитие метода прямых, обобщенная форма И. с. м.
с введением сглаживающих функций дана в [2], раз-
разработка и развитие метода — о [3].
Пусть имеется система дифференциальных уравнений
с частными производными в дивергентном виде
— Р; (х, у, u-l, и2, ..., ик) -]-
I — 1, ?, .. ., К,
где Р,-, Qi, Pi — заданные функции от независимых
х, у н искомых ult u2,..., иь переменных. Пусть реше-
решение системы A) ищется в криволинейном прямоуголь-
прямоугольнике с границами х=а, х—Ь, у=0, у=А(х), на к-рых
ставится 2к условий, из них к условий на границах х=
= а и х=Ъ. Если заранее функция Д (х) неизвестна, то
требуется одно дополнительное условие. При наличии
на границе особых точек вместо соответствующих гра-
граничных условий используются условия регулярности.
В Л"-м приближении область интегрирования разби-
разбивается на N непересекающихся полос системой линий
y = yn(x) = nA(x)lN, и=1,..., N. Для каждого N вы-
выбирается замкнутая система из N линейно независимых
функций fn(y). При умножении каждого исходного
уравнения A) на функции /„(?/) и интегрировании по у
поперек всех полос получают kN интегральных соот-
соотношений вида
Aix)fn(y)Pdy-A'(x)fn(A(x)P +
О # = Л (х)
+/„ (д И) Q\y=A w-fn @) Q @)-
Подынтегральные функции Р, Q, F аппроксимируют^:
при помощи интерполяционных формул через их зна-
значения Рп, Qn, Fn на границах полос; интегралы, входя-
входящие в интегральные соотношения, имеют вид
где Сп — численные коэффициенты, зависящие от вы-
выбора интерполяционных формул и вида функций /„(;/).
В результате получается аппроксимирующая система
обыкновенных дифференциальных уравнений по х
относительно i?(./V-|-l) значений искомых функций и,,
на всех границах полос. Эта система замыкается А-
граничными условиями при у=0 и у=А(х).
Функции fn(y) выбираются достаточно произвольно.
Применение в качестве fn(y) б-функции /п(г/) = б(г/—//„).
ге=1, 2,..., N, приводит к методу прямых, в к-ром про-
производные по у заменяются разностными выражениями,
отвечающими выбранным интерполяционным форму-
формулам. При использовании ступенчатых функций
0 при у < j/n_1?
fn (у) \ 1 при Уп-1<У<Уп, п=1, 2, ..., N,
У
г 0
0 при у > уп
говорят о простом И. с. м., где исходные уравнения
интегрируются поперек каждой полосы. При этом выра-
выраженные исходной системой A) законы сохранения запи-
запишутся для полос в виде следующих интегральных соот-
соотношений
J iln—i
[у Fdy.
-l
Сходимость и погрешность И. с. м. исследовались
для систем квазилинейных уравнений гиперболич. типа
[4]. Здесь были установлены результаты, показывающие
преимущество И. с. м. над методом прямых. В более
поздних работах проводилось аналогичное исследова-
исследование для уравнений эллиптич. типа.
К достоинствам И. с. м. относятся: возможность вы-
выбора интерполяционных формул и функций f{y) с уче-
учетом поведения решения, точное интегрирование по од-
одной из переменных (вследствие дивергентной формы
записи исходных уравнений), простота вычислитель-
вычислительного алгоритма, небольшой объем машинной памяти
при расчетах на ЭВМ. В И. с. м. аппроксимируется
интеграл: это повышает точность аппроксимации за счет
уменьшения коэффициента остаточного члена; интеграл
представляет собой более гладкую функцию, чем под-
интегральная функция, что позволяет уменьшить число
узлов интерполяции. В случае разрыва первого рода
поцинтегральнои функции интеграл непрерывен. И. с. м.
наиболее эффективен, когда решение с хорошей точ-
точностью получается при малом числе полос.
Проведением аппроксимаций по двум переменным
И. с. м. обобщается на случай уравнений с тремя неза-
независимыми переменными. Аппроксимации по двум пере-
переменным можно проводить и в двумерном случае (при
этом область интегрирования разбивается не на полосы,
а на подобласти), тогда аппроксимирующая система
будет системой нелинейных алгебраич. или трансцен-
трансцендентных уравнений. Элементы И. с. м. применяются в
др. численных методах, напр, в крупных частиц методе.
И. с. м. наиболее приложим в газовой динамике, где
с его помощью был решен цикл практически важных
задач. При этом выделяют три схемы И. с. м.: 1) область
интегрирования разбивается линиями, проходящими
между поверхностью тела и ударной волной (рис. а);
2) область интегрирования разбивается линиями, про-
проходящими менаду осью симметрии и граничной характе-
характеристикой (рис. б); 3) производится разбиение на подоб-
подобласти двумя семействами пересекающихся линий
(рис. в).
И. с. м. для расчета сверхзвукового обтекания но-
носовой части затупленного тела с отошедшей ударной
волной был разработан в [5], где впервые получено
численное решение этой задачи в прямой постановке.
Проведено решение этой задачи для самых общих слу-
случаев (тела разнообразной формы, пространственное об-
обтекание, течения реального газа при наличии равно-
равновесных и неравновесных физико-химич. превращений и
излучения, нестационарное движение, течение вязкого
газа [6]). И. с. м. применялся для численного иссле-
исследования потенциальных течений газа [7], для решения
нек-рых смешанных задач: течение в дозвуковой и транс-
трансзвуковой части сопла [8]. Рассматривалось закрити-
ческое обтекание профиля под углом атаки с местной
сверхзвуковой зоной [9]. И. с. м. рассчитывались сверх-
сверхзвуковые конич. течения газа.
Широкое применение И. с. м. нашел при расчетах
движения вязкого газа в рамках теории пограничного
слоя. Для ламинарного несжимаемого случая было по-
получено решение вплоть до точки отрыва [2]. Далее рас-
рассчитывался ламинарный пограничный слой в газе с
учетом вдува или отсоса, излучения, теплопроводности.
И. с. м. получено решение нестационарной задачи о
точечном одномерном взрыве в газе с учетом противо-
противодавления [10], а также в газе с бесконечной проводи-
проводимостью в присутствии магнитного поля и в горючем газе.
Лит.: [1] Дородницын А. А., в кн.: Тр. 3 Всесоюз-
Всесоюзного математического съезда. 1950, т. 3, М., 1958, с. 447—53;
[2] его же, «Ж. прикл. механ. и техн. физ.», I960, № 3,
с. 111 —18; [3] Белоцерковский О. М., Ч у га-
гаки н П. И., «Ж. вычисл. матем. и матем. физ.», 1962, т. 2,
№5, с. 731—59; [4J Бобков В. В., Крылов В. И,,
«Дифференциальные уравнения», 1965, т. 1, № 2, с. 230—43;
[5] Белоцерковский О. М., «Докл. АН СССР», 1957,
т. 113, в. 3, с. 509—12; [6] Белоцерковский О.М. и др.,
Обтекание затупленных тел сверхзвуковым потоком газа. Тео-
?|етические и экспериментальные исследования, 2 изд., М., 1967;
7] Чушки н П. И., «Вычисл. математика», 1957, № 2, с. 20—
44; [8] А л и ха шк и н Я. И., Ф а в о р с к и й А. П., Ч у га-
гаки н II. И., «Ж. вычисл. матем. и матем. физ.», 1963, т. 3,
№6,0.1130 — 34 [9]Tai Т. С., «J. AIAA», 1974, v. 12, р. 798 —
804; [10] Коробейников В. П., Чушкин П. И.,
«Тр. Матем. ин-та АН СССР», 1966, т. 87, с. 4—34.
Ю. М. Давыдов.
ИНТЕГРИРОВАНИЕ — операция отыскания ин-
интеграла. Под И. понимают также решение дифферен-
дифференциальных уравнений.
ИНТЕГРИРОВАНИЕ ДИФФЕРЕНЦИАЛЬНЫХ
УРАВНЕНИЙ В ЗАМКНУТОЙ ФОРМЕ — представле-
представление решений дифференциальных уравнений аналитич.
формулами, использующими указанный априори запас
функций и перечисленный заранее набор математич.
операций.
Если в качестве функций допускаются элементарные
функции и функции, входящие в уравнение, а иод
операциями понимаются конечные последовательности
алгебраич. операций и операций взятия неопределен-
неопределенного интеграла (квадратуры) от допустимых
функций, то говорят об и н т е г р и р о в а н и и (т. с.
решении) дифференциальных уравне-
уравнений в квадратурах. Примером обыкновен-
обыкновенного дифференциального уравнения, интегрируемого
в квадратурах, служит Бернулли уравнение. Ж. Лиу-
вилль (см. [1]) впервые указал уравнение, интегриро-
интегрирование к-рого в квадратурах невозможно. Так, решения
уравнения
у" + ху = 0 (*)
нельзя выразить через элементарные функции и интег-
интегралы от них (см. [2]). Обыкновенные дифференциальные
уравнения удается проинтегрировать в квадратурах
крайне редко. Наиболее глубокие результаты о воз-
возможности интегрирования в квадратурах получаются
на основе восходящей к С. Ли (см. [3]) теории непре-
непрерывных групп преобразований (см. [4], [5]).
И. д. у. в з. ф. допускает привлечение специальных
функций, представление решений в виде сходящихся
рядов и т. д. Любое конкретное линейное дифферен-
дифференциальное уравнение с переменными коэффициентами
интегрируется в замкнутой форме, если включить
в допустимые конечное число функций (вообще го-
говоря, специальных), составляющих фундаментальную
систему решений этого уравнения. Например, если
ввести Бесселя функции, то с их помощью записывается
формула для общего решения уравнения (*). Таким
образом, дифференциальные уравнения являются источ-
источником специальных функций, включение к-рых в число
допустимых позволяет расширять класс уравнений,
разрешимых в замкнутой форме. Однако проблема
интегрирования в замкнутой форме нелинейного урав-
уравнения в общем случае не сводится к пополнению мно-
множества допустимых функций конечным числом специ-
специальных функций.
Для дифференциальных уравнений с частными про-
производными формулы для решений удается получить
лишь в отдельных специальных случаях (см., напр.,
Д'Аламбера формула). При отыскании формул для
решений таких уравнений большое значение имеют
групповые методы (см. [5]).
Лит.: [1] L i о u v i 1 1 е J., «J. math, pures et appl.»,
ser. 1, 1841, v. 6; [2] Капланский И., Введение в диф-
дифференциальную алгебру, пер. с англ., М., 1959; [31 L i e S.,
Scneffers G., Vorlesungen tlber Differentialgleichunsen
mit bekannten infinitesimalen Transtormationen, Lpz., 1891; Ul
А й H с Э. Л., Обыкновенные дифференциальные уравнения,
пер. с англ., Хар., 1939; [5] Овсянников Л. В., Груп-
Групповые свойства дифференциальных уравнений, Новосиб., 1962;
[6J Камке Э., Справочник по обыкновенным дифференци-
дифференциальным уравнениям, пер. с нем., 5 изд., М., 1976; [7J его
ж е, Справочник по дифференциальным уравнениям в частных
производных первого порядка, пер. с нем., М., 1966.
Н. X. Розов.
ИНТЕГРИРОВАНИЕ ПО ЧАСТЯМ — один из спо-
способов вычисления интеграла, состоящий в представле-
представлении интеграла от выражения вида u(x)dv{x) через ин-
интеграл от v(x)du(x). Для определенного интеграла фор-
формула И. по ч. имеет вид
dv (x) =u(b)v (b) — и (a) v (о) —
v (х) du (х) A)
и справедлива в предположении, что функции и(х) и
v(x) и их производные и (х) и v'(х) непрерывны на
Аналогом этой формулы для неопределенного интег-
интеграла является соотношение
\ и (х) dv (x) = u{x)v (х) — [ v (х) du (x). B)
Аналогом формулы A) для кратных интегралов яв-
является соотношение
ds~\DvщdXt C)
где D — область в пространстве Rm с гладкой (или хотя
бы кусочно гладкой) границей Г, х= (хг, х2,..., хт),
(ж/., н) — угол между осью Ох^ и внешней нормалью к
поверхности Г. Формула C) справедлива, напр., для
непрерывных в (-О + Г) функций и (х) и v (x) и их частных
производных 1-го порядка. Если интегралы в C) пони-
понимаются в смысле Лебега, то для справедливости этой
формулы достаточно, чтобы и(х) и v(x) принадлежали
Соболева пространству и(х) ? Wp (D), v (x) ? W\ (D)
при любых р>1, д>1 таких, что j <1-|-—.
Лит.: [1] И л ь и и В. А., П о з н я к Э. Г., Основы ма-
математического анализа, ч. 1—2, М., 1971—73; [2J Куд-
Кудрявцев Л. Д., Математический анализ, ч. 1—2, М., 1970;
[3J Никольский СМ., Курс математического анализа,
т. 1 — 2, М., 1973. В. А. Ильин, Т. П. Лукашенко,
ИНТЕГРИРОВАНИЕ ПОДСТАНОВКОЙ, замена
переменного в интеграл е,— один из спо-
способов вычисления интеграла, состоящий в преобразо-
преобразовании интеграла посредством перехода к другой пере-
переменной интегрирования. Для определенного интеграла
от функции одной переменной формула имеет вид
A)
и справедлива при следующих предположениях: f(x)
непрерывна на отрезке [я, 6], к-рый является множест-
множеством значений нек-рой функции x=q>(t), определенной и
непрерывной вместе со своей производной <р' (t) на от-
отрезке сс<г<Р и ф(а)=я, ф(Р) = 6.
Аналогом формулы A) для неопределенного интег-
интеграла является соотношение
Если функция x=q>(t) определена и дифференцируема
на нек-ром промежутке {t}, а функция f(x) имеет перво-
первообразную на множестве всех значений функции ж=фB),
то и функция /[ф(?)]ф' (t) имеет первообразную на ука-
указанном промежутке, причем имеет место равенство B).
В случае кратного интеграла Римана по ограничен-
ограниченной замкнутой m-мерной кубнруемой области G анало-
аналогом формулы A) является соотношение
\ f(x)dx=\ f [ф (t)\ ' '%2' '"'Xgl dt, C)
Jo JC D(t,,t,,...,tm)
справедливое при следующих предположениях: функ-
функция f(x)—f(xlt x2,..., х,„) непрерывна в области G;
преобразование я/=ф,-(*1, t2,..., tm), i=l, 2,..., т,
взаимно однозначно переводит область G' в пространстве
переменных 1г, t2,. . ., tm, в область G в пространстве
переменных xl7 х2,. . ., хт функции Xi=<pi(t1, t2,. .., tm)
имеют в G' непрерывные частные производные первого
порядка и отличный от нуля якобиан х"' '"' х"> .
Формула C) справедлива и при более общих предполо-
предположениях (не обязательно требовать непрерывности f(x) в
области G, а можно допустить обращение в нуль якобиана
на множестве точек m-мерноп меры нуль).
Лит.: [1] Ильин В. А., II о з н я к Э. Г., Основы ма-
математического анализа, ч. 1—2, М,, 1971—73; [2] Кудряв-
Кудрявцев Л. Д., Математический анализ, т. 1—2, М., 1970; [3]
Никольский СМ., Курс математического анализа, М.,
1973. В. А. Ильин.
ИНТЕГРИРОВАНИЕ ЧИСЛЕННОЕ — нахождение
интеграла численными методами. И. ч. применяется,
если подинтегральная функция задана приближенно
(таблицей), или если она задана точно, то использование
методов И. ч. быстрее приводит к получению результата
с заданной точностью, чем использование точных мето-
методов, или, наконец, если использование точных методов
невозможно, так как интеграл не выражается в извест-
известных функциях. Для И. ч. осуществляют построение
квадратурных формул (в случае функций одного пере-
переменного) и кубатурных формул (для вычисления крат-
кратных интегралов). См. также Интерполирование в вы-
вычислительной математике.
ИНТЕГРИРУЕМАЯ СИСТЕМА — дифференциальная
система размерности р на n-мерном дифференцируемом
многообразии М", к-рая в окрестности каждой точки
х?Мп обладает (п—р)-параметрич. семейством р-
мерных интегральных многообразий. Часто в этом
случае говорят о вполне интегрируемой дифференциаль-
дифференциальной системе; более точно она определяется следующим
образом. Пусть в каждой точке х?Мп выделено нек-рое
подпространство D (х) размерности р касательного век-
векторного пространства Тх(Мп), так, что на Мп задана
дифференциальная система, пли распределение
D класса С'2, г^1 размерности р. Система D наз. впол-
вполне интегрируемой, если для любой точки
а?М" найдется система координат (U, ф), х? U, <$(х)=
= х1,. . ., х", такая, что для любых постоянных с/,
р</<:?г многообразие ?<тс= {¦?? U; xJ = c-i} является
интегральным подмногообразием, т. е. его касательное
пространство в произвольной его точке х совпадает с
D(x). Аналитич. условия, необходимые и достаточные
для этого, см. в ст. Инволютивное распределение.
Ю. Г. Лумисте.
ИНТЕГРИРУЕМАЯ ФУНКЦИЯ — см. Интеграл.
ИНТЕГРИРУЕМОЕ ПРЕДСТАВЛЕНИЕ — непрерыв
ное неприводимое унитарное представление я локально
компактной унпмодулярион группы G в гильбертовом
пространстве И такое, что для нек-рого ненулевого
вектора ?,?Н функция g^-(n(g)l, g), g?G, является
интегрируемой относительно меры Хаара на G. В этом
случае представление л — квадратично интегрируемое
представление, причем существует такое плотное в Н
векторное подпространство Н'CZH', что функция
g—^(n(g)?,, T|), g? G, интегрируема относительно меры
Хаари на группе G для всех g. ц?1Г. Если {л}—
элемент в дуальном пространстве G группы G, опреде-
определенный классом унитарной эквивалентности представ-
представления л, и Gr — носитель регулярного представления
группы G в пространстве G, то {я} — одновременно
открытая и замкнутая точка в Gr. а. и. Штерн.
ИНТЕГРИРУЮЩИЙ МНОЖИТЕЛЬ для обыкновен-
обыкновенного дифференциального уравнения 1-го порядка
Р(х, y)dx+Q(x, y)dy=0 A)
— функция \i=\i(x, у)=?0, обладающая тем свойством,
что уравнение
[х (х, у)Р(х, y)dx-\-\i(x, y)Q(x, y)dy=O
является дифференциальным уравнением в полных
дифференциалах. Напр., для линейного уравнения
y'+a(x)y=f(x), или (а(х)у—f (x))dx+dy=0, И. м. слу-
служит функция [д,= ехр \ a(x)dx. Если уравнение A) в об-
области D, где P2JrQ2=/^0, имеет гладкий общий интег-
интеграл U(x, у) = С, то оно имеет бесконечно много И.м.
Если функции Р(х, у), Q(x, у) имеют непрерывные
частные производные в односвязной области D, где
^2+<?2=7^0, то в качестве И. м. можно взять любое
частное (нетривиальное) решение уравнения с частными
производными
(см. [1]). Однако общего метода отыскания решений
уравнения B) не существует и поэтому фактическое
нахождение И. м. для конкретного уравнения A) уда-
удастся лишь в исключительных случаях (см. [2]).
Лит.: [1] Степанов В. В., Курс дифференциальных
уравнений, 9 изд., М., 1966; [2] Камке Э., Справочник по
обыкновенным дифференциальным уравнениям, пер. с нем.,
5 изд., М., 1976. Н. X. Розов.
ИНТЕГРО-ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕ-
УРАВНЕНИЕ — уравнение, содержащее неизвестную функцию
под знаками дифференциальных и интегральных опера-
операций. И.-д. у. включают и интегральные и дифференци-
дифференциальные уравнения.
Линейные И.-д. у. Пусть / (х) — заданная функ-
функция,
[
— дифференциальные выражения с достаточно гладки-
гладкими коэффициентами pi(x) и q,-(y) на [a, b], a K{x, у) —
известная функция, достаточно гладкая в квадрате
[а, Ь]Х[а, Ь]. Уравнение вида
K(x,y)My[U]dy + j(x) A)
наз. линейным И.-д. у.; здесь Я — параметр. Если в
И.-д. У- A) функция К(х, г/)^гО при у>х, то уравнение
A) наз. И.-д. у. с переменным пределом интегрирования:
его можно записать в форме:
K(x, y)My[U]dy + f(x). B)
Для И.-д. у. A) или B) можно ставить задачу Коши
(ищется решение, удовлетворяющее условиям ?Л')сс=с,-,
i=0, 1,. . ., 1—1, где с; — заданные числа, I — порядок
выражения LX[U], а а?[а, Ь]) и различные граничные
задачи (напр., задачу о периодических решениях).
В ряде случаев (см. [3] — [4]) задачи для A) или B)
можно упростить или даже свести соответственно к
интегральным уравнениям Фредгольма 2-го рода или
уравнениям Вольтерра. Вместе с тем для И.-д. у. воз-
возможен ряд специфич. явлений, не характерных ни для
дифференциальных, ни для интегральных уравнений.
Простейшее нелинейное И.-д. у. имеет вид:
F(x, у, U (y),V (у), ..., №> {y))dy + f (x).
К исследованию этого уравнения применимы метод
сжатых изображений, принцип Шаудера и другие мето-
методы нелинейного анализа.
Для И.-д. у. изучаются вопросы устойчивости реше-
решений, разложения по собственным функциям, асимпто-
асимптотика по малому параметру и др. В приложениях встре-
встречаются также И.-д. у. с частными производными и с
кратными интегралами. Таковы, напр., уравнение
Больцмана, уравнение Колмогорова — Феллера.
Лит.: [1] Volterra V., Lemons sur les equations in-
tegrales et les equations integrodirferentielles, P., 1913; [2] его
ж е, Математическая теория борьбы за существование, пер.
с франц., М., 1976; [3] Быков Я. В., О некоторых задачах
теории интегро-дифференциальных уравнений, Фр., 1957;
[4J В а й н б е р г М. М,, в кн.: Итоги науки. Математический
анализ. Теория вероятностей. Регулирование. 1962, М., 1964,
с. 5—37; [5] Филатов А. Н., Асимптотические методы в тео-
теории дифференциальных и интегро-дифференциальных уравне-
уравнений, Таш., 1974. В. А. Треногий.
ИНТЕГРО-СТЕПЕННОЙ РЯД — ряд, содержащий сте-
степени переменной функции под знаком интеграла. Пусть
K(s, tl7 ..., t/;) — функция непрерывная по совокуп-
совокупности переменных в кубе [a, b\k + 1 и пусть U (s) — про-
произвольная непрерывная на [а, Ь] функция. Выражение
...Uab(tk)dtl...dtk,
где сс0, ах,. . ., а^ — неотрицательные целые числа и
ao+cci+. . . + (*?= m, наз. интегро-степенным
членом степени т относительно U. Два интегросте-
пенных члена степени т принадлежат к одному типу,
если они отличаются лишь своими ядрами А". Сумма
конечного числа интегро-степенных членов степени т,
принадлежащих различным типам, наз. интегро-
степенной формой степени т относительно
функции U и обозначается Wm ( г/ )• Пусть \W\m(rj) —
интегро-степенная форма, в к-рой все ядра К заменены
на \К\, пусть
{7 = max|?/(S)|, Wm = max | W \m (*
[а,Ъ] [а,Ь]
тогда
W ( s \ \ ^с W Пт
" т \U )\ т '
Выражение
наз. интегро-степенным рядом. Если
сходится числовой ряд #0-f Wi^U + W2U-+ ..., то
И.-с. р. наз. регулярно сходящимся.
В этом случае И.-с. р. сходится абсолютно и равномер-
равномерно и сумма его непрерывна на [а, Ь].
Аналогично вводится И.-с. р. от нескольких функ-
функциональных аргументов, а также И.-с. р., в к-рых вме-
вместо [а, Ь] фигурирует нек-рое замкнутое ограниченное
множество конечномерного евклидова пространства.
И.-с. р.— частный случай более общего понятия абст-
абстрактных степенных рядов.
Лит.: [1] Ляпунов А. М., О фигурах равновесия, мало
отличающихся от эллипсоидов вращающейся однородной массы
жидкости. Собр. соч., т. 4, М., 1959; [2] Schmidt E., «Math.
Ann.», 1908, Bd 65, S. 370 — 99; [3] В а й н б е р г М. М.,
Треноги н В. А., Теория ветвления решений нелинейных
уравнений, М., 1969. В. А. Треногий.
ИНТЕРВАЛ — 1) см. Интервал и сегмент. 2) И.
пространства-времени — величина, ха-
характеризующая связь между двумя событиями, разде-
разделенными пространственным расстоянием и промежут-
промежутком времени. В специальной теории относительности
квадрат И. равен
где с — скорость света, х,, у;, г,- — пространственные
координаты, ti — соответствующие моменты времени
(подробнее см. Минковского пространство).
В общей теории относительности рассматривается
И. между двумя бесконечно близкими событиями:
где dxl — бесконечно малые разности координат двух
событий, gjk — метрический тензор. а. б. Иванов.
ИНТЕРВАЛ И СЕГМЕНТ — простейшие множества
точек на прямой. Интервалом (или проме-
промежутком) наз. множество точек прямой, заключенных
между фиксированными точками А и В, причем сами
точки А и В не причисляются к интервалу. Сегмен-
Сегментом (или отрезком) наз. множество точек прямой,
лежащих между точками А и В, к к-рому присоеди-
присоединены и сами эти точки. Термины «интервал» и «сегмент»
применяются также для обозначения соответствующих
множеств действительных чисел: интервал состоит из
чисел х, удовлетворяющих неравенствам я<а:<&, а
сегмент — из чисел х, удовлетворяющих неравенствам
а<:ж<:Ь. Интервал обозначается (а, Ь), иногда ]а, b[,
а сегмент [а, Ь].
Термин «интервал» употребляется также в более
широком смысле для обозначения произвольного связ-
связного множества на прямой. В этом случае к интервалам
относятся собственно интервал (я, Ь), бесконечные, или
несобственные, интервалы (—<х>, а), (я, +°°). (—°°>
+ оо), сегмент [а, Ь] и полуинтервалы [а, Ь), (а, Ь],
(—оо, а], [а, +оо). При этом круглая скобка обозна-
обозначает, что соответствующий конец интервала не принад-
принадлежит к рассматриваемому множеству, а квадратная —
что принадлежит. БСЭ-з.
Более общим является понятие интервала в
частично упорядоченном множест-
в е. Интервалом [а, Ъ] здесь наз. совокупность всех
таких элементов х данного частично упорядоченного
множества, к-рые удовлетворяют неравенству a<s?x<:b.
Интервал частично упорядоченного множества, состоя-
состоящий в точности из двух элементов, наз. простым.
Л. А. Скорняков.
ИНТЕРВАЛ СХОДИМОСТИ степенного
ряда — интервал действительных значений перемен-
переменного, обладающий тем свойством, что в каждой точке
этого интервала степенной ряд сходится, а в каждой
точке, не принадлежащей к этому интервалу и не являю-
являющейся его концом,— расходится. БСЭ-з.
ИНТЕРВАЛЬНАЯ ОЦЕНКА для неизвестного истин-
истинного значения скалярного параметра вероятностного
распределения — интервал, принадлежащий множест-
множеству допустимых значений параметра, границы к-рого
суть функции от результатов наблюдений, подчиняю-
подчиняющихся данному распределению. Пусть X — случайная
величина, принимающая значения в выборочном про-
пространстве Ct, 33, Ре), 9 ?6, в — интервал на действи-
действительной прямой, причем истинное значение параметра 8
неизвестно. Интервал (^(Х), я2(Х))С1в, границы к-рого
являются функциями от подлежащего наблюдению
значения случайной величины X, наз. И. о., или д о-
верительным интервалом для 6, число
р= inf P{«i(X) < 9< я2(Х)|9}
бев
наз. коэффициентом доверия этого дове-
доверительного интервала, а величины аг (X) и аг(Х) —
нижним и верхним доверительными
пределами соответственно. Понятие И. о. распро-
распространяется на более общий случай, когда требуется
оценить нек-рую функцию или только одно ее значение,
зависящую от параметра 8.
Пусть на множестве TczR1 задано семейство функций
и F, ¦) = («! F, •). и2 (9, •).•¦•, «ft (9, •)): 7-»UcR*,
е = (еь..., em) eecR",
и пусть по реализации случайного вектора Х= (Хи. . .,
Хп), принимающего значения в выборочном простран-
пространстве (¦?, SJ3, Pq), JdR", Э?в, требуется оценить функ-
функцию u(Q, •), отвечающую неизвестному истинному
значению параметра 8. Каждому t?T в П отвечает
множество B(t), являющееся образом множества в
при отображении и(-, t) : 0—кВ (f)dU. По определе-
определению, множество С(Х, t)dB(t) называется довери-
доверительным множеством для значения и (8, t)
функции и (в, ¦) в точке t, t?T, имеющим довери-
доверительную вероятность.
Р{и(9, 0 €C(X,t)\Q)=p(Q,t)
и коэффициент доверия
p(t)= inf p(Q,t).
вев
Совокупность всех доверительных множеств С(Х, t)
образует в11 доверительную зону С(Х) для
функции и (9, •) : T-vlI, имеющую доверитель-
доверительную вероятность
Р{С(Х)Э «(в, .):T^U\Q) = p(Q)
и коэффициент доверия
р= inf р(в).
Множества типа С(Х, t) и С(X) наз. И. о. для одного
значения и@, t) функции «@, •) в точке t и самой
функции и (9, •) соответственно.
Существует несколько подходов к построению И. о.
для неизвестных параметров распределений. Наиболее
распространенными являются бейесовский подход, ос-
основанный на теореме Бейеса, метод Фишера, связан-
связанный с введением фидуциалъных распределений (о методе
Фишера см. [3] — [5]), Неймана метод доверительных
интервалов ([5], [81, [9]) и метод, предложенный
Л. Н. Болыиевым [6].
Лит.: [1] Крамер Г., Математические методы статис-
статистики, пер. с англ., 2 изд., М., 1975; L2J Fisher R. А.,
Statistical Methods and Scientific Inferense, N. Y. — L., 1973;
[3] Бернштейн С. Н., «Изв. АН СССР». Сер. матем.»,
1941, т. 5, с. 85—93; [4] Б о л ь ш е в Л. Н., Комментарии
к статье О «доверительных» вероятностях Фишера, в кн.: Берн-
Бернштейн С. Н., Собр. соч., т. 4, М., 1964, с. 566—9; [5] N е у-
man У., «J. Operat. Res. Soc. Japan», 1961, v. 3, №4, p.
145 —154; [6] Б о л ь ш е в Л. Н. «Теория вероят. и ее при-
мен.», 1965, т. 10, в, 1, с. 187—92; [7] Большее Л. Н.,
Логинов Э. А., «Теория вероят. и ее примен.», 1966, т. 11,
в. 1, с. 94—107; [8] N е у m a n J., «Biometrika», 1941, v. 32,
,N!> 2, p. 128—150; [9] его ж е, «Phil. Trans. Roy. Soc. London»,
1937, v. 236, p. 333—80. M. С. Никулин.
ИНТЕРВАЛЬНЫЙ АНАЛИЗ — теория, предназна-
предназначенная для учета ошибок округления при проведении
расчетов на цифровых вычислительных машинах
(ЦВМ). Так как точное представление чисел невозможно
в машине с конечной разрядной сеткой, то результат
каждого достаточно сложного расчета содержит нек-рую
ошибку, обусловленную погрешностями округлений
входных данных и промежуточных результатов. Для
учета этой ошибки можно каждую величину предста-
представить парой чисел, к-рые ограничивают ее снизу и сверху
и имеют точное представление в ЦВМ. Таким образом,
каждая величина заменяется нек-рым, содержащим ее
интервалом. При выполнении арифметич. действий но-
новый интервал вычисляется с помощью специальных
операций.
Пусть G — множество интервалов {[а, Ь]}. Элемен-
Элементарные арифметнч. операции над интервалами опре-
определяются следующим образом:
где *? {+, —?¦>/}• Деление возможно лишь в том слу-
случае, если интервал, являющийся делителем, не содер-
содержит нуля. Множество G образует полугрупп}' но сложе-
сложению и умножению. Имеют место следующие равенства:
— К) = (/ + /) -\-К ассоциативность сложения,
/ •(/-К)= A J)K ассоциативность умножения,
/j-/ = /-}/ коммутативность сложения,
I -J — J -I коммутативность умножения.
Нулем и единицей служат соответственно интервалы
0=[0, 0], 1 = [1, 1]. Особенностью этой алгебраич.
структуры является то, что обратные элементы как по
сложению, так и по умножению определяются не един-
единственным образом, т. е. уравнения (относительно X)
I-\-X—J, I-X=J имеют, вообще говоря, не единствен-
единственное решение. Кроме того, не выполняется закон дист-
дистрибутивности, напр.
[1, 2]-([1, 2]-[1,2])=[1,2]-[-1, 1] = [-2, 2],
тогда как
[1, 2].[1, 2]-[1, 2][1, 2] = [1, 4]-[1, 4] = [-3, 3].
Имеет место лишь субдистрибутивность:
Операции над интервалами монотонны по включению.
Если IczK, JdL, то
I+JcK + L, I—JczK—L, I.JczKL, I/JczK/L.
В множестве G вводится топология с помощью метрики
р(/, /)=max(|c—o|, \d—b\), I=[a, b], J=[c, d], и ча-
частичная упорядоченность /</, если 6<:с, и /=/, ес-
если а=с, b=d.
Однозначное отображение G в G наз. интерваль-
интервальной функцией. Обычным образом вводится поня-
понятие непрерывности функции. Определяется производная
интервальной функции, определенный и неопределен-
неопределенный интегралы.
И. а. успешно применяется при решении нек-рых
задач. Однако применение этого метода значительно
увеличивает объем работы (более чем вдвое), требует
вдвое больше памяти и времени счета. Кроме того,
в достаточно больших задачах интервал, содержащий
окончательный ответ часто бывает настолько большим,
что практически не дает решения задачи. Для преодо-
преодоления последней трудности развивают И. а. со струк-
структурами теории вероятностей (см. [3]).
Лит.: [1] Moore R. E., Interval Analysis, 1966; [2]
Хемминг Р. В., Численные методы, пер. с англ., М.,
1968; [31 Interval Mathematics, N.Y., 1975 (Lect. Notes Com-
Computer Sience, v. 29). В. В. Поспелов.
ИНТЕРКВАНТИЛЬНАЯ ШИРОТА — расстояние
между нижней и верхней квантилями одинакового уров-
уровня. Пусть F(x) — строго монотонная функция непре-
непрерывного распределения и пусть р — произвольное
число из интервала 0<p<V2. И. ш. уровня р опреде-
определяется как разность xi^p—Хр, где х„ и х\ - р— решения
уравнений F(xp)=p и F(xi-p)=l—р соответственно.
II. ш. определенным образом подобранного уровня р
используется в математической статистике и теории
вероятностей для характеризации рассеяния распреде-
распределения вероятностей. Напр., разность хо^7ь—х0 гъ,
отвечающая значению р = 0,25, носит название и н т е'р-
кварт ильной широты, и в случае нормаль-
нормального распределения она равна 1,349 а (а — естествен-
естественная мера рассеяния, называемая квадратичным откло-
отклонением); половину интерквартильной широты наз.
еероятным отклонением. Если р=1/с, 1Г Р==1Ло, то
И. ш. наз. интерсекстильной и интерде-
ЦВЛЬЕОЙ Соответственно. Л. Н. Большее.
ИНТЕРПОЛИРОВАНИЕ, интерполяцп я,—
в простейшем, классическом смысле — конструктивное
восстановление (быть может, приближенное) функции
определенного класса по известным ее значениям или
значениям ее производных в данных точках.
Пусть даны п-j-l точек {.гд,}?=о сегмента Д=[а, Ь],
причем а-<.хо<^х1-С.. .<^„_1<а:„<:Ь, и набор из re-f-1
чисел {yk)k=o (не обязательно различных). Пусть из-
известно, что нек-рая функция f(x), принадлежащая
тому или иному фиксированному классу К функций,
определенных во всяком случае на Л (напр., /?яЛ;
где я„ — множество всех алгебраич. многочленов сте-
степени <;ге, или /?С'! + 1(Д)), удовлетворяет системе
соотношений:
Точки х^, в к-рых задаются значения f(xk)=ijk, наз.
узлами интерполяции, или полюсами
интерполяции для /. Естественно возникли
главным образом из потребностей приближенных вы-
вычислений следующие две задачи, к-рые и явились от-
отправными моментами развития всей теории И. А имен-
именно, спрашивается, как, обладая перечисленными выше
сведениями (А) относительно /, можно с определенной
точностью получить информацию: 1) о поведении f(x)
на интервалах (х^-х, х^), к=\, 2,. . ., га, то есть между
(лат. inter) полюсами х^, & = 0, 1,. .., п, и 2) вне (лат.
extra) сегмента [х0, хп], содержащего все полюсы
{жи}/г=о? Упомянутые здесь лат. слова inter и extra
привели соответственно к образованию терминов в слу-
случае 1) задачи интерполирования (или интерполяции)
функции /ив случае 2) задачи экстраполирования
(или экстраполяции) функции /, к-рые впоследствии
слились в одну проблему интерполирования (А).
Задача (А), понимаемая как задача точного восста-
восстановления функции, имеет единственное решение, напр.
в классе К=лп. Ее решением в я„ является интерполя-
интерполяционный многочлен Лагранжа
Однако, если f(x) принадлежит классу, в каком-то
смысле «более обширному», чем я„, то интерполяционная
задача (А), вообще говоря, не имеет единственного
решения. Тем не менее многочлен Ln(x) в нек-рой мере
позволяет судить о поведении f(x) на Д, если считать,
что
f(x)xL!n (x), x?A. A)
В связи с этим возникает потребность в оценке погреш-
погрешности
Rfn(x)=f(r)-Lfn(X)
для х? Д, к-рая во многом зависит от того, какому клас-
классу функций К принадлежит f(x), другими словами,
Rn(x) зависит от наперед известных свойств, к-рыми
обладает f(x). Напр., если А'=СК + 1(Д), то для задачи
(А) остаточный член имеет вид
где а<?<Р, a
А <*> = Ш=о(л-**>-
Здесь через аир обозначены соответственно наимень-
наименьшее и наибольшее из чисел х0, хп и х. Приведенная
формула остаточного члена принадлежит О. Коши
(A. Cauchy, см. [3]). Величина Rn(x) во многом зависит
от характера распределения и числа узлов интерполя-
интерполяции {xb}k=o на Д. При этом естественно предположить,
что чем больше узлов интерполяции х% будет взято и
чем «равномерней» они будут расположены на Д, тем
«точнее» будет выполняться соотношение A). Эти сооб-
соображения в свою очередь приводят к еще более важной
интерполяционной задаче, тесно примыкающей к проб-
проблеме (А).
Пусть f(x) принадлежит классу функций К, опреде-
определенных на Д, и таких, что ппфК при уге, ге=0, 1,. . ..
Предположим, что множество узлов интерполяции
{xfi)czA, x^Xj при кф], счетно, и задана последова-
тельность чисел {yft }й*=о- Спрашивается, как по имею-
имеющимся данным
f(r)?K; f(xk) = yk, k = 0, 1, 2, ..., (Б)
восстановить/(ж)? Поставленная задача в общем случае
далеко не всегда разрешима и требует ряда уточнений,
но это будет сделано несколько позже, а сейчас укажем
только абрис одного весьма естественного и важного
подхода к решению проблемы (Б). Обычно вначале
решается «усеченная» задача (А):
H.xkj) = ykj, / = 1> 2. ••¦> ге + 1,
в классе я„. Пусть Ln(x) — интерполяционный поли-
полином, являющийся решением этой усеченной задачи и
записанный, например, в виде многочлена Лагранжа.
Затем рассматривается возможность осуществления в
том или ином смысле предельного перехода Ln{x)-+f(x)
при я—юо (что равносильно, в частности, исследованию
вопроса о стремлении к нулю остаточного члена Rn{x)
при и—>-оо в рассматриваемом смысле). Приведенный
эскиз схемы решения задачи (Б) лежит в основе теории
сходимости (и расходимости) интерполяционных про-
процессов; он является одним из основных методов решения
задач интерполирования и имеет приложения не только
в различных разделах чистой математики (напр., в тео-
теории чисел, см. [3]), но и в методах вычислений (см.
Интерполирование в вычислительной математике, а
также [1]).
В последующем, наряду с интерполяционными зада-
задачами рассмотренного здесь вида, определяемыми прос-
простейшими функционалами j(xk), стали исследоваться и
другие, в к-рых, напр., задаются значения производ-
производных /(я)(хл)) "i=0, 1,..., nk, или иные более сложные
функционалы. При их решении стали применяться ин-
интерполяционные процессы, в к-рых в роли отправного
интерполирующего класса вместо класса л„ исполь-
используются другие множества функций, напр, классы Т„
тригонометрич. полиномов степени <:гс, классы ра-
рациональных функций nm,n=pjqn, где рт?л,п, а
9/1 €я« и <7и^0> классы целых функций специального
вида и т. д. . См. также интерполяционная формула.
Проблема И. в своей общей постановке заключается в
следующем. Пусть X и Y — два непустых множества;
задано семейство отображений {/a}a?jt, /а : X-+Y,
уа, а(;Э[. Если {уа}, а?9(, — некоторый заданный
набор элементов (не обязательно различных) множе-
множества У, то естественно возникает задача об отыскании
множества всех х^Х, удовлетворяющих следующей
системе равенств
{1а)(х) = Уа, Va, а?Ж. (В)
Вообще говоря, не для всякого априори заданного
набора элементов {[/а], ос?31, задача (В) обязана
иметь решения х, х?Х. Поэтому сформулированная
проблема требует ряда уточнений своей постановки.
Эти уточнения состоят в следующем.
I. Выяснить, каково множество Е=Е(Х; /а) всех
наборов {ya}, a(;S(, для к-рых система уравнений (В)
(быть может, бесконечная) имеет хотя бы одно решение
х, х?Х. Другими словами, требуется дать конструк-
конструктивное описание множества Е всех допустимых наборов
{уа}, сс?2[, для заданного фиксированного семейства
отображений {fa}, х?Ч1, для к-рых система (В) непро-
непротиворечива в X.
II. Пусть {i/a}, сс?91, — фиксированный допустимый
набор элементов из Y (т. е. принадлежащий множеству Е
из пункта I) задачи (В); требуется найти множество
всех решений х, л?Х, системы (В).
При решении задач I и II особое значение имеют от-
ответы на следующие вопросы более частного характера.
III. Каково подмножество Xt, XdX, на к-ром систе-
система уравнений (В) имеет единственное решение х, x?Xlt
для каждого допустимого для Хх набора {уа}, h
IV. Пусть Ех — некоторое подмножество Е, опреде-
определяемое обычно заданием лишь некоего ограничитель-
ограничительного свойства. Требуется дать конструктивную харак-
характеристику множества решений х, х?Х, системы (В)
при условии, что правые части в (В) «пробегают» все Ех.
Задание множества X, У и семейства отображений
{fa}, а?21(/а : X—>-У при уа, а?21) в совокупности с
сформулированными вопросами I и II (и обычно при-
присоединяемым к ним III, а иногда и IV) определяют
интерполяционную задачу (В). Класс задач описанного
вида иногда наз. классом прямых задач интер-
интерполирования.
Каждый в отдельности из перечисленных выше
пунктов I, II, III и IV представляет и сам по себе науч-
научный интерес. Пункт I имеет «пограничный характер»:
им занимаются теория чисел, функциональный анализ,
теория функций и др. Пусть, напр., х является действи-
действительным числом, ж?К, и {х} — его дробная часть.
Семейство отображений /„ : X-^-Y, n?N, задается сле-
следующим образом: XdR, У=[0, 1), fn{x)={xn}, n=
= 1, 2,..., и рассматривается следующая конкретиза-
конкретизация интерполяционной задачи (В):
Для нек-рых подмножеств X, IcR, пункт I задачи B)
в какой-то мере исследован, но в целом проблема B)
трудна: до сих пор A978), напр., нет ответа на вопрос о
распределении дробных долей {еп} степени числа е,
что является весьма частным подвопросом пункта I
задачи B). Связь между вопросом I и проблемами ба-
зисности системы элементов в различных функциональ-
функциональных пространствах отмечались, напр., в [9].
Вопрос II самый старый в теории И., он лежит у
истоков всей теории И. и связан с именами И. Ньюто-
Ньютона (I. Newton), Ж. Лагранжа (J. Lagrange), H. Абеля
(N. Abel), III. Эрмита (Ch. Hermite) и др. До 20 в. задачи
I, II и IV почти не рассматривались, а решение задачи
II, как правило, носило формальный характер.
Пункт III тесно примыкает к пункту II, но представ-
представляет интерес еще и потому, что во многих задачах он
эквивалентен проблеме полноты, а иногда и базисностя
различных систем элементов {fa}, a?31, в соответст-
соответствующих функциональных пространствах (полнота обыч-
обычно устанавливается с помощью критерия С. Банаха
(S. Banach), в к-ром доказана эквивалентность проб-
проблемы полноты нек-рой задаче единственности).
Важным примером исследований, относящихся к
пункту IV, являются задачи, посвященные изучению
классов функций, принимающих целые значения на
заданном множестве точек (напр., F(п) или F(qn), n—
= 0. 1, 2,..., являются целыми числами). Эта область
особенно бурно развивалась после получения Д. Пойа
(G. Polya) следующего результата: если целая функция
F (z) экспоненциального типа о", ст<1п2, такова, что ее
значения F{n), уп, п=0, 1, 2, ..., являются целыми
числами, то F (z) — полином. Константа 1п2 в приве-
приведенной теореме точная, ибо функция F(z) = 2ir=ez 'n2
является целой экспоненциального типа ст=1п 2, отлич-
отлична от многочлена и принимает в точках п=0, 1, 2,...
целые значения (см., напр., [5], [10]).
В том случае, когда в задаче (В) множество X явля-
является топологич. пространством и редуцированная в
каком-то смысле задача (В) имеет сравнительно простое
решение х*, одним из методов ее решения является
интерполяционный процесс, при к-ром исследуется
сходимость решений х* к решению х системы (В). О ча-
частном виде подобного рода процессов упоминалось
выше. Однако во многих случаях задачи типа (В) эффек-
эффективно решаются функциональными методами (см.,
напр., [10]).
Помимо прямых интерполяционных проблем опреде-
определенный интерес представляют обратные задачи
интерполирования. Основное содержание
исследований в этом направлении состоит в следующем.
Заданы непустые множества X и Y и нек-рый класс F
семейств отображений {{fa}, а?31}, действующих из
Л' в Y. Пусть М={{уа), а?Щ — некоторая сово-
совокупность наборов {уа} элементов из множества Y. За-
Задача состоит в нахождении необходимых и достаточных
условий, к-рым должен удовлетворять подкласс Fyu,
FjiCF, для того, чтобы существовало семейство
{fa}a^i^Fj\j. обладающее следующим свойством: мно-
множество {/а (х), а?81} совпадает с М (или czM, или ZDM),
когда переменная х пробегает всю совокупность
значений X. Выбор F и М тесно между собой связан.
Поэтому в исследованиях, относящихся к разделу
обратных задач И., обычно пара (F, М) естественным
образом составляет единое целое. В качестве примера
обратной задачи описанного здесь вида возьмем одну
из формулировок из круга вопросов, примыкающих к
известной интерполяционной проблеме Н е-
ванлпнны — Пика. Пусть {z^} — последова-
последовательность точек открытого единичного круга |z| <1 ком-
комплексной плоскости С. Каждой функции x(z) из класса
Н" (Н°° — класс функций, аналитических и ограни-
ограниченных в круге \z\ <1) ставится в соответствие последо-
последовательность ее значений в точках z^:
к — 1
Такимобразом, задан нек-рый вид F отображений Х=
=#°°в У— С. Пусть в качестве М берется пространство 1"°
(множество всех ограниченных последовательностей
комплексных чисел с=(с1, с2,. ..) с нормой ||c||=sup|cft|).
h
В рассматриваемом случае обратная'задача конкретизи-
конкретизируется следующим образом: требуется дать описание
множества всех последовательностей точек {z^} единич-
единичного круга |z|<l (т. е. класса F^[=Floo отображений
специального вида f^(x)=x(zk)), обладающих следую-
следующим свойством: оператор S (х) отображает все 7/~ на
I*. Последовательности {г^}, обладающие указанными
качествами, наз. интерполяционными.
Таким образом, множество всех интерполяционных
последовательностей {z^} и определяет в данной ситуа-
ситуации класс Fyi;=F/Oo- Ответ на поставленный вопрос дает
теорема Карлесона: для того чтобы после-
последовательность точек {zj.} открытого единичного круга
|г| <1 была интерполяционной, необходимо и доста-
достаточно, чтобы существовало б>0 такое, что
п,
б, fc =
(так наз. условие разделения). Обратные
задачи И., типа решенной Л. Карлесоном (L. Carleson),
рассматривались и для других классов функций и
соответствующих пространств числовых последователь-
последовательностей (см., напр., [9], [12], [13], [14]).
См. также Абеля — Гончарова проблема.
JIuvi.: [1] Б е р е з и н II. С, Ж и д к о в Н. П., Методы
вычислений, т. 1, 3 изд., М., 1966, т. 2, 2 изд., М., 1962; [2]
Гельфонд А. О., Исчисление конечных разностей, М.—
Л,, 1952; [3] Г о н ч а р о в В. Л., Теория интерполирования
и приближения функций, 2 изд., М., 1954; [4] У о л ш
Дж.-Л., Интерполяция и аппроксимация рациональными функ-
функциями в комплексной области, пер. с англ., М., 1961; L5] Б и-
б ер б ах Л., Аналитическое продолжение, пер. с нем., М.,
1967; [6] N б г 1 u n d N. Е., Vorlesungen uber Differenzenre-
chnung, В., 1924; [7] e г о же, Lecons sur les series d'interpo-
lation, P., 1926; [8] Whittaker J. M., The interpolator
function theory, Camb., 1Я35; [9] D u ren P. L., Theorie of Hp
spaces, N.Y.—L., 1970; LlO] Казьмин Ю. А., Методы ин-
интерполяции аналитических функций и их приложения, Докт.
цисс, М., 1972; [11] Коробейник Ю. Ф., «Матем. сб.»,
1975, т. 97, .№ 2, с. 193—229; т. 98, № 1, с. 3—26; [12) К а-
б а й л а В., «Литов. матем. сб.», 1963, т. 3, М 1, с. 141—47;
113] С е д л е ц к и й А. М., «Докл. АН СССР», 1973, т. 208,
№ 6, с. 1293—95; [14] Ш в е д е н к о С. В., «Матем. заметки»,
1977, т. 21, X» 4, с. 503—08. Ю. А. Казыиин.
ИНТЕРПОЛИРОВАНИЕ в вычислительной
математике — способ приближенного пли точ-
точного нахождения какой-либо величины по известным
отдельным значениям этой же или других величин, свя-
связанных с ней. На основе И. построен ряд приближен-
приближенных методов решения математич. задач.
Наибольшее значение в вычислительной математике
имеет задача построения способов интерполирования
функций. Интерполяция функционалов и операторов
также широко используется при построении прибли-
приближенных методов.
Приближенное представление и
вычисление функций. И. функций рассмат-
рассматривается как один из способов их приближения. И.
функции f (х) на отрезке [а, Ь] по значениям ее в узлах
Xk сетки Ап= {а^ха<хг<-. .<xn*?b} означает построе-
построение другой функции L,,(x)^Ln(f; х) такой, что Ьп(хь) =
=t{xk), k=0, I,..., п. В более общей постановке задача
И. функции f(x) состоит в построении Ln(x) не только
из условия совпадения значений функций Ln (x) и
f(x) на сетке Д„, но и из требования совпадения в
отдельных узлах их производных до какого-то порядка
или нек-рых других соотношений, связывающих }(х) и
Ln(x).
Обычно Ln (x) строится в виде
гДе {ф/(ж)} — некоторая заранее выбранная система
линейно независимых функций. Такое И. наз. линейным
относительно еистемы {q>i(x)}, а1„(г)-пнтерп о-
л я ц и о н н ы м полиномом по системе
(ф,-(*)}.
Выбор системы {ф<(;г)} определяется свойством того
класса функций, для приближения к-рых предназнача-
предназначаются интерполяционные формулы. Напр., для при-
приближения 2я-периоднческих функций на [0, 2я] за
{ф,(ж)} естественно взять тригонометрическую систему
функций, для приближения на полуоси [0, оо) огра-
ограниченных или возрастающих функций — систему раци-
рациональных или показательных функций, учитывающих
поведение приближаемых функций на бесконечности и
т. д.
Чаще всего используется алгебраич. И.: <pi(x) = x1',
простейший вариант которого — линейное ин-
интерполирование с двумя узлами И. х^ и
— определяется формулой
Алгебраическое И. более высокого порядка в задаче
приближения функций на всем отрезке [а, Ь] приме-
применяется на практике сравнительно редко. Обычно огра-
ограничиваются линейным И. по формуле A) или квад-
квадратичным интерполированием с тре-
тремя узлами на частичных отрезках сетки по формуле
'¦Xk-i хк'1-хк-1 xk + i>
-г (т _т uz—z Г ' ( к> '
(х-х fi_1)(x-Xfl)
xk>
f(xk+l), B)
Имеются различные варианты записи алгебраич. ин-
интерполяционных многочленов (см. Интерполяционная
формула).
Находит все большее применение И. сплайнами (см.
Интерполяционный сплайн).
На практике чаще всего используются параболичес-
параболические или кубические сплайны. Интерполяционным ку-
кубическим сплайном дефекта 1 для функции /(ж) относи-
относительно сетки Дк наз. функцию S3(x)=S3(f; x), являю-
являющуюся многочленом третьей степени на каждом из
отрезков [xft_b xk], принадлежащую классу дважды не-
непрерывно-дифференцируемых функций и удовлетворяю-
удовлетворяющую условиям
При таком определении имеется еще два свободных
параметра, для нахождения к-рых налагаются дополни-
дополнительные краевые условия: S3l) (a) = Sl3(b), i=l, 2; S3(a)=
= <!„ и S3{b)=bn или нек-рые другие.
Как непосредственно для задачи приближения функ-
функций, так и при решении других задач используются
сплайны, к-рые в точках сетки Дк совпадают не только
со значениями функций f{x), но и со значениями про-
производных этой функции до нек-рого порядка.
Часто при обработке эмпирических данных {у ь}
коэффициенты а,- в Ln (x) определяются, исходя из требо-
требования минимизации суммы
Такое построение функции Ln(x) наз. интерполи-
интерполированием по методу наименьших
квадратов.
И. функций многих переменных имеет ряд принципи-
принципиальных и вычислительных трудностей. Напр., в случае
алгебраич. И. интерполяционный многочлен Лагранжа
фиксированной степени, вообще говоря, не существует
для произвольной системы различных узлов И. В част-
частности, для функций двух переменных / (х, у) такой мно-
многочлен Ln(x, у) суммарной степени не выше п может
быть построен по узлам (х^, у^) лишь при условии,
что эти узлы не лежат на алгебраич. кривой порядка п.
Другой подход к И. функций многих переменных
f{xx,..., хт) состоит в том, что сначала интерполируется
функция по переменной хх при фиксированных х^,
к = 2, 3,. . ., т, потом по следующей переменной при
фиксированных остальных х^ и т. д. При таком способе
построения интерполяционный алгебраич. многочлен
Ln,. ¦¦пт(х1,. . ., хт) для функции f(xx,. .., хт) с узлами
(*i''"'zmm)' xJ^xr v=?\i; kj=O, 1, ..., nj;
имеет вид
/ = 1, 2 m,
t (xx )-У1 "и
(*?• **r)
X
где
Интерполяционные сплайны для функций многих пере-
переменных определяются на многомерной сетке при соответ-
соответствующих изменениях по аналогии с одномерным слу-
случаем. И. функций используется для замены сложно
вычисляемой функции другой, вычисляемой быстрее;
для приближенного восстановления функции на всей
области задания по значениям ее в отдельных точках;
для получения сглаживающих функций, описывающих
плавный процесс. Такого рода задачи имеют как само,
стоятельное значение, так и возникают в качестве вспо-
вспомогательных при решении более сложных задач во мно-
многих областях науки и техники. И. функций применяется
также для приближенного нахождения предельных
значений функций, в задачах ускорения сходимости
последовательностей и рядов и в других вопросах.
Численное решение нелинейных
уравнений и систем. Общие идеи построения
интерполяционных методов решения уравнения f(x) = 0
и систем уравнений fi(-r1, х2,. . ., жт) = 0, ?=1, 2,...,
т, одни и те же. Трудности задачи И. функции многих
переменных особенно сказываются при исследовании и
практич. использовании такого рода методов для боль-
большого числа уравнений. В основу получения интерполя-
интерполяционных методов решения уравнения f(x) = 0 положена
замена функции / (х) ее интерполяционным полиномом
Ь,г(х) и последующим решением уравнения Ln(x)=0.
Корни уравнения Ln(x) = 0 берутся за приближенные
решения уравнения /(х) = 0. Интерполяционный поли-
полином Ln(x) используется также при построении итера-
итерационных методов решения уравнения f(x) = 0.
Напр., взяв за хп + 1 корень линейного интерполяци-
интерполяционного алгебраич. многочлена, построенного по значени-
значениям f(xn) и /' (хп) в узле х„, или по значениям /(x4_i)
и }(х„) в узлах хп_х и хп, приходят соответственно
к методам Ньютона и секущих:
х ==х" — - -
f'(xn) ' /(ж„_!, хп)
где /(?„_!, xn) — разделенная разность функции f(x)
для узлов х„_! и хп. При выполнении нек-рых условий
последовательность значении хп будет стремиться при
п—^-оо к решению уравнения f(x) = 0.
Другой подход к построению методов решения урав-
уравнения /(х) = 0 основан на И. обратной функции х=
= g(y). Пусть в качестве интерполяционной формулы
для функции x=g(y) взят интерполяционный алгебраич.
многочлен Лагранжа
¦^uk = oii)'n{ijk)(y-yk)
Предполагается, что обратная функция существует
в окрестности искомого корня уравнения f(x)—0
и составлена таблица значений х^ и ijk=f(xk), k=
= 0, 1, ..., п. За следующее приближенное значение
Xk + л принимается значение интерполяционного много-
многочлена в нуле:
Численное интегрирование. Аппарат
И. функций лежит в основе построения многих квадра-
квадратурных и кубатурных формул. Такого рода формулы
строятся путем замены интегрируемой функции на всей
области или на ее составных частях интерполяцион-
интерполяционными полиномами того или иного вида и последующим
интегрированием этих полиномов.
Напр., квадратурные формулы наивысшей алгеб-
алгебраич. степени точности, так наз. Гаусса квадратурные
формулы
где р (х) — знакопостоянная весовая функция, полу-
получаются в результате замены функции / (ж) интерполя-
интерполяционным алгебраич. многочленом, построенным по
корням хь ортогонального относительно веса р(х)
многочлена степени п.
Если разделить весь отрезок интегрирования [а, Ъ]
на четное число п равных частей длины h= —(Ь—а)
н на каждом сдвоенном частичном отрезке заменить
1(х) ее квадратичным интерполяционным многочленом
с узлами в крайних и средней точках, то придем к со-
составной Симпсона формуле
(*) dx^~ [/„ + /„ + 2 (/2 + /4+ . . . + /„-.) +
где fk=f(a+kh), к = 0, 1, . . ., п.
Можно взять за основу и интерполяционные сплайны
какой-то фиксированной степени. Изложенная выше
схема построения формул для приближенного вы-
вычисления интегралов применима и в многомерном
случае.
Численное дифференцирование.
Формулы численного дифференцирования получаются
в результате дифференцирования интерполяционных
формул. При этом, как правило, заранее известна
нск-рая априорная информация о дифференцируемой
функции, касающаяся ее гладкости.
Пусть Ln(x) — интерполяционный полином нек-рого
вида для функции f(x), a Rn(x) — остаток интерполя-
интерполяционной формулы:
f(x) = L,,(x)+Rn(x).
Если в равенстве
пренебречь величиной Rn\x), то это приведет к фор-
формуле для приближенного вычисления i-й производной
функции f(x):
/<'•> (х) « ?{*> (х). C)
Формулы численного дифференцирования, в основе
к-рых лежит И., получаются из приближенного равен-
равенства C) в зависимости от выбора интерполяционного
полинома Ln(x). При численном дифференцировании
используются, как правило, приближенные значения
функции в узлах; погрешность формул численного
дифференцирования зависит не только от способа И. и
шага И., но и от ошибки используемых значений функ-
функции в узлах. Напр., в случае линейного И. A):
{/М], D)
причем для остатка R\ (x) имеет место представление:
Если f(xit + 1) n f (аг^известны соответственно с погреш-
погрешностями 6^+ i и 6^, &k + v?=?k, T° погрешность формулы D)
будет содержать еще член (e^ + i—Bk)/h, к-рый с умень-
уменьшением шага h возрастает. При использовании формул
численного дифференцирования шаг И. должен согласо-
согласовываться с погрешностью значений функции. Поэтому на
практике нередки случаи, когда известная с нек-рой
погрешностью на густой сетке функция используется
в данной задаче не во всех точках, а на более редкой
сетке.
Численное решение интегральных
уравнений. Неизвестная функция <р(х) заме-
заменяется в интегральном уравнении какой-либо интер-
интерполяционной формулой (интерполяционным полино-
полиномом, интерполяционным сплайном и т. д.) с узлами И.
x/i, а приближенные значения для ^(х^) находятся
из системы, полученной после подстановки вместо не-
независимой переменной х узлов И. хк.
I Напр., для линейного интегрального уравнения Фрод-
гольма 2-го рода
Ф (х) = к J * К (*, s) Ф (s) ds + / (i) E)
можно воспользоваться лагранжевым представлением
интерполяционного многочлена:
где Rn{x) — остаток И.,
1к(х) = со,, (т)/и^ (,rfr) (ж — хА), шп(г) =Д^=0 (х — хк).
Замена функции <р(х) в E) ее интерполяционным много-
многочленом Ln(x) и х на ж,-, приводит к линейной системе
уравнений
т;, s)lh(s)ds, i = 0, 1, ..., в,
для нахождения приближенных значений ф,- решения
ф(х) уравнения E) в узлах х;. В случае нелинейных
интегральных уравнений приближенные значения ф,-
находятся соответственно из нелинейной системы.
Численное решение дифференци-
дифференциальных уравнений. Построение численных
методов решения дифференциальных уравнений состоит
в замене производных искомых функций интерполя-
интерполяционными формулами численного дифференцирования,
а в ряде случаев и заменой интерполяционными фор-
формулами других функций и выражений, входящих
в уравнения.
Пусть имеются формулы численного дифференци-
дифференцирования
y^-»^± (в)
для равноотстоящих узлов х^=жо+АЛ, получаемые
соответственно дифференцированием формул линейной
и квадратичной И. A) и B). Тогда для обыкновенного
дифференциального уравнения 2-го порядка
F(x, у, у', г/") = °
при нек-рых дополнительных условиях получается
с учетом F) уравнение в конечных разностях
Уь ~hhlJh, -p" &2Ук\ =0,
из к-рого вместе с уравнениями, полученными из до-
дополнительных условий, находятся приближенные зна-
значения уь решения у(х) в узлах х^.
Сведение дифференциальных уравнений с частными
производными к соответствующим уравнениям в ко-
конечных разностях производится часто также с исполь-
использованием формул численного дифференцирования.
Интерполяционный метод применим для решения
дифференциальных уравнений, записанных в интег-
интегральной форме. Напр., для нахождения приближенного
решения задачи Коши
y'=f(x, у), у(хо) = уо G>
в точках xk=x0-\-kh, k = 0, I, . .., используются раз-
разностные формулы типа
Уп + 1= Уп + h ^"= j Bjf {xn-j, Уп-j),
получаемые заменой функции под знаком интеграла
в равенстве
\X x, y)dx
интерполяционным полиномом и последующим интег-
интегрированием. В частности, таким образом получены
формулы Адамса для уравнения 1-го порядка G) фор-
формулы Стёрмера для уравнений 2-го порядка и т. д.
Такой подход позволяет строить вычислительные
алгоритмы для широкого класса дифференциальных
уравнений в том числе и для уравнений в частных про-
производных. Исследование разрешимости, точности и
устойчивости решения возникающих конечно разност-
разностных уравнений представляет собой основную и наибо-
наиболее трудную часть теории численного решения диффе-
дифференциальных уравнений.
Интерполирование операторов и
некоторые общие подходы к пост-
построению численных методов. Построение
численных методов решения математич. задач, записан-
записанных в виде у=Ах, где элементы х и у принадлежат
нек-рым множествам X и Y, а А — заданный оператор,
состоит в замене множеств X и Y и оператора А или
только нек-рых из этих трех объектов другими, удоб-
удобными для вычислительных целей. При этом замена
должна быть сделана так, чтобы решение новой за-
задачи
У = Ах,
состоящей в нахождении у или х, было в каком-то
смысле близко к решению первоначальной задачи.
Один из способов замены оператора А его приближе-
приближением А состоит в использовании интерполирования опе-
операторов. Имеются различные формулировки задачи
Я. операторов. Линейный интерполяционный оператор
Lf(F; x) для данного оператора записывается в виде
Ьг(Р; x)=F(xo)+F(xo, Xl){x-xa), (8)
где х0 и хх — узлы П., F(x0, хх) — оператор разделенной
разности 1-го порядка, определяемый как линейный
оператор, удовлетворяющий условию
F(x0, x1)(x0—x1)=F{x0) — F(x1).
Данное определение оператора разделенной разности
в ряде случаев конкретизируется. С использованием
линейного И. (8) «метод секущих» для уравнения
F(x) = O записывается в виде
хп + 1 = хп — Р~1 {xn--i, xn)F(xn),
где F~1(xn-1, xn) — оператор, обратный к F(xn-1, х„).
Постановка задачи И. функционалов, представляю-
представляющая интерес для теории приближенных методов такова.
Пусть {г|з/(ж)}, i = 0, 1, . . ., п,— некоторые фиксиро-
фиксированные функционалы или классы функционалов, оп-
определенные на X. Функционал Ln[F; x] наз. интер-
интерполяционным функциональным мно-
многочленом для данного функционала F(x) и сис-
системы точек {x/i} из X, если выполняются соотношения
Ln[F; xk}=F (хк), Ln[^i; x] = -ф,- (х),
i = 0, 1, .. ., п.
И. функционалов используется при построении при-
приближенных методов вычисления континуальных интег-
интегралов, для нахождения экстремальных значений функ-
функционалов и ряда других задач.
Напр., приближенные интерполяционные формулы
для вычисления континуальных интегралов имеют вид
при этом интеграл от интерполяционного полинома
Ln[F; x] для нек-рых мер ц может вычисляться точно
или сводиться к конечномерным интегралам. Интер-
Интерполяционный полином LX[F; x], когда X есть прост-
пространство непрерывных на отрезке [а, Ь] функций С [а, Ь],
представляется в виде интеграла Стилтьеса
L,[F; x]=F(xo) +
., т) fo (¦)
где ?„(?) и ar^i) — узлы И., а функция
Если F(a:) — постоянный или линейный функционал,
то Lt[Fi x]-^F(x).
Применение И. к нахождению экстремальных зна-
значений функционалов может быть проиллюстрировано
двумя интерполяционными аналогами метода градиента
для нахождения локальной точки безусловного мини-
минимума функционала F(x), определенного на нек-ром
гильбертовом пространстве. Первый из этих методов
получается, если в градиентном методе заменить
grad F(xn) на F(xn-lt xn), т. е.
xn + i = xn+znF (хп-х, яп). &п > 0, ге = 1, 2, ... (9)
Второй метод использует градиент интерполяционного
полинома. По приближениям х„_2. ^«-i, xn к экстре-
экстремальной точке х* функционала F(x) строится квадра-
квадратичный интерполяционный функционал
L2[F; x]=F{xn) + F(xn_1, хп)(х~х„) +
+ F(xn_2, з-„_ь хп) (х — хп_х) (х — хп),
где F(xn-2, x-n-i> хп) — разделенная разность 2-го по-
порядка функционала F(x) относительно узлов ?„_2, г„_ь
х-п, и новое приближение хп + 1 находится по формуле
xn + i:=xn — engradL2 [F; хп], A0)
е„ > 0, и = 2, 3, ...
Итерационные методы (9) и A0) используют соответст-
соответственно два и три начальных приближения.
Применение И. функционалов и операторов для по-
построения вычислительных алгоритмов решения кон-
конкретных задач основано на использовании интерполя-
интерполяционных формул с малой величиной погрешности.
Такого рода формулы должны строиться для отдель-
отдельных классов функционалов и операторов с учетом спе-
специфики этих классов.
Лит.: [1] Гончаров В. Л., Теория интерполирования
и приближения функций, 2 изд., М., 1954; [2] Б е \\ е з и н
И. С., Ж и д к о в Н. П., Методы вычислений, т. 1—2, М.,
1959—60; [3] Бахвалов Н. С, Численные методы,
2 изд., М., 1975; [4] Крылов В. И., Б о б к о в В. В.,
М о н а с т ы р н ы й П. И., Вычислительные методы, т. 1 — ?
М., 197A—77; [5] С т е ч к и н СБ., Субботин Ю. Н.,
Сплайны в вычислительной математике, М., 1970; [С] Сама \>-
с к и й А. А., Введение в теорию разностных схем, М., 1SI71;
[7] Янович Л. А., Приближенное вычисление континуальных
интегралов по гауссовым мерам, Минск, 1976. Л.А. Я)ювич
ИНТЕРПОЛИРОВАНИЕ ОПЕРАТОРОВ — получе-
получение из известных свойств оператора в двух или не-
нескольких пространствах выводов о свойствах этого
оператора в нек-рых в определенном смысле промежу-
промежуточных пространствах. Банаховой парой А, В
наз. два банаховых пространства, алгебраически и
непрерывно вложенные в отделимое линейное тополо-
гич. пространство 2(. На пересечении A f\B вводится
норма
1Ми {[И| |||!}
на арифметич. сумме А +Д — норма
IMU+b= inf {||
Пространства ^Г)# и АЛ~В банаховы. Банахово
пространство Е наз. промежуточным для пары
А, В, если Af\B a E a A + В.
Линейное отображение Т, действующее из А +5
в C+Z>, наз. ограниченным оператором
из пары А, В в пару С, D, если его сужение на А
(соответственно В) является ограниченным операто-
оператором из А (соответственно В) в С (соответственно D).
Тройка пространств {А, В, Е) наз. интерполя-
интерполяционной относительно тройки
(С, D, F}, Cf\DczFczC+D, пространство Е (соответ-
(соответственно F) — промежуточное для пары Л, В (соответ-
(соответственно С, D), если всякий ограниченный оператор
из пары А, В в пару С, D отображает Е в F. Если
Л—С, B=D и E—-F, то пространство /? наз. и н т е р-
поляц ионным между Л и В. Для интерполяци-
интерполяционных троек существует константа с такая, что
| Г [|л ^ с, || 7 ||а _ D }.
Первая интерполяционная теорема получена М. Рис-
сои (М. Riesz, 1926): тропка пространств {Lpa, Lp , ?р}
является интерполяционной относительно тройки
fL<7.' L<v L<?}' еслп ! <;»(>> Pi. ?o, ?i<°° и при нек-ром
в
'~е i ° L
Мера, по к-рой строятся перечисленные пространства,
может быть своей для каждой тройки. Аналог этой
теоремы может не быть справедливым для других
классич. семейств пространств; напр., пространство
С1 @, 1) не является интерполяционным между С @, 1)
п С2@, 1).
Интерполяционным функтором F
наз. функтор, ставящий в соответствие каждой бана-
банаховой паре А, В промежуточное пространство F(A. В),
причем для любых двух банаховых пар А, В и С, D
тройки {А, В, F(A, В)} и {С, D, F(C, D)} являются
друг относительно друга интерполяционными. Имеется
ряд методов построения интерполяционных функторов.
Наибольшее число приложений нашли два из них.
К-м етод Петре. Для банаховой пары А, В
строится функционал
K(t, х)= inf {[|u|U + <|M|B},
Х= U + V
эквивалентный при каждом t норме в А-\-В. Банахово
пространство G измеримых на полуоси функций наз.
идеальным пространством, если из того,
что |/(t)| <\g(t)\ почти всюду на @, <х>) и g?G, выте-
вытекает f?G и ||/|1о<11#11о- Рассматриваются все элементы х
из А-\-В, для к-рых K(t, x)^G. Они образуют ба-
банахово пространство (А, В)§ относительно нормы
||i|l к= Н-ЙГ(*. *)Hg- Пространство (А, В)о будет
{А, B)q
ненулевым и промежуточным для А, В в том и только
в том случае, когда функция min {t, 1} принадлежит G.
В этом случае функтор F(A, B)=(A, В)д будет ин-
интерполяционным. Для нек-рых банаховых пар функ-
функционал K(t, x) вычисляется, и это позволяет эффек-
эффективно строить интерполяционные пространства. Для
пары Lj и Loo
K(t, х)=^'.г*(т) di,
где х*(х) — равноизмерпмая с функцией х невозрас-
тающая непрерывная справа функция на @, <х>). Для
пары С к С1
K(t, x) = -^aBt, x),
где со (?, х) — модуль непрерывности функции х, а знак
-— означает переход к наименьшей выпуклой мажоранте
функции на @, оо). Для пары Lp(Rn) и Wlp(Rn) {Со-
{Соболева пространство)
где
«/, p(t, x)= sup j|Aft.r (s)l\L ,
\h\<,l. P
За пространство G часто принимается пространство
с нормой
0>-е1/(*I^}1Л7' 0 < 9 < 1, l^g^oo.
Соответствующий функтор обозначается (A, B)q, р .
Важную роль в теории уравнений с частными произ-
производными играют пространства Бесова
где т=8/. Ряд класси:. неравенств анализа уточняется
в терминах пространств Лоренца
Комплексный метод Кальдерона—
Л и о н с а. Для банаховой пары А, В через Ф (А, В)
обозначается пространство, состоящее из всех функ-
функции <p(z), определенных в полосе П : 0«:Re zsg:l комп-
комплексной плоскости, со значениями в пространстве
А-\-В, обладающих свойствами: 1) <p(z) непрерывна
и ограничена по норме Л+В в П, 2) <p(z) аналитична
относительно нормы в А-\-В внутри П, 3) <р(гт) непре-
непрерывна и ограничена по норме Л, 4) <рA-(-гт) непрерывна
и ограничена по норме В. Пространство [А, В]а,
0<а<:1, определяется как совокупность всех элемен-
элементов х?А+В, представимых в виде ;г=<р(а) при
?Ф(Л, В). В нем вводится норма
Таким образом строится интерполяционный функтор
[А, В]а. Если Л = Лр и B=Lpi, i*cp0, р1-^.оо, то
[Lpa, Lpi]a =Lp, где °l/p = (l—aj/po+a/p!. Если Go
и Gx— два идеальных пространства, и хотя бы в одном
из них норма абсолютно непрерывна, то пространство
[Go, GJa состоит из всех функций x(t), для к-рых
x(t) \— \xo(t)\1-a\x1(t)\a при нек-рых xQ?G0, x1^:G1.
Если для двух комплексных гильбертовых пространств
Но и Н1 имеется вложение Н^сНц, то пространства
[Но, Ht] ? образуют важное для приложений семейство
пространств, наз. гильбертовой шкалой.
Если #0=L2 и Н1= W-2, то [#0, Н1]а= W?1 (пространство
Соболева с дробными индексами). О других методах
построения интерполяционных функторов, а также об
их связях с теорией шкал банаховых пространств см.
[1], [3], [5], [8].
Особую роль в теории И. о. играет направление,
связанное с интерполяционной теоремой М а р-
ц и н к е в п ч а об операторах слабого типа: опера-
оператор Т, действующий из банахова пространства А в про-
пространство всех измеримых функций, напр., на полуоси,
наз. оператором слабого типа {A, i|>),
если (Tx)*(t)^-r~\\x\\A. При этом предполагается, что
функции 1|)(г) и f/i|j(t) не убывают (напр., \p(t)=ta,
0<сс<:1). Теоремы типа теоремы Марцпнкевича по-
позволяют для операторов Т слабых типов (Ао, i|H)
и (Аг, \рг) одновременно (Ао, А±— банахова пара) опи-
описывать пары пространств А,Е, для к-рых TAczE.
Во многих случаях достаточно проверить, что из А
в Е действует оператор
1 is / Фо (О
где K(t, x) — функционал Петре для пространств
Ао, Ах. Если действие из А в Е показано для всех ли-
нсйных операторов слабых типов (А;, г|з,), то оно будет
иметь место и для квазиаддитивных операторов (со
свойством | T(x+y)(t)\ <Zb(\Tj(t)\ + \Ty(t)\) слабых ти-
типов (А I, г)),-), г=0, 1. Многие важные операторы анали-
анализа (напр., сингулярный оператор Гильберта) имеют сла-
слабый тип в естественных пространствах и поэтому со-
соответствующие интерполяционные теоремы получили
многочисленные применения.
Лит.: [1] Butzer P.,Berens H., Semi-groups of
Operators and Approximation, В., 1967; M Зигмунд А.,
Тригонометрические ряды, пер. с англ., М., 1965; [3] Крсйн
С. Г., Петунии Ю. И., «Успехи матем. наук», 1966,
т. 21, в. 2, с. 89—168; [4] Лионе Ж.-Л., Мадженес Э.,
Неоднородные граничные задачи и их приложения, пер. с франц.,
М., 1971; [5] Мадженес Э., «Успехи матем. наук», 1966,
т. 21, в. 2, с. 169—218; [6] Стейн И., В е й с Г., Введение
в гармонический анализ на евклидовых пространствах, пер.
с англ., М., 1974; [7] Функциональный анализ, [Справочная
математическая библиотека], 2 изд., М., 1972; [8] В е г g h
Т. L of strom, Interpolation spaces, В., 1976. С. Г. Крейн.
ИНТЕРПОЛЯЦИОННАЯ ФОРМУЛА — формула для
приближенного вычисления значений функции f(x),
основанного на замене приближаемой функции / (ж)
более простой в каком-то смысле функцией
g (x) = g(x; ай, oj, . . ., а„)
наперед заданного класса, причем параметры в/,
t=0, 1, ..., п, выбираются таким образом, чтобы зна-
значения g(x) совпадали с известными заранее значениями
/ (х) для данного множества ге+1 попарно различных
значений аргумента:
*(**) = /(**). * = 0, 1, ..., п. A)
Такой способ приближенного представления функций
наз. интерполированием, или интерполяцией,
а точки хк, для к-рых должны выполняться усло-
условия A),— узлами интерполяции. Вместо
простейших условий A) могут быть заданы значения
каких-либо иных величин,' связанных с f(x), напр,
значения производных функции f(x) в узлах интер-
интерполяции.
Среди методов интерполирования самым распрост-
распространенным является линейное интерполи-
интерполирование, когда приближение ищется в классе
(обобщенных) полипомов
g (х; а0, аг, . ..,а„)=> а;^(х) B)
по некоторой системе функций фо(-с), fi(x), ¦ . ., <рп(х)-
Для того, чтобы для любой функции/(х), определенной
на отрезке [а, Ь], и для любого набора га-f-l узлов
х0, х1, ..., хп, х;?[а, Ь], х;Фху при 1Ф] существовал
интерполяционный полином B), необ-
необходимо и достаточно, чтобы система функций {(р,(х)}
являлась Чебышева системой на отрезке [а, Ь]. При
этом интерполяционный полином будет единственным
и его коэффициенты а/ можно найти непосредственным
решением системы A).
Чаще всего в качестве {ц>;(х)} берут последователь-
последовательность степеней х:
\ Т Г2 гп
±, л, л j ...» ^ , •>•;
последовательность тригонометрических функций:
1, sin х, cos .r, sin 2x, cos2x, ...,
или последовательность показательных функций
1, еа'х, еа'х, ...,
где {а,-} — некоторая подпоследовательность попарно
различных действительных чисел.
В случае интерполирования алгебраич. многочле-
многочленами
система функций {ф,(ж)} такова:
ф, (*) = *'¦, « = 0, 1, ..., п, D)
а система уравнений A) имеет вид
?"_ я,-4 = /Ы, ft = 0, 1, ...,«. E)
Система D) является системой Чебышева, что обеспе-
обеспечивает существование и единственность интерполяцион-
интерполяционного многочлена вида C). Особенностью системы D)
является возможность получения явного представле-
представления интерполяционного многочлена C), не прибегая
к непосредственному решению системы E). Одну из
явных форм интерполяционного многочлена C):
наз. интерполяционным многочленом
Л а г р а н ж а. В предположении непрерывности про-
производной f + 1(x) остаточный член интерполяционного
многочлена F) может быть записан в форме
Ап + 1) /?\
f(*)-gn(*) = - („ + О| -<П„ (*), G)
здесь !/1=min(x0,x1,.. ., хп, х), у2=тах(х0,х1, . . .,х„,х).
Величина остаточного члена G) зависит, в частности,
от значения многочлена со„(х). Представляет интерес
такой выбор узлов интерполяции, при к-ром supl ш- (х)\
[а, 6]
был наименьшим. Распределение узлов будет оптималь-
оптимальным в указанном смысле, если в качестве узлов интер-
интерполяции взяты корни
хк=~(Ь^а)+^(Ь-а)с08-§^-п, к = 0, 1, ...,п,
наименее уклоняющегося от нуля на отрезке [а, Ь]
многочлена
b-a
где Tn + i(z) — Чебышева многочлен степени ге+1.
Существует ряд других явных представлений интер-
интерполяционного алгебраич. многочлена C), более при-
приспособленных для решения тех или иных практич.
задач интерполяции (см., напр., Бесселя интерполя-
интерполяционная формула, Гаусса интерполяционная формула,
Ньютона интерполяционная формула, Стирлинга ин-
интерполяционная формула, Стеффенсена интерполя-
интерполяционная формула, Эверетта интерполяционная фор-
формула). Если заранее трудно оценить степень интерпо-
интерполяционного многочлена, требуемую для достижения
заданной точности (напр., при интерполировании таб-
таблиц), то прибегают к использованию Эйткена схемы,
по к-рой интерполяционные многочлены все более
высокой степени строятся последовательно, что позво-
позволяет контролировать точность в процессе вычислений.
Другой подход к построению И. ф. см. в ст. Фрезера
диаграмма.
Решение задачи алгебрапч. интерполирования по
значениям функции и ее производных в узлах интер-
интерполяции дается Эрмита интерполяционной формулой.
Лит.: [1] Б е р е з и н И. С, Жидков Н. П., Методы
вычислений, 3 изд., т. 1, М., 1966; [2] Бахвалов Н. С,
Численные методы, 2 изд., М., 197Г>- М. К. Самарин.
ИНТЕРПОЛЯЦИОННЫЙ ПРОЦЕСС — процесс по-
получения последовательности интерполирующих функ-
функции {/„(z)} при неограниченном возрастании числа п
условий интерполирования. Если интерполирующие
функции fn(z) представлены в виде частных сумм неко-
некоторого функционального ряда, то последний иногда наз.
интерполяционным рядом. Целью пост-
построения И. п. чаще всего является, по крайней мере
в простейших первоначальных задачах интерполиро-
интерполирования, приближение в каком-то смысле посредством
интерполирующих функций /n(z) исходной функции / (г),
о к-рой или имеется неполная информация или форма
к-рой слишком сложна для непосредственного исполь-
использования.
Довольно общая ситуация, связанная с построением
И. п., описывается следующим образом. Пусть (а/ь),
0<&</, /=0, 1, . . .— бесконечная треугольная таб-
таблица произвольно заданных комплексных чисел
«оо
Я10 Оц
A)
°ло ал1 ••• апп
наз. узлами интерполяции. Пусть, наряду
с таблицей A), имеется таблица аналогичного вида
(w/k), 0•<*•</, /=0, 1, ..., также составленная из
произвольно заданных комплексных чисел wjk-
Если в л-й строке ani,, к = 0, 1, . . ., п, таблицы уз-
узлов A) нет совпадающих чисел, или, как еще говорят,
вся эта строка состоит из простых узлов, то,
пользуясь, напр., Лагранжа интерполяционной фор-
формулой, строится (единственный) алгебраический интер-
интерполяционный многочлен рп (z) степени ве выше п,
удовлетворяющий простым условиям ин-
интерполяции
Pn(ank) = wnk- /f = 0, 1, .. ., п. B)
Если же точка ап0 является кратным узлом
кратности vo>l в и-й строке, т. е. встречается в этой
строке v0 раз: anb=ank=. . . = onfev 1? то соответствую-
соответствующие условия кратного интерполирова-
интерполирования в узле ат имеют вид
Рп (апо) = Рп (а„о) = ш„о. C)
В общем случае при наличии кратных узлов (единст-
(единственный) алгебраический интерполяционный многочлен
р„(г) степени не выше п строится по этим условиям,
напр., по дрмита интерполяционной формуле. В ка-
качестве примера системы узлов A) можно привести си-
систему /+1, /=0, 1, ..., равноотстоящих узлов я//ь=
_е2л(А/(/+1) на единичной окружности, применяемую
в случае так наз. интерполяции в корнях
из единицы (см. [5]).
В результате осуществляемого таким путем И. п.
получается последовательность интерполяционных
многочленов {pn{z)}, определяемая таблицами (o.jk) и
(юуй). Основными вопросами, здесь возникающими,
являются: определить в зависимости от (оу^) и (Wjk)
множество EczC точек сходимости последовательности
0>n(z)b В к-рых существует предел lim pn(z)=q(z);
п-ы:
определить характер предельной функции q(z); опре-
определить множество FCZ.E, на к-ром сходимость p,,(z)-+-
-yq(z) равномерная; и т. д.
В теории функций комплексного переменного наи-
наиболее изучен случай, когда таблица (wjk) строится
по значениям регулярной аналитич. функции f(z)
и ее производных в узлах интерполяции так, что (при-
(применительно к узлу ап0 кратности vo^l; ср. C))
Рп (а„о) = РпО> («ло) = / ("по).
"п У по' ~ I 1ило'' ¦•¦' "л ("по>~~1 \апо>-
В этом случае интерполяционный многочлен p,,(z)
можно записать по формуле Эрмита в виде
интеграла по контуру Г, охватывающему узлы а„^,
к = 0, 1, . . ., п, на к-ром и внутри к-рого /(г) регу-
регулярна:
«>,,(z) = (z — апо) (z~anl) ¦ ¦ ¦ (z — ann)-
Из формулы D) легко получается и интегральное пред-
представление остаточного члена интерпо-
интерполяции Rn(z) — f(z)—pn(z). Вообще говоря, последо-
последовательность {pn(z)}, построенная по f(z), может рас-
расходиться. Если же она сходится, то предельная функ-
функция q(z) может не совпадать с /(z). Основным вопросом
является изучение сходимости \pn(z)} к /(z) и нахож-
нахождение таких систем узлов (а^), для к-рых сходимость
в каком-то смысле оптимальная. Пусть, напр., функ-
функция /(г) регулярна на континууме КсС, содержащем
не менее двух точек, дополнение к-рого до расширен-
расширенной плоскости С есть односвязная область, содержа-
содержащая бесконечно удаленную точку. Пусть узлы (а/*.)
принадлежат К. Тогда для того, чтобы И. п. {pn(z)}
равномерно сходился на К к f{z), необходимо и доста-
достаточно, чтобы выполнялось условие
где Afn=sup {|con(z)|; z?dK}, с— емкость множества
К (см. [4]).
Классический вариант И. п. получается, когда узлы
ajk~ak, 0 •<&•</, /=0, 1, ..., составляют последова-
последовательность {а*}, из к-рой на ?г-м шаге для получения
многочлена pn(z) используются первые ге-f-l узлов
а0, at, ..., ап. В этом случае для регулярной функции
/(z) многочлены pn(z) суть частные суммы интер-
интерполяционного ряда Ньютона
— ал) . . . (z — an),
1 (I) dt
При вычислениях интерполяционный ряд вида E)
имеет то преимущество перед последовательностью
{p,,(z)}, что для перехода от уже известного многочлена
Pn(z) к pn + 1(z) необходимо вычислить только один коэф-
коэффициент ряда сп + 1. В зависимости от расположения
узлов a/i и значений коэффициентов с^, областью схо-
сходимости ряда Ньютона может быть любая односвязная
область плоскости С с аналитич. границей. В част-
частности, напр., если последовательность узлов {а/,}
имеет предельную точку только в бесконечности,
^fc=ml/|a^| <оо и ряд E) сходится хотя бы в одной
точке гй-фаъ, к = 0, 1, ..., то он сходится равномерно
в любом круге \z\<R и, следовательно, его сумма q(z)
есть целая функция. Интерполяционный
ряд Стирлпнга есть частный случай ряда Нью-
Ньютона для последовательности узлов яо = О, а1=—1,
«2"!» •••* a2ft-i=—k, аъь = к, .... Исследованы и
другие разновидности интерполяционных рядов (см.
[3], [5]).
Объектами изучения являются также И. п. с неал-
гебраическнми интерполяционными полиномами pn(z)^=
= ]7iv=06v(pv(z), составленными по другим системам
функций {cpv (z)}, отличным от системы степеней {zv },
напр., по системе {еЖл'г} (см. [4], [6]).
Изучение И. п. в действительной области имеет свою
специфику как в постановке задач, так и в результа-
тах (см. [2], [41). Эта специфика обусловлена прежде
всего естественным в действительной области отказом
от требования регулярности интерполируемой функ-
функции f(x). Известно, напр., что никакая система узлов
на отрезке [а, Ь] не гарантирует сходимости И. п. для
произвольной непрерывной функции f(x), х ? fa, 6].
С другой стороны, если непрерывная функция / (х)
наперед задана, то всегда можно выбрать систему уз-
узлов так, чтобы II. п. сходился к f(x).
Кроме И. п. с интерполяционными полиномами
pn(z) внимание исследователей привлекают И. п. с ра-
рациональными функциями rn(z), напр, вида rn(z) =
= gn(z)/wn_i(z), где 4>n-1(z)=(z—b0) ... (z— bn-i) nqn(z)
— многочлен степени не выше п. Условия интерполя-
интерполяции A) — C) остаются в силе, но теперь должно быть
добавлено условие на полюсы Ь^, к = 0, 1,...,к-рые
в простейшем случае задаются в виде треугольной таб-
таблицы (b/k), 0<Л-</, у = 0, 1, ..., аналогичной A).
См. также Абеля — Гончарова проблема, Бернштейна
интерполяционный процесс.
Лит.: [1] Маркушевич А. И., Теория аналитических
функций, т. 1, 2 изд., М., 1967; [2] Гончаров В. Л.,
Теория интерполирования и приближения функций, 2 изд.,
М., 1954; [3] Г е л ь ф о н д А. О., Исчисление конечных раз-
разностей, 2 изд., М., 1959; [4] Смирнов В. II., Лебе-
Лебедев Н. А., Конструктивная теория функций комплексного
переменного, М., 1964; [5] Уолш Дж. Л., Интерполяция и
аппроксимация рациональными функциями в комплексной об-
области, пер. с англ., М., 1961; [6] Леонтьев А. Ф., Ряды
экспонент, JNI., 1976. -Е. Д. Соломеицев.
ИНТЕРПОЛЯЦИОННЫЙ СПЛАЙН — сплайн
где
"{о,
хп-\
совпадающий с данной функцией в заданных различ-
различных точках {х[}. Обычно при т=2к-\-1 полагают
xi=x;, г=0, 1, . . ., п, и так как при этом у сплайна
S-2k+i(&n> x) остается еще 2ft свободных параметров,
то на сплайн налагают еще по к условий в точках х0 и хп,
1,
напр., Sik+i{hn, z)=i/J\ /=1, 2, ..., к, z=x0,
где //г"— заданные числа. Если числа у(г1} линейно за-
зависят от данной функции, то соответствующий И. с.
линейно зависит от этой функции. Для т=2к полагают
Обычно ХО=ХО, Хп=Хп, X; = (ж,-_! -j- X;)/2, 1=1, 2, . . .,
п—1, и по к условий задают в точках х0 и хп. Если
сплайн Sт{\п, х) в точках хг, . . ., хп^г имеет непре>
рывную (т—s)-to производную, а (т—s-f-l)-H производ-
производная в них разрывна, то при s^2 в этих точках задают
еще производные сплайна от 1-го до (s—1)-го порядка,
требуя, чтобы эти производные совпадали с соответст-
соответствующими производными интерполируемой функции.
Рассматриваются также интерполяционные L- и Lq-
сплайны и И. с. многих переменных. И. с. применяются
для приближенного представления функций по их
значениям на сетке. В отличие от интерполяционных
полиномов для И. с. существуют матрицы узлов, для
к-рых И. с. сходятся к произвольно заданной непре-
непрерывной интерполируемой функции.
Лит.: [1] С т е ч к и н С. Б., С у б б о т и н Ю. Н.,
Сплайны в вычислительной математике, М., 1976; [2] А л б е р г
Д ж., Ни ль сон Э., Уолш Д ж., Теория сплайнов и ее
приложения, пер. с англ., М., 1972. Ю. Н. Субботин.
ИНТЕРПОЛЯЦИЯ — то же, что интерполирование.
ИНТЕРПРЕТАЦИЯ — задание значения (смысла) ма-
тематич. выражений (символов, формул и т. д.). В ма-
математике такими значениями служат математич. объек-
объекты (множества, операции, выражения и т. д.). Сами
эти значения также наз. И. соответствующих вы-
выражений.
Примеры. Значением (или П.) символа • может
быть операция умножения действительных чисел, опе-
операция сложения целых чисел и т. д. Пусть в качестве
И. символа • выбрана первая из этих операций. Если
символы х и у понимаются как действительные пере-
переменные (т. о. переменные, областью изменения к-рых
является множество всех действительных чисел), то
значением выражения х-у является отображение,
переводящее всякую пару действительных чисел в их
произведение; если значениями символов хи у являются
соответственно числа 6 и 2,5, то значением выражения
х-у является число 15. Значением (или И.) высказыва-
высказывания в языке плоской геометрии Лобачевского при интер-
интерпретации Пуанкаре может служить соответствующее
высказывание в языке плоской евклидовой геометрии.
Важнейшим видом И. являются теоретико-множест-
теоретико-множественные И. выражений логпч. языков. Когда речь идет
об одновременной И. всех выражений языка, то говорят
об И. языка. Теоретико-множественная И. логич.
языка включает задание значений констант — пред-
предметных, функциональных, предикатных и констант
более высоких ступеней (констант для предикатов от
предикатов и т. д.), а также задание областей измене-
изменения переменных — предметных, функциональных и т. д.
В многосортных И. различные предметные перемен-
переменные могут иметь различные области изменения, то же
касается функциональных и т. д. переменных. Наиболее
употребительными, однако, являются П., при к-рых
все предметные переменные, так же как и функцио-
функциональные переменные с одинаковым числом аргумен-
аргументов и т. д., имеют одинаковые области изменения. Если
областью изменения предметных переменных (иногда
называемой областью, или носителем, И.) служит
множество Do, то областью изменения ге-местных
функциональных переменных служит нек-рое мно-
множество Вп гс-местных операций на множестве Do.
В качестве множества Dn часто выбирается множество
всех re-местных операций на Во, в таком случае упоми-
упоминание об области изменения функциональных пере-
переменных обычно опускается. Значениями предметных
констант служат элементы пз Do, функциональных кон-
констант — элементы из Dlt D2, ... .
При теоретико-множественной И. логич. языка под
И. терма (т. е. под значением терма при данной И.)
понимается отображение, к-рое каждому набору зна-
значений переменных рассматриваемого языка (или, при
несколько ином определении, набору значений пере-
переменных, входящих в терм) по определенному правилу
сопоставляет элемент области И. Это отображение
обычно задается индукцией по построению термов.
Для получения И. формул языка необходимо, кроме
перечисленных выше компонент И., задать нек-рое
непустое множество А, называемое множеством логи-
логических значений. И. re-местных предикатных констант
являются отображениями из Do в А; в частности, И.
?г-местных предикатных констант — это элементы А.
Если в языке имеются нульместные, одноместные и т. д.
предикатные переменные, то их областями изменения
служат, соответственно, множество А, нек-рое под-
подмножество множества AD°, содержащее И. всех одно-
одноместных предикатных констант и т. д. Интерпретация
формулы определяется аналогично И. терма как ото-
отображение, сопоставляющее всякому набору значений
предметных, функциональных и предикатных пере-
переменных языка элемент множества А. Важным видом
теоретико-множественных И. являются алгебраич. И.,
при к-рых в качестве значений (И.) логич. связок
языка выбираются операции на множестве А, в ка-
качестве значений кванторов — отображения из мно-
множества всех подмножеств А в А (обобщенные операции
на А), и И. формулы определяется индукцией по пост-
роению. Среди других теоретико-множественных И.
важнейшими являются Крипке модели.
Булевозначные алгебраические И. характеризуются
тем, что множество А является полной булевой алгеб-
алгеброй, а значениями связок и кванторов являются: для
конъюнкции — пересечение, для квантора существо-
существования — взятие точной верхней грани и т. д. Особо
важную роль играют классические И., к-рые можно
определить как булевозначные И. с двухэлементной
Нулевой алгеброй А.
Понятие истинности формулы в данной И. опроде-
опроденется с помощью выделения в А нек-рых элементов.
Напр.,при классической И. единственным выделенным
элементом является единица булевой алгебры (обозна-
(обозначаемая также «истина»). Формула наз. истинной при
данной И., если ее И. принимает только выделенные
значения. Моделью (или правильной И., или просто И.)
системы формул нек-рого языка наз. И. языка, при
к-рой все формулы системы истинны.
Термин стандартная И. употребляется, когда среди
всевозможных значений (И.) нек-рого выражения
имеется одно общепринятое. Напр., стандартной И.
символа = в классических II. является совпадение
элементов, стандартными И. символов + и • языка
арифметики являются сложение и умножение нату-
натуральных чисел. Соответственно вводится понятие стан-
стандартной II. языка и стандартной модели. В частности,
классическую И. языка арифметики первого порядка
с предикатной константой = и функциональными
константами + и •, интерпретируемыми, как указано
выше, наз. стандартной.
Кроме теоретико-множественных И. логич. языков
используются и другие. Напр., II., при к-рых выраже-
выражения нек-рого логич. языка интерпретируются выра-
выражениями другого логич. языка, применяются при до-
доказательствах разрешимости, неразрешимости и отно-
относительной непротиворечивости логнч. теорий. См.
также Конструктивная логика.
Лит.: [1] Р а с е в а Е., С п к о р с к и й Р., Математика
метаматематики, пер. с англ., М., 1972; [2] Ч ё р ч А., Введе-
Введение в математическую логику, пер. с англ., т. 1, М., I960;
[3] Мендельсон Э., Введение в математическую логику,
пер. с англ., 2 изд., М., 1976. А. Л. Семенов.
ИНТУИЦИОНИЗМ — совокупность философских и
математич. идей и методов, рассматривающих матема-
математику как науку об умственных построениях. С точки
зрения И., основным критерием истинности математич.
суждения является интуитивная убедительность воз-
возможности построения мысленного эксперимента, свя-
связываемого с этим суждением. Поэтому в интуицио-
интуиционистской математике отвергается теоретико-множест-
теоретико-множественный подход к определению математич. понятий,
а также нск-рыо способы рассуждения, принятые в
классич. логике.
Истоки И. можно проследить еще в античной мате-
математике, а позднее в высказываниях таких ученых, как
К. Гаусс (С. Gauss), Л. Кронекер (L. Kronecker),
А. Пуанкаре (Н. Poincare), А. Лебег (Н. Lebcsgue),
Э. Борель (Е. Borel). Начиная с 1904 в ряде статей
выступил с развернутой критикой нек-рых концепций
классич. математики Л. Э. Я. Брауэр (L. E. J. Brou-
wer). В основе этой критики лежит обсуждение статуса
существования в математике: в каком смысле следует
считать установленным существование актуально за-
заданного бесконечного множества и могут ли быть
построены в виде потенциально осуществимой конст-
конструкции такие объекты исследования, как неизмеримое
множество действительных чисел, нигде не дифферен-
дифференцируемая функция? Естественно предположить, что
можно построить произвольное натуральное число
в виде последовательного ряда однородных предметов,
напр, ряда параллельных черточек. В рамках такой же
идеализации можно допустить, что, построив нек-рое
натуральное число, можно построить затем и следующее
добавив к уже построенному еще одну черточку. Но,
возникает вопрос о том, с какого рода построением
связано множество всех действительных чисел или
множество всех натуральных чисел как единый объект
исследования. Современные физич. воззрения также
как будто не дают оснований полагать, что в окружаю-
окружающем нас мире актуально существуют бесконечные мно-
множества объектов. Есть серьезные основания считать,
что объекты, существование к-рых устанавливается
без использования абстракции актуальной бесконеч~
ноепш, а лишь в рамках гораздо более скромной абст-
абстракции потенциальной осуществимости., имеют более
непосредственное отношение к реальной действитель-
действительности. Однако при обычной теоретико-множественной
трактовке не делается никакого различия между объек-
объектами, существование к-рых можно подтвердить с по-
помощью нек-рого потенциально осуществимого пост-
построения, и абстрактными теоретико-множественными
объектами исследования. Способы установления свойств
обоих типов объектов в класенч. математике основаны
на законах логики, возникших в результате экстрапо-
экстраполяции законов, верных для конечных совокупностей,
на бесконечные множества. В области бесконечного
эти законы не ориентированы на эффективное построе-
построение объектов, существование к-рых утверждается.
Фактически такое положение дел приводит к появле-
появлению в математике так наз. «теорем чистого существо-
существования», в к-рых утверждается существование нек-рых
объектов и в то же время не указывается никакого
способа отыскания этих объектов. Такова, напр., из-
известная теорема классич. анализа, утверждающая, что
всякая непрерывная действительная функция, задан-
заданная на замкнутом ограниченном множестве, имеет
максимум. Обычное доказательство этой теоремы не
дает никаких указаний на метод построения искомого
максимума. Это обстоятельство может и не смущать те-
теоретико-множественно настроенного математика: он
может считать, что максимум «есть» у всякой функции
рассматриваемого класса, независимо от того, можно
его отыскать в каждом частном случае или нот, «есть»
как объект нек-рого воображаемого мира («платонист-
ского мира», см. [6], с. 399). Однако такой подход не
удовлетворяет, если принять во внимание возможности
субъекта-иеследователя. Имеется ли способ отыскания
максимума, и если этот способ не указан, то в каком
смысле верно, что максимум существует у всякой
функции рассматриваемого класса? Известно, сколь
трудной является задача поиска экстремума у функций
даже весьма узкого класса (многочлены с рациональ-
рациональными коэффициентами от нескольких переменных),
и, что существенно, указанная теорема нисколько не
помогает в решении этой задачи. Заметим, что описан-
описанная выше критика классич. математики не связана
непосредственно с антиномиями теории множеств.
Появление антиномий можно рассматривать как до-
дополнительный довод в пользу неудовлетворительности
теоретико-множественного подхода, но критика отно-
относится и к таким разделам математики, где антиномий
не возникает.
Описанная критика теоретико-множественного под-
подхода к математике исторически привела к возникнове-
возникновению двух путей преодоления трудностей в обосновании
математики — интуиционизма Л. Э. Я. Брауэра и
формализма Д. Гильберта (D. Hilbert). Обе концепции,
развиваясь, оказывают в настоящее время A970-е гг.)
значительное влияние друг на друга. Так, при обосно-
обосновании непротиворечивости формальных теорий необ-
необходимо уточнить приемы содержательных умозаключе-
умозаключений в метаматематике, что делается обычно в рамках
тех или иных интуиционистских концепций. С другой
стороны, именно с помощью формализации метода
удалось получить ряд важнейших результатов о ло-
логике интуиционизма.
Интуиционистская математика есть наука об интуи-
интуитивно убедительных мысленных построениях. Сам
Л. Э. Я. Брауэр трактовал эту интуитивную убеди-
убедительность идеалистически, рассматривая мысленные
построения как таковые «безотносительно к таким воп-
вопросам о природе конструируемых объектов, как вопрос,
существуют ли эти объекты независимо от нашего
знания о них» (см. [1]). Однако возможно и материа-
листич. толкование «интуиции» И. как наглядной
умственной убедительности простейших конструктив-
конструктивных процессов реальной действительности. И незави-
независимо от философских установок, конкретные матема-
тич. результаты, относящиеся к интуиционистской
математике и логике, представляют большую научную
ценность.
При построении интуиционистской математики
обычные логич. связки, употребляемые для формули-
формулировки математич. суждений, истолковываются спосо-
способом, отличным от классического. Суждение считается
истинным, только если исследователь имеет возмож-
возможность его доказать. Доказательство же всегда связано
с построением нек-рой мысленной конструкции. Так,
утверждение, начинающееся с квантора существо-
существования ЪхА (х), может быть доказано только путем
построения объекта х, для к-рого доказывается суж-
суждение А{х). Дизъюнкция А у В суждений А и В счи-
считается доказанной, только если исследователь распо-
располагает методом доказательства одного из суждений А
или В. С этой точки зрения суждение вида А V ~]А
может быть и не истинным, если проблема А не ре-
решена и не опровергнута к настоящему времени. От-
Отсюда видно, что исключенного третьего закон непри-
неприемлем в интуиционистской математике в качестве
логич. принципа. Истинное математнч. суждение пред-
представляет собой сообщение о выполненных построениях,
и эффективный характер этих построений предпола-
предполагает использование особой интуиционистской логики,
отличной от классической. При этом эффективность
в И. понимается достаточно широко, она не обяза-
обязательно связана с наличием алгоритма в точном пони-
понимании этого термина и может носить, напр., характер
историч. наступления события, зависеть от фактич.
решения проблем, от физпч. факторов.
Объектами исследования интуиционистской матема-
математики являются прежде всего конструктивные объекты,
такие, как натуральные числа, рациональные числа,
конечные множества конструктивных объектов, за-
заданные списком своих элементов. Своеобразным объек-
объектом исследования являются так наз. свободно ста-
становящиеся последовательности (с. с. п.; в другой
терминологии — последовательности вы-
выбора). С. с. п. можно представлять себе как функ-
функцию, определенную на натуральном ряде, принимаю-
принимающую в качестве значений объекты исследования неко-
некоторого класса (в простейшем случае — натуральные
числа) и такую, что всякое ее значение эффективно
становится доступным исследователю. Точный анализ
показывает, что следует различать несколько видов
с. с. п. в зависимости от степени информации, извест-
известной исследователю относительно с. с. п. Так, если
полностью известен закон образования с. с. п., напр.
в виде записи соответствующего алгоритма, то такую
с. с. п. наз. заданной законом. Другой край-
крайний случай имеет место, если в каждый момент времени
исследователю известен лишь нек-рый начальный отре-
отрезок с. с. п. и нет никакой информации относительно
ее дальнейшего поведения; такие с. с. п. наз. без-
беззаконными. Эти различия, игнорируемые в клас-
сич. математике, в интуиционистской математике могут
быть отражены посредством точных математич. прин-
принципов, свидетельствующих о разных способах обра-
обращения с такими с. с. п. Наконец, объектами исследо-
исследования интуиционистской математики могут быть и
так наз. интуиционистские виды. Вид — свойство,
к-рым могут обладать объекты исследования. Объекты,
удовлетворяющие этому свойству, наз. элементами
вида, или его членами. Во избежание появления анти-
антиномий среди видов можно ввести иерархию, подобную
типов теории, а именно, требовать, чтобы элементы
вида были определены независимо от определения са-
самого вида. Разумеется, при широком введении видов
в интуиционистскую математику в ней возникают
проблемы, характерные для абстрактной теории мно-
множеств, такие, как предикативность, возникновение
антиномий и т. п. Следует, однако, иметь в виду, что,
с одной стороны, обращение с видами во многом от-
отлично от обращения с множествами в классич. мате-
математике и, с другой стороны, в практически разраба-
разрабатываемой интуиционистской математике виды занимают
весьма скромное место. В действительности подавляю-
подавляющую часть результатов можно сформулировать и до-
доказать вообще без употребления видов как самостоя-
самостоятельных объектов исследования. Это связано с естест-
естественной тенденцией И. рассматривать в качестве объекта
исследования эффективно конструируемые или эффек-
эффективно порождаемые объекты. В рамках И. рассматри-
рассматриваются и другие, «нетрадиционные» объекты. Перспек-
Перспективным оказалось изучение аффективных функциона-
функционалов конечного типа, с помощью к-рых в рамках И.
удалось построить интерпретацию для классич. ана-
анализа [П. С. Новиков, К. Гёдоль (К. Godcl), К. Спектор
(С. Spector)].
Отказ от рассмотрения актуально заданных беско-
бесконечных множеств и требование эффективности всех
осуществляемых построений приводят к тому, что
нек-рые разделы традиционной математики приобре-
приобретают в И. весьма необычный вид. Числовой конти-
континуум трактуется не как совокупность отдельных
точек, а как «среда становления», поток измельчаю-
измельчающихся рациональных интервалов. Каждое отдельное
интуиционистское действительное число определяется
с. с. п., значениями к-рой являются неограниченно
уменьшающиеся вложенные друг в друга рациональ-
рациональные интервалы. В рассуждениях об интуиционистском
числовом континууме применяются такие специфич.
принципы, как бар-индукция и теорема о веере. Следст-
Следствием этого является, напр., то обстоятельство, что
в естественной системе понятий всякая интуиционист-
интуиционистская действительная функция, определенная на от-
отрезке, равномерно непрерывна. Интуиционистская ма-
математика является достаточно разработанным направ-
направлением в математике, содержащим много продвину-
продвинутых результатов, в том числе и в таких областях, как
теория меры, функциональный анализ, топология,
теория дифференциальных уравнений.
Несколько в стороне от этих исследований стоит
попытка Г. Вепля (Н. Weyl, 1918) построить матема-
математику на основе предикативного подхода. Соглашаясь
в целом с интуиционистской критикой, Г. Вейль пред-
предложил ограничиться конструктивными объектами ис-
исследования и задавать множества в виде условий
в нек-ром языке, определяемом таким образом, чтобы
не нарушалась предикативность определения мно-
множеств. Впоследствии Г. Вейль присоединился к раз-
развитой интуиционистской концепции построения мате-
математики, его взгляды положили начало глубоким
исследованиям в основаниях математики.
Считая критерием верности построений прежде
всего интуицию и в противовес формализму,
Л. Э. Я. Брауэр возражал против попыток формализа-
формализации интуиционистской математики и, в частности, ин-
интуиционистской логики. Однако значительные успехи
в изучении интуиционистской логики были достигнуты
именно после того, как ее основные законы были точно
сформулированы в виде исчислений, к к-рым можно
было применять точные методы математич. логики.
В разработке интуиционистской логики приняли зна-
значительное участие и математики, не считающие себя
«интуиционистами». Более того, вопрос «веры в ин-
интуиционизм» становится второстепенным — специаль-
специальные интуиционистские исчисления имеют большой
чисто математич. интерес, как проясняющие различ-
различные идеи эффективности в математике. Современная
тенденция в развитии И. сближает его с конструктив-
конструктивной математикой в самом широком понимании по-
последнего термина.
После точной формулировки А. Рейтингом (А. Неу-
ting) интуиционистского исчисления предикатов (см.
Интуиционистская логика) была открыта топологпч.
интерпретация этого исчисления [А. Тарский (A. Tar-
ski)] и интерпретация интуиционистского исчисления
предикатов в виде исчисления задач (А. Н. Колмого-
Колмогоров). Была доказана независимость логич. связок и
невозможность представления интуиционистской ло-
логики высказываний в виде конечнозначной логики
(К. Гёдоль). А. Рейтинг описал интуиционист-
интуиционистское арифметическое исчисление,
к-рое получается, если классическое арифметич. исчис-
исчисление рассматривать на базе интуиционистского исчис-
исчисления предикатов. Для исчисления предикатов и
арифметич. исчисления А. Н. Колмогоров и К. Гё-
дель предложили погружающую операцию классич.
исчисления в негативный фрагмент соответствующего
интуиционистского исчисления, из к-рой, в частности,
следует непротиворечивость классич. исчисления, если
интуиционистское считать содержательно истинным.
Были установлены свойства интуиционистской дизъюн-
дизъюнкции и существования, состоящие в том, что если вы-
выводимо утверждение ЭхА (х), то для нек-рого терма t
выводимо A (t), а из выводимости АуВ следует выво-
выводимость А или выводимость В. Некоторый вариант
интуиционистского понимания суждений был пред-
предложен С. К. К лини (S. С. Kleene) в форме рекурсивной
реализуемости. Именно такое понимание характерно
для конструктивного направления в математике, раз-
развиваемого в Советском Союзе научной школой
А. А. Маркова. Понимая термин «И.» достаточно ши-
широко, можно рассматривать конструктивное направле-
направление в математике как разновидность И., для к-рого
характерно исследование конструктивных объектов и
конструктивных процессов алгоритмич. методами.
Исследовался вопрос о семантической полноте интуи-
интуиционистского исчисления предикатов. Исчерпывающая
алгебраич. характеристика выводимости дана в теории
моделей интуиционистской логики Э. Бета (Е. Beth)
и С. Крипке (S. Kripke). Эти теории имеют значитель-
значительные приложения и в других разделах интуиционист-
интуиционистской математики. Интуиционистская логика полна от-
относительно нек-рых концепций с. с. п. и, в то же время,
не полна относительно рекурсивной реализуемости.
Интуиционистское понимание кванторов позволяет
сформулировать в арифметике в виде математич. ут-
утверждения Чё'рча тезис, напр, в форме: «если для вся-
всякого натурального числа х существует натуральное у,
удовлетворяющее отношению А (х, у), то существует
общерекурсивная функция / такая, что для всякого х
имеет место А (х, f{x))>>, при этом отношение А (х, у)
но должно содержать неконструктивных параметров
типа с. с. п. В языке арифметики можно естественно
сформулировать и конструктивного подбора принцип
А. А. Маркова. Анализ взаимоотношений этих фунда-
ментальных принципов в интуиционистских теориях
является предметом ряда современных исследований.
Удовлетворительное построение теории с. с. п. и
более высоких разделов интуиционистской математики
было завершено к 70-м гг. 20 в. Обычный язык формаль-
формальной теории интуиционистского ана-
анализа содержит два сорта переменных: переменные
х, у, z, ... для натуральных чисел и переменные а,
Р, у, ... для с. с. п., перерабатывающих натуральные
числа в натуральные. В качестве термов теория содер-
содержит символы примитивно-рекурсивных операций над
функциями и числами. Атомарные формулы имеют вид
равенства двух термов, кванторы употребляются по
обоим сортам переменных. Теория содержит все посту-
постулаты интуиционистского арифметич. исчисления. Эта
группа постулатов обеспечивает возможность вывести
в теории все основные свойства примитивно-рекурсив-
примитивно-рекурсивных преобразований чисел и функций. Так, в теории
можно описать взаимно однозначный способ кодиро-
кодирования конечных последовательностей (кортежей) на-
натуральных чисел натуральными числами. Пусть
(х1} . . ., хп) означает номер кортежа с числами х1%
. .., хп в качестве членов; х*у есть операция сочле-
сочленения кортежей, заданных номерами, т. е. если
х=(х1, ..., хп) и у~ (уг, ..., ут), то х*у={хи ...,
хп, ух, ..., //,„). Номер одночленного кортежа (х)
обозначим через х. Пусть ах означает кортеж (ос@),
..., а(ге—1)). Введем предикат «а есть непрерывный
оператор» следующим определением: а?К означает
VP3x(a('prx) > 0) &уху (ах > 0z>a (x*y) = a (х)),
результаты применения непрерывного оператора
к с. с. п. определяются следующим образом: г/=а(|3)
означает
За (у+ 1 =«(?*))
и 7=(а|Р) означает
Пусть, далее, (fi)x означает такую функцию а, что
уу(а(у) = $«х, у»).
С помощью приведенных определений можно точно
сформулировать несколько фундаментальных принци-
принципов, относящихся собственно к с. с. п. Это прежде
всего интуиционистская аксиома вы-
выбора:
ухЭаА (х, a.)=K$VxA (х, ф)х),
принцип непрерывности Брауэра
VaaM (a, Р)=>(Эу?К)А(а, (у | а))
и бар-индукция. Эти принципы задают формальную
теорию с. с. п., предложенную С. Клини, теорию, дос-
достаточную для получения в ней всех основных теорем
интуиционистского анализа, включая теорему о веере,
равномерную непрерывность действительных функ-
функций и др. Следует иметь в виду, что эта теория отра-
отражает лишь один вид интуиционистских последователь-
последовательностей, вид, особенно пригодный для построения интуи-
интуиционистского анализа. Другой характерный вид
с. с. п.— беззаконные последовательности, упомяну-
упомянутые выше. Следующий принцип Крайзеля
отражает то обстоятельство, что вся информация о без-
беззаконной с. с. п. может быть извлечена лишь путем
исследования ее начальных отрезков:
где a — единственный параметр А (а) по с. с. п.
Еще один вид с. с. п. возникает при попытке от-
отобразить в формальной теории существование с. с. п.,
зависящих от решения проблем. Для таких с. с. п.
истинна так нав. схема Крипке:
За ((V*a (*)=() = ~\А)А(Эха(х) ф 0=)Л)).
Различные интуиционистские принципы имеют место
по отношению к определенным видам с. с. п. Так, для
беззаконных последовательностей не выполняется в об-
общем виде интуиционистская аксиома выбора, а после-
последовательности, зависящие от решения проблем, не
удовлетворяют принципу непрерывности Брауэра в том
его виде, к-рый был указан выше. Гораздо менее раз-
разработаны формальные теории для отражения интуи-
интуиционистской теории видов. Однако и здесь имеются
попытки сформулировать специфически интуиционист-
интуиционистские способы обращения с видами. Напр., если X —
переменная для видов натуральных чисел, то можно
принять следующую схему аксиом, предложенную
А. Троэльстра [4]:
yXjxA (х, Х)^ЗхуХА (х, X).
До 2-й половины 20 в. идеи Л. Э. Я. Брауэра в полном
объеме оставались достоянием узкой группы матема-
тиков-интуиционистов, хотя они и оказали большое
влияние на все дальнейшие исследования по основа-
основаниям математики. В последнее время положение изме-
изменилось. Развитие теории доказательств позволило
оформить в виде точных исчислений основные интуи-
интуиционистские теории и подвергнуть их точному иссле-
исследованию. Развитие вычислительной тенденции в мате-
математике пробудило интерес к логич. анализу эффек-
эффективных средств доказательства и изучению абстрак-
абстракций, применяемых в математике. Возникли различные
программы конструктивной перестройки математики
в той или иной концепции конструктивности. Синтез
традиционных методов И. с современными методами
теории доказательств позволил значительно продви-
продвинуться в И.
Лит.- [1] Гейтинг А., Интуиционизм, пер. с англ.
М., 1965; [2] К 1 е е n e S. С, V е s 1 е у R. Е., The foun-
foundations of intuitionistic mathematics, Amst., 1965; [3] Krei-
sel G. Troelstra A. S., «Ann. Math. Logic», 1970, v. 1
N, 3, p. 229—387; [4] TroelstraA. S., Metamathematical
investigation of intuitionistic Arithmetic and Analysis, В., 1973
(Lect. Notes in Math., №344); [5] Мартин-Лёф П.,
Очерки по конструктивной математике, пер. с англ., М., 1975;
[6] Френкель А., Бар-ХиллелИ., Основания тео-
теории множеств, пер. с англ., М., 1966. А. Г. Драгалин.
ИНТУИЦИОНИСТСКАЯ ЛОГИКА — совокупность
приемлемых с точки зрения интуиционизма методов
доказательства утверждений. В более узком смысле
под И. л. понимается интуиционистское
исчисление предикатов, сформулирован-
сформулированное А. Рейтингом (A. Heyting) в 1930. Это исчисление
формулируется обычно в стандартном языке предика-
предикатов исчисления, содержит все схемы аксиом и правила
вывода интуиционистского исчисления высказываний
(но для языка исчисления предикатов) и, кроме того,
следующие кванторные аксиомы и правила
вывода. Аксиомы:
ухА (х)-=>А (t) и A (t)^jxA (x).
Два правила вывода:
CD А (х) А
(х) ' Эх/1(х)ОС '
где х — переменная, t — терм языка, формула С не
содержит х в качестве параметра.
Полнота интуиционистского исчисления предикатов
зависит от семантич. принципов, к-рые лежат в основе
рассматриваемой интуиционистской теории. Так, прин-
принцип конструктивного подбора Маркова (см. Конструк-
Конструктивного подбора принцип) в форме
Чх(Р (x)v~\P(x))A
не выводится в интуиционистском исчислении преди-
предикатов, но принимается как истинный в нек-рых разно-
разновидностях конструктивизма. Другой пример такого
рода — так наз. принцип униформиза-
ц и и:
являющийся истинным в нек-рых интуиционистских
интерпретациях и в то же время несовместный с прин-
принципом конструктивного подбора в рамках арифметнч.
теории с Чёрча тезисом. Приведенные примеры пока-
показывают, что не существует единого полного интуицио-
интуиционистского исчисления предикатов, к-рое могло бы
служить логич. базисом всех прикладных интуицио-
интуиционистских теорий. В зависимости от применяемых се-
мантич. соглашений возможны существенно различные
варианты И. л. Развитие интуиционистской теории ви-
видов позволяет в рамках интуиционизма точно формули-
формулировать многие семантич. проблемы. Так. К. Гёдель
(К. Godel) показал, что полнота интуиционистского
исчисления предикатов относительно интуиционист-
интуиционистской теории видов влечет принцип конструктивного
подбора Маркова для примитивно-рекурсивных преди-
предикатов, что является аргументом в пользу неполноты
исчисления предикатов с точки зрения такой семан-
семантики. С другой стороны, были найдены интуиционистски
приемлемые доказательства полноты И. л. относи-
относительно алгебраич. семантик типа моделей Бета или
моделей Крипке.
Лит.: [1] Гейтинг А., Интуиционизм, пер. с англ.,
М., 1965; [2] К л и н и С. К., Введение в метаматематику,
пер. с англ., М., 1957. А. Г. Драгалин.
ИНТУИЦИОНИСТСКОЕ АРИФМЕТИЧЕСКОЕ ИС-
ИСЧИСЛЕНИЕ — см. Интуиционизм.
ИНТУИЦИОНИСТСКОЕ ИСЧИСЛЕНИЕ ВЫСКА-
ВЫСКАЗЫВАНИЙ — логическое исчисление, описывающее спо-
способы вывода высказываний, истинных с точки зрения
интуиционизма. Общепринятая (к 1978) формули-
формулировка И. и. в. была предложена А. Рейтингом (А. Неу-
ting) в 1930. Основное ее отличие от классич. исчисле-
исчисления высказываний состоит в замене исключенного тре-
третьего закона (или эквивалентного ему закона сня-
снятия двойного отрицания) более слабым
принципом противоречия:
Один из распространенных вариантов И. и. в. фор-
формулируется следующим образом. Пусть А, В, С —
произвольные формулы рассматриваемого логич. языка.
Аксиомы исчисления суть формулы следующего вида:
2.
3.
4.
5.
6.
7.
8.
9.
10.
Единственное правило вывода И. и. в.— правило
modus ponens: если выведены формулы А
и A'ZiB, то выводима и формула В.
Всякая выводимая формула этого исчисления прием-
приемлема с интуиционистской точки зрения; более сложен
вопрос о полноте описанного исчисления. И. и. в.
оказывается, напр., полным относительно алгебраич.
семантик — моделей Крипке и моделей Бета, но не-
неполным относительно естественной конструктивной
семантики — рекурсивной реализуемости Клини; см.
также Конструктивное исчисление высказываний.
Лит. см. при ст. Интуиционизм. А. Г. Драгалин.
ИНТУИЦИОНИСТСКОЕ ИСЧИСЛЕНИЕ ПРЕДИКА-
ПРЕДИКАТОВ — см. Интуиционистская логика.
ИНФИНИТЕЗИМАЛЬНАЯ СВЯЗНОСТЬ — первона-
первоначальное название дифференциально-геометрич. струк-
структуры на расслоенном пространстве, к-рую впоследст-
впоследствии стали называть просто связность. Ю. Г. Лумисте.
ИНФИНИТЕЗИМАЛЬНАЯ СТРУКТУРА — струк-
структура на п-мерном дифференцируемом многообразии
Мп, к-рая определяется приведением структурной
дифференциальной группы Drn главного расслоения ре-
поров r-го порядка на Мп, т. е. обратимых г-струй
из R" в Мп с началом O?R", к нек-рой своей под-
подгруппе Ли G. Другими словами, на Мп задана И. с.
r-го порядка, если в факторрасслоении главного рас-
расслоения реперов r-го порядка на Мп по подгруппе Ли
G<zDrn выделено нек-рое сечение. При г=1 И. с. наз.
также G-структурой на Мп, а при г>1 наз.
G-структурой высшего порядка. Если
Drn заменяется проективной дифференциальной груп-
группой PDn — нек-рой своей факторгруппой группы D1^1,
ю соответствующая И. с. наз. проективной
и н ф и н и т е з и м а л ь н о й структурой.
Аппаратом для изучения И. с. являются ее струк-
структурные уравнения. Основные задачи при исследовании
И. с.— нахождение топологич. характеристик много-
многообразия Мп, допускающего ту или иную И. с, выде-
выделение И. с, получаемых продолжением нек-рой И. с.
более низкого порядка, проблема интегрируемости
И. с. и др.
Лит.: [1] Лаптев Г. Ф., «Тр. геометрич. семинара
ВИНИТИ», т. 1, 1966, с. 139—89; [2] С h е г n S. S., «Bull.
Amer. Math. Soc», 1966, v. 72, № 2, p. 167—219.
Ю. Г. Лумисте.
ИНФИНИТЕЗИМАЛЬНЫЙ ОПЕРАТОР — наимено-
наименование линейных операторов, являющихся дифферен-
дифференциалами отображений нек-рых классов. Так, на диф-
дифференцируемом многообразии И. о., или и н ф и н и-
тезимальное преобразовани е,— то же,
что и векторное поле, в теории полугрупп (операторов,
преобразований) — то же, что и (ннфинитезимальный)
производящий оператор. М. И. Войцеховский.
ИНФОРМАНТ — градиент логарифмической функции
правдоподобия. Понятие И. возникает в так наз. пара-
метрич. задачах математич. статистики. Имеется ап-
априорная информация, что наблюдаемое случайное
явление описывается распределением вероятностей
P®(d(?)) ил семейства {Р*, ??в}, где t — числовой или
векторный параметр, однако истинное значение 8
неизвестно. Проведенное наблюдение (серия незави-
независимых наблюдений) явления привело к исходу <в (серии
соA), . . .. co(jV)). По исходам наблюдения требуется
оценить 0. Пусть семейство {Р*} задается семейством
плотностей р(ю; t) относительно моры \i(ddt) на прост-
пространстве Q всех исходов явления. Когда Q дискретно,
за р(ш; t) можно принять сами вероятности Р'(ш) ис-
исходов. При фиксированном ш величина р(ш; t) как
функция параметра t=(t1, . . ., tm) наз. функцией
правдоподобия, а ее натуральный логарифм —
логарифмической функцией правдо-
правдоподобия.
Для гладких семейств удобно вводить И. как вектор
gradf In р (ш; t) =
1 dp (ц>; t) I dp (ц>; t)
Р(со; t) att ' • • •' p(w; t) atn
к-рый, в отличие от логарифмической функции правдо-
правдоподобия, не зависит от выбора меры (х. И. содержит
всю существенную для задачи оценки 6 информацию,
как получаемую из наблюдений, так и известную за-
ранее. Кроме того, он аддитивен: при независимых
наблюдениях, т. е. когда
., w<№; t) = ft" ] Pk
И. суммируется:
grad In р (ш*1», ...,ш<ЛГ>; 0=2- gracl ln Рк
В теории статистич. оценивания существенны свой-
свойства И. как случайной вектор-функции. В предполо-
предположении, что логарифмич. функция правдоподобия регу-
регулярна, в частности дважды дифференцируема, ее про-
производные интегрируемы и что дифференцирование по
параметру перестановочно с интегрированием по ис-
исходам, справедливы тождества:
aln %/"••*> Р(ш; 0 4 0 Vfe;
9' ln p (со; t) T . . д ln p д In p
/ « J K
Ковариационная матрица ||//fc(?)ll7? *=i наз- информа-
информационной матрицей. Через эту матрицу выписывается
неравенство информации, дающее границу точности
статистич. оценок параметра 0.
При оценке 0 методом максимума правдоподобия
наблюденному исходу со (или серии шA), ..., со(ЛГ))
сопоставляется наиболее правдоподобное, т. е. макси-
максимизирующее функцию правдоподобия и логарифмич.
функцию правдоподобия, значение i=0*(co). В точке
экстремума И. должен обращаться в нуль. Однако
возникающее уравнение правдоподобия
grad In р(ш; ?)=0
может иметь лишние корни сверх *=9*, к-рые отвеча-
отвечают локальным максимумам (или минимумам) логариф-
логарифмич. функции правдоподобия и к-рые следует отбрасы-
отбрасывать. Если в нек-рой окрестности значения ?—0
то из приведенных свойств И. следует асимптотич.
оптимальность оценки Qn максимума правдоподобия
при возрастании числа N используемых независимых
наблюдений.
Лит.: [1] Уилкс С, Математическая статистика, пер.
с англ., М., 1967. Н. Н. Ченцо,:.
ИНФОРМАЦИИ КОЛИЧЕСТВО — теоретико-инфор-
теоретико-информационная мера величины информации, содержащейся
в одной случайной величине относительно другой.
Пусть | и т| — случайные величины, определенные на
нек-ром вероятностном пространстве (Q, 31, Р) и
принимающие значения в измеримых пространствах
(Ж, Sj) и (;)}, SS]) соответственно, а р^{С), C^S^XS^,
р*(А), A?SS, pr\(B), 5g5,a—их совместное и мар-
маргинальные распределения вероятностей. Если распре-
распределение ?!„(•) абсолютно непрерывно относительно
прямого произведения мер р^Хрп(-), а^(-) — плот-
плотность (по Радону — Никодиму) меры /и I ¦) относительно
меры р^Хрц(-), и i^(-)=log a^(-) — информационная
плотность (логарифмы обычно берутся по основанию 2
или е), то, по определению, И. к. дается формулой
Если же мера Pt^A-) не является абсолютно непрерыв-
непрерывной относительно произведения мер р%Хрц(-), то, по
определению, /(g, т))= + <».
В случае, когда величины | и ц принимают конечной
число значений, выражение для И. к. 1"(|, т|) приобре-
приобретает следующий вид:
где
{Pi, i = l, ..., re}, {?/, / = 1, ..., m},
{Pi7> *=1i • • -i re> /= 1 > • •., w} — распределения вероят-
вероятностей |, т) и пары (|, т)) соответственно (в частности,
I (|, I) = - 2"= j P/ log pf = Я (?)
является энтропией случайной величины |), а если
i, т) — случайные векторы и существуют плотности
Р%(х), Рц(у), P\r\{x> у) случайных векторов |, т) и пары
(|, т)) соответственно, то
В общем случае
1A, T|) = sup/(q>(|), i|>(i))),
где верхняя грань берется по всем измеримым функ-
функциям ср( •) и ф (•) с конечным числом значений. Понятие
И. к. используется главным образом в теории передачи
информации.
Лит. см. [1], [2], [4] при ст. Информации передача.
Р. Л. Добрушин, В. В Прелое.
ИНФОРМАЦИИ ПЕРЕДАЧА — составная часть
информации теории, относящаяся к изучению процесса
переноса информации от источника сообщений к полу-
получателю сообщений (адресату). В теории И. п. изучаются
оптимальные и близкие к оптимальным методы И. п.
по каналам связи в предположении, что можно в ши-
широких пределах варьировать методы кодирования сооб-
сообщений в сигналы на входе канала и декодирования сиг-
сигналов на выходе канала в сообщения на выходе (см.
Кодирование и декодирование).
Общую схему системы И. п., впервые рассмотренную
К. Шенноном (С. Shannon, [1]), можно описать сле-
следующим образом. Источник сообщений вырабатывает
сообщения, подлежащие передаче по каналу связи от
источника к получателю. Обычно предполагают, что
это сообщение — случайная величина |, определен-
определенная на нек-ром вероятностном пространстве (Q, 31,
Р), принимающая значения в нек-ром измеримом
пространстве (Ж, S^ ) и имеющая распределение вероят-
вероятностей р{-)- Часто |= {|(?), *?Д}, где Д — множество
значений параметра t, является случайным процессом
с дискретным или непрерывным временем со значениями
в нек-ром измеримом пространстве (X, Sx)- Напр.,
в случае дискретного времени |= {!#, k=i, 2, ...}
или |= {gft, &=..., —1, 0, 1, ...} случайные вели-
величины |fc, принимающие значения в измеримом прост-
пространстве (X, Sx}, наз. компонентами сообщения на
входе и часто трактуются как сообщения, вырабаты-
вырабатываемые источником в моменты времени к. Наборы §"=
= (?г, . .., !„), принимающие значения в пространстве
(Хп, Sxn), т. е. в ?г-кратном произведении пространств
(X, Sx), наз. отрезками сообщений длины п на входе.
Аналогичным образом определяются соответствующие
понятия и в случае, когда сообщение — случайный
процесс с непрерывным временем.
Сообщение на выходе, получаемое адресатом,— это
тоже случайная величина f, определенная на том же
вероятностном пространстве (Q, Ж, Р) и принимающая
значения в измеримом пространстве (ЭВ, S~) (вообще
говоря, отличном от (ЭВ, S^)). В случае, когда f яв-
ляется случайным процессом с дискретным или не-
непрерывным временем, аналогичным образом вводятся
понятия пространства (X, S~) значений компонент
сообщения на выходе и пространства (Хп, S~n) зна-
значений отрезков длины п сообщения на выходе.
Мерой качества передачи сообщений по каналу связи
является сообщений точность воспроизведения. Как
правило, если передача ведется по каналу связи с по-
помехами, даже если множества ЗЕ и J совпадают, нельзя
добиться абсолютной точности, т. о. полного совпаде-
совпадения посылаемого и получаемого сообщений. Обычно
требования, предъявляемые к точности, трактуют ста-
статистически, выделяя класс W допустимых совмест-
совместных распределений вероятностей для пары (?, f) пере-
передаваемого и получаемого сообщений в множестве всех
вероятностных мер в произведении (Э? X 2t, S^XS^).
Класс W часто задается при помощи измеримой не-
неотрицательной функции р(х, х), z?$, х?$, и числа
а>0: считают, что распределение вероятностей (|, ?)
принадлежит W, лишь если
Ер (?, !)<;«• A)
Таким образом, условие точности воспроизведения
показывает, насколько полученное сообщение может
отличаться от переданного.
Сообщения, вырабатываемые источником, передаются
по каналу связи. Каналом (Q, V) наз. совокуп-
совокупность двух измеримых пространств (;)!, 5?,), (§}, ?§),
переходной функции Q(y, А), у?3}, Л^5,^, являю-
являющейся измеримой относительно сг-алгебры S^ при
фиксированном A ?-Sg и вероятностной мерой на
(?Т, Sy) при фиксированном г/ОК и подмножества V
в пространстве всех вероятностных мер в пространстве
C), Sg). Пространства (§.}, 5а), (SI, S$) наз. соот-
соответственно пространствами сигналов на входе и выходе
канала, а подмножество V — ограничением на рас-
распределение сигнала на входе. Говорят, что две слу-
случайные величины т) и т) (определенные на вероятност-
вероятностном пространстве (Q, 31, Р)) связаны каналом (Q, V),
если они принимают значения в (;Л, $%), (VI, $щ)
соответственно и для любого A ?<S|j с вероятностью 1
условная вероятность
|п}= <?(гь А), B)
и распределение вероятностей случайной величины т)
принадлежит V. Наиболее часто ограничение V за-
задается с помощью измеримой функции п(у), г/?3(,
и числа Ь>0: считают, что распределение вероятностей
т) принадлежит V, лишь если
Ея(т|)<Ь. C)
В случае дискретных каналов V обычно совпадает
с совокупностью всех распределений вероятностей,
т. е. ограничение отсутствует.
С наглядной точки зрения, 3) — это совокупность
сигналов, передаваемых передатчиком, а ;Л — сово-
совокупность сигналов, принимаемых приемником (в при-
приложениях пространства 5J и §J часто совпадают).
Если задано случайное значение т) сигнала на входе,
то B) позволяет найти условное распределение сигнала
на выходе т). Введение ограничения V связано с тем,
что во многих приложениях нельзя считать распреде-
распределение входного сигнала произвольным [типична, напр.,
ситуация, когда предполагается, что среднее значение
квадрата (мощность) входного сигнала не превосходит
заданной константы]. В приложениях особенно важен
случай, когда сигналами на входе и выходе канала
являются случайные процессы Т1={т|(*)}, 'П={г|(*)}
с дискретным или непрерывным временем, определен-
определенные на нек-ром конечном или бесконечном (в одну или
обе стороны) интервале действительной оси и прини-
принимающие значения в нек-рых измеримых пространствах
(У, Sy) и (У, Sy) соответственно. Напр., если г\=
= {%, г|2, ...} и г|= {%, г|2, . ..} — случайные последо-
последовательности, то канал связи, для к-рого последователь-
последовательности т) и г| служат сигналами на входе и выходе, часто
рассматривают как последовательность каналов (в опи-
описанном выше смысле), называемых отрезками данного
канала; сигналами на входе и выходе этих отрезков
канала служат векторы
!)"=(%, ..., Г)„) И Г\п = (Т\1, ..., Т)„), Л = 1, 2, ...
Для того чтобы превратить сообщение на входе
в сигнал, передаваемый по каналу связи, а сигнал,
полученный на выходе канала,— в сообщение на вы-
выходе, необходимо провести операции кодирования и
декодирования сообщений. Кодированием наз.
функцию / (х) от х ? ЗЕ со значениями в "}}, а дек о-
дированием — функцию g (у) от у ? $} со значения-
значениями в I. Множество значений функции f(x), ж^ЗЁ,
часто наз. кодом, а отдельные элементы этого мно-
множества — кодовыми словами. Использование ко-
кодирования f(x) и декодирования g(y) означает, что ес-
если сообщение приняло значение х?Ж, то по каналу
передается сигнал y=f(x); если на выходе канала по-
получен сигнал у ? §}, то его декодируют в сообщение на
выходе x=g(y). В теории передачи информации ча-
часто рассматривают случайное кодирование,
когда кодовые слова выбираются' случайно в соответ-
соответствии с нек-рым распределением вероятностей.
Сообщение с распределением вероятностей р(-),
вырабатываемое источником, может быть передано с
точностью воспроизведения W по каналу (Q, V) при
помощи кодирования /(•) и декодирования g(-), если
могут быть построены случайные величины ?, ц, г\у
|, образующие цепь Маркова такую, что ? имеет рас-
распределение вероятностей р(-), распределение вероят-
вероятностей пары (?, 1) принадлежит W- пара (г|, т)) связана
каналом (Q, V) и
Предположение о том, что |, ц, г\, ? образуют цепь
Маркова, сводится к предположению о том, что ус-
условное распределение г| при заданных значениях | и т|
зависит лишь от т), т. е. оно означает, что при передаче
сигнал на выходе зависит лишь от сигнала на входе,
а не от того, какое значение сообщения им закоди-
закодировано.
Основную проблему, исследуемую в И. п., можно
сформулировать следующим образом. Считаются из-
известными и фиксированными источник, порождающий
сообщения с распределением вероятностей р(-), канал
связи ((?, V) и условия точности воспроизведения W.
Задача состоит в том, чтобы выяснить, при каких ус-
условиях существуют методы кодирования /(•) и декоди-
декодирования g(-) такие, что сообщение, вырабатываемое
данным источником, может быть передано с заданной
точностью воспроизведения W по данному каналу
(Q, V). Решения этой проблемы при разных предполо-
предположениях наз. теоремами кодирования, или теоремами
Шеннона. Естественно возникает также другая про-
проблема о том, как в случае, когда передача возможна,
построить наиболее простым и эффективным образом
кодирование и декодирование, осуществляющие эту
передачу.
К. Шеннон [1] ввел величины, позволяющие сформу-
сформулировать ответ на первую из поставленных проблем.
Главной среди них является информации количество,
или просто информация, /(-, ¦)• Если
С = С (Q, F) = sup/(Ti, ц) E)
— пропускная способность канала (Q, V) (см. Канала
пропускная способность), где верхняя грань берется
по всем парам величин (т), т)), связанным каналом
(Q, V), и если число
Hw(p) = mU(l, I) F)
есть VF-энтропия (см. Энтропия) сообщения, где ниж-
нижняя грань берется по всем парам (?, |) таким, что
совместное распределение вероятностей пары (?, ?)
принадлежит W, а % имеет распределение вероят-
вероятностей р(-), то справедлива следующая теорема Шен-
Шеннона (обращение теоремы кодирования): если сообще-
сообщение с распределением вероятностей р (•) может быть
передано по каналу (Q, V) с условием точности воспро-
воспроизведения W, то
Hw(p)<zC(Q, V). G)
Достаточные условия для возможности И. п. по-
получить сложнее. Так, условие G) достаточно для воз-
возможности И. п. лишь в некотором асимптотич. смысле,
и при этом главным является предположение о том,
что Д^(р)—^-оо, следовательно условие G) необходимо
и достаточно лишь, грубо говоря, применительно
к задаче о передаче довольно большого количества ин-
информации. Остальные нужные предположения носят
характер предположений регулярности, к-рые в кон-
конкретных ситуациях обычно выполняются. Чтобы сфор-
сформулировать достаточные условия для возможности
передачи в точных терминах, необходимы нек-рые
дополнительные понятия.
Последовательность пар случайных величин (?', ?*,
<=1, 2, . ..) наз. информационно-устойчивой, если
KtftaKV)
lim -2_s = 1 (8)
в смысле сходимости по вероятности. Здесь i&~t(-, •) —
информационная плотность (см. Информации коли-
количество) пары (g*, Z;*). Последовательность каналов
{(<?*, Vf), i=l, 2, ...} с C(Q\ У')<оо наз. информа-
информационно-устойчивой, если существует информационно-
устойчивая последовательность пар (т]*, т)*), связанных
каналом (Qt, Vf), такая, что
lim У-ч">*>=1. (9)
t -* и C^Q*, V')
Последовательность сообщений с распределением ве-
вероятностей р'(-) и условиями точности И7' с Н't(pl)<
<оо, 2=1, 2, . . ., наз. информационно-устойчивой,
если существует последовательность пар (с,1, \() такая,
что Ъ* имеет распределение вероятностей р'(-), распре-
распределение вероятностей пары (?*, f') принадлежит W* и
W
(р1)
A0)
Пусть Vs — множество распределений вероятностей,
для к-рого справедливо C) с заменой Ъ на b-\~e, a We —•
условие точности, задаваемое неравенством A), в к-ром
а заменено на а+е, е>0. Имеет место теорема коди-
кодирования (теорема Шеннона): пусть заданы информа-
информационно-устойчивая последовательность сообщений с рас-
распределением вероятностей р*{-) и условиями точности
W1 и информационно-устойчивая последовательность ка-
каналов (Qf, V1) такие, что функции itf(-) ир'(-, •) равно-
равномерно ограничены по t; пусть Н t(p*)—*-°° ПРИ *—>-°° и
lim ciRhjlL > 1, (И)
тогда для любого е>0 существует столь большое t0,
что при всех t^t0 сообщение с распределением вероят-
вероятностей р'(-) может быть передано через канал (Q*, Ve)
с точностью воспроизведения We. Эта формулировка
прямого утверждения теоремы кодирования является
одной из наиболее общих. Предположение об ограни-
ограниченности функций я'(-) и р'(-, •) может быть сущест-
существенно ослаблено. Информационная устойчивость по-
последовательности сообщений и каналов всегда имеет
место в большом числе практически интересных част-
частных случаев. Наконец, при нек-рых условиях в сфор-
сформулированной теореме можно заменить We на W1 и Т'Ё
на Т''.
Для описания реальных ситуаций наиболее интере-
интересен случай, когда последовательность каналов, рас-
рассматриваемая в теореме, есть последовательность от-
отрезков данного фиксированного канала, а последова-
последовательность сообщений — это последовательность от-
отрезков сообщений фиксированного источника с расту-
растущим числом компонент. Наглядно это соответствует
функционированию системы связи во времени. Ниже
для этой ситуации сформулированы нек-рый вариант
теоремы кодирования и его обращение в несколько
отличной от предыдущей форме. При этом рассматри-
рассматриваются дискретный стационарный источник и канал
без памяти.
Пусть дискретный стационарный источник U, вы-
вырабатывающих! сообщение %= {|k, &=..., —1, О,
1, . . .}, где отдельные компоненты (буквы сообщения
5ft) принимают значения из нек-рого конечного мно-
множества алфавита X объема М, производит буквы сооб-
сообщения со скоростью одна буква в единицу времени.
Компоненты сообщения f= {%k, k=..., —1, 0, 1, . . .},
получаемого адресатом, принимают значения из того же
алфавита X (т. е. Х=Х). Пусть, далее, используется
дискретный канал без памяти, передача по к-рому ве-
ведется со скоростью один символ в интервал времени т.
Ограничения на распределение сигнала на входе ка-
канала отсутствуют. Пусть отрезок сообщения ? '=
= (li, . . ., 5л) длины L=Ly передается по отрезку
канала длины N=--[Llx\ (где [х] — целая часть числа х)
с помощью нек-рых методов кодирования и декодиро-
декодирования описанного выше типа. Если при этом \ =
= (li, ..., ^i) — соответствующий отрезок сообщения,
полученный адресатом, а Ре— средняя вероятность
ошибки на букву источника, определяемая формулой
то справедлива следующая теорема.
Обращение теоремы кодирования.
Пусть Н(U) —скорость создания сообщений данным
дискретным стационарным источником ж С — пропуск-
пропускная способность (на передаваемый символ) используе-
используемого канала без памяти. Тогда при всех L справедли-
справедливо неравенство
где
h (з-) = — х log x— A— x) log(l— x).
Таким образом, если скорость создания сообщений
Н(U) больше, чем — С (пропускная способность канала
на букву источника), то средняя вероятность ошибки
на букву источника при любом L и для любых методов
кодирования и декодирования ограничена снизу от-
отличной от нуля константой и, значит, не стремится
к нулю даже при L-^-oo. Чтобы сформулировать прямое
утверждение теоремы кодирования, необходима ве-
величина
RN=^l^l. A4)
В случае, когда М=2 и Луу/т — целое" число, Луу=т,
т. е. RN в битах является числом двоичных символов,
вырабатываемых источником за время передачи одного
символа по каналу. Кроме того, i?w совпадает со ско-
скоростью создания сообщений Н (U) источником U с не-
независимыми и равномерно распределенными компо-
компонентами. Вероятность ошибки и средняя вероятность
ошибки на блок источника определяются соответст-
соответственно формулами:
Pe = ^xLP{iL=xL}Pe,xL, A6)
здесь Р L(-) — условная вероятность при условии,
что ^ =ii^Ii. Справедлива следующая тео-
теорема кодирования. Для всех N и любого
Д<С существуют методы кодирования и декодирования
такие, что при Е^^Е для всех xL ? Х?
A7)
(оценка A7) справедлива и для Ре), причем для
функция Е (Е) выпуклая, положительная и убывает
с ростом Е (см. также Ошибочного декодирования вероят-
вероятность). Таким образом, эта теорема показывает, что
для всех Е <С вероятность ошибки с ростом N стре-
стремится к нулю и притом экспоненциально быстро.
Имеются обобщения теорем Шеннона на случай так
наз. составных каналов и сообщений с неизвестными
параметрами. Интерес к подобным обобщениям выз-
вызван тем, что обычно на практике нельзя считать пол-
полностью известными статистич. параметры источника
сообщений и канала связи, тем более что эти пара-
параметры могут иногда меняться в процессе передачи.
Поэтому приходится предполагать, что источник сооб-
сообщений и канал связи принадлежат нек-рому классу
возможных источников сообщений и каналов. При
этом вводится минимаксный критерий качества пере-
передачи, при к-ром качество данного метода передачи
оценивается для наихудших возможных источников
сообщений и каналов, принадлежащих рассматривае-
рассматриваемому классу.
Имеются также обобщения теорем Шеннона на слу-
случай И. п. по каналу с обратной связью. Наличие полной
обратной связи означает, что в момент времени t на
передающей стороне канала (т. е. на его входе) счи-
считаются известными точные значения сигналов на вы-
выходе канала для всех моментов времени t' <?. В част-
частности, для каналов без памяти с обратной связью ос-
основной результат состоит в том, что наличие обратной
связи не увеличивает пропускную способность канала,
хотя и может существенно уменьшить сложность коди-
кодирующих и декодирующих устройств.
Из других обобщений следует отметить теорию И. п.
по каналам с ошибками синхронизации, в к-рых воз-
можны случайные сбои синхронизации, в результате
чего нарушается однозначность соответствия между
сигналами на входе и выходе канала, а также теорию
передачи по каналам многосторонним, когда имеется
несколько источников и получателей информации и
передача может осуществляться по нескольким на-
направлениям одновременно.
Лит.: [1] Шеннон К., Работы по теории информации
и кибернетике, пер. с англ., М., 1963, с. 243—332; [2] Добру-
ши н Р. Л., «Успехи матем. наук», 1959, т. 14, в. 6, с. 3—104;
[3] Вольфовиц Д ж., Теоремы кодирования теории ин-
информации, пер. с англ., М., 1967; [4] Г а л л а г е р Р., Теория
информации и надежная связь, пер. с англ., М., 1974; L5J Ф а й н-
стейн А., Основы теории информации, пер. с англ., М.,
1900; [6] Ф а н о Р. М., Передача информации. Статистическая
теория связи, пер. с англ., М., 1965; [7J Харкевич А. А.,
Борьба с помехами, 2 изд., М., 1965; [8] В о з е н к р а ф т Д ж.,
Джекобе И., Теоретические основы техники связи, пер.
с англ., М., 1969; [9] Колмогоров А. Н., «Пробл. пере-
передачи информ.», 1965, т. 1, № 1, с. 3—11; [10] Пинскер М. С,
в сб.: Проблемы передачи информации, в. 7, 1960, М., с. 1—201;
[11] Левин Б. Р., Теоретические основы статистической ра-
радиотехники, 2 изд., М., 1974; [1 2] К о л м о г о р о в А. Н.,
в кн.: Сессия АН СССР по научным проблемам автоматизации
производства. 15—20 октября 1956 г. Т. 1. Пленарные заседа-
заседания, М., 1957, с. 66—99; [13] Key papers in the development of
information theory, N.Y., 1974; [14] Proceeding of the 1975 IEEE-
USSR Joint Workshop on Information Theory. Moscow. 15—19
December, 1975, N.Y., 1976. P. Л. Добрушин, В. В. Прелое.
ИНФОРМАЦИИ СКОРОСТЬ ПЕРЕДАЧИ — величи-
величина, характеризующая информации количество, к-рая
содержится в сигнале на выходе канала связи относи-
относительно сигнала на входе канала в расчете на единицу
времени. Если
Т1={Т1 (*). — °° < ' < °°}> Г)={Т1((), — оо < t < оо}
— случайные процессы с непрерывным или дискретным
временем, являющиеся сигналами на входе и выходе
нек-рого канала связи, то И. с. п. наз. величину
R= lim ^—. /О/., ц1), (*)
1 г
если такой предел существует; здесь /(•, •) — коли-
количество информации, r\t = {r\(s), t'Cs^.T} — отрезок
(t, T] процесса т), аналогично определяется щ . Сущест-
Существование предела (*) доказано для достаточно широкого
класса каналов, в к-рых сигналы г\ и г\ являются
стационарными и стационарно связанными случай-
случайными процессами. Явное вычисление И. с. п. воз-
возможно, в частности, для стационарных каналов без
памяти и каналов гауссовских. Напр., для гауссовского
канала, сигналы г| и г| на входе и выходе к-рого яв-
являются гауссовскими стационарными процессами, об-
образующими совместно гауссовскую стационарную пару
процессов, И. с. п. задается формулой
гДе fn М и /rifi^) — спектральные плотности процес-
процессов т] и г| соответственно, а /Г|^(^) — их взаимная спект-
спектральная плотность.
Лит.:[1] Галлагер Р., Теория информации и надежная
связь, пер. с англ., М., 1974; [2] Пинскер М. С, в сб.:
Проблемы передачи информации, в. 7, М., 1960, с. 1—201.
Р. Л. Добрушин, В. В. Прелое.
ИНФОРМАЦИИ ТЕОРИЯ — раздел прикладной ма-
математики и кибернетики, связанный с математич.
описанием и оценкой качества передачи, хранения,
извлечения и классификации информации. Термин
«И. т.», возникший в 50-х гг. 20 в., до сих пор (к 1978)
не имеет единого общепринятого толкования. В раз-
разных источниках по-разному определяется перечень
разделов наук, включаемых в И. т., а при логич. тол-
толковании в И. т. надо включать и нек-рые разделы науки,
традиционно в нее не включаемые. Важной чертой,
объединяющей различные разделы науки, относимые
к И. т., является широкое использование статистич.
методов. Это обусловлено тем, что процесс извлечения
информации связывают с уменьшением неопределен-
неопределенности наших сведений об объекте, а естественной число-
числовой мерой неопределенности нек-рого события является
его вероятность.
Важнейшая составная часть И. т. при любых трак-
трактовках — теория информации передачи. Часто, осо-
особенно в чисто математич. литературе, термин «И. т.»
используют как синоним термина «теория передачи
информации». Теория передачи информации изучает
оптимальные и близкие к оптимальным методы пере-
передачи информации по каналам связи в предположении,
что можно в широких пределах варьировать методы
кодирования сообщений в сигналы на входе канала
связи и декодирование сигналов в сообщения на вы-
выходе.
Возникновение теории передачи информации связано
с именем К. Шеннона (С. Shannon), предложившего
в 1948 решение основной проблемы о нахождении ско-
скорости передачи информации, к-рую можно достичь
при оптимальном методе кодирования и декодирования
так, чтобы вероятность ошибки при передаче инфор-
информации была как угодно мала. Эта оптимальная ско-
скорость передачи, называемая канала пропускной спо-
способностью, выражается через введенную К. Шенноном
величину, называемую информации количеством. По-
Понятие количества информации представляется весьма
важным и находит многочисленные важные приложе-
приложения и в других разделах И. т., хотя далеко не все
попытки его приложения адекватны существу рас-
рассматриваемых проблем.
Задачи, связанные с оптимальным способом хране-
хранения информации, принципиально не отличаются от
задач оптимальной передачи информации, так как хра-
хранение информации можно рассматривать как передачу
информации, но не в пространстве, а во времени.
Основные теоремы теории передачи информации пер-
первоначально носили характер теорем существования,
в к-рых доказывалось существование оптимальных ме-
методов кодирования и декодирования, но не указывались
способы их построения и технич. реализации этих ме-
методов. Поэтому позже получила широкое развитие
теория кодирования, посвященная построению кон-
конкретных и относительно простых алгоритмов кодиро-
кодирования и декодирования, приближающихся по своим
возможностям к оптимальным алгоритмам, существо-
существование к-рых доказывалось в теории передачи инфор-
информации. Теорию кодирования отличает то, что наряду
со статистич. методами она использует для построения
конкретных кодов глубокие алгебраические и комби-
комбинаторные идеи.
Обычно к И. т. относят также всю совокупность ис-
исследований, посвященных приложениям теории ста-
статистич. методов для описания способов преобразований
сигналов на входе и выходе каналов связи. С математич.
точки зрения, это просто нек-рые приложения мате-
математич. статистики (в первую очередь статистики слу-
случайных процессов), теории прогнозирования и фильтра-
фильтрации стационарных случайных процессов, теории
игр и пр. Таким образом, этот раздел И. т. не имеет
специфического математич. аппарата и в своем развитии
все более сближается с другими разделами прикладной
теории вероятностей.
В И. т. часто включают также теорию распознавания
образов, разрабатывающую алгоритмы распределения
объектов по нек-рым классам объектов, к-рые описаны
лишь на интуитивном уровне и не имеют четкого мате-
математич. описания. Такие алгоритмы всегда включают
в себя процесс обучения по нек-рому списку заранее
классифицированных человеком объектов.
Попытка определить границы И. т., исходя из ее
общепринятых определений, и включить в нее все раз-
разделы математики, имеющие дело с понятием информа-
информации в его общелексической трактовке, привела бы к не-
неоправданной, по крайней мере на современном этапе,
расширенной трактовке понятия И. т. Так, вся мате-
матич. статистика имеет дело с проблемами извлече-
извлечения информации, теория алгоритмов — с проблемами
переработки информации, теория формальных язы-
языков — с проблемами записи информации и т. д.
Понятие информации и его приложения весьма много-
многообразны, и этим можно объяснить то, что в настоящее
время (к 1978) комплекс наук об информации представ-
представляет собой совокупность довольно разрозненных науч-
научных дисциплин, каждая из к-рых связана с изучением
одного из аспектов этого понятия. Несмотря на интен-
интенсивные усилия ученых процесс сближения этих науч-
научных дисциплин идет довольно медленно, и создание
единой и всеохватывающей И. т. представляется делом
не слишком близкого будущего.
Лит.: [1] Галлагер Р., Теория информации и надеж-
надежная связь, пер. с англ., М., 1974; [2] Колмогоров А. Н.,
«Пробл. передачи информ.», 1965, т. 1, № 1, с. 3—11; [3] X а р-
кевич А. А., Борьба с помехами, 2 изд., М., 1965; [43 Бри л-
люэн Л., Наука и теория информации, пер. с англ., М.,
1960; [5] Ч е р р и К., Человек и информация, пер. с англ.,
М., 1972; [6] Яг лом А. М., Яг л ом И. М., Вероятность
и информация, 3 изд., М., 1973; [7] Возенкрафт Д ж.,
Джекобе И., Теоретические основы техники связи, пер.
с англ., М., 1989; [8] Левин Б. Р., Теоретические основы
статистической радиотехники, 2 изд., М., 1974.
Р. Л. Добрушии, В. В. Прелое.
ИНФОРМАЦИОННАЯ МАТРИЦА, информа-
информация по Фишер у,— матрица ковариаций инфор-
информанта. Для доминированного семейства распределений
вероятностей .P'(dco) с плотностями р(со; t), достаточно
гладко зависящими от векторного (в частности, число-
числового) параметра t=(tt, . .., tm)?Q, элементы И. м.
при t= 6 определяются как
Ijk{Q)=C amp («.-.о. amp («,;!> в) ^ A)
Q /
где /, А=1, . . ., т. При скалярном параметре t И. м.
описывается единственным числом — дисперсией ин-
информанта.
И. м. /F) определяет неотрицательную дифферен-
дифференциальную квадратичную форму
^iJkIjk{Q)dtjdtk = ^ B)
снабжающую семейство {Pt} римановой метрикой.
Когда пространство О, исходов со конечно,
д/> = 2у (dFjJ/Pf, Pj = Р (а>/), Vco/ ? Й.
Дифференциальная квадратичная форма Фишера B)
является единственной (с точностью до постоянного
множителя) дифференциальной квадратичной формой,
инвариантной относительно категории статистических
решающих правил. Ввиду этого она возникает в фор-
формулировке многих статистич. закономерностей.
Любое измеримое отображение / пространства Q
исходов порождает новое гладкое семейство распределе-
распределений Qt=Ptf~1 с И. м. IQ(Q). При этом И. м. монотонно
не возрастает:
каковы бы ни были zlt . . ., zm. И. м. обладает также
свойством аддитивности. Если /<'"> (8) — И. м. для се-
семейства с плотностью Р/(ш'; t), то для семейства
р(ш^ со(Л'); *) = Д^_ p,-(fi><'>; t)
будет /Л/(9)=2.1-/"')(9). В частности, IA(Q)=NI(Q)
при N независимых одинаково распределенных испы-
испытаниях. И. м. позволяет охарактеризовать статистич.
точность решающих правил в задаче оценки параметра
закона распределения. Для дисперсии любой несме-
несмещенной оценки т (со)=т(сйA), ..., со(ЛГ)) скалярного па-
параметра t справедливо
Аналогичное матричное неравенство информации вы-
выполняется для оценок векторного параметра. Его ска-
скалярное следствие
показывает, что несмещенное оценивание нигде не мо-
может быть слишком точным. Для произвольных оценок
последнее неверно. Однако остаются ограничения,
напр., на среднюю точность
2Лв-Ее<т —е|/(9)|т —e>=s=m7V-1 + o(iV-1), D)
где усреднение 2R левой части C) проведено по инва-
инвариантному объему V любой компактной подобласти
в'(=в,
dV F)= }/~det/ (9) dQ1...ddm;
остаточный член зависит от размеров в'.Неравенства D)
асимптотически точны, и асимптотически оптимальной
в этом смысле оказывается оценка максимума правдо-
правдоподобия.
В точках вырождения, det /(8)=0, совместная оценка
параметров затруднена", если det/(8) = O в нек-рой
области, то совместная оценка вообще невозможна.
Таким образом, следуя Р. Фишеру [1], с известной ос-
осторожностью можно сказать, что И. м. описывает
среднее количество информации о параметрах закона
распределения, содержащееся в случайной выборке.
Лит.: [1] Fisher R. А., «Ргос. Cambr. Phil. Soc>>,
1925, v. 22, p. 700—25; [2] Барра Ж.-Р., Основные понятия
математической статистики, пер. с франц., М., 1974; [3] Чеп-
Чепцов Н. Н., Статистические решающие правила и оптималь-
оптимальные выводы, М., 1972. Н. Я. Ченцои.
ИНФОРМАЦИОННОЕ МНОЖЕСТВО (в теории
игр) — известная игроку в данный момент совокуп-
совокупность возможных состояний (позиций) игры, среди
к-рых находится ее действительное состояние. И. м.
характеризует знания игрока о прошлых состояниях
и выборах как своих (память), так и чужих (информа-
(информация). Находясь в И. м., игрок должен принять одно
решение (выбрать альтернативу И. м.,т. е. по
одной альтернативе сразу для всех позиций из И. м.),
к-рое лишь конкретизируется как альтернатива позиции
при реальном разыгрывании игры. И. н. Врублевская.
ИНФОРМАЦИОННОЕ РАССТОЯНИЕ — метрика или
псевдометрика на совокупности распределений вероят-
вероятностей, характеризующая «непохожесть» описываемых
этими распределениями случайных явлений. Наиболее
интересны И. p. p(P, Q), связанные с мерами информа-
информативности эксперимента в задаче различения Р и Q
по наблюдениям.
В любой конкретной задаче статистик, обработав
материалы наблюдений, должен сделать выводы о на-
наблюденном явлении. Эти выводы не будут, вообще
говоря, совершенно точными, поскольку исходы на-
наблюдений случайны. Интуитивно понятно, что каждая
выборка несет какое-то количество полезной инфор-
информации, причем: А) при обработке информация может
только теряться, Б) информация, доставляемая неза-
независимыми источниками, напр, независимыми выбор-
выборками, суммируется. Таким образом, если ввести и н-
формативность эксперимента как
среднее количество информации в наблюдении, то для
информативности выполнены аксиомы А и Б. И хотя
понятие информации остается интуитивным, иногда
можно указать величину /, удовлетворяющую аксио-
аксиомам А и Б, к-рая описывает асимптотику средней точ-
ности выводов в задаче с ростом числа наблюдений и
к-рую потому естественно принять за информативность.
Информативность может быть как числовой, так и
матричной величиной. Важный пример — информа-
информационная матрица в задаче оценки параметра закона
распределения.
Согласно аксиоме Б, информативности складываются
как квадраты длин (катетов), т. е. квадрат разумного
И. р. должен обладать свойством аддитивности. Прос-
Простейшие И. р.— расстояние по вариации:
Pv(P, <?)=$ |Р(*п)-<?(Л»)|.
и расстояние в инвариантной рима-
новой метрике Фишера:
Pf(P> <?) = 2arccos С У~Р (dm) Q (Ло),
последним свойством не обладают и собственного ста-
тистич. смысла не имеют.
По теории Неймана — Пирсона вся полезная инфор-
информация о различении распределений вероятностей P(d(o)
и Q (d<?>) на общем пространстве Q исходов со содер-
содержится в отношении правдоподобия или его логарифме
In р (со) - In ? (со) = In-!! (со),
определенном с точностью до значений на множестве
исходов вероятности нуль. Математическое ожидание
_ С ГР (da» j P (da»
наз. (средней) информацией различе-
различения (по Кульбаку) в пользу Р про-
против Q, а также относительной энтро-
энтропией, информационным уклонением.
Неотрицательная (может быть, бесконечная) величина
I(P '¦ Q) удовлетворяет аксиомам А и Б. Она характе-
характеризует точность одностороннего различения Р от Q,
определяя максимальный порядок убывания вероят-
вероятности Рдг ошибки второго рода (т. е. ошибочного при-
принятия гипотезы Р, когда она неверна), при росте
числа ./V независимых наблюдений:
Рлг~ехр[—ЛГ./(Р:<?)],
при фиксированном уровне значимости — вероятности
ад/ ошибки первого рода, 0<я0<:ад'<:а1<1.
Аналогичная величина I (Q : Р) определяет макси-
максимальный порядок убывания ajV при 0<60<P^v<:61<l.
Отношение «сходства», в частности «сходства» случай-
случайных явлений, не симметрично и, как правило, I(Р:(?)Ф
ф!(Q : Р). Геометрич. интерпретация I (P : Q) как
половины квадрата несимметричного расстояния от Q
до Р оказалась естественной в ряде вопросов статис-
статистики. Для такого И. р. неравенство треугольника не-
неверно, но справедлив несимметричный аналог теоремы
Пифагора:
/(Я:Р) = /(Я
если
ь ] q (dm) = \ Пп Щ\ R (dffl).
qL v (a>) J v *¦ ' J в L p (to) J v ;
Симметричная характеристика непохожести Р и Q
возникает при их минимаксном тестировании. Для
оптимального теста
ctjv= Рл' — exp l—NIpq],
/p0 = _ln min С |P(dw)|»| <? (dco)p-» =
0<а<1Ja
= min max {/ (R:P), I(R:Q)}.
С информационным уклонением связаны также
нек-рые другие И. р. (см. [1], [2]). Для бесконечно
близких Р и Q главная часть информационного укло-
уклонения, равно как и квадрата любого разумного И. р.,
задается, с точностью до постоянного множителя сA),
квадратичной формой Фишера. Для информационного
уклонения
4
Лит.: [1] К у л ь б а к С, Теория информации и статис-
статистика, пер. с англ., М., 1967; [2] Ченцов Н. Н., Статисти-
Статистические решающие правила и оптимальные выводы, М., 1972.
ИНФОРМАЦИОННЫЙ КОЭФФИЦИЕНТ КОРРЕ-
КОРРЕЛЯЦИИ — мера зависимости между двумя случайными
величинами X и У, определяемая как функция от ве-
величины количества информации в одной случайной
величине относительно другой:
где I(X, Y) — информации количество.
Свойства И. к. к. R(X, Y) как меры зависимости
полностью определяются свойствами величины I (X, Y),
к-рая сама служит характеристикой зависимости слу-
случайных величин X и У. Однако использование И. к. к.
R в качестве самостоятельной меры зависимости как
информационного аналога обычного коэффициента кор-
корреляции р оправдано тем, что для произвольных слу-
случайных величин И. к. к. имеет преимущество перед
р, так как в силу свойств информации Я = 0 тогда и
только тогда, когда X и Y независимы. Если
X и У имеют совместное нормальное распределение,
то эти два коэффициента совпадают, так как в этом
случае
Практическое исследование зависимости с помощью
И. к. к. равносильно анализу количества информации
в таблицах типа таблиц сопряженности признаков.
Выборочным аналогом R служит коэффициент
вычисляемый через информационную статистику /•
где п — число наблюдений, s и t — числа классов
группировки по двум признакам, и,-у — число наблю-
наблюдений в классе (г, ;), п.. = "У п.., п..— "Vs га... Таким
образом, вопрос о распределении выборочного И. к. к.
сводится к вопросу о распределении выборочной ин-
информации. Анализ выборочной информации как меры
зависимости затрудняется тем, что / сильно зависит от
группировки наблюдений.
Лит.: [1] L i n f о о t E., «Information and Control», 1957,.
v. 1, Ns 1, 85—89; [2] К у л ь б а к С, Теория информации и
статистика, пер. с англ., М., 1967. А. В. Прохоров.
ИНФОРМАЦИЯ — основное понятие кибернетики.
Кибернетика изучает машины и живые организмы
исключительно с точки зрения их способности воспри-
воспринимать определенную И., сохранять эту И. в «памяти»,
передавать ее по каналам связи и перерабатывать ее
в «сигналы», направляющие их деятельность в соот-
соответствующую сторону. Интуитивное представление
об И. относительно каких-либо величин или явлений,
содержащейся в нек-рых данных, в кибернетике огра-
ограничивается и уточняется.
В нек-рых случаях возможность сравнения различ-
различных групп данных по содержащейся в них И. столь же
естественна, как возможность сравнения плоских фи-
гур по их «площади»: независимо от способа измерения
площадей можно сказать, что фигура А имеет не боль-
большую площадь, чем В, если А может быть целиком по-
помещена в В (ср. примеры 1—3 ниже). Более глубокий
факт — возможность выразить площадь числом и на
этой основе сравнивать между собой фигуры произ-
произвольной формы — является результатом развитой ма-
тематич. теории. Подобно этому фундаментальным ре-
результатом теории И. является утверждение о том, что
в определенных, весьма широких, условиях можно
пренебречь качественными особенностями И. и выра-
выразить ее количество числом. Только этим числом опре-
определяются возможности передачи И. по каналам связи
и ее хранения в запоминающих устройствах.
Пример 1. Знание положения и скорости час-
частицы, движущейся в силовом поле, дает И. о ее поло-
положении в любой будущий момент времени, притом пол-
полную, т. к. это положение может быть предсказано
точно. Знание энергии частицы также дает И., но,
очевидно, неполную.
Пример 2. Равенство
а=Ъ A)
дает II. относительно переменных а и Ъ. Равенство
я2=62 B)
дает меньшую И. [т. к. из A) следует B), но эти ра-
равенства не равносильны]. Наконец, равенство
а3=Ь3, C)
равносильное A), дает ту же П., то есть A) и C) — это
различные формы задания одной и той же И.
Пример 3. Результаты произведенных с ошиб-
ошибками независимых измерений к.-л. физич. величины
дают И. о ее точном значении. Увеличение числа
наблюдений увеличивает эту И. Пример За. Сред-
Среднее арифметическое результатов наблюдений также
содержит нек-рую И. относительно рассматриваемой
величины. Как показывает математич. статистика,
в случае нормального распределения вероятностей
ошибок с известной дисперсией среднее арифметиче-
арифметическое содержит всю И.
Пример 4. Пусть результатом нек-рого измере-
измерения является случайная величина ?. При передаче
по нек-рому каналу связи ? искажается, в результате
чего на приемном конце получают величину
где 6 не зависит от ? (в смысле теории вероятностей).
«Выход» п дает И. о «входе» |, причем естественно ожи-
ожидать, что эта И. тем меньше, чем больше «рассеяние»
значений 6.
В каждом из приведенных примеров данные сравни-
сравнивались по большей или меньшей полноте содержащейся
в них И. В примерах 1—3 смысл такого сравнения ясен
и сводится к анализу равносильности или неравно-
неравносильности нек-рых соотношений. В примерах За и 4
этот смысл требует уточнения. Это уточнение дается,
соответственно, математич. статистикой и теорией И.
(для к-рых эти примеры являются типичными).
В основе информации теории лежит предложенный
в 1948 К. Шенноном (С. Shannon) способ измерения
количества И., содержащейся в одном случайном
объекте (событии, величине, функции и т. п.) относи-
относительно другого случайного объекта. Этот способ при-
приводит к выражению количества И. числом. Положение
можно всего лучше объяснить в простейшей обста-
обстановке, когда рассматриваемые случайные объекты яв-
являются случайными величинами, принимающими лишь
конечное число значений. Пусть ? — случайная вели-
величина, принимающая значения хг, х2, . . ., хп с вероят-
вероятностями р1, р2, ..., рп, а т) — случайная величина,
принимающая значения j/1? t/2> • • •> Ут с вероятностями
qt, q%, ..., qm. Тогда И. /(?, r|) относительно л, содер-
содержащаяся в |, определяется формулой
I F. П) =S,./Vl0g2 (pu/pigJ}' D)
где p.. — вероятность совмещения событий \=х[ и
г|= г/у и логарифмы берутся по основанию 2. И. 1A, т|)
обладает рядом свойств, к-рые естественно требовать
от меры количества И. Так, всегда /(?, г|)>0 и ра-
равенство / (?, г|) = 0 возможно тогда и только тогда,
когда pjz=pq.- при всех г и ;, т. е. когда случайные
величины | и г| независимы. Далее, всегда
I(%, л)<:/(г|, л,) и равенство возможно только в случае,
когда г| есть функция от % (напр., т)=^2 и т. д.). Не-
Неожиданным может казаться лишь равенство I (\, т])=
Величина #(?) = /(?, D=?.plog2(l/p.) носит на-
название энтропии случайной величины |. Понятие
энтропии относится к числу основных понятий теории
И. Количество И. и энтропия связаны соотношением
I(l,i\) = H(l)+H(i\)-H(l,i\), E)
где 11A, Ц) -- энтропия пары (?, г|), т. с.
Величина энтропии указывает среднее число двоичных
знаков, необходимое для различения (или записи)
возможных значений случайной величины. Это об-
обстоятельство позволяет понять роль количества И. D)
при «хранении» И. в запоминающих устройствах. Если
случайные величины | и г\ независимы, то для записи
значения ? требуется в среднем Н (?) двоичных зна-
знаков, для значения л требуется //(г|) двоичных знаков,
а для пары (?, т]) требуется //(?)+#"(л) двоичных зна-
знаков. Если же случайные величины \ и г\ зависимы, то
среднее число двоичных знаков, необходимое для за-
записи пары (|, г|), оказывается меньшим суммы //(!)-)-
+ 7/G1), так как //(?, г)) = 11A)+Н(ц)-1 (I, л).
С помощью значительно более глубоких теорем вы-
выясняется роль количества И. D) в вопросах передачи
И. по каналам связи. Основная информационная ха-
характеристика каналов, так наз. емкость, опреде-
определяется через понятие «И.».
Если ? и т] могут принимать бесконечное число зна-
значений, то предельным переходом из D) получается
формула
IG,n) = Npl*,»)log*?g$jr)dxdy, F)
где буквами р и q обозначены соответствующие плотно-
плотности вероятности. При этом энтропии Н (Ъ,) и Н(г\) не
существуют, но имеет место формула, аналогичная E)
1A, n) = AF) + ft(ri)-A(|, л), G)
где
* (?) = S Р (*) bg2 ^ Аг
— дифференциальная энтропия | [/j (tj) и h (|, л) оп-
определяются подобным же образом].
Пример 5. Пусть в условиях примера 4 случай-
случайные величины Ъ, и 0 имеют нормальное распределение
вероятностей с нулевыми средними значениями и дис-
дисперсиями, равными соответственно ol и ад. Тогда,
как можно подсчитать по формулам F) или G): / (л, ?)=
= /(?, т])= -у Iog2[l+ а|/ае]. Таким образом, коли-
количество И. в «принятом сигнале» т] относительно «пере-
«переданного сигнала» ? стремится к нулю при возрастании
уровня «помех» 8 (т. е. при o"q—>-оо) и неограниченно
возрастает при исчезающе малом влиянии «помех»
(т. е. при а?,—>-0).
Особенный интерес для теории связи представляет
случай, когда в обстановке примеров 4 и 5 случайные
величины | и ц заменяются случайными функциями
(или, как говорят, случайными процессами) ? (t) и
i]((), к-рые описывают изменение нек-рой величины на
входе и на выходе передающего устройства. Коли-
Количество И. в r|(t) относительно ?(() при заданном уровне
помех («шумов», по акустич. терминологии) 8 (t) может
служить критерием качества самого этого устройства.
В задачах математич. статистики также пользуются
понятием И. (ср. примеры 3 и За). Однако как по
своему формальному определению, так и по своему
назначению оно отличается от вышеприведенного (из
теории П.). Статистика имеет дело с большим числом
результатов наблюдений и заменяет обычно их полное
перечисление указанием нек-рых сводных характе-
характеристик. Иногда при такой замене происходит потеря
II., но при нек-рых условиях сводные характеристики
содержат всю П., содержащуюся в полных данных
(разъяснение смысла этого высказывания дано в конце
примера 6). Понятие И. в статистике было введено
Р. Фишером (R. Fisher) в 1921.
Пример 6. Пусть ?t, ?2, ..., Ъ,п — результаты п
независимых наблюдений нек-рой величины, распреде-
распределенные по нормальному закону с плотностью вероят-
вероятности
р (х; а, ст2) = =- ехр I— (х — аJ/2ст21,
оУ2л
где параметры а и а2 (среднее и дисперсия) неизвестны
и должны быть оценены по результатам наблюдений.
Достаточными статистиками (т. е.
функциями от результатов наблюдений, содержащими
нею И. о неизвестных параметрах) в этом примере яв-
являются среднее арифметическое
и так наз. эмпирическая дисперсия
Если параметр а2 известен, то достаточной статистикой
будет только \ (ср. пример За выше).
Смысл выражения «вся И.» может быть пояснен
следующим образом. Пусть имеется к.-л. функция
неизвестных параметров ф=ф(я, а2) и пусть ф* =
=Ф*(?Х, ?2, ..., ?„) — к.-л. ее оценка, лишенная си-
стематич. ошибки. Пусть качество оценки (ее точность)
измеряется (как это обычно делается в задачах мате-
математич. статистики) дисперсией разности ф*—ф. Тогда
существует другая оценка ф**, зависящая не от от-
отдельных величин \i, а только от сводных характери-
характеристик \ и s2, не худшая (в смысле упомянутого крите-
критерия), чем ф*. Р. Фишером была предложена также ме-
мера (среднего) количества И. относительно неизвестного
параметра, содержащейся в одном наблюдении. Смысл
этого понятия раскрывается в теории статистич. оце-
оценок.
Лит. см. при ст. Информации передача. Ю. В. Прохоров.
ИНФРАБОЧЕЧНОЕ ПРОСТРАНСТВО — локально
выпуклое линейное топологич. пространство, в к-ром
каждая бочка (т. е. поглощающее выпуклое зам-
замкнутое уравновешенное множество), поглощающая лю-
любое ограниченное множество, является окрестностью
нуля. Важный класс И. п. доставляют бочечные про-
пространства.
Произведение любого числа и индуктивный предел
II. п. есть И. п.; локально выпуклое пространство ин-
фрабочечно тогда и только тогда, когда либо каждая
ограниченная полунепрерывная снизу полунорма яв-
является непрерывной, либо каждое сильно ограничен-
ное подмножество в сопряженном пространстве равно-
равностепенно непрерывно. В частности, каждое борнологи-
ческое пространство (т. е. пространство, в к-ром каж-
каждая ограниченная полунорма непрерывна) является
И. п. В секвенциально полном линейном топологич.
пространстве из инфрабочечности следует бочечность,
И. п., подобно бочечным, могут быть охарактеризо-
охарактеризованы через отображения в банаховы пространства:
локально выпуклое линейное топологич. пространство
X является И. п. тогда и только тогда, когда для вся-
всякого банахова пространства Y каждое линейное отобра-
отображение из X в У, имеющее замкнутый график и пере-
переводящее ограниченные множества в ограниченные, не-
непрерывно. См. также Улыпрабочечное пространство.
Лит.: [1] Бур баки Н., Топологические векторные
пространства, пер. с франц., М., 1959; [2] Эдварде Р.-Э.,
Функциональный анализ. Теория и приложения, пер. с англ.
М., 1969. В. М. Тихомиров.
ИНЦИДЕНТНОСТИ КОЭФФИЦИЕНТ — число, ха
рактеризующее когерентность ориентации инцидентных
элементов симплициального, полиэдрального (клеточ-
(клеточного) и других комплексов. Понятие И. к. и его свой-
свойства необходимо входят в определение любого аб-
абстрактного комплекса.
Пусть tn = (a0, ..., ап) — ориентированный симплекс
в пространстве R^, т. о. симплекс, в к-ром выбран
указанный порядок его вершин as, a t"~1=(a0, . . .,
а,-_!, a/ + i, • • ., о-п) — ег0 ориентированная грань,
противоположная вершине я,-. Если i — четное, то V1
и if ориентированы когерентно, а
ориентация грани if индуцирована ориента-
ориентацией симплекса tn; в этом случае симплексам приписы-
приписывается И. к. [tn: i"~1] = + l. Если i — нечетное, то
tn и i" ориентированы некогерентно, и им приписы-
приписывается И. к. [tn : t1'1]=— 1.
Пусть теперь tn и t"-1—элементы (симплексы)
симплициалъного комплекса в R^. Тогда их И. к.
определяется следующим образом: если tn и tn~l не-
неинцидентны, то [tn : tn~1] = 0, если tn и t"'1 инцидентны,
то [tn : i"~1] = + l или —1 в зависимости от того, коге-
когерентно ориентированы tn и i"-1 или нет.
Свойства И. к.
[—t":tn-1] = [tn: — tn-1] = —[tn:t"-1], A)
где —t" — противоположно ориентированный сим-
симплекс, т. с. симплекс, получающийся нечетной переста-
перестановкой вершин симплекса t";
2Л*в:'Г1]['2~1:«"] = 0, B)
где суммирование распространяется на все как-либо
ориентированные симплексы ijj (для выполнимости
B) при нек-рых определениях симплициального ком-
комплекса требуется его полнота).
Аналогично, при надлежащем определении коге-
рентностей ориентации, вводится И. к. элементов
полиэдрального комплекса. Пусть R — подпрост-
подпространство в R", R" — одно из полупространств, ограни-
ограниченных R", и пусть R™ ориентировано выбором
нек-рого векторного базиса (еи . . ., еп). Тогда R" ц
R™~1 наз. когерентно ориентирован-
ориентированными, если (е2, ¦ ¦ ., еп) — базис в R", а ег направ*
лен в полупространство R". Клетки аг и а'' коге-
когерентно ориентированы, если они содержатся соответ-
соответственно в нек-рых когерентно ориентированных полу-
полупространстве и подпространстве.
Лит.: [1] Александров П.С, Введение в гомологи-
гомологическую теорию размерности и общую комбинаторную тополо-
топологию, М., 1975; [2] Хилтон П.-Д ж., У а й л и С, Теория
гомологии. Введение в алгебраическую топологию, пер. с англ.t
М., 1966; [3] Д о л ь д А., Лекции по алгебраической тополо-
топологии, пер. с англ., М., 1976. М. И. Войцеховский.
ИНЦИДЕНТНОСТИ СИСТЕМА — совокупность
S=(A, SB, /) двух множеств А и 53 с отношением ин-
инцидентности / между их элементами, к-рое записы-
записывается как а1В для а?А, В ?23; в этом случае говорят,
что элемент а инцидентен элементу В, или В инциден-
инцидентен а. Понятие «И. с.» вводится с целью использова-
использования геометрич. языка при рассмотрении общих ком-
комбинаторных проблем существования и построения;
при этом отношению инцидентности предписываются
нек-рые свойства, приводящие к тем или иным комби-
комбинаторным конфигурациям.
Примером используемых в комбинаторике И. с.
служат (конечные) геометрии: элементы (конечных)
множеств А и SB наз. соответственно точками и пря-
прямыми, а отношению / предписываются свойства, обыч-
обычные в теории проективных или аффинных геометрий.
Другим характерным примером И. с. являются блок-
схемы, к-рые получаются, если потребовать, чтобы:
1) каждый элемент а?А был инцидентен в точности
г элементам из SB, 2) каждый элемент fi?SB был ин-
инцидентен в точности к элементам из А; 3) каждая пара
{а, а' } различных элементов из А была инцидентна
в точности Я элементам из 23- Часто в качестве 23 бе-
берется нек-рое множество подмножеств множества А,
тогда а1В есть не что иное, как а?В.
И. с. S = (A, 23, /) и S' = (A', 93', /') наз. изо-
изоморфны м и, если существуют такие взаимно одно-
однозначные соответствия а : А+-+А' и р1 : SB<-»5B', что
а1В ФФ (ал) Г фВ).
Если А={а, я2, ...} и 23=16!, В2, ...} —конечные
множества, то удобно описывать свойства И. с. S с по-
помощью матрицы инцидентности Ца^Ц,
где а,-у=1, когда aj?B{ и a.ij=O — в противном слу-
случае; матрица ||a,yl| определя.ет И. с. S с точностью до
изоморфизма.
Лит.: Н] Холл М., Комбинаторика, пер. с англ., М.
1970; [2] Dembowski P., Finite Geometries, В.—N.Y.,
1968. В. Е. Тараканов.
ИНЦИДЕНТНОСТЬ — геометрический термин, упо-
употребляемый для обозначения (?) отношения принад-
принадлежности (связи, соединения) между основными объек-
объектами геометрии: точками, прямыми, плоскостями.
Свойства И. характеризуются так наз. аксиомами
принадлежности (см., например, Гильберта система
аксиом). А. Б. Иванов.
ИНЪЕКТИВНЫЙ МОДУЛЬ — инъективный объект
в категории модулей над кольцом R, т. е. такой Л-
модуль Е над ассоциативным кольцом R с единицей,
что для любых Л-модулей М, N, для любого мономор-
мономорфизма i : N—*M и для любого гомоморфизма / : N—*E
найдется такой гомоморфизм g : М-*Е, что диаграмма
коммутативна (все Л-модули пред-
предполагаются правыми). Следующие ы
условия на Л-модуль Е равносиль-
равносильны его инъективности: 1) для лю-
любой точной последовательности
0 _» N ->M->L-> О
индуцированная последовательность
0—>HomR(N, Е) —*liomR(M, Е) —*¦ Hom# (L, Е)—*-0
точна; 2) любая точная последовательность Л-модулей,
имеющая вид *
расщепляется, т. е. подмодуль Im a=Ker P выделяется
в М прямым слагаемым; 3) Ext# (С, Е)=0 для всех
Л-модулей С; 4) для всякого правого идеала / кольца R
любой гомоморфизм Л-модулей / : /->¦? может быть
продолжен до гомоморфизма Л-модулей g : R-+E (к р и-
терий Бэра).
В категории Д-модулей «достаточно много» инъек-
тивных объектов: каждый Д-модуль М можно вложить
в И. м. Более того, каждый модуль М содержится
в своей инъективной оболочке Е(М),
то есть в И. м. Е(М), каждый ненулевой подмодуль
к-рого имеет ненулевое пересечение с М. Любое вло-
вложение модуля М в И. м. Е продолжается до вложения
инъективной оболочки Е(М) в Е. Каждый Л-модуль М
обладает инъективной резольвентой
О —>- М —>- Eq ¦—> Ei —>- ... —>- Еп —> ...,
т. е. точной последовательностью модулей, в к-рой
все модули Ei, i^O, инъективны. Длина самой корот-
короткой инъективной резольвенты наз. инъективной
размерностью модуля (см. также Гомологи-
Гомологическая размерность).
Прямое произведение И. м. есть И. м. Инъективный
модуль Е равен Ег для любого элемента г ? Л, не являю-
являющегося левым делителем нуля в Л, т. е. И. м.— де-
делимый модуль. В частности, абелева группа является
И.м. над кольцом % тогда и только тогда, когда она
делимая. Над коммутативным нётеровым кольцом 1{
каждый И. м.— прямая сумма инъективных оболочек
модулей вида R/P, где Р — простой идеал кольца R.
И. м. широко используются при описании различ-
различных классов колец (см. Гомологическая классификация
колец). Так, все модули над кольцом инъективны
тогда и только тогда, когда кольцо классически полу-
полупросто. Равносильны условия: Л — нётерово справа
кольцо; любая прямая сумма инъективных Л-модулей
инъективна; любой инъективный Л-модуль разлагается
в прямую сумму неразложимых Л-модулей. Артино-
вость справа кольца Л равносильна тому, что каждый
И. м. является прямой суммой инъективных оболочек
простых модулей. Наследственность справа кольца
равносильна инъективности всех фактормодулеи инъек-
инъективных Л-модулей, а также тому, что сумма двух инъек-
инъективных подмодулей в произвольном Л-модуле инъек-
инъективна. Если кольцо Л наследственно справа и нётерово
справа, то каждый Л-модуль содержит наибольший
инъективный подмодуль. Проективность (инъектив-
ность) всех инъективных (проективных) Л-модулей
эквивалентна тому, что Л является квазифробениусо-
вым кольцом.
Инъективная оболочка модуля Д# играет важную
роль в теории колец частных. Напр., если правый
сингулярный идеал кольца Л равен нулю, Е — инъек-
инъективная оболочка модуля RR, А=Нот#(Е, E) — ее
кольцо эндоморфизмов, то Л-модули Ад и Er изо-
изоморфны, Е является кольцом, изоморфным кольцу Л,
и это кольцо оказывается максимальным правым
кольцом частных кольца Л, причем А.~Е — само-
инъективное справа регулярное (в смысле Неймана)
кольцо.
В связи с различными задачами продолжения гомо-
гомоморфизмов модулей рассматриваются классы модулей
М, близких к инъективным: квазиинъектив-
н ы е (если 0-+N—>М и / : N—*M, то / продолжается
до эндоморфизма модуля М); псевдоинъек-
т и в н ы е (если О—>JV—*M, f : N-+M и / — моно-
мономорфизм, то / продолжается до эндоморфизма модуля
М); малоинъективные (все эндоморфизмы
подмодулей продолжаются до эндоморфизмов модуля
М). Квазиинъективность модуля М равносильна ин-
инвариантности модуля М в своей инъективной оболочке
относительно ее эндоморфизмов.
Лит.: [1] Картав А., Эйленберг С, Гомологи-
Гомологическая алгебра, пер. с англ., М., 1960; [2] Маклейн С,
Гомология, пер. с англ., М., 1966; [3] Faith С, Lectures
on inlective modules and quotient rings, B.—Hdlb.—N.Y.,
1967; [4] Sharpe D. W., Vamos P., Injective modules,
Camb., 1972. А. В. Михалев, А. А. Тугапбаев.
ИНЪЕКТИВНЫЙ ОБЪЕКТ — такой объект / абе-
левой категории С, что для каждого мономорфизма
а : А' -+А отображение
Ноте (А, -0—>-Нотс(^', /), где (pi—*¦ (р°сс
является сюръективным. Всяких! инъективный под-
объект / объекта А выделяется прямым слагаемым.
Произведение И. о. — всегда И. о. В случае, когда
каждый объект в С изоморфен подобъекту нек-рого
И. о. категории С, говорят, что С — категория
с достаточно многими инъектив-
инъективными объектами (такова, напр., категория
Гротепдика). В этих категориях объект инъективен
тогда и только тогда, когда он выделяется прямым
слагаемым из любого объекта, его содержащего. Для
объектов таких категорий можно строить резольвенты,
состоящие из И.о. (инъективные резоль-
резольвенты), что позволяет развивать в этих категориях
гомологическую алгебру.
В локально нётеровых категориях (см. Топологизи-
рованиая категория) прямая сумма И. о. является И. о.,
а каждый И. о. изоморфен прямой сумме неразложи-
неразложимых И.о. и это представление однозначно [3]. Если
С — категория модулей над нётеровым коммутатив-
коммутативным кольцом Л, то неразложимые инъективные модули
суть инъективные оболочки полей частных факторко-
лец А/р, где ? — произвольный простой идеал в Л [4].
Примеры: 1) Категория абелевых групп имеет
достаточно много И. о. Таковыми объектами являются
полные (делимые) группы.
2) Категория Сл правых Л-модулей содержит до-
достаточно много И. о. (см. Инъективнай модуль).
3) Категория пучков модулей на окольцованном то-
пологич. пространстве (X, Ох) содержит достаточно
много И. о. Примерами таких И. о. служат пучки F,
все слои к-рых Fх являются инъективными Ох, х-
модулями. В случае, когда (X, Ох) есть схема, для
квазикогерентных Ох, ^-модулей верно и обратное
утверждение: всякий И. о. есть пучок, все слои к-рого
являются инъективными Ох, л-модулями.
Лит.: [1] Б у к у р И., Деляну А., Введение в теорию
категорий и функторов, пер. с англ., М., 1972; L2] Г р о т е н-
д и к А., О некоторых вопросах гомологической алгебры, пер.
с франц. М., 1961; ГЗ] Gabriel P., «Bull. Soc. Math. France»,
1962, t. 90, p. 323—448; [4] M a t 1 i s E., «Pacific J. Math.»,
1958, v. 8, p. 511—28. И. В. Долгачев.
ИНЪЕКЦИЯ, инъективное отображе-
отображение, множества А в множество В — отображение
f : А—*В, при к-ром различные элементы из А имеют
различные образы в В. И. наз. также взаимно
однозначным отображением множества
А в множество В, или вложением.
О. А. Иванова.
ИОАХИМСТАЛЯ ПОВЕРХНОСТЬ — поверхность,
образованная ортогональными траекториями однопара-
метрического семейства сфер с центрами на одной
прямой. Если за эту прямую принять ось z, аппликату
центра сферы обозначить через и, а радиус сферы —
через R = R(u), то радиус-вектор И. п. есть:
j R cos v R sin и . D ., \
r~\—г—i —п—i и 4-R tax i ,
\ ch т ' ch x ' ' J '
где
Одно из семейств линий кривизны (v= const) И. п.
расположено в плоскостях одного пучка. Изучена
Ф. Иоахимсталем [1].
Лит.: [1] Joachimsthal P., «J. reine und angew.
Math.», 1846, Bd 30, S. 347—50. И. Х. Сабитов.
ИРРАЦИОНАЛЬНОЕ ЧИСЛО — число, не являю-
являющееся рациональным (т. е. целым или дробным) чис-
числом. Геометрически И. ч. выражает собой длину от-
резка, несоизмеримого с отрезком единичной длины.
О существовании несоизмеримых отрезков знали уже
древние математики: им была известна, напр., несоиз-
несоизмеримость диагонали и стороны квадрата, что равно-
равносильно иррациональности числа У2.
Всякое действительное число может быть записано
бесконечной десятичной дробью, при этом И. ч. и
только они записываются непериодическими десятич-
десятичными дробями, напр. 1^2=1,41..., я=3,14... . И. ч.
определяют сечения (см. Дедекиндово сечение) в мно-
множестве рациональных чисел, у к-рых в нижнем классе
нет наибольшего, а в верхнем нет наименьшего числа.
Множество И. ч. всюду плотно на числовой прямой:
между любыми двумя числами имеется И. ч. Множество
И. ч. несчетно, является множеством второй категории
и имеет тип Об ¦
Иррациональные алгебраические
числа (в отличие от трансцендентных чисел) не
допускают аппроксимаций любого порядка рацио-
рациональными дробями. Точнее, для всякого иррациональ-
иррационального алгебраического числа степени п числа \ сущест-
существует такое с>0, что при любых целых р и q (?>0)
выполняется неравенство
Квадратичные иррациональности и только они изоб-
изображаются периодическими цепными дробями.
Л. Д. Кудрявцев.
ИРРАЦИОНАЛЬНОСТИ МЕРА действитель-
действительного числа Ъ, — функция
L&, H)=mm\h1l + h0\, -
где минимум берется по всевозможным парам ft0, hx
целых рациональных чисел таких, что
|*о 1<#, |М<Я. l*ol + IM?*0.
Понятие И. м. является частным случаем понятий
линейной независимости меры и трансцендентности
меры. И. м. показывает, насколько «хорошо» может
число | быть приближено рациональными дробями. Для
всех действительных иррациональных чисел ? выпол-
выполняется неравенство
L&, Н) <-^гН-\
но при любом е>0 для почти всех (в смысле меры Ле-
Лебега) действительных \
Щ, Н) > СН~1-г,
где С = С(в, 5)>0. Однако для любой функции ц>(Н)—>0
при Н—юо и ф(/Г)>0 существует число ?ф такое, что
при всех Н^\
0 < L (?ф, И)< Ф (Н).
Лит.: [1] Хин чин А. Я., Цепные дроби, 3 изд., М. 1978.
А. И. Галочкии.
ИРРЕГУЛЯРНАЯ ГРАНИЧНАЯ ТОЧКА — точка
i/o границы Г области D, для к-рой существует такая
непрерывная граничная функция f(y) на Г, что обоб-
обобщенное решение Дирихле задачи в смысле Винера —
Перрона (см. Перрона метод) и{х) не принимает в точке
у0 граничного значения fd/q), т. е. либо предел
lim и (х)
?
не существует, либо не совпадает с /(j/0)- Для плоских
областей D И. г. т. является всякая изолированная
точка границы Г. В случае области D в евклидовом
пространстве R", и^З, А. Лебег (Н. Lebesgue, 1912)
впервые обнаружил, что И. г. т. может быть вершина
весьма заостренного входящего в D острия. Напр.,
И. г. т. является начало координат O?R.3, если в его
окрестности граница области имеет вид входящего
острия, получаемого вращением кривой у—е~1'х ,
х>0, вокруг положительной полуоси Ох (острие
Лебега). Обобщенное решение задачи Дирихле не
принимает в И. г. т. граничного значения }(у0) в том
случае, если f(y0) является верхней или нижней гранью
значений f(y) на Г; при этом классическое решение
не существует. Множество И. г. т. в определенном
смысле разреженное, оно имеет тип Fa, является по-
полярным множеством и имеет нулевую емкость.
См. также Барьер, Регулярная граничная точка.
Лит.: [1] Л а н д к о ф Н. С, Основы современной теории
потенциала, М., 1966; [2] Брело М., Основы классической
теории потенциала, пер. с франц., М., 1964. Е. Д. Соломенцев.
ИРРЕГУЛЯРНАЯ ОСОБАЯ ТОЧКА — понятие, воз-
возникающее в аналитич. теории линейных дифференци-
дифференциальных уравнений. Пусть (гаХ га)-матрица A (t) голо-
голоморфна в проколотой окрестности точки t0~t=oo и име-
имеет особенность в точке ?0; точка ?0 наз. тогда особой
точкой системы
x = A(t)x. (*)
Существует два неэквивалентных определения И. о. т.
Согласно первому определению, точка t0 наз. И. о. т.
системы (*), если A (t) имеет в точке t0 полюс по-
порядка выше первого (см. Аналитическая теория диф-
дифференциальных уравнений, а также [2]). Согласно
второму определению, точка t0 наз. И. о. т. системы
(*), если не существует такого числа ст>0, что каж-
каждое решение x(t) растет не быстрее \t—to\~° при t—>t0
по лучам (см. [3]). Случай t0=oo сводится к случаю
?0=0 с заменой t-^-t~1. И. о. т. наз. иногда сильно
особой точкой (см., напр., Бесселя уравнение).
В окрестности И. о. т. решения допускают асимптотич.
разложения, изученные впервые А. Пуанкаре [1].
Лит.: [1] Poincare H., «Acta math.», 1886, v. 8,
p. 295—344; [2] В а з о в В., Асимптотические разложения
решений дифференциальных уравнений, пер. с англ., М., 1968;
[3] Коддингтон Э. А., Левинсон Н., Теория
обыкновенных дифференциальных уравнений, пер. с англ.,
М., 1958. Ю. С. Илъяшенко.
ИРРЕГУЛЯРНОЕ ПРОСТОЕ ЧИСЛО — простое не-
нечетное число р, для к-рого число классов идеалов
кругового поля R (e2jI1//p) делится на р. Все остальные
простые нечетные числа наз. регулярными.
Признак Кум мера позволяет для каждого
данного простого числа решить вопрос о том, будет ли
оно регулярным или нет: для того чтобы нечетное
простое число р было регулярным, необходимо и доста-
достаточно, чтобы ни один из числителей первых 2^ Бер-
нулли чисел В2, Bit . .., В^_3 не делился на р (см. [1]).
В связи с этим результатом возник вопрос о распре-
распределении регулярных и иррегулярных чисел. Таб-
Таблицы бернуллиевых чисел и признак Куммера пока-
показывают, что в пределах первой сотни только три про-
простых числа: 37,59 и 67 — иррегулярны (числители В32,
B4i и 558—кратны соответственно 37, 59 и 67). Э. Кум-
мер предположил, что регулярных чисел в среднем
в два раза больше, чем иррегулярных. Позднее К. Зи-
гель [2] выдвинул предположение, состоявшее в том,
что отношение числа И. п. ч. к4 числу регулярных
простых чисел, содержащихся в промежутке A, х),
при х—юо стремится к пределу уе—1, где е — основа-
основание натуральных логарифмов. К настоящему времени
A978) известно только, что число И. п. ч. бесконечно
и что среди нечетных простых чисел, меньших 5500,
имеется 439 регулярных и 285 И. п. ч. [3].
Для всякого регулярного р уравнение Ферма
не имеет ненулевых решений в рациональных числах [1].
Пусть р — некоторое И. п. ч., 2ах, ..., 2а^.— ин-
индексы бернуллиевых чисел из В2, 54, ..., Вр-3, числи-
числители к-рых делятся на р, а к и t — натуральные числа
такие, что q=i-\-pk — простое, меньшее р (р — 1) и
tft^l (mod q). И пусть
D = 4 т-т(Р-1)/2 ^ftr_jjrp-l -2а_
Если для каждого а=а,-, г=1, 2, . . ., s,
-D&s^l (mod?),
то для иррегулярного простого р справедлива теорема
Ферма, т. е. уравнение Ферма неразрешимо в рацио-
рациональных числах, отличных от 0. Этот признак наз.
признаком Ванд и вер а. С помощью этого
признака установлена справедливость теоремы Ферма
для всех показателей, меньших 5500 (см. [4]).
Лит.: [1] К u m m e r E. E., «J. reine und angew. Math.»,
1850, Bd 40, S. 130—38; [2] Siegel C. Z., «Nachr. Akad.
Wiss. Gottingen. Math.-Phys. Kl.», 1904, S. 5 1 — 57; [3] Б o-
ревич З. И., Шафаревич И. Р., Теория чисел, 2 изд.,
М., 1972; [4] Vandiver H. S., «Proc. Nat. Acad.», 1954,
v. 40, № 8, p. 732—35. В. А. Демьяненко.
ИРРЕГУЛЯРНОСТЬ — численный инвариант неосо-
неособого проектного алгебраич. многообразия, равный
размерности его Пикара многообразия. В случае,
когда основное поле имеет характеристику нуль (или,
более общо, если схема Пикара многообразия X при-
приведена), И. совпадает с размерностью пространства
#Х(Х, Ох) первых когомологий с коэффициентами
в структурном пучке.
Многообразия с ненулевой И. наз. иррегуляр-
иррегулярными, а многообразия с нулевой И.— регуляр-
н ы м и. Иногда для полной линейной системы \D\
на многообразии X ?-й иррегулярностью
системы \D\ наз. число
o-''(?>) = dimtf' (X, OX(D)),
где l«:i«:dim X.
Лит.: [1] Бальдассарри М., Алгебраические много-
многообразия, пер. с англ., М., 1961; [2] М а м ф о р д Д., Лекции
о кривых на алгебраической поверхности, пер. с англ., М.,
1968. И. В. Долгачее.
ИСКАЖЕНИЯ ТЕОРЕМЫ при конформ-
конформных отображениях плоских облас-
областей — теоремы, характеризующие искажение линей-
линейных элементов в данной точке области, а также иска-
искажение области и ее подмножеств, и искажение границы
области при конформном отображении. К И. т. в пер-
первую очередь относятся оценки модуля производной
функции в данной точке области. Так, И. т. в классе
2 функций
F (?)= ^
мероморфных и однолистных в области |?|>1, состоит
в утверждении, что при любом ?0, 1<|?0|<оо, имеют
место точные неравенства
Равенство в левой части A) имеет место только для
функции
а в правой части — только для функции
где сс0 и ро— произвольные фиксированные числа.
Функция w=F1{^) отображает область |?!>1 на плос-
плоскость w с разрезом по отрезку, соединяющему точки
cc0—2 -tVh oc0+2 -p- ,a функция w~F2 (?) отображает
область | ?| >1 на плоскость w с разрезом по дуге ок-
окружности \w—Pol = 1 Sol со средней точкой |30—?„.
Неравенства A) легко получаются из неравен-
неравенства Грунского
определяющего область значений функционала In F'(Zo)
на классе 2. С другой стороны, неравенства A) явля-
являются прямым следствием теоремы Голузина:
если ./?(?) ?2, то для любых точек ^ и ?2, j ?tI = J g2f=p,
1<р<оо, справедливо точное неравенство
B)
причем знак равенства имеет место для функции F(t,)—
= ?+eta/?, где а — действительная постоянная. Из
неравенства B) следует также теорема иска-
искажения хорд (см. [1]): если функция F(?)?2, то
для любых точек ^ и ?2 на окружности |?|1
справедливо точное неравенство
при этом знак равенства имеет место только для функ-
функции
где С — постоянная, ф= — (arg $x+arg $2). Известны
различные обобщения неравенства B), определяющие
области значений соответствующих функционалов и
составляющие усиления И. т. в классе 2 и его под-
подклассах (см., напр., [1]).
В классе S функций
регулярных и однолистных в круге \z\ <1, при 0<|z0| <1
справедливы следующие точные неравенства:
1—1
1 + 1 г„ |
1-1 z.l
Оценки D) и E) следуют из оценок C). Совокупность
неравенств C) — E) наз. И. т. в классе S. Нижние
границы в оценках C) — E) реализуются только
функцией
верхние границы — только функцией
где a=argz0. Функции w=fa(z), 0<а<2я, известные
как функции Кёбе, отображают круг \z\ <1
на плоскость w с разрезом но лучу arg w=a, |ш|>1/4,
и являются экстремальными в ряде задач теории одно-
однолистных функций. Имеет место теорема Кёбе
об V4: область, являющаяся образом круга |г|<1
при отображении w=f(z), f(z)?S, всегда содержит
круг |w|<V4, причем точка шо= — е1а принадлежит
границе этой области только для функции f(z)=fa(z).
Оценки C) — E) являются простыми следствиями
результатов об областях значений функционалов
на классе S (см. [2]).
Пусть 20— класс функций F(t,)?I., 7?(?)^=0 при
1<1?1<°о. Имеет место следующая связь между
функциями классов 5 и 20: если /(z)?S, то F(Z,) =
Т7Г) €2о. и обратно, если 7?(?) g 20, to/(z)=1
=77Т7Г) 7^
Поэтому область значений к.-л. функционала (или
системы функционалов) на классе S определяет об-
область значений соответствующего функционала (или
системы функционалов) на классе 20, и обратно.
Напр., из области значений функционала In ,
0<|z0|<l, на классе S легко получается область зна-
значений функционала In * , 1<|?0[ <оо, на классе 20.
Для функций, регулярных и ограниченных в круге,
примерами И. т. являются Шварца лемма (см. [1]) и
ее обобщения, а также следующая теорема Лёв-
нера о граничном искажении: для
функции ф(г), регулярной в круге |z|<l, ф@) = 0
|ф(г)|<1 в |г|<1 и |ф(г)| = 1 на дуге А окружность.
|z| = l, длина образа дуги А не меньше длины самой
дуги .4 , и равенство длин этих дуг имеет место только
для функции q>(z) = elaz, где а — действительное число.
В классе функций, однолистных в данной много-
многосвязной области, минимум (соответственно максимум)
модуля производной функции в данной точке области
реализуется только отображениями этой области на
область с радиальными (соответственно с концентри-
концентрическими круговыми) разрезами. Для случая неограни-
неограниченных отображений имеет место следующая теорема.
Пусть D — конечносвязная область плоскости ?, со-
содержащая бесконечно удаленную точку, 2 (D) — класс
функций F(?,), однолистных в D и имеющих в окрест-
окрестности ?= оо разложение
F (?)^?-|-ао+.2!.+ ...,
?0^оо — точка области D. Пусть Fed), Fe(?,0) ()>
есть функция класса 2 (D), отображающая D на плос-
плоскость с разрезами по дугам логарифмич. спиралей,
образующих угол 8 с лучами, выходящими из начала
(достаточно считать —я/2<:6<:я/2; при 8=0 логариф-
логарифмич. спираль вырождается в луч, выходящий из на-
начала, а при 8=±л/2 — в окружность с центром в на-
начале),
p(S) = K^o(S)^/2(S). «(С) = 1^0 (?)/*"„/, E),
где ветви корней выбраны так, что коэффициенты при
? в разложениях Лорана функций р{?) и q(t) в окрест-
окрестности ?= оо равны 1. Тогда область значений функцио-
функционала In F'(t,0) на классе 2 (D) представляет собой круг,
определяемый неравенством:
причем каждой точке границы этого круга соответст-
соответствует только функция F(?,)=Fe(QJrC с надлежащим 0,
С — постоянная. В частности, справедливы точные
неравенства:
К (?о) I <; I ^'(So) I < кя/2 (So) |,
Лит.: [1] Го л у зин Г. М., Геометрическая теория
функций комплексного переменного, 2 изд., М., 1966; [2]
Дженкинс Д. А., Однолистные функции и конфор-
конформные отображения, пер. с англ., М., 1962; [3] Ч е р н и-
к о в В. В., в кн.: Итоги исследований по математике и меха-
нике за 50 лет. 1917—1967, Томск, 1967, с. 23—51; [4] Баз и-
л е в и ч И. Е., в кн.: «Математика в СССР за 40 лет», М.,
1959, с. 444—72; [5] Белинский П. П., Общие свойства
квазиконформных отображений, Новосиб., 1974; [б] Kiili-
nau R., «Math. Nachr.», 1971, Bd 48, S. 77 — 105.
E. Г. Голузина.
ИСКЛЮЧЕНИЯ ТЕОРИЯ — теория исключения не-
неизвестных из системы алгебраич. уравнений. Более
точно, пусть имеется система уравнений
/,¦(*!, ..., х„) = 0, i = l, ..., то, A)
где /,- — многочлены с коэффициентами из заданного
поля Р. Задача исключения неизвестных xlt ..., х^
из системы A) (неоднородная задача тео-
теории исключения) может быть сформулиро-
сформулирована следующим образом; найти проекцию множества
решений системы A) на пространство координат
хь+1, ..., хп. В том случае, когда каждое из уравне-
уравнений однородно по совокупности неизвестных хл, . . ., х^,
рассматривается также однородная зада-
задача теории исключения (неоднородная за-
задача в этом случае тривиальна): найти проекцию на
пространство координат г^+1, ..., хп множества тех
решений системы A), в к-рых не все неизвестные хг,
..., Xk равны нулю.
Неоднородная задача И. т. может также тракто-
трактоваться как нахождение условий на коэффициенты си-
системы алгебраич. уравнений, при к-рых эта система
совместна, а однородная задача И. т.— как нахожде-
нахождение условий на коэффициенты системы однородных
алгебраич. уравнений, при к-рых эта система имеет
ненулевое решение.
Основные результаты И. т. заключаются в том, что
если поле Р алгебраически замкнуто, то решение одно-
однородной задачи И. т. является алгебраическим
множеством, т. е. множеством решений системы
алгебраич. уравнений, а решение неоднородной за-
задачи — конструктивным множеством
в смысле алгебраич. геометрии, т. е. конечным объеди-
объединением множеств вида M\N, где М и N суть алгеб-
алгебраич. множества. В нек-рых простейших случаях ре-
решение задач И. т. известно в явном виде.
1) Пусть рассматриваемая система уравнений ли-
линейна и однородна относительно xlt . .., х^, т. е. имеет
вид
где ац — многочлены от х^ + ], . . ., хп. При заданных
значениях хь+1, ..., хп система B) имеет ненулевое ре-
решение тогда и только тогда, когда ранг матрицы A = (а,-у)
меньше к (см. Линейное уравнение). Решением однород-
однородной задачи И. т. в этом случае будет множество в про-
пространстве координат xk+i, ..., хп, выделяемое усло-
условиями равенства нулю всех миноров порядка к мат-
матрицы А.
2) Пусть рассматриваемая система уравнений линейна
относительно х1,..., х^, т. е. имеет вид
где я,у, Ъ, — многочлены от х^ + 1, . . ., хп. Пусть А —
матрица, получаемая приписыванием к матрице А —
= (я,у) столбца (Ь;). При заданных значениях хь+i, ...,
хп система C) совместна тогда и только тогда, когда
ранг матрицы А равен рангу матрицы А. Следователь-
Следовательно, результатом исключения хх, ..., хп из системы C)
является
где Мг — множество точек (xk + i, ¦ ¦ ., хп), в к-рых
гкА <г, а Nг — множество точек, в к-рых гкА <г (мно-
(множества Мг и Nг алгебраические).
3) Пусть &=2, поле Р алгебраически замкнуто и рас-
рассматриваемая система состоит из двух уравнений,
однородных по х1, хг:
аох? + а1х1~1х2 + ... + апх" = О, ,,
D)
+ ЪТО
где я0, аг, . .., ап, Ьо, Ъ1,. .., Ът — многочлены от х3, ...,
хп- При заданных значениях хя, . . ., хп система D)
имеет ненулевое решение тогда и только тогда, когда
равен нулю результант
R (я0, аъ ..., ап; b0, bi ..., Ът) =
а0 аг ... а„_1 ап
а-й а„_!
do п\
bo bi ... Ът_х Ът
Ъп bm-i
строк
п строк
Это и дает решение однородной задачи И. т. в рассмат-
рассматриваемом случае.
4) Пусть А=1, поле Р алгебраически замкнуто и
рассматриваемая система состоит из двух уравнений:
¦..+*„,= о,
где а0, aj, . . ., ап> Ьо> Ь17 . . ., 6т — многочлены от х2, ...,
хп. При заданных значениях х2,. .., хп, не обращающих-
обращающихся в нуль а0 или 60, система E) совместна тогда и только
тогда, когда
R (а0, аъ ..., ап; Ьо, 61? .... Ьт)=0.
Если же ао=Ьо=О, то следует рассмотреть
R (aj, ..., а„; Ьх, ..., Ьт)
и т. д. Это позволяет описать в явном виде результат
исключения хх из системы E).
Исключение неизвестных из произвольной системы
алгебраич. уравнений может быть проведено последо-
последовательно (т. е. исключается сначала одно неизвестное,
затем другое и т. д.) при помощи описываемых ниже
«элементарных преобразований». Поскольку после иск-
исключения одного неизвестного получается, вообще гово-
говоря, не алгебраическое, но конструктивное множество,
то следует рассмотреть задачу проектирования на
пространство координат х2, . . ., хп произвольного кон-
конструктивного множества в Рп.
Всякое конструктивное множество ХаРп может
быть представлено как объединение множеств решений
совокупности систем алгебраич. уравнений и неравенств.
(Под алгебраич. неравенством здесь понимается нера-
неравенство вида f(xx, . . ., хп)ф0, где / — многочлен.) Эле-
Элементарным преобразованием такой совокупности наз.
преобразование одного из следующих типов: в одной
из систем к одному из уравнений прибавляется другое,
умноженное на многочлен; в системе, содержащей не-
неравенство /#0, одно из уравнений умножается на /;
в одной из систем к одному из неравенств прибавляется
одно из уравнений, умноженное на многочлен; одна из
систем заменяется на две, получаемые из нее приписы-
приписыванием уравнения /=0 и неравенства 7V=0 соответствен-
соответственно (/ — нек-рый многочлен); в одной из систем два
неравенства заменяются их произведением.
Элементарные преобразования не изменяют объедине-
объединения множеств решений систем, входящих в данную
совокупность. Применяя элементарные преобразования,
можно привести любую совокупность систем алгебраич.
уравнений и неравенств с неизвестными х±, ..., хп к
такому виду, когда в каждую из систем входит не
более одного уравнения или неравенства, содержащего
zj, причем наряду с таким уравнением /=0 или неравен-
неравенством /=^0 в эту же систему входит неравенство /0=^0,
где /„ — многочлен от х2, . .., хп, являющийся старшим
коэффициентом в разложении / по степеням жх. Если
поле Р алгебраически замкнуто, то, отбросив в системах
полученной совокупности уравнения и неравенства,
содержащие ж1, получают совокупность систем алгебра-
алгебраич. уравнений и неравенств с неизвестными х2, ..., хп,
к-рая и задает проекцию множества X на пространство
координат х2, . . ., хп.
Последовательное исключение неизвестных с помо-
помощью элементарных преобразований позволяет в прин-
принципе свести решение произвольной системы алгебраич.
уравнений с п неизвестными к решению ряда алгебраич.
уравнений с одним неизвестным.
Лит.: [1] X о д ж В., Пидо Д., Метод алгебраической
геометрии, пер. с англ., т. 1, М., 1954; [2] Ван-дер-Вар-
ден Б. Л., Алгебра, пер. с нем., М., 1976. Э. Б. Винберг.
ИСКЛЮЧЕННОГО ТРЕТЬЕГО ЗАКОН — закон
классической логики, состоящий в том, что одно из двух
высказываний «Л» и «не А» является истинным. В мате-
математической логике И. т. з. выражается формулой А V ~\А,
где v — знак дизъюнкции, ~~| — знак отрицания.
С интуиционистской (конструктивной) точки зрения
установление истинности высказывания вида А V "]А
означает установление истинности А или истинности
~]А. Поскольку не существует общего метода, позво-
позволяющего для каждого высказывания за конечное число
шагов установить его истинность или истинность его
отрицания, И. т. з. подвергается критике со стороны
представителей интуиционистского и конструктивного
направлений в основаниях математики (см. Интуици-
Интуиционизм, Конструктивная математика). В. Е. Плиско.
ИСКЛЮЧИТЕЛЬНОЕ АНАЛИТИЧЕСКОЕ МНОЖЕ-
МНОЖЕСТВО — аналитич. множество А в комплексном про-
пространстве X, допускающем такое аналитич. отображе-
отображение / : X—yY, что f(A)=y — точка комплексного про-
пространства Y, а/ : X\A-^>-Y\{y} — аналитич. изомор-
изоморфизм. Модификация / наз. стягиванием мно-
множества А в точку у.
Задача о характеризации исключительных множеств
возникла в алгебраич. геометрии в связи с изучением
бирационалъных преобразований (см. также Исключи-
Исключительное подмногообразие). В аналитич. геометрии найде-
найдены весьма общие критерии исключительности множества.
А именно, пусть А — связное компактное аналитич.
множество положительной размерности в комплексном
пространстве X. Множество А исключительно тогда и
только тогда, когда оно обладает в X относительно
компактной псевдовыпуклой окрестностью, в к-рой А
является максимальным компактным аналитич. под-
подмножеством. Пусть ЭД1 — когерентный пучок идеалов,
множество нулей к-рого совпадает с Л и пусть N—
ограничение на А двойственного к 9Л линейного про-
пространства над X (см. Векторное аналитическое расслое-
расслоение). Для исключительности множества А достаточно,
чтобы N было слабо отрицательным (см. Положительное
расслоение). Если X — многообразие, а Л — его под-
подмногообразие, то N — это нормальное расслоение над
X. В нек-рых случаях слабая отрицательность расслое-
расслоения N является и необходимой (напр., если А — под-
подмногообразие коразмерности 1, изоморфное Р*(С), или
если X — двумерное многообразие). В частности, кри-
кривая А на комплексной поверхности X исключительна
тогда и только тогда, когда матрица {A(Aj) пересечений
ее неприводимых компонент отрицательно определена
(см. [1], [2]). Строение окрестности И. а. м. AczX пол-
полностью определяется окольцованным пространством
(А, C-ХУЗЛ Ща) при достаточно большом jj,. И. а. м.
обладают следующим свойством транзитивности: если
ВаА — компактные аналитич. пространства в X,
причем В исключительно в А, а. А — в X, то В исклю-
исключительно в X. Существует относительное обобщение
понятия И. а. м., рассматривающее, грубо говоря,
одновременное стягивание семейства аналитич. мно-
жзств в аналитич. семействе комплексных пространств.
Здесь также справедлив критерий, аналогичный сфор-
сформулированному выше критерию Грауэрта (см. [2]).
Другое естественное обобщение понятия И. а. м. со-
состоит в следующем. Пусть А — подпространство в
X и пусть задано собственное сюръективное голоморф-
голоморфное отображение ф : А—*-В. Стягиванием про-
пространства X вдоль ср наз. такое собственное
сюръективное голоморфное отображение / : X—у У, где
У содержит В в качестве подпространства, что /|л = ср
и что / индуцирует изоморфизм X\A-*-Y\B. В случае,
когда X—многообразие, dim Х^З, А — его компактное
подмногообразие коразмерности 1, а ср — расслоение со
слоем РГ(С), г>1, необходимое и достаточное условие
стягиваемости пространства X вдоль ср на многообразие
У состоит в следующем: нормальное расслоение jV
над А (совпадающее в этом случае с расслоением, отве-
отвечающим дивизору А) должно индуцировать на каждом
слое <р-1(Ь)=Рг(С) расслоение—L, где/, определяется
гиперплоскостью в РГ(С); соответствующее стягивание
обратно к моноидальному преобразованию с центром в В
[3]. С другой стороны, для всякой модификации / : X—>-У,
где У — многообразие, B—f(A) — его подмногообразие,
dim B<dimA и /: X\A-*Y\B — изоморфизм, отобра-
отображение /U является расслоением со слоем РГ(С). Извест-
Известны критерии стягиваемости вдоль ср и в более общей си-
ситуации (см. [2]). Если А исключительно в X и является
его голоморфным ретрактом (напр., А — нулевое се-
сечение слабо отрицательного векторного расслоения),
то X допускает стягивание вдоль любого ср. Если при
этом размерности слоев ретракции Х—>А равны по край-
крайней мере dim Л+2, то по полученному после стягивания
пространству У можно полностью восстановить исход-
исходные данные [5].
Лит..: [1] Грауэрт Г., сб. пер.'. Комплексные прост-
пространства, М., 1965, с. 45—104; [2] Итоги науки. Алгебра. Топо-
Топология. Геометрия, т. 15, М., 1977, с. 93—171; [З] Pujiki A.,
N a k a n о S., «Publs Res. Inst. Math. Sci.», 1972, v. 7, № 3,
p. 637—44; [4] Итоги науки. Алгебра. Топология. Геометрия,
т. 12, М., 1974 с. 77—170;" [5] Т a k i ) i m а К., SuzukiT.,
«Trans. Amer. Math. Soc», 1976, v. 219, p. 369—77.
А. Л. Онищик.
ИСКЛЮЧИТЕЛЬНОЕ ЗНАЧЕНИЕ — понятие тео-
теории распределения значений. Пусть /(z) — мероморф-
ная во всей плоскости z функция, a n(r, а, /) означает
число ее я-точек (с учетом их кратностей) в круге |z|<r.
Согласно первой основной теореме Р. Неванлинны (см.
[1], с. 164), при г—>-оо имеет место соотношение
N (г, a, f) + m(r,a,f) = T (r, f) + О A),
где T(r, f) — характеристическая функция, не завися-
зависящая от a, N(r, а, /) — считающая функция (логариф-
(логарифмическое усреднение п(г, я, /)) ито(г, а, /)>0 — функ-
функция, отражающая среднюю близость значений / к числу
а на окружности \z\=r (см. Распределения значений тео-
теория). Для большинства значений я величины N (г, я, /)
и Т(г, /) при г—>-оо эквивалентны; число а (конечное
или бесконечное) наз. исключительным зна-
значением, если эта эквивалентность при г—>-оо наруша-
нарушается. Различают несколько типов И. з.
Число а наз. И. з. функции /в смысле Пика-
р а, если число а-точек функции / во всей плоскости
конечно (см. [1], с. 22, [2], с. 68), в частности если/(г)^а
для любого z.
Число а наз. И. з. /в смыслеВореля, если
при г—уоо функция п(г, а, /) растет в определенном
смысле медленнее функции Т(г, /) (см. [1], с. 266, [2],
с. 69).
Число а наз. И. з./в смысле Неванлинны
([1] с. 271), если его дефект (см. Дефектное значение)
Число а наз. И. з. /в смысле Валирона,
Число а, для к-рого
также наз. И. з. / (z). При этом величина C (а, /) (по-
(положительное отклонение / (z)) характеризу-
характеризует скорость асимптотического приближения / (z) к чи-
числу а (см. [3]).
Лит.: [1] Неванлинна Р., Однозначные аналитиче-
аналитические функции, пер. с нем., М.— Л., 1941; [2] Г о л ь д б е р г
А. А., Островский И. В., Распределение значений ме-
роморфных функций, М., 1970; [3] П с т р е н к о В. П., «Изв.
АН СССР. Сер. матем.», 1969, т. 33, Л» 2, с. 414 — 54.
В. П. Петре}то.
ИСКЛЮЧИТЕЛЬНОЕ ПОДМНОГООБРАЗИЕ — зам-
замкнутое подмногообразие У алгебраич. многообразия X
определенного над алгебраич. замкнутым полем, к-рое
при помощи некоторого собственного бирационального
морфнзма / : X—>-Х' может быть отображено на под-
подмногообразие У меньшей размерности и при этом / :
: X\Y ~^ X'—f(Y) — изоморфизм. Морфизм / наз.
стягиванием подмногообразия У на У=/(У);
это понятие является частным случаем понятия моди-
модификации алгебраич. пространств [3]. В случае, когда
X, Y, X' и У являются гладкими неприводимыми
многообразиями, И. п. У наз. исключитель-
исключительным подмногообразием 1-го рода.
Если И. п. Y имеет коразмерность 1 в X, то оно наз.
также исключительным дивизором.
Исключительный дивизор на алгебраич. поверхности
наз. исключительной кривой.
Понятие И. п. естественным образом распространя-
распространяется на схемы, комплексные аналитич. и алгебраич.
пространства. Соответствующий морфизм при этом
также наз. стягиванием; естественным образом
определяется понятие И. п. 1-го рода. И. п. комплексно-
комплексного аналитич. пространства наз. также исключительным
аналитич. множеством.
Характеризация И. п. внутри объемлющего много-
многообразия — одна из основных задач бирациональной гео-
геометрии. Исторически первый пример такой характери-
зации — критерий Кастельнуово — Эн-
р и к е с а: неприводимая полная кривая Y на глад-
гладкой поверхности X тогда и только тогда является И. п.
1-го рода, когда она изоморфна проективной прямой Р1
и индекс ее самопересечения (Y -Y) на X равен —1 (см.
[1], [9]). Этот критерий допускает обобщение на одно-
одномерные подсхемы двумерных регулярных схем (см.
16], [10]). Если Y=2ji=iYi — произвольная связная
полная кривая с неприводимыми компонентами У,- на
гладкой проективной поверхности X, то необходимое
(но не достаточное) условие исключительности кривой У
состоит в отрицательной определенности матрицы (У,Х
X Yj) (см. [2]). В случаях связной компактной комплекс-
комплексной кривой на гладкой комплексной поверхности и
связной полной кривой на гладком двумерном алгебра-
алгебраич. пространстве аналогичное условие является необ-
необходимым и достаточным условием исключительности.
Многомерное обобщение критерия Кастельнуово —
Энрикеса для стягивания в точку имеет следующий
вид [5]: неприводимое полное подмногообразие У в
гладком алгебраич. многообразии X тогда и только тог-
тогда является И. п. 1-го рода относительно стягивания в
точку, когда выполняются следующие два условия:
a) Y^Pr, где r=dim X—1; б) нормальное расслоение
NY/x к У в Z определяется дивизором —Я, где Н —
гиперплоскость в Рг. При этом X' проективно. Соответ-
Соответствующее стягивание / является моноидалъным преоб-
преобразованием с центром в точке /(У) (см. [7], [8]).
В аналитич. случае найдены необходимые и доста-
достаточные условия того, чтобы связное компактное комп-
комплексное подмногообразие У в комплексном многообра-
многообразии X было И. п. 1-го рода; соответствующее стягивание
/ необходимо является моноидальным преобразованием
с центром в Y'=f(Y) (см. Исключительное аналитичес-
аналитическое множество). Аналогичный критерий справедлив
для алгебраич. пространств [3]. Для алгебраич. мно-
многообразий соответствующие условия необходимы, но не
всегда достаточны.
При стягивании / : Х-*-Х' И. п. 1-го рода Y в алгеб-
алгебраич. проективном многообразии X на подмногообра-
подмногообразие ненулевой размерности У' в X' алгебраич. многооб-
многообразие А" может уже не быть проективным. Более того,
если алгебраич. многообразия X и Y определены над
полем комплексных чисел, то при аналитич. стягивании
/ И. п. 1-го рода У не в точку многообразие X' в общем
случае не является алгебраическим.
Если рассматривать вопрос о стягиваемости в точку
И. п. (не обязательно 1-го рода), то для полного связ-
связного алгебраич. подпространства У гладкого алгебраич.
пространства X достаточным (но не необходимым при
dim A>2) условием исключительности является отри-
отрицательность нормального расслоения NY,X. Аналогич-
Аналогичный факт имеет место для комплексных пространств.
В случае алгебраич. пространств наиболее общий
критерий исключительности утверждает, что в катего-
категории нётеровых алгебраич. пространств подпространство
У в X тогда и только тогда является И. п., когда фор-
формальное пополнение У в X вдоль является И. п. в ка-
категории формальных алгебраич. пространств [3]. Иными
словами, стягивание алгебраич. подпространства воз-
возможно тогда и только тогда, когда возможно его соот-
соответствующее формальное стягивание.
Лит.: [1] Алгебраические поверхности, М., 1965, «Тр. Ма-
тем. ин-та АН СССР»- [2] Ар тин М., «Математика», 1965,
т. 9, .№ 3, с. 3 — 14; [3] Art in M., «Ann. math.», 1970, v. 91,
№ 1, p. 88—135; [4] Г р а у э р т Г., в кн.: Комплексные про-
пространства, М., 1965, с. 45 —104; [5] К о d a i r а К., «Ann. math»,
1954, v. 60, p. 28—48; [6] Lichtenbaum S., «Amer.
J. math.», 1968, v. 90, J\S 2, p. 380—405; [7] N a k a n о S.
«Publs Res. Inst. Math. Sci.», 1971 V. 6, Ki 3, p. 483—502-
[8] Fujiki A., N a k a n о S., там же, 1972, v. 7, № 3,
p. 637—44; [9] Шафареаич И. Р., Основы алгебраиче-
алгебраической геометрии, М., 1972; [10] его же, Lectures on minimal
models and borational transformations of two dimensional sche-
schemes, Bombay, 1966. В. А. Псковских.
ИСПЫТАНИЕ — один из основных терминов клас-
сич. вероятностей теории. При аксиоматич. подходе
определяется как любое разбиение пространства эле-
элементарных событий на попарно непересекающиеся со-
события, к-рые наз. «исходами испытания», а элементы
порождаемой ими сг-алгебры — «событиями, связанны-
связанными с данными испытаниями». Термин «И.» употребля-
употребляется в основном в сочетаниях «повторные И.», «неза-
«независимые И.», «И., связанные в цепь Маркова».
Ю. В. Прохоров.
ИССЛЕДОВАНИЕ ОПЕРАЦИЙ — построение, раз-
разработка и приложения математич. моделей принятия
оптимальных решений. Содержанием теоретич. аспекта
И. о. являются анализ и решение математич. задач вы-
выбора в заданном множестве допустимых реше-
решений X элемента, удовлетворяющего тем или иным
критериям оптимальности и называемого оптималь-
оптимальным решением задачи. При этом иногда выби-
выбирается «обобщенный» элемент X: подмножество X или
функция со значениями в X (в том числе случайная ве-
величина со значениями в X). Такие задачи наз. опти-
оптимизационными. Прикладной аспект И. о. состо-
ит в составлении оптимизационных задач и реализации
их решений.
Постановка задачи И. о. охватывает прежде всего
формальное описание множества допустимых решений X
и критериев оптимальности выбора. Оно должно соот-
соответствовать содержательным представлениям о возмож-
возможном и целесообразном в данных условиях. Напротив,
проверка адекватности самих содержательных пред-
представлений объективной реальности уже выходит за
пределы И. о. Все решения (в том числе оптимальные)
принимаются всегда на основе информации, к-рой рас-
располагает принимающий решения субъект (или субъекты),
и только на ней. Поэтому каждая задача И. о. должна
в своей постановке отражать знания принимающего
решение субъекта о множестве допустимых решений и
о критерии оптимальности. Так, если принятие решения
происходит в наперед известном и не изменяющемся
информационном состоянии, то задача наз. стати-
статической. В таких условиях весь процесс принятия
решения может быть сведен к единому мгновенному
акту. В противном случае, если приходится иметь
.тло с несколькими различными информационными
состояниями, то решение будет заключаться в установ-
установлении соответствия между каждым информационным со-
состоянием и доступной в нем альтернативой, т. е. в вы-
выборе функции, выражающей это соответствие. Если
информационные состояния в ходе принятия решения
сменяют друг друга, то задача наз. динамичес-
динамической; в ней часто целесообразно принимать поэтапные,
«многошаговые» решения или даже развертывать при-
принятие решения в непрерывный во времени процесс.
Информационные состояния принимающего решения
субъекта могут по-разному характеризовать его истин-
истинное («физическое») состояние. Может оказаться, что
одно информационное состояние субъекта охватывает
целое множество его физич. состояний. В этом случае
задача принятия решений наз. неопределенной.
Такие задачи И. о. рассматриваются в игр теории.
Если информационное множество содержит несколько
физич. состояний, но субъект кроме их множества знает
еще и (априорные) вероятности каждого из этих физич.
состояний, то задача наз. стохастической.
Наконец, если информационное состояние состоит из
единственного физич. состояния, то задача наз. д е-
терминированной. Иногда представляет
интерес одновременно рассматривать семейства задач,
зависящих от численного, векторного или пробегающе-
пробегающего значения из к.-л. другого множества параметра,
объединяя их в единую параметрическую
задачу. Отличие ее от неопределенной задачи состоит в
том, что решение первой заключается в решении всех
задач, отвечающих конкретным значениям параметра,
а решение второй — в нахождении такого допустимого
решения, к-рое было бы в известной мере желательным,
как бы конкретно ни реализовалась неопределенность.
Вместе с тем решение стохастич. задачи состоит в
нахождении такого допустимого решения, к-рое было бы
оптимальным «в среднем» по всему множеству отдель-
отдельных задач.
Теоретически мыслимы задачи И. о. с любыми множе-
множествами допустимых решений X и с весьма произволь-
произвольными критериями оптимальности. Последние могут
иметь вид требований о максимизации (или минимиза-
минимизации) значений нек-рой числовой или векторной функции
/ на X. Эта функция обычно наз. целевой функцией.
В первом случае говорят о задаче математического про-
программирования (оптимального програм-
программирования, что не следует смешивать с програм-
программированием на ЭВМ), а во втором — о задаче
векторной оптимизации, или о многокри-
многокритериальной задаче. Рассматриваются также критерии,
выражаемые бинарным отношением предпочтения ?>-
на X. Это отношение не обязано быть отношением ли-
линейного или хотя бы частичного упорядочения.
В математич. программировании чаще других рас-
рассматриваются задачи, в к-рых X есть подмножество ко-
конечномерного евклидова пространства Еп. Если при
этом X — выпуклый многогранник с конечным числом
вершин, а целевая функция / линейна, то имеют дело
с задачами линейного программирования; если X —¦
произвольное выпуклое множество, а / — выпуклая
функция, то — с задачей выпуклого программирования.
Естественным образом определяются задачи, относя-
относящиеся к кусочно линейному программированию, квад-
квадратичному программированию и т. д. Множество допу-
допустимых решений X может быть также подмножеством
функционального пространства, и формально вариаци-
вариационное исчисление, а также круг вопросов, связанный с
принципом максимума Понтрягина, поэтому могут быть
также отнесены к оптимальному программированию.
В других задачах оптимального программирования X
может быть конечным множеством; такие задачи отно-
относятся к дискретному программированию. В них допу-
допустимые решения могут быть точками целочисленной
решетки в Еп (целочисленное програм-
программирование) или векторами, каждая компонента
к-рых принимает лишь два значения (булево про-
программирование). В отдельных задачах элемен-
элементы X суть перестановки конечного числа символов,
пути в заданном графе и т. д. Особым случаем задач
оптимального программирования является нахождение
м а к с и м и н а, т.е. максимального значения функции,
имеющей вид минимума (аналогично—м и и и м а к с а).
Теория решения стохастич. задач линейного програм-
программирования составляет предмет стохастического про-
программирования. Многокритериальные задачи, а также
задачи с отношением предпочтения по существу отно-
относятся к теории игр; их классификация проводится по
теоретико-игровым признакам.
Одной из тенденций современного G0-е гг. 20 в.)
И. о. является переход от рассмотрения отдельных
задач И. о. к изучению систем, пространств, исчислений
таких задач и исследование связей между различными
задачами или сведений одних задач к другим, более
просто устроенным. Математич. аппарат, предназначен-
предназначенный и разрабатываемый для целей решения задач И. о.,
принято называть математич. методами И. о. По своему
характеру математич. методы И. о. в принципе не от-
отличаются от математич. методов любой другой матема-
математич. дисциплины, имеющей содержательные приложе-
приложения или хотя бы интерпретации. Разработанность
математич. методов для разных задач И. о. и их классов
неодинакова. Наиболее разработанной является теория
линейного и выпуклого программирования.
Некоторые параметрич. задачи И. о., выделяемые
специфическими содержательными интерпретациями,
проблематикой и терминологией, носят название м о-
д е л е й И. о. Обычно каждая модель И. о. имеет при-
присущие ей методы решения. Диапазон калибров моделей
И. о. весьма широк: от конкретных задач, различаю-
различающихся лишь численными значениями входящих в них
параметров (к их числу можно отнести задачу о назна-
назначениях, транспортную задачу и несколько более слож-
сложные задачи о раскрое, задачу о размещении и теорию
сетевых графиков), до таких разветвленных дисциплин,
как теория управления запасами, теория расписаний
(иногда называемая календарным планированием) или
теория надежности. Большое число моделей И. о. дает
теория игр (игры с выбором момента времени, игры типа
Блотто, игры типа покера, дифференциальные игры
преследования и др.). К числу моделей И. о. принято
несколько авансированно относить теорию массового
обслуживания, хотя большинство ее задач пока еще не
приобрело оптимизационного характера.
Решение каждой задачи И. о. начинается с выбора
принципа оптимальности. Если задача относится к оп-
оптимальному программированию, то этот выбор тривиа-
тривиален: принцип оптимальности состоит в максимизации
(соответственно минимизации) целевой функции. Таким
образом, в этом случае принцип оптимальности задачи
формально совпадает с ее критерием оптимальности.
В остальных случаях нахождение принципа оптималь-
оптимальности оказывается существенным этапом решения
задачи и может реализоваться неоднозначно. Употреби-
Употребительны приемы сведения векторного критерия или
отношения предпочтения к численным критериям.
Напр., в случае многокритериальной задачи принцип
оптимальности может состоять в придании отдельным
компонентам векторного критерия тех или иных весов и
рассмотрении в качестве целевой функции взвешенной
суммы; другой принцип оптимальности в этой задаче
может заключаться в максимизации минимальной
компоненты вектора критерия (принцип максимнна) и
т. д. Весьма разнообразными могут быть принципы опти-
оптимальности в задачах с отношением предпочтения (см.. на-
напр., Игр теория). Возможности и пути замены отноше-
отношений предпочтения численными критериями составляют
один из основных вопросов полезности теории. Т.. о.,
критерий задачи И. о. есть часть ее условия, а принцип
оптимальности — часть ответа. Для большинства мо-
моделей И. о. принципы оптимальности фиксированы.
Следующим после выбора принципа оптимальности
этапом решения задачи И. о. является установление его
реализуемости (т. е. существование решений задачи в
смысле этого принципа). Нереализуемость принципа
оптимальности в классе заданных в условиях задачи
допустимых решений иногда преодолевается путем
введения в том или ином смысле обобщенных решений:
подмножеств множества допустимых решений или функ-
функций со значениями в этом множестве.
Так как существование оптимальных решений задачи
И. о. нередко доказывается неконструктивно (напр.,
на основании тех или иных теорем о неподвижной точ-
точке), а иногда конструктивным образом, но обеспечиваю-
обеспечивающим фактическое его нахождение лишь потенциально
(но не практически), получение оптимального решения
задачи И. о. является третьим этапом ее разработки.
Задачи И. о. обладают рядом черт, обусловливающих
методику их составления и решения. Во-первых, даже
для наиболее простых параметрич. классов задач не
удается представить решение в виде единообразного
аналитич. выражения от соответствующих параметров.
Поэтому задачи И. о. в подавляющем большинстве не
поддаются аналитич. решению и должны решаться чис-
численно. Во-вторых, большинство практически интерес-
интересных задач И. о. содержит в своих формулировках весь-
весьма большое количество числового материала, не сво-
сводящегося к аналитич. выражениям, поэтому численное
решение этих задач возможно лишь с использованием
ЭВМ. В-третьих, процесс решения многих задач И. о.
заключается в выполнении простых однотипных опера-
операций над числами, составляющих большие массивы.
Поэтому задачи И. о. предъявляют к ЭВМ требования,
касающиеся в большей степени их памяти, чем быстро-
быстродействия. Фактически требования И. о. оказывают
значительное влияние на развитие ЭВМ и формирование
их парка.
Круг приложений И. о. весьма широк. И. о. исполь-
используется для решения технических (причем не столько
конструкторских, сколько технологических), технико-
экономических, социально-экономических задач, а так-
также задач управления в различных сферах и на раз-
различных уровнях, вытесняя постепенно традиционные
«интуитивные» методы принятия решений.
Практическое внедрение результатов И. о. встреча-
встречается с трудностями различного рода. Первая из них,
преодолеваемая еще сравнительно легко, связана с по-
построением концептуальной структуры модели реальной
задачи принятия решения (или с подбором уже имею-
имеющейся структуры модели). Этим устанавливается прин-
принципиальная возможность моделирования класса реаль-
реальных задач, включающего рассматриваемую задачу,
нек-рым классом задач И. о. Следующая трудность
состоит в выборе из этого класса задач И. о. именно той,
к-рая моделирует интересующую исследователя кон-
конкретную задачу. Для этого, в частности, необходимо
измерить значения параметров, определяющих решае-
решаемую задачу. Но поскольку эти параметры имеют не
обязательно физический или технический, а часто
экономический пли даже социально-экономич. характер,
их измерение с требуемой точностью может представлять
самостоятельную проблему. Эту трудность сбора инфор-
информации для построения конкретной модели можно
считать основным препятствием на пути выработки
оптимального решения. Затем, после построения моде-
модели, возникают чисто математич. и в том числе вычисли-
вычислительные трудности ее анализа и решения. В сущности
именно их преодоление и составляет содержание И. о.
Наконец, после нахождения решения возникает послед-
последняя трудность, уже организационного и психологич.
плана: найденное решение нередко существенно отли-
отличается от традиционных и потому может восприниматься
с недоверием. Все это ограничивает практич. примене-
применения И. о. Для более успешного их преодоления коллек-
коллективы, работающие в области И. о., формируются как
комплексные: в них включаются кроме математиков
обычно и инженеры, и экономисты, и специалисты в
области конкретных дисциплин, иногда — психологи,
администраторы и т. д.
Лит.: [1] М о р з Ф. М., К я м б е л л Д. Е., Методы ис-
исследования операций, пер. с англ., М., 1956; [2] Саати Т.-Л.,
Математические методы исследования операций, пер. с англ.,
М., 1963; [3] Кофман А., Ф о р Р., Займемся исследова-
исследованием операций, пер. с франц., М., 1966; [4] К о ф м а н А., Ме-
Методы и модели исследования операций, пер. с франц., М., 1966;
[5] Черчмен У., А к о ф Р., Арноф Л., Введение
в исследование операций, пер. с англ., М., 1968; [61 Чу ев
Ю. В., Исследование операций в военном деле, М., 1970;
[7] ГермейерЮ. Б., Введение в теорию исследования опе-
операций, М., 1971; [81 А к о ф Р., С а с и е н и М., Основы ис-
исследования операций, пер. с англ., М., 1971: L9] В е н т-
це ль Е. С, Исследование операций, М., 1972; [10] В агнер Г.,
Основы исследования операций, т. 1—3, пер. с англ., М., 1972—
1973; [11] Исследование операций. Методологические аспекты,
М., 1972; [12] Mathematische Standardmodelle der Operations-
forschung, В., 1971; [13] Mathematische Standardmodelle der
Operationsforschung. Mathematische Grundlagen, Methoden und
Modelle, Bd 1—3, В., 1971—73. H. H. Воробьев,
ИСТИННОСТНАЯ ТАБЛИЦА — таблица, выражаю-
выражающая истинностное значение сложного высказывания
через истинностные значения входящих в него простых
высказываний. И. т. имеет вид (см. таблицу, И означа-
означает «истина», Л — «ложь»).
Здесь Аи ..., Л„ —пропози-
—пропозициональные переменные,
9l(^i, ..., Ап) — высказы-
вательная форма, причем
истинностное значение вы-
высказывания Ш(Аг, ..., Ап)
определяется истинностны-
истинностными значениями высказыва-
высказываний Ах, ...,Ап. Каждаястро-
ка таблицы соответствует
одной из 2" возможных комбинаций истинностных зна-
значений п высказываний. При этом F,- есть истинностное
значение высказывания 91 (Лц . .., А„), если высказы-
высказывания Ai, ...,An имеют истинностные значения, ука-
указанные в i-й строке. С помощью И. т. в математич. логи-
логике определяются истинностные функции, соответствую-
соответствующие таким логич. связкам, как отрицание, конъюнкция,
дизъюнкция, импликация, эквивалентность. В клас-
сич. логике высказываний И. т. применяются для про-
проверки общезначимости формул: формула общезначима
A,
И
И
Л
Аг
И
и
л
Ап\щАи...,Ап)
И
Л
л
V2
тогда и только тогда, когда в последнем столбце таблицы
все Vi суть И. в. Е. Плиско.
ИСТИННОСТНОЕ ЗНАЧЕНИЕ — одно из двух зна-
значений — «истина» (И) или «ложь» (Л),— которое может
принимать данная логич. формула в рассматриваемой
интерпретации (модели). И. з. И иногда в литературе
обозначается также 1, Т, t, а И. з. Л — О, F, /. Если
в модели ЯЛ заданы И. з. элементарных формул, то
И. з. \\А || всякой формулы А определяется индуктивно
следующим образом (для классич. логики):
|| = Я и \\С\\ = И,
|| = Я или || С || = Я,
|| = ./7 или ||СЦ = Я,
|| VxB (х) || = Я О для всех а из ЯЛ || В (а) || = Я,
||Э*В(:г)|| = Я«Ф для нек-рого я из ЯЛ ||В(а)[| = Я.
Иногда рассматриваются интерпретации, в к-рых ло-
логич. формула, кроме И и Л, может принимать и другие
«промежуточные» И. з. В таких интерпретациях И. з.
формул могут быть, напр., элементами булевых алгебр
(так наз. булевозначные модели для классической логи-
логики), элементами псевдобулевых алгебр или открытыми
множествами топологич. пространств (для интуицио-
интуиционистской логики), элементами топологических булевых
алгебр (для модальной логики 54) (см. [2]). При этом,
если в булевозначной модели Щ} заданы И. я. элементар-
элементарных формул, то И. з. сложных формул определяются
так:
HI ВЦП || С [|,
где ||В|| есть дополнение к элементу \\B\\. Напр., в
топологич. моделях для интуиционистской логики
И. з. сложных формул определяются так:
П В ||= hit (|| В ||),
\\^xB(x)\\=\Ja(.m\\B(a)l
где Int (X) обозначает внутренность множества X.
Лит.: [1] Новиков П. С, Элементы математической
логики, 2 изд., М., 1973; [2] Р а с е в а Е., Сикорский Р.,
Математика метаматематики, пер. с англ., М., 1972.
С. К. Соболев.
ИСТИННЫЙ ЦИКЛ метрического про-
пространства — последовательность zn= {z", . ..,
zfe, . ..} бициклов с условием е^-»-0 при к~>-оо. Компакт,
на к-ром лежат все вершины всех циклов всех симплек-
симплексов И. ц., наз. компактным носителем z.
Если /: Х~>-Х — некоторое непрерывное отображение,
то /z — также И. ц., деформация отображения / инду-
индуцирует деформацию истинного цикла.
См. Вьеториса гомологии. а. А. Мальцев.
ИСТОЧНИК векторного поля — точка век-
векторного поля а, обладающая тем свойством, что поток Q
поля через любую окружающую ее замкнутую поверх-
поверхность 0V (и не окружающую др. источников) положи-
положителен. Поток
Q = ]]dv(n, a)ds,
где п — вектор внешней нормали к dV, s — элемент
площади dV, называется мощностью И. Если
поток Q отрицателен, то говорят о стоке. Если
И. распределены непрерывно по рассматриваемой облас-
области V, то предел
lim
наз. плотностью (интенсивностью) И.
в точке Af п равен дивергенции векторного поля а в
Точке М. А. Б. Пеанов.
ИСТОЧНИК СООБЩЕНИЙ — объект, вырабатываю-
вырабатывающий сообщения, подлежащие передаче по канал]/ связи.
Сообщение, вырабатываемое И. с. U, есть случайная ве-
величина 5, определенная на нек-ром вероятностном
пространстве (Я, 2t, P), принимающая значения в
нек-ром измеримом пространстве (J, 5 ) и имеющая
распределение вероятностей /)(•)•
Обычно
где (Х(, 5^ ) — экземпляры одного и того же измери-
измеримого пространства (X, Sx), а П — прямое произведе-
произведение пространств (Xf, S х ), когда параметр t пробегает
множество Д, являющееся, как правило, либо нек-рым
интервалом (конечным, полубесконечным или бесконеч-
бесконечным в обе стороны) действительной оси, либо нек-рым
дискретным подмножеством этой оси (в последнем слу-
случае обычно Д= {..., — 1,0, 1,...} илиД={1, 2,...}).
В первом из этих случаев говорят об И. с. с непре-
непрерывным временем, а во втором — об И. с. с
дискретным временем. Ив том, и в другом
случае сообщением служит случайный процесс \= {?(?),
г?Д} со значениями в пространстве (X, Sx); в прило-
приложениях g (t) трактуется как сообщение, вырабатываемое
И. с. в момент времени t. Наборы случайных величин
ll={l(s), t<s<T} наз. отрезками (t, Т] с о о б-
щ е н и й.
И. с. делятся на различные классы в зависимости
от типа сообщения — случайного процесса ?(?), выра-
вырабатываемого И. с. Напр., если g (t) — случайный про-
процесс с независимыми одинаково распределенными зна-
значениями или стационарный, эргодический, марковский,
гауссовский и т. д. процесс, то И. с. наз. соответствен-
соответственно И. с. без памяти, стационарным,
эргодическ им, марковским, гауссов-
с к и м и т. д.
Одной из задач в теории информации передачи яв-
является задача кодирования И. с. При этом различают,
напр., кодирование И. с. кодами фиксированной длины,
переменной длины, кодирование И. с. при заданных
условиях точности и др. (в приложениях нек-рые задачи
кодирования И. с. наз. квантованием сообщений, сжа-
сжатием сообщений и т. д.). Напр., пусть U — И. с. без
памяти с дискретным временем, вырабатывающий сооб-
сообщение ?=(..., 5_ь §о, 5i>- . .), компоненты 5^ к-рого
принимают значения из нек-рого конечного множества
(алфавита) X. Пусть имеется другое конечное множество
X (множество значений компонент |^ воспроизводимого
сообщения i=(...,!_b lb, f1;...)). Кодирова-
Кодированием объема М отрезка Si=Ei,- • ¦> \й сообщения
длины L наз. отображение XL в множество из М элемен-
элементов XL, и пусть xL (xL) — образ элемента xL ? XL при
таком отображении (здесь XL — прямое произведение
L экземпляров множества X). Пусть, далее, сообщений
точность воспроизведения задается действительнознач-
действительнозначной неотрицательной функцией р(ж, х), х?Х, х?Х,—
мерой искажения, так что средняя мера ис-
кажения нек-рого кодирования задается равенством
где
если xL=(x1,. . ., xL) и xL=(xu.. ., xL). е-энтропией
И. с. без памяти наз. величина
He(U) = inlIGu&, B)
где /(•,•) — информации количество, а нижняя грань
берется по всевозможным совместным распределениям
пары (gi, fj), ?,i?X, %г?Х, таким, что распределение
Xt совпадает с распределением отдельной компоненты
И. с. U и
Теорема кодирования И. с. Пусть
Нг(и) есть е-энтропия дискретного источника U без
памяти с конечной мерой искажения р(-,-) и пусть
Af=exp {Li?}. Тогда: 1) для любого е>0, любого
6>0, любого R~>Hz(U) и достаточно большого L су-
существует кодирование объема М отрезка сообщения
длины L такое, что среднее искажение р^ удовлетворя-
удовлетворяет неравенству р/<;е+б; 2) если R<,HS{U), то при
любом кодировании объема М отрезка сообщения дли-
длины L среднее искажение рд удовлетворяет неравенству
рд>8. Эта теорема кодирования обобщается и на более
общий класс И. с, напр, для И. с. с непрерывным про-
пространством X значений компонент. В этом случае вместо
кодирования объема М говорят о квантовании
И. с. объема М. Следует заметить, что е-энтропия
He{U), входящая в формулировку теоремы, при е=0
и мере искажения
( 0, еслн х = х,
р(х, х) ----- > _ при Х = Х
\ 1, если х Ф х,
совпадает со скоростью создания сообщений заданным
И. с.
Лит.: [1] Шеннон К., Работы по теории информации
и кибернетике, пер. с англ., М., 1963; [2] Д о б р у ш и н Р. Л.,
«Успехи матем. наук», 1959, т. 14, в. 6, с. 3—104; L3] Г а л-
лагер Р., Теория информации и надежная связь, пер.
с англ., М., 1974; [4] Berger Т., Rate distortion theory,
N.Y., 1971. Р. Л. Добрушин, В. В. Прелое.
ИСЧЕРПАНИЕ ОБЛАСТИ, аппроксимирую-
аппроксимирующая последовательность облас-
т е й,— для данной области D топологического про-
пространства X последовательность в определенном смысле
регулярных областей {Dk)k=\CzD такая, что DkCZD^+i
н \Jk=\Dfc=D. Для любой области D комплексного про-
пространства С" существует, напр., И. о., состоящее из
областей D ^, ограниченных кусочно гладкими кривыми
в С1 или кусочно гладкими поверхностями в С", ге>1.
Для любой открытой римановой поверхности S сущест-
существует полиэдрическое исчерпание
{IIfc}ftLi, состоящее из полиэдрических об-
областей П^, представляющих собой, каждая в от-
отдельности, связное объединение конечного числа тре-
треугольников триангуляции S, причем:
иГ=1П^=5 и границей каждой из областей, составляю-
составляющих открытое множество 5\П^ при достаточно большом
к является лишь один из граничных контуров П&.
Лит.: [1J Стой лов С, Теория функций комплексного
переменного, пер. с рум., т. 2, М., 1962, гл. 5 и ел.
Е. Д. Соломенцев.
ИСЧЕРПЫВАНИЯ МЕТОД — метод доказательства,
применявшийся математиками древности при нахожде-
нии площадей и объемов. Назв. «метод исчерпывания»
введено в 17 в.
Типичная схема доказательства при помощи И. м.
может быть изложена в современных обозначениях так:
для определения величины А строится нек-рая последо-
последовательность величин С1У С2, . .., Сп, ... так, что
С„ < А; A)
предполагают также известным такое В, что
С„<В f2)
и при любом целом К для достаточно больших п удов-
удовлетворяются неравенства
K(A-Cn)<D, K(B-Cn)<D, C)
где D — постоянно. С современной точки зрения, для
перехода от неравенства C) к равенству
А = В D)
достаточно заметить, что из условий A), B) и C) сле-
следует
lim (А — С„) = 0, lim (В — С„) = 0
п —*¦ ее п -> со
А= lim С„ = В.
Математики древности, не располагавшие теорией пре-
пределов, обращались к доказательству от противного и
доказывали невозможность каждого из неравенств
А<В, В<А. Чтобы опровергнуть первое из них, при
помощи Архимеда аксиомы устанавливали, что для
R=B—А существует такое К, что KR~>D, и в силу ус-
условия A) получали
К{В — Сп) >К(В — А) > D,
что противоречит второму из неравенств C). Аналогич-
Аналогично опровергалось другое предположение. После этого
оставалось принять только равенство D).
Введение И. м. вместе с лежащей в его основе аксио-
аксиомой приписывается Евдоксу Книдскому. Этим методом
широко пользовался Евклид, а с особенным искусством
и разнообразием — Архимед. Напр., для определения
площади сегмента А параболы Архимед строит площади
С,, С2,.. ., «исчерпывающие» при их постепенном нара-
нарастании площадь А сегмента.
При этом
С2 = Cj-f -j- Clt
Вместо того чтобы прибегнуть к предельному переходу
А= lim Cn
Архимед геометрически доказывает, что при любом п
А-СпК-ф^Сг.
Вводя площадь
Архимед получает, что
и, следуя изложенному выше порядку, заканчивает
доказательство того, что
±
БСЭ-З.
ИСЧИСЛЕНИЕ — 1) Составная часть названия
нек-рых разделов математики, трактующих правила вы-
числений и оперирования с объектами того или иного ти-
типа; напр., дифференциальное И., вариационное И. 2) Д е-
дуктивная система, т. е. способ задания мно-
множества путем указания исходных элементов (аксиом
исчисления) и вывода правил, каждое из к-рых описы-
описывает, как строить новые элементы из исходных и уже
построенных. Выводом в И. S наз. такое линейно
упорядоченное множество, что всякий его элемент Р
является либо аксиомой И. S, либо заключением при-
применения к.-л. принадлежащего Е правила вывода, при-
причем все посылки этого применения предшествуют Р
в выводе. Элемент наз. выводимым в Е, если в В
можно построить вывод, кончающийся этим элементом.
Для удобства изучения выводов они иногда записывают-
записываются в виде нелинейной структуры (см. Вывода дерево);
выводы могут быть снабжены анализом, т. е. до-
дополнительной информацией, облегчающей проверку
правильности вывода (напр., при каждом элементе вы-
вывода пишутся код правила и номера предшествующих
элементов, при помощи к-рых получен данный элемент).
Пример. Рассмотрим исчисление S, задающее
множество М записей в однобуквенном алфавите {| }
всех чисел вида 2" при н —1, 2, ... И. Е имеет одну ак-
аксиому || и одно правило вывода «Из слова Р можно
получить РР». Легко убедиться, что слова из М и толь-
только они выводимы в Е.
И. может иногда порождать также нск-рые вспомо-
вспомогательные элементы, в таком случае задается нек-рый
алгоритм, позволяющий отличать основные элементы от
вспомогательных. При отсутствии вспомогательных
элементов говорят о строгом представле-
н и и. множества М исчислением 3. Таков, в частности,
приведенный выше пример.
Используются и более сложные формы задания мно-
множеств посредством И., когда вместо элементов множе-
множества порождаются их коды (т. е. нужен еще дополни-
дополнительный алгоритм, декодирующий основные элементы).
Так, широко распространены кодировки нелинейных
объектов словами, кодировки слов и n-к чисел нату-
натуральными числами и др. Важным частным случаем
нестрогого представления является ступенчатое
построение II., когда выводимые объекты пре-
предыдущих ступеней носят вспомогательный характер при
формировании следующей ступени (такие построения
особенно xai актерны для логико-математич. теорий,
к-рые оказываются верхней ступенью над рядом П., за-
задающих язык теории).
Понятие И. является формализацией интуитивного
представления об индуктивно порождаемом множестве.
Такие множества широко используются в математике;
в частности, формализация любой развитой теории опи-
опирается на большое количество индуктивно определяе-
определяемых множеств, начиная с простейших (множества пере-
переменных, термов, формул и т. п.) и кончая множеством
теорем, к-рые выводятся из аксиом теории при помощи
соответствующих логич. переходов. Неудивительно
поэтому, что И. являются одним из основных аппаратов
математич. логики. Именно логические исчисления были
первыми примерами полностью формализованных дедук-
дедуктивных систем (на базе этих И. вырабатывались основ-
основные понятия и методы общей теории И., возникли да-
далеко идущие обобщения И.; см., напр., Карнапа прави-
правило). Нек-рые специальные виды И. хорошо пригодны для
описания формальных грамматик (чем определяется
роль И. в математической лингвистике) и для задания
множеств, распознаваемых автоматами конечными.
Одной из основных сфер применения общей теории
И. является алгоритмов теория. Это объясняется тем,
что понятие И. имеет такой же фундаментальный харак-
характер, как и понятие алгоритма. Действительно, класс
множеств, к-рые могут быть заданы при помощи
И., совпадает с классом алгоритмически перечислимых
множеств слов (если оставаться в рамках общеприня-
общепринятых уточнений понятия И. и не прибегать к обобщени-
обобщениям, нарушающим потенциальную возможность порож-
порождения каждого выводимого элемента). Отсюда вытекает
существование такого И., для к-рого неразрешима про-
проблема выводимости, т. е. невозможен алго-
алгоритм, к-рый для всех слов (в языке И.) кончал бы рабо-
работу с правильным ответом (напр., давал бы 0 на всех
выводимых словах и 1 на остальных). Из возможности
задания сколь угодно сложных перечислимых множеств
вытекает также существование универсальных в том
или ином смысле И. (т. е. И., моделирующих все другие
И. фиксированного языка, см. Креативное множество).
Эти факты, в сочетании с изучением различных модифи-
модификации п специализаций общего понятия И., открывают
возможности получения интересных алгоритмически
неразрешимых проблем. Основополагающее значение
для этого направления имела работа Э. Поста (см. [1]),
в к-роп впервые было предложено понятие дедуктивной
системы, пригодной для порождения произвольных
перечислимых множеств слов (см. Поста каноническая
система). Широкие возможности в оформлении пра-
правил вывода канонических И. позволяют хорошо обслу-
обслуживать процессы индуктивного порождения множеств;
подавляющее большинство построенных конкретных И.
легко и естественно можно сформулировать как частные
случаи канонических И.
Ассоциативные исчисления, называемые также си-
системами Т у э, служат удобным средством зада-
задания и изучения групп и полугрупп.
Лит.: [ll Post E. L., «Amer. J. Math.», 1943, V. 65,
Кг 2, р. 197—215; [2] Марков А. А., Теория алгорифмов,
М.— Л., 1954 («Тр. матем. ин-та АН СССР», т. 42); [3] «Тр.
матем. ин-та АН СССР», 1964, т. 72, с. 5—56; 1967,т. 93, с. 3 — 42.
С. Ю. Маслов.
ИТЕРАЦИОННЫЕ МЕТОДЫ решения проб-
проблемы собственных значений матри-
матрицы — методы нахождения собственных значений и
собственных векторов (или корневого базиса) матрицы,
минующие предварительное вычисление характеристич.
многочлена. Эти методы существенно различаются
для задач среднего размера, матрицы к-рых могут быть
целиком размещены в оперативной памяти вычислитель-
вычислительной машины, и для задач большого порядка, в к-рых
хранение информации обычно осуществляется в ком-
компактной форме.
Первый И. м. был предложен К. Якоби [1] для вы-
вычисления собственных значений и векторов действи-
действительных симметричных матриц (см. Вращений метод).
Метод переносится на комплексные эрмитовы матрицы,
а также на более широкий класс нормальных матриц.
Имеется ряд обобщений метода Якоби для матриц
произвольного вида. Типичный алгоритм этого класса
состоит из последовательности элементарных шагов,
выполняемых по схеме:
При этом роль подобного преобразования с (элемен-
(элементарной) матрицей S & состоит в уменьшении евклидовой
нормы текущей матрицы А /г, т. е. в приближении ее к
нек-рой нормальной матрице. В качестве Т/г обычно
берется матрица вращений или ее унитарный аналог.
Смысл подобного преобразования с этой матрицей, как
и в классич. методе Якоби, заключается в аннулирова-
аннулировании внедиагонального элемента в нек-рой эрмитовой
матрице, связанной с матрицей A^+i, напр, в матрице
A k+i~\-A k+i- С ростом к матрицы А ь сходятся к матрице
диагонального или квазидиагонального вида, а накоп-
накопленное произведение матриц S^ и Т^ дает матрицу,
столбцами к-рой являются приближенные собственные
векторы либо векторы, образующие базисы инвариант-
пых подпространств матрицы (см. [2], [3]).
Наряду с вышеописанными методами развиваются
алгоритмы другого класса, так. наз. степенные
методы. Самым эффективным методом этого направ-
направления, наиболее широко применяющимся для решения
задач среднего размера, является QR -алгоритм
(см. [4], [5]). Итерации ()Л-алгоритма проводятся по
следующей схеме:
Ak=QkRk, Ak+1 = RkQk, A)
здесь Qk — ортогональная или унитарная, а Л а —
правая треугольная матрица. Для перехода от А ^ к
A k+i сначала находится ортогонально-треугольное
разложение матрицы A s, после чего матрицы Qk и Л/,
перемножаются в обратном порядке. Если положить
Qk=Qi- ¦ -Qk, Rk=Rk- ¦ -ffi, то из A) следует схема
Ak+x=QUiQk, A\=QkRk. B)
Таким образом, (^Л-алгоритм генерирует последова-
последовательность матриц Аи, ортогонально подобных исходной
матрице А^; при этом трансформирующая матрица
Qk является ортогональной компонентой в разложении
B) матрицы Ai.
При итерации по схеме A) матрицы А ^ сходятся к
правой треугольной или квазитреугольной матрице,
причем скорость сходимости поддиагональных элемен-
элементов к нулю управляется отношениями модулей различ-
различных собственных значений и является, вообще говоря,
довольно медленной. Для ускорения сходимости QR-
алгоритма используются так наз. сдвиги, что при-
приводит к следующему видоизменению схемы A):
Ak-y.kI=QhRk, Ak+l = RkQk + y.kI. C)
Обычно применение сдвигов (напр., у.и=^пп) позволяет
получить быструю сходимость внедиагональных эле-
элементов последней строки к нулю (асимптотически
квадратичную в общем случае и кубическую для эрми-
эрмитовых матриц) и соответственно быструю стабилизацию
диагонального элемента (га, га). После того, как значе-
значение этого элемента установилось, дальнейшие итерации
проводят с главной подматрицей порядка п—1, и т. д.
Собственные векторы результирующей треугольной
матрицы после умножения на накопленное произведе-
произведение ортогональных матриц Qk дают собственные векто-
векторы исходной матрицы Ах.
Итерации по схеме A) либо C) применяют к матрице,
предварительно приведенной к так наз. форме Хесеен-
берга. Говорят, что матрица А имеет правую форму
X ессенберга, если я/у=0 при г>/ + 1- (?Л-алго-
ритм обладает свойством сохранять форму Хессенберга
исходной матрицы, что намного удешевляет стоимость
каждой итерации. Есть и другие важные возможности
уменьшения объема вычислений, напр., неявное ис-
использование сдвигов, что позволяет находить комплекс-
комплексно сопряженные собственные значения действительных
матриц, не прибегая к комплексной арифметике.
В задачах высокого порядка (от нескольких сотен
до нескольких тысяч) матрицы обычно бывают разре-
разреженными, т. е. имеют относительно небольшое число
ненулевых элементов. При этом, как правило, нужно
вычислять не все, а лишь нескелько собственных зна-
значений и соответствующие собственные векторы. В ти-
типичном случае требуемые собственные значения —
наибольшие или наименьшие по модулю.
Описанные выше методы, основанные на подобных
преобразованиях, разрушают разреженность матрицы и
потому неприемлемы. Основными для задач высокого
порядка являются методы, элементарная операция ко-
которых — умножение матрицы на вектор. При их опи-
сании в дальнейшем предполагается, что собственные
значения заданной матрицы А занумерованы в порядке
убывания модулей так, что
Наиболее широкую область применимости имеет
степенной метод для вычисления собственного значе-
значения >ч с максимальным модулем. Исходя из начального
приближения х0 строится последовательность нормиро-
нормированных векторов
Р = 1/||ЛжА||. D)
Эта последовательность сходится к собственному век-
вектору, отвечающему кг, при выполнении следующих ус-
условий: 1) все элементарные делители матрицы А, от-
относящиеся к Xj,— линейные; 2) нет других собствен-
собственных значений с тем же модулем; 3) в разложении ис-
исходного вектора х0 по корневому базису матрицы А
имеется нетривиальная компонента по собственному
подпространству для Х±. Однако сходимость степен-
степенного метода, как правило, медленная и определяется
отношением величин двух старших по модулю собствен-
собственных значений.
Если известно приближение Хв к желаемому собст-
собственному значению А,,-, то быстрая сходимость может быть
достигнута посредством метода обратных итераций.
Вместо D) строится последовательность, определяемая
соотношениями
(Л— lol)xk + 1 = pkxk, ]\xk\\ = i, yk. E)
Метод обратных итераций есть по существу степенной
метод для матрицы (А—Xgl)'1, имеющей сильно до-
доминирующее собственное значение 1/(Я0—Яо). Реали-
Реализация формулы E) требует, однако, решения линейной
системы с матрицей А —Хо/ и даже при использовании
специальных методов для разреженных систем предъяв-
предъявляет повышенные требования к оперативной памяти по
сравнению со степенным методом.
Для вычисления группы собственных значений при-
применяются так наз. методы одновременных итераций.
Они представляют собой обобщение степенного метода,
где вместо итераций одного вектора фактически строят-
строятся итерации матрицей А целого подпространства. Типич-
Типичным для этой группвг методов является метод Сть го-
ар т а [6]. Пусть собственные значения матрицы А удов-
удовлетворяют соотношениям
Выбирается начальная nXr-матрица Qo с ортонорми-
рованными столбцами. Исходя из QQ, строится после-
последовательность матриц Qk по схеме:
Во второй из этих формул ifft+i — правая треуголь-
треугольная rXr-матрица, а матрица Qk+i имеет ортонорми-
рованные столбцы. Цель этого разложения, к-рое может
выполняться не на каждой итерации, состоит в том, что-
чтобы обеспечить линейную независимость столбцов по-
последовательно получаемых матриц Qk, к-рая в прак-
практическом смысле может быть утеряна в результате мно-
многократного итерирования матрицей А. Важную роль
в ускорении сходимости метода играет третья формула
F). Ортогональная rXr-матрица, участвующая в этой
формуле, имеет следующий смысл. Если обозначить че-
через fift+i rX г-матрицу QkAQh, то Wu+i приводит -S^+i
к ф о р м е Шура, т. е. правой треугольной матрице.
Матрица Wk + i может быть построена посредством QR-
алгоритма; ее столбцы образуют базис Шура
матрицы Bk+i, характеризуемый тем, что при любом
к, 1 <:&<:;-, линейная оболочка первых к векторов
есть инвариантное подпространство матрицы В^+1.
Матрицы Qk метода Стьюарта сходятся к матрице Q,
столбцы к-рой дают базис Шура для инвариантного
подпространства матрицы А, отвечающего собственным
значениям Х1; . . ., Хг. При этом скорость сходимости
1-го столбца определяется отношением |Xr+il/|^,|.
В случае действительной симметричной матрицы по-
появляются дополнительные возможности, связанные с
трактовкой собственных значений как стационарных
точек функционала Рэлея:
, х)=(Ах, х)/(х, х), хфО. G)
Для нахождения крайних точек спектра могут быть
применены методы безусловной оптимизации функцио-
функционала G). Получающаяся здесь теория параллельна те-
теории итерационных методов для решения положительно
определенных линейных систем и приводит к тем же
самым алгоритмам: координатной релаксации, последо-
последовательной сверхрелаксации, наискорейшего спуска,
сопряженных градиентов (см. [7]).
Перечисленные методы находят собственные значения
«по одному». Для одновременного вычисления группы
собственных значений симметричной матрицы исполь-
используется метод Л а е ц о ж а [8], к-рый предназначал-
предназначался для трехдиагонализации симметричной матрицы по-
порядка п. В основу метода положено следующее наблю-
наблюдение: если последовательность векторов р0, Ар0, ¦ ¦ ¦,
Ар1~~Х линейно независима, то в базисе q1, q2, . . ., qn'
полученном из нее процессом ортонормализации, мат-
матрица приводится к трехдиагональной форме Тп. Век-
Векторы од. строятся по трехчленным рекуррентным форму-
формулам
коэффициенты а^ и р^,&=1, . . ., и, определяют матрицу
Тп. После к шагов процесса ортогонализации известны
векторы qlt . . ., qu и главная подматрица Ть матрицы
Тп. Во многих случаях уже при k <^ n часть собст-
собственных значений матрицы Т^ достаточно точно прибли-
приближает нек-рые собственные значения Тп; соответствую-
соответствующие собственные векторы Т ^ могут быть использованы
для построения приближений к собственным векторам
А. Если же достигнутая точность еще не удовлетвори-
удовлетворительна, то можно выбрать новое начальное приближе-
приближение р0 в линейной оболочке векторов qx, . . ., q^ и повто-
повторить процесс, проведя к шагов, и т. д. В этом и со-
состоит итерационная трактовка метода Ланцоша (см. [9]).
Нахождение внутренних точек спектра для разрежен-
разреженных матриц высокого порядка еще не имеет удовлетво-
удовлетворительного численного решения.
Лит.: [1] J а с о b i С. G., «J. reine und angew. Math.»,
1846, Bd 30, № 1, S. 51—94; [2] E b e r 1 e i n P. J., «J. Soc.
Industr. and Appl. Math.», 1962, v. 101, N° 1, p. 74—88; [3] В о-
еводин В. В., «Вычисл. методы и программирование», 1965,
J* 3, с. 89 — 105; [4] К у б л а н о в с к а я В. Н., «Ж. вычисл.
матем. и матем. физ.», 1961, т. 1 № 4, с. 555—70; [5] F г а п-
cis J. G. F., «Comput. J.», 1961, v. 4, Л» 3, p. 265—71; 1962,
v. 4, ,№ 4, p. 332—45; [6] Stewart G. W., «Numer. Math.»,
1976, v. 25, M!> 2, p. 123—36; [7] Ruhe A., Computation of
engenvalues and eigenvectors, В., 1977; [8] L a n с z о s C,
«J. Res. Nat. Bur. Standards», 1950, v. 45, Л» 4, p. 255—82;
[9] Paige C. C, «J. Inst. Math, and Appl.», 1972, v. 10,
p. 373—81. X. Д. Икрамов.
ИТЕРАЦИОННЫЙ АЛГОРИТМ — рекурсивный ал-
алгоритм, реализующий в нек-ром топологич. пространст-
пространстве V последовательность точечно-множественных отоб-
отображений A k : V—r V, при помощи к-рых по начальной
точке м° ^ V вычисляют последовательность точек uk ^ V
согласно формулам
uk + i = Akub, к = 0, 1, .... A)
Операцию A) наз. итерацией, а последователь-
последовательность ик — итерационной последова-
последовательностью.
И. а. (или методы последовательных
приближений) применяют как для нахождения
решения операторного уравнения
Au=f, B)
или минимума нек-рого функционала, или собственных
значений и элементов уравнения Аи=ки и т. п., так
и для доказательства существования решений этих за-
задач. И. а. A) наз. сходящимся при начальном
приближении м° к решению и упомянутых задач, если
и*—>-и при /с_>-оо.
Операторы А д. для решения уравнения B), заданного
в линейном метрич. пространстве V, обычно строят по
формулам
Akuk=uk — Hk{Aub — f), C)
где #k(V—+V) — некоторая, определяющая тип И. а.,
последовательность операторов. В основе построения
И. а. типа A), C) лежат или сжатых отображений прин-
принцип и его обобщения, или вариационные методы миними-
минимизации нек-рого связанного с задачей функционала.
При этом используются различные методы построения
операторов А^, напр, варианты Ньютона метода,
или спуска метода. Операторы Н^ стараются выб-
выбрать так, чтобы быстрая сходимость uk к и обеспе-
обеспечивалась при условии, что численная реализация опе-
операции Af.uk при заданном объеме памяти ЭВМ была до-
достаточно проста, нетрудоемка по количеству операций и
устойчива к ошибкам округления.
Хорошо разработаны и исследованы И. а. решения
линейных задач. И. а. делятся при этом на линейные
и нелинейные. К линейным относятся, напр., Гаусса
метод, Зейделя метод, верхней релаксации метод,
И. а. с чебышевскими параметрами; к нелинейным —
вариационные методы: наискорейшего спуска метод,
сопряженных градиентов метод, минимизации невя-
невязок метод и т. д. Одним из эффективных И. а. явля-
является метод с использованием чебышевских
параметров, когда А — самосопряженный опе-
оператор со спектром на отрезке [т, М], где М>т>0.
Этот метод дает оптимальную (при данной информации о
границах спектра) оценку сходимости на заранее за-
задаваемом JV-м шаге. Записывается метод в виде
где
2.7ь-1 N
i — (M — m) cos-
2N
N —ожидаемое число итераций, в нем используется ид'=
= 0i> Hi ¦ • ¦• In) — специальная перестановка TV-го по-
порядка, хорошо перемешивающая для устойчивости счета
корни многочлена Чебышева. Для 7V=2" перестановку
идг можно построить, напр., так: и2=A, 2), и если из-
известна перестановка и ,-_i= (/i, j2, ¦ ¦ ¦, j i-i), то и ,¦=
= Gl, 2- + 1-/!, j2, 2Ч-1-72, ...)• При Лг=16 эта
перестановка имеет вид: A, 16, 8, 9, 4, 13, 5, 12, 2,
15, 7, 10, 3, 14, 6, 11).
Существуют И. а., использующие г предыдущих
приближений ик, ц*-1, . . ., ик~г + 1\ они наз. г-шаговы-
ми и обладают повышенной скоростью сходимости.
И. а. широко применяются при решении многомер-
многомерных задач математич. физики, для нек-рых классов
таких задач существуют специальные быстросходящиеся
И. а. Напр., переменных направлений метод, метод,
изложенный в [7] для эллиптических краевых задач,
нек-рые методы для задач переноса частиц или излу-
излучений (см. [1] — [7]).
Лит.: [1] Канторович Л. В., А к и л о в Г. П.,
Функциональный анализ, 2 изд., М., 1977; [2] К о л л а т ц Л.,
Функциональный анализ и вычислительная математика, пер.
с нем., М., 1969; [3] М а р ч у к Г. И., Л е б е д е в В. И., Чи-
Численные методы в теории переноса нейтронов, М., 1971; [4J
Бахвалов Н. С, Численные методы, 2 изд., М., 1975; [5]
Красносель ский М. А. и др., Приближенное решение
операторных уравнений, М., 1969; [6J Лебедев В. И.,
в кн.: Тр. института кибернетики АН УССР, К., 1972, с. 109—
135; [7] Ф е д о р е н к о Р. П., «Успехи матем. наук», 1973,
т. 28, в. 2, с. 121—82. В. И. Лебедев.
ИТЕРАЦИЯ — результат повторного применения ка-
какой-либо математич. операции. Так, если
есть нек-рая функция от х, то функции
/.W=/[/lWI, /з (¦*)=/ [/2 И], ...,/„(*)=/[/„-!(*)]
наз. соответственно второй, третьей, .. ., ;г-й итера-
итерациям и функции f(x). Напр., полагая/(х) = га, полу-
получают
Индекс и наз. показателем И., а переход от
функции /(х) к функциям f2(x), /3 (•*¦)' • • •— и т с р и-
р о в а н и е м. Для нек-рых классов функций можно
определить И. с произвольным действительным и даже
комплексным показателем. И..используются при реше-
решении различного рода уравнений и систем уравнений
итерационными методами. Подробнее см. Последова-
Последовательных приближений метод.
Лит.: Н] К о л л а т ц Л., Функциональный анализ и вы-
вычислительная математика, пер. с нем., М., 1969. БСЭ-3.
ИТЕРИРОВАННОЕ ЯДРО — функция (х, s) H>
\-*Кп{х, s), к-рая образуется из данного ядра К ин-
интегрального оператора
K(x, t)q(t)dt,
по рекуррентным соотношениям:
Кг{х, s) = K(x, s), К„(х, s)={ibaKn-i(x, t)K(t, s)dt;
Кп наз. ге-й итерацией, или га-м итерирован-
итерированным ядром, ядра К. И. я. иногда наз. повтор-
н ы м ядро м. Если ядро К непрерывно или интегри-
интегрируемо с квадратом, то все его И. я. непрерывны, соответ-
соответственно, интегрируемы с квадратом. Если К — симмет-
симметричное ядро, то все его И. я. также симметричны. Ядро
Кп является ядром оператора А". Имеет место равен-
равенство
Кп (х, s) = \ Кп-т (¦*¦> *) Km (t, s) dt, 1 sj: msj: и — 1.
Лит.: [1] Смирнов В. И., Курс высшей математики,
т. 4, ч. 1, 6 изд., М., 1974; [2] М и х л и н С. Г., Лекции по ли-
линейным интегральным уравнениям, М., 1959. Б. В. Хведелидзе.
ИТО ПРОЦЕСС — случайный процесс, имеющий
стохастический дифференциал. Точнее, непрерывный
случайный процесс Xt, заданный на вероятностном про-
пространстве (Q, F, Р) с нек-рым неубывающим семейст-
семейством {Ff} ст-подалгебр событий ?1, наз. процессом
И т о по отношению к {Ft}, если существуют процес-
процессы a(t) и o(t) (называемые коэффициентом
сноса и коэффициентом диффузии
соответственно), измеримые при каждом t относительно
Ft, и винеровскии процесс Wf относительно {Ft} такие,
что
И. п. назван по имени К. Ито (К. Ito). Один и тот же
процесс Xf может быть И. п. по отношению к двум
различным семействам {Ft}. При этом соответствующие
стохастич. дифференциалы могут существенно отли-
отличаться. И. п. наз. процессом диффузион-
диффузионного типа, если его коэффициенты сноса a(t) и диф-
диффузии о(() измеримы при каждом t относительно а-ал-
гебры
X
s,
При некоторых достаточно общих условиях оказы-
оказывается возможным представление И. п. в виде процесса
диффузионного типа, но, вообще говоря, с некоторым
новым винеровским процессом (см. [3]). Если И. п. Xt
представим в виде диффузионного И. п. с некоторым
винеровским процессом Wt и выполняется равенство
FY= Ff, то Wt наз. обновляющим процес-
процессом для Xf.
Пример. Пусть задан некоторый винеровскии про-
процесс Wt, ?>0, относительно {Ft} и
dXt = Y dt-\-dWt,
где Y — нормально распределенная случайная величи-
величина, имеющая среднее т и дисперсию у; Y измерима от-
относительно Fo.
Процесс Xt, рассматриваемый относительно Ff, име-
имеет стохастнч. дифференциал
где новый винеровскии процесс Wt, определяемый
равенством
является обновляющим процессом для А';.
Лит.: [1] Г и р с а н о в И. В., «Теория веропт. и ее при-
мен.», 1960, т. 5, в. 3, с. 314—30; [2] Л и п ц е р Р. III., Ш и-
р я е в А. Н., Статистика случайных процессов, М., 1974;
[3] Ширяев А. Н., «Проблемы передачи информации»,
1966, т. 11, в. 3, с. 3—22. А. А. Новиков.
ИТО ФОРМУЛА — формула, по к-рой вычисляется
стохастический дифференциал функции от Ито про-
процесса. Пусть (неслучайная) функция f(t, x), определен-
определенная при действительных tux, дважды непрерывно
дифференцируема по х, один раз непрерывно дифферен-
дифференцируема по t и пусть у процесса Xt существует стохас-
стохастич. дифференциал
dXt = a (t) dt + o(t) dWt;
тогда стохастич. дифференциал процесса f(t, Xt) имеет
вид
df(t, Xt) = [f't(t, Xt) + a(t)f'x(t, Xt)^r
+ 1/^2(t)f"xx(t, Xt)]dt + a(t)f'x(t, Xt)dWt.
Эта формула была получена К. Ито [1]. Аналогичная
формула имеет место и для векторных Xt и f(t, x).
И. ф. распространяется на некоторые классы негладких
функций [2J и семимартингалое.
Лит.: [1] Ito К., «Nagoya Math. J.», 1951, v. 3, p. 55—65;
см. также «Математика», 1959, № 3, в. 5, с. 131—41; [2] Кры-
Крылов Н. В., «Теория вероят. и ее примен.», 1969, т. 14, в. 2,
с. 340—48. А. А. Новиков,
ИЕТСА ПОПРАВКА — поправка, применяемая в
нек-рых задачах математич. статистики (напр., в зада-
задаче о стохастич. независимости) и позволяющая иногда
улучшить результаты, полученные с помощью обычных
таблиц ^-распределения. Предложена Ф. Йетсом [i].
Лит.: [i] Yates J., «Т. Roy. Statist. Soc», 1034, v. 1,
p. 217; [2] Крамер Г., Математические методы статистики,
пер. с англ., 2 изд., М., 1975. В. В. Сенатов.
ИОРДАНОВА АЛГЕБРА — алгебра, в к-рой справед-
справедливы тождества
ху = ух,
(х*у)х=х2{ух).
Такие алгебры впервые возникли в работе П. Йордана
11], посвященной аксиоматизации основ квантовой
механики (см. также [2]), а затем нашли применения
в алгебре, анализе и геометрии.
Пусть А — ассоциативная алгебра над полем харак-
характеристики Ф2. Множество А с операциями сложения и
й о р д а н о в а умножения
aob==1/2 (ab-[ Ъа)
образует алгебру А<- + ), к-рая является йордановой.
Й. а., изоморфная подалгебре алгебры Ai + ) для нек-
некрой ассоциативной алгебры А , наз. специальной.
Роль специальных алгебр в теории Й. а. во многом
аналогична роли ассоциативных алгебр в теории альтер-
альтернативных алгебр. В основе этой аналогии лежит теоре-
теорема о том, что всякая двупорожденная подалгебра Й. а.
специальна. (Всякая двупорожденная подалгебра аль-
альтернативной алгебры — ассоциативна.) Однако класс
специальных Й. а. не является многообразием, т. е.
не задается тождествами, поскольку специальные алгеб-
алгебры могут иметь неспеццальные гомоморфные образы.
Тем не менее, найден ряд тождеств 8-й и 9-й степеней,
которым удовлетворяет всякая специальная Й. а. и не
удовлетворяют нек-рые неспециальные алгебры, а
также доказано, что таких тождеств степени <7 не су-
существует. Необходимое и достаточное условие специаль-
специальности алгебры: Й. а. специальна тогда и только тогда,
когда она изоморфно вложима в Й. а., каждое счетное
подмножество к-рой лежит в подалгебре, порожденной
двумя элементами.
Примеры. 1) Пусть V — векторное пространство
над полем F с симметрической билинейной формой
f(x, у), a F-eQ+V — пространство на единицу боль-
большей размерности, на к-ром формулой
(а, Р ?F, и, v?V) определяется умножение. Возни-
Возникающая таким образом алгебра наз. алгеброй
симметрической билинейной формы
/. Она изоморфно вкладывается в алгебру C(V, /)( + ),
где C(V, /) — алгебра Клиффорда формы /, и потому
является специальной Й. а.
2) Пусть А — ассоциативная алгебра и / — ее инво-
инволюция (антиизоморфизм порядка два). Множество
Н (А, )) = {а ? А \а/ = а}
является подалгеброй в Л< + ) и образует специальную
Й. а.
3) Пусть С — альтернативная неассоциативная ал-
алгебра над полем F с инволюцией с^-с, неподвижные
элементы к-рой лежат в ассоциативном центре алгебры
С. В алгебре матриц С3 третьего порядка над С под-
подмножество
#(С3, Т) = {Х?СЯ\Х = Г-1Х'Г},
где
r = diag {71, 72, Тз}. Vi^O, yt^F,
относительно операций сложения и йорданова умноже-
умножения образует неспециальную Й. а. Такая алгебра не
является гомоморфным образом никакой специальной
алгебры.
Конечномерные простые Й. а. над алгебраически
замкнутым полем F характеристики ф2 полностью
классифицированы (см. [3]). Центральные простые
конечномерные Й. а. разбиваются на пять серий. Серии
(А) —(D) бесконечны и состоят из специальных алгебр,
серия (Е) состоит из одной неспециальной алгебры:
(A) /у + >;
(B) H(Fn, А), где Jx : X-+X';
(C) H(F2m Js), где/5: X-^S'X'S, S=diag {Q, <?,...,
Qh <?=Q;
(D) F-e^V— алгебра симметрической невырожден-
невырожденной билинейной формы;
(E) Н(С3, /j), где С — алгебра Кэли — Диксона со
стандартной инволюцией. Эта алгебра 27-мерна над F.
Во всякой конечномерной Й. а. J радикал (наиболь-
(наибольший шшьидеал) N ьильпотентен и факторалгебра
/ = У/Л есть конечная прямая сумма простых Й. а.
Если факторалгебра / сепарабельна, то алгебра /
обладает разложением J=N-\-W в сумму радикала и
полупростой подалгебры W, изоморфной /. В случае
поля характеристики 0 все полупростые слагаемые W
сопряжены относительно автоморфизмов специального
вида (см. [3]). С некоторыми ограничениями на алгебру
это верно и в случае поля характеристики р>0.
Обобщением теории конечномерных Й. а. является
теория Й. а. с условием минимальности для квадратич-
квадратичных (внутренних) идеалов (см. [3], [4], [5]). Квадра-
Квадратичный идеал (? алгебры / — это такое подпро-
подпространство, что {qxq } ?Q для всех q?Q и x?J, где {abc}=
= (ab)c-{-(bc)a—(са)Ь— тройное йорданово произведение.
Если / — Й. а. с условием минимальности для квадра-
квадратичных идеалов и R — ее квазирегулярный радикал, то
факторалгебра JlR есть конечная прямая сумма про-
простых алгебр, к-рые описаны за исключением Й. а. с деле-
делением. В случае, когда алгебра / специальна, доказано,
что радикал R нильпотентен и конечномерен.
Алгебраическая специальная Й. а., удовлетворяю-
удовлетворяющая нетривиальному (для специальных алгебр) тож-
тождеству, локально конечномерна; специальная йордано-
йорданова нильалгебра с нетривиальным тождеством локально
нильпотентна [6]. В частности, специальная алгебраи-
алгебраическая (ниль) Й. а. ограниченного индекса является
локально конечномерной (нильпотентной). Конечно по-
порожденная разрешимая Й. а. нильпотентна, в общем
случае это не верно даже для специальных алгебр.
Йорданово Ф-опораторное кольцо, являющееся конечно
порожденным Ф-модулем с нильпотентными порож-
порождающими элементами, нильпотентно [7].
Каждо11 Й. а. можно различными способами сопостав-
сопоставлять алгебры Ли (см. [3], [8]). Ряд теорем о Й. а. полу-
получен с помощью известных теорем об алгебрах Ли. Так,
напр., доказано, что полупростая конечномерная Й. а.
над алгебраически замкнутым нолем характеристики О
имеет базис с целочисленными структурными кон-
константами. Для теории алгебр Ли эти конструкции также
полезны, так как с их помощью реализуются нек-рые
важные классы алгебр Ли. Напр., алгебра Ли диффе-
дифференцирований простой Й. а. типа (Е) есть исключитель-
исключительная простая алгебра Ли Ft, а алгебра линейных пре-
преобразований этой же алгебры, оставляющих инвариант-
инвариантной нек-рую кубич. форму, есть исключительная про-
простая алгебра Ли Ек. При помощи другой конструкции,
сопоставляющей альтернативной алгебре степени 2 и
Й. а. степени 3 некоторую алгебру Ли, можно реализо-
реализовать все пять простых исключительных алгебр Ли
типов G2, Ft, Ев, Е-,, Еа.
Интересно, наконец, отметить, что нек-рые алгебры,
возникающие в генетике, являются йордановыми
[Ю].
Лит.: [1] Jordan P., «Nachr. Akad. Wiss. Gottingen.
Math.-Phys. Kl. 2A», 1933, S. 209—17; [2] Э м х Ж., Алгебраи-
Алгебраические методы в статистической механике и квантовой теории
поля, пер. с англ., М., 1976; [3] Jacob son N., Structure
and representations of Jordan algebras, Providence, 1968; [4]
Me С г i m га о n K., «Prof. Nat. Acad. Sci USA», 1969, v. 02,
Л5 3, p. 671 — 78; [5J С л и н ь к о А. М., «Алгебра и логика»,
1972, т. 11, № 6, с. 711 — 24; [61 Ширшов А. И., «Матем. сб.»,
1957. т. 41, Ni 3, с. 381 — 94; (.7] Ш е с т а к о в И. П., «Алгебра
и логика», 1971, т. 10, № 4, с. 407 — 48; L8] S с h a f e r R. 1).,
An introduction to nonassociative algebras, N. Y., 1У66; [9] Gor-
Gordon S. K., «J. of Algebra», 1973, v. 24, p. 258 — 82; [10] S с h a
fer R. D., «Amer. J. Math.», 1949, v. 71, p. 121 — 35; [HI
Koecher M., An elementary approach to bounded symmetric
domains, Houston, 1969; [12] С л и н ь к о А. М. и д р.,
Йордановы алгебры, в. 1, Новосиб., 1976. А. М. Слинъко.
КАВАГУТИ ПРОСТРАНСТВО — гладкое п-мерное
многообразие Vn, в к-ром элемент дуги ds регулярной
кривой x=x(t), t?[t0, tj], выражается формулой:
, A)
причем метрическая функция F подчиняется условиям
Цермело:
У" sx^'Fis)i = F, У"
r = 2, 3,..., p,
где
*•"# л eF
dt* "" gxWl
Условия B) обеспечивают независимость элемента дуги
ds от параметризации кривой x=x(t).
Общая теория К. п. впервые изложена А. Кавагути
(см. [1]). Основанием для рассмотрения К. п. послу-
послужило то, что элементы дуги вида A) встречались в
различных однородных пространствах (напр., афинная
дуга, проективная дуга). Впоследствии было установ-
установлено (см. [2]), что в любом однородном пространстве
существует инвариантная метрика Кавагути A), группа
автоморфизмов к-рой совпадает с группой преобразова-
преобразований однородного пространства. Основы общей теории
К. п. развивались на формальном пути обобщения
тензорного аппарата и параллельного перенесения.
А. Кавагути в качестве основного пространства рассмат-
рассматривал расслоенное пространство, базой к-рого является
пространство линейных элементов (х', x{si'), s=l, 2,. . .,
q, порядка q=2p—1, а слоями — и-мерные векторные
пространства Тп, касательные к Vn. Ковариантное
дифференцирование контравариантных векторов V'(xk,
Х(Я?) определяется с помощью операторов ковариант-
ного дифференцирования
. . .. . ^п (S) ......
s = l, 2, ..., q,
где Fft/, }if, АУь зависят от линейного элемента порядка
q=2p — 1. Эти операторы могут быть построены с по-
помощью трехкратного продолжения метрич. функции и
определяемого ею метрич. тензора qij, зависящего так-
также от линейного элемента порядка 2р — 1. Так, построен-
построенная общая теория К. п. не получила глубокого развития
отчасти ввиду того, что порядок q базисного простран-
пространства линейных элементов оказался выше, чем порядок р
пространства, на к-ром задана метрич. функция F и на
к-ром должны определяться все дифференциальные ин-
инварианты К. п.
Другие возможности исследования К. п. основаны на
современной теории расслоенных пространств, теории
струй и теории нелинейных связностей. На этом пути с
применением дифференциально-алгебраич. метода про-
продолжений и охватов для широкого класса К. п. найдена
нек-рая редуктивная линейная связность в подходя-
щим образом подобранном расслоенном пространстве,
базой к-рого служит пространство линейных элементов
порядка р. Структурные уравнения форм этой связно-
связности дают полную систему тензорных инвариантов
К. п., на основе к-рой формулируются инвариантные
признаки нек-рых важных классов К. п.
В дифференциальной геометрии обобщенных про-
пространств большое место занимает исследование специ-
специальных К. п. с метрикой вида
где А( и В — функции х' и х'', что сближает такие
пространства с финслеровыми пространствами. В этом
случае общая теория А. Кавагути оказывается непри-
неприменимой, так как метрич. тензор g,-j становится вырож-
вырожденным. Поэтому вводится несимметрич. тензор
к-рый в общем случае не вырожден. В отличие от таких
пространств, К. п. общего типа представляют собой диф-
ференциально-геометрич. структуру высшего порядка.
Изучение К. п. служит также для поиска геометрич.
подходов к исследованию вариационной задачи для
интегралов вида
S =
Г'2 v ( <** dPx
J<t V dt dtP
Лит.: [1] Kawaguchi A., «Proc. Imp. Acad. Tokyo»,
1937, v. 13, p. 237—40; [2] Л о с и к М. В., б кн.: Тр. семи-
семинара по векторному и тензорному анализу, 1963, в. 12,
с. 213—37; [3] Б л и з н и к а с В. И., в кн.: Итоги науки.
Алгебра. Топология. Геометрия. 1967, М., 1969, с. 73 — 125.
Л. Е. Евтушик.
КАВАЛЬЕРИ ПРИНЦИП: объемы (или площади)
двух тел (фигур) равны, если равны между собой пло-
площади (длины) соответствующих сечений, проведенных
параллельно нек-рой данной плоскости (прямой). Это
положение, известное еще древнегреческим математи-
математикам, наз. обычно К. п., хотя Б. Кавальери (В. Cava-
lieri, 1635) не принимал его за принцип, а доказывал.
КАЗИМИРА ЭЛЕМЕНТ, оператор К а з и м и-
р а,— центральный элемент специального вида в уни-
универсальной обертывающей алгебре полупростой алгеб-
алгебры Ли. Такие операторы в одном частном случае были
впервые введены X. Казимиром [1].
Пусть (й — полупростая конечномерная алгебра Ли
над полем характеристики О, В — билинейная симмет-
симметричная инвариантная (т. е. В([х, у], z) = B(x,
[у, z\) для всех х, у, z?{sS) форма на @, невырожден-
невырожденная на идеале №ос:(Я К. э. алгебры (й (отно-
(относительно формы В) наз. элемент универсальной
обертывающей алгебры U(<3), представимый в виде
где {е/}, {/,} — дуальные базисы ®0 относительно
формы В, т. е. B(ei, /,) = б,-у-, i=l,. .., I, б/;-— символ
Кронекера, &=dim ©0. Элемент b не зависит от выбора
дуальных базисов в ©0 и содержится в центре t/(№).
Если алгебра ® проста, то К. э. алгебры ©, определяе-
определяемый Киллинга формой в В, является единственным, с
точностью до числового множителя, центральным эле-
ментом в U(®), представимым в виде однородного
квадратичного полинома от элементов алгебры ©.
Каждое линейное представление ф полупростой алгеб-
алгебры (S) в конечномерном пространстве V определяет
билинейную симметрическую инвариантную форму
Вч(х, ») = Тг(ф(*)фЫ)
на (.si, невырожденную на идеале ®ос:@, дополни-
дополнительном ккегф, и тем самым нек-рый К. э. b^^U(О).
Если ф неприводимо, то продолжение представления ф
на О'(Щ переводит 6Ф в ^ Е.
Лит.: [llCas i m ir H., van derWardenB. L.,
«Math. Ann.», 1935, Bd 111, S. 1 — 12; [2] БурбакиН.,
Группы и алгебры Ли, пер. с франц., М., 1976; [3] С е р р Ж.-П.,
Алгебры Ли и группы Ли, пер. с англ. и франц., М., 1969; [4]
Джекоб сон Н., Алгебры Ли, пер. с англ., М., 1964; [5]
Н а й м а р к М. А., Теория представлений групп, М., 1976;
[6] D i х m i e r J., Algebres enveloppantes, P., 1974.
Д . П. Желобеппо.
КАКТОИД — локально связный континуум С, к-рый
является замыканием суммы не более чем счетного числа
сфер Si и простых дуг D,-, расположенных в евклидовом
пространстве Е3, причем для каждого простого замкну-
замкнутого контура LczC существует одна и только одна сфера
S/, его содержащая. К. и только они являются монотон-
монотонными образами двумерной сферы S2; более того, всякий
К.— монотонно открытый образ S2. Б. А. Ефимов.
КАКУТАНИ ТЕОРЕМА: пусть X — непустое вы-
выпуклое компактное множество в R", X*—множество
ого подмножеств и / : X—>-Х* — такое полунепрерывное
сверху отображение, что для каждой точки х?Х мно-
множество f (х) непусто, замкнуто и выпукло; тогда отобра-
отображение / имеет неподвижную точку. С. Какутани [1] по-
показал, что из этой теоремы вытекает минимакса принцип
для конечных игр.
Лит.: [1] Kakutani S,, «Duke Math. J.», 1941, v. 8,
•Nb 3, p. 457 — 59; [2] К у Fan, «Proc. Nat. Acad. Sci. USA»,
1952, v. 38, p. 121—26; [3] H и"к а й д о X., Выпуклые струк-
структуры и математическая экономика, пер. с англ., М., 1972.
А. Я. Кирута.
КАЛИБР топологического простран-
пространства X — кардинальное число т такое, что всякое
семейство SB мощности т, состоящее из непустых откры-
открытых подмножеств топологич. пространства X, содержит
подсемейство SB'cSB также мощности т с непустым
пересечением, т. е. Г) {U:U ? SB'} ф 0- Регулярное
несчетное кардинальное число т является К. топологи-
топологического произведения ПХа, я?А, тогда и только
тогда, когда т — К. каждого сомножителя Ха- Свойство
быть К. сохраняется при непрерывных отображениях;
всякое несчетное регулярное кардинальное число
является К. любого диадического бикомпакта. Если
первое несчетное кардинальное число — К. простран-
пространства X, то X удовлетворяет Суслина условию. В неко-
некоторых моделях аксиоматич. теории множеств верно поч-
почти обратное утверждение, а именно, аксиома Мартина и
условие $г <2" ° влекут следующее: если пространство
X удовлетворяет условию Суслина, то всякое несчетное
семейство непустых открытых в X множеств содержит
несчетное центрированное подсемейство. В частности, в
этой модели кардинальное число Цг является К. для
всякого бикомпакта с условием Суслина. В некоторых
иных моделях теории множеств существует бикомпакт
с условием Суслина, для к-рого {i1 не является К.
Лит.: [1] Шанин Н. А., О произведении топологиче-
топологических пространств, М.— Л., 1948 (Тр. матем. ин-та АН СССР,
т. 24). Б. А. Ефимов-
КАЛЬДЕРОНА — ЗИГМУНДА ОПЕРАТОР — опб-
ратор К, определяемый на достаточно гладких финит-
финитных функциях ц>(х), заданных в евклидовом простран-
пространстве R", формулой
Кц>(х)= lim \ k (х— г/)ф (у) dy,
О J | |
= lim \ k (х— г/)
е->- О J | х-у | > е
где ядро к (х) — однородная функция степени п с ну-
нулевым средним значением по единичной сфере S=
= {х; x(?Rn, \x\ = l}. Ядро к (х) имеет вид
k(x) = Q(x)/\z\»,
где функция ?2 (х) — характеристика к (х) — удовлетво-
удовлетворяет условиям
?} (tx) = ?} (я) при t > О, ?1 (х) ? Lx (S),
Преобразование К.— 3. о. записывают часто в виде
/Cq>(*)=v.p. [Dn<f{y)r^-dy;
J R" \x-y\n
при этом интеграл понимается в смысле главного зна-
значения. В одномерном случае К.— 3. о. превращается
в оператор Гильберта Н:
К.— 3. о. по непрерывности расширяется на простран-
пространство Lp(Rn) функций f(x), суммируемых в степени р,
1 <р<оо, по R" и непрерывно отображает это простран-
пространство в себя. Если функция ?i (х) удовлетворяет усло-
условиям (*) и, кроме того, условию Днни:
^<», a(t)= sup \Q(x)-Q(x')\;
U| = |x'|=l
Kef(x)=[ °Mf(x-y)dy
J I У I > e | у I"
для 1<р<оо и f(?Lp(Rn), то:
а) существует постоянная Ар (не зависящая от /
и е) такая, что
II Ке/Hz.^ 4, ||/||^;
б) предел lim K&f=Kf существует в смысле сходи-
мости в Lp и
К.— 3. о. рассмотрен А. Кальдсроном и А. Зигмун-
Зигмундом [1].
Лит.: [1] С а 1 d е г о n A. P., Zygmund A., «Acta
Math.», 1952, v. 88, № 1—2, p. 85 — 139; [2] M и х л и н С. Г.,
Многомерные сингулярные интегралы и интегральные уравне-
уравнения, М., 1962; [3] С т е й н И., Сингулярные интегралы и диф-
дифференциальные свойства функций, пер. с англ., М., 1973.
Л. И. Лизоркин.
КАМЕРА в конечномерном действительном аффинном
пространстве Е относительно локально конечного
множества % гиперплоскостей в Е — связная компо-
компонента множества E\\J Ие%11. К. является открытым
выпуклым множеством в Е.
Пусть % — такое множество гиперплоскостей в Е,
что группа XV движений пространства Е, порожденная
ортогональными отражениями относительно гиперпло-
гиперплоскостей из %, есть дискретная группа преобразований
пространства Е, причем система % инвариантна отно-
относительно W. В этом случае говорят о К. относительно
W. Группа W действует на множестве всех К. просто
транзитивно и порождена множеством S ортогональных
отражений относительно гиперплоскостей системы $,
содержащих (dim E—1)-мерные грани, любой фиксиро-
фиксированной К. С, причем пара (W, S) является системой
Кокстера, а замыкание К. С — фундаментальной
областью группы W. Строение С (описание двугранных
углов между стенками) полностью определяет структуру
группы W как абстрактной группы. Изучение этого
строения является важным моментом в получении
полной классификации дискретных групп, порожден-
порожденных отражениями в Е (см. Кокстера группа). Вместе
с этой классификацией получается и полное описание
строения К. для таких групп W.
В том случае, когда W является группой Вейля си-
системы корней полупростой алгебры Ли, К. относитель-
относительно W наз. камерой Вейля группы W.
Понятие К. может быть введено и для гиперплоско-
гиперплоскостей и дискретных групп, порожденных отражениями
в пространстве Лобачевского или на сфере [2].
Лит.: [1] Бурбаки Н., Группы и алгебры Ли, пер.
сфранц., М., 1972, гл. 4; [2J В и н б е р г Э. Б., «Изв. АН СССР.
Сер. матем.», 1971, т. 35, К, 5, с. 1072—112. В. Л. Попов.
КАНАЛ БЕЗ ПАМЯТИ — канал связи, для к-рого
статистич. свойства сигнала на выходе в момент вре-
времени t определяются только сигналом на входе, пере-
переданном в этот момент времени t (и, следовательно, не
зависят от сигналов, переданных до и после этого мо-
момента времени t). Точнее, канал связи с дискретным
временем, сигналами на входе и выходе к-рого служат
случайные последовательности t] = (t]i, г\2, . . .) и ц =
= (rli' Л2> • • •) с пространствами значений (Y, Sy) и
(Y, Sy) соответственно, наз. К. б. п., если для любого
натурального п и любых множеств А1,. . ., Ап,
k=l, ..., га, справедливо равенство
= р {% € ^i ИЛ ¦ ¦ • р Ы € An I лп}>
где т]™= (t]i,. . ., г\п). Если к тому же условные веро-
вероятности P{r|fc? Ak\r\k} не зависят от к, то К. б. п. наз.
однородным.
Если обозначить через Сп канала пропускную способ-
способность отрезка длины га однородного К. б. п., то Сп =
= пС1. В случае, когда УиУ — конечные (или счетные)
множества, однородный К. б. п. полностью задается
матрицей переходных вероятностей {q(y, у),
где
Лит. см. [1], [3], [4], [5] при ст. Канал связи.
Р. Л. Добрушин, В. В. Прелое.
КАНАЛ ГАУССОВСКИЙ — канал связи, переходная
функция к-рого задает условное гауссовское распреде-
распределение. Точнее, канал связи (Q, V) наз. К. г. на конечном
отрезке [0, 7"], если выполнены условия: 1) простран-
пространствами значений сигналов на входе и выходе (g/, Sjy)
и (Й/, Soy) являются пространства функций y(t) и у (t),
i?[0, 7"], с действительными значениями и обычным
образом вводимой ст-алгеброй измеримых множеств
(т. е. сигналами на входе и выходе К. г. служат случай-
случайные процессы ti= {т) (t), ?[0, Т] } и ц= {rf (t), t?[0, T]}
соответственно), 2) переходная функция Q(y,-) канала
задает при любом фиксированном у ? Y условное гаус-
гауссовское распределение (говорят, что нек-рая совокуп-
совокупность случайных величин имеет условное гаус-
гауссовское распределение, если любая конеч-
конечная подсовокупность имеет условное конечномерное
нормальное распределение со вторыми моментами, не
зависящими от этого условия) и 3) ограничение V на-
наложено лишь на вторые моменты случайной величины г\.
Примером К. г., определенного на интервале (— оо,
оо), является канал, сигналом на входе к-рого служит
стационарная случайная последовательность г\=(...,
т]-!, г|0, гц, ...), а сигналом на выходе — стационарная
случайная последовательность г\=(..., г)_ 15 т]0, т|1? ...),
получаемая по формулам
где ?=--(..., 5-i, ?о> Si, • • •) — не зависящая от i] ста-
стационарная гауссовская случайная последовательность
с е?/=0, i=0, —i, — 2, . . ., и спектральной плотно-
плотностью fi(k), —1/2<Ъ<?1/2- Ограничение на входной
сигнал имеет вид
где fr\ (к) — спектральная плотность т), Ф (А,) — некото-
некоторая функция и S — константа. Пропускная способ-
способность такого канала задается формулой
где a(X) = ^/e=_ooa/,e-2ro*\ a ц определяется из урав-
уравнения ~ °°
Лит.; [1] Возенкрафт Д ж., Джекобе И., Тео-
Теоретические основы техники связи, пер. с англ., М., 196Н.
См. также [1], [4], [6] при ст. Канал связи.
Р. Л. Добрг/шин, В. В. Прелое.
КАНАЛ МНОГОСТОРОННИЙ — канал связи, для
к-рого возможна передача информации одновременно в
нескольких направлениях. Ниже описан К. м. без па-
памяти с дискретным временем и конечными алфавитами
на входах и выходах. Пусть заданы s конечных множеств
Ylt . . ., Ys, где (алфавит) У,- — совокупность возмож-
возможных сигналов, передаваемых г-м передатчиком, г конеч-
конечных множеств Ylt . . ., Yr, где (алфавит) Yj — совокуп-
совокупность возможных сигналов, принимаемых /-м прием-
приемником, и стохастическая матрица
1 (г/i, • ¦ ., Vs\ Уъ ¦¦¦¦, У г),
Говорят, что два набора случайных векторов (г|A). . . .,
Ti<«>) и (^(i), ..., т^")), где ti<*>=(ti1*), . . ., r\(sk)), т)(*>=
= (r|i ', . . ., Т]г '), определенных на нек-ром вероятност-
вероятностном пространстве (Q, Ш, Р), связаны отрезком длины
п однородного К. м. с s входами и г выходами, если г|?
и r]J-ft), i=l, .. ., s; / = 1, . • ., г; к=1, . . ., п, принимают
значения в множествах У,- и Yj, соответственно, и спра-
справедлива формула
Пп / (&) (k) ~ (k) ~ (k)\
к^хЧ\Уг •••••> У* \ Уг ,-.-•> Уг )
ПрИ Любых */^ — (yi , - . ., 7/s ) И y*"^=={yi t .... ?//- ),
Л=1, ..., n, ylk')€Yi~yf)€Yj,i=\, ...,s; /=1, ..., г.
Наглядно можно представить, что каждый вход и
каждый выход К. м. расположены в разных терм и-
налах (концах) К. м. (т. е. всего имеется s+r тер-
терминалов). Это означает, что передатчик или приемник,
расположенный в нек-ром терминале, не может исполь-
использовать информацию, известную передатчикам или при-
приемникам других терминалов. К. м., обладающие ука-
указанным свойством, часто наз. ч и с т ы м и в отличие от
смешанных К. м., для к-рых существуют терми-
терминалы, содержащие одновременно нек-рые входы и вы-
выходы канала. Сложность исследования смешанных
К. м. связана с тем обстоятельством, что передатчики
нек-рого терминала при выборе очередного сигнала для
передачи могут использовать информацию, получен-
полученную к данному моменту времени всеми приемниками
данного терминала; в свою очередь и приемники этого
терминала могут использовать всю информацию, имею-
имеющуюся на данный момент в терминале.
Наиболее общая задача передачи информации по
наглядно описанному выше чистому К. м. без памяти
состоит в следующем. Пусть имеется sBr—1) дискрет-
дискретных стационарных источников сообщений U(i, Л),
г=1, ..., s; Д?Л, где D — множество всех непустых
подмножеств совокупности индексов {1, ..., г}, выра-
вырабатывающих сообщения |(i, A)={gfe(t, A), k= ..-,
—1, 0, 1, . . .}, причем отдельные компоненты сооб-
сообщения ?ft(t, А) принимают значения из нек-рого мно-
множества X(i, А) объема M(i, A); ?(г, А) можно трак-
трактовать как сообщение, предназначенное для передачи
с i-ro входа К. м. во все выходы с номерами ; ? Д. Сооб-
Сообщением на /-м, /=1, .... г, выходе служит набор слу-
случайных процессов {g(i, А; /), i=l, . . ., s, и А таковы,что
?А} где
1(<А- /) = {Ы«\ Д; /). *=.... -1, о, 1, ...}
и компоненты ffc(?, A; j) принимают значения в мно-
множестве X(i, Д). Пусть отрезки сообщений
{lL(i, A) = (|!(i, A), ..., \L(i, Д)), i = l, ..., s; A??>}
длины L передаются по отрезку К. м. без памяти дли-
длины N с использованием следующих блочных методов
кодирования и декодирования. Кодирование задается
набором из s кодирующих отображений // таких, что
f ¦ • I Г v /,• л \ \rN j л
(Yi — прямое произведение N экземпляров множеств
Yj), а декодирование — набором декодирующих отоб-
отображений
Sj-i, A:Yf — *(*. А), 7 = 1, ..., г; i = l, ..., s,
и А таковы, что ;^А.
Набор кодирующих функций {/,¦} устанавливает
функциональную зависимость между отрезками сооб-
сообщении длины L всевозможных источников и отрезками
длины N сигналов на входах К. м. Набор декодирующих
функций {g.. (• д} устанавливает функциональную за-
зависимость между отрезками длины N сигналов на вы-
выходах канала и отрезками длины L сообщений, воспро-
воспроизводимых на каждом выходе. Если известно совместное
распределение отрезков сообщений %L(l, Д) длины L,
кодирующие и декодирующие функции {/,¦} и {gy-; l д}
и переходные вероятности К. м. без памяти, то может
быть вычислена вероятность ошибки ре, определяемая
формулой pe — P{?L(i, А) Ф \L ((, А; /) хотя бы при
одном i=l, ..., s;/=l, . .., г и А таком, что j:? А}.
Множество 9i наборов (векторов) скоростей Д =
= {R (г, Д), г=1, . . ., s; A?D} в s Br—1)-мерном ев-
евклидовом пространстве наз. областью про-
пропускной способности рассматриваемого
К. м., если для любого е>0 существуют N, кодиро-
кодирование {/,¦} и декодирование {gj. i } такие, что
Задача об описании области 9{ является одной из
основных задач теории К. м. В общем случае эта задача
не решена. Ее окончательное решение получено лишь
в нек-рых частных случаях, напр, для каналов с много-
многократным доступом (то есть К. м. с г=1) и для неко-
некоторого класса широковещательных каналов (то есть
К. м. с s=l).
Лит.: [1] Шеннон К., Работы по теории информации
и кибернетике, пер. с англ., М., 1963, с. 622—63; [2] Van
der Meulen E. С, в кн.: Proceedings of the 1975 IEEE-
USSR Joint Workshop on Information Theory. Moscow. Decem-
December 1875, N.Y., 1976, p. 227 — 47; [3] Cover T. M. «JEEE
Trans. Inform. Theory», 1972, v. 18, Ks 1, p. 2 — 14; [4] S 1 e-
p i a n D., Wolf J. K., «Bell System Techn. J.», 1973
v. 52, Mi 7, p. 1037—76. P. Л. Добрушин, В. В. Прелое.
КАНАЛ С КОНЕЧНОЙ ПАМЯТЬЮ — канал связи,
для к-рого статистические свойства сигнала на выходе
в момент времени t определяются сигналами на входе,
переданными в момент времени t', t—m«:?' <:? (и, следо-
следовательно, не зависят от сигналов, переданных до момен-
момента времени t—т); число т наз. величиной (длиной) па-
памяти К. с к. п.
Точнее, канал связи с дискретным временем, сигна-
сигналами на входе и выходе к-рого служат случайные по-
последовательности Т] = (. . ., Т|_!, Т)о, ГЦ,. . .) И Г| = (Т)_1,
ц0, г\,. . .) с пространствами значений (У, 5» и (У, 5у)
соответственно, наз. К. с к. п., если согласованный на-
набор условных распределений
с помощью к-рого может быть определен такой канал,
при любых к, п п А удовлетворяет условию
Р { ц1 ? А | т?„} = Р { г% € А' | rLm).
Здесь r(k=(y\k, i]ft + i. •••, т]п), ii"«,= (..., 11„_,, т)„),
.4 — некоторое множество из прямого произведения
;г—fc-j-1 экземпляров пространств (У, 5у). Аналогично
определяется К. с к. п. с непрерывным временем.
Лит.: [1] Хинчин А. Я., «Успехи матем. наук», 1956,
т. 11, в. 1, с. 17—75; 12] Файнстейн А., Основы теории
информации, пер. с англ., М., I960.
Р. Л. Добрушин, В. В. Прелое.
КАНАЛ С КОНЕЧНЫМ ЧИСЛОМ СОСТОЯНИЙ -
канал связи, для к-рого статистич. свойства сигнала на
выходе в момент времени t определяются сигналом на
входе в этот момент времени и состоянием канала в
предыдущий момент времени, причем множество воз-
возможных состояний канала конечно. Можно также опре-
определить К. с к. ч. с. как канал, заданный конечным
автоматом вероятностным. Ниже приведено строгое
определение однородного К. с к. ч. с. с дискрет-
дискретным временем и конечными пространствами У и У
значений компонент сигналов на входе и выходе. Пусть
заданы функция q(y, s'; у, s"), y?Y, y~?Y, s', s"?S,
где S — конечное множество, называемое множест-
множеством состояний канала, и распределение
вероятностей {pSo> so€^}- Наглядно функция q(y,
s'; у, s") определяет условную вероятность того, что
в момент времени кх на выходе К. с к. ч. с. появится
сигнал у и канал перейдет в состояние s" при условии,
что передавался сигнал у и в предыдущий момент вре-
времени (к—1)т канал находился в состоянии s'. Распреде-
Распределение {pSa, s0?S} трактуют как распределение вероят-
вероятностей начального состояния канала (т. е. состояние
канала в начальный момент времени). Рекуррентным
образом с помощью равенств определяют функцию
Qn(y", «о; У", О =
=2« «= 9 Ч(У"' s«"i; Уп' sn)Qn-i(y"~1, sol У"*1, »B-i),
Qi(y, «о; у, si) = q(y, s0; у, *i),
где уп = (у1,..., уп), yi?Y, y~i?Y, i=i,..., n
k = 0, 1, . . ., n.
Пусть
Qn(y", »o; y") = 2s cSQn(y", s0; y", «„)•
Тогда переходная функция
отрезка длины га К. с к. ч. с. при любом га, по опреде-
определению, равна
Qn(y", 2/") = 2SoSSpSo<?«(</", «о; у"),
здесь т)п=(т]1, ..., г\п) и ¦пп=(т11 г\„) — отрезки
длины п сигналов на входе и выходе канала.
Лита. см. [3], [4] при ст. Напал связи.
Р. Л. Добрушин, В. В. Прелое.
КАНАЛ С ОБРАТНОЙ СВЯЗЬЮ — канал связи,
используемый для передачи сообщений от источника
сообщений к получателю, на входе к-рого в любой мо-
момент времени известна нек-рая информация о сигналах,
полученных на его выходе до этого момента времени;
эта информация может быть использована для выбора
очередного сигнала, подлежащего передаче по каналу.
Ниже приведено описание одной из возможных схем
передачи информации по каналу с дискретным време-
временем при наличии полной обратной связи. Пусть сооб-
сообщением на входе канала служит случайная величина ?,
принимающая значения в нек-ром измеримом простран-
пространстве (I, 5 ^). Сообщение, доставляемое адресату (полу-
(получателю),— случайная величина |, принимающая зна-
значения в измеримом пространстве (J, S~). Пусть для
передачи сообщения § используется отрезок длины п
нек-рого канала с дискретным временем. Сигналами на
входе (%,..., цп) н выходе (г\1г..., г\п) этого отрезка
канала служат случайные векторы, компоненты к-рых
принимают значения в измеримых пространствах (Y,
Sy) и (У, Sy) соответственно. Метод передачи по тако-
такому каналу с использованием полной обратной связи
задается набором из п кодирующих функций
/iW, /2 (¦*, vi), i3 (*, г/ь У2), ¦¦-, fn(x,y~u ¦¦¦, yn-i),
со значениями в множестве Y и декодирующей функцией
/?(;/!• . . .,_у„), Vi(zY, i—1> • • ч п, со. значениями в мно-
множестве ЭЁ, с помощью соотношений
Эти соотношения показывают, что выбор очередного
сигнала гц для передачи по К. с о. с. зависит как от пе-
передаваемого сообщения ?, так и от сигналов л1; . . .,
Hii-i, полученных на выходе канала до этого момента
времени. Реально это означает, что имеется возмож-
возможность мгновенно и без помех доставлять на вход канала
сведения о полученном сигнале на его выходе. В этом
случае часто говорят, что наряду с каналом, осуществ-
осуществляющим передачу в прямом направлении (т. е. от источ-
источника сообщений адресату), имеется канал обрат-
обратной с в я з и (т. е. канал, осуществляющий передачу
в обратном направлении) с бесконечной пропускной
способностью (см. Канала пропускная способность).
Более реальным является предположение о том, что
канал обратной связи не является бесшумным, т. е.
сведения о сигналах на выходе канала, поступающие
на ого вход, могут содержать случайные ошибки. В этом
случае говорят о канале с неполной обрат-
обратной связью.
Так же, как и в обычном случае, вводится понятие
пропускной способности канала с обратной связью как
верхней грани скоростей передачи, при к-рых мож-
можно вести передачу, используя описанные выше методы
кодирования и декодирования при сколь угодно малой
вероятности ошибки. В общем случае пропускная спо-
способность К. с о. с. больше обычной пропускной способ-
способности канала. Установлено, однако, что для каналов
без памяти эти пропускные способности совпадают.
Для каналов с полной обратной связью предложены
просто описываемые и высоко эффективные алгоритмы
кодирования и декодирования.
Лит.: [1] Д о б р у ш и н Р. Л., «Теория вероятн. и ее
применен.», 1958, т. 3, № 4, с. 395—412; [2] Feedback communi-
communication systems, N.Y., 1961; [3] Зигангиров К. Ш.,
«Пробл. передачи информ.», 1970, т. 6, № 2, с. 87—92.
Р. Л. Добрушин, В. В. Прелое.
КАНАЛ СВЯЗИ — одна нз основных составных час-
частей систем передачи информации, рассматриваемых в
теории передачи информации. Используется при мате-
матич. описании реального канала связи, т. е.
совокупности технических устройств, обеспечивающих
передачу сообщений от передатчика к приемнику по
физической линии связи, и среды, в к-рой распростра-
распространяются сигналы от передатчика к приемнику.
К. с. с одним передатчиком и одним приемником,
используемый для передачи информации в одном на-
направлении (от передатчика к приемнику), задается
совокупностью двух измеримых пространств B/, S*y),
B/, Sjjj) (пространств сигналов, передаваемых передат-
передатчиком и принимаемых приемником соответственно),
переходной функцией Q(y, А), г/?й/, A^Soy, измери-
измеримой относительно а-алгебры S оу при фиксированном А
п являющейся вероятностной мерой на B/, Sщ) при
фиксированном у (функция Q(y, А) задает условное
распределение сигнала, получаемого приемником, при
условии, что передатчик передал сигнал у), и подмно-
подмножеством V в пространстве всех вероятностных мер в
пространстве B/, Sa/) (V задает ограничение на рас-
распределении сигнала, передаваемого передатчиком).
Говорят, что две случайные величины г\ и л, опреде-
определенные на нек-ром вероятностном пространстве (Q,
ЗГ, P), связаны каналом (Q, V), если они принимают
значения в пространствах (g/, Soy) и (g7, S^y) соответ-
соответственно, для любого А ? S~u с вероятностью 1 условная
вероятность Р {т] ? А | r\} = Q (ц, А), и распределение
ц принадлежит V.
В приложениях часто рассматривают К. с, для к-рых
(g/, S^y) и B/, Sоу) являются пространствами измери-
измеримых функций, определенных на отрезке [а, Ь] и прини-
принимающих значения в нек-рых измеримых пространствах
(У, Sy) и (У, Sy) соответственно с а-алгеброй, порож-
порожденной измеримыми цилиндрическими множествами.
В этом случае пишут B/, Suy) = (Yba, Syb), (g/, Sy) =
= (Ya, S~b\ и говорят о К. с. с непрерывным
Ya>
временем на отрезке [а, Ь], для к-рого г| =
= {rl№> t^ia, b}} и r\={r](t), t?[a, b]} — случайные
процессы со значениями в пространствах (Y, Sy) и
(У, Sy) соответственно; значения r\(t) и r\ (t) трактуются
тогда как переданный и получаемый сигнал в момент
времени t. Аналогично, в случае дискретного
времени сигналами на входе и выходе К. с. служат
случайные векторы т)?= (r\k, r\k + 1, ..., т]„) и т]Л=('П«t»
ц/г + i, ¦ . ., т)„), компоненты к-рых принимают значения в
измеримых пространствах (У, Sy) и (У, Sy) соответ-
соответственно; при этом x\i и г]у трактуются как переданный
и полученный сигналы в момент времени / т, где х—
= const — промежуток времени между двумя последо-
последовательными передачами сигналов по К. с.
Часто рассматривают также К. с. с непрерывным или
дискретным временем t на полубесконечном или беско-
бесконечном в обе стороны интервале. Напр., под К. с.
(Q, V) с непрерывным временем на полубесконечном
интервале [0, оо) подразумевают обычно совокупность
описанных выше К. с. (Qo , Fo ), заданных на всех ко-
конечных отрезках [0, Т] и удовлетворяющих нек-рым
условиям согласованности. Каждый К. с. (Qo, Fo
наз. в этом случае отрезком [О, Г] К. с. (Q, V).
Один из возможных вариантов условий согласованности
может быть сформулирован следующим образом. Пусть
Ац — произвольное множество из SyT; у0 — произ-
произвольная функция из Уо и I/O = (г/о, 2/s) для нек-poro s,
0<s<7\ где г/о€У(ь ys ?YS . Условия согласован-
согласованности, наложенные на переходные функции Qa (., .),
состоят тогда в требовании, чтобы для любого конеч-
конечного отрезка [0, 7"], любых s, 0<s<71, множества
Лj?5ps н функции ya = (yso, y!)€Y%, г/о^Уо, yf ?У[,
выполнялось равенство
где ^4oXys — цилиндрическое множество в простран-
пространство Уо . порожденное множеством АI из пространства
Уо. Ограничения Vo , 0<7'<oo накладываемые на
т т
вероятностные меры в пространствах (Уо , So), также
должны удовлетворять нек-рым условиям согласован-
согласованности.
Аналогично вводят понятие К. с. (Q, V) с непрерыв-
непрерывным временем на бесконечном в обе стороны интервале
(—оо, оо). Условия согласованности, необходимые при
задании такого К. с, формулируются обычно специ-
специфически для каждого типа этого канала. Иногда в кон-
конкретных ситуациях понятие К. с. на бесконечных интер-
интервалах [0, оо) и (— оо, оо) вводится и непосредственно
(без рассмотрения конечных отрезков этих каналов)
с помощью явного описания преобразования, совершае-
совершаемого над входным сигналом К. с. при получении сигна-
сигнала на выходе К. с. (см., напр., Канал гауссоеский, Шум
аддитивный). Все сказанное о К. с. (Q, V) с непрерыв-
непрерывным временем на интервалах [0, оо) или (— оо, оо) сох-
сохраняет силу и для аналогичных К. с. с дискретным
временем.
К. с. делятся на различные классы в зависимости
от типов условных распределений Q и ограничений
V (см., напр., Канал без памяти, Канал с конечной па-
памятью, Канал с конечным числом состояний, Канал га-
гауссоеский, Канал симметричный). Основной характе-
характеристикой К. с. является канала пропускная способность,
к-рая характеризует максимально возможную инфор-
информации скорость передачи по этому К. с.
Возможны различные обобщения приведенного опре-
определения К. с, соответствующие более общим и сложным
системам передачи информации (см., напр., Канал с об-
обратной связью, Канал многосторонний).
Лит.: [1] Ш е к н о к К., Работы по теории информации и
кибернетике, пер. с англ., М., 1963, с. 243—332; [2] Добру-
ш и н Р. Л., «Успехи матем. наук», 1959, т. 14, в. 6, с. 3 —104;
[3] Вольфовиц Дж., Теоремы кодирования теории ин-
информации, пер. с англ., М., 1967; [4] Г а л л а г е р Р., Теория
информации и надежная связь, пер. с англ., М., 1974; [5]
Файнстейн А., Основы теории информации, пер. с англ.,
М., 1960; [6] Ф а н о Р., Передача информации. Статистиче-
Статистическая теория связи, пер. с англ., М., 1965.
Р. Л. Добрушин, В. В. Прелое.
КАНАЛ СВЯЗИ КВАНТОВЫЙ — система передачи
(преобразования) информации, использующая в каче-
качестве носителя сообщений квантово-мехаиич. объект.
В отличие от классического сообщения, описываемого
распределением вероятностей на пространстве сигна-
сигналов X, квантовое сообщение представляется оператором
плотности (состоянием) в гильбертовом пространстве //,
соответствующем данному квантово-механич. объекту.
Всякий канал связи можно рассматривать как аффин-
аффинное (сохраняющее выпуклые комбинации) отображение
(выпуклого) множества сообщений на входе в множество
сообщений на выходе. В частности, квантовое
кодирование есть аффинное отображение С
лшожества S (X) распределений вероятностен на про-
странстве входных сигналов X в 2 (Я), множество
всех операторов плотности в Я. Собственно К. с. к. есть
аффинное отображение L из 2 (Я) в 2 (Я'), где Я. И' —
гильбертовы пространства, описывающие соответственно
вход и выход канала. Квантовое декодиро-
декодирование есть аффинное отображенпе D из 2 (Я') в S (У),
где У — пространство сигналов на выходе. Передача
сообщений, как и в классической теории информации,
описывается схемой
S (X) Л 2 (Я) Л 2 (Я') Л S (Y). A)
Важной задачей является нахождение оптимального
способа передачи сообщения по заданному квантовому
каналу L. При фиксированном L условное распределе-
распределение сигнала на выходе относительно сигнала на вхо-
входе является функцией Рс ?,(dy\x) кодирования С ц
декодирования D. Задается некоторый функционал
Q{Pc, D(dy\x)} и требуется найти экстремум этого
функционала по С и D. Наиболее изучен случай, ког-
когда С также фиксированно и нужно найти оптималь-
оптимальное D. Тогда схема A) сводится к более простой:
S (X) Л 2 (Я) Л S (У). B)
Чтобы задать кодирование, достаточно указать образы
рх распределений, сосредоточенных в точках х?Х.
Декодирование удобно описывать У-и з м е р е н п е м,
к-рое определяется как мера М(dy) на У со значениями
в множестве неотрицательных эрмитовых операторов
в Я, причем M(Y) равно единичному оператору. Вза-
Взаимно однозначное соответствие между декодированием
и измерениями задается формулой
Dp (dy) = Tr pM (dy),
так что условное распределение сигнала на выходе
схемы B) относительно сигнала на входе есть
Р
В случае конечных X, Y для оптимальности измере-
измерения {Л1(у)} необходимо, чтобы оператор
где
был эрмитов и удовлетворял условию
(F(y)~K)M(y) = 0, y?Y. C)
Если Q — аффинная функция (как в случае бейесовс-
кого риска), то для оптимальности (в смысле минимума
Q) необходимо и достаточно, чтобы оператор Л, кроле
C), удовлетворял условию A<^:F(y), y?Y. Аналогич-
Аналогичные условия имеют место для достаточно произволь-
произвольных X, Y.
Существует параллель между квантовыми измерения-
измерениями и решающими процедурами в классической теории
статистич. решений, причем детерминированным про-
процедурам соответствуют простые измерения, определяе-
определяемые проекторнозначными мерами M(dy). Однако, в от-
отличие от классич. статистики, где оптимальная проце-
процедура, как правило, сводится к детерминированной, в
квантовом случае уже для бейесовской задачи с конеч-
конечным числом решений оптимальное измерение, вообще
говоря, не может быть выбрано простым. Геометриче-
Геометрически это объясняется тем, что оптимум достигается на
крайних точках выпуклого множества всех измерений,
а в квантовом случае класс простых измерений содер-
содержится в множестве крайних точек, не совпадая с ним.
Как и в классич. теории статистич. решений, возмож-
возможно ограничение клавса измерений требованиями инва-
инвариантности или несмещенности. Известны квантовые
аналоги неравенства Рао — Крамера, дающие нижнюю
границу для среднеквадратичной погрешности измере-
ння. В приложениях теории много внимания уделяется
бозонным гауссовским каналам связи, для к-рых в
ряде случаев дано явное описание оптимальных из-
измерений.
Лит.: [llHelstrom С. W., Quantum detect iv and estima-
estimation theory, N. Y., 1976; [2] X о л е в о А. С, Исследования
по общей теории статистических решений, М., 1976; [3] его
же, «Repts Math. Phys.», 1977, v. 12, p. 273 — 78.
А. С. Халсво.
КАНАЛ СИММЕТРИЧНЫЙ — канал связи, пере-
переходная функция к-рого обладает тем или иным свойст-
свойством симметрии. Однородный канал без памяти с диск-
дискретным временем и конечными пространствами состоя-
состояний Y и У=У компонент сигналов на входе и выходе,
задаваемый матрицей переходных вероятностей {q(y, у),
У< H^Y}, наз. К. с, если
( q при у = у,
Цу,у) = ^ у_ при у ф - W
где п — число элементов множества Y, 0<:<7<:1. Наи-
Наиболее изученным примером К. с. без памяти является
двоичный К. с. с матрицей переходных вероят-
вероятностей
— Q Q II '
Для К. с. многие важные теоретико-информационные
характеристики могут быть либо вычислены явно, либо
их вычисление значительно упрощается по сравнению
с несимметричными каналами. Напр., для К. с. без
памяти с матрицей {q(y, у), у, y?Y) вида (*) канала
пропускная способность С дается равенством
С = log п + q log q + A — q) log ^ .
Лит. см. [1], [4] при ст. Канал связи.
Р. Л. Добрушин, В. В. Прелое,
КАНАЛА ПРОПУСКНАЯ СПОСОБНОСТЬ — теоре-
теоретико-информационная мера возможности передачи ин-
информации по каналу связи. Пусть т) и т) — случайные
величины, связанные каналом связи (Q, V) . К. п. с. С
такого канала определяется равенством
С = sup/(г), ц), A)
где /(т), rj) — информации количество в т) относительно
t), а верхняя грань берется по всем парам случайных
величин (т), т)), связанным каналом ((>, V). В случае,
когда сигналы на входе и выходе канала т)={т)D),
— оо <?<оо } и т)= {т) (?), —оо <i<oo } являются случай-
случайными процессами с непрерывным или дискретным вре-
временем, под К. п. с. обычно понимают среднюю
К. п. с, приходящуюся на единицу времени или на
один символ передаваемого сигнала, т. е., по определе-
определению, полагают
С = r_lim ^sup / (г,Г, ^ Г), B)
если такой предел существует; здесь верхняя грань
берется по всевозможным парам случайных величин
r\f={i](s), i<s<r}, Т|Г= {"П (s)' *<s<r}, связанных
соответствующим отрезком данного канала. Существо-
Существование предела B) доказано для достаточно широкого
класса каналов, напр, для однородных каналов с ко-
конечной памятью и необращающимися в нуль вероятно-
вероятностями перехода.
Известно, что в достаточно широком классе случаев
(напр., для упомянутых выше каналов с конечной па-
памятью) справедливо равенство
! П) C)
где верхняя грань берется по всем парам стационарно
связанных случайных процессов ц (t), r\(t), —oo<f<oo,
таким, что при любых — oo<t<T<oo случайные вели-
величины т)Г={т)(«). t<s*?T} и ^гг={^E), г<л<Г} связа-
связаны соответствующим отрезком рассматриваемого кана-
канала. Равенство C) показывает, таким образом, что
К. п. с. совпадает с максимально возможной информации
скоростью передачи по этому каналу.
Явное вычисление К. п. с. оказывается возможным
лишь в ряде частных случаев, напр, для каналов симмет-
симметричных без памяти и каналов гауссовских. Поэтому зна-
значительный интерес представляют различные асимпто-
асимптотические формулы для К. п. с. Напр., для канала
(Q, V), сигналы на входе и выходе к-рого принимают зна-
значения в n-мерном евклидовом пространстве R", пере-
переходная функция канала Q(y, •) задается плотностью
q(y, у) (относительно меры Лебега), у, j^R", и огра-
ограничение V состоит в ограничении на среднюю мощность
сигнала на входе Elii^-ssS1 (где |т)| — длина вектора г\
в R."), iS>0 — фиксированное число, известны следую-
следующие результаты (см. [1]).
1) Пусть q(y, y) = q(y—y), т. е. рассматривается ка-
канал с аддитивным шумом, так что сигнал на выходе п
равен сумме r\ = r\-\-t> сигнала на входе ц и не зависящего
от него шума ?, и пусть Е|?|2^Л". Тогда при jV—>-0
(при слабых дополнительных условиях) справедлива
асимптотическая формула
С = — й (?) -4- — log —— + —^- N + о (Л ),
где h(t,) — дифференциальная энтропия Z,, a o(N)/N—>-0
при JV—>-0. Эта формула соответствует случаю малого
шума.
2) Пусть q(y, у) — произвольно, но ?—>-0. Тогда
(
V у
где
Лит.: [1] П р е л о в В. В., «Пробл. передачи пнформ.»,
1969, т. 5, J* 2, с. 31—36; 1972, т. 8, ЛЬ 4, с. 22—27.
См. также [1], L3]—[6] при ст. Капал связи.
Р. Л. Добрушин, В. В. Прелое.
КАНАЛОВАЯ ПОВЕРХНОСТЬ — поверхность, одно
семейство линий кривизны к-рой состоит из окружно-
окружностей, плоскость каждой такой окружности пересекает
К. п. под постоянным углом. Одна полость эволюты
К. п. вырождается в кривую Г, так что К. п. является
огибающей однопараметрич. семейства сфер. Если p(s) —
радиус-вектор кривой Г — множества центров сфер
семейства, R (s) — радиус соответствующей сферы
(s — длина дуги Г), то радиус-вектор К. п. определя-
определяется из уравнений:
(г-рJ = Д2, (г-р, р')-(Л, Л')=0,
причем |Л'1<1. Если /?=const, то К. п.— трубча-
трубчатая поверхность, таков, напр., тор.
И. X. Сабитов.
КАНОНИЧЕСКАЯ КОРРЕЛЯЦИЯ — корреляция
между линейными функциями двух множеств случайных
величин, характеризуемая максимально возможными
значениями коэффициентов корреляции. В теории
К. к. случайные величины Хг, . . ., Xsn Xs + ], . . .. Xs + t,
s<:i, линейно преобразуются в так наз. канонические
случайные величины Y1, ..., Ys и Ys + 1, . . ., Ys + t—
такие, что: а) все величины Y имеют нулевое матема-
тич. ожидание и единичную дисперсию, б) внутри
каждого из двух множеств величины Y некоррелиро-
ваны, в) любая величина Y из 1-го множества коррелп-
рована лишь с одной величиной из 2-го множества, г)
ненулевые коэффициенты корреляции между величи-
величинами Y из разных множеств имеют максимальное
значение.
В частном случае s=l К. к. представляет собой мно-
множественную корреляцию между Хг и Х2, . . ., X\ + t-
Преобразование к каноническим случайным величинам
соответствует алгебраич. задаче приведения квадратич-
квадратичных форм к канонич. виду. В многомерном статистич.
анализе с помощью метода К. к. при изучении взаимо-
взаимосвязи двух множеств компонент вектора наблюдений
осуществляется переход к новой системе координат, в
к-рой корреляция между Хи . . ., Xs и Xs + i, . . ., Xs + t
проявляется наиболее отчетливо. В результате анализа
К. к. может оказаться, что взаимосвязь между двумя
множествами полностью описывается корреляцией
между несколькими каноническими случайными вели-
величинами.
Лит.: [1] Hotell ing H., «Biometrika», 1936, v. 28,
p. 321—77; [2] Андерсон Т., Введение в многомерный
статистический анализ, пер. с англ., М., 1963; [31 К е н д а л л
М. Д., Стьюарт А., Многомерный статистический анализ и
временные ряды, пер. с англ., М., 1976. А. В. Прохоров.
КАНОНИЧЕСКАЯ КРИВАЯ — образ алгебраич.
кривой при каноническом погружении. Если кривая X
не является гиперэллиптической и имеет род #>2,
то ее образ в проективном пространстве Pg-i при ка-
канонич. погружении имеет степень 2g—2 и является
нормальной кривой. Обратно, любая нормальная кри-
кривая степени 2g—2 в проективном пространстве Pg-i
будет канонич. кривой для нек-рой кривой рода g.
Алгебраич. кривые (с указанным выше условием) бира-
циональио изоморфны тогда и только тогда, когда их
К. к. проективно эквивалентны. Это сводит проблему
классификации кривых к задаче теории проективных
инвариантов и дает возможность построить многообра-
многообразие модулей алгебраич. кривых [2]. Для небольших g
можно дать явное геометрич. описание К. к. рода g-
Так, для рода 4 К. к. совпадают с пересечениями
квадрики и кубики в Р3, а для рода 5 — с пересечением
трех квадрик в Р4.
Лит.: [1] Ш а ф а р с в и ч И. Р., Основы алгебраической
геометрии, Ы., 1972; [2] Дьёдонне Ж., К е р р о л Д ж.,
М а м ф о р д Д., Геометрическая теория инвариантов, пер.
с англ., М., 1974; [3J У о к е р Р., Алгебраические кривые, пер.
с англ., М., 1952; [4] S e v е г i F., Vorlesungen uber algebra-
ische Geometrie, Lpz., 1921. A. H. Паршин.
КАНОНИЧЕСКИЕ КОЭФФИЦИЕНТЫ КОРРЕЛЯ-
КОРРЕЛЯЦИИ — максимальные значения коэффициентов кор-
корреляции между парами линейных функций
U — a.iXi.-lr .. . 4-asXs, V=$iXs + 1, ..., $tXs + t
от двух множеств случайных величин Хг, . . ., Xs и
Xs + i, . . ., Xs + -t, для к-рых U ж V являются каноничес-
каноническими случайными величинами (см. Каноническая кор-
корреляция). Задача определения максимума коэффициен-
коэффициента корреляции между U и V при условиях E[/=EF=O
и E[/2=EF2=1 решается с помощью неопределенных
множителей Лагранжа. К. к. к. являются корнями
X^h^. . .^Я^>0 уравнения
где 2ц п 2]2 соответственные матрицы ковариаций
величин Хг, . . ., Xs п Xs + i, . . ., Xs + t, а 212=2Г1 —
матрица ковариаций между величинами 1-го и 2-го
множеств. При этом r-й корень уравнения наз. г-м
К. к. к. между Xlt . . ., Xs и Xs + u ¦ • -, Xs + t и равен
максимальному значению коэффициентов корреляции
между парой линейных функций U(r"> и Vir) канони-
канонических случайных величин, каждая из к-рых имеет
единичную дисперсию и некоррелирована с первыми
г—1 парами величин U и V. Коэффициенты а(г)=
(i, • •. ai°)T, Р(П = (Р{П, • • •, р(/')Глииейныхфунк-
р(/')Глииейныхфункций ?/(г' и F(r) удовлетворяют уравнению
2 1V I i D J = 0
21 —АЛУ V P
при условии \ = Xr. И. О. Сарманов.
КАНОНИЧЕСКИЕ РАЗРЕЗЫ, канонические
сечения,— система
S — {a1, 61, а2, Ь3, ..., ag, bg, lu ..., lv)
2g-\-v кривых на конечной римановой поверхности Н
рода g с v компонентами края, после удаления точек
к-рых из R, т. е. разрезания R вдоль кривых
системы 5, остается (плоская) односвязная область R*.
Точнее, система S образована из К. р., если каждому
замкнутому, или циклическому, разрезу,
или, короче, циклу ау, /=1, . . ., g, в S соответствует
ровно один так называемый сопряженный цикл
bj, пересекающий цикл о,- в одной и только в одной фик-
фиксированной точке po?R> общей для всех разрезов
системы S. Остальные циклы oft, 6ft, &^=/, и кривые
ls, s=l, . . ., v, лишь имеют точку р0 общей, но не пере-
переходят с одного берега разреза а;- на другой; каждая
кривая ls соединяет р0 с соответствующей компонентой
края. На данной римановой поверхности R существует
бесконечное множество систем S К. р. В частности,
какова бы ни была односвязная область DcR, вместе
со своим замыканием D расположенная строго внутри
R, можно выбрать систему К. р. так, чтобы DcR*.
Далее, всегда можно найти систему К. p. S, состоя-
состоящую только из аналитич. кривых. Единственность
системы 5 аналитич. К. р. можно обеспечить, напр.,
потребовав дополнительно, чтобы достигался экстре-
экстремум нек-рого функционала, связанного с 5. В частно-
частности, можно проводить циклич. К. p. aj, bj системы S
так, чтобы достигалось наибольшее в классе систем,
гомотопных S, значение Робена постоянной в точке
р0 для определенной области DcR, po?D. Единствен-
Единственности разрезов ls также можно добиться, исходя из
требования максимизации постоянных Робена в опре-
определенной паре точек (см. [2]).
Лит.: [1] Г у р в и ц А., Курант Р., Теория функций,
пер. с нем., М., 1968; [2] Ш и ф ф е р М., Спенсер Д. К.,
Функционалы на конечных римановых поверхностях, пер.
с англ., М., 1957. Е. Д. Соломенцев.
КАНОНИЧЕСКИЙ КЛАСС — класс Кх дивизоров
относительно линейной эквивалентности на алгебраич.
многообразии X, являющихся дивизорами дифферен-
дифференциальных форм со максимальной степени. Если X —
пеособое алгебраич. многообразие и dim X=n, то в ло-
локальных координатах хг, . .., хп форма (о имеет вид
« = / (xi, . ¦ ¦, <г„) dx1 А . . . A dxn.
Дивизор (ю) формы со локально равен дивизору (/)
рациональной функции /. Эта конструкция не зависит
от выбора локальных координат и дает дивизор (со)
формы на всем многообразии X. Поскольку для любой
другой формы ю' той же степени, что и «а, имеет место
равенство co' = gco, то (<a')=(g)+(<a) и соответствующие
дивизоры эквивалентны. Построенный так К. к. Кх
является первым Чжэня классом пучка Qx регулярных
дифференциальных форм степени п. Его численные
характеристики (степень, индекс самопересечения и
т. д.) являются эффективно вычисляемыми инвариантами
алгебраич. многообразия.
Если X — неособая проективная кривая рода g, то
deg Kx=2g—2. Для эллиптич. кривых и, более общо,
для абелевых многообразий Кх = 0- Если X — неособая
гиперповерхность степени d в проективном простран-
пространстве Р„, то Kx=(d — п — 1) //, где Н — ее гиперпло-
гиперплоское сечение.
См. также Каноническое погружение.
Лит.: [1] Ш а ф а р е в и ч И. Р., Основы алгебраической
геометрии, М., 1972. А. Н. Паршин.
КАНОНИЧЕСКОЕ МНОЖЕСТВО замкнутое,
ия-м ножество,— множество М топологич. про-
пространства, являющееся замыканием открытого множе-
множества; другими словами, это — множество, являющееся
замыканием своего открытого ядра <М> : М—
= [<Л/">]. В каждом замкнутом множестве F содер-
содержится максимальное хя-множество: Л —[<^>]. Сумма
двух иа-множеств есть ха-множество, однако пересе-
пересечение их может н не быть таковым. Множество, являю-
являющееся пересечением конечного числа ха-множеств, наз.
я-м ножество м.
Множество, являющееся (открытым) ядром замкну-
замкнутого множества, наз. каноническим множе-
множеством открытым или хо-множеством; другими сло-
словами, это — множество, совпадающее с ядром своего
замыкания: М= <\М]>. Всякое открытое множество G
содержится в наименьшем хо-множестве: В— <[G]>.
Открытые К. м. могут быть определены и как дополне-
дополнения к замкнутым К. м., и наоборот.
Лит.: [1] Александров П. С, Введение в теорию
множеств и общую топологию, М., 1977; Г2] А р х а н г е л ь-
ск и й А. В., Пономарев В. И., Основы общей топо-
топологии в задачах и упражнениях, М., 1974. М. И. Войцеховский.
КАНОНИЧЕСКОЕ ПОГРУЖЕНИЕ — отображение
алгебраич. многообразия X в проективное пространство
с помощью степеней канонического класса Кх (см. Ли-
Линейная система). Пусть X — неособая проективная
кривая рода g", отображение, определяемое классом
пКу, будет вложением для нек-рого п только, если
#>1. Причем можно взять п=1 для негиперэллиптич.
кривых, п=2 для гиперэллиптич. кривых рода g>2 и
в=3 для кривых рода g=2. Эти результаты использу-
используются для классификации алгебраич. кривых рода g>l
(см. Каноническая кривая).
Аналогичные вопросы для многообразий размернос-
размерности больше единицы рассматривались в основном для
поверхностей. При этом роль кривых рода ?>1 играют
поверхности, у к-рых нек-рая степень пКх канонич.
класса дает бирациональное вложение поверхности в
проективное пространство. Они наз. поверхно-
поверхностями общего типа; основной результат об
этих поверхностях состоит в том, что для них уже класс
5КХ определяет регулярное отображение в проектив-
проективное пространство, являющееся бирацпональным вло-
вложением. Напр., неособые поверхности степени т. в Р3
являются поверхностями общего типа, если т>4. В этом
случае бирациональное вложение дает уже каноничес-
канонический класс Кх- Если КХКХ>2 и pg(X)>l (здесь
КхК-х — индекс самопересечения, a pg(X) — геомет-
геометрический род), то вместо 5КХ можно взять даже ЗКу-
Поверхности, для к-рых никакая степень пКх не дает
вложения, разбиваются на следующие пять семейств:
рациональные поверхности, линейчатые поверхности,
абелевы многообразия, .КЗ-поверхности и поверхности
с пучком эллиптич. кривых. При этом рациональные и
линейчатые поверхности — аналоги рациональных
кривых, а остальные три семейства — аналоги эллип-
эллиптич. кривых.
Получены первые обобщения этих результатов и на
многообразия произвольной размерности [5].
Лит.: [1] Шафаревич И. Р., Основы алгебраической
геометрии, М., 1972; [2] Severi F., Vorlesungen iiber al-
gebraische Geometrie, Lpz., 1921; Гз] Алгебраические поверх-
поверхности, M,, 1965 (Тр. Матем. ин-та АН СССР, т. 75); [4] В о т-
b i e r i E., Husemoller D., «Ргос. Sympos. Pur. Math.»,
1975, v. 29, p. 329—420; [5] Ueno К., в кн.; Lecture Notes
in Mathematics, v. 412, В.—Hdlb.—N.Y., 1974, p. 288 — 332.
A. H. Паршин.
КАНОНИЧЕСКОЕ ПРОИЗВЕДЕНИЕ, канониче-
каноническое произведение Вейерштрасса, —
целая функция, все нули к-рой составляют заданную
последовательность комплексных чисел {а.^}. Пусть
нули а^О расположены в порядке неубывания их
модулей, |afr! <:|a/;+1|, и не имеют предельных точек в
конечной плоскости (необходимое условие), т. е.
Urn а/;=оо. Тогда К. п. имеет вид
где
W ( — , qu) —п ервичные, или примерные,
\ak I
множители Вейерштрасса. Показатели
Gй выбираются так, чтобы К. п. абсолютно и равномерно
сходилось на любом компакте; напр., достаточно взять
Чь~^к — 1- Если последовательность { laft I } имеет
конечный показатель сходимости
то все qk можно взять одинаковыми, исходя, напр.,
из минимального требования 9^ = </<Р<9~1-1; такое
число q наз. родом К. п. Если E = оо, т.е. если
ряды У lakl~x расходятся при любом ?. > 0, то
*™ k=\
имеем К. п. бесконечного рода. Порядок К. п. р=Р
(об определении типа К. п. см. [1]).
Лит.: [1] Левин Б. Я., Распределение корней целых
функций, М., 1956. Е. Д. Соломенцев.
КАНТОРА АКСИОМА — одна из аксиом, характе-
характеризующих непрерывность прямой линии; заключается в
следующем: любая последовательность вложенных друг
в друга отрезков, длины к-рых стремятся к нулю, име-
имеет одну общую точку. Сформулирована Г. Кантором
(G. Ca'ntor, 872). БСЭ-з.
КАНТОРА ПАРАДОКС — см. Антиномия.
КАНТОРА ТЕОРЕМА — 1) Множество 2А, состоя-
состоящее из всех подмножеств множества А, не равномощно
ни самому А, ни его подмножеству. Идея доказательст-
доказательства этой теоремы, принадлежащая Г. Кантору (G.Can-
(G.Cantor, 1878), получила название «канторова диагональ-
диагонального метода» и играет существенную роль в теории мно-
множеств. Из К. т. следует, что никакие два из множеств А ,
2Л, 22 , 222 ,. . . не равномощны. Таким способом
получается бесконечно много различных кардинальных
чисел. Из К. т. вытекает, что не существует множества
всех множеств. Это означает, что нельзя принять
аксиому теории множеств, утверждающую существо-
ванне для каждой высказывательной функции Ф (х)
множества, состоящего из элементов х, удовлетворяю-
удовлетворяющих Ф(х) (СМ. [1], [2], [3], [8]). Б. А. Ефимов.
2) Любая последовательность убывающих ограничен-
ограниченных замкнутых множеств действительных чисел имеет
непустое пересечение. Обобщается на компактные
подмножества метрич. пространства. Свойство: диамет-
диаметры замкнутых множеств метрич. пространства Л', после-
последовательно вложенных друг в друга, стремятся к ну-
нулю — одно из определений полноты X. Свойство:
вполне упорядоченная система убывающих замкнутых
множеств топологич. пространства X — одно из оп-
определений бикомпактности X (см. [1], [2], [4], [5], [11]).
3) Всякое множество действительных чисел есть объ-
объединение совершенного множества своих конденсации
точек и счетного множества; иногда наз. теоре-
теоремой Кантора — Бендиксона. Обобщена на
случай подмножеств метрич. пространства со счетной
базой (теорема Линделёфа) (си. [1], [2], [3J,
[14], [15]).
4) Если из двух множеств каждое эквивалентно
части другого, то эти два множества эквивалентны
между собою. Аналогичное утверждение справедливо
и для вполне упорядоченных множеств. Иногда наз.
теоремой Кантора — Вернштейна или
просто теоремой Бернштейна (последний
дал корректное доказательство этой теоремы) (см. [1],
[2], [3], [10], [12], [16]).
5) Если
Ап — ап cos пхл-Ьп sin nx —^0
для всех, кроме конечного числа, точек отрезка [—я, я],
то ап, Ъп—»-0. Обобщена на случаи, когда Л„—>-0 на
множестве положительной меры (теорема Ле-
Лебега), когда А„—>-0 на множестве второй категории
(теорема Ю н г а), и на другие ситуации. Важ-
Важнейшим следствием являются различные теоремы о
множествах единственности тригонометрич. рядов (см.
[1], [В], [7], [9], [18], [19]).
6) Функция, непрерывная на замкнутом отрезке дей-
действительной оси, равномерно непрерывна на нем.
Обобщена на случай непрерывных отображений биком-
бикомпактного пространства в равномерное пространство.
Иногда наз. теоремой Гейне — Кантора (см. [1],
[4], [5], [13]).
Лит.: [1] Cantor G., Gesammelte Abhandlungen, В.,
1932; [2] Хаусдорф Ф., Теория множеств, пер. с нем.,
М.— Л., 1937; [3] К у р а т о в с к и й К., Мостовский
А., Теория множеств, пер. с англ., М., 1970; [4] Александ-
Александров П. С, Введение в теорию множеств и общую топологию,
М., 1977; [5] Б у р б а к и Н., Общая топология. Основные
структуры, пер. с франц., М., 1968; [6] Бари Н. К., Тригоно-
Тригонометрические ряды, М., 1961; [7] Уиттекер Э. Т., Ват-
сон Д ж. Н., Курс современного анализа, 2 изд., т. 1, пер.
с англ., М., 1963; [8] С a n t о г G., «J. reine und angew. Math.»,
1878, Bd 84, S. 242—58; [9] e г о же, «Math. Ann.», 1871,
Bd 4, S. 139—43; [10] его же, там же, 1897, Bd 49, S. 207—46;
[11] его же, там же, 1880, Bd 17, S. 355 — 58; [12] В о-
r e 1 E., Lecons sur la theorie des fonctlons, P., 1898; [131 Hei-
Heine E., «J. reine und angew. Math.», 1872, Bd 74, S. 172; [14]
Lin del of E., «Acta math.», 1905, v. 29, p. 183—90; [15]
Cantor G., «J. zeine und angew. Math.», 1870, Bd 72, S.
130 — 42; [16] его же, «Math. Ann.», 1883, Bd 21, S. 51 — 58;
[17] Bendixson I., «Actamath.», 1883, v. 2, p. 415 —29; [18]
Lebessue H., Lemons sur les series trigonometriques...,
P., 1906; [19] Young W. H., «Proc. Roy. Soc», 1912,
v. 87, p. 331 — 39; [20] Б у р б а к и Н., Очерки по истории
математики, пер. с франц., М., 1963. М. И. Войцехоеский.
КАНТОРОВ ДИСКОНТИНУУМ, канторово
совершенное множеств о,— то же, что
Канторово множество. В. В. Фсдорчуп.
КАНТОРОВА КРИВАЯ — метризуемый одномерный
континуум. Первоначально К. к. наз. плоский нигде не
плотный континуум, и это была первая (хотя и не внут-
внутренняя) характеристика одномерных замкнутых связ-
связных подмножеств плоскости, рассмотренная Г. Канто-
Кантором (G. Cantor). К. к. содержит нигде не плотный
подконтинуум тогда и только тогда, когда замыкание
множества всех точек ветвления одномерно. В то же
время, если К. к. не содержит нигде неплотного под-
подконтинуума, то все ее точки имеют конечный индекс
ветвления. К. к. без точек ветвления является или
простой дугой, или простой замкнутой линией. Множе-
Множество концевых точек К. к., т. е. множество точек
индекса 1, нульмерно, но может быть всюду плотным.
Если все точки К. к. имеют одинаковый конечный ин-
индекс ветвления, то эта К. к. является простой замкну-
замкнутой линией. Построена универсальная К. к. (к р п-
в а я 31 е н г е р а), то есть К. к., к-рая содержит топо-
логич. образ всякой К. к.
Лит.: [1] Урысон П. С, Тр. по топологии и другим
областям математики, т. 2, М.— Л., 1951; [2} Menger К.,
Kurventheorie, Lpz. —В., 1932. В. В. Федорчук.
КАНТОРОВИЧА ПРОЦЕСС — итерационный метод
уточнения значения корня нелинейного функциональ-
функционального (операторного) уравнения (обобщение метода
Ньютона). Для уравнения Р(х)=0, где Р — нелинейная
операция, действующая из одного банахова пространст-
пространства в другое, вычислительная формула метода имеет
следующий вид
(здесь Р' — производная Фреше). Иногда использу-
используется модифицированный процесс, определяемый фор-
формулой
Пусть операция Р дважды непрерывно дифференци-
дифференцируема п выполняются условия (см. [2]):
1) существует линейная операция Т0=[Р' (хо)]~х,
2) ЩУ>(;го)||<:ть
3) \\Т0Р"(x)\UK при \\х-хо\\<г,
4) h=Ki)<.1/2,
5) r>ro=(l — l/Ч—2h)r\/h.
Тогда уравнение Р(х)=0 имеет решение х* такое,
что
|).г*— аго|]<го.
К этому решению сходятся последовательности хп и
хп, причем
и в случае
К. п. всегда сходится к корню х* уравнения Р(х)=0,
если только Р достаточно гладкая, существует [Р' (х*)\~1
и начальное приближение х0 избрано достаточно близ-
близким к х*. Если существует непрерывная Р"(х), то схо-
сходимость основного процесса квадратическая. Модифи-
Модифицированный процесс сходится с быстротой убывающей
геометрич. прогрессии; знаменатель этой прогрессии
стремится к нулю, когда хо—>-х*.
К. п. предложен Л. В. Канторовичем [1].
Лит.: [1] Канторович Л. В., «Докл. АН СССР»,
1948, т. 59, № 6, с. 1237—40; [2] Канторович Л. В.,
А к и л о в Г. П., Функциональный анализ в нормированных
пространствах, М., 1959; [4] Красносельский М. А.
и др., Приближенное решение операторных уравнений, М.,
1969; [4] К о л л а т ц Л., Функциональный анализ и вычис-
вычислительная математика, лер. с нем., М., 1969. И. К. Даугаеет.
КАНТОРОВО МНОГООБРАЗИЕ — re-мерный биком-
бикомпакт X, dim Х = и, в к-ром любая перегородка В между
непустыми множествами имеет размерность dimB^n—1.
Эквивалентное определение: n-мерное К. м. есть п-мер-
ный бикомпакт X, обладающий тем свойством, что при
всяком представлении его в виде суммы двух непустых
и отличных от всего пространства X замкнутых множеств
Хг и Х2 пересечение Хг Л Х2 имеет размерность dim (Х1 П
f|J2)^n—1. Одномерные метризуемые К. м. суть од-
одномерные континуумы, или канторовы кривые.
Понятие К. м. было введено П. С. Урысоном (см.
[1]). n-мерный замкнутый шар и, значит, п-мерное
замкнутое многообразие являются К. м.; п-мерное
евклидово пространство нельзя разбить множеством
размерности <гя—2 (при и = 3 — теорема Уры-
с о н а, при п>3—теорема Александрова).
(п — 1)-мерным К. м. является совместная граница двух
областей n-мерного евклидова пространства, одна из
к-рых ограничена (теорема Александрова).
Основной факт теории К. м.: всякий n-мерный бикомпакт
содержит n-мерное канторово подмногообразие (т е о-
рема Александрова).
Всякое лежащее в n-мерном бикомпакте X максималь-
максимальное n-мерное К. м. наз. размерностной ком-
компонентой бикомпакта X. Всякое n-мерное канто-
канторово подмногообразие бикомпакта X лежит в единст-
единственной размерностной компоненте X. Пересечение
двух различных размерностных компонент п-мерного
бикомпакта X имеет размерность <:п—2. В частности,
размерностные компоненты одномерного бикомпакта
суть его компоненты. Множество размерностных ком-
компонент конечномерного компакта конечно, счетно или
имеет мощность континуума. Справедливо неравенство:
iim(A Г\В)<?п—2, где А — произвольная размерност-
размерностная компонента совершенно нормального бикомпакта
X, а В — объединение всех остальных размерностных
компонент (теорема Александрова). В нас-
наследственно нормальном бикомпакте с 1-й аксиомой
счетности размерностная компонента может содержаться
в сумме остальных размерностных компонент.
Объединение Л.'^ всех размерностных компонент
«-мерного бикомпакта X наз. его внутренним
размерностным ядром. Ввиду монотон-
монотонности размерности в совершенно нормальном бикомпак-
бикомпакте X всегда dim A'x=dim X и dim(Z\Xx)<dim X.
Множество Х\Кх не содержит никакого n-мерного би-
бикомпакта. Но даже для компактов неизвестно A978),
может ли dim(A"\A."^-)=dim X. Что касается наследст-
наследственно нормальных бикомпактов, то в них внутреннее
размерностное ядро п его дополнение могут иметь все
допустимые размерности, а именно, в предположении
континуум-гипотезы, для всякой тройки целых чисел п,
л, п п2 с п^\, п{^п и п2^0 существует такой наслед-
наследственно нормальный n-мерный бикомпакт X, что
dim K-x= n\ и dim (Х\Кх)=п2.
Если dim X=ind X, то KxCZNx, где Nx (определен-
(определенное по Урысону) — индуктивное размер-
размерностное я д р о, т. е. множество всех точек х?Х,
в к-рых indxX = n. Индуктивное размерностное ядро
Nx компакта X всегда имеет тип Fa. Неизвестно,
так ли обстоит дело с внутренним размерностным ядром
компакта. Что касается бикомпактов, то в них ни
индуктивное, ни внутреннее размерностные ядра не
обязаны иметь тип Fa. Для всякой точки x?Nx
"ш&х Nx= indx X,
где X — компакт (теорема М е н г е р а). Поэтому
для произвольного компакта X его внутреннее размер-
размерностное ядро Кх всюду плотно в индуктивном размер-
ностном ядре Атх- На бикомпакты это утверждение уже
не переносится. Нерешенным остается вопрос A978),
всякая ли точка содержится в индуктивном размер-
ностном ядре вместе с нек-рым невырожденным конти-
континуумом.
Конечномерный континуум X, внутреннее размер-
размерностное ядро Кх к-рого всюду плотно в X, наз. обоб-
обобщенным канторовым многообрази-
е м. Совместная граница двух открытых подмножеств
л-мерного евклидова пространства является (п—1)-мер-
ным обобщенным К. м. В метризуемом n-мерном обоб-
обобщенном К. м. X может быть всюду плотно множество
тех точек х, в к-рых iadxX<Cn. Ни произведения, ни
непрерывные отображения не сохраняют свойство быть
обобщенными К. м., равно как и свойство быть К. м.
Бикомпакт X наз. бесконечномерным
канторовым многообразием, если его
нельзя разбить никаким способом слабо бесконечномер-
бесконечномерным замкнутым подмножеством. Во всяком бесконечно-
бесконечномерном бикомпакте содержится бесконечномерное К. м.
Лит.: [1] Урысон П. С, Тр. по топологии и другим
областям математики, т. 1, М.— Л., 1951; [2] Александ-
Александров П. С, «Ann. Math.», 1929, v. 30, p. 101—87; [3] его
ж е, «Proc. Roy. Soc. London. Ser. A», 1947, v. 189, p. 11 — 39;
[4] Александров П. С, Пасынков Б. А., Вве-
Введение в теорию размерности ..., М., 1973; [5] Федорчук
В. В., «Докл. АН СССР», 1974, т. 215, JV» 2, с. 289—92; [6]
Jlengcr К., Dimensionstheorie, Lpz.—В., 1928; [7] С к л я-
ренко В. Г., «Изв. АН СССР. Сер. матем.», 1959, т. 23,
№2, с. 197—212. В. В. Федорчук.
КАНТОРОВО МНОЖЕСТВО — подмножество отрез-
отрезка [0, 1] числовой осп, состоящее из всех чисел вида
2j ._ —— , где е,- равно 0 или 2. Построено Г. Кантором
(G. Cantor, 1883). Геометрич. его описание (см. рис.):
из отрезка [0, 1] выбрасывается его средняя треть —•
/1 2 \
интервал ( "о" ' ~5~ ) > затем из оставшихся отрезков
[1 ~! П ° ~1 /12
О, у и |,f выбрасываются интервалы Г -д- , —
G Я \
-Q- , -<г ) , из оставшихся четырех отрезков также вы-
У У /
брасываются их средние трети, и т. д.; то, что останется
после выбрасывания всех этих интервалов (смежных
интервалов), суммарная длина к-рых равна 1, и
есть канторово совершенное множе-
множество (Кантора множество; канторов
дисконтинуум); оно нигде не плотно на число-
числовой прямой, имеет мощность континуума.
С топологич. точки зрения К. м.— нульмерный со-
совершенный (т. е. без изолированных точек), компакт,
причем с точностью до гомеоморфизма существует един-
единственный такой компакт. Все ограниченные совершен-
совершенные нигде не плотные множества на числовой прямой
суть подобные множества. К. м. гомеоморфно счетной
степени D ° простого двоеточия D и является простран-
пространством топологич. группы Z^fo ; К. м. универсально в
двух смыслах: во-первых, всякое нульмерное простран-
пространство со счетной базой гомеоморфно подмножеству К. м.;
2) во-вторых, всякий компакт является непрерывным
образом К. м. (теорема Александрова).
Эта теорема кладет начало теории диадических биком-
бикомпактов и показывает, что многие компакты похожи друг
на друга с функциональной точки зрения. Так, в част-
частности, все совершенные компакты имеют одинаковые
булевы алгебры всех канонич. открытых множеств.
Существование специальных отображений К. м. на
компакты позволяет доказать, что банаховы алгебры
всех непрерывных функций на двух произвольных
совершенных компактах (напр., на отрезке и квад-
квадрате) линейно гомеоморфны. Далее, К. м. и возмож-
возможность отобразить его на произвольный компакт лежат
в основе построения многих примеров, интересных с
точки зрения топологии и теории функций. Одним из
них является так наз. канторова лестница —
график непрерывного монотонного отображения отрез-
отрезка [0, 1] на себя, производная к-рого определена и рав-
равна нулю на множестве меры 1. Хотя стандартное К. м.
имеет меру нуль, существуют нигде не плотные на от-
отрезке совершенные компакты меры, сколь угодно близ-
близкой к единице.
Лит.: [1] Александров П. С, Введение в теорию
множеств и общую топологию, М., 1977. В. В. Федорчук.
КАППА — плоская алгебраическая кривая 4-го по-
порядка, уравнение к-рой в декартовых прямоугольных
координатах имеет вид:
(х2+г/2)г/2=я2ха;
в полярных координатах:
р=а ctgep.
Начало координат — узло-
узловая точка с совпавшими
касательными х=0 (см. рис.). Асимптоты — прямые у=
= ita. Относится к так наз. узлам.
Лит.: [1] С а в е л о в А. А., Плоские кривые, М., 1960.
Д. Д. Соколов.
КАРАТЕОДОРИ КЛАСС — класс С функций
регулярных в круге | z\ <1 и имеющих в нем положитель-
положительную действительную часть. Класс назван по имени
К. Каратеодори, определившего точное множество
значений системы коэффициентов{с1; с2, . . ., сп}, п^1,
на классе С (см. [1], [2]).
Теорема Рисса — Герглотца. Для того
чтобы функция /(z) принадлежала классу С, необходи-
необходимо и достаточно, чтобы она допускала представление
интегралом Стилтьеса
f B) = \ -7J ^ С).
J -я е'1 - 2
где jx(t) — функция, неубывающая на отрезке [—я, я]
п такая, что и. (я)—(г(— я)=1.
С помощью этого представления легко выводятся
интегральные параметрич. представления для классов
функций, выпуклых и однолистных в круге, звездооб-
звездообразных и однолистных в круге и др.
Теорема Каратеодори — Теплица.
Множество значений системы {сь с2, . . ., с„}, л^1, на
классе С есть замкнутое выпуклое ограниченное мно-
множество Кп точек n-мерного комплексного евклидова
пространства, в к-рых определители
Aft =
ck
ck ck_1 ... 2
либо все положительны, либо положительны до какого-
то номера, начиная с к-рого все равны нулю. В послед-
последнем случае получается поверхность П„ тела К„. Каж-
Каждой точке П„ отвечает только одна функция класса С
и она имеет вид
V
где
2у=г Р/ = !. Py" > °- 1 < jV < n, — я < *y < л, tj ^th
при /=^=A, ft, / = 1, ..., yV.
Множество значений коэффициента с„, n=l, 2, . . .,
на классе С есть круг |с„|<:2; окружности |с„|=2 соот-
соответствуют только функции
Множество значений /(z0) (z0 фиксировано, |zo| <1)
на классе С есть круг, диаметром к-рого является
отрезок -—р^- , 'г° I ; границе этого круга соот-
ветствуют только функции
Рассматривались множества значений систем функ-
функционалов и более общего вида (см. [6]). Для класса
С получены вариационные формулы, с помощью к-рых
показано, что ряд экстремальных задач в классе С
решается функциями /д;(г), JV<:2 (см. [6]).
Основной подкласс С — класс Сг функций /(z)?C,
имеющих действительные коэффициенты с„, п=1, 2, ....
Для того чтобы функция f(z) принадлежала классу Сг,
необходимо и достаточно, чтобы она допускала пред-
представление
1-22 cos t + z> d»^>
где ц(/) — функция, неубывающая на [0, 2я], ,иBя)—
—j.i@)=l. С помощью этого представления решаются
многие экстремальные задачи на классе Сг.
Лит.: 11) С а г a t h ё о d о г у С, «Math. Ann.», 1907,
Bd 64-, S. По —115; [2] его же, «Rend. Circolo mat. Palermo»,
1911, v. 32, p. 193—217; L3J T о e p 1 i t z О., там же, р. 1Э1 —
92; [4] Riesz F., «Ann. scient. Ecole norm, super.», 1911,
t. 28, p. 33—62; [5] Herglotz G., «Ber. Vertiandl. Sach-
sisch. Akad. Wiss. Leipzig. Math.-naturwiss. Kl.», 1911, Bd 63,
S. 501—11; [6] Го л узин Г. М., Геометрическая теория
функций комплексного переменного, 2 изд., М., 19<>6.
КАРАТЕОДОРИ МЕРА — мера ц, порожденная
внешней мерой Каратеодори [j,*, где
внешняя мера Каратеодори есть внешняя мера, опре-
определенная на классе всех подмножеств метрич. простран-
пространства М (с метрикой р) и такая, что
ц* (A UВ) = ii* (А) ^^* (В),
если р(А, В)>0. Введена К. Каратеодори [1]. Множе-
Множество ЕсМ принадлежит области определения и., т. е.
*имеи тогда и только тогда, когда
и* (Л) = ц* {А[\Е)+р* (A
для любого AczM (здесь ЕС=М\Е); если Е (^-измери-
(^-измеримо, то \i(E)=\i*(E). Область определения К. м. со-
содержит все борелевские множества. Если и,* — внеш-
внешняя мера в классе всех подмножеств метрич. простран-
пространства такая, что всякое открытое множество ^-изме-
^-измеримо, то (j.* — внешняя К. м.
Лит.: [1] Caratheodory С,, «Nachr. Ges. Wiss.
Gottingen», 1014, 404—26; [21 Сакс С, Теория интеграла,
пер. с англ., М., 1949; [3] X а л м о ш П., Теория меры, пер.
с англ., М., 1»53. В. В. Сазонов.
КАРАТЕОДОРИ ОБЛАСТЬ — ограниченная одно-
связная область G комплексной плоскости такая, что
граница G совпадает с границей области G^, смежной с
областью G и содержащей точку оо. К К. о. относятся,
напр., все области, ограниченные кривыми Жордана.
Каждая К. о. может быть представлена в виде ядра
убывающей сходящейся последовательности односвяз-
ных областей {Gn}:
и каждая область G, для к-рой существует такая после-
последовательность, есть К. о. (теорема Кара-
Каратеодори, см. [1]).
Лит.: [1] Caratheodory С, «Math. Ann.», 1912,
Bd 72, S. 107 — 44; [2] M a p к у ш е в и ч А. И., Теория ана-
аналитических функций, т. 2, 2 изд., М., 1968. Е. Г. Голцзина.
КАРАТЕОДОРИ ТЕОРЕМА о конформном отображе-
отображении областей с переменными границами — один из
основных результатов теории конформных отображений
областей с переменными границами: получен К. Кара-
Каратеодори [1].
Пусть дана последовательность односвязных облас-
областей Вп, п=1, 2, ..., плоскости z, содержащих фиксиро-
фиксированную точку z0, г0=й=оо. Если существует круг \z—zo|<
<р, р>0, принадлежащий всем областям Вп, то я д-
ром последовательности Вп, ;г = 1, 2, ...,
относительно точки z0 нал. наибольшая область В, со-
содержащая точку z0 и обладающая тем свойством, что
для всякого компакта Е, принадлежащего В, сущест-
существует такое число vV, что Е принадлежит областям Вп
при n~^N. Наибольшая область понимается в том смыс-
смысле, что она содержит любую другую область, обладаю-
обладающую тем же свойством. Если указанного круга не су-
существует, то под ядром В последовательности Вп. п=
= 1, 2, . . ., понимается точка z0 (в этом случае говорят,
что последовательность областей Вп, и=1, 2, . .., имеет
вырожденное ядро). Последовательность об-
областей Вп: 7i=l, 2,..., сходится к ядру В, если лю-
любая последовательность из Вп имеет своим ядром так-
также В.
Теорема Каратеодори. Пусть дана после-
последовательность функций z=/n(?), /n(?o) = zo- /A(?o)>Oi
тг=1, 2,..., регулярных и однолистных в круге
| ?— ?0| <1 и отображающих | ?— ?о| <1 соответственно на
области Вп. Для того чтобы функции /„(?), n = i, 2,...,
сходились в круге |?—?ol<l K конечной функции /(?),
необходимо и достаточно, чтобы последовательность
областей Вп, п=1, 2,..., сходилась к ядру В, к-рое
есть либо точка z0, либо область, имеющая более од-
одной граничной точки. При этом сходимость равномер-
равномерна внутри круга | ?— ?01<1. Если предельная функ-
функция /(Q^const, то она однолистно отображает круг
|?— Sol <1 на ядро 5, а обратные функции ф„(г), п =
= 1,2,.. ., равномерно сходятся внутри В к функции ep(z),
обратной к /(?).
Аналогично рассматривается вопрос о сходимости
последовательности функций, однолистных в многосвяз-
многосвязных областях. Ниже приводится одна из таких теорем
для неограниченных областей. Пусть дана последова-
последовательность любых областей Вп, n—i, 2,..., плоскости
г, содержащих нек-рую фиксированную окрестность
точки 2= оо. Ядром последовательности
Вп, п=1, 2,..., относительно точки z= оо наз. наиболь-
наибольшая область В, содержащая z—оо, любая замкнутая
подобласть к-рой принадлежит всем Вп, начиная с не-
некоторого п. Сходимость последовательности областей
Вп, п=1, 2,..., к ядру В определяется, как и выше.
Имеет место следующая теорема [2]. Пусть в плоскости
z дана последовательность областей Ап, и=1, 2,...,
содержащих z= оо и сходящихся к ядру А, и пусть
функции ? —/,,(z), n=i, 2,..., однолистно отображают
их соответственно на области Вп, содержащие ?=оо,
/„(оо)=оо, /^(оо)=1, п=1, 2.. . . Для того чтобы функ-
функции /„(г), ге=1, 2,..., равномерно сходились внутри
области А к однолистной функции /(г), необходимо и
достаточно, чтобы последовательность областей Вп,
n—i, 2,..., имела ядро В и сходилась к нему, причем
тогда функция ?=/(z) однолистно отображает А на В.
Можно указать и другие теоремы о сходимости по-
последовательностей однолистных функций в зависимос-
зависимости от способа их нормировки (см.. [2]).
Лит.: [1] Caratheodory С, «Math. Ann.», 1912,
Bd 72, S. 107—44; [2] Г о л у з и н Г. М., Геометрическая тео-
теория функций комплексного переменного, 2 изд., М., 1966.
Г. В. Кузьмина,
КАРАТЕОДОРИ — ФЕЙЕРА ЗАДАЧА — задача о
продолжимости многочлена от z до степенного ряда,
представляющего собой регулярную в круге |z|<l
функцию, реализующую наименьшее значение супре-
супремума модуля в круге \z\ <1 в классе всех регулярных
в |z|<l функций, к-рые имеют начальным отрезком
своего разложения в ряд Маклорена данный многочлен.
Решение этой задачи дается следующей теоремой.
Теорема Каратеодорп — Фей ера [1].
Пусть
— данный многочлен, Р (z)?=0. Существует единственная
рациональная функция R (z)=R(z, с0, с1,. . ., с,,-!)
вида
+ а г + anzn~
'1ГП-, Х>0,
а„ + <x,z + ... + «¦„_! г
регулярная в |z|<<:1 и имеющая в своем разложении в
ряд Маклорена п первых коэффициентов, равных
соответственно с0, с1,. . ., <¦„_). Эта функция, и только
она, реализует наименьшее значение
М;= sup |/(z)|
|*|< l
в классе всех регулярных в круге |z| <1 функций f(z)
вида
п указанное наименьшее значение равно Х=Х(са, сь. ..,
)
Число Х(с0, cj,. . ., с„_х)равно наибольшему положи-
положительному корню уравнения 2п-й степени
— X 0 ... О С„ Cj . . . Cn_t
О — X ... О 0 с0 ... сп_2
О О ... — X 0 0 ... с0
со О... О —А О... О
с", с0 ... О О —Л ... О
Сп-1 СЯ-2
с0 О О
— X
= 0.
Если с0, с15. . ., с„_! — действительные числа, то Х(с0,
С],..., cn_t) является наибольшим из абсолютных
значений корней уравнения п-й степени
— X 0 ... О с0
О-Л...с„с, =о>
Лит.: [1] Caratheodory С, Pejer L. «Rend.
Circolo mat. Palermo», 1911, v. 32, p. 218—39; [2] Г о л у-
зин Г. М., Геометрическая теория функций комплексного
переменного, 2 изд., М., 1966. Г. В. Кузьмина.
КАРДАНО ФОРМУЛА — формула для отыскания
корней кубического уравнения над полем комплексных
чисел
x^rpx+q=0. A)
К такому виду может быть приведено любое кубич.
уравнение. К. ф. для уравнения A) имеет вид:
Применяя эту формулу, нужно для каждого из трех
значений кубич. корпя
« = V -
брать то значение корня
для к-рого выполняется условие ар" = —р/3 (такое зна-
значение корня E всегда существует). В К. ф. числа р и
q — любые комплексные. В случае действительных
коэффициентов рад свойство корней уравнения быть
действительными или мнимыми зависит от знака диск-
дискриминанта уравнения
D = — 27?2 — 4р3 = —108 {?. + IL\ .
При D>0 все три корня уравнения действительны и
различны. Но по К. ф. корни выражаются через кубич.
радикалы с мнимыми подкоренными выражениями.
Хотя в атом случае как коэффициенты, так и корни дей-
действительны, корни не могут быть выражены через
коэффициенты при помощи радикалов из действитель-
действительных чисел, ввиду чего данный случай получил назва-
название неприводимого. При D = Q все корни действитель-
действительны, причем при р и q, отличных от нуля, имеется один
двукратпый и один однократный корень, а при р =
=q=Q — один трехкратный корень. При /><0всетри
корня различны, причем один корень является дейст-
действительным, а два других — сопряженными мнимыми
числами.
К. ф. названа по имени Дж. Кардано (G. Cardano),
впервые опубликовавшего ее в 1545.
Лит.: [1] К у р о ш А. Г., Курс высшей алгебры, 11 изд..
М., 1975. II. В. Проскуряков.
КАРДИНАЛЬНОЕ ЧИСЛО, трансфинитное
число, мощность по Кантору, карди-
кардинал множества А,— такое свойство этого мно-
множества, к-рое присуще любому множеству В, равно-
мощному А. При этом два множества А и В наз. р а в-
н о м о щ н ы м и, если существует взаимно однознач-
однозначная функция / : А—*-В с областью определения А и мно-
множеством значений В. Г. Кантор (G. Cantor) определял
К. ч. множества А как такое его свойство, к-рое оста-
остается после абстрагирования от качества элементов мно-
множества А и от их порядка. Чтобы подчеркнуть этот
двойной акт абстрагирования, Г. Кантор для обозна-
обозначения К. ч. множества А ввел символ А. Из других обоз-
обозначений К. ч. множества А наиболее употребительны
символы card А и |Л|. Если А — конечное множество,
содержащее п элементов, то card A = n. Если g +—мно-
+—множество всех натуральных чисел, то card Z + = Но (см-
Алефы). Если R — множество всех действительных чи-
чисел, то card R = с — мощность континуума. Множество
2А всех подмножеств множества А не равномощно ни
самому А, ни его подмножеству (теорема Кан-
Кантора). В частности, никакие два из множеств
А, 2А, 2*А, 22*А, ... A)
не равномощны. При А= Ъ+ получается бесконечно
много различных бесконечных К. ч. Другие К. ч. полу-
получаются, если взять объединение Q множеств, входящих
в A), и построить последовательность, аналогичную
A), положив A = Q. Этот процесс можно продолжать
бесконечно. Шкала всех бесконечных К. ч. намного
богаче шкалы конечных мощностей. Более того, их так
много, что нельзя образовать множества, содержащего
по крайней мере по одному К. ч.
Для К. ч. определяются операции сложения, умноже-
умножения, возведения в степень, а также взятие логарифма и
извлечение корня. Так, К.' ч. б=а+E наз. суммой
К. ч. а и р", если каждое множество мощности б можно
представить в виде объединения двух непересекающих-
непересекающихся множеств А и В мощностей а и Р соответственно;
К. ч. у— ар наз. произведением К. ч. а и C,
если у является К. ч. декартова произведения АХВ,
причем card Л=а и card5=p\ Сложение и умножение
К. ч. коммутативно и ассоциативно, а умножение дист-
дистрибутивно относительно сложения. К. ч. х=аР наз.
степенью с основанием а и показателем E, если
каждое множество мощности х равномощно множеству
Ав. где card А = а и card i} = p\ К. ч. а не больше К- ч.
Р, а<р, если каждое множество мощности а равномощ-
равномощно нек-рому подмножеству множества мощности р.
Если а<Р и P«ga, то а=Р (теорема Кантор а—
Б е р н ш т е й н а ), так что шкала К. ч. линейно
упорядочена. Более того, для каждого К. ч. E множе-
множество {а. : а<{5} вполне упорядочено, что позволяет
определить логарифм logaP К. ч. Р по основанию
К. ч. а, а<|3 как наименьшее К. ч. у такое, что av^p
и к о р е н ь a-й степени Р'/« из К. ч. Р, а<Р, как наи-
наименьшее К. ч. б такое, что ба^р.
Любое К. ч. а можно отождествить с наименьшим
порядковым числом мощности а. В частности, Но соот-
соответствует порядковому числу соо, Hi — порядковому
числу o)i, и т. д. Таким образом, шкала К. ч. является
подшкалой шкалы порядковых чисел. Ряд свойств
порядковых чисел переносится на К. ч., однако эти
же свойства можно определить и «внутренним» спосо-
способом. Если at<$t Для каждого t? T и card T^cog, то
2 B)
(теорема К ё ни г а). Если в B) положить 7=
и 1<а„<ап + х, то
C)
В частности, ни для какого К. ч. а^2 степень аш» нель-
нельзя представить в виде суммы членов бесконечно воз-
возрастающей последовательности меньших К. ч. Для
каждого К. ч. а определяется К. ч. с/(а) — к о н ф и -
на льны и характер а, как наименьшее К. ч. у
такое, что а=2 {Р(, t?T}, если р\<а для всех t ?2" и
card Т=у. Если с/(а) = а, то а наз. регулярным.
К. ч., не являющееся регулярным, наз. сингуляр-
н ы м. Для любого К. ч. а наименьшее К. ч. <х + , сле-
следующее за а, является регулярным. Примером сингу-
сингулярного К. ч. является К. ч. ащ0 из левой части фор-
формулы C) при условии, что (»(!<«!. В этом случае
К ч. а наз. предельным, если для любого
К. ч. E<а существует К. ч. у такое, что E<у<а-
Примеры предельных К. ч.: со0 и ссШо. Непредельным
К. ч. является «>j. Регулярное и предельное К. ч.
называется слабо недостижимым. К. ч. а
называется доминантным, если для любого E<а
выполняется 2Р <а. Доминантное и регулярное К. ч.
наз. сильно недостижимым. Из обобщенной
континуум-гипотезы вытекает, что класс сильно недо-
недостижимых К. ч. совпадает с классом слабо недостижи-
недостижимых К. ч. Классы недостижимых К. ч. допускают даль-
дальнейшую классификацию (так наэ. с х е м а М а л о),
к-рая приводит к определению гипернедостижимых
К. ч. Существование сильно (слабо) недостижимых
К. ч., больших со0, оказывается независимым от обыч-
обычных аксиом как аксиоматической, так и наивной теории
множеств.
К. ч. а наз. измеримым (точнее, {0, 1 }-нзмеримым),
если существует множество А мощности а и функция
fi, определенная на всех элементах семейства 2А, при-
принимающая значения 0 или 1 и такая, что \i(A)=l,
ji{а}=0 для любого а?А и если {Хп : п?со0} — после-
последовательность, состоящая из попарно непересекающих-
непересекающихся подмножеств А, то
u.(U {ЛГ„:«€<»о})=2{^ (*«)•«?<«о}-
Каждое К. ч., меньшее первого несчетного сильно не-
недостижимого К. ч., неизмеримо (теорема Ула-
м а), так что первое измеримое К. ч. непременно сильно
недостижимо. Однако первое измеримое К. ч. значи-
значительно больше, чем первое несчетное сильно недостижи-
недостижимое К. ч. (теорема Т а р с к о г о). Неизвестно
A978), противоречит ли аксиомам теории множеств
гипотеза о существовании измеримых К. ч.
Лит.: [l] Александров П. С, Введение в теорию
множеств и общую топологию, М., 1977; [2] Кантор Г.,
в кн.: Новые идеи в математике, сб. 6, СПБ, 1914, с. 90—184;
[3] Хаусдорф Ф., Теория множеств, пер. с нем., М.— Л.,
1937; [4] Куратовский К., Мостов с кий А.,
Теория множеств, пер. сангл., М., 1970; [5] Sierp ill ski W.,
Cardinal and ordinal numbers, Warsz., 1958 B wyd. 1965).
Б. А. Ефимов.
КАРДИОИДА — плоская алгебраич. кривая 4-го
порядка, к-рая описывается точкой М окружности ра-
радиуса г, катящейся по окружности с таким же радиусом
г; эпициклоида с модулем т=1. Уравнение К. в поляр-
полярных координатах:
р = 2г A—cos ф),
в декартовых прямоугольных координатах:
(x2-j-z/2-^-2rxJ^4r2 (х2 -{- г/2).
Длина дуги от точки возврата:
I = 16r sin2 ~.
4
Радиус кривизны:
__ 8г . ф
Площадь, ограниченная кривой: 5=6лг2. Длина кри-
кривой: 1бг. К. является конхоидой окружности, частным
случаем Паскаля улитки и синусоидальных спиралей.
Лит.: [1] Саве лов А. А., Плоские кривые, М., 1960.
КАРЛЕМАНА ГРАНИЧНАЯ ЗАДАЧА — граничная
задача аналитич. функций со сдвигом, изменяющим
направление обхода контура на обратное; впервые рас-
рассмотрена Т. Карлеманом [1]. Пусть L — простая замк-
замкнутая кривая Ляпунова на плоскости комплексного
переменного z, D — конечная область, ограниченная
кривой L. Пусть дифференцируемая комплексная функ-
функция а (г), заданная на L, осуществляет взаимно одно-
однозначное отображение контура L самого на себя с изме-
изменением направления обхода L на обратное и удовлетво-
удовлетворяет дополнительному условию Карлемана;
a[a(t)] = t, t?L, (*)
(предполагается еще, что производная a (t) удовлетво-
удовлетворяет условию Гёльдера). К. г. з. состоит в нахождении
аналитической в Z), за исключением конечного числа
полюсов, и непрерывной в D[JL функции Ф (z) по гра-
граничному условию
где заданные на L функции G(t) и g(t) удовлетворяют
условию Гёльдера и G(t)^O на L.
Изучалась также К. г. з. с условием
am(t) = t, с.1 («)=а (t). а* @ = а (а*-1 (t)), A=2,3,.. .,т,
более общим, чем (*), и К. г. з. для нескольких неизве-
неизвестных функций (см. [2], [3]).
Лит.:[1] Carleman Т., в сб.: Verhandlungen des Inter-
Internationale^ Mathematiker-Kongresses, Bd 1, Z.—Lpz., 1932,
S. 138 — 51; 12] M у с х е л и ш в и л и Н. И., Сингулярные
интегральные уравнения, 3 изд., М., 1968; [3] В е к у а Н. П.,
Системы сингулярных интегральных уравнений и некоторые
граничные задачи, 2 изд., М., 1970. Е. Д. Соломенцев.
КАРЛЕМАНА НЕРАВЕНСТВО — неравенство для
произвольных неотрицательных чисел ап^0
найдено Т. Карлеманом [1]. Константу е здесь умень-
уменьшить нельзя. Аналог К. н. для интегралов имеет вид:
Рехр I-L [x \n f (t) dt) <e[°° f(x) dx, f(x)^0.
Jo ( x Jo ) Jo
Имеются и другие обобщения К. н. [3].
Лит.: [1] Carleman Т., в кн.: Wissenschaftliche Vort-
rage gehalten auf dem funften Kongress der skandinavischen Ma-
thematiker, Hels., 1923, S. 181—96; [2] X a p д и Г., Л ит т ль-
льву д Д., Полна Г., Неравенства, пер. с англ., М., 1948.
Е. Д. Соломенцев.
КАРЛЕМАНА ТЕОРЕМА — 1) К. т. о к в а з и-
аналитических классах функций —
необходимое и достаточное условие квазианалитичности
в смысле Адамара, найденное Т. Карлеманом [1] (см.
также [5]). Класс К действительных функций f{x),
бесконечно дифференцируемых на отрезке [а, Ъ], наз.
квазианалитическим в смысле Ада-
Адамара, если из равенств /"(с)=0, п = 0, 1,. .., в какой-
либо точке с, а <с<6, следует, что / (х)=0. Формулиров-
Формулировка теоремы: класс К квазианалитический тогда и только
тогда, когда
где
М„ (/) = max |/<п> (х) |,
а < дг< b
А (/) — константа, а последовательность {а„} удовлет-
удовлетворяет одному из равносильных условий:
С со In T (r) dr ,
^ ' . B)
где
Т (г) = sup (r"/an).
п >- 1
В теории квазианалитич. классов функций это —
один п.ч первых законченных результатов. Квазиана-
Квазианалитич. классы, определяемые условиями A), B), часто
наз. классами Карлсмана.
2) К. т. об условиях определенно-
определенности проблемы моментов: если последователь-
последовательность положительных чисел sn, ге = 0, 1,..., удовлетво-
удовлетворяет условию
то проблема моментов
tkdo(t), k = 0, 1, ..., C)
со
является определенной. Это означает, что существует
неубывающая функция a(t), —oo<i<+oo, для к-рой
выполняются равенства C), единственная с точностью
до прибавления любой функции, постоянной в окрест-
окрестности каждой точки ее непрерывности. Теорема уста-
установлена Т. Карлеманом (см. [1], [2]).
3) К. т. о равномерном приближении
целыми функциями: если f(x) — любая не-
непрерывная функция на действительной оси, а 8(г),
0<г<+°°,— положительная непрерывная функция,
сколь угодно быстро убывающая при г—»-+оо, то суще-
существует целая функция g(z) комплексного переменного
z—x^-iy такая, что
\f(x)—g(r)\<e(\x\), —<x < *< + оо.
Эта теорема, установленная Т. Карлеманом [3], яви-
явилась исходным пунктом исследований по приближе-
приближениям целыми функциями. В частности, континуум Е
на плоскости z наз. континуумом Карле-
м а н а, если для любой непрерывной на Е комплексной
функции /(z) и произвольно быстро убывающей при
/¦—>-оо положительной функции г (г), нижняя грань к-рой
на любом конечном интервале положительна, сущест-
существует целая функция g(z), удовлетворяющая неравенству
\f(z)-g(z)\ < 8(|z|), z?E.
Необходимые и достаточные условия, при к-рых
замкнутое множество Е является континуумом Кар-
лемана, получены в теореме Келдыша—Лаврентьева
(см. [6]). Напр., континуумом Карлемана является
замкнутое множество, составленное из лучей вида
arg z = const, | z | > с > 0.
4) К. т. о приближении аналитичес-
аналитических функций полиномами в с р е д н е м
по площади области: пусть D — конечная
область на плоскости комплексного переменного z=
= x-\-iy, ограниченная жордановон кривой Г, и пусть
/(z) — регулярная аналитич. функция в D такая, что
оо, р>0;
тогда для любого числа 8>0 найдется такой полином
P(z), что
и.
) — P(z)\Pdxdy< 8.
Этот результат установлен Т. Карлеманом [4]. Анало-
Аналогичное утверждение верно и для случая приближения с
любым положительным непрерывным весом, причем
граница Г может быть и более общей природы. Система
степеней {z"}, п=0, 1,..., полна относительно любого
такого веса. Ортогонализация и нормирование этой
системы дает полиномы Pn(z) степеней п, часто наз.
полиномами Карлемана.
Лит.: [1] Carl em an Т., Les fonctions quasi-analyti-
ques, P., 1926; [2] его же, Sur les equations integrates singu-
lieres anoyau reel et symetrique, Uppsala, 1923; [3] e г о же,
«Arkiv mat., astron., fys.», 1927, Bd 20, №4; [4] его же,
там же, 1922, Bd 17, JN« 9; [5] M а н Д е л ь б р о й т С, Примы-
Примыкающие ряды. Регуляризация последовательностей. Примене-
Применения, пер. с франц., М., 1955; [6] Мергеля н С. Н., «Успехи
матем. наук», 1952, т. 7, в. 2, с. 31 —122. Е. Д. Сояо.ченцев.
КАРЛЕМАНА ЯДРО — измеримая, вообще говоря,
комшгекснозначная функция К (х, s), удовлетворяющая
условиям: 1) К(х, s)=K(s, х) почти всюду на ЕХЕ,
где Е — измеримое в смысле Лебега точечное мно-
множество в конечномерном евклидовом пространстве;
2) \ JK(x, s){2ds<oo для почти всех х?Е.
Лит.: [1] А х и е з е р Н. И., Г л а з м а н И. М., Тео-
Теория линейных операторов в гильбертовом пространстве, 2 изд.,
М,, 1966. Б. В. Хведелидзе.
КАРЛЕСОНА МНОЖЕСТВО — замкнутое множество
Е с [0, 2л), на к-ром всякая функция f(t), заданная
и непрерывная на этом множестве, представима рядом
вида 2„=о апе'п\ гДе 2л=о1алК+°°- Введено Л. Кар-
лесоном [1]. К. м. образуют важный класс так наз.
тонких множеств. Для того чтобы замкнутое множество
Ес[0, 2л) было К. п., необходимо и достаточно, чтобы
существовала такая постоянная е>0, что коэффициенты
Фурье — Стилтьеса
всякой меры и., сосредоточенной на Е, удовлетворяли
неравенству
sup|cn(n)| >
л>0
Лит.: [1] Carleson L.,«Acta math.», 1952, v. 87,
JNi 3—4, 325—45; [2] Wik I., «Arkiv mat.», 1960, v. 4, Л& 2—3,
209—18; [3] К ah an e J.-P., Salem R., Ensembles
parfaits et series trigonometriqucs, P., 1963, p. 142; [4] К а-
x а н Ж.-П., Абсолютно сходящиеся ряды Фурье, пер.
с франц., М., 1976. Б. И. Голубое.
КАРЛЕСОНА ТЕОРЕМА: для функции из прост-
пространства L2 @, 2л) ее ряд Фурье по тригонометрической
системе сходится почти всюду. В качестве гипотезы эта
теорема была высказана Н. Н. Лузиным [1], доказана
Л. Карлесоном [2]. Утверждение К. т. справедливо
также для всех функций пространства if при р > 1
(см. [3]). То, что для р=1 это не так, показывает по-
построенный А. Н. Колмогоровым [4] пример функции
из L1, тригопометрич. ряд Фурье к-рой почти всюду
расходится.
Лит.: [1] Лузин Н. Н., Интеграл и тригонометрический
ряд, М., 1915; [2] Carleson L., «Acta math.», 1966, v. 116,
p. 135 — 57 (см. также «Математика», 1967, т. 11, JV» 4, с. 113—
132); [3] Hunt R., в кн.; Orthogonal expansions and their
continuons analogues, Carbondale — L.— Amst., 1968, p. 235—
255; [4] Колмогорова. H.,«Fundam. Math.», 1923, t. 4, p.
324—28. С. А. Теляковский.
КАРЛСОНА МЕТОД, 5„-м е т о д,— одни из числен-
численных методов решения кинетического уравнения пере-
переноса нейтронов в ядерных реакторах. Первый вариант
метода для сферически симметричной геометрии, пред-
предложенный Б. Карлсоном (В. Carlson, 1953), был основан
на кусочно линейном представлении потока нейтронов
как функции косинуса угла между вектором скорости
нейтрона и радиусом. После интегрирования по угло-
угловой переменной в пределах элементарной ячейки полу-
получается система уравнений, в каждое из к-рых входят
лишь два направления скорости нейтрона, если счи-
считать известным из предыдущего приближения интеграл
столкновений (к-рый вычисляется по формуле трапе-
трапеций). Иными словами, как и в Владимирова методе,
решение уравнения переноса ведется методом последо-
последовательных приближений по интегралу столкновении.
В каждом приближении система распадается на отдель-
отдельные уравнения, если ввести дополнительное уравнение
для направления вдоль радиуса, к-рое интегрируется от
внешней границы шара к его центру. Каждое следующее
направление в уравнениях системы будет теперь свя-
связано с предыдущим, для к-рого неизвестная функция
уже определена. Интегрирование для отрицательных
значений косинуса, определяющего направление, ве-
ведется от внешней границы к центру, а для положитель-
положительных значений косинуса — от центра к краю.
Немонотонный характер решения уравнения перено-
переноса К. м. (возможность появления осцилляции и отрица-
отрицательных значений потока нейтронов) привел к необхо-
необходимости дальнейшего развития К. м. Широко исполь-
используется дискретный К. м.: DSn-si e т о д. В этом методе
разностные уравнения выводятся из физических сооб-
соображений методом баланса частиц в ячейке фазового
пространства. В низком приближении Л5„-метод не
обеспечивает требуемой точности в неодномерных гео-
геометриях. Одним из выходов из этой ситуации являет-
является добавление в систему уравнений ХMп-метода слага-
слагаемых так. обр., чтобы с помощью линейного преобра-
преобразования неизвестных она переводилась в систему уравне-
уравнений, возникающую в сферических гармоник методе.
Большое число расчетов ядерных реакторов К. м.
(и его модификациями) дает хорошие результаты, со-
согласующиеся с результатами других численных мето-
методов решения уравнения переноса нейтронов.
Лит.: [1] М я р ч у к Г. И., Методы расчёта яперных реак-
реакторов, М., 1961; [2] Вычислительные методы в физике реакторов,
пер. с англ., М., 1972; [31 Белл Д ж., Г лесс тон С,
Теория ядерных реакторов, пер. с англ., М., 1974.
В. А. Чуянов.
КАРЛСОНА НЕРАВЕНСТВО: пусть {ап, 1<и<
<оо } — не все равные нулю неотрицательные действи-
действительные числа, тогда:
Установлено Ф. Карлсоном [1]. Интегральный аналог
К. п.: если f(x)>0, /(s)=2E0, f, xf?L2(O, oo), то
> ^ X f lr\ Jr\ <r— т2 ' Г °° /2 tr\ Jr\ ' С M T-2f2 lf\ iJr\ IO\
\ \ 0 / \x) ax } s? It i \ 0 / \x) ax ) \ \ 0 x 1 (x) ax i ¦ №)
Константа я2 является наилучшей в том смысле, что
существует последовательность ап такая, для к-рой
правая часть A) сколь угодно близка к левой, и суще-
существует функция / (х) такая, для к-рой знак равенства в
B) достигается.
Лит.: [lj Carlson F., «Ark, mat., astron. ocEi fys.», 1934,
Bd 2jA, >i 7, S. 1 — 13; 12] X a p д и Г. Г., Л и т т л ь в у д
Д ж. Е., Полна Г., Неравенства, пер. с англ., М.,
1948. М, И. Войцеховский.
КАРНАПА ПРАВИЛО, правило бесконеч-
бесконечной п н д у к ц и и, ш-п р а в и л о, — вывода пра-
правило, состоящее в том, что если для арифметич. формулы
(р(х) доказаны предложения ф@), <рA),. . ., <р(ге),...,
то можно считать доказанным предложение V-cfp(^).
Это правило впервые введено в рассмотрение Р. Карна-
пом [1]. К. п. использует бесконечное множество посы-
посылок и потому неприемлемо при построении формаль-
формальных теорий по Д. Гильберту (D. Hilbertj. Понятие
вывода в системе с К. п. является неразрешимым. В
математич. логике при исследовании формальной ариф-
арифметики используется конструктивное К. п.:
если имеется алгоритм, к-рый по натуральному числу п
дает вывод формулы ф(«), то можно считать доказанным
предложение V хц>(х) (ограниченное со-п р а -
вило, правило конструктивно-бес-
конструктивно-бесконечной и н д у к ц и и). Классическое арифме-
тич. исчисление, неполное в силу теоремы Ге'деля,
становится полным после добавления конструктивного
К. п. (см. [2], [3]).
Лит.: [1] Carnap R., Der logische Syntax der Sprache,
W., 1934; [2] Кузнецов А. В., «Успехи матем. наук»,
1957, т. 12, в. 4, с.'218 —19; [3] Shoenlield J. R., «Bull.
Acad. poloi). sci. Cl. Ill», 1959, t. 7, № 7, s. 405 — 07.
В. Е. Плиско.
KAPHO ТЕОРЕМА — теорема о произведении про-
простых отношений, в к-рых точки пересечения алгебраич.
линии со сторонами треугольника делят эти стороны.
Пусть алгебраич. линия I порядка ге не проходит ни
через одну из вершин треугольника ABC и пересекает
каждую из его сторон или ее продолжение в п точках:
сторону АВ — в точках С1, С2,. .., С'„; сторону ВС —
в точках Аг, А2...., А„; сторону СА — в точках Вг,
В2,. . ., Вп. Тогда произведение Зге простых отношений
С;В А(С В;А
равно —1, если п — число нечетное, и -f-1, если п —•
четное.
Эта формулировка эквивалентна следующей: произ-
произведение Зга отношений
В(А
i = l, 2, ..., п,
равно +1.
Частный случай этой теоремы был доказан Л. Карно
Ш-
Если I — прямая линия, то получается Менелая тео-
теорема.
Обобщение К. т. : пусть алгебраич. линия порядка
п пересекает каждую из прямых Л,Л,-+1, i = l,2,...,
т, Ат + 1 = А), лежащих в плоскости этой линии, ровно
r п точках Bjj, г'=1,2,..., т; /=1,2,..., п. Тогда
П. ?и—
¦LA'./ ^—. ~
Лит.: [1] Carnot L., Geometrie de position. P., 1803.
П. С. Моденов.
КАРСОНА ПРЕОБРАЗОВАНИЕ — преобразование
функции f(t), определенной при —оо<г<оо и равной
нулю при i<0, в функцию
где s — комплексная переменная. Формула обращения:
-:—г \ — F (s) est ds.
2лг Jo,-t« s
К. п. функции /(/) отличается от Лапласа преобра-
преобразования этой же функции наличием множителя s.
А. Б. Иванов.
КАРТА, криволинейная система ко-
координат, параметризация множест-
множества М,— взаимно однозначное отображение
множества М на открытое подмножество D арифмети-
арифметического векторного пространства R". Число ге наз.
размерностью карты, а компоненты х'(р)
вектора х(р) ?R" — координатами точки
р?М относительно карты х.
Примером К. служит декартова прямоугольная систе-
система координат на плоскости и в пространстве, введенная
П. Ферма (P. Fermat) и Р. Декартом (R. Descartes) и
положепная ими в основу аналитич. геометрии. К.
(криволинейные координаты) на поверхности в геомет-
рич. исследованиях впервые использовал Л. Эйлер
(L. Euler). Б. Риман (В. Riemann) положил понятие
К. в основу нового инфинитезимального подхода к обос-
обоснованию геометрии (см. [1]). Согласно концепции
Б. Римана, основным объектом исследования геометрии
является многообразие — множество М, снабженное
К. Современное понятие многообразия является есте-
естественным обобщением определения Б. Римана.
Карта х : U-+-D нек-рого подмножества U множества
М наз. локальной картой множества М с
областью определения U. Если множество М снабжено
структурой топологич. пространства, то при этом
дополнительно требуется, чтобы область определения U
была открытым подмно?кеством в М, а отображение х
было бы гомеоморфизмом. Аналогично определяется К.
со значениями в F", где F — произвольное нормиро-
нормированное поле, и вообще К. со значениями в топологиче-
топологическом векторном пространстве. Две локальные К. (x,U),
(у, V) с областями определения U, V множества М наз.
согласованными класса С1, если: 1) их
общая область определения W=Uf\V изображается
на каждой из них открытым множеством (т. е. множест-
множества х(W) и у(W) открыты в R"), 2) координаты точки из
общей области определения W относительно одной из
этих К. являются I раз непрерывно дифференцируемыми
функциями от координат этой же точки относительно
другой К., т. е. вектор-функция
I раз непрерывно дифференцируема. Множество А =
= {{ха, Ua)} попарно согласованных между собой ло-
локальных К. (ха, Uа) множества М, покрывающих все
M([)aUa=M) наз. атласом множества М. Задание
атласа определяет на М структуру дифференцируемого
многообразия, а локальные К., согласованные со всеми
К. этого атласа, наз. допустимыми (или Сг-гладкими).
Инфинитезимальным аналогом понятия К. является
понятие и н ф и н и т е з и м а л ь н о й карты
порядка к (или, иначе, k-c труп карты, или
корепера порядка к). Говорят, что две сог-
согласованные между собой локальные карты (х, U) (у, V)
множества М касаются друг друга до порядка к
в точке р ? Uf\ V, если х(р) = ц (р) и все частные произ-
производные до порядка к включительно вектор-функции
уох'1: х-^-у(х) обращаются в точке х(р) в нуль. Класс
]р(х) локальных К., касающихся в точке p^U до-
допустимой локальной К. (.г, V) многообразия М, наз.
инфинитезимальной К. порядка к в точке р.
Выбор К. многообразия М позволяет рассматри-
рассматривать различные полевые величины на М как числовые
функции и применять к ним методы анализа. Вообще
говоря, значение полевой величины в точке зависит от
выбора К. (Величины, не зависящие от выбора К.,
наз. скалярными и описываются функциями на многооб-
многообразии М.) Однако для широкого и наиболее важного
класса величин (см. Геометрических объектов теория)
их значение в точке зависит только от устройства К.
в инфинитезимальной окрестности fc-ro порядка этой
точки. Такие величины (примерами к-рых являются
тензорные поля) описываются функциями на множе-
множестве всех кореперов порядка к на М. Вместе с тем
изучаются такие свойства величин, к-рые не зависят от
выбора К. В связи с этим весьма эффективным окалы-
окалывается инвариантный бескоординатный подход к зада-
задачам дифференциальной геометрии.
Лит.: [1] Риман Б., Соч., пер. с нем., М.— Л., 1948,
с. 279—93; [21 Рашевский П. К., Риманова геометрия и
тензорный анали?, 3 изд., М., 1967; [3] Зуланке Р.,
Винтген П., Дифференциальная геометрия и расслоения,
пер. с нем., М., 1075; [4] Лихнерович А., Теория связ-
ностей в целом и группы голономий, пер. о франц., М., 1960.
Д. В. Алексеевский.
КАРТАНА ЛЕММА: если для 2р линейных форм ср,-,
ov от п переменных равна нулю сумма внешних произве-
произведений
и формы о' линейно независимы, то ср,- будут линейными
комбинациями а1 с симметричными коэффициентами:
Установлена Э. Картаном (Ё. Cartan) в 1899.
Лит.: [1] К а р т а н Э., Внешние дифференциальные
системы..., пер. с франц., М., 1962. М. И. Войцеховский.
КАРТАНА МАТРИЦА — 1) К. м. конечномер-
конечномерной полупростой алгебры Ли д над
алгебраически замкнутым полем к
характеристики 0 — матрица
А =|| 2 (а,-, ау)/(ау, а,-) || i, j = i, ..., г,
где а!,..., аг — какая-либо система простых корней
алгебры Д относительно фиксированной Картана под-
подалгебры t, а ( , ) — скалярное произведение на про-
пространстве, дуальном к t, определенное Киллинга фор-
формой на Д. (О К. м. произвольной системы корней см.
Корневая система.) С точностью до преобразования,
индуцированного перестановкой индексов 1,. . ., г, К. м.
является инвариантом алгебры Д, т. е. не зависит от
выбора t и системы простых корней. Этот инвариант
полностью определяет д: две полуиростые алгебры Ли
изоморфны тогда и только тогда, когда их К. м. сов-
совпадают, с точностью до преобразования, индуцирован-
индуцированного перестановкой индексов. Полупростая алгебра Лп
проста тогда и только тогда, когда ее К. м. н е р а з л о-
ж и м а, т. е. не представнма в виде блочно-днаго-
нальной матрицы после нёк-рой перестановки индексов.
Пусть Д = Дх +• • • + fl/я — разложение алгебры Д
в прямую сумму простых идеалов и Aу — К. м. про-
простой алгебры Ли Ду. Тогда блочно-днагональная мат-
матрица
х 0
0 А
является К. м. алгебры Лп д (явный вид К. м. прос-
простых алгебр Ли см. Ли полупростая алгебра).
Элементы а,у= 2 (а,-, ау)/(ау, ау) К. м. обладают сле-
следующими свойствами:
«и =2; а,-у-<0, а/у С Z при i Ф j \ .
а,7 = 0=>а// = 0. f * ;
К. м. тесно связаны с заданием д образующими и
соотношениями. А именно, в алгебре д существуют
линейно независимые образующие е/, //, /г,-, г=1,...,
г (так наз. канонические образующие),
связанные следующими соотношениями:
[«г. fj] = Sijhr, [hi,ej]=aiJej;
[hi, fj]=-aijfj; [hi, hj]=O. B)
Любые две систел1ы канонических образующих перево-
переводятся друг в друга автоморфизмом алгебры д. Кроме
B), канонические образующие удовлетворяют также
соотношениям
(adei-)"a'/ + 1e/ = O, (ad/1-)"°'V + 1/y = 0, tj=f, C)
где, по определению, (ad x)y=[x, ;/]. Соотношения B)
и C) являются определяющими для алгебры д при
выбранной системе образующих е/, /,-, /г,-, г=1,..., г
(см. [2]).
Для любой матрицы А , удовлетворяющей условиям
A), алгебра Ли fl (А) над полем к с образующими е/,
/,-, h{, j=l,..., r и определяющими соотношениями B)
и C) конечномерна тогда и только тогда, когда А есть
К. м. конечномерной полупростой алгебры Ли [3].
Лит.: [1] Д ж е к о б с о н Н., Алгебры Ли, пер. с англ.,
М., 1964; [2] Серр Ж.-П., Алгебры Ли и группы Ли,
пер. с англ. и франц., М., 1969; [3] К а ц В. Г. «Изв. АН СССР.
Сер. матем.», 1968, т. 32, № 6, с. 1323—67.
2) К. м. конечномерной ассоциатив-
ассоциативной алгебры j4 с единицей над полем
к — матрица (c[j), i, ]—i,. .., s, определяемая полным
набором Nlt. . ., Ns конечномерных неприводимых
левых /1-модулей. А именно, сц есть кратность вхожде-
вхождения N j в композиционный ряд такого неразложимого
проективного левого А -модуля Р;, для к-рого Нот
(Pi, N/)^0. Модуль Р{ существует для каждого JV/ и
определен однозначно с точностью до изоморфизма.
В некоторых случаях К. и. С оказывается симметри-
симметричной, положительно определенной и даже C=D^D,
где D — целочисленная, не обязательно квадратная
матрица (Т — знак транспонирования). Такова К. м.
групповой алгебры A = kG конечной группы G над полем
к характеристики р>0 (см. [1]), причем Pl,...,Ps
в этом случае — полный набор неизоморфных глав-
главных неразложимых левых Л-моду-
л е н, т. е. неразложимых Л-модулей, в прямую сумму
к-рых раскладывается левый Л-модуль А. Другой
пример, когда такое равенство для К. м. имеет место:
А — ограниченная универсальная обертывающая ал-
алгебра алгебры Лн g над алгебраически замкнутым
полем характеристики р>0, полученной из полупростой
комплексной алгебры Ли д редукцией в характеристи-
характеристику р (см. [2]).
Лит.: [1] К э р т и с Ч., равнее П., Теория представ-
представлений конечных групп и ассоциативных алгебр, пер. с англ.,
М., 1969; [2] Humphreys J. E., «J. Algebra», 1971, v. 19,
p. 51—79. В. Л. Попов.
КАРТАНА МЕТОД ВНЕШНИХ ФОРМ — дифферен-
дифференциально-алгебраический метод исследования систем
дифференциальных уравнений и многообразий с различ-
различными структурами. Алгебраич. основу метода состав-
составляет алгебра Грассмана. Пусть V есть 2"-мерное век-
векторное пространство над произвольным полем К с ба-
базисными векторами е°, е', e'J, e'jk, ..., el2%n, !</<&.
Кроме векторов базиса для произвольного натурального
числа q, определяются векторы еЧЧ'-'q , ix, i2,. . .. iq=
= 1, 2,. . ., п, по следующему закону: если среди нату-
натуральных чисел г'1; г2,. . ., iq есть хотя бы одна пара
одинаковых, то еН--'д=0; если все числа г,,..., iq
попарно различны и числа Д<;.,<...<jq являются
перестановкой чисел ц, t2,..., iq, то eii"'q=eh"JQ,
когда подстановка (?*)+(/)*—четная, и eii'"lq =
=—eii"'Jq , когда эта подстановка нечетная. В вектор-
векторном пространстве V вводится внешнее умножение:
еЧ'г---'р Aeftift2---ft?=e»i---ijpfti---ft?, при этом требуется
выполнение обычных для гиперкомплексной системы
(алгебры) законов. Построенная алгебра ранга 2" наз.
алгеброй Грассмана. Вектор
наз. мономом степени р, Х?К. Сумма мономов
одинаковой степени р>1 наз. внешней формой
степени р; сумма мономов первой степени наз. лине й-
н о й формой. Элементы поля К являются, по опре-
определению, формами нулевой степени. Векторы е' и любые
п их линейно независимых комбинаций
ai = a{ei, det ( а[) ф 0, а[ ? К,
образуют линейный базис алгебры Грассмана. Здесь и
в дальнейшем по одинаковым индексам, встречающимся
один раз снизу и один раз сверху, производится сумми-
суммирование в соответствующих пределах.
Алгебраической производной 1-го
порядка от внешней формы
Qp = al _ j е'1 Л . . . Л еР
дО.
степени р по символу е' наз. форма Qp-1 =—-¦ степени
г ве
p—i, к-рая получается из формы Qp заменой нулем
всех мономов, не содержащих символа е', и заменой еди-
единицей символа е' в остальных мономах после перенесе-
перенесения символа е' на первое место с соблюдением закона
антикоммутативности при каждой последовательной
перестановке. Ассоциированной систе-
м о й линейных форм внешней формы Qp наз. совокуп-
совокупность всех ненулевых алгебраических производных
(р—1)-го порядка от формы Qp. Рангом внешней
формы Qp наз. ранг ее ассоциированной системы. Он
совпадает с минимальным числом линейных форм, через
к-рые, используя операцию внешнего умножения,
можно выразить форму Qp. Для исследования системы
дифференциальных уравнений в R» используется диффе-
дифференциальная алгебра Грассмана, когда в качестве К
рассматривается множество аналитич. функций от п
действительных переменных х', определенных в нек-рой
области пространства R", а векторы е' обозначаются
символами dx'. Линейные формы в ней наз. 1-ф о р м а -
м и, или формами Пфаффа. В них символы dx'
являются дифференциалами переменных х'. Внешние
формы степени р>1 наз. р-ф о р м а м и, или внеш-
внешними дифференциальными формами
степени р. Внешним дифференциалом р-
формы
QP = atl...i dxh Л ... Л dxP
наз. (р+1)-форма
DQp = dah i Л dz'1 Л .. . Л dx'P.
Внешнее дифференцирование обладает следующими
свойствами:
D (Qp ± Qp) = DQp ± PQP,
D (DQp) = 0,
где Qp, Qp — произвольные р-формы, a Qq — произ-
произвольная д-форма.
Форма Пфаффа co=a,da:' тогда и только тогда является
полным дифференциалом нек-рой функции /, когда ее
внешний дифференциал равен нулю. Пусть
Qa~bZ(xb, zP)dx" + cf(x», zP)dzl-~dza = 0, A)
?., р = 1, ..., s; a, 6 = 1, ..., т; §,r| = s + l, ..., г;
р, g = l, . . ., г,
— произвольная система линейно независимых уравне-
уравнений Пфаффа cm независимыми переменными ха и
г неизвестными функциями zP. Система ZNa=0 наз.
замыканием системы A). Замыкание наз. чис-
чистым замыканием (обозначается ?>6а=0), если
в нем алгебраически учтена исходная система A), то
есть если в квадратичные формы DQa подставлены
значения dza из уравнений A). Система 8а=0, ?>6а=0
или эквивалентная ей система 6a=0, DBa=0 наз. зам-
замкнутой системой. Система A) тогда и только
тогда вполне интегрируема, когда ?>6а=0. Приравнивая
нулю алгебраические производные от D6a no dxa и dz*,
a=l, . . ., rn, g = s+l,. . ., г, и присоединяя уравнения
Пфаффа к исходной системе A), получают вполне
интегрируемую систему уравнений, к-рая наз. х а р а к-
тер ист и ческой системой системы A).
Множество ее независимых первых интегралов обра-
образует наименьшую совокупность переменных, через
к-рые можно выразить все уравнения системы A).
Пусть m?ft — результат подстановки в алгебраич.
производную dD6a/ddz^ вместо dxa, dz* произвольных
переменных Хн, Д, h—i, 2,..., то—1. С системой A)
ассоциируется последовательность матриц
Числа
s2 = rang М2 — rang
sm = r — s —rang Mm_!
наз. характерами, число
Q=si + 2s2 +. . .+ms,e
наз. числом К а р т а н а системы A). Присоединяя
к замкнутой системе 6а=0, DQa=O уравнения dz?=
= badxa, где frf — новые неизвестные функции, по-
получают первое продолжение системы A). Пусть N —
число функционально независимых функции из ь|>
(> 1)
ф фуц
всегда УУ<(>. Если N=Q, то система A) — в инволю-
инволюции и ее общее решение зависит от sm произвольных
функций т. аргументов, sm_j функций m—1 аргумента,
и т. д., Si функций одного аргумента и s произволь-
произвольных постоянных. Если же N<LQ, то систему A) надо
продолжать, причем в результате конечного числа про-
продолжений получается либо система в инволюции, либо
противоречивая система.
Пусть, напр., имеется система
dzx = udx -\- х2 dy, dz2 = и dy -j- У2 dx
с независимыми переменными х, у и неизвестными фун-
функциями и, z-i, z2 (s=2,m=2, r=3). Чистое замыкание ее
имеет вид:
duAdx^r2x dxAdy = 0, duAdy-r2y dy/\dx = 0.
Для этой системы:
= i, s2 = 0, Q=i, Л' = 0.
Система не находится в инволюции. Продолженная
система
dz± —и dx А-х1 dy, dz2 = u dy-\- у2 dx, du = 2 (у dx-\- x dy)
вполне интегрируема и ее общее решение имеет вид:
2, z2 = y (xy-\-Cj)-\-c3,
где с1т с2, с3 — произвольные постоянные.
Использование К. м. в. ф. значительно упрощает фор-
формулировки и доказательства многих теорем математи-
математики и теоретич. механики. Напр., теорема Остроградского
записывается формулой
где М — аналитическое ориентируемое (т+1)-мерное
многообразие, Г — его m-мерная гладкая граница,
Q — m-форма, a DQ — ее внешний дифференциал.
Формула замены переменных в кратном интеграле
/ = С ... С / (х1, . .., х") dx1 A dx2 л ... Л dx"
при отображении р : A—kD, определенном формулами
ж' = ф' (и1, и2,..., и"), где D, Ас:Лп, получается не-
посредственной заменой переменных х' и их дифферен-
дифференциалов dxl = —-duJ. Так как
ди>
dx1 Л ... Л dx" =afa''---- Ф%Ц1 Л ... Л du«,
а (и1 и")
/=
=Г..Г
J j
К. м. в. ф. широко применяется при исследовании
многообразий с различными структурами. Пусть М —
дифференцируемое многообразие класса С", F=^
= С°°(М) — множество дифференцируемых функций на
М, D1 — множество всех векторных полей на М, Ш$—
множество кососимметричных ^-полилинейных отобра-
отображений модуля D1 X . . . X D1 (s раз, s>l — натуральное
число).
Пусть <й0= F, а через 21 обозначена прямая сумма F-
модулей %.s:
Элементы модуля Э? наз. внешними диффе-
дифференциальными формами на М; элементы
модуля 219 наз. s-ф о р м а м и. Пусть
/, е g с» (М); е е Кп о е я„ a:, g dk
Тогда внешнее умножение Л определится формулами:
/ л« = /г, (/л 6)(ХЪ ..., А'г)=/б(А-1, ..., хг),
(QAg)(Xu ..., Jf,) = gQ(.Y1, ..., X,),
F AQ)ft, ..., Хг + ,) =
где Sr+S — группа подстановок множества 1, 2,...,
r+s, а е(а)^1 или —1, в зависимости от того, четной
или нечетной подстановкой является а. Модуль 3[
кососимметрических ^'-полилинейных функций с внеш-
внешним умножением паз. алгеброй Грассмана
над многообразием М. Если М совпа-
совпадает с R", то получается рассмотренная выше диффе-
дифференциальная алгебра Грассмана. Внешним дифферен-
дифференцированием наз. Л-линейное отображение D : 31-*-2(,
обладающее следующими свойствами: О^.5с:Ж3 + 1 для
каждого s^O, если /?Э@=С°о(М), то Df есть 1-форма,
определенная равенством Df(X) = X{f), где X ^Д1;
Z>-?> = 0, ?>@aQ) = ?>6aQ+( — l)rQADQ, если 0^
?51,., Q^SI. Пусть, напр., М — многообразие с заданной
аффинной связностью. Аффинная связность на многооб-
многообразии М — это правило у, к-рое сопоставляет каждому
X^D1 линейное отображение ух векторного простран-
пространства D1 в себя, удовлетворяющее следующим двум
условиям:
e4Y; vx (fY)=fvx <X)
для /, g(zC°° (M), X, Y(zD1. Оператор \х наз. к о в а-
риантной производной относительно X.
Пусть Ф — диффеоморфизм многообразия М, у —• аф-
аффинная связность на М. Формула
где X, Y^D1, определяет на М новую аффинную связ-
связность. Аффинная связность у наз. инвариантной отно-
относительно Ф, если v' = v- В этом случае Ф наз. аффин~
ным преобразованием многообразия М. Пусть
[X, Y] = XY — YX,
Т(Х, Y)^fy(Y)~Vyty*i — lX, Y],
It (X, Y) = \xS/y— V fVX— V [Xi у-]
для всех X, Y^D1, и пусть D1 — модуль, двойствен-
двойственный /"-модулю D1. /'-полилинейное отображение (со,
X, У)->шG"(Х, У)), где a^D1 — форма Пфаффа, наз.
тензорным полем кручения и обозна-
обозначается через 7"; /"-полилинейное отображение (со, Z,
X, У)—>-со (R (X, Y) -Z) наз. тензорным полем
кривизны и обозначается через R. Пусть р?М и Х^,. . .,
Хп — базис для векторных полей в нек-рой окрестности
Up точки р. Функции Tjj, T/j, Rjj определяются на
Up формулами
VXji^-J) — -1 IJAK' 1 (А/; AJ)~ ' 1JAK'
Для 1-форм ш1, aj, определенных на Up формулами
справедливы структурные уравнения
К а р т а н а:
Дсо, =10^ л шк + Y R'lKL<i>K л aL-
Система уравнений Пфаффа
Ma = Xfco', I, ), к=1, . . ., т; а, Ъ = т + \, ...,п,
задает m-мерное подмногообразие 9ЛшсЛГ. Продол-
Продолжая эту систему с использованием структурных урав-
уравнений Картана, получают последовательность фунда-
фундаментальных геометрич. объектов подмногообразия
первого, второго и т. д. порядков. В общем случае
существует фундамептальнын геометрич. объект
конечного порядка к, определяющий подмногообразие
'Him c точностью до постоянных. При исследовании
подмногообразий многообразия М К. м. в. ф. обычно
используется совместно с методом подвижного репера
(см., напр., [4]).
Метод назван по имени Э. Картана (Е. Cartan), к-рый
широко использовал внешние формы с 1899.
Лит.: [1] К ар тан Э., Внешние дифференциальные си-
системы и их геометрические приложения, пер. с франц., М.,
1962; [2] Фиников С. П., Метод внешних форм Картана
в дифференциальной геометрии, М.— Л., 1948; 131 X е л г а-
сон С, Дифференциальная геометрия и симметрические про-
пространства, пер. с англ., М., 1964; L4] Карта н Э., Риманова
геометрия в ортогональном репере, пер. с франц., М., 1900.
В. С. Малаховский.
КАРТАНА ПОДАЛГЕБРА к о и е ч н о м е р н о и
алгебры Л и j н а д полем к — нильпотентная
подалгебра в Д, совпадающая со своим нормализато-
нормализатором в Д. Напр., если д — алгебра Ли всех комплекс-
комплексных квадратных матриц фиксированного порядка, то
подалгебра всех диагональных матриц является К. п.
в д. К. п. может быть определена также как ниль-
нильпотентная подалгебра t в д, совпадающая со своей
ф и т т п н г о в о й н у л ь-к омпонвнтой
ft,= {x 6 й|(а<1Я)п*.Я(.Х)=0, ff6t,Bi,ff€Zl,
где ad обозначает присоединенное представление д.
Пусть, далее, характеристика к равна 0. Для произ-
произвольного регулярного элемента Х?д множество
П(Х, Д) всех элементов из д, аннулируемых степе-
степенями оператора ad X, является К. п. в Д и всякая К. п.
в Д имеет вид П(Х, д) для подходящего регулярного
элемента X. Всякий регулярный элемент принадлежит
одной и только одной К. п. Размерности всех К. п. в
g одинаковы и равны рангу алгебры д. Всякая мак-
максимальная ннльпотентная подалгебра в q размерности,
равной рангу $, есть К. п. (но не всякая максимальная
нпльпотентная подалгебра есть К. п.). Образ К. п. при
сюръективном гомоморфизме алгебр есть К. п. Если
поле к алгебраически замкнуто, то все К. п. в д сопря-
сопряжены, а точнее, преобразуются друг в друга операто-
операторами из алгебраич. группы D автоморфизмов алгебры
С[, алгебра Ли к-рой есть коммутант алгебры ad Я-
Если Д разрешима, это утверждение справедливо и без
предположения об алгебраич. замкнутости к.
Пусть G — либо неприводимая алгебраич. линейная
группа над к, либо связная группа Ли, и а, — ее ал-
алгебра Ли. Тогда подалгебра t в д будет К. п. в д, если
и только если она является алгеброй Ли Картана
подгруппы в G.
Пусть CJ — подалгебра алгебры fll(F) всех эндо-
эндоморфизмов конечномерного векторного пространства V
над к, а Д — наименьшая Ли алгебраическая алгебра
в Д1(К), содержащая д. Тогда, если t — К. п. в д,
то tflfl — К. п. в ц, и если t — К. п. в д, a t —
наименьшая алгебраич. подалгебра в cj((F), содержа-
содержащая t, то t — К. п. в д и t=tfl4-
Если kdK — некоторое расширение полей, то подал-
подалгебра t в д есть К. п. тогда и только тогда, когда
t(Y)kK есть К. п. в $(X)kK.
Особо важную роль К. п. играют, когда Д — по-
полупростая алгебра Ли (это было использовано Э. Кар-
таном [1]). В этом случае всякая К. п. t в д абелева и
состоит из полупростых элементов (см. Жордана раз-
разложение), а ограничение Киллинга формы на t невырож-
невырождено.
Лит.: [1] С а г t a n Е., Sur la structure des groupes de
transformations finis et continus, Pj, 1894; [2] Джекоб-
сон H., Алгебры Ли, пер. сангл., М., 1964; [3] Ш е в а лл е К.,
Теория групп Ли, т. 3, пер. с франц., М., 1958; [4] Теория ал-
алгебр Ли. Топология групп Ли, пер. с франц., М., 1962.
В. Л. Попов.
КАРТАНА ПОДГРУППА группы G — макси-
максимальная нильпотентная подгруппа С в G, всякий нор-
нормальный делитель конечного индекса к-рой является
подгруппой конечного индекса в своем нормализаторе в
G. Если G — связная линейная алгебраич. группа
над полем характеристики 0, то К. п. в G могут быть
определены п как замкнутые связные подгруппы, ал-
алгебры Ли к-рых являются Картана подалгебрами ал-
алгебры Ли группы G. Примером К. п. может служить
подгруппа D всех дпагональных матриц в группе GLn(k)
всех невырожденных матриц.
В связной линейной алгебрапч. группе G К. п. может
быть определена также как централизатор максималь-
максимального тора группы G или как связная замкнутая нильпо-
нильпотентная подгруппа, совпадающая со связной компонен-
компонентой единицы своего нормализатора в G. Множества Cs
и Си всех полупростых и унипотентных элементов в С
(см. Жордана разложение) являются замкнутыми под-
подгруппами в С и C=CSX Си. При этом Cs — единственный
максимальный тор группы G, лежащий в С. Размер-
Размерность К. п. группы G наз. рангом группы G. Объе-
Объединение всех К. п. группы G содержит открытое в то-
топологии Зариского подмножество в G (но, вообще гово-
говоря, не совпадает с G). Всякий полупростой элемент в G
лежит по крайней мере в одной К. п., а всякий регуляр-
регулярный элемент — ровно в одной К. п. Если <р : G—yG' —
сюръективный морфпзм линейных алгебраич. групп,
то К. п. в С — образы К. п. в G относительно <р. Любые
две К. п. в G сопряжены.
Пусть группа G определена над полем к, тогда в G
существует К. п., также определенная над к, более
того, G порождается своими К. п., определенными
над к. Две определенные над к К. п. в G могут быть и
не сопряжены над к (но в случае, когда G разрешима.
они сопряжены). Многообразие К. п. группы G рацио-
рационально над к. К. п. связной полупростой (или, более-
общо, редуктивнои) группы G является максимальным
тором в G.
Пусть G—связная вещественная группа Ли с алгеброй
Ли д. Тогда К. п. группы G замкнуты в G (но не обяза-
обязательно связны) и их алгебрами Ли являются подалгебры
Картана алгебры Д. Если G — аналитич. подгруппа в
GLn(R), a G—наименьшая содержащая G алгебраич. под-
подгруппа в GLn(R), то К. п. в G являются пересечениями О
с К. п. в G. В случае, когда G компактна, К. п. связны,
абелевы (являются максимальными торами) и сопряже-
сопряжены между собой, а всякий элемент в G лежит в нек-рой
К. п.
Лит.: [1! Ш е в а л л е К., Теория групп Ли, пер. с франц.,
т. 3, М., 1958; Г2] Б о р е л ь А., Линейные алгебраические
группы, пер. с англ., М., 1972; [3] Б о р е л ь А., Тите Ж.,
«Математика», 1967, т. 11, Ml 1, с. 43—111; .№2, с. 3—31; [4]
Dem azure М., Grothendteck A., Schemas en grou-
pes, Seminaire de geometrie algebrique, P., 1964. В.Л.Попов.
КАРТАНА РАЗЛОЖЕНИЕ — представление дей-
действительной некомпактной Ли полупростой алгебры Д
в виде прямой суммы векторных пространств. Пусть
С Г
д — комплексная ооолочка д, тогда в д существует
действительная компактная подалгебра дА' той же
размерности, что и д, такая, что имеют место следую-
следующие разложения в прямые суммы векторных пространств
где I — подалгебра инвариантных элементов нек-рого
инволютивного автоморфизма <р алгебры д*, а |) —
множество антиинвариантных элементов автоморфизма
<р. Вторая формула и есть К. р. алгебры д (см. [1]).
К. р. сводит классификацию действительных неком-
некомпактных полупростых алгебр Ли к классификации
компактных полупростых алгебр Ли и инволютивных
автоморфизмов в них.
Лит.: X е л г л с о н С, Дифференциальная геометрия
и симметрические пространства, пер. с англ., М., 1964.
А. С. Феденко.
КАРТАНА ТЕОРЕМА — 1) К. т. о старшем
векторе: пусть д — комплексная полупростая ал-
алгебра Ли, е,-, /,-, h,, j=l,. . ., г — ее канониче-
канонические образующие, т. е. линейно независи-
независимые образующие, между к-рыми имеются следующие
соотношения:
[«(. //] = $/A- [hi, ej]=aijej, \hh tj\=—aijfj,
где я,7=2, a;j —неположительные целые числа при
i^j, i, /=1,. . ., г, aij = O влечет за собой ау-,-=0, и пусть
t — подалгебра Картана алгебры д, являющаяся
линейной оболочкой элементов hi,. . ., hr. Пусть также
р — линейное представление д в комплексном конеч-
конечномерном пространстве V. Тогда существует ненулевой
вектор v?V, для которого:
р(е,-)г; = О, р (hj) v = k;v, i = i, ..., г,
где k; — некоторые числа. К. т. установлена Э. Кар-
таном [1]. Вектор v наз. старшим вектором
представления р, а линейная функция Л на t, опре-
определенная условиями k(hi)=ki, г=1, . . ., г, наз. стар-
старшим весом представления р, соответствующим v.
Упорядоченный набор чисел (к1,..., кг) наз. набо-
набором числовых отметок старшего
веса Л. К. т. дает полную классификацию неприво-
неприводимых конечномерных линейных представлений комп-
комплексной полупростой конечномерной алгебры Лп.
Она утверждает, что всякое конечномерное комплек-
комплексное неприводимое представление д обладает един-
единственным, с точностью до пропорциональности, стар-
шим вектором, причем соответствующие ему числовые
отметки — неотрицательные целые числа; два конеч-
конечномерных неприводимых представления эквивалентны
тогда и только тогда, когда соответствующие старшие
веса совпадают и любой набор неотрицательных целых
чисел является набором числовых отметок старшего
веса нек-рого конечномерного комплексного неприводи-
неприводимого представления.
Лит.: [1] Cart an E., «Bull. Sci. math.», 1925, t. 49,
p. 130—52: [2] Д ж е к О б с о н Н., Алгебры Ли, пер. с англ.,
М., 1964; [3] Теория алгебр Ли. Топология групп Ли, пер.
с франц., М., 1962; [4] Же л обе н ко Д. П., Компактные
группы Ли и их представления, М., 1970; [5] Dixmier J-,
Algebres enveloppantes, P., 1974; [6] Семинар по алгебраиче-
алгебраическим группам, пер. с англ., М., 1973. В. Л. Попои-
2) К. т. в теории функций многих
комплексных переменных — так наз. тео-
теоремы А и В о когерентных аналитич. пучках на мно-
многообразиях Штейна, впервые доказанные А. Картаном
(Н. Cartan, [1]). Пусть Q — пучок ростков голоморфных
функций на комплексном многообразии X. Пучок 0-
модулей ?f на X наз. когерентным аналити-
аналитическим, если в окрестности каждой точки х?Х
существует точная последовательность пучков
QP _^ Qq _^ $> _^ о
для нек-рых натуральных р, q. Такими являются, на-
например, все локально конечно порожденные подпучки
в Qp.
Теорема А. Пусть ?f — когерентный аналитич.
пучок на многообразии Штейна X. Тогда для каждой
точки х?Х найдется конечное число глобальных се-
сечений «!,..., sу пучка of таких, что любой элемент s
слоя ?f x представляется в виде
где все hj?Qx. (Другими словами, пучок ?f локаль-
локально конечно порожден над Q своими глобальными сече-
сечениями. )
Теорема В. Пусть <ff — когерентный аналитич.
пучок на многообразии Штейна X. Тогда все группы
когомологий порядка p^i многообразия X с коэффи-
коэффициентами в пучке ?f тривиальны:
HP (X, сУ) = О при p=al.
К. т. имеют много приложений. Из теоремы А полу-
получаются различные теоремы существования глобальных
аналитич. объектов на многообразиях Штейна. Основ-
Основным следствием теоремы В является разрешимость д-
проблемы: на многообразии Штейна уравнение df—g
с условием согласования dg=O всегда разрешимо.
Схема применения теоремы В такова: если
— точная последовательность пучков на X, то после-
последовательность
<ff)-^HP(X, F)^HP(X, G)—>
тоже точна. Если X — многообразие Штейна, то
HP (X, <У) = 0,
и, значит, ф0 есть отображение на, a <fp, p^i,— изо-
изоморфизмы.
Теорема В точна: если на комплексном многообразии
X группы Н1(Х, #")=0 для любого когерентного ана-
аналитич. пучка ЗР, то X — многообразие Штейна. Теоремы
А и В вместе с их многочисленными следствиями
составляют т. наз. теорию Ока — Кар тана о
многообразиях Штейна. Из этих теорем следует разре-
разрешимость на многообразиях Штейна всех классич. про-
проблем многомерного комплексного анализа — проблема
Кузена, Леви, Пуанкаре и др. Теоремы А и В и их
следствия допускают дословное обобщение на простран-
пространства Штейна.
Лит.: [11 К а р т а н А., в кн.: Расслоенные пространства
и их приложения, М., 1958, с. 352—62; [2] Г а н н и н г Р.,
Росси X., Аналитические функции многих комплексных
переменных, пер. с англ., М., 1969; [3] Хёрмандер Л.,
Введение в теорию функций нескольких комплексных перемен-
переменных, пер. с англ., М., 1968. Е. М. Чирка.
КАРТАНА — ВЕЙЛЯ БАЗИС конечномерной
полупростой комплексной алгебры
Ли д — базис д, составленный из элементов Картана
подалгебры алгебры д и корневых векторов Ха, а?Д,
где Д — система всех ненулевых корней алгебры д от-
относительно т. К.— В. б. выбирается неоднозначно.
Корень <x(h), h?x, как линейная форма над т, отожде-
отождествляется с вектором Ла?т, для которого a(h)= (hath),
где (х, у) — Киллинга форма в алгебре д. При этом
[h, Xa] = (ha, h)Xa
для всякого /г?т. Если сс?Д, то — сс?Д, причем
можно выбрать Ха так, чтобы выполнялось равен-
равенство [Ха, X-a] = ha- Если а+|3?Д, то
[Ха, Хр] = Л-арХа+э,
где Na$?=0. Если а, р, у?Д, а+р+-\>=0, то iVap=
= NPy=Nya- Существует нормировка векторов Ха,
при которой iVap=—iV-a,-p, причем числа iVap полу-
получаются рациональными. Существует нормировка век-
векторов Ха, при которой все Na$ — целые (см. Шевалле
группа). Определение К.— В. б. (введенное Г. Вейлем в
[1]), а также все сказанное выше о векторах Ха, ha и
числах iVap дословно переносится на случай произволь-
произвольной конечномерной полупростой расщепляемой алгебры
Ли над полем нулевой характеристики и ее корневого
разложения относительно расщепляющей подалгебры
Картана.
Лит.: Ll] W е у 1 Н., «Math. Z.»>, 1924, Bd 23, S. 271 — 304;
[2] Джекобсон Н., Алгебры Ли, пер. с англ., М., 1964;
[3] Теория алгебр Ли. Тополо1ия групп Ли, пер. с франц..
М., 1962. Д. П. Желобенко.
КАРТЕРА ПОДГРУППА — максимальная нилыю-
тентная подгруппа группы, совпадающая со своим нор-
нормализатором. Введена Р. Картером [1]. Любая конечная
разрешимая группа G обладает К. п., причем все К. п. в
группе G сопряжены (теорема Картера).
Лит.: [1] Carter R. W., «Math. Z.», 1961, Bd 75, M 2
S. 136—39; [2] Итоги науки. Алгебра. 1964, М., 1966, с. 23—24.
Н. Н. Вильяме.
КАРТОГРАФИИ МАТЕМАТИЧЕСКИЕ ЗАДАЧИ —
задачи, возникающие при построении математич. основы
географических и специальных карт, именно, при раз-
разработке теории картографических проекций, исследо-
исследовании их свойств, преобразований, методов изысканий и
др. Поверхность Земли при этом принимают либо за
сферу, либо за эллипсоид вращения.
Основным объектом изучения в математич. картогра-
картографии является картографич. проекция: отображение
на плоскости всей поверхности земного эллипсоида
(шара) или какой-либо ее части:
x=hiu, v), У=/2(«. v), Г1)
где и — широта, v — долгота точки Р? Д (Д — одно-
связная область эллипсоида); х, у определяют на
плоскости точку Q — изображение точки Р, Q?D,
D — область изображения Д. Функции /х и /2 удовлет-
удовлетворяют следующим условиям: они однозначные, дважды
непрерывно дифференцируемые, имеют якобиан А=
= д(ж, уIд(и, v)=?0 (для сохраняющих ориентацию
отображений, используемых в геодезии и картографии,
й>0). Большинство фактов математич. картографии от-
относится не только к отображениям эллипсоида на пло-
плоскость, но и к отображениям произвольных поверх-
ностей, поэтому далее под картография, проекцией
A) понимается отображение Ac:5j на DdS2, где
5i:ds2 = A!(u, v) [du^ + dv2]; B)
S2:da2Al(x, у) [dzt^-dyZ]
любые регулярные поверхности; А и D — односвяз-
ные области. Выбор для целей отображения таких коор-
координат, кроме простоты записи в них линейного элемента
поверхности и выгоды их использования при последую-
последующих вычислениях, обусловлен еще и тем, что переход к
ним от произвольных криволинейных координат на
поверхности непосредственно доставляет конформное
отображение поверхности на плоскость (см. [6], [3]).
Эти координаты даже на произвольной поверхности наз.
иногда картографическими координатами (см. [9]);
в геодезии и картографии их наз. изометрическими
координатами.
Знание уравнений A) отображения S1 на S2 позволяет
изучить метрич. свойства отображения (см. [7], [2]),
т. е. найти его характеристики: масштаб отображения
\a=da/ds, причем д.= ц(м, v; а), и, в частности, масшта-
масштабы по направлениям координатных линий m=[i\v = consi,
п=V-\u = const-
поворот г() изображения в направлении линии и и его
поворот % в направлении линии и:
tg 4' = Уи/Хи, tg х = yv/xv;
угол 6 между образами параметрич. линий:
искажение этого угла:
масштаб площади:
наибольшее искажение углов:
ю а-Ь
sm-- = —г-;
2 а + Ь '
и др. Большое значение имеют главные мае ш-
т а б ы а=цтах и b=umjn, связанные с т,, га, 6 теоре-
теоремами Аполлония:
a2+&2=m2+»2, ab=mn sin 6=p,
и соответствующие им главные направления, ортого-
ортогональные как на 5Х (tg 2ao=2//(e—g-), где
так и на S2 (tg Ao=- tg ae). С указанной сетью Тиссо
на 52 связывается индикатриса отображения — эллипс
искажений {а, Ь, Ао, \р}, трактуемый в касательной
плоскости к S2 в точке Q как эллипс, подобный и по-
подобно расположенный тому бесконечно малому эллипсу
(главной части отображения), к-рый является — с точ-
точностью до о(р) — изображением окружности бесконечно
малого радиуса р, взятой в касательной плоскости к
Sx в точке Р. Из приведенных характеристик, выра-
выраженных через коэффициенты первых квадратичных
форм взаимно отображаемых поверхностей B) и частные
производные 1-го порядка отображающих функций A),
независимы только четыре. Выбор групп независимых
характеристик неоднозначен, и вместо {a, b, Ao, \j)}
часто берут {т, п, if. 6}.
По характеру искажений среди картографич. проек-
проекций выделяют следующие проекции: а) к о н ф о р м-
н ы е, или равноугольные (т=п, 6=я/2);
б) эквивалентные, или равновеликие
(р= 1); в) эквидистантные, или равнопро-
межуточные (а=1, или 6=1); г) геодези-
геодезические, в картографии наз. ортодромиче-
с к и м и (ортодрома — геодезическая на сфере), при
к-рых геодезические на Sx переходят в геодезические на
S2; и др. Построение проекций, обладающих объеди-
объединением хотя бы двух из перечисленных свойств а) —
г), возможно только при отображении поверхности на
изометричные ей поверхности и в нек-рых других три-
тривиальных случаях. Так как условия конформности и
эквивалентности для целей картографии не совместимы,
то для нее особое значение имеют проекции эквидистант-
эквидистантные, к-рые по характеру искажений занимают проме-
промежуточное место между отображениями а) и б). Вы-
Выделение отдельных совокупностей картографич. про-
проекций делают обычно указанием присущих им свойств,
напр, вида а) — в), т. е. заданием их уравнениями в
характеристиках, к-рые с учетом формул теории иска-
искажений легко преобразуются в уравнения с частными
производными 1-го порядка. Множество решений кон-
конкретной системы двух таких уравнений описывает опре-
определенный класс проекций. По типу этих урав-
уравнений проекциям приписывают соответствующий тип
(эллиптический, гиперболический и т. д.).
Использование в картографии приведенных выше фор-
формул теории искажений позволяет выполнить выбор
нужной для конкретной цели проекции: установив
каким-либо образом уравнения проекции A) (напр.,
задав на плоскости общий вид изображения координат-
координатных линий эллипсоида и, возможно, использовав при
этом нек-рые дополнительные условия — конформ-
конформности, эквивалентности и др.), можно на основании этих
формул исследовать отображение и, варьируя его пара-
параметрами, подобрать наиболее подходящую проекцию
для картографирования заданной Acz5x. Кроме такого
решения прямой задачи, в ней используются и иные
методы (геометрические, графоаналитические и др.).
В обратных задачах картографии проекции изыски-
изыскивают на основе априорного задания искажений в них
(см. [11]). При этом первоочередное значение имеет
вопрос существования требуемых проекций. Ответ на
этот вопрос дает основная система уравнений в теории
отображения поверхностей (см. [4]):
ml — пи со& 6-1- i|3Hre*sin 6 + 6ыге* sin 6 = 0, 1
i|)j,m* — /?Msin 6 — ij)Hre*cos 6 — 6ыге* cos 6 = 0, J
в к-рой
к2 (X, у) ' Х2 (ж, у)
При отображении поверхности на плоскость: к2 (х, г/)=1,
при отображении плоских областей друг на друга так-
также nlj (и, у)=1. Система C)— недоопределенная: двумя
ее уравнениями связаны четыре независимые характе-
характеристики отображения; различные способы доопределе-
доопределения и интерпретации системы дают возможности разно-
разнообразным ее приложениям. Система C) — квазилиней-
квазилинейная относительно любой пары характеристик. Имеют
место следующие теоремы.
Теорема 1. Характеристики т, п, г)з, 6 отобра-
отображения области Ас:^! на область ?>cS2, осуществляемо-
осуществляемого однозначными дважды непрерывно дифференцируе-
дифференцируемыми функциями A) с якобианом, сохраняющим знак в
области Д, удовлетворяют во всех точках этой области
системе C).
Теорема2. Пусть выделена односвязная область
А данной регулярной поверхности и пусть в области Д
заданы четыре функции ф,-=ф,-(и, v), непрерывные
в А вместе со своими частными производными 1-го по-
рядка и принимающие значения из любой односвязной
области П, принадлежащей 4-мерному параллелепипеду
[О < срд. < кх; 0 < <р2 < &2,' ft/= const, г' = 1, 2;
— я < <р3^л; 0 < <р4 < Я1-
Если эти функции принять за характеристики нек-рого
отображения AdS1 на плоскость
т = фь и = <р2, г|з = ф3, 6 = <р4.
и если они удовлетворяют в А системе C), то восста-
восстанавливаемое по ним отображение АаЗ± на нек-рую
область D плоскости хОу гомеоморфно, дважды не-
непрерывно дифференцируемо, имеет в Д якобиан Л>0
и переводит любую точку (и0, ио)?А в заданную точку
(Xq, у0) ПЛОСКОСТИ XI/.
Теорема 2 дает при заданном распределении характе-
характеристик условия существования отображений односвяз-
односвязной области Д поверхности S1 на нек-рую область
D плоскости S2 при соответствии одной внутренней
точки (и0, и0) своему изображению (х0, уа) на плоскости;
граница области D при этом неизвестна. Незнание об-
области изображения характерно для К. м. з.: она либо
определяется после установления отображающих функ-
функций A), либо должна быть найдена на основе допол-
дополнительных условий, напр, условий минимизации иска-
искажений в проекции.
При отображениях сферы на плоскость система C)
переходит в так наз. систему Эйлера — У р-
м а е в а (см. [5], [11]), а при отображениях плоских
областей, когда система C) доопределена записанной в
характеристиках системой уравнений отображения, она
дает как следствие производную систему квазиконформ-
квазиконформных отображений (см. [12]). Сведение отображений по-
поверхностей к квазиконформным отображениям плоских
областей (с ограниченным искажением) вполне естест-
естественно, и первые, т. е. отображения A) заданной области
AaSx на заданную область Dcz.S1, могут интерпрети-
интерпретироваться как «тройная» проекция: область AcSj кон-
конформно отображается на область Д плоскости uv, об-
область Dcz.S.2 конформно отображается на область D
плоскости хОу; область А плоскости uOv квазиконформ-
квазиконформно преобразуется в область D плоскости хОу. Квазикон-
Квазиконформное отображение плоских областей Д на Й, сопут-
сопутствующее отображению Дс?, на DdS2, имеет сле-
следующие характеристики: V=m*. oc=ip, W=n* sin 6,
угол В имеет тот же смысл, что и выше. Связь рассмат-
рассматриваемых изображений дала возможность (см. [4])
использовать в К. м. а. теорию квазиконформных
отображений плоских областей. При этом систему
уравнений любого класса картографич. проекций или,
более общо, всякую нелинейную систему дифференци-
дифференциальных уравнений вида
Fi(u, г;, хи, xv, yu, yv) = 0, г = 1, 2, D)
после ее записи в характеристиках
Ji(u, v, m*, n*, \Jj, 9) = 0, i = l, 2, E)
удается редуцировать к квазилинейной системе, к-рая
следует из системы C) после ее доопределения системой
E) и к-рая трактуется как производная система исход-
исходной системы D). При этом, однако, остается открытым
вопрос о соотношении типов этих двух систем: исход-
исходной и производной.
Аппарат квазиконформных отображений плоских об-
областей (с двумя парами характеристик) может быть
привлечен также в качестве теоретич. основы прибор-
приборного (с использованием механич., оптич., электронных
и других устройств) преобразования картографич.
проекций, точнее, преобразования двух заданных
односвязных плоских областей друг в друга, каждая из
к-рых является результатом картографирования одной
и той же области земного эллипсоида, но в различных
проекциях.
Одной из основных задач картографии (в области соз-
создания мелкомасштабных и частично среднемасштабных
карт) является проблема наивыгоднейших картографич.
проекций, т. е. таких отображений заданной области Д
поверхности S на плоскость, в к-рых искажения (в не-
к-ром заранее оговоренном смысле) сведены к минимуму
(см. [2]). Наиболее распространенными критериями
достоинств картографич. проекций являются следую-
следующие:
критерий Э й р и:
критерий Иордана:
критерий Эйри — Каврайского:
Фе-к= $ 4 dA 4
критерий Иордана — К авра некого:
причем все они суть вариационного типа, и
критерий Чебышева — критерий мини-
минимаксного типа, согласно к-рому качества проекции оце-
оцениваются либо величиной
¦ _ supaU
шь\а '
либо ее логарифмом, либо просто максимумом модуля ло-
логарифма масштаба в пределах отображаемой территории.
В соответствии с тем, критерий какого вида исполь-
используется при построении проекции, различают выгодней-
выгоднейшие проекции вариационного и минимаксного типов.
Таким образом, проблемы построения наивыгоднейших
проекций заключаются в том, что для заданной одно-
связной области А поверхности S требуется отыскать
(при условии минимума одного нз приведенных функ-
функционалов Ф или величины б) проекцию А на плоскость
либо из всего их множества A) — такие проекции наз.
идеальными, либо из какой-либо их совокупности
(напр., из класса проекций, описываемых решениями
соответствующей ему системы D)) — такие проекции
наз. наилучшими проекциями данной их совокуп-
совокупности (класса). Для каждой такой задачи должна быть
исследована корректность ее постановки.
Для сферич. сегмента (области сферы, ограниченной
окружностью малого круга) в соответствии с критерием
Чебышева идеальной проекцией (см. [2], [13]) является
равнопромежуточная проекция Постеля; наилучшей
конформной — стереографическая (см. [8]); наилучшей
эквивалентной — равновеликая проекция Ламберта
(см. [2]). На основании вариационного критерия для
сферич. сег.мента Эйри (см. [14]) была вычислена наи-
наилучшая азимутальная проекция. Для сферич. трапе-
трапеции — области сферы, ограниченной дугами двух ме-
меридианов и двух параллелей, и (в некотором смысле)
близких к ней областей при картографировании ис-
используют конические проекции.
Среди этих проекций, предназначенных для картогра-
картографирования сферич. трапеций, известны наилучшие про-
проекции минимаксного типа (проекции Маркова, см. [10]),
а также наилучшие (того же типа) конформные и экви-
эквивалентные (см. [2]). Разработана общая методика по-
построения наилучших по критерию Эйри конич. проекций
(конформных, эквивалентных, равнопромежуточных)
для односвязных областей произвольных очертаний (см.
[15], [2]). Однако для сферич. трапеции при изображе-
изображении ее на плоскости в конформной проекции наимень-
наименьшее колебание логарифма масштаба имеет место в про-
проекциях, рассчитанных (см. [9], [11]) в соответствии с
теоремой Чебышева — Граве (см. [8], [9]):
для того чтобы в конформной проекции (т=ге, е=0)
на плоскость односвязной области А поверхности S,
имеющей полную кривизну одного и того же знака, ло-
логарифм масштаба наименее уклонялся от нуля, необхо-
необходимо и достаточно постоянство масштаба на контуре изо-
изображаемой территории. Конформные проекции, удов-
удовлетворяющие условиям этой теоремы, наз. ч е б ы ш е в-
скими проекциями. Они обладают рядом
supmA .
полезных свойств (в них -lf :—= mm, O/_A-=min, ми-
минимальна средняя кривизна изображений геодезич. ли-
линий поверхности S, тахд|1п р\ =min), за счет к-рых
они ценны для практики. П. Л. Чебышев решил задачу
отыскания для Acz5 конформной проекции с минимумом
искажения площадей, т. е. конформной проекции,
наиболее близкой к эквивалентным.
Важна и обратная задача: среди всех эквивалентных
проекций области Acz5 на плоскость найти проекцию с
минимумом искажений форм. Один из подходов к этой
задаче таков. Ввиду разной мощности двух рассматри-
рассматриваемых множеств проекций (множество конфор.мных
описывается системой двух уравнений с частными
производными т=п, е=0, а эквивалентных — одним
p—tnn cos e=l) сначала из совокупности эквивалентных
проекций выделяется нек-рый класс проекций, близких
к конформным, а затем уже в нем ищется проекция с
минимумом искажений форм. Из классич. наследия был
известен один класс таких проекций, именно, класс эй-
эйлеровых проекций: р = 1, е=0 (см. [5]), ныне предложе-
предложены и другие классы эквивалентных проекций, близких к
конформным, напр, класс: р=1, (т—re) + fte=0, k =
=к(и, v) — параметр класса (см. [4]).
Исследование указанных и других новых классов
картографич. проекций и поиски в них наивыгоднейших
проекций минимаксного типа привели к постановке за-
задач на условный минимакс (см. [16]). Сущность таких
задач заключается в том, что для данной системы диф-
дифференциальных уравнений с частными производными,
решения к-рой должны быть найдены в заданной области
Л, требуется установить те дополнительные условия
(краевые, начальные и т. д.) и в нек-рых случаях еще
определить вид тех кривых, к к-рым должны быть
отнесены эти условия, чтобы при интегрировании си-
системы с ними одно из ее решений в области А наименее
уклонялось бы от нуля. Известны только частные
случаи исследования таких задач, основанные на мето-
методе априорных оценок решений дифференциальных
уравнений. Достигнутые результаты для систем эллип-
тпч. типа — распространение теоремы Чебышева —
Граве на два новых класса проекций: класс, описывае-
описываемый системой уравнений в характеристиках re=ftm,
е = 0, /c = const>0 (см. [17]), и класс т=пс, е=0, с =
-^const>0 (см. [19]). Для гипсрболич. системы, описы-
описывающей эйлеровы проекции, методом характеристик
установлены такие начальные условия на меридиане
(см. [16]) и на параллели (см. [18]), при к-рых одно из
решений системы (логарифм масштаба) в области влия-
влияния начальных данных наименее уклоняется от нуля.
Картографический смысл этого аналога теоремы Чебы-
Чебышева таков: «носительница» данных Коши должна быть
линией конформности, т. е. масштаб на ней равен
единице. Этот результат при задании начальных усло-
условий на меридиане справедлив и для более широкого
класса проекций: т=пс, е=0, c=const (см. [19]). Иссле-
Исследован случай эйлеровых проекций для заданной сферич.
трапеции, в к-ром при рассмотрении — с привлечением
интеграла энергии — смешанной задачи установлены
начальные (для южной стороны трапеции) и краевые
(на дугах, ограничивающих ее меридианов) условия,
обеспечивающие получение для этой области наилуч-
наилучших эйлеровых проекций вариационного типа: на ука-
указанных трех сторонах области масштаб должен быть
равен единице (см. [20]). Общая методика изыскания
наивыгоднейших проекций вариационного типа для
произвольной области AdS сводится к решению ва-
вариационных задач со свободными краями (см. [4]).
Лит.: [1] Итоги науки и техники. Картография, т. 7, М.,
1976, с. 45 —57; [2J К'а в р а й с к и й В. В., Избр. труды,
т. 2, в. 1 — 3, М., 1958 — 1960; [3] К а г а н В. Ф., Основы тео-
теории поверхностей ..., ч. 1—2, М.— Л., 1947—48; [4] М е щ е-
р я к о в Г. А., Теоретические основы математической карто-
картографии, М., 1968; [5] Эйлер Л., Избр. картографические
статьи, пер. с нем., М., 1959; [6] Гаусс К. Ф., Избр. геоде-
геодезические соч., т. 2, М., 1958; [7] Т и с с о М. А., Изображение
одной поверхности на другой и составление географических
карт, пер. с франц., М., 1899; [8] Чебышев П. Л.. Соч.,
т. 1, СПБ, 1899; [9] Г р а в е Д. А., Об основных задачах мате-
математической теории построения географических карт, СПБ, 1896;
[10] Марков А. А., «Изв. АН», сер. 5, 1895, т. 2, Х° 3,
с. 177—87; Г11] У р м а е в Н. А., Методы изыскания новых
картографических проекций, М., 1947; [12] Лаврентьев
М. А., Вариационный метод в краевых задачах для систем урав-
уравнений эллиптического типа, М., 1962; [13] Milnor J «Amer.
Math. Monthly», 1969, v. 76, p. 1101 — 12; [14] Airy G. В.,
«Philos. Mag.», 1861, Ser. 4, v. 22, p. 409—21; [15] Цингер
H. Я., «Изв. AH», 1916, сер. 6, т. 10, ,\g 17, с. 1693 — 1704; [IB]
Мещеряков Г. А., «Докл. АН СССР», 1961, т. 136, У° 5,
с. 1026—29; [17] Топчи лов М. А., «Изв. ВУЗов. Геод. а
аэрофотосъемка», 1970, №4, с. 91 — 96; [18] Тучин Я. И.,
«Тр. Новосиб. ин-та инженеров геод., аэрофотосъемки и карто-
картографии», 1973, т. 30, с. 65—67; [19] Юзефович Ю. М.,
«Сб. научн. трудов Белорусск. сельхоз. академии», 1972, т. 86,
с. 245—53; [20] Тучин Я. И., «Тр. Новосиб. ин-та инженеров,
геод., аэрофотосъемки и картографии», 1975, т. 34, с. 55—64.
Г. А. Мещеряков.
КАРТОГРАФИЧЕСКАЯ ПРОЕКЦИЯ — отображе-
отображение всей поверхности земного эллипсоида или какой-
либо ее части на плоскость, получаемое в основном с.
целью построения карты.
К. п. чертят в определенном масштабе. Уменьшая
мысленно земной эллипсоид в М раз, получают его
геометрич. модель — глобус, изображение к-рого в
натуральную величину на плоскости дает карту по-
поверхности этого эллипсоида. Величина 1 : М определяет
главный, или об щ и й, м а с ш т а б карты. Однако
основной характеристикой К. п. в любой ее точке яв-
является частный масштаб ц. Это — величина,
обратная отношению бесконечно малого отрезка dS на
земном эллипсоиде к его изображению da на плоскости:
i/\y=dS!da, причем |i зависит от положения точки на
эллипсоиде и от направления выбранного отрезка.
Отношение \i!M наз. относительным масш-
масштабом, или увеличением длины, разность (\х,/М—1) —
искажением длины. Численное значение глав-
главного масштаба М учитывается только при вычислениях
координат точек К. п. п при использовании карты, а
при исследованиях К. п. полагают М=1.
В картографии часто ограничиваются рассмотрением
отображений на плоскость сферы нек-рого радиуса R,
отклонениями к-рой от земного эллипсоида можно
пренебречь или каким-либо способом их учесть. По-
Поэтому далее имеются в виду отображения на плоскость
хОу сферы, отнесенной к географнч. координатам ц>
(широта) и А, (долгота).
Уравнения К. п. имеют вид
ж=Д(ф, ^). г/=.Мф. *¦). (*)
где /х н /2 — функции, удовлетворяющие нек-рым
общим условиям (К. п. может быть определена также
уравнениями, в к-рых фигурируют не прямоугольные
координаты плоскости х, у, а какие-либо иные). Изоб-
Изображения меридианов A,=const и параллелей cp=const в
данной К. п. образуют картографическую
сетку.
КАРТОГРАФИЧЕСКИЕ ПРОЕКЦИИ
1. СЕТИ СФЕРИЧЕСКИХ
КООРДИНАТНЫХ ЛИНИЙ
2. ШАР И ЕГО ОРТОГРАФИЧЕСКИЕ
ПРОЕКЦИИ
Б. ПОПЕРЕЧНАЯ
3. ЦИЛИНДРИЧЕСКИЕ ПРОЕКЦИИ
А. РАВНОУГОЛЬНАЯ МЕРКАТОРА
85
30
0
30
-
f
I
\
и
1
9
J
/
(
1
So
i
1
-
г-
С
)
7
И
1
/
1
Г3
)=
-'С
л|
91
-к
/
*|
&
0
^1
%
г-
1
<
/
(•
—!
if
1
9
0,
'¦
г,
0
л
¦ 1
Тл.
3
"я
А
-
'С
s
\
-si
80
А. НОРМАЛЬНАЯ
Б. РАВНОПРОМЕЖУТОЧНАЯ (ПРЯМОУГОЛЬНАЯ)
В. РАВНОВЕЛИКАЯ (ИЗОЦИЛИНДРИЧЕСКАЯ)
...
*
...
1
1
"Ч,
1
9
I
\
^-
¦¦¦:?
1
м
\)
V
«¦
{-
г
(
^
V
%
\
\
(
3S
*:
1-
id
%
iS
V
/
i
у
i
t
Щ
«
Л
\
04
¦/f
1
0
%
4
1
¦4
%
4
:i
(
i'1
f
IE
4v
0
i
¦-
i
9
:-
О
s
f
c
К
\
)
i
<¦
r
)
)
{
A4
К
(
J
~\
J
i
к
g
1
li
w
i
/
ь
8
\
1
i
A
J
I
i
ч
,/>
-\
%
5-
\
re
s
...
КАРТОГРАФИЧЕСКИЕ ПРОЕКЦИИ
1. СЕТИ СФЕРИЧЕСКИХ
КООРДИНАТНЫХ ЛИНИЙ
2. ШАР И ЕГО ОРТОГРАФИЧЕСКИЕ
ПРОЕКЦИИ
Б. ПОПЕРЕЧНАЯ
3. ЦИЛИНДРИЧЕСКИЕ ПРОЕКЦИИ
А. РАВНОУГОЛЬНАЯ МЕРКАТОРА
85
30
0
30
-
Г
-f>
Г
1
).
\
и
%
-\
9
-S
i
\
1,
о»
/
(
A
i
1
4-
-
с
7
и
¦>r
1
/
I
*
a|
91
/
n
<•
tl
0
M
-,g
%
1
$
/
-*¦
—j
/
If
9
rv
Ok
I
r,
0
Л
_j
¦ 1
4?
•-!
N
3
"^
л
-
X
\
V
\
-si
80
-,
А. НОРМАЛЬНАЯ
Б. РАВНОПРОМЕЖУТОЧНАЯ (ПРЯМОУГОЛЬНАЯ)
В. РАВНОВЕЛИКАЯ (ИЗОЦИЛИНДРИЧЕСКАЯ)
...
...
1
1
"")
zj
с
i
1
9
1
У
¦¦¦:?
1
%
м
V
«¦
щ
г
л
(
^
V
й-
%
\
\
(
J
*:
1-
V
/
(-
i
у
i
t
щ
ш
s
я?
Л
;.'•
s>
1
04
1
%
4
1
;В
(Я
Ч
У
f
IE
0
30
0
4
¦-
1
X
9
?¦
?
о
?
i
\
)
:^
f
¦У:
]
f
А4
V
f
(.
)
г?1
Г
¦?
g
*F
«
i
%
f
j
6
й
U
%
'А
h
S
&
а
\
%
Й
1
А
J
\
1
¦i
ч
А
1
'I
t
te
-
КАРТОГРАФИЧЕСКИЕ ПРОЕКЦИИ
4. КОНИЧЕСКИЕ ПРОЕКЦИИ
А. РАВНОУГОЛЬНАЯ
В- РАВНОВЕЛИКАЯ
5. АЗИМУТАЛЬНЫЕ ПРОЕКЦИИ
А. РАВНОУГОЛЬНАЯ
(СТЕРЕОГРАФИЧЕСКАЯ)
ПОПЕРЕЧНА
/0
1——14 1 i f Г"~
1 -1
i f Г
1 ' Г ' f
•^ -r-
\
A
п. равнопромея;уточная
В. РАВНОВЕЛИКАЯ
ПОПЕРЕЧНАЯ КОСАЯ
6. ПСЕВДОКОНИЧЕСКАЯ РАВНОВЕЛИКАЯ
ПРОЕКЦИЯ БОННА
7. КОСАЯ ПЕРСПЕКТИВНО-ЦИЛИНДРИЧЕСКАЯ
ПРОЕКЦИЯ М.Д. СОЛОВЬЕВА
КАРТОГРАФИЧЕСКИЕ ПРОЕКЦИИ
4. КОНИЧЕСКИЕ ПРОЕКЦИИ
А. РАВНОУГОЛЬНАЯ
Б. РАВНОПРОМЕЖУТОЧНАЯ
90 9о
В- РАВНОВЕЛИКАЯ
5. АЗИМУТАЛЬНЫЕ ПРОЕКЦИИ
А. РАВНОУГОЛЬНАЯ
(СТЕРЕОГРАФИЧЕСКАЯ)
ПОПЕРЕЧНА
1 -f- »
П. РАВНОПРОМЕЖУТОЧНАЯ
В. РАВНОВЕЛИКАЯ
ПОПЕРЕЧНАЯ КОСАЯ
6. ПСЕВДОКОНИЧЕСКАЯ РАВНОВЕЛИКАЯ
ПРОЕКЦИЯ БОННА
7. КОСАЯ ПЕРСПЕКТИВНО-ЦИЛИНДРИЧЕСКАЯ
ПРОЕКЦИЯ М.Д. СОЛОВЬЕВА
30 60
КАРТОГРАФИЧЕСКИЕ ПРОЕКЦИИ
8. ПСЕВДОЦИЛИНДРИЧЕСКИК ПРОЕКЦИИ
А. РАВНОВЕЛИКАЯ ПРОЕКЦИЯ МОЛЬВЕЙДЕ В. ПРОИЗВОЛЬНАЯ ПРОЕКЦИЯ ЦНИИГАиК
Изображен;-;?! меридианов-эллипсы. Длины сохраняются вдоль параллелей
с широтами у = i40°,7
Б. РАВНОВЕЛИКАЯ СИНУСОИДАЛЬНАЯ ПРОЕКЦИЯ В.В. КАВРАЙСКОГО
\Ш\\\\\\
Длины сохраняются вдоль экватора по всем меридианам
Г. ПРОЕКЦИЯ БСАМ
Изображения мер ид из нов-дуги синусоид. Длины сохраняются вдоль параллелей
с широтами гр =146°,5
Использован способ Гуда построения надрезанной проекции: допущены разрывы
изображения на океанах с целью уменьшения искажений на континентах
А. ПРОСТАЯ
9. ПОЛИКОНИЧЕСКИЕ ПРОЕКЦИИ
Б. ПРОИЗВОЛЬНАЯ ПРОЕКЦИЯ Г.Л. ГИНЗБУРГА
Длины сохраняются вдоль параллелей с широтами ш =i45°
Проекции произвольна?. Длины сохраняются вдоль всех параллелей
и по среднему меридиану
КАРТОГРАФИЧЕСКИЕ ПРОЕКЦИИ
8. ПСЕВДОЦИЛИНДРИЧЕСКИЕ ПРОЕКЦИИ
А. РАВНОВЕЛИКАЯ ПРОЕКЦИЯ МОЛЬВЕЙДЕ
В. ПРОИЗВОЛЬНАЯ ПРОЕКЦИЯ ЦНИИГАиК
Изображения меридианов-эллипсы. Длины сохраняются вдоль параллелей
с широтами tf = ^40°,7
Б. РАВНОВЕЛИКАЯ СИНУСОИДАЛЬНАЯ ПРОЕКЦИЯ В.В. КАВРАЙСКОГО
Длины сохраняются вдоль экватора по всем меридианам
Г. ПРОЕКЦИЯ БСАМ
Изображения меридианов-дуги синусоид. Длины сохраняются вдоль параллелей
с ширит i f =146°,5
Использован способ Гула построения надрезанной проекции: допущены разрывы
изображения на океанах с целью уменьшения искажений на континентах
А. ПРОСТАЯ
9. ПОЛИКОНИЧЕСКИЕ ПРОЕКЦИИ
Б. ПРОИЗВОЛЬНАЯ ПРОЕКЦИЯ Г.Л. ГИНЗБУРГА
Длины сохраняются вдоль параллелей с широтами ш =i45°
Проекции произвольна?. Длины сохраняются вдоль всех параллелей
и по среднему меридиану
При картографировании областей, содержащих гео-
географич. полюсы, иногда применяют не географич.
координаты, а другие, в к-рых полюсы оказываются
обыкновенными точками координации. Напр., исполь-
используют сферич. координаты, координатные линии к-рых—
так наз. вертикалы (условная долгота на них
o=const) и альмукантараты (где полярные
расстояния z=const)—аналогичны географич. меридиа-
меридианам и параллелям, но их полюс Zo(<Po, ^o) не совпадает
с географич. полюсом Ро (рис. 1). Всякая К. п., данная
уравнениями (*), наз. нормальной, или пря-
прямой (фо=я/2). Если та же самая проекция сферы
вычисляется по формулам (*), в к-рых вместо ф, к фи-
фигурируют z, а, то эта проекция наз. поперечной
при фо=О, и к о с о й, если 0<ф0<я/2. На рис. 2 пока-
показаны нормальная (А), поперечная (Б) и косая (В) орто-
рафич. проекции шара.
Искажения в бесконечно малой области около какой-
либо точки проекции подчиняются нек-рым общим за-
законам. Во всякой точке карты, составленной в проек-
проекции, не являющейся равноугольной (см. ниже), суще-
существует два таких взаимно перпендикулярных направ-
направления, к-рым на отображаемой поверхности соответ-
соответствуют также взаимно перпендикулярные направления—
так наз. главные направления отображения. Масштабы
по этим направлениям имеют экстремальные значения
Р-тах=а н !-imin=b- Если в какой-либо К. п. изображе-
изображения меридианов и параллелей пересекаются под прямым
углом, то их направления и есть главные для данной
К. п. Искажения длин в данной точке К. п. наглядно
представляет эллипс и с к а ж е н и и, подобный и
подобно расположенный изображению бесконечно малой
окружности, описанной вокруг соответствующей точки
отображаемой поверхности. Полудиаметры этого эллип-
эллипса численно равны частным масштабам в данной точке
в соответствующих направлениях, полуоси эллипса
равны экстремальным масштабам, а направления их —
главные.
В равноугольных (конформных)
К. п. масштаб зависит только от положения точки и
не зависит от направления. Эллипсы искажения —
окружности. Примеры: проекция Меркатора, стереогра-
стереографическая проекция, равноугольная коническая проек-
проекция и др. (см. рис. ЗА, 5А, 4А).
В равновеликих (эквивалентных)
К. п. сохраняются площади; точнее, площади фигур
на картах, составленных в таких проекциях, пропорцио-
пропорциональны площадям соответствующих фигур в натуре,
причем коэффициент пропорциональности — величина,
обратная квадрату главного масштаба карты. Эллипсы
искажений всюду имеют одинаковую площадь, разли-
различаясь формой и ориентировкой; см., например, рис. ЗВ,
4В, 5В.
Произвольные К. п. (см., напр., рис. 7) не
относятся ни к равноугольным, ни к равновеликим. Из
них выделяют равнопромежуточные, в
к-рых один из главных масштабов равен единице (см.
рис. ЗВ, 4Б, 5Б), и ортодромические, в
к-рых большие круги сферы (ортодромы) изображаются
прямыми.
При изображении сферы на плоскости свойства рав-
ноугольности, равновеликости, равнопромежуточности
и ортодромичности несовместимы.
Для показа искажений в разных местах изображае-
изображаемой области применяют: эллипсы искажений (см., напр.,
рис. 3, 4); изоколы — линии равного значения ис-
искажений (на рис. 8 В см. изоколы наибольшего искаже-
искажения углов о и изоколы масштаба площадей р); изобра-
изображения в нек-рых местах карты нек-рых сферич. линий,
обычно ортодромий «О» и изогональных траекторий ме-
меридианов-локсодромий «Л» (см., напр., рис. ЗА, ЗБ).
По виду картографической сетки к. п. подразделяют
на следующие группы.
Цилиндрические проекции — про-
проекции, в к-рых меридианы изображаются равноотстоя-
равноотстоящими параллельными прямыми, а параллели — пря-
прямыми, перпендикулярными меридианам (см. рис. 3).
Конические проекции — проекции, в
к-рых параллели изображаются концентрич. окруж-
окружностями, меридианы — ортогональными им прямыми,
причем углы между последними пропорциональны
соответствующим разностям долгот (см. рис. 4).
Азимутальные проекции — проекции,
в к-рых параллели изображаются концентрич. окруж-
окружностями, меридианы — их радиусами, при этом углы
между последними равны соответствующим разностям
долгот (см. рис. 5).
Псевдоконпческие проекции — про-
проекции, в к-рых параллели изображаются концентрич.
окружностями, средний меридиан — прямой линией,
остальные меридианы — кривыми симметричными от-
относительно изображения среднего меридиана (см.,напр.,
рис. 6).
Псевдоцилиндрические проек-
ц и и — проекции, в к-рых параллели изображаются
параллэльнымп прямыми, средний меридиан — пря-
прямой линией, перпендикулярной этим прямым, осталь-
остальные меридианы — кривыми (см. рис. 8).
Пол и конические проекции — проек-
проекции, в к-рых параллели изображаются окружностями с
центрами, расположенными на одной прямой, изобра-
изображающей средний меридиан, остальные меридианы —
кривыми, также симметричными относительно этой
прямой (см. рис 9). При построении конкретных поли-
поликонических проекций ставятся дополнительные усло-
условия.
Существуют и другие проекции, не относящиеся к
указанным видам. Цилиндрические, конические и ази-
азимутальные проекции, называемые простейшим и,
часто относят к круговым проекциям в широком смыс-
смысле, выделяя из них круговые проекции в узком смысле—
проекции, в к-рых все меридианы и параллели изобра-
изображаются окружностями.
Об использовании, выборе, исследованиях свойств,
преобразованиях К. п. см. статью Картографии мате-
математические задачи И ЛИТ. при ней. Г. Л. Мещеряков.
КАСАНИЕ — геометрическое понятие, обозначаю-
обозначающее, что в некоторой точке две кривые (кривая и поверх-
поверхность) имеют общую касательную прямую или две по-
поверхности имеют общую касательную плоскость. Поря-
Порядок К.— характеристика близости двух кривых (кри-
(кривой и поверхности или двух поверхностей) в окрестно-
окрестности их общей точки. См. Соприкосновение. БСЭ-i.
КАСАТЕЛЬНАЯ к кривой л и н и и — прямая,
представляющая предельное положение секущей. Пусть
М — точка кривой L (рис. 1). На L выбирается вторая
точка М' и проводится прямая ММ'. Точка М считается
Рис. 1. Рис.
неподвижной, а точка М' приближается к М по кривой
L. Если при неограниченном приближении М' к М
прямая ММ' стремится к определенной кривой М Т, то
МТ наз. касательной к кривой L в точке Д/.
Не у всякой непрерывной кривой имеются К., посколь-
поскольку прямая ММ' может не стремиться к предельному
положению или может стремиться к двум разным пре-
предельным положениям, когда М' стремится к М с разных
сторон от М (рис. 2). Если кривая на плоскости в
прямоугольных координатах определяется уравнением
y=f(x* п f(x) дифференцируема в точке х0, то угловой
коэффициент К. в точке М с абсциссой х0 равен значе-
значению производной /' (х0) в точке х0; уравнение К. в этой
точке имеет вид:
y—f(xo)=f (хв)(х—х0).
Уравнение К. к пространственной кривой r=r(t):
К. к поверхности S в точке М наз. прямая, проходя-
проходящая через точку М и лежащая в касательной плоскости
к S в точке М. БСЭ-з.
КАСАТЕЛЬНАЯ ПЛОСКОСТЬ к поверхности
S ъ точке М — плоскость, проходящая через точку
М и характеризующаяся тем свойством, что расстояние
от этой плоскости до переменной точки М' поверхности
S при произвольном стремлении М' к М является бес-
бесконечно малым по сравнению с расстоянием ММ'. Если
поверхность S задана уравнением z=f(x, у), то урав-
уравнение К. п. с точке (х0, у0, z0), где zo=f(xo, у0), имеет
вид:
z—zo=A (x—xo)+B(y—ya)
в том и только том случае, когда функция f(x, у) имеет
в точке (х0, г/0) полный дифференциал. В этом случае
А и В суть значения частных производных dfldx и
vfldy в точке (х0, г/0). БСЭ-з.
КАСАТЕЛЬНОЕ ПРЕОБРАЗОВАНИЕ — см. При-
Прикосновения преобразование.
КАСАТЕЛЬНОЕ РАССЛОЕНИЕ дифферен-
дифференцируемого многообразия М — вектор-
векторное расслоение т : ТМ—*-М, пространство к-рого ТМ
является касательным пространством к М (объедине-
(объединением касательных пространств ТМ\Х в точке х?М),
состоящим из касательных векторов к М, а проекция т
отображает ТМ\Х в х. Сечение К. р. х(М) — векторное
поле на многообразии М. Атлас многообразия ТМ
определяется атласом многообразиям и
условием локальной тривиальности расслоения т (М).
Функции перехода К. р. являются матрицами Якоби
функций перехода атласа многообразия.
К К. р. присоединено главное расслоение реперов
многообразия М. Расслоение т* (М), двойственное
К. р. х(М), наз. кокасательным рассло-
расслоением, а его пространство Т*М— кокасатель-
кокасательным пространством. Сечениями его яв-
являются линейные дифференциальные формы (Пфаффа
формы).
Дифференцируемое отображение h : М—vjV индуци-
индуцирует морфизм К. р. х(М)—>-t(VV); соответствующее
отображение касательных пространств hT : TM^>-TN
наз. касательным к h отображением. В част-
частности, если i : M—*-N — иммерсия, то х(М) является
подрасслоением индуцированного расслоения i*t(jV).
Факторрасслоение v(i) = i*x(M)/x(M) наз. нормаль-
нормальным расслоением иммерсии. Двойственно, если
/ : M^-N—субмерсия, то факторрасслоенпе x(M)/i*r(M)
наз. с у б р а с с л о е н и е м /. Если в качестве М и N
взяты соответственно ТМ и М, a h=x : ТМ—*-М, то
х*х(М) наз. вторым касательным рассло-
расслоение м.
Если К. р. х(М) — тривиально, то М наз. паралле-
лизуемым многообразием.
Лит.: [1] Г о д б и й о н К., Дифференциальная геометрия
и аналитическая механика, пер. с франц., М., 1973.
М. И. Войцеховский.
КАСАТЕЛЬНЫЙ КОНУС—1) К. к. квыпуклой
поверхности S в точке О—поверхность V(O)
конуса, образованного полупрямыми, исходящими из О
и пересекающими выпуклое тело, ограниченное S по
крайней мере в одной еще точке, отличной от О (сам
этот конус иногда наз. телесным К. к.). Другими
словами, V(O) — граница пересечения всех полупро-
полупространств, содержащих S и определяемых опорными
плоскостями к S в точке О. Если V(O) — плоскость,
то О наз. гладкой точкой 5, если V(O) — дву-
двугранный угол, то О наз. ребристой точкой,
наконец, если V(O) — невырожденный (выпуклый)
конус, то О наз. конической точкой поверхно-
поверхности S.
Лит.: [1] Погорелое А. В., Внешняя геометрия
выпуклых поверхностей, М., 1969. М. И. Войцехоеский.
2). К. к. к алгебраическому многооб-
разиюХв точке х—множество предельных поло-
положений секущих прямых, проходящих через х. Точнее,
если алгебраич. многообразие X вложено в аффинное
пространство А" и задается идеалом ЭГ кольца к[Тх,...,
Тп\, а точка х?Х имеет координаты @, ...,0), то ка-
касательный конус С(Х, х) к X в точке х задается идеа-
идеалом начальных форм многочленов из Ш. (если F=Fi,-\-
+^ft+1+...—разложение F на однородные многочле-
многочлены и Р^ФО, то Fk наз. начальной формой F).
Существует другое определение, пригодное для про-
произвольных нётеровых схем (см. [1]): пусть Ох,х—
локальное кольцо схемы X в точке х, 9Л — его макси-
максимальный идеал, тогда спектр градуированного кольца
наз. касательным конусом к X в
точке х.
Многообразие X в окрестности точки х в некотором
смысле устроено так же, как К. к. Напр., если К. к.
приведенный, нормальный или регулярный, то та-
таким же будет локальное кольцо Qx,x- Размерность и
кратность X в точке х совпадают с размерностью К. к.
и кратностью его в вершине. К. к. совпадает с Зарис-
кого касательным пространством тогда и только тогда,
когда х — неособая точка X. Морфизм многообразий
индуцирует отображение К. к.
Лит.: [1] I g u s a J., «Mem. Coll. Sci. Univ. Kyoto», 1951,
v. 27, p. 189—201; L2] Samuel P., Methodes d'algebre abst-
racte en geometrie algebrique, В., 1967; [3] Хиронака
Ж., «Математика», 1965, т. 9, №. 6, с. 2—70; [4] W h I t n е у Н.,
Differential and Combinatorial Topology, N.Y., 1965, p. 205—44,
В. И. Данилов.
КАСАТЕЛЬНЫЙ ПОТОК — поток в пространстве
й/г ортонормированных /с-реперов re-мерного риманова
многообразия М, обладающий следующим свойством.
Пусть со (г) — произвольная траектория потока; по
определению пространства Q^, со (t) есть нек-рый/с-ре-
пер li(i), ¦••, 5/г(*) в нек-рой точке x(t)?M (т. е. в
касательном пространстве к М в этой точке). Требуется,
чтобы dx(t)ldt='E>1(t) (вариант; требуется, чтобы сопро-
сопровождающий репер параметризованной кривой x(t) в М
имел своими первыми к векторами как раз ^(t), ...,
5/г(г))- Для получения содержательных результатов о
К. п. приходится накладывать различные дополнитель-
дополнительные условия. Полученные результаты обобщают нек-рые
из свойств геодезических потоков (являющихся частным
случаем К. п., когда к=1 и ковариантная производная
Dydt=0). См. [1], [2].
Иногда касательными потоками наз. различные ти-
типы потоков в касательном пространстве к нек-рому
многообразию М (или — считая, что М снабжено ри-
мановой или финслеровой метрикой,— в простран-
пространстве единичных касательных векторов). Напр., К. п.
наз. пульверизации (вообще, уравнения 2-го порядка)
на М и уравнения в вариациях для нек-рого потока на
М. Но такое словоупотребление не получило распро-
странения — со временем находились более употреби-
употребительные термины.
Лит.: [1] Арнольд В. И., «Докл. АН СССР», 1961,
т. 138, №2, с. 255—57; [2] е г о же, «Сиб. матем. ж.», 1961,
т. 2, № 6, с. 807—13. д. в. Лкосов!
КАСАТЕЛЬНЫЙ ПУЧОК в алгебраиче-
алгебраической геометрии— пучок в^ на алгебраич. мно-
многообразии или схеме X над полем к, сечения к-рого над
открытым аффинным подмножеством U=Spec(A) со-
составляют Л-модуль ^-дифференцирований Derk(A, A)
кольца А. Эквивалентное определение состоит в том,
что @х есть пучок гомоморфизмов Kom(Q1x/k, Ox)
пучка дифференциалов Qx/fc в структурный пучок Ох
(см. Дифференциалов модуль).
Для любой рациональной А-точки х?Х слой ®х(х)
пучка &х совпадает с касательным прост-
пространством Зариского Тх,х к схеме X в точке
х, т. е. с векторным ^-пространством Нот/г(Ш1х/Ш1|,Л),
где ЗЛх — максимальный идеал локального кольца
®Х,х- К- п. в^ служит пучком ростков сечений вектор-
векторного расслоения V(Qx;k), двойственного пучку Qx (ка-
(касательного расслоения к схеме X). В случае, когда
X — гладкая связная &-схема, пучок @% является ло-
локально свободным пучком на X ранга, равного раз-
размерности X.
Лит.: [1] Шафаревич И. Р., Основы алгебраической
геометрии, М., 1972. И. В. Долгачее.
КАСАТЕЛЬНЫХ ИНДИКАТРИСА к р и в о й Г в ев-
евклидовом пространстве Е"—расположенная на
сфере SndEn кривая Г*, радиус-векторы точек тк-рой
параллельны касательным векторам т кривой Г. Для
того чтобы сферич. кривая L была К. и. нек-рой замк-
замкнутой кривой в Е", необходимо и достаточно, чтобы L
не могла поместиться ни в какой открытой полусфере
(теорема К р е й н а).
Лит.: [1] В ы г о д с к и й М. Я., Дифференциальная гео-
геометрия, М.— Л., 1949. ' Ы. И. Войцеховский.
КАСКАД в теории динамических сис-
систем, динамическая система с диск-
дискретным времене м,— динамическая система,
определяемая действием аддитивной группы целых
чисел z (или аддитивной полугруппы натуральных чи-
чисел М) на нек-ром фазовом пространстве W. Согласно
общему определению действия группы (полугруппы),
это означает, что каждому целому (натуральному)
числу п сопоставлено нек-рое преобразование Sn : И7—>-
-+W, причем
Sn + m(w)=Sn(Sm(w)) (*)
для всех w?W. Поэтому все преобразования Sn по-
получаются из одного преобразования S=S1 посредством
итерирования и (если и<0) обращения:
Sn=(S)" при n>0, Sn=(S-1)n при и<0.
Тем самым изучение К. по существу сводится к изуче-
изучению свойств порождающего его преобразования S,
и в этом смысле К. являются простейшими динамич. сис-
системами. Поэтому К. исследуются весьма интенсивно,
хотя в приложениях чаще всего встречаются динамич.
системы с непрерывным временем (потоки). Принци-
Принципиальная сторона дела для потоков и К. обычно одина-
одинакова, но случай К. несколько проще технически, и в
то же время полученные для них результаты часто без
особого труда удается перенести на потоки — иногда
путем формальной редукции свойств потоков к свой-
свойствам К., но чаще путем нек-рого видоизменения дока-
доказательств.
Как и для любых динамич. систем, обычно фазовое
пространство W наделено нек-рой структурой, и пре-
преобразования Sn ее сохраняют. Напр., W может быть
гладким многообразием, топологич. пространством или
пространством с мерой; соответственно говорят о н е-
прерывном, гладком или из меримом К. |
(впрочем, в последнем случае определение обычно не-
несколько видоизменяют, требуя, чтобы каждое Sn было
определено почти всюду и чтобы при любых п, т ра-
равенство (*) имело место при почти всех w). Преобра-
Преобразование S, порождающее К., является в этих слу-
случаях диффеоморфизмом, гомеоморфизмом или автомор-
автоморфизмом пространства с мерой (если речь идет о груп-
группе преобразований), либо гладким отображением, не-
непрерывным отображением или эндоморфизмом про-
пространства с мерой (если К. является полугруппой).
КАСКАДНЫЙ МЕТОД, метод Л а и л а с"ец —
метод теории дифференциальных уравнений с частными
производными, позволяющий в нек-рых случаях нахо-
находить общее решение линейного уравнения с частными
производными гиперболич. типа
Lussuxy + a(x, у) их + Ь (х, у)иу + с(х, у) u = f(x, у), A)
построив последовательность уравнений
Lius=uxv-\~ai(x, y)ux-\-bt(x, у) uy-\-Ci(x, y)u =
=f,-(x, у), B,-)
?= ±1, ±2,..., через решения к-рых выражается реше-
решение уравнения A).
Уравнение A) может быть записано в одном из сле-
следующих видов:
vx-\-bv — hu = f, Wy^aw — ku = f,
где
— с, к = Ьу-гаЬ— с,
Функции h и к наз. инвариантами уравнения A).
При h=0 решение уравнения A) сводится к интегри-
интегрированию обыкновенных дифференциальных уравнений
и его решение имеет вид:
- I ady г- ) с [bdx \ \ady-bdx
и = е ¦> \ X -\-\ \Y -\-\ fe' dx > е-'
где X и У — произвольные функции, зависящие соот-
соответственно от х и у. Аналогично, если &=0, то реше-
решение уравнения A) запишется следующим образом:
— \bdx\ г- ) [> [ady \ I bdx-ady
и=е J \Y-\-\\X-\-\feJ dy ( eJ <
L J ' J )
В случае кфО, решение и уравнения A) может быть по-
получено из решения ut уравнения B^, коэффициенты а1г
Ь1? с1 и правая часть /х к-рого имеют вид:
ах = а~ (\nh)y, ЪХ = Ъ, c1 = c — ax^-by — b(lnh)y,
h = f-(a-(lnh)y),
по формуле
Для уравнения BХ) инварианты h^ и к1 выражаются по
формулам
Если кг=0, то решение иг уравнения BХ) получается
описанным выше способом; если И^фО, то процесс про-
продолжается дальше построением уравнений B,), при г=
= 2, 3,..., через решения последовательности уравне-
уравнений с помощью квадратур выражается решение урав-
уравнения A). В случае кфО, можно построить аналогичную
цепочку уравнений B,) при i= —1, —2, .... Если на
каком-нибудь шаге h{ (или /с,) обратится в нуль, то
общее решение уравнения A) находится в квадратурах.
К. м. может быть использован для перехода от дан-
данного уравнения к уравнению, для к-рого легче приме-
нить какой-лпоо другой из известных аналитических
или численных методов решения; для получения се-
семейств уравнений, решения к-рых известны п коэффи-
коэффициенты к-рых достаточно хорошо аппроксимируют ко-
коэффициенты уравнений, встречающихся в важных при-
прикладных задачах; для получения основных операторов в
теории возмущений операторов.
К. м. указан П. Лапласом [1] в 1773 и развит Г. Дар-
% [2].
Лит.: [1] Laplace P. S., Oeuvres completes, t. 9, P.,
1893, p. о—68; [2] Darboux G., Lecons sur la theorie
gengrale des surfaces, 2 ed., t. 2, P., 1915; [3] T p и к о м и Ф.,
Лекции по уравнениям в частных производных, пер. с итал.,
М., 1957, с". 177—86; [4] Б а б и ч В. М. и др., Линейные
уравнения математической физики, М., 1964; [5] Д о м б р о в-
ский Г. А., Метод аппроксимации адиабаты в теории пло-
плоских течений газа, М., 1964; [6] Ч е к м а р е в Т. В. «Изв.
ВУЗов. Математика», 1972, №11, с. 72—9; [7] Пашков-
с к и й В. И., «Дифференциальные уравнения», 1976, т. 12,
J45 1, С. 118 — 28. В. II. Пашковский.
КАСП, обыкновенная точка возвра-
возврата,— особая точка алгебраич. кривой специального
типа. А именно, особая точка х алгебраич. кривой X
над алгебраически замкнутым полом к наз. К., если
пополнение ее локального кольца f)y,x изоморфно
пополнению локального кольца плоской алгебраич.
кривой ;/2+ж3=0 в начале координат.
КАССЙНИ ОВАЛ — плоская алгебрапч. кривая 4-го
порядка, уравнение к-рой в декартовых прямоуголь-
прямоугольных координатах имеет вид:
М (ж2+г/2J — 2с2 (z2—у2) = я4^<г>.
К. о. — множество точек (см.
Трис), произведение расстояний
каждой из к-рых до двух за-
заданных точек F(—с, 0) и fj (с, 0)
(фокусов) есть величина пос-
постоянная. При я>с|Л> К. о.—
овальная линия, при с<я<с У2 —
кривая с «талией», при а=с —
Бернулли лемниската, при а<^с —
два овала. К. о. относятся к
лемнискатам. К. о. рассматри-
рассматривались Дж. Кассинп (G. Cassi-
ni, 17 в.) при попытках опреде-
определить орбиту Земли.
Лит.: [1] Саве лов А. А., Плоские кривые, М., 1960.
Д. Д. Соколов.
КАТАЛАНА ПОВЕРХНОСТЬ — линейчатая поверх-
поверхность, прямолинейные образующие к-рой параллельны
одной и той же плоскости. Ее стрикционная линия
плоская. Радиус-вектор К. п.: r=p(u)-\-vl(u), причем
Г(и)=/=0, (I, V, Г)=0. Если все образующие К. п. пере-
пересекают одну и ту же прямую, то она является коноидом.
Лит..: [1] Catalan E., Memoire sur les surfaces grauches
a plan directeur, P., 1843. II. X. Сабитов.
КАТЕГОРИЧНАЯ СИСТЕМА АКСИОМ — всякая
система аксиом 2 , для к-рой все алгебраические системы
сигнатуры 2, удовлетворяющие этим аксиомам, изо-
изоморфны. Из теоремы Мальцева — Тарского об элемен-
элементарном расширении следует, что модели категоричной
системы 2 аксиом 1-го порядка имеют конечную мощ-
мощность. Верно и обратное: для любой конечной алгебраич.
системы А существует категоричная система 2 аксиом
1-го порядка, модели к-рой изоморфны А. Пусть 20 —
множество универсальных замыканий формул
1H#х + 1, 2) x + i = yA-\-^x=y,
3) x-ir0 = x, 4) x+(y-\- z) = (.r-L;/H z,
5) х-0^0, 6) x-(y + i) = (x.y)+x,
7) (ф @) & V* (Ф (х) —+ ф (х + 1))) —> V«p П,
где ф(ж) — любая формула сигнатуры ( +, •, 0, 1).
Система аксиом 20 известна под названием арифме-
арифметики Пеан о. Арифметика натуральных чисел N
будет моделью для 20. Однако существуют модели 20,
не изоморфные N. Пусть система 2t получается из 20
заменой схемы элементарной индукции 7) на аксиому
полной индукции
VP ЦР @)&Vx (Р (х) —* Р (х + 1))) -^ ухР (х)),
записанную на языке 2-го порядка. Система 2 х является
категоричной, и все модели 2Х изоморфны арифметике
натуральных чисел N. Другой способ категоричного
описания арифметики N состоит в добавлении к 20
следующей бесконечной аксиомы (языка La ш):
V-r (х = 0 v х---- 1 V ... vi = "V . . •),
где п — сокращение для суммы 1-J-. . . + 1 из и единиц.
Лит.: [1] Ш е н ф и л д Д ж., Математическая логика,
пер. с англ., М., 1975. Е. А. Палютин.
КАТЕГОРИЧНОСТЬ В МОЩНОСТИ х — свойство
класса алгебраич. систем, заключающееся в изомор-
изоморфизме всех систем из этого класса, имеющих мощность
'/.. Теория Т 1-го порядка наз. категоричной в
мощности х, если все модели Т мощности к изо-
изоморфны одной алгебраич. системе. Счетная полная
теория Т категорична в счетной мощности тогда и только
тогда, когда для любого натурального числа п суще-
существует такое конечное множество Fn формул сигнатуры
Т со свободными переменными хг, ..., х,„ что любая
формула сигнатуры Г со свободными переменными^, ...,
хп эквивалентна в теории Т одной из формул множества
Fn. Совокупность аксиом:
1) х < у —* ~| (у < х),
2) (х < у & у < z) —-*- х < z,
3) х < у v x=y v у < х,
4) Jujv3t(x<y —m<x<v<y<t)
определяет теорию То плотных линейных порядков,
к-рая категорична в счетной мощности и не категорична
во всех несчетных мощностях. Теория Тг алгебраически
замкнутых полей характеристики 0 категорична во всех
несчетных мощностях, но не категорична в счетной
мощности. Верна общая теорема: если счетная теория Т
1-го порядка категорична в какой-нибудь несчетной
мощности, то она категорична во всех несчетных мощ-
мощностях. Этот результат обобщен на несчетные теории Т
с заменой в условии несчетных мощностей на мощности,
большие мощности теории Т. Квазитождест-
Квазитождеством наз. универсальное замыкание формулы
(<?„&<?!& ... &?„) — Р,
где Qi и Р — атомарные формулы. В счетных теориях
7", аксиоматизируемых с помощью квазитождеств, воз-
возможностей распределения категоричности еще меньше:
если такая теория Т' категорична в счетной мощности,
то она категорична во всех мощностях. Если к аксио-
аксиомам теории То добавить аксиомы для констант с,-
5,0 с,- < ci + 1,
где i пробегает все натуральные числа, то полученная
теория Т3 имеет ровно три счетных модели (с точностью
до изоморфизма), так как возможны лишь 3 случая:
множество {с0, с,, ..., с„, ...} не имеет верхней грани,
имеет верхнюю грань, но не имеет наименьшей верхней
грани, и, наконец, имеет наименьшую верхнюю грань.
Если в счетных моделях Мг и М2 теории Т3 имеет
место один и тот же из описанных случаев, то Мг изо-
изоморфна М2. Оказывается, что среди теорий, категорич-
категоричных в несчетных мощностях, аналогичного примера
найти нельзя. А именно: если теория Т 1-го порядка
категорична в несчетной мощности, то число счетных
моделей Т (с точностью до изоморфизма) либо равно 1,
либо бесконечно.
Лит.: [1] Сакс Д ж., Теория насыщенных моделей, пер.
с англ., М., 1976; 12] Палютин Е. А., «Алгебра и логика»,
1975 т. 14, Хе 2, с. 145—85; [3] S h е 1 a h S., «Proc. of Symp.
Pure Math.», 1974, v. 13, Ni 2, p. 187 — 203. E. А. Палютин.
КАТЕГОРИЯ — понятие, выделяющее ряд алгебра-
ич. свойств совокупностей морфизмов однотипных ма-
тематич. объектов (множеств, топологич. пространств,
групп и т. п.) друг в друга при условии, что эти сово-
совокупности содержат тождественные отображения и замк-
замкнуты относительно последовательного выполнения (су-
(суперпозиции или умножения) отображений. К. SI состоит
из класса ОЬ.Я1, элементы к-рого наз. объектами
категории, и класса МогЙ, элементы к-рого наз.
морфизмами категории. Эти классы долж-
должны удовлетворять следующим условиям:
1) Каждой упорядоченной паре объектов А, В со-
сопоставлено множество Hst (А, В) (обозначаемое также
Нот (Л, В) пли Н(А, В)) из Мог; если а?Н(А, В),
то говорят, что А — начало, или область определения,
морфнзма <х, а В — конец, или область значений а;
а,
часто вместо а?Н(А, В) пишут а : А—уВ или А-+В.
2) Каждый морфпзм К. принадлежит одному и только
одному множеству Н& (А, В).
3) В классе Мог Л задан частичный закон умноже-
умножения: произведение морфизмов а : А-^-В и р1 : C-+-D
определено тогда и только тогда, когда В=С, п принад-
принадлежит множеству Н(А, D), произведение а и р1 обо-
обозначается сф или j3a.
4) Для любых морфизмов а : А—уВ, р4 : В-^-С и
у : С—yD справедлив закон ассоциативности:
5) В каждом множестве Hg {А, А) содержится такой
морфпзм 1д, что a-lj = a и I^.f5=p для любых мор-
фнзмов a : X—>-А и $ : А^>-У; морфизмы 1А наз. е д и-
н и ч н ы м и, тождественными, или е д и-
н и ц а м и.
Входящее в определение К. понятие класс предпола-
предполагает использование такой аксиоматики теории мно-
множеств, к-рая различает множества и классы. Наиболее
употребительной является аксиоматика Гёделя — Берн-
сайда — Неймана.
Иногда в определении К. не требуют, чтобы клас-
классы Н(А, В) являлись множествами. Иногда вместо
использования классов предполагается существование
универсального множества и требуется принадлежность
классов ОЫХ и MorJi фиксированному универсально-
универсальному множеству.
Поскольку между единицами К. Я1 п классом ОЬ$
имеется биективное соответствие, К. можно определить
как класс морфизмов с частичным умножением, удов-
удовлетворяющим дополнительным требованиям (см.,
напр., [6], [9]).
Понятно К. было введено в 1945 [8]. Своим происхож-
происхождением и первоначальными стимулами развития теория
К. обязана алгебраич. топологии. Последующие иссле-
исследования выявили объединяющую и унифицирующую
роль понятия К. и связанного с ним понятия функтора
для многих разделов математики.
Примеры К.:
1) Категория множеств Ens; класс Ob Ens
состоит из всевозможных множеств, класс Мог Ens —
из всевозможных отображений множеств друг в дру-
друга, а умножение совпадает с последовательным выпол-
выполнением отображений (см. Множеств категория).
2) Категория топологических про-
пространств Тор (или %); класс Ob Top состоит из
всевозможных топологич. пространств, класс Мог Тор —
из всех непрерывных отображений топологич. прост-
пространств, а умножение снова совпадает с последователь-
последовательным выполнением отображений.
3) Категория групп Gr (или ®); класс
Ob Gr состоит из всевозможных групп, класс Мог Gr —
из всех гомоморфизмов групп, а умножение опять сов-
совпадает с последовательным выполнением гомоморфизмов
(см. Групп категория). По аналогии с этими примерами
можно ввести К. векторных пространств над нек-рым
телом, К. колец и т. п.
4) Категория бинарных отношений мно-
множеств Rel Ens (или i?C)); класс объектов этой К.
совпадает с классом Ob Ens, а морфнзмами множества
А в множество В служат бинарные отношения этих мно-
множеств, т. е. всевозможные подмножества декартова
произведения Ах В; умножение совпадает с умноже-
умножением бинарных отношений.
5) Полугруппа с единицей является К. с одним объ-
объектом, п наоборот, каждая К., состоящая из одного
объекта, есть полугруппа с единицей.
6) Предупорядоченное множество N можно рас-
рассматривать как К. Щ, для которой Ob9J=JV и МогЭ?=
= {(а, Ъ)\а, &?ЛГ, а<&}, а умножение определяется ра-
равенством (я, Ь)(Ь, с)=(а, с).
Все перечисленные выше К. допускают изоморфное
вложение в К. множеств. К., обладающие указанным
свойством, наз. конкретными К. Не всякая К.
конкретна, напр., такова К., объектами к-рой являются
все топологич. пространства, а морфизмами — классы
гомотопных отображений [10].
Запас примеров К. можно значительно расширить
при помощи различных конструкций и прежде всего
при помощи К. функторов или К. диаграмм.
Отображение F :Й—>-Я' категории Я1 в категорию Я"
наз. ковариантным функтором, если
для каждого объекта /4?0ЬЯ объект F(A)?ObSX',
для каждого морфизма а?Ня (А, В) образ F(oi)?
?Hb'(F(A),F(B)),причем F(lA)=lF{AlvF(a$)= F(a)X
XF(E) всякий раз, когда определено произведение оф.
Если объекты К. Я составляют множество, то можно
построить К. д и а г р а м м Funct(S, ) или F($t, Я'),
объектами к-рой являются всевозможные ковариантные
функторы из Я в Я, а морфизмами — всевозможные
естественные преобразования этих функторов.
Каждой К. Я может быть сопоставлена двойст-
двойственная, или дуальная, К. Я*, или Я7", для
которой ОЬЯ* = ОЬЯ и Hs\'(A, B) = Hsx(B,A) для
любых А, Б?ОЬЯ. Ковариантный функтор из St* в
Я' наз. контравар п антным функтором
из Я в Я- Наряду с функторами одного аргумента мож-
можно рассматривать многоместные функторы или функто-
функторы от многих аргументов.
Для каждого предложения теории К. существует
двойственное (дуальное) предложение, к-рое получается
формальным «обращением стрелок». При этом справед-
справедлив так наз. принцип двойственности: предложение р
истинно в теории К. тогда и только тогда, когда в этой
теории истинно двойственное предложение р*.
Многие понятия и результаты в математике оказа-
оказались двойственными друг другу с категорией точки
зрения: ннъектпвность и проективность, нильпотент-
нильпотентность и К. топологич. пространства в смысле Люстер-
ника — Шнирельмана, многообразия и радикалы в ал-
алгебре и т. д.
Теоретпко-категорный анализ основ теории гомо-
гомологии привел к выделению в середине 50-х гг. 20 в. так
наз. абелевых категорий, в рамках к-рых оказалось
возможным осуществить основные построения гомоло-
гич. алгебры [2]. В 60-е гг. 20 в. определился возрастаю-
возрастающий интерес к неабелевым К., вызванный задачами ло-
логики, общей алгебры, топологии и алгебранч. геомет-
геометрии. Интенсивное развитие универсальной алгебры и
аксиоматич. построения теории гомотопий положили на-
начало различным направлениям исследований: категор-
ному изучению многообразий универсальных алгебр,
теории изоморфизмов прямых разложений, теории сопря-
сопряженных функторов и теории двойственности функторов.
Последующее развитие обнаружило существенные вза-
имосвязи между этими исследованиями. Благодаря воз-
возникшей в последние годы теории относительных К.,
широко использующей технику сопряженных функторов
и замкнутых К., была установлена двойственность
между теорией гомотопий и теорией универсальных ал-
алгебр, основанная на интерпретации категорных опре-
определений моноида и комоноида в подходящих К. функто-
функторов (см., напр., [7]). Наряду с развитием общей теории
относительных К., шло выделение специальных клас-
классов таких К.: 2-категории, или формальные К., К. с
инволюцией, или 1-категории, включающие, в част-
частности, К. бинарных отношений, и т. д. В частности, 2-
категорней является К. малых К., к-рая может быть
положена в основу аксиоматического построения мате-
математики.
Перечисленные классы К. характеризуются тем, что
их множестваморфизмовН(А,В) обладают дополнитель-
дополнительной структурой. Другой способ введения дополнитель-
дополнительных структур в К. связан с заданием в К. топологии
и построении К. пучков над топологизированной К.
(так наз. топосы).
Лит.: [1] Б у к у р И., Деляну А., Введение в теорию
категорий и функторов, пер. с англ., М., 1972; [2] Гроте н-
ди к А., О некоторых вопросах гомологической алгебры, пер.
с франц., М., 19E1; [3] К у р о ш А. Г., Л и в ш и ц А. X.,
Шульгейфер Е. Г., «Успехи матем. наук», 1960, т. 15,
в. 6, с. 3—52; [4] Итоги науки. Алгебра. Топология. 1962, М.,
1963, с. 90—106; [5] Итоги науки. Алгебра. Топология. Геомет-
Геометрия. 1967, М., 1969, с. 9—57; [6] Ц а л е н к о М. Ш., Шуль-
Шульгейфер Е. Г., Основы теории категорий, М., 1974; [7]
Binge M., «J. Algebra», 1969, v. 11, р. 64—101; [8] Е i I e п-
h erg S., Mac Lane S., «Trans. Amer. Math. Soc»,
1945, v. 58, p. 231—94; [9] Preyd P., Abelian categories,
N. Y., 1964; [10] его же, «Symposia mathem.», IV, S. 431 —
56; [11] Mac Lane S., Kategorien. Begriffssprache und
mathematische Theorie, В., 1972; [12] Schubert H., Kate-
Korien, Bd 1—2, В., 1970; [13] Mitchell В., Theory of ca-
tegorie, N. Y., 1965. M. Ш. Цаленпо.
КАТЕГОРИЯ (в смысле Люстерника — Шнирельма-
на) — характеристика топологич. пространства Е —
минимальное число catE' таких замкнутых множеств
AiCZE, к-рыми можно покрыть Е и каждое из к-рых
может быть стянуто в точку посредством непрерывной
деформации в Е. К. является гомотопич. инвариантом
(т. е. совпадает для всех топологич. пространств одно-
одного гомотопического типа). К. имеет важное значение
для вариационного исчисления в целом, так как она
оценивает снизу число стационарных (критических) то-
точек гладкой функции на замкнутом многообразии. Уже
простейшие примеры вроде функции f(x) = x, рассматри-
рассматриваемой на всей действительной оси и вообще не имею-
имеющей крнтпч. точек, показывают, что за пределами клас-
класса замкнутых многообразий нельзя ожидать, чтобы та-
такая оценка выполнялась для всех гладких функций.
Тем не менее в ряде случаев удается получить аналогич-
аналогичную оценку для числа критич. точек различных изу-
изучаемых в вариационном исчислении функционалов, рас-
рассматриваемых как функции на бесконечномерных функ-
функциональных пространствах. Общих методов вычисления
К. не имеется (хотя известно ее значение для некото-
некоторых конкретных пространств), известна только оценка
cat ?>long ?-1-1,
где (когомологическая) длина long E
определяется как наибольшее число классов кого-
мологий положительной размерности, произведение
которых может быть отлично от нуля. Поэтому иногда
рассуждения проводят непосредственно в терминах ко-
когомологического умножения (или, двойственно, пере-
пересечения циклов), не обращаясь к К.
К. введена в [1], впервые вычислена в нетривиальном
случае (для действительного проективного пространст-
пространства) и сразу же использована для решения ряда задач,
в том числе задачи Пуанкаре о трех замкнутых геодези-
геодезических на поверхностях, гомеоморфных двумерной
сфере [2].
Лит.: [1] Lusternik L., в кн.: «Atti del Gongresso
Internazionale dei Matematica», Bologna, 1931, t. 4, p. 291—96;
[2] Люстерник Л. А., Шнирельман Л. Г., «Ус-
«Успехи матем. наук», 1947, т. 2, № 1, с. 166—217. Д. В. Аносов.
КАТЕГОРИЯ МНОЖЕСТВА — топологическая ха-
характеристика «массивности» множества. Множество Е
топологич. пространства X наз. множеством
первой категории на X, если оно представи-
мо в виде конечной или счетной суммы множеств, нигде
не плотных на X. В противном случае Е наз. множе-
множеством второй категории. Иногда множест-
множеством второй категории наз. также дополнение в X к мно-
множеству первой категории. В современной литературе
(см. [2]) иногда (в случае Бэра пространства) такие
множества наз. р е з и д у а л ь н ы м и, или оста-
остаточными. Непустое замкнутое числовое множество,
в частности отрезок, не является множеством первой
категории на самом себе [1]. Имеется обобщение этого
результата на случай любого полного метрич. простран-
пространства. Это обобщение имеет большое применение в ана-
анализе. Роль множества первой категории в топологии
аналогична роли множества меры нуль в теории меры.
Однако множество первой категории может быть мно-
множества полной меры, а среди множеств меры нуль име-
имеются множества второй категории.
Лит.: [1] Бэр Р., Теория разрывных функций, пер. с
франц., М.— Л., 1932; [2] О к с т о б и Д., Мера и категория,
пер. с англ., М., 1974. В. А. Снзорцав.
КАТЕГОРИЯ С ИНВОЛЮЦИЕЙ — категория, об-
обладающая рядом характерных свойств категории би-
бинарных отношений. К. с и. наз. категория, в к-рой
каждое множество Н(А, В) частично упорядочено
отношением а, а также задано отображение *, наз. ин-
инволюцией, сопоставляющее морфизму а морфизм а*
и удовлетворяющее следующим условиям:
а) если а?Н(А, В), то а*?#(В, А);
б) а## = а;
в) если а ? Я (Д,/?), $?Н(В, С), то (аР)#=Р#а*;
г) если а<гр\ а, fi?H(A, В) и у?Н(В, С), то
ayczfiy.
В каждой К. си. утверждение, двойственное истинно-
истинному утверждению, также истинно (усиленный
принцип двойственности). Категория,
двойственная К. с и., является К. с и. Всякая группа
может рассматриваться как К. с и., состоящая из од-
одного объекта, если в качестве отношения порядка взять
отношение тождества (тривиальный частичный порядок),
а в качестве инволюции — отображение, сопоставляю-
сопоставляющее элементу группы обратный к нему элемент.
Важный пример К. с и.— категория бинар-
бинарных отношений 3t(@) над категорией множеств
©строится следующим образом. 0b9f(B) = 0b2, мор-
физмы §R(@) — бинарные отношения с обычным умноже-
умножением бинарных отношений и частичной упорядочен-
упорядоченностью, индуцируемой отношением включения подмно-
подмножеств декартова произведения. Инволюция в этой кате-
категории определяется с помощью перестановки множите-
множителей в декартовом произведении. Аналогично можно
построить категории бинарных отношений над катего-
категориями групп, колец, топологич. групп и т. п. Однако
для категории всех топологич. пространств описанное
выше построение зависит от выбора структуры бикате-
гории и может привести к неассоциативному умножению.
Описание строения разных классов К. с и., их связей
с классами точных, абелевых, регулярных категорий и
их использование в гомологич. алгебре можно найти в
[1] - [4].
Лит.: [1] В г I n k m а п п Н. В., Р и р р е D., Abelsche
und exakte Kategorien, В. — Hdlb.-N. Y., 1969; [2] К a \t a-
h a r a J., «Memoirs Рас. Sci., Kyushu Univ. Ser. A. Math.»,
1973, v. 27, № 1, p. 149—73; [3] его me, там же, 1973, v. 27,
№ 2, p. 249—73; [4] Ц а л е н к о М. Ш., «Докл. АН СССР»,
1973, т. 211, № 2, с. 297—9. М. Ш. Цаленкд.
КАТЕНОИД — поверхность, об- /X /\
разуемая вращением цепной ли- / \^__^i \
нии y=ach — вокруг оси Ох,
принадлежит к числу минималь-
минимальных поверхностей. Форму К. при-
принимает мильная пленка (см. рис.),
«натянутая» на 2 проволочных
круга, плоскости к-рых перпенди-
перпендикулярны линии, соединяющей их центры. БСЭ-з-
КАТЕТ — сторона прямоугольного треугольника,
прилегающая к прямому углу.
КАУСТИКА — огибающая лучей, отраженных или
преломленных данной линией. К. отраженных лучей
наз. к а т а к а у с т п к о й, К. преломленных лучей —
диакаустикой. Напр., катакаустика параллель-
Рис. 1.
А'
Рис. 2.
ного пучка лучей, отраженного от полуокружности,—
часть эпициклоиды (см. рис. 1); диакаустика пучка
лучей, исходящего из точки А, лежащей в более плот-
плотной среде, и преломленного прямой,— часть астроиды
с острием в точке А', лежащей на расстоянии в п раз
(п — показатель преломления) более близком от пря-
прямой, чем сама точка А (см. рис. 2).
Лит.: Ш Саве лов А. А., Плоские кривые, М., 1960.
А. Б. Иванов.
КАЧЕСТВЕННАЯ ТЕОРИЯ ДИФФЕРЕНЦИАЛЬ-
ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ — математическая дисциплина,
изучающая свойства решений обыкновенных дифферен-
дифференциальных уравнений без нахождения самих решений.
Основы К. т. д. у. были заложены в конце 19 в.
А. Пуанкаре (см. [1], [2]) и А. М. Ляпуновым (см. [3],
[4]). А. Пуанкаре широко пользовался геометрич. мето-
методами, рассматривая решения систем дифференциальных
уравнений как кривые в соответствующем пространст-
пространстве. На основе этого рассмотрения он создал общую тео-
теорию поведения решений дифференциальных уравнений
(д. у.) 2-го порядка, разрешил ряд фундаментальных
проблем о зависимости решений от параметров (см.
ниже). А. М. Ляпунов изучал поведение решений в ок-
окрестности состояния равновесия. Он создал современ-
современную теорию устойчивости движения (см. Устойчивости
теория}.
Геометрическое направление А. Пуанкаре было раз-
развито в 20-х гг. 20 в. Дж. Биркгофом, открывшим мно-
многие важные факты качественной теории многомерных
систем д. у. (см. [5]. [6]).
Линейные системы. Рассматривается система д. у.
|=--РМ», г/€к". A)
где Р (х) — квадратная матрица порядка п. Предпола-
Предполагается, что Р (х) ограничена (в случае неограниченности
имеется лишь небольшое число весьма специальных
исследований). В К. т. д. у. изучается асимптотич. по-
поведение решений системы A) при х—voo.
Характеристическим показате-
показателем решения у(х) наз. величина
характеризующая рост решения в сравнении с экспо-
экспоненциальной функцией. Каждое ненулевое решение
системы A) имеет конечный характеристич. показатель.
Характористич. показатели ненулевых решений наз.
также характеристическими показате-
л я м и системы. Линейная система не может иметь
более чем п различных характеристич. показателей.
Характерпстич. показатели системы не меняются при
линейной замене переменных:
*=U(z)y, B)
в к-рой матрица U (х) ограничена вместе с —р и и~х.
Такие преобразования наз. преобразования-
преобразованиями Ляпунова.
В случае, когда матрица Р(х) постоянна, характери-
характеристич. показатели системы A) суть действительные части
собственных значений матрицы Р.
Линейная система наз. приводимой, если су-
существует преобразование Ляпунова B), приводящее
эту систему к виду A), но с постоянной матрицей Р
(см. [7], [8]).
В случае, когда матрица Р (х) имеет период со, фун-
фундаментальная матрица Ф (х) (т. е. матрица,
составленная из линейно независимых решений) пред-
представляется по теореме Флоке (см. [9]) в следующем виде:
Ф(г)=? (х) еАх, C)
где Q(x) есть ш-пернодическая, а. А — постоянная мат-
матрицы. При этом, если Р (х) — вещественная матрица,
не всегда можно А и Q (х) выбрать вещественными,
однако в представлении C) их можно выбрать таковыми
при условии, что Q (х) имеет период 2ш. Из формулы
C) следует, что система A) с периодич. матрицей Р(л)
приводима (теорема Ляпунова). Формула C)
показывает, что для вычисления характеристич. пока-
показателей требуется знать лишь Ф(ш), т. е. надо вычис-
вычислить п различных решений на промежутке 0<?.r«:co.
Линейные системы с периодич. коэффициентами изу-
изучены весьма подробно (см. [8], а также Линейная систе-
система дифференциальных уравнений с периодическими ко-
коэффициентами).
Линейная система обладает свойством устойчивости
асимптотич. поведения решений по отношению к малым
возмущениям самой системы. Важной характеристикой
линейной системы с этой точки зрения является пра-
правильность в смысле Ляпунова (см. [3]).
А. М. Ляпунов доказал (это составляет сущность его
первого метода в теории устойчивости), что правильная
система устойчива по отношению к аналитическим не-
нелинейным возмущениям.
Одной из интересных задач качественной теории
линейных д. у. является проблема колеблемости реше-
решений таких уравнений (см. Колеблющееся решение), т. е.
проблема распределения нулей решений. Напр., если
р(х)^>а^>0 при всех х, то всякое решение уравнения
d?tJ- р М у = о
имеет бесконечно много нулей на промежутке 0<
<z<+oo, причем нули двух линейно независимых
решений чередуются (см. [10]).
Нелинейные системы. Рассматриваются общие сис-
системы нелинейных д. у. в нормальной форме:
^ = Y(y,x), y?Rn. D)
Наиболее детально изучены автономные системы:
Пространство векторов ;/ для системы E) наз. ф а з о-
в ы м. Система D) приводится к автономному виду E)
с помощью увеличения порядка на единицу. Автоном-
Автономная система вида E), в случае если все ее решения про-
должимы на всю ось —оо<?<+оо, определяет дина-
динамическую систему.
Пусть у=у{х, г/0) — решение системы E) с началь-
начальными данными х=0, г/=г/о- Кривая фазового простран-
пространства у=у(х, у0), —оо<х<+оо, наз. траекторией,
а ее части, соответствующие х^О, х«:0,— полу-
полутраекториями. Особую роль играют траектории,
вырождающиеся в точку: у{х, уо)=уо; это происходит,
если Y (уо) = О. Такие точки наз. состояниями
равновесия. Другой важный тип траекторий —
траектории периоднч. решений, представляющие собой
замкнутые кривые в фазовом пространстве. Замкнутую
траекторию наз. предельным циклом, если к ней стре-
стремится хотя бы одна траектория, отличная от нее.
Важная задача качественной теории нелинейных
систем — изучение асимптотнч. поведения всех реше-
решений при х—>-±оо. Для автономных систем вида E) эта
задача сводится к изучению структуры предельных
множеств всех полутраекторнй и способов приближения
траекторий к этим множествам. Предельное множество
всякой полутраекторин замкнуто и инвариантно (мно-
(множество фазового пространства наз. инвариант-
н ы м, если оно состоит из целых траекторий). Если
полутраекторня ограничена, то ее предельное множест-
множество связно.
В случае, когда ?г=2, т. е. когда фазовое простран-
пространство представляет собой плоскость, А. Пуанкаре (см.
[1]) и И. Бендиксон (I. Bendixon, см. [11]) дали исчер-
исчерпывающее описание возможного расположения траек-
траекторий. В предположении, что уравнение У(г/) = О имеет
лишь конечное число решений в ограниченной части
плоскости, они доказали, что предельное множество
любой ограниченной полутраектории может быть одного
из трех следующих типов^ 1) одно состояние равнове-
равновесия, 2) одна замкнутая траектория, 3) конечное число
состоянии равновесия и траектории, стремящиеся к
этим состояниям равновесия при х—>-±оо. А. Пуанкаре
[1] и А. Данжуа [12] рассмотрели случай уравнения
1-го порядка вида D) с правой частью, периодичной по
обоим аргументам у и х. Такие уравнения удобно рас-
рассматривать на торе (см. Дифференциальные уравнения
на торе). Расположение решений в этом случае сущест-
существенно зависит от числа вращения, определяе-
определяемого формулой
ц= Jim v <*¦ »»> .
Если и. рационально, то существуют периодические
решения; если ц иррационально, то пориодич. ре-
решений нет. При этом, если функция Y достаточно глад-
гладкая, то вое решения суть квазипериодич. функции
с двумя частотами.
В случае ;?>2 такого четкого описания возможного
поведения траекторий дать не удается. Однако имеется
много сведений, касающихся предельного поведения
решений многомерных автономных систем. Имеет ме-
место следующий результат Дж. Биркгофа. Пусть зам-
замкнутое, ограниченное, инвариантное множество фазо-
фазового пространства наз. минимальны м, если оно
не содержит истинного подмножества с теми же свойст-
свойствами. Всякое минимальное множество представляет
собой замыкание рекуррентной траектории. Таким об-
образом, в предельном множестве всякой ограниченной
полутраекторпи содержится рекуррентная траектория.
В том важном частном случае, когда система имеет
инвариантную меру, исследование общих закономер-
закономерностей поведения решений проведено весьма детально
(см. [5], [22]).
Особый интерес для приложений представляют гру-
грубые системы, т. е. системы, устойчивые по отношению
к малым в смысле С1 возмущениям правых частей.
Для случая и=2 А. А. Андронов и Л. С. Понтрягия
[13] сформулировали условия, необходимые и достаточ-
достаточные для грубости. В частности, они показали, что в
ограниченной части плоскости существует лишь конеч-
конечное число периодич. решений. В случае п>2 поведение
грубых систем значительно сложнее. С. Смойл (S. Sma-
1е, [14]) указал пример грубой системы, имеющей бес-
бесконечно много периодич. решений в ограниченной части
фазового пространства.
Многочисленные исследования посвящены изучению
глобальных свойств конкретных систем д. у. В связи с
запросами теории автоматич. управления в 50-х гг.
20 в. была развита новая отрасль К. т. д. у.— теория
устойчивости движения в целом. Важную роль в теории
колебаний играют диссипативные систе-
системы — системы вида D), у к-рых все решения с ростом
времени попадают в нек-рую ограниченную область.
Свойства диссипативных систем изучены весьма де-
детально. Построены сравнительно надежные методы,
позволяющие устанавливать диссипативность конкрет-
конкретных систем (см. [15]).
Одной из проблем К. т. д. у. является проблема су-
существования периодич. решении. Для доказательства
существования таких решений часто используют топо-
логич. приемы, в частности различные критерии суще-
существования неподвижной точки. Многие теоремы такого
рода были доказаны применением принципа тора. При
п=2 этот принцип вырождается в классический прин-
принцип кольца Пуанкаре.
Полное качественное исследование нелинейных си-
систем д. у. удается дать лишь в весьма частных случаях.
Напр., было доказано (см. [16]), что Лъенара уравнение
при весьма естественных предположениях имеет един-
единственное периодич. решение, а все остальные его ре-
решения стремятся к этому периодическому.
Относительно уравнения Ван дер Поля с возмуще-
возмущением
при больших значениях параметра к были установлены
в числе других следующие интересные факты (см. [17]).
При специальном выборе параметра Ь уравнение имеет
два асимптотически устойчивых решения с периодами
Bп+1Jл/Я и Bп— 1Jл/Я, где п — натуральное доста-
точпо большое число, «большинство» остальных реше-
решений стремится к этим двум. Имеется, кроме того, счет-
счетное множество неустойчивых периодич. решений и
континуум рекуррентных непериодических.
Локальная теория. Качественное исследование не-
нелинейной системы д. у. D) значительно упрощается,
если его требуется провести не во всем пространстве
у, х, а лишь в окрестности заданного решения. В этом
случае простой заменой переменных проблема сводится
к изучению следующей системы д. у.:
$L = PWy + Y(y, х), j/?R«, F)
где вектор-функция У в определенном смысле мала
в сравнении с у. Исследование поведения решений
системы F) в окрестности состояния равновесия г/=0
и составляет предмет локальной К. т. д. у.
Важное место в этой теории занимает проблема
устойчивости нулевого решения системы F). Нулевое
решение наз. устойчивым, если решение г/=
= 2/(х! г/о) непрерывно по у0 при уо=О равномерно
относительно х^О.
В локальной К. т. д. у. наиболее полно исследован
случай постоянной матрицы Р(х). К этому случаю
сводится проблема исследования окрестности состояния
равновесия и периодич. решения автономной системы.
Описание поведения решений системы F) в окрест-
окрестности г/—О сравнительно просто, если матрица Р по-
постоянная и все ее собственные значения имеют нену-
ненулевые действительные части. В этом случае дело сво-
сводится к следующему фундаментальному
результату Ляпунова — Перрона (см.
[1], [18]). Пусть к собственных значений постоянной
матрицы Р имеют отрицательные действительные части,
а остальные п—к собственных значений имеют положи-
положительные действительные части. Тогда в пространстве у
существуют два многообразия М и N размерности к и
п—к, соответственно, такие, что если у0 ?М, то у (х, у0) ->
-»-0 при х—>-+оо, а если yo?N, то у(х, уо)—>-О при х->-
-*¦—оо; все остальные решения покидают окрестность
начала координат как при возрастании, так и при
убывании х. Случаи, когда матрица Р имеет собственные
числа с нулевыми действительными частями, наз. к р и-
т и ч е с к и м и.
А. М. Ляпунов дал исчерпывающее описание пове-
поведения решений системы F) в окрестности начала коор-
координат в случаях, когда постоянная матрица Р имеет
одно нулевое или два чисто мнимых собственных числа,
все остальные собственные числа имеют отрицательные
действительные части, а вектор-функция Y не зависит
от х и аналитнчна (см. [3]). Основополагающие резуль-
результаты в локальной качественной теории автономных
систем 2-го порядка принадлежат Л. Пуанкаре [1],
А. М. Ляпунову [3, 4], И. Бендиксону [11] и М. Фром-
ыеру (М. Frommer, [19]).
Пусть рассматривается система уравнений
%г=Рт(у, *) + У(У, *), ~=Qm(y, *) + Z(y, г), G)
где Рт и Qm — формы степени т, а функции Y и Z ма-
малы в сравнении с величиной (;y2+z2)'m'2. Пусть состояние
равновесия, расположенное в начале координат, изо-
изолировано. В этом случае для системы G) либо сущест-
существует решение, стремящееся к началу, либо в любой
окрестности начала существует замкнутая траектория.
Во втором случае либо все траектории, лежащие в ок-
окрестности начала, замкнуты (расположение типа центр),
либо в любой окрестности начала существуют как замк-
замкнутые, так и незамкнутые траектории (расположение
типа центрофокус). Показано, что в случае аналити-
аналитических Y и Z центрофокус невозможен (см. [20]).
Далее, если траектория стремится к началу координат,
то либо она имеет в начале определенную касательную,
либо вдоль нее полярный угол не ограничен. В послед-
последнем случае — расположение типа фокус. Касательными
к траекториям, стремящимся к началу, могут быть лишь
прямые, на к-рых аннулируется величина Qту—Ртъ.
Такие прямые наз. исключительными на-
направлениями. Для достаточно гладких Y a Z
разработаны алгоритмы, позволяющие выяснить нали-
наличие и количество траекторий, входящих в начало
вдоль данного исключительного направления. Это
позволяет в случаях, когда существуют траектории,
входящие в начало с определенной касательной, пол-
полностью описать поведение траекторий в окрестности
начала.
Если исключительные направления отсутствуют или
все они «проходятся» решениями (т. е. не существует
решений, входящих в начало с определенной касатель-
касательной), то возникает центра и фокуса проблема.
Зависимость поведения решений от параметров сис-
системы. Одной из центральных проблем К. т. д. у. яв-
является проблема поведения решений системы, близкой к
данной, при условии, что свойства этой последней из-
известны. Рассматривается система
% y, x, р), (8)
где |л — параметр. Пусть порождающая сис-
система, т. е. система (8) при ц=0, обладает нек-рым
свойством. Ставится вопрос, обладает ли тем же свой-
свойством система (8) при малых, но отличных от нуля, ц.
Классическим примером такой задачи является з а-
дача Пуанкаре (см. [2]) о существовании перио-
периодических решений. Пусть векторы Y и R имеют пе-
период со по х, а порождающая система обладает со-перио-
дическим решением. В этом случае проблема сводится
к рассмотрению квазилинейной системы
^=Ау + уМ(у, х, Ц), (9)
где А — постоянная матрица. Оказывается, что если
собственные числа А отличны от 2я/шсо; где к — целое
число, то система (9) имеет при достаточно малых ^
единственное со-периодич. решение (р(х, li), непрерыв-
непрерывное по |х, и ф(х, 0) = 0. В случае, когда матрица А
имеет собственные числа вида 2л7п/м, вопрос о суще-
существовании и количестве периодич. решений существенно
зависит от вида возмущения R(y, x, \х). При решении
проблемы существования периоднч. решений в этом
случае весьма полезным оказывается метод усреднения
(см. Крылова — Боголюбова метод усреднения).
Аналогичные вопросы ставятся и для других типов
решений: ограниченных, рекуррентных, почти перио-
периодических и т. д. Напр., если вектор R равномерно почти
периодичен по х, а все собственные числа матрицы А
имеют ненулевые действительные части, то система (9)
при достаточно малом д. имеет единственное почти пе-
рподич. решение (см. [21]).
Малого параметра методом исследуются также во-
вопросы существования у системы (8) интегральных
множеств с определенными свойствами. Н. Н. Боголю-
Боголюбов (см. [21]) рассмотрел с этой точки зрения следующую
важную для приложений систему:
$ = а--г|гФ(*, Ф, t, u), ^
% = Ах-f y.R(x, ф, t, ц),
где ф есть А—мерный, х есть re-мерный векторы, а — по-
постоянный i-морный вектор, А — постоянная матрица,
все собственные числа к-рой имеют ненулевые вещест-
вещественные части. Векторы Лиф имеют период 2я по ком-
компонентам вектора ф. При ji=0 система A0) имеет интег-
интегральную поверхность х=0. Н. Н. Боголюбов доказал,
что при достаточно малом ц система A0) имеет интег-
интегральную поверхность:
x=f(t, ф, ц),
где функция / имеет период 2я по компонентам ф и
f(t, ф, 0) = 0. При этом, если векторы Ф и R являются
со-периоднчными по ?, то вектор / также со-периодичен
по t. Если все собственные числа матрицы А имеют
отрицательные действительные части, то интегральная
поверхность x—f асимптотически устойчива. Отсюда,
в частности, вытекает, что если в системе (8) вектор Y
но зависит от х и при |и=0 эта система имеет асимпто-
асимптотически устойчивое по первому приближению периодич.
решение, то при достаточно малых ц. система (8) имеет
в пространстве у, х двумерное, цилиндрическое асимп-
асимптотически устойчивое интегральное многообразие.
Лит.: [1] Пуанкаре А.. О кривых, определяемых диф-
дифференциальными уравнениями, пер. с франц., М., 1947; 12]
Р о i n с а г ё H., Les methodes nouvelles de la mecanique ce-
celeste, t. 1—3, P., 1892—99; [3] Ляпунов А. М., Общая за-
задача об устойчивости движения, М.— Л., 1950; [4] его же,
«Матем. сб.», 1893, т. 17, в. 2, с. 253 —333; [5] Биркгоф
Д. Д., Динамические системы, пер. с англ., М., 1941; [в] В i r k-
h о f f G. D., «Acta Math.», 1922, v. 43, p. 1—119: [71 E p y-
гин Н. П., Приводимые системы, Л.— М., 1946; [8] его
ж е, Линейные системы обыкновенных дифференциальных урав-
уравнений с периодическими и квазипериодическими коэффициента-
коэффициентами, Минск, 1963; [9] F 1 о q u e t M. G., «Ann. sci. Ecole norm.
super.», 1883, ser. 2, t. 12, p. 47—89; [10] Sturm J. С h.,
«J. math, pures et appl.», 1836, p. 106—86; [11] Б е н д и к-
сон И., «Успехи матем. наук», 1941, в. 9, с. 191—211;
[12] D e n ] о у A., «J. math., pures et appl.», 1932, ser. 9, t. 11,
J4i 3, p. 333—75; [13] Андронов А. А., Понтря-
г и н Л. С, «Докл. АН СССР», 1937, т. 14, Л1» 5, с. 247 — 50; [14]
С м е й л С, «Успехи матем. наук», 1970, т. 25, в. 1, с. 113—85;
[15] Плис с В. А., Нелокальные проблемы теории колебаний,
М.— Л., 1964; [16] L e v i n s о n N., S m i t h О. К., «Duke
Math. J.», 1942, v. 9, .Mi 2, p. 382—403; [17] L i t t 1 e w o-
odJ. E. «Acta math.», 1937, v. 97, Л<° 3—4, p. 267—308; [18]
Perron O., «Math. Z.», 1928, Bd 29, S. 129 — 60; [19]
Ф р о м м е р М., «Успехи матем. наук», 1941, в. 9, с. 212—53;
[20] D u 1 а с Н., «Bull. Soc. math. France», 1923, t. 51; [21]
БоголюбовН. Н.,0 некоторых статистических методах в
математической физике, К., 1945; [22] Н е м ы ц к и й В. В.,
Степанов В. В., Качественная теория дифференциальных
уравнений, М., 1949; [23] Андронов А. А. и др., Качест-
Качественная теория динамических систем второго порядка, М., 1966;
[24] Коддингтон Э. А., Левин сон Н., Теория
обыкновенных дифференциальных уравнений, пер. с англ., М.,
1958; [25] Лефшец С, Геометрическая теория дифферен-
дифференциальных уравнений, пер. с англ., М., 1961. В. А. Плисе.
КАЧЕСТВЕННАЯ ТЕОРИЯ ДИФФЕРЕНЦИАЛЬ-
ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИИ вбанаховом простран-
пространстве — раздел функционального анализа, в к-ром
исследуется поведение на действительной оси / или на
положительной (отрицательной) полуоси /+ (/~)
решений эволюционных уравнений в банаховом простран-
пространстве. Рассматриваются уравнения
I. и = А (t) и;
II. й = А (t)u ± /(*);
III. 'и = А (t)u + f(t, и),
где u(t) — искомая, a f(t) — заданная функция со
значениями в комплексном банаховом пространстве Е,
A (t) — линейный оператор, f(t, и) — нелинейный опе-
оператор в Е. Под производной и понимается предел по
норме пространства Е отношения — при At—v0.
Для дифференциального уравнения I имеется рав-
равномерная устойчивость (р. у.), если су-
существует константа М такая, что для любого решения
||«(i)||<:Af||и(«)||, t^s, и экспоненциальная
устойчивость (э. у.), если для всех решений
||«(t);!<Me-a<'-s>||u(s)|| при нек-рых М и а>0.
Для уравнения I с постоянным ограниченным опера-
оператором A (t)=^A решение задачи Коши (u(s) задано)
имеет вид и (t) = ea-siA и (s). Справедлива оценка
\\eAl\\<cMeot, где а — число, большее всех действитель-
действительных частей точек спектра оператора А. Таким образом,
для э. у. необходимо и достаточно, чтобы спектр А
лежал внутри левой полуплоскости. В гильбертовом
пространстве это имеет место тогда и только тогда, когда
существует положительно определенная форма (Wx,y),
для к-рой -4- jf( Wu, u)=Re( Wu, iii)<-a(u, и) на
любом решении уравнения (теорема Ляпуно-
в а). Если спектр А расположен по обе стороны от
мнимой оси и не пересекается с ней, то пространство Е
разлагается в прямую сумму инвариантных относитель-
относительно А подпространств Е+ и ?_, причем все решения в
Е+(Е-.) экспоненциально возрастают (убывают) при
t—>-oo. В этом случае для уравнения имеет место экс-
экспоненциальная дихотомия (э. д.).
Если оператор А неограничен, замкнут и имеет плот-
плотную в Е область определения, то задача Коши с и@) =
= и0, вообще говоря, не является корректной. Существо-
Существование и свойства ее решений не определяются только
расположением спектра оператора А, необходимо еще
определенное поведение его резольвенты (А—XI)-1.
Употребительными условиями, обеспечивающими рав-
равномерную корректность задачи Коши на / + , являются
неравенства
' a-o)r-
для выполнения к-рых достаточно условие X и л-
ле — Иосиды
или неравенство
i| (А— XI)-1 f,^ M/\X—a\, Re Я > а.
При выполнении их решение задачи Коши имеет вид
u(t)=T(t—s)u(s), где T{t) — сильно непрерывная при
t^O полугруппа операторов, причем \\Т (t)\\^.Meat.
Для р. у. (э. у.) достаточно, чтобы было сг=О (а<0).
Если оператор А порождает сильно непрерывную полу-
полугруппу в гильбертовом пространстве, то для него спра-
справедлива достаточная часть теоремы Ляпунова, а если —
группу, то — и необходимая. В гильбертовом простран-
пространстве э. у. эквивалентна ?2-устойчивости, т. е. тому, что
для всех решений ||T(t)ito||?L2(O, оо).
Важным для приложений свойством решений и (t)
является почти периодичность (п. п.) или
слабая почти периодичность (то есть
п. п. скалярных функций (u(t), ср) для всех ср?.Е*).
Все значения п. п. решения лежат в компактном
множестве — решение компактно. Из компактности и
слабой п. п. следует п. п. Для уравнения и=А (и)
вопрос о п. п. решений связан со структурой пересече-
пересечения спектра А с мнимой осью. Если А — производящий
оператор ограниченной сильно непрерывной полугруп-
полугруппы и указанное пересечение счетно, то для п. п. опреде-
определенного на всей оси и ограниченного решения необхо-
необходимо п достаточно, чтобы существовал предел
Пте(Л—Х-\-е)~1и@) в каждой предельной точке спект-
ра X на мнимой оси. При этом всякое равномерно непре-
непрерывное решение слабо п. п.; оно п. п., если оно слабо
компактно, или если Е не содержит подпространств,
изоморфных пространству Со последовательностей, стре-
стремящихся к нулю с нормой max. Если А — производя-
производящий оператор сильно непрерывной полугруппы T(t),
к-рая обладает тем свойством, что функции \\Т* (?)ф||
ограничены на /+ для плотного в Е* множества функ-
функционалов ф, то из компактности решения следует п. п.
Для уравнения I с ограниченным и непрерывным по
t оператором A (t) решения задачи Коши определены
на всей оси, и с помощью эволюционного оператора
U(t, s) записываются в виде u(t)= U(t, s) «(s). Свойст-
Свойство p. у. эквивалентно тому, что \\U(t, s)||<gAf, свойство
э. у.— тому, что \\U(t, s)\\^.Me-a(t~s). Если оператор
S^ + l
\\А (т)||Л<оо,
t
то генеральный показатель
x=lim '"Я ^ <' + '¦'> В
конечен. Если % <0, то имеет место э. у. Для уравнений
с постоянным или периодич. оператором A (t) справед-
справедлива формула%=lim 'nll"(t'0> ". В общем случае она
неверпа. Генеральный показатель не изменяется, если
оператор A (t) возмущается слагаемым B(t), для к-рого
В (?)—>-0 при t—>-oo или для к-рого сходится на оо интег-
интеграл \ \\B(t)\\dt. Величина генерального показателя за-
зависит от поведения А (?) на бесконечности. Если суще-
существует предел А <*, =\imA (t) и спектр А„ лежит внутри
левой полуплоскости, то к <0. Если операторы A (t), 0<
<g?<oo, образуют компактное множество в простран-
пространстве ограниченных операторов, спектры всех предель-
предельных операторов лежат в полуплоскости ReX<—v<0
и оператор-функция A (t) мало осциллирует, напр.,
имеет вид В (et) при достаточно малом е или при до-
достаточно больших t удовлетворяет условию Липшица
\\А (t)—Л(т)||<:еи—т| с достаточно малым е, то %<0.
В гильбертовом пространстве условие у, <0 эквива-
эквивалентно существованию эрмитовой формы {W(t)x, у) та-
такой, что 0 < аг (х, x)<(W(t)x, х)<а2(х, х) и
¦jf (W (t) и, и) < — а (и, и) для любого решения u(t).
Если оператор A (t) периодичен с периодом со, A (t-\-
+ ш) = /1 (?), то оператор U(t, s) обладает свойством
С/(г+со, O)=U(t, 0)[/(со, 0). Оператор [/(со)= [/(со, 0)
наз. оператором монодромии уравнения I.
Его спектральный радиус ги{ю) связан с генеральным
показателем х формулой х = — In ги(@).Уравнение име-
имеет периодич. решения тогда и только тогда, когда 1
является собственным числом [/(со). Если оператор
[/(со) обладает логарифмом, то справедливо пред-
представление Флоке U(t, O) = Q(t)etT, где Q (t) пе-
периодичен с периодом со, а Т=1 In [/(со). В частности,
представление Флоке имеет место, если спектр [/(со) не
окружает нуля, для чего достаточно, чтобы - \ \\А (t)\\dt
было меньше нек-рой константы, зависящей от гео-
геометрии сферы в Е и не меньшей 1п4. Для гильбертова
пространства эта константа равна я. Представление
Флоке сводит вопрос о поведении решений уравнения с
нериодич. оператором к такому же вопросу для урав-
уравнения v=Tv с постоянным оператором Г.
Для уравнения I имеет место экспоненциаль-
экспоненциальная дихотомия (э. д.): если для нек-рого s про-
пространство Е разлагается в прямую сумму подпрост-
подпространств E + (s) и ?_(s) так, что
\\U (t, s) x\]^IV1e-Vl<-i~s) \\x\\, Vj > 0,
при x?E_(s), t^ss, и
¦\U (t, s)*j[s?AV~V2('~s)IMI, v2 > 0,
при х?Е + (s), t-^s. При этом предполагается, что подпро-
подпространства U(t, s)E + (s) и U(t, s)E_ (s) в определенном
смысле не должны сближаться. В случае конечности
генерального показателя последнее условие выполня-
выполняется автоматически. Для того чтобы для уравнения с
периоднч. A (t) имела место э. д., необходимо и доста-
достаточно, чтобы спектр оператора монодромии распола-
располагался вне и внутри единичного круга, но не пересе-
пересекался с единичной окружностью.
Для уравнения I с неограниченным оператором A (t)
с не зависящей от t областью определения, удовлетво-
удовлетворяющим условиям корректности задачи Коши (см. вы-
выше) при каждом t, при дополнительных условиях глад-
гладкости доказано существование эволюционного опера-
оператора U(t, s), определенного и сильно непрерывного по
( и s при t^s. Это позволяет перенести на этот случай
ряд понятий и результатов, описанных выше. Однако
здесь встречаются трудности. Так, представление Флоке
получено лишь для уравнений в гильбертовом про-
пространстве, когда A (t) = A+B (t), где А —отрицатель-
—отрицательно определенный самосопряженный оператор, а В (t) —
ограниченный периодич. оператор, удовлетворяющий
нек-рым дополнительным условиям.
Пусть A (t) периодичен, и задача Коши для уравне-
уравнения I равномерно корректна. Если пересечение спек-
спектра оператора монодромии [/(со) с единичной окруж-
окружностью счетно, то каждое ограниченное равномерно
непрерывное на / решение слабо п. п. Оно — п. п. в
случае слабой компактности или если Е не содержит с0.
В рефлексивном пространстве Е существует разложение
в прямую сумму Ег-}-Ег такое, что Ех и Е2 инвариантны
относительно [/(со), и все решения, начинающиеся в Ег,
являются п. п., а начинающиеся в Ег — в определен-
определенном смысле убывают: при U2@)^E2, t
Для решения неоднородного уравнения II справед-
справедлива формула
u(t) = U (t, s) u(s)+^s U (t, т) / (x) di.
Для уравнения с ограниченным оператором ато равен-
равенство эквивалентно дифференциальному уравнению. В
случае неограниченного оператора, это, вообще говоря,
не так, но тогда это равенство принимается за опре-
определение (обобщенного) решения. Основной задачей для
уравнения II является исследование свойств решений
при заданных свойствах правой части. Эти свойства
обычно описываются как принадлежность функции ка-
какому-либо банахову пространству функций на / или
/+ со значениями в Е. Если каждой непрерывной
ограниченной функции / (i) € С (Е) отвечает хотя бы
одно ограниченное решение, то оператор i=——A (t)
наз. слабо регулярным. Если каждой f?()
отвечает единственное решение и?С(Е), то L наз. р е-
г у л я р н ы м. Для ограниченного постоянного А из
слабой регулярности следует регулярность. Для
неограниченного А или ограниченного периодического
A (t) этот факт уже может быть неверным даже в гиль-
гильбертовом пространстве. Если генеральный показатель
уравнения и=А (t)u конечен, то э. д. для этого урав-
уравнения эквивалентна регулярности оператора L на /.
Для того чтобы э. д. имела место на полуоси / + , необ-
необходимо и достаточно, чтобы оператор L на /+ был слабо
регулярным и чтобы множество тех начальных значе-
значений и@), к-г>ым отвечают ограниченные решения урав-
уравнений I, было дополняемым подпространством Е.
Если для всех решений уравнения II выполнено нера-
неравенство
* sup К'
а для решений формально сопряженного уравнения
— %=А* (t)v+ g(t)— неравенство \\v(t)\\^k sup||#(i)||, то
операторы L и ?* = — м —A* (t) регулярны. Неизве-
Неизвестно A978), сохранится ли регулярность, если справа
в первом неравенстве стоит к sup||/(t)\\. Для регуля;)
t
ности L и L* обе априорные оценки необходимы.
Если A (t) периодичен, то для существования пери-
одич. решения при всякой периодич. f(t) необходимо и
достаточно, чтобы отображение /—U(u>) было сюръек-
тивным, а для того чтобы такое решение было един-
единственным, необходимо и достаточно, чтобы оператор
/—U (а) был обратимым.
Проверка регулярности при известных условиях мо-
может быть сведена к проверке регулярности операторов
с постоянными коэффициентами. В случае сильной ос-
осцилляции A (t) (напр., A (t)=B (at) с большим ш)
при условии существования среднего
Т + а
A--=lim ±- \ A(t)dt
Т->-эо IT J
Т + а
равномерно по а ? / оператор A (t) регулярен тогда
d ~т
и только тогда, когда регулярен оператор jt — •«.
Для почти периодических решений специфика беско-
бесконечномерного пространства сказывается уже на обобще-
обобщении известной теоремы Боля-Бора о п. п. ограниченно-
ограниченного интеграла от п. п. функции, то есть о п. п. ограничен-
ограниченного решения простейшего уравнения u=f(t). Если нео-
неопределенный интеграл от п. п. функции со значениями в
Е ограничен и Е не содержит с0, то он является п. п.
В пространстве с0 теорема Бо.1я-Бора неверна. Если
A (t) периодичен, / (() —почти периодична и пересечение
спектра оператора монодромии U(a) с единичной ок-
окружностью счетно, то справедливы те же выводы о п. п.
решения, к-рые сформулированы выше для однородного
уравнения. Если A (t) почти периодичен (как функция
со значениями в пространстве ограниченных операторов
b?"),to для того чтобы при всякой п. п./ (t) существовало
единственное п. п. решение, необходимо и достаточно,
чтобы оператор ? был регулярным. Если у равнение II име-
имеет (слабо) компактное при г>0 решение, и нетривиальные
(слабо) компактные решения однородного уравнения
u=A{t)u обладают тем свойством, что ]im||«(i)ll>0, то
уравнение II имеет (слабо) п. п. решение.
При качественном исследовании нелинейного урав-
уравнения z=F(t, z) обычно ааранее предполагаются вы-
выполненными условия, обеспечивающие существование
решений на / или на / + , что налагает существенные
ограничения на вид нелинейности F(t, z). Решение zo(t)
на /+ наз. равномерно устойчивым (р.
у.), если для всякого е существует б такое, что для вся-
всякого другого решения z(t) из неравенства ||z(s) —zo(s)|]<
<б, s>0. следует, что z(t) определено при t^ss и \\z(t) —
—z0 (t) ||<:8. Решение наз. асимптотически
устойчивым (а. у.), если оно р. у. п при нек-ром
б из неравенства \\z(s)—zo(s) ||<:б следует, что
lim]|z(i)—zo(()||=O. Если в уравнении сделать замену
u=z—zo(t), то после линеаризации (если она возможна)
оно принимает вид III, где A (t) = F'z(t, zo(t)), а нелиней-
нелинейность обладает тем свойством, что /(?, 0)=0. Таким
образом, задача о р. у. или а. у. решения zo(t) сводится
к задаче о р. у. или а. у. нулевого решения уравнения
III. Уравнение и=А (t)u при этом наз. уравнени-
уравнением в вариациях для исходного уравнения отно-
относительно решения zo(t). .
Если нелинейная часть f(t, и) достаточно мала, то
свойства решений определяются свойствами решений
уравнения в вариациях. Если генеральный показатель
уравнения в вариациях отрицателен, и выполнено не-
неравенство ||/(t, ц)||<:</||и||, ОО, ||м||<:р, то при доста-
достаточно малом q нулевое решение уравнения III будет
а. у. Если A (t)=A и спектр А не пересекается с мнимой
осью и имеет точки в правой полуплоскости, то при
достаточно малом q нулевое решение неустойчиво.
Если выполнено неравенство
| / (t, и) |К с !1 и li1+P' Р > °> * Зг 0, || и || < р,
то требование отсутствия точек спектра на мнимой оси
можно отбросить.
Если для уравнения в вариациях имеет место э. д.
на /, то для каждого р>0 существуют такие М и с,
зависящие только от A (t) и р, что из неравенств
II/(t, u)\\^M
||/(*, u)—f(t, v)\\^c\\u — v\\, t?J, \\u\\, |М|<р,
следует существование в нек-рой окрестности нуля
многообразий М + и М_, пересекающихся в одной точке
jt0, таких, что решение uo(t), начинающееся в щ, огра-
ограничено на всей оси, и ||мо(()||<р; решения, начинающие-
начинающиеся на Л/_ (М + ), экспоненциально приближаются при
г_>оо (t—>•—оо) к uQ{t) и удаляются от него при t, неогра-
неограниченно изменяющемся в противоположном направ-
направлении. При этом М + (М_) гомеоморфны окрестностям
пространств Е + @) и ?"_ @), участвующих в определении
з. д. Если в предыдущих условиях A (t)=A и f(t, и)
п. п. по t при каждом и с ||ц||<:р, то решение uo(t) п. п.
Пусть автономное уравнение z=F(z) имеет со-периодич.
решение zo(t), тогда уравнение в вариациях u=Fz(zg(t))u
имеет одно периодич. решение zo(t) и, следовательно,
его оператор монодромии U(a>) имеет 1 собственным
числом. Если это число простое и остальной спектр
1/(ш) лежит внутри единичного круга и не окружает
нуля, то существуют такие числа fi>0, то и N, что для
всех других решений исходного уравнения \\z(t—z0) —
—z(t)\\<cNe~)xt. Указанное свойство наз. асимп-
асимптотической орбитальной устойчи-
устойчивостью периодич. решения. Имеются исследова-
исследования и других устойчивых инвариантных многообразий
для нелинейных уравнений.
Уравнения вида III с неограниченным оператором
A (t) в приложениях соответствуют квазилинейным
уравнениям параболич. и гиперболич. типа. Развита те-
теория «истинно» нелинейных эволюционных уравнений
определенного типа. Так, если В — непрерывный всюду
определенный диссипативный оператор, то задача Ко-
ши и — Ви, и@)=и0 однозначно разрешима на полу-
полуоси /+ при любом щ?Е. Определение диссипативного
оператора естественно переносится на случай много-
многозначного оператора, и для таких операторов вместо диф-
дифференциального уравнения рассматривается диф-
дифференциальное включение и?Ви. Если в рефлексив-
рефлексивном пространстве оператор В замкнут, диссипативен
и значения оператора /—В покрывают все пространство
Е, то задача Коши однозначно разрешима на /+ при
каждом и0 из области определения оператора В. Име-
Имеется много вариантов последнего утверждения. Решение
задается формулой м(г)= SA)щ, где S(t) — полугруппа
нелинейных операторов S(t-\-x)x=S (t)(S (t)x), t, t^jO.
Для уравнений с диссипативными операторами имеются
также теоремы существования периодпч. и почти пе-
периодич. решений.
Лит.: [1] Д а л е ц к и й Ю. Л., К р е й н М. Г., Устой-
Устойчивость решений дифференциальных уравнений в банаховом
пространстве, М., 1970; L2J Массера Х.-Л., Шефер
Х.-Х., Линейные дифференциальные уравнения и функцио-
функциональные пространства, пер. с англ., М., 1970; [3] И о с и д а К.,
Функциональный анализ, пер. с англ., М., 1967; [4] Крейн
С. Г., Линейные дифференциальные уравнения в банаховых
пространствах, М., 1967; [5] В а г b u Лг., Nonlinear semigroups
and differential equations in banach spaces, Netherlands, 1976;
[6] Баскаков А. Г., «Тр. матем. ф-та Воронеж, ун-та»,
1973, в. 10, с. 9 6—101; [7] Ж и к о в В. В., «Изв. АН СССР.
Сер. матем.», 1976, т. 40, с. 1380 —1408, № 6; [8] Ж И к о в В. В.,
Левитан Б. М., «Успехи матем. наук», 1977, т. 32, в. 2,
с. 123—71; [9] М и л о с л а в с к и й А. И., «Функц. анализ
и его прилож.», 1976,т. 10, Xi 2, с. 80—81; [10] Т ю р и н В. М.,
в кн.: «Функциональный анализ», в. J, Ульяновск, 1973; [11]
Левитан Б. М., Ж и к о в В. В., Почти периодические
функции и дифференциальные уравнения, М., 1977. С. Г. Крейн.
КВАДРАНТ — 1) К. плоскости — любая из
четырех областей (углов), на к-рые плоскость делится
двумя взаимно перпендикулярными прямыми, приня-
принятыми в качестве осей координат. 2) К. к р у г а — сек-
сектор с центральным углом в 90°, V, часть круга. БСЭ-з.
КВАДРАТ — 1) Равносторонний прямоугольник. К.
является правильным многоугольником. 2) К. числа а —
произведение а-а=а2; название связано с тем, что та-
таким произведением выражается площадь К., сторона
к-рого равна а. всэ-з
КВАДРАТИЧЕСКАЯ ИРРАЦИОНАЛЬНОСТЬ -
корень неприводимого над полем рациональных чисел
квадратного трехчлена с рациональными коэффициен-
коэффициентами. К. и. представима в виде а-\-Ь Y~d, где а и Ь —
рациональные числа, ЬфО, ad — целое число, не яв-
являющееся полным квадратом. Действительное число се
тогда и только тогда является К. и., когда оно допускает
разложение в бесконечную периодическую цепную
Дробь. А. II. Галочкин.
КВАДРАТИЧНАЯ ОШИБКА — см. Квадратичное
отклонение.
КВАДРАТИЧНАЯ ФОРМА над коммутатив-
коммутативным кольцом с единицей — однородный
многочлен
q = q (x) = q (xu ..., *„) = '? .qij^i^j,
от n=n(q) переменных с коэффициентами q;/(zR-
Обычно R — это поле С, R или Q, либо кольцо Z, коль-
кольцо целых элементов алгебраич. числового поля, а так-
также их пополнения по неархимедовым нормам.
Симметрическая квадратная матрица А =А (q) = (a;j)
порядка п, где ац=2дц, <4f=aji=q;j, 1<:Z</«:n, наз.
к р о н е к е р о в о й матрицей К. ф. д(х); обо-
обозначение Зигеля: д(х)=-^-А [х]. Если дискриминант
D (q) К. ф. q не равен 0, то q наз. невырожден-
н о и, а если равен 0, то — в ы р о ж д е н н о й.
К. ф. q(x) наз. гауссово й, если она допускает
симметрическую запись:
т.е. найдутся bjj=bji?R, для к-рых д,-у = 26,у, 1<:?<
</<:». Симметрическая квадратная матрица B — B(q) =
= (bjj) наз. матрицей (или гауссовой мат-
матрицей) К. ф. q(x). Величина d = d(q) — det В наз.
определителем К. ф. q (x); при этом
D (?) = (— 1)п''-2" d (q), если п (q) четно,
= (— l)(n-1)/'-2n-1d(q), если n(q) нечетно.
Если R — поле характеристики, отличной от 2, то вся-
всякая К. ф. над R гауссова. Если Л вкладывается в поле
F характеристики, отличной от 2, то К. ф. q(x) над R
можно рассматривать как гауссову, но с матрицей В =
=B(q) над F и d(q)?F.
К. ф. q1 и q2 эквивалентны над R (q1^^q2),
если одна из них преобразуется в другую обратимой в
R линейной однородной подстановкой переменных,
т. е. если найдется такая обратимая квадратная ма-
матрица U над Л, что A (q1)= UTA (q2)U. Совокупность
К. ф. над Л, эквивалентных над R данной, называется
классом К. ф. Дискриминант К. ф., с точностью
до квадрата обратимого в R элемента,— инвариант
класса.
Другая точка зрения на К. ф. состоит в следующем.
Пусть V — унитарный Л-модуль; отображение q : F-^-i?
наз. квадратичным отображением (или
квадратичной формой на модуле V,
если 1) q(ax) = a-q(x), a?R, x?V; 2) отображение bq:
VX V—>-R, задаваемое равенством
bq (x, y) = q{x + y)~q(x) — q(y),
является билинейной формой на модуле V. Пара (F, q)
наз. квадратичным модулем. Форма bq
всегда является симметрической.
Всякой билинейной форме Ь(х, у) на V отвечает К. ф.
q(x) = qb(x)=b(x,x); при этом bgb(x, y)=b(x, y)+b(y,x).
Если в кольце R элемент 2 имеет обратный 1/2, то
<;<—>— Ь„ есть взаимно однозначное соответствие между
квадратичными и симметричными билинейными фор-
формами на модуле V. Если V — свободный Л-модуль ран-
ранга п и q — К. ф. на V, то каждому базису е1, . .. , еп
модуля V отвечает К. ф. в классическом понимании
q (хъ . . ., хп) = q (x1e1^r . . . +хпеп) = 2t
где <lii=q(ei), Qij==bg(eh ej)i l<:i<;-<n. Каждая К. ф.
q(xr, . . . , xn) над Л получается таким способом из
нек-рого квадратичного модуля (Л", q). При замене ба-
базиса К. ф. q(xl, ... , хп) переходит в эквивалентную
К. ф., и обратно.
Говорят, что элемент y?R представим К. ф. д (пли
что форма q представляет у), если у является значением
этой формы при нек-рых значениях переменных. Экви-
Эквивалентные К. ф. представляют одни и те же элементы.
К. ф. q (x) над упорядоченным нолем наз. неопре-
неопределенной, если она представляет как положитель-
положительные, так и отрицательные элементы, и наз. положи-
тельно (отрицательно) определен-
определенной, если д(х)>0 (соответственно q(x)<CO) при всех
х^О. Невырожденная К. ф., представляющая 0 не-
нетривиально, наз. изотропной, в противном слу-
случае — анизотропной. Аналогично, К. ф. r(yt,
. .. , ут) наз. представ л мой К. ф. д, если q
превращается в г при подстановке нек-рых линейных
форм от j,, ... , ут вместо переменных в q, т. е. если
существует прямоугольная матрица S порядка тХп
над R такая, что A (r)=ST A (q)S (T — знак транспо-
транспонирования).
Алгебраическая теория К. ф.— теория
К. ф. над полями.
Пусть F — произвольное поле характеристики, от-
отличной от 2. Задача о представлении формы г формой q
над F сводится к проблеме эквивалентности форм над F,
ибо (теорема Полла) для того, чтобы невырож-
невырожденная К. ф. г была представима невырожденной К. ф.
q над Л, необходимо и достаточно, чтобы нашлась такая
форма h = h(xrB + x, ... , хп), что К. ф. r-\-h и q эквива-
эквивалентны над /•'. Здесь r-\-h — ортогональная прямая
с у м м а форм, т. е. г и h не имеют общих переменных.
Теорема В и т т а о сокращении: если h-\-
Всякая К. ф. над F эквивалентна диагональной:
<> 9 2 2
О j_i-'i ~[ п%3*% —у~ . . . —j- О, р'Х f — . , , —j— п jj3. ft.
Можно считать, что ах, . . . , аг^=0, а аг+х=. . . = ап = 0.
Число г называется рангом К. ф. q п совпадает
с рангом матрицы A (q). Если в F существует квадрат-
квадратный корень из любого элемента, то К. ф. над F эквива-
эквивалентна форме х\~-. . .Л'Х'Г (нормальный вид
К. ф.)..
Всякая невырожденная К. ф. q эквивалентна форме
ч' = <?о + Х=1 (-г?-—2/f).
где q0 анизотропна; при этом q однозначно определяет к
и класс формы q0 над F, называемый анизотроп-
н.ы м ядром формы q (см. также Bumma разложе-
разложение). Две формы qx и q2, имеющие одно и то же анизо-
анизотропное ядро, наз. подобными по В и т т у. На
классах подобия форм определена структура кольца
(см. Bumma кольцо).
Пусть F — упорядоченное поле (в частности, поле R)
и всякий положительный элемент в F является квадра-
квадратом. Тогда всякая К. ф. q приводима к форме вида
3i- . +3-1 — J-s+i— • •— 37-s.
При этом числа s и г — з (положительный и
отрицательный индексы инерции) оп-
определены формой однозначно (см. Инерции закон). Тем
самым для этих полей разрешается проблема эквива-
эквивалентности К. ф.
Над полем Q проблема эквивалентности сводится к
аналогичной проблеме для полей р-адических чисел:
для того чтобы К. ф. qx и g2 были эквивалентны над Q,
необходимо и достаточно, чтобы qx и д2 были эквива-
эквивалентны над Qp для всех простых чисел р и над QOO=R
(теорема Минковского — Хассе). Анало-
Аналогичное утверждение справедливо и для А- п о л е й —
алгебраических числовых полей и полей алгебрапч.
функций от одной переменной над конечным полем кон-
констант. Это — частные случаи общего Хассе принципа.
В поле Qp (рфоо) проблема эквивалентности решается
с помощью Хассе инварианта.
К. ф. q над полем F наз. мультипликатив-
мультипликативной над F, если
где z,- суть рациональные функции от хх, . . . , хп, ух,
... , уп над F. Если при этом z/ — билинейные функ-
ции, то говорят, что форма обладает компози-
композицией. Композиция возможна лишь в случаях п = 2, 4,
8 (т е о р е м а Г у р в и ц а). Существует простое опи-
описание мультипликативных форм [16].
Изложенная алгебраич. теория К. ф. обобщена [7]
на случай поля характеристики 2.
Арифметическая теория К. ф.— теория
К. ф. над кольцами. Она возникла в связи с задачей о
решении диофантовых уравнений 2-й степени. Вопрос
о решении таких уравнений сводится к задаче о пред-
представлении целых чисел целочисленной К. ф. д, т. е. к
задаче решения в % уравнения b=q(x1, ... , хп). Из-
Известны алгоритмы, сводящие нахождение (описание)
всех решений этого уравнения к проблеме эквивалент-
эквивалентности К. ф. над Ж, т. е. к задаче отыскания по заданным
К. ф. q{x) = 4rA[x] п q1(x) = 4rA1{x] обратимых матриц
U над 2, удовлетворяющих условию UTAU=A1. Для
п=2 эти алгоритмы были построены Ж. Лагранжем
(J. Lagrange) и К. Гауссом (С. Gauss), к-рые создали
общую теорию бинарных К. ф. На произвольное п они
обобщены Г. Смитом (Н. Smith) и Г. Минковским
(Н. Minkowski).
Одной из центральных проблем арифметич. теории яв-
является задача отыскания простых критериев существо-
существования представлений S формы г(ж) = — В [х] формой
д(х)= — А [х], т. е. решений матричного уравнения
STAS = B, A)
а также задача построения формул для числа R(q, r) =
= R(A, В) таких представлений. При этом, если число
представлений бесконечно, то речь идет о числе R'(q, r)
«существенно различных» представлений (представле-
(представления S и S' отождествляются, если S'=VS, где V —
целочисленный автоморфизм формы
q(x), т. е. YTAV=A). Необходимым условием существо-
существования представлений является разрешимость уравне-
уравнения A) над IR и разрешимость над % матричного срав-
сравнения
STAS = В (mod g) B)
по любому g. (Для разрешимости всех сравнений B)
достаточна разрешимость B) при g= go=SD (q)D (г).)
Эти необходимые условия, наз. «родовым и», рав-
равносильны разрешимости A) над Zp для любого простого
числа р и над Z» = R. Они равносильны также разре-
разрешимости A) над полем рациональных чисел Q «без су-
существенного знаменателя», т. е. существованию рацио-
рационального решения S с общим знаменателем, взаимно
простым с любым наперед заданным числом g (достаточ-
(достаточно ограничиться числом g=g0). Условия разрешимости
сравнений B) можно выразить через родовые инвариан-
инварианты форм q и г. Число решений сравнения B) находится
с помощью сумм Гаусса.
Род К. ф. над 2— множество К. ф. над 21> эквива-
эквивалентных друг другу над lip для всех простых р, вклю-
включая z» = R. Род К. ф. состоит из конечного числа клас-
классов одного и того же дискриминанта. Род К. ф. q(x) =
= —Л [х] может быть задан конечным набором родовых
инвариантов — инвариантов порядка, выражаемых че-
через элементарные делители матрицы А, и характеров
рода у_(д)=±1. Род может быть задан также значения-
значениями сумм Гаусса. Существенную роль в теории К. ф.
играет также понятие сшшорного рода, более тонкое,
чем понятие рода.
Число R'(q, r) существенно различных представле-
представлении формы г формой q просто связано с числом Ro(q, r)
существенно различных примитивных
представлений, т. е. таких представлений S,
что наибольший общий делитель миноров порядка т
матрицы равен 1. Для величины
(усреднения функции R'0(q, г) по роду формы q), где
qx, . . . , qi — представители всех классов рода формы
q (из каждого класса по одному), имеются (см. [11],
[15]) формулы, выражающие S0(q, r) через число реше-
решений нек-рых сравнений. В случае, когда род формы q
состоит из одного класса, эти формулы полностью ре-
решают вопрос о числе представлений. В случае много-
многоклассных родов известны лишь асимптотич. формулы
для Я (д, г), а также точные формулы для нек-рых кон-
конкретных К. ф.
Аналитическая теория К. ф. Аналитич.
методы в теорию К. ф. были введены П. Дирихле (P. Di-
richlet). Развивая эти методы, К. Зигель (К. Siegel)
пришел к общим формулам для числа представлений
формы родом форм.
Пусть q(Xl,... , хп)=4г А [х] и r(Xl, ... , хт)=
= — В [х] — положительно определенные К. ф. над 2-
Число
наз. знгелевым средним по роду для
числа представлений R (q, г) формы г формой q. Здесь
E(qi) — число автоморфизмов формы $г/,
— вес рода К. ф. q. Пусть
где Ф — окрестность точки г=г(х) в т(т-г1)/2-мерном
пространстве то-арных К. ф. над R, f>' — соответствую-
соответствующая область решений Sx матричного уравнения A) над
R, a V(&) и F(d') — их объемы.
Формула Зигеля для К. ф. q и г имеет вид
Я (9. г) = тх» (q, r)H (q, г), C)
где t=V2, если и=то>1 или п=т-\-1 и т=1 в осталь-
остальных случаях. Здесь
Rg («• г)
Н (q, r)= lim -=-
^ ' a{& nm-m
где предел берется по таким последовательностям g, что
любое натуральное число является делителем почти всех
g, а соо(?) — число различных простых делителей g,
(о„_m(g) = 0, если п>т, a Rg(q, г) — число представле-
представлений формы г формой q по модулю g, т. е. число решений
матричного сравнения
SEs-i-fi (modg).
Справедливо равенство
н(9,г)=- ,g./°g'_m,m+1w.2, go = SD (q) D (г).
Имеется ряд равносильных определений для Н(q, t)
и (см. [17]) выражение через обобщенные суммы Гаус-
Гаусса. Формула C) содержит, как частный случай, фор-
формулу Минковского для веса рода:
XT
р f-p <9- 9)
последняя в случае п=2 дает формулу Дирихле для
числа классов.
Формулы, аналогичные C), имеют место и для неопре-
неопределенных К. ф. и форм с целыми алгебраич. коэффици-
коэффициентами (см. [17], [18]).
Приложение теории модулярных форм к исследова-
исследованию мультипликативных свойств количества представ-
представлений чисел положительными К. ф. с четным числом
переменных было дано Э. Хекке (Е. Неске, [10]). Теория
модулярных форм позволяет получать формулы для
R(q, Ь) (см. обзор [5]).
К вопросу о представлении чисел К. ф. от четырех
и более переменных применяется круговой метод (см.
[4]). Если q — положительно определенная К. ф. над
Z, то применение кругового метода приводит для 4
к аспмптотич. формуле
п 1
л/2 .л/2 - 1 -, у + Е
R(Q,b)=^—^ -H{q, Ь) О4 4
г (? )«»<,>
Подобные асимптотич. формулы могут быть получены
круговым методом и для неопределенных К. ф. при п^
>4.
Для исследования R(q, b) в случае п=3 применяется
дискретный оргодпческий метод Линника (см. [3], [4]).
Он заключается в том, что на нек-ром множестве пред-
представлений чисел тернарными К. ф. устраивается эрго-
дический поток представлений, управляемый операто-
оператором, связанным с задачей представления чисел квате-
рнарными К. ф. Эргодическпй метод приводит (при
выполнении необходимых условий) к оценке типа
R (q, Ь) > ch(-Ab), c = c(q) > 0;
в ряде случаев получены и асимптотич. формулы.
Для исследования таких вопросов теории К. ф., как
теория приведения, автоморфизмы, арифметпч. мини-
минимумы К. ф., Ш. Эрмнтом (Ch. Hermite) был развит метод
непрерывных параметров, превратившийся затем в об-
обширный раздел теории К. ф.— геометрическую
теорию К. ф., или геометрию К. ф. (к-рую
можно рассматривать и как часть Геометрии чисел).
Идея метода состоит в следующем. Заданной га-мерной
точечной решетке Л ставится в соответствие та или иная
арифметич. величина а=а(Л) и рассматривается пове-
поведение функции а (Л) при малых изменениях параметров
решетки Л. Характерной чертог! геометрии К. ф. яв-
является систематич. использование гс(?г+1)/2-мерного
пространства коэффициентов (параметров), в к-ром
решетка Л изображается точкой. Пусть
i
— К. ф. с действительными коэффициентами я,-у = а,-,-
(;, 7=1, . . . , п). Форме / ставится в соответствие точка
/=(«11, ... , апп, а12. ... , «„_!,„) в Л'-мерном евкли-
евклидовом пространстве.Л'=ге(п-|--1)/2, называемом прост-
пространством коэффициентов. Положительно
определенным формам / при этом отвечает открытый
выпуклый конус $р с вершиной в начале координат, на-
называемый конусом положительности. Ре-
шетгсс Л соотносится класс эквивалентных гс-арных по-
положительно определенных К. ф.; при базисе [аг, ...,
ап] решетки Л ей ставится в соответствие форма
Тем самым решетке Л соответствует бесконечное дис-
дискретное множество точек конуса положительности $р.
Если выбрать точную область приведения ус§Р поло-
положительно определенных К. ф., то каждой решетке будет
взаимно однозначно соответствовать точка f?$ прост-
пространства коэффициентов. Малым изменениям параметров
решетки Л отвечают малые изменения точки /.
Геометрическая теория К. ф. распадается на ряд до-
достаточно самостоятельных теорий, связанных единым
методом исследования. Фундаментом ее является теория
приведения положительных К. ф., к-рая, изучая обла-
области приведения %, решает проблему эквивалентности
положительных К. ф.— одну из центральных задач
арифметич. теории К. ф. (см. Квадратичных форм при-
приведение).
Существенную роль играет теория Вороного типов
решетки. Она имеет важные приложения в теории па-
раллелоэдров. Теория типов получила применение в ре-
решении задач об экономнейшем решеточном покрытии п-
мерного пространства шарами.
Другой традиционный раздел геометрич. теории
К. ф.— теория совершенных форм, также созданная
Г. Ф. Вороным. Эта теория позволила решить Эрмита
проблему арифметич. минимумов положительных К. ф.,
равнозначную задаче о плотнейшей решетчатой упаков-
упаковке шаров в «-мерном пространстве. Задача о плотней-
плотнейшей решетчатой упаковке шаров и задача об эконом-
экономнейшем решетчатом покрытии шарами — наиболее из-
известные примеры экстремальных задач, составляющих
значительную часть К. ф. геометрии.
К геометрической теории К. ф. можно также отнести
нек-рые обобщения алгоритма цепных дробей, напр,
алгоритм Вороного вычисления единиц кубического по-
поля, теорию фундаментальных областей автоморфизмов
неопределенных К. ф.
Лит.: [1] Б о р е в и ч 3. И., Шафаревич II. Р.,
Теория чисел, 2 изд., М., 1972; [2] Делоне Б. Н., «Успехи
матем. наук», 1937, в. 3, с. 16—62; 1938, в. 4, с. 102—64;
[3] Л и н н и к Ю. В., Эргодические свойства алгебраических
полей, Л., 1967; [4] М а л ы ш е в А. В., О представлении целых
чисел положительными квадратичными формами, М.— Л., 1962;
[5] его ж е, в кн.: Актуальные проблемы аналитической тео-
теории чисел, Минск, 1974, с. 119—37; [6] С е р р Ж. - П., Курс
арифметики, пер. с франц., М., 1972; [7] A rf С, «J. reine und
angew. Math.», 1941, Bd 183, S. 148—67; [8] Eichler M.,
Quadratische Formen und orthogonale Gruppen, 2 Aufl., В., 1974;
[9] Hasse H., «J. reine und angew. Math.», 1923, Bd 152,
S. 129 —48 205—24; 1924, Bd 153, S. 12—43, 76—93, 113—30,
158—62, 186—207; [10] He eke E., Mathematische Werke,
Gott., 1959; til] Jones B. W., The arithmetic theory of
quadratic forms, N. Y., 1950; [12] L a m T. Y., The algebraic
theory of quadratic forms, Reading, 1973; [13] Minkowski H.,
Gesammelte Abhandlungen, Bd 1—2, Lpz. — В., 1911; [14]
O'M e a r а О. Т., Introduction to quadratic forms, В., 1963; [15]
Pall G., «Canad. J. Math.», 1949, v. 1, p. 344—64; [16]
Pfister A., «Arch. Math.», 1965, Bd 16, S. 363—70; [17]
S i e g e 1 C. L., Lecturis on the analytical theory of quadratic
forms, 3 ed., Gott., 1963; [18] его же, Gesammelte Abhan-
Abhandlungen, Bd 1—3, В., 1966; [19] Smith H. J. S., The
collected mathematical papers, y. 1—2, Oxf., 1894; [20] Wat-
Watson G. L., Integral quadratic forms, Camb., 1960: [21]
Фоменко О. M., Итоги науки и техники. Алгебра. Тополо-
Топология. Геометрия, т. 15, М., 1977, с. 5 — 91. А. В. Малышев.
КВАДРАТИЧНОЕ ОТКЛОНЕНИЕ, квадратич-
квадратичное уклонение, стандартное отклоне-
отклонение величин аг1; х2, . .. , хп от а — квадратный ко-
корень из выражения
(x,-a.J + (.v,-aJ + ... +{хп-аJ
Наименьшее значение К. о. имеет при а=х, где х
среднее арифметическое величин xL, х2, . . . , хп:
В этом случае К. о. может служить мерой рассеяния
системы величин хг, х„, . . . , хп. Употребляют также
более общее понятие взвешенного К. о.
ViPi (xi — a)*^. . . +рп (х„ — аJ]/(р1 + . . . -р„),
числа pj, . . . , рп наз. при этом весами, соответст-
соответствующими величинам хг, . . . , хп. Взвешенное К. о.
достигает наименьшего значения при а, равном взве-
взвешенному среднему:
(Pl*l + • • • + Pnxn)l(Pl + • • • + Рп) ¦
В теории вероятностей К. о. а у случайной величины
X (от ее математич. ожидания) наз. квадратный корень
из дисперсии j/~D(X).
К. о. употребляют как меру качества статнстнч. оце-
оценок и наз. в этом случае квадратичной о ш и б-
к о й. БСЭ-в.
КВАДРАТИЧНОЕ ПОЛЕ — расширение степени 2
поля рациональных чисел Q. Любое К. п. имеет вид
Q{Y~d), где rf?Q, VcK^Q, т. е. получается присоеди-
присоединением к полю Q элемента Yd~. С( |/"й,)=0( Yd2) тогда
и только тогда, когда d1=c2d2, где с?0. Поэтому любое
К. п. имеет вид Q(Y~d), где d — целое рациональное
число свободное от квадратов, однозначно определяемое
этим К. п. В дальнейшем d предполагается именно та-
таким.
При d>0 поле Q ( ]/ d) наз. вещественным
К. п., а при rf<0 — мнимы м.
В качестве фундаментального базиса поля Q( Y~d),
т. е. базиса кольца целых чисел поля Q( Yd) над коль-
кольцом целых рациональных чисел 2, можно взять
1, -1±L± | при d = I (mod 4)
{l, Y"d) при d=2, 3 (mod 4).
Дискриминант D поля Q(Y~d) равен соответственной
при d=l (mod 4) и Ad при ds2, 3 (mod 4).
Мнимые К. п.— единственный тип полей (кроме Q)
с конечной группой единиц. Эта группа имеет порядок
4 для Q( }/ —1) (и образующую Y—1)> порядок 6 для
Q( V7—3) (и образующую -г-\—^-), порядок 2 (и об-
образующую — 1) для всех остальных мнимых К. п.
Для вещественных К.'п. группа единиц изоморфна
прямому произведению {rtl}x {e}, где {—1} — группа
порядка 2, порожденная числом —1, и {s} — бесконеч-
бесконечная циклическая группа, порожденная основной еди-
единицей е. Напр., для поля Q( |/) е=1+|/.
Закон разложения простых дивизоров в К. п. допу-
допускает простую формулировку: полю <Q( Y~d) можно со-
сопоставить квадратичный характер j на 2 по модулю
\D\. Если р —простое число и (Z),p)=l, то дивизор
(р) прост в С( Yd) при %(р) =—1, и распадается в про-
произведение двух простых дивизоров при х(р)=1.
Группа классов дивизоров К. п. изучена лучше, чем
для других классов полей. В случае мнимых К. п. тео-
теорема Бруэра — 3 п геля (утверждающая, что
для полей алгебраических чисел фиксированной степени
выполняется асимптотич. соотношение
In (hR) , . г-. |
— >¦ 1 при D —у оо,
In I | D I F I I
где h, R и D — число классов, регулятор и дискрими-
дискриминант поля) показывает, что число классов дивизоров
стремится к бесконечности при d—>•—оо. Имеется ровно
9 одноклассных мнимых К. п. (при d= — 1, —2, —3, —7,
— И, —19. —43, —67, —163, см. [2]). Для вещественных
К. п. неизвестно A978) конечно или бесконечно число
одноклассных полей. Существует бесконечно много
К. п. (как мнимых, так и вещественных), число классов
к-рых делится на данное натуральное число (см. [3],
[4]). Аналогичное свойство для 2-компоненты группы
классов следует из теории родов Гаусса.
Абелевы расширения мнимых К. п. в явном виде
позволяет строить теория комплексного умножения
(см. [5]).
Мнстиз арифмотич. свойства К. п. допускают пере-
форм57лировку в терминах теории бинарных квадратич-
квадратичных форм.
Лит.: [1] Б о р е в и ч 3. И., Шафаревич И. Р.,
Теория чисел, 2 изд., М., 1972; [2] Stark H. M., «Mich.
Math J.», 1967, v. 14, p. 1—27; [3] Ankeny N. С, С h o-
w 1 a S., «Pacific. J. Math.», 1955, v. b, p. 321—24; [4] Jam a-
m о t о J., «Osaka J. Math.», 1970, v. 7, p. 57—7B; [5] Алгебра-
Алгебраическая теория чисел, пер. с англ., М., 1969, гл. 13.
Л В. Нузъмин.
КВАДРАТИЧНОЕ ПРОГРАММИРОВАНИЕ — раз-
раздел выпуклого программирования, посвященный теории
и методам решения задач минимизации выпуклых квад-
квадратичных функций на множествах, задаваемых систе-
системами линейных неравенств и равенств. Существует за-
законченная теория К. п., и разработаны численные ме-
методы решения задач К. п., в том числе методы типа симп-
симплексного метода, приводящие к решению за конечное
число шагов (итераций).
Реальные задачи технико-зкономич. содержания, ма-
тематнч. моделями к-рых являются задачи К. п., не-
немногочисленны. Однако задачи К. п. возникают как
вспомогательные при решении различных задач матема-
математического программирования. Так, в одном из вариантов
метода возможных направлений для численного реше-
решения задач нелинейного программирования проблему
выбора направления спуска на каждой итерации сводят
к решению задачи К. п. Задачи безусловной минимиза-
минимизации квадратичных функций, а также задачи К. п. с ог-
ограничениями простейшего вида (напр., когда ограниче-
ограничениями являются условия неотрицательности перемен-
переменных) возникают в результате применения метода регу-
регуляризации для решения неустойчивых (некорректных)
задач линейного программироваття и штрафных функ-
ций метода для решения задач линейного программи-
программирования.
Лит.: [11 ТТшеничны и Б. Н., Данилин IO. М.,
Численные методы в экстремальных задачах, М., 1975; [2J
Хедли Д ж., Нелинейное и динамическое программирова-
программирование, пер. с англ., М., 1967; [3] 3 а н г в и л л у. И.. Нели-
Нелинейное программирование. Единый подход, пер. с англ., М.,
1973; [4] Кюнци Г. П., Крелле В., Нелинейное про-
программирование, пер. с нем., М., 1905; [5] Демьянов В. Ф.,
М а л о з е м о в В. Н., Введение в минимакс, М., 1972.
В. Г. Карманов.
КВАДРАТИЧНОЕ СРЕДНЕЕ — число s, равное кор-
шо квадратному из среднего арифметического квадратов
данных чисел а1? а2, . . . , ап:
s = V (at 4- a\ -f- . . . -г а„)In.
КВАДРАТИЧНЫЕ ФОРМЫ ПОВЕРХНОСТИ - об-
общее наименование квадратичных форм от дифференци-
дифференциалов координат на поверхности, инвариантных при
преобразованиях этих координат. К. ф. п. характери-
характеризуют основные внутренние свойства поверхности и ее
расположение в пространстве в окрестности данной точ-
точки; обычно выделяют так наз. первую, вторую и третью
основные квадратичные формы.
Первая квадратичная форма поверх-
поверхности характеризует внутреннюю геометрию поверх-
поверхности в окрестности данной точки. Это означает, что с
ее помощью можно производить измерения на поверх-
поверхности. Пусть поверхность зада-
задана уравнением: ^~~—-^ d
r=r(u, v),
где и и i; — координаты
поверхности;
d>'= vu du -\- T,v do
— дифференциал радиус-вектора г (и, и) вдоль выбран-
выбранного направления смещения из точки М в бесконечно
близкую точку М' (см. рис. 1). Главная линейная часть
приращения длины дуги ММ' выражается квадратом
дифференциала dr:
I=ds2 = dr2=E (и, v) du2 -f 2F (и, v) du dv 4- G (u, v) dv2,
где Е(и, v)=r2u, F(u, v) = (ru, rv),G(u, v) = r\ .Форма I
и наз. первой основной К. ф. п. См. также
Первая квадратичная форма поверхности.
Вторая квадратичная форма поверх-
поверхности характеризует локальную структуру поверх-
поверхности в окрестности обыкновенной точки. Именно, пусть
— единичный вектор нормали к поверхности в точке М,
где e=-Ll, если тройка векторов {ru, rv, n}— правой
ориентации, и 8=—1 — в противоположном случае.
Удвоенная главная линей-
линейная часть 26 отклонения точ-
точки М' (см. рис. 2) поверх-
поверхности от касательной плоско-
плоскости в ее точке М равна
11 = 26 = {—dr, dn) =
= L (и, v)du2-+-
+2М(и, v) dudv -+- N (и, v) dv2,
где L=(rllu, n), M=(rav, n). N={rvv, n). ФормаП наз.
второй основной К. ф. п. См. также Вторая
квадратичная форма поверхности.
Первая и вторая К. ф. п. обладают двумя важными
совместными скалярными инвариантами относительно
преобразования координат на поверхности. Именно,
отношение дискриминантов этих форм равно гауссовой
кривизне поверхности в точке:
к =
LM-N
EG - F'
а выражение
EN-2FM + GL
EG-F*
тределяет среднюю кривизну поверхности в точке.
Задание первой (положительно определенной) и вто-
второй К. ф. п. определяет поверхность с точностью до
движения (Бонне теорема).
Третья квадратичная форма поверх-
поверхности представляет собой квадрат дифференциала
единичного вектора п нор-
нормали к поверхности в точке
М (см. рис. 3 : ('
III = dn2 = -n
-f- 2nunv du dv -\- nv dv'1.
Третья К. ф. п. равна глав-
главной линейной части прира-
приращения угла между вектора-
векторами пи л'при смещении по
поверхности из точки М в точку М'\ она является пер-
первой К. ф. п. сферического изображения поверхности.
Три основные К. ф. п. связаны линейной зависи-
зависимостью:
\-К — II-2Я — 111 = 0.
Кроме перечисленных выше иногда рассматривают и
другие К. ф. п. (см., напр., [3]).
Лит.: [1] Каган В. Ф., Основы теории поверхностей
в тензорном изложении, ч. 1, М.— Л., 1947; [2] Р а ш е в-
с к и й П. К., Курс дифференциальной геометрии, 4 изд., М.,
1956; [3] III у л и к о в с к и й В. И., Классическая диффе-
дифференциальная геометрия в тензорном изложении, М., 1963.
КВАДРАТИЧНЫЙ ВЫЧЕТ п о модулю "т"—
целое число а, для которого разрешимо сравнение
i2sa (mod m).
Если указанное сравнение не разрешимо, то число а
наз. квадратичным невычетом по моду-
модулю т. Критерий Эйлера: пусть р>2 простое.
Число а, взаимно простое с р, является К. в. по модулю
р тогда п только тогда, когда
р-г
а 2 !Е= 1 (mod p),
и является квадратичным невычетом по модулю р тогда
. и только тогда, когда
р-1
а 2 =— 1 (mod /?).
Лит.: [1] Виноградов И. М., Основы теории чисел,
8 изд., М., 1972. С. А. Степанов.
КВАДРАТИЧНЫЙ ДИФФЕРЕНЦИАЛ на р и м а-
новой поверхности/? — правило, которое каж-
каждому локальному параметру z, отображающему пара-
метрнч. окрестность UcR в замкнутую комплексную
плоскость C(z : ?/—>-С), ставит в соответствие функцию
Qz : z(?/¦)—>- С такую, что для всяких локальных пара-
параметров z1 : D\—>-С и z2 : ?'2—>-С с непустым пересечением
иг П t в последнем выполнено соотношение
A)
здесь z(U) — образ U в С при отображении z. К. д. ча-
часто обозначается символом Q(z)dz2, к-рому приписыва-
приписывается указанная инвариантность относительно выбора ло-
локального параметра z. Иначе говоря, К. д.— это нели-
нелинейный дифференциал типа B,0) на римановой поверх-
поверхности. '
Функции Qz(-), входящие в определение К. д., обыч-
обычно предполагаются измеримыми или даже аналитиче-
аналитическими. В последнем случае К. д. наз. аналитиче-
аналитически м. Точка р ? R наз. нулем или полюсом порядка к
дифференциала Q(z)dz2, если для каждого локального
параметра z функция Qz(-) имеет в р соответственно
нуль или полюс порядка к. Нули и полюсы К. д. наз.
его критическими точками. Нули и простые
полюсы наз. конечными критич. точками, и их совокуп-
совокупность обозначают С. Множество всех полюсов порядка
к ^2 обозначают Н.
Если кривая yczR имеет в каждой своей точке q отно-
относительно локального параметра z касательную с на-
направляющим вектором az(q) и
<?, (* (<?)) (аг (д)J > 0, V9GY. B)
то К. д. Q(z)dz- наз. положительным и пишут
Q(z)dz2>0 на кривой у. Если в B) вместо знака >
имеет место знак <, то К. д. Q (z)dz2 отрицателен
(Q(z)dz2<C0) на кривой у. Всякая максимальная
на R регулярная кривая, на к-рой Q(z)dz2>0 (либо
Q(z)dz2<CO), наз. траекторией дифференци-
дифференциала Q (z)dz- (соответственно ортогональной
траекторией).
К. д. Q(z)dz2, определенный на конечной римановой
поверхности R, принадлежит R, если край
OR поверхности R либо пуст, либо состоит из конечного
числа точек />(? Н и дуг у, на каждой из к-рых диффе-
дифференциал Q (z)dz2 регулярен и положителен пли отрица-
отрицателен. Если к тому же край OR пуст или если диффе-
дифференциал Q (z)dz2 на OR регулярен и положителен, то
Q (z)dz2 наз. положительным К. д. на R.
Метрика |(?(z)| /2|dz|, называемая Q-м с т р и к о й,
однозначна на R и инвариантна относительно выбора
локального параметра z.
В нек-рой окрестности U любой точки p?R\(C\JH)
функция
Q(z
(р) v v
регулярна, однозначна и однолистна при каждом выбо-
выборе знака подинтегрального выражения, причем всякая
максимальная дуга траектории (или ортогональной
траектории) из U при отображении Z (q) переходит в го-
горизонтальный (соответственно вертикальный) прямо-
прямолинейный интервал. Поэтому через каждую точку
p(zR\(C\JH) проходит траектория, являющаяся либо
открытой дугой, либо жордановой кривой на R. Топо-
Топологическая и конформная структуры семейства траек-
траекторий в малой окрестности всякой критич. точки г пол-
полностью классифицированы в зависимости от порядка
крптпч. точки г и (если г — полюс 2-го порядка и
z(r) = O) от
wglim Qz(z(q))z(q)*
(см. Локальная структура траекторий). Описание гло-
глобальной структуры траекторий известно для конечных
Романовых поверхностей и имеет много важных прило-
приложений (см. также [1]).
О. Тайхмюллер (О. Teichmiiller) исследовал роль по-
понятия К. д. для теории экстремальных конформных и
квазиконформных отображений и для решения пробле-
проблемы модулей рнмановых поверхностей (см. [1] — [3]).
Он сформулировал принцип, согласно к-рому экстре-
экстремальным задачам геометрич. теории функций ставятся
в соответствие нек-рые К. Д., причем каждому типу
экстремальных задач соответствуют определенные осо-
особенности (полюсы) К. д., а геометрич. свойства решения
связаны надлежащим образом со структурой траекто-
траекторий К. д. В терминах К. д. доказаны неравенства для
коэффициентов однолистных функций. Общее неравен-
неравенство для коэффициентов однолистных функций в семей-
семействах областей, расположенных на конечной римановой
поверхности, носит название общей теоремы о
коэффициентах и является конкретным вопло-
воплощением принципа Таихмюллера для широкого класса
задач (см. [1], [4]). Принцип Таихмюллера позволил так-
также установить специальную теорему о коэффициентах и
решить большое число конкретных экстремальных за-
задач (см. [1], [5]).
Лит.: [1] Дженкинс Д ж., Однолистные функции и
конформные отображения, пер. с англ., М., 1962; [2] Ш и ф-
фер М., Спенсер Д. К., Функционалы на конечных ри-
мановых поверхностях, пер. с англ., М., 1957; [3] А л ь ф о р с
Л., Б е р с Л., Пространства римановых поверхностей и квази-
квазиконформные отображения, пер. с англ., М., 1961; [4J Т а м р а-
зов П. М., «Матем. CO.», 1967, т. 72, JsiS 1, с. 59—71;
[о] Jenkins .Т. A., «111. J. Math.», 1964, v. 8, К 1,
p. 80 — 09. П. М. Тамрпзов.
КВАДРАТИЧНЫЙ ЗАКОН ВЗАИМНОСТИ — соот-
соотношение
связывающее Лежандра символы (—) и (—) для различ-
различных нечетных простых чисел р и q. Имеются два допол-
дополнения к указанному квадратичному закону взаимно-
взаимности, а именно:
( JL\ = (_i)(p2-1'''8
К. Гаусс (С. Gauss) дал первое полное доказательство
К. з. в., в связи с чем К. з. в. наз. также Гаусса законом
взаимности.
Из К. з. в. непосредственно следует, что при задан-
заданном целом d, не делящемся на квадрат целого числа,
простые р, для к-рых d является квадратичным вычетом
по модулю р, лежат в нескольких арифметич. прогрес-
прогрессиях с разностью 2\d\ или A\d\. Число этих прогрессий
равно -|-фB|й|) или -i-<pD|d|), где ф(ге) — Эйлера, функ-
функция. К. з. в. дает возможность установить законы раз-
разложения в квадратичном расширении R ( Yd) поля ра-
циональных чисел, поскольку в Rd^d) разложение
простого числа р, не делящего d, на простые дивизоры
зависит от того, приводим или нет многочлен ж2—d по
модулю р.
Лит.: [1] Виноградов И. М., Основы теории чисел,
8 изд., М., 1972; [2] Боревич 3. П., Шафаревич
И. Р., Теория чисел, 2 изд., М., 1972. С. А. Степанов.
КВАДРАТИЧНЫХ ФОРМ ПРИВЕДЕНИЕ — выде-
выделение в каждом классе квадратичных форм (к. ф.)над
данным кольцом R приведенных форм — «стандартных»
форм класса (одной или нескольких). Основной целью
К. ф. п. является решение проблемы эквивалентности
к. ф.: установить, эквивалентны над R данные к. ф. q
и г или нет. и в случае их эквивалентности найти (опи-
(описать) все обратимые матрицы V над R, переводящие q
в г (см. Квадратичная форма). Для решения последней
задачи достаточно знать одну такую матрицу Uo и все
автоморфизмы V формы q, ибо тогда U=VU0. Обычно
имеется в виду эквивалентность к. ф. над 2, причем
часто рассматривается вся совокупность к. ф. над R.
и их классы над %. Имеются принципиальные различия
в теории приведения положительных (положительно
определенных) и неопределенных к. ф.
Приведение положительных к. ф. Имеются различные
способы приведения над Z действительных положитель-
положительных к. ф. Из них наиболее распространенный и изучен-
изученный — способ приведения по Минковскому (или по
Эрмнту — Минковскому), наиболее общий — по Венко-
ву. Распространено также приведение по Зелингу
Gг=3) и по Шарву (га=4).
Определить приведенную к. ф.
значит задать в конусе положительности $Р пространст-
пространства коэффициентов R^, JV=n(re-f-l)/2, область приведе-
приведения (М так, чтобы q(x) была приведенной тогда и только
тогда, когда </=(&ii, ... , bn-i,n)?©. Желательно,
чтобы © обладала хорошими геометрия, свойствами (бы-
(была односвязной, выпуклой и т. п.) и была фундамен-
фундаментальной областью группы Г целочисленных подстановок
определителя ±1. Область Fczty наз. фундамен-
фундаментальной областью приведения положи-
положительных к. ф., если F—открытая область в RN и: 1) для
всякой к. ф. д?§Р найдется эквивалентная к. ф. hc^
c^qiZ), для к-рои h?~F; 2) если А1; h^^F и h1z±Jii(%),
то h1=h2-
а) Приведение к. ф. по М и н к о в с к о м у.
Положительная к. ф. q(x) приведена по Минковскому,
если для любого к=1, ... , п и любых целых чисел llt
... , ln с условием н. о. д. (lk,. . ., ln)=l,
q(h, ..., ln)^bkk. A)
Из бесконечного числа неравенств (Г) для коэффициен-
коэффициентов b{j можно выбирать конечное число так, что осталь-
остальные неравенства из них следуют. В пространстве коэф-
коэффициентов R множество приведенных по Минковскому
форм образует бесконечную выпуклую пирамиду (гоно-
эдр) с конечным числом граней, наз. областью
приведения Минковского (или г о н о э д-
ром Эр ми та — Минковского) 6 =6„; 6—
замкнутое множество, 6с§р. Для ге<7 вычислены гра-
грани области (?„ (см. [9]).
Существует такая постоянная Я„, что если к. ф. q(x)
приведена по Минковскому, то
где d(g)=det\\bij\\ — определитель к. ф. q(x).
Всякая действительная положительная к. ф. эквива-
эквивалентна над % приведенной по Минковскому к. ф. Имеет-
ся алгоритм приведения (отыскания приведенной фор-
формы, эквивалентной данной) (см. [8], [15]).
Для п=2, q=q{x, г/) = (а, Ъ, с)= ах2-\-2Ьху-\-сц2, а, Ъ,
c?R, a>0, d(g)>0 условия приведения имеют вид
О ==? 26 < а < с.
Если ограничиться собственной эквивалентностью (ког-
(когда допускаются целочисленные преобразования только
определителя +1), то область приведения имеет вид
0<2|Ь| «:а<с (условия приведения Лагран-
жа — Гаусса). Множество всех неэквивалентных
(собственно) приведенных к. ф. записывается как объ-
объединение F U F! U F2, где
F:2\b\<a<c, Ft:0 =sS26 < а = с, F2:0 < 2Ь = а <с.
Для п=2 имеется алгоритм приведения Гаусса, соглас-
согласно к-рому от формы, не удовлетворяющей условиям
Лагранжа — Гаусса, следует перейти к ее «соседней»:
(а1, Ь', с') = (а, Ь, с)
0 —1
1 к
а =с,
где целое число к выбирается так, что \Ь'\ -<е/2. Для лю-
любой действительной к. ф. (а, Ъ, с) алгоритм обрывается
через конечное число шагов.
Если q=(a, Ь, с), а, Ь, c?z, н. о. д. (а, Ь, с)=1, то
для d(q)=ac— Ь2>3 имеется лишь два автоморфизма
(определителя +1), для d(g)=3 — шесть автоморфиз-
автоморфизмов, для d(q)=i —четыре автоморфизма.
б) Приведение к. ф. по Венкову. Это —
способ приведения C5ф), зависящий от параметра ф —
произвольно задаваемой действительной положитель-
положительной re-арной к. ф. (см. [3]). Говорят, что к. ф. q ф-п р и-
ведена, если
(д, ф) =sS (g, ф5)
для всех целочисленных геХге-матриц S определителя
1; здесь ф=^(ф)ф-1 — форма, взаимная с ф, <pS —
к. ф., получающаяся из ф подстановкой S, (qt, q2) —
полуинвариант Вороного, определяемый
так: если q^BJx], В^ЦЬ'^Ц, дг=В2[х],В2=[Ь^\\, то
(Чъ дг) = 2.1, /_i ЬЧ ЬЧ ¦
Совокупность ф-приведенных к. ф. образует в про-
пространстве коэффициентов RN выпуклый гоноэдр SB<p с
конечным числом граней, лежащий в 5р. Если ф=жЦ-
+ .. .+^,2, и п<:6, то Жф совпадает с областью приведения
Мипковского.
в) Приведение к. ф. по Зелингу и Шар-
в у. Если в приведении по Венкову положить ф=ф<[0) =
= 2- -xixj't гДе ф'г"' — первая совершенная форма Во-
Вороного, то для 7г=3 получается приведение по Зелингу,
а для 7г=4 — приведение по Шарву (см. [5], [6]).
Приведение неопределенных к. ф. принципиально
сложнее, чем приведение положительных к. ф. Для них
нет фундаментальных областей. Только для ге=2 имеет-
имеется законченная теория приведения к. ф. над %.
а) Приведение неопределенных
бинарных к. ф. Пусть
q = q(x, у) = (а, Ь, с) =ах2 + 2Ъху + cj/2, a, 6, cgZ,
к. ф. определителя d=ac—Ь2= — |d| и \d\ не есть
полный квадрат. Форме q сопоставляется квадратное
уравнение az2-\-2bz-\-c=0 и его различные иррациональ-
иррациональные корни
= Q(g)= ^ t to = co(g)= —!—L.
Форма q наз. приведенной, если | Q| >1, | ю| <1,
Qco<O. Эти условия равносильны условиям
О < УЩ—Ь < | а | < УЩ+ Ъ
(а также условиям 0< Y\d\ — o<\c\ < ]/ \d\-\-b). Число
приведенных целочисленных к. ф. данного определите-
определителя конечно. Каждая к. ф. эквивалентна приведенной.
Существует алгоритм приведения, использующий цеп-
цепные дроби (см. [1]).
Для приведенной к. ф. существует ровно одна «со-
«соседняя справа» и ровно одна «соседняя слева» приведен-
приведенная к. ф. (см. [1], с. 100). Исходя из приведенной к. ф.,
переходя к «соседним», получают двояко бесконечную
цепь приведенных форм. Эта цепь периодична. Конеч-
Конечный отрезок неэквивалентных форм этой цепи наз. п е-
р и о д о м. Две приведенные формы собственно экви-
эквивалентны тогда п только тогда, когда одна из них встре-
встречается в периоде другой.
Изложенная теория справедлива и для форм с дейст-
действительными коэффициентами я, 6, с, если Q (q) и u>(q) —
различные иррациональные корни, но цепь приведен-
приведенных форм при этом может не быть периодичной.
Все собственные автоморфизмы (определителя +1)
к. ф. с н. о. д. (а, Ъ, е)=1, н. о. д. (а, 26, с) = о, d=
= ас—62<0 имеют вид
= 0, ±
где (t, и) пробегает все решения Пелля уравнения ?24-
-\-йи2 = аг, (Т, V) — фундаментальное решение этого
уравнения, т. е. наименьшее положительное решение.
Несобственные автоморфизмы (определителя —1) име-
имеются лишь у двусторонних форм — форм,
класс к-рых совпадает с обратным (см. [1], с. 111). Под-
Подгруппа собственных автоморфизмов двусторонней фор-
формы имеет индекс 2 в группе всех автоморфизмов.
Неопределенные целочисленные к. ф. определителя
d=—s-, s>0, s?3, приводятся к виду @, —s, г), где
r?Z, 0<r<2s. К. ф. @,—s, гх) и @, —s, г2), 0<г1)г2<2*
собственно эквивалентны тогда и только тогда, когда
= г2. Все автоморфизмы таких форм суть —\\l ill (см.
] с. 107).
б) Приведение неопределенных ге-а р-
н ы х к. ф. Пусть q(x)=B \х\ = хтВх — такая форма
с действительными коэффициентами и d (<?)=^=0. Тогда
существует такая подстановка переменных (над R):
x=Sy, что
t-bu
о
аи
о
си
о
t + bu
о
— 4-
1 T-bU
о
aU
а
Т
cU
а
+ьи
о
г1 =
[1],
б
— г/1
у) —
где (t, n — i) — сигнатура к. ф. q. Пусть
1 0
1
— 1
t строк
n—t строк
и B=SrDS. К. ф. q(x) сопоставляется положительная
к. ф.
hs{x)=y\+ ...
г у\
у\ = STS [х].
Форма q наз. приведенной (по Эрмиту), если найдется
такое преобразование S формы q к сумме квадратов, что
положительная к. ф. ks (z) является приведенной (напр.,
по Минковскому).
Равносильное этому определение приведенной к. ф.
следующее [13], [14]. Пусть Ф (q) — множество матриц
If над R положительных n-арных к. ф., удовлетворяю-
удовлетворяющих равенству НВ~1Н=В. Это связное t(n—?)-мерное
многообразие конуса положительности 5pczR (выпи-
сываемое в явном виде). Пусть Fd^— область приве-
приведения положительных к. ф. Форма q наз. приведенной,
если Ф(д)П^ не пусто.
Число классов целочисленных неопределенных к. ф.
от п переменных с данным определителем d конечно (это
верно и для положительных к. ф.). Число приведенных
форм в данном классе также конечно. Если две целочис-
целочисленные к. ф. q1 и q,2 эквивалентны, то найдется целочис-
целочисленная подстановка S, абсолютные величины элемен-
элементов к-рой ограничены постоянной, зависящей только от
п и d, переводящая д1 в д.,. Тем самым проблема установ-
установления эквивалентности или неэквивалентности двух
неопределенных целочисленных к. ф. решается в конеч-
конечное число шагов.
в) Автоморфизмы неопределенных
к. ф. Проблема описания всех автоморфизмов неопре-
неопределенной целочисленной к. ф. имеет два аспекта: 1) по-
построить фундаментальную область группы автоморфиз-
автоморфизмов и 2) описать общий вид автоморфизмов (подобно
описанию автоморфизмов через уравнение Пелля).
Общий вид автоморфизмов к. ф. был описан Ш. Эр-
мптом (Ch. Hermite) для га=3 и А. Кэли (A. Cayley) для
произвольного п (см. [10]).
Построена фундаментальная область группы авто-
автоморфизмов неопределенной целочисленной к. ф. q (x) в
многообразии Ф (q), ограниченная конечным числом
алгебрацч. поверхностей, и вычислен ее объем [13].
В случае (=1 в га-мерном пространстве переменных по-
построена фундаментальная область группы автоморфиз-
автоморфизмов к. ф. q(x) в виде бесконечной пирамиды с конечным
числом плоских граней [2], [4].
Построена теория приведения к. ф. в алгебрапч. чис-
числовых полях (см. [11]).
Лит.: [1] Венков Б. А., Элементарная теория чисел,
М,—Л., 1937; [2] его ж е, «Изв. АН СССР. Сер. матем.»,
1937, т. 1, с. 139—70; [3] его же там же, 1940, т. 4, с. 37—52;
[4] его же, «Тр. Матем. ин-та АН СССР», 1951, т. 38, с. 30—
41; [5] Делоне Б. Н., «Успехи матем. наук», 1937, в. 3,
с. 16—62; 1938, в. 4, с. 104 — 64; [6] Делоне Б. Н., Г а л н-
у л и н Р. В., III т о р г п н М. И., в кн.; Современные проб-
проблемы математики, т. 2, М., 1973, с. 119—254; [7] Лежен-
Дирихле П. Г., Лекции по теории чисел, пер. с нем., М.—
Л.. 1936; [8] Р ы ш к о в С. С. «Зап. науч. семинаров ЛОМИ»,
1973, т. 33, с. 37 — 64; [9] Т а м м е л а П. П., там же, 1975,
т. 50, с. 6—96; 1977, т. 67, с. 108—43; [10] В а с h m a n n P., Die
Arithmetik der quadratischen Formen, Abt. 1—2, Lpz., 1923—25;
[11] Humbert P., «Comment, math, helv.», 1949, t. 23, p. 50—
63; L12J Minkowski H. «J. relne und angew. Math.»,
1905, Bd 129, S. 220 —74; [13]Siegel С L.,«Abh. Math.
Semin. Univ. Hamburg», 1940, Bdl3, S. 209—39; [14] его же,
«N'achr. Akad. Wiss. Gottineen. Math.-phys. Kl.», 1972, S. 21—Hi;
[15] Van der Waerden B. L. «Acta math.», 1956, v. 96,
p. 265 — 309. А. В. Малышев.
КВАДРАТНОГО КОРНЯ МЕТОД — метод решения
системы линейных алгебраич. уравнений Ах=Ъ с эрми-
эрмитовой невырожденной матрицей А. Среди прямых ме-
методов он наиболее эффективен при реализации на ЭВМ.
Вычислительная схема метода в общем случае осно-
основана на факторизации эрмитовой матрицы А в виде
A=S*DS, A)
где S — правая треугольная матрица с действительными
положительными диагональными элементами, D — ди-
диагональная матрица с элементами 1 или —1 на диаго-
диагонали. Из A) непосредственно получаются рекуррент-
рекуррентные соотношения для вычисления элементов si/ и da
матриц S и D:
,7 = sign (пц — 2*1\ I ski I2 dkk),
\ B)
После того как факторизация A) выполнена, решение
исходной системы сводится к последовательному реше-
решению двух систем S*Dy=b и Sx=y с треугольными мат-
рицами. В этой части К. к. м. совпадает с обратным
ходом большинства прямых методов решения систем
(см. Гаусса метод).
В действительном случае, когда А — симметрич. мат-
матрица, схема B) соответствует разложению A — S'DS с
действительной матрицей S и несколько упрощается.
Существенное упрощение схемы B) происходит, когда
А — положительно определенная матрица. В этом слу-
случае D = E, A = S*S.
Известны схемы К. к. м. для неположительно опре-
определенных матриц, основанные на факторизации вида
A = S*S. Для вычисления элементов S имеют место ре-
рекуррентные соотношения, аналогичные B). Однако эта
факторизация но эффективна для реализации на ЭВМ
в случае, когда А — действительная матрица, так как
при вычислении матрицы S возможен выход в комплекс-
комплексную арифметику.
Из характеристик К. к. м. важны следующие.
1) Среди прямых методов решения систем, основан-
основанных на факторизации матрицы, К. к. м. обладает самым
высоким быстродействием (в два раза выше, чем у ме-
метода Гаусса).
2) Для факторизации матрицы по К. к. м. достаточно
задавать компактную информацию о матрице в виде эле-
элементов ее треугольной половины. Кроме того, схема B)
позволяет записывать в память ЭВМ матрицу S на
месте исходной информации об А. Это существенно уве-
увеличивает порядок решаемых систем.
3) Вычислительная схема К. к. м. допускает сегмен-
сегментированную обработку исходной матрицы участками из
нескольких последовательных строк. Использование
внешней памяти при этом позволяет решать системы
высокого порядка.
4) К. к. м. сохраняет ленточную структуру матрицы,
т. е. матрица S будет иметь тот же вид, что и верхняя
половина исходной матрицы.
5) Особенно эффективен К. к. м. для систем с поло-
положительно определенными матрицами. В данном случае
нет роста элементов матрицы в процессе вычислений.
Это свойство обеспечивает устойчивость вычислитель-
вычислительного процесса к ошибкам округления. Мажорантная
оценка точности вычисленного решения в этом слу-
случае — минимальная в классе прямых методов. Пониже-
Понижению общего уровня ошибок способствует и возможность
вычисления скалярного произведения векторов в схеме
B) в режиме накопления с удвоенной точностью.
Отсутствие роста элементов в процессе вычислений
делает удобным реализацию К. к. м. на ЭВМ, работаю-
работающих в арифметике с фиксированной запятой.
6) Разложение A) по К. к. м. может быть использо-
использовано для вычисления определителя матрицы, обраще-
обращения матрицы.
Лит.: [1] Воеводин В. В., Численные методы алгебры,
М., 1SH6; [2] Бахвалов Н. С, Численные методы, М.,
1974; [4] У и л к и н с о н Д ж. X., Алгебраическая проблема
собственных значений, пер. с англ., М.. 1970: 14] Воеводин
В. В., Вычислительные основы линейной алгебры, М. 1977.
Г. Д. Ким.
КВАДРАТНОЕ УРАВНЕНИЕ — алгебраическое
уравнение 2-й степени. Общий вид К. у.
ax2+bx+c=0, афО.
В поле комплексных чисел К. у. имеет два решения,
выражающиеся в радикалах через коэффициенты этого
уравнения:
х -Ь ± Vb'- -1щс , ,
1-2 = ja • (*>
При 62>4ac оба решения К. у. действительные и раз-
различные, при !J<4ас решения — комплексные (комп-
(комплексно сопряженные) числа, при 62 = 4ас уравнение
имеет кратный корень хг~х2=—Ь/2а.
Для приведенного К. у.
x*+px+q=0
формула (*) имеет вид
1Г — 9-
Корни и коэффициенты К. у. связаны соотношени-
соотношениями: Xj+a;2=——, х1х2= — (Виета теорема).
О. А. Иванова.
КВАДРАТРИСА — плоская кривая, используемая
для решения задачи квадратуры круга. Напр.: Дино-
страта квадратриса, кохлеоида, квадратриса
Чирнгаузена:
квадратриса Оцанама:
о: = 2а sin2 f- .
la
А. Б. Иванов,
КВАДРАТУРА — 1) Построение квадрата, равнове-
равновеликого данной фигуре (см., напр., Квадратура круга).
2) Вычисление площади или интеграла (от функции од-
одного переменного).
КВАДРАТУРА КРУГА — задача на построение
квадрата, равновеликого данному кругу; одна из клас-
сич. задач древности на точное построение циркулем и
линейкой. Сторона квадрата, равновеликого кругу ра-
радиуса г, равна г У п. Таким образом, задача о К. к. сво-
сводится к следующей: построить отрезок длины Ул. Такое
построение неосуществимо с помощью циркуля и ли-
линейки, так как ,ч — трансцендентное число, что было
доказано в 1882 Ф. Линдеманом (F. Lindemann). Однако
задача о К. к. разрешима, если расширить средства по-
построения, напр., используя нек-рые трансцендентные
кривые, наз. квадратрисами.
Лит.: [1] Энциклопедия элементарной математики, кн. 4,
Геометрия, М., 1963, с. 205—27. Е. Г. Соболевская.
КВАДРАТУРНАЯ ФОРМУЛА — приближенная фор-
формула для вычисления определенного интеграла:
РИ/ (x)dx~^_Cjf(zj); A)
в левой части стоит интеграл, подлежащий вычислению.
Подинтсгральная функция записана в виде произведе-
произведения двух функций. Первая из них р (х) считается фик-
фиксированной для данной К. ф. и наз. весовой ф у н к-
ц и е й, функция f(x) принадлежит достаточно широ-
широкому классу функций, напр, непрерывных и таких,
что интеграл в левой части A) существует. Сумма в пра-
правой части A) наз. квадратурной суммой,
числа Xj наз. узлами К. ф., а числа Су — коэф-
коэффициентами К. ф. Нахождение приближенного
значения интеграла с помощью формулы A) сводится к
вычислению квадратурной суммы; при этом значения
узлов и коэффициентов обычно берутся из таблиц (см.,
напр.. [3]).
Наибольшее распространение получили К. ф., осно-
основанные на алгебраическом интерполировании. Пусть
х., . . ., хх— попарно различные точки (обычно ж/?[я,
Ь], хотя это требование не является обязательным) и
Р(х) — интерполяционный многочлен функции f(x),
построенный по ее значениям в этих точках:
здесь L,-(x) — многочлен влияния г'-го узла: Ь,-(х/)—5,у
(б,-у — символ Кронекера). Интеграл по [а, Ь] от
p(x)f(x) приближенно заменяется интегралом от
р(х)Р(х); получается приближенное равенство вида
A), в к-ром
^b (x)Li(x)dx, j = l, 2, ..., N. B)
Существование интегралов в B) равносильно существо-
существованию моментов весовой функции
pk=^ba p (х) х* dz, k = O,l,...,JV
(здесь и далее предполагается, что требуемые моменты
р (х) существуют, в частности в случае р(ж) = 1 проме-
промежуток [а, Ь] считается конечным).
К. ф. A), коэффициенты к-рой определяются равенст-
равенствами B), наз. интерполяционной. Целое чис-
число d^O наз. алгебраической степенью
точности К. ф. A), если эта формула точна, когда
f(x) — любой многочлен степени выше d, и не точна для
f(x) = xd + x. Чтобы К. ф. A) была интерполяционной, не-
необходимо и достаточно, чтобы для ее алгебраич. степени
точности d выполнялось неравенство d'^N—1.
Пусть р(х)=1 и [а, Ь] конечен. Интерполяционная
К. ф. с равноотстоящими узлами
Tj = a — ih, } = 0, 1, ..., п, h = {b—a)jn, C)
где п — натуральное число, iV=ra+l, наз. Ньютона —
Нотеса квадратурной формулой; такая К. ф. имеет
алгебраич. степень точности d = re при п нечетном и
d=re+l при п четном. Интерполяционная К. ф. с одним
узлом
наз. прямоугольников формулой, ее алгебрапч. степень
точности d=i, когда % = (а-\-Ь)/2, н d = Q в остальных
случаях.
Пусть
р (х)^0 на [а, Ъ], ц0 > 0 D)
Интерполяционная К. ф. A), у к-рой узлами являются
корни ортогонального на [а, Ь] с весом р (х) многочлена
степени N, наз. квадратурной формулой
гауссова типа; ее называют также квадратур-
квадратурной формулой наивысшей алгебраич. сте-
степени точности, так как при условиях D) ника-
никакая К. ф. с N узлами не может быть точна для х-'х. Наи-
Наиболее употребительны К. ф. гауссова типа, к-рые опре-
определяются следующими частными случаями веса р (х) и
промежутка [а, Ь]:
вес Якоби A—х)аA+х)?> (а> —1, Р> —1), [ —1, 1]
при значениях параметров: a) a~fi = O (Гаусса квадра-
квадратурная формула), б) а=E=—1/2 (Мелера квадратурная
формула), в) а=Р = 1/2, г) а= —р = 1/2;
вес Эрмита е—х" (— оо, +°°);
вес Лагерра хае~х(а> — 1), @, +оо).
Существуют К. ф., в к-рых часть узлог. заранее фик-
фиксирована, а остальные узлы выбираются так. чтобы
К. ф. имела наивысшую алгебраич. степень точности.
Таковы, в частности, Лобатто квадратурная формула
и Радо квадратурная формула для вычисления интег-
интеграла по [ — 1, 1] с весом 1. В первой из них фиксирован-
фиксированными узлами являются —1, 1, а во второй — одна иа
этих точек.
Две К. ф. с весом 1
d S^^^iГ/ф(Т/)
наз. подобными, если tj—c=s(xj—у), Cj—sT ¦, j-—l, 2r
. . ., т, где s определяется равенством d—c=sF—у).
В случае конечного [а, Ь]
где х; определяются равенствами C). Если для вычис-
вычисления интегралов по промежуткам [ж,-, #/ + i] применя-
применяются К. ф., подобные одной и той же К. ф., то равенст-
E) приведет к составной К. ф. для вычисления
интеграла, стоящего в левой его части. Такова, напр.,
составная К. ф. прямоугольников:
—1) А), Ша,
В случае Ъ—а=2я эта К. ф. точна для cos kx, sin kx при
Л = 0, 1, ..., /г—1.
Можно рассматривать интерполяционные К. ф., к-рые
получаются интегрированием интерполяционного мно-
многочлена Эрмита функции f(x). В квадратурную сумму
такой К. ф. входит не только значение самой функции
в узле, но и значения ее последовательных производных
до нек-рого порядка. Значения производных подинтег-
ральной функции на концах промежутка интегрирова-
интегрирования используются и в Эйлера —• Маклорена формуле.
Для погрешности К. ф. A)
p и / (*)dx- S/=i °jf (*/)
имеются представления, в к-рые входит производная
JU">(x). Эти представления мало пригодны для фактиче-
фактической оценки R(f), так как при этом требуется оценка
производной f{ri(x). Погрешность R (/) является адди-
аддитивным и однородным функционалом на векторном про-
пространстве функций, для к-рых она определена.
Другой подход основан на минимизации нормы функ-
функционала погрешности R (/) построению К. ф.
Пусть R (/) — погрешность К. ф., к-рая точна для
всех многочленов степени не выше ;—1, при этом [а, Ь] =
= [0, 1] и p(x)=i, и W-p (<7>1, г — натуральное чис-
число) — векторное пространство функций f(x), к-рые на
{0, 1] имеют абсолютно непрерывную производную по-
порядка г—1 и суммируемую со степенью q производную
порядка г. Две функции из WlP считают эквивалент-
эквивалентными, если их разность есть многочлен степени не выше
г—1. Множество классов эквивалентности (факторпрост-
ранство W-n по векторному пространству многочленов
степени не выше г—1) является векторным пространст-
пространством, к-рое обозначают L(rK В L(r> можно ввести норму,
полагая для класса ???)
def def / /. i -, l/q
\ \\f()kl\\fw()\Qd\
где / — любая функция, принадлежащая г|\ Функцио-
Функционал погрешности К. ф. рассматривают на LlP, полагая
if A|з)=Л (/), /6Ч1- Функционал ЛA|з) непрерывен в ли-
жейном нормированном пространстве L(!">. Его норма
\\R\\ характеризует точность К. ф. для всех функций из
Win: для любой fQ_W<n справедливо неравенство
\R(f)\<L\\R\V\\i^\\L ,
я
it-poe является точным. Ясно, что \\R \\ есть функция
параметров xk, ck, /r=l, 2, . . ., JV, К. ф., и естественно
ш.ттаться их выбрать так, чтобы ||Я|| принимала наимень-
наименьшее значение. Это приводит к такой К. ф. (из класса
рассматриваемых), погрешность к-рой имеет минималь-
минимальную оценку для всех функций пространства W(P. Та-
Таким образом, построение К. ф. сводится к решению экс-
экстремальной задачи. Эта задача уже в рассмотренном
частном случае весьма сложна и ее решение получено
A978) лишь при г=1 и г=2.
Лит.: [1] Крылов В. И., Приближенное вычисление
интегралов, 2 изд., М., 1967; [2] Никольский С. М.,
Квадратурные формулы, 2 изд., М., 1974; [3] К р ы л о в В. И.,
Шульгина Л. Т., Справочная книга по численному ин-
интегрированию, М., 1966. И. П. Мысовских.
КВАДРАТУРНЫХ СУММ МЕТОД — метод аппрок-
аппроксимации интегрального оператора при построении чис-
численных методов решения интегральных уравнений.
Простейший вариант К. с. м. состоит в замене интег-
интегрального оператора, напр, вида
К (х, s) ф (s) ds
в интегральном уравнении
Лф (х) -j- \ К (х, s) ф (s) ds = f (s)g
на оператор с конечномерной областью значений по
правилу
; к (х, S) ф (»)» 2Г=, а^>к (*• ч) ф (»')• (*)
Интегральное уравнение в свою очередь аппроксими-
аппроксимируется линейным алгебраич. уравнением
В правой части приближенного равенства A) стоит квад-
квадратурная формула для интеграла по s. Возможны раз-
разнообразные обобщения аппроксимации A) вида:
(х, s) ф (s) ds я: \j. ai (х) ф (si')i B)
где af.N)(x) — некоторые функции, строящиеся по ядру
К(х, s). К. с. м., обобщенный в виде B), может приме-
применяться при аппроксимации интегральных операторов
с особенностями в ядре и даже сингулярных интеграль-
интегральных операторов.
Лит.; [1] Канторович Л. В., Крылов В. И.,
Приближенные методы высшего анализа, 5 изд., М.— Л., 19В2.
А. Б. Бакушинский.
КВАДРИКА — 1) К.— поверхность 2-го порядка.
В трехмерном пространстве (проективном, аффинном
или евклидовом) К. есть множество точек, однородные
координаты х0, хх, х2, х3 к-рых (относительно проектив-
проективной, аффинной или декартовой системы координат)
удовлетворяют однородному уравнению 2-й степени:
Билинейная симметричная форма
наз. полярной формой относительно F(x).
Две точки М'(х'о, х[, х'2, х'3), М"(х"й, x"v x"v x?, для кото-
которых Ф (х', х")=0, наз. полярно сопряженны-
сопряженными точками относительно К. Если прямая (М',
М") пересекает К. в точках Nlt N2 и точки М', М" по-
полярно сопряжены относительно К., то точки Nx, N2 и
М', М" образуют гармоническую четверку. Точки К.
и только они являются самосопряженными. Прямая,
каждая точка к-рой принадлежит К., наз. прямолиней-
прямолинейной образующей К. Полюсом данной плоскости от-
относительно К. наз. точка, полярно сопряженная со все-
всеми точками этой плоскости. Множество точек простран-
пространства, полярно сопряженных с данной точкой М' отно-
относительно К., наз. полярой точки М' относительно
К. Касательная плоскость к К.— поляра точки каса-
касания. Поляра точки М' определяется линейным уравне-
уравнением Ф (х, а;') = 0 относительно координат х0, хг, х2, х3.
Если Ф(х, х')^0, то поляра точки М' —плоскость;
если ф (х, a;')sE=O, то поляра точки М' — все простран-
пространство. В этом случае точка М' принадлежит К. и наз. ее
особой точкой. Если число i? = rang(a,y)=4, то
К. не имеет особых точек и наз. невырождающейся К.
В проективном пространстве это — мнимый овалоид,
действительный овалоид или линейчатая К. Невырож-
дающаяся К. определяет корреляцию — биективное
отображение множества точек проективного простран-
ства на множество плоскостей. Линейчатая невырожда-
ющаяся К. имеет два различных семейства прямолиней-
прямолинейных образующих, расположенных на К. так, что всякие
две прямые одного семейства не пересекаются, а две
прямые разных семейств пересекаются в одной точке.
Если Д=3, то К. является конусом (действительным
или мнимым) с вершиной в единственной особой точке.
Действительный конус имеет единственное семейство
прямолинейных образующих, проходящих через его
вершину. Если Д = 2, то К. распадается на пару пло-
плоскостей (действительных или мнимых), пересекающихся
по прямой, состоящей из особых точек. Если Д=1, то
К. является сдвоенной действительной плоскостью, об-
образованной особыми точками К. Аффинные свойства К.
выделяются спецификой расположения К., ассоцииро-
ассоциированных с Ней точек, прямых и плоскостей относительно
выделенной плоскости хо=О — несобственной плоско-
плоскости. Напр., эллипсоид (гиперболоид, параболоид) —
невырожденная К., не пересекающая (пересекающая,
касающаяся) несобственную плоскость. Центр К.—
полюс несобственной плоскости; диаметр — пря-
прямая, полярно сопряженная несобственной прямой.
Лит.: [1] Фиников С. П., Аналитическая геометрия,
2 изд., М., 1952; [2] Ефимов Н. В., Краткий курс анали-
аналитической геометрии, 5 изд., М., 1960. В. С. Малаховский.
2) К. в алгебраической геометрии —
проективное алгебраическое многообразие, определяе-
определяемое однородным квадратным уравнением
2" /=ой'
в проективном пространстве Рп над основным полем к.
Пусть далее основное поле алгебраически замкнуто с
характеристикой, не равной 2. Пусть Q — К. в Рп и
s(Q) — множество ее особых точек. Тогда s(Q) — пустое
множество, если и только если rk (Q)=n-\-i, где rk (Q) —
ранг соответствующей квадратичной формы. Если s(Q)
не пусто, то Q — конус над гладкой К. размерности
rk(Q) — 1, вершиной к-рого является проективное под-
подпространство s(Q) в Рп размерности n—rk(Q). Все К. с
rk(Q)=r проективно эквиваленты К.
z:l **=«•
Пусть s(Q) пусто и EczQ — линейное подпространство
максимальной размерности (оно наз. образующей
квадрики Q), тогда
а) если dim Q=2m, то dim Е— т;
б) если dim Q=2m-\-l, то dim E=m.
Кроме того, семейство всех подпространств Е макси-
максимальной размерности на Q является замкнутым неосо-
неособым подмножеством G грассманова многообразия под-
подпространств размерности dim E в Р", причем, если
dim Q=2m, то G=GjlJG2; G,-, i=l, 2,— непересекаю-
непересекающиеся неособые неприводимые рациональные многооб-
многообразия одинаковой размерности (J!+1), a E и Е' принад-
принадлежат одной и той же компоненте, если и только если
dim (Ef]E') == dim E (mod 2).
Если же dim Q=2m-\-i, то G является неособым и не-
неприводимым рациональным многообразием размерности
(т+2)
В случае, когда s(Q) пусто и dim Q=2, Q^,P1XP1;
если же dim Q=?2, то Pic((?)^=Z.
Любая К. рациональна: бирациональный изомор-
изоморфизм К. Q с проективным пространством задается стере-
ографич. проекцией К. Q из нек-рой точки q(:Q,
q(f,s(Q). Многообразия, являющиеся полными пересече-
пересечениями К., изучаются с точки зрения бирациональной
геометрии [3]. Пересечения двух К. изучены в [2],
трех — в [4].
Любое проективное многообразие X может быть так
погружено в проективное пространство PN (для доста-
достаточно большого N), что его образ является пересечением
(как правило, неполным) К., его содержащих [1].
Изучение К. над незамкнутыми нолями тесно связано
с арифметикой квадратичных форм.
Лит.: [1] Mumford D., С. I. M. E. Ill ciclo. Varenna,
1969, Roma, 1970, p. 29 — 100; [21 Reid M., The complete
intersection of two or more quadrics, These D. Ph. Cambridge
Univ., 1972; [3l Roth L., Algebraic threefols (with special
regard to problems of rationality), B.—Hdlb.—N.Y., 1955;
[4] Тюрин А. Н., «Успехи матем. наук», 1975, т. 30, Хг 6,
с. 51—99. В. А. Псковских.
КВАДРИРУЕМОСТЬ — измеримость по Жордану
множества на плоскости (см. Жордана мера). Не всякая
область (т. е. открытое связное множество) и даже но
всякая жордаиова область (т. е. область, имеющая своей
границей простую замкнутую кривую) квадрируема.
С другой стороны, множество, граница к-рого спрямляе-
спрямляемая кривая, квадрируемо.
Лит.: [1] Никольский С. М., Курс математического
анализа, т. 2, М., 1973. В. В. Сазонов.
КВАЗИАБЕЛЕВА ФУНКЦИЯ — обобщение абеле-
вой функции. Мероморфная в комплексном пространстве
С", п>1, функция f(z), 2=(z1, . . ., zn), наз. к в а з и-
абелевоп функцией, если она имеет т, 0<
<т<2я, линейно независимых периодов; в случае абе-
левых функций т=2п. К. ф. могут рассматриваться как
предельный случай абелевых функций, когда нек-ры&
периоды неограниченно возрастают.
Лит.: [ll Severi F., Funzioni quasi-abeliane, Roma,
1947. E. Д. Соломепцев.
КВАЗИАНАЛИТИЧЕСКИЙ КЛАСС функций —
класс функций, характеризуемый свойством единствен-
единственности: если две функции класса совпадают «в малом»,
то они тождественны. Простейшим К. к. является
класс функций, аналитических на отрезке [а, Ь] дейст-
действительной оси (функция этого класса представляется в
достаточно малой окрестности каждой точки отрезка ря-
рядом Тейлора): если две аналитические на [а, Ъ] функции
равны на интервале (а, E)с[а, 6], то они тождественны
[совпадение «в малом» здесь означает равенство функ-
функций на внутреннем интервале (а, E)]. Совпадение «в ма-
малом» для аналитич. функций может означать и равенст-
равенство функций вместе со всеми производными в нек-рой точ-
точке х0, 0<x0^b. Из совпадения «в малом» в этом новом
смысле также следует тождественность функций на всем
отрезке.
Э. Борель (Е. Borel) обнаружил, что свойство единст-
единственности может иметь место не только для аналитич.
функций. В связи с этим Ж. Адамар (J. Hadamard, 1912)
поставил следующую проблему. Пусть {Мп} — после-
последовательность положительных чисел и [а, Ь] — некото-
некоторый отрезок действительной оси. Пусть С{Мп} — мно-
множество бесконечно дифференцируемых на [а, Ъ] функций
}(х) таких, что
|/(п) (х) \<К"М„, a^xs^b, 7i = 0, 1, 2, ...,
где K=K(f) — постоянная, не зависящая от п. При
этом функция f(x) является аналитической на [а, Ь] тог-
тогда и только тогда, когда при некотором K=K(f)
|/(п) (ж) | < Кпп\, а<а-<6, га = 0, 1, 2, ... A)
Таким образом, класс аналитических на [я, Ь] функций
есть класс С{п\]. Проблема Адамара состоит в указании
условий на числа Мп таких, чтобы всякая функция из
класса С{Мп}, обращающаяся в нуль вместе со всеми
своими производными в нек-рой точке а0, а<:ао<:Ь. была
тождественно равна нулю (или, что то же, чтобы две-
функции из С{Мп}, равные вместе со всеми производ-
производными в точке а0, были всюду равны). Класс С{Мп} с та-
таким свойством наз. кваз и аналитическим;
н а [а, 6]. Класс С{п\}, согласно сказанному выше,—
квазианалитпческий на [а, Ь].
А. Данжуа (A. Denjoy, 1921) привел достаточные усло-
условия квазианалитичности. Он указал, что если
Мп = п\ (In га)», Мп = п\ (In га)» (In lnre)«, ...,
то С{Мп} — квазианалитический (эти классы, в силу
{1), шире класса аналитич. функций).
Т. Карлеман (Т. Carleman) полностью решил пробле-
проблему Адамара, дав необходимые и достаточные условия
квазианалитичности. Эти условия в дальнейшем видоиз-
видоизменялись. Теорема Данжуа — Карле ма-
на о квазианалитичности формулируется
так: каждое из следующих условий является необходи-
необходимым и достаточным для квазианалитичности класса
с{мпу.
а) если положить
ТО
б) если положить
Т (г) = sup ?- ,
то
в) либо
lim M\ln < оо,
либо
lim М\!п = оо
П -»- СО ,
-^-=00.
где {М'п} — выпуклая регуляризация посредством ло-
логарифмов последовательности {Мп}. [Условие а) наз.
условием Карлемана, б) — условием
Островского, в) — условием Банта —
М андельбройта].
В случае Мп=п\=пп/(е-\-е.п)п (е„—>-0 при п—>-оо) имеем
Р„«п/е, выполняется условие а), и снова получаем, что
С{п\} — квазианалитич. класс. В случае Мп=п\(\п п)п
имеем $п~(п In n)/e, выполняется условие а) и потому
класс Данжуа С {re! (In re)™} — квазианалитпче-
ский. В случае Мп=п\ Aп1+еге)п, е>0, имеем
вследствие чего С{Мп] — не К. к.
С. Н. Бернштейн ввел другие К. к. функций. Он по-
показал, что функция f(x) является аналитической на от-
отрезке [а, Ь] тогда и только тогда, когда
ЕпA) < Мр", п = 0, 1, 2, ..., р < 1,
где M=M(f\ и р = р(/) не зависят от п, a En(f) — наи-
наилучшее приближение функции / (х) на [а, Ь] многочле-
многочленами степени п. Имея это ввиду, он рассмотрел класс
функций f(x) на [а, Ь], удовлетворяющих условию
En(i) < Мр", р < 1, п = пъ п2, ..., B)
где п1, ;?„, ... — некоторая бесконечная возрастающая
последовательность целых чисел, и доказал, что если на
нек-ром интервале (а, $)а[а, Ь] функция этого класса
равна нулю, то она тождественно равна нулю. Класс
функций С, заданных на [а, Ь], наз. квазианали-
квазианалитическим (по Б е р н ш т е й н у), если ¦ две
функции этого класса, совпадающие в нек-рой частя
(а, Р)с[а, Ь], необходимо совпадают на всем отрезке
[а, Ъ]. Класс B) — квазианалитический в этом смысле.
Следует заметить, что из условия B) не вытекает, что
f(x) — бесконечно дифференцируемая функция (имеют-
(имеются соответствующие примеры).
Изучаются и другие проблемы квазианалитичности.
Напр., решается вопрос о скорости убывания коэффи-
коэффициентов ап и Ьп в ряде
/ И = 2Г=о (пп C0S пх+Ъп sin лх)'
при к-рой класс таких функций квазианалитический;
находятся условия на числа Мп такие, чтобы функций
/(z), аналитические в круге |z[<l, бесконечно диффе-
дифференцируемые в замкнутом круге \z\ <:1 и удовлетворяю-
удовлетворяющие условиям
|/<«)(г)|</С"Мп, п = 0, 1, 2, ..., |z|<l,
образовывали К. к., и т. д.
Лит.: [1] Берн штейн С. Н., Собр. соч., т. 2, М.,
1954; [2] М а н д е л ь б р о й т С, Квазианалитические классы
функций, пер. с франц., Л.— М., 1937; L3] его же, Примы-
Примыкающие ряды, регуляризация последовательностей. Примене-
Применения, пер. с франц., М., 1955. А. Ф. Леонтьев.
КВАЗИАФФИННАЯ СХЕМА — схема, изоморфная
открытой квазикомпактной подсхеме аффинной схемы.
Квазикомпактная схема X квазиаффинна, если выпол-
выполняется любое из следующих условий: канонический
морфизм X—>-Spec Г(Х, Qx) является открытым вложе-
вложением; любой квазикогерентный пучок бх"М0ДУлей по-
порождается глобальными сечениями. Морфизм схем
f : X—>Y наз. кваз и аффинным, если для любой
открытой аффинной подсхемы U в Y прообраз f~1(U)
Является К. С. В. И. Данилов.
КВАЗИГЕОДЕЗИЧЕСКАЯ ЛИНИЯ, квазигео-
дез и ческа я,— кривая на поверхности, на любом
отрезке к-рой повороты справа и слева имеют одинако-
одинаковый знак (см. Извивание кривой). Напр., ребро лин-
линзы — К. л.
Класс К. л. существенно дополняет класс геодезич.
линий, делая его семейства (ограниченные по длине и
расположению) компактными. В двумерном многооб-
многообразии М ограниченной кривизны из каждой точки в
каждом направлении идет хотя бы одна К. л.; она всегда
может быть продолжена. Отрезки К. л. (в пределах
к-рых на М нет точек с кривизной 2я) суть пределы
геодезических, лежащих на гладких поверхностях, пра-
правильно сходящихся к М.
Лит.: [1] Александров А. Д., Б у р а г о Ю. Д.,
«Тр. матем. ин-та АН СССР», 1965, т. 76, с. 49—63.
-В. А. Залгаллеъ.
КВАЗИГИПЕРБОЛИЧЕСКОЕ ПРОСТРАНСТВО -
проективное «-пространство, в к-ром метрика опреде-
определяется абсолютом, заданным совокупностью абсолют-
абсолютного конуса Qa индекса к с (п—т-—1)-вершиной (абсо-
(абсолютная плоскость То) и (п—m—2)-квадрикой (абсолют-
(абсолютная квадрика Qr) индекса I на этой (п—m—1)-плоско-
сти. Определяемое таким образом пространство наз.
кваз и гиперболическим пространст-
пространством индексов к и I, обозначается символом !ilSm, где
т<«. К. п. является частным случаем полугиперболиче-
ских пространств. К. п. Ы8™ получается предельным
переходом из гиперболич. пространства lSn таким об-
образом, что при этом абсолют гиперболич. пространства
переходит в абсолют К. п.
При т=0 конус Qu является парой слившихся пло-
плоскостей, совпадающих с плоскостью То, а абсолют про-
пространства совпадает с абсолютом псевдоевклидова про-
пространства lRn. При т=1 конус Qo является парой дей-
действительных плоскостей; в частности, для usl плоскость
То является прямой пересечения этих двух плоскостей,
а квадрика Q1 — парой точек на прямой То. В случае
m = re—1 конус Qo имеет точечную вершину, и абсолют
пространства klS'^~1 совпадает с абсолютом копсевдоев-
клидова пространства lR*n.
К. п. являются пространствами более общего проек-
проективного типа по отношению к копсевдоевклидовым про-
пространствам.
Проективная метрика К. п. klS'™ определяется таким
образом, чтобы при т=0 получалась метрика псевдо-
псевдоевклидова пространства lRn, а при т=ге—1 — метрика
копсевдоевклидова пространства kR*n-
В К. п. различают прямые четырех типов: эллип-
эллиптические прямые, пересекающие абсолютный
конус в двух мнимо сопряженных точках; гиперболи-
гиперболические прямые, пересекающие абсолютный конус
в двух действительных точках; параболиче-
параболические прямые, проходящие через вершину абсо-
абсолютного конуса; изотропные прямые, про-
проходящие через вершину абсолютного конуса и касаю-
касающиеся его.
Расстояние б между двумя точками X и У опреде-
определяется в случае, когда прямая XY не пересекается с
(в—т— 1)-плоскостыо Го, с помощью соотношения
cos2 — = (¦у0?°?^J
где Ео — линейный оператор, определяющий скалярное
произведение в псевдоевклидовом (т-|-1)-пространстве
kRm + i', oc°=(xa, a^im), ?/°=(yb, 6<m) — векторы точек
X и Y, р — действительное число. Расстояние между
двумя точками, не лежащими на параболич. прямой,
равно расстоянию между проекциями этих точек на т-
плоскость жх=0 в направлении (п—т—1)-плоскости То.
В случае, когда прямая XY пересекает (п—m—^-пло-
(п—m—^-плоскость То, то расстояние d вычисляется с помощью раз-
разности а=7/1—аз1, где жх—(хи, u>m); y1=(yv, v>m) —
векторы точек X и Y в псевдоевклидовом пространстве
Rn-m; d(XY) = aE1a, здесь Et— линейный оператор,
определяющий скалярное произведение в этом прост-
пространстве.
За угол между двумя плоскостями пространства
klS™ принимается (нормированное) расстояние между
двумя соответствующими точками в двойственном ему
пространстве ikgn-m-i по принципу двойственности
проективного re-пространства. Координаты этих точек
численно равны проективным координатам данных пло-
плоскостей. В случае, когда (и—2)-плоскость пересечения
двух данных плоскостей пересекается с (п—т—1)-
плоскостью То, этот угол всегда равен нулю, но тогда
применяется способ измерения, аналогичный измере-
измерению расстояний в подобном случае. В частности, при
п = 2 углы между 1-плоскостями являются углами меж-
между прямыми и, в зависимости от расположения 2-пло-
скости относительно плоскости То, на этой плоскости
возможны три типа геометрий — евклидова, псевдо-
псевдоевклидова или копсевдоевклидова.
Движениями К. п. являются коллинеации, сохра-
сохраняющие расстояние между точками и переводящие аб-
абсолютный конус Qo, (п—m—1)-вершину То и(п—m—2)-
квадрику Qx в То в себя. Движения описываются псевдо-
псевдоортогональными операторами индекса I. В К. п. llSt2m + \,
двойственном самому себе, определяется к о д в и ж е-
н и е — корреляция, переводящая всякие две точки в
две плоскости, угол между к-рыми пропорционален рас-
расстоянию между двумя данными точками, а всякие две
плоскости — в две точки, расстояние между которы-
которыми пропорционально углу между плоскостями. Ко-
движения описываются псовдоортогональными опера-
операторами индекса I. Движения образуют группу Ли, как
и движения и кодвпжения двойственного самому себе
К. п.
Квазигиперболическое 3-пространство с проективной
эллиптич. метрикой на прямых — olsl — имеет коевкли-
дову метрику на 2-плоскостях и псевдоевклидову
метрику индекса 1 в связках плоскостей. Квазигипер-
Квазигиперболическое 3-прострапство с гиперболической проектив-
проективной метрикой расстояний может быть двух типов —
10Sl и 1:LSl, отличающихся метриками в связках пло-
плоскостей: в первом — евклидова, во втором — псевдо-
псевдоевклидова метрика индекса 1. Метрика на 2-плоскостях
одна и та же — копсевдоевклидова индекса 1.
Квазигиперболическое 3-пространство u?i может
быть интерпретировано как группа движений псевдо-
псевдоевклидовой 2-плоскости индекса 1. Многообразие ги-
перболич. прямых указанного квазигиперболического
3-пространства допускает интерпретацию на паре таких
псевдоевклидовых плоскостей. Пространства 10Ss и
01S^, двойственные друг другу, допускают интерпрета-
интерпретации на комплексной 2-плоскости.
Лит.: [1] Розенфельд Б. А., Неевклидовы прост-
пространства, М., 1969; [2] Я г л о м И. М., Розенфельд
Б. А., Ясинская Е. У., «Успехи матем. наук», 1964,
т. 19, в. 5, с. 51 — 113. Л. А. Сидоров.
КВАЗИГРУППА — множество с одной бинарной
операцией (наз. обычно умножением), в к-ром каждое из
уравнений ах~ Ь и г/а= Ъ имеет единственное решение
для любых элементов а, Ъ этого множества. К. с едини-
единицей наз. лупой.
К.— естественное обобщение понятия группы. К.
возникают в различных областях математики, напр, в
теории проективных плоскостей, неассоциатпвных тел,
в ряде вопросов комбинаторного анализа и т. п. Термин
«К.» введен Р. Муфанг (R. Moufang); с ее работ по недо-
зарговым плоскостям A935), в к-рых выяснялась связь
таких плоскостей с К., собственно и началось развитие
теории К.
Основные понятия. Отображения Ra : х^>-ха и La: x—t-
—>-ах наз. правой и левой трансляциями
(или сдвигами) относительно элемента а. В К.
трансляции являются подстановками множества ее эле-
элементов. Подгруппа G группы подстановок множества Q,
порожденная всеми трансляциями К. Q(-), наз. груп-
группой, ассоциированной с квазигруп-
квазигруппой <?(•)• Существует тесная связь между строением
группы G и К. (?(¦)•
Гомоморфный образ К., вообще говоря, не К., а
группоид с делением. Гомоморфизмам К. на К. соответ-
соответствуют так наз. нормальные конгруэнции
(конгруэнция Э на Q(-) нормальна, если каждое из со-
соотношений acQbc и caQcb влечет aQb). В группах все
конгруэнции нормальны. Подквазигруппа Н наз. нор-
нормальной, если существует такая нормальная кон-
конгруэнция 6, что Н совпадает с одним из классов кон-
конгруэнции. Существуют К., в к-рых два или даже все
классы по конгруэнции 6 — подквазигруппы.
С каждой квазигрупповой операцией на множестве
связаны еще две операции, наз. левой и правой обрат-
обратной операциями, обозначаемые (/) и (\) соответствен-
соответственно. Они определяются следующим образом: zly=x и
x\z=y, если x-y=z. Рассматривая всевозможные пере-
перестановки трех элементов х, у, z, можно получить пять
обратных операций, не считая исходной. Переход от ос-
основной операции к одной из них наз. парастрофи-
е й. К., в к-рых все обратные операции совпадают с ос-
основной, наз. тотально-симметрически-
м и, или TS-к вазигруппами. TS-квазпгруппы
можно определить также как К., удовлетворяющие тож-
тождествам: ху = ух и х(ху) = у. Идемпотентные TS-квази-
группы (т. е. с дополнительным тождеством х2=х) наз.
квазигруппами Штейнера. Они тесно свя-
связаны с системами троек Штейнера (см. Штейнера сис-
система).
Одним из самых важных понятий в теории К. являет-
является понятие изотопии. Изотопия может быть определена
и для К., заданных на разных (но равномощных) мно-
множествах. Число неизотопных К., к-рые могут быть зада-
заданы на конечном множестве мощности п, известно A978)
только для ге<:8.
Основные классы квазигрупп. Самые первые работы
по К. относятся к таким обобщениям групп, в к-рых
требование ассоциативности заменяется более слабыми
условиями, теперь называемыми постулатами
«А» и «Б» С у ш к е в и ч а. К. удовлетворяет постулату
Сушкевича «А», если решение х уравнения (ab)c=a(bx)
зависит только от Ъ и с, и постулату «Б», если это реше-
решение зависит только от с. Доказано, что К. этих классов
изотопны группам. В случае, когда решение такого
уравнения зависит от а и с, К. наз. левой F-к в а з и-
группо й. Аналогично, при помощи уравнения
(аЪ)с=х(Ьс) определяется правая F-к в а з и г р у п-
п а. К., являющаяся левой и правой F-квазигруппой
одновременно, наз. F-к вазигруппой. Сущест-
Существуют F-квазигруппы, не изотопные группам. Идемпо-
тентная /'-квазигруппа наз. дистрибутивной
квазигруппой и может быть определена тожде-
тождествами:
(yz)x=(yx)(zx), x(yz)={xy)(xz),
наз. тождествами дистрибутивности.
Доказано, что дистрибутивные К. изотопны лупам Му-
фанг (см. Лупа). К. Q (•) м е д и а л ь н а, если выпол-
выполняется тождество
(xy)(uv)=(xu){yv).
Всякая медиальная К. изотопна абелевой группе <?(+)
и изотопия имеет вид
где ф, ijJ — коммутирующие1 автоморфизмы группы, а
с — некоторый элемент Q (теорема Тоёды).
Системы квазигрупп и функциональные уравнения.
Пусть на множестве Q задана нек-рая система К. В этом
случае операции удобнее обозначать буквами: вместо
аЪ=с писать, напр., А (а, Ь) = с. Квазигрупповые опе-
операции на Q предполагаются связанными между собой
нек-рым образом, чаще всего какими-либо тождествами,
называемыми в этом случае «функциональными уравне-
уравнениями». Обычно решается задача нахождения системы
К. на Q по заданным функциональным уравнениям.
Напр., решено уравнение общей ассоциа-
ассоциативности:
A1[A2(x,y),z\ = A3[x,Ai(y,z)], A)
а именно, доказано, что если четыре К. удовлетворяют
A), то они изотопны одной группе (?(•), а общее реше-
решение дается равенствами:
Ai_(x, у)=ах-$у, А^(х, у) = а-1(ц>х-лру),
где а, Р, ф, г)), 0 — любые подстановки множества Q.
Очень похоже решается уравнение общей ме-
диальности:
А1[А2(х, у), А3(и, v)] = Ai[Ab{x, и), Ае(у, v)].
Все шесть К. здесь оказываются изотопными одной абе-
абелевой группе.
»г-арные квазигруппы. Множество с одной ге-арной
операцией наз. re-квазигруппой, если каждое из урав-
уравнений
а^аг . . . aj-1xai + i ... ап = Ъ
(где Ъ, ах, а2, . .. , an?Q, i=\, 2, . .. , re) имеет единст-
единственное решение. На re-квазигруппы переносятся основ-
основные понятия теории К. (изотопия, парастрофия и т. д.).
Каждая ^-квазигруппа изотопна нек-рой re-лупе (см.
Лупа).
Некоторые классы обычных бинарных К. (такие как
классы медиальных, TS-квазигрупп и др.) имеют аналог
в гс-арном случае. Операция А арности п п р и в о д п-
м а, если существуют две такие операции В ж С арно-
арности не меньше двух, что
А (хъ х2, ..., хп) =
= ?(*!, х2, ...,х(_ъ С (xi, ...,xj), xj + u ...,хп)
г
(сокращенная запись А=В-\-С). В противном случае А
наз. неприводимой. Для re-арных К. верна
теорема, аналогичная теореме о канонич. разложении
натурального числа на простые множители.
Комбинаторные вопросы. Таблица умножения конеч-
конечной К., т. е. ееКэли таблица, в комбинаторике известна
под названием латинский квадрат. Одна из задач ком-
комбинаторной теории К.— отыскание систем взаимно ор-
ортогональных К. на заданном множестве — важна для
построения конечных проективных плоскостей. Две К.
А и В, заданные на множестве Q, ортогональны,
если система уравнений А (х, г/) = а, В (х, у)=Ь имеет
единственное решение для любых а и Ъ из Q. Ортого-
Ортогональность конечных К. эквивалентна ортогональности
их латинских квадратов. Доказано, что система взаимно
ортогональных К., определенных на множестве из п
элементов, не может содержать более чем п—1 К.
Другим комбинаторным понятием, связанным с К.,
является понятие полной подстановки. Под-
Подстановка ф К. <?(•) наз. полной, если отображение
ц>':х—>-хц>х также подстановка множества Q. Не всякая
К. обладает полной подстановкой. К., обладающая полной
подстановкой, наз. допустимой. Для допустимой
группы существует ортогональная к ней К., и обратно:
если для группы существует ортогональная к ней К.,
то группа допустима. Если конечная К. порядка п до-
допустима, то из нее специальным процессом (продолже-
(продолжением) можно получить К. порядка п+1.
Алгебраические сети. К. имеют естественную гео-
метрич. интерпретацию с помощью алгебраич. сетей,
называемых также алгебраич. тканями (см. Тканей
геометрия). Алгебраической сетью наз.
множество, состоящее из элементов двух видов — линий
и точек — с некоторым отношением инцидентности ме-
между ними. (Вместо слова «инцидентна» употребляются
также выражения «проходит через», «лежит на».) Пусть
множество линий N разбито на три класса так, что вы-
выполняются аксиомы: 1) две линии из различных клас-
классов инцидентны ровно одной общей точке из N; 2) каж-
каждая точка инцидентна ровно одной линии каждого клас-
класса. Тогда N наз. 3-сетью. Аналогично, разбиением на к
классов могут быть определены fc-сети. Число (мощ-
(мощность множества) линий в каждом классе одинаково и
равно числу (мощности множества) точек любой линии
сети. Оно наз. порядком сети. Сети могут быть
координатизированы с помощью К. следующим обра-
образом. Пусть дана 3-сеть Лг с множеством линий ?х, L2, L3
и Q — множество, мощность к-рого равна порядку сети
N. И пусть фиксированы нек-рые взаимно однозначные
соответствия между Q и каждым из L;, т. е. каждой ли-
линии класса L; дана нек-рая координата в Q. Множество
Q становится К. (координатная квазигруп-
квазигруппа сети), если на нем определить следующую опера-
операцию: xy=z, тогда и только тогда, когда общая точка ли-
линии с координатой х из Ьг и линии с координатой у из
L2 лежит на линии с координатой z из L3. Обратно,
каждая К. является координатной К. некоторой 3-сети.
При различных взаимно однозначных соответствиях
между Q и L[ получаются различные, но изотопные К.
на множестве Q. Каждой 3-сети, в к-рой зафиксирован
порядок классов Llt L2, L3, соответствует класс всех
изотопных между собой К. Перенумерации классов сети
соответствует парастрофия координатных К.
Каждому свойству 3-сети соответствует инвариантное
при изотопии (т. е. универсальное) свойство К. Такими
свойствами являются, напр., замыкания условия, наибо-
наиболее известны из к-рых условия замыкания Томсена,
Рейдемейстера, Бола, шестиугольника. Условие Том-
Томсена для коордипатной К. означает, что из соотношений
ЧУ?.=хъУ\ и х1у3=х3у1 для ее элементов хг, хг, х3, уи у2,
у3 следует соотношение х2у3 = х3у2. В К. выполняется
условие Томсена тогда и только тогда, когда она изотоп-
изотопна абелевой группе. Аналогичные характеристики К.
получены и для других условий замыкания.
А-сети координатизируются с помощью к—2 взаимно
ортогональных К.
Лит.: Ll] Белоусов В. Д., Основы теории квазигрупп
и луп, М., 1967; [2] Итоги науки, Алгебра. Топология. Геомет-
Геометрия, 1965, М., 1967, с. 63—81; [3] В ruck R. H., A Survey
of Binary Systems, 3ed., В., 1971; [4] его же, «Studies in
math.», 1963, v. 2, p. 59—99; [5] Aczel J.,«Adv. Math.», 1965,
V. 1, № 3, p. 383 — 450. В. Д. Белоусов.
КВАЗИДИСКРЕТНЫЙ СПЕКТР — термин эргодич.
теории и топологии, динамики, употребляемый в оборо-
оборотах: «динамическая система (поток, каскад или порож-
порождающее последний преобразование) имеет К. с. (или
является системой, потоком и т. д. с К. с.)».
В эргодич. теории понятие «преобразование с К. с.»
фактически рассматривается только применительно к
эргодич. автоморфизму Т Лебега пространства (X, \х)
(хотя приводимое ниже определение формально годит-
годится и в более общей ситуации). Для Т индуктивно опре-
определяются квазисобственные функции
(к. ф.) и квазисобственные значения
(к. з.) re-го порядка. К. ф. 1-го порядка — это обычные
собственные функции соответствующего оператора
сдвига
UT:f(x)^f(Tx) в L*{X, ц),
т. е. такие ненулевые f?L2(X, |л), что f(Tx)=Xf(x) (поч-
(почти всюду; ниже подобная оговорка опускается), где А, —
некоторая константа (собственное значение; оно яв-
является к. з. 1-го порядка). Если f?L2(X, |л), /фО и
f(Tx) = (f(x)f(x), где ф — некоторая к. ф. re-го порядка,
то / наз. к. ф. (n--f-l)-ro порядка, а ф — соответствую-
соответствующим к. з. (того же порядка). (В [2] вместо к. ф. и к. з.
говорится об обобщенных собственных
функциях иобобщенных собственных
значениях.) Из эргодичности Т следует, что
|/(ж)| = const для любой к. ф. /, а если / еще и к. з., то
|/(ж)| = 1. Поэтому часто в определение к. ф. включают
условие нормировки |/(д:)| = 1. Говорят, что Т и м е е т
К. с, если к. ф. всевозможных порядков образуют пол-
полную систему в L2(X, (л). Законченные результаты отно-
относятся к тому случаю, когда в дополнение к сказанному Т
вполне эргодичен (т. е. все его степени эрго-
дичны). Имеется полная метрическая классификация
таких Т и их свойства хорошо изучены [3]. Понятие
К. с. и соответствующую теорию можно обобщить для
локально компактных коммутативных групп преобра-
преобразований пространств Лебега (в частности, для измери-
измеримых потоков) — см. изложение результатов Т. Уитинга
(Т. Wieting) в [4].
Хотя внешне термин «К. с.» выглядит так, как если
бы речь шла о нек-ром типе спектра динамич. системы,
на самом деле свойство каскада {Тп} иметь К. с. не
является спектральным, т. е. не может быть выражено в
терминах спектральных свойств оператора сдвига Uj.
Даже если известно, что каскад имеет К. с, спектр еще
но определяет однозначно его метрич. свойства. К. с.
иыл введен именно в связи с первым примером метриче-
метрически неизоморфных эргодич. каскадов с одинаковым
спектром ([1], см. также [2]). В этом примере каскады
имеют К. с, но у одного из них имеются к. ф. 3-го по-
порядка, а у другого — нет.
В топология, динамике понятие К. с. вводится при-
применительно к гомеоморфизму Т компакта X, предпола-
предполагаемому вполне минимальным (т. е. каждая
его степень минимальна). К. ф. и к. з. определяются
аналогично предыдущему с заменой TJ(X, ц) на С (X)
(непрерывные функции с комплексными значениями).
Т имеет К. с, если к. ф. разделяют точки X. Топологич.
вариант теории во многом аналогичен метрическому
(см. [5] — [7]). Однако при переходе в топологич. теории
от каскадов к потокам с К. с. требуются существенно
иные соображения и даже в нек-рой степени приходится
выходить за рамки обычных понятий топологич. дина-
динамики (оказывается целесообразным рассматривать по-
потоки {Tf} с разрывной зависимостью гомеоморфизмов
Tt от t) (см. [8], [9]).
Лит.: [1] Н а 1 m о s P. R., Neumann J., «Ann.
Math.», 1942, v. 43, №2, p. 332—50; [2] Халмош П. Р.,
Лекции по эргодической теории, М., 1959; [3] Абрамов
Л. М., «Изв. АН СССР. Сер. матем.», 1962, т. 26, № 4, с. 513—
30; [4] Z i m m е г R. J., «111. J. Math.», 1976, v. 20, № 4,
p. 555—88; [5] Hahn F., Parry W., «,T. London Math.
Soc», 1965. v. 40, № 2, p. 309 — 23; [6] их же «Math, systems
theory», 1968, v. 2, №2, p. 179—90; [7] Brown J. R., Er-
?odic theory and topological dynamics, N.Y.—S.F.—L., 1976;
8] Hahn P., «Israel J. Math.», 1973, v. 16, J« 1, p. 20 — 37;
19] Parry W., там же, р. 38—45. Д. В. Аносов.
КВАЗИДИЭДРАЛЬНАЯ ГРУППА — конечная 2-
группа, задаваемая в образующих х, у определяющими
соотношениями
где т5=4. Порядок К. г. равен 2т\ группа обладает цик-
циклической инвариантной подгруппой индекса 2. Назва-
Название дано по причине сходства определяющих соотноше-
соотношений с определяющими соотношениями диэдра групп,
к-рым, однако, эта группа не изоморфна ни при одном
значении т. К. г. иногда наз. также с е м и д и э д-
р а л ь н о й.
Лит.: [1] Hup pert В., Endliche Gruppen, В., 1967.
Н. Н. Вильяме.
КВАЗИЕВКЛИДОВО ПРОСТРАНСТВО — двумерное
пространство, в к-ром каждое направление, заданное в
его точке, может быть включено в поле, направления
к-рого переносятся параллельно по любому пути (т. е.
К. п. допускает абсолютный параллелизм). Геодезиче-
Геодезические линии К. п. распадаются на оо1 семейств вектор-
векторных линий полей абсолютно параллельных направле-
направлений, причем каждое такое семейство образует с тремя
другими постоянное ангармоническое отношение:
где k = du?ldu1 — угловой коэффициент направления.
Всякое семейство геодезических определяется через три
данных уравнением 1-го порядка:
a duP
= с = const.
Лит.: [1] Н о р д е н А. П., Пространства аффинной связ-
связности, 2 изд., М., 1976. А. Б. Иванов.
КВАЗИИНВАРИАНТНАЯ МЕРА — мера на неко-
некотором пространстве, остающаяся эквивалентной себе
при «сдвигах» этого пространства. Более точно: пусть
(X, В) — измеримое пространство (т. е. множество X с
выделенной ст-алгеброй В его подмножеств) и G — неко-
некоторая группа его автоморфизмов (т. е. взаимно одно-
однозначных преобразований g : X—уХ, измеримых вместе
со своими обратными g-1 относительно а-алгебры В).
Мера (л на {X, В) наз. квазиинвариантной
(относительно G), если при любом g?G преобразованная
мера gix(A)=\n(g-1A), А ?В, эквивалентна мере (л (т. е.
эти меры взаимно абсолютно непрерывны). В случае,
когда X — топологическое однородное пространство с
непрерывной локально компактной группой автомор-
автоморфизмов G (т. е. группа G действует на X транзитивно и
снабжена такой топологией, что отображение GXX—*¦
—>-Х : (g, x)—t-gx непрерывно относительно произведения
топологий в GXX), & В — борелевская о"-алгебра отно-
относительно введенной в X топологии, существует единст-
единственная с точностью до эквивалентности К. м. [1]. В ча-
частности, мера в пространстве R™ квазиинвариантна от-
относительно всех сдвигов х—>~х-\-а, х, a?R", в том и
только том случае, когда она эквивалентна Лебега мере.
В случае, когда группа преобразований не локально
компактна, К. м. может не существовать: это имеет ме-
место, напр., у широкого класса бесконечномерных топо-
логич. векторных пространств [2].
Лит.: [1] Бурбаки Н., Интегрирование. Векторное
интегрирование. Мера Хаара. Свертка и представления, пер.
с франц., М., 1970; [2] Г е л ь ф а н д И. М., В и л е н к и н
Н. Я., Некоторые применения гармонического анализа. Осна-
Оснащенные гильбертовы пространства, М., 1961. Р. А. Минлос.
КВАЗИИНФОРМАЦИОННОЕ РАСШИРЕНИЕ бес-
бескоалиционной ПГры Г= (/, {5,}isJ, {#,}isj) —
бескоалиционная игра Г=(/, {>S,}isJ, {H;}iej), ДЛЯ
к-рой заданы отображения я: S—>-5 и с,-: Si—>-S;, i^
удовлетворяющие при всех i?J, s,^5,-, 3 ?S ус-
условиям: 1) H{=Hi°n, 2) rt,(s||c,(s,)) = s,-, где я,-—ком-
я,-—композиция отображения я и проекции 5->-5,-. К. р. игры Г
может интерпретироваться как результат установления
определенной схемы взаимодействия игроков в процессе
выбора ими своих стратегий s,- в игре Г. Стратегии s; со-
соответствуют правилам, определяющим поведение игро-
игрока г в любой ситуации, с к-рой он может встретиться.
Отображение я сопоставляет набору правил поведения
игроков их реализацию, т. е. набор стратегий s,-, i?/,
к-рые будут выбраны игроками, придерживающимися
данных правил. Условие 1), определения К. р. является
тогда определением функций выигрыша новой игры Г,
а условие 2) выражает сохранение у каждого игрока
старых стратегий Si?S;.
Ситуация s* игры Г тогда и только тогда является об-
образом ситуации равновесия какого-либо К. р. Г игры Г
при соответствующем отображении я, когда для любо-
любого i?J и любой Sj^Si найдется такая ситуация s?S,
что
Я,-(*
Особенно широко понятие К. р. используется в тео-
теории игр с иерархической структурой, где неформальная
задача оптимизации информационной схемы трансфор-
трансформируется в задачу построения К. р. заданной игры,
дающего первому игроку наилучший результат. Рас-
Рассматриваются также классы К. р., удовлетворяющих
условиям, выражающим те или иные ограничения на
информированность игроков. Напр., если Г — игра
двух лиц (J= {1, 2}), то говорят, что в К. р. игрок 1 не
имеет (собственной) информации о стратегии s2, если для
каждой s1^S1 найдется такая Sj^Sj, что я^, S2)—
5 {si)X52. Наилучшим среди К. р., удовлетворяющих
этому условию, является, напр., «игра Г3», в то время
как наилучшим среди всех К. р. является «игра Г2».
Лит.: [1] Герме й ер Ю. Б., Игры с непротивололож-
ными интересами, М., 1976; Г2] Кукушкин Н. С, Моро-
Морозов В. В., Теория неантагонистических игр, ч. 2, М., 1977.
Н. С Нупушкин.
КВАЗИКЛАССИЧЕСКОЕ ПРИБЛИЖЕНИЕ — асим-
асимптотическое представление, асимптотика решений урав-
уравнений квантовой механики при h—y-0 (h — постоянная
Планка). Уравнение Шрёдингера
^ = -^^ + У{х)у, x?Rn, A)
описывает движение квантовомеханич. частицы в по-
тепциальном поле V(x). Движение классич. частицы
описывается уравнением Гамильтона — Якоби
! --(TO) + F(*)=0 B)
или системой Гамильтона
§=* ^ = -^(х). О)
Задаче Кошп для уравнения Шрёдингера
D)
сопоставляется задача Коши для системы C)
x\t=o = y, P\t=o=vSo(y), y?R" E)
(здесь функции ф, So, V — гладкие, So, V — действи-
действительные, ф — финитна). Асимптотика решения ty(t, х)
при h-+b, 0<г<7" и при малых Т>0 имеет вид:
г|з (t, х) ~ exp \±- S (t, s)] ХГ=О <~ "^ Ф/ (t, *), F)
здесь S(t, x) — решение уравнения B) с данными Ко-
Коши S\t=o=S0(x) (классическое действие), а
= Ф @,
где x=x{t, у), р=р (t, у) — решение задачи C), E).
Функции фу при /5=1 определяются из рекуррентной
системы уравнений переноса (это обыкновенные диф-
дифференциальные уравнения вдоль траекторий системы
C)), так что все члены асимптотики выражаются в тер-
терминах классич. механики. Принцип соответствия Бора
утверждает: «Если h стремится к нулю, то квантовые
законы должны переходить в законы классические».
Метод отыскания асимптотики в виде F) был предложен
П. Дебаем (P. Debye) и широко применяется в кванто-
квантовой механике.
Асимптотика решения задачи A), D) в большом (т. е.
за любое конечное время) строится с помощью канонич.
оператора В. П. Маслова [3]. Данные Коши E) заполня-
заполняют ?г-мерное лагранжево многообразие А" в фазовом
пространстве Rj"p. Его сдвиги \'}=gtAn вдоль траекто-
траекторий системы C) — также лагранжевы многообразия;
их объединение Ап + 1= U_O0<t<0C^" есть (ге+1)-мерное
лагранжево многообразие в фазовом пространстве
R2« + 2 с координатами (t, x, р0, р). Для канонич. опера-
оператора К= КАп + 1, отвечающего Ап + \ справедлива фор-
формула коммутации
?/Сф = — ihKq> + O(h*), G)
где ф — производная в силу системы C), L — оператор
Шрёдингера. Асимптотика решения г|з в большом дается
формулой
* С. г) ~
где функции %j определяются из данных Коши D) с по-
помощью уравнений переноса и выражаются в терминах
классич. механики. В нефокальной точке (t0, x°) асимп-
асимптотика имеет вид
где сумма берется по всем лучам, приходящим в эту
точку, S/ и Jj — действие и якобиан для /-го луча,
lj — индекс Морса ;'-го луча. Для стационарного урав-
уравнения Шрёдингера в К. п. исследованы задача о рас-
рассеянии, задача о поле точечного источника, получены
квазиклассич. серии (типа бальмеровских) собственных
значений.
Квази классическое приближение в
широком смысле слова (синонимы: высоко-
высокочастотная асимптотика, коротковолновое приближение,
приближение геометрич. оптики, метод ВКБ, метод эй-
эйконала) — асимптотика решений дифференциальных
уравнений с частными производными с действительными
характеристиками вида
Hx.k-Wx; (iX)-1)u(x)--=0, x?R", (9)
а также систем дифференциальных и псевдодифференци-
псевдодифференциальных уравнений. Здесь X—>-оо — большой параметр,
символ L(x, p; е) слабо зависит от е. Уравнению (9)
отвечают уравнения классич. механики — уравнение
Гамильтона — Якоби
L0(x, VS(x)) = O
и система Гамильтона
dt dp ' dt dx ' ^ I
где L"=L(x, p; 0). К. п. строится с помощью канонич.
оператора, отвечающего инвариантным относительно
дпнамич. системы A0) лагранжевым многообразиям, и
имеет вид, аналогичный (8).
К. п. широко применяется в современной физике, в
задачах о распространении звуковых, упругих, элек-
электромагнитных волн, в нерелятивистской и релятивист-
релятивистской квантовой механике и других вопросах.
Лит.: [1] Б р и л л ю э н Л., Атом Бора, пер. с франц.,
Д.—М., 1935; [2] Ландау Л. Д., Лившиц Е. М.,
Квантовая механика, 2 изд., М., 1963 (Теоретическая физика,
т. 3); [3] М а с л о в В. П., Теория возмущений и асимптоти-
асимптотические методы, М., 1965; [4] Мае лов В. П., Федорюк
М. В., Квазиклассическое приближение для уравнений кван-
квантовой механики, М., 1976; [5] Фок В. А., Проблемы дифрак-
дифракции и распространения электромагнитных волн, М., 1970;
[6] Бабич В. М., Булдырев В. С, Асимптотические
методы в задачах дифракции коротких волн, М., 1972; L7] М а с-
л о в В. П., Операторные методы, М., 1973. М. В. Федорюк.
КВАЗИКОГЕРЕНТНЫЙ ПУЧОК — пучок модулей,
локально задаваемый образующими и соотношениями.
Точнее, пусть X — топологич. пространство и А — пу-
пучок колец на X, пучок „-/-модулей JF наз. к в а з и к о-
герентным, если для любой точки х?X найдется
открытая окрестность U и точная последовательность
пучков (^|;у)-модулей
где I n J — некоторые множества, \и означает ограни-
ограничение пучка на U, а Л*-1*1 есть прямая сумма / экземпля-
экземпляров ,Л- Аналогично определяется К. и. на топологизи-
рованной категории с пучком колец.
Если (X, А) — аффинная схема, то сопоставление
jpi_»r(X,JF) осуществляет эквивалентность категории
квазикогерентных пучков ^/-модулей с категорией
V(X, ^-модулей. Благодаря этому К. п. находят ши-
широкое применение в теории схем. См. также Когерент-
Когерентный пучок. В. И. Данилов.
КВАЗИКОМПАКТНОЕ ПРОСТРАНСТВО — тополо-
топологическое пространство X, в к-ром всякий фильтр имеет
по крайней мере одну точку прикосновения. Этому ус-
условию эквивалентны следующие три условия: 1) всякое
семейство замкнутых множеств в X, пересечение к-рого
пусто, содержит конечное подсемейство с пустым пере-
пересечением; 2) всякий ультрафильтр в X сходится; 3) вся-
всякое открытое покрытие пространства X содержит ко-
конечное открытое покрытие этого пространства (условие
Бореля — Лебега). К. п. наз. компактом (или биком-
бикомпактом), если оно отделимо (или хаусдорфово). Напр.,
всякое пространство, в к-ром имеется только конечное
число открытых множеств, является К. п. В частности,
таково любое конечное пространство. Непрерывный об-
образ К. п. является К. п. Топологич. произведение К. п.
в любом числе есть К. п. (т е о р е м а Тихонова).
Лит,: [1] Б у р б а к и Н., Общая топология. Основные
структуры, пер. с франц., М., 1968. Б. А. Ефимов.
КВАЗИКОНФОРМНОЕ ОТОБРАЖЕНИЕ — отобра-
отображение с ограниченным искажением или ограниченным
отклонением от конформного. Числовой характеристи-
характеристикой искажения при отображении / : D-+D' в точке a?D
является коэффициент k(f, а) квазикон-
квазиконформности (или дилатация) отображения /
в этой точке:
sup \f(x)-f(a)\
k <'' а> = ™ inf |/(х)-/(а)| •
г " \х-а\ = г
Величина
k (/) = sup k (/, х)
наз. коэффициентом квазиконформ-
квазиконформности (или д и л а т а ц и е й) отображения /в об-
области D. Сохраняющее ориентацию отображение
/ : D-+D' наз. квазиконформным (или отоб-
отображением с ограниченным искаже-
искажение м), если к (/)<оо; оно наз. к-к вазиконформ-
н ы м, если fc (/)-<&. Для конформного отображения
/с (/) = &(/, а:)=1. Если / дифференцируемо в точке a?D,
то линейное отображение /' (а) преобразует шар каса-
касательного пространства в эллипсоид, отношением наи-
наибольшей полуоси к-рого к наименьшей будет k(f, a).
Наряду с данным определением часто используются
следующие эквивалентные ему условия квазиконформ-
квазиконформности / в области Z>czR" : /? ~W\ (т. е. / имеет обобщен-
обобщенные производные, локально суммируемые в D в степени
п) и существует такое действительное число к, что
| grad / (х) \" < knn/i det /' (х)
почти во всех точках z?D.
Термин «К. о.», как правило, предполагает гомеомор-
гомеоморфность отображения. Негомеоморфные отображения с
ограниченным искажением обычно наз. квазирегу-
квазирегулярными. Теория К. о. областей в R" при п=2 и
га^З, если не считать общих для них и, как правило,
более простых вопросов, имеет ярко выраженную спе-
специфику.
Двумерная теория. В этом случае диффе-
дифференциал отображения в точке z?D может быть записан
в виде
df(z) = fz{z)dz-\f-(z)dz.
С точностью до множителя он определяется соотноше-
соотношением
Ь(*) = ц (*)/*(*)• A)
Функция fx(z) наз. комплексной характе-
характеристикой отображения /в точке z; 1 ц (z)|<
<1 для отображений с положительным якобианом /=
= |/z]2—\f- |2. Для аналитич. отображений [x(z)=O —
условия Коши — Римана. Коэффициент к (/, z) квази-
квазиконформности отображения в точке выражается через
(x(z) в виде
к U . z) — 1 _ , ц (Z) | '
поэтому условие квазиконформности отображения /?
? W-z в терминах комплексной характеристики есть
IHUDK1.
Обычно соотношение A) появляется как уравнение
относительно / при известной функции ц; оно наз.
уравнением (или системой) Бельтрами.
Напр., задача конформного отображения одной обла-
области D на другую D' есть задача отыскания гомеоморфиз-
ма / : D-*-D', удовлетворяющего в D уравнению Бель-
трами с n(z)=O.
К решению общего уравнения A) сводится, напр.,
классич. задача об одновременном во всей области D
приведении к канонич. виду заданной в D положитель-
положительно определенной квадратичной формы от двух перемен-
переменных или, что то же самое, задача построения конформ-
конформно евклидовых координат на двумерной поверхности
(см. [2]).
Основной факт двумерной теории К. о., аналогичный
Римана теореме для конформных отображений, состоит
в следующем: для всякой измеримой в области DaC
функции |x(z) такой, что ||lu||(xl(Z>)<l, найдется квази-
квазиконформный гомеоморфизм / области D с комплексной
характеристикой \x(z); общее решение уравнения A) в
области D имеет вид Fof(z), где / — построенный ква-
квазиконформный гомеоморфизм, a F — любая аналитич.
функция.
Если D — единичный круг, то / можно выбрать так,
что f(D)=D. Тогда / продолжается до гомеоморфизма
замкнутого круга на себя и условия нормировки/@)=0,
/A) = 1 выделяют единственный гомеоморфизм/ : D-+D,
удовлетворяющий уравнению Бельтрами. Если, кроме
того. n?C'S(D), 0<а<1, m>0, то f?C?+1(D), где
CS.(D) — пространство функций, имеющих в D т не-
непрерывных производных, причем последняя удовлетво-
удовлетворяет в D условию Гёльдера с показателем а. Если по-
последовательность /„ нормированных квазиконформных
автоморфизмов круга D такова, что |jxn(z)[ -<|х<1 и
11Цл1!»(-О)-»-0 при n^-оо, то
II /« (z) — z |]c (Z3) —> о.
К. о. как гомеоморфные решения сильно эллиптических
систем
Ф/ (¦*•, У, и, v, ux, vx\ uy, vy) = 0, i = l, 2, B)
так же естественно связаны с проблемами струйных те-
течений дозвуковой газовой динамики, как конформные
отображения, удовлетворяя системе Кощи — Римана,
связаны с течением несжимаемой идеальной жидкости
(см. [1], [5]).
Общая задача построения К. о. одной односвязной
области на другую, удовлетворяющего системе B), бы-
была поставлена и решена М. А. Лаврентьевым [1] — од-
одним из основателей теории К. о. В явном виде понятие
К. о. появилось у X. Грётша (Н. Grotzsch, см. [3]) в
связи со следующей экстремальной задачей (задачей
Грётша): среди отображений с соответствием вер-
вершин квадрата на прямоугольник, не являющийся квад-
квадратом, найти наиболее близкое к конформному. Чтобы
охарактеризовать меру этой близости, пришлось ввести
коэффициент квазиконформности — начальное поня-
понятие геометрич. теории К. о.
В двумерной теории К. о., как и в теории аналитич.
функций, исследованы общие вопросы компактности —
нормальности семейства отображений; построена тео-
теория соответствия границ, показавшая, что это соответ-
соответствие осуществляется по тем же простым концам в смыс-
смысле Каратеодори (см. Граничные элементы), как и в кон-
конформном случае; изучены условия устранимости множе-
множества особенностей; разработаны вариационные принци-
принципы решения основных экстремальных задач на классе
квазиконформных гомеоморфизмов (см. [4], [7]).
Важное применение в геометрич. теории функций дву-
двумерные К. о. получили в исследованиях по проблеме
модулей римановых поверхностей в связи с Тайхмюллера
пространством и деформацией клейновых групп (см.
[7]).
Пространственная теория. Теория К.
о. областей пространства R", ге^З, также имеет свою
специфику. Прежде всего это связано с отсутствием
конформных отображений: по т е о р е м е Л и у в и л-
л я всякое достаточно гладкое конформное отображе-
отображение области Z>czR", п^З, является м ё б и у с о в ы м,
т. е. суперпозицией инверсий и вращений. Суть этого
факта в том, что условия конформности отображения
при п>3, в отличие от условий К огни — Римана при
п=2, составляют переопределенную систему уравнений
с частными производными.
Ниже указаны нек-рые важные результаты простран-
пространственной теории К. о. Теорема Лиувилля остается в си-
силе как в случае гильбертова пространства, так и при
минимальных априорных условиях регулярности отоб-
отображения. В теореме Лиувилля имеет место устойчивость
в том смысле, что существуют константы к-^ и к2 и функ-
функция Я(е)=0(е) при е-^-0, обладающие следующими свой-
свойствами: а) если y=f(x) есть К. о. шара \х\ <1 с k(f)Kk1,
то существует мёбиусово отображение L (у) такое, что
sup | L о / (х) | < оо,
Iх\ < 1
и образ единичного шара при отображении L°f содержит
шар Ы<1; б) если fc(/)<l+e<&2, то
\Loj (x1)-Lof(Xt) | < к (е) | Xl-xt |аЧ
где
limfe(e) = l и lima(e) = l;
е->-0 е->-0
в) если А(/)<1+8, то
|?о/(*)-*!<;А, (е)
во всем шаре |г|<1. Устойчивость имеет место также в
нек-рых классах областей с нерегулярной границей.
Подобно тому, как 1-квазиконформное отображение
оказывается мёбиусовым даже без априорного предпо-
предположения гомеоморфности, К. о. локально гомеоморфно
как только его коэффициент квазиконформности доста-
достаточно близок к 1. В отличие от плоского случая, всякое
локально гомеоморфное К. о. единичного шара в R",
ге^З, автоматически гомеоморфно в нек-ром шаре Ы<
<:г(;г, й)<1, где г зависит только от размерности я про-
пространства и коэффициента квазиконформности k=k(f)
отображения. В частности, локально гомеоморфное К. о.
всего пространства R", п^З, глобально гомеоморфно и
/(R")=R".
Граничное поведение: если / : R+—>- R+ есть К. о.
полупространства ж„>0 пространства R", п^2, на
себя, то / продолжается до гомеоморфизма замкнутых
областей; при этом индуцированный на границе <?R" =
= R"-1 гомеоморфизм ср : R"-1—^R"-1 в случае гс=2
удовлетворяет ЛГ-условию;
а в случае п^Ъ является квазиконформным. Каждое из
последних двух условий в своей размерности не только
необходимо, но и достаточно для того, чтобы отображе-
отображение ф : 9R+—^9R™ было граничным следом нек-рого
К. о. (при п = 4 это пока A978) не доказано).
Вытекающая отсюда возможность продолжить квази-
квазиконформный автоморфизм пространства Лобачевского
до К. о. абсолюта в совокупности с тем, что 1-квази-
1-квазиконформное отображение сферы конформно и является
следом конформного автоморфизма шара, лежит в осно-
основе доказательства жесткости пространственных гипер-
болич. форм: если два замкнутых римановых многооб-
многообразия размерности га^З одной и той же постоянной от-
отрицательной кривизны гомеоморфны, то они изометрич-
ны (см. [9]).
Лит.: [1] Лаврентьев М. А., Вариационный метод
в краевых задачах для систем уравнений эллиптического типа.
М., 1962; [2] В е к у а И. Н., Обобщенные аналитические
функции, М., 1959; [3] А л ь ф о р с Л., Лекции по квазикон-
квазиконформным отображениям, пер. с англ., М., 1969; [4] Белин-
Белинский П. П., Общие свойства квазиконформных отображе-
отображений, Новоспб., 1974; [5] Б е р с Л., Математические вопросы
дозвуковой и околозвуковой газовой динамики, пер. с англ.,
М., 1961; [6] V Sis a la Jussi, Lectures on n-dimensional
quasiconformal mappings, В., 1971; [7] К р у ш к а л ь С. Л.,
Квазиконформные отображения и римановы поверхности, Но-
восиб., 1975; [8] Lento О., V i г t a n e n К. I., Quasi-
conforme Abbildungen, В., 1965; [9] Мостов Г. Д., «Мате-
«Математика», 1972, т. 16, N° 5, с. 105 — 57. В. А. Зорич.
КВАЗИЛИНЕАРИЗАЦИЯ — совокупность приемов
численного решения нелинейных задач путем сведения
их к последовательности линейных задач. В основе ап-
аппарата квазилинеаризации лежит метод Ньютона и его
обобщение на функциональные пространства, теория
дифференциальных неравенств п метод динамич. про-
программирования. Наиболее простым примером, иллю-
иллюстрирующим приемы К., является использование метода
Ньютона — Рафсона для отыскапия корня г скалярной
монотонно убывающей строго выпуклой функции f(x).
В этом случае на каждом шаге итеративного процесса
исходная нелинейная функция / (ж) аппроксимируется
линейной ф(л-), отыскивается корень ф(ж), к-рый служит
следующим приближением, так что
хп + 1 = хп — f (xn)lf (ж„), п = 0,1, ...
Построенная последовательность обладает свойством
монотонности (жо<х1<л:2<. . .О) и квадратичной схо-
сходимости
Применение К. для решения уравнения Риккати
v' + v*+p (t)v+q(«) = 0, v@) = c,
(предполагается, что решение существует на отрезке
[0, to\) выглядит следующим образом. Исходное уравне-
уравнение заменяется эквивалентным
v' =min [и2—2uv-\-p (t) v — q (t)],
и
где минимум берется по функциям u(t), заданным на
[0, t0]. Данное уравнение обладает рядом свойств,
присущих линейным уравнениям, и для его решения
используется линейное дифференциальное уравнение
ш' = м2—2uw—p(t)w—q(t), ш@) = с,
где u(t) — некоторая фиксированная функция. Опи-
Опираясь на свойство v(t)<?w(t) (причем равенство имеет
место при u(t)=v(t)), можно построить систему после-
последовательных приближений
удовлетворяющих линейным уравнениям
v'n+i= v% — 2vnvn + 1 — p (t) vn + 1—q (t), vn + 1 @) = c.
To же самое рекуррентное соотношение может быть по-
получено путем применения метода Ньютона — Канторо-
Канторовича к исходному нелинейному уравнению.
Использование схемы К. при решении краевой зада-
задачи для нелинейных дифференциальных уравнений вто-
второго порядка
u"=f(u', и, t), t1^:t^.t2,
g^uitj), u'(t2)) = 0, g2(u(t2), u'(t2)) = 0
приводит к следующей последовательности функций
iun{t)}, удовлетворяющих линейным уравнениям
"л+1 =/("«, ип, *) + /„,( «п. ип, <) («п+1 —«п) +
+ fn(u'n, un: t) (Un + 1 — Un),
с линеаризованными краевыми условиями
gj{un (t;), u'n(ti))+gla (un(ti), u'n(
+ giu> («„ (ti), u'n (*,¦)) ('
Существование, единственность и квадратичная схо-
сходимость последовательности следуют из соответствую-
соответствующей выпуклости функций /, glt g2 при достаточно малом
интервале [ilt t2].
Метод К. находит применение при решении двухто-
двухточечных и многоточечных краевых задач для линейных
и нелинейных обыкновенных дифференциальных урав-
уравнений, краевых задач для оллиптич. и параболич.
уравнений в частных производных, вариациопных за-
задач, дифференциально-разностных и функционально-
дифференциальных уравнений и т. д. Как и всякая ите-
итеративная схема, метод К. удобен для реализации на
ЭВМ, допускает различные модификации, позволяющие
ускорить сходимость для более узких классов задач.
Существуют разнообразные примеры его использования
как эвристического способа решения ряда физических,
технических и экономических задач.
Лит.: [1] Б е л л м а н Р., К а л а б а Р., Квазилинеари-
Квазилинеаризация и нелинейные краевые задачи, пер. с англ., М., 1968.
И. А. Вателъ, Ф. И. Ерешгм.
КВАЗИЛИНЕЙНОЕ УРАВНЕНИЕ — дифференци-
дифференциальное уравнение с частными производными, линейное
относительно старших производных от неизвестной
функции. Так, напр., уравнение
ЭиЛ2 дЫ , ди_ д2и , 2 „
~Ьх) Ш i ~ду ду?~г и ~U
— К. у. 2-го порядка относительно неизвестной функ-
функции и.
КВАЗИЛИНЕЙНЫЕ ГИПЕРБОЛИЧЕСКИЕ УРАВ-
УРАВНЕНИЯ И СИСТЕМЫ — уравнения и системы диффе-
дифференциальных уравнений вида:
aaDau = f, A)
где оператор L характерен тем, что в каждой точке су-
существует проходящий через нее вектор ? такой, что для
произвольного непараллельного к ? вектора г\ характе-
характеристическое уравнение
Q(K+r\)=O B)
относительно параметра к имеет тк действительных
корней (каждый корень считается столько раз, какова
его кратность).
Система уравнений A) рассматривается относительно
искомой вектор-функции и(х) с компонентами щ(х),
... , и^х) (в случае одного уравнения &=1). Коэффи-
Коэффициенты аа — матрицы, элементы к-рых зависят от не-
независимых пространственных переменных г=(ж0, ... ,
хп), вектор-функции и (х) и ее частных производных до
порядка т—1 включительно. От этих же аргументов
зависит правая часть/. Если аа являются квадратными
матрицами порядка, совпадающего с числом компонент
вектор-функции и(х), система A) наз. определен-
определенной системой. Характеристическая
форма:
Q(l) = Q (lo, . ¦ ¦, 1„) = det j 2, ttl=m a" ^ I
определяется по главной части 2|И \=maaDa
оператора L.
Элементы поверхности, к-рые проходят через нек-рую
точку Р и ортогональны векторам ?, наз. элемента-
элементами пространственного типа. Векторы ?,
проходящие через ?, определяют так наз. конус нор-
нормалей. Любое направление, выходящее из точки во
внешней полости конуса нормалей, наз. направле-
направлением временного типа. Кривая, к-рая в
каждой точке пространства переменных х имеет на-
направление временного типа, наз. кривой времен-
временного типа.
Среди задач для К. г. у. и с. центральное место зани-
занимает задача Коши — задача нахождения решения и(х)
системы A), если на нек-рой гладкой я-мерной гипер-
гиперповерхности П, определенной уравнением
известны значения вектора-функции и (х) и ее частных
производных по какому-нибудь нетангенциальному к
П направлению до порядка т—1 включительно. Если
такое решение всегда можно найти, то гиперповерхность
П наз. свободной относительно оператора L.
Если коэффициенты системы A) и условия Коши,
заданные на аналитической свободной гиперповерхно-
гиперповерхности П, аналитичны, то аналитическое в окрестности П
решение единственно; если, помимо этого, условия Ко-
Коши определяют на П все производные до порядка т.— 1,
то, согласно теореме Коши — Ковалевской, в достаточ-
достаточно малой окрестности любой точки поверхности П ана-
литич. решение отсутствует. Эта теорема применима ко
всем аналитич. уравнениям и системам независимо от
того, какому типу они принадлежат. При неаналити-
неаналитических же данных теорема не дает ответа о существова-
существовании таких решений.
Если никакая часть гиперповерхности П не свободна,
то ее наз. характеристической поверх-
поверхностью относительно оператора L. Чтобы гиперпо-
гиперповерхность П была характеристической относительно
оператора L, необходимо и достаточно выполнение ус-
условия
<?Ш=0, C)
где 1 = (|о. ••• » ?л) — нормаль к поверхности П. Ха-
рактеристнч. матрица, характеристич. форма и харак-
теристич. поверхность инвариантны относительно не-
неособых преобразований. Характеристич. поверхности
играют важную роль при исследовании многих задач для
уравнений и систем вида A).
Многие задачи математич. .физики сводятся к симмет-
симметрическим гиперболич. уравнениям и системам. Квази-
Квазилинейная система 1-го порядка
наз. симметрической, если все матрицы а1
симметричны. Симметрич. система A') наз. гипер-
гиперболической симметрической системой
в точке Р, если одна из матриц а1 или какая-либо ли-
линейная комбинация 5'а' знакоопределенна. Одно урав-
уравнение или система уравнений высшего порядка наз.
симметрическими гиперболически-
м и, если они эквивалентны какой-нибудь симметриче-
симметрической гиперболич. системе 1-го порядка. Систему A')
при положительно определенном коэффициенте а0 с по-
помощью линейного преобразования можно привести к
виду
ut-'rM[u]=f, t^x0 (I")
с симметрич. оператором М. При помощи энергетиче-
энергетических неравенств и метода итераций доказывается су-
существование решения задачи Коши для квазилинейных
систем 2-го порядка и для одного нелинейного уравне-
уравнения произвольного порядка.
Так как характеристики и бихарактеристики для ги-
гиперболич. уравнений и систем, как линейных, так и
квазилинейных, определяются одинаково, известные
факты о распределении разрывов младших производ-
производных решений линейных уравнений и систем относятся
и к случаю квазилинейных уравнений. Распростране-
Распространение разрывов решения и(х) гиперболич. систем рассмот-
рассмотрено для законов сохранения, т. е. для
систем 1-го порядка, имеющих следующий вид:
Е" 5§7^/-/(*.")=0, У = 1, 2 *, D)
при условии, что поверхность ударной волны является
нехарактеристической.
Много работ посвящено исследованию К. г. у. и с. в
случае двух пространственных переменных х и t. Важ-
Важную часть этих исследований составляют квазилиней-
квазилинейные системы 1-го порядка, к-рые имеют вид:
L [и] = Aux-^But = C, E)
где А и В — квадратные матрицы порядка к, вектор С
зависят от переменныхх, t и от вектора и(х, t)= {ux(x,t),
. .. , и^(х, t)}. Если от искомой вектор-функции и
(х, t) зависит только правая часть С, E) наз. почти
линейной системой. Почти линейные систе-
системы 1-го порядка эквивалентно сводятся к симметрич.
системам линейными преобразованиями. Квазилиней-
Квазилинейная система E) при предположении det ВфО имеет
следующий вид:
щ + Аих = С. F)
Матрицу А можно преобразовать к диагональному виду
с элементами у.;, где векторы (х,-, 1) определяют харак-
теристич. направления; эта запись наз. нормальной
формой системы E). Для систем вида F) справедлива
теорема единственности, независимо от того, зависят
их характеристики от решения и (ж, t) или нет.
Если коэффициенты А, С и начальные значения реше-
решения и(х, t) при t=0 имеют первые производные по всем
аргументам и эти производные удовлетворяют Липшица
условию, то можно указать окрестность 0<г<Л отрезка
оси ?=0, в к-рой существует единственное решение за-
задачи Коши с первыми производными, удовлетворяю-
удовлетворяющими условию Липшица. При этом вводятся вектор-
функции v(x, t), к-рые при г=0 совпадают с заданными
начальными данными, а их первые производные удов-
удовлетворяют условию Липшица. После подстановки v(x,t)
в коэффициенты А ж С решается задача Коши с задан-
заданными начальными данными для линейного уравнения.
Каждой функции v(x, t) ставится в соответствие реше-
решение и(х, t) и решение задачи для системы F) выводится
как неподвижный элемент преобразования u=9T[i;], или
как продел равномерно сходящейся последовательности
{z4n}n-i,2...i полученный в результате итерационного
процесса
Аналогичный результат получается при достаточно гла-
гладких коэффициентах А, Си начальных данных путем
редукции задачи к системе интегральных уравнений,
разрешимость к-рой доказывается на основе сжатых
отображений принципа.
Квазилинейная система 1-го порядка E) наз. слабо
нелинейной системой, если соответствующая
ей нормальная форма
щ+Аих=С G)
такова, что для каждого элемента а" диагональной
матрицы выполняется условие:
JLa" (x, t, иъ ..., uk) = 0, i = l, 2, ..., к.
В других случаях E) наз. сильно нелинейной
системой. Если решение слабо нелинейной систе-
системы при А:=2 ограничено, то задача Коши всегда разре-
разрешима в области определенности.
Кроме задачи с начальными данными, для квазили-
квазилинейных систем 1-го порядка поставлены и исследованы
и другие задачи. Напр., так наз. смешанные задачи, за-
заключающиеся в нахождении решения и(х, t) системы
G), к-рое наряду с начальными условиями и(х, 0)=
=ty(x) при г=0, а<ж<E удовлетворяет краевым усло-
условиям на нек-рых гладких кривых 1\ и Г2, выходящих
из точек (а, 0) и ф, 0) соответственно. Эти краевые ус-
ловия относительно решения и(х, t) могут быть как
линейными, так и нелинейными. В нек-рых случаях при
соблюдении специальных условий удается проверить
корректность постановки задач указанного типа.
Для сильно нелинейной системы F) в случае А;=2
исследована следующая задача: пусть Т1 — кривая
выходящая из начала координатной системы и заданная
уравнением x=x(t), кривая 1\ предполагается характе-
характеристической, имеющей непрерывную касательную. Сле-
Следует определить решение системы F) в нек-рой области,
ограниченной характеристикой 1\ и еще одной кривой
Г2, выходящей тоже из начала координат, если известно
решение и{х, t) на 1\ при дополнительном условии, что
одна из компонент вектора и(х, t) имеет определенную
особенность в точке пересечения граничных кривых.
Известна разрешимость подобных задач при г<б для
достаточно малых б.
Среди задач, поставленных для квазилинейных ги-
гиперболич. систем 1-го порядка, имеется ряд важных
прикладных задач: задача о распаде произвольного
взрыва, задача хроматографии, задача фильтрации и др.
Изложенные выше результаты носят локальный ха-
характер, касаются только регулярных решений. Если же
решения не являются дифференцируемыми или даже
непрерывными функциями, вводятся понятия так наз.
слабых решений, определяемых различными способами,
для к-рых доказываются теоремы единственности и су-
существования решения задачи Кошы глобально. Как
правило, эти решения определяются в довольно широ-
широких классах функций (ограниченные измеримые функ-
функции, локально суммируемые функции и др.). Они удов-
удовлетворяют уравнению или системе в каком-нибудь смыс-
смысле, напр, в смысле теории обобщенных функций, или
подчинены вполне определенным интегральным соот-
соотношениям. Слабое решение в нек-рых случаях принято
наз. решением задачи Коши, если' разность решения и
начальных данных слабо стремится к нулю при стрем-
стремлении точки к носителю начальных данных.
Известно несколько путей построения глобальных
слабых решений задачи Коти для законов сохранения в
случае многих переменных с начальными данными до-
вольпо общего вида. Напр., метод сглаживания, конеч-
конечно разностные схемы решения задач с начальными дан-
данными.
Общие нелинейные гиперболич. уравнения и системы
путем дифференцирования по независимым переменным
сводятся к квазилинейным гиперболич. системам 1-го
порядка. Любое гиперболич. уравнение 2-го порядка ре-
редуцируется к симметрической гиперболич. системе 1-го
порядка, и факты, относящиеся к гпперболич. системам
1-го порядка, остаются в силе и для одного гиперболич.
уравнения 2-го порядка.
Теорема существования решения задачи Коши для
одного гиперболич. уравнения высшего порядка была
получена при требовании достаточно высокой гладкости
коэффициентов уравнения (см. [9]).
Задача Коши для гиперболических квазилинейных
уравнений высшего порядка была исследована при по-
помощи редукции к аналогичной задаче для квазилиней-
квазилинейных систем 1-го порядка. Для уравнений 2-го порядка,
кроме этого, используется и другой метод, заключаю-
заключающийся в введении характеристич. системы координат
(се, Р). Получается система уравнений относительно х, t
функции и и ее производных 1-го и 2-го порядков, к-рые
рассматриваются как функции характеристич. перемен-
переменных. Система эта состоит из шести уравнений 1-го по-
порядка относительно функций
х=х(а, Р), у = у(а, р), и = и (а, р), р= их (а, Р),
д = иу (а, Р),
одно из к-рых является следствием всех остальных.
Можно рассматривать определенную систему из пяти
квазилинейных уравнений с пятью неизвестными функ-
функциями. Для подобных систем и, следовательно, для
квазилинейных уравнений имеются теоремы существо-
существования и единственности решения задачи Коши. Этот
метод без существенных изменений применяется и для
квазилинейных систем уравнений 2-го порядка
где коэффициенты зависят от х, t и функций мЛ
Лит.; [1] Glimm J., «Comm. pure and appl. Math.»,
1965, № 18 p. 697—715; [2] D о ug 1 i s A., «Ann. Inst. Fou-
Fourier», 1072, t. 22, p. 141—227; [3] Кружков С. Н., «Докл.
АН СССР», 1989, т. 187, №1, с. 29—32; [4] Кузнецов
Н. Н., «Матем. заметки», 1967, т. 2, Jw 4, с. 401—10; [5] С о и-
r a n t R., Lax P., «Comm. pure and appl. Math.», 1949, v. 2,
p. 255—73; [6] С о n w а у Б., S m о 1 1 e r J., «Comm. pure
and appl. Math.», 1966, v. 19, p. 95—105; [7] Lax P., «Comm.
pure and appl. Math.», 1953, v. 6, p. 231 — 58; [8] L e w у H.,
«Math. Ann.», 1927, Bd 98, p. 179—91; [9] Levl E., «Rend,
reale accad. Lincei», 1908, ser. 5, v. 17, p. 331—39; [10] Le-
ray J., Hyperbolic differential equations, Prinston, 1953;
[11] Lee Da-tsin, Yu Wen-tzu, «Scientia sinica»,
1964, t. 13, N° 4, p. 529—62; [12] О л е Й н и к О. А., «Успехи
матем. наук», 1957, т. 12, в. 3, с. 3—73; [13] Петровский
И. Г., «Матем. сб.», 1937, т. 2, в. 5, с. 815—66; [14] Рож-
Рождественский Б. Л., Яненко Н. Н., Системы ква-
квазилинейных уравнений, М., 1968; [15] Priedrichs К.,
«Amer. J. Math.», 1948, v. 70, p. 555—89: [16] Hartman P..
Wintner A., «Amer. J. Math.», 1952, v. 74, p. 834—64;
[17] Schauder J., «Comment, math, helv.», 1936, v. 9,
p. 263—283. Д. К. Гвазпва.
КВАЗИМНОГООБРАЗИЕ — см. Алгебраических сис-
систем квазимногообразие.
КВАЗИНОРМА — неотрицательная функция ||ж||,
определенная на линейном пространстве R и удовлетво-
удовлетворяющая тем же аксиомам, что и норма, кроме аксиомы
сложения ||г+(/||<Цж|]+||г/||, к-рая заменяется более
слабым требованием: существует постоянная с>0 такая,
что для всех х ? R и у ? R выполняется неравенство
||г+2/Ц<сAЫ1+1Ы1)- Л. Д. Кудрявцев.
КВАЗИНОРМАЛЬНОЕ ПРОСТРАНСТВО — регуляр-
регулярное пространство, в к-ром два непересекающихся п-мно-
жества имеют непересекающиеся окрестности. Всякое
Т\-пространство, в к-ром любые два непересекающихся
я-множества имеют непересекающиеся окрестности, яв-
является К. п. Для К. п. п только для такого простран-
пространства Стоуна — Чеха бикомпактное расширение f>X сов-
совпадает с соцА'-пространством. Большой запас ненормаль-
ненормальных К. п. дает теорема: произведение любого числа
метрических пространств есть К. п.
Лит.: [1] Зайцев В. И., «Тр. Моск. матем. об-ва»,
1972, т. 27, с. 129—93; [2] Щ е п и н Е. В., «Матем. сб.»,
1972, т. 88, N, 2, с. 316—25. В. В. Федорчук.
КВАЗИНОРМИРОВАННОЕ ПРОСТРАНСТВО — ли-
линейное пространство, в к-ром задана квазинорма. При-
Примерами К. п., не являющихся нормированными, служат
Лебега пространства Ьр(Е) при 0<р<1, в к-рых ква-
квазинормой является выражение
Л. Д. Кудрявцев.
КВАЗИПЕРИОДИЧЕСКАЯ ФУНКЦИЯ с периодами
%, со2, ... , со,, — функция f(t) такая, что /(*)=
= F(t,t, ... , t) для нек-рой непрерывной функции
F{tt, t2, . .. , tn) от п переменных, периодической по
tt, <2, ... , tn с периодами и>1, ю2, ... , со„ соответст-
соответственно. Все со!, со2, ... , со„ строго положительны, и их
обратные величины рг, р2, ... , рп являются рацио-
рационально линейно независимыми.
Если ft(t) и /2(i) — непрерывные периодич. функции
с периодами ш1 и со2 соответственно, причем отношение
собеса иррационально, то g(t)=fi(t)+fz(t) и h{t)~
= max {^(i), /2(i)} суть К. ф.
Теория К. ф. послужила основой для создания теории
почти периодических функций. В случае непрерывных
функций К. ф. являются обобщением периодич. функ-
функций, но частным случаем почти периодических.
К. ф. допускает представление вида
„,bV, l(klPl + ... + k Vn)t
l\l)—?jckl...kne >
если Cit,i...ktf=ck таковы, что 2к/г12<°°- К. ф. обладают
следующими свойствами: сложение и умножение К. ф.
дают снова К. ф.; равномерно сходящаяся последова-
последовательность К. ф. при t?R дает в пределе почти периодич.
функцию; если g(t) — почти периодич. функция и е>0,
то существует такая К. ф. f(t), что
\f(t)-g(t)\ < e при teR-
Лит.: [1] Боль П. Г., Избр. труды, цер. с нем., Рига,
1961; [2] X а р а с а х а л В. X., Почти-периодические реше-
решения обыкновенных дифференциальных уравнений, А.-А., 1970.
Ю. В. Номленпо, Е, Л. Топкое.
КВАЗИПЕРИОДИЧЕСКОЕ ДВИЖЕНИЕ — прямо-
прямолинейное движение материальной точки, закон к-рого
выражается квазипериодической функцией.
КВАЗИПРОЕКТИВНАЯ СХЕМА — локально замк-
замкнутая подсхема проективного пространства Р". Иначе
говоря, К. с.— это открытая подсхема проективной
схемы. Схема X над полем квазипроективна тогда и
только тогда, когда на X существует обратимый обиль-
обильный пучок. Обобщение понятия «К. с.» — квазипро-
квазипроективный м о р ф и з м, т. е. морфизм схем, яв-
являющийся композицией открытого вложения и проек-
проективного морфизма. Схема, одновременно квазипроек-
квазипроективная и полная, является проективной, в И. Данилов.
КВАЗИПРОСТОЕ ПРЕДСТАВЛЕНИЕ — непрерыв-
непрерывное линейное представление я связной полупростой дей-
действительной группы Ли G в банаховом пространстве Е
такое, что: 1) оператор я (ж) является скалярным крат-
кратным единичного оператора в пространстве Е для любого
элемента х из центра группы G; 2) если F — пространст-
пространство аналитич. векторов в Е относительно я и если пр—
представление универсальной обертывающей алгебры
$ алгебры Ли группы G в векторном пространстве F,
то оператор np(z) является скалярным кратным единич-
единичного оператора в пространстве F для всех элементов z
из центра алгебры g. Эти скалярные кратные опреде-
определяют характер центра алгебры g, наз. и н ф и н и т е-
зимальным характером К. п. Два К. п.
наз. инфинитезимально эквивалент-
эквивалентными, если определяемые ими представления уни-
универсальной обертывающей алгебры в соответствующих
векторных пространствах аналитич. векторов эквива-
эквивалентны. Всякое вполне неприводимое представление
группы в банаховом пространстве есть К. п., и любое
неприводимое К. п. группы G в банаховом пространстве
инфинитезимально эквивалентно нек-рому вполне не-
неприводимому представлению; последнее является огра-
ограничением на инвариантное подпространство нек-рого
факторпредставлешш представления (вообще говоря,
неунитарного) из основной серии представлений груп-
группы G.
Лит.: [1] Harish-Chandra, «Trans. Ашег. Math.
Soc», 1953, v. 75, p. 185—243; 1954, v. 76, p. 26—65; [2] L e-
pofsky J., там же, 1973, v. 176, p. 1—44; [3] Фомин
А. И., «Функцией, анализ и его прилож.», 1976, т. 10, № 3,
с. 95 — 96. А. И. Штерн.
КВАЗИПРОСТОЕ ЧИСЛО — натуральное число п,
не имеющее малых простых делителей. Это означает, что
все простые делители числа п должны быть больше
3*(п), где Цр(п) — некоторая функция, растущая мед-
медленнее, чем п. Напр.,
К. ч. хорошо распределены в арифметич. прогрессиях с
большим модулем. Б. М. Бредихин.
КВАЗИРАВНОМЕРНАЯ СХОДИМОСТЬ — обобще-
обобщение равномерной сходимости. Поточечная сходимость
последовательности отображений {/„} топологич. про-
пространства X в метрнч. пространство У к отображению /
наз. К. с, если для всякого е > U и всякого натурально-
натурального числа N существует такое не более чем счетное от-
открытое покрытие {Го, Г1, ... , Г^, ...} пространства X
и такая последовательность л0, пг, . . . , ns, ... нату-
натуральных чисел, больших N, что р(/(ж), / (ж))<е для
всякого x^Tft- Из равномерной сходимости вытекает
К. с. Для последовательностей непрерывных функций
К. с. является необходимым и достаточным условием
непрерывности предельной функции (теорема А р-
целя — Александрова).
Лит.: [1] Александров П. С, Введение в общую
теорию множеств и функций, М.— Л., 1948. В. В. Федорчук.
КВАЗИРАЗЛОЖИМАЯ ГРУППА, квазирас-
щепимая группа, над полем к — аффинная ал-
гебраич. группа, определенная над полем к, содержа-
содержащая Бореля подгруппу, определенную над тем же полем.
Всякая аффинная алгебраич. группа становится К. г.
при нек-ром расширении основного поля, напр, над
алгебраическим замыканием этого поля. Всякая аффин-
аффинная алгебраич. группа, определенная над конечным по-
полем к, квазиразложима над к. См. также Разложимая
группа. в. Л. Попов.
КВАЗИРЕГУЛЯРНОЕ КОЛЬЦО — кольцо, в к-ром
каждый элемент квазирегулярен. Элемент а альтерна-
альтернативного (в частности, ассоциативного) кольца R наз.
кваз и регулярным, если существует такой
элемент а'?Д, что
' -f- аа' = а+ a' -J- а' а= 0.
Элемент а' наз. квазиобратным для элемента
а. Если R — кольцо с единицей 1, то элемент a?R яв-
является квазирегулярным с квазиобратным а' тогда и
только тогда, когда элемент l-f-а обратим в Л с обрат-
обратным 1 + а'. Всякий нильпотентный элемент квазнрегу-
лярен. В ассоциативном кольце множество всех квази-
квазирегулярных элементов образует группу относительно
операции круговой композиции: х-у=х-\-у-\-ху. Важ-
Важным примером К. к. является кольцо (некоммутатив-
(некоммутативных) формальных степенных рядов без свободных чле-
членов. Существуют простые ассоциативные К. к. [2].
Лит.: [1] Д ж е к о б с о н Н., Строение колец, пер. с
англ., М., 1961; [2] Sasiada E., Colin P. M., «J. Al-
Algebra», 1967, v. 5, № 3, р. 373—77. И. П. Шестанов.
КВАЗИРЕГУЛЯРНЫЙ РАДИКАЛ кольца — на-
наибольший квазирегулярный идеал данного кольца.
Идеал А кольца R наз. квазирегулярным, если А яв-
является квазирегулярным кольцом. Во всяком альтерна-
альтернативном (в частности, ассоциативном) кольце существует
К. р.; он совпадает с суммой всех правых (левых) ква-
квазирегулярных идеалов (см. [1], [10]). К. р. ассоциатив-
ассоциативного кольца наз. также Джекобсона радикалом.
К. p. J(R) произвольного альтернативного кольца Я
равен пересечению всех максимальных модулярных
правых (левых) идеалов кольца R; J (R) равен также пе-
пересечению ядер всех неприводимых правых (левых)
представлений кольца R (см. [1], [5] — [8]). Кольцо R
наз. /-п олупростым (или просто полупростым),
если J(R) = 0. Факторкольцо R/J{R) всегда полупро-
полупросто. Всякое полупростое кольцо изоморфно подпрямой
сумме примитивных колец [1], [8]. Если R удовлетворят
условию минимальности для правых (левых) идеалов,
то радикал J(R) нильпотентен, а факторкольцо RlJ(R)
изоморфно конечной прямой сумме полных матричных
колец над телами и алгебр Кэли — Диксона (последние
слагаемые в ассоциативном случае отсутствуют), см.
[1]—[3]. Пусть А — двусторонний идеал кольца R,
тогда
J(A) = A(]J(R)
(см. [1], [4]); если R ассоциативно и Rn — кольцо всех
матриц порядка п над R, то
Если R — ассоциативная алгебра над полем F и мощ-
мощность F больше размерности R над F либо R является
алгебраической над F, то J(R) — нильидеал. К. р. ко-
конечно порожденного альтернативного кольца, удовле-
удовлетворяющего существенному тождественному соотноше-
соотношению, совпадает с нижним нильрадикалом (см. Радикалы
колец и алгебр) [6]. Некоторый аналог К. р. существует
во всякой йордановой алгебре.
Лит.: [1] Джекобсон Н., Строение колец, пер. с
англ., М., 1961; [2] Ж е в л а к о в К. А., «Алгебра и логика»,
1965, т. 4, Л"» 4, с. 87—102; [3] его ж е, там же, 1966, т. Ь, № 3,
с. 11—36; [4] его же, там же, 1969, т. 8, ЛЬ 2, с. 176—80;
[5] его же, там же, Л» 3, с. 309—19; [6] е г о ж е, там же,
1972, т. 11, ЛЬ 2, с. 140 — 61; [7] С л и н ь к о А. М., Ш е с т а-
к о в И. П., там же, 1974, т. 13, ЛЬ 5, с. 544—88; [8] Klein-
f el d E., «Amer. J. Math.», 1955, v. 77, p. 725—30; 19] M c-
Crimmon K., «Proc. Nat. Acad. Sci. USA», 1969, v. 62,
p. 671—78; [10] Smiley M. F., «Ann. Math.», 1948, v. 49,
№ 3, p. 702—09. II. П. Шестаков.
КВАЗИРЕШЕНИЕ — обобщенное решение некор-
некорректных задач, к-рое (при достаточно общих условиях),
в отличие от истинного решения, удовлетворяет услови-
условиям корректности по Адамару.
Пусть X, Y — метрические пространства, А : X-+-Y,
М — множество из А'. К в а з и р е ш е н и е м урав-
уравнения
Ах=у A)
на множестве М при заданном у из Y наз. элемент х
из М, минимизирующий уклонение р(Ах, у) при х из М.
Если уравнение A) имеет на М истинное решение х0, то
г0 будет также и К.
Зависимость множества К. от у удобно представить
как суперпозицию двух отображений
х=А~1Ру,
где А ~1 — обращение (вообще — многозначное) ото-
отображения А, а Р — оператор метрич. проектирования в
пространстве Y на множество N=AM. Такая суперпо-
суперпозиция позволяет свести исследование свойств К. к ис-
исследованию отображений Д-'иР, Напр., если множе-
множество N — чебышевское, а отображение А~г — одно-
однозначно и непрерывно на Лг, то задача нахождения К.
является корректной. Если Р или А~х многозначны, то
устойчивость множества К формулируется в терминах
В-ненрерывности (непрерывности функций от множеств).
Обычно в качестве X п Y берутся линейные нормиро-
нормированные пространства, что позволяет получить наиболее
полные и законченные результаты. Так, задача нахож-
нахождения К. корректна, если Y — строго выпукло, А —
линейный непрерывный обратимый оператор, М — вы-
выпуклый компакт. Имеется ряд других комбинаций ус-
условий, обеспечивающих корректность задачи нахожде-
нахождения К., в к-рых одни условия усиливаются, другие ос-
ослабляются (напр., А — линейный замкнутый оператор,
но F — гильбертово).
Существует ряд способов задания множества М, обес-
обеспечивающих возможность эффективного нахождения К.
Один из наиболее распространенных способов состоит
в следующем. Рассматривается третье пространство Z
(все или нек-рые из пространств X, Y, Z могут совпа-
совпадать) и линейный оператор В : Z-^-X такой, что В-1 —
неограничен. За множество М=МГ принимается образ
шара:
Mr = BSr; Sr = {z?Z: ||z||<r}.
В такой форме задача нахождения К. является задачей
математич. программирования: минимизировать функ-
функционал
f(z) = \\ABz-y{\
при ограничении ||z||«:r. Для гильбертовых Y и Z полу-
получается задача квадратичного программирования.
В случаях корректности К. важное значение для при-
приложений имеют оценки устойчивости, в к-рых дается за-
висимость \\хг— х2\\ от \}у1— у2\\. При приведенном выше
способе задания множества М устойчивость К. харак-
характеризуется функцией:
Q (Т, г) = sup || л-! — х2\\; xi = Bzi, ||z,-||<r,
II Ахх— Лл
Имеет место соотношение
Q(t, г)=со(т, 2г),
где со(т, г) есть решение экстремальной задачи со (т, г)=
= sup ||Вг||при ||z||<r, \\ABz\\*?T.
Для гильбертовых Z и Y имеются выражения для
со (т, г) в замкнутой форме.
Лит.: [1] Иванов В. К., «Докл. АН СССР», 1962,
т. 145, X» 2, с. 270—72; [2] его ж е, «Матем. сб.», 1963,
т. 61, N5 2, с. 211—23; [3] Л и с к о в е ц О. А., «Дифферен-
«Дифференциальные уравнения», 1971, т. 7, № 9, с. 1707—09; [4] Мор о-
з о в В. А., в сб.: Итоги науки и техники. Математический
анализ, т. 11, М., 1973, с. 129—78; [5] Тихонов А. Н.,
Арсенин В. Я Методы решения некорректных задач,
М., 1974; [6] Крылов В. И., Б о б к о в В. В., М о-
настырный П. И., Вычислительные методы высшей ма-
математики, т. 1—2, Минск, 1972—75. В. К. Иванов.
КВАЗИСИМПЛЕКТИЧЕСКОЕ ПРОСТРАНСТВО —
нечетномерное проективное пространство Р2и-и в к-ром
заданы нульспстемы:
Первая нульсистема переводит точки пространства в
гиперплоскости, проходящие через Bп—2т—1)-пло-
скость
вторая нульсистема — в точки этой же плоскости.
Плоскость ха = хт + а =0 наз. абсолютной, а обе нуль-
системы — абсолютными нульсистемами К. п. S~^a~ .
1 2л-1
К. п. является частным случаем полусимплектических
пространств.
Коллинеации пространства ?Л™ , переводящие в
1 2л-1
себя абсолютную плоскость, имеют вид:
0</с, К<2т — 2, 2т — 1 < ц, «<2гс — 1,
и матрицы Ufa и V"— симплектич. матрицы порядков
2т и Bп—2т); Т% — прямоугольная матрица с 2га
столбцами и Bп—2т) строками.
Эти коллинеации наз. квазисимплектиче-
скими преобразованиями пространства
Spl~_ . Они перестановочны с заданными нульсистема-
мп пространства. Квазисимплектич. инвариант двух
прямых определяется по аналогии с симплектич. инва-
инвариантом прямых симплектического пространства.
К. п. S2?n~i может быть получено из симплектиче-
ского S г, путем предельного перехода от абсолюта
1 2Я-1
пространства S т, к абсолюту пространства Sp~: .
Именно, первая из заданных нульсистем переводит все
точки пространства в плоскости, проходящие через аб-
абсолютную плоскость, а вторая — переводит все пло-
плоскости в точки той же плоскости.
Квазисимплектич. преобразования образуют группу,
являющуюся группой Ли.
Лит.: [1] Р о з е н ф е л ь д Б. А., Неевклидовы прост-
пространства, М., 1969. Л. А. Сидоров.
КВАЗИСРЕДНИХ МЕТОД — конструктивная схема
исследования систем со спонтанным нарушением сим-
симметрии, основанная на фундаментальной концепции
квазисредних (Н. Н. Боголюбов [1], 1961).
Кваз и средние — термодинамические (в ста-
статистической механике) или вакуумные (в квантовой тео-
теории поля) средние от динамических величин в специаль-
специальным образом модифицированной процедуре усреднения,
позволяющей учесть эффекты влияния вырождения
состояния системы.
В статист и ч. механике при спонтанном на-
нарушении симметрии на основе К. м. могут быть описа-
описаны макроскопические наблюдаемые в рамках микроско-
микроскопического подхода.
В задачах с вырождением одному уровню энергии от-
отвечает более одного независимых состоянии системы;
среднее же значение (А ) любой динамической величи-
величины А определенно однозначно:
где Н — гамильтониан системы, р — обратная темпера-
температура. Если состояние статистического равновесия систе-
системы обладает более низкой симметрией, чем гамильто-
гамильтониан системы (так наз. спонтанное нарушение симметрии
см. [2] — [5]), то операцию усреднения A) необходи-
необходимо дополнить правилом, запрещающим «лишнее» усред-
усреднение по различным значениям рассматриваемой макро-
макроскопической величины, изменение к-рой не сопровож-
сопровождается изменением энергии.
Это достигается введением квазисредних, т. е. сред-
средних по гамильтониану, дополненному бесконечно малы-
малыми членами, нарушающими аддитивные законы сохра-
сохранения. Термодинамические средние могут оказаться не-
неустойчивыми по отношению к такому изменению исход-
исходного гамильтониана, что и свидетельствует о вырожде-
вырождении состояния статистического равновесия.
Итак, квазисреднее -<Л>- динамической величины А
для системы с гамильтонианом Н определяется как пре-
предел
<Л>Н= lim lim <A>H(V>, B)
П V — OV-voo V
где через (... )н обозначено обычное среднее, взятое по
гамильтониану Ну, содержащему малые нарушающие
симметрию члены, вводимые параметром включения v,
исчезающие при v—>-0. Согласно определению B) обыч-
обычное термодинамическое среднее получается дополнитель-
дополнительным усреднением квазисреднего по группе нарушенной
симметрии.
Значение квазисреднего B) может зависеть от кон-
конкретной структуры добавочного члена АН=Н v—Н', если
усредняемая динамическая величина А неинварнантна
относительно группы симметрии исходного гамильто-
гамильтониана Н. При стремлении параметров включения источ-
источников v к нулю произвольным образом предел обычных
средних B) для вырожденного состояния не существует.
Для полного определения квазисредних необходимо
указать способ стремления этих параметров к нулю,
обеспечивающий сходимость (см., напр., [5]). С другой
стороны, для снятия вырождения достаточно нарушить
при построении Hv лишь те аддитивные законы сохра-
сохранения, «выключение» к-рых приводит к неустойчивости
обычных средних. При этом для квазисредних не будут
выполняться именно те правила отбора корреляцион-
корреляционных функций, к-рые обусловлены указанными закона-
законами сохранения.
К. м. непосредственно связан с принципом ослабле-
ослабления корреляции (см. [8], [9]): корреляционные функции
<иг (хъ t,) ... Us (xs, ts) ... Un (xn, tn)>, C)
где Us(xs, ts) — полевые функции в Гейзенберга пред-
представлении W(xs, ts) илихИ' + (х5, ts), распадаются на про-
произведение
X<Us(xs, ts) ... Un(xn, *„)>, D)
если совокупность точек хг, ..., xs-r бесконечно уда-
удаляется от совокупности точек xs, . . . , хп при фиксиро-
фиксированных временных переменных tx, t2, ... , tn. В случае
вырождения рассматриваемого состояния выражения
<(. . .)>, входящие в эту формулировку, с необходимостью
должны пониматься как квазисредние: приведенная вы-
выше формулировка принципа ослабления корреляции
становится прямо неверной, если считать <.. .)> обычны-
обычными средними.
Для построения неравновесного статистического опе-
оператора рассматриваются бесконечно малые возмущения,
нарушающие симметрию (Лиувилля уравнения) относи-
относительно обращения времени. Применение этой операции
эквивалентно отбору запаздывающих решений уравне-
уравнения Лиувилля (см. [7]).
Вопросы о выборе способа стремления параметров
включения источников v к нулю, обеспечивающего схо-
сходимость обычных средних в определении квазисредних
B) рассмотрены в рамках метода аппроксимирующих
гамильтонианов, где исходный гамильтониан заменяет-
заменяется на специальным образом конструируемый путем за-
замены динамических величин, коммутирующих со всей
алгеброй локальных наблюдаемых в пределе большой
системы, на с-числа, так наз. аппроксимирующей га-
гамильтониан, так что этот последний гамильтониан яв-
является много проще исходного (и в широком ряде физи-
физически важных случаев допускается точное решение) и
является ему эквивалентным при К->-оо (см. [7]). При
построении добавочного члена АН следует взять его
пропорциональным решениям в общем случае мини-
минимаксной задачи для предельной (F->oo) функции сво-
свободной энергии аппроксимирующего гамильтониана.
Тогда произвольная последовательность вещественных
положительных v, сходящаяся к нулю, обеспечивает
сходимость в определении B), при этом таким образом
построенные квазисредние оказываются равными соот-
соответствующим решениям указанной минимаксной задачи.
В рамках метода аппроксимирующих гамильтонианов
указан другой альтернативный способ определения ква-
квазисредних без введения дополнительных членов в га-
гамильтониан //. В этом подходе при вычислении квази-
квазисреднего <^АУч-1 рассматриваемая динамическая величи-
величина А домножается на нек-рый, в определенном смысле
стремящийся к единице при F—»-оо, множитель L, га-
гамильтониан Н остается неизменным [4]:
lim{i-i>. E)
Квазисредние, определенные согласно B) и E), совпа-
совпадают.
Математический аппарат К. м. включает Боголюбова
теорему об особенностях типа 1/д2 и Боголюбова нера-
неравенства для Грина функций и корреляционных функций;
содержит в себе алгоритмы установления нетриви-
нетривиальных оценок для равновесия квазисредних, позволяю-
позволяющих исследовать проблему упорядочения в статистич.
системах и выяснять структуру энергетического спектра
низколежащих возбужденных состояний (см. [4], [8]).
Концепция квазисредних непосредственно связана с
теорией фазовых переходов (см. [6], [7], [9]): неустойчи-
неустойчивость термодинамических средних по отношению к воз-
возмущениям гамильтониана, нарушающим инвариант-
инвариантность относительно нек-рой группы преобразований,
означает, что в системе происходит переход в экстре-
экстремальное состояние.
В квантовой теории поля для ряда модель-
модельных систем доказано наличие фазового перехода и ус-
тановлена справедливость теоремы Боголюбова об осо-
особенностях типа 1/<72; исследована возможность локаль-
локальной неустойчивости вакуума и появления у него домен-
доменной структуры.
Лит.: [1] Боголюбов Н. Н., Избр. труды, т. 3, К.,
1971; [2] Статистическая физика и квантовая теория поля, М.,
1973; [3] Гриб А. А., Д а м а с к и н с к и й Е. В., Мак-
Максимов В. М., «Успехи физ. наук», 1970, т. 102, с. 587—620;
[4] Боголюбов Н. Н. (м л.), Садовников Б. И.,
Некоторые вопросы статистической механики, М., 1975; [5]
Боголюбов Н. Н. (м л.). Метод исследования модель-
модельных гамильтонианов, М., 1974; [6] Б р а у т Р., Фазовые пере-
переходы, пер. с англ., М., 1967; [7] Р ю э л ь Д., Статистическая
механика. Строгие результаты, пер. с англ., М., 1971; [8] А х и-
езерА. И., Пелетминский СВ., Методы статисти-
статистической физики, М., 1977; [9] Престон К., Гиббсовские
состояния на счетных множествах, пер. с англ., М., 1977.
А. Я. Ермилов, А. М. Курбатов.
КВАЗИТОЖДЕСТВО, условное тождест-
в о,— формулы логического языка 1-й ступени вида
(V*i ...*„) (^i& ¦ • • &Ар —>. А),
где через Alt ... , А р, А обозначены простейшие фор-
формулы вида
f=g, Р(аг, ..., ат),
а /, g, аь . . . , ат— термы от ж1? .. . , хп, Р — сигна-
сигнатурный предикатный символ. Квазитождествами опре-
определяются алгебраических систем квазимногообразия.
Тождество — чаСТНЫЙ случай К. О. А. Иванова.
КВАЗИФРОБЕНИУСОВО КОЛЬЦО, QF-к о л ь-
ц о,— артиново кольцо (слева и справа), удовлетворя-
удовлетворяющее аннуляторным условиям:
для каждого левого (правого) идеала L(H) (см. Аннуля-
тор). Артиново слева кольцо, удовлетворяющее лишь
одному из аннуляторных условий, может не быть К. к.
Интерес к К. к. обусловлен наличием двойственности:
артиново слева кольцо R является К. к. тогда и только
тогда, когда отображение
М н-> Нот# (М, R)
определяет двойственность категорий левых и правых
конечно порожденных Л-модулей. Конечномерная ал-
алгебра А над полем Р оказывается К. к. в том и только
том случае, когда каждое неприводимое прямое слагае-
слагаемое левого /1-модуля Нотр(А ^, Р) изоморфно нек-рому
минимальному левому идеалу алгебры А. А это равно-
равносильно самодуальности решеток левых и правых иде-
идеалов алгебры А.
К. к. были введены как обобщение фробениусовых
алгебр, определяемых требованием эквивалентности
правого и левого регулярных представлений. Первона-
Первоначально свойство артинова слева и справа кольца R быть
квазифробениусовым определялось следующим усло-
условием: если ег, . . . , е„ — полный список примитивных
идемпотентов из R (т. е. Re/^kRej при 1ф] и, каков бы
ни был примитивный идемпотент е, Re~Rei для нек-ро-
го г), / — радикал кольца R и ср : R-+R/J — естествен-
естественный гомоморфизм, то найдется такая перестановка я
множества {1, ... , п), что
Soc (eiR) = ф ( enU)R) и Soc (Ren([)) = ср (Re;),
где Soc M — цоколь модуля М. Квазифробениусовость
кольца R эквивалентна также каждому из следующих
свойств: A) R нётерово слева, i]r(>]e(H))=H для каж-
каждого правого идеала Н и
для любых левых идеалов Lx и L2; B) R удовлетворяет
условию максимальности для левых (или правых) анну-
аннуляторных идеалов (в частности, если R нётерово слева
или справа) и самоинъективно слева или справа; C) R
артиново справа и самоинъоктивно слева или справа;
D) каждый инъективный (проективный) левый Л-мо-
дуль проективен (инъективен1); E) все плоские левые
Л-модули инъективны; F) Л самоинъективно слева и
справа и совершенно справа; G) Л самоинъективно сле-
слева и справа и каждый его правый идеал является аннуля-
тором нек-рого конечного множества из Л; (8) Л совер-
совершенно справа и каждый конечно порожденный левый Л-
модуль вкладывается в проективный модуль; (9) R ко-
когерентно и совершенно справа и Ext#(Af, R)=0 для
всех конечно представимых левых Л-модулей М; A0) Л
удовлетворяет условию максимальности для левых ан-
нуляторов и Ext^(Af, Л) = 0 для всех конечно предста-
представимых левых Д-модулей М; A1) Л артиново слева и
справа и для всякого конечно порожденного левого Л-
модуля М длины модулей М и Нотд(М, Л) совпадают;
A2) кольцо эндоморфизмов каждого свободного левого
Л-модуля самоинъективно слева; A3) конечно порож-
порожденные односторонние идеалы кольца эндоморфизмов
любого проективного образующего (инъективного кооб-
разующего) категории левых Л-модулей являются анну-
ляторами.
Инъективные модули над К. к. разлагаются в прямую
сумму циклических. Для коммутативных колец спра-
справедливо и обратное. Если радикал Джекобсона / коль-
кольца Л трансфинитно нильпотентен (т. е. /а=0 для нек-ро-
нек-рого трансфинита а, где /!=/, Ja=Ja~1J и /«= Г)|3«х/^
для предельного а), то Л — К. к. тогда и только тогда,
когда Л самоинъективно слева и все его односторонние
идеалы аннуляторные. Левый модуль над К. к. Л точен
в том и только в том случае, когда он является образую-
образующим категории левых Л-модулей. Групповое кольцо RG
является К. к. тогда и только тогда, когда группа G
конечна, а кольцо Л квазифробениусово.
Изучаются также нек-рые обобщения К. к.: левое
QF-3-к о л ь ц о Л определяется требованием сущест-
существования точного левого Л-модуля, вкладывающегося
в качестве прямого слагаемого в любой точный левый
Л-модуль; левое QF-З'-к о л ь ц о Л определяет-
определяется требованием вложимости инъективной оболочки ле-
левого Л-модуля Л в прямое произведение пек-рого мно-
множества экземпляров модуля Л. Левое псевдо-
фробениусово кольцо (или левое PF-
кольцо) определяется каждым из следующих
свойств: а) Л — инъективный кообразующий категории
левых Л-модулей; б) каждый точный левый Л-модуль
является образующим категории левых Л-модулей;
в) Л — левое <//<'-3-кольцо и аннулятор любого отлич-
отличного от Л правого идеала отличен от нуля.
Лит.: [1] К э р т и с Ч., Р а й н е р И., Теория представ-
представлений конечных групп и ассоциативных алгебр, пер. с англ.,
М., 1969; L2] Модули, [в.] 2, Нпвосиб., 1973, с. 42—48; [3]
Ф е й с К., Алгебра: кольца, модули и категории, пер. с англ.,
т. 1—2, М., 1977—78. Л. А. Скорняков.
КВАЗИХАРАКТЕР — непрерывный гомоморфизм
с абелевой топологич. группы G в мультипликативную
группу комплексных чисел. В качестве G обычно рас-
рассматривается мультипликативная группа А;* нек-рого
локального поля к.
Ограничение К. с на любую компактную подгруппу
группы G является характером этой подгруппы. В ча-
частности, если || || — нормирование поля к и Г/=
= {а?к*\ ||я||=1}, то с индуцирует нек-рый характер %
группы U, совпадающей в неархимедовом случае с груп-
группой единиц поля к. Если c{U)—i, то К. наз. н е р а з-
ветвленным. Любой неразветвленный К. имеет
вид
В общем случае К. группы к* имеет вид с^^ЦяЦ*, где
s — комплексное число, а с^я) — характер группы к*.
Действительная часть числа s однозначно определяется
К.си наз. вещественной частью К. с.
В неархимедовом случае для всякого К. с найдется
натуральное т, для которого
где ЯЛ — максимальный идеал кольца целых поля к.
Минимальное число т с этим свойством наз. степенью
ветвления К. с, а идеал 9Jim — ведущим
модулем К. с.
Лит.: [11 Ленг С, Алгебраические числа, пер. с англ.,
М., 1966; [2] Ш а ф а р е в и ч И. Р., Дзета-функция, М., 1969.
Л. В. Кузьмин.
КВАЗИЦИКЛИЧЕСКАЯ ГРУППА, группа
типа р°°,— бесконечная абелева р-группа, все собст-
собственные подгруппы к-рой циклические. Для каждого
простого р существует единственная с точностью до изо-
изоморфизма К. г. Эта группа изоморфна мультипликатив-
мультипликативной группе всех корней уравнений
хр" = 1, ге = 1, 2, ...,
в поле комплексных чисел с обычным умножением, а
также факторгруппе Qp/r?p, где Qp— аддитивная груп-
группа поля рациональных р-адических чисел, а Ър— адди-
аддитивная группа кольца всех целых р-адических чисел.
К. г. есть объединение возрастающей последовательности
циклич. групп Сп порядка р", тг=1, 2, ... , точнее —•
индуктивный предел
lim Cn
относительно индуктивной системы (С„, ф„). В терми-
терминах образующих и определяющих соотношений эта груп-
группа может быть определена как группа со счетной систе-
системой образующих а1у а2, ... , ап, ... и определяющими
соотношениями
*п+1 =
п = 2, 3, ... .
К. г. являются единственными бесконечными абеле-
выми (а также единственными локально конечными бес-
бесконечными) группами, все подгруппы к-рых конечны.
Вопрос о существовании бесконечных неабелевых групп
с указанным свойством еще не решен A978) и состав-
составляет одну из проблем О. Ю. Шмидта.
К. г. являются полными абелевыми группами, и вся-
всякая полная абелева группа есть прямая сумма нек-рого
множества групп, изоморфных аддитивной группе ра-
рациональных чисел и К. г. для нек-рых простых чисел
р. Группы типа р°° являются максимальными р-под-
группами мультипликативной группы комплексных чи-
чисел, а также максимальными р-подгруппами аддитив-
аддитивной группы рациональных чисел по модулю 1. Кольцо
эндоморфизмов группы типа р°° изоморфно кольцу це-
целых р-адических чисел. К. г. совпадает со своей Фрат-
тини подгруппой.
Лит.: [1] К у р о ш А. Г., Теория групп, 3 изд., М., 1967;
[2] Каргаполов М. И., Мерзляков Ю. И., Ос-
Основы теории групп, М., 1972. Н. Н. Вильяме.
КВАЗИЭКВИВАЛЕНТНЫЕ ПРЕДСТАВЛЕНИЯ —
унитарные представления лг, я2 группы X (или симмет-
симметричные представления симметричной алгебры X) в гиль-
гильбертовых пространствах Нг и Н2 соответственно, удов-
удовлетворяющие одному из следующих четырех эквива-
эквивалентных условий: 1) существуют такие унитарно экви-
эквивалентные представления pt и р2, что рх есть кратное
представления я1? а р2 — кратное представления я2;
2) ненулевые подпредставления представления % не
дизъюнктны с я2, а ненулевые подпредставления пред-
представления я2 не дизъюнктны с ях; 3) я2 унитарно экви-
эквивалентно подпредстявлению нек-рого представления рх,
кратного представлению ях, имеющему единичный цент-
центральный носитель; 4) существует изоморфизм Ф Нейма-
на алгебры, порожденной множеством щ(Х), на алгеб-
алгебру Неймана, порожденную множеством п2(Х), удовле-
удовлетворяющий условию Ф (л1{х)) = л2(х) для всех х?Х.
Унитарно эквивалентные представления суть К. п.;
неприводимые К. п. унитарно эквивалентны. Если ях н
я2 — К. п., и ях — факторпредставление, то и я2 —
факторпредставление; факторпредставлепие и его нену-
ненулевое подпредставление суть К. п.; два факторпредстав-
ления либо дизъюнктны, либо являются К. п. Понятие
К. п. приводит к понятию квазпдуального объекта и
квазиспектра для локально компактных групп и сим-
симметричных алгебр соответственно.
Лит.: [1] Диксмье Ж., С*-алгебры и их представле-
представления, пер. с франц., М., 1974. А. И. Штерн.
КВАЗИЭЛЛИПТИЧЕСКОЕ ПРОСТРАНСТВО — про-
проективное n-пространство, проективная метрика к-рого
определяется абсолютом, состоящим из совокупности
мнимого конуса (абсолютный копус Qo) с (п—т—1)-
вершиной (абсолютная плоскость То) и мнимой
(и—m—2)-квадрикой Qt на этой (п—m—1)-плоскости
(абсолютная квадрика Qj); обозначается символом 51™,
т<ге. К. п. является пространством более общего
проективного типа по отношению к евклидову прост-
пространству и коевклидову пространству, метрики послед-
последних получаются из метрики первого. К. п. является
частным случаем полуэллиптических пространств. При
т=0 абсолютный конус является парой слившихся
(п—1)-плоскостей, совпадающих с (п—1)-абсолютной
плоскостью То, а абсолюты совпадают с абсолютом
евклидова n-пространства. При m=n—1 конус Qa
является конусом с точечной вершиной, абсолют
в этом случае совпадает с абсолютом коевклидова
«-пространства. При т=1 конус Qo является парой
мнимых (п—1)-плоскостей. В частности, конус Qo
квазиэллиптического 3-пространства S\ является парой
мнимых 2-плоскостей, прямая A-плоскость) То является
действительной прямой их пересечения, а квадрика
Q1— парой мнимых точек на прямой То.
Расстояние б между двумя точками X и Y опреде-
определяется в случае, когда прямая XY не пересекает
(п—m—1)-плоскость То, с помощью соотношения
wo p - (x°E*x°) (у«Е,у°) '
где
y»=(yb, b<m)
— векторы точек X и Y, Ea— линейный оператор,
определяющий скалярное произведение в пространстве
этих векторов, р — действительное число; в случае,
когда прямая XY пересекает плоскость То, расстоя-
расстояние d между этими точками определяется с помощью
разности векторов точек X и Y:
ж = ух — ж1, аз1 = (.т°, а > т),
У1=(уь, Ъ > т).
где Ег— линейный оператор, определяющий скалярное
произведение в пространстве этих векторов.
Угол между двумя плоскостями, (п—2)-плоскость
пересечения к-рых не пересекается с (п—т—^-плос-
(п—т—^-плоскостью То, определяется как (нормированное) расстоя-
расстояние между соответствующими точками в двойственном
К. п. Six''1, координаты к-рых численно равны или
пропорциональны проективным координатам плоскос-
плоскостей в пространстве S™. Если (п—2)-плоскость пересе-
пересечения данных двух плоскостей пересекается с (п—m—1)-
плоскостью Тй, то угол между плоскостями и в этом
случае определяется как нормированное расстояние.
При га=2 углы между плоскостями являются углами
между прямыми.
Движениями К. п. S™ являются коллинеации этого
пространства, переводящие конус Qo, плоскость То
и квадрику Qt в себя. Группа движений является груп-
группой Ли, а движения описываются ортогональными опе-
операторами. В К. п. iSam+i, двойственном самому себе,
определяются к о д в и ж е н и я — корреляции, пере-
переводящие каждые две точки в две 2т-плоскости, угол
между к-рыми пропорционален расстоянию между
точками, а каждые две 2т-плоскости — в две точки,
расстояние между к-рыми пропорционально углу
между плоскостями. Движения и кодвижения прост-
пространства SZln+i образуют группу, являющуюся группой
Ли. Геометрия 2-плоскости S° совпадает с геометрией
евклидовой, а геометрия 2-плоскости si— с геометрией
коевклидовой плоскости.
Геометрия 3-пространства Si определяется эллипти-
эллиптической проективной метрикой на прямых, коовклидо-
вой — на плоскостях и евклидовой — в связках пло-
плоскостей. Геометрия 3-пространства Sjj совпадает с ев-
евклидовой, а геометрия 3-пространства S%— с геомет-
геометрией коевклидова 3-пространства. Пространство S\
с радиусом кривизны V2 изометрично связной группе
движений евклидовой 2-плоскости со специально вве-
введенной метрикой. Связная группа движений К. п.
S\ изоморфна прямому произведению двух связных
групп движений евклидовой 2-плоскости.
Лит.: [1] Розенфельд Б. А., Неевклидовы прост-
пространства, М., 1969. Л. А. Сидоров.
КВАНТИЛЬ — одна из числовых характеристик
распределения вероятностей. Для действительной слу-
случайной величины X с функцией распределения F(x)
квант и лью порядка р, 0 < р < 1, наз. число
Кр такое, что F (Кр) < р, F (Кр + 0) Ss p. Если F (х) —
непрерывная строго монотонная функция, то Кр —
единственное решение уравнения F (х) = р, то естъКр—
функция р, обратная функции F (х). Если F (х) не-
непрерывна и р' > р, то вероятность неравенства
Км х
Кр < X < Кр' равна р'—р. Квантиль Ki/% есть ме-
медиана случайной величины X. Квантили Кщ и Кзц
наз. квартилями, а КоЛ, К0<2, ¦•-, Ка>9—
д е ц и л я м и. Знание К. для подходяще выбран-
выбранных значений р позволяет составить представление
о виде функции распределения.
Напр., для нормального распределения (рис.)
Ф (*) = -!= Г*
У 2я J -о
график функции Ф(х) можно вычертить по децилям:
Я01=—1,28; Z0l2=-0,84; Z03=-0,52; ЛГ0>4=—0,25;
Х0,5=0; tfOi6=O,25; tfo,7=O,52; Z0,8=0,84; AT0i9==l,28.
Квартили нормального распределения Ф(х)' равны
Кщ=— 0,67; i?3/4=0,67. В. В. Сенатов.
КВАНТОВАЯ ТЕОРИЯ ПОЛЯ — теория релятивист-
релятивистских квантовых систем. Возникновение К. т. п. свя-
связано с задачами о взаимодействии вещества с излуче-
излучением и с попытками построения релятивистской кван-
товой механики [П. Дирак (P.A.M. Dirac, 1927),
В. Гейзенберг (W. Heisenberg), В. Паули (W. Pauli) и
др.]. При релятивистских (т.е. больших) энергиях не
может быть последовательной квантовой механики
частицы, так как релятивистская квантовая частица
способна порождать новые (такие же или другие) ча-
частицы, а сама — исчезать. Вследствие этого нельзя
выделить нек-рое число механич. степеней свободы,
связанных с этой частицей, а приходится говорить
о системе с переменным, вообще говоря, бесконечным
числом степеней свободы. К. т. п. объединяет описа-
описание полей и частиц, к-рые в классич. физике высту-
выступают как две разные сущности.
Центральную роль в теории играет понятие кванто-
квантового поля. Удобно пояснить, как оно вводится, на
примере электромагнитного поля, так как это единст-
единственное поле, имеющее ясное содержание и в классиче-
классическом и в квантовом случаях.
Классическое электромагнитное поле удовлетворяет
уравнениям Максвелла. Эти уравнения можно пере-
переписать в виде канонических уравнений Гамильтона, так
что потенциал поля играет роль координаты, а его про-
производная по времени — импульса в соответствующем
фазовом пространстве. Поле представляется как кано-
каноническая система с бесконечным числом степеней сво-
свободы, так как потенциал в каждой пространственной
точке есть независимая координата. Эту систему можно
квантовать так же, как обычную механич. систему.
В квантовой картине основные понятия — это состоя-
состояния, описываемые векторами гильбертова пространства,
и наблюдаемые, описываемые самосопряженными опе-
операторами, действующими в этом пространстве. Кван-
Квантование состоит в замене канонических координат и
импульсов на операторы таким образом, чтобы скобке
Пуассона сопоставлялся коммутатор соответствующих
операторов. Квантовое поле становится оператором,
действующим на векторы состояния и вызывающим
переходы между состояниями с различным числом
квантовых частиц — фотонов, т. е. описывающим рож-
рождение и уничтожение (излучение и поглощение) квантов
поля.
Аналогично квантовое поле может быть поставлено
в соответствие любым другим фундаментальным части-
частицам. Уравнения для оператора свободного поля полу-
получаются из основного требования теории относитель-
относительности — условия инвариантности относительно Пуан-
Пуанкаре группы. Сорт частиц характеризуется массой по-
покоя т, спином, т. е. собственным моментом s, прини-
принимающим целые и полуцелые значения, включая нуль,
и различными зарядами (электрическим, барионным,
лептонным и т. д.). Первые два числа [т, s] определяют
неприводимое представление группы Пуанкаре, по
к-рому преобразуется поле, а тем самым и уравне-
уравнения поля.
Свободное классическое скалярное поле и{х) подчи-
подчиняется уравнению (х = (х°, ж) ? R4)
(П + т2)и(х)=0, [J^d^^dl—dl — dl — dl. A)
Это — вариационное уравнение Эйлера для функцио-
функционала действия
с плотностью лагранжиана
Яо {и (х)) = 4- д^ид^и — Щ- иК
Если рассматривать и (ж), a??R3 как каноническую
координату, то сопряженный импульс есть р(ас)=
= dJ?jdu(x)—u(oo) (точка означает производную по
времени). Квантование выполняется посредством со-
доставления функциям и (ас), р (ж) операторных функций
<р (ж), к (ее), удовлетворяющих коммутационным соотно-
соотношениям (квантовой скобке Пуассона)
(л-—постоянная Планка, далее принимается ti=i).
Оператор Гамильтона имеет вид:
#0= \ЛсЯ0(ф(ж), я(ж)) =
= С <2ж | : -s- я2 (.») -f — (уф (ж)J+ ^- ф2 (as): )
т. е. Яо— та же функция квантовых операторов ф и я,
что и классич. гамильтониан, с точностью до порядка
{не коммутирующих) операторов. Символ :: нормаль-
нормального произведения уточняет этот порядок. Гамильто-
новы уравнения движения
ф(ж) = г [#0, <р(ж)],
я (ж) = i [Яо, я (ж)]
эквивалентны уравнению
(? + ™2)Ф(*) = О. B)
Квантовое поле в 4-мерном пространстве-времени необ-
необходимо является обобщенной, а не обыкновенной опе-
раторнозначной функцией, поэтому (р(х) следует по-
понимать только как символическую запись.
Математич. смысл этим символам придается в фор-
формализме пространства Фока, представляющего собой
реализацию пространства состояний в К. т. п. Состо-
Состояние одной частицы в заданный момент времени опи-
описывается комплексной функцией "F (р), квадратично ин-
интегрируемой по релятивистски инвариантной мере
где ч>(р)=(рг-\-т~уи— релятивистская энергия час-
частицы с массой т. Такие функции образуют гильбертово
пространство ^j(=L2(da). Система из п тождествен-
тождественных частиц описывается квадратично интегрируемой
функцией х?п(р1,..., рп), симметричной (для бозонов —
частиц с целым спином) или антисимметричной (для
фермионов — частиц с полуцелым спином) относительно
перестановки любых двух координат. Эти функции
(для бозонов) принадлежат гильбертову пространст-
пространству efn — снмметризованному тензорному произведе-
произведению п экземпляров ^f. Для описания систем с пере-
переменным числом частиц вводится прямая сумма про-
пространств ^"„—фоковское пространство <У=Ф„'^"'"
|Р0=С. Вектор Q0=(l, 0, 0, .. .) наз. вакуумом
и интерпретируется как состояние системы без ча-
частиц. Векторы вида @, 0, .... ?„, 0, . . .) наз. ча-
частичными векторами и отождествляются
с Vn. Удобно рассматривать функции W (р) из 3% как
функции 4-вектора р = (ро,Р), где рй=ш(р). Тогда
представление группы Пуанкаре U(a, А) дается фор-
формулой
(U(a, Л)^)(р) = е-'<Р'а>^(Л-1р),
где (р, a) = pfxa^==p°a°—pa — лоренц-инвариантная би-
билинейная форма. Представление, заданное в ,^f, ес-
естественным образом индуцирует представление во
всем фоковском пространстве ,|Г. Генератор сдвигов
вдоль оси р0 совпадает с гамильтонианом 7/0. Здесь
описано простейшее представление группы Пуанкаре,
соответствующее спину s=0.
Различные операторы в фоковском пространстве вы-
выражаются через операторы рождения и уничтожения.
Пусть f(p)— одночастичная волновая функция (т. е.
/€$?)• Тогда оператор уничтожения a(f) :
определяется по формуле
„ (Рь ..., р„) / (рп) da (pn),
а оператор рождения a*(f) : JF'п-\ -*Wn — как ему сопря-
сопряженный. В частности, a*(/)Q0=@, f(p), 0, . . .), т. е.
оператор a*(f) рождает из вакуума частицу с волновой
функцией f(p), а а(/)йо=О. Операторы рождения и
уничтожения принято записывать в символическом
виде
а (/) = ^ а (р) f (p) da (р), а* (/) = $ а* (р) f (p) da (p).
Фурье-преобразование суммы операторов рождения и
уничтожения <р(/)=а(/)+а*(/) является для действи-
действительных f?L2(R%) симметрическим оператором и наз.
свободным (скалярным) квантовым полем в нулевой
момент времени. Квантовое поле в момент времени
х° имеет вид
ф(я», f) = eix°H°<?(f) e~ix°H°
и как операторная обобщенная функция ср (х) удовле-
удовлетворяет на своей области определения уравнению
B) и каноническим коммутационным соотношениям
[ф (/), п Ш = '\ f (a?) g (ж) dec. C)
Таким образом, в фоковском пространстве реализуется
каноническое квантование, описанное выше.
Теория свободного квантового поля может быть
изложена математически строго и последовательно.
Для взаимодействующих полой положение иное. Хотя
в К. т. п. и получен целый ряд важных результатов
по проблемам, допускающим корректную математиче-
математическую постановку, но до сих пор но решена принци-
принципиальная задача обоснования теории взаимодействую-
взаимодействующих полей: но построено нетривиального примера,
удовлетворяющего всем физич. требованиям. Конкрет-
Конкретные физич. расчеты опираются на эвристическую
схему К. т. п., в основе к-рой в большинстве случаев
лежит теория возмущений. Уравнение для взаимо-
взаимодействующего поля содержит нелинейный член —
](Ф(х)):
(П+/п!)Ф(г)-1(ФA)). D)
Это уравнение, так же как A), может быть получено
как вариационное уравнение для %=Хй-\-Х-1Г^, при-
приЛагранжиан взаимодействия jf 1т(Ф) выбирается в виде
нелинейной инвариантной комбинации полей, участ-
участвующих во взаимодействии, и их производных. В про-
простейшем случае скалярного поля, взаимодействующего
с самим собой, j?int = —ХФ4(ж). При Х~0 получает-
получается свободное поле. Взаимодействующее квантовое по-
поле Ф(х) можно явно выразить через начальные дан-
данные Ф(ж) н П(ж)=Ф(ж) по формуле
где, однако, в экспоненте стоит уже полный гамильто-
гамильтониан
oa |яо(Ф(я5), П(я5)) + Х:Ф«(а5
Выбирая в качестве начальных данных значения сво-
свободного поля ф(я?) и я (ж), можно выразить решение
нелинейного уравнения D) через операторы рождения
и уничтожения а*{р) и а(р) свободных частиц.
В этой схеме приходится вводить в рассмотрение
невзаимодействующие частицы и рассматривать взаимо-
взаимодействие как дополнительный фактор, к-рый в после-
последовательном изложении приходится «включать» и
«выключать» с помощью специальной адиабатической
процедуры (см. [5]). Между тем взаимодействие может
весьма заметно менять спектр и другие характеристики
рассматриваемых полей. В стандартных методах счи-
считается, что полю Ф отвечает именно та частица, к-рая
проявляется в линеаризованном уравнении. Только
для достаточно слабого взаимодействия типа А.Ф4
ложно доказать, что это так. Однако и в теории возму-
возмущений спектр, вообще говоря, меняется. Собственный
вектор Q, отвечающий минимальному собственному
значению дискретного спектра // (точнее, следовало бы
говорить об операторе массы) наз. перенормированным
вакуумом и интерпретируется как состояние без час-
частиц. Собственные значения, отвечающие остальным
точкам дискретного спектра, называются перенорми-
перенормированными одночастичными состояниями (обычно счи-
считается, что имеется одно такое состояние). Оно отли-
отличается от состояния a*(f)Q0 и имеет массу М, отличную
от затравочной массы т.
Прямое применение теории возмущений дает бес-
бессмысленные расходящиеся выражения (так наз. «ульт-
«ультрафиолетовые расходимости»). Если регуляризацию
этих расходимостеп проводить в соответствии с физи-
физическими принципами (главным условием оказалась
релятивистская и калибровочная инвариантность всей
процедуры), то весь произвол (в электродинамике)
сводится к формально бесконечной перенормировке
массы и заряда электрона, как было показано в 1948
Ю. Швингером (J. Schwinger), P. Фейнманом (R. Р.
Feynman) и Ф. Дайсоном (F. J. Dyson).
Окончательную формулировку и строгий математич.
анализ К. т. п. в рамках теории возмущений дал
Н. Н. Боголюбов A951—55). Он указал, что ультра-
ультрафиолетовые расходимости в теории возмущений по-
появляются вследствие перемножения обобщенных функ-
функций в точках, где их носители пересекаются, и сформу-
сформулировал такой способ их перемножения, при к-ром
выполняются физич. требования релятивистской ин-
инвариантности, причинности и др. В практич. расчетах
теория возмущении применяется не непосредственно
к уравнению D), а к различным другим объектам,
к-рые могут быть из него получены, напр, к 5-матрице
(см. Рассеяния матрица) или к функциям Грина. Вы-
Вычисление 5-матрицы является одной из главных задач в
физике элементарных частиц. Ее матричные элементы
просто выражаются через функции Грина поля Ф(х):
Сп(хъ ..., xn) = (Q, Т(Ф(хл) ...Ф(хп))й),
где Т(. . .) — символ хронологического упорядочения
Г (Ф (a-i) .. . Ф (*„)) = Ф (*,-,) .. . Ф (х!п), если
Разлагая Gn в ряд по степеням JPjnt, используя, напр.,
представление для Gn в виде функциональною интег-
интеграла
Gn (хъ ..., хп) =
(хх) ...и (х„) е J v 1Щ Tlxdu (ж),
E)
можно выразить ее в каждом порядке теории возмуще-
возмущений через интегралы от произведений простейших функ-
функций Грина свободного поля
D (х1~х2) = (й„, Г (ф (Xl) ф (х2)) й0) =
^ С j (p. *1-*»>
Для вычислений по теории возмущений разработана
техника диаграмм Фейнмана. При этом возникают
произведения функций Грина D (х) в совпадающих
точках. Напр., функция G2(xly х2) для модели J?jnt=
= —ЯФ4 во втором порядке по Я пропорциональна вы-
выражению
y2)D (y2-r2). F)
Этот интеграл расходится, однако его можно регуля-
ризовать, т. е. сопоставить ему нек-рое осмысленное
выражение. Прежде всего следует придать смысл про-
произведению обобщенных функций D3(z). Это можно
сделать следующим образом. Рассматривается сглажен-
сглаженная функция
(х)
_J_ f
<2л)« J '
где е>0, а ри(|) — такая функция, что Dy,?{x) —
достаточно гладкая, напр., Ph(D=A+Ii'y-)~n, N>2
и DK<e(x)—>-D (х) при х—voo, 8—>-0 (х — называется
ультрафиолетовым обрезанием). Можно считать, что
лагранжиан X в E) заменен на
.Sfoo =-1 Зцир (?) д^и — -^1 и* — ки*.
Найдутся такие константы ак и Ьк (расходящиеся
при х—у°о), что в смысле обобщенных функций сущест-
существует предел
D3reg (х) = lim | lim ?>?, е (я) —ах П б (*) —М (х)\ .
И->- со (.? -* 0 /
Функция D3Tes(x) и является регуляризацией Da(x).
Она определяется с точностью до слагаемых a?j6(;r)-j-
-гбб(я), где а и 6 — произвольные константы. Та-
Таким же образом регуляризуется и все выражение F).
при этом нового произвола не появляется. Аналогичнс
регуляризуются все функции Грина во всех порядках
теории возмущений по X. Подобную процедуру можно
провести для Х\п\, равного любому полиному. Для
=Sfjnt=—ЯФ4 процедуру регуляризации можно провести
самосогласованно во всех порядках теории возмущений
по Я, в следующем смысле. Существуют такие константы
Ay., By,, Су. (представимые в виде рядов по Я, степени
два и выше; для их вычисления разработаны простые
правила), что при подстановке в E) вместо лагран-
лагранжиана J?<ю — перенормированного лагранжиана
в каждом порядке разложения в ряд по Я при х—>-ос
получаются конечные выражения. Х^п называется
перенормированным лагранжианом, и говорят, чтч
к исходному X добавлены расходящиеся контрчлены.
Эти контрчлены имеют ту же структуру, что и исход-
исходный лагранжиан (т. е. являются линейной комбина-
комбинацией выражений д^ид^и, и2, м4). Вследствие этого не-
неоднозначность в величинах А и, By, Су. можно фикси-
фиксировать, если считать заданными массу и заряд систем!,:
(масса определяется как значение р2, при к-ром G2(/'2)
имеет полюс, а заряд — как значение G4 в нек-роп
определенной точке). Анализ этой неоднозначности
приводит к важному понятию ренормализационши:
группы [5].
Если в данной модели возможно устранить ультра-
ультрафиолетовые расходимости с помощью добавления контр-
контрчленов той же структуры, чяо и исходный лагранжиан,
то такая модель называется перенормируемой; в про-
противном случае — неперенормируемой. Все модели ска-
скалярного поля, взаимодействие в к-рых есть полином
степени выше четвертой — неперенормируемы. Это
относится только к теории возмущений. Последова-
тельная формулировка описанного способа отделения
«бесконечностей», возникающих при перемножении
сингулярных обобщенных функций во всех порядках
теории возмущений, составляет содержание так наз.
теоремы об «Д-операции» Н. Н. Боголюбова и О. С. Па-
расюка A956) [5], [19]. Тем самым была доказана тео-
теорема существования квантовой теории взаимодейст-
взаимодействующих полей во всех порядках теории возмущений.
Последующие исследования показали, что ряд теории
возмущений является в лучшем случае асимптотиче-
асимптотическим, и оценки на его основе применимы только при
не слишком больших энергиях участвующих в процессе
частиц. Устранение ультрафиолетовых расходимостей
удается последовательно провести только в рамках
теории возмущений.
Все вышесказанное относилось к реальному четырех-
четырехмерному пространству-времени. В трехмерном прост-
пространстве-времени взаимодействие становится менее син-
сингулярным и можно ограничиться добавлением контр-
контрчлена fix : и2, причем Вх имеет второй порядок по Я.
В двумерном пространстве-времени контрчлены не
нужны.
Здесь описана только простейшая модель скаляр-
скалярного поля с взаимодействием Я.Ф4. В К. т. п. имеют дело
с более сложными многокомпонентными системами
взаимодействующих ферми- и бозе-полей. Напр., ки-
ральные поля уже на классич. уровне принимают зна-
значения в нек-рых не обязательно линейных однородных
пространствах (напр., на сфере); калибровочные поля
являются связностями в нек-рых векторных расслое-
шгях — к ним относятся электромагнитное поле, гра-
гравитационное поле и поле Янга — Миллса (см. [11],
[15]).
Метод возмущений не применим в тех случаях, когда
константа взаимодействия — основной параметр раз-
разложения — заведомо больше единицы, как для силь-
сильных ядерных взаимодействий мезонов и нуклонов.
Для сильных взаимодействий пользуются другими ме-
методами, в к-рых существенную роль играют рассмотре-
рассмотрение 5-матрицы в целом и изучение общих свойств ее
матричных элементов, прямо описывающих интересные
для опыта величины — амплитуды процессов рассея-
рассеяния и рождения. При этом квантовые поля (или токи),
к-рые могут быть выражены через 5-матрицу, играют
важную роль, поскольку на 5-матрицу накладывается
центральное условие причинности (Н. Н. Боголюбов,
1955) как ограничение на носитель определенных мат-
матричных элементов 5-матрицы. Вместе с другими физич.
требованиями, такими, как релятивистская инвариант-
инвариантность и характер энергетического спектра, условие
причинности позволяет установить свойства голоморф-
голоморфности обобщенных функций — амплитуд рассеяния
как функций нескольких комплексных переменных.
Эти аналитич. свойства оказываются достаточными
для вывода специального рода интегральных представ-
представлений для амплитуды рассеяния — «дисперсионных
соотношений». Строгое доказательство дисперсионных
соотношений [4] потребовало развития специальных
математич. методов, лежащих на стыке теории обоб-
обобщенных функций и теории функций многих комплекс-
комплексных переменных и, в частности, доказательства теоре-
теоремы об острие клина Н. Н. Боголюбова и о С-выпуклой
оболочке В. С. Владимирова [8]. Дисперсионные соотно-
соотношения стали основой большей части конкретных мето-
методов расчета в теории сильных взаимодействий [А. А. Ло-
Логунов, С. Мандельстам (S. Mandelstam) и др.]. Они
примыкают к так наз. аксиоматической теории поля, в
к-рой выясняются совместность аксиом и их следст-
следствия, касающиеся вопросов существования и свойств
квантовых полей.
Метод теории возмущений предполагает, что для
уравнения D), решением к-ро.го является квантовое поле
Ф(х), выбираются простейшие начальные данные q>, n,
заданные в фоковском пространстве свободных частиц.
Существует много унитарно неэквивалентных реализа-
реализаций (представлений) коммутационных соотношений C),
и в этом состоит отличие К. т. п. как системы с беско-
бесконечным числом степеней свободы от квантовой меха-
механики, где имеется теорема Неймана о единственности
этих представлений. Для физики интересны любые
реализации начальных данных, для к-рых уравне-
уравнение D) имеет решения Ф{х), и гамильтониан // ограни-
ограничен снизу. Гильбертово пространство, в к-ром реали-
реализовано такое представление, наз. сектором. Нек-рые
модели могут иметь по нескольку фаз (фаза — сектор
с единственным вакуумом), напр., ЯФ4-модель имеет
при достаточно больших X две фазы — происходит
фазовый переход. При построении фаз применяется
квазисредних метод. Представление о фазовом переходе
и связанном с ним явлении спонтанного нарушения
симметрии сыграло важную роль в частности в единой
теории слабых и электромагнитных взаимодействий.
В 1974 было показано, что в нек-рых двумерных моде-
моделях имеются так наз. солитонные сектора, в к-рых ва-
вакуум отсутствует, но к-рые имеют богатый спектр час-
частиц, аналогичный спектру частиц соответствующе!]
классич. модели (Л. Д. Фаддеев и др.).
В К. т. п. имеется много задач, требующих для своего
решения методов из различных областей математики,
в настоящее время интенсивно исследуемых. Условно
их можно разбить на следующие группы.
1) Анализ аксиом и их следствий для квантовых по-
полей и ^-матрицы. Помимо средств функционального
анализа — теории самосопряженных операторов, обоб-
обобщенных функций, представлений групп,— здесь ис-
используются методы теории функций многих комплекс-
комплексных переменных, С*-алгебры и алгебры Неймана,
в последнее время — методы теории вероятностей. Ос-
Основные величины — функции Грина или функции
Уайтмана у^п(хи • • м хп) — являются граничными
значениями функций, голоморфных в некоторых обла-
областях Dncz.Cin. Нерешенная задача здесь — построе-
построение оболочек голоморфности S^(Dn). Область Dn со-
содержит евклидовы точки вида (mJ, Я5Х, srf, cc2, ...).
Для ряда моделей в двух- и трехмерном простравпетве-
времени доказано, что значения функции Уайтмана
в этих точках являются моментами вероятностной
меры. Заслуживает внимания дальнейший анализ та-
такого евклидова подхода к К. т. п. с точки зрения тео-
теории вероятностей.
Имеется общий алгебраич. подход к теории поля,
при к-ром в основу теории кладутся алгебры наблюдае-
наблюдаемых — т. е. С*-алгебры или алгебры Неймана, наде-
наделенные нек-рыми естественными с физич. точки зрения
структурными свойствами. Здесь одна из основных
задач состоит в анализе связи между алгебрами полей
и алгебрами наблюдаемых, а также задача об описании
динамики в рамках этого подхода.
2) Конструктивная К. т. п. имеет важнейшей задачей
доказательство существования моделей К. т. п. в 4-
мерном пространстве-времени. В двух- и трехмерном
случае существование ряда моделей доказано на основе
евклидова (вероятностного) • подхода с применением
методов, развитых по аналогии со статистической меха-
механикой; здесь требуется дальнейший математич. анализ
таких вопросов, как спектр гамильтониана, фазовые
переходы, свойства 5-матрицы и др.
3) В формальной К. т. п., существование к-рой из-
известно в каждом порядке теории возмущений, также
имеется ряд проблем, допускающих математич. форму-
формулировку. Сюда относятся, напр., анализ рядов теории
возмущений (в частности, аналитич. свойства диаграмм
Фейнмана), изучение классич. уравнений теории поля
я кпазиклассических поправок к ним — здесь возни-
возникают нелинейные уравнения эллиптического и гипербо-
гиперболического типов, для анализа к-рых применяются,
в частности, метод обратной задачи рассеяния, методы
дифференциальной и алгебраической геометрии и то-
топологии, и др.
Лит.: [1] А х и е з е р А. И., Берестецкий В. Б.,
Квантовая электродинамика, 3 изд., М., 1969; [2] Б е р е-
зин Ф. А., Метод вторичного квантования, М., 1965; [3]
Боголюбов Н. Н., Логунов А. А., Т о д о р о в И. Т.,
Основы аксиоматического подхода к квантовой теории поля, М.,
1969; f/jj Боголюбов Н. Н., Медведев Б. В.,
Поливанов М. К., Вопросы теории дисперсионных соот-
соотношений, М., 1958; [5] Б о г о л ю б о в Н. Н., Ш и р к о в Д. В.,
Введение в теорию квантованных полей, 3 изд., М., 1976; [6]
Байтман А., Проблемы в релятивистской динамике кван-
квантованных полей, пер. с англ., М., 1968; [7] В а с и л ь е в А. Н.,
Функциональные методы в квантовой теории поля и стати-
статистике, Л., 1976; [8] В л а д и м и р о в В. С, Методы теории
функций многих комплексных переменных, М., 1964; [9] Й о с т
Р., Общая теория квантованных полей, пер. с англ., М., 1967;
[10] Конструктивная теория поля, пер. с англ., М., 1977; [11]
Попов В. Н., Континуальные интегралы в квантовой теории
поля и стилистической физике, М., 1976; [12] Рид М., Сай-
Саймон Б., Методы современной математической физики, пер. с
англ., т. 1, М., 1977, т. 2, М., 1978; [13] Саймон Б., Модель
Р(ФJ эвклидовой квантовой теории поля, пер. с англ., М., 1976;
[14] Сигал И., Математические проблемы релятивистской
физики, пер. с англ., М., 1968; [15] С л а в н о в А. А., Фад-
Фаддеев Л. Д., Введение в теорию калибровочных полей, М.,
1978; [16] С т р и т е р Р., В а й т м а н А., РСТ, спин и ста-
статистика и все такое, пер. с англ.,М., 1966; [17] Ф амФ., Вве-
Введение в топологическое исследование особенностей Ландау, пер.
с франц., М., 1970; [18] Фридрихе К., Возмущение спектра
операторов в гильбертовом пространстве, пер. с англ., М., 1969;
[1!I X е п п К., Теория перенормировок, пер. с франц., М., 1974;
[20] Шварц А. С, Математические основы квантовой теории
поля, М., 1975; [21] Ш в е б е р С, Введение в релятивистскую
квантовую теорию поля, пер. с англ., М., 1963; [22] Квантовая
теория калибровочных полей, пер. с англ., М., 1977.
И. В. Волович, М. К. Поливанов.
КВАНТОР — общее название для логических опе-
операций, к-рые по предикату Р (х) строят высказывание,
характеризующее область истинности предиката Р(х).
В математич. логике наиболее употребительны кван-
квантор всеобщности уи квантор суще-
существования 3- Высказывание VxP(x) означает,
что область истинности предиката Р (х) совпадает
с областью значений переменной х. Высказывание
ЗхР(х) означает, что область истинности предиката
Р(х) непуста. Если интересуются поведением преди-
предиката Р (х) не на всей области значений переменной х,
а лишь на ее части, выделяемой предикатом R(x), то
часто употребляют так наз. ограниченные
кванторы Cx)rix) и (V^)#(xb ПРИ этом высказы-
высказывание Cx)R(x)P(x) означает то же, что и 3x(R (x)&P(x)),
а (\/х)щХ) Р(х) — то же, что yx(R (x)'Z)P(x)), где
& — знак конъюнкции, ID — знак импликации.
В. Е. Плиспо.
КВАРТИЛЬ в теории вероятностей —
частный случай квантили. К. наз. квантили Кр, соот-
соответствующие значениям р, равным '^(нижняя К.)
и 3/4 (верхняя К.).
КВАТЕРНАРНАЯ КВАДРАТИЧНАЯ ФОРМА —
квадратичная форма от четырех переменных. К. к. ф.
над полем F связаны с алгебрами кватернионов над
тем же полем, а именно, алгебре с базисом [1, ц, i2, i3],
j'J=—a^jF, i'l=—a2^F, i1i2=—i2il=i3 отвечает
К. к. ф.— норма кватерниона,
q (х0, хъ х2, xs) = N (xo + z1l
= .го -j- а.\х\ 4- а2х1 -j-
Для К. к. ф., отвечающих кватернионным алгебрам, и
только для таких определена композиция квадратич-
квадратичных форм:
(
где координаты вектора z суть билинейные формы
от х и у. Композиция возможна лишь для квадратич-
квадратичных форм от двух, четырех и восьми переменных.
А. В. Малышев.
КВАТЕРНАРНАЯ ФОРМА — форма от четырех пе-
переменных, т. е. однородный многочлен от четырех
неизвестных с коэффициентами из заданного коммута-
коммутативного кольца С единицей. О. А. Иванова.
КВАТЕРНИОН — гиперкомплексное число, геомет-
геометрически реализуемое в четырехмерном пространстве.
Система К. предложена в 1843 У. Гамильтоном (W. Ha-
Hamilton). К. явились исторически первым примером
гиперкомплексной системы, возникшей при попытках
найти обобщение комплексных чисел. Комплексные
числа изображаются геометрически точками плоскости,
и действия над ними соответствуют простейшим гео-
метрич. преобразованиям плоскости. Из точек прост-
пространства трех и выше измерений нельзя «устроить»
числовую систему, подобную полю действительных или
комплексных чисел. Однако, если отказаться от комму-
коммутативности умножения, то из точек 4-мерного прост-
пространства можно устроить числовую систему (в прост-
пространстве трех, пяти и выше измерений нельзя по-
построить даже такую систему).
К. образуют 4-мерную алгебру над полем действи-
действительных чисел с базой 1, i, j, k («базисные единицы») и
следующей таблицей умножения «базисных единиц»:
1.1 = 1 \.i = i l-/ = / l.fc = *
M = i j.j = —-1 i-j = k i.k = —j
7-1=7 j-i — —k j ¦ j = —1 j-k=i
k-l = k k-i = j k-j = —i k-k = —1.
Всякий К. может быть записан в виде
X = x0A-\-x1i-\-xij+xsk
или (поскольку 1 играет роль обычной единицы и в за-
записи К. может быть опущена) в виде
X=xo+x1i+x2j+x3k.
Различаются скалярная часть К. х0 и
векторная часть
V=x1i+x2j+x3k,
так что Х=хо-\-У. Если хо=О, то кватернион V наз.
вектором, и он может отождествляться с обычным
3-мерным вектором, поскольку умножение в алгебре К.
двух таких векторов Vt и Fa связано со скалярным
(V1, F2) и векторным [F1; F2] произведениями векторов
V1 и F2 в 3-мерном пространстве формулой
VtV^-lVi, Vt)+[Vlt F2].
Это показывает тесную связь К. с векторным исчисле-
исчислением. Исторически последнее и возникло из теории К.
Всякому К. X=xo-\-V сопоставляется сопря-
сопряженный кватернион Х=х0— V, при этом
X -X =Х-X =
Это действительное число наз. нормой кватер-
кватерниона X и обозначается N(X). Норма К. удовлет-
удовлетворяет соотношению
Любое вращение 3-мерного пространства вокруг на-
начала координат может быть задано при помощи ква-
кватерниона Р с нормой 1. Вращение, соответствующее Р,
переводит вектор X — x^-^xj+xgk в вектор 1^=^+
+yai+yak=PXP-\
Алгебра К. является единственной ассоциативной,
но не коммутативной, конечномерной нормированной
алгеброй над полем действительных чисел, обладаю-
обладающей единицей. Алгебра К.— тело, т. е. в ней опреде-
определено деление, причем К., обратным к К. X, является
^ X. Тело К. единственная конечномерная дейст-
вительная ассоциативная, но не коммутативная ал-
алгебра без делителей нуля (см. также Фробениуса тео-
теорема).
Лит.: [1] К а л у ж н и н Л. А., Введение в общую алгебру,
М., 1973; И Кантор И. Л., С о л о д о в н и к о в А. С,
Гиперкомплексные числа, М., 1973; [3] К у р о ш А. Г., Лек-
Лекции по общей алгебре, 2 изд., М., 1973. Н. Н. Вильяме.
КВАТЕРНИОННАЯ СТРУКТУРА — 1) К. с. на
вещественном векторном простран-
пространстве V — структура модуля над телом кватернио-
кватернионов Н, т. е. подалгебра Н алгебры End V эндоморфиз-
эндоморфизмов пространства V, порожденная двумя антикоммути-
рующидш комплексными структурами /х, J2 на прост-
пространстве V. Эндоморфизмы /1? J 2 наз. стандарт-
стандартными образующими К. с. Н, а определяе-
определяемый ими базнс {id, Ju J2, J3 = JtJ2} алгебры // —
стандартным базисом. Стандартный базис
определен с точностью до автоморфизмов алгебры Н.
Алгебра Н изоморфна алгебре кватернионов. Автомор-
Автоморфизм А векторного пространства V наз. автомор-
автоморфизмом К. с, если индуцированное им преобразо-
преобразование Ad А пространства автоморфизмов сохраняет Н,
т. е. (Ad A)H=AHA ~1=Н. Если при этом на Н инду-
индуцируется тождественный автоморфизм, то А наз.
специальным автоморфизмом К. с.
Группа всех специальных автоморфизмов К. с. изо-
изоморфна полной линейной группе GL(m, К) над те-
телом К, при этом 4m = dim V. Группа всех автоморфиз-
автоморфизмов К. с. изоморфна прямому произведению с объеди-
объединенной подгруппой группы GL(m, H) и группы единич-
единичных кватернионов /fTssSp(l).
2) К. с. на дифференцируемом много-
многообразии — ноле кватернионных структур на каса-
касательных пространствах, т. е. подрасслоение л : Н-^-М
расслоения End T(M)-+M эндоморфизмов касательных
пространств, слой ffl p =я~1(р) к-рого суть К. с. на
касательном пространстве. ТрМ для любого р?М.
Специальной К. с. наз. пара антикоммутирую-
щих почти комплексных структур Jlt /2 на многообра-
многообразии М. Она порождает К. с. //, где
2, к[ ^ fKj.
К. с. Н на многообразии М порождается нек-рой спе-
специальной К. с. тогда и только тогда, когда расслое-
расслоение Н-+-М тривиально. К. с. на многообразии можно
рассматривать как Sp (l)-GL(m, Н)-структуру, а спе-
специальную К. с— как GL(m, Н)-структуру в смысле
теории G-структур. Отсюда следует, что для существо-
существования на многообразии М нек-рой К. с. (специальной
К. с.) необходимо и достаточно, чтобы структурная
группа его касательного расслоения редуцировалась
к группе Sp(l)-Sp(ni) (соответственно, Sp(m)). Пер-
Первое продолжение специальной К. с, рассматриваемой
как GL(m, Н)-структура, есть е-структура (поле ре-
реперов), к-рая определяет каноническую линейную
связность, ассоциированную со специальной К. с.
Обращение в нуль кривизны и кручения этой связности
является необходимым и достаточным условием того,
чтобы специальная К. с. была локально эквивалентна
стандартной плоской специальной К. с. на векторном
пространстве R4ra.
Аналогом кэлерова многообразия для К. с. служит
кватернионное риманово многооб-
многообразие. Оно определяется как риманово многооб-
многообразие М размерности 4т, группа голономии Г к-рого
содержится в группе Sp(l)-Sp(m). Если TcSp(m), то
кватернионное риманово многообразие наз. специ-
специальным, или кватернионным кэлеро-
в ы м, многообразием и при т>1 имеет ну-
нулевую кривизну Риччи. Кватернионное риманово
многообразие можно охарактеризовать как риманово
многообразие Л/, в к-ром существует К. с. Н, инвари-
инвариантная относительно параллельного переноса Леви-
Чивиты. Аналогично, специальное кватернионное ри-
маново многообразие есть риманово многообразие,
в к-ром существует специальная К. с. (J1, /2), инва-
инвариантная относительно параллельных переносов Леви-
Чивиты: у/1 = у/2=0, где у — оператор ковариант-
ной производной связности Леви-Чивиты.
В кватернионном римановом многообразии сущест-
существует каноническая параллельная 4-форма, к-рая опре
деляет ряд операторов в кольце Л (М) дифференциаль-
дифференциальных форм на М, перестановочных с оператором Бель
трами — Лапласа (оператор внешнего умножения, опе-
операторы свертки). Это позволяет построить содержатель-
содержательную теорию гармонических дифференциальных форм
на кватернионных римановых многообразиях [2], анало-
аналогичную теории Ходжа на кэлеровых многообразиях, и
получить оценки для чисел Бетти многообразия М.
Все однородные специальные кватернионные римановы
многообразия исчерпываются локально евклидовыми
пространствами. Примером однородного кватернион-
ного риманова многообразия, не являющегося спе-
специальным, служит кватернионное проективное прост-
пространство, а также другие симметрич. пространства
Вольфа, к-рые находятся во взаимно однозначном
соответствии с простыми компактными группами Ли
без центра. Ими исчерпываются все компактные одно-
однородные кватернионные римановы многообразия. Широ-
Широкий класс некомпактных несимметрических однород-
однородных кватернионных римановых многообразий строится
с помощью модулей над алгеброй Клиффорда (см. [5]).
Лит.: [1] Chern S. S., в кн.: Algebraic geometry and
topology. A symposium in honor of S. Lefschetz, N. Y., 1957,
p. 103—21; [2] К r a i n e s V. Y., «Trans. Amcr. Math. Soc»,
19tSB, v. 122, p. 357 — 67; [3] J a n о К., A k о М., «.T. of diff.
geom.», 1973, v. 8, №3, p. 341---47; [4] S о m m.,e s e A. J.,
«Math. Ann.», 1975, Bd 212, S. 191—214; [5] Алексеев-
c к и й Д. В., «Изв. АН СССР. Сер. матем.», 1975, т. 39, Л". 2,
с. 315—62; [6] W о 1 1 J. A., «J. Math, and Mech.», 1965, v. 14,
Xi 6, p. 1033—47; [7] Итоги науки и техники. Алгебра. Топо-
Топология. Геометрия, т. 11, М., 1974, с. 37—123.
Д. В. Алексеевский.
КВАТЕРНИОНОВ ГРУППА — метабелева 2-группа
порядка 8, задаваемая в образующих х, у определяю-
определяющими соотношениями
ж4 = х2у2 = ху ху~1 = 1.
К. г. может быть изоморфно вложена в мультипли-
мультипликативную группу алгебры кватернионов (вложение
определяется соответствием х—yi, y-^-j). Более того,
алгебра кватернионов является групповой алгеброй
К. г. над полем действительных чисел. Соответствие
II 0 1 II || 0 i
задает точное представление К. г. матрицами 2-го по-
порядка с комплексными элементами.
Обобщенная группа кватернионов
(частным случаем к-рой при ?г=2 является К. г.) —
группа, задаваемая в образующих х и у определяю-
определяющими соотношениями
(где п — фиксированное число). Эта группа является
2-группой порядка 2п + 1 и класса нильпотентности п.
К. г. является гамилыпоновой группой и минималь-
минимальной гамильтоновой группой в том смысле, что любая
гамильтонова группа содержит подгруппу, изоморф-
изоморфную К. г. Пересечение всех неединичных подгрупп
К. г. (а также любой обобщенной К. г.) является нееди-
неединичной подгруппой. Всякая некоммутативная конеч-
конечная группа, обладающая этим же свойством, будет
одной из обобщенных К. г. Среди конечных абелевых
групп таким свойством обладают циклические р-группы
и только они. Обобщенные К. г. и циклические р-груп-
пы являются единственными р-группами, допускаю-
щпми собственный L-гомоморфизм, т. е. гомоморфизм
решеток подгрупп на нек-рую решетку L, не являю-
являющийся изоморфизмом.
Иногда термин «К. г.» используется для обозначения
различных подгрупп мультипликативной группы ал-
алгебры кватернионов и соответствующих топологич.
групп.
Лит.: [1] X о л л М., Теория групп, пер. с англ., М., 1962.
Н. Н. Вильяме.
КЁБЕ ТЕОРЕМА — 1) К. т. покрытия: су-
существует абсолютная постоянная if >0 (постоян-
(постоянная К ё б е) такая, что если f?S (S — класс функ-
функций / (z) = z -р . .. , регулярных и однолистных в
|z| < 1), то множество значений функции w=f(z) при
|z|<l заполняет круг |ц>| <СК, причем А' — наибольшее
из чисел, для к-рых это справедливо. Л. Бибербах (L.
Bieberbach, 1916) доказал, что K=1/i п что на окруж-
окружности \w\=1/i только в том случае имеются точки, не
принадлежащие образу круга |z| <1 при отображении
w=f(z), если
где а '¦— действительное число. К. т. покрытия иногда
формулируют так: если функция w=f{z), /@) = 0,
регулярна и однолистна в |z|<l и отображает круг
\z\ <1 на область, не содержащую точку с, то |/'@)| <:4с.
2) К. т. искажения, а) Существуют такие поло-
положительные числа m1(r), Mt(r), зависящие только от г,
что для f?S, \z\ = r имеют место неравенства:
m1(r)<\f(z)\<M1(r).
б) Существует число М(г), зависящее только от г
и такое, что для f?S, \zt\<.r, |z2|<:r справедливы не-
неравенства:
Г <2>> I ^ л/г i-\
М(г)
Г (г,)
Эту теорему можно также сформулировать следующим
образом: существуют положительные числа т2(г),
М2(г), зависящие только от г и такие, что для ?S
|z|<r
Л. Бибербах показал, что наилучшие границы в К. т.
искажения таковы:
1 +
3) К. т. об отображении конечно
связных областей на канонические
области, а) Всякую га-связную область В плос-
плоскости z можно однолистно отобразить на круговую
область (т. е. на область, ограниченную конечным
числом полных окружностей без общих точек, причем
нек-рые из них могут вырождаться в точки) плоскости ?.
Среди этих отображений существует только одно нор-
нормированное отображение, переводящее заданную точку
z=af В в J= оо и такое, что разложение отображаю-
отображающей функции в окрестности z=a имеет вид
¦7r^-^ai(z — а)+ ¦ ¦ ¦ или 2 + ^-+---.
смотря по тому, конечно а или нет.
б) Всякую га-связную область В плоскости z с гра-
граничными континуумами Кг, . . ., Кп можно однолистно
отобразить на плоскость ? с п разрезами по дугам ло-
гарифмич. спиралей соответственно наклонов 9lt . . .,
8,„ O<0v<:jt/2, v=1, ..., га, к радиальным направле-
направлениям и притом так, что континуумы KVl v=l, ..., п,
переходят соответственно в дуги наклонов 0V , заданные
точки a, b?B переходят в 0 и оо и разложение отобра-
отображающей функции в окрестности z=b имеет вид
-j^- 4- а0 4- <Xi (z — Ъ) 4- .. . или z + Оо + -^ + • • • ,
смотря по тому, конечно 6 или нет. Отображение един-
единственно.
Теоремы 1) — 3) установлены П. Кёбе (см.[1] — [4]).
Лит.: [1] К о е b e P., «Nachr. Kgl. Ges. Wiss. Gott. Math -
Phys. Kl.», 1907, Bd 2, S. 191—210; 1909, Bd 4, S. 68 — 76; [2]
его же, «Math. Ann.», 1910, Bd 69, S. 1—81; 13] e г о же,
«Acta Math.», 1918, v. 41, p. 305—44; [4] e г о же, «Math. Z.»,
1918, Bd 2, S. 198 — 236; [5] Г о л у з и н Г. М., «Успехи матем.
наук», 1939, в. 6, с. 26—89; [6] е г о же, Геометрическая тео-
теория функций комплексного переменного, 2 изд., М., 1966; [7)
Дженкинс Дж., Однолистные функции и конформные
отображения, пер. с англ., М., 1962. Е. Г. Голузина.
КЁБЕ ФУНКЦИЯ — функция
где 9?[0, 2л). Эта функция была впервые изучена
П. Кёбе [1]. К. ф. отображает круг \z\ <1 на плоскость
1 -а
w с разрезом по лучу, исходящему из точки гг'"
и содержащему на своем продолжении точку w=0.
К. ф. является экстремальной функцией ряда задач
теории однолистных функций.
Лит.: [1] К о е b e P., «Math. Ann.», 1910, Bd 69, S. 1—81;
[2] H а у m a n W. K., «J. London Math. Soc», 1965, v. 40,
Л» 3, p." 385 — 406; [3] Го л узин Г. М., Геометрическая
теория функций комплексного переменного, 2 изд., М., 1966.
Е. Г. Голузина.
КЕЛДЫША ТЕОРЕМА — 1) К. т. о прибли-
приближении непрерывных функций мно-
многочленами: пусть функция f(z) комплексного
переменного z голоморфна в области G и непрерывна
в замкнутой области G; тогда, для того чтобы при лю-
любом е>0 существовал многочлен P(z) такой, что
|/(*)-/> (г) |< е, z?G,
необходимо и достаточно, чтобы дополнение CG со-
состояло нз одной единственной области G*, содержащей
бесконечно удаленную точку. Установлена М. В. Кел-
Келдышем [1]. Эта теорема является одним из основных
результатов теории равномерных приближений функ-
функций многочленами в комплексной области (см. [2]).
2) К. т. в теории потенциала — теоремы
о разрешимости и устойчивости Дирихле задачи, уста-
установленные М. В. Келдышем в 1938—41.
а) Пусть D — ограниченная область евклидова про-
пространства R", и>2, с границей T=dD. Тогда на Г
существует счетное множество иррегулярных граничных
точек {?/ft}, &=1, 2, . . ., такое, что для разрешимости
задачи Дирихле в области D с непрерывной граничной
функцией f(y) на Г необходимо и достаточно, чтобы
эта задача была разрешима в точках yk, k=i, 2, . ..,
т. е. чтобы
lim и (x) = f(yh), k=i, 2, . ..,
v -* yk. xeD
где и(х) — обобщенное в смысле Винера — Перрона
решение задачи Дирихле (см. Перрона метод, а также
[3]. [4]).
б) Пусть оператор А действует из пространства С (Г)
непрерывных функций на Г в пространство ограни-
ограниченных гармонических в D функций и удовлетворяет
следующим условиям: (a) A (a.f-\-$g)=a.A {f)-\-$A (g),
fi g<zC(t), где a, p —действительные числа, т. е. опе-
оператору! линейный; (б) если/(г/)^0, /?С(Г), но A (f)(x)~^
^0; (в) если для функции /?С(Г) задача Дирихле
разрешима, то А (/) дает решение этой задачи. При
этих условиях оператор А единственный и А (/) для
всех /?С(Г) дает обобщенное в смысле Винера —
Перрона решение задачи Дирихле (см. [5]—[7]).
в) Для того чтобы всякая разрешимая в D задача
Дирихле была устойчивой в D, необходимо и доста-
достаточно, чтобы множество иррегулярных граничных
точек множества CD совпадало с множеством иррегу-
иррегулярных граничных точек множества CD. Задача Ди-
Дирихле с любой функцией /?С(Г) устойчива внутри D
тогда и только тогда, когда множество иррегулярных
граничных точек CD, принадлежащих Г, имеет в D
гармонич. меру нуль (см. [4]).
Лит.: [1) Келдыш М. в., «Матем. сб.», 1945, т. 16,
№ 3, с. 249—58; [2] М е р г е л я н С. Н., «Успехи матем.
наук», 1952, т. 7, в. 2, с. 3—122; [3] К е л д ы ш М. В., «Докл.
АН СССР», 1938, т. 18, с. 315—18; [4] е г о же, «Успехи матем.
паук», 1941, т. 8, с. 171—292; [5] е г о же, «Докл. АН СССР»,
1941, т. 32, с. 308—9; [6] Л а н д к о ф Н. С, Основы совре-
современной теории потенциала, М., 1966, гл. 4, 5; [7] Б р е л о М.,
Основы классической теории потенциала, пер. с франц., М.,
1904. Е. Д. Соломенцев.
КЕЛДЫША — ЛАВРЕНТЬЕВА ПРИМЕР — пример
односвязной области Д плоскости комплексного пере-
переменного z, ограниченной спрямляемой кривой Жордана,
но не принадлежащей классу областей Смирнова S.
Пусть функция z=f(w) реализует конформное ото-
отображение единичного круга Е= {w; | w\ <1} на одно-
связную область D, ограниченную спрямляемой кри-
кривой Жордана. Известно, что f(w) непрерывна в замкну-
замкнутом круге Е, а логарифм модуля производной In |/'(ш)|
представим в Е интегралом Пуассона — Стилтьеса
1+р;.2';ср;5,ф_е) dv. (9), <*)
где A — нормированная борелевская мера на дЕ,
=1. Класс S состоит из таких областей D,
для к-рых мера ц в представлении (*) абсолютно не-
непрерывна по мере Лебега на дЕ и интеграл (*) прев-
превращается в интеграл Пуассона — Лебега от сущест-
существующих почти всюду на дЕ граничных значений
In |/'(e«e)|.
М. В. Келдыш и М. А. Лаврентьев [1] построили для
любого h, 0</}<l, односвязную область Д, ограни-
ограниченную спрямляемой кривой Жордана Г, расположен-
расположенную в круге |z|<A, 0?Д и такую, что при конформном
отображении области Д на круг Е,
произвольной дуге кривой Г на окружности дЕ—
= {w, \w\ = l} соответствует дуга той же длины. Эта
область Д не принадлежит классу S, так как In |/'(e'")| =
= 0 почти всюду на дЕ.
Проблема характеризации областей класса S (облас-
(областей типа Смирнова) до сих пор A978) полного решения
не получила (см. [2], [3]).
Лит.: [1] Келдыш М. В., Лаврентьев М. А.,
«Ann. Ecole norm, super.», 1937, t. 54, p. 1—38; [2] Прива-
Привалов И. И., Граничные свойства аналитических функций,
2 изд., М.— Л., 1950; [3] Л о в а т е р Д ж., в кн.: Итоги науки
и техники. Математический анализ, т. 11, М., 1973, с. 99—179.
Е. Д. Соломенцев.
КЕЛДЫША — ЛАВРЕНТЬЕВА ТЕОРЕМА о рав-
равномерном приближении целыми функ-
функциями: для того чтобы для любой непрерывной комп-
комплексной функции f(z) на континууме Е и произвольно
быстро убывающей при г-*-оо положительной функции
е(г), 0о, нижняя грань к-рой на любом конечном
интервале положительна, существовала целая функция
g(z) такая, что
\f(z)-g(z)\<s(\z\), z?E,
необходимо и достаточно, чтобы Е не содержал внут-
внутренних точек и существовала растущая к + °° функция
г) D), 0<г<+оо, такая, что любую точку z дополнения
СЕ можно соединить с оо жордановой кривой, распо-
расположенной вне Е п вне круга \t,\ <t)(|z|).
Этот результат М. В. Келдыша и М. А. Лаврентьева
[1] подвел итог многочисленным исследованиям по
приближениям целыми функциями, начатым Карле-
мана теоремой (п. 3, см. также [2]).
Лит.: Ш Келдыш М. В., Л а в р е н т ь е в М. А.,
«Докл. АН СССР», 1939, т. 23, MS 8, с. 746—48; [2] М е р г е-
л я н С. Н., «Успехи матем. наук», 1952, т. 7, в. 2, с. 31 —112.
Е. Д. Соломенцев.
КЕЛЛОГА ТЕОРЕМА: пусть функция w=f(z) реали-
реализует однолистное конформное отображение круга
{z?C; |z|<l} на область D, ограниченную гладкой
замкнутой жордановой кривой S, у к-рой угол наклона
вA) касательной к действительной оси, как функция
длины дуги I кривой S, удовлетворяет условию Гёль-
дера:
I 6 (lx)-e (l2) \<K\ h-hl*, 0<о<1;
тогда производная f(z) непрерывна в замкнутом круге
Ы<:1, а на окружности |z| = l выполняются условия
Гёльдера с тем же показателем а:
| ь /' (e'eO-in /' (**в«) | < к21 вх-е, jа.
К. т. непосредственно следует из более общих резуль-
результатов О. Келлога (см. [1], [2]) о граничном поведении
частных производных порядков г^1 гармонич. функ-
функции и(х), являющейся решением Дирихле задачи для
области D евклидова пространства R", гаЭ=2, ограни-
ограниченной достаточно гладкой поверхностью Ляпунова S
(при гС^Ъ) или кривой Ляпунова S (при га=2; см. Ля-
Ляпунова поверхности и кривые), причем заданная на
границе S функция f(y) также предполагается доста-
достаточно гладкой.
Другие результаты о граничном поведении производ-
производной f(z) отображающей функции см. в [3], [4].
Лит.: [1] Kellogg О. D., «Trans. Amer. Math. Soc»,
1912, v. 13, № 1, p. 109—32; [2] e г о же, там же, 1931, v. 33,
MS 2, p. 486—510; [3] Г о л у з и н Г. М., Геометрическая тео-
теория функций комплексного переменного, 2 изд., М., 1966; [4]
Warschawski S. E., «Proc. Amer. Math. Soc», 1961,
v. 12, p. 614—20. E. Д. Соломенцев.
КЕЛЛОГА — ЭВАНСА ТЕОРЕМА, лемма Кел-
Келлога: множество всех иррегулярных точек границы
произвольной области D евклидова пространства R",
и^2, относительно обобщенного решения Дирихле за-
задачи для D в смысле Винера — Перрона (см. Перрона
метод) имеет нулевую емкость, является полярным
множеством и имеет тип Fa. Следствие К.— Э. т.:
если К — компакт положительной емкости в Rn и
D — связная компонента дополнения СК, содержащая
бесконечно удаленную точку, то на границе dDdK
существует по крайней мере одна регулярная точка.
К.— Э. т. была высказана О. Келлогом [1] в виде ги-
гипотезы, доказана впервые Г. Эвансом [2].
Лит.: [1] К е 1 1 о g g О. D., Foundations of potential theo-
theory, В., 1929; [2] E v a n s G. C, «Proc. Nut. Arnd. Sci. USA>>
1933, v. 19 p. 457—61; [3] К е л Д ы ш Ы. В., «Успехи матем.
наук», 1941, в. 8, с. 171—231; [4] Брело М., Основы клас-
классической теории потенциала, пер. с франц., М., 1964.
Е. Д. Соломенцев.
КЕЛЬВИНА ПРЕОБРАЗОВАНИЕ — преобразование
функций, определенных в областях евклидова прост-
пространства R", п^З, при к-ром гармонические функции
переходят в гармонические. Получено У. Томсоном
(лордом Кельвином, [1]).
Если и (х) — гармонич. функция в области
то ее К. п. есть функция
гармоническая в области D*, получающейся из D
и и перс it ей относительно сферы S^—-
= {ж : \x\ = R}, т.е. отображением пространства R",
определяемым формулами
х —>• У = ! х , , -г, 0—> оо,
где ж=(л1, ..., *„), |i| = (^+...+^)'/..
При инверсии бесконечно удаленная точка оо ком-
компактифицированного по Александрову пространства R"
переходит в начало координат О, и наоборот. При К. п.
гармонич. функции и(х) в областях D, содержащих оо,
регулярные в оо, т. е. такие, что lim и(х)=0,
переходят в гармонич. функции v(у) в ограничен-
ограниченных областях D*, содержащих начало координат О,
причем и@)=0. Благодаря этому свойству, К. п. по-
позволяет сводить внешние краевые задачи теории по-
потенциала к внутренним, и наоборот (см. [2], [3]).
Кроме К. п., гармоничность функций в R™, ге^З,
сохраняется при аналитич. преобразованиях вида
"B/) = фЫ u(ty(y)) только в случае, когда y(y)^sl и i|)
есть отображение подобия, движение или симметрия
относительно плоскости; при и=2 этим свойством об-
обладает широкий класс конформных отображений i|).
Лит.: [1] Т h о m s о n W., «J. math, pures et appl.», 1847,
v. 12, p. 256—64; [2] Владимиров В. С, Уравнения ма-
математической физики, 3 изд., М., 1976, гл. 5; [3] Б р е л о М.,
Основы классической теории потенциала, пер. с франц., М.,
1964. Е. Д. Соломенцев.
КЕЛЬВИНА ФУНКЦИИ, функции Томсо-
н а,— функции ber(z) и bei(z), her(z) и hei(z), ker(z) и
kei(z), к-рые определяются следующими соотноше-
соотношениями:
berv(z) ± beiv(z) = /v( ze± З'я'4),
herv (z) + i heiv (z) = H'vu ( z
kerv (z) + i heiv (z) = f
где Hi/ — Ганкеля функция, Jv — Бесселя функция.
При v=0 индекс у знака функции опускается. К. ф.
составляют фундаментальную систему решений урав-
уравнения
переходящего при z= Уi x в уравнение Бесселя.
Представление в виде ряда:
(-1)* zik
Ьег (z) =
bei («) = У
ker (z)=(h T~C)heT (Z) + Tbei
*y2ft
kei (z)= (in -f — c) bei (z)—-? Ьег (z
Асимптотическое представление:
еа(г)
ber(z) = -—=cosP(z),
V 2Я2
еа(г)
bei(z)= y__ sinP(z),
ker (z) = Yjl e* () cos P (- г)>
|argz| < -|-я,
где
25 13
Г 384z3l/2 128z4
1 1 25
^У ' VI 8 8z T/ 16z* 384z3/- ' "' "
Функции введены У. Томсоном (лордом Кельвином,
[1]).
Лит.: [1] Thomson W., Mathematical and Physical pa-
papers, v. 3, Camb., 1890, p. 492; [2] Янке Е., Эмде Ф.,
Лёш Ф., Специальные функции. Формулы, графики, таблицы,
пер. с нем., 1964; [3] Рыжик И. М., Г р а д ш т е й н И. С,
Таблицы интегралов, сумм, рядов и произведений, 3 изд.,
М.— Л., 1951. А. Б. Иванов.
КЕНДАЛЛА КОЭФФИЦИЕНТ РАНГОВОЙ КОРРЕ-
КОРРЕЛЯЦИИ — одна из выборочных мер зависимости двух
случайных величин (признаков) X и Y, основанная па
ранжировании элементов выборки (Хх, Уг), ..., (Х„,
У„). К. к. р. к. относится, таким образом, к ранговым
статистикам и определяется формулой
2SC-, г„)
ТЦП-1)
где п— ранг Y, принадлежащего той паре (X, Y),
для к-рой ранг X равен i, ? = 2iV—га (га—1)/2, N—
число элементов выборки, для к-рых одновременно
/>i и rj>ri. Всегда —1<:т<:1. В качестве выборочной
меры зависимости К. к. р. к. широко использовался
М. Кендаллом (М. Kendall, см. [1]).
К. к. р. к. применяется для проверки гипотезы неза-
независимости случайных величин. Если гипотеза незави-
независимости верна, то Ех=0 и ?>т=2 Bга+5)/9га(«— 1). При
небольшом объеме выборки D<га<:10) проверка ста-
тистич. гипотезы независимости производится с по-
помощью специальных таблиц (см. [311. При гс>10 поль-
пользуются нормальным приближением для распределе-
распределения т: если
М >иа/2 V2Bn
то гипотеза о независимости отвергается, в противном
случае принимается. Здесь а — уровень значимости.
"а/2 есть 100-"-процентная точка нормального распре-
распределения. К. к. р. к., как и любая ранговая статистика,
может использоваться для обнаружения зависимости
двух качественных признаков, если только элементы
выборки можно упорядочить относительно этих при-
признаков. Если X, Y имеют совместное нормальное рас-
распределение с коэффициентом корреляции р, то связь
между К. к. р. к. и имеет вид:
Ет = — arcsin p.
См. также Спирмена, коэффициент ранговой корреля-
корреляции, Ранговый критерий.
Лит.: [1] Кендэл М., Ранговые корреляции, пер. <
англ., М., 1975; [2] Ван дер Варден Б. Л., Математиче-
Математическая статистика, пер. с нем., М., 1960; [3] Б о л ь ш е в Л. Н.,
Смирнов Н. В., Таблицы математической статистики, М.,
1965. А. В. Прохоров.
КЁНИГА ТЕОРЕМА: если прямоугольная матрица
составлена из нулей и единиц, то минимальное число
линий, содержащих все единицы, равно максималь-
максимальному числу единиц, к-рые могут быть выбраны так,
чтобы никакие две из них не лежали на одной и той же
линии (термин «линия» обозначает либо строку, либо
столбец в матрице). Сформулирована и доказана
Д. Кёнигом [1]. К. т., одна из основных в комбинато-
комбинаторике, представляет собой матричный аналог критерия
Холла существования системы различных представи-
телей у семейства, подмножеств конечного множества
(см. Выбора теоремы). Распространена также форму-
формулировка К. т. в терминах графов: в графе двудольном
число ребер в наибольшем паросочетании равно числу
вершинного покрытия.
К. т. часто используется в различных комбинаторных
вопросах, связанных с проблемами выбора и экстре-
экстремальными задачами. Известны ее обобщения на случай
бесконечных матриц [3].
Лит.: [l]K6uig D., «Mat. lapok», 1931, v. 38, p. 116—19;
[2] X a p a p и Ф., Теория графов, пер. с англ., М., 1973; [3]
Тараканов В. Е., в кн.: Вопросы кибернетики. Тр.
Семинара по комбинаторной математике, М., 1973, с. 185—99.
В. Е. Тараканов.
КЕПЛЕРА УРАВНЕНИЕ — трансцендентное урав-
уравнение вида
у —с sin y=x.
Для приложений важен случай |с|<1, когда у опреде-
определяется по заданным с и х единственным образом. К. у.
впервые рассматривалось И. Кеп-
Кеплером (J. Kepler, 1609) в свя-
связи с задачей: на диаметре А В
полукруга АОВМ дана точка D;
провести прямую DM так, чтобы
D q B она делила площадь полукруга
в заданном отношении (см. рис.).
К. у. играет важную роль в астрономии при определе-
определении элементов эллиптич. орбит планет. В небесной
механике это уравнение обычно записывают в форме
Е—е sin E=M,
где е — эксцентриситет эллипса, М — средняя ано-
аномалия, Е — эксцентрическая аномалия.
Лит.: [1] Субботин М. Ф., Курс небесной механики,
2 изд., т. 1, Л.— М. 1941. БСЭ-З.
КЕРВЕРА ИНВАРИАНТ,—инвариант почти парал-
лелизуемого гладкого многообразия М размерности
'ifc+2, определяемый как ari-инвариант квадратичной
формы по модулю 2, возникающий на решетке B&+1)-
мерных гомологии многообразия М.
Пусть М — односвязное почти нараллелизуемое зам-
замкнутое гладкое многообразие размерности 4к~2, го-
мологич. группы Я,-(ЛГ; Z) к-рого при 0<i<4fc+2.
кроме V=H2k+i(M; Z), равны нулю.
На свободной абелевой группе Г имеется кососпм-
метрическая форма пересечения циклов Ф(х, у), Ф :
VX V—*-Z и размерность целочисленной решетки V
равна 2т. На группе V существует функция Фо : V—>-22>
определяемая следующим образом: если z?V, то су-
существует гладкое вложение сферы S'2k + l в М, реали-
реализующее данный элемент х, k^ssi. Трубчатая окрест-
окрестность этой сферы S2ft + 1 в М параллелизуема, она может
быть либо тривиальной, либо изоморфной трубчатой
окрестности диагонали в произведении 5* + 1Х Л'2* + а.
При этом трубчатая окрестность диагонали в S-k + 1X
х52* + 1тогдаи только тогда нетривиальна, когда 2А:+1=#=
=^=1, 3, 7 (см. Хопфа инвариант). Значение функции Фо
равно нулю или единице в зависимости от тривиаль-
тривиальности или нетривиальности трубчатой окрестности
сферы S2!i + 1, реализующей элемент х в М, 2кАс\ф
= 1, 3, 7. Так определенная функция Фо : V—*-Z.2
удовлетворяет свойству
Фо(х+у) = Фо{х) + Фо{у)+Ф{х, y)mod 2.
arf-инвариант для функции Фо и наз. инвариан-
инвариантом Кервера многообразия M*k + 2, 2A-+ 1ф1, 3, 7.
Если К. и. многообразия Mik + 2 равен нулю, то су-
существует симплектич. базис (е/, //) для V такой, что
Фо(е/)==Фо(//)~О. В этом случае многообразие Л/4* + 2
есть связная сумма произведения сфер
Если же К. и. многообразия Л/4* + 2не равен нулю, то
существует симплектич. базис {е;, /;) для V такой, чти
Ф0(е,)=Ф0(/,)=0 для 1ф1 иФ0(е1)=Ф0(/1)=1. В этом слу-
случае объединение трубчатых окрестностей двух B&+ 11-
мерных сфер, вложенных в Mik + 2 с трансверсальны.ч
пересечением в одной точке и реализующих элементы
elt Д, дает нек-рое многообразие Kik^2, наз. много-
многообразием Кервера (см. Древовидное многооб-
многообразие); его край дК4к + 2 диффеоморфен стандартной
сфере, а само многообразие М4* + 2 представляет собой
связную сумму
где гладкое замкнутое многообразие К* +2 получено
из Kik+" добавлением клетки.
Если М*к + 2,кф0, 1, 3, есть гладкое параллелизуе-
мое BА-)-связное многообразие с краем, к-рый является
гомотоппч. сферой, то точно так же определен К. и.
многообразия М4к + 2 с теми же свойствами, что и выше,
с той разницей, что в разложении М1к + 2 в связную
сумму простейших многообразий слагаемое К% а,
являющееся многообразием Кервера, будет иметь крап
dKik + i=dMik + i (вообще говоря, не диффеоморфный
стандартной сфере).
В случае к=0, 1, 3 исходные многообразия М2, Ме,
Ми представляют собой связную сумму E2А + 1х
XS2* + 1!#..4(-?2* + 1X52* + 1) (если край пуст),
пли {S2k + 1X 52* + 1)o4t('S2* + 1X5a* + 1I#. . .#(S** + 1X
Хб'й + 1)я_1, (если край непуст), где E2S + 1X'52* + 1H
получено выкидыванием открытой клетки из многооб-
многообразия 52* + 1Х52* + 1.
Однако К. и. для замкнутых многообразий М2, М6,
Мы может быть все же определен (см. Понтрягина ин-
инвариант, Кервера — Милнора инвариант) и зависит
в этих размерностях от выбора оснащения, т. е. яв-
является инвариантом оснащенных перестроек пары
(М4А' + 3, fr),k=O, 1, 3. В размерностях кфО, 1, 3 много-
многообразие Milt + - тогда и только тогда перестраивается
до сферы Sik + 2, когда пара (Л/4* + 2, fr) оснащение пере-
перестраивается до нары (Sik + 2, fr) при любом выборе осна-
оснащения fr на исходном многообразии Mik + i (см. Пере-
Перестройка на многообразии).
К. п. определен для любого стабильно параллелизуе-
мого многообразия Л/4'с~2 как инвариант оснащенных
перестроек и любой элемент в стабильных гомотопич.
группах сфер может быть представлен либо гомотопич.
сферой с оснащением, либо замкнутым гладким много-
многообразием Кервера с оснащением (в этом случае т —
= 4/с+2, кфО, 1,3), либо многообразием S2k + 1XS2k + 1
с оснащением, если к=0, 1, 3.
Иначе говоря, К. п. можно рассматривать как пре-
препятствие к тому, чтобы заданное оснащение на много-
многообразии «перенести» на сферу той же размерности,
кфО, 1, 3. В этом смысле К. и. для значений к=0, 1, 3
выполняет ту же роль: заданное оснащение на много-
многообразии S-h + l>iS2k+1, к=0, 1, 3, вообще говоря, не
всегда может быть «перенесено» на сферу 54* + 2, к =
= 0, 1, 3, с помощью оснащенных перестроек.
Впервые такое оснащение на многообразии S2k + 1X
X S2k + 1 было построено Л. С. Ионтрягиным для случая
к = 0, т. е. оснащение на двумерном торе ((S'X^1), fr),
которое нельзя «перенести» на S2. Существуют такие же
примеры оснащения на многообразиях S3X S3 ж S7X S7.
Основная задача, касающаяся К. и., заключается
в следующем: для каких нечетных значений и сущест-
существует пара (M2n, fr) с отличным от нуля К. и.? Ответ
на этот вопрос отрицателен для пф2'—1 и положите-
положителен для ге=2' — 1, где г=1 (Л. С. Понтрягин, см. [2]),
?=2, 3 (М. Кервер — Дж. Милнор, [5], [6]), i=4
(У. Браудер, [3]), г=5, 6 [М. Баррат (М. Barratt), Ma-
ховальд (М. Mahowald), А. Мильграм (A. Milgram)].
Для остальных значений i ответ неизвестен A978).
Лит.: [1] Н о в и к о в С. П., «Изв. АН СССР. Сер. матем.»,
19&4, т. 28, № 2, с. 365—474; [2] П о н т р я г и н Л. С, Глад-
Гладкие многообразия и их применения в теории гомотопий, 2 изд.,
М., 1976; [3] В г о w d е г W., «Ann. Math.», 1969, v. 90, p. 157—
86' [4] его же, Surgery on simply-connected manifolds, В., 1972;
[5] К е г v a i r e M., «Comm. math, helv.», 1960, v. 34, p. 257—
70; [6] К e r v a i г e M. A., M i 1 n о r J. W., «Ann. Math.»,
1963, v. 77, № 3, p. 504 — 37. M. А. Штанъпо.
KEPBEPA — МИЛНОРА ИНВАРИАНТ — инвариант
оснащенных перестроек замкнутого 6- пли 14-мерного
многообразия с заданным на нем оснащением.
Пусть Мв— стабильно параллелезуемое 2-связное
многообразие, на к-ром задано стабильное Л'-мерное
оснащение (М6, U), т. е. тривпалнзация стабильного
Л'-мерного нормального расслоения. Пусть S3.— сфе-
сферы, реализующие базис 3-мерных гомологии много-
многообразия М6. Суммированием заданной Л'-трнвпалпза-
цшг U с некоторыми тривиализацпямп а,-?л3F'О3)
трубчатых окрестностей сфер S3 в Ms получаются
(Л*+3)-мерные тривиализацни стабильных нормальных
расслоений к сферам S3. и возникают элементы а1. ?
?лзEОд- + з). Коядро гомоморфизма стабилизации
s ; nn(SOn)->-nn(SOj\' + n) изоморфно Z2 для л = 3, так
что каждой сфере S3. сопоставляется элемент из группы
ns(SO/^ + 3)/Ims (по значению элементов сф к-рое они
принимают в группе 22 после факторизации по а\).
Это значение не зависит от выбора элементов а/, а за-
зависит только от классов гомологии, реализуемых сфе-
сферами S3., и оснащения U. ari-инвариант получающейся
функции ф0 : Н3(М6, %)-+Ъ2, обладающей свойством
Фо(ж гг/)=Фо(-г;)+Фр(^)+ФC:. .'/) mod 2. где у(х, у) —
форма пересечений 3-мерных гомологии на многообра-
многообразии М6, и наз. инвариантом Кервера —
М и л н о р а этого многообразия с оснащением U. Пара
(Af6, U) оснащенно перестраивается до пары (Se, V) то-
тогда и только тогда, когда К.— М. и. пары {Ms, U) равен
нулю.
Аналогичные построения проводятся и для Ми.
К.— М. и. в размерности шесть является единственным
инвариантом стабильного 6-мерного оснащенного ко-
бордизма и задает изоморфизм nn + e{Sn)**i Z2, к>7,
в размерности же четырнадцать это — не единствен-
единственный инвариант стабильного четырнадцатпмерного осна-
оснащенного кобордизма, т. е. стабильная группа nn + 14(Sr"),
п^16, определяется оснащениями на сфере Su и осна-
оснащениями на S7XS7.
Лит. см. при статье Нервера инвариант. М. А. Штанъко.
КЕРНФУНКЦИЯ — см. Бергмана кернфункция.
КЕРРА МЕТРИКА — решение уравнений Эйнштейна,
описывающее внешнее гравитационное поле вращаю-
вращающегося источника с массой т. и угловым моментом L.
Относится к типу D по классификации А. 3. Петрова.
Наиболее просто записывается в виде метрики Керра —
Шильда: _
где К\х—нулевой (изотропный) вектор (A'^A'vg^v=0),
касательный к специальной главной нулевой кон-
конгруэнции с вращением (неградиентного типа), т)^—
метрический тензор пространства Минковского. Ха-
Характерный параметр К. м. a=L/m. В общем случае
при наличии заряда е (метрика Керра — Ньюмена)
скалярная функция h имеет вид
где
Поле сингулярно на кольцевой нити радиуса а (при
р=0). При а=0 сингулярность стягивается в точку;
при а=е=0 переходит в Шварцшилъда метрику.
К. м. получена Р. П. Керром [1].
Лит.: Li J К err В. Р., «Phys. Hew. Letters», 1963, v. 11,
p. 237—38; [2] Мёл пер К., Теория относительности, пер.
с англ., 2 изд., М., 1975; [3] Р и с М., Р у ф ф и н и Р., У и л е р
Дж., Черные дыры, гравитационные волны и космология,
пер. с англ., М., 1977. А. Я. Буринский.
КИБЕРНЕТИКА — наука об управлении, связи и
переработке информации (буквально «искусство уп-
управления рулем»). Первым, кто употребил этот термин
для управления в общем смысле, был, по-видимому,
древнегреческий философ Платон. А. М. Ампер
(А. М. Ampere, 1834) предложил называть К. науку
об управлении человеческим обществом. Н. Винер
(N. Wiener, 1948) назвал К. науку об управлении и
связи в живом организме и машине. На дальнейшее
становление К. огромное влияние оказали электрон-
электронные вычислительные машины (ЭВМ). К началу 70-х гг.
20 в. К. окончательно оформилась как наука фнзико-
математ. профиля с собственным предметом исследо-
исследования — так наз. 'кибернетич. системами. К и б е р-
н е т и ч е с к и е системы представляют собой
абстракцию под определенным (информационным) уг-
углом зрения сложных систем, изучаемых широким спект-
спектром естественных, технических и социальных наук
(под своими специфическими углами зрения). Выявляя
общие аспекты в системах столь различной природы,
К. вместе с тем дает общин и притом принципиально
новый метод их изучения. Это — так наз. метод м а-
ш и иного эксперимента, промежуточный
между классическим дедуктивным и классическим экс-
экспериментальным методами. Благодаря этому К., по-
подобно математике, можно использовать в качестве
аппарата исследования в других науках. Причем спектр
проблем, доступных исследованию кибернетич. мето-
методами, по сравнению с классическими (аналитическими)
математич. методами значительно шире и охватывает
практически все науки. Кибернетическая система
в простейшем случае может сводиться к одному эле-
элементу. Элемент А кибернетич. системы, рассматривае-
рассматриваемый в абстрактном плане, представляет собой набор
(х, у. 2, /. g) пяти объектов. Через x=x(t) обозначается
так наз. входной сигнал элемента, т. о. ко-
конечное множество функций времени t : x— (z1(t), . . .,
xk(t)). Во многих конкретных кибернетич. системах
время рассматривается как параметр, принимающий
лишь дискретные множества значений (обычно цело-
целочисленные значения). Однако можно, не нарушая общ-
общности, рассматривать и обычное «непрерывное» время
(ниже рассматривается именно атот случай). Области
значений функций x,(t) в одном и том же элементе
могут быть различными множествами действительных
чисел. Чаще всего в качестве областей значений фигу-
фигурируют обычные непрерывные числовые интервалы,
множество целых чисел и различные его конечные
подмножества. Сами функции x;(t) обычно предпола-
предполагаются кусочно непрерывными. Буквой у обозначается
выходной сигнал y=y(t) элемента, представ-
представляющий собой конечное множество функций //= lii^it),
.... !i,r(t)) той же самой природы, что входные функ-
функции xj(i). Через z=z(t) обозначено внутреннее
состояние элемента А, также характеризую-
характеризующееся коночным множеством функций z= (z1(t). . . .,
zn(t)) той же природы. Через / и g обозначены функ-
функционалы, задающие текущие значения внутреннего
состояния z(t) и выходного сигнала у(t):
z(t) = f(t,x(t),Dtz(t)); y(t)=g(t, x(t), Dtz(t)). A)
Здесь через Diz(t) обозначено сужение векторной функ-
функции z(t)— (z1(t), . . ., zn(t)) на область, задаваемую систе-
системой полуоткрытых интервалов [тх, t), . . ., [т„, t), где
%l=%i(t) — заданные кусочно непрерывные функции
от t, удовлетворяющие условию x,-<i, i=l, 2, ..., п.
Приведенное определение элемента кибернетич. си-
системы предполагает, что время t может принимать
любые действительные значения. На практике в боль-
большинстве случаев эти значения ограничиваются лишь
неотрицательными числами. При этом определение
элемента должно быть дополнено заданием его началь-
начального состояния zo=z(O), а также, возможно, заданием
начального выходного сигнала Уо=у(О). Зависимости
A) рассматриваются в таком случае лишь при положи-
положительных значениях t. Другое обстоятельство связано
с том,что наряду с детерминированными элементами в
кибернетич. системах часто приходится иметь дело со
стохастич. элементами. Для этого обычно оказывается
достаточным в правые части соотношений A) добавить
в качестве аргументов функционалов случайную функ-
функцию со (г), принимающую значения на непрерывном или
дискретном множестве действительных чисел.
Возможны и другие варианты обобщений этого опре-
определения, в частности введение бесконечномерных век-
векторных функций для входных и выходных сигналов,
а также для внутреннего состояния элемента. Однако
следует иметь в виду, что, в отличие от математики, для
К. характерен конструктивный подход к изучаемым
объектам. Это означает возможность фактического вы-
вычисления (с той или иной степенью точности) значений
всех рассматриваемых функций. Поэтому на практике
рано или поздно при изучении кибернетич. систем,
а следовательно, и их элементов приходится перехо-
переходить к конечным аппроксимациям.
Многоэлементные кибернетичес-
кибернетические системы строятся из набора (обычно конеч-
конечного) М элементов путем отождествления выходных
сигналов одних элементов с входными сигналами дру-
других. Формально такие отождествления задаются систе-
системой равенств
j?Jp, B)
где через xp.(t) обозначена.i-я компонента входного сиг-
сигнала р-го элемента, а через yr-(t) — /-я компонента вы-
выходного сигнала r-го элемента. При подобном отож-
отождествлении (соединении элементов в систему) часть
компонент входных сигналов тех или иных элементов
может оказаться свободной, т. е. не отождествленной
ни с какими выходными компонентами. Все такие ком-
компоненты объединяются в векторный входной сигнал
x(t) построенной системы S. Оставшиеся свободными
компоненты выходных сигналов образуют выходной
сигнал у (t) построенной системы. В отличие от входного
сигнала в выходной сигнал у (i) могут быть включены
(по определению строящейся системы) также любые
несвободные компоненты выходных сигналов, состав-
составляющих систему S элементов. Начальным состоянием
системы, по определению, считается вектор, состав-
составленный из компонент начальных состояний всех ее
элементов (упорядоченных тем или иным образом).
Аналогичным образом определяется и вектор z(t) со-
состояния системы в произвольный момент времени.
Определяя систему множеством элементов и множест-
множеством отождествляющих соотношений B), необходимо
обеспечить корректность такого определе-
определения, под к-рой понимается возможность фактического
вычисления выходного сигнала у (t) для всех t>0
при задании начального состояния системы г@) и
входного сигнала x(t) для всех t^O. Необходимым ус-
условием корректности определения системы является,
напр., вхождение области значений функции yr,(t)
в соотношениях B) в область значений функции xR(t).
Для упрощения задачи обеспечения корректности оп-
определения систем обычно вводится запрет на отождеств-
лепше любой входной компоненты более чем с одной
выходной компонентой.
Множество соотношений B) задает структуру
киСзрнетич. системы (не путать с абстрактным поня-
тием структуры в математике!). В ряде приложений
оказывается полезным рассмотрение систем с перемен-
переменной структурой. При этом, вводя дополнительные ком-
коммутационные элементы, можно любую систему с пере-
переменной структурой свести к системе с постоянной
структурой.
Приведенное определение абстрактной кибернетич.
системы охватывает весьма большой круг конкретных
систем, рассматриваемых в различных областях зна-
знания. К их числу относятся логические сети и сети
абстрактных автоматов, механические динамич. сис-
системы, различного рода электромеханические и элект-
электронные устройства (включая ЭВМ), биологич. орга-
организмы и различные их подсистемы (напр., нервная сис-
система), экологические, экономические и социальные
системы. Для возможности рассмотрения конкретных
биологических, технических и социальных систем
в качестве абстрактных кибернетич. систем необхо-
необходимо отвлечься от большинства их специальных свойств
(размеров, массы, химич. состава, многих конкретных
форм представления сигналов и состояний и т. д.).
Кибернетический аспект рассмотрения систем яв-
является аспектом чисто информационным. Иными сло-
словами, состояния элементов и взаимодействие элементов
друг с другом описываются системой кодов прежде
всего для установления меры их различия (при задан-
заданной точности описания), а не для фактич. измерения
тех или иных реальных физич. величин. Напр., при
наличии в электрлч. сети лишь двух уровней напря-
напряжения i>j и v2 их можно задать числовыми кодами
О и 1, независимо от фактич. величин этих напряже-
нп". Заметим, что хотя в приведенном выше опреде-
определении кибернетич. системы употреблялись лишь число-
числовые коды, их нетрудно, в случае необходимости, за-
заменить буквенно-цифровыми кодами с использованием
букв любых конечных алфавитов.
Всякая система, имеющая нетривиальный входной
сигнал x(t) и выходной сигнал y(t), может рассматри-
рассматриваться как преобразователь ннформа-
ц и и, перерабатывающий поток информации х (t) в по-
поток информации у (t). В случае дискретного времени и
конечных областей определения функций x(t) и у(t)
преобразование (при соответствующем кодировании
входной информации) можно интерпретировать как
соответствие между словами в той или иной паре фик-
фиксированных алфавитов. В этом случае система может
рассматриваться как дискретный преобразователь ин-
информации. Системы с нетривиальным входным сигна-
сигналом x(t) наз. открытыми. В отличие от них
замкнутые системы не оставляют свободных
входных компонент ни у одного из своих элементов.
Вектор входного сигнала х(t) в таких системах имеет
нулевое число компонент и не может, следовательно,
нести никакой информации. Замкнутые системы в стро-
строгом смысле слова не должны иметь не только входа,
но и выхода. Однако даже в этом случае их можно
интерпретировать как генераторы информации, рас-
рассматривая изменение их внутреннего состояния z(t)
во времени. В дальнейшем генерацию удобно рас-
рассматривать как частный случай преобразования ин-
информации.
Для кибернетич. систем важное значение имеют
задачи их анализа и синтеза. Задача анализа
системы состоит в нахождении различного рода свойств
задаваемого системой преобразования информации,
в частности представление в удобной форме алгоритма
преобразования. В последнем случае речь идет факти-
фактически об агрегации (композиции) системы в один
единственный элемент. Задача синтеза сис-
системы противоположна задаче анализа. Необходимо
по описанию осуществляемого системой преобразова-
преобразования построить систему, фактически выполняющую это
A
I'
В
преобразование. При этом должен быть предварительно
определен класс элементов, из к-рых должна строиться
искомая система.
Важное значение имеет задача нахождения формаль-
формальных преобразований кибернетич. систем, не меняю-
меняющих задаваемых ими преобразований (а, возможно, и
нек-рые другие инварианты). Тем самым вводятся раз-
различные определения эквивалентности систем, делающие
возможными постановку задач оптимизации
систем, т. е. задач нахождения в классе эквивалентных
систем системы с экстремальными значениями опреде-
определяемых на системах функционалов.
Задача декомпозиции системы означает
представление части системы или всех ее элементов
в виде систем, состоящих из более мелких элементов
(подсистем). Для большого числа применений важное
значение имеют системы, представляемые в виде ком-
комбинации двух подсистем (элементов), наз. обычно у п-
равляющей системой и объектом уп-
управления. Для наглядности подобную систему
можно представить в виде графа (см.
рис.), где через А обозначена управля-
управляющая система, через В — объект уп-
управления; буквой х обозначен так
наз. канал прямой связи
|й (выход элемента А, отождествленный
t с входом элемента В), через у — канал
обратной связи, через а — входной сигнал сис-
системы (воздействие окружающей среды, различного
рода помехи) и через Ь — выходной сигнал, характери-
характеризующий качество функционирования подсистемы В
(качество управления).
Для подобных систем задача синтеза ставится обычно
следующим образом: при заданной системе В, задан-
заданном классе внешних воздействий а и заданном крите-
критерии качества управления Ь пострбить управляющую
систему А, обеспечивающую заданное поведение кри-
критерия качества Ь. Под такое определение попадают за-
задачи синтеза систем программного управления (Ь —
заданная векторная функция времени), следящие сис-
системы (минимизирующие в том или ином смысле вектор
Ь—а), системы оптимального управления (системы,
выводящие объект управления в желательную область
значений его состояния за кратчайшее время) и т. п.
Важное место в теории кибернетич. систем занимают
задачи обеспечения надежности их функционирования.
Причем, кибернетич. аспект надежности связан не
с обеспечением физич. надежности элементов и связей
между ними, а с вопросами организации самой системы
(избыточность элементов и связей, специальные сис-
системы кодирования и т. п.).
Для достаточно простых систем большинство из
перечисленных задач (если не в полных, то хотя бы
в упрощенных постановках) могут быть решены средст-
средствами классич. математики, дополненными тривиальным
перебором вариантов. Для сложных систем, с к-рыми
приходится обычно иметь дело на практике, эти методы
оказываются, как правило, непригодными. При этом
сложность систем в К. понимается не только и не
столько в простом количественном смысле (число эле-
элементов системы, число связей, размерность векторов
состояний, входов и выходов), а прежде всего — в прин-
принципиальном качественном смысле. Сложной в этом
смысле наз. система, не имеющая простых описаний.
А это предполагает наряду с большими количествами
используемых элементов и параметров большое их
разнообразие (но сводящееся к простым закономер-
закономерностям), а также большое разнообразие п нерегуляр-
нерегулярность связей между элементами. Эффективное исследо-
исследование таких систем классическими дедуктивными мето-
методами оказывается практически невозможным. Класси-
Классический экспериментальный метод исследования также
оказывается применимым лишь в весьма ограниченных
пределах. Во многих случаях его применение ограни-
ограничивается высокой стоимостью эксперимента, а в ряде
случаев (метеорология, экология, макроэкономика и
др.) натурные эксперименты становятся либо вовсе
невозможными, либо по крайней мере чересчур рис-
рискованными.
Поэтому в качестве основного метода исследования
сложных систем К. использует метод машинного экспе-
эксперимента, превратившийся в новый мощный универ-
универсальный метод научного познания в результате появ-
появления быстродействующих универсальных ЭВМ. Метоя
машинного эксперимента в чистом виде осногсан на
использовании так наз. имитационных мо-
моделей. Такие модели по существу являются простым
переложением на машинный язык описаний моделируе-
моделируемых систем. Специальные программы, обслуживающие-
модель, генерируют различные конкретные реализа-
реализации входного сигнала х(t) моделируемой системы и
строят в соответствии с введенным в ЭВМ описанием
системы (включая ее начальное состояние) выходной
сигнал y(t). Далее, как и в обычном (натурном) экспе-
эксперименте, полученные результаты обрабатываются с по-
помощью специальных программ, строящих, напр., гисто-
гистограммы распределений тех или иных величин, характе-
характеризующих поведение исследуемой системы, определяю-
определяющих различные качественные характеристики (при-
(принадлежность системы и определяемого ею преобразо-
преобразования информации к тому или иному классу), и т. п.
Таким способом решаются прежде всего.задачи анализа
кибернетич. систем. Для решения задач синтеза и опти-
оптимизации методом машинного эксперимента обслужи-
обслуживающая эксперимент система машинных программ до-
дополняется средствами, обеспечивающими диалог ЭВМ
с человеком-исследователем, внесение изменений в опи-
описание моделируемой системы по подсказке человека,
а также процедуры направленного перебора для орга-
организации подобных изменений в автоматич. режиме.
Перевод описаний кибернетич. систем на машинный
язык представляет собой достаточно трудоемкую про-
процедуру. Поэтому в современные средства машинного-
эксперимента включаются специальные программы
трансляторы (или интерпретаторы), автоматизирующий
перевод на машинный язык описаний систем на спе-
специально разрабатываемых для этой цели языках сис-
системного моделирования. Основу таких языков состав-
составляют средства (удобные для исследователя) фактич.
описания параметров, функций и связей, входящих
в описание систем. Сохраняя, как правило, универ-
универсальность (т. е. возможность описания произвольных
систем), языки моделирования обычно ориентированы
на более простое и легкое описание систем тех или иных
специальных классов. Кроме того, в языки системного-
моделирования включаются дополнительные средства
для описания процедур, обслуживающих машинный
эксперимент, к-рые были описаны выше. В настоящее-
время A978) разработаны многие десятки универсаль-
универсальных и специализированных языков системного модели-
моделирования и основанных на них систем машинного экспе-
эксперимента: иностранные языки—симула, симскрипт, оте-
отечественные — слэнг, недис и др.
Во многих системах машинного эксперимента имита-
имитационное моделирование дополняется возможностями
использования аналитич. аппарата тех или иных раз-
разделов математики (напр., теории массового обслужи-
обслуживания), а также современных вычислительных методов.
В первую очередь это касается различного рода опти-
оптимизационных методов: линейное программирование,
динамич. программирование, градиентные методы, сто-
хастич. программирование и др.
В ряде случаев для изучения кибернетич. систем
оказывается целесообразным дополнять машинный экс-
перимент натурным. Некоторые части моделируемой
кибернетич. системы при этом подключаются к универ-
универсальной ЭВМ (через специальные преобразователи)
в виде натурных моделей, моделирование же остальных
частей, управление экспериментом и обработка его
результатов производятся в универсальной ЭВМ уже
описанным способом. Использование универсальных и
специализированных ЭВМ для автоматизации управле-
управления натурными экспериментами, а также для сбора
и обработки получаемых экспериментальных данных
является важным направлением совершенствования
исследовательского процесса во всех эксперименталь-
экспериментальных науках. Не менее широкие возможности примене-
применения имеет и чистый машинный эксперимент.
Взаимоотношения К. с математикой не ограничи-
ограничиваются одним лишь использованием К. математич.
методов. Математика и К. имеют и общие объекты ис-
исследования. Так, напр., алгоритмы, являющиеся объек-
объектом исследования в математнч. теории алгоритмов,
могут рассматриваться в то же время как кибернетнч.
системы и служить для К. не только средством, но
и объектом исследования. Однако подход к изучению
этого объекта, а следовательно, и возникающие при
этом задачи у математики и К. сильно отличаются
друг от друга. Для математики алгоритм выступает
прежде всего как одно из фундаментальных понятий
оснований математики. Поэтому главная задача состоит
в изучении общих свойств этого понятия, для чего
необходимо свести его определение к минимальному
числу простейших фундаментальных понятий п опе-
операций. К. ставит своей задачей разрабатывать практи-
практически удобные методы синтеза конкретных систем,
в том числе и алгоритмов. Эта практическая направ-
направленность приводит к необходимости разработки доста-
достаточно удобных для пользования процедурно и проблем-
проблемно ориентированных алгоритмических языков. Вместо
характерного для математики интереса к принципиаль-
принципиальной возможности установления эквивалентности в тех
или иных классах алгоритмов, К. интересуется прежде
всего созданием аппарата, удобного для фактич. вы-
выполнения эквивалентных преобразований алгоритмов.
Вместо простейшей формы представления информации
в виде слов в абстрактном алфавите, К. изучает слож-
сложные структуры данных, необходимые для эффективной
реализации алгоритмов на ЭВМ. Приведенные примеры
достаточно ясно характеризуют особенности подхода
К. к изучаемым ею математич. объектам. То же раз-
различие подходов обнаруживается при изучении К. дру-
других математич. объектов (абстрактные автоматы, ло-
гич. сети и т. п.).
Особый интерес с точки зрения взаимоотношения
К. с математикой представляет их подход к аппарату
классической математич. логики. Математич. аспект
предполагает максимальное упрощение системы аксиом
и правил вывода, без чего невозможен эффективный
анализ общих свойств и возможностей логических исчис-
исчислений. К., ставящая задачу автоматизации дедуктив-
дедуктивных построений на практический путь, начала разви-
развивать язык практической математич. логики. Этот язык
относится к языку классической математич. логики,
а как современный язык программирования (напр.,
алгол-ЧЪ) — к языку алгоритмов Поста или нормаль-
нормальных алгорифмов Маркова. Правила вывода в этом
языке (во взаимодействии с конкретными содержа-
содержательными математич. текстами) имеют доказательную
силу, не меньшую, чем сила, к-рая скрывается за сло-
словом «очевидно» в современных математич. монографиях.
Автоматизация дедуктивных построений представ-
представляет собой одну из наиболее важных частей раздела
К., получившего наименование «искусственный интел-
интеллект». Естественный человеческий интеллект (мозг
вместе с органами восприятия информации и выдачи
ее во вне) представляет собой одну из наиболее инте-
интересных и сложных кибернетич. систем. Вопрос о том,
как человек мыслит, был и продолжает оставаться од-
одним из самых интересных и увлекательных научных
вопросов. К. подходит к его решению не только с тео-
теоретической, но н спрактич. стороны. Речь идет об авто-
автоматизации (полной или частичной — с подсказкой че-
человека) различных аспектов интеллектуальной дея-
деятельности человека, а в конце концов — и всего интел-
интеллекта в целом.
Помимо автоматизации логич. мышления (дедуктив-
(дедуктивных построений), важными составными частями проб-
проблемы «искусственного интеллекта» являются задачи
распознавания образов (прежде всего зрительных и
слуховых), операции в естественных человеческих язы-
языках (распознавание смысла фраз и выражений, поддер-
поддержание диалога и т. п.), задачи обучения и самообуче-
самообучения и т. д. Важное значение имеют задачи изучения и
синтеза эффективных алгоритмов управления движе-
движениями искусственных конечностей человекоподобных
роботов, синтеза искусственного голоса, управления
им и др. Особая группа задач возникает при изучении
целенаправленного поведения, методов выбора целей
и подцелей и планов их достижения. Практический
путь к созданию искусственного интеллекта лежит
в создании диалоговых (человеко-машинных) систем,
повышающих производительность труда человека в раз-
различных областях умственной деятельности (логич.
вывод, переводы с одних естественных языков на дру-
другие, шахматная игра и т. п.). По мере их совершенст-
совершенствования доля ЭВМ в совместной работе будет непре-
непрерывно повышаться вплоть до достижения полной авто-
автоматизации соответствующего процесса.
Очень важным является вопрос о взаимоотношениях
К. с современной вычислительной техникой. Эти взаи-
взаимоотношения имеют две различные стороны. Во-пер-
Во-первых, ЭВМ являются для К. основным инструментом
исследований, а во-вторых, будучи сами сложными
кибернетич. системами, они выступают в качестве
важного объекта исследований К. Разумеется, в задачу
К. не входят многие технич. вопросы, разрешающиеся
при реальном проектировании ЭВМ. Однако вопросы
архитектуры ЭВМ и вычислительных систем, органи-
организация управления вычислительным процессом (включая
организацию баз данных) входят в компетенцию К.
и представляют один из важных ее разделов. На это
обстоятельство следует обратить особое внимание,
ибо оно отличает понимание предмета К., сложившееся
в СССР, от западного (прежде всего американского)
понимания, где вопросы архитектуры и управления
вычислит, системами относят к специальной компью-
компьютерной науке (computer science) и не включают их в К.
Кибернетнч. системы встречаются практически во
всех областях знания. Отличаясь теми или иными спе-
цифич. свойствами, такие системы могут изучаться
кибернетич. методами, специально приспособленными
к системам соответствующих классов. Тем самым ста-
становится возможным более глубокое их изучение. Так
возникли и продолжают развиваться специализирован-
специализированные прикладные разделы К.: техническая К., экономи-
экономическая К., биологическая К., медицинская К., воен-
военная К. Применение математических и кибернетических
методов в языкознании привело к возникновению так
наз. математической лингвистики. Эта наука имеет
непосредственное отношение к языковым проблемам
искусственного интеллекта.
Лит.: [11 Винер Н., Кибернетика..., пер. с англ., 2 изд.,
М., 1968; [2] Э ш б и У. Р., Введение в кибернетику, пер.
с англ., М,, 1959; [3] Г л у ш к о в В. М., Введение в кибер-
кибернетику, К., 1964; [4] Энциклопедия кибернетики, т. 1—2, К.,
1974. В. М. Глушков.
КИЛЛИНГА ВЕКТОР, точнее—к и л л и н г а в е к-
i торное поле, или и н ф и н и т е з и м а л ь н о е
движение,— поле скоростей (локальной) одно-
параметрич. группы движений риманова пространства
М. Точнее, векторное поле X на М наз. векторным по-
полем Киллинга (к. в. п.), если оно удовлетворяет сле-
следующему уравнению Киллинга
где Lx~ производная Ли по направлению X, a g —
тензорное поле на М, определяющее структуру рима-
риманова пространства (риманова метрика). К. в. п. впер-
впервые были систематически изучены В. Киллингом [1],
к-рый вывел также для них уравнение (*). В полном
рпмановом пространстве любое к. в. п. полно, т. е.
является полем скоростей однопараметрич. группы
движений. Множество i(M) всех к. в. п. на М образует
алгебру Ли размерности не более ге(ге+1)/2, где п =
= dim M, причем эта размерность равна ге(и+1)/2
только для пространств постоянной кривизны. Мно-
Множество всех полных к. в. п. образует подалгебру
в i{M), Являющуюся алгеброй Ли группы движений
пространства М. Производная Ли по направлению
к. в. п. аннулирует не только метрику g, но и все дру-
другие поля, к-рые канонически строятся по метрике,
напр, тензор кривизны Римана, оператор Риччи и т. д.
Это позволяет установить связь между свойствами
к. в. п. и тензором кривизны. Так, напр., в точке, где
собственные значения оператора Риччи попарно раз-
различны, к. в. п. не мок;ет обращаться в нуль.
К. в. п. X, рассматриваемое как функция
X: Т*М Э а -^ а (X)
па кокасательном многообразии Т*М, является первым
интегралом (гамильтонова) геодезич. потока на Т*М,
определяемого римановол метрикой. По аналогии,
поле S контравариантных симметрич. тензоров на М наз.
тензорным полем К и л л я н г а, если соот-
соответствующая ему (полиномиальная по слоям) функция
S : a-+S(a, ..., а)
на Т*М является первым интегралом геодезич. потока.
Уравнение, задающее тензорное поле Киллинга, также
наз. уравнением Киллинга. Множество
всех тензорных полей Киллинга, рассматриваемых
как функции на Т*М, образует (вообще говоря, бес-
бесконечномерную) алгебру Ли относительно скобки
Пуассона, задаваемой стандартной симплектич. струк-
структурой на Т*М.
Более общо, пусть Q : Rep*jl#—>-VK — геометрич.
объект порядка к на многообразии М, т. е. GLk(n)-
эквивариантное отображение многообразия реперов
порядка к на М в пространство W, на к-ром действует
группа GL'<(n) А--струй в нуле диффеоморфизмов R",
сохраняющих начало координат. Векторное поле X
на М наз. инфинитезимальным авто-
автоморфизмом, или полем Киллинга объ-
объекта Q, если соответствующая ему (локальная) одно-
однопараметрич. группа преобразований ц>) многообразия М
индуцирует группу ц>'(к) преобразований многообразия
реперов Rep*M", сохраняющую Q : Q о tp<fc) = (>. Урав-
Уравнение, задающее поля Киллинга объекта Q, наз. урав-
уравнением Ли — К и л л и п г а, а соответствующий
ему оператор — оператором Ли.
Лит.: [1] Killing W., «J. reine und angew. Math.», 1892,
Bd 109, S. 121—8E; L2] Pa me в с кий II. К., Риманова
геометрия и тензорный анализ, 3 изд., М., 1967; [3] Э й з е н-
харт Л. П., Риманова геометрия, пер. с англ., М., 1948;
[4] X е л г а с он С, Дифференциальная геометрия и сим-
симметрические пространства, пер. с англ., М., 1964; [5] К о b a-
yashi S., Transformation groups in differential geometry,
В.— Hdlb.— N. Y., 1972; [6] К u m p e r a A., Spencer D.
Lie equations. V. 1. General theory, N. Y., 1972; [7] К о b a y-
ashi S.,Nomizu K., Foundations of differential geometry,
v. 2, N. Y., 1969; [8] E г о р о в И. П., Движения в простран-
пространствах аффинной связности, Казань, 1965, с. 5—179.
Д. В. Алепсеевский.
КИЛЛИНГА ФОРМА — билинейная форма специаль-
специального вида на конечномерной алгебре Ли7 введенная
В. Киллингом [1]. Пусть © — конечномерная алгебра
Ли над полем к. К. ф. на алгебре © наз. билинейная
форма
В (х, !/) = tr(ad .r-ad у), х, j/g©,
где tr обозначает след линейного оператора, a ad x —
образ х при присоединенном представлении алгебры ©,
т. е. линейный оператор на векторном пространстве ©,
определенный правилом z-+[x, г], [,] — операция ком-
коммутирования в алгебре Ли ©. К. ф. симметрична. Опе-
Операторы adz, #?©, кососимметрпчны относительно
К. ф., т. е.
В ({х, у], z) = B(x, [у, z]) для всех х, у, z?@.
Если @0— идеал алгебры ©, то сужение К. ф. на ©0
совпадает с К. ф. алгебры ©0. Всякий коммутативный
идеал ©0 содержится в ядре К. ф. Если К. ф. невырож-
невырождена, то алгебра © полупроста.
Пусть характеристика поля к равна 0. Радикал
алгебры © совпадает с ортогональным дополнением
относительно К. ф. к производной подалгебре W' =
= [©, ©]• Алгебра © разрешима тогда и только тогда,
когда ©_L@', т. е. когда В([х, у], г) = 0 для всех х, у,
z?© (критерий разрешимости К ар-
тана). Если алгебра © нильпотентна, то В(х, у) = 0
для всех х, #?©. Алгебра © полупроста тогда и
только тогда, когда К. ф. невырождена (критерий
полупростоты К а р т а н а).
Каждая комплексная полупростая алгебра Ли содер-
содержит вещественную форму Г (компактную форму Венля)
(см. Комплексификация алгебры Ли), на к-рой К. ф.
отрицательно определена.
Лит.: Ll) Killing W., «Math. Ann.» 1888, Bd 31, S.
252 — 90; 1889, Bd 33, S. 1 — 48; 1889, Bd 34, S. 57 — 122; 1890,
Bd 36, S. 161—89; 12] К а р т а н Э., Геометрия групп Ли и
симметрические пространства, пер. с франц., М., 1949, с. 259 —
261; [3] Б у р б а к и Н., Группы и алгебры Ли, пер. сфранц,,
М., 1976; [4] К а ила некий И., Алгебры Ли и локально
компактные группы, пер. с англ., М., 1974; [5] Наймарк
М. А., Теория представлений групп, М., 1У7И.
Д. П. Желобенка.
КИНЕТИЧЕСКОЕ УРАВНЕНИЕ — уравнение не-
неравновесной статистич. физики, используемое в теории
газов, аэродинамике, физике плазмы, теории прохож-
прохождения частиц через вещество, теории переноса излуче-
излучения. Решение К. у. определяет функцию распределе-
распределения динамич. состояний одной частицы, обычно в за-
зависимости от времени, координаты и скорости.
В 80-х гг. 19 в. Л. Больцман (L. Boltzmann) сформу-
сформулировал основное К. у. теории газов — нелинейное
интегро-диффоренциальное уравнение (см. Волъцмаиа
уравнение), к-рое описывает движение молекул как
нек-рый случайный процесс, определяемый механиз-
механизмом бинарных соударений молекул. Входящие в урав-
уравнение коэффициенты (эффективные сечения) рассчиты-
рассчитываются из уравнений классич. механики. Исследуя
свойства решений кинетич. уравнения, Л. Больцман
дал молекулярно-кинетнч. истолкование . второго на-
начала термодинамики it установил статистич. смысл
понятия энтропии (см. Волъцмаиа Н-теорема). В кван-
квантовой статистич. физике в простейшем случае уравне-
уравнение Больцмана записывается аналогично классич.
случаю, но с использованием квантовых эффективных
сечений и с учетом требований симметрии. Для реля-
релятивистского газа уравнение Больцмана формулируется
в ковариантном виде. Развит метод получения К. у.
теории газа, учитывающий корреляции между динамич.
состояниями молекул (см. Боголюбова цепочка урав~
нений). Исходя из Лиувилля уравнения, этим методом
можно в низшем приближении получить уравнение
Больцмана, если использовать разложения по степе-
степеням плотности газа.
Разложение по степеням малости энергии взаимо-
взаимодействия приводит к Власова кинетическому уравнению
с самосогласованным полем, а в следующем приближе-
приближении в пространственно однородном случае — к кинети-
кинетическому уравнению Ландау, описывающему так наз.
«диффузию в пространстве скоростей».
Известно небольшое число точных решений нелиней-
нелинейного К. у. Его численные решения трудны и при ис-
использовании ЭВМ. Более исследовано линеаризован-
линеаризованное К. у., описывающее малые отклонения от равно-
равновесного решения нелинейного уравнения. По форме
оно совпадает с линейными уравнениями переноса,
возникающими в теории переноса излучения и нейтро-
нейтронов (см. Переноса излучения теория), а также в теории
прохождения частиц через вещество.
Теория переноса излучения по своим задачам и ме-
методам их решения близка к теории переноса нейтро-
нейтронов. Расчет ядерных реакторов и защиты от ядерных
излучений потребовал создания эффективных методов
решения К. у. переноса нейтронов и гамма-квантов,
а также способствовал созданию математич. теории
линейного К. у. Если для нелинейного уравнения
Больцмана теоремы существования и единственности
решения и его асимптотич. поведение исследованы лишь
в простейших случаях [1], то для линейного уравнения
они получены в самой общей постановке математиче-
математической теории ядерных реакторов [2], [3], [4]. Ряд задач
решается аналитическими методами, в общем случае
разработаны многочисл. приближенные методы реше-
решения, приспособленные для удобного программирова-
программирования на ЭВМ (см. Переноса уравнения, численные ме-
методы решения).
Задача о прохождении заряженных частиц через
вещество сводится часто к решению линейного урав-
уравнения переноса при анизотропном рассеянии или
к решению линеаризованного уравнения Ландау (напр.,
при определении углового распределения частиц, вы-
вылетающих с поверхности тела, или при определении
энергетич. спектра заряженных частиц в веществе).
Лит.: [1] Карлеман Т., Математические задачи ки-
кинетической теории газов, пер. с франц., М., 1960; [2] Влади-
Владимиров В. С, «Тр. матем. ин-та АН СССР», 1961, № 61; [3]
Ш и х о в С. Б., Вопросы математической теории реакторов.
Линейный анализ, М., 1973; [4] К е й з К., Ц в а й ф е л ь П.,
Линейная теория переноса, пер. с англ., М., 1972; [5] К о-
ган М. Н., Динамика разреженного газа (кинетическая
теория), М., 1967; [6] С и л и н В. П., Введение в кинетиче-
кинетическую теорию газов, М., 1971; [7] С о б о л е в В. В., Перенос
лучистой энергии в атмосферах звезд и планет, М., 1956.
В. А. Чуянов.
КИРХГОФА МЕТОД — метод приближенного реше-
решения задач теории дифракции коротких волн; предложен
Г. Кирхгофом (G. Kirchhoff). В своем простейшем
варианте К. м. сводится к следующему: пусть волновой
процесс описывается уравнением Гельмгольца и рас-
рассматривается задача рассеяния плоской волны огра-
ограниченным выпуклым препятствием 2, на к-ром вы-
выполняется классическое краевое условие и\^ =0. Ре-
Решение сводится к нахождению функции, удовлетво-
удовлетворяющей уравнению Гельмгольца (А+/с2)и=0, для ука-
указанного краевого условия и представляющейся в виде
суммы u=elkx-\-U, где U отвечает излучения усло-
условиям Зоммерфельда. Решение задачи существует и для
него имеет место интегральное представление
х=(хъ х2, х3), х' = (х[, х'г, х'3),
где д/дпх' —дифференцирование по нормали к 2.
Нормаль берется внешней по отношению к бесконечной
области, ограниченной 2. Предполагается, что на
части 2, освещенной плоской волной е'кх, duldnX'
приближенно равна тому выражению, к-рое получается
по лучевому методу. На теневой части полагают
ди(х')/дпХ' = 0. Полученное таким путем выражение
ид- наз. приближением по Кирхгофу для и.
В освещенной области ик и геометрич. приближении
для и в главных членах совпадают. В окрестности гра-
границы, отделяющей освещенную область от зоны тени,
главный член асимптотич. разложения ик выражается
га
через интеграл Френеля \ exp ia2da, в зоне тени
ик=ОA/к) (на самом деле и в зоне тени убывает го-
гораздо быстрее, чем \1к).
К. м. дает асимптотически правильную в главных
членах формулу для и, сохраняющую свою справед-
справедливость и при |л;|->оо. В следующих порядках по к
приближение по Кирхгофу уже неприменимо.
Лит.: [1] Хёнл X., Мауэ А., Вестпфаль К.,
Теория дифракции, пер. с нем., М., 1964. В. М. Бабич.
КИРХГОФА ФОРМУЛА, Кирхгофа интег-
р а л,— формула
которая выражает значение и (х, t) решения неодно-
неоднородного волнового уравнения
в любой точке х=(хг, хг, x3)?Q в момент времени t
через запаздывающий объемный потенциал
с плотностью / и через значения функции и (у, t) и ее
производных 1-го порядка на границе а области Q
в момент времени r=i—г. Здесь Q — ограниченная
область трехмерного евклидова пространства с кусочно
гладкой границей а, п — внешняя нормаль к ст, г=
= \х—у\ — расстояние между точками х и у.
Пусть
о 9* п
где
9* ц, (У, t-r)_ 1 дгд»2(у, t-r) , ,Э(|/г)
дЧ г 7 дп at С2 1 г> дп ¦
Интегралы v-y{x, t) и v2(x, t) наз. запаздываю-
запаздывающими потенциалами простого и
двойного слоев.
К. ф. A) означает, что любое дважды непрерывно
дифференцируемое решение и(х, t) уравнения B) пред-
представляется в виде суммы запаздывающих потенциалов
простого слоя, двойного слоя и объемного потенциала:
и(х, t)=vy(x, t)+v2(x, t)+v3(x, t).
В случае, когда и(х, t)=u(x), f(x, t)=f(x) не зависят
от t, К. ф. принимает вид
и дает решение уравнения Пуассона Аи=—f(x).
К. ф. широко применяется при решении целого ряда
задач. Например, если Q — шар \у—х\ <:г радиуса t
с центром в точке х, то формула A) преобразуется в
соотношение
<
C)
где
— среднее значение функции ф(я) по поверхности
сферы \у—x\ = t,
<р (л:) = и
1|з (.г) = щ
D)
Если ф(я) н ty(x) — заданные в шаре |ж|<:Л функции,
имеющие непрерывные частные производные 3-го и 2-го
порядков соответственно, a f(x, t) дважды непрерывно
дифференцируема при |г|<Л, 0<<<Л—\х\, то функ-
функция и(х, t), заданная формулой C), является регуляр-
регулярным решением Коши задачи D) для уравнения B) при
\x\<R и t<R-~\x\.
Формула C) также наз. К. ф.
К. ф. в виде
и(х, t) = tMt [W + -§
для волнового уравнения
hu—utf E)
примечательна тем, что из нее следует Гюйгенса прин-
принцип: решение (волна) и (х, t) уравнения E) в точке
(х, t) пространства независимых переменных х±, хг,
х3, t вполне определяется значениями ф, d<f/dn и г|з
на сфере \у—x\ = t с центром в точке х и радиуса \t\.
Пусть дано уравнение нормально гипер-
гиперболического типа
2";_', aU (х) их. у. +2Р/ Ь> (х) их/ + е(х) « = /(*)
F)
с достаточно гладкими в нек-рой (т+1 (-мерной об-
области Qm + 1 коэффициентами а'Цх), Ы(х), с{х) и правой
частью f(x), т. е. уравнение, форма
к-рого в любой точке x?Qm + 1 с помощью невырожден-
невырожденного линейного преобразования приводится к виду
К. ф. обобщена на уравнение F) в случае, когда число
т+1 независимых переменных хи . . ., хт + 1 четно [4].
При атом существенным моментом было построение
k
функции ф, обобщающей на случай уравнения F)
ньютоновский потенциал Vr. Для частного случая
уравнения F)
а«-2Г=1м*/*/ = 0> msl(mod2) G)
обобщенная К. ф. принимает вид
д'и
k-i+l
где у — некоторое положительное число, а — кусочно
гладкая граница m-мерной ограниченной области Qm,
содержащей внутри себя точку у, п — внешняя нор-
нормаль к а;
г h
<p = Y,T-*-' + 1, ф = г2-"», г = \у — х\\
, i = l, ..., к — 1; к=(т —
[г|з] означает запаздывающее значение ty(x, t):
[i|>(*, t)]=ty(x, t-r).
Формулу (8) для уравнения F) иногда наз. форму
лой Кирхгофа — Соболева.
Лит.: [1] Б и ц а д з е А. В., Уравнения математической
физики, М., 1976; 12] Владимиров В. С, Уравнения
математической физики, 3 изд., М., 1976; [3] Bateman H.,
Partial Differential equations of Mathematical Physics, N. Y.,
1944, Camb., 1959; [4] M a t h i s s о n M., «Math."Ann.», 1932,
Bd 107, S. 400—19: [5] e г о же, «Acta Math.», 1939, v. 71,
№ 3—4, p. 249—82; [6]I M и х л и н С. Г., Линейные уравнения
в частных производных, М., 1977; [7] Соболев С. Л.,
«Докл. АН СССР», 1933, т. 1, JVS 6, с. 256—62; [8] е г о же,
Некоторые применения функционального анализа в матема-
математической физике, Новосиб., 1962; [9] Смирнов В. И.,
Курс высшей математики, т. 4, 3 изд., М., 1957; [10] Тихо-
Тихонов А. Н., Самарский А. А., Уравнения математиче-
математической физики, 4 изд., М., 1972. А. М. Нахушев.
КИТАЙСКАЯ ТЕОРЕМА ОБ ОСТАТКАХ: пусть
А — ассоциативное и коммутативное кольцо с единицей
и аи ..., а„—такая совокупность идеалов кольца А,
что а,- + uj = A для любых 1ф]'\ тогда для любого
набора элементов хх, ..., хп?А найдется элемент
х?А такой, что хз^х{ (mod а,-), ?=1, . . ., п. В частном
случае, когда А — кольцо целых чисел 2, К. т. об
о. утверждает, что для любого набора попарно взаимно
простых чисел аг, . . ., ап найдется целое число х, даю-
дающее заданные остатки при делении его на ах, ..., а„.
В этой форме К. т. об о. была известна еще в Древнем
Китае, с чем и связано название теоремы.
Наиболее часто К. т. об о. применяется в случае,
когда А — дедекиндово кольцо и a1 = pj', . . ., а„=
= ^п. где plt ..., J)n —различные простые идеалы
в А (если идеалы аг, ..., ап удовлетворяют условию
теоремы, то этим же свойством обладают и идеалы
а\\ ..., апп для любых натуральных su ..., sn).
К. т. об о. в этом случае показывает, что для любого
набора Sj, . . ., sn найдется х?А такой, что разложение
главного идеала (х) в произведение простых идеалов
имеет вид
где идеалы )}1, ..., рп, qlt ..., qm попарно различны
(теорема о независимости показа-
показателе й).
Лит.: [1] Кострикин А. И., Введение в алгебру,
М., 1977; [2] Ленг С, Алгебра, пер. с англ., М., 1968; [3]
его же, Алгебраические числа, пер. с англ., М., 1966.
Л. В. Кузьмин.
КЛАСС — 1) Термин, употребляемый в математике
в основном как синоним термина «множество» для обо-
обозначения произвольных совокупностей объектов, об-
обладающих каким-либо определенным свойством или
признаком (напр., в алгебре—классы эквивалентности
относительно данного отношения эквивалентности).
Иногда К. предпочитают наз. совокупности, элемен-
элементами которых являются множества (напр., в рекур-
рекурсивной теории — перечислимые классы). В некоторых
случаях под влиянием аксиоматической теории мно-
множеств (см. п. 2) термин «К.» применяется для того,
чтобы подчеркнуть, что данная совокупность оказы-
оказывается собственно К., а не множеством в узком
смысле (напр., в алгебре — примитивные классы уни-
универсальных алгебр, называемые также многообра-
многообразиями). Теоретико-множественные операции над К.
определяются так же, как и над множествами.
2) К. в аксиоматической теории мно-
множеств (точнее, в аксиоматич. системе Гёделя —
Бернайса) — один из видов исходных объектов, рас-
рассматриваемых в этих системах, причем различие между
множествами и К. состоит в том, что элементами К.
и множеств, рассматриваемых в данной теории, могут
быть только множества, но не классы. Идея введения
так понимаемых К. в теорию множеств принадлежит
Дж. Нейману (J. Neumann) и основывается на его за-
замечании, что известные противоречия канторовской
теории множеств возникают не из-за допущения обра-
образования очень больших множеств, а из-за того, что
таким множествам разрешается быть элементами дру-
других множеств. Кроме указанного ограничения, в на-
названных аксиоматич. системах допускаются все обыч-
обычные теоретико-множественные операции над К., при-
приводящие к К., а не к множествам; к тому же для вся-
всякого в нек-ром смысле допустимого предиката, опре-
определенного на множествах, существует К., состоящий
в точности из множеств, удовлетворяющих рассматри-
рассматриваемому предикату. Доказано, что непротиворечивость
каждой из систем Гёделя — Бернайса и Цермело —
Френкеля следует нз непротиворечивости другой (чем
подтверждается точка зрения Дж. Неймана). См.
также Аксиоматическая теория множеств.
Лит.: [1] К о э н II о л Д ж., Теория множеств и конти-
континуум-гипотеза, пер. с англ., М., 1969; [2] Френкель А.-А.,
Б а р-Х и л л е л И., Основания теории множеств, пер. с англ.,
М.. 196В. В. А. Душский.
3) К. риманова пространства V1— чис-
число р такое, что V1 может быть локально изометрически
вложено в (/+р)-мерное евклидово пространство Е1+Р
и не может быть вложено в евклидово пространство
меньшего числа измерений. От вложения требуется
достаточно высокая регулярность (т. к. риманово
пространство V1 допускает локальное изометрическое
вложение в виде С1-гладкой гиперповерхности в El + 1
(теорема Наша)); класс аналитич. риманова
пространства V1 не превосходит Z(Z+l)/2 (теорема
Жане — Картана).
К. риманова пространства равен нулю в том и только
том случае, если тензор кривизны многообразия V1
тождественно равен нулю. Метрики постоянной поло-
положительной кривизны имеют К. 1 и реализуются в виде
гиперсфер евклидова пространства. К. /-мерного прост-
пространства постоянной отрицательной кривизны равен
I — 1 (теорема К а р т а н а). К. риманова многооб-
многообразия V1 строго отрицательной двумерной секционной
кривизны не меньше I—1 (см. [3]). Если риманово
многообразие V1 имеет отрицательную /с-мерную сек-
секционную кривизну, где к — четно, то К.р^A—1)/(к—1).
Найден алгебраич. критерий [4], позволяющий уста-
установить, будет ли К. данного многообразия равен 1,
основанный на том факте, что для метрик К. 1 при
нек-рых дополнительных условиях уравнения Петер-
сона — Кодацци являются следствием уравнений Га-
Гаусса.
Если риманово многообразие V1 является метрич.
произведением римановых многообразий V ':
причем V '— пространства К. 1, то V1 есть пространство
К. р = к (см. [5]). Если многообразия V ' имеют по-
постоянную отрицательную секционную кривизну, то
К. их метрич. произведения равен /—к (см. [5]).
К. двумерных рнмановых многообразий знакопо-
знакопостоянной кривизны равен 1. Вопрос остается открытым
A978) в случае метрики знакопеременной кривизны.
Построен [6] пример двумерного риманова многообра-
многообразия класса С2Л, не допускающего локально изометрич-
ного погружения класса С2 в Е3. Однако любая ком-
компактная часть полной метрики на плоскости изомет-
рично погружается в Я4 (причем, если метрика имела
регулярность С3а, то поверхность принадлежит классу
С2'а), т. е. К. не больше двух [7].
Понятие К. погружения вводится и для псевдорима-
нова пространства. Пусть V"(p, q) — псевдориманово
многообразие, метрический тензор которого имеет
р положительных и q отрицательных собственных
значений, p-\-q=n, а Еп(р, д) — псевдоевклидово про-
пространство с метрикой
Пусть к0— наименьшее неотрицательное целое число
такое, что Vn(p, q) допускает погружение в пространство
с En + ka(p, q-\~k0). Для каждого к из 0<:/с<:/с0 опреде-
определяется к-ж К. погружения многообразия Yn(p, q) как
такое наименьшее число N к, что V"(j>, q) допускает
погружение в En + Nk(p + ak, q+k), где ak=Nk—k.
К. погружения многообразия Vn(p, q) определяется
как min N/,.
0«;ft<ho
Любое псевдориманово многообразие V(p, q) с ана-
литич. метрикой допускает аналитич. и изометрич.
погружение в Em(r, s), где m=n(n+l)/2, ar,j — любые
заданные целые числа, удовлетворяющие условию
r^p, s~^q, т. е. vV^<:n(re+l)/2 для всех к [8]. Если тен-
тензор Риччи для V"(p, q) равен нулю, то N \*ф\.
Если V(p, q) имеет постоянную кривизну, то его
К. равен 1, т. е. существует пространство En + '(r, s)
с r^p, s~^q такое, что Vn(p, q) локально изомотрично
части гиперсферы в En + 1(r, s). Для пространств по-
постоянной отрицательной кривизны N0=n— 1, тогда
как N=i (см. [9]).
Лит.: [1] Э й з е н х а р т Л. П., Риманова геометрия,
пер. с нем., М., 1948; [2l Moor J., «Pacif. J. Math.», 1972,
v. 40, JMs 1, p. 157 — 66; [3] Б о р и с е н к о А. А., «Укр. гео-
геометр, сб.», 1973, в. 13, с. 15—18; [4] Розенсон Н. А.,
«Изв. АН СССР. Сер. Матем.», 1941, т. 5, с. 325 — 52; 1943.
т. 7, с. 253—84; [5] Moor J., «J. Diff. Geometry», 1971,
v. 5, Ml—2, p. 159 —89; [6] П о г о р е л о в А. В., «Докл.
АН СССР», 1971, т. 198, № 1, с. 42—43; [7] П о з и я к Э. Г.,
«Успехи матем. наук», 1973, т. 28, К: 4, с. 47—76; [н] Фрид-
Фридман А., в кн.: Гравитация и топология, пер. с англ., М.,
1966, с. 182—88; [9] Б о р и с е н к о А. А., «Укр. геометр,
сб.», 1976, в. 19, с. 11 —18. А. А. Бориа'нпо.
КЛАССИФИЦИРУЮЩЕЕ ПРОСТРАНСТВО — база
Во универсального расслоения ?= (Ео, р0, Во).
Универсальность расслоения | понимается в следую-
следующем смысле. Пусть ко(Х) — множество классов экви-
эквивалентности (относительно изоморфизма, накрываю-
накрывающего тождественное отображение X) локально триви-
тривиальных расслоений над клеточным разбиением X со
структурной группой G. Если | = (?, р, В) — локально
тривиальное расслоение со структурной группой G,
В'— топологич. пространство, /, g : В'^>~В — гомотоп-
гомотопные отображения, то индуцированные расслоения
/*(?) и g*(?,) над В' принадлежат одному и тому же
классу ко(В'). Локально тривиальное расслоение §G=
= (EG, p, BG) наз. универсальным, если отоб-
отображение [X, BG]—>ko(X), /->/*(|G) взаимно одно-
однозначно. Пространство BG в этом случае наз. также
классифицирующим пространством
группы G. Главное расслоение со структурной груп-
группой G универсально (в классе локально тривиальных
расслоений над клеточными разбиениями), если про-
пространство расслоения имеет нулевые гомотопич. группы.
Важнейшие примеры К. п. ВОп, BSOn, BL'ni BSUn
для групп О,г, SOn, Un, SUn соответственно конструи-
конструируются следующим образом. Пусть G(n, к) — Грасс-
мана многообразие, оно является базой главного Оп-
расслоения с Штифеля многообразием V(n, к) в ка-
качестве пространства расслоения. Естественные вложе-
вложения G(n, fc)<zG(n., jfc-f-l) и V(n, k)dV(n, A-+1) позво-
позволяют строить объединения G(n)= U ~=1G(n, к) и V(n)=-
= Uj?=iV(n, к). Расслоение (V(n), p0, G(n)) универсаль-
универсально, a G(n) = BOn есть К. п. для группы О„(л;У(п, /с) =
=0 при i<,k—1 и niV(n) = 0 для всех i). Многообразие
Грассмана G(n, к) (пространство с фиксированной ори-
ориентацией) приводит аналогично к К. п. \Jk=iG(n, k)=
= G(n) = BSOn для группы SOn. .К. п. групп BUn и
BSUn строятся так же, с той разницей, что здесь рас-
рассматриваются комплексные многообразия Грассмана.
Для любого ©„-расслоения (Е, р, В) (В — клеточ-
клеточное разбиение) существует отображение / : B^-G(n),
при к-ром индуцированное расслоение над В изоморфно
(Е, р. В). В случае, когда В — гладкое n-мерное много-
многообразие, а главное О„-расслоение (Е, р, В) ассоцииро-
ассоциировано с касательным векторным расслоением к В, пост-
построение отображения / особенно просто: многообра-
многообразие В вкладывается в евклидово пространство R« + * при
достаточно большому и полагается f(x), х ? В, совпадаю-
совпадающим с n-мерным подпространством в R" + '^ к-рое полу-
получается сдвигом касательного пространства к В в точке х.
Многообразия Грассмана дают удобный способ конст-
конструкции К. п. для векторных расслоений. Имеются
также конструкции, позволяющие функториально
строить К. п. для любой топологич. группы. Наиболее
употребительная из них — конструкция Мил-
н о р a <?>q (см. Главное расслоение), причем расслое-
расслоение (Oq универсально в более широкой категории всех
нумерируемых G-расслоений над произвольным топо-
топологич. пространством.
Важную роль играют К. п. для сферических расслое-
расслоений BGn над клеточным разбиением В; для построения
пространств BGn (и BSGn для ориентированных сферич.
расслоений) конструкция Милнора не пригодна, так
как множество гомотопич. эквивалентностей Sn^-Sn
не группа, а Я-пространство. Явная конструкция этих
пространств изложена в [2].
Существуют также К. п. ВР1п и ВТорп для кусочно
линейных и топологич. микрорасслоений.
Имеется естественное отображение ВО,г-+ВОп + 1, со-
соответствующее прибавлению к векторному расслоению
одномерного тривиального расслоения. Отображение
это можно считать вложением, так что имеет смысл
объединение ВО= \Jn=iBOn в топологии индуктивного
предела. Совершенно аналогично строятся пространства
BSO, BU, BSU, BG, BSG, BPl, Bfop и т. д. Это —
К. п. для классов стационарной эквивалентности рас-
расслоений, заданных над связными конечными клеточны-
клеточными разбиениями. Все эти пространства имеют струк-
структуру //-пространств, связанную с операцией суммы
Уитни расслоений.
Термин «К. п.» употребляется не всегда в связи
с расслоениями. Иногда К. п. наз. представляющее
пространство (объект) для произвольного представи-
мого функтора Т : H^t-Ens гомотопич. категории в ка-
категорию множеств. Примером такого К. п. является
пространство ВГд, классифицирующее в нек-ром смысле
слоения коразмерности q на многообразии, или, более
общо, ^-структуры Хефлигера на произвольном топо-
топологич. пространстве.
Лит.: [1]Хьюзмоллер Д., Расслоенные пространства,
пер. с англ., М., 1970; [2] Бордман Д ж., Фогт Р.,
Гомотопически инвариантные алгебраические структуры на
топологических пространствах, пер. с англ., М., 1977.
А. Ф. Харшиладзс.
КЛАССИЧЕСКАЯ ГРУППА — группа автоморфиз-
автоморфизмов нек-рой полу то ралине иной формы f на правом
А'-модуле Е, где К — кольцо; при этом / и Е (а иногда
и А ) удовлетворяют дополнительным условиям. Точ-
Точного определения К. г. нет. Предполагается, что / —
либо нулевая, либо невырожденная рефлексивная
форма; иногда считается, что Е — свободный модуль
конечного типа. Часто под К. г. понимают также и
другие группы, тесно связанные с группами автомор-
автоморфизмов форм (напр., их коммутанты или факторы по
центру) или нек-рые их расширения (напр., группы
полулинейных преобразований модуля Е, сохраняю-
сохраняющие / с точностью до множителя и применения авто-
автоморфизма кольца К).
К. г. тесно связаны с геометрией: они могут быть
охарактеризованы как группы таких преобразований
проективных пространств (а также нек-рых многооб-
многообразий, связанных с грассманианами, см. [2]), к-рые
сохраняют естественные отношения инцидентности.
Напр., согласно основной теореме проективной гео-
геометрии, группа всех преобразований re-мерного про-
проективного пространства Р над телом К, переводящих
любые три коллинеарные точки снова в три коллинеар-
коллинеарные точки, совпадает при ге>3 с К. г. всех проектив-
проективных коллинеаций пространства Р. По этой причине
изучение структуры К. г. имеет геометрический смысл —
оно равносильно изучению симметрии (автоморфизмов)
соответствующей геометрии.
Теория К. г. наиболее глубоко развита для случая,
когда К — тело, а Е — векторное пространство над
К конечной размерности п. Далее эти условия предпо-
предполагаются выполненными; в этой ситуации классически-
классическими наз. обычно группы из следующих (описываемых
ниже) серий: GLn(K), SLn(K), SPn(K), О„(К, /). Un(K,f).
1) Пусть / — нулевая форма. Группа всех автомор-
автоморфизмов формы / совпадает с группой всех автоморфиз-
автоморфизмов пространства Е (т. е. биективных линейных отобра-
отображений Е в Е)\ она обозначается GLn(K) и наз. п о .1
ной линейной группой от п перемен-
переменных над телом К. Подгруппа в GLn(K), порож-
порожденная всеми трансвекциями, обозначается SLn (К) п
наз. специальной линейной группой
(или унимодулярной группой) от п
переменных над телом К. Она совпадает
с множеством автоморфизмов, имеющих определитель,
равный 1.
2) Пусть / — невырожденная полуторалинепная фор-
форма (относительно инволюции / тела А'), для которой
отношение ортогональности симметрично, т. е.
Такан форма наз. рефлексивной. Группа
Un(K, f) автоморфизмов формы / наз. унитарной
группой от п переменных над телом
К относительно формы /. Имеются лишь
две возможности: либо К — поле, /=1 и / — кососим-
метрическая билинейная форма, либо, умножая / на
подходящий скаляр и меняя /, можно добиться того.
чтобы / стала эрмитовой формой или косозрмитовон
формой. Для кососимметрич. формы / группа Un(K, /'
наз. симплектической группой от пере-
переменных над телом К (если char АГ=2, нужно
считать, что / — знакопеременная форма); она обозна-
обозначается Spn(K). Это обозначение не содержит /, по-
поскольку все невырожденные знакопеременные формы
на Е эквивалентны и определяют изоморфные симплек-
тич. группы. В этом случае п четно. Для эрмитовых
и косоэрмитовых форм выделяется случай, когда К —
поле характеристики, отличной от 2, /=1, а / — сим-
симметрическая билинейная форма. Тогда Un{K, f) наз.
ортогональной группой от п пере-
переменных над полем К относительно
формы /и обозначается Оп(К, /). Ортогональные
группы могут быть определены (особым способом) и
для полей характеристики 2 (см. [2]). Часто термин
«унитарная группа» употребляется в более узком
смысле — для групп Un(K, /), не являющихся ортого-
ортогональными или симплектическими, т. е. соответствую-
соответствующих нетривиальным инволюциям /.
К каждой из основных серий К. г. относят также и:
их проективные образы PGLn(K), PSLn(K), PSpn(K),
РОп(К, /), PUn(K, /), т. е. их факторгруппы по пере-
пересечениям с центром Zn группы GLn(K). Группу
OUK, f) = On(K, f) r\SLn(K),
коммутант Qn(K, f) группы Оп(К, f) и группу
Ut(K, f) = Un(K, f)OSLa(K)
и их проективные образы также относят к сериям орто-
ортогональных и унитарных К. г. соответственно.
Классическим направлением в теории К. г. является
выяснение их алгебраич. строения, к-рое сводится
к описанию нормальных рядов подгрупп и их после-
последовательных факторов (в частности, к описанию нор-
нормальных делителей и выяснению вопроса о простоте),
описанию автоморфизмов и изоморфизмов К. г. (и,
более общо, гомоморфизмов), описанию различных
типов систем порождающих элементов и соотношений
между ними и т. п. Так, основные утверждения о строе-
строении групп типа GLn{K) и SLn(K) следующие. Комму-
Коммутантом GLn(K), n^s2, является SLn(K), кроме случая
и—-2 и AT=F2 (здесь F?— поле из q элементов). Центр
Zn группы GLn(K) состоит из всех гомотетий х^г-ха, где
а — элемент центра группы К*. Имеется нормальный
ряд подгрупп
GLn (К) ZD SLn (К) =) SLn (К) П 2„ з {1}.
Группа GLn(K)ISLn(K) изоморфна К*/С, где К* —
мультипликативная группа тела К, а С — ее комму-
коммутант. Группа SLn(K)[)Zn является центром в SLn(K)
и факторгруппа
SLn (K)l(SLa (К) П Zn) = PSLn (К)
является простой во всех случаях, кроме ге=2, K=f2
пли F3. Подробнее см. Полная линейная группа, Спе-
Специальная линейная группа, Симплектическая группа,
Ортогональная группа, Унитарная группа. Строение
К. г. существенно зависит от ее типа, тела К, свойств
формы / и числа п. Для одних типов К. г. оно выяснено
весьма детально, для других имеются еще открытые
вопросы (последнее относится в основном к случаю
групп типа U„(К, /), где / — анизотропная форма).
Типичным в построении структурной теории К. г.
является наличие утверждений, справедливых почти
для всех К, f и п, и исследование различных исключи-
исключительных случаев, когда эти утверждения не выпол-
выполняются (такие исключения возникают, напр., для не-
небольших значений п, для конечных полей К маленького
порядка или для специальных значений индекса
формы /).
Особое место занимает вопрос об изоморфизмах К. г.
Среди всего множества изоморфизмов выделяются т и-
повые изоморфизмы — изоморфизмы между
G(n, К, f) и G'(n', K',f), определение к-рых не зависит
от специальных свойств тела К (кроме, быть может, его
коммутативности). Все прочие изоморфизмы наз.
нотиповыми. Напр., существует (типовой) изо-
изоморфизм Sp2(K) на SL2{K), где К — любое поле, или
Vt(K, f) на SL2(K0), где К — любое поле, 1ф1, f —
форма индекса 1 и А'о— поле инвариантов инволюции
/. Подробное описание известных типовых изоморфиз-
изоморфизмов см. [2], [3]. Из нетиповых изоморфизмов известны
следующие:
PSL2 (F4) s» PSL2 (F6), PSL2 (F7) s= PSL3 (F2),
Известно также, что группы PSLn(K) и PSLm(K'),
п~^2, ni^2, могут быть изоморфны только при п=т,
кроме случая
PSL2 (F7) 3s PSL3 (F2);
при от— ге>2 изоморфизм возможен лишь, если тела
К и К' изоморфны или антиизоморфны, это же верно
при т—п=2, если К и К'— поля, кроме случая
PSL2 (F4) as PSL2 (F6).
Группы PSpn(K) и PSpm(K') могут быть изоморфны
только, если ;г=т и К~К', кроме случая т=п=2,
Z-=F4, К' = ?ъ. Между группами PSLn(K), PSpm(K),
PQq (К, /), где К — конечное поле, нет никаких дру-
других изоморфизмов, кроме указанных выше.
Перечисленные результаты о строении К. г. и их
изоморфизмах получены классич. методами линейной
алгебры и проективной геометрии. Их основу состав-
составляет исследование специальных типов преобразований
из К. г. и их геометрия, свойств главным образом, изу-
изучение инволюций и плоских вращений. Позднее в тео-
теорию К. г. были введены методы теории групп Ли и
алгебраич. геометрии, после чего теория К. г. стала
частью общей теории полупростых алгебраич. линейных
групп, в к-рой К. г. появляются в качестве форм: вся-
всякая форма простой алгебраической линейной группы
классич. типа (т. е. типа Ап, Вп, Сп или Dn) является
К. г. (исключение составляет форма D4, связанная
с внешним автоморфизмом третьего порядка). В случае,
когда К есть R или С, К. г. естественно снабжается
структурой группы Ли, а для р-адических полей —
структурой р-адической аналитич. группы. Это позво-
позволяет использовать при изучении таких К. г. тополо-
гич. методы, а также, наоборот, получать информацию
о топологич. строении многообразия К. г. (напр.,
о его конечно клеточном разбиении) из знания ее ал-
алгебраич. структуры.
В более общей ситуации (когда Е — модуль над
кольцом К) результаты о К. г. не столь исчерпывающи
(см. [3]). В этой своей части теория К. г. смыкается
с алгебраической /f-теорией.
Лит.: [1] Ар тин Э., Геометрическая алгебра, пер. с
англ., М., 1969; [2]Дьедонне Ж., Геометрия классических
групп, пер. с франц., М., 1974; [3] Автоморфизмы классических
групп, сб. пер., пер. с англ. и франц., М., 1976; [4] Б у р б а-
к и Н., Алгебра. Модули, кольца, формы, пер. с франц., М.,
1966. В. Л. Попов.
КЛАССИЧЕСКИ ПОЛУПРОСТОЕ КОЛЬЦО — ассо-
ассоциативное артиново справа (или, что равносильно,
артиново слева) кольцо с нулевым Джекобсона радика-
радикалом. Строение К. п. к. описывает Веддерберна — Ар-
тина теорема. Класс К. п. к. может быть охаракте-
охарактеризован и гомологическими свойствами (см. Гомологиче-
Гомологическая классификация колец). К. п. к. является каждая
групповая алгебра конечной группы над полем, харак-
характеристика к-рого взаимно проста с порядком этой
группы. Коммутативные К. п. к. суть конечные пря-
прямые суммы полей. С К. п. к. связана теорема
Г о л д и, утверждающая, что кольцо обладает левым
классическим кольцом частных, являющимся К. п. к.,
тогда и только тогда, когда оно удовлетворяет условию
максимальности для левых аннуляторов и не содер-
содержит прямых сумм левых идеалов. Л.А.Скорняков.
КЛАССИЧЕСКИЕ ОРТОГОНАЛЬНЫЕ МНОГОЧЛЕ-
МНОГОЧЛЕНЫ — общее название Якоби многочленов, Эрмита
многочленов, Лагерра многочленов и Чебышева многочле-
многочленов. Эти системы ортогональных многочленов обладают
общими свойствами:
1) Весовая функция <р(х) на интервале ортогональ-
ортогональности (а, Ь) удовлетворяет дифференциальному урав-
уравнению Пирсона
Ф'Ос) _ Ро + р.ж __А (х) -
qo + qix+q2xz — В (х) ' •<" С V". »),
причем на концах интервала ортогональности выпол-
выполняются условия
lim <p (х) В (х) = lim <p (х) В (х) = 0.
х-* а + 0 i-ii-0
2) Многочлен у=Рп(х) порядка п удовлетворяет диф-
дифференциальному уравнению
В(х)у"+[А (х)+В'(х)]у'-п lpi+(n+i)g2]y=0.
3) Имеет место обобщенная Родрига формула
где сп— некоторый нормировочный коэффициент.
4) Производные К. о. м. суть также К. о. м. и орто-
ортогональны на том же интервале ортогональности, вообще
говоря, с другим весом.
5) Для производящей функции
F(x, u,) = ^_ ^ш», х?(а, Ъ),
имеет место представление
где к=к(х, w) — тот корень квадратного уравнения
?—х—wB (t,)=0, который при малых \w\ ближе распо-
расположен к точке х.
Этими свойствами обладают только три из указан-
указанных систем ортогональных многочленов, а также си-
системы, полученные из этих трех линейными преобра-
преобразованиями независимого переменного.
В обобщенной формуле Родрига нормировочный ко-
коэффициент сп обычно выбирается тремя различными
способами с целью получения ортонормированных мно-
многочленов, либо ортогональных многочленов с единич-
единичным старшим коэффициентом, либо так наз. стандарти-
стандартизованных ортогональных многочленов, к-рые вводятся
потому, что наиболее удобны в применениях и основные
формулы для них имеют наиболее простой вид.
К. о. м. являются собственными функциями нек-рых
задач на собственные значения для уравнений типа
Штурма — Лиувилля, причем в этих задачах каждая
система ортогональных многочленов (многочлены S. ко-
би, многочлены Эрмита, многочлены Лагерра) является
единственной последовательностью решений соответст-
соответствующей системы уравнений (см. [4], с. 110).
Частные случаи К. о. м. определяются следующим вы-
выбором весовой функции и интервала ортогональности:
1) Многочлены Якоби {Рп(х; а, 'Р)} ортогональны на
сегменте [—1,1] с весом (р(х)=A— z)a(l+z)P, где
а>—1, Р> — 1. В частности, при а=Р имеем ультра-
ультрасферические многочлены, или многочлены Гегенбауэра
{Рп(х; а)}. Лежандра многочлены {Рп{х)} соответст-
соответствуют значениям а=р=0 и ортогональны на сегменте
[—1,1] с весом (р(х)==1. Если а=Р=—1/2, т. е. ц>(х)=
= [A—x)({-\-x)Y~1l*, то имеем многочлены Чебышева
первого рода {Тп(х)}, а при a=P=V2 — многочлены
Чебышева второго рода {Un(x)}.
2) Многочлены Эрмита {Нп(х)} ортогональны на ин-
интервале (—оо, оо) с весом ф(ж) = ехр(—х2)
3) Многочлены Лагерра {Ln(x\ a)} ортогональны на
интервале @, сю) с весом (р{х)=хае~х, где а> — 1.
Лит.: [1] Г е р о н и м у с Я. Л., Теория ортогональных
многочленов, М.— Л., 1950; [2] Б е й т м е н Г., Э р д е й и А.,
Высшие трансцендентные функции. Т. 2, Функции Бесселя,
функции параболического цилиндра, ортогональные много-
многочлены, пер. с англ., 2 изд., М., 1974; [3] Джексон Д.,
Ряды Фурье и ортогональные полиномы, пер. с англ., М., 1948;
[4] Н и к и ф о р о в А. Ф., Уваров В. Б., Основы теории
специальных функций, М., 1974; [5] Суетин П. К., Клас-
Классические ортогональные многочлены, М., 19 76. См. также лит.
при ст. Ортогональные многочлены. П. К. Суетин.
КЛАССИЧЕСКОЙ НЕБЕСНОЙ МЕХАНИКИ МАТЕ-
МАТЕМАТИЧЕСКИЕ ЗАДАЧИ — задачи, возникающие в
астрономии в связи с изучением движения небесных
тел в гравитационном поле. Классическими объектами,
изучаемыми небесной механикой, являются планеты и
спутники Солнечной системы. Движение звезд и звезд-
звездных систем изучает звездная астрономия (см. Звездной
астрономии математические задачи). Движение ис-
искусственных небесных тел исследует астродинамика.
Так как расстояния между телами Солнечной системы
велики по сравнению с размерами самих тел, то посту-
поступательное и вращательное движения можно изучать
отдельно, причем при изучении поступательного дви-
движения все тела Солнечной системы можно рассматри-
рассматривать как материальные точки, взаимодействующие по
закону тяготения Ньютона,— так наз. задача JV
тел. Идеализированной схемой этой задачи описы-
описывается большая часть задач классической небесной ме-
механики. Единственным универсальным методом полу-
получения решений этой задачи для произвольных началь-
начальных значений является численное интегрирование.
Однако численное интегрирование не в состоянии вы-
выявить эволюцию системы на достаточно больших интер-
интервалах времени. Известны нек-рые частные классы ре-
решений, пригодные для любого момента времени, (напр.,
периодич. решения Эйлера и Лагранжа, см. [1]). Более
полно изучены общие свойства трех тел задачи.
В 1912 было найдено аналитич. решение этой задачи и
координаты тел в виде рядов по степеням времени,
сходящихся для любого момента. Однако эти ряды не-
непригодны для практич. вычислений из-за их крайне-
медленной сходимости. Большая часть результатов,
относящихся к задаче iV тел, получена с помощью ме-
методов теории возмущений для планетной проблемы,
т. е. в случае, когда масса N—1 тел мала по сравнению
с массой центрального тела. Если пренебречь возмуще-
возмущениями, то уравнения движения вырождаются в урав-
уравнения задачи двух тел и интегрируются в замкнутой
форме. Движение планеты подчиняется при этом зако-
законам Кеплера. Для достаточно малых масс удается полу-
получить аналитич. продолжение нек-рых важных классов
решений: периодических и квазипериодических. Пока-
Показано, что наиболее общим видом движения является
квазипериодич. движение с несоизмеримыми частотами.
Эти результаты позволяют приблизиться к решению-
проблемы устойчивости Солнечной системы под дейст-
действием взаимных возмущений планет.
Наиболее полно исследована ограниченная
задача трех тел, в к-рой два тела конечной
массы движутся вокруг центра инерции по эллинтич.
орбитам, а третье имеет пренебрежимо малую массу.
Довольно полно исследована также задача Хил-
л а, описывающая движение спутника, подвергающего-
подвергающегося возмущениям со стороны весьма удаленного, но мас-
массивного тела. Ограниченная задача имеет важное зна-
значение для теории движения малых планет, задача Хил—
ла — для теории движения Луны.
Для построения теорий движения конкретных не-
небесных тел разработаны эффективные вычислительные-
методы, основанные на разложении решения в ряд по
степеням малого параметра. Эти методы могут быть
разбиты на две группы в зависимости от того, входит
ли время только в аргументы тригонометрич. функций
в выражениях для возмущений или эти выражения
могут содержать время и в явном виде (так наз. веко-
вековые возмущения). Методы первой группы зна-
значительно сложнее и используются в тех случаях, когда
необходимо получить решение на интервалах времени
достаточно больших по сравнению с периодами невозму-
невозмущенного движения (как, напр., в теории движения
Луны). Для вычислительных методов небесной меха-
механики характерной чертой является необходимость вы-
выполнения большого объема вычислений.
Теория движений больших планет сводится к реше-
решению задачи N тел при Л"=10, под к-рыми понимается
Солнце и девять планет. Уравнения движения интег-
интегрируются приближенно с помощью разложений в ряды
(аналитич. методы) или численным интегрированием.
Идеальная теория движения больших планет должна
удовлетворять следующим четырем условиям: 1) она_
должна быть построена на основе единого математич.
метода, 2) постоянные интегрирования должны быть
определены, исходя из согласованной системы астроно-
мич. постоянных, 3) точность теории должна соответ-
соответствовать требованиям современных космич. экспери-
экспериментов, 4) теория должна быть пригодной на длитель-
длительные промежутки времени. Существующая к 70-м гг.
20 в. (и лежащая в основе всех астрономич. эфемерид)
теория не удовлетворяет указанным выше требованиям.
Она была создана разными авторами, различными мето-
чами и в разное время. Создание теории, удовлетворяю-
удовлетворяющей современным требованиям, немыслимо без широко-
широкого использования ЭВМ и совершенных наблюдений.
Теория движения спутников во многом аналогична
теории движения больших планет, однако особенностью
пой задачи является то обстоятельство, что масса пла-
планеты, относительно к-рой вращается спутник, значи-
значительно меньше массы Солнца, притяжение к-рого
существенно возмущает движение спутников. Для близ-
близких спутников необходимо также учитывать несферич-
несферичность центрального тела. В связи с этим важное зна-
значение приобретает задача двух неподвижных центров,
поскольку потенциал несферической планеты может
быть довольно точно аппроксимирован потенциалом двух
соответствующим образом подобранных точечных масс.
Лит.: [1] Д у б о ш и н Г. Н., Небесная механика, 2 изд.,
М., 1968; [2] Справочное руководство по небесной механике и
астродинамике, М., 1971. Г. А. Чеботарев.
КЛАССОВ ДИВИЗОРОВ ГРУППА — факторгруппа
группы дивизориалъных идеалов D (А) Крулля кольца А
по подгруппе главных идеалов F(A). К. д. г. явдяется
абелевой группой и обычно обозначается С (А). Группа
С (А) порождается классами простых идеалов высоты
1 в кольце А.
В некотором смысле К. д. г. измеряет отклонение
от однозначности разложения элементов кольца А
на неразложимые множители. Так, факториальное коль-
кольцо имеет пулевую К. д. г.
Пусть ф : А-+В — гомоморфизм колец Крулля, тогда
при некоторых дополнительных предположениях (напр.,
в случае, когда В — целое или плоское расширение
кольца А) определен канонич. гомоморфизм К. д. г.
<р* : С(А)^-С(В). Если В — локализация кольца А
по мультипликативной системе 'S, то ф* сюръективно
и ядро ф* порождается простыми дивизориальными
идеалами кольца А, пересекающимися с S (теорема
Н а г а т а). Если В — кольцо многочленов над А,
то канонич. гомоморфизм ф* биективен (это является
обобщением теоремы Гаусса о факториальности кольца
многочленов над полем). В более общем случае, когда
В — симметрическая нётерова алгебра Л-модуля М,
канонич. гомоморфизм ф* будет биективен при условии,
что все симметрия, степени S' (М) рефлексивны. Если
В — кольцо формальных степенных рядов над А, то го-
гомоморфизм ф* инъективен (и даже обратим слева),
но. вообще говоря, не биективен.
Подгруппа группы С (А), порожденная обратимыми
идеалами, изоморфна Пикара группе Pic(A) кольца
А, н функторнальные свойства Pic (А) и С (А) согласо-
согласованы. Так, если В — строго плоское расширение коль-
кольца А и гомоморфизм ф* : PicA—>-Pic В инъективен, то
инъективен и ф* : С (А)—>С(В). В частности, если по-
пополнение А локального кольца А факториально, то
факториально и А (теорема Мор и).
Пусть А — нормальное нётерово кольцо. Группа
Pic (А) совпадает с С (А) тогда и только тогда, когда
А — локально факториальное коль-
кольцо, т. е. все локальные кольца А т факториальны
(напр., когда А — регулярное кольцо). Более точно,
если F= {jJ^Spec (A), Ap — факториально}, то
?(Л) = 1'т Pic (U), где U пробегают систему открытых
подсхем в Spec (Л), содержащих F. Это позволяет
определить К. д. г. нормальной схемы [5] — группу
классов дивизоров Вейля (см. Дивизор).
Первоначально изучались К. д. г. колец алгебраич.
чисел, первые результаты о конечности этой группы
были получены еще Э. Куммером (Е. Kummer). Имеется
•тесная связь свойств К. д. г. с теоретико-числовыми
вопросами, напр. с теоремой Ферма. Таблицы порядков
К. д. г. некоторых колец алгебраич. чисел приведены
в [1].
Современную общность теория К. д. г. получила в
работах В. Крулля (W. Krull); П. Самюэль (P. Sa-
Samuel) изучил функториальный характер К. д. г. и
предложил несколько методов ее вычисления (как,
напр., метод спуска). Другие подходы к изучению
К. д. г. основаны на сравнении ее с группой Пикара,
при этом применяются когомологич. и алгебро-геомет-
рич. средства.
Для любой абелевой группы существует изоморфная
ей К. д. г.
Лит.: [1] Б о р е в и ч 3. И., Ш а ф а р е в и ч И. Р.,
Теория чисел, М., 1964; [2] Бур баки Н., Коммутативная
алгебра, пер. с франц., М., 1971; [3] S a m u e I P., Topology,
[1964], v. 3, Suppl. I, S. 81—96; [4] V о s s и m R. M., The
divisor class group of a Krull domain, В., 1973; [5] G г о t h e n-
dieck A., Dieudonne J., «Publ. Math. IHES», 1967,
t. 32. • В. И. Данилов.
КЛАССОВ ИСЧИСЛЕНИЕ — традиционное, восхо-
восходящее к Дж. Булю (G. Boole) название раздела матема-
тич. логики, изучающего логику классов. К. и. фак-
фактически представляет собой логику высказываний, в
к-рой дополнительно рассматривается субъектно-пре-
дикатная структура элементарных высказываний (т. е.
элементарные высказывания имеют вид «элемент х об-
обладает свойством Р»), причем с каждым предикатом
(свойством) Р связывается класс элементов из рассмат-
рассматриваемой области, обладающих этим свойством. К. п.
было задумано как математич. эквивалент аристотеле-
аристотелевой силлогистики, однако оно не является таковым, по-
поскольку допустимые в К. и. пустой и одноэлементные
классы Аристотелем не рассматривались. К. и. обыч-
обычно не выделяют в самостоятельный раздел математич.
логики, так как все его выразительные возможности
перекрываются исчислением одноместных предикатов
(являющимся, в свою очередь, разрешимым фрагмен-
фрагментом узкого исчисления предикатов, см. Логические ис-
исчисления). Аристотелева силлогистика адекватным об-
образом формализована Я. Лукасевичем [4].
Лит.: [1] Гильберт Д., Аккерман В., Основы
теоретической логики, пер. с нем., М., 1947; 12] К у т ю р а Л.,
Алгебра логики, [пер. с франц.], Одесса, 1909; [3] W а ] s-
b e r gM., «Monatsch. fur Math, und Phys.», 1933, Bd 40, S. 113—
26; [4] Л у к а с е в и ч Ян, Аристотелевская силлогистика с
точки зрения современной формальной логики, пер. с англ.,
М., 1959; [5] Яновская С, Логика классов, в кн.: Фило-
Философская энциклопедия, т. 3, М., 1964, с. 224—26.
В. А. Душспий.
КЛЕБША УСЛОВИЕ — необходимое условие опти-
оптимальности в задаче вариационного исчисления на ус-
условный экстремум; установлено Р. Клебшем [1]. Если
экстремаль x(t), x : R—>-R", доставляет условный ми-
минимум функционалу в Больца задаче:
(t> г, xjdt+git^ x(h), U, x(t2)),
/:RxR"xR"—>• R, g:RxR"xRxR"—> R,
<f>(t,x, i)=0, cp:RxR"XlRn—*-Rra, m < n,
'a
то согласно правилу множителей она является безус-
безусловной экстремалью функционала
где
F (t, х, х, Я) =>
а
— Лагранжа множители, определяемые вместе с x(t)
из необходимых условий экстремума функционала A).
Одним из таких необходимых условий является К. у.
Для того, чтобы экстремаль х (t) доставляла минимум в
рассматриваемой задаче, необходимо выполнение
К. у., требующего, чтобы для любой ненулевой сово-
совокупности чисел |/, i=l,..., п, удовлетворяющей урав-
уравнениям
((, x, x)
Эх,
., т,
имела место неотрицательность квадратичной формы
д'-F (t, x, X, к)
К,.,
;/sy ^
Необходимое К. у. непосредственно связано с более
сильным необходимым Вейерштрасса условием и может
быть получено из последнего как следствие.
В задачах вариационного исчисления на безусловный
экстремум, в частности в простейшей задаче вариацион-
вариационного исчисления, аналогом К. у. является Лежандра
условие.
В задачах оптимального управления К. у. эквива-
эквивалентно неположительности второго дифференциала
Гамильтона функции, что является необходимым ус-
условием выполнения Понтрягина принципа максимума
при изменении оптимального управления в открытой
области.
Лит.: [llClebsch R. F. A., «J. fur Math.», 1858, Bd 55,
S. 2J4; [2] Б л и с с Г. А., Лекции по вариационному исчис-
И.Б.Вапнярскай.
Г. А.,
лению, пер. с англ., М., 1950.
КЛЕЙНА ИНТЕРПРЕТАЦИЯ — модель, реализую-
реализующая систему аксиом геометрии Лобачевского. В К. и.
плоскость Лобачевского интерпретируется как внутрен-
внутренность действительного невырожденного абсолюта (ова-
(овала) на евклидовой плоскости. Прямые линии плоскости
Лобачевского реализуются
хордами 'абсолюта (без кон-
концевых точек). Параллели
через точку Р к прямой
MN реализуются прямыми
PU и РТ, пересекающими
прямую MN в точках V
и Т на абсолюте (см. рис.).
Движениями в К. и. служат
проективные преобразования, оставляющие абсолют
инвариантным. Метрическими величинами служат
численные инварианты этих преобразований: расстоя-
расстояния выражаются с помощью ангармонических отноше-
отношений четверок точек, углы — с помощью ангармоничес-
ангармонических отношений четверок прямых. Абсолют можно
рассматривать как совокупность бесконечно удаленных
точек плоскости Лобачевского. К. и. обобщается на
многомерный случай.
К. и. предложена Ф. Клейном в [1].
Лит.: 11] Klein F., «Gott. Nachr.», 1871, 419—33; [2l
Каган В. Ф., Основания геометрии, ч. 2, М., 1956; [3]
Ефимов Н. В., Высшая геометрия, 5 изд., М., 1971; [4]
II о г о р е л о в А. В., Основания геометрии, 3 изд., М.,
1968. А. В. Иванов.
КЛЕЙНА КООРДИНАТЫ — см. Плюккеровы коор-
координаты.
КЛЕЙНА ПОВЕРХНОСТЬ, бутылка Клей-
н а,— замкнутая односторонняя поверхность рода I
Рис. 1.
1/
(см. рис. 1, а, б). К. п. может
быть получена из квадрата A BCD
(см. рис. 2) отождествлением
точек отрезков А В и CD, лежа-
лежащих на прямых, параллельных
стороне AD, и точек отрезков
ВС и AD, симметричных отно-
относительно центра квадрата A BCD.
К. и. топологически вкладывает-
вкладывается в 4-мерное евклидово прост-
пространство и не вкладывается в 3- Рис' "'
мерное евклидово пространство.
К. п. введена в рассмотрение Ф. Клейном (F. Klein,
1874). Е. В. Шикин.
КЛЕЙНА ПРОСТРАНСТВО, однородное
пространств о,— топологическое пространство, в
к-ром определена группа гомооморфных отображе-
отображений этого пространства на себя, обладающая тем свойст-
свойством, что для каждых двух точек пространства А и В
существует преобразование этой группы, переводя-
переводящее точку А в точку В.
Происхождение термина «К. п.» связано с эрланген-
ской программой ф. Клейна (F. Klein, 1872), в к-рой
различные геометрии определялись с точки зрения соот-
соответствующих групп преобразований. а. б. Иванов.
КЛЕЙНА — ГОРДОНА УРАВНЕНИЕ — релятивист
ски инвариантное квантовое уравнение, описывающем-
бесспиновые скалярные или псевдоскалярные частицы,
напр, я-, А-мезоны. Уравнение установлено О. Клей-
Клейном [1] н несколько позднее В. Л. Фоком как волновое
уравнение при условии цикличности по пятой коор-
координате н вскоре было выведено без привлечения пятой
координаты многими авторами (напр., В. Гордоном
[2]).
Последовательное применение К.—Г. у. как квантово-
квантового релятивистского уравнения возможно лишь в кван-
квантовой теории поля, а не в квантовой механике. В [3]
была дана интерпретация К.—Г. у. как уравнения для
полей частиц спина нуль. К.—Г. у. применяется для
описания я-мезоатомов и соответствующих полей; играет
роль одного из фундаментальных уравнений квантовой
теории поля.
К.—Г. у. — линейное однородное дифференциальное
уравнение с частными производными 2-го порядка с
постоянными коэффициентами:
г . дг , S2 82 „ \ п ...
-ар —air —^aTF —^2; Ф = О, A)
где ф(ж, t) — (псовдо) скалярная функция, в общем
случае комплексная, \у=тс!%, т — масса покоя частиц.
Если ф — действительная функция, то К.—Г. у. описы-
описывает нейтральные (псевдо) скалярные частицы, а при
комплексном ф — заряженные. В последнем случае
уравнение A) дополняют уравнением для комплексно
сопряженной функции ф*:
\дх--^ду*^ dzz c=s/2 Ц. у ф — и. w
Взаимодействие (псевдо) скалярных частиц с электро-
магнитным полем описывается минимальной подстанов-
подстановкой —-—>-—-—геАа- К.—Г. у. удовлетворяет также
дха дха
каждая компонента волновой функции частиц любого
спина, но только для случая спина 0 функция является
инвариантной относительно Лоренца—Пуанкаре груп-
группы.
К.—Г. у. может быть получено с помощью соотноше-
соотношения между энергией Е и импульсом р частицы в спе-.
циалыюй теории относительности
сг & —Рх—Ру — Pz—m c
путем замены величин операторами (см. [4], [5]):
R'-i.—iLJl _». A JL
Как все релятивистские уравнения К.—Г. у. может быть
представлено в форме Дирака уравнения, т. е. приведено
к линейному уравнению первого порядка:
\ дха )
где коэффициенты Га — матрицы, аналогичные Дирака
матрицам уа. В случае К.—Г. у. матрицы Га удовлет-
удовлетворяют перестановочным соотношениям:
напр., Г^=0 (матрицы Кеммер а—Д у ф ф и-
н а). Здесь r)|xV — метрический тензор пространства
Минковского. Все Га являются особенными матрицами
(det Га=0) и не имеют обратных матриц.
Наряду с тривиальным решением D) Га=0, i|)=0
и в виде пятирядных матриц, описывающим скалярное
поле самой функцией ф и четырьмя компонентами ее
градиента, соотношение D) имеет еще решение в виде
матриц десятого ранга. Соответствующая десятикомпо-
нентная функция содержит 4 компоненты потенциала
Аа ш 6 компонент напряженности Faa = 2d,aA«-,, т. е.
уравнения C), D) могут одновременно давать пред-
представление для уравнения Прока, описывающего вектор-
векторные частицы спина 1; при (х=0 и действительной ф
дают представление уравнений Максвелла.
При учете взаимодействия (псевдо) скалярных частиц
с гравитационным полем в соответствии с общей тео-
теорией относительности К.—Г. у. обобщается на произ-
произвольное риманово пространство в виде:
1 э
У~—„ „ а
гДе ?аЗ — метрический тензор, g — определитель
матрицы Hgapll- Часто в уравнение E) добавляют член
Rqi/б, где R — скалярная кривизна, благодаря чему
при ц=0 общерелятивистское К.—Г. у.
становится конформно инвариантным.
Лит.: [1] Klein О., «'/,. Phys.», 1926, Bd 37, S. 895—906;
[2] G or d on W., там же, 1926/1927, Bd 40, S. 117-33; [3]Pau-
li W.,Weisskopf V., «Helv. phys. acta», 1934, Bd 7,
S. 709—31; M Боголюбов Н. Н., Ш и р к о в Д. В.,
Введение в теорию квантованных полей, 3 изд., М., 1976; [5]
Ш в е б е р С, Введение в релятивистскую квантовую тео-
теорию поля, пер. с англ., М., 1963. В. Г. К)>ечет.
КЛЕЙНОВА ГРУППА — дискретная подгруппа Г
группы всех дробно-линейных отображений
, ч ах ->-Ь
v(z) = ;
' v ' cz + d
ad — ос =
расширенной комплексной плоскости С, являющаяся
собственно разрывной. Это означает, что множество
Л (Г) точек накопления орбит (v(z0)}, у?Г, для всех
точек zo?C, называемое предельным множе-
множеством группы Г, есть собственное подмножество
С. Дополнение Q (Г)=С\Л (Г), называемое множе-
множеством разрывности группы Г, откры-
открыто и обладает тем свойством, что каждая его точка z
имеет окрестность Uz, для к-рой y(Uz)[\Uz=<3 при
всех т?Г\Гг, где
— стабилизатор точки z в Г. Если точка z?Q(F) от-
отлична от неподвижных точек эллиптич. элементов
Г, то Гг= {/}, где / — тождественное отображение,
а для каждой эллиптической неподвижной точки Гг —
циклическая группа конечного порядка. Основы теории
К. г. были заложены в фундаментальных работах
А. Пуанкаре [1] и Ф. Клейна [2] еще в 19 в., название
«К. г.» восходит к А. Пуанкаре.
Предельное множество Л(Г) либо пусто, либо со-
состоит из одной или двух точек, либо бесконечно. Пер-
Первые два случая соответствуют элементарным
группам (сюда, в частности, входят все циклич.
группы). Если Л (Г) бесконечно, то оно есть нигде не
плотное в С совершенное множество положительной
логарифмич. емкости. Часто элементарные группы не
включают в К. г.
Факторпространство О(Г)/Г имеет естественную
комплексную (конформную) структуру, в к-рой проек-
проекция
ji:Q (Г) -+Q (Г)/Г
голоморфна, и представляет собой конечное или счет-
счетное объединение \JjSj римановых поверхностей Sf,
это накрытие будет разветвленным над проекциями
точек z?Q(T) с нетривиальными стабилизаторами Гг.
Само Q(F) распадается на компоненты связности Qy,
число к-рых равно 1,2 или оо. Если подгруппа
совпадает с Г, то компонента Qf наз. инвариант-
инвариантной. Инвариантных компонент может быть не больше
двух. К. г. с инвариантными компонентами получили
название функциональных.
Примеры. 1) Фуксовы группы. Каждая такая
группа оставляет инвариантной нек-рую окружность
(прямую) I с сохранением направления обхода, и
Л(Г)с:?. Для того чтобы (неэлементарная) К. г. Г
была фуксовой, необходимо и достаточно, чтобы она не
содержала локсодромических элементов. По те о р е м е
Клейна — Пуанкаре об униформиза-
ц и и всякая риманова поверхность, за исключением
нескольких простейших случаев, унпформизируется
фуксовой группой, действующей, напр., в верхней по-
полуплоскости /?={z^C : Imz>0}, т. е. с точностью до
конформной эквивалентности представляется в виде
Н/Г. Если в Н ввести гиперболич. метрику Пуанкаре
\ dz\
то элементы Г становятся неевклидовыми (гиперболи-
(гиперболическими) движениями. А. Пуанкаре предложил подоб-
подобную интерпретацию и для произвольной К. г. Г, ос-
основанную на продолжении действия Г в полупростран-
полупространство
Именно, поскольку всякий элемент Г есть суперпо-
суперпозиция четного числа инверсий относительно окруж-
окружностей Z/CC, можно рассмотреть инверсии относительно
соответствующих полусфер в R+, опирающихся на L.
Продолженная таким образом группа Г действует в
R+ разрывно, а ее элементы становятся гиперболич.
движениями R+.
2)Квазифуксовы группы. Они служат
непосредственным обобщением фуксовых групп. Ква-
зифуксовой наз. К. г. Г, оставляющая инвариантной
нек-рую ориентированную жорданову кривую ZczC.
Тогда A(T)czZ. Если Л(Г)=/, то Г наз. группой пер-
первого рода, а при /\Л(Г)=^0— второго ро-
д а. Римановы поверхности DJT и DJT, где D1 — внут-
внутренность, a D2 — внешность I, гомеоморфны; более
того, напр., любые две гомеоморфные римановы поверх-
поверхности конечного типа (т. е. замкнутые поверхности с
конечным числом проколов) могут быть униформизиро-
ваны одной квазифуксовон группой. Конечно порож-
порожденные квазифуксовы группы сводятся к фуксовым
(сопрягаются с ними) с помощью квазиконформных
автоморфизмов плоскости.
3) Группы Шотки. Каждая такая группа
есть К. г. Г с образующими у1,. . ., ур, р^1, для к-рых
существуют 2р непересекающихся жордановых кри-
кривых 1г, l[,. . ., lp, l'p, ограничивающих 2р-связную
область D такую, что
yj(D)[\D = 0, Y/('/) = */• / = *, •¦-,?•
При этом Г свободна, О(Г)/Г — замкнутая поверхность
рода р, а все элементы т?Г\{/} — гиперболические
или локсодромические. Группами Шотки униформизи-
руются все замкнутые римановы поверхности (это —
у н и ф о р м и з а ц и я по Кебе).
4) Вырожденные группы. Это — неэле-
неэлементарные конечно порожденные К. г., у к-рых множе-
множества разрывности являются односвязными областями.
Имеется весьма-сложное доказательство существования
таких групп, однако явных их примеров пока A978) не
построено. Вырожденные группы являются частным
случаем групп с одной инвариантной односвязной ком-
компонентой, называемых Ь-т р у п п а м и.
В основе геометрич. подхода к исследованию К. г.
лежит понятие фундаментальной области,
т. е. множества соСЙ(Г), содержащего по одной точке
из каждой орбиты Гг0, го?Й(Г), и такого, что каждая
непустая его компонента юГ)Йу связна. Напр., для
групп Шотки в качестве w можно взять указанную
область D, присоединив к ней точки кривых lt,. .., lp.
Часто фундаментальной областью наз. только внутрен-
внутренность w. Для любой К. г. можно выбрать канониче-
каноническую фундаментальную область, ограниченную дугами
окружностей. Свойства фундаментальной области поз-
позволяют выяснить структуру К. г. Г. Одним из методов
построения К. г. служат так наз. комбинацион-
комбинационные теоремы, дающие условия, когда группа Г,
порожденная данными К. г., снова является К. г.
Напр., если взять фуксовы группы Tlt. . ., Г„, дейст-
действующие соответственно в кругах Ux,. . ., Un, достаточно
удаленных друг от друга, и представляющие компакт-
компактные поверхности Uj/tj соответственно родов ру, то Г =
= (Гх,. . ., Г„) — функциональная группа, представляю-
представляющая п-\-1 поверхностей родов р1,. . ., р„ и pi~\-. . .+рп.
Весьма полезными оказались методы трехмерной топо-
топологии, связанные с рассмотрением 3-многообразия
(К+иЩПУГ, у к-рого О(Г)/Г служит краем.
Аналитический подход в теории К. г. связан с рас-
рассмотрением автпоморфных форм. Если Г — неэлемен-
неэлементарная К. г. и оо?0(Г), то при целых q^i сходится
Ряд2уег1т'(-I9 (в точках 2?О(Г) с Г2= {/}); соот-
соответствующие тета-ряды Пуанкаре
где / — мороморфная функция в Q(T), дают автоморф-
ные формы веса (—2д). Для конечно порожденных
К. г. размерность пространств таких форм подсчиты-
вается с помощью Римана—Роха теоремы. Геометрич.
структура таких групп Г описывается теоремой
А л ь ф о р с а, согласно к-рой пространство О(Г)/Г
для них состоит из конечного числа поверхностей Slt. . .,
Sn конечного типа, а я может быть разветвлено над
каждой Sj лишь в конечном числе точек. Этот результат
допускает количественные уточнения. Используются и
когомологич. методы, основанные на рассмотрении
действия группы Г в векторных пространствах полино-
полиномов (см. [5]). Существенную роль в теории К. г. на
плоскости играют методы теории квазиконформных
отображений [6], [7]. На них опирается, в частности,
теория деформаций К. г., тесно связанная с теорией
модулей римановых поверхностей (см. также Римановых
поверхностей конформные классы). На этом пути были
выявлены и нек-рые новые классы К. г. Однако пока
еще не получено полной классификации даже конечно
порожденных К. г.
По сравнению с плоскими гораздо слабее изучены
К. г. в многомерном евклидовом пространстве R",
п>2, определяемые как собственно разрывные подгруп-
подгруппы группы конформных автоморфизмов пространства
R"=R"(J {оо}; здесь появляется ряд совершенно но-
новых эффектов.
Лит.: [1] Р о i n с а г ё Н., «Acta math.», 1883, v. 3, p. 49 —
92; [2] Klein С h. F., «Math. Ann.», 1883, Bd 21, S. 141—218;
[3] Форд Л. Р., Автоморфные функции, пер. с англ., М.— Л.,
1936; [4] L e h n e r J., Discontinuous groups and automorphic
functions, Providence, 1964; [5] К р а И., Автоморфные функции
и клейновы группы, пер. с англ., М., 1975; [6] Крушкаль
С. Л., Квазиконформные отображения и римановы поверх-
поверхности, Новосиб., 1975; [7] A crash course on Kleinian groups
В.— Hdlb.— N. Y., 1974. С. Л. Нрушкалъ.
КЛЕРО УРАВНЕНИЕ — обыкновенное дифферен-
дифференциальное уравнение 1-го порядка, не разрешенное от-
относительно производной:
y=xy'+f(y'), A)
где f(t) — нелинейная функция. Уравнение A) назы-
называется по имени А. Клеро [1], к-рый впервые указал
на различие общего и особого решений уравнения тако-
такого вида. К. у. является частным случаем уравнения Ла-
гранжа.
Если f(t)?C1(a, Ъ) и f (ь)Ф0 при t?(a, Ъ), то мно-
множество интегральных кривых уравнения A) включает
в себя: параметрически заданную кривую
x=~f'(t), y=-tf'(t)+f(t), a<t<b; B)
однопараметрич. семейство прямых
y = Cx + f(C), С?(а,Ь), C)
касательных к кривой B); кривые, составленные из
произвольного участка кривой B) и двух прямых се-
семейства C), касающихся кривой B) в концах этого
участка. Семейство прямых C) представляет собой
общее решение, а кривая B), являющаяся огибающей
семейства C),— особое решение (см. [2]). Семейство ка-
касательных к гладкой нелинейной кривой удовлетворяет
К. у. Поэтому к К. у. приводят геометрич. задачи, в
к-рых требуется определить кривую по заданному свой-
свойству ее касательных (общему для всех точек кривой).
Уравнением Клеро наз. также уравнение с частными
производными 1-го порядка
_ дг . dz . , ( dz dz
оно имеет интеграл
где (а, Р) — произвольная точка области определе-
определения функции f(p q) (см. [3]).
Лит.: [1] Glairaut А., в кн.: Histoire de l'Academie
Royal des sciences. Annee 1734, P., 1736, p. 196—215; [2] Сте-
Степанов В. В., Курс дифференциальных уравнений, 8 изд.,
М., 1959; [3] Камке Э., Справочник по дифференциальным
уравнениям в частных производных первого порядка, пер. с
нем., М., 1966. Н. X. Розов.
КЛЕТОЧНОЕ ОТОБРАЖЕНИЕ — отображение
/ : (X, A)—*-(Y, В) одного относительного клеточного
разбиения (X, А) в другое клеточное разбиение (У, В)
такое, что/((X, A)r)c(Y, В)р, где (X, A)Pn(Y, В)Р—
р-мерные остовы пространств X и Y относительно А
и В соответственно. В случае, когда А, В=ф полу-
получается К. о. / клеточного разбиения X в клеточное
разбиение Y.
Гомотопия F : (X, A)XI^(Y, В), где /=[0, И,
наз. клеточной, если F( {X, А)Х1?С2(У, В)Р
для всех р. Следующая теорема о клеточной аппрокси-
аппроксимации является аналогом теоремы о симплициальной
аппроксимации (см. Симплициалъное отображение):
пусть дано отображение /: {X, A)-+(Y, В) одного
относительного клеточного разбиения (X, А) в другое
(Y, В), ограничение к-рого на некоторый подкомплекс
(L, Л')с:(Х, А) является клеточным. Тогда существует
клеточное отображение g : (X, А)—>-(У, В), гомотопное
относительно L отображению /.
Лит. см. при ст. Клеточное разбиение. д q Баладзе
КЛЕТОЧНОЕ ПРОСТРАНСТВО — хаусдорфово про-
пространство, наделенное клеточным разбиением. Напр.,
каждое симплициалъное пространство является К. п.
Обратно, для любого К. п. существует гомотопически
эквивалентное ему симплициальное пространство той же
размерности.
Лит.: [1] Рохлин В. А., Фукс Д. Б., Начальный
курс топологии. Геометрические главы, М., 1977.
С. Н. Малыгин.
КЛЕТОЧНОЕ РАЗБИЕНИЕ, CW -комплекс,—
клеточный комплекс X, удовлетворяющий следующим
условиям: (С) Для любой точки х?Х комплекс X(х)
является конечным, т. е. состоит из конечного числа
клеток (для произвольного подмножества А клеточного
комплекса X через X (А) обозначается пересечение
всех подкомплексов комплекса X, содержащих мно-
множество A). (W) Если F — нек-рое множество клеточного
комплекса X, и для любой клетки t из клеточного
комплекса X пересечение /Т)*замкнут° B t (а следова-
следовательно и в X), то F является замкнутым подмножеством
в X. При этом каждая точка х? X принадлежит неко-
некоторой определенной клетке tx из клеточного комплекса
X, и выполняется равенство Х(х)=Х(tx)=X(tx).
Обозначение CW получено из первых букв англ.
названий вышеприведенных двух условий: (С) — Closure
finiteness (конечность замыкания) и (W) — Weak to-
topology (слабая топология).
Конечный клеточный комплекс X удовлетворяет
обоим условиям (С) и (W). Вообще, клеточный комплекс
X, в к-ром каждая точка х содержится в нек-ром конеч-
конечном подкомплексе Y(х), есть К. р. Пусть для нек-рого
множества F из X множество Ff\t замкнуто в t при
любом выборе клетки t из X. Тогда для любой точки
х?Х множество F[\Y(x) замкнуто в X. Если теперь
точка х не принадлежит множеству F, то открытое
множество Ux=X\(Ff\Y(х)) содержит точку х и не
пересекается с F. Множество X\F=\JxeX\f Vх—
открыто, а множество F — замкнуто.
Класс К. р. (или класс пространств, каждое из к-рых
имеет гомотопический тип К. р.) является наиболее
подходящим классом топологнч. пространств для по-
построения содержательной теории гомотошш. Так:
если подмножество А К. р. X замкнуто, то отобра-
отображение / топологич. пространства А в топологич. про-
пространство У непрерывно тогда и только тогда, когда
непрерывны ограничения отображения / на замыкания
клеток комплекса X. Если С — компактное подмно-
подмножество К. р. X, то комплекс X(С) конечный. Для любой
клетки t из К. р. X существует множество D, открытое
в t, к-рое допускает в качестве деформационного
ретракта множество t\t.
Практически К. р. строятся последовательно: каж-
каждая стадия состоит в приклеивании клеток данной раз-
размерности к результату предшествующей стадии. Клеточ-
Клеточная структура такого комплекса находится в прямой
связи с его гомотопич. свойствами. Даже для таких
«хороших» пространств, как полиэдры, полезно рассмат-
рассматривать их представление в виде К. р.: в таком пред-
представлении они обычно имеют меньше клеток, чем при
симплициальной триангуляции. Если пространство X
получено приклеиванием гг-мерных клеток к простран-
ству А, то подмножество XX0\JAXl, где /=[0, 1]
является сильным деформационным ретрактом простран-
пространства XXI.
Относительным К. р. наз. пара (X, А),
состоящая из топологич. пространства X и его замкну-
замкнутого подпространства А, а также такой последователь-
последовательности замкнутых подпространств (X, AI*, k^g=O, что вы-
выполняются следующие условия: а) пространство (X, А)°
получено из А приклеиванием нульмерных клеток;
б) при /с^1 пространство (X, А)к получается при-
приклеиванием ^-мерных клеток к пространству (А', А)к~г\
в) пространство X=U(X, А)к\ г) топология простран-
пространства X согласована с семейством {{X, А)к}. Простран-
Пространство (X, А)к наз. к-м ерным остовом прост-
пространства X относительно А. При А = ф относительное
К. р. (X, ф)—Х есть К. р. в прежнем смысле, его к-
мерный остов — Хк.
Примеры: 1) Пара (К, L) симплициальных комп-
комплексов К и L, LaK определяет относительное К. р.
(\К\, \L\), где (\К\, \L\)k=(Kk\JD. 2) Шар V" есть
К. p.: (Vn)k = p0 при fc<re—I, (K4)"-1=Sn-1 и (Vn)k
при к^и. Сфера S"-1 есть подразбиение этого К. р.
V". 3) Если пара (X, А) есть относительное К. р., то
(XXI, А XI) — также К. р., и (XXI, АХ.1)к=((Х,
A)kX0xl)(j((X, А)к~1Х1). 4) Если (X, А) есть от-
относительное К. р.,тоХ/Л есть К. р., при этом (Х/А)к=
= (X,A)lt /А , где Х/А—факторпространство простран-
пространства X, полученное отождествлением всех точек мно-
множества А с одной точкой.
Лит.: [1] Телеман К., Элементы топологии и диффе-
дифференцируемые многообразия, пер. с рум., М., 1967; [2]
С п е н ь е р Э., Алгебраическая топология, пер. с англ., М.,
1971; [3] Дольд А., Лекции по алгебраической топологии,
пер. с англ., М., 1976. Д. О. Баладзе.
КЛЕТОЧНЫЙ КОМПЛЕКС — отделимое простран-
пространство X являющееся объединением непересекающихся
клеток. При этом р-м ерной клеткой наз. топо-
топологич. пространство, гомеоморфное внутренности еди-
единичного куба размерности р. Если: 1) для каждой р-
мерной клетки tP пространства X задано непрерывное
отображение / р-мерного куба IP в пространство X,
причем ограничение /' отображения / па внутренность
1Р куба IP взаимно однозначно, и образ f(IP) совпа-
совпадает с замыканием tP в X клетки tP (т. е. /' — гомео-
гомеоморфизм. IP на tP) и 2) множество f(OIP), где д1Р —
граница куба IP, включено в объединение ХР~г клеток
tP~г пространства X, то X наз. клеточным ком-
комплексом; объединение ХР~г наз. остовом
размерности р — 1 К. к. X. Пример К. к.— симпли-
циальный полиэдр.
Подмножество L К. к. X наз. подкомплек-
с о м, если L является объединением клеток из X,
к-рое вместе с клетками содержит их замыкание. Так,
«-мерный остов X" К. к. X является его подкомплек-
подкомплексом. Любое объединение и любое пересечение подкомп-
подкомплексов К. к. X являются подкомплексами X.
Любое топологич. пространство можно рассматри-
рассматривать как К. к.— объединение его точек, к-рые являют-
являются клетками размерности нуль. Этот пример показы-
показывает, что понятие К.к. слишком обширно и потому для
приложений важны более узкие классы К. к., напр.
класс клеточных разбиений, или CW-комплексов.
Д. О. Балпдзе.
КЛИН в векторном пространстве —
выпуклое множество, инвариантное относительно пре-
преобразования х-^Хх, Я^О, т. е. множество К такое, что
если х, у?К, а числа X, |i^U то Хх-^щ/^К. К., удов-
удовлетворяющий условию: если х, —х?К, то х^=0 наз.
конусом (выпуклым). Всякий К. порождает в
векторном пространстве структуру квазинорядка:
х^у, когда х—у?К. К. К в пространстве X наз.
воспроизводящим, если К—К=Х.
Б. 3. Вулих.
КЛИНИ — МОСТОВСКОГО КЛАССИФИКАЦИЯ —
классификация теоретико-числовых предикатов, вве-
введенная независимо С. Клини [1] и А. Мостовским [2].
Через По и одновременно через 20 обозначается класс
всех рекурсивных предикатов. Для всякого /с>0 класс
2fc определяется как класс всех предикатов, выразимых
в виде 3yR(y, %i,. ¦ ., хп), где 3 — квантор суще-
существования, R (у, х^,. . ., хп) — предикат из класса П^_1,
а класс П^ определяется как класс предикатов, вырази-
выразимых в виде 4yR(y, xt,. . ., хп), где v — квантор все-
всеобщности, R (у, з:ь. . ., хп) — предикат из класса 2^_1.
Таким образом получается последовательность классов:
Если предикат принадлежит классу 2 ^ или Пд., то он
принадлежит классам Пу и 2 j для любого />/с, т. е.
!*^2уГ|П/ и ИА^2уПП/ для любого j>k. Если
/с>0, то существуют предикаты из класса 2 ?. не при-
принадлежащие Ид., а также предикаты из класса П^,
не принадлежащие 2ц,т. e.2ft— Пд, Ф 0 и ПА — 2Й т= 0-
Предикат принадлежит одному из классов 2 д. или Пд,
тогда и только тогда, когда он выразим в языке арифме-
арифметики формальной. Если предикат Q(xx,. . ., хп) принад-
принадлежит классу 2^ (или Пд.), то предикат ~^Q(xly. . ., х„),
где "| — знак отрицания, принадлежит классу Щ
(соответственно 2^). Предикат Q{xx, .. ., хп) рекурсивен
тогда и только тогда, когда предикаты Q(xy, . . ., хп) и
'1?(ж11--ч хп) принадлежат классу 21; т. е. 21ПП1 =
^2„=П0. Если Л>0,то BА + 1Г)Пй + 1)-BАиЩ) #0.
На классификации предикатов основана класси-
классификация множеств, определимых в языке
бормальноп арифметики: множество М принадлежит
классу П^ или 2 д., если этому классу принадлежит
предикат «х?М».
Лит.: [1] К 1 е е n e S. С, «Trans. Amfir. Math. Soc», 1943,
v. 53 p. 41 — 73: [2] М о s t о w s k i A., «Fund, math.», 1947,
v. 34, p. 81 —112. В.Е.Плиско.
КЛИФФОРДА АЛГЕБРА — конечномерная ассо-
ассоциативная алгебра над коммутативным кольцом, впер-
пые рассмотренная У. Клиффордом (W. Clifford) в
i S76. Пусть К — коммутативное кольцо с едини-
единицей, Е — свободный А"-модуль, Q — квадратичная
|>орма на Е. К. а. квадратичной формы Q (или нары
(Г., Q)) наз. факторалгебра С(Q) тензорной алгебры
Т(Е) Х-модуля Е по двустороннему идеалу, порожден-
порожденному элементами вида х(у)х—Q(x)A, где х?Е. Элемен-
Элементы из Е отождествляются с соответствующими классами
смежности в C(Q). Для любых х, у ?Е имеет место
тождество ху^-ух — Ф(х,у)А, где Ф : ЕХЕ-+-К — ассо-
ассоциированная с Q симметрическая билинейная форма.
Для нулевой квадратичной формы Q алгебра С(Q)
совпадает с внешней алгеброй А(Е) ЛГ-модуля Е. Если
if=R — поле действительных чисел, a Q — невырож-
невырожденная квадратичная форма на га-мерном векторном
пространстве Е над R, то C{Q) совпадает с алгеброй
М„ + 1 альтернионов, где I — число положительных
квадратов в канонич. виде формы Q.
Пусть <?!,..., е„ —базис ЛГ-модуля Е, тогда эле-
элементы 1, е. ... <?. (*!<... <ifc) образуют базис К-
модуля C(Q). В частности, C(Q) является свободным
Х-модулем ранга 2". Если, кроме того, elt. . ., еп орто-
ортогональны относительно Q. то C(Q) можно задать как
.ЙГ-алгебру с образующими 1, elt . . ., еп и определяю-
определяющими соотношениями е/еу=—е]е;Aф{) и e'2i = Q(el).
Подмодуль C(Q), порожденный произведениями чет-
четного числа элементов из Е, образует подалгебру в
C(Q), к-рая обозначается через С+ (Q).
Пусть К — поле и квадратичная форма Q невырож-
невырождена. При четном га алгебра C(Q) является центральной
чростой алгеброй над К размерности 2", подалгебра
С+(Q) сопарабельна, а ее центр Z имеет размерность
2 над К. Если К алгебраически замкнуто, то при
четном, п C(Q) — матричная алгебра, a C+(Q) — про-
произведение двух матричных алгебр (если же п нечетно,
то, наоборот, C+(Q) — матричная, а С(Q) — произ-
произведение двух матричных алгебр).
Обратимые элементы s алгебры С (Q) (соответственно
C+(Q)) такие, что sEs~1 = E, образуют группу
Клиффорда G(Q) квадратичной формы Q (соот-
(соответственно специальную группу Клиф-
Клиффорда G + (<?)). Ограничение преобразований
на подпространство Е определяет гомоморфизм q>: G (<?)-*•
-*¦ OiQ), Где O(Q) — ортогональная группа квадратич-
квадратичной формы Q. Ядро Кег ф состоит из обратимых элемен-
элементов алгебры Z и Кег ф(~|<5+ (Q)~ Л'*. Если п четно, то
(p(G(Q)) = O(G), a (p(G+(<?))=-0+(?) есть подгруппа ин-
индекса 2 в O(Q), совпадающая со специальной ортого-
ортогональной группой SO(Q) в случае, когда характеристика
К отлична от 2. Если п нечетно, то
ф(С«?))=ф(Сн
Пусть Р : C(Q)-+C(Q) — антиавтоморфизм К. а.
С (Q), индуцированный антиавтоморфизмом
Xt (X) . . . (X) Х„ ->- Хп (X) . . . (X) .Г!
тензорной алгебры Т(Е). Группа
Spin (Q) = {s?G + @ I P («) = *~1}
наз. с п и н о р н о й группой квадратичной формы
Q (или К. а. С(<?)).
Гомоморфизм ф : Spin (O)-vO+(<?) имеет ядро {±1}.
Если А- =С или A-=R и Q положительно определена, то
1тф--0+ (Q)=SO(Q) и Spin(O) совпадает с класси-
классической спинорной группой.
Лит.: [11 Бур баки Н., Элементы математики, пер.
с франц., М., 1966; [2] Дьёдонне Ж., Геометрия класси-
классических групп, пер. с франц., М., 1974; [3] Кириллов А. А.,
Элементы теории представлений, М., 1972; [4] С art an E.,
Lecons sur la theorie des spineurs, P., 1938. И. В. Долгачсв.
КЛИФФОРДА ПАРАЛЛЕЛЬ — прямая эллиптич.
пространства, отстоящая от данной (базисной) прямой
на постоянном расстоянии. Через каждую точку, ле-
лежащую вне данной прямой и вне полярной ей прямой,
проходят две К. п. к данной прямой. Поверхность,
образуемая вращением К. п. вокруг ее базисной пря-
прямой, наз. поверхностью Клиффорда.
Поверхность Клиффорда имеет постоянную нулевую
гауссову кривизну.
На существование К. п. впервые указал У. Клиффорд
(VV. Clifford, 1873).
Лит.: [1] Богомолов С. А., Введение в неевклидову
геометрию Римана, Л.— М., 1934; [2] Р о з е н ф е л ь д Б. А.,
Неевклидовы пространства, М., 1969. А. Б. Иванов.
КЛИФФОРДА ТЕОРЕМА — теорема, устанавливаю-
устанавливающая неравенство между степенью и размерностью спе-
специального дивизора на алгебраич. кривой. Доказана
У. Клиффордом (\V. Clifford).
Пусть X — гладкая проективная кривая над ал-
алгебраически замкнутым полем и D — дивизор на X.
Пусть deg D — степень, a l(D) — размерность диви-
дивизора D. Положительный дивизор наз. специальным,
если ЦК—?М>0, где А' — канонический дивизор на
X. К. т. утверждает: для любого специального диви-
дивизора D справедливо неравенство deg D^2l(D)—2, при-
причем равенство имеет место, если ?>=0 или D = K или
X — гиперэллиптич. кривая и D—кратность единствен-
единственного специального дивизора степени 2 на А". Из К. т.
следует, что данное неравенство справедливо для лю-
любого дивизора D на А' такого, что 0<:deg D<.2g—2,
где g=l(K) — род кривой X.
Лит.: [1] Уокер Р., Алгебраические кривые, пер. с
англ., М., 1952; [2] Ч с 0 о т а р е в Н. Г., Теория алгебраи-
алгебраических функций, М.— Л., 1948; [3] Шафаревич И. Р.,
Основы алгебраической геометрии, М., 1972. В. А. Псковских.
КЛИФФОРДОВА ПОЛУГРУППА, вполне
регулярная полугрупп а,— полугруппа,
каждый элемент к-рой является г р у п п о в ы м, т. е.
принадлежит нек-рой подгруппе. Элемент полугруппы
будет групповым тогда и только тогда, когда он вполне
регулярен (см. Регулярный элемент). Свойство полу-
полугруппы S быть К. п. эквивалентно каждому из следую-
следующих: 1) для любого a?S имеет место a?a2Sf\Sa2,
2) каждый односторонний идеал / из S изолиро-
изолирован, т. е. из того, что #(?/, следует хп&1 при лю-
любом натуральном п.
К. п. наряду с инверсными полугруппами представ-
представляют собой один из важнейших типов регулярных по-
полугрупп. Их изучение началось с основополагающей
работы А. Клиффорда [1]. Произвольная К. п. облада-
обладает (единственным) разбиением на группы, классы к-рого
суть в точности J^f-классы (см. Грина отношения эк-
эквивалентности). Указанное разбиение не всегда будет
связкой (см. Связка полугрупп); условия, когда это так,
известны (см. [3]). Отношения Грина ?f и <2) на К. п.
совпадают. Всякая вполне простая полугруппа будет
К. п., причем для К. п. свойство быть вполне простой
эквивалентно идеальной простоте (см. Простая полу-
полугруппа). Произвольная К. п. S разлагается в полу-
полуструктуру вполне простых полугрупп, это разложение
единственно, его компоненты суть в точности ^-классы,
а соответствующая факторполуструктура изоморфна
полуструктуре главных идеалов полугруппы S; обрат-
обратно, всякая полугруппа, разложимая в полуструктуру
вполне простых полугрупп, есть К. п.
Для К. п. S следующие условия эквивалентны:
1) S инверсна; 2) каждый идемпотент из S лежит в
центре, т. е. перестановочен с любым элементом из
Si 3) каждый односторонний идеал полугруппы S
является двусторонним; 4) отношения Грина ffl и <%)
на S совпадают; 5) S есть полуструктура групп; 6) S
разложима в подпрямое произведение групп и групп
с присоединенным нулем.
Указанное выше разложение произвольной К. п. в
полуструктуру вполне простых полугрупп определяет
ее «грубое строение». Закон перемножения элементов
в компонентах этого разложения описывает теорема
Риса (см. Вполне простая полугруппа). Дальнейшее
изучение К. п. в значительной степени направлено
на выяснение «тонкого строения», т. е. закона пере-
перемножения элементов из различных компонент. В случае,
когда эти компоненты — группы, т. е. для инверсных
К. п., известно следующее конструктивное описание в
терминах так наз. суммы прямого спектра
групп. Пусть {Ga.}a€A — семейство попарно не-
непересекающихся групп, А — полуструктура (см. Идем-
потентов полугруппа) и каждой паре элементов а, Р?Л
таких, что а^Р, поставлен в соответствие гомоморфизм
<Ра, Р-' Ga-+Gfi, причем фа, а для любого а есть тождест-
тождественный автоморфизм и для любых а^Р^-у имеет место
Фа, р'Фр, у = Фа, у На объединении S= \Ja6AGa зада-
задается умножение •, а именно, а-Ь=афа ао6фо аа для
любых a?Ga и &?Gp.
Тогда S превращается в инверсную К. п. Обратно,
каждая инверсная К. п. может быть получена указан-
указанным способом.
В общем случае проблема «тонкого строения» К. п.
чрезвычайно усложняется, и удовлетворительного ее
решения пока A978) нет. Некоторые весьма сложные
конструкции, описывающие К. п. в терминах вполне
простых полугрупп, их сдвиговых оболочек, полустру-
полуструктур, отображений со специальными свойствами, при-
приведены в [5]. Больший прогресс достигнут в случае
ортодоксальных К. п. (см. Регулярная полугруппа);
такие полугруппы наз. ортогруппами. Для них
имеется несколько обозримых, хотя и довольно гро-
моздких конструкций (см. [2]). Все упомянутые кон-
конструкции так или иначе обобщают приведенное выше
описание инверсных К. п., полученное в [1].
Лит.: [1] Clifford A., «Ann. Math.», 1941, v. 42, JV. 4,
p. 1037—49; [2] e г о же, «J. Pure and Appl. Algebra», 1976,
v. 8, № 1, p. 23—50; [3] К л и ф ф о р д А., П р е с т о н Г.,
Алгебраическая теория полугрупп, пер. с англ., т. 1—2, М.,
1972; [4] Л я п и н Е. С, Полугруппы, М., 1900; [5] Р е-
t r i с h M., «Trans. Amer. Math. Soc», 1974, v. 189, p. 211—36.
Л. H. Шеврин.
КЛОН о п е р а ц и и — всякое замкнутое относительно
композиции множество конечноместных операций ви-
вида а: Ап ->¦ А, содержащее все единичные операции
ш^: А" ->- А, т. е. такие, что
для любого набора (а1,..., а,-,..., ап) нз Ап, где
п~>А, i = l,2,..., A—произвольное фиксированное
множество. Под композицией операций
(Ох (хъ..., xj,..., хп) и ш2 (уъ..., ут) понимается опера-
операция a>3(z1,..., zz)> задаваемая с помощью формулы
вида
«1 (Xlt..., Ж/-!, С02 (i/l,--., Ут),
где для множеств переменных X = {жь..., х}-,..., хп},
Y = {y\,..., ут} и Z = {z1,..., z,} выполнено
В. Б. Кудрявцев.
КЛОТОИДА — то же, что Корню спираль.
КНАСТЕРА КОНТИНУУМ, наследственно
неразложимый континуум,— континуум,
всякий подконтинуум к-рого неразложим. Пространст-
Пространство X наз. неразложимым, если оно связно л не
допускает представления в виде объединения двух
замкнутых связных множеств, отличных от X. Первое
доказательство существования К. к. было дано Б. Кна-
Кнастером [1]. В пространстве всех подконтинуумов обы-
обычного квадрата Р множество всех К. к. составляет
всюду плотное G&- множество [2].
Лит.: [1] Knaster В., «Fundam. math.», 1922, t. 3,
s. 247—86; [2] M а г u r k i e w i с z S., там же, 1930, t. 16,
S. 151 — 59. Л. Г. Замбахидзе.
КНЕЗЕРА ТЕОРЕМА об одномерных слоениях без
особенностей на замкнутых поверхностях рода нуль —
теорема, устанавливающая свойства такого слоения
в зависимости от наличия или отсутствия у него замк-
замкнутых слоев и описывающая поведение незамкнутых
слоев в областях, ограничиваемых замкнутыми слоями.
К. т. принадлежит X. Кнезеру (говорившему не о
слоениях, а о «регулярных семействах кривых на по-
поверхности» [1]; модзрнизироваиное изложение основ-
основных аспектов К. т. см. в [2], [3]). Чаще всего К. т.
упоминается в связи с траекториями потока без поло-
положений равновесия на торе или Клейна поверхности:
эти траектории образуют слоение рассматриваемого в
К. т. типа.
Одномерное слоение (без особенностей)
на поверхности — это целиком заполняющее последнюю
семейство непересекающихся кривых («слоев»), причем
у каждой точки имеется такая координатная окрест-
окрестность U, что в терминах соответствующих локальных
координат хг, хг слоение локально выглядит как се-
семейство прямых х2=const (точнее, такое уравнение
имеют связные компоненты пересечений слоев с U).
Слоение наз. ориентируемым, если можно
так определить нек-рое «положительное» направление
на каждом его слое (ориентировать слои), чтобы для
различных слоев эти направления были согласо-
согласованы — при непрерывном переходе от слоя к слою
положительное направление нигде не менялось скачком.
Ориентируемы те и только те слоения, к-рые состоят
из траекторий нек-рых потоков без положений равно-
равновесия.
Пусть на поверхности М задано поле направ-
направлений (поле линейных элементов) —
каждой точке х?М сопоставлено одномерное подпро-
подпространство I (х) касательной плоскости ТХМ в этой точке
(если М лежит в евклидовом
пространстве, то 1(х) пред-
представляется прямой, касающей-
касающейся М в точке х, см. рис. 1).
Если 1(х) гладко зависит от х,
то интегральные кривые этого
поля направлений образуют
одномерное слоение, к-рое мо-
может и не быть ориентируе-
ориентируемым.
Основное содержание К. т. относится к тому случаю,
когда у слоения имеются как замкнутые, так и незамк-
незамкнутые слои. Утверждается, что последние заполняют
области, ограниченные первыми, причем эти области
могут быть трех типов — см. рис. 2, где подразуме-
подразумевается, что у каждого прямоугольника а), б) и в) надо
Рис. 1.
В' В'
А' А'
If \\
В А
б
Рис. 2.
В А
верхнюю сторону склеить с нижней, причем А склеи-
склеивается с А', а В — с В'; (напр.. из а) при этом полу-
получается «кольцо Кнезера», см. рис.' в ст. Дифференци-
Дифференциальные уравнения на торе. Если на поверхности име-
имеется только один замкнутый слой, то у прямоугольника
надо дополнительно склеить еще левую и правую сто-
стороны.
Незамкнутый слой, лежащий в одной из этих облас-
областей, при неограниченном продолжении в одну сторону
навивается на замкнутый слой, ограничивающий данную
область, или на один из двух ограничивающих ее замк-
замкнутых слоев. При продолжении в другую сторону неза-
незамкнутый слой навивается, соответственно, на тот же
замкнутый слой (но с другой стороны) или на второй из
упомянутых замкнутых слоев.
Областей типа а) и б) может быть лишь конечное
число, причел неориентируемая область типа б) воз-
возможна только на поверхности Клейна и только для
неориентируемого слоения, областей типа в) — конеч-
конечное или счетное число.
X. Кнезер доказал также, что тот случай, когда у
слоения нет замкнутых слоев, возможен только для
ориентируемого слоения на торе, и что в этом случае
имеется замкнутая линия L, трансверсальная к слое-
слоению и пересекающая все слои. (В общем случае, когда
не предполагается, что слои гладкие и что слоение за-
задается нек-рым полем направлений, трансверсальность
понимается в том смысле, что у каждой точки линии L
имеется координатная окрестность, в к-рой слои зада-
задаются уравнением ^2 = const, а ? — уравнением ^ = 0.)
См. об этом также в ст. Дифференциальные уравнения
на тире.
Лит.: [ljKneser H., «Math. Ann.», 192-4, Bd 91, М 1—2,
S. 135—54; [2] R e i n h а г t B. L., «Amer. J. Math.», 1959,
v. 81, № 3, p. 617—31; [3] A e p p 1 у A., M ar k u s L., «Amer.
J. Math.», 1963, v. 85, №4, p. 633 — 54. Д. В. Аносов.
КНЕЗЕРА — ТИТСА ГИПОТЕЗА — гипотеза о строе-
строении /с-простых односвязных изотропных над полем к
алгебраич. групп. А именно, К.— Т. г. состоит в том,
что группа Gk /с-рациональных точек /с-простой одно-
связной и изотропной над к алгебраич. группы О порож-
порождается унипотентными элементами. В несколько менее
общей форме это утверждение было высказано М. Кне-
зером (М. Kneser), общая формулировка принадлежит
Ж. Титсу [1]. Для групп типа Ап (см. Полупростая
алгебраическая группа) К.— Т. г. эквивалентна про-
проблеме Таннака — Артина о совпадении
подгруппы SL(i, D) элементов единичной приведенной
нормы конечномерного тела D с коммутантом [D*,
D*] его мультипликативной группы. К.— Т. г. имеет
тесную связь с вопросами аппроксимации в алгебраич.
группах, рациональности групповых многообразий и
алгебраич. АГ-теории.
Справедливость К.— Т. г. доказана в случае локаль-
локально компактных полей [2], а также для глобальных функ-
функциональных полей [3]. Более того, для глобальных по-
полей нулевой характеристики метод спуска из [2] дал
возможность доказать справедливость К.— Т. г. для
всех алгебраич. групп за исключением типов Е6 и Es.
Однако в общем случае К.— Т. г. не верна, что следует
из отрицательного решения проблемы Таннака — Ар-
тина [4]. Вследствие этого выдвинулись задачи иссле-
исследования меры отклонения SL(l, D) от [D*, D*], вы-
выражаемой приведенной группой Уайтхеда. Результаты,
полученные в этом направлении ([5] — [6]), составили
основы приведенной АГ-теории. В [7] показано, что
К.— Т. г. неверна и в случае унитарных групп, что, в
свою очередь, открывает путь к развитию приведенной
унитарной ЛГ-теории.
Лит.: [1] Т i t s J., «Ann. Math.», 1964, v. 80, JV« 2, p. 313 —
29; [2] П л а т о н о в В. П., «Изв. АН СССР. Сер. матем.»,
1969, т. 33, М 6, с. 1211—20; [3] е г о ж е, «Proc. Intern. Congr.
Math. Vancouver», 1974, p. 471—76; [4] его же, «Докл. АН
СССР», 1975, т. 221, Mi 5, с. 1038—41; [5) е г о же, «Изв. АН
СССР. Сер. матем.», 1976, т. 40, № 2, с. 227—61; [6] е г о же,
«Матем. сб » 1976 т. 100 JV» 2 с. 191—200; [7] Платонов
В. П., Я н ч е в с к и й В. И., «Докл. АН СССР», 1975, т. 225,
№ 1, с. 48—51. В. И. Янчевский.
КНОППА МЕТОД СУММИРОВАНИЯ — суммиро-
суммирования метод числовых и функциональных рядов; яв-
является обобщением Эйлера метода суммирования и
носит в литературе название Эйлера — Кноппа
метод суммирования. И. И. Волков.
КОАЛГЕБРА — модуль А над коммутативным коль-
кольцом К с такими двумя гомоморфизмами ф : АЛ
и 8 : А—>-/с, что диаграммы
коммутативны, т. е. К. поня-
тие Дуальное (в СМЬ1сле тео-
теории категорий) к понятию ас-
ассоциативной алгебры над коль-
кольцом К.
К. приобрели значение в
связи с множеством топологич. приложений, так, на-
например, симплициальный комплекс топологического
пространства является К. Тесно связаны с К. Хопфа
алгебры, несущие на себе структуры алгебры и К.
одновременно.
Лит.: [1] Маклейн С, Гомология, пер. с англ., М
1966. В. Е. Говоров.
КОАЛИЦИОННАЯ ИГРА — игра, в к-рой коалиции
действия Std и коалиции интересов Slu составляют
различные семейства (вообще говоря, пересекающихся)
подмножеств множества игроков /, а отношение пред-
предпочтения для каждой из коалиций интересов К?Яи
описывается ее функцией выигрыша Нь (см. Игр те-
теория). Исследовался случай, когда Ми S
Множество Я'й естественно и полезно понимать как
симплициальный комплекс с множеством вершин /.
Некоторые топологнч. свойства $\д имеют теоретико-
игровой смысл; в частности, если комплекс ,!?<} нульме-
нульмерен, то игра оказывается бескоалиционной.
Протекание К. и можно интерпретировать как согла-
согласованный набор игроками («на по-коалицпонных со-
совещаниях») коалиционных стратегий для каждой коа-
коалиции действия, после чего в сложившейся ситуации
s каждая коалиция интересов К получает выигрыш
HK(s).
Оптимальность в К. п. можно понимать как своего
рода «локализацию конфликтов», а именно как устой-
устойчивость ситуации s в смысле выполнения набора усло-
условий следующего вида: коалиция интересов К не заинте-
заинтересована в отклонении от своей коалиционной страте-
стратегии в s, даже если нек-рая коалиция действия К' от-
отклонится от своей стратегии. Равновесность по Нэшу
охватывается этим принципом.
Лит.: [1] В о р о б ь е в Н. Н., «Теория вероятн. и ее
примен.», 1967, т. 12, №2, с. 289 — 306. Н. Н. Воробьев.
КОАЛИЦИЯ (в теории игр) — группа лиц или сторо-
сторона, принимающая решение в конфликте (коалиция
действия), либо отстаивающая нек-рые интересы
(коалиция интересов). См. Игр теория.
А. С. Михайлова.
КОБАЗИС — базис двойственного, или сопряженного
пространства.
КОБОЛ — алгоритмический язык, ориентированный
на задачи обработки данных (COBOL — сокр. от
Common Business Oriented Language). Способ записи
программы приближен к естественному английскому
языку, удобен в изучении, документировании и пере-
переносе программы с одной ЭВМ на другую. К. разрабаты-
разрабатывается в США, начиная с 1959; получил широкое рас-
распространение, стал национальным стандартом [1].
Русский вариант К. опубликован в 1968 [2], с 1978
вводится государственный стандарт [3].
Программа на К. состоит из четырех разделов:
1) Раздел идентификации содержит
имя программы, автора, дату и другую справочную
информацию.
2) Раздел оборудования определяет кон-
конфигурацию транслирующей и рабочей ЭВМ, специфи-
специфические особенности оборудования и управления вводом-
выводом.
3) Раздел данных содержит машинно-неза-
машинно-независимое описание вида и структуры входных, проме-
промежуточных и выходных данных. Допускаются цифровые
и нецифровые элементарные данные, к-рые могут объе-
объединяться в группы, группы групп и т. д. Такая струк-
структурная иерархия задается с помощью номеров уровней.
Высший уровень присваивается логической записи.
Совокупности однородных или разнородных записей
образуют файл ы. Допустимы указания, повышаю-
повышающие эффективность внутренней интерпретации формата
данных.
4) Раздел процедур задает операции обра-
обработки данных в виде последовательности предложе-
предложений, именованных параграфов и секций, составленных
ил повелительных, условных и управляющих трансля-
трансляцией операторов.
По назначению элементы К. разделяются на ядро
и 11 функциональных обрабатываю-
обрабатывающих модуле й. Ядро содержит элементы языка,
необходимые для обработки данных во внутренней
памяти ЭВМ. Функциональные модули соответственно
содержат средства: обработки таблиц; пос-
последовательного, относительного и
индексного ввода-вывода для органи-
организации доступа к внешним файлам; сортировки-
слияния; генерации отчетов; с е г-
м е н т а ц и и программы для совмещения памяти в
рабочее время; модификации и включения в программу
текстов на К. вз библиотеки; отладки и
контроля данных и процедур; организации межпро-
межпрограммных связей с другими программами;
а также коммуникативные средства посылки и получе-
получения сообщений.
Гибкость выбора стандартных подмно-
подмножеств К. при разработке конкретных трансляторов
основана на выделении в ядре и функциональных
модулях фиксированных уровней. Элементы языка
распределены по уровням так, что более высокие уровни
обеспечивают большую полноту реализации соответ-
соответствующей функции и содержат нижние уровни как
собственные подмножества. Для некоторых функцио-
функциональных модулей в качестве самого низкого уровня
допускается пустое множество.
Основные направления дальнейшего развития К.—
организация взаимодействия с базами данных и исполь-
использование идей структурного программирования.
Лит.: [1] American National Standard. Programming Lan-
Language COBOL. ANSI X3.23 —1974; [2] Бабенко Л. П.
[и др.], в кн.: Тр. 1 Всесоюзной конференции по программи-
программированию. И. Алгоритмические языки, К. 1968, с. 3—15; [3]
ГОСТ 22558—77. «Язык программирования КОБОЛ»; [4]
Ющенно Е. Л. [и др.], КОБОЛ, 2 изд., К., 1974.
Г. К. Столяров.
КОБОРДИЗМ, кобордизмов теори я,—
обобщенная теория когомологий, определенная спект-
спектрами пространств Тома и связанная с различными
структурами в стабильном касательном или нормаль-
нормальном расслоении к многообразию. Теория К. двойствен-
двойственна (в смысле S-двойстеенности) теории бордизмов.
Простейшим примером К. являются ортогональные,
или неориентированные К. Пусть Ог — группа орто-
ортогональных преобразований евклидова пространства
Rr, ВОг — ее классифицирующее пространство. Стан-
Стандартное вложение О,—»-Ог + 1 задает отображение /г :
: ВОг-+-ВОг + 1, переводящее универсальное расслоение
Уг + i над ВОг + 1 в расслоение Y,-(r,9, где G — одномер-
одномерное тривиальное расслоение над ВОГ. Если ТВОГ —
Тома пространство расслоения уг, то получается ин-
индуцированное отображением ir отображение sr: STBOr-*
—*-ТВОг+1, где S — оператор надстройки. Последова-
Последовательность {ТВОГ, sr} образует спектр пространств и,
следовательно, задает теорию когомологий, наз. тео-
теорией ортогональных К., или О-К., обозна-
обозначаемую О*. Группа Оп(Х, А) «-мерных О-К. пары
пространств (X, А) определяется как
lim [S'(X/A), TBOi + n],
где [Р, О] — множество гомотопич. классов отображе-
отображений из Р в О. При этом О"(Х) = Оп(Х, ф), где ф —
пустое множество, а под Х1ф=Х+ понимается несвяз-
несвязное объединение X и точки. Группа Оп(Х, ха), где хо?Х,
наз. приведенной группой «-мерных О-К.
О" (X) пространства X. Обобщенная теория гомологии,
двойственная теории О-К., наз. теорией 0-бордиз-
мов. Группы Оп(Х, А) n-мерных бордизмов пары
(X, А) определяются как
lim л! + п((Х/А)л ТВО-).
Группы д-мерных О-К. точки обозначаются через
QJJ, а д-мерных О-бордизмов точки — через Q,°; пос-
последние описываются чисто геометрически. При этом
?1-п-~Я°г^лп+х{ТВ0х), N%-n, так что ее можно ин-
интерпретировать как группу К. и как группу бордизмов
(см. Бордизм), где она обозначена У1п. Полная группа
коэффициентов теории О-К.— градуированная группа
Qo—(t + ~Qn— является кольцом: умножение индуци-
индуцировано прямым произведением многообразий. Более
того, для любого конечного Cjy-комплекса X группа
О(Х)=®+™_ооОп(Х) является естественным по X коль-
кольцом, поскольку индуцированное вложением ОгпХОп—»-
-+-От±п отображение ВОтХВОп->-ВОт + п задает отоб-
отображение ТВОтлТВОп-+ТВОт + п, так что {ТВОГ} —
мультипликативный спектр пространств.
Общая ситуация описывается следующим образом.
Структурной серией (В, <р) наз. последо-
последовательность расслоений q>r : ВГ^*-ВОГ и отображений
ir : Вr-^-Вг + 1 таких, что фг+1 ° ir—jr ° Фг- Отображе-
Отображение фг задает векторное расслоение |;-=ф*уг наД Вг,
причем г*|г+1=|г+ф*Э. Пусть Г.В,. — пространство
Тома расслоения %г; указанное равенство задает отоб-
отображение sr : S ТВr-^-ТВг + 1, так что последовательность
Г(Б, ф)= {TBr, sr} является спектром пространств и,
следовательно, задает теорию когомологий, наз. тео-
теорией (В, ф)-К., обозначаемую (В, ц>)*. Таким образом
(В«р)'(Х, А)= lim [S"(X/A), TBi+N].
JV-*oa
Группа коэффициентов теории (В, ц>) -К. обозначается
через Й(В> ф)-вПри этом Qf' ф)=й<^ V) = ni +N{TBу),
N^>i, где Q(( ' <i>>— группа коэффициентов двойствен-
двойственной теории (В, ф)-бордизмов, которая допускает геомет-
геометрическое определение, использующее понятие так наз.
(В, ц>)-структуры: определяется (В, ф)-б о р д а н т-
н о с т ь и элементы Q( • ч)) интерпретируются как
классы (В, ф)-бордантных многообразий.
Первые примеры теорий К. возникают из серий ли-
линейных групп. Напр., серия ортогональных групп
{Ог} определяет структурную серию {Вг, фг), где
Br=BOr, (fr=id. Серия {SOr} определяет структурную
серию {Вг, фг}, где Br=BSOr, ц>г : BSOr—>-BOr —
универсальное двулистное накрытие, соответствующее
включению S0rd0r. Соответствующая теория К. наз.
теорией ориентированных К. и обозна-
обозначается через SO*. Серия унитарных групп {Uг) опре-
определяет теорию унитарных, или квази-
квазикомплексных К., обозначаемую U*. Здесь серия
{В, ф} строится так: B2r=B2r + 1=BUr — класси-
классифицирующее пространство группы Ur, а отображения
фг — отображения классифицирующих пространств
ВUг->ВОгг—*-BO2r + i, индуцированные естественными
вложениями Urd0ird02r + i- Серия симплектических
групп {5рг} определяет теорию симплекти-
симплектических К. Sp*, здесь B4r=Bir + i=Bir+2=Bir + 3=
=В Spr, и отображения фг строятся так же, как н в
случае унитарных К. Имеются также теории К., соот-
соответствующие сериям групп {Spin,.}, {SUr}, и т. д. Нако-
Наконец, серия единичных групп {Ег}, где фг : ВГ—^ВОГ—
расслоение со стягиваемым Вг, дает теорию К., совпа-
совпадающую с теорией стабильных когомотопических групп,
и потому двойственная теория бордизмов изоморфна
теории стабильных гомотопических групп, Ei(X)~
~я,- + ^(S^X), N^>i. Я-многообразие наз. оснащенным,
так как ^-структура — это в точности оснащение (трп-
виализация) стабильного нормального расслоения.
Теория Е-К. наз. теорией оснащенных К.,
а ее j-мерная группа коэффициентов обозначается
через Qlfr [так что Qfr =Qj =jii + ^(SN)]; это — пер-
первый пример К.; он появился у Л. С. Понтрягина A955),
проинтерпретировавшего стабильные гомотопич. груп-
группы сфер как (определяемые геометрически) группы
оснащенных К. точки Q1 с целью вычисления группы
Все описанные теории К., возникающие из серий
линейных групп, являются мультипликативными, н
потому для любого конечного CW-комплекса Х пол-
полная (градуированная) группа К. является кольцом.
Например, для серии групп {Uг} имеется вложение
UmX Un—>-Um + n, порождающее отображение
BUmXBUn-+BUm+n
и, следовательно, отображение TBUm Л TBU,,~>
-+TBUт + п. Спектр {Мг}, представляющий теорию {/*,
имеет вид M2r=TBUr, M2r + 1=STBUr и потому су-
существуют отображения Мr,\Ms-*-Mr + s, так что спектр
пространств {Мг} мультипликативен.
Развитие теории К. началось с геометрич. определе-
определения и вычисления групп Q/?, Qq, Qso- Важную роль
сыграла теорема Понтрягина о том, что О-бордантные
многообразия имеют одни и те же числа Штифеля. Ис-
Исследование К. было продвинуто Р. Томом (R. Thorn).
Он ввел пространства TBOjy, TBSOjy и доказал изо-
морфизм nj + NiTBO^^Qgi, что позволило привлечь к
вычислению колец К. точки методы гомотопич. тополо-
топологии. Конструкции Тома стимулировали введение TBUny
TBSpn и т. д. и соответствующих К. Основной задачей
первого этапа развития теории К. и было вычисление
колец К. точки.
При изучении К. точки большую роль играют харак-
характеристические классы — Чжэня для Qy. Штифеля
для Qo, Понтрягина и Штифеля для Qso- Вообще, для
любой структурной серии (В, q>) и любой мультипли-
мультипликативной теории когомологий h*, в к-рой все расслоения
|г над Вг ориентируемы, можно определить харак-
характеристические классы как элементы группы h*(B), где
В = lim(-Br, ir). При этом соответствующие характе-
ристич. числа, являющиеся элементами кольца h*
(точка), будут инвариантны относительно (В, ср)-бор-
дантности. Пусть ж,- — образующие By для классов
Чжэня и Sat — симметрич. функция от п переменных,
соответствующая нек-рому разбиению w=(i1, . . .. гд.)
числа п. Характеристич. класс S а(х1,. .., хп) обо-
обозначается через 5щ. Аналогичные конструкции для
классов Понтрягина и Штифеля обозначаются через.
5ю и 5ю соответственно.
1) Унитарные К. Кольцо Qy — свободная гра-
градуированная полиномиальная алгебра от счетного числа
однородных образующих
®и = Ж [*i. • ¦ .. *п, • • •]. deg л-,- —— 2г.
Множество {х„}, degxn=~~2n является системой поли-
полиномиальных образующих тогда и только тогда, когда
с < ±1,и ф рг — 1 ни для какого простого р-
Sin)(xn) = { и целого г,
[ ±р, и = рг — 1 для некоторого простого р,.
где (и) — разбиение числа и, состоящее из одно-
одного слагаемого. Одну из систем полиномиальных
образующих кольца йу можно описать так. Пусть
СРп есть и-мерное комплексное проективное простран-
пространство. Комплексная алгебраич. гиперповерхность би-
степени A,1) в CP'xCPJ является комплексным мно-
многообразием. Класс его унитарных К. обозначим H,j,
dimR#,-?y=2(i+/ — 1). Оказывается, что S; + /-i(//,-,/) =
= (|-+'). так что подходящая целочисленная линейная
комбинация элементов Hij задает образующую кольца
Q[/ степени 2A — i—/).
Из отсутствия кручения в кольце Q/j и того, что>
Я* (BU; Ъ)= ZUi, . . ., с,,...], где сп— Чжэня классы,
deg cn=2n, следует, что Чжэня числа полностью опре-
определяют класс унитарных К. квазикомплексного много-
многообразия.
Пусть п — натуральное число (i1?..., ift), isy-0,
^г-5 = и — его разбиение. Каждому 2и-мерному (раз-
(размерность действительная) квазикомплексному многооб-
разию М соответствует набор {а. . }= {с, .. .с. (М)}
V"'fc ' 'ft
целых чисел, где мультииндекс ilt. . .i^ пробегает все
разбиения числа п. Набор таких целых чисел {6,- ,. ..,
^tft} реализуется как набор чисел Чжэня нек-рого
квазикомплексного многообразия в следующей ситуа-
ситуации. Пусть Sc (е)?Л** (BU; Q) — характеристичес-
характеристический класс, заданный симметрич. функцией 5И от пере-
переменных ех' —1, г=1, 2,..., | ш|, а Т?Н** (BU; Q) —
характеристический класс, заданный произве-
произведением функций х,-/(ех'—1), где xi — образующие By.
Пусть х(М) — значение характеристич. класса х?
?H"(BU; Q) на фундаментальном классе [М] ?Н„(М,
Ъ) квазиксмплексного многообразия М с касательным
расслоением ТМ.
Для гомоморфизма ср : H"(BU; Q)—y-Q тогда и только
тогда существует такое замкнутое квазикомплексное
многообразие М, что ср(.г) = ж(Л/) для всех x?H"{BU;
Q), когда ср принимает целые значения на всех и-мер-
ных компонентах каждого характеристич. класса
S (е)Т (теорема Стонга). Эквивалентно, гомо-
гомоморфизм Гуревича
где N^k,— мономорфизм на прямое слагаемое (т е о-
рема X аттори). Здесь К — приведенная К-теория.
2) Неориентированные, или ортого-
ортогональные, К. Каждый элемент кольца Qg имеет
порядок 2, и
a0Z2ki, ...,*„, •-.], degxi = — i, i ф 2* —1,
т. e. Qn—свободная полиномиальная 22-алгебра. В ка-
качестве образующей х; можно выбрать любой элемент
[М] с Sfi)(M)^0, напр. x2i=Rp21. В этой теории есть
аналоги многообразий Н; j, если вместо СРк брать
RP1'; подходящее многообразие H;j может служить
образующей степени 1 — г—/. Шти'феля числа полно-
полностью определяют класс неориентируемых К. многообра-
многообразия, соотношения между числами Штифеля дает сле-
следующая теорема: для гомоморфизма ср: Н"(ВО; Z2)—»¦
Ъг. Тогда и только тогда существует такое и-мерное
замкнутое многообразие 71/, что у{х)=х{М) для всех
x?H"(BO;Z2), когда<p(Sqb+vb)=O для всех Ь?Н* (ВО;
Ж2), где v=Sq~1w. Здесь Sq=Sq1-\-Sq2-\-. . . — полная
Стинрода операция, u.'=U/i1-f-ui2-|-. . . — полный класс
Штифеля. Образом гомоморфизма Qy->Q0 является
кольцо (Q0J
3) Ориентированные К. с кольцом Qso-
Все элементы подгруппы кручения Tors этого кольца
имеют порядок 2. Кольцо Q^o/Tors является кольцом
полиномов над Z от классов ж,- степени — 4г, образую-
образующие выделяются условием
( il, 2г = рГ — 1 для некоторого простого р
S^(xf)= ' _ и целого г,
\ ±р, 2' = рг-1 для некоторого простого р.
Класс SO -К. многообразия определяется Понтрягина
числами и числами Штифеля. Инвариантом класса К.
является также сигнатура многообразия. Соотношения
между числами Штифеля вытекают из следующего фак-
факта: образ гомоморфизма «забывания» Qs0—>-Q0 состоит
точно из тех классов К., у которых все числа, содержа-
содержащие класс Ц71? равны нулю. Для любого разбиения
<a=(ii, . . .,ift) имеет место
Р(Л (М) mod 2 = w\a = [»,,-, WiU ... w2;k (M)],
где pa — соответствующее число Пснтрягина. Не су-
существует 2-примарьь.х соотношений между числами
Понтрягина.
Подобно тому, как для унитарных К. вводились
с
классы S (/), вводятся классы Sp(e) — симметрич.
(Л
функции от ехi -\-e~xi—2. Пусть L — характеристич.
класс, задающий L-pod Хирцебруха. Все соотношения
между числами Понтрягина следуют из того, что числа
Понтрягина целые, и (S&{e)L) [Af]? Zt1^- Гомомор-
Гомоморфизм Q(j—>-Qso/Tors эпиморфен.
4) Специальные унитарные К. с коль-
кольцом Qsu- {/-многообразие М допускает S {/-структуру
тогда и только тогда, когда Сг (М)—0. Все элементы под-
подгруппы кручения Tors имеют порядок 2. Ядро гомомор-
гомоморфизма Qsu—*-®u есть в точности Tors. Группы Qsu ко-
конечно порождены, и Qsu@Q есть кольцо полиномов
над Q от классов ж,- степени —2s, s>l. Подгруппа
кручопия Tors имеет вид Tors~"=0 при пф8к-\-1,
8к+2, а для n=8A+l, 8к+2 группа Tors~« есть
векторное пространство над 22, размерность к-рого
равна числу разбиений числа к. Два S {/-многообразия
бордантны тогда и только тогда, когда они имеют одни
и те же характеристич. числа в целочисленных кого-
мологиях и в ЙО-теории.
Все соотношения между числами Чжэня для и-мер-
ных S {/-многообразий вытекают из следующих:
с1сш(М)=0 для всех со; (Sa(e)T) [M]?z для всех со;
если п=А mod8, то (S&(e)T) [Af]?2Z для всех со.
Образ гомоморфизма Qsu—*-®o состоит из классов [М]а,
где М — ориентированное многообразие, у к-рого все
числа Понтрягина, содержащие класс plt четны.
Полностью вычислены также кольца ^gDjn и ^
Кольца Qsp и Qfr до сих пор A978) не вычислены.
Кольцо Qsp®1, [V2] является кольцом полиномов от
(—4;)-мерных образующих. Все известные A978) эле-
элементы группы Tors Qsp имеют порядок 2. Что касает-
касается кольца Qfr, то здесь основным результатом явля-
является теорема Серра о конечности этих групп. Изучается
также кольцо самосопряженных К. Qsc, гДе объекты—
квазикомплексные многообразия с заданным в нормаль-
нормальном расслоении оператором, изоморфно отображающим
комплексную структуру на сопряженную. Спектр
TBSC построен; о группах Qso известно, что там есть
лишь 2-примарное кручение, но, в отличие от Qsp,
найдены элементы порядка 4* с любым к, именно
[Rpik~3]. Вычислен также образ im(Qsc—*-Qq) с по-
помощью техники формальных групп.
Отображение одной теории К. в другую, напр. SU*—*¦
-*-{/*, индуцирует отображение спектров TBSU—^TBU.
Конус этого отображения в категорию спектров задает
обобщенную теорию когомологий. Кольцо точки полу-
полученной теории имеет следующую геометрич. интерпре-
интерпретацию. Пусть (U, SU) — [/-многообразие, на краю
к-рого (возможно, пустом) фиксирована S {/-структура.
Введением для ([/, S {/(-многообразий соответствую-
соответствующего отношения бордантности получается кольцо Qu,su-
Так же вводятся группы йу, /г, Qo.so и ДР-
Выше рассматривались гладкие многообразия или,
эквивалентно, линейные представления групп (струк-
турпыэ серии возникали из расслоений над SOr). Мож-
Можно рассматривать различные структуры на топологич.
многообразиях, т. е. исходить из группы гомеоморфиз-
гомеоморфизмов (и даже собственных гомотопич. эквивалентностей)
пространства Rr. Здесь известны следующие примеры
(буква S везде означает переход к ориентированному
случаю).
5) Кусочно линейные К. Объекты — ку-
кусочно линейные многообразия. Соответствующее отно-
отношение бордантности приводит к группам Qpi, Qspl-
Определив группу PLn (соответственно SPLn) как
группу кусочно линейных гомеоморфизмов простран-
пространства к." на себя, сохраняющих начало координат (соот-
петственно и сохраняющих ориентацию), можно ввести
классифицирующие пространства BPLn, BSPLn и про-
пространства Тома TBPLn, TBSPLn и построить теории
К. PL, SPL. При этом Qpl^ni(TBPL), QspL^
~ni(TBSPL). Группы Qpi вычислены. Класс К. ку-
кусочно линейного многообразия полностью определяется
своими характеристич. числами, т. е. элементами груп-
группы Н* (BPL; z2).
6) Топологические К. Объекты — тополо-
гич. многообразия, для к-рых определяются группы
Qrop, QsTop- Рассматривая группу Торп, сохраняющих
начало координат гомеоморфизмов пространства R" на
себя, можно определить пространства ВТор и ТВТорп.
Группы nt(TBTop) и Н* (ВТор, z2) вычислены. Однако
изоморфизм Q^-jj ^п;(ТВТор) установлен при всех i,
кроме г'=4. Отсутствие доказательства этого изомор-
изоморфизма связано с тем, что теорема трансверсальности,
на к-рой основан изоморфизм Qg1' «я,-(:Г (В, q>)),
для топологич. многообразий, в общем случае не дока-
доказана (но и не опровергнута, 1978).
7) К. комплексов Пуанкаре Qa, &SO-
Объекты — комплексы с Пуанкаре двойственностью,
бордантность — соответствующее отношение эквива-
эквивалентности. Такие комплексы имеют нормальное сферич.
расслоение, к-рое индуцируется из универсального
расслоения над BG^(viaaBSG^). Здесь Gjy (соответствен-
(соответственно SGjy) — Н-пространство гомотопич. эквивалентно-
стей (соответственно степени 1) сферы SN на себя. Воз-
Возникающие спектры Тома TBG и TBSG имеют конечные
гомотопич. группы, в то время как сигнатура задает
нетривиальный гомоморфизм а : Qg?j*—>-Z, так что
отображение fi^cr"*ni + N{TBGw) заведомо не изомор-
изоморфизм.
Еще одну серию примеров дают К. многообразий с
особенностями специального типа. На этом пути можно
построить теорию К., совпадающую с обычной теорией
сингулярных когомологий, и теорию К., совпадающую
со связной Я-теорией.
Второй этап развития теории К. связан с изучением
К. как специфических обобщенных теорий когомологий.
Пусть F — одно из полей R, С или тело кватернионов
И, GF — соответствующая серия групп (GRn=On,
GCn=Un, GtHn=Spn) и GF* — соответствующая теория
К. Мультипликативная обобщенная теория когомоло-
когомологий h* наз. F-o риентируемой, если любое
F-векторное расслоение Л "-ориентируемо или, эквива-
эквивалентно, каноническое одномерное F-векторное расслое-
расслоение ?,^>-FP°°, где FP°°—проективное пространство, h*
ориентируемо, ^-ориентацией теории h* наз. /^-ориен-
/^-ориентация ?//j(i)?fe* (FP°°) расслоения |, и теория с вы-
выбранной ориентацией наз. ориентированной.
Теории GF-K. имеют канонич. ориентацию благодаря
отождествлению FP°°= TBGF-^. Теория GF* является
универсальной в классе /^-ориентированных теорий,
т. е. для любой ^-ориентированной теории h* с /^-ори-
/^-ориентацией Ultd) существует единственный мультипли-
мультипликативный гомоморфизм теорий фл : GF*->-h*, при к-ром
канонич. ориентация теории GF* переходит в U^. При
этом, когда Fo— одно из полей R, С, то для любой ^V
ориентированной теорииh* и любого конечного CW-kom-
плекса X существуют спектральные последовательности
Erp,q(X) и ЕР/"(Х) с
Е%, q (X) = TorBCF0 (GF*, (X), h* (точка)),
Ep2'i(X) = Ext%4 (GFl(X), h* (точка)),
GF0
сходящиеся к h* (X) и естественные по X и h*, где
й*(точка) сделано ?3<з/го"моДУлем посредством гомо-
гомоморфизма фл(точка). Если h* — теория гомологии,
двойственная /""-ориентированной теории когомологий
h*, то имеется гомоморфизм q>/j : GF%-^-h*. В случае,
когда Л» — обычная теория гомологии, он совпадает с
гомоморфизмом Стинрода—Тома реализации циклов
(см. Стинрода задача).
Наиболее важные и удачные применения теории К.:
доказательство теоремы Атьи—Зингера об индексе эл-
липтич. оператора и общей теоремы Римана—Роха; изу-
изучение неподвижных точек действий групп; классифика-
классификация гладких (кусочно линейных) многообразий данного
гомотопич. типа; доказательство теоремы о топологич.
инвариантности рациональных классов Понтрягина
и решение проблемы триангулируемости топологич.
многообразия.
Лит.: [1] Стонг Р., Заметки по теории кобордизмов,
пер. с англ., М., 1973; [2] К о н н е р П., Ф л о й д Э., Гладкие-
периодические отображения, пер. с англ., М., 1969; [3] Н о-
виков СП., «Изв. АН СССР. Сер. матем.», 1967, т. 31
№4, с. 855—951; [4] В г б с k e г Т., Dieck Т., Kobordis--
mentheorie, В., 1970; [5] Бухштабер В. М., Итоги науки
и техники. Алгебра. Геометрия. Топология, т. 13, М., 197 5,
с. 231 — 72. См. также лит. при статье Бордизм. Ю.Б.Рудяк.
Л-КОБОРДИЗМ — бордизм (W; Мо, Мг), где W ~
компактное многообразие, край к-рого dW — объеди-
объединение непересекающихся замкнутых многообразий Мо
и Mi, являющихся деформационными ретрактами W.
Простейший пример — тривиальный h-K.
(AfX[0, 1]; Мх{0}, Mx{i}).
Многообразия Мо и Мх наз. h-к обордантными,
если существует h-K. W, соединяющий их.
Если (W, М„, Мх) — такой h-K., что W, Мо, Мх —
односвязные дифференцируемые (кусочно линейные)
многообразия и dim W^6, то W диффеоморфно (кусочно
линейно изоморфно) Af0X[0, 1]: W^M0X[0, 1] и,
следовательно, М0«лМ1 (теорема об h-к о б о р-
д и з м е [4]). Таким образом, установление изомор-
изоморфизма MotaMi сводится к установлению их fe-кобор—
дантности, что удается сделать методами алгебраич. то-
топологии, и по этой причине эта теорема является
основным средством перехода от гомотопич. классифика-
классификации односвязных многообразий к их классификации с
точностью до диффеоморфизма (кусочно линейного изо-
изоморфизма). Так, если W", и^б,— дифференцируемое-
компактное многообразие односвязным краем, то оно
диффеоморфно диску D". Если Мп, п^5,— многооб-
многообразие, гомотопически эквивалентное сфере S", то он»
гомеоморфно (и даже кусочно линейно изоморфно)
сфере S" (обобщенная гипотеза Пуан-
Пуанкаре).
Теорема об h-K. позволила классифицировать диф-
дифференцируемые структуры на сфере, S", ?г>5 [6], а
также на гомотопическом типе произвольного замкну-
замкнутого односвязного многообразия [1].
В случае h-K. (W; Ма, Мг) с itjWV^l} диффеомор-
диффеоморфизма W«Af0X[0, 1], вообще говоря, нет.
Все h-K. (W\ Mo, Mi) с dim W~^6 и фиксирован-
фиксированным Мо классифицируются нек-рой абелевои группой —
Уайтхеда группой Whnx группы щМй. Данному /j-K.
соответствует элемент Шгл17 являющийся инвариан-
инвариантом пары (W, Мо); он обозначается %(W, Ma) и наз.
кручением (иногда кручением Уайт-
Уайтхеда) данного h-K. Если т( W, М0) = 0 (или равносиль-
равносильно x(W, Мх) = 0), то h-K. наз. s-к о б о р д и :i м о м.
Если (W; Мо, Мг) — такой h-K., что dim W^6, то
кручение т( W, Мо) обращается в нуль тогда п только то-
тогда, когда W~M0X [0, 1] (теорема об s-к обо р-
д и з м е). Теорема об h-K. есть частный случаи этой тео-
теоремы ввиду Wh {l}=0. Теорема об s-кобордизме спра-
справедлива и для топологич. многообразий [9].
Для h-K. (W; Mo, Mi) наряду с t(W, Mo) определя-
определяется кручение т( W, Мх); если данный h-K. ориентируем,
то t(W, M0)=( — l)n~1x*(W, Mi), где л —dim W, ауле-
мент т* сопряжен к т в группе WTwXj. В частности, если
я1 конечна и абелева, то т* = т.
Если два h-K. (W; Mo, Mt) и (W"'; М1, М~) склеены
по М1 в h-K. (W{]W\ Мо, Мх), то
t(W{JW, M0)=x(W, Ma)+x(W\ Mx).
Если склеить две копии W по Мг, причем dim W
нечетно и я1=2в. то получится Л-К. BW, Л/"о, Мо), где
Л/о----Л/о при отсутствии диффеоморфизма W^M0X
X [0, 1], т. е. из МокМ1 не следует тривиальность
¦связывающего их h-K.
Если Мо—замкнутое связное многообразие, и dimM0>
S=5, то для любого %^Whn1M0 существует h-K. (W;
Af0, Af^c t(W, Afo) = x. Если h-K. (W; Mo, Mx) и (W;
Мо. M\) с dim W^6 имеют одинаковые кручения
t(W, M0) = t(W, Mo), to W^W rel Mo. При четной
¦dim Л/о и конечной п-^Мд существует конечное мно-
множество различных многообразий, /г-кобордантных Ма,
в случае нечетной размерности это не так.
Если гомотопич. эквивалентные многообразия М1
и М2 вложены в R-W с достаточно большим N, и их нор-
нормальные расслоения тривиальны, то многообразия AftX
X SN и М2 X SN /г-кобордантны. Если же Mt и М2 —
•одного и того же простого гомотопического типа, т. е.
кручение этой гомотопич. эквивалентности равно
нулю, то М1Х.9Л'^ЛГ2Х5Л'.
Для h-K. (W; Мо, Мг) и замкнутого многообразия
Р имеет место h-K. (WXP, М0ХР, М1ХР), причем
t(WXP, M0XP) = t(W, М0)х(Р), гдех(Р) — эйлерова
характеристика Р. Если dim W^S и Р = 51, то
WxSl~M0XSiX[0, i]^M1XS1X[0, 1].
В частности, Мох S1^M1 xS1; кроме того, замкнутые
многообразия Мо и М1 одинакрвой размерности ^5
А-кобордантны тогда и только тогда, когда A/qXR1»
«^xR1.
Структура h-K. при п<6 полностью не выяснена
A978). Так, имеет место [8] следующий отрицатель-
отрицательный результат: существует h-K. (W; Т*, Г4), где Г4—
четырехмерный тор, где нет диффеоморфизма W~TiX
X [0, 1], п поскольку Whn1Ti=0, то теорема об s-
кобордизме при ге=5 неверна.
Лига.: [1] Н о в и к о в С. П., «Изв. АН СССР. Сер. матем.»,
19В4, т. 28, .4s 2, с. ЗВ5 —474; [2] М и л н о р Д ж., Теорема об
h-кобордизме, пер. с англ., М., 1969; [3] е г о же, «Матема-
«Математика» 1967, т. 11, Л5 1, с. 3—43; [4] Смей л С, там же, 1964,
т. 8, № 4, с. 95—108; 151 М i 1 п о г J., (.Bull. Soc. Math. France»,
1959, t. 87, p. 439 — 44; [6] К е г v a i r e M., MilnorJ., «Ann.
Math.», 1963, v. 77, p. 504—37; [7] M a z u г В., там же, р.
232—49; [8j Siebenmann L., Topology of Manifolds, Chi.,
19ЙЗ; [a] Kirby R., S i e b e n m a n n L., «Bull. Amer.
Math. Зое», 1969, v. 75, p. 742—49; [10] К erv a i r e M.,
«Lect. Notes Math.», 1967, v. 48, p. 83—95; [11] Thorn
R., Topologia algebraico, Мёх., 1958; [12] Рурк К., С а н-
дерсон Б., Введение в кусочно линейную топологию, пер.
с англ., М., 1974. Ю. Б. Рудяк.
КОВАРИАНТ тензора t на конечномерном век-
векторном пространстве V — такое отображение q> про-
пространства Т тензоров фиксированного типа на V в неко-
некоторое пространство S ковариантных тензоров на V,
что (fi(g(t)) = g((f(t)) для любого невырожденного линей-
линейного преобразования g пространства V и любого t?T.
Это — определение коварианта тензора относительно
полной линейной группы GL(V). Если же g не любое, а
принадлежит фиксированной подгруппе GdGL(V), то
получается определение К. тензора относительно груп-
группы G, или просто К. группы G.
На координатном языке К. тензора на конечномер-
конечномерном векторном пространстве представляет собой на-
¦бор функций
«<=ф/ (*ь ••-, tn), i = l, .... пг,
от координат тензора t, обладающий свойством: при
.1:вменении набора чисел ij,. . ., ?„, определенным невы-
невырожденным линейным преобразованием g?G, набор
чисел si,. . ., sm меняется так же, как меняются коорди-
координаты нек-рого ковариантного тензора s на V при
преобразовании g. Аналогично (рассматривая вместо
одного тензора t конечный набор тензоров) определя-
определяется совместный К. системы тензоров. Если же
вместо ковариантности тензора s требовать контравари-
антность, получится понятие контраварианта.
Понятие К. возникло в классической теории инвари-
инвариантов и является частным случаем понятия комитанта.
Координаты любого тензора на V могут рассматриваться
как коэффициенты соответствующей формы от несколь-
нескольких контравариантных и ковариантных векторов (т. е.
векторов пространства V и его сопряженного про-
пространства V*}. Пусть тензору t соответствует таким
образом форма /, а его коварианту s — форма h. Тогда
h — форма только от контравариантных векторов.
В классич. теории инвариантов форма h называлась К.
формы /. Особенно часто рассматривался случай, когда
k — форма от одного контравариантного вектора. Сте-
Степень этой формы наз. порядком К. Если коэффи-
коэффициенты формы h являются многочленами от коэффициен-
коэффициентов формы /, то наивысшая из степеней этих много-
многочленов наз. степенью К.
Пример. Пусть / = \\ аи ...» ж'' ¦ ¦ -х'г — и-арная
форма порядка г, где ж1,. .., хг— координаты контрава-
контравариантного вектора. Форма / соответствует симметри-
симметрическому ковариантному тензору t г-ж валентности с
координатами яA ... ir. Пусть
}*/ дЧ
А = -
дх1 дхп
' дЧ дЧ
дхп дх1 ' ' ' (джлJ
Тогда коэффициенты формы h являются координатами
нек-рого ковариантного тензора х. Тензор s (форма h)
есть К. тензора t (формы /). Фо;ша h наз. гессиа-
гессианом формы /.
Лит.: ШГуревич Г. Б., Основы теории алгебраиче-
алгебраических инвариантов, М.— Л., 1948. В.Л.Попов.
КОВАРИАНТНАЯ ПРОИЗВОДНАЯ — обобщение по-
понятия производной для полей различных геометричес-
геометрических объектов на многообразиях — векторов, тензоров,
форм и т. д. Это — линейный оператор у „, действую-
действующий на модуле тензорных полей У? данной валентно-
валентности и определяемый по векторному полю X на многооб-
многообразии М следующими свойствами:
1) U fU U
2) Vx J
где U?Ts(M), f, g — дифференцируемые функции на
М. По линейности это отображение распространяется
на алгебру тензорных полей, причем для тензорного
произведения (X) тензоров U и V:
v (U 1Я) 1Л — v TT ($\V А- II 1Я) v V
V y v Ч-У i — * х ^-У * vjy ^ х
Таким образом, отображение у„ является дифферен-
дифференцированием алгебры тензорных полей; оно обладает
дополнительными свойствами перестановочности с опе-
операциями свертки, альтернирования и симметрирования
тензоров.
Свойства 1) и 2) отображения у^. позволяют ввести
на М линейную связность (и соответствующее парал-
параллельное перенесение) и на ее основе дать локальное опре-
определение К. п., к-рая, будучи распространенной на все
многообразие, совпадает с определенны»' здесь опера-
оператором у„; см. также Ковариантное дифференцирование.
И. X. Сабитов.
КОВАРИАНТНОЕ ДИФФЕРЕНЦИРОВАНИЕ, аб-
абсолютное дифференцирование, — опе-
операция, инвариантным образом определяющая понятия
производной и дифференциала для полей геометрич.
объектов на многообразиях — векторов, тензоров,
форм и т. д. Основные понятия теории К. д. (под наз-
названием абсолютное дифференциальное исчисление) были
даны в конце 19 в. в работах Г. Риччи (G. Ricci) и в
наиболее полкой форме изложены им в 1901 в совмест-
совместной работе его с Т. Леви-Чивита (Т. Levi-Civita) (см.
[1]). Сначала теория К. д. строилась на римановых мно-
многообразиях и предназначалась в первую очередь для
исследования инвариантов дифференциальных форм.
Впоследствии оказалось, что определение и свойства
К. д. естественным образом связаны с введенными
позже понятиями связности и параллельного перенесе-
перенесения на многообразиях, и теперь теория К. д. строится в
общих рамках теории связпостей. Как аппарат тензор-
тензорного анализа, К. д. широко употребляется в теоротич.
физике, особенно в общей теории относительности.
Пусть на и-мерном многообразии М введена аффинная
связность и соответствующее параллельное перенесение
векторов и вообще тензоров. Пусть X — гладкое век-
векторное поле, ХрТ^О, р?М, и U—тензорное поле типа
(г, s), т. е. г раз контравариантное и s раз ковариант-
ное; ковариантной производной (относи-
(относительно данной связности) тензорного поля U в точке
pQM вдоль векторного поля X наз. тензор того же
типа (г, s)
где x(t) — точка интегральной кривой ух векторного
поля X с начальным условием х@) = р, Uр и U х^—
локализации (значения) тензорного поля U в точках р
и x(t) соответственно, тТ1( Ux^)) — результат параллель-
параллельного перенесения тензора Uxa) вдоль ух из x(t) в р.
Таким образом, основная идея определения ковариантной
производной тензорного поля U вдоль векторного поля
X заключается в том, что ввиду отсутствия операций
между тензорами Uр и UX(t), принадлежащими разным
слоям тензорного расслоения над М, т. е. принадле-
принадлежащими тензорным пространствам Trs над разными каса-
касательными к М плоскостями ТрМ и Т'хц)М, в качестве
«приращения» тензора U рассматривается разность
между Up(zTrs(TрМ) и образом параллельно перене-
сенпого в Trs{TрМ) вдоль ух тензора t/x(f>? Trs(Tx^)M),
и дальше, как обычно, берется предел отношения этого
«приращения» к приращению аргумента 4. В частности,
если для точек x(t), близких к р, поле U получено
параллельным перенесением тензора Uр вдоль ")>х> то
(у^6г)р=0, и тем самым в общем случае ковариант-
ная производная поля U в точке р вдоль X определяет
начальную скорость отличия поля U вдоль у ^от резуль-
результата параллельного перенесения Vр вдоль у%. Для тен-
тензорных полей нулевой валентности, т. е. для функций
/ из кольца дифференцируемых функций S~ на М
(V^ ^\
что приводит к совпадению (yxf)p c производной /
по вектору Xр, т. е. с Xpf. При Х^=0 для любого тен-
тензорного поля U, по определению, считается (vy^Op ==0-
Введение ковариантной производной позволяет опре-
определить ковариантный дифференциал
DU для тензорного поля U вдоль гладкой кривой y(t)
как
и его можно рассматривать как главную линейную
часть «приращения» тензора U (в описанном выше смыс-
смысле) при перемещении точки вдоль у на бесконечно ма-
малый участок ау = у (O)dt.
Знание s/xU для тензорного поля U типа (г, s)
в каждой точке р?М вдоль каждого векторного по-
поля X позволяет ввести два поля: 1) поле ковариантного
дифференциала D U как тензорной 1-формы со значе-
значениями в модуле Trs(M), определенной на векторах X
по формуле (D U)(X) = s/xU; 2) поле ковариантиой про-
производим"! уU как тензорного поля типа (г, s+1), кано-
канонически соответствующего форме DU и действующего
на 1-формах со' и векторах X; по формуле
.., W; Xlt ..., Xs, X) =
o1, .... W; Xu ..., Xs).
Обычно под ковариантным дифференциалом понимается
не сама 1-форма DU, а ее значения на векторах X, и в
таком толковании (DU)(X) тоже превращается в тен-
тензорное поле типа (г, s), локализация к-рого, в частно-
частности, при р = у@) и Х = у совпадает с введенным выше
ковариантным дифференциалом (D ?/)y«» вдоль кривой
y(t). Иногда ковариантная производная у U называется
градиентом тензора U; а производная —
ковариантным дифференциалом.
а
Если х1 — локальные координаты, е; = Г7 \р — ба-
базисные векторпые поля, е1 — сопряженные базисные
1-формы, X' и U-1'" -г — координаты векторного и
' k
тензорного полей в этих базисах, 1\-/ — коэффициен-
коэффициенты введенной на М аффинной связности, то, обозначая
через Vft^i'"'/ или U,l'"{ координаты тензор-
Jl'"Js l" s, k
ного поля \jU, получают следующие выражения (для
примера взяты r=2, s=l)
Г'
km
j +lkmUj —lkjUm J Л =
DU =
где C-i — операция свертки по последним (третьему)
коптравариантному и (второму) ковариантному индек-
индексам.
Если М — аффинное пространство, х' — аффинные
координаты, то (sjxU)p является обычной производной
тензорного поля V по векторному полю X, (sikU)p —
частными производными U в точке р по xk, (DU)yU) —
обычным дифференциалом U вдоль кривой y(t) и, та-
таким образом, К. д. выступает как обобщение обычного
дифференцирования с сохранением известных связей
между частными производными и дифференциалами
первого порядка.
Значение К. д. заключается в том, что оно дает удоб-
удобный аналитический аппарат для изучения и записи
свойств геомотрич. объектов и операций в инвариант-
инвариантной форме. Напр., условие параллельного перенесения
тензора U вдоль кривой у дается уравнением у G=0,
уравнение геодезической у записывается в виде и f=0,
условие интегрируемости системы уравнений в ковари-
антных производных 1-го порядка сводится к нек-рому
уравнению для альтернированной разности S/^sj^U—
— Vu,Va U; внешнее дифференцирование форм на мно-
многообразии и в расслоениях над ним можно также выра-
выразить через К. д., и т. д.
Определение ковариантных производных высших
порядков дается индуктивно: у U— y(ym~xU).
Вообще говоря, получаемый при этом тензор s]mU не
симметричен относительно последних ковариантных
индексов; высшие ковариантные производные вдоль
разных векторных полей также зависят от порядка
дифференцирования. Альтернированные разности ком-
компонент ковариантных производных высших порядков
выражаются через кривизны тензор R^kl и кручения
тензор Sljk, совместно характеризующих отличие мно-
многообразия М с данной связностью от аффинного про-
пространства. Напр.,
(тождество Риччи)
x x
где [X. Y]—коммутатор векторов ХиУ, а
Определение К. д. и его свойства остаются в силе и в
более общем случае, когда вместо сечения U тензорного
расслоения с аффинной связностью рассматривается
сечение ср произвольного (действительного или комп-
комплексного) векторного расслоения, ассоциированного
нек-рому главному расслоению со связностью Г и со
структурной группой G, к-рая действует на слое своим
представлением в группе невырожденных матриц.
Существуют определения К. д. в более общей ситуации,
когда расслоение не обязательно является векторным;
общий смысл [9] этих определений заключается в ана-
аналитическом выражении параллельного перенесения
объекта или параллельности определяющего его сече-
сечения как равенства нулю результата К. д. Подобные
подходы имеются и для бесконечномерных многообра-
многообразий.
Лит.: [1] R i с с i G., Lcvi-Civita Т., «Math. Ann.»
1901, Bd 54, №1, S. 125—201; [2] P а ш е в с к и й П. К.,
Риманова геометрия и тензорный анализ, М., 1967; [3] Н о р-
ден А. П., Пространства аффинной связности, 2 изд., М.,
1976; [4]Лихнерович А., Теория связности в целом и
группы голономий, пер. с франц., М., 1960; [5]Хелгасон С,
Дифференциальная геометрия и симметрические пространства,
пер. с англ., М., 1964; [6] Бишоп Р., Криттенден Р.,
Геометрия многообразий, пер. с англ., М., 1967; [7] Г р о м о л Д.,
Клингенберг В., Мейер В., Риманова геометрия в
целом, пер. с нем., М., 1971; М К о Ь а у a s h i S., N о m i-
zu K., Foundations of differential geometry, v. 1—2, N. Y.—
L., 1963—69; [9] Итоги науки. Алгебра. Топология. Геомет-
Геометрия. 1969, М., 1971,с.123—68; [10] 3 уланке Р., Винт-
ген П., Дифференциальная геометрия и расслоения, пер. с
нем., М., 1975. И. X. Сабитов.
КОВАРИАНТНЫЙ ВЕКТОР — элемент векторного
пространства Е*, сопряженного к м-мерному вектор-
векторному пространству Е, то есть линейный функционал
(линейная форма) на Е. В упорядоченной паре (Е, Е*)
элемент пространства Е наз. контр авар иантным век-
вектором. В общей схеме построения тензоров К. в. отож-
отождествляется с ковариантным тензором валентности 1.
Координатная запись К. в. особенно проста, если в
Е и Е* выбрапы так наз. взаимные, или дуальные,
базисы «!,..., еп в Ей е1,. . ., еп в Е*, т. е. такие
базисы, что (e'ey)=6j- (где б/ — Кронекера символ);
тогда произвольный К. в. а?Е* представляется в виде
со=//е' (суммирование по г от 1 до и), где /,¦ — значение
линейной формы со их вектора е;. При переходе от вза-
взаимных базисов (е,-) и (е-1) к взаимным базисам (е;-) и
(е>') по формулам
координаты ж' контравариантного вектора x=x'ej
изменяются по контравариантному закону xi' = qi'xi',
а координаты /,• К. в. со изменяются по ковариантному
(соизменяющемуся с базисом) закону fi> = p\>ti.
Лит.: [1] Широков П. А., Тензорное исчисление,
2 изд., Казань, 1961; [2] Беклемишев Д. В., Курс ана-
аналитической геометрии и линейной алгебры, М., 1971 ;[3] С х о у-
тен Я. А., Тензорный анализ для физиков, пер. с англ., М.,
1965. И. X. Сабитов.
КОВАРИАНТНЫЙ ДИФФЕРЕНЦИАЛ — обобщение
понятия дифференциала для полей различных геометрич.
объектов. Это — тензорная 1-форма D U на многообра-
многообразии со значениями в модуле тензорных полей U, опре-
определенных формулой
(DU)(X)=VxU,
где Vy^ — ковариантная производная поля U вдоль
X. См. также Коеариаптное дифференцирование.
И. X. Сабитов.
КОВАРИАНТНЫЙ ТЕНЗОР валентности s>1 -
тензор типа @, s), элемент тензорного произведения
TS{E) = E*Q). . .(Х)?* s экземпляров пространства Е*,
сопряженного (дуального) к векторному пространству
Е над полем К. Относительно операции сложения К. т.
одной и той же валентности и умножения их на скаляр
TS(E) является в свою очередь векторным пространст-
пространством над К. Пусть Е — конечномерно и пусть ех,. ..,
еп— базис в й, а с1,..., е" — сопряженный с ним ба-
базис в Е*. Тогда dim Ts(E) = ns и базис в TS(E) состоит
из всевозможных разложимых тензоров вида ег'(Х). ..
(g)els, 1<г!,..., is<n. Любой К. т. t?Ts(E) может
быть представлен в виде t=ti i ег'(Х). . .(Х)ег$. Числа
? ¦ наз. координатами или компонентами К. т.
относительно базиса е1?. . ., е„ в Е. При изменении ба-
базиса в Е по формулам ei'=a\'ej и соответственно бази-
базиса в ТS(E) координаты К. т. t изменяются по так наз.
ковариантному закону
Ч is .
При валентности s^2 К. т. наз. коеариантным век-
вектором; при s^2 К. т. можно инвариантным обра-
образом связагь с s-линейным отображением прямого про-
произведения ES = EX . . .ХЕ (s раз) в К, приняв коорди-
координаты К. т. t относительно базиса elt ..., еп за значения
r-линейпого отображения t на базисных в Es векторах
(eiit. .., eis), и обратно; поэтому иногда К. т. опреде-
определяют как полилинейный функционал на Es.
Лит. см. при статье Ковариантный вектор.
И. X. Сабитов.
КОВАРИАЦИОННАЯ МАТРИЦА — матрица, обра-
образованная из попарных ковариаций нескольких случай-
случайных величин; точнее, для ^-мерного случайного векто-
вектора Х= (Xlt..., Хи) К. м. наз. квадратная матрица
2 = Е[(Х-ЕХ)(Х-ЕХ)Л, где EX=(EXj EXft) -
вектор средних значений. Компоненты К. м. равны
0/у=
Е [(Xt-EXi) (АГу-ЕХ,)] =cov (Xh Xf),
i, 7 = 1, ..., k,
п при i=j совпадают с DXt (т. е. на главной диагонали
К. м. находятся дисперсии величин X;). К. м. пред-
представляет собой симметричную неотрицательно опреде-
определенную матрицу. Если К. м. является положительно
определенной, то распределение X — невырожденное
распределение, в противном случае — вырожденное.
Для случайного вектора X К. м. играет роль дисперсии.
Если дисперсии случайных величин Xlf. . ., Xf, равны
1, то К. м. для вектора Х=(Х1,..., Х^) совпадает
с корреляционной матрицей.
Выборочная К. м. для выборки Х{1\. . ., Х{п), где
Хш), т=1,..., п — независимые одинаково распре-
распределенные случайные /с-мерные векторы, состоит из
оценок дисперсий и ковариаций:
где X — вектор арифметического среднего Ха\. ..,
Х{п). Если случайные векторы ХA).. . ., Х(п) имеют
нормальное распределение с К. м. 2, то S является
оценкой максимального правдоподобия 2 ; в этом случае
совместное распределение элементов матрицы (и—1M
наз. Уишарта распределением, оно является одним Из
основных распределений в многомерном статисгич.
анализе, с помощью к-рого проверяются гипотезы о
К. М. 2. А. В. Прохоров.
КОВАРИАЦИОННЫЙ АНАЛИЗ — совокупность ме-
методов математич. статистики, относящихся к анализу
моделей зависимости среднего значения нек-рой слу-
случайной величины У от набора неколичественных фак-
факторов F и, одновременно, от набора количественных
факторов х. По отношению к У переменные х наз.
сопутствующими; факторы F задают сочета-
сочетания условий качественной природы, при к-рых получе-
получены наблюдения У и х, и описываются с помощью так
наз. индикаторных переменных; среди сопут-
сопутствующих и индикаторных переменных могут быть как
случайные, так и не случайные (контролируемые в эк-
эксперименте); если случайная величина У является
вектором, то говорят о многомерном К. а.
Основные теоретические и прикладные проблемы
К. а. относятся к линейным моделям. Ё частности,
если анализируется схема из и наблюдений Уь. ..,
У„ с р сопутствующими переменными и к возможными
типами условий эксперимента, то линейная модель
соответствующего К. а. задается уравнениями
где индикаторные переменные /,у равны 1, если у-е
условие эксперимента имело место при наблюдении
Y{, и равны 0 в ином случае; коэффициенты 6у опреде-
определяют эффект влияния /-го условия; xis> — значение
сопутствующей переменной x(s), при к-рой получено
наблюдение У,-, i=l,.... n; s=l,. . ., р; P^(-f;) — зна-
значения соответствующих коэффициентов регрессии У
по xis), вообще говоря, зависящие от конкретного соче-
сочетания условий эксперимента, т. е. от вектора F,-=
— (/iii-• •> fik)\ ?i(Fi) ~ случайные ошибки, имеющие
нулевые средние значения. Основное содержание К. а.—
в построении статистич. оценок для неизвестных пара-
параметров 9j,. . ., 6^; pj,. . ., $р и статистич. критериев для
проверки различных гипотез относительно значений
этих параметров.
Если в модели (*) постулировать априори $!=...=
= рр=О, то получится модель дисперсионного анализа;
если из (*) исключить влияние неколичественных фак-
факторов (положить Q1=... =6fc=0), то получится модель
регрессионного анализа. Своим названием К. а. обязан
тому обстоятельству, что в его вычислениях исполь-
зуются разбиения коеариации величин Y и X точно
так же, как в дисперсионном анализе используются
разбиения суммы квадратов отклонений Y.
Лит.: [1] Ш е ф ф е Г., Дисперсионный анализ, пер. с англ.,
М., 1963; 12] К е н д а л л М. Д ж., С т ь ю а р т А., Много-
Многомерный статистический анализ и временные ряды, пер. с англ.
М., 1976; [3J «Biometrics», 1957, v. 13, Х° 3. С. А. Айвазян.
КОВАРИАЦИЯ — числовая характеристика совмест-
совместного распределения двух случайных величин, равная
матрматич. ожиданию произведения отклонений слу-
случайных величин от их математич. ожиданий. К. опре-
определяется для случайных величин Хг и Х2 с конечными
дисперсиями и обычно обозначается cov (Xlt Х2).
Таким образом,
cov(Xb Х2) = Е[(Х1-ЕХ1)(Х2-ЕХ2)],
при этом cov (X,, X2)=cov(X2, XJ; cov (X, X) = DX.
К. естественным образом появляется в выражении для
дисперсии суммы случайных величин
+ 2cov(X1, Х2).
Если величины Хх и Х2 независимы, то cov (Xj, Х2) =
= 0. К. служит характеристикой взаимозависимости
случайных величин, с помощью К. определяется кор-
корреляции коэффициент. В математич. статистике оцен-
оценкой К. служит выборочная К., вычисляемая по формуле
где (Xi\ Хг}), i=l,..., п, — независимые величины,
а Хг и Х2 — арифметические средние, а. в. Прохоров.
КОВАРИАЦИЯ ЧИСЛА РЕШЕНИЙ — понятие в
дисперсионном методе, вводимое при сравнении чисел
решений уравнений
и n=q>+D'v A)
, B)
где ф иг|) принадлежат к некоторым последовательностям
натуральных чисел, D' пробегает некоторую заданную
систему чисел сегмента
(D)=[D1, D!+D2],
v пробегает систему чисел сегмента
(v) = [v0, Vo-j-Vo].
Пусть
тогда дисперсия разности решений уравнений A) и B)
будет
V' —У (Y'Y'V
у —Zi
где
Применяя идею И. М. Виноградова по сглаживанию
двойных сумм, можно распространить суммирование по
D' на все D из (D). Дисперсия при этом может только
увеличиться; таким образом
V <V=V1-2V2+V3,
где
здесь
По аналогии с теоретико-вероятностными концепциями
выражение F2 наз. к о в а р нацией числа ре-
решений уравнений A) и B). Асимптотический расчет
Fj, V3 и ковариации F2 может показать, что дисперсия
V' относительно мала, а это существенно при рассмот-
рассмотрении аддитивных задач, приводимых к уравнениям
A) и B).
Лит.: [1] Линии к Ю. В., Дисперсионный метод в би-
бинарных аддитивных задачах, Л., 1961. В. М. Бредихин.
КОГЕРЕНТНОЕ КОЛЬЦО — кольцо, в к-ром каждый
конечно порожденный левый идеал является конеч-
конечно и р е д с т а в и м ы м, т. е. фактормодулем конечно
порожденного свободного модуля по конечно порож-
порожденному свободному подмодулю. Такое К. к. наз.
когерентным слева кольцом, анало-
аналогично, но с помощью правых идеалов, может быть опре-
определено когерентное справа кольцо.
Когерентное слева кольцо R может быть определено
также любым из следующих двух эквивалентных ус-
условий: 1) каждый левый конечно порожденный под-
подмодуль конечно представимого Д-модуля конечно пред-
представим; 2) прямое произведение левых плоских Д-мо-
дулей — левый плоский /?-модуль.
Многие конструкции, известные для модулей над
нётероеыми кольцами, оказались осуществимыми и для
модулей над К. к. Напр., всякий конечно порожденный
модуль над К. к. обладает проективной резольвентой
из конечно порожденных модулей. В то же время класс
К. к. шире класса нё'теровых колец, так как включает
в себя, напр., все регулярные кольца (в смысле Ней-
Неймана) и кольца многочленов над нётеровыми кольцами
от любого (конечного или бесконечного) числа пере-
переменных.
Лит.: [1] Бурбаки Н., Коммутативная алгебра, пер.
с франц., М., 1971. В. Е. Говоров.
КОГЕРЕНТНЫЕ ЧИСЛА — натуральные числа, от-
отличающиеся друг от друга только квазинростыми
множителями (см. Квазипростое число). При решении
аддитивных проблем часто используется тот факт, что
числа решений некоторых аддитивных уравнений,
относящихся к различным К. ч., асимптотически совпа-
совпадают. ?• -М- Бредихин.
КОГЕРЕНТНЫЙ АЛГЕБРАИЧЕСКИЙ ПУЧОК —
когерентный пучок модулей на алгебраич. многообразии
Или схеме. Структурный пучок нётеровой схемы и, в
частности, алгебраич. многообразия является когерент-
когерентным.
К. а. п.— удобное средство исследования алгебраич.
многообразий. Интуитивно К. а. п. соответствуют пред-
представлению о непрерывной алгебраич. системе линейных
пространств на многообразии (см. Векторное расслоение
на алгебраическом многообразии) и возникают при рас-
рассмотрении линейных и алгебраич. семейств дивизоров,
вложений многообразия в проективное пространство,
дифференциальных форм, векторных полей и автомор-
автоморфизмов, деформаций многообразий и подмногообразий,
одним словом — при линеаризации всевозможных задач
алгебраич. геометрии (см. [3]). Результаты при этом
формулируются в терминах когомологий К. а. п. Тео-
Теория когомологий К. а. п. включает: а) конечности тео-
теоремы (в алгебраической геометрии), утверждающие
конечномерность пространств когомологий Н'(Х, §г),
г^О, когерентного пучка JF на полном многообразии
X; б) Римана — Роха теорему, вычисляющую характе-
характеристику Эйлера — Пуанкаре К. а. п.; в) теоремы об
обращении в нуль высших когомологий типа теоремы
Серра (см. А ффинная схема) пли Нодаиры теоремы (см.
[4], [5]); г) теоремы двойственности (см. Двойствен-
Двойственность в алгебраической геометрии), связывающие
г-мерные и (п—г)-мерные когомологии пучков на гладком
многообразии размерности га; д) Кюннета формулы,
выражающие когомологии некоторых пучков на про-
произведении многообразий; е) сравнения теоремы в ал-
гебраич. геометрии с другими теориями когомологии—
аналитическими, формальными, этальными; ж) теорию
локальных когомологии, полезную при изучении К. а. п.
на неполных многообразиях. Одно из важнейших ее
применений относится к Лефшеца теореме, сравнива-
сравнивающей свойства многообразия и его гиперплоского се-
сечения.
Многие результаты обобщаются на случай, когда одно
многообразие X заменяется семейством многообразий,
т. е. на случай морфизма / : X—>Y. Пространства
когомологии заменяются при этом пучками Rnf* про-
производных от функтора прямого образа /*; большую
роль здесь играет поведение этих функторов при замена
базы.
См, также Квазикогерентиый пучок, Когомологии
со значениями в пучке.
Лит.: [1] Серр Ж.-П., в сб.: Расслоенные пространства,
пер. с англ., М., 1958, с. 372 — 450; [2] G г о t h e n d i e с к А.,
Elements de geometric algebrique, t. 3, P., 1961 (Publs math.
IHES, № 11); [3] M а м ф о р д Д., Лекции о кривых на ал-
алгебраической поверхности, пер. с англ., М., 1968; [4] К о-
даира К., «Математика», 1958, т. 2 № 6, с. 126 — 31; [5]
М u m f о г d D., «Amer. J. Math.», 1967, v. 89, Л» 1, p. 94—
104; [6] Итоги науки и техники. Алгебра. Геометрия. Топо-
Топология, т. 10, М., 1972, с. 47 — 112. В. И. Данилов.
КОГЕРЕНТНЫЙ АНАЛИТИЧЕСКИЙ ПУЧОК —
когерентный пучок E~М0ДУлеи на аналитическом про-
пространстве (X, 6). Пространство (X, Q) наз. коге-
когерентным, если Q — когерентный пучок колец.
Любое аналитич. пространство над алгебраически
замкнутым полем когерентно. Важнейшими примерами
К. а. п. на таком пространстве (X, Q) являются любой
локально свободный пучок (т. е. ана-
аналитич. пучок, локально изоморфный пучку QP), а также
пучок идеалов аналитического мно-
множества YdX, т. е. пучок ростков аналитич.
функций, равных 0 на У [1].
Если |Г — К. а. п. на комплексном аналитич. про-
пространстве (X, 0), то пространство его сечений Г(Х,
F) снабжается естественной топологией, превращающей
его в пространство Фреше, если X сопарабельно. Для
F=Q эта топология совпадает с топологией равномер-
равномерной сходимости аналитич. функций на компактах.
При этом |Г превращается в п у ч о к Ф р е ш е, т. е.
для любых открытых множеств t/cFel отображение
ограничения T(V, ^")->r(f/, !f) непрерывно. Анали-
Аналитич. гомоморфизм когерентных пучков |Г—>-$ порож-
порождает непрерывное линейное отображение Т(Х, ^F)—>-
Т(Х, %). Если §~ — К. а. п. на X и М — подмодуль
в W xi Х?Х, то Для любой окрестности U точки х под-
подмодуль {s?T(U, §')\s(x)^M) замкнут в ГA7, <jF).
Пространства когомологии IIP(X, ^f) также обладают
естественной топологией, к-рая, вообще говоря, не
отделима для р >0 (они являются факторпространст-
вамн пространств Фреше) [2], [4].
К. а. п. были введены в связи с задачами теории
аналитич. функций в областях пространства С" (см.
[3], [5]). Впоследствии К. а. п. и их когомологии стали
основным аппаратом глобальной теории аналитич.
пространств. Важную роль в этой теории играют крите-
критерии обращения в 0 когомологии со значениями в К. а. п.
(см. Кодаиры теорема. Обильное векторное расслоение,
Штейна пространство), а также критерии их конечно-
конечномерности и отделимости (см. Конечности теоремы в те-
теории аналитических пространств).
См. также Векторное аналитическое расслоение, Двой-
Двойственность в теории аналитических пространств.
Лит.: [1] A b h у а п к а г S. S., Local analytic geometry,
N. Y.— L., 1964; [2] В a n i с a C., S t a n a 5 i 1 a 0., Metode
altrebrice In teoria globala a spatiilor complexo, Buc, 1974; [3]
С a r t a n H., «Bull. Soc. math. "France», 1950, t. 78, p. 28 — 64;
[4] Г a 11 н и и г Р., Р о с с и X., Аналитические функции
многих комплексных переменных, пер. с англ., М., 1969; [5]
Ока К., «Bull. Soc. math. France», 1950, t. 78, p. 1 — 27.
А. Л. Онищик.
КОГЕРЕНТНЫЙ ПУЧОК на окольцован-
окольцованном пространстве (X, 0) — пучок модулей
If над пучком колец 0, обладающий следующими
свойствами: 1) |Г — пучок конечного типа, т. е.
локально порождается над 0 конечным числом сечений;
2) ядро любого гомоморфизма пучков модулой 0Р\[/->-
-KFIlt над открытым множеством UdX является пуч-
пучком конечного типа. Если в точной последовательности
0-+§~1-+$г2—>-$~3->.0 пучков (о-модулей два из трех
лучков $~i когерентны, то и третий пучок когерентен.
Если ф : ff'—^tff — гомоморфизм когерентных пучков
0-модулей, то Кег ф, Coker cp, Im ф — также коге-
когерентные пучки. Если f и <ff когерентны, то §~(X)paf и
Horrid (§~, if) также когерентны [4]. ^
Структурный пучок 0 наз. когерентным пуч-
пучком колец, если 0 когерентен как пучок модулей
над самими собой, что сводится к выполнению условия
2). Если 0 — когерентный пучок колец, то пучок E-мо-
дулей |р когерентен тогда и только тогда, когда каждая
точка пространства X обладает окрестностью U, над
которой существует точная последовательность пучков
0-модулей:
[4]. Далее, при этом условии для любых когерентных
JT, <У пучки Ext?- {F, iff) когерентны для всех р (см. [2]).
Основными классами окольцованных пространств с
когерентным структурным пучком Q являются: анали-
тич. пространства над алгебраически замкнутым полем
[1], нётеровы схемы и, в частности, алгебраич. много-
многообразия [4]. Классический частный случай представляет
собой пучок 0 ростков голоморфных функций в об-
области пространства С; утверждение о его когерент-
когерентности известно как теорема О к а [3], [5]. Струк-
Структурный пучок вещественного аналитич. пространства,
вообще говоря, не когерентен.
См. также Когерентный аналитический пучок, Коге-
Когерентный алгебраический пучок.
Лит.: [1] A b h у a n k а г S. S., Local analytic geometry,
N. Y.— L., 1964; [2] В a n i с a C., S t a n a 5 i 1 a O., Metodo
algebrice in teoria globala a spatiilor complexe, Buc, 1974; [3]
Г а н 11 и h г Р., Р о с с и X., Аналитические функции многих
комплексных переменных, пер. с англ., М., 1969; [4] Серр
Ж.-П., в сб.: Расслоенные пространства и их приложения,
пер. с франц., М., 1958, с. 372—450; [5] Ф у к с Б. А., Специ-
Специальные главы теории аналитических функций многих ком-
комплексных переменных, М., 1963. А. Л. Онищип.
КОГОМОЛОГИИ — термин, употребляемый по от-
отношению к функторам гомологической природы, ко-
которые, в отличие от гомологии, как правило, контра-
варпантно зависят от объектов основной категории, на
которой они определены. В отличие от гомологии,
связывающие гомоморфизмы в когомологической точ-
бой последовательности повышают размерность. В
типичных ситуациях когомологии возникают одновре-
одновременно с соответствующими гомологиями.
Е. Г. Скляренпо.
Когомологии топологического
пространства — градуированная группа
Н*{Х, 0)=%п>оЛп{Х, G),
которая ставится в соответствие топологич. простран-
'тву и абелевой группе G. Понятие К. двойственно
понятию гомологии (см. Гомологии теория, Гомологии
руппа, Александрова — Чеха гомологии и когомологии).
Если G — кольцо, то в группе Н* (X, G) определено
естественное умножение (произведение Кол-
Колмогорова — Алекса н дера или [)-п р о и з-
ведение), превращающее эту группу в градуиро-
градуированное кольцо (к о л ь ц о к о г о м о л о г и й). В слу-
случае, когда X — дифференцируемое многообразие,
кольцо когомологии Н*{Х, R) может быть вычислено
при помощи дифференциальных форм на X (см. де
Рама теорема).
Когомологии со значениями в пуч-
пучке абелевых групп — обобщение обычных
когомологии топологич. пространств. Имеются две
теории когомологии со значениями (или с коэффициен-
коэффициентами) в пучках абелевых групп: когомологии Чеха и
когомологии Гротендика.
Когомологии Чеха. Пусть X — топологич.
пространство, §~ — пучок абелевых групп на X,
{}]= {U,}ig T — открытое покрытие пространства X.
n-мерной коцепью покрытия ?J наз. отображение /,
к-рое всякому упорядоченному набору г0, ..., ?„?/,
такому, что
сопоставляет сечение /; i пучка F над U\ г . Мно-
Множество всех и-мерных коцепей С"(Щ, JF) является
абелевой группой относительно сложения. Кограничный
оператор
определяется следующим образом:
где символ Л означает, что соответствующий индекс
опускается.
Последовательность
является комплексом (комплекс Чеха). Кого-
Когомологии этого комплекса обозначаются Н" (j}, JF) и
наз. когомологиями Чеха покрытия
Jf со значениями в §~. Группа Н°C), §~)
совпадает с группой Г(Х, |Г) сечений пучка $~. При
вычислении этих когомологии комплекс Чеха можно
заменить его подкомплексом, состоящим из альтерни-
альтернированных коцепей, т. е. коцепей, меняющих знак при
перестановке двух индексов и равных 0 в случае, когда
два индекса совпадают.
Если покрытие J) вписано в d)= {F/}, т. е. для каж-
каждого г?/ указано t(s)?/ так, что Ui^V%a), то опреде-
определен канонический гомоморфизм Н"(&\, of)—v//" (9t,
§~), не зависящий от вписывания т. re-мерная группа
когомологии Чеха пространства X со значениями в JF
определяется формулой:
Йп(Х, F) = lim#" (*}, |"),
где индуктивный предел берется по направленному (по
отношению вписанности) множеству классов открытых
покрытий (два покрытия эквивалентны тогда и только
тогда, когда каждое из них можно вписать в другое).
Определение когомологии Чеха применимо и к предпуч-
кам.
Недостатком когомологии Чеха является то, что они
(для непаракомпактных пространств) не образуют
когомологич. функтора (см. Гомологический функтор).
В случае, когда ff~ — постоянный пучок, соответствую-
соответствующий абелевой группе JF, группы И"{Х, {f) совпадают
с когомологиями Александрова — Чеха с коэффициента-
коэффициентами в группе §~.
Когомологии Гротопдика. Рассматри-
Рассматривается функтор <^->Г(Х, <fF) из категории пучков абе-
абелевых групп наХв категорию абелевых групп. Правые
производные этого функтора наз. я-м е р н ы м и
группами когомологии Гротендика
со значениями впучке JF и обозначаются
Л"(Х, |F), п—0, 1,. .. . Точной последовательности
пучков абелевых групп
соответствует точная последовательность
т.е. {Я"(Х, !F)n=0 i образуют когомологич. функ-
функтор. При этом н'°(х','дг)=Т(Х,§г). Если ^ — вя-
вялый пучок, то Нп(Х, $~)=0 (re>0). Эти три свойства
когомологнй Гротендика характеризуют функтор JFH»
\-*{Нп(Х, §~)}п=й 1 однозначно с точностью до
изоморфизма.
Для вычисления когомологии Гротендика пучка %f
можно воспользоваться левой резольвентой пучка <5Г,
состоящей из пучков, когомологии Гротендика к-рых
равны 0 в положительных размерностях. Напр., на про-
произвольных топологич. пространствах можно взять ре-
резольвенту из вялых пучков, а на паракомпактных про-
пространствах — из мягких пучков или из тонких пучков.
Когомологии Гротендика связаны с когомологиямн
покрытий следующим образом. Пусть 3>={?//}i6l—
открытое покрытие пространства А". Тогда существует
спектральная последовательность {Ef'4}, сходящаяся
к {Н"(Х, §~)} и такая, что
где fflq(X, eF) ~ предпучок, сопоставляющий откры-
открытому множеству VdX группу H^(V, §r). Если когомо-
когомологии всех Uj i со значениями в §~ равны 0 в поло-
положительных размерностях, то последовательность вы-
вырождается и
Я» (?}, Ю = Я» (X, ^), я = 0, 1, ...,
(теорема Лере). В общем случае спектральная
последовательность определяет функторный гомомор-
гомоморфизм
я»а w)-^-H"(x, л
и, после перехода к пределу,— функторный гомомор-
гомоморфизм
Й"(Х, ^)-^Нп(Х, |").
Последний гомоморфизм биективен для и=0, 1, инъек-
тивен (но, вообще говоря, не сюръективен) для и=2 и
биективен для всех и, если X паракомпактно. Таким
образом, для паракомпактного пространства X
Н" (X, f) as H" (X, f), и = 0, 1, ...
Обобщением определенных выше групп когомологии
являются группы когомологии Яф(Х, §~)
сносите л ями всемействеф. Семейство Ф
замкнутых подмножеств пространства X наз. семей-
семейством носителей, если 1) замкнутое подмно-
подмножество любого множества из Ф принадлежит Ф; 2)
объединение любых двух подмножеств из Ф лежит в
Ф. Группы Яф(Х, |F) определяются как правые
производные функтора f Н-Гф(Х, f), где ГФ(Х,
|Г)=Яф(Х, |F) — группа сечений пучка $', носители
к-рых лежат в Ф. Они образуют когомологич. функтор.
Если Ф — семейство всех замкнутых множеств, то
Нф(Х, <f) = Hn{X, §~). Другой важный частный слу-
случай: Ф = с — семейство всех компактных подмножеств.
Группы Л"(Х, ,f) наз. группами когомоло-
гий с компактными носителями.
В случае, когда §~ — пучок колец, в группе
естественным образом определяется умножение, превра-
превращающее ее в градуированное кольцо (кольцо ко-
кого м о л о г в й). При этом ассоциативность в пучке JF
влечет за собой ассоциативность умножения в Н* {X,
§~), а пучок коммутативных колец или колец Ли при-
приводит к градуированно-коммутативному кольцу или
градуированному кольцу Ли когомологий соответ-
соответственно. Если |р — пучок модулей над пучком колец
Л, то Нп(Х, §~) являются модулями над кольцом
Г(Х, Л).
О когомологиях со значениями в пучке неабелевых
групп см. Неабелевы когомологий.
Лит.: [1] Гротендик А., О некоторых вопросах го-
гомологической алгебры, пер. с франц., М., 1961; [2] Годе-
м а н Р., Алгебраическая топология и теория пучков, пер. с
франц., М., 1961; L3] Серр Ж.-П., в сб.: Расслоенные прост-
пространства, М., 1958, с. 372—450. Д. А. Пономарев.
Когомологий пространства с опе-
операторами — когомологические инварианты топо-
логич. пространства с заданным на нем действием груп-
группы. Пусть группа G действует на пространстве X, причем
для каждого g?G отображение xH>gx является гомео-
гомеоморфизмом X—>-Х, тогда G-пучком абелевых групп на
X наз. пучок абелевых групп на X вместе с заданным
на нем действием группы G, к-рое непрерывно, согласо-
согласовано с действием на X и изоморфно отображает слои
пучка друг на друга. В группе сечений G-пучка JF
(и вообще в группах когомологий Нп(Х, qF)) определена
естественная структура G-модуля. G-пучки абелевых
групп на X образуют абелеву категорию, всякий объ-
объект к-рой вкладывается в инъективный объект. Функтор
|ГН-Г(Х, IFH из этой категории в категорию абелевых
групп, где Г(Х, §~)° — группа G-инвариантных се-
сечений G-пучка JF, обладает правыми производными
функторами <f^Hn{X, G, &) (ге=0, 1, 2, . . .), где
Н°(Х, G, §r)=T(X, if)°, составляющими когомоло-
гич. функтор. Группы Нп(Х, G, JF) играют основную
роль в изучении связи между когомологиями простран-
пространства X, факторпространства У= X/G и группы G. Суще-
Существует спектральная последовательность {Ег} со вто-
вторым членом Ер q = HP(G, Hi(X, §~)), сходящаяся к
Н* (X, G, JF). Пусть ?f° — пучок инвариантов пря-
прямого образа /ф|Г (/ : X-+Y— естественная проекция),
рассматриваемого как G-пучок на пространстве У,
на к-ром G действует тривиально. Если G действует на
X собственно разрывно (см. Дискретная группа
преобразований) и свободно, то Н* (X, G, §~)=Н* (У,
JF°) (см. [1]). В частности, если А — некоторый G-
модуль, то постоянный пучок 3~=А на X обладает
естественной структурой G-пучка, а пучок g~G на У
будет локально постоянным. В этом случае спектраль-
спектральная последовательность {Ег} удовлетворяет условию
EZ-q=HP(G, H«(X, А)) и сходится к II* (У, fG)
(спектральная последовательность
накрытия). Если при этом X связно и НЧ(Х, А)=0
дляд>0,то HP(G, A)^=HP(Y, g~°), что дает топологич.
интерпретацию когомологий группы G [2]. Если G
собственно разрывна и У паракомпактно, то группы
Н"(Х, G, §~) можно вычислять аналогично когомоло-
гиям Чеха при помощи G-инвариантных покрытий
пространства X (см. [1]).
В случае, когда G — группа Ли, дифференцируемо
и свободно действующая на дифференцируемом многооб-
разии X, причем X/G — дифференцируемое многооб-
многообразие, известен аналог {Ег} спектральной последо-
последовательности накрытия [3]. Последовательность {Ёг}
сходится к когомологиям комплекса G-инвариантных
дифференциальных форм на X и Ё?' д=
= HP(G, Н'1(Х, R)), где когомологий группы G вычис-
вычисляются при помощи коцепей класса С°°.
См. также Когомологий групп, Эквивариантные кого-
когомологий.
Лит.: [1] ГротендикА.,0 некоторых вопросах гомоло-
гомологической алгебры, пер. с франц., М., 1961; |2]КартанА.,Эй-
ленберг С, Гомологическая алгебра, пер. с англ., М.,
19К0; [3] van Est W. Т., «Proc. Nederl. Akad. Wetensch.
Ser. A», 1958, v. 61, p. 399—413.
А. Л. Онищип, Д. А. Пономарев.
КОГОМОЛОГИЙ АЛГЕБР — группы
II" (R, A)^Ext^(K, A), n Ss О,
(см. Функтор Ext), где Я — ассоциативная алгебра
над коммутативным кольцом К с фиксированным гомо-
гомоморфизмом А'-алгебр s : R^K, позволяющим рассмат-
рассматривать кольцо К как iJ-модуль, а А есть iJ-модуль. Это
определение охватывает наиболее распространенные тео-
теории когомологий нек-рых типов (универсальных) алгебр.
Впервые группы когомологий групп во всех размер-
размерностях были введены С. Эпленбергом и С. Маклейном
[3] в связи с топологич. исследованиями и Д. К. Фадде-
евым [5] — с чисто алгебраич. точки зрения — как
группы классов обобщенных систем факторов, в 40-х гг.
20 в. Ранее изучались в той или иной форме когомологий
групп в малых размерностях (см. [1], [2], [4]).
Примеры групп когомологий. 1) Если
К =%— кольцо целых чисел, G — группа, R=%G —
групповая алгебра группы G над %,
то группы Hn(R, А) наз. группами когомо-
когомологий г р у п п ы G с коэффициентами (или со зна-
значениями) в Д-модуле А и обозначаются Hn(G, A).
Можно вместо группы G рассмотреть моноид G и ана-
аналогично получить группы когомологий
Hn(G, А) м о н о и д a G. 2) Если S — ассоциативная
if-алгебра, 5° — антиизоморфная ей if-алгебра,
то группы Hn(R, А) наз. группами когомо-
когомологий ассоциативно it алгебры S с ко-
коэффициентами в 5-бимодуле А (т. е. в Д-модуле А) и
обозначаются Hn(S, А). Если К — поле, то группы
Hn(S, А) наз. группами когомологий
Хохшильда К -алгебры S.
3) Если 5-алгебра Ли над полем К, Я= Us — ее
универсальная обертывающая алгебра с пополнением
8 : R-+K, то группы H"(R, А) наз. группами
когомологийалгебры Ли5с коэффициен-
коэффициентами в ?/$-модуле А (т. е. в лиевом 5-модуле А) и
обозначаются H"(S, A).
При и=0, 1, 2 группы когомологий в ряде случаев
допускают простую интерпретацию.
а) Если G — группа, то группа H°(G, А) изоморфна
группе
инвариантных элементов; группа H1(G, А) изоморфна
факторгруппе Der(G, A)/lder (G, А), где
Der(G, A) = {f:G-+ A\f (xy) = xf (y) + f (z), \fx,
— группа дифференцирований (или скрещенных гомо-
гомоморфизмов),
Ider(G, A) = {f:G—> A\ia?A, f (x) = xa — a, Vx?G}
— группа внутренних дифференцирований (или глав-
ных скрещенных гомоморфизмов), при этом точна после-
последов ател ьность
0—+AG—+A—+DeT(G, A)—+m(G, A)—ч-0;
для абелевой группы G группа H2(G, А) изоморфна
группе расширений группы А с помощью группы G
(см. Бэра умножение); третья группа когомологий груп-
группы G связана с препятствиями для расширений (см.
[9], гл. IV).
б) Если S — ассоциативная /f-алгебра, то группа
Н° (S, А) изоморфна группе
группа Я1 (S, А) изоморфна факторгруппе
Der(S, A)/ldei(S, A),
где
Der (S, A) = {f:S®KS°-+A\f (ху) = xf (у) -L/(x) у,
Ider(S, A) = {f:S @
группа H2(S, А) описывает сингулярные расширения
5-бимодуля А с помощью кольца S (см. [14]).
в) Если S — алгебра Ли, то группа H°(S, А) изоморф-
изоморфна /f-модулю {а?А\ха=0, Vx?S); группа ЯХE, А)
изоморфна факторгруппе
Der E, 4)/Ider(S, A),
где
Der E, A) = {f:S-+A\f([x, y]) = xf (y)~yf (x),
Ider(S, A)=:{f:S—+ A
двумерная группа когомологий H2(S, А) алгебры Ли
соответствуют /f-расщепляющимся расширениям ал-
алгебр Ли (см. [6], гл. XVI); в нек-рых случаях элементы
группы H3(S, А) являются препятствиями в задаче о
расширении.
Группы когомологий находят широкое применение в
различных областях алгебры. Так, напр., если G —
группа и H2(G, А) = 0 для всех ZG-модулей А, то G —¦
свободная группа (теорема Столлингса, см.
Гомологическая размерность). Если G — группа, С* —
мультипликативная группа поля комплексных чисел, то
группа M(G) = H2(G, С*) наз. мультипликато-
мультипликатором Шура группы G. Она играет важную роль при
изучении центральных расширений групп и в теории
проективных представлений конечных групп [1]. Если
G— группа, А — ZG-модуль и рА=0 для простого
числа р, то
ExtnzQ(Z, A)^ExinkG(k, A),
где k=GF(p) — поле из р элементов. Если G — конеч-
конечная р-группа, то d(G) = dim* H1(G, k) — минимальное
число образующих группы G, r(G) = dim.k H2(G, k) —
минимальное число определяющих соотношений для
G, рассматриваемой как про-р-группа, r(G)<:i?(G),
где R (G) — минимальное число соотношений дискрет-
дискретной группы G. Тот факт, что r(G) — d(G) стремится к
бесконечности при d(G)-voo, приводит к отрицательно-
отрицательному решению проблемы башни полей, проблемы Куроша
о нильалгебрах и общей проблемы Бернсайда [10].
Если G — про-р-группа, {?/,-, г?/} — семейство всех
ее открытых нормальных делителей, то группа
\imH»{G/Ui, AUi)
наз. ге-й группой когомологий пр о-р-
группы С с коэффициентами в gG-модуле А и
обозначается Hn{G, А). Если Е — расширение Галуа
поля L с группой Галуа G=G(ElL), то группа G яв-
является про-р-группой, группы H"(G, А) наз. группами
когомологий Галуа. Важную роль играют группы
Hq{G, Е*), где Е* — мультипликативная группа ноля
Е. Так, Hl(G, E*)=0, а следствием этого факта является
известная теорема Гильберта (о циклических расшире-
расширениях) 90. Если же Е — сепарабельное замыкание поля
L, то группа H2(G(E/L), Е*) наз. группой Бра-
уэра поля L (см. Брауэра группа). В настоящее
время A978) развита теория Галуа коммутативных
колец, в к-рой существенную роль играют когомологий
Галуа коммутативных колец и группа Брауэра.
Если S — ассоциативная алгебра, то из H2(S, S) = 0
следует, что алгебра S жесткая (см. Деформация ал-
алгебры).
Группы когомологпй IIn(R, А) в нек-ром смысле
двойственны группам гомологии
Я„(Д, А) = Тот*(А, К)
ассоциативной jff-алгебры Л с коэффициентами в Д-мо-
дуле А. Если С — группа, R=r?G и A' -Z, то группы
Hn(R, A) наз. группамиго молог и й груп-
группы G с коэффициентами в .й-модуле А и обозначаются
Hn(G, А); если S — ассоциативная if-алгебра и R =
= S@j(S~, то группы Hn(R, А) наз. группами
гомологии ассоциативной алгебры
S с коэффициентами в 5-бимодуле А и обозначаются
Hn(S, А); если S — алгебра Ли и R=Us— ее уни-
универсальная обертывающая алгебра, то группы Hn(R,
А) наз. группами гомологии алгебры
Л и S с коэффициентами в лиевом ^-модуле А и обо-
обозначаются Hn(S, А). Группы гомологии в малых раз-
размерностях в ряде случаев также допускают простую
интерпретацию. Так, если G — группа, то II0(G, %) =
~Ъ, H1(G, 1)=GI[G, G].
Если в абелевой категории функтор Нот обладает
производным функтором Ext и определен функтор (g)
с его производным функтором Тог, то приведенная
схема определяет теории гомологии и когомологий в
этой категории. Весьма общий подход к построению
теории когомологий может быть развит с использова-
использованием котроек [11]. Понятие (ко)тройки возникло при
анализе минимальных средств, необходимых для по-
построения симплициальных резольвент. Тройкой
Т= (Т, к, р) над категорией 21 наз. совокуп-
совокупность функтора Т : 31—>-31 и двух естественных преобра-
преобразований функторов к : 1И—>-Г, р : Г2-^-Г, подчиненных
условиям
poTk = p°kT = 1, роТр = рорТ.
Понятие котройки двойственно, т. е. получается из
приведенного обращением стрелок. Если объект X?Щ.
п морфизм q : T(X)-*-X удовлетворяют условиям
док(Х)=1х- Х-+Х, qoT(q) = qop(X) : T2(X)-+X, то па-
пару (X, q) наз. Г-алгеброй. Пусть 31Г — категория
Г-алгебр. Если Х?21, то F(X)=(T(X), p(X))?%T.
Тем самым определен функтор jP : Щ —*- Шт (в нек-ром
смысле F(X) — объект, свободный над X). Пусть
U : 5G —>-21 — функтор, забывающий Г-структуру.
Тогда функторы F и U сопряжены, UF=T, a G=FU :
: 9tr-^-2tr с I : G-^-l9lr, q : G-+G2 определяют котройку
(G, I, g) и комплекс
d0 dl da
X^-G (X) +— G2 (X) «— С3 (X) «— ...
с дифференцированием dn=^li=0( — l)iG"-'lGi (этот
комплекс является аналогом свободной резольвенты
объекта X). Если категория 21Г абелева и полученный
комплекс ацикличен, то стандартное применение функ-
функтора Нот (соответственно B>) приводит к построению
групп когомологпй (соответственно гомологии) объекта
X. В общем случае над Г-алгеброй (X, д) надо постро-
построить новую абелеву категорию (X, <?)-модулей, на к-рой
имеется естественная структура котройки, позволяю-
позволяющая уже построить группы, называющиеся группами
когомологий первоначальной категории (аналогично
построению групп когомологий для категорий групп,
ассоциативных алгебр н алгебр Ли). В эту схему вклю-
включаются как когомолопш групп, ассоциативных алгебр,
алгебр Ли, так и ряд других теорий когомологий (ко-
(когомологий коммутативных алгебр Харрисона, когомо-
когомологий Андре — Квиллена, когомологий Амицура и др.,
см. [8]).
Все приведенные конструкции относились так или
иначе к абелевым категориям. В то же время ряд раз-
разделов математики (напр., теория расширений групп)
приводит к необходимости построения теории когомо-
когомологий с коэффициентами в неабелевой категории (напр.,
в неабелевом G-модуле А в случае группы G) (см. [8),
[11]). Отправной точкой для построения различных
теорий неабслевых когомологий алгебр служат интер-
интерпретации когомолопш в размерностях 0 и 1, но при
этом приходится отказываться от нек-рых привычных
аспектов классической теории (структуры группы на
когомологиях и др.). Рассматривались когомологий то-
топологических алгебраических структур (напр., кого-
когомологий топологич. групп [5], банаховых алгебр и др.).
Лит.: [1] Schur J., «J. reine und angew. Math.», 1907,
Bd 132, S. 85 — 137; [2] Baer R., «Math. Z.», 1934, Bd 38,
S. 374—416; [3] Eilenberg S., MacLane S., «Proc.
Nath. Acad. Sci. USA», 1943, v. 29, p. 155 — 58; [4] Hopf H.,
«Comment, math, helv.», 1944/45, v. 17, p. 39—79; [5] Фад-
Фаддеев Д. К., «Докл. АН СССР», 1947, т. 58, № 3, с. 361 — 64;
[6] К а р т а н А., Эйленберг С, Гомологическая алгебра,
пер. с англ., М., 1960; [7] Гротендик А., О некоторых
вопросах гомологической алгебры, пер. с франц., М., 1961;
[8] Итоги науки. Алгебра. 1964, М., 1966, с. 203—35; [9] М а it-
лей н С, Гомология, пер. с англ., М., 1966; [10J С е р р Ж.-П.,
Когомологий Галуа, пер. с франц., М., 1968; [11] Seminar on
Triples and Categorical Homology Theory. Zurich. 1966—67,
В.— Hdlb.—N. Y., 1969; [12] Gruenberg K. W., Coho-
mological topics in group theory, B,— Hdlb.— N. Y., 1970;
[13] S t a m in b а с h U r s., Homology in group theory, B.—
Hdlb.— N. Y., 1973; [14] Possum R., Griflitli Ph.,
Reiter I., Trivial extensions of abelian categories. Homolo-
gical algebra of trivial extensions of abelian categories with app-
application to ring theory, В.— Hdlb.— N. Y., 1975.
В. E. Говоров, А. В. Михалев.
КОГОМОЛОГИЙ АЛГЕБР ЛИ — специальный слу-
случай когомологий алгебр. Пусть © — алгебра Ли над
коммутативным кольцом К с единицей и пусть задан
левый ©-модуль V, т. е. линейное над К представле-
представление алгебры © в К -модуле V. Модулем р-м е р -
ных когомологий алгебры Ли б) со
значениями в V наз. НР(®, F)=Ext^/M (К, V),
р = 0, 1, 2,. . ., где Uts) — универсальная обертываю-
обертывающая алгебра алгебры © [3]. Иначе говоря, соответствие
V\-*HP{®,V) есть р-й правый производный функтор для
функтора V-^-F® из категории ©-модулей в кате-
категорию К -модулей, где \r<3= {v? V\xv=G (.т^ 14)}. Функ-
Функтор V-+H* (©, V)--=^p>0HP(®, V) является когомо-
когомологическим (см. Гомологический функтор).
В малых размерностях К. а. Ли интерпретируются
следующим образом. Модуль Н° (®, V) совпадает с
Уы. Если V', V" — ©-модули, то Н1(®,Яот^ (V", V'))
можно отождествить с множеством классов эквивалент-
эквивалентных расширений ©-модуля V" с ядром V. Если рас-
рассматривать © как ©-модуль относительно присоеди-
присоединенного представления ad, то .Н1 (©,($) изоморфен
фактормодулю Der ©/ad ® модуля всех дифференци-
дифференцирований по подмодулю внутренних дифференцирований.
Если © есть свободный /f-модуль (напр., К — поле), то
Я2(©, V) отождествляется с множеством классов
эквивалентных расширений алгебры ©, ядром к-рых
служит абелева алгебра Ли V с заданным представле-
представлением алгебры @. Модуль #2(®, ®) интерпретируется
также как множество инфинитсзимальных деформаций
алгебры Ли ©.
Имеется следующая связь между К. а. Ли и когомо-
логиями ассоциативных алгебр; если ® — свободный
jf-модуль и V — произвольный двусторонний ?/©-мо-
дуль, то HP(U®, V)~HP(®, V), где представление
алгебры ® в V определяется формулой (х. v)\->xv—vx.
Другой способ введения К. а. Ли (см. [6], [14]) исполь-
использует коцепной комплекс С* (©, V) = ^v> 0СР (®, V),
где Ср(®, V)!=Cp — модуль всех кососимметрических
/(-линейных отображений ®P-+V, снабженный когра-
кограницей d : СР-+СР+Х вида
Xp + 1)
где знак л показывает, что соответствующий аргудгент
пропускается. В случае, когда ® — свободный К-
модуль, когомологии этого комплекса естественно
изоморфны модулям ЛР{®, V). С каждой подалгеброй
fed© связывается подкомплекс С* (©, Jp; F)cz6'* (©, V),
приводящий к относительным кого мол о-
г л я м Н* (©, ?; F) = 2p>o///'(®. •&; V). Если V -
алгебра над К, на к-рой @ действует дифференциро-
дифференцированиями, то в когомологиях возникает естественное
умножение, к-рос превращает II* (@, ij; V) в граду-
градуированную алгебру.
Пусть ©=3:(Af) — алгебра Ли (над R) гладких
векторных полей на дифференцируемом многообразии
М, V=--F(M) — пространство гладких функций на М
с естественной структурой ©-модуля. Определение
кограницы в С* (И{М), F(M)) формально совпадает с
определением внешнего дифференциала дифференци-
дифференциальной формы. Точнее, комплекс де Рама есть под-
подкомплекс в С* (?(ЛЛ, F(M)), состоящий из коце-
коцепей, линейных над F{M). С другой стороны, если
(S — алгебра Ли связной вещественной группы Ли G,
то комплекс С* (®, R) отождествляется с комплексом
левоинвариантных дифференциальных форм на G.
Аналогично, если § — подалгебра, отвечающая связ-
связной замкнутой подгруппе HczG, то С* (®, ?*; R) есте-
естественно изоморфен комплексу G-инвариантных диффе-
дифференциальных форм на многообразии GIH. В частности,
если G компактна, то отсюда получаются изоморфизмы
градуированных алгебр:
#*(©, R)s=#*(G, R); #*(©, §; R)?sЯ*(G/^^, R).
Именно эти факты послужили отправной точкой при
определении К. а. Ли. На них основаны и приложения
аппарата К. а. Ли к изучению когомологии главных
расслоений и однородных пространств (см. [8], [14]).
Двойственным образом определяются гомологии
алгебры Ли © с коэффициентами в
правом ®-м о д у л е V. А именно, р-мерная группа
гомологии есть /f-модуль Нр(®, V) = Tot^s (V, К).
В частности, Яо(©, V)=V/V®, а если V — тривиаль-
тривиальный ©-модуль, то #!(©, F)^F(g)A-®/[®, ©].
При вычислении К. а. Ли широко используются
следующие спектральные последовательности, часто
наз. спектральными последователь-
последовательностями Хохшильда — Серра. Пусть fi —
идеал в ® и V — некоторый ® - модуль. Если § и
®/6 — свободные А'-модули, то существует спектраль-
спектральная последовательность {E?'v} с Е$' Ч = НР (©/?>,
Hi(fc, V)), сходящаяся к //*(©, V) (см. [3], [141).
Аналогичная спектральная последовательность суще-
существует для гомологии [3]. Далее, пусть ® — конечно-
мерная алгебра Ли над полем К характеристики О,
©"с®' — ее подалгебры, причем ©' редуктивна в
©, V — ©-модуль, являющийся полупростым ©-моду-
©-модулем. Тогда существует спектральная последовательность
{Fpr'q} с Ff=Hp(.&, &'; V)&f[</(&', №"; К), схо-
сходящаяся к Н* (©, ©"; V) (см. [12], [14]).
Полностью изучены когомологии конечномерных ре-
дуктивных и, в частности, полупростых алгебр Ли над
полем характеристики 0. Если © — полупростая ко-
конечномерная алгебра Ли над таким полем, то для лю-
любого конечномерного ©-модуля V имеют место равен-
равенства
Я1 (®, V) = 0; #2(®, V) = 0
(леммы У а й т х е д а). Первое из этих свойств
является и достаточным условием полупростоты конеч-
конечномерной алгебры © и равносильно также полупро-
полупростоте всех конечномерных ©-модулей. Второе свойство
равносильно теореме Леви (см. Леей, — Мальцева раз-
разложение) для алгебр Ли с абелевым радикалом [1], [5],
[14]. Если © — редуктивная алгебра Ли, ?> — ее
подалгебра и V — конечномерный полупростой модуль,
то И* (©, §; V)=H* (©,§; Fffl), что сводит вычисле-
вычисление когомологии к случаю тривиального ©-модуля
V=K (см. [5], [14]). Алгебра когомологии Н* (©, К)
редуктивной алгебры Ли © естественно изоморфна ал-
алгебре С* (©, /?)а коцепей, инвариантных относитель-
относительно ad. В этом случае Н* (©, К) является алгеброй Хоп-
фа и, следовательно, есть внешняя алгебра над про-
пространством Р($ примитивных элементов, градуирован-
градуированных нечетными степенями 2т,-—1, г=1,..., г. В част-
частности, dim H1 (©,К) = dim Р\ есть размерность центра
алгебры @, а Р^ изоморфно пространству инвариант-
инвариантных квадратичных форм на © (см. [12], [14]). Если К
алгебраически замкнуто, то г есть ранг алгебры ©,
т. е. размерность ее подалгебры Картана 3(, а то,- суть
степени свободных образующих в алгебре многочленов
на ©, инвариантных относительно ad (или в изоморфной
ей алгебре многочленов на 31, инвариантных относитель-
относительно группы Вейля). В этом случае числа 2т/ — 1 совпа-
совпадают с размерностями примитивных классов когомо-
когомологии соответствующей компактной группы Ли.
Алгебра гомологии Н* (©, К) редуктивной алгеб-
алгебры Ли © над полем характеристики 0 есть внешняя
алгебра, двойственная к Н* (©, К). Для любой
n-мерной унимодулярной алгебры Ли ® справедлив
аналог двойственности Пуанкаре:
HP {Од, & К)е*Н„-т-р(®, $>; К),
где 0<:р<:п—т и § — любая m-мерная редуктивная в
© подалгебра (см. [14], [16]).
Для когомологии разрешимых алгебр Ли известны
лишь немногие сколько-нибудь общие утверждения.
Напр., пусть © — конечномерная нильпотентная
алгебра Ли над бесконечным полем, а V — конечномер-
конечномерный ©-модуль. Тогда ЦР(®, V) = 0 для всех р, если
в V нет тривиальных ©-подмодулей, и НР(®, V)^=0 для
р = 0, l,...,n = dim ©, причем dim H?(®, #)>2
для 1 <:/)<«—1, если такой ©-подмодуль существует
(см. [7]). Хорошо изучены группы Нр(П, V), где п —
нильпотентный радикал параболической подалгеб-
подалгебры $р в некоторой полупростой алгебре Ли © над ал-
алгебраически замкнутым полем характеристики 0, а
представление алгебры Ц в V является ограничением
некоторого представления алгебры © в V (см. [11]).
Эти когомологии тесно связаны с когомологиями ком-
комплексного однородного пространства G/P, отвечающего
паре ©ZMp, со значениями в пучках ростков голоморф-
голоморфных сечений однородных векторных расслоений над
GlP. Для вычисления когомологий неполупростых
конечномерных алгебр Ли над полем характеристики
О полезна формула
Я* (®, V) а= Н* (®Д), К) ® Н* (й, vf,
где i) — идеал в ©, причем ©Я) полупроста [14].
В некоторых случаях можно установить связь между
К. а. Ли и когомологиями групп. Пусть G — связная
вещественная группа Ли, К — ее максимальная ком-
компактная подалгебра, ®:эЯ — их алгебры Ли, V —
конечномерный гладкий G-модуль. Если определить
в V естественную структуру й-модуля, то когомологий
//* F5, St; V) изоморфны когомологиям группы G
{как абстрактной группы), вычисленным с помощью
непрерывных коцепей [10]. С другой стороны, пусть
<5) — алгебра Ли односвязной разрешимой группы Ли
G, Г — решетка в G и р : G-+GL ( V) — гладкое ко-
конечномерное линейное представление. Если р(Г)Х
ХАAГ плотна по Зарискому в алгебраич. замыкании
группы p(G)XAdG, то Я* (®, V)=H* (Г, V) (см. [4]).
В общем случае dim #/>(I\F)>dim HP(®V)(p=0,1,...).
Для нильпотентной © достаточно потребовать, чтобы
р было унипотентным. Если решетка Г в односвязной
разрешимой группе G такова, что Ad Г плотна в алгеб-
алгебраич. замыкании группы Ad Г (напр., G нильпотентна),
то Н*(&, R)=H*(G/r, R).
В последние годы стали систематически изучаться
когомологий некоторых бесконечномерных алгебр Ли.
К ним относятся алгебра Э?(М) векторных полей на
дифференцируемом многообразии М, алгебра Ли фор-
формальных векторных полей, подалгебры этих алгебр,
состоящие из без дивергентных, гамильтоновых или
канонических векторных полей (см. [2], [13]), а также
некоторые классические банаховы алгебры Ли [9].
Лит.: [1] Джекобсон Н., Алгебры Ли, пер. с англ.,
М., 1964; [2] Итоги науки. Алгебра. Топология. Геометрия,
т. 11, М., 1974, с. 37—123; [3] К а р т>а н А., Э й л е н б е р г С,
Гомологическая алгебра, пер. с англ., М., 1960; [4] Р а г у н а-
тан М., Дискретные подгруппы групп Ли, пер. с англ., М.,
1977; [5J Теория алгебр Ли. Топология групп Ли. Семинар «Со-
фус Ли», пер. с франц., М., 1961; [6] С h e v a I 1 е у С, Е i I e п-
berg S., «Trans. Amer. Math. Soc», 1948, v. 63, p. 85—124;
Й] Dixmicr J., «Acta scient. mat. Szeged», 1955, v. 16,
№ 3—4, p. 246—50; [8] G r e u b W., H a 1 p e r i n S., V a n-
stone R., Connections, curvature and cohomology. Vol. 3;
Cohomology of principal bundles and homogeneous spaces, N. Y.—
L., 1975; [9] d e la Harpe P., Classical Banach — Lie al-
algebras and Banach — Lie groups of operators in Hilbert space,
В.— Hdlb.— N. Y., 1972; [10] Hochschild G., M о s-
tow G. D., «111. J. Math.», 1962, v. 6. № 3, p. 367 — 401; [11]
К о s t a n t В., «Ann. Math.», 1961, v. 74, № 2, p. 329 — 87;
[12] К о s z u 1 J. L., «Bull. Soc. math. France», 1950, t. 78,
p. 65 —127; [13] Lichnerowicz A., «J. math, pures appl.»,
1974, t. 53, Л» 4, p. 459—83; [14] Verona A., Introducere
in coomologia algebrelor Lie, Buc. 1974. А. Л. Онищик.
КОГОМОЛОГИЙ БАНАНОВЫХ АЛГЕБР — груп-
группы Нп(А, X), п>0, где X — банахов бимодуль над
банаховой алгеброй А, определяемые как когомологий
коцепного комплекса
0—>-С0 (А, Х)—+. . .—+С" (А,
ые
и о
б"/
n-мерные цепи к-рого являются непрерывными «-ли-
«-линейными операторами из Л в X, а
+ (_!)/. + !/ (аъ ..., an)an+1.
К. б. а. могут быть также введены с помощью банахова
аналога функтора Ext, есть и их аксиоматическое оп-
определение.
Аналогично когомологиям алгебр, элементы одномер-
одномерных К. б. а. реализуются как непрерывные дифферен-
дифференцирования из А в X «по модулю внутренних», а эле-
элементы двумерных — как препятствия к расщепимости
сингулярных расширений А с ядром X. В то же время
на языке К. б. а. выражается ряд специфических
понятий анализа и топологии.
Алгебра А такая, что Нг(А, Х) = 0 для всех X, наз.
вполне отделимой; эти алгебры характери-
характеризуются тем, что все их сингулярные расширения рас-
щепимы. Специфика банаховых структур сказывается
в том, что такое требование является весьма жестким:
вполне отделимая коммутативная банахова алгебра
необходимо имеет конечный спектр (пространство
максимальных идеалов). В частности, вполне отделимая
алгебра функций совпадает с прямой суммой конечного
числа полей комплексных чисел.
Класс банаховых алгебр с тривиальными когомологи-
ями в высших (п^Э=3) размерностях уже не столь узок:
таковы, напр., бипроективные алгебры — алгебры А,
проективные, как банахов 4-бимодуль. Бипроектив-
ными являются L1- и С*-алгебра компактной группы, а
также алгебры ядерных операторов во всех класси-
классических примерах банаховых пространств. При нек-рых
условиях на банахову структуру топологически про-
простые бипроективные алгебры допускают полное опи-
описание, а любая полупростая бипроективная алгебра
разлагается в их топологич. прямую сумму.
Коммутативная алгебра наз. слабо наследственной,
если ее максимальные идеалы проективны. Это свойст-
свойство эквивалентно тривиальности Н2(А, X) с теми X,
у к-рых ха=Хх при всех х?Х, а?А. Для пректив-
ности идеала в коммутативной банаховой алгебре А
необходимо, а при A = C(Q) и достаточно, чтобы его
спектр был паракомпактен. В частности, слабая нас-
наследственность алгебры С (Q) эквивалентна паракомпакт-
паракомпактности всех множеств вида Q\{i}, t?Q.
Пространство, сопряженное к Л-бимодулю X, само
есть Л-бимодуль. Алгебры с Нп(А, Х*) = 0 при всех
X и п>0 наз. аменабельными, поскольку для
A = LX(G) такое свойство равносильно аменабельности
(усреднимости) самой G. В общем случае А аменабельна
тогда и только тогда, когда алгебра
обладает ограниченной аппроксимативной единицей.
Лит.: [1) Johnson В. Е., «Mem. Amer. Math. Soc»,
1972, № 127; [2] X e л е м с к и й А. Я., Труды семинара им.
Петровского, 1978, в. 3, с. 223—42. А. Я. Хелемский.
КОГОМОЛОГИИ ГРУПП — исторически первая тео-
теория когомологий алгебр.
Любой паре (G, А), где G — группа, а Л — левый
G-модуль, т. е. модуль над целочисленным групповым
кольцом Z(G), сопоставляется последовательность абе-
левых групп Hn(G, А), называемых группами
когомологий группы G с коэффици-
коэффициентами в А. Число п, пробегающее все целые не-
неотрицательные значения, наз. размерностью
группы Hn(G, А). Группы К. г. являются важными
инвариантами, содержащими информацию как о группе
G, так и о модуле А.
Группа HU(G, А) равна, по определению, НогпоB,
д)~А°, Где А0 — подмодуль G-инвариантных элемен-
элементов в А. Группы H"(G, А) для гС^\ определяются
как значения n-го производного функтора от функтора
A^/H°(G, А). Пусть
dn dn-i
...~*Рп * Pn-i — • ¦ • —" Ро —* Z -* О
— некоторая проективная резольвента тривиального
G-модуля % в категории G-модулей, т. е. точная после-
последовательность, в которой все модули Pj проектив-
проективны. Тогда Hn(G, А) — это п-я группа когомологий ком-
комплекса
<*'о
О -—>- Ното (^о, -4) —•" Homo (Plt A) —»-...,
где отображения dn индуцированы отображениями dn,
т.е. Hn(G, A)=Kerd'n/Imdn-1.
Группы гомологии групп определяются
при помощи двойственной конструкции с заменой всюду
функтора Homo функтором ®q.
Набор функторов A^JHn(G, А), ге=0, 1,. . ., яв-
является когомологическим функтором (см. Гомологичес-
Гомологический функтор) на категории левых G-модулей.
Модуль вида B=Hom (Z [G], X), где X — абелева
группа, a G действует на В по формуле
наз. ко индуцированным. Для инъективных
и коиндуцированных модулей A Hn(G, A)=0 при п^\.
Любой модуль А изоморфен подмодулю нек-рого коин-
дуцированного модуля В, Точная когомологическая
последовательность для последовательности
О —> А —* В —* В/А —>¦ О
определяет изоморфизмы Hn(G, BlA)~Hn + 1{G, A)
(l) и точную последовательность
Таким образом, вычисление n-j-1-мерной группы кого-
мологий для модуля А сводится к вычислению п-мер-
ной группы когомологий для модуля В/А. Этот прием
наз. сдвигом размерностей.
Сдвиг размерностей позволяет дать аксиоматичес-
аксиоматическое определение групп когомологий, а именно, их мож-
можно определить как последовательность функторов
A^\/Hn(G, А) из категории G-модулей в категорию абе-
левых групп, образующую когомологический функтор и
удовлетворяющую условию H"(G, B) = 0 при п^1 для
любого коиндуцированного модуля В.
Группы H"(G, А) можно рпределить также как
классы эквивалентности точных последовательностей
G-модулей вида
о—*а —* мх —* ...—+ мп-^х—+о
относительно подходящим образом определенной экви-
эквивалентности (см. [1], гл. 3, 4).
Для вычисления групп когомологий обычно исполь-
используют стандартную резольвенту тривиального G-модуля
Z, в которой РП=Ч [G" + 1] и для (g0,. . ., gk)?Gn'+1
где знак л означает, что член g,- опущен. Коцепи из
Ното(^п, ^4) — это функции /(g0,..., gn) такие, что
g/(go.---< gn)=f(ggo,- ¦ ¦, ggn)- Делая замену перемен-
переменных по формулам go=l, gi=hu g2=hlhi, gn=h1h2. . .hn,
можно перейти к неоднородным коцепям f(hi,...,hn).
Действие кограничного оператора на них таково:
d'f(hlt ..., An + i) = fci/ (йг, ..., Л„ + 1) +
+ (-l)a + 4(hi, ..., К),
напр., одномерный коцикл — это функция / : С—^А
такая, что f(gig2)=gif(g2)+f(gi) Для gx, g2?G, а когра-
кограница — функция вида f(g) = ga—а для нек-рого а?А.
Одномерный коцикл наз. также скрещенным
гомоморфизмом, а одномерная коцепь —
тривиальным скрещенным гомомор-
гомоморфизм о м. В случае, когда G действует на А тривиаль-
тривиально, скрещенные гомоморфизмы совпадают с обычными
гомоморфизмами, а все тривиальные скрещенные го-
гомоморфизмы равны 0, т. е. в этом случае H1(G, A) =
= Hom (G, А).
Элементы группы H1(G, А) можно интерпретировать
как классы автоморфизмов группы F, содержащейся
в точной последовательности 1_>_у1—>F—>-G—vl, тожде-
тождественные на А и на G по модулю сопряжений элемен-
элементами а?А. Элементы группы Н2 (G, А) интерпретиру-
интерпретируются как классы расширений группы А с помощью С.
Наконец, группа Н3 (G, А) допускает интерпрета-
интерпретацию в качестве препятствий для расширений неабелевой
группы Н с центром А с помощью G (см. [1]). Для п>3
аналогичная интерпретация групп Hn(G, А) неизвест-
неизвестна A978).
Если Н — подгруппа группы G, то ограничение
коциклов с G на Н определяет для всех п функториаль-
функториальные гомоморфизмы ограничения
res: Hn(G, А)—+Цп(Н, А).
При n=0 res совпадает с вложением AOczA^. Если
GIH — некоторая факторгруппа группы G, то подъем
коциклов с GlH на G индуцирует функториальные гомо-
гомоморфизмы инфляции
inf: H"(G/H, AH)-^H*(G, A).
Пусть ф : G'^-G — некоторый гомоморфизм. Тогда
любой G-модуль А ложно превратить в G'-модуль,
полагая для g' ?G', g'a=q>(g')a. Комбинируя отобра-
отображения res и inf, получают отображения II" (G, Л)—>-
-^H"(G', А). В этом смысле H^(G, А) является кон-
травариантным функтором по G. Если П — некоторая
группа автоморфизмов группы G, то группы H"(G, A)
можно превратить в П-модули. Напр., если Н — нор-
нормальный делитель в G, то группы Н"(Н, А) можно
снабдить естественной структурой GAff-модулей. Это
возможно благодаря тому, что внутренние автоморфиз-
автоморфизмы группы G индуцируют тождественные отображения
на группах II"(G, А). В частности, для нормального
делителя Н?G Im resc=#"(#, A)G/H.
Пусть Н — подгруппа группы G конечного индекса.
Тогда отображение нормы NqIH : A H-+A ° позволяет,
при помощи сдвига размерностей, определить для всех
п функториальные гомоморфизмы коограничения
cores: II" (II, A)-^Hn(G, A),
удовлетворяющие соотношению cores -res— (G : Н).
Если Н — нормальный делитель в G, то существует
спектральная последовательность Линдона, со вторым
членом E?-" = Hp(G/H, НЧ(Н,А)\, сходящаяся к
когомологиям @nHn(G, А) (см. [1], гл. 2).В малых
размерностях она приводит к точной последователь-
последовательности
inf res G /Htr
О —>¦ II1 (G/H, АН) —> m (G, A) —+ H' (tf, A) —>-
, AH)
где tr — отображение трансгрессии.
Для конечной группы G норменное отображение Nд:
А-4-А индуцирует отображение Nq : H0(G, A)-+H°(G,
А), где H0(G, A) = AUqA и Jo — идеал кольца % (G),
порожденный всеми элементами вида g—1 для g?G.
Отображение Nq позволяет срастить точные последо-
последовательности когомологий и гомологии. Точнее, можно
определить модифицированные группы когомологий —
//"(G, А) (называемые также когомологиями
Т е й т а) для всех целых п. При этом
Нп (G, A) = Hn(G, А) для п5э1,
Нп (G, .4)n=#_n_i(G, А) для п< —1,
Н-'Чв, Л) = КегЛ'о и #0(G, A) = CokevNa.
Для этих когомологий существует точная бесконечная
в обе стороны когомологическая последовательность.
G-модуль А наз. когомологически три-
тривиальным, если Нп(Н, А ) = 0 для всех п и любой
подгруппы H^G. Модуль А когомологически тривиа-
тривиален тогда и только тогда, когда для нек-рого iH' (Я, А) =
=0 п Hi + l(H, A) = 0 для любой подгруппы H^G.
Любой модуль А можно представить как подмодуль
или фактормодуль когомологически тривиального мо-
модуля, что позволяет применять сдвиг размерностей как
для повышения, так и для понижения размерности.
В частности, сдвиг размерностей позволяет определить
отображения res и cores (но не inf) для всех целых п.
Для конечно порожденного G-модуля А группы
Hn(G, А) конечны.
Группы Н" (G, А) аннулируются умножением на по-
порядок G, а отображения II(G, A)-+QpH"(Gp, А), ин-
индуцированные ограничениями, где Gp — некоторая
силовская р-подгруппа группы G, мономорфны. Это
позволяет сводить ряд вопросов о когомологиях ко-
конечных групп к рассмотрению когомологий р-групп.
Когомологии циклической группы имеют период 2,
т. е. для любого п Hn(G, A)~H" + 2(G, А).
Для любых целых п и т определено отображение
(наз. w-n р о и з в е д е н и е м)
Я» (G, A)%Hm (G, В) —* Нп + т (G, А ®?),
где тензорное произведение групп А и В рассматри-
рассматривается как G-модуль. В частном случае, когда А —
кольцо, и операции из группы G являются автоморфиз-
автоморфизмами, то ^-произведение превращает группу (+)nHn(G,
А) в градуированное кольцо. Теорема двойст-
двойственности для w-n р о и з в е д е н и я утверж-
утверждает, что для любой полной абелевой группы С и G-
модуля А w-пропзведение
H"(G, A)@H-"-1(G, Horn (A, C))—+H-X(G, С)
определяет изоморфизм между группами H"(G, А) п
Horn (H-"-1(G,llom(A, С)), H~1(G, С)) (см. [2]).
^-произведение определено и для бесконечной группы
G при условии, что п, т>0.
Многие задачи приводят к необходимости рассмотре-
рассмотрения когомологий топологич. группы G, непрерывно
действующей на топологич. модуле А. В частности,
если G — проконечная группа (случай наиболее близкий
конечным группам) и А — дискретная абелева группа,
являющаяся непрерывным С-модулем, то можно рас-
рассмотреть когомологии группы G с коэффициентами в
А, вычисляемые в терминах непрерывных коцепей [5].
Эти группы можно определить также как пределы
\imHn(GlU, Au) относительно отображений инфля-
инфляции, где U пробегает все открытые нормальные делители
в G. Эти когомологии обладают всеми основными свой-
свойствами когомологий конечных групп. Если G — про-р-
группа, то размерности над Z/pZ первой и второй групп
ее когомологий с коэффициентами в z/pZ интерпрети-
интерпретируются как минимальное число образующих и соотно-
соотношений (между этими образующими) группы G.
О различных вариантах непрерывных когомологий, а
также нек-рых других типах групп когомологий см.
[6]. О К. г. с неабелевой группой коэффициентов см.
Неабелевы когомологии.
Лит.: [1] Маклейн С, Гомология, пер. с англ., М.,
1966: 12] К а р т а н А., Эйленберг С, Гомологическая
алгебра, пер. с англ., М., 1960; [3] Алгебраическая теория чисел,
пер. с англ., М., 1969; [4] С е р р Ж.-П., Когомологии Галуа,
пер. с франц., М., 1968; [5] К о х X., Теория Галуа р-расши-
рсний, пер. с нем., М., 1973; [6] Итоги науки. Математика. Ал-
Алгебра. 1964, М 1966, с. 203—35. Л. В. Кузьмин.
КОГОМОЛбГИИ КОМПЛЕКСА — см. Гомологии
комплекса.
КОГОМОЛОГИП ГРУППА коцепи ого ком-
комплекса К'= (К", dn) абелевых групп — гра-
градуированная группа IT (К) = @Нп(К), где Нп(К) =
*= Ker dn+l/lm dn (см. Комплекс). Группа Нп{К) наз.
n-мерной, или ге-й, К. г. комплекса К' Это понятие
двойственно понятию группы гомологии цепного ком-
комплекса (см. Гомологии комплекса).
Модули когомологий коцепного комплекса в катего-
категории модулей также часто наз. К. г.
Когомологий группа цепного ком-
комплекса К.= (Кп, dn) Л-модулей с коэффициентами,
или со значениями, в А, где А — некоторое ассоциатив-
ассоциативное кольцо с единицей, а А — Л-модуль, есть К. г.
1Г (К., Л) =®//«(?., А)
коцепного комплекса
НотА(К., А) = (НотА(Кп, A), d*n),
где d*n{y) — yodn, ¦у?Нотл(,К'„, А). Частным случаем
этой конструкции являются К. г. полиэдра, сингуляр-
сингулярные К. г. топологич. пространства, К. г. групп, ал-
алгебр и т. д.
Если 0-^К.^Ь.^М.—>-0 — точная последователь-
последовательность комплексов Л-модулей, причем образы Кп —
прямые слагаемые в /,л, то естественным образом воз-
возникает точная последовательность
а* Р* d*
С другой сторопы, если К.— комплекс Л-модулей,
причем все Кп проективны, то с каждой точной по-
последовательностью 0-+А-+В-+С-+0 Л-модулей связана
точная последовательность К. г.
...—>Я» (К., А) —* Н" (К., В) —>¦ Н" (А'., С) —>
О К. г. топологич. пространства см. Гомологии груп-
группа топологич. пространства, Когомологий.
Лит.: [1] К а р т а н А., Эйленберг С, Гомологиче-
Гомологическая алгебра, пер. с англ., М., 1960; [2] Годеман Р., Ал-
Алгебраическая топология и теория пучков, пер. с франц., М.,
1961; [3] Маклейн С, Гомология, пер. с англ., М., 1966.
Л. В. Кузьмин.
КОГОМОЛОГИЙ КОЛЬЦО — кольцо, аддитивной
группой к-рого является градуированная группа кого-
когомологий
ф:=онп(Х, а),
где X — некоторый цепной комплекс, А — группа коэф-
коэффициентов, а умножение определяется по линейности
набором отображений
vm,n: Hn(X, А)®Н"(Х, 4)-*#*» + "(*, А)
для всех т, п^О, являющихся внутренними когомо-
логич. умножениями. К. к. оказывается при этом снаб-
снабженным структурой градуированного кольца.
Для существования отображений vm> „ достаточно
иметь набор отображений vm> „ : Хя + „—>-Хя(Х)Х„, удов-
удовлетворяющих нек-рым дополнительным свойствам, и
отображение А(?)А—*-А, т. е. умножение в группе
коэффициентов А (см. [2]). Тогда отображения vm> „
индуцируют отображения
Нот(Хи, А)®Шт(Хп, А) — Нот (Хт + а, А),
к-рые в свою очередь индуцируют на когомологиях ото"
браженпя vm? „.
В частности, структура кольца определена на гра-
градуированной группе Н(G, Z)—(?)n=otfn(G, Z), где
G — некоторая группа и % — кольцо целых чисел с
тривиальным действием группы G. Соответствующие
отображения vOT? „ совпадают с ^-произведением. Это
ассоциативное кольцо с единицей, а для однородных
элементов a, b?H(G, Ж) степеней р и q соответственно
выполняется соотношение ab=(—\)Pqba.
Аналогично, w-произведение определяет структуру
кольца па группе ф~=оЯ"(Х, Z), где II"(X, %) —
тг-мерная группа сингулярных когомологий топологпч.
пространства X с коэффициентами в %.
Лит.: [1] К а р т а н А., Эйленберг С, Гомологиче-
Гомологическая алгебра, пер. с англ., М., 1960; [2] МаклейнС, Го-
Гомология, пер. с англ., М., 1966. Л. В. Кузьмин.
КОГОМОЛОГИЧЕСКАЯ ОПЕРАЦИЯ — естествен-
естественное преобразование одних когомологич. функторов в
другие (чаще всего — в себя).
Когомологической операцией типа
(п, т.; л, G), п, т — целые числа, я, G — абелевы
группы, наз. такое семейство заданных для любого
пространства X отображений (не обязательно гомомор-
гомоморфизмов) групп когомологии вх : Н"(Х\ л)-+Нт(Х; G),
что для любого непрерывного отображения / : X—>-
—>-F, 6x°/*=/*°0V (естественность). Множество всех
К. о. типа (п, то; л, G) образует абелеву группу отно-
относительно сложения: (9+1(з)х=9\'+'1С\'' обозначаемую
О(п, т; я, G).
Примеры К. о.: Стинрода приведенные степени
Sql и %pl\ Понтрягина квадрат ^р1; Постникова квад-
квадрат; возведение в к-ю степень [ц.: для x?Hs(X; л),
где я — кольцо, j.1/,(x)^=xk, \ik?O(s, ks, л, я); гомо-
гомоморфизм Бокштейна Р; К. о., индуцированные гомомор-
гомоморфизмами л—>-G групп коэффициентов, например mod
р :НП(Х)-*.Н"(Х; %р).
К. о. представляют собой дополнительную структуру
в когомологич. функторах, ввиду чего они позволяют
решать такие задачи гомотопич. топологии, к-рые нель-
нельзя решить «на уровне» групп когомологии. Приме-
р ы: 1) пусть X и Y — два пространства и х?Н"(Х; я),
y?Hn(Y\ л) — два элемента. Существует ли отоб-
отображение / : X-+Y с /* (у) = х? Первым достаточным
условием отсутствия такого / является отсутствие го-
гомоморфизма g : H* (Y; я)—кЯ* (X; я) с g(y) = x (таким
приемом доказывается, напр., Бр'ауэра теорема о
неподвижной точке). Если g существует, то несущест-
несуществование отображения / можно установить так: пусть
имеется К. о. 8?0(п, т; я, G) с 6к(г/) = 0, вх(х)ф0.
Тогда 0^8x(x)=Qx(f*(ij))=f* {QY(l/))=f* @) = 0, что не-
невозможно; в частности 6(О) = 0. 2) Существенно ли
отображение / : Sm-+Sn? Пусть Сf=Sn^fem. Тогда
(при тфп) Hm + 1(Cf; G) = G, Hn(Cf\ я) = я. Если суще-
существует К. о. в?О(п, то+1; я, G) с 8С ФО, то / сущест-
существенно. В этом случае операция 6 детектирует
отображение / или элемент [/] ?лт E")-
Имеет место изоморфизм группы О(п, т; я, G)«
~Нт(К(л, n)\ G), где К(л, п) — Эйленберга—Мак-
лейна пространство, и потому О(п, т; л, G)==
~[К(л, п), K(G,m,)] (см. 11редставимый функтор).
Группы Пт(К(п, и); G) вычислены для всех т и п и
любых конечно порожденных я и G [9].
Когомологическая надстройка
Щ^О(п~ 1, m — i; я, G) над К. о. 9?<9(п, т; я, G),
определяется отображением 10х, заданным композицией
Дп-ЦХ; л) —> Я" (SX; л) —* II<" (SX; С) -^
^^ffrn-l (X; G),
где SX — надстройка над X. Напр., 1|ц.—О, 1S5' =
= Sq', 13ii=Sii. При т<2п—11(в) есть изоморфизм.
Для любого X 16^ есть гомоморфизм групп.
Стабильной (или стационарной) ко-
когомологической операцией типа (я, G)
степени к наз. набор {6„}!^ с 6„?0(п, п+к; я, G) и
16п=0п-1- Такие К. о. образуют абелеву группу
Os(k; я, G), изоморфную группе lim_ Нп + к(К(л, п)\ G)
п
— обратному пределу последовательности
. ..*— Нп + к (К (я, п); G) *—
^ Hn+k-i(K (я, n — i); G)-1—...
Группа (?)kOs(k; я, G) обозначается 0${л, G). '
Примеры стабильных К. о.: степени
Стинрода5д'?05(г; %г, %2) а Р1' gO5B (pi— 1); %р, г?р),
/>>2 — простое, и гомоморфизмы Бокштепна C ?
€os(i; z», 2Я).
Если 6?0(п, то; я, G) и cp?0(m, Z; G, т), то опреде-
определена К. о. ц>эв?О(п, I; л, т). В частности, можно опре-
определить композицию (рэв?О$(л, т) любых двух стабиль-
стабильных К. о. в^О$(л, G) н <p?Os(G, т), так что группа
0s(it, л) является кольцом; O$(Iip, Г&р) наз. Стиирода
алгеброй А „.
К. о. впервые появилась при решении задачи клас-
классификации отображений (п+1)-мерного полиэдра в п-
мерную сферу (п^=2 в [1] и и>2 в [2]). Теорема
классификации [2]. Имеет место точная после-
последовательность групп:
О—
mod 2
[ЛГ, 5«] —->- ker (II" (X) >¦ II" (X; Z2)
»0.
Теорема продолжения [2]. Пусть Y —
(п+2)-мерный полиэдр, У + 1— его (п-г1)-мернын ос-
остов. Отображение f : Yn + 1-^-S" определяет элемент
i/=f*(s)^H"(Y" + 1), где s?H"(S") — образующая. Это
отображение продолжается до g : Y—+-S" тогда и только
тогда, когда Sq2 (у mod 2) — 0.
Отвечающее К. о. 6?0(n, m; я, G) отображение
6 : К(л, n)-+K(G, m) из стандартного Серра расслоения
K(G, то —1)—>-PA'(G, m)—*A'(G, то)
индуцирует расслоение
F = K(G, т — 1) -^-? (9) —*А'(я,п) =fi.
Вторичные когомологические опе-
операции — классы когомологий пространств Я F). Бо-
Более точно, пусть задан элемент tf^Hq(E(Q); Н), Н —
абелева группа. Для любого и^Н"(Х; я) с вх(и)=0
существует и?[Х, Е(Q)] ср#а=в, где р#: [X, ?"F)]—>.
-^>-[Х, В] — индуцированное р отображение, и элемент
!?=<рэи = и*(ср) ?IIQ(X; H), зависящий от выбора элемен-
элемента и. Произвол в выборе и определяется прообразом
p-1(u), т. е. орбитой действия группы [X, F] = Hm~1
(X; G) на множестве [X, Е(в)]. При т<2п— 1 и q<2n—1
i# н <Р# будут гомоморфизмами групп, и потому при
другом выборе и элемент v может измениться лишь на
нек-рый элемент подгруппы lm(t*<p : Hm(X\ G)—>.
-v//?(X; H)) = Q группы НЧ(Х; Н). Определим вто-
вторичную К. о. Ф, полагая Ф^- (и) — и -\- Q (смежный класс
u-\-Q однозначно определен элементом и). Таким обра-
образом, отображение Фу определено на подгруппе Кег 6д-
и принимает значения в факторгруппе Нд(Х; II)/Q,
где Q наз. неопределенностью К. о. Ф.
Другое название: Ф — частичная многозна-
многозначная К. о. из #"(•; я) в Н9(-; И).
Вторичные К. о. естественны в следующем смысле:
для любого / : Y-+X ц любого к^Кег QczH"(X; n)
имеет место: /*(Фд(м))с:ФИ/*(и)) [3]. Если i*((p)--=-0,
то <р=р*(9') для нек-poii 6' ^НЧ(В\ Н), так что и*(ф) =
= 6'(и), и потому Фи=в*(в')=9'(и) с нулевой неопре-
неопределенностью. При этом для К. о. 6" ?Нт(В; Н) с
р*F") = ф и элемента и?Кег 6 выполнено 6'(«) — 6"(и),
так что К. о. Ф является однозначной К. о. 6', ограни-
ограниченной на Кег 0.
Каждой вторичной К. о. отвечает нек-рое соотноше-
соотношение между обычными (п р и м а р н ы м и) К. о. Если
q<2m—1, то К. о. ?*(ф) ?H4(K(G, то—1); Я) одно-
однозначно представляется в виде 1-1)з с т|>?Я'? + 1 (K(G, m^r
+ 1); Я) и i|joe=0. Если ф'?Ят(?F); Я) такова, что
?*(ф—ф')=0, то К. о. Ф' отвечает то же самое соотно-
соотношение ijx>6=0. Обратно, любому соотношению вида
i|>o6~0 отвечает множество вторичных К. о. {Ф}, лю-
любые две из к-рых отличаются друг от друга на при-
марную К. о., определенную на ядре К. о. 6.
Более общее понятие вторичной К. о. получается,
если исходить из набора 6=F1, ..., 6„) с в,-?Нт1
(К (я, п); G) и соотношения ^Ч^-об/^О (см. [3]).
Пример вторичной К. о. Пусть
и пусть q>?ff" + 3(?(9); Z2)—22-образующая. Воз-
Возникает вторичная К. о. а ://"(•; ^)_>_//« + 3(.; й2),
соответствующая соотношению Sq2o(Sqi^mod 2)—0. Она
позволяет классифицировать отображения (ге+2)-мер-
ного полиэдра в n-мерную сферу, п>2. Решение соот-
соответствующей задачи продолжения таково. Пусть
У— (п+3)-мерный полиэдр и пусть дано отображение
/: Yn + l-+Sn, так что имеется элемент y?Hn(Yn + 1),
y?f*(s). Для продолжения / на У» + 2 необходимо ус-
условие Sq2(y mod 2) = 0; если / продолжается на У" + 2,
то на у определена а. Оказывается, что / можно про-
продолжить на У тогда и только тогда, когда 0?а(у).
При этом а детектирует отображение 6'" + 2-^-Sn + 1-^-5n,
являющееся композицией надстроек над отображением
Хопфа 53—>-5а и задающее образующую группы я„ + 2
(S«)^Z2.
С помощью вторичных К. о. было дано также первое
решение проблемы «нечетного инварианта Хопфа» [7].
Для отображения / : S2"-1-^>-S" инвариантХоп-
фа H(f)?Z определяется формулой u2=H(f)v, где
v?H2"(Sn^fe2n)=Z, u?Hn(Sn^fe2")=Z —образующие.
Нечетность Н (f) равносильна условию Sqnun=^=0, где
un^H»(Sn^fein\ Z2)=Z2- При n^2s операция Sq"
разложима в классе примерных операций, т. е. Sqn=
=2 at^?*> так чт0 Н if) может быть нечетным лишь
при n=2s. Но в классе вторичных операций Sq2S раз-
разложимы при s=ytl, 2, 3, и поэтому И (/) нечетно лишь
при ге=2, 4, 8.
Наряду с вторичными К. о. существуют третичные
К. о. и вообще К. о. любого порядка. Примарной опе-
операции 6 и элементу (p?HQ(E(Q); Н), определяющим
вторичную К. о. Ф, отвечает отображение ЯF)—>-
-+К(Н; q), индуцирующее из расслоения Серра над
К(Н; q) расслоение К(Н, q—l)-^E (Ф)^-Е (Q); при
этом Е(Ф) наз. пространством когомоло-
когомологической операцииФ. Имея класс когомоло-
гий ч?Нг(Е(Ф)\ А), можно построить третичную
К. о. Г : Нп(Х; л)-+Нг(Х; А), определенную на Кег Ф,
неопределенность к-рой (при подходящих размерно-
стных ограничениях) есть1т(г*7). Этой К. о. отвечает
соотношение т|ьФ =0, где лр — примарная К. о., 1i))= i*y.
Индуктивное продолжение этого процесса приводит
к определению когомологической опера-
операции п-го порядка. Иными словами, для К. о.
| гг-го порядка, пространство к-рой есть -Е(|), и эле-
элемента XQHS(E(|); С) строится К. о. (п+1)-го порядка
Л, определенная на Кег 1. При этом пространство
Е (А) является пространством расслоения, индуциро-
индуцированного из расслоения Серра над К (С, s) отображе-
отображением X : ?(!)—*-К(С, s). Построена [12] аксиоматика
высших К. о.
Простейшими примерами высших К. о. являются
высшие гомоморфизмы Бокштейна.
Пусть дана точная последовательность групп
и соответствующая точная последовательность
р mod p 6
...Н"(Х)—+Н»(Х) >¦ Н" (Х;ХР) ~+ И»*1 (Х)—+ ...
Гомоморфизм P=mod роб : Я"(Х; zp)-^Hn + 1(X; %p)
И есть гомоморфизм Бокштейна; р ^(9^A; 2„, Zp).
Имеет место fbp=O; этому соотношению отвечает вто-
вторичная К. о. Р2. При этом рор2=0, так что возникает
третичная К. о. C3- И вообще рг— это К. о. порядка г,
построенная по соотношению рорг_] = 0. При этом РГ
определен на Ker Pr-j. Явное описание К. о. рг вы-
выглядит так: пусть х?Нп(Х; Ър) и пусть с — пред-
представляющий его коцикл с коэффициентами в %„\
равенство $г-гх=0 означает, что существует цело-
целочисленный представитель z коцикла с, кограница 6z
которого делится на рг. Тогда $гх — класс когомоло-
гий mod р коцикла —- . Таким образом, информация
р
о действии высших К. о. Бокштейна в группах Н*{Х;
Жр) позволяет полностью вычислить свободную часть
и р-компоненту группы Н*{Х) = Н*(Х; %,).
Каждой частичной К. о. Ф отвечает гомотопическп
простое пространство Е(Ф) с конечным числом (нетри-
(нетривиальных) гомотопич. групп. Обратно, каждому та-
такому пространству Е можно сопоставить К. о. Ф, для
к-рой Е и Е (Ф) слабо гомотопически эквивалентны,
Е^.Е(Ф). Напр., если Е — пространство с двумя
нетривиальными гомотопич. группами л„(?)=я, лт
(E) = G1 m>ra, то имеется отображение Е-+К(л, п),
индуцирующее изоморфизм лп{Е)-+лп(К (я, п)). Это
отображение можно превратить в расслоение, слоем
к-рого будет К(G, то); это расслоение индуцируется из
расслоения Серра над K(G, m-\-\) нек-рым отображе-
отображением К (л, n)-+K(G, m-\-i), последнее задает К. о.
В?О(п, то+1; я, G).
Эти соображения позволяют описать слабый гомо-
гомотопич. тип любого пространства, сопоставив ему на-
набор частичных К. о. {kn}™_i , наз. его n-ми постни-
ковскими факторами (см. Постникова системы). Напр.,
для сферы Sn, ге>3, первым постниковским фактором
является Sq2, а вторым — а.
Другим важным типом К. о. являются функцио-
функциональные когомологические опера-
операции [3]. Для их определения задается отображение
/: У-^-Х («функция») и К. о. в?О(п, то; я, G). При
m«:2n—2 6 лежит в образе когомологич. надстройки и
является гомоморфизмом групп. Если / — замкнутое
вложение (корасслоение) и ; : Х-^-(Х, Y) —включение,
то функциональная К. о. 6^: П"(Х; л)-^//"*-1 (Y, G)
определяется как частичное многозначное отображение
/* 6(Х,У) 6
Bf.H" (X; я) ¦<— Я" (X, Y; я) >¦ Нт (X, Y; G) ¦<—
6^=6-1oGo(;'*)-1. Эта К. о. определена на подгруппе
Кег /* f"|Ker Qx группы НП(Х, я), а ее неопределенность
есть подгруппа 1шA6г/)-|-1т(/*) группы H"-1(Y; G).
Конструкция функциональной К. о. естественна по /.
Пример: если для отображения / : Y-^-X сущест-
существует такая (примарная) К. о. 6 и такой класс когомоло-
гий и пространства X, что Of (и) определена и 0(?6^(ц),
то отображение / существенно. Функциональные и вто-
вторичные К. о. связаны между собой формулами Петер-
сона — Штейна (см. [31), позволяющими в ряде случаев
сводить вычисление вторичных К. о. к вычислению
примарных и функциональных К. о. Существуют также
функциональные К. о. высшего порядка [6].
Конструкцией, аналогичной по построению и при-
приложениям высшим К. о., является Масси произведение.
Понятие К. о. было перенесено и в обобщенные тео-
теории когомологий. К. о. типа (п, т) в обобщенной теории
когомологий h* наз. естественное по X преобразование
h"(X)-^t-hm(X). Эти К. о. образуют группу, изоморф-
изоморфную группе hm(Mn), где {М^, s^} — Q-спектр, пред-
представляющий теорию h*. Группа всех стабильных К. о.
является (относительно композиции) кольцом Ah, так
что h*(X) — естественный по X Лй-модуль. Понятия
частичной и функциональной К. о. также имеют ана-
аналоги в обобщенных теориях когомологий.
С помощью частичных К. о. в обычной теории кого-
когомологий можно решить в принципе любую гомотопич.
задачу, однако практич. применение К. о. порядка
гс>3 весьма трудоемко. В то же время часто бывает,
что задача, требующая для своего решения обычных
К. о. высшего порядка, может быть решена примене-
применением примарных К. о. в подходяще выбранной обоб-
обобщенной теории когомологпй. Напр., проблема «инва-
«инварианта Хопфа» легко решается с помощью примарных
когомологич. операций Адамса 1|з* в К -теории [10].
Эти К. о., введенные [8] для решения задачи о вектор-
векторных полях на сферах, явились первым примером К. о.
в обобщенной теории когомологий.
Алгебра Ah вычислена [4] для h= U*— теории уни-
унитарных кобордизмов и использована при построении
спектральной последовательности типа Адамса, началь-
начальный член к-рой есть когомологин алгебры Аи. Ин-
Информация о действии кольца Ah в группах h*(X) ока-
оказывается полезной при вычислении спектральной после-
последовательности Атья — Хирцебруха в теории h* [11].
Лит.: [1] П о н т р я г и н Л. С, «Матем. сб.», 1941, т. 9,
с. 331—63; [2] Steenrod N., «Ann. Math.», 1947, v. 48,
p. 290 — 320; [3] M о ш е р Р., Т а н г о р а М., Когомологи-
Когомологические операции и их приложения в теории гомотопий, пер. с
англ., М., 1970; [4] Новиков С. П,, «Изв. АН СССР. Сер.
матем.», 1967, т. 31, №4, с. 855 — 951; [5] Стинрод Н.,
«Математика», 1958, т. 2, № 6, с. 11—48; [6]Петерсон Ф.,
там же, 1958, т. 2, № 2, с. 47—60; [7] А д а м с Д ж., там же,
1961, т. 5, № 4, с- 3—86; [8] е г о ж е, там же, 1963, т. 7, № 6,
с. 49—79; [9] К а р т а н А., там же, 1959, т. 3, № 5, с. 3—50;
т. 3, № 6, с. 3—45; [10] Атья М., Лекции по К-геории, пер.
с англ., М., 1967; [11] Бухштабер В. М., «Матем. сб.»,
1969, т. 78, с. 307—20; 1974, т. 83, с. 61 — 76; [12] М a u n d e г С,
«Proc. Lond. Math. Soc», 1963, v. 13, p. 125 — 154.
Ю. Б. Рудяк.
КОГОМОЛОГИЧЕСКАЯ ПОСЛЕДОВАТЕЛЬ-
ПОСЛЕДОВАТЕЛЬНОСТЬ — см. Гомологическая последовательность.
КОГОМОЛОГИЧЕСКАЯ РАЗМЕРНОСТЬ — 1)
К. p. (dimaX) топологического прост-
пространства X относительно группы
коэффициентов G — максимальное целое чис-
число р, для к-рого в X найдутся замкнутые подмножества
А такие, что когомологий НР(Х, А\ G) отличны от нуля.
Аналогично определяется гомологическая размерность
h uiiUqX. Конечная лебегова размерность совпадает
с dimo (с ndimG), если G — целые числа (приведен-
(приведенные по модулю 1 действительные числа). В евклидовом
пространстве XdR" равенство dimgX=p равно-
равносильно тому, что X локально зацепляется (га—р — 1)-
мерными циклами (с коэффициентами в G). Для пара-
компактных пространств X неравенство сИтдХ-^гр
равносильно существованию мягких резольвент для G
длины р. Поскольку мягкие пучки ацикличны, этим
устанавливается связь с общим определением размер-
размерности в гомологич. алгебре, напр, инъективная (про-
(проективная) размерности модуля <:р, если он обладает
инъективными (проективными) резольвентами длины р;
глобальная размерность кольца есть максимум инъек-
тивных (проективных) размерностей модулей над коль-
кольцом и является аналогом лебеговой размерности X.
Лит.: [1] Александров П. С, «Ann. Math.», 1929,
v. 30, p. 101—87; [2] е г о же, «Math. Ann.», 1932, Bd 106,
S. 161—238; [3] e г о же, Введение в гомологическую теорию
размерности и общую комбинаторную топологию, М., 1975;
Г4] X а р л а п А. Э., «Матем. сб.», 1975, т. 96, № 3, с. 347—73;
[5] К у з ь м и н о в В. И., «Успехи матем. наук», 1968, т. 23,
Х° 5, с. 3—49; [6] В г е d о n G. E., Sheat theory, N. Y., 1967;
[7] К а р т а н А., Э й л е н б е р г С, Гомологическая ал-
алгебра, пер. с англ., М., 1960. Е. Г. Скляренко.
2) К. р. схемы — аналог понятия когомологиче-
когомологической размерности топологич. пространства для алгеб-
раич. многообразия или схемы с выбранной теорией
когомологий на них. Пусть X — алгебраич. многооб-
многообразие или нётерова схема размерности п. К. р. схемы X
наз. целое число cd(X), равное нижней грани в тех i,
для к-рых HJ(X, йП = О для всех абелевых пучков на
топологическом пространстве X при />г. Справедливо
неравенство
Когерентной когомологической раз-
размерностью схемы X наз. число cohcd(X), равное
нижней грани тех i, для к~рых IU{X, 5~) = 0 для всех
когерентных алгебраич. пучков ^ на X при />?. В силу
определения cohcd(X)«xd(X). По теореме С е р-
р a cohcd(X) = 0 тогда и только тогда, когда X —
аффинная схема. С другой стороны, если X — алгеб-
алгебраич. многообразие над полем к, то cohcd(X) = « тогда
и только тогда, когда X собственно над к (теорема
Л и х т е н б а у м а) (см. [3]).
Пусть X — собственная схема над полем к, Y —
ее замкнутая подсхема коразмерности d и U=X — Y.
Тогда имеют место следующие утверждения ([2] — [4]).
Если Y — теоретико-множественное полное пересе-
пересечение обильных дивизоров на X, то
если X — проективное многообразие Коэна — Мако-
лея (напр., неособое проективное многообразие) и У
нульмерно, то cohed (U)=n—1. Условие cohed (?/)<.
<:ге—2 равносильно тому, что Y связно. Если Х = Рп-~
проективное пространство и У связно и размерности
cohed (?/)<»—1.
Если X — алгебраич. комплексное многообразие, то
можно рассматривать гомологич. размерность соответ-
соответствующего топологич. пространства X (С). В общем
случае, когда X — нётерова схема, аналогом гомоло-
гомологич. размерности является понятие этальной
когомологической размерности
схемы X. Точнее, пусть Xef— этальная топология
Гротендика схемы X и I — простое число. Когомо-
Когомологической l-тр аз мерностью схемы
X (или э т а л ь н о й К. р.) наз. число cd;(X), равное-
нижней грани тех г, для к-рых HJ(Xef, §~) = 0 для всех
Z-периодических абелевых пучков JF на Xet при />t.
Если Z = Spec A — аффинная схема, то cd^Spec А)
наз. также К. р. кольца А. В частности, если А —
поле, то понятие cd;(.<4) совпадает с понятием К. р.
поля, к-рое изучается в теории Галуа когомологий.
Если X — алгебраич. многообразие размерности п
над полем к и Iфchar к, то cAt(X) <2ra+cdz(fc). В част-
частности, если к — сепарабельно замкнутое поле, то
cAi(X)^2n. Если X — аффинное алгебраич. многооб-
многообразие над сепарабельно замкнутым полем к, то cd;(X)<:
<dim X.
Пусть к — поле конечной характеристики р, тогда
для любой нётеровой схемы X над полем к имеет место
неравенство
В частности, для любого нётерова коммутативного
кольца А
Если X — квазипроективное алгебраич. многооб-
многообразие над сепарабельно замкнутым полем к, то cdj0(X)<:
<:dim X, где р — характеристика к.
Лит.: [1] Гротендик А., О некоторых вопросах го-
гомологической алгебры, пер. с франц., М., 1961; [2] Н а г t s h о г-
n e R., «Ann. Math.», 1968, v. 88, p. 403—50; [3] e г о же,
Ample subvarieties of algebraic varieties, В., 1970; [4] e г о же,
«Compositio math.», 1971, t. 23, № 3, p. 257—64; [5] Theorie des
topos et cohomologie etale des schemas, B.— Hdlb.— N. Y., t. 2,
1972; t. 3, 1973. И. В. Долгачев.
КОГОМОЛОГИЧЕСКИЙ ФУНКТОР -- см. Гомоло-
Гомологический функтор.
КОГОМОЛОГИЧЕСКОЕ МНОГООБРАЗИЕ — см.
Гомологическое многообразие.
КОГОМОТОПИЧЕСКАЯ ГРУППА — одно из обобще-
обобщений одномерной группы когомологий, понятие, в нок-
ром смысле дуальное понятию гомотопической группы.
Пусть п"(Х) = [Х, S"] — множество гомотопич. клас-
классов непрерывных отображений пунктрировапного топо-
логич. пространства X в пунктированную сферу.
Множество я"(Х) не всегда имеет естественную струк-
структуру группы (это так лишь при га=1, 3, 7, поскольку
тогда S" является Н-пространством). Группа ^{Х)
совпадает с Hi(X, 3).
Если X — клеточное разбиение размерности, не пре-
превосходящей 2ге—2, то на множестве л"(Х) следующим
образом] задается структура группы. Для [а], [0] ?
?лп(Х) рассматривается отображение
(а X Р) ° А:X ~^Sn X S»,
здесь А : Х—уХХХ — диагональное отображение, а,
Р : X-+Sn— представители классов [а], [Р]. Ввиду
ограничения на размерность X существует единствен-
единственный гомотоптгч. класс отображений / : X—*-S" v S"
(здесь S"vS"— букет пунктированных сфер), компо-
композиция к-рого с естественным включением SnvS"cz
dS-'XS" совпадает с гомотоппч. классом отображения
(ахР)оД. Гомотоппч. класс [6о/]?я"(Х) отображения
8з/ : X-+-S", где 9 : S"\/Sn—*-Sn— складываннцее ото-
отображение, полагается равным [сс] + [Р]? л"{Х). Отно-
Относительно описанной операции множество п"{Х) пред-
представляет собой абелеву группу, поэтому часто функтор
л" рассматривается как функтор, определенный лишь
на категории клеточных разбиений размерности, не
превосходящей 2и—2, со значениями в категории абе-
левых групп. Для клеточных разбиений X размер-
размерности, меньшей п, л"{Х) = 0. Таким образом, функ-
функтор я" представляет интерес в размерностях от п до
2п—2, т. е. в так наз. стабильных раз-
размерностях.
Если dim X<2«—2, то nh(X)~nn + \SX), где SX —
надстройка над X. Этот изоморфизм задается функ-
функтором надстройки: [X, S"]-+-[SX, SS"] = [SX, Sn + 1].
Если X — произвольное конечномерное клеточное раз-
разбиение, то при достаточно большом Аг множество
nn + N{SNX) имеет структуру группы (при yV^dim X—
—2п+2 выполнено соотношение dim(SN X) = N-{-
+dim Х«2(/1+Л0—2. Группа n§(X)=n" + *{S#X) при
iV^dim X—2н-Ь2 наз. стабильной к о г о м о-
топ и ческой группой клеточного разбиения,
она определена для любого конечномерного клеточного
разбиения. Группы я§(Х) определены при всех це-
целых п (а не только при положительных). Если в ка-
качестве X взять две точки (одна из к-рых отмечена),
то л§(Х) = 0 при ге>0, л%(Х)=Ж, a ns(X) = nN-n(S*)
¦— стабильные гомотоппч. группы сфер при га<0.
Если (X, А) — пара клеточных разбиений размер-
размерности т, то при m<:2n—2 определена от нос и тель-
тельная когомотопическая группа я"(Х,
А) — пп(Х/А). Имеет место точная последователь-
последовательность абелевых групп
л> (X) —>¦ л< (А) —>¦ п' + г (X, А) —¦+ jt' + J (X) —*¦
продолжающаяся вправо неограниченно, однако, начи-
начиная с нек-рого места, все группы будут нулевыми:
п'(Х, А) = л'(Х) = л'(А) = 0 при г>т. Влево эта после-
последовательность продолжается лишь до тех значений г,
при к-рых ??к2г—2. В этой последовательности гомо-
гомоморфизмы к'(Х)~^л'(А) и n'\X/A)-+-7t'{X) индуциро-
индуцированы естественными отображениями АаХ и X—*-Х/А.
Гомоморфизм л'(А)-^-л' + 1(Х/А) устроен следующим
образом. Для класса [/] ?л'(А) = [А, S'] и для его
представителя / : A—yS' выбирается продолжение
F : X—>Dl+x отображения /, заданного на подпрост-
подпространстве АаХ со значениями в S'czD' + 1. Отображе-
Отображение F индуцирует отображение Х/А—^D' + 1I S' = Si+1,
гомотопич. класс к-рого (элемент группы л' + 1(Х, А))
ставится в соответствие с классом \j]Qn'(A).
Если (X, А) — пара пунктированных клеточных
разбиений конечной размерности, то для стабильных
К. г. имеет место точная последовательность
... -> я^ (X) ->-я^ {А) ^я'/1 (X, A) ^nij+1 (X)-» ...,
продолжающаяся неограниченно в обе стороны. Это
обстоятельство позволяет превратить стабильные К. г.
в обобщенную теорию когомолоиш. Для произвольного
(непунктированяого) конечномерного клеточного раз-
разбиения X пусть ns(X) = nls{X{Jx0, х0), где (X\Jx0, хп) —
пунктированное клеточное разбиение, полученное из X
несвязным присоединенном отмеченной точки. Функ-
Функтор ns< определенный на категории конечномерных кле-
клеточных разбиений, задает обобщенную теорию когомо-
логпй, если положить
л*3 (X, А) =л*8 (Х/А) = Кег [n*s (Х/А) -ч-я| (ft)].
Значение на точке этой теории совпадает со стабиль-
стабильными гомотопич. группами сфер.
К. г., так же как и гомотопические, не могут быть
явно вычислены даже в самых простых случаях, и зто
сильно ограничивает возможность практич. примене-
применения описанных выше функторов.
Лит.: [1] X у С ы-ц з я н, Теория гомотопий, пер. с англ.,
М., 1984; [2] С п е н ь с р Э., Алгебраическая топология, пер.
с англ., М., 1971. А. Ф. Харшиладзе.
КОД — конечное или счетное множество слов в нек-
ром алфавите, изучаемое в теории кодирования и деко-
декодирования. См. Код с исправлением арифметических
ошибок, Код с исправлением выпадений и вставок, Код
с исправлением ошибок.
КОД С ИСПРАВЛЕНИЕМ АРИФМЕТИЧЕСКИХ
ОШИБОК, код, исправляющий арифме-
арифметические ошибки,— код, предназначенный
для контроля работы сумматора. При сложении чисел,
представленных в двоичной системе счисления, оди-
одиночный сбой в работе сумматора приводит, как пра-
правило, к изменению результата на нек-рую степень
числа два. В связи с этим в кольце целых чисел %
вводится понятие (одиночной) арифметиче-
арифметической о ш и б к и как преобразования числа Лг
в число N' = N^2>, 2=0, 1, ... . Функция p(A'j, N%)
на Z X Z, определяемая как минимальное число ариф-
метич. ошибок, преобразующих Л^ в Л'2, является мет-
метрикой. Произвольное конечное подмножество (код)
Koz. 7L характеризуется расстоянием
P(fl=min p^Vj, N2),
где минимум берется по всем различным Nlt N2?K.
Последовательности из t или менее арифметич. ошибок
преобразуют любое число Л" в метрический шар ра-
радиуса t с центром в N. Поэтому если метрические шары
радиуса t, описанные вокруг любых двух чисел кода,
не пересекаются (т. е. расстояние кода больше 2t),
то код наз. кодом, исправляющим t ариф-
арифметических ошибок. Если же метрический
шар радиуса s, описанный вокруг любого числа кода,
не содержит других чисел кода (т. е. расстояние кода
больше s), то код наз. кодом, обнаружива то-
тощим s арифметических ошибок. Мет-
Метрика р допускает другое описание:
Где w(N) — (арифметический) вес числа N, равный
минимально возможному числу ненулевых коэффици-
коэффициентов в представлениях
Для каждого числа Л" существует единственное пред-
представление (*), в к-ром JVk=?O и N{Ni + x=0, i=0, 1,
..., к—1, число ненулевых коэффициентов в этом пред-
представлении равно w(N). Напр., 23=2"+22+21+2°=
= 25—23—2° и шB3) = 3. Так как p(Nx+N, N2+N)=
= р(Лт1, Л'2) для любых N±, JVa, N?z, то ограничи-
ограничиваются рассмотрением кодов, не содержащих отрица-
отрицательных чисел. Длиной кода К наз. величина
[log2 В(К)]-\-1, где В (К) — наибольшее число кода К.
Произвольному числу В кода длины п однозначно со-
соответствует слово р(Д)=Ь„_г.. .&х&0 в алфавите {0, 1}
такое, что В=^.=о Ь,-2'. Если код KCLTL исправ-
исправляет t арифметич. ошибок, то код (РE) : В?К} ис-
исправляет t ошибок (типа замещения) в силу того, что
d($(Bx), РE2))>рE1? В2), где <*(., •) — метрика Хем-
мннга (см. Код с исправлением ошибок). При исследо-
исследовании задачи контроля сумматора обычно рассма-
рассматривают кодирования /:{0, 1, ..., М — 1}-—>-~Z. (см.
Кодирование и декодирование), обладающие свойст-
свойством /(J+/)=/(i)+/(/l при г+/<М (что равносильно
j{i)=A-i, где A=f(\)). В этом случае операция коди-
кодирования состоит в умножении кодируемого числа на А ,
а обнаружение ошибок в работе сумматора заклю-
заключается в проверке делимости на А результата сложе-
сложения. Код Ка% м= {0. А, .. ., А (М— 1)} наз. 4-кодом
мощности М. Расстояние Л-кода равно минималь-
минимальному w(A -i), i=l, ..., М—1. Напр., расстояние 3-кода
произвольной мощности равно 2, код обнаруживает
одиночные арифметич. ошибки и часто применяется
в ЭВМ (в виде контроля по модулю-3). Наиболее иссле-
исследованы (циклические и негациклические) А -коды мощ-
мощности M=2n^fl/A, характеризующиеся тем свойством,
что вместе с числом 5 = ^(=г0 Ь,-2', &;=0, 1, число 5' =
= —b/i-i+2"=i &'2' также принадлежит коду. Та-
Такие коды, называемые (л, А)-к одами, удобно рас-
рассматривать как подмножества метрического простран-
пространства Nm= {0, 1, ..., т—1}, то=2л=р1 с метрикой
Рт (х< >j)=^wm(x — y) = mm{w(x — y), w(x~y — m)}.
Расстояния (га, /1)-кода в метриках риря равны. С каж-
каждым (и, А )-кодом связан (п, Л*)-код, где АА* = т,
называемый двойственным. Если 2 или —2 —
первообразный корень по модулю простого числа р,
то ((р—1)/2, р)-код исправляет одиночные арифметич.
ошибки и является совершенным в метрике рт, т. е.
метрические шары радиуса 1, описанные вокруг чисел
кода, не только попарно не пересекаются, но и запол-
заполняют все NOT. В двойственном коде все расстояния
между различными числами кода равны] (р-{-\I&[. Пере-
Перечисленные результаты для кодов имеют аналоги в клас-
классе двоичных линейных циклических кодов, исправ-
исправляющих ошибки. В то же время не известны арифметич.
аналоги БЧХ-кодов, а также не известны верхние
границы мощности кодов с заданными длиной и рас-
расстоянием, аналогичные границам для кодов, исправ-
исправляющих ошибки. Еще большей спецификой обладают
коды, исправляющие д-ичные (?>2) арифметич. ошибки
(<7-и чной арифметической ошибкой
наз. преобразование числа N в число N' = N±aq',
а=1, ..., ?—.1; i=0, 1, . ..), интерес к к-рым возрастает
с развитием вычислительной техники. Так, в отличие
от кодов, исправляющих ошибки при q=2l (Z>1), не
существует совершенных Л-кодов, исправляющих оди-
одиночные д-ичные арифметич. ошибки, а при q= 6 из-
известны примеры таких кодов. Условия существования
совершенных А -кодов имеют теоретико-числовой ха-
рактер и связаны с изучением законов взаимности
в числовых полях.
Лит.: [1] Дадаев Ю. Г., Арифметические коды, исправ-
исправляющие ошибки, М., 1969; [2]Питерсон У., У э л д о н Э.,
Коды, исправляющие ошибки, пер. с англ., 2 изд., М., 1976; [3]
Massey J. L., Garcia О. N., в кн.: Advances in Infor-
Information Systems Science, v. 4, N. Y.—L., 1972, p. 273 — 326; [4]
Бояринов И. М., К а б а т я н с к и й Г. А., «Проблемы
передачи информации», 1976, т. 12, в. 1, с. 16—23.
Г. А. Кабптянский.
КОД С ИСПРАВЛЕНИЕМ ВЫПАДЕНИЙ И ВСТА-
ВСТАВОК — код, предназначенный для исправления оши-
ошибок двух типов, встречающихся при передаче и пер-
перфорации информации. Выпадением буквы в сло-
слове р=61. ..6П длины п в нек-ром алфавите В наз. пре-
преобразование слова Р в слово Р' = 6Х.. .&,_16;+1.. .Ьп
длины п—1, 1<:г«:га. Для числа Ns(§) слов, получае-
получаемых из слова Р выпадениями s букв, справедливы
следующие оценки С\ (p)_s + 1 «S Л^ (р1) «S C\ (P) + S_X ,
где т(Р) — число серий слова р (с е р и е й слова
Р=Ь1... Ьп наз. слово Ь,-+1Ь;+2.. .bj, />j-j-l, такое,
что 1) &( + 1=.. .= &,-, 2) если jjjsl, то Ь,-=^6,- + 1, 3) если
/<ге, то bj + 1=?bj). В частности, N1($) = i($). Встав-
Вставкой буквы в слове Р=61...6„ наз. преобразование
слова C в слово Р' = Ь1.. .Ь,-Ь&,- + 1.. .6„ длины п+1, где
Ь?В и 0<j<w. Число слов, получаемых из произволь-
произвольного слова р длины п вставками s букв алфавита В,
равно 2*-о C'n+S(r — 1У> гДе г ~~ чпсло букв алфа-
алфавита В. Множество К слов в алфавите В наз. кодом
с исправлением s выпадений (вставок, выпадений или
вставок), если никакое слово в алфавите В не может
быть получено из двух различных слов из К а результа-
результате s пли менее выпадений (вставок, выпадений или вста-
вставок) букв в каждом из них. Функция, определенная на
парах (р1? Р2) слов в алфавите В и равная минимальному
числу выпадений и вставок букв, преобразующих РХ'
в Р2, является метрикой. Множество К слов в алфавите
В является кодом с исправлением s выпадений (вставок,
выпадений или вставок) тогда и только тогда, когда
расстояние между любыми двумя различными словами
из К больше 2s, так что указанные три определения
кодов эквивалентны. Примером кода с исправлением
одного выпадения или одной вставки является мно-
множество слов {Р=&! ... Ъп} длины п в алфавите В=
= {0, 1}, для к-рых 2«=1^'—0 (mod n+1). Число слов
в этом коде равно о ^ , ^ У л ер (d) 2(" + 1)/d, где сум-
суммирование производится по всем нечетным делителям d
числа га+1 и ф(<2) — функция Эйлера, и является
асимптотически максимальным при п—>-оо.
В. Л. Левенштейн.
КОД С ИСПРАВЛЕНИЕМ ОШИБОК, код, кор-
корректирующий ошибки,— множество сооб-
сообщений, предназначенных для передачи по каналу связи
с шумами, обладающее тем свойством, что окрестность
ошибок каждого сообщения (т. е. совокупность иска-
искаженных вариантов этого сообщения) не пересекается
с окрестностями ошибок других сообщений. Это свойст-
свойство К. с и. о. позволяет правильно корректиро-
корректировать ошибки (т. е. правильно восстанавливать пере- •
данное сообщение) в тех (полученных на выходе кана-
канала) искаженных сообщениях, к-рые принадлежат своей
окрестности ошибок. Элементы К. с и. о. используют-
используются при кодировании последовательностей информацион-
информационных символов, вырабатываемых источником сообщений.
Кодирование заключается в представлении информа-
информационной последовательности в специальной форме и
введении в нее дополнительной информации (избыточ-
(избыточности). Избыточность обычно вводят путем добавления
в сообщение тем или иным способом дополнительных
символов. Напр., последовательность символов разби-
вается на блоки фиксированной длины к, а затем неза-
независимо один от другого блоки заменяются другими бло-
блоками большей длины га, к-рые являются элементами
так наз. блокового К. си. о. Известны [1] и
другие способы введения избыточности и связанные
с ними К. с и. о.
Элементы блокового К. с и. о. выбираются из
нек-рого множества га-мерных векторов L", снабженного
метрикой %(,), а их окрестности ошибок задаются в виде
шара с центром в элементе кода. Радиус этого шара оп-
определяет корректирующую способность блокового кода.
Метрика Х(,) зависит от характера ошибок, для исправ-
исправления к-рых предназначен код. Дальнейшее изложение
касается только блоковых К. с и. о. как наиболее рас-
распространенных.
Для того чтобы иметь возможность передать макси-
максимальное количество сообщений по каналу связи, не-
необходимо использовать коды с максимальным числом
элементов при заданной корректирующей способности.
Построение таких кодов является одной из основных
задач теории К. с и. о. Эта задача достаточно далеко
продвинута только для нек-рых рассматриваемых ниже
конечных множеств L". В то же время как для прило-
приложений, так и для теории интересны коды на нек-рых
бесконечных множествах, напр, на сфере в евклидовом
пространстве R".
При практическом использовании К. с и. о. возни-
возникают задачи отображения информации, предназначен-
предназначенной для передачи в множество элементов К. с и. о.
и нахождения по принятому элементу х' переданного
элемента кода х. Первая задача наз. задачей ко-
кодирования, вторая — задачей декоди-
декодирования. Сложность кодирования и декодирова-
декодирования в значительной мере определяется свойствами
используемого К. с и.о. Это обстоятельство приводит к
изучению относительно узких' классов кодов, как, на-
например, рассматриваемых ниже двоичных линейных
кодов.
Наиболее широко исследовались блоковые
г-и чные коды в метрике Хемминга, ввиду того
что они находят многочисленные применения, а методы
их построения связаны с известными ранее математи-
математическими структурами. Элементами этих кодов явля-
являются нек-рые элементы множества Д", состоящего из
всех векторов длины п, координаты к-рых принадле-
принадлежат множеству из г элементов. Расстоянием
Хемкпнга d(x, у) между векторами х, у из В" наз.
число их несовпадающих координат. Окрестность оши-
ошибок Uf(x) кратности t (t — целое) вектора х состоит
из всех векторов из В1}, отличающихся от х не более
чем в г координатах, т. е. Ut(x) — шар в метрике d(,)
радиуса ? с центром в точке х. В частности, t/j (x) со-
состоит из (>—1)п+1 векторов. Для произвольного мно-
множества КаВ" функция d(K)= min d(x, у) наз.
х, уеК, хфу
кодовым расстоянием г-ичного кода К.
Код К является К. с и. о. кратности t, если d(K)^2t-\-i.
При выполнении последнего неравенства каждая ок-
окрестность ошибок U-t(x), x?K, не пересекается ни с
какой другой окрестностью ошибок кратности t век-
вектора у из К.
Значительный прогресс в изучении r-ичных кодов по-
получен для случая, когда г является степенью простого
числа. В этом случае в качестве множества координат
берут конечное поле GF(q) из q элементов и используют
алгебраические свойства этого понятия. Ниже предпо-
предполагается, что координатами элементов множества Bq
являются элементы поля GF(q). Множество В^ являет-
является линейным пространством над полем GF(q). Если
векторы кода К образуют линейное подпространство про-
странства В", то код наз. линейным. Линейный
код К может быть задан как своим базисом, так и ба-
базисом линейного пространства, двойственного к К.
Последний способ более распространен. Матрица А,
строками к-рой служат базисные векторы пространства,
двойственного к К, наз. проверочной матри-
ц е й К. Для векторов х?К справедливо соотношение:
хАт=0, где Ат— транспонированная матрица А. Да-
Далее п — длина кода, к — размерность линейного кода и
d — кодовое расстояние. Код над В% наз. двоич-
двоичным кодом.
Для оценки качества конкретных кодов изучают
поведение функции m(n, d), равной максимальному
числу векторов двоичного кода длины п с кодовым рас-
расстоянием d. Относительно хорошо функция т(п, d)
изучена при больших d, 2d^n, и малых d, d=const,
га—»- оо. В первом случае величина т(п, d) не превос-
превосходит 2ге при 2d~n и 2d/Bd—га) при 2d—га>0, а во
втором — равна по порядку п~х2п при |2=2г+1-
Если d=3, n=2l—l, то m (га, 3) = 2"/(га+1).
Код, на к-ром достигается последнее равенство, но-
носит название двоичного кода Хемминга.
Двоичный код Хемминга, корректирующий ошибки
кратности t=l, обладает следующим свойством: шары
радиуса i=l с центрами в точках кода не пересекаются
и в то же время заполняют все множество В". Подобные
коды наз. совершенными. Известно, что, кро-
кроме кодов Хемминга, существует еще лишь конечное
число нетривиальных двоичных совершенных кодов.
В случае ге—>-оо, d/re—>-б, 0<б<1/2, изучают функцию
(логарифмич. асимптотику т(п, d)), называемую ско-
скоростью передачи максимальным кодом с от-
относительным кодовым расстоянием б. Для скорости
R (б) известны существенно различающиеся верхние и
нижние оценки. Нижняя оценка (оценка Вар-
шамова — Гилберта) имеет вид
где
Я (б) = б log2 -j- + A - б) log2 -^ ,
и гарантирует существование кодов с указанными па-
параметрами. Коды с параметрами, лежащими на грани-
границе (*), к настоящему времени A978) могут быть построе-
построены только методом перебора. Существенно новые верх-
верхние оценки получены в [6], [7]. Весьма правдоподобна
гипотеза, по к-рой ЯF)=1 — #F).
Далее рассматриваются конструктивные
методы (т. е. методы, требующие для своей реали-
реализации относительно небольшого числа операций) по-
построения К. с и. о. К важнейшим конструктивным ко-
кодам относятся: коды Рида — Соломона
(PC-коды), коды Боуза — Чоудхури —
Хоквингема (БЧХ-коды) и коды Ри-
Рида — Маллера (РМ-коды). Перечисленные коды
являются линейными. Отправной конструкцией для
построения первых двух служит матрица А г с элемен-
элементами из GF(q):
1 ... aJ ... а9
где а — первообразный корень GF(q). Матрица Аг
является проверочной матрицей PC-кода Сг над GF(q),
к-рый имеет следующие параметры: n=q—1, /с=?—г,
d=r. Кодовое расстояние кода СТ является макси-
максимальным среди всех линейных кодов длины q—1 и
размерности q—r. Двоичный БЧХ-код Нг состоит
пз всех векторов PC-кода Сг над GFBl), координаты
к-рых принадлежат полю GFB), т. е. НГ=СГ[\В1-
БЧХ-код Нг при г=2г+1 имеет следующие па-
параметры: n=2l — I, k^n—lt, d^2t-{-l. Упомянутый
выше код Хемминга совпадает с БЧХ-кодом Н3.
Если г<2^' + 1'/2^([х] — целая часть х), то размер-
размерность кода #2f + i равна п—It. БЧХ-код является ц и к-
лическим, т.е. обладает тем свойством, что вмес-
вместе с вектором х содержит все его циклнч. сдвиги.
Число векторов БЧХ-кодов в случае п —>- оо, r=const
совпадает по порядку с мощностью наилучшего кода
т(п, г).
Двоичный РМ-код определяется как множество дво-
двоичных векторов вида (f(a1), /(a2), ...,/(а„)), где п=
=2l, ocj, ..., а„— всевозможные двоичные векторы дли-
длины г и {(х) пробегает множество всех функций алгебра
логики, представнмых в виде многочлена над GFB) сте-
степени не выше г от I двоичных переменных. РМ-код име-
имеет следующие параметры: n = 2l, k= 2/=о^'/' d=2l~r-
Скорость передачи R{K) двоичного кода К длины п
с числом векторов т определяется как
Если К — линейный код, то R(K)=k/n. Скорость
передачи перечисленных выше конструктивных кодов
при п —у- оо, d/n—>-&, S>0, стремится к 0. Известны
конструктивные коды со скоростью передачи большей
нуля при п —>- оо, din —>- б, 1/2>6>0, но меньшей ско-
скорости передачи кодов, существование к-рых устанавли-
устанавливает граница (*).
При практическом использовании К. с и. о. крат-
кратности t для коррекции ошибок канала связи необхо-
необходимо устройство (декодер), к-рое по искажен-
искаженному вектору х' ? U-t(x) указывает переданный кодовый
вектор х. При этом предпочтительно использовать такие
К. с и. о., для к-рых декодер имеет небольшую слож-
сложность. Под сложностью декодера двоич-
двоичного кода К с кодовым расстоянием 2г+1 пони-
понимается, напр., минимальное число функциональных
элементов, к-рое необходимо для реализации булева
оператора F(x')=x, x'?Ut(x), x?K. Малую сложность
декодера имеют рассмотренные конструктивные коды.
Кроме того, известны другие К. с и. о. со скоростью
передачи, не стремящейся к 0 при п—>-оо, d/ra_>-6, 6>0,
и малой сложностью декодера. К таким кодам отно-
относятся, напр., каскадные коды и коды с малой плот-
плотностью проверок на четность. Каскадный код
в простейшем случае представляет собой итерацию
PC-кода над полем GFBl) и двоичного кода длины пг
размерности I с кодовым расстоянием dt. С помощью
какого-либо линейного отображения устанавливается
взаимно однозначное соответствие между элементами
поля GFBl) и векторами двоичного кода. Затем коор-
координаты PC-кода заменяются соответствующими векто-
векторами двоичного кода. В результате получается двоичный
линейный каскадный код с параметрами п=п1B1—1),
k = lBl—г), d~^T\. Лучшие результаты достига-
достигаются, если для замены различных разрядов РС-кода
использовать различные двоичные коды. Таким спосо-
способом могут быть получены коды длины п, исправляющие
с помощью декодера со сложностью, равной по порядку
п log и, фиксированную долю от п ошибок. Ансамбль
двоичных кодов с малой плотно-
плотностью проверок на четность опреде-
определяется ансамблем проверочных матриц {А }, состоящим
из двоичных матриц нек-рого вида, размера пХг,
к-рые содержат в каждом столбце и каждой строке
соответственно I и h единиц, 4<Z</t. При фиксиро-
фиксированных I и h и га-*-оо типичный код длины п ансамбля I
с помощью декодера со сложностью, по порядку рав-
равной п log n, может исправлять фиксированную долю
от п ошибок. Скорость передачи как каскадных, так
и кодов с малой плотностью проверок лежит ниже
оценки (*).
Достаточно широко исследовались коды на множест-
множествах В^ в метриках, отличных от метрики Хемминга.
Направление и результаты этих исследований во мно-
многом сходны с соответствующими результатами для мет-
метрики Хемминга. В частности, рассматривались коды в
метриках, связанных с синхронизационными ошибками,
с ошибками в арифметич. устройствах ЭВМ (а р и ф-
метические коды), с пачками ошибок, с не-
несимметричными ошибками, с ошибками в непрерывном
канале связи. Напр., в последнем случае множеством Ln
является сфера единичного радиуса S" в евклидовом
пространстве R" с центром в начале координат, а ок-
окрестностью ошибок 1Тц{х), x?S",— поверхность, высе-
высекаемая из Sn~1 круговым конусом с полууглом ф и с
осью, проходящей через точки 0 и х. Следует также
заметить, что коды в евклидовом пространстве R"
в несколько иной трактовке рассматривались, начиная
с конца 19 в., в геометрии.
Развитие теории К. си. о. стимулировалось работами
К. Шеннона (С. Shannon) по теории информации, в к-рых
была показана принципиальная возможность передачи
по каналу связи с шумами информации со скоростью
меньшей пропускной способности канала и произволь-
произвольной малой ошибкой. Первоначально теория К. с и. о.
удовлетворяла потребности техники связи в математи-
математических конструкциях, обеспечивающих надежную пе-
передачу информации при ограничениях на число и вид
ошибок в сообщении. Затем результаты и методы тео-
теории К. с и. о. нашли применение в других областях.
В частности, в математике этими методами удалось
получить наилучшие (к 1978) оценки плотности уклад-
укладки шаров в евклидовом пространстве, получить зна-
значительное продвижение при оценке сложности тупико-
тупиковых дизъюнктивных форм для почти всех функций ал-
алгебры логики, построить нек-рые новые объекты в ком-
комбинаторике, построить самокорректирующиеся схемы
из функциональных элементов и т. д.
Лит.: [1] Питерсон У., У э л д о н Э., Коды, исправ-
исправляющие ошибки, пер. с англ., 2 изд., М., 1976; [2] Б е р л е-
кэмп Э., Алгебраическая теория кодирования, пер. с англ.,
М., 1971; [3] Дискретная математика и математические вопросы
кибернетики, т. 1, М., 1974; [4] Блох Э. Л., 3 я б л о в В. В.,
Обобщенные каскадные коды, М., 1976; [5] Колес-
н и к В. Д., МирончиковЕ. Т., Декодирование цикли-
циклических кодов, М., 1968; [6] С и дольни ков В. М., «Пробл.
передачи информ.», 1974, т. 10, в. 2, с. 43 — 51; [7] Левей-
штейн В. И., там же, с. 26—42; [8] Зяб лов В. В.,
Пинскер М. С, «Пробл. передачи информ.», 1975, т. 11,
в. 1, с. 23 — 36. В. М. Сиделъников.
КОДАИРЫ РАЗМЕРНОСТЬ — численный инвариант
алгебраич. многообразия, названный по имени К. Ко-
даиры (К. Kodaira), впервые указавшего на важность
этого инварианта в теории классификации алгебрапч.
многообразий.
Пусть V — неособое алгебраич. многообразие и
Фи : V-+P(n) — рациональное отображение, опреде-
определяемое линейной системой \mKv\, где Ку—канони-
Ку—канонический класс многообразия V. Размерность
К о д а и р ы х (Т') многообразия V определяется как
max^j (dim Фт(П}. При этом, если \mKv\ = 0 для
всех m^l, то считается, что х(И= —«». К. р. является
бирациональным инвариантом, т. е. не зависит от пред-
представителя в классе бирациональной эквивалентности.
Пусть основное поле есть поле комплексных чисел С.
Если т достаточно большое, то имеет место оценка
am^b^diml mKv | < Pm* (V),
где a, p — некоторые положительные числа. Если
к (V) >0, то существует сюрьективный морфизм / : V*—>-
—*-W алгебраич. многообразий такой, что: а) V* бира-
ционально эквивалентно V; б) x(F)=dim W; в) для
некоторого плотного открытого множества UcW
все слои /~1(со), cogf/, являются многообразиями
параболич. типа.
Существует обобщение понятия К. р. (см. [2]) на
случай, когда в линейной системе |тоЯу| канонич.
класс Ку заменяется на произвольный дивизор D.
Лит.: [1] Алгебраические поверхности, М., 1965 (Тр.
Матем. ин-та АН СССР, т. 75); [2] U e n о К., Classification
theory of algebraic varieties and compact complex spaces, B.—
Hdlb.— N. Y., 1975; [3] I i t a k a S., «J. Math. Soc. Jap.», 1971,
V. 23, p. 256 — 73. И. В. Долгачев.
КОДАИРЫ ТЕОРЕМА об обращении в
нуль, теорема Кодаиры об исчезло-
в е н и и,— теорема о равенстве нулю групп когомоло-
гий Н'(Х, Q(L)), i<dim X, где Q(L) — пучок голоморф-
голоморфных сечений отрицательного векторного расслоения L
ранга 1 на компактном комплексном многообразии X.
Эквивалентная формулировка К. т. состоит в том, что
НЦХ, 6A,®**)) = О, 1 >0,
для любого положительного векторного расслоения
ранга 1 (здесь К% обозначает каноническое линейное
расслоение на X). В терминах дивизоров К. т. форму-
формулируется как равенство Н'(Х, Ox(—D)) = 0 для i<
<dim X и любого дивизора D такого, что для некото-
некоторого rC^\ nD является гиперплоским сечением в каком-
либо проективном вложении многообразия X.
К. т. была доказана трансцендентными методами К.
Кодаирой [1] (см. также [2]) как обобщение на случай
произвольной размерности классич. теоремы о регу-
регулярности присоединенной системы на алгебраич. по-
поверхности. Существует пример нормальной алгебраич.
поверхности над полем положительной характерис-
характеристики, для к-рой К. т. неверна [4]. Неизвестно A978),
справедлива ли К. т. для неособого алгебраич. много-
многообразия над полем положительной характеристики.
К. т. справедлива п для голоморфных векторных
расслоений произвольного ранга, отрицательных в
смысле Накано. Обобщением К. т. является также
следующий результат:
Н'(Х, QP(L))=0 для p-rfSsdimX + r,
где L — слабо положительное векторное расслоение
ранга г на компактном комплексном многообразии X,
Qp(L)=QP(?N{L) — пучок голоморфных форм степени
р со значениями в L. Для слабо отрицательных вектор-
векторных расслоений L обращение в 0 имеет место при
p+i«:dim X—г. Аналоги этих теорем получены для
слабо 1-полных многообразий X,
т. е. многообразий, допускающих гладкую плюрисуб-
гармонич. функцию т|з такую, что множества {х?Х,
i|}(.r)<c} относительно компактны в X для всех c?(R,
и для компактных комплексных пространств X, об-
обладающих ra=dim X алгебраически независимыми ме-
роморфными функциями [5].
Лит.: [1] К о d a i г а К., «Ргос. Nat. Acad. Sci. USA»,
1953, v. 39, p. 1268 — 73; [2] Уэллс Р., Дифференциальное
исчисление на комплексных многообразных, М., 1976; [3] М u m-
f ord D., «Amer. J. Math.», 1967, v. 89, № 1, p. 94—104; [4]
Zariski O., Algebraic surfaces, В.— Hdlb.— N. Y., 1971;
[5] Итоги науки. Алгебра. Топология. Геометрия, т. 15, М.,
1977, с. 93—171. И. В. Долгачев.
КОДИРОВАНИЕ АЛФАВИТНОЕ, к о д и р о в а-
ние неравномерное,— представление инфор-
информации в стандартной форме, при к-рой
элементарным синтаксическим единицам языка сооб-
сообщений (буквам алфавита языка) последовательно сопо-
сопоставляются кодовые комбинации символов из нек-рого
заданного алфавита (здесь под информацией пони-
понимается линейная запись букв). Примером К. а. может
служить известный код Морзе, в к-ром слова коди-
кодируются побуквенно, а буквам сопоставлены слова
в алфавите трех символов {¦, —, Л }, где Л — пробел.
Примером естественно сложившегося кодирования,
к-рое не укладывается в модель К. а., является деся-
десятичная система счисления. Источником идей для раз-
развития теории К. а. являются кибернетич. точка зре-
зрения на информационные процессы и системы, с одной
стороны, и потребность техники связи (где часто воз-
возникает необходимость преобразования информации
к более удобной в каком-то отношении форме) — с дру-
другой; отправным пунктом была фундаментальная работа
К. Шеннона [1], опубликованная в 1948. Теория К. а.—
раздел прикладной математики, включающий в себя
изучение различных математич. моделей каналов
связи с использованием разнообразных математич.
методов. Лучше всего изучено равномерное или блоч-
блочное кодирование, при к-ром кодовые комбинации
имеют фиксированную длину. Для этого класса имеется
развитый математич. аппарат (см. Код с исправлением
ошибок). Более общей абстрактной схемой является
автоматное кодирование, при к-ром соответствие реа-
реализуется конечным автоматом. В практич. отношении
равномерное кодирование обеспечивает, как правило,
удовлетворительные результаты, поэтому использова-
использование других методов кодирования должно иметь очень
веские достоинства (напр., существенное сжатие инфор-
информации) при не слишком серьезных недостатках (услож-
(усложнение кодирования и декодирования).
Основные результаты общего характера можно сфор-
сформулировать для случая побуквенного К. а. (когда коди-
кодирующий автомат имеет одно внутреннее состояние), так
как известные обобщения не имеют принципиального
значения, а исследования, связанные с другими моде-
моделями, не получили еще значительного теоретич. разви-
развития. Рассматривается следующая модель канала связи:
источ-
источник
сооб-
сообщений
схема
кодирования
рхема
декоди-
декодирования
адресат
А= {ах, .. ., ап} — алфавит канала связи, т, е. перечень
сигналов, к-рые могут передаваться по каналу, т(а,) —
длительность сигнала а,-, В = {bj, . . ., Ът } — алфавит
языка сообщений. В простейшем случае источник сооб-
сообщений есть вероятностная схема, на выходе к-рон
в каждый момент дискретного времени появляется
одна из букв В, причем вероятности р,=р(&,) появ-
появления букв не зависят от времени. Схема кодирования
/ отображает буквы В в слова Л* (А*— моноид, по-
порожденный A), i(bi)=V( и слова В* кодируются по-
буквенно: f{bh ... 6,-ft) = /(b,-1). . ./(fe,-ft). Таким об-
образом, отображение / полностью задается кодом V=
= {«!, ¦ • •, vm}- Если / взаимно однозначно, то зада-
задача схемы декодирования — восстановить переданное
сообщение, реализуя отображение /-1.
Оценочными факторами для модели являются инфор-
информации скорость передачи и сложность декодирова-
декодирования, определяемые выбором кода V. Скорость пе-
р е д а ч и характеризуется количественно величи-
величиной математич. ожидания времени, к-рое требуется для
передачи одной буквы сообщения: длительность пере-
передачи буквы Ь[ есть
') = 2/= 1
где со,у— число вхождений буквы ау в слово и,-, а ис-
искомое математическое ожидание есть
(Е f наз. также стоимостью кодирования
/). В общем случае Е^ зависит от структуры кода, к-рая
описывается структурным многочленом
— производящей функцией, перечисляющей слова кода
по их составу. В частном случае, когда т(а1)=...=
—¦т(а„)=т, имеем Ef=T^i=slpili, т. е. Еу определяется
только спектром длин слов кода {1Х, 12, . .., 1т),
где lj— длина слова и,-. Для этого случая проблема
выбора оптимального кода (т. е. минимизи-
минимизирующего стоимость) решается полностью; доказано [2]
необходимое и достаточное спектральное условие для
существования однозначно декодируемого кода
Показано [4], что вместе с неравенством A) условие
необходимо и достаточно для существования кода
с данным спектром, имеющего так наз. свойство
самосинхронизации, к-рое состоит в том,
что ошибка при декодировании автоматически локали-
локализуется с вероятностью 1.
Для сложности декодирования, с аб-
абстрактной точки зрения, наиболее интересна качест-
качественная мера: наличие свойства конечности задержки
декодирования, означающее возможность реализации
декодирования конечным автоматом (количественные
оценки сложности схемной реализации автоматов вы-
выходят за рамки теории кодирования). Так наз. и р е-
флксные коды (свойство префиксностн состоит
в том, что никакое слово V не является начальным от-
отрезком другого слова из V) ,все имеют это свойство.
Было показано [2], что любой код, для к-рого / взаимно
однозначно, спектрально эквивалентен нек-рому пре-
префиксному коду. Класс префиксных кодов относительно
хорошо обозрим, чем и объясняется результативность
исследования случая т(ах)=. . . = т(а„).
В общем случае известны алгоритмич. решения воп-
вопросов распознавания свойств взаимной однозначнести
кодирования п конечности задержки декодирования.
Свойство взаимной однозначности / можно рассматри-
рассматривать как минимальный уровень помехоустойчивости
кода V. Имеется алгоритмич. решение задачи вычисле-
вычисления фактической корректирующей способности произ-
произвольного кода в общем случае и с дополнительным тре-
требованием конечной задержки декодирования. Класс
всех свободных кодов (т. е. однозначно декодируемых)
устроен весьма сложно, но экстремальные требования
к кодам часто приводят к существенным ограничениям.
Напр., показано, что для максимальных по включению
кодов (для к-рых неравенство A) обращается в равен-
равенство п к-рые наз. полными, так как для них н только
для них алфавит канала используется полностью в том
смысле, что любое слово из А* является частью
нек-рого закодированного сообщения) свойство конечной
задержки имеет место в том и только в том случае,
если код префиксный.
1ит.: [1] Шеннон К., Работы по теории информации
и кибернетике, пер. с англ., М., 1963; [2] М а к-М и л л а и Б.,
-хчшернетич. сб.», 1961, в. 3, о. 88—92; [3] X а ф ф м е н Д.,
там же, с. 79—87; [4] Schiitzenberger M. P., «Infor-
«Information and Control», 1967, v. 1), p. 396 — 401; [5] Марков
Ал. А., «Пробл. кибернетики» 1962, в. 8 с. 169—86; 1964
в. 12, с. 137 — 53; 1967, в. 19, с. 307—09; 1976, в. 31, с. 77 — 108.
Ал. А. Марков.
КОДИРОВАНИЕ И ДЕКОДИРОВАНИЕ — процесс
представления информации в определенной стандарт-
стандартной форме и обратный процесс восстановления инфор-
информации по ее такому представлению. В математич.
литературе кодированием наз. отображение про-
произвольного множества А в множество конечных после-
довательностей (слов) в нек-ром алфавите В, а д е к о-
д и р о в а н и е м — обратное отображение. Приме-
Примерами кодирования являются: представление натураль-
натуральных чисел в 7-ичной системе счисления, при к-ром
каждому числу Лг— 1, 2, ... ставится в соответствие
слово b1b2 ... 6; в алфавите В г — {0, 1, . . ., г—1} такое,
что Ь^фй и birl-1Jr...^rbl-1rJrbl=N\ преобразование
текстов на русском языке с помощью телеграфного
кода в последовательности, составленные из посылок
тока и пауз различной длительности; отображение, при-
применяемое при написании цифр почтового индекса (см.
рис.). В последнем случае каждой десятичной цифре со-
соответствует слово в алфавите В2= {0, 1} длины 9, в ко-
котором символами 1 отмечены номера использованных ли-
линий (напр., цифре 5 соответствует слово 110010011).
Исследование различных свойств
г—'.-д К. и д. и построение эффективных в опре-
21 $f''\i деленном смысле кодирований, обладаю-
обладающих требуемыми свойствами, составляет
c~~~j, проблематику теории кодирова-
н и я. Обычно критерий эффективности
кодирования так или иначе связан с мини-
7/
«I
V.....
мизацией длин кодовых слов (образов
элементов множества А), а требуемые свойства кодиро-
кодирования связаны с обеспечением заданного уровня поме-
помехоустойчивости, понимаемой в том или ином смысле. В
частности, под помехоустойчивостью понимается воз-
возможность однозначного декодирования при отсутствии
или допустимом уровне искажений в кодовых словах.
Помимо помехоустойчивости, к кодированию может
предъявляться ряд дополнительных требований. Напр.,
при выборе кодирования для цифр почтового индекса
необходимо согласование с обычным способом написа-
написания цифр. В качестве дополнительных требований часто
используются ограничения, связанные с допустимой
сложностью схем, осуществляющих К. и д. Пробле-
Проблематика теории кодирования в основном создавалась под
влиянием разработанной К. Шенноном (С. Shannon,
[1]) теории передачи информации. Источником новых
задач теории кодирования служат создание и совер-
совершенствование автоматизированных систем сбора, хра-
хранения, передачи и обработки информации. Методы ре-
решения задач теории кодирования главным образом ком-
комбинаторные, теоретико-вероятностные и алгебраические.
Произвольное кодирование / множества (алфавита) А
словами в алфавите В можно распространить на мно-
множество А * всех слов в А (сообщений) следующим об-
образом:
.ak) = f(a1) f (й2) . . ./ (oft),
где а;(^А, г=1, 2, ..., к. Такое отображение / : А*~>-В*
наз. побуквенным кодированием сооб-
сообщений. Более общий класс кодирований сообщений об-
образуют автоматные кодирования, реа-
реализуемые инициальными асинхронными автоматами,
выдающими в каждый момент времени нек-рое (быть
может, пустое) слово в алфавите В. Содержательный
смысл этого обобщения заключается в том, что автомат
в разных состояниях реализует различные кодирования
букв алфавита сообщений. Побуквенное кодирование —
это автоматное кодирование, реализуемое автоматом
с одним состоянием. Одним из направлений теории
кодирования является изучение общих свойств коди-
кодирования и построение алгоритмов распознавания этих
свойств (см. Кодирование алфавитное). В частности, для
побуквенных и автоматных кодирований найдены не-
необходимые и достаточные условия для того, чтобы:
1) декодирование было однозначным, 2) существовал
декодирующий автомат, т. е. автомат, реализующий де-
декодирование с нек-рой ограниченной задержкой, 3) су-
существовал самонастраивающийся декодирующий авто-
автомат (позволяющий в течение ограниченного промежутка
времени устранить влияние сбоя во входной последо-
последовательности или в работе самого автомата).
Большинство задач теории кодирования сводится
к изучению конечных или счетных множеств слов в ал-
алфавите Вг. Такие множества наз. кодами. В част-
частности, каждому однозначному кодированию / : Вт-+В*
(и побуквенному кодированию / : В*т—^В*Г) соответст-
соответствует код {/@), ..., f(m—i)}aB*. Одно из основных
утверждений теории кодирования состоит в том, что
условие взаимной однозначности побуквенного коди-
кодирования / : Вт-+Вг накладывает следующее ограни-
ограничение на длины /, = //(/) кодовых слов f(i):
Справедливо и обратное утверждение: если A0, ...,
1т-х) — набор натуральных чисел, удовлетворяю-
удовлетворяющих A), то существует взаимно однозначное побуквен-
ное кодирование / : Вщ—^В* такое, что слово /(г) имеет
длину 1{. При этом, если числа Z,- упорядочены по возрас-
возрастанию, то в качестве f(i) можно взять первые после за-
пятой I, символов разложения числа 2j'=or B Г"ИЧНУК)
дробь (метод Шеннона).
Наиболее законченные результаты в теории кодиро-
кодирования связаны с построением эффективных взаимно
однозначных кодирований. Описанные здесь конструк-
конструкции используются на практике для сжатия информации
и выборки информации из памяти. Понятие эффектив-
эффективности кодирования зависит от выбора критерия стои-
стоимости. При определении стоимости L(f) взаимно
однозначного побуквенного кодирования / : Вт-*.В*
предполагается, что каждому числу i?Bm поставлено
в соответствие положительное число р,- и Р= {р0, ...,
Pn-i). Исследованы следующие варианты определения
стоимости L(f):
3) L' (/) = max (h — Pi),
0 < i < m - 1
причем предполагается, что в первых двух случаях р,- —
вероятности, с к-рыми некоторый бернуллиевый источ-
источник порождает соответствующие буквы алфавита Вт
B^=оРг= 1)> а в третьем случае р,— заданные длины
кодовых слов. При первом определении стоимость
равна средней длине кодового слова, при втором опреде-
определении с ростом параметра t более длинные кодовые
слова оказывают все большее влияние на стоимость
(L(t)(f)—>-?ср(/) при t—>-0 и L(t)(f)—>-max I; при t—»-°°), при
0<i<m— I
третьем определении стоимость равна максимальному
превышению длины I; кодового слова над заданной
длиной pi. Задача построения взаимно однозначного по-
побуквенного кодирования/ : В^—^В*, минимизирующего
стоимость L(f), равносильна задаче минимизации фун-
функции L (/) на наборах (/0. • •., lm-i) из натуральных чи-
чисел, удовлетворяющих A). Решение этой задачи извест-
известно при каждом из указанных определений стоимости.
Пусть минимум величины L(f) на наборах (Zo, ...,
lm-i) из произвольных (не обязательно натуральных)
чисел равен Lr(P) и достигается на наборе Aо(Р), ¦..,
lm-!(P)). Неотрицательная величина I (f)-=L(f)—Lr(P)
наз. избыточностью, а величина / (f)lL (/) —
относительной избыточностью коди-
кодирования /. Для избыточности взаимно однозначного
кодирования / : В*т-+В*г, построенного по методу
Шеннона для длин I;, г,(/')<г,<г,(/))+1, справедливо
неравенство /(/)<1. При первом, наиболее употреби-
употребительном, определении стоимости как среднего числа
кодовых символов, приходящихся на одну букву по-
порождаемого источником сообщения, величина Lr(P)
равна энтропии Шеннона
источника, вычисленной по основанию г, а г,(/>)=
= —logrp,-. Граница избыточности I (f)= Ltp(f)—H Г(Р)<
<1 может быть улучшена с помощью так наз. коди-
кодирования блоками длины к, при к-ром сооб-
сообщения длины к (а не отдельные буквы) кодируются по
методу Шеннона. Избыточность такого кодирования
не превышает Ilk. Этот же прием используется для эф-
эффективного кодирования зависимых источников. В свя-
связи с тем, что определение длин 1[ при кодировании по
методу Шеннона основано на знании статистики источ-
источника, для нек-рых классов источников разработаны
методы построения универсального кодирования, га-
гарантирующего определенную верхнюю границу избы-
избыточности для любого источника из этого класса. В част-
частности, построено кодирование блоками длины к, избы-
избыточность к-рого для любого бернуллиевого источника
асимптотически не превышает ^^ logrk (при фикси-
рованных т, г и &_уоо), причем эта асимптотическая
граница не может быть улучшена.
Наряду с задачами эффективного сжатия информации
рассмотрены задачи оценки избыточности конкретных
видов сообщений. Напр., была оценена относительная
избыточность нек-рых естественных языков (в част-
частности, английского и русского) в предположении, что
тексты на них порождаются марковскими источниками
с большим числом состояний.
При исследовании задач построения эффективных
помехоустойчивых кодирований обычно рассматривают
кодирования / : В т—*-В*г, к-рым соответствуют коды
{/@), ..., f(m— 1)}, принадлежащие множеству В"г
слов длины п в алфавите В г, и предполагают, что буквы
алфавита сообщений Вт равновероятны. Эффективность
такого кодирования оценивают избыточностью / (/)=
= п—logrm или скоростью передачи Я (/)=
= — logrm. При определении помехоустойчивости коди-
кодирования формализуется понятие ошибки и вводится
в рассмотрение нек-рая модель образования ошибок.
Ошибкой типа замещения (или просто
ошибкой) наз. преобразование слова, состоящее
в замещении одного из его символов другим символом
алфавита Вг. Напр., проведение лишней линии при
написании цифры почтового индекса приводит к заме-
замещению в кодовом слове символа 0 символом 1, а отсут-
отсутствие нужной линии — к замещению символа 1 симво-
символом 0. Возможность обнаружения и исправления оши-
ошибок основана на том, что для кодирования /, обладаю-
обладающего ненулевой избыточностью, декодирование /-1
может быть произвольным образом доопределено на
г"—т словах из В", не являющихся кодовыми. В част-
частности, если множество В" разбито на т непересекаю-
непересекающихся подмножеств D0, ..., Dm_1 таких, что /(i)G#/,
а декодирование /-1 доопределено так, что f~1(D;)=i,
то при декодировании будут исправлены все ошибки,
преобразующие кодовое слово /(?) в D/, ?=0, ...,
т—1. Аналогичная возможность имеется и в случае
ошибок других типов таких, как стирание символа
(замещение символом другого алфавита), изменение
числового значения кодового слова на rt&r', 6=1, ...,
г—1, г=0, 1, ... (арифметическая ошибка), выпадение
или вставка символа и т. п.
В теории передачи информации (см. Информации пе-
передача) рассматриваются вероятностные модели обра-
образования ошибок, называемые каналами. Простей-
ший канал без памяти задается вероятностями рц за-
замещения символа i символом у. Для канала определяет-
определяется величина (пропускная способность)
С= max2; Zj %ll 4iPtj log, {ptjjj^lo qhPh') '
где максимум берется по всем наборам (q0, ..., qm-^)
таким, что 9(^0 и 2г=о 9'=^- Эффективность кодиро-
кодирования / характеризуется скоростью передачи R(f),
а помехоустойчивость — средней вероятностью ошибки
декодирования Р (/) (при наилучшем разбиении В"
на подмножества /?,-). Основной результат теории пере-
передачи информации (теорема Шеннона) сос-
состоит в том, что пропускная способность С является верх-
верхней гранью чисел R таких, что для любого е>0 при
всех п, начиная с нек-рого, существует кодирование
/ : Вт-+Впг,р,лп к-рого R{f)>R и Р(/)<е.
Другая модель образования ошибок (см. Код с ис-
исправлением ошибок, Код с исправлением арифметиче-
арифметических ошибок, Код с исправлением выпадений и вставок)
характеризуется тем, что в каждом слове длины п про-
происходит не более заданного числа t ошибок. Пусть
E/(t) — множество слов, получаемых из f(i) в резуль-
результате t или менее ошибок. Если для кода
{/@), ..., f(m-i))cBnr
множества ?/(*), г=0, ..., т—1, попарно не пересе-
пересекаются, то при декодировании таком, что ?,-(t)czZ)/,
будут исправлены все ошибки, допустимые рассматри-
рассматриваемой моделью образования ошибок, и такой код наз.
кодом с исправлением t ошибок. Для
многих типов ошибок (напр., замещений, арифметич.
ошибок, выпадений и вставок) функция d(x, у), равная
минимальному числу ошибок данного типа, преобра-
преобразующих слово х?В" в слово у?В", является метри-
метрикой, а множества E,(t) — метрическими шарами ра-
радиуса t. Поэтому задача построения наиболее эффектив-
эффективного (т. е. максимального по числу слов т) кода в Впг
с исправлением t ошибок равносильна задаче плотней-
шей упаковки метрического пространства В" шарами
радиуса t. Код для цифр почтового индекса не яв-
является кодом с исправлением одной ошибки, так как
d(f(O), /(8))=1 и d(fE), /(8))=2, хотя все другие рас-
расстояния между кодовыми словами не менее 3.
Задача исследования величины I r(n, t) — мини-
минимальной избыточности кода в Bi с исправлением t
ошибок типа замещения распадается на два основных
случая. В первом случае, когда t фиксировано, а и_>-оо,
справедлива асимптотика
h(n, t)~t log2ra, B)
причем достигается «мощностная» граница, основан-
основанная на подсчете числа слов длины п в шаре радиуса t.
Асимптотика величины Ir(n, t) при г>2, а также при
г=2 для многих других типов ошибок (напр., ариф-
арифметич. ошибок, выпадений и вставок) не известна A978).
Во втором случае, когда t=lpn], где р — некоторое
фиксированное число, 0<р<(*—1)/2г, а п—>-оо, «мощ-
«мощностная» граница
1г(п,
где Тг(р)=— р logr(p/(r— 1))—A— р) logr(l— p), суще-
существенно улучшена. Имеется предположение, что верх-
верхняя граница
Тг(п, [рп]ХпТгBр), C)
полученная методом случайного выбора кода, является
асимптотически точной, т. е. Iг(п, \рп))~пТгBр). До-
Доказательство или опровержение этого предположе-
предположения — одна из центральных задач теории кодирования.
Большинство конструкций помехоустойчивых кодов
являются эффективными, когда длина п кода доста-
достаточно велика. В связи с этим особое значение приобре-
приобретают вопросы, связанные со сложностью устройств,
осуществляющих кодирование и декодирование (коде-
(кодера и декодера). Ограничения на допустимый тип деко-
декодера или его сложность могут приводить к увеличе-
увеличению избыточности, необходимой для обеспечения за-
заданной помехоустойчивости. Напр., минимальная избы-
избыточность кода в В", для к-рого существует декодер,
состоящий из регистра сдвига и одного мажоритарного
элемента и исправляющий одну ошибку, имеет порядок
У~п (ср. с B)). В качестве математич. модели кодера
и декодера обычно рассматривают схемы из функцио-
функциональных элементов и под сложностью понимают число
элементов в схеме. Для известных классов кодов с ис-
исправлением ошибок проведено исследование возмож-
возможных алгоритмов К. и д. и получены верхние границы
сложности кодера и декодера. Найдены также нек-рые
соотношения между скоростью передачи кодирования,
помехоустойчивостью кодирования и сложностью де-
декодера (см. [5]).
Еще одно направление исследований в теории коди-
кодирования связано с тем, что многие результаты (напр.,
теорема Шеннона и граница C)) не являются «конструк-
«конструктивными», а представляют собой теоремы существова-
существования бесконечных последовательностей {Кп} кодов
КпЯ^В1. В связи с этим предпринимаются усилия,
чтобы доказать эти результаты в классе таких последо-
последовательностей {Кп} кодов, для к-рых существует ма-
машина Тьюринга, распознающая принадлежность про-
произвольного слова длины I множеству \Jn=iKn за время,
имеющее медленный порядок роста относительно I
(напр., llogl).
Нек-рые новые конструкции и методы получения гра-
границ, разработанные в теории кодирования, привели
к существенному продвижению в вопросах, на первый
взгляд весьма далеких от традиционных задач теории
кодирования. Здесь следует указать на использование
максимального кода с исправлением одной ошибки
в асимптотически оптимальном методе реализации функ-
функций алгебры логики контактными схемами; на прин-
принципиальное улучшение верхней границы для плотности
упаковки га-мерного евклидова пространства равными
шарами; на использование неравенства A) при оценке
сложности реализации формулами одного класса функ-
функций алгебры логики. Идеи и результаты теории коди-
кодирования находят свое дальнейшее развитие в задачах
синтеза самокорректирующихся схем и надежных схем
из ненадежных элементов.
Лит.: [1] Шеннон К., Работы по теории информации
и кибернетике, пер. с англ., М., 1963; [2] Берлекэмп Э.,
Алгебраическая теория кодирования, пер. с англ., М., 1971;
[3] Питерсон У., Уэлдон Э., Коды, исправляющие
ошибки, пер. с англ., 2 изд., М., 1976; [4] Дискретная матема-
математика и математические вопросы кибернетики,т. 1, М., 1974,
раздел 5; [5] Б а с с а л ы г о Л. А., 3 я б л о в В. В., II и н-
скер М. С, «Пробл. передачи информации», 1977, т. 13,
№ 3, с. 5—17; [6] С и д е л ь н и к о в В. М., «Матем. сб.»,
1974, т. 95, в. 1, с. 148—58. В. И. Левенштейн.
КОЕВКЛИДОВО ПРОСТРАНСТВО — пространство,
получаемое из евклидова применением принципа двой-
двойственности проективного пространства такой же раз-
размерности. Обозначается R*n, где га — размерность
пространства. К. п. Rn является пространством с про-
проективной метрикой, к-рая задается в соответствии
с общей схемой введения проективных метрик. Если
проективная метрика евклидова пространства Rn опре-
определяется абсолютом, состоящим из совокупности
(п—1)-плоскости и (п—2)-мнимой квадрики в этой плос-
плоскости, го проективная метрика К. п. R« определяется
двойственным абсолютом: мнимым конусом 2-го по-
порядка, к-рый наз. абсолютным конусом, с вершиной
в качестве абсолютной точки абсолюта.
Расстояние между точками в пространстве Rn опре-
определяется в соответствии с общей схемой определения
расстояния между точками в пространствах с проек-
проективной метрикой с учетом двойственного характера
этого пространства по отношению к Rn. Пусть
(и, as
— нормальные уравнения нек-рых плоскостей в евкли-
евклидовом пространстве Rn, двойственном для R*n, где
(и, и) = 1, (v, v) = \, (и, ж)
— скалярное произведение векторов в Rn. В прост-
пространстве Rn этим плоскостям ставятся в соответствие
точки X (я:0, х) и У (у0, у) с координатами
координаты этих точек нормированы условиями
(as. ж) = р2 > 0, (у, у) = р2 > О
(х° и j/°— координаты точек X и У в бесконечно уда-
удаленной плоскости). Расстояние б между точками
X и Y определяется соотношением
C0S p -<.Г,Х) (,/, ,,)'
т. е. выражается через величину угла между плоско-
плоскостями, двойственными точкам X и У. В соответствии
с нормировкой векторов точек X и У это соотношение
можно записать в виде
cos-5- = -~H(a5, y)\.
Действительное число р наз. радиусом кривизны К. п.
В случае, когда точкам X, y?R« в двойственном
пространстве Rn соответствуют параллельные плос-
плоскости, то 6=0, а расстояние между точками X и У
определяются как евклидово расстояние между этими
параллельными плоскостями.
Углы между двумя плоскостями определяются в R«
как нормированное евклидово расстояние между соот-
соответствующими по принципу двойственности двумя
точками в Rn. Этот угол равен также нормированному
расстоянию между точками данных плоскостей в RjJ,
являющихся полюсами (п—2)-плоскости их пересече-
пересечения относительно квадрик, высекаемых абсолютным
конусом на этих плоскостях. При этом всегда опреде-
определяется тот из углов между плоскостями, к-рый не со-
содержит абсолютной точки. В частности, между двумя
прямыми на коевклидовой плоскости R2 он равен
нормированному расстоянию между такими двумя
точками этих прямых, к-рые вместе с точкой пересече-
пересечения данных прямых гармонически делят точки пересе-
пересечения прямых с абсолютными прямыми.
Движения К. п. R^ определяются как преобразо-
преобразования этого пространства, индуцируемые движениями
соответствующего двойственного пространства R,,, тем
самым движения К. п. R^ описываются ортогональ-
ортогональными операторами.
Геометрия коевклидовой плоскости R* обладает
свойствами, двойственными свойствам плоскости R».
Так, из инвариантности длин сторон в треугольни-
треугольнике ABC относительно движений плоскости R2 следует,
что угловой избыток А=А-{-С—В инвариантен при
движениях плоскости Ra и всегда положителен.
(Здесь и далее предполагается, что внутренний угол В
треугольника ABC в R2 содержит абсолютную точку.)
За площадь S треугольника на плоскости R^ берется
величина, пропорциональная угловому избытку, к-рый
является аддитивной функцией треугольника: 5=р2Д.
Вследствие двойственного характера величин углов
и длин сторон треугольника на плоскости R-> имеют
место следующие тригонометрич. соотношения в тре-
треугольнике ABC:
Ь а 1-е,
А2 = В2 4- С2 — гСВ cos — ,
р
а . Ь .с
sin — sin — sin —
Р Р Р
ABC
На плоскости R2 метрика расстояний (на прямых)
является проективной эллиптической, метрика углов —
параболической. В пространстве Rl проективная мет-
метрика расстояний (на прямых) — эллиптическая, в плос-
плоскостях — также эллиптическая, а в пучках плоскос-
плоскостей — параболическая.
К. п. R« является предельным случаем как эллипти-
эллиптического пространства, так и Лобачевского простран-
пространства: проективная метрика К. п. Rn может быть полу-
получена предельными переходами из проективных метрик
указанных пространств.
Лит.: [1] Р о з е н ф е л ь д Б. А., Неевклидовы простран-
пространства, М., 1969. Л. А. Сидоров.
КОКСТЕРА ГРУППА — группа с отмеченной си-
системой образующих {г,-: i?I}, допускающая определяю-
определяющую систему соотношений
(г/, гу)"'/ = 1, i, j?I,
где И(( = 1 (так что г? =1 при любом i) и га/у=«у,- при
1ф] — целое число Js2 или сю (в последнем случае со-
соотношения между г/ и rj нет). При этих условиях пц
совпадает с порядком элемента r^j. Если ге,у=2, то г,-
и tj коммутируют. Матрица (га(/), i, ) ?/ наз. м а т р и-
цей Кокстера данной К. г. Эта матрица (л,
тем самым, группа) может быть задана посредством
графа Кокстера — графа с вершинами а,-
(г?/), в к-ром вершины а,- и а;- соединены (щ/—2)-
кратным ребром, если га,у<оо (в частности, вообще не
соединены, если га,у=2), и соединены жирным ребром,
если n;j= 00. В другой системе обозначений вершины
а,- и aj графа Кокстера соединяются простым ребром
с отметкой пц.
Примеры. 1. Всякая группа, порождаемая дву-
двумя элементами порядка 2, есть К. г. с графом
2. Симметрическая группа S,, является К. г. отно-
относительно образующих r,-=(t, i+1), г=1, . . ., п — 1; ее
граф Кокстера имеет вид
3. Группа PGL^%) = GL^/L)l{r±L\} является К. г.
относительно образующих
ri = <±
—1 О
О 1
\
—1 О
1 1
s={±
|0 —1
1 0
ее граф имеет вид
Группа PGL2('?) содержит подгруппу PSL.2(z)~
2{±l} индекса 2, изоморфную модулярной
группе Клейна.
Понятие К. г. возникло в теории дискретных групп,
порождаемых отражениями относительно гиперплос-
гиперплоскостей (см. Отражений группа, в дальнейшем — о. г.).
Всякая о. г. является К. г., если в качестве образую-
образующих взять отражения относительно гиперплоскостей,
ограничивающих ее фундаментальный многогранник.
К числу о. г. относятся Вейля группы (обычные и
аффинные) полупростых групп Ли.
В 1934 X. С" М. Кокстер [1] перечислил все о. г.
в и-мерном евклидовом пространстве Е" и доказал, что
все они являются, как говорят сейчас, К. г. В следую-
следующей работе [2] он доказал, что всякая конечная
К. г. изоморфна некоторой о. г. в Е", элементы кото-
которой имеют общую неподвижную точку, и тем самым
получил классификацию конечных К. г. (см. табл. 1).
Табл. 1,—Неразложимые конечные К. г.
Обозначение группы
А„ л г 1
В„ или Сп< " ¦
Dn л ? 4
°2
Ее граф Кокстера
Ее показатели
1,2 п
1,3 21-1
I, 3 2п-3, л-1
1,4,5,7,8, II
1,5,7,9,11,13.17
1,7,11,13,17,19,23,29
1, 5, 7, II
I, т-\
I, 5, 9
I, 11,19,29
Число образующих равно нижнему индексу
в обозначении группы.
Среди бесконечных К. г. выделяются параболи-
параболические и гиперболические К. г. По
определению, К. г. является параболической (соот-
(соответственно гиперболической), если она изоморфна о. г.
в Е" (соответственно в пространстве Лобачевского L"),
элементы к-рой не имеют общей инвариантной плос-
плоскости размерности <ге (в гиперболическом случае плос-
плоскостью следует считать и бесконечно удаленную точку).
Табл. 2. —Н е р а з л о ж и м ы е
пара бо лическиеК.г.
Обозначение группы
/1Л ,"*2
В„ , л > 3
С/7 i n *¦ 2
Л, .04
Ее граф Кокстера
Число образующих на единицу больше
индекса в обозначении группы.
Параболические К. г. перечислены X. С. М. Кокстером
(см. табл. 2); они возникают в теории полупростых
групп Ли как аффинные группы Вейля.
К. г. с к образующими является двумерной гипер-
гиперболической К. г. тогда и только тогда, когда, при под-
подходящей нумерации образующих,
-L. + -L.+ ...+—<1
и п,у=оо при \1—)\~>i. Что касается n-мерных гипер-
гиперболических К. г. при ?г>2, то их полное перечисление
не представляется возможным, хотя были достигнуты
определенные успехи в изучении наиболее важных
классов таких групп (см. Отражений группа).
Конечные, параболические и гиперболические К. г.
и их прямые произведения составляют лишь неболь-
небольшую часть К. г. Произвольная К. г. с конечным числом
образующих допускает конечномерное вещественное
линейное представление, указанное явно X. С. М. Кок-
Кокстером [2], при к-ром образующие переходят в линей-
линейные отражения. Доказано [4], что это представление
является точным, из чего вытекает, в частности, реше-
решение проблемы тождества слов в К. г. [5].
Стандартные подгруппы К. г. Пусть
G — К. г. с системой образующих {г/, i?l). Для лю-
любого подмножества /с/ подгруппа Gj, порожденная
множеством {г,-, ??/}, является К. г., причем r^Gj
при ;(?/. Подгруппы такого вида наз. стандарт-
н ы м и. Всякая максимальная конечная подгруппа
К. г. сопряжена стандартной подгруппе.
К. г. наз. неразложимой, если она не яв-
является прямым произведением двух нетривиальных
стандартных подгрупп; это эквивалентно связности
ее графа Кокстера. Все конечные (соответственно пара-
параболические) К. г. суть прямые произведения неразло-
неразложимых К. г. того же типа; все гиперболические К. г.
неразложимы. Неразложимая К. г. является конеч-
конечной (соответственно параболической, гиперболической)
тогда и только тогда, когда симметрическая матрица
—cos -2- положительно определенна (соответственно
неотрицательно определенна и вырождена, имеет
отрицательный индекс инерции 1).
В теории конечных К. г. важную роль играют так
наз. показатели (см. табл. 1) — уменьшенные
на единицу степени образующих инвариантов соот-
соответствующей о. г. Через показатели выражаются по-
порядок группы, число отражений (элементов, сопряжен-
сопряженных образующим) н пр.— см. Отражений группа.
Произведение всех образующих конечной К. г. с точ-
точностью до сопряженности не зависит от порядка мно-
множителей и наз. элементом К и л л и н г а —¦
Кокстера.
Лит.: [1] С о х е t е г Н. S. M., «Ann. Math.», 1934, v.
35 p. 588 — 621; [2] e г о же, «J. London Math. Soc», 1935 v.
10, p. 21 — 25; [3] его же, «Duke Math. J.», 1951, v. 18, p.
765—82; [4] Б у р б а к и Н-, Группы и алгебры Ли, пер. с
франц., М., 1972, гл. 4—6; [а] Т i t s J., в кн.: Symposia Ma-
thematica, v. 1, L.— N. Y., 1969, p. 175—85. Э. В. Випберг.
КОЛЕБАНИЕ ФУНКЦИИ на множестве
Е — разность между верхней п нижней гранями зна-
значений функции на множестве Е. Иначе, К. ф. равно
©?(/)= SUP {\f(P')-f(P")\}-
Р', Р"еЕ
Если функция не ограничена на множестве Е, К. ф.
полагается равным оо. Для постоянных на Е функций
(н только для них) колебание на Е равно нулю. Если
функция / определена на подмножестве Е пространства
R", то К. ф. в любой точке Q замыкания Е определя-
определяется по формуле
где нижняя грань берется по всем окрестностям точки Q.
Если Q?E, то для непрерывности / в точке Q по мно-
множеству Е необходимо и достаточно, чтобы coq fi(/) = 0.
А. А. Нонюшпов.
КОЛЕБАНИЙ ТЕОРИЯ — раздел прикладной теории
дифференциальных уравнений, связанный с изучением
колебательных явлений в естествознании и технике.
Основные проблемы К. т. состоят в доказательстве
существования и фактич. отыскании колебательных
(периодических, почти периодических и др.) движе-
движений — решений заданной системы, и исследовании по-
поведения остальных решений по отношению к данным
колебательным. Различают теорию линейных колеба-
колебаний и теорию нелинейных колебаний.
В теории линейных колебаний дело
сведится к изучению линейных систем дифференци-
дифференциальных уравнений, это обычно бывает связано с тем,
что рассматриваемые величины (искомые функции
системы дифференциальных уравнений) столь малы,
что оказывается возможным пренебречь нелинейными
членами в правых частях системы. Рассматриваются
линейные системы дифференциальных уравнений:
2L = P{t)x + f(t), A)
где x(t) и f(t) суть га-мерные векторы, аР(() — квадрат-
квадратная матрица порядка га, причем Р(t) и f(t) чаще всего
являются периодич. или почти периодич. функциями.
Основные проблемы теории линейных колебаний: по-
построение периодич. и почти периодич. решений системы
A) и исследование свойств их устойчивости. Наиболее
детально с этих точек зрения изучены случаи, когда
заданная система близка к системе уже изученной, ины-
иными словами, те случаи, когда удается ввести малый па-
параметр следующим образом:
^ B)
в предположении, что система
2L = P(t)x C)
полностью исследована, а \х — малый параметр. Для та-
таких систем в большинстве случаев удается исследовать
вопрос о существовании периодических (соответственно
почти периодических) решений и фактически построить
их. При весьма широких предположениях относитель-
относительно матриц Р и Q дается представление характеристич.
показателей системы C) в виде функций параметра
(см. [7), [10]), в частности исследовано интересное яв-
явление параметрич. резонанса в линейных системах [5].
В теории нелинейных колебаний как
по постановке задач, так и по методам исследования
существенным образом различаются так наз. локаль-
локальные и нелокальные проблемы. К первым из них отно-
относятся такие задачи, в к-рых удается выделить какие-
либо «малости» (напр., малы сами исследуемые вели-
величины, или в системе имеются малые параметры).
Если в исследуемой задаче искомые функции можно
считать малыми, то дело сводится к исследованию
окрестности состояния равновесия для системы диф-
дифференциальных уравнений
где x(t) и Х(х, t) суть га-мерные векторы и Х@, t)s=O.
Здесь широко применяются методы локальной качест-
качественной теории дифференциальных уравнений [4] и
методы теории устойчивости движения в смысле Ля-
Ляпунова [1]. Весьма важный результат для теории нели-
нелинейных колебаний был получен А. Н. Колмогоровым
и его последователями (см. [4]): было доказано сущест-
вование квазипориодич. решении в окрестности состоя-
состояния равновесия х=0 для системы D).
Часто в заданные системы дифференциальных урав-
уравнений входят малые параметры, т. е. рассматриваются
системы вида
?L=X(x, t) + llR(x, t, ц), E)
где A — малый параметр. С такого рода системами свя-
связывают следующую проблему: наряду с системой E)
рассматривают так наз. «порождающую» систему —
ту, в к-рую обращается система E) при ji=0, т. е. си-
систему вида D). Предполагается, что «порождающая»
система обладает нек-рым свойством; ставится вопрос:
не будет ли и система E) обладать тем же свойством
при малых, но отличных от нуля \i. Напр., пусть сис-
система D) имеет периодич. или почти периодич. решение
ж=г|)(/), будет ли при этом система E) обладать пе-
периодич. или почти периодич. решением ж=ф(г, (х)
таким, что
lim ф(«, ц) = -ф(«)?
Еще А. Пуанкаре [2] разработал мощные методы для
решения такого рода проблем. В ряде случаев им было
не только доказано существование периодич. решения,
но и указан алгоритм для его построения (см., напр.,[5]).
Н. М. Крылов, Н. Н. Боголюбов и их ученики
(см. [3], [6J, [11]) развивали для систем вида E) асим-
птотич. методы. Среди этих методов особо важную
роль играет метод осреднения, к-рый состоит в следую-
следующем. Рассматривается так наз. стандартная система:
^. = цХ(х, t, ц). F)
Оказывается, что к такой системе могут быть сведены
многие системы теории нелинейных колебаний. Наряду
с системой F) рассматривается «осредненная» система
7Г = цУ(у), G)
где
У = lim — Г X (х, т, 0)dx.
t ч- 00 * J 0
Н. М. Крылов и Н. Н. Боголюбов показали, что система
G) приближает систему F) с точностью до величин
порядка (г2. С помощью дальнейших осреднений можно
избавиться от зависимости от f в членах сколь угодно
высокого порядка малости по \i. Однако этот процесс,
как правило, расходится, так что описанный метод
является по существу асимптотическим.
Весьма важную роль в теории нелинейных колебаний
играет метод интегральных поверхностей. Основы
этого метода были заложены А. М. Ляпуновым [1].
При весьма общих предположениях было доказано
(см. [3], [6], [11]), что если «порождающая» система D)
имеет интегральную поверхность с определенными свой-
свойствами, то и система E) обладает такой же интеграль-
интегральной поверхностью.
С описанным кругом проблем тесно связана теория
релаксационных колебаний. Эти колебания описываются
системами дифференциальных уравнений с малыми
параметрами при производных:
% = Х(х, у, t, ц), цЦ- = У(х, у, t, (i), (8)
где х и X — re-мерные векторы, у и У — m-мерные век-
векторы, а (х — малый параметр. Наряду с системой (8)
рассматривается вырожденная система:
?^Х(х, у, t,0), Y(x, у, t, 0) = 0. (9)
Если система (9) имеет специальное «разрывное» перио-
периодическое решение, то и (8) в ряде случаев располагает
при малых |х истинным периодич. решением (см. [12]).
В приложениях весьма часто встречаются системы
дифференциальных уравнений, в к-рых нельзя выде-
выделить никаких малостей. Здесь сталкиваются с нелокаль-
нелокальными проблемами К. т. При исследовании нелокаль-
нелокальных проблем возникают весьма серьезные трудности.
Однако в ряде частных, но важных для приложений,
случаев удается провести полное исследование соот-
соответствующей системы или получить достаточно сущест-
существенную информацию о поведении ее решений. Напр.,
для уравнения
'x+f(x)x + g(x) = 0, A0)
представляющего собой обобщение Ван дер Поля урав-
уравнения, Н. Левинсон и О. Смит [15] доказали существо-
существование, устойчивость и единственность предельного
цикла. При доказательстве существенно использовался
тот факт, что уравнение A0) есть уравнение 2-го по-
порядка. В дальнейшем было доказано существование
периодич. решения у нелинейного уравнения 3-го поряд-
порядка и различных автономных систем высших порядков.
При исследовании периодических неавтономных сис-
систем, т. е. систем вида D), у к-рых X (х, t-\-<o)=X (x, t),
с системой связывают ее преобразование Пуанкаре Т,
вводимое формулой Тхо=х(а>, 0, х0), где x(t, t0, x0) —
решение системы D) такое, что x(t0, to, Хо)=хо- Если
х* есть неподвижная точка преобразования Т, то ре-
решение x(t, 0, х*) имеет период со по г. Это дает воз-
возможность для доказательства существования периодич.
решений применять различные теоремы о существо-
существовании неподвижной точки (см. [8], [9]).
В теории нелинейных колебаний важную роль иг-
играют диссппативные системы (это такие системы вида
D), у к-рых все решения при достаточно больших t
остаются в фиксированном шаре) и системы с конвер-
конвергенцией (у таких систем все решения сходятся к одному
устойчивому); разработаны достаточно надежные ме-
методы доказательства конвергентности и диссипативности
конкретных систем [8].
Поведение решений диссипативной периодич. сис-
системы во многом определяется структурой нек-рого
асимптотически устойчивого интегрального множества
этой системы. Поэтому для теории нелинейных коле-
колебаний существенно исследование структуры таких
множеств. В случае, если заданная система имеет лишь
конечное число периодич. решений, такое множество
удается охарактеризовать достаточно полно [13].
Если же система имеет бесконечно много периодич.
решений, то в этом случае оказывается, что асимпто-
асимптотически устойчивые интегральные множества имеют
чрезвычайно сложную структуру [13]. Исследование
таких систем связано, как правило, с преодолением
значительных трудностей, и его удается провести лишь в
исключительных случаях. Пример такого исследова-
исследования дан М. Картрайт и Дж. Литлвудом [16] при ис-
исследовании уравнения Ван дер Поля с вынужденней:
"х + к(хг — 1) x-\-x=kbsint.
В частности, они показали, что это уравнение при
соответствующем выборе параметров Ь и к имеет бес-
бесконечно много периодич. решений.
Лит.: [1] Л я п у н о в А. М., Общая задача об устойчи-
устойчивости движения, Хар., 1892; [2] Р о i n с а г е Н., Les methodes
nouvelles de la mecanique celeste, t. 1, P., 1892; [3] К р ы л о в
Н. М., Б о г о л ю б о в Н. Н., Новые методы нелинейной меха-
механики, М.—Л., 1934; [4] Н е м ы ц к и й В. В., С т е п а н о в В. В.,
Качественная теория дифференциальных уравнений, М.— Л.,
1949; [5] М а л к и н И. Г., Некоторые задачи теории нелиней-
нелинейных колебаний, М.—Л., 1956; [6] Б о г о л ю б о в Н. Н., М и т-
ропольский Ю. А., Асимптотические методы в теории нели-
нелинейных колебаний, 3 изд., М., 1963; [7] Еругин Н. П., Ли-
. нейные системы обыкновенных дифференциальных уравнений с
периодическими и квазипериодическими коэффициентами, Минск,
1963; [8J II л и с с В. А., Нелокальные проблемы теории коле-
колебаний, М.—Л., 1964; [9] Красносельский М. А.,
Оператор сдвига по траекториям дифференциальных уравнений,
М., 1966; [10] Якубович В. А..Старшинский В. М.,
Линейные дифференциальные уравнения с периодическими
коэффициентами, М., 1972; [11] М и т р о п о л ь с к и й Ю. А.,
Лыкова О. Б., Интегральные многообразия в нелинейной меха-
механике, 1973; [12] Мищенко Е. Ф., Розов Н. X., Диф-
Дифференциальные уравнения с малым параметром и релаксацион-
релаксационные колебания, М., 1975; [13] Пл исс В. А., Интегральные мно-
множества периодических систем дифференциальных уравнений, М.,
1977; [14] Арнольд В. И., «Успехи матем. наук», 1963, т. 18,
в. 6, с. 91 — 192; [15] Levinson N.. Srait О. К. «Duke
Math. J.», 1942, v. 9, p. 382—403; [16] Little wo о dJ E.,
«Acta math.», 1957, v. 97, № 3 — 4, p.267—308. В. А. Плисе.
КОЛЕБЛЮЩЕЕСЯ РЕШЕНИЕ — решение x(t)
дифференциального уравнения
a-<«) = /(t, ж, г', ....a-'"-1)), t?[t0, oo), (*)
обладающее свойством: для любого t{^t0 найдется
точка t2'>t1, при переходе через к-рую функция x(t)
меняет знак. Во многих прикладных задачах возникает
вопрос о существовании К. р. или о колеблемости всех
решений уравнения (*). Известно много достаточных
условий, при к-рых уравнение (*) имеет К. р. (см.
[1] — [3]). Напр., любое нетривиальное решение урав-
уравнения х"-\~28х'-\-а>2х=0 с постоянными коэффициен-
коэффициентами колеблется, если 82<<в2; любое нетривиальное
решение уравнения
x"+p(t)x'-\-q{t)x=O
с со-периодическими коэффициентами колеблется, если
^—5- ( 1 —exp
и д (t) =?0 на [0, со].
В ряде приложений возникает вопрос о К. р. (в оп-
определенном смысле) системы обыкновенных дифферен-
дифференциальных уравнений. Напр., в теории регулирования
изучают колеблемость относительно заданной гипер-
гиперплоскости ^fr-jc/*! —0 решений x(t)=(x1(t), ..., xn(t))
системы уравнений x'=f(t, x), т. е. вопрос о колеб-
колеблемости функции a(t) = 2- cixi (')• Изучают также
[ос, Р]-колеблющиеся решения, при этом ограниченное
решение x(t) системы х' =/ (t, х) наз.[а, |3]-к о л е б л ю-
щ и м с я, если функция a(t) колеблется и для любо-
любого t^to найдутся точки t2 и t3 такие, что t1<Ct2<Ct3,
a(f2Xa, a(i3)>p\ причем а<0<р\ Для системы B)
существуют и др. определения колеблемости решений.
Лит.: [1] X артман Ф., Обыкновенные дифференциаль-
дифференциальные уравнения, пер. с англ., М., 1970; [2] S w а п s о п С. А.,
Comparison and oscillation theory of linear differential equations,
N. Y.— L., 1968; [3] К и г у р а д з е И. Т., Некоторые сингу-
сингулярные краевые задачи для обыкновенных дифференциальных
уравнений, Тб., 1975. Ю. В. Комленко, Е. Л. Тонкое.
КОЛЕЦ МНОГООБРАЗИЕ — класс колец ЯЛ, удов-
удовлетворяющих заданной системе полиномиальных тож-
тождеств. К. м. можно определить аксиоматически, как
наследственный класс алгебр, замкнутый относительно
взятия гомоморфных образов и полных прямых сумм
(см. Алгебраических систем многообразие). Так как
совокупность полиномиальных тождеств, выполни-
выполнимых в данном кольце, образует вполне характеристич.
идеал (Т-идеал) свободного кольца, то существует
взаимно однозначное соответствие между многообра-
многообразиями колец и Г-идеалами счетно порожденного сво-
свободного кольца. Если для К. м. имеет место включение
3?с=9Л, то говорят, что 9с является подмногообра-
подмногообразием в ЯЛ. Многообразие, соответствующее Г-идеалу
тождеств кольца А, наз. многообразием, порожденным
кольцом А. Каждое многообразие колец порождается
своим «универсальным объектом» — свободным коль-
цом данного многообразия, к-рое обладает свободной
системой образующих: всякое отображение множества
свободных образующих в произвольное кольцо из
многообразия продолжается до гомоморфизма.
Пусть Мп— многообразие, порожденное алгеброй
квадратных матриц порядка п. Для всякого многооб-
многообразия ассоциативных колец нулевой характеристики
(т. е. колец, аддитивная группа к-рых без кручения)
существует такое натуральное число ;i=rc(ffll)> чт0
М„'=Ш, но Мп+1^>Ж. Многообразие колец наз.
шпехтовым, если всякое его кольцо обладает
конечным базисом тождеств. Многообразие, порожден-
порожденное конечным ассоциативным кольцом или конечным
кольцом Ли, является шпехтовым. Вопрос о том, всякое
ли многообразие ассоциативных алгебр шпехтово, соста-
составляет содержание (пока открытой, 1978) проблемы
Ш и е х т а. Если многообразие Ш порождено ассоциа-
ассоциативной алгеброй с конечным числом образующих над по-
полем нулевой характеристики и М2(?Ж1, то ЗЛ шпехтово.
См. также Vl-алгебра.
Лит.: [1] Procesi С, Rings with polynomial identities,
N. Y., 1973; [2] К о н П., Универсальная алгебра, пер. с англ.,
М., 1968. В. Н. Латышев.
КОЛЛИНЕАРНЫЕ ВЕКТОРЫ — векторы, лежащие
на одной прямой или на параллельных прямых. Для
того чтобы два ненулевых вектора были коллинеарны,
необходимо и достаточно, чтобы их координаты были
пропорциональны. Нулевой вектор коллинеарен вся-
всякому вектору. Аналогично, коллинеарными наз. точки,
Лежащие на ОДНОЙ ПРЯМОЙ. А. Б. Иванов.
КОЛЛИНЕАЦИЯ — проективное преобразование
проективного пространства П„, представимое в виде
произведения конечного числа перспектив; если v
есть К., то для любого подпространства Sg сущест-
существует такое произведение п не более чем q—1 перспек-
перспектив, что v(Sp) = n(Sp) для .любого SpdSg. Напр.,
проективное преобразование, оставляющее неподвиж-
неподвижной каждую точку нек-рой прямой, является К.,—
это гомология (в узком смысле).
Пусть П„ интерпретируется как совокупность под-
подпространств линейного пространства Aen+i(K) над те-
телом К. Для того чтобы проективное преобразование
было К., необходимо и достаточно, чтобы оно индуци-
индуцировалось линейным преобразованием Ап+х(К). Сово-
Совокупность всех К. образует подгруппу Go группы про-
проективных преобразований G, являющуюся нормальным
делителем G.
К. тогда и только тогда исчерпывают все проективные
преобразования, когда каждый автоморфизм тела К
является внутренним. Поле обладает этим свойством
в том и только в том случае, когда любой его автомор-
автоморфизм — тождественный, таково, напр., поле действи-
действительных чисел R. Поле комплексных чисел С этим
свойством не обладает, в то время как каждый авто-
автоморфизм тела кватернионов Н является внутренним.
Если К — некоммутативное тело, то существует
нетождественная К., оставляющая неподвижной каж-
каждую точку данного симплекса. Каждый симплекс тогда
и только тогда отображается на любой другой симплекс
¦одной и только одной К., когда К — поле (вторая
основная теорема проективной гео-
геометр и и). М- И. Вопцеховский.
КОЛЛОКАЦИИ МЕТОД — проекционный метод ре-
решения интегральных и дифференциальных уравнений,
в к-ром приближенное решение определяется из усло-
условия удовлетворения уравнению в нек-рых заданных
точках. Напр., для приближенного решения интеграль-
интегрального уравнения
и (*)=(" К (t, s, и (s)) ds + f (t)
¦выбираются нек-рое п-параметрич. семейство функций
cp(t, cx, . .., cn) и нек-рые точки (узлы коллока-
ц п и) tv •.., t,, на отрезке [а, Ь]. Приближенное ре-
решение un(t) = ff(t, cu ..., с„) определяется из условий
s,un(s))ds-\-f(ti), i=l, ...,гс,
представляющих собой систему п уравнений относи-
относительно неизвестных clt . . ., с„. Если данное уравнение
линейно, а приближенное решение ищется в виде линей-
линейной комбинации ип (t) = c1cfl (() -j- . .. -j- с„ф„ (t) задан-
заданных (так наз. координатных) функций ф1; . . ., ф„, то и
система уравнений относительно сх, . . ., сп получает-
получается линейная.
Сходимость К. м. для линейны х к р а е-
вых задач. Пусть поставлена краевая задача
(t) мея-1)+ ...+ат (t)u^f(t), A)
— 1 < t < 1;
27=0V1) + P'V"<;)(l)]=0, i = l, .... m. B)
Приближенное решение задачи разыскивается в виде
где фу(*) — некоторый многочлен степени m-\-j—1,
удовлетворяющий краевым условиям B). Коэффици-
Коэффициенты сх, ..., с„ определяются из линейной системы
[Lun — f]t=tl = 0, 1 = 1, ...,п, C)
с чебышевскими узлами t, = tf) = cos 2п я, i = 1,. . . ,n.
Справедлива следующая теорема [1]. Пусть функции
/ и ay, ; = 1, . .., m, непрерывны на [—1, 1] и пусть
краевая задача A), B) имеет единственное реше-
решение u(t). Тогда существует ге0 такое, что при п
система C) однозначно разрешима, и
max | uf (t) — u^) (t) | < cEn (u<-*)) -^ 0,
-i<t<l
k = 0, 1, .... m-1,
1 |u(m) «)_„<"» /,\|2 | 1/2
( Г1 |u(m) «)_„<"»
IJ-i vi-t«
где с=const,
Еп (v) = min max
Аналогичный результат верен (см. [1]), если узлы
корни ортогональных по какому-либо весу многочле-
многочленов. При равноотстоящих узлах рассматриваемый
метод расходится.
Развиваются также эффективные вычислительные
схемы К. м. с координатными сплайн-функциями
(см. [2], [3]).
Лит.: [1] Приближенное решение операторных уравнений,
М., 1969; [2] R u s s е 1 1 R. D., Shampine L. F. «Nume-
rische Mathematik», 1972, Bd 19, № 1, S. 1—28; [3] В о о г С.
de, S w a r t z В., «SIAM Journal of Numerical Analysis», 1973,
v. 10, № 4, p. 582—606. Г. М. Вайникко.
КОЛМОГОРОВА АКСИОМА, аксиома Го,—
самая слабая из всех отделимости аксиом в общей то-
топологии; введена А. Н. Колмогоровым. Топологич.
пространство удовлетворяет этой аксиоме, или есть
Г0-п ространство, пространство Кол-
Колмогорова, если, каковы бы ни были две различные
точки пространства, в этом пространстве существует
открытое множество, содержащее одну из этих точек, но
не содержащее другую. Если потребовать, чтобы каждая
из двух (произвольно данных) точек содержалась в от-
открытом множестве, не содержащем другую точку, то
получим следующую по силе аксиому отделимости,
называемую аксиомой 2Y, удовлетворяющие ей тодо-
логич. пространства наз. Г]-пространствами. Простей-
Простейшим примером Г0-пространства, не являющегося Тх-
пространством, служит связное двоеточие.
В Т0-пространстве одноточечные множества могут не
быть замкнутыми; Tj-пространства могут быть опре-
определены как такие Г0-пространства, в к-рых все одно-
одноточечные множества замкнуты. Г0-пространство, в
к-ром пересечение любого числа открытых множеств
открыто, наз. дискретным (в широком смысле)
пространством. В таком и только в таком про-
пространстве замыкание объединения любого числа мно-
множеств совпадает с объединением замыканий этих мно-
множеств. В любом дискретном пространстве и даже в лю-
любом пространстве Колмогорова может быть определен
(частичный) порядок между его точками хну: пишем
¦rsgj/, если точка х содержится в замыкании одноточеч-
одноточечного множества, состоящего из точки у. Обратно, опре-
определяя в произвольном частично упорядоченном мно-
множестве замыкание какой-либо точки х как множество
всех точек х'^х и называя замыканием любого мно-
множества объединение замыканий всех его точек, получим
дискретное пространство. Таким образом, изучение
дискретных пространств равносильно изучению час-
тично-упорядоченных множеств. К важным примерам
дискретных пространств относятся симплициальные
(и более общие) комплексы комбинаторной топологии:
для симплексов х, у отношение порядка х^.у означает,
что х есть грань (возможно, несобственная) симплек-
симплекса у.
Лит.: [1] Александров П. С, Введение в теорию
множеств и общую топологию, М., 1977. В. И. Зайцев.
КОЛМОГОРОВА ДВОЙСТВЕННОСТЬ — двойствен-
двойственность в алгебраич. топологии, состоящая в изомор-
изоморфизме
Hr(A, G)~Hr + 1(R\A, G)
r-мерной группы гомологии Н r(A, G) замкнутого мно-
множества А хаусдорфова локально компактного прост-
пространства R с нулевыми г- и (г+1)-мерными группами
гомологии (г+1)-мерной группе гомологии с абелевой
группой коэффициентов G дополнения Д\Л и в изо-
изоморфизме
Hr(A, G) ~Hr + 1(R\A, G)
соответствующих групп когомологии при Hr(R, G)=0
и Hr + 1(R, G)=0.
Группы гомологии и когомологии, участвующие
в этих изоморфизмах, определяются так. За г-м е р-
н у ю цепь принимается любая кососимметриче-
ская, аддитивная относительно каждого аргумента
функция сг(е0, ех, . . ., ег) от г+1 подмножеств прост-
пространства R, имеющих компактные замыкания, прини-
принимающая значения из G и равная нулю, когда пересе-
пересечение е0 Г) • • • Г\вг пусто. Граничный опера-
оператор д определяется по формуле
дсг (е0, . . ., er_i) =cr (V, е0, ..., ег_х),
где U — любое открытое множество из R с компактным
замыканием, содержащее eo\J- ¦ -\Jer-i- Циклами
считаются цепи сг с нулевыми границами, йсг=О,
а циклами, гомологичными нул ю,—
цепи сг, являющиеся границами, сг=дсг+1. Группа
Zr(R, G) всех г-мерных циклов по обычному сложению
функций содержит группу Br(R, G) всех г-мерных
границ в качестве подгруппы. Факторгруппа Zr(R, G)/
IBr(R, G) и есть группа Hr(R, G). Группу G коэффициен-
коэффициентов А. Н. Колмогоров всегда рассматривал как ком-
компактную группу и компактно топологизировал и группу
гомологии. Однако на построение группы гомологии то-
топология группы коэффициентов не оказывает влияния,
и гомологии можно брать над любой абелевой группой.
Для определения коцепей рассматриваются такие
кососимметрические функции f(x0, х1У ..., хг) от г+1
точек х0, xlt ..., хг пространства R со значениями
в G, что для каждой f существует конечная система
S,r попарно непересекающихся подмножеств из Л
с компактными замыканиями, удовлетворяющая усло-
условиям: f(x0, . . ., xr) = f(x'o, . . ., х'г), если x-t и xi принад-
принадлежат одному и тому же элементу системы S f для лю-
любого г; f(x0, . . ., хг) = 0, если хотя бы одно х; не со-
содержится ни в каком элементе из Sfr. К о г р а н и ч-
ный оператор б определяется по формуле
Rjr (^ т \
О/ V^Ol • • ч хГ + \) —
Функции f[ и fi считаются эквивалентными, если каж-
каждая точка х из R имеет такую окрестность U, что
fi(xa, . . ., xr)=ii(x0, . . ., хг), как только все xt принад-
принадлежат U, и за коцепь принимается класс экви-
эквивалентных функций. Кограница коцепи определяется
как класс кограниц входящих в эту коцепь функций.
Коцикл есть коцепь сг с нулевой кограницей,
бсг=О, а когомологпчным нулю счи-
считается коцикл, являющийся кограницей, сг=Ьсг~1-
Группа Br(R, G) всех r-мерных кограниц есть подгруппа
группы Zr(R, G) всех r-мерных коциклов; фактор-
факторгруппа Zr{R, G)/Br(R, G) и есть группа Hr(R, G).
Определенные так группы гомологии и когомологии,
часто называемые функциональными, были
введены А. Н. Колмогоровым [1]. Тогда же, кроме
выше указанных изоморфизмов двойственностей, им
были доказаны двойственность между гомологиями и
когомологиями Hr(R, G*)\Hr(R, G) в смысле теории
характеров Понтрягина, когда компактная группа G*
двойственна группе G, и двойственности Пуанкаре
Hr(R,G*)~H"~r(R, G*), Hr(R, G)~Hn-r(R, G),
где R — открытое re-мерное многообразие, Hr(R, G*)
и Hr(R, G) •— функциональные группы над компактной
(соответственно, дискретной) группой G* (соответст-
(соответственно G), H"-r(R, G*) и IIn-r(R, G) — группы когомо-
когомологии (соответственно гомологии) бесконечных ко-
коцепей (соответственно конечных цепей) произвольного
клеточного разбиения многообразия R.
В случае, когда R есть n-мерное евклидово прост-
пространство, из указанных двойственностей получается
теорема двойственности Понтрягина (см. Александера
двойственность). Частным случаем этих двойственно-
двойственностей является и теорема двойственности Стинрода
(см. Двойственноетъ в алгебраич. топологии), поскольку
К. д. для гомологии справедлива и для произвольной
группы коэффициентов [2].
Функциональные группы гомологии изоморфны:
группам Вьеториса (см. Въеториса гомологии) в случае
компактных метрич. пространств и компактной группы
коэффициентов [1]; спектральным группам гомологии
Александрова относительно особых подкомплексов [3]
в случае локально компактных пространств и компакт-
компактной группы коэффициентов [4] и, следовательно: группам
гомологии Александрова — Чеха одноточечной ком-
пактификации данного локально компактного прост-
пространства [5]; группам гомологии Стинрода [8] в случае
компактных метрич. пространств п произвольной
группы коэффициентов [7]. Таким образом, гомологии
Колмогорова, введенные на четыре года раньше гомо-
гомологии Стинрода, представляют собой и их обобщение
на более широкий класс пространств.
Функциональные гомологии и когомологии удовлетво-
удовлетворяют всем Стинрода — Эйленберга аксиомам на кате-
категории локально компактных пространств с допусти-
мыми отображениями (т. е. когда прообраз каждого
компактного множества компактен) [6] и, кроме того,
двум аксиомам Милнора на категории компактных
метрич. пространств [7].
Лит.: [1] Колмогоров А. Н., «С. г. Acad. sci.», 1936,
t. 202. p. 1144—47; 1325 — 27; 1558 — 60; 1641 — 43; [2] M д з и-
н а р и ш в и л и Л. Д., «Докл. АН СССР», 1974, т. 216, № 3,
с. 502—04; [3] Александров П. С, «Уч. зап. МГУ»,
1940, т. 45, с. 1 — 60; [4] Ч о г о ш в и л и Г. С, «Изв. АН СССР.
Сер. матем.», 1951, т. 15, N° о, с. 421 — 38; [5] С т и н р о д Н.,
Эйленберг С, Основания алгебраической топологии,
М., 1958; [6] Б а л а в ад з е М. Б., «Тр. Тбил. матем. ин-та»,
1972, т. 41, с. 5—40; 171 М д з и н а р и ш в и л и Л. Д., «Тр.
Тбил. матем. ин-та», 1972, т. 41, с. 143—63; [8] S t e e n r о d
N.. «Ann. Math.», 1940, v. 41, p. 831 — 51. Г. С. Чогошвили.
КОЛМОГОРОВА ИНТЕГРАЛ — общая схема по-
построения интеграла, включающая в себя Лебега —
Стилтьеса интеграл, Бёркиля интеграл, Хеллингера
интеграл и др. Предложена А. Н. Колмогоровым [1].
Рассматривается направленное семейство разбиений
пространства Е произвольной природы. На элементах
разбиения определена функция множества Ф, вообще
говоря многозначная. Сумма значений этой функции,
взятая по всем элементам разбиения, задает много-
многозначную функцию разбиения. Эта сумма представ-
представляет собой, в частности, обобщение суммы Рнмана
2/7A|)Д^/, где многозначность является следствием
произвольности выбора точек |,- на элементах разбие-
разбиения. Предел многозначной функции разбиения по на-
направлению и определяет К. и. ffdO. К. и. рассматри-
рассматривается как для конечных, так и для счетных разбиений.
Можно рассматривать К. и. от функций со значениями
в коммутативной топологич. группе.
Лит.: [1] Колмогоров А. Н. «Math. Ann.», 1930,
Bd 103, S. 654 — 96. В. А. Скворцов.
КОЛМОГОРОВА КРИТЕРИЙ — статистический кри-
критерии, применяемый для проверки простой непарамет-
непараметрической гипотезы Но, согласно к-рой независимые
одинаково распределенные случайные величины Х1}
. . ., Хп имеют заданную непрерывную функцию рас-
распределения F(.r), причем альтернативная гипотеза Нг
предполагается двусторонней:
\EFn(x)-F(x)\>0, ¦
где ?Fn— математическое ожидание функции эмпи-
эмпирического распределения Fn(x). Критическое множест-
множество К. к. выражается неравенством
/>„= sup \Fn(x)-F(x)\>Xn ¦
и основано на теореме, доказанной А. Н. Колмогоро-
Колмогоровым в 1933: в случае справедливости гипотезы Но рас-
распределение статистики Dn не зависит от функции F(x),
причем если п—»-оо, то
где /C(A) = V (_i)»i
^¦771 = — 00
В 1948 Н. В. Смирнов [4] табулировал функцию
распределения Колмогорова К (к).
Согласно К. к. с уровнем значимости а, 0<а<0,5,
гипотезу Но следует отвергнуть, если Dn^kn(a),
где ^п(а) — критическое значение К. к., соответст-
соответствующее заданному уровню значимости а и являющееся
корнем уравнения Р {Dn^s X} = а.
Для определения Я,„(а) рекомендуется пользоваться
аппроксимацией допредельного закона статистики Кол-
Колмогорова Dn ее предельным распределением; см. [3],
где показано, что если п—>-оо и 0<А.0<Л=О(/г1//з), то
-['-»(•?)][' + »(?)]• м
Применение аппроксимации (*) дает следующее при-
приближение критического значения
u«> »¦/!-?•
где z — корень уравнения 1—/С
На практике для вычисления значения статистики
Dn пользуются тем обстоятельством, что
где
Dn= max
1 <m<n
/>й= max
1 < m < n
m- 1
(dB,-<. . .<ДГ(П)— вариационный ряд, построен-
построенный по выборке Xj, ... ,ХИ. К. к. имеет следующее
геометрич. истолкование (см. рис.). Изобразим на
плоскости жОу графики функций Fn(x), Fn(x)±kn(a).
Заштрихованная область является доверительной зо-
зоной уровня 1—а для функции распределения F(x),
так как если гипотеза Яо верна, то согласно теореме
Колмогорова
P{Fn(x)-Xn(a) <F (x)< Fn(x) + ln(a)}xl-a.
Если график функции F(x) не выходит из заштрихо-
заштрихованной области, то по К. к. с уровнем значимости а
гипотезу Но следует принять, в противном случае ги-
гипотеза Но отвергается.
К. к. дал мощный толчок развитию математич. ста-
статистики, в результате чего были получены совершенно
новые методы статистич. исследований, к-рые легли
в основу непараметрич. статистики.
Лит.: [1] Колмогоров А. Н., «Giorn. Istit. Ital. At-
tuari» 1933, v. 4, p. 83—91; L2] Смирнов Н. В., «Бюлл.
МГУ», секц. А, 1939, т. 2, в. 2, с. 3—14; [3J Б о л ь ш е в Л. Н.,
«Теория вероятн. и ее примен.», 1963, т. 8, с. 129—55; 14]
Большее Л. Н., Смирнов Н. В., Таблицы матема-
математической статистики, 2 изд., М., 1968. М. С. Никулин.
КОЛМОГОРОВА НЕРАВЕНСТВО — 1) К. н. в тео-
теории приближений — мультипликативное нера-
неравенство между нормами в пространствах LS(J) функций
и их производных на действительной оси (или полуоси):
Lr р
гдеО<^</г, v=(n — k — ± + -L\!fn — ± + ±.\
а С не зависит от х. Впервые такие неравенства изучали
Г. Харди (G. Hardy, 1912), Дж. Литлвуд (J. Little-
wood, 1912), Э. Ландау (Е. Landau, 1913), Ж. Адамар
(J. Hadamard, 1914). А. Н. Колмогоров [1] нашел
наименьшую константу С для наиболее важного слу-
случая /=(—оо, +«>), р = д=г~оо и любых k, п.
К. н. связаны с задачей наилучшего численного диф-
дифференцирования и устойчивого вычисления (неогра-
(неограниченного) оператора Dk ^-кратного дифференциро-
дифференцирования. Именно, модуль непрерывности
со (б) = sup { || *<*> \\Lq: I x hr < 6, |] *(»> ||ip ^ 1}
оператора Dk на классе {z?Lr: | \xn\ \L <1} выра-
выражается формулой соF)= соAN, т. е. имеет место К. н.
с константой С= со A).
К. н.— частный случай неравенств, связанных с вло-
вложением классов дифференцируемых функций (см. Вло-
Вложения теоремы).
Лит.: [1] Колмогоров А. Н., «Ученые зап. Моск.
ун-та, математика», 1939, в. 30, кн. 3, с. 3—16; [2] С т е ч-
кин С. Б., «Матем. заметки», 1967, т. 1, в. 2, с. 137—48;
[3] Т а й к о в Л. В., «Матем. заметки», 1968, т. 4, в. 2, с. 233—
238; [4] А р е с т о в В. В., «Acta Sci. Math.», 1972, v. 33,
p. 243—67. JO. H. Субботин.
2) К. н. в теории вероятностей — неравен-
неравенство для максимума сумм независимых случайных ве-
величин — обобщение классического Чебышева неравен-
неравенства. Пусть Хг, Х2, • ¦ ., Xп, . . .— независимые случай-
случайные величины с конечными математич. ожиданиями
йп=еХ„ и дисперсиями a«=DXn. Тогда для любого е>0
и если величины ограничены (|Х,|<:с с вероятно-
вероятностью 1), то
(е + 2с)г ( _
1—ГГ^ Г<Р<* max ym (Xk — ak)
1 <m
К. н. установлено А. Н. Колмогоровым [1]. К. н.
замечательно как доказательством — способ рассуж-
рассуждений был новым в теории вероятностей, так и самим
результатом — оценка для максимума сумм такова же,
что и для последней суммы в неравенстве Чебышева.
При доказательстве К. н. существенно используются
вытекающие из взаимной независимости X ь свойства
условных математич. ожиданий функций от сумм
Sk+p при условии, что Хх, . . ., Xk фиксированы.
К. н. допускает многочисленные обобщения, из ко-
которых можно отметить следующие:
1) К. н. остается справедливым, если условие взаим-
взаимной независимости величин Хп заменить условием,
что {^п} есть абсолютно беспристрастная последо-
последовательность, т. е. что последовательность сумм Sn=
= 2» гХk образует мартингал.
2) Если g(iM=0 — выпуклая монотонная функция,
то
Р{ max |5m|S=
\l<m<n
3) Если X^, fc=l, ..., и, симметричны относительно
начала координат, то
Р/ max |5m|S
СМ. Леей неравенство.
4) Для произвольных независимых случайных вели-
величин Xlt Х2, . . ., Хп, . ..
Р/ max |Sm| > д + е\<гЬр{|Я„| > е},
\1<т <п |
еели только числа б>0 и 0<р<1 выбраны так, что
Р { | Sm | > 6}<р при всех т, 1<т<ге.
Во всех вариантах К. н. можно увидеть следующее
свойство сумм независимых величин — «размах» мак-
максимальной суммы имеет тот же порядок, что и «размах»
последней суммы.
Как неравенство Чебышева применяется при выводе
больших чисел закона, так и К. н. применяется при до-
доказательстве больших чисел усиленного закона (крите-
(критерий Колмогорова сходимости Sjn-^-О почти всюду).
На использовании К. н. основано доказательство тео-
теорем о сходимости рядов из случайных величин.
Лит.: [1] Колмогоров А. Н., «Math. Ann.», 1928, Bd
99, S. 309—19; 1929, Bd 102, S. 484—88; [2] e г о же, Основные
понятия теории вероятностей, 2 изд., М., 1974; [3] Л о э в М.,
Теория вероятностей, пер. с англ., М., 1962. А. В. Прохоров.
КОЛМОГОРОВА ПРОСТРАНСТВО — топологиче-
топологическое пространство, удовлетворяющее Колмогорова ак-
аксиоме.
КОЛМОГОРОВА УРАВНЕНИЕ — уравнение вида
(обратное, или первое, уравнение; s < t)
или вида
Э/ Л * /о,
St=Ati B>
(прямое, или второе, уравнение; t > s)
для переходной функции [f=P(s, х; t, Г), 0<;««:<<оо,
х?Е, Г?$, (?, ?8)— измеримое пространство] или
ее плотности [f=p(s, x; t, Г), если она существует],
к уравнению A) для переходной функции P(s, x; t, Г)
присоединяется условие
limP (s, x; t, T)=IT(x),
а к уравнению B) — условие
limP(s, х; t, Г) = 1т(х),
Us
где Ir(x) — индикатор множества Г; в этом случае
оператор As— оператор, действующий в пространстве
функций, a A*t —в пространстве обобщенных мер.
Для марковских процессов со счетным множеством
состояний переходная функция полностью определя-
определяется вероятностями перехода p,-j(s, t) = P(s, i; t, {/})
(из состояния i в момент s в состояние / в момент t),
для к-рой обратное и прямое уравнения Колмогорова
имеют (при некоторых дополнительных предположе-
предположениях) следующий вид:
Эр, , («, t) ^
—^—=2dfe aik (s) Pkj(Si г)> s<t' C)
dp,- ,¦ (s, t) xr*
—-~ - = 2^kPik(s,t)akJ(t), t > s, D)
где
,,<) E)
В случае конечного числа состояний уравнения C),
D) справедливы, если только предположить существо-
существование пределов в E).
Другой важный класс процессов, для к-рых де-
детально изучен вопрос о справедливости уравнений A)
и B), — это процессы диффузионного типа, опреде-
определяемые тем, что их переходная функция P(s, x; t, Г),
x?R, r?23(R) удовлетворяет следующим условиям:
а) для всякого x?R и е>0 равномерно по s, s<(,
б) существуют функции a(s, x) и b(s, x) такие, что
для всякого х и е>0 равномерно по s, s<Ct,
(y x)P(s,x;t,dy) a(s,x)(s) + o(ts),
I x~У I ^* ?
f (y — x)*P(s,x;t,dy) = b(s,x)(t — s) + o(t—s).
J I X-V I < E4
Тогда, если существует плотность p^pis, x; t, у),
то (при некоторых дополнительных предположениях)
справедливо (по t>s и y?R) прямое уравнение
др д . . , 1 Эг
W = {ap) + -?
(называемое также уравнением Фоккера — Планка),
а обратное уравнение (по s<f и i^R) имеет следую-
следующий вид
Эр Эр 1 ,2 д'р
Лит.: [1] Колмогоров А. Н., «Успехи матем. наук»,
1938, в. 5, с. 5—41; [2] Г и х м а н И. И., С к о р о х о д А. В.,
Теория случайных процессов, т. 2, М., 1973. А. Н. Ширяев,
КОЛМОГОРОВА — СЕЛИВЕРСТОВА ТЕОРЕМА:
если выполнено условие
с W(n) = \ogn, то ряд Фурье
-|-° + /^ 1 (aneosnx+bnsmnx)
сходится почти всюду. Установлена А. Н. Колмогоро-
Колмогоровым и Г. А. Селиверстовым (см. [1], [2]). В [1] доказано,
что можно брать W(n) = log1+0rc для любого б>0, а в [2]
было усилено это утверждение: доказана его справед-
справедливость и при 6=0. Это усиление было получено также
А. И. Плеснером [3]. До К.—С. т. была известна теоре-
теорема Г. X. Харди (G. H. Hardy, 1916), где W(n) = log2n.
К.—С. т. оставалась наиболее сильным результатом
в этом направлении до 1966, когда была доказана Кар-
лесона теорема, согласно К-рой можно брать W(n)=l.
С. Качмаж [4] перенес К.—С. т. с тригонометрической
системы на произвольные ортонормированные системы,
показав, что для сходимости рядов по таким системам
почти всюду на нек-ром множестве в качестве W(п)
можно брать монотонную мажоранту функций Лебега
на этом множестве.
Лит : [1] Колмогорова. Н., Селиверстов Г. А.,
«С. г. Acad. sci.», 1924, t. 178, p. 303—06; [2] и х ж е, «Atti
Accad. naz. Lincei», 1926. v. 3, p. 307—10; [3] Plessner
A., «J. reine und angew Math.», 1925, Bd 155, S. 15—25; [4]
Kaczmarz S., «Studia math.», 1929, t. l,p. 87—121.
С. А. Теляковский.
КОЛМОГОРОВА — СМИРНОВА КРИТЕРИЙ — нс-
параметрическнй критерий, применяемый для проверки
гипотезы Но, согласно к-рой независимые случайные
величины Хг, . . ., Хп имеют заданную непрерыв-
непрерывную функцию распределения F(x) против односто-
односторонней альтернативы ЯГ : sup (EFn(x)— F (.r)) > 0,
I х |< а>
где ?.Fn(x) — математическое ожидание функции эм-
эмпирического распределения Fn(x). К.— С. к. построен
на статистике
Z>+= sup (Fn(x)~F(x))= max ( -?-- F (X im))) ,
| x I < x 1 < m^.n\ /
где XA)<X(,)<:. . .<:X(-,) — вариационный ряд, полу-
полученный по выборке Хг, ¦ . ., Хп. Таким образом, К.—•
С. к. является вариантом Колмогорова критерия для
проверки гипотезы Но против односторонней альтер-
альтернативы Н{. Изучая распределение статистики D%,
Н. В. Смирнов [1] показал, что
где 0<Я<1, [о] — целая часть числа а. Кроме точного
распределения A) статистики D%, H. В. Смирнов по-
получил также ее предельное распределение, именно:
если п-*-°о и 0<ко<\= О(«'''"), то
где Я.о— любое положительное число. С помощью техни-
техники асимптотических пирсоновских преобразований бы-
было показано [2], что если ге—>-оо и 0<Я.0<А.= О(ге''3), то
B)
Согласно К.— С. к. с уровнем значимости а гипотезу
#о следует отвергнуть, коль скоро
ехр [ —
причем, в силу B),
Аналогично поступают при проверке гипотезы Но
против альтернативы Hi : inf (EFrl(x)— F (x)) < 0.
В этом случае статистикой К.— С. к. является случай-
случайная величина
D~ = - inf (Fn(x)-F(x))=
|x| < oo
распределение к-рой, при справедливости гипотезы Но,
совпадает с распределением статистики D%.
Лит.: [1] С м и р н о в Н. В., «Успехи матем. наук», 1944,
в. 10, с. 179—206; [2] Большее Л. Н., «Теория вероятно-
вероятностей и ее применения», 1963, т. 8, в. 2, с. 129 — 55; [3] Б о л ь^
шев Л. Н., Смирнов Н. В., Таблицы математической
статистики, 2 изд., М., 1968; [4] Ван дер ВарденБ. Л.,
Математическая статистика, пер. с нем., М., 1960.
М. С. Никулин.
КОЛМОГОРОВА — ЧЕПМЕНА УРАВНЕНИЕ —
уравнение вида
Р (s, х; и, T)=\jEP (s, x; t, dy) P (t, у; и, Г), s < t < и,
то есть условие, налагаемое на переходную функцию
P(s, x; t, r)(CKss?«< оо, х?Е, Г?5Ц, (Е, SB) —
измеримое пространство), позволяющее (при некоторых
условиях на (Е, 53)) построить марковский процесс,
для которого условная вероятность Ps,x(xt^^) совпа-
совпадает с Р(s, x; t, Г). Обратно, для марковского процесса
его переходная функция Р (s, х; t, Г), по определению
равная Ps x(xt ? Г), удовлетворяет К.—Ч. у., что не-
непосредственно следует из общих свойств условных
вероятностей. Указано С. Чепменом [1], исследовано
А. Н. Колмогоровым в 1931 (см. [2]).
Лит.: [1] С h a p m a n S., «Pros. Roy. Soc, Ser. A», 1928*
v. 119, p. 34—54; [2] Колмогоров А. Н., «Успехи матем.
наук», 1938, в. 5, с. 5—41; [3] Г и х м а н И. И., Скороход
А. В., Теория случайных процессов, т. 2, М., 1973.
А. Н. Ширяев.
КОЛОКОЛООБРАЗНАЯ ИГРА — игра на единич-
единичном квадрате, у к-рой функция выигрыша имеет вид
<р(х—у), где ф — положительная аналитическая р е-
гулярная частотная функция Пой а,
то есть: 1) ф(«) определена при всех м?(—оо, оо),
2) для любого п и любых наборов —оо<^1<. . .<х„<с»
и —оо <г/х<.. .<г/„<°° имеет место неравен-
неравенство det[ |ф (ж,—?//) ||^0, 3) для любого набора
{хь} (соответственно {j/fc}) найдется такой набор
{Ук) (соответственно {х^}), что det| |ф(л-,—^-)| |>0,
4) \ ф(м)йгг<оо. Примером К. и. может служить игра
с функцией выигрыша е-<-х-У>2. Оптимальные стратегии
игроков в К. и. единственны и являются кусочно по-
постоянными распределениями с конечным числом скач-
скачков. Значение игры с функцией выигрыша (р(К(х—у))
при X—>-оо стремится к нулю, а число точек в носителе
оптимальных стратегий неограниченно возрастает.
Лит.: [1] К а р л и н С, Математические методы в теории
игр, программировании и экономике, пер. с англ., М., 1964.
В. К. Доманский.
КОЛЬЦА И АЛГЕБРЫ — множества с двумя би-
бинарными операциями, к-рые обычно принято наз. сло-
сложением и умножением. Кольцом наз. множество:
1) являющееся абелевой группой относительно сложе-
сложения (в частности, в кольце существует нулевой эле-
элемент, обозначаемый 0, и противоположный элемент —х
для каждого элемента х), 2) операция умножения в к-ром
удовлетворяет правому и левому законам дистрибутив-
дистрибутивности относительно сложения, т. е. x(y-Arz) = xy-\-xz и
(y^-z)x=yx-\-zx, для любых элементов х, у, z из кольца.
Если кольцо К не имеет делителей нуля, т. е. хуфО
для любых ненулевых элементов х, у?К, то множество
взех ненулевых элементов кольца будет группоидом
относительно умножения. Кольцо будет телом, если
множество его ненулевых элементов образует группу
относительно умножения. Кольцо К наз. ассоциа-
ассоциативным, если умножение в нем удовлетворяет
закону ассоциативности, т. е. (xy)z=x(yz), для любых
х, у, z из К. Если умножение в кольце коммутативно,
то кольцо наз. коммутативным. Едини-
Единицей наз. такой элемент 1 кольца, что
л>1= 1 -х=х
для всех х?К. Кольцо, вообще говоря, не обязано об-
обладать единицей. Любое тело является ассоциативным
кольцом с единицей и без делителей нуля. Ассоциа-
Ассоциативно-коммутативное кольцо без делителей нуля и с еди-
единицей наз. областью целостности.
Пусть Ф — произвольное ассоциативное кольцо с еди-
единицей 1. Кольцо А (не обязательно ассоциативное)
наз. алгеброй над Ф, или операторным кольцом
с кольцом операторов Ф, если для любых элементов
а?Ф, а?А однозначно определено произведение аа? А,
причем так, что для всех а, {5?Ф, а, Ь?А справедливы
соотношения
(а-~р) а =аа л-$а, а
, 1а = а, a (ab) = (ал) Ъ.
Если кольцо Ф коммутативно, то принято требовать
усиления последнего из условий A):
а (аЬ)= (аа)Ь=а (аЬ).
Любое кольцо можно считать алгеброй над кольцом
целых чисел, если понимать произведение па (где п —
целое число) обычно, т.е. как а-\-а-\-. . ,-\-а. Поэтому
п раз
кольца можно рассматривать как частный случай
алгебр.
Если А — алгебра над полем Ф, то, по определению,
А является векторным пространством над Ф, а значит,
имеет базис. Это дает возможность строить алгебры над
полем по базису, для чего достаточно задать таблицу
умножения базисных элементов. Алгебра над нолем
наз. конечномерной, если она имеет конечный
базис, т. е. если она конечномерна как векторное прост-
пространство над своим полем.
Наиболее известными примерами алгебр являются
алгебры квадратных матриц, алгебры многочленов и
алгебры формальных степенных рядов над нолями.
В теории К. п а., как и в любой другой алгебраич.
теории, большую роль играют понятия гомоморфизма
и изоморфизма. Многие рассуждения и описания про-
проводятся «с точностью до изоморфизма», т. е. изоморф-
изоморфные кольца п алгебры не различаются. Понятие гомо-
гомоморфизма тесно связано с понятиями идеала и подал-
подалгебры (подкольца).
Пусть А и В — две алгебры (над некоторым фикси-
фиксированным кольцом Ф с единицей). Отображение
ф : А-+.В множества А в множество В наз. гомомор-
гомоморфизмом алгебры А в алгебру В, если оно
«сохраняет операции алгебры», т. е.
для любых х, у?А, а?Ф. Гомоморфизм ф наз. и з о-
м о р ф и з м о м, если ф — взаимно однозначное ото-
отображение множества А на множество В. Послед-
Последнее равносильно тому, что образ гомомор-
гомоморфизма ф:
вообще говоря, являющийся подалгеброй алгебры В,
совпадает со всей алгеброй В, а ядро гомомор-
гомоморфизма (р:
Кегф={я?А |ф(а)=0},
вообще говоря, являющееся двусторонним идеалом
в А, в этом случае — нулевой идеал. Двусторонние
идеалы алгебры А и только они служат ядрами гомо-
гомоморфизмов этой алгебры, а гомоморфные образы А,
с точностью до изоморфизма, исчерпываются фактор-
алгебрами алгебры А по всевозможным ее двусторон-
двусторонним идеалам.
Переход от алгебры к ее подалгебрам и гомоморфным
образам является одним из способов получения новых
алгебр. Так, напр., из алгебры многочленов (от доста-
достаточно большого числа переменных) над полем Ф можно
получить, в качестве гомоморфного образа, любую
ассоциативно-коммутативную алгебру над ф. Среди
других часто применяемых конструкций следует отме-
отметить прямые суммы, прямые и подпрямые произведе-
произведения К. и а.
Историческая справка. Примерно до середины 19 в.
были известны лишь отдельные примеры колец: число-
числовые кольца, т. е. подкольца поля комплексных чисел,
появившиеся в связи с потребностями теории алге-
браич. уравнений, кольца вычетов целых чисел — в те-
теории чисел. Общего понятия кольца не существовало.
Первые примеры некоммутативных К. и а. встре-
встречаются A843—44) в работах У. Р. Гамильтона (W. R.
Hamilton) и Г. Грассмана (Н. Grassman). Это — тело
кватернионов, алгебра бикватернионов, внешняя ал-
алгебра. Начинает формироваться понятие гнперком-
плексной системы, т. е., в современной терминологии,
конечномерной ассоциативной алгебры над полем R
действительных чисел либо над полем С комплексных
чисел. К 1870 в работах Б. Пирса (В. Peirce) появились
понятия идемпотентного элемента (идемпотента) и
нильпотентного элемента и было доказано, что если
не все элементы гиперкомплексной системы нильпо-
тентны, то в ней имеется хотя бы один ненулевой пдем-
потент. Полученные результаты позволили развить
«технику идемпотентов>> и «пирсовских разложении»,
широко применявшихся при изучении конечномерных
алгебр.
После 1870 начинается общее исследование гппер-
комплексных систем. В работах Р. Дедекпнда (R. De-
dekind) встречается общее понятие (ассоциативного)
кольца, тела и алгебры над полем (гиперкомплексной
системы), хотя кольцо у него называлось не кольцом,
а порядком. Термин «кольцо» был введен Д. Гильбертом
(D. Hilbert) позднее. К. Вейерштрасс (К. Weierstrass)
и Р. Дедекинд доказали, что любая конечномерная
ассоциативно-коммутативная алгебра без нильпотент-
ных элементов над полем действительных чисел яв-
является прямой суммой полей, изоморфных либо полю
R действительных чисел, либо полю С комплексных
чисел. Г. Фробениус (G. Frobenius) в 1878 доказал, что
единственное некоммутативное тело конечной размер-
размерности над полем действительных чисел — тело кватер-
кватернионов.
К началу 20 в. в работах С. Э. Молина и Э. Картана
(Е. Cartan) были получены наиболее значительные ре-
результаты по теории гиперкомплексных систем. К этому
времени уже была достаточно развита теория гомомор-
гомоморфизмов, выяснена связь их с идеалами, появилось
понятие прямой суммы алгебр. С. Э. Молин, рассмат-
рассматривая конечномерные ассоциативные алгебры над
полем С комплексных чисел, ввел понятие простой
алгебры и доказал, что простые алгебры — это в точ-
точности полные алгебры матриц над полем С. Он же
ввел понятие радикала (теперь называемого классиче-
классическим радикалом) и доказал, по существу, что если ра-
дикал алгебры равен нулю, то алгебра является прямой
суммой простых алгебр. Эти результаты были вновь
найдены Э. Картаном, к-рый, кроме того, распростра-
лил их на алгебры над полем R действительных чисел.
В начале 20 в. начинают рассматривать алгебры
{ассоциативные и конечномерные) над произвольным
полем, а не только над полями действительных или
комплексных чисел. Дж. М. Веддерберн (J. M. Wedder-
burn), совершенствуя технику идемпотентов Пирса,
перенес результаты С. Э. Молина и Э. Картана на слу-
случай произвольного поля. Он же доказал, что любое
конечное тело коммутативно.
Наконец, в 20—30-х гг. 20 в. стали изучать произ-
произвольные ассоциативные кольца и алгебры. При этом
большую роль начинают играть ле^вые и правые идеалы
колец. В. Крулль (W. Krull) и Э. Нётер (Е. Noether)
в 1925—26 ввели и систематически использовали усло-
условие максимальности и минимальности для левых идеа-
идеалов. В 1927 Э. Артнн (Е. Artin) перенес результаты
Дж. М. Веддерберна о разложении полупростых
алгебр на все ассоциативные кольца и алгебры, левые
идеалы к-рых одновременно удовлетворяют и условию
максимальности и условию минимальности. В 1929
Э. Нётер показала, что при этом достаточно требовать
только условий минимальности. К 1939 было доказано,
что при условии минимальности (также как и при ус-
условии максимальности) радикал кольца является его
наибольшим нильпотентным левым идеалом (см. Ар-
тиново кольцо, Нётерово кольцо). Таким образом,
к 1940 теория Молина — Картана — Веддерберна была
перенесена на случай ассоциативных колец и алгебр
с условием минимальности для левых (или правых)
идеалов.
Основные направления теории колец и алгебр. Струк-
Структурная теория дает описание алгебр (как правило,
удовлетворяющих нек-рым услрвиям конечности), пред-
представляя их в виде прямой суммы или подпрямого про-
произведения более просто устроенных алгебр. К настоя-
настоящему времени G0-е гг. 20 в.) для ассоциативных К. и а.
классич. теория Молина — Картана — Веддерберна —
Артина перенесена на случай К. и а. с условием мини-
минимальности для главных левых идеалов. При этом же
условии доказано, что если алгебра не имеет кильпо-
тентных идеалов, то она разлагается в прямую (не обя-
обязательно конечную) сумму простых алгебр, а если она
не имеет даже нилыготентных элементов, то — в пря-
прямую сумму тел. В случае, когда алгебра имеет нильпо-
тентные идеалы, ее строение значительно сложнее.
Наиболее известной теоремой о таких алгебрах яв-
является Веддерберна — Мальцева теорема «об отщепле-
отщеплении радикала» — о разложении конечномерной ассо-
ассоциативной алгебры в полупрямую сумму радикала и
полупростой подалгебры. Содержательная структур-
структурная теория создана для альтернативных алгебр (см.
Альтернативные кольца и алгебры), на к-рые факти-
фактически перенесена вся теория Молина — Картана —
Веддерберна — Артина, а также для йордановых алгебр.
Ряд структурных теорем получен и без условий
конечности. Еще В. Крулль доказал, что любое ассоциа-
ассоциативно-коммутативное кольцо без нильпотентных эле-
элементов разлагается в подпрямое произведение колец
без делителей нуля. В дальнейшем было доказано, что
в теореме Крулля требование коммутативности можно
опустить, а затем был найден ряд критериев разложи-
разложимости произвольной неассоциативной алгебры в под-
подпрямое произведение алгебр без делителей нуля и ал-
алгебр с однозначным делением.
Теория простых алгебр и тел тесно связана со струк-
структурной теорией, так как многие структурные теоремы
сводят изучение рассматриваемых колец и алгебр
к изучению простых алгебр и тел. Получено описание
ассоциативных простых алгебр с единицей, обладаю-
щих минимальными левыми идеалами, а также ко-
конечномерных альтернативных н йордановых простых
алгебр. Рассмотрены автоморфизмы и дифференциро-
дифференцирования простых ассоциативных алгебр и тел (см. Алгеб-
Алгебраической системы автоморфизм, Дифференциальная
алгебра).
Теория радикалов также тесно связана со структур-
структурной теорией; сами структурные теоремы — это, как
правило, теоремы о К. и а. полупростых в смысле
некоторого радикала. Для получения новых структур-
структурных теорем было введено множество различных ради-
радикалов: нижний нильрадикал Бэра, локально нильпо-
тентный радикал Левицкого, квазирегулярный Дже-
кобсона радикал, радикал Брауна — Маккоя и др.
В начале 50-х гг. 20 в. была создана общая теория ра-
радикалов, тесно связанная с теорией модулей и пред-
представлений (см. Радикалы колец и алгебр).
Алгебры с тождественными соотношениями начали
привлекать внимание алгебраистов с тех пор, как
обнаружилось, что наличие (нетривиального) тож-
тождества сильно влияет на строение К. и а. В этом от-
отношении показательна теорема Капланского об ассо-
ассоциативных алгебрах: если А — примитивная алгебра
с полиномиальным тождеством степени d, то А — ко-
конечномерная простая алгебра над своим центром и еэ
размерность не превосходит [d/2]2 (см. [6]). Имеется
немало результатов и о неассоциативных алгебрах
с тождественными соотношениями (см. Колец много-
многообразие).
Свободные алгебры и свободные произведения алгебр
являются важными конструкциями в теории К. и а.,
поскольку любая алгебра (некоторого многообразия)
является гомоморфным образом свободной алгебры
этого многообразия. Доказано, что любая подалгебра
свободной неассоциативной алгебры сама свободна,
а также что свободны все подалгебры свободных ком-
коммутативных, антикоммутативных алгебр и свободных
алгебр Ли. Исследования в этой области тесно связаны
с исследованиями алгебр с тождественными соотноше-
соотношениями и многообразий алгебр, так как тождества дан-
данного многообразия — это определяющие соотношения
в свободной алгебре данного многообразия.
Теория вложений изучает в основном вопросы вло-
вложения ассоциативных К. и а. в тела или простые ал-
алгебры, в к-рых разрешимы те или иные уравнения
(см. Вложение кольца). Стимулом к развитию этой
теории послужил пример ассоциативной алгебры без
делителей нуля, не вложимой в тело. Затем был най-
найден критерий существования (классического) тела дро-
дробей для ассоциативных К. и а. без делителей нуля,
а также необходимые и достаточные условия вложи-
мости кольца в тело. К теории вложений можно от-
отнести и теорию колец частных (см. Частных кольцо).
Аддитивная теория идеалов возникла при обобще-
обобщении основной теоремы арифметики, равносильной тео-
теореме о представлении любого идеала кольца целых
чисел в виде пересечения степеней простых идеалов, на
произвольные ассоциативно-коммутативные кольца с ус-
условием максимальности (т. е. нётеровы кольца). Основ-
Основная цель этой теории — представление любого идеала
кольца в виде пересечения конечного числа идеалов
нек-рого специального вида (примарных, примальных,
терциарных и т. д.). При этом вид «специальных»
идеалов и вид разложений подбирается так, что при
нек-рых условиях конечности верны и «теоремы су-
существования» (т. е. любой идеал имеет разложение) и
«теорема единственности» (с каждым идеалом связы-
связывается нек-рое множество простых идеалов, не завися-
зависящее от разложения). Для нётеровых колец эта цель
была достигнута в классической нётеровой теории при-
примарных идеалов. Найдено обобщение этой теории и на
некоммутативный случай.
Коммутативная алгебра занималась сначала число-
числовыми кольцами, возникшими в теории алгебраич.
чисел. В настоящее время теория коммутативных колец
является бурно развивающейся областью на границе
алгебры и алгебраич. геометрии.
Нормированные, топологические, упорядоченные и
нек-рые другие К. и а. с дополнительными структурами
часто встречаются в функциональном анализе и дру-
других областях математики. Подробнее о кольцах с до-
дополнительными структурами см. Нормированное кольцо,
Топологическая алгебра, Упорядоченное кольцо.
Лит.: ШБурбаки Н., Очерки по истории математики,
пер. с франц., М., 1963; [2] е г о же, Алгебра. Многочлены
и поля. Упорядоченные группы, пер. с франц., М., 1965; [31
его же, Алгебра. Модули, кольца, формы, пер. с франц.,
М., 1966; [4] е г о же, Коммутативная алгебра, пер. с франц.,
М., 1971; [5] Д ж е к о б с о н Н., Теория колец, пер. с англ.,
М., 1947; [6] е г о же, Строение колец, пер. с англ., М., 1961;
[7J е г о же, Алгебры Ли, пер. с англ., М., 1964; [8] 3 а р и с-
ский О., Самюэль П., Коммутативная алгебра, т. 1—2,
пер. с англ., М., 1963; [9] А т ь я М., Макдональд И.,
Введение в коммутативную алгебру, пер. с англ., М., 1972;
[10] Херстейн И., Некоммутативные кольца, пер. с англ.,
М., 1972; [11] К у р о ш А. Г., Лекции по общей алгебре, М.,
1%2; [12] Ленг С, Алгебра, пер. с англ., М., 1968; [13]
В а н -д е р-В а р д е н Б. Л., Алгебра, М., 1976; [14] П о н-
трягин Л. С, Непрерывные группы, 3 изд., М., 1973; 115]
Наймарк М. А., Нормированные кольца, 2 изд., М., 1968;
[16] Фейс К., Алгебра. Кольца, модули и категории, т. 1,
пер. с англ., М., 1977. В. А. Андрунакиевич.
КОЛЬЦЕВАЯ ГРАНИЦА — подмножество Г прост-
пространства М д максимальных идеалов коммутативной
банаховой алгебры А с единицей над полем С комп-
комплексных чисел, на к-ром модули Гельфанда предста-
представлений а всех элементов а?А достигают максимума.
Напр., можно положить Т=МА (тривиальная граница).
Интерес представляют нетривиальные границы с тем
или иным свойством минимальности. Среди замкнутых
границ ТаМА существует минимальная дМд— такая
замкнутая граница, что дМдСТ для каждой замкну-
замкнутой границы Г; она наз. границей Шилова.
Точки границы Шилова характеризуются тем, что для
каждой окрестности VdMд такой точки | и каждого
е>0 существует элемент а?А, для к-рого тах|а| = 1
п |а|<8 вне F. Точки ?,?дМд составляют «наиболее
устойчивую» часть множества М д максимальных идеа-
идеалов: если В — коммутативное банахово расширение
алгебры А, то максимальные идеалы (мультипликатив-
(мультипликативные функционалы), отвечающие таким точкам, расши-
расширяются до максимальных идеалов (мультипликативных
функционалов) алгебры В, тогда как за пределами
дМд такое расширение, вообще говоря, невозможно.
Это обстоятельство аналогично устойчивости границы
спектра ограниченного линейного оператора банахова
пространства. Типичный пример: алгебра А состоит
из непрерывных функций в диске |Я,|<:1, аналитических
при |А.|<1- В этом случае Мд отождествляется с замк-
замкнутым диском, а дМд— с его топологич. границей;
максимальные идеалы, отвечающие внутренним точ-
точкам диска, не продолжаются до максимальных идеалов
алгебры всех непрерывных функций на границе,
в к-рую естественно (согласно принципу максимума)
вкладывается А, а максимальные идеалы, отвечающие
граничным точкам,— продолжаются.
Подобно алгебрам аналитич. функций, для общих
коммутативных банаховых алгебр имеет место л о-
кальный принцип максимума моду-
л я: если V — открытое подмножество пространства
МА, то
для всех а?А, где V — замыкание и 0V — топологич.
граница множества V в Мд. Грубо говоря, это озна-
означает, что точка локального максимума непременно
является точкой глобального максимума (нек-рого,
быть может, другого элемента).
Понятие К. г. используется при изучении равно-
равномерных алгебр, т. е. замкнутых, разделяю-
разделяющих точки и содержащих константы подалгебр А ал-
алгебры С{Х) всех непрерывных функций на компакте X.
В данной ситуации дМАсХаМд. Для каждой точки
|?МА существует представляющая мера,
сосредоточенная на границе Шилова, т. е. такая ве-
вероятностная мера |а, что
при всех а?А (это верно для произвольных коммута-
коммутативных банаховых алгебр). В простейшем (описанном
выше) случае диска и алгебры аналитич. функций
последняя формула сводится к Пуассона формуле.
Вообще говоря, представляющая мера ц не единственна.
Для точек |, принадлежащих одной и той же доле
Глисона (см. Алгебра функций), меры |х можно выби-
выбирать взаимно абсолютно непрерывными, что при нек-рых
дополнительных условиях типа единственности пред-
представляющих мер позволяет наделять доли Глисона
пространства максимальных идеалов одномерной ана- •
литич. структурой, согласованной с алгеброй. Каждая
точка границы Шилова равномерной алгебры состав-
составляет одноточечную долю Глисона, но обратное, вообще
говоря, неверно.
Равенство дМд=Х=МЛ для равномерных алгебр
служит простейшим необходимым условием совпаде-
совпадения А с С(Х). Без дополнительных предположений
оно не является достаточным для такого совпадения
даже в случае алгебр A = R(X) равномерных пределов
рациональных функций на плоском компакте X.
Пусть X — метризуемый компакт и А — равномер-
равномерная алгебра на X. Тогда существует минимальная
среди всех границ: д0М А. Замыкание минимальной
границы совпадает с дМд, однако, вообще говоря,
д0Мд не замкнуто: пример доставляет подалгебра тех
аналитич. внутри диска |Я,|<:1 функций, для к-рых
/@) = /A). Граница д0М д совпадает с множеством
точек пика относительно А, т.е. таких точек
Ъ,?Мд, для к-рых существует а?А с |а(|)| >|а(т])|
при всех т)=7^=5- С Другой стороны, известно формально
гораздо более слабое достаточное условие принадлеж-
принадлежности к д0Мд. Именно, если точка ??Л/^ такова, что
при нек-рых 0<с<1 и d~^\ для каждой окрестности V
точки | в А имеется элемент а, для к-рого а(?)=1,
max|a] = d и |a(t))|<c при t](?f, то 1?д0МА. Абстракт-
Абстрактная формула Пуассона усиливается следующим обра-
образом: для любой точки |?Л/д существует представляю-
представляющая мера, сосредоточенная на д0Мд (при этом д0Мд
есть (?й-множество), и в таком виде она с успехом при-
применяется в нек-рых вопросах теории приближений.
Точки \?д0МА характеризуются тем, что для них такая
мера единственна и совпадает с б-мерой, т. е. минималь-
минимальная граница есть частный случай границы Шоке.
Для алгебры A = R(X) равномерных пределов ра-
рациональных функций на плоском компакте X совпаде-
совпадение А с С (X) равносильно совпадению Х= МА с д0Мд.
Для произвольных равномерных алгебр это не так:
существует равномерная алгебра А , отличная от С (Мд),
для к-рой МА метризуемо, и каждая точка \?МА
является точкой пика (т. е. д0Мд=МА). Существует
и такая равномерная алгебра, что все доли Глисона
тривиальны (одноточечны), однако даже граница Ши-
Шилова составляет собственную часть пространства макси-
максимальных идеалов.
Одно из алгебраич. обобщений понятия границы
Шилова заключается в следующем. Пусть дхМд=дМд
и / — замкнутый идеал, порожденный набором эле-
элементов аи ... , а„_!^Л, п^2. Пространство MA/1
естественно отождествляется с множеством общих
нулей функций alt . . . , ап-\- Замыкание объединения
границ дМА/1 по всем (п—1)-наборам обозначается
дпМд. Напр.. для алгебры непрерывных функций в би-
диске |А,Х|<:1, |Я2|<:1, аналитических внутри его,
д^М А— остов 1^1=1^21 = 1, д2МА—топология, гра-
граница 1^1=1, 1^1 <i-, l^Ki, |X2|=i, д3мА=мА.
Эти обобщения полезны при доказательстве теорем
о многомерной аналитич. структуре в пространстве
максимальных идеалов.
Понятия К. г. (или функциональных границ), ана-
аналогичные описанным, встречаются в теории аналитич.
функций (граница Бергмана), теории вероятностей
(граница Мартина) и в ряде других разделов матема-
математики. При этом исходный запас функциональных эле-
элементов не обязательно предполагается составляющим
алгебру или кольцо.
Лит.: [1] Basener R., «Proc. Amer. Math. Soc», 1975,
V. 47, № 1, p. 98—104; [2] В г о w d e r A., Introduction to fun-
function algebras, N. Y.—Amst., 1969; [3] Гаме ли н Т. В.,
Равномерные алгебры, пер. с англ., М., 1973; [4]Гельфанд
И. М., Райков Д. А., Шилов Г. Е., Коммутативные
нормированные кольца, М., 1960; [5] Г о н ч а р А. А., «Изв.
АН СССР. Сер. матем.», 1963, т. 27, № 4, с. 949—55; [6] Ф е л п с
Р., Лекции о теоремах Шоке, пер. с англ., М., 1968.
Е. А. Горин.
КОЛЬЦЕВАЯ ОБЛАСТЬ — 1) Двусвязпая плоская
область между двумя замкнутыми жордановыми кри-
кривыми без общих точек, из к-рых одна охватывает дру-
другую. 2) К. о. относительно квадратичного дифферен-
дифференциала — см. Глобальная структура траекторий квад-
квадратичного дифференциала. Е. Д. Соломенцее.
КОЛЬЦО — множество R, в к-ром заданы две би-
бинарные алгебраич. операции: сложение и умножение,
причем по сложению это множество — абелева группа
(аддитивная группа кольца R), а умно-
умножение связано со сложением законами дистрибутив-
дистрибутивности:
a(b-{-c) = ab-\-ac, (b-\-c)a= ba+ca,
где а, Ъ, c?R. На умножение в общем случае не накла-
накладывается никаких ограничений, т. е. R по умноже-
умножению — группоид (наз. мультипликативным
группоидом кольца R).
Непустое подмножество AczR наз. п о д к о л ь-
ц о м в Л, если А само является кольцом относительно
операций, определенных в R, т. е. А должно быть под-
подгруппой аддитивной группы кольца R и подгруппоидом
мультипликативного группоида этого кольца. Естест-
Естественно, подкольцами всякого кольца служат само это
кольцо и нульподкольцо, состоящее из одного нуля.
Пересечение (теоретико-множественное) подколец лю-
любого кольца есть подкольцо. Объединением подколец
Аа, а?/, кольца R наз. пересечение всех подколец,
каждое из к-рых содержит все Аа. Множество всех
подколец данного кольца является решеткой S (R) от-
относительно операций пересечения и объединения под-
подколец. Множество идеалов этого кольца образуют под-
решетку в S(R).
О направлениях в теории колец см. Кольца и алгебры,
Ассоциативные кольца и алгебры, Неассоциативные
кольца и алгебры. о. А. Иванова
КОЛЬЦО С ДЕЛЕНИЕМ — кольцо (не обязательно
ассоциативное), в к-ром для любых элементов а и Ь,
где афО, уравнения
ax=b, ya=b
обладают решениями. Если решения этих уравнений
определены однозначно, то К. с д. наз. к в а з и т е-
л о м. Квазитело, в отличие от произвольного К. с д.,
не может содержать делителей нуля; ненулевые эле-
элементы квазитела составляют по умножению квази-
квазигруппу. Всякое (не обязательно ассоциативное) кольцо
без делителей нуля вкладывается в квазитело. Ассоциа-
тивное К. с д. является (ассоциативным) телом. См.
также Алгебра с делением.
Лит.: [1] К у р о ш А. Г., Лекции по общей алгебре, 2 изд.,
М., 1973. О. А. Иванова.
КОЛЬЦОИД — обобщение понятия ассоциативного
кольца. Пусть (Q, Л) — многообразие универсальных
алгебр сигнатуры Q. Алгебра О= {G, fi(J(-)} наз.
кольцоидом над алгеброй G+ многооб-
многообразия (Q, Л), или (Q, Л)-к о л ь ц о и д о м, если
G + = {G, Q} принадлежит многообразию (Q, Л), по
умножению (•) алгебра G является полугруппой и
выполняется закон дистрибутивности на втором месте
относительно умножения
.хпш)-у = (х1у)(х2у)...(хпу)и>,
Операции из Q наз. аддитивными опера-
операциями кольцоида G, a G+ — аддитив-
аддитивной алгеброй кольцоида. К. наз. дист-
дистрибутивным, если законы дистрибутивности вы-
выполняются также и на первом месте, т. е.:
у (х-уХъ. . . хпа>) = (ух{) (ух2). . . (ухп) оз.
Обычное ассоциативное кольцо G есть дистрибутив-
дистрибутивный К. над абелевой группой (и G+ — аддитивная
группа кольца G). К. над группой наз. почти-
кольцом, К. над полугруппой — полуколь-
ц о м, К. над лупой — неокольцом. Рассматри-
Рассматривались также (под разными названиями, одно из ко-
которых — менгерова алгебра) К. над коль-
кольцами.
Лит.: [1] К у р о ш А. Г., Общая алгебра, лекции 1969—
1970 учебного года, М., 1974. О. А. Иванова.
КОМБИНАТОРИКА — см. Комбинаторный анализ.
КОМБИНАТОРНАЯ ГЕОМЕТРИЯ — раздел мате-
математики, объединяющий круг задач, в к-рых исследуются
экстремальные свойства комбинаторного характера
для систем фигур. Эти задачи связаны, в первую оче-
очередь, с оптимальным в нек-ром смысле расположением
выпуклых множеств. Примером одной из старейших
задач такого рода может служить задача о 13
шарах: каково максимальное число равных мате-
материальных шаров, к-рые можно приложить к равному
всем им шару в евклидовом пространстве? И. Кеплер
(J. Kepler, 1611) указал число 12, но строгое решение
этой задачи было дано в сер. 20 в. Б. Л. Ван дер Вар-
деном (В. L. Van der Waerden) и К. Шютте (К. Schiitte).
Термин «К. г.», по-видимому, впервые появился
в 1955 (см. [1]). Обычно с этим годом связывают воз-
возникновение К. г. как направления в математике, хотя
к ней можно отнести и более ранние результаты (см.,
напр., [2]). Для К. г. характерна наглядность ее задач.
В К. г. широко используются комбинаторные сообра-
соображения и сочетания приемов из различных областей
математики (топологии, функционального анализа,
геометрии в целом, теории графов и др.).
Одной из центральных групп задач К. г. являются
задачи о разбиении фигур на части, напр. Борсука
проблема.
Большую группу задач К. г. составляют задачи
о покрытиях, в к-рых исследуется возможность покры-
покрытия заданного множества фигурами специального вида
(см., напр., Хадвигера гипотезу о покрытии выпуклого
тела минимальным числом меньших гомотетичных ему
тел с коэффициентом гомотетии k, 0<&<1); освещения
задачи о минимальном числе направлений пучков
параллельных лучей или источников, освещающих гра-
границу выпуклого тела и др.
К. г. родственна дискретной геометрии, см., напр.,
определенным образом связанную с гипотезой Хадви-
Хадвигера и задачами освещения Эрдёша задачу о нахожде-
нахождении максимального числа точек евклидова прост-
пространства R", любые три из к-рых образуют треуголь-
треугольник с углами, не превосходящими я/2.
К. г. тесно примыкает к теории выпуклых множеств.
См., напр., Хелли теорему, к-рая описывает пересече-
пересечения нек-рых семейств выпуклых множеств в зависи-
зависимости от пересечения их подсемейств.
Лит.: [1] Hadwiger H., «J. reine angew. Math.», 1955,
Bd 194, S. 101 — 10; [2] Alexandroff P., Hopf H.,
Topologie, Bd 1, В., 1935; [3] X а д в и г е р Г., Д е б р у н-
н е р Г., Комбинаторная геометрия плоскости, пер. с нем., М.,
1Й65; [4] Грюнбаум Б., Этюды по комбинаторной гео-
геометрии и теории выпуклых тел, пер. с англ., М., 1971; [5] Had-
Hadwiger Н., Debrunner H., Combinatorial Geomelry in
the Plane, N. Y., 1964; [6j Я г л о м И. М., О комбинаторной
геометрии, М., 1971; [7] Болтянский В. Г., Сол-
тан П. С, Комбинаторная геометрия различных классов вы-
выпуклых множеств, Киш., 1978. П. С. Солтан.
КОМБИНАТОРНАЯ ГЕОМЕТРИЯ — конечное мно-
множество S вместе с отношением замыкания
А -> Т,
определенным для всех подмножеств А из S (т. е. А^А,
А<=В влечет А^В и 4=Л, но не обязательно А []В~
= A[jB), удовлетворяющим условиям: 1) 0 = 0 для
пустого множества 0; 2) р=р для каждого элемента
3) если р, q?S it AczS и если ?? A \Jp, но q%A,
то Р (zA\Jq (свойство вамен ы). Замкнутые
множества, пли плоскости (А=А), образуют гео-
геометрическую решетку. Подмножество /с=5
независимо, если рц:1\р для всех р?/; все макси-
максимальные независимые множества, или базисы, имеют
одинаковую мощность. Обычным образом определяются
прямая сумма К. г. и сужение К. г. на подмножество А.
Мощность базисов сужения К. г. на А наз. рангом
г(А) множества А. Ранг удовлетворяет условию:
Множество vlcz;S, для к-рого г(Л)<|Л|, наз. зависи-
зависимым; минимальные зависимые множества К. г. наз.
циклами. Опуская условия 1) и 2) в определении К. г.,
получают определение п р е д г е о м е т р и и, или
матроида. Рассматриваются также бесконечные К. г.,
при этом требуется конечность базисов.
Пример К. г.— подмножество S векторного про-
пространства V с отношением
А -> T=sp (A)f\S,
определенным для всех A^S, где sp(vl) — линейная
оболочка, натянутая на А в V.
Одной из основных проблем в теории К. г. является
так наз. критическая проблема. Для
К. г., заданной множеством S в проективном прост-
пространстве размерности п над полем Галуа, эта проблема
состоит в том, чтобы найти наименьшее положительное
целое число А; (критическую экспоненту),
для к-рого существует семейство гиперплоскостей
Нг, . .., Hk-, различающих S (семейство гиперплоскос-
гиперплоскостей различает множество S, если для всякого
t?S существует хотя бы одна гиперплоскость, не со-
содержащая t).
Лит.: [1] Whitney H., «Amer. J. Math.», 1935, v. 57,
p. 509—33; [2] С г а р о Н. Н., Н о t a G. С, On the founda-
foundations of combinatorial theory: combinatorial geometries, Camb.—
L., 1970; [3] T u t t e W. Т., Introduction to the theory of ma-
troids, N. Y., 1971; [4] У и л с о н Р., Введение в теорию гра-
графов, пер. с англ., М., 1977; [5] Р ы б н и к о в К. А., Введение
в комбинаторный анализ, М., 1972. А. М. Рееякин.
КОМБИНАТОРНАЯ ЛОГИКА — раздел логики, по-
посвященный изучению и анализу таких понятий и ме-
методов, как переменная, функция, операция подста-
подстановки, классификация предметов по типам или кате-
категориям и другие.
В качестве основных понятий в К. л. выбираются
одноместная функция и операция применения функ-
ции к аргументу (аппликация), при этом поня-
понятие функции рассматривается как первичное по отно-
отношению к понятию множества и обобщается таким обра-
образом, что функция может принимать объекты одного
с ней уровня как в качестве аргументов, так и в ка-
качестве значении. В частности, аргументом функции /
может служить сама эта функция. Поскольку функции
могут выступать в качестве как аргументов, так и зна-
значений, понятие многоместной функции сводится к по-
понятию одноместной функции. Результат аппликации
функции /к аргументу х обозначают (fx). Для простоты
часто скобки опускают, понимая при этом запись
}х^2. . .хп как (. . .{(fxj)x2). . .хп). Функция /, удовлет-
удовлетворяющая равенству
где хх, х2, ... , х„, ra^l, — произвольные функции,
a J — объект, построенный из этих функций (быть
может, не из всех) с помощью операции аппликации,
наз. комбинатором (существование комбина-
комбинаторов неявно постулируется). Всякий комбинатор
может быть выражен через два комбинатора S и К,
удовлетворяющих следующим равенствам:
Sxyz=xz(yz), Kxy=x
(здесь х, у, z — произвольные функции).
Одной из первых в К. л. была задача, к-рая состояла
в сведении первичных логич. понятий к минимальному
числу достаточно простых понятий. Была введена ин-
индивидуальная функция U, к-рая обобщала штрих
Шеффера [если / и g — одноместные пропозициональные
функции, то Ufg интерпретируется как (ijx)(f(x)=±>
=^>~\g(x)], и было показано, что каждую формулу ис-
исчисления предикатов можно представить в виде комби-
комбинации из букв U, S, К (и скобок), откуда и название
«К. л.» [X. Карри (Н. Curry), 1930]. Переменные
в таком представлении совсем не использовались, что
позволило избавиться от переменной как исходного
понятия (понятия индивидуальной константы, выска-
высказывания и пропозициональной функции при этом также
элиминировались как исходные понятия). Однако,
как показало дальнейшее развитие К. л., построение
на такой основе логич. систем встретило значительные
трудности. Первые логич. исчисления такого типа,
предложенные А. Чёрчем (A. Church) и X. Карри, ока-
оказались противоречивыми (парадокс К л и н и —
Р о с с е р а, см. [4]). Чтобы избежать этого противо-
противоречия, К. л. приходится строить либо как обладающую
очень бедными дедуктивными возможностями, либо
как содержащую объекты разных категорий. Основное
развитие К. л. пошло по второму пути.
Часть К. л., к-рая не имеет дела с «логикой», а ин-
интересуется только свойствами комбинаторов, наз.
теорией комбинаторов. Показано, что эта
теория непротиворечива. В результате формализации
она принимает вид различных исчислений. Все они
распадаются на два внешне различных класса: и с-
числения комбинаторов и Я-и с ч и с л е-
н и я.
Лит.: [1] Curry Н., Р е у s R., Combinatory logic, v. 1
Amst., 1958; [2] С u г г у H., H i n d 1 e у J., Seldin J.,
Combinatory logic, v. 2, Amst.— L., 1972; [3] С h u г с h A.,
The calculi of lambda-conversion, Princeton, 1941; [4] К 1 e e-
ne S., Rosser J., «Ann. Math.», 1935, v. 36, p. 630—36;
[5] Я н о в с к а я С. А., Логика комбинаторная, в кн.: Фило-
Философская энциклопедия, т. 3, М., 1964, с. 226—27; [6] К у з и-
чев А. С, в сб.: История и методология естественных наук,
в. 14, 1973, с. 131—41. Л. В. Шабунин.
КОМБИНАТОРНАЯ МАТЕМАТИКА — см. Ком-
Комбинаторный анализ.
КОМБИНАТОРНАЯ ТОПОЛОГИЯ — раздел топо-
топологии, в к-ром топологич. свойства геометрич. фигур
изучаются при помощи их разбиений на более элемен-
элементарные фигуры (напр., разбиение полиэдров на сим-
плексы) или при помощи покрытий системами мно-
множеств. Эти методы применимы в самых широких пред-
предположениях об изучаемых фигурах.
Лит.: [1] А л е к с а н д р о в П. С, Комбинаторная топо-
топология, М.— Л., 1947; [2] П о н т р я г и н Л. С, Основы ком-
Винаторной топологии, 2 изд., М., 1976. С. П. Новиков.
КОМБИНАТОРНЫЕ ЗАДАЧИ классические —
задачи выбора и расположения элементов конечного
множества, имеющие в качестве исходной нек-рую фор-
формулировку развлекательного содержания типа голово-
головоломок.
Одной из классических К. з., фигурирующей еще
в мифах Древнего Востока, является построение м а-
гического квадрата, т. е. расположение пер-
первых га2 натуральных чисел в квадрате пХп так, чтобы
все суммы по строкам, столбцам и диагоналям были
равны одному и тому же числу. Напр.,
4 9 2
3 5 7
8 1 6
— магический квадрат при ?г=3. Известен ряд методов
построения таких квадратов (см., напр., [1]). Опреде-
Определение числа магических квадратов порядка п при ге>4
представляет трудную еще нерешенную A978) задачу.
Ряд К. з. был рассмотрен Л. Эйлером (L. Euler).
Одна из них — задача о 36 офицерах, со-
состоящая в том, чтобы указанное число офицеров б раз-
различных воинских званий и из 6 различных полков так
расположить в ячейках квадрата 6X6 (каре), чтобы
каждая колонна и каждая шеренга содержали одновре-
одновременно одного и только одного офицера каждого ранга
н каждого полка. Квадрат размером гаХге, содержащий
в ячейках элементы 1,2, . .., п, наз. латинским,
если элементы в каждой строке и каждом столбце раз-
различны. Два латинских квадрата'наз. ортогональ-
ортогональным и, если при их наложении все га2 пар элементов
в ячейках различны. Задача о 36 офицерах эквивалентна
задаче о существовании пары ортогональных латинских
кнадратов порядка 6. Л. Эйлер высказал гипотезу
о несуществовании ортогональных латинских квадра-
квадратов порядка re=4fc+2, k=i, 2, ... В 1900 Г. Тарри
(G. Tarry) подтвердил эту гттпотезу для ге=6 и тем
самым доказал, что задача о 36 офицерах не имеет ре-
решения. В 1959—60 была доказана теорема о существо-
существовании пары ортогональных латинских квадратов для
каждого «=4fc-f-2, &=2, 3, ... (см. [2]).
Другая задача, рассмотренная Л. Эйлером,— зада-
задача о кёнигсбергских мостах, форму-
формулируемая следующим образом. Имеется семь мостов,
соединяющих берега реки, протекающей через город,
и два острова, расположенные на ней.
Спрашивается, можно ли обойти все мо-
мосты, проходя по каждому только один
раз, и возвратиться в исходную точку,
i с Полагая, что вершины соответствуют
районам суши, а ребра — мостам, эту
задачу можно сформулировать в виде
вопроса о возможности последователь-
последовательного обхода графа, изображенного на
рис. 1, с условием однократного исполь-
использования его ребер и возвращения в исход-
исходную точку (см. Графа обход). Если в графе такой об-
обход возможен, то говорят, что он обладает эйлеровым
циклом. Л. Эйлер установил, что такой цикл в графе
существует тогда и только тогда, когда он связен, и
число ребер, инцидентных каждой вершине, четно.
Так как граф на рис. 1 не удовлетворяет этому требо-
требованию, то задача о кёнигсбергских мостах неразре-
неразрешима. Она неразрешима и в том случае, если отбросить
требование совпадения точек начала и конца обхода.
В этом случае решается вопрос о существовании эйле-
ровой цепи в графе. Граф обладает эйлеровой
цепью тогда и только тогда, когда он связен и число
вершин, инцидентных нечетному числу ребер, равно
О или 2. Граф на рис. 1 не удовлетворяет и этому усло-
условию (см. [3]).
В 1859 У. Гамильтон (W. Hamilton) придумал игру
«Кругосветное путешествие», состоящую в отыскании
такого пути, проходящего через все вершины (города)
графа, изображенного на рис. 2,
чтобы посетить каждую вершину
однократно и вернуться в ис-
исходную. Пути в графах, обла-
обладающие таким свойством, наз.
гамильтоновыми цик-
циклами. Необходимые и доста-
достаточные условия существования
гамильтонова цикла в графе пока
A978) неизвестны (см. [3]).
Задача о гамильтоновых цик- Рис. 2.
лах в графе получила различ-
различные обобщения. Одно из этих обобщений —
задача коммивояжера, имеющая ряд при-
приложений в исследовании операций, в частности при
решении нек-рых транспортных проблем. Она состоит
в следующем: имеется нек-рое количество городов,
расстояния между к-рыми известны; нужно найти
кратчайший путь, проходящий через все города и воз-
возвращающийся в исходный.
В 1847 Р. Киркман (R. Th. Kirkman) поставил и
решил задачу о 15 школьницах. Они
должны были гулять ежедневно пятью группами по
три в каждой группе. При этом необходимо было так
составить расписание для их прогулок, чтобы каждая
школьница в течение семи дней смогла точно один раз
попасть в одну группу с каждой из остальных. Эта за-
задача связана с задачей построения системы троек, по-
поставленной Я. Штейнером (J. Steiner, 1853). Систе-
Системой троек Штейнера порядка v наз. такой
набор троек из множества, содержащего и элементов,
что каждая пара элементов входит точно в одну тройку.
Системы троек Штейнера описаны для р<15. Оказы-
Оказывается, что для t>=3, 7, 9 системы троек единственны
с точностью до эквивалентности (подстановка v элемен-
элементов, перестановка троек); для f=13 существуют две
неэквивалентные системы троек; при i>=15 таких троек
80. Для f >15 число различных систем троек Штейнера
пока A978) неизвестно. При i->3 система троек Штей-
Штейнера является частным случаем неполной частично
уравновешенной блок-схемы.
Классическая задача о встречах состоит
в следующем. Имеются две одинаковые колоды из п
различных карт каждая. Необходимо определить Dnr,
г=0, 1, ... , п,— число расположений карт во второй
колоде таких, что при сравнении соответствующих
карт первой и второй колоды число совпадений равно
г, г=0, 1, ... , п. Частный случаи этой задачи при г=0
впервые был сформулирован П. Монмором (P. Mont-
mort, 1708). Л. Эйлер рассматривал задачу отыскания
числа членов определителя, не имеющих общих эле-
элементов с главной диагональю, эквивалентную опреде-
определению Dno.
Задача о встречах была исходным пунктом для воз-
возникновения раздела комбинаторного анализа, связан-
связанного с исследованием перестановок с ограниченными
позициями. На совокупности Sn подстановок степени га,
действующих на множестве X, можно ввести расстоя-
расстояние р, полагая
p(s,s') = \{x:s(x)=?s' (x), x?X}\, s, s'?Sn.
Тогда
Dnr=\{s'-P{s> s') = n — r,s?Sn}\,
причем
В терминах расстояний между подстановками можно
сформулировать и другую классическую К. з., назы-
называемую обычно задачей о супружеских
парах. Она состоит в определении числа М„ рас-
рассаживаний п супружеских пар на 2га местах за круглым
столом так, чтобы ни один муж не сидел рядом со своей
женой. Тогда
Mn = 2.n\Un. Un=\{s:p(s,e) = n, p (s, с) = „, s?Sn}\,
где е — единичная подстановка, а с—A, 2, ..., п).
Получена формула:
Если
Un(slt s2) = \{s:p (s, «!) = >?, p(s, s2) = n, s?Sn}\,
то величина Un(s1, s2) зависит только от цикловой
структуры «Г1*2 и может быть выражена в виде формулы
с использованием Чебашева многочленов (см. [4]).
Тесную связь с приведенными задачами имеет проб-
проблема определения числа Ь^п латинских прямоугольни-
прямоугольников кХп и числа Ln латинских квадратов. Латинский
прямоугольник кХп может рассматриваться как упо-
упорядоченных"! набор подстановок slt s2, . .., s/, степени
п таких, что p(s,-, sj)=n, 1ф]. Показано, что
Lln = n\, L2n=Dnn\, Dn=Dn0
Установлено, что при к<п 3~Е, е>0,
где б„—>-0 при п—>-оо. Число латинских квадратов по-
порядка п известно до п=9 включительно.
Задача о числе разбиений нату-
натурального числа п на слагаемые впервые появи-
появилась в письме Г. Лейбница (G. Leibniz) к Я. Бер-
нулли (J. Bernoulli) в 1669. Однако разработка мето-
методов решения целого класса задач такого типа была
осуществлена Л. Эйлером, к-рып эффективно исполь-
использовал для этой цели производящие функции, задавае-
задаваемые в виде бесконечных произведений. Он, в частности,
установил, что число разбиений т+ге на п слагаемых
равно числу разбиений т на не более чем п слагаемых,
равно числу разбиений т. на слагаемые, не превосходя-
превосходящие п, и равно числу разбиений т+Ct1) на п раз-
различных слагаемых.
Классическая задача размещения состоит
в определении числа Спт(г) способов размещения т
различных предметов в п различных ячейках с задан-
заданным числом г пустых ячеек. Получено, что
C»« (г) = (") А""'О", г=0,1. ...,и,
где
Исследования здесь велись в плане теоретико-вероят-
теоретико-вероятностных приложений, включая разнообразные обоб-
обобщения и модификации. Наиболее интересная часть
этих исследований касается получения различных
асимптотических результатов, когда тип неограни-
неограниченно возрастают.
Лит.: [1] Постников М. М., Магические квадраты,
М., 1964; [2] Холл М., Комбинаторика, пер. с англ., М.,
1970; [3] О р е О., Теория графов, пер. с англ., М., 1968;
[4] Р и о р д а н Д ж., Введение в комбинаторный анализ, пер.
с англ., М., 1963; [5] X а р а р и Ф., Теория графов, пер. с
англ., М., 1973. В. Н. Сачков.
КОМБИНАТОРНЫЙ АНАЛИЗ, комбинатор-
комбинаторная математика, комби натори к а,—
раздел математики, посвященный решению задач вы-
выбора и расположения элементов нек-рого, обычно
конечного, множества в соответствии с заданными пра-
правилами. Каждое такое правило определяет способ пост-
построения нек-рой конструкции из элементов исходного
множества, называемой комбинаторной кон-
конфигурацией. Поэтому можно сказать, что целью
К. а. является изучение комбинаторных конфигураций.
Это изучение включает в себя вопросы существования
комбинаторных конфигураций, алгоритмы их построе-
построения, оптимизацию таких алгоритмов, а также решение
задач перечисления, в частности определение числа
конфигураций данного класса. Простейшими приме-
примерами комбинаторных конфигураций являются переста-
перестановки, сочетания и размещения.
Множество X из п элементов наз. л-м ножеством;
любое его /«-подмножество, т<:я, наз. сочетанием
объема т. Число сочетаний объема т из п различных
элементов равно
Имеет место формула:
обычно называемая формулой бинома Нью-
Ньютона. Числа (т) наз. биномиальными ко-
коэффициентами. Упорядоченное т-подмножество
наз. размещением объема т. Число размеще-
размещений объема т из п различных элементов равно
А (п, т)=п(п—1). . .{п—т+1).
При т=/г размещение представляет собой переста-
перестановку элементов множества X, причем число таких
перестановок равно Р(ге) = ге!
Возникновение основных понятий и развитие К. а.
шло параллельно с развитием других разделов мате-
математики, таких, как алгебра, теория чисел, теория ве-
вероятностей, с к-рыми К. а. тесно связан. Еще матема-
математикам Древнего Востока были известны формула, вы-
выражающая число сочетаний через биномиальные коэф-
коэффициенты, и формула бинома Ньютона с натуральным
показателем п. С мистическими целями изучались маги-
магические квадраты 3-го порядка. Рождение К. а. как
раздела математики связано с трудами Б. Паскаля
(В. Pascal) и П. Ферма (P. Fermat) по теории азартных
игр. Эти труды, составившие основу теории вероят-
вероятностей, одновременно содержали принципы определе-
определения числа комбинаций элементов конечного множества,
устанавливая тем самым ставшую затем традиционной
связь К. а. с теорией вероятностей.
Большой вклад в систематическое развитие комбина-
комбинаторных методов был сделан Г. Лейбницем (G. Leibniz)
в его диссертации «Ars Combinatoria» («Комбинатор-
(«Комбинаторное искусство»), где, по-видимому, впервые появился
термин «комбинаторный». Большое значение для ста-
становления К. а. имела работа Я. Бернулли (J. Ber-
Bernoulli) «Ars conjectandi» («Искусство предположений»),
посвященная основным понятиям теории вероятностей,
где обстоятельно изложен ряд комбинаторных понятий
и указаны их применения для вычисления вероятнос-
вероятностей. Можно считать, что с появлением работ Г. Лейб-
Лейбница и Я. Бернулли комбинаторные методы выдели-
выделились в самостоятельную часть математики.
Большой вклад в развитие комбинаторных методов
сделал Л. Эйлер (L. Euler). В его работах по разбие-
ниям и композициям натуральных чисел на слагаемые
было положено начало одному из основных методов
перечисления комбинаторных конфигураций — методу
производящих функций.
Возрождение интереса к К. а. относится к 50-м гг.
20 в. в связи с бурным развитием кибернетики и дис-
дискретной математики и широким использованием элект-
электронно-вычислительной техники. В этот период активи-
активизировался интерес к классическим комбинаторным
задачам.
На формирование направлений исследований в даль-
дальнейшем оказывают влияние два фактора. С одной сто-
стороны, выбор объектов исследований, с другой сто-
стороны — формулировка целей исследования, завися-
зависящая в конечном счете от сложности изучаемых объек-
объектов. Если исследуемая комбинаторная конфигурация
имеет сложный характер, то целью исследования яв-
является выяснение условий ее существования и разра-
разработка алгоритмов построения.
Большой развивающийся раздел К. а. составляет
теория блок-схем (см. также [2], [3], [10]); основные
проблемы этого раздела связаны с вопросами классифи-
классификации, условиями существования и методами построе-
построения нек-рых классов блок-схем. Частным случаем
блок-схем являются так наз. уравновешенные неполные
блок-схемы, или (b, v, г, к, >.)-конфпгу рации, к-рые
определяются как совокупности из Ь Жг-подмножеств
нек-рого и-множества, называемых блоками, с услови-
условием, что каждый элемент появляется в г блоках, а каждая
пара элементов — в А, блоках. При 6= v и, следова-
следовательно, г=к (Ь, и, г, к, А,)-конфигурация наз. (и, к, %)-
конфигурацией, или симметричной уравнове-
уравновешенной неполной блок-схемой. Даже для (и, к, Я)-
конфнгураций вопрос о необходимых и достаточных
условиях их существования остается пока A978) от-
открытым. Для существования (v, к, ^-конфигураций
необходимо, чтобы при v четном к—Я было квадратом,
а при v нечетном уравнение
z2 = (к — Х) х2 + (—l^o-1)'* Ху*
имело решение в целых числах х, у, z, одновременно не
равных нулю'.
При i?=ra2+rc+l, /е=ге-|-1, Я=1 (v, к, А,)-конфигу-
рацня представляет собой проективную плос-
плоскость порядка п, являющуюся частным случаем
конечной геометрии, содержащей коночное
число точек и прямых с заданными условиями их ин-
инцидентности. Каждой проективной плоскости порядка
п—1 можно поставить во взаимно однозначное соот-
соответствие полное множество из п—1 попарно ортого-
ортогональных латинских квадратов порядка п. Для су-
существования проективной плоскости порядка п необ-
необходимо, чтобы при ге=1, 2 (mod 4) существовали целые
числа а и 6, удовлетворяющие равенству
Вопрос о существовании проективных плоскостей по-
порядка п решен положительно только для п=ра, где р —
простое, а а — натуральное числа. Даже для ге—10
этот вопрос является открытым A978). К этому кругу
вопросов относится результат, связанный с опровер-
опровержением гипотезы Эйлера о несуществовании пары орто-
ортогональных латинских квадратов порядка ге=4&+2,
А=1, 2, ... (см. Комбинаторные задачи).
Другое направление К. а. связано с выбора теоре-
теоремами. В основе целого ряда результатов этого направ-
направления лежит теорема Ф. Холла о существо-
существовании системы различных представителей (транс-
в е р с а л и) семейства подмножеств (ЛГХ, ..., Хп)
множества X, т. е. системы элементов (хг, . . ., хп)
такой, что х,?Х и х;фх/ при гфу. тращсверсаль су-
существует тогда и только тогда, когда для любых г1; ...
..., ik таких, что l<:jj<.. .<г^<ге, 1<:&<:п, справед-
справедливо неравенство
где \Y\ — число элементов в множестве Y. Из теоремы
Ф. Холла вытекает теорема о существовании латин-
латинского квадрата, состоящая в том, что любой латинский
прямоугольник размера кХп, 1<:А;<:ге—1, можно до-
дополнить до латинского квадрата порядка п. Другое
следствие теоремы ф. Холла: любую неотрицательную
матрицу А — [|а,у||, г, /=1, . .., п, такую, что
можно представить в виде
где FIj, ..., Xls— матрицы подстановки порядка п
и s^.(n—1J-{-1. Из теоремы Ф. Холла следует также
теорема о том, что минимальное число строк и столб-
столбцов неотрицательной матрицы, содержащих все поло-
положительные элементы, равно максимальному числу
элементов, попарно не расположенных в одной и топ же
строке пли в одном и том же столбце. Экстремальное
свойство частично упорядоченных множеств, анало-
аналогичное этой теореме, устанавливает теорема, утверж-
утверждающая, что минимальное число непересекающихся
цепей совпадает с объемом максимального подмно-
подмножества, состоящего из попарно несравнимых элемен-
элементов. Экстремальный характер носит и следующая
теорема: если для «-множества X составить все (")
сочетаний по г элементов и разбить их на к непересе-
непересекающихся классов, то для целого т существует число
reo==reo(m> г> к) такое, что при гС^щ найдется подмно-
подмножество из т элементов YaX, для к-рого все (™) соче-
сочетаний принадлежат одному классу.
Экстремальной является задача коммивояжера, за-
заключающаяся в составлении кратчайшего маршрута
посещения га городов с возвращением в исходный пункт
при условии, что расстояния между городами известны.
Эта задача имеет приложения к изучению транспорт-
транспортных сетей. Комбинаторные задачи экстремального
характера рассматриваются в теории потоков в сетях
и в теории графов.
Значительную часть К. а. составляют перечис-
перечислительные задачи. При их решении либо
указывается метод перебора комбинаторных конфигу-
конфигураций и.ч данного класса, либо определяется их число,
либо делается то и другое. Типичные результаты пере-
перечислительных задач: число подстановок степени пек
циклами равно \S(n, к)\, где S(n, к) — числа С т и р-
л и н г а 1-го рода, определяемые равенством
число разбиений множества из п элементов на к под-
подмножеств равно числу Стирлпнга 2-rd
число размещений т различных предметов в п различ-
различных ячейках, когда пустых ячеек нет, равно п\а{т, п).
Полезным инструментом для решений перечислитель-
перечислительных задач является перманент матрицы.
Перманент матрицы Л = ||а;;||, г=1, ..., га, /=1, ...,
т, ?г<:т, с элементами из нек-рого кольца определяется
равенством
per Л = 2^. ....//У,*»/.-¦•«»/„•
где суммирование производится по всевозможным
размещениям объема п из т различных элементов,
Число трансверсалей нек-рого семейства подмножеств
конечного множества равно перманенту соответствую-
соответствующей матрицы инцидентности.
К вычислению перманентов сводится целый класс
задач по определению числа перестановок
с ограниченными позициями. Эти задачи
для удобства иногда формулируются как задачи о рас-
расстановке взаимно неатакующих фигур на шахматной
доске размером пХп. С определенном перманентов
нек-рых классов матриц связаны варианты задачи
о д и м е р а х, возникающей при изучении явления
адсорбции и заключающейся в определении числа спо-
способов объединения атомов в двухатомные молекулы на
нек-рой поверхности. Ее решение может быть также
получено через пфаффианы — некоторые функции от
матриц, близкие к определителям. Проблема о числе
латинских прямоугольников (квадратов) также свя-
связана с разработкой эффективных методов вычисления
перманентов нек-рых @, 1)-матриц.
Для вычисления перманентов применяется формула:
Имеется большое число неравенств, дающих оценку
величины перманента в нек-рых классах матриц. Пред-
Представляет интерес определение экстремальных значений
перманента в определенных классах неотрицательных
матриц, однако эта задача не решена A978) даже для
(О, 1)-матриц с заданным значением числа единиц
в строках и столбцах. К этой проблеме примыкает ги-
гипотеза Ван дер Вардена о том, что минимум перма-
перманента дважды стохастической матрицы порядка п ра-
равен п\1пп, подтвержденная только для положительно
полуопределенных матриц.
Большую роль в решении перечислительных задач
играет метод производящих функций. Производящая
функция
ставится в соответствие последовательности (а0, alt
. . .) с элементами из нек-рого поля и рассматривается
как формальный степенной ряд. При таком определе-
определении производящие функции эффективно используются
для решения перечислительных задач параллельно с
методами рекуррентных соотношений и конечно разност-
разностных уравнений. При получении асимптотических фор-
формул в качестве производящих функций обычно исполь-
используются аналитические функции действительного или
комплексного переменного. В последнем случае для
отыскания выражений коэффициентов применяют ин-
интегральную формулу Коши.
Имеются результаты в направлении возможной уни-
унификации методов перечисления, связанные с рассмот-
рассмотрением так наз. алгебр инцидентности и использованием
функции Мёбиуса на частично упорядоченных множест-
множествах (см., напр., [10]). При решении перечислительных
задач существенную роль играет формализация понятия
неразличимости объектов. Использование для этих
целей понятия эквивалентности объектов относительно
нек-рой группы подстановок в сочетании с применением
метода производящих функций было положено в ос-
основу так наз. теории перечисления
П о й а (см. [10]). Сущность этой теории состоит в сле-
следующем. Рассматривается Yx — множество конфигу-
конфигураций
/:АГ->У. |А'|=ш, | У | = и.
На множестве X действует группа подстановок А,
определяющая на Yx отношение эквивалентности ~,
при к-ром f~f1, если существует такое и?А, что
f(a(x)) = f1(x) для всех х?Х, /, f1^iYx. Каждому y?Y
ставится в соответствие характеристика [y]=(s1, . .., s:z),
где s,-, i=l, . .., к,— элементы абелевой группы.
Характеристика конфигурации / задается равенством
Если а^, . . ., s^) — число элементов j^Kc заданным
значением характеристики и bm(s1, . .., sk) — число
неэквивалентных конфигураций x
2(Sl,... s , ^^
то основная теорема Пой а утверждает, что
Фт(Уъ ¦¦-,Ук) =
= Z(F(yi, ...,yk), F(y\, ...,y%), ...,F(yf ут)),
где Z есть циклический индекс группы
А, определяемый равенством
С (/!, . . ., ]т; A) t1' . . . t'
т
C(/j, . . ., ]„; А) —число элементов циклового класса
{lJi2hi. . .т3т} группы А. Эта теорема основана на
лемме Б е р н с а и д а: число классов эквивалент-
эквивалентности N(A), определяемых на множестве X группой
подстановок А, дается формулой
1 ' -<—*аеЛ
где /х(а) — число единичных циклов а ? А. Теория
Iloiia имеет применения при решении перечислительных
задач теории графов и перечислении углеродных хими-
химических соединений. Имеется обобщение теории Пойа
на случай, когда эквивалентность конфигураций опре-
определяется двумя группами G и Н, действующими на X
и У соответственно (см. [4] и [10]). В таком виде она
применяется, напр., для определения числа неизоморф-
неизоморфных абстрактных автоматов.
Если Х= {1, . .., т}, Y= {alt . . ., ап) и а : Х^У",
где a.j используется a.j раз в качестве образа, то вы-
выражение
наз. первичной спецификацией ст. Если
числа ос1? а2, ..., ап содержат E0 нулей, Pt единиц и т. д.,
то выражение
наз. вторичной спецификацией. При
нек-рой специализации групп G и Н, определяющих
эквивалентность конфигураций а : X-yY, можно ука-
указать способ построения производящих функций для
перечисления неэквивалентных конфигураций. Этот
способ, называемый общей комбинаторной
схемой, подразделяется на четыре частных слу-
случая в соответствии с тем, принимают группы G и II
значения единичной Е или симметрической Sn групп
соответствующих степеней. Эти частные случаи яв-
являются моделями для большинства известных комбина-
комбинаторных схем (см. [9], [10]).
1. Коммутативный несимметрич-
несимметричный случай: G=Sm, 11= Е. Моделирует схемы
сочетаний, заполнений одинаковых предметов в раз-
различные ячейки и др. Производящая функция для пере-
числения неэквивалентных конфигураций а таких, что
М = К1 •¦¦<#•].
а|-€Л|-?ЛГ0 = {0,1, ...}, Л = (ЛЬ ...,Л„),
имеет вид:
2. Некоммутативный несимметрич-
несимметричный случай: G=E, H=E. Моделирует схемы раз-
размещений, заполнений различимых предметов в различ-
различные ячейки п др. Производящая функция для пере-
перечисления неэквивалентных конфигураций а таких, что
[а] = [а?.. .а««], а,• ^Л,-, Л = (Лг Л„),
имеет вид:
3. Коммутативный симметричный
случай: G=Sm, H=Sn. Моделирует схемы запол-
заполнения одинаковых предметов в одинаковые ячейки,
перечисления разбиений натуральных чисел и др.
Перечисление конфигурации а таких, что
л = (Л1,л2, ...),
основано на использовании производящей функции
вида:
4. Некоммутативный симметричный
случай: G=E, H=Sn. Моделирует схемы разбие-
разбиений конечных множеств на блоки, заполнения различи-
различимых предметов в одинаковые ячейки и др. Перечисле-
Перечисление конфигураций а таких, что
[[0p«lPl...mp«]]. Ру€Лу, Л-(Лх, Л„ . . .),
основано на использовании производящей функции
вида:
/=1хр.еЛ.
Значительное место в К. а. занимают асимптотические
методы. Они применяются как для упрощения сложных
конечных выражений при больших значениях входя-
входящих в них параметров, так и при получении прибли-
приближенных формул обходными путями, когда точные фор-
формулы неизвестны. Комбинаторную задачу перечисли-
перечислительного характера иногда удобно сформулировать
как задачу отыскания характеристик распределения
нек-рой случайной величины. Такая интерпретация
дает возможность применять развитый аппарат теории
вероятностей, а для отыскания асимптотик — предель-
предельные теоремы. Детальному исследованию с этих пози-
позиций подвергнута классическая схема случайных раз-
размещений предметов в ячейки, случайные разбиения
множеств, цикловая структура случайных подстано-
подстановок, а также различные классы случайных графов,
включая графы отображений (см. [8], [9]).
Вероятностный подход применяется при изучении
комбинаторных свойств симметрических групп и по-
полугрупп. Исследовано предельное распределение по-
порядка случайного элемента симметрической группы Sn
при п—>-оо, а также асимптотика вероятности порож-
порождения ее случайными элементами. Для нек-рых классов
случайных неотрицательных матриц изучались рас-
распределения числа нулевых линий в матрице и перма-
перманентов, даны оценки вероятности примитивности таких
матриц. Для доказательства существования комбина-
комбинаторных конфигураций без их конструирования иногда
используется нек-рый специфический вероятностный
прием. Сущность этого приема заключается в установ-
установлении существования конфигурации без ее конструи-
конструирования с помощью оценки вероятности нек-рого со-
события (см. [7]).
Лит.: [1] Риордан Д ж.. Введение в комбинаторный
анализ, пер. с англ., М., 1963; [2] Р а й з е р Г.-Д ж., Комби-
Комбинаторная математика, пер. с англ., М., 1966; [3] Холл М-,
Комбинаторика, пер. с англ., М., 1970; [4] Прикладная комби-
комбинаторная математика, сб. статей, пер. с англ., М., 1968;
[5J X а р а р и Ф., Теория графов, пер. с англ., М., 1973; L6] X а-
рари Ф, П а л м е р Э., Перечисление графов, пер. с англ.,
М., 1977; [7] Эрдёш П., Спенсер Д ж., Вероятностные
методы в комбинаторике, пер. с англ., М., 1976; [8] К о л ч и и
В. Ф., Чистяков В. П., в кн.: Итоги науки и техни-
техники. Теория вероятностей. Математическая статистика. Тео-
Теоретическая кибернетика, т. 11, М., 1974, с. 5—45; [9] Сач-
Сачков В. Н., в кн.: Вопросы кибернетики. Тр. семинара по
комбинаторной математике, М., 1973, с. 146—64; [10] его же,
Комбинаторные методы дискретной математики, М., 1977.
В. Н. Сачков.
КОМИТАНТ, к о н к о м и т а н т, группы G, дей-
действующей на множествах X и У,— такое отображение
Ф : X-+Y, что
для любых g?G, x?X. В этом случае говорят также,
что ф коммутирует с действием G, или, что ф — э к в и-
вариантное отображение. Если G дейст-
действует на каждом множестве семейства {X;, г?/}, то К.
JJ. Х[—»-У наз. совместным (или одновре-
одновременным) К. группы G.
Понятие К. происходит из классической инвариантов
теории, в к-рой, однако, К. понимается в более узком
смысле: G — полная линейная группа нек-рого ко-
конечномерного линейного пространства U, X и У —
пространства тензоров на U определенного (вообще
говоря, различного) типа, на к-рых G действует естест-
естественным образом, а ф — эквивариантное полиномиаль-
полиномиальное отображение X в У. Если, кроме того, У есть
пространство ковариантных тензоров, то К. наз. к о-
вариантом группы G, а если У — пространство
контравариантных тензоров, то К. наз. контрава-
р и а н т о м группы G.
Пример. Пусть / — бинарная кубическая форма
от переменных х и у:
Ее коэффициенты являются координатами ковариапт-
ного симметрического тензора. Коэффициенты гессиана
формы /, т. е. формы
д-f дЧ
1_ дх2 дх ду
" ~ 36 Э2/ дЧ_
дхду ду*
= (аоа2 — а|) я2 + (аовз — аха2) ху-{-(а1а3 — af)y2
также являются координатами ковариантного симмет-
симметрического тензора и отображение
(а„, alta2, a3) i—*• fa0a2 — af, — (аоа3 —
соответствующих пространств тензоров есть К. (так
наз. К. формы /). Аналогично можно определить гес-
гессиан произвольной формы, к-рый также дает пример К.
(см. Коеариант).
В современной геометрич. теории инвариантов под К.
часто понимают любой эквивариантный морфизм X—*-Y,
где X и У — алгебраич. многообразия, снабженные
регулярным действием алгебраич. группы G. Если
X и У аффинны, то К. определяет гомоморфизм (и сам
определяется им) &[У]-+А-[Х] G-модулей регулярных
функций на многообразиях У и X соответственно
(к — основное поле).
Лит.: ШГуревичГ. Б., Основы теории алгебраических
инвариантов, М.— Л., 1948; [2]Дьедонне Ж., К е р р о л
Д ж., М а м ф о р д Д., Геометрическая теория инвариантов,
пер. с англ., М., 1974. В. Л. Попав.
КОММУТАНТ группы, производная груп-
группа, второй член нижнего централь-
центрального ряда группы,— подгруппа, порождаемая
в группе G всевозможными коммутаторами элементов
группы G. Обычно К. группы G обозначается [G, G],
или G', или T2(G). К. группы является вполне характе-
характеристической подгруппой, а любая подгруппа, содержа-
содержащая К., является нормальным делителем этой группы.
Факторгруппа по некоторому нормальному делителю
абелева тогда и только тогда, когда этот нормальный
делитель содержит К. группы.
К. кольца R — идеал, порожденный всеми про-
произведениями ab, a, b?R; он наз. также квадратом
кольца R и обозначается [R, R] или R2.
Оба введенные понятия — частные случаи понятия К.
мультиоператорной Q-группы G, оп-
определяемого как идеал, порожденный всеми коммутато-
коммутаторами и элементами вида
— ajag. . .апш — ЬХЬ2. . A,co-j-
• • • ian ~~ Ъп) СО,
где со—га-арная операция пз Q, а
аъ а2, . . ., а„, bltb2 bn?G.
Н. В. Вильяме, О. А. Иванова.
КОММУТАТИВНАЯ АЛГЕБРА — раздел алгебры,
изучающий свойства коммутативных колец и связанных
с ними объектов (идеалов, модулей, нормирований и т. д.).
К. а. выросла из задач, возникавших в теории чисел
и алгебраич. геометрии. Задачи эти, как правило, отно-
относились к конкретным классам колец. Фундаменталь-
Фундаментальным объектом теории чисел является кольцо % целых
рациональных чисел, и основной факт его арифметики
состоит в том, что любое целое число по существу одно-
однозначно разлагается в произведение простых чисел.
В ЗО-е гг. 19 в. К. Гауссом (С. Gauss), Э. Куммером
(Е. Kummer) и другими была обнаружена связь различ-
различных вопросов теории чисел (напр., квадратичные фор-
формы, теорема Ферма) с арифметикой квадратичных и
круговых расширений поля рациональных чисел Q
(см. [11]). Распространению классических рассуждений
на кольца алгебраич. чисел препятствовало, однако, то
обстоятельство, что разложение на далее неразложимые
множители в них перестает быть однозначным (см. Ал-
Алгебраическая теория чисел). Догадка Э. Куммера сос-
состояла в том, что если добавить к обычным числам некие
«идеальные» числа (подобно тому, как в проективной
геометрии добавляются бесконечно удаленные точки),
однозначность разложения сохранится (см. Идеальное
число).
Э. Куммеру удалось построить такие «идеальные»
числа, или, как сейчас говорят, дивизоры, только для
круговых полей; однако его результаты побудили Р. Де-
декинда (R. Dedekind) и Л. Кронекера (L. Kronecker)
распространить теорию дивизоров на произвольные
кольца алгебраич. чисел. В построенной Р. Дедекин-
дом к 1882 теории была выявлена роль целых элементов
поля; но что еще более важно — это появление поня-
понятия идеала и простого идеала. Так были заложены ос-
основы одномерной К. а.
Параллельно в алгебраич. геометрии происходило
формирование многомерной К. а. Алгебраич. геометрия
того времени изучала свойства алгебраич. кривых на
плоскости, а также более общих алгебраич. многооб-
многообразий, задаваемых как множество MczCn общих нулей
нескольких многочленов Рх, . .., P^^Clxy, ..., хп]
(различие между аффинными и проективными много-
многообразиями здесь не существенно). То же многообразие
М можно задавать и другими уравнениями, так что
более инвариантно с многообразием М связывается
идеал Щ всех многочленов, обращающихся в нуль
на М. Это еще один путь, приводящий к понятию
идеала. Однако до 1890 алгебраич. основы алгебраич.
геометрии находились в зачаточном состоянии. Поло-
Положение изменилось после опубликования работ Д. Гиль-
Гильберта (D. Hilbert). В 1893 он доказал теорему о нулях
(см. Гильберта теорема). Несколько раньше он же
установил следующие факты, во многом определившие
дальнейшее направление развития К. а.: теорему о ба-
базисе (любой идеал в С \xt, ..., зсп] порождается конеч-
конечным числом многочленов), теорему о сизигиях и сущест-
существование Гильберта многочлена для однородного идеала
в кольце многочленов.
Опыт работы с алгебраич. многообразиями малой
размерности убеждал в том, что они состоят из конеч-
конечного числа неприводимых подмногообразий, что при-
приводило к алгебраич. задаче о представлении идеала
в виде пересечения более просто устроенных идеалов.
Эта задача была решена Э. Ласкером (Е. Lasker, см. [4]),
к-рый ввел понятие примарного идеала, заменяющего
в многомерном случае степень простого идеала, и ассо-
ассоциированного с ним простого идеала, а также доказал
существование примарного разложения произвольного
идеала в кольце многочленов. Вопрос об однознач-
однозначности такого разложения рассматривался Ф. Маколеем
(F. Macaulay, 1913). Было установлено, что хотя само
примарное разложение и не однозначно, множество
ассоциированных с ним простых идеалов определяется
однозначно, как п «изолированные» примерные ком-
компоненты. Естественное стремление избавиться от не-
неоднозначности примарного разложения побудило
Б. Л. Ван дер Вардена (В. L. Van der Waerden, 1931)
ввести более грубое отношение эквивалентности для
идеалов, чем равенство. Это привело к теории дивизо-
риалъных идеалов, или дивизоров, и позволило обоб-
обобщить теорию Куммера — Дедекинда на более широкий
класс колец (см. Крулля кольцо).
Начиная с Л. Кронекера и Э. Ласкера, с простыми
идеалами в кольце многочленов связывают их раз-
размерность, определяемую пока как степень трансцен-
трансцендентности соответствующего факторкольца; современ-
современное комбинаторное определение размерности было
предложено В. Круллем (W. Krull) позже. Если псе
простые идеалы, ассоциированные с идеалом 31, имеют
одну размерность, то идеал Ш наз. н е с м е ш а н-
н ы м. В кольце многочленов идеалы главного ряда
несмешаны, пли, в современной терминологии, кольцо
многочленов является Коэна — Маколея кольцом.
Наконец, ряд своих результатов Э. Ласкер распрост-
распространил на кольцо сходящихся степенных рядов, рас-
рассматривая последнее с алгебраич. точки зрения.
К началу 20 в. были получены результаты, относя-
относящиеся к кольцам алгебраич. чисел и многочленов.
Здесь же стоит упомянуть о конструктивном направ-
направлении, отыскивающем явные алгоритмы для установ-
установления принадлежности многочлена нек-рому идеалу.
Однако конкретность материала мешала увидеть об-
общие закономерности и связи. Толчком к развитию
современной К. а. послужила теория р-адпческих чисел
К. Гензеля (К. Hensel); именно возможность приме-
применения классических методов к такому нетрадиционному
объекту позволила осознать и выделить общие идеи,
применимые к произвольным кольцам (удовлетворяю-
(удовлетворяющим тем или иным условиям, напр, условиям конеч-
конечности). Начинается новый этап — этап абстрактной
К. а., системами, изучение строения различных клас-
классов коммутативных колец. Это проявилось уже в ра-
работах Э. Нётер (Е. Noethei). Связав условие конечности
базиса для любого идеала с условием максимальности,
т. е. с условием обрыва возрастающих цепочек идеалов
(кольца с этим условием наз. нётеровыми), она получила
в наиболее общем виде теорию примерных разложений
Л аскера — Маколея, казавшуюся ранее сугубо вы-
вычислительной и громоздкой. Ею было дано также ак-
сиоматич. описание дедекиндовых колец. В то же время
Э. Артин (Е. Artin) изучает кольца с условием мини-
минимальности — артиновы кольца; X. Грелль (Н. Grell)
вводит понятие локализации целостного кольца — опе-
операции, обобщенной затем К. Шевалло (С. Chevalley) и
А. И. Узковым. В. Крулль доказывает теорему о глав-
главном идеале, положившую начало теории размерности
нётеровых колец, а также теорему о пересечении степе-
степеней идеала в нётеровом кольце, являющуюся основой
при изучении 21-адических топологий. Теория дивизо-
рцальных идеалов A931) и теория нормирования обоб-
обобщают более ранние исследования К. Гензедя и А. Ост-
Островского (A. Ostrowski). Наконец, следует упомянуть
теорему Нётер о нормализации, выяснение роли поня-
понятия целой зависимости в рамках общей теории комму-
коммутативных колец, а также теоремы Крулля о подъеме
простых идеалов для целых расширений.
Новое направление открыла работа В. Крулля о ло-
локальных кольцах [7]. Так называются кольца, имеющие
единственный максимальный идеал; примером может
служить кольцо ростков аналитич. функций на ком-
комплексном многообразии. В абстрактном случае к ло-
локальным кольцам приводят операции локализации и
пополнения, а также операция перехода к Гензеля
кольцу. В. Крулль развил теорию размерности локаль-
локальных колец и ввел понятие регулярного локального
кольца, соответствующего гоомотрич. понятию неосо-
бон точки многообразия. В 40-е гг. 20 в. интенсивно
развивается локальная алгебра и ее алгебро-геометрич.
приложения. Локальное кольцо снабжается естествен-
естественной топологией; это позволяет использовать операцию
пополнения и сравнивать свойства кольца и его попол-
пополнения. Устанавливается, чтб для колец алгебраич.
геометрии (геометрич. кольца) переход к пополнению
сохраняет ряд важных свойств. Вместе с исследова-
исследованиями о конечности целого замыкания это сформиро-
сформировалось в целое направление теории колец (см. Превос-
Превосходное кольцо). В 1946 И. С. Коэн (I. S. Cohen) описал
структуру полных локальных колец. Другое направле-
направление связано с обоснованием теории пересечений. Раз-
Развивая идеи В. Крулля, П. Самюэль (P. Samuel) вводит
понятие градуированного кольца, связанного с локаль-
локальным кольцом, возрождает характерпстич. функции
Гильберта, приводящие к еще одному определению
размерности локального кольца, определяет кратность
идеала.
Последующее развитие идей К. а. связано с гомоло-
гич. методами, функториальным подходом и дальнейшей
геометризацией. Этому способствовала восходящая
к Р. Дедекинду и Э. Нётер тенденция к линеаризации
К. а., в соответствии с к-рой идеалы кольца рассматри-
рассматриваются как частный случай модулей. Последние яв-
являются обобщением векторных пространств и в гео-
геометрич. представлении соответствуют понятию се-
семейства векторных пространств. К модулям применимы
обычные конструкции линейной алгебры — прямой
суммы, модуля гомоморфизмов, тензорного произве-
произведения. Плодотворность такого более широкого взгляда
видна уже из возможности применять резольвенты,
а вместе с ними и гомологнч. алгебру, сформировав-
сформировавшуюся к 50-м гг. 20 в. и представляющую далеко иду-
идущее обобщение теории сизигий. Это привлекло внима-
внимание к модулям специального вида (см. Проективный
модуль, Инъективный модуль, Плоский модуль). Изу-
Изучение любого класса колец тесно связано с изучением
модулей над ними (см. Гомологическая классификация
колец). Серьезное продвижение было достигнуто в ло-
локальной алгебре: Ж. П. Серр (J.-P. Serre) охарактери-
зовал регулярные кольца как кольца конечной гомо-
логич. размерности и установил Тог-формулу для крат-
кратности пересечений, М. Ауслендер и Д. А. Буксбаум
(М. Auslander, D. A. Buchsbaum) доказали факториаль-
ность регулярного локального кольца. Началось изу-
изучение функторов Ext и Тог, связанных с гомоморфиз-
гомоморфизмами и тензорными произведениями модулей, Горен-
шгпейна колец и колец Коэна — Маколея, допускающих
гомологич. описание, чисел Бетти локальных колец.
Другая особенность современной К. а.— функто-
риальный подход, проявляющийся в изучении свойств
не изолированного кольца или модуля, а целой системы
таких объектов, связанных между собой морфпзмами.
Замена базисного кольца, теория спуска, изучение раз-
различных функториальных конструкций — все это отра-
отражение упомянутой тенденции. Так, напр., сохранение
многих свойств при локализации и пополнении связа-
связано с плоскостностью соответствующего расширения.
Третья особенность — геометризация. Она соответст-
соответствует взгляду (естественному в алгебраич. геометрии
и функциональном анализе) на элементы кольца как
на функции на нек-ром пространстве. В качестве такого
пространства предлагалось брать сначала множество
максимальных идеалов кольца, а затем множество
всех простых идеалов, снабженное Зариского тополо-
топологией (простой спектр кольца). В частности, появилась
возможность использовать теорию пучков и их когомо-
логий. К. а. становится составной частью алгебраич.
геометрии, значительно расширившей благодаря этому
свои рамки и возможности. Напр., появилась возмож-
возможность использовать и интерпретировать в геометрич.
терминах кольца с делителями нуля и нильпотентнымп
элементами. В свою очередь геометрич. методы ожи-
оживили те направления К. а., к-рые можно назвать гло-
глобальной К. а. К ним относятся инвариантов теория,
алгебраическая К-теория, когомологич. образования
(Пикара группа, Брауэра группа и др.), изучение груп-
группы автоморфизмов и различных инвариантов колец,
теория разрешения особенностей и т. д. Однако здесь
уже стираются грани между К. а. и алгебраич. геомет-
геометрией.
Лит.: [1] К u m m е г Е., «J. reine und angew. Math.», 1847,
Bd 35, S. 319—26; [2j Dedekind R., Gesammelto mathc-
matische Werkc, Bd 3, Braunschweig, 1932; [3J H i 1 b e г t D.,
Gesammelte Abhandlungen, Bd 2, В., 1933; [4] LaskerE.,
«Math. Ann.», 1905, Bd 60, S. 20—116; [51 Noether E.,
«Math. Ann.», 1921, Bd 83, S. 24—66; [6] e e ж е, там же, 1926,
Bd 96, S. 26—61; [7] К г u 1 1 W., «J. reine und angew. Math.»,
1938, Bd 179, S. 204—26; [8] Cepp Ж.-П., «Математика»,
1963, т. 7, в. 5, с. 3—93; [9] Ван-дер-Варден Б. л..
Современная алгебра, т. 2, пер. с нем., М.— Л. 1947; [10]
Krull W., Idealtheorie, В., 193ft: [И] Боревич 3. И.,
III а ф а Р е в и ч И. Р., Теория чисел, 2 изд., М., 1972; [12]
Зарисский О., Самюэль П., Коммутативная алгебра,
т. 1—2, пер. с англ., М., 1963; [13] Nagata M., Local
rings, N. Y., 1962; [14] Б у р б а к и Н., Коммутативная ал-
алгебра, пер. с франц., М., 1971; [15] К а р 1 a n s k у I., Com-
Commutative rings, Boston, 1970. В. И. Данилов.
КОММУТАТИВНАЯ БАНАХОВА АЛГЕБРА — ба-
банахова алгебра А с единицей над полем С, в к-рой
ху~ух для всех х, у^А.
Всякий максимальный идеал К. б. а. А является
ядром нек-рого линейного непрерывного мультипли-
мультипликативного функционала ср на А, т. е. гомоморфизма
алгебры А в поле комплексных чисел. Обратно, всякий
линейный мультипликативный функционал на К. б. а.
непрерывен, имеет норму 1, и его ядром служит макси-
максимальный идеал в А. Пусть ф — множество линейных
мультипликативных функционалов на А. Элемент
а?А тогда и только тогда обратил!, когда ср(а)^=О для
всех ф?Ф. Более того, спектр а (а) состоит в точ-
точности из чисел вида ц>(а). Если линейный непрерывный
функционал 1|э на А таков, что ty(a)?o(a) для любого
а?А, то \р — мультипликативный функционал; для
алгебр над полем действительных чисел это, вообще
говоря, уже неверно.
Примеры описания максимальных идеалов в К. б. а.
Пусть Л = С(ЛГ) — алгебра всех непрерывных функций
на компакте X. Если х0— фиксированная точка из X,
то совокупность функций f?A, для к-рых f(xo)=O,
образует максимальный идеал, и в С(X) нет других
максимальных идеалов. Если X — компакт на ком-
комплексной плоскости л A = R(X) — замкнутая подал-
подалгебра в С(Х), состоящая из функций, к-рыо равномерно
аппроксимируются на X рациональными функциями
с полюсами вне X, то максимальные идеалы в R(X)
устроены так же, как и в С(Х). Пусть ^(G) — груп-
групповая алгебра, где G — дискретная аболева группа,
и каждому элементу f^L1(G) ставится в соответствие
его преобразование Фурье. Если ср — мультипликатив-
мультипликативный линейный функционал на L1(G), то ф(/) = /(%о)
для нек-рого %0 лз группы характеров G группы G,
поэтому множество максимальных идеалов в Z-1(G)
находится во взаимно однозначном соответствии с мно-
множеством элементов группы G. В применении к группе
целых чисел Z последний пример приводит к доказа-
доказательству известной теоремы Винера: если функция /(()
разлагается в абсолютно сходящийся тригонометрич. ряд
и не обращается в нуль на [0, 2я], то i/f(t) также раз-
разлагается в абсолютно сходящийся тригонометрич. ряд.
Так как мультипликативные линейные функционалы
имеют норму 1. то каждый такой функционал является
элементом из единичной сферы банахова пространства,
сопряженного А. Множество Ф всех мультипликатив-
мультипликативных линейных функционалов на А замкнуто в слабой
топологии сопряженного пространства. Так как еди-
единичный тар сопряженного пространства ость компакт
в слабой топологии сопряженного пространства, то
и Ф в этой топологии является компактом, к-рый
наз. пространством максимальных
идеалов алгебры А и обозначается через 2Л.
Если К. б. а. содержит нетривиальный идемпотент,
т. е. такой элемент / ?А, что {фО, }фе и /2=/, то прост-
пространство максимальных идеалов алгебры А несвязно.
Обратно, если пространство X максимальных идеалов
алгебры А представимо в виде объединения двух непере-
непересекающихся замкнутых множеств Хо и Х17 то сущест-
существует элемент f?A такой, что /|^0 = 0 и /|у,= 1 (т е о-
р е м а Ш и л о в а). В частности, пространство мак-
максимальных идеалов К. б. а. связно тогда и только то-
тогда, когда эта алгебра не может быть представлена в
виде прямой суммы двух своих нетривиальных идеалов.
Пусть ?Х{А) — подгруппа в группе г(А) обратимых
эле.ментов алгебры А, состоящая из экспонент, т. е.
элементов вида exp a=2j ^-. Подгруппа е^А) об-
образует связную компоненту единицы в группе г(А).
Для любого компакта X имеется канонический изо-
изоморфизм между группами ЯХ(Х, %) и е(С)/е1(С), где
С=С(Х) — алгебра всех непрерывных функций на X
(теорема Брушл и некого — Эйленбер-
г а). Оказывается, этот изоморфизм естественно инду-
индуцирует изоморфизм между Я1(Х, Ъ) и г(АIг1{А),
где А — любая К. б. а., пространством максимальных
идеалов к-рой является X (теорема Аренса —
Р о й д е н а). В нек-рых случаях аналогичную интер-
интерпретацию допускают группы Н1{Х, Z) с нечетным q.
Алгебра А допускает следующее каноническое пред-
представление в алгебру С(9Л). Преобразованием
Гельфанда элемента а?Л наз. функция а на 2J},
значение к-рой в каждой точке х?Ш1 определяется пра-
правилом а(х) = <рх(а), где <рх— линейный мультиплика-
мультипликативный функционал, соответствующий точке ж?ЯI. Яд-
Ядром гомоморфизма а\-^а служит совокупность элементов
а?А. принадлежащих всем максимальным идеалам,
т. е. радикал алгебры А. Если алгебра А полупроста,
т. е. Rad A={0}, то гомоморфизм а\-*а оказывается
(алгебраическим) изоморфизмом А в С (ЯЛ). Полупростые
К. б. а. часто наз. алгебрами функций.
Представление Гельфанда хорошо приспособлено
для изучения полупростых алгебр: один из основных
результатов теории К. б. а. есть возможность изоморф-
изоморфного представления полупростой алгебры в алгебру
непрерывных функций на пространстве максимальных
идеалов. Об общих алгебрах с радикалом известно
гораздо меньше, чем о полупростых. Описаны все
идеалы в алгебре комплексных полиномов степени <:га.
Эта алгебра состоит из формальных полиномов |=
= ao+a1X-f-. . .Jramkm, к-рые перемножаются по обыч-
обычным правилам, но с учетом соотношения Хт + 1 = 0.
Такая алгебра конечномерна, все нормы в ней экви-
эквивалентны и любой идеал замкнут. Совокупность I ^
тех |, для к-рых ау=О при ]'<к, образует замкнутый
идеал; других идеалов в этой алгебре нет. Всякая ал-
алгебра с единственным нетривиальным идеалом изо-
изоморфна алгебре полиномов первой степени. До сих
пор неизвестно A978), верно ли это для алгебр с единст-
единственным замкнутым идеалом.
Естественным бесконечномерным аналогом алгебры
полиномов служат алгебры бесконечных комплексных
формальных степенных рядов l^aQ-j-ajX-j-ajA,3-{-...
с обычными операциями и нормой ||i|| = 5i la*laft,
где a#— положительная последовательность, удовлет-
удовлетворяющая условию а^+г<:а^.аг. Если а^й—»-0 при
&—>-оо, то единственным нетривиальным гомоморфизмом
алгебры в поле комплексных чисел служит ||-^в0. Та-
Таким образом, /х является единственным максимальным
идеалом, и этот идеал совпадает с радикалом. Идеалы
Ik, определяемые аналогично конечномерному случаю,
дают счетный набор различных замкнутых идеалов.
Если последовательность ak+1la/l монотонна, то этим
набором идеалов исчерпываются все замкнутые идеалы.
В общем случае алгебра может содержать континуаль-
континуальное семейство различных замкнутых идеалов.
При надлежащем выборе последовательности ak
в рассматриваемой алгебре (не имеющей нетривиаль-
нетривиальных нильпотонтов) можно задать ненулевое непрерыв-
непрерывное дифференцирование, т. е. ограниченный линейный
оператор D такой, что D (|т|) = Д B)^)т]+|(-От)). В полу-
полупростых алгебрах нет нетривиальных непрерывных
дифференцирований, так как в любой (не обязательно
коммутативной) алгебре имеет место тождество
если | и D\ коммутируют. В частности, если D непреры-
непрерывен, то Д| — обобщенный нилыготент.
Любая конечномерная алгебра разлагается в прямую
сумму радикала и полупростой алгебры. В бесконечно-
бесконечномерном случае аналогичное утверждение, вообще го-
говоря, перестает быть справедливым даже для К. б. а.
Кроме того, приходится различать случаи алгебраиче-
алгебраической и сильной (топологической) разложимости.
Оказывается, никакие условия, наложенные только
на радикал, не обеспечивают даже алгебраич. разложи-
разложимости: радикал может быть одномерным и аннулирую-
аннулирующим нек-рый максимальный идеал и, тем не менее, не
выделяться в качестве прямого слагаемого хотя бы
в алгебраич. смысле.
С другой стороны, если радикал конечномерен, а
факторалгебра есть алгебра всех непрерывных функций
(или алгебра всех операторов в гильбертовом прост-
пространстве), то имеется сильная разложимость. Если
факторалгебра есть алгебра всех непрерывных функ-
функций и Л — ее аннуляторный радгткал (т. е. такой, что-
квадрат любого элемента в R равен нулю) и А имеет
банахово дополнение, то А сильно разложима; вместо
условия дополняемости R можно потребовать, чтобы
пространство максимальных идеалов А удовлетворяло
первой аксиоме счетности в каждой точке.
Полностью исследован также случай, когда фактор-
алгебра по радикалу есть алгебра непрерывных функ-
функций на вполне несвязном компакте: необходимое и
достаточное условие сильной разложимости состоит
в равномерной ограниченности идемпотентов исходной
алгебры.
Пусть V — некоторая ограниченная область в С"
и А —замкнутая подалгебра алгебры C(V), состоящая
из функций, голоморфных на V. Известно, что в доста-
достаточно общих предположениях относительно V любой
максимальный идеал алгебры А, отвечающий точке
?>={г\, . .., z°)?F, конечно порожден, а именно, по-
порождается функциями /,-=z,—z\. Это утверждение до-
допускает следующее локальное обращение. Пусть А —
полупростая К. б. а. с пространством максимальных
идеалов X. Если максимальный идеал, соответствую-
соответствующий нек-рой точке хй?Х, порожден конечным набором
элементов /х, . . ., fn?A, то максимальные идеалы, со-
соответствующие точкам из нек-рой окрестности точки х0,
порождаются элементами вида /,-—Я,е, отображение
•ф : x(-^(/j(x), . . ., jn(x)) взаимно однозначно в нек-рой
окрестности точки ха, функция golf для любого g?A
голоморфна в нек-рой фиксированной окрестности
начала координат в С" и, кроме того, X вблизи х0
допускает введение нек-рой естественной аналитиче-
аналитической структуры.
Множество S элементов алгебры А наз. системой
образующих, если наименьшей замкнутой под-
подалгеброй с единицей в А, содержащей множество S,
служит сама алгебра А. Единица обычно не включается
в число образующих. Если существует конечная сис-
система S с указанными свойствами, то А наз. алгеб-
алгеброй с конечным числом образую-
щ и х. Числом образующих алгебры А называют в этом
случае наименьшее возможное число элементов в сис-
системе образующих.
Если Д, ..., /„—система образующих нек-рой ал-
тебры, то отображение x\-^-(f1(x), . .., fn{x)) осуществляет
гомеоморфизм пространства максимальных идеалов
этой алгебры на нек-рый полиномиально выпуклый
компакт в С". Всякий полиномиально выпуклый ком-
компакт в С" служит пространством максимальных идеа-
идеалов нек-рой банаховой алгебры (напр., алгебры равно-
равномерных на этом компакте пределов полиномов).
Пространство максимальных идеалов алгебры с га
образующими удовлетворяет условию dim X <:2п и
обладает рядом других свойств; напр., Н' (X, С)=0
при г^ге. Отсюда, в частности, следует, что число об-
образующих в алгебре C(Sn), где S" есть n-мерная сфера,
равно ге+1; аналогичный результат имеет место для
любого n-мерного компактного многообразия X. Для
любого конечного клеточного «-мерного полиэдра X
алгебра С(Х) допускает систему из ге+1 образующей.
Наименьшее замкнутое множество TczX, где X —
пространство максушальных идеалов алгебры А, на
к-ром все функции |/| достигают максимума, наз.
траницей Шилова пространства X. Для
любой К. б. а. с единицей такое множество сущест-
существует и единственно.
Точка хо?Х тогда и только тогда принадлежит Г,
когда для любой ее окрестности U существует такой
элемент /?Л, для к-рого max |/| = 1, но |/(ж)[<1 вне U.
X
Более того, если U — открытое множество в X и су-
существует такое замкнутое множество FdU и такой
элемент g?A, что |g(x)| <max|g\ для точек x?U\F,
F
то пересечение Tf\U непусто. В частности, если Х =
= [0, 1], то Т=Х.
Любой мультипликативный линейный функционал ф
непрерывен относительно нормы, определяемой спект-
спектральным радиусом; более того, |ф(г)| <:max[/j, где X —
X
пространство максимальных идеалов. В этом нера-
неравенстве можно, по определению границы Шилова,
заменить X на Г; поэтому существует положительная
регулярная мера и. на Г, «представляющая» функцио-
функционал ф, т. е. такая, что для любого /?А имеет место
равенство ф(/)=\ fd\i. Для случая алгебры аналитич.
функций в круге эта формула сводится к классической
формуле Пуассона. Среди представляющих мер сущест-
существует мера ц., удовлетворяющая неравенству Иенсена
для всех fQ_A.
Пусть В есть К. б. а. с единицей и А — некоторая
ее замкнутая подалгебра. Алгебра А наз. макс и-
мальной подалгеброй алгебры В, если В
не содержит никакой замкнутой собственной подал-
подалгебры, содержащей А и не совпадающей с А. Во всякой
достаточно широкой алгебре В имеются максимальные
подалгебры с единицей и даже замкнутые подалгебры
коразмерности 1. Действительно, если ф1? ф2— два
различных гомоморфизма алгебры В в поле комплекс-
комплексных чисел и 'ф=ф1—ф2, то ядро функционала \р яв-
является замкнутой подалгеброй А алгебры В такой, что
dim B/A = l. Аналогично, ядро «точечного дифферен-
дифференцирования», т. е. функционала \р такого, что "ty(fg) =
=гИ/)ф(?)~ггИ?)гИ/)> гДе Ф — мультипликативный
функционал, есть подалгебра коразмерности 1. В ком-
комплексном случае эти примеры исчерпывают всевозмож-
всевозможные подалгебры коразмерности 1. В частности, всякая
такая подалгебра алгебры С (X) не разделяет точки
компакта X, так как на С(Х) нет никаких (даже раз-
разрывных) дифференцирований. Близкое описание до-
допускают все подалгебры конечной коразмерности.
Алгебра А тех непрерывных функций на единичной
окружности, к-рые допускают аналитич. продолжение
внутрь единичного круга, является максимальной под-
подалгеброй алгебры непрерывных функций на окруж-
окружности; это утверждение может рассматриваться как
обобщение теоремы Вейерщтрасса, к-рая означает,
что замкнутая подалгебра алгебры С (Г), где Г=
= {z:|z[ = l}, содержащая А и функцию z, совпадает
с С (Г). Алгебра L+(R)= {/^i^R) : f(t)=O при г<0}
является замкнутой подалгеброй алгебры -Z>1(R); эта
подалгебра максимальна.
Пусть а — иррациональное число, Аа— алгебра,
состоящая из всех тех непрерывных функций на дву-
двумерном торе, коэффициенты Фурье к-рых стп=0 при
т+геа<0. Эта алгебра является максимальной под-
подалгеброй алгебры всех непрерывных функций тора.
Тор служит границей Шилова относительно А а, и Аа
есть алгебра Дирихле. Если тор реализовать в виде
остова единичного бицилиндра в С2, то пространство
максимальных идеалов А а идентифицируется с под-
подмножеством бицилиндра, к-рое описывается уравне-
уравнением |zi| = |z2|a. Точка @, 0) не принадлежит границе
Шилова, но является одноточечной долей Глисона (два
мультипликативных функционала ц>1 и ф2 на равно-
равномерной алгебре принадлежат, по определению, одной
и той же доле, если |!фх—ф2||<2). Алгебра Аа анали-
тична (в смысле свойства единственности: /=0, если
/E) = 0 для точек непустого открытого множества)
на пространстве максимальных идеалов, хотя вещест-
вещественная размерность пространства максимальных идеа-
идеалов равна 3. Алгебра непрерывных функций на
«-мерном торе, допускающих распространение внутрь
соответствующего полицилиндра, не является мак-
максимальной при л>1, но она максимальна в классе
подалгебр, инвариантных относительно голоморфных
автоморфизмов тора.
Лит. см. при статье Банахова алгебра. Е. А. Горин.
КОММУТАТИВНАЯ ГРУППА — то же, что абелева
группа.
КОММУТАТИВНАЯ ГРУППОВАЯ СХЕМА — груп-
групповая схема G над базисной схемой S, значение к-рой
на любой 5-схеме является абелевой группой. Приме-
Примерами К. г. с. служат абелева схемы и алгебраические
торы. Обобщением алгебраич. торов в рамках теории
групповых схем служит следующее понятие. Говорят,
что К. г. с. есть групповая схема мульти-
мультипликативного типа, если для любой точки
s 6 $ существует открытая окрестность U 3 s и абсолют-
абсолютно плоский квазикомпактный морфизм / : ?/—»-?/ такой,
чте К. г. с. G' = GX[/U' является диагонализируемой
над U'. При этом диагонализируемой
групповой схемой наз. групповая схема
DS (М) = Spec Fs (M)),
где М — абелева группа и 6s(M) — ее групповая ал-
алгебра с коэффициентами в структурном пучке 0s
схемы S. В случае, когда S есть спектр алгебраически
замкнутого поля, это понятие сводится к понятию диаго-
диагонализируемой группы. Если М = Z — аддитивная
группа целых чисел, то D$(M) совпадает с мультипли-
мультипликативной групповой схемой Gm< $.
Пусть G — групповая схема над S, слой к-рой над
точкой s?S является групповой схемой мультиплика-
мультипликативного типа над полем вычетов k(s). Тогда сущест-
существует окрестность U точки s такая, что Gx$U является
групповой схемой мультипликативного типа над U
(теорема жесткости Гротендика).
Строение К. г. с. изучено лишь в случае, когда ба-
базисная схема S есть спектр поля к, а К. г. с. G имеет
конечный тип над к. В этом случае К. г. с. содержит
максимальную инвариантную групповую аффинную
подсхему, фактор по к-рой является абелевым много-
многообразием. Любая аффинная К. г. с. G такого типа об-
обладает максимальной инвариантной групповой под-
подсхемой Gm мультипликативного типа, фактор по к-рой
является унипотентной группой. Если поле к совер-
совершенно, то Gd*GmxGn, где G" — максимальная унипо-
тентная подгруппа в G.
Лит.: [1J С е р р Ж.-II., Алгебраические группы и поля
классов, пер. с франц., М., 1968; [2J Grothendieck A.,
в кн.: Schemas en groupes, t. 2, В.— Hdlb.— N. Y., 1970, p.
1—179; [3] Demazure M., Gabriel P., Groupes al-
gebriques, P.— Amst., 1970; [4] О о rt F., Commutative group
schemes. В.— Hdlb.— N. Y., 1966. И. В. Долгачев.
КОММУТАТИВНОЕ КОЛЬЦО — кольцо, умножение
в к-ром удовлетворяет закону коммутативности. Тео-
Теория ассоциативно-коммутативных колец с единицей
наз. коммутативной алгеброй. Примером неассоциа-
неассоциативных К. к. могут служить йордаповы кольца (см.
Йорданоеа алгебра). О А Иванова.
КОММУТАТИВНОСТЬ, перестановоч-
перестановочно с т ь,— свойство алгебраической операции. Для сло-
сложения и умножения К. выражается формулами
а-\-Ь=Ь-{-а и ab=ba.
Произвольная бинарная операция * коммутативна
(или, что то же, для * выполняется закон ком-
коммутативности), если в данной алгебрапч. сис-
системе СПравеДЛИВО ТОЖДеСТВО X * у = у * X. Д. Ы. Смирнов.
КОММУТАТОР элементов аи 6 мульти-
операторной группы — элемент '
—а~ Ь+а+Ь.
Для групп без мультиоператоров (где операцию при-
принято наз. умножением) К. элементов а и Ъ будет эле-
элемент a~1b~1ab. Множество всевозможных К. в группе G
порождает подгруппу, наз. коммутантом группы G.
В ассоциативной алгебре произведением
Л и, или К. элементов аи Ь, наз. элемент [х, у] = ху—ух.
О. А. Иванова.
КОММУТАЦИОННЫХ И АНТИКОММУТАЦИОН-
АНТИКОММУТАЦИОННЫХ СООТНОШЕНИЙ ПРЕДСТАВЛЕНИЕ — линей-
линейное слабо непрерывное отображение /—+ар / ? L, нек-рого
предгильбертова пространства L в совокупность (во-
(вообще говоря, неограниченных) операторов, действую-
действующих в каком-либо гильбертовом пространстве Н,.
такое, что выполнены либо соотношения коммутации
aJaJ~a'fah = (f1, f^) E, afafi — afafl = Q, A>
либо соотношения антикоммутации
afflJ + a)ffi=(fi'1%)E, aflaf2 + ahafl = 0, B)
где а/, f?L,— оператор в Н, сопряженный оператору
а/, Е — единичный оператор в Н и (•, ¦) — скалярное
произведение в L.
В случае, когда пространство L конечномерно, вс&
неприводимые представления как соотношений A),
так и соотношений B) унитарно эквивалентны друг
другу. В случае бесконечномерного пространства су-
существует бесконечно много различных (не унитарно'
эквивалентных) неприводимых представлений соотно-
соотношений A) и B); для полного сепарабельного прост-
пространства L все они описаны [2] — [5].
Операторы а^ f?L, удовлетворяющие соотноше-
соотношениям A) и B), лежат в основе формализма так наз.
вторичного квантования (где а у наз. обычно опера-
оператором уничтожения частицы в состоянии
f?L, а оператор at—• оператором рожде-
рождения этой частицы), часто используемого при исследо-
исследовании квантовых физич. систем с большим числом сте-
степеней свободы. Однако во вторичном квантовании
используются в основном наиболее простые, так наз.
фоковские, К. и а. с. п., то есть неприводимые пред-
представления, у к-рых пространство индексов L — сепара-
бельное гильбертово пространство, а в пространстве
Н существует так наз. вакуумный вектор, обращаемый
всеми операторами a,, Y^f^L, в нуль.
Лит.: [1] Березян Ф. А., Метод вторичного кванто-
квантования, М., 1965; [2] Г е л ь ф а н д И. М., ВиленкинН. Я.,
Обобщенные функции, в. 4, М., 1961; [3] Г о л о д е ц В. Я.,
«Успехи матем. наук», 1969, т. 24, в. 4, с. 3—64; [4] G 4 г d i n g
L., Wightman A., «Proc. Nat. Acad. Sci. USA», 1954,.
v. 40, № 7, p. 617—26; [5] S e g a 1 I. E., «Trans. Amer. Math.
Soc», 1958, v. 88, JVs 1, p. 12 — 41. P. А. Минлос.
КОМПАКТ — метризуемое бикомпактное прост-
пространство. Примеры К.: отрезок, окружность, п-мерные
куб, шар, сфера, канторово множество, гильбертов
кирпич; re-мерное евклидово пространство не является
К., а подмножество такого пространства будет К. тогда
и только тогда, когда оно замкнуто и ограничено.
Замкнутое подмножество К. есть К., и всякий К. го-
меоморфен замкнутому подмножеству гильбертова кир-
кирпича (теорема У р ы с о н а). Для существования
гомеоморфизма К. в евклидово пространство необхо-
необходимо и достаточно, чтобы он был конечномерен (т е о-
рема Понтрягина — Небел и н г а). Не-
Непрерывный образ К., являющийся Г ^пространством,
есть К., и всякий К. есть непрерывный образ канто-
рова множества (теорема Александрова).
Произведение конечного или счетного множества К.
есть К. Любой К. сепарабелен; среди всех бикомпактов.
К. характеризуются тем, что обладают конечной или
счетной базой. К. характеризуется также тем, что он
вполне ограничен относительно какой-нибудь метрики,
совместимой его топологией (теорема Хаус-
до р ф а).
К.— один из важнейших классов топологич. прост-
пространств. Свойство метризуемого пространства быть К.
равносильно каждому из следующих свойств.
1) Из любого счетного открытого покрытия прост-
пространства X можно выделить конечное подпокрытие (ана-
(аналог леммы Гейне — Бореля — Лебега о покрытии от-
отрезка интервалами).
2) Любая счетная система таких замкнутых в X
непустых множеств F,-, что Fi + 1cFj, i=l, 2, ..., имеет
непустое пересечение (обобщение принципа вложенных
отрезков Кантора).
3) Из любой последовательности точек пространства
X можно выделить сходящуюся в X подпоследователь-
подпоследовательность (обобщенная теорема Больцано — Вейерштрасса).
4) Любое бесконечное подмножество пространства X
имеет в X хотя бы одну предельную точку (обобщенная
теорема Больцано — Вейерштрасса).
5) Любая непрерывная на X функция ограничена
(обобщенная теорема Вейерштрасса).
6) Любая непрерывная на X функция принимает
в нек-рой точке максимальное (минимальное) значение
(обобщенная теорема Вейерштрасса).
7) Любая непрерывная на X функция равномерно
непрерывна на X относительно какой-либо метрики,
совместимой с топологией пространства X (обобщенная
теорема Гейне — Кантора).
Лит.: [1] Александров П. С, Введение в общую
теорию множеств и функций, М.— Л., 1948; [2] Колмого-
Колмогоров А. Н., Фомин С. В., Элементы теории функций и
функционального анализа, 4 изд., М., 1976, гл.. 2.
Б. А. Пасынков.
КОМПАКТНАЯ ГРУППА — топологическая группа,
компактная как топологич. пространство. Напр., вся-
всякая конечная группа (в дискретной топологии) являет-
является К. г. Алгебраическая группа, хотя она и является
компактным топологич. пространством (относительно
топологии Зариского), не будет топологич. группой
относительно этой топологии и потому не будет К. г.
Два важнейших типа К. г. представляют следующие
группы. 1) Локально связные компакт-
компактные группы. Примерами таких К. г. являются
группа U(n, С) всех унитарных комплексных матриц
порядка п, группа О(п, R) всех ортогональных вещест-
вещественных матриц порядка п (с топологией, индуцирован-
индуцированной топологией полей С и R соответственно, определен-
определенной обычным абсолютным значением) и, более общо,
любая компактная вещественная группа Ли. 2) Впол-
Вполне несвязные компактные группы.
Такова группа GL(n, %p) невырожденных матриц по-
• рядка п с коэффициентами в кольце Zp целых р-
адпческих чисел (с топологией, индуцированной топо-
топологией кольца %р, определенной р-адическим нормиро-
нормированием) (см. Вполне несвязное пространство).
Любая вполне несвязная К. г. является проконеч-
ной группой, и обратно, всякая проконечная группа
будет вполне несвязной К. г. Вполне несвязные хаус-
дорфовы К. г. могут быть охарактеризованы как К. г.
нулевой топологич. размерности. Если же G локально
связна и конечномерна, то G — вещественная группа
Ли [1]. Структура К. г. общего вида до нек-рой сте-
степени определена структурой этих двух типов К. г. А
именно: в произвольной конечномерной К. г. G имеется
такой нульмерный нормальный делитель N (лежащий
в центре группы G), что G/N — вещественная группа
Ли и, более того, нек-рая окрестность единицы в G
является прямым произведением группы N и вещест-
вещественной Ли локальной группы. Всякая связная конеч-
конечномерная К. г. имеет вид (PxC)/Z, где Р — односвяз-
ная компактная полупростая вещественная группа Ли,
С—связная конечномерная коммутативная К. г.,
a Z — конечный центральный нормальный делитель, у
к-рого лишь единица лежит в С. Изучение строения
связных компактных вещественных групп Ли доведено
до их полной классификации (см. Ли компактная груп-
группа); строение коммутативных К. г. выясняется в тео-
теории двойственности Поитрягина. Любая К. г. (не
обязательно конечномерная) является проективным
пределом компактных вещественных групп Ли [2].
Топологич. строение указанных двух типов К. г. сле-
следующее: всякая локально связная конечномерная К. г.
является топологич. многообразием, а всякая беско-
бесконечная нульмерная К. г. со счетной базой гомеоморф-
на канторову совершенному множеству.
Изучение строения К. г. основано на том, что вся-
всякая К. г. G обладает достаточной систе-
системой конечномерных линейных пред-
представлений, т. е. для любого элемента g?G су-
существует такое непрерывное конечномерное линейное
представление р, для к-рого g^Kev p. Этот факт яв-
является одним из важных результатов далеко раз-
развитой общей теории линейных представлений К. г.
Эта теория существенно использует то, что каж-
каждая К. г. обладает двусторонне инвариантной мерой
\i{g), к-рая позволяет определить на G инвариантное
интегрирование. Важнейшие факты этой теории сос-
состоят в следующем. Всякое непрерывное представление
К. г. G в предгильбертовом пространстве эквивалентно
унитарному представлению. Пусть L2(G) — гильбер-
гильбертово пространство интегрируемых с квадратом по ин-
инвариантной мере \i(g) комплекснозначных функций на G.
Действие группы G на функции левыми и правыми
сдвигами определяет на L2(G) структуры левого и пра-
правого G-модулей. Соответствующие представления наз.
соответственно левым и правым регуляр-
регулярным представлением группы G; они унитарны и
унитарно эквивалентны. Пусть {Ra, cc?/} — се-
семейство всевозможных попарно неэквивалентных ко-
конечномерных неприводимых унитарных представлений
К. г. G и mfj(g), i,/=l, 2, . . ., rea = dim Ra—набор мат-
матричных элементов представления Ra в некотором орто-
нормированном базисе. Тогда функции mfj{g) лежат
в L2(G) и образуют там полную ортонормированную
систему, причем норма функции mfj(g) равна ге~1/2. Лю-
Любая непрерывная на G комплекснозначная функция может
быть с любой точностью равномерно аппроксимирована
конечными линейными комбинациями функций mfj(g)
(теорема Петера — Вей л я). Характеры не-
неприводимых унитарных конечномерных представлений
попарно ортогональны и имеют норму 1. Непрерывные
конечномерные унитарные представления эквивалентны
тогда и только тогда, когда их характеры равны. Не-
Непрерывное конечномерное унитарное представление
неприводимо тогда и только тогда, когда норма его
характера (который лежит в L2(G)) равна 1. Всякое
неприводимое непрерывное унитарное представление
группы G в гильбертовом пространстве конечномерно.
Всякое непрерывное унитарное представление группы
в гильбертовом пространстве является ортогональной
прямой суммой унитарных представлений, кратных
конечномерным неприводимым представлениям. В част-
частности, кратность вхождения представления Ra в пра-
правое регулярное представление равна rea=dim Ra; при
этом сумма всех G-подмодулей в G-модуле L2(G), изо-
изоморфных Ra, является в точности линейной оболочкой
всех функций mfj(g).
Лит.: [1] П о н т р я г и н Л. С, Непрерывные группы,
3 изд., М., 1973; [2] Вейль А., Интегрирование в тополо-
топологических группах и его применения, М., 1950; [3] Н а й м а р к
М. А., Теория представлений групп, М., 1976; [4] Ж е л о б е н-
к о Д. П., Компактные группы Ли и их представления, М.,
1970. В.Л.Попов.
КОМПАКТНОЕ МНОЖЕСТВО — подмножество М
топологич. пространства X такое, что каждая беско-
бесконечная последовательность {#,-, i?g} содержит под-
подпоследовательность, сходящуюся к нек-рой точке х0
пространства X. Если хо?М, то М наз. компакт-
компактным в себе множеством. Оно является
компактным пространством в индуцированной из X
топологии. Обратно, всякое К. м. метрич. пространства
является в такой топологии компактным пространством.
Множество, замыкание к-рого — К. м., наз. относи-
относительно компактным множеством.
М. И. Войцеховский.
КОМПАКТНОЕ ПРОСТРАНСТВО — топологич. про-
пространство, обладающее свойством компактности. Мет-
рцзуемое К. п. является компактом. Иногда под К. п.
понимается бикомпактное пространство, причем тре-
требуется его отделимость; пространство без этого условия
наз. кваз и компактным. Пространство, пред-
ставпмое в виде счетного объединения К. п., наз.
G-К О М П а К т Н Ы М. М. И. Войцеховский.
КОМПАКТНОЙ СХОДИМОСТИ ТОПОЛОГИЯ — од-
одна из топологий в пространстве непрерывных отобра-
отображений, по существу, то же, что и бикомпактно откры-
открытая топология, в определении к-рой бикомпактность
заменена свойством компактности (в том или ином
смысле). Для пространства отображений L(E, F) ло-
локально выпуклых пространств Е и F К. с. т.— одна из
сг - т о п о л о г и й, т.е. топологий равномерной сходи-
сходимости на множествах из семейства а ограниченных мно-
множеств в Е; она согласуется со структурой векторного
пространства L(E, F) и локально выпукла.
М. И. Войцеховский.
КОМПАКТНОСТИ ПРИНЦИП в теории функ-
функций комплексного переменного — усло-
условие компактности семейств аналитических функ-
функции. Бесконечное семейство CD={/(z)} голоморфных
функций в области D комплексной плоскости z называ-
называется компактным, если из любой последователь-
последовательности {/й(г)}сФ можно выделить подпоследователь-
подпоследовательность, сходящуюся к аналитической функции в D
или, что то же самое, равномерно сходящуюся вну-
внутри D, т. е. равномерно сходящуюся на любом ком-
компакте KaD. К. п. был дан П. Монтолем (P. Montel,
1927, см. [1]): для того чтобы семейство Ф было компакт-
компактным, необходимо и достаточно, чтобы оно было равно-
равномерно ограниченным внутри D, т. е. равномерно огра-
ограниченным на любом компакте KdD.
Пусть Нd — комплексное векторное пространство
голоморфных функций в области D пространства С",
п^1, с топологией равномерной сходимости на ком-
компактах KcD. К. п. можно сформулировать и в более
абстрактной форме: замкнутое множество ФсЯд
компактно в Но тогда и только тогда, когда оно огра-
ограничено в Н?>. Понятие компактных семейств аналитич.
функций тесно связано с нормальными семействами.
См. также Витали теорема.
Лит.: [1] М о н т е л ь П., Нормальные семейства аналити-
аналитических функций, пер. с франц., М.— Л., 1936; [2] М а л ь-
г р а н ж Б., Лекции по теории функций нескольких комплекс-
комплексных переменных, пер. с англ., М., 1969. Е. Д. Соломенцев.
КОМПАКТНОСТЬ — свойство топологич. простран-
пространства, состоящее в том, что каждое бесконечное его под-
подмножество имеет предельную точку. Для метрич.
пространства понятие К. совпадает с понятием би-
компактпости. Свойство К. может быть выражено
в такой форме: всякое счетное подмножество имеет
предельную точку, так что компактные пространства
естественно называть компактными для мощности ?J0.
В связи с этим возникают понятия инициальной и
финальной К. пли, более общо, компактности
в отрезке мощностей, [а, 6], или [а, 6]-
компактности, выражаемой в трех эквивалент-
эквивалентных формах: 1) всякое множество Мс! мощности
го?[а, 6] имеет точку полного накопления, т. е. такую
точку |, что для каждой ее окрестности Og множество
О| f| М имеет ту же мощность, что и М\ 2) всякая вполне
упорядоченная система порядкового типа а)?[о)а, а>ь]
замкнутых множеств имеет непустое пересечение;
3) всякое открытое покрытие мощности тс[а, Ь] со-
держит покрытие мощности <т. Если а=Цд, то X
наз. инициально компактным вплоть до
мощности Ъ. Просто К. означает инициальную К. до
мощности #0 и поэтому иногда К. наз. счетной
К. Если Ь^а — любое, то X наз. финально
компактным, начиная с мощности а; так, всякое
пространство со счетной базой финально компактно
с a—Zfj. Бикомпактные пространства инициально ком-
компактны до любой (бесконечной) мощности и одновре-
одновременно финально компактны, начиная с любой мощ-
мощности,— отсюда их название. Таким образом, всякое
бикомпактное пространство компактно, но не наобо-
наоборот: пространство W^atj) всех порядковых чисел О^
компактно, но не бикомпактно. Из К. пространства X,
вообще говоря, но следует, что X является компактным
множеством, напр, в пространстве (неметризуемом) Iе
существует замкнутое (и следовательно бикомпактное)
множество, не содержащее никакой нестационарной
сходящейся последовательности. м. И. Войцеховский
КОМПАКТНЫЙ ОПЕРАТОР — оператор А, опре-
определенный на множестве М топологич. векторного
пространства X, со значениями в топологич. векторном
пространстве Y такой, что всякое ограниченное подмно-
подмножество множества М он отображает в предкомпактное
множество пространства Y. Если, кроме того, опера-
оператор А непрерывен на М, то он наз. вполне не-
непрерывным на этом множестве. В случае, когда
X и Y банаховы или, более общо, борнологические
пространства, а оператор А : X—*-Y линеен, то поня-
понятия компактного и вполне непрерывного оператора
совпадают. Если А — компактный, а В — непрерыв-
непрерывный операторы, то АоВ и ВоА — К. о., так что мно-
множество К. о. есть двусторонний идеал в кольце веек
непрерывных операторов. В частности, К. о. не имеет
непрерывного обратного. Свойство компактности иг-
играет существенную роль в теории неподвижных точек
оператора и при изучении его спектра, к-рый в этом
случае обладает рядом «хороших» свойств.
Примерами К. о. являются интегральные опе-
операторы Фредгольма
Ах = [Ь К (t, s) x(s) ds,
Гаммерштейна
Ах=<\)Ьа K(t,s) g(s,x(s))ds,
и Урысона
\bK(t, s,x(s))ds
в нек-рых функциональных пространствах при соот-
соответствующих ограничениях на функции K(t, s), g(t, и)
и K(t, s, и).
Лит.: ШЛюстерник Л. А., Соболев В. И., Эле-
Элементы функционального анализа, 2 изд., М., 1965; [2] И о с и-
д а К., Функциональный анализ, пер. с англ., М., 1967; [3]
Р у ди н У., Функциональный анализ, пер. с англ., М., 1975;
[4] Красносельский М. А. и др., Интегральные опе-
операторы в пространствах суммируемых функций, М., 1966.
В. И. Соболев.
КОМПАКТНЫЙ ЭЛЕМЕНТ решетки — элемент
а решетки L, для которого условие
влечет
a^xjy ...\jxjk
для некоторого конечного подмножества {/,, . . ., //г}с/.
Т. С. Фофанова.
КОМПЛАНАРНЫЕ ВЕКТОРЫ — векторы, парал-
параллельные одной плоскости. Необходимым и достаточным
условием компланарности трех векторов
«1 = {¦*•!, Уъ zi}, аг = {х2, у2, z2}, а3={х3, у3, z3}
является равенство:
хх ух Zl
А
КОМПЛЕКС — частично упорядоченное рефлексив-
рефлексивным, правильным и транзитивным отношением <
множество К= {t} каких-либо элементов t, вместе с
целочисленной функцией dim t, называемой раз-
размерностью элемента t, [t '¦ t'], называе-
называемой коэффициентом инцидентности
элементов t и t', которые удовлетворяют условиям:
1) из t' <t следует, что dim t'<dim t; 2) [f. t']=[t': t\\
3) из [t : t']=?0 следует, что либо t'<t, либо t<t',
и |dim t—dim t'\ = i; 4) для любой пары элементов t, t",
из К, размерности к-рых отличаются на две единицы,
в К найдется не более, чем конечное число таких эле-
элементов t', что
[(:('][1':('];40е2,[(:1'] [t':t"]=O.
Заменой [t : t'] на a(t)a(t') [t : t'], где a(t) — функ-
функция со значениями —I, получается К., отождествляе-
отождествляемый с К; иначе говоря, инциденции [t : t'] задаются
с точностью до множителя a(t)a.(t'); переход от одного
значения к другому наз. переменой ориен-
ориентации К. К; элемент t сохраняет или меняет ориен-
ориентацию, смотря по тому, что a(t)= — i или, соответст-
соответственно, —1.
К. К наз. конечномерным, а именно —
re-мерным, если п есть максимальная размерность
симплексов из К; если же в К не существует сим-
симплекса максимальной размерности, то К наз. бес-
бесконечномерным. Звездой элемента t
К. К наз. множество всех таких элементов t' из К, что
t' >i. Замыканием элемента г из К наз.
множество всех таких элементов t' из К, что t' <i.
Границей элемента t из К наз. множество
всех таких элементов t' из К, что t' <t и t'=?t- Элемент
t' наз. гранью элемента (из К, если t' <?;
грань t' элемента t наз. истинной гранью,
если 1'ФХ. Элементы t и f из К наз. инцидент-
инцидентным и, если t' Kt или t<Zt'. К. К наз. конечным,
если множество его элементов конечно. К. наз. звезд-
звездно конечным, или замкнуто конеч-
конечным, если звезда (соответственно замыкание каждого
его элемента) состоит из конечного числа элементов.
К. на;;, локально конечным, если он яв-
является и звездно коночным, ц замкнуто конечным.
Подкомплексом К. К наз. любое подмно-
подмножество множества К, являющееся К. при тех же раз-
размерностях и коэффициентах инцидентности, что и в К.
Подкомплекс наз. замкнутым, если он содержит
замыкание каждого своего элемента, и открытым,
если он содержит звезду каждого своего элемента.
Дополнение замкнутого К. есть открытый К., и наобо-
наоборот. Звезда каждого элемента любого К. является
открытым подкомплексом, а замыкание и граница —
замкнутыми подкомплексами, r-мерным осто-
остовом Кг К. К наз. множество всех таких элементов
t из К, что dim t<.r\ он является замкнутым подком-
подкомплексом.
К. К= {t} и L наз. изоморфными, если су-
существует такое взаимно однозначное отображение /
множества К на множество L, что dim/(()=dim(
я lt:t']=lf(t):f(t')].
Важнейшим типом К. является симплициальный К.,
к-рый в свою очередь имеет две разновидности: абстрак-
абстрактный К. п геометрический К.
Абстрактный симплициальный
комплекс К имеет элементами абстрактные сим-
симплексы различных размерностей, r-мерный симплекс V
есть множество каких-либо г-j-l объектов а°, а1, . .., аг.
Эти объекты, т. е. О-мерные симплексы, наз. верши-
вершинами К. К. Симплекс ориентирован, если
множество его вершин упорядочено, причем порядки,
отличающиеся друг от друга четной перестановке,!:,
задают одну и ту же ориентацию, s - м е р н ы м и
гранями симплекса f наз. s-мерные симплексы.
вершины к-рых содержатся среди вершин f. Вместе
с данным симплексом симплициальный К. содержит
и все его грани. Порядок ts*Ctr означает, что ts есть
грань tr. Грани (а0, . .., as) и (а5 + 1, .. ., аг) наз. п р о-
тивоположными гранями симплекса f.
Если tr~1 есть грань tr, противоположная вершине а', то
смотря по тому, ориентирован ли f так же, как aitr~1,
или нет. Если f~x но есть грань tr, то
Ориентацией каждого симплекса симплициального К.
получается ориентированный К.
Абстрактный симшшциальный К. определен, если
известны множество его вершин и система, так на.ч.
схема, всех тех конечных подмножеств этого мно-
множества, к-рые приняты за симплексы; при этом тре-
требуется, чтобы каждая вершина принадлежала хотя бы
одному элементу системы и чтобы с каждым входящим
в систему элементом ей принадлежали л все подмно-
подмножества этого элемента. Размерность, ориентация и т. д.
определяются как и выше.
Полиэдральный (клеточный) ком-
комплекс re-мерного евклидова пространства Еп есть
счетный локально конечный К. К, элементами к-рого
являются r-мерные клетки f — ограниченные выпук-
выпуклые открытые подмножества нек-рого Ег из Е", 0<:г<:гс,
причем клетки попарно не пересекаются, объединение
клеток, принадлежащих замыканию элемента f, есть
топологич. замыкание tr множества f в Ег, и топологич.
замыкание объединения клеток, не принадлежащих
звезде элемента f, не пересекается с f¦ При этом
tr<ts означает, что либо tr=ts, либо f(^ts\ls, a
[ir~1 : f] определяется с помощью коэффициента ин-
инцидентности [El-1 : ЯЧ=—[Я^1 : Ег], где Е^1 и Е'-Г1—
те две области, на к-рые пространство Ег~х, содержа-
содержащее 1Г~Х, делит пространство Ег. Объединение клеток
полученного таким образом полиэдрального К. К с ин-
индуцированной из Е" топологией, наз. полиэдром
и обычно обозначается через \К\. Частным видом
полиэдрального К. является евклидов геометри-
геометрический симплициальный К., элементы
к-рого — евклидовы симплексы из Еп. г-мерный
евклидов симплекс f состоит из точек
х=(х1, . .., хп)^Е", заданных соотношениями
где я' = (<4, . . ., а1п), ?=0, . . ., г — независимые точки
из Еп (т. е. но содержащиеся ни в одном Ег~х из Е"),
0<Х'<1,
2^_0^'=1 (если г = 0, ж=а°),
а1 наз. вершинами tr, Я! — барицентри-
барицентрическими координатами точки х, a f —
геометрическим симплексом, порож-
порожденным абстрактным симплексом (а0, а1, . .., аг).
Пусть К — счетный локально конечный абстракт-
абстрактный симшшцпальный К., вершины к-рого принадле-
принадлежат Еп, причем если какие-либо вершины образуют
симплекс, то они независимы, если два симплекса из К
не имеют общей вершины, то порожденные ими геомет-
рич. симплексы не пересекаются, и замыкание объеди-
нения всех тех геометрич. симплексов, к-рые порож-
порождены симплексами из К и к-рые не принадлежат одному
какому-либо из этих порожденных симплексов, не пере-
пересекаются с последним. На множество порожденных
геометрич. симплексов переносятся из К понятия
размерности, порядка, инцидентности, и т. п., это
превращает указанное множество в полиэдральный К.,
наз. евклидовой реализацией К.
Геометрич. реализация, не обязательно евклидова,
возможна и для любого абстрактного симплициального
К. Пусть {а'} — совокупность вершин произвольного
абстрактного симплициального К. К, обозначенных ин-
индексами i из нек-рого вполне упорядоченного мно-
множества /, \К\ —множество всех таких систем {X,},
i?/, неотрицательных действительных чисел X/, что
вершины, соответствующие отличным от нуля коорди-
координатам Х,-о, . . ., А,; системы {Я,-}, образуют симплекс
(а'°, . . ., а г) из К (число таких координат конечно) и
^^.А,,-= 1. Симплексу ?г=(а'°, . .., а г) из К ставится
в соответствие множество \tr\ всех таких систем {А.,},
что А,,=^=0 тогда и только тогда, когда i есть один из
i0, ..., ir; тогда \К\ есть объединение множеств \f\-
Пусть \f\ гомеоморфно вложено в Er+1: точке {А-,}
из \tr\ соответствует точка {Х;в, . . ., Х{ } из Er + 1. Это
вносит топологию в \tr\ п в \К\: множество из \К\ счи-
считается открытым, если его пересечение с каждым
|/г| открыто в \f\. Полиэдр \К\ и наз. геометри-
геометрической р е а л и з а ц н е Й К. Л', а К — т р и-
а н г у л я ц и е й полиэдра \К\. К. К конечен
(соответственно локально конечен) тогда и только
тогда, когда \К\ является компактным (соответственно
локально компактным) пространством. Локальная ко-
конечность К. К является также необходимым и доста-
достаточным условием метризуемости | К\, причем метрика
задается формулой
Если К — счетный локально конечный n-мерный К.,
то он может быть реализован в Bге+1)-мерном евкли-
евклидовом пространстве Е2п + 1. К. К реализуем в гильберто-
гильбертовом пространстве, если \К\ можно гомеоморфно вло-
вложить в это пространство так, чтобы каждый замкнутый
симплекс из \К\ получал евклидову реализацию; это
возможно тогда и только тогда, когда К есть счетный
локально конечный симшшциальный К.
Конечный геометрический К. есть та-
такое множество открытых геометрич. симплексов, к-рое
вместе с нек-рым симплексом содержит и все его грани,
а пересечение различных симплексов пусто. При рас-
рассмотрении замкнутых симплексов второе условие за-
заменяется требованием, чтобы пересечение двух замкну-
замкнутых симплексов было пусто или являлось замкнутой
гранью обоих этих симплексов.
Понятие К. находит наибольшее применение в тео-
теории гомологии. Использование симплнциальных К.
при вычислении топодогпч. инвариантов полиэдров
осложняется тем, что при триангуляции полиэдра
может понадобиться слишком много симплексов. В этом
отношении преимущество принадлежит клеточному
разбиению, при к-ром количество клеток может быть
гораздо меньшим, чем количество симплексов при лю-
любом симплициальном разбиении этого полиэдра. С дру-
другой стороны, и симплициальные комплексы н триангу-
триангуляции имеют свои преимущества, напр, при симпли-
циальной аппроксимации непрерывного отображения,
при составлении и применении матриц инцидентности,
при использовании комплексов для гомологич. исследо-
исследования общих топологич. пространств и т. п.
Симплнциальным отображением К.
К в К. L наз. функция / : K-^t-L, ставящая в соответст-
соответствие каждой вершине а К. К нек-рую вершину f(a) К. L
так, что если накие-либо вершины а'0, ..., а г К. К
образуют в нем симплекс, то и вершины /(а'°), . ..,
f(a г), среди к-рых могут быть и совпадающие, должны
образовывать симплекс К. L. функция / каждому
симплексу tr К. К приводит в соответствие нек-рый
симплекс ts=f(tr) К. L. С и м п л и ц и а л ь н ы м
отображением /: (К, L)-+(K', L') пары
(К, L) в пару (К', L'), где L, L'— замкнутые подком-
подкомплексы комплексов К, К' соответственно, наз. такое
симплициальное отображение / : K^t-К', что f(L)dL'.
Множество всех симплициальных К. и всех их симпли-
циальных отображений также, как и множество всех
пар симплициальных К. и всех их симплициальных
отображений, образуют категории.
Гомологии К., выражавшиеся сначала числовыми
инвариантами, позднее стали представляться алгеб-
раич. средствами — группами, модулями, пучками и
т. п. Схема их построения такова. Пусть К — произ-
произвольный К., a G — абелева группа; г-мерпой
цепью (вообще говоря, бесконечной) К. К над
группой коэффициентов G наз. функция сг, областью
определения к-рой является множество всех г-мерных
элементов К. К, а множеством значений — группа G.
Совокупность {сг} всех r-мерных цепей сг К. К, обозна-
обозначаемая через Сr(K\ G) относительно операции сложения
образует группу, наз. группой r-мерных цепей
К. К над G. В предположении, что К — звездпо ко-
конечный К., в Cr(K; G) вводится граничный
оператор дг с помощью формулы
к-рый определяет гомоморфизм
ЭГ:СГ(К; G)^Cr-1{K; G).
В силу равенства дг_1дг=О получается цепной К.
{Сr{K; G), дг}, группа гомологии НГ(К\ G) к-рого,
т. е. факторгруппа группы Кег дг по подгруппе Im дг + 1,
наз. r-мерной группой гомологии К.
К над G (группа Кег дг часто обозначается через
Zr (К; G) и наз. группой r-мерных цик-
циклов К. К над G, а группа Im dr + 1 обозначается через
Br(K; G) и наз. группой r-мерных огра-
ограничивающих циклов К. К над G).
Наряду с группами гомологии для К. определяются
группы когомологии. При их определении исходной
является опять же группа цепей, называемая в этом
случае группой коцепей и обозначаемая через Cr(K; G).
К. К предполагается здесь замкнуто конечным, а к о-
граничный оператор б' задается формулой
определяющей гомоморфизм
br-.Cr(K; G) -^Cr+1(K; G).
Когомологическая группа IIr(K; G) этого коцепного>
комплекса {С(К\ G), бг}, бг + 1б''=О, т. е. факторгруппа
группы Кег бг по подгруппе Im Ьг~1, наз. г - м е р-
ной когомологической группой К.
К над G (группа Кег бг часто обозначается через
Zr(K; G) и наз. группой r-мерных коцик-
коциклов К. К над G, а группа 1тбг-1 обозначается через
В'(К; G) и наз. группой r-мерных коог-
раничивающих коциклов К. К над G).
Звездная (соответственно замкнутая) конечность К.
требуется для того, чтобы суммирование при опреде-
определении граничного (соответственно кограничного) опе-
оператора было конечным. В случае звездно конечного К.
определяются гомологии про-лзвольных (бесконочных)
циклов и когомологии конечных коциклов. В случае
замкнуто конечного К.— когомологпи бесконечных
коциклов и гомологии конечных циклов. В случае ло-
локально конечного К. определяются как конечные, так
(I бесконечные гомологии и когомологпи. Если К. произ-
произвольный, то его группы гомологии (соответственно кого-
когомологии) определяются как пределы прямого (соответст-
(соответственно обратного) спектра групп гомологии (соответст-
(соответственно когомологип) всех локально конечных подком-
подкомплексов данного К., упорядоченных по возрастанию.
При исследовании гомологии и когомологии К. рас-
рассматривается категория пар спмплициальных К. (К, L)
и их симплициальных отображенпй / : (К, L)-+-(K', L' \
и группы Cr(K, L; G) r-мерных конечных цепей К. К
по модулю L над G, являющаяся факторгруппой группы
СГ(К; G) r-мерных цепей К. К над G по подгруппе
Сr(L; G) r-мерных цепей К. L над G. Гомологическая
группа НГ(К, L; G) цепного комплекса {Сr(K; L; G), дг}
ваз. г-мерной относительной груп-
группой гомологии К. К по модулю L над группой
коэффициентов G.
Симплицнальное отображение / порождает гомомор-
гомоморфизм /х группы СГ(К\ G) в группу Сr(K'; G) по формуле
где cr?Cr(K\ G), а сумма распространяется на все
такие симплексы tR из К, к-рые отображаются на
данный симплекс i^v из К', причем знак -f" или —
берется в зависимости от того, совпадают или не сов-
совпадают ориентации t/с, и f(tk)- Гомоморфизм /х, рас-
распространенный на факторгруппы, порождает гомомор-
гомоморфизм группы Cr(K, L; G) в Сr(K', L', G); последний
гомоморфизм коммутирует с граничным оператором дг,
так что получается гомоморфизм относительных групп
гомологии
f,r:Hr(K,L;G)-+ffr(K', L'; G),
наз. гомоморфизмом, индуцирован-
индуцированным симплициальным отображени-
отображением/. Пара (Нr, f%r) является ковариантным функто-
функтором из категории пар симплициальных К. и симпли-
симплициальных отображений в категорию абелевых групп.
ф Ф
Отображения включения LdKc(K, L), где L и К —
пары (L, 0) и (К, 0), порождают точную последова-
последовательность
0-»Cf (L; G) -Д. Сг (К; G) -\ Сг (К, L; G) ->0.
Пусть zr — произвольный цикл К. К по модулю L
из любого элемента hr группы Нr(K, L; G); существует
такая цепь сг К. К, что г|з (cr) = zr (if — эпиморфизм),
цепь ty(drcr) — dr\p(cr)=drzr К. К лежит на L (т. е.
равняется нулю на симплексах из K\L) и принадле-
принадлежит Кег-ф; совпадающая с ней цепь — прообраз
tf-1(drzr) при мономорфизме ф — является циклом К. L,
Данному элементу hr ставится в соответствие класс
.•омологии /ir_] ^ flrr_](L; G) соответствующего цикла,
и получается гомоморфизм
д*г:Нг (К, L; G) -> Нг_г (L; G),
наз. связывающим гомоморфизмом.
Он согласован с функтором {Нп f^r), т. е. имеет место
равенство ^*r/*r=(/]i)*/-^*r. гДе 1\l — ограничение /
на L. Отображения вложения <р : LcK, -ф : Кс(К, L)
порождают точную последовательность групп
.. .«-!¦— IIг-1 {lA G) ^ Пг (К, L; G) ч-С
^_ Нг (К; G) bL Hr (L; G) !^-— >....
наз. гомологической последователь-
последовательностью пары (К, L).
Симплициальные отображения /, g : (К, L)^(K', L')
наз. смежными, если для каждого симплекса f
из К симплексы f(tr) и g(tr) являются гранями од-
одного и того же симплекса из К'. В категории пар сим-
плициальных К. и их симплициальных отображений
это отношение играет роль отношения гомотопности:
для любых смежных симплициальных отображений
/, g : {К, L)—,-(K', L') и для любого г индуцированные
гомоморфизмы f%r, g%r группы НГ(К, L; G) в группу
IIГ(К', L'; G) совпадают.
Вложение i : [Кг, Lj)c:(K, L) наз. отображе-
отображением вырезания, если Кх—Ly= К—L. С в о й-
ство вырезания состоит в том, что всякое
отображение вырезания симплициальных пар i для
любого г индуцирует изоморфизм i^.r : НГ(К^ Ьг; G)«
я*Нг(К, L; G). r-мерная группа гомологии любого К.
К, состоящего из одной точки над произвольной груп-
группой коэффициентов G, является нулевой группой для
всех гфО и изоморфна группе G при г=0.
Таким образом, тройка (Нг, /*,., д„,г) представляет
собой теорию гомологии в смысле Стинрода — Эйлен-
берга (см. Стинрода — Эйленберга аксиомы).
Аналогично строится теория когомологии. Группа
С(К, L; G) r-мерных бесконечных коцепей К. К по
модулю подкомплекса L над G является множеством
всех таких r-мерных коцепей сг К. К, к-рые равны
нулю на симплексах f подкомплекса L К. К, а
r-мерная относительная группа ко-
когомологии Hr(K, L; G) К. К по модулю L над
группой коэффициентов G есть когомологич. группа
коцепного комплекса {Cr(K, L; G), бл}.
Симшшциальное отображение / порождает гомомор-
гомоморфизм Z1 группы Cr(K'\ G) в группу С (К; G)
Гомоморфизм Z1 порождает также гомоморфизм группы
Cr(K', L'; G) в группу С (К, L; G); последний гомомор-
гомоморфизм коммутирует с кограничным оператором бг, и
получается гоморфизм f*r относительных групп кого-
когомологии
f*r-.Hr (К1, L'; G) -> Нг (К, L; G),
наз. гомоморфизмом, индуцированным
симплициальным отображением /.
Пара {Hr, f*r) является контравариантным функтором
из категории пар симплициальных К. и симплпциаль-
ных отображений в категорию абелевых групп.
Имеет место точная последовательность
О +— Cr (L; G) Л- С- (К; G) Л- С" (К, L, G) ^— О,
порожденная вложениями <р : LcK, г|) : Ка(К, L).
В классе когомологии hr ^Hr(L\ G) произвольный коцикл
zr?Zr(L; G) распространяется до коцепи z[?Cr(K; G)
произвольно, когда tr не принадлежит подкомплексу
L К. К. Кограница &rz[ получающейся коцепи равна
нулю на L и принадлежит группе Zr + 1(K, L; G). Класс
когомологии 6rhr^Hr + 1(K, L; G) этого коцикла при-
приводится в соответствие выбранному классу hr. Это
соответствие hr^-6rhr определяет гомоморфизм
6*r:Hr (L; G) -> ЦГ + 1 (К, L; G),
наз. связывающим гомоморфизмом.
Гомоморфизм б*г согласован с функтором {Hr, f*r},
т. е. имеет место равенство 6*r(f\L)*r=f*r?i*''.
Прямая последовательность групп
т*г б*г
^Hr + ^(K; G)>Я' +
G)
где ф : LcK и if : Kd(K, L) — отображения вложе-
вложения, является точной последовательностью и наз.
когомологической последователь-
последовательностью пары (К, L).
Для любых смежных симплициальных отображений
/, g : (К, L)—>-(K', L') и любого г индуцированные гомо-
гомоморфизмы f*r, g*r группы Hr(K', L', G) в группу
Hr(K, L; G) совпадают; всякое отображение вырезания
симшшциальных пар i : (Л^, LX)(^(K, L) индуцирует
изоморфизм i*r : Hr{K, L; G)^Hr(K1, Lx\ G). Для лю-
любого одноточечного К. К группы Hr(K\ G) = 0 для всех
;-^0, a II°(K; G)^G. Таким образом, тройка (Нг,
f*r) §*а) является теорией когомологии (в смысле
Стинрода — Эйленберга).
Лит.: [1] А л е к с а н д р о в П. С, Комбинаторная топо-
топология, М.— Л., 1947; [2] е г о же, Введение в гомологическую
теорию размерности и общую комбинаторную топологию, М.,
1975; [3] Лефшец С, Алгебраическая топология, пер. с
англ., М., 1948; [4] Хилтон П.-Д т., У а й л и С, Теория
гомологии. Введение в алгебраическую топологию, пер. с англ.,
1966; [5] П о н т р я г и н Л. С, Основы комбинаторной топо-
топологии, 2 изд., М., 197С. Д. О. Баладзе.
КОМПЛЕКС — одно из основных понятий гомологи-
гомологической алгебры. Пусть А — абелева категория. Граду-
Градуированным объектом наз. последовательность
К=(Кп) г™ объектов Кп из А. Последовательность
а=(ап) морфизмов ап : К.'п-*-Кп наз. м орфизм ом
а : К'—>К граду и рованых объектов. По-
Полагая K(h)n= Kn + h, можно определить объект К {К).
Морфизм градуированных объектов K'^K(h) наз.
морфизмом степени h из К' в К. Градуированный
объект наз. положительны м, если Кп=0 для
п<0, ограниченным снизу, если K(h) по-
положителен для нек-рого h, и конечным, если
Кп=0 для всех, кроме конечного множества, чисел п.
Цепной комплекс в категории А состоит из
градуированного объекта К и морфизма d : К-^К
степени — 1 такого, что сР = 0. Подробнее: d=(dn),
где dn : Кп-^-К„^1 и dtl-1dn=O для любого п. М о р-
физм цепных комплексов
(К', d') —у (К, d)
это морфизм а : K'^t-К градуированных объектов та-
такой, что ad' = da. Двойственным образом (как градуи-
градуированный объект с морфизмом d степени +1) опреде-
определяется коцепной комплекс.
Наиболее часто рассматриваются К. в категориях
абелевых групп, модулей, пучков абелевых групп на
топологич. пространстве. Так, К. абелевых групп
есть градуированная дифференциальная группа, диф-
дифференциал в к-роп имеет степень — 1 или -f-1.
С каждым цепным К. К связаны три градуированные
объекта:
В = В (К): Вп=1т (Кп+1 >- Кп)~границы;
Z = Z(K): Zn = Кег (Кп -^ Х„_ х) — циклы;
Н=Н{К) : Hn=Zn/Bn— re-мерные гомологии (см.
Гомологии комплекса).
Для коцепного К. аналогичные объекты наз. к о-
границами, коциклами и когомоло-
г и я м и.
Если Н{К) = 0, то говорят, что К. К — ацикли-
ацикличен.
Морфизм а : К'-+К комплексов индуцирует мор-
физмы
Z (К') —+ Z (К), В (К1) —»¦ В (К)
и, следовательно, морфизм гомологии или когомологий
Н(а):Н (К')—+Н (К).
Два морфизма a, b : К'—>~К паз. гомотопными
(что обозначается а^Ь), если существует такой мор-
морфизм s : К'—>-K(i) (или s : К'-+К( — 1) для коцепных
К.) градуированных объектов (называемый г о м о-
т о и и е и), что
а — b=ds-\-sd'
(откуда следует, что Н(а) — Н(Ь)). Комплекс К наз.
стягиваемым, если 1д-^*0 (в этом случае К. К
ацикличен).
Если О—>К'—>К—>К"—>-0 — точная последовательность
К., то существует связывающий морфизм
д : II(К")^Н(К) степени — 1 (+1), естественный от-
относительно морфизмов точных последовательностей я
такой, что ассоциированная с ним длинная го-
гомологическая последовательность
(т. е. последовательность
... — Нп (К') -* IIп (К) —* Н„ (К") Л
Л #„_!(*') — #„_!(*)— ...
для цепного К. и последовательность
. . . — Нп (К') —> Н„ (К) —* Нп (К") Л
>¦ Нп+1 (К ) >¦ IIп+\ (К) ¦—>¦ . ..
для коцепного К.) является точной.
Конус морфизма цепных комплек-
комплексов а : К'—^К есть К. МС(а), определенный следую-
следующим образом:
Разложение К. МК(а) в прямую сумму приводит
к точной последовательности К.
для к-рой ассоциированная длинная гомологич. после-
последовательность изоморфна последовательности
...-*Н„ (К) — Нп (МК (а)) — Нп_1 (А")
> Я„_! (К) —^ Нп.х (МК (а)) — ...
Следовательно, цепной К. МК(а) ацикличен тогда и
только тогда, когда Н (а) — изоморфизм. Аналогичные
понятия и факты имеют место для коцепных К.
Лит.: [1] Б а с с X., Алгебраическая К-теория, пер. с англ.,
М., 1973. А. В. Михалев.
КОМПЛЕКС прямых — множество К прямых
в трехмерном пространстве (проективном, аффинном,
евклидовом), зависящее от трех параметров. Прямая
1?К наз. лучом К. Через каждую точку М прост-
пространства проходит однопараметрическая совокупность
лучей К.— конус К м- К. определяет соответствие
между точками луча К. и плоскостями, проходящими
через этот луч: каждой точке М луча I соответствует
плоскость П, касательная к конусу А"д1 в точке М.
Такое соответствие наз. нормальной корре-
корреляцией. В каждой плоскости пространства рас-
располагается однопараметрическое семейство лучей К.,
огибающих плоскую кривую s. Инфлекц ионным
центром луча Z? К наз. точка М?1, в к-рой кри-
кривая s плоскости П, соответствующей точке М в нормаль-
ной корреляции, имеет возврат. На каждом луче К.
имеется в общем случае четыре инфлекционных центра.
Точкой прикосновения линейчатой по-
поверхности К. наз. такая точка М на ее образующей,
в к-рой касательная плоскость поверхности совпадает
с плоскостью П, соответствующей точке М в нормаль-
нормальной корреляции. На каждой образующей линейчатой
поверхности К. имеется в общем случае две и только
две точки прикосновения. Линии, описанные этими
точками, наз. линиями прикосновения
линейчатой поверхности. Главными поверх-
поверхностями К. наз. линейчатые поверхности, у к-рых
линии прикосновения суть их асимптотич. линии.
Проективную классификацию К. можно осуществлять
по кратности инфлекцнонных центров их лучей.
В евклидовом пространстве на каждом луче I опре-
определяется инвариантная точка С (центр луча),
в к-рой вектор нормали к плоскости П. соответствую-
соответствующей в нормальной корреляции точке С, ортогонален
нормали к плоскости П, соответствующей несобствен-
несобственной точке луча I. Примеры К.: специальный К.—
множество всех касательных к ¦ данной поверхности;
линейный К., задаваемый линейным однородным урав-
уравнением относительно грассмановых координат луча К.;
специальный линейный К.— множество прямых трех-
трехмерного пространства, пересекающих данную прямую.
Наряду с К. прямых рассматривают К. (трехпара-
метрич. семейства) плоскостей, коник, квадрик и дру-
других фигур (см. Фигур многообразие).
Лит.: [1] Ф и н и к о в С. П., Теория конгруэнции, М.— Л.,
1950; [2] К о в а н ц о в Н. И., Теория комплексов, К., 1963.
B.C. Малаховский.
КОМПЛЕКСИФИКАЦИЯ АЛГЕБРЫ ЛИ © над
R — комплексная алгебра Ли E'<р, являющаяся тен-
тензорным произведением алгебры © на поле комплексных
чисел С над полем действительных чисел R:
Таким образом, К. а. Ли (Я получается из © расшире-
расширением поля скаляров с R до С. Элементами алгебры ©^
можно считать пары (и, у), и, у?©; тогда операции в
<5V будут определяться формулами:
)(и, v) = (au—fiv, cci> + |5u) для любых a,
[(«1, ^i), («2, ^2)] =([«1. «2] — [. vd, [vi, ] + [«i, v2]).
Алгебра ©^ наз. также комплексной обо-
оболочкой алгебры Ли®.
Нек-рые важные свойства алгебр наследуются при
комплексификации: (й~ нильпотентна, разрешима или
полупроста тогда и только тогда, когда © обладает
этим свойством. Однако простота © не влечет, вообще
говоря, простоту ©?•
Понятие К. а. Ли тесно связано с понятием вещест-
вещественной формы комплексной алгебры Ли. Вещественная
подалгебра Ли f в комплексной алгебре Ли 1) наз.
вещественной формой алгебры Л и [),
если всякий элемент х?1) однозначно представим в
виде x=u-\-iv, где и, у?[. К. а. Ли f естественно изо-
изоморфна алгебре I). Не всякая комплексная алгебра Ли
имеет вещественную форму. С другой стороны, за-
заданная комплексная алгебра Ли, вообще, может иметь
несколько неизоморфных вещественных форм. Так, ал-
алгебра Ли всех вещественных матриц порядка п и ал-
алгебра Ли всех антиэрмитовых матриц порядка п яв-
являются неизоморфными вещественными формами ал-
алгебры Ли всех комплексных матриц порядка п (у к-рой
имеются и другие вещественные формы).
Лит.: [1] Н а й м а р к М. А., Теория представлений групп,
М., 1976; [2] Ж е л о б е н к о Д. П., Компактные группы Ли
и их представления, М., 1970; [3]Гантмахер Ф., «Матем.
сб.», 1939, т. 5, в. 2, с. 217—50. В. Л. Попав.
КОМПЛЕКСИФИКАЦИЯ ВЕКТОРНОГО ПРОСТ-
ПРОСТРАНСТВА — комплексное векторное пространство У ,
полученное из вещественного векторного пространства
V путем расширения поля скаляров. Пространство V
определяется как тензорное произведение Т(укС.
Его можно определить также как множество формаль-
яых выражений x-\-iy, где х, y?V, с естественно за-
заданными операциями сложения и умножения на ком-
С
плексные числа. Пространство V вкладывается в V
в качестве вещественного подпространства и наз.
р
вещественной формой пространства V .
Всякий базис пространства V будет базисом простран-
р р
ства V (над С). В частности, dim^F =dimR V.
С
Операция Fi—>V является функтором из категории
векторных пространств над R в категорию векторных
пространств над С. А.л.Онищик.
КОМПЛЕКСИФИКАЦИЯ ГРУППЫ ЛИ G над
R — комплексная группа Ли Gp, содержащая G
в качестве вещественной подгруппы Ли и такая, что ал-
алгебра Ли © группы G является вещественной формой
алгебры Ли (ftp группы Gp (см. Комплексификация ал-
алгебры Ли). Группа G при этом наз. вещественной
формой группы Ли Gp. Напр., группа U(п)
всех унитарных матриц порядка п является вещест-
вещественной формой группы GL (п, С) всех невырожденных
матриц порядка п с комплексными элементами.
Имеется взаимно однозначное соответствие между
комплексно аналитическими линейными представления-
представлениями связной односвязной комплексной группы Ли Gp и
вещественно аналитич. представлениями ее связной ве-
вещественной формы G, при к-ром неприводимым пред-
представлениям соответствуют неприводимые. Это соответ-
соответствие устанавливается следующим образом: если р —
(неприводимое) конечномерное комплексно аналитиче-
аналитическое представление группы Gp, то ограничение р на
G является (неприводимым) вещественно аналитич.
представлением группы G.
Не всякая вещественная группа Ли обладает ком-
плекснфикацией. В частности, связная полупростая
группа Ли G обладает комплексификацией тогда и
только тогда, когда G линейна, т. е. изоморфна под-
подгруппе некоторой группы GL(n, С). Например, уни-
универсальная накрывающая группы вещественных ма-
матриц второго порядка с определителем 1 не имеет
комплексификации. Однако всякая компактная группа
Ли комплексификацией обладает.
Отсутствие комплексификации у нек-рых вещест-
вещественных групп Ли инспирировало введение более об-
общего понятия — универсальной комплек-
комплексификации (G, т) вещественной группы Ли G.
Здесь G — комплексная группа Ли, т : G^-G — ве-
вещественно аналитич. гомоморфизм такой, что для лю-
любой комплексной группы Ли Н и любого вещественно
аналитич. гомоморфизма а : G—>-// существует единст-
единственный комплексно аналитич. гомоморфизм Р : G—>~H,
для к-рого а=Рот. Универсальная К. г. Ли всегда су-
существует и определена однозначно [3]. Однознач-
Однозначность означает, что если (G', %') — другая универсаль-
универсальная К. г. Ли G, то существует единственный изомор-
изоморфизм X : G—>-G', для к-рого Хот=т'. В общем случав
dim^G^dim G, если же G односвязна, то dim^G=
= dim G и ядро гомоморфизма т дискретно.
См. также Форма группы Ли.
Лит.: [1]Наймарк М. А., Теория представлений групп,
М., 1976; [2] Ж е л о б е н к о Д. П., Компактные группы Ли
и их представления, М., 1970; [3] Б у р б а к и Н., Группы и
алгебры Ли. Алгебры Ли, свободные алгебры Ли и группы
Ли, пер. с франц., М., 1976. В. Л. Попов.
КОМПЛЕКСНАЯ СТРУКТУРА — 1) К. с. и а
действительном векторном прост-
пространстве V — структура комплексного векторного
пространства на V, согласованная с исходной структу-
структурой. К. с. на V полностью определяется заданием опе-
оператора умножения на число г, роль к-poro может играть
произвольное линейное преобразование / : F—э-F, удов-
удовлетворяющее условию /-=—Е. Поэтому преобразова-
преобразование такого типа часто наз. К. с. на V. Если V снаб-
снабжено К. с. и ъ\, ..., у„—базис этого пространства
над С, то v1, . .., vn, Ivu ..., Ivn образуют его базис
над R, так что dim V=2 diin^F. Если / — К. с. на V,
то комплексифпкация V пространства V распадается
С
в прямую сумму V = F++F_, где VM — собственные
подпространства преобразования /, продолженного
на V , отвечающие собственным значениям =ti, при-
причем F_ = F + . Обратно, всякое комплексное подпрост-
ранство ScV такое, что V =S-\-S, определяет
на V К. с, для к-рой V+ = S.
Любые две К. с. на 2л-мерном действительном прост-
пространстве V переводятся друг в друга нек-рым автомор-
автоморфизмом пространства V. Множество всех К. с. на V
является, таким образом, однородным пространством
группы GLBn, R) и отождествляется с факторпрост-
ранством GLBn, R)/H, где H=GL(n, С) — подгруппа,
состоящая из невырожденных матриц вида _д
2) К. с.— структура комплексного аналитического
многообразия. Если М — дифференцируемое многооб-
многообразие, то К. с. на М — это комплексный аналитич.
атлас на М, согласованный с заданным на М действи-
действительным дифференцируемым атласом. При этом dim M=
Ы.
=2 dixn^M. К. с. на М индуцирует К. с. на каждом
касательном пространстве ТХ(М) и тем самым индуци-
индуцирует на М почти комплексную структуру, к-рая ее
полностью определяет.
Лит.: ШЛихнерович А., Теория связностей в целом
и группы голономий, пер. с франц., М., i960; [2] у э л л с Р.,
Дифференциальное исчисление на комплексных многообразиях,
пер. с англ., М 1976. А. Л. Онищип.
КОМПЛЕКСНОГО ИНТЕГРИРОВАНИЯ МЕТОД,
контурного интегрирования мето д,—
один из наиболее универсальных методов исследова-
исследования и приложений дзета-функций, L-функций, вооб-
вообще, функций, определяемых рядами Дирихле.
К. и. м. в теорию чисел впервые ввел Б. Риман
(В. Riemann) [1] в 1876 в связи с изучением свойств
дзета-функции. Известные в настоящее время приме-
применения К. и. м., опирающиеся на теорему Котпи о вы-
вычетах, теорему Фрагмена — Линделёфа для рядов
Дирихле, метод перевала и т. п., весьма разнообразны
по своей форме и содержанию. К. и. м. используется
для аналитич. продолжения и вывода функциональных
уравнений функций Дирихле; для вывода приближен-
приближенных функциональных уравнений этих функций; для оце-
оценок числа их нетривиальных нулей и оценок плотно-
плотности распределения таких нулей в той или иной части
критической полосы; для получения асимптотич. формул
и разного рода оценок важнейших арифметич. функций.
Классический вариант К. и. м. иллюстрируется
нижеследующим примером аналитич. продолжения и
вывода функционального уравнения дзета-функции Ри-
мана (см. [2], [3]). При s=a+it, a>0, ге>0
га-*Г (s)= п.-* [Ж е-х xs-^dx= f Ж е-"*х s~1 dx.
После суммирования получается, что функция t,(s),
первоначально определенная рядом ? (s) = 'S\ , n-*,
при сг>1, представляется также формулой
Пусть рассматривается интеграл
взятый вдоль (бесконечного) контура С=а-{-$-\-у, где
а, у проходят по нижнему и верхнему краям разреза
вдоль отрицательной действительной оси плоскости z,
обходя начало координат по окружности C радиуса
г<2л. Интеграл J (s) сходится при всех s и притом
равномерно в любом круге |s|<A, ибо на а и у подин-
тегральная функция меньше g-o.sizi для всех |ж|>
>zo(A). По теореме Коши он не зависит от г и, значит,
представляет целую функцию s. Полагая, что на а, C, у
соответственно г=6е-'я, z=re'9, г=бе'я и/(z)=l/(ez—1),
легко расписать J (s) в виде интегралов по действитель-
действительным переменным:
В круге |г|<л будет |г/(г)|<Л. Поэтому второе слагае-
слагаемое правой части этого равенства меньше, чем
2nAra-1eJrtt\, что для любого фиксированного s с сг>1
стремится к нулю при г—>0. Следовательно, в силу
формулы A), л J (s)= sin ksT (s)?(s) и
IJ() = A— s)J(s). B)
ъ v ' sin jisF (s)
Эта формула, доказанная в предположении 0>1, дает
продолжение функции ? (s) на всю плоскость. Из нее
видно, что ^ (s) является однозначной аналитич. функ-
функцией во всей плоскости s, имеющей единственной осо-
особенностью простой полюс в точке *= 1 с вычетом \.
Для вывода функционального уравнения ? (s) пред-
предполагается, что сг<0, N — целое >4. Пусть
где С (N) — контур, отличающийся от прежнего кон-
контура замыканием а, у дугой окружности радиуса
Д = 2Лг+1 с центром в начале координат. Интеграл
по внешней дуге контура С (N) оценивается в виде
АЯаел1", что при сг<0 стремится к нулю при TV—>-°о.
Отсюда, Jx(s)—>-J (s) при JV->-oo. С другой стороны по
теореме о вычетах
= 2 (гя)^-1 sin -212^n_ l п*-1.
Поэтому при сг<0
/(s) = lim/A,(s)=2Bn)^-1sin^-C(l — s).
Это равенство в соединении с формулой B) дает соот-
соотношение:
I (I -s) =2 Bл)-* cos -f. Г (s) ? (s),
к-рое по теории аналитич. продолжения имеет место
уже во всей плоскости s и наз. функциональ-
функциональным уравнением дзета-функции Ри-
Рима н а.
К. и. м. играет большую роль в получении прибли-
приближенных функциональных уравнений, к-рые лежат в ос-
основе современных оценок функций Дирихле (см. [4],
[5]).
К. и. м. является основным в исследованиях распре-
распределения нулей функций ?(s), L(s, y_) и др. До недавнего
времени здесь он применялся в форме известных тео-
теоремы Литлвуда о числе нулей в прямоугольнике регу-
регулярной при 0>О функции F(s) и теоремы Баклуыда об
arg F(s), а также теорем о выпуклости средних значе-
значений аналитич. функций (см. [2]). В 1969 X. Монтгомери
(G. Montgomeric) [6] нашел новый прямой и более
сильный путь использования К. и. м. для этих целей.
К. и. м. в приложениях к теории чисел естественно
лозникает в связи с формулой суммирования коэффи-
коэффициентов рядов Дирихле (см. [2], [7]).
Лит.: [1] Риман Б., Сочинения, пер. с нем., М.— Л.,
1948; [2]Титчмарш Е. К., Теория дзета-функции Римана,
пер. с англ., М., 1953; [3] П р а х а р К., Распределение про-
простых чисел, пер. с нем., М., 1967; 14] Л а в р и к А. Ф., «Изв.
АН СССР. Сер. матем.», 1967, т. 31, X, 2, с. 431—42; [о] его
я; е, «Изв. АН СССР. Сер. матем.», 1968, т. 32, Л6 1, с. 134—185;
[fi] Монтгомери X., Мультипликативная теория чисел,
пер. с англ., М., 1974; [7] К а р а ц у 6 а А. А., «Изв. АН СССР.
Сер. матем.», 1972, т. 36, Ли 3, о. 475 83. А. Ф. Лаерик.
КОМПЛЕКСНОЕ МНОГООБРАЗИЕ, комплек-
комплексное аналитическое многообра-
з и е,— аналитическое многообразие над полем ком-
комплексных чисел.
КОМПЛЕКСНОЕ ПРОСТРАНСТВО, комплек-
комплексное аналитическое пространст-
пространство,— аналитическое пространство над полем комплекс-
комплексных чисел. Наиболее простым и употребительным К. п.
является числовое комплексное пространство С",
точками, или элементами, к-рого являются всевозмож-
всевозможные п-строки z=(z1, . . ., г„), z' = (zi, . . ., z'n), ..., сос-
составленные из произвольных комплексных чисел zv=
=iv+ijv, zv=^v+ij/v, v=l, 2, . . ., га. К. п. С" есть
векторное пространство над полем комплексных чи-
чисел С с операциями сложения
и умножения на число
hz = (kzi, .. ., Xzn),
а также метрическое пространство с евклидовой мет-
метрикой
Иначе говоря, К. п. С" получается в результате ком-
плексификации числового действительного прост-
пространства R2". К. п. С" есть топологич. произведение п
комплексных плоскостей С1 = С, С"=СХ...ХС.
Лит.: [1] Ш а б а т Б. В., Введение в комплексный анализ,
2 изд., М., 1976; [2] Бур баки Н., Общая топология. То-
Топологические группы. Числа и связанные с ними группы и про-
пространства, пер. с франц., М., 1969. Е. Д. Соломенцев.
КОМПЛЕКСНОЕ ЧИСЛО — число вида j^x+iy,
где х и у — действительные числа, а г= У—1 — так
наз. мнимая единиц а, т. е. число, квадрат
к-рого равен —1 (в технической литературе приме-
применяется также обозначение /= У—1); х наз. д е й с т в и-
т е л ь н о и, пли вещественной, частью К. ч.
z, а у — его мнимой частью (обозначения
x=Re z, !/ = Im z). Действительные числа — частный
случай К. ч. при у-=0; К. ч.. не являющиеся действи-
действительными, т. е. такие, что уфО, иногда наз. мнимыми
числами. В приведенных терминах, в основном
традиционного происхождения, нашел свое отражение
сложный исторический процесс развития понятия К. ч.
Алгебраическая природа К. ч. состоит в том, что
К. ч. есть элемент (алгебраического) расширения С поля
действительных чисел R, получаемого алгебраич.
присоединением к полю R корня i многочлена Х2-\-1.
Получающееся таким путем поле С наз. полем
комплексных чисел. Наиболее важное свой-
свойство поля С состоит в том, что опо алгебраически зам-
замкнуто, т. о. любой многочлен с коэффициентами из С
разлагается на линейные множители. Иначе это свой-
свойство алгебрапч. замкнутости выражается в том, что
любой многочлен степени ге^г! с коэффициентами из С
имеет в С по крайней мере один корень (теорема
Д'А ламбера — Гаусса).
Фактическое построение поля С осуществляется
следующим обраяом. В качестве элементов z-=(x, у),
z' = (x', у'), . . ., или комплексных чисел,
принимаются точки (х, у), (х', у'), . . ., плоскости R?
с декартовыми прямоугольными координатами х и у,
х' ну', . . ., причем суммой К. ч. z=(x, у) и z' =
= (х', у') наз. К. ч. (х-\-х', у~гУ'), т. е.
z+z' = (x, y)-\-{x', у')={х-'гх', у+у'), A)
а произведением этих К. ч. наз. К. ч.
(хх'—уу1, ху'+х'у), т.е.
zz' = (x, y)(x', у') = (хх'-уу', ху'+х'у). B)
Нулевой элемент 0=@, 0) совпадает с началом коорди-
координат, К. ч. A, 0) есть единица поля С.
Плоскость R2, точки к-рой отождествлены с элемен-
элементами поля С, наз. комплексной плоско-
плоскостью. Действительные числа х, а-', ... отождествля-
отождествляются при этом с точками (ж, 0), (х', 0), ... оси абсцисс,
к-рая применительно к плоскости С наз. д е й с т в и-
тельной, или вещественной, осью.
Точки @, y)^=iy, @, y')=iy', . . . располагаются на оси
ординат, называемой на комплексной плоскости С
м н и м о и ось ю; числа вида iy, iy', ... наз. чисто
мнимыми. Это представление элементов z, z', ...
поля С, или К. ч., в виде точек комплексной плоскости
с правилами действий A) и B) равносильно указанной
выше наиболее употребительной форме записи К. ч.:
z=(x, y) = x-\-iy, z'--={x', y') = x'-\-iy', . . .,
называемой также алгебраической, или д е-
картовой, формой записи К. ч. Применительно
к алгебраич. форме правила A) и B) сводятся к прос-
простому условию, что все действия с К. ч. выполняются
как с многочленами с учетом свойства мнимой еди-
единицы: i-j=j2=—1.
К. ч. z=(x, y)—x-{-iy и z=(x, —у) = х—iy наз. сопря-
сопряженными, на плоскости С онп располагаются
симметрично относительно действительной оси. Сумма
и произведение сопряженных К. ч. суть действитель-
действительные числа:
z+~z=2 Re z, zz=|z|2,
где \z\ = г = y~x2JrУ2 наз- модулем, или абсо-
абсолютной в е л ц ч п н о и, К. ч. z.
Всегда
К. ч. z отлично от 0 тогда и только тогда, когда |z|>0.
Отображение z-+z есть автоморфизм комплексной пло-
плоскости порядка 2 (т. е. z—>-z=z), оставляющий на месте
все точки действительной оси. При этом z-\-z' = z-\-z',
Операции сложения и умножения A) н B) коммута-
коммутативны и ассоциативны, связаны соотношением дистри-
дистрибутивности и для них существуют обратные действия
вычитания и деления (кроме деления на
нуль), записываемые в алгебрапч. форме следующим
образом:
z — z' = (x-\- ly) — (x' + iy') = (х — х<) -<r i {у— у'),
z' х'+ it/ z'z хх' + уу' , . ух' — ху' , ^ C)
"V" x + iy \z |2"~ х2 + у2" ^ 1 х2 + уг ' z ^ '
Деление К. ч. z' на К. ч. z=^=0 сводится, таким образом,
к умножению z' на К. ч.
z х у
На важный вопрос о том, является ли построенное
расширение С поля действительных чисел с указан-
указанными выше правилами действий единственно возмож-
возможным пли же мыслимы существенно иные варианты,
дает ответ теорема единственности: вся-
всякое (алгебраическое) расширение поля R, получаю-
получающееся из R присоединением корня i уравнения Х2^1=
= 0, изоморфно С, т. е. с требованием алгебранч. при-
присоединения корня i совместимы только указанные выше
правила действий с К. ч. Этому факту, однако, не про-
противоречит наличие других интерпретаций К. ч., от-
отличных от истолкования К. ч. как точек комплексной
плоскости. Наиболее часто в приложениях исполь-
используются следующие две интерпретации.
Векторная интерпретация. К. ч. z=
= x-\-iy можно отождествить с вектором (х, у) с коорди-
координатами х и у, приложенным в начале координат (см.
рис.). При такой интерпретации сложение и вычитание
К. ч. производится по правилам сложения и вычита-
вычитания векторов. Однако умножение и деление К. ч., со-
совершаемые необходимо по формулам B) и C), не имеют
непосредственных аналогов в векторной алгебре (см.
[4], [5]). Векторная интерпретация К. ч. непосредственно
применяется, напр., в электротехнике для изображения
переменных синусоидальных токов и напряжений.
Матричная интерпретация. К. ч. w=
= M-f-jy можно отождествить с матрицей второго по-
порядка специального вида
и v
V U
причем действия сложения, вычитания и умножения
выполняются по обычным правилам матричной ал-
алгебры.
Применяя полярные координаты на комплексной
плоскости С, т. е.
радиус-вектор
ный
мый
К. ч.
z\ и поляр-
угол cp=Arg z, называе-
здесь аргументом
z (иногда также ф а-
-У-
-iZ = X-iy
з о и, или амплитудой,
К. ч. z), получают триго-
тригонометрическую, пли
полярную, форму К. ч.:
z=r(cos ф-j-i sin ф),
гсозф=Нег, г sin ф=1т
Аргумент ф=Arg z являет-
является многозначной депствитель-
z=^0, значения к-рой для дан-
от другого на целое кратное
' '
ной функцией К. ч.
ного z отличаются одно ру ц р
2я; аргумент К. ч. z=0 не определен. Обычно исполь-
используется главное значение аргумента
Ф=а^ z, определяемое дополнительным условием
—ji<arg г<гя. Эйлера формулы e±l(p=cos ф±1 sin ф
преобразуют тригонометрич. форму D) в показа-
показательную форму К. ч.:
z = гес4>. E)
Формы D) и E) особенно удобны для выполнения умно-
умножения и деления К. ч.:
zz' = rr'[cos (ф-f ф')-{-i sin
= rr'e'
-j- = ^r [сов(ф' —
' — ф)]=-^- е1 «Р-Ч>'\ г>0.
При умножении (делении) К. ч. модули перемножаются
(модуль делимого делится на модуль делителя), а ар-
гументы складываются (из аргумента делимого вычи-
вычитается аргумент делителя). Возведение в степень К. ч.
и извлечение корня из К. ч. производятся по так наз.
формулам Муавра:
,п = rn (cos ге ф-f i sin re ф) = гпе1пц>,
л/ z — -г/ г [ cos 1 - ism — ) =
_ . <p + 2kn
= у/ге'—^—, к = 0, 1, ..., га-1,
причем первая из них применима н для целых отрица-
отрицательных показателей п. Геометрически умножение
К. ч. z на К. ч. z' — r'e'w сводится к повороту вектора z
на угол ф' (против часовой стрелки при ср' >0) и после-
последующему изменению его длины в lz'| = r' раз; в част-
частности, умножение на К. ч. z'-~el<v\ по модулю равное-
единице, есть не что иное как поворот на угол ф'.
Таким образом, К. ч. могут быть истолкованы и как
операторы специального вида (аффиноры). В связи
с этим иногда удобна смешанная векторно-матричная.
интерпретация умножения К. ч.:
(х> УУ _ " ^1 =--(xu~yv, xv + yu),
при к-poii множимое трактуется как матрица-векторг
а множитель — как матрица-оператор.
Биективное отображение (х, y)-+x-{-iy переносит
в поле К. ч. С топологию двумерного действительного
числового пространства R2, эта топология согласуется
со структурой поля С и, таким образом, С есть тополо-
топологическое тело. Модуль \z\ есть евклидова норма К. ч.
z = (x, у), и поле С, наделенное этой нормой, есть ком-
комплексное одномерное евклидово пространство, называе-
называемое также плоскостью комплексного-
переменного С. Топологии, произведение С" =
= Сх...хС (п раз, rLSsi) есть комплексное /г-мерное
евклидово пространство. Вследствие алгебраич. замк-
замкнутости поля К. ч. С, изучение функций и математич.
анализ вообще приобретают должную полноту и закон-
законченность только при рассмотрении поведения функции
в комплексной области. В частности, даже поведение
таких элементарных функций, как z", cos z, sin z, ez,
может быть правильно понято только при условии их
рассмотрения как функций комплексного переменного-
(см. Аналитическая функция).
Впервые, по-видимому, мнимые величины появились.
в известном труде «Великое искусство, или об алгебраи-
алгебраических правилах» Дж. Кардано (G. Cardano, 1545),
к-рый счел их бесполезными, непригодными к употребле-
употреблению. Пользу мнимых величин, в частности при решении
кубического уравнения в так наз. неприводимом случае-
(когда действительные корни выражаются через куби-
кубические корни из мнимых величин) впервые оценил
Р. Бо.мбелли (R. Bombelli, 1572). Он же дал нек-рыс
простейшие правила действий с К. ч. Вообще, выраже-
выражения вида а-\-ЬУ~—1, ЪфО, появляющиеся при решении
квадратных и кубических уравнений, стали называть,
в 16—17 вв. «мнимыми». Однако даже для многих
крупных ученых 17 в. алгебраич. и геометрич. сущ-
сущность мнимых величин представлялась неясной и
даже загадочной и мистической. Известно, напр., что-
И. Ньютон (I. Newton) не включал мнимые величины
в понятие числа, а Г. Лейбницу (G. Leibniz) принад-
принадлежит фраза: «Мнимые числа — это прекрасное и
чудесное убежище божественного духа, почти что-
амфибия бытия с небытием».
Задача о выражении корней степени п из данного
числа была в основном решена в работах А. Муавра
(A. de Moivre, 1707, 1724) и Р. Котеса (R. Cotes, 1722).
Символ ?= У—1 предложил Л. Эйлер (L. Euler,
1777, опубл. 1794). Он же высказал в 1751 мысль о&
алгебраич. замкнутости поля С, к такому же выводу
пришел Ж. Д'Аламбер (J. D'Alembert, 1747), но пер-
первое строгое доказательство этого факта принадлежит
К. Гауссу (С. Gauss, 1799). Он же ввел в употребление
термин «К. ч.» в 1831. Полное геометрнч. истолкова-
истолкование К. ч. и действий над ними появилось впервые в ра-
работе К. Весселя (С. Wessel, 1799). Геометрия, представ-
представление К. ч., иногда называемое «диаграммой Аргаиа»,
вошло в обиход после опубликования в 1806 и 1814
работы Ж. Р. Аргана (J. R. Argand), повторявшей
в основном независимо выводы К. Весселя.
Чисто арифметич. теория К. ч. как пар действитель-
действительных чисел была построена У. Гамильтоном (W. Hamil-
Hamilton, 1837). Ему же принадлежит важное пространст-
пространственное обобщение К. ч.— кватернионы, алгебра к-рых
некоммутативна. Вообще, в конце 19 в. было доказано,
что всякое расширение понятия числа за пределы по-
поля К. ч. возможно только при отказе от каких-либо
обычных действий (прежде всего коммутативности).
См. также Гиперкомплексное число, Двойные и дуаль-
дуальные числа, Кэли число.
Лит.: [lJ К у р о ш А. Г., Курс высшей алгебры, 9 изд.,
М., 1968; [2] К о с т р и к и н А. И., Введение в алгебру, М.,
1977; [3J Маркушевич А. И., Теория аналитических
функций, т. 1, 2 изд., М., 1967; [4] Ш а б а т Б. В., Введение
в комплексный анализ, ч. 1, 2 изд., М., 1976; [5] Лавренть-
Лаврентьев М. А., Шабат Б. В., Проблемы гидродинамики и их
математические модели, 2 изд., М., 1977; [6] Гурвиц А.,
Курант Р., Теория функций, пер. с нем., М., 1968; [7]
Харди Г. X., Курс чистой математики, пер. с англ., М.,
1949; [8] Б у р б а к и Н., Общая топология. Топологические
труппы. Числа и связанные с ними пространства, пер. с франц.,
М., 1969. Е. Д. Соломенцев.
КОМПЛЕКСНЫЙ ТОР — комплексная абелева груп-
ла Ли, получаемая из n-мерного комплексного прост-
пространства С" факторизацией по решетке ГсгС" ранга In.
К. т.— это единственные связные компактные ком-
комплексные группы Ли [1]. Каждое эрмитово скалярное
произведение в С" определяет 'на Т= С "/Г кэлерову
метрику, инвариантную относительно сдвигов. К. т.
могут быть охарактеризованы также как единственные
компактные кэлеровы параллелизуемые многообра-
многообразия [2]. Группа автоморфизмов комплексного много-
многообразия Т совпадает с голоморфом группы Т как ком-
комплексной группы Ли.
Голоморфные р-формы на К. т. Т имеют вид
тде а,-г . .,¦ ?С, a Zj, ..., гп — координаты в С", и кольцо
"когомологий Дольбо ?j Qsa0Hp'9(T) естественно изо-
изоморфно AC"*(x)ACn* (см. [1]).
Как вещественные группы Ли все n-мерные К. т.
являются 2ге-мерными торами и изоморфны между собой
при фиксированном п. С точки зрения комплексной
структуры положение гораздо сложнее. Базис решетки
ГсСи можно задать матрицей Q размера пХ2п, наз.
матрицей периодов тора Т=С"/Г. Торы
Tj=Cn/Tj с матрицами периодов Q,- (?=1, 2) изоморфны
между собой (как комплексные группы Ли или как
комплексные многообразия) тогда и только тогда,
когда существуют такие матрицы C?GL(n, С) и Z?
?GL{2n, Z), что QZ=CQ1Z.
Матрицу периодов любого n-мерного тора можно
привести к виду Ц-Б4Ц, где Im|A|>0. Торы с матри-
матрицами такого вида образуют голоморфное семейство,
дающее эффективно параметризованную версальную
деформацию любого re-мерного К. т., зависящую от га2
параметров [3]. В частности, при ге=1 пространство
параметров есть верхняя полуплоскость Im a>0 и
множество классов изоморфных одномерных К. т.
отождествляется с фактором {Im а>0}/А, где Д —
модулярная группа.
К. т., являющиеся алгебраич. многообразиями, наз.
абелевыми многообразиями. К. т. С"/Г — абелево мно-
многообразие тогда и только тогда, когда в С" существует
эрмитово скалярное произведение, мнимая часть к-рого
целочцсленна на ГХГ [1]. В терминах матрицы перио-
периодов это условие выражается как условие Ри-
мана — Фробениуса: должна существовать та-
такая кососимметрич. матрица Q?GLBn, %), что
Q()Q' = 0 и что —iQQii' положительно определена.
При п= 1 эти условия всегда выполнены; соответствую-
соответствующие алгебраич. кривые суть эллиптические кривые.
Матрица периодов
0 iV~2 i\T
0 1
дает пример двумерного К. т., но являющегося абеле-
вым многообразием. На этом торе не существует даже
непостоянных мероморфных функций [5]. Необходи-
Необходимым и достаточным условием алгебраичностп «-мерного
К. т. является также наличие на нем п алгебраически
независимых мероморфпых функций.
Интерес к К. т. возник в 19 в. в связи с изучением
абелевых функций, а также Якоби многообразий ал-
алгебраич. кривых. С любым re-мерным компактным кэ-
леровым многообразием М связан набор п К. т.— его
многообразий Якоби, к-рые являются абелевыми много-
многообразиями, если М алгобраично [7].
Лит.: [1J Мамфорд Д., Абелевы многообразия, пер. о
англ., М., 1971; [2] W a n g Н. С, «Proc. Amer. Math. Soc.»
1954, v. 5, p. 771—76; [3] К о d a i г а К., Spencer D. С,
«Ann. Math.», 1958, v. 67, p. 328—466; L4] В ей ль А., Вве-
Введение в теорию кэлеровых многообразий, пер. с франц., М., 1961;
[5] 3 и г е л ь К. Л., Автоморфные функции нескольких ком-
комплексных переменных, пер. с англ., М., 1954; [6] Уэллс Р.,
Дифференциальное исчисление на комплексных многообразиях,
пер. с англ., М., 1976; [7] Ч ж е н ь Щ э н-ш э н ь, Комплекс-
Комплексные многообразия, пер. с англ., М., 1961. А. Л. Онищик.
КОМПОЗИТ расширении поля — наимень-
наименьшее подрасширение А -В расширения Q поля к, со-
содержащее заданные два подрасширения А с Q и B<z.Q;
оно совпадает с образом гомоморфизма ср : А@^В—»-й,
сопоставляющего тензорному произведению а(хN про-
произведение ab?Q.
КОМПОЗИЦИОННЫЙ РЯД — конечное подмножест-
подмножество {а0, ох, ..., ап} частично упорядоченного множества
с наименьшим элементом 0 и наибольшим элементом 1
такое, что
0 = а0 < аг < ... < ап = 1
и все интервалы [а,-, а/ + 3] являются простыми интер-
интервалами. Можно говорить также о К. р. любого интер-
интервала [а, Ь] частично упорядоченного множества. К. р.
существует далеко не всегда.
Под К. р. универсальной алгебры понимается К. р.
в решетке ее конгруэнции. Поскольку конгруэнции
в группах определяются нормальными подгруппами,
К. р. группы может быть определен как ее нор-
нормальный ряд (см. Подгрупп ряды), не имеющий отлич-
отличных от него самого уплотнений (без повторений). Ряд
будет К. р. группы G тогда и только тогда, когда
всякая подгруппа G;_lt ?=1, 2, . . ., к, является мак-
максимальным истинным нормальным делителем подгруп-
подгруппы G;.
Все факторы К. р. будут простыми группами. Всякий
нормальный ряд, изоморфный с некоторым К. р., сам
будет композиционным. Для К. р. групп имеет место
Жор дана — Гёлъдера теорема. Аналогично опреде-
определяются и аналогичными свойствами обладают К. р.
колец и, вообще, Q-групп (см. [2]).
Лит.: [1] К о н П. М., Универсальная алгебра, пер. с англ.,
М., 1968; [2] К у р о ш А. Г., Лекции по общей алгебре, 2 изд.,
М., 1973. О. А. Иванова, Л. А. Скорняте.
КОМПОЗИЦИЯ — бинарная алгебраическая опера-
операция. Напр., К. (или суперпозицией) двух функций f(x)
и g(x) наз. функция h(x) = f[g(x)\. О К. в теории вероят-
вероятностей см. Свертка.
КОМПОНЕНТА вектора а по ос и — век-
вектор, образованный проекциями концов вектора а на
эту ось.
КОМПОНЕНТА пространства — связное
подмножество С топологич. пространства X, обладаю-
обладающее следующим свойством: для любого связного мно-
множества СгсХ из включения CdCl вытекает, что
С=С1. К. пространства являются непересекающимися
множествами. Всякое непустое связное множество со-
содержится в одной и только одной К. Если С — К.
пространства X, и при этом CdY<z.X, то С ость К.
подпространства Y. Если / : X—*Y — монотонное не-
непрерывное отображение на, то множество С является
компонентой Y тогда и только тогда, когда f~1(C) —
К. X.
Лит.: [1] Куратовский К., Топология, т. 2, пер. с
англ., М., 1969. Б. А. Ефимов.
КОНГРУЭНТНОСТЬ — отношение эквивалентности
на множестве геометрич. фигур (отрезков, углов и т. д.).
Оно вводится либо аксиоматически (см. Гильберта
система аксиом), либо на основе какой-либо группы
преобразований, чаще всего движений. Так, в евклидо-
евклидовой геометрии (и вообще в геометрии пространств
постоянной кривизны) две фигуры наз. конгру-
конгруэнтными, или равными, если одна из них
движением может быть переведена в другую.
М. И. Войцеховский.
КОНГРУЭНЦ-ПОДГРУППА — подгруппа Н полной
линейной группы GL(n, R) над кольцом R, обладающая
следующим свойством: существует такой ненулевой
двусторонний идеал §р кольца R, что H^GL(n, R, 5$),
где
GL(n, R, 5p) = Ker(GL(re, R)—+GL (n,
т. е. Н содержит все матрицы из GL(n, R), сравнимые
с единичной матрицей по модулю §р. Более общо,
подгруппа Н линейной группы Г степени п над R наз.
К.-п., если для некоторого ненулевого двустороннего
идеала §р^Я
Н ^Tr\GL(n, R, $).
В случае
ff=Vr\GL(n, R, Щ
подгруппа Н наз. главной К. - п., соответствую-
соответствующей идеалу Щ. Понятие К.-п. первоначально возникло
для R=%. Оно особенно эффективно и важно с точки
зрения применений для дедекиндова кольца R и Г=С^,
где G — алгебраическая группа, определенная над
полем отношений кольца R.
Лит.: Ll] Басе X., Ми л нор Д ж., Серр Ж.-П.,
«Математика», 1970, т. 14, № 6, с. 64—128. В. П. Платонов.
КОНГРУЭНЦ-ПРОБЛЕМА: всякая ли подгруппа ко-
конечного индекса группы Go, где О — кольцо целых эле-
элементов поля алгебраич. чисел k, a G — связная линей-
линейная алгебраическая /с-определенная группа, является
конгруэнц-подгруппой? Это — классическая постановка
К.-п. Современный вариант К.-п. основывается на
понятии конгруэнц-ядра, выражающего меру откло-
отклонения от ее положительного решения. А именно, пусть
Go и Go — пополнения группы О — точек Go в тополо-
топологии, определяемой соответственно всеми подгруппами
конечного индекса и конгруэнц-подгруппами группы Go.
Тогда существует сюръективный и непрерывный гомо-
гомоморфизм л : G0-^.G0. Ядро Ker n наз. конгруэнц-ядром
и обозначается через c(G). Положительное решение
К.-п. в классической постановке эквивалентно c(G)=l.
К.-п. в современной форме заключается в вычислении
конгруэнц-ядра c(G).
Для G0=SL(n, Z), где Z —кольцо целых чисел,
еще в конце 19 в. было известно, что при ге=2 К.-ц.
решается отрицательно. В 1965 было показано, что при
ге>2 всякая подгруппа конечного индекса группы
SL(n, %) является конгруэнц-подгруппой (см. [1]).
Вслед за этим было получено [1] решение К.-п. для
G0=SL(n, О), п>2, или SpBn, О), ге>1, где Sp обо-
обозначает симплектическую группу. Для этих групп ре-
результат таков: с{в)ф\ только для вполне мнимого
поля к, для к-рого конгруэнц-ядро c(G) изоморфно
циклической группе корней из единицы, содержа-
содержащихся в к. Оказывается, точно такой же результат
справедлив для всех односвязных групп Шевалле,
кроме SL B) (см. [3]). Условие односвязности является
существенным, ибо из теоремы о сильной аппрокси-
аппроксимации следует, что для неодносвязной полупростой
группы G конгру;щц-ядро c(G) бесконечно. Для неполу-
простой группы G всегда c(G) = c(S), где S — макси-
максимальная полупростая подгруппа в G; в частности, для
разрешимой G всегда c(G)=l.
Более общая форма К.-п. получается заменой кольца
О на кольцо
Оу= {х? к | v (х) < 1, при всех v (? V},
где V — произвольное конечное множество неэквива-
неэквивалентных нормирований поля к, содержащее все архиме-
архимедовы нормирования. В этой ситуации конгруэнц-ядро,
обозначаемое c(G, V), существенно зависит от V (см.
[4], [5]).
Лит.: [1] Басе X., М и л н о р Д ж., С е р р Ж.-П.
«Математика», 1970, т. 14, № 6 с 64—128; 1971, т. 15, № 1, о.
44—60; [2] Серр Ж.-П., «Математика», 1971, т. 15, Mi, с,
12—45; [3]Matsumoto H., «Ann. sci. Ecole norm, super.»
1969, t. 2, № 1, p. 1—62; [4] Итоги науки и техники. Алгебра
Топология. Геометрия, т. 11, М., 1974, с. 5—37; [5] Raghu
nathan M., «Publ. Math. IHES», 1976, №46, p. 107—61
В. П. Платонов
КОНГРУЭНЦИЯ — отношение эквивалентности л
на универсальной алгебре Л={Л, Q}, перестановочное
с любой операцией из Q, т. е. такое отношение эквива-
эквивалентности, для которого из а{па\ следует (аг, . . ., а„и>)х
Хя(я!, . . ., ап(а), где а,-, а,-?Л, i=l, . . ., п, u>?Q —
re-арная операция. Аналогично определяется К. в ал-
гебраич. системе. Таким образом классы по К. я об-
образуют однотипную с А универсальную алгебру (ал-
гебраич. систему) А /я, называемую фактора л-
геброй (факторсистемой) по К. я. Ес-
Естественное отображение А на А /я (сопоставляющее
элементу а класс по я, к-рому он принадлежит) яв-
является сюръективным гомоморфизмом. Обратно, вся-
всякий гомоморфизм ф : А—кВ определяет однозначно К.,
классами к-рой служат полные прообразы элементов В.
Пересечение К. я/, г?/, в решетке соответствий на
универсальной алгебре (алгебраич. системе) является
К. Объединение К. в решетке соответствий, вообще
говоря, не обязано быть К. Произведение л1я2 К. ях
и я2 тогда и только тогда будет К., когда ях и я2 пере-
перестановочны, т. е. я1я2=я2я1.
Лит.: [1] Курош А. Г., Общая алгебра. Лекции...,
М., 1974. В. С. Малаховский.
КОНГРУЭНЦИЯ прямых — множество С пря-
прямых трехмерного пространства (проективного, аффин-
аффинного, евклидова), зависящее от двух параметров.
Прямая 1? С наз. лучом К. Порядком К.
наз. число прямых К., проходящих через произволь-
произвольную точку пространства; классом — число пря-
прямых К., лежащих в произвольной плоскости.
Лучи К. можно двумя способами разложить на одно-
параметрич. семейство торсов так, что через каждый
ЛУЧ 1?С проходят два торса действительных различ-
различных (гиперболический луч), мнимых ( э л-
липтический луч) или действительных сов-
совпадающих (параболический луч). Точки
касания луча 1?С с ребрами возврата этих торсов наз.
фокусами луча I. Поверхности, образованные
фокусами лучей К., наз. ее фокальными по-
поверхностями. Касательные плоскости к фо-
фокальным поверхностям, проходящие через луч I К.,
наз. фокальными плоскостями луча I.
Торсы К. высекают на каждой фокальной поверхности
сеть линий, к-рая Ha:s. фокальной сетью К.
Фокальная сеть линий на каждой фокальной поверх-
поверхности сопряжена. В гнперболич. области К. представ-
представляет собой множество общих касательных двух фо-
фокальных поверхностей; в эллиптпч. области К. обра-
образована действительными общими касательными двух
сопряженных мнимых поверхностей; в параболич.
области К. образована касательными к одному семей-
семейству асимптотич. линий единственной фокальной по-
поверхности. Центром луча К. наз. середина
отрезка, определяемого фокусами луча. Поверхность,
описанная центрами лучей, наз. средней повер-
поверхностью К. Основания общих перпендикуляров
двух смежных лучей I (и, v) и l'(u-\-du, v-\-dv) запол-
заполняют на луче I отрезок, концы к-рого наз. г р а н и ч-
н ы м и точками луча. Плоскости, перпендику-
перпендикулярные к направлению общего перпендикуляра в гра-
граничных точках, наз. главными плоскостями;
линейчатые поверхности, линии сжатия к-рых пересе-
пересекают лучи в их граничных точках, наз. главными
поверхностями. Множество граничных точек
луча наз. граничной поверхностью.
Пример ы К.: И'-конгруэнция, у к-рой асимпто-
асимптотич. линии на фокальных поверхностях соответствуют
ДРУГ другу; линейная К.— множество прямых прост-
пространства, пересекающих две данные прямые, называе-
называемые директрисами; нормальная К.— множество
нормален нек-рой поверхности; изотропная К.— К. с не-
неопределенными главными поверхностями.
Наряду с К. прямых рассматриваются К. (двупара-
метрнч. семейства) плоскостей, коник, квадрик и дру-
других фигур (см. Фигур многообразие). К. произвольных
линий в пространстве называются криволиней-
криволинейными К.
Лит.: [1] Ф и н и к о в С. П., Теория конгруэнции, М.—
Л., 1950. В. С. Малаховский.
КОНДЕНСАЦИИ ТОЧКА множества М, лежащего
в евклидовом пространстве Е,— точка из Е, в любой
окрестности к-рой содержится несчетное множество
точек множества М. Множество К. т. любого множества
замкнуто; если оно непусто, то является совершенным
множеством п имеет мощность континуума. Понятие
К. т. обобщается для произвольного топологич. прост-
пространства. Б. А. Ефимов.
КОНДУКТОР характера — целое число, со-
сопоставляемое характеру нек-рого представления груп-
группы Галуа конечного расширения локальных полей.
Пусть К — полное поле дискретного нормирования с
полем вычетов к характеристики р^О, ЫК — его рас-
расширение Галуа степени п с группой Галуа G. Если % —
характер некоторого конечномерного комплексного
представления группы G, то его К. /(%) определяется
формулой:
где
У
G x(g)
причем П обозначает простой элемент поля L, & \L —
соответствующее нормирование. Для (ге, р)=1 будет
G0=G, С/={1}для !>0н/(х)=хA)-х№). Еслих-
характер рационального представления М, то % (?,¦)=
= dim MGi. К. f(%) является целым положительным
числом, равным 0 только, если гс=1.
Лит.: [1] Алгебраическая теория чисел, пер. с англ., М.,
1969; И А г t i и Е., Т a t e J., Class field theory, N. Y.— Amst,
1967; 13] Сер р Ж.-И., Абелевы (-адические представления
и эллиптические кривые, пер. с англ., М., 1973.
И. В. Долгачев.
КОНДУКТОР целого я а м ы к а и и я —идеал
целостного коммутативного кольца А, являющийся ан-
нулятором Л-модуля А/А, где А —целое замыкание
кольца А в его поле частных. Иногда К. рассматривает-
рассматривается также как идеал кольца А. Если А является А -моду-
-модулем конечного ттша (напр., когда А — геометрич.
кольцо), то простой идеал 5р кольца А содержит К.
тогда и только тогда, когда локализация А„ не являет-
является цслозамкнутым локальным кольцом. В геометрич.
терминах это означает, что К. определяет замкнутую
подсхему аффинной схемы Spec (Л), состоящую из то-
точек, не являющихся нормальными точками.
Лит.: [1] Б у р б а к и Н., Коммутативная алгебра, пер.
с франц., М., 1971; [2] Зарисский О., Самюэль П.,
Коммутативная алгебра, пер. с англ., т. 1, М., 1963.
И. В. Долгачев.
КОНЕЧНАЯ ГРУППА — группа с конечным числом
элементов. Это число наз. порядком группы.
Исторически К. г. послужили исходным материалом
для формирования многих понятий абстрактной теории
групп.
Обычно говорят, что целью теории К. г. является
описание, с точностью до изоморфизма, групп любого
порядка. Это верно лишь отчасти. Наивный подход,
основанный на полном переборе всех групп, заведомо
обречен на неудачу. Напр., составление списка всех не-
неизоморфных групп сравнительно небольшого порядка
1024 явилось бы трудным испытанием для лучших со-
современных ЭВМ. Вообще, перебор конечных /5-групп
(групп порядка р, где р — простое число) — «дикая»,
пли плохо поставленная задача. Напротив, существуют
некие экстремальные классы групп, играющие принци-
принципиальную роль в теории, для к-рых проблема класси-
классификации (перечисления с точностью до изоморфизма)
либо решена, лнбо представляется вполне осмысленной.
Так, для абелевых К. г. имеется законченная теория
(см. Абелева группа). Отдельные типы конечных р-групп
(регулярные, свободные экспоненты р, максимального
класса, заданные образующими и минимально возмож-
возможным числом соотношений) также допускают качествен-
качественное описание. Простые группы (т. е. группы с триви-
тривиальными нормальными подгруппами), являющиеся
«строительными блоками» для всех К. г., несмотря на
настойчивые попытки пока не удается описать. Сущест-
Существует гипотеза, что должно существовать не более двух
(чаще всего — нуль) неизоморфных простых групп лю-
любого фиксированного порядка п. Это проверено для
ге<106. При конкретном анализе простых групп ока-
оказалось успешным применение ЭВМ, хотя, разумеется,
их роль — чисто вспомогательная. Гораздо более зна-
значительными являются теоретические результаты о про-
простых группах (см. Простая конечная группа). К настоя-
настоящему времени A978) известно несколько бесконечных
серий простых групп (Шевалле группы) и около трех
десятков изолированных примеров (спорадические про-
простые группы). Описание конечных групп целочислен-
целочисленных матриц — еще один пример важной классифика-
классификационной задачи, решенной лишь для небольших разме-
размеров матриц.
После периода становления в теории К. г., связан-
связанного с именами О. Копти (A. Cauchy), Ж. Лагранжа
(J. Lagrange), К. Гаусса (С. Gauss), H. Абеля (N. Abel)
и, в первую очередь, Э. Галуа (Е. Galois), К. г. изуча-
изучались почти исключительно как группы перестановок
(см. неудачно укоренившийся термин подстановок
группа), причем эта точка зрения остается плодотвор-
ной и в наши дни. Напр., если абстрактная К. г. G
допускает реализацию (вложение в симметрия, группу
Sm) в виде кратно-транзитивной группы перестановок,
то в ряде случаев G определяется однозначно с точ-
точностью до изоморфизма. Классификационные резуль-
результаты, относящиеся к простым 2-транзитпвным группам
перестановок, составляют богатый раздел теории К. г.,
начало к-рому было заложено более ста лет тому назад
К. Жорданом (С. Jordan). Вычислительные методы в
теории групп перестановок, развившиеся за последние
годы, отчасти вызваны к жизни запросами комбина-
комбинаторики, теории графов, теории кодирования, необхо-
необходимостью проверки различных гипотез.
В начале 20 в. трудами Г. фробениуса (G. Frobenius),
У. Бёрнсайда (W. Burnside), И. Шура (I. Schur) и др.
была развита теория линейных представлений К. г. (см.
Конечной группы представление), давшая мощный ин-
инструмент исследования абстрактных групп и послужив-
послужившая прототипом для аналогичной теории представлений
групп Ли, а затем и других алгебраич. систем. Выраже-
Выражение свойств групп и их представлений на языке теории
характеров — одно из проявлений взаимных связей
между различными разделами алгебры. Интенсивно изу-
изучаются представления К. г. над коммутативными коль-
кольцами и над полями ненулевой характеристики (Р. Брау-
эр (R. Brauer) и др., см. [2]). Выделившаяся в результате
этих исследований область конечных линейных групп
изобилует многими глубокими результатами.
Почти очевидное соображение, что свойства конечной
группы G должны быть в какой-то мере арифметически-
арифметическими, зависящими от канонического разложения |G| =
=р™1. . .р^к ее порядка, нашло свое воплощение в Сило-
ва теоремах о существовании и сопряженности под-
подгрупп порядка pni. Если \G\ = nm, где гейт. — произ-
произвольные взаимно простые натуральные числа, тс под-
подгруппа порядка п, называемая холловской, существует,
вообще говоря, не всегда, но для обширного класса
разрешимых групп холловские подгруппы полностью
наследуют свойства силовских. Открытая У. Бёрнсай-
дом разрешимость групп порядка paqb (p, q — простые
числа) — типичный пример арифметич. свойства. Раз-
Разрешимость групп нечетного порядка, установленная
много лет спустя Дж. Томпсоном й У. Фейтом (J. Thomp-
Thompson, W. Feit, см. Вёрнсайда. проблема 1),— достиже-
достижение, к-рое поставило теорию К. г. на принципиально
новую основу. Существование инволюций (элементов
порядка два) в неразрешимых группах — иная форму-
формулировка теоремы Томпсона — Фейта и выражение
свойств группы в терминах централизаторов инволю-
инволюций — одно из главных направлений исследований в
области К. г. за последние два десятилетия.
Длительное время изучаются свойства групп, пред-
ставимых в виде произведения подгрупп специальных
типов. Если, напр., G=AB, где А и В — нильпотент-
ные подгруппы, то G — разрешимая группа. Произ-
Произвольная 2-транзитивная группа преобразований допу-
допускает факторизацию G—ABA, где А — стабилизатор
точки, а В — подгруппа порядка 2. Остается недока-
недоказанной пока A978) гипотеза С. А. Чунихина о непросто-
непростоте К. г., предетавимой в виде произведения централиза-
централизаторов двух неединичных элементов.
Видное место занимает изучение К. г. с выделенным
действием на них групп автоморфизмов. Согласно не
доказанной в полной общности гипотезе, К. г. G с авто-
автоморфизмом ф, оставляющим на месте лишь единич-
единичный элемент из G, должна быть разрешимой. Если G —
простого порядка, то G нильпотентна, и уже отсюда сле-
следует, что К. г., обладающая нильпотентной максималь-
максимальной подгруппой нечетного порядка, разрешима. Как
видно, критерии разрешимости К. р. могут быть самой
различной природы.
Расширения К. г. изучаются средствами теории ко-
гомологий (см. Когомологии групп), имеющей самосто-
самостоятельное значение.
Лит.: [1] Клейн Ф., Лекции о развитии математики в
XIX столетии, пер. с нем., ч. 1, М.—Л., 1937; L2J К э р т и с Ч.,
Р айн ер И., Теория представлений конечных групп и ассоциа-
ассоциативных алгебр, пер. с англ., М., 19E9; [3] Каргаполов
М. И., Мерзляков 10. И., Основы теории групп, 2 изд., М.,
1977; [4] К о с т р и к и н А. И., в кн.: Итоги науки. Алгеб-
Алгебра. 1964, М., 1966, с. 1—46; to] ЧунихинС. А., Шемет-
ков Л. А., в кн.; Итоги науки. Алгебра. Топология. Геометрия.
1969, М., 1971, с. 7 — 70; [6] Мазуров В. Д., в кн.: Ито-
Итоги науки и техники. Алгебра. Топология. Геометрия, т. l'i.
М. 1976 с. 5 — 56; [7] Speiser A., Die Theorie der Gruppen
von endlicher Ordnung, 4 Auf]., Basel, 1956; [8] WielandtH..
Finite permutations groups, N. Y.— L., 1964; [9] Huppert В.,
Endliche Gruppen, В.—Hdlb.—N. Y., 1967; [10] G о г е r.-
stein D., Finite groups, N. Y., 1968; [11] I s а а с s I. M.,
Character theory of finite groups, N. Y., 1976. А. И. Кострикик.
КОНЕЧНАЯ ГРУППОВАЯ СХЕМА — групповая
схема, конечная и плоская над базисной схемой. Ес-
Если G — К. г. с. над схемой (S, Qs), то G=Spec(.^), где
Jl — коночный плоский квазикогерентный пучок ал-
алгебр над Qs- В дальнейшем предполагается, что S ло-
локально нётерова. В этом случае пучок Л является ло-
локально свободным. Если S связна, то ранг алгебры
<Л>\ р k(s) над полем вычетов k (s) точки s?S ие зави-
зависит отsи наз. рангом К. г. с. Пусть па' G—*-Gморфизм
5-схем, отображающий элемент x?G(T) в элемент
x"?G(T) для любой S-схемы Т. Морфизм по является
нулевым, если ранг G делит п и S — приведенная схема
или G — коммутативная К. г. с. (см. Коммутативная
групповая схема). К. г. с. ранга р, где р — простое чис-
число, коммутативна [2].
Если G — подгруппа коммутативной К. г. с. G, то
определяется К. г. с. GIG', причем ранг схемы G равен
произведению рангов схем G' и GIG'.
Примеры. 1) Пусть G = Gm$ — мультипликатив-
мультипликативная групповая схема (соответственно абелева схема ,А
над S); тогда Ker uq является К. г. с. ранга \п\ (соот-
(соответственно | п\" dlm '¦'*). 2) Пусть S — схема над простым
полем ?р и F : GaS-^-GaS — гомоморфизм Фробениуса
аддитивной групповой схемы Ga 5. Тогда Ker F яв-
является К. г. с. ранга р. 3) Для любой конечной абст-
абстрактной группы Г порядка п постоянная групповая
схема Т$ является К. г. с. ранга п.
Классификация К. г. с. над произвольными базами
проведена только для случая, когда ранг схемы G
есть простое число [2]. Хорошо изучен случай, когда
G — коммутативная К. г. с, a S — спектр поля харак-
характеристики р (см. [1], [3], [7]).
Лит.: [1] Мании Ю. Н., «Успехи матем. наук», 1963,
т. 18, в. 6, с. 3 — 90; [2] Тэйт Дж., О орт Ф., «Математика»,
1973, т. 16, № 1, с. 165—83; [3] D e m a z u г е М., G a b г i e 1 Р..
Groupes algfibriques, t. 1, P.— Amst., 1970; [4] О о г t F., Com-
Commutative group schemes, В.— Hdlb.— N. Y., 1966; [5] S h a t z
S., «Ann. Math.», 1964, v. 79, p. 411 — 49; [6] M a z и г В., «Ann.
sci. Ecole norm, super.», 1973, t. 6, p. 521—52; L7] Kraft H.,
Kommutative algebraische Gruppen und Ringe, B.— Hdlb.—
N. Y., 1975. И. В. Долгачев.
КОНЕЧНАЯ МАТЕМАТИКА — область математи-
математики, занимающаяся изучением свойств структур финит-
финитного (конечного) характера, к-рыо возникают как вну-
внутри математики, так и в ее приложениях. К числу таких
конечных структур могут быть отнесены, напр., конеч-
конечные группы, коночные графи, а также нек-рые матема-
тич. модели преобразователей информации, автоматы
конечные, Тьюринга машина и т. п. Иногда допускают
расширение предмета К. м. до произвольных дискрет-
дискретных структур и приходят к дискретной мате-
математик е, отождествляя последнюю с К. м. К таким
структурам могут быть отнесены нек-рые алгебраические
системы, бесконечные графы, определенные виды вы-
вычислительных схем, клеточные автоматы и т. д. В ка-
качестве синонима понятий «К. м.» и «дискретная матема-
математика» употребляется термин дискретный анализ.
КОНЕЧНАЯ РАЗНОСТЬ — см. Конечных разностей
исчисление.
КОНЕЧНАЯ РИМАНОВА ПОВЕРХНОСТЬ — ри-
манова поверхность конечного рода, имеющая конечное
число невырожденных компонент края. К. р. п. может
быть вложена в замкнутую риманову поверхность —
дубль римановой поверхности.
Лит.: [1] Ш и ф ф е р М., Спенсер Д. К., Функцио-
Функционалы на конечных римановых поверхностях, пер. с англ., М.,
1957. Е. Д. Соломенцев.
КОНЕЧНО ОПРЕДЕЛЕННАЯ ГРУППА — группа,
обладающая конечным числом образующих и задавае-
задаваемая в этих образующих конечным числом соотношений.
Таких групп с точностью до изоморфизма счетное мно-
множество. Для любой конечной системы образующих К. о. г.
из всякой системы определяющих соотношений, связы-
связывающих эти образующие, можно выбрать конечную под-
подсистему, уже достаточную для задания группы.
Лит.: [1] К у р о ш А. Г., Теория групп, 3 изд., М., 1967.
О. А. Иванова.
КОНЕЧНО ПОРОЖДЕННАЯ ГРУППА — группа
G, обладающая конечным порождающим множеством
М= {«j, .... ad}. Состоит из всевозможных произве-
произведений o?t» ... af?, где ik? {I, . . . , d}, eft=±l. Если
M содержит d элементов, то G наз. d-n о р о ж д е н-
н о й. Из любого порождающего множества К. п. г.
можно выбрать конечное порождающее множество.
1-порожденные группы наз. циклическими (они
исчерпываются с точностью до изоморфизма группой %
целых чисел относительно сложения и группами %п
классов вычетов по данному модулю п относительно
сложения, ге=1, 2, . . .).
Множество всех неизоморфных 2-порожденных групп
имеет мощность континуума. Всякая счетная группа
изоморфно вкладывается в нек-рую 2-порожденную
группу; можно считать при этом, что последняя проста,
а ее порождающие элементы имеют порядки 2 и 3. Вся-
Всякая счетная n-ступенно разрешимая группа изоморфно
вкладывается в 2-порожденную (п+2)-ступенно разре-
разрешимую группу. Подгруппа конечного индекса в К. п. г.
сама является К. п. г. Во всякой К. п. г. имеется лишь
конечное число подгрупп данного конечного индекса.
К. п. г. может быть бесконечной периодической; более
того, для всякого натурального числа d~^2 и всякого
нечетного числа ге^665 существует бесконечная d-no-
рождонная группа периода п (см. Вёрнсайда проблема).
К. п. г. может быть нехопфовой, т. е. изоморф-
изоморфной своей истинной факторгруппе; более того, существу-
существуют разрешимые нехопфовы К. п. г. Если К. п. г. фи-
финитно аппроксимируема (см. Финитно аппроксимируе-
аппроксимируемая группа), то она хопфова. Всякая К. п. г. матриц
над полем финитно аппроксимируема. Существуют бес-
бесконечные К. п. г., и даже конечно определенные группы,
являющиеся простыми.
Лит.: Г1] К а р г а п о л о в М. И., Мерзляков Ю. И.,
Основы теории групп, 2 изд., М., 1977. Ю. И. Мерзлякос.
КОНЕЧНОЕ ПОЛЕ — см. Галуа поле.
КОНЕЧНОЙ ГРУППЫ ПРЕДСТАВЛЕНИЕ — гомо-
гомоморфизм конечной группы G в группу обратимых ли-
линейных операторов в векторном пространстве над полем
К. Теория К. г. п. является наиболее разработанным
(и одним из наиболее важных) разделом теории пред-
представлений групп.
Теория К. г. п. над полем С является частью
теории представлении компактных групп, и все ре-
результаты этой теории (теорема Петера — Вейля, тео-
теория характеров, соотношения ортогональности и т. д.)
справедливы (и притом упрощаются) для К. г. п.
В частности, любое К. г. п. в топологич. вектор-
векторном пространстве является суммой представлений,
кратных неприводимым. С другой стороны, в теории
К. г. п. есть ряд существенных результатов, исполь-
использующих специфику конечных групп. Напр., для данной
конечной группы G число различных классов эквива-
эквивалентности К. г. п. равно числу классов сопряженных
элементов в G; сумма квадратов размерностей предста-
представителей классов эквивалентности К. г. п. равна поряд-
порядку \G\ группы G; размерность любого неприводимого
К. г. п. является делителем индекса любого абелева
нормального делителя в G (в частности, делителем по-
порядка \G\) и не превосходит индекса абелевых подгрупп
в G. Если % — характер К. г. п. я, d — размерность л,
то для всех s^Gn всех классов сопряженных элементов
QczG числа %xs) nd~1^ „%(s) являются целыми алгеб-
раическими. Каждый характер группы G является ли-
линейной комбинацией характеров К. г. п., индуцирован-
индуцированных (см. Индуцированное представление) представле-
представлениями ее циклических подгрупп и линейной комбина-
комбинацией с целыми коэффициентами характеров К. г. п.,
индуцированных одномерными представлениями под-
подгрупп. Группа // наз. р-элементарной, если она являет-
является произведением группы, порядок к-рой равен степени
простого числа р, и циклич. группы порядка, взаимно
простого с р; группа Н наз. элементарной, если она р-
элементарна для нек-рого простого р. Любой характер
конечной группы G является линейной комбинацией с
целыми коэффициентами характеров К. г. п., индуци-
индуцированных представлениями элементарных подгрупп
HcG (теорема Брауэра, допускающая обобщение на
случай поля произвольной характеристики). Если груп-
группа G сверхразрешима, т. е. допускает композиционный
ряд из нормальных делителей с циклическими факто-
факторами, то любое неприводимое К. г. п. для G индуциро-
индуцировано одномерным представлением нек-рой подгруппы.
В случае, если характеристика р поля К не является
делителем порядка | G|, теория мало отличается от слу-
случая К=С. В частности, любое конечномерное К. г. п.
вполне приводимо; если К — алгебраически замкнутое
поло, то число классов эквивалентности неприводимых
К. г. п. над К равно числу классов сопряженных эле-
элементов группы, а сумма квадратов размерностей пред-
представителей этих классов раина порядку группы. Но для
алгебраичесьи замкнутого поля К могут существовать
представления, неприводимые над К, но приводимые
над его расширениями; поле К наз. полем разложения
неприводимого К. г. п. я, если л остается неприводи-
неприводимым над любым расширением поля К, и — полем разло-
разложения для G, если К есть поле разложения для любого
неприводимого К. г. п. для G. Если К — поле характе-
характеристики нуль или конечное поле, содержащее корни из
единицы степени т, где т — наименьшее общее кратное
порядков элелтпитов группы G, то К — поле разложе-
разложения для G; ¦¦•>!>сия К. г. п. над полем, не являющимся
полем разделения, связана с группой Галуа расшире-
расширения данного ноля, получаемого присоединением всех
корней т-тк степени из единицы. В частности, число
классов неприводимых представлений группы G над
полем рациональных чисел равно числу классов сопря-
сопряженности циклич. подгрупп этой группы; если К — со-
совершенное поле, то существует поле разложения для G,
конечное над К. Для любого поля К характер любого
К. г. п. принимает значение во множестве конечных
сумм корней из единицы в поле К, и для матричных эле-
элементов и характеров справедлив аналог соотношений
ортогональности и их следствий; в частности", если К —
поле разложения для G характеристики нуль, то К. г. п.
с характером % неприводимо тогда и только тогда, когда
51 Х(ё)х(ё~'У—\&\- Если характеристика р поля
К — делитель порядка \G\, то групповая алгебра груп-
группы G над полем К не полупроста, и существуют не впол-
вполне приводимые К. г. п. над К. Пусть к — локальное
поле характеристики нуль, полное относительно не-
нек-рого дискретного нормирования, К — конечное поле
классов вычетов поля к с характеристикой р\ К. г. п.
группы G над К наз. модулярными. Теория моду-
модулярных К. г. п. устанавливает более глубокие связи
между строением группы и свойствами представлений
этой группы, чем теория К. г. п. над С. Теория упро-
упрощается в случае, если к и К содержат все корни т-й
степени из единицы (и поэтому являются полями раз-
разложения); в этом случае для матричных элементов и
характеров справедлив аналог соотношений ортого-
ортогональности. Пусть л — К. г. п. над К, % — его харак-
характер, Д — первообразный корень m-ii степени из еди-
шшы в поле к, б — его канонический образ в К\ пусть
s?G— элемент, порядок к-рого взаимно прост с р,
т. е. р-регулярный элемент, Greg — множество р-регу-
лярных элементов. Преобразование n(s) диагонализуе-
мо и % (s) = 6ai+. . .-\-6а" для нек-рых целых ах, ..., ап;
формула t](s) = Aa> + - ¦ •+ Aa" определяет функцию
ц : Gtcs—>~k, наз. характером Брауэра пред-
представления я; он однозначно определяет композици-
композиционные факторы представления л над К. Неразложимые
двусторонние идеалы в групповой алгебре K(G) груп-
группы G над полем К наз. блоками; существует классифи-
классификация неэквивалентных неприводимых представлений
над к, неизоморфных представлений над К и неизоморф-
ных компонент разложения левого регулярного пред-
представления группы G над К в алгебре K(G) в прямую
сумму ненулевых неразложимых представлений в тер-
терминах блоков; эти результаты допускают распростра-
распространение на случай, когда поля к и К не являются полями
разложения для G.
Лит.: [1] К э р т и с Ч., Р а й н е р II., Теория представ-
представлений конечных групп и ассоциативных алгебр., пер. с англ.,
М., 1069; [2] К и р и л л о в А. А., Элементы теории представ-
представлений, М., 1972; [3] Н а й м а р к М. А., Теория представлений
групп, М., 1976; [4] Л е н г С, Алгебра, пер. с англ., М., 1968;
[5] С е р р Ж.-П., Линейные представления конечных групп,
пер. с франц., М., 1970. Л. И. Штерн.
КОНЕЧНОКРАТНОЕ ОТрБРАЖЕНИЕ — отображе-
отображение / ." X—*-Y такое, что прообраз f~xy любой точки у? Y
состоит из конечного числа пу точек. Если пу=п — од-
одно и то же для всех у, то / наз. re-кратным от-
отображением.
Понятию К. о. в дифференцируемом случае соответст-
соответствует понятие конечного отображения. Дифференцируе-
Дифференцируемое отображение дифференцируемых многообразий
/ : X—*-Y наз. конечным в точке х? X, если раз-
размерность локального кольца Rf{x) отображения / в точке
х конечна. Все отображения такого рода являются
К. о. на компактных подмножествах X, более того, су-
существует открытая окрестность U точки х такая, что
f~1(f(x))C\ U состоит только из одной точки. Число к=
= dim Rj{x) измеряет кратность х как корня уравнения
/(у)—г: существует окрестность V точки х такая, что
для всякого у, достаточно близкого к f(x), множество
/-1(у)П V состоит не более, чем из к точек.
Если dim Z<:dim Y, то конечные отображения обра-
образуют массивное множество в пространстве С°°(Х, У),
более того, множество неконечных отображений имеет в
этом пространстве бесконечную кораз.мерность (т е о-
р е м а Т у ж р о н а).
Лит.: [1] Архангельский А. В., Понома-
Пономарев В. И., Основы общей топологии в задачах и упражнениях,
М., 1974; [2] Голубицкий М., Гийемин В., Устой-
Устойчивые отображения и их особенности, пер. с англ., М., 1977.
М. И. Войцеховский.
КОНЕЧНОМЕРНАЯ АССОЦИАТИВНАЯ АЛГЕБ-
АЛГЕБРА — ассоциативное кольцо А, являющееся одновре-
одновременно конечномерным векторным пространством над
полом F, в к-ром выполняется следующее условие
для всех а, Ь?А и a?F. Размерность n^dimpA прост-
пространства А над полем F наз. размерностью алгебры А
над F. Принято также говорить, что алгебра А являет-
является п-морнон. Всякая n-мерная ассоциативная алгебра А
над полем F имеет точное представление матрицами по-
рядка ге+1 над F, т. е. существует изоморфизм алгебры
А на нек-рую подалгебру алгебры всех квадратных мат-
матриц порядка (ге+1)Х (ге-j-l) над F. Если, кроме того,
алгебра А содержит единицу, то она имеет точное пред-
представление матрицами порядка п над F.
Пусть ех, ... , еп — некоторый базис векторного про-
пространства А над F (он наз. также базисом алгеб-
алгебры А) и ,.
Элементы yfj, поля F наз. структурными кон-
константами алгебры А в данном базисе. Они
образуют тензор третьего ранга в пространстве А.
Основные теоремы о К. а. а. Радикал
Джокобсона К. а. а. нильпотентен и, если основное по-
поле сепарабельно, отщепляется полупрямым слагаемым
(см. Веддерберна — Мальцева теорема). Полупростая
К. а. а. над полем разлагается в прямую сумму матрич-
матричных алгебр над телами. Если основное поле F алгебра-
алгебраически замкнуто, то полупростая К. а. а. распадается
в прямую сумму матричных алгебр над F. Простые ко-
конечномерные алгебры исчерпываются полными матрич-
матричными алгебрами над телами (теорема Веддер-
Веддерберна). В частности, К. а. а. без делителей нуля ока-
оказывается телом. Над полем действительных чисел
К. а. а. с делением (т. е. тела) исчерпываются следую-
следующими примерами: поле действительных чисел, поле
комплексных чисел, тело кватернионов (теорема
Фробениуса).
Многие из упомянутых структурных свойств К. а. а.
имеют место и в более широких классах нётеровых и
артиновых колец (см., напр., Веддерберна — Артина
теорема).
Лит.: [II Ван дер Варден Б. Л., Алгебра, пер. с
нем., М. 1976; [2] А 1 b e r t A. A., Structure of algebras, N. Y.,
1939. В. Н. Латышев.
КОНЕЧНОМЕРНОЕ ПРЕДСТАВЛЕНИЕ — линейное
представление топологич. группы в конечномерном
векторном пространстве. Теория К. п. является одним
из наиболее разработанных и важных разделов общей
теории представлений групп. Неприводимое К. п. впол-
вполне неприводимо (см. Шура лемма), но операторно не-
неприводимое К. п. может быть приводимым. Измеримое
К. п. локально компактной группы совпадает локально
почти всюду с нек-рым непрерывным К. п. Ограничен-
Ограниченное К. п. локально компактной группы эквивалентно
унитарному представлению. Локально компактная
группа, имеющая точное К. п., является группой Ли
[7].
Унитарное К. п. есть прямая сумма неприводимых
унитарных К. п. Пересечение ядер непрерывных гомо-
гомоморфизмов топологич. группы G совпадает с пересече-
пересечением ядер неприводимых унитарных К. п. группы G;
если это множество содержит лишь единичный элемент
группы G, то группа G допускает непрерывный мономор-
мономорфизм в нек-рую компактную группу и группа G наз.
в л о ж и м о и в компактную группу, или макс и-
м а л ь н о й почти периодической (МПП-
группой). Если G — МПП-группа, то семейство матрич-
матричных элементов неприводимых унитарных К. и. группы
G разделяет точки группы G. Коммутативные и компакт-
компактные группы являются МПП-груипами; связная локаль-
локально компактная группа тогда и только тогда является
МПП-группой, когда она есть прямое произведение
связной компактной группы и группы R™ (см. [5]).
МПП-группа может иметь бесконечномерные неприво-
неприводимые унитарные представления и даже быть группой
не типа 1. Для того чтобы любое непрерывное неприво-
неприводимое унитарное представление локально компактной
группы G было К. п., необходимо и достаточно [8], чтобы
группа G являлась проективным пределом конечных
расширений групп Н вида (K-D)XV, где К, D, V —
замкнутые подгруппы группы Я, причем группа V изо-
изоморфна R", К — компактная группа, D — дискретная
группа, центральная в Н; достаточно, чтобы фактор-
факторгруппа группы G по ое центру была компактна. Кролю
того, для многих локально компактных групп (в част-
частности, для некомпактных простых групп Ли) единст-
единственным неприводимым унитарным К. п. является еди-
единичное представление.
Неунитарные К. п. топологип. грунн расклассифици-
расклассифицированы (с точностью до эквивалентности) лишь для
нек-рых групп, в частности для групп Rug, где за-
задача описания К. п. решается приведением матрицы к
жордановой форме и — в случае группы R — связана
с теорией обыкновенных дифференциальных уравнений
с постоянными коэффициентами, так как пространство
решений такого уравнения является конечномерным
инвариантным подпространством регулярного пред-
представления группы R в пространстве непрорывных функ-
функций на R. Кроме того, известны К. п. связных полу-
полупростых групп Ли. А именно, К. п. таких групп яв-
являются прямыми суммами неприводимых К. п., к-рые
описываются следующим образом. Если G — нолупро-
стая комплексная группа Ли, U — ее максимальная
компактная подгруппа, то любое непрерывное непри-
неприводимое унитарное представление я группы U в про-
пространстве Е может быть продолжено: 1) до неприводи-
неприводимого представления я0 группы G в Е, матричные эле-
элементы к-рого являются аналитич. функциями на G;
2) до неприводимого представления группы яО группы
G, матричные элементы к-рого комплексно сопряжены
аналптич. функциями на G; представления я0 и я<3
определяются представлением л однозначно. Тензорное
произведение я/^я-з является неприводимым К. п.
группы G для любых неприводимых унитарных К. п.
ях, я2 группы G, и любое неприводимое К. п. группы G
эквивалентно одному из представлений вида яр(>?)Я2 .
Описание К. п. односвязной связной комплексной полу-
полупростой группы Ли может быть дано также в терминах
экспонент К. п. ее алгебры Ли, а также с помощью Гаус-
Гаусса разложения Gz^Z-DZ +. группы G: пусть а — такая
непрерывная функция на G, что a(z_6z + )=aF) для
всех z _?.Z_, b?D, z+?Z+, и пусть линейная обо-
оболочка Фа функций g—va(gg0), go?G конечномерна; тогда
формула [Ta(g0)f]{g)=f(ggB), g, go?G, /?Ф«, опреде-
определяет неприводимое К. п. группы G, и все неприводимые
К. п. группы G могут быть получены таким образом.
Если G — действительная полупростая группа Ли,
С
имеющая комплексную форму G , то любое неприводи-
неприводимое К. п. группы G является сужением на G нек-рого
однозначно определенного неприводимого К. п. группы
С С
G , матричные элементы к-рого аналитичпы на G (так
что теория К. п. полупростых связных групп Ли по су-
существу сводится к теории представлений компактных
групп Ли). К. п. любой группы Ли является действи-
действительно аналитическим; если G — односвязная группа
Ли, то между К. п. группы G и ее алгебры Ли сущест-
существует взаимно однозначное соответствие (сопоставляю-
(сопоставляющее представлению группы Ли его дифференциал; об-
обратное соответствие сопоставляет представлению алгеб-
алгебры Ли его экспоненту). Но классификация К. п. про-
произвольных групп Ли далека A978) от полного решения
даже для частных случаев групп R™, ге^2, как и для
групп Z", «5=2 (см. [6]). С другой стороны, неприводи-
неприводимые К. п. я связной группы Ли G известны [2]: они име-
имеют вид я=х0яо, где х — одномерное представление
группы G (т. е. фактически — ее коммутативной фак-
факторгруппы по коммутанту), а я0 — К. п. полупростой
факторгруппы группы G по максимальному связному
разрешимому нормальному делителю группы G (см.
Леей—Мальцева разложение).
Лит.: [1] К и р и л л о в А. А., Элементы теории представ-
представлений, М., 1972; [2] Ж е л о б е н к о Д. П., Компактные
группы Ли и их представления, М., 1970; [3J Н а й м а р к М. А.,
Теория представлений групп, М., 1976; [4] Д и к с м ь е Ж.,
С*-алгебры и н\ представления, пер. с франц., М., 1974; to]
В е й л ь А., Интегрирование в топологических группах и его
применения, пер. с франц., М., 1950; [6] Г е л ь ф а н д И. М.,
Пономарёв В. А., «Функциональный анализ и его приме-
применения», 1969, т. 3, JVs 4, с. 81—82; L7J Г л у ш к о в В. М.,
«Успехи матем. наук», 1957, т. 12, Ks 2, с. 3 — 41; [8J Штерн
А. И., «Матем сб.», 1973, т. 90, № 1, с. 86 — 95. А. И. Штерн.
КОНЕЧНОСТИ ТЕОРЕМЫ — 1) К. т. в алгеб-
алгебраической геометрии — утверждения о раз-
различных объектах алгебраич. геометрии (пространствах
когомологий, алгебрапч. многообразиях, схемах, рас-
расслоениях и т. п.), состоящие в том, что эти объекты за-
зависят от конечного числа параметров или жо образуют
конечное множество.
Первый круг теорем конечности относится к простран-
пространствам когомологий когерентных алгебраич. пучков.
Фундаментальная теорема состоит в том, что эти прост-
пространства конечномерны над основным полем к, если мно-
многообразие собственно (для к=С это свойство равносиль-
равносильно компактности) (см. [2]). В рамках теории схем были
получены весьма широкие обобщения этой теоремы.
Одно из них обобщает данную теорему на случай
собственных морфизмов схем и утверждает, что прямой
образ когерентного пучка относительно такого отобра-
отображения когерентен (см. [3], [4]). Другое обобщение отно-
относится к изучению когомологий несобственных многооб-
многообразий. Оказывается, что если рассматриваемое многооб-
многообразие X получается выбрасыванием нек-рого подмного-
подмногообразия Y из собственного многообразия, то можно
оценить те размерности, в к-рых группы когомологий
конечномерны. Эти оценки зависят от коразмерности
многообразия Y и свойств его особых точек (см. [5], [6J).
Известны также соответствующие К. т. для этальных
когомологий.
Другой круг К. т. относится к подсхемам и, более
общо, когерентным пучкам на фиксированной собствен-
собственной схеме. Эти объекты могут быть параметризованы в
весьма широкой ситуации Гильберта схемами (или для
обратимых пучков — Пикара схемами). Наиболее об-
общая из таких К. т. утверждает, что эти схемы квази-
проективны, если ограничиться подсхемами или пучка-
пучками с одним и тем же Гильберта многочленом [4]. Ее
частным случаем является тот факт, и что алгебраич.
подмногообразия данной степени в проективном про-
пространстве зависят от конечного числа параметров, а
также теорема о конечности базиса Нерона — Севери
группы.
Эти теоремы находят применение в целом ряде про-
проблем конечности, возникающих в диофантовой геомет-
геометрии. Среди таких проблем: вопрос о конечности множе-
множества рациональных точек алгебраич. многообразия,
определенного над глобальным полем (многомерный
аналог гипотезы Морделла), гипотеза Шафаревича о
конечности числа алгебрапч. кривых, определенных над
данным глобальным нолем и с фиксированными вырож-
вырождениями, вопрос о конечной порождонности группы
рациональных точек алгобраич. группы.
Лит.: [1] S erre J.-P., «J. math, pures et appl.», 1957,
t. 36, № 5, p. 1 —16; [2] Расслоение пространства и их прило-
приложения М., 1958, с. 372—450; [3] Grothendieck A.
Elements de geometrie algebrique, ch. 3, pt 2, P., 1963 (Publ.
Math. IHKS, jvft 17); [4] e г о же, Fondcments de gfiometrie
algebriquo, P., 1962; [5]Hartshorne R., Ample Subvarie-
ties of Algebraic Varieties, В.—Hdlb.—N. Y., 1970; [6] Ogus
A., «Ann. Math.», 1973, v. 98, Nt 2, p. 327 — 65; [7] Щ а ф а р e-
вич И. Р., в кн.: Proceedings of the International Congress
of Mathematicians, Stoakh., 1962, p. 163—76; l8j Араке-
л о и С. Ю., «Изв. АН СССР. Сер. матем.», 1971, т. 35, Л5 6,
с. 1269—93. А. Н. Паршин.
2) К. т. в теории аналитических про-
пространств — критерии конечномерности групп ко-
когомологий со значениями в когерентных аналитических
пучках. Первой общей теоремой такого рода явилась
теорема конечности Картана — С е р-
р а [1]: если X — компактное комплексное простран-
пространство п §~ — когерентный аналитпч. пучок на X, то
пространства когомологий Нк(Х, §~) конечномерны н
отделимы для всех к^О. Обобщение этой теоремы на
случай выпукло-вогнутых пространств [2], [3] утверж-
утверждает: если X — сильно (р, ^-выпукло-вогнутое про-
пространство (см. Псевдовыпуклость и псевдовогнутость) и
$~ — когерентный аналптпч. пучок на X, то Hk(X, If)
конечномерны при p-sg/c-agprofj"—q—1 и отделимы при
p</c<prof gf—q, a Hkc (X, §~) конечномерны при ?+1<
<r/c<:prof EF—р п отделимы при g-rl<:fe<:prof |f—р+1.
К К. т. относят также обобщения указанных выше те-
теорем на относительный случай, т. е. критерии когерент-
когерентности прямых образов когерентных аналитпч. пучков
при аналитич. отображениях. Обобщением теоремы
Картана — Серра является следующая теорема
Грауэрта [4], [5]: если я : X—>Y — собственное
аналитпч. отображение комплексных пространств и
F — когерентный аналнтич. пучок на X, то прямые
образы Rkn^gF когерентны при всех к^О. Это свойство
оказывается и достаточным для собственности отобра-
отображения я. Аналогичные К. т. доказаны для сильно р-
выпуклых и сильно дг-вогнутых отображений (см. [6]).
Аналог теоремы Грауэрта доказан также для жестких
аналитических пространств над полем с неархимедовым
нормированием [7].
С К. т. тесно связаны теоремы об оценке степени
трансцендентности поля мероморфных функций на раз-
различных классах комплексных пространств (см. Зигеля
теорема). Простым следствием теоремы Грауэрта яв-
является следующая теорема Реммерта [4]:
если я : X—>-Y — собственное аналтгаич. отображение
комплексных пространств и Z — аналитич. множество
в X, то множество n(Z) аналитично в Y. Эта теорема
переносится и на случай жестких пространств [7].
Лит.: [1] С art an H., Serre J.-P., «С. г. Acad. sci.»,
1953, t. 237, p. 128 — 30; [2]Андреотти А., Г р а у э р т Г.,
в кн.: Комплексные пространства, М., 1965, с. 105—89, пер.
с франц.; [31 R am i s J. P., «Ann. Scuola norm, super. Pisa.
Sci. fis. e mat.», 1973, ser. 3, t. 27, Xi 4, p. 933—97; [4] Г р a y-
э р т Г. в кн.: Комплексные пространства, М., 1965, с. 205 —
299, пер. с нем.; [5] В S n i с а С, S t a n a s i 1 а О., Metode
algebrice In teoria globala a spatiilor complexe, Buc, 1974;
[6] Итоги науки. Алгебра. Топология. Геометрия, т. 15, М.,
197Т, с. 93—171; [7] Klehl R., «Invent, math.», 1967, Bd 2,
Лп. 3, S. 191 — 214. А. Л. Онищик.
КОНЕЧНОСТРОЧНЫЙ МЕТОД СУММИРОВА-
СУММИРОВАНИЯ — матричный метод суммирования, определен-
определенный конечнострочной матрицей — матрицей, каждая
строка к-poir содержит только конечное число отличных
от нуля элементов. Важным частным случаем К. м. с.
являются треугольные методы суммирования.
Для любого регулярного матричного метода сумми-
суммирования последовательностей можно построить К. м. с.
равносильный и совместный (см. Включение методов
суммирования и Совместность методов суммирования)
с ним на множестве ограниченных последовательностей
(см. [3]). Однако существуют регулярные матричные
методы суммирования, для к-рых нет равносильных
К. м. с. на множестве всех последовательностей (при-
(пример см. [4]).
Лит.: [1] Харди Г., Расходящиеся ряды, пер. с англ.,
М., 1951; [21 Кук Р., Бесконечные матрицы и пространства
последовательностей, пер. с англ., М., I960' [3] Б р у д н о А. Л.,
«Матем сб » 1945, т. 16, с. 191 — 247; [4] Е г d о s P., P i г а-
nian G., «Proc. Amer. Math. Soc», 1950, v. 1, p. 397—401.
И. И. Волков.
КОНЕЧНЫХ ПРИРАЩЕНИЙ ФОРМУЛА, фор-
формула конечных приращений Лагран-
ж а,— формула, выражающая приращение функции
через значение производной в промежуточной точке.
Если функция / непрерывна на отрезке [а, Ь] числовой
оси и дифференцируема в его внутренних точках, тогда
f(b)~f(a)=f'\l)(b-a), a<l<b.
К. п. ф. записывают также в виде
j(x+\x)—f(x) = f'(x+Q\x)\x, a<Q<\.
Геометрпч. смысл К. п. ф.: для хорды графика функции
/ с концами в точках (a, f(a)), (Ь, f(b)) существует такая
точка \, а<?<6, что касательная к графику функции
в точке (g, /(?)) параллельна указанной хорде (см.
рис.).
К. п. ф. обобщается на функции многих переменных:
если функция / дифференцируема в каждой точке вы-
У
f(b)
пуклой области G n-мерного евклидова пространства,
то для каждой пары точек х=(х1, . . . , xn)?G, г+Дл: —
-'(^itAij, ..., xn-\-Axn)^G существует такая точка
!—(ij, ¦.. , |„), лежащая на отрезке с концами в точ-
точках х и х-\-Ах, что
Л. Д. Кудрявцев.
КОНЕЧНЫХ РАЗНОСТЕЙ ИСЧИСЛЕНИЕ — раз-
раздел математики, в к-ром изучаются функции при ди-
дискретном изменении аргумента, в отличие от дифферен-
дифференциального и интегрального исчислений, где аргумент
изменяется непрерывно. Пусть функция y=f(x) зада-
задана в точках xk=xo-\-kh (k — постоянная, к — целое).
Тогда
— (конечные) разности первого поря д-
к а,
— разности второго порядка,
— разности re-го порядка. Разности удоб-
удобно располагать в таблицу:
X
x0
Xi
x2
x3
У
Уо
Ух
У1
Дм
Д.Уо
Ду,
Ду 2
Ду3
Д2У
А2у0
А2у±
ДЗу
Д3У1
Разность re-го порядка через величины у0, ylt ... вы-
выражается формулой:
к + п~2~ ¦ ¦ ¦ +(—1)" Ук-
Наряду с разностями вперед Аук употреб-
употребляются разности назад:
В ряде вопросов (в частности, при построении интер-
интерполяционных формул) используют центральные
разности:
к-рые определяются следующим образом:
&У. х =yi+i~yi,
62y,' = 6i/ —8у ,
«' н— (
2 2
б2"*;/ i ^ги-г^^^гт-г^
Между центральными bnyt и обычными разностями
A"i/fc имеется связь
tf—
2
В случае, когда промежутки х(,+х—х& не постоянны,
рассматривают так наз. разделенные разно-
с т и:
L-^o» xiJ —т _ х *
_Jxt:x,:-:xB_1]-[xt;x,; -:хн]
[^о, хи ¦¦¦, хп\— ; т-—:.
Имеет место формула
Иногда вместо [ж0; ^il • • ¦ ; жп1 употребляется обозначе-
обозначение /(ж0; ^5 ... ; ж„). Если ж„=жо+п/г, ге=0, 1, 2, ... ,
Если функция /(ж) в интервале ж^<ж<ж^ + п имеет ге-ю
производную f" (ж), то
К. р. и. тесно связано с общей теорией приближения
функций, используется в приближенном дифференциро-
дифференцировании и интегрировании, в приближенном решении
дифференциальных уравнений и других вопросах. Пусть
поставлена задача (интерполяционная задача) о восста-
восстановлении функции f(x), если известны значения /(ж) в
точках хд, хг, . . . , хп. Строится многочлен Р (?) степе-
степени ге, к-рый в указанных точках принимает те же зна-
значения, что и f(x). Его можно записать в различных фор-
формах — в форме Лагранжа, в форме Ньютона и т. д.
В форме Ньютона интерполяционный многочлен имеет
вид:
i, х2] (х~х0) (x —
а в случае равноотстоящих значений независимого пере-
переменного:
Р« П =1 Ы + У
=1 А! Л*
Функцию f(x) принимают приближенно равной Рп(х).
Если f(x) имеет ге-j-l производную, то ошибка от замены
f(x) на Рп(х) оценивается соотношением
ЛП
где | лежит в интервале, в к-ром находятся точки х,
х0, . . . , хп. В случае, если f(x) — многочлен степени
<п, то f(x) = Pn(x).
При неограниченном увеличении числа узлов интер-
интерполяции многочлен Рп(х) становится в пределе много-
многочленом Р (х) «бесконечной» степени н естественно воз-
возникает вопрос: когда f(x)=P(x), т. е. когда будет вы-
выполняться равенство
/(*) = /Ы + УЮ Д*/(*-> (g-д-о) ... (т-хк_х) A)
ft=1 ft! Л*
(для простоты рассматривается случай равноотстоящих
узлов). Пусть хо=0, Л=1, так что хп=п(п^0). Если ряд
A) сходится в точке а, отличной от узлов (ряд A) всег-
всегда сходится в узлах х0, хх, . ..), то он сходится в полу-
полуплоскости Re ж>а и представляет собой в этой полу-
полуплоскости аналптнч. функцию, к-рая в полуплоскости
Re x^p>a удовлетворяет условию (е>0):
1
а | ье
/ (ге'Ф) | < cerh <Ф'г 2
h (ф) — cos ф In B cos ф) + ф sin ф.
Обратно, если f(x) аналптична в нек-рой полуплоскости
н тшеет оценку роста, подобную указанной (несколько
лучше ее), то она представляется рядом A). Таким об-
образом, в ряд A) (так наз. ряд Ньютона) разла-
разлагаются функции из весьма узкого класса (только аналп-
аналптнч. функции с определенным ростом). Изучаются ря-
ряды Ньютона, когда узлы — вообще комплексные числа.
Такие ряды нашли большое применение в теории транс-
трансцендентных чисел. Пусть теперь узлы интерполяции об-
образуют треугольную матрицу
хо, о
Х1, О х\,1.
п, 0
и интерполяционный многочлен Рп(х) строится по уз-
узлам, расположенным в (ге+1)-й строчке. Класс функ-
функций, для к-рых Рп{х) стремится к f(x) при га—>оо, зави-
зависит от матрицы узлов. Напр., в случае, когда
..., П,
(хп ^ — корни Чебышева многочлена), для сходимости
интерполяционного процесса на отрезке [ —1,1] доста-
достаточно выполнения условия
lim со A/л) In re = 0,
п —*- х
где со (б) — непрерывности модуль f (х) на [ —1,1].
Другая важная задача К. р. и.— задача суммирова-
суммирования функций. Пусть дана нек-рая функция f(x). Тре-
Требуется найти в конечном виде, точно или приближенно,
сумму
Sn = / (*о) г/ (хо + К) -f- ... + / (.т0 -!- nk),
при фиксированных х0 и h и большом и, если известны
нек-рые аналитнч. свойства f(x). Иначе говоря, иссло-
дуется асимптотнч. поведение Sn npTi п—»-оо. Пусть
хо=0, Д=1 (для простоты) и найдена функция F(x) та-
такая, что
F(x) = f(x). B)
Тогда
Sn = F(n + i)-F@). C)
Напр., пусть f(x) = x2. Решение уравнения B) ищется
в виде многочлена третьей степени
с неопределенными коэффициентами. При подстановке
в уравнение B) и приравнивании коэффициентов левой
и правой частей при соответствующих степенях много-
многочлен имеет вид:
л (n+1) Bn+ 1)
6
He всегда удается в конечном виде получить решение
уравнения B). Поэтому полезно иметь приближенные
формулы для Sn. Такой формулой является Эйлера —
Маклорена формула суммирования. В случае, если /(х)
имеет к производных и к — четное, формулу Эйлера —
Маклорена можно записать в виде
^г U"-» (и)-/^-» @)} +
+?5Г>
п ¦ -""^ж = 0
где 0<9<1 (9 вообще зависит от п), Bv — Бернулли
числа. Если f(x) — многочлен степени, меньшей к, то
остаточный член равен нулю.
Имеется аналогия между задачами К. р. и. и диффе-
дифференциальным и интегральным исчислениями. Операция
разыскания разности соответствует нахождению произ-
производной; решение уравнения B) как операция, обратная
разысканию конечной разности, соответствует нахож-
нахождению первообразной, т. е. неопределенному интегри-
интегрированию. Формула C) есть прямой аналог Ньютона —
Лейбница формулы. Эта аналогия проявляется при рас-
рассмотрении уравнений в коночных разностях. Уравнени-
Уравнением в конечных разностях наз. соотношение
F (г, /(.г), Л/ (х), ..., &nf {*))--О,
где F — заданная функция, a f(x) — искомая. Если
выразить все Anf(x) через /(х), f(x-\-i), ... ,f(x~\-n),
то уравнение в конечных разностях запишется в виде
Ф(х, /(*),/(*+!), -.. ,/(х+/г)) = 0. D)
Его решение относительно /(х+тг):
/(х+/г)-ф(х, f(x), ... , /(я+п-1)). E)
При задании начальных значений f{x0), /(го+1), ••• >
j(xo~j-n—1) можно последовательно найти f(xo-\-n),
/ (хо+тг+1) и т. д. После решения уравнения D) отно-
относительно f (х):
можно, положив х=х0—1, найти f(x0—1), затем найти
/(х0—2) и т. д. Таким образом, из уравнения через на-
начальные данные могут быть найдены значения /(х) во
всех точках хо-\-к, где к — целое. Пусть рассматривает-
рассматривается линейное уравнение
/ (*+*)+/>! (*) / (Х+ к- 1) + . . . + Рк (х) f (X) =
= <?(*), х = 0, 1, ..., F)
где P-i(x), . . . , Pk(x) и Q(x) —- заданные функции на
множестве х=0, 1,2... . Общее решение неоднородно-
неоднородного уравнения F) есть сумма частного решения неодно-
родного уравнения и общего решения однородного урав-
уравнения
f(x+k) + Pt(x)f(x + k-l)+...+Pk(x)fW=O. G)
Если /j(x), . .. , fk(x) — линейно независимые решения
уравнения G), то общее решение уравнения G) выража-
выражается формулой
где сх, . . . , cf. — произвольные постоянные. Постоян-
Постоянные сх, . .. , с? можно найти, задав начальные условия,
значения /@), /A), ... , f(k—1). Линейно независимые
решения f^x), . . . , fk(x) (фундаментальная система)
легко находятся в случае уравнения с постоянными ко-
коэффициентам
f(x + k) + a1](x + k-\)+...+arJ{x) = Q. (8)
Решение уравнения (8) ищется в виде f(x) = Xx. Харак-
Характеристическое уравнение для X:
Пусть A,j, . . . , Я,й — его корни и все они различны.
Тогда фундаментальная система решений уравнения (8)
есть система А,*, ... , Х\ и общее решение уравнения (8)
представляется формулой:
Если Xj есть s-кратный корень характерпстич. уравне-
уравнения, то ему соответствуют частные решения Х\, хХ\, . ..,
Пусть, напр., рассматривается последовательность
чисел, начинающаяся с нуля и единицы, в к-рой каждый
последующий член равен сумме двух непосредственно
предшествующих ему: 0, 1, 1, 2, 3, 5, 8, 15, . . . (Фибонач-
(Фибоначчи числа). Ищется выражение для общего члена после-
последовательности. Пусть /(х), х=0, 1, 2, 3, ... ,— общий
член последовательности; условие
f(x+2) = f(x+l)+f{x), /@) = 0, /A)=1,
является разностным уравнением с заданными началь-
начальными условиями. Характеристическое уравнение имеет
вид: X.2—X—1=0, его корни Хх=1 + У^ , Х2=1-^??,
поэтому
c1= 1/1^5 u c2 =—1/У~Ъ находятся из начальных ус-
условий.
Уравнение D) можно изучать не только тогда, когда
х изменяется дискретно, принимая значения 0, 1,2,
... , но и тогда, когда х изменяется непрерывно. Пусть
}(х) задана произвольно в полуинтервале [0, п). Из E),
положив х=0, получают /(ге). Если /(х) задана непре-
непрерывной в [0, ге), то в замкнутом интервале [0, п] функ-
функция }(х) может оказаться разрывной. Желая иметь дело
с непрерывными решениями, надо f(x) так задать в
[О, п), чтобы, в силу E), /(х) оказалась непрерывной в
[О, ге]. Зная /(х) в [0, ге], из E) находят f(x) для х^(п,
ге+1], затем для х?(п.+ 1, re-f-2] и т. д.
Более общим, чем уравнение (8), является уравнение
О < «1 < h2 < ¦ ¦ ¦ < hk.
Здесь hly . . . , к^ — необязательно целые и необяза-
необязательно соизмеримы между собой. Уравнение (9) имеет
частные решения
где а — корень уравнения
L(X)^i
Это уравнение имеет бесконечно много корней кг, Я2,
.... Следовательно, уравнение (9) имеет бесконечно
много частных решений е^'"х, т=1, 2, ... . Пусть все
корни простые. Для выражения решения уравнения (9)
через эти элементарные частные решения уравнение
удобнее записать в виде:
f(X^-t)do(t) = 0,a=hk, A0)
где a(t) — кусочно постоянная функция, имеющая скач-
скачки в точках 0, /гх, ... , Л^, равные соответственно 1,
ах, . . . , аА. Пусть
Функции i|)v(i) обладают свойством:
(Smv=l, если m=v, и 6mv=0, если тфч), т. е. они об-
образуют систему, бтюртогональную к системе {е ¦"'}. На
этом основании решению f(x) уравнения A0) приводит-
приводится в соответствие ряд
В случае, когда уравнение (9) имеет штд
}(х^2п)-}(х)-Л) A2)
(т. е. f(x) — периодическая функция с периодом 2я);
L(k)=e2st*-—1; корни уравнения L(X) = 0 суть mi;
(т=0, ±1, . . .) и ряд A1) есть ряд Фурье для функции
}(х), записанный в комплексной форме. Ряд A1) можно
рассматривать как обобщение на случай разностного
уравнения (9) обычного ряда Фурье, соответствующего
простейшему разностному уравнению A2). При опре-
определенных условиях ряд A1) сходится к решению f(x).
Если f(x) — аналитическая функция, то уравнение (9)
представнмо в виде бесконечного порядка уравнения
Аналогично разностям функций одного переменного
вводятся разности функций многих переменных. Так,
напр., пусть требуется решить задачу численного реше-
решения уравнения Лапласа
ёж5 ' ey1^
в прямоугольнике 0<:х<:а, 0<:г/<й, при заданных зна-
значениях и(х, у) на граннце прямоугольника. Прямо-
Прямоугольник разбивается на мелкие прямоугольные ячей-
ячейки со сторонами Ax=a/N, Ay=b/M. В вершинах этих
ячеек ищутся значения решения. В вершинах, к-рые
лежат на границе исходного прямоугольника, значения
и(х, у) известны. Принимая приближенно (в числите-
числителях стоят разности второго порядка)
д-и _^ и (х + Дх, ;/)-2« (х, у) + и (х-Дх, у)
Эх5 ~ Дх5 ' '
д2и ^ и (х, у+Ау)-2и (ж, у) + и (х, у-Ау)
?Пр Ау1 '
вместо уравнения Лапласа получают спстему уравнений
и (х + Ах, у) — 2и (х, у) + и (х-Ах, у) .
, и (ж, у + Ау)-2и (х, у) + и(х, у-Ау) п
-1 д^ -"¦
Точка (х, у) пробегает те вершины ячеек, к-рые распо-
расположены внутри основного прямоугольника. Тем самым
строится система (N — 1)(М — 1) уравнений, содержащая
то же число неизвестных. Решая эту адгебраич. систему
уравнений, получают значения и(х, у) в вершинах яче-
ячеек. Когда Ах и Ау малы, а решение задачи имеет опре-
определенную гладкость, найденные значения близки к точ-
точным значениям.
К. р. и. развивалось параллельно с развитием основ-
основных разделов математич. анализа. Начала К. р. и. со-
содержатся в трудах П. Форма (P. Fermat), И. Барроу
(I. Barrow), Г. Лейбница (G. Leibniz). В 18 в. К. р. п.
приобрело характер самостоятельной математпч. дис-
дисциплины. Первое снстематнч. изложение К. р. и. было
дано Б. Тейлором (В. Taylor) в 1715. Труды математи-
математиков 19 в. подготовили почву для современных глав
К. р. и. Идеи и методы К. р. и. получили существенное
развитие в применении к аналитнч. функциям комплекс-
комплексного переменного и задачам вычислительной матема-
математики.
Лит.: [1] М а р к о в А. А., Исчисление конечных разно-
разностей, 2 изд., Од., 1910; L2] Б е р е з и н И. С, Ж и д к о в
Н. П., Методы вычислений, т. 1 — 2, 3 изд., М., 196Ё; [3] Гель-
фонд А. О., Исчисление конечных разностей, 3 изд., М.,
1Я67; [4] Б а х в а л о в Н. С, Численные методы, 2 изд., М.,
19751 А. Ф. Леонтьев.
КОНИКА — линия 2-го порядка, т. е. множество
точек плоскости (проективной, аффинной, евклидовой),
однородные координаты х0, хх, х2 к-рых (относительно
проективной, аффинной или декартовой систем коор-
координат) удовлетворяют однородному уравнению второй
степени:
Билинейная симметричная форма
ф (х х\ __ V1" а. .х-х-
наз. полярной формой относительно F{x). Две
точки М'(х'о, .Ti, x',), M"(x'o, x'l, x'i), для к-рых Ф (х',х") =
= 0. наз. полярно сопряженными относительно К. Ес-
Если прямая (М', М") пересекает К. в точках Л\, N2 и
точки М', М" полярно сопряжены относительно К., то
точки Nx, N2 и М', М" образуют гармоннч. четверку.
Точки К. и только они являются самосопряженными от-
относительно К.Полюсом данной прямой относитель-
относительно К. наз. точка, полярно сопряженная со всеми точ-
точками этой прямой. Множество точек плоскости, поляр-
полярно сопряженных с данной точкой М' относительно К.,
наз. полярой точки М' относительно К. Поляра
точки М' определяется линейным уравнением Ф (х, х')-—
= 0 относительно координат х0, хх, х2. Если Ф (х, х')^0,
то поляра точки М'— прямая линия; если Ф (х, х') = О
то поляра точки М' — вся плоскость. В этом случае
точка М' принадлежит К. и наз. ее о с о б о й т о ч-
к о и. Если число ^ = rang(e,y) = 3, то К. не имеет осо-
особых точек и наз. невырождающейся, или нераспадаю-
нераспадающейся. На проективной плоскости это — действитель-
действительный овал, или мнимый овал. Нераспадающаяся К. оп-
определяет на проективной плоскости корреляцию —
биективное отображение множества точек на множество
прямых. Касательная к нераспадающейся К.
есть поляра точки касания. Если Л = 2, то К. является
парой действительных или парой мнимых прямых, пере-
пересекающихся в особой точке. Если Д=1, то каждая точ-
точка К. является особой, а сама К.— парой совпадающих
действительных прямых (сдвоенной прямой). Аффинные
свойства К. выделяются спецификой ее расположения
и ассоциированных с ней точек и прямых относительно
выделенной прямой яо=О — несобственной прямой.
К. имеет гиперболический, эллиптический или парабо-
параболический тип в зависимости оттого, пересекает она не-
собственную прямую (б<0, 6 =
a.2la.12
), не пересекает
F>0) или касается ее F — 0). Центр К.— полюс несоб-
несобственной прямой, диаметр — поляра несобствен-
несобственной точки, асимптота — касательная к К. в не-
несобственной точке. Два диаметра сопряжены относи-
относительно К., если их несобственные точки полярно со-
сопряжены относительно К.
Метрические свойства К. выделяются из аффинных
инвариантностью расстояния между двумя произволь-
произвольными точками. Диаметр К., ортогональный сопряженно-
сопряженному с ним диаметру, является осью симметрии К. it на.!,
ее осью. Директриса К.— поляра ее фокуса.
Лит.: [1] Фиников С. П., Аналитическая геометрия,
2 изд., М., 1952; 1.2] Ефимов Н. В., Краткий курс анали-
аналитической геометрии, 5 изд., М. I960. В. С. Малаховский.
КОНИЧЕСКАЯ КОНСТРУКЦИЯ — сопоставление с
каждым непрерывным отображением топологпч. про-
пространств / : X—>-У топологпч. пространства CfD Y, к-рое
получается из топологнч. суммы (несвязногоt объедине-
объединения CX'+sY (здесь CX=(XX[0,l])f(XX {0}) — конус
над X) отождествлением гХ {1}=/(х), х?Х. Простран-
Пространство С j на.!, конусом отображения /. Если
пространства X, Y пунктированы отмеченными точка-
точками х?Х, y?Y, то дополнительно стягивается в точку
образующая ,тХ[0, 1] конуса СХ, и само С j наз. стя-
стянутым конусом отображения /. Для
любого пунктированного топологич. пространства К по-
последовательность X-+YczCj индуцирует точную после-
последовательность
[А', А'] <- [Y, К] *- [С,, К]
пунктированных множеств. Отображение / гомотопно по-
постоянному отображению в отмеченную точку тогда и
только тогда, когда У является ретрактом простран-
пространства СI.
Лит.: ШСпеньср Э., Алгебраическая топология, пер.
с англ., М., 1971; [2] М о ш е р Р. Э., Т а н г о р а М. К.,
Когомологические операции и их приложения в теории гомо-
топий пер. с англ., М. 1970. ' А. Ф. Харшиладзе.
КОНИЧЕСКАЯ ПОВЕРХНОСТЬ, конус, — по-
поверхность, образуемая движением прямой (образую-
щ е й). проходящей через данную точку (вершину
К. п.) и пересекающей данную линию (направляю-
щ у ю). К. п. имеет две полости, расположенные сим-
симметрично относительно вершины.
Коническая поверхность 2-го по-
порядка — один из видов поверхностей второго поряд-
порядка. Каноническое уравнение действительной К.
п. 2-го порядка:
о2 ¦ Ь2 с2 >
если а—й, то К. п. наз. круглой (круговой)
К. п., или К. п. в р а щ е н и я; каноническое уравне-
уравнение м н и м о п К. п. 2-го порядка:
Т2 7/2 72
О2 Т Ь2 Г С2 V'>
единственная действительная точка мнимой II. и.—
точка @, 0, 0).
Конической поверхностью »-го по-
порядка наз. алгебраич. поверхность, задаваемая в
аффинной системе координат х, у, z уравнением:
f{x,y,z) = O,
где f(x, у, z) есть однородный многочлен (форма ге-й
степени от переменных х, у, z). Если точка М (х0, у0, z0)
лежит на К. п., то и вся прямая ОМ лежит на К. п.
(точка О — начало координат). Справедливо и обрат-
обратное утверждение: всякая алгебрапч. поверхность, к-рая
состоит из прямых, проходящих через одну точку, есть
К. П. А. Б. Иванов.
КОНИЧЕСКАЯ СЕТЬ — сопряженная сеть на по-
поверхности трехмерного пространства, образованная ко-
пческими линиями, т. е. линиями касания конусов,
описанных около поверхности. Поверхности, несущие
К. с, на». Нетерсона поверхностями. Переноса сеть
можно рассматривать как частный случай К. с. Верши-
Вершины конусов К. с. расположены на двух кривых. К. с.
зависят самое большее от четырех параметров. Только
невырожденные поверхности 2-го порядка несут 4-па-
раметрнческое семейство К. с. Поверхности, несущие
2-нараметрнческое семейство К. с,— линейчатые, при-
принадлежащие линейной конгруэнции (т. е. конгруэн-
конгруэнции, образованной общими секущими двух прямых).
Лит.: [1] Бланк Я. II., «Тр. геометр, семинара. Ин-т
науч. информ. АН СССР», 1971, т. 3, с. 5—27. В. Т. Базылев.
КОНИЧЕСКИЕ СЕЧЕНИЯ — линии, к-рые полу-
получаются сечением прямого кругового конуса плоскос-
плоскостями, не проходящими чере.ч его вершину. К. с. мо-
могут быть трех типоп:
1) секущая плоскость
пересекает все обра-
образующие конуса в
точках одной его по-
полости (рис., а): линия
перосечеппя есть зам-
замкнутая овальная кри-
кривая — эллипс; окруж-
окружность как частный
случай эллипса полу-
получается, когда секущая
плоскость перпенди-
перпендикулярна осп конуса. 2) Секущая плоскость параллель-
параллельна одной из касательных плоскостей конуса (рис., б); в
сечении получается незамкнутая, уходящая в беско-
бесконечность кривая — парабола, целиком лежащая на од-
одной плоскости. 3) Секущая плоскость пересекает обе
полости конуса (рис., в); линия пересечения — гипер-
гипербола — состоит пз двух одинаковых незамкнутых, про-
простирающихся в бесконечность частей (ветвей гипербо-
гиперболы), лежащих на обеих полостях конуса.
С точки зрения аналитич. геометрии К. с.— действи-
действительные нераспадающиеся линии второго порядка.
В тех случаях, когда К. с. имеет центр симметрии
(цент р), т. е. является эллипсом или гиперболой,
его уравнение может быть приведено (путем перенесе-
перенесения начала координат в центр) к виду:
апх2 + 2я, гху -+ а22у2 — а33.
Дальнейшие исследования таких (наз. централ ь-
н ы м и) К. с. показывают, что их уравнения могут
быть приведены к еще более простому виду:
если за направления осей координат выбрать так на;!,
главные направления — направления главных
осей (осей симметрии) К. с. Если А и В имеют оди-
одинаковые знаки (совпадающие со знаком С), то уравне-
уравнение (*) определяет эллипс; если А и В разного знака,
то — гиперболу.
Уравнение параболы привести к виду (*) нельзя.
При надлежащем выборе осей координат (одна ось ко-
координат — единственная ось симметрии параболы, дру-
другая — перпендикулярная к ней прямая, проходящая
через вершину параболы) ее уравнение можно привести
к виду:
г/2 = 2рх.
К. с. были известны уже математикам Древней Гре-
Греции. Наиболее полным сочинением, посвященным этим
кривым, были «Конические сечения» Аполлония Перг-
ского (ок. 200 до н. э.). Дальнейшие успехи теории К. с.
связаны с созданием в 17 в. новых геометрич. методов:
проективного [Ж. Дезарг (G. Desargues), Б. Паскаль
(В. Pascal)] и в особенности координатного [Р. Декарт
(R. Descartes), П. Ферма (P. Fermat)].
При надлежащем выборе системы координат (ось
абсцисс — ось симметрии К. с, ось ординат — каса-
касательная в вершине К. с.) уравнение К. с. может быть
приведено к виду:
(р и X — постоянные). Если р=т^0, то оно определяет
параболу при А,= 0, эллипс при Я<0, гиперболу при
Я>0. Геометрич. свойство К. с, содержащееся в по-
последнем уравнении, было известно уже древнегреч.
геометрам п послужило для Аполлония Пергского пово-
поводом присвоить отдельным типам К. с. названия, сохра-
сохранившиеся до сих пор: слово «парабола» (греч. parabole)
означает приложение (т. к. в греч. геометрии превра-
превращение прямоугольника данной площади у2 в равновели-
равновеликий ему прямоугольник с данным основанием 1р наз.
приложением данного прямоугольника к этому
основанию); слово «эллипс» (греч. cileipsis) — недоста-
недостаток (приложение с недостатком); слово «гипербола»
(гроч. hyperbole) — избыток (приложение с избытком).
С переходом к современным методам исследования
стереометрия, определенно К. с. было заменено плани-
мотрич. определениями этих кривых как множеств то-
точек на плоскости. Так, напр., эллипс определяется как
множество точек, для к-рых сумма расстояний от двух
данных точек (фокусов) имеет данное значение. Можно
дать другое планпметрпч. определение К. с, охваты-
охватывающее все три типа этих кривых: К. с.— множество
точек, для каждой из к-рых отношение ее расстояний
до данной точки (фокуса) к расстоянию до данной пря-
прямой (директрисы) равно данному положительному чис-
числу (эксцентриситету) е. Если при этом е<1, то К. с.—
эллипс; если е>1, то — гипербола; если е=1, то — па-
парабола.
Лит.: [1] Александров П. С, Лекции по аналити-
аналитической геометрии, М., 1968; [2] В а н дер В а р д е н Б. Л.,
Пробуждающаяся наука, пер. с голл,, М., 1959.
В. И. Битюцков.
КОННЕКС, к о и н е к с К л е б ш а,— связь точек
п прямых на плоскости, выражаемая уравнением
/(х\ х\ х\ ih, и2, и3) = 0, A)
где х1 и и,- — однородные координаты соответственно
точки и прямой. Напр., уравнение
u1x1+uix2+u3x3=0 B)
задает так наз. главный коннекс, выражаю-
выражающий инцидентность точки х н прямой и. То, что два К.
имеют общее, наз. к о н ц и д е н ц и е п. Понятие К.
введено А. Клебшем (A. Clebsch) в 1871 для однородной
формулировки дифференциальных уравнений.
Так, уравнение
определяется конциденцией К. A) п B), и задача инте-
интегрирования C) заключается в том, чтобы из х опреде-
определенных таким образом соответствующих точек и пря-
прямых и составить кривые, для к-рых х и и являются со-
соответствующими точками интегральной кривой и каса-
касательными к ней. Введение такой проектной точки зре-
зрения (равноправности координат х и и) дает также не-
к-рый принцип классификации дифференциальных
уравнений.
Аналогичные построения могут быть проведены для
уравнений с частными производными, причем но обяза-
обязательно первого порядка.
Лит.: [1] Клейн Ф., Высшая геометрия, пер. с нем.,
М.— Л., 1939. М. II. Войцеховский.
КОНОИД — Каталана поверхность, все прямоли-
прямолинейные образующие к-рой пересекают фиксированную
прямую — ось К. Напр., гиперболпч. параболоид
есть К. с двумя осями.
Радиус-вектор К.
г= {и cos y+a/(w), и sin v-{-$f(v), yf(v)},
где {a, P, 7} — единичный вектор, имеющий направле-
направление оси 1С, f(v) — некоторая функция. Для прямого К.
а=Р-=0, у=1, и тогда его ось является стрикцпонной
линией. Прямой К. с f(v)=av есть геликоид.
11. X. Сабитов.
КОНОРМАЛЬ — термин, употребляемый в теории
краевых задач для дифференциальных уравнений с част-
частными производными. Пусть V—(Vj, ... , vn)—внешняя
нормаль в точке х к гладкой поверхности S, располо-
расположенной в евклидовом пространстве Е" с координатами
х1, . . . , х", g'J — контравариантный невырожденный
тензор, обычно представляющий коэффициенты нек-рого
дифференциального оператора второго порядка D =
.. д в
= g'J • —;•. Тогда конор малью (относительно D)
дх dyJ
наз. вектор
re=(v1, . . . , v"),
где v' = glkvk. Другими словами, К.— контравариантная
запись (в пространстве с метрикой, определяемой тен-
тензором, обратным g'J) нормального к S ковариантного
(в пространстве с евклидовой метрикой) вектора v.
Лит.: [1] Б и ц а д з е А. В., Уравнения математической
физики, М., 197В; [2] Миранда К., Уравнения с частными
производными эллиптического типа, пер. с итал., Ы.. 1957.
М- И. Boviit-'.ховскип.
КОНСТАНТА в математической логи-
логике — символ формального языка для обозначения неко-
некоторого фиксированного элемента (индивида), фиксиро-
фиксированной операции или отношения на какой-либо струк-
структуре, описываемой этим языком. В соответствии с этим
различают индивидные константы, функциональ-
функциональные константы и предикатные кон-
константы. Совокупность всех К. языка наз. с и г н а-
т у р о й этого языка. Напр., сигнатура языка ариф-
арифметики формальной состоит из индивидной К. «О»
(нуль), двуместных функциональных К. «+» (сложение)
и «•» (умножение), одноместной функциональной К. «'»
(прибавление единицы) и двуместной предикатной К.
«—» (равенство). С. К. Соболев
КОНСТРУКТИВНАЯ КВАНТОВАЯ ТЕОРИЯ ПО-
ПОЛЯ — раздел математической физики, изучающий свой-
свойства моделей квантовой теории поля (к. т. п.). Одна из
задач К. к. т. и. состоит в исследовании квантовых по-
полей в реальном 4-мерном пространстве-времени. Однако
само существование этих полей остается A978) матема-
математически недоказанным. Основные усилия были направ-
направлены на изучение менее сингулярных моделей к. т. п.
в 2- и 3-мерном пространстве-времени. К. к. т. п. пред-
представляет собой синтез идей и методов аксиоматич. тео-
теории поля и теории перенормировок с современными ма-
тематич. методами. Само понятие релятивистского кван-
квантового поля допускает различные эквивалентные мате-
матич. интерпретации, что позволяет использовать в
к. т. п. методы различных областей математики.
Квантовое поле можно трактовать либо в терминах
теории нелинейных гиперболич. уравнений для опера-
операторных обобщенных функций, либо в терминах тео-
теории обобщенных случайных полей (устанавливая тес-
тесный контакт со статистич. механикой), либо как систему
аналитпч. функций многих комплексных переменных
(при изучении аналитич. свойств 5-матрицы), либо же
рассматривать его с точки зрения С*-алгебр и теории
представлений.
В первых работах по К. к. т. п. использовались в ос-
основном средства функционального анализа. Реляти-
Релятивистское квантовое поле в 2-мерном пространстве-вре-
пространстве-времени, удовлетворяющее аксиомам Уайтмана, впервые
удалось построить [8], только используя евклидову фор-
мулировку [9] к. т. п., позволившую привлечь методы
теории вероятностей п статистич. механики.
Релятивистское квантовое поле полностью характе-
характеризуется последовательностью своих функции Уайтма-
на VFn(.Tj, . . . , ,г„). Эквивалентная евклидова форму-
формулировка к. т. п. дается последовательностью функций
Швингера Sn(xl, . .. , хп) (они получаются из Wп ана-
лнтпч. продолжением в евклидовы точки (ix\, act, ix\ ,
а%, . . .)), удовлетворяющих аксиомам Остервальдера —
Шрадера (ОШ). При некоторых дополнительных пред-
предположениях можно доказать, что Sn являются момен-
моментами вероятностной .меря, обладающей специальными
свойствами. Способ построения моделей к. т. п., при
к-ром сначала строится вероятностная мера, а затем
проверяются аксиомы ОШ для ее моментов, оказался
наиболее удобным и является общепринятым.
В простейшем случае одного скалярного поля рас-
рассматривается измеримое пространство (of'(Rd), <S&), где
гУ(йа) — пространство обобщенных функции умерен-
умеренного роста, иЗ есть ст-алгобра, генерируемая цилиндри-
цилиндрическими множествами, и класс вероятностных мер и.
на (сУ, <$), обладающих следующими специальными
свойствами.
1) На (of1, а8) задано естественное представление
связной компоненты единицы G евклидовой группы дви-
движении Rd автоморфизмами а-алгебры иЗ. Требуется,
чтобы мера и была G-инвариантна. Это условие
есть евклидово выражение релятивистской инвариант-
инвариантности.
2) Пусть Ф (/) — непосредственно заданное обобщен-
обобщенное случайное поле на Qf', иЗ, (х), т. е. Ф (/)(ш)= со (/),
f»^af' ,/(;?У. Для любой функции ^(со)на &' определя-
определяется Fe((o)=F(a>()), где ше(/)=ш(/е), fQ(xu . .. , xd)=
= /(.xj, ... , —*rf). Пусть & + — о-алгебра, генерируе-
генерируемая функциями Ф (/) с supp fd{x?Rd, xa>0}. Требует-
Требуется выполнение условия положительности ОШ:
для любой & + -измеримой функции F насУ'.Это усло-
условие выражает положительную определенность скаляр-
скалярного произведения в релятивистском гильбертовом про-
пространстве. Для двумерных моделей широко использует-
используется несколько более сильное условие марковости поля
)
(/)
3) Требуется существование нормы ||-|| на <ff(Rd)
такой, что
равномерно ограничена и непрерывна по норме
4) Подгруппа трансляций группы G должна дейст-
действовать эргодпческл. Это есть выражение единствен-
единственности вакуума в релятивистской теории.
Если мера и, удовлетворяет условиям 1—4, то она
называется квантовой мерой, а соответствую-
соответствующее обобщенное случайное поле Ф (/) наз. евклидо-
евклидовым полем. Моменты квантовой меры
Sa(fi, .... /Я)
— функции Швингера, удовлетворяют аксиомам ОШ.
Существует единственное релятивистское квантовее
поле, удовлетворяющее всем аксиомам Уайтмана, талое,
что аналитич. продолжение его функций Уайтмана в ев-
евклидовы точки совпадает с функциями Швпнгера дан-
данной квантовой мерог ц. Если некоторая мера и. удов-
удовлетворяет лишь условиям 1 — 3, то для всех ее эргоднч.
компонент выполняются условия 1—4.
Один класс квантовых мер строится легко — это га-
гауссовы меры (зависящие от параметра ;ге>0) с характе-
ристнч. функционалом
/-4- (/, (-Д-f m)-1/) |
здесь Д — оператор Лапласа (при d^3 допускается
7/г=0). Соответствующее евклидово поле называют сво-
свободным (скалярным) евклидовым полем массы т.
Построение негауссовых мер представляет боль-
большие трудности, ir результаты существенно зависят
от размерности d. Обычная процедура следующая. Стро-
Строится нек-рая функция У (А., х) на $" (потенциал взаимо-
взаимодействия), зависящая от параметров Л, наз. объемным
обрезанием, и х, наз. ультрафиолетовым обрезанием.
Эвристически V——Jifint (CM- Квантовая теория поля).
Желательно, чтобы Г(Л, х) обладала свойствами а д-
д и т и в н о г о функционала. Затем строится мера
(определение dv^ см. ниже) н изучаются пределы по-
последовательности мер d\ix и при Л, х—>-оо. Для некото-
некоторых потенциалов V (каких именно — определяется из
физич. соображений; вид V и задает модель) предельная
мера (х будет удовлетворять условиям 1—4. Сходимость
мер обычно понимается в смысле сходимости всех мо-
моментов и характеристич. функционалов.
Напр., для модели со взаимодействием А.Ф4 при d=2
эта процедура конкретизируется следующим образом.
Пусть d\'^— гауссова мера на (<fjP', <3$) с характеристич.
функционалом
exp{i(D(/)}dv?=exp {--5-(A (-^A + m')~1f)L>} .
где ДЛ— самосопряженное расширение оператора Лап-
Лапласа с нек-рыми краевыми условиями на границе дА
области Л на плоскости R2 (обычно Л — прямоуголь-
прямоугольник); ядром (—&.А-{-т?)~1(х, у) может быть, папрнмер,
функция Грина для задачи Дирихле. Пусть, да-
далее, hK?3P и hK{x—y)^-b(x—y) при ?—>-оо. Случайная
величина Ф (ж)=Ф (Лх(ж—.)) при х<оо является
гладкой функцией параметра х ? R2 и
Фх (х) f (х) йх^Ф (/)
при х—>-оо. Положим
V(A, х) =
где : Фи(х): виковская степень случайной величины
() ( Фа прос) Т
-к (Л,
д и() у
Ф (х) (см. Фока пространство). Тогда
Пусть, наконец,
При х—>-оо, Л—>-R2 все моменты и характеристич. функ-
функционалы мер u, v и сходятся к моментам и характери-
характеристич. функционалу нек-poii квантовой меры [X. Оказы-
Оказывается, что при достаточно больших Хмеры |j,A=lim (Л^ к
с разными краевыми условиями на дА имеют, вооб-
вообще говоря, разные пределы при A^R2. В этом случае
говорят, что имеет место фазовый переход.
Задача К. к. т. п. состоит в том, чтобы описать все
квантовые меры (фазы), отвечающие данному потении-
алу взаимодействия, п исследовать свойства соответст-
соответствующих релятивистских квантовых полей. В первую
очередь интересуются спектральными свойствами опе-
оператора массы группы Пуанкаре (его изучение сводится
к рассмотрению поведения функций Швпнгера на боль- |
ншх расстояниях) и свойствами ^-матрицы — анали-
аналитичность, унитарность п другие E-матрица изучается
при помощи аналитического продолжения функций
Швтшгера).
Существование квантовых мер при d= 2 доказано A978)
для потенциалов взаимодействия У=Р(Ф), Р — любой
полуограниченный снизу полином, V=X cos §Ф (урав-
(уравнение синус-Гордона) и нек-рых других неполиномиаль-
неполиномиальных взаимодействий, а также для нек-рых многокомпо-
многокомпонентных полей Ф = (ФХ, ... , Фд')- Для полиномиаль-
полиномиального достаточно слабого взаимодействия начато изуче-
изучение спектра массового оператора в зависимости от вида
полинома и установлено существование S-матрицы.
Исследуется также взаимодействие Юкавы ферлшонных
и скалярных полей. Евклидово фермионное поле не
является обобщенным случайным полем, оно прини-
принимает значения в алгебре Грассмана. Однако по фермп-
онным переменным можно «проинтегрировать», и задача
сводится к оценкам нек-рых континуальных интегралов
по обычным гауссовым мерам. Все эти модели при не-
нек-рых значениях параметров имеют фазовые переходы.
Описанная выше конструкция релятивистских кван-
квантовых полей приводит только к так называемым вакуум-
вакуумным секторам, т. е. к квантовым полям, удовлетворяю-
удовлетворяющим аксиомам Уайтмана, включая существование ва-
вакуума. Эти поля являются решением нелинейных урав-
уравнений с простейшими начальными условиями. Для ряда
2-мерных моделей (синус-Гордона и др.) построены со-
литонные сектора, у которых вакуум отсутствует, но
которые имеют весьма интересный с физич. точки зре-
зрения спектр оператора массы. Эти новые сектора стро-
строятся при помощи специальных автоморфизмов С*-ал-
С*-алгебры, наблюдаемых в вакуумном секторе.
При d=3 доказано существование квантовых мер
для модели с Х(Ф, ФJ взаимодействием, где
Потенциал взаимодействия здесь имеет вид
V (Л, у.) = Х ^ ^:(ФИ (.т), фи (x))
, Фк(х)):с1х+СК<А,
где бтх и Ск Л — некоторые определенные функции от
х и Л, т. е. добавлены контрчлены. В этой модели также
происходит фазовый переход при достаточно больших
X, причем ен сопровождается нарушением 0(ЛО-сим-
метрип.
Лит.: [1] Б о г о л ю б о в Н. Н., Логунов А. А.,
Тодоров И. Т., Основы аксиоматического подхода в кван-
квантовой теории поля, М., 1969; [2J Конструктивная теория поля,
пер. с англ., М., 1977; [3] Рид М., Саймон Б., Методы
современной математической физики, пер. с англ., М., т. 1,
1977, т. 2, 1978; [4] С а й м о н Б., Модель Р (фJ эвклидовой
квантовой теории поля, пер. с англ., М., 1976; [5] X е п п К.,
Теория перенормировок, пер. с франц., М., 1974; [б] Эвклидова
квантовая теория поля. Марковский подход, пер. с англ., М.,
1978; [7] Д о б р у ш и н Р. Л., М и н л о с Р. А., «Успехи
матем. наук» 1977, т. 32, в. 2 с. 67 — 122; [8] Climm J.,
Jaffe A. Spencer Т. «Ann. Math.» 1974, v. 100, JVi 3,
p. 585—632; [91 Nelson E., «J. Funct. Anal.», 1973, v. 12,
,"№ 1, p. 97 — 112; [10] Fr ohl i ch J., «Adv. Math.», 1977, v. 23,
№2, p. 119—81. И. В. Волович, М. К. Поливанов.
КОНСТРУКТИВНАЯ ЛОГИКА — раздел математи-
математической логики, изучающий рассуждения о конструктив-
конструктивных объектах и конструкциях. При таком понимании
К. л. шире, чем логика конструктивной математики.
Самое заметное отличие от традиционной (классиче-
ской) логики состоит в отсутствии исключенного третьего
закона А\/~~}А н двойного отрицания закона ~| ~~]А—*-А.
При обозначении систем чдстой логики (исчисление
высказываний, предикатов) термины «конструктивное»,
«интуиционистское», «гейтинговское» часто считаются
синонимами (см. Рейтинга формальная система). Под
конструктивной арифметикой иногда
понимают гмтшговскую арифметику, а иногда — ее
расширение, нолучаемое добавлением принципа Марко-
Маркова (см. Конструктивного подбора принцип) и схемы
А*-*Зе(е г А), выражающей эквивалентность формулы и
утверждения о ее реализуемости (см. Конструктивная
семантика). Эта расширенная система, достаточная для
доказательства основных результатов конструктивного
математич. анализа, но является, в отличие от гейтпн-
говскнх систем, подсистемой классич. арифметики: в
ней опровергается закон исключенного третьего
4x(A(x)v~\A(x)).
Иногда к К. л. относят системы интуиционистской ло-
логики, содержащие средства описания специфически
интуиционистских понятий. Общая черта подавляюще-
подавляющего большинства систем К. л., отражающая специфику
конструктивного понимания связки у и квантора 3,—
явная реализация этих связок: выводимость А\В (со-
(соответственно ВхА (x)) влечет выводимость одной из фор-
формул А, В (соответственно A (t) для нек-рого терма t).
При этом в случае прикладных слсте.м (арифметика,
анализ) требуется замкнутость рассматриваемых фор-
формул. Большинство систем К. л. (включая все геитпнгов-
ские системы) корректны относительно различных по-
понятий реализуемости, включая реализуемость по К лини
и Гёделя интерпретацию: все выводимые формулы
реализуемы, в частности истинны, в конструктивной
семантике. С другой стороны, формальные системы К. я.
обычно неполны относительно естественной конструк-
конструктивной семантики. Для систем, содержащих арифмети-
арифметику, это следует из Гёделя теоремы о неполноте.
Множество реализуемых предикатных формул неие-
речислимо, поэтому конструктивное исчисление иреди-
катов неполно относительно реализуемости, а из его
полноты относительно «наивной» конструктивной се-
семантики следовала бы интуиционистская истинность
принципа конструктивного подбора. Конструктивное
исчисление высказываний также неполно относительно
реализуемости, но полно при нек-рой интерпретации в
терминах систем Поста. Арифметическая по-
полуформальная система, полная относи-
относительно конструктивной семантики Маркова — Шанина,
получается, если добавить к формальной конструктив-
конструктивной арифметике со схемой А<—>Ве(егА) и принципом
конструктивного подбора эффективное со-п р а-
в и л о: из А @), А A), . . . вывести ЧхА (х). Для гей-
Пшговскпх систем установлены теоремы полноты отно-
относительно теоретико-модельных семантик Крипке и Бе-
Бета, использующих «возможные миры» (эти семантики
связаны с теоретико-множественным вынужденней), а
также относительно алгебраических и топологических
моделей.
классические формальные системы обычно погру-
жаю.тся в соответствующие системы К. л. (с сохране-
сохранением отношения выводимости из гипотез) с помощью
негативного перевода, т. е. приписыва-
приписывания двойного отрицания ~] ~~\ перед всеми подформула-
подформулами. Поэтому системы арифметики, анализа и типов
теории, основанные на классич. логике, изоморфно
вкладываются в соответствующие системы, основанные
на К. л. Имеются системы теории множеств, основан-
основанные на К. л., в к-рые погружаются классич. системы.
Гептинговские системы погружаются в модельные рас-
расширения классических с помощью d-перевода,
т. е. приписывания знака необходимости D перед всеми
подформулами. При этом D можно читать «доказуемо».
В нек-рых системах К. л. справедливы суждения,
ложные при классическом истолковании, напр, отрица-
отрицание закона исключенного третьего или специфически
интуиционистские утверждения о последовательностях.
Такие системы S сводятся к классическим системам S°
с помощью подходящего понятия реализуемости р. До-
Доказывают, что S\—А влечет существование t такого, что
S"\—(tpA), причем если А — числовое равенство, то
S°\—(А*—ырА). Отсюда следует непротиворечивость &
относительно 5°.
К. л. исследует истинность суждений также в нетра-
нетрадиционных языках, отличных от языков логики преди-
предикатов арифметики, анализа и т. д. Наряду с традици-
традиционным отрицанием ~), основанным на приведении к про-
противоречию, изучается сильное отрицание ~,
предусматривающее построение контрпримера. Для ~
справедливы многие из законов классич. логики, напр.
но теорема об эквивалентной замене верна лишь в виде
((р <-> 9) & (~ /, <-> ~_ д)) Z) (А (р) <-> А (д)).
К системе сильного отрицания близки системы, осно-
основанные на симметричной трактовке истинности и лож-
ложности. Семантика для них предусматривает указание
но только вида конструкций, обосновывающих истин-
истинность, но и вида конструкций, обосновывающих лож-
ложность рассматриваемого суждения.
Безотрицательная логика Грисса — Нель-
Нельсона стремится избежать использования отрицания и
ограничить класс свойств, о к-рых делаются утверж-
утверждения, такими, для к-рых уже построены объекты, удов-
удовлетворяющие этим свойствам. Язык такой логики со-
содержит связку -> причем А ~>-В понимается при-
приблизительно как
V.!1 (A ZD В) & ЗхА.
В т е о р и и конструкций исследуются сами
правила построения и доказательства, лежащие в осно-
основе конструктивной математики. Конструкции строятся
из исходных с помощью фиксированного набора комби-
комбинаторов и операции применения функции к аргументу.
Формулы строятся из равенства с помощью связок ло-
логики высказываний и предиката доказуемости я, причем
л(а, х-а(х)) читается «а есть доказательство того, что
а(х) верно для всех .т>>. В качество аксиом берутся, в
частности, всо классические тавтологии (включая закон
исключенного третьего), т. е. отношение «быть доказа-
доказательством» предполагается разрешимым. Имеется кор-
корректная и точная интерпретация гейтинговскпх систем
в теории конструкций.
Рассмотрение в К. л. бескванторных систем вызвано
стремлением получить финитные (в том или ином смыс-
смысле) доказательства рассматриваемых суждений или их
мажорант (см. Конструктивная семантика). Многие
традиционные системы S К. л. погружаются в бескван-
бескванторные системы S~ таким образом, что выводимость в S
суждения \jx^yR (х, у) с бескванторной формулой Л
влечет выводимость п S~ формулы li(x, <р(х)) для под-
подходящего ф. Если S — арифметика без индукции, то
S~ примитивно рекурсивная арифметика; если S —
гейтинговская арифметика, то S~ — система гёделев-
ских примитивно рекурсивных функционалов.
Для формальных систем К. л. доказаны теоремы
нормализации: любой вывод может быть конеч-
конечным числом стандартных преобразований (редукций)
приведен к нормальной форме, не содержащей «лишних»
участков (см. Генцеиа формальная система). Нормаль-
Нормальные выводы обладают (в полной мере или, в случае
арифметики и более широких систем, частично) свойст-
свойством подформульности.
Имеются связи между К. л. п теорией категорий. Так,
понятию «декартовой замкнутой категории» соответст-
соответствует гейтинговское исчисление высказываний.
Иногда к К. л. относят все логические рассмотрения,
в к-рых требуется, чтобы все изучаемые объекты были
конструктивными, независимо от применяемой логики.
С этой тенденцией связано название конструктивных
по Гёделю множеств.
Лит.: [1] К л и н и С. К., Введение в метаматематику, пер.
с англ., М., 1957; [2] Troelstra A. S., в кн.: Metamathema-
tical investigation of intuitionistic arithmetic and analysis,
В. —Hdlb.—N. Y., 1973; [3] H о в и к о в П. С, Конструктив-
Конструктивная математическая логика с точки зрения классической,. М.,
1977; [4] Kreisel G., Mathematical logic, в кн.: Lectures on
modern mathematics, v. 3, N. Y., 1965, p. 95 —195. Г. Е. Минц.
КОНСТРУКТИВНАЯ МАТЕМАТИКА, конст-
конструктивное направление в математи-
математике,— математика, строящаяся в соответствии с тем
или иным конструктивным математич. мировоззрением,
обыкновенно стремящимся связывать утверждения о
существовании математич. объектов с возможностью их
построения и отвергающим в силу этого ряд установок
традиционной теоретико-множественной математики,
приводящих к появлению чистых теорем существо-
существования (в частности, абстракцию актуальной бесконечно-
бесконечности и универсальный характер исключенного третьего
закона). Конструктивная тенденция в математике про-
проявлялась в той или иной форме на протяжении всей ее
истории, хотя, по-видимому, только К. Гаусс (С. Gauss)
впервые отчетливо выразил принципиальное для К. м.
различие становящейся (потенциальной) и актуальной
математич. бесконечности и возразил против употреб-
употребления последней. Дальнейшие критические шаги в этом
направлении были сделаны Л. Кронекером (L. Кгоие-
cker), А. Пуанкаре (Н. Poincare) и особенно Л. Брауэ-
ром (L. Brouwer). В критике Л. Брауэра, совпавшей по
времени с кризисом оснований математики конца 19 —
нач. 20 вв., энергично отвергалась как вера в экзи-
экзистенциальный характер бесконечных множеств, так и
убеждение в допустимости неограниченной экстраполя-
экстраполяции классических логических принципов, в особенности
закона исключенного третьего. В качестве альтернати-
альтернативы теоретико-множественному подходу Л. Брауэр, а
затем и его последователи, разработали оригинальную
программу построения математики, известную ныне под
названием интуиционизм. Интуиционистскую матема-
математику Л. Брауэра можно считать первой систематич.
попыткой построения математики на конструктивной
основе. Параллельно успехам интуиционистов в создан-
созданной Д. Гильбертом (D. Hilbert) с целью обоснования
теоретико-множественной математики доказательств
теории был четко выявлен ряд первоначальных поня-
понятий, послуживший впоследствии отправной точкой от-
отличных от интуиционизма конструктивных течений.
Значительная часть соответствующих работ (при этом
обнаружился достаточно широкий спектр толкования
различными исследователями терминов «конструктив-
«конструктивный», «эффективный» и пр.) опиралась на успехи, достиг-
достигнутые (опять-таки под влиянием идей Д. Гильберта) в
изучении матоматпч. понятия алгоритма. Один из наи-
наиболее последовательных и законченных подходов к по-
построению К. м. на этой основе доставляется основанной
А. А. Марковым советской школой К. м., формирование
основных понятий к-рой относится к 50-м гг. 20 в. Сам
термин «К. м.» (конструктивное направление в матема-
математике) часто употребляется в узком смысле слова для
именования математики, строящейся советским конст-
конструктивным направлением; ниже этот термин будет ис-
использоваться именно в указанном только что смысле.
К. м. может быть коротко охарактеризована следую-
следующими основными чертами: A) предметом изучения яв-
являются конструктивные процессы и возникающие в ре-
результате их выполнения конструктивные объекты;
B) рассмотрение конструктивных процессов п объектов
производится в рамках абстракции потенциальной осу-
осуществимости с полным исключением идеи актуальной
бесконечности; C) интуитивное понятие эффективности
связывается с точным понятием алгоритма; D) исполь-
используется специальная, учитывающая специфику конст-
конструктивных процессов и объектов конструктивная ло-
логика.
Понятия конструктивного процесса и конструктивно-
конструктивного объекта являются первоначальными; представления
о них пмеют своим источником практическую матери-
материальную деятельность человека. Примерами конструк-
конструктивных процессов могут служить сборка часов на кон-
конвейере, полная пли частичная разборка их в ремонтной
мастерской, набор текстов (с корректурами) в типогра-
типографии, формирование и расформирование железнодорож-
железнодорожных составов и пр. Характерной чертой конструктивных
процессов является протекающее по отдельным шагам
оперирование в рамках нек-рых четко указанных пра-
правил с элементарными, заведомо отличимыми друг от дру-
друга объектами, считающимися неразложимыми в ходе
этих процессов. Возникающие в результате фигуры, со-
составленные из исходных элементарных объектов, и счи-
считаются конструктивными объектами.
К. м. не имеет необходимости углубляться в общее по-
понятие конструктивного процесса и объекта, поскольку
для ее нужд оказывается вполне достаточным один спе-
специальный вид конструктивных объектов — слова в том
или ином алфавите.
Рассмотрение слов (это понятие также представляется
первоначальным) происходит на следующей основе.
Вначале фиксируется нек-рый алфавит, т. е. список
неразложимых, уверенно отличимых друг от друга эле-
элементарных знаков (бук в). Каждая буква алфавита
может копироваться; возникающие в результате после-
последовательных актов такого копирования прямолинейные
цепочки знаков считаются словами в исходном ал-
алфавите. К словам в данном алфавите удобно отнести
также и и у с т о е слово, т. е. цепочку, не содер-
содержащую ни одного знака. Напр., цепочки E) «авввеед» и
F) «книга» являются словами в русском алфавите. При
обращении со словами К. м.— и в этом проявляется ее
абстрактный характер — использует абстракции отож-
отождествления и потенциальной осуществимости. Первая
из них позволяет, отвлекаясь от различий копий и ори-
оригинала, говорить о разных копиях данной буквы и о ней
самой, как об одной букве. Напр., говорят, что в слово
E) три раза входит буква «в» русского алфавита, тогда
как в действительности при написании данного слова
воспроизводились три различных конкретных копии
исходной буквы. Это соглашение естественным образом
распространяется на одинаковые по написанию (гра-
(графически равные) слова. Напр., о двух конкретных сло-
словах: слове «книга» и слове F) говорят как об одном
слове. В допущении абстракции отождествления прояв-
проявляется предполагаемая К. м. первоначальная способ-
способность человека к «чтению» слов, т. е. к многократному
и устойчивому опознанию знаковых цепочек как оди-
одинаковых или различных. На это обстоятельство как
минимальную предпосылку любой научной деятельно-
деятельности указывал Д. Гильберт. Абстракция потенциальной
осуществимости позволяет пренебрегать в рассуждени-
рассуждениях о написании слов реальными ограничениями в про-
пространстве, времени и материале. Таким образом, о вооб-
воображаемых очень длинных словах начинают рассуждать
как о реально существующих, в частности считается воз-
возможным к любому данному слову приписать справа (или
слева) любое другое слово. Отсюда вытекает и возмож-
возможность рассмотрения сколь угодно больших натуральных
чисел, а также сложения любых двух- натуральных
чисел, поскольку натуральными числами можно, напр.,
считать слова вида 0, 0|, 0|| и т. д. в алфавите 0|. Вме-
сте с тем абстракция потенциальной осуществимости не
позволяет рассматривать как своего рода завершенные
объекты «бесконечные» слова и совокупность «всех» слов
в данном алфавите (в частности, не рассматривается как
завершенный объект и натуральный ряд). Такого рода
рассмотрения требуют привлечения более сильной абст-
абстракции — абстракции актуальной бесконечности, к-рая
отвергается К. м.
Принятие абстракции потенциальной осуществимости
приводит к тому, что наряду с элементарными, целиком
обозримыми конструктивными процессами (напр., на-
написанием коротких слов) рассматриваются воображае-
воображаемые, не подлежащие реальному воспроизведению конст-
конструктивные процессы. Такие процессы задаются своими
предписаниями; сами эти предписания по существу я
становятся предметом исследования. Задающее конст-
конструктивный процесс предписание (для простоты речь идет
о процессах, оперирующих со словами) должно быть
общепонятным и совершенно однозначно определять
шаг за шагом последовательное построение слов, причем
шаги должны быть элементарными, т. е. не предпола-
предполагать ничего, кроме умения читать, писать (и стирать)
слова. Шаги эти, таким образом, сводятся к написанию
и графическому сравнению нек-рых слов, а также к за-
замене вхождений одних слов в другие третьими словами.
Окончание процесса определяется самим предписанием
и может зависеть от результатов, полученных на шагах,
предшествующих заключительному, причем принятие
решения о заключительном характере данного шага
также должно носить описанный только что элементар-
элементарный характер. Возможна ситуация, когда никакой шаг
не оказывается заключительным, т. е. после каждого
совершенного шага данное предписание требует совер-
совершить следующий шаг. Такому предписанию не соответ-
соответствует никакой потенциально выполнимый конструк-
конструктивный процесс, однако здесь оказывается удобной ус-
условная терминология, согласно к-рой соответствующее
предписание определяет неограниченно продолжаемый
(потенциально бесконечный) процесс. Для оправдания
этой терминологии можно было бы также расширить
исходные представления о конструктивных процессах,
рассматривая наряду с потенциально реализуемыми
процессами более абстрактные образования — процес-
процессы, отождествляемые с их предписаниями. В связи с
появлением неограниченно продолжаемых конструк-
конструктивных процессов возникает вопрос о средствах, прп
помощи к-рых можно убедиться в обрываемости зада-
задаваемого данным предписанием конструктивного процес-
процесса. К. м. принимает здесь важный принцип, называемый
конструктивного подбора принципом п позволяющий
устанавливать такие факты методом от противного,
т. е. приводя к нелепости предположение о неограни-
неограниченной продолжаемости соответствующего конструк-
конструктивного процесса. Примеры предписаний: G) написать
|; (8) к произвольному слову в алфавите 0| приписать
справа |; (9) п. 1: написать | и перейти к п. 2; п. 2: сте-
стереть | (т. е. заменить эту букву пустым словом) и перей-
перейти к п. 1; A0) п. 1: к произвольному слову в алфавите 0|
приписать справа | и перейти к п. 2; п. 2: если обрабаты-
обрабатываемое в данный момент слово совпадает с 0| |, то закон-
закончить процесс, в противном случае вернуться к п. 1;
A1) п. 1: написать 0 и перейти к п. 2; п. 2: к обрабаты-
обрабатываемому в данный момент слову приписать справа |
и перейти к п. 3; п. 3: если получилось совершенное на-
натуральное число, то закончить процесс, в противном
случае приписать к обрабатываемому в данный момент
слову справа | и перейти к п. 2. Предписание G) задает
конструктивный процесс, оканчивающийся за один
шаг написанием однобуквенного слова |. Процесс вы-
выполнения (9) неограниченно продолжаем. В настоящее
время (к 1978) неизвестно, заканчивается ли конструк-
конструктивный процесс, задаваемый A1) (в A1) для краткости
использовались понятия теории чисел; ясно, что воз-
возможно более длинное предписание этого рода, опираю-
опирающееся исключительно на возможности чтения, написа-
написания и сравнения слов в алфавите 0|). Несколько особый
характер имеют предписания (8) и A0): их выполнение
может начинаться с любого слова в указанном алфави-
алфавите, при этом конструктивный процесс, определяемый
(8), всегда заканчивается, в то время как в случае пред-
предписания A0) он неограниченно продолжаем при нек-рых
исходных словах. Предписания указанных типов при-
принято называть алгоритмами (в данном контек-
контексте речь идет об алгоритмах, оперирующих со словами).
К необходимости рассмотрения алгоритмов приводит
конструктивная трактовка экзистенциальных утверж-
утверждений. Утверждение о существовании конструктивного
объекта с данным свойством, т. е. утверждение вида A2)
ЗхА (х), в соответствии с представлениями о конструк-
конструктивных объектах как результатах конструктивных про-
процессов считается в К. м. установленным только в том
случае, когда указан потенциально выполнимый конст-
конструктивный процесс, заканчивающийся построением ис-
искомого объекта. Соответственно установление парамет-
параметрического утверждения существования A3) ухЗуА (х, у)
(«для всякого х существует у такой, что А (х, у)»)
предполагает указание «общего» конструктивного про-
процесса, начинающегося с произвольного конструктивно-
конструктивного объекта х данного исходного типа и заканчивающего-
заканчивающегося построением искомого у. Другими словами, A3) вы-
выражает существование алгоритма, находящего у, исхо-
исходя из х. Из такой трактовки существования вытекает и
конструктивное понимание дизъюнкции: суждение А у В
(«Л или В») считается установленным, только если
предъявлен конструктивный процесс, заканчивающийся
указанием его верного члена. Дальнейшее разъяснение
смысла суждений более сложной структуры и выработ-
выработка правил обращения с ними, соответствующих исход-
исходным конструктивным установкам, составляет задачу
конструктивной семантики и конструктивной логики.
Приведенная конструктивная трактовка утверждений
существования и дизъюнкции существенно отличается
от традиционной: в теоретико-множественной матема-
математике, напр., суждение A2) может быть доказано приве-
приведением к нелепости его отрицания. Такое доказатель-
доказательство обыкновенно не содержит никакого способа по-
построения искомого конструктивного объекта. К. м. счи-
считает, что подобное рассуждение доказывает не A2), а
его «двойное отрицание», т.е. '^~\ЗхА(х). Последнее
суждение рассматривается в К. м. как, вообще говоря,
более слабое, чем A2). Таким образом, К. м. не прини-
принимает закона снятия двойного отрицания, а, следова-
следовательно, н закона исключенного третьего (на отсутствие
оснований для принятия последнего указывает и конст-
конструктивная трактовка дизъюнкции).
Первоначальные математич. структуры — натураль-
натуральные, целые и рациональные числа — непосредственно
могут трактоваться как слова нек-рых простых типов в
фиксированном алфавите, при этом соответствующие от-
отношения равенства и порядка легко сводятся к графнч.
совпадению п различию слов. Введение более сложных
структур — действительных чисел, функции над ними
и т. д.— осуществляется в К. м. на основе понятия ал-
алгоритма, играющего в ней примерно такую же роль,
какую играет в традиционной математике понятие
функции. Считая интуитивные представления об алго-
алгоритмах слишком расплывчатыми для таких построении,
К. м. делает здесь принципиальный шаг, стандартизи-
стандартизируя используемые алгоритмы посредством принятия
одного из современных точных определений этого поня-
понятия вместе с соответствующей гипотезой типа Чёрча те-
тезиса, принципа нормализации и т. д., утверждающей
совпадение оперативных возможностей, доставляемых
алгоритмами в интуитивном и точном смысле слова.
Фактически наибольшее применение в К. м. получили
нормальные алгорифмы Маркова. К необходимости
уточнения понятия алгоритма приводит также и конст-
конструктивная трактовка существования. Напр., отрицание
суждения A3) есть утверждение о невозможности не-
к-рого алгоритма, между тем интуитивные представле-
представления, достаточные для опознания в качестве алгоритма
того или иного конкретного предписания, в принципе
не позволяют получать сколько-нибудь нетривиальные
теоремы невозможности. На основе изложенных прин-
принципов и опираясь на современную теорию алгоритмов,
К. м. строит ряд математич. дисциплин, в том числе и
конструктивный математич. анализ, включая сюда
элементы функционального анализа, дифференциаль-
дифференциальные уравнения, теорию функций комплексного пере-
переменного и т. д. (см. Конструктивный анализ). Получае-
Получаемые таким образом теоретпч. модели, основанные на
более скромной чем обычно системе абстракций, хотя и
уступают традиционным в прозрачности и элегантно-
элегантности, тем не менее, по-видимому, способны обслужить
тот же круг приложений.
Имея общий критический источник с интуиционист-
интуиционистской математикой Л. Брауэра и заимствовав из нее ряд
конструкций и идей, К. м. обнаруживает определенное
сходство с последней. Вместе с тем, здесь имеются и
принципиальные отличия как общефилософского, так и
конкретно математич. характера. Прежде всего К. м.
не разделяет свойственное интуиционизму убеждение в
первоначальном характере математич. интуиции, счи-
считая, что сама эта интуиция формируется под влиянием
практической деятельности человека. Соответственно
абстрагирование в К. м. идет не от умственных построе-
построений как в интуиционизме, а от простейших реально на-
наблюдаемых конструктивных процессов. В математич.
плане К. м. не принимает выводящую за рамки конст-
конструктивных процессов п объектов концепцию свободно
становящейся последовательности и основанную на ней
интуиционистскую теорию континуума как среды сво-
свободного становления. С другой стороны, интуиционист-
интуиционистская математика не принимает правила конструктивно-
конструктивного подбора и не считает необходимым элиминировать ин-
интуитивные алгоритмы при помощи соответствующих точ-
точных определений. Следует заметить, что в. последние-
годы наметилась определенная тенденция к сближению
конструктивного и интуиционистского подходов: в не-
к-рых конструктивных исследованиях, в особенности
относящихся к семантике, используются индуктивные
определения и соответствующие им индуктивные дока-
доказательства, напоминающие построения Л. Брауэра при
доказательство его так наз. бар-теоремы (см. Вар-индук-
Вар-индукция), занимающей одно из центральных мест в интуи-
интуиционистской математике.
Лит.: [1] Френкель А.-А., Б а р-Х и л л е л И.,.
Основания теории множеств, пер. с англ., М., 1966; 12] Г е й-
тинг А., Интуиционизм. Введение, пер. с англ., М., 1965;
[3] Гильберт Д., Основания геометрии, пер. с нем. М.„
1948; [4] Constructivity in mathematics, Amst., 1959; [5] Map-
нов А. А., Теория алгорифмов, М., 1954 (Тр. Матем. ин-та
АН СССР, т. 42); [6] е г о ж е, О логике конструктивной ма-
математики, М., 1972; [7] Проблемы конструктивного направ-
направления в математике, в. 1—6, М.— Л., 1958—73 (Тр. Матем.
ин-та АН СССР, т. 52, 67, 72, 93, 113, 129).
См. также лит. при ст. Конструктивный анализ.
КОНСТРУКТИВНАЯ СЕМАНТИКА — совокуп-
совокупность способов понимания суждений в конструктивной
математике. Необходимость в особой семантике вы-
вызвана различием общих принципов, лежащих в основе
традиционной (классической) и конструктивной мате-
математики (далее последний термин будет в основном отно-
относиться к подходу, развитому в советской школе конст-
конструктивной математики). Основное внимание К. с. уде-
уделяет суждениям о конструктивных объектах в H;u>iKaN
первого порядка, то есть, по существу, арифметич.
суждениям (см. Арифметика формальная). Принцппи-
альные различия с традиционной семантикой в понима-
понимании дизъюнкции Ап\/А1 (и суждений о существовании
ЭхА (х)) сформулированы Л. Брауэром (L. Brouwer).
Конструктивное обоснование таких суждений требует
решения задачи: найти число ?<:1 такое, что верно Л;
(соответственно найти число п такое, что А (п)). Общие
принципы описания задач, соотиетствующпх более слож-
сложным формулам, были намечены А. Рейтингом (А. Неу-
ting) и А. Н. Колмогоровым. Точная формулировка
(к-рая стала возможной после появления математич.
определения алгоритма) была дана С. Клинн (S. Kleene)
в виде понятия реализации замкнутой арифметич. фор-
формулы (см. Рекурсивная реализуемость). Реализа-
Реализация верного равенства t=r есть фиксиро-
фиксированная константа, напр, число 0, а ложное равенство не
имеет реализаций. Реализация к о н ъ го н к-
ц и и А&В — это пара (а, Ь), где а — реализация Л,
Ь — реализация В. Реализация д п з ъ ю н к-
ц и и AowАх — это пара (г, я), где г=0,1 и а — реа-
реализация суждения А,-. Реализация суждения ЗхА (х) —
это пара (и, а), где п — число, а — реализация суж-
суждения А (и). Реализация суждения УхА (х) — это об-
общий метод /, к-рый по всякому натуральному п выдает
реализацию /(«) суждения А (п). Реализация суждения
A ZDB — это общий метод /, к-рый по всякой реализации
а суждения А выдает реализацию f(a) суждения В (и
может быть не определен для аргументов а, не являю-
являющихся реализациями А). При этом общин метод пони-
понимается как алгоритм (частично рекурсивная функция).
Используя кодирование алгоритмов числами, можно за-
записать условие «число е есть реализация формулы Л» в
виде арифметич. формулы (егА), не содержащей дизъ-
дизъюнкции V и содержащей существование 3 только три-
тривиальным образом — перед равенствами. Такие форму-
формулы наз. почти нормальными. Суждение
Эе (егА) (читаемое «А реализуема») может служить кон-
конструктивным разъяснением Суждения А. При таком
понимании закон исключенного третьего Ух(Л (х)\/
V ~]А (.г)) опровергается, напр., для Л (х) = ЗуТ(х, х, у),
где Т(е, х, у) означает, что алгоритм (с кодом) е за-
заканчивает работу над аргументом х за у шагов. Опровер-
Опровергается и закон двойного отрицания \jx(~\~\B(х)^>
ZDB(x)), напр, для В(х) = А (х)\/^А(х). Приведенное
определение связывает конструктивную задачу (поиск
реализации) со всяким суждением А, даже если А не
содержит V, 3. Предложенный Н. А. Шаниным алго-
алгоритм выявления конструктивной задачи не меняет фор-
формул без v,3 (нормальных формул) и экви-
эквивалентен реализуемости в формальной интуиционист-
интуиционистской арифметике с бескванторной индукцией. Произ-
Произвольные формулы сводятся к почти нормальным, так
как обоснование З.гА (х) состоит в предъявлении числа
п и обосновании А (п). К. с. для почти нормальных фор-
формул определяется разными авторами по-разному, однако
ни в одном случае не получается столь существенного
расхождения с классическим пониманием, как для фор-
формул, содержащих V и нетривиальное 3.
А. А. Марков определяет истинность для почти нор-
нормальных формул с помощью выводимости по обычным
правилам для рассматриваемых логических связок плюс
эффективное to-правпло: если имеется общий метод,
позволяющий для любого п устанавливать выводимость
А (п) из суждения А', то VxA (x) выводимо из К. Истин-
Истинность определяется постепенно. Язык Яш, состоящий из
всех почти нормальных формул, делится на слои >7Х,
Л2, ... ; язык Яг состоит из формул без з, V; язык
Яп + 1, и^1, включает Яп и формулы, к-рые можно по-
построить из формул языка Яп одним применением им-
импликации и любым числом применений V, &. Истин-
Истинность для ^-формул — это выводимость по обычным
правилам для &, 3, V- Истинность для /72"Ф°РМУЛ
определяется через допустимость соответствующего
правила. Напр., истинность ^xR(ж)зЗг/Т(у) означает
наличие алгоритма ср такого, что Л(л)эТ(ф(в)) для
любого числа п. Для >7„ + 1-формул при и>1 истинность
конъюнкций и V-формул определяется обычным обра-
образом через истинность компонент, а истинность импли-
импликации A zdB означает выводимость В из А по нек-рым
правилам Sn, о к-рых уже доказано, что они сохраняют
истинность ^„-формул. Системы Sn содержат со-пра-
внло, а в качестве аксиом — все истинные >7„-формулы.
Понятие выводимости в Sn вводится обобщенным ин-
индуктивным определением, а для доказательства мета-
теорем применяется соответствующий принцип индук-
индукции. Индукцией по 52-выводу доказывается допусти-
допустимость правила 4d"| 1з^Д|—ЛЗЗ^Д. Оно включается в
S3 и дает принцип Маркова ~\ ~\3xR^>3xR. Системы
5„ + 3, п^1, состоят из обычных правил для рассматри-
рассматриваемых связок, включая to-правило. Оказывается, что
почти нормальная формула А истинна по Маркову тогда
и только тогда, когда примитивно рекурсивное дерево Т&
поиска вывода формулы А без сечения (но с со-правилом
и принципом Маркова) является выводом в смысле ин-
индуктивного определения. Это эквивалентно (в рамках
классической математики) классической истинности А.
В мажорантной семантике Н. А. Шанина для каждой
почти нормальной формулы А определяется трансфи-
трансфинитная иерархия {Ла} формул простой структуры, при-
причем Аа1эА доказуемо в подходящей формальной систе-
системе. Формула Ла наз. мажорантой для А , и А счи-
считается истинной формулой ранга а, если Аа верна. Точ-
Точность аппроксимации растет с ростом а: а<р"з(-4а:э
1ЭА Р). Если отвлечься от технических детален, то фор-
формула А строится с помощью а-кратного вынесения
кванторов, согласно эквивалентности
Ц (Bx'^\~\3uWC (и, v))<r*
3Uyv~\ ~\(Bv 1 "\3uVvC (и, v)vC(u, v)),
и сворачивания цепочек кванторов с помощью алгорит-
алгоритма выявления конструктивной задачи. Это дает дока-
доказуемую в арифметике с трансфинитной индукцией до а
эквивалентность
А <-» 3W 11A1 ЪюСа уDa)
с бескванторной формулой Са, так что
A<*- = 3uyv3wCa(u, v, w)
оказывается мажорантой для А. Суждение Аа оказы-
оказывается, с точностью до технических деталей, эквивалент-
эквивалентным утверждению о существовании вывода высоты <а
для исходной формулы с использованием ш-правила.
В этом смысле мажорантная семантика эквивалентна
ступенчатой семантике А. А. Маркова. После фиксации
нек-рого класса в общерекурсивных функций (напр.,
класса всех функций, определимых рекурсией до а)
определяются мажоранты еще более простой структуры:
а, (и, v, ф (v)) для
Если А' — бескванторное исчисление для класса в, то
А'-истннность формулы 3uyvC(u, v) определяется как
выводимость формулы C(t, v) с переменной v для не-
нек-рого постоянного терма t. Если в качестве К взято
стандартное исчисление равенств для функций, опреде-
определимых рекурсией до ординалов, меньших а, то А-истин-
нымн оказываются формулы, выводимые в формальной
интуиционистской арифметике, пополненной принци-
принципом Маркова, соотношениями, определяющими алго-
алгоритм выявления конструктивной задачи, и правилом ин-
индукции до ординалов E таких, что е(Р)<:а, где е(Р) —¦
первое е-число, большее р. В частности, а=е0 для |3— со,
т. е. для обычной индукции.
Доведение обоснования до бескванторного уровня
(.ЙТ-истинность) связано со стремлением остаться по воз-
возможности в рамках финитизма, т. е. бескванторного
языка и соответствующих логических средств. С этим же
связано стремление ограничиться небольшими а. Для
большей части «работающего» конструктивного анализа
(включая теорему о непрерывности эффективных опера-
операторов) достаточно конечных а.
Лит.: [1] М а р к о в А. А., в сб.: Исследования по теории
алгорифмов и математической логике, М., 1976, т. 2, с.З—31;
МШанин Н. А., «Тр. Матем. ин-та АН СССР», 1973, т. 129,
с. 203—66; [3] К л и н и С. К., Введение в метаматематику,
пер. с англ., М., 1957. Г. Е. Минц.
КОНСТРУКТИВНАЯ ТЕОРИЯ ФУНКЦИИ — поня
тие, введенное С. Н. Бернштейном, назвавшим К. т. ф.
«направление теории функций, которое ставит себе
целью дать возможно более простую и удобную основу
для качественного изучения и вычисления как эмпири-
эмпирических функций, так и всяких функций, являющихся
решениями естественно поставленных задач математи-
математического анализа» [1]. Имелось в виду, что К. т. ф. долж-
должна содержать теорию приближения (аппроксимации)
функции в качестве одного из своих разделов. Однако
фактически название К. т. ф. получило употребление
в более узком смысле, как другое название теории
приближения функций. В последнее время термин
«К. т. ф.» используется реже.
Лит.: [1] Бернштейн С. Н., «Изв. АН СССР. Сер.
матем.», 1945, т. 9, № 3, с. 145—58 (Собр. соч., т. 2, М., 1954,
С. 349—60). С. А. Телякивский.
КОНСТРУКТИВНАЯ ФУНКЦИЯ ДЕЙСТВИТЕЛЬ-
ДЕЙСТВИТЕЛЬНОГО ПЕРЕМЕННОГО, конструктивная
ф у н к ц и я,— понятие функции одного и многих дей-
действительных переменных, используемое в конструктив-
конструктивной математике. Предложено А. А. Марковым. Может
трактоваться как частный случай понятия алгоритмиче-
алгоритмического оператора в конструктивных метрич. пространст-
пространствах. См. также Конструктивный анализ, Конструктив-
Конструктивное метрическое пространство. Б. А. Кушнер.
КОНСТРУКТИВНОГО ПОДБОРА ПРИНЦИП,
принцип Маркова,— логико-философский прин-
принцип конструктивной математики, выдвинутый
А. А. Марковым [1], [2] и в общей форме утверждающий,
что если конструктивный процесс, заданный нек-рым
предписанием, не является неограниченно продолжае-
продолжаемым, то он заканчивается. В конструктивной математи-
математике получили применение несколько конкретных, содер-
содержательно эквивалентных разновидностей этого прин-
принципа. 1) Пусть W — нормальный алгорифм, Р — слово в
его алфавите. Тогда, если опровергнуто предположение
о неприменимости Ч' к Р, то W применим к Р; символи-
символически
2) Б арифметике формальной К. п. п. может быть выра-
выражен следующей арифметич. формулой
VzVx[-|V2/IT^z, x, y)ZD3yT1(z, х, у)],
где Т1 — примитивно рекурсивный предикат такой, что
частично рекурсивная функция с гёделевым номером z
определена на х тогда и только тогда, когда jyT^z, x, у)
(ср. [3]). 3) Если рекурсивно перечислимое множество
непусто, то оно содержит нек-рый элемент. 4) Пусть А —
алгоритмически проверяемое свойство натуральных чи-
чисел. Тогда, если опровергнуто предположение о том, что
не существует числа со свойством А, то найдется нату-
натуральное число со свойством А. Соответствующая логи-
логическая схема записывается в виде
ух (A Wvli (*)) ZD П^ЭхА (х) ZD Зу А (у)).
Иногда термин «К. п. п.» специально связывается имен-
именно с этой последней формой рассуждений, поскольку
искомое число «подбирается» в ходе следующего конст-
конструктивного процесса: проверяют А @), если это верно,
то берут 0 в качестве искомого числа, в противном слу-
случае переходят к проверке А A) н т. д.
Интуитивное оправдание К. п. п. в рамках применяе-
применяемой в конструктивной математике системы абстракций
состоит в том, что если невозможность неограниченного
продолжения данного конструктивного процесса убе-
убедительно доказана, то потенциально достижимо окон-
окончание атого процесса в результате его последовательно-
последовательного выполнения шаг за шагом. Таким образом, при ут-
утверждении существования конструктивного объекта
(напр., результата применения нормального алгорифма
к слову) на основании К. п. п. не происходит выхода за
рамки абстракции потенциальной осуществимости.
К. п. п. безусловно допустим с точки зрения клас-
снч. логики, поскольку он является частным случаед(
общего закона снятия двойного отрицания и закона ис-
исключенного третьего. Применение этих логических за-
законов сводится к К. п. п. во многих конструкциях тео-
теории рекурсивных функций, что делает эти конструкций
достоянием конструктивной математики. Использова-
Использование К. п. п. позволяет также получить ряд значитель-
значительных результатов в конструктивном анализе, в частности
теорему о непрерывности алгорптмпч. операторов и о
продолжимости эффективных функционалов до частично
рекурсивных функционалов (см. также Конструктивное
метрическое пространство). Другой сферой приложе-
приложений К. п. и. является конструктивная семантика [4].
Еще задолго до формулировки К. п. п. в качестве об-
общего принципа конструктивной математики проводи-
проводились исследования по обоснованию различных форм это-
этого принципа в рамках того или иного круга допускае-
допускаемых конструктивных средств. Здесь следует указать
следующий основополагающий результат П. С. Нови-
Новикова, полученный в 1943 (см. [5]): пусть для формулы
А (х) с одной переменной в конструктивной формальной
арифметике выводимо А (п)\/ "]А (п) для каждого пив
классической арифметике выводимо ЭхА (х); тогда фор-
формула ЭхА (х) выводима и в конструктивной арифмети-
арифметике. В работе [6] было получено обоснование К. п. п. в
рамках новой системы конструктивной семантики, раз-
развиваемой в последние годы А. А. Марковым.
Являясь, по-видимому, наименее непосредственной из
первоначальных установок конструктивной математи-
математики, К. п. п. принимается нек-рымп сторонниками по-
последней с известными оговорками. К. п. п. отвергается
также интуиционистской математикой как недостаточно
убедительный интуитивно. С другой стороны, в связи с
формализацией ряда разделов интуиционистской мате-
математики детально изучались вопросы о соотношениях со-
соответствующих систем с формальными схемами, выра-
выражающими К. п. п. В частности, установлена независи-
независимость схем B) и D) от аксиом интуиционистского исчис-
исчисления предикатов, арифметики и анализа (см. [2], [7],
[8]).
Лит,: L1J Марков А. А., «Успехи матем. наук», 1954,
т. 9, в. 3, с. 226—30; [2] е г о ж е, в кн.: Тр. 3 Всесоюзного
математического съезда, т. 2, М,, 1956, с. 146—47; [3] К л и-
н и С. К., Введение в метаматематику, пер. с англ., М., 1957;
[4] Ш а н и н Н. А., «Тр. матем. ин-та АН СССР», 1958, т. 52,
с. 226—311; [5] Н о в и к о в П. С, «Матем. сб.», 1943, т. 12,
в. 2, с. 231—61; [6] М а р к о в А. А. «Докл. АН СССР», 1974,
т. 214, Л» 4, с. 765—68, т. 215, № 1, с. 57—60; [7] К ли ни С,
В е с л я Р., Основания интуиционистской математики с точ-
точки зрения теории рекурсивных функций, пер. с англ., М.,
1978; [8] Т г о е 1 s t г a A. S., в кн.: ISILC. Proof theory sym-
posion, В., 1975, p. 370—83. Б. А. Кушпер.
КОНСТРУКТИВНОЕ ДЕЙСТВИТЕЛЬНОЕ ЧИСЛО—
понятие действительного числа, употребляемое в конст-
конструктивной математике. В более широком смысле —
действительное число, конструируемое в соответствии
с тем или иным кругом конструктивных средств. Близ-
Близкое значение имеет термин «вычислимое действительное
число», обычно употребляемый и тех ситуациях, когда
не ставится цель изначального, нетрадиционного по-
построения континуума, а речь идет просто о классиче-
ских действительных числах, вычислимых в том или
ином смысле посредством нек-рых алгоритмов. (См. так-
также Конструктивный анализ.) Б. А. Нушнер.
КОНСТРУКТИВНОЕ ИСЧИСЛЕНИЕ ВЫСКАЗЫ-
ВЫСКАЗЫВАНИИ — логическое исчисление, описывающее способы
вывода высказываний, истинных с точки зрения конст-
конструктивной математики. Обычно этот термин рассмат-
рассматривается как синоним термина интуиционистское исчис-
исчисление высказываний. Однако, при нек-рых специальных
интерпретациях конструктивизма интуиционистское ис-
исчисление высказываний оказывается неполным. Напр.,
известная формула Роуз а:
где А — формула ~]р v ~\ q, a p, q — пропозициональные
переменные, не выводится в интуиционистском исчисле-
исчислении высказываний и в то же время тождественно истин-
истинна в интерпретации рекурсивной реализуемости Клпни,
по крайней мере, если признавать конструктивного под-
подбора принцип. Актуальной задачей является исследова-
исследование полноты К. и. в. для различных вариантов семанти-
семантики конструктивной математики.
Лит.: [1] К лини С. К., Введение в метаматематику,
пер. с англ., М., 1957; [2] R о s e G. F., «Trans. Amer. Math.
Soc», 1953, v. 75, p. 1 — 19. А. Г. Драгалин.
КОНСТРУКТИВНОЕ МЕТРИЧЕСКОЕ ПРОСТРАН-
ПРОСТРАНСТВО — концепция метрич. пространства, используе-
используемая в конструктивной математике. Близкий смысл
имеет также понятие рекурсивного метрического про-
пространства.
Список {5Ш, р}, где ffli •— некоторое множество конст-
конструктивных объектов (обычно слов в том или ином ал-
алфавите), р — алгоритм, переводящий любую пару эле-
элементов 9J! в конструктивное действительное число (к. д.
ч., см. Конструктивный анализ), наз. К. м. п., если при
любых X, У, Z?3ft выполняется: 1) р(Х, Х)=0,
2) р(Х, У)<р(Х, Z)+p(Y, Z) (здесь и ниже термин «ал-
«алгоритм» употребляется в смысле одного из точных поня-
понятий алгоритма). Множество Щ1 и алгоритм р наз. носи-
носителем и метрическим алгоритмом со-
соответствующего К. м. п., а элементы 5Л — точка-
м и этого К. м. п. Из аксиом 1), 2) следует, что всегда
p(,Y, У)>0 и р(Х, Y)=p(Y, X). Две точки X, У?2Л
называются эквивалентными (различными)
в К. м. п. {ЯП, р}, если р(Х У) = 0 (соответственно
р(Х, У)ФО).
Примеры К. м. п.: а) пространство натуральных
чисел Ы. Носителем Н является множество натуральных
чисел (натуральные числа трактуются как слова вида О,
01, 011, .. .), а метрич. алгоритм р таков, что р(т, п) =
= |то—п\. Аналогично определяются пространства R и
Ех — рациональных и конструктивных действительных
чисел, соответственно; б) n-мерное евклидово простран-
пространство Еп. Носителем Еп является множество слов вида
хх*. . .*хп, где х{, 1<:г«:п, есть к. д. ч., а метрич. алго-
алгоритм р строится так, что
• -*г/п)= у
в) пространство С равномерно непрерывных на единич-
единичном сегменте конструктивных функций. Носителем С
является множество слов вида е/з*еуз, где / — всюду
определенная на единичном сегменте конструктивная
функция, а у — алгоритм, переводящий всякое нату-
натуральное число в натуральное число, причем
0*Цхъ хг < 1& | хг — х2 | < 2-V <«>) ZD
(еЭ1з означает запись (код) алгоритма 31). Метрич. ал-
алгоритм р строится так, что
р (t7i3*ev13, е/2з«еу2з) = max (J /i (a-) — /2 (•*•)!)-
О < ж< 1
Сложный вид носителя пространства С обусловлен
требованием эффективной вычислимости метрики; г) бэ-
ровское пространство В общерекурсивных функций. Но-
Носителем В является множество гёделевых номеров обще-
рекурсивных функций, а метрич. алгоритм р строится
так, что если ф„ и фи — общерекурсивные функции с
номерами пи т, то р(п, т) = 0, если фП(') = фт(') ПРИ
любом г, и р(п, лг) = 2 *, если <pn(i) = <fm{i) при i<Ck
и <рп(к)ф<рт{к).
Пусть М= {ffll, р} — К. м. п. Алгоритм Р наз. пос-
последовательностью точек М, если при
всяком п имеем Р(п)?Щ1. Последовательность Р наз.
регулярной, если при т~^п имеем р(Р(та), Р(п))<
<2~". Регулярная последовательность р сходится к
точке X К. м. п. М, если при любом п имеем р(Х,
P(n))<:2~". К. м. п. М наз. полным, если сущест-
существует алгоритм, находящий для каждой регулярной по-
последовательности р (точек М) точку М, к к-рой сходится
р. К. м. п. М наз. сепарабельным, если суще-
существуют алгоритмы а, б такие, что ос — последователь-
последовательность точек М, и при любом Х?М и любом п имеем:
Ь(Х*п) есть натуральное число, причем р(аF(Х*п)),
Х)<_2~п. Все пространства Н, R, Ех, Еп, С, В примеров
а) — г) сепарабельны, пространства Н, EL, En, С, кро-
кроме того, полны. Пример несепарабельного К. м. п. дает
рассмотрение подпространства Н, индуцированного не
рекурсивно перечислимым множеством. В терминах
К. м. п. могут быть изложены многие результаты клас-
сич. теории метрич. пространств; в частности, большое
значение имеет конструктивный вариант
теоремы Хаусдорфа, утверждающий, что
для каждого К. м. п. может быть построено его попол-
пополнение.
Процесс пополнения К. м. п. является сильным сред-
средством введения тех или иных структур конструктивной
математики. На этом пути вводятся к. д. ч., могут быть
определены естественные аналоги классич. понятий из-
измеримых множеств и функций, интегрируемых по Лебе-
Лебегу функций, и т. д. Одной из основных целей теории
К. м. п. является исследование алгоритмич. отображе-
отображений, корректных относительно тех или иных вычисли-
вычислимых метрик.
Пусть Afx= {ffl?!, рх}, М2= {аЛ2, Р2) — К- м. п. А л-
горитмическим оператором типа Мх-*-
-?-М2 наз. алгоритм if, удовлетворяющий условиям:
а) если X^2Rj и определено V(X), то ЧГ(Х)^9Л2; б) ес-
если X, У — эквивалентные точки Mt (т. е. Pj(X, У) = 0)
и определено ^?(Х), то определено ? (У), причем ЧГ(Х),
Т(У) — эквивалентные точки М2. Алгоритмич. опера-
операторы типа Е1~^Е:1, Еп-*Е1 суть конструктивные функ-
функции одной и п переменных; алгорптмнч. операторы типа
В^-Н принято наз. эффективными функци-
функционалами.
Основным результатом теории алгоритмических
операторов является теорема Ц е и т и н а, ут-
утверждающая, что в случае полного сепарабельного
К. м. п. М1 для любого алгоритмич. оператора Т типа
М^-^М^, при каждом п можно построить алгоритмиче-
алгоритмически (рекурсивно) перечислимое множество шаров, по-
покрывающее область определения Т, такое, что колеба-
колебание W на любом шаре этого множества не превосходит
2~". Из этой теоремы вытекает известный результат о
продолжимости эффективных функционалов до частич-
частично-рекурсивных функционалов. Другим важным след-
следствием приведенного результата является теорема о не-
непрерывности алгорптмич. операторов: если М1 — пол-
полное и сепарабельное К. м. п., М2 — произвольное К.
м. п., то по любому алгоритмич. оператору Т типа
М1-?М2 можно построить алгоритм а такой, что для
любых X, У из области определения Т и любого п число
а(Х, п) есть натуральное, причем из рЛХ, Y)<2—a<-X> n)
следует p2(V(X), Чг(У))<2-«.
В таком же порядке идей, что п в случае К. м. п.,
может быть развита теория конструктивных нормиро-
нормированных и гильбертовых пространств.
Лит.: [1] Цейтин Г. С. «Тр. матем. ин-та АН СССР»,
1962, т. 67, с. 295—361; [2] М о s с h о v a k i s G. N., «Fun-
dam, math.», 1964, v. 55, Mi 3 p. 215—38; [3] III а н и н Н. А.,
«Тр. матем. ин-та АН СССР», 1962, т. 67, с. 15—294; [4] К у ш-
н е р Б. А., Лекции по конструктивному математическому
анализу, М., 1973. Б. А. Нушнер.
КОНСТРУКТИВНОЕ ПО ГЁДЕЛЮ МНОЖЕСТВО —
множество, возникающее в описанном ниже процессе
построения множеств. Пусть X — множество и Rc^XX
XX. Рассмотрим язык 1-й ступени L(R, X), содержа-
содержащий один 2-местный предикатный символ, обозначаю-
обозначающий отношение R, и индивидные константы, обозначаю-
обозначающие элементы множества X (для каждого х?Х своя
константа х). Суждение «формула ф языка L(R, X) ис-
истинна в модели М^=(Х, R)» записывается следующим
образом:
М |= <р.
Множество Y^X наз. определимым в моде-
л и М=(Х, R) (иначе М-о п р е д е л и м ы м), если
существует формула ф(у) языка L(R, X) с одной сво-
свободной переменной v такая, что
Пусть Def M обозначает множество всех Л/-определи-
мых множеств. Каждому ординальному числу а сопос-
таппм множество La, определяемое рекурсивным соот-
соотношением:
^а= Up <a
где ?\Lo есть отношение принадлежности, ограничен-
ограниченное множеством Lo. Отсюда следует:
Lo^0,L1 = {0}, L2 = {0, {0}}, ..., LWo= и„<шЛ<. •••
Множество z наз. конструктивным, если су-
существует ординал а такой, что z?La. Класс всех конст-
конструктивных множеств обозначается через L. К. Гёдель
(К. Godel) ввел следующую аксиому констру-
конструктивности: всякое множество конструктивно. Он
доказал, что в классе L выполняются все аксиомы систе-
системы ZF, а также аксиома конструктивности, и что аксио-
аксиома выбора и обобщенная контннуум-ги-
п о т е з а («для всякого ординала а имеет место 2 а=
= tfa+i») следуют в ZF из аксиомы конструктивности.
Класс L можно охарактеризовать также как наимень-
наименьший класс, являющийся моделью ZF и содержащий все
ординальные числа; имеются и другие определения
класса L (см. [2] — [4]). Отношение x?La можно выра-
выразить формулой языка ZF и притом простой синтаксиче-
синтаксической структуры (так наз. Д^-формулой, см. [4]).
Среди результатов, относящихся к К. м., упомянем
следующие. Множество конструктивных действитель-
действительных чисел, т. е. множество Rf\L, где R — множество
всех действительных чисел, т. е. последовательностей
нулей и единиц, является А2-множеством (см. [5]).
Было показано, что из аксиомы конструктивности выте-
вытекает существование неизмеримого по Лебегу множества
действительных чисел типа А2 (см. [6]), отрицание Сус-
лина гипотезы и несуществование измеримого кардина-
кардинала (см. [2]).
Лит.: [1] Гёдель К., «Успехи матем. наук», 1948, т. 3,
вьш. 1, с. 96—149; [2] Й е х Т., Теория множеств и метод фор-
форсинга, пер. с англ., М., 1973; [3] М о с т о в с к и й А., Кон-
Конструктивные множества и их применения, пер. с англ., М.,
1973; [4] К а г р С, A proof of the relative consistency of the
continuum Hypothesis, в кн.: Sets models and recursion theory,
Amsterdam, 1967; [5] A d d i s о n J. W., «Fund. Math.», 1959,
v. 4fi, № 3, p. 337—57; [6] H о в и к о в П. С, «Тр. матем. ин-та
АН СССР», 1951, т. 38, с. 279—316; [7] Feigner U., Models
of ZF-Set theory, В.—Hdlb.—N.Y., 1971 (Lect. notes in mathe-
mathematics, v. 223). В. Н. Гришин.
КОНСТРУКТИВНОЕ ПОДМНОЖЕСТВО алгеб-
алгебраического многообразия — конечное объ-
объединение локально замкнутых (в Зариского топологии)
подмножеств. Локально замкнутым под-
подмножеством наз. пересечение открытого и зам-
замкнутого подмножеств. К. п. образуют булеву алгеб-
алгебру и могут быть определены как элементы булевой ал-
алгебры, порожденной алгебраич. подмногообразиями.
Роль К. п. в алгебраич. геометрии объясняет следую-
следующая теорема Шевалле: если / : X—*-Y — мор-
физм алгебрапч. многообразий, то f(X) (и более того,
образ любого К. п. пз X) является К. п. в У. С этим
фактом связано то, что «алгебраические» условия выде-
выделяют конструктивные подмножества алгебраич. много-
многообразий.
Отображение h : X-+T наз. конструктивным,
если h(X) конечно и для любой точки t? T прообраз
h,'1^) есть К. п. в X.
Лит.: [llGrothendieck A., Elements de geometrie
algebrique, t. 4, P., 1964; [2] Б op ель А., Линейные алге-
алгебраические группы, пер. с англ., М., 1972. В. И. Данилов.
КОНСТРУКТИВНЫЙ АНАЛИЗ, рекурсивный
анализ, вычислимый анали з,— назва-
название, объединяющее различные течения в основаниях
математики и математич. анализе. При развитии К. а.,
как правило, преследуются обе или вторая из следую-
следующих двух принципиальных целей: A) нетрадиционное
построение тех или иных фрагментов анализа на основе
более ясных и в большей степени учитывающих реаль-
реальные вычислительные возможности исходных концеп-
концепций, нежели теоретико-множественные посылки обыч-
обычного анализа; B) изучение эффективности в анализе;
введение и изучение вычислимых объектов анализа, в
частности исследование вопроса о том, по каким исход-
исходным данным можно эффективно находить те или инме
вычислимые объекты. В соответствии с этими целями,
исследования по К. а. можно грубо разделить на два
типа: претендующие и не претендующие на достижение
цели A). Для исследований первого типа характерно
либо использование нестандартных логик, либо суще-
существенные ограничения в употреблении традиционных
логических и математических средств, в то время как в
работах второго типа свободно используются традици-
традиционная математика и логика. Ко второму типу относятся
основополагающие работы (см. [1]—[4]), в к-рых были
выработаны современные концепции вычислимого дейст-
действительного числа (см. также [5]—[12]). К первому типу
относятся исследования по интуиционистскому анализу
(см. Интуиционизм), возникшие в связи с выдвинутой
Л. Э. Я. Брауэром (L. E. J. Brower) интуиционистской
программой построения математики и оказавшие су-
существенное влияние на формирование задач и методов
К. а., рекурсивный анализ Р. Л. Гудстейна (R. L. Со-
odstein, см. [12]), а также оригинальная и чрезвычайно
далеко продвинутая система К. а., развитая Э. Би-
Бишопом (см. [13]). (Конструктивный анализ Бишопа за-
занимает промежуточное положение между интуицио-
интуиционистским анализом и системами, использующими точ-
точные концепции алгоритма.) Своеобразная трактовка
К. а. (в частности, теории меры) была предложена в
1970 П. Мартином-Лёфом [14]. В СССР начиная с 50-х
гг. в трудах А. А. Маркова, Н. А. Шанина и их учени-
учеников (см. [15], [16], [19]) интенсивно разрабатывалась сис-
система К. а., относящаяся к первому типу и укладываю-
укладывающаяся в рамки конструктивного направления в мате-
математике. Являясь частью конструктивной математики,
эта система (за к-рой ниже для краткости закрепляется
термин «К. а.») сохраняет характерные черты последней.
В частности, рассмотрения ограничиваются конструк-
конструктивными объектами (чаще всего словами в нек-рых
алфавитах пли объектами, допускающими очевидное
кодирование словами) и проводятся в рамках абст-
ракции потенциальной осуществимости с применением
специальной конструктивной логики, вырабатываемой
с учетом специфики конструктивных объектов как ре-
результатов потенциально выполнимых конечных пост-
построений. При этом полностью исключается использова-
использование абстракции актуальной бесконечности, и интуитив-
интуитивное понятие «эффективности» связывается с одним из
точных понятий алгоритма (в большинстве работ, отно-
относящихся к рассматриваемой системе К. а., использует-
используется понятие нормального алгорифма). В рамках К. а. по-
получено большое число результатов, интересных как с
точки зрения круга вопросов A), так и с точки зрения
круга вопросов B). По существу показана возможность
построения средствами конструктивной математики
ряда теорий, таких, как теория элементарных функций,
теория рядов, интегрирования по Римануи Лебегу, те-
теория функций комплексного переменного, теория об-
обобщенных функций и т. п. Получающиеся конструктив-
конструктивные теории наряду со сходством с одноименными тради-
традиционными теориями обладают заметными отличиями от
них; впрочем эти отличия проявляются не столько в
конкретных вопросах, связанных с приложениями ана-
анализа, сколько в теоретич. концепциях (таких, напр., как
концепция компактности и т. д.).
Фундаментальными понятиями К. а. являются по-
понятия конструктивного действительного числа и конст-
конструктивной функции действительного переменного. Кон-
Конструктивные действительные числа можно ввести раз-
различными (не всегда эквивалентными) способами. Опи-
Опишем один из таких способов, следующий канторовскому
построению классического континуума и приводящий к
наиболее употребительной и естественной концепции
конструктивного (вычислимого) действительного числа.
Сначала вводятся натуральные числа как слова вида
О, 01,011, ... в двухбуквенном алфавите {01}. Анало-
Аналогично определяются рациональные числа как слова не-
к-рого типа в алфавите {01 — /"}. Определяются отноше-
отношения порядка и равенства над рациональными числами,
а также арифметич. операции над ними. Конструк-
Конструктивной последовательностью нату-
натуральных чисел (к. п. н. ч.) наз. (нормальный)
алгорифм, перерабатывающий всякое натуральное чис-
число в натуральное число. Аналогичным образом тракту-
трактуется понятие конструктивной последова-
последовательности рациональных чисел (к. п.
р. ч.). Схемы нормальных алгорифмов однозначным об-
образом кодируются словами в алфавите {01}; код данно-
данного алгорифма наз. его записью. К. п. н. ч. а наз.
регулятором фундаментальности к.
п. р. ч. р\ если для любых натуральных I, m, n таких,
что I, т^а(п), выполняется неравенство |Р(/) —
р" (?и) | <2~". К. п. р. ч. наз. фундаментальной,
если можно построить ее регулятор фундаментальности.
Конструктивными действительными
числами (к. д. ч.) наз. рациональные числа, а также
слова в алфавите {01<3>} вида U(}V (<(> играет роль раз-
разделительного знака), где U — запись некоторой к. п. р.
ч., V — запись к. п. н. ч., являющейся регулятором
фундаментальности этой к. п. р. ч. Описанное понятие
к. д. ч. (предложенное Н. А. Шаниным, см. [20], на-
называвшим такие к. д. ч. «7<7?-числами» или «дуплекса-
«дуплексами») хорошо согласуется с интуитивным представлени-
представлением о вычислимых действительных числах как объектах,
допускающих эффективную сколь угодно точную аппро-
аппроксимацию рациональными числами. Для к. д. ч. можно
определить естественным образом отношения порядка и
равенства и арифметич. операции (причем последние за-
задаются алгоритмами). Система к. д. ч. с этими отноше-
отношениями равенства и порядка и арифметич. операциями
оказывается полем. Далее, можно ввести в рассмотре-
рассмотрение конструктивные последовательности к. д. ч. (к. п.
д. ч.) и определить в том же порядке идей, что и выше,
понятие фундаментальной к. п. д. ч. и понятие конст-
конструктивной сходимости к. п. д. ч. к данному к. д. ч. От-
Относительно такого понятия сходимости система к. д. ч.
оказывается полной: существует алгоритм, находя-
находящий, исходя из записи всякой фундаментальной к. п. д.
ч. у и записи ее регулятора фундаментальности, такое
к. д. ч., к к-рому (конструктивно) сходится у (т е о р е-
ма о полноте системы к. д. ч.). Методом,
аналогичным канторовскому, можно доказать также
теорему о конструктивной несчет-
несчетности множества всех к. д. ч.: осуществим
алгоритм, перерабатывающий запись всякой к. п. д. ч.
в к. д. ч., отличное (в смысле равенства к. д. ч.) от всех
членов этой к. п. д. ч. Теорема о полноте придает .•зна-
.•значительное сходство конструктивной и классич. теорпя.ч
пределов, особенно сильно проявляющееся в вопросах
сходимости тех или иных конкретных используемых в
анализе последовательностей и рядов. Вместе с тем
здесь имеются и существенные отличия, проявляющие-
проявляющиеся, напр., в следующем результате Э. Шпеккера (см.
[4]): можно построить возрастающую к. п. р. ч. E такую,
что всегда 0<E(«)<1 и, несмотря на это, {5 не является
фундаментальной (и, следовательно, не сходится (кон-
(конструктивно) ни к какому к. д. ч.). Кроме того, п,ч Р
нельзя выбрать сходящейся (конструктпвной) подпосле-
подпоследовательности, и множество значений {5 не имеет в кон-
конструктивном континууме точной верхней границы. Дру-
Другим напрашивающимся способом введения к. д. ч. яв-
является конструктивизация понятия систематической
дроби в той или иной системе счисления. Именно, кон-
конструктивной /ге-и ч н о ii дробью (т>1)
наз. (нормальный) алгорифм а такой, что а@) есть це-
целое число и а (г) при г>0 есть натуральное число, при-
причем 0<:а(г)<:то—1 (с т-пчаой дробью а связывается
к. п. р. ч. a-@)+^k=xm-'lo.(k)). Несмотря на простоту
такого понятия к. д. ч., оно не получило распростране-
распространения, поскольку обладает рядом существенных не-
неудобств: напр., не сохраняется теорема о полноте и не-
невозможен алгорифм, осуществляющий сложение любых
двух m-пчных дробей.
Понятие конструктивной функции (к. ф.) является
естественным уточнением интуитивного понятия точеч-
точечной вычислимой функции над вычислимыми действи-
действительными числами. Конструктивной ф у н к-
ц и е ii (одной действительной переменной) наз. (нор-
(нормальный) алгорифм F такой, что для любых равных
к. д. ч. х я у, если F применим к х, то F применим к у и
F(x), F(y) суть равные к. д. ч. В терминах к. ф. могут
быть введены элементарные функции (показательная
функция, тригонометрич. функции и др.), обладающие
обычными свойствами; для конструктивных функций
могут быть развиты теории дифференцирования, интег-
интегрирования по Риману и т. д., близкие к традиционным.
Вместе с тем возможны и необычные с традиционной точ-
точки зрения функции: напр., построена к. ф., всюду оп-
определенная, непрерывная на единичном сегмопте и не
ограниченная на нем (см. [17]). Не имеет аналогов в тра-
традиционном анализе и теорема, согласно к-рой всякая
к. ф. конструктивно непрерывна в любой точке, в к-рой
она определена (см. [18]).
Система понятий п методы К. а., позволяя существен-
существенно продвинуться с точки зрения цели A), оказались так-
также удобными для выявления вычислительных связей в
анализе, поскольку многие теоремы К. а. являются
либо утверждениями об осуществимости алгоритмов,
строящих нек-рые конструктивные объекты по тем или
иным исходным данным, либо утверждениями, что такие
алгоритмы невозможны. В настоящее время (к 1978)
установлена неразрешимость большого числа естествен-
естественных массовых проблем анализа. Результаты этого типа
(совершенно отсутствующие в курсах традиционного
анализа) имеют очевидную теоретич. и практич. цен-
ценность, так как они выявляют потенциальные вычисли-
вычислительные тупики и способствуют четкому уяснению прин-
принципиальных границ вычислительных возможностей.
Так, доказана невозможность следующих алгоритмов (в
смысле одного из уточнений понятия алгоритма): 1) рас-
распознающего для произвольного конструктивного дей-
действительного числа равно оно нулю или нет; 2) находя-
находящего для каждой сходящейся к. п. р. ч. то к. д. ч., к
к-рому она сходится; 3) находящего для каждой совме-
совместной системы линейных уравнений (над полем к. д. ч.)
какое-либо ее решение; 4) находящего для каждой не-
непрерывной кусочно линейной знакопеременной функции
корень этой функции; 5) находящего для всякой непре-
непрерывной кусочно линейной на единичном сегменте функ-
функции ее интеграл Рпмана по этому сегменту. К этому же
кругу результатов принадлежит и следующая теорема,
полностью решающая вопрос о возможности эффектив-
эффективного перехода от одной системы счисления к другой:
алгоритм, находящий для всякой 7п-нчной конструк-
конструктивной дроби равную ей n-ичную конструктивную
дробь, возможен тогда и только тогда, когда множество
простых делителей п содержится в множестве простых
делителей т (см. [6]). (В частности, возможен алгоритм
перехода от десятичной системы счисления к двоичной,
но невозможен алгоритм перехода от двоичной системы
к десятичной.) Теоремы о невозможности алгоритмов
часто сопровождаются в К. а. теоремами о существова-
существовании алгоритмов, решающих рассматриваемые задачи по
более полным исходным данным (ср. теорему о полноте
к. д. ч. и пример 2)) или с произвольной наперед задан-
заданной точностью (напр., можно построить алгоритм, на-
находящий для каждой всюду определенной знакопере-
знакопеременной к. ф. / и каждого п к. д. ч. х^ п такое, что
\1(xf ti)\ <^%~")¦ Сопоставление таких результатов по-
позволяет во многих случаях i получить отчетливое пред-
представление о том, как можно корректно ставить ту или
иную алгоритмич. проблему.
Лит.: [1] Turing A. M., «Proc. London Math. Soc. Ser.
II», 1937, v. 42, p. 230—65; v. 43, part 6, p. 544—46; [2] В а-
n а с h S., M a z u r S., «Ann. polon. math.», 1937, v. 16, p. 223'
[3] M a z u r S., Computable analysis, Warszawa, 1963; [4]
Speck er E., «J. Symbol. Log.», 1949, v. 14, №3, p. 145—
158; [5]Grzegorczyk A. «Fundam. math.», 1955, v. 42,
p. 168—202, 232—39; 1957", v. 44, № 1, p. 61—71; [6] M о s t о w s-
k i А., там же, p. 37—51; [7] К 1 a u a D., Konstruktive Ana-
Analysis В., 1961; [8] К r e i s с 1 G., L а с о m b e D., S с h o-
e n f i e 1 d J. R., «C. r. Acad. sci.», 1957, t. 245, № 4, p.
399—402; [9] К r e i s e 1 G., L а с о m b e D., там же, № 14,
p. 1106—1109; [10] La com be D., там же, 1955, t. 240,
№26, p. 2478—80- t. 241, № 1, p. 13—14, №2, p. 151 — 53,
№ 19, p. 1250 — 52; 1957, t. 244, J* 7, p. 838—40, № 8, p. 996 —
97; t. 245, № 13, p. 1040—43; 1958, t. 246, № 1, p. 28—31;
[11] Успенский В. А., Лекции о вычислимых функци-
функциях, М., 1960; [12] Гудстейн Р. Л-, Рекурсивный математи-
математический анализ, пер. с англ., М., 1970; [13] Bishop E., Foun-
Foundations of constructive analysis, N. Y., 1967; [14] Мартин-
Л ё ф П., Очерки по конструктивной математике, пер. с англ.,
М., 1975; [151 Марков А. А., Теория алгорифмов, М.— Л.,
1954; [16] Шанин Н. А., «Тр. матем. ин-та АН СССР», 1962,
т. 67, с. 15—294; [17] Заславский И. Д., там же,
с. 385—457; [18] Цейтин Г. С, там же, с. 295—361; [19]
Кушнер Б. А., Лекции по конструктивному математиче-
математическому анализу, М-, 1973. Б. А. Кушнер.
КОНСТРУКТИВНЫЙ ОБЪЕКТ — название, уста-
установившееся за математич. объектами, возникающими в
результате развертывания так называемых кон-
конструктивных процессов. При описании того
или иного конкретного конструктивного процесса обыч-
обычно «...предполагается, что отчетливо охарактеризованы
объекты, которые в данном рассмотрении фигурируют в
качестве нерасчленяемых на части исходных объектов;
предполагается, что задан список тех правил образова-
образования новых объектов из ранее построенных, которые в
данном рассмотрении фигурируют в качестве описаний
допустимых шагов конструктивных процессов; предпо-
предполагается, что процессы построения осуществляются от-
отдельными шагами, причем выбор каждого очередного
шага произволен в тех границах, которые определяются
списком ранее построенных объектов и совокупностью
тех правил образования, которые фактически можно
применить к ранее построенным объектам» (см. [3J,
с. 16). Такое описание конструктивного процесса, а тем
самым и К. о., разумеется, не может претендовать на то,
чтобы быть точным математич. определением. Однако
конкретные математич. теории всегда имеют дело лишь
с такими конкретными типами К. о., к-рые допу-
допускают точную характеризацию. Приведенное выше опи-
описание К. о. служит в таких ситуациях ориентиром для
выбора соответствующих точных определений.
Примером точно определенного типа К. о. могут слу-
служить слова в к.-л. фиксированном алфавите (буквы этого
алфавита играют роль исходных объектов; новые слова
получаются из уже имеющихся путем приписывания к
последним справа букв рассматриваемого алфавита).
Другими примерами типов К. о. могут служить конеч-
конечные графи, конечные абстрактные топологические ком-
комплексы, релейно-контактные схемы (выбор соответствую-
соответствующих исходных объектов и правил образования не пред-
представляет труда). Как К. о. могут быть также определе-
определены рациональные числа, алгебраические многочлены,
алгоритмы и исчисления различных точно определенных
типов, автоматы конечные, конечно определенные груп-
группы и другие им подобные математпч. объекты.
К. о. играют важную роль в тех математич. теориях,
в к-рых возникает потребность в рассмотрении объектов,
допускающих отчетливое индивидуальное задание сред-
средствами той или иной математич. символики. В рамках
теоретико-множественной математики, неограниченно
использующей абстракцию актуальной бесконечности,
К. о. и произвольные множества К. о. рассматриваются
одновременно и наравне с прочими математич. объек-
объектами, среди к-рых К. о. выделяются лишь своей боль-
большей «осязаемостью». В рамках конструктивной мате-
математики К. о. (или объекты, задаваемые ими) представ-
представляют собой единственно допускаемый к рассмотрению
тип математич. объектов, и рассмотрение их здесь ве-
ведется на базе отказа от применения абстракции акту-
актуальной бесконечности и на основе специальной конст-
конструктивной логики, учитывающей, в частности, специ-
специфику определения К. о. См. также Конструктивная
математика.
Лит.: [1] М а р к о в А. А., «Тр. Матем. ин-та АН СССР»,
1962, т. 67, с. 8—14; [2] е г о ж е, О логике конструктивной
математики, М., 1972; [3] Ш а н и н Н. А., «Тр. матем. ин-та
АН СССР», 1962, т. 67, с. 15 — 294. Н. М. Нагорный.
КОНСТРУКТИВНЫХ МОДЕЛЕЙ ТЕОРИЯ — один
из разделов математики, возникший на границе моделей
теории, алгебры и теории рекурсивных функций и свя-
связанный с изучением вопросов эффективности в моделях
и алгебрах.
Статья А. И. Мальцева «Конструктивные алгебры»-
[1] явилась первой обзорной работой по конструктив-
конструктивным моделям, в к-рой были выработаны и систематизи-
систематизированы основные понятия и намечены дальнейшие пути
развития этой теории. Большую роль в становлении п
развитии этого раздела математики сыграли работы
Ю. Л. Ершова и его учеников, в к-рых был решен ряд,
основных проблем, выработаны новые понятия и опре-
определены новые направления в исследовании конструктив-
конструктивных моделей (см. [2]).
Ниже сформулированы основные понятия и резуль-
результаты К. м. т. Все рассмотрения обычно ведутся в нек-рой
фиксированной сигнатуре
а„±;<Р"«, .... Рр, ...>к<ш
такой, что функция / : f(k)t^nk общерекурсивна. Если
рассматриваются алгебраич. системы, то в сигнатуре
могут быть и функциональные символы. Используется
также сигнатура
a-y, ..., ak,...yk<m,
к-рая получается присоединением к ст0 счетного числа
символов для констант. Всегда предполагается, что по=
= 2 и предикат Pi на любой модели определен как ра-
равенство. Пусть L{, ?=0,1,— совокупность всех формул
узкого исчисления предикатов с равенством (Ра) сиг-
сигнатуры а;, ?=0,1, и g— некоторая фиксированная гёде-
левская нумерация (см. [3]) множества Lt(g : N—t-Lj).
Подмножество St^L1 наз. разрешимым, если
множество g~1(S) рекурсивно. Нумерованной
моделью (сигнатуры а0) наз. пара (Щ}, v), гдеЩ}=
= Ш, Р^°, • • • , Рик' ¦ • •>&«¦> — модель сигнатуры
0О, a v — нумерация основного множества М модели ШЪ
Нумерованная модель EШ, v) наз. конструктив-
конструктивной моделью, если множество
рекурсивно.
По каждой нумерованной модели (*Ш, v) можно кано-
нич. образом построить нек-рое ах-о богащение
ffllv модели ЯЛ, т. е. модель сигнатуры ст17 основное
множество к-рой есть основное множество модели Щ},
лредикаты из о"„ в 2RV совпадают с соответствующими
предикатами Щ], а константы определены следующим об-
образом: в качестве значения а^, к<_и>, полагают элемент
v (к) ? М. Пусть Тк(Ш) — элементарная тео-
теория модели Ш1, т. е. множество всех замкнутых
формул сигнатуры а0. истинных на модели Щ}, а 7%(9Л,
v) — элементарная теория нумерованной модели OJlv
Нумерованная модель (Щ}, v) наз. сильно конст-
конструктивной, если теория Th EШ, v) разрешима.
Непосредственно из определения видно, что сильно кон-
конструктивная модель конструктивна.
Одной из основных проблем К. м. т. является пробле-
проблема существования конструктивных моделей с различны-
различными элементарными свойствами, т. е. свойствами, запи-
записываемыми на языке узкого исчисления предикатов.
В этом направлении получен (к 1978) ряд интересных и
важных теорем. Существование широкого класса силь-
сильно конструктивных моделей дает следующая теорема:
если T~L0 — разрешимая теория, то существует такая
последовательность сильно конструктивных моделей
(ЯП.. v0), (ШЬ, vj, ..., (?Dlftl Vft), ..., *<ш,
что: T=r\k<aTh(TiW, множество {(z,y)\g(y)?
? 77i (Ш1у, Vj)} является рекурсивным. Было замечено,
что существуют формулы, не имеющие конструктивных
моделей. Следующие две теоремы дают нек-рые доста-
достаточные условия существования конструктивных моде-
моделей у теорий с рекурсивно перечпслпмым множеством
аксиом.
Если Т — рекурсивно перечпслимая УЭ-теория,
имеющая модель Ш1 с рекурсивно перечислимой з-тео-
рией, то теория Т имеет конструктивную модель.
Теория Т конечной сигнатуры сг= (Р7^0, ¦.., Р\к ,
с0, ... , с{) наз. v-к о н е ч н о й, если универсальная
теория любого расширения Т'^>Т (той же сигнатуры)
конечно аксиоматизируема (универсальными предло-
предложениями). Теория Т наз. сильно V-к о н е ч н о и,
если для любого конечного множества (с[ + 1, . .., сдг)
константных символов теория Т*, определенная теори-
теорией Т в языке сигнатуры о*~о[) (с[ + 1, ... , сдг), яв-
является V-конечной.
Если теория Т сильно V-конечна, а Т' — рекурсив-
рекурсивно перечислимое расширение Т, то 7" имеет конст-
конструктивную модель.
Другой круг исследуемых вопросов связан с пробле-
проблемой существования для заданной модели Щ} нумерации
v такой, чтобы пара (!Ш, v) стала (сильно) конструктив-
конструктивной моделью. Модель, для к-рой существует такая ну-
мерация, наз. (сильно) конструктивней-
р у е м о и, а соответствующая нумерация (с и л ь-
ной) конструктивизацией. Для решения ряда
вопросов, связанных с конструктивизируемостыо мо-
моделей, оказывается полезной теорема Ершова
о ядре, применение к-рой к конкретным алгебраич.
системам позволяет решить ряд естественных вопро-
вопросов. В частности, установлено: 1) для любой конструк-
конструктивной локально ннльпотентной группы без кручения
существует конструктивное пополнение; 2) если (F,v) —
конструктивное поле, Fo — алгебраич. расширение по-
поля F, то v продолжается до конструктивизации поля
Fo тогда и только тогда, когда семейство конечных
множеств многочленов над F от счетного числа пере-
переменных, имеющих корень в F, рекурсивно перечислимо.
Большой класс конструктивизируемых моделей дает
следующая теорема: любая счетная модель ftj-катего-
рпчной разрешимой теории сильно конструктивпзируе-
ма. Интересным является вопрос о (сильной) конструк-
тивизируемости специальных моделей полных теорий,
в ¦частности простых и универсальных. Найдены необ-
необходимые и достаточные условия (сильной) конструкти-
визируемости простой (и счетной насыщенной) модели
полной теории; построены примеры полных теорий с не-
конструктивизируемыми простой и универсальной мо-
моделями. Доказано, что простая модель полной разреши-
разрешимой теории, имеющей сильно конструктивизпруемую
универсальную модель или конечное число попарно
неизоморфных счетных моделей, всегда сильно конст-
руктивизируема.
Изучался вопрос о числе неэквивалентных конструк-
тпвизаций для данной модели. Две конструктивизации
v и (х модели ffll нач. (рекурсивно) эквива-
эквивалентными, если существуют изоморфизм ф(ф-=
= 1<1!М) и рекурсивная функция / такие, что (pv^jx/. Мо-
Модель наз. (рекурсивно устойчивой) ав-
автоустойчивой, если любые две се конструктнви-
зации (рекурсивно) эквивалентны.
Для широкого класса алгебрапч. систем показано,
что существует либо только одна (с точностью до экви-
эквивалентности), либо счетное число неэквивалентных кон-
конструктивизации [4], [5]. Полностью решен вопрос о
числе неэквивалентных конструктивизации и описаны
автоустойчивые модели для полей, булевых алгебр и
абелевых групп без кручения. А также показано, что
вопросы автоустойчпвости связаны с изучением вычис-
вычислимости классов конструктивных моделей.
Лит.: [l] M а л ь ц е в А. И., «Успехи матем. наук», 1961
т. 16, № 3, с. 3—60; [2] Е р ш о в Ю. Л., Теория нумераций
ч. 3 — Конструктивные модели, Новосиб., -1974; [3] Ершов
Ю. Л. и др., «Успехи матем. наук», 1965, т. 20, М« 4, с. 37—108-
[4] Гончаров С. С, «Алгебра и логика», 1975, т. 14, № б'
с. 647—80; [5] Н у р т а з и н А. Т., там же, 1974, т. 13, М« 3, с!
311—23; [6] С о b h a m А., в кн.: Summaries of talks presented
at the Summer Institute for Symbolic Logic Cornell University
1957, Wash., 1960, p. 391—95; [7] F г б h 1 i с h A., Shep-
h e r d s о n J. C, «Phil. Trans. Royal Soc. London», 1956
ser. A, v. 248, p. 407—32; [8] Mostowski A., «Fundam'
math.», 1955, v. 42, № 1, p. 125—40: [9] Rabin M. O., «Trans'
Amer. Math, Soc», 1960, v. 95, № 2, p. 341—60; [10] V a u g h t
R. L., «J. Symb. Logic», 1960, v. 25, Ml 1, p. 39 — 53.
С. С. Гончаров.
КОНТАКТНАЯ СТРУКТУРА — инфинитезималь-
ная структура 1-го порядка на гладком многообразии
М2"^1 нечетной размерности, к-рая определяется зада-
заданием на М2п + 1 такой 1-формы а, что а^(йа)пф0. Здесь
а наз. контактной формой на М2п + 1. К. с.
существует только на'ориентируемом м2п + 1 и опреде-
определяет единственное векторное поле У на М2п + 1 такое,
что ос(У)—-1 и da(Y, X) = 0 для любого векторного поля
X; поле У наз. динамич. системой на М2п + 1, соответст-
соответствующей контактной форме а. К. с. находит применения
в аналитич. механике благодаря тому, что на любом
подмногообразии уровня гамильтониана, заданного на
фазовом пространстве, возникает естественная К. с.
Лит.: [1] Годбийон К., Дифференциальная геометрия
и аналитическая механика, пер. с франц., М., 1973.
Ю. Г. Лумисте.
КОНТАКТНАЯ СХЕМА — специальная управляю-
управляющая система, одна из математических моделей реальных
устройств, построенных из контактов реле. К. с.— мо-
модельный класс управляющих систем, и для него рас-
рассматриваются все те же задачи, что и для прочих клас-
классов управляющих систем; он особенно удобен при изу-
изучении «геометрических» свойств управляющих систем.
К. с. получается в результате приписывания каждому
ребру нек-рого графа с выделенными вершинами одной
из букв конечного алфавита {хг, хх, ... , хп, хп}. Выде-
Выделенные вершины наз. полюсами схемы. Ребро с
приписанной ему буквой ж,- (х-,) наз. замыкающим
(размыкающим) контактом. Последова-
Последовательность контактов между полюсами а и Ъ схемы S, со-
соответствующая простой цепи (см. Граф) в графе схемы
5, наз. цепью между полюсами а и 6 схемы S; конъ-
конъюнкция соответствующих букв наз. проводи-
проводимостью данной цепи. Проводимость между полю-
полюсами а и Ъ схемы есть функция алгебры логики /а;,(х1,
.... хп), равная дизъюнкции проводимостей всех це-
цепей между этими полюсами (в случае, если множество
цепей между а и Ъ пусто, /аь=^0; при а, совпадающем с
6, faap=i). Всякой К. с. сопоставляется матрица прово-
проводимостей ||/а(,||, элементами к-рой являются проводимо-
проводимости между парами полюсов. При этом fab-fbc<fac- Об-
Обратно, если задана матрица из функций алгебры логи-
логики \\fab\\ такая, ЧТО/аа=1, fab = fba п fab-fbc<fac Дл«
любых а, Ъ, с, то существует К. с. с данными полюсами,
для которых проводимости совпадают с заданными fab.
В частности, для любой / существует двухполюсная
схема, проводимость между полюсами к-рой равна /.
В этом случае говорят, что схема реализует
функцию /. Напр., схема рис. 1 реализует линей-
линейную функцию / = х1 + . . . -г *п+ 1 (mod 2). Всякая
функция алгебры логики реализуема некоторой К. с.
РИС. 1.
Рис. 2.
Иногда в К. с. множество всех полюсов разбито на два
подмножества — входов и выходов. К. с. с г входами и s
выходами называется контактным (г, s)-n o-
люсником. К. с, проводимости между любыми
парами выходов (входов) которой равны нулю, называ-
называется разделительной относительно выходов (входов).
Примером разделительного (относительно выходов)
A, 2")-полюсника может служить контактное дерево
(рис. 2). К. с. наз. плоской, если соответствующий
ей граф, дополненный псточннковым ребром (т. е.
ребром, соединяющим полюсы, к-рому не приписана
никакая буква рассматрива-
рассматриваемого алфавита), является
\ плоским (см. Граф плоский).
¦ Плоская К. с. S* наз. д в о й-
/ ственной к плоской К. с.
/ S, если граф Г* схемы S* (с
источшшовым ребром) являет-
является двойственным к аналогич-
аналогичному графу Г схемы S, причем
нсточниковому ребру графа Г
соответствует таковое в графе
Г*, а остальные соответствующие друг другу ребра
несут одинаковые буквы (рис. 3). Схемы S и S*
имеют одинаковое число контактов и реализуют двойст-
двойственные функции (принцип двойственности). При замене
Рис. 3.
контактов в схеме S* на противоположные получается
схема для отрицания функции, реализуемой схемой S.
Для неплоских К. с, вообще говоря, не существует воз-
возможности перехода к схемам с тем же числом контак-
контактов, реализующим двойственные функции. П-схема (па-
(параллельно-последовательная схема) может быть опре-
определена индуктивно: К. с, состоящая из единственного
контакта, соединяющего полюсы, есть П-схема; К. с,
построенная из двух П-схем, соединенных параллельно
или последовательно, есть П-схема. Су-
Существуют К. с, не являющиеся П-схе-
мами, напр, схема рис. 4. К. с., двойст-
двойственная к П-схеме, есть П-схема. Су-
Существует соответствие между П-схемами
и формулами в базисе {&,V,~}. При
этом всякая П-схема реализует ту же самую функцию,
что и соответствующая ей формула, и содержит столько
же контактов, сколько букв содержит формула. Напр.,
схеме рис. 5 соответствует ф-ла
Рис. 4 .
V а-'
V
V
V
Под сложностью К. с. понима-
понимается число всех ее контактов. Ми-
Минимальное число контактов, доста-
достаточное для реализации контакт-
контактной схемой произвольной функ-
функции алгебры логики, зависящей
от п переменных, асимптотически
равно 2"/к; минимальное число
контактов, достаточное для реа-
реализации П-схемой, асимптотиче-
асимптотически равно 2"/log п (см. Синтеза задачи).
Две К. с. наз. эквивалентными (при задан-
заданном взаимно однозначном соответствии между их полю-
полюсами), если проводимости между любой парой соответ-
соответствующих полюсов этих схем совпадают. При замене в
любой К. с. S любой ее подсхемы S' на эквивалентную
получается схема, эквивалентная S. (При замене необ-
необходимо рассматривать г . _.—,_
как полюсы S' все по-
попавшие в 5' полюсы Si! 2,
все вершпны S', ннцн- о—2__—2-^> -.—.- о о
дентные не попавшим в ' 2
S' контактам 5'.) Если r v
Slt S2—эквивалентные
К. с, то правило
&!<—>?а эквивалентного
преобразования К. с.
разрешает в любой схе-
схеме заменить подсхему,
полученную из St (или
5Ч) переименованием
букв, на К. с, получен-
полученную из S2(St) тем же
переименованием. Для
каждого п существует
конечная полная систе- Рис. 6.
переводить друг в
с числом перемен-
ма правил (рис. 6), позволяющая
друга любые эквивалентные К. с.
ных, не превосходящим п. Для класса же всех К. с.
(без ограничения числа переменных) конечной полной
системы правил не существует (если при применении
правил допускать только переименования букв).
Лит.: [1] Ш е с т а к о в В. И., «Автоматика и телемеха-
телемеханика», 1941, т. 6, №2, с. 15—24; [2] Шеннон К., Работы
по теории информации и кибернетике, пер. с англ., М., 1963,
с. 9—45; 13] N a k a s i m a A., «Nippon Electr. Comm. Eng.»
1938, MsJMi 9, 10, 13, 14; [4] Я б л о н с к и й С. В., <<Тр. Матем
ин-та АН СССР», 1958, т. 51, с. 5—142- [5] К у з н е ц о в А. В
там же, с. 174—85; [6] Ч е г и с И. А., Я б л о н с к и й СВ.,
там же, с. 270—360; [7] Л у п а н о в О. В., «Проблемы кибер-
кибернетики», 1963, в. 10, с. 63—97; [8] Мурский В. Л.,
там же, 1961, в. 5, с. 61—76. Н. А. Карпова.
КОНТАКТНОЕ ПРЕОБРАЗОВАНИЕ — преобразо-
преобразование кривых на плоскости, при к-ром касающиеся кри-
кривые переходят в касающиеся же кривые. Аналогично
определяется К. п. поверхностен в пространстве. Про-
Простейший пример К. п.— Лежандра преобразование.
Более общо, контактное преобразова-
преобразование — такой диффеоморфизм / контактного
многообразия (т. е. многообразия М2" + 1, снаб-
снабженного контактной структурой с формой г|), что
/*г| = ал, где а — ненулевая функция на М2. При
а— 1 / наз. строго контактным преобра-
преобразованием. Векторное поле X на контактном много-
многообразии наз. контактным (строго кон-
контактным) и н ф и н и т е з и м а л ь н ы м пре-
преобразованием, если 1'хЦ =ат], (L^n = 0), где
Lx — Ли производная вдоль X. К. п. иногда наз. пре-
преобразованиями прикосновения.
Лит.: [1] Рашевский П. К., Геометрическая теория
уравнений с частными производными, М.— Л., 1947; [2J Э й-
зенхарт Л. П., Непрерывные группы преобразований, пер.
с англ., М., 1947; [3] К о н-Ф о с с е н С. Э., Некоторые вопросы
дифференциальной геометрии в целом, М., 1959; [4] Г о д б и й о н
К., Дифференциальная геометрия и аналитическая механика,
пер. с франц., М., 1973; [5] Итоги науки. Алгебра. Топология.
Геометрия, 1967, М., 1969, с. 127 — 188. М. П. Войцеховский.
КОНТАКТНЫЕ ЗАДАЧИ ТЕОРИИ ТЕПЛОПРО-
ТЕПЛОПРОВОДНОСТИ — задачи распространения тепла (стацио-
(стационарные и нестационарные для эллиптич. п параболич.
уравнений соответственно) в случае, когда вещество
является термически неоднородным — состоит из не-
нескольких частей с различными коэффициентами тепло-
теплопроводности к, теплоемкости с и плотности р. Входящие
в дифференциальное уравнение коэффициенты к, с, р,
имеют разрывы 1-го рода, что приводит к задачам со сла-
слабыми разрывами решений — непрерывной температу-
температурой Т п разрывными ее производными. Однако поток
тепла w задается непрерывным.
Пусть, напр., имеется одномерное по х, 0<z<Z, урав-
уравнение теплопроводности
п пусть в точке 0<Сх—х°<С1 функции к(х), с(х), р(х)
имеют разрыв 1-го рода
[к] =к(х°-\-0) — к(х0 — 0) ^0, [cp] ?b0.
Тогда в точке х=хц должны выполняться условия (см.
[1], [2]) непрерывности температуры Т и потока w=
— ~к(х)дТ1дх (условия сопряжения)
[74 = 0, [w] = 0, i>0. B)
В других точках отрезка температура Т(х, t) должна
удовлетворять уравнению A) при ?>0, начальным усло-
условиям при ?—0, а также граничным условиям при ,г=0,
x=l, t>0.
В многомерном случае для параболич. уравнения
+ YP Ьа(.г, t)-?L — q(x, t)T:f(x, t),
х = (х1, х2, ..., хр)
на поверхности Г° разрыва коэффициентов также ставят-
ставятся условия B) непрерывности функции Т и потока
где и° — нормаль к поверхности Г° (см. [3], [4]).
В стационарном случае (dT/dts^O) условия A) на
разрыве сохраняются. Иногда ставятся более общие ус-
условия сопряжения (см. [2], [4]). Так, в одномерном слу-
случае рассматриваются условия
[Г]=-г@, [adT/dx]=k(t), x = x°, t^sO.
К К. з. т. т. относится также задача о распределе-
распределении тепла в средах, агрегатное состояние к-рых может
меняться при определенном значении температуры Т*
(температуры фазового перехода) с выделением или по-
поглощением теплоты фазового перехода X (задача
Стефана [5]). На искомой границе x=x°(t) раздела
фаз в одномерном случае ставятся условия
Г (а;0 («)-]-0, t) = T (х° (<) — 0, t) = Т*,
дх J dt '
Имеется большое число контактных задач для системы
уравнений теплопроводности и газовой динамики, маг-
магнитной гидродинамики.
Лит.: [1] С а м а р с к и й А. А., «Докл. АН СССР», 1958,
т. 121 Л» 2, с. 225—28- [2] К а м ы н и н Л. И., «Сиб. матем.
ж.», 1963, т. 4, №5, с. 1071 — 1105; [3] Олейник О. А.,
«Изв. АН СССР. Сер. матем.», 1901, т. 25, № 1, с. 3—20; [4] К а-
м ы и и н Л. И., «Дифференциальные уравнения», 1967, т. 3,
№ 6, с. 948—964; [5] Т и х о н о в А. Н., Самарский А. А.,
Уравнения математической физики. 4 изд., М., 1972; [6] Л а д ы-
женская О. А., Солониикив В. А., Уральцева
Н. Н., Линейные и квазилинейные уравнения параболического
типа, М., 1967. И. В. Фрязинов.
КОНТАКТНЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ —
задачи распределения деформации и напряжения в сис-
системе твердых тел, имеющих общие участки границ (по-
(поверхности соприкосновения). В общей постановке ре-
результаты по контактной задаче (к. з.) ограничиваются
теоремами существования и нок-рыми приближенными
способами решения. Более полные результаты относят-
относятся к тому случаю, когда одно из контактирующих тел яв-
является упругой полуплоскостью (пли полупространст-
полупространством), а другое — абсолютно жестким телом, вдавливае-
вдавливаемым в полуплоскость (полупространство) заданными
силами (задачи о штампах). Вне основания штампа,
приходящего в соприкосновение с упругим телом, на
границе последнего граничные условия могут задавать-
задаваться, из числа допустимых, произвольно, а на участке
под штампом граничные условия формулируются в за-
зависимости от характера контакта. Так, если упругое
тело жестко сцеплено с прижимаемым к нему твердым
телом, под штампом могут считаться заданными переме-
перемещения; если же допускается скольжение упругого тела
по контактной поверхности жесткого штампа, то под
штампом известны нормальная составляющая переме-
перемещения и нек-рое линейное соотношение между нормаль-
нормальным и касательным напряжением, зависящее от коэф-
коэффициента трения (закон Кулона). Могут реализоваться
и другие граничные условия. Все случаи упругого по-
полупространства (полуплоскости) приводят к смешанной
задаче с различными граничными условиями на раз-
различных участках границы. Развитие методов решения
этих задач, включая тот случай, когда оба контакти-
контактирующих тела являются упругими, составляет содержа-
содержание работ, посвященных задачам о штампах. Эти методы
близки друг другу и в плоской задаче, в конечном счете,
сводятся к методу сопряжения кусочно голоморфных
функций (метод задачи Римана — Гильберта), с по-
помощью к-рого к. з. решаются в квадратурах. Задача о
соприкосновении двух упругих тел в трехмерном слу-
случае была впервые поставлена и решена Г. Герцем
(Н. Hertz), к-рый считал площадку соприкосновения
весьма малой, а уравнения недеформированных по-
поверхностен вблизи места соприкосновения — уравне-
уравнениями поверхностей 2-го порядка. При этом оказалось
возможным воспользоваться одной электростатич. ана-
аналогией, и функция, выражающая давление на участке
контакта, была найдена в виде электростатич. потен-
потенциала нек-рого эллипсоида. В плоском случае задача
Герца приводится к уравнению Фредгольма 1-го рода
1Де р (f)— искомое давление одного тела на другое в
точке t участка соприкосновения ab, a }(t) — заданная
функция; эта же задача приводится к разрешимому в
замкнутом виде сингулярному интегральному уравне-
нню.
В общей постановке к. ;s. формулируются следующим
образом.
Задача I. Пусть в бесконечном изотропном уп-
упругом теле с постоянными Ламе Яо, (х0 имеются т упру-
упругих изотропных изолированных включении с постоян-
постоянными Я/,, |л/г, /с=1, ... , т, ограниченных гладкими по-
поверхностями iS/j произвольной конфигурации. Считая
включения жестко сцепленными с основной средой
вдоль контактных поверхностен Sk, требуется опреде-
определить напряженное состояние тела под влиянием задан-
заданных объемных сил.
Задача II. В конечном изотропном упругом теле
с произвольной гладкой границей So и постоянными
Я-о. Цо имеется т упругих изотропных изолированных
включений, ограниченных поверхностями Sk, k=i,
.... т, жестко сцепленных с несущей средой вдоль S^.
Требуется найти упругое состояние тела, возникающее
под действием заданных объемных сил и заданных гра-
граничных условий на So.
Эти же задачи ставятся для анизотропных тел, а так-
также при других допущениях относительно характера кон-
контактов вдоль Sк, fc=l, ... , '»• Для указанных задач
доказаны теоремы существования, в изотропном слу-
случае — методом сингулярных потенциалов и сингуляр-
сингулярных интегральных уравнении, для анизотропных тел —
методами функционального анализа.
В изотропном случае найдены также способы при-
приближенного решения в квадратурах. Пусть х, у —
точки трехмерного пространства Е3, D^ — область,
ограниченная поверхностью S^, D + =[}™=ХО#, D~' =
= E3\D +, Tb(jr—y) — матрица размера 3x3 фунда-
фундаментальных решений для области Dь, &=1, ... , т,
Г" (.г—у) — та же матрица для области D~, и(х) —
вектор смещения в точке .т, Т — оператор напряжения,
Ти (х) — вектор напряжения, соответствующий сме-
смещению и в точке х, ТГр(х—у), р=1, 2, 3,— вектор на-
напряжения, соответствующий смещению Г 0(х—у) в
области Dк для хфу, ТТк(х—у) — матрица размера
3x3, составленная из ТТр(х—у), р = 1, 2, 3, как из
столбцов, (ТТк(х—у))' — союзная матрица; Mk{x, у) и
М°(х, у) — прямоугольные матрицы размера 3x6, оп-
определенные следующим образом
Мк(х, у) =
y?Sk, fc=l, то,
0 y?Sj, /-1, ..., тп,
||3Х6,
М*{х, у) = (| (IТ» (х-у))', _ Г» (*-!
Задача I, без ограничения общности, есть задача об
определении смещения из условий
graddiv u = 0,
graddiv и = Ф* (х),
: linl u(x)= lim u(x),
D+ эх-* v D~ эх ->¦ у
lim Tu{x)= lim Tu(x), к=\, ..., т.
эх-t-y
Пусть значения пределов с обеих сторон контактных
границ для и(х) и Ти(х) обозначены через и (у), Ти(у),
UfeLi^b тогДа Для регулярного решения:
Ьк{х)и{х)=\ T"(x-y)Tu{y)dyS-
Г (TT*[x-y))' u{y)dyS, k = l, ...,m;
.m s.
t=1 (
-Cm 5.
A)
где
для x?Dk и 8k(x)=0 для x?Es\Dk, a 6(z)=0 для х?
€ UjLi^i n S(x) = 2 для x?D~.
Формулы A) могут быть записаны в виде:
Чх?Е3\П~ь:\..т s M* (х, у) к (у) dS = 0, k = I то;
J U,-=1 г
где к(у)=(и(у), Ти(у)) — шестимерный вектор. Первое
из этих раненств верно для всех х, принадлежащих
Ез~\^к, а второе — для всех х, принадлежащих
Ui=1Di- Соответствующею произвольно заданные зна-
значения переменной х проводят к бесконечному множеству
равенств
\.,m s. M*$j; y)k(y)dyS =0,
,ms.M0(l),y)\(y)dvS=F(\%... \ B)
h, й = 1, ..., m; / = 1, 2, ... .
Пусть {ф"(г/) }о° — множество шестимерных векторов
...,(rrj(if-y). — r^feT1 —j,)),
у€ UJ^s,-, p = i, 2, 3,
соотиетственно пронумерованное, напр., по диагональ-
диагональному правилу. Это множество линейно независимо и
полно в <5?2(UJ=i'S/)- В левых частях равенств B) сто-
стоят скалярные произведения (к, <р") для любого значе-
значения индекса п в качестве составляющих заданных
векторов и, следовательно, эти произведения также
заданы. Вследствие полноты {ф"(г/)}о> в ifj((jLS()
неизвестный вектор к=(и, Ти) может быть аппрокси-
аппроксимирован линейной комбинацией ^, _.an4>"(y), если по-
N
стоянные аа найдены из условия минимума нормы
Это приводит к системе линейных алгебраич. уравне-
уравнений
к-рая разрешима. iV-e — приближение №(у) для векто-
вектора к (у) выражается формулой kN (y)=^j n=lan wn(y).
Подстановка первых трех составляющих АА(г/), как
вектора, вместо и(у), а вторых трех составляющих вме-
вместо Ти(у) под интегралами в A), приводит к приближен-
приближенному решению в квадратурах задачи I. Точное решение
есть равномерный при N—voo предел приближенного в
произвольной внутренней точке области.
Формулы для решения задачи II остаются теми же,
с одним изменением: вместо матрицы Т°(х—у) исполь-
используется тензор Грпна для полной области, ограниченной
поверхностью So, соответствующей заданным на So
граничным условиям.
Лит.: [1] М у с х е л и ш в и л и Н. И., Некоторые основ-
основные задачи математической теории упругости, 5 изд., М.,
1966; [2] Г а л и н Л. А., Контактные задачи теории упругости,
М., 1953; [3] Ш т а е р м а н И. Я., Контактная задача теории
упругости, М.— Л, 1949; [4] К у п р а д з е В. Д. и д р., Трех-
Трехмерные задачи математической теории упругости и термоупру-
термоупругости, 2 изд., М., 1976; [5] Фи к ер а Г., Теоремы существо-
существования в теории упругости, пер. с англ., М., 1974.
В. Д. Нупрадве.
КОНТИНГЕНЦИЯ подмножества Е ев-
евклидова пространства в точкеЛ^В >—
объединение лучей А В с началом А таких, что сущест-
существует последовательность точек Вп?Е, сходящаяся к А,
и последовательность лучей АВп сходится к А В; обо-
обозначается contg (E, А). Для m-мерного дифференцируе-
дифференцируемого многообразия Е contg(E,A) совпадает с т-мер-
вой плоскостью, касательной к ? в точке А. Поня-
Понятие оказалось полезным при изучении дифференци-
дифференциальных свойств функций. Если для любой точки А
плоского множества Е contg(?', А) не совпадает со
всей плоскостью, то Е распадается на счетное число
частей, расположенных на сирямляемых кривых. Эта
теорема неоднократно обобщалась и уточнялась, напр,
лшожество конечной р-меры Хаусдорфа р = 1, . . ., п—1,
расположенное в n-мерном евклидовом пространстве,
распадается на счетное число 'частей, одна из к-рых
имеет нулевую меру Фавара порядка р, а каждая из
остальных расположена на нек-рой липшицовой по-
поверхности размерности р; для почти всех х?Е в смы-
смысле р-меры Хаусдорфа contg (E, А) является плоскостью
размерности р, если все вариации множества Е ко-
конечны и, начиная с (р+1)-й, равны нулю.
Лит.: [1] В о u I i g a n d G., Introduction a la geometrie
infinitesimale directe, P., 1932; [2] С а к с С, Теория интеграла,
пер. с англ., М., 1949; [3] Federer H., Geometric measure
theory, В., 1969; [4] И в а н о в Л. Д., Вариации множеств и
функций, М., 1975. Л. Д. Исанов.
КОНТИНУАЛЬНЫЙ ИНТЕГРАЛ — см. Интеграл
по траекториям.
КОНТИНУУМ — непустое связное хаусдорфово
бикомпактное пространство. К. наз. вырожден-
вырожденным, если он состоит из одной точки. Особо важным
является класс метризуемых К. Примеры К.: замкну-
замкнутый отрезок, окружность, выпуклый многогранник
и т. д. Компакт (X, р) (т. е. метризуемый бикомпакт с
метрикой р) есть К. в том и только в том случае, если
для каждой пары точек а, Ь?Х и для любого е>0 най-
найдется конечная 8-цепь, соединяющая эти точки, т. е.
последовательность {хп}п=\ точек в X такая, что х1 = а,
Xk=b и р(хп, жп + 1)<е. Объединение двух К., имеющих
общую точку, есть К. Топологич. произведение К.
есть К., непрерывный образ К. есть К., компоненты
бикомпакта суть К., пересечение убывающей последо-
последовательности К. есть К. Никакой К. нельзя разложить
в объединение счетного семейства непересекающихся
замкнутых множеств (теорема Серпинь-
с к о г о).
Каждый локально связный метрич. К. является не-
непрерывным образом замкнутого отрезка (теорема
Хана — Мазуркевича). Невырожденный К.
неприводим между двумя своими точками, если
никакой его собственный подконтинуум не содержит
этих двух точек К., неприводимый между некоторыми
двумя своими точками, наз. неприводимым
континуумом. Всякий локально связный непри-
неприводимый К. есть простая дуга, т. е. гомеоморфен от-
отрезку.
Невырожденный К. наз. неразложимым,
если его нельзя представить в виде суммы двух соб-
собственных подконтинуумов, и — наследственно
; неразложимым, если неразложим он сам, и
неразложимы все его подконтинуумы. К. неразложим
тогда и только тогда, когда в нем существуют три такие
точки, что он неприводим между любыми двумя из них;
все наследственно неразложимые К. гомеоморфны
между собой.
Лит.: [1] Куратовский К., Топология, пер. с англ.,
т. 2, М. 1969. //. С. Александров, Л. Г. Замбахивзе.
КОНТИНУУМА МОЩНОСТЬ — кардинальное чи-
число с=2^°, являющееся мощностью множества всех
подмножеств натуральных чисел. Следующие множества
имеют К. м.: 1) множество R всех действительных чисел,
2) множество всех точек интервала @, 1); 3) множество
всех иррациональных чисел из этого интервала, 4) .мно-
.множество всех точек пространства R", где п — нату-
натуральное; 5) множество всех трансцендентных чисел;
6) множество всех непрерывных функций действитель-
действительного переменного К. м. нельзя представить в виде счет-
счетной суммы меньших кардинальных чисел. Для любого
кардинального числа а такого, что 2<:<х«г:с, выполня-
выполняется »
в частности,
2Хо =3«. = ... =-_ n*°= tf?" = c*» = c.
Континуум-гипотеза утверждает, что К. м. является
первым несчетным кардинальным числом, т. е.
c=lfi.
Лит.:М Куратовский К., Мостовский А.,
Теория множеств, пер. с англ., М., 1970. Б. А. Ефимов.
КОНТИНУУМ-ГИПОТЕЗА - гипотеза Г. Кантора
(G. Cantor, 1878), состоящая в том, что всякое беско-
бесконечное подмножество континуума R равномощно либо
многкеству натуральных чисел, либо R. Эквивалентная
формулировка (при наличии выбора аксиомы):
(см. Алефы). Обобщение этого равенства на произволь-
произвольные кардинальные числа наз. обобщенной
континуум-гипотезой: для всякого орди-
ординального числа а
2*а = Ка+1. A)
В отсутствии аксиомы выбора обобщенная К.-г. фор-
формулируется в виде
Vfel3m (ft < m < 2*), B)
где k, m — переменные для бесконечных кардинальных
чисел. Из B) вытекают аксиома выбора и A), а из A) и
аксиомы выбора вытекает B).
Д. Гнльберт (D. Hilbert) в своем знаменитом списке
проблем поставил под номером 1 проблему доказать
гипотезу континуума Кантора (проблема кон-
континуума). В рамках традиционного теоретико-
множественного решения проблема не поддавалась ре-
решению. Среди математиков росло убеждение в принци-
принципиальной неразрешимости проблемы континуума. Лишь
после того, как был найден способ сведения математпч.
понятий к теоретико-множественным, выявлены акси-
аксиомы, сформулированные на теоретико-множественном
языке, к-рые можно положить в основу реально встре-
встречающихся математич. доказательств, и формализованы
логич. средства вывода, стало возможным точно поста-
поставить, а затем и решить вопрос о формальной неразре-
неразрешимости К.-г. Формальная неразрешимость понимается
в смысле не существования формального вывода в
системе Цермело — Френкеля ZF как для К.-г., так
и для ее отрицания.
В 1939 К. Гёдель (К. Godel) установил недоказуе-
недоказуемость отрицания обобщенной К.-г. (а следовательно,
II недоказуемость отрицания К.-г.) в системе ZF с
аксиомой выбора (системе ZFC), в предположении, что
ZF непротиворечива (см. Конструктивное по Гёделю
множество). В 1963 П. Коэн (P. Cohen) показал невы-
невыводимость К.-г. (а следовательно, и невыводимость
обобщенной К.-г.) из аксиом ZFC при условии непро-
непротиворечивости ZF (см. Вынуждения метод).
Являются ли эти результаты окончательными в проб-
проблеме континуума? Ответ на этот вопрос зависит от от-
отношения к посылке о непротиворечивости ZF и, что
более существенно, к тому экспериментальному факту,
что всякое содержательное математнч. доказательство
(традиционной классич. математики), после того как
оно найдено, может быть адекватным образом формали-
формализовано в системе ZFC. Факт этот нельзя не только до-
доказать, но даже точно сформулировать, поскольку
всякое уточнение поднимает аналогичный вопрос об
адекватности уточнения уточняемому.
На теоретико-модельном языке К. Гёдель и П. Коэн
построили модели для ZFC, в к-рых
9ft / т, если к < т,
\ fc+, если
где т — произвольный, наперед заданный несчетный
регулярный кардинал, а к+ — первое кардинальное
число, большее к. Каково возможное поведение функции
2* в различных моделях ZFC?
Известно, что на регулярных кардиналах к функ-
функция эта может вести себя как угодно, подчиняясь
лишь условиям
к^к'~*2*<2fe', k<cfBk),
где cf (т.) — наименьший кардинал конфинальный т
(см. Кардинальное число). Для сингулярных (т. е. не
регулярных) к значение функции 2* может зависеть от
ее поведения на меньших кардинальных числах. Так,
напр., если равенство A) имеет место для всех a<wlt
то оно имеет место и для a= wr
Лит.: [1] К о э н П. Д ж., Теория множеств и континуум-
гипотеза, пер. с англ., М., 1969; [2] Baumgartner J. Е.,
Prikry K.,«Amer. Math. Monthly», 1977, v. 84, № 2, p. 108—
ИЗ. В. Н. Гришин.
КОНТОРОВИЧА — ЛЕБЕДЕВА ПРЕОБРАЗОВА-
ПРЕОБРАЗОВАНИЕ — интегральное преобразование вида
F(x) = ^ Kix(x)f{x)dx,
где Ку(х) — Макдональда функция.
Если функция f(x) имеет ограниченное изменение в
окрестности точки х=яо>О и
то справедлива формула обращения
=ik; \ о ки(Zo) T sh ят F (T) йх-
Пусть fi(x), j= 1,2,— действительные функции,
причем
JO л V x
< w L? fi <>dx-
JO л V x
Тогда
J " (т) di, = J o" U (*) h
(равенство Парсеваля).
Конечное К.— Л. п. имеет вид
f (T)I
т>0, /v (x) — модифицированная функция Бесселя
(см. [3]).
Исследование таких преобразований было начато
М. И. Конторовичем и Н. Н. Лебедевым (см. [1J, [2]).
Лит.: ШКонторович М. II., Лебедев Н. Н.,
«Ж. экспер. и теор. физ.», 1938, т. 8, М« 10—11, с. 1192—206;
[2] Лебедев Н. Н., «Докл. АН СССР», 1946, т. 52, № 5,
с. 395—98; [3] У ф л я н д Я. С, Ю ш к о в а Е. А., там же,
1965, т. 164, № 1, с. 70—72; [4] Д и т к и н В. А., П р у д н и-
ков А. П., Интегральные преобразования и операционное
исчисление, 2 изд., М., 1974. Ю. А. Брычков, А. П. Прудников.
КОНТРАВАРИАНТНЫЙ ВЕКТОР — наименование
элемента векторного пространства Е в ситуации, когда
наряду с Е рассматривается сопряженное ему простран-
пространство Е*. Элементы пространства Е* наз. тогда ковари-
антпими векторами. М. И. Войцеховский.
КОНТРАВАРИАНТНЫЙ ТЕНЗОР валентно-
валентности /Csl — тензор типа (г, 0), элемент тензорного-
произведения
г экземпляров векторного пространства Е над полем К.
Относительно операции сложения К. т. одной и той же
валентности и умножения их на скаляр ТГ(Е) явля-
является векторным пространством над К. Пусть Е — ко-
конечномерно и пусть е1( . . ., еп — базис в Е. Тогда раз-
размерность ТГ(Е) равна пг\ базис в ТГ(Е) состоит из все-
всевозможных К. т. вида
еи® ¦¦ ¦ ® etr, 1 < «1. • • •, «V < п.
Любой К. т. t?Tr(E) представляется в виде
Числа t наз. координатами, или ком-
компонентами, К. т. t относительно базиса ех, . . ., еп
в Е. При переходе в Е к новому базису по формулам
координаты К. т. t изменяются по так наз. контрава-
риантному закону
При валентности г=1 К. т. совпадает с вектором —
элементом пространства Е\ при г^2 К. т. можно
инвариантным образом связать с r-линейным отобра-
отображением в К прямого произведения
Ег* =Е*Х...У.Е*
г экземпляров сопряженного к Е пространства Е*.
Для этого достаточно принять за координаты К. т. t
значения r-линейного отображения t на векторах
(ег', . . ., ег)?Ег* (где е1, . . ., е" — элементы базиса
в Е*, сопряженного к ег, . . ., еп, т. е. е'(еу)=б}), и
обратно; поэтому иногда К. т. сразу определяют как
ПОЛПЛИНеЙНЫЙ фуНКЦИОНаЛ на Ег*. И. X. Сабитов.
КОНТРАГРЕДИЕНТНОЕ ПРЕДСТАВЛЕНИЕ к
представлению (р группы G в линей-
линейном пространстве V — представление (р*
этой же группы G в двойственном к V пространстве V*,
определяемое правилом:
для любого g?G, где * означает переход к сопряженному
оператору.
Более общо, если W — линейное пространство над
тем же полем к, что н пространство V, а ( , ) —
невырожденная билинейная форма (спаривание) на
Vy W со значениями в к, то представление^ группы G
в W наз. К. п. к представлению <р отно-
относительно формы ( , ), если
(<p(g)x, y)--=(x, ^(g-^y)
для любых ? ? y?
Напр., если G — полная линейная группа конечно-
конечномерного пространства Г, то естественное представление
G в пространстве ковариантных тензоров фиксирован-
фиксированного ранга на V является К. п. относительно канони-
канонического спаривания к естественному представлению G
в пространстве контравариантных тензоров того же
ранга на V.
Пусть V конечномерно над к и (е) — его базис, а
if) — дуальный к (е) базис в V*. Тогда для любого g
из G матрица оператора <р* (g) в базисе (/) получается
из матрицы оператора <р (g) в базисе (е) транспони-
транспонированием и переходом к обратной. Если ф неприводи-
ию, то и ф* неприводпмо. Если G — группа Ли с алгеб-
алгеброй Ли д, a d<f и <Л|: — представления алгебры д,
индуцированные соответственно представлениями ф и
-ф группы G в пространствах V и W, контрагредиентны-
ми относительно спаривания ( , ), то
(Ap(X)(x), у)--=-(х, d^(X)y) (*)
для всех Х?д, х?\~, y?W. Представления алгебры
Ли д, удовлетворяющие условию (*), также наз. К. п.
относительно ( , ).
Пусть далее G — комплексная связная односвязная
полупростая группа Ли и ф — ее неприводимое ко-
конечномерное представление в линейном пространстве
Г. Веса представления ф* противоположны весам пред-
представления ф (см. Вес представления), младший вес
представления ф* противоположен старшему весу
представления ф (см. К ар тана теорема о старшем век-
векторе). Представления ф и ф* эквивалентны тогда и
только тогда, когда на Г существует ненулевая инвари-
инвариантная относительно ф(б) билинейная форма. Если та-
такая форма существует, то она невырождена и либо сим-
симметрична, либо кососимметрична. Набор числовых от-
отметок старшего веса представления ф* получается из
набора числовых отметок представления ф применени-
применением подстановки, индуцированной следующим автомор-
автоморфизмом у схемы простых корней Д группы G:
а) v переводит каждую связную компоненту Д,-,
г=1, . . ., I, схемы Д в себя;
б) если Д,- — схема типа Ar, ZJr + iiMii Ев, то суже-
сужение v на Д, однозначно определяется как единственный
элемент второго порядка в группе автоморфизмов схе-
схемы Д,-, в остальных случаях сужение v на Д,- тождест-
тождественно .
Лит.: [1] Н а й м а р к М. А., Теория представлений групп,
М., 197В; [2] Кириллов А. А., Элементы теории пред-
представлений, М., 1972; [3J Ж е л о б е н к о Д. П., Компактные
О н и щ и к А. Л., Семинар по алгебраическим группам и
группам Ли. 1967/68, М., 1969. В. Л. Попов.
КОНТРАГРЕДИЕНТНЫЙ АВТОМОРФИЗМ к а в-
т о м о р ф ичм у ф правого модуля М
над кольцом А — автоморфизм <р левого Л-мо-
Л-модуля М* (*обозначает переход к сопряженному моду-
модулю), сопряженный к автоморфизму, обратному ф. Более
общо, если я|з—изоморфизм правого А -модуля Мг
и правого Л-модуля Д/2, то контрагредиент-
н ы м к г|з изоморфизмом наз. изоморфизм
левого А -модуля М[ на левый А -модуль м\, сопря-
сопряженный к изоморфизму, обратному г|). Пусть ( , )^
и ( i )г — канонические билинейные формы на
Л/jXAfx и M2xMl. Тогда гр определяется следующим
тождеством относительно
Если il/j н Мг обладают конечными базисами, то if —
изоморфизм, контрагредиентный к i|).
Пусть А — кольцо с единицей и М — правый А -мо-
-модуль, обладающий конечным базисом, q> — некоторый
автоморфизм модуля М и X — матрица ф в фиксиро-
фиксированном базисе (эта матрица обратима). Тогда в сопря-
сопряженном базисе матрица К. a. q> имеет вид
Х = (ТХ)-1 = Т (Х-1)
(индекс т означает транспонирование). Матрица X
наз. к о н т р а г р е д н е н т н о й матрицей к об-
обратимой матрице X.
Лит.: [1] Б у р б а к и Н., Алгебра. Алгебраические струк-
структуры. Линейная и полилинейная алгебра, пер. с франц., М.,
1962. В. Л. Попов.
КОНТРАПОЗИЦИИ ЗАКОН — логический принцип,
согласно к-рому если из одного утверждения следует
другое, то отрицание последнего влечет отрицание
первого:
(А зД)=>ПД=> -]А).
К. з. принимается как классической, так и конструк-
конструктивной ЛОГИКОЙ. С. И. Соболев,
КОНТРАСТ, сравнение,— ейалярпое произве-
произведение QT-с вектора 6=FХ, ..., 6^)г, координаты к-рого
суть неизвестные параметры, на заданный вектор
с--- (сх, . . ., ck)T такой, что cx-J- . . . -\-ck=0. Напр.,
разность 6Х—G2=(91, G2) A, —1)г неизвестных мате-
матпч. ожиданий Gt и 92 двух одномерных нормальных
распределений является К. Среди всех функций, за-
зависящих от неизвестного вектора 6= (91; . . ., 6^)г,
только для К. существует линейная несмещенная оцен-
оценка, и наоборот. В дисперсионном анализе часто рас-
рассматривается задача множественного сравнения, кото-
которая заключается в проверке гипотез о численных значе-
значениях К.
Лит.: [1] Шеффе Г., Дисперсионный анализ, пер. с
англ., М., 1963. М.С. Никулин.
КОНТУРНОГО ИНТЕГРИРОВАНИЯ МЕТОД —
один из основных методов геометрич. теории функций
комплексного переменного, позволяющий получать
различные неравенства, выражающие экстремальные
свойства однолистных и многолистных функций, а
также тождества, связывающие основные функции об-
областей теории конформного отображения. Метод су-
существенно связан с использованием свойств функций,
конформно отображающих данную область на различные
канонические области. С помощью таких функций мо-
можно строить функции области, обладающие следую-
следующим контурным свойством: на каждой
граничной компоненте области значения функции раз-
разнятся на аддитивную постоянную от комплексно со-
сопряженных значений соответствующей другой функ-
функции. К. и. м. состоит в основном в следующем.
Рассматривается нек-рый интеграл, взятый по всему
контуру данной области (обычно контур можно счи-
считать состоящим из конечного числа простых замкнутых
аналнтич. кривых). Этот интеграл выбирается так, что-
чтобы подинтегральное выражение содержало множители
с указанным выше контурным свойством и чтобы после
использования этого свойства получался интеграл,
вычисляемый с помощью теоремы о вычетах. Если из
других соображений известны либо значение исходного
интеграла, либо его знак, то в результате получается
или нек-рое соотношение между использованными функ~
циями, пли нек-рое неравенство, связывающее их.
Часто контурный интеграл, к к-рому удается приме^
нить указанный метод, появляется в результате пре-
преобразования по формуле Грина неотрицательного двой-
двойного интеграла — интеграла от квадрата модуля про-
производной нек-рой функции, регулярной в данной об-
области. Отсюда — связь К. и. м. с площадей методом.
С помощью К. и. м. были получены результаты, каса-
касающиеся искажения теорем для однолистных конфор-
конформных отображений многосвязных областей (см. [1], [2]);
необходимые и достаточные условия для коэффициентов
однолистных функций (см. [3]); тождества, связывающие
основные функции областей теории конформного отоб-
отображения (см. [4]).
К. и. м. применялся для исследования однолистных
функций также в следующей форме. Пусть, напр.,
В — область плоскости w с контуром С, состоящим из
конечного числа простых замкнутых аналитич. кривых;
S(w) — функция, гармоническая в полной плоскости
ш за исключением конечного числа точек области В;
p(w) — функция, обладающая свойством: разность
S (w) — p (w) является гармонической в области В
и непрерывной в этой замкнутой области, р(ш)|с=0.
Тогда
где д/дп обозначает дифференцирование по направле-
направлению внешней нормали к области В. Если а(и>) и
q(w) — аналитич. функции, для к-рых S= Re {а},
p=Re {q}, то последнее неравенство может быть пере-
переписано в виде
В этом неравенстве интеграл вычисляется по теореме
о вычетах. Выбирая различные функции S (w) и p{w),
надлежаще связанные с исследуемыми функциями,
можно таким образом получать различные новые нера-
неравенства для однолистных функций (см. [5] — [7]).
К. и. м. успешно использовался и при исследовании
неоднолистных конформных отображений. Так, этим
методом был установлен ряд новых экстремальных
свойств функций, мероморфных в многосвязной области
и удовлетворяющих нек-рым дополнительным условиям
(см. [8]); получено обобщение на многосвязные области,
на случай нескольких полюсов и на функции, р-листные
в соответствующем обобщенном смысле теоремы площа-
площадей Голузина для функций, р-листных в круге (см.
[9]). Упомянутые выше функции области тесно связаны
с Бергмана кернфункциями, и результаты, получаемые
К. и. м., часто выражаются через них. Отсюда же сле-
следует связь К. и. м. с теорией ортонормальных систем
аналитич. функций.
Лит.: [1] Grunsky H., «Schriften math. Semin. und
Inst. angew. Math. Univ. Berlin», 1932, S. 95—140; [2] Г о-
лузин Г. М., «Матем. сб.», 1937, т. 2, №1, с. 37—63; [3]
Grunsky H., «Math. Z.», 1939, Bd 45, S. 29—61; [4] G а г а-
bedian P. R., Schiffer M., «Trans. Amer. Math. Soc»,
1949 v. 65, № 2, p. 187—238; [5] N e h a r i Z., «Trans. Amer.
Math. Soc», 1953, v. 75, № 2, p. 256—86; [6] Аленицын
Ю Е., «Матем. сб.», 1956, т. 39, JM5 3, с. 315—36; [7] е г о же,
«Тр матем. ин-та АН СССР», 1967, т. 94, с. 4—18; [8] М е s с h-
kowski H., «Math. Ann.», 1954, Bd 127, S. 107—29; [9]
Аленицын Ю. Е., «Изв. АН СССР. Сер. матем.», 1973,
т. 37, в. 5, с. 1132—54; [10] Голузин Г. М., Геометрическая
теория функций комплексного переменного, 2 изд., М., 1966,
с. 221—26. Ю. Е. Аленицын.
КОНУС — 1) К. в евклидовом прост-
пространстве — множество К, составленное из полупря-
полупрямых, исходящих из нек-рой точки О — вершины
К. Границу дК множества К (составленную из полу-
полупрямых, наз. образующими К.) — часть ко-
конической поверхности — также иногда наз. К. Наконец,
часто К. наз. пересечение К с полупространством, со-
содержащим О и ограниченным плоскостью, не проходя-
проходящей через О. В этой ситуации часть плоскости, лежащая
внутри конич. поверхности, наз. основанием К.,
а часть конич. поверхности, заключенная между вер-
вершиной и основанием,— боковой поверхно-
поверхностью К.
Если основание К. есть круг, то К. наз. к р у г о в ы м.
Круговой К. наз. прямым, если ортогональная
проекция его вершины на плоскость основания совпа-
совпадает с центром основания. Прямая, проходящая через
вершину К. перпендикулярно основанию, наз. осью
К., а ее отрезок между вершиной и основанием —
высотой К. Объем прямого кругового К. равен
яй2й/3, где h — высота, R — радиус основания; пло-
площадь боковой поверхности равна nRl, где I — длина
отрезка образующей между вершиной и основанием.
Подмножество К., заключенное между двумя парал-
параллельными плоскостями, наз. усеченным К., или
коническим слоем. Слой прямого кругового
К. между плоскостями, параллельными основанию,
имеет объем я(Я2+г2+Лг) Л/3, где R, г — радиусы
оснований, h — высота (расстояние между основания-
основаниями); площадь боковой поверхности n(R^-r) I, где
I — длина отрезка образующей. а. б. Иванов.
2) К. над тополог л ч. пространством
X (основанием К.) — пространство СХ, полу-
получающееся из произведения XX [0, 1] стягиванием под-
подпространства X X {0} в одну точку ^(вершину К):
Другими словами, СХ — цилиндр постоянного отоб-
отображения X-+-W (см. Цилиндрическая конструкция)
или конус тождественного отображения id : Х-+Х
(см. Коническая конструкция). Пространство X стяги-
стягиваемо тогда и только тогда, когда оно является ретрак-
том всякого К. над X.
Понятие К. над топологии, пространством обобща-
обобщается в рамках теории категорий: множество морфизмов
а,- : А—*-А;, i ? /, произвольной категории 91 с общим
началом в объекте А наз. конусом морфиз-
морфизмов с вершиной А; двойственно, коконус мор-
морфизмов есть множество морфизмов E,- : A i—+A,
i^I с общим концом в объекте А. См. [4], [5], [в].
М. И. Войцеховский.
3)К. отображения — топологпч. простран-
пространство, сопоставляемое непрерывному отображению
/ : X-+Y топологич. пространств конической конструк-
конструкцией. Пусть Ci — конус вложения YaCj, C2— конус
вложения Cf(Z.C1 и т. д. Получающаяся последователь-
последовательность
X -U Y с Cf С Cj с С2 с. ..
наз. последовательностью Пуппе; здесь
C-l-SX, C2~SY и т. д., где SX(SY) — надстройка
над X (над Y).
Аналогично определяется приведенный конус С j
отображения пунктированных пространств. При атом,
как и в ситуации с корасслоением, для любого пункти-
пунктированного пространства А последовательность гомо-
топич. классов, индуцированная последовательностью
Пуппе,
[X, Л]^-[У, А]+-[Сг, А]*—[С„ А]*—...,
точна; в ней все члены, начиная с четвертого,— группы,
а начиная с седьмого — абелевы группы. См. [4], [5].
А. Ф. Харшиладзе.
4) К. в действительном векторном
пространстве Е — множество КаЕ такое, что
ККаК для любого Х>0. К. наз. заостренным,
если 0(-К, а заостренный К.— выступающим,
если К не содержит никакого одномерного подпростран-
подпространства. Невыступающий К. иногда наз. клином.
К., являющийся выпуклым множеством в Е, наз.
выпуклым. Таким образом, подмножество К в Ё
является выпуклым К. тогда и только тогда, когда
ХКаК для всякого Х>0 и К-\-КаК. В атом случае
векторное подпространство в Е, порожденное выпук-
выпуклым К. К, совпадает с множеством К—К. Если К.
заострен, то Kf] (—К) — наибольшее векторное под-
подпространство, содержащееся в К. Заостренный выпук-
выпуклый К. будет выступающим тогда и только тогда,
когда ЯГИ — К) = 0-
Если Е — полуупорядоченное пространство, то п о-
лож и тельный конус Р= {х : х^Е, х^О }
является выступающим, заостренным, выпуклым К.
Обратно, любой такой К. К в векторном пространстве Е
порождает отношение порядка: x1^sx2, если хх—х2?К.
К. К наз. воспроизводящим, если любой элемент
х?Е представим в виде разности элементов из К. Напр.,
воспроизводящими являются К. неотрицательных не-
непрерывных (или суммируемых) функций на отрезке
[О, 1], множество положительных операторов в про-
пространстве ограниченных самосопряженных операторов,
действующих в гильбертовом пространстве. Однако К.
неотрицательных неубывающих непрерывных функций
таковым не является.
Наличие топологии в Е наделяет понятие К. более
богатым содержанием, позволяющим получать нетри-
нетривиальные результаты. Напр., пусть Е — отделимое
локально выпуклое пространство и К — выступающий
заостренный выпуклый К. в Е, имеющий непустую
внутренность (такие К. наз. телесным и). Тогда
каждая линейная форма на Е, положительная на К,
непрерывна; если М — векторное подпространство в Е,
пересекающееся с внутренностью К, и / — линейная
форма на М, положительная на К(\м, то на Е су-
существует линейная форма /, продолжающая / и поло-
положительная на К. См. [1], [2], [3]. М. И. Войцеховский.
Более других развита теория К. в банаховых
пространствах. Пусть К — К. в банаховом
пространстве Е, порождающий в Е нек-рое отношение
порядка ^. Если К. замкнут, то для Е имеет место
принцип Архимеда: если х?-Е, а числа Х„>0
и Х„ —>-оо, и при этом существует такое у, что Х„х<:г,
при всех п, то zs?;0. Для телесного К. верно и обрат-
обратное: из архимедовости Е вытекает замкнутость К.
Пусть К'— сопряженный клин, т. е. совокупность
всех положительных линейных непрерывных функцио-
функционалов на Е (/ положителен, если /(х)^0 для любого
х(-К). К'— К. тогда и только тогда, когда К — про-
пространственный, т. е. замыкание К — К=Х. Если К
замкнут, то для любого ?0>0 (соответственно х
существует такой f?K', что /(хо)>О (/(хо)<0).
К. К наз. несплющенным, если для любого
х?Е существуют такие и, v?-K, что
x=u-v, а ||и||, M<iW||x||,
где М= const.
Если К. замкнутый и воспроизводящий, то он
несплющен (теорема Крейна — Шмульяна).
К. К наз. нормальным, если
Нормальность К. равносильна полумонотонно-
полумонотонности нормы: 0<:г,<:х влечет ||j,||<:M||x||, где М=
= const. Для того чтобы клин К' был воспроизводящим
в сопряженном пространстве, необходимо и достаточно,
чтобы К. был нормальным (теорема Крейна).
Двойственно: если К' — нормальный К., соответствую-
соответствующий замкнутому К. К, то К. К воспроизводящий.
Существует взаимно однозначное линейное и непрерыв-
непрерывное отображение пространства Е с нормальным К. К в
подпространство пространства С (Q) непрерывных функ-
функций на некотором бикомпакте Q, при котором элементы
из К и только они переходят в неотрицательные
функции.
К. К наз. правильным (вполне пра-
правильным), если всякая последовательность эле-
элементов из К, возрастающая и ограниченная по поряд-
порядку (по норме), сходится. Если К замкнут и правилен,
то он нормален, а всякий вполне правильный конус
нормален и правилен. Если же К правилен и телесен,
то он вполне правилен. Правильность К. связана со
свойством монотонной непрерывности
нормы: если ха \ О, т. е. семейство {ха } — убываю-
убывающее направление, и inf ха = 0, то ||ха||—>-0. Правильность
замкнутого К. К равносильна тому, что пространство Е
дедекиндово полно, а норма в Е монотонно непрерывна.
Правильность телесного К. К влечет монотонную не-
непрерывность нормы в Е.
К. К наз. оштукатуриваемым, если суще-
существуют К. K1(Z.X и число б>0 такие, что для любого
х?К шар S(x; д\\х\\)<^К1. Оштукатуриваемость К
равносильна существованию в Е эквивалентной нормы,
аддитивной на К. Оштукатуриваемый К. вполне пра-
правилен.
Теория К. развита и для произвольных нормирован-
нормированных пространств. Однако в этом общем случае нек-рые
из вышеприведенных результатов не сохраняются, напр.,
перестает быть верной теорема Крейна — Шмульяна, а
правильность замкнутого К. не влечет его нормаль-
нормальность. См. [1], [7], [8], [9], [10]. Б.З.Вулих.
Лит.: [1] Функциональный анализ, 2 изд., М., 1972, гл. 8
(Справочная матем. библиотека); [2] Э д в а р д с Р. Э., Функ-
Функциональный анализ. Теория и приложения, пер. с англ., М.,
1969; 13] Ш е ф е р X., Топологические векторные пространства,
пер. с англ., М., 1971; [4] Д о л ь д А., Лекции по алгебраиче-
алгебраической топологии, пер. с англ., М., 1976; [5] С пень ер Э.,
Алгебраическая топология, пер. с англ., М., 1971; [6] Ц а л е н-
к о М. Ш., Шульгейфер Е. Г., Основы теории катего-
категорий, М., 1974; [7] Красносельский М. А., Положи-
Положительные решения операторных уравнений, М., 1962; [8] В у-
л и х Б. 3., Введение в теорию конусов в нормированных про-
пространствах, Калинин, 1977; [9] е г о же, Специальные во-
вопросы геометрии конусов в нормированных пространствах,
Калинин, 1977; [10] К р е й н М. Г., Р у т м а н М. А., «Ус-
«Успехи матем. наук», 1948, т. 3, в. 1, с. 3—95.
КОНУСА УСЛОВИЕ — условие на область евклидо-
евклидова пространства, отражающее нек-рым образом ее не-
несплющенность. Открытое множество G?En удовлетво-
удовлетворяет слабому условию конуса, если
x+V(e(x), H)cG для всех x?G, где V(e{x), H) — пря-
прямой круговой конус с вершиной в начале координат,
фиксированного раствора е и высоты Н, 0<#<оо, и с
зависящим от х вектором е(х) направления оси. От-
Открытое множество G удовлетворяет сильному
условию конуса, если существует покрытие
замыкания G открытыми множествами G^, что для лю-
любого x^-G^G^ конус x-\-V(e(x), H) содержится в G
(растворы этих конусов могут зависеть от к). В свя-
связи с интегральными представлениями функций и вло-
вложения теоремами рассматриваются анизотропные обоб-
обобщения К. у.— напр., условия слабого, сильного /-рога
(см. [1], с. 117 и далее), условия куба и т. п.
Лит.: [1] Б е С о в О. В., И л ь и н В. П., Николь-
Никольский СМ., Интегральные представления функций и теоремы
вложения, М., 1975. М. И. Войцеховский.
КОНФИГУРАЦИЯ — конечное множество точек, пря-
прямых, плоскостей, связанных между собой взаимными
инцидентностями. К. могут быть как плоскими, так
и пространственными.
Плоская конфигурация — конечная
система р точек и g прямых на плоскости, расположен-
расположенных таким образом, что всякая точка системы инци-
инцидентна с одним и тем же числом у прямых этой системы,
а всякая прямая инцидентна с одним и тем же числом
я точек этой системы. Минимальная система точек дан-
данной К., из к-рой вся К. может быть получена путем
инциденций пар точек с прямыми и пересечений пар
прямых, наз. системой образующих дан-
данной К. Числа р, g, у, п связаны соотношением py=gn, a
К. обозначается символом (ру, gn). К., содержащая
одинаковое число точек и прямых, обозначается симво-
символом (Ру).
Примеры плоских К.: 1) Одна точка и одна пря-
прямая, инцидентные между собой, образуют К. AХ).
2) Три точки, не лежащие на одной прямой, и три пря-
прямые, инцидентные с каждой парой, образуют К. C2),
Л эта фигура — трех-
вершинник (или
трехсторонник) на
плоскости. 3) Пол-
_ . „ ный четырехсторон-
_\дЛ?
в
рис
" ник — четыре пря-
прямые и шесть точек
их попарного пере-
сечения образуют
К. F2, 43). Однако
здесь не все пря-
прямые, соединяющие
попарно точки К., являются прямыми этой К.; точки
R, Р, Q и прямые RP, RQ, PQ не принадлежат
ей (рис. 1).
Автоморфизмом К. наз. отображение К. на
себя, при к-ром точки К. переходят в точки, прямые —
в прямые этой же К., и при этом ни одна инцидентность
не пропадает, и не добавляется новых. К. наз. пра-
правильной, если группа автоморфизмов этой К.
транзитивна.
Для данной К. (ру, gn) двойственной наз. К.
(#я, Ру)- К. типа (ру) и только такие, двойственно соот-
соответствуют К. такого же типа, они наз. двойствен-
двойственно-инвариантными.
К. наз. проективной, если инцидентность ее
элементов сохраняется при проективных преобразова-
преобразованиях. Напр., инцидентность элементов нек-рой К.,
расположенной на проективной плоскости, обеспечи-
обеспечивается выполнением аксиом связи ее, и потому инци-
инцидентность точек и прямых К. сохраняется при проек-
проективных преобразованиях этой плоскости, а К. будет
проективной. Все инцидентности и элементы такой пло-
плоской К. могут быть изображены на чертеже с помощью
только одной линейки. Плоская К. всегда имеет двой-
двойственную вследствие принципа двойственности.
К. может быть определена также как конечная час-
частичная плоскость. Возможность существования нек-рой
К. определяется из геометрич. и
комбинаторных соотношений меж-
между количеством точек и прямых и
количеством взаимных инциден-
ций. К. задается и с помощью
абстрактных схем, напр, на таб-
таблице (рис. 2) указаны инцидент-
инцидентности (обозначенные крестиком)
четырех точек, вершин А,-, и че-
четырех плоскостей, граней D,• те-
тетраэдра. После того как нек-рая
К. определена абстрактно, возни-
возникает вопрос о ее реализации, т. е. о
возможности построения всех инциденций по данной
системе образующих. Реализуемость К. как конечной
частичной плоскости означает возможность изоморф-
изоморфного отображения ее на нек-рую подплоскость какой-
либо плоскости.
К. (р2), Р>3, реализуется в виде р-сторонника так,
что вершины и стороны его попарно инцидентны.
Абстрактную схему К. C2) можно построить, напр.,
таблицей, как на рис. 2. Плоские К. (р3) возможны лишь
при р^7, так как через каждую точку К. должны прохо-
проходить три прямые и на каждой из них должны лежать
еще две другие точки К. (число р должно удовлетво-
удовлетворять неравенству р (р — 1)/2^3р). К. типа (р3) допускают
модификации, количество к-рых зависит от р. К. G3)
представляется схемой (рис. 3), где цифра за фигурной
лг
D2
•
X
X
X
X
•
X
X
X
X
•
X
X
X
X
•
Рис. 2.
скобкой означает точку пересечения прямых, прохо-
проходящих через пары точек, записанные слева от скобки,
цифры за вертикальной чертой обозначают те точки,
к-рые должны быть коллинеарпымп при выполнении
всех указанных слева инци-
денций. На действительной
проективной плоскости все
инцидентности реализуются
в полном четырехвершинни-
ке(рис. 4), однако последняя
13 ] 12] 14]
241 34| 23
7 567
Рис. 3.
инциденция (коллинеарность трех точек) здесь не имеет
места. К. (93) допускает три различные модификации,
одна из к-рых (93)i наз. конфигурацией Б р и-
аншона — Паскаля (рис. 5): каждая прямая Ii
"--^Прямые (,-
Точки о;
@
1
2
3
B)
1
4
5
C)
1
6
7
D)
2
4
8
E)
2
7
9
F)
3
6
8
G)
3
5
9
(8)
4
6
9
(9)
5
7
8
Рис. 5.
инцидентна с тремя различными точками а;, а каждая
точка — с тремя различными прямыми. Эта К. может
быть реализована на проективной плоскости (рис. 6),
она является проективной, правильной, двойственно
инвариантной (см.
Брианшона теоре-
ма, Паскаля теоре-
ма). Две другие
модификации К.
(9,),, <9„), (рис. 7)
существенно отли-
отличаются от конфигу-
конфигурации Б рианшона
—Паскаля. Напр.,
К. (93K не являет-
является правильной, а
для построения К.
) б
G)
5 .
Рис. 6.
(93J необходима
вспомогат е л ь н а я
кривая 2-го порядка. К. A03) имеет уже десять раз-
различных модификаций, из к-рых важнейшей является
конфигурация Дезарга (рис. 8). Она реа-
реализуется на действительной проективной плоскости,
является проективной, правильной, двойственно инва-
инвариантной. Другие девять модификаций К. A03) не вы-
выражают никакой общей геометрич. теоремы, причем
лишь восемь из них могут быть реализованы на дей-
ствительной проективной плоскости, но для их постро-
построения требуется специальное расположение системы обра-
образующих точек (в частности, К. такого типа реализуются
Рис. 9.
Рис. 8.
в виде правильных многосторонников (рис. 9). В при-
приведенной на чертеже последовательности вершин также
получается вписанный и одновременно описанный деся-
тпсторонник. К. (93) п A03) также допускают геометрич.
построение с помощью многосторонников, вписанных и
описанных вокруг самих себя, так, К. (93)i представля-
представляется в виде девятнсторонника B, 3, 6, 1, 5, 9, 4, 8, 7, 2)
(рис. 6), конфигурация Дезар-
га — в виде десятисторонника
(рис. 8)A, 2,3,4,5,6,7, 8,9,
10, 1). Такие представления
этих К. единственны с точно-
7 1-Й—N стыо до автоморфизмов.
Вообще, построение р-сторон-
ников, одновременно вписан-
вписанных и описанных вокруг са-
самих себя, приводит к К.
типа (р3). Существуют также
представления К. типа (р3)
в виде нескольких многосто-
многосторонников, вписанных и опи-
описанных вокруг друг друга.
Напр., конфигурация Дезарга допускает единственный
способ (с точностью до автоморфизма) представления
парой взаимно вписанных и описанных пятисто ройников
A, 9, 7, 5, 3) и (8, 4, 10, 6, 2) (рис. 8). При увеличении
числа р количество модификаций К. типа (р3) быстро
растет.
Пространственная конфигура-
конфигурация — конечная система точек и плоскостей такая,
что каждая точка инцидентна с одним и тем же числом
плоскостей, а каждая плоскость — с одним и тем же
числом точек. Наряду с К., состоящей из точек и пло-
плоскостей, в пространстве рассматриваются и К., состоя-
состоящие из точек и прямых. Так, рассмотренная выше кон-
конфигурация Дезарга, состоящая из точек и прямых,
представляет собой также и пространственную К. A03)
(рис. 8), если соответствующие трехсторонники лежат
в различных плоскостях; одновременно ее можно рас-
рассматривать как К. (Ю3, 5в), составленную из точек и
плоскостей: шесть вершин соответствующих трехсто-
ронников, центр перспективы и три точки на оси пер-
перспективы, в к-рых сходятся соответствующие стороны
трехсторонников, дают всего десять точек, а три пло-
плоскости, образованные соответствующими сторонами
трехсторонников, и две плоскости самих трехсторон-
трехсторонников дают всего пять плоскостей. В каждой плоскости
шесть точек К., и каждая точка инцидентна трем раз-
различным плоскостям.
Тривиальной пространственной К. типа (ру) явля-
является К. D3), ее схема — на рис. 2; она изображается
тетраэдром. К. типа (р4) для р<:7 невозможна, при р=8
имеется пять различных схем К., одна из к-рых, так
наз. конфигурация Мёбиуса, состоит из
двух тетраэдров, вписанных и описанных друг около
друга. Каждой из восьми точек — вершин тетраэд-
тетраэдров — инцидентны четыре плоскости граней тетраэд-
тетраэдров, а каждой из восьми плоскостей инцидентны четы-
четыре точки — вершины. При переходе к К. более вы-
высокого порядка число возможных модификаций быст-
быстро возрастает, напр., К. (94) имеет уже 26 геометрия,
осуществимых модификаций.
Из пространственных К. более высокого порядка
примечательны конфигурация Рейе и конфигурация
Шлефли. Конфигурацией Рейе наз. состо-
состоящая из точек и плоскостей К. A2в). В действительном
проективном пространстве ее можно построить, напр.,
из вершин нек-рого куба, его центра, трех (бесконечно
удаленных) точек, в к-рых сходятся параллельные ребра
куба, а плоскостями этой К. являются шесть граней
с/
Рис. 10.
куба и шесть его диагональных плоскостей, проходящих
через пары противоположных ребер (рис. 10). Конфигу-
Конфигурация Рейе является проективной, правильной и двой-
двойственно инвариантной, причем изображение этой К.
можно построить (сог-
(согласно большому прин-
принципу двойственности),
используя вместо ку-
куба октаэдр (рис. 11).
Конфигурацию Рейе
можно рассматривать
также как простран-
пространственную К. точек и
прямых A24, 163). К.
C02, 125), состоящая
из точек и прямых,
наз. двойным ше-
стисторо н н и-
ком Шлефли.
Он изображается в
пространстве, напр.,
в виде симметрично
расположенных прямых и точек на каждой
куба (по одной из двух шестерок) (рис. 12).
Не всякая плоская К. может быть реализована на
действительной проективной плоскости. Напр., К.
G3) и (83) не реализуются на ней, в связи с чем возни-
возникает задача реализации К. на каких-либо других про-
проективных плоскостях. Каждое предложение, утвержда-
утверждающее, что из реализуемости в данной плоскости нек-рой
К. со всеми инцидентностями, кроме, быть может,
одной, вытекает реализуемость К. со всеми ее инци-
инцидентностями, называется конфигурационным
предложением данной плоскости. Таким об-
образом, если все инцидентности некоторой К. реали-
реализуются на данной плоскости вследствие геометрических
свойств этой плоскости, то К. реализуется на этой
плоскости. Например, К. (93)x всегда реализу-
Рис. И.
грани
ется на действительной проективной плоскости, так
как из реализуемости всех инциденций, кроме одной,
последняя инцидентность выполняется всегда вследствие
теорем Брианшона и Паскаля, т. е. эти теоремы являются
конфигурационными предложениями. Выполнение по-
последней инцидентности в К. G3) (рис. 4) на такой пло-
плоскости не имеет места (так как диагональные точки
полного четырехвершинннка не принадлежат одной
прямой), поэтому такое утверждение не является кон-
конфигурационным предложением. Однако оно будет тако-
таковым в комплексной проективной плоскости. Подобным
образом рассматривается и реализуемость других
К.; в частности, К. (83) может быть реализована в
конечных папповых плоскостях, построенных над по-
полями Галуа с тремя и четырьмя элементами.
Конфигурационные предложения, справедливые в
данной плоскости, определенным образом организуют
элементы этой плоскости и потому играют роль при
аксиоматическом построении геометрии этой плоско-
плоскости. Напр., если в данной плоскости выполняются все
аксиомы связи проективной плоскости, но не реализу-
реализуется конфигурация Дезарга, то данная плоскость несет
на себе так наз. недезаргову геометрию. Конфигура-
Конфигурационное предложение может быть также записано в
алгебрапч. форме в виде нек-рого алгебраич. тождест-
тождества. В произвольной проективной плоскости конфигура-
конфигурационные предложения могут вводиться лишь в ка-
качестве новых аксиом, причем постулирование одного
какого-нибудь конфигурационного предложения может
повлечь за собой справедливость других конфигураци-
конфигурационных предложений в этой плоскости. Вообще говоря,
всякому алгебраич. тождеству соответствует конфигу-
конфигурационное предложение, к-рое наз. геометрич. пред-
представлением этого тождества в определенной плоскости,
где реализуется К. (однако не установлено, всякое ли
конфигурационное предложение является геометрич.
представлением определенного вида тождества в алге-
алгебре тернаров и натуральных тел проективной плоско-
плоскости). Исследование подобных алгебраич. эквивалентов
позволяет изучать как свойства К., так и возможность
их реализуемости как конечной частичной плоскости в
определенной проективной плоскости, а также логиче-
логическую связь между различными конфигурационными
предложениями.
Теория К. находит применение в решении ряда гео-
геометрич. вопросов. Так, плоская К. (83) играет важную
роль в теории плоских кривых третьего порядка, не
имеющих двойных точек, в частности, при исследова-
исследовании их точек перегиба. Конфигурация Рейе применя-
применяется при изучении правильных многогранников в четы-
четырехмерном евклидовом пространстве Ё4. Правильный
многогранник в ?4 ограничен областями, являющимися
правильными трехмерными многогранниками. Пра-
Правильный многогранник в Е* наз. га-я ч е й к о й, если
он ограничен п правильными многогранниками. Напр.,
5-ячейка ограничена пятью трехмерными тетраэдрами,
8-ячейка — восемью кубами и т. д., причем 5-ячейка и
24-ячейка являются двойственными сами себе (точки
соответствуют пространствам, а прямые — плоскостям).
Изучение правильных ячеек проводится исследованием
их проекций в Е3. Если в качестве пространства проек-
проекции выбирается для 24-ячейки нек-рая трехмерная
Рис. 13.
грань, то получается разделение пространства на 12-ок-
таэдров, из к-рых все, не считая среднего, простира-
простираются в бесконечность, что приводит к такому виду про-
проекции, к-рая составляет конфигурацию Рейе (рис. 10).
Если в качестве пространства проекции берется трех-
трехмерное пространство, проходящее через вершину
24-ячейки, то получается также конфигурация Рейе
(рис. 11). (Проекция 24-ячейки в трехмерное простран-
пространство — на рис. 13.) Конфигурация Рейе возникает и в
системе точек и осей подобия четырех гааров, центры
к-рых не лежат все в одной плоскости. В этой системе
каждая ось инцидентна с тремя точками, и каждая точ-
точка—с четырьмя осями, получается пространственная
К. A24, 163) точек и прямых. Каждые три точки —
центры подобия — определяют по одной плоскости,
каждые две оси, инцидентные с точкой подобия, обра-
образуют еще восемь различных плоскостей, всего 12, каж-
каждая из к-рых инцидентна с шестью точками подобия,
а каждая из двенадцати точек подобия — с шестью пло-
плоскостями, т. е. получается К. A26). К., представляемая
двойным шестисторонником Шлефли, применяется для
изучения свойств алгебраич. поверхностей третьего
порядка, к-рая определяется 19 точками н всегда про-
проходит через нек-рый двойной шестисторонник Шлефли.
При этом существенным является то, что любые четыре
прямые его имеют гиперболоидальное расположение.
Конфигурационные предложения о реализации ин-
цидентностей на плоскости применяются для изучения
свойств многосторонников (многовершинников) и для
решения задач на построение при различных ограниче-
ограничениях (построение с недоступными элементами, построе-
построение одной линейкой и т. д.). В кинематике и графиче-
графической статике находит практическое применение теория
К. полиэдров.
Возможны К., составленные из других геометрич. эле-
элементов, напр, из кругов произвольной размерности и
единичного радиуса в Еп.
Лит.: [1] Гильберт Д., Кон-Фоссен С, Нагляд-
Наглядная геометрия, пер. с нем., 2 изд., М.—Л., 1951; [2] Скор-
Скорняков Л. А., «Успехи матем. наук», 1951, т. 6, в. 6, с. 112—
154; [3] Аргунов Б. И.,«Матем. сб.», 1950, т. 26, Яг 3, с.
425—56; [4] Levi F., Geometrische Konfigurationenen, Lpz.,
1929. Л. А. Сидоров.
КОНФЛЮЭНТНАЯ ГИПЕРГЕОМЕТРИЧЕСКАЯ
ФУНКЦИЯ — то же, что вырожденная гипергеометри-
гипергеометрическая функция.
КОНФЛЮЭНТНЫЙ АНАЛИЗ — совокупность ме-
методов математической статистики, относящихся к ана-
анализу априори постулируемых функциональных связей
между количественными (случайными или неслучай-
неслучайными) переменными ХA), . . ., XW в условиях, когда
наблюдаются не сами переменные X(i), а случайные
величины
где ejs) — случайная ошибка измерения x\s) перемен-
переменной Xis) в г-м наблюдении, п — общее число наблюде-
наблюдений. При этом общий вид исследуемых функциональных
(«структурных») соотношений между ненаблюдаемыми
переменными ХA>, . . ., Х(Р) считается заданным. В за-
задачу К. а. входит построение статистич. оценок для
неизвестных значений параметров, участвующих в
уравнениях исследуемых «структурных» соотношений,
а также — статистич. критериев, предназначенных для
проверки различных гипотез о природе анализируемых
связен.
Разработка теоретических и прикладных аспектов
К. а. ведется главным образом применительно к линей-
линейному (или линеаризуемому с помощью подходящих
преобразований исходных переменных) виду исследу-
исследуемых структурных соотношений. В рамках линейной
модели К. а. априорное постулирование т линейных
связей между р, т<р, переменными может быть сфор-
сформулировано как допущение о существовании р — т
«общих» факторов F'1', . . ., У(р-т) таких, что
X<s> = Xs ,уа>+ ... + XS, y^YV—", s = l, 2, ..., р, B)
причем матрица Л= ||Я,^^||, s=l, . . ., р,А=1,. . ., р — то,
имеет ранг р—т. Параметризация модели К. а. в виде
A) — B) позволяет сформулировать основные задачи
в терминах статистич. оценивания неизвестных значе-
значений параметров Л^ и статистич. проверки гипотез, с
ними связанных. Формально модель A) — B) выглядит
так же, как модель факторного анализа, однако задачи
К. а. и факторного анализа почти не пересекаются:
если цель К. а. в описании структурных соотношений,
существующих между переменными ХA), . . . , Х(//),
то в факторном анализе основной задачей является по-
построение и интерпретация общих факторов У1', . . .,
у(р-т). В то же время можно говорить о родственном
характере задач К. а. и регрессионного анализа: неко-
некоторые частные схемы К. а. укладываются в рамки схе-
схемы регрессионного анализа (напр., если по наблюдениям
A) надо выявить единственную зависимость переменной
X{i), измеряемой с ошибкой, от остальных переменных,
измеряемых без ошибок).
Лит.: [1] Frisch R., Statistical Confluence Analysis by
Means of Complete Regression Systems, Oslo, 1934; [2] К о о р-
m a n s Т. С, Linear Regression Analysis of Economic Time
Series, Haarlem, 1937; [3]КендаллМ. Дш., СтьюартА.,
Статистические выводы и связи, пер. с англ., М., 1973, гл. 29;
[4] М а л е н в о Э., Статистические методы эконометрии, в. 1,
пер. с франц., М., 1975, гл. 10; [5] А й в а з я н С. А., Бог-
дановский И. М., «Заводск. лаборатория», 1974, т. 40,
№ 3, с. 285 — 95. С. А. Айвазян
КОНФОКАЛЬНЫЕ КРИВЫЕ — то же, что софо-
кусные кривые.
КОНФОРМНАЯ ГЕОМЕТРИЯ — раздел геометрии,
в к-ром изучаются свойства фигур, неизменные при
конформных преобразованиях. Основным инвариантом
К. г. является угол между направлениями.
К. г.— это геометрия, определенная в евклидовом
пространстве, дополненном одной бесконечно удален-
ной (несобственной) точкой, с фундаментальной группой
точечных преобразований, переводящих сферы в сферы.
Указанное пространство наз. конформным про-
пространством М„, а фундаментальная группа —
группой конформных преобразова-
н и й. В конформном пространстве плоскость является
сферой, проходящей через бесконечно удаленную точку.
Приведенное определение К. г. справедливо для про-
пространства любого числа измерений; в двумерном случае
вместо сфер говорят о кругах (точнее окружностях).
При числе измерений п^З преобразования, переводя-
переводящие сферы в сферы, исчерпывают все преобразования,
сохраняющие углы (теорема Л и у в и л л я).
При тг=2 группа преобразований, сохраняющих углы,
шире, однако и здесь название К. г. сохраняется за гео-
геометрией с фундаментальной группой точечных преоб-
преобразований, переводящих круги в круги.
Всякое преобразование из фундаментальной группы
К. г. состоит из конечного числа движений, подобных
преобразований и инверсий.
Фундаментальная группа К. г. плоскости М2 изо-
изоморфна нек-роп подгруппе проективной группы, именно
подгруппе проективных преобразований трехмерного
проективного пространства Р3, переводящих в себя
овальную поверхность 2-го порядка, т. е. группе ги-
перболич. движений трехмерного пространства. Это
позволяет применять для К. г. удобный аналитич.
аппарат, к-рый используется в неевклидовых геомет-
геометриях.
Всякая точка Р3 определяется четырьмя однород-
однородными координатами Х(, ;=1,4, или псевдовектором ж
с этими координатами. Пусть
{pay) =
— форма от векторов аз, //; К — овальная поверхность
2-го порядка Р3, задаваемая уравнением х\-\-х\-}-х\—
—Х4=0, или (j"as) = O. Для точек вне К (а?а?)>0, внут-
внутри — (жаз) <0. С помощью абсолюта К осуществляется
стереографическая проекция точек абсолюта и точек вне
абсолюта на конформную плоскость. Координаты я/,
г=1,4, точек Р3 наз. тетрациклическими координатами
точек и кругов на плоскости Мг. Так как при стерео-
графич. проекции точки на абсолюте переходят в точки
на плоскости, а точки вне абсолюта — в круги на пло-
плоскости, то группе гиперболич. движений bF, с абсолю-
абсолютом К будет соответствовать группа преобразований
на плоскости, при к-рых точки переходят в точки,
а круги — в круги, т. е. фундаментальная группа К. г.
плоскости. Аналитически эта группа задается формулами
**=2Lip**'; *=1> ••¦'4; DetWll*o,
где М (х() н М* (х1) — точки до и после преобразова-
преобразований, причем форма
(айв) = х\ + х\-\-х1 — х\
отличается от формы
(х*х*) = х{ +4 +хз —4
только множителем. Если ввести
то условия сохранения квадратичной формы запишутся
в виде
при 1Ф].
При конформных преобразованиях несобственная
точка может переходить в любую другую точку, поэто-
поэтому круг может перейти в прямую, и обратно. Если по-
потребовать, чтобы несобственная точка переходила в
себя, т. е. чтобы прямые переходили в прямые, то под-
группа таких преобразований представляет группу
подобных преобразований (гомотетия и евклидово
движение). В Р3 подгруппе подобия соответствует под-
подгруппа гиперболич. движений, оставляющих непод-
неподвижной нек-рую фиксированную точку абсолюта.
Другим важным классом конформных преобразований
является инверсия. В Р3 инверсии соответствует п о-
лярная гомология, т. е. такое гиперболич.
движение, при к-ром каждая пара соответствующих
точек М и М* лежит на прямой, проходящей через нек-
рую фиксированную точку С вне абсолюта, и удовлетво-
удовлетворяется условие: двойное отношение D(M, M*, С, N)=
= —1, где N — точка пересечения указанной прямой с
плоскостью, полярной точке С относительно абсолюта.
Также как всякое гиперболич. движение можно полу-
получить с помощью конечного числа полярных гомологии,
так и любое конформное преобразование можно полу-
получить с помощью конечного числа инверсий.
Основным инвариантом К. г. на плоскости является
угол ф между двумя кругами. Он выражается по форму-
формуле
где ж и у — векторы, соответствующие двум кругам с
тетрациклич. координатами х,- и у{, i=l~4l В гипербо-
гиперболич. геометрии Р3 угол между кругами на плоскости
равен неевклидову расстоянию между точками в про-
пространстве, соответствующими кругам. Инвариантность
угла следует из инвари-
инвариантности расстояния.
Условие ортогонально-
ортогональности двух кругов (ору) =
= 0, условие касания
(кж)(уу) — (ж?/J=0. Ес-
Если один из кругов обра-
обращается в точку: (хж)=0,
то получается условие
инцидентности точки и
круга (аз?/)=0.
Простейшим образом
в М 2 является пучок
кругов. Он задается урав-
уравнением t=ap-{-$q, где
р и q — фиксированные
круги пучка. В зави-
зависимости от знака Д =
= (рр) (qq)--(pqJ пуч-
пучки бывают: а) эллипти-
эллиптические (Д>0), б) гипер-
гиперболические (Д <0),
в) параболические (Д=0)
рис. 1. (см. рис. 1). В Р3 пуч-
пучкам кругов соответст-
соответствуют прямые. Эллиптическому пучку — прямая, не пере-
пересекающая абсолют, гиперболическому — прямая, пе-
пересекающая абсолют, параболическому — прямая, ка-
касающаяся абсолюта. Так как у всякой прямой Р3 есть
сопряженная ей, то и у всякого пучка в М2 имеется
сопряженный пучок. I
Преобразования фундаментальной группы К. г.
плоскости это — преобразования, задаваемые дробно-
линейной функцией комплексного переменного.
В К. г. трехмерного пространства М3 основными
образами являются точки и сферы. Задаются они
пентасферическими координатами Х{, г'=1,5, или псев-
псевдовектором ж пятимерного пространства. Угол между
сферами определяется по той же формуле, что и угол
между кругами на плоскости.
Простейшие образы в М3: пучки сфер w—ay-\-$z,
двупараметрич. связки M>=aa?+Pj/+Ys и трехпара-
метрпч. связки w=ax-\-$y-\-y2^rot сфер.
Круг в Мя задается с помощью эллиптич. пучка
сфер, т. е. формулой
при дополнительном условии
(a^aSi) (as2as2) — (ж1ж2J > 0.
Угол 9 между кругом, заданным с помощью сфер азХ1 а?2
и сферой ?/, определяется по формуле
со»'6 =
где Аа?> — алгебраич. дополнения элементов определи-
определителя, составленного из Аа$~жаж$; а, Р=1, 2. Пара
кругов
ж = 2?=, а''*,- и аз = 2?= j Р'**
имеет два абсолютных инварианта
fe = -4 и h = —
АА 2
где
A{j=(a>ia>j), Л,7 = (аз,-азу-), 4 =Det [|
i=DetM,7||, 5,7 = (ж,-жу), 5 = Det||5,7l|.
Для каждой пары кругов из составляющих их пучков
можно выделить главные сферы. Это сферы, к-рые удов-
удовлетворяют УСЛОВИЯМ All=Asi—A11=A22==l, •^12=
=Л12=0, 512^521^0. Через эти сферы сами пучки
задаются в виде
аз = cos фа?! + sin q>o?2, ж = cos фхазх + sin ф]Ж2,
где ф(фх) — угол между сферой аз (ж) и сферой аз1(аз1).
Углы 9Х и 92, под к-рыми пересекаются главные сферы
первого круга со вторым кругом, наз. главными угла-
углами пары кругов (они совпадают с углами, под к-рыми
главные сферы второго круга пересекаются с первым
кругом). Через главные углы инварианты пары кругов
выражаются следующим образом:
k = cos2 9j cos2 92, h = 4- (cos2 9t + cos2 92).
Главные углы Q± и 92 определяют экстремальные зна-
значения углов, к-рые сферы одного круга образуют с
другим. Если 01=92, то для всех сфер пары 9=91=02,
и такая пара кругов наз. изогональной. С помощью
инвариантов пары кругов можно охарактеризовать
взаимное расположение двух кругов: а) зацепленные
A — 2/i+k>0), б) изолированные A — 2h+k<0), в) пе-
пересекающиеся A—2h-\-k=Q), и условие линейной неза-
независимости сфер ж; и аз,- (см. рис. 2). Необходимое и до-
достаточное условие изогональности пары кругов Л2—&= 0.
Использование в К. г. методов математич. анализа
привело к созданию конформно-дифференциальной гео-
геометрии. На основе К. г. построена геометрия простран-
пространства конформной связности, относящаяся к К. г. как
риманова геометрия к евклидовой. Для К. г. на пло-
плоскости употребительны также названия геометр и я
обратных радиусов, круговая гео-
метри я, инверсионная геометрия, а
также геометрия Мёбиуса (по имени А. Мё-
Мёбиуса, A. Mobius), впервые изучавшего геометрию кру-
круговых преобразований.
Лит.: [1] Клейн Ф., Высшая геометрия, пер. с нем.,
М.— Л., 1939; [2] Blaschke W., Vorlesungen iiber Diffe-
rential-Geometrle, Bd 3, В., 1929; [3] Бушманова Г. В.,
Норден А. II., Элементы конформной геометрии, Казань,
1972. Г. В. Вушмпнова.
КОНФОРМНАЯ СВЯЗНОСТЬ — дифференциально-
геометрическая структура на гладком многообразии
М, специальный вид связности на многообразии, когда
приклеенное к М гладкое расслоенное пространство Е
имеет своим типовым слоем конформное пространство
Сп размерности re=dimM. Структурой такого простран-
пространства Е к каждой точке х ? М присоединяется экземпляр
конформного пространства {Сп)х, к-рый отождествляется
(с точностью до конформных преобразований, сохраня-
сохраняющих х и все направления в ней) с касательным про-
пространством ТХ(М), дополненным одной бесконечно уда-
удаленной точкой. К. с, как связность в таком Е, пре-
предусматривает сопоставление каждой гладкой кривой
J&cM с началом х0 и каждой ее точке х,( конформное
отображение Yt '• (Сп)х ~^(^п)х так, что удовлетворяется
нек-рое условие (см. ниже условие на yt). Пусть про-
пространство Сп отнесено к реперу, к-рый состоит из двух
точек (вершин) и из п проходящих через них попарно
ортогональных гиперсфер. Такой репер интерпретирует-
интерпретируется в псевдоевклидовом пространстве 1Rn + 2 как класс
эквивалентных базисов, удовлетворяющих условиям
(<"о> e,, + i) = (ei, e{)= ...=(е„, е„), \
(е0, eo) = (en + i, е„ + ,) = (е,-, е/) = 0, \ A)
i, i—i, . .., п, i Ф /, )
относительно эквивалентности
Пусть М покрыто координатными областями и в каж-
каждой области фиксировано гладкое поле репера в (Сп)х,
у к-рого вершина, определяемая вектором е0, совпадает
с х. Условие на у^ следующее: при ?—»-0, когда Xf пере-
перемещается по X до х0, yt должно стремиться к тождест-
тождественному отображению, причем главная часть его от-
отклонения от последнего должна определяться относи-
относительно поля репера в нек-рой окрестности точки х0 мат-
матрицей вида
=II41=
} = 0, а, Р =
со»! со'„
со»! 4
0 ; - со»
0
1=1,
из -у(га+1) (п-{-2) линейных дифференциальных форм
со?,
шо,
(г<;), со0 типа
det |
0.
Другими словами, образ репера в точке
жен быть определен векторами
C)
при yt дол-
долгде X — касательный вектор к X в точке х0 и
lim
- = 0.
При преобразовании репера поля в произвольной
точке х согласно формулам еа,=Аи,ел> eg=^e'ea" со~
храняющим условия A), т. е. при переходе к произ-
вольному элементу главного расслоенного пространства
П реперов в пространствах (Сп)х, формы C) заменяются
следующими 1-формами на П:
образующими также матрицу со' вида B). 2-формы
образуют матрицу Q'=||Q^]| такой же структуры, как
B), и выражаются по формулам Qa', = Aa'A% Qy через
формы Q|5=dcoa-f-co!)>A(o<L являющиеся в силу C)
линейными комбинациями от dxk /\dxl, а следовательно
и от ЮоЛсоо. Для элементов матрицы со' имеют место
структурные уравнения К. с. (где для простоты опу-
опущены штрихи):
dcoS + со" Л соо = &о,
d(o{ + со? Л cof + со'0 Л со? Н- со? Л со'о = Q/, ( < /, ' D)
Здесь правые части полубазовы, т. е. являются линей-
линейными комбинациями только от ЮоЛсоо; они составля-
составляют систему форм кручения-кривизны К. с. и преобра-
преобразуются по законам
о0' л о (/| о'о° ' Л°'о'\
"о' ~Аа'\Ач "о~Л! "о/'
Равенства йо = О имеют инвариантный смысл и выде-
выдеК П
р
ляют К. с. нулевого кручения. Пусть
тогда при Qo=0:
Лш°;
k'Al'bprs
и для Cik=C'ikj:
Инвариантные тождества йо=?2о^0, C/ft=0 выделяет
специальный класс так называемых (по Картану) нор-
нормальных К. с.
Формы C), образующие матрицу вида B), опреде-
определяют К. с. на М однозначно: образ репера в точке xt
при yf. (Cn)x -+(Cn)Xtj определяется решением {ea(t)}
системы
при начальных условиях иа@)=еа, где x' = x'(t) —
уравнения кривой X в нек-рой координатной окрест-
окрестности ее точки ха с координатами х'@). Любые 1-фор-
мы coo, coo, co{(i</), <x>i на П, удовлетворяющие урав-
уравнениям D) с правыми частями, выражающимися через
сооЛШо, где а>о (i=l, . . ., п) — линейно независимы,
определяют в указанном смысле нек-рую К. с. на М.
К. с. дают удобный аппарат для исследования кон-
конформных отображений римановых пространств. К. с.
сводится к Леви-Чивита связности нек-рого риманова
пространства, если на М существуют локальные поля
реперов, относительно к-рых
Qf> = <2/COo Л И».
Для тензора кривизны Я\ы этой связности, определяе-
определяемого равенством
du>'i + (o'k л co* = -i- Я/лдоо Л «4,
имеет место
В'ш = b[Pik ~ фи - Ь\Р{Ь + 6< Р/7 + С[ы.
Обратно, для каждой связности Леви-Чивита риманова
пространства существует единственная нормальная
К. с, из к-рой она получается указанным способом.
При этом Qf=O и P;j выражается через тензор Риччи
Riii=R{kj и скалярную кривизну Я = 2-^м формулой
*»7 ~~п-2 ПН °1 2 (п-1) (п-2) '
Соответствующий тензор C/fc/ наз. тензором кон-
конформной кривизны связности Леви-Чивита.
Два римановых пространства конформно эквивалент-
эквивалентны, если их связности Леви-Чивита имеют совпадаю-
совпадающие нормальные К. с. В частности, риманово про-
пространство прип>3 конформно евклидово тогда п толь-
только тогда, когда для него //^;
Лит.: [1] С art an E., «Ann. polon. math.», 1923,
t. 2, s. 171—221; [2] К а р т а н Э., Пространства аффинной,
проективной и конформной связности, пер. с франц., Казань,
1962; [3] Ogiue К.. «Kodai Math. Semin. Repts», 1967 v. 19,
p. 193—224. Ю.Г.Лумисте.
КОНФОРМНАЯ СТРУКТУРА — 1) К. с. на век-
векторном пространстве V — класс К по-
попарно гомотетичных евклидовых метрик пространства V.
Любая евклидова метрика g пространства V определяет
К. с.
которая наз. К. с, порожденной евклидо-
евклидовой метрикой g. Автоморфизм А пространства V
наз. автоморфизмом К. с. К, если индуциро-
индуцированное им преобразование пространства билинейных
форм сохраняет множество К. Группа автоморфизмов
К. с. изоморфна линейной конформной группе
СО (n) = R+XO (re), n = dimF,
являющейся прямым произведением мультипликатив-
мультипликативной группы положительных чисел и ортогональной
группы.
2) К. с. н а многообразии — поле конформ-
конформных структур касательных пространств, т. е. подрас-
слоение я: К-^-М расслоения симметрических билиней-
билинейных форм на многообразии М, слои Кр=л~1(р) к-рого
суть К. с. соответствующих касательных пространств
Т „М. Расслоение я является топологически триви-
тривиальным, и любое его сечение g (представляющее из себя
риманову метрику на М) однозначно определяет К. с.
по формуле
Kp={Xgp, к > 0}.
Сечение g наз. римановой метрикой, под-
подчиненной К. с. К. Любое другое сечение g1 рас-
расслоения имеет вид g^fg, где / — положительная функ-
функция на М, т. е. римановы метрики gx и g конформно
эквивалентны. Поэтому К. с. можно определить также
как класс конформно эквивалентных римановых метрик.
К. с. К на многообразии М можно отождествить с
СО (п)-структурой В на М, состоящей из всех реперов
на М, ортонормпрованных относительно хотя бы одной
римановой метрики, подчиненной структуре К. Основ-
Основные свойства К. с. определяются тем, что СО (^-струк-
(^-структура В является G-структурой второго порядка: ее
первое продолжение есть К"-структура Вт-+В на В,
а второе продолжение — е-структура (поле реперов)
на В1-1''. Отсюда в частности следует, что группа автомор-
физмов К. с. К (к-рая совпадает с группой конформных
преобразований любой подчиненной К римановой ме-
метрики) есть группа Ли размерности <1/2(ге+1)(?г+2), а
представление изотропии ее стационарной подгруппы в
касательном пространстве второго порядка точно.
Как правило, группа автоморфизмов К. с. К совпа-
совпадает с группой движений нек-рой подчиненной ей ри-
римановой метрики. Исключениями являются только
стандартные конформные структуры Ко на сфере S" и
евклидовом пространстве Е", порожденные стандарт-
стандартными римановыми метриками. К. с. на многообразии М
наз. локально плоской, если она локально
эквивалентна стандартной К. с. Ко евклидова простран-
пространства Еп, т. е. если в окрестности любой точки р?М су-
существует подчиненная К плоская риманова метрика.
Для того чтобы К. с. была локально плоской, необхо-
необходимо и достаточно, чтобы тензор конформной кривизны
Вейля нек-рой (а тем самым и любой) подчиненной ей
римановой метрики был равен нулю. Примерами ло-
локально плоских К. с. являются стандартные К. с. в
евклидовом пространстве Е", на сфере Sn, в простран-
пространстве Лобачевского Л", а также в пространствах A"iX Sn*
и ЛпХЕ1, порожденные стандартными метриками. Ими
исчерпываются все локально плоские К. с. на односвяз-
ных многообразиях, обладающие транзитивной груп-
группой автоморфизмов. Стандартная К. с. Ко на сфере Sn
выделяется среди всех К. с. как единственная К. с,
имеющая максимальную (в смысле размерности) группу
автоморфизмов. Сфера S", снабженная К. с. Ко, наз.
конформным пространством.
Понятие К. с. тесно связано с понятием конформной
связности на М: заданием такой связности всегда опре-
определена нек-рая К. с. на М; с другой стороны, конформ-
конформная связность — это связность в приведенном главном
расслоении, к-рое определяет данная К. с.
Лит.: Ш К о b а у a s h i S., Transformation groups in dif-
differential geometry, В.— Hdlb.— N. Y., 197:'.: Г21 С т с р н б е р г
С, Лекции по дифференциальной геометрии, пер. с англ., М.,
1970; [3] Кимельфельд Б. Н., «Матем. заметки», 1970,
т. 8, Ка 3, с. 321—28; [4] А л е к с е е в с к и й Д. В., «Матем.
сб.», 1972, т. 89, № 2, с. 280—96.
Д. Б. Алексеевский, Ю. Г. Лумисте.,
КОНФОРМНО-ГЕОДЕЗИЧЕСКАЯ СЕТЬ — сеть на
двумерной поверхности евклидова пространства, допу-
допускающая конформное отображение на геодезическую
сеть. При повороте на прямой угол К.-г. с. переходит в
ромбическую сеть, и обратно. в. Т- Базылев.
КОНФОРМНО-ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТ-
ГЕОМЕТРИЯ — раздел конформной геометрии, в котором гео-
геометрические образы, инвариантные при конформных
преобразованиях, изучаются методами анализа беско-
бесконечно малых, в первую очередь дифференциального ис-
исчисления.
В конформной плоскости Л/2 каждая точка и круг
определяются вектором а5(хх, х2, х3, xt), где a;/, i=l,2,
3,4 — тетрациклические координаты. Для точки
(asas) = х\агх\-\- х% — 4 = 0,
для круга (жаз)>0. К.-д. г. плоскости изучает последова-
последовательности и конгруэнции кругов. Последовательности
кругов соответствует в трехмерном гиперболич. про-
пространстве кривая, конгруэнции кругов — поверхность.
Последовательность задается параметрич. уравнением
oc=oc(t). Параметр t можно специализировать, взяв
в качестве него
da — угол между двумя бесконечно близкими круга-
кругами последовательности. Особое значение в теории после-
последовательностей имеют две ветви огибающей этой после-
последовательности v= v (t) и v=v(t), их соприкасающиеся
круги. Как и в обычной дифференциальной геометрии
кривых можно записать деривационные формулы для
последовательности кругов, разложив производные
векторов ж, z=d.v/de. v, v по ним самим:
<*•*¦_ „ dz - , -
35-"-.' ^^-х-г^т-с»,
Можно получить два инварианта Ь=—2сс и g=c'/c.
Инвариант Ъ выражается через угол ф между соприка-
соприкасающимися кругами огибающей: b=l/sin2 ср/2. Теория
кривых конформной плоскости строится на основе тео-
теории последовательности кругов: каждая кривая рас-
рассматривается как огибающая: последовательности, у
к-рой инвариант g=±i. Если при этом инвариант Ь
постоянный, то кривая оказывается изогональной тра-
траекторией пучка кругов, т. е. локсодромой.
В трехмерном конформном пространстве М3 урав-
уравнение x=x(t) задает последовательность сфер. При
ее изучении важную роль играет ее огибающая поверх-
поверхность, так наз. каналовая поверхность. Каждая после-
последовательность сфер характеризуется тремя инвариан-
инвариантами, выражающимися через нек-рые углы, связанные
со сферами последовательности.
Конгруэнция кругов в М2 задается уравнением
ж=аз(м1, и2). На поверхности, соответствующей ей в
гиперболич. пространстве, удобно ввести полярную
нормализацию, приняв за нормаль 1-го рода прямую, ор-
ортогональную касательной плоскости поверхности в точ-
точке яп, а за нормаль 2-го рода — поляру нормали 1 рода
•относительно абсолюта К (см. [3]). В М3 нормализации
поверхности соответствует нормализация конгруэнции:
каждому кругу х конгруэнции ставится в соответствие
круг х, ортогональный кругу ж и всякому бесконечно
близкому кругу, и два круга yi, определяющие пучок
кругов, сопряженный пучку {аз, ж}: j/,=5,as. В соответ-
соответствии с инвариантами поверхности в гиперболич. про-
пространстве на М2 определяются инварианты конгруэнции
кругов, выделяются специальные виды конгруэнции.
В теории поверхностей М3 вводится оснащение по-
поверхности с помощью нормализующих кругов, ортого-
ортогональных в каждой точке всем касательным сферам по-
поверхности; связывается с каждой точкой конформный
репер, состоящий из точки поверхности ж, двух коор-
координатных сфер у{, г=1, 2, определяющих нормализую-
нормализующий круг, касательной в точке х сферы я и точки X
пересечения этой сферы и нормализующего круга.
В общей теории нормализации поверхностей использу-
используется изоморфизм теории нормализованных поверхностей
конформного пространства и теории внутренних по-
полярных нормализации абсолюта гиперболнч. простран-
пространства. Внутренняя геометрия нормализованной поверх-
поверхности Мп есть геометрия Вейля, основной тензор к-рой
совпадает с тензором угловой метрики поверхности, а
дополнительный тензор есть нормализатор, определяю-
определяющий опорные координатные сферы.
Результаты, полученные для нормализованной по-
поверхности, справедливы и для нормализованного кон-
конформного пространства.
Лит.: Ш D а г b о u x G., Lecjons sur la theorie generate des
surfaus, pt. 1—4, P., 1887—96; 2 ed., pt. 1—2, P., 1914—26; [21
Blase like W., Vorlesungen uber Differentialgeometrie, Bd
3, В., 1929; [3] H о р п е н А. П., Пространства аффинной связ-
связности, 2 изд., М., 197В; [41 Б у ш м а н о в а Г. В., Н о р-
ден А. П., Элементы конформной геометрии, Казань, 1972.
Г. В. Бушмапова.
КОНФОРМНОЕ ОТОБРАЖЕНИЕ — непрерывное
отображение, сохраняющее форму бесконечно малых
фигур.
Основные понятия. Непрерывное отображение
w=f(z) области G ?;-мерного евклидова пространства
(«J&2) в ?г-мерное евклидово пространство наз. кон-
формным в точке zo?G, если оно в этой точке
обладает свойствами постоянства растяжений и сохране-
сохранения углов. Свойство постоянства рас-
растяжений в точке z0 при отображении w=/(z) со-
состоит в том, что отношение |/(z)—/(zo)|/jz— z0
расстояния между образами /(z) и /(z0) точек z и z0 к
расстоянию между z и z0 стремится к определенному
пределу k-=k(z0, /), когда z стремится к z0 произвольным
образом; число к наз. коэффициентом рас-
растяжения в точке z0 при рассматриваемом отобра-
отображении. Свойство сохранения (консер-
(консерватизма) углов в точке zo?G при отображении
w=f(z) состоит в том, что любая пара непрерывных кри-
кривых 1Х, 12, расположенных в G и пересекающихся в точке
z0 под углом а (т. е. имеющих касательные в точке z0,
образующие между собой угол а), при рассматриваемом
отображении переходит в пару непрерывных кривых
Z/-L. L2, пересекающихся в точке k>0=/(z0) под тем же
углом а. Непрерывное отображение области G наз.
конформным, если оно конформно в каждой
точке этой области. По определению, К. о. области G
обязано быть непрерывным и конформным лишь во
внутренних точках G, и если говорят о К. о. замкнутой
области, то, как правило, имеют в виду непрерывное
отображение замкнутой области, конформное в ее вну-
внутренних точках.
В наиболее важном случае п=2 область G и ее образ
f(G) при отображении / лежат в плоскости, к-рую удобно
рассматривать как плоскость С комплексного перемен-
переменного z; соответственно отображение w=f(z) является
комплекснозначной функцией комплексного перемен-
переменного z?G. При этом если в точке z0 отображение w=
=/(z) сохраняет углы, то криволинейные углы с вер-
вершиной z0 при этом отображении либо все сохраняют свою
абсолютную величину и знак, либо все сохраняют свою
абсолютную величину, изменяя знак на противополож-
противоположный. В первом случае говорят, что отображение в точке
z0 является К. о. п е р в о г о р о д а, во втором —
К. о. второго рода. Если функция w=/(z) за-
задает К. о. второго рода в точке z0, то комплексно со-
сопряженная функция u?=/(z) задает К. о. первого рода в
точке г0, н наоборот. Поэтому изучаются лишь К. о.
первого рода, и именно их обычно имеют в виду, когда
говорят о К. о., не уточняя их род.
Если отображение w=f(z) конформно в точке z0,
то при z—*-z0 существует конечный предел отношения
(/(г) — /(zo))/(z—z0), т. е. существует производная
/'(z0). При дополнительном предположении, что /'(го)=И=О,
верно н обратное.
Таким образом, если существует /' (zo)^=O, то каждый
бесконечно малый вектор с началом в точке z0 при отоб-
отображении ц)=/(г) растягивается в к (z0, /)= \f (zo)j раз,
поворачивается на угол arg /' (z0) и параллельно сдви-
сдвигается на вектор /(z0) — z0; бесконечно малые круги
с центром z0 переходят в бесконечно малые круги.
Отображение k>=/(z) является конформным в обла-
области G конечной комплексной плоскости С тогда и только
тогда, когда функция f(z), z?G, является аналитиче-
аналитической и /' (z)=^0 в G. Для конформности отображения
w=j(z) (и аналитичности /(z)) в области G достаточно
потребовать, чтобы непрерывная функция /(z) обла-
обладала в каждой точке z?G лишь свойством сохранения
углов (с сохранением не только величин углов при этом
отображении, но и их знаков). Если же от непрерывного
отображения w^f(z), z?G, потребовать однолистности
его (т. е. взаимной однозначности) и постоянства рас-
растяжений в каждой точке, то это отображение будет кон-
конформным первого или второго рода, так что либо /(z),
либо f(z) является аналитич. функцией, производная
к-рон всюду в G отлична от нуля. В случае аналитично-
аналитичности i(z) в нек-рой окрестности точки zo?C следующие
три свойства эквивалентны: а) отображение w=f(z)
конформно (первого рода) в точке z0, б) функция /(z)
(локально) однолистна в точке z0, в) /' (zo)=^=O. Всякая
однолистная аналитическая в области G функция совер-
совершает К. о. области G на область f(G) той же связности;
при этом обратная функция f~1(z) является в области
f(G) однолистной аналнтич. функцией с ненулевой
производной. Существуют и неоднолистные К. о. (на-
(например, отображение w=zi конформно и не однолист-
однолистно в полуплоскости Im z>0, a w=ez — во всей пло-
плоскости С).
В теории плоских К. о. и ее приложениях принципи-
принципиальным является вопрос о возможности однолистно и
конформно отобразить одну заданную область на дру-
другую, а в практических приложениях — вопрос о воз-
возможности это сделать посредством сравнительно про-
простых функций. Первую задачу для случая односвязных
областей, границы к-рых не пусты и не вырождаются
в точки, решает в положительном смысле Римана теоре-
теорема о конформном отображении. Вторая задача для нек-
рых областей специального вида решается применением
элементарных функций комплексного переменного (см.
ниже), Кристоффеля — Шварца формулы для отобра-
отображения полуплоскости пли круга на многоугольник,
применением симметрии принципа и приближенных
методов К. о. По теореме Римана, все односвязные об-
области расширенной комплексной плоскости с непустыми
границами, не вырождающимися в точки, конформно
эквивалентны. Иначе обстоит дело с К. о. многосвязных
областей. Поскольку однолистное К. о. нек-рой обла-
области G1 на другую область G2 является взаимно однознач-
однозначным и взаимно непрерывным, то для существования
такого отображения необходимо, чтобы Gt и G2 имели
один и тот же порядок связности, т. е. они одновремен-
одновременно должны быть либо односвязными, либо двусвязны-
ми и т. д., либо бесконечносвязными. Однако это не-
необходимое условие не является достаточным, что про-
проявляется уже в случае односвязных областей. Так,
круг ' z\ <1 нельзя однолистно и конформно отобразить
на конечную плоскость С, а расширенную комплексную
плоскость С нельзя конформно и однолистно отобразить
на круг |г|<1 или плоскость С (на самом деле, послед-
последние два отображения невозможно выполнить даже то-
топологически). Еще более жесткая ситуация имеет место
в случае многосвязных областей. Напр., круговое коль-
кольцо Gj= {z : rj<jzj<flj} можно однолистно и конформ-
конформно отобразить на другое круговое кольцо G2= {z : r2<
<]z <Я2}, rj>0, г2>0, тогда и только тогда, когда
эти кольца подобны, т. е. Яг : г2^В2 : г2; в этом случае
всякое К. о. G1 на G2 является целой линейной функцией
вида e'Pr2z/Vj, где р — некоторое действительное число.
Однако всякую конечносвязную область G расширенной
комплексной плоскости с непустой границей можно
однолистно и конформно отобразить на любую из так
наз. канонических областей той же связ-
связности, содержащую точку то, а именно: на расширенную
плоскость с конечными горизонтальными разрезами,
на расширенную плоскость с исключенными конечными
не пересекающимися замкнутыми кругами, на расши-
расширенную плоскость с исключенными замкнутыми дугами
логарифмич. спиралей заданного наклона 6; при этом
отдельные отрезки, круги и дуги спиралей могут вы-
вырождаться в точки. Если потребовать, чтобы заданная
точка a?G при таком отображении перешла в оо и
при z-^-a выполнялось соотношение f(z) = (z—а)-1+
-r"O(z—а) при аФоо или соотношение f(z) = z-\~O(\.lz)
при а=оо, то в случае канонич. областей первых двух
перечисленных типов отображающая функция w=
—f(z) существует, определяется единственным образом
н наз. каноническим К. о. Эти теоремы спра-
справедливы и для бесконечносвязных областей.
Всякое однолистное К. о. области Glt ограниченной
конечным числом непересекающихся окружностей (при
этом прямая считается окружностью бесконечно боль-
большого радиуса), на область G2 этого же типа является
дробно-линейным отображением. В теории аналитич.
функций рассматриваются также неоднолистные отоб-
отображения областей разной связности друг на друга по-
посредством аналитич. функций, в том числе К. о. круга
на многосвязные области, отображение n-связных об-
областей на п-лпстный круг, вообще, отображения одной
римановой поверхности на другую.
В теории К. о. и ее приложениях важную роль иг-
играют так наз. условия нормировки, или
условия единственности, К. о., обеспе-
обеспечивающие выделение одной единственной функции из
рассматриваемого бесконечного класса К. о. одной
заданной области на другую (в случае односвязных об-
областей) или заданной области на каноническую область
определенного типа (в случае областей любой связно-
связности). Наиболее употребительные условия нормировки
К. о. в случае односвязных областей Gx, G2 с непустыми
границами Гр Г2 соответственно, не вырождающимися
в точки, таковы: 1) заданная конечная точка a^iGl
переходит в заданную конечную точку b?G2, причем
arg/' (а)=а, где а — наперед заданное действительное
число, 0<:а<2я (см. Римана теорема о К. о.); 2) за-
заданная точка a?G1 переходит в заданную точку b?G2, a
заданная достижимая граничная точка (или граничный
элемент) ?х области Gx переходит в заданную достижи-
достижимую граничную точку (граничный элемент) ах области G2
(см. Конформных отображений граничные свойства):
3) заданные три различные достижимые граничные точ-
точки (граничные элементы) ^, ?2, ?3 области Gt переходят
соответственно в заданные достижимые граничные точ-
точки (граничные элементы) colt ш2, ш3 области G2, при
этом, если при движении по 1\ от ?г к ?3 через ?2 область
Gj остается слева (справа), то при движении по Г2
от щ к ш3 через ш2 область G2 также должна оставаться
слева (соответственно справа). Последними двумя ти-
типами нормировок проще всего пользоваться в случае
областей, ограниченных замкнутыми жордановыми
кривыми, так как в этом случае понятия достижимой
граничной точки и граничного элемента области экви-
эквивалентны понятию граничной точки области. Об усло-
условиях нормировки в случае отображения области про-
произвольной связности на каноническую область сказано
выше.
К. о. областей «-мерного евклидова пространства
при njs=3 образуют весьма узкий класс так наз. м ё-
биусовых отображений, каждое из к-рых
является либо линейным преобразованием подобия, ли-
либо композицией такого линейного преобразования по-
подобия и одной инверсии (т. е. симметрии относительно
нек-рой сферы в пространстве, или преобразования об-
обратных радиусов) (теорема Л и у в и л л я).
Существенно более обширный класс отображений при
п^2 образуют так наз. квазиконформные отображения.
При этих отображениях формы бесконечно малых фигур
искажаются, но в ограниченных пределах, в частности
в ограниченных пределах меняются величины углов, а
бесконечно малые шары переходят в бесконечно малые
эллипсоиды с ограниченным отношением наибольшей
полуоси к наименьшей. Большую роль играют К. о.
двумерных областей не только плоских, но и лежащих на
гладких поверхностях. Примеры таких К. о. дают
стереографическая проекция и проекция Меркатора
сферы на плоскость. Они были открыты и нашли при-
применение в картографии (см. Картографии математиче-
математические задачи, Картографическая проекция). Заметим, что
постановка в общем виде задачи о К. о. поверхностей
в свое время привела к возникновению и развитию общей
теории поверхностей. К. о. имеют обширные применения
в теории функций, теории потенциала, при решении
краевых задач для уравнении математической физики,
прежде всего при решении первой краевой задачи для
уравнений Лапласа и Пуассона.
Конформное отображение некоторых односвязных
областей. Растяжения, повороты и параллельные пе-
переносы областей комплексной плоскости осуществляют
целые линейные функции вида w=az-\-b. Однолистные
К. о. полуплоскостей, кругов и внешностей кругов друг
на друга осуществляются посредством дробно-линей-
дробно-линейных функций. При этом каковы бы ни были три раз-
различные точки ?1, ?s, ?3 границы одной и той же области
Gt (занумерованные так, что при движении по границе
G1 от gj к ?3 через ?2 область G1 остается слева) и раз-
различные точки (Oj, (o2, (о3 границы другой такой области
G2 (занумерованные аналогичным образом), существует,
и притом единственная, дробно-линейная функция
w=L(z), однолистно н конформно отображающая Gx
на G2 с условиями нормировки третьего типа: L(t>/1)=
= а>?, к=1, 2, 3. Эта функция находится из уравнения
ж-(О2'<о3-<в2
в к-ром каждый числитель или знаменатель заменяется
числом 1, если в его запись должна войти точка (о^=оо
или точка t,f,= oo. В частности, общий вид отображений
единичного круга D= {z : |г| <1} на себя:
а общий вид отображения верхней полуплоскости
Р= {z : Im z>0} на этот круг:
Здесь а и с — соответственно прообразы точки 0 при
этих отображениях, a=arg Lx (a) = arg L2(c), 0<:a<
<2я. Числа a, о|<1, с, Im e>0, и а, 0<а<2л, могут
задаваться произвольно. Таким образом, указанный
общий вид однолистных К. о. единичного круга и верх-
верхней полуплоскости на единичный круг позволяет легко
учитывать условия нормировки первого типа при этих
отображениях. Условия нормировки второго типа с
&=0 при этих же отображениях также легко выполнить,
если воспользоваться указанным общим видом с за-
заданным а (пли с), поело чего остается только подобрать
множитель eia из условия соответствия заданных гра-
граничных точек ? и to.
Простота выполнения условий нормировки при отоб-
отображении единичного круга на себя или верхней полу-
полуплоскости на себя лежит в основе следующего употре-
употребительного приема, с помощью к-рого учитывают усло-
условия нормировки при однолистных К. о. произвольных
областей Gt, G2 с непустыми невырожденными границами
друг на друга. Именно, обе области Gx и G2 каким-либо
образом конформно и однолистно отображают на D
(или на Р) с помощью нек-рых функций u"=/j (z) и
w=f% (z) соответственно, после чего задача об отобра-
отображении Gt на G2 с нек-рыми условиями нормировки сво-
сводится к задаче о дробно-линейном отображении ц>=
= L(z) круга D (соответственно полуплоскости Р)
на себя с выполнением соответствующих условий нор-
нормировки. Если функция L найдена, to/(z) = /2~1(/>(/1(z)))
решает исходную задачу. Ввиду этого обстоятельства
ниже приводятся лишь однолистные К. о. различных
областей на единичный круг D или на верхнюю полу-
полуплоскость Р без каких-либо условии нормировки.
1) Горизонтальную полосу {z=x-riy : 0<(/ < я}
на верхнюю полуплоскость отображает функция w =
= ег = ех (cos y-\- i sin у). Эта функция каждую горизон-
горизонталь у = с переводит в луч Arg w=c; каждый верти-
вертикальный отрезок {x-f-iy '¦ x—d, a<i/<P} — в дугу
{w : \w\~ed, a<:Arg u>f5}
2) Вертикальную полосу {x-\-iy :—-j-<x<-j-) Ha
круг D отображает функция w=tg z. При этом верти-
вертикаль х=с, —т-<^с ¦<-?", переходит в «меридиан» —
дугу окружности с концами in —i, проходящую через
точку w=tg с, а горизонтальный отрезок {x-{-iy : —-г-<
:-^-, y=d}, —°° <d<oo, переходит в «параллель» —
дугу окружности, ортогональную «меридианам», со-
соединяющую левую часть единичной окружности с ее
правой частью и проходящую через точку z=iih d.
3) Полуполоса {x-\-iy : — •*-<?<-"-, ^>0} отобра-
отображается на Р функцией u?=sin z. При этом горизонталь-
горизонтальные отрезки переходят в дуги эллипсов с фокусами
—1, +1, а вертикальные — в дуги гипербол с теми же
фокусами.
4) Угол Va= {z : 0<arg z<ct}, 0<а<2я, на угол
Fp= {z : 0<arg z<p}, 0<Р<2я (vn = P), отображает
функция
w^exp (-|lnz]=|z|P/«(cos(|-argz) +
+ isin (^-?-arg
— однозначная аналитическая ветвь функции w=z$/a •
При этом луч arg z=c переходит в луч arg w=$c/a,
дуга окружности ]z| = d — в дугу окружности |w|=dP/a .
5) Внутренность или внешность двуугольника с вер-
вершинами а и Ь (афЪ), образованного двумя дугами ок-
окружностей или дугой окружности п отрезком прямой,
имеющими общие концы в этих точках, может быть ото-
отображена на Р следующим образом. Сначала дробно-
линейным преобразованием w1= (z—a)l(z—Ь) отобра-
отображают данную область на угол Vc вершиной в О, затем
поворотом w2=eiyw1 на нек-рын угол у переводят V
в нек-рый угол Va (см. п. 4), после чего пользуются пре-
преобразованием п. 4 с р=я.
6) Внешность эллипса -^- + rir=l с фокусным рас-
расстоянием с= У а2—Ь2>0 отображается однозначной
аналитической ветвью функции (см. Жуковского функ-
функция)
выделяемой условием |ц>|<1, на круг \w\ <c/(a-\-b), а
второй ее ветвью, выделяемой условием |и>|>1, —на
область |w|>(a+b)/e. Эти же ветви отображают рас-
расширенную плоскость С с удаленным отрезком [—с, с]
соответственно на внутренность и внешность единич-
единичной окружности |z| = l. Внутренность эллипса нельзя
отобразить на D или Р посредством композиции эле-
элементарных функций; это отображение осуществляется
посредством композиции элементарных функций и эл-
липтич. синуса sn z.
7) Часть G плоскости С, заключенная между ветвями
гиперболы ^j-—'тт={ с фокусным расстоянием с=
= \^а2^~Ь2, отображается на Р функций
где однозначная аналитич. ветвь функции t=z-\- Y~z2—с?
в области G выделяется условием Im i>0, Y=arctg — ,
Внутренность правой ветви этой гиперболы отобража-
отображается на верхнюю полуплоскость однозначной ветвью
аналнтич. функции
где arch t, означает (единственное) решение уравнения
ch сэ=?, принадлежащее полосе {z : 0<Im г<я} с
присоединенной действительной положительной полу-
полуосью.
8) Внешность параболы уг=2рх отображается на Р
однозначной аналнтич. ветвью функции
выделяемой условием Im w>0, т. е. функцией
|Cos-|-arg(z— -|-
-f- г sin — arg [ z —
где значения квадратного корня берутся положитель-
положительные. Внутренность этой параболы отображает на Р од-
однозначная аналитнч. функция
w = i ch я
где
-./ZZT
У 2р 4 '
О < arg I < 2я.
9) Прямоугольник Q— {x-^iy :
отображается на Р с помощью эллиптнч. синуса, а Р
отображается на Q одной из однозначных аналптнч.
ветвей функции
где к зависит от отношения alb, ас — от величины а! К,
Лит.: [1] Лаврентьев М. А., Ш а б а т Б. В., Ме-
Методы теории функций комплексного переменного, 4 изд., М.,
1973; [2] Г о л у з и н Г. М., Геометрическая теория функций
комплексного переменного, 2 изд., М., 1966; [3] Келдыш
М. В., «Успехи матем. наук», 1939, т. 6, с. 90—119; [4] При-
Привалов И. И., Граничные свойства аналитических функций,
2 изд., М.—Л., 1950; [5] Л а в р е н т ь е в М. А., Конформные
отображения с приложениями к некоторым вопросам механики,
М.— Л., 1946; [6]Коппенфельс В., Штальман Ф.,
Практика конформных отображений, пер. с нем., М., 1963;
[7] Л а в р и к В. И., С а в е н к о в В. Н., Справочник по
конформным отображениям, К., 1970; [8] Фильчакова
В. П., Конформные отображения областей специального типа,
К., 1972; [9]Каратеодори К., Конформное отображение,
пер. с англ., М.— Л., 1934; [10] Бицадзе А. В., Основы
теории аналитических функций комплексного переменного,
2 изд., М., 1972; [11] Лаврентьев М. А., Ш а б а т Б. В.,
Проблемы гидродинамики и их математические модели, 2 изд.,
М., 1977. Е. П. Долженко.
КОНФОРМНОЕ ПРЕОБРАЗОВАНИЕ — взаимно од-
однозначное конформное отображение. К. п. в п-мерном,
га>2, евклидовом пространстве, образует (п+1) (п+2)/2-
параметрическую конформную группу.
М. И. Войцеховский.
КОНФОРМНОЕ ПРОСТРАНСТВО Мп — евклидово
пространство Еп, дополненное одной несобственной
(бесконечно удаленной) точкой. Рассматривается в
конформной геометрии, в к-рой в этом пространстве
задается фундаментальная группа, состоящая из то-
точечных преобразований, переводящих сферы (в М2 ок-
окружности) в сферы. С помощью стереографической про-
проекции К. п. Мп отображается на абсолют Кп простран-
пространства Pn + i с гиперболич. метрикой, а фундамен-
тальная группа конформной геометрии изоморфна
группе гиперболич. движений этого Рп + \.
Наличие одной несобственной точки обеспечивает
взаимную однозначность стереографпч. проекции. При
преобразованиях конформной группы несобственная
точка может переходить в обычную точку. Поэтому в
К. п. сфера неразличима с плоскостью. Плоскость —•
это сфера, проходящая через несобственную точку.
Г. В. Бцшмаповп.
КОНФОРМНО-ЕВКЛИДОВО ПРОСТРАНСТВО — ри
маново пространство, допускающее конформное отоб-
отображение на евклидово пространство. Тензор кривизны
К.-е. п. имеет вид
где
При п=2 всякое Vn есть К.-е. п. Для того чтобы про-
пространство при п>3 было К.-е. п., необходимо и доста-
достаточно, чтобы существовал тензор pij, удовлетворяющий
условиям (*) и V[feP/j/=O. Иногда К.-е. п. наз. про-
пространство Вейля, допускающее конформное отображе-
отображение на евклидово пространство (см. [2]).
Лит.: [1] С х о у т е н И. А., С т р о й к Д. Д ж., Введение
в новые методы дифференциальной геометрии, пер- с англ.,
т. 2, М.— Л., 1948; [2] Н о р д е н А<П., Пространства аффинной
связности, 2 изд., М., 1976. Г. В. Бушмапова.
КОНФОРМНО-ИНВАРИАНТНАЯ МЕТРИКА н а
ри меновой поверхности R — правило,
к-рое каждому локальному параметру z, отображающе-
отображающему параметрич. окрестность UaR в замкнутую комплек-
комплексную плоскость С (z : U-*-C), ставит в соответствие дей-
действительную функцию
pz:z (V) —у [0, + оо]
такую, что для всяких локальных параметров zx : fj-vC
и z2 : E/j—vC с непустым пересечением U1f\U2 в по-
последнем выполнено соотношение
р., С*, <р))
dz2 (p)
где z(U) — образ U в С при отображении z. К.-и. м.
часто обозначается символом p(z)|dz|, к-рому приписы-
приписывается указанная инвариантность относительно выбора
локального параметра z.
Всякий линейный дифференциал X(z) dz или квадра-
квадратичный дифференциал Q(z) dz2 порождает К.-л. м.
соответственно \X(z) | -\dz\ или \Q(z)\lU \dz\. Понятие
К.-и. м. позволяет ввести понятие длины для кривых на
Я, а также понятия экстремальной длины и модуля
семейств кривых, являющиеся весьма общей формой
определения конформных инвариантов (см. Экстре-
Экстремальной метрики метод, а также [1]). Определение
К.-и. м. может быть перенесено на римановы многооб-
многообразия любой размерности.
Лит.: [1] Дженкинс Дж., Однолистные функции и
конформные отображения, пер. с англ., М., 1962; [2] Ш и ф-
фер М., Спенсер д. К., Функционалы на конечных ри-
мановых поверхностях, лер. с англ., М., 1957; [3] А л ь ф о р с Л.,
Б е р с Л., Пространства римановых поверхностей и квазикон-
квазиконформные отображения, пер. с англ., М., 1961. П. М. Тажразов.
КОНФОРМНЫЙ РАДИУС области — характе-
характеристика конформного отображения односвязной
области, определяемая следующим образом. Пусть
D — односвязная область плоскости z, имеющая
более одной граничной точки. Пусть z0— точка D.
Если Zq^oo, to существует единственная функция
w=/(z), регулярная в D, нормированная условиями
/(zo)=O, /' (zo)=l и однолистно отображающая область
D на круг |ц?|<г. Радиус r=r(z0, D) указанного круга
наз. К. р. области D в точке z0. Если oo?D, то
существует единственная функция w=f(z), регулярная
в области D за исключением точки оо, в окрестности
к-рой она имеет разложение в ряд Лорана вида
и однолистно отображающая D на область |ш| >г. В этом
случае величина r=r(oo, D) наз. К. р. области D
в точке то. К. р. области D, oo?D, в точке оо
равен трансфинитному диаметру границы С области
D, или емкости множества С.
Расширением понятия К. р. области на случай произ-
произвольной области D комплексной плоскости z является
понятие внутреннего радиуса области D в точке zo?D
(в зарубежной литературе термин «внутренний радиус»
употребляется и в случае односвязной области). Пусть
D — область комплексной плоскости z, z0 — точка D
и пусть существует функция Грина g(z, z0) области D
с полюсом в точке z0. Пусть у — постоянная
Р о б э н а области D относительно точки z0:
lim [g (z, z0) + In | z — z0 |] при zo?!:cc,
=\
lim [g (z, oo) — In | z |] при
Величина r=eV наз. внутренним радиусом
области D в точке z0. Если D — односвязная об-
область, граница к-рой содержит не менее двух точек,
то внутренний радиус области D в точке zo?D равен
К. р. области D в точке z0. Внутренний радиус области
не убывает с расширением области: если области D,
D± имеют функции Грина g(z, z0), gi (z, z0) соответствен-
соответственно) 2о6^П^1' и если Dcz.D1, то для внутренних ради-
радиусов г, /-J областей D, Dt в точке z0 справедливо нера-
неравенство
Внутренний радиус произвольной области D в точке
zo?D определяется как точная верхняя граница мно-
множества внутренних радиусов в точке z0 всех областей,
содержащих z0, содержащихся в D и имеющих функцию
Грина. В соответствии с этим определением, если об-
область D не обладает функцией Грина, то внутренний
радиус г области D в точке zo?D равен оо.
Лит.: [1] Г о л у з и н Г. М., Геометрическая теория функ-
функций комплексного переменного, 2 изд., М., 1966; [2] Смир-
Смирнов В. И., Лебедев Н. А., Конструктивная теория функ-
функций комплексного переменного, М.— Л., 1964; [3] Хейман
В. К., Многолистные функции, лер. с англ., М., 1960.
Г. В. Кузьмина,
КОНФОРМНЫХ ОТОБРАЖЕНИЙ ГРАНИЧНЫЕ
СВОЙСТВА — свойства функций, конформно отобра-
отображающих одну область комплексной плоскости на дру-
другую, проявляющиеся вблизи границы отображаемой
области и на самой границе. К числу таких свойств от-
относятся: возможность непрерывного продолжения функ-
функции w=f(z), конформно отображающей рассматривае-
рассматриваемую область Gj на область G2, в нек-рую точку Z, гра-
границы Т1 области Gj или на всю границу Гг этой области;
характер разрыва в случае невозможности такого про-
продолжения; наличие конформности продолженного ото-
отображения в граничных точках ? ? Г]; дифференциально-
гладкостные свойства продолженной функции на Г1
и на замкнутой области G1=G1(jrl; принадлежность
производной /' (z), z^Glt отображающей функции к
различным классам функций, аналитических в Glt
и т. п. Эти свойства изучаются в зависимости от свойств
границ областей Gx и G2. Из самых общих К. о. г. с.
можно выделить следующее: каковы бы ни были одно-
связные области Gj и G2 и однолистное конформное ото-
отображение w=f(z) области G1 на G2, это отображение
устанавливает взаимно однозначное соответствие между
граничными элементами этих областей в том смысле,
что класс всех эквивалентных путей, лежащих в обла-
области Gx и определяющих нек-рый граничный элемент ?
области G1? переходит при этом отображении в класс
всех эквивалентных путей, лежащих в области G2 и
определяющих нек-рый граничный элемент со области
G2 (обратное отображение z=f~1(w), w?G.-,. переводит
класс эквивалентных путей, определяющих со, в класс
эквивалентных путей, определяющих ?). При этом в
специальной топологии / задает гомеоморфизм области
G2 с присоединенными ее граничными элементами (рас-
(рассматриваемыми наряду с точками z^G1 как точки то-
пологич. пространства) на область G2 с присоединен-
присоединенными граничными элементами. Обычно рассматрива-
рассматривается случай, когда одна из областей Gj, G2 является
единичным кругом D={z: |г|<1} (реже полуплоско-
полуплоскостью или углом), общий же случай сводится к этому
частному случаю.
Пусть w=f(z) — однолистное конформное отображе-
отображение круга D с границей С= {z : |z| = 1} на ограничен-
ограниченную односвязную область G с границей Г, z=<p(w) —
обратное конформное отображение: ср (/(z)) = z при z^_D.
Имеют место следующие результаты.
1) Для того чтобы отображение w=f(z) непрерывно
продолжалось в точку ??С, необходимо и достаточно,
чтобы граничный элемент области G, соответствующий
точке ?, при этом отображении, был граничным эле-
элементом 1 рода (т. е. состоял из единственной точки).
Для непрерывной продолжимости функции z=<p(w) в
точку со?Г необходимо и достаточно, чтобы со входила
в состав лишь одного граничного элемента (точнее, в
состав лишь одного носителя граничного элемента об-
области G). Если Г — замкнутая жорданова кривая, то
/ непрерывно продолжается на С, а ср — на Г, так что
продолженные функции осуществляют взаимно одно-
однозначное и взаимно непрерывное отображение (гомео-
(гомеоморфизм) замкнутых областей D и G друг на друга.
Всюду ниже Г обозначает жорданову кривую и пред-
предполагается, что функции / и ф уже продолжены по
непрерывности на С и Г соответственно.
2) Если Г — замкнутая жорданова спрямляемая
кривая, то граничные функции /(?), ??С, и ср(со),
со?Г, являются абсолютно непрерывными. Таким об-
образом, отображения со=/(?), ??С, и ?=ср(со), со?Г,
переводят граничные множества меры нуль в граничные
множества меры нуль. Функция f(z) имеет конечную
ненулевую производную относительно замкнутого кру-
круга Ъ почти в каждой точке ??Г, а функция ср(к>) имеет
конечную ненулевую производную почти в каждой точ-
точке со?Г. Следовательно, эти отображения обладают
свойством конформности (т. е. свойством постоян-
постоянства растяжений и сохранения углов) почти в каждой
граничной точке соответствующей области. Функция
/' (z) принадлежит классу Хардп Н1.
3) Пусть Г — спрямляемая жорданова замкнутая
кривая со свойством: для любой пары различных точек
coj ? Г, со2 ? Г отношение длины меньшей из дуг, на
к-рые эти точки разбивают кривую Г, к расстоянию
| со, — со2| между этими точками ограничено сверху нек-
некрой величиной d, не зависящей от сох и со2. Тогда функ-
функция / (z) удовлетворяет на D условию Гёльдера порядка
2(l + dJ
( + )
4) Пусть Г — гладкая замкнутая жорданова кривая.
Зафиксируем нек-рую точку со0?Г и при —oo<s<
<оо отложим вдоль Г дугу длины \s\ в положительном
(при s>0) или отрицательном (при s<0) направлении
обхода области G. Пусть со (s) — конец отложенной ду-
дуги, a t(s) — угол между положительным направлением
действительной оси и положительным направлением
касательной в точке co(s) (значение угла x(s) выби-
выбирается так, чтобы функция x(s) была непрерывной).
Если при нек-ром р=0, \, . . . существует производ-
ная x'/'^s), удовлетворяющая условию Гёльдера нек-
рого положительного порядка а<1, то функция
/<^ + 1>(z) непрерывна и удовлетворяет условию Гёльдера
того же порядка а на замкнутом круге D nf'(z) ф О
на D, а ф(^ + 1'(!у) непрерывна и удовлетворяет условию
Гёльдера порядка а на G а ср'' (w) ф 0 на G.
Лит.: [1] М а р к у ш е в и ч А. И., Теория аналитических
функций, 2 изд., т. 2, М., 1968; [2] К о л л и н г в у д Э., Л о-
ватер А., Теория предельных множеств, пер. с англ., М.,
1971; [3] П р и в а л о в И. И., Граничные свойства аналити-
аналитических функций, 2 изд., М.— Л., 1950; [4] Г о л у з и н Г. М.,
Геометрическая теория функций комплексного переменного,
2 изд., М., 1966; [5] W a r s с h a w s k i S. E., «Proc. Amer.
Math. Soc», 1961, v. 12, Mi 4, p. 614—20; [6] Kellogg
O. D., «Trans. Amer. Math. Soc», 1912, v. 13, № 1, p. 109—32;
[7] Долженко Е. П., «Изв. АН СССР. Сер. матем.», 1965,
т. 29, с. 1069—84. Е. П. Долженко.
КОН-ФОССЕНА ПРЕОБРАЗОВАНИЕ — соответст-
соответствие между парой изометричных поверхностей F1 и F2
и бесконечно малым изгибанием Z так наз. срединной
поверхности Fcp: если хх пх2— радиус-векторы поверх-
поверхностей F1 и F2, то радиус-вектор хср поверхности
Fcp равен -^-(х1-!гх2), а поле скоростей z бесконечно
малого изгибания Z равно -^(х1— х2); введено С. Э.
Кон-Фоссеном [1]. Если F1 и F,— гладкие поверхно-
поверхности и если углы между полукасательными х1 и т2 к
соответствующим по изометрии кривым поверхностей
Fj и F2 меньше я, то Fcp оказывается гладкой. Этот факт
позволяет в ряде случаев сводить исследование изо-
метрпп Fj и F2 к изучению бесконечно малых изгибаний
FCT>. Для фиксированной точки Мх на Рг (и соответствен-
соответственно М2 на F2) К.-Ф. п. определяет преобразование Кэлн
ортогональной матрицы О, преобразующей касатель-
касательный пучок на Fj в изометричный ему пучок на F2, в
кососимметрическую матрицу К, описывающую бес-
бесконечно малое изгибание FCv Так как О полностью
определяется вектором V= V sin — и скаляром р=
= cos-^-, где V — орт оси поворота соответствующих
пучков, X — угол поворота (см. Поворотов диаграмма),
а К — вектором вращения у, то К.-Ф. п. можно выра-
выразить формулой: у= V/p.
К.-Ф. п. обобщается на случай пространств постоян-
постоянной кривизны [2].
Лит.: [1] К о н-Ф о с с е н С. Э., Некоторые вопросы диф-
дифференциальной геометрии в целом, М., 1959; [2] П о г о р е-
лов А. В., Внешняя геометрия выпуклых поверхностей, М.,
1969. М. И. Войцеховский.
КОНХОИДА кривой — плоская кривая, полу-
получающаяся при увеличении или уменьшении радиус-век-
радиус-вектора каждой точки данной плоской кривой на постоян-
постоянный отрезок I. Если уравнение данной кривой в по-
полярных координатах: р=/(ф), то уравнение ее К. имеет
вид: p=/((p)±Z. Примеры: К. прямой — Никомеда кон-
конхоида, К. окружности — Паскаля улитка.
Д. Д. Соколов.
КОНЦЕНТРАЦИИ ФУНКЦИЯ случайной ве-
величины X — функция Q(l, X), определенная для
всех неотрицательных I и случайной величины X со-
соотношением
Q(l,X)= sup P{x<X<x + l}.
К. ф. Q(l, X) является неотрицательной, полуаддитив-
ной, монотонно неубывающей функцией при 1^0, не-
непрерывной справа и такой, что
lim Q (I, A)=l.
Обратно, любая функция, обладающая этими свойст-
свойствами, может рассматриваться, как К. ф. нек-рой слу-
случайной величины.
К. ф. является удобной характеристикой разброса
значений случайной величины, особенно для количест-
венного выражения факта увеличения разброса при
суммировании независимых случайных величин. Пер-
Первая абсолютная, т. е. содержащая лишь абсолютные
константы, оценка для концентрации суммы при задан-
заданных концентрациях слагаемых была получена А. Н.
Колмогоровым [4] методом, развивающим метод П. Ле-
ви [2]. В дальнейшем этот результат был усилен
(см. [5]); была получена формулировка, включающая в
качестве частных случаев все ранее найденные резуль-
результаты:
где
Хх, . . ., Хп— совокупность независимых случайных
величин, l^lj, ?=1, 2, . . ., re, и С — абсолютная по-
постоянная. Выделены два типа оценок: оценки Q(l, S)
локального типа (см. [6]); оценки Q(l, S) интегрального
типа (см. [7]).
Двойственной характеристикой разброса, тесно свя-
связанной с К. ф., является функция рассеивания случай-
случайной величины X:
D(q, X)=iai{l:Q (I, XOsq)
при 0<:д<1. Имеет место (см. [8]) следующее неравен-
неравенство, связывающее К. ф. и характеристич. функцию
f(t) случайной величины X:
а также неравенства
Q(l, X%+X2)^Q(l, Xi), ? = 1, 2,
где Х1 и Х2— независимые случайные величины. Име-
Имеются попытки перенести нек-рые результаты, касаю-
касающиеся К. ф. на случай суммирования независимых слу-
случайных векторов (см. [9J).
Лит.: [1] Doeblin W., Levy Р., «С. г. Acad. sci.»,
1936, t. 202, p. 2027—29; [2] Levy P., Theorie de Paddition
des variables aleatoire, 2 ed., P., 1954; [3] Doeblin W.,
«Bull. sci. math.», 1939, t. 63, p. 23—64; [4] К о 1 m о g о г о v A.,
«Ann. de l'lnst. H. Poincare», 1958, t. 16, p. 27—34; [5] P о г о-
зин Б. А., «Теория вероят. и ее примен.», 1961, т. 6, в. 1,
с. 103—108; [6] К е s t e n H., «Math. Scand.», 1969, v. 25,
p. 133—44; [7] Рогозин Б. А., «Докл. АН СССР», 1973,
т. 211, с. 1067—70; [8] П е т р о в В. В., Суммы независимых
случайных величин, М., 1972; [9] Е s s е е п С. G., «Z. Wahr-
scheinlichkeitstheor. und verw. Geb.>>, 1968, Bd 9, S. 290—308.
Б. А. Роговин.
КОНЪЮНКТИВНАЯ НОРМАЛЬНАЯ ФОРМА —
пропозициональная формула, имеющая вид
где каждое С,у, ?=1, . . ., п; j=i, ¦ . ., m;, есть либо
переменная, либо отрицание переменной. К. н. ф. (*}
является тавтологией тогда и только тогда, когда для
любого I среди Си, . . ., Cim. встречаются обе формулы
р и ~]р для нек-рой переменной р. Для всякой пропози-
пропозициональной формулы А можно построить эквивалент-
эквивалентную ей К. н. ф. В, содержащую те же переменные, чта
и А. Такая формула В наз. К. н. ф. формулы А.
С. К. Соболева
КОНЪЮНКЦИЯ — логическая one- .
рация, служащая для образования вы-
высказывания «А и В» из высказываний
А и В. В формализованных языках К.
высказываний А и В обозначается
посредством А&В, А /\В, А -В, АВ.
Высказывания А и В наз. конъюнк-
конъюнктивными членами высказыва-
высказывания А&В. Употреблению К. в математической логике
соответствует следующая истинностная таблица (см.
выше). В- Е- Плиска*
А
И
И
Л
л
в
и
л
и
л
А&В
И
Л
л
л
КООПЕРАТИВНАЯ ИГРА — нестратегическая игра
{см. Игр теория), задаваемая тройкой (/, v, H), где
/ — множество (обычно конечное), элементы к-рого
наз. игроками, а подмножества Kal — коали-
коалициями, v — вещественная функция, определенная
на множестве коалиций и называемая характе-
характеристической функцией игры, Н — неко-
некоторое подмножество векторов ж/ (компоненты х\ к-рых
соответствуют игрокам ; из /), называемых деле-
дележами. К. и. впервые были введены Дж. Нейманом
(J. Neumann, 1929) как аппарат кооперативной теории
{бескоалиционных) игр.
В классической теории К. и. принимается:
На множестве Н вводится бинарное отношение >¦
к
доминирования (предпочтения) дележей по
коалиции Kcl.:
xi > У> (i € K).
Если х/У-yj для нек-рого Kcz.1, то полагают
к
Относительно этого отношения доминирования форму-
формулируются понятия оптимальности дележей.
Значительная часть содержания теории К. и. состо-
состоит ь разработке понятий оптимальности, в доказатель-
доказательствах их реализуемости для различных частных клас-
классов К. и. и фактическом нахождении таких реализаций.
К числу принципов оптимальности, разрабатываемых
применительно к К. п., относятся: двойная (т. е. внеш-
внешняя и внутренняя) устойчивость, реализуемая в форме
решений по Нейману — Моргенштерну (Н—М-решения);
недоминируемость дележей (см. Ядро в теории игр);
устойчивость относительно угроз; устойчивость в смы-
смысле минимизации наибольшей неудовлетворенности
(см. Устойчивость в теории игр), справедливость (см.
Шепли вектор) и др.
Введение на классе К. и. алгебраич. операций при-
приводит к исчислениям К. и. и к исследованию
взаимосвязей между этими операциями и различными
принципами оптимальности. Специальному изучению
подвергались различные частные классы К. и., описан-
описанные ниже.
Простая игра — К. и., в к-рой характери-
стич. функция v принимает ровно два значения (обычно
О и 1); при этом коалиции К, на к-рых достигается мак-
максимальное значение v(K), наз. в ы п г р ы в а ю щ и-
м п. Частным случаем простых игр является взве-
взвешенная мажоритарная игра, в к-рой
коалиция К является выигрывающей, если VV ш,->
>е\\ w;, где u'i(i^I) и c?(V2, 1) — некоторые задан-
заданные числа.
Сбалансированная игра — К. и., для
характеристической функции которой
¦у (К) < и{1),
если семейство коалиций Я и числа Яд-(А'^.Й') таковы,
что
v @ = li @ Лля всех ' € Т,
где tK{i)= 1, если i ? К, и 0 в противном случае.
Сбалансированные игры и только они имеют непустое
с-ядро.
Выпуклая игра — К. и., для характеристич.
функции к-рой при К, Lczl
В выпуклой игре с-ядро непусто и совпадает с единст-
единственным Н — М-решением. Если К. и. строго выпуклая
(т.е. неравенство (*) строгое), то вектор Шепли явля-
является центром тяжести с-ядра.
Игра с квотой — К. и. с характеристич. функ-
функцией v, для к-рой существует такой вектор ш? (w,-)igj ,
ЧТ0 2- гш'=у(^)' п для любых игроков i, j?I Aф])
имеет место v({i, /})=ш, + о)у.
Игра рынка — К. и., порожденная рынком,
к-рый понимается как система
где / — множество участников рынка (с т товарами),
а1 ? R™ — начальный набор товаров s-ro участника,
и' (х!) — функция полезности г-го участника, определен-
определенная на R™. На основе этого рынка строится К. и., в
к-рой
Я = {»/•• У/= в/(*0 (* €Л.
*'€*? («ел, 2,6/*'=2, «=/«'}.
а характернстич. функция определяется равенством
Теория классич. К. и. подвергалась обобщениям в
различных направлениях (см. также Неатомическая
игра).
Игры без побочных платежей —
нестратегич. игры, задаваемые тройкой </, v, H), где v
(в отличие от классических К. и.) — функция, к-рая
каждой коалиции К ставит в соответствие множество
v(K) векторов х,, удовлетворяющее условиям: 1) v(K)
замкнуто и выпукло; 2) если xr?v(K) и у,-<:^,- (i?K),
то yi^v(K); 3)если Sf\K=0, то v(S)r\v(K)Cv(S()K);
4) 1*(К)Ф0 для всех Кс1\ 5) xf?v(I) тогда и только
тогда, когда ж/<:^/ для нек-рого yi^H.
Доминирование в игре без побочных платежей оп-
определяется следующим образом: х^у;, если сущест-
существует такая непустая коалиция Kdl, что
х\ > у; (i G к) и xi G v (К)-
Игра в форме функции разбиени я—
нестратегическая игра, задаваемая множеством игро-
игроков / и функцией v, к-рая каждому разбиению !р—
= (Р1, • • ., Рп) множества / ставит в соответствие вектор
VJ —(yJ (Pj), . . . , V-* (Pn))- Максимальный выигрыш,
к-рый может гарантировать себе коалиция К, определя-
определяется формулой u(/<Q=min v^ (К). Дележ в игре в форме
функции разбиения определяется как вектор хр удов-
удовлетворяющий условиям: xi^u({i}) (i?I)\ \\. x[=
= V ^ E)=||53[| Для нек-рого^- Дележ хг доми-
доминирует дележ у/ по коалиции К, если: ж,->
(<K) 2 Kxi<u(KS>'< существует такое 53, что
Лит.: [1] Нейман Дж., Моргенштерн О., Тео-
Теория игр и экономическое поведение, пер. с англ., М., 1970; [2]
Воробьев Н. Н., «Успехи матем. наук», 1970, т. 25, № 2,
с. 81 —140; [3] Розенмюллер И., Кооперативные игры
и рынки, пер. с англ., М., 1974.
Н. Н. Воробьев, А. И. Соболев.