УДК 517
ББК 22.161.1
К88
Кудрявцев Л. Д. Краткий курс математического анализа. Т. 1. Диф-
Дифференциальное и интегральное исчисления функций одной переменной.
Ряды: Учебник. — 3-е изд., перераб. — М.: ФИЗМАТЛИТ, 2005. — 400 с. —
ISBN 5-9221-0184-6.
Излагаются традиционные разделы математического анализа: диффе-
дифференциальное и интегральное исчисления функций одной переменной, теория
рядов.
Второе издание — 1998 г.
Для студентов физико-математических и инженерно-физических спе-
специальностей.
Ил. 128.
Рецензенты:
заведующий кафедрой общей математики факультета ВМиК МГУ
им. М.В.Ломоносова, академик В.А. Ильин;
профессор МФТИ, академик СМ. Никольский.
ISBN 5-9221-0184-6 (Т. 1)	© ФИЗМАТЛИТ, 2003, 2005
ISBN 5-9221-0183-8	© Л.Д. Кудрявцев, 2003, 2005

ОГЛАВЛЕНИЕ
Предисловие
ГЛАВА 1
ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ
ОДНОЙ ПЕРЕМЕННОЙ
\ 1. Функции и множества 	 11
1.1. Множества A1). 1.2. Функции A3).
J2. Числа	 15
2.1. Действительные числа A5). 2.2. Расширенная числовая пря-
прямая. Окрестности A9). 2.3. Комплексные числа B0). 2.4. Пере-
Перестановки и сочетания B9). 2.5. Формула бинома Ньютона C1).
\ 3. Элементарные функции	 32
3.1. Числовые функции C2). 3.2. Понятие элементарной функ-
функции C3). 3.3. Многочлены C4). 3.4. Разложение многочленов
на множители C7). 3.5. Рациональные дроби D0). 3.6. Графи-
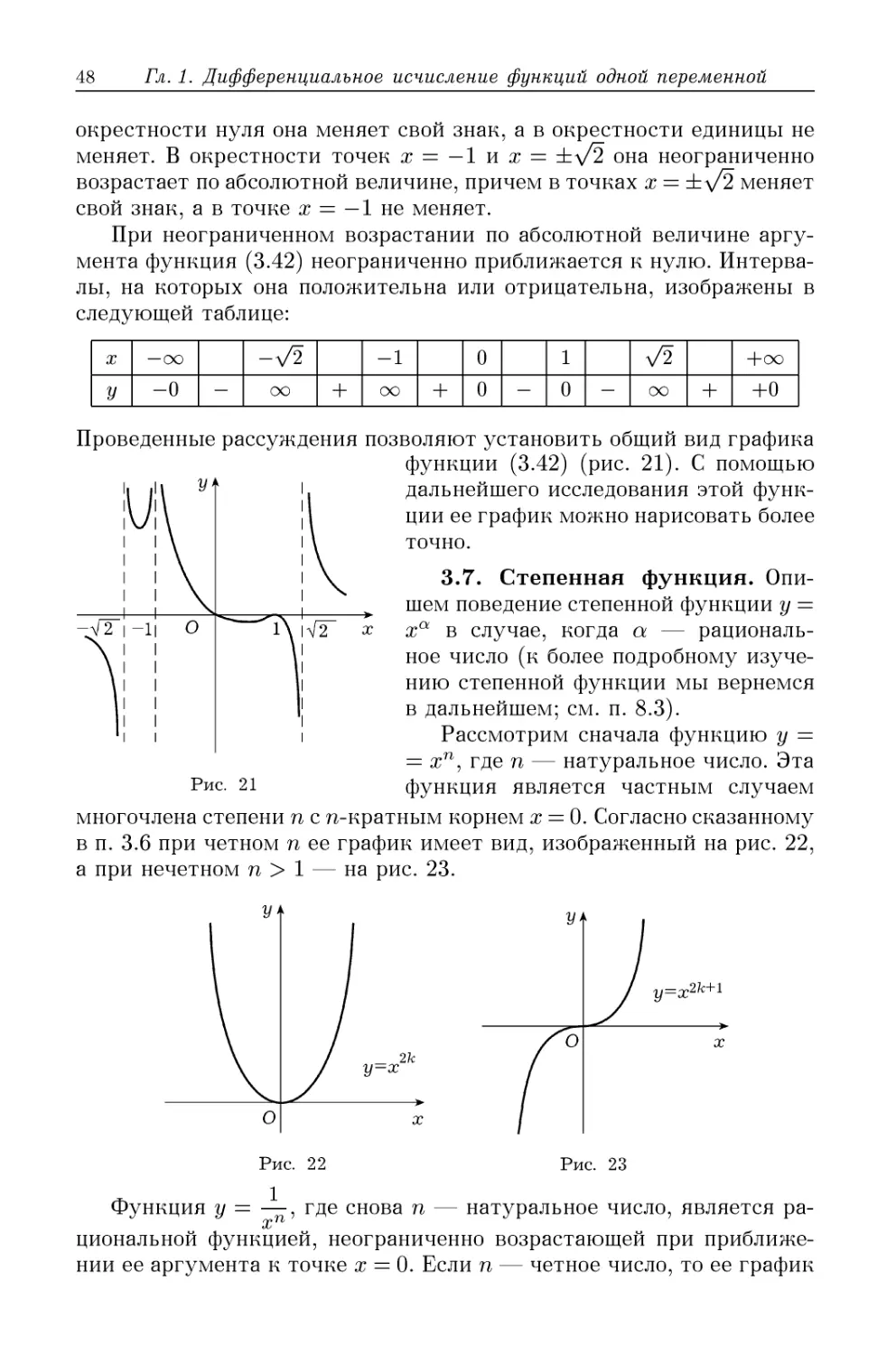
Графики рациональных функций D5). 3.7. Степенная функция D8).
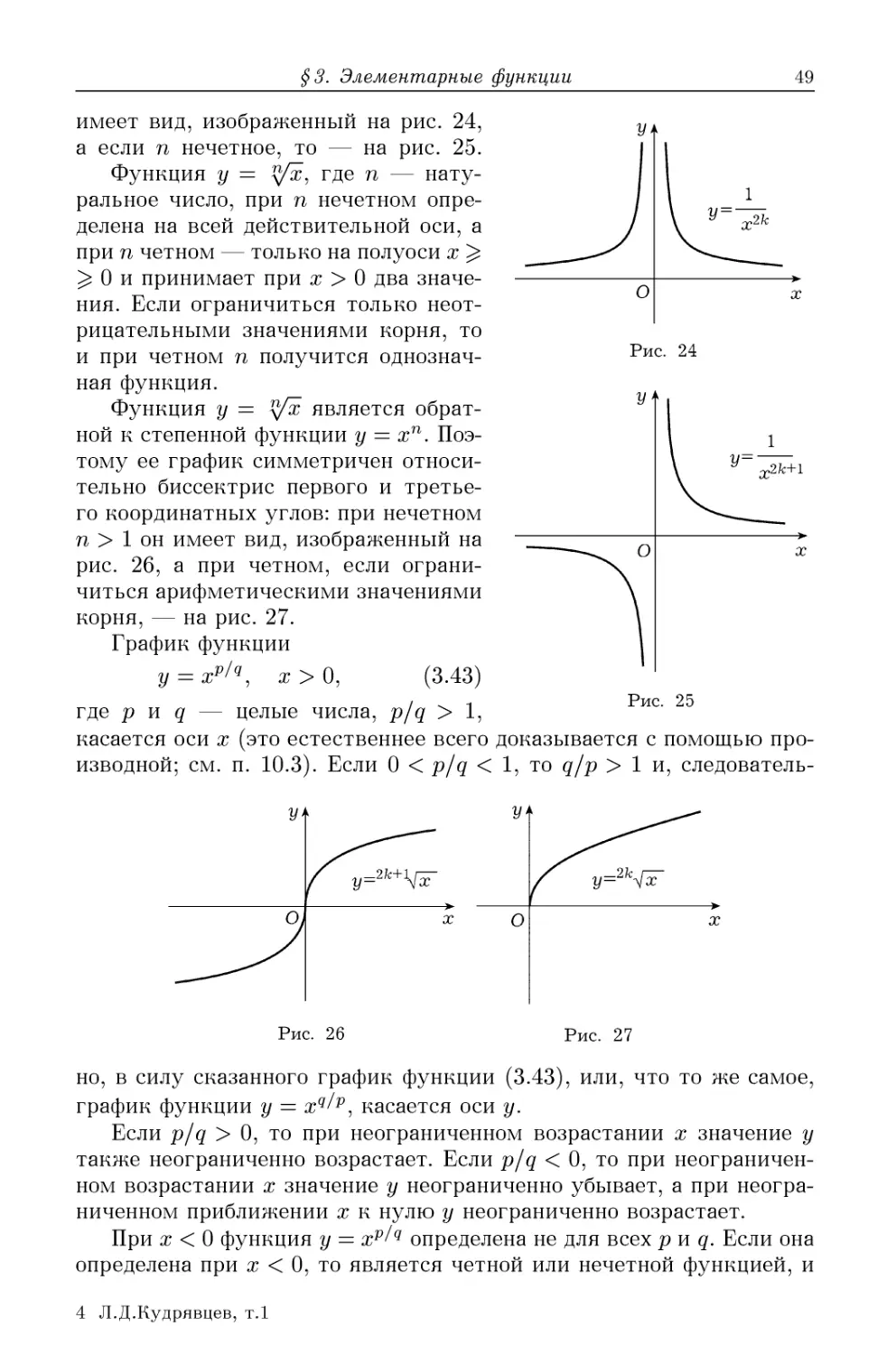
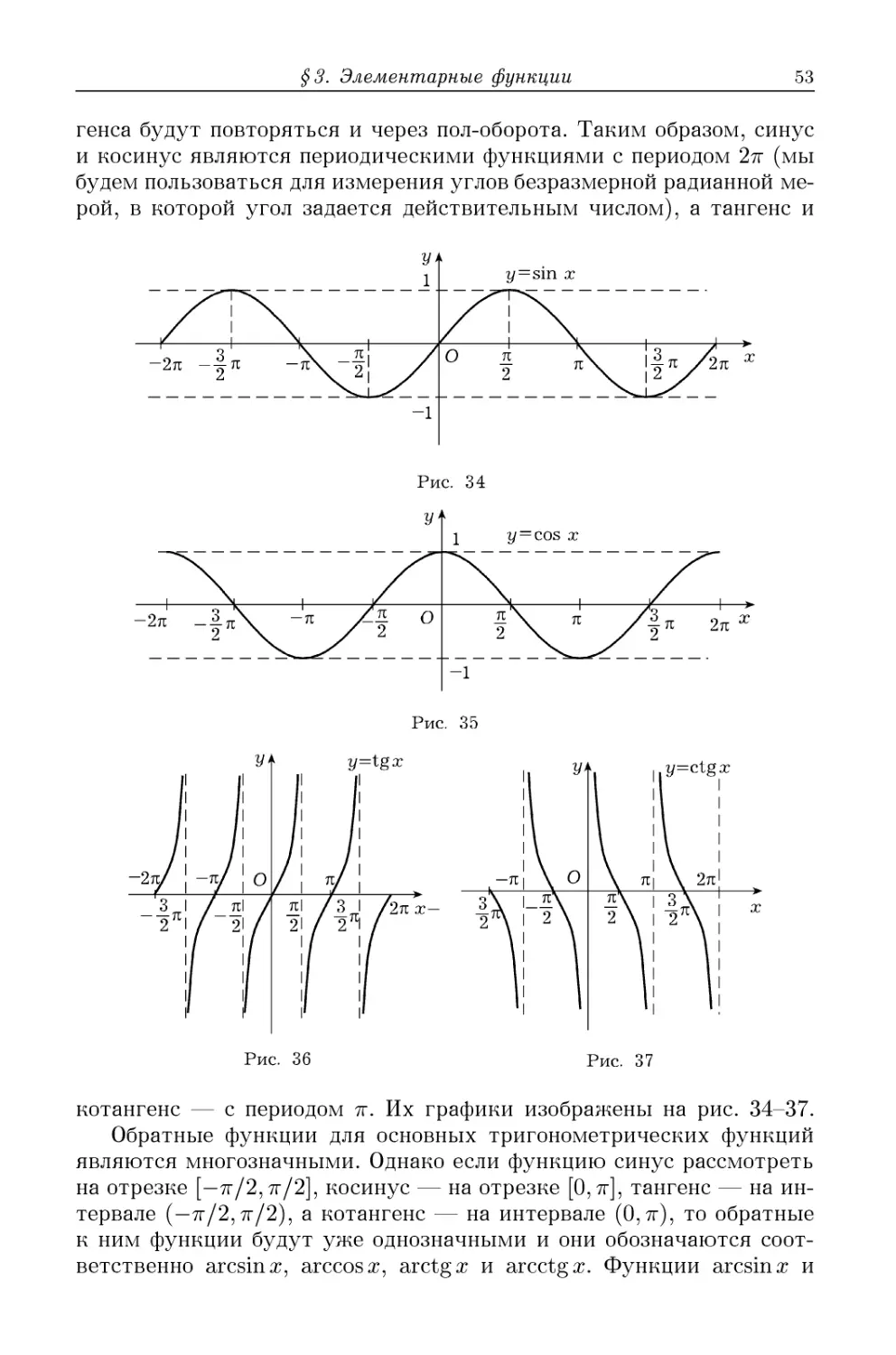
3.8. Показательная и логарифмическая функции E0). 3.9. Три-
Тригонометрические и обратные тригонометрические функции E1).
3.10. Параллельный перенос и растяжение графиков E4).
\ 4. Числовые множества	 55
4.1. Ограниченные и неограниченные множества E5). 4.2. Верх-
Верхняя и нижняя грани E6). 4.3*. Арифметические свойства верх-
верхних и нижних граней E8). 4.4. Принцип Архимеда F1). 4.5. Прин-
Принцип вложенных отрезков F1). 4.6*. Счетность рациональных
чисел. Несчетность действительных чисел F3).
\ 5. Предел числовой последовательности 	 67
5.1.	Определение предела числовой последовательности F7).
5.2.	Единственность предела последовательности G1). 5.3. Пере-
Переход к пределу в неравенствах G1). 5.4. Ограниченность сходя-
сходящихся последовательностей G4). 5.5. Бесконечно малые последо-
последовательности G5). 5.6. Свойства пределов, связанные с арифмети-

Оглавление
ческими действиями над числовыми последовательностями G7).
5.7.	Монотонные последовательности (80). 5.8. Принцип ком-
компактности (83). 5.9. Критерий Коши (86). 5.10*. Изображение
действительных чисел бесконечными десятичными дробями (88).
5.11. Предел последовательности комплексных чисел (94).
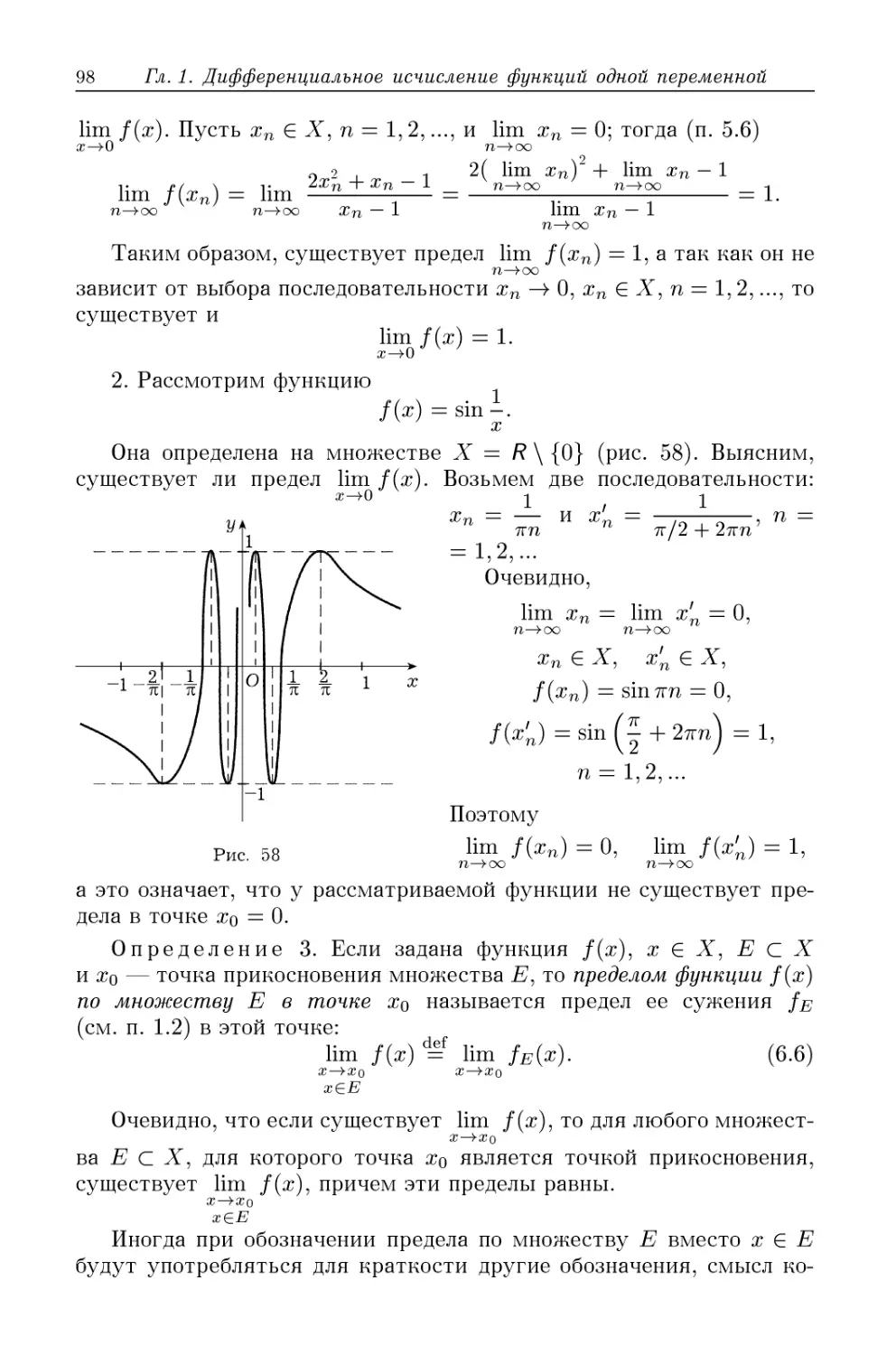
§ 6. Предел и непрерывность функций	 95
6.1. Первое определение предела функции (95). 6.2. Опреде-
Определение непрерывности функции A00). 6.3. Второе определение
предела функции A01). 6.4. Условие существования предела
функции A03). 6.5. Предел функции по объединению мно-
множеств A04). 6.6. Односторонние пределы и односторонняя
непрерывность A05). 6.7. Свойства пределов функций A07).
6.8.	Бесконечно малые A10). 6.9. Непрерывные функции A11).
6.10. Классификация точек разрыва A14). 6.11. Пределы мо-
монотонных функций A15). 6.12. Критерий Коши существования
предела функции A18). 6.13. Предел и непрерывность компо-
композиции функций A19). 6.14. Предел и непрерывность функций
комплексного аргумента A20).
§ 7. Свойства непрерывных функций	 122
7.1. Ограниченность непрерывных функций. Достижимость эк-
экстремальных значений A22). 7.2. Промежуточные значения не-
непрерывных функций A23). 7.3. Обратные функции A24). 7.4. Рав-
Равномерная непрерывность A28).
§ 8. Непрерывность элементарных функций	 130
8.1.Многочлены и рациональные функции A30). 8.2. Показатель-
Показательная и логарифмическая функции A31). 8.3. Степенная функ-
функция A38). 8.4. Тригонометрические и обратные тригонометри-
тригонометрические функции A39). 8.5. Элементарные функции A40).
§ 9. Сравнение функций	 140
9.1. Замечательные пределы A40). 9.2. Сравнение функций в
окрестности заданной точки A43). 9.3. Эквивалентные функ-
функции A46).
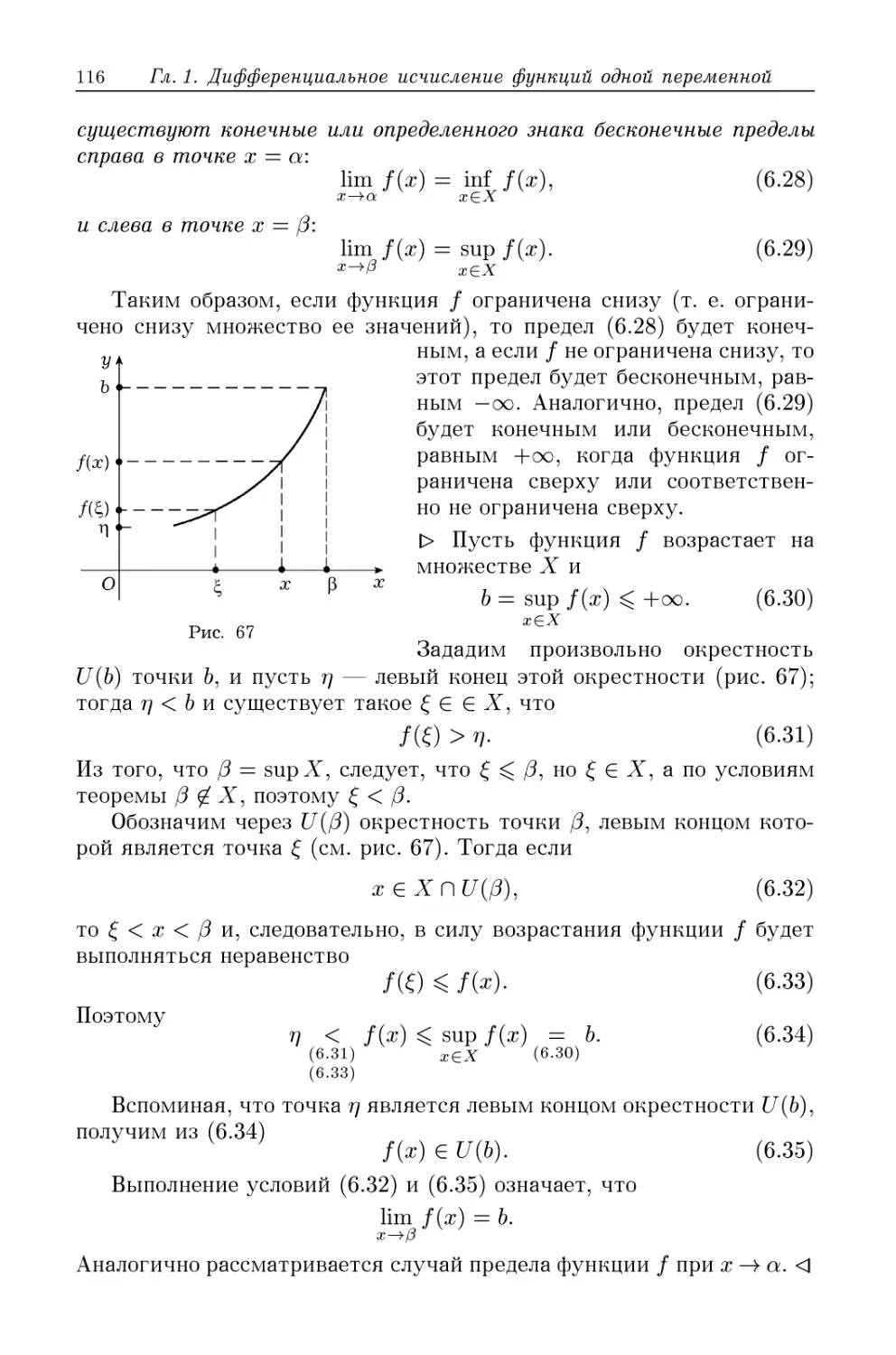
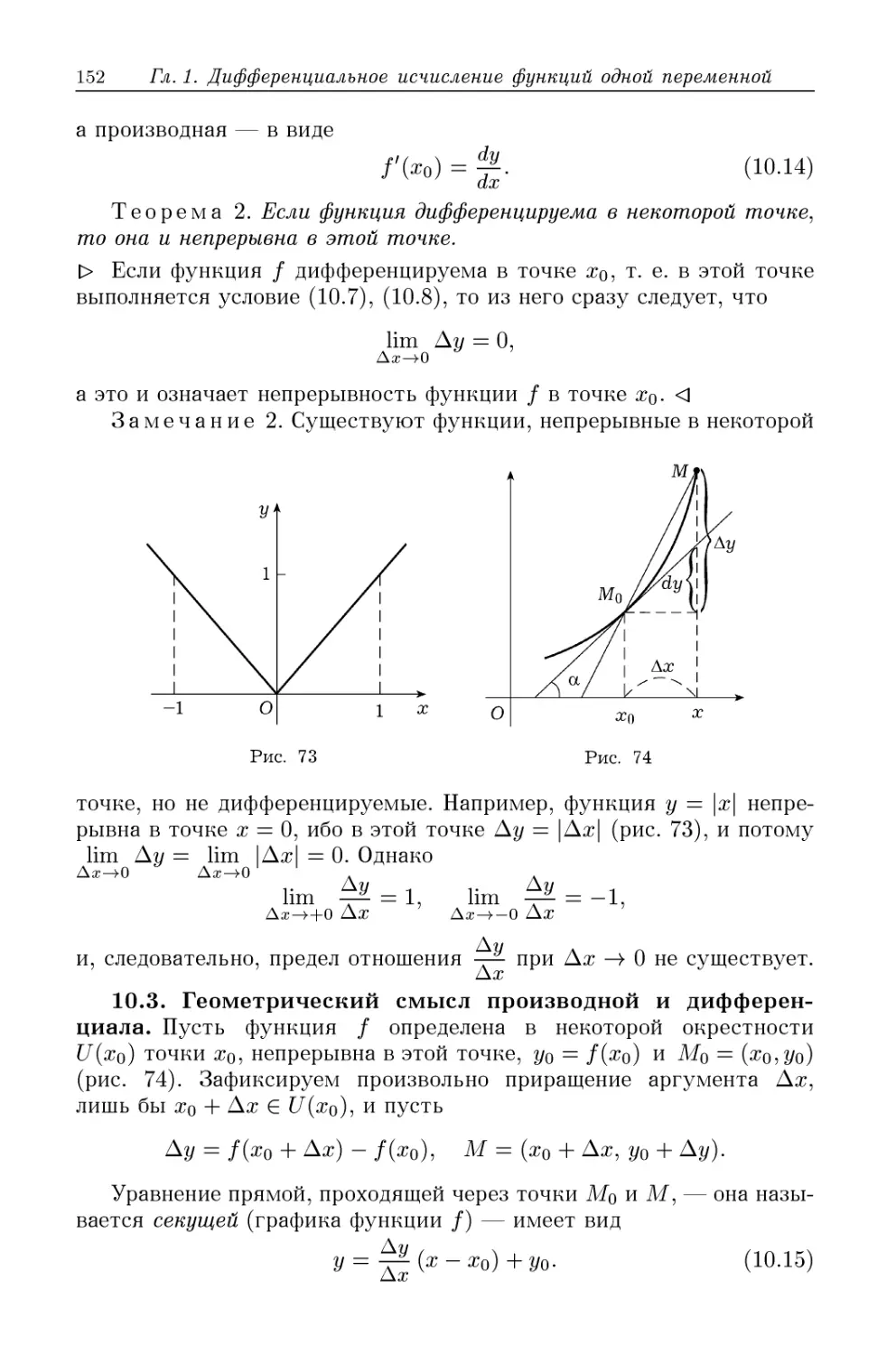
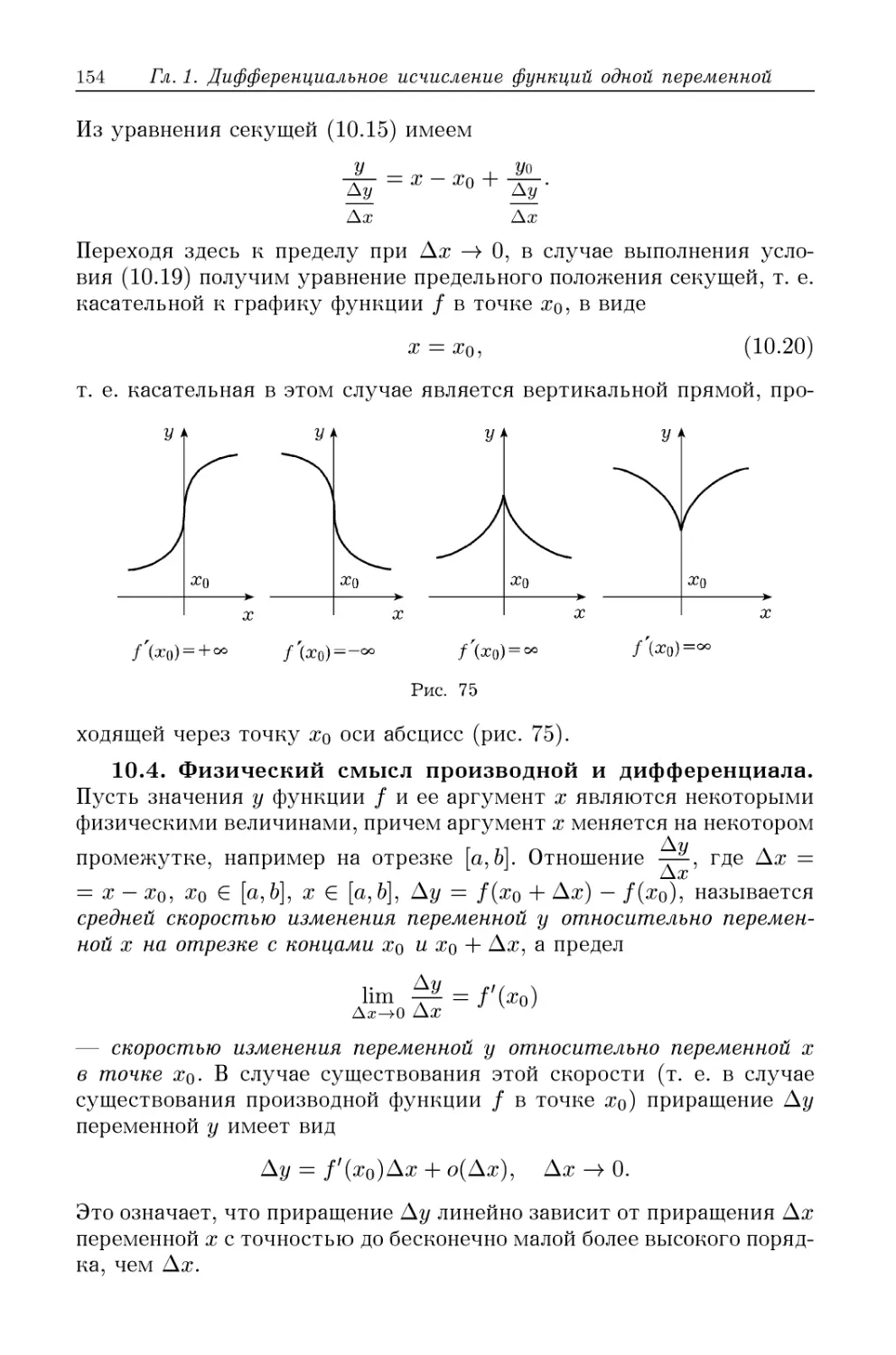
§ 10. Производная и дифференциал	 148
10.1. Определение производной A48). 10.2. Дифференциал функ-
функции A50). 10.3. Геометрический смысл производной и диф-
дифференциала A52). 10.4. Физический смысл производной и
дифференциала A54). 10.5. Свойства производных, связанные с
арифметическими действиями над функциями A55). 10.6. Про-
Производная обратной функции A57). 10.7. Производная и диффе-
дифференциал сложной функции A58). 10.8. Гиперболические функции
и их производные A60). 10.9. Производные комплекснозначных
функций действительного аргумента A60).
§ 11. Производные и дифференциалы высших порядков	 161
11.1. Производные высших порядков A61). 11.2. Производные

Оглавление
высших порядков сложных функций, обратных функций и функ-
функций, заданных параметрически A63). 11.3. Дифференциалы выс-
высших порядков A64).
\ 12. Дифференциальные теоремы о среднем	 165
12.1. Теорема Ферма A65). 12.2. Теоремы Ролля, Лагранжа и
Коши о средних значениях A67).
\ 13. Раскрытие неопределенностей по правилу Лопиталя	 172
13.1. Неопределенности вида jj A72). 13.2. Неопределенности
вида g A73).
\ 14. Формула Тейлора	 178
14.1. Вывод формулы Тейлора A78). 14.2. Примеры разложения
по формуле Тейлора A82). 14.3*. Применение метода выделения
главной части функций для вычисления пределов A85).
\ 15. Исследование функций	 186
15.1. Признак монотонности функций A86). 15.2. Локальные
экстремумы функций A87). 15.3. Выпуклость и точки переги-
перегиба A94). 15.4. Асимптоты A98). 15.5*. Построение графиков
функций B00).
\ 16. Векторные функции	 201
16.1.Предел и непрерывность векторной функции B01). 16.2. Про-
Производная и дифференциал векторной функции B05).
\ 17. Длина кривой 	 211
17.1. Понятие кривой B11). 17.2. Касательная к кривой B16).
17.3.	Определение длины кривой. Спрямляемые кривые B18).
\ 18. Кривизна кривой	 223
18.1.	Определение кривизны и радиуса кривизны кривой B23).
18.2.	Формула для кривизны B24). 18.3. Главная нормаль. Со-
Соприкасающаяся плоскость B25). 18.4. Центр кривизны. Эволю-
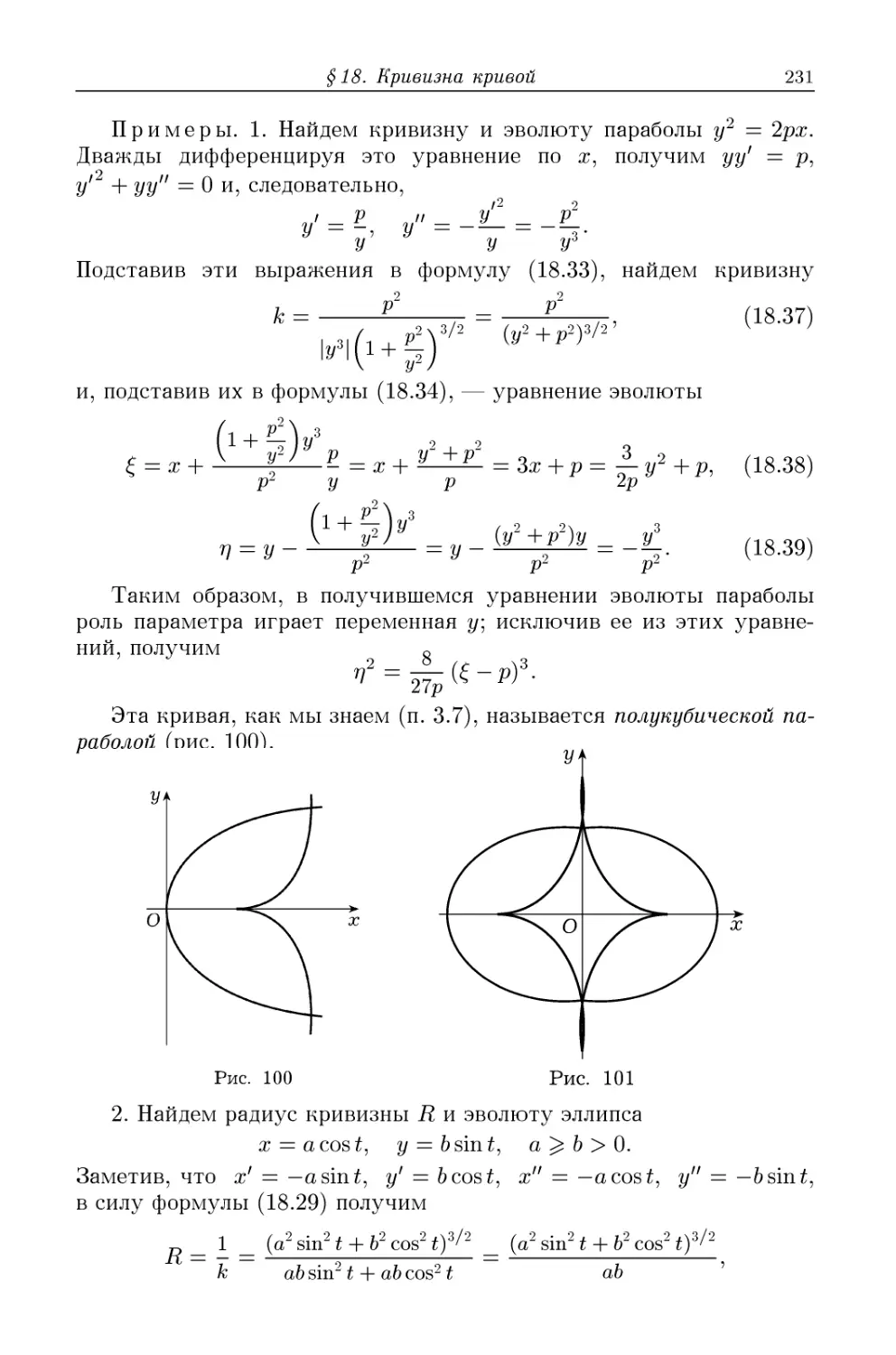
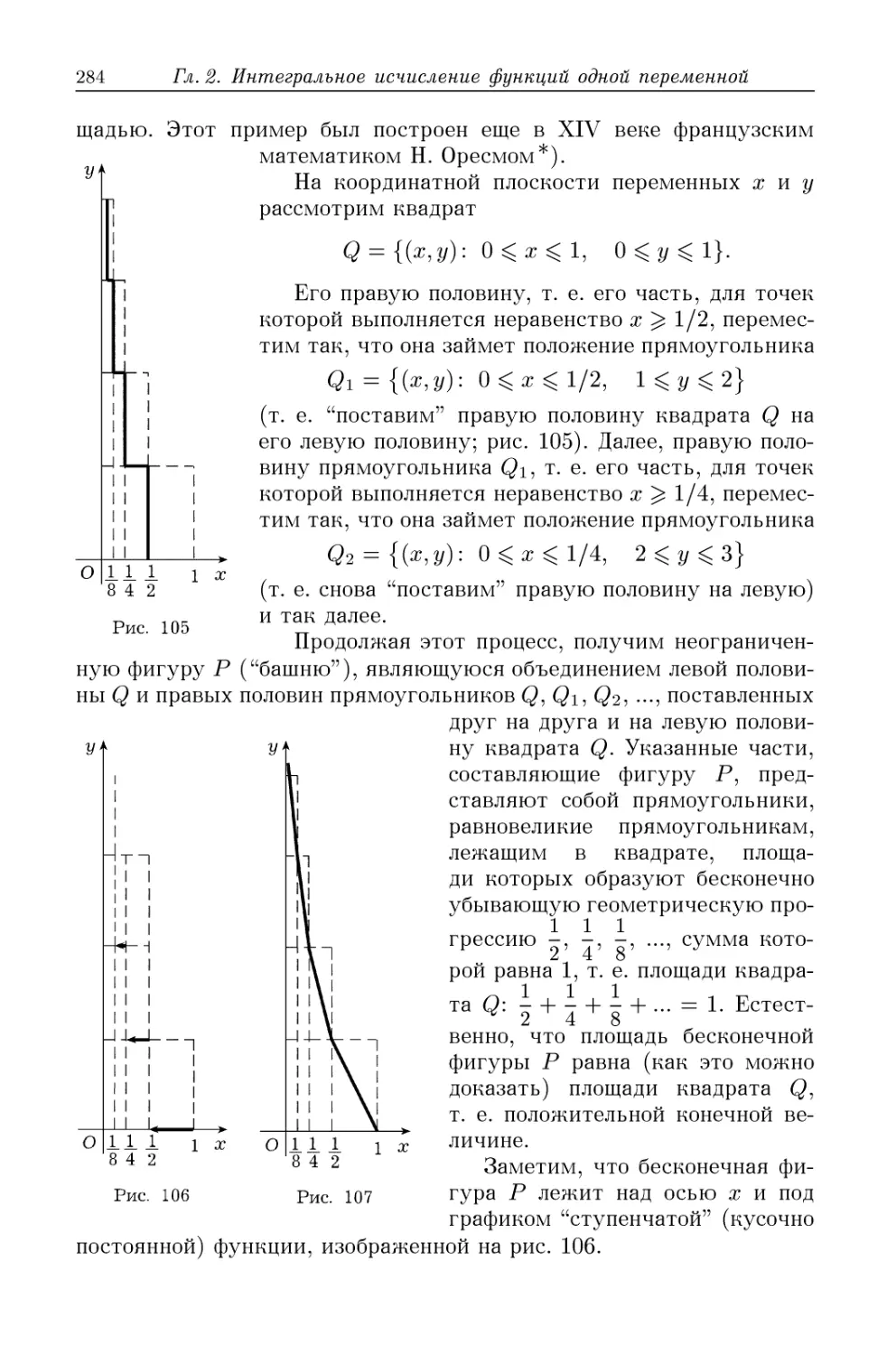
Эволюта B28). 18.5. Кривизна и эволюта плоской кривой B29).
ГЛАВА 2
ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ
ОДНОЙ ПЕРЕМЕННОЙ
\ 19. Определение и свойства неопределенного интеграла 	 233
19.1.Первообразная и неопределенный интеграл B33). 19.2. Основ-
Основные свойства интеграла B35). 19.3. Табличные интегралы B37).
19.4.	Формула замены переменной B38). 19.5. Формула интегри-
интегрирования по частям B41).
\ 20. Интегрирование рациональных дробей 	 242
20.1.	Интегрирование элементарных рациональных дробей B42).
20.2.	Общий случай B44).

Оглавление
§21. Интегрирование некоторых иррациональностей 	 244
21.1. Рациональные функции от функций B44). 21.2. Интегралы
вида J R (ж, (дд^)Г1 ? • ••? (сж+сг)ГП) ^ж B45). 21.3*. Интегралы от
дифференциального бинома B46).
§ 22. Интегрирование некоторых трансцендентных функций	 247
22.1. Интегралы J R(sinx, cos ж) dx B47). 22.2. Интегралы
J sinm ж cosn ж dx B48). 22.3. Интегралы J sinax cos f3x dx,
J sin ax sin f3x dx, J cos ax cos f3x dx B49). 22.4. Интегралы от
трансцендентных функций, вычисляющиеся с помощью интег-
интегрирования по частям B50).
§ 23. Определенный интеграл 	 251
23.1.Определенный интеграл Римана B51). 23.2. Ограниченность
интегрируемых функций B53). 23.3. Верхние и нижние суммы
Дарбу B55). 23.4. Нижний и верхний интегралы B58). 23.5. Не-
Необходимые и достаточные условия интегрируемости функ-
функций B59). 23.6. Интегрируемость непрерывных и монотонных
функций B60).
§ 24. Свойства интегрируемых функций	 262
24.1.Основные свойства определенного интеграла B62). 24.2. Ин-
Интегральная теорема о среднем B71).
§ 25. Определенный и неопределенный интегралы 	 274
25.1. Дифференцирование определенного интеграла по пределам
интегрирования B74). 25.2. Существование первообразной B76).
§ 26. Формулы замены переменной и интегрирования по частям в опре-
определенном интеграле	 278
26.1. Формула замены переменной B78). 26.2. Формула интег-
интегрирования по частям B79).
§ 27. Площади и объемы	 282
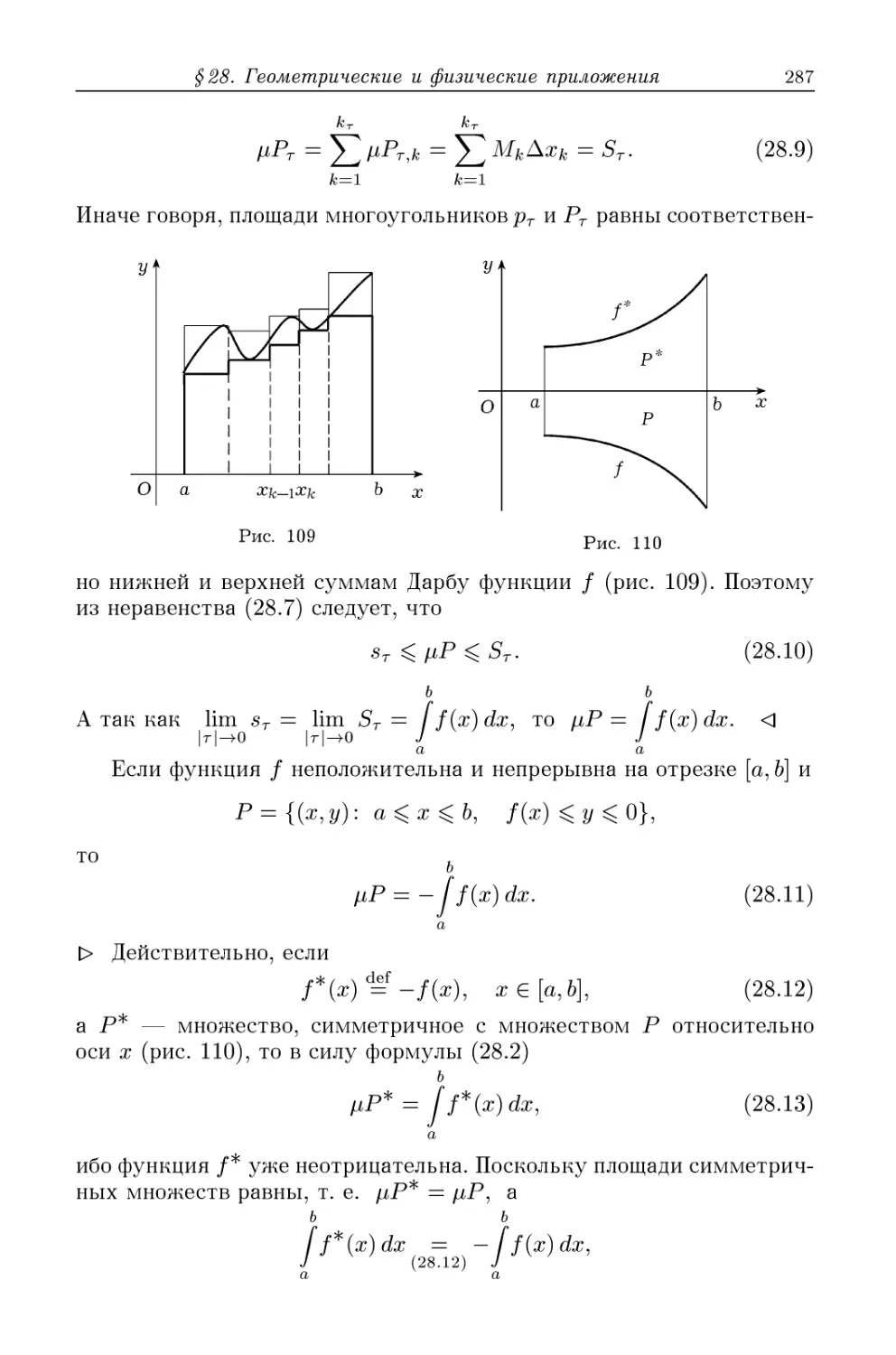
27.1. Понятие площади плоского множества B82). 27.2*. При-
Пример неограниченного множества положительной конечной пло-
площади B83). 27.3. Понятие объема B85).
§ 28. Геометрические и физические приложения определенного интег-
интеграла 	 286
28.1.	Вычисление площадей криволинейных трапеций B86).
28.2.	Вычисление площадей в полярных координатах. B88).
28.3.	Вычисление длины кривой B90). 28.4. Площадь поверхнос-
поверхности вращения B90). 28.5. Объем тел вращения B94). 28.6*. Тео-
Теоремы Гульдина. Центры тяжести плоских фигур и их моменты
относительно осей B94).
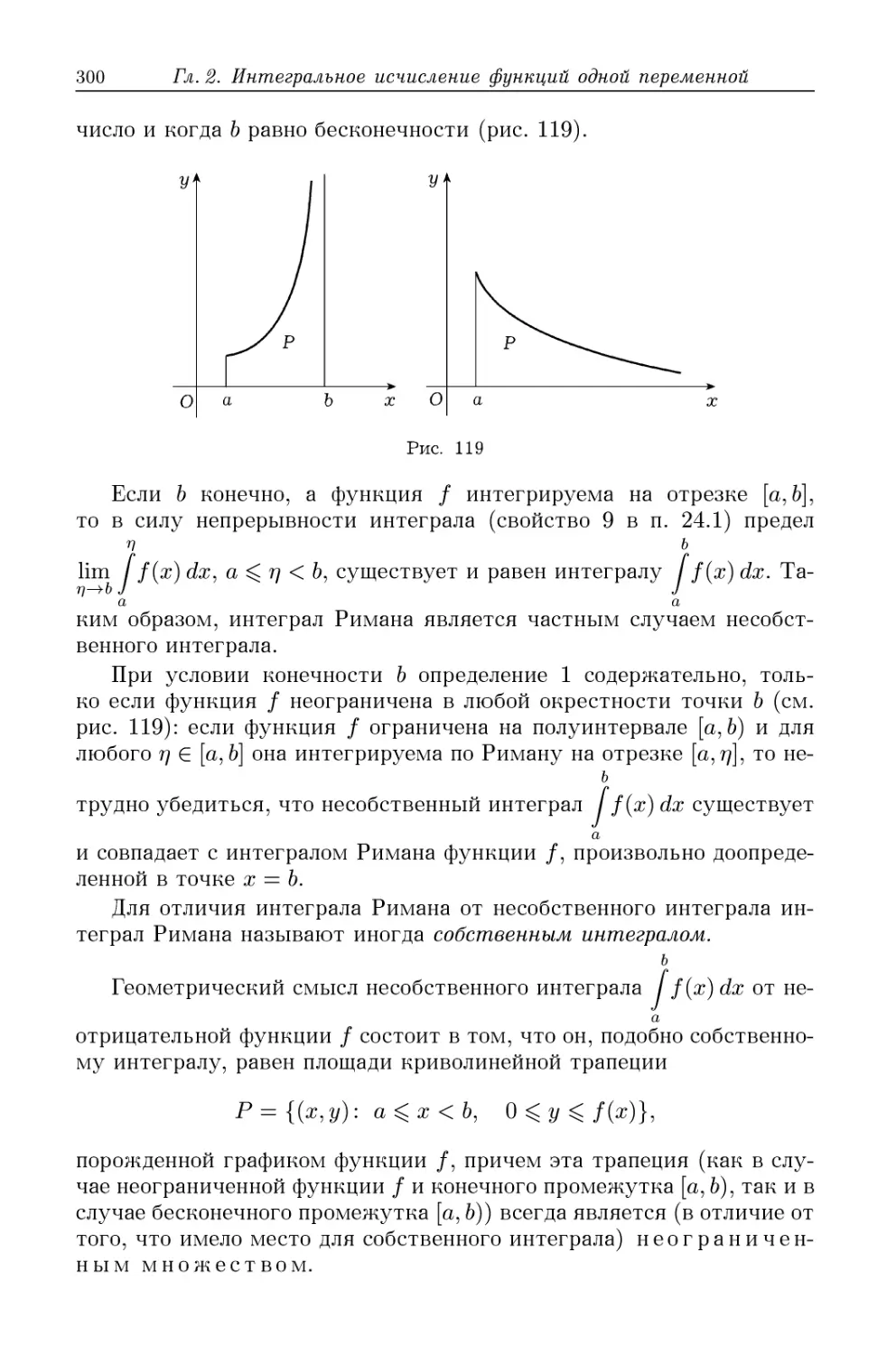
§ 29. Несобственные интегралы	 299
29.1. Определение несобственных интегралов B99). 29.2. Фор-
Формулы интегрального исчисления для несобственных интегра-
интегралов C04). 29.3. Несобственные интегралы от неотрицательных
функций C07). 29.4. Критерий Коши C12). 29.5. Абсолютно схо-
сходящиеся интегралы C13). 29.6. Признаки сходимости Дирихле

Оглавление
и Абеля C16). 29.7. Интегралы от комплекснозначных функций
действительного аргумента C19).
глава з
РЯДЫ
§ 30. Числовые ряды 	 321
30.1. Определение ряда C21). 30.2. Свойства сходящихся ря-
рядов C22). 30.3. Критерий Коши C24). 30.4. Признаки сходимос-
сходимости рядов с неотрицательными членами C25). 30.5. Знакочере-
Знакочередующиеся ряды C32). 30.6. Абсолютно сходящиеся ряды C34).
30.7. Условно сходящиеся ряды C38). 30.8*. Признаки сходимос-
сходимости рядов Дирихле и Абеля C42). 30.9. Исследование сходимости
рядов методом выделения главной части ряда C45). 30.10. Сум-
Суммирование рядов методом средних арифметических C47).
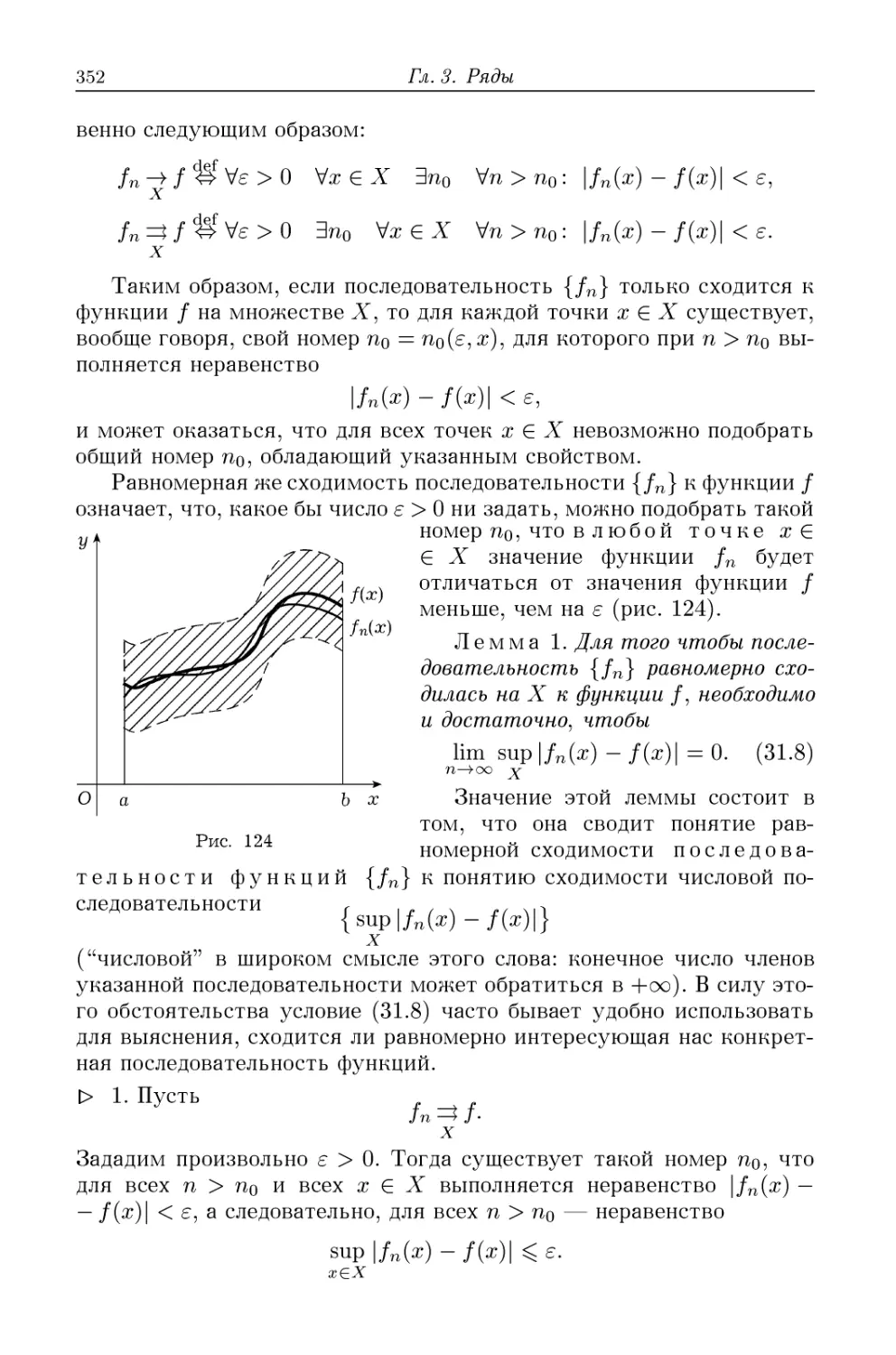
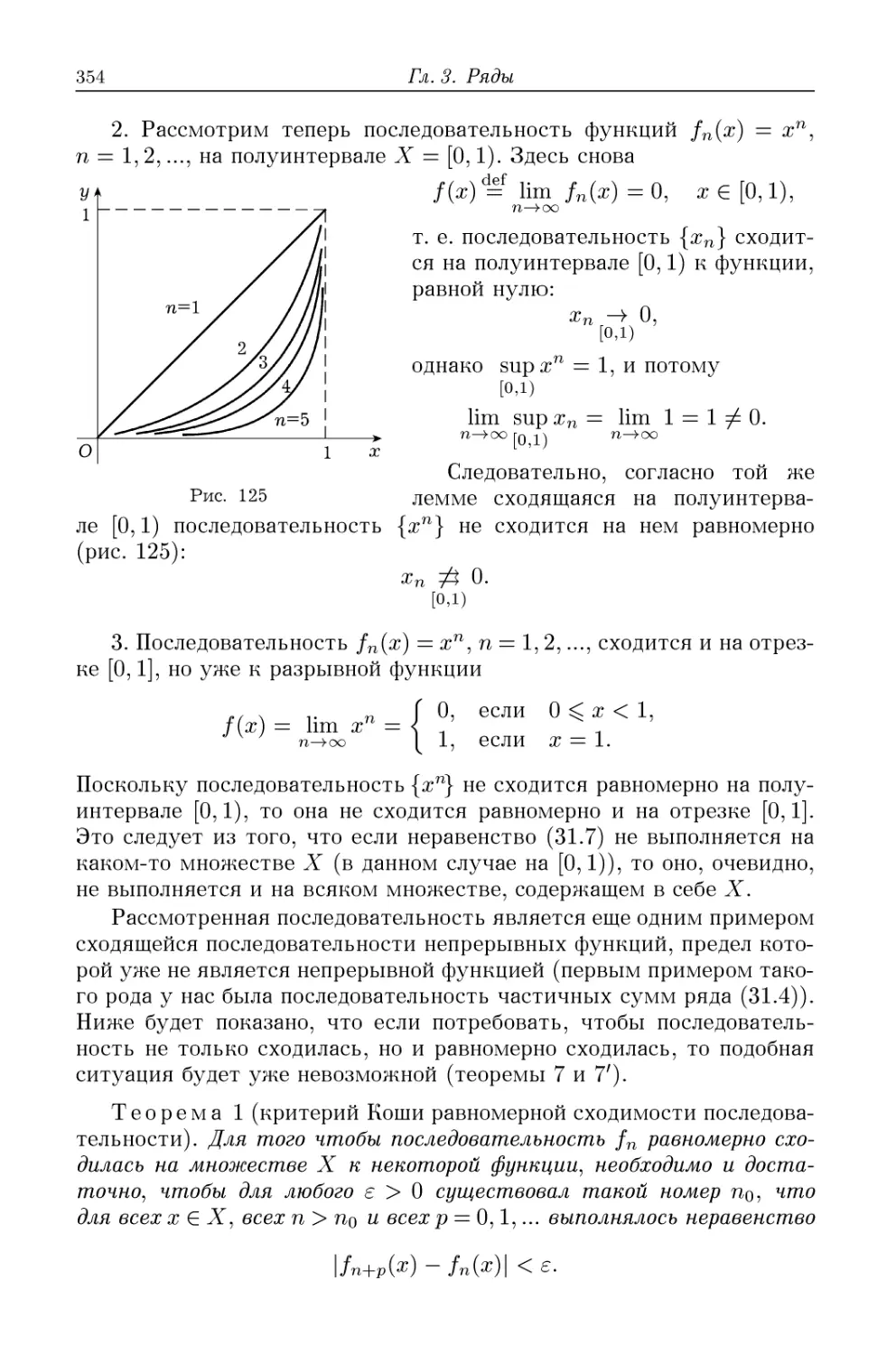
§31. Функциональные последовательности и ряды	 349
31.1. Сходимость функциональных последовательностей и ря-
рядов C49). 31.2. Равномерная сходимость функциональных по-
последовательностей и рядов C51). 31.3*. Специальные признаки
равномерной сходимости рядов C59). 31.4. Свойства равномерно
сходящихся последовательностей и рядов C62).
§ 32. Степенные ряды	 369
32.1. Радиус сходимости и круг сходимости C69). 32.2. Анали-
Аналитические функции в действительной области C76). 32.3. Раз-
Разложение функций в степенные ряды. Различные способы записи
остаточного члена формулы Тейлора C78). 32.4. Разложение эле-
элементарных функций в ряд Тейлора C83). 32.5. Формула Стир-
линга C93).
Предметный указатель	 395

ПРЕДИСЛОВИЕ
В основе настоящего учебника лежит классический метод изло-
изложения материала, характерный для математических дисциплин, т. е.
метод, при котором ни одно принципиально важное для построения
курса утверждение, требующее доказательства, не остается без та-
такового. Автору представляется, что изложение математической дис-
дисциплины, при которой ряд фактов (часто основополагающих) прини-
принимается без доказательства, затрудняет изучение предмета и актив-
активное использование его в дальнейшем. В качестве оправдания такого
"нестрогого" изложения обычно приводится довод о невозможности в
отведенные учебным планом часы дать обоснованное изложение всего
материала. Однако в высших учебных заведениях, в которых на курс
математики отводится 350-510 часов, вопросы математического ана-
анализа можно изложить неформально, с общепринятой в математике
строгостью. Один из возможных путей такого изложения без отказа
от наглядности и обстоятельности предлагается в данном курсе. В
полном объеме весь материал, содержащийся в учебнике, можно под-
подробно в умеренном темпе рассказать за 75 лекций (каждая из двух
частей по 40 минут). Это подтверждается многолетним опытом чте-
чтения автором курса математического анализа на различных факуль-
факультетах Московского физико-технического института.
Некоторые вопросы, рассматриваемые в учебнике, отмечены звез-
звездочкой. Это означает, что их целесообразнее разобрать не на лекциях,
а на семинарских занятиях, или предоставить студентам самостоя-
самостоятельно ознакомиться с ними. Во-первых, это вопросы, касающиеся на-
напоминания некоторых понятий элементарной математики, известных
из курса средней школы. Во-вторых, это вопросы, которые можно ис-
исключить из лекций без нарушения логической завершенности курса,
что имеет смысл сделать в том случае, когда эти вопросы не входят в
обязательную программу (например, в случае, когда на курс высшей
математики отводится 350 часов). К ним относятся счетность ра-
рациональных и несчетность иррациональных чисел, теорема о записи
действительных чисел бесконечными десятичными дробями, элемен-
элементы теории функций комплексного переменного, теория обобщенных

Предисловие	9
функций и т. п.
В первую лекцию целесообразно включить пп. 2.1, 2.2, 4.1 и 4.2.
Тем самым первая лекция будет завершаться доказательством теоре-
теоремы о существовании точной верхней грани у ограниченного сверху
числового множества, которая является одной из фундаментальных
теорем, лежащих в основе математического анализа.
Существенное отличие предлагаемого учебника от большинства
других состоит в изложении теории предела функции. В основе этого
изложения лежит рассмотрение предела функции в точке не только
по ее проколотой окрестности, а по любому множеству, содержаще-
содержащемуся в области задания функции. Это позволяет изучать свойства
функций глубже, чем при рассмотрении предела только по проколотой
окрестности. В учебнике определение предела lim f(x) = а числовой
X—УХо
функции /, заданной на множестве X, формулируется, например, в
терминах последовательностей следующим образом: для любой после-
последовательности хп ->• жо, хп е X, имеет место f(xn) ->• а, п = 1,2,...
При этом допускаются оба случая, ж0 G X и ж0 0 X, а тем самым при
таком определении предела функции не предполагается, что хп Ф х§.
Это упрощает формулировки и доказательства теорем (по сравнению
с обычным определением здесь одним условием меньше), что особен-
особенно хорошо видно на примере теоремы о пределе сложной функции и
позволяет наглядно и убедительно показать, что в математике дис-
дискретное является частным случаем непрерывного. Подробный срав-
сравнительный анализ с точки зрения различных определений предела
функции содержится в статье L.D. Kudryavtsev "Introducihg limits at
the undergraduate level" (Int. J. Math. Educ. Sci. Technol., 1992, V. 23,
№4, 517-523).
Автор старался отобрать минимальное количество вопросов, кото-
которые все вместе составляют логически завершенное изложение курса
математического анализа, освоив который, студент сможет актив-
активно использовать его методы для решения задач и будет достаточно
хорошо подготовлен для изучения других математических курсов.
Чтобы не отвлекать читателя от основного содержания учебника,
иногда опускаются доказательства, представляющие собой техничес-
техническое усложнение тех, которые имеются в курсе. Например, формула
интегрирования по частям доказывается для непрерывно дифферен-
дифференцируемых функций, а для непрерывных и кусочно непрерывно диф-
дифференцируемых формулируется без доказательства. Лишь для функ-
функций многих переменных имеются отдельные исключительные случаи,
когда доказательство теоремы в приведенной общей формулировке
требует существенного развития методов, примененных при ее дока-
доказательстве в тексте при более сильных ограничениях. Это относится
прежде всего к теоремам Грина и Гаусса-Остроградского для произ-
произвольных областей с кусочно гладкой границей.

10	Предисловие
Автор выражает свою глубокую благодарность рецензентам пер-
первого и второго издания учебника академикам РАН В.А. Ильину и
СМ. Никольскому, члену-корреспонденту РАН СИ. Похожаеву, про-
профессору A.M. Седлецкому, доцентам Л.А. Кузнецову, В.П. Пикулину
и научному редактору доценту В.Н. Седову, а также редактору из-
издательства "Альфа" М.Д. Жабцевой, внимательно прочитавшим ру-
рукопись и сделавшим много полезных замечаний, которые все были
учтены при окончательном редактировании текста, что, безусловно,
содействовало улучшению предлагаемого учебника.
Особую признательность автор испытывает к академику СМ. Ни-
Никольскому, члену-корреспонденту РАН О.В. Бесову и профессору
С.А. Теляковскому, с которыми в продолжение многих лет читает
в МФТИ курс математического анализа студентам параллельных по-
потоков. Постоянные обсуждения с ними содержания курса и методики
изложения материала нашло свое воплощение при освещении ряда во-
вопросов в предлагаемом учебнике.
В третьем издании по-новому изложен рад вопросов дифференци-
дифференциального и интегрального исчисления функции многих переменных.
Автор выражает свою искреннюю благодарность студентам МФТИ
В. Акимову, А. Малашевичу и А. Чудновскому, сделавшим ряд полез-
полезных замечаний к тексту и составившим список опечаток в предыду-
предыдущих изданиях этой книги, исправленных в настоящем издании.

ГЛАВА 1
ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ
§ 1. Функции и множества
1.1. Множества. Напомним некоторые обозначения, часто упо-
употребляемые в математике, и дополним их некоторыми новыми, быть
может, не встречавшимися раньше читателю. Большими буквами,
как правило, будем обозначать множества: А, В, С, X, У, ..., а ма-
малыми — их элементы: а, Ь, с, ж, у, ... и т. д. Запись А = {а, 6, с,...}
означает, что множество А состоит из элементов а, Ь, с, ..., а запись
А = {х : ...} или А = {х\...} означает, что множество А состоит из
всех таких элементов ж, которые удовлетворяют условию, написан-
написанному после двоеточия или соответственно после вертикальной черты
(двоеточие и вертикальная черта в этом случае читаются как "таких
что").
Отметим следующее: запись А = {а} может означать либо, что
множество А состоит из одного элемента а, либо, что оно состоит из
множества каких-то элементов, каждый из которых обозначен бук-
буквой а. Какой именно из указанных двух случаев имеет место, будет
всегда ясно из контекста.
Через a Е А и А Э а обозначается принадлежность элемента а мно-
множеству А, а а 0 А или А^ а означает, что элемент а не принадлежит
множеству А. Для удобства вводится понятие пустого множества,
которое обозначается символом 0. Пустое множество не содержит
элементов. Символы А С В и В D А выражают собой включение мно-
множества А в множество В. В этом случае множество А называется
подмножеством множества В. В частности, здесь возможен случай
А — В. Если Ас5иА/5, тоА называется собственным подмно-
подмножеством множества В.
Символом A U В обозначается объединение множеств А и В; т. е.
множество всех элементов, каждый из которых принадлежит хотя бы
одному из множеств Аи В, символом А П В — пересечение множеств
А и В, т. е. множество всех элементов, принадлежащих одновремен-
одновременно А и В; символом А \ В — разность множеств А и В, т. е. мно-
множество всех элементов, принадлежащих множеству А, но не принад-
принадлежащих множеству В (рис. 1).
В случае семейства множеств {Аа}, a G 21, где 21 — некоторое

12 Гл. 1. Дифференциальное исчисление функций одной переменной
множество индексов а, символом (J Аа обозначается объединение
а
всех множеств Аа, a Е 21, а символом Q Аа — их пересечение.
а
Вместо слов "существует", "найдется", "имеется" в логических
формулах употребляется символ 3 (перевернутая первая буква анг-
английского слова exist — существо-
вать), называемый символом сущест-
существования, а вместо слов "любой",
"каждый", "произвольный", "какой
бы ни" — символ V (переверну-
(перевернутая первая буква английского сло-
слова all — "все"), называемый сим-
символом всеобщности. Так, запись Зх
читается "существует ж", а запись
Уж — "любое ж" или "для любого ж"
или "для всех ж". Соответственно запись Зж, Зу, или, короче, Зх,у
означает "существуют ж и ?/", а запись Уж, У?/, или, короче, Уж,?/ —
"любые ж и у" или "для любых х и у".
Знак => означает "следует", "вытекает", а знак <^=> — "равносиль-
"равносильно". В этих обозначениях формула
АсВо(хеА^хеВ)
означает, что утверждение "множество А является подмножеством
множества В" равносильно утверждению "из того, что элемент ж при-
принадлежит множеству А, следует, что он принадлежит множеству ?Г.
г	def
Символ = означает определение выражения, стоящего слева от этого
символа (def — первые три буквы английского слова definition, что
означает "определение"). Например, определение объединения (J Аа
а
и пересечения Q Аа системы множеств Аа можно записать в виде
а
формул следующим образом:
[jAad^{x: За, ж G Aa}, f]Aad^ {x: \/a x e Аа}.
а	а	п
Определение часто используемого в математике символа V^ a/.
k=i
для обозначения суммы слагаемых а/, можно записать следующим
образом:	п
^ аи = а\ + а2 + ... + ап.
k=i
Знак тождества между двумя уже ранее введенными символами
означает, что они обозначают один и тот же объект. Например,
п
22 ак = о>\ + а2 + ... + ап.
к=1

§1. Функции и множества	13
Наконец, символами 1> и <| будут отмечаться начало и конец до-
доказательства высказываемого утверждения.
1.2. Функции. Наряду с понятиями множества и элемента в ма-
математике первичным понятием является понятие соответствия. Это
понятие неявным образом присутствует и в понятии множества, по-
поскольку понятие множества предполагает, что каждый элемент дан-
данного множества обладает определенным свойством, отличающим его
от элементов, не входящих в это множество. Иначе говоря, каждому
из рассматриваемых элементов поставлено в соответствие некоторое
свойство, позволяющее судить о том, является этот элемент элемен-
элементом данного множества или нет.
Среди всевозможных соответствий важную роль в математике иг-
играют соответствия, называемые функциями. Опишем эти соот-
соответствия.
Пусть заданы непустые множества X и У. Соответствие, при ко-
котором каждому элементу х е X соответствует единственый элемент
у Е У, называется функцией, заданной (определенной) на множест-
множестве X со значениями в множестве У, или отображением множества X
в множество Y. Такая функция (такое отображение) обозначается с
помощью некоторой буквы, например, буквы /, одним из следующих
способов:
у = /(ж), х Е X, или /: X —> У, или /: х н-» у, х Е X, у Е Y.
Наряду с терминами "функция", "отображение" употребляются
равнозначные термины "преобразование", "морфизм".
Элемент х Е X называется независимым переменным или аргумен-
аргументом, а соответствующий элемент у Е Y — зависимым переменным.
Множество X называется множеством задания (определения) функ-
функции /, а множество тех у Е F, каждый из которых поставлен в соот-
соответствие хотя бы одному х Е X, — множеством значений функции
/ и обозначается Yf. Очевидно, Yf С Y. Если Yf = У, то отображе-
отображение / называется отображением X на множество Y или сюръекцией.
Если при х ф х1 выполняется неравенство f(x) ф f(x'), то отобра-
отображение / называется взаимно однозначным отображением X в Y или
инъекцией. Если / является взаимно однозначным отображением X
на У, т. е. является одновременно сюръекцией и инъекцией, то оно
называется биекцией.
Если задано отображение /: X —> У, то элементы множеств X
и У часто называются точками.
Символом f(x) обозначается как сама функция, так и элемент,
соответствующий элементу х при этой функции. Обозначение одним
и тем же символом /(ж) как самой функции, так и ее значения в
точке х не приводит к недоразумениям, так как всегда из контекста
ясно, о чем идет речь.

14 Гл. 1. Дифференциальное исчисление функций одной переменной
%0
Значение функции / в точке ж0 обозначается также /(ж)
0
Если /: X —У Y и Е — подмножество множества X, то функция
fE : Е ->• У, такая, что для каждого х е Е выполняется равенство
!е{х) = f(x),	A.1)
называется сужением функции f на множество Е. Таким образом,
сужение fE функции / принимает в точках х множества Е те же
значения, что и функция /. Иногда сужение /# функции / обознача-
обозначают тем же символом /, что и саму исходную функцию, и называют
функцией / на множестве Е.
Пусть заданы функция /: X —>Y и А С X. Множество всех
у G У, являющихся значениями функции / в точках х е А, называется
образом множества А при отображении / и обозначается f(A), т. е.
/(V={</: Эх* A, №=у}.	A.2)
В частности, образ множества X есть множество значений функции:
f(X) = YS.
Если В С У, то множество всех тех точек х Е X, значения функ-
функции / в которых принадлежат множеству В, называется прообразом
множества В. То есть прообразом множества В является множество
{х: f(x)€B}.	A.3)
Пусть Z — некоторое множество и Y = &(Z) — множество всех
его подмножеств. Если /: X —У У, то значение /(ж) функции / в точке
х G X является в этом случае некоторым подмножеством множества
Z: f(x) С Z. Если среди подмножеств /(ж), х е X, имеется по крайней
мере одно непустое множество, содержащее более одного элемента,
то функция / называется многозначной функцией. При этом всякий
элемент z G Z, принадлежащий множеству /(ж) С Z, т. е. z G /(ж),
часто также называется значением функции / в точке ж G X.
Если каждое из множеств /(ж) состоит только из одного элемента,
то функцию / называют однозначной функцией.
Пусть 3?{Х) — множество всех подмножеств множества X. Функ-
Функция, определенная на множестве Yf = f(X) значений функции
/: X —У У, с областью значений, принадлежащей множеству ^(Х),
и ставящая в соответствие каждому элементу у G У/ его прообраз
{ж : /(ж) = у}, называемся обратной к f функцией и обозначается
через f~l: Yf —> 3?{Х). Обратная функция является, вообще говоря,
многозначной функцией.
Если отображение / взаимно однозначно (т. е. является инъек-
инъекцией), то обратная функция является однозначной.
Если отображение / является взаимно однозначным отображени-
отображением X на У, то обратное отображение f~l является взаимно однознач-
однозначным отображением Y на X (т. е. если /: X —> Y — биекция, то и

§2. Числа	15
f~1\ Y ->• X — биекция), и поэтому / является в свою очередь отобра-
отображением, обратным к отображению j~x. Это означает, что при любом
х Е X имеет место равенство j~x j[x) = ж, а при любом у Е f{X) —
равенство ff~1(y) = У- При этом для заданного инъективного
отображения / : X —> Y каждое из указанных двух условий одно-
однозначно определяет обратное отображение f~l.
Если /: X ->• F и д: Y ^ Z, то функция F: X ->• Z, ставящая в
соответствие каждому элементу х Е X элемент F{x) = g(f(x)), на-
называется композицией функций fug (иногда — суперпозицией этих
функций или сложной функцией) и обозначается д о /. Таким обра-
образом, согласно определению для каждого х Е X имеет место равенство
d	)¦	A.4)
§ 2. Числа
2.1. Действительные числа. Из элементарной математики из-
известно, что действительные числа можно складывать, вычитать,
умножать, делить и сравнивать по величине. Перечислим основные
свойства, которыми обладают эти операции. Множество всех дейст-
действительных чисел будем обозначать через /?, а его подмножества на-
называть числовыми множествами.
I. Операция сложения. Для любой пары действительных чи-
чисел а и Ъ определено единственное число, называемое их суммой и
обозначаемое а + Ь, так, что при этом выполняются следующие ус-
условия:
I±. a + b = b + a, a,b G R.
12.	a + (b + с) = (a + b) + с, a,b,ce R.
13.	Существует такое число, называемое нулем и обозначаемое О,
что для любого a G R выполняется условие а + 0 = а.
14.	Для любого числа a G R существует число, называемое ему
противоположным и обозначаемое -а, для которого а + (-а) = 0.
Число а + (—6), а, b G /?, называется разностью чисел а и b и
обозначается а — Ь.
П. Операция умножения. Для любой пары действительных
чисел а и b определено единственное число, называемое их произведе-
произведением и обозначаемое ab, такое, что выполняются следующие условия:
Hi. оЪ = ba, a, b G R.
П2. а(Ьс) = (ab)c, a,b,c G /?.
П3. Существует такое число, называемое единицей и обозна-
обозначаемое 1, что для любого а е R выполняется условие а • 1 = а.
Щ. Для любого числа а / 0 существует число, называемое ему
обратным и обозначаемое - или 1/а, для которого а • - = 1.
а	а

16 Гл. 1. Дифференциальное исчисление функций одной переменной
Число а • -, b ^ 0, называется частным от деления а на Ъ и обо-
о
значается а : Ъ или - или а/Ъ.
III.	Связь операций сложения и умножения:
для любых a,b,c Е /? выполняется условие (а + Ъ)с — ас-\- be.
IV.	Упорядоченность. Для действительных чисел определено
отношение порядка. Оно состоит в следующем.
Для любых двух различных чисел а и Ъ имеет место одно из двух
соотношений: либо а < Ъ (читается "а меньше 6"), или, что то же
самое, Ъ > а (читается "Ь больше а"), либо а > Ь, или, что то же са-
самое, Ъ < а. При этом предполагается, что выполняются следующие
условия:
IVi. Транзитивность. Если а<Ъ и Ъ < с, то а < с.
IV2- Если а < Ь, то для любого числа с имеет место а + с < b + с.
IV3. Если а > Ь и с > 0, то ас> be.
Соотношения порядка называют также сравнением действитель-
действительных чисел по величине или неравенствами. Запись а ^ Ь, равносиль-
равносильная записи Ъ ^ а, означает, что либо а < 6, либо а = Ъ.
Из выполнения условий IV2 и IV3 вытекает одно важное свойст-
свойство, называемое плотностью действительных чисел: для любых двух
различных действительных чисел а и Ь, например, таких, что а < Ь,
существует такое число с, что а < с < Ъ. В самом деле, сложив каждое
из равенств a = a,b = bc неравенством а < Ь, получим 2a<a + b<2b,
^а+Ь , а+Ъ
откуда а < 	 < 6, т. е. в качестве числа с можно взять 	.
Множество действительных чисел обладает еще свойством непре-
непрерывности.
V.	Непрерывность. Для любых непустых числовых множеств
X и Y таких, что для каждой пары чисел х ? X и у ?Y выполняется
неравенство х ^ у, существует число а, удовлетворяющее условию
х	Y	х ^а^у, х е X, у eY
^+		 * (рис. 2).
У	Перечисленные свойства полностью
с>	определяют множество действитель-
действительных чисел в том смысле, что из этих свойств следуют и все осталь-
остальные его свойства. Поэтому можно дать аксиоматическое определе-
определение множества действительных чисел следующим образом.
Определение 1. Множество элементов, обладающих свойства-
свойствами I-V, содержащее более одного элемента, называется множеством
действительных чисел, а каждый его элемент — действительным
числом.

§2. Числа	17
Это определение однозначно задает множество действительных
чисел с точностью до конкретной природы его элементов. Оговорка о
том, что в множестве содержится более одного элемента, необходима
потому, что множество, состоящее из одного только нуля, очевидным
образом удовлетворяет условиям I-V.
Числа 1,2 = 1 + 1,3 = 2 + 1,... и т. д. называются натуральны-
натуральными числами, и их множество обозначается N.
Из определения множества натуральных чисел вытекает, что оно
обладает следующим характеристическим свойством: если
1)	А С Л/,
2)	1 е А,
3)	если для каждого элемента х Е А имеет место включение
х + 1 е А, то A=N.
\> Действительно, согласно условию 2) имеем 1 Е А, поэтому по свой-
свойству 3) и 2 Е А, а тогда согласно тому же свойству получим 3 Е А.
Поскольку любое натуральное число п получается из 1 последователь-
последовательным прибавлением к ней той же 1, то п Е А, т. е. Л/ С А, а так как по
условию 1 выполняется включение А С А/, то А = N. <\
На этом свойстве натуральных чисел основан принцип доказа-
доказательства методом математической индукции. Если имеется мно-
множество утверждений, каждому из которых приписано натуральное
число (его номер) п = 1,2,..., и если доказано, что:
1)	справедливо утверждение с номером 1;
2)	из справедливости утверждения с любым номером п е N сле-
следует справедливость утверждения с номером п + 1;
то тем самым доказана справедливость всех утверждений, т. е. лю-
любого утверждения с произвольным номером п Е N.
Примером доказательства методом математической индукции яв-
является доказательство теоремы 1 в п. 2.4.
Числа 0, ±1, ±2,... называют целыми числами, их множество обо-
обозначают Z.
Числа вида —, где тип целые, а п ф 0, называются рационалъ-
п
ными числами. Множество всех рациональных чисел обозначают Q,
т. е.
Q = ix e R : х = —, т G Z, n G Z, п ф о|.
Действительные числа, не являющиеся рациональными, называ-
называются иррациональными, их множество обозначается /.
Кроме четырех арифметических действий над числами можно
производить действия возведения в степень и извлечения корня.
Для любого числа a G R и натурального п степень ап определя-
2 Л.Д.Кудрявцев, т.1

18 Гл. 1. Дифференциальное исчисление функций одной переменной
ется как произведение п сомножителей, равных а:
п def
а = а • а • ... • а .
п раз
По определению а° = 1, а > О, а~п = —, а ф О, п — натуральное
число.	а
Пусть а > О, а п — натуральное число. Число Ъ называется корнем
n-й степени из числа а, если Ъп = а. В этом случае пишет-
пишется Ъ = д/а. Существование и единственность положительного кор-
корня любой степени п из любого положительного числа будет доказано
ниже в п. 7.3.
Корень четной степени 2^а, а ф 0, имеет два значения: если 6 =
= 2-(/а, k e N, то и -Ь= 2^/а. Действительно, из Ъ2к = а следует, что
Неотрицательное значение у/а называется его арифметическим
значением.
Если г = -, где р и q целые, q ф 0, т. е. г — рациональное
число, то для а > О
vIя. я/ ~v	to I ^
а — v & •	\ )
Таким образом, степень аг определена для любого рационального
числа г. Из ее определения следует, что для любого рационального г
имеет место равенство
аТ
Степень ах (число х называется показателем степени) для лю-
любого действительного числа х получается с помощью непрерывного
распространения степени с рациональным показателем (см. об этом
в п. 8.2).
Для любого числа a G R неотрицательное число
если а ^ О,
если а < О,
def Г а,
" \ -а,
называется его абсолютной величиной или модулем. Для абсолютных
величин чисел справедливы неравенства
а + Ь\ ^ \а\ + |Ь|,
Ь\\ ^ \а - b\, a,b G R.
Они доказываются с помощью свойств I-IV действительных чисел.

§2. Числа	19
2.2. Расширенная числовая прямая. Окрестности. Геомет-
Геометрически множество действительных чисел изображается направлен-
направленной (ориентированной) прямой, а от-
отдельные числа — точками этой прямой	jjj	^ J ? *
(рис. 3). Поэтому совокупность дейст-
действительных чисел часто называют чис- Рис- 3
ловой прямой или числовой осью, а отдельные числа — ее точками. В
связи с этим иногда вместо а < Ъ (соответственно вместо Ъ > а) гово-
говорят, что точка а лежит левее точки Ъ (точка Ъ лежит правее точки а).
Часто бывает удобно дополнить множество действительных чи-
чисел элементами, обозначаемыми через +оо и — оо и называемыми со-
соответственно плюс бесконечностью и минус бесконечностью, считая
при этом по определению, что для любого числа х Е R выполняется
неравенство	/rt ^ч
^	-оо < х < +оо.	B.2)
Множество действительных чисел R, дополненное элементами +оо
и —оо, называется расширенным множеством действительных чисел
(расширенной числовой прямой) и обозначается R.
Иногда бывает удобно дополнить множество действительных чи-
чисел R одним элементом оо (бесконечностью без знака), в этом случае
бесконечность оо уже не связана соотношением порядка с действи-
действительными числами. Бесконечности +оо, -оо и оо называются также
бесконечно удаленными точками числовой прямой, в отличие от ее
остальных точек, которые называются конечными точками числовой
прямой.
Напомним определения некоторых важных типов подмножеств
расширенной числовой прямой R. Пусть a Е R, Ъ Е /?, а ^ Ъ. Множество
[а, Ъ] = {х: х G /?, а ^ х ^ Ь}
называется отрезком, множество
(a,b)d= {х: х G /?, а < х < Ь}
—	интервалом, множества
[а, Ь) = {х: х G /?, а ^ х < Ъ},
[а,Ъ] = {х: х G /?, а < х ^ 6}
—	полуинтервалами, а все они — промежутками расширенной чис-
числовой оси. Точки а и Ъ называются концами этих промежутков, а
точки х такие, что а < х < Ъ, — их внутренними точками. Если а
и Ъ — числа, а ^ Ъ, то число 6 — а называется длиной соответствую-
соответствующего промежутка, а сам промежуток называется конечным.
Важным для дальнейшего является понятие окрестности конечной
или бесконечно удаленной точки числовой прямой.

20 Гл. 1. Дифференциальное исчисление функций одной переменной
Если а е /?, т. е. когда а является действительным числом, то
для любого г > 0 ^-окрестностью U{a,s) числа а называется интер-
интервал (а - г, а + е), т. е.
def
Aj	j/(a е) = (а-г, а + г).
а+е	\
В случае а = +оо
а=+оо
0 +!/е	?/(+оо, е) d= A/e, +oo],
_1/е о	а в случае а = — оо
тт/	\ def г	-1 / \
Рис. 4	С/(-оо, г) = [-оо, -1/г)
(рис. 4).
Таким образом, во всех случаях с убыванием г соответствующая
окрестность точки а уменьшается. Всякая ^-окрестность конечной
или бесконечно удаленной точки a G R на-
	г
а = -оо
Ща)
а
Щ-оо)
ч
/
-е-
—1	7	>
ь
Щ+оо)
1 *
Ь = +оо
С7(+оо)
( >
/ . ч	ч	зывается ее окрестностью. Иногда окрест-
а	ъ	ность обозначается просто U(a).
-оо<а<ъ<+оо	Важным свойством точек расширенной
прямой, следующим непосредственно из
определения их окрестностей, является то,
что у двух любых различных точек расши-
расширенной числовой прямой имеются непересе-
непересекающиеся окрестности (рис. 5).
Нужным бывает и понятие окрестнос-
окрестности для бесконечности без знака оо. Ее
^-окрестность, е > 0, определяется равен-
равенством (рис. 6)
U(oo,s)d={x: же/?, \х\ >1/г}и{оо}.
Легко убедиться, что пересечение двух
окрестностей точки (конечной или беско-
-1/8 о +1/8	нечно удаленной) является также окрест-
Рис- 6	ностью этой точки.
2.3. Комплексные числа. Рассмотрим элементы вида x + yi,
где х и у — действительные числа, а г — некоторый элемент, назы-
называемый мнимой единицей (см. с. 25).
Элемент z = х + yi называют комплексным числом, х — его
действительной, а у — мнимой частью и пишут
x = Kez, у = Imz*).
Два комплексных числа считаются равными тогда и только тогда,
когда равны их действительные и мнимые части.
?) От латинских слов realus — действительный, imaginarius — мнимый.

§2. Числа	21
Вместо х + Ог и 0 + уг пишут соответственно х и yi, в частнос-
частности, 0 + Ог = 0; вместо 1г пишут г. Число х + yi, у которого ?/ ф 0, назы-
называют существенно комплексным числом, а число вида yi, у ф 0, —
чисто мнимым.
Множество всех комплексных чисел обозначают через С.
Арифметические операции. С помощью операций сложения и ум-
умножения действительных чисел в множестве комплексных чисел так-
также можно ввести операции сложения и умножения.
Для комплексных чисел z\ = х\ + y\i и z2 = Ж2 + 2/2^ их сум-
сумма z\ + z2 определяется как комплексное число, действительная и
мнимая части которого получаются в результате сложения соответ-
соответственно действительных и мнимых частей чисел z\ и z2'.
zi+ z2 = Oi + x2) + (j/i + у2)г.
Для определения произведения комплексных чисел сначала опре-
определим квадрат мнимой единицы:
.о • • def 1
г = гг = —1,
а затем — произведение двух произвольных комплексных чисел
zi = х\ + г/1 г и ^2 = Ж2 + yii как результат почленного умноже-
умножения x\+y\i на Ж2 + y2i с использованием соотношения г2 = —1 и
последующего сложения полученных результатов:
Ol + 2/1*)(^2 + 2/2*) =	+	i +	^ +	2
- У1У2) + (Х1У2 + ^22/1J. B.3)
Замечание. При определении умножения комплексных чисел
можно было бы предварительно не определять, что г2 = —1, и не
использовать правила почленного умножения, а сразу определить
произведение по формуле B.3). Тогда из нее бы уже следовало,
что г2 = —1. В самом деле,
п = (о + 1-г)(О + 1-г) = -1.
Вычитание определяется как действие, обратное сложению: z =
= 21 — 22, если z\ — z2 + 2, а деление — как действие, обратное ум-
умножению: 2 = z\jz2^ z2 ф 0, если 2i = z2z.
Определенные указанным образом арифметические операции
над комплексными числами удовлетворяют группам аксиом I, II, III,
п. 2.1.
Теперь можно сформулировать более полное и более точное опре-
определение множества комплексных чисел С.
Определение 2. Множество всех элементов x + yi, в котором
заданы операции сложения, вычитания, умножения и деления сог-
согласно выше сформулированным правилам, называется множеством

22 Гл. 1. Дифференциальное исчисление функций одной переменной
комплексных чисел, а каждый его элемент — комплексным числом.
Обозначение х + yi комплексных чисел называется их алгебраи-
алгебраической формой записи.
Векторная интерпретация. Каждому комплексному числу z =
= ж + yi соответствует упорядоченная пара действительных чи-
чисел (ж, у), и наоборот, каждой упорядоченной паре действитель-
действительных чисел (ж, у) соответствует комплексное число z = ж + yi, и эти
соответствия взаимно однозначны. С упорядоченными же парами
действительных чисел (ж, у) на плоскости (при фиксированной
системе декартовых координат) находятся
У \	~^т *	во взаимно однозначном соответствии век-
векторы этой плоскости, имеющие числа х и у
своими координатами. В результате комп-
комплексное число z = х + yi можно рассматри-
О	х ~~^ вать как вектор на плоскости с координата-
координатами ж, у. Этот вектор мы будем обозначать
Рис- 7	той же буквой z — (ж, у) (рис. 7).
Целесообразность такой интерпретации комплексных чисел сле-
следует из того, что при сложении комплексных чисел складываются и
соответствующие им векторы: при сложении векторов их координаты
складываются, поэтому суммой векторов z\ = [х\, у\) и z2 = [х2, у2)
является вектор
z\-\- z2 — {х\ + х2, у\ + у2),
т. е. вектор, соответствующий сумме z\ + z2 комплексных чисел z\ —
— xi + 2/1 г и z2 = х2 + y2i (рис. 8).
Поскольку вычитание как для комплексных чисел, так и для век-
2/1+У2
3/2
3/1
о
Рис. 8
Рис. 9
торов является действием, обратным сложению, то при вычитании
комплексных чисел соответствующие им векторы также вычитаются
(рис. 9).
Координатная плоскость, векторы z = (ж, у) которой интерпрети-
интерпретируются как комплексные числа, называется комплексной плоскостью,
ее ось ж — действительной осью, а ось у — мнимой.

§2. Числа
23
Длина \z\ вектора z = (ж, у) называется модулем или абсолютной
величиной комплексного числа z = ж + уг. Очевидно,
\z\ = л/х2+у2.	B.4)
Поскольку длина каждой стороны треугольника не превосходит
суммы длин двух других его сторон, а абсолютная величина разности
длин двух сторон треугольника не меньше длины третьей стороны, то
для любых двух комплексных чисел z\ и z^ имеют место неравенства
(см. рис. 8 и рис. 9)
22 | ^ \zi\ + \z2\,
N|^ki-^|.	B.5)
Аргумент комплексного числа. Если ip — угол, образованный не-
ненулевым вектором z с действительной осью, то всякий угол вида
(р + 2тгп, где п — целое число, и угол только такого вида, также бу-
будет углом, образованным вектором z с действительной осью.
Множество всех углов, которые образует ненулевой вектор z =
= (ж, у) с действительной осью, называется аргументом комплекс-
комплексного числа z = х + уг и обозначается argz. Каждый элемент это-
этого множества называется значением аргумента числа z (рис. 10).
Часто для краткости вместо "значение
аргумента" говорят "аргумент" и обознача- У>
ют его тем же символом argz, что и все
множество (подобно тому, как в теории
неопределенных интегралов множество всех
первообразных данной функции / обозна-
обозначается тем же символом //(ж) dx, что
и произвольный элемент этого множества;	Рис 10
см. п. 28.1).
Поскольку ненулевой вектор плоскости однозначно определяется
своей длиной и углом, который он образует с осью ж, то два комп-
комплексных числа, отличные от нуля, равны тогда и только тогда, когда
равны их абсолютные величины и аргументы.
Если на значения аргумента ip числа z наложить, например, усло-
условие 0 ^ ср < 2тг или условие —тг < ср ^ тг, то значение аргумента будет
определено однозначно. Это ограничение, однако, как мы в этом убе-
убедимся в дальнейшем, не всегда удобно.
Из определения аргумента следует, что tgip = у/х. Здесь при
х = 0, у ф 0 считается у/0 = оо.
Тригонометрическая форма записи комплексного числа. Действи-
Действительная и мнимая части комплексного числа z = х + уг ф 0 выра-
выражаются через его модуль г = \z\ и аргумент ip следующим образом:
B.6)
argz

24 Гл. 1. Дифференциальное исчисление функций одной переменной
Отсюда
z = х + уг = г {cos if + г sin у?).	B.7)
Правая часть этого равенства называется тригонометрической
формой записи комплексного числа z. Мы будем ее употреблять и для
z = 0; в этом случае г = 0, а у? может принимать любое значение — ар-
аргумент числа 0 не определен. Итак, всякое комплексное число можно
записать в тригонометрической форме.
Ясно также, что если комплексное число z записано в виде z =
= г (cos ip + г sin у?), г ^ 0, то число г является его модулем (ибо г =
J + (r sin ifJ ), a (^ — одним из значений его аргумента.
Запись операций умножения, деления и возведения в степень в
тригонометрической форме. Тригонометрическую форму записи
комплексных чисел бывает удобно использовать при перемножении
комплексных чисел, в частности, она позволяет выяснить геометри-
геометрический смысл произведения комплексных чисел.
Найдем формулы для умножения и деления комплексных чисел
при тригонометрической форме их записи. Если
zi = п (cos if\ + г sin cpi), z^ = г 2 (cos cp2 + г sin if 2),
то по правилу умножения комплексных чисел получим
Z\Z2 =
= Т\Т2 [(cos if 1 cos if 2 — sin if 1 sin if 2) + г (cos if\ sin if 2 + sin if\ cos ^2)] =
Таким образом, при умножении комплексных чисел их абсолют-
абсолютные величины перемножаются, а аргументы складываются:
\ziz2\ = ЫЫ, &rg(z1z2) = arg^i +argz2	B.8)
(второе равенство является равенством двух множеств). Отметим,
что эту простую формулу для аргумента произведения комплексных
чисел нельзя было бы написать, если бы мы с самого начала огра-
ограничились однозначным выбором аргументов комплексных чисел, на-
например, с помощью неравенств
—тг < argz ^ тг,	B.9)
так как сумма arg^i +argZ2 могла бы уже не удовлетворять этому
неравенству, хотя arg^i и argz2 ему удовлетворяли.
Применив последовательно формулы B.8) к произведению п
комплексных чисел zi, z2,..., zn, получим
\Z1Z2...Z71\
cng(z1z2...zn) = arg
Если z\ — Z2 — ... = zn, то из полученных равенств следует, что
\zn\ = |z|n argzn = nargz + 27rA: fe = 0, ±1, ±2,...	B.10)

§2. Числа	25
Следует обратить внимание на то, что вторая формула B.10) пред-
представляет собой равенство множеств: если ср — какое-либо значение
аргумента числа z и, следовательно, тр — значение аргумента zn, то
левая часть равенства состоит из всех чисел вида
тр + 2тгт, т = 0, =Ы, ±2,...,
а правая — из всех чисел вида
п(ср + 2тгт) + 2тгк = пер + 2тг(пт + к),
m = 0,±1,±2,..., к = 0,±1,±2,...
Нетрудно убедиться, что эти два множества состоят из одних и тех
же чисел. Отсюда видно, что argzn ф nargz, так как здесь правая
часть состоит лишь из чисел вида п((р + 2тгт) = тр + 2тгпт, т. е.
таких чисел, которые получаются прибавлением к числу тр не все-
всевозможных чисел вида 2тгт, т. е. чисел, кратных 2тг, а лишь чисел,
кратных числу 2тгп.
Отметим еще, что формула B.10) равносильна утверждению: если
ю G argz, то
mpe&rgz71.	B.11)
Поэтому если z = r(cos(p + г sin у?), то
^n _ rn(COsn(^ + isinn(p).	B.12)
Отсюда для комплексного числа, абсолютная величина которого рав-
равна 1 (следовательно, оно имеет вид z = cos(p + г sin у?), получаем
(cos (^ + г sin Lp)n = cos n(p + г sin n(p.
Эта формула называется формулой Муавра*).
Если г = Zi/z2j z^ ф 0, т. е. z\ = 2:22:, то \z\\ =
= arg^2 + argz. Таким образом,
Иначе говоря, при делении комплексных чисел их модули делятся,
а аргументы вычитаются.
Извлечение корня. Если п — натуральное число, z G С, то корнем
n-й степени Vfz из комплексного числа z называется такое число w,
что
^п = z.	B.13)
Например, числа г и —г являются корнями степени 2 (квадратны-
(квадратными корнями) из числа z — —1, так как г2 = —1 и (—гJ = —1. На
этом примере уже видно, что число yfz определено неоднозначно:
для z = — 1 может быть д/~Т = г, а может быть и д/~Т = —г. При
:|<) А. Муавр A667-1754) — английский математик.

26 Гл. 1. Дифференциальное исчисление функций одной переменной
этом, в отличие от области действительных чисел, когда можно бы-
было рассматривать положительные и отрицательные значения корня,
говорить о знаке корня в комплексной области нельзя, так как су-
существенно комплексные числа не разбиваются на положительные и
отрицательные: у существенно комплексного числа "нет знака". Поэ-
Поэтому при употреблении записи y/z, z G С, всегда надо отдавать себе
отчет в том, что именно в рассматриваемом случае обозначает собой
символ yfz.
Если z = r{cosif + г sin у?), w = p(cosip + г sin^) и wn = z, то
рп(cosnip + i slump) = r(cos(p + i simp).
B.13)
B.12)
Отсюда pn = г, а следовательно, ^ = >/r, где корень п-й степени по-
понимается в арифметическом смысле, т. е. р ^ 0, и
nip = (р + 2тг&, fe = О, ±1, ±2,...,
или
^ = - Н	к.
п п
Для того чтобы получить все возможные различные значения кор-
корней n-й степени, здесь достаточно ограничиться лишь значениями
& = 0,1,...,п-1:
фк = ? + tL к, к = 0,1,..., п - 1,	B.14)
так как при к = п получим грп = — + 2тг, т. е. значение аргумента грп
п
отличается от значения аргумента гр0 = — на 2тг и при остальных
п
значениях & будут получаться значения угла гр, отличающиеся от од-
одного из значений т/^, к = 0,1,..., п — 1, на кратное числа 2тг, а поэтому
соответствующее значение корня будет совпадать с одним из чисел
k +ismipk), к = 0,1,...,п - 1.	B.15)
Таким образом, корень n-й степени из числа z = r(cos(p + г sin у?)
имеет п значений Wk, к = 0,1,...,п-1, для которых справедливы
формулы B.14) и B.15). Все значения корня yfz имеют одинаковые
модули у/г, а аргумент грк корня wk получается из аргумента ipk-i
корня Wk-i, к = 1, 2,..., п — 1, так же, как и аргумент ^о = <^/п кор-
корня wo, — из аргумента грп-\ корня wn-i прибавлением числа 2тг/п.
Отсюда следует, что если начало всех векторов Wk, к = 0,1, ...,п —
1, поместить в начало координат, то их концы будут находиться
в вершинах правильного n-угольника. На рис. 11 изображены кор-
корни
Сопряженные комплексные числа. Для каждого комплексного
числа z = х + уг число х — уг называется ему сопряженным и обоз-
обозначается ~z. Геометрический вектор ~z симметричен с вектором z

§2. Числа
27
относительно действительной оси (рис. 12).
w2
w4
Рис. 11	Рис. 12
Перечислим основные свойства сопряженных чисел.
1°. \z\ =
2°. zz =
z\, aigz = -arg2:.
z\\
4°. Z\ + Z2=Z! + Z2.
5°. Zl-Z2 = z1-z2.
6°. ¦ZTz^ = z1 -z2.
7°. B:1/2:2) =Z!/z2.
Докажем 1°: \z\ = л/х2 + ^/2 = |*|; если 2: = r(cos(^ + г siny?), то ~z —
r(cos(p — i simp) = r(cos(—ф) + г sin(—(/?)), и потому argz = — arg2:.
Докажем 2°: z~z — (x + 2/г)(ж - 2/г) = ж2 + у2 = |2:|2.
Так же просто доказывается ~z = x + yi = x — yi = x + yi =
Рис. 13	Рис. 14
Свойства 4° и 5° вытекают из симметричности сопряженных чи-
чисел относительно действительной оси (рис. 13 и рис. 14), из которой

28 Гл. 1. Дифференциальное исчисление функций одной переменной
следует, что число z\ + z2 симметрично с z\ + z2, а число z\ - z2 сим-
симметрично С Z\ — Z2-
Проверим теперь, что в формуле 6° абсолютные величины и аргу-
аргументы чисел, стоящих в левой и правой частях равенства, равны:
| = \Zl\\Z2\ =8)
B.8)
g^i - argz2 = arg^i + argz2 = arg(^iz2).
B.8)
Аналогично доказывается свойство 7°.
Используя сопряженные комплексные числа, можно получить фор-
формулу для частного комплексных чисел в алгебраической форме: ум-
умножив числитель и знаменатель дроби ——— на число ж2 — yoi, co-
пряженное знаменателю, получим
xi -\-yii _ (xi +yii)(x2 - V2J) _ xix2 + г/iг/2 , У1Х2 - xiy2 .
x2+y2i (x2 + y2i)(x2 — г/2 г)	х\ + y\	x\ + y\
При построении теории комплексных чисел мы исходили из того,
что комплексным числом называют объекты вида z — х + г/г, где ж и
у — действительные числа, а г — некоторый новый элемент, назы-
называемый мнимой единицей. Этому определению можно легко придать
строго логическую форму следующим образом.
Назовем комплексным числом упорядоченную пару (ж, у) дейст-
действительных чисел х и у. Операции сложения и умножения для двух
комплексных чисел (ж, у) и (х',у') определим по формулам
(ж, у) + (х',у') = (х + х', у + у'),	B.16)
(ж, у)(х',у') = (хх' -уу', ху' + х'у).	B.17)
Комплексные числа вида (ж,0) будем обозначать просто символом ж:
(ж,0)=ж,	B.18)
а комплексное число @,1) — символом г. Из формулы B.17) следует,
что
Для любого комплексного числа (х,у) имеет место легко прове-
проверяемое тождество (ж, у) = ж + уг. В самом деле,
(х,у) = (ж,0) + @,2/) = (ж,0) + @,1)(?/,0) = x + yi.
B.16)	B.17)	B.18)
Таким образом, мы пришли к первоначальной записи комплекс-
комплексных чисел.

§2. Числа	29
2.4. Перестановки и сочетания. Пусть задано конечное мно-
множество элементов. Выясним, сколькими различными способами мож-
можно упорядочить элементы этого множества.
Определение 3. Группы элементов, состоящие из одних и тех
же элементов и отличающиеся друг от друга только их порядком,
называются перестановками этих элементов.
Число всевозможных перестановок п элементов обозначается Рп.
Как это будет ниже показано, оно равно произведению всех натураль-
натуральных чисел от 1 до п. Для краткости это произведение обозначают
символом п! (читается "эн факториал"), т. е. п! = 1 • 2 • 3 • ... • п. Для
удобства полагают
О! = 1.	B.19)
Пример 1. Группы {1,2,3}, {1,3,2}, {2,1,3}, {2,3,1}, {3,1,2}
и {3,2,1} являются всевозможными перестановками элементов 1,
2 и 3.
Лемма. Если Р^ — число всех перестановок из к элементов и
к > 1, то
Рк=кРк-г.	B.20)
|> Множество всех перестановок из заданных к элементов разбива-
разбивается на группы, в каждой из которых на первом месте стоит один и
тот же элемент. Число таких групп равно к — числу всех элементов.
В перестановках, входящих в одну и ту же группу, на последую-
последующих к - 1 местах могут располагаться оставшиеся к - 1 элементов в
любом порядке. Поэтому число перестановок в каждой группе рав-
равно /Vi.
Каждая перестановка из к элементов попадает в одну из описан-
описанных групп и в точности один раз. Поэтому для числа Р\~ всех пере-
перестановок из к элементов имеет место соотношение B.20). <1
Теорема 1. Число всевозможных перестановок из п элементов
равно п\\
Рп = п\.	B.21)
|> Докажем теорему методом математической индукции. Если
п = 1, то, очевидно, Р\ = 1 = 1!. Если для некоторого k Е А/ имеет место
формула Pk = к\, то согласно лемме Pk+i = (к + 1)Рк = (к + 1)к\ =
= (* + 1)!.<1	B'20)
Выясним теперь, сколько подмножеств, содержащих т элементов,
имеет множество, состоящее из п элементов, 1 ^ т ^ п.
Определение 4. Каждое множество, содержащее т элементов
из числа п заданных, называется сочетанием из п элементов по т.
Подчеркнем, что сочетание определено как множество некоторых
элементов без рассмотрения порядка, в котором они расположены.
Число всех сочетаний из п элементов по т обозначается С™.

30 Гл. 1. Дифференциальное исчисление функций одной переменной
Пример 2. Множества {1, 2}, {1, 3} и {2, 3} образуют всевозмож-
всевозможные сочетания из трех элементов 1,2,3 по два.
Из определения сочетаний вытекают следующие два свойства.
1°. Имеет место формула
Скп = С™-\ к = 0,1,2,...,п,	B.22)
гдв	С1 ИГ 1.	B.23)
|> Действительно, если из п элементов выбрать какое-либо сочета-
сочетание, содержащее к элементов, то элементы, не вошедшие в него, со-
составят сочетание изп - к элементов. Причем, таким путем получатся
все сочетания из п элементов по п — к и каждое по одному разу. Поэ-
Поэтому число сочетаний из п элементов по &, т. е. С%, равняется числу
сочетаний из п элементов по п — к, т. е. числу С™~к. <1
2°. Имеет место формула
СкпХ\=Скп + Скп+\ & = 0,1,...,п-1.	B.24)
|> Пусть дано п + 1 элементов. Зафиксируем один из элементов и
разобьем все сочетания по к + 1 элементов на две группы: содер-
содержащие этот элемент и не содержащие его. Число первых равно С%
(ибо если удалить фиксированный элемент из каждого содержащего
его сочетания по к + 1 элементов, то получатся всевозможные соче-
сочетания из п элементов по к и каждое по одному разу), число вто-
вторых равно Ск+1 (ибо они образуют всевозможные сочетания по к + 1
элементов из п элементов, получающихся удалением фиксированного
элемента из п + 1 заданных). Это и означает справедливость форму-
формулы B.24). <
Докажем теперь формулу для числа всевозможных сочетаний
из п элементов по т.
Теорема 2. Для числа сочетаний имеет место формула
С™ = р-р5—•	B.25)
-* га-* п—т
|> Множество всех перестановок из заданных п элементов разбива-
разбивается на группы, в каждой из которых на т первых местах стоят одни
и те же элементы (в том или ином порядке), а следовательно, и на по-
последних п — т местах также находятся одни и те же элементы. Число
таких групп равно числу способов, которыми из данных п элементов
можно выбрать т элементов, т. е равно числу С™.
В перестановках, входящих в одну и ту же группу, на m первых
местах выбранные элементы могут быть расположены любым спосо-
способом, а число таких способов равно числу Рш всевозможных переста-
перестановок из т элементов. Элементы же, стоящие на п — т последних
местах, также могут находиться в любом порядке, т. е. из них мо-
может быть образована любая перестановка из п — т элементов, а число
таких перестановок равно Рп-т.

§2. Числа	31
Таким образом, число перестановок в каждой группе равно
РтРп-т, и поскольку число всех групп равно С™, причем каждая
перестановка из п заданных элементов входит только один раз в од-
одну из указанных групп, то для числа всех перестановок Рп получаем
формулу
р _ /-1ТП р р
1 п — ^п т п—тч
из которой и следует формула B.25). <1
Следствие.
С™ = n'	B.26)
т\(п — ту
> Формула B.26) вытекает из формулы B.25) в силу равенст-
равенства B.21). <
Отметим, что формулы B.22) и B.24) можно доказать, подставив
в них значения сочетаний согласно формуле B.26) и проведя в случае
формулы B.24) нужные вычисления. Однако приведенные выше дока-
доказательства раскрывают смысл формул и дают возможность получить
их, не зная заранее, как они выглядят.
Числа С* можно последовательно находить с помощью следую-
следующей треугольной таблицы, называемой треугольником Паскаля*), в
которой первые и последние числа во всех строчках равны единице,
и, начиная с третьей строчки, каждое число в строчке, отличное от
первого и последнего, получается сложением двух ближайших к нему
чисел предшествующей строчки:
1
1 2 1
13 3 1
14 6 4 1
1 5 10 10 5 1
В силу формулы B.24) в n-й строчке будут стоять числа
^n' ^n' •••¦) ^n' •••¦) ^n'
2.5. Формула бинома Ньютона**). Многочлены, являющиеся
суммой двух слагаемых, называются биномами. Формула для n-й сте-
степени бинома х + а
(х + а)п = хп + С^ах71-1 + С2па2хп-2 + ... + С1~хап~хх + ап B.27)
называется формулой бинома Ньютона.
*) Б. Паскаль A623-1662) — французский философ, писатель, физик и мате-
математик.
**) И. Ньютон A643-1727) — английский физик, механик, астроном, матема-
математик и теолог.

32 Гл. 1. Дифференциальное исчисление функций одной переменной
Применив символ Y1 Для обозначения суммы и вспомнив, что
С% = С% = 1, формулу B.27) можно записать в виде
п
(гп _|_ п\п — \ л rik k п-k	/су <уг>\
yJL ~Г UjJ — 7 Ly^U/ Jb	.	y^i.^iOJ
k=0
\> Для доказательства B.28) рассмотрим произведение п биномов
(х + а\)(х + а2)... (х + ап).	B.29)
Открыв скобки, получим
(х + а\)(х + а2)... (х + ап) = жп + (а\ + а2 + ... + ап)хп~1 +
Коэффициент при жп-1 является суммой всевозможных сочетаний
из элементов ai,a2, ...,an по одному элементу, поэтому число слагае-
слагаемых равно С\. Коэффициент у хп~2 является суммой произведений
элементов всевозможных сочетаний из тех же элементов ai,a2, ...,an
по два элемента, а следовательно, число слагаемых равно С2. Вооб-
Вообще, коэффициент хк, к = 0,1,2,...,п, является суммой произведений
элементов всевозможных сочетаний из элементов ai,a2,...,an по к
элементов, и поэтому число таких слагаемых равно С* .
Если а\ — а2 = ... = ап = а, то из формулы B.30) следует, что
(\ гул	гул у"~у "I rt~)	"I	x^~y2 2 '/'?	2	/^~^i iv A* */^	A*	r\~)
tiy I vAj J		 tiy	I V_y /yj H/tiy	I V_y /yj vAj tiy	| • • • | Ч_У /yj vAj tiy	| • • • | vAj •
т. е. формула B.27) доказана. <|
Замечание. Положив в формуле B.28) х — а = 1, получим
п	п
\~^ С* = 2П, а положив ж = 1, а = —1, получим V^(—1)^G^ = 0.
§ 3. Элементарные функции
3.1. Числовые функции. Если функции принимают числовые
значения (такие функции называются числовыми или скалярными),
то над ними можно производить арифметические операции. Пусть
даны две функции /: 1ч7и^: X —>Y, где X — произвольное
множество, а У — подмножество множества комплексных чисел С
(в частности, действительных чисел /?); тогда значения суммы f + g,
разности f — д, произведения fg и частного - функций / и д по опре-
9
делению в каждой точке х G X задаются следующими формулами:
(/ + 9)(*) d= fix) + 9(х), (fg)(x) Hf f(x)g(x),

§3. Элементарные функции	33
Конечно, в последней формуле предполагается, что для всех ж е X
выполняется неравенство д{х) ф 0.
Значение функции / в точке жо, как это отмечалось в п. 1.2, обо-
обозначается символами /(жо), f(x)\ . Символ /(ж) означает разность
значений функции / в точках Ъ и а:
f(x)\ba=ff(b)-f(a).	C.1)
Функция /, заданная на подмножестве X числовой прямой, на-
называется периодической с периодом Т > 0, если для любого х Е X
выполняются условия
х±ТеХ и /(ж + Т) = /(ж).	C.2)
Значение функции / в точке ж0 называется наибольшим, если для
всех точек х Е X выполняется неравенство /(ж) ^ /(жо)? и наимень-
наименьшим, если имеет место неравенство /(ж) ^ f(xo)-
Если функция / задана на подмножестве X числовой оси и прини-
принимает действительные значения, то ее графиком называется множество
на координатной плоскости, состоящее из всех точек вида (ж,/(ж)),
ж Е X (координатной плоскостью называется плоскость, на которой
задана некоторая прямоугольная декартова система координат).
Если функция у = /(ж) и у = д(х) взаимно обратны: д = /-1, то их
графики симметричны относительно биссектрис первого и третьего
координатных углов (эти биссектрисы, очевидно, составляют прямую
линию).
В ближайших параграфах будут рассматриваться только функции,
у которых как их значения, так и значения их аргументов являются
действительными числами (если, конечно, не будет специально ого-
оговорено что-либо другое).
3.2. Понятие элементарной функции. Функции:
постоянная у — с (с — константа);
степенная у — ха, a G /?;
показательеая у = ах', а > 0;
логарифмическая у = loga ж, а > 0, а ^ 1;
тригонометрические 2/ = sin ж, у = cos ж, у = tgx, у = ctgж;
обратные тригонометрические 2/ = arcsinx, у = агссовж,
2/ = arctgж и у = arcctgж;
называются основными элементарными функциями.
Всякая функция /, которая может быть задана с помощью форму-
формулы у = /(ж), содержащей лишь конечное множество арифметических
операций над основными элементарными функциями и композиций,
называется элементарной функцией.
В множестве элементарных функций выделяются следующие
классы.
3 Л.Д.Кудрявцев, т.1

34 Гл. 1. Дифференциальное исчисление функций одной переменной
1. Многочлены {полиномы), или, подробнее, алгебраические много-
многочлены (полиномы), — функции вида
Р(х) = апхп + ... + (цх + а0.	C.3)
Многочлены определены на всей числовой оси.
Если ап ф 0, то целое неотрицательное число п называется сте-
степенью многочлена Р(х). Функция, тождественно равная нулю, явля-
является в силу данного определения многочленом, который называется
нулевым многочленом. Степень многочленов обладает тем свойством,
что при перемножении ненулевых многочленов степень произведе-
произведения равна сумме степеней сомножителей (см. п. 3.3*). Чтобы это
свойство сохранялось и при умножении на нулевой многочлен, сте-
степенью нулевого многочлена называется минус бесконечность (—оо).
По определению полагается, что сумма —оо и любого числа снова рав-
def , /	ч def	^ r>	. /	\ def
на —оо: —оо + х = х + (—сю) = —оо, х Е п, и —оо + (—сю) = —оо.
Напомним еще (см. B.2)), что —оо меньше любого числа х: —оо < х.
2.	Рациональные функции (рациональные дроби)— функции /(ж),
представимые в виде
™ = Шу	C-4)
где Р(х) и Q(x) — многочлены (Q(x) — ненулевой многочлен). Функ-
Функция f(x) определена во всех точках числовой оси, кроме тех ее точек,
в которых знаменатель Q(x) обращается в нуль.
3.	Иррациональные функции, т. е. такие функции, не являющиеся
рациональными, которые могут быть заданы композицией конечного
числа рациональных функций, степенных функций с рациональными
показателями и четырех арифметических действий.
4.	Трансцендентные функции — элементарные функции, не являю-
являющиеся рациональными или иррациональными.
Все перечисленные функции можно рассматривать и в комплекс-
комплексной области (т. е. когда их аргументы и их значения могут быть
комплексными числами), но, конечно, в этом случае функции wz,
logzw, sinz, cosz, z G C, w G С, требуют специальных определений
(см. п. 41.4).
3.3*. Многочлены. Для изучения ряда свойств многочленов в
действительной области, т. е. функций вида
Р{х) = апхп + ... + а\х + а0,
где ao,ai,...,an и х — действительные числа, оказывается целесооб-
целесообразным рассмотреть более общие функции: многочлены в комплекс-
комплексной области, т. е. функции вида
P(z) = anzn + ... + axz + а0,	C.5)

§3. Элементарные функции
35
где ao,ai, ...,an и z — комплексные числа. Числа ao,ai, ...,an называ-
называются коэффициентами многочлена P(z). Если ап ф О, то, как и вы-
выше, неотрицательное целое число п называется степенью многочле-
многочлена P(z), который в этом случае обозначают иногда Pn(z).
Два многочлена, P(z) и
Q(z) = bmzm +
равны тогда и только тогда, когда
т = n, a0 = bo, ai
bxz
an = bn.
C.6)
C.7)
l> В самом деле, если выполняются эти равенства, то ясно, что мно-
многочлены C.5) и C.6) принимают одинаковые значения при всех z G С.
Наоборот, пусть при всех z справедливо равенство
a0 = bm
b0.
C.8)
Без ограничения общности можно предполагать, что т = п, так как
при т ф п можно добавить недостающие члены с нулевыми коэффи-
коэффициентами. Перенесем в равенстве C.8) все члены в одну сторону и
положим
Ло = а0 - bo, Ai = а\ — b\, ..., An = ап - bn.	C.9)
В результате получим, что для всех z G С выполняется равенство
A0 + Aiz + ... + Anzn = 0.	C.10)
В частности, это равенство имеет место для произвольно фиксиро-
фиксированных п + 1 значений z\, ...,zn+\, отличных друг от друга: z\ ф Zj,
i,j = l,2,...,n + l. Подставим z\, ...,zn+\ в равенство C.10). Полу-
Получим систему п + 1 линейных уравнений относительно п + 1 неизвест-
неизвестных Ао, Аь..., Ап
k =
C.11)
с определителем
1
1
1
Z2
Zn+1
Zl
4
Zn+l
... zx
... Z%
Zn+l
Из курса алгебры известно, что этот определитель, называемый
определителем Вандермонда*), равен произведению всевозможных
разностей Zj — Zi, j > i, и, следовательно, не равен нулю. Поэтому
система C.11) имеет единственное решение
Ао = Ai = ... = An+i = 0.
*) А. Вандермонд A735-1796) — французский математик.
3*

36 Гл. 1. Дифференциальное исчисление функций одной переменной
Отсюда, в силу формулы C.9), следует, что для коэффициентов мно-
многочленов C.5) и C.6) действительно имеют место равенства C.7). <1
Сумма и произведение двух многочленов являются, очевидно, так-
также многочленами. Чтобы перемножить два многочлена, достаточно
перемножить их почленно и полученные результаты сложить:
P{z)Q{z) = anbmzn+m + {апЪш^ + ап-1Ът)гп+т-1 + ... + aobo.
C.5)
C.6)
Из этой формулы видно, что если ни один из перемножаемых мно-
многочленов не нулевой, то степень их произведения равна сумме их
степеней. Если же по крайней мере один из них нулевой, то это
свойство сохраняется в силу того, что степень нулевого многочлена
равна —оо (см. п. 3.2).
Если степень многочлена P(z) не меньше степени многочлена Q(z),
то существуют единственные многочлены S(z) и R(z) такие, что
P(z) = S{z)Q(z) + R(z),	C.12)
где степень многочлена R(z) меньше степени многочлена Q(z). При
этом степень многочлена S(z) равна разности степеней многочле-
многочленов P(z) и Q(z).
Многочлен S(z) называется частным от деления многочлена P(z)
на Q(z), а многочлен R(z) — остатком. Если R(z) = 0, то говорят,
что P(z) делится на Q(z).
Существование и единственность многочленов S(z) и R(z), удов-
удовлетворяющих соотношению C.12) при заданных многочленах C.5) и
C.6), Ъш ф 0, можно доказать методом неопределенных коэффици-
коэффициентов.
|> Запишем многочлены S(z) и R(z) в виде
R(z) = cm-xzm~x + ... + cxz + с0,
S(z) = cnzn-m + ... + cm+1z + cm.
Подставим эти формулы в равенство C.12):
anzn + an-izn~1 + ... + a\z + a0 =
= (cnzn-m + ... + cm+1z + cm)(bmzm + ... + blZ + bo) +
+ cm-xzm-x + ... + az + c0, C.13)
произведем почленное умножение, сложим получившиеся результа-
результаты, сделаем приведение подобных членов и приравняем коэффициен-
коэффициенты в левой и правой частях равенства при одинаковых степенях z. В
результате получится система из п + 1 линейных уравнений относи-
относительно п + 1 неизвестных
с0, сь ..., ст_ь ст, ..., сп.	C.14)

§3. Элементарные функции	37
Можно показать, что эта система имеет единственное решение, и
даже найти его в явном виде методом математической индукции. В
самом деле, для определения коэффициента сп из равенства C.13) по-
получаем одно уравнение
ап = спЪт, Ът ф 0.
Далее возможны два случая: т < п и т = п. Если т < п, то для
коэффициента cn_i из равенства C.13) получается уравнение
an-i = сп-\Ьш + cnbm_i,
в котором все коэффициенты, кроме cn_i, известны. Если же т = п,
то S(z) = сп, а Д(г) = со + c\z + ... + Cn-i^™, и для коэффициен-
коэффициента cn_i из C.13) получаем уравнение
an-i = cnbn-i + cn_i.
Таким образом последовательно и однозначно находятся все коэф-
коэффициенты C.14). <|
3.4. Разложение многочленов на множители. Число z0 e С
называется корнем многочлена P(z), если
= о.
Поделив многочлен P(z) степени п на z — z$ (здесь z$ не обязательно
корень P(z)), получим
P(z) = Q(z)(z-zo)+r,	C.15)
где Q(z) — многочлен степени п — 1, а остаток от деления г — пос-
постоянная: г G С.
Если в равенстве C.15) положить z = zo, то получим
г = РЫ,	C-16)
т. е. остаток от деления многочлена P{z) на z — zo равняется значе-
значению этого многочлена в точке z = zq. Это утверждение называется
теоремой Безу*).
Если zq — корень многочлена P(z), то из равенства C.16) следует,
что г = 0. Наоборот, если г = 0, то из C.16) имеем P(z0) = 0. Таким
образом, число zo является корнем многочлена P(z) тогда и только
тогда, когда этот многочлен делится на z — z$.
В курсе алгебры доказывается, что всякий многочлен степени, рав-
равной единице, или более высокой имеет корень (основная теорема ал-
алгебры).
Пусть Pn(z) — многочлен степени п ^ 1 и z\ — его корень. Тогда,
согласно теореме Везу, многочлен Pn(z) можно представить в виде
?K. Безу A730-1783) — французский математик.

38 Гл. 1. Дифференциальное исчисление функций одной переменной
где Qn-i — многочлен степени п - 1. При этом либо Qn-i(zi) ф О,
либо Qn-i(zi) = 0. Во втором случае, снова согласно теореме Безу,
многочлен Qn-i(zi) можно представить в виде
Qn-l(zi) = (Z~ Z!)Qn-2(z),
где Qn-2(z) — многочлен уже степени п — 2. В результате в этом
случае
Pn(z) = (z-ZlJQn-2(z),
т. е. многочлен Pn(z) делится на (z — z\J.
Целое неотрицательное число к\ называется кратностью корня z\
многочлена Pn(z), если этот многочлен делится на (z — z\)kl и не де-
делится на (z — zi)kl+l.
Однократный корень называется простым, а корень кратности,
большей единицы, — кратным.
Если z\ является корнем кратности к\ многочлена Pn(z) =
= anzn + ... + a\z + ао, то, применяя последовательно теорему Безу,
получим
Pn(z) = (z- z^Qn-^iz), Qn-kl(zi) Ф 0
{Qn-kAz) — многочлен степени n — ki). Согласно основной теореме
алгебры многочлен Qn-k1{z) при п — к\ ^ 1 имеет корень. Обозначим
его через Z2, и пусть его кратность равна k<i\ тогда
Qn-kl(z) = (z- z2)k2Qn-kl-k2(x), Qn-kl-k2(z2) ф 0,
и, следовательно,
Pn(z) = {z- Zl)^{z - z2)k2Qn-kl-k2(z).
Продолжив последовательно этот процесс, через конечное число
шагов (каждый раз степень многочлена понижается) получим
Pn(z) = an(z - Zl)kl... (z - zN)kN,	C.17)
где Zj ф z\ при j ф /, j, / = 1,2,..., N. Ясно, что к\ + ... + км = п. Чис-
Числа 2i,22,...,2/v и только они являются корнями многочлена Pn(z).
Для многочлена Pn(z) = anzn + an-i^™ + ... + a\z + a0 положим
^ / ч def — n	—	—
Рп(з) = anz + ... + a\z + a0.
Многочлен Pn(z) называется многочленом, сопряженным много-
многочлену Pn(z). В силу свойств сопряженных комплексных чисел будем
иметь
Pn(z) = anzn + dn-iz71-1 + ... + a\z + a0 =

§3. Элементарные функции	39
Если zo — корень кратности к для многочлена Pn(z), то z0 яв-
является корнем той же кратности сопряженного многочлена Pn(z).
Действительно, если
Pn(z) = (z- zv)kQn-k{z), Qn-k(zo) Ф О,
то
Pn(z) = (z-Z0)kQn-k(z), Qn-кЫ ф О,
откуда
Pn(z) = PJ?) = (z - zo)kQn-k(z) = (z- zo)kQn_k(z),
причем,
Это и означает, что ~zq — корень кратности к многочлена Pn(z).
Пусть теперь коэффициенты многочлена Pn{z) — действительные
числа. Тогда ясно, что Pn(z) = Pn(z), и если z0 = а + Ы — корень
кратности к такого многочлена Pn(z), то и z0 = а - Ы — корень крат-
кратности к этого же многочлена, так как он совпадает со своим сопря-
сопряженным.
В дальнейшем в случае многочлена с действительными коэффици-
коэффициентами будем вместо переменной z писать, как это обычно принято,
переменную х.
Заметим, что
(ж — zo)(z — z~o) = (ж — а — bi)(z — а + Ы) = (ж — аJ + Ь2 =
= ж2 - 2ах + а2 + b2 =x2 +px + q, C.18)
где р = -2а, q = а2 + Ь2 и, следовательно,
2
?- - q = -b2 < 0	C.19)
при b ф 0, т. е. когда zo = а + Ы является существенно комплексным
числом.
Теперь мы видим, что если в разложении C.17) многочлена с
действительными коэффициентами объединить скобки с сопряжен-
сопряженными корнями согласно формуле C.18) и обозначить действительные
корни Ж1,ж2, ...,жг, то получим разложение вида
или, короче,
Рп(х) = ап

40 Гл. 1. Дифференциальное исчисление функций одной переменной
где
3 = 1	1=1
(при перемножении многочленов их степени складываются),
*L-qi<Q, / = 1,2,..., s
(это следует из C.19)), pi,qi — действительные числа, a kj и т/ —
натуральные, j = 1, 2,..., г, / = 1, 2,..., s.
3.5. Рациональные дроби. Как в случае многочленов, мы рас-
рассмотрим рациональные дроби в комплексной области.
Пусть P(z) и Q(z) — многочлены с, вообще говоря, комплексными
коэффициентами и Q(z) не является нулевым многочленом. Рацио-
Рациональная дробь —)—!- называется правильной, если степень многочле-
Q\z)
на P(z) меньше степени многочлена Q(z), и неправильной, если сте-
степень многочлена P(z) не меньше степени многочлена Q(z).
Всякая рациональная дробь является либо правильной, либо не-
неправильной.
P(z)
Если рациональная дробь	неправильная, то, произведя деле-
деление числителя на знаменатель по правилу деления многочленов, т. е.
представив числитель в виде
где S(z) и R(z) — некоторые многочлены, причем степень многочле-
многочлена R(z) меньше степени многочлена Q(z), получим
Q(z) u{Z) + Q(z)-
Здесь в силу уже сказанного дробь	является правильной.
Qyz)
Займемся более подробно изучением правильных рациональных
дробей.
P(z)
Лемма 1. Если	— правильная рациональная дробь и чис-
число zo G С является корнем кратности к ^ 1 ее знаменателя, т. е.
Q(z) = (z-zo)kQ1(z), Qi(*o)#0,	C.22)
то существуют единственное число A G С и многочлен Pi (z) такие,
Г(*)- А ¦	*(*)	C23)

§3. Элементарные функции	41
где дробь 	^	 также является правильной.
(z — zo)k~1Qi(z)
Если коэффициенты многочленов P(z) и Q(z) — действительные
числа и корень z$ многочлена Q(z) — также действительное число,
то число А также является действительным числом, а многочлены
Pi(z) и Qi(z) можно выбрать с действительными коэффициентами.
Отметим, что здесь у многочленов P\{z) и Q\{z) единица является
просто индексом, а не их степенью.
P(z)
\> Каково бы ни было число A Е С, прибавляя к дроби	=
Q\z)
дробь	—, а затем вычитая ее, получим
(z-zo)kQi(z)	(z-zo)k
Г P(z)	А_] =
l(z-zo)kQi(z) (z-zo)k\
=	=
Q(z) (z-zo)kQi(z) (z-zo)k l(z - zo)kQ!(z) (z-zo)k
A
- {z_zo)t + {z_Zo)kQl{zy №)
Степень многочлена P(z) по условию меньше степени многочле-
многочлена Q(z) — {z — zo)kQi(z), а степень многочлена Qi(z) меньше степени
многочлена Q(z), поскольку Q(z) получается из Qi(z) умножением на
многочлен (z - zo)k, k ^ 1. Поэтому при любом выборе числа А е С
ДР°бЬ	P(z)-AQliz)
является правильной: степень ее числителя меньше степени знамена-
знаменателя.
Для того чтобы дробь C.25) имела вид
необходимо и достаточно, чтобы ее можно было сократить на множи-
множитель (z — zo), а это можно сделать в том и только том случае, когда
числитель дроби C.25) делится на (z — zo), что согласно теореме Безу
равносильно тому, что число z0 является корнем многочлена, стояще-
стоящего в числителе этой дроби, т. е. когда
P(zo)-AQ1(zo)=0.
Поскольку по условию Qi(zo) ф 0, то это равносильно тому, что
А ~ Ш^У	C-27)
При таком и только таком выборе числа А дробь C.25) сократится
на [z — 20), в результате в этом и только этом случае после сокраще-
сокращения дроби C.25) получится дробь вида C.26). Подставив эту дробь
в равенство C.24), получим разложение C.23), в котором коэффици-
коэффициент А однозначно определен.

42 Гл. 1. Дифференциальное исчисление функций одной переменной
Если корень z0, а также коэффициенты многочленов P(z) и Q(z)
являются действительными числами, то из равенства C.22) следует,
что и многочлен Q\{z) имеет действительные коэффициенты. Поэ-
Поэтому в силу формулы C.27) число А оказывается действительным,
откуда следует, что и все коэффициенты многочленов, стоящих в чис-
числителе дроби C.25), — также действительные числа. Следователь-
Следовательно, сокращая эту дробь на множитель (z - z0), имеющий действи-
действительные коэффициенты, можно записать результат в виде рациональ-
рациональной дроби, у которой в числителе и знаменателе стоят многочлены с
действительными коэффициентами. <|
P(z)
Теорема 1. Если	— правильная рациональная дробь и
Qyz)
Q(z) = (z- Zl)kl(z - z2)k\.. (z - zN)kN,	C.28)
где zi, ^2,..., zn — попарно различные корни многочлена Q(z), то су-
существуют единственные комплексные числа Aj\ Aj\ ..., Aj ,
j = 1,2,..., TV, такие, что
? ?] (,29)
P(z)
\> Применив последовательно k\ раз лемму к дроби —^ при z0 =
= zi, получим
P(z) = A{kl)	P^z)
Q(z) (z-ztfi ^ (z - ztfi-iQ^z)
{^1)	P2(z)
A^
(z - Zl)ki (z- Zl)k^ (z- Zl)k^Q2(z) '
= —21	+ —^	+ + l
=	+	+ +	+
'" (z - Zl)k^ (z- Zl)k^	z-zi Q*(z)'
где комплексные числа А\ г\...,A[' определяются последователь-
последовательно единственным образом, P*(z) и Q*(z) — многочлены, причем
P*(z)
у ' — правильная рациональная дробь и
Q*(z) = (z-z2)k*...(z-zN)k».
Применив теперь аналогичным образом последовательно к2 раз
Р* (z)
лемму 1 к дроби	при z$ = 2:2, затем к% раз при z$ = z% и т. д.,
Q \z)
kjy раз при zo = zn, получим формулу C.29). <1
Докажем еще одну лемму для правильных рациональных дробей,
в числителях и знаменателях которых стоят многочлены с действи-
действительными коэффициентами.

§3. Элементарные функции	43
Лемма 2. Пусть Р(х) и Q(x) — многочлены с действительны-
действительными коэффициентами, причем ; { — правильная рациональная дробь.
Q(x)
Если число zo = хо + ?/о 2, xo Е /?, у о Е /?, ?/о т^ 0? является кор-
корнем кратности т ^ 1 многочлена Q(x), т. е.
Q(x) = (x2+px + 4)mQi(x),	C.30)
где
Qi(z0) 7^ 0, х2 + рж + gr = (х - zo)(x - z0),	C.31)
mo существуют такие единственные действительные числа В, С и
многочлен Р\{х) с действительными коэффициентами, что
Р(х) = Вх + С	Pi (ж)	( ,
q)™ (x2+px + q)™-lQi(xy	У' }
Q(x) (a
где дробь
Pl!.l-^^	(з-зз)
также является правильной.
\> Для любых действительных В и С имеем
Q{x) (з.зо) (ж2
_ Вх + С	Г	Р(ж)
(*т»2 _|_ /г)/г» _|_ /у )Ш	[ /v»2 _|_ /ri/r» _|_ ft\l
(x2+px + q)m (ж2 +px + q)mQi(x) v ' J
Рассуждениями, аналогичными проведенным при доказательстве
леммы 1, легко убедиться, что дробь
V / [-DX —|— Ly Jvc^llX)	/ J-. г» h'\
—г^	.	, .	(o.ooj
является правильной и что коэффициенты многочленов, стоящих у
нее в числителе и знаменателе, являются действительными.
Для того чтобы дробь C.35) имела вид
*(f> ч,	(з-зб)
необходимо и достаточно, чтобы ее можно было сократить на множи-
множитель х2 + рх + q = (х - zo)(x - ^о), а это можно сделать тогда и толь-
только тогда, когда числитель дроби C.35) делится на (ж — zq){x — ~г~о),
что согласно теореме Безу равносильно тому, что число zo являет-
является корнем многочлена, стоящего в числителе дроби C.35), т. е. когда
P(zo)-(Bzo + C)Q1(zo)=0.

44 Гл. 1. Дифференциальное исчисление функций одной переменной
Поскольку Qi(zo) ф О, то
^	C-37)
Пусть у 0) = а + Ы. Тогда равенство C.37) можно записать сле-
следующим образом:
Приравняв действительные и мнимые части комплексных чисел,
стоящих в разных частях этого равенства, получим В = —, С =
2/о
= а	 Ь. При таком выборе В и С они, во-первых, являются дейст-
2/о
вительными числами, во-вторых, в этом и только этом случае чис-
число zo, а следовательно, и сопряженное ему число ^о, являются кор-
корнями многочлена C.37). При таком и только таком выборе чисел В
и С дробь C.35) сократится на (х - zo)(x - z0). В результате в
этом и только этом случае после сокращения дроби C.35) получит-
получится дробь вида C.36). Подставив эту дробь в равенство C.34) вместо
дроби C.35), получим разложение C.32), в котором действительные
коэффициенты В и С однозначно определены. <|
Р(х)
Теорема 2. Пусть	— правильная рациональная дробь, Р(х)
Q(x)
и Q(x) — многочлены с действительными коэффициентами. Если
Q{x) =
3 = 1	1=1
где Xj — попарно различные действительные корни многочлена Q{x)
кратности kj, j = 1,2,...,г, а х2 + pix + qi = (ж — zi){x — ~z\\
где zi,~z~i — попарно различные существенно комплексные корни мно-
многочлена Q(x) кратности m/, I = 1, 2,..., s, то существуют единст-
единственные действительные числа
А?\А?\ ..., Af > з = 1,2,...,г,
„A) „B)	„(mz) ^A) r{2)	r(mi) / _ -i 9
такие, что
U - x,- ^ (x- Xjy ^ - ^ (X - Xj)kj
I
^\+pi + qi (+pi + qiJ '" (x2
l> Аналогично тому, как это было сделано в доказательстве теоре-
теоремы 1, сначала последовательно применим лемму 1 к\ раз при zq = х\,

§3. Элементарные функции	45
затем к2 раз при z0 = х2 и т. д., кг раз при z0 = жг. В результате по-
ЛУЧИМ	.	m	.,*л
где действительные числа ^Ц- , ..., А^ э определяются последова-
последовательно единственным образом, коэффициенты многочленов Р*(ж),
^>*/ \ «	р*(ж)
Q (х) — действительные числа, — правильная рациональная
Q ух)
дробь, а	в
f
1=1
Р*(х)
Применив к дроби	последовательно лемму 2 mi раз при zq =
затем m2 раз при z0 = z2 и т. д., ms раз при z0 = zs, получим
'"
Q*(x) Z^\x2+pix + qi '" (х2
Подставив это выражение для ^ ^ в C.39), получим доказывае-
доказываемую формулу C.38). <1
Рациональные дроби вида
А	Бж + С ^<
Ц—, ^- - q < 0, meN, neN,
¦ q)n 4
называются элементарными, поэтому теоремы 1 и 2 называются те-
теоремами о разложении правильных рациональных дробей на сумму
элементарных (соответственно в комплексной и действительной об-
областях).
3.6. Графики рациональных функций. График всякого мно-
многочлена степени п с действительными коэффициентами пересекает
ось х в тех точках, абсциссы которых являются его действительны-
действительными корнями и тем самым не более чем в п точках, так как он имеет
не более чем п корней.
Поведение многочлена при неограниченном возрастании или не-
неограниченном убывании его аргумента зависит от четности степе-
степени многочлена и знака при старшем члене. Если п — четное чис-
число и коэффициент при старшем члене многочлена больше нуля, то
как при неограниченном возрастании аргумента, так и при неограни-
неограниченном его убывании значения многочлена неограниченно возраста-
возрастают (рис.15). Если п — нечетное число, то при положительном коэф-
коэффициенте при старшем числе многочлена значения многочлена не-
неограниченно растут при неограниченном возрастании аргумента и

46 Гл. 1. Дифференциальное исчисление функций одной переменной
неограниченно убывают при неограниченном его убывании (рис. 16).
О
чу \7
Рис. 15	Рис. 16
Если же коэффициент при старшем члене многочлена отрицателен, то
при п четном многочлен неограниченно убывает как при неограни-
неограниченном возрастании, так и при неограниченном убывании аргумента
У\
\
Рис. 17	Рис. 18
(рис. 17), а в случае п четного многочлен неограниченно убывает при
неограниченном возрастании аргумента и неограниченно возрастает
при неограниченном его убывании (рис. 18).
Если Р{х) — многочлен первого порядка:
Р{х) = ах + Ь,
то его графиком является прямая линия. Коэффициент а равен тан-
тангенсу угла (см. п. 3.9), который эта прямая образует с осью ж, а Ъ
равно ординате точки пересечения прямой с осью у (рис. 19).
О
4а
tgcp=a
О
у=ах2+Ъх+с
2а
Рис. 20
Рис. 19
В случае когда рассматриваемый многочлен является квадрат-
квадратным трехчленом ах2 + Ъх + с, его график называется параболой.

§3. Элементарные функции	47
Поскольку	2
2/ = аж2 + 6ж + с = а(ж + ^-) +с-^-,	C.40)
V 2а/	4а
то график функции 2/ = аж2 + 6ж + с получается из параболы у = ж2
Ь	i i
ее переносом на — — параллельно оси ж, растяжением в а раз вдоль
2а
оси ж, симметрией относительно оси ж при а < 0 и переносом на
с—-— параллельно оси 2/ (рис. 20). Из этого следует, что прямая
4а
ж =	является осью симметрии параболы C.40), ибо ось у является
2а
осью симметрии параболы у = ж2. Точка (	, с	) называется
вершиной параболы C.40).
Рациональная функция
где Р(х) и Q(x) — многочлены с действительными коэффициента-
коэффициентами, не имеющие общих действительных корней (если бы нашелся та-
такой корень ж0, то дробь C.41) можно было бы сократить на ж - ж0),
обращается в нуль в тех точках, в которых обращается в нуль ее
числитель Р(х). При этом если кратность нуля числителя четная, то
,	Р(х)
функция —)—!- не меняет знака в его окрестности, а если нечетная,
Q(x)
то меняет. В окрестности нулей знаменателя значения рациональ-
рациональной функции неограниченно возрастают по абсолютной величине при
приближении к указанным нулям.
Если степень числителя рациональной функции C.41) больше сте-
степени ее знаменателя, то при неограниченном возрастании по абсо-
абсолютной величине аргумента она также неограниченно возрастает по
абсолютной величине; если степень знаменателя больше степени чис-
числителя, то она неограниченно убывает по абсолютной величине; если
же степень числителя равна степени знаменателя, то она неограни-
неограниченно приближается к отношению коэффициентов при старших чле-
членах многочленов Р{х) и Q{x).
Изучению поведения рациональных функций помогает определе-
определение интервалов, на которых рассматриваемая функция C.41) сохра-
сохраняет постоянный знак. Все эти соображения полезно использовать при
построении графиков рациональных функций.
В качестве примера построим график функции
х(х-1J
У (х + 1)*(х*-2У	[ >
Эта функция обращается в нуль в точках х = 0 и х = 1, причем в

48 Гл. 1. Дифференциальное исчисление функций одной переменной
окрестности нуля она меняет свой знак, а в окрестности единицы не
меняет. В окрестности точек х = — 1 и х = ±у/2 она неограниченно
возрастает по абсолютной величине, причем в точках х = ±л/2 меняет
свой знак, а в точке х = — 1 не меняет.
При неограниченном возрастании по абсолютной величине аргу-
аргумента функция C.42) неограниченно приближается к нулю. Интерва-
Интервалы, на которых она положительна или отрицательна, изображены в
следующей таблице:
X
У
—оо
-0
-
-л/2
оо
+
-1
оо
+
0
0
-
1
0
-
л/2
оо
+
+ ОО
+0
и
Проведенные рассуждения позволяют установить общий вид графика
функции C.42) (рис. 21). С помощью
дальнейшего исследования этой функ-
функции ее график можно нарисовать более
точно.
3.7. Степенная функция. Опи-
Опишем поведение степенной функции у =
с ха в случае, когда а — рациональ-
рациональное число (к более подробному изуче-
изучению степенной функции мы вернемся
в дальнейшем; см. п. 8.3).
Рассмотрим сначала функцию у =
-и о
Рис. 21
= жп, где п — натуральное число. Эта
функция является частным случаем
многочлена степени п с n-кратным корнем х = 0. Согласно сказанному
в п. 3.6 при четном п ее график имеет вид, изображенный на рис. 22,
а при нечетном п > 1 — на рис. 23.
О
У=х
У'
г
' 1
1 y=x2k+1
X
Рис. 22
Функция у = —, где снова п
Рис. 23
натуральное число, является ра-
рациональной функцией, неограниченно возрастающей при приближе-
приближении ее аргумента к точке х = 0. Если п — четное число, то ее график

§3. Элементарные функции
О
Рис. 24
имеет вид, изображенный на рис. 24,
а если п нечетное, то — на рис. 25.
Функция у = у/х, где п — нату-
натуральное число, при п нечетном опре-
определена на всей действительной оси, а
при п четном — только на полуоси х ^
^ 0 и принимает при х > 0 два значе-
значения. Если ограничиться только неот-
неотрицательными значениями корня, то
и при четном п получится однознач-
однозначная функция.
Функция у = у/х является обрат-
обратной к степенной функции у = хп. Поэ-
Поэтому ее график симметричен относи-
относительно биссектрис первого и третье-
третьего координатных углов: при нечетном
п > 1 он имеет вид, изображенный на
рис. 26, а при четном, если ограни-
ограничиться арифметическими значениями
корня, — на рис. 27.
График функции
	 p/q	^ г\	/о л о\
где р и q — целые числа, p/q > 1,	ис'
касается оси х (это естественнее всего доказывается с помощью про-
производной; см. п. 10.3). Если 0 < p/q < 1, то q/p > 1 и, следователь-
х2к+1
О
Рис. 26
Рис. 27
но, в силу сказанного график функции C.43), или, что то же самое,
график функции у = xqlv', касается оси у.
Если p/q > 0, то при неограниченном возрастании х значение у
также неограниченно возрастает. Если p/q < 0, то при неограничен-
неограниченном возрастании х значение у неограниченно убывает, а при неогра-
неограниченном приближении х к нулю у неограниченно возрастает.
При х < 0 функция у = xvlq определена не для всех р и q. Если она
определена при х < 0, то является четной или нечетной функцией, и
4 Л.Д.Кудрявцев, т.1

50
Гл. 1. Дифференциальное исчисление функций одной переменной
потому ее график при х < 0 получается из ее графика при х > 0 с
помощью той или иной симметрии.
В качестве примера рассмотрим функцию у = ж2/3. Здесь р = 2,
q = 3, следовательно, 0 < p/q < 1, и функция определена при всех х.
О
Рис. 28
О
Рис. 29
В силу сказанного выше ее график (он называется полукубической
параболой) имеет вид, изображенный на рис. 28.
В качестве второго примера рассмотрим функцию у = ж~2//3. Ее
график изображен на рис. 29.
3.8. Показательная и логарифмическая функции. У степен-
степенной функции у = ха показатель степени постоянен, а основание сте-
степени меняется. Функция, у которой постоянно основание степени, а
меняется ее показатель, называется показательной.
Если а < 0, то степень ах имеет смысл не для всех х. В случае а = 0
при х > 0 имеет место равенство 0х = 0. Поэтому под показательной
функцией понимается функция у = ах', где а > 0. Она принимает по-
положительные значения при всех значениях х. Если а = 1, то у = 1.
При х = 0 показательная функция ах обращается в 1, так как а0 = 1.
Если а > 1, то функция у — ах возрастает при возрастании аргумен-
аргумента, и, следовательно, при х > 0 выполняется неравенство аж > а0 = 1,
а при х < 0 — неравенство аж < а0 = 1. При неограниченном убы-
убывании аргумента показательная функция в этом случае неограни-
неограниченно приближается к нулю, а при его неограниченном возрастании
также неограниченно возрастает. Если же а < 1, то показательная
функция убывает при возрастании
ее аргумента; она больше единицы
при х < 0, меньше единицы при
х > 0 и при неограниченном воз-
возрастании аргумента неограни-
неограниченно приближается к нулю, а при
его неограниченном убывании не-
Рис зо	ограниченно возрастает (рис. 30).
Если а > 0, а ф 1, Ъ > 0, то показатель степени а, в который надо
возвести число а, чтобы получить число Ь, называется логарифмом
а>\
О

§3. Элементарные функции
51
числа b по основанию а и обозначается loga Ъ.
Таким образом,
Функция у = logax, а > 0, а ф 1, называет-
называется логарифмической функцией. Она определена при
х > 0. Функции у = ах и у = loga ж взаимно об-
ратны друг другу, ибо у = aloga у и loga аж = х.
Поэтому график функции у = loga x симметричен
графику функции у — ах относительно биссектрис
первого и третьего координатных углов (рис. 31).
Если а > 1, то логарифм loga x положителен
при х > 1 и отрицателен при 0 < х < 1, а если 0 <	Рис. 31
< a < 1, то, наоборот, положителен при 0 < х < 1 и отрицателен при
ж > 1. Если a > 1, то логарифмическая функция у = loga ж возрастает,
причем при неограниченном возрастании аргумента она неограничен-
неограниченно возрастает, а при неограниченном его приближении к нулю она не-
неограниченно убывает. Если же 0 < а < 1, то логарифмическая функция
при возрастании аргумента убывает, причем при его неограниченном
возрастании неограниченно убывает, а при его неограниченном при-
приближении к нулю неограниченно возрастает, при любом а > 0, а ф 1,
имеет место равенство loga 1 = 0.
Логарифмическая функция по основанию 10 обозначается симво-
символом lg.
3.9. Тригонометрические и обратные тригонометричес-
тригонометрические функции. В прямоугольном треугольнике отношение катета,
противолежащего данному углу а треугольника, к гипотенузе назы-
называется синусом (sin а) этого угла, а отношение прилежащего катета к
гипотенузе — косинусом (cos а) угла а; отношение противолежащего
катета к прилежащему — тангенсом (tga), а прилежащего к противо-
противолежащему — котангенсом (ctga) уг-
угла а (рис. 32). Из свойств подобных
треугольников следует, что синус, ко-
косинус, тангенс и котангенс не зависят
от размеров треугольника, а однознач-
однозначно определяются углом а,
Легко видеть, что они связаны соот-
соотношениями
sin2 a + cos2 a = 1,
tga =
г2,
sin a
а
sin a= —
с
cos a
ctga = —
C.44)
cos a' ~	sina	Рис. 32
Для определения синуса, косинуса, тангенса и котангенса в случае
4*

52
Гл. 1. Дифференциальное исчисление функций одной переменной
произвольного угла а, -оо < а < +оо, рассмотрим на координат-
координатной плоскости переменных х,у окруж-
окружность радиуса 1 с центром О в начале
координат (рис. 33). Обозначим а угол,
который образует вектор О А, идущий
из начала координат в точку А = (ж, у),
с положительным направлением оси ж,
иначе говоря, угол, на который надо
повернуть единичный вектор оси ж,
чтобы он совпал с вектором О А. При
этом угол, который получается ука-
указанным вращением, считается положи-
положительным, если вращение производится
против часовой стрелки, и отрицатель-
отрицательным, если по часовой стрелке. Таким
образом, угол а, который образует вектор О А с осью ж, определен
с точностью до целого, кратного полному обороту в ту или другую
сторону. Следовательно, если а — величина угла в радианной мере,
образованного вектором О А с осью ж, то при любом целом п угол
а + 2тгп также будет углом, образованным этим вектором с осью ж.
Если 0 < а < тг/2, то согласно данному выше определению
s'ma = х, cosa = y.	C.45)
Если а — произвольный угол, —оо < а < +оо, и О А — единичный
вектор с координатами х,у, образующий угол а с осью ж, то форму
лы C.45) принимаются за определение значений синуса и косинуса
этого угла. Из них следует, что
Рис. 33
sm(a ± тг) = — sin a, cos(a ± тг) = — cos a.
C.46)
Тангенс и котангенс произвольного угла а определяются по фор-
формулам
sin а	/ тг	,	cos а
tga=	, а Ф—V тгп: ctga =	,
cos а	2	sin а
п = 0, ±1, ±2,...
а
тгп:
C.47)
Таким образом, они определены для всех тех а, для которых зна-
знаменатели в правых частях равенств C.47) не обращаются в нуль.
Синус, косинус, тангенс и котангенс называются основными три-
тригонометрическими функциями. Из их определения следует, что они
являются периодическими функциями: при полном обороте (на 360°
в градусной мере или на 2тг в радианной) в том или ином направле-
направлении радиус О А займет прежнее положение, т. е. будет иметь те же
самые координаты, а следовательно, синус, косинус, тангенс и котан-
котангенс примут прежние значения.
Из формул C.46) и C.47) следует, что значения тангенса и котан-

§3. Элементарные функции
53
генса будут повторяться и через пол-оборота. Таким образом, синус
и косинус являются периодическими функциями с периодом 2тг (мы
будем пользоваться для измерения углов безразмерной радианной ме-
мерой, в которой угол задается действительным числом), а тангенс и
Рис. 36
Рис. 37
котангенс — с периодом тг. Их графики изображены на рис. 34-37.
Обратные функции для основных тригонометрических функций
являются многозначными. Однако если функцию синус рассмотреть
на отрезке [—тг/2,тг/2], косинус — на отрезке [0,тг], тангенс — на ин-
интервале (—7г/2,тг/2), а котангенс — на интервале @,тг), то обратные
к ним функции будут уже однозначными и они обозначаются соот-
соответственно arcsinx, arccosx, arctgx и arcctgx. Функции arcsinx и

54 Гл. 1. Дифференциальное исчисление функций одной переменной
arccosx определены на отрезке [—1,1], a arctgx и arcctgx — на всей
-1
1
1
1
У'
л
~2
/
t/=arcsinx

/\ >
О 1 х
п
2
Рис. 38
t/=arctgx
Рис. 40
Рис. 41
числовой прямой. Их графики изображены на рис. 38-41.
3.10. Параллельный перенос и растяжение графиков. Если
известен график функции у = /(ж), то с его помощью легко получить
график функции вида у = kf(ax + b) + I. Опишем это построение по
этапам. Из графика функции /(ж):
1)	график функции /(аж), а > 0, получается сжатием графика f(x)
вдоль оси х в а раз ("сжатие" с коэффициентом а, 0 < а < 1, является
растяжением в 1/а раз);
2)	график функции f(—x) — преобразованием симметрии отно-
относительно оси у;
3)	график функции f(x + b) — переносом параллельно оси х на
отрезок длины \Ь\ влево, если b > 0, и вправо, если b < 0;
4)	график функции kf(x), k > 0, — растяжением вдоль оси у в к
раз ("растяжение" с коэффициентом fc, 0 < fc < 1, является сжатием
в 1/к раз);
5)	график функции —f(x) — преобразованием симметрии отно-
относительно оси х;
6)	график функции /(ж) + I — переносом параллельно оси у на
отрезок длины |2| вверх, если I > 0, и вниз, если I < 0.
Применив эти операции, из графика функции f(x) можно полу-

§4- Числовые множества
55
чить график функции
kf(ax + b) + / = kf(a(x + -)) + Z, а ф 0.
Для этого согласно указанному выше надо последовательно по-
построить графики функций
f(ax), f(a(x + -)>\ = f(ax + b), kf(ax + b) kf(ax + b) + l
(на рис. 42 схематически изображено построение графика функ-
kf{ax+b)+l
kf(ax+b)
I f(ax+b)
f(x)
Рис. 42
ции kf(ax + b) + l в случае, когда а > 0, 6 > 0, fc > 0, Z > 0).
Вместо последовательного построения этих графиков можно сде-
сделать преобразование координат: соот-
соответствующий параллельный перенос,
изменение масштабов, а если надо, и
ориентации координатных осей. Имен-
Именно, график самой функции f(x) ста-
станет графиком функции kf(ax + b) + I,
а ф 0, к ф 0, если перенести начало
&?—т)? увеличить
координат в точку
О
масштаб по оси х в
а| раз, уменьшить
Рис. 43
его по оси у в |fc| раз и при а < 0, соот-
соответственно при fc < 0, изменить ориентацию оси х соответственно
оси у (рис. 43).
§ 4. Числовые множества
4.1. Ограниченные и неограниченные множества.
Определение 1. Множество X С /? называется ограниченным
сверху, если существует такое число b € R, что для всех ж G X имеет
место неравенство х ^ Ь. Число b называется в этом случае числом,
ограничивающим сверху множество X.

56 Гл. 1. Дифференциальное исчисление функций одной переменной
Множество X называется ограниченным снизу, если существует
такое число a Е /?, что для всех х Е X выполняется неравенство
х ^ а. Число а называется в этом случае числом, ограничивающим
снизу множество X.
Множество, ограниченное сверху и снизу, называется ограни-
ограниченным.
С помощью логических символов существования и всеобщности
определение, например, ограниченного сверху множества можно за-
записать следующим образом:
3be R УхеХ: х^Ь	D.1)
(здесь двоеточие означает "имеет место" или "выполняется усло-
условие").
Множество, не являющееся ограниченным сверху, называется
неограниченным сверху.
Определение неограниченного сверху множества можно сформу-
сформулировать и в позитивной форме, т. е. без отрицаний (без частицы
"не"), следующим образом; множество X называется неограничен-
неограниченным сверху, если для любого числа Ъ Е R найдется такой х Е X, что
х > Ъ.
Запишем это определение с помощью логических символов:
\/Ъе R Зх еХ: х> Ъ.	D.2)
Сравнивая определения D.1) и D.2), видим, что при построении
отрицания символ существования заменился на символ всеобщнос-
всеобщности, а символ всеобщности — на символ существования. Этим фор-
формальным правилом можно пользоваться при построении отрицаний в
позитивной форме.
Аналогично, множество, не являющееся ограниченным снизу, на-
называется неограниченным снизу.
Множество, не являющееся ограниченным, называется неограни-
неограниченным.
Множество натуральных чисел Л/ является примером ограничен-
ограниченного снизу множества. Если а Е R и Ъ Е /?, то отрезок [а, Ь] пред-
представляет собой ограниченное множество. Множества рациональных
чисел Q, иррациональных чисел /, вообще всех чисел R дают приме-
примеры неограниченных множеств.
4.2. Верхняя и нижняя грани.
Определение 2. Пусть числовое множество X ограничено свер-
сверху. Наименьшее среди всех чисел, ограничивающих сверху множест-
множество X С /?, называется его верхней гранью и обозначается supX или
sup х (от латинского слова supremum — наибольший).
хех
Если числовое множество X ограничено снизу, то наибольшее сре-
среди всех чисел, ограничивающих снизу множество X, называется его

§4- Числовые множества	57
нижней гранью и обозначается inf X или inf х ( от латинского слова
хех
infinum — наименьший).
Итак, C = supX, если, во-первых, число C ограничивает сверху
множество X, т. е. для всех х Е X выполняется неравенство х ^ /3, а
во-вторых, число /3 является наименьшим среди всех чисел, ограни-
ограничивающих сверху множество X (т. е. если /3' < /3, то число C' уже не
ограничивает сверху множество X, а это означает, что существует
такое х Е X, что х > (З1).
Таким образом, определение верхней грани можно перефразиро-
перефразировать в следующем виде.
Определение 2'. Число C называется верхней гранью числового
множества X, если:
1)	для любого х е X выполняется неравенство х ^ /3;
2)	для любого /3' < /3 существует такой х е X, что х > /3' (рис. 44).
Р=р-?	х	Р	ах	а=а+в
Рис. 44	Рис. 45
Аналогично, число а называется нижней гранью числового мно-
множества X, если:
1)	для любого х Е X выполняется неравенство х ^ а;
2)	для любого а' > а существует такой х G X, что х < а' (рис. 45).
Если во втором условии положить г = /3 - /3' (соответственно г =
= а' — а), то это условие можно перефразировать следующим обра-
образом:
2') для любого е > 0 существует такой х G X, что х > C — е (соот-
(соответственно х < а + г).
Пример. Пусть aGRnbGR,a^b; тогда
sup [a, b] = sup (а, b) = b, inf [а, b] = inf (а, Ь) = а.
Эти примеры показывают, в частности, что нижняя и верхняя
грани могут как принадлежать, так и не принадлежать самому мно-
множеству.
В силу самого своего определения верхняя и нижняя грани мно-
множества единственны. В самом деле, если в некотором множестве, при-
принадлежащем даже расширенной числовой прямой /?, существует наи-
наименьший (наибольший) элемент, то он единственен, так как из двух
разных элементов множества больший из них не может быть наи-
наименьшим элементом, а меньший — наибольшим.
Теорема 1. Всякое ограниченное сверху непустое числовое мно-
множество имеет верхнюю грань, а всякое ограниченное снизу непустое
числовое множество имеет нижнюю грань.
|> Пусть числовое множество А ограничено сверху, А ф 0, а В —

58 Гл. 1. Дифференциальное исчисление функций одной переменной
множество всех чисел, ограничивающих сверху множество А. Если
a Е А и Ъ Е В, то из определения числа, ограничивающего сверху
множество, следует, что а ^Ь. Следовательно, по свойству непрерыв-
непрерывности действительных чисел (п. 2.1, свойство V) существует такое
число /3, что для всех a Е А и всех Ъ Е В будет выполняться нера-
неравенство а ^ /3 ^ Ъ. Неравенство
а ^ C, a Е А,
означает, что число C ограничивает сверху множество А, а нера-
неравенство
(З^Ъ, be В,
— что число /3 является наименьшим среди всех чисел, ограничи-
ограничивающих сверху множество А. Следовательно, /3 = sup A.
Аналогично доказывается, что ограниченное снизу числовое мно-
множество имеет нижнюю грань. <|
Замечание 1. Если числовое множество X неограничено свер-
сверху, то у него не существует верхней грани в смысле определения 2.
В этом случае по определению полагаем, что верхней гранью мно-
множества X является +оо:
лг def ,
SUp A = +00.
Отметим, что при таком определении условия 1) и 2) определения 2'
оказываются выполненными, если использовать соглашение B.2)
(п. 2.2).
Если числовое множество X неограничено снизу, то его нижней
гранью является —оо:
. р ^r def
mi А = —оо.
Благодаря этому соглашению и теореме 1 всякое непустое число-
числовое множество имеет единственную верхнюю (нижнюю) грань, ко-
конечную, если оно ограничено сверху (снизу), и бесконечную, если оно
не ограничено сверху (снизу).
Замечание 2. Если X — числовое множество и для некоторого
числа а и всех х G X выполняется неравенство х ^ а (соответственно
х ^ а), то sup ^ а ( inf х ^ а), так как supX (соответственно inf X)
хеХ \хех	J
является наименьшим (наибольшим) среди всех чисел, ограничи-
ограничивающих сверху (снизу) множество X. Иначе говоря, в неравенствах
можно переходить к верхним и нижним граням.
4.3*. Арифметические свойства верхних и нижних гра-
граней. Отметим три свойства верхних и нижних граней, связанные с
арифметическими операциями над числовыми множествами. Прежде
всего определим такие операции.

§4- Числовые множества	59
Арифметической суммой Х\ + ... + Хп числовых множеств Хь...
...,ХП называется множество всех чисел ж, представимых в виде
х = xi + ... + xn, xi Gli, ..., хп G Хп.
Арифметической разностью X - Y числовых множеств X и Y на-
называется множество всех чисел z, представимых в виде
z = х - у, х е х, у eY.
Следует, конечно, отличать понятие арифметической суммы
Х\ + ... + Хп и разности X — Y от понятия теоретико-множественной
суммы Х\ U ... U Хп и разности X \ Y тех же множеств.
Произведением XX числа Л на числовое множество X называется
множество всех чисел вида Аж, х G X.
>
то
1°.
Если ж
хк ^su
Пусть
supp?
inf р
GXi + ...
ipXk, к =
ж = ж
теперь
\ + ..
^1 + •
+ хп
1,2,.
1 + ...
. + Хп) = SUpX;
.. + Xn) = inf X]
, т. е. ж = х\ + ..
i + ... + supXn,
L + ... + inf Xn.
• • \ хП) Х\ G Л-i, ..., ж
..,п, и, следовательно,
+ жп ^ supXi + ... + supXn.
D.3)
D.4)
nexn,
D.5)
у < sup Xi + ... + sup Xn.	D.6)
Рассмотрим сначала случай, когда все верхние	грани supX/,,
к = 1,2,...,п, конечные. В этом случае представим	число у в виде
у = ?/i + ...+ 2/nj где
2/fc<supXfc, fe = 1,2,..., п.	D.7)
В качестве у\~ можно взять
def	Л7-	?	/, п\
2/л = supXfc - -,	D.8)
где
г = supXi + ... + supXn - у > 0.	D.9)
Действительно, в этом случае у\~ < supX/, и
""D-8)
(sup Хп-^) =
= (supXi + ...+ supXn) - г =
D.9)
Из неравенств D.7) следует, что существуют такие Xk G Х&, что
ук <хк ^ supXfe, fe = 1,2,...
Полагая ж = xi + ... + хп, получим
х G Xi + ... + Xnj ж = xi + ... + хп > У1 + ... + Уп = у. D.10)

60 Гл. 1. Дифференциальное исчисление функций одной переменной
Таким образом, выполняются оба условия определения верхней
грани (см. D.5) и D.10)), т. е. supXi + ... + supXn действительно
является верхней гранью множества Х\ + ... + Хп.
Пусть теперь хотя бы одна из верхних граней supX/,, k = 1,2,...
...,п, бесконечная, т. е. равна +оо, например supXi = +оо. Докажем,
что тогда
sup(Xi + ... + ХП) = +оо = supXi + ... + supXn*).
Пусть задано какое-либо у Е R. Зафиксируем произвольно Xk ? X/,,
к = 2,...,п. Тогда из условия supXi = +оо следует, что существует
такое х\ G Xi, что х\ > у — х<± — ... — хп, т. е.
def	,
X = Х\ + Х2 + ... + Хп > у.
Так как у — произвольное число, а х G Х\ + ... + Хп, то это и озна-
означает, что sup (Xi + ... + Хп) = +оо.
Аналогично доказывается формула D.4). <|
2°. Если Л > 0, то
supAX = AsupX,	D.11)
infAX = AinfX,	D.12)
а если А < 0, то
sup AX = AinfX,	D.13)
inf XX = AsupX.	D.14)
l> Пусть A > 0. Если у е XX, т. е. у = Аж, где х е X и, следовательно,
х ^ supX, то у = Хх ^ A supX. Если у < AsupX, т. е. у/Х < supX,
то найдется такое х G X, что х > у/Х и, следовательно, Хх > у,
где Хх G АХ. Таким образом, AsupX является верхней гранью мно-
множества АХ, т. е. формула D.11) доказана. Аналогично доказывается
и формула D.12).
Пусть теперь А < 0. Если у е АХ, т. е. у = Хх, где х е X и, следова-
следовательно, х ^ inf X, то Хх ^ A inf X. Если 2/ < A inf X, т. е. у/Х > inf X, то
найдется такое х G X, что ж < ?//А, а потому Аж > у, где Ах G АХ. Это
и означает, что A inf X является верхней гранью множества АХ. Ра-
Равенство D.13) доказано. Аналогично доказывается равенство D.14). <|
Положим теперь для каждого множества X
-X=f(-l)X.	D.15)
Очевидно, что из определения суммы X + Y и разности X — Y мно-
множеств следует
X-Y = X + (-Y).	D.16)
В силу определения D.15) из второго свойства при А = — 1 полу-
получаем
sup(-X) = -infX, inf (-X) = -supX.	D.17)
?) Мы полагаем, что а + (+оо) = +оо + а = +оо для любого числа а.

§4- Числовые множества	61
3°.
sup (X-Y) = sup X - inf Y.	D.18)
Следует сразу из первого свойства и формул D.16) и D.17).
4.4.	Принцип Архимеда.
Теорема 2. Каково бы ни было действительное число а, сущест-
существует такое натуральное число п, что п > а.
\> Если бы утверждение теоремы не имело места, то нашлось бы
такое число а, что для всех натуральных чисел п выполнялось
бы неравенство п ^ а, т. е. множество натуральных чисел Л/ было
бы ограничено сверху. Тогда, согласно теореме 1, у множества Л/
существовала бы конечная верхняя грань:
/3 = sup7V < +оо.	D.19)
Поскольку C — 1 < /3, то в силу определения верхней грани (см.
свойство 2 в определении 2' в п. 4.2) найдется такое натуральное
число п, что п > C — 1, т. е.
п + 1 > C,	D.20)
но п + 1 — также натуральное число: п + 1 G А/, поэтому неравенст-
неравенство D.20) противоречит условию D.19). <1
Следствие (принцип Архимеда*)). Для любых чисел а иЪ та-
таких, что 0 < а < Ь, существует нату-	^_	_^
ралъное число п, для которого выполня- /S _ _ _ -Гч».
ется неравенство (рис. 46)	о а	Ъ па
па > Ь.	D.21)	Рис. 46
|> Действительно, согласно теореме 2 для числа Ъ/а существует та-
такое натуральное число п, что п > b/а, откуда сразу и следует D.21). <|
4.5.	Принцип вложенных отрезков.
Определение 3. Система числовых отрезков
[ai,bi], [а2,Ь2], -.., [ап,Ьп], .., aneR, bneR, n = l,2,.., D.22)
называется системой вложенных от-
отрезков, если	^^-^-z~Z^--^
i1in i и м ii м111 м|i1>
D.23) а\ а2 ап Ъп Ъ2 bi
т. е. если (рис. 47)
Г	, 1	Г	7 1	Г	7 1	РИС- 47
[ai,bi] Э [а2,Ь2] D ••• D [ап,Ъп\ D ...
Теорема 3. Всякая система вложенных числовых отрезков име-
имеет непустое пересечение.
?) Архимед B87-212 до н.э.) — древнегреческий математик и механик.

62 Гл. 1. Дифференциальное исчисление функций одной переменной
\> Пусть задана система вложенных отрезков D.22). Обозначим че-
через А множество всех левых концов ап от- резков этой системы, а
через В — множество их правых концов Ъп. Из неравенств D.23) сле-
следует, что для любых номеров тип выполняется неравенство ат ^ Ъп.
Поэтому по свойству непрерывности действительных чисел (п. 2.1,
свойство V) существует такое число ?, что для всех номеров тип
выполняется неравенство
в частности, неравенство ап ^ ? ^ bn, n = 1, 2,... Это и означает, что
точка ? принадлежит всем отрезкам [ап,Ьп]. <\
Укажем условие, при котором пересечение системы вложенных
отрезков состоит из единственной точки.
Определение 4. Длины Ъп — ап отрезков [an,bn], an Е /?, Ъп Е
G /?, ап ^ bn, n = 1,2,..., называются стремящимися к нулю, если
для любого числа г > 0 существует такой номер п?, что для всех но-
номеров п > п? выполняется неравенство
Ьп - ап < е.	D.24)
Теорема 4. Для всякой системы вложенных отрезков [ап,Ьп],
п = 1,2,..., длины которых стремятся к нулю, существует единст-
единственная точка ?, принадлежащая всем отрезкам данной системы; при
этом
? = sup{an} = inf{6n}.	D.25)
|> Если точки ? и п принадлежат всем отрезкам рассматриваемой
системы, т. е.
€€[о>п,Ьп], f]e[an,bn], п = 1,2,...,
то ясно, что для всех номеров п выполняются неравенства
1^7 - fl ^ Ъп-ап,
а следовательно, в силу условия D.24) для любого г > 0 справедливо
неравенство
\V-Z\<e.	D.26)
Поскольку г > 0 — произвольное число, то это возможно только
тогда, когда ? = п (если бы ? ф п, то, например, при г = \п — ?| нера-
неравенство D.26) было бы противоречиво). Это означает, что существу-
существует единственное число ?, принадлежащее всем отрезкам [anjbn]:
ап^?, ^bn, n = 1,2,...
Из этих неравенств видно, что число ? ограничивает сверху числа ап
и снизу числа Ьп, поэтому если а = sup{an}, C = inf {6n}, то в си-
силу определения верхней и нижней граней будут выполняться нера-
неравенства
an^a^^f3^bn, n = 1, 2,...	D.27)

§4- Числовые множества	63
Таким образом, числа а, /3 и ? принадлежат всем отрезкам [ап,Ьп],
а следовательно, по доказанному выше они равны, т. е. выполняется
условие D.25). <1
Замечание 1. Для интервалов и полуинтервалов множества
действительных чисел аналог принципа вложенных отрезков не име-
имеет места. Например,
пел/
Замечание 2. Для множества одних только рациональных чисел
принцип вложенных отрезков несправедлив. При этом под отрезком
в множестве рациональных чисел понимается пересечение обычного
отрезка, концы которого являются рациональными числами, с мно-
множеством рациональных чисел:
[а, Ъ] П Q = {х е Q: а ^ х ^ Ь}, а е Q, be Q.
Например, пусть числа ап и Ъп представляют собой десятичные при-
приближения числа у/2 с недостатком и с избытком и имеют по п деся-
десятичных знаков после запятой, п = 1,2,..., тогда
так как Q [ап,6п] = {л/2} и у/2 — иррациональное число: у/2 0 Q.
neN
4.6*. Счетность рациональных чисел. Несчетность дейст-
действительных чисел. Сравнение множеств осуществляется с помощью
понятия взаимно однозначного соответствия.
Определение 5. Два множества, между элементами которых
можно установить взаимно однозначное соответствие (биекцию),
называются равномощными.
Замечание. Нетрудно убедиться, что если множество X равно-
мощно множеству F, а множество Y равномощно Z, то и множест-
множество X равномощно множеству Z.
Множество X называется конечным, если существует такое нату-
натуральное число п (называемое числом элементов множества X), что
между элементами множества X и элементами множества {1,2,...
...,п —1,п} можно установить взаимно однозначное соответствие.
Очевидно, два конечных множества равномощны тогда и толь-
только тогда, когда они содержат одинаковое число элементов. Пустое
множество по определению считается конечным. Множества, не яв-
являющиеся конечными, называются бесконечными.
Приведем примеры равномощных бесконечных множеств.
Примеры. 1. Множество четных натуральных чисел равномощ-
равномощно множеству всех натуральных чисел. Действительно, соответствие

64 Гл. 1. Дифференциальное исчисление функций одной переменной
п и-» 2n, n = 1,2,..., является биекцией множества натуральных чи-
чисел Л/ и множества всех четных натуральных чисел.
2.	Множество всех целых чисел равномощно множеству натураль-
натуральных чисел. В самом деле, соответствие
2п ь->- п, п = 1, 2,...,
2п + 1 н> -n, n = 0,1,2,...,
является биекцией множества натуральных чисел Л/ и множества це-
целых чисел Z.
3.	Любые два конечных интервала (соответственно отрезка) чис-
числовой прямой равномощны. Если заданы два интервала (а, Ъ) и (с, б?),
то отображение
(а — c)t + Ъс — ad	, 7
ж =	^	, a<t<b,
Ъ — а
является биекцией интервалов (а, 6) и (с, б?) (соответственно отрез-
отрезков [а, Ъ] и [с, б?]).
4.	Множество всех действительных чисел R равномощно любому
конечному интервалу числовой оси. В силу замечания после опреде-
определения 5 и примера 3 достаточно показать, что множество действи-
действительных чисел равномощно хотя бы одному интервалу, поэтому дос-
достаточно заметить, что функция у =	 устанавливает взаимно од-
однозначное соответствие между точками интервала (—1,1) и точками
всей числовой оси.
Примеры 1, 2 и 4 показывают, что в случае бесконечных множеств
собственное подмножество бесконечного множества может оказаться
равномощным всему множеству.
5.	Пусть задано некоторое множество X. Всякое отображение мно-
множества натуральных чисел А/ в множество X, т. е. отображение вида
/ : А/ —У X, называется последовательностью элементов множест-
множества X. Элемент /(n), n Е А/, обозначается через хп и называется п-м
членом последовательности /: N —> X, число п — его номером, и сам
элемент /(n) G X — значением этого члена.
Последовательность /: /V ->• X обозначается также {хп} или жп,
п = 1,2,...
Отметим, что член последовательности задается его значением и
номером. Если п > т, то член последовательности хп называется чле-
членом, следующим за членом хт.
Множество членов последовательности равномощно с множеством
натуральных чисел, так как каждому натуральному числу соответ-
соответствует член последовательности и разным натуральным числам соот-
соответствуют разные члены последовательности, отличающиеся друг от
друга по крайней мере номерами. Таким образом, множество членов
последовательности всегда бесконечно, в то время как множество зна-
значений членов последовательности, т. е. множество значений функции

§4- Числовые множества	65
f:N->X (иначе говоря, подмножество множества X, на которое по-
посредством отображения / отображается множество Л/ натуральных
чисел), может оказаться конечным множеством, в частности состо-
состоять из одного элемента. В последнем случае, т. е. тогда, когда у после-
последовательности все значения ее элементов совпадают, она называется
стационарной.
Определение 6. Множество, равномощное множеству нату-
натуральных чисел, называется счетным.
Из рассмотренных выше примеров 1, 2 и 5 следует, что множества
всех четных чисел, всех целых чисел и всех членов любой последова-
последовательности являются счетными.
Пусть X — счетное множество, т. е. существует взаимно одно-
однозначное отображение (биекция) множества натуральных чисел Л/ на
множество X. Элемент множества X, соответствующий при этом ото-
отображении числу п, обозначим, как и в случае последовательности,
хп и будем называть число п его номером. Поэтому можно сказать,
что множество является счетным, если его элементы можно пере-
перенумеровать натуральными числами. Отличие определения счетного
множества от последовательности состоит в том, что в случае после-
последовательности рассматриваемое отображение множества натураль-
натуральных чисел не обязано быть биекцией: не исключается случай, когда
разным натуральным числам окажется поставленным в соответствие
один и тот же элемент. Отсюда следует, что множество значений чле-
членов последовательности либо конечно, либо счетно, т. е., как говорят,
не более чем счетно.
Лемма 1. Любое бесконечное множество содержит бесконечное
счетное подмножество.
Х> Пусть X — бесконечное множество; тогда оно во всяком случае
непусто, т. е. в нем существует по крайней мере один элемент, обозна-
обозначим его через х\. Поскольку множество X бесконечно, то множество
X \ {xi} также непусто, т. е. содержит по крайней мере один элемент,
обозначим его х2. Продолжая этот процесс, на n-м шаге получим
элемент хп. Поскольку X — бесконечное множество, то множест-
множество X \{х\,Х2, ...,хп} непусто, т. е. содержит по крайней мере один
элемент, обозначим его хп+\ и т. д. Множество {xi,X2, ...,жп,...} —
искомое счетное подмножество множества X. <|
Лемма 2. Любое бесконечное подмножество счетного множества
счетно.
\> Пусть X — счетное множество: X = {xi,X2, ...,жп,...} и Y С X.
Обозначим через у\ элемент из У, имеющий наименьший номер в X,
через ?/2 — элемент множества У, имеющий следующий ближайший
номер, и т. д. Поскольку каждый элемент множества Y является неко-
некоторым элементом хп множества X и, следовательно, имеет номер п,
5 Л.Д.Кудрявцев, т.1

66 Гл. 1. Дифференциальное исчисление функций одной переменной
то через конечное число шагов (не больше, чем п) он получает неко-
некоторый номер т и в множестве У, т. е. будет обозначен ут, причем,
поскольку множество Y бесконечно, этот процесс может быть про-
продолжен неограниченно. Таким образом, все элементы множества Y
окажутся перенумерованными, что и означает счетность этого мно-
множества. <|
Теорема 5. Множество всех рациональных чисел счетно.
\> Расположим все рациональные числа в таблицу, содержащую бес-
бесконечное число строк и столбцов, следующим образом (см. таб-
таблицу):
0
1
2
1
1
1
2
1
-1
3
2
2
3
2
-2 ...
5
2 •"
С J С J
Здесь в n-ю строчку помещены рациональные числа, записывае-
записываемые несократимыми рациональными дробями со знаменателем п и
О/Т\ /Т\ /Т\ упорядоченные по возрастанию их абсо-
\—' \У \—' лютных величин, причем непосредственно
0/^\ /^\ /^\ за каждым положительным числом следует
ч?у \JL/ K-J емУ противоположное. Очевидно, что каж-
каждое рациональное число находится на каком-
то месте в этой таблице.
Занумеруем теперь элементы получив-
получившейся таблицы согласно следующей схеме,
в которой в кружочках стоят номера соот-
соответствующих элементов, а стрелки указывают направление нумера-
нумерации.
В результате все рациональные числа оказываются занумерован-
занумерованными, т. е. множество Q рациональных чисел счетно. <|
Возникает естественный вопрос, существуют ли несчетные
множества, т. е. бесконечные множества, не являющиеся счетными,
а если существуют, то интересно построить пример несчетного мно-
множества.
Лемма 3. Любой отрезок множества действительных чисел со-
состоит из несчетного множества точек.
\> Допустим противное: пусть точки некоторого отрезка [а, 6], a Е /?,
Ъ Е /?, а < 6, можно занумеровать: [а, Ъ] = {xi, Х2,..., хп,...}. Выберем
какой-либо отрезок [ai,bi], лежащий на
,^^^ х^^\	\а-> Ь] и не содержащий точки х\ (рис. 48):
ч	1	1	1—i—н—i	1—>
а х\ а\ х2 а2 Ъ2 Ь\ Ь	Х\ 0 [ai,bi] С [а, Ь].
Рис. 48	Далее выберем отрезок [а2, Ъ2], лежащий

§ 5. Предел числовой последовательности	67
на [ai,bi] и не содержащий точки ж2, и т. д. Таким образом, если
выбран отрезок [an,6n], то выберем отрезок [an+i,6n+i], лежащий
на [anjbn] и не содержащий точки хп+\. Продолжая этот процесс,
получим систему вложенных отрезков [an, bn], n = 1, 2,..., такую, что
хп &[ап,Ъп], п = 1,2,...	D.28)
Следовательно, ни одна точка хп не принадлежит пересечению
оо
Р| [an, bn], но согласно принципу вложенных отрезков (см. п. 4.5, тео-
71=1
рема 3) существует точка, обозначим ее ?, принадлежащая всем от-
отрезкам \ап.Ьп]:
11	?€[ап,Ьп], п = 1,2,...,	D.29)
а поэтому и отрезку [а, 6], ибо [ап,Ьп] С [а, 6] при всех п = 1,2,...
А так как все точки отрезка [a, b] по предположению перенумерованы,
то точка ? также должна иметь какой-то номер, т. е. существует такое
натуральное число по, что ? = жПо, и тогда согласно D.29) получим
Zno €[a>n,bn], га = 1,2,...	D.30)
В частности, жПо G [аПо,6По], а это противоречит условию D.28). <1
Теорема б (Кантор*)). Множество всех действительных чисел
несчетно.
\> Если бы множество всех действительных чисел было счетным, то
было бы счетным, согласно лемме 2, и любое его подмножество, в
частности, любой отрезок, что противоречит лемме 3. <1
§ 5. Предел числовой последовательности
5.1. Определение предела числовой последовательности.
Одним из важнейших понятий математического анализа является по-
понятие предела. Начнем его изучение с предела последовательности
действительных чисел. Напомним (см. п. 4.6*, пример 5), что после-
последовательностью {хп} элементов некоторого множества X называется
отображение множества натуральных чисел в это множество X. Об-
Образ при этом отображении натурального числа п (член последователь-
последовательности с номером п) в множестве X обозначается через хп. В частнос-
частности, последовательностью действительных чисел является "занумеро-
"занумерованное" натуральными числами некоторое множество Х\,Х2, ...,жп,...
действительных чисел, причем члены последовательности с разными
номерами могут иметь одно и то же значение. Примерами последо-
последовательностей являются 1, -, -,..., -,... и 1,1,1,..., 1,... В дальнейшем
2 6 п
в этом параграфе буквой п всегда обозначаются натуральные числа.
?) Г. Кантор A845-1918) — немецкий математик.

68 Гл. 1. Дифференциальное исчисление функций одной переменной
Под бесконечно удаленной точкой числовой прямой будем пони-
понимать одну из бесконечностей +оо, —оо или оо (см. п. 2.2).
Определение 1. Конечная или бесконечно удаленная точка
числовой прямой называется пределом некоторой числовой после-
последовательности действительных чисел, если какова бы ни была
окрестность точки а, она содержит все члены рассматриваемой
последовательности, начиная с некоторого номера.
Этот номер зависит, вообще говоря, от выбора окрестности точ-
точки а. Сформулированное условие равносильно тому, что вне любой
окрестности точки а находится лишь конечное число членов рассмат-
рассматриваемой последовательности. Вспомнив, что окрестности конечных
и бесконечно удаленных точек числовой прямой определяются зада-
заданием некоторого числа г > 0 (п. 2.2), определение предела последо-
последовательности действительных чисел можно перефразировать следую-
следующим образом.
Точка а (конечная или бесконечно удаленнная) числовой прямой
называется пределом последовательности {хп} действительных чи-
чисел, если для любого г > 0 существует такой номер п?, что для всех
номеров п > п? члены хп содержатся в окрестности U(a\e):
хп е U(a;e), п>п?.	E.1)
Если выполняется это условие, то пишут lim хп = а или хп —У а
п—юо
при п —У оо (а иногда пишут хп —> а, п = 1, 2,...) и говорят, что члены
последовательности {хп} стремятся к а.
С помощью логических символов существования и всеобщности
определение предела записывается следующим образом:
а = lim хп <Й> \/г > 0 Зп? : Vn > п? хп G U(a;e).	E.2)
п—>-оо
Если предел последовательности действительных чисел является
конечной точкой числовой прямой, т. е. числом, то говорят, что по-
последовательность имеет конечный предел.
Определение 2. Если числовая последовательность имеет ко-
конечный предел, то она называется сходящейся.
Для случая конечного предела определение 1 предела можно пере-
перефразировать следующим образом.
Число а является пределом последовательности {хп} действи-
действительных чисел, если для любого г > 0 существует такой номер п?,
что для всех номеров п > п? выполняется неравенство
\хп — а\ < г.	E.3)
В логических символах эта формулировка выглядит следующим
образом:
а = lim хп <Й> \/г > 0 Зп? Vn > п?: \хп — а\ < г.	E-4)

§ 5. Предел числовой последовательности	69
Очевидно, что неравенство E.3) равносильно неравенству
а - е < хп < а + е.	E.5)
Аналогичным образом формулируются и определения предела
числовой последовательности в случае, когда этот предел является
той или иной бесконечно удаленной точкой (или, как говорят, равен
бесконечности).
Например, согласно определению E.2) оо является пределом по-
последовательности {жп}, если для любого е > 0 существует такой но-
номер п?, что для всех номеров п > п? выполняется включение
хпе?/(ос;г),	E.6)
или, что то же самое, неравенство
хп\ > 1/е.	E.7)
В логических символах это утверждение записывается следую-
следующим образом:
lim хп = оо *Ш Vs > 0 Зп? Vn > п?: \хп\ > 1/е.	E.8)
п—Уоо
Аналогичным образом определение предела последовательности
перефразируется для случая, когда этот предел равен бесконечности
со знаком. Для краткости ограничимся записью этих определений
только с помощью логических символов:
def
lim хп = +оо <^> Vs > 0 Зп? Vn > п?: хп > 1/е,
п—>-оо
lim хп = —оо <Й> Vs > 0 Зп? Vn > п?: хп < —1/е.
Заметим, что если е — произвольное положительное число, то
и 1/е — также произвольное положительное число.
Очевидно, что если lim хп = +оо или lim хп = —оо, то и
п—>-оо	п—>-оо
lim xn = оо.
п—>-оо
Определение 3. Последовательность, пределом которой явля-
является бесконечность (со знаком или без знака), называется бесконечно
большой.
Примеры. 1. Последовательность хп = 1/п, п — 1,2,..., сходит-
сходится и имеет своим пределом нуль. Действительно, каково бы ни было
е > 0, согласно принципу Архимеда существует натуральное п?, боль-
большее, чем 1/е, т. е. п? > 1/е и, следовательно, 1/п? < е, а тогда для
всех натуральных п > п? имеет место неравенство
П?

70 Гл. 1. Дифференциальное исчисление функций одной переменной
Таким образом, при п > п? выполняется условие
а это и означает, что lim — = 0.
п—Уоо П
2.	Последовательность хп = (—l)n, n = 1,2,..., не имеет преде-
предела, так как какое бы число а ни взять, вне любой его ^-окрестности
при г < 1 будет находиться бесконечно много членов указанной
последовательности.
3.	Последовательность хп = п2, п = 1,2,..., бесконечно большая и
lim п2 = +оо. В самом деле, согласно принципу Архимеда для любо-
п—уоо
го е > 0 существует такое натуральное число п?, что пе > 1/е. Для
любого же номера п > 1, очевидно, имеет место неравенство п2 > п,
поэтому при п > п? выполняется условие
п2 > п > п? > 1/е,
т. е. если п > п?, то п2 > 1/е, а это и означает, что lim п2 = +оо.
п—уоо
4.	Докажем, что если а > 1, то
lim ап = +оо, lim — = 0.	E.9)
п—уоо	п—уоо ап
|> В самом деле, положим а = а - 1; тогда а > 0 и по формуле
бинома Ньютона
ап = A + а)п = 1 + па + п(п ~ Х) а2 + ... + ап > па.	E.10)
Для любого г > 0 существует такое по, что по > —. Поэтому
as
для всех п > по имеем
ап > па> поа > -	E.11)
E.10)	?
И	1
-<е.	E.12)
А это по определению предела и означает справедливость ра-
равенств E.9). <1
Определение предела числовой последовательности обобщается
на последовательности точек расширенной числовой прямой /?,
т. е. числовой прямой, дополненной отрицательной (—оо) и поло-
положительной (+оо) бесконечностями (п. 2.2). По форме оно полностью
совпадает с определением 1.
Определение 4. Точка а расширенной числовой прямой назы-
называется пределом последовательности точек этой прямой, если какова

§ 5. Предел числовой последовательности	71
бы ни была окрестность точки а, она содержит все члены рассматри-
рассматриваемой последовательности, начиная с некоторого номера.
Отличие от вышерассмотренного случая состоит в том, что здесь
членами последовательности могут быть не только действительные
числа, но и бесконечности со знаками.
Конечно, понятие предела можно обобщить и на случай последова-
последовательности точек прямой, расширенной с помощью только одной бес-
бесконечно удаленной точки — бесконечности без знака, однако в даль-
дальнейшем у нас такие последовательности не будут встречаться.
5.2.	Единственность предела последовательности. Докажем
теорему о единственности предела последовательности.
Теорема 1. Последовательность точек расширенной числовой
прямой R может иметь на этой прямой только один предел.
\> Допустим противное. Пусть существует такая последовательность
хп G /?, п = 1, 2,..., что lim хп = а и lim хп = Ь, причем афЬ, a G /?,
п—>-оо	п—>-оо
Ъ Е R. Возьмем какие-либо непересекающиеся окрестности U = U(a)
и V = V(Ь) точек а и Ъ (рис. 49): U П V = 0. Согласно определению
предела вне окрестности U точки а, в
частности, в окрестности V точки Ь, со-	U	U
держится лишь конечное число членов (^Т^)	Г"^) >
последовательности {хп}. Однако точ-	а	ъ
ка Ъ также является ее пределом, и	Рис 49
потому в ее окрестности V должны
находиться все члены последовательности {жп}, начиная с некоторо-
некоторого номера, а следовательно, бесконечно много ее членов. Получилось
противоречие. <\
5.3.	Переход к пределу в неравенствах. Сформулируем и до-
докажем три часто используемые свойства пределов последовательнос-
последовательностей точек расширенной числовой прямой, связанные с равенствами и
неравенствами для членов последовательностей.
1°. Если для всех п = 1,2,... имеет место равенство хп = a G /?,
то lim xn = а.
п—>-оо
|> Действительно, в этом случае для любой окрестности U(a) точки а
в качестве номера п?, указанного в определении предела последова-
последовательности, можно взять п? = 1, так как для всех п = 1,2,... имеет
место включение
хп = a G U(a). <\
2°. Если хп е 7?, yne~R, zne~R,
Xn^Vn^Zn, 71=1,2,...,	E.13)
и
lim xn = lim zn = a G /?,	E-14)
П—Y(X>	П—Y(X>

72 Гл. 1. Дифференциальное исчисление функций одной переменной
то
lim yn = а.	E.15)
п—>-оо
|> Зафиксируем произвольно окрестность U(a)	точки а. В силу
условий E.14) существует такой номер ni, что	для всех номеров
п > п\ выполняется включение
хп е U(a),	E.16)
и такой номер п2, что для всех номеров п > п2 выполняется вклю-
включение
Ща)	zn е U(a).	E.17)
^^*~"~	""""^^^	Положим п0 = max{ni,n2}. Тогда
при п > по будут одновременно выпол-
хп ^ yn zn	няться включения E.16) и E.17), а сле-
Рис 50	довательно, [жп,2п] G С/(а) (рис. 50). Но
в силу условия E.13) уп G [xn,zn], поэ-
поэтому для всех п > по будет выполняться включение ?/n G ?7(a), a это
и означает справедливость утверждения E.15). <1
С л е д ст вие. Если хп ^ уп, хп G /?, yn ? R, n = l,2,..., u
lim жп = +оо,	E.18)
п>оо
п—>-оо
то
lim 2/n = +оо,	E.19)
п—>-оо
а если Нт 2/п = —оо, то Нт жп = —оо.
п—>-оо	п—>-оо
|> Пусть выполнено условие E.18). Рассмотрим вспомогательную по-
последовательность zn = +00, п = 1,2,...; тогда, очевидно, для последо-
последовательностей {жп}, {^п}5 {^п} выполняются условия E.13) и E.14)
при а = +00, а поэтому в силу E.15) имеет место и равенство E.19).
Аналогично рассматривается и случай lim yn = -оо. <1
п—>-оо
3°. Если хп е ~R, yn?~R, n = l,2,...,
lim жп = a, lim yn = b,	E.20)
n—>-oo	n—>-oo
[i	_	_
a<6, a eft, iiGfi,	E.21)
mo существует такой номер no, '/mo <?ля всех номеров п>по
выполняется неравенство
Хп < Уп-	E.22)
|> Пусть U = U(а) и V = V(b) — какие-либо непересекающиеся ок-
окрестности точек а и 6 (см. рис. 49); тогда из условия а < Ъ следует,
что для любых х G U и у G V выполняется неравенство
х < у.	E.23)

§ 5. Предел числовой последовательности	73
В силу условия E.20) существует такой номер п0, что для всех номе-
номеров и > по выполняются включения
хп еи, упе У,	E.24)
а поэтому согласно E.23) имеют место неравенства E.22). <|
Следствие 1. Пусть а, Ъ и хп, и = 1, 2,..., принадлежат R. Если
lim хп = а и а < Ъ (а > Ь), то существует такой номер по, что для
всех номеров п > по выполняется неравенство
хп < Ъ {соответственно хп> Ъ).	E.25)
|> Пусть а < Ъ. Рассмотрим вспомогательную последовательность
уп = Ь, п = 1,2,...; тогда для последовательностей {хп} и {уп} вы-
выполняются условия E.20) и E.21), а следовательно, и условие E.22),
которое в данном случае превращается в E.25). Аналогично рассмат-
рассматривается случай а > Ь. <\
Следствие 2. Если lim хп = a, lim уп = 6, хп Е /?, 2М ? ^
п—>-оо	п—>-оо
п = 1,2,..., а G /?, & G /?, ?/ для всех п = 1,2,... выполняется нера-
неравенство	, ч
хп ^ уп,	E.26)
Ш°	а ^ Ъ.	E.27)
|> Пусть выполнено условие E.26). Если бы оказалось, что а < Ь, со-
согласно свойству 3° нашелся бы такой номер по, что для всех номе-
номеров п > по выполнялось бы неравенство хп < уп, что противоречит
условию E.26). Следовательно, выполняется неравенство E.27). <1
Из следствия 2, в частности, вытекает, что если хп ^ b, n = 1, 2,...,
и lim хп = а, то имеет место неравенство а ^ Ъ.
п—уоо
\> В самом деле, если взять вспомогательную стационарную после-
последовательность уп — Ь, п — 1,2,..., то для последовательностей {хп}
и {уп} будут выполняться условия следствия 2, т. е. lim xn = a G /?,
п—>-оо
жп G /?, п = 1,2,..., и для всех п = 1,2,... справедливы неравенства
n ^ U — Уп-
Поэтому согласно следствию 2 имеет место и неравенство
а ^ 6. <1	E.28)
Следствие 2 означает, что если последовательности {хп} и {^/п}
имеют пределы lim хп = a, lim уп = b, a G /?, 6 G /?, то в нера-
п—>-оо	п—>-оо
венствах жп > уп и жп ^ 2/п можно переходить к пределу, причем даже
в первом случае в результате получается, вообще говоря, нестрогое
неравенство
а = lim xn ^ lim уп = Ъ.

74 Гл. 1. Дифференциальное исчисление функций одной переменной
Пример. Если для всех п = 1,2,... выполняется включение
хп Е U(a, 1/n), хп Е /?, где либо а Е /?, либо а = оо, либо а = +оо,
либо а = —оо, то
lim хп = а.
п—>-оо
|> В самом деле, если a Е /?, то условие жп Е ?/(а, 1/п) равносильно
условию |жп — а\ < 1/п, а так как \хп - а\ ^ 0 и lim 1/п = 0, то сог-
п—>-оо
ласно свойству 2° имеет место равенство lim \xn — а\ =0. Отсюда
п—>-оо
сразу и следует, что
lim xn = а.
п—>-оо
Если а = оо, то условие хп е С/(а, 1/п) равносильно условию |жп| >
> п. Отсюда в силу следствия из свойства 2° имеем lim \хп\ = +оо.
п—>-оо
Это и означает, что lim жп = оо.
п—>-оо
Аналогично рассматриваются случаи а = +оо и а = —оо. <1
В дальнейшем в этом параграфе будут рассматриваться только по-
последовательности, все члены которых являются числами, т. е. толь-
только числовые последовательности, а не последовательности элементов
расширенной числовой прямой, как это делалось выше.
5.4. Ограниченность сходящихся последовательностей.
Определение 5. Числовая последовательность называется огра-
ограниченной сверху (снизу), если множество ее значений ограничено
сверху (снизу).
Иначе говоря, числовая последовательность {хп} ограничена свер-
сверху (снизу), если существует такое число с G /?, что для всех номеров п
выполняется неравенство хп ^ с (соответственно неравенство хп ^ с).
Последовательность, ограниченная как сверху, так и снизу, назы-
называется ограниченной.
Таким образом, числовая последовательность {хп} ограничена, ес-
если существуют такие числа a G R и Ъ G /?, что для всех номеров п
выполняется условие а ^ хп ^Ъ. Это условие, очевидно, равносильно
тому, что существует такое число с > 0, что для всех номеров п имеет
место неравенство
\Хп\ ^ С.
Последовательность, не являющаяся ограниченной сверху (сни-
(снизу), называется неограниченной сверху (снизу), а последовательность,
не являющаяся ограниченной, называется неограниченой. Примером
неограниченных последовательностей являются бесконечно большие
последовательности (см. п. 5.1, определение 3). Следует заметить, од-
однако, что не всякая неограниченная последовательность является бес-
бесконечно большой. Так, последовательность
хп = (-l)nn + n

§ 5. Предел числовой последовательности	75
неограниченная, но не бесконечно большая.
Теорема 2. Если числовая последовательность имеет конечный
предел, то она ограничена.
|> Пусть последовательность хп е /?, п = 1, 2,..., имеет конечный пре-
предел lim хп = а е R. Тогда согласно определению предела Последова-
Последовать—>-оо
тельности (см. п. 5.1, определение 1), взяв г = 1, получим, что сущест-
существует такой номер п\, что для всех номеров п > п\ будет выполняться
неравенство
\хп -а\<1	E.29) ^ а[_г ^+1;	a+lin/
(в определении предела последователь-
последовательности можно взять любое г > 0; мы
взяли е = 1; рис. 51). Обозначим через б? наибольшее из чисел 1,
\х\— а|, ..., \хП1 — а\. Тогда, очевидно, в силу условия E.29) для всех
п G А/ будет иметь место неравенство
\хп - а
или, что равносильно,
а — d ^ хп ^ а + d.
Это и означает, что последовательность {хп} ограничена. <|
5.5. Бесконечно малые последовательности. Над числовы-
числовыми последовательностями можно производить арифметические опе-
операции. Определим их.
Определение 6. Пусть {хп} и {уп} — числовые последователь-
последовательности. Тогда числовая последовательность {хп + уп} называется
их суммой {хп} + {уп}, {хп-уп} — их разностью {хп} - {уп},
{хпУп} — их произведением {хп}{уп}, а если для всех номеров п
выполняется неравенство уп ф 0, то последовательность I — > на-
называется частным ±?Щ. данных последовательностей.
&п}
Если Л — действительное число, то произведением \{хп} число-
числовой последовательности {хп} на число Л называется последователь-
последовательность {Ххп}. Таким образом, получается тот же результат, что и от
умножения стационарной последовательности {Л} на последователь-
последовательность {хп}:
•^пу — \ЛХп} — t^J X^nj •
Определение 1. Числовая последовательность, предел которой
равен нулю, называется бесконечно малой.
Рассмотрим свойства бесконечно малых.
1°. Любая конечная линейная комбинация бесконечно малых явля-
является бесконечно малой.

76 Гл. 1. Дифференциальное исчисление функций одной переменной
\> Пусть числовые последовательности {ап} и {/Зп} бесконечно ма-
малые, т. е.
lim ап = lim /Зп = 0,	E.30)
п—>-оо	п—>-оо
а Л и \i — какие-либо действительные числа. Покажем, что после-
последовательность {Хап + /i/?n} также бесконечно малая. Зададим произ-
произвольно г > 0 и возьмем какое-либо число с такое, что
О |А| + Н.	E.31)
Тогда, согласно определению предела, из E.30) следует, что сущест-
существует такой номер по, что для всех номеров п > по выполняются не-
неравенства
К| <е/с, \рп\ <е/с	E.32)
и, следовательно, неравенство
E.32)	С	E.31)
Это и означает, что
lim (Хап + /i/3n) = О,
га-юо
т. е. что последовательность {Хап + /л/Зп} бесконечно малая. Соответ-
Соответствующее утверждение для любой конечной линейной комбинации
бесконечно малых следует из доказанного методом математической
индукции. <|
2° Произведение бесконечно малой последовательности на ограни-
ограниченную последовательность является бесконечно малой.
|> Пусть
lim an = 0	E.33)
п—>-оо
и {хп} — ограниченная последовательность, т. е. существует такое
с > 0, что для всех номеров п выполняется неравенство
\хп\ ^с.	E.34)
Зафиксируем произвольное г > 0, тогда согласно определению преде-
предела из условия E.33) следует, что существует такой номер по, что для
всех номеров п > по имеет место неравенство
К| <е/с,	E.35)
а следовательно, и неравенство
I	_| и |	? _
E.34) С
E.35)
Это и означает, что lim апхп = 0, т. е. что последовательность {апхп}
п—>-оо
бесконечно малая. <|
Следствие. Произведение конечного числа бесконечно малых по-
последовательностей является бесконечно малой.

§ 5. Предел числовой последовательности	77
|> Если lim ап = lim /Зп = 0, то зоследовательность {/Зп}, имея
п—>-оо	п—>-оо
конечный предел, является ограниченной последовательностью. По-
Поэтому произведение {ап/Зп} бесконечно малых последовательностей
{ап} и {/Зп} можно рассматривать как произведение бесконечно ма-
малой на ограниченную последовательность, и, следовательно, согласно
свойству 2° это произведение является бесконечно малой последова-
последовательностью.
Соответствующее утверждение для любого конечного числа бес-
бесконечно малых последовательностей получается из данного методом
математической индукции. <|
5.6. Свойства пределов, связанные с арифметическими
действиями над числовыми последовательностями. Беско-
Бесконечно малые последовательности играют в теории пределов особую
роль, так как понятие конечного предела последовательности можно
в определенном смысле свести к понятию бесконечно малой. Сформу-
Сформулируем это утверждение в виде леммы.
Лемма 1. Числовая последовательность {хп} имеет конечный
предел, равный числу а, тогда и только тогда, когда последователь-
последовательность
ап = хп-а, п = 1,2,...,
является бесконечно малой:
lim ап = 0.	E.36)
п—>-оо
|> Пусть заданы числовая последовательность {хп} и число а. Если
ап = хп - а, то условие lim xn = а согласно определению предела по-
п—>-оо
следовательности равносильно тому, что для любого г > 0 существует
такой номер п?, что для всех номеров п > п? выполняется неравен-
неравенство \хп — а\ < е, т. е. неравенство \ап\ < г, а это равносильно тому,
что lim ап = 0, т. е. тому, что последовательность {ап} бесконечно
малая. <|
Утверждение леммы можно перефразировать следующим обра-
образом: число а является пределом последовательности {хп} тогда и
только тогда, когда хп = а + ап, где {ап} — бесконечно малая по-
последовательность.
Рассмотрим свойства пределов числовых последовательностей.
1°. Если последовательность {хп} сходится, то сходится и по-
последовательность {|жп|}, причем, если lim xn = а, то
п—>-оо
lim \xn\ = \а\.	E.37)
п—>-оо
|> Если lim хп = а, то для любого г > 0 существует такой номер п?,
п—>-оо
что для всех номеров п > п? выполняется неравенство \хп — а\ < г, а

78 Гл. 1. Дифференциальное исчисление функций одной переменной
поскольку ||жп| - |а|| ^ \хп - а|, то выполняется и неравенство
\\хп\ - \а\\ < г,
а это и означает выполнение равенства E.37). <1
2°. Конечная линейная комбинация сходящихся последовательнос-
последовательностей также является сходящейся последовательностью, и ее предел
равен такой же линейной комбинации пределов данных последователь-
последовательностей.
|> Пусть
lim хп = а е /?, lim уп = Ъ е R.	E.38)
п—>-оо	п—>-оо
Тогда в силу необходимости условий E.36) для существования со-
соответствующих конечных пределов члены последовательностей {хп}
и {уп} можно представить в виде
хп = а + ап, Уп = Ь + рп, п = 1,2,...,	E.39)
где {ап} и {(Зп} бесконечно малые:
lim ап = lim (Зп = 0.	E.40)
п—>-оо	п—>-оо
Пусть теперь Аи/i — какие-либо числа. Тогда члены последова-
последовательности {\хп + /луп} представимы в виде
\xn+fiyn = \a + fib + Xan + /i/3n, n = l,2,...,	E.41)
(^5.39 J
где последовательность {Лап + /i/3n} в силу бесконечной малости по-
последовательностей {ап} и {(Зп} также бесконечная малая (см. свойст-
свойство 1° бесконечно малых последовательностей в п. 5.5):
lim (Xan + fi{3n) = 0.	E.42)
п^оо	E.40)
Поэтому в силу достаточности условий E.36) для существования со-
соответствующего конечного предела из равенств E.41) следует, что
последовательность {Ххп + fiyn} имеет предел, равный Ха + fib:
lim (Xxn + цуп) = Ха + fib,
п—>-оо
или (см. E.38))
lim (Лжп + fiyn) = Л lim xn + /i lim 2/n.	E.43)
п—>-оо	n—>-oo	n—>-oo
Соответствующее утверждение для любой конечной линейной
комбинации сходящихся последовательностей получается из доказан-
доказанного методом математической индукции. <|
3°. Если последовательности {хп} и {уп} сходятся, то их произ-
произведение {хпуп} также сходится:
lim xnyn = lim xn lim yn,	E.44)
п—уоо	п—уоо п—уоо

§ 5. Предел числовой последовательности	79
т. е. предел произведения сходящихся последовательностей сущест-
существует и равен произведению пределов данных последовательностей.
\> Пусть lim xn — a G R, lim уп = Ь G /?; тогда хп = а + ап, ?/п =
п—Усю	п—Усю
= Ь + /Зп, п = 1, 2,..., где lim ап = lim /Зп = 0. Поэтому
п—>-оо
ХпУп = (а + ап)(Ь + Рп) = ab+ (Ьап + а/Зп + ап(Зп),	E.45)
причем последовательность {Ьап + а/Зп} бесконечно малая как линей-
линейная комбинация бесконечно малых последовательностей {ап}
и {/Зп}, а последовательность {ап/Зп} бесконечно малая как произ-
произведение тех же последовательностей, поэтому бесконечно малой яв-
является и их сумма {Ьап + а(Зп + ап(Зп}:
lim (Ъап + а/Зп + ап/Зп) = 0.	E.46)
п—уоо
Из равенств E.45) и E.46) следует, что
lim xnyn = ab= lim xn lim 2/n. <
п—уоо	п—уоо п—уоо
Следствие. Если последовательность {хп} сходящаяся и т —
натуральное число, то
lim х™ = ( lim хп ) .
п—уоо	V п—уоо J
Это непосредственно следует из свойства 3°, так как возведение
числа в целую положительную степень т сводится к повторному ум-
умножению на это число т раз.
4°. Если последовательности {хп} и {уп} сходятся, для всех но-
номеров п имеет место неравенство уп ф 0 и lim yn ф 0, то последо-
вательность < — > сходится, причем
1 У™ J	lim хп
п^оо уп lim yn '
п—>-оо
т. е. при сделанных предположениях предел частного сходящихся по-
последовательностей существует и равен частному от пределов дан-
данных последовательностей.
> Пусть lim хп = а е /?, lim уп = b e R, b ф 0, уп ф 0, п = 1,2,...
п—>-оо	п—>-оо
Тогда жп = а + ап, уп = ^ + /^n5 lim an = lim /3n = 0- Из условия
п—уоо	п—уоо
lim уп = Ъ согласно свойству 1° следует, что lim \уп\ = |Ь|. Посколь-
п—уоо	п—уоо
ку \Ь\ > 0 (ибо Ъ ф 0) и 0 < \Ъ\/2 < \Ъ\, то согласно следствию 1 из
свойства 3° пределов последовательностей (п. 5.3) существует такой
номер п0, что для всех п > п0 выполняется неравенство \уп\ > \Ь\/2 и,
следовательно, неравенство
нк щ	<5-47)

80 Гл. 1. Дифференциальное исчисление функций одной переменной
(поскольку все уп ф 0, то на уп можно делить).
Теперь имеем
хп а а-\-ап а	1 ,,	„ ,	sk aq\
	Г = Т~ГЪ	Г = и и i а \УЬап - аРп)'	E.48)
Здесь последовательность
I Ъ(Ъ + /3n) J
ограничена, ибо для всех п > п0 выполняется неравенство
1
2
E.47) \Ц2 '
а последовательность {Ьап — а(Зп} бесконечно малая как линейная
комбинация бесконечно малых последовательностей {ап} и {/Зп}. По-
Поэтому бесконечно малой является и последовательность
как произведение ограниченной последовательности на бесконечно
малую.
Следовательно, из равенства E.48) вытекает, что
lim хп
lim = =	, <
п^оо г/п 6 lim г/п
п—>-оо
5.7. Монотонные последовательности.
Определение 8. Верхняя (нижняя) грань множества значений
числовой последовательности {хп} называется верхней (нижней)
гранью этой последовательности и обозначается sup{xn} (соот-
(соответственно inf {xn}).
Иначе говоря, если хп G /?, п = 1,2,..., и если /3 = sup{xn}, то:
1)	для всех п е N имеет место неравенство хп ^ /3;
2)	для любого /3' < /3 существует такое n0 G А/, что жПо > /^.
Аналогично, если а = inf {жп}, то:
1)	для всех п G А/ имеет место неравенство жп ^ а;
2)	для любого <У > а существует такое no G А/, что жПо < а7.
Примеры.
1.	sup(-) = 1, inf (-) =0.
2.	sup {n} = +oo, inf {n} = 1.
Определение 9. Числовая последовательность {хп} называе-
называется возрастающей (убывающей), если для всех п е N выполняется
неравенство хп ^ жп+1 ( соответственно неравенство хп ^ xn+i).
Возрастающая (убывающая) последовательность обозначает-
обозначается хп t (соответственно хп \). Если возрастающая (убывающая)
последовательность имеет предел, равный а, то пишут хп "[ а (со-
(соответственно хп la).

§ 5. Предел числовой последовательности	81
Последовательность {хп} называется строго возрастающей
(строго убывающей), если для всех п Е А/ выполняется неравенст-
неравенство хп < хп+1 (соответственно неравенство хп > xn+i)- Строго
возрастающая (строго убывающая) последовательность обозначает-
обозначается хп tt (соответственно хп Ц).
Убывающие и возрастающие последовательности называются мо-
монотонными, а строго убывающие и строго возрастающие — строго
монотонными.
Примеры.
3.	Последовательность {1/п} строго убывает.
4.	Последовательность {п} строго возрастает.
5.	Последовательность {(-1)п} немонотонная.
Теорема 3 (Вейерштрасс*)). Всякая возрастающая числовая по-
последовательность {хп} имеет предел: конечный, если она ограничена
сверху, и бесконечный, если она неограничена сверху, причем
lim xn = sup{xn}.	E.49)
>оо
п—>-оо
Аналогично, если {хп} — убывающая последовательность, то су-
существует (конечный или бесконечный) предел
lim xn = inf {xn\,	E.50)
и, следовательно, этот предел конечен, если последовательность {хп}
ограничена снизу, и бесконечен, если она неограничена снизу.
|> Пусть последовательность {хп} возрастает. Докажем равенст-
равенство E.49). Остальные утверждения теоремы для возрастающих после-
последовательностей следуют из него оче-
очевидным образом.
Пусть C = sup{xn}, значение C
может быть как конечным, так и
бесконечным. Возьмем произвольную
окрестность U(C) точки C и обозначим
через /3' ее левый конец (рис. 52). Оче-
видно, /3' < /3. Согласно определению
верхней грани:
1)	для любого номера п G А/ имеет
место неравенство
хп <: C;	E.51)
2)	существует такой номер по, что
хпо> C .	E.52)
В силу возрастания последовательности {хп} из E.51) и E.52)
*) К. Вейерштрасс A815-1897) — немецкий математик.
6 Л.Д.Кудрявцев, т.1

82 Гл. 1. Дифференциальное исчисление функций одной переменной
следует, что для всех номеров п > п0 выполняется неравенство
/3' < хпо ^хп^/3,	E.53)
и поскольку (/3',/3] С U(/3), то при п > по имеет место включение
хп € Щ0),	E.54)
а это и означает, что C является пределом последовательности {хп}.
Аналогично рассматривается случай хп I. <\
Замечание. Если [ап,Ьп], п = 1,2,..., — система вложенных от-
отрезков, длины которых стремятся к нулю, а ? — точка, принадлежа-
принадлежащая всем отрезкам этой системы, то
? = lim an = lim Ъп.	E.55)
п—>-оо	п—>-оо
В самом деле, последовательность {ап} возрастает, а {6П} убыва-
убывает, кроме того (см. D.25) в п. 4.5), было показано, что ? = sup{an} =
= inf{bn}. Поэтому равенство E.55) сразу следует из теоремы 3.
Пример б (число е). Рассмотрим последовательность
n = l,2,...,	E.56)
и покажем, что она строго возрастает и ограничена сверху, а следо-
следовательно, согласно теореме 3 имеет конечный предел.
Применив формулу бинома Ньютона, получим
\ га/	п
п	2 п2
ra(ra-l)(ra-2)...(ra-jfe + l) I	ra(ra-l)...l 1
к\	пк '"	га!	пп
1 ' 2!
... + -^fl --)...(l-—Y E.57)
n! V га/ V	га /
Из выражения, стоящего в правой части равенства, видно, что при
переходе от га к п + 1 число слагаемых (которые все положительны)
в написанной сумме возрастает на единицу и каждое слагаемое, на-
начиная с третьего, увеличивается, так как становится больше выра-
выражение, стоящее в каждых круглых скобках, ибо
п	га + 1'
Это означает строгое возрастание последовательности E.56):
хп<хп+и га = 1,2,...	E.58)
Далее, поскольку
1 — — \ 1, Ь — 1, Z, .... /7/ — 1, П — Z. о, ...,	{Э.ЭУ)
П

§ 5. Предел числовой последовательности	83
2й-1 = 1-2-2-...-2 ^ 1 • 2 • 3 • ... • п = п!,
п сомножителей
и поэтому
^^Т, п = 1,2,...,	E.60)
то при п > 1 из равенства E.57) получим
<2++Ь+ + Ь<2+\ + + +^<
п=0	'
(мы заменили сумму конечной геометрической прогрессии суммой
бесконечной геометрической прогрессии, так как у последней проще
формула). Итак,
хп < 3,	E.61)
т. е. последовательность E.56) ограничена сверху. Из E.58) и E.61)
следует, что она имеет конечный предел. Он обозначается через е:
е =f lim (l + -Y.	E.62)
Поскольку 2 < xn < 3 и xn t, то 2 < e ^ 3. Можно показать, что е —
иррациональное число и что с точностью до 10~15
е« 2, 718 281 828 459 045.
5.8. Принцип компактности. Если дана последовательность
{хп} и из некоторых ее членов хПк, взятых в порядке возрастания но-
номеров пи (к > к' равносильно п/. > п/./), составлена новая последова-
последовательность {хПк}, то она называется подпоследовательностью после-
последовательности {хп}.
В подпоследовательности {хПк} к является номером члена этой
последовательности, а п\~ — его номером в исходной последователь-
последовательности. Ясно, что для всех к = 1,2,... имеет место неравенство пи ^ к,
и поэтому lim n/. = +оо.
к—><х)
Подпоследовательности {хПк} последовательности {хп} считают-
считаются различными, если они соответствуют различным наборам номе-
номеров {nk}. Различные подпоследовательности одной и той же после-
последовательности, рассматриваемые как последовательности, могут
оказаться одинаковыми. Так, последовательность хп = 0, п = 1,2,...,
как и любая последовательность, имеет бесконечно много различных
подпоследовательностей (можно, например, выбрать четные номера,
нечетные, кратные трем, четырем и т. д.), но все эти подпоследо-
подпоследовательности как последовательности совпадают, очевидно, с данной
последовательностью хп = 0, п = 1, 2,...
6*

84 Гл. 1. Дифференциальное исчисление функций одной переменной
Выше было показано (см. п. 5.4), что если числовая последователь-
последовательность имеет конечный предел, то она ограничена. Обратное, конечно,
неверно. Например, последовательность хп = (—l)n, n = 1,2,..., огра-
ограничена, но не имеет предела. Вместе с тем, если вся ограниченная
последовательность не имеет предела, то у нее всегда существует
подпоследовательность, которая имеет предел. Точнее, имеет место
следующий факт.
Теорема 4. Из любой ограниченной числовой последовательнос-
последовательности можно выделить сходящуюся подпоследовательность, а из любой
неограниченной сверху [неограниченной снизу) числовой последова-
последовательности — последовательность, имеющую своим пределом +оо
[соответственно — об).
Х> Рассмотрим сначала случай, когда последовательность {хп}
ограничена, т. е. существуют такие a Е R и Ъ Е /?, что для всех
номеров п выполняется неравенство а ^ хп ^ Ъ.
Разделим отрезок [а, Ь] на два равных отрезка точкой 	. Тогда
по крайней мере на одном из них — обозначим его [ai,bi] — ока-
окажется бесконечно много членов последовательности {хп}. Выберем
произвольно какой-либо член этой последовательности, содержащий-
содержащийся в отрезке [ai,bi]. Пусть его номер равен п\\
хП1 € [аъ &i], Ь1-а1 = —^А	E.63)
Снова разделим отрезок [ai,bi] на два равных отрезка и тот из них,
на котором лежит бесконечно много членов последовательности (по
крайней мере для одного из них это условие выполняется), обозна-
обозначим [а2,&2]. Поскольку на отрезке [02,62] лежит бесконечно много
членов последовательности {жп}, то среди них заведомо есть члены
с номерами, большими чем щ. Выберем один из таких членов. Если
его номер П2, то
хП2 ? [«2,62] С [ai,bi], n2 > пь	E.64)
Ь2-а2 = Ь-^ = Ь-^.	E.65)
Продолжая этот процесс, получим такую подпоследователь-
подпоследовательность {хПк} (т. е. п\ < П2 < ... <nk < ...) последовательности {жп}, что
at ^ хПк ^ Ьк,	E.66)
[a>k,bk] С [ak-i,bk-i],	E.67)
Ък-ак = Ь-^, А: = 1,2,...,	E.68)
и, следовательно, lira (Ък — ак) = Нт —— = 0.

§ 5. Предел числовой последовательности	85
В результате получилась система вложенных отрезков [а^,^],
к = 1, 2,..., длины которых стремятся к нулю. Поэтому (см. п. 4.5) су-
существует единственная точка ?, принадлежащая всем этим отрезкам,
причем (см. E.55)) lim а/. = lim bk = ?, а тогда в силу свойства 2°
к^-оо	к^-оо
пределов (см. п. 5.3) из неравенства E.66) следует, что
lim хПк = f.
Это означает, что подпоследовательность {хПк} имеет конечный пре-
предел, т. е. сходится.
Пусть теперь последовательность {жп}, п = 1,2,..., не ограничена
сверху. Тогда существует такой номер ni, что хП1 > 1. Поскольку по-
последовательность жП1+1,жП1+2, •••? получающаяся из данной последо-
последовательности {хп} отбрасыванием конечного числа ее членов Х\,Х2,...
...,хП1, также не ограничена сверху, то найдется такой номер n<i > ni,
что хП2 > 2. Продолжая этот процесс, получим такие члены хПк по-
последовательности {жп}, что
ni < п2 < ... <пк < ...,	E.69)
хПк >к, к = 1,2,...	E.70)
Условие E.69) означает, что последовательность {хПк} является под-
подпоследовательностью последовательности {жп}, а из условия E.70) в
силу следствия свойства 2° пределов (п. 5.3) вытекает, что
lim хПк = +оо.	E-^1)
к—><х)
Аналогично рассматривается случай последовательности, не огра-
ограниченной снизу. <|
Замечание 1. Первое утверждение теоремы 4, т. е. то, что из
всякой ограниченной числовой последовательности можно выделить
сходящуюся, называется теоремой Болъцано-Вейерштрасса*) или
принципом компактности отрезка.
Замечание 2. Поскольку всякая неограниченная последователь-
последовательность не ограничена по крайней мере либо сверху, либо снизу, то из
второго утверждения теоремы 4 следует, что всякая неограничен-
неограниченная последовательность содержит бесконечно большую подпоследо-
подпоследовательность, причем ее всегда можно выбрать таким образом, что ее
пределом будет являться бесконечность со знаком.
Определение 10. Предел, конечный или определенного знака
бесконечный, подпоследовательности числовой последовательности
называется частичным пределом этой последовательности.
Из теоремы 4 следует, что у любой числовой последовательности
всегда существует по крайней мере один частичный предел (заведомо
конечный, если последовательность ограничена, и бесконечный, если
она не ограничена).
?) Б. Больцано A781-1848) — чешский математик.

86 Гл. 1. Дифференциальное исчисление функций одной переменной
5.9. Критерий Коши. В этом пункте дается критерий*) сходи-
сходимости последовательности, т. е. критерий существования у нее ко-
конечного предела, в терминах только самих членов данной последова-
последовательности, иначе говоря, без привлечения значения самого предела.
Определение 11. Числовая последовательность {хп}, п = 1,
2,..., называется фундаментальной последовательностью, если она
удовлетворяет следующему условию: для любого г > 0 существует
такой номер по, что для всех п > по и т > по выполняется нера-
неравенство	.	.	/к _ЛЧ
\Хп - хт\ < е.	E.72)
Это условие называется условием Коши**). Его можно записать
в несколько другом виде: для любого г > 0 существует такой номер
по, что для всех п > по и всех целых р ^ 0 выполняется неравенство
\хп+Р -хп\ < г.	E.73)
Чтобы убедиться в равносильности этих утверждений, достаточ-
достаточно заметить, что из двух номеров тип всегда один не превышает
другого, например, т ^ п, и тогда, положив р = т — п, мы перейдем
от записи E.73) к записи E.72).
Докажем несколько лемм о фундаментальных последователь-
последовательностях.
Лемма 2. Если последовательность имеет конечный предел, то
она фундаментальная.
|> Действительно, если последовательность {хп} сходящаяся и а —
ее предел: lim xn = а, то согласно определению предела для любого
п—>-оо
г > 0 существует такой номер п0, что для всех п > п0 выполняется
неравенство
\хп -а\< г/2.	E.74)
Поэтому если т > по и п > по, то
\хп-х
= \(хп-а) + (а-хт)\
хп-а\
т|	| |
Лемма 3. Если последовательность фундаментальная, то она
ограниченная.
|> Действительно, пусть последовательность {хп} фундаментальная.
Тогда согласно условию Коши существует такой номер по, что для
всех т > по и п > по имеет место неравенство
\хп-хт\<1	E.75)
(в условии Коши (см. определение 11) можно взять любое е > 0; мы
взяли здесь г = 1). В частности, при т = по + 1 из E.75) следует,
*) Термин "критерий" употреблен здесь в смысле "необходимое и достаточное
условие".
**) О. Коши A789-1857) — французский математик.

§ 5. Предел числовой последовательности	87
что \хп -хП0+1\ < 1, или
жПо+1 - 1 < хп < жПо+1 + 1, п = по + 1, по + 2, ...,
т. е. последовательность жПо+1,жПо+2, •••? получающаяся из данной по-
последовательности {хп} отбрасыванием первых ее по членов xi,X2,...
...,жПо, является ограниченной последовательностью. Поэтому огра-
ограничена, очевидно, и вся последовательность {хп}. <\
Лемма 4. Если некоторая подпоследовательность фундамен-
фундаментальной последовательности сходится, то ее предел является и
пределом всей последовательности.
|> Пусть {хп} — фундаментальная последовательность, {хПк} — ее
сходящаяся подпоследовательность и
lim хПк = а.	E.76)
k—too
Зададим произвольно е > 0. Согласно условию Коши существу-
существует такой номер по, что для всех п,т > по выполнятся неравенство
\хп -хт\ < г/2.	E.77)
Выберем теперь номер ко так, чтобы при всех к > ко имело место
неравенство	^	/к ~оЛ
к	пк> по	E.78)
(это возможно сделать в силу того, что lim n/. = +оо). Тогда при
к—>-оо
всех п > по и к > ко справедливо неравенство
E.77) 2
E.78)
Перейдя здесь к пределу при к —у оо, в силу условия E.76) полу-
получим, что для всех п > по выполняется неравенство
-а\ ^ | <е.
Это и означает, что lim xn = а. <1
/с—>-оо
Теорема 5 (критерий Коши). Для того чтобы последователь-
последовательность имела конечный предел, необходимо и достаточно, чтобы она
удовлетворяла условию Коши.
\> Действительно, необходимость выполнения условия Коши для
сходящейся последовательности составляет содержание леммы 2.
Если же последовательность удовлетворяет условию Коши, т. е.
является фундаментальной, то согласно лемме 3 она ограничена, и,
следовательно, в силу принципа компактности (см. теорему 4) из нее
можно выделить подпоследовательность, имеющую конечный предел.
Тогда из леммы 4 следует, что вся заданная последовательность схо-
сходится к тому же пределу. <|
Упражнение. Доказать, что не всякая фундаментальная после-
последовательность рациональных чисел имеет рациональный предел.

Гл. 1. Дифференциальное исчисление функций одной переменной
5.10*. Изображение действительных чисел бесконечными
десятичными дробями. Пусть задано действительное число а ^ 0.
В силу принципа Архимеда существует натуральное число п > а. В
множестве чисел 1,2,...,п возьмем наименьшее среди тех, которые
больше числа а, т. е. такое натуральное число по, что
по — 1 ^ а < по.
Обозначим по — 1 через ао, а отрезок [ао, ао + 1] — через /q. Тогда
a Е /о = \_olo] ао + 1], а ф ао Н~ 1
(поскольку в этом пункте концы отрезков будут обозначаться деся-
десятичными дробями, то в качестве разделительного знака между кон-
концами отрезков удобнее употреблять не запятую, а точку с запятой,
т. е. вместо [а, Ь] писать [а; Ь]).
Разобьем отрезок /о на 10 равных отрезков и каждому отрезку
слева направо припишем последовательно индексы 0,1, 2,..., 9. Точ-
Рис. 54
ка а либо принадлежит только одному из этих отрезков, обозначим
его 1\ (рис. 53 и рис. 54), либо двум соседним, если она является их
общим концом (рис. 55). В последнем
случае для однозначности выбора от-
отрезков обозначим через 1\ тот из двух
соседних отрезков, для которого точ-
точка а является левым концом (целесооб-
Рис. 55	разность такого выбора будет пояснена
ниже). Итак, в обоих случаях точка а лежит на отрезке 1\ и не явля-
является его правым концом.
Обозначим левый конец отрезка Д десятичной дробью «o,«i, где
ct\ — индекс отрезка 1\ (одна из цифр 0,1,2, ...,9), тогда правый ко-
конец будет записываться числом «o,«i + Ю. Таким образом,
а е h = [«o,«i; «o,«i + 10—1], а ф «o,«i + 10.
Разобьем отрезок 1\ в свою очередь на десять равных отрезков и
обозначим через 1^ = [ao,«i«25 ao5«i«2 + Ю~2] тот из них, который
содержит точку а, причем она не является его правым концом. Про-
Продолжая этот процесс, получим систему вложенных отрезков
/о D h D h D .- D In D -..,	E.79)

§ 5. Предел числовой последовательности
содержащих точку а, причем она не является правым концом ни од-
одного из них:	_
а е In = [ao,OL1...an',ao,a1...an +10 п],
_	E.80)
а ф ol^,ol1...olti + Ю~п, п = 1,2,...
Поскольку длина отрезка 1п равна 10~п и lim 10~n = 0, то точ-
п—юо
ка а является единственной точкой, принадлежащей всем отрез-
отрезкам /п, п = 1,2,... Отрезок 1п будем называть отрезком ранга п.
Таким образом, каждому действительному числу а ^ 0 однознач-
однозначным образом поставлена в соответствие последовательность вложен-
вложенных отрезков {/п}5 длины которых стремятся к нулю. А именно,
последовательность {/п}, пересечение отрезков которой состоит из
числа а:	°°
П In = W-	E.81)
га=1
При этом разным числам оказываются поставленными в соот-
соответствие разные последовательности вложенных отрезков {/п}5 так
как в силу стремления к нулю длин отрезков 1п пересечение рас-
рассматриваемой последовательности {/п} состоит из единственной точ-
точки а и, следовательно, разные точки числовой прямой принадлежат
разным последовательностям {/п}, т. е. на некотором n-м шаге они
окажутся в разных отрезках ранга п.
Каждая последовательность {/п}5 очевидно, полностью описы-
описывается последовательностью своих левых концов «о, aia2...an
(правый конец получается добавлением числа 10~п к левому кон-
цуM п = 1,2,..., а следовательно, и бесконечной десятичной дробью
ао, aia2...an..., так как левый конец каждого отрезка 1п получается
из этой бесконечной десятичной дроби отбрасыванием всех ее цифр
после запятой, начиная с (п + 1)-й.
В результате каждому действительному числу а ^ 0 оказывает-
оказывается поставленной в соответствие указанным образом бесконечная де-
десятичная дробь «о, aia2...an... Если числу а соответствует дробь
ао, aia2...an..., то пишут
а = «о, aia2-..an...	E.82)
Подчеркнем, что в этой записи через ао обозначается соответствую-
соответствующее неотрицательное целое число, а через an, п = 1,2,..., — одна из
цифр 0,1,2,..., 9.
Получающиеся в результате описанной конструкции бесконечные
десятичные дроби E.82) не могут иметь периода, состоящего только
из цифры 9. В самом деле, пусть некоторому действительному числу
соответствует дробь
«о, aia2...ano99...9..., no ^ 0,	E.83)
имеющая период, состоящий из цифры 9 и начинающийся с
(по + 1)-го места после запятой. Обозначим через {/п} последова-
последовательность отрезков, соответствующих дроби E.83) в том смысле, что

90 Гл. 1. Дифференциальное исчисление функций одной переменной
левым концом отрезка /n, n = 1,2,..., этой последовательности явля-
является число «о, aia2...anj получающееся из дроби E.83) отбрасыва-
отбрасыванием всех десятичных знаков после запятой, начиная с (п + 1)-го, а
правым — число «о, aia2...an + 10~п. Такая последовательность от-
отрезков является вложенной системой отрезков, длины которых стре-
стремятся к нулю, и, следовательно, существует единственное число а,
принадлежащее всем отрезкам 1п этой системы. Поскольку в дро-
дроби E.83), начиная с (по + 1)-го места после запятой, стоит цифра 9,
то точка а, начиная с отрезков ранга по + 1, будет находиться на от-
отрезке с индексом 9, т. е. на самом правом отрезке. Этим свойством
обладает только правый конец отрезка /По, таким образом, число а
совпадает с правым концом отрезка /По.
При описанной же конструкции соответствия чисел а^Ои беско-
бесконечных десятичных дробей (см. E.72)-E.82)) всегда предполагалось,
что число а не является правым концом ни одного из отрезков соот-
соответствующей ему системы вложенных отрезков {/п} (см- E.79)) — в
этом состояло одно из условий E.80). Полученное противоречие по-
показывает, что при указанной конструкции соответствия чисел а ^ 0
и бесконечных десятичных дробей не участвуют дроби вида E.83),
т. е. с периодом, состоящим из одной лишь цифры 9.
Вместе с тем каждая бесконечная десятичная дробь
«о, а1а2...ап...,	E.84)
не имеющая периода, состоящего только из одной цифры 9, оказы-
оказывается поставленной в соответствие единственному числу а ^ 0, яв-
являющемуся точкой пересечения отрезков
1п = [а0, ai...an] (*о, ai...an + 10~n], га = 1,2,...	E.85)
В самом деле, последовательность отрезков E.85) является вло-
вложенной системой отрезков, длины которых 10~п стремятся к нулю,
а потому существует единственное число а, принадлежащее всем от-
отрезкам a Е /n, n = 1,2,...
Покажем, что дробь E.84) поставлена в соответствие этому чис-
числу а, т. е. что выполнены условия E.79)-E.81). Очевидно, следует
лишь показать, что число а не является правым концом ни одного из
отрезков 1п. Если бы оказалось, что число а является правым концом
некоторого отрезка 1По ранга по системы {/п}5 то число а было бы и
правым концом всех отрезков 1п ранга п > по, т. е. принадлежало бы
отрезкам ранга п > по с индексом 9. Это означает, что в дроби E.84),
начиная с (п0 + 1)-го места после запятой, все время стоит цифра 9 —
противоречие. Итак, действительно, каждая бесконечная десятичная
дробь, не имеющая периода, состоящего из одной цифры 9, поставлена
в соответствие некоторому числу а ^ 0.
В результате установлено взаимно однозначное соответствие
между всеми неотрицательными действительными числами и всеми

§ 5. Предел числовой последовательности	91
бесконечными десятичными дробями, не имеющими периода, состо-
состоящего только из цифры 9.
Бесконечные десятичные дроби с периодом, состоящим только из
нуля, обычно записываются в виде конечной десятичной дроби, т. е.
вместо «о, aia2...an00...0... пишут «о, aia2...an-
Подчеркнем, что при конструкции соответствия E.79)-E.82) меж-
между неотрицательными действительными числами и десятичными дро-
дробями это соответствие оказалось взаимно однозначным в силу того,
что рассматривались лишь десятичные дроби, не имеющие периода,
состоящего только из цифры 9, и требовалось, чтобы никакое а не яв-
являлось правым концом ни одного отрезка 1п соответствующей этому
числу а системы {1п}. При отказе от выполнения этих условий для
каждого числа, являющегося концом некоторого отрезка ранга п, су-
существовали бы две его записи в виде бесконечной десятичной дроби:
ао, ai...an99...9... = ao, ai...(an + 1H0...0..., ап ф 9,
например,
1 = 1,00...0 = 0,99...9...
Если а > 0 и а соответствует дробь ao, aia2...an..., то отрица-
отрицательному числу —а поставим в соответствие ту же дробь, только со
знаком минус, и будем писать
-а = —ao, aia2...an...	E.86)
Запись действительных чисел в виде E.82) и E.86) называется их
десятичной записью.
Бесконечные десятичные дроби ±ao, aia2...an..., не имеющие
периода, состоящего только из одних девяток, называются допус-
допустимыми.
Из всего сказанного видно, что десятичная запись действитель-
действительных чисел устанавливает между всеми действительными числами и
всеми допустимыми десятичными дробями взаимно однозначное со-
соответствие.
Конечно, нужно не только уметь записывать каждое действитель-
действительное число в виде десятичной дроби, но и уметь производить с по-
помощью этой записи различные операции над числами: сравнивать
их по величине, складывать, вычитать, умножать, делить и т.д. Пе-
Перейдем к рассмотрению этих вопросов.
Пусть снова а ^ 0 и а = ao, aia2-..an... Введем обозначения
ап = aOj ai...anj an = an + 10~n, n = 0,1,2,...	E.87)
Если же a<0 и а = —ao, aia2...an..., то положим
an = -а0, a1a2...an - 10~n, an = an + 10~n, n = 0,1, 2,... E.88)

92 Гл. 1. Дифференциальное исчисление функций одной переменной
Из этих формул сразу следует, что если Ъ < 0 и Ъ = -а, а > 0, то
(рис. 56)
hn = -an, bn = -anJ п = 0,1,2,...	E.89)
Конечная десятичная дробь ап (как в случае E.87), так и в слу-
случае E.88)) называется нижним десятичным приближением порядка п
числа а, а дробь ап — его верх-
Ъ=\~а	| ? | > ним десятичным приближением того
Ьп=-ап Ъп=-ап ап ап же порядка. Очевидно, что в случае
а ^ 0 конечные десятичные дроби ап
Рис- 56	и ап являются концами отрезка 1п
(см. E.80)) последовательности вложенных отрезков {/п}5 поставлен-
поставленной в соответствие числу а = а0, aia2...an..., т. е.
1п = \ап,пп], п = 1,2,...,	E.90)
и, таким образом,
ап^а^ап, п = 1,2,...	E.91)
В силу соотношений E.89) система отрезков E.90) является сис-
системой вложенных отрезков и при а < 0; выполняется в этом случае
и неравенство E.91). Из того, что система отрезков E.90) является
системой вложенных отрезков, следует, что
an^an+1, an+i^an, п = 1,2,...,	E.92)
т. е. что последовательность нижних десятичных приближений пред-
представляет собой возрастающую последовательность, а верхних — убы-
убывающую.
Наконец, из E.87) и E.88) непосредственно следует, что
ап-ап = 10~п,	E.93)
а так как lim 10~n = 0, то для любого действительного числа а после-
п—>-оо
довательность отрезков E.90) образует систему вложенных отрезков,
длины которых стремятся к нулю и единственной точкой пересече-
пересечения которых является точка а. Отсюда имеем (см. замечание в п. 5.7)
lim an = lim an = а.	E.94)
п—>-оо	п—>-оо
Таким образом, доказано следующее свойство десятичных при-
приближений.
1°. Каково бы ни было действительное число а, последователь-
последовательность его нижних десятичных приближений {ап} возрастает, верх-
верхних {ап} убывает, и имеет место равенство E.94).
Следствие. Всякое действительное число является пределом
последовательности рациональных чисел.

§ 5. Предел числовой последовательности	93
|> В самом деле, нижние и верхние десятичные приближения лю-
любого числа, представляя собой конечные десятичные дроби, являют-
являются рациональными числами, поэтому утверждение следствия непос-
непосредственно вытекает из равенства E.94). <|
Перейдем теперь к сравнению по величине действительных чисел
посредством их десятичной записи.
2°. Если a Е /?, Ъ Е /?, то а < Ъ в том и только том случае, ког-
когда существует такое неотрицательное целое число п0, что для всех
п > по выполняется неравенство
Ъп.	E.95)
Ъп
|> Если а < Ь, то из условия E.94) согласно свойству 3° пределов
(п. 5.3) сразу следует существование такого п0, что для п > п0 вы-
выполняется условие E.95). Обратно, если существует такое по, что для
всех п > по выполняется неравенство E.95), то, перейдя в нем к пре-
пределу при п —У оо, получим а ^ Ь, но случай а = Ъ невозможен, так
как тогда в силу однозначности десятичной записи чисел для всех
п = 0,1,2,... имело бы место равенство ап = Ьп, что противоречило
бы условию E.95).
Следовательно, а < Ь. <\
С помощью арифметических операций над нижними и верхни-
верхними десятичными приближениями чисел можно получить нужный ре-
результат соответствующих операций над самими числами с любой на-
наперед заданной точностью. Это видно из следующего утверждения.
3°. Если а е R,be /?, то
lim (an -Ъп)=а-Ъ,
п—>-оо
lim anhn = аб,
а при Ь ф О
а„ а
п—>-оо
О
\> Эти формулы сразу следуют из равенств E.94) и свойств пределов
числовых последовательностей (п. 5.6). Отметим лишь, что из условия
lim Ъ = Ъ ф 0 следует существование такого номера по, что для всех
п—>-оо
п > п0 выполняется неравенство Ьп ф 0 (см. следствие 1 свойства 3°
пределов, п. 5.3) и при рассмотрении предела lim ^ берутся только
п—>-оо Оп
дроби =ZI, для которых Ъп ф 0, что заведомо имеет место при п > по- <\
-п

94 Гл. 1. Дифференциальное исчисление функций одной переменной
5.11. Предел последовательности комплексных чисел. Мно-
Многие из понятий, введенных для последовательностей действительных
чисел, обобщаются на последовательности комплексных чисел, при-
причем с сохранением ряда свойств.
Комплексное число z$ называется пределом последовательности
комплексных чисел {zn}, если для любого г > 0 существует такой но-
номер п?, что для всех п > п? выполняется неравенство
\zn - zq\ < e.
В этом случае пишут lim zn = z0 и говорят, что последователь-
п—>-оо
ность {zn} сходится к числу zq.
Таким образом, по форме это определение совершенно такое же,
как для предела последовательности действительных чисел, однако
геометрический смысл его иной: на комплексной плоскости нера-
неравенство \z - zo\ < г задает открытый круг (т. е. круг без ограничи-
ограничивающей его окружности) радиуса г с центром в точке z0. Этот круг
называется г-окрестностью (или, короче,
окрестностью) точки z0; будем его обозначать
U = U(zo,e).
Условие lim zn = z$ означает, что, какова бы
п—уоо
ни была окрестность U точки zo, найдется та-
такой номер по, что все члены последовательности
{zn} с номерами, большими по, будут содержать-
содержаться в этой окрестности (рис. 57). Тем самым вне
Рис" 57	этой окрестности будет находиться только ко-
конечное множество членов рассматриваемой последовательности.
Существование предела lim zn = zo в силу самого определения
п—>-оо
предела равносильно существованию предела
lim \zn-z0\ =0,	E.96)
п—>-оо
т. е. сходимости к нулю последовательности действительных чисел
\zn -20|, п = 1,2,...
Если zn = хп + упг, zo = х0 + уог, хп, уп, х0, Уо G /?, то
1
^ —
\ ?
\
\
\
\
\
Zn/
\zn - ^о| = у/(хп ~ хоJ + (уи ~ УоJ	E.97)
и, следовательно,
\хп ~ хо\ ^\z- zo\, \уп - 2/о| ^ \z - zo\.	E.98)
Из соотношений E.97), E.98) следует, что условие lim \zn — zo I =
= 0 равносильно условиям lim xn = жо, lim yn = y0. Это означает,
n—>-oo	n—>-oo
что последовательность комплексных чисел zn = хп + ynh ^ = 1,2,...,
имеет своим пределом число z$ = хо + yoi в том и только том слу-
случае, когда последовательности действительных {хп} и мнимых {уп}

§ 6. Предел и непрерывность функций	95
частей членов последовательности {zn} имеют своими пределами со-
соответственно хо и Не-
Непоследовательность {zn} комплексных чисел называется ограни-
ограниченной, если ограничена последовательность действительных чи-
чисел {\zn\} (т. е. если ограничена последовательность абсолютных ве-
величин членов данной последовательности).
На последовательности комплексных чисел обобщаются многие
предложения, доказанные для последовательностей действительных
чисел. Так, если последовательность комплексных чисел имеет пре-
предел, то он единствен; всякая последовательность комплексных чисел,
имеющая предел, ограничена; из всякой ограниченной последователь-
последовательности комплексных чисел можно выделить сходящуюся; для последо-
последовательностей комплексных чисел имеет место аналог критерия Коши
сходимости последовательностей действительных чисел; переносятся
на последовательности комплексных чисел и свойства пределов, свя-
связанные с арифметическими операциями над последовательностями.
Все это следует, например, из того, что сходимость последовательнос-
последовательности комплексных чисел равносильна сходимости последовательностей
их действительных и мнимых частей.
Аналогично случаю последовательностей действительных чисел
для последовательностей комплексных чисел определяется и беско-
бесконечный предел (без знака, так как комплексные числа не имеют зна-
знака): lim zn = оо означает по определению, что lim \zn\ = +оо.
п—юо	п—юо
Замечание. Обычно, когда говорят, что некоторая последова-
последовательность комплексных (в частности, действительных) чисел имеет
предел, то под этим подразумевают, что этот предел конечный, а слу-
случай бесконечного предела оговаривается особо.
§ 6. Предел и непрерывность функций
6.1. Первое определение предела функции. В дальнейшем
под термином "элемент", "точка" будет пониматься либо действи-
действительное число, либо одна из бесконечностей оо, +оо и -оо (бесконеч-
(бесконечно удаленные точки).
Сформулируем сначала определение предела функции /: X —>¦/?,
X С /?, в терминах пределов последовательностей. Это определение
часто называют определением предела функции по Гейне*).
Определение 1. Точка а называется пределом значений функ-
функции /(ж), х Е X (или, короче, пределом функции /), в точке хо (или,
что то же самое, при х —> жо*), если для любой последовательности
*) Г. Гейне A821-1881) — немецкий математик.
*) Читается "при ж, стремящемся к хоп.

96 Гл. 1. Дифференциальное исчисление функций одной переменной
точек хп е X, п = 1,2,..., имеющей своим пределом точку ж0, т. е.
такой, что
lim хп = ж0,	F.1)
п—юо
последовательность {f(xn)} значений функции / в точках жп, п =
= 1, 2,..., имеет своим пределом точку а, т. е.
lim f(xn) = а.	F.2)
п—>-оо
В этом случае пишут
lim /(ж) = а или /(ж) —у а при ж —у жо,	F.3)
ж—^жо
а если жо — конечная точка: жо G /?, то также
lim fix) = a.
ж-жо^О V '
В символической записи с помощью логических символов это
определение выглядит следующим образом:
lim /(ж) = а <Й>
ж—^жо
% {Ужп G X, п = 1, 2,...: lim жп = ж0 => lim /(жп) = а}. F.4)
п—Усю	п—Усю
Двоеточием здесь, как и раньше в символических формулах (см.
п. 1.1), отделяются описания рассматриваемых в условии элементов.
В данном случае рассматриваются элементы хп G X, п = 1,2,..., та-
такие, что lim хп = ж0.
п—>-оо
Если в формуле F.4) а является числом, то говорят, что функция /
имеет в точке жо конечный предел (равный а).
Сформулированное определение предела при заданной функции
/(ж), ж G X, содержательно только тогда, когда для точки жо сущест-
существуют последовательности точек хп G X, п = 1,2,..., имеющие своим
пределом (конечным или бесконечным) точку ж0: lim хп = ж0.
п—>-оо
Определение 2. Пусть X G /?. Точка жо, для которой существу-
существует последовательность хп G X, п = 1,2,..., имеющая своим пределом
точку жо,
lim хп = жо,	F.5)
называется точкой прикосновения множества X.
Если точка прикосновения жо является одной из бесконечнос-
бесконечностей оо, +оо или —оо, то она называется также бесконечно удален-
удаленной точкой прикосновения (множества X). Очевидно, что точка ж0 =
= оо является бесконечно удаленной точкой прикосновения мно-
множества X тогда и только тогда, когда множество X неограничен-
неограниченно, точка жо = +00 — тогда и только тогда, когда множество X неог-
неограниченно сверху, а жо = —оо — тогда и только тогда, когда X не-
неограниченно снизу.

§ 6. Предел и непрерывность функций	97
Очевидно, что любая точка ж0, принадлежащая самому множест-
множеству X, является его точкой прикосновения, так как стационарная по-
последовательность хп = хо Е X, п = 1, 2,..., удовлетворяет условию F.5).
Точками самого множества не исчерпываются, вообще говоря, все его
точки прикосновения: могут существовать точки прикосновения, и
не принадлежащие ему. Например, точки х = а и х = Ъ являются точ-
точками прикосновения интервала (а, Ъ) и не содержатся в нем.
Замечание 1. Точка является точкой прикосновения данного
множества тогда и только тогда, когда любая ее окрестность пересе-
пересекается с этим множеством.
В самом деле, если жо — точка прикосновения множества X, то
существует последовательность хп —> жо, хп Е X, п = 1, 2,..., и, следо-
следовательно, в любой окрестности точки жо будут содержаться все чле-
члены этой последовательности, начиная с некоторого, и они являются
точками множества X.
Наоборот, если в любой окрестности точки жо имеются точки мно-
множества X, то выберем по точке множества X в каждой окрестности
U(xo, 1/п) и обозначим эти точки через жп, т. е.
хп е X П U(xo, 1/п), п = 1, 2,...
Если жо Е R, т. е. жо является числом, то хп G U(xo, 1/n) означает,
что \хп — хо\ < 1/п. Отсюда при п —> оо следует, что lim \хп — хо\ = О,
п—>-оо
т.е. lim жп = жо- Если же жо — бесконечно удаленная точка, напри-
п—>-оо
мер, жо = оо, то хп G С/(оо, 1/п) означает, что (см. п. 2.2) |жп| > —^— =
= п. Отсюда при п —>- оо вытекает, что lim жп = оо. Аналогично рас-
п—>-оо
матриваются случаи ж0 = +оо и ж0 = -оо. Таким образом, всегда из
условия хп G U(xo, 1/п) следует, что lim хп = жо-
п—>-оо
Отметим, что нижняя и верхняя грани множества (конечные или
бесконечные) являются его точками прикосновения.
Поскольку понятие предела функции /: X ->• R в точке ж0 содержа-
содержательно только тогда, когда эта точка является точкой прикосновения
множества X, то в дальнейшем при рассмотрении предела функции /
в точке жо будем всегда предполагать (как правило, специально это не
оговаривая), что точка жо является точкой прикосновения множест-
множества X.
Примеры. 1. Рассмотрим функцию
г/ \ 2х -\- х — 1
/и
определенную на множестве X = R\ {1}. Выясним, существует ли
7 Л.Д.Кудрявцев, т.1

Гл. 1. Дифференциальное исчисление функций одной переменной
lim /(ж). Пусть хп е X, п = 1, 2,..., и lim хп = 0; тогда (п. 5.6)
lim f(xn) = lim
2x1
Хп-1
Хп -
2( lim жп) + lim жп — 1
п—>-оо	п—>-оо
lim жп — 1
= 1.
Таким образом, существует предел lim f(xn) = 1, а так как он не
п—>-оо
зависит от выбора последовательности жп —у 0, жп G X, п = 1, 2,..., то
существует и
lim /(ж) = 1.
2. Рассмотрим функцию
1
f (ж) = sin -.
ж
Она определена на множестве X = R \ {0} (рис. 58). Выясним,
существует ли предел lim /(ж). Возьмем две последовательности:
Ж"°	± и х>	Х
У
= 1,2,...
Очевидно,
	:	,
тг/2 + 2тгп'
П =
lim хп = lim х' = 0,
П—>-ОО	П—У(Х>
хп ех, х'пе х,
f(xn) = sinnn = 0,
Рис. 58
Поэтому
lim f(xn) = 0, lim
^) = 1,
а это означает, что у рассматриваемой функции не существует пре-
предела в точке хо = 0.
Определение 3. Если задана функция /(ж), х G X, Е С X
и жо — точка прикосновения множества Е, то пределом функции /(ж)
по множеству Е в точке ж0 называется предел ее сужения fE
(см. п. 1.2) в этой точке:
lim /(ж) d= lim fE(x).	F.6)
X—УХо	X—УХо
хЕЕ
Очевидно, что если существует lim /(ж), то для любого множест-
множестве—>Хо
ва Е С X, для которого точка жо является точкой прикосновения,
существует lim /(ж), причем эти пределы равны.
XYX
Иногда при обозначении предела по множеству Е вместо ж G Е
будут употребляться для краткости другие обозначения, смысл ко-

§ 6. Предел и непрерывность функций
99
торых будет ясен из контекста. Например, при Е = X \ {ж0} будем
писать lim /(ж), а при Е = {хо} будем писать lim f{x).
х—Ухо, хфхо	х—Ухо, х=хо
3. Пусть
f(r\ - 1 !> если х ? С
Л ;~\0, если х е /.
Эта функция называется функцией Дирихле*). Имеем
а предел Нт /(ж) по всему множеству определения функции /, т. е.
х—>0
по всему множеству действительных чисел, не существует.
Часто пределы функций рассматриваются по пересечениям об-
областей определения этих функций с так называемыми проколотыми
окрестностями.
о
Определение 4. Проколотой г-окрестностью U(xo,e) точки хо
называется множество, получающееся удалением точки ж0 из ее
^-окрестности:
def
U(xo,e) = U(xo,e) \{x0}.
F.7)
Проколотую окрестность будем также обозначать и через U(xo).
Пример 4. Пусть
1, если х > О,
О, если х = О,
-1, если х < 0.
def
sign ж =
Тогда (рис. 59 и рис. 60) предел lim |signx| функции |signx| по всей
х—>0
	>
1
о
y=sign;r
X
= \signx\
Рис. 59
Рис. 60
ее области задания, т. е. по всей числовой прямой (или, что равно-
равносильно, по любой окрестности U@) точки хо = 0), не существует, а
о
предел этой функции по проколотой окрестности U@) точки хо = 0
существует и равен 1: lim Isignxl = 1.
х—уО
хе и(х)
?) Л. Дирихле A805-1859) — немецкий математик.
7*

100 Гл. 1. Дифференциальное исчисление функций одной переменной
о
Действительно, для любой последовательности жп? U@), n =
= 1, 2,..., lim хп = 0, имеем f(xn) = 1, а поэтому lim f(xn) = 1. Это
п—Уоо	п—>-оо
означает, что lim f(x) = 1, т. е. что предел по проколотой окрест-
х>0
ности существует и равен 1. Если же х'п = 1/п, ж" = 0, п = 1, 2,..., то
lim х'п = lim < = 0, и /«) = 1, /«) = 0. Поэтому lim f(x'n) =
п-У оо	га-юо	га-юо
= 1, a lim fix1') = 0. Это означает, что предел lim fix) no всей
га-юо	ж-И)
()
окрестности t/@) не существует.
Замечание 2. Пусть заданы последовательность {хп} и функ-
функция ip: N ^ N. Введем обозначение ip(k) = пи и рассмотрим последова-
последовательность {xnfc}. Иначе говоря, из значений последовательности {хп}
образуем новую последовательность {хПк}, в которой порядок членов
может не совпадать с их порядком в исходной последовательности.
Таким образом, последовательность {хПк} не является, вообще гово-
говоря, подпоследовательностью последовательности {хп}.
В этих обозначениях справедливо следующее утверждение.
Лемма 1. Если существует конечный или бесконечный предел
lim xn = а и lim n/. = оо, то lim хПк = а.
п—>-оо	к—уоо	к—уоо
|> Действительно, из условия lim xn = а следует, что для любого
п—>-оо
г > 0 существует такой номер по, что для всех номеров п > по вы-
выполняется включение хп е U(a,e), а из условия lim пи = оо, — что
k—too
для по существует такой номер ко, что для всех к > ко выполняется
неравенство пи > п0 и, следовательно, включение хПк е U(a,e). Это
и означает, что lim хПк = а. <\
к^-оо
Из леммы 1 следует, что понятие предела последовательности яв-
является частным случаем понятия предела функции.
|> Действительно, пусть предел последовательности {хп} равен а:
lim хп = а. Рассмотрим функцию /(п) = жп, п G N. В силу леммы 1
п—>-оо
для любой последовательности вида {хПк}, п\~ G A/, lim п\~ — оо, име-
к—>-оо
ем lim xnfc = а, т. е. lim f(rik) = а. Согласно определению 1 это и
/с—>-оо	/с—>-оо
означает, что lim /(n) = а. <1
п—>-оо
6.2. Определение непрерывности функции. При рассмотре-
рассмотрении предела функции /(ж), х е X, в точке ж0 случай, когда ж0 G X,
представляет особый интерес — он приводит к понятию непрерывной
функции.
Если хо G X и существует предел lim /(ж), то он равен /(ж0):
lim /(ж) = /(жоГ	F.8)
X—YXQ

§ 6. Предел и непрерывность функций	101
В самом деле, поскольку ж0 G X, то в качестве последовательности
хп Е X, п = 1, 2,..., lim жп = жо, в этом случае можно взять стацио-
п—Уоо
нарную последовательность хп = жо, п = 1,2,... Для нее имеем
lim f(xn) = lim /(ж0) = f(x0).	F.9)
п—>-оо	n—>-oo
Если существует предел lim /(ж), то, согласно его определению,
Х^Хо
для любой последовательности хп ? X, п = 1,2,..., для которой
lim жп = жо, существует предел последовательности /(жп), п = 1, 2,...,
п—Уоо
и все пределы таких последовательностей равны между собой. Поэ-
Поэтому из равенства F.9) следует выполнение условия F.8).
Определение 5. Если
lim /(ж) = /Оо),
X—УХо
то функция f(x) называется непрерывной в точке х0.
Согласно сказанному выше функция /(ж) непрерывна в точке жо
тогда и только тогда, когда существует предел (по множеству X)
2,х -\- х	1
lim fix) и жо G X. Например, функция fix) = 	 является
х—ухо	X — 1
непрерывной в точке ж = 0 (как и во всякой другой точке ж ф 1), ибо,
как это было показано в п. 6.1,
Функция же	•
-/ ч I sin-, если ж ф О,
I О,	если ж = О,
не является непрерывной в точке ж = 0, так как предел lim sin - не
существует.
6.3. Второе определение предела функции. Существует дру-
другое определение предела функций, в котором используется понятие
окрестности, оно называется определением по Коши.
Определение 6. Точку а называют пределом функции /(ж),
ж G X, при ж —> жо (или, что то же самое, в точке жо) и пишут
lim /(ж) = а, если для любой окрестности U(a) точки а существует
X—УХо
такая окрестность U{xq) точки жо, что
f(XnU(xo))cU(a).
Используя логические символы, это определение можно записать
в следующем виде:
lim /(ж) = a d4 \/U(a) 3?/(ж0): f(X П U(x0)) С U(a),
Х^УХо

102 Гл. 1. Дифференциальное исчисление функций одной переменной
или, что равносильно,
lim /(ж) = a d4 \/U(a) 3U(x0) Уж G X П U(x0): /(ж) G U(a) F.10)
x—Vxq
(в подобных символических записях двоеточие читается как "имеет
место").
Вспоминая определения окрестностей, эти определения для соот-
соответствующих конкретных случаев можно перефразировать в терми-
терминах неравенств. Рассмотрим важный случай, когда хо и а — дейст-
действительные числа.
Число а называется пределом функции /(ж), х Е X, в точке жо Е /?,
если для любого г > 0 существует такое 6 > 0, что для всех ж, удов-
удовлетворяющих условию |ж — хо\ < й, х G X, выполняется неравенство
\f(x)-a\<e.
Это определение действительно равно-
равносильно определению F.10) в случае, если
хо G R и a G /?, так как условие \х — хо\ < S
равносильно условию
х е U(x0) = U(xo,S),
а условие \f(x) — а\ < е — условию
а+г
(рис. 61).
Рис. 61	о	«л.
В символической форме для рассмат-
рассматриваемого случая определение предела функции имеет вид
lim /(ж) = а *Ш Уг > 0 36 > 0 Уж G X, |ж - жо| < 5: |/(ж) - а| < г.
X^-Xq
В частности, если функция / непрерывна в точке жо G X С /? и
а = /(жо) (в этом случае жо и а являются числами), то определение
непрерывности в символической записи имеет вид
lim /(ж) = /(ж0)
X—YXQ
36 > 0
, |ж-жо|<E:
г.
В качестве примера бесконечных пределов рассмотрим определе-
определение предела lim /(ж) = —оо:
ж-^+оо
lim /(ж) = -оо *Ш Уг > 0 36 > 0 Уж G X, ж > ^ : /(ж) < --.
х—у-\-оо	о	е
Теорема 1. Определения 1 и б предела функции в точке прикос-
прикосновения множества задания функции равносильны.
\> Пусть функция / задана на множестве X и жо — точка прикос-
прикосновения этого множества. Предположим сначала, что lim /(ж) = а в

§ 6. Предел и непрерывность функций	103
смысле определения 1, и покажем, что тогда число а является и пре-
пределом функции в смысле определения 6. Допустим, что это не так,
т. е. (см. F.10)), что существует такая окрестность ?/(а), что для
любой окрестности U(xo) найдется такая точка ж Е XnU(xo), что
f(x) 0 U(a), или, в символической записи,
3U(a) W(x0) 3xeXnU(xo): f(x)?U(a).	F.11)
В частности, указанные точки х найдутся в каждой окрестности
U(xo, 1/п), п = 1, 2,..., точки хо. Обозначим эти точки жп, т. е.
хп е ХГШ(жо,1/п),	F.12)
f(xn)#U(a).	F.13)
Из условия F.12) следует (см. пример в п. 5.3), что
lim хп = ж0.	F.14)
п—Уоо
Поскольку а = lim /(ж) в смысле определения 1, то из выполнения
х->хо
условия F.14) следует, что lim f(xn) = а. Следовательно, для любой
п—Уоо
окрестности С/(а), в частности, и для окрестности С/(а), указанной в
условии F.13), существует такой номер по, что для всех п > по вы-
выполняется включение
f(xn) e U(а),	F.15)
что противоречит условию F.13). В одну сторону утверждение тео-
теоремы доказано.
Пусть теперь а = lim f(x) в смысле определения б предела функ-
X—УХо
ции /: X —>¦/?, хо — точка прикосновения множества X и хп —> жо,
жп G X, п = 1, 2,... Покажем, что lim f(xn) = а. Зададим произволь-
п—>-оо
но окрестность U(a) точки а и выберем для нее окрестность U(xo)
точки ж0, удовлетворяющую условию F.10). Для окрестности U(xo)
в силу условия lim хп = хо существует такой номер по, что для
п—уоо
всех п > по выполняется включение хп G U(xo), а так как хп G X,
п = 1, 2,..., то при п> по будем иметь xnGlfl ?7(жо). Следовательно,
в силу F.10) при п > по имеет место включение f(xn) G U(a), т. е.
lim f(xn) = a.
п—>-оо
Это и означает, что lim /(ж) = а в смысле определения 1. <|
X—YXQ
6.4. Условие существования предела функции. Согласно
определению предела функции (п. 6.1) для того, чтобы существовал
предел lim /(ж) функции /(ж), ж G X, нужно, чтобы для любых
X—УХо
последовательностей хп ->• ж0, жп G X, п = 1,2,..., существовали пре-
пределы lim f(xn) и они были равны между собой. Покажем, что второе
п—Уоо
условие вытекает из первого. То есть, не предполагая равенство этих

104 Гл. 1. Дифференциальное исчисление функций одной переменной
пределов, а предполагая только их существование, можно доказать
их равенство, а следовательно, и существование предела функции.
Точнее, докажем следующее утверждение.
Лемма 2. Для того чтобы функция /(ж), ж Е X, имела конечный
или определенного знака бесконечный предел в точке жо, являющейся
конечной или бесконечно удаленной точкой прикосновения множест-
множества X, необходимо и достаточно, чтобы для любой последовательнос-
последовательности хп —У жо, хп Е X, п = 1,2,..., последовательность соответст-
соответствующих значений функции {/(жп)} имела предел (конечный или
определенного знака бесконечный).
\> Необходимость сформулированного условия для существова-
существования lim f(x) содержится в самом определении предела функции
х—Vxq
(см. F.4)), в котором утверждается существование пределов
lim f(xn) для всех указанных в условиях леммы ПОСЛеДОВатеЛЬНОС-
тй—>-оо
тей {хп}.
Докажем достаточность этого условия для существования преде-
предела функции. Пусть х'п —> жо, ж" —> жо, х'п Е X, ж" Е X, п = 1, 2,..., и
существуют пределы lim fix') Е /?, lim fix1') E R. Покажем, что
они равны. Положим
x'k, если n = 2k-l,
,,	o7	ft, — 1, Z, ...
^, если п = 2Ат,
Тогда lim xn = жо и жп G X, n = 1, 2,... Согласно условиям леммы
п—Yoo
существуют пределы
lim f(x'n), lim /(ж^), lim /(жп),
п—>-оо	п—>-оо	п—>-оо
причем {/(ж^)} и {/(ж^)} являются подпоследовательностями после-
последовательности {/(жп)}.
Поскольку из существования у последовательности предела (ко-
(конечного или бесконечного) следует существование того же предела у
любой ее подпоследовательности, то будем иметь
lim f(x'n) = lim f(xn) = lim /«).
n—>-oo	n—>-oo	n—>-oo
Таким образом, пределы последовательностей {/(жп)}, где хп —>¦
->• ж0, inGl, n = 1,2,..., не зависят от выбора указанных после-
последовательностей {хп}. Обозначив общее значение пределов последо-
последовательностей {/(жп)} через а, получим lim /(ж) = а. <\
х^х0
6.5. Предел функции по объединению множеств.
Лемма 3. Пусть функция / задана на объединении Х\ U Х<± мно-
множеств Х\ и Х2, а жо является точкой их прикосновения. Тогда ес-
если при х —> жо функция f имеет равные пределы по множествам Х\

§ 6. Предел и непрерывность функций	105
и Х2, то она имеет тот же предел и по их объединению.
> Если
lim /(ж) = lim /(ж) = a,
то для любой окрестности U(a) точки а существует такая окрест-
окрестность U(xo) точки жо, что образы ее пересечений Х\ П U{xo) и
Х<± П U(xo) с множествами Х\ и Х2 содержатся в окрестности ?/(а),
а тогда и образ их объединения (Xl U X2) П С/(жо) также содержится
в t/(a). Это и означает, что
lira /(ж) = a. <\
Х^-Хо
хехгих2
6.6. Односторонние пределы и односторонняя непрерыв-
непрерывность. Введем обозначения: для любого числового множества X и
любой точки хо расширенной числовой прямой R положим
Х+(х0) = {х е X: х ^ ж0}, Х_(хо) = {х е X: х ^ х0}.
Если х0 G X, то х0 G Х+, ж0 G Х_, а если ж0 0 X, то ж0 0 Х+,
хо $. Х-. Очевидно, если ж0 = +оо, то Х+(х0) = 0, а если ж0 = —оо,
то Х_(ж0) = 0.
В случае когда множество Х+(х0) (соответственно множест-
множество Х-(хо)) непусто, условие, что хо является его точкой прикосно-
прикосновения, равносильно тому, что хо = inf Х+(хо) (соответственно хо =
Определение 7. Пусть задана функция /(ж), х G X и хо G /?.
Точка а называется пределом функции f слева при ж ->• ж0 (соответст-
(соответственно справа), если она является пределом при х —У хо функции / по
множеству Х-(хо) (соответственно по множеству Х+(жо)), т- е- если
lira f(x) = а (соответственно lira f(x) = a).
X—VXq	X—YXq
xeX-(xo)	xex+(x0)
В силу этого определения предел lim f(x) причисляется к пре-
пресс—>-|-оо
делам слева, а lim f(x) — к пределам справа.
х—> — оо
Иначе говоря, предел функции / слева в точке хо — это предел в
этой точке сужения функции / на множество Х+(жо), а предел спра-
справа — это предел сужения / на множество X-{xq).
Для пределов справа и слева сужения функции / на множество
X \ {жо}, т. е. для случая, когда предел берется по множеству, не
содержащему точку жо, имеются специальные обозначения: для пре-
предела слева /(жо — 0) и lim /(ж), а для предела справа /(жо + 0) и
X—YXq— О
lim /(ж). При этом в случае жо = 0 вместо 0 + 0 и 0 — 0 пишут +0
х^ж+0

106 Гл. 1. Дифференциальное исчисление функций одной переменной
и -0, а в случае ж0 = +оо (соответственно ж0 = —оо) вместо +оо - 0
(—оо + О) пишут просто +оо (соответственно —оо).
Если множества Х_(жо) \ {^о}, Х+(жо) \ {^о} не пусты, жо явля-
является их точкой прикосновения и существует предел lim /(ж) по мно-
X—УХо
жеству X, то он называется также двусторонним пределом.
Пример 1. Для функции у = sign ж (см. рис. 59) имеем
lim sign ж = 1, lim sign ж = — 1.
ж^+О	х^0
Теорема 2. Если функция f(x) задана на множестве X, жо =
= supX_(x0) = inf Х+(ж0), Х-(хо) ф 0, Х+(х0) ф 0, то для того,
чтобы у функции f существовал предел lim /(ж), необходимо и дос-
X—YXq
таточно, чтобы в точке ж0 существовали пределы слева и справа и
они были равны (общее значение этих пределов является двусторон-
двусторонним пределом функции / в точке жо).
\> Если у функции / существует предел в точке жо, то тот же предел
существует у этой функции при ж —> жо и по любому подмножеству
Е С X, для которого точка жо является его точкой прикосновения, в
частности по множествам Х_(ж0) и Х+(ж0). Обратно, если у функ-
функции / существуют равные пределы по множествам Х_(жо) и Х+(жо),
то по лемме 3 у нее существует тот же предел и по их объединению,
т. е. по множеству X = Х_(жо) U Х+(жо). <\
Определение 8. Функция /(ж), ж G X, называется непрерывной
слева (справа) в точке жо G X, если
lim /(ж) = /(жо) (соответственно lim /(ж) = /(жо)).
X—УХо	X—УХо
Из теоремы 2 следует, что если функция / непрерывна слева и
справа в точке жо, то она непрерывна в этой точке (напомним, что
непрерывность функции / в точке жо
означает, что в жо существует предел
i функции / по множеству, содержащему
! эту точку: lim /(ж) = /(жо), т. е. в дан-
I	х—ухо
I ном случае ж0 G Х+(ж0) и ж0 G Х_(ж0) и,
| следовательно, жо G X).
!	Пример 2. Символом [ж] обозна-
—'—> чается целая часть числа ж G /?, т. е.
4 х наибольшее целое число, не превосходя-
превосходящее ж (рис. 62). Таким образом, [ж] =
= п G Z, n ^ ж, но п + 1 > ж. Функ-
Функция ^/ = [ж] непрерывна справа во всех
точках числовой оси и не является непрерывной слева во всех цело-
целочисленных точках ж = ±п, п = 0,1, 2,...
-1 о
Рис- 62

§ 6. Предел и непрерывность функций	107
6.7. Свойства пределов функций. В пп. 6.7-6.12 все рассмат-
рассматриваемые функции определены на некотором фиксированном мно-
множестве X С R и хо — его точка прикосновения, конечная или беско-
бесконечно удаленная.
Функция называется ограниченной (сверху или снизу), если мно-
множество ее значений ограничено (соответственно сверху или снизу).
1°. Если функция f имеет в точке ж0 конечный предел, то сущест-
существует такая окрестность U(xo) точки ж0, что функция f ограничена
на пересечении X П U{xq).
\> Если lim /(ж) = a Е /?, то существует такая окрестность U{xq)
Х^Хо
точки жо, что для всех х Е X П U{xq) выполняется включение /(ж) Е
Е U(a, 1) (здесь в качестве окрестности U(a) в определении 6 взята
окрестность С/(а, 1)), т. е. неравенство а - 1 < f(x) < а + 1. <
Следствие. Если функция f непрерывна в точке хо, то сущест-
существует такая окрестность U(xo) точки жо, что функция / ограни-
ограничена на
Это следует из того, что если функция / непрерывна в точке ж0,
то она имеет в этой точке конечный предел.
2° (лемма о сохранении знака). Если функция f имеет в точке жо
не равный нулю конечный предел lim /(ж) = а ф 0, то существуют
Х^-Хо
такие окрестность U{xq) точки жо и число с > 0, что для всех точек
х G X П U(xo) выполняются неравенства
/(ж) > с, если а > 0;
/(ж) < —с, если а < 0.
> Поскольку а ф 0, то — > 0. Возьмем в качестве окрестности U(a)
в определении 6 окрестность Ula, —)• Тогда согласно этому опре-
определению существует такая окрестность U(xq) точки жо, что для всех
точек ж G X Г\17(хо) выполняется включение /(ж) G C/fa,-L-J, т. е.
справедливо неравенство
Отсюда имеем при а > О
f{x) > а - ^ = $ > О,
а при а < О
|
Таким образом, неравенства F.16) выполняются при с = —-. <1

108 Гл. 1. Дифференциальное исчисление функций одной переменной
Следствие. Если функция f непрерывна в точке ж0 и /(ж0) ф 0,
то существуют такие окрестность U{xq) точки жо и постоян-
постоянная с > 0, что для всех х Е X П U{xq) выполняются неравенства:
/(ж) > с, если /Оо) > 0;
/(ж) < -с, если /(ж0) < 0.
Это сразу вытекает из свойства 2°, поскольку непрерывность в
точке хо означает существование у функции / в точке хо конечного
предела, равного /(ж0). В качестве с можно взять ^ ^°^.
Замечание. Если у функции / в точке хо существует один из
бесконечных пределов оо, +оо и —оо, то для любого числа с > 0
существует такая окрестность U(xo) точки ж0, что для любой точки
х е X П U(xo) выполняются неравенства:
|/(ж)| > с, если lim f(x) = оо;
X—YXq
f(x) > с, если lim f(x) = +оо;
X—YXq
f(x) < -с, если lim f(x) = -оо.
х—>хо
Это следует из определения 5 предела функции, в котором в ка-
качестве окрестности U(a) бесконечно удаленной точки в этом случае
следует взять окрестность Uya, -).
3°. Если f(x) —с — постоянная, х G X, то lim f(x) = с.
х—>хо
Это означает, в частности, что постоянная функция является не-
непрерывной.
4°. Если f(x)^a, х G X и существует конечный или определен-
определенного знака бесконечный предел lim /(ж), то lim f(x) ^ a.
X—YXq	X—YXq
5°. Если ср(х) ^ /(ж) ^ ф(х), х G X и существуют конечные или
определенного знака бесконечные пределы lim cp(x), lim ф(х) и они
Х^-Хо	Х^-Хо
равны между собой, то существует lim /(ж) и
lim /(ж) = lim ip(x) = lim ф(х).
X—УХо	X—УХо	X—УХо
6°. Если существуют конечные пределы lim /(ж) и lim g(x), то
X^-Xq	X^-Xq
существуют и конечные пределы
lim [А/(ж) + уд(х)] = A lim /(ж) + \i lim g(x), A G /?, ц G /?,
ж—>-жо	ж—>-жо	ж—>-жо
F.17)
lim f(x)g(x) = lim /(ж) lim #(ж),	F.18)
Ж—УХо	X—УХо	X—УХо
Шод(х)*0,тои
Нш Щ = х-^—у	F.19)
ж-^ж0 дух) lim р(ж)

§ 6. Предел и непрерывность функций	109
fix)
В последнем случае функция ^-4- рассматривается только для
д(х)
тех ж, для которых д[х) ф 0 (см. свойство 2°).
|> Утверждения 3°-б° следуют из соответствующих утверждений
для пределов последовательностей (см. пп. 5.3, 5.6) Докажем, напри-
например, формулу F.18). Пусть lim f(x) = а е /?, lim д(х) = b e R. Возь-
X—YXq	X—YXq
мем какую-либо последовательность хп е X, п = 1,2,..., имеющую
своим пределом ж0. Тогда согласно определению 1 lim f(xn) = a,
п—Уоо
lim g{xn) = 6, поэтому в силу свойства пределов ПОСЛеДОВатеЛЬНОС-
ть—Уоо
тей (свойство 3° в п. 5.6)
lim f(xn)g(xn) = lim f(xn) lim g(xn) = ab,
n—Уоо	n—Уоо	n—Уоо
и поскольку последовательность {хп} является произвольной после-
последовательностью такой, что хп ->• хо и хп е X, п = 1, 2,..., то согласно
тому же определению 1 предела функции получим
lim f{x)g{x) = ab = lim f(x) lim
ж^ж	ж^ж	ж^ж
Следствие. Е'сли функции fug непрерывны в точке хо G X,
то функции Xf(x) + /ид(х), X G /?, \i G /?, f(x)g(x), а если д(хо) ф 0,
/(ж)
то и ^-гг, непрерывны в точке х0.
дух)
\> Докажем, например, непрерывность произведения f(x)g(x). Если
функции / и д непрерывны в точке ж0, то в этой точке они имеют
конечные пределы /(жо) и 9(хо)- Поэтому согласно формуле F.18) по-
получим
lim f(x)g(x) = lim f(x) lim g(x) = f(xo)g(xo).
ж->-жо	ж->-жо	ж->-жо
Это и означает непрерывность произведения / д. <\
Отметим, что проведенное доказательство можно было бы и не
проводить, так как непрерывность функции в точке означает, что
(см. п. 6.2) эта точка принадлежит множеству задания функции и
что у функции в этой точке существует предел по указанному мно-
множеству. Поскольку функции / и д заданы в точке ж0, то, очевидно,
fix)
и функции А/(ж) + /ig(x), f(x)g(x), а при д(хо) /0 и (~^? заданы в
9\х)
этой точке. В силу свойства 6° у перечисленных функций существуют
пределы в точке жо, принадлежащей в данном случае их множеству
задания, что и означает их непрерывность в точке xq. Иначе говоря,
утверждение следствия является просто частным случаем утвержде-
утверждения 6°, когда точка, в которой рассматривается предел, принадлежит
области определения функций.

110 Гл. 1. Дифференциальное исчисление функций одной переменной
6.8. Бесконечно малые.
Определение 9. Функция а(х), х Е X, называется бесконечно
малой при х —У жо, если lim a(x) = 0.
X—УХо
Бесконечно малые функции играют в теории пределов функций
роль, аналогичную той, которую играют бесконечно малые последо-
последовательности в теории пределов последовательностей (п. 5.5).
Лемма 3. Для того чтобы у функции /(ж), х Е X, существовал в
точке хо конечный предел, равный а, необходимо и достаточно, чтобы
функция а(х) = f(x) — а была бесконечно малой при х —У xq.
>	Действительно, существование конечного предела lim f(x) = a
Х^-Хо
равносильно тому, что (см. п. 6.4) для любого г > 0 существует такая
окрестность U{xq) точки хо, что для всех х Е X П U{xq) выполняется
неравенство \f(x) — а\ < ?, т. е. |а(ж)| < г, что и означает бесконечную
малость функции а(х) при х —у xq. <\
Теорема 3. Линейная комбинация конечного числа бесконечно
малых при х —> хо функций является бесконечно малой при х —> хо
функцией.
Произведение бесконечно малой при х —У хо функции на ограничен-
ограниченную функцию является бесконечно малой при х —У хо функцией.
Следствие. Произведение конечного числа бесконечно малых при
х —У хо функций является бесконечно малой при х —У хо функцией.
>	Первое утверждение теоремы сразу следует из свойства предела
линейной комбинации функций (см. F.17)). Докажем второе: пусть
lim а(х) = 0,	F.20)
X—YXQ
а функция / ограничена на множестве X, т. е. существует такая
постоянная с > 0, что для всех х G X выполняется неравенство
|/(х)|^с.	F.21)
Тогда для произвольной последовательности хп ->• ж0, хп е X, п =
= 1, 2,..., последовательность {а(хп)} будет в силу условия F.20) бес-
бесконечно малой, а последовательность {f(xn)} в силу условия F.21) —
ограниченной. Поэтому (см. п. 5.5) их произведение является беско-
бесконечно малой последовательностью, т. е. lim f(xn)a(xn) = 0. Посколь-
КУ {хп} — произвольная последовательность такая, что хп —У жо,
хп е X, п = 1, 2,..., то это означает, что
lim f{x)a{x) = 0.
X^XQ
Для доказательства следствия из теоремы достаточно заметить, что
всякая бесконечно малая при х —У хо функция, имея в точке хо конеч-
конечный предел, ограничена в некоторой окрестности этой точки. Поэто-
Поэтому в некоторой окрестности точки xq произведение конечного числа

5. Предел и непрерывность функций
111
бесконечно малых при х ->• х0 функций можно рассматривать как
произведение бесконечно малой при х —У хо функции на ограничен-
ограниченную. <|
6.9. Непрерывные функции. Согласно определению (определе-
(определение 5, п. 6.2) функция у = f(x) непрерывна в точке хо Е /?, если
\imj(x) = f(xo).	F.22)
Это означает (определение 1, п. 6.1), что если хп ->• ж0, хп е X, то
f(xn) —У f(xo), п = 1,2,..., а также (см. определение б и теорему 1 в
п. 6.4), что для любого е > 0 существует такое S > 0, что для всех
х Е X, удовлетворяющих условию \х — хо\ < S, выполняется нера-
неравенство \f(x) - f(xo)\ < е.
Из F.22) следует, что
lim \f{x) - /(
О] = 0.	F.23)
х — х о—?"U
Введем обозначения:
Ах d= х - хо, Ay d= f(x) - f(x0) = Джо + Ах) - f(x0).
Тогда равенство F.23) можно записать в виде
lim Ay = 0.	F.24)
С точки зрения приближенного вычисления значений функций вы-
выполнение равенства F.22), т. е. непрерывность функции, означает,
что по достаточно точным приближеным
значениям аргумента можно вычислять
сколь угодно точно значения функции.
В качестве примера использования за-
записи условия непрерывности в виде F.24)
покажем, что функция /(ж) = 1/х (рис. 63)
непрерывна во всех точках хо ф 0. Имеем
Ау = f(x0 + Ах) - f(x0) =
_ 1	1 _	Ах	v п
Рис. 63
хо + Ах хо	(хо ¦
при Ах ->• 0.
Бывает полезным условие непрерыв-
непрерывности функции в точке, основанное на
рассмотрении предела функции по проколотой окрестности этой точ-
точки (см. определение 4 в п. 6.1).
Лемма 5. Если функция f задана на множестве X, хо G X и
существует предел
lim f(x) = a,	F.25)
х—Ухо, хфхо
то функция / непрерывна в точке хо тогда и только тогда, когда
а = f(x0).

112 Гл. 1. Дифференциальное исчисление функций одной переменной
\> Если функция / непрерывна в точке ж0, т. е. выполняется усло-
условие F.22), то
lim /(ж) = lim /(ж) = f(x0)
X—УХо, X^Xq	X—YXq
(предел по подмножеству совпадает с пределом по множеству, если
последний существует). Таким образом, предел F.25) равен f(xo).
Пусть, наоборот, выполняется условие а = /(жо), т- е-
lim f(x) = f(x0),	F.26)
ж-^ж0, хфх0	F.25)
очевидно, и
lim /(ж) = lim /(ж0) = /(ж0).
x—>xo, хфхо	x—>xq
Таким образом, по двум множествам X \ {жо} и {хо} функция /
при х —> хо имеет один и тот же предел /(жо). Поэтому она согласно
лемме 3 из п. 6.5 имеет тот же предел и по их объединению
(Х\{хо})и{хо} = х,
т. е.
lim /(ж) = /Оо).
X—YXQ
Это означает, что из выполнения условия а = /(жо) следует вы-
выполнение условия F.22), т. е. того, что функция / непрерывна в точ-
точке Xq. <\
Условие непрерывности леммы 5 бывает полезно, в частности, в
случае односторонних пределов, когда пределы слева и справа берут-
берутся по множествам, не содержащим точки ж0, т. е. когда рассматрива-
рассматриваются пределы /(жо — 0) и /(жо + 0). Именно, имеет место следующее
утверждение.
Если хо G X и
lim f(x)= lim f(x) = f(x0),	F.27)
X—YXq— 0	X—>-Жо+О
то функция f непрерывна в точке ж0.
> Действительно, из условия F.27) следует, что lim /(ж) =
х—Ухо, хфхо
— /(жо), а поэтому согласно лемме 5 функция / непрерывна в точ-
точке Жо- <\
Для дальнейшего анализа свойства непрерывности функции вве-
введем понятия изолированных и предельных точек множества.
Определение 10. Точка жо называется изолированной точкой
множества X С /?, если существует окрестность С/(жо), пересечение
которой с множеством X состоит только из самой точки жо:
и(х0) Ш = {ж0}.
Определение 11. Точка жо называется предельной точкой мно-
множества X G /?, если в любой ее окрестности содержится точка
множества X, отличная от самой точки жо-

§ 6. Предел и непрерывность функций	113
Например, все точки множества натуральных чисел Л/ изолирова-
изолированы, а множество Q всех рациональных чисел вовсе не имеет изолиро-
изолированных точек. Каждая точка числовой прямой R является предельной
точкой для множеств Q, / и R.
Предельная точка множества может как принадлежать самому
множеству, так и не принадлежать ему. Так, например, концы а и Ъ
отрезка [а, Ь] и интервала (а, Ь) являются предельными точками и то-
того, и другого промежутка, но в первом случае они принадлежат ему,
а во втором — нет.
Каждая точка прикосновения множества X является либо его изо-
изолированной точкой, либо его предельной точкой. В самом деле, либо у
нее существует окрестность, не содержащая других точек множества,
кроме нее самой, тогда она изолированная, либо в любой ее окрест-
окрестности имеются точки множества X, отличные от нее, тогда она пре-
предельная.
Лемма 6. Всякая функция непрерывна в каждой изолированной
точке множества своего определения.
|> Пусть на множестве X задана функция / и ж0 — изолированная
точка множества X. Тогда существует такая окрестность U(xo) точ-
точки, что
U(x0) Ш = {ж0}.
Какова бы ни была последовательность хп Е X, п = 1, 2,..., такая, что
lim хп = жо, существует такой номер по, что для всех п > по выпол-
выполняется условие хп Е U(xo), и так как хп Е X, то при п > по имеет
место равенство хп = жо, а следовательно, и /(жп) = /(жо) (т. е., на-
начиная с номера по + 1, последовательность {/(жп)} делается стацио-
стационарной), а потому lim /(жп) = /(ж0). В силу произвольного выбора
п—>-оо
последовательности хп ->• ж0, хп Е X, п = 1,2,..., это означает, что
lim f(x) = f(x0). <\
Например, функции, определенные лишь на одной точке или на
двух точках, или, более общо, на любом конечном множестве то-
точек, являются непрерывными. Непрерывной является и элементарная
функция
у = 1 +
определенная только для целочисленных значений аргумента, т. е.
для х = О, =Ы, ±2,..., в которых она равна 1 (в остальных точках вы-
выражение под знаком корня отрицательно, и поэтому функция не опре-
определена). График этой функции состоит из отдельных изолированных
8 Л.Д.Кудрявцев, т.1

114 Гл. 1. Дифференциальное исчисление функций одной переменной
-2 -1 О
Рис. 64
()()()()()
(рис. 64).
Таким образом, при изучении воп-
вопроса о непрерывности функции в неко-
торой точке следует рассматривать лишь
предельные точки ее множества опре-
определения, так как, согласно доказанно-
доказанному, во всех изолированных точках этого
множества она заведомо непрерывна.
В этом смысле дискретное в математике является частным слу-
случаем непрерывного.
6.10. Классификация точек разрыва.
Определение 12. Пусть функция / определена в некоторой
окрестности точки жо, кроме, быть может, самой точки xq. Тогда
хо называется точкой разрыва функции /, либо если функция / не
определена в самой точке жо, либо если она определена в этой точке,
но не является в ней непрерывной.
Образно говоря, точка ж0 является точкой разрыва функции, ес-
если хо является значением аргумента, при котором происходит "раз-
"разрыв графика функции".
Например, точка х = 0 является точкой разрыва функции /(ж) =
= 1/ж, так как эта функция не определена при ж = 0. Та же точ-
точка ж = 0 является и точкой разрыва функции
1/ж, если х^О,
если ж = 0,
так как в этом случае, хотя функция / и определена при ж = 0, но она
не непрерывна при ж = 0.
Если в точке разрыва существуют конечные пределы /(ж0 - 0) и
/(жо + 0), то она называется точкой разрыва первого рода, а величи-
величина /(жо + 0) — /(жо — 0) — скачком функции / в точке жо (рис. 65).
t(х)
рр
Г 1/ж
\ 0,
Дхо+в)
/(Хо-8)
о
У
О
Рис. 65
х0
Рис. 66
Если скачок функции в точке жо равен нулю, то точка
ется точкой устранимого разрыва (рис. 66).
называ-

называ§ 6. Предел и непрерывность функций	115
Точка разрыва, не являющаяся точкой разрыва первого рода, на-
называется точкой разрыва второго рода.
Примеры. 1. У функции
f(x) = sign ж
(см. рис. 59) точка жо = 0 является точкой разрыва первого рода, и
скачок в ней равен 2:
sign(+0) -sign(-O) = 2.
Та же точка ж0 = О является для функции /(ж) = |signx| (см. рис. 60)
точкой устранимого разрыва:
|sign(+0)|-|sign(-0)| =0.
2. Точка хо = 0 для функций /(ж) = - и /(ж) = sin - является
х	х
точкой разрыва второго рода.
6.11. Пределы монотонных функций.
Определение 13. Функцию /(ж), х Е X, называют возрастаю-
возрастающей (соответственно убывающей) на множестве X и пишут / t
(соответственно / \), если для любых х\ Е X и х2 Е X таких, что
х\ < ж2, выполняется неравенство f(xi) ^ /(ж2) (соответственно
f(xi) > /Ы).
Возрастающие и убывающие функции называются монотонными.
Если из неравенства х\ < ж2, xi E X, х2 ? X, следует, что
f(xi) < f{x2) (соответственно, что f{x\) > /(^2)), то функ-
функцию / называют строго возрастающей (строго убывающей) и пи-
ШУТ / tt (соответственно / Ц). Строго возрастающие и строго
убывающие функции называются строго монотонными. Если функ-
функция / (строго) возрастает на множестве X, то функция —/ (строго)
убывает на этом множестве.
Верхней гранью sup/ функции /(ж), х G X (или, в другой записи,
sup f(x)), называется верхняя грань значений этой функции на мно-
хех
жестве ее задания X:
sup/ = sup {/(ж)},
хех
а нижней гранью inf / (или inf f(x)) — нижняя грань ее значений:
хех
inf/= inf {/(ж)}.
X t A
Если функция / принимает в точке хо наибольшее значение на
множестве X, то, очевидно, /(жо) = sup/, а если она принимает в
точке хо наименьшее значение, то f(xo) = inf/.
Теорема 4. Пусть функция /(ж), ж G X, возрастает на мно-
множестве X, а = inf X, /3 = supX, a ^ X, /3 ^ X. Тогда у функции /

116 Гл. 1. Дифференциальное исчисление функций одной переменной
существуют конечные или определенного знака бесконечные пределы
справа в точке х = а:
lim /(ж) = inf /(ж),	F.28)
х-нх	хЕХ
и слева в точке х = C:
lim /(ж) = sup /(ж).	F.29)
Х^Р	хех
Таким образом, если функция / ограничена снизу (т. е. ограни-
ограничено снизу множество ее значений), то предел F.28) будет конеч-
конечным, а если / не ограничена снизу, то
этот предел будет бесконечным, рав-
равным — оо. Аналогично, предел F.29)
будет конечным или бесконечным,
равным +оо, когда функция / ог-
ограничена сверху или соответствен-
соответственно не ограничена сверху.
|> Пусть функция / возрастает на
множестве X и
Ъ = sup /(ж) ^ +оо.	F.30)
хех
Зададим произвольно окрестность
U{b) точки 6, и пусть г\ — левый конец этой окрестности (рис. 67);
тогда г\ < Ъ и существует такое ? Е G X, что
ПО > v-	F-31)
Из того, что C = supX, следует, что ? ^ /3, но ? G X, а по условиям
теоремы /3 0 X, поэтому ? < /3.
Обозначим через U(/3) окрестность точки /3, левым концом кото-
которой является точка ? (см. рис. 67). Тогда если
хехпи(р),	F.32)
то ? < х < C и, следовательно, в силу возрастания функции / будет
выполняться неравенство
/(О ^ К*).	(б.зз)
Поэтому
г] < f{x) ^ sup f{x) = Ъ.	F.34)
F.31)	хеХ	F.30)
F.33)
Вспоминая, что точка г] является левым концом окрестности U(b),
получим из F.34)
fix) G ЩЬ).	F.35)
Выполнение условий F.32) и F.35) означает, что
lim fix) = Ь.
х^C
Аналогично рассматривается случай предела функции / при х —> а. <\

5. Предел и непрерывность функций
117
Следствие. Если функция f возрастает на множестве X, ж0 0
0 X, множества Х_(жо), Х+(жо) не пусты и точка жо является их
точкой прикосновения, то функция f имеет в этой точке конечные
пределы /(жо — 0) и /(жо + 0), причем
/(жо-0К/(жо
F.36)
Напомним, что запись х —> хо + 0 (соответственно запись х —у
—> хо — 0) означает, что рассматривается предел справа (слева) по
множеству, не содержащему точки ж0.
|> Если функция / возрастает на множестве X, то для любых х' е
е Х_(ж0) и х" е Х+(хо) выполняется неравенство
f(x') ^ f{xn).	F.37)
Иначе говоря, возрастающая функция / ограничена числом fix")
сверху на множестве Х_(жо) и числом fix') снизу на множест-
множестве Х_|_(жо). Поэтому согласно теореме 4 существуют конечные преде-
пределы f(xo — 0) и /(жо + 0). Перейдя к верхней грани в левой части не-
неравенства F.37), получим
sup fix) <: fix"),
х<хо
а перейдя здесь в правой части к нижней грани, будем иметь
sup fix) <: inf fix).
x<x0	x>x
F.38)
Согласно теореме 4
f(x0 - 0) = sup f(x), f(x0 + 0) = inf f(x), xeX.
x<x0	x>x0
Поэтому неравенство F.38) совпадает с неравенством F.36). <1
Замечание 1. Теорема, аналогичная теореме 4, справедлива и
для убывающих функций.
Замечание 2. Если функция / возрастает на множестве X,
f] = supX и f3 G X, то предел lim /(ж) функции / по всякому X (т. е.
включая C) может существовать (рис. 68), тогда функция / будет
У\	Т
о
о
Рис. 68
Рис. 69

118 Гл. 1. Дифференциальное исчисление функций одной переменной
непрерывна в точке х = /3 (см. п. 6.2), а может и не существовать
(рис. 69), тогда точка C будет точкой разрыва функции /. Подчерк-
Подчеркнем, однако, что согласно теореме 4 предел lim f(x) всегда сущест-
ж->¦/?—о
вует.
6.12. Критерий Коши существования предела функции.
Теорема 5 (критерий Коши). Для того чтобы функция /(ж),
х Е X, имела в (конечной или бесконечно удаленной) точке хо ко-
конечный предел, необходимо и достаточно, чтобы для любого г > О
существовала такая окрестность U(xo) точки ж0, что для любых
x'GlH U(xo) и х" Е X П U(xo) выполнялось бы неравенство
\f(x")-f(x')\<e.	F.39)
> Докажем необходимость условия F.39). Пусть lim f(x) =
X—УХо
= a Е /?, тогда для любого г > 0 существует такая окрестность U(xq)
точки ж0, что для каждого х е XnU(xo) справедливо неравенство
\f(x)-a\<e/2.
Поэтому если х' G X П U(xq) и / GXflG(xo), to
\f(x") - f(x')\ = \[f(x") -a] + [a- f(x')}\ ^
Докажем достаточность условий F.39) для существования ко-
конечного предела lim fix). Пусть произвольно фиксировано е > 0; тог-
х^х0
да существует такая окрестность U(xo), что для всех х' Е X Г\ U(xq)
и всех х" G X П U(xq) выполняется неравенство \f(x") — f(x')\ < e.
Возьмем какую-либо последовательность хп ->• ж0, хп е X, п = 1, 2,...
В силу определения предела последовательности существует такой
номер по, что для всех п > по имеет место включение хп G U(xo), a
поскольку хп G X, то и включение xn G X П С/(жо). Тогда для всех но-
номеров п> по и т> по будем иметь хп G X П ?/(ж0), жт G X П ?/(ж0),
и, следовательно, будет выполняться неравенство \f(xn) — f(xm)\ < e.
Это означает, что последовательность {f(xn)} удовлетворяет кри-
критерию сходимости Коши для последовательностей и, следовательно,
имеет конечный предел.
Таким образом, для любой последовательности хп —> жо, хп G X,
п = 1,2,..., последовательность {f(xn)} имеет конечный предел. От-
Отсюда в силу леммы п. 6.3 сразу следует, что функция / имеет в точке
хо конечный предел. <|
Замечание. Сформулируем критерий Коши существования ко-
конечного предела функции в терминах неравенств для случая, ког-
когда хо — действительное число:

§ 6. Предел и непрерывность функций	119
функция /(ж), х е X, имеет в точке х0 е R конечный предел тогда
и только тогда, когда для любого г > 0 существует такое S > О, что
для всех точек х' Е X, х" Е X, \х' — хо\ < S, \x" — хо\ < S, выполня-
выполняется неравенство \f(x") — f(x')\ < s.
6.13. Предел и непрерывность композиции функций.
Теорема 6. Пусть функция f задана на множестве X, функ-
функция g — на множестве Y и f(X) С Y. Если существуют конечные
или бесконечные пределы
lim /(ж) = у,,,	F.40)
Х^Хо
lim g(y)=z0,	F.41)
У^У
то при х —> хо существует предел (конечный или бесконечный) слож-
сложной функции g[f(x)], причем
lim g[f(x)] = lim g(y).	F.42)
ж^ж0	у>Уо
\> Пусть хп —У хо, xnGl, n = 1,2,...; тогда в силу F.40) имеем
Уп = 1(хп)^Уо, Уп^У, га = 1,2,...
Поэтому в силу F.41) д(уп) ~^ zo, но Уп = f(xn), следовательно,
g[f(xn)] —> zo, n = 1,2,..., т. е. имеет место равенство F.42). <|
Замечание 1. Если функция д непрерывна в точке уо, т. е.
lim д(у)=д(у0),	F.43)
У^Уо
то формулу F.42) можно записать в виде
lim g[f(x)]=g( lim f(x)).	F.44)
X—>Xq	\ X—>Xq	/
Иначе говоря, предельный переход перестановочен с операцией взя-
взятия непрерывной функции. В самом деле, согласно теореме б
lim q\f(x)] = lim а (у) = а (у о) = Q\ Hm f(x)).
x^xoUUy И F.42) У^Уо УКУ) F.43) УКУ J F.40)^ \x^x0JK Ч
Отсюда следует, в частности, что непрерывная функция от непрерыв-
непрерывной функции непрерывна, точнее:
Следствие. Если функция / непрерывна в точке хо, а функция д
непрерывна в точке у о = /(жо)? то и их композиция д о / непрерывна
в точке хо-
\> Действительно, непрерывность функции / в точке хо означает, что
lim f(x) = /Ы =2/о,	F.45)
X—УХо
поэтому в силу непрерывности функции д в точке уо из формулы F.44)
получим
lim g[f(x)] = д\ lim f(x)\ = g(f(x0)),
x^xo	F.44) La?^a?o J F.45)

120 Гл. 1. Дифференциальное исчисление функций одной переменной
т.е. функция g о f непрерывна в точке ж0. <1
Замечание 2. Обычно, когда говорят, что некоторая функция в
данной точке имеет предел, то имеют в виду, что этот предел конеч-
конечный, а случай бесконечного предела оговаривают особо.
6.14. Предел и непрерывность функций комплексного ар-
аргумента. Понятия предела и непрерывности функции обобщают-
обобщаются на случай функций, значениями которых являются комплексные
числа и которые заданы на подмножествах множества комплексных
чисел.
К таким функциям относятся, например, функции f(z) = \z\,
f(z) = г, f(z) = z2, f(z) = 1/z. Первые три определены на всей комп-
комплексной плоскости С, а последняя — на комплексной плоскости, из
которой удалена точка 0; первая принимает только неотрицатель-
неотрицательные действительные значения, три последние — существенно комп-
комплексные.
Итак, будем здесь предполагать, что функция / задана на некото-
некотором подмножестве Z множества комплексных чисел С и принимает
комплексные значения, т. е. что
/(*) еС, z е Z С С.
Комплексное число wo называется пределом функции / в точке zo
(или, что то же самое, при z —> zo), если для любой последовательнос-
последовательности комплексных чисел zn Е Z, п = 1,2,..., для которой lim zn = z$
(см. п. 5.11), имеет место равенство lim f(zn) = w^. В этом случае
п—>-оо
пишут lim f(z) = w0.
Z^-Zo
В терминах окрестностей точек на комплексной плоскости (п. 5.11)
это определение равносильно следующему.
Комплексное число wo называется пределом функции / в точке zo,
если для любой окрестности V точки wo существует такая окрест-
окрестность U ТОЧКИ Zo, ЧТО
f(unz) cv.
На "языке е-б" это означает следующее: для любого г > 0 су-
существует такое S > 0, что для всех z G Z, для которых \z - zo\ < S,
выполняется неравенство
\f(z)-wo\ <e.
Доказательство эквивалентности двух сформулированных опре-
определений предела функции комплексного переменного — в терминах
последовательностей и в терминах окрестностей — проводится ана-
аналогично случаю функций действительного аргумента, принимающих
действительные значения.
При рассмотрении предела функции / в точке z$ возможны два
случая: zq принадлежит множеству Z, на котором задана функция /,

§ 6. Предел и непрерывность функций	121
или не принадлежит ему. Если z0 G Z, то существование предела
функции / в точке zo означает, что
lim f(z) = /(гь).
Z—tZo
В этом случае функция / называется непрерывной в точке zq.
Если f(z) = u(z) + v(z)i, w0 = u0 + voi, u(z),v(z),u0,v0 G /?, то
существование предела lim f(z) = w^ равносильно, как это легко ви-
Z—>Zq
деть, существованию пределов lim u(z) = щ и lim v(z) = г70, причем
в случае существования указанных пределов имеет место равенство
lim f(z) = lim u{z) + lim v(z)i.
Z—YZq	Z—YZq	Z—YZq
В частности, функция f(z) непрерывна в точке z$ тогда и только
тогда, когда в этой точке непрерывны функции u(z) и v(z).
Заметим, что функции u(z) и v(z) принимают действительные
значения, но их аргументы — комплексные числа, поэтому пределы
этих функций и их непрерывность понимаются в смысле сделанных
выше определений для функций комплексного переменного.
На комплекснозначные функции комплексного аргумента перено-
переносятся многие свойства предела функций, доказанные выше в этом
параграфе для действительных функций действительного аргумента.
Например, предел линейной комбинации функций, имеющих преде-
пределы в некоторой точке, равен такой же линейной комбинации этих
пределов.
Функция f(z) называется ограниченной на множестве Z С С, если
на этом множестве ограничена ее абсолютная величина |/(г)|.
Как и раньше, справедливо утверждение: если функция f имеет
предел при z —У zo, то она ограничена в некоторой окрестности точ-
точки Zo.
Переносятся на случай функций комплексного аргумента поня-
понятие предела при стремлении аргумента к бесконечности и понятие
бесконечного предела. Ограничимся формулировкой общего понятия
предела (конечного и бесконечного) лишь в терминах последователь-
последовательностей.
Бесконечность оо называется бесконечно удаленной точкой комп-
комплексной плоскости С, в связи с чем точки самой комплексной плос-
плоскости С называются также и конечными точками.
Конечная или бесконечно удаленная точка w^ комплексной плос-
плоскости С называется пределом функции f при z ->• z0, где z0 — также
конечная или бесконечно удаленная точка, если для любой последо-
последовательности zn G Z, п = 1, 2,..., для которой lim zn = zo, имеет место
( .	7WOO
lim f(zn) = w0.
п—уоо
Это определение предела (как и все сформулированные выше) со-
содержательно, конечно, лишь в том случае, когда существует такая

122 Гл. 1. Дифференциальное исчисление функций одной переменной
последовательность zn e Z, п = 1, 2,..., что lim zn = z0. В этом случае
п—>-оо
точка zo называется соответственно конечной или бесконечно удален-
удаленной точкой прикосновения множества Z.
§ 7. Свойства непрерывных функций
7.1. Ограниченность непрерывных функций. Достижи-
Достижимость экстремальных значений.
Определение 1. Функция называется непрерывной на множест-
множестве, если она непрерывна в каждой его точке.
Теорема 1 (Вейерштрасс). Всякая непрерывная на отрезке функ-
функция ограничена и достигает на нем своей верхней и своей нижней
граней.
Иначе говоря, непрерывная на отрезке функция принимает как
свое наибольшее, так и свое наименьшее значение (см. п. 3.1).
|> Пусть функция / непрерывна на отрезке [а, Ь] и /3 = sup/(ж). По-
[а,Ь]
кажем, что C < +оо и что существует такое хо Е [а, Ь], что /(жо) = C.
Пусть {уп} — такая последовательность, что
2/п-^А Уп<Р, п = 1,2,...	G.1)
Согласно определению верхней грани для каждого п = 1, 2,... най-
найдется такое хп G [а,Ь], что
f(xn) >yn, п = 1,2,...	G.2)
С другой стороны, поскольку /3 — верхняя грань функции /, то для
любого х е [а,Ь] выполняется неравенство f(x) ^ /3, в частности
f(xn) ^ 0- Итак, уп < f(xn) ^ /?, п = 1, 2,..., а поэтому
lim f(xn) = C.	G.3)
n-^oo	G.1)
Последовательность {хп} ограничена: а ^ хп ^ 6, п = 1, 2,... Сле-
Следовательно, по теореме Больцано-Вейерштрасса она содержит сходя-
сходящуюся подпоследовательность {хПк}. Обозначим ее предел через х$:
lim хПк =х0.	G.4)
к—>-оо
Поскольку а ^ xnfc ^ b, то
а ^ ж0 ^ Ъ.	G.5)
А так как {f(xnk)} является подпоследовательностью последователь-
последовательности {/(жп)}, то из G.3) имеем
lim f(xnh)=/3.	G.6)
к—уоо

§ 7. Свойства непрерывных функций	123
Но функция / непрерывна на отрезке [а, 6], в частности, в точ-
точке жо, поэтому из G.4) вытекает, что
lim f(xnh) =/Oo).	G.7)
к—>-оо
Следовательно, /3 = /(ж0) < +оо.
G.6)
G.7)
Аналогично доказывается ограниченность снизу функции / и до-
достижимость ее нижней грани. <|
7.2. Промежуточные значения непрерывных функций.
Теорема 2 (Больцано-Коши). Если функция / непрерывна на от-
отрезке [а, Ь], /(а) — А и f(b) = В, то для любого числа С, заключенного
между А и В, существует такая точка ? G [а, Ъ], что
ДО = С.	G.8)
Следствие 1. Функция, непрерывная на конечном или бесконеч-
бесконечном промежутке (отрезке, интервале, полуинтервале), принимая два
каких-либо значения, принимает и все промежуточные.
|> Пусть для определенности /(а) = А < В = f(b) и, следовательно,
А < С < В. Разделим отрезок [а, Ь] на два равных отрезка точкой
	. Если / (	) = С, то точка ? найдена (см. G.8)): ? =	.
А	\ А J	А
Если / (^) 7^ С, то либо / (^) < С, либо / (^) > С. В первом
случае выберем отрезок 	, 6 , а во втором — отрезок а,	 ;
выбранный отрезок обозначим [ai,bi]. Очевидно, f(a\) < С < /(bi) и
6: — а\ — 	. Разделим отрезок [ai,bi] его средней точкой —	-
на два равных отрезка.
Если /(—2~) = С, то ? = —^—. Если же f{-^—) Ф С, то
выберем из получившихся отрезков тот, на левом конце которого зна-
значение функции меньше С, а на правом — больше С, и т. д. Тогда
либо через конечное число шагов мы получим такую среднюю точку
? некоторого отрезка, что /(?) = С, тогда теорема доказана, либо —
такую систему вложенных отрезков [ап,Ъп], что
/К) < С < f(bn), n = l,2,...,	G.9)
Ьп ~ ап = -7^~ -*¦ 0 при п -> оо.	G-Ю)
А
Пусть ? — общая точка, принадлежащая всем отрезкам [ап,Ьп];
тогда (см. замечание в п. 5.7)
lim ап = lim Ьп = ?
п—>-оо	п—>-оо
и, следовательно, в силу непрерывности функции /
lim /(an)= lim f(bn)=№.	G.11)

124 Гл. 1. Дифференциальное исчисление функций одной переменной
Но в силу G.9)
lim f(an)^C^ lim f(bn).	G.12)
nюо	n>oo
Из соотношений G.11) и G.12) следует, что /(?) ^ С ^ /(?)? т. е. что
/(О = С. <
Следствие 2. Если функция непрерывна на отрезке и на его кон-
концах принимает значения разных знаков, то на этом отрезке сущест-
существует хотя бы одна точка, в которой функция обращается в нуль.
Следствие 1 вытекает из того, что, принимая какие-либо значения
в двух точках некоторого промежутка, непрерывная на нем функция,
согласно теореме 2, принимает все промежуточные значения на от-
отрезке с концами в этих точках. А этот отрезок, очевидно, содержит-
содержится в рассматриваемом промежутке. Следствие 2 является частным
случаем теоремы 2.
7.3. Обратные функции.
Лемма. Если функция f строго возрастает (см. п. 6.11) на мно-
множестве X и f(X) = У, то обратная функция j~x (см. п. 1.2) является
однозначной строго возрастающей на множестве У функцией.
|> Докажем сначала однозначность обратной функции j~x. Допустим
противное: пусть существует такая точка у Е Y, что ее прообраз со-
содержит по крайней мере две различные точки х\ и ж2, т. е. х\ ф ж2
и f(xi) = /(ж2). Возможны два случая: либо х\ < ж2, либо х\ > х2. В
первом случае в силу строгого возрастания функции / должно быть
f(xi) < /(^2), а во втором — f{x\) > /(#2). И то, и другое невозмож-
невозможно, так как f(x\) = /(#2).
Докажем теперь, что обратная функция j~x строго возрастает на
множестве Y = f(X). Пусть ух < у2, yi G Y, y2 G Y, хх = f~l(yi),
Х2 = f~1(y2) и, следовательно, f(x\) = у\, f{x^) — у2- Если бы х\ — ж2,
то f(x-\) = /(#2), т- е- имело бы место равенство у\ — у2, а если бы
х\ > Х2ч то в силу строгого возрастания функции / имело бы место
неравенство f(xi) > /(ж2), т. е. у\ > у2. И то, и другое противоречит
условию ух < 2/2- Таким образом, остается возможным только слу-
случай Х\ < Ж2. <|
Теорема 3. Если функция / строго возрастает и непрерывна на
отрезке [а, 6], /(а) = A, f(b) = В, то
f([a,b]) = [A,B]	G.13)
и обратная функция является однозначной строго возрастающей не-
непрерывной на отрезке [А, В] функцией.
|> Докажем сначала равенство G.13). Если а ^ х ^ Ь, то в силу воз-
возрастания функции / на отрезке [а, Ь] выполняется неравенство
А = /(о) ^ f(x) ^ № = В.

§ 7. Свойства непрерывных функций
125
С другой стороны, для любой точки у е [А, В] согласно теореме 2
о промежуточных значениях непрерывной функции найдется такая
точка х Е [а,Ь], что /(ж) = у. Это и означает, что образом отрезка
[а, Ь] при отображении / является отрезок [-4,5] и, тем самым, от-
отрезок [-4,5] является множеством, на котором определено обратное
отображение (обратная функция) f~l.
Однозначность функции j~x и ее строгое возрастание на отрезке
[А, В] следуют из леммы. Докажем ее непрерывность на этом отрезке.
Выберем произвольно уо Е [А, 5], и пусть lim уп = уо, уп Е [А, 5],
п—юо
п = 1,2,... Тогда из равенства G.13) следует, что существуют такие
точки хо Е [а, Ь] и хп G [а, 6], что
/(so) = 2/о, /(жп) =
т. е. /~1(?/о) =ж0, 1~1{Уп) = хп,п = 1,2,...
Покажем, что lim хп = ж0, т. е. что
G.14)
lim / (yn) = /
n—>-oo
Допустим, что это не так. Тогда найдется такое е > 0, что вне
окрестности U(xo,e) лежит бесконеч-
бесконечно много элементов последовательнос-
последовательности {жп}, а поэтому у нее существу-
существует подпоследовательность {хПк}, все
члены которой также лежат вне ок-
окрестности U(xo,e):
хПк 0 U(xo,e),
и, следовательно,
ьпк
е[а,Ъ]\Щхо,е), к = 1,2,...
О
а хпк х* XQ-e хо хо+г х
Рис. 70
G.15)
Множество [a,b]\U(xo,e) являет-
является либо отрезком, либо объединением
двух отрезков (рис. 70). По теореме
Больцано-Вейерштрасса у подпоследо-
подпоследовательности {хПк} существует ее подпоследовательность {хПкз}, схо-
сходящаяся к некоторой точке ж*:
lim хПк = ж*,
s—>-оо s
причем в силу G.15)
x*e[a,b]\U(xo,e).
Из этого включения, очевидно, вытекает, что
Х0 ф X*
G.16)

126 Гл. 1. Дифференциальное исчисление функций одной переменной
Из непрерывности функции / в точке ж* следует, что
Но предел подпоследовательности {f(xnks)} последовательности уп =
— f(xn), n = 1,2,..., равен пределу всей последовательности, поэтому
/(ж*) = lim f(xn ) = lim f(xn) = lim yn = 2/0-
s—>-oo	n—>-oo	G.14) n—>-oo
А так как з/0 = /(ж0), то получилось, что /(ж*) = /(ж0). Это же
в силу взаимной однозначности отображения / противоречит нера-
неравенству G.16). Следовательно,
lim Г1(уп)=Г1Ы,
га-юо
т. е. обратная функция /-1 непрерывна в произвольно выбранной точ-
точке у0 е [А, В]. <
Теорема 4. Если функция f непрерывна и строго возрастает на
интервале (а, Ь),
А = lim /(ж), В = lim /(ж),	G.17)
х—>а	х—>Ъ
то f((a,b)) = (А, В) и обратная функция f~x является однознач-
однозначной строго возрастающей непрерывной на интервале (А, В) функцией.
Х> Поскольку из G.17) следует, что
А = inf /(ж), В = sup /(ж)	G.18)
(а>&)	(а,Ъ)
(см. теорему 4 из п. 6.11), то для любого ж G (а, 6) в силу определения
нижней и верхней граней функции имеет место неравенство
Более того, для всех ж, а < ж < Ь, выполняется строгое неравенство
А < /(ж) < В. В самом деле, если бы нашлась, например, такая точка
ж е (а, 6), что /(ж) = А, то для любой точки ж', а < ж; < ж, в силу
строгого возрастания функции / имело бы место неравенство
f(x')<f(x)=A=mi f(x),
(a,b)
что противоречит определению нижней грани. Итак,
/((М))С(А,В).	G.19)
Пусть теперь
А = inf / < у < sup f = В.
Тогда согласно определению нижней и верхней граней функции су-
существуют такие точки х\ G (а, Ь) и Ж2 G (а, Ь), что
А < /(ж:) < ?/ < /(ж2) < В.

§ 7. Свойства непрерывных функций	127
В силу строгого возрастания и непрерывности сужения функции / на
отрезок [ж1,Ж2] обратная для него функция определена и непрерывна
на отрезке [f(xi),f(x2)] (см. теорему 3). А тогда, во-первых, сущест-
существует такая точка х Е (жь^г) С (а, Ь), что /(ж) = у и, следователь-
следовательно, f((a,b)) = (А, 5), а во-вторых, сужение на отрезок [/(xi),/(x2)]
обратной функции f~l непрерывно во внутренней точке у отрез-
отрезка [/(xi), /(ж2)], а поэтому в этой точке непрерывна и обратная функ-
функция /-1, рассматриваемая на всем множестве своего определения,
т. е. на интервале (А, В).
Отметим, что последнее заключение следует из того, что если
сужение какой-либо функции на множество, содержащее некоторую
окрестность заданной точки, непрерывно в этой точке, то и сама
функция, рассматриваемая на всем множестве своего определения,
непрерывна в указанной точке, так как непрерывность в точке зави-
зависит лишь от значений функции в достаточно малой окрестности этой
точки. <|
Отметим, что в теореме 4 интервалы (а, Ъ) и (А, В) могут быть
как конечными, так и бесконечными: —оо ^ а < Ъ ^ +оо, —оо ^ А <
<	В ^ +оо.
Утверждения, аналогичные теоремам 3 и 4, имеют место и для
строго убывающих функций.
Пример. Функция у = хп, п Е А/, строго возрастает на полуоси
х > 0 и непрерывна на всей числовой оси. Действительно, если 0 <
<	х\ < ж2, то, умножая п раз это неравенство само на себя, получим
О < х™ < х^; это и означает строгое возрастание рассматриваемой
функции. Для доказательства ее непрерывности заметим, что функ-
функция у — х непрерывна на всей числовой оси. В самом деле, каковы бы
ни были хо Е R и е > 0, возьмем S = е. Если уо = жо, то Ау = у — у0 =
= х — хо = Ах. Поэтому при |Аж| < S получим \Ау\ = |Аж| < S = г,
т. е. lim Ay = 0, а это и является условием непрерывности функции
у — х. Функция же у = хп непрерывна на всей числовой оси (в част-
частности, при х > 0) как произведение п непрерывных функций у = х.
Из того, что lim хп = 0 и lim xn = +оо, следует согласно теоре-
х—>0	х—>-|-оо
ме 4, что множество значений функции у = хп на интервале @, +оо)
также является интервалом @,+оо). Отсюда согласно той же теоре-
теореме вытекает, что обратная функция х = ^/у определена, строго воз-
возрастает и непрерывна на интервале @,+оо). Поэтому, в частности,
из любого положительного числа можно извлечь положительный ко-
корень п-й степени, и притом единственный, а следовательно, для лю-
любого рационального числа г однозначно определена степень аг, а > О,
такая, что аг > 0 (см. п. 2.1).
Замечание. Аналоги теорем 3 и 4 имеют место и для функций,
строго монотонных и непрерывных на конечных или бесконечных

128 Гл. 1. Дифференциальное исчисление функций одной переменной
полуинтервалах вида [а, Ъ) и (а, Ь]. Их формулировка и доказательство
по мере потребности предоставляются читателю.
7.4. Равномерная непрерывность. Если функция / непрерыв-
непрерывна на отрезке, то это означает, что любой точки ж этого отрезка и для
любого числа е > 0 найдется такое число S > 0 (зависящее от точки ж
и числа г), что для всех точек х' отрезка, для которых
х' - х\ < 5,	G.20)
выполняется неравенство
\f(x')-f(x)\<e.	G.21)
Если число S можно выбрать не зависящим от точки х так, чтобы при
выполнении условия G.20) выполнялось условие G.21), то функция /
называется равномерно непрерывной. Сформулируем определение это-
этого важного понятия более подробно.
Определение 2. Функция /, заданная на отрезке [а, 6], называ-
называется равномерно непрерывной на нем, если для любого г > 0 существу-
существует такое S > 0, что для любых двух точек х е [а, Ь] и х' е [а, Ь] таких,
что \х' — х\ < S, выполняется неравенство \f{x') — /(ж)| < г.
В символической записи определение непрерывности функции на
отрезке выглядит следующим образом:
\/х Уг>0 36 > 0 Уж', \x'-x\<6: \f(x')-f(x)\<e,
а определение равномерной непрерывности выглядит так:
Уг>0 Э5>0 Уж,ж;, \х'-х\ <5: \f(x')-f(x)\ < г. G.22)
Здесь точки х и х' принадлежат отрезку, на котором задана функ-
функция /.
Примеры. 1. Функция /(ж) = х равномерно непрерывна на всей
числовой оси R. Действительно, если задано г > 0, то, выбрав S = г,
получим, что для любых точек х и х' таких, что \х' — х\ < S, выпол-
выполняется неравенство
\f(x')-f(x)\ = \x'-x\<6 = e,
т. е. условия определения 1 выполнены.
2. Функция /(ж) = х2 не равномерно непрерывна на всей числовой
оси R.
Это следует из того, что для любого h ф 0 имеет место
lim [f(x + К) - f(x)\ = lim \(х + КJ - х2] = lim Bhx + h2) = оо.
х—>-оо	х—>-оо	х—>-оо
G.23)
Поэтому, если задано г > 0, то, каково бы ни было S > 0, зафиксиро-
зафиксировав h ф 0, \h\ < S, можно в силу G.23) так выбрать ж, что для то-
точек х' = х + h и ж будем иметь

§ 7. Свойства непрерывных функций	129
и в то же время
\х' — х\ = \h\ < S.
Ясно, что всякая равномерно непрерывная на отрезке функция
непрерывна на нем: если в определении равномерной непрерывности
зафиксировать точку ж, то получится определение непрерывности в
этой точке. Верно и обратное утверждение.
Теорема 5 (Кантор). Функция, непрерывная на отрезке, равно-
равномерно непрерывна на нем.
\> Докажем теорему от противного. Допустим, что существует не-
непрерывная на некотором отрезке [а, Ь] функция /, которая, однако,
на нем не равномерно непрерывна. Это означает (см. G.22)), что
существует такое г0 > 0, что для любого S > 0 найдутся такие точки
х Е [а, Ь] и х' Е [а, Ь], что \х' — х\ < ?, но \f{x') —/(ж)| ^ г. В част-
частности, для S = 1/п найдутся такие точки, обозначим их хп и х'п, что
\х'п-хп\<^	G.24)
\J\xn) — J\xn)\ ^ to-	\(.?д)
Из последовательности точек {хп} в силу свойства компактности
отрезка (см. теорему 4 в п. 5.8) можно выделить сходящуюся под-
подпоследовательность {хПк}. Обозначим ее предел ж0:
lim хПк = х0.	G.26)
к—>-оо
Поскольку а ^ хПк ^ Ь, к = 1,2,..., то а ^ хо ^ 6. Функция / не-
непрерывна в точке ж0, поэтому
lim f(xnk) = f(x0).	G.27)
к—уоо	G.26)
Подпоследовательность {х'Пк} последовательности {х'п} также схо-
сходится в точке жо, ибо
гр 	 ПГп ^ ПГ 	 Т*	—I— Т* 	 Т*г> <^ 	 —I— Т* 	 Т^п 	^ О
I Пи	U | "^ I Пь.	пк I ^^ I nk	U	^	^^ I ?^fc	U	^ w
G.24) Пд,	G.26)
при к ^ оо. Поэтому
\imQf(x'nk)=f(x0).	G.28)
Из G.27) и G.28) следует, что
JmiJ/(<J - f(xnh)] = f(x0) - f{xo) = О,
а это противоречит условию, что при всех к = 1,2,... выполняется
неравенство
I/0O-/0OI ^ ^о>о.
G.25)
Полученное противоречие доказывает теорему. <|
Условие равномерной непрерывности можно сфомулировать в тер-
терминах так называемых колебаний функции на отрезках.
9 Л.Д.Кудрявцев, т.1

130 Гл. 1. Дифференциальное исчисление функций одной переменной
Определение 3. Пусть функция / задана на отрезке [а, Ъ]. Тогда
величина
oo(f;[a,b})= sup \f(x')-f(x)\	G.29)
x,x'e[a,b]
называется колебанием функции f на отрезке [а,Ь].
Из двух значений f(x') - f(x) и f(x) - f(x') одно неотрицатель-
неотрицательно и, следовательно, не меньше второго, поэтому величина верхней
грани и в правой части равенства не изменится, если вместо абсо-
абсолютной величины |/(V) — f(x)\ разности f(x') — f(x) взять саму эту
разность:
u(f;[a,b])= sup (f(x')-f(x)).
x,x'e[a,b]
Справедливо следующее утверждение.
Для того чтобы функция f была равномерно непрерывна на отрез-
отрезке [а, Ь], необходимо и достаточно, чтобы для любого г > 0 существо-
существовало такое S > 0, что для любого отрезка [ж, х'] С [а, Ь] такого, что
0 < х' — х < S, выполнялось неравенство
uj(f;[x,x'})<e.	G.30)
|> Действительно, поскольку х,х' G [ж,ж;], то из неравенства G.30)
следует, что |/(V) — f(x)\ < г, а поэтому выполняется утвержде-
утверждение G.22).
Обратно, если справедливо утверждение G.22), то для любого г >
> 0 найдется такое S > 0, что для любых двух точек х и х' отрез-
отрезка [а, 6], удовлетворяющих условию \х' — х\ < 5, имеет место нера-
неравенство \f(x') — f(x)\ < г/2. В частности, это неравенство выполня-
выполняется и для всех таких точек х,х' G [а, Ь], для которых 0 < х' — х < S.
Но для любых двух точек ? и г\ отрезка [х,х'] выполняется, очевид-
очевидно, неравенство 0 < \rj - ?| < х' - х < S, а следовательно, и нера-
неравенство 1/G7) — /(?I < ?/2- Поэтому для любого отрезка [х,х'\ тако-
такого, что 0 < х' — х < 5, имеем
^(/;[х,х/])= sup
Z,r,e[x,x
Утверждение доказано. <|
§ 8. Непрерывность элементарных функций
8.1. Многочлены и рациональные функции.
Теорема 1. Многочлен непрерывен на всей числовой оси.
|> Действительно, во-первых, постоянная на всей числовой оси функ-
функция непрерывна во всех точках (см. свойство 3° пределов функций

§8. Непрерывность элементарных функций	131
в п. 6.7); во-вторых, функции хк, к = 1,2,..., также непрерывны на
всей числовой оси (см. пример в п. 7.3), а любой многочлен Рп{х) =
= ао + а\х + ... + anxn является линейной комбинацией функций 1,
ж, ж2, ..., хп с коэффициентами ао, ai,..., ап, поэтому, согласно следст-
следствию из свойства 6° пределов функции в п. 6.7, он непрерывен на всей
числовой оси. <|
Р(х)
Теорема 2. Рациональная функция —±—!-, где Р(х) uQ(x) —мно-
Q(x)
гочлены, непрерывна во всех точках числовой оси, в которых Q(x) ф 0.
|> Это сразу следует из непрерывности многочленов Р(х) и Q(x) на
всей числовой оси и непрерывности частного непрерывных функций
во всех точках, в которых знаменатель не обращается в нуль (см.
следствие из свойства 6° пределов функций в п. 6.7). <1
8.2. Показательная и логарифмическая функции. Перечис-
Перечислим основные свойства степеней аг, а > 0, с рациональными показа-
показателями г Е Q (см. п. 2.1).
1°. Пусть Т\ < г2. Если а > 1, mo ari < аГ2, а если а < 1,
то аГ1 > аГ2.
2°. аГ1аГ2 =аГ1+Г2.
3°. (аГ1)Г2 =аГ1Г2.
Эти свойства доказываются в курсе элементарной математики в
предположении существования и однозначной определенности аг для
любого рационального г, а > 0, а это было доказано в п. 7.3.
Вспомним еще, что а0 = 1 и что а~г = —.
аг
Из свойства 1° вытекает, что для любого г G Q выполняется не-
неравенство аг > 0. В самом деле, если а ^ 1 и г ^ 0, то по свойству 1°
аг ^ а0 = 1 > 0. Отсюда следует, что а~г = — > 0. Аналогично рас-
аг
сматривается случай 0 < а < 1.
Нашей ближайшей задачей является определение значения выра-
выражения ах для любого действительного числа х и а > 0. Затем будут
изучены свойства функции ах.
Лемма 1. Для любого а > 0 имеет место равенство
lim a1'71 = lim оГ1'71 = 1.	(8.1)
п—>-оо	п—>-оо
Следствие. Для любого а > 0 имеет место равенство
lim ar = 1.	(8.2)
r^0,r?Q
|> Пусть сначала а > 1. Для любого n G А/ положим
хп = а1/- - 1.	(8.3)
9*

132 Гл. 1. Дифференциальное исчисление функций одной переменной
Поскольку — > 0, то а1//п > а0 = 1 и, следовательно,
п
жп>0, п = 1,2,...	(8.4)
Из (8.3) и (8.4) вытекает, что
а = A + хп)п = 1 + пхп + ... > пхп.
Отсюда и из неравенства (8.4) получаем 0 < хп < -, а так как lim - =
П	п—)-оо П
= 0, то lim жп = 0, что в силу (8.3) и означает, что
п—юо
lim a1/n = 1.	(8.5)
п—>-оо
Если а<1, то Ь = - > 1, и потому
а
Нт а1/п = lim -^— = 	5__ = 1.
frV	1/
п—юо
Наконец, если а = 1, то утверждение (8.1) очевидно, так как
Из доказанного следует, что при любом а > 0 имеет место и ра-
равенство	i
lim а 'п =	-г- = 1. <1
/woo	lim ai/n
п—юо
Докажем следствие.
|> Для всех а > 0 функция аг монотонна на множестве рациональных
чисел Q. Для каждого действительного числа х множества рациональ-
рациональных чисел г<хиг>хне пусты и точка х является их точкой
прикосновения. Поэтому, согласно следствию из теоремы 4 п. 6.11,
существуют односторонние пределы lim ar и lim ar, r Е Q. В
частности, указанные пределы существуют для х = 0. Согласно опре-
определению предела функции в терминах последовательностей их зна-
значения равны соответственно значению последовательностей аГп при
любых последовательностях тп < 0 и тп > 0, стремящихся к нулю,
гп е (?, п = 1,2,... Выбрав гп =	и гп = -, для которых пределы
уже вычислены (см. (8.1)), в силу сказанного получим
lim ar = lim а~1/п = 1, lim ar = lim a1/n = 1,	(8.6)
г—У—0	п—>-оо	г—^+0	п—>-оо
т. е. односторонние пределы в точке х = 0 функции ar, r G Q, г ф 0,
равны и, следовательно, согласно теореме 2 п. 6.6, существует дву-
двусторонний предел lim ar = 1. Он совпадает со значением а0 = 1
г-И), г^О

§8. Непрерывность элементарных функций	133
функции аг при г = 0, а поэтому (см. лемму 5 в п. 6.9) она непрерывна
в нуле:
lim ar = а0 = 1, г е Q, а > 0.
Равенство (8.2) доказано. <|
Определение. Пусть а > 0 и ж Е /?. Определим аж как предел аг
по множеству рациональных чисел Q, когда г ->• ж, т. е.
аж=? limar.	(8.7)
г—)-ж
Докажем, что это определение корректно, т. е. покажем, используя
критерий Коши для предела функции (см. теорему 5 в п. 6.12), что
предел (8.7) существует.
|> Пусть a ) 1 и х G /?. В силу принципа Архимеда существует на-
натуральное п такое, что	/о оЧ
п > х.	(8.8)
Зададим произвольно г > 0. Согласно следствию леммы 1 сущест-
существует такое S > 0, что для всех рациональных г, удовлетворяющих
неравенству
|г| < S,	(8.9)
выполняется неравенство
\аг - 1| < ^.	(8.10)
Если это условие выполняется для некоторого S > 0, то оно заведо-
заведомо выполняется и для всякого меньшего положительного S. Поэтому
указанное S > 0 можно всегда выбрать так, чтобы выполнялось нера-
неравенство (см. (8.8))	е
х+°- <п.	(8.11)
Если рациональные числа г' и г" принадлежат --окрестности
точки х:	л	л
и, следовательно,
- Т\ < _
х\ ^ 2'
_ х\
^ + ^ = 5,	(8.12)
то, заметив, что г' < х -\— < п, будем иметь
2 (8.11)
< ап\аг"-г' -1| < ап— = г.
(8.8)	(8.9), (8.10) ап
(8.11)	(8.12)
Таким образом, для произвольно заданного г > 0 существует та-
такое S > 0, что из выполнения условий \г' — х\ < -, \г" — х\ < - вы-

134 Гл. 1. Дифференциальное исчисление функций одной переменной
текает неравенство
\аг" -аг'\ <е.
Согласно критерию Коши это означает существование конечного
предела lim ar для всех х Е /?, а ^ 1. Этот предел обозначается ах.
г—Ух, г?ф
Если 0 < а < 1, то Ь = - > 1, и для любого х Е R предел
CL
lim а = 	?
r-^ж	lim Ъ
reQ	r^x, reQ
также существует. <|
Отметим, что если х Е Q, то определение (8.7) совпадает с уже
известным определением рациональной степени аг числа а, г Е Q.
Действительно, в силу доказанного предел lim ar = ах сущест-
г—ух, r?Q
вует и для любой последовательности гп ->• ж, rn e (?, п = 1,2,...,
равен пределу lim аГп. В случае х = г G Q за указанную последо-
п—>-оо
вательность можно взять стационарную последовательность гп = г,
п = 1,2,... Тогда будем иметь
ах = lim аГп = lim ar — аг.
п—уоо	п—уоо
Из определения функции ах следует, что для любого действитель-
действительного числа х выполняется равенство
1
ах
U3)
Действительно, это равенство имеет место для рациональных значе-
значений х = г G Q, поэтому для любого действительного х получаем
-х	v	-г v 1	1
а = lim а = lim — = —.
(8.7) — г—У — х	г—ух аг (8.7) CL
Функция f(x) = аж, а > 0, х е /?, называется показательной функ-
функцией.
В случае а = е функция еж обозначается также ехр х и называ-
называется экспонентой.
Теорема 3. Показательная функция ах, а > 0, обладает следую-
следующими свойствами.
1°. При а > 1 она строго возрастает, а при а < 1 строго убывает
на всей числовой оси.
2°. Для любых х е R и у е R имеет место равенство ахау = аж+2/.
3°. Для любых х е R и у е R имеет место равенство (ах)у = аху.
4°. Функция ах непрерывна на всей числовой оси.
5°. Областью значений функции ах является множество всех по-
положительных чисел, т. е. бесконечный интервал @,+оо).

§8. Непрерывность элементарных функций	135
|> Доказательство. 1°. Пусть для определенности а > 1 и ж < у.
Существуют такие рациональные числа г' и г", что
х < г' < г" < у.
Возьмем последовательности рациональных чисел г'п -у х и г" -у 2/
такие, что г^ < г' < г" < г", n = 1,2,... Тогда в силу свойства 1°
степеней с рациональными показателями будем иметь
аг>п < аг> < аг" < аг™ , п = 1, 2,...
Переходя в этом неравенстве к пределу при п —у оо, получим
ах = lim ar- ^ аг' < ar" ^ lim аг- = ау',
п—>-оо
т. е. при ж < у имеет место неравенство ах < ау.
Отметим, что из 1° и того, что для любого рационального г имеет
место неравенство аг > 0, следует, что для любого действительного
числа х выполняется неравенство
ах > 0.	(8.14)
В самом деле, если, например, а ^ 1 и х G /?, то, выбрав рацио-
рациональное число г так, чтобы выполнялось неравенство г < ж, полу-
получим ах > аг > 0. Аналогично рассматривается случай 0 < а < 1.
Доказательство. 2°. Пусть ж G /?, у ? R, r'n G Q, r[[ G (J,
г^ —>¦ ж, г^ —>¦ ^/ и, следовательно, г^ + г^ —>¦ ж + 2/, п = 1, 2,... Тогда
aV = lim ar- lim a< = lim ar-ar- = lim a<+< = аж+2/.
(8.7) n—>-oo	n—>-oo	n. 6.7 n—>-oo	n—>-oo	(8.7)
Доказательство. 4° (свойство 3° будет доказано позже). По-
Покажем, что функция ах непрерывна на всей числовой оси. Пусть
жо G /?. В силу монотонности функции аж (см. свойство 1°) сущест-
существуют конечные односторонние пределы lim ax и lim ax. Яс-
х—ухо— 0	ж—^жо+0
но, что они совпадают соответственно с односторонними пределами
lim ar и lim ar сужения функции ах на множество ра-
r^xo-o,reQ r^xo+o,reQ
циональных чисел Q, из которого удалена точка жо, если она рацио-
рациональная. Эти пределы в свою очередь совпадают с двусторонним пре-
пределом lim ar = ах° (см. формулу (8.7)). Таким образом,
г—>xo,r?Q
lim ax = lim ar = ах° = lim ar = lim ax.
ж-^жо-0	г->жо-О,г?(?	г-^жо+О,геР	ж-^жо+О
В силу равенства односторонних пределов
lim ах = аХо = lim ax
х—>xq— 0	ж—>-жо+О

136 Гл. 1. Дифференциальное исчисление функций одной переменной
согласно теореме 2 из п. 6.6 существует двусторонний предел
lim ax=aXo.
х—>хо, хфхо
Отсюда в силу леммы 5 из п. 6.9 следует, что в точке хо предел функ-
функции ах существует и без ограничения х ф хо, т. е.
lim ax =аХо.	(8.15)
X—УХо
Это и означает, что функция ах, х е /?, непрерывна в любой точ-
точке Хо Е R.
Доказательство. 3°. Пусть сначала у = р — натуральное чис-
число; тогда, применив р раз свойство 2°, получим
рраз
{ах)р = ах ¦ ах ¦... ¦ ах, =ах+х+-+х= ахр.	(8.16)
р раз
Если у = 1/д, где q — натуральное число, то
{axI/q = ax/q.	(8.17)
В самом деле, согласно определению корня для доказательства спра-
справедливости равенства (8.17) надо показать, что
а это равенство сразу следует из свойства (8.16):
(ax/q)q = a^xlq^q = ах
(8.16)
Если у = p/q, где р и q — натуральные числа, то
(ax)p/q = [(ax)p]1/q = (axpI/q = axp/q.	(8.18)
(8.16)	(8.17)
Если же у = —p/q, то
(ax\-p/q _	1	_	1	_ а~хР/я	(g 19)
(8.13) (ах)Р/У (8.18) ажР/4 (8.13)
Наконец, при у = 0, очевидно,
(ж\0 	 1 	 0 	 Х'О	/о оп\
а ) =1 = а =а .	(o.zUJ
Таким образом, для любого рационального числа г справедливо ра-
равенство
(ах)г = ахг.	(8.21)

§8. Непрерывность элементарных функций	137
Пусть теперь у — произвольное действительное число. Возьмем
какую-либо последовательность рациональных чисел {гп}, имеющую
своим пределом число у, т. е. гп —У у, rn Е Q, п = 1, 2,... Тогда
(ахуп = ахгп^	(8<22)
(8.21)
Поскольку lim хгп = ху, то в силу непрерывности функции ах на
п—>-оо
всей числовой оси имеет место равенство
Нт аХГп = аху,	(8.23)
гаюо
га-юо
а в силу определения (8.7) степени числа — равенство
lim (ах)Гп = (ах)у.	(8.24)
га-юо
Переходя к пределу при п ->• оо в равенстве (8.22), в силу (8.23)
и (8.24) получим (ах)У = аху.
Доказательство. 5°. Поскольку функция аж строго монотон-
монотонная, то для того чтобы доказать, что ее областью значений является
бесконечный интервал @,+оо), надо согласно теореме 4 п. 7.3 дока-
доказать, например, при а > 1, что
lim ах = 0, lim ax = +оо.	(8.25)
х—У — сю	х—>-|-оо
Эти пределы (конечные или бесконечные) в силу монотонности
функции всегда существуют (см. п. 6.11), поэтому достаточно лишь
доказать, что для каких-либо фиксированных последовательностей
хп —у —оо и х' —> +оо имеют место равенства lim аХп = 0, lim aXn =
п—>-оо	п—>-оо
= +00, например, что эти равенства справедливы для последователь-
последовательностей хп = — п и х'п = п, п = 1,2,... А это было доказано выше
(см. пример 4 в п. 5.1).
Функция, обратная к показательной функции у = ах, а > 0, а/
7^ 1, называется логарифмической и обозначается loga 2/. В силу свойст-
свойства 5° показательной функции логарифм loga у определен для любого
положительного числа. Число а называется основанием логарифмичес-
логарифмической функции у = loga х. Особую роль в математическом анализе играет
логарифмическая функция с основанием а = е, она обозначается In ж
и называется натуральным логарифмом.
Согласно определению обратной функции справедливо тождество
alo^x =x.	(8.26)
Теорема 4. Логарифмическая функция у = loga ж, а > 0, а ф 1,
определена и непрерывна при любом х > 0. При этом она строго воз-
возрастает при а > 1 и строго убывает при 0 < а < 1.

138 Гл. 1. Дифференциальное исчисление функций одной переменной
\> Это непосредственно следует из свойств 1°, 4° и 5° показательной
функции (теорема 3) и теоремы 4 из п. 7.3. <1
Подчеркнем, что нами, в частности, доказано, что при любом ос-
основании а > 0, а ф 1, логарифм loga x определен для любого положи-
положительного числа х.
Из свойств 2° и 3° показательной функции следуют соответствую-
соответствующие свойства логарифма произведения и степени:
\ogaxy = \ogax + \ogay, ж>0, у>0,	(8.27)
loga ха = a loga ж, х > 0, a е /?.	(8.28)
Докажем, например, формулу (8.28). Согласно свойству 3° показа-
показательной функции из теоремы 3 имеем
(аР)а = а^, /Зе /?, a G /?.	(8.29)
Поэтому
logж" = log>los*Х)а Ъ log
Из формул (8.27) и (8.28) следует формула для логарифма
частного:
lQga 7 = 10§а Ж^-1 , = 10§а Ж + 10§а У~\ = , 1о^ Ж ~ loga У-
у	(8.27)	(8.28)
С помощью перечисленных свойств показательной и логарифми-
логарифмической функций можно получить и другие их свойства.
Докажем, например, равенство
(ab)x=axbx, а>0, Ъ > 0.
В случае а = 1 или 6 = 1 написанное равенство очевидно. Если же
а/ 1 и &/ 1, то
(
(8.26)
= axaxlogab
(8.28)	(8.26)
8.3. Степенная функция. Функция у = ха, х > 0, называется
степенной функцией (а G /?).
Теорема 4. При любом a G /? степенная функция ха непрерывна
при всех х > 0.
|> Это сразу следует из того, что степенную функцию ха можно
представить как композицию непрерывных функций — логарифми-
логарифмической и показательной. В самом деле, поскольку х = е1пж, то
у = ха = еа1пх = еи, и = а\пх. <

§8. Непрерывность элементарных функций
139
В точке х = 0 функция ха определена не для всех значений пока-
показателя а. Если а > 0, то существует предел lim xa = lim ealnx = 0.
По определению полагают
0а = 0, а > 0.	(8.30)
Это определение согласуется с тем, что при рациональных а = г > 0
имеет место 0г = 0. Кроме того, естественность определения (8.30)
оправдывается и тем, что, если в определении (8.7) взять а = 0 (рань-
(раньше предполагалось, что а > 0), то будем иметь
0а = Hm 0r = 0, а > 0.
При определении (8.30) функция ха оказывается непрерывной
справа в точке х = 0 при любом а > 0.
Функция жа может оказаться определенной при некоторых рацио-
рациональных а^Ои для х < 0, например, ж±п, x±1/Bn~1^), n G А/. Степенная
функция жа непрерывна во всех точках, в которых она определена.
Это следует из того, что если она определена при х < 0, то является
четной или нечетной функцией.
8.4. Тригонометрические и обратные тригонометричес-
тригонометрические функции.
Лемма 2. Для любого действительного числа х имеет место
неравенство
sinx| ^ \х\.	(8.31)
|> Рассмотрим на координатной плоскости
круг радиуса R с центром в начале коорди-
координат О. Если 0 < х
(рис. 71), то
|, О А = R, LAOC = х
\АВ\
2R
где \АВ\ — длина хорды, соединяющей точ-
точки А и В, \АВ\ — длина дуги окружности,
Рис. 71
соединяющей эти точки, а отношение
\АВ
R
равно радианной мере уг-
угла ААОВ, т. е. равно 2х. Таким образом, неравенство (8.31) для слу-
случая 0 ^ х ^ ^ доказано.
Если
ж < 0, то 0 < —х ^ —, и потому по уже доказанному
| sin ж| = sin(—х) ^ —х = |ж|, т. е. в этом случае неравенство (8.31)
также справедливо.
Наконец, если |ж| > — > 1, то неравенство (8.31) очевидно, ибо
I sinxl < 1. <1

140 Гл. 1. Дифференциальное исчисление функций одной переменной
Теорема 5. Функции у = sin ж и у = cos ж непрерывны на всей
числовой оси.
\> Докажем, например, непрерывность функции у = sin ж:
\Ау\ = | sin(x + Ах) - sinx| = 2 cos (x + ^) 11 sin ^ <С |Аж|, (8.32)
V	2 / \ \	Z
ибо
COS Ж+ —- ^ 1,
sin ¦
Ах
\Ах\
Из неравенства (8.32) сразу следует, что lim Ay = 0; это и озна-
Аж-^О
чает непрерывность функции у = sin ж в произвольной точке х Е R. <\
„	..	sin ж ,	cos ж
Следствие. Функции tgx = 	 u ctgx = —— непрерывны во
cos ж	sin ж
всех точках числовой оси, кроме тех, в которых их знаменатели об-
обращаются в нуль.
\> Это сразу следует из непрерывности частного непрерывных
функций в точках, в которых делитель не обращается в нуль (см.
следствие из свойства 6° пределов функций в п. 6.7). <1
Теорема 6. Каждая из обратных тригонометрических функций
у = arcsinx, у = arccosx, у = arctgx и у — arcctgx непрерывна в об-
области своего определения.
\> Это в силу теоремы о непрерывности обратных функций
(см. п. 7.3) сразу следует из теорем 3 и 4. <|
8.5. Элементарные функции.
Теорема 7. Каждая элементарная функция непрерывна в облас-
области своего определения.
\> В самом деле, согласно теоремам 1-6 все основные элементарные
функции непрерывны на множествах, на которых они определены. По-
Поэтому непрерывна в области своего определения и каждая функция,
которая может быть получена из основных элементарных функций с
помощью четырех арифметических действий и операции композиции
функций, т. е. каждая элементарная функция (определение элемен-
элементарной функции см. в п. 3.2). <|
§ 9. Сравнение функций
9.1. Замечательные пределы. В этом пункте будут вычисле-
r sinx .. ( ,i/x .. ln(l + х) ,. ах — 1
ны пределы lim	, limfl + x) ' , lim —	-, lim	, которые
х^О X х^О	х^О X	х^О X
обычно называются замечательными пределами.
I. Докажем, что
sin? ^	^ j

9. Сравнение функций
141
|> Рассмотрим в координатной плоскости круг радиуса R с цент-
центром в начале координат. Если (рис. 72) О А =
= R, LAOB = ж, 0 < х < ?, АС ±ОА, то
пл. АОАБ < пл. сектора ОАВ < пл.
т. е. -R2smx < - R2x < -R2tgx;
отсюда
ИЛИ
sin ж < x < tgx,
ж	1
1 <
sin ж
COS Ж
Ж
и
1
это
В силу четности функций
sin ж cos ж
неравенство справедливо и для	< х < 0.	рИс. 72
Перейдя в этом неравенстве к пределу при х —> 0 и заметив, что в
силу непрерывности функции cos ж при х = 0 имеет место равенство
lim cos x = 1, получим
lim
Sin Ж
= 1,
что равносильно равенству (9.1). <1
С помощью предела (9.1) вычисляется ряд других пределов,
например,
r tgx r /sin x 1 \ 1
lim -5— = lim 	•	 = 1,
^о ж	^о \ х cos ж У
lim
П. Докажем, что
ж
arcsin ж
Sin ?/
=е.
= 1.
(9.2)
\> Мы уже знаем (см. п. 5.7), что
/	1 \ п
lim A + -) =е.
п—юо V	пУ
Более того, из замечания 2 в п. 6.1 следует, что для любой по-
последовательности Пк G А/, п/. —>¦ +оо, & = 1,2,..., также имеет место
равенство	. л \nh
lirn^ ^1 + — J = е.	(9.3)
Пусть Хк > 0 и ж/, —>- 0, к = 1, 2,... Положим п/. = — , где — —
1	Lx^J	1хк\
целая часть числа —, тогда
— < пк + 1
и, следовательно,
+
< ^^ ^ —.
(9.4)
(9.5)

142 Гл. 1. Дифференциальное исчисление функций одной переменной
Кроме того, согласно условию Хк —> 0 имеем	> оо, откуда в силу
неравенства (9.4) следует, что
lim nk = +оо.	(9.6)
к^оо
В результате имеем
(9.7)
где
i V
)
lim A + ^—) =^\ "к^;\ = е, (9.8)
fc^ooV	nk + U	lim Л	1 \ (9.3)
fc^oo V nk + lj
lim (l + —)= lim (l + —Yh lim A + —) = e. (9.9)
k—yoo V	Tlfc /	k^-oo \	n^ / k^-oo \	n^ / (9.3)
Из (9.7), (9.8) и (9.9) следует, что (см. обозначения в п. 6.6)
lim (l + xI/x =е.	(9.10)
ж-^+О
Пусть теперь Хк < 0 и ж/, ->• 0, к = 1, 2,... Положим ^ = —ж&, тог-
тогда ук > 0 и 2/А; —>- 0, fc = 1, 2,... Без ограничения общности будем счи-
считать, что ук < 1 (с некоторого номера это неравенство заведомо
выполняется). Имеем
lim A + Хк)г/Хк = Hm A - Ук)'1^1* = Hm
f 1 ч	1?*—)	. (9.11)
\	1-J/jfe/
1-Ук
Положим теперь Zk = ———. Очевидно,
zfe > 0, zfe -> 0.	(9.12)
Поэтому
lim (I + ж^I/жй = lim (I + zkI/zh+1 =
fe-^oo	(9.11) fe-^oo
= lim A + ^)!/^ Hm (l + zk) = e. (9.13)
к^оо	ж^оо	(9.10)
(9.12)
Таким образом,
lim A + жI/ж= lim A + жI/х = e.
ж^+0	ж^-0	(9.10)
(9.13)

9. Сравнение функций	143
Отсюда в силу теоремы 2 из п. 6.6 и следует равенство (9.2). <|
Вычислим с помощью (9.2) некоторые другие пределы. Покажем
прежде всего, что
Umloga(l + x)= 1	аф	(9Л4)
ж^о	ж	In a
в частности,
Ит ln(l±?) = L
ж^О Ж
В самом деле,
lim logjl + ж) = Ит iOg A + x)i/x = ioga lim (I + xflx = loga e = -Ц
ж^о ж	ж^о av	у	аж^оч	у	a In a
Докажем еще, что
lim —— = In a, a > 0, a ^ 1,	(9.16)
ж—)-О Ж
в частности, что	Рх _ i
lim ?	1 = i.	(9.17)
ж^О X
Действительно, положив у = ах - 1 и, следовательно, ж = -5^-	—,
ma
получим lira у = 0, а поэтому
ж—^0	^ .	.
г ал - 1 г г/In a	,
lira 	 = lira —7;	 = In a.
ж^О X	у^О 1пA + 2/) (9.15)
9.2. Сравнение функций в окрестности заданной точки.
Как известно, сумма, разность и произведение бесконечно малых яв-
являются бесконечно малыми. Частное же бесконечно малых может
быть и не бесконечно малой, однако отношение бесконечно малых
позволяет сравнивать их "по порядку убывания". Аналогично мож-
можно сравнивать "по порядку роста" бесконечно большие. Перейдем к
точным определениям.
Пусть функции fug заданы на множестве X и хо — конечная
или бесконечная удаленная точка прикосновения этого множества.
При этом возможны случаи, когда хо G X и когда хо 0 X.
Будем предполагать, что существуют такие окрестность U =
= U(xo) точки хо и функция ср, заданная на X П U, что для всех
х G X П U выполняется равенство
f(x)=<p(x)g(x).	(9.18)
В частности, если функции / и д заданы в точке хо, то и функция ср
задана в этой точке, а если / и д не заданы в ней, то не задана в ней
и функция ср.
Определение 1. Функция / называется функцией, ограниченной
относительно функции д в окрестности точки жо, если функция ip
ограниченна.

144 Гл. 1. Дифференциальное исчисление функций одной переменной
В этом случае существует такая постоянная с > О, что для всех
х Е X П U выполняется неравенство
\ф)\^с,	(9.19)
а следовательно, и неравенство
\f(x)\ ^ c\g(x)\.	(9.20)
(9.18)
(9.19)
Условие (9.20) равносильно условиям (9.18) и (9.19). Действитель-
Действительно, если выполняется условие (9.20), то при
если
У 0, если д(х) = 0,
выполняются условия (9.18) и (9.19).
Если функция / ограничена относительно функции д в окрестнос-
окрестности точки жо, то пишут
f = O(g), x^x0	(9.21)
(читается: / есть "О большое" от д).
Определение 2. Функция / называется функцией того же по-
порядка при х —У жо, что и функция д, если существуют такие постоян-
постоянные с\ > 0 и С2 > 0, что для всех х G X П U выполняется неравенство
С1 ^ \ф)\ ^ с2.	(9.22)
В этом случае для всех х G X П U выполняется неравенство
ci|^(x)|^|/(x)|^c2|^(x)|.	(9.23)
Если функция / того же порядка при х ->• ж0, что и функция #, то
пишут / = д, х —У хо.
Очевидно, что функция / того же порядка при х —У хо, что и функ-
функция д, тогда и только тогда, когда / = О(д) и д = О(/), ж —у xq.
Определение 3. Функция / называется бесконечно малой от-
относительно функции д при х —У жо, если функция ip бесконечно малая
при х ->• ж0, т. е. если
lim у?(ж) = 0.	(9.24)
х—Vxq
В этом случае пишут
f = o(g), х^х0	(9.25)
(читается: / есть "о малое" от д при ж —У хо).
Определение 4. Функция / называется эквивалентной функ-
функции д (или асимптотически равной ей) при х —У жо, если
lim <р(ж) = 1.	(9.26)
ж

9. Сравнение функций	145
В этом случае пишут
f ~ д, х -> х0.
Замечание 1. Если хо Е X, то, как известно (см. п. 6.2), из
существования предела lim (р(х) следует, что lim (р(х) = (р(х0). По-
X—YXq	X—YXq
этому в случае (9.24) имеем ср(хо) = 0, а в случае (9.26) — Ц>(хо) = 1.
Если / = о(д), х —У хо и lim gix) = 0, то функция / называется
бесконечно малой более высокого порядка, чем бесконечно малая д. В
случае / = о(дп), х —> жо, бесконечно малую / называют бесконечно
малой порядка п относительно бесконечно малой д.
Замечание 2. Если в условиях определений 3 или 4 функция д
не обращается в нуль на множестве X П U и хо 0 X, то условие (9.24)
можно записать в виде
Нт /М = 0,	(9.27)
х^хо д(х)
lim Щ = 1.	(9.28)
^х д(х)
а условие (9.26) — в виде
Замечание 3. Если хо 0 X и существует конечный предел
Нт Щ = к,	(9.29)
х^х0 д(х)
то функция ^-7—7 ограничена на пересечении некоторой окрестнос-
д(х)
ти U(xo) точки хо с множеством X (см. свойство 1° пределов функций
в п. 6.7), т. е. существует такая постоянная с > 0, что для всех х G
fix)
G X П U(xq) выполняется неравенство
с, т. е.
откуда следует, что при выполнении условия (9.29) имеет место со-
соотношение
f(x) = O(g(x)), х^х0.
Замечание 4. В определениях 1-4 функции / и д могут быть
последовательностями / = {жп}, д = {уп}, и, таким образом, указан-
указанные определения содержат в себе определения следующих понятий:
а)	последовательности, ограниченной относительно другой после-
последовательности: хп = О(уп), п ->• оо;
б)	последовательностей одного порядка: хп = уп, п ->• оо;
в)	асимптотически равных последовательностей: хп ~ уп, п —> оо;
г)	последовательности, бесконечно малой по сравнению с другой
последовательностью: хп = о(уп), п —> оо.
10 Л.Д.Кудрявцев, т.1

146 Гл. 1. Дифференциальное исчисление функций одной переменной
Примеры. 1. sin2x = 0(ж), ж ->• 0, ибо
|вт2ж| ^ 2|ж|.	(9.30)
Верно и соотношение ж = O(sin2x), ж ->• 0, ибо существует ко-
X	\	X
нечный предел lim	= -, и, следовательно, функция 	 огра-
ж^о sin 2x 2	sin 2x
ничена в некоторой окрестности С/@) точки ж = 0 (см. свойство 1°
пределов функций в п. 6.7). Иначе говоря, существует такая постоян-
постоянная с > 0, что для всех ж Е U@) выполняется неравенство
х/0, поэтому
ж G U@).	(9.31)
Из (9.30) и (9.31) следует, что при ж ->• 0 функции ?/ = ж и ?/ = sin 2ж
одного порядка:
sin2x = ж, ж ->• 0.
2.	ж3 = о(ж2), ж —>¦ 0, ибо ж3 = ж • ж2 и lim ж = 0.
ж-И)
3.	ж2 = о(ж3), ж —У оо, ибо ж2 = - • ж3 и lim - = 0.
Ж	ж-Юо X
sin ж
4.	Поскольку lim	= 1, то функции у — х и у — sin ж экви-
эквивалентны при ж —у 0:
sin ж ~ ж, ж —>¦ 0.
Замечание 5. Символы О(д) и о(#) по существу обозначают це-
целые классы функций, обладающих по сравнению с данной функцией
определенным свойством, поэтому равенства типа /(ж) = О(д(х)) и
f[x) = о(д(х)), х —> жо, следует читать только слева направо, напри-
например, ж2 = о(ж), ж —> 0. Здесь верно то, что функция у — х2 является при
ж ->• 0 бесконечно малой по сравнению с функцией ^/ = ж, но не всякая
функция, бесконечно малая по сравнению с функцией у — ж, является
функцией у = ж2. Равенства с символами О и о не обладают и ря-
рядом других свойств равенств, например, свойством транзитивности:
х2 = о(ж), ж3 = о(ж), ж —>¦ 0,
но ж2 ф ж3.
9.3. Эквивалентные функции. Примеры эквивалентных функ-
функций (см. определение 3 в п. 9.2) легко получить из результатов в п. 9.1:
ж ~ sin ж ~ tgx ~ arcsinx ~ arctgж ~ 1пA + ж) ~ еж — 1, ж —>¦ 0.
Теорема 1. Для того чтобы функции /(ж) и д{х) были эквива-
эквивалентны при х —У 0, необходимо и достаточно, чтобы
f(x)=g(x)+o(g(x)), x -»• 0.	(9.32)

9. Сравнение функций	147
|> Формула (9.32) является просто другой записью определе-
определения 4. Действительно, условие (9.26) lim ср(х) = 1 равносильно усло-
вию ip(x) = 1 + s(x), где lim s(x) = 0. Поэтому условие
X—УХо
f{x) = ф)д(х), lim tp(x) = 1,	(9.33)
X—YXq
равносильно условию
f{x) = A + е{х))д{х) = д{х) + е{х)д{х), lim е{х) = 0, (9.34)
х—>хо
т. е. условию /(ж) = д{х) + о{д{х)), х —>- жо- <1
Замечание 1. Если д{х) / 0, х G I, ж / жо, то условие (9.32)
можно записать в виде
Шп faM = о.
х^х0 д(х)
^	fix) — д(х)
Оно означает, что относительная погрешность	, ч между эк-
Бивалентными функциями fug является бесконечно малой при
х —У хо.
Пример 5. ctg х — —h о( — ), ж —>¦ 0. Чтобы в этом убедиться, в
х \х /
силу теоремы 1 достаточно показать, что ctg ж ~ -, ж ->• 0. Это же
х
сразу следует из того, что lim -^— = 1 (см. п. 9.1), ибо
ж-^0 X
,. ctg ж ,. х 1
lim —7— = lim 	 = 1.
х^О 1/Х	х^О tgX
Теорема 2. Если f(x) ~ fi(x), g{x) ~ gi(x), х —У жо, то преде-
пределы (конечные или бесконечные) lim ^7-7 и lim ,{ одновременно
х^х0 д(х) х^х0 gi(x)
существуют или нет, при этом, если они существуют, то они равны
Шп Щ = Ит AM.	(9.35)
х^х0 д(х) х^х0 gi(x)
\> Условия / ~ /i и д ~ gi, х —> хо означают, что существуют такие
окрестность U = U(xo) и функции (риф, определенные на пересече-
пересечении X nU, что
/(ж) = <p(x)fi(x), g(x) = ф(х)д1(х), xeXnU, (9.36)
lim (p(x) = lim ф(х) = 1.	(9.37)
X—YXq	X—YXq
Поэтому функции ^-7—г и , { отличаются друг от друга на множи-
д(х) gi(x)
тель }, {, имеющий в точке жо предел, равный 1:
ф(х)
f(x) ip(x) fi(x)	/q^
g[x) ф[х)91[хУ	^'6Ь)
10*

148 Гл. 1. Дифференциальное исчисление функций одной переменной
lim ф)
lim Щ = 'Г*0,, = 1.	(9.39)
X—YXq
Поэтому ±-)—^ и ; : одновременно имеют или нет конечный или
g(x) gi(x)
бесконечный предел в точке xq. Если он существует, то
г /0*0	у ф) у fi(x)	у h(x) ^
х^х0 д(х) (9.38) х^х0 гр{х) х^х0 gi(x) (9.39) х^х0 gi(x)
Пример 6. Найдем lim —	-. Поскольку
ж-^ж0 smzx
ln(l + х) rsj х, sin 2х ~ 2х, х —У О,
то ,. 1пA + ж) г х 1
lim —^	 = lim — = -.
ж-^ж0 2х 2
Замечание 2. Понятия функции, ограниченной по сравнению
с другой функцией, функций одного порядка, функций, эквивалент-
эквивалентных между собой, функции, бесконечно малой по сравнению с дру-
другой функцией, переносятся и на случай комплекснозначных функций
комплексного аргумента. Все сформулированные выше определения
остаются по форме прежними, только аргумент и значения рассмат-
рассматриваемых функций могут принимать комплексные значения и предел
понимания в смысле предела функций комплексного переменного (см.
п. 6.14).
Остаются верными и аналоги теорем 1 и 2. Правда, многие из
данных выше примеров нуждаются в определениях рассматриваемых
в них функций (синуса, косинуса и т.д.) для комплексных значений
аргумента; к этому мы вернемся в п. 41.4.
§ 10. Производная и дифференциал
10.1. Определение производной. Пусть функция у = /(ж) за-
задана в окрестности U(xq) точки хо Е /?, х G U(xq) и, следовательно,
ФУНКЦИЯ	/(»)
х -
определена на проколотой окрестности JJ
Определение 1. Если существует предел
lim
ж—^жо

§10. Производная и дифференциал	149
то он называется производной функции f в точке ж0 и обознача-
обозначается /'Оо).
Таким образом,
Hf Я)
/'Ы Hf Ит Я*)-/(*°).	A0Л)
ж-)>ж0 X — Хо
Образно говоря, это равенство означает, что производная f'(xo) функ-
функции у = /(ж) в точке хо равна скорости изменения переменной у от-
относительно переменной х в указанной точке.
Если положить Ах = х - ж0, Ау = /(ж) - /(ж0) = /(ж0 + Ах) -
—/(жо), не писать аргумент и обозначить производную через у'', то
получим определение A0.1) в виде
у' = Hm ^.	A0.2)
Аж^О Аж
Иногда производная обозначается не только штрихом, но еще ука-
указывается в виде нижнего индекса переменная, по которой берется
производная, т. е. пишут у'х, а также просто ух.
Если предел A0.1) равен оо, +оо и —оо, то производная f'(xo)
называется бесконечной.
Всегда, когда говорится о существовании производной (конечной
или бесконечной) в некоторой точке, подразумевается (согласно опре-
определению производной), что функция определена в какой-то окрестнос-
окрестности рассматриваемой точки.
Под производной всегда понимается конечная производная: в слу-
случае, когда допускаются бесконечные производные (определенно-
(определенного знака или знаконеопределенные), это специально оговаривается.
Если функция / определена на некотором отрезке [а, Ь], то под ее
производной в точках хо = а и хо = Ъ обычно понимается соответст-
f(x) - Ы
f() /Ы
венно предел справа или слева отношения ^-^———- при х —> жп.
х - хо
Эти пределы называют также производными соответственно справа
и слева.
Операция вычисления производной функции называется опера-
операцией дифференцирования.
Примеры. 1. у = с — постоянная функция. Имеем Ау = с — с = 0,
Ау
следовательно, у' = Hm —^ = 0, т. е. с' = 0.
А^О Ах
Ах
2. у = sin ж. Имеем
Ay _ sin(x + Ах) — sin ж _ / Ax\
А^ "	А^	" C°S Г + ~Y)
sin(Ax/2)
Аж/2 '
поэтому
/ г Ay v ( , Ах\ r sin(Ax/2)
у = hm —2-= hm cos ж Н	hm —?—1J—L = cos ж,
Аж^О Ах Аж^О	V	2 / Аж^О Аж/2 (9.1)

150 Гл. 1. Дифференциальное исчисление функций одной переменной
т. е. (sin ж)' = cos ж.
Аналогично,
(cos ж/ = — sin ж.
3. у = ах, а > 0. Имеем
Ау _ ах+Ах - ах _ х аАх - 1
Ах ~ Ах ~	Ах '
поэтому
, Л. Ау т ,. аАх - 1	г,
у = lim —— = a lim —^^	 = а 1п а.
Аж^О Ах	Аж^О Ах (9.16)
Таким образом, (ах)' = аж1па, в частности (ех)' = еж.
10.2. Дифференциал функции.
Определение 2. Функция 2/ = /(ж), заданная в некоторой окрест-
окрестности ?/(жо) точки жо Е /?, называется дифференцируемой в этой точ-
точке, если ее приращение
Ау = /(ж0 + Аж) - /(ж0), Аж = ж - ж0,
представимо в этой окрестности в виде
Ау = ААж + о(Аж), Аж-^0,	A0.3)
где А — постоянная.
Линейная функция ААх (аргумента Аж) называется дифферен-
дифференциалом функции f в точке жо и обозначается df(xo) или, короче, dy.
Таким образом,
Ay = dy + o(Ax), Ах -> 0,	A0.4)
dy = ААх.	A0.5)
Так как при А ф 0 имеет место равенство (двустороннее)
о(Аж) = о(ААх),
то из соотношения A0.3) при АфО следует, что Ay = dy + o(dy),
Ах —У 0, т. е. что функции Ау и dy переменной Аж эквивалент-
эквивалентны при Аж —> 0 (см. теорему 1 в п. 9.3), причем, dy — линейная
функция аргумента Аж, а Ау, вообще говоря, — функция более слож-
сложной структуры.
Для симметрии записи приращение независимого переменного Аж
обозначается dx, т. е. dx = Аж. Поэтому формулу A0.5) можно запи-
записать в виде
dy = Adx.	A0.6)
Вспомнив определение о(Аж) (см. определение 3 в п. 9.2), усло-
условие A0.3) можно переписать в виде
Ау = ААх + г(Аж) Аж,	A0.7)
lim e(Ax) = 0.	A0.8)

§10. Производная и дифференциал	151
Здесь функция г(Ах) определена для тех Ах, для которых определе-
определена функция о(Ах) = Ау — ААх в формуле A0.3) (см. определение 4
в п. 9.2), т. е. для всех таких Ах, что хо + Ах Е U{xq) (cm. опреде-
определение 2), в частности для Ах = 0. Именно по множеству таких Ах
и берется предел A0.8), а так как точка Ах = 0 принадлежит этому
множеству, то функция г(Ах) непрерывна в этой точке (см. п. 6.2),
и, следовательно, в силу A0.8) имеем
е@) = 0.	A0.9)
Теорема 1. Функция дифференцируема в некоторой точке в том
и только том случае, когда она в этой точке имеет конечную произ-
производную.
|> 1) Пусть у функции / существует конечная производная
т. е. существует конечный предел lim —^ = f'(xo). Это равносильно
Дж-И) Аж
тому, что
^ = f'(xo) + e(Ax),	A0.10)
где lim е(Ах) = 0 (левая часть формулы A0.10) не определена
Дж-И), АхфЪ
при Ах = 0, следовательно, и функция е(Ах) не определена при Ах =
= 0). Поэтому
Ay = f'(xo)Ax + г(Аж)Аж.
Доопределив функцию г(Ах) нулем в точке Ах = 0, т. е. положив
е@) = 0, получим
г(Аж)Аж = о(Аж), Ах -> 0,
и, следовательно,
Ay = f((x0)Ax + o(Ax), Аж-^0.	A0.11)
Это и есть условие A0.3) дифференцируемости функции / в точке хо,
причем
/'Ы = А.	A0.12)
2) Пусть теперь, наоборот, функция / дифференцируема в точ-
точке хо, т. е выполняется условие A0.3), или, что то же самое, условия
A0.7), A0.8). Тогда при Ах ф 0 будем иметь —- = А + е(Ах), откуда
lim ^ = А,
Аж^О Ах A0.8)
т. е. в точке хо у функции / существует производная, причем имеет
место равенство A0.12). <|
Замечание 1. Из формул A0.6) и A0.12) следует, что диффе-
дифференциал dy функции у = f(x) записывается в виде
dy = f(xo)dx,	A0.13)

152 Гл. 1. Дифференциальное исчисление функций одной переменной
а производная — в виде
A0.14)
Теорема 2. Если функция дифференцируема в некоторой точке,
то она и непрерывна в этой точке.
|> Если функция / дифференцируема в точке ж0, т. е. в этой точке
выполняется условие A0.7), A0.8), то из него сразу следует, что
lim Ay = 0,
Дж-И)
а это и означает непрерывность функции / в точке xq. <\
Замечание 2. Существуют функции, непрерывные в некоторой
-1
О
Рис. 73
О
Рис. 74
точке, но не дифференцируемые. Например, функция у = |ж| непре-
непрерывна в точке х = 0, ибо в этой точке Ау = \Ах\ (рис. 73), и потому
lim Ay = lim |Аж| = 0. Однако
А^О	А^О
lim %L =
lim ^ = -
Ау
и, следовательно, предел отношения —— при Ах ->• 0 не существует.
Ах
10.3. Геометрический смысл производной и дифферен-
дифференциала. Пусть функция / определена в некоторой окрестности
U(xo) точки жо, непрерывна в этой точке, уо = /(жо) и Mq = (хо,уо)
(рис. 74). Зафиксируем произвольно приращение аргумента Ах,
лишь бы хо + Ах G U(xo), и пусть
Ау = f(x0 + Ах) -
М = (х0 + Аж, у0 + Ау).
Уравнение прямой, проходящей через точки Мо и М, — она назы-
называется секущей (графика функции /) — имеет вид
Ay ,	ч
У = д^ (ж~жо) +^о-
A0.15)

§10. Производная и дифференциал	153
Подчеркнем, что здесь Ах фиксировано, а х и у — текущие коор-
координаты точек прямой.
Если задано семейство прямых уравнениями
a(t)x + b(t)y + c(t) = 0,	A0.16)
где t — параметр (в случае уравнения A0.15) параметром слу-
служит Ах), и существуют конечные пределы
lim a(t) = ao, Hm b(t) = bo, lim c(t) = Co,
ttt	t^t	t^t
то говорят, что прямые A0.16) стремятся при t -> to к предельно-
предельному положению — к прямой, уравнением которой является уравнение
аох + Ъоу + с0 = 0.
Для того чтобы секущая A0.15) при Ах —У 0 стремилась к пре-
предельному положению, отличному от вертикальной прямой, необхо-
необходимо и достаточно, чтобы существовал конечный предел lim —^,
т. е. чтобы существовала конечная производная. При этом уравнение
предельного положения секущей, которое называется касательной к
графику функции / в точке Mq, имеет вид
y = ff(xo)(x-xo)+yo.	A0.17)
Отметим, что из непрерывности функции / в точке хо следует, что
lim Ay = 0, а поскольку |М0М| = \/Ах2 + Ау2, то и lim |МоМ|=0,
Аж-^О	Аж-^0
т. е. точка М "стремится к точке Mq" по графику функции /.
Вспомнив геометрический смысл коэффициента при х - х0 в
уравнении A0.17), получим
f'(x0) =tga,
где а — угол наклона касательной к оси Ох (см. рис. 74).
Обозначим ординату касательной через укас; тогда, положив
х — хо = Ах, запишем уравнение касательной A0.17) в виде
Укас ~У0= f'(xO)Ax.
В правой части этого равенства стоит дифференциал dy функции / в
точке хо. Таким образом,
dy = уКас -Уо	A0.18)
— дифференциал функции равен приращению ординаты касательной.
Рассмотрим случай бесконечной производной
f(x0) = оо.	A0.19)

154 Гл. 1. Дифференциальное исчисление функций одной переменной
Из уравнения секущей A0.15) имеем
Ау
Ах
Ау '
Ах
Переходя здесь к пределу при Ах —у 0, в случае выполнения усло-
условия A0.19) получим уравнение предельного положения секущей, т. е.
касательной к графику функции / в точке ж0, в виде
ж = ж0,	A0.20)
т. е. касательная в этом случае является вертикальной прямой, про-
У ^	У
Рис. 75
ходящей через точку ж0 оси абсцисс (рис. 75).
10.4. Физический смысл производной и дифференциала.
Пусть значения у функции / и ее аргумент х являются некоторыми
физическими величинами, причем аргумент х меняется на некотором
Аи
промежутке, например на отрезке [а, Ь]. Отношение —-, где Ах =
= х - хо, х0 е [а, Ь], х е [а, Ь], Ау = f(x0 + Ах) - f(x0), называется
средней скоростью изменения переменной у относительно перемен-
переменной х на отрезке с концами хо и хо + Ах, а предел
lim —- = f'(xo)
— скоростью изменения переменной у относительно переменной х
в точке хо- В случае существования этой скорости (т. е. в случае
существования производной функции / в точке хо) приращение Ау
переменной у имеет вид
Ay = f'(xo)Ax + о(Ах), Ах -у 0.
Это означает, что приращение Ау линейно зависит от приращения Ах
переменной х с точностью до бесконечно малой более высокого поряд-
порядка, чем Ах.

§10. Производная и дифференциал	155
Иначе говоря, существование скорости означает, что в малом
физический процесс, описываемый функцией /, протекает почти
линейно. Этим обстоятельством и объясняется
широкое применение дифференциального ис-
исчисления при изучении самых разнообразных
явлений.
Примеры. 1. Если s = s(t) — длина пути,
проходимого материальной точкой за время t,
отсчитываемое от некоторого момента време-
времени t0, As = s(t + At) - s(t) (рис. 76), то — на-
называется в физике величиной средней скорости
движения за промежуток времени At, начиная	Рис. 76
с момента времени t, и обозначается vcp = ——. Предел же lim vcp = v
называется величиной мгновенной скорости движения в момент вре-
времени t. Таким образом, v = —.
at
Дифференциал ds = vAt равен пути, который прошла бы рассмат-
рассматриваемая точка за промежуток времени At, начиная с момента t, если
бы движение на этом участке пути было равномерно со скоростью v.
Этот путь отличается от истинного пути As на бесконечно малую
более высокого порядка, чем At: As = ds + o(At), At ->• 0.
2. Если q = q(t) — количество электричества, протекающего че-
через поперечное сечение проводника в момент времени t, то Ад =
= q{t + At) — q{t) равно количеству электричества, протекающего че-
через указанное сечение за промежуток времени от момента t до мо-
момента t + At. Отношение —- называется средней силой тока за ука-
указанный промежуток времени длительностью At и обозначается /ср.
Предел же lim /ср = / называется силой тока в данный момет Вре-
мени t. Таким образом, / = -р.
at
Дифференциал dq = /At равен количеству электричества, кото-
которое бы протекло через поперечное сечение проводника за промежуток
времени At, если бы сила тока была постоянной и равной силе тока в
момент времени t. Как всегда, Aq — dq — o(At), At —> 0.
10.5. Свойства производных, связанные с арифметичес-
арифметическими действиями над функциями.
Теорема 3. Если функции у\ — Д (ж) и у2 = /2(х) заданы в окрест-
окрестности точки хо G /?, а в самой точке хо имеют конечные производные,
то функции Xifi(x) + А2/2(ж), Ai G /?, А2 G /?, Л(ж)/2(ж), а в случае
f2(xo) ф 0 и функции ^ также имеют в точке хо конечные про-

156 Гл. 1. Дифференциальное исчисление функций одной переменной
изводные; при этом имеют место формулы
(Ai2/i + Х2У2У = Aij/i + A22/?,	A0.21)
(У1У2У = У[У2+У1У'2,	(Ю.22)
A0<23)
2/2/	2/2
(в формулах A0.21)—A0.23) значения всех функций взяты при х = жо).
> Прежде всего заметим, что в силу условий теоремы в точке хо
существуют конечные пределы
Аж^О Аж У1 Аж^О Аж UI
Докажем теперь последовательно формулы A0.21)—A0.23).
1)	Пусть у = Aij/i + Л22/2; тогда
Ay = (AiB/1 + А2/1) + Л2B/2 + А2/2)) - (Ai2/i + Л22/2) = А1А2/1 + A2A^2
и, следовательно,
^=Al^ + A2^.
Аж	Аж	Аж
Перейдя здесь к пределу при Ах —> 0, получим формулу A0.21).
2)	Пусть у = 2/12/2; тогда
Д2/ = B/1 + д2/1)B/2 + Aj/2) - 2/12/2 = 2/2А2/1 + 2/1A2/2 + АугАу2,
откуда
^ = ^У2+У1^ + ^ДУ2.	A0.24)
Аж Аж	Аж Аж
Заметив, что в силу непрерывности функции /2 в точке ж0 выпол-
выполняется условие lim Ay2 = 0, и, перейдя в равенстве A0.24) к пределу
Аж-^О
при Аж —У 0, получим формулу A0.22).
3. Пусть /2(ж0)^0 и у = У1/у2; тогда
д _ 2/i + Ащ _ ш _ y2Ayi -yiAy2
у2 + Ау2 у2 у2(у2
следовательно,
A?/i	А?/2
^2^
Аж
Перейдя здесь к пределу при Аж ->• 0, получим формулу A0.23). <
Отметим, что из формулы A0.21) при 2/2 = 0 (так же, как и из фор-
формулы A0.22), когда функция у2 равна постоянной, а поэтому у'2 = 0)
следует, что постоянную можно выносить из-под знака дифференци-
дифференцирования, т. е.
(Ay)' = Ay', A € /?.

§10. Производная и дифференциал	157
Пример. Вычислим производную функции tgx. Применяя фор-
формулу A0.23), получим
/, ч/ /sinxV cos2 x + sin2 х	1
(tgx/ = 	 =	 = 	—.
Vcosx/	cos2 ж	cos2 ж
Итак,
Аналогично вычисляется
(ctgrc)' = —V-
sin ж
Замечание. Поскольку dy = y'dx, то, умножая формулы A0.21)—
A0.23) на dx, получим
d(X1y1 + A22/2) = Aidj/i + A2d2/2,
7 Ш _ 2/2cfa/i
—	2
2/2 г/г
10.6. Производная обратной функции.
Теорема 4. #а/ш функция f непрерывна и строго монотонна в
окрестности точки х0 и имеет в точке х0 производную f'(xo) ф 0,
то обратная функция j~x имеет производную в точке у о = /(жо) и
^М	1 .	(Ю.26)
dy
dx
> Пусть функция / строго монотонна и непрерывна в окрестности
U = U(xo) точки жо; тогда обратная функция j~x строго монотонна
и непрерывна на интервале V = f(U) (см. теорему 4 п. 7.3). Поэтому
если Ах = ж — жо, Д?/ = у — уо, то для функции 2/ = /(ж) имеет место
lim Ay = 0 и Ay ф 0 при Аж ф 0, а для функции ж = f~1(y) — соот-
Аж—^0
ветственно lim Аж = 0 и Аж ф 0 при Ау ф 0. Заметив это, вычислим
< A0.27)
производную обратной функции следующим образом:
dx
—
dy
,. Аж ,.1	1	1
= lim —- = lim -г— = 	т— = -г-
А	^	^	d
у=Уо
Ау
Ах Аж—^о Аж dx
Замечание. Если функция / непрерывна и строго монотон-
монотонна в окрестности точки ж0 и существует f'(xo) = 0, то обратная
функция /-1 имеет в точке у0 = /(ж0) бесконечную производную
т = оо. Это сразу следует из соотношения A0.27).
dx

158 Гл. 1. Дифференциальное исчисление функций одной переменной
Примеры. 1. Если
U 	 dl Uolll Jb ^	X -^ Jb <^ X ^	— -^ (y -^ — •j	Jb 	 Dill U ^
T°	,	. w dy	1	1	1	1
(агсвтж) = —- = -г- = 	 = —#	= #
аж «ж cos 2/ y/i _ sin2 у у/1-х2
2. Если у = агссояж, -1 ^ ж ^ 1, 0 ^ у ^ тг, х = cosy, то
(агссозжУ = -У- = -г- = —:— =	,	=
- cos2
/1-ж2
3.	Если ?/ = arctgx, —оо < ж < +оо, ——< у < —, х = tg?/, то
• , ч/ С?г/	1	2	1	1
(arctgx) = -г- = -г- = cos у =	г— = 	-.
v ь } dx dx_	y 1+tg2^/ 1 + ж2
dy
4.	Аналогично,
5. Если ?/ = loga ж, а > 0, а ф 1, ж > 0, —оо < у < +оо, ж = ау, то
в частности,
Aпж)' = -.
X
10.7. Производная и дифференциал сложной функции.
Пусть функция у = /(ж) задана в некоторой окрестности U = U(xq)
точки ж0, а функция z = ^B/) — в некоторой окрестности V = У(з/о)
точки уо = /(жо), причем f(U) С У и, следовательно, определена слож-
сложная функция
F(x) = g(f(x)).
Теорема 5. Если функция у = /(ж) имеет производную в точ-
точке ж0, а функция z = д(у) имеет производную в точке у0 = /(ж0), то
сложная функция z = F(x) = g(f(x)) также имеет в точке ж0 произ-
производную', причем
F'(x0) = g'(yo)f(xo),	A0.28)
или, опуская значение аргумента,
zfx=zfyyfx.	A0.29)
|> Пусть, как всегда, Аж = ж - ж0, Aj/ = у - уо и Az = ^B/) - ^B/0);
тогда в силу дифференцируемости функции д в точке уо будем иметь
(см. A0.11))
Az = д'(уо)Ау + е(Ау)Ау, lim s(Ay) = 0.	A0.30)

§10. Производная и дифференциал	159
Поскольку функция у = f(x) непрерывна при х = ж0, то lim Ay =
Дж-И)
= 0 и, следовательно, в силу теоремы о пределе сложной функции
(см. F.41) в п. 6.13) имеем
lim е(Ау) = 0.	A0.31)
Дж-И)
Поделив обе части первого равенства A0.30) на Ах ф 0, получим
??=9'ЫЦ+е(Л9>§|.	A0.32)
В силу равенств A0.31) и lim —— = /Чж0) предел правой части ра-
Дж-И) /лх
венства A0.32) при Ах -у 0 существует и равен gf(yo)ff(xo), следова-
следовательно, существует и предел левой части, т. е. существует
F'(x0) = Hm ^,
v J Дж^о Ах
причем
F'(z0) = g'(yo)f'(xo). <
Следствие (инвариантность формы дифференциала).
dz = F'(xo)dx = g'(yo)dy,	A0.33)
илщ короче,
dz = zxdx = zydy.
Эта формула показывает, что формально записи дифференциала
сложной функции посредством независимой переменной х и пос-
посредством зависимой переменной у имеют один и тот же вид, но сле-
следует иметь в виду, что здесь dx = Ах — приращение независимой
переменной ж, a dy — дифференциал функции у = /(ж), т. е. главная
линейная часть приращения Ау зависимой переменной ("главная" в
том смысле, что разность Ау — dy является при Ах —у 0 бесконечно
малой более высокого порядка, чем само Ах).
Докажем формулу A0.33):
dz = dF(x0) = F'(xo)dx = g'(yo)f(xo)dx = g'(yo)dy.
A0.13)	A0.28)	A0.13)
Пример. Вычислим производную функции у = ха, х > 0, a G /?,
с помощью формулы A0.28). Для этого представим функцию у = ха
dij
как композицию функций у = еи и и = а\пх. Заметив, что -^ = еи,
аи
du a
— = —, получим
dx х
(Х*У = (еаЫх)' = (еи)'ии'х = еи- = еаЫх- = ха- = аха~\
т. е.
(ха)' = аха~1.	A0.34)

160 Гл. 1. Дифференциальное исчисление функций одной переменной
10.8. Гиперболические функции и их производные. Неред-
ех - е~х
ко в математическом анализе встречаются функции 	 и
&х -Ь в х
	. Они имеют специальные названия: первая из них называет-
называется гиперболический синус и обозначается shx, а вторая — гиперболи-
гиперболический косинус chx. Таким образом,
A0.35)
, def ех +е х	,ЛГ. пг,
chx =	.	A0.36)
Эти функции обладают некоторыми свойствами, похожими на
свойства обычных (круговых) синусов и косинусов, например,
ch2x - sh2x = ^(e2x + 2 - е~2х - е2х + 2 - е~2х) = 1, A0.37)
ПГ*		 qn	qn		 qn	O qn		 О qn
Ю^ 	 p Л p^ _|_ p Л	в		 в
zbiixcnx —z ^	2 ~~	2	~~	^iu.oo;
Слово "гиперболический" в названии функций A0.35) и A0.36)
объясняется тем, что уравнения
x = acht, у = asht, а > 0, — оо < t < +оо,
являются, в силу формулы A0.37), параметрическими уравнениями
правой ветви гиперболы х2 — у2 = а2, подобно тому, как уравнения
х = a cost, у = asint, 0 ^ t ^ 2тг,
являются параметрическими уравнениями окружности х2 + у2 = а2.
Вычислим производные гиперболических синуса, косинуса:
(shx)' = {f ~^ Х)' = еЖ+26 = chx,	A0.39)
(chx)f = {f ^^ X)f = бЖ~е = shx.	A0.40)
10.9. Производные комплекснозначных функций действи-
действительного аргумента. Если функция f(x) задана в некоторой ок-
окрестности U точки хо числовой оси и принимает, вообще говоря,
комплексные значения, т. е. имеет вид
f[x) = и(х) + iv(x), u(x) G /?, v(x) G /?, х G U,
то ее производная в точке хо определяется равенством
(^Хо) = и {Хо) + гг' (жо)	A0.41)
(само собой разумеется, что это определение имеет смысл только тог-
тогда, когда у фyнкциq и(х) и v(x) существуют производные в точке xq).

§11. Производные и дифференциалы высших порядков	161
При таком определении операция дифференцирования остается
линейной:
(Ai/i + Л2/2)' = Ai/{ + Л2/2, Ai е С, Л2 G С.
Пример. Если /(ж) = cos ах + г s'max, то
/'(ж) = —a sin ах + ia cos ах = ia( cos ах + ism ах) = iaf(x).
A0.41)
Можно обобщить понятие производной на случай комплекснознач-
ных функций комплексного переменного. Это понятие приводит к
большому качественному многообразию новых явлений и потому
изучается в отдельном курсе теории функций комплексного перемен-
переменного.
§ 11. Производные и дифференциалы высших порядков
11.1. Производные высших порядков. Пусть функция у =
= /(ж) имеет производную у' = f'{x) во всех точках некоторой окрест-
окрестности точки жо- Если функция /'(ж) в свою очередь имеет в точ-
точке хо производную [//(ж)]/|ж_ж •> то она называется второй производ-
производной функции f в точке хо и обозначается f"(xo) или f^xo. Таким
образом, опуская обозначения аргумента, имеем
(о)	и def / /ч/
yW = у" = (у1I.
Аналогично определяются и производные у^ более высоких по-
порядков п:
У(п+1) = [У{П)}', п = 0,1,...,	A1.1)
где для удобства считается, что у^ = у.
Примеры. 1. Если у = аж, а > 0, то у' = аж1па, у" = ах In2 а,
вообще, з/п) = ах 1пп а, п = 0,1,2,... В частности, если у = еж, то
(еж)(п) =ех.	A1.2)
2. Если ^/ = sin ж, y' = cosx, у^ = -s'mx, у^ = - cos ж, у^ =
= sin ж. Заметив, что cos a = sin (а-\— J, получим
у' = sin (a + f), 2/B) = cos (ж + |) = sin (ж + 2 |).
Вообще,
(sina;)(n) = sin (x + п |).	A1.3)
Аналогично,
(со8ж)(п) =cos^ + n|), п = 0,1,...	A1.4)
11 Л.Д.Кудрявцев, т.1

162 Гл. 1. Дифференциальное исчисление функций одной переменной
Теорема 1. Если функции у\ — j\{x) и у2 = /2(х) имеют в точ-
точке хо производные порядка п Е Л/, то любая их линейная комбина-
комбинация \\у\ + А22/2, Ai Е /?, А2 G /?, и их произведение у\у2 имеют в точ-
точке хо производные порядка п, причем
(Ац/1 + A2j,2)(») = Al2/<n) + Л22/(и),	A1.5)
(У1У2){п) = J2 Ckny{rk)VBk) = B/1 + У2){п}, п е N. A1.6)
Все производные в формулах A1.5) и A1.6) берутся в точке жо,
п!
С^ = —у——ггт — биномиальные коэффициенты.
Символическая запись (^/i +2/2)"^ означает, что это выражение
(см. среднюю часть формулы A1.6)) по своей структуре напоминает
формулу бинома Ньютона
{yi+y2)n = J2cnVi~ky^
только вместо степеней у\ и у<± берутся производные соответствую-
соответствующих порядков функций у\ и ?/2- Формула A1.6) называется формулой
Лейбница*).
\> Докажем формулы A1.5) и A1.6) методом математической индук-
индукции. В п. 10.5 формула A1.5) была доказана для п = 1:
(Ai2/i + A22/2)' = Ai2/i + A22/2.	A1.7)
Пусть справедлива формула A1.5); покажем, что тогда будет спра-
справедлива и аналогичная формула для производной порядка п + 1:
= [(Ai2/i+A22/2)n]' = (iy[ + 2У2У
A1.1)	A1.5)	A1.7)
(l=7) AiB/i ) +А2(?/2
Формула A1.5) доказана; докажем формулу A1.6).
Пусть справедлива формула A1.6) для производной порядка п от
произведения функций. Докажем, что тогда будет справедлива и ана-
аналогичная формула для производной порядка п + 1:
к,—О
к=0
?) Г.В. Лейбниц A646-1716) — немецкий математик, физик, философ.

§11. Производные и дифференциалы высших порядков	163
Вспомнив, что (см. п. 2.4)
s~ik _|_ s~ik — l 	 /ofe	/iO 	 гчп 	 /оО 	 s~in-\-l
°П "•" °П	— °П+15	°П " °П " °П+1 — Un+1 —
получим
n+1
11.2. Производные высших порядков сложных функций,
обратных функций и функций, заданных параметрически. С
помощью формулы производной сложной функции (см. п. 10.7) можно
вычислять и производные высших порядков сложной функции. Пусть
функция у — у(х) дважды дифференцируема в точке жо, а функция
z = z(y) дважды дифференцируема в точке уо = у(хо) и имеет смысл
сложная функция z = z(y(x)). Вычислим вторую производную z"x
сложной функции z = z(y(x)) (для простоты записи аргумент писать
не будем):
= {г'уУуУ'хУ* + 2'уУ™ = 2ууУ'*2 + zWxx- (П-8)
Аналогично вычисляются и производные более высоких порядков.
С помощью формул производных обратной функции (см. п. 10.6) и
сложной функции (см. п. 10.7) можно вычислять производные высших
порядков обратных функций. Вычислим, например, вторую производ-
производную. Пусть функция у = у(х) дважды дифференцируема в точке жо, а
в ее окрестности непрерывна и строго монотонна, причем у'(хо) ф 0.
Тогда для второй производной х'уу имеем в точке уо = у(хо)
w [vh Ky'Jy \у'х)хУ y'x2 y'x
Рассмотрим теперь параметрическое задание функций. Пусть на
некотором множестве Е задана пара функций
x = x(t), y = y(t),	A1.9)
причем одна из них, например, х = ж(?), строго монотонна на этом
множестве и, следовательно, существует обратная функция t = ?(ж),
11*

164 Гл. 1. Дифференциальное исчисление функций одной переменной
для которой Е является множеством значений. Тогда функция у =
= y(t(x)) называется параметрически заданной функцией (уравне-
(уравнениями A1.9)). Она определена на множестве значений функции x(t).
Если функции x(t) и y(t) дифференцируемы в точке to, функ-
функция x(t) непрерывна и строго монотонна в окрестности этой точки
и х'(to) ф 0, то функция y(t(x)) дифференцируема в точке хо = x(to),
причем
x't'
ибо t'x = l/x't.
Аналогично вычисляются и производные высших порядков. На-
Например, если функции A1.9) дважды дифференцируемы в точке ?0
их'(to) фО,то
у" = (у1 У = (Ш-\ t' = ШЩ ~ VtXtt
Ухх УУх>х{11шщ \xlt)t *	(ж/K	•
Выведенные здесь формулы не предназначены для запоминания.
Достаточно усвоить метод их получения.
11.3. Дифференциалы высших порядков. Дифференциал от
дифференциала первого порядка
dy = f'(x)dx	A1.11)
функции у = /(ж), рассматриваемого только как функция пере-
переменной х (т. е. приращение dx аргумента х предполагается
постоянным), при условии, что повторное приращение независи-
независимой переменной х совпадает с первоначальным, называется вторым
дифференциалом d2 f(x) функции f в данной точке х. Таким образом,
d2f(x) d= d(df(x)) = d(f'(x)dx) = d(f'(x))dx = f"(x)dxdx.
Вместо dxdx пишут dx2:
d2f(x) = f"(x)dx2,
или
d2y = y"dx2,	A1-12)
откуда у" = —|.
dxz
Аналогично, дифференциалом п-го порядка, п = 2,3,..., называет-
называется дифференциал от дифференциала порядка п — 1 при условии, что
в дифференциалах все время берутся одни и те же приращения dx
независимой переменной х:
dny Hf d(dn~ly).	A1.13)

§11. Производные и дифференциалы высших порядков	165
При этом оказывается справедливой формула
dny = y^dxn,	A1.14)
где dxn = (dx)n.
Формула A1.14) легко доказывается по индукции: при п = 1 она
доказана; если она доказана при некотором п, то
d d(dny)
Из формулы A1.14) следует, что
В силу формулы A1.14) высказывания "функция имеет в точке п
производных" и "функция п раз дифференцируема в этой точке" (т. е.
у нее существует дифференциал порядка п) равносильны.
Дифференциалы высших порядков dny, n ^ 2, не обладают свойст-
свойством инвариантности формы относительно выбора переменных: если,
например, z = z(y), у = у(х) — дважды дифференцируемые функции
и имеет смысл композиция z(y(x)), то
dz = zl.dy,
у	A1 16)
где, вообще говоря, d2y ф 0. Заметим, что если обе части фор-
формулы A1.16) поделить на dx, то в силу A1.15) получится форму-
формула A1.8).
§ 12. Дифференциальные теоремы о среднем
12.1. Теорема Ферма*). Пусть функция / задана на множест-
множестве X и хо G X. Напомним, что если для всех точек х G X выполняется
неравенство f(x) ^ /(ж0) (соответственно неравенство f(x) ^ /(ж0)),
то говорят, что функция / принимает в точке ж0 наибольшее (наи-
(наименьшее) значение на множестве X (см. п. 3.1).
Если в неравенстве /(ж) ^ /(^о) (соответственно в неравенстве
f(x) ^ f(xo)) заменить при х ф хо знак нестрогого неравенства на
знак строгого неравенства, то получится определение точки жо, в ко-
которой функция / принимает строго наибольшее (строго наименьшее)
значение на множестве X.
Теорема 1 (Ферма). Если функция определена в некоторой
окрестности точки, принимает в этой точке наибольшее (наимень-
(наименьшее) значение и имеет конечную или определенного знака бесконечную
производную, то эта производная равна нулю.
*) П. Ферма A601-1665) — французский математик.

166
Гл. 1. Дифференциальное исчисление функций одной переменной
\> Пусть функция / определена на окрестности U(xo) точки ж0 и
принимает в этой точке, например, наибольшее значение, т. е. для
любой точки х Е U(xo) выполняется неравенство /(ж) ^ f(xo). Тогда
если х < хо, то	?( , ?( ,
f(x)-Kxo) ^0	A2Л)
х хо
а если х > xq, to
х -
0.
A2.2)
По условию теоремы существует конечный или определенного зна-
знака бесконечный предел lim ^-^—JV^l _ f4Xo\ поэтому в нера-
х—>хо X — Хо
венствах A2.1) и A2.2) можно перейти к пределу при х —У хо (см.
свойство 4° пределов функций в п. 6.7). В результате получим соот-
соответственно f'(xo) ^ 0 и f'(xo) ^ 0. Следовательно, f'(xo) = 0. <1
Замечание 1. Формулировка теоремы Ферма на первый взгляд
может показаться неестественной: в предположениях говорится о бес-
бесконечных производных, а в утверждении — о равенстве нулю про-
производной. Однако на самом деле формулировка теоремы вполне кор-
корректна: a priori предполагается, что в точке существует производная
(конечная или определенного знака бесконечная), и доказывается, что
при выполнении дополнительного условия о достижении в рассматри-
рассматриваемой точке наибольшего или наименьшего значения указанная про-
производная равна нулю. Иначе говоря, доказывается, что в точке, в ко-
которой принимается наибольшее в некоторой ее окрестности значение
функции, не может существовать ни конечная, не равная нулю про-
производная функции, ни определенного знака бесконечная производная.
Поэтому в точке, в которой достигается наибольшее или наимень-
наименьшее в ее окрестности значение функции, возможны следующие слу-
случаи: в этой точке существует конечная равная нулю производная; су-
существует знаконеопределенная бесконечная производная; не сущест-
существует никакой производной (ни конечной, ни бесконечной). Приме-
Примером функции, для которой осуществляется первый случай, является
функция fi(x) = ж2; второй случай: /2(х) = \fx*\ третий: /з(ж) =
-1
-1
О
1 х
О	1 х
fi{x) = x2	f2
Рис. 77
(рис. 77). Все эти функции принимают при х = 0 наименьшее значе-

§12. Дифференциальные теоремы о среднем
167
У\
ние, /{@)=0, /2@) = оо, а производная (конечная или бесконечная)
функции /з в точке х = 0 не существует.
Замечание 2. В теореме Ферма существенно, что точка, в ко-
которой достигается экстремальное значение, является внутренней для
рассматриваемого промежутка. Так, например, функция f(x) = ж,
рассматриваемая только на отрезке [0,1], принимает наибольшее и
наименьшее значения на его концах, а производная в них не обраща-
обращается в нуль.
12.2. Теоремы Ролля, Лагранжа и Коши о средних значе-
значениях.
Теорема 2 (Ролль*)). Если функция /:
1)	непрерывна на отрезке [а,Ь];
2)	имеет в каждой точке интервала (а, Ь) конечную или опреде-
определенного знака бесконечную производную;
3)	принимает равные значения на
концах отрезка [а, 6], т. е.
/(а) = /(Ь);	A2.3)
то существует по крайней мере одна
такая точка ? Е (а, Ь), что
/'(О = О-	A2.4)
Геометрический смысл теоремы Рол-
Ролля состоит в том, что на графике функции, удовлетворяющей усло-
условиям теоремы Ролля, имеется по крайней мере одна точка, в которой
касательная горизонтальна (рис. 78).
|> Если для любой точки х интервала (а, Ь) выполняется равенст-
равенство f(x) = /(а) = /(&), то функция / является постоянной на этом
интервале, и потому для любой точки ? G (а, Ь) выполняется усло-
условие A2.4).
Пусть существует точка хо G (а, Ь), для которой /(жо) Ф /(аM на-
например /(жо) > /(а). Согласно теореме Вейерштрасса о достижимости
непрерывной на отрезке функцией своих наибольшего и наименьшего
значений (см. теорему 1 в п. 7.1), существует такая точка ? G [а, 6],
в которой функция / принимает наибольшее значение. Тогда
-2
-1
2 х
-1
Рис. 78
Поэтому ? ф а и ? ф Ь, т. е. точка ? принадлежит интервалу (а, Ь)
и функция / принимает в ней наибольшее значение. Следователь-
Следовательно, согласно теореме Ферма (см. теорему 1 в п. 12.1), выполняется ра-
равенство /'(?) = 0. <1
?) М. Ролль A652-1719) — французский математик.

168
Гл. 1. Дифференциальное исчисление функций одной переменной
Замечание 3. Все условия теоремы Ролля существенны. На
о
-1
о
1 х
-1 О
1 х
О
1 х
х=1 — точка
разрыва
а
/'@)=оо
б
Рис.
/ @) не
существует
в
79
/@)^/A)
г
рис. 79 изображены графики четырех функций, определенных на от-
отрезке [—1,1]; у каждой из ниех не выполняется лишь одно из трех
условий теоремы Ролля и не существует такой точки ?, что /'(?) — 0.
Пример функции /(ж) = л/ж2" (см. рис. 79, б) показывает также, что
условие существования определенного знака бесконечной производ-
производной нельзя заменить условием существования просто бесконечной
производной. У функции f(x) = ух? в точке х = 0 производная рав-
равна бесконечности, но без определенного знака, т. е. /'@) = оо, и не
существует такой точки ?, что /'(?) — 0.
Примером функции, удовлетворяющей условиям теоремы Ролля и
имеющей в некоторой точке определенного знака бесконечную про-
производную, является функция
л/1-(*-1J, о ^ х <: 2,
Эта функция непрерывна на отрезке [—2, 2], дифференцируема во всех
точках интервала (—2,2), кроме точки х = 0, в которой f'@) = +оо,
и /(—2) = /B) (см. рис. 78). В согласии с теоремой Ролля у нее име-
имеются точки, в которых производная равна нулю: ими являются точ-
точки х = ±1. Графиком этой функции являются две полуокружности
радиуса единица, сопряженные в точке @,0).
Замечание 4. В дальнейшем нам понадобится следующее
свойство бесконечных производных. Если функции у\ = fi(x) и г/2 =
= /2 (ж) определены в окрестности точки хо, функция Д имеет в точ-
точке хо бесконечную производную (определенного знака или нет),
а функция /2 имеет в точке хо конечную производную, то функ-
функция у = fi(x) + /2(х) имеет в точке хо такую же бесконечную про-
производную, как и функция Д. Для того чтобы в этом убедиться, надо
перейти к пределу при Ах —У 0 в равенстве
Ау _ Ау± Ау2
Ах Ах Ах

§12. Дифференциальные теоремы о среднем	169
Теорема 3 (Лагранж*)). Если функция f непрерывна на отрез-
отрезке [а, Ъ] и в каждой точке интервала (а, Ъ) имеет конечную или опре-
определенного знака бесконечную производную, то существует такая точ-
точка ? Е (а, Ь), что
f(b)-f(a) = f'(O(b-a).	A2.5)
Это равенство называется формулой конечных приращений
Лагранжа.
\> Рассмотрим вспомогательную функцию
F(x) = f(x) - Ах,	A2.6)
где А — некоторое число. Эта функция непрерывна на отрезке [а, Ь] и
в каждой точке интервала (а, Ь) имеет конечную или определенного
знака бесконечную производную (см. замечание 4). Подберем число А
так, чтобы выполнялось соотношение
F(a)=F(b);	A2.7)
тогда функция F будет удовлетворять всем условиям теоремы Ролля.
Из условий A2.6) и A2.7) имеем равенство /(а) — А(а) = f(b) — Xb,
°ткуда	л - т -/(а)	т 8)
А - ъ_а .	A2.8)
При этом А, согласно теореме Ролля, существует такая точка ? G (а, Ь),
что
F @ = 0,	A2.9)
и так как из A2.6) следует, что F'(x) = f'(x) - А, то из A2.8) и A2.9)
получаем	f(n
/W	b- a	'
что равносильно равенству A2.5). <l
Геометрический смысл теоремы Лагранжа состоит в том, что на
дуге АВ (рис. 80) графика функции / с концами в точках А = (а, /(а))
и В = F, f(b)) найдется точка М = (?,/(?)), касательная в которой
параллельна хорде АВ. Действительно, со-
согласно теореме Лагранжа
^ = /'(О,	A2-10)
где ^-^—^-^- — тангенс угла наклона хор-
о — а
ды АВ, а /;(?) — тангенс угла наклона ка-
сательной к дуге АВ в точке М = (?,/(?)),
?е (а, 6).	Рис. 80
*)Ж. Л. Лагранж A736-1813) — французский математик и механик.

170 Гл. 1. Дифференциальное исчисление функций одной переменной
Если положить в = т	•> а < f; < Ь, то, очевидно, 0 < в < 1 и
о — а
? = а + #(& — а). Поэтому формулу Лагранжа можно также записать
в виде
/(&) - /(а) = f (а + в{Ъ - а))(Ъ - а), 0 < в < 1,
или, полагая Ъ — а = Дж, а = ж и, следовательно, 6 = ж + Дж, в виде
/(ж + Дж) - /(ж) = /(ж + 6>Дж)Дж.	A2.11)
Заметим, что равенство A2.10) остается верным и при Ъ < а
(а поэтому и равенство A2.11) при Дж < 0), так как при перемене
местами а и Ъ его левая часть не меняет знака, причем в этом
случае также ? = а + в(Ь - а), 0<#< 1 (здесь 6-а<0, ? — а < 0).
Следствие 1. Если фукция непрерывна и имеет производную,
равную нулю, во всех точках некоторого промежутка (конечного или
бесконечного), то она на нем постоянна.
|> Действительно, пусть функция / удовлетворяет сформулирован-
сформулированным условиям на некотором промежутке и Ж1, Ж2 — две произвольные
его точки, х\ < ж2. Тогда функция / непрерывна и дифференцируема
на отрезке [ж1,Ж2] (на концах этого отрезка в смысле соответствен-
соответственно односторонней непрерывности и односторонних производных). По
теореме Лагранжа
/Ы - /(Xi) = /'@(*2 " Ж!), Ж! < ^ < Ж2.	A2.12)
Во всех точках промежутка, на котором рассматривается функция /,
по условию f'(x) = 0, в частности /'(?) = 0. Поэтому из равенст-
равенства A2.12) следует, что f(xi) = /(ж2).
Поскольку х\ и Ж2 — произвольные точки указанного промежут-
промежутка, то это и означает, что функция / на нем постоянна. <|
Следствие 2. Если функция f непрерывна в окрестности U(xq)
о
точки жо, дифференцируема в проколотой окрестности U(xq) и су-
существует конечный или бесконечный предел
limo f(x),
х—>хо, ж??/(жо)
то существует конечная или бесконечная производная f'(xo) и
В частности, производная не может иметь устранимую точку раз-
разрыва.
|> В самом деле, согласно теореме Лагранжа для любой точки ж G
о
е U(xo) справедливо равенство
Ы = /'@,	A2.13)

§12. Дифференциальные теоремы о среднем	171
где ? = ?(ж) лежит между точками ж0 и ж, и, следовательно, lim ?(ж) =
X—YXQ
= ж0, а потому
limo /'(?) =	limo /'(ж).	A2.14)
ж-)>ж0, же С/(жо)	ж-)>ж0, же С/(жо)
Из этого равенства следует, что левая часть равенства A2.13)
имеет конечный или бесконечный предел, т. е. существует конеч-
конечная или бесконечная производная /'(^о), причем
/'(so) = Hm /(ж) ~ /Ы =	lim	/'(ж). <
Х^Х° Х~Х°	х^хо,хеЩхо)
Утверждение, аналогичное следствию 2, имеет место и для одно-
односторонних производных.
Замечание 5. Из следствия 2 вытекает, что если функция /
непрерывна на некотором промежутке (конечном или бесконечном) и
имеет производную, равную нулю во всех точках этого промежутка,
кроме, быть может, конечного множества его точек, то функция /
постоянна на указанном промежутке.
Действительно, в этом случае в достаточно малых проколотых
окрестностях точек рассматриваемого конечного множества произ-
производная функции равна нулю и, следовательно, имеет в этих точках
предел, равный нулю по проколотым окрестностям. Согласно следст-
следствию 2 в указанных точках также существует производная и она рав-
равна нулю. Поэтому в силу следствия 1 функция является постоянной.
Теорема 4 (Коши). Если функции fug:
1)	непрерывны на отрезке [а, 6];
2)	дифференцируемы в каждой точке интервала (а, Ь);
3)	д'(х) ф 0 во всех точках х Е (а, Ь);
то существует такая точка ? G (а, Ь), что
№ - /(а) _ f'(Z)	,	.
9(Ъ)-д(а) ~ Ш	(	}
> Прежде всего заметим, что для функции д справедливо нера-
неравенство
д{а)фд{Ъ),	A2.16)
так как если бы имело место равенство д(а) = д(Ь), то в силу теоремы
Ролля нашлась бы такая точка хо G (а, Ь), что д'(хо) = 0, а это про-
противоречило бы условиям теоремы. В силу неравенства A2.16) левая
часть формулы A2.15) имеет смысл.
Рассмотрим теперь функцию
F(x)=f(x)-\g(x),	A2.17)
где число Л подберем таким образом, чтобы имело место равенство
F(a) = F(b).	A2.18)

172 Гл. 1. Дифференциальное исчисление функций одной переменной
Тогда функция F будет удовлетворять на отрезке [а, Ъ] условиям
теоремы Ролля. Из соотношений A2.17) и A2.18) имеем
f(a)-\g(a) = f(b)-\g(b),
0ТКуДа	fib) - fia)
Л* *)а1	A2.19)
А=	I
g(b) - g(a)
При таком выборе числа Л существует ? G (а, Ь), для которого
(?) = 0, но F'(x) = f'(x) - Xg'(x), следовательно,
и поэтому	,
Л-Ш.	A2.20)
Из A2.19) и A2.20) следует A2.15). <
§ 13. Раскрытие неопределенностей по правилу Лопиталя
13.1. Неопределенности вида -.
Теорема 1. Если функции fug определены в окрестности точ-
точки Хо,
/Ы = д(х0) = 0,	A3.1)
существуют конечные производные д'(хо) ф 0 и f'(xo), то сущест-
существует предел
цш ZM = 1Щ.	A3.2)
> Действительно,	/(я) _ /(яо)
4
О
/	\			11111	•	ч	•	ч			. ,
х^х0 д(х) A3.1) х^х0 д(х) - д(хр) д'(
Геометрический смысл равенства A3.2) состоит в том, что предел
отношения ординат графиков функций / и д равен пределу отноше-
отношения ординат их касательных у = f'(xo)(x -
-хо) и у = д'(хо)(х - хо), которое постоян-
постоянно и равно ,; °ч (рис. 81).
д'Ы
Теорема 2. Если:
1) функции fug дифференцируемы на ин-
_^ тервале (а, Ь);
х	2) д'(х) ф 0 для всех х G (а, Ь);
3) lim f(x) = lim g(x) = 0;
x—>a
Рис. 81	4) существует конечный или бесконеч-

§13. Раскрытие неопределенностей по правилу Лопиталя	173
f'(x)	fix)
ный предел lim ; '; то существует и предел lim ^Ц—7, причем
ж-^а р (ж)	ж->-а д(ж)
lim М = lim Ш.	A3.3)
ж->-а д(ж) ж->-а g'(х)
> Доопределим функции / и g в точке ж = а по непрерывности, т. е.
положим
/(а) = <?(а) = 0.	A3.4)
Тогда для любого х Е (а, Ь) продолженные функции на отрезке [а, х]
будут удовлетворять условиям теоремы Коши о среднем значении,
и потому будет существовать такая точка ? = ?(ж), а < ? < ж, что
/0*0 = №-№ = /40	A35)
0(ж) A3.4) р(ж)-р(а) р'@'
Поскольку lim ?(ж) = а и предел lim ,) ! существует, то
ж^а	ж^а р (ж)
Нт Ш = Hm 4т4	A3.6)
х^а 9 (О ж^а Р (ж)
и, следовательно, существует
х^а д(х) A3.5) х^а д'{?) A3.6) х
ОО
13.2. Неопределенности вида —.
оо
Теорема 3. Если:
1)	функции fug дифференцируемы на интервале (а, Ь);
2)	д'[х) ф 0 для всех х е (а, 6);
3)	lim f(x) = lim g(x) = оо;	A3.7)
ж—Уа	х—Уа
f'(x)
4)	существует конечный или бесконечный предел lim ,,{'•>
то существует предел lim ^j4 u
х—va дух)
lim ^4—г = Нт ^ , .	A3.8)
|> Пусть существует конечный или бесконечный предел
lim Ц& = к.	A3.9)
Покажем, что при выполнении остальных условий теоремы
Нт Щ = к.	A3.10)
х^а д(х)

174 Гл. 1. Дифференциальное исчисление функций одной переменной
Если а < х < хо < Ь, то на отрезке [ж,ж0] функции / и g удов-
удовлетворяют условиям теоремы Коши (см. теорему 4 в п. 12.2), а поэ-
поэтому существует такая точка ? = ?(жо,ж), что
Далее, в силу A3.7) существует такая точка х\ — х\{х§), a < %i <
< жо, что при всех х Е (a, xi) выполняются неравенства
f(x) ф О,
9(х) ф О,
f(x) Ф f(x0),
и, следовательно, можно производить деление на /(ж), д(х) и 1 — °
fa также и на 1 — ° , поскольку в силу условий теоремы д{х) ф
Ф д(хо); см. A2.16) в доказательстве теоремы 4 из п. 12.2 J. Для этих
значений х из A3.11) вытекает равенство
1 _/ы
/(Ж) /о»;) _ /40
_
/40
В правой части равенства первый сомножитель .,{ стремится к
9 (О
числу к при хо —у а (ибо а < ? < жо, и поэтому lim ? = а), а второй
жо—^а
в силу условия A3.7) стремится к 1 при i-Уаи фиксированном ж0:
lim 	§&- = i.	A3.13)
ж^а , _ /(жр)
/(^)
Непосредственно перейти к пределу в равенстве A3.12) нельзя,
так как указанные выше предельные переходы в сомножителях в пра-
правой части равенства происходят при разных условиях: при ж0 -У а и
при фиксированном ж0, но х -у а. Однако если задать произвольно
окрестность U(k) предела к отношения производных A3.9), то мож-
можно сначала зафиксировать точку хо столь близко к точке а, что отно-
f4?)
шение f попадет в эту окрестность, ибо а < ? < xq. Согласно же

§13. Раскрытие неопределенностей по правилу Лопиталя	175
условию A3.13) для всех точек ж, достаточно близких к а, отноше-
f(x)
ние ^Ц—г (см. A3.12)) также будет принадлежать указанной окрест-
9\х)
ности U(к), а это означает справедливость утверждения A3.10).
Проведенное рассуждение нетрудно записать с помощью нера-
неравенств.
Пусть сначала предел A3.9) конечный. Положим
а(х) = ?{g - *.	A3.14)
Тогда из A3.9) будем иметь lim а(х) = 0, и, следовательно, для лю-
х—>а
бого произвольно фиксированного г > 0 существует такое жо, что для
всех ж Е (а, жо) выполняется неравенство
\а(х)\ < |.	A3.15)
Если положить еще
^	A3.16)
то в силу условия A3.7)
lim /3(х) = 0.	A3.17)
х—>а
Теперь имеем
Ш AзЪ)
A3.14), A3.16)	= к + а(^) + ^(д.) + а(^)/3(ж), A3.18)
ж < ^ < жо; при этом в силу A3.17) существует такое S > 0, а < а + 5 <
< жо, что при ж G (а,а + 5) выполняется неравенство
\k(i(x)+a{0(i(x)\<?-.	A3.19)
В результате получаем, что для всех ж G (а, а + 5) выполняется
неравенство
-к
A3.18)	A3.15)
A3.19)
а это и означает выполнение равенства A3.10).
Если теперь	,
lim 4т^г = оо,

176 Гл. 1. Дифференциальное исчисление функций одной переменной
Q (X )	О (X )
то lim nl/ \ = 0, откуда по уже доказанному lim ^-^- = 0, и потому
х^а f'(x)	х^а f(x)
lim Щ = оо.	A3.21)
х^а д(х)
Из A3.20) и A3.21) следует, что A3.8) справедливо и в этом
случае.
Аналогично рассматривается и случай бесконечного предела со
знаком. Более того, можно показать, что в условиях теоремы беско-
бесконечный предел A3.9) всегда является бесконечностью со знаком. <|
В теоремах 2 и 3 был рассмотрен случай, когда аргумент стре-
стремился к числу а справа. К этому случаю сводятся случаи, когда аргу-
аргумент х стремится к числу а слева или произвольным образом, а также
случаи, когда а является одной из бесконечностей оо, +оо или —оо.
Во всех этих случаях при соответствующих предположениях имеет
место формула	,
Нт 1Щ = lim 1Ш.	A3.22)
ж-^а дух) х^а д'ух)
Рассмотрим, например, случай стремления аргумента к +оо для
функций / и д, заданных на полуинтервале вида [с,+оо), где с —
некоторое число. Этот случай сводится к случаю, рассмотренному
в теореме 3 с помощью замены переменного х = 1/t. В самом деле,
Шп № = Нт ЯШ = Um J
ж^+оо д(х) x=1/tt^+o g(l/t) (i3.7)t^+o ±
dt
= Нт	= Нт ^М
gf(l/t)(-l/t2) t^+o g'(l/t) t=i/x ж^+оо д'(х)
(здесь штрихом обозначены производные функций / и д по первона-
первоначальному аргументу х).
fix)
Правило вычисления предела отношений функций ^4—г по форму-
формуле A3.22) называется правилом Лопиталя*).
Примеры. 1. Если а > 0, то
Нт — = 0,	A3.23)
х—>-|-оо Ха
т. е. любая положительная степень х возрастает быстрее In ж при
х —> +00. Действительно, применив правило Лопиталя, получим
r In ж г	1/х 1 г 1^
lim 	 = lim ——— = — lim — =0.
x—^+oo Xa	x—>-|-oo OLXa i OL x—>-|-oo Xa
?) Г. Лопиталь A661-1704) — французский математик.

§13. Раскрытие неопределенностей по правилу Лопиталя	177
2. Если а > 0 и а > 1, то
Нт ^ = 0,	A3.24)
т. е. при х —У +оо любая степень жа, а > 0, растет медленнее пока-
показательной функции с основанием, большим единицы. В самом деле,
сделав указанные ниже преобразования и применив правило Лопита-
Лопиталя, получим
Ха	( X	\а	(	пг	\Ы
lim — = lim —-г- — lim
—^-) = (
j_ аж/а \naJ	Vina/ lim а
а	ж—>-+оо
=Г=0.
2
х sin —
—
3. Найдем lim	—. Здесь отношение производных числите-
ж-^о sin ж
ля и знаменателя
[ ж sin - ) 2ж sin	cos -
X	X
2 • Л'
г sin -
х) _
(sinxO	cos ж
не стремится ни к какому пределу при х —У 0 и, следовательно, пра-
правило Лопиталя неприменимо. В этом случае предел находится непо-
непосредственно:
х2 sin —
~	ж	/	1 \
lim —:—— = lim —— lim ( х sin - ) =1-0 = 0.
ж-^о sin ж ж-^о sin ж ж-^о V ж/
Из этого примера следует, что предел
lim Щ	A3.25)
ж^ж0 д(х)
может существовать в случае, когда предел
lim 4т4	A3-26)
ж^ж0 д'(х)
не существует, и, тем самым, здесь для нахождения предела A3.25)
правило Лопиталя A3.22) неприменимо.
4. Предел неопределенностей типа 0°, оо° или 1°° можно найти,
предварительно прологарифмировав функции, предел которых ищет-
ищется. Например, чтобы найти предел lim xx, найдем сначала предел
ж^+0
In х	1/х
lim \nxx = lim ж In ж = lim —— = — lim ——^ — — lim x — 0.
ж-^+0	ж-^+0	ж-^+0 1/Ж A3.8) ж-^0 1/Ж2	ж-^+0
Отсюда в силу непрерывности показательной функции будем
иметь
lim ж In ж
lim хх = lim exlnx = е^+° = е° = 1.
ж-^+0
12 Л.Д.Кудрявцев, т.1

178 Гл. 1. Дифференциальное исчисление функций одной переменной
В частности, при х — — получим
п
lim (i
lim y/n =
5. Пределы неопределенностей типов 0 • oo и оо — oo целесообразно
О	оо тт
привести к виду - или —. Например,
О	оо
,. /1 , о А т sin2 ж — ж2 cos2 ж
lim — - ctg x = hm	-—2	=
ЖЧО \Г	/ ж^О	Х2Ъ\ТГХ
,. / sin ж + ж cos ж sin ж — ж cos ж \
= hm 	:	—	 .
ж^О V	Sin Ж	Ж2 SHI Ж У
Предел первого сомножителя в правой части находится непос-
непосредственно:
,. втж + жсовж ,. Л ж	\ о
lim 	:	 = lim I 1 + —— cos x I = 2,
ж—^o V sin ж	/
втж
а предел второго — с помощью правила Лопиталя:
,. sin ж —ж cos ж ,. ж sin ж	,.	1
lim 	—	 = lim 	:	 = lim
ж2 sin ж	ж-^о 2ж sin ж + ж2 cos ж -^^п 2 | Х сое ж
sin ж
Таким образом, lim (— — ctg2x) = -.
ж-^о \xz	/3
§ 14. Формула Тейлора
14.1. Вывод формулы Тейлора. Рассмотрим следующую зада-
задачу. Пусть функция у = f(x) имеет в точке ж0 производные до поряд-
порядка п включительно. Требуется найти такой многочлен Рп(х) степени
не выше, чем п, что
Pkk)(xo) = fW(xo), k = 0,l,...,n,	A4.1)
rn(x) d= f(x) - Pn(x) = o((x - xo)n), x ->¦ x0.	A4.2)
В случае п = 1 нам уже известно, что эта задача имеет решение
и что ее решением является многочлен
Pi{x)=f(xo)+f'{xo)(x-xo),	A4.3)
так как
Pi(x0) = f(x0), P{(xo)=f'(xo),
П(х) = f(x) - Pi (ж) = f(x) - f(x0) - f'(xo)(x - x0) =
= Ay- f'(xo)Ax = Ay-dy = o(Ax), Ax ->• 0,

§Ц. Формула Тейлора	179
где, как обычно, Ах = ж - ж0, Ау = /(ж) - /(ж0).
По аналогии с формулой A4.3) будем искать многочлен Рп(ж),
удовлетворяющий условиям A4.1) и A4.2), в виде
Рп(х) =ао + а1(х- ж0) + ... + ап(х - хо)п.	A4.4)
Положив х = жо, в силу условия A4.1) при к = 0 получим
а0 = /Ы-	A4.5)
Дифференцируя равенство A4.4), будем иметь
Р'п(х) = ах + 2а2(ж - ж0) + ... + пап(х - жо)™.
Положив здесь ж = жо, в силу условия A4.1) при к = 1 получим
а1=/'Ы-	A4.6)
Вообще, продифференцировав равенство A4.4) к раз:
PW (ж) = fe! ак + (fe + 1)... 2а*+1(ж - ж0) + ...
... + п(п - 1)... (п-к + 1)ап(ж - хо)п~к,
и положив ж = жо, в силу условия A4.1) получим
f{k)(Tn)
ак=к\> к = 0>1>->п-	A4-7)
Таким образом, если коэффициенты многочлена A4.4) выбраны
согласно формулам A4.7), то этот многочлен удовлетворяет усло-
условию A4.1). Покажем, что он удовлетворяет и условию A4.2). Для это-
этого прежде всего отметим, что в силу условий A4.1) для функции
гп(ж)=?/(ж)-Рп(ж)	A4.8)
имеет место
гп(ж0) = г'п(х0) = ... = г^(жо) = 0.	A4.9)
Из того, что функция /(ж) имеет в точке ж0 производную поряд-
порядка п, вытекает, что у нее в некоторой окрестности этой точки сущест-
существуют производные до порядка п — 1 включительно и все производные
функции /(ж), а следовательно, в силу равенства A4.8) и производ-
производные функции гп(ж), до порядка п — 1 включительно непрерывны в
указанной точке ж0 и
lim г?\х) = г(/е)(ж0) = 0, /с = 0,1,...,п-1.
х^хо	A4.9)
Для вычисления предела lim -— \ применим сначала п — 1
х^х0 (Х - Хо)п
раз правило Лопиталя — теорему 2 из п. 13.1, а затем оттуда же
12*

180 Гл. 1. Дифференциальное исчисление функций одной переменной
теорему 1:
hm , v \ = lim ——^^Ц—т = ... = hm —	Щ- =
х^хо (X — Хо)п A3.3) х^хо П(Х — Хо)п L A3.3) A3.3) х^х0 П\ (X — Хо) A3.2)
=	=Q
A3.2) п\
Это и означает выполнение условия A4.2). Итак, доказана сле-
следующая
Теорема 1. Если функция f п раз дифференцируема в точке хо,
то в некоторой окрестности этой точки
f(x) = /Ы + ^ (х - х0) + ...
Многочлен
Рп(х) = f(x0) + ?М (х -
f(n){xo]
1 n!
_A J
fc=O
Жо)"
), ж -
Xq)
;0) ,
i . . .
> ж0.
/-1
A4-
A4-
Л 1 Г\\
10)
И)
называется многочленом Тейлора*) (порядка п), формула A4.10) —
формулой Тейлора (порядка п) для функции / в точке х = жо, а функ-
rn(x) = /(x)-Pn(x)	A4.12)
— остаточным членом (порядка п) формулы Тейлора, а его представ-
представление в виде A4.2), т. е.
гп(х) = о((х - жо)п), х -»> ж0,
— записью остаточного члена в виде Пеано**)
).
Частный случай формулы Тейлора A4.10) при хо = 0 называется
формулой Маклорена***)
f(x) = f2^^xk+rn(x),	A4.13)
k=0
где, согласно A4.2), остаточный член гп(х) можно записать в виде
rn(x)=o(xn), х^О.	A4.14)
Из нижеследующей теоремы будет следовать, что многочлен Тей-
Тейлора единствен в своем роде. Именно, никакой другой многочлен не
?) Б. Тейлор A685-1731) — английский математик.
?) Д. Пеано A858-1932) — итальянский математик.
?) К. Маклорен A698-1746) — шотландский математик.

§14- Формула Тейлора	181
приближает функцию, заданную в окрестности точки х0 с точностью
до бесконечно малых того же порядка относительно х — хо, х —У хо,
что и многочлен Тейлора.
п
Предварительно отметим, что любой многочлен Рп(х) = У^ аххк
к=0
п
степени п для любого хо может быть записан в виде Рп(х) = 2^ Ък(х —
к=0
— хо)к. Действительно, положив h = х — хо, использовав формулу би-
бинома Ньютона и собрав члены с одинаковыми степенями /i, получим
п	п	п	п
к=0	к=0	к=0	к=0
где Ък — некоторые постоянные.
Теорема 2. Если функция / задана в окрестности точки хо и
имеет представление
п
/(х) = ^ak(x -xo)k +о((х -хо)п), х -> х0,	A4.15)
k=o
то такое представление единственно.
|> Пусть наряду с представлением A4.15) имеет место представление
п
/(х) = ^ Ък{х — хо)к + о((х - хо)п), х ->• х0.	A4.16)
Тогда, положив
ск=Ьк-ак, к = 0,1,...,п,	A4.17)
и вычтя из равенства A4.16) равенство A4.15), получим
п
,(х - хо)* + о((х - хо)п) = 0, х -)> х0.	A4.18)
Перейдя в этом равенстве к пределу при х —>- хо, получим со = 0.
Заметим, что о((х — хо)т) = е(х)(х — хо)т, Нт е(х) = 0, и, сле-
следовательно, при х т^ хо, т = 1, 2,...
—	——- = е(х)(х — хо)т~1 = о((х — хоO"), х —> xq.
Сократив на х - х0, х т^ х0, левую часть равенства A4.18) (в нем,
как уже доказано, со = 0), получим
п-1
^2ск(х- хо)к~г + о((х - хоO1) = 0, х -)> х0.

182 Гл. 1. Дифференциальное исчисление функций одной переменной
Перейдя в этом равенстве к пределу при ж ->• ж0, ж ф ж0, получим
с\ = 0. Продолжая этот процесс после ттг-го шага, 0 ^ m ^ п, получим
2k{x — xq) m + o((x — xo)n m) = 0, ж —у жо,
A;=ra
отсюда при ж —>¦ жо следует, что сш = 0, т = 0,1, ...,п.
Таким образом, в силу равенств A4.17)
аи = bfc, fc = 0,1, ...,n. <l
Теорема 2 называется обычно теоремой единственности. Из нее
следует, что если для п раз дифференцируемой в точке функции / по-
получено представление ее в виде A4.15), то это представление являет-
является ее разложением по формуле Тейлора. В самом деле, при сделанных
предположениях, согласно теореме 1, такое представление существу-
существует, а другого в силу теоремы 2 нет.
14.2. Примеры разложения по формуле Тейлора.
Примеры. 1. Напишем формулу Маклорена для функции /(ж) =
sin ж.
Так как (sina;)^ = sin (ж + п ^ J (см. п. 11.1), то
0,	если п — 2к,	_
(—1) , если n = 2fc + l,	->->->
Поэтому
2. Для функции /(ж) = cos ж имеем аналогично
(cos x) (п) = cos (х + п — J,
+ 1'	* = 0,1,2
[ (—1) ? если п =
поэтому
cosa; = !_?_ + ... + (_l)»^_+o(a;2n+i)) ж^0.	A4.20)
3. Рассмотрим функцию f(x) = ех.
Так как (еж)(п) = еж, то /^п^@) = 1 и, следовательно,
еж = 1 + ж + |- + ... + ^+о(жп), ж^0.	A4.21)
Отсюда следует, что
^ ...(-1)п^ + о(жп), ж ^ 0.	A4.22)

§Ц. Формула Тейлора	183
Складывая и вычитая соотношения A4.21) и A4.22), после умножения
результата на 1/2 получим
e^	^	^+o(x2n+l), х^О, A4.23)
. A4.24)
В силу теоремы единственности (см. теорему 2 в п. 14.1) полу-
полученные разложения являются разложениями функций chx и shx по
формуле Тейлора.
4. Если /(ж) = A + х)а, а е /?, а 0 Л/, то
/(™)(х) = а(а - 1)... (а - п + 1)A + ж)а~п.
Поэтому
/(")@)=а(а-1)...(а-п + 1), п = 1,2,..., /@) = 1;
отсюда
Если а = т — натуральное число, то при п ^ т будем иметь
A + х)ш = Рт(х) +0, где Рт(х) — многочлен степени т. Отсюда,
согласно теореме единственности, следует, что Рт(х) является мно-
многочленом Тейлора, и, следовательно, в силу A4.25)
т. е. в этом случае формула A4.25) превращается в формулу бинома
Ньютона.
5. Пусть /(ж) = In A + ж); тогда
/'(*) = гГх = A + х)~^ f"{x) = ()A + ж)~2'
вообще, f{n){x) = (-1)п+1(п - 1)!A + х)~п, поэтому
/(")@) = (-1)"+1(п-1)!, п = 1,2,...,
и так как /@) = 0, то
\пA + х)=х-^- + ... + {-1)п+1—+о{хп), х^О. A4.26)

184 Гл. 1. Дифференциальное исчисление функций одной переменной
Замечание. Отметим, что
ахп + о(хп) = О(жп), х -+ 0.	A4.27)
Действительно, о(хп) = г(х)хп, где lim six) = 0. Поэтому сущест-
ж-И)
вует такое 8 > 0, что при |ж| < 6 имеем \е(х)\ ^ 1 и, следовательно,
ахп + о(хп)\ = \ахп + г(ж)жп| ^ (\а\ + 1)|жп .
Это и означает, что выполняется равенство A4.27).
Если в формуле Маклорена A4.13), A4.14) заменить п на п + 1
(в предположении, конечно, существовании производной порядка п +
+ 1 при х = 0) и воспользоваться равенством A4.27), то получим
Получившаяся оценка остатка гп(х) = О(жп+1) является, очевидно,
более сильной, чем его оценка в формуле A4.13), где
гп(х) = о(жп), х -> 0.
Поэтому формула Тейлора для sinx, cosx, еж, shx, chx, A + х)а
и In A + х) можно при х —У 0 записать в виде
„.2*5 + 1
-1)ft(iTi)!+^2"+3)'
fc=o	v	;
k=o
k=0
п
+ ^2 ~ "г., ~—-^ ж^ + 0(жп+1),
А;=1
k=i

§14- Формула Тейлора	185
14.3*. Применение метода выделения главной части функ-
функций для вычисления пределов. Пусть функция / представлена в
окрестности точки жо по формуле Тейлора в виде
/(ж) = Р(х) + о((х - жо)п), ж -у ж0.
Многочлен Тейлора Р(х) (если он не тождественный нуль) называ-
называют главной частью функции f в рассматриваемой окрестности. Ее
выделение полезно применять для нахождения пределов функций. По-
Покажем на примерах, как это делается.
Примеры. 1. Найти lim	.
х^О Ж3
Представим sin ж, согласно формуле Тейлора, в виде
sin ж = ж —— + о(ж4), ж —у 0.
6
В соответствии с теоремой 1 п. 9.3
/Ж3	4 \	Ж3	4	Ж3
x-sinx = х- [х- — +о(ж4) = — +о(ж4) ~ —, ж -у 0.
V 6	/6	6
Поэтому, применив теорему 2 п. 9.3, получим
о тт „ ,.
2. Найти lim
ж-^0	In A + ж) — Ж
Имеем
A + о(ж)) = ж + о(ж2),
2жI/2 = 1 + ж--ж2+ о(ж2),
In A + ж) = ж	ж2 + о(ж2), ж ->• 0.
Поэтому, согласно теоремам 1 и 2 из п. 9.3, с помощью этих соот-
соотношений будем иметь
,. l + xcosx-VT+2^ ..
lim	—	 = lim
I A + )
= lim	=
In A + ж) — Ж	ж-^0	т — -
х	ж2 + о(ж2) — ж
1 .2
- ж + о(ж ) - ж
= lim -Д:	 = lim —Л	 = —1.
Мы воспользовались здесь тем, что
- ж2 + о(ж2) ~ - х2 и	ж2 + о(ж2) ~ — ж2, ж -у 0.

186 Гл. 1. Дифференциальное исчисление функций одной переменной
3. Найти предел lim(cosx)ctg x.
ж-ИГ	J
Заметив, что (cosx)ctg х = ectg ж1псо8Ж5 найдем предел натураль-
натурального логарифма функции, стоящей под знаком предела, т. е. предел
Имеем
lim (ctg 2х In cos х).
ж-И)
cos ж = 1 —— + о[х ), х ->• 0.
Поэтому
lncosx = In (l - у + о(ж2)) = -у + Ф2), ж ^ 0.
Далее,
ctff 2Т = сов^я = A + ^)J = 1 + ФО т , 0
ё	sin2 ж (ж + о(ж)J ж2 + о(ж2)'
Следовательно,
(l+o(x
lim (ctg ж In cos ж) = lim
= lim —f	——- = lim
Тем самым найден и искомый предел:
lim(cosx)ctg2* = 4=.
§ 15. Исследование функций
15.1. Признак монотонности функций.
Теорема 1. Для того чтобы дифференцируемая на интервале
функция возрастала [убывала) на этом интервале, необходимо и
достаточно, чтобы ее производная была во всех точках интервала
неотрицательна [неположительна).
Если производная функция во всех точках интервала положитель-
положительна [отрицательна), то функция строго возрастает [строго убывает).
\> Докажем, например, что если на интервале (а, Ъ) производная
функции / неотрицательна [f'[x) ^ 0 для всех х G [а,Ъ)), то функ-
функция / возрастает на (а, Ъ). Действительно, если х\ G (а, Ь), х<± G (а, Ь)
и х\ < Ж2, то по теореме Лагранжа
/Ы - f[xx) = ГШХ2 ~ Xl), Xl < ^ < X2,	A5.1)
а так как по условию /'(?) ^ 05 то из равенства A5.1) следует, что
f[xi) ^ f[x2).	A5.2)

§15. Исследование функций
187
При этом если для всех ж G (а, Ь) выполняется неравенство f'(x) > О
следовательно, в равенстве A5.1) /'(?) > О, то
т. е.
f(x2)
— f(x\) > О,
A5.3)
f(xi)
— функция / строго возрастает.
Пусть теперь функция / возрастает на интервале (а, Ь) и имеет в
точке xq Е (а, Ь) производную. Возьмем Ах > О, тогда
и, следовательно,
f(x0 + Ах) ^ f(x0)
/(ж0 + Ах) - /(ж0)
A5.4)
1 х
Рис. 82
Переходя в этом неравенстве к пределу при Ах —У 0, получим
/'Ы ^ 0.	A5.5)
Аналогично теорема 1 доказывается для
убывающих функций. <|
Замечание 1. Как было показано, усло-
условие положительности производной на ин-
интервале является достаточным условием
строгого возрастания. Отметим, что это
условие не является, однако, необходимым
условием строгого возрастания. Действи-
Действительно, например, функция f(x) = х3 строго
возрастает на всей числовой оси, однако ее
производная f'(x) = Зх2 не всюду положительна — она обращается в
нуль при х = 0 (рис. 82).
15.2. Локальные экстремумы функций. Пусть функция / за-
задана на некотором множестве X С R и ж0 G X.
Определение 1. Точка хо называется точкой локального мак-
максимума (минимума) функции /, если существует такая окрестность
U(xo) точки жо, что для всех х G X П U{xq) выполняется неравенство
/(ж) ^ f(x0) (соответственно /(ж) ^ /(жо))-
Если для всех х е X П U(xo) иж/ж0 выполняется неравенство
/(ж) < /(жо) (соответственно /(ж) > /(жо)), то точка жо называется
точкой строгого локального максимума (минимума).
В дальнейшем для простоты точки (строгого) локального макси-
максимума и минимума функции будем кратко называть ее точками (стро-
(строгого) максимума и минимума.
Точки максимума и минимума (строгого) функции называют ее
точками экстремума (строгого).

188 Гл. 1. Дифференциальное исчисление функций одной переменной
Из теоремы Ферма (см. п. 12.1) для функций, определенных в не-
некоторой окрестности точки, сразу следует необходимое условие ло-
локального экстремума в этом точке.
Теорема 2 (необходимое условие экстремума). Если функция
имеет в точке локального экстремума производную, то эта произ-
производная равна нулю.
\> Действительно, из того, что у функции в точке существует про-
производная, следует, что функция определена в некоторой окрестности
этой точки, а так как эта точка является точкой локального экстре-
экстремума, то ее окрестность можно выбрать так, что сужение на выбран-
выбранную окрестность функции примет в рассматриваемой точке наиболь-
наибольшее или наименьшее значение. Из теоремы Ферма, примененной к
указанному сужению функции, следует, что если в указанной точке
производная существует, то она равна нулю. <|
Замечание 2. Напомним, что под производной всегда понима-
понимается конечная производная, если специально не оговорено, что допус-
допускаются и бесконечные производные (см. п. 10.1). Из комментариев к
теореме Ферма (замечание 1 в п. 12.1) следует, что в точке локально-
локального экстремума может существовать знаконеопределенная бесконеч-
бесконечная производная, но не может существовать бесконечная производ-
производная определенного знака. Может случиться, что в точке локального
экстремума вообще не существует производной — ни конечной, ни
бесконечной (см. рис. 77).
Отметим, что условия равенства нулю производной или ее несу-
несуществования в данной точке, будучи необходимыми условиями
экстремума, не являются достаточными условиями для наличия
экстремума в этой точке. Например, у функции /(ж) = ж3 производ-
производная f'(x) = Зж2 в точке х = 0 равна нулю, а экстремума в этой точке
нет (рис. 82).
Определение 2. Если функция определена в некоторой окрест-
окрестности точки хо и в этой точке производная функции либо существует
и равна нулю, либо не существует, то точка хо называется критичес-
критической точкой этой функции.
Критические точки функции, в которых производная функции
равна нулю, называются также и стационарными точками.
Теорема 2 означает, что все точки локального экстремума функ-
функции находятся среди множества ее критических точек.
Определение 3. Точка жо называется точкой возрастания
(убывания) функции /, если у ж0 существует такая окрестность
U(xo), что при х е X П U(xo), х < ж0, выполняется неравенство f(x) ^
^ /(жо) (соответственно /(ж) ^ /(жо)), а при х > жо — неравенст-
неравенство /(ж) ^ /(жо) (соответственно /(ж) ^ /(жо)).
Если при ж ф жо выполняется, кроме того, неравенство /(ж) ф

§15. Исследование функций	189
Ф /(жо), то точка хо называется точкой строгого возрастания (стро-
(строгого убывания) функции /.
Точки строгого экстремума, точки строгого возрастания и убы-
убывания удобно описывать в терминах знака приращения
Ay = f(x0 + Ах) - /Ы	A5.6)
функции /.
В точке строгого максимума приращение функции в некоторой
окрестности этой точки имеет отрицательное значение при Ах ф О,
в точке строгого минимума — положительное, в точке строгого воз-
возрастания при Ах < 0 — отрицательное, при Ах > 0 — положительное,
а в точке строгого убывания — положительное при Ах < 0 и отрица-
отрицательное при Ах > 0 (рис. 83). Конечно, здесь всегда предполагается,
Ау<0 ] Ау>0 Ау>0 | Ау<0^ Ау<0 I Лу<0 ^ Ay>0 | Ау>0
Точка строгого Точка строгого Точка строгого Точка строгого
возрастания	убывания	максимума	минимума
Рис. 83
что приращение аргумента Ах таково, что точка хо + Ах принадле-
принадлежит области определения X функции /.
Таким образом, при переходе через точку строгого экстремума хо
(т. е. при изменении знака приращения аргумента Ах) приращение
функции не меняет знака, а при переходе через точки строгого воз-
возрастания и убывания меняет знак.
Нетрудно сформулировать в терминах знака производной в точ-
точке достаточные условия того, что эта точка является точкой строго-
строгого возрастания или убывания (в этом случае согласно определению
производной функция заведомо определена в некоторой окрестности
рассматриваемой точки).
Лемма. Если в точке конечная или бесконечная производная поло-
положительна (соответственно отрицательна), то эта точка является
точкой строгого возрастания (строгого убывания) функции.
\> Если функция / имеет в точке хо положительную производную
то для всех достаточно малых Ах выполняется неравенство
1Г- > 0-	A5.8)
Ах A5.7)

190 Гл. 1. Дифференциальное исчисление функций одной переменной
Отсюда следует, что при Ах < 0 имеет место Ау < 0, а при Ах > 0
также и Ау > 0, т. е. точка хо является точкой строгого возрастания.
Аналогично рассматривается случай f'(xo) < 0. <1
Таким образом, если в точке хо существует не равная нулю произ-
производная (конечная или определенного знака бесконечная), то эта точ-
точка является либо точкой строгого возрастания, либо точкой строгого
убывания, а следовательно, не может быть точкой экстремума. Тем
самым мы еще раз доказали, что если в точке экстремума сущест-
существует конечная или определенного знака бесконечная производная, то
она равна нулю (см. теорему 1 в п. 12.1).
Отметим, что доказанная лемма дает лишь достаточные, но не не-
необходимые условия для точек строгого возрастания и строгого убы-
убывания функций, имеющих в этих точках конечные или бесконечные
производные. Это видно уже на примере функции f(x) = ж3, у кото-
которой точка х = 0 является точкой строгого возрастания, а производная
в ней равна нулю: f'@) = 0 (см. рис. 82).
Замечание 3. Аналогично лемме нетрудно доказать, что ес-
если в точке производная, конечная или бесконечная, неотрицательна
(неположительна), то эта точка является точкой возрастания (соот-
(соответственно убывания) функции, но, вообще говоря, нестрогого.
Отметим, что у функции, равной тождественно постоянной на
множестве ее задания, все точки этого множества являются как точ-
точками экстремума, так и точками возрастания и убывания функции.
Все это делает целесообразным введение понятий как точек
экстремума, точек возрастания и убывания функции, так и точек
строгого экстремума, точек строгого возрастания и строгого убыва-
убывания функции.
Теорема 3. Пусть функция непрерывна в некоторой окрестнос-
окрестности точки, дифференцируема в ее проколотой окрестности, и произ-
производная с каждой стороны от рассматриваемой точки сохраняет один
и тот же знак.
Для того чтобы функция в этой точке имела строгий максимум
(строгий минимум), необходимо и достаточно, чтобы при переходе
через нее производная меняла знак с плюса на минус (соответственно
с минуса на плюс).
Для того чтобы эта точка была точкой строгого возрастания
(строгого убывания) функции, необходимо и достаточно, чтобы про-
производная с обеих сторон от рассматриваемой точки была положи-
положительной (отрицательной).
Таким образом, образно говоря, в условиях теоремы точка явля-
является точкой строгого максимума (строгого минимума) функции тог-
тогда и только тогда, когда в этой точке строгое возрастание (строгое
убывание) функции сменяется ее строгим убыванием (соответствен-
(соответственно строгим возрастанием). Подобным образом точка является точкой

§15. Исследование функций	191
строгого возрастания (строгого убывания) функции тогда и только
тогда, когда с обеих сторон от этой точки функция строго возрастает
(соответственно строго убывает) (см. теорему 1).
|> Пусть функция / непрерывна в окрестности U(xo) точки жо, диф-
о
ференцируема в проколотой окрестности U(x0) и производная сох-
сохраняет постоянный знак во всех точках проколотой окрестнос-
о
ти U(xo), лежащих с каждой стороны от точки xq. Для любой точ-
о
ки х Е U(xo), согласно формуле Лагранжа, имеем Ау = /'(?)Дж, где
точка ? лежит между точками хо и х = хо + Ах. Таким образом,
^ = /'(?)•	A5-9)
Поэтому если производная f'(x) меняет знак с плюса на минус
при переходе через точку ж0 : f'(x) > 0 при Ах < 0 и f'(x) < 0 при
Ах > 0, то —- > 0 при Ах < 0 и —- < 0 при Ах > 0. Отсюда
Ах A5.9)	о	Ах A5.9)
Ау < 0 при всех Ах, хо + Ах Е U(xo), т. е. приращение функции Ау
не меняет знака при переходе через точку хо и является отрицатель-
отрицательным. Это означает, что точка хо является точкой строгого локального
максимума.
Аналогично, из формулы A5.9) следует, что если производ-
производная f'(x) меняет знак с минуса на плюс при переходе через точку ж0,
Ау	Ау
то —^ < 0 при Ах < 0 и —^ > 0 при Ах > 0, а поэтому при пе-
Аж A5.9)	Аж A5.9)
реходе через точку ж0 приращение функции Ау не меняет знака и
положительно. Это означает, что точка хо является точкой строгого
локального минимума.
Если производная f'(x) не меняет знака при переходе через точ-
/\у
ку хо, то из формулы A5.9) следует, что и отношение —- также не
меняет знака при переходе через эту точку и его знак совпадает со
о
знаком производной. Поэтому если ff(x) > 0, х G U(xo), то Ау < 0 при
Ах < 0 и Ау > 0 при Ах > 0, т. е. точка ж0 является точкой строгого
о
возрастания, а если f'(x) < 0, х G U(xo), то аналогично получаем, что
точка хо является точкой строгого убывания. <|
Мы доказали, что каждое из рассмотренных условий о знаке про-
производной с разных сторон от точки ж0 является достаточным усло-
условием соответственно для строгого локального максимума, строгого
локального минимума, строгого возрастания или убывания функции
в точке. Поскольку были рассмотрены все возможные случаи знаков
производной с каждой стороны от точки хо, то все сформулирован-
сформулированные условия являются не только достаточными, но и необходимыми

192 Гл. 1. Дифференциальное исчисление функций одной переменной
для соответствующих утверждений (рис. 84).
I
! -
^о	^0	OCq	Xq
Рис. 84
Следует обратить внимание на то, что рассмотренным здесь слу-
случаем, когда производная с каждой стороны от данной точки не ме-
меняет своего знака (а поэтому можно говорить об изменении знака
производной при переходе через точку), не исчерпываются возмож-
возможные ситуации даже для дифференцируемых функций: может случить-
случиться, что для сколь угодно малой окрестности по одну из сторон от
точки хо или по обе стороны производная меняет знак. В этих точ-
точках приходится применять другие методы для исследования функ-
функций на экстремум. Таким образом, в более широком классе функций,
дифференцируемых в окрестности рассматриваемой точки, кроме,
быть может, самой этой точки, условие изменения знака производной
в данной точке является лишь достаточным условием экстремума.
Докажем еще одни достаточные условия для точек строгого эк-
экстремума и точек строгого возрастания (строгого убывания) в тер-
терминах производных любого порядка в данной точке. Эти условия для
точек строгого возрастания и убывания обобщают условия, указан-
указанные в приведенной выше лемме. Для задачи же об экстремумах они
представляют собой принципиально новый подход к отысканию точек
экстремума, имеющий широкие обобщения.
Теорема 4. Пусть функция y = f(x) n раз дифференцируема в
точке жо, п ^ 1 и
fw(x0) = 0, к = 1, 2,..., п - 1, /(п) Ы ф 0.	A5.10)
Тогда если п = 2m, т Е А/, т. е. п — четное число, то функция /
имеет в точке хо строгий экстремум, а именно строгий максимум
при /Bт)(жо) < 0 и строгий минимум при /^2т^(жо) > 0.
Если же п = 2т — 1, т G А/, т. е. п — нечетное число, то функ-
функция f не имеет в точке хо экстремума; в этом случае при
/^2т~1^(жо) > 0 точка хо является точкой строгого возрастания
функции /, а при fBm~1\xo) < 0 — ее точкой строгого убывания.
Предпошлем доказательству одно простое замечание: если /3(х) =
= о(а(х)), х —У хо, где функции а и C заданы в некоторой окрестнос-
окрестности точки хо G R, то существует такая окрестность U(xo) этой точки,
что при х G U(xo) справедливо неравенство
\р{х)\<\\а{х)\.	A5.11)

§15. Исследование функций	193
В самом деле,
Р(х) =е(х)а(х),	A5.12)
где lim e(x) = 0, и, следовательно, существует такая окрестность
U(xo), что при х е U(xo) выполняется неравенство
\е(х)\ < \.	A5.13)
Из A5.12) и A5.13) следует неравенство A5.11).
> Напишем формулу Тейлора порядка п для функции / в окрестнос-
окрестности точки хо (см. п. 14.1).
В силу условий A5.10) будем иметь
Ау = f(x0 + Ах) - f(x0) = f П (,Жо) Ахп + о(Ажп), Ах -+ 0. A5.14)
п!
Так как /(п)(^о) ф 0, то
о(Ажп) = о
т. е. второй член правой части равенства A5.14) является бесконечно
малым по сравнению с первым. Поэтому, согласно A5.11), существу-
существует такая окрестность U{xq) точки жо, что при х G U{xq) для функ-
функции о(Ахп) в формуле A5.14) выполняется неравенство
и, следовательно, при достаточно малых Ах ф 0 знак правой части ра-
равенства A5.14), а потому и знак приращения функции Ау, совпадает
со знаком первого слагаемого правой части.
Если п = 2fc, то в формуле A5.14) приращение аргумента Ах воз-
возводится в четную степень, поэтому знак приращения функции Ау не
зависит от знака Ах ф 0 и, следовательно, хо является точкой строго-
строгого экстремума, причем строгого максимума при fBk\xo) < 0 (в этом
случае Ау < 0, Ах ф 0) и строгого минимума при fBk\xo) > 0 (в
этом случае Ау > 0, Ах ф 0).
Если же п = 2fc — 1, то Ах возводится в нечетную степень, и поэто-
поэтому знак Ау меняется вместе с изменением знака Аж, следовательно,
точка хо не является точкой экстремума. Если Ах меняет знак с ми-
минуса на плюс, то при f<y2k~1\xo) > 0 приращение Ау также меняет
знак с минуса на плюс и, следовательно, хо является точкой возрас-
возрастания функции /, а при f^2k~1\xo) < 0 приращение Ау меняет знак с
плюса на минус и, следовательно, точка хо является точкой убывания
функции /. <\
Отметим специально частный случай теоремы 4 при п = 2.
13 Л.Д.Кудрявцев, т.1

194 Гл. 1. Дифференциальное исчисление функций одной переменной
Л*о)>О
Если f'(xo) = 0, a f"(xo) > О, то точка ж0 является точкой строго-
строгого минимума, а если f'(xo) = 0, /"(жо) < 0 (рис. 85), то — точкой
строгого максимума.
Подчеркнем, что все условия эк-
экстремума, полученные в этом парагра-
параграфе, относились к внутренним точкам
промежутка, на котором была опре-
определена функция. На концах проме-
промежутка требуется проводить отдельные
исследования и при применении ме-
методов дифференциального исчисления
Минимум
х0
Максимум
Рис. 85
использовать в концевых точках понятие односторонних производ-
производных (см. п. 10.1).
15.3. Выпуклость и точки перегиба. Пусть функция / задана
на интервале (а, Ь) и а < х\ < х<± < Ъ. Проведем прямую через точки
А = (xi,f(xi)) и В = (ж2,/(ж2)), лежащие на графике функции /.
Уравнение этой прямой можно записать в виде
_ f(x2)(x-xi)-
У
¦ f(xi)(x2 - X)
Х2 - XI
A5.15)
Обозначим правую часть этого уравнения через 1(х), тогда оно за-
запишется в виде
1()
Определение 4. Функция / называется выпуклой вверх на ин-
интервале (а, 6), если, каковы бы ни были точки х\ и х2, а < х\ < х2 <
< 6, для любой точки х интервала (xi,x2) выполняется неравенство
l(x) sC f(x). A5.16)
Если же для всех то-
точек х е (xi,x2) выполняет-
выполняется противоположное нера-
неравенство
lyjL J ^ J \Jb ) •)	ул-О. л. I J
то функция / называется
выпуклой вниз на интерва-
интервале (а,Ь).
Это означает, что любая
точка хорды АВ (т. е. отрезка прямой A5.15) с концами в точках
А и В), например, в случае выпуклости вниз расположена не ниже
точки графика функции /, соответствующей тому же значению ар-
аргумента (рис. 86).
Заметим, что функция / выпукла вверх тогда и только тогда, ког-
когда функция —/ выпукла вниз.
Х\
Х2
Рис.

§15. Исследование функций	195
Если вместо неравенств A5.16) и A5.17) выполняются строгие не-
неравенства 1(х) < f(x) и 1(х) > /(ж), а < х\ < х < Х2 < Ъ, то функция /
называется строго выпуклой вверх, соответственно строго выпуклой
вниз на интервале (а,Ъ). В этом случае любая точка хорды АВ, кро-
кроме ее концов, лежит ниже (выше) соответствующей точки графика
функции.
Всякий интервал, на котором функция (строго) выпукла вверх, со-
соответственно (строго) выпукла вниз, называется интервалом (стро-
(строгой) выпуклости вверх, соответственно вниз этой функции.
Теорема 5 (достаточные условия строгой выпуклости). Если
вторая производная функции отрицательна (положительна) во всех
точках интервала, то функция строго выпукла вверх (соответствен-
(соответственно строго выпукла вниз) на этом интервале.
\> Если а < х\ < х < х2 < Ь, то
Kx)-f(x) = /(Ж2)(Ж ~ Ж0 + /(ж0(ж2 - X)	,, . (х - Xi) + (Х2 ~ X) _
К } П ;A5.15)	Ж2-Ж1	П }	Х2-Х1
= [f(x2) - f(x)](x - Xl) - [f(x) - f(Xl)](x2 - х) ^
Х2 — Х\
Применив к разностям значений функций, стоящим в квадратных
скобках, теорему о среднем Лагранжа (п. 12.2), получим
(Ж2 - х)(х - xi) - f'(Q(x
где xi < ? < х < Т] < Х2- Применим теперь теорему о среднем Лагран-
Лагранжа к разности значений производной f (rf) — /'(?)> тогда будем иметь
()/()	, ?<С<,
Здесь знак правой части равенства совпадает со знаком f"(() (все
остальные сомножители положительны). Поэтому если /" < 0 на (а, Ъ),
то l(x) < f(x), т. е. функция / строго выпукла вверх; если же /" > О
на (а,Ъ), то l(x) > f(x), т. е. функция / строго выпукла вниз. <|
Отметим, что условие постоянства знака второй производной, яв-
являясь достаточным условием строгой выпуклости вверх или вниз, не
является необходимым: на интервалах строгой выпуклости вверх или
вниз вторая производная может обращаться в нуль. Например, функ-
функция у = ж4 строго выпукла вниз на всей числовой прямой, однако ее
вторая производная у" = 12ж2 обращается в нуль при х = 0.
Замечание 4. Из доказательства теоремы 5 видно, что если
условие положительности второй производной на интервале заменить
условием ее неотрицательности, то функция будет выпукла вниз на
13*

196 Гл. 1. Дифференциальное исчисление функций одной переменной
этом интервале. Соответственно, если вторая производная неположи-
неположительна на интервале, то функция выпукла вверх на этом интервале.
Покажем, что расположение графика дважды дифференцируемой
функции относительно касательной к этому графику также зависит
от знака второй производной.
Теорема 6. Пусть функция f имеет во всех точках ж интервала
(а, Ь) положительную (отрицательную) вторую производную f"(x) > О
(соответственно f"(x) < 0). Тогда, какова бы ни была точка хо Е
Е (а, Ь), все точки (ж,/(ж)), х Е (а, Ь), графика функции f лежат вы-
выше (соответственно ниже) касательной, проведенной к нему в точке
(ж0, /(ж0)), кроме самой этой точки, которая лежит на касательной.
\> Если у функции / существует вторая производная в точке жо, то в
этой точке существует конечная первая производная, а следователь-
следовательно, график функции имеет в точке (жо, f(xo)) наклонную касательную
y = f'(xo)(x-xo) + f(xo).	A5.18)
Обозначим правую часть этого уравнения через Ь(х), тогда
f{x) - L{x) = \f{x) - /Ы] - f'(xo)(x - х0).
A5.18J
Применив к разности /(ж) — /(жо) теорему о среднем Лагранжа, по-
получим
fix) - Цх) = f'iOix ~ х0) - f'(xo)(x - х0) = [/'(?) - f'ixo)]ix - х0),
где а < жо < Ъ, а < ж < Ъ, а ? лежит между жо и ж.
Применив еще раз теорему Лагранжа, но уже к разности произ-
производных /'(?) — f'(xo), будем иметь
fix) - Цх) = f"(ri)(Z - xo)ix - х0),	A5.19)
где точка г] лежит между ? и жо. Поскольку точка ? лежит между
точками ж и жо, то точки ? и ж расположены по одну сторону от
точки жо, и поэтому (? — жо)(ж — жо) > 0. В силу этого знак разности
/(ж) — L(x) при ж ф жо совпадает со знаком второй производной f"(rj).
Следовательно, если на интервале (а,Ь) вторая производная положи-
положительна, то /(ж) > 1/(ж), т. е. график функции / лежит над касательной,
а если вторая производная отрицательна, то /(ж) < L(x), т. е. гра-
график функции лежит под касательной у = L(x), ж G (а, Ь), ж ф xq. <l
Определение 5. Пусть функция / дифференцируема при ж = жо
и пусть у = L(x) — уравнение наклонной касательной к графику
функции / в точке (жо, f(xo)) (см. A5.18)). Если разность /(ж) — L(x)
меняет знак при переходе через точку жо, то жо называется точкой
перегиба функции /.

§15. Исследование функций	197
Если хо — точка перегиба функции,
то точка (жо,/(жо)) называется точкой
перегиба графика функции /. В точке
(жо,/(жо)) гРаФик функции / перехо-
переходит с одной стороны наклонной касатель-
касательной A5.18) на другую сторону (рис. 87).
Пример. Рассмотрим функцию /(ж) =
= ж3. Поскольку f"(x) = 6ж, то f"(x) < 	'	^
< 0 для всех х < 0 и f"(x) > 0 для	х°
всех х > 0. Следовательно (теорема 5),	Рис- 87
функция /(ж) = ж3 выпукла вверх на бесконечном интервале (—оо,0)
и выпукла вниз на @,+оо) (см. рис. 82). Уравнение касательной к
ее графику в точке @, 0) имеет вид у = 0. Поэтому поскольку при
ж < 0 выполняется неравенство /(ж) < 0, а при ж > 0 — неравенство
/(ж) > 0, то точка ж = 0 является точкой перегиба функции /(ж) = ж3.
Теорема 7 (необходимое условие точки перегиба). Если в точ-
точке перегиба функции существует вторая производная, то она равна
нулю.
> Действительно, пусть функция / имеет в точке жо вторую произ-
производную и, как и выше, у = L(x) — уравнение касательной к графику
функции / в точке (жо,/(жо)), т. е.
Тогда в силу формулы Тейлора
fix) - L{x) =
= (/(ж0) + /'(жо)(ж - ж0) + J У^о) (ж - ж0J + о((ж - ж0J) - L(x) =
Z
Если бы f"(xo) ф 0, то знак разности /(ж) — 1/(ж) в некоторой
окрестности точки жо совпадал бы со знаком числа /"(жо). В этом
случае разность /(ж) - Ь(х) не меняла бы знака в точке ж0 и, сле-
следовательно, эта точка не была бы точкой перегиба. Итак, если жо —
точка перегиба функции /, то /"(жо) = 0. <1
Теорема 8 (первое достаточное условие точек перегиба). Если
функция f дифференцируема в точке жо, дважды дифференцируема в
некоторой проколотой окрестности этой точки и ее вторая произ-
производная меняет знак при переходе аргумента через точку жо, то жо
является точкой перегиба функции /.
|> Действительно, запишем, как и выше, уравнение касательной
A5.18) к графику функции / в точке (жо,/(жо)) в виде у = L(x). При

198 Гл. 1. Дифференциальное исчисление функций одной переменной
доказательстве теоремы б было показано (см. A5.19)), что
где точки ?, г\ и х лежат по одну сторону от точки жо, и, следователь-
следовательно, всегда
(? ~ хо)(х - хо) > 0, хф ж0,
кроме того, когда точка х переходит с одной стороны от точки жо на
другую, то то же происходит и с точкой rj.
В силу этого разность /(ж) — 1/(ж), x ф жо, имеет тот же знак, что
и вторая производная f"(rj), и так как по условию эта производная в
точке хо меняет знак, то меняет знак в этой точке и разность f(x) -
— L(x). Это и означает, что ж0 является точкой перегиба. <
Теорема 9 (второе достаточное условие точек перегиба). Если в
некоторой точке вторая производная функция равна нулю, а третья
не равна нулю, то эта точка является точкой перегиба.
\> Пусть f"(xo) = 0, f'"(xo) ф 0. Согласно формуле Тейлора и в силу
условия f"(xo) = 0 имеем
/Or) = /Ы + f'(xo)(x - х0) + ^^(х - xof + о((х - х0K),
X —У Xq.
Отсюда, применив обозначение L(x) = /(ж0) + f'(xo)(x - ж0) (у —
= L(x) — уравнение касательной к графику функции f(x) в точ-
точке (жо,/(жо))), получим
/(ж) - L(x) = f~^P^(x ~ xof + о((х - ж0K), ж ^ ж0.
Отсюда следует, что в некоторой окрестности точки жо разность
/(ж) — 1/(ж), т. е. разность ординат графика функции и касательной
к нему, при ж ф хо имеет тот же знак, что v; у (ж - ж0) , а сле-
следовательно, меняет его при переходе через точку жо (разность ж — жо
возводится в нечетную степень). Это и означает, что жо является точ-
точкой перегиба функции /. <|
15.4. Асимптоты.
Определение 6. Если функция / задана для всех х > а (соот-
(соответственно для всех ж < а) и существует такая прямая
y = kx + l,	A5.20)
что
lim [/(ж) -(кх + 1)] = 0	A5.21)
х—у-\-оо
(соответственно при ж —у — оо), то эта прямая называется асимптотой
функции f при ж —у +оо (соответственно при ж —у —оо).

§15. Исследование функций	199
Конечно, далеко не всякая функция имеет асимптоты. Сущест-
Существование асимптоты функции означает, что при х —У +оо (или при
х —У — оо) функция ведет себя "почти как линейная функция", т. е.
отличается от линейной функции на бесконечно малую.
Укажем методы отыскания асимптот A5.20). Будем рассматри-
рассматривать лишь случай х —> +оо; для х —> — оо вывод уравнения асимптоты
производится аналогичным способом. Пусть функция / при х ->• +оо
имеет асимптоту A5.20). Тогда поскольку lim - = 0, то из усло-
ж-Ц-оо X
вия A5.21) следует, что тем более
lim
- (/(ж) -kx-l)=O, т. е. lim (^ - к - -) = О,
х W V J	У	'	ж^+оо V X	Х)	'
Hm ^ = к.	A5.22)
ж —>-|-оо X
Если значение к найдено, то значение I находится из условия A5.21):
/= lim [f(x) -kx].	A5.23)
х—у-\-оо
Очевидно, справедливо и обратное утверждение: если существу-
существуют такие числа к и I, что выполняется условие A5.23), то прямая у =
= кх + 1 является асимптотой функции / при х ->• +оо, так как
из A5.23) сразу следует условие A5.21).
Пример. Найдем асимптоту функции
у = X°'t-V-	A5-24)
X I X I 1
Согласно формулам A5.22) и A5.23) имеем к = lim —	— = 1,
ж-^оо Х\Х — 1)
7 ,. /ж2+ж + 1 \ г 2ж + 1
/ = lim	ж = lim 	 = 2.
ж-^оо V X — 1	/ ж-^оо Ж — 1
Отсюда следует, что асимптотой функции A5.24) является прямая
у = х + 2.
Уравнениями вида A5.20) описываются все прямые, которые не
параллельны оси Оу, т. е. не вертикальны. Поэтому асимптоты ви-
вида A5.20) называют также и наклонными асимптотами. Сформули-
Сформулируем теперь определение вертикальных асимптот.
Определение 7. Если для функции / выполнено хотя бы одно
из условий
lim f(x) = оо или lim f(x) = оо,	A5.25)
ж—^жо—0	ж—^жо+0
то прямая х = хо называется вертикальной асимптотой функции /.
Для того чтобы имело смысл рассматривать первый (второй) пре-
предел A5.25), здесь предполагается, что функция / задана на пересече-
пересечении некоторой окрестности точки xq с лучом х < xq (с лучом х > xq).

200 Гл. 1. Дифференциальное исчисление функций одной переменной
Чтобы найти вертикальные асимптоты функции /, надо найти
такие значения хо, для которых выполняются одно или оба усло-
условия A5.25). Например, для функции A5.24) вертикальной асимптотой
является прямая х = 1, ибо
Л. х2+х + 1
lim 	 = оо.
х->1 X — 1
15.5*. Построение графиков функций. С помощью развито-
развитого в этом параграфе математического аппарата можно изучать по-
поведение функций и строить их графики. Общее изучение заданной
функции целесообразно проводить в следующем порядке.
1.	Определить область существования функции, область непрерыв-
непрерывности и точки разрыва.
2.	Найти асимптоты.
3.	Приблизительно, вчерне, нарисовать график функции.
4.	Вычислить первую, а если нужно, и вторую производные (без
производных более высокого порядка обычно удается обойтись). Най-
Найти точки, в которых первая и вторая производные либо не существу-
существуют, либо равны нулю. Составить таблицу изменения знака первой и
второй производных.
5.	Определить интервалы возрастания, убывания, выпуклости
вверх и вниз функции, найти точки экстремума (в том числе и кон-
концевые) и точки перегиба.
6.	Окончательно вычертить график.
В результате, действуя подобным образом, мы, как правило, суме-
сумеем провести лишь качественное исследование заданной функции, так
как, например, для нахождения точек экстремума согласно теореме 2
надо решить уравнение f'(x) = 0, а может оказаться, что точные зна-
значения корней этого уравнения мы не сумеем найти, а сумеем лишь
с большей или меньшей точностью найти интервалы, где они нахо-
находятся. В этом случае методы математического анализа позволяют,
вообще говоря, осуществлять лишь качественное изучение поведения
функции, а их количественное изучение осуществляется с помощью
численных методов, возможности которых существенно расширяет
использование современных вычислительных машин.
Пример. Построить график функции
f(x) = х l/(x-lJ.	A5.26)
Функция / определена и непрерывна на всей числовой оси, по-
f(x)
этому у нее нет вертикальных асимптот. Поскольку lim ^-^ =
х—>-±оо X
= lim U(x — IJ = +оо, то у нее нет и наклонных асимптот.
ж->-±оо
Функция / неотрицательна при положительных значениях аргу-
аргумента х и отрицательна при его отрицательных значениях; /@) =

§16. Векторные функции
201
lim /(ж) = +oo, lim /(ж) = —оо.
х—^+оо	х—У — оо
Легко видеть, что /(ж) ~ ж при ж —>¦ 0, /(ж) ~ ж5/3 как при ж —>¦ +оо,
так и при ж —>¦ —оо.
На основе полученных данных мож-
можно построить эскиз графика функции
A5.26) — он изображен на рис. 88.
Для уточнения вида графика вычислим
первую и вторую производные функ-
функции A5.26):
О
Поскольку /'C/5) = 0 и производная в	Рис- 88
точке ж = 3/5 меняет знак с плюса на минус (отметим, что в доста-
достаточно малой окрестности точки ж = 3/5 знаменатель у выражения
для /'(ж) отрицателен), то эта точка является точкой максимума,
что соответствует виду графика на
рис. 85.
В точке ж = 1 существует бесконеч-
бесконечная производная, поэтому график функ-
функции A5.26) имеет в точке A,0) верти-
вертикальную касательную.
Наконец, /"F/5) = 0, и в точке ж =
= 6/5 вторая производная меняет знак.
Это означает, что точка ж = 6/5 является
точкой перегиба. Принимая во внимание
все дополнительные исследования, можно
существенно уточнить вид графика функ-
функции A5.26). Уточненный вид графика этой функции изображен на
рис. 89.
§ 16. Векторные функции
16.1. Предел и непрерывность векторной функции. В этом
параграфе будут изучаться функции, значениями которых являются
векторы, а аргументами — числа. Такие функции называют вектор-
функциями или векторными функциями (числового аргумента). Они
обозначаются жирным шрифтом: г(?), или с помощью черты над зна-
значениями функции: OM(t), t G X, где X — некоторое числовое мно-

202 Гл. 1. Дифференциальное исчисление функций одной переменной
жество.
В этом определении в зависимости от рассматриваемых задач под
векторами r(t) могут пониматься как свободные векторы, так и век-
векторы с закрепленными началами. Если начала всех векторов закреп-
закреплены в одной и той же точке (обычно — начало координат), то такие
векторы называются радиус-векторами.
Если в трехмерном евклидовом пространстве задана прямоуголь-
прямоугольная система координат, то, как хорошо известно, каждому вектору
соответствует упорядоченная тройка действительных чисел — его
координат и, наоборот, каждой упорядоченной тройке чисел соот-
соответствует вектор, для которого числа, входящие в эту тройку, явля-
являются его координатами. Поэтому задание вектор-функции r(t), t Е X,
эквивалентно заданию трех скалярных, т. е. числовых, функций x(t),
y(t), z(t), t e X, являющихся его координатами:
r(t) = (x(t),y(t),z(t)), teX.
Длина (абсолютная величина) всякого вектора а, обозначается |а|
скалярное произведение векторов а и b — через ab или (а, Ь), а век-
векторное — через а х b или [а, Ь].
Определим понятия предела, непрерывности, производной и диф-
дифференциала для векторных функций.
Определение 1. Вектор а называют пределом вектор-функ-
вектор-функции r(t), t Е X, при t —> to (или в точке t = to) и пишут
lim r(t) = a,	A6.1)
ttt
если
lim |r(t) - а| = 0.	A6.2)
t^t ' w '	v J
В этом определении |r(t) — a| — числовая функция. Таким обра-
образом, понятие предела векторной функции сводится к понятию предела
скалярной функции. Вспомнив определение этого понятия, получим,
что A6.1) означает, что для любого г > 0 существет такое 8 > 0, что
для всех
teXDU(to,S)	A6.3)
выполняется неравенство
|r(t) - а| < г.	A6.4)
Как и в случае скалярных функций, будем предполагать, что to яв-
является точкой прикосновения (конечной или бесконечно удаленной)
множества X. Если to — конечная точка, то условие A6.3) можно
записать в виде
|t-to|<E, teX,	A6.5)
а если t0 — одна из бесконечно удаленных точек оо, +оо или -оо, то
соответственно в одном из следующих трех видов:
|t| > 1/8, t > 1/8, t < -1/8,	A6.6)

§16. Векторные функции
203
и, конечно, всегда t G X.
Если начало всех векторов r(t) поместить в одну точку (например,
в начало координат), то условие A6.4) будет означать, что концы всех
векторов r(t) при t G X П ?/(to,?) лежат в шаре радиуса г с центром
в конце вектора а (рис. 90).
Если r(t) = (x(t),y(t),z(t)) и а = (аьа2,аз),
то
Ш - а| =
[y(t) - а2]2 + [z(t) - а3]2 A6.7)
A6.8)
и, следовательно,
|x(t) — CL\\ ^ |r(t) —
\y(t) -CL2\ ^ |r(t) -
z(t) - a3\ ^ |r(t) - a|.
Поэтому предел
lim r(t) = a	A6.9)
векторной функции r(t) существует в том и только том случае, когда
существуют пределы ее координат
lim y(t) = a2, lim
Рис. 90
lim x(t) =
= a3.
A6.10)
Действительно, в силу соотношений A6.7) и A6.8) для того, чтобы
выполнялось условие A6.2), необходимо и достаточно, чтобы
lim \x(t) — а\\ =0, lim \y(t) — a2| =0, lim \z(t) — as\ =0.
t—tto	t^-to	t^-to
Аналогично случаю числовых функций, если to G X и на мно-
множестве X существует предел lim r(t), то этот предел равен зна-
t—tto
чению функции r(t) в точке to: lim r(t) = г (to).
Определение 2. Если to — конечная точка и для функции r(t),
t GX, имеет место равенство
lim r(t) =r(t0),	A6.11)
то эта функция называется непрерывной в точке to.
Как и в случае скалярных функций, условие A6.11) выполняется
тогда и только тогда, когда существует lim r(t) и to G X.
Если положить At = t — to, Ar = r(t0 + At) - r(t0), то усло-
условие A6.11) примет вид lim Ar = 0.
At^O
Из эквивалентности условий A6.9) и A6.10) следует, что вектор-
векторная функция непрерывна в некоторой точке тогда и только тогда,
когда в этой точке непрерывны все ее координатные функции.

204 Гл. 1. Дифференциальное исчисление функций одной переменной
Отметим основные свойства пределов векторных функций.
1°. Если lim r(t) = а, то lim |r(t)| = |а|.
t—tto	t^-to
Это непосредственно следует из неравенства ||г| — |а|| ^ |г — а|.
Геометрический смысл этого неравенства состоит в том, что раз-
разность длин двух сторон треугольника не превышает длины его
третьей стороны.
2°. lim [nCt) + r2(?)l = lim n(t) + lim r2(?).
3°. lim f(t)r(t) = lim f(t) lim r(t) (f(t) — скалярная функция).
4°. lim ri(t)r2(t) = lim n(t) lim r2(t).
5°. lim ri(t) x r2(t) = lim ri(t) x lim r2(t).
t—tto	t—tto	t—tto
В свойствах 2°-5° все рассматриваемые функции определены на
некотором множестве X С /?; предполагается, что все пределы, вхо-
входящие в правые части равенств, существуют, и утверждается, что
существуют пределы, стоящие в левых частях, причем имеют место
написанные формулы.
Все эти свойства доказываются методом, аналогичным методу, ко-
которым доказывались свойства пределов скалярных функций в п. 6.7.
|> Докажем в качестве примера свойство 5°. Заметим предваритель-
предварительно, что для любых двух векторов р и q справедливо неравенство
Р х q| = |p||q| sinpq ^ |p||q|.	A6.12)
Поэтому если р = р(?), q = q(t), причем lim |p(t)| = 0, a |q(t)| —
ограниченная функция, то в силу неравенства A6.12)
lim |p х q| = 0.	A6.13)
Пусть теперь lim i*i(t) = a, lim r2(?) = b. Положим
a(t) =f n(t) - a, 0(t) d= r2(t) - b,	A6.14)
тогда, согласно A6.2),
\\mo\ct(t)\ = limjC(t)\ = 0-	A6-15)
Преобразуем произведение i*i(t) x r2(t) с помощью формул	A6.14):
ri(t) xr2(t) = [a + a(t)] x [b + 0(t)] =
= a x b + a x C(t) + ct(t) x b + ct(t) x C(t). A6.16)
Здесь в силу A6.13)
lim |а x C(t)\ = lim \ct(t) x b| = lim \ct(t) x C(t)\ = 0,
ttt	ttt	ttt
а так как
|а х C{t) + cx{t) x b + cx{t) x C{t)\ ^
^ |a x C(t)\ + \ct(t) x b| + \ct(t) x C(t)\,

§16. Векторные функции	205
то lim |a x C(t) + oc(t) х b + oc(t) x C(t)\ = 0.
t—Но
Отсюда в силу A6.16) имеем lim |i*i(t) х T2(t) — а х Ь| =0, что
согласно определению 1 (см. A6.2)) и доказывает свойство 5°. <1
Из свойств пределов векторных функций и определения их непре-
непрерывности следует, что сумма, скалярное и векторное произведения
векторных функций, а также произведение скалярных функций на
векторные непрерывны в некоторой точке, если в этой точке непре-
непрерывны все слагаемые или соответственно сомножители.
16.2. Производная и дифференциал векторной функции.
Пусть векторная функция r(t) задана в некоторой окрестности точ-
.	r(t) - r(t0)
ки to; тогда соотношение —^	—- определено в соответствующей
t — to
проколотой окрестности точки t0.
Определение 3. Предел lim -^—-^- (если он, конечно, су-
t—tto	t — to
ществует) называется производной векторной функции r(t) в точке to
и обозначается г'(to) или г (to).
Если положить At = t — to, Ar = r(t) — r(to) = r(to + At) — r(to), то
r'(io)=f Hm ?.	A6.17)
At->0 At
Пусть r(t) = (x(t),y(t),z(t)). Так как
r(t) - r(t0) = /x(t)-x(to) y(t) - y(tp) z(t)-z(tp)\
t — to	V t — to	t — to	t — to )
то в силу A6.9), A6.10) для того, чтобы векторная функция r(t) =
= (x(t),y(t),z(t)) имела производную в точке to, необходимо и
достаточно, чтобы ее координаты x(t), y(t), z(t) имели производные
в точке t0, причем в этом случае
r/(to) = (x/(to),2//(^o)^/(^o)).	A6.18)
Производную r'(t) вектор-функции r(t) называют также ско-
скоростью изменения вектора r(t) относительно параметра t. В случае
когда длина вектора r(t) не меняется, производная r'(t) называется
также и скоростью вращения вектора r(t), а ее абсолютная величи-
величина — численным значением скорости его вращения.
Замечание 1. По аналогии со случаем скалярных функций век-
векторную функцию a(t), t G X, называют бесконечно малой по сравне-
сравнению со скалярной функцией /3(t), t G X, при t —> to и пишут cx(t) =
= o(/3(t)), t ->• t0, если существует векторная функция e(t), опреде-
определенная на том же множестве X, что и функции a(t), /3(t), такая,
что в некоторой окрестности точки t = to имеет место равенство
a(t) =e(t)/3(t), teX,n
lim e(t) = 0.
t^t

206 Гл. 1. Дифференциальное исчисление функций одной переменной
Как и для скалярных функций, если t0 € X, то функция e(t) непре-
непрерывна в точке to, и потому s(to) = 0.
Замечание 2. Вектор-функция аргумента t называется линей-
линейной, если она имеет вид at + b, где а и b — какие-либо два фиксиро-
фиксированных вектора.
После этих вводных замечаний можно определить понятие диф-
ференцируемости и дифференциала вектор-функции.
Определение 4. Вектор-функция r(t), заданная в некоторой
окрестности точки t0, называется дифференцируемой при t = t0, ес-
если ее приращение Ar = r(to + At) — r(to) в точке to представимо в
виде
Ar = aAt + o(At), At-^O.	A6.19)
При этом линейная вектор-функция aAt приращения аргумен-
аргумента At называется дифференциалом функции r(t) в точке t0 и обозна-
обозначается через <ir, т. е. dr = aAt.
Таким образом,
Ar = dr + o(At), At^O.	A6.20)
Здесь функция o(At) определена при At = 0; в этой точке она равна
нулю:
o(At)	= (Ar - aAt)
At=0
= 0.
At=0
Следовательно, если представить эту функцию o(At) в виде (см.
замечание 1) o(At) = s(At)At, то функция s(At) также будет оп-
определена при At = 0, а поэтому, как было отмечено выше, в этом
случае s@) = 0. Благодаря этому здесь предел
lim s(At) = 0	A6.21)
рассматривается не по проколотой, а по целой окрестности точки
At = O.
Формулу A6.19) теперь можно записать в виде
Ar = aAt + s(At)At, lim s(At) = 0.	A6.22)
Докажем несколько простых утверждений о дифференцируемых
векторных функциях, аналогичных соответствующим утверждениям
для скалярных функций.
I. Если векторная функция дифференцируема в некоторой точке,
то она и непрерывна в этой точке.
\> lim Ar = lim (aAt + s(At)At) = 0. <l
At^O A6.22) At^O
П. Если векторная функция r(t) дифференцируема в точке to, то
она имеет в этой точке производную и
г'(t0) = a,

§16. Векторные функции	207
где вектор а определяется формулой A6.19).
\> lim -— = lim а -\	^—- = а. <|
At^O At A6.19) At^O V	At J
Верным является и обратное утверждение.
III.	Векторная функция, имеющая в некоторой точке производную,
дифференцируема в этой точке.
\> Если существует производная г'(to) = lim —— и, следовательно,
At—>0 At
г7(to) = ? + e(At), At ф 0, где lim e(At) = 0, то
At	At^0,At^0
Ar = r'(to)At + e(At)At.
Полагая e@) = 0, получим, что условие lim e(t) = 0 выполняется
и без ограничения At ф 0.
Таким образом, имеет место A6.22) при а = г'(to), т. е. функ-
функция r(t) дифференцируема в точке to и
dr(t0) =r/(t0)At. <
def
По определению считается, что dt = At. Поэтому (опуская для
dr
простоты обозначения аргумента) имеем dr = r'dt, или rf = —.
IV.	Если t = ?(т) — дифференцируемая в точке г0 числовая функ-
функция, a r(t) — дифференцируемая в точке to =t(ro) векторная функция,
то сложная функция r(t(r)) дифференцируема в точке то и
r'T(t(To))=r't(to)tfT(To),
или, короче	dr drdf
Т~ = ~Л1~'	A6.23)
dr dt dr
l> Из соотношения A6.22) имеем при Аг ф 0
По условию функция t = t(r) дифференцируема в точке то, т. е.
существует конечный предел
Hm ^ =t'(T0).	A6.25)
Ar^O Ar
Отсюда следует, что эта функция в рассматриваемой точке непре-
непрерывна:
н	lim At = 0.
Ar^O
Отсюда и из условия A6.21) вытекает, что lim s(At) = 0.
Ar—^0

208 Гл. 1. Дифференциальное исчисление функций одной переменной
Из всего сказанного следует, что при Ат ->• 0 правая часть ра-
равенства A6.24), а следовательно, и его левая часть имеют конечные
пределы. Это означает, что в точке то существует производная т'т и
что
Из формулы A6.23) аналогично случаю скалярных функций вы-
вытекает инвариантность записи дифференциала векторной функции:
как для зависимой переменной t, так и для независимой т имеем
dr = r't dt, dr = r(Tdr,	A6.26)
т. е. чтобы из второй формулы получить первую, надо подставить во
вторую формулу r'T = r't • t'T и заметить, что t'Tdr = dt.
V. Для производных вектор-функций имеют место формулы, ана-
аналогичные соответствующим формулам для скалярных функций:
(ri X Y2)' = r[ X Г2 + Г1 X Г2.
Здесь все производные берутся в одной и той же точке. Предпола-
Предполагается, что производные, стоящие в правой части каждого равенства,
существуют, и утверждается, что в этом случае существуют и про-
производные, находящиеся в левых частях равенств.
> Доказываются эти формулы аналогично скалярному случаю. До-
Докажем, например, последнюю из них.
Заметив, что п (?0 + At) = ri (t0) + Ari, r2(t0 + At) = r2(t0) + Ar2,
получим
/ x r у	= lim riftp + At) x r2(t0 + At) - n(to) x r2(t0)
= lim
t=t0 At^o	At
Ит (ri(tp) + An) x (r2(t0) + Ar2) - ri(tp) x r2(t0)
At^o	At
= г;(*0) xr2(to)+r!(to) xr2(t0). <
Для дальнейшего нам будет полезна следующая
Лемма. Если вектор-функция r(t) дифференцируема в точке to и
все векторы r(t) имеют одну и ту же длину в некоторой окрестности
точки t0, то производная г'(to) ортогональна вектору г (to):
r/(t0)r(t0) = 0.	A6.27)

§16. Векторные функции	209
|> Действительно, если в указанной окрестности |r(t)| = с, где с —
константа, то |г|2 = с2, т. е. г2 = с. Дифференцируя это равенство,
получим 2гг/ = 0, что равносильно равенству A6.27). <1
Утверждение леммы содержательно лишь в случае, когда г'(to) ф
Ф 0 (если г'(to) = 0, то условие A6.27), очевидно, выполняется и без
условия постоянства длины вектора r(t)). В этом случае физический
смысл формулы A6.27) состоит в том, что у материальной точки,
движущейся по поверхности шара (r(t) — радиус-вектор этой точки,
t — время движения, с — радиус указанного шара), скорость v = —
всегда направлена при v ф 0 по касательной к поверхности шара, т. е.
перпендикулярно радиусу шара.
Производные высших порядков для вектор-функции определяют-
определяются по индукции: если у вектор-функции r(t) в некоторой окрест-
окрестности точки to задана производная An\t) порядка n, n = 0,1,2,...
(r(°)(t) = r(t)), то производная порядка п + 1 в этой точке (если эта
производная, конечно, существует) определяется по формуле
t=to
Если векторная функция имеет в некоторой точке п производ-
производных, то говорят также, что она в этой точке п раз дифференцируема.
Можно и для векторных функций по аналогии со скалярными ввес-
ввести понятие дифференциалов высших порядков, но не будем на этом
останавливаться.
Если векторная функция r(t) = (x(t),?/(t), z{t)) n раз дифферен-
дифференцируема в точке t = to, то в некоторой окрестности этой точки для
функции r(t) имеет место формула
Ar = r(t0 + At) - r(t0) = Y^ nJ^ Afk + °(АГ)> At "> °>
k=i
называемая по аналогии со скалярным случаем формулой Тейлора (по-
(порядка п) функции r(t) с остаточным членом в виде Пеано. Эта фор-
формула непосредственно следует из разложений по формуле Тейлора
координат x(t), y(t), z(t) векторной функции r(t).
Из всего сказанного видно, что рассмотренные определения и
утверждения для векторных функций получаются перенесением со-
соответствующих определений и утверждений из теории скалярных
функций.
Замечание 3. Следует, однако, иметь в виду, что не все, что
справедливо для скалярных функций, имеет прямой аналог в вектор-
векторном случае. Это относится, например, к теореме Ролля, а следова-
следовательно, и к теореме Лагранжа, частным случаем которой является
теорема Ролля.
14 Л.Д.Кудрявцев, т.1

210 Гл. 1. Дифференциальное исчисление функций одной переменной
В самом деле, рассмотрим дифференцируемую векторную функ-
функцию r(?) = (cost, sin?), 0 ^ t ^ 2тг (третья координата функции r(t) —
тождественный нуль). Поскольку г'(?) = (—sint, cost), то |r'(t)| =
= л/sin2 t + cos2 t = 1 при любом t G [0,2тг], и, следовательно, не су-
существует такой точки ? Е [0,2тг], для которой было бы г'(?) = 0, не-
несмотря на то, что г@) = гBтг).
Для векторных функций вместо прямого аналога теоремы Лагран-
жа можно доказать нижеследующую теорему 1.
Ее формулировке и доказательству предпошлем два замечания.
Замечание 4. Если вектор х ненулевой и xq — единичный век-
вектор в направлении вектора х, т. е. xq = x/|x|, то
|х|=хх0.	A6.28)
В самом деле, согласно определению скалярного произведения
хх0 = |х||хо| cosxxj.	A6.29)
Здесь по условию |xq| = 1, a xxq = 0 и, следовательно, cosxxq = 1,
т. е. равенство A6.29) превращается в равенство A6.28).
Замечание 5. Для любых векторов х и у имеет место нера-
ВеНСТВ°	ху^|х||у|.	A6.30)
|> Действительно,
ху ^ |ху| = ||x||y|cosxy| = |х||у| |cosxy| ^ |х||у|. <|
Теорема 1. Если вектор-функция г(?) непрерывна на	отрез-
на	отрезке [а, Ь] и дифференцируема внутри него, то существует	такая
точка ? е (а, Ь), что
|г(Ь)-г(а)| ^ |г'(О1(Ь-а).	A6.31)
|> Если г(а) = гF), то неравенство A6.31) справедливо при любом
выборе точки ? G (а,Ь), так как его левая часть обращается в нуль.
Пусть г(а) ф r(b) и, следовательно, r(b) — г(а) ф 0. Если е — еди-
единичный вектор в направлении вектора г(Ь) —г(а), то согласно заме-
замечанию 4
|г(Ь) - т(а)\ = (г(Ь) - г(а))е = г(Ь)е - г(а)е,
т. е. получилась разность значений скалярной функции
f(t)d=r(t)e	A6.32)
на концах отрезка [а, Ь]:
\r(b)-r(a)\=f(b)-f(a).	A6.33)
Из формулы A6.32) следует, что функция / непрерывна на от-
отрезке [а, Ь] и дифференцируема во всех его внутренних точках, ибо

§17. Длина кривой	211
согласно условиям теоремы этими свойствами обладает функция г(?).
Поэтому в силу формулы конечных приращений Лагранжа существу-
существует такая точка ? Е (а, Ь), что f(b) — /(а) = /'(?)(Ь — а). Но согласно
правилу дифференцирования скалярного произведения имеем f'(t) =
= г'(?)е, вследствие чего
№ - f(a) = г'(Ое(Ь - а), а < ? < Ь.	A6.34)
Поскольку в силу неравенства A6.30) имеет место неравенство
г'(Ое^|г'(О1|е| = |г'(О1,	A6.35)
ТО
|г(Ь)-г(а)| = №-f(a) ^ |г'(О1(Ь-а), а < ? < Ъ.
A6.33)	A6.34)
A6.35)
Неравенство A6.31) доказано. <
§ 17. Длина кривой
17.1. Понятие кривой. Рассмотрим отображение некоторого
отрезка [а, Ь] числовой прямой R в пространство /?3, т. е. такое
отображение, которое каждой точке t G [а, Ь] ставит в соответствие
точку M(t) пространства R3. Если в пространстве R3 задана пря-
прямоугольная декартова система координат x,y,z, то между точками
пространства R3 и тройками чисел x,y,z имеется взаимно одно-
однозначное соответствие, а поэтому задание отображения M(t) e /?3,
t G [а,Ь], равносильно заданию трех числовых функций (называе-
(называемых координатными) x(t), y(t), z(t), где x(t), y(t) и z(t) являются
координатами точки M(t).
Отображение M(t) G /?3, t G [a,b], называется непрерывным на
отрезке [а, 6], если на этом отрезке непрерывны все его координат-
координатные функции ж(?), y(t), z(t).
Определение 1. Непрерывное отображение отрезка в прост-
пространство называется кривой.
Кривые будем обозначать большими греческими буквами Г, Л.
Если М(?), а ^ ? ^ Ь, — непрерывное отображение какого-либо отрез-
отрезка [а, Ь] в пространство, т. е. кривая Г, то будем писать
Г = {М(?); а ^ t ^ &},	A7.1)
или
T = {x(t\y(t\z(t)\ a^t^b},	A7.2)
где x(t), y(t), z(t) — координатные функции отображения M(t), a ^
^ t ^ Ь.
14*

212 Гл. 1. Дифференциальное исчисление функций одной переменной
Координатные функции ж(?), y(t), z(t) отображения М(?), t e [а, Ь],
однозначно задают вектор-функцию г(?), координатами которой они
являются:
r(?) = (x(t),y(t),z(t)), a^t^b.	A7.3)
Эта вектор-функция называется векторным представлением кри-
кривой A7.1). Если начало вектора г(?) поместить в начало координат,
то его концом будет точка M(t). При задании кривой Г ее векторным
представлением A7.3) пишут
Г = {r(i); a ^ t О}-	A7-4)
Множество точек пространства /?3, на которое отображение A7.1)
отображает отрезок [а, 6], называется носителем кривой Г.
Иногда там, где это не может привести к недоразумению, носи-
носитель кривой называется также кривой.
Если О — начало координат в пространстве /?3, то конец радиус-
вектора OM(t) при изменении параметра t на отрезке [а, Ъ] пробегает
носитель кривой Г. В дальнейшем, когда будут рассматриваться век-
векторные представления A7.4) кривой Г, всегда будет предполагаться,
что вектор г(?) является радиус-вектором с началом в начале коор-
координат, т. е. что r(?) = OM(t).
Переменная t называется параметром на кривой Г. Всякая строго
монотонная непрерывная на некотором отрезке [а,/3] функция
t = t(r), а^т^/3,	A7.5)
отображающая отрезок [а,/3] на отрезок [а, 6], для которой, следова-
следовательно, в случае ее строгого возрастания выполняется условие
t(a) = a, t(/3) = Ъ,
а в случае строгого убывания — условие
t(a) = Ъ, t(/3) = a
(рис. 91), называется преобразованием параметра t кривой A7.1) (или,
t,
ъ
а
О
1
1
1
а
1
i
i ,
C т
Рис. 91
полнее, преобразованием параметра t к параметру г). Обратная к

§17. Длина кривой	213
функции t = t(r) функция г = r(t) является, очевидно, преобразова-
преобразованием параметра для кривой {М(?(т)); а ^ т ^ /3}.
При преобразовании параметра t = t(r) из равенства М(?) =
= M(t(r)), а ^ г ^ /3, следует, что исходная кривая и кривая, полу-
получающаяся из нее с помощью преобразования параметра, имеют один
и тот же носитель.
Если t = ?(т), а ^ г ^ C, — преобразование параметра, то кри-
кривые {M(t)\ a^t^b} и {M(t(r))\ а ^ т ^ /3} часто называют одной
и той же кривой с разными параметризациями.
Если координатные функции ж(?), y(t), z(t) отображения A7.1) п
раз дифференцируемы или п раз непрерывно дифференцируемы (т. е.
имеют п непрерывных производных) на отрезке [а, Ь], то кривая Г
называется п раз дифференцируемой или, соответственно, п раз не-
непрерывно дифференцируемой кривой.
Преобразованиями параметра п раз [непрерывно) дифференцируе-
дифференцируемой кривой называются такие п раз (непрерывно) дифференцируемые
строго монотонные функции A7.5), у которых во всех точках отрез-
отрезка [а,/3] их производная не равна нулю:
Это условие нужно для того, чтобы обратная функция т = т(?), а ^ t ^
^ 6, была также преобразованием параметра т кривой M(t(r)), a ^
^ т ^ C (см. формулы для производной обратной функции в п. 10.6).
Для того чтобы кривая Г была п раз дифференцируема (соответ-
(соответственно п раз непрерывно дифференцируема, п = 1, 2,...), необходимо
и достаточно, чтобы ее векторное представление A7.2) было п раз
дифференцируемо (соответственно п раз непрерывно дифференци-
дифференцируемо). Это следует из того, что непрерывность (дифференцируе-
мость) векторной функции равносильна непрерывности (дифферен-
цируемости) ее координат (п. 16.2).
Точка носителя кривой Г, в которую при отображении A7.1)
отображаются по крайней мере две разные точки отрезка [а, 6],
называется кратной точкой носителя этой кривой или точкой
самопересечений кривой. Если кратная точка носителя кривой Г
имеет в точности п прообразов при отображении M(t), a ^ t ^ b, то
эта точка называется п-кратной.
Если носитель кривой Г не имеет кратных точек, т. е. отобра-
отображение A7.1) взаимно однозначно отображает отрезок [а, Ъ] в прост-
пространство /?3, то кривая Г называется просто дугой.
Точкой кривой A7.1) называется пара (М,?), где М = M(t) G /?3,
a t G [а, Ь]. Точка М G R3 называется носителем точки (М, t).
Носитель точки кривой там, где это не может привести к недора-
недоразумению, называется иногда также точкой кривой.

214 Гл. 1. Дифференциальное исчисление функций одной переменной
Если Мо = М(а), a Mi = M(b), то точка (М0,а) называется нача-
началом кривой Г, а точка (Mi, b) — ее концом (впрочем, иногда обе точки
(Мо,а) и (Mi, b) называют концами кривой Г). Если носители начала
и конца кривой Г совпадают: М(а) = МF), то кривая Г называется
замкнутой.
Если у носителя замкнутой кривой нет других кратных точек,
кроме носителя ее начала и конца, который является двукратной
точкой, то кривая Г называется простым замкнутым контуром.
Там, где это не может привести к недоразумениям (например,
для простых дуг), точка (М,t) кривой Г часто обозначается M(t),
т. е. тем же символом, что и носитель указанной точки.
Если ti G [a, b], t2 ? [а, Ь], h < t2, то кривая {М(?); t\ ^ t ^ ?2}
называется частью кривой A7.1) или ее дугой
M(h)M(t2)
с началом в точке M(ti) и концом в M(t2).
Если носитель кривой Г лежит в некоторой плоскости, то эта кри-
кривая называется плоской.
Примеры. 1. Рассмотрим две замкнутые плоские кривые:
х = cost, у = sint, 0 ^ t ^ 2тг,	A7.6)
х = cost, у = sin?, 0 ^ t ^ 4тг.	A7.7)
Их носителями является одна и та же окружность х2 + ^/2 = 1, но
это две разные кривые: у кривой A7.6) параметр t изменяется от О
до 2тг, и эта окружность проходится один раз, а у кривой A7.7) пара-
параметр t изменяется от 0 до 4тг, и та же окружность проходится два раза.
Носитель кривой A7.6) имеет только одну кратную точку — носи-
носитель начала и конца этой кривой. У носителя кривой A7.7) все точки
кратные.
2. Непрерывная на некотором отрезке [а, Ь] функция у = /(ж),
а ^ х ^Ь, задает плоскую кривую х = t, у = /(t), a ^b, являющуюся,
очевидно, простой дугой. Ее носителем является график функции /,
а параметром — переменная х. В этом случае пишут
и говорят, что кривая Г имеет явное представление — функцию /.
Упорядоченность точек отрезка [а, Ь] порождает с помощью ото-
отображения M(t), a ^ t ^ 6, упорядоченность точек на кривой Г =
= {M(t); a ^ t ^ Ъ}. Если t\ < t2, то точка M(ti) кривой Г называет-
называется точкой, предшествующей точке M(t2) этой кривой. Этот порядок
точек называется ориентацией кривой, а кривая, на которой задана
ориентация, называется ориентированной кривой.

§17. Длина кривой	215
Порядок точек на кривой
+ b-t); a^t^b}	A7.8)
называется противоположным порядку точек кривой Г{М(?); а ^ t ^
^ Ъ} {противоположной ориентацией кривой), а сама кривая A7.8) —
кривой, ориентированной противоположно к данной кривой Г.
Для ориентированной кривой преобразованием параметра называ-
называются только строго возрастающие функции — они не меняют поря-
порядок точек, в то время как строго убывающие меняют их порядок на
противоположный.
Замечание 1. Задания кривой Г в виде М(?), (x(t),y(t),z(t))
и r(t), a ^ t ^ b, называют ее параметрическими заданиями, а саму
кривую Г называют также параметрически заданной непрерывной
кривой.
Замечание 2. Если для плоской кривой Г существует такая
функция F(x,y), что координаты всех точек (х,у) носителя кривой Г
удовлетворяют условию
F(x,y)=0,	A7.9)
то говорят, что уравнение A7.9) является неявным заданием кривой Г.
Следует иметь в виду, что, вообще говоря, множество всех то-
точек, удовлетворяющих уравнению вида A7.9), не является носителем
некоторой кривой в определенном выше смысле даже для достаточ-
достаточно "хороших" функций F(x,y). Например, множество точек, коорди-
координаты которых удовлетворяют уравнению
Ог2+у2)Ог2+у2-1)=0,
представляет собой окружность х2 + у2 = 1 и точку @,0).
Замечание 3. В случае кривых, лежащих на плоскости, иногда
бывает удобно их задавать в полярных координатах р, ср (p — поляр-
полярный радиус точки плоскости, a ip — угол, образованный им с полярной
осью), которые связаны с декартовыми координатами х,у соотноше-
соотношениями	. ч
х — р cos if, У — Р sin if. A7.10)
В полярных координатах кривая задается уравнениями вида
a^ip^f3.	A7.11)
С помощью формул A7.10) задание кривой уравнением A7.11) сразу
сводится к ее параметрическому заданию
х = p(ip) cos ip, у = p(ip)simp, a^ip^/3,
где за параметр взят полярный угол ip.
Замечание 4. Отметим еще, что сформулированное определение
кривой не охватывает все то, что интуитивно естественно отнести

216 Гл. 1. Дифференциальное исчисление функций одной переменной
к понятию кривой, например, прямую линию, гиперболу, параболу
и т. п. Чтобы охватить определением и подобные "кривые", следу-
следует рассмотреть отображения в пространство не только отрезков, но
и других промежутков числовой оси: интервалов и полуинтервалов.
17.2. Касательная к кривой. Пусть задана кривая Г = {М(?);
а ^ t ^ b}, r(t) = OM(t) — радиус-вектор точки M(t), вектор-функ-
вектор-функция r(t) дифференцируема в точке to Е [а, Ъ] и г7(to) ф 0. В силу опре-
определения дифференцируемости
Аг = r(t0 + At) - r(t0) = r/(t0)At + o(At), At -+ 0.
Из этой формулы и из условия г7(to) ф 0 следует, что для всех доста-
достаточно малых At ф 0 имеет место неравенство Аг ф 0, т. е. r(to + At) ф
Ф r(to), а поэтому точки Mq = M(to) и М = M(to + At) различны.
Проведем через них прямую (она обычно называется секущей) MqM.
Очевидно, вектор Аг, а следовательно, и вектор Ar/At, At ф 0, отли-
отличающийся от вектора Аг только скалярным множителем I/At, парал-
параллельны секущей MqM. По условию в точке to существует производная
г7(to) = Hm —. Геометрически это
означает, что векторы Ar/At, парал-
параллельные секущей MqM, при At —У 0
стремятся к некоторому предельному
вектору г7(to), по условию не равному
нулю, а так как все секущие MqM про-
проходят через одну и ту же точку Мо, то
прямую, проходящую через эту точку
в направлении вектора г7(to), называ-
называют предельным положением секущих
MqM при At —> 0 (рис. 92) или каса-
касательной к кривой Г в точке M(to).
Если начало вектора r^to) помес-
поместить в точку M(to), то он будет нап-
направлен по касательной, поэтому ее уравнение в векторной форме
имеет вид
/о = г(*о)+г'(*о)г, -оо < т < +оо	A7.12)
(р — текущий радиус-вектор касательной), а в координатной —
x = xo+x'(to)r, y = yo + y'(to)r, z = z0 + z'(to)r,
A7.13)
r(to+At)
Рис. 92
или
— 00 < Т < +00,
X -Хр _ У - УО _ Z - Zp
Хп	2/g	Zft
xo
zo
(здесь p=(x,y,z),
= (xf0,yf0,zf0)).

§17. Длина кривой	217
Точка кривой Г, в которой г'(to) = 0, называется особой, а точка,
в которой г'(to) ф 0, — неособой.
Из сказанного выше следует, что геометрический смысл произ-
производной r'(t) вектор-функции r(t) состоит в том, что в неособой точке
вектор г'(to) направлен по касательной к кривой в конце радиус-
вектора г (to). В этом случае вектор г1 (to) называется вектором,
касательным к кривой в соответствующей точке.
Если г'(t0) = ... = г^-^Оо) = 0, а г(п)(?0) ф 0, то по формуле
Тейлора	{п)( .
дг = т^-±М At71 + o(Atn).	A7.14)
n!
Вектор Ar/Atn направлен по секущей MqM, где, как и раньше,
Определяя и в этом случае касательную к кривой Г в точке Мо
как предельное положение секущих М0М при At ->• 0, т. е. как пря-
прямую, проходящую через точку Mq в направлении вектора г(п)(?о),
получим ее уравнение в виде
р(Т) = r(t0) + r^ (to)r, -oo < г < +оо.	A7.15)
Замечание 1. Если рассматривается плоская кривая r(t) =
= (x(t),y(t)), a ^ t ^ Ь, и r;(to) ф 0, то уравнение A7.14) касатель-
касательной прямой превращается в уравнение прямой
^ =	A7.16)
лежащей в плоскости кривой.
Если эта кривая задается непрерывной функцией у = /(ж),
а ^ х ^ 6, дифференцируемой в точке хо (за параметр на кривой взята
переменная ж), то уравнение касательной в точке (жо,2/о)? ^° =
в силу формулы A7.16) имеет вид	 =	, т. е.
1	/ (%о)
y = f'(xo)(x-xo)+yo.	A7.17)
Таким образом, получилось, конечно, то же самое уравнение ка-
касательной к графику функции, что и раньше (п. 10.3).
Сформулируем еще несколько определений, которые будут исполь-
использоваться в дальнейшем.
Непрерывно дифференцируемая кривая без особых точек называ-
называется гладкой кривой.
Кривая Г = {r(t); а ^ t ^ Ь} называется объединением кривых Г^,
если
Г; = {r(t); U-г ^ t ^ U], г = 1,2,..., п,
а = to < t\ < ... < tn-\ < tn = b.

218 Гл. 1. Дифференциальное исчисление функций одной переменной
Очевидно, что в этом случае начало кривой 1\ является и началом
кривой Г, конец кривой Гп — концом Г, а конец каждой кривой Г^ —
началом ГУц, г = 1, 2,..., п — 1.
Кривая, являющаяся объединением конечного числа гладких кри-
кривых, называется кусочно гладкой.
Замечание 2. Понятие кривой имеет в своей основе понятие
траектории движущейся материальной точки. Если конец радиус-
вектора г(?) описывает траекторию движения этой точки, а пара-
,	dr
метр t является временем движения, то производная — равна мгно-
dt
венной скорости в данный момент времени.
17.3. Определение длины кривой. Спрямляемые кривые.
Под длиной кривой понимается точная верхняя грань длин вписан-
вписанных в эту кривую ломаных. Сформули-
Сформулируем это определение более подробно.
Введем сначала понятие разбиения от-
отрезка — понятие, которое будет неодно-
неоднократно встречаться в дальнейшем.
Определение 2. Для отрезка [а, Ь]
всякая система т = {?гК=сГ точек U, i =
= 0,1, 2,..., гг, таких, что
а = to < t\ < ... < tin
называется его разбиением.
Пусть задана кривая
Г = {r(?) ; a <: t <:
Рис. 93
= b,
Ь]
и пусть т = {ti}^llT — некоторое разбиение отрезка [а, Ь]. Положим
A7.18)
т. е. ат — это длина ломаной с вершинами в точках Mi, являющихся
концами радиус-векторов г(^), г = 0,1,...,гг, иначе говоря, ломаной,
вписанной в кривую Г (рис. 93).
Определение 3. Верхняя грань длин всевозможных ломаных,
вписанных в данную кривую, называется ее длиной.
Таким образом, длина 5г кривой Г определяется формулой
def
= sup сгг,
A7.19)
где верхняя грань берется по всевозможным разбиениям т отрез-
отрезка [а, Ь]. Очевидно, 0 ^ 5г ^ +оо.
Если 5г < +оо, то кривая Г называется спрямляемой.

§17. Длина кривой	219
Теорема 1. Если кривая Г = {r(?); a ^ t ^ Ъ] непрерывно диф-
дифференцируема, то она спрямляема и ее длина 5г удовлетворяет не-
неравенству
\r(b)-r(a)\^Sr^c(b-a),	A7.20)
где
c = max|r'(?)|.	A7.21)
[а,Ъ]
|> Прежде всего заметим, что в силу непрерывности на отрезке [а, Ь]
производной г'(?) числовая функция \r'(t)\ также непрерывна на этом
отрезке, а следовательно, ограничена и принимает на нем наибольшее
значение. Поэтому существует число с = тах|г'(?)| < +оо.
[а,Ъ] ^
Возьмем какое-либо разбиение г = {?гК=сГ 0ТРезка [а,Ъ]. Тогда,
используя очевидное векторное тождество
r(ti)-r(tj_i)	A7.22)
1=1
и применяя теорему 1 из п. 16.2, получим
|Г(Ь)-Г(О)| =
i=l	i=l
<У]|г'(^)К*<-*<-1) ^ cV]tj-ti_i=c(b-a), A7.23)
где ti-i < & <ti,i = l,2,...,ir. Так как У^ |г(^) - r(?;_i)| = ат —
i^l	A7.18)
длина вписанной в кривую Г ломаной, соответствующей разбиению г,
то из неравенства A7.23) следует, что
г(Ь) - r(a)| ^ ат ^ сF - а).
Перейдя в этом неравенстве к верхней грани по всевозможным раз-
разбиениям т отрезка [а, 6], получим, в силу определения A7.19), нера-
неравенство A7.20)
|г(Ь) — r(a)| ^ 5г = supат ^ сF — а).
Поэтому 5г < +оо, т. е. кривая Г спрямляема. <|
Теорема 2. Если кривая Г = {r(t) = (x(t),y(t),z(t))] a ^ t ^ b}
непрерывно дифференцируема, то переменная длина дуги s = s(t), от-
отсчитываемая от начала кривой Г, является возрастающей непрерыв-
непрерывно дифференцируемой функцией параметра t и
ds_
dt
(dx\2 (dy\2 (dz\2

220 Гл. 1. Дифференциальное исчисление функций одной переменной
\> Как и выше, будем через M(t) обозначать конец радиус-векто-
радиус-вектора r(t). Пусть s(t) — длина дуги кривой Г от точки М(а) до точ-
точки M(t), t e[a,b], t + At e [a, b], и As = s(t + At) - s(t0). Очевидно,
что \As\ является длиной дуги с концами в точках M(t) и M(t + At).
Поэтому согласно теореме 1 для Ar = r(t + At) — r(t) имеет место
неравенство
|Ar| = |r(t + At) - r(t)| <С |As| ^ c|At|,	A7.25)
где с — наибольшее значение |r'(t)| на отрезке с концами в точках t
и t + At. Обозначим через ? = ?(At) точку этого отрезка, в которой
|г'@1=с	A7.26)
Поделим обе части равенства A7.25) на |At|, At ф 0:
Ar
At
As
At
W<«|-
A7.27)
Функция s = s(t) возрастает (с увеличением дуги ее длина возрас-
возрастает). Поэтому если At > 0, то As ^ 0, а если At < 0, то As ^ 0 и,
следовательно, всегда —- ^ 0, иначе говоря,
As
At
As
At'
Таким образом, неравенство A7.27) можно записать в виде
% ^ №1-	A7-28)
О один
Аг
At
Левая и правая части этого неравенства имеют при At
и тот же предел, равный |r'(t)|.
В самом деле, в силу определения производной
lira
r(t + At) - r(t)
At
lira
r(t + At) - r(t)
At
Из выполнения же условия ? G [t,t + At] при At > 0 или условия ? G
e [t + At, t] при At < 0 следует, что lim ? = t, а так как функция |r'(t)|
At—>0
непрерывна, то отсюда вытекает, что lim |r'(?)| = |r'(t)|. А тогда
At->0
As
из неравенства A7.28) получаем, что предел lira —— существует и
дг->-о At
также равен |r'(t)|. Это означает, что существует производная s'(t) и
что s'(t) = |r'(t)|.
Если r(t) = (x(t),y(t),z(t)), то r'(t) = (x'ifyy'ifyz'it)), а потому
s'(t) =
A7.29)
Замечание 1. Если длина а дуг кривой Г отсчитывается от ее
о	da	1
конца, то а = Ьг — s и, следовательно, —- = —1, поэтому
as
da _ da ds _ ds _ ,, ч,
~dt ~ ~ds~di ~ ~di ~ Г ^ "'

§17. Длина кривой	221
Замечание 2. Если непрерывно дифференцируемая кривая Г =
= {r(?); a ^ t ^ Ъ} не имеет особых точек (г'(?) ф 0 на отрезке [а, 6]),
т. е. Г — гладкая кривая, то в силу теоремы 2 переменная длина ду-
дуги s = s(t), отсчитываемая от начала М(а) кривой Г, является строго
возрастающей непрерывно дифференцируемой функцией с производ-
производной, положительной во всех точках отрезка [a, b]: s'(t) = \r'(t)\ > 0.
А так как s(a) = 0, s(b) = 5г, то обратная функция t = t(s) однозначна,
строго возрастает, непрерывно дифференцируема на отрезке [0, Sr] и
ds ds_	y	J
dt
Таким образом, для всякой гладкой кривой ее параметр является
строго возрастающей непрерывно дифференцируемой функцией пере-
переменной длины дуги и производная этой функции нигде не обращается
в нуль.
Следовательно, функция t = t(s) есть допустимое преобразование
параметра в смысле п. 17.1 и, следовательно, на гладкой кривой в
качестве параметра можно взять переменную длину ее дуг. Из ска-
сказанного вытекает также, что имеет смысл производная
т = §?•	A7-31)
as at ds
т-,	dr	dt
Вектор — только числовым множителем — отличается от каса-
ds	ds
тельного вектора — ф 0 и поэтому также направлен по касательной.
dt
Докажем, что вектор — является единичным вектором,
as
Теорема 3. Если на кривой Г = {r(s); 0 ^ s ^ S} парамет-
параметром является длина дуги и кривая непрерывно дяфференцируема, то
dr
ds
= 1.	A7.32)
|> Из формулы A7.24) при t = s имеем
ds ds
Поскольку на гладкой кривой можно взять за параметр длину ду-
дуги, то формула A7.32) имеет место для гладких кривых.
Разъясним геометрический смысл равенства A7.32).
Отрезок, соединяющий две точки кривой, называется хордой, стя-
стягивающей дугу кривой с концами в этих точках. Пусть кривая Г
гладкая и r(s), 0 ^ s ^ S, — ее векторное представление, в котором в
качестве параметра выбрана переменная длина дуги кривой s G [О, S].
Длина хорды, соединяющей концы радиус-векторов r(so) и
r(s0 + As), so G [0, 5], so + As G [0, 5], равна длине | Аг| вектора Ar =

222 Гл. 1. Дифференциальное исчисление функций одной переменной
= r(s0 + As) — r(so) (рис. 94). В силу равенства A7.32) для предела
M(to)	отношения ——- при
ZAS
As
lim
О имеем
= 1,
r(to+At)
|Ar| ,. Ar	dr
1—L = hm -— = —
|Zas| As—>0 As	as
A7.33)
т. е. отношение длины хорды к длине
стягиваемой ею дуги стремится к еди-
когда As —У 0.
Замечание 3. Координатами вся-
рис 94	кого единичного вектора являются его
направляющие косинусы, т. е. косинусы
углов, которые он образует с осями координат. Поэтому если обозна-
обозначить через а, C и j углы, которые образует с координатными осями
переменных ж, у и z единичный вектор —, то
as
dr
— = (cos a, cos/3, cos 7).
as
dr _ (dx dy dz
A7.34)
С другой стороны,
Сравнив формулы A7.34) и A7.35), получим
dx	dy	o dz	(ЛП ~п,
— = cosa, -^- = cosp, --=cos7.	A7.36)
ds	ds	ds
Замечание 4. Если плоская кривая является графиком функ-
функции у = /(ж), а ^ х ^ Ь, т. е. параметром кривой является перемен-
переменная ж, то ж; = 1, и поэтому
1
Замечание 5. Если кривая Г гладкая и в качестве параметра на
ней взята переменная длина дуги s, 0 ^ s ^ 5, то единичный касатель-
dr
ный вектор т = — является непрерывной функцией переменной s.
as
Если какая-то функция является непрерывной функцией парамет-
параметра кривой, то будем говорить, что она непрерывна вдоль кривой. Те-
Теперь можно сказать, что на ориентированной гладкой кривой имеется
непрерывный вдоль нее единичный касательный вектор. При измене-
изменении ориентации кривой, т. е. при переходе к параметру s* = S - s, ка-
касательный вектор меняет свое направление. Действительно, посколь-
ds _ .	х _ dr _ dr ds _ dr _
КУ ds^~~ ' T° Г " ds^ ~ ds"^ ~~Ts~~T'
Таким образом, ориентации гладкой кривой однозначным образом
соответствует выбор непрерывного единичного касательного вектора
вдоль кривой т или г*.

§18. Кривизна кривой	223
Пусть Г — плоская кривая и на плоскости фиксирован базис i,j.
В этом случае каждому касательному вектору гит* соответствует
единственный перпендикулярный к нему единичный вектор и и со-
соответственно v* (нормаль к кривой) такой, что пары векторов t,is
и т*,г/* ориентированы так же как пара i,j векторов базиса (т. е.
так, что определители преобразования этих пар положительны). Оче-
Очевидно, что is* = -г/, и нормали v и и* также являются непрерывны-
непрерывными функциями вдоль кривой Г. Из сказанного ясно, что при фик-
фиксированной системе координат ориентация плоской кривой может
быть задана непрерывной вдоль этой кривой единичной нормалью.
§ 18. Кривизна кривой
18.1. Определение кривизны и радиуса кривизны кривой.
Важной характеристикой кривой является ее кривизна. Определим
это понятие.
Определение 1. Абсолютная величина (длина) скорости вра-
вращения единичного касательного вектора к кривой в данной ее точке
относительно переменной длины дуги называется кривизной кривой в
этой точке.
Если Г = {r(?); a ^ t ^ Ъ] — гладкая кривая, as = s(t) — пере-
переменная длина ее дуги, отсчитываемая от начала кривой Г, то вектор
является единичным касательным вектором (теорема 3 в п. 17.3) к
кривой Г. Поэтому кривизна кривой в данной ее точке, обозначаемая
обычно через &, согласно данному определению задается формулой
dr
к = ——	A8 2)
ds
Отсюда в силу соотношения A8.1) следует, что
к = Ш-	A8-3)
Из этой формулы видно, что определение A8.2) имеет смысл тогда,
когда функция r(s) является по крайней мере дважды дифференци-
дифференцируемой.
Величина, обратная кривизне, называется радиусом кривизны кри-
кривой в данной точке и обозначается через R. Таким образом,
R=\.	A8.4)
Пример. Покажем, что для окружности ее радиус совпадает с
радиусом кривизны, и поэтому ее кривизна одна и та же во всех
точках и равна обратной величине радиуса.

224 Гл. 1. Дифференциальное исчисление функций одной переменной
Рассмотрим окружность радиуса R с центром в точке О. Пусть
А — фиксированная точка окружности. Угол а, образованный ра-
радиусом-вектором г некоторой точки
окружности (обозначим ее В) с осью
ОА и угол, образованный единичным
касательным к окружности в точке В
вектором т с касательным вектором в
точке А, равны как углы со взаимно
перпендикулярными сторонами (рис. 95).
Если s — длина дуги окружности, от-
отсчитываемая от точки А в направлении
s
возрастания угла а, то а = — и, следова-
следовательно, ,
Рис. 95
Для единичной окружности длина ее
дуги совпадает со значением соответствующего ей угла а, и так как
\т\ = 1, то
= 1.	A8.6)
dr_
da
A7.32)
Поэтому для окружности радиуса R имеем
к =
dr_
ds
dr\
da\
Ida
Ids
A8.5) R'
A8.6)
A8.7)
18.2. Формула для кривизны. Пусть
T = {r(t); a^t^b}	A8.8)
— дважды дифференцируемая кривая без особых точек. Тогда су-
существует дважды непрерывно дифференцируемое преобразование
параметра t к переменной длине s дуги кривой Г: t = t(s), 0 ^ s ^ 5г
(см. замечание 2 в п. 17.3), причем
вектор г = — является единичным касательным к кривой Г векто-
ds
ром и имеет производную
dr
Is
d r
A8.9)
а следовательно, для рассматриваемой кривой в каждой ее точке опре-
определена кривизна к (см. A8.2)) и для нее справедлива формула A8.3).
Теорема 1. Если Г = {r(t); a ^ t ^ Ь} — дважды дифференцируе-
дифференцируемая кривая без особых точек, то в каждой точке кривой существует
кривизна к и для нее справедлива формула
к =
A8.10)

§18. Кривизна кривой
225
Штрихом здесь и в дальнейшем обозначаются производные по па-
параметру ?, производные же по длине дуги будут обозначаться че-
|> Касательный вектор т = — единичный, т. е. имеет постоянную
ds
длину, равную единице. Поэтому его производная — ему перпен-
ds
дикулярна (см. лемму из п. 16.2). Длина векторного произведения
т х —— равна произведению длин сомножителей \т = 1 и
as
dr_
ds
= k
A8.2)
на значение синуса угла между ними, т. е. на единицу, так как ука-
указанный угол прямой. Поэтому
dr
Т X
ds
= k.
По правилу дифференцирования сложной функции имеем
dr , dt rf
т = — = г— = —
ds	ds s'
^L - ^L - —( — \ - f — \— -
ds ds2 ds\s'J \s') ds
A8.11)
A8.12)
A8.13)
Следовательно,
dr
k =
A8.11)
r x
ds
A8.12)
A8.13)
I, A8.14)
ибо г' х г' = 0. <]
Из формулы A8.10) можно получить формулу, выражающую кри-
кривизну через производные координатных функций: если i, j и к —
единичные векторы координатных осей переменных x,y,z и
r(?) = x(t) i + y(t) j + z(t) k,	A8.15)
TO
r' = x1 i + y' j + z1 k, r" = x" i + y" j + z" k,	A8.16)
Г X Г =
У"
A8.17)
A8.18)
откуда
|г; х r"| = y/(y'z" - y"z'J + (z'x" - z"x'J + (x'y" - x"y'J. A8.19)
Подставив A8.17) и A8.19) в формулу A8.10), получим искомое
выражение для кривизны.
18.3. Главная нормаль. Соприкасающаяся плоскость. Для
того чтобы изучить расположение кривой относительно ее касатель-
касательной в окрестности точки касания, полезно ввести понятие главной
нормали.
15 Л.Д.Кудрявцев, т.1

226 Гл. 1. Дифференциальное исчисление функций одной переменной
Определение 2. Если в некоторой точке кривой ее кривизна не
равна нулю (к ф 0), т. е. существует производная —— ф 0, то единич-
ds
ный вектор в направлении вектора — называется вектором главной
as
нормали (короче, главной нормалью) и обозначается через v.
dr
Так как
ds
= k (см. A8.2)), то
*L = kv, |i/| = 1.	A8.20)
as
Эта формула называется формулой Френе*).
То, что вектор и называется нормалью, оправдывается тем
обстоятельством, что вектор и как вектор, параллельный производ-
„ dr
ной —— единичного вектора т, перпендикулярен касательному векто-
ds
ру т (см. лемму в п. 16.2).
Отметим два свойства главной нормали.
1°. Направление главной нормали не зависит от выбора ориента-
ориентации кривой.
В самом деле, если а — переменная длина дуги кривой Г, от-
отсчитываемая в противоположном, чем длина дуги s, направлении, и,
с	da
следовательно, если а = Ьг — s, то, заметив, что — = —1, получим
ds
dr dr da	dr
ds da ds	da'
а поэтому
d2r _ d /dr\ _ d / _ dr\ da _ d2r
ds2 dsxdsJ da \ da J ds da2
Таким образом, вектор —— = —— не зависит от выбора начала
ds ds1
2	отсчета дуг на кривой, т. е. не зависит
- v + o(As ) от ее ориентации. Главная нормаль
гу = 1 —, кфО,	A8.21)
имеет то же направление, что и век-
dr
тор ——, поэтому она также не зависит
ds
от ориентации кривой.
2°. Главная нормаль с точностью
с'	до бесконечно малых более высокого по-
порядка, чем As2, As —> 0, направлена в сторону отклонения кривой от
касательной (рис. 96).
. Френе A816-1900) — французский математик.

§18. Кривизна кривой	227
Разложим векторную функцию г = r(s) в окрестности точки
по формуле Тейлора:
ds	Zi cLs
A8.22)
~	dr	d2r	,
Отсюда, вспомнив, что — = т, -—¦ = kv, получим
as A8.1) dsz A8.21)
Ar = Asr + ^kAs2*/ + o(As2), As -+ 0.	A8.23)
Поскольку - k As2 > 0, то разность Ar — Asr, т. е. отклонение
z
кривой от касательной, с точностью до o(As2), As —>¦ 0, направлена
по вектору г/:
Аг - Asr =\k As2v + o(As2), As ->> 0.
Определение З. Всякая прямая, проходящая через точку кри-
кривой и перепендикулярная касательной в этой точке, называется нор-
нормалью к кривой в данной точке. Нормаль к кривой, параллельная век-
вектору г/, называется главной нормалью.
Таким образом, главной нормалью называют как вектор г/, так
и параллельную ему прямую, проходящую через соответствующую
точку кривой.
Определение 4. Плоскость, проходящая через касательную и
главную нормаль в данной точке кривой, называется соприкасающей-
соприкасающейся плоскостью в этой точке.
Эта плоскость обладает тем свойством, что дважды непрерывно
дифференцируемая кривая в окрестности каждой своей точки, в ко-
которой кривизна не равна нулю, лежит "почти" в соприкасающейся
плоскости. Это означает, что конец радиус-вектора r(so + As) отсто-
отстоит от конца радиус-вектора r(so) + Asr + - k As2v, лежащего, оче-
очевидно, на соприкасающейся плоскости, на величину, бесконечно ма-
малую по сравнению с As2.
Это сразу следует из равенства A8.22):
фо + As) - (r(s0) + Asr + | fe As2i/) = o(As2).
В силу определения соприкасающаяся плоскость однозначно опре-
определена для точек, в которых кривизна к ф 0. Напишем уравнение этой
плоскости для кривой, заданной произвольным дважды дифференци-
дифференцируемым векторным представлением г = г(?).
Как всегда, производные по переменной t будем обозначать штри-
штрихом, а производные по длине дуги s — символом —. Дифференцируя
as
15*

228 Гл. 1. Дифференциальное исчисление функций одной переменной
векторную функцию г = г(?) как композицию функций г = r(s) и
s = s(t), получим
г' = — s' = s'r,
A8.24)
Таким образом, векторы г' и г" являются линейными комбина-
комбинациями векторов т и г/ и, следовательно, также параллельны соприка-
соприкасающейся плоскости. В силу же условия к ф 0 выполняется неравен-
неравенство |г' х г"| ф 0 (см. A8.10)), поэтому векторы г' и г" не коллинеар-
ны, а тем самым однозначно определяют параллельную им плоскость,
проходящую через заданную точку.
Обозначим тезерь через го, г0 и г0' радиус-
векторы г, г' и г", соответствующие некото-
некоторой фиксированной точке данной кривой, а
через р обозначим текущий радиус-вектор со-
соприкасающейся плоскости в этой точке. Тог-
Тогда смешанное произведение векторов р — го,
Го и Го должно быть равно нулю, так как все
они параллельны соприкасающейся плоскости
(рис. 97):
Рис- 97	(р-го,г[),г[)/) = 0.	A8.25)
Это и есть уравнение соприкасающейся плоскости в векторном ви-
виде. Если р= (x,y,z), r0 = (xo,yo,zo), r0 = (жо,2/о,2:о), г0; = (х'^уЦ^Ц),
то уравнение A8.25) можно переписать в виде
х - х0 у -уо z- z{
У'о
УН
у"
= 0.
18.4. Центр кривизны. Эволюта.
Определение 5. Точка пространства, находящаяся на расстоя-
расстоянии, равном радиусу кривизны от точки кривой в направлении век-
вектора главной нормали, называется центром кривизны кривой в рас-
рассматриваемой точке этой кривой.
Пусть R — радиус кривизны кривой Г в
точке Mq. Если р — радиус-вектор центра
кривизны М, а г, как обычно, есть радиус-
вектор данной точки Mq кривой, то (рис. 98)
р = г + itV, или, что то же самое (см. A8.4)
и A8.21)),	л *
Найдем выражение вектора р через производные векторной функ-
функции г по произвольному параметру t.

§18. Кривизна кривой	229
d2r
Подставив в формулу A8.26) выражение для —— через производ-
dsl
ные по t (см. A8.13)) и выражение для кривизны
i ' v "
A8.10) \Г'\6
|г'|6 sV-sV
получим р = г + —^—Ц-	^	, а так как Ir'l = s' (предпола-
|г; X Г/;|	s'3	A7.24)
гается, что при возрастании параметра t длина дуги s = s(t) также
возрастает), то	/3
где sf = |г;| = ух'2 + у'2 + z'2, а поэтому
8„ = хх +уу +zz _	A8_28)
Формулу A8.27) можно рассматривать как векторное представле-
представление некоторой кривой, точками носителя которой являются центры
кривизны данной кривой. Эта кривая называется эволютой данной
кривой.
18.5. Кривизна и эволюта плоской кривой. Пусть кривая
Г = {r(?); a ^ t ^ Ъ] лежит в некоторой плоскости; тогда и все произ-
производные векторной функции г(?), если их начало поместить на эту
плоскость, будут также в ней лежать. В самом деле, приращение
Ar = r(? + At) — r(t) лежит в этой плоскости, поэтому лежит в ней
Ar	Ar ,
и отношение -—, а следовательно, и его предел lim -— = г . Приме-
At'	д	'	р д At^o At	p
нив те же рассуждения к г;, получим, что и г" лежит в указанной
плоскости и т. д. Отсюда следует, что если кривая лежит в некоторой
плоскости, то касательная к кривой (а если ее кривизна к ф 0, то и
главная нормаль) лежит в той же плоскости. Поэтому эта плоскость
является соприкасающейся плоскостью для рассматриваемой кривой.
Запишем некоторые из формул, полученных в п. 18.4, более под-
подробно для случая, когда кривая Г = {r(?); a ^ t ^ Ъ] лежит в плоскости
переменных х и у. r(?) = (x(t),y(t)). В этом случае
г' = (х1, у'), г" = (х", у"), |г'| = (х'2 + у2/
г"=@,0,
у"
х'у"-х"у'\
Поэтому из формул A8.4) и A8.10) получаем следующую формулу
для кривизны:
\*'v"-*"v'
R

230 Гл. 1. Дифференциальное исчисление функций одной переменной
Обозначим через (?, rj) центр кривизны кривой Г. Из формул A8.27)
и A8.28) следует, что
„,2I/2
Аналогично,
A8.28)
Х'у" - Х"у'
х' + у'
В случае когда кривая задается явно, т. е. функцией
y = f(x), a^x^b
A8.31)
A8.32)
(в этом случае х = ?, х' = 1, х" = 0) s' = A + 2/'2I/2, формулы A8.29),
A8.30), A8.31) принимают вид
j-,	A8.33)
/(х)
€ = x-±-^f-y', v = y + ^-.	A8.34)
На примере кривой, имеющей явное задание, поясним, что кривиз-
кривизна кривой является угловой скоростью
вращения касательной к этой кривой от-
относительно длины ее дуги.
Обозначим через а угол, образован-
образованный касательной к кривой A8.7) с осью х
(рис. 99), и будем его рассматривать как
функцию длины дуги s этой кривой, a s,
в свою очередь, — как функцию перемен-
переменной х.
Дифференцируя no x равенство у' =
О
= tga, получим
Рис. 99
у" =
+ tg а) — s , A8.35)
a	ds
где (см. замечание 4 в п. 17.3) s' = A + у' I//2. Поэтому у" = A +
-\-у> K/2 и^ таким образом,
da
\У"
= *,
A8.36)
" A+2/2K/2
т. е. действительно кривизна кривой к равна абсолютной величине
угловой скорости — вращения касательной,
as

§18. Кривизна кривой
231
Примеры. 1. Найдем кривизну и эволюту параболы у2 = 2рх.
Дважды дифференцируя это уравнение по ж, получим уу' = р,
у'2 + УУ" = 0 и, следовательно,
у' = ?, у" = -? = -?.
У У' У	У	У3
Подставив эти выражения в формулу A8.33), найдем кривизну
к =
Р
Р
3/2
A8.37)
и, подставив их в формулы A8.34), — уравнение эволюты
v у
-Р=х+У +р
, A8.38)
A8.39)
Таким образом, в получившемся уравнении эволюты параболы
роль параметра играет переменная у; исключив ее из этих уравне-
уравнений, получим	о
Эта кривая, как мы знаем (п. 3.7), называется полукубической па-
параболой (пис. 10СП.
Рис. 100	Рис. 101
2. Найдем радиус кривизны R и эволюту эллипса
t, у = bsint, a^b>0.
Заметив, что х' = —asint, у' = Ъcost, х" = —acost, у" = — frsint,
в силу формулы A8.29) получим
1 _ (a2 sin21 + b2 cos21K/2 _ (a2 sin21 + b2 cos21K/2
k	ab sin21-\-ab cos21	ab

232 Гл. 1. Дифференциальное исчисление функций одной переменной
а из формул A8.30), A8.31) получим уравнение эволюты
2 • 2 i . 7 2 2/	2 72
, , a sin t + b cos t a —b 3 ,
xi = a cost - b cos ?	=	cos t,
ab	a
, . ,	. , a2 sin21 + b2 cos21 62 - a2 . 3 ,
77 = о sin t — a sin ?	;	= —;— sin t.
ab	b
Исключив из этих уравнений параметр t (для чего достаточно воз-
возвести их в степень 2/3 и сложить их), найдем уравнение эволюты в
неявном виде
/
Полученная кривая называется астроидой (рис. 101).

ГЛАВА 2
ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ
ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ
§ 19. Определение и свойства неопределенного интеграла
19.1. Первообразная и неопределенный интеграл. В этом
параграфе рассматривается задача отыскания функции, для которой
заданная функция является производной.
Пусть А — конечный или бесконечный промежуток числовой оси,
т. е. интервал, полуинтервал или отрезок*), и на А заданы функ-
функции / и F.
Определение 1. Функция F называется первообразной функ-
функцией (или, короче, первообразной) функции / на промежутке А,
если F дифференцируема на А и в каждой точке этого промежутка
производная функции F равна значению функции /:
F'(x)=f(x), же А.	A9.1)
При этом если некоторый конец промежутка А принадлежит это-
этому промежутку, то под производной в этом конце, естественно, по-
понимается соответствующая односторонняя производная. Поскольку
функция, имеющая в данной точке производную, непрерывна в этой
точке (односторонне непрерывна, если речь идет об односторонней
производной), то первообразная F функции / непрерывна на проме-
промежутке А.
Пример. Функция F(x) = х3/3 является первообразной функции
f(x) = х2 на всей числовой оси.
Иногда вместо слов "первообразная данной функции" говорят
"первообразная для данной функции".
Первообразная любой функции непрерывна, так как она имеет
производную. Функция же, у которой существует первообразная, не
обязательно непрерывна, например, у разрывной в нуле функции
г/ ч I 2xsin	cos- при х Ф О,
fix) = <	х	х
у	0	при х = О
*) Если рассматриваемый промежуток является отрезком, то само собой ра-
разумеется, что он может быть только конечным.

234	Гл. 2. Интегральное исчисление функций одной переменной
на всей числовой оси существует первообразная
Pf ч I х2 sin - при х Ф О,
f(x) = <	х
у 0	при х = 0.
Лемма 1. Для того чтобы две дифференцируемые на некотором
промежутке функции были первообразными одной и той же функции,
необходимо и достаточно, чтобы они на этом промежутке отлича-
отличались на постоянную.
Иначе говоря, функции F(x) и Ф(х) являются на промежутке А
первообразными одной и той же функции тогда и только тогда, когда
Ф(х) = F(x) + С, х е А, С — константа.	A9.2)
|> Если F — первообразная функции /, т. е. F' = /, то функция
F + С является первообразной той же функции /, ибо (F + С)' =
= F' = f.
Если F и Ф — первообразные для одной и той же функции /,
т. е. F' = Ф' = /, то (F - Ф)' = F' - Ф' = 0 и, следовательно, согласно
следствию 1 теоремы Лагранжа (п. 12.2, теорема 3) разность F — Ф =
= С является постоянной на промежутке А. <|
Определение 2. Пусть функция / задана на некотором проме-
промежутке А. Совокупность всех ее первообразных на этом промежут-
промежутке называется неопределенным интегралом от функции / и обозна-
чается	Jf(x)dx.	A9.3)
Если множество первообразных некоторой функции не пусто, то
говорят, что у нее существует неопределенный интеграл. Таким
образом, существование интеграла f(x)dx (на промежутке А) рав-
равносильно существованию у функции / первообразной на рассматри-
рассматриваемом промежутке.
Если F — какая-либо первообразная функции / на рассматривае-
рассматриваемом промежутке, то пишут
Jf(x)dx = F(x) + C,	A9.4)
хотя правильнее было бы писать f(x)dx = {f(x) + С} (здесь и в
дальнейшем С — произвольная постоянная).
Иногда под f(x) dx понимается не совокупность всех первообраз-
первообразных функции /, а произвольный элемент этого множества, т. е. про-
произвольная первообразная рассматриваемой функции. С разночтением
одного и того же обозначения мы встречались и раньше, например,
символом /(ж) обозначается как сама функция, так и ее значение в
точке х. Из контекста обычно всегда бывает ясно, в каком смысле в
данном месте употреблено то или иное обозначение. Следует, однако,
иметь в виду, что всякое равенство, в обеих частях которого стоят
неопределенные интегралы, есть равенство между множествами.

§19. Определение и свойства неопределенного интеграла	235
Под знаком интеграла пишут для удобства не саму функцию /,
а ее произведение на дифференциал dx. Это делается, например, для
того, чтобы указать, по какой переменной ищут первообразную:
Г 2 7 x?>z , ri f 2 7 X2Z2 , ri
I x z dx =	ho, / x z dz =	h С
Здесь в обоих случаях подынтегральная функция равна x2z, но ее не-
неопределенные интегралы в первом и втором случаях различны, так
как в первом случае она рассматривается как функция от перемен-
переменной ж, а во втором — как функция от z.
Другие принципиально более важные удобства, вытекающие из
использования записи f(x)dx, будут указаны в дальнейшем (см.
замену переменной в интеграле в п. 19.4).
Если F — какая-либо первообразная функции / на промежутке
А, то согласно формуле A9.4) под знаком интеграла стоит дифферен-
дифференциал функции F:
dF(x) = F'(x) dx = f(x) dx.	A9.5)
Будем считать по определению, что этот дифференциал под знаком
интеграла можно записывать в любом из указанных видов, т. е. со-
согласно этому соглашению
ff(x) dx = [f'(x) dx = fdF(x).	A9.6)
19.2. Основные свойства интеграла. Все рассматриваемые в
этом пункте функции определены на некотором фиксированном про-
промежутке А. Перечислим свойства неопределенного интеграла, выте-
вытекающие непосредственно из его определения.
1°. Если функция F дифференцируема на промежутке А, то
dF(x) = F(x) + С, или, что то же самое,
[F'(x)dx = F(x) + C.
Это сразу следует из определения неопределенного интеграла как
совокупности всех дифференцируемых функций, дифференциал ко-
которых стоит под знаком интеграла.
2°. Пусть функция f имеет первообразную на промежутке А; тог-
тогда для всех х е А имеет место равенство
dff(x)dx = f(x)dx.	A9.7)
Отметим, что в этом равенстве под интегралом f(x) dx понима-
понимается произвольная первообразная F функции /. Поэтому A9.7) можно
записать в виде равенства dF(x) = f(x) dx, справедливость которого
следует из того, что F — первообразная / (т. е. из A9.1)).

236	Гл. 2. Интегральное исчисление функций одной переменной
3°. Если функции Д и /2 имеют первообразные на промежутке А,
то и функция Д + /2 имеет первообразную на этом промежутке,
причем
f{fi{x) + /2(ж)) dx = jh{x) dx + jf2{x) dx.	A9.8)
Это равенство выражает собой совпадение двух множеств функ-
функций. В правой его части стоит арифметическая сумма множеств (ее
определение см. в п. 4.3). Оно означает, что сумма каких-либо перво-
первообразных для функций Д и /2 является первообразной для функции
Д + /2 и что, наоборот, всякая первообразная для функции Д + /2
является суммой некоторых первообразных для функций Д и Д.
|> Пусть F\ и i<2 — первообразные соответственно функций Д и Д,
т. е. в каждой точке х Е А выполняются равенства F[{x) = Д(ж),
i^2(ж) = Д (ж). Тогда неопределенные интегралы fi(x)dxn //2(ж) dx
состоят соответственно из функций вида i*i(x)+Ci и ^(яО + Сгэ
где Ci и G2 — произвольные постоянные. Положим F(x) = Fi(x) +
+ ^(ж), тогда функция F будет первообразной для функции Д + Д,
ибо F;(x) =F{(x)+Fl(x) =Д(х)+/2(х), х G А.
Следовательно, интеграл / (Д (ж) +/2(ж)) б?ж состоит из функций
F(x) + C = Fi(x) + i^(^) + С, в то время как сумма интегралов
fi(x)dx+ U2(x)dx — из функций вида i*\(ж) + Ci + F2(ж) + С2.
Поскольку С, Ci, C2 — произвольные постоянные, то оба эти мно-
множества, т. е. левая и правая части равенства A9.8), совпадают. <|
4°. Если функция f имеет первообразную на промежутке Auk —
число, то функция kf также имеет на А первообразную и при к ф О
справедливо равенство
fkf(x) dx = kff(x) dx.	A9.9)
Это равенство так же, как равенство A9.8), является равенством
множеств.
|> Пусть F — первообразная функция /, т. е. F'{x) = /(ж), х G А.
Тогда функция kF является первообразной функции kf на проме-
промежутке А при любом к G /?, ибо (kF(x))' = kF'(x) = kf(x), x G A.
Поэтому интеграл / kf(x) dx состоит из всевозможных функций вида
kF + С\ а интеграл к f(x)dx — из всевозможных функций
k(F + С) = kF + кС. В силу произвольности постоянной С и условия
& ^ 0 обе совокупности функций совпадают. Это и означает справед-
справедливость равенства A9.9). <1
Следствие (линейность интеграла). Если функции Д и Д иже-
ют первообразные на промежутке A, a Ai G R и Л2 G /? — такие числа,

§19. Определение и свойства неопределенного интеграла	237
что \\ + XI > О, то функция Ai/i + Л2/2 также имеет первообразную
на А, причем
f(\ifi(x)+\2f2(x))dx = \1ff1(x)dx + \2ff2(x)dx.
Это непосредственно следует из свойств 3° и 4°.
Вопрос о существовании первообразной будет изучаться несколь-
несколько позже (п. 25.2), а теперь рассмотрим простейшие методы вычис-
вычисления интегралов для элементарных функций.
19.3. Табличные интегралы. Из всякой формулы для произ-
производной некоторой функции
F'(x) = /(ж)	A9.10)
следует формула для неопределенного интеграла
ff(x)dx = F(x) + C.	A9.11)
Иначе говоря, чтобы проверить формулу A9.11) для конкретных
функций, надо проверить для них справедливость равенства A9.10)
во всех точках рассматриваемого промежутка. Таким способом мож-
можно доказать справедливость следующих пятнадцати формул, назы-
называемых табличными интегралами.
. xadx = ^—— + С, аф-\.
J	а + 1
2. Г— =1п|ж|+С.
J х
ах dx =	\- С, а > 0, а ф 1, в частности, / ех dx = ех + С.
та	J
4.	/ sin xdx — — cos x + С.
5.	/ cos xdx — sin x + С.
6.
7.	fJ^ = -c
J sin x
8.	shxdx = chx + C.
9.	chxdx = shx + C.
10.
11.
12. / —	 = - arctg - + С = -- arcctg - + C.
' x2 + a2 a	a	a	a

238	Гл. 2. Интегральное исчисление функций одной переменной
2а
х — а
х + а
с.
X	X
= arcsin - + С = - arccos - + С, х\ < a.
a	a
,	 = In \x + лДс2 =Ь a21 + С (если под корнем стоит
х2 ± а2
то |х| > |а|).
Само собой разумеется, что если знаменатель подынтегральной
функции обращается в нуль в некоторой точке, то написанные фор-
формулы будут справедливы лишь для тех промежутков, в которых не
происходит обращение в нуль указанного знаменателя.
19.4. Формула замены переменной. Познакомимся в заключе-
заключение этого параграфа с двумя свойствами неопределенного интеграла,
весьма полезными, в частности, для вычисления интегралов.
Пусть функции /(ж) и ip(t) заданы соответственно на промежут-
промежутках Ах и At, причем функция ip отображает промежуток At на про-
промежуток Ах, т. е.	/ л ч л	/
ip(At) = Ax,	A9.12)
и, следовательно, имеет смысл сложная функция f(ip(t)), t G At.
Пусть, кроме того, функция ip(t) дифференцируема на промежут-
промежутке At и ее производная не меняет знака на А^, т. е. для всех t e At
имеет место либо неравенство ip'(t) > 0, либо ip'(t) < 0, а следовательно
(см. п. 15.1), функция cp{t) строго монотонна на промежутке А^. Тогда
(см. п. 7.3) у функции ip(t) существует обратная однозначная функ-
функция (р~1(х), определенная на промежутке Ах.
В формулируемой ниже теореме будем предполагать, что все пе-
перечисленные условия выполняются.
Теорема 1. Существование на промежутке Ах интеграла
ff(x)dx	A9.13)
и существование на промежутке At интеграла
t)dt	A9.14)
равносильны, и имеет место формула
A9.15)
ние
f
f
Эта формула называется формулой замены переменной в неопреде-
неопределенном интеграле: переменная х заменяется переменной t по форму-
формуле х = (f(t).
Если в формуле A9.15) в обеих частях равенства перейти к пере-
переменной t по формуле х = ip(t), то, меняя местами левую и правую
части равенства, получим
[f{<p{t))<p'(t)dt= ff(x)dx	A9.16)
J	J	X = (p(t)

§19. Определение и свойства неопределенного интеграла	239
Иначе говоря, сделав сначала подстановку ip(t) = ж, а затем взяв
интеграл или сначала взяв интеграл, а потом сделав указанную под-
подстановку, получим один и тот же результат.
Формула A9.16) обычно называется формулой интегрирования под-
подстановкой. Эту формулу можно записать также в виде
/С
fUp(t)) diptt) = / fix) dx
J	x=<p(t)
Ее применение к вычислению интегралов состоит в том, что вмес-
вместо интеграла f(<p(t))dip(t) вычисляется интеграл f(x)dx, а затем
полагается ж = ip(t). Формула замены переменной A9.15) и соответ-
соответственно, формула интегрирования подстановкой A9.16) применяют-
применяются тогда, когда интегралы, стоящие в их правых частях, в каком-то
смысле проще интегралов, стоящих в их левых частях. Ниже, после
доказательства теоремы, это будет пояснено на примерах.
> Докажем сначала, что существование интегралов A9.13) и A9.14)
равносильно, т. е. что равносильно существование первообразных у
функции /(ж) на промежутке Ах и функции f(ip(t))(p'(t) на проме-
промежутке At.
Пусть у функции /(ж) на промежутке Ах существует первообраз-
первообразная F(x), т. е.
dF{x) _ ,, ч	д	AQ 17^
dx
В силу условия A9.12) имеет смысл сложная функция F(ip(t)). По-
Покажем, что она является на промежутке At первообразной функции
f(ip(t)) т • Действительно, по правилу дифференцирования слож-
dt
ных функций имеем
x=cp(t) dt A9.17)
Наоборот, пусть теперь функция f(ip(t))	имеет первообраз-
первообразную. Обозначим ее Ф(?):
—L_i — f(ip(ty) ——.	A9.19)
В силу условий, которым удовлетворяет функция (р, обратная к ней
функция if~x дифференцируема во всех точках промежутка Аж, и
имеет место формула (см. п. 10.6)
й-^ = ш ' хеА~ A9-20)
dt + — т-^(тЛ

240
Гл. 2. Интегральное исчисление функций одной переменной
Покажем, что функция Ф((р 1(х)) является на промежутке Ах пер-
первообразной для функции /(ж). В самом деле,
dx
dt t=<fi-1(x) dx A9.19)
A9=19) №»
dt
t=tp-1(x) dx A9.20)
= fix).
Итак, интегралы A9.13) и A9.14) одновременно существуют или
нет. При этом
ff(x)dx = F(x)+C,
J	A9.17)
ff(<p(tW(t)dt = F(<p(t))+C,
а так как
TO
F(<p(t))
ff(x)dx = F(x)+C = F(<p(t))
J	A9.21)	A9.23)
= F(x),
t=(P~1(x)
A9.21)
A9.22)
A9.23)
= ff(<p(t))<p'(t)dt
Примеры. 1°. Вычислим с помощью формулы замены перемен-
переменной A9.13) интеграл
/ л/l - х2 dx, -
1 ^ х ^ 1.
Сделав замену переменной х = sint,	^ t ^ —, получим
j^l-x2dx = jVl-sin2tcostdt = I cos2 tdt = jl + ™s2t dt =
= I f dt+ I [cos2tdt = l- + ^s
2J	2 J	2 4:
= l- + i
2 2
+ С =
= - (arcsinx + xyl — x2) + C.
Аналогично вычисляется и интеграл / у/1 + х2 dx, только здесь
целесообразно положить х = sht:
= J
= Jch2tdt =
В полученном выражении надо вернуться к переменной х. Име-
Имеем sht = ж, cht = л/1 + sh2t = л/1 + ж2- Переменную же ? найдем из

§19. Определение и свойства неопределенного интеграла	241
е* - е~1
уравнения х = sht, т. е. из уравнения х = 	. Из него следует,
что у = е1 удовлетворяет квадратному уравнению у2 — 2ху — 1 = 0 и,
следовательно, е1 — х + л/1 - х2 (другой корень указанного квадрат-
квадратного уравнения отрицателен, а е* принимает только положительные
значения), откуда t = In (x + л/1 + х2).
В результате окончательно получим
= | (In (ж
2°. Вычисление интегралов с помощью формулы подстанов-
подстановки A9.16) целесообразно, например, применять к интегралам вида
: , <ix. Применив в них подстановку ip(x) = и, получим
i
(ff(x) , fd<p(x) fdu
dx\ / = / —
J	J
[фух) ,	fd<p(x) fdu	n | , л^|	i i / м , io
/ / ч dx—\ ; / = / —	= (In ix + C) \ _ , >. = In Ыж) + G.
J <p(x)	J <p(x)	J U u=cp(x)	\u-<p{x)
К такому типу интегралов относится интеграл
/7 Г sin х dx Г d cos ж	, ,	^
tgxdx = /	 = - /	 = - In cos x + С.
J COS Ж J COS Ж
Иногда, прежде чем применить метод интегрирования подстанов-
подстановкой, приходится проделать некоторые преобразования подынтеграль-
подынтегральной функции:
X
dx _ Г	dx	_ Г 1 dx _ Г g 2 _ i
^~bsin|cos| "У^|2со82| " '^f~
19.5. Формула интегрирования по частям.
Теорема 2. Если функции и(х) и v(x) дифференцируемы на не-
некотором промежутке и на этом промежутке существует интеграл
vdu, то на нем существует и интеграл udv, причем
udv = uv — vdu.	A9.24)
Эта формула называется формулой интегрирования по частям не-
неопределенного интеграла.
|> Пусть функции и и v дифференцируемы на промежутке А; тогда
по правилу дифференцирования произведения d(uv) = vdu + udv, и
П0Т°МУ	udv = d(uv) - vdu.	A9.25)
Интеграл от каждого слагаемого правой части существует: интег-
интеграл vdu существует по условию, а по свойству 1° из п. 19.2 имеем
fd(uv) =uv + C.	A9.26)
16 Л.Д.Кудрявцев, т.1

242	Гл. 2. Интегральное исчисление функций одной переменной
Поэтому, согласно свойству 3° из п. 19.2, существует и интеграл
udv, причем
udv = d(uv) — v du = uv — v du,
J	A9.25) J	J	A9.26)	J
где постоянная интегрирования С (см. A9.26)) отнесена к интегра-
интегралу v du. Формула A9.24) доказана. <|
Пример. Для вычисления интеграла / х In х dx положим и = In ж,
,	,	, dx	х2
dv = x dx; тогда du — —, v = — и, следовательно,
х\пх dx = \пх d — =	\ xdx — — (In ж	) + С.
J	J	2	2	2J	2 V	2/
§ 20. Интегрирование рациональных дробей
20.1. Интегрирование элементарных рациональных дро-
дробей. В этом параграфе будут рассматриваться рациональные дроби,
у которых в числителе и знаменателе стоят многочлены с действи-
действительными коэффициентами. Будет всегда предполагаться, что коэф-
коэффициент у старшего члена многочлена, стоящего в знаменателе, ра-
равен 1 (этого, очевидно, всегда можно достичь, поделив числитель и
знаменатель дроби на указанный коэффициент).
Будут изложены методы, с помощью которых можно вычислить,
т. е. выразить через элементарные функции, интегралы от рациональ-
рациональных дробей.
Рассмотрим сначала элементарные дроби вида	—. Если
(х — а)п
п > 1, то
4 - а^х -а^ = А{х~гГ+с=
Если п = 1, то
|А d = A In \х - а\ + С.	B0.2)
|
х — а
Вычислим теперь интеграл от элементарной дроби вида
Вх + D	/ _	— 19
Заметив, что
х2

§20. Интегрирование рациональных дробей	243
где а2 = q — ^— > О, и положив t = ж + -, будем иметь
/• ? ж + D	_ г	Вх + Р	_ ГВУ~ 2)+В1,_
J (x*+px + q)" йХ ~ J ffx + P\2 + q_?\n	J (t2 + «2)n
tdt +(n ^ f dt
= в f tdt +(n- ^ f
J (t2 + a2)n V	2 JJ (t2
rr	*	f Bx + D
Таким образом, вычисление интеграла / ——	г— ах сводится
J (x2 +px + q)n
к вычислению интегралов, стоящих в правой части получившегося
равенства.
Если п = 1, то
g+a	B0.4)
a	a
Если же п > 1, то
t dt	1 /* / 19	9 \	r>
/
B0.5)
jj	T def /" dt	^ 1
Для интеграла Yn = / -^	r—, n > 1, выведем с помощью
J (tz + a^)n
интегрирования по частям рекуррентную формулу, т. е. выразим 1п
через /п_ь
- _ f dt _ ! ft
n — /,2 _|_ 2Vn ~ ~ I
т-
п =
_ 1 /" ^	1 f tdt	_
~ ~^J (t2 + a2)n-1 ~ ~^J (t2 + a2)^ B0ЛЗ)
= 1/ ,-lf	*	+ X /	^	U
B0.5) a2 n~1 a2 V 2(n - l)(t2 + a2)^ 2(n - 1) J (t2 + a2)n~l J
~ а2 п-1 + 2a2(n - l)(t2 + a2O1 ~ 2a2(n - 1) n~b
т. e.
In= 2a2(n-l)(t2 + a2)^ +M1- 2(n-l))fw"b n = 2'3'- B0'6)
Так как интеграл Д уже вычислен (см. B0.4)), по формуле B0.6)
можно последовательно вычислить /2, /з и т. д.
Таким образом, интеграл от любой элементарной дроби находится
в явном виде и является элементарной функцией.
16*

244	Гл. 2. Интегральное исчисление функций одной переменной
20.2. Общий случай. Любую рациональную дробь можно пред-
представить в виде суммы многочлена и правильной рациональной дро-
дроби, а всякая правильная рациональная дробь раскладывается в сум-
сумму элементарных рациональных дробей (см. п. 3.5), поэтому задача
интегрирования рациональных дробей сводится к интегрированию
многочленов и элементарных рациональных дробей, т. е. функций, от
которых мы уже умеем вычислять интегралы. Имеет место следую-
следующая
Теорема 1. Неопределенный интеграл от любой рациональной
дроби на всяком промежутке, на котором ее знаменатель не обраща-
обращается в нуль, существует и выражается через элементарные функции,
являющиеся линейной комбинацией композиций рациональных дробей,
логарифмов и арктангенсов.
\> Для доказательства достаточно, поделив числитель на знамена-
Р(х)	Р(х)
тель, данную рациональную дробь ; ' представить в виде ) ; =
R(x)	™ж)	Q(x>
= S(x) +	, где S(x) и R{x) — многочлены, причем степень мно-
Q\x)	щх\
гочлена R(x) меньше степени многочлена Q(x), т. е.	— правиль-
Q(x)
ная рациональная дробь. Разложив ее согласно теореме 2 из п. 3.5 на
элементарные, получим, что всякая рациональная дробь является ли-
либо многочленом, либо суммой многочлена и конечного числа элемен-
элементарных рациональных дробей. Интеграл от каждого слагаемого этой
суммы (см. п. 19.3 и п. 20.1) имеет вид, указанный в теореме. <\
Следует отметить, что при применении описанного метода интег-
интегрирования рациональных дробей на практике он приводит к окон-
окончательному результату, т. е. к элементарной функции, только в том
случае, когда удается найти все корни знаменателя интегрируемой
рациональной дроби.
§ 21. Интегрирование некоторых иррациональностей
21.1. Рациональные функции от функций. Функции вида
гп\ rri2	тап
Р(иии2,...,ип) = Yl Y1 - Yl ak1k2...knu\1uk22...uknn
k1=0k2=0 kn=0
,	P(U\,U2, ...,Un)	т->	гл
называются многочленами, а функции —-.—¦—¦—¦	-, где Р и и —
Q(ilUU)
многочлены, называются рациональными дробями (или рациональны-
рациональными функциями) от переменных щ,и2, ...,ип.
Композиция рациональных дробей ь—h^i—Vd. c функциями
Q(UU	U

§21. Интегрирование некоторых иррационалъностей	245
= fi(x), u2 = /2(ж), ..., ип = /п(ж), т. е. функции вида
называются рациональными функциями от функций /i(x), /2(ж), ...
..., /п(ж) и обозначаются i?(/i(x),/2(ж),...,/п(ж)).
• 2
sin ж Ч~ cos ж
Например, i?(sinx,cosx) = —	рациональная функция
cos2 ж — sin х
от sin ж и cos ж, а R(y/x, %/х) = ^Ж 3	— рациональная функ-
функция от у/х и у/х.
о-! о тт	f r>( fax + byi /ax + byn\
21.2. Интегралы вида I ЩхА	 ,....	 ] ах.
J V \сх + а/	\сх + а/ /
г»	/*D/r (ах + ЪУ1 (ах +
Рассмотрим интеграл п[х,	 ,....
к	7 V ' \cx + d) ' ' Vcx +
с одним и тем же знаменателем: п = —, т — натуральное число,
т
Будем предполагать, что числа ri,...,rn рациональны и записаны
т —
Pi целые, i = 1, 2,..., п, и что определитель	, не равен 0. Если бы
с а
, = 0, то существовали бы такие числа Л, /i, что А2 + /i2 / 0 и
с а
Ха + \ic — 0, ХЬ + /id = 0, а тогда, например, при Л ф 0 имело бы место
равенство
ах + Ъ _ Хах + ХЪ _ —ficx — fid _ fi
ex + d X(cx + d) X(cx + d)	X
и, следовательно, функция /t ж,	 ,...,		была бы
V \сх + d/	ex + dJ )
просто рациональной функцией.
Сделаем в рассматриваемом интеграле замену переменной
го = ах±Ъ	B1Л)
сх + d	y J
откуда
at — о def / .ч	/Л1 ~ч
х = ^^ = РИ)-	B1-2)
Здесь p(t) — рациональная функция, поэтому p'(t) — также ра-
рациональная функция. Поскольку
dx-p(t)dt, ycx + d) B-i}l* ) -t , j-M,...,n,
TO
= fR(p(t),t*,...,i"»)p'(*) dt = JR*{t) dt,
где R*(t) = R(p(t),tPl, ...,tPn)p'(t) — рациональная функция.
16*

246	Гл. 2. Интегральное исчисление функций одной переменной
Таким образом, замена переменной B1.1) сводит интеграл
№Ьтх) '-'(^Td) )dx BL3)
к интегралу от рациональной функции.
К рассмотренному типу интегралов относятся интегралы вида
[r(x, (ах + Ъ)Г1,..., (ах + h)rn)dx, а ф О,
в частности интегралы / R(x,xri, ...,жГп) dx.
/dx
	—. Сделаем согласно формуле B1.1) замену пе-
J- ~т~ уX
ременной t2 = ж, t > 0, откуда б?ж = 2?d? и, следовательно,
dt 2dt
д/	1 + t	\J	J l+t)
= 2(t - In |1 + t\) + С = 2(л/ж - In A
К интегралам вида B1.3) иногда удается свести интегралы дру-
других типов, например, интегралы вида / R(x, д/ж2 + рх + q) dx, ког-
когда квадратный трехчлен х2 + рх + q имеет действительные корни. В
самом деле, если х2 + рх + q = (х — а)(х — Ь), то
R(x, л/х2 + рх + q) = Л(ж, д/(ж - а)(х — Ь)) =
где Ri — рациональная функция. Поэтому
jR(x, Vx2+px + q) dx = JR1 (x, (^I/2) dx
и в правой части получился интеграл типа B1.3).
21.3*. Интегралы от дифференциального бинома. Рассмот-
Рассмотрим интеграл вида
f(a + bxp)ax^dx;	B1.4)
его подынтегральное выражение называется дифференциальным би-
биномом. Будем рассматривать случаи, когда а, C и 7 являются рацио-
рациональными, а а и Ъ — произвольными действительными числами.
Сделаем в интеграле B1.4) замену переменной
B1.5)

§22. Интегрирование некоторых трансцендентных функций	247
тогда dx = — t1l^~1 dt и, следовательно,
J{
{a + bxp)ax^ dx = iy (a + fa)^7+1^-1 dt.	B1.6)
Таким образом, интеграл B1.4) с помощью подстановки B1.5) сво-
сводится к интегралу вида
f(a + bt)atxdt,	B1.7)
Т Н~ 1
где а и Л — рациональные числа, Л = -^—	1.
Рассмотрим три случая.
1.	a — целое число. Пусть Л = т/п, где m и п > 0 — целые чис-
числа. Согласно результатам п. 21.1 подстановка и = ?1//п сводит интеграл
B1.7) к интегралу от рациональной дроби.
2.	Л — целое число. Пусть теперь а = т/п, где т и п > 0 —
целые числа. Тогда согласно тому же п. 21.1 интеграл B1.7) приво-
приводится к интегралу от рациональной функции с помощью подстановки
и = (а + ЫI/71.
3.	а + \ — целое число. Пусть, как и выше, а = ттг/n, где т и
п > 0 — целые числа. Имеем Г (а + bt)atx dt = Г f^±^\ °V+A dt.
Снова получился интеграл типа, рассмотренного в п. 21.1: под-
(а + Ы\11п
становка и = (	) сводит его к интегралу от рациональной
функции.
Итак, в трех случаях, когда а, Л или а + Л являются целыми чис-
числами, интеграл B1.7) сводится к интегралу от рациональных функ-
ции. Поэтому если хотя бы одно из чисел a, J—— или -L—	ha в
первоначальном интеграле B1.4) является целым числом, то этот ин-
интеграл сводится к интегралу от рациональных функций и, следова-
следовательно, выражается через элементарные функции.
Русский математик П.Л. Чебышев*) показал, что ни в каком
другом случае рациональных показателей а, C и 7 интеграл B1.4)
не выражается через элементарные функции.
§ 22. Интегрирование некоторых трансцендентных функций
22.1. Интегралы R(sm x, cos x) dx. Интеграл / R(smx, cos ж) dx
сводится подстановкой
u = tg|, -^<x<^,	B2.1)
*)П.Л. Чебышев A821-1894) — русский математик.
16*

248	Гл. 2. Интегральное исчисление функций одной переменной
к интегралу от рациональной функции. Действительно,
2 sin | cos |	2tg|	2u
Cos^|-sin^| _ l-tg^| _
sin2 I +cos2| l + tg2|
,	2du
x = 2arctg/u, dx = 	-,
1 + ul
поэтому
R(smx,cosx)dx = 2
т. е. получился интеграл от рациональной функции.
При вычислении интегралов типа / R(smx, cos ж) dx часто оказы-
оказываются полезными также и подстановки
и = sin ж, I/= cos ж, u = tgx.	B2.2)
В ряде случаев при интегрировании с помощью этих подстановок тре-
требуется провести меньше вычислений, чем при интегрировании с по-
помощью подстановки B2.1).
Примеры. 1. Применим подстановку B2.1) для вычисления ин-
интеграла
Г dx
J I — sin x '
Имеем
J -L	Dill *h	|1
dx	n f	du	_ c> [ du _ 2	„ _
, ,x ~ J (I-UY- ~ l-U
2 +C.
1-tef
2. Для вычисления интеграла / —— применим подстановку
J cos6 ж
= tgx:
22.2. Интегралы / sinm xcosnx<ix. В случае когда тип — ра-
рациональные числа, интеграл / sinm xcosn xdx подстановкой u — sin ж
или v = cos ж сводится к интегралу от иррациональной функции, а
именно к интегралу от дифференциального бинома (п. 21.3*).

§22. Интегрирование некоторых трансцендентных функций	249
В самом деле, если, например, и = sin ж, то
и, следовательно,
smmxcosnxdx =
т. е. действительно получился интеграл от дифференциального бино-
бинома и, таким образом, выражается ли он через элементарные функции,
зависит от того, какие при этом получились показатели степеней (см.
п. 21.3*).
В случае когда тип — целые числа, интеграл / sinm x cosn x dx
относится к типу интегралов, рассмотренных в предыдущем пункте,
и для его вычисления целесообразно использовать подстановки B2.2).
Например,
/sin3 х -. С sin2 х -. С 1 — cos2 x 7
—— dx = — / —— d cos x = — /	a cos x =
COS2 X J COS2 X J COS2 X	u=COS x
= — / —-— du — du — / — = u -\	V С — cos x Л	V С.
u=COSX J Uz	J	J Uz	U	COS Ж
Если m = 2& + l и п = 21 + 1 — нечетные числа, то полезна
подстановка t = cos2x:
/ sin2/e+1 x cos2/+1 xdx — -\ sin2fe x cos2/ x sin 2ж dx —
= ~жУ С	2	J (J
2
т. е. получился интеграл от рациональной дроби (к и I могут быть
отрицательными).
Если тип — четные числа, то полезна подстановка u = tgx —
см. пример 2 в п. 22.1.
Если оба показателя тип неотрицательные и четные, то, приме-
,	.2 1 — cos 2х	2 1 + cos 2х
нив формулы sin х =	, cosz x =	, получим интег-
интеграл того же типа, но с меньшими показателями, например,
/.2 у Г1 — cos 2x , х sin 2x ,~
sin xdx — \	dx —	V С.
J Z Z 4
Отметим, что методами, аналогичными методам, описанным в
этом пункте, берутся интегралы вида shmxchnxdx.
f	f
22.3. Интегралы / sinaxcos/3xdx, / sinaxsin/3xdx,
cos ax cos /3x dx. Интегралы / sinaxcos Cx dx, / sinaxsin Cx dx,
cos ax cos Cx dx вычисляются, если их подынтегральные выраже-
16*

250	Гл. 2. Интегральное исчисление функций одной переменной
ния преобразовать по формулам
sin ах cos /Зх = - [sin(a + C)х + sin(a — /3)х],
sin аж sin /Зх = - [cos(a — /3)ж — cos(a + C)х\,
cos аж cos /Зх = - [cos(a + /3)ж + cos(a — /3)ж].
Например,
/1 г	1 г	1	1
sin ж cos 2xdx — - \ sin Зх dx — - sin xdx = —- cos Зж + - cos ж + С
22.4. Интегралы от трансцендентных функций, вычис-
вычисляющиеся с помощью интегрирования по частям. К интегра-
интегралам от трансцендентных функций, вычисляющимся с помощью
интегрирования по частям, относится много разнообразных интег-
интегралов, например,
еах cosflxdx, eax sinflx dx, xncosaxdx,
xnsmaxdx, xneax dx, xn aicsinx dx,
/xn arccosxdx, xnarctgxdx, xnarcctgxdx, xnlnxdx.
Здесь везде п — целое неотрицательное число.
Для вычисления интегралов / еах cos /Зх dx и / еах sin /Зх dx
следует их дважды проинтегрировать по частям, в результате для
каждого из них получится линейное уравнение, из которого они сра-
сразу находятся. Например,
/ = Геах sin Cxdx = ~ Jeaxd cos /Зх = _e^c°s/^ +
а Г ах о , eaxcosf3x , а Г ах , . о еах cos /Зх ,
+ - / еах cos /Зх dx =	--^— + — eaxdsmCx =	—^— +
г ol ( ах . о С ах • о 1 \ (asm/Зх -/3 cos/Зх) еах а2 Т
+ Tji ( е sm (Зх-а еах sin (Зх dx) = ^	^	^	— /;
г asin/Зх — /3 cos /Зж ^г , ^
отсюда / = 	—0—^-—^— еаж + С.
а2 + /З2
В интегралах xncosaxdx, xnsmaxdx, xneax dx после од-
однократного интегрирования по частям получаются интегралы тех
же типов, но с меньшими показателями степени.
Рассмотрим пример:
/Г	Г
х sin ж dx = - / ж d cos ж = -ж cos ж + / cos ж dx = -ж cos ж + sin ж + С
j	j
В интегралах хп aicsinx dx, xn arccos ж б?ж, хп aictgx dx,

d(l — x ) = xarcsinx +
§23. Определенный интеграл	251
/ xn arcctg x dx, xn\nxdx в результате однократного интегрирова-
интегрирования по частям пропадает трансцендентная функция, причем в первых
двух получаются интегралы от иррациональных функций, выражаю-
выражающиеся через элементарные функции, а в трех последних — интегралы
от рациональных функций и, следовательно, также выражающиеся
через элементарные функции. Например,
/С х dx
arcsin xdx — х arcsin x — I ,	=
J л/l -x2
= x arcsin x +
В заключение подчеркнем, что далеко не всякий интеграл от эле-
элементарной функции выражается через элементарные функции. Среди
таких интегралов встречаются интегралы, которые находят большое
применение в различных разделах математики. К числу их относят-
/2
е~х dx, интегральный лога-
, Г dx „ fsinx ,
рифм / -—, интегральный синус /	dx.
J 111 JL	J JL
§ 23. Определенный интеграл
23.1. Определенный интеграл Римана*). Напомним, что
множество г = {xk}1^^ точек отрезка [а, Ь] таких, что
а = х0 < хх < ... < хкт-1 < хкт = Ь,
называется разбиением отрезка [а, 6], a G /?, Ъ G R.
Точки хк называются точками разбиения г, отрезки [xk-i,Xk] —
отрезками разбиения г; их длины обозначаются Аж^, т. е.
= Xk-Xk-i, к = 1,2,...,&г, а число
называемся мелкостью разбиения т.
Разбиение г* = {x^}kZ0T* называется разбиением, вписанным в
разбиение г, если г С г*, т. е. если каждая точка разбиения т со-
содержится в разбиении г*. В этом случае каждый отрезок [х^_1,х^\
разбиения содержится в некотором отрезке [xj-i,Xj] разбиения г,
j = l,2,...,fcr.
Разбиение г*, вписанное в разбиение г, называется также раз-
разбиением, следующим за разбиением г, и пишут г* >- т. В этом случае
говорят также, что разбиение т предшествует разбиению г*, и пи-
пишут Т -< Г*.
?) Б. Риман A826-1866) — немецкий математик.

252
Гл. 2. Интегральное исчисление функций одной переменной
Существенными являются следующие два свойства разбие-
разбиений отрезка.
1°. Если т -< т', а т' -< г", то г -< г".
|> Действительно, если каждый отрезок разбиения г" содержится
в некотором отрезке разбиения т', а каждый отрезок разбиения т'
содержится в некотором отрезке разбиения т, то каждый отрезок
разбиения т" содержится в соответствующем отрезке разбиения т. <1
2°. Для любых разбиений т' и т" существует такое разбиение г,
что г У г' и т У т".
|> В самом деле, таким разбиением является, например, разбиение,
состоящее из всех точек обоих разбиений т' и т". <1
Пусть функция / определена на отрезке [а, 6], а < 6, и т =
= {xjfe}j^QT — некоторое разбиение этого отрезка. Всякая сумма ат
вида
У
называется интегральной суммой Римана функции /.
В случае если функция / неотри-
неотрицательна, то интегральная сумма оТ
равна площади фигуры, составлен-
составленной из прямоугольников с основани-
основанием [Xk-ljXk] И ВЫСОТОЙ ДЛИНЫ f(?k)
(рис. 102).
Определение 1. Функция / на-
называется интегрируемой по Риману
на отрезке [а, 6], если для любой по-
~? следовательности разбиений
О
I
hn
i
i
i
i
i
i
Рис. 102

Тп —
ik=0
отрезка [а, 6], мелкость которых стремится к нулю: lim \rn\ = 0, и
п—>-оо
для любого выбора точек ?^ G [х^_1,х^], к = 1,2, ...,fcr, последова-
последовательности интегральных сумм
д. f-p.c(n) An) \ п = 1 2
имеют и притом один и тот же предел.
Этот предел называется интегралом Римана функции / по отрез-
ь
ку [а, Ь]. Его обозначают f(x)dx и пишут
ъ
lim аТ = f(x
B3.1)

§23. Определенный интеграл	253
Согласно определению это означает, что если
то	ь
; ^и),..., ^l) = jf{x) dx,
если только lim \rn\ = 0.
n—>-oo
Можно сформулировать определение интеграла Римана, и не
используя понятия предела последовательности, а, как говорят,
на "языке е-б".
Определение 2. Число / называется интегралом Римана от
функции f на отрезке [а, 6], если для любого г > 0 существует такое
S > 0, что, каково бы ни было разбиение г = {xk}1^^ отрезка [а, 6],
мелкость которого меньше S: |т| < ?, и каковы бы ни были точки
€k ? [^/г-ъ^/г], & = 1Э 2, ...,fcr, выполняется неравенство
Аналогично равносильности определений предела функции в тер-
терминах последовательностей и в терминах окрестностей доказывается
и равносильность определений 1 и 2 интеграла Римана. Это рекомен-
рекомендуется читателю проделать самостоятельно.
ъ
В интеграле I f{x)dx число а называется нижним, а число Ь —
а
верхним пределом интегрирования.
В дальнейшем для краткости вместо "функция, интегрируемая по
Риману", будем говорить "интегрируемая функция", а вместо "ин-
"интеграл Римана" — просто "интеграл".
Дополним определение интеграла следующими соглашениями.
а
Если функция / задана в точке х = а, то по определению / /(ж) dx =
а
= 0. Если функция / интегрируема на отрезке [а, 6], то положим
а	Ъ
f(x)dxd= - f(x)dx.
b	a
23.2. Ограниченность интегрируемых функций. Изучение
определенного интеграла начнем с исследования необходимых, а за-
затем и достаточных условий интегрируемости функций.
Теорема 1. Если функция интегрируема на некотором отрезке,
то она ограничена на нем.

254	Гл. 2. Интегральное исчисление функций одной переменной
Ъ
\> Пусть функция / интегрируема на отрезке [а, Ь] и f(x)dx = /.
а
Зафиксируем какое-либо г > О, например г = 1. Согласно опреде-
определению 2 интеграла существует такое S > О, что для любой интег-
интегральной суммы аТ, соответствующей разбиению т мелкости \т\ < ?,
выполняется неравенство \ST — /| < 1, а следовательно, и неравенство
1-1<<тт<1+1,	B3.2)
т. е. множество {стт} значений интегральных сумм ат, \т\ < S, функ-
функции / ограничено.
Допустим теперь, что существует функция /, интегрируемая на
некотором отрезке [а, 6], и неограниченная на этом отрезке. Возьмем
произвольное разбиение т — {xk}^^ отрезка [а, Ь]. Из того, что функ-
функция / неограниченна на отрезке [а, 6], следует, что она неограничен-
неограниченна и по крайней мере на одном из отрезков разбиения т. Пусть для
определенности функция / неограниченна на отрезке [xo,xi]. Из ее
неограниченности на этом отрезке следует, что для любого числа п
на нем существует такая точка, обозначим ее ?,[ , что
Отсюда, очевидно, следует, что
lim /(^n)) = оо.	B3.3)
п—>-оо
Зафиксируем какие-либо точки ?& в остальных отрезках разбие-
разбиения т:
Тогда сумма	ит
^2f(^k)Axk	B3.4)
будет иметь вполне определенное значение. Добавив к этой сумме сла-
слагаемое /(?i )Дж]_, получим интегральную сумму aT(f; {;[, ?2, •••??&)?
причем в силу условия B3.3) и постоянства суммы B3.4) будем иметь
кт
п—Уоо	т	п—Уоо L	^-^
к=2
а следовательно, для любого разбиения т множество значений ин-
интегральных сумм 0>(/;?i 5 ?2, ...,6гх) неограниченно. Поэтому неогра-
неограниченно и множество {сгт}, \т\ < S (число S > 0 было выбрано выше),
что противоречит неравенству B3.2). <|
Замечание. Условие ограниченности функции, являясь необхо-
необходимым условием интегрируемости функции по Риману, не является

§23. Определенный интеграл	255
достаточным условием для этого. В самом деле, рассмотрим, напри-
например, функцию Дирихле
,, \ _ f 1? если х рационально,
•^ \ 0, если х иррационально.
Каковы бы ни были отрезок [а, Ь] и его разбиение г = {xk}JjZ^)T, выбрав
все точки ?ь Е [хк-1,хк] рациональными, в силу условия /(?&) = 1,
к = 1, 2,..., кт, получим	,_
/С — Т
а выбрав точки ^ иррациональными, в силу условия /(?&) = 0, к =
= 1, 2,..., &г, будем иметь	к
X>, = o.
Поэтому интегральные суммы сгг функции Дирихле заведомо не име-
имеют предела при \т\ —У 0.
Тем самым функция Дирихле дает пример функции, ограниченной
на любом отрезке, но неинтегрируемой на нем.
23.3. Верхние и нижние суммы Дарбу*). Пусть функция /
определена на отрезке [а, Ь], т = {ж/е}^^ — разбиение этого отрезка,
Ак = [хк-1,хк], Ахк=хк-хк-1. Положим
Мк = sup /(ж), га/. = inf /(ж), fc = 1,2,...,&г, B3.5)
5Г = ST(f) = 5]MfeAxb 8r = sr(/) = ^mfeAxfe. B3.6)
A;=l	k=l
Сумма 5r, называется верхней, а сумма sr — нижней суммой Дарбу
функции /. Очевидно, что в случае, когда функция / ограничена, то
нижние тпк и верхние Мк грани B3.5) конечны, и потому суммы
Дарбу B3.6) при любом разбиении принимают конечные значения. В
дальнейшем будем предполагать, что функция / ограниченна — это
естественно, так как нас будут интересовать свойства интеграла от
функции /, а он, согласно теореме 1, может существовать только в
том случае, когда функция ограниченна.
Из того, что выполняется неравенство тпк ^ Мк, к = 1, 2,..., кт,
следует, что при любом разбиении т выполняется неравенство
sT ^ ST.	B3.7)
Очевидно также, что в силу определения B3.5) чисел тпк и Мк для
любых ?к е Ак имеет место неравенство
тк
?) Г. Дарбу A842-1917) — французский математик.

256	Гл. 2. Интегральное исчисление функций одной переменной
Отсюда следует справедливость неравенства
sT <С оТ = <7Г(/;&,...,&Т) ^ St.	B3.8)
Отметим еще следующие свойства сумм Дарбу.
1°. Каждая нижняя сумма Дарбу не превосходит любой верхней:
*п «S ST2	B3.9)
(т\ и Т2 — разбиения отрезка [а, Ь]).
иения
> Пусть сначала т*Ут, т = {хк}%1о , г* = {%*}]={т* — разб:
отрезка [а, Ь],
Ак = [хк-ихк], А* = [х*_15х*],
mfe = inf /(ж), fc = 1,2,...,&г, ш* = inf /(ж), j = l,2,...,jr*.
Условие г* ^ г означает, что каждый отрезок Ак разбиения т яв-
является объединением некоторых отрезков разбиения г*. Обозначим
эти отрезки A*fc, тогда Д/, = (J A*fc, где суммирование ведется по
Зк
всем таким индексам jk, что A*fc С Ак. Отсюда следует, что
Ахк =^Ах*к.	B3.10)
Зк
Кроме того, выполняются неравенства
тк^т*к,	B3.11)
так как при переходе от отрезка Ак к содержащемуся в нем от-
отрезку A*fc нижняя грань значений функции может только увели-
увеличиваться.
Теперь легко доказать неравенство
sT <С s*.	B3.12)
В самом деле,
4^	B3Л°) и к	°к B3Л1) 4^	°к
л	"^	Зк	л Jfc
J
Аналогично доказывается неравенство
5r* ^ 5Г.	B3.13)
Пусть теперь Т\ и т2 — два произвольных разбиения отрезка [а, Ь].
Возьмем какое-либо разбиение г, вписанное в разбиения т\ и Т2, т. е.
т У т\ и г У т2. Тогда неравенство B3.9) вытекает из следующей це-
цепочки неравенств:
sTl ^ sT ^ ST ^ ST2. <\
B3.12) B3.7) B3.13)

§23. Определенный интеграл	257
2°. Нижняя {верхняя) сумма Дарбу является нижней {верхней)
гранью интегральных сумм Римана, соответствующих данному
разбиению:
sT= inf aT(/;?b-,6J,	B3.14)
?iv,?fcx
5r= sup <7r(/;fi,...,&J.	B3.15)
l> Пусть r = {x/e}^QX — разбиение отрезка [a, b] и ?k e Ak =
= [xfc_i,Xjfe], & = 1,2, ...,fcr. Тогда в силу того, что нижняя грань ариф-
арифметической суммы числовых множеств равна сумме нижних граней
этих множеств, и того, что положительный постоянный множитель
можно внести под знак нижней грани (п. 4.3*), получим
sT = У2ткАхк = У2 т{ f(€k)Axk =
= inf
k=l,2,...,kT k~1	k=l,2,...,kT
т. е. равенство B3.14) доказано. Аналогично доказывается равенст-
равенство B3.15). <
3°. Имеет место равенство
кТ
ST-sT = J2^k{f)Axk,	B3.16)
к=1
где uok{f) — колебание функции f на отрезке [xk-\,xk] разбиения г,
к = 1,2, ...,fcr (см. п. 7.4).
|> Формула B3.16) следует из того, что для любого множества X С
С Rn справедливо равенство
sup(X — X) = sup {x' — х) = supX — inf X,
х,х'ех
т. е. разность верхней и нижней граней двух множеств (в данном слу-
случае одного и того же) равна верхней грани разности этих множеств
(п. 4.3*). В самом деле, так как
Мк-тк = sup f{x) - inf f{x) = sup [f{x') - f{x)} = uk(f),
B3.5) xeAk	xeAk	x',xeAk
ST-sT = ^{Mk -mk)Axk =
17 Л.Д.Кудрявцев, т.1

258	Гл. 2. Интегральное исчисление функций одной переменной
При заданной на отрезке [а, Ъ] ограниченной функции / верхние
и нижние суммы Дарбу являются функциями, заданными на мно-
множестве {г} всех разбиений отрезка [а, Ь]. Для таких функций можно
определить их предел по аналогии с понятием предела интегральных
сумм Римана.
Пусть на множестве {г} всех разбиений т отрезка [а, Ь] задана
функция F: т \-^ F(r) G R.
Определение 3. Число А назовем пределом функции F{r) при
\т\ —у О, если для любой последовательности {тп} разбиений тп отрез-
отрезка [а,Ь] такой, что lim \тп\ = 0, имеет место
П—У СО
lim F(rn) = A.
п—у со
Если А — предел функции F(r) при \т\ —у 0, то пишут
lim F(r) = A.	B3.17)
\т\-УО
Определение предела B3.17) можно сформулировать и на "язы-
"языке е-6п.
Определение 4. Число А называется пределом функции F(x)
при \т\ —У 0, если для любого г > 0 существует такое S > 0, что для
всех разбиений т отрезка [а, 6], имеющих мелкость \т\ < S, выполня-
выполняется неравенство
\F(t) -A\<e.
Поскольку определения предела B3.17) так же, как и определения
предела интегральных сумм B3.1), могут быть сформулированы в
терминах пределов последовательностей, то на эти пределы перено-
переносятся обычные свойства пределов, в частности возможность предель-
предельного перехода в неравенствах.
В смысле предела B3.17) мы и будем в дальнейшем говорить о
пределах нижних и верхних сумм Дарбу: lim sT и lim ST.
\т\-УО	\т\-уО
23.4. Нижний и верхний интегралы. Пусть функция / огра-
ограничена на отрезке [а, Ь]. Рассмотрим верхнюю грань /* всевозможных
ее нижних сумм Дарбу и нижнюю грань /* всебозможных верхних
сумм Дарбу:
/* = supsr, /* = inf ST.	B3.18)
т	т
Число /* называется нижним, а число /* — верхним интегралом
функции /. Из неравенства B3.9) следует, что если функция / огра-
ограничена на отрезке [а, 6], то ее нижний и верхний интегралы конечны
и для них выполняется неравенство
/* ^ /*.	B3.19)

§23. Определенный интеграл	259
|> В самом деле, перейдя в левой части неравенства B3.9) к верхней
грани по разбиениям Т\, получим, что для любого разбиения т^ вы-
выполняется неравенство /* ^ ST2. Перейдя здесь к нижней грани по Т2,
получим /* ^ /*. <|
Интегралы /* и /* понадобятся нам ниже при доказательстве кри-
критерия интегрируемости функции.
23.5. Необходимые и достаточные условия интегрируе-
интегрируемости функций.
Теорема 2. Для того чтобы ограниченная на некотором отрезке
функция была интегрируема на нем, необходимо и достаточно, что-
чтобы разность верхних и нижних сумм Дарбу стремилась к нулю, когда
мелкость разбиений отрезка стремится к нулю:
lim (Sr - sr) = 0.	B3.20)
\T\->°
Следствие. Для того чтобы ограниченная на отрезке [а, Ь] функ-
функция f была на нем интегрируема, необходимо и достаточно, чтобы
ljmo5>*(/)Az*=0,	B3.21)
где т — {xk}\z^T — разбиение отрезка [a,b], a uJk(f) — колебание
функции / на отрезке [xk-i,Xk], к = 1, 2,..., кТ.
\> Необходимость. Пусть ограниченная на отрезке [а,Ь] функ-
ъ
ция / интегрируема на этом отрезке и / = / fix) dx. Тогда lim aT =
J	\т\->о
а
= /. Поэтому для любого г > 0 существует такое S > 0, что, каковы
бы ни были разбиение т = {ж/е}^^ отрезка [а, Ъ], имеющее мелкость
\т\ < S, и точки ?д. G [xk-ijXk]j к = 1,2,..., кт, для интегральной суммы
ат = о>(/;?]_, ...,?jfeT) выполняется неравенство \ат — 1\ < е, а следова-
следовательно, и неравенство
I -е <ат < 1 + е.	B3.22)
Переходя в неравенстве B3.22) к нижней и верхней граням от-
относительно точек ?ъ?2?---?6;т? в силу свойств сумм Дарбу B3.14) и
B3.15) получим
I-e^sT^ST^I + e.
Таким образом, если \т\ < S, то 0 ^ ST — sT ^ 2г. Отсюда сразу и
следует, что
lim (ST ~ sT) = 0.
|r|^0
Достаточность. Пусть функция / ограничена на отрезке [а,Ь]
и для ее сумм Дарбу выполняется условие B3.20). Из определения
17*

260	Гл. 2. Интегральное исчисление функций одной переменной
нижнего /* и верхнего /* интегралов (см. п. 23.4) и неравенст-
неравенства B3.19) имеем
sT <С h ^ /* ^ ST.	B3.23)
Поэтому 0 ^ /* - /* ^ ST - sT. Отсюда в силу условия B3.20) следует,
что /*—/* = 0. Обозначим общее значение нижнего и верхнего интег-
интегралов через /, т. е. / = /*=/*. Из B3.23) будем иметь sT ^ / ^ ST, но
любая интегральная сумма аТ также лежит между суммами Дарбу sT
и ST (см. B3.8)): sT ^ ат ^ ST, поэтому \ат - I\ ^ ST - sT. Отсюда в
силу условия B3.20) следует, что lim \ат — /| = 0. Это означает, что
существует предел интегральных сумм
lim от = /,	B3.24)
т. е. что функция / интегрируема, причем
ъ
!f(x)dx = I. <\	B3.25)
а
Следствие непосредственно вытекает из свойства B3.16) сумм
Дарбу: условие B3.21) равносильно в силу указанного свойства усло-
условию B3.20).
Теорема 3. Если функция f интегрируема на отрезке [а,Ъ], a sT
и ST — ее суммы Дарбу, то
ъ
lim sT = lim ST = ff(x)dx.	B3.26)
a
l> Если функция / интегрируема на отрезке [a,b], то согласно тео-
теореме 2 выполняется условие B3.20). При доказательстве теоремы 2
было показано, что при выполнении этого условия верхний интеграл
функции совпадает с ее нижним интегралом: /* = /* = / (а поэто-
ъ
му в силу B3.23) sT ^ / ^ ST), и что / = f(x)dx. Следовательно,
а
0 ^ / — sT ^ ST — sT, 0 ^ ST — I ^ ST — sT. Отсюда в силу выполне-
выполнения условия B3.20) следует, что lim (/ — sT) = 0 и lim (ST — /) = 0.
А это равносильно существованию пределов B3.26). <1
23.6. Интегрируемость непрерывных и монотонных функ-
функций.
Теорема 4. Функция, непрерывная на отрезке, интегрируема на
нем.
\> Если функция / непрерывна на отрезке [а,Ь], то она, во-первых,
ограничена на нем, а во-вторых, равномерно непрерывна. Последнее
означает, что для любого г > 0 существует такое S > 0, что для всех

§23. Определенный интеграл	261
точек х е [а,Ь] и х' е [а,Ь] таких, что \х' - х\ < S, выполняется нера-
неравенство \f{x') — f(x)\ < г.
Возьмем для отрезка [а, Ь] какое-либо разбиение г = {хи}1^^ мел-
мелкости \т\ < S. Тогда для любых двух точек х и х', принадлежащих
одному и тому же отрезку разбиения т, х е [xk-i,Xk], x' e [xk-i,Xk],
имеет место неравенство \х' — х\ ^ Xk — Xk-i = Дж/г ^ \т\ < й, а
поэтому и неравенство |/(V) — f(x)\ < г. Отсюда следует, что колеба-
колебание ujk(f) функции / на отрезке [xk-i,Xk] удовлетворяет неравенству
МЛ = SUP 1/0*0 - /0*01 ^ е, к = 1,2,..., кт. B3.27)
x,x'e[xk-i,xk]
Следовательно,
О^У^МЛ^к <: eJ2Axk=e(b-a).	B3.28)
ti	B3-27) ti
Поскольку г было произвольным положительным числом, то нера-
кт
венство B3.28) означает, что lim У^^(/)Аж^ = 0. Поэтому в силу
следствия 1 теоремы 2 функция / интегрируема на отрезке [а, Ь]. <\
Теорема 5. Функция, монотонная на отрезке, интегрируема
на нем.
\> Пусть для определенности функция / возрастает на отрезке [а, Ь].
Тогда, в частности, для любого х G [а, Ь] выполняется неравенство
/И ^ fix) ^ №,
и, следовательно, функция / ограничена на отрезке [а, Ь]. Очевид-
Очевидно также, что в силу возрастания функции / для любого разбиения
г = {xk}lZQT отрезка [а, Ь] имеют место равенства
тк = inf f(x) = f(xk-i),
xe[xk-i,xk]
Мк= sup f(x)=f(xk).	B3.29)
xe[xk-i,xk]
Поэтому, заметив, что
xk - хк-г = Axk <: |r|, к = 1, 2,.., fer,	B3.30)
и что хо = a, XkT = b, получим
к	к
- f(x0)) + (f(x2) -
B3.30)
= [№ -

262	Гл. 2. Интегральное исчисление функций одной переменной
Отсюда следует, что lim (ST - sT) = 0, и потому, согласно теореме 2,
|т|-И)
функция / интегрируема на отрезке [а, Ь]. <\
Замечание. Отметим, что монотонные на отрезке функции
могут быть и разрывными. Так, например, функция f(x) = sign ж
монотонна и разрывна на любом отрезке, содержащем точку х = 0.
Поскольку же всякая монотонная функция, в частности, /(ж) = sign ж,
согласно теореме 4, интегрируема, то отсюда следует, что существу-
существуют разрывные интегрируемые функции.
§ 24. Свойства интегрируемых функций
24.1. Основные свойства определенного интеграла. Пере-
Перечислим свойства определенного интеграла, вытекающие непосредст-
непосредственно из того, что он является пределом интегральных сумм.
ъ
1°. [dx = b-a.
|> В данном случае подынтегральная функция тождественно равна 1,
и потому при любом разбиении т = {xjYjZ^ все интегральные суммы
Римана равны b - а:
от = у Axj = b — a,
следовательно,
/ dx = lim oT — b — a. <l
a
2°. Линейность интеграла. Если функции fug интегрируе-
интегрируемы на отрезке [а, 6], то при любых X G R и \i G R функция А/ + \ig
также интегрируема на отрезке [а, Ь] и
f[Xf(x) + iig(x)] dx = Л ff(x) dx + /i fg(x) dx.	B4.1)
a	a	a
\> Каковы бы ни были разбиение г = {xk}1^^ отрезка [а, Ь] и точ-
точки & е [хк-1,хк], к = 1,2,...,&г, будем иметь
aT(Xf + fig) =
Аат(/)+/и7гE). B4.2)
k=l	k=l

§24- Свойства интегрируемых функций	263
Поскольку при \т\ ->• 0 предел правой части этого равенства в силу
интегрируемости функций / и д существует, то существует при этом
условии и предел левой части lim aT(\f + ид), что означает интег-
|т|-Ю
рируемость функции А/ + \ig. Перейдя в равенстве B4.2) к пределу
при \т\ —У О, получим формулу B4.1). <|
3°. Если функция f интегрируема на отрезке [а, 6], то она интег-
интегрируема и на любом отрезке [а*, 6*] С [а, Ь].
\> Из интегрируемости функции / на отрезке [а, Ь] следует ее огра-
ограниченность на нем, а следовательно, и на отрезке [а*, 6*]. Если т* =
= {x*}^Zqx* — какое-либо разбиение отрезка [а*, 6*], то всегда, доба-
добавив к нему соответствующее конечное множество точек, лежащих на
отрезках [а, Ь], но уже вне отрезка [а*, Ь*], можно получить разбиение
г = {xk}lZQT, кТ ^ 2т* •> отрезка [а, Ь] той же мелкости
М = |т*
B4.3)
Обозначив посредством uok{f) и и^A) колебания функции / соответ-
кт
ственно на отрезках [xk-i,Xk] и [ж*_1?ж*] и заметив, что У^
к=1
отличается от ^*(/)А* A	А*
k=Xk — Xk-i, Аж* = ж* = ж* - ж*_15
на неотрицательные слагаемые вида cj^(/)Ax^, соответствующие от-
отрезкам [xk-i,Xk] разбиения г, лежащим вне отрезка [а*, 6*], получим
.	B4.4)
3 = 1	к=1
Из интегрируемости функции / на отрезке [а, 6], согласно след-
кт
ствию 1 теоремы 2 из п. 23.5, вытекает, что lim S^ujk(f)/\xk = 0,
поэтому в силу B4.3) и B4.4) lim V^cj*(/)Ax* = 0, а это, согласно
тому же следствию теоремы 2 п. 23.5, и означает интегрируемость
функции / на отрезке [а*, 6*]. <1
4°. Аддитивность интеграла. Если функция f интегрируе-
интегрируема на отрезке [а,Ь] и а < с < Ь, то
Ь	с	Ь
ff(x) dx = ff(x) dx + ff(x) dx.	B4.5)

264	Гл. 2. Интегральное исчисление функций одной переменной
\> Если тса и тьс — разбиения соответственно отрезков [а, с] и [с, Ь], то
объединение этих разбиений т = т^ U тьс является разбиением отрез-
отрезка [а, Ь], причем
К1^И, \тьс\^\т\.	B4.6)
Пусть атс и сггь — какие-либо интегральные суммы Римана функ-
функции /, соответствующие разбиениям тса и тс6; тогда
от = атс + сггь	B4.7)
— интегральная сумма Римана функции / на отрезке [а, Ь].
Согласно свойству 2° из интегрируемости функции / на отрез-
отрезке [а, Ь] следует ее интегрируемость на отрезках [а, с] и [с, Ь]. Следова-
Следовательно, интегральные суммы ат, атс и отъ при условии, что мелкости
разбиений т, т? и тьс стремятся к нулю, имеют конечные пределы —
интегралы от функции по указанным отрезкам:
с	Ь	Ь
lim атс = fix) dx. lim ать = f(x) dx. lim aT = / /(ж) <ix.
|racH0 a У W	|rbH0 c У	|т|-Ю	У
a	c	a
Поэтому, перейдя к пределу в равенстве B4.7) при условии \т\ ->• О
(при этом в силу B4.6) \т%\ ->• 0 и |тс6 ->• 0), получим формулу B4.5). <
Замечание 1. В силу определения интеграла / f(x) dx при Ъ ^ а
а
(см. п. 23.1) формула B4.5) остается в силе и при с ^ 6, если только
функция / интегрируема на отрезке [а, с].	ъ
/г г
+ / = / и, следо-
п h п
г г г г г	а ь а
вательно, / = / — / = / + /. <|
ч/	ч/	ч/	ч/	ч/
а	а \)	а с
Замечание 2. Если функция / интегрируема на отрезках [а, с]
и [с, 6], то она интегрируема и на отрезке [а, 6], а следовательно, для
нее в силу свойства 3° имеет место формула B4.5).
|> Действительно, если функция / интегрируема на отрезках [а, с]
и [с, 6], то она ограничена на них, а поэтому ограничена и на отрез-
отрезке [а, Ь]. Далее, всякое разбиение т отрезка [а, 6], не содержащее точ-
точки х = с, добавлением этой точки превращается в разбиение т', ко-
которое является объединением разбиений отрезков [а, с] и [с, Ь]. Если
точка х = с входит в разбиение г, то положим т' = т. Тогда \т'\ ^ |т|.
Рассмотрим такие интегральные суммы сгг и ат>, что у них на от-
отрезках разбиений т и т', не содержащих точки х — с, выбраны оди-
одинаковые точки, в которых берутся значения функции /. Эти суммы

§24- Свойства интегрируемых функций	265
отличаются друг от друга не более чем на три слагаемых. Поэтому,
если \f(x)\ ^ М, а ^ х ^ 6, то
\аТ - сгг/1 ^ ЗМ\т\ -+ 0 при \т\ -+ 0.
А так как существует предел
с	Ъ
/г
fix) dx + I fix) dx,
J
а	с
то существует и равный ему предел
lim от,
|т|-И)
т. е. функция / интегрируема на отрезке [а, Ь]. <\
Замечание 3. Из свойства аддитивности интеграла и из теоре-
теоремы 4 п. 23.6 следует интегрируемость так называемых кусочно не-
непрерывных на отрезке функций.
Функция называется кусочно непрерывной на отрезке, если она
имеет на нем только конечное множество точек разрыва, и притом
только первого рода. На концах отрезка функция может быть не опре-
определена.
Таким образом, функция / кусочно непрерывна на отрезке [а, 6],
если найдется такое разбиение г = {xk}1^^ этого отрезка, что для
всех к = 1,2,..., кт существуют конечные пределы /(xfc-i + O) и
f(xk -0). В точках Xk, к = 0,1, 2,..., &г, функция / может быть
определена или не определена.
Если положить
def f f(xk-i + 0) при x = xk-i,
fk(z) = < /О)	при хк-Х < х < хк,
{f(xk-0) при х = хк,
то функция fk будет непрерывна, а поэтому, согласно теореме 4 п. 23.6,
и интегрируема на отрезке [хк-1,хк], к = 1, 2,..., кт.
Отсюда следует интегрируемость функции / на отрезке [а, Ь] (зна-
(значения функции / в тех точках хк, в которых она не определена, можно
задавать произвольно: это не влияет ни на существование, ни на зна-
значение интеграла) и справедливость формулы
Ъ	кт хк
Г /О) dx = ^2 J fk(x) dx-
а	к=1 хк_х
5°. Интегрируемость произведения интегрируемых
функций. Если функции fug интегрируемы на некотором от-
отрезке, то их произведение также интегрируемо на этом отрезке.
|> Если функции / и g интегрируемы на отрезке [а, Ь], то они на нем

266	Гл. 2. Интегральное исчисление функций одной переменной
ограничены, т. е. существует такая постоянная А > О, что для всех
х Е [а, Ъ] выполняются неравенства
\f(x)\^A, \g(x)\^A,	B4.8)
а следовательно, и \f(x)g{x)\ ^ А2 , т. е. произведение fg ограничено
на отрезке [а, Ь]. Проверим для него выполнимость критерия B3.21)
интегрируемости функций. Из тождества
f(x')g(x') - f(x)g(x) = [f(x') - f(x)]g(x') + [g(x') - g(x)]f(x),
xe[a,b], x'€[a,b],
имеем
\f(x')g(x') ~ f(x)g(x)\ < \f(x') - f(x)\\g(x')\ + \g(x') - g(x)\\f(x)\ <
^ A[\f(x') - f(x)\ + \g(x') - g(x)\]. B4.9)
Если г = {x/e}^QX — разбиение отрезка [а, 6], то, выбирая точки х
иж'в одном и том же отрезке [xk-i,Xk] этого разбиения и переходя в
неравенстве B4.9) к верхним граням по всевозможным х е [xk-i,Xk]
и х' G [xk-i,Xk], получим
: A[uk(f) + uk(g)], k = 1, 2,.., kT;
здесь cjjfe(-), как обычно, — колебание соответствующей функции на
отрезке [xk-i,Xk]. Отсюда
к=1	к=1	к=1
В силу интегрируемости функций / и д на отрезке [а, Ь] имеем
(см. B3.21))
lim V^cj(/)Ax^ = lim V^c^^Ax/. =0.
Поэтому из неравенства B4.10) следует, что lim 2^uk(f 9)^xk = 0,
откуда в силу того же критерия B3.21) и вытекает интегрируемость
произведения fg. <\
6°. Интегрирование частного интегрируемых функ-
функций. Если функции fug интегрируемы на некотором отрезке и абсо-
абсолютная величина функции д ограничена на нем снизу положительной
постоянной, то частное — также интегрируемо на этом отрезке.
9
|> Покажем, что при сделанных предположениях функция - интег-
9
рируема. Пусть функция д интегрируема на отрезке [а, Ь] и существу-
существует такая постоянная с > 0, что для всех точек х G [а, Ь] выполняется

§24- Свойства интегрируемых функций	267
неравенство \д(х)\ ^ с. Тогда для любых точек х,х' е [а,Ь] имеем
1	1
\д(х)-д(х')\ 1	,
с)| ^ С2 \9\х) У\х Л-
0(ж') р(ж)
Если т = {x^}^qx — разбиение отрезка [а, Ъ] и точки ж, ж' со-
содержатся в одном и том же отрезке [xk-i->Xk]-> к = 1, 2,..., fcr, разбие-
разбиения г, то переходя к верхним граням в полученном неравенстве, бу-
будем иметь
Отсюда
кт
к=1	к=0
В силу интегрируемости функции д правая часть неравенства стре-
стремится к нулю при \т\ —У 0. Поэтому стремится к нулю и его левая
часть. Это означает интегрируемость функции - на отрезке [а, Ь].
Если функция / также интегрируема на этом отрезке, то частное -,
9
будучи произведением интегрируемых функций /и -, сог-
9
ласно свойству 5° также интегрируемо. <|
7°. Интегрирование неравенств. Если функции fug ин-
интегрируемы на отрезке [а,Ь] и
f(r) > п(т) т ^ \п Ы	B4 1Л
то
ъ	ъ
ff(x)dx ^ fg(x)dx.	B4.12)
а	а
В частности, если f(x) ^ 0, х е [а, 6], то
ъ
ff(x)dx ^0.	B4.13)
а
\> Из неравенства B4.11) следует, что для любых интегральных
сумм (TT(f) и сгт{д) соответственно функций / и д выполняется нера-
неравенство
кт	кт
ат(Л = ^2f(b)Axk ^ ^2д(?к)Ахк = <тт(д),	B4.14)
к=1	к=1
ибо f(?k) ^ g(?,k), к = 1, 2,..., кт. Переходя в неравенстве B4.14)
B4.11)
к пределу при \т\ —У 0, получим неравенство B4.12).
Неравенство B4.13) следует из неравенства B4.12) при д(х) = 0. <1

268	Гл. 2. Интегральное исчисление функций одной переменной
8°. Если функция f интегрируема и неотрицательна на отрез-
отрезке [а, Ь], существует точка хо Е [а, Ь], в которой функция f непрерыв-
непрерывна, и f(x0) > О, то	ь
ff(x)dx > О.
а
> Если функция / непрерывна в точке хо Е [а, Ь] и /(жо) > О, то из
очевидного неравенства /(жо) >	> 0 согласно "лемме о сохра-
нении знака" (см. следствие из следствия 2° в п. 6.7) следует, что
существует такой отрезок [а,/3], что хо Е [а,/3] С [а,Ь], а < C, и для
всех точек х G [а, C] выполняется неравенство
№) 2 ^f1,	B4.15)
а тогда
Ъ
ff(x)dx = [f(x)dx+ [f(x)dx+ [f(x)dx
{ B4-з)/ I i
B4-з)/
f(x)dx
B4.13)./	B4.12) J 2	B4.1) 2
B4.15) a
9°. Если функция f интегрируема на отрезке [а, Ь], то ее абсолют-
абсолютная величина |/| интегрируема на нем и
ь	ь
\jf(x)dx\ <С f\f(x)\dx.	B4.16)
а	а
\> Прежде всего из интегрируемости функции / следует ее ограни-
ограниченность, а следовательно, и ограниченность функции |/|. Покажем,
что для функции |/| выполняется критерий интегрируемости B3.21).
Заметив, что для любых двух точек х Е [а, Ь] и х' Е [а, Ь] спра-
справедливо неравенство
рассмотрим какое-либо разбиение т — {хк}\^т отрезка [а, Ъ]. Тогда,
выбирая точки х и х' из одного и того же отрезка [хк-1,хк] этого
разбиения, х Е [хк-1,хк], х' Е [хк-1,хк], и переходя в обеих частях
неравенства B4.17) к верхним граням, будем иметь
х'х'е[хк-1'Хк]	^ sup \f(x')-f(x)\=uk(f),
Х,х'е[хк-1,Хк]
где (Jk(\f\) и Uk(f) — колебания соответственно функций |/| и / на
отрезке [xk-i,Xk], к = 1, 2,..., кт. Поэтому
кт	кт
О ^ ^uk(\f\)bxk ^ ^
к=0	к=1

§24- Свойства интегрируемых функций	269
а поскольку, согласно уже упоминавшемуся критерию интегрируе-
интегрируемости B3.21), для интегрируемой функции / выполняется условие
lim S^tok(f)Axk = 0, то и lim "S^ u>k(\f\)Axk = О, откуда и сле-
дует интегрируемость функции |/|.
Если теперь crr(/) = ^/(^)Axfe, €k€[xk-i,xk], k = 1, 2,..., fcrj
т. e. (TT(f) — интегральная сумма Римана функции /, то
kT	kT
Ч E l/«*)lA^ =MI/I),	B4.18)
где в правой части неравенства стоит интегральная сумма Римана
ъ	ъ
функции |/|. Так как lim crT(f) = lf{x)dx, lim oy(|/|) = l\f{x)\dx,
Irl^O	J	|r|->0	У
a	a
то, перейдя в неравенстве B4.18) к пределу при \т\ ->• 0, получим
J\f(x)
dx.
Заметим, что если не предполагать, что а < Ъ (см. п. 23.1), то вмес-
вместо неравенства B4.16) следует писать
ъ	ъ
\jf(x)dx\ <: \f\f(x)\dx\.	B4.19)
а	а
10°. Непрерывность интеграла. Если функция f интегри-
интегрируема на отрезке [а, 6], то функции
X
F(x) Hf ff{t) dt,	B4.20)
a
b
G(x)d= Jf(t)dt	B4.21)
x
непрерывны на этом отрезке.
Следствие. Если функция f интегрируема на отрезке [а, 6], то
Ъ-е	Ъ
lim I f(x) dx = ff(x) dx, 0 < г < b - a.	B4.22)
a+e	a
\> Функция /, будучи интегрируемой на отрезке [a, 6], ограничена
на нем, поэтому существует такая постоянная с > 0, что для всех
х G [a, b] выполняется неравенство
\f(x)\^c.	B4.23)

270
Гл. 2. Интегральное исчисление функций одной переменной
ж+Аж
Представим интеграл / f(i)dt в виде суммы (см. B4.3)):
а
ж	ж	ж+Дж
f(t)dt = Jf(t)dt+ I f(x)dt	B4.24)
ж+Дж
(отметим, что это равенство верно как при Ах ^ 0, так и при Ах <
< 0, лишь бы х Е [а, Ь] и х + Ах Е [а, Ь]). Теперь видно, что прираще-
приращение AF(x) функции F(x) (см. B4.20)) можно записать в виде
ж+Дж
AF(x) = F(x + Ax) - F(x) = / f(t) dt - ff(t) dt =
B4.20) J	J	B4.2
B4.24)
B4.24)
B4.25)
Поэтому
I дед i = I nt)dt
ж+Дж
ж+Дж
B4.19)
Г \f(t)\dt
ж+Дж
B4.23)
I dt =с|Дж|.
Отсюда, очевидно, сразу следует, что lim AF(x) = 0, т. е. непрерыв-
Аж-^О
ность функции F{x).
Непрерывность функции G(x) следует из непрерывности функ-
х	Ъ	Ъ
ции F(x). В самом деле, поскольку f(t)dt+ f(t)dt = f(t)dt,
B4.26)
постоянная величина, то непрерыв-
непрерывЬ	а
т. e.F(x)+G(x) = ff(t)dt, то
{	ь
G(x)=ff(t)dt-F(x),
ь	а
а так как интеграл f(t)dt —
ен
ность функции F влечет за собой непрерывность функции G. <\
Свойство непрерывности функции F называется непрерывностью
х
интеграла f(t)dt no верхнему пределу интегрирования, соответст-
а
венно свойство непрерывности функции G — непрерывностью интег-
интеграла по нижнему пределу интегрирования.
\> Для того чтобы убедиться в справедливости равенства B4.22), вы-
С	X
берем какую-либо точку с G (а, Ь), тогда функции //(?) dt и //(?) dt
X	С
в силу свойства 9° непрерывны соответственно в точках х = а и

§24- Свойства интегрируемых функций
271
х = Ь, поэтому при 0 < г < Ъ - а будем иметь
Ь—е	с	Ь—е
lim / fix) dx = lim [ / fix) dx + Г fix) dx] =
e^O J J X J B4.3) s^O L J V J	J V J J
a+e
b-e
= lim / fix) dx + lim / fix) dx = / f(ж) dx + fix) dx =
e^O J K J	s^O J J K J св. 9° У V У	У V У B4.
B4.3)
B4.
a
24.2. Интегральная теорема о среднем.
Теорема. Пусть на отрезке [a, b]:
1) функции fug интегрируемы;
2)т^ f(x) <: М;
3) функция д не меняет знака.
Тогда существует такое число /i, m ^ \i ^ M, что
6
= ff(x)dx.
4.3) У V У
и	и
J f(x)g(x) dx = iiJg(x) dx.
B4.27)
B4.28)
Следствие. Если в дополнение к условиям теоремы функция f
непрерывна на отрезке [а, 6], то на интервале (а,Ь) существует
такая точка ?, что
ъ
Jf{x)g{x)dx =
а	Ъ
= f@J9(x) dx, a<?<b, B4.29)
а
в частности, при д(х) = 1 на [а, Ь]
ь
а	О
(рис. 103).
> Умножив неравенство B4.27) на	Рис' 103
д(х), получим, что для всех х Е [а, Ь] в случае д(х) ^ 0 выполняется
неравенство	. ч ., ч . ч	. ч
тд(х) ^ f{x)g(x) ^ Мд(х),
а в случае д(ж) ^0 — неравенство
™#(ж) ^ f(x)g(x) ^ Мд(х).
Интегрируя эти неравенства, будем иметь
ъ	ъ	ъ
т Гд(х) dx ^ ff(x)g(x) dx ^ М Гд(х) dx,	B4.30)

272	Гл. 2. Интегральное исчисление функций одной переменной
или соответственно
ъ
Если
т fg(x) dx ^ ff(x)g(x) dx ^ М Гд(х) dx.	B4.31)
а	а	а
Ъ
Гд(х) dx = О,	B4.32)
то как в первом, так и во втором случае
ъ
Jf(x)g(x)dx = 0	B4.33)
а
и, следовательно, равенство B4.28) верно при любом /i, так как обе
его части, согласно B4.32) и B4.33), обращаются в нуль.
ъ	ъ
д(х) dx ф 0, то при д(х) ^ 0 имеем / д(х) dx > 0, а при
h	^
а	°	а
д(х) ^0 — соответственно д(х) dx < 0.
{	ь
Поделив обе части неравенств B4.30) и B4.31) на интеграл д(х) dx,
а
в обоих случаях получим одно и то же неравенство
ъ
jf(x)g(x)dx
т ^ ^—ь	 ^ М.	B4.34)
Jg{x)dx
Определим число \i равенством
ъ
jf(x)g(x)dx
A
B4-35)
Jg(x)dx
Ь	Ь
/Г
f(x)g(x)dx = /л g(x)dx, причем в силу B4.34) и B4.35) вы-
а	а
полняется неравенство т ^ \i ^ М. <\
Докажем следствие.
|> Если функция / непрерывна на отрезке [а, 6], то согласно теореме
Вейерштрасса она достигает своих наибольшего и наменьшего значе-
значений в некоторых точках а и /3 этого отрезка:
f(a) = min/(x), f(/3) = max/(ж).	B4.36)
[a, b]	[a,b]

§24- Свойства интегрируемых функций	273
m = /(a), M = f(/3)	B4.37)
выполняется условие B4.27) теоремы и, следовательно, существует
такое число /i,
m^ja^M,	B4.38)
для которого выполняется равенство B4.28).
В силу условий B4.37), B4.38), согласно теореме Больцано-Коши
о промежуточных значениях непрерывной функции, на отрезке [а, Ь]
существует точка ?, для которой имеет место равенство /(?) = /i, a
поэтому и равенство B4.29). Покажем, что, более того, точку ? всегда
можно выбрать так, что она будет лежать на интервале (а, Ь).
ъ	ъ
Если д(х) dx = 0, то из формулы B4.28) следует f(x)g(x) dx =
а	а
= 0, поэтому равенство B4.29) выполняется при любом выборе точ-
точки ? е (а, Ъ).
Пусть теперь	ъ
Jg{x) dx ф 0,	B4.39)
а
и для определенности д{х) ^ 0 во всех точках х отрезка [а, 6], а сле-
следовательно,	ь
fg(x) dx^O	B4.40)
а
(случай д(х) ^ 0, а ^ х ^ 6, сводится к рассматриваемому заменой
функции д(х) на функцию —д(х): применив к неотрицательной функ-
функции д(х) формулу B4.29) и умножив обе части равенства на —1, по-
получим и в этом случае формулу B4.29)).
Из выполнения условий B4.39) и B4.40) следует, что
ь
fg(x) dx > 0.	B4.41)
а
В силу неравенства B4.38) возможны три случая: т < \i < М,
\i — М и \i — т. Если т < \i < М, то из условий B4.37) согласно
теореме Больцано-Коши о промежуточных значениях непрерывной
на отрезке функции следует, что между точками а и /3, а следова-
следовательно, на интервале (а, Ь) существует такая точка ?, что /(?) = \i.
Если же \i — М, то равенство B4.28) примет вид
ь	ь
Jf(x)g(x) dx = Mjg(x) dx,
a	a
откуда	b
f(M - f(x))g(x) dx = 0.	B4.42)
a
18 Л.Д.Кудрявцев, т.1

274	Гл. 2. Интегральное исчисление функций одной переменной
Из неравенства B4.41) в силу следствия из свойства 10° опреде-
определенного интеграла (см. п. 24.1) существует такое г > 0, что
Ь-е
[ g(x) dx > 0.	B4.43)
а+е
Если бы на интервале (а, Ь) не существовала точка ?, в которой
/(?) = М, то непрерывная функция М — f(x) была бы положитель-
положительной во всех точках отрезка [а + е,Ь - е], а следовательно, и в точке
хо Е [а + е,Ь — е], в которой она принимает наименьшее значение на
этом отрезке; т. е., если
M-f(xo)= min (М-/(ж)),	B4.44)
[а+е, Ь-е]
ТО
М - f(x0) > 0.	B4.45)
Поэтому
Ъ	Ь-е
[(M-f(x))g(x)dx> [ (M-f(x))g(x)dx >
I	a{e	<24'44) h
b-e
> (M-f(x0)) f g(x)dx > 0,
B4.44)	J	B4.43)
a+?	B4.45)
что противоречит равенству B4.42). А это означает, что на интерва-
интервале (а, Ъ) существует такая точка ?, что /л = М = /(?).
Случай \i-vn рассматривается аналогично. <\
§ 25. Определенный и неопределенный интегралы
25.1. Дифференцирование определенного интеграла по
пределам интегрирования. При изучении свойств интеграла была
установлена (см. свойство 10° в п. 24.1) его непрерывность по преде-
пределам интегрирования, т. е. непрерывность функций
х	Ъ
F(x) = ff(t)dt, G(x)=Jf(t)dt
а	х
на отрезке [а, Ь]. Оказывается, что с "улУчшением" свойств подын-
подынтегральной функции / "улУчшаются" и свойства функций F и G.
Так, например, если функция / непрерывна на отрезке [а, Ь], то будет
показано, что функции F и G являются уже дифференцируемыми.
Докажем даже более точную теорему о дифференцируемости
функции F в точке xq.

§25. Определенный и неопределенный интегралы
275
Теорема 1. Если функция f интегрируема на отрезке [а,Ь] и не-
X
прерывна в точке хо Е [а,Ь], то функция F{x) = / f(t)dt дифферен-
дифференцируема в этой точке и	а
F'(x0) = f(x0).	B5.1)
Следствие. Всякая непрерывная на отрезке функция имеет на
нем первообразную.
|> Используя представление приращения AF(xo) в виде (см. B4.25))
AF(x0) = J f(t) dt, xo e [a, b], x0 + Ax e [a, b],
XQ
и тождество -— / dt = 1, будем иметь
Ax J
XQ + /1
~Ax~ J
AF(xq)
Ах
XQ
жо+Аж
/ dt
Ax J
XQ
. B5.2)
XQ
XQ
Зададим произвольно г > 0. В силу непрерывности функции / в
точке хо существует такое S > 0, что если \t — хо\ < S и t G [a, Ь], то
\f(t) - f(xo)\ < г.	B5.3)
Пусть Ах таково, что |Аж| < S; тогда для всех значений ?, при-
принадлежащих отрезку с концами хо и хо + Ах (по которому ведется
интегрирование в неравенстве B5.2)), будем иметь \t — хо\ ^ |Аж| < S
и, следовательно,
\f(t)-f(xo)\<e.	B5.4)
Поэтому
1
-/(*)
B5?2)
\№-f(xo)\dt
XQ
B5.4)
е
B5?4) 1А^
/
XQ
dt
= г.
г,	у AF(xq)
Это, согласно определению предела, и означает, что lim —-^—- =
= /(жо), и, таким образом, формула B5.1) доказана. <\
Для доказательства следствия достаточно заметить, что равенст-
равенство B5.1) в случае непрерывной на отрезке функции имеет место во
всех точках этого отрезка.
18*

276	Гл. 2. Интегральное исчисление функций одной переменной
Замечание. Из доказанного следует, что в условиях теоремы 1
функция	ъ
G(x)=jf(t)dt
X
также имеет производную в точке ж0 и
G'(x0) = -/(я*).	B5.5)
Это сразу следует из формулы B5.1), ибо (см. B4.26))
ь
G{x) = Jf(t) dt - F(x)
и //(*)
dt — постоянная величина.
Если функция / непрерывна на отрезке [а, 6], то для каждой его
точки х справедливы формулы
х	ь
?//(*) dt = Дат), ?//(*) dt = -/(*).	B5.6)
а	х
25.2. Существование первообразной.
Теорема 2. Если функция f непрерывна во всех точках неко-
некоторого промежутка А, то на этом промежутке у нее существует
первообразная; при этом если х0 — какая-либо точка рассматривае-
рассматриваемого промежутка А, то функция
X
F(x) = [f(t)dt, жеД,	B5.7)
XQ
является одной из первообразных функций f на промежутке А.
|> Достаточно проверить, что функция B5.7) действительно явля-
является первообразной функции /. Если х > ж0, х е А, то равенство
F'(x) = f{x) сразу следует из теоремы 1. Если же х < хо, х G А, то
XQ	X
Замечание 1. Совокупность всех первообразных непрерывной
на некотором промежутке А функции / составляет неопределенный
X
интеграл f(x) dx, x G А, а определенный интеграл //(?) dt, x0 G А,
XQ
х е А, является одной из первообразных функции / на А. Поскольку
две любые первообразные отличаются на постоянную, то
х
Jf(x) dt = Jf(t) dt + С,	B5.8)

§25. Определенный и неопределенный интегралы	277
где С — произвольная постоянная. Так выглядит связь между не-
неопределенным и определенным интегралами. Из теоремы 2 следует,
что у всякой непрерывной на некотором промежутке функции су-
существует на этом промежутке неопределенный интеграл.
Теорема 3 (основная теорема интегрального исчисления). Ес-
Если функция f непрерывна на отрезке [а, 6], то, какова бы ни была на
этом отрезке ее первообразная Ф, справедлива формула
о),	B5.9)
называемая формулой Ньютона-Лейбница.
X
|> По теореме 2 функция F(x) = f(t)dt является первообразной
а
функции / на отрезке [а, Ь]. Если Ф — какая-либо первообразная
на [а, Ь] той же функции /, то они отличаются на постоянную, т. е.
существует такая постоянная С, что для всех х Е [а, Ь] имеет место
равенство
f	B5.10)
а
Положив здесь х = а и вспомнив, что f(t)dt = 0, получим С =
а
= —Ф(а). Подставив это значение в формулу B5.10), будем иметь
= Ф(ж) -Ф(а), хе [а,Ъ].
i
Формула B5.9) получается отсюда при х = Ъ. <\
Отметим, что формула Ньютона-Лейбница B5.9) справедлива и
для а > Ъ. Действительно, если в ней поменять местами а и Ь, то обе
части равенства B5.9) изменят знак на противоположный.
Замечание 2. В формуле B5.9) Ф'(?) = f(t). Поэтому ее можно
записать в виде	ъ
-Ф(а),	B5.11)
т. е. интеграл от непрерывной производной равен разности значений
самой функции на концах отрезка, по которому производится интег-
интегрирование.
Замечание 3. С помощью формулы B5.11) нетрудно показать,
что формула Ньютона-Лейбница B5.9) остается верной и в случае,
когда функция Ф непрерывна, а ее производная / кусочно непрерывна
на отрезке [а, Ь] (см. замечание 3 в п. 24.1), а равенство Ф'(х) = f(x)
выполняется во всех точках непрерывности функции /.

278
Гл. 2. Интегральное исчисление функций одной переменной
Примером непрерывной первообразной кусочно непрерывной
функции / является, например (см. теорему 1), функция
F(x)=ff(t)dt.
а
1
Примеры. 1. Вычислить значение интеграла х3 dx. Посколь-
А
ку х3 dx =	\-С, то по формуле Ньютона-Лейбница получим
} з ^ *4
/ х dx = —
1 _ 1
о ~ 4*
тг/2
2. Найдем значение интеграла / cosxdx. Имеем
-тг/2
тг/2	^
/ cos х dx = sin ж
-тг/2
-тг/2
= 2.
§ 26. Формулы замены переменной и интегрирования
по частям в определенном интеграле
26.1. Формула замены переменной. Пусть функция f(x) за-
задана на промежутке Дж, а функция ip(t) — на промежутке At и
tp(At) С Ах. Тогда имеет смысл ком-
композиция / о (^, т. е. сложная функ-
функция f(<p(x)).
Теорема 1. Если функция f(x) не-
непрерывна на промежутке Дж, а функ-
функция if(t) непрерывна вместе со своей
производной (p'(t) на промежутке At, то
Ъ	C
ff(x)dx = ff(<p(t))<p'(t)dt, B6.1)
Ч ъ
\ а
О
где
Рис. 104
(рис. 104).
Формула B6.1) называется форму-
формулой замены переменной в определенном интеграле.
> Пусть F(x) — какая-либо перво образная для функции f(x) на
промежутке Аж; тогда функция F((p(t)) является первообразной для

§26. Формулы замены переменной и интегрирования по частям 279
функции f((p(t))(p'(t) на промежутке At, ибо
| F(<p(t)) =
Поэтому по теореме Ньютона-Лейбница
C	Ъ
= F(b)-F(a) = Jf(x)dx. <
а	а
26.2. Формула интегрирования по частям.
Теорема 2. Если функции и(х) и v(x) непрерывны вместе со
своими производными на отрезке [а, 6], то
ъ	ъ
udv = uv\a — vdu.	B6.2)
а	а
Формула B6.2) называется формулой интегрирования по частям
для определенного интеграла.
|> Имеем ,	,	1.1.
0	0	0	0
(uv)' dx = / (uv' + u'v) dx = ludv+ I vdu.	B6.3)
a	a	a	a
Все интегралы в B6.3) существуют, поскольку подынтегральные
функции непрерывны. Для интеграла в левой части равенства, со-
согласно формуле Ньютона-Лейбница, имеем
ъ
(uv)' dx = uv
I {
Подставив выражение, стоящее в правой части последнего равенства,
в B6.3), получим	ъ	ъ
I udv + v du = uv\a,
а	а
что равносильно B6.2). <|
Замечание. Можно доказать, что формула интегрирования по
частям B6.2) остается верной и в том случае, когда функции и и v
непрерывны, а их производные кусочно непрерывны (см. п. 24.1).
Примеры. 1. Применим формулу интегрирования по частям для
2
вычисления интеграла / \nxdx:
2	1	2
/ \nxdx = ж1пж|^ — / dx = 2 In 2 — 1.
i	i
2. Приведем пример интеграла, при вычислении которого приме-
применим и замену переменной, и интегрирование по частям. Вычислим
интеграл /= / sin х л/1 + cos2 x dx.

280
Гл. 2. Интегральное исчисление функций одной переменной
Сделав сначала замену переменной t = cos ж, а затем проинтег-
проинтегрировав по частям, получим
/=
-1
1
t2dt= [ )
J VT
-1
T1?
dt =
= ln
л/2 + 1
л/2 — 1
-1
-1
1 +12
..-/•
л/2) + 2л/2 -
Из получившегося относительно / уравнения находим
Заметим, рассмотренный интеграл можно вычислить, и приме-
применяя только замену переменной. Для этого можно воспользоваться, на-
например, уже вычисленным неопределенным интегралом / у 1 + х2 dx
(пример в п. 19.4).
3*. Покажем, что для любого п = 1, 2,...
тг/2
тг/2
(п-1)!! тг
In = sinnxdx= / cosn
У	J
п — при п четном,
(п-1)!!
при п нечетном.
B6.4)
Под n!!, n Е А/, понимается произведение всех натуральных чисел,
не превышающих п и имеющих ту же четность, что и число п:
Bп)!! = 2-4- ...• Bп-2) • 2п,
Bп + 1)!! = 1 • 3 • 5... • Bп - 1) • Bп + 1).
По определению 0!! = 1.
тг/2
Положив для удобства /0 = \ dx — ^- и проинтегрировав по час-
о
тям интеграл 1п при n ^ 2, имеем
тг/2	тг/2
In = smnxdx= / sin71 xd(— cos ж) =
о	о
тг/2
= — sin71 xcosx|q + (n — 1) / sinn~2 x cos2 x dx =
о
7Г/2
= (n-l) Г sinn~2 жA - sin2 ж) dx = (n- l)/n_2 - (n - l)/n,

§26. Формулы замены переменной и интегрирования по частям 281
откуда	_
1п = ^1п-2-	B6.5)
Заметим, что
тг/2
/о = —, h = / sinxdx = 1.	B6.6)
о
Поэтому при п = 2& + 1, т. е. при нечетном п,
2fe	_ _
2^TT 2'-1 " - " (
l)...l 7l " B1fe + l)!!
а при n = 2k, т. е. при четном п,
, 2fc-l	Bfc-l)Bfc-3)-l r Bfc-l)!! 7Г
к ZK"Z -	2JfeB1fe-2)...2 u	B1fe)!! 2* v J
тг/2	тг/2
Равенство интегралов / sinn x dx и / cosn x dx сразу получа-
о о
ется с помощью замены переменных х =	?, 0 ^ ? ^ —. Таким
образом, формулы B6.4) доказаны. Из них легко получается формула
Валлиса*)
тг ,.
— = lim
2 ~ пЛ™2п + \\{2п-\)\\) •	^•">
В самом деле, проинтегрировав по отрезку [0,тг/2] неравенства
sin2n+1 х <С sin2n х ^ sin271 х, п = 1, 2,..,
получим
тг/2	тг/2	тг/2
/2Г7-И	С - 2Г7	/"	2Г7 —1
О	0	0
т. е.
Wl ^/2n^/2n-l.	B6.10)
Отсюда в силу формул B6.4) имеем
^^ет^^т^ттт-	B6-11)
Bn +
Если ввести обозначения
_ / () N _
Хп ~ 2^ТТ lBnl)!lJ ' Уп ~ 2^
то неравенства B6.11) можно записать в виде
хп < | ^ 2/п,	B6.13)
:|<) Дж. Валлис A616-1703) — английский математик.

282	Гл. 2. Интегральное исчисление функций одной переменной
где
.	1 7Г	~
^	у О при п —> оо,
B6.13) 2n 2
и, следовательно, lim (?/п — хп) = 0, т. е. длины отрезков \хп,уп],
содержащих точку тг/2, стремятся к нулю, а это означает, что
lim хп = lim ?/п = ^.
Равенство lim жп = — в силу первой формулы B6.12) и пред-
га-юо	2
ставляет собой формулу Валлиса.
§ 27. Площади и объемы
27.1. Понятие площади плоского множества. Проведем на
координатной плоскости х,у для каждого к = 0,1, 2,... всевозможные
прямые	,	,
х = 10~ V, 2/ = Ю~Ч р G Z, <? G Z.
В результате при фиксированном к получим разбиение плоскости на
замкнутые квадраты {(ж, у): 10~кр ^ ж ^ 10~fe(p + 1), К)"*5*? ^ 2/ ^
^ 10~k(q + 1)} со сторонами длины lCT^. Квадраты, из которых со-
состоит это разбиение, будем называть квадратами ранга к. Очевидно,
что каждый квадрат ранга к состоит из 100 равных квадратов ран-
ранга к + 1.
Пусть X — множество на плоскости х,у. Обозначим через Sk =
= Sk(X) объединение всех квадратов ранга к, содержащихся в мно-
множестве X. Все квадраты ранга к + 1, которые получаются разбиением
квадратов ранга к, содержащихся в Sk, заведомо принадлежат Sfc+i.
Поэтому при переходе от к и к + 1 множество Sk может только уве-
увеличиться за счет тех квадратов ранга к + 1, которые содержатся в X,
но не содержатся в квадратах ранга к, принадлежащих Sk. Таким об-
разом'	So с в1 с ... с sk с ... с х.	B7.1)
Каждое Sk состоит из конечного или бесконечного множества квад-
квадратов ранга к. Если их конечное множество, то через /iSk обозначим
площадь многоугольника Sk- Если же Sk состоит из бесконечного мно-
множества квадратов ранга &, то Sk не может иметь конечной площади.
В этом случае будем писать fiSk = +оо.
Очевидно, что если некоторое множество Sk состоит из бесконеч-
бесконечного множества квадратов ранга к, то и для всех к' > к множества s^
также состоят из бесконечного множества квадратов ранга к', так как

§27. Площади и объемы	283
уже тех квадратов ранга к', которые содержатся в квадратах ранга к,
принадлежащих Sk, будет бесконечно много. Поэтому если fiSk = +00,
то и для всех к' > к имеет место [iSk> = +00.
Из включений B7.1) следует, что
fiso ^ /xsi ^ ... ^ fiSk ^ ...,	B7.2)
иначе говоря, последовательность {/ask} точек, вообще говоря, рас-
расширенной числовой прямой R возрастает и потому имеет конечный
или бесконечный предел lim /ask, называемый площадью или мерой
к^-оо
множества X и обозначаемый \iX. Таким образом,
d= lim iisk(X).	B7.3)
к—юо
Согласно этому определению каждое множество на плоскости име-
имеет конечную или бесконечную площадь. Площадь всякого ограничен-
ограниченного множества конечна. В самом деле, если множество X ограни-
ограничено, то оно содержится в некотором многоугольнике So, состоящем
из конечного числа квадратов нулевого ранга и имеющем поэтому
конечную площадь. В силу этого при любом к = 0,1,2,... Sk(X) С
С X С So и, следовательно, /iSk(X) ^ /iSo < +00, т. е. последова-
последовательность {(/iSk(X)} ограничена сверху, а поэтому имеет конечный
предел.
Иногда меру \iX называют внутренней мерой множества X по
причинам, которые будут ясны из дальнейшего.
Из курса элементарной математики известно, что если мно-
множество X является многоугольником, замкнутым или открытым
(т. е. включающим ограничивающую его ломаную или нет), кругом,
его сектором или сегментом, то площади совпадают с определенны-
определенными нами площадями \iX.
Теорема 1. Если Х\ и Х<± — подмножества координатной плос-
плоскости переменных ж, у и Х\ С Х^, то
^Хг ^ цХ2.	B7.4)
|> Если Sk(Xi) и Sk(X2) — совокупность всех квадратов ранга к,
содержащихся соответственно в множествах Х\ и Х2, к — 0,1,2,...,
то из условия Х\ С Х2, очевидно, следует, что Sk(Xi) С Sk(X2), a
потому fiSk(Xi) ^ /iSk(X2). Переходя в этом неравенстве к пределу
при к —> оо, получим неравенство B7.4). <|
27.2*. Пример неограниченного множества положитель-
положительной конечной площади. Всякое ограниченное множество, как это
было показано выше, имеет конечную площадь. Однако существуют и
неограниченные множества с конечной площадью. Примером неогра-
неограниченного множества нулевой площади является прямая. Приведем
пример неограниченного множества с положительной конечной пло-

284
Гл. 2. Интегральное исчисление функций одной переменной
щадью. Этот пример был построен еще в XIV веке французским
математиком Н. Оресмом*).
На координатной плоскости переменных х и у
рассмотрим квадрат
Его правую половину, т. е. его часть, для точек
которой выполняется неравенство х ^ 1/2, перемес-
переместим так, что она займет положение прямоугольника
Qi = {(х,у): (К ж ^ 1/2, 1^у^2}
(т. е. "поставим" правую половину квадрата Q на
его левую половину; рис. 105). Далее, правую поло-
половину прямоугольника Qi, т. е. его часть, для точек
которой выполняется неравенство х ^ 1/4, перемес-
переместим так, что она займет положение прямоугольника
О
111 1 х
8 4 2
Рис. 105
(т. е. снова "поставим" правую половину на левую)
и так далее.
Продолжая этот процесс, получим неограничен-
неограниченную фигуру Р ("башню"), являющуюся объединением левой полови-
половины Q и правых половин прямоугольников Q, Qi, Q2, ..., поставленных
друг на друга и на левую полови-
половину квадрата Q. Указанные части,
составляющие фигуру Р, пред-
представляют собой прямоугольники,
равновеликие прямоугольникам,
лежащим в квадрате, площа-
площади которых образуют бесконечно
убывающую геометрическую про-
1 1 1
О
±11 1 х
8 4 2
Рис. 106
грессию -, -, -,
1
сумма кото-
которой равна 1, т. е. площади квадра-
квадрата Q: i + i + i + ... = 1. Естест-
Естественно, что площадь бесконечной
фигуры Р равна (как это можно
доказать) площади квадрата Q,
т. е. положительной конечной ве-
величине.
Заметим, что бесконечная фи-
фигура Р лежит над осью х и под
графиком "ступенчатой" (кусочно
постоянной) функции, изображенной на рис. 106.

§27. Площади и объемы	285
Нетрудно получить и бесконечное множество конечной площади,
ограниченное графиком непрерывной на полуинтервале @,1] функ-
функции, положительной полуосью оси у, отрезком 0 ^ х ^ 1, у = 0, оси х.
Чтобы получить график такой функции, достаточно, например, со-
соединить прямолинейными отрезками правые концы ступенек графи-
графика функции, изображенной на рис. 106. В результате получится функ-
функция, график которой изображен на рис. 107.
Отметим, что эта функция, будучи неограниченной, неинтегри-
руема по Риману.
27.3. Понятие объема. Пусть в трехмерном пространстве R3
фиксирована декартова прямоугольная система координат ж, у, z.
Аналогично разбиению плоскости на квадраты ранга к = 0,1,2,...
можно произвести разбиение пространства R3 на кубы с помощью
плоскостей, параллельных координатным плоскостям и отстоящих
последовательно друг от друга на расстояние 10~fe, точнее, с помо-
помощью плоскостей х = 10~кр, у = 10~kq, z = 10~*т, p,q,r Е Z, т. е. на
кубы
{(х, у, z): 10- кр ^х^ 10-к(р + 1), 10~kq ^у^ 1(Г*(д + 1),
10~kr ^z ^ 10~fe(r + l)}.
При фиксированном к получится разбиение пространства R3 на ку-
кубы с ребрами длины 10-/\ Кубы этого разбиения называются кубами
ранга к.
Для любого множества X С R3 через Sk(X) обозначается совокуп-
совокупность всех кубов ранга к, содержащихся в множестве X. Очевидно,
как и в случае плоскости,
so(X) С Sl(X) С ... С зк(Х) С ... С X,	B7.5)
и, следовательно, последовательность объемов /iSk(X) конечных
или бесконечных многогранников Sk(X), к = 0,1,2,..., является
возрастающей:
fiso(X) <: fjLSl(X) ^ ... ^ fjLsk(X) ^ ...	B7.6)
Объем (мера) \iX множества X (или, подробнее, внутренний
объем, внутренняя мера) определяется как конечный или бесконеч-
бесконечный предел этой последовательности:
fiXd= lim nsk{X).	B7.7)
к—^оо
Таким образом, всякое множество трехмерного пространства R3
имеет конечный или бесконечный объем. Как и в случае плоскости,
доказывается, что если
IiCl2C/?3,	B7.8)
то
4: ЦХ2.	B7.9)

286
Гл. 2. Интегральное исчисление функций одной переменной
§ 28. Геометрические и физические приложения
определенного интеграла
28.1. Вычисление площадей криволинейных трапеций.
Теорема 1. Если функция f неотрицательна и интегрируема на
отрезке [а, 6], а
Р = {(х,у): а^х^Ъ, O^y^f(x)},	B8.1)
то площадь S множества Р выражается формулой
ь
S=ff(x)dx.	B8.2)
Множество вида B8.1) называется криволинейной трапецией,
порожденной графиком функции /
(рис. 108).
/ у/	Х> Пусть т — {x/.}^~qx — разбиение
отрезка [а, Ь],
О
mk = inf /(ж), Mk = sup /(ж),
k	X^Ak
k = 1,1,..., kT.
B8.3)
Рис. 108
Обозначим соответственно через
рт и Рт замкнутые прямоугольники, составленные из всех прямо-
прямоугольников вида
Рт,к — \\хтУ) • хк — 1 <^ х <^ хк, и ^ у ^ ni<kj,	у^о.Ч:)
т,к — \\хчУ) • Хк — \ ^ Ж ^ Ж&, U ^ у ^ N1}*^,	\Ao.o)
т. е.
кт	кт
Рт= U Рт,к, Рт= U ^г,Л.
B8.6)
Из B8.3) следует, что для любого разбиения т выполняется вклю-
включение рт С Р С Рт, а следовательно (см. теорему в п. 27.1),
fipT^fiP^fiPT.	B8.7)
Из B8.4) и B8.5) следует, что /xpr>A. = ткАхк, \iPT,k = MkAxk, и
так как прямоугольники Рг,^, соответственно рт,к, не имеют общих
внутренних точек, то в силу B8.6)
кт
кт
/ipT =
B8i

Геометрические и физические приложения
287
кТ
Иначе говоря, площади многоугольников рт и Рт равны соответствен-
У
о
Рис. 109
Рис. ПО
но нижней и верхней суммам Дарбу функции / (рис. 109). Поэтому
из неравенства B8.7) следует, что
ST.
B8.10)
ъ	ъ
/г
f(x)dx, то /jlP = f(x)dx. <
J
1 '	' '	а	а
Если функция / неположительна и непрерывна на отрезке [а, Ь] и
то
ь
= - ff(x)dx.
> Действительно, если
), хе[а,Ь],
B8.11)
B8.12)
а Р* — множество, симметричное с множеством Р относительно
оси х (рис. 110), то в силу формулы B8.2)
ъ
^Р* = ff*(x)dx,	B8.13)
а
ибо функция /* уже неотрицательна. Поскольку площади симметрич-
симметричных множеств равны, т. е. /лР* = \лР', а
ъ	ъ
[f*(x)dx = -ff(x)dx,
J	B8.12) J

288
Гл. 2. Интегральное исчисление функций одной переменной
то из равенства B8.13) сразу следует формула B8.11). <|
Если функция / непрерывна и знакопеременна на отрезке [а, Ь], то
интеграл от нее равен "алгебраической сумме", вообще говоря, бес-
бесконечного числа слагаемых, равных площадям криволинейных тра-
трапеций, образованных частями графика функции /, расположенными
соответственно в полуплоскостях у ^ 0 и у ^ 0, причем площади пер-
первых берутся со знаком плюс, а площади вторых — со знаком минус.
Примеры. 1. Найдем площадь, образованную одной аркой си-
синусоиды:
У\
i
sin ж dx = — cosx|0 = 2.
Рис. Ill
2. Найдем площадь S(x) криволи-
криволинейной трапеции, ограниченной ду-
дугой гиперболы у = 1/ж, отрезком [1,ж]
оси х и соответствующими отрезка-
отрезками, параллельными оси у (рис. 111):
=\nx.
S(x) = [j =
28.2. Вычисление площадей в полярных координатах.
Пусть Р — замкнутое множество, граница которого состоит из
некоторой кривой, заданной урав-
уравнением в полярных координатах
р = р((р), а ^ (р ^ C (р((р) — не-
непрерывная функция), и двух отрез-
отрезков (которые могут превращаться
в точки) лучей ip = а и ip = C
(рис. 112), т. е.
О
Рис. 112
Найдем формулу для вычисле-
вычисления площади S = цР множества Р.
Возьмем какое-либо разбиение т = {^Pk}kZoT отрезка [а,/3] и положим
mk = inf
Mk = sup
=(рк

'. Геометрические и физические приложения
289
/с — 1, z,..., /сг,
к
т= U Рт,к,
к
Множества рг^ и Рг^ представляют собой круговые секторы с уг-
углом A(pk и радиусами соответственно т/. и М/,, арт и Рт — ступенча-
ступенчатые фигуры, составленные из указанных секторов и соответственно
содержащиеся в множестве Р и содержащие его: рт С Р С Рг. Из этих
включений следует, что
/ipr ^/iP ^ /iPr.	B8.14)
Согласно формуле для площади сектора
lA	Р	M
поэтому
АФт =
h
2
Получившиеся суммы являются соответственно нижней sr и верх-
верхней Sr суммами Дарбу функции - /Я2((р): sr = /ipr, 5r = /iPr- Таким
образом, в силу B8.14)
sT^S = iiP ^ 5r.	B8.15)
Поскольку суммы Дарбу sr и 5Г при |г| ->• 0 стремятся к одному и
тому же пределу — интегралу от функции - р2((р):
Р 2
1 г
lim sr = lim 5r = - p2 (if) dip,
то из неравенств B8.15) следует, что
S = -
B8.16)
Пример. Найдем площадь S множества, ограниченного кривой
р = а(\ + cosy?), О ^ if ^ 2тг	у
(она называется кардиоидой] рис. 113):	aj
2тг
2тг	2 27Г
+ а / cos (p dtp + —	—^- dy? =
J	Z J	Z
Рис. ИЗ
19 Л.Д.Кудрявцев, т.1

290
Гл. 2. Интегральное исчисление функций одной переменной
28.3. Вычисление длины кривой. Применение определенного
интеграла к задачам вычисления площадей множеств было основано
на его равенстве пределу интегральных сумм. Приведем теперь при-
пример применения определенного интеграла, который основан на фор-
формуле Ньютона-Лейбница, позволяющий найти значение функции, ес-
если известна ее производная.
Пусть Г — кривая, заданная своим непрерывно дифференцируе-
дифференцируемым векторным представлением г = r(?), a ^ t ^ b; тогда она спрям-
спрямляема, и если s = s(t) — ее переменная длина дуги, отсчитываемая
от начала, то функция s(t) дифференцируема и s'(t) = |г'(?)|.
По формуле Ньютона-Лейбница для длины S = s(b) кривой имеем
формулу
ь	ь
S = s{b)-s{a) = Js'{t)dt = j\v'{t)\dt (s(a) = 0).	B8.17)
Если r(t) = (x{t),y(t),z(t)), то
b
B8.18)
В случае, когда кривая Г является графиком функции у = /(ж),
а ^ х ^ Ь, для ее длины S в силу B8.18)
справедлива формула
ъ
S = fy/l + y'^dx.	B8.19)
а
Пример. Вычислим длину астроиды
х = a cos3 ?, у = a sin3 t
(рис. 114). В силу симметричности аст-
астроиды относительно координатных осей
ее длина S равна учетверенной длине ее
части, лежащей в первом координатном
угле, т. е. соответствующей изменению параметра на отрезке [0,тг/2].
Заметив, что
х' = -3a cos2 t sin t, у' = За sin2 t cos t,
согласно формуле B8.18), в которой надо положить z' = 0, получим
тг/2	тг/2
5 = 4/ л/9a2 cos4 t sin2 t + 9a2 sin4 t cos2 tdt = 6a / sin 2t dt = 6a.
о	о
28.4. Площадь поверхности вращения. Пусть на отрезке [а, Ъ]
задана неотрицательная функция у = f(x):
f(x) ^0, a^x^b.

'. Геометрические и физические приложения
291
Множество, получающееся вращением графика функции f(x) во-
вокруг оси Ох, называется поверхностью вращения (этого графика).
Определим ее площадь. Пусть г = {хк}1^^ — какое-либо разбиение
отрезка [а, Ь]. Впишем в график функции / ломаную Лг, соответст-
соответствующую разбиению т, т. е. ломаную с вершинами в точках (хк,Ук),
где
Vk = f(xk), к = О,1,...,кт B8.20)
(рис. 115). Звено этой ломаной с кон-
концами в точках {хк-иУк-i) и (хк,Ук)
(будем называть его к-м звеном ло-
ломаной Хт) при вращении его вокруг
оси х описывает боковую поверхность
усеченного конуса (в частности, при
ук_1 = ук — боковую поверхность ци-
цилиндра), площадь которой равна
х1+Ау1 B8.21)
Рис. 115
где yk-i и ук — соответственно радиусы оснований усеченного кону-
конуса, а у/' Ах\ + Ау\ — длина его образующей, Ахк — Хк — Xk-i, Ay к =
— Ук — Ук-it к = 1,2,..., кт. Поэтому площадь LT поверхности, полу-
получающейся от вращения ломаной Лг вокруг оси Ох, выражается фор-
формулой
кт
Ьт = 7г
B8.22)
к=1
Если существует предел lim LT, то он называется площадью по-
поверхности вращения, образованной вращением графика функции во-
вокруг оси х. Таким образом, обозначив через L площадь указанной
поверхности вращения, будем иметь
B8.23)
Т def т т
L = lim LT.
||0
Пусть теперь функция / непрерывно дифференцируема на отрез-
отрезке [а, 6]; тогда для площади поверхности L можно получить удобную
для вычислений формулу в виде некоторого интеграла.
Теорема 2. Если функция f непрерывно дифференцируема и не-
неотрицательна на отрезке [а, 6], то для площади поверхности враще-
вращения, образованной вращением графика функции / вокруг оси Ох, имеет
место формула
L =
|> Функция / непрерывно дифференцируема на отрезке [а,Ь], т. е. ее
производная непрерывна, и, следовательно, ограничена на этом от-
19*

292
Гл. 2. Интегральное исчисление функций одной переменной
резке. Это означает, что существует такая постоянная с > О, что для
всех точек х Е [а, Ъ] выполняется неравенство
|/'(аОКс.	B8.24)
По формуле конечных приращений Лагранжа имеем
Аук = Ук -Ук-i = f'(
Поэтому л/Ах2к + Ayl = у/1 + f/2(?k)Axk, откуда
B8.22)
B8.25)
Эта сумма не является интегральной, так как в ней значения уи-i —
= f{xk-i), Ук = f(xk) и /'F) берутся в разных точках xk-i, xk и ^
отрезка [ж^_1,ж^] разбиения г. Сравним ее с интегральной суммой
К
B8.26)
функции 2тг/(ж)л/1 + //2(ж).
Снова применив формулу Лагранжа, получим
/(&) - J/fc-i =
ft - /F) =
- /F) = f(Ck
B8.27)
Теперь имеем
B8.24)
B8.24)
B8.27)
B8.24)
B8.27)
c(xk -?k)
Поэтому
|crr-Lr|
B8.25)
B8.26)
B8.25)
B8.26)
2тгс
B8.28)
B8.28)
B8.28)

'. Геометрические и физические приложения	293
Отсюда следует, что
lim (аТ - LT) = 0.	B8.29)
Но оТ является интегральной суммой функции 2ъуу/\ + у'2,
где у = /(ж), поэтому
ъ
lim аТ = 2тг fyy/l + y'2dx.	B8.30)
'Г'^	а
И так как в силу формулы B8.29) lim LT = lim aT, то для площа-
площади L поверхности вращения получается формула
ъ
L = lim LT = 2тг yy/l + у'2 dx. <\	B8.31)
B8.23) \т\^0	B8.29) J
B8.30) а
Вспоминая, что у/Т^у^2 dx = (is (см. п. 17.3), т. е. является диф-
дифференциалом длины дуги, формулу B8.31) для площади L поверх-
поверхности вращения можно записать в более компактном виде
ъ
L = 27rfyds.	B8.32)
а
Можно показать, что эта формула остается справедливой для пло-
площади поверхности вращения, образованной вращением вокруг оси х
любой непрерывно дифференцируемой кривой, заданной параметри-
параметрическим представлением х = x(t), у = y(t), a ^ t ^ Ъ, и не пересекаю-
пересекающей ось х. В этом случае в развернутом виде формула B8.32) имеет
вид
о
L = 2ж1Ул/х'2 + у12 dt.	B8.33)
а
Пример. Найдем площадь L поверхности, полученной вращением
вокруг оси х одной арки синусоиды у = sin x. Согласно формуле B8.31)
имеем
L = 2тг / sin х л/l + cos2 xdx.
Интеграл, стоящий в правой части этого равенства, был вычислен
раньше (пример 2 в п. 26.2), он равен 1пA + у/2) + л/2- Поэтому сра-
сразу находим значение искомой площади
L = 2тгAп A + л/2) + л/2).

294
Гл. 2. Интегральное исчисление функций одной переменной
28.5. Объем тел вращения. Пусть функция / неотрицательна и
непрерывна на отрезке [а, Ь], a Q — множество, полученное вращени-
вращением вокруг оси Ох криволинейной трапеции Р, порожденной графиком
функции у = f(x) (см. B8.1) и рис. 108). Такого типа множества на-
называются телами вращения. Покажем, что для объема V этого тела
имеет место формула	ь
B8.34)
V = тг у2 dx.
Обозначим через qT и QT тела, образованные вращением вокруг
оси х ступенчатых фигур рТ и Рт (см. B8.6)), соответствующих неко-
некоторому разбиению т отрезка [а, Ъ]. Из включения рт С р С Рт следует
включение qT С Q С Qr, a следовательно, и неравенство
V =
\iQT.
B8.35)
Объемы \iqT и \iQT равны суммам объемов составляющих их цилинд-
цилиндров, образованных вращением прямоугольников рт k и Рт k (см. B8.4)
к=1	к=1
(рис. 116). Из этих равенств видно, что \iqT и \iQT являются соот-
соотУ
Ъ ос
ветственно нижними и верхними сум-
суммами Дарбу функции тг/2(ж), поэтому
ь
lim {iqT = lim {iQT = тг f2(x) dx,
|т|-И)	IrUO	i
a
откуда в силу B8.35) и следует, что
V = тг f2(x) dx.
B8.36)
Рис. 116
Пример. Найдем объем тела, получающегося от вращения вок-
вокруг оси х одной арки синусоиды у = sin ж:
7Г	7Г	7Г	2
У = тг / sin2 хdx = ^- dx — ^- cos2xdx = ^-.
о	оо
28.6*. Теоремы Гульдина. Центры тяжести плоских фигур
и их моменты относительно осей. Пусть Г — график неотри-
неотрицательной непрерывно дифференцируемой на отрезке [a, b] функции
/5 г = {x^}^qx — разбиение этого отрезка, а Ат — ломаная, соот-
соответствующая этому разбиению и вписанная в кривую Г. Будем кри-
кривую Г и ломаные Аг рассматривать как материальные кривые, т. е.
как имеющие массу. Будем предполагать, что их линейные плот-

'. Геометрические и физические приложения	295
ности равны единице. Это означает, что массы их частей совпадают
с длинами этих частей.
Как и выше (см. п. 28.4), положим
Ук = f(xk), Axk = хк - хк-1, Аук =ук- Ук-i,
А(ХТ)к =
6fe € [хк-1,хк], к = 1,2,...,&г.
Рассмотрим физический смысл суммы
кт	кт
к=1	к=1
являющейся, очевидно, интегральной суммой функции у у/1 + у'2,
у = /(ж), и потому имеющей своим пределом при \т\ ->• 0 интеграл
ъ	ъ
'2dx = jyds.	B8.38)
Каждое слагаемое /(^)А(ЛГ)^ суммы B8.37) является произведени-
произведением массы А(ЛГ)^ fc-ro звена ломаной Лг на некоторое среднее рас-
расстояние f(?k) этого звена от оси ж, т. е. /(^)А(ЛГ)^ является при-
приближенным значением момента fc-ro звена ломаной Лг относительно
оси ж, а вся сумма B8.37) представляет собой приближенное значение
момента этой ломаной относительно той же оси. Предел этих прибли-
приближенных значений моментов ломаных Лг при \т\ —У 0 равен момен-
моменту Мх кривой Г относительно оси х. Поскольку сумма B8.37) при
\т\ —> 0 стремится к интегралу B8.38), то
ъ
Мх= [yds.	B8.39)
а
Этот момент равен моменту относительно оси х материальной точки,
масса которой равна массе кривой Г (в данном случае совпадающей с
ее длиной 5), помещенной в центр тяжести (жо,2/о) этои кривой. Мо-
Момент относительно оси х материальной точки массы 5, находящейся
в точке (жо,2/о)? Равен &Уо- В силу сказанного он совпадает с момен-
моментом Мт. т. е.	п ъ л-	/^о лгл\
Syo = Mx.	B8.40)
Используя формулу B8.39), это равенство можно записать в виде
ъ	ъ
Sy0 = yds. Умножив обе его части на 2тг и вспомнив, что 2тг yds
а	а
является площадью L поверхности вращения (см. п. 28.4), получим,
что
B8.41)

296
Гл. 2. Интегральное исчисление функций одной переменной
Мы доказали эту формулу в предположении, что кривая Г явля-
является графиком функции / (имеет явное представление). Можно пока-
показать, что формула B8.40), а следовательно, и формула B8.41), остает-
остается справедливой и для любой непрерывно дифференцируемой кривой,
замкнутой или незамкнутой, не пересекающей ось х. Таким образом,
верна следующая
Теорема 1 (первая теорема Гульдина*)). Площадь поверхности,
полученной вращением кривой вокруг оси, равна длине кривой, умно-
умноженной на длину окружности, описанной центром тяжести кривой.
В этой теореме предполагается, что кривая, которая вращается
около оси, непрерывно дифференцируема, лежит в одной плоскости с
указанной осью и по одну сторону
от нее.
Эта теорема позволяет иногда нахо-
находить площади поверхностей вращения
без вычисления интегралов. Например,
найдем площадь поверхности тора, т. е.
поверхности, образованной вращением
вокруг оси окружности радиуса г, центр
которой находится на расстоянии а от
оси. При этом будем считать, что ось и
окружность лежат в одной плоскости и не пересекаются, т. е. а > г
(рис. 117).
Поскольку длина вращаемой окружности равна 2тгг, а ее центр яв-
является и ее центром тяжести, то согласно формуле B8.41)
L = 2тга • 2тгг = 4тг2аг.
Отметим, что аналогично формуле B8.40) для другой координаты хо
центра тяжести кривой Г имеет место формула
Sx0 = Му.
Рис. 117
у.
B8.42)
Из соотношений B8.40) и B8.42) следуют формулы для коорди-
координат хо, уо центра тяжести кривой Г, именно,
B8.43)
х0 = My/S, уо = Mx/S,
где момент Му кривой Г относительно оси у может быть вычислен
по формуле, аналогичной формуле B8.39) для момента Мх:
ъ
Му = I xds.
а
Если кривая Г не удовлетворяет условиям, при которых получена
формула B8.39), то можно попытаться разбить кривую Г на конеч-
конечное число кривых, каждая из которых уже удовлетворяет указанным
*) П. Гульдин A577-1633) — швейцарский математик.

'. Геометрические и физические приложения
297
условиям, и воспользоваться тем, что момент относительно оси объе-
объединения тел равен сумме их моментов.
Перейдем ко второй теореме Гульдина.
Пусть функции / и д непрерывны на отрезке [а, Ь], 0 ^ д(х) ^ /(ж),
хе[а,Ь],
х^ Ъ, д(х) ^ у ^ /(х)};	B8.44)
разбиение отрезка [а, 6],
Ахк =хк -хк-1, & е [хк-1,хк],
а Рт — на этот раз ступенчатая фигура, состоящая из прямоуголь-
прямоугольников
Рт,к = {(х,у): хк-\ ^ х ^ хк,
&) < У
как всегда, т =
Рис. 118
с основаниями и высотами, равными со-
соответственно Ахк и f(?k) — 9(€k), к =
= 1,2,...,/сг (рис.118):
кт
Рт= U Рт,к-
Будем рассматривать фигуры Р и
Рт как материальные, т. е. как фигу-
фигуры, имеющие массу с плотностью 1.
Это означает, что масса каждой из их частей совпадает с площадью
этой части.
Центр тяжести прямоугольника Рт^ находится в его центре и, сле-
следовательно, на расстоянии
i[/F) + <?F)]	B8.45)
ОТ ОСИ X.
Момент прямоугольника Рт^ относительно оси х равен произведе-
произведению ординаты его центра тяжести B8.45) на его массу, т. е. в данном
случае на площадь [/(?&) —#(?&)]Джь Таким образом, этот момент
равен
Для момента же Мт ступенчатой фигуры Рг, равного сумме мо-
моментов составляющих его прямоугольников Рт^-> имеем формулу
B8.46)
к=1
Момент Мх самой фигуры Р относительно оси х равен пределу
моментов Мт ступенчатых фигур при \т\ ->• 0:
Мх = lim MT.	B8.47)
||И)

298	Гл. 2. Интегральное исчисление функций одной переменной
Сумма, стоящая в правой части равенства B8.46), представляет
собой интегральную сумму функции - [f2(x) — д2(х)], поэтому име-
имеем также	ъ
lim MT = \ f[f(x) - д2(х)} dx.	B8.48)
|т|-И)	^ J
а
Таким образом, из B8.47) и B8.48) следует, что момент Мх фигу-
фигуры Р относительно оси х равен интегралу, стоящему в правой части
формулы B8.48):	ъ
Mx=l-f[f{x)-g2{x)]dx.	B8.49)
а
Момент фигуры относительно оси равен моменту материальной
точки, масса которой равна массе фигуры и которая помещена в центр
тяжести фигуры.
Поэтому если (жо,2/о) — центр тяжести фигуры Р, то, так как ее
масса в данном случае совпадает с ее площадью S, получим
Мх = Sy0,	B8.50)
или, в силу B8.49),	ъ
Sy^\j[f2{x)-g2{x)]dx.
а
Умножим обе части последнего равенства на 2тг:
ъ	ъ
S • 2ти/о = тг If (x) dx - тг /д2(х) dx.
а	а
В правой части этого равенства стоит разность объемов тел, получен-
полученных вращением вокруг оси х криволинейных трапеций, порожденных
графиками соответственно функций / и д (п. 28.5), т. е. объем V тела,
получающегося вращением фигуры Р вокруг оси х:
B8.51)
Таким образом, доказана следующая
Теорема 2 (вторая теорема Гуль дина). Объем тела, получен-
полученного вращением плоской фигуры вокруг оси, равен площади фигуры,
умноженной на длину окружности, описываемой центром тяжести
фигуры.
Здесь под плоской фигурой понимается множество Р рассмотрен-
рассмотренного выше типа (см. B8.44)), а под ее вращением — вращение этой
фигуры вокруг оси, лежащей с фигурой в одной плоскости и не пере-
пересекающей ее.
Пример. Найдем объем V тора, рассмотренного в качестве при-
примера применения первой теоремы Гульдина. Поскольку площадь вра-
вращаемой фигуры (в данном случае круга) равна тгг2, то в силу форму-
формулы B8.51)	ЛТ	о ел	ел 2 2
v ;	V = тгг2 • 2тта = 2тг2г2а.

'. Несобственные интегралы	299
Отметим в заключение, что для координаты ж0 центра тяжести
фигуры Р имеет место формула (аналогичная формуле B8.50))
Му = Sx0,	B8.52)
где момент Му фигуры Р находится по формуле, аналогичной фор-
формуле B8.49).
Из формул B8.50) и B8.52) получаются следующие формулы для
координат центра тяжести (жо,2/о) ФИГУРЫ Р-
х0 = My/S, уо = Mx/S.
§ 29. Несобственные интегралы
29.1. Определение несобственных интегралов. Пусть функ-
функция / определена на конечном или бесконечном полуинтервале [а, 6),
— оо < а < Ъ ^ +оо, и для любого числа r\ Е [а, Ъ) интегрируема на
отрезке [а, 77].	ц
Определение 1. Функция F(rj) = f(x)dx верхнего предела
а
интегрирования, а ^ г\ < 6, называется несобственным интегралом
и обозначается
ъ
f(x) dx.
ч
Если существует конечный предел lim f(x)dx, то несобствен-
ный интеграл f(x)dx называется сходящимся, а если этот предел
а
не существует, то — расходящимся.
В случае когда несобственный интеграл сходится, говорят также,
что он существует, а если расходится, то не существует.
Ъ	V
Если интеграл f(x)dx сходится, то предел lim f(x)dx обозна-
J	г)—уЪ J
а	ъ
чается тем же символом, что и сам интеграл, т. е.
Ъ	г]
ff(x) dx =f lim ff(x) dx,	B9.1)
J	r]^b J
a	a
и для краткости также называется несобственным интегралом (иног-
(иногда — его значением).
Подчеркнем, что здесь возможны два случая: когда Ъ — конечное

300
Гл. 2. Интегральное исчисление функций одной переменной
число и когда Ь равно бесконечности (рис. 119).
о
а
х О
Рис. 119
Если Ъ конечно, а функция / интегрируема на отрезке [а, 6],
то в силу непрерывности интеграла (свойство 9 в п. 24.1) предел
г]	Ъ
fix) dx, а ^ г) < 6, существует и равен интегралу / fix) dx. Ta-
J
а	а
ким образом, интеграл Римана является частным случаем несобст-
несобственного интеграла.
При условии конечности Ъ определение 1 содержательно, толь-
только если функция / неограничена в любой окрестности точки Ъ (см.
рис. 119): если функция / ограничена на полуинтервале [а, Ъ) и для
любого r\ G [а, Ь] она интегрируема по Риману на отрезке [а, 77], то не-
ъ
трудно убедиться, что несобственный интеграл f(x) dx существует
а
и совпадает с интегралом Римана функции /, произвольно доопреде-
доопределенной в точке х = Ъ.
Для отличия интеграла Римана от несобственного интеграла ин-
интеграл Римана называют иногда собственным интегралом.
ъ
г
Геометрический смысл несобственного интеграла / f(x) dx от не-
а
отрицательной функции / состоит в том, что он, подобно собственно-
собственному интегралу, равен площади криволинейной трапеции
порожденной графиком функции /, причем эта трапеция (как в слу-
случае неограниченной функции / и конечного промежутка [а, 6), так и в
случае бесконечного промежутка [а, Ь)) всегда является (в отличие от
того, что имело место для собственного интеграла) неограничен-
неограниченным множеством.

'. Несобственные интегралы	301
Если а < с < Ь, то из равенства
Г]	С	Г]
ff(x) dx = ff(x) dx + ff(x) dx	B9.2)
а	а	с
сразу видно, что несобственный интеграл B9.1) существует в том
и только том случае, когда существует несобственный интеграл
Ь	V
f(x)dx = lim f(x)dx, причем в случае существования этих ин-
J	г]^Ь J
с	с
тегралов, перейдя в равенстве B9.1) к пределу при rj —У Ь, получим
Ъ	с	Ъ
ff(x) dx = ff(x) dx + ff(x) dx.	B9.3)
a
b	b
В этом равенстве / и / — несобственные интегралы, а / — собст-
собственный интеграл. а с	а
Если функция / определена на полуинтервале (а, 6], —оо ^ а <
< Ъ < +оо, и при любом ? G (а, Ь] интегрируема по Риману на отрез-
отрезке [?, Ь], то аналогично формуле B9.1) несобственный интеграл
ъ	ъ
f(x)dx определяется как функция F(?) = f(x)dx нижнего пре-
а	?
дела интегрирования, а < ? ^ Ъ.	ъ
Если существует конечный предел lim / f(x)dx, то несобствен-
?—Уа J
ный интеграл называется сходящимся, а если этот предел не сущест-
существует, то — расходящимся.
Здесь, как и выше, в случае, когда несобственный интеграл схо-
сходится, говорят, что он существует, а когда расходится, что он не
существует.	ь	ь
Если интеграл f(x)dx сходится, то предел lim f(x)dx обозна-
J	?-)>a J
а	?
чается тем же символом, что и сам интеграл, т. е.
ъ	ъ
ff(x)dxd=\im [f(x)dx,	B9.4)
J	?-)>a J
а	?
и для краткости также называется несобственным интегралом (иног-
(иногда — его значением).
Для интеграла B9.4) имеет место свойство, аналогичное свойст-
свойству B9.3) для интеграла B9.1).
Если функция / определена на интервале (а, 6), —оо ^ а <Ъ ^ +оо,
ъ
и с G (а, Ь), то несобственным интегралом f(x)dx называется пара

302	Гл. 2. Интегральное исчисление функций одной переменной
с	Ъ
несобственных интегралов f(x)dx, f(x)dx. Если оба эти интег-
а Ъ	с
рала сходятся, то интеграл f(x)dx называется сходящимся, а ес-
а
ли хотя бы один расходится, то — расходящимся. Если интегралы
с	Ъ
f(x) dx и / f(x) dx сходятся, то их сумма обозначается тем же сим-
I j
а	ос
волом //(ж)б?ж, т. е.
а	Ъ	с	Ъ
ff(x) dx =f ff(x) dx + ff(x) dx.	B9.5)
а	а	с
Из свойства B9.3) и аналогичного свойства для интеграла B9.4)
следует, что существование и значение несобственного интеграла
ъ
f(x)dx не зависят в рассматриваемом случае от выбора точ-
а
ки с G (а, Ь).
Определим теперь общее понятие несобственного интеграла от
функции / по промежутку А с концами а и Ь, —оо ^ а ^ Ъ ^ +оо.
Всякое множество точек X = {xk}^Zo расширенной числовой пря-
прямой называется правильным разбиением промежутка А относитель-
относительно функции /, если:
1)	а = хо < х\ < ... < хп = Ь]
2)	функция / интегрируема по Риману на любом конечном от-
отрезке, лежащем на промежутке А и не содержащем точек множест-
множества X.
Ясно, что на каждом из промежутков (xo,^i), (xi,X2), ..., (xn-i,xn)
имеет смысл несобственный интеграл от функции / одного из трех
рассмотренных выше типов,
Совокупность интегралов
хк
I f(x)dx, fc = l,2,...,n,	B9.6)
ki	ь
называется в этом случае несобственным интегралом f(x)dx.
ъ
Если все интегралы B9.6) сходятся, то интеграл f(x)dx назы-
а
вается сходящимся, а если хотя бы один из них расходится, то —
расходящимся.	ъ	ъ
В случае когда интеграл f(x)dx сходится, через f(x)dx обо-

'. Несобственные интегралы	303
хк
J
значается и сумма интегралов B9.6), т. е.
Ь	п X},
f(x)dx,
и эта сумма также называется несобственным интегралом (иногда —
его значением).
Сходимость и расходимость несобственного интеграла, как и его
значение, если он сходится, не зависят от выбора правильного раз-
разбиения промежутка А относительно заданной функции /.
Заметим, что если к правильному разбиению X промежутка А
добавить любое конечное множество точек расширенной числовой
прямой, принадлежащих этому промежутку, то полученное множест-
множество также будет, очевидно, правильным разбиением А относительно
функции /.
Перейдем к рассмотрению примеров. Вычислим несобственные
интегралы от функции f(x) = —, а > 0, на полуинтервале @,1] (где
она неограниченна) и на бесконечном промежутке [1,+оо).
/dx	Г dx	11
— = lim / — = lim lnxL = +oo.
X B9.4) ?-)>() J X	?->¦()	'?
i	i	x_a Л
2. а Ф 1, / — = lim / x~a dx = lim
J Xa B9.4) С^О У	^0 1 - a
если a < 1,
если a > 1.
Обратим внимание на то, что при 0 < а < 1 несобственный ин-
интеграл / — существует, в то время как собственный интеграл / —
J ха	J ха
о	о
заведомо не существует, поскольку функция х~а при любом ее до-
доопределении в точке х = 0 будет неограниченной на отрезке [0,1].
Этот пример говорит о том, что в случае конечного промежутка
понятие несобственного интеграла шире понятия собственного интег-
интеграла. В случае же бесконечного промежутка понятия собственного
интеграла просто нет.
Итак, интеграл / -^ сходится при а < 1 и расходится при а ^ 1
J х
о
(при а < 0 этот интеграл является интегралом Римана).
+ ОО	Г]
dx	,. Г dx
. / — = lim /— = lim In ж
J X B9.1) ry^+oo J X	ry^+oo

304	Гл. 2. Интегральное исчисление функций одной переменной
+ ОО	Г]	_
/dx С dx х ^
— = Hm / — = Hm 	 =
Ха B9.1) г]^+оо J Ха ?7-^+оо 1 — а 1
1 1
{+оо, если а < 1,
	, если а > 1.
а — 1
+ ОО
Итак, интеграл / -^ сходится при а > 1 и расходится при а ^ 1.
1
29.2. Формулы интегрального исчисления для несобствен-
несобственных интегралов. В силу свойства предела функций и определения
значения несобственного интеграла как предела функции, являющей-
являющейся интегралом Римана с переменным пределом интегрирования, на
собственные интегралы предельным переходом переносятся многие
свойства определенного интеграла.
В дальнейшем в этом параграфе для простоты в вопросах теории
будем рассматривать случай несобственного интеграла от функций,
определенных на полуинтервале [а, Ь) и интегрируемых по Риману на
любом отрезке [а, 77], —оо < а ^Т] <Ъ ^ +оо (определение B9.1)), если,
конечно, специально не оговорено что-либо другое.
Аналогичные определения и теоремы для интегралов B9.4) и B9.5)
читатель без труда сформулирует самостоятельно.
Для общего несобственного интеграла B9.6) утверждения, анало-
аналогичные тем, которые будут сформулированы ниже для интеграла ви-
вида B9.1), также справедливы и в случае необходимости могут быть
сформулированы читателем.
1°. Формула Ньютона-Лейбница. Если функция f непре-
непрерывна на промежутке [а, Ь) и Ф — какая-либо ее первообразная, то
ъ
ff(x) dx = Ф(Ь - 0) - Ф(а).	B9.7)
i>
В этом равенстве либо обе части одновременно имеют смысл, и
тогда они равны, либо они одновременно не имеют смысла, т. е.
стоящие в них пределы не существуют.
|> Справедливость формулы B9.7) следует из того, что для любо-
любого Т] G [а, Ь), согласно формуле Ньютона-Лейбница для интеграла Ри-
Римана (теорема 3 из п. 25.2), имеет место равенство
Ф(а).	B9.8)
Из него следует, что предел lira f(x)dx существует тогда и только
г]^Ь J
а
тогда, когда существует предел lira Ф(?7), причем, если эти пределы

'. Несобственные интегралы	305
существуют, то, перейдя в равенстве B9.8) к пределу при rj -> Ь,
получим формулу B9.7). <1
2°. Линейность интеграла. Если несобственные интегралы
ь	ь
f(x)dx и g(x)dx сходятся, то для любых чисел X и /а несобст-
а	а	Ь
венный интеграл I [А/(ж) + /J>g(x)] dx также сходится и
Ъ а	ъ	Ъ
J[\f(x) + /ig(x)} dx = XJf(x) dx + /ijg(x) dx.	B9.9)
a	a	a
\> Действительно, на основании соответствующих свойств предела и
линейности интеграла Римана имеем
Ъ	г]
f[Xf(x) + 1лд{х)] dx = lim f[Xf(x) + цд(х)] dx =
J	B9.1) 77-^6 J
B9.1) 77-^6
a
77
= lim A / fix) dx + \i\ gix) dx = A lim / f(x) dx + \i lim / g[x) dx =
77-^6 V J	J	J	77-^6 J	77-^6 J	B9.Г
a	a	a	a
77	77
= A / fix) dx + и gix) dx. <\
B9.1) J	J
0
3°. Интегрирование неравенств. Если интегралы f(x) dx
ь	i
и g(x)dx сходятся и для всех х е [а,Ь) выполняется неравенст-
а
во f(x) ^g(x), то	ь	ь
I f(x)dx ^ I g(x)dx.	B9.10)
а	а
\> В силу соответствующего свойства интеграла Римана (см. след-
следствие свойства 6° в п. 24.1) для любого Т] G [а, Ь) выполняется нера-
неравенство	v	v
I f{x) dx ^ g(x) dx.
a	a
Перейдя в нем к пределу при rj —> b, получим неравенство B9.10). <1
Аналогичным образом, исходя из соответствующих свойств ин-
интеграла Римана, с помощью предельного перехода доказываются и
следующие два свойства несобственных интегралов (проведение до-
доказательств которых предоставляется читателю).
4°. Правило замены переменной. Если функция f(x) не-
непрерывна на полуинтервале Ах = [а, Ь), функция ip(t) непрерывно диф-
дифференцируема на полуинтервале At = [«,/3), —00 < а < /3 ^ +оо, и
20 Л.Д.Кудрявцев, т.1

306	Гл. 2. Интегральное исчисление функций одной переменной
выполняются условия
СДЖ, a = tp(a), Ь= lim tp(t),
mo	b	0
Jf(x) dx = ff(<p(t))<p'(t) dt,	B9.11)
a	a
причем из существования интеграла, стоящего слева в этом ра-
равенстве, следует существование интеграла, стоящего справа.
Если функция (р такова, что обратная функция (р~г однозначна
и удовлетворяет условиям, аналогичным условиям, наложенным на
функцию ср, и, следовательно, в интеграле, стоящем в правой час-
части равенства B9.11), можно сделать замену переменной t = ср~1(х),
то оба интеграла в этом равенстве сходятся или расходятся
одновременно.
С помощью замены переменной из условий сходимости интегра-
интегралов, рассмотренных в примерах 1 и 2 п. 29.1, следует, что интегралы
ъ	ъ
Г dx	Г dx	^^l^,	^ л
\	— и / -	—, —оо < а <о < +00, сходятся при а < 1 и расхо-
J (х — а)а J (b — х)а
а	а
дятся при а ^ 1. В самом деле, первый интеграл с помощью замены
переменной t = х — а, а второй с помощью t = Ъ — х приводятся к
Ъ—а
Г dt
интегралу J —.
о
5°. Правило интегрирования по ч а с т ям. Если функции
и и v непрерывны на промежутке [а,Ъ), а их производные кусочно не-
непрерывны на любом отрезке [а,т]), а < т\ < Ъ, то
ъ	ъ
fudv = uv\b~° - fvdu.	B9.12)
а	а
При этом из существования любых двух из следующих трех
пределов:
Ъ г]	Ъ г]
/Г	Г Г
udv = lim / и dv,	v du = lim / v du,
r\—>b J	J r\—>b J
uv\ = lim u(r])v(r]) — u(a)v(a)
a 77—^6
следует существование оставшегося.
Замечание. Отметим, что не все свойства интеграла Римана пе-
переносятся на несобственные интегралы. Например, интеграл от про-
произведения двух функций может расходится в случае, когда интеграл
от каждого из сомножителей сходится: если /(ж) = —=, то интеграл
Vх

'. Несобственные интегралы	307
11	11
f(x)dx = / —-=. сходится, а интеграл f2(x)dx — \— расходится,
оо	оо
Примеры. 1. Посредством замены переменной х — 1/t вычислим
интеграл
Г dx	С dt	. ,ii тг
I xVx^T = I 7Т=? = arCSmtlo = 2 '
1	0
+оо
2. Вычислим интеграл 1п = хпе~х dx, n = 0,1,2,... Проинтег-
о
рировав по частям при п > 0, будем иметь
+ ОО	+ОО
/_	_ 1-1-оо	С —Л —
х de = —х е | +п х е dx = nIn-\. B9.13)
о	о
+ ОО
Поскольку /0 = / е~х dx = е~ж|0°° = 1, то, применив последова-
о
тельно рекуррентную формулу B9.13), получим
In = nln-i = п(п — 1)/п-2 = ••• = п\ 1о = п\.
29.3. Несобственные интегралы от неотрицательных функ-
функций. Установим признаки сходимости для несобственных интегралов
от неотрицательных функций.
Лемма 1. Если функция f неотрицательна на полуинтервале
ъ
[а,Ь), то для сходимости интеграла f(x)dx необходимо и доста-
а	у
точно, чтобы множество всех интегралов f(x)dx, r\ е [а,Ь), бы-
а
ло ограничено сверху, т. е. чтобы существовала такая постоянная
с > 0, что для всех r\ G [а, Ь) выполнялось бы неравенство
Г]
ff(x)dx ^c.	B9.14)
а
\> Положим
Г]
<р(г)) =f ff(x)dx.	B9.15)
а
Если а ^ Т] < г]' < Ъ, то
Г)'	Г)	7]
ip(jj ) = / f{x) dx = / f(x) dx ¦
a	a
20*

308	Гл. 2. Интегральное исчисление функций одной переменной
ибо в силу неотрицательности функции / имеет место неравенство
ч'
f(x)dx ^ 0, т. е. функция ip(rj) возрастает на полуинтервале [а, Ь).
г]	Ъ
Существование несобственного интеграла f(x)dx означает сущест-
сущесть	а
= ff(x)dx,
J
вование конечного предела
J
а
что имеет место тогда и только тогда, когда функция ip(rj) ограничена
сверху (см. теорему 4 в п. 6.11), а это в силу B9.15) равносильно
условию B9.14). <\
Замечание. При доказательстве леммы 1 было показано, что в
случае неотрицательности функции / функция (p(rj) (см. B9.15)) воз-
возрастает на [а, Ь) и, следовательно, всегда имеет при rj —> Ъ конечный
или бесконечный, равный +оо, предел в зависимости от того, огра-
ограничена она или нет. Если функция ср(г)) неограничена на [а, 6), то
v
lim / f(x) dx = lim ip(ri) = +00,
ri^bJ	B9.15) r]^b
B9.15)
a
и в этом случае пишут ъ
f(x) dx = +00
а
(как мы уже и поступали в примерах п. 29.1).
Теорема 1 (признак сравнения). Пусть
0 ^ д(х) ^ /(ж), х е [а, Ь).	B9.16)
Тогда:	ь
1)	если интеграл f(x)dx сходится, то сходится и интеграл
ь	{
g(x)dx;
а	Ь
2)	если интеграл g(x) dx расходится, то расходится и интеграл
ь	I
I f(x) dx.
а
Следствие 1. Пусть функции fug неотрицательны на про-
промежутке [а, b), g(x) ф 0 при всех х G [а, Ь) и существует конечный
или бесконечный предел
Нт Щ = к.	B9.17)
х^ъ g(x)	v	J
Тогда:	ь
1) если интеграл g(x)dx сходится и 0 ^ к < +оо, то и ин-

'. Несобственные интегралы	309
ъ
теграл f(x)dx сходится;
а	ь
2) если интеграл g(x) dx расходится и 0 < к ^ +оо, то и ин-
ъ	{
теграл I f (x) dx расходится.
а
Следствие 2. Если функции f(x) и д(х) эквивалентны при
х ->• Ь, т. е. f(x) = ip(x)g(x), а ^ х < b, lim ip(x) = 1, то интегра-
ъ	ъ	х^ь
лы f(x)dx и g(x)dx одновременно сходятся или расходятся.
а	а
> Докажем теорему. Для любого r\ e [a, b) в силу неравенства B9.16)
имеем
77	Г]
7	]
Jg(x)dx ^ jf(x)dx.
а	а
Ъ
Поэтому если интеграл I f{x)dx сходится и, следовательно, согласно
лемме 1 ограничен сверху интеграл / /(ж) dx, то будет ограничен
}	а
сверху и интеграл g(x)dx, откуда, согласно той же лемме, интег-
ъ	{
рал / g(ж) dx сходится.
{	ьг
Если же расходится интеграл / g(x) dx, то в силу уже доказанного
ь	i
интеграл / f(x) dx не может сходиться, так как тогда бы сходился
{ ь
и интеграл g(x)dx, а это противоречит условию. Таким образом,
а
Ъ
интеграл f(x)dx расходится. <|
а
Докажем теперь следствие 1.
> Пусть выполняется условие B9.17) и 0 ^ к < +оо. Из того,
7	л.	/О)	г.
что к является пределом функции ±Jj-^- при х —У 6, и из нера-
9Ух)
9У)
венства к < к + 1 следует существование такого г] G [а, Ь), что ес-
()
-\-1, т. е.
f(x) <(k + l)g(x).	B9.18)
f(x)
ли г] < х < Ъ, то ^"Т <к-\-1, т. е.

310	Гл. 2. Интегральное исчисление функций одной переменной
Ъ
Если сходится несобственный интеграл / g(x)dx, то сходится ин-
г	а
теграл / (k + l)g(x) dx (см. B9.3) и B9.9)); следовательно, в силу не-
негу	ъ	ъ
равенства B9.18) интеграл / f(x)dx, а поэтому и интеграл I f{x)dx
сходятся. ^ а
Пусть теперь условие B9.17) выполняется при 0 < к ^ +оо. Тог-
Тогда зафиксируем произвольно такое к', что 0 < к' < к. Из того, что к
fix)
является пределом функции ^4 при х —> 6, и из неравенства к' < к
д(х)
следует существование такого rj G [а, Ь), что для всех х G (rj, b) выпол-
к', т. е. нераве
f{x) > к'д{х).
fix) 1f
няется неравенство ^"т > к , т. е. неравенство
9\р)
Отсюда в силу расходимости интеграла д(х) dx следует расходи-
1	j
Г
мость интеграла / к'д(х) dx, а следовательно, по теореме 1 и расхо-
а ь
димость интеграла f(x)dx. <\
а
Докажем теперь следствие 2.
|> Из условия lim (p(x) = 1 следует, что существует такое число с,
х—>Ъ
1	3
а < с <Ъ, что при с ^ х < Ь выполняется неравенство - ^ Ц>(х) ^ -•
А так как f(x) = cp(x)g(x), то
о
Отсюда в силу теоремы и следует, что интегралы f(x)dx и
jg(x) dx
ь
одновременно сходятся или расходятся
При применении признака сходимости для исследования интегра-
интеграла обычно начинают со сравнения подынтегральной функции с функ-
функциями
1	1	1
(х-а)а' (Ь-х)а' ха'
сходимость интегралов от которых уже известна (примеры п. 29.1 и
п. 29.2).

Примеры. 1. Выясним, сходится ли интеграл
'. Несобственные интегралы	311
B9.19)
о
ж3 ж3 1 1
Имеем f(x) = 4	= 4	4	~ -^	—, х —> 1,
? с/ж
а так как интеграл /	г сходится, то сходится и интег-
</ A — жI/4
рал B9.19).	°
2.	Исследуем интеграл i
flnxdx.	B9.20)
о
Для любого а > 0, применив правило Лопиталя, получим
lim а = lim	 а+1 =	lim xa = 0,
в частности, это равенство имеет место при 0 < а < 1. Но при 0 < а < 1
/с/ж
—— сходится, следовательно, сходится и интеграл B9.20).
ж
о
3.	Рассмотрим интеграл ±
It	<29-21>
о
Поскольку In х = In [I + (х — 1)] ~ х — 1 при ж —>¦ 1 и интеграл
/с/ж
	 расходится, то расходится и интеграл B9.21).
ж — 1
о
4.	Рассмотрим на бесконечном промежутке @, +оо) интеграл
+ ОО
[xne~xdx, n = 0,1,2,...	B9.22)
о
Заметим, что
хпе~х	хп
lim —-т- = lim —r- = 0
(в этом легко можно убедиться по правилу Лопиталя) и что интег-
+ ОО
/ e~xl2 dx,
о
рал / e~xl2 dx, очевидно, сходится:
о	+о°
о
Отсюда в силу следствия теоремы 1 при f(x) = хпе~х и д(х) = е~Ж//2
вытекает, что интеграл B9.22) сходится.

312
Гл. 2. Интегральное исчисление функций одной переменной
29.4. Критерий Коши.
Теорема 2 (критерий Коши сходимости интеграла). Несобст-
ъ
венный интеграл f(x)dx сходится тогда и только тогда, когда для
а х\' ц" Ь х
Рис. 120
О
Рис. 121
любого г > 0 существует такое 77, что для всех rj' и rj", удовлетво-
удовлетворяющих условию
г)<г)' <Ъ, г)<г)" <Ъ,	B9.23)
выполняется неравенство
(рис. 120 и рис. 121).
|> Если положить
п
\ff(x)dx
< г
'/
= Jf(x)dx,
B9.24)
B9.25)
и
то сходимость интеграла f(x) dx будет означать существование ко-
а
нечного предела функции ср(г)) при г] —У Ъ. Согласно критерию Коши
существования предела функции (п. 6.12) для существования указан-
указанного предела необходимо и достаточно, чтобы для любого е > 0 на-
нашлось такое ?7, что если rj < rj' < Ь, Т] < Т]" < b, то
B9.26)
Так как
'/	'/	'/
), = Л ff(x)dx- ff(x)dx= ff(x)dx,
то неравенство B9.24) совпадает с неравенством B9.26). <l

'. Несобственные интегралы
313
29.5. Абсолютно сходящиеся интегралы. Как и выше, будем
предполагать, что функция / задана на полуинтервале [а, Ъ), —оо <
< а < Ъ ^ +оо, и интегрируема по Риману на любом отрезке [a,rj\,
а<т]<Ь.	b
г
Определение 2. Несобственный интеграл / f(x) dx называется
а
Ъ
абсолютно сходящимся, если сходится интеграл / |/(ж)| dx.
а
Теорема 3 (критерий Коши абсолютной сходимости интеграла).
ъ
Для того чтобы интеграл f(x)dx абсолютно сходился, необходимо
а
и достаточно, чтобы для любого г > 0 существовало такое r\, a ^
^ г\ < Ъ, что если г\ < ?/ < Ъ, г\ < г]" < Ъ, то
Г]"
(х) I dx
< г.
B9.27)
|> Применив критерий Коши сходимости несобственного интегра-
ъ
ла (теорема 2) к интегралу \f(x)\dx, получим утверждение тео-
теоремы 3. <1	а
Теорема 4. Если несобственный интеграл абсолютно сходится,
то он и просто сходится.
ъ
Х> Если интеграл f(x)dx абсолютно сходится, то согласно необхо-
а
димости выполнения условий критерия Коши абсолютной сходимости
интеграла для любого г > 0 существует такое Т], что если
г) <т]' <Ъ, г) <т]" <Ъ,	B9.28)
то
Но
Г]
ff{x)
dx
поэтому,если выполнено условие B9.28), то
Г]
jf{x)dx
B9.29)
B9.30)
B9.31)
< г.
B9.30)
V	B9.29)
В силу достаточности выполнения условий критерия Коши для схо-

314
Гл. 2. Интегральное исчисление функций одной переменной
димости интеграла из B9.28) и B9.31) следует сходимость интеграла
ъ
ff(x)dx. <
а
Если интеграл от абсолютной величины функции сходится, то она
называется абсолютно интегрируемой (в несобственном смысле) на
соответствующем промежутке.
Теорема 4 показывает, что если функция абсолютно интегрируе-
интегрируема, то она и просто интегрируема в несобственном смысле. Обратное
утверждение неверно. Действительно, рассмотрим интеграл
+ ОО
dx.
B9.32)
Прежде всего, если доопределить подынтегральную функцию при
S1I1 Г?
х = 0 единицей, то, поскольку lim	 = 1, получившаяся функция
ж-^0 X
будет непрерывной, а следовательно, интегрируемой по Риману на
любом отрезке [0,77], г\ > 0. Поэтому определение B9.1) несобственно-
несобственного интеграла B9.32) имеет смысл. Кроме того, интеграл B9.32) схо-
сходится или расходится одновременно с интегралом
+оо
dx.
B9.33)
Для выяснения сходимости этого интеграла проинтегрируем его
по частям: если в результате получатся выражения, имеющие смысл
и принимающие конечные значения, то это будет являться обоснова-
обоснованием возможности интегрирования по частям и будет означать схо-
сходимость интеграла B9.33). Имеем
+оо
/sin
X
Sin Ж 7	fly	COS Ж
ах = — / —acosх =
J х
х
+ оо
+ оо
+
Г	7/1\
/ cosха - =
J	\х/
+00
= cos 1 —
+
Г ?2|? dx. B9.34)
J х
Получившийся интеграл
абсолютно сходится, ибо
+оо
dx
1
COS Ж
1
—, а интеграл
X
Г dx_
J ~&
B9.35)
сходится.
Следовательно, интегралы B9.35), а потому и B9.33) сходятся.
Покажем теперь, что интеграл B9.33) не сходится абсолютно, т. е.

'. Несобственные интегралы	315
+оо,
/sin х
	dx расходится. Из неравенства
х
sinx| ^ sin ж = 		B9.36)
следует, что для любого г\ > 0 выполняется неравенство
Г]	Г]	Г]
/I sin ж , . 1 С dx I /cos2x ,	/ЛЛ о^_ч
J	dx ^ - /	 /	dx.	29.37
ж	B9.36) 2 J X	2 J X
+оо
ах
Интеграл / — расходится, т. е.
J х	7
lim /— = +оо,	B9.38)
1
+ ОО
cos2x
а интеграл / C0S <ix сходится. Действительно, аналогично случаю
J х
1
интеграла B9.33) имеем
/ 	dx — - \ - afsin 2ж) =	 	/ sin 2ж а - =
Уж	2 J х у	J 2ж 1	2J	Чж/
1
+ ОО
1 /" sin2x , /оп опч
- / —^— б?ж, B9.39)
л J х
+ ОО
sin 2
2
+00
sin 2x . 1	Г sin 2x , ^
и поскольку —-— ^ —, то интеграл / —— dx абсолютно, а сле-
X1	X1	J	X1
1
довательно, и просто сходится. Поэтому из равенства B9.39) следует,
+ ОО
/cos 2x
—-— dx сходится, т. е. существует конечный предел
X
1	г)	+оо
lim [S^±ldx= f^pdx.	B9.40)
77-Ц-00 J X1	J X1
1	1
Из неравенства B9.37) и выполнения условий B9.38) и B9.40) полу-
получаем	+ ОО	Г]
Г sin ж ,	,.	Л sin ж ,
/ J	-dx— lim	dx = +00,
J x	77-^+00 J x
1	1
т. е. действительно интеграл B9.33) не сходится абсолютно.
Замечание. Отметим одно простое свойство абсолютно сходя-
ъ
щихся интегралов. Если интеграл f(x)dx абсолютно сходится, а
а
функция д(х) интегрируема по Риману на любом отрезке [а, 77] С [а, Ъ)

316	Гл. 2. Интегральное исчисление функций одной переменной
Ъ
и ограничена на полуинтервале [а, 6), то интеграл / f(x)g(x) dx также
абсолютно сходится.	а
В самом деле, произведение интегрируемых по Риману функций
также интегрируемо по Риману (свойство 5 в п. 24.1), поэтому функ-
функция f(x)g(x) интегрируема на любом отрезке [a,rj\ С [а, Ь), и, следо-
ъ
вательно, можно говорить о несобственном интеграле f(x)g(x) dx.
а
Из ограниченности функции д(х) следует, что существует такая
постоянная с > 0, что для всех х е [а, Ь) выполняется неравенство
\д(х)\ ^ с, а поэтому и неравенство \f(x)g(x)\ ^ с|/(ж)|, из которого
ъ
явствует, что сходимость интеграла l\f{x)g{x)\dx вытекает, соглас-
согласно признаку сравнения для сходимости интегралов от неотрицатель-
ъ
ных функций, из сходимости интеграла \f(x)\dx.
а
Определение абсолютно сходящегося интеграла естественным об-
образом обобщается на несобственный интеграл общего вида, определяе-
определяемый с помощью правильных разбиений промежутка интегрирования
(см. п. 29.1), и для него остаются верными аналоги теорем, дока-
доказанных выше в этом пункте для абсолютно сходящихся интегралов
специального вида (определение 1, п. 29.1).
29.6. Признаки сходимости Дирихле и Абеля.
Теорема 5 (признак Дирихле). Если на полуоси х ^ а:
1)	функция / непрерывна и имеет ограниченную первообразную;
2)	функция д непрерывно дифференцируема и убывает, стремясь к
нулю при х —> +оо, т. е. lim g(x) = 0;
х—>-+оо
то интеграл	+оо
I f(x)g(x)dx	B9.41)
сходится.	а
\> Пусть F — ограниченная первообразная функции / на полуоси
х ^ a, F'(x) = f(x). По условию функция / непрерывна, поэтому
функция F непрерывно дифференцируема. Проинтегрируем по час-
ъ
тям интеграл / f(x)g(x) dx, a < b < +оо:
ъ	а ъ	ъ
ff(x)g(x) dx = jg[x) dF(x) = F(b)g(b) - F(a)g(a) - JF(x)g'(x) dx.
B9.42)
Поскольку по условию функция F ограничена на полуоси х ^ а, то

'. Несобственные интегралы	317
существует такая постоянная с > О, что для всех х ^ а выполняется
неравенство
\F(x)\ ^c	B9.43)
и, следовательно, \F(b)g(b)\ ^ с|#(Ь)|. В силу стремления к нулю
функции д при х ->• +оо отсюда получаем
lim F(b)g(b) = 0.	B9.44)
6^+оо	ь
Докажем теперь, что интеграл F(x)g'(x)dx, стоящий в правой
а
части равенства B9.42), абсолютно сходится. Из убывания функ-
функции д(х) (второе условие теоремы) вытекает, что д'(х) ^ 0 при х ^ а,
\д'(х)\ = -д'(х).	B9.45)
Далее, из того, что функция д при х ^ а, убывая, стремится к нулю,
когда х —> +оо, следует, что д(х) ^ 0 при х ^ а, в частности,
5(Ь) ^ 0.	B9.46)
В результате
ъ	ъ	ъ
f\F{x)g'{x)\dx = -f\F{x)\g'{x)dx <: -cfg((x)dx =
= с[д(а) - д(Ь)] ^ ср(а).
B9.46)
Ъ
Таким образом, множество интегралов / \F(x)gf(x)\ dx при всех b ^ a
а
ограничено сверху, а это, согласно лемме п. 29.3, и означает сходи-
+ ОО	+ОО
мость интеграла / \F(x)g'(x)\dx. Итак, интеграл / F{x)g'{x)dx аб-
абсолютно, а следовательно, и просто сходится, т. е. существует конеч-
конечный предел	ь
lim [F(x)g'(x)dx= f F{x)g'{x)dx.	B9.47)
a	a
В силу выполнения условий B9.44) и B9.47) из равенства B9.42)
следует существование конечного предела
Ъ	+оо
lim ff(x)g(x)dx = -F(a)g(a)- Г F(x)g'(x)dx,
а	а
что и означает сходимость интеграла B9.41). <|
Теорема б (признак Абеля). Если на полуоси х ^ а:
1) функция f непрерывна и интеграл
+ ОО
[ f(x)dx	B9.48)
сходится:	а

318	Гл. 2. Интегральное исчисление функций одной переменной
2) функция g непрерывно дифференцируема, ограничена и моно-
монотонна]
то интеграл	+оо
J f(x)g(x)dx
сходится.
Х> Покажем, что эта теорема вытекает из предыдущей. Прежде всего
отметим, что интегралы
+ ОО	+ОО
j f(x)g(x) dx и j f(x)[-g(x)] dx
а	а
сходятся или расходятся одновременно и что в силу монотонности
функции g одна из функций g или — g убывает. Пусть для определен-
определенности убывает функция д. В силу ее ограниченности и монотонности
существует конечный предел
lim g(x) = с,
х—>-+оо
а так как функция д убывает, то, убывая, стремится к нулю и раз-
разность д{х) — с при х —У +оо.
Представим произведение f(x)g(x) в виде
f(x)g(x) = f(x)[g(x) - с] + cf(x).	B9.49)
+ ОО
В силу первого условия теоремы интеграл / cf(x) dx сходится. Из
a J
этого же условия следует, что интеграл F(x) = / f(t) dt, х ^ а, огра-
а
ничен. В самом деле, из существования конечного предела
X
lim F(x) = f(t)dt следует ограниченность функции F в некото-
х—>-|-оо	J
а
рой окрестности С/(+оо) = {х: х>Ъ} бесконечно удаленной точки +оо
(свойство 1° из п. 6.7). На отрезке же [а, Ъ] функция F ограничена,
ибо она непрерывна. В результате функция F ограничена на всей по-
полупрямой х ^ а. Функция F является первообразной функции /, тем
самым функция / имеет ограниченную первообразную при х ^ а.
+ ОО
Таким образом, для интеграла / f(x)[g(x) — с] dx выполнены все
а
условия признака Дирихле, и потому этот интеграл сходится. В си-
силу доказанного из равенства B9.49) следует сходимость интеграла
+ ОО
j f(x)g(x)dx. <\

'. Несобственные интегралы	319
+ ОО .
Примеры. 1. Интеграл / —— dx в силу признака Дирихле схо-
J х
а
дится при всех а > 0. Действительно, функция f(x) = sin ж имеет
ограниченную первообразную F(x) = — cos ж, а функция д(х) = 1/ха,
убывая, стремится к нулю.
2. Интеграл / 	— dx, а > 0, в силу признака Абеля схо-
J	ха
а	+оо .
„	Г sin ж ,
дится. В самом деле, как мы уже знаем, интеграл / —— dx сходится,
j х
а
а функция д(х) = arctgx ограниченна и монотонна.
Замечание. Усовершенствовав доказательства теорем 5 и б,
можно показать, что признаки Дирихле и Абеля сходимости интег-
интегралов остаются справедливыми, если у функции / условие ее непре-
непрерывности заменить условием ее интегрируемости на любом конечном
отрезке [а,Ь], а у функции д отбросить требование ее непрерывной
дифференцируемости, оставив все остальные.
29.7. Интегралы от комплекснозначных функций дейст-
действительного аргумента. Если функция f(x) определена на проме-
промежутке с концами а и Ъ, — оо ^ а < Ъ ^ +оо, и ее значениями явля-
являются комплексные числа, т. е.
/(ж) = и(х) + iv(x), u(x) e R, v(x) e R,	B9.50)
ъ
то интеграл f(x)dx (собственный или несобственный) определяет-
определяется
ся равенством ъ	ъ	ъ
ff(x) dx = Ги(х) dx + i fv(x) dx.	B9.51)
a	a	a
Это определение имеет, конечно, смысл только тогда, когда оба
интеграла в правой части равенства существуют.
ъ
Интеграл f(x) dx называется несобственным, если хотя бы один
а Ъ	Ъ
из интегралов u(x)dx, v(x)dx несобственный. При этом несобст-
а Ъ	а
венный интеграл / f(x) dx называется сходящимся, если сходятся оба
Ъ	а Ъ
интеграла u(x)dx, v(x)dx. В этом случае, согласно определению,
а	а
имеет место равенство B9.51).
Функция f(x) называется абсолютно интегрируемой, если абсо-
абсолютно интегрируемы функции и(х) и г?(ж).

320	Гл. 2. Интегральное исчисление функций одной переменной
Определение B9.51) сохраняет свойство линейности:
ъ	ъ	ъ
J(Xifi(x) + A2/2(») dx = Xijfi(x) dx + X2Jf2(x) dx,
a	a	a
Ai e C, A2 G С
Ряд свойств интеграла от действительных функций (аддитивность
по множествам интегрирования, формула Ньютона-Лейбница, прави-
правила замены переменной и интегрирования по частям) также перено-
переносится и на случай комплекснозначных функций.
Если /(ж) = и(х) + iv(x), причем действительные функции и(х) и
ь
v(x) интегрируемы по Риману на отрезке [а, Ь], то интеграл / /(ж) dx,
а
также называемый в этом случае интегралом Римана, является пре-
кТ
делом (комплекснозначных) интегральных сумм ат = V^/(
к=1
где т = {xk}kZoT — разбиение отрезка [а, Ь], хк-Х ^ & ^ хк,
= хк -хк-1, к = 1,2,...,&г:	ь
lim ат = / fix) dx,
|т|-И)	У
\т\ — мелкость разбиения т.
Отсюда тем же методом, что и для действительных функций, лег-
легко показать, что если для функции / существует интеграл Римана,
то он существует и для ее абсолютной величины, причем
ь	ь
rf(x)dx <: f\f(x)\dx.
Предельным переходом справедливость этого неравенства уста-
устанавливается и для абсолютно интегрируемых в несобственном смысле
комплекснозначных функций.
Подобным же образом вводится и понятие неопределенного интег-
интеграла от функции B9.50):
ff(x) dx = Ги(х) dx + i fv(x) dx.	B9.52)
Для этого интеграла также имеет место свойство линейности,
справедливы формулы замены переменной и интегрирования по час-
частям, которые в силу формулы B9.52) вытекают из соответствующих
свойств интегралов от функций действительного аргумента, прини-
принимающих только действительные значения.
Для непрерывных функций / определенный и неопределенный ин-
интегралы B9.51) и B9.52), как и в действительной области, связаны
соотношением	х
J f(x)dx = J f(t)dt + C.

ГЛАВА 3
РЯДЫ
§ 30. Числовые ряды
30.1. Определение ряда.
Определение 1. Пара последовательностей {ип} и {sn}, где
un, sn G С, п = 1, 2,...,
sn = Ul +u2 + ... + ип, га = 1,2,...,	C0.1)
называется рядом (а также бесконечной суммой) и обозначается
^1 + ^2 + ." + ^п + ."
ИЛИ	°°
$^п.	C0.2)
n=l
Элементы последовательности {ип} называются членами ряда, а
элементы последовательности {sn} — его частичными суммами.
Если существует конечный предел
lim sn = s,	C0.3)
га-юо
то он называется суммой ряда. В этом случае ряд называется сходя-
сходящимся и пишут	оо
п=1
Если последовательность частичных сумм {sn} не стремится к
конечному пределу, то ряд C0.2) называется расходящимся.
Очевидно, что
u1=s1, un = sn-sn-1, га = 2,3,...	C0.4)
Из формул C0.1) и C0.4) видно, что каждая из последователь-
последовательностей {ип} и {sn} однозначно определяет другую. Таким образом,
чтобы задать ряд C0.2), достаточно задать одну из последователь-
последовательностей {ип} или {sn}. В этом смысле изучение рядов равносильно
изучению последовательностей.
Часто нумерацию членов ряда производят не натуральными чис-
числами, а целыми, начиная с нуля, т. е. числами 0,1,2,..., а иногда —
начиная с некоторого целого п0, т. е. числами по,по + 1,...
Примеры. 1. Примером сходящегося ряда является ряд
оо
^</\	C0.5)
21 Л.Д.Кудрявцев, т.1

322	Гл. 3. Ряды
членами которого являются элементы геометрической прогрес-
прогрессии {q71}, q G С, \q\ < 1. В самом деле, в этом случае
_ -, п-0,1,2,...,
к=о	ч
и потому
г l-4n+1 г
Hm s^ = Hm _ 	= hm
n—>-oo \ 1 — (/ 1 — С
1
r n
hm gfn =
1 — q 1 — g n-^oo	1 —
Следовательно, ряд C0.5) при \q\ < 1 сходится и
(X)
2. Примером расходящегося ряда является ряд, все члены которо-
п
го равны единице: ип = 1, п = 1,2,... В этом случае sn = ^ 1 = п,
поэтому
Hm sn = +оо.
п—^оо
30.2. Свойства сходящихся рядов.
Теорема 1 (необходимые условия сходимости ряда). Если ряд
сходится, то последовательность его членов стремится к нулю.
ОО
|> Если ряд 2_, ип сходится, т. е. существует конечный предел
п=1
Hm sn = s его частичных сумм, то из равенства
п—>-оо
			 с\ о
следует, что
Hm ип = Hm sn — Hm sn_i = s — s = 0. <l
n—^oo	n—^oo	n—^oo
Пример. Ряд C0.5), членами которого являются члены геомет-
геометрической прогрессии {q71}, в случае, когда знаменатель прогрессии q
по абсолютной величине не менее единицы, т. е. \q\ ^ I, q e С, рас-
расходится, так как последовательность его членов {qn} не стремится к
нулю, ибо \qn\ ^ 1.
ОО	ОО
Теорема 2. Если ряды ^ ип и ^^vn сходятся, то для любых
00	п=1	п=1
Л G С, \i G С ряд 2_, ^ип + №п сходится и
п=1
ОО	ОО	ОО

§ 30. Числовые ряды	323
|> Положим sn = 2_.uk, &n = y.Vk, тогда
OO	OO
Если ряды ^^ип и ^^vn сходятся, т. е. существуют конечные
71=1	71=1
ОО	ОО
пределы lim sn = У^ ип и lim ап = У^г>п, то существует и ко-
п—юо	^—'	п—^оо	^—'
нечный предел
п	оо
lim У^ Aix^ + /i^jfe = Л lim sn + \i lim crn = Л У^ ип +
n—>-oo -^—'	n—>-oo	n—>-oo	-^—^
A;=l	n=l
что и означает справедливость утверждения теоремы. <|
оо
Определение 2. Для ряда У^ ип ряд
п=1
к=1
называется п-м остатком данного ряда.
Если n-и остаток ряда сходится, то его сумму будем обозна-
обозначать гп, т. е.	^
к=1
Теорема 3. Если ряд сходится, то и любой его остаток сходит-
сходится. Если какой-то остаток ряда сходится, то сам ряд также схо-
сходится, причем, если
оо	п	оо
f\ I	^	^—^ Ж	f\ I j	/V»	^—^ Ж	/II	j	I ¦ I I / I
n=l	fe=l	fe=l
то при любом п = 1,2,...
s = sn+rn.	C0.7)
|> Пусть sn и Sm являются соответственно п-й частичной суммой
оо
ряда У^ ип и ттг-й частичной суммой его остатка C0.6):
71=1
тогда
Sn+m^Sn + S^.	C0.8)
21*

324	Гл. 3. Ряды
Поэтому при произвольно фиксированном п пределы lim sn+rn и
га—>-оо
lim s$ одновременно существуют или не существуют. СущеСТВО-
га>оо
оо
вание первого из этих пределов означает сходимость ряда 2_,uk, a
существование второго — сходимость остатка C0.6) V^ un+k этого
к=1
ряда. Если оба рассматриваемых предела существуют, то, перейдя к
пределу при т ->• оо в равенстве C0.8), получим формулу C0.7). <1
оо
Отметим, что если ряд V^ un сходится, то его остатки стремятся
71=1
к нулю. Это сразу следует из формулы C0.7), так как сходимость
ряда означает, что lim sn = s, и поэтому
п—юо
lim rn — lim (s — sn) = 0.
п—>-оо C0.7) п—>-оо
30.3. Критерий Коши.
Теорема 4 (критерий Коши сходимости ряда). Для того что-
оо
бы ряд 2^ ип сходился, необходимо и достаточно, чтобы для любо-
71=1
го г > 0 существовало такое по, что для всех п > щ и всех це-
целых р ^ 0 имеет место неравенство
\ип + iAn+i + ... + iAn+p| < г.	C0.9)
> Это утверждение сразу следует из критерия Коши существова-
существования конечного предела последовательности, примененного к последо-
последовательности частичных сумм {sn} данного ряда, ибо
ип + un+i + ... + ип+р = sn+p - sn-i. <\
Замечание. При р = 0 из теоремы следует, что если ряд V^ un
71=1
сходится, то для любого г > 0 существует такой номер п0, что для
всех п > по выполняется неравенство |i&n| < г, а это означает, что
lim un = 0. Таким образом, мы получим еще одно доказательство
п—уоо
необходимого условия сходимости ряда (см. теорему 1).
Пример. Рассмотрим ряд
C0.10)

§30. Числовые ряды	325
называемый гармоническим, и докажем, что он расходится. При лю-
любом натуральном п имеем
1
н
п
1
1
п
1
+
п
1
слагаемых
1
2п-
•1 "
1
2п
1
2п '"
п слагаемых
1
2п
1
2
Поэтому если 0 < г < -, то для ряда C0.10) нельзя подобрать номе-
номера по, указанного в критерии Коши, так как при любом п = 1,2,...
и р = п - 1 не выполняется условие C0.9). Следовательно, гармони-
гармонический ряд расходится.
Отметим, что последовательность \-\ членов гармонического ря-
ряда стремится к нулю:	п
Нт - = 0.
п—юо П
Таким образом, условие стремления к нулю последовательности
членов ряда, являсь необходимым условием сходимости ряда, не яв-
является достаточным для этого.
30.4. Признаки сходимости рядов с неотрицательными
членами.
Лемма 1. Если члены ряда неотрицательны, то он сходится тог-
тогда и только тогда, когда его частичные суммы ограничены сверху.
|> Если члены ряда	^
]Гип	C0.11)
71=1
неотрицательны (ип ^ 0, п = 1,2,...), то
ч ,1—4 -А- и , 1 > ч	D0 19)
т. е. последовательность частичных сумм {sn} данного ряда возраста-
возрастает, а возрастающая последовательность имеет конечный предел тогда
и только тогда, когда она ограничена сверху. <|
Замечание 1. Если члены ряда C0.11) неотрицательны, то
последовательность его частичных сумм {sn}, согласно C0.12), воз-
возрастает и, следовательно, всегда имеет конечный или бесконечный
предел s, причем
s= lim sn = 8upsn,	C0.13)
n-^oo	n
и поэтому
sn ^ s, n = l,2,...	C0.14)
(X)
Если s = +00, то пишут ^ un = +00.
71=1

326
Гл. 3. Ряды
Замечание 2. Ряд с неотрицательными членами сходится тогда
и только тогда, когда сходится п о крайней мере одна подпос-
подпоследовательность последовательности его частичных сумм. Дей-
Действительно, последовательность частичных сумм ряда с неотрица-
неотрицательными членами возрастает и потому всегда имеет конечный или
бесконечный предел, совпадающий, конечно, с пределом любой ее под-
подпоследовательности.
Теорема 5 (интегральный признак Коши сходимости ряда). Ес-
Если функция / неотрицательна и убывает на полупрямой х ^ 1, то
для того чтобы ряд	^
?/(п)	C0.15)
71=1
сходился, необходимо и достаточно, чтобы сходился интеграл
+ ОО
I f(x)dx.	C0.16)
1
|> В силу монотонности функции / на промежутке [1,+оо) она ин-
интегрируема по Риману на любом конеч-
конечном отрезке [1, rj\, r\ e [1, +оо), и потому
имеет смысл говорить о несобственном
интеграле C0.16).
Если
ГЬ ^ X ^ ГЬ ~\ А. ,	ГЬ 	 -L , Л, . . . ,
х то в силу убывания функции / будем
иметь
О
/с+1
Рис-122
Проинтегрировав это неравенство по отрезку [к, к + 1] длины 1
(рис. 122), получим
к+1	к+1	к+1
f(k) I dx^ I f{x) dx > f(k + 1) I dx,
к	к	к
т. е.	fc+i
Просуммировав получившиеся неравенства по к от 1 до п, придем к
основному неравенству
п к+1
Е
к=1
т. е. к неравенству
к=1 к
к=1
п+1
sn+1 - /A) ^ J f(x) dx ^ sn,
C0.17)

§ 30. Числовые ряды	327
где
k=i
+ ОО
Если интеграл / f(x)dx сходится, то из неравенства C0.17) в
1
силу неотрицательности подынтегральной функции следует, что
71+1	+ОО
sn+1 <С /A) + I /(ж) dx <С /A) + J f{x) dx < +oo,	C0.18)
1	1
а поэтому последовательность частичных сумм sn, n = 1,2,..., ря-
ряда C0.13) с неотрицательными членами ограничена сверху числом
+ ОО
/A) + / f(x)dx. Отсюда согласно лемме 1 следует, что этот ряд
1
сходится.
+ оо
Если же интеграл / /(ж) dx расходится, то в силу неотрицатель-
1
ности подынтегральной функции /(ж) имеем
77+1	+ОО
lim / /(ж) dx = [ f(x) dx = +оо,	C0.19)
п—>-оо J	J
1	1
а так как согласно неравенству C0.17)
п+1
sn^ J f(x)dx,
1
то, перейдя к пределу в этом неравенстве при п ->• оо, получим
lim sn = +oo. Это означает, что ряд C0.13) расходится. <\
п-^оо C0.19)
Для применения интегрального признака к исследованию сходи-
(X)
мости ряда V^ un с неотрицательными членами надо подобрать
п=1
такую убывающую функцию /, что f(n) = ип, п = 1,2,..., и затем
исследовать сходимость интеграла C0.16).
Применим этот метод к исследованию сходимости рядов вида
^	C0-2°)
В этом случае при а ^ 0 требуемой функцией, очевидно, являет-
является функция /(ж) = —. Поскольку интеграл
Х	+ОО
Г dx
J ~x^
1

328	Гл. 3. Ряды
сходится при а > 1 и расходится при а ^ 1, то и ряд C0.20) сходится
при а > 1 и расходится при а ^ 1. Расходимость ряда C0.20) при а < 0
ясна непосредственно: последовательность его членов не стремится к
нулю, ибо — ^ 1 при а < 0.
Теорема б (признак сравнения). Пусть
0^un^vn, п = 1,2,...	C0.21)
Тогда:
(X)	(X)
1)	если ряд ^ ип сходится, то и ряд ^ ип сходится;
п=1	п=1
оо	оо
2)	если ряд 2_,ип расходится, то расходится и ряд у^ уп.
С лед ст вие. Пусть ип ^ 0, г;п > 0, n = l,2,..., u
lim ^ = 1.	C0.22)
п—>-оо Vn
Тогда:
(X)
1)	если ряд V^ i7n сходится и 0 ^ / < +оо, то сходится
и ряд 2^ип;
п=1
(X)
2)	если ряд V^ vn расходится и 0 < I ^ +оо, то расходится и
П=1	(X)	(X)
^ частности, если Нт — = 1, то ряды У^ un u У^ г;п схо-
дятся и расходятся одновременно.	п~	п~
оо
|> Доказательство теоремы. Если ряд V^ vn сходится, т. е.
71=1
(X)	П
имеет конечную сумму а = J^^n, и crn = ^^/г, то для любого
71=1	fc = l
п = 1,2,... выполняется неравенство
ап ^ а.	C0.23)
C0.14)
Следовательно,
п	п
J2	*Vk=<jn ^ а,	C0.24)
(X)
а это в силу леммы означает, что ряд ^ ип сходится.
71=1

§ 30. Числовые ряды	329
оо	оо
Если ряд 2_,ип расходится, то расходится и ряд /_^^п5 так как
если бы он сходился, то в силу уже доказанного сходился бы и ряд
оо
У2ип. <\
71=1
ОО
|> Доказательство следствия. Пусть ряд ^ vn сходится.
71=1
Поскольку I < +оо, то в силу условия C0.22) существует такой но-
номер по, что для всех и > по выполняется неравенство — < I + 1, а
следовательно, и неравенство
un<(l + l)vn, n>n0.	C0.25)
оо	оо
Если ряд 2_^Vn сходится, то сходится и ряд 2_^ + ^-)vn (теоре-
71=1	71=1
ма 2), а поэтому по признаку сравнения (теорема 6) в силу неравенст-
оо
ва C0.25) сходится и ряд *S^uno+k, а тогда (см. теорему 3) сходится
и ряд 2_^ип.
71=1
оо
Пусть ряд ^^vn расходится. По условию / > 0; выберем число /'
71=1
так, чтобы 0 < V < I. В силу условия C0.22) существует такой номер
по, что для всех п > по выполняется неравенство — > V. а следова-
Vn
тельно, и неравенство
ип>Гуп, п>п0.	C0.26)
оо
Поскольку из расходимости ряда 2^ vn вытекает, очевидно, и расхо-
00	п=1
димость ряда ^^l'vn, то согласно второму утверждению теоремы 6
71=1	°°
из неравенства C0.26) следует расходимость ряда 2_.un0+k, а потому
°2^	к=1
и ряда V^ un. <\
71=1
Заметим, что при применении признака сравнения для исследова-
исследования сходимости ряда с неотрицательными членами в качестве ряда, с
которым сравнивается данный ряд, часто бывает удобным брать ряд
^ 1
71=1

330	Гл. 3. Ряды
При меры. 1. Ряд у,	2— сходится, ибо
п
71=1
n sin2 па 1	— 1 о
U ^ - ^ —, п — 1, z,...,
оо	nz	nz
и ряд V^ — сходится.
71=1
оо
1
2. Ряд У^	— расходится, ибо
*-^ 1 + Jn
п=1	v	-^	-^	-^
1-\-л/п ^ л/п-\-л/п 2л/п'
(X)
и ряд 2^ —/= расходится.
п=1
Теорема 7 (признак Даламбера). Пусть для ряда
(X)
^2ип, ип>0, п = 1,2,...,	C0.27)
га=1
существует предел
lim _^_ = /.	C0.28)
n>oo U
n—>-oo Un — i
Тогда если I < 1, то ряд C0.27) сходится, а если I > 1, то рас-
расходится.
> Пусть сначала / < 1. Выберем число g так, чтобы / < q < 1. Тог-
Тогда в силу условия C0.28) существует такой номер по > 1, что для
всех п > по выполняется неравенство —^— < g и, следовательно,
^71-1
неравенство i&n < qun-\. Применяя это неравенство последователь-
последовательно для , п = по + 1, по + 2,..., получим
^no + l < QUno,
Но ряд 2^ Qkun0 = иПо 2^ Qk в силу условия 0 < q < 1 сходится,
к=1	к=1	°°
поэтому, согласно признаку сравнения, сходится и ряд 2^ип0+к,
а следовательно, и ряд C0.27).	fe=1
Пусть теперь I > 1; тогда в силу условия C0.28) существует такой
номер по, что для всех п > по выполняется неравенство —^— > 1,
а поэтому и неравенство г&п > ип-\. Применяя его последовательно

§30. Числовые ряды	331
для и = п0 + 1, п0 + 2,..., получим
ип+1 > ип> ... > ит+1 > ипо > 0.
Поэтому последовательность членов ряда C0.27) не стремится к ну-
нулю, откуда и следует его расходимость. <|
Теорема 8 (признак Коши). Пусть для ряда
ОО
^ип, ип^0,	C0.29)
71=1
существует предел
lim *Уг^ = /.	C0.30)
п—Уоо
Тогда если Z < 1, то ряд C0.29) сходится, а если I > 1, то рас-
расходится.
|> Пусть сначала I < 1. Выберем число q так, чтобы / < q < 1. Тог-
Тогда в силу условия C0.30) существует такой номер по, что для всех
п > по выполняется неравенство ^/п^, < q и, следовательно, i&n < ^п.
оо	оо
Поскольку ряд 2^ Qn сходится, то сходится ряд 2_^un0+k, a поэтому
и ряд C0.29). n=°	k=1
Если I > 1, то в силу условия C0.30) существует такой номер п0,
что при п > п0 выполняется неравенство ^/г^ > 1, т. е. ип > 1, и,
следовательно, последовательность членов ряда C0.29) не стремится
к нулю, поэтому этот ряд расходится. <|
Примеры. 3. Ряд V^ — сходится. Это устанавливается, напри-
п=1
мер, с помощью признака Даламбера:
lim —-—'-——- = lim - = 0.
п—уоо i-/\Tl — 1)' п—уоо п
оо
4.	Ряд ^ — сходится. Это сразу можно установить с помощью
п=1
признака Коши:	l 1
оо П
5.	Для ряда с общим членом ип — —, а > 0, имеем
Un+l	Па	(	П \а
lim —— = lim	—- = lim	 = 1,
п—Уоо Un	п—Уоо \П + 1)а	\ п—Уоо П + 1 /
lim ?/п^= lim ?/—- =
п—уоо	п—уоо у па ( lim
п—Уоо
(см. пример 4 в п. 13.2). Таким образом, при применении признаков
Даламбера и Коши соответствующие пределы равны единице, т. е. при

332	Гл. 3. Ряды
помощи этих признаков нельзя определить, сходятся или расходятся
рассматриваемые ряды. Среди них есть как сходящиеся при а > 1, так
оо
и расходящиеся при а ^ 1. Иначе говоря, среди рядов V^ un с неот-
неотрицательными членами, для которых lim n+1 = 1, соответственно
п—юо Un	оо
lim ^/пп~ — 1, имеются как сходящиеся (например, V^ — ), так и
п—>-оо	оо	V	-^—' 77- /
расходящиеся (например, У^ —) ряды.
п=1
30.5. Знакочередующиеся ряды.
Теорема 9 (Лейбниц). Если последовательность {ип} убывает
и стремится к нулю, т. е.
Un^Un+i, ra = l,2,..., \imun = 0,	C0.31)
п—^оо
то ряд	оо
(—1) ^ ип	C0.32)
п=1
оо	п
сходится, причем, если s = V^(—l)n+1ixn, sn = V^(—l)fe+1ix^, mo
n=l	k=l
при любом п = 1,2,... выполняется неравенство
\sn-s\ ^г/n+i.	C0.33)
Прежде всего отметим, что из условия C0.31) следует, что
ип ^ 0,	C0.34)
в силу чего члены ряда C0.32) поочередно то ^ 0, то ^ 0.
Ряды вида C0.32) при ип > 0 называются знакочередующимися.
\> Частичные суммы с четными номерами ряда C0.32) возрастают
и неотрицательны. В самом деле,
— S2n + (^2n+l — ^2п+2) ^ S2n ^0, П = 2, 3, ..., C0.35)
ибо в силу убывания последовательности {ип} значения всех выра-
выражений, стоящих в круглых скобках, неотрицательны. Кроме того, по-
последовательность {s2n} ограничена сверху:
ибо
ик — uk+i ^0, к = 1, 2,..., и2п ^ 0.
C0.34)
Поскольку последовательность {s2n} возрастает и ограничена

§ 30. Числовые ряды	333
сверху, то она имеет конечный предел
s = lim s2n,	C0.37)
п—>-оо
при этом из неравенств C0.35) и C0.36) следует, что (рис. 123)
(Ks^ui. C0.38) 	1	•	1	1
S2 S S2+1 U\
Покажем, что тот же предел	Рис 123
имеет и последовательность час-
частичных сумм с нечетными номерами. Действительно,
lim u2n+i = 0,
п-юо	C0.31)
поэтому
lim S2n+i — lim S2n + lim U2n+i — 5-	C0.39)
n—>-oo	n—>-oo	n—>-oo	C0.37)
Из C0.37), C0.39) следует, что последовательность {sn} всех час-
частичных сумм ряда C0.32) имеет конечный предел s, т. е. этот ряд
сходится, и s является его суммой.
Докажем неравенство C0.33). Имеем
(X)	(X)
s-sn = ^(-l)"+ft+1Mn+fc = (-1)" ^(-l)fc+1Un+ft,
k=l	k=l
где в правой части стоит ряд У^(—V)k+1un+k- Применив к нему не-
неравенство C0.38), получим к=1
поэтому
При
"К"\ f~\ "Л Т Т Т 11
мер.
s -
Ряд
0
±
(X)
к=1
к=1
К (~1)П
1 п
L
ип+1.
сходится. Это сразу следует из тео-
теоЗамечание. Выше (см. следствие теоремы б в п. 30.4) было по-
(X)	(X)
казано, что если у двух знакопостоянных рядов V^ un и V^ vn
п=1	п=1
их члены эквивалентны: ип ~ vn, п —> оо (см. C0.22)), то они од-
одновременно сходятся или расходятся. Для не знакопостоянных рядов
аналогичное утверждение уже не имеет места. Например, если
(-1)п	(-1)п , 1
аП —	i— 1	иП —	i—	\	1

334	Гл. 3. Ряды
то
«»= Шп
т. е. ип ~ vn, п —у оо. Однако в силу признака Лейбница ряд V^ -—yL-
оо
_ л/™
сходится, а ряд V^ (-—г=—|— ) расходится, ибо расходится гармо-
*-^ V л/га га/
71=1
нический ряд У^ -.
*-^ п
71=1
Очевидно, что — = о(-—т=^Ь п-Уоо. Таким образом, добавляя к
га V л/га /
членам ряда бесконечно малые более высокого порядка по сравнению
с членами ряда, можно изменить сходимость ряда: из сходящегося
ряда получить расходящийся.
30.6. Абсолютно сходящиеся ряды.
Определение 3. Ряд
оо
^ип, ипеС,	C0.40)
71=1
называется абсолютно сходящимся, если ряд, членами которого
являются абсолютные величины членов данного ряда, т. е.
оо
J^KI,	C0.41)
71=1
СХОДИТСЯ.
Теорема 10 (критерий Коши абсолютной сходимости ряда). Для
того чтобы ряд C0.40) абсолютно сходился, необходимо и достаточ-
достаточно, чтобы для любого г > 0 существовало такое щ, что для всех
номеров п > по и всех р = 0,1,... выполнялось бы неравенство
к=0
> Это сразу следует из определения абсолютно сходящегося ряда и
критерия Коши сходимости ряда (теорема 4 из п. 30.3). <\
Теорема 11. Если ряд абсолютно сходится, то он сходится.
\> Это следует из неравенства
^2\ип+к\.	C0.42)
к=0	к=0
В самом деле, в силу критерия Коши абсолютной сходимости ря-
ряда C0.40) для любого г > 0 существует такое по, что для всех п > по и
всех р ^ 0 правая часть неравенства C0.42) меньше г. Следовательно,

§ 30. Числовые ряды	335
и левая часть этого неравенства окажется меньше г, т. е. для ря-
ряда C0.40) выполняется критерий Коши сходимости рядов, и потому
ряд C0.40) сходится. <|
оо .п
Примеры. 1. Ряд Y^ %-— абсолютно, а значит, и просто схо-
п=0	^п
дится. Это следует из равенства
= — и сходимости ряда ^ —.
п=1
2. Ряд 2_, — сходится (см. п. 30.5), но не абсолютно, так как
п=1
ряд, составленный из абсолютных величин его членов, т. е. гармони-
оо
ческий ряд У^ —, расходится (см. п. 30.3).
п=1
Теорема 12. Линейная комбинация абсолютно сходящихся рядов
является абсолютно сходящимся рядом.
оо	оо
|> Если ряды ^^ип и ^^vn абсолютно сходятся, а \,ц G С, то
оо
сходится и ряд У^ |A||ixn| + |/i||i7n|. Отсюда в силу неравенств
71=1
\\ип + /ivn\ ^ |A||un| + |/i||vn|, n = 1,2,...,
по признаку сравнения (см. теорему 6) следует сходимость ряда
оо	оо
\Хип + /ivn\, т. е. абсолютная сходимость ряда y^(Aixn + /ivn). <l
71=1	71=1
оо
Теорема 13. ^сли ря^ C0.40) абсолютно сходится, то любой ряд
C0-43)
7П=1
составленный из тех же членов, что и данный ряд, но взятых, вообще
говоря, в другом порядке, также абсолютно сходится и имеет ту же
сумму
т—1	п—1
\> Пусть ряд C0.40) абсолютно сходится. Докажем, во-первых, что
ряд C0.43) сходится и имеет ту же сумму, что и ряд C0.40), а во-
вторых, что ряд C0.43) абсолютно сходится. Пусть
71=1	k = l	k = l	71=1	k = l

336	Гл. 3. Ряды
Зафиксируем произвольно г > 0. В силу абсолютной сходимости
ряда C0.40) существует такой номер по, что
оо
Y^ \un\ = s-sno < |	C0.44)
и, следовательно, выполняется неравенство
оо
- Snn I =
оо
ип
<
е
—
2'
C0.45)
Выберем номер m0 так, чтобы частичная сумма s^0 ряда C0.43)
содержала в качестве своих слагаемых все члены ряда C0.40), входя-
входящие в сумму sno. Для всякого т > то положим
С=4г-*п0.	C0.46)
В силу выбора номера m0 слагаемыми суммы s^* являются чле-
члены ряда C0.40) с номерами, большими по- Поскольку абсолютная ве-
величина суммы s^ не превышает абсолютных величин ее слагаемых,
то
1U	оо
=no
Поэтому при m > mo будем иметь
C0<4)I-
n=no+l	v	'
()	()
C0.47)
Это означает, что lim s* = s. Иначе говоря, ряд C0.43) сходится и
га—^оо
его сумма равна s, т. е. равна сумме ряда C0.40):
оо	оо
J2 < =s = Е "«•
?тг=1	п=1
Второе утверждение — абсолютная сходимость ряда C0.43) —
следует из уже доказанного первого утверждения, если его приме-
применить к ряду	qq
Х>»1-	C0.48)
71=1
В самом деле, если ряд C0.40) абсолютно сходится, то сходится
ряд C0.48), причем он, очевидно, сходится абсолютно, так как его чле-
члены неотрицательны. Поэтому согласно доказанному сходится и любой
ряд, получающийся перестановкой членов ряда C0.48), в частности,
оо	оо
сходится ряд V^ \um\- А это и означает, что ряд V^ и*ш абсолютно
сходится. <| m=1	m=1

§30. Числовые ряды
337
Теорема 14. Если ряды
п=1
n=l
C0.49)
абсолютно сходятся, то ряд, составленный из всевозможных попар-
попарных произведений umvn членов этих рядов, также абсолютно сходит-
сходится, причем его сумма s равна произведению сумм данных рядов: если
C0.50)
C0.51)
п=1
то
s = s's".
Коротко говоря, утверждение теоремы означает, что абсолютно
сходящиеся ряды можно перемножать почленно.
|> Докажем абсолютную сходимость ряда, составленного из всевоз-
всевозможных попарных произведений umvn членов рядов C0.49). Заметим,
что если будет показано, что ряд из этих произведений абсолютно
сходится при каком-то их порядке, то согласно предыдущей теореме
отсюда будет следовать, что он абсолютно сходится и при любом дру-
другом порядке своих членов. Поэтому расположим произведения umvn в
конкретном порядке, удобном для доказательства теоремы. Для опи-
описания этого порядка составим следующую таблицу:
U2V2
UmV2 ...
C0.52)
Рассмотрим составленный из элементов таблицы C0.52) ряд
U1V2 + U2V2 + U2V1 + ...,	C0.53)
в котором порядок членов выбран согласно нумерации элементов таб-
таблицы C0.52) по схеме
C0.54)
1
4
Г
2
з
8
5
6
7
Докажем абсолютную сходимость ряда C0.53), т. е. сходимость ряда
Vl\ + ...	C0.55)
22 Л.Д.Кудрявцев, т.1

338	Гл. 3. Ряды
Положим
га=1	п=1	к=1	к=1
а через 7in обозначим частичные суммы ряда C0.55). Тогда
sn2 = МН + \ux\\v2\ + \u2\\v2\ + ЫЫ + ... + К1Ы =
C0.55)
= (Ы + ... + Ы)(Ы + ... + Ы) = ?К. C0.56)
Перейдя в этом равенстве к пределу при п ->• оо, получим
lim 5^2 = ?'?".
п—>-оо
Но последовательность {S^} всех частичных сумм ряда C0.55) в
силу неотрицательности его членов возрастает и потому имеет пре-
предел, конечный или бесконечный, совпадающий, конечно, с пределом
любой ее подпоследовательности, в частности, с пределом 5" подпосле-
подпоследовательности {3^2}. Таким образом, существует конечный предел
lim Ип = 7= ?/?//,
п—>-оо
т. е. ряд C0.53) абсолютно сходится, и, следовательно, абсолютно схо-
сходится любой ряд, полученный перестановкой его членов.
Докажем теперь формулу C0.51). Обозначим через sn частичные
суммы ряда C0.53) и положим
к=1	к=1
Аналогично C0.56) имеем
sn2 = (щ + ... + un)(vi + ... + vn) = «.	C0.57)
Поскольку уже доказано, что ряд C0.53) абсолютно, а следова-
следовательно, и просто сходится, то существует конечный предел
lim sn = s.	C0.58)
п—>-оо
Поэтому
s = lim sn= lim sn2 = lim s' s" = lim s' lim s" = s's".<\
C0.58) n-^00	n-^00	C0.57) n-^00	n-^00 n-^00 C0.50)
30.7. Условно сходящиеся ряды.
Определение 4. Сходящийся, но не абсолютно сходящийся ряд
называется условно сходящимся рядом.
Примером условно сходящегося ряда является ряд \^ -——
^-^ п
(пример 2 из п. 30.6).	1
п=1

§ 30. Числовые ряды	339
Для ряда	^
]Гип	C0.59)
71=1
с действительными членами обозначим через и+,и^,...,м+,... и
—Ui,—U2,...,—u~,... соответственно его неотрицательные и отрица-
отрицательные члены, взятые в том же порядке, в котором они расположены
в ряде C0.59). Очевидно, и~ > 0, п = 1, 2,...
Если одно из множеств {и~} или {и+} окажется конечным, то,
отбросив в ряде C0.59) соответствующее конечное число первых чле-
членов (от чего сходимость ряда не нарушится), получим остаток ряда,
члены которого будут неотрицательны или неположительны и, сле-
следовательно, во втором случае неотрицательны после умножения всех
членов на —1. И в том, и в другом случае, если исходный ряд сходит-
сходится, то он очевидным образом абсолютно сходится. Таким образом,
если ряд C0.59) условно сходится, то оба множества {и+} и {и~}
бесконечны, т. е. являются последовательностями. Рассмотрим ряды
ОО
Y1 ип>	C0.60)
71=1
ОО
5>".	C0.61)
71=1
Согласно определению члены этих рядов и+ и и~ неотрицательны,
поэтому если они расходятся, то
71=1	71=1
Лемма 2. Если ряд C0.59) условно сходится, то оба ряда C0.60)
и C0.61) расходятся.
> Положим
к=1	к=1	к=1	к=1
Поскольку все слагаемые последних трех сумм 7in, s+ и s~ неотри-
неотрицательны, то последовательности этих сумм возрастают и, следова-
следовательно, имеют конечные или бесконечные пределы.
Суммы sn и !$п можно представить в виде
к	т
Sn = J2Ut-J2U7 = St-Sm,	C0.62)
г=1	j=l
к	т
t + ? UJ = 4
22*
Ut + ? UJ = 4 + Sm	C0-63)
3=1	г=1

340	Гл. 3. Ряды
(для заданного ряда тик зависят от n = Hm); при этом усло-
условие стремления п к бесконечности равносильно стремлению к бес-
бесконечности каждого из индексов тик. Действительно, если бы при
п —У оо номера т = т(п) (соответственно к = к(п)) не стремились к
бесконечности, то это означало бы, что в ряде C0.59) имеется лишь
конечное число неотрицательных (соответственно отрицательных)
членов, а в этом случае ряд C0.59) абсолютно сходился бы, что про-
противоречило бы его условной сходимости. То, что при к —У оо (соответ-
(соответственно при т —у оо) имеет место п —У оо, очевидно в силу равенст-
равенства п = к + т.
В силу сходимости ряда C0.59) последовательность {sn} сходится.
Если бы сходилась одна из последовательностей {s^} или {s^} (т. е.
сходился бы один из рядов C0.60) или C0.61)), то из равенства C0.62)
следовало бы, что сходится и другая, а тогда в силу равенства C0.63)
оказалось бы, что сходится последовательность {sn}. Это же означает
абсолютную сходимость ряда C0.59), что противоречит сделанному
предположению. Поэтому ряды C0.60) и C0.61) расходятся. <|
Теорема 15 (Риман). Если ряд с действительными членами
условно сходится, то, каково бы ни было действительное число s,
можно так переставить члены этого ряда, что сумма получившего-
получившегося ряда будет равна s.
\> Пусть члены ряда C0.59) — действительные числа, и пусть про-
произвольно задано число s. Рассмотрим ряды C0.60) и C0.61) Наберем
из C0.60) подряд столько членов, чтобы их сумма превышала s и
чтобы сумма меньшего числа этих членов была не больше s. Точнее,
обозначим через п\ наименьшее натуральное число, при котором вы-
выполняется условие
и^ + ... + и+г > s.	C0.64)
Тогда при ni > 1 имеет место неравенство
^ + ... + ix+i_1 ^ s.	C0.65)
Возможность выбора такого числа п\ следует из расходимости ря-
ряда C0.60).
Наберем теперь из C0.61) подряд столько членов, чтобы, вычтя
их сумму из суммы уже набранных из ряда C0.60) членов, получить
значение, меньшее s, и чтобы меньшее число указанных членов ря-
ряда C0.61) не обладало этим свойством. Точнее, обозначим через п^
такое наименьшее натуральное число П2, что
uf + ... + гг+ - щ - ... - и~2 < s,	C0.66)
и если п2 > 1, то
и+ + ... + < - Щ - ... - г/-2_х ^ s.	C0.67)

§30. Числовые ряды	341
Существование такого числа п2 следует из расходимости ряда C0.61).
Далее обозначим через пз такое наименьшее натуральное число,
что
uf + ... + и+ - щ - ... - и~2 + и++1 + ... + и+з > s,
и если п3 > п\ + 1, то
Очевидно, всегда пз > ni. Продолжая этот процесс, т. е. набирая со-
соответствующие суммы членов поочередно то из ряда C0.60), то из
ряда C0.61), получим ряд
и++ ... + гг+ - щ - ... - и~2 + гг++1 + ... + гг+з - и~2+1 - ... - гг~4 + ...
C0.68)
Обозначим через sn, n = 1,2,..., частичные суммы этого ряда. В
силу выбора номеров П1,П2,пз,П4,... будем иметь
sni > s,	и если	п\ > 1,	то	sni_i ^ s,
Sni+na < ^,	и если	п2 > 1,	то	sni+n2_i ^ s,
5п2+п3 > 5,	и если	пз > ni + 1,	то	зП2+Пз_1 ^ s,
8Пз+п4 < s,	и если	п4 > п2 + 1,	то	sn3+n4-i ^ s,	C0.69)
П1 < Пз < ... < П2?;+1 < ...,	П2 <П4 < ... < П2(к+1) < -j
Л; = 0,1,2,...
Их этих неравенств следует, что частичная сумма вида snm+nm+1
отличается от числа s не более чем на абсолютную величину послед-
последнего ее члена, т. е. для всех т = 1,2,... имеют место неравенства
\snm+nm+1-s\^utm+1,	C0.70)
где и^т+1 является абсолютной величиной последнего слагаемого сум-
суммы 5Пт+Пт+1 (член и^т г может принадлежать как ряду C0.60), так
и ряду C0.61), поэтому в качестве верхнего индекса написано ±).
По условию ряд C0.59) сходится, следовательно,
lim un = 0.
п—>-оо
Отсюда в силу неравенства C0.70) получаем, что
lim snm+nm+1 = s.	C0.71)
Для любой же частичной суммы sn ряда C0.68) в силу его пост-
построения существует такое ш, что выполняется либо неравенство

342	Гл. 3. Ряды
либо
Поэтому из равенства C0.71) следует, что и последовательность всех
частичных сумм sn ряда C0.68) имеет своим пределом число s:
lim sn = s,
n—>-oo
т. е. число s является суммой ряда C0.68). <l
Теорема Римана показывает, что одно из основных свойств конеч-
конечных сумм чисел — независимость их суммы от порядка слагаемых
(коммутативность сложения) — не переносится на сходящиеся ряды,
т. е. на бесконечные суммы: если ряд сходится, но не абсолютно, то
его сумма зависит от порядка слагаемых.
Отметим, что и ассоциативный закон сложения непосредственно
не переносится на ряды; так, например, ряд
1 - 1 + 1 - 1 + 1 - 1 + ... + (-l)n+1 + ...
расходится, а ряды
A -1) + A -1) + A -1) +... + A -1) +...,
1 - A -1) - A -1) -... - A -1) -...,
полученные из него указанным объединением его членов, сходятся;
при этом сумма первого ряда равна 0, а второго 1.
30.8*. Признаки сходимости рядов Дирихле и Абеля. Рас-
п
смотрим одно преобразование конечных сумм вида ^^ajbj, принад-
з=1
лежащее Абелю и часто весьма полезное при исследовании сходимос-
сходимости рядов.
Пусть ctj е С, bj G С, Bj = Ъ\ + ... + bj, j = 1,2, ...,п, и, следова-
следовательно, bi = Bi, bj = Bj — Bj-i, j = 2,3, ...,n. Тогда
a\b\ + a2b2 + ... + anbn = a\B\ + a2(B2 - B\) + ... + an(Bn - Bn-i) =
= (ai - а2)Вг + (a2 - a3)B2 + ... + (an_i - an)?(n_i) + anBn,
или, используя знак суммирования,
п	п—1
Yl aJbJ = ^2(aJ - aJ+^)BJ + a^Bn-	C0.72)
3=1	3=1
Это равенство называется преобразованием Абеля суммы
Если его переписать в виде
п	п—1
^2aj(Bj - Bj-г) = апВп - ахВх - ^(«j+i - a,j)Bj,
3=2	3 = 1

§30. Числовые ряды
343
то видно, что его можно рассматривать как дискретный аналог ин-
интегрирования по частям.
В дальнейшем числа ctj будут действительными, a bj, вообще го-
говоря, комплексными.
Лемма 3 (Абель). Если для всех j = l,2,...,n —1 выполняются
неравенства
ctj ^ aj+i UJlu aj ^ aj+b	C0.73)
и для всех j = l,2,...,n — неравенства
: в,	C0.74)
то
C0.75)
|> Имеем
п-1
C0.72) Т^
п-1
C0.74)
C0.74)
._-.
C0.73)
-ап\ + \ап\)
+
ы) =
+ 2|ап|).
Мы воспользовались здесь очевидным равенством
п-1
\аз~аз+Л =
Теорема 16 (признак Дирихле).
монотонная и	,.	л
hm an = 0,
п—>-оо
(ап_1-ап)| = |ai-an|.<
последовательность {ап}
C0.76)
а последовательность частичных сумм ряда \. Ьп ограничена, то ряд
оо	п=1
Y, anbn	C0.77)
п=1
|> Из ограниченности последовательности частичных сумм Вп =
п	оо
= ^^ 6^, п = 1, 2,..., ряда ^~^ 6П следует, что существует такое чис-
ло В > 0, что для всех п = 1, 2,... выполняются неравенства \Вп\ ^ 5
и, следовательно, для всех п = 2, 3,... и всех р = 0,1,... — неравенства
v
2В.	C0.78)
|
к=0

344	Гл. 3. Ряды
Зафиксируем произвольно г > 0. В силу условия C0.76) сущест-
существует такой номер по, что для всех п > по имеет место неравенство
К\ < ^б-	C0.79)
Поэтому для всех п > по и всех р = 0,1, 2,... будем иметь
V
n i - - i	- - ¦ л- i ' •	ч	«/? 7~~>	/? 7~~> /	5
C0.75)	C0.79)
C0.78)
т. е. ряд C0.77) удовлетворяет критерию Коши сходимости рядов и,
следовательно, сходится. <|
Теорема 17 (признак Абеля). Если последовательность {ап}
ограничена и монотонна, а ряд ^
JT Ъп	C0.80)
71=1
сходится, то сходится и ряд ^
J2anbn.	C0.81)
71=1
> Из ограниченности и монотонности последовательности {ап} сле-
следует существование конечного предела lim an = а, и потому последо-
п—>-оо
вательность {ап - а} монотонная и стремится к нулю. Из сходимости
же ряда C0.80) следует, что последовательность {Вп} его частичных
п
сумм Вп = \^ bk ограниченная. Теперь имеем
Второй ряд в правой части равенства сходится по условию теоре-
теоремы, а первый — в силу признака Дирихле. Поэтому сходится и ряд,
стоящий в левой части равенства, т. е. ряд C0.81). <1
Примеры. 1. Ряд	^
gsinna
^ п	v	J
га=1
сходится. Действительно, последовательность ап = —, п = 1,2,...,
п
монотонно убывая, стремится к нулю, а
п	п
>^ sin ка =	т^г /^ 2 sin /ca sin — =
cos (к - -)а - cos (к + -)а\ =

§30. Числовые ряды
345
а	( 1\
;- -cos {п+-)а
Поэтому
2sinf
, аф2ттг, т = 0,=Ы,...
sin ка
а
cos-
+
2
cos (п + - j a
sin —
^ 1
. а
sin-
k=i
т. е. при а ф 2ттг, m = О, =Ы,..., все рассматриваемые суммы ограни-
ограничены. Отсюда в силу признака Дирихле следует, что при а ф 2ттг,
m = 0,=Ы,..., ряд C0.82) сходится. Он сходится, очевидно, и при
а = 2ттг, m = 0,=Ы,..., так как в этом случае все члены его обра-
обращаются в нуль.
Итак, ряд C0.82) сходится при всех a Е R.
2. Ряд
V ^^ cos -	C0.83)
*-^ п	п
п=2
сходится по признаку Абеля, ибо сходится ряд C0.82), а последова-
последовательность I cos — > ограниченна и монотонна.
30.9. Исследование сходимости рядов методом выделения
главной части ряда. Для того чтобы выяснить, сходится или рас-
оо
ходится данный ряд 2^ит бывает полезно разложить с помощью
п=1
формулы Тейлора члены ряда ип по степеням — при подходящем
п
показателе а > 0, т. е. представить ип в виде (см. п. 14.2)
C0.84)
где число т выбрано так, что та > 1. Тогда ряд 2_^Vn с членами
/ 1 \	п=1
vn = О(	) сходится абсолютно по признаку сравнения, так как
\пта )
существует такая постоянная с > 0, что для всех п = 1,2,... выпол-
няется неравенство
сходится.
v
—— (см. (9.20)), и ряд
1ша
, та > 1,
71=1
Таким образом, сходимость данного ряда N. ип сводится к иссле-
исследованию сходимости рядов	п=1
(X)
ап,к
—г^, к = 0,1, ...,т — 1.
пка '	->->->
1
71=1

346	Гл. 3. Ряды
Примеры. 1. Рассмотрим ряд с общим членом ип = In cos—.
п
Используя разложение функций cos и In по формуле Тейлора
(см. п. 14.2), получим
2n2 ' \n*
ОО	ОО
и РЯД	"=1 те n=l
оо	оо
Поскольку ряды >^	 и >^0(—г) сходятся, то сходится
*-^ 2п2	*-^ \п4/
71=1
(X)
Eln cos -.
п
п=1
2. Рассмотрим ряд с общим членом ип = In cos A. . Имеем
(X)	(X)
Ряд У^--^— расходится, а ряд У^0( —
' ¦ ATI	\ Tl
1
сходится, поэтому
\ п~ /
п=1	п=1
данный ряд	^
Eln cos -—rL-
у/п
расходится.
3. Рассмотрим ряд с общим членом ип = In A + -—-/=- ). Заме-
V	у/п /
ТИМ, ЧТО	2
In A + х) = х - у + О(х3), ж -)> 0;
в частности, при х = -—-jL- имеем
где
= In A + ЦТ) = ЦТ - J- + О(^-) = ап + Ъп + сп, C0.85)
V	л/п У	л/п 2п	\п3/2/
def (-l)n , def 1	^/ 1 1
оо
Ряд V^ ап знакочередующийся; он сходится по признаку Лейб-
71=1
ОО
ница. Ряд ^ Ъп расходится, так как он только постоянным множи-
71=1

§ 30. Числовые ряды	347
1	v^
телем — - отличается от гармонического ряда, а ряд 2_^сп сходится.
71=1
Поэтому в силу равенства C0.85) данный ряд
расходится.
оо	оо
Таким образом, ряды V^ an и V^ un являются еще одним при-
п=1	п=1
мером рядов, члены которых эквивалентны: ип = ап + о(ап), п —У оо,
но один из них сходится, а другой расходится (см. замечание в
п. 30.5).
30.10. Суммирование рядов методом средних арифмети-
арифметических. Если заданный числовой ряд расходится, то иногда оказы-
оказывается полезным определить сумму ряда не обычным способом —
как предел его частичных сумм — а каким-либо другим. Рассмотрим
один из таких способов, называемый суммированием рядов методом
средних арифметических.
оо
Для ряда 2_^ип, ип Е С, составим из его частичных сумм sn их
п=1
средние арифметические
vn=Sl+S2+n- + Sn, n = l,2,...
Если существует конечный предел lim on — а, то заданный
п—>-оо
ряд называется суммируемым методом средних арифметических к
числу а.
Пример. Расходящийся ряд 1 — 1 + 1 — 1 + ... суммируется ме-
методом средних арифметических к числу -.
В самом деле, в этом случае s2n = 0, s2k-i = 1, &2k = тг> 0fc-i =
к	1	2
= —	, к = 1,2,..., и, следовательно, lim an = -.
JifZ	I	Ti—^ОО	Zi
Таким образом, если под 1 — 1 + 1 — 1 + ... понимать число, к ко-
которому этот ряд суммируется методом средних арифметических, то
получится равенство
1-1 + 1-1 + ... = |.	C0.86)
Замечательно то, что если в формулу
оо
п=0

348
Гл. 3. Ряды
для суммы геометрической прогрессии {(-1)пжп} подставить х = 1,
то получим	оо
т. е. снова формулу C0.86).
Понятие суммируемости ряда методом средних арифметических
является обобщением понятия сходимости ряда, так как, с одной сто-
стороны, существуют расходящиеся ряды, суммируемые методом сред-
средних арифметических, а с другой — всякий сходящийся ряд сумми-
суммируем методом средних арифметических к своей сумме. Покажем это.
Лемма 4. Если последовательность zn e С, п — 1,2,..., сходится,
то последовательность средних арифметических ее членов
wn =
Z\ ~\- Z2 ~\~ ••• ~\~
C0.87)
также сходится, и притом к тому же пределу, что и сама последо-
последовательность {zn}.
|> Пусть \imzn = z0. Для любых натуральных чисел п0 и п > п0 вы-
выполняется следующее тождество:
wn -
C0.86)
Z\
(Znp+1 - Zp)
Зафиксируем произвольно г > 0. Согласно определению предела
последовательности существует такой номер по, что для всех п > по
имеет место неравенство
\zn-z0
C0.89)
Поскольку z\ + ... + zno — noZo — фиксированное число, a lim — =
n—>-oo П
= 0, то существует такой номер mo, что для всех п > то выполняется
неравенство
C0.90)
п	2
Если теперь п? = max{no,mo} и п > по, то
C0.88)
C0.89)
C0.90)
Это и означает, что lim wn
п—>-оо
C0.89)
C0.90)
= zo. <\

§31. Функциональные последовательности и ряды	349
Теорема 18. Если ряд сходится, то он суммируется методом
средних арифметических к своей сумме.
оо
|> Сходимость ряда 2_\ ип означает, что последовательность его час-
71=1
тичных сумм {sn} имеет конечный предел, а тогда, согласно лемме 4,
и последовательность средних арифметических {ап} членов последо-
последовательности {sn} имеет тот же предел
lim оп — lim sn. <l
§ 31. Функциональные последовательности и ряды
31.1. Сходимость функциональных последовательностей
и рядов. Пусть на некотором множестве X (произвольной природы)
задана последовательность функций
fn, П = 1,2,...,	C1.1)
принимающих числовые значения (вообще говоря, комплексные, в
частности, только действительные). Элементы множества X будем
называть точками.
Последовательность C1.1) называется ограниченной на множест-
множестве X, если существует такое число с > 0, что для всех п = 1,2,... и
всех точек х е X выполняется неравенство
\fn(x)\^C.
Последовательность C1.1) называется сходящейся на множест-
множестве X, если при любом фиксированном х G X числовая последователь-
последовательность {/п(#)} СХОДИТСЯ.
Если последовательность C1.1) сходится на множестве X, то
функция /, определенная при каждом х G X равенством
f(x) = lim /п(ж),
п—>-оо
называется пределом последовательности C1.1).
Пусть на множестве X задана последовательность числовых функ-
(X)
ций ип(х), п = 1,2,... Множество всех числовых рядов ^^ип(х), в
71=1
каждом из которых точка х G X произвольно фиксирована, называ-
называется рядом	оо
^>п(аО	C1.2)
71=1
на множестве X, а функции ип(х), п = 1, 2,..., — его членами.

350	Гл. 3. Ряды
Аналогично случаю числовых рядов сумма
к=1
называется частичной суммой ряда C1.2) п-го порядка, а ряд
оо
^ un+k — его п-м остатком.
k=i
Ряд C1.2) называется сходящимся на множестве X, если последо-
последовательность {sn(x)} его частичных сумм сходится на этом множест-
множестве. При этом предел частичных сумм
lim sn(x) = s(x), x G X,
n—юо
называется суммой ряда C1.2). В этом случае пишут
ОО
s(x) = ^2ип(х)
п=1
и говорят, что функция s(x) раскладывается в ряд C1.2).
Если ряд C1.2) при любом фиксированном х Е X сходится аб-
абсолютно, то он называется абсолютно сходящимся на множестве X.
Примеры. 1. Рассмотрим ряд, членами которого являются
функции	zn
un(z) = ^р п = 0,1,2,...,
определенные на комплексной плоскости С, т. е. ряд
1 + ^ + у + ... + ^ +.., z e С.	C1.3)
Исследуем абсолютную сходимость этого ряда при фиксированном z
с помощью признака Даламбера:
Шп Щф = lim JfL = 0.
Таким образом, при любом z G С ряд C1.3) абсолютно, а следователь-
следовательно, и просто сходится; иначе говоря, ряд C1.3) сходится, и притом
абсолютно, на всей комплексной плоскости.
2. Рассмотрим ряд
При х = 0 все его члены обращаются в нуль и, следовательно, его
сумма s(x) также равна нулю:
s@) = 0.	C1.5)
При х ф 0 ряд C1.4) представляет собой сумму членов бесконечной
геометрической прогрессии со знаменателем

§31. Функциональные последовательности и ряды	351
и поэтому
s(x) = 1 + ж— = 1.	C1.6)
Из формул C1.5) и C1.6) следует, что ряд C1.4) сходится на всей
числовой оси и его сумма
1 при х/0
S^ -10 при х =
оказывается разрывной в точке ж = 0 функцией (см. рис. 60), хотя
все его члены, очевидно, непрерывны на всей числовой оси.
Этот пример показывает, что сумма сходящегося и даже абсо-
абсолютно сходящегося на некотором множестве ряда (члены ряда C1.4)
неотрицательны, и потому ясно, что он абсолютно сходится), все чле-
члены которого непрерывны, может оказаться разрывной функцией. Та-
Таким образом, на сходящиеся и даже на абсолютно сходящиеся ряды
функций не переносится свойство конечных сумм: сумма конечной
совокупности непрерывных на некотором множестве функций так-
также непрерывна на нем. Для того чтобы описать ряды функций, на
которые переносится это свойство, введем понятие равномерно схо-
сходящихся рядов.
31.2. Равномерная сходимость функциональных последо-
последовательностей и рядов.
Определение 1. Функциональная последовательность C1.1)
называется равномерно сходящейся к функции f на множестве X, ес-
если для любого г > 0 существует такой номер по, что для всех то-
точек х Е X и всех номеров п > по выполняется неравенство
\fn(x)-f(x)\<e.	C1.7)
Очевидно, что если последовательность C1.1) равномерно сходит-
сходится на множестве X к функции /, то эта последовательность сходится
к функции / на рассматриваемом множестве (определение сходимос-
сходимости последовательности функций на множестве см. в п. 31.1).
Если последовательность {/п} сходится на множестве X к функ-
функции /, то пишут
а если эта последовательность сходится равномерно к / на указанном
множестве, то пишут
ff
В символической записи определения сходящейся и равномерно
сходящейся на множестве последовательности выглядят соответст-

352
Гл. 3. Ряды
венно следующим образом:
ef v
fn^f
fn^f
X
0
3n0
ef ,
\fn(x)-f(x)
\fn(x)-f(x)
e.
Таким образом, если последовательность {/п} только сходится к
функции / на множестве X, то для каждой точки х Е X существует,
вообще говоря, свой номер п0 = по(г,ж), для которого при и > п0 вы-
выполняется неравенство
\fn(x)-f(x)\<e,
и может оказаться, что для всех точек х Е X невозможно подобрать
общий номер по, обладающий указанным свойством.
Равномерная же сходимость последовательности {/п} к функции /
означает, что, какое бы число г > 0 ни задать, можно подобрать такой
номер по, что в л юб ой точке жЕ
Е X значение функции /п будет
отличаться от значения функции /
меньше, чем на г (рис. 124).
Лемма 1. Для того чтобы после-
последовательность {fn} равномерно схо-
сходилась на X к функции /, необходимо
и достаточно, чтобы
lim sup|/n(x)-/(x)| =0.
п—>-оо j^
C1.8)
О
Ь х
Значение этой леммы состоит в
том, что она сводит понятие рав-
равномерной сходимости последова-
последовательности функций {/п} к понятию сходимости числовой по-
последовательности
Рис. 124
{|()()|}
X
("числовой" в широком смысле этого слова: конечное число членов
указанной последовательности может обратиться в +оо). В силу это-
этого обстоятельства условие C1.8) часто бывает удобно использовать
для выяснения, сходится ли равномерно интересующая нас конкрет-
конкретная последовательность функций.
> 1. Пусть
Jn
X
Зададим произвольно г > 0. Тогда существует такой номер п0, что
для всех п > по и всех х Е X выполняется неравенство \fn(x) —
— f(x)\ < г, а следовательно, для всех п > по — неравенство
\Jn\X) — J\X)\ ^ S.
хех

§31. Функциональные последовательности и ряды	353
Это и означает выполнение условия C1.8).
2. Пусть выполнено условие C1.8). Зададим произвольно г > 0.
Тогда в силу определения предела числовой последовательности су-
существует такой номер п0, что для всех п > п0 выполняется нера-
неравенство	| , ( ч ?( \\
sup|/n(x) - f(x)\ <е,
х
а следовательно, для всех п > по и всех х Е X — неравенство
\fn(x)-f(x)\<e.
Это означает, что
Следствие. #а/ш существует стремящаяся к нулю последова-
последовательность \ап}:
lim an = 0,
п—>-оо
такая, что для всех х ? X выполняется неравенство
\fn(x)-f(x)\ ^an,	C1.9)
то последовательность {fn(x)} равномерно сходится к функции f(x)
на множестве X.
|> Действительно, поскольку неравенство C1.9) выполняется для
всех х G X, то
sup|/n(x) - f(x)\ ^ anj
х
а поэтому из условия lim an = 0 получаем, что
п—>-оо
lim sup \fn(x) - f(x)\ =0. <l
7WOO X
Замечание 1. Очевидно, что из определения равномерной схо-
сходимости последовательности функций следует, что если какие-то по-
последовательности равномерно сходятся на некотором множестве, то
и любая их конечная линейная комбинация равномерно сходится на
этом множестве.
Примеры. 1.Пусть /п(ж)=жп, га = 1,2,..., X = [0,q], 0<q<l.
Предел lim fn(x), x G [0,g], существует и равен нулю:
п—>-оо
/(ж) d= lim fn(x) = 0.
п—>-оо
Так как supxn = gn, то
[М	lim supxn= lim qn = 0.
Следовательно, согласно лемме 1, последовательность {х71} равномер-
равномерно сходится к нулю на отрезке [0,д]:
хп ^ 0, Q<q<l.
23 Л.Д.Кудрявцев, т.1

354
Гл. 3. Ряды
2. Рассмотрим теперь последовательность функций fn(x) = жп,
п = 1, 2,..., на полуинтервале X = [О,1). Здесь снова
е [0,1),
d= lim /„(*)= О,
га-юо
т. е. последовательность {хп} сходит-
сходится на полуинтервале [0,1) к функции,
равной нулю:
хп -+ О,
[ОД)
однако supxn = 1, и потому
[ОД)
lim sup xn — Hm 1 = 1^0.
П—>-ОО Гд -]\	П—>-ОО
Следовательно, согласно той же
лемме сходящаяся на полуинтерва-
полуинтервале [0,1) последовательность {хп} не сходится на нем равномерно
(рис. 125):
хп JX 0.
[ОД)
3. Последовательность fn(x) = жп, п = 1, 2,..., сходится и на отрез-
отрезке [0,1], но уже к разрывной функции
О
Рис. 125
f(x) = lim xn =
п—>-оо
0, если 0 ^ х < 1,
если х =
Поскольку последовательность {х71} не сходится равномерно на полу-
полуинтервале [0,1), то она не сходится равномерно и на отрезке [0,1].
Это следует из того, что если неравенство C1.7) не выполняется на
каком-то множестве X (в данном случае на [0,1)), то оно, очевидно,
не выполняется и на всяком множестве, содержащем в себе X.
Рассмотренная последовательность является еще одним примером
сходящейся последовательности непрерывных функций, предел кото-
которой уже не является непрерывной функцией (первым примером тако-
такого рода у нас была последовательность частичных сумм ряда C1.4)).
Ниже будет показано, что если потребовать, чтобы последователь-
последовательность не только сходилась, но и равномерно сходилась, то подобная
ситуация будет уже невозможной (теоремы 7 и 7').
Теорема 1 (критерий Коши равномерной сходимости последова-
последовательности). Для того чтобы последовательность fn равномерно схо-
сходилась на множестве X к некоторой функции, необходимо и доста-
достаточно, чтобы для любого е > 0 существовал такой номер по, что
для всех х G X, всех п > по и всех р = 0,1,... выполнялось неравенство
\fn+P{x) - fn{x)\

§31. Функциональные последовательности и ряды	355
В символической записи это условие выглядит следующим об-
образом:
Ve>0 Зп0 МхеХ Уп>п0 Мр^ 0: \fn+p(x) - fn(x)\ <e. C1.10)
> 1. Пусть
fn^f-
х
Зафиксируем произвольно г > 0. Для него в силу C1.7) существует
такой номер по, что для всех п > по и всех х Е X выполняется нера-
неравенство
\fn(x)-f(x)\<e/2.
Поэтому для всех точек х е X, всех номеров п > п0 и всех р = 0,1, 2,...
имеем
\fn+p(x) ~ fn(x)\ = \[fn+p(x) ~ f(x)] + [f(x) - fn(x)]\ ^
<C \fn+p(x) - f(x)\ + \fn(x) - f(x)\ < | + | =e,
т. е. выполняется условие C1.10).
2. Пусть выполняется условие C1.10); тогда в каждой точке х G
е X последовательность {fn(X)} удовлетворяет критерию Коши схо-
сходимости числовых последовательностей и, следовательно, сходится.
Обозначим предел последовательности {/п} на множестве X через /:
f(x) = lim /n(x), xeX.	C1.11)
п—>-оо
Перейдя к пределу в последнем неравенстве C1.10) при р —У оо, в
силу C1.11) получим, что для всех номеров п > по и всех точек х G X
выполняется неравенство \f(x) — fn(x)\ ^ e.
Это и означает равномерную сходимость последовательности
функций {/п} к функции / на множестве X. <\
Определение 2. Ряд
(X)
^2ип(х), хеХ,	C1.12)
71=1
называется равномерно сходящимся на множестве ж, если на х равно-
равномерно сходится последовательность его частичных сумм.
Очевидно, что ряд, равномерно сходящийся на множестве X, схо-
сходится на этом множестве. Пусть
оо	п
s(x) = ^2 ип(х)^ sn(x) = ^2Uk^
71=1	k = l
и rn(x) = s(x) — sn(x) = 22 uk(x) — остаток ряда. Равномерная
k=n+l
23*

356	Гл. 3. Ряды
оо
сходимость ряда 2_,ип(%) согласно определению означает, что
sn(x)=ls(x).	C1.13)
X
Это условие равносильно условию
s(x) -sn(a;)=4 0.
х
Поэтому условие C1.13) равномерной сходимости на множестве X
ряда равносильно условию
Иначе говоря, равномерная сходимость ряда на множестве X оз-
означает равномерную сходимость на X к нулю последовательности
его остатков. Отсюда в силу леммы получаем, что для того чтобы
ряд C1.12) равномерно сходился на множестве X, необходимо и
достаточно, чтобы
lim sup|rn(x)| = 0.	C1.15)
П-ЮО Х
Замечание 2. Если какие-то ряды равномерно сходятся на не-
некотором множестве, то и любая их конечная линейная комбинация
равномерно сходится на этом множестве (см. замечание 1).
Теорема 2 (необходимое условие равномерной сходимости ря-
ряда). Если ряд C1.12) равномерно сходится на множестве X, то по-
последовательность его членов равномерно стремится к нулю на этом
множестве.
|> В самом деле,
ип(х) =sn(x) -sn_i(x), n = 2,3,...	C1.16)
В случае равномерной сходимости на множестве X ряда C1.12) после-
последовательности {sn(x)} и {sn-i(x)} его частичных сумм равномерно
стремятся на X к его сумме s(x):
поэтому
а это в силу
C1
S
.16)
п(х)
=U(x),
X
sn(x) -
и означает,
s
зп-г
что
n-l(x)
X
X
s(x),
ип(х)^0. <	C1.17)
х
Отметим, что согласно лемме 1 для того, чтобы было выполнено
условие C1.17), необходимо и достаточно, чтобы выполнялось усло-
lim sup\un(x)\ = 0.	C1.18)

§31. Функциональные последовательности и ряды	357
Теорема 3 (критерий Коши равномерной сходимости ряда). Для
того чтобы ряд C1.12) равномерно сходился на множестве X, необ-
необходимо и достаточно, чтобы для любого г > 0 существовал такой
номер по, что для всех п > по, всех р = 0,1, 2,... и всех х Е X выпол-
выполнялось неравенство
\ип(х) + ип+1(х) + ... + ип+р(х)\ < г.
\> В силу равенства
ип(х) + ип+1(х) + ... + ип+р(х) = sn+p(x) - sn-!(x),
где sn(x) — частичные суммы рассматриваемого ряда, критерий Ко-
Коши равномерной сходимости рядов сразу следует из критерия Коши
равномерной сходимости последовательностей. <\
Замечание 3. В дальнейшем нам понадобится следующее прос-
простое свойство равномерно сходящихся рядов.
Если ряд C1.12) равномерно сходится на множестве X, а функ-
(X)
ция / ограничена на этом множестве, то ряд *S^f(x)un(x) также
равномерно сходится на X.	п=1
\> Действительно, ограниченность функции / означает, что сущест-
существует такая постоянная с > 0, что для всех х G X выполняется нера-
неравенство \f(x)\ ^ с. Поэтому для любых целых п ^ 1, р ^ 0 и любой
точки х е X имеет место неравенство
\f(x)un(x) + f(x)un+1(x) + ... + f(x)un+p(x)\ =
= \f(x)\\un(x) + un+1(x) + ... + un+p(x)\ ^
^ c\un(x) + un+1(x) + ... + un+p(x)\.
(X)
Из этого неравенства следует, что ряд *S^ f(x)un(x) удовлетворя-
п=1
ет на множестве X критерию Коши равномерной сходимости ряда,
ибо этому критерию удовлетворяет исходный ряд C1.12). <|
Теорема 4 (признак Вейерштрасса). Если числовой ряд
ап, ап^0,	C1.19)
71=1
сходится и для всех х G X и для всех п = 1,2,... выполняется не-
неравенство
\ип(х)\ ^ ап,	C1.20)
то ряд C1.12) абсолютно и равномерно сходится на множестве X.
\> Абсолютная сходимость ряда C1.12) в каждой точке х множест-
множества X следует, согласно признаку сравнения (теорема б в п. 30.4), из
неравенства C1.20) и сходимости ряда C1.19).

358
Гл. 3. Ряды
Докажем равномерную сходимость ряда C1.12). Пусть гп(х) и еп
ОО
являются остатками порядка п соответственно рядов у^ ип(х),
ОО	(X)	(X)
хеХ, и ^ап, т.е. гп(х)=
71=1
(X)
uk(x)
к=п+1
к=п+1
ик(х)
п—1
к=п+1
Из сходимости ряда V^ ап следует, что lim еп — О, а тогда в
^—'	п>оо
п=1
силу следствия из леммы 1 имеем
Это и означает, что ряд C1.12) равномерно сходится на множест-
множестве X. <\
Примеры. 4. В п. 31.1 было показано, что ряд
±-
п=0
C1.21)
сходится при любом z G С, в частности, для любого г > 0 сходится ряд
Уг-
п=0
Поскольку из неравенства \z\ ^ r следует неравенство
то
из признака Вейерштрасса следует, что ряд C1.21) абсолютно и рав-
равномерно сходится в круге Kr = {z: \z\ ^ г} любого радиуса г. Однако
ряд C1.21) не сходится равномерно на всей комплексной плоскости С.
Это следует из того, что последовательность членов ряда C1.21) не
стремится равномерно к нулю на С, ибо при любом п = 1, 2,... имеет
место равенство
sup
с
= +00,
и потому условие C1.18) заведомо не выполнено.
Итак, ряд C1.21) равномерно сходится в круге Кг сколь угодно
большого радиуса г, но не сходится равномерно на всей плоскости С.
Это означает, что если обозначить через s(z) и sn(z) соответственно
сумму и частичные суммы ряда C1.21), то для любого г > 0 при за-
заданном круге Кг можно так выбрать номер п0, что для всех п > п0 и
всех z G Кг будет выполняться неравенство \s(z) — sn(z)\ < г. Номер
по зависит не только от г, но и от г, т. е. по = по(е, г), причем при не-
неограниченном возрастании радиуса г номер по также неограниченно
возрастает: lim no(e, г) = +оо (если бы это было не так, то ряд C1.21)

§31. Функциональные последовательности и ряды	359
сходился бы равномерно на всей комплексной плоскости), т. е. невоз-
невозможно выбрать такой номер по, чтобы при всех п > по неравенство
\s(z) — sn(z)\ < г выполнялось для всех z Е С.
оо
5. Ряд У^ ?n, z Е С, сходится в открытом круге К = {z: \z\ < 1}
n=0
и при любом г, 0 ^ г < 1, сходится равномерно в замкнутом круге
Kr = {z : |z| ^ r}. Это следует, например, из признака сходимости
оо
Вейерштрасса, так как при \z\ ^ r имеем \zn\ = \z\n ^ rn и ряд У^ гп
п=0
сходится. В круге if заданный ряд не сходится равномерно, так как
lim sup \zn\ = lim sup \z\n = lim 1 = 1 и, следовательно, в кру-
п—^оо ы<1	п—^оо ui^i	п—^оо
re if не выполняется необходимое условие равномерной сходимости
ряда (см. теорему 2).
При \z\ < 1 члены ряда ^ zn образуют убывающую геометричес-
-=°оо
кую прогрессию, и поэтому
п=0
Если z = r(cos(p + г sin у?), то
(X)	(X)
Е?п = У^ rn (cos n(z? + г sin no?) =
1 — г cos ш — ir sin <z?
n=0	n=0	^	^
_ 1 — r cos (p + ir sin 9?
1 — 2r cos cp + r2 '
0 ^ r < 1, -oo < <? < +oo.
Приравняв действительную и мнимую части этого равенства, полу-
получим
оо	оо
V^ п	1 — г cos ш	\-^ п .	г sin ш
> г cosrup =	—-,	> г smncp =	-.
*-^	^ 1 - 2r cos ip + г2	^	^ 1 - 2r cos ip + r2
п=0	п=1
При фиксированном г, 0 ^ г < 1, эти ряды как функции перемен-
переменной if абсолютно и равномерно сходятся на множестве R всех дейст-
действительных чисел. Это следует, например, из признака равномерной
сходимости Вейерштрасса, так как \rn cosmp\ ^ rn, |rnsinn(^| ^ rn,
оо
и при 0 ^ г < 1 ряд У^ гп сходится.
п=0
31.3*. Специальные признаки равномерной сходимости
рядов. Для рядов функций справедливы признаки равномерной
сходимости, аналогичные признакам Дирихле и Абеля сходимости
числовых рядов.

360	Гл. 3. Ряды
Теорема 5 (признак Дирихле-Харди*)). Если последователь-
последовательность функций ап{х) Е /?, п = 1, 2,..., равномерно стремится на мно-
множестве X к нулю, т. е.
ап(х)^0,	C1.22)
х
и в каждой точке х Е X монотонна, а последовательность функций
Ъп(х) е С, п = 1,2,..., х е X, такова, что последовательность час-
частичных сумм ряда	оо
$>»(*)	C1.23)
П=1
ограничена на X, то ряд ^
Y,an(x)hn(x)	C1.24)
п=1
равномерно сходится на множестве X.
\> Согласно условию последовательность частичных сумм
Вп(х) = h(x) + ... + Ъп(х), п = 1, 2,...,
ряда C1.23) ограничена на множестве X, поэтому существует такая
постоянная В > 0, что для всех х G X и всех п = 1, 2,... выполняется
неравенство
|Вп(ж)| ^В.
Отсюда для всех х G X, всех п = 2,3,... и всех р = 0,1,2,... имеем
, bk(x)\ = \Вп+р(х) - В„_1(ж)| ^ |В„+Р(а;)| + |Bn-i(a0| ^ Ч.В.
k—n
C1.25)
Зафиксируем произвольно г > 0. Из условия C1.22) следует, что
существует такой номер п0, что для всех х е X и всех номеров п> п0
выполняется неравенство
\ап(х)\ < g|.	C1.26)
Поэтому для любого х G X, любого п > по и любого р = 0,1, 2,..., со-
согласно неравенству Абеля C0.75), будем иметь
(\()\ \+р()\)
C0.75)	C1.26)
к~П	C1.25)
Таким образом, ряд C1.24) удовлетворяет на множестве X критерию
Коши равномерной сходимости ряда. <|
Теорема б (признак Абеля-Харди). Если последовательность
функций ап(х) G /?, п = 1,2,..., ограничена на множестве X и мо-
монотонна в каждой точке х G X, а ряд C1.23) равномерно сходится
?) Г. Харди A877-1947) — английский математик.

§31. Функциональные последовательности и ряды
361
на X, то и ряд C1.24) также равномерно сходится на множестве X.
\> В силу ограниченности на множестве X последовательности
{ап(х)} существует такая постоянная А > О, что для всех х е X и
всех п = 1,2,... выполняется неравенство
\ап(х)\^А.	C1.27)
В силу же равномерной сходимости ряда C1.23) для произвольно
фиксированного г > 0 существует такой номер п0, что для всех х е X,
всех п > п0 и всех р = 0,1, 2,... имеет место неравенство
В результате, согласно неравенству Абеля C0.75), для всех х G X,
всех п > по и всех р = 0,1, 2... будет выполняться неравенство
п+р
C0.75)
C1.28)
C1.27)
т. е. снова ряд C1.24) удовлетворяет на множестве X критерию Коши
равномерной сходимости ряда. <|
Пример. В п. 30.8* было показано, что ряд
sinnx
C1.29)
п=1
сходится на всей числовой оси R. Там же было показано, что
п,
1
sinkx
k = l
. X
sin —
2
2тггтг, т = 0,±l,±2,...
C1.30)
Поэтому если положить ап = 1/n, bn(x) = sinnx, n = 1,2,..., то пос-
последовательность {ап} будет монотонной и, как всякая сходящаяся
числовая последовательность, может рассматриваться как равномер-
равномерно сходящаяся, например, на R. Последовательность {Ьп(х)} ограни-
ограниченна на любом отрезке [а, Ь], не содержащем точек вида х = 2тгт,
т = 0, =Ы, ±2,..., так как для любой точки х такого отрезка
k=i
sin kx
k=i
C1.30)
X
sm-
max
[a,b]
x
sm-
< +00,
и, следовательно, последовательность
k=i
, n = 1,2,..., ограни-
ограниченна сверху на отрезке [а, Ь] числом max
[а,Ъ]
х
sm-
. Таким образом,

362	Гл. 3. Ряды
на всяком отрезке [а, 6], не содержащем точек вида х = 2тгт, т =
= О, =Ы, ±2,..., ряд C1.29) удовлетворяет условиям признака Дирихле-
Харди и потому равномерно сходится.
Можно показать, что если отрезок [а, Ъ] содержит точку вида х =
= 2тгт при некотором т = О, =Ы, ±2,..., то ряд C1.29) не сходится
равномерно на этом отрезке.
31.4. Свойства равномерно сходящихся последовательнос-
последовательностей и рядов. До сих пор при изучении последовательностей и рядов
функций эти функции предполагались заданными на произвольном
множестве X. Теперь мы перейдем к изучению свойств непрерыв-
непрерывности, дифференцируемости и интегрируемости, в связи с чем мно-
множество X будет являться подмножеством числовой прямой.
При изучении вопроса о непрерывности суммы ряда будем рас-
оо
сматривать ряды ^~^г?п(ж), где х Е X С /?, ип(х) Е С, п — 1,2,...
п=1
Теорема 7. Если ряд равномерно сходится на некотором мно-
множестве и в какой-то точке этого множества все члены ряда неп-
непрерывны, то сумма ряда непрерывна в этой точке.
\> Пусть ряд	оо
X>n(s), xex,	C1.31)
71=1
(X)
равномерно сходится на множестве X, s(x) = ^^ип(х) — его сум-
сумма, а	п	п=1
Sn(x) = J2 ^fr)' П=1>2> -'	C1-32)
k=l
— его частичные суммы.
Зафиксируем произвольно е > 0. Равномерная сходимость ряда
C1.31) означает, что последовательность {sn(x)} равномерно сходит-
сходится на множестве X к функции s(x). Поэтому существует такой но-
номер п, что для всех точек х е X выполняется неравенство
\s(x) - sn(x)\ < 1,	C1.33)
так как такое неравенство имеет место для всех номеров, начиная с
некоторого. Зафиксируем указанный номер п.
Функция sn(x), являясь конечной суммой непрерывных (соглас-
(согласно условиям теоремы) в точке хо G X функций ui(x),U2(x),...,un(x),
сама непрерывна в этой точке. Поэтому существует такое S > 0, что
для всех точек х G X, удовлетворяющих условию х G U(xo; S), выпол-
выполняется неравенство
г(х)-зп(х0)\ <|.	C1.34)

§31. Функциональные последовательности и ряды	363
В силу сказанного для любой точки х е X П U(xo]S) имеем
\s(x) - s(xo)\ = \[s(x) - sn(x)] + [sn(x) - sn(x0)] + [sn(x0) - s(xo)]\ ^
^ \s(x) - sn(x)\ + \sn(x) - sn(x0)\ + \sn(x0) - s(xo)\	<
C1.33), C1.34)
C1.33), C1.34) 3 3 3
Это и означает непрерывность функции s(x) в точке xq. <\
оо
Отметим, что в условиях теоремы в точке хо Е X для ряда V^ un(x)
возможен почленный переход к пределу, т. е.	п=1
оо
lim У^ ип(х) = У^ lim un(x).
ж)ж ^^	^^ ж^ж
> Действительно, в силу непрерывности функций s(x) и ип(х) в точ-
точке хо имеем lim s(x) =s(xo), lim un(x) = un(xo), n = 1, 2,..., поэтому
ж—>-жо	ж—>-жо
оо	оо	оо
lim У^ ип(х) = lim s(x) = s(x0) = У^^п(ж0) = У^ lim un(x). <\
ж—>-жо ^——^	ж—>-жо	^——^	^——^ ж—Ухо
п=1	п=1	п=1
Заметим, что в теореме 7 условие равномерной сходимости ряда
на множестве нельзя заменить условием только его сходимости на
этом множестве. Это показывает пример 2 в п. 31.1: ряд C1.4) схо-
сходится на всей числовой прямой, его члены являются непрерывными
на ней функциями, а сумма ряда — разрывная в точке х = 0 функция.
Выше отмечалось, что изучение рядов равносильно изучению по-
последовательностей (п. 30.1), поэтому каждое предложение о рядах
можно перефразировать в соответствующее предложение о последо-
последовательностях.
Будем рассматривать последовательности {/п(ж)}, х G X С /?,
/п(ж) е С, п = 1,2,... Теорема 7 в терминах последовательностей
равносильна следующей теореме.
Теорема 7'. Если последовательность функций равномерно схо-
сходится на некотором множестве и в некоторой точке множества все
члены последовательности непрерывны, то и предельная функция по-
последовательности непрерывна в этой точке.
Заметим, что если
X
и все функции непрерывны в точке ж0 G X, то
lim lim fn(x) = lim lim fn(x),
n—>-oo ж—>xo	x—>xo n—>-oo
т. е. при сделанных предложениях предельные переходы при п —> оо
и при х —> xq перестановочны.

364	Гл. 3. Ряды
Действительно,
lim lim fn(x) = lim fn(xo) = /(#o) = lim f(x) = lim lim fn(x).
n—>-oo ж-^жо	n—>-oo	ж-^жо	ж-^жо n—юо
Пример З в п. 31.2 еще раз подтверждает, что условие равномер-
равномерной сходимости в теоремах 7 и 7' существенно.
Теорема 8. Пусть функции ип(х) е /?, п = 1,2,..., ж G [а, 6],
непрерывны на отрезке [а, 6] и ряд
ОО
$^п(ж)	C1.35)
71=1
равномерно сходится на этом отрезке. Тогда, какова бы ни была точ-
точка х0 е [а, Ь], ряд	оо ж
]Г jun(t)dt	C1.36)
71=1 Ж0
также равномерно сходится на отрезке [а,Ь] и
|(	)	/««(*) di-	C1-37)
Xq 71=1	71=1 Жд
Равенство C1.37) означает, что в условиях теоремы ряд C1.35)
можно почленно интегрировать.
> В силу равномерной сходимости ряда C1.35) и непрерывности его
членов на отрезке [а, Ь] его сумма
X (X)	(X) Ж
( )
оо
<j уж J 	 7 Ubiyiyaj j	^Ol.OUy
71=1
также непрерывна на этом отрезке (теорема 7), а следовательно, и ин-
интегрируема по Риману на отрезке [а, Ь], а поэтому и на любом отрезке
с концами в точках ж0 G [а, Ь] и ж G [а, Ь].
Покажем, что ряд C1.36) равномерно сходится к функции
ж
a(x)d= Js(t)dt.	C1.39)
жд
Как всегда, положим
п
def V ^ / \	/ \ def / \	/ \	/О1 лгл\
к(х), rn(x) = s(x)-sn(x),	C1.40)
A;=l
а через сгп(ж) обозначим частичные суммы ряда C1.36):
= Jsn(t)dt, n = 1,2,...
Жд
C1.41)

§31. Функциональные последовательности и ряды
365
Для любого х е [а, Ь] имеем
XX	X
т(х) - ап(х)\ = I fa(t) dt - fan(t) dt	^ I /|e(*) - an(t)\ dt
C1 .39 J \ J	J	\ J
C1.41) x°	x°	x°
C1.40)
C1.40)
X	X
J\rn(t)\dt\ ^sup|rn(t)||y<ft
X0	L">"J	XQ
= x — xo\ sup \rn(t)\ ^ (b — a) sup |rn(t)|. C1.42)
[a,b]	[a,b]
Отсюда следует, что
sup \a(x) - <тп(х)\ ^(b-a) sup \rn(x)\.
[a,b]	[a,b]
Из равномерной сходимости на отрезке [а, Ь] ряда C1.35) следует, что
Следовательно,
lim sup |гп(ж)| = 0.
п^°° [а,Ъ]
lim sup \cr(x) - ап(х)\ = 0,
n^°° [a,b]
что, согласно лемме 1, означает, что последовательность {ап(х)} рав-
равномерно на отрезке [а, Ь] сходится к функции сг(х), т. е. что ряд C1.36)
равномерно сходится на указанном отрезке и что его сумма равна
(X) X
<X) = Y. jun{t)dt.
П=1 XQ
Последнее равенство в силу C1.39) можно записать в виде
X	(X) X
fs(t)dt =
XQ
ra=l
что согласно C1.38) равносильно равенству C1.37). <l smallskip
Перефразировка теоремы 8 в терминах последовательностей име-
имеет следующий вид.
Теорема 8;. Если последовательность непрерывных на отрез-
отрезке [а,Ь] функций fn(x) G /?, п = 1,2,..., равномерно сходится на этом
отрезке к функции /(ж), то, какова бы ни была точка х0 е [а, 6], по-
X
следовательность fn(t)dt сходится равномерно на отрезке [а, Ь] к
функции I f(t) dt.
XQ

366	Гл. 3. Ряды
Из этой теоремы следует, в частности, что
X	XX
lim [fn(t)dt= ff(t)dt= f lim fn(t)dt,
n—yoo J	J	J n—yoo
Xq	Xq	Xq
т. е. что в данном случае можно переходить к пределу под знаком
интеграла, или, коротко: в рассматриваемом случае
предел интегралов равен интегралу от предела.
Замечание. Условия равномерной сходимости в
теореме 8' являются существенными. Подтвердим это
примером.
Функции fn(x), 0 ^ х ^ 1, зададим для наглядности
графически (рис. 126). Для любой точки х G [0,1] име-
ем lim fn(x) = 0 и, следовательно, / lim fn(x)dx =
п—>-оо	J п—уоо
О	1
= 0. При любом же п = 1,2,... интеграл fn(x)dx = l
о
равен площади треугольника ААОВ. Поэтому в этом случае
1	1
lim fn(x)dx = 1^0= / lim fn(x) dx.
n—уоо J	J n—уоо
0	0
Теорема 9. Пусть функции un{x) G /?, n = 1,2,..., непрерывно
дифференцируемы на отрезке [а, Ъ] и ряд, составленный из их произ-
производных:	оо
Е<0*0'	C1.43)
71=1
равномерно сходится на отрезке [а,Ь]. Тогда если ряд
(X)
5>п(х)	C1.44)
71=1
сходится хотя бы в одной точке хо G [а, Ь], то он сходится равномер-
равномерно на всем отрезке [а, 6], его сумма
оо
Un(x)	C1.45)
71=1
является непрерывно дифференцируемой функцией и
оо
s'(x) = J2<(x)-	C1-46)
71=1
В силу формулы C1.45) последнее равенство можно записать в
виде
)
71=1	71=1

§31. Функциональные последовательности и ряды	367
Таким образом, в условиях теоремы ряд C1.44) можно почленно диф-
дифференцировать.
|> Положим
ОО
<7(aOd= ?<(*)•	C1-47)
71=1
По теореме 8 этот ряд можно почленно интегрировать:
X	ОО X	ОО
j	/«»(*) dt = E^W - "»(*<>)]	C1-48)
Xq	71=1 Xq	71=1
(мы использовали формулу Ньютона-Лейбница), причем ряд, стоя-
стоящий в правой части равенства, в силу той же теоремы 8 равномерно
сходится на отрезке [а, Ь].
оо
По условию теоремы числовой ряд 2^y"n(xo) сходится, причем,
71=1
как и для всякого числового ряда, у него сходимость совпадает с рав-
равномерной сходимостью. Сумма двух равномерно сходящихся на от-
(X)	(X)	(X)
резке [а, Ь] рядов ^2[ип(х) - ип(х0)] и ^г1п(ж0)> т- е- РЯД
п=1	п=1	п
также, очевидно, равномерно сходится на отрезке [а, Ь]. В силу дока-
доказанной сходимости ряда C1.44) формулу C1.48) можно записать в
виде
Jcr(t) dt =
Xq
х
или (см. C1.45))
fa(t) dt = s(x) - s(x0).	C1.49)
XQ
Функция a(t) является суммой равномерно сходящегося ряда не-
непрерывных функций на отрезке [а, Ъ] (см. C1.47)), и поэтому она сама
X
непрерывна на этом отрезке, а тогда функция a(t)dt непрерывно
дифференцируема на [а, Ь] (см. п. 25.1) и	х°
j- a(t)dt = a(x).	C1.50)
ох j
Xq
В силу формулы C1.49) это означает, что функция s(x) непрерыв-
непрерывно дифференцируема и что
X	(X)
s'(x) = ^-[a(t)dt = <г(х) = V<(x). <
К JC1A9)dxJ W C1.50) V J C1.47) ^^
Ж0	71=1

368	Гл. 3. Ряды
Для последовательностей функций аналогичная теорема выглядит
следующим образом.
Теорема 9'. Если последовательность непрерывно дифференци-
дифференцируемых на отрезке [а, Ъ] функций fn(x) Е /?, п = 1, 2,..., сходится в не-
некоторой точке хо Е [а, Ь], а последовательность их производных f'n(x)^
п = 1,2,..., равномерно сходится на [а,Ь] к некоторой функции (р(х),
то и последовательность {fn(x)} сходится равномерно на отрезке
[а, Ь] к непрерывно дифференцируемой функции f и f = ср.
Из рассуждений, проведенных при доказательстве теоремы 9, сле-
следует, что если функции /п, п = 1, 2,..., непрерывно дифференцируемы
и последовательность их производных {/^} равномерно сходится на
отрезке [а, 6], то условия:
1) существует такая точка хо Е [а, Ь], что числовая последователь-
последовательность {/пОо)} сходится;
[а,Ъ]
3) /п =4 /;
[а,Ч
равносильны (то, что из условия 1) следуют условия 2) и 3), было
доказано; что из 3) следует 1) — очевидно). Поэтому теорема 9 рав-
равносильна следующему утверждению.
Если
fn =r / и /; =* <л
[а,Ь]	[а,Ь]
то существует производная f и f = ср, т. е. в этом случае предел
производных равен производной от предела.
В терминах рядов это утверждение (равносильное теореме 9) мож-
можно сформулировать следующим образом: если функции ип(х) непре-
оо	оо
рывно дифференцируемы, а ряды 2^ип(х) = s(x) и 2^u'n(x) = а(х)
п=1	п=1
равномерно сходятся на отрезке [а, 6], то у суммы ряда s(x) сущест-
существует производная s'(x) и s'(x) = а(х).
Эти формулировки отражают сущность условий, при выполнении
которых возможно почленное дифференцирование последовательнос-
последовательностей и рядов. Но, конечно, на практике очень удобно, что сходимость
последовательностей и рядов достаточно проверять лишь в одной точ-
точке и не доказывать их равномерную сходимость (конечно, равномер-
равномерную сходимость последовательностей и рядов производных необхо-
необходимо установить).
Пример. Рассмотрим функцию
71=1

§ 32. Степенные ряды	369
называемую функцией Римана (ряд, стоящий в правой части ра-
равенства, сходится при х > 1; см. C0.20)).
Каково бы ни было а > 1, ряд У^ — и ряд, получающийся его
^—' пж
формальным дифференцированием, т. е. ряд — V^ ——, равномерно
71=1
сходятся на полуинтервале [а,+оо). Это сразу вытекает в силу при-
признака Вейерштрасса из неравенств
1 1 ~ Inn In n	1	~	л
— < —, 0 < —^ < —— <-^37, х > а, 0 <е <а-1,
справедливых при фиксированном г для достаточно больших п, и из
сходимости рядов >^ —, >^	, 0 < г < а — 1.
*-^ па *-^ па~?
п=1	п=1
В силу теоремы 9 при любом х > а имеет место равенство
а поскольку а > 1 было выбрано произвольно, то это равенство верно
и при любом х > 1.
§ 32. Степенные ряды
32.1. Радиус сходимости и круг сходимости. Степенным
рядом называется ряд вида
оо
J2an(z-z0)n, zeC, zoeC,	C2.1)
n=0
числа an G С, п = 1,2,..., называются коэффициентами ряда C2.1).
С помощью замены переменного ^ — z — z^ ряд C2.1) может быть
преобразован к виду	^
YJanZn.	C2.2)
п=0
Поэтому, как правило, мы ограничиваемся рассмотрением рядов ви-
вида C2.2).
Теорема 1 (первая теорема Абеля). Если степенной ряд C2.2)
сходится при z = zo, то при любом z таком, что \z\ < \zo\, ряд C2.2)
сходится абсолютно.
Следствие. Если ряд C2.2) расходится в точке zo, то в любой
точке z такой, что \z\ > \zo\, он также расходится.
24 Л.Д.Кудрявцев, т.1

370
Гл. 3. Ряды
\> Если ряд
ОО
Е<
п=0
C2.3)
сходится, то lim anz^ — 0, и потому существует такая постоянная
п—>-оо
с > 0, что для всех п = 1, 2,... выполняется неравенство
|<Wo I ^ С'	C2-4)
Следовательно, при ^о ф 0 (в случае ^о = 0 утверждение теоремы оче-
очевидно и бессодержательно, так как множество таких z, что \z\ < О,
пусто) имеем
Z	C2.5)
= \anz$\
C2.4)
и если
ТО РЯД
нечно убывающей
У
/ ^
\
\
\
\
\
\
\
О
- _
/ \
\
1
1
/
/
у
ОО
Е
п=0
геометрической прогрессии (е
z п \z\	\	^
— = -!—у < 1). Поэтому
ку сравнения сходимости рядов из нера-
неравенства C2.5) следует, что сходится ряд
сходится, ибо является суммой беско-
бескопрогрессии (ее знаменатель
Ы	^
по призна-
признаРис. 127
|anzn|, т. е. ряд C2.2) абсолютно схо-
дится (рис. 127). <1
Следствие сразу вытекает из теоре-
теоремы: если в точке z0 ряд C2.2) рас-
расходится, то при \z\ > \zo\ он не мо-
может сходиться в точке z, так как
тогда бы он по доказанной теореме схо-
сходился (и даже абсолютно) в точке zq.
Рассмотрим степенной ряд C2.2). Он заведомо сходится в точ-
точке z = 0. Обозначим через X множество всех таких действительных
неотрицательных чисел х G /?, что при z — х ряд C2.2) сходится. По-
Поскольку 0 е X, то X ф 0. Пусть
R = supX.	C2.6)
Очевидно, 0 ^ R ^ +оо.
Неравенство \z\ ^ R задает на комплексной плоскости С замкну-
замкнутый круг радиуса R с центром в точке z = 0. При R = 0 этот круг
вырождается в точку z = 0, а при R = +оо превращается во всю
комплексную плоскость.
Определение 1. Число R = supX (конечное или бесконечное)
называется радиусом сходимости ряда C2.2), а круг {z:
его кругом сходимости.

§ 32. Степенные ряды
371
Теорема 2. Пусть R — радиус сходимости ряда C2.2). Тогда
если \z\ < R, то ряд C2.2) сходится абсолютно, если \z\ > R, то
ряд C2.2) расходится, а если 0 ^ г < R, то в круге {z : \z\ ^ r}
ряд C2.2) сходится равномерно.
\> Если R = 0, то точек z Е С таких, что \z\ < R нет. Если же 0 <
< R ^ +оо и z Е С таково, что \z\ < R, то согласно определению
верхней грани из равенства R = supX следует, что существует такое
х е X, что \z\ < х < R, а так как по определению множества X во
ОО
всех его точках х ряд V^ апжп сходится, то по первой теореме Абеля
n=0
он абсолютно сходится в точке z.
Если R = +00, то точек z e С таких, что \z\ > R, нет.
Если же R < +00 и z Е С таково, что \z\ > R, то для любой точ-
точки х такой, что R < х < \z\, согласно
определению R = supX имеем х 0 X,
а поэтому в силу определения мно-
жества X ряд
оо
Е
п=0
апх
расходится.
Следовательно, в силу следствия из
теоремы 1 ряд C2.2) расходится в рас-
рассматриваемой точке z.
Если теперь
О ^ г < R,	C2.7)
то покажем, что ряд C2.2) сходится рав-
равномерно в круге \z\ ^ г (рис. 128). Действительно, если \z\
\апгп
Рис. 128
J г, то
C2.8)
Из неравенства C2.7), согласно вышедоказанному свойству ради-
радиуса сходимости, вытекает, что ряд C2.2) при z = г абсолютно сходит-
ся, т. е. сходится ряд
, а тогда в силу признака равномерной
п=0
сходимости Вейерштрасса (п. 31.2) из неравенства C2.8) следует, что
ряд C2.2) равномерно сходится в круге {z: \z\ ^ г}. <
оо
Рассмотрим степенной ряд общего вида 2_^ an(z — ^о)п- Он сходит-
ся или расходится в точке z тогда и только тогда, когда соответствен-
оо
но сходится или расходится в точке ( = z — z$ ряд 2^ап(п- Радиус
п=0
сходимости R последнего ряда называется и радиусом сходимости
24*

372	Гл. 3. Ряды
исходного ряда V^ an(z — zo)n.
п=0
При замене переменного ( = z — z$ кругу сходимости {(: \(\ ^ R}
ОО
ряда ^ап(п соответствует круг {z : \z - zo\ ^ R}. Он называется
п=0
оо
кругом сходимости ряда V^ an(^ — ^о)п-
п=0
Из теоремы 2 следует, что если Л является радиусом сходимос-
оо
ти ряда V^ an(z — zo)n, то при \z — zo\ < R этот ряд абсолютно схо-
п=0
дится, при \z — zo\ > R он расходится, а если 0 ^ г < Л, то в круге
{z: \z — zo\ ^ r} ряд равномерно сходится.
Отметим, что из равномерной сходимости ряда C2.1) в любом
круге \z — zo\ ^ R, где 0 ^ г < Л, и непрерывности каждого члена
этого ряда следует, что сумма каждого степенного ряда непрерывна
внутри его круга сходимости R > 0.
Действительно, для любого z, \z\ < R, можно выбрать такое г,
что \z\ < г < R. В круге \z\ ^ r рассматриваемый ряд сходится рав-
равномерно, а так как его члены — непрерывные функции, то его сум-
сумма также непрерывна на этом круге, в частности в точке z (см.
теорему 7 в п. 31.4).
Примеры. 1. Рассмотрим ряд
\zn.	C2.9)
п=0
Для исследования его абсолютной сходимости применим признак Да-
ламбера (п. 30.4):
г |(п + 1)Ьп+1| , г . , Л. Г+оо, если z^O,
hm	гЦ	L = \z hm (n + 1) = < n	n
n^oo \n\zn\	' n^oov J { 0, если 2 = 0.
Следовательно, ряд C2.9) сходится только при z = 0, а потому его
радиус сходимости равен нулю: R = 0.
2.	Радиус сходимости Л ряда
Е ^	C2Л°)
п=0
равен +оо, так как в п. 31.1 было показано, что этот ряд сходится при
любом z G С.
3.	Радиус сходимости суммы бесконечной геометрической прог-
прогрессии	°°
J>"	C2.11)
71=1

§ 32. Степенные ряды
373
равен 1, так как ряд C2.11) сходится при \z\ < 1 и расходится при
\z\ > 1 (п. 30.1, 30.2). На границе {z: \z\ = 1} круга сходимости име-
имеем \z\ = 1 и, следовательно, последовательность членов ряда C2.11)
не стремится к нулю, откуда явствует, что во всех точках границы
своего круга сходимости ряд C2.11) расходится.
4.	У ряда
C2.12)
радиус сходимости также равен 1. Действительно, при \z\ < 1 выпол-
выполняется неравенство
C2.13)
и, следовательно, согласно признаку равномерной сходимости Вейер-
штрасса, ряд C2.12) равномерно, а следовательно, и просто сходится.
7П\
При Ы > 1 имеем lim —^ = +оо, т. е. не выполняется необходимое
условие сходимости ряда (см. теорему 1 из п. 30.1), и, таким образом,
ряд C2.12) при \z\ > 1 расходится.
Отметим, что во всех точках границы круга сходимости, т. е. при
= 1, в силу того же неравенства C2.13) ряд C2.12) сходится.
5.	Радиус сходимости R ряда
71=1
можно найти, применив признак Даламбера: имеем
lim
п + 1 _
= Ы lim
П + 1
< 1 и расходится при \z\ > 1.
Поэтому ряд C2.14) сходится при
Таким образом, R = 1.
В точке z — \ границы круга сходимости ряд C2.14) превращается
в гармонический ряд и, следовательно, расходится, а при z = — 1 по-
——. Итак, у ряда C2.14) на границе
лучается сходящийся ряд
круга сходимости имеются как точки, в которых он сходится, так и
точки, в которых он расходится.
Разобранные примеры показывают, что существуют степенные
ряды, у которых радиус сходимости равен нулю (ряд C2.9)), равен
конечному положительному числу (ряд C2.11)) и равен бесконечнос-
бесконечности (ряд C2.10)). На границе круга сходимости ряд может во всех
точках сходиться (ряд C2.12)), а может и сходиться в одних точках

374	Гл. 3. Ряды
и расходиться в других (ряд C2.14)) или расходиться во всех точках
(ряд C2.11)).
Функции, раскладывающиеся в степенные ряды, называются ана-
аналитическими. Точнее, имеет место следующее
Определение 2. Функция / называется аналитической в точ-
точке 2о, если в некоторой окрестности (см. п. 5.11) этой точки функ-
функция / раскладывается в степенной ряд:
п=0
Поскольку в силу определения окрестности точки все точки, до-
достаточно близкие к данной точке, принадлежат ее окрестности, то
радиус сходимости написанного ряда положителен.
Теорема 3* (вторая теорема Абеля). Если R — радиус сходимос-
сходимости степенного ряда C2.2), R < +оо, и этот ряд сходится при z = R,
то он сходится равномерно на отрезке [О, R] действительной оси.
Следствие. Если ряд C2.2) сходится при z = R, то его сумма
непрерывна на отрезке [О, R] действительной оси.
\> Доказательство теоремы. Имеем
(!) ,	C2.15)
ОО
причем, по условию теоремы ряд ^ anRn сходится. Поскольку этот
ряд числовой, то его сходимость можно рассматривать как равномер-
равномерную сходимость на отрезке [О, R]. Последовательность
(x/R)n, n = l,2,...,
ограничена на отрезке [О, Д], ибо если 0 ^ х ^ R, то
О ^ (x/R)n ^ 1,
и монотонна при любом х G [0,Д]. Следовательно, в силу признака
равномерной сходимости Абеля (п. 31.3*) ряд C2.2) равномерно схо-
сходится на отрезке [О, R]. <\
Утверждение следствия вытекает из непрерывности каждого чле-
члена ряда C2.2) на отрезке [О, R] и доказанной равномерной сходимости
этого ряда на указанном отрезке.
Докажем еще одну лемму для степенных рядов в комплексной об-
области, которая будет использована в следующем параграфе.

§ 32. Степенные ряды
375
Лемма 1. Радиусы сходимости R, Ri и R2 соответственно рядов
п=0
п + 1
п=0
ОО
Е
п=1
nanz
n-l
равны:
R — R\ — R2 •
C2.16)
C2.17)
C2.18)
C2.19)
Таким образом, ряды C2.17) и C2.18), получающиеся из C2.16)
соответственно с помощью "формального интегрирования и диффе-
дифференцирования", имеют те же радиусы сходимости, что и исходный
ряд. Интегрирование и дифференцирование названо здесь формаль-
формальным, поскольку для функций комплексного аргумента эти операции
у нас не были определены и они были произведены так, как если
бы ап и z были действительными числами.
> Из неравенства
7п+1
1
z\\anz
следует, что если в точке z абсолютно сходится ряд C2.16), то в этой
точке абсолютно сходится и ряд C2.17), а это означает, что ради-
радиус сходимости R\ ряда C2.17) не меньше радиуса сходимости R ря-
ряда C2.16): R\ ^ R. Из неравенства же
следует, что если в точке z абсолютно сходится ряд C2.18), то в этой
точке абсолютно сходится и ряд C2.16), т. е. R ^ R2.
Таким образом,
Rx^R^ R2.	C2.20)
Покажем теперь, что
R2^Rl	C2.21)
Возьмем какую-либо точку z ф 0 внутри круга сходимости ря-
ряда C2.17) и докажем, что в ней сходится ряд C2.18). Посколь-
Поскольку \z\ < Ri, то существует такое действительное число г, что
\z\ < г < Дь	C2.22)
Запишем абсолютную величину члена ряда C2.18) следующим об-
образом:
\пап
1)
п+1
г.П+1
п+1
C2.23)

376
Гл. 3. Ряды
Положим q =
. В силу условия C2.22) 0 < q < 1. Ряд
п=0
п(п+ 1)
n(n
п=0
сходится (в этом легко убедиться, например, с помощью призна-
признака Даламбера). Поэтому последовательность его членов стремится к
нулю и, следовательно, ограничена, т. е. существует такая постоян-
постоянная с > 0, что для всех п = 0,1, 2,... выполняется неравенство
п(п + 1) n+i
Из C2.23) и C2.24) следует неравенство
C2.24)
n-li
nanz
Поскольку г ^ Д]_, то ряд
C2.22)
71+ 1
П+ 1
rn+1 абсолютно сходится, т. е.
сходится ряд
71+1
, а поэтому по признаку сравнения схо-
сходится и ряд 2_,пап%п 1- Итак, из условия \z\ < Ri, следует абсОЛЮТ-
ная сходимость ряда C2.18). Это и означает выполнение неравенст-
неравенства C2.21).
Из неравенств C2.20) и C2.21) следует, что имеет место равенст-
равенство C2.19). <
32.2. Аналитические функции в действительной области.
Рассмотрим теперь аналитические функции, раскладывающиеся в
степенной ряд с действительными коэффициентами в некоторой
окрестности точки действительной оси R. Такие функции называ-
называются действительными аналитическими функциями. Это означает,
что действительная аналитическая в точке хо Е R функция / в неко-
некоторой окрестности этой точки на действительной оси представима в
виде степенного ряда	^
х) — > ап\х — Хо)	yoZi.Zio)
с действительными коэффициентами ап, п = 0,1, 2,...
Очевидно, что действительные аналитические функции являют-
являются частным случаем аналитических функций, и поэтому при изуче-
изучении их можно использовать свойства степенных рядов в комплексной
области. Рассмотрим некоторые свойства действительных аналити-
аналитических функций. Прежде всего заметим, что для всякого степенного

§ 32. Степенные ряды	377
ряда C2.25) с действительными коэффициентами (как и для всяко-
всякого степенного ряда) существует радиус сходимости R (теорема 2 из
п. 32.1). В действительной области радиус сходимости R ряда C2.25)
обладает тем свойством, что для всех х Е (хо — R,xo + R) рассмат-
рассматриваемый ряд абсолютно сходится, а при х 0 [хо — R,xo + R] расхо-
расходится. При R > 0 интервал (хо — R, хо + R) называется интервалом
сходимости степенного ряда C2.25).
Теорема 4. Если функция f раскладывается в окрестности х0
в степенной ряд C2.25) с радиусом сходимости R (и, следовательно,
радиус сходимости R этого ряда положителен: R > 0), то:
1)	функция f имеет на интервале {хо — R,xo + R) производные
всех порядков, которые могут быть найдены из ряда C2.25) почлен-
почленным дифференцированием:
ОО
f^m\x) = 2^ п(п ~ 1) ••• (п — т -\- 1)ап(х — хо)п~т, т = 1, 2,...;
п=т
C2.26)
2)	для любого х Е (хо — R,xo -\- R)
X	ОО
ff(t) аИ = У2 -^— (х - жо)п+1;	C2.27)
х0	п=0
таким образом, ряд C2.25) можно почленно интегрировать на интер-
интервале (хо — R,xo -\- R)]
3)	ряды C2.25), C2.26) и C2.27) имеют одинаковые радиусы схо-
сходимости.
Короче, внутри интервала сходимости степенного ряда ряд можно
почленно интегрировать и дифференцировать любое число раз.
|> В силу леммы п. 32.1 ряды C2.26) и C2.27), получающиеся из ря-
ряда C2.25) почленным дифференцированием и интегрированием, име-
имеют тот же радиус сходимости, что и ряд C2.25). Так как всякий
степенной ряд вида C2.25) с радиусом сходимости R > 0 на любом
отрезке [хо — г, хо +г], 0 < г < R, сходится равномерно (теорема 2
из п. 32.1), то утверждения 1) и 2) доказываемой теоремы непос-
непосредственно следуют из общих теорем о дифференцируемости и ин-
интегрируемости функциональных рядов (теоремы 8 и 9 из п. 31.4). <|
Теорема 5. Если функция f раскладывается в некоторой окрест-
окрестности точки хо в степенной ряд:
1п(х-х0)п,	C2.28)
то
ап = ^Р^, п = 0,1,2,...,	C2.29)

378	Гл. 3. Ряды
и, следовательно, справедлива формула
		{х-хо)п.	C2.30)
п=О
Следствие. Если в некоторой окрестности заданной точки
функция раскладывается в степенной ряд, то это разложение единст-
единственно.
\> Из формулы C2.26) при х = хо имеем /(т)(жо) = т\ат, т =
= 0,1, 2,... Отсюда и следует равенство C2.29).
Единственность разложения C2.28) следует из того, что его
коэффициенты задаются формулами C2.29). <1
32.3. Разложение функций в степенные ряды. Различные
способы записи остаточного члена формулы Тейлора.
Определение 3. Пусть действительная функция / определена
в некоторой окрестности точки хо и имеет в этой точке производные
всех порядков. Тогда ряд
/(П^Жо) (х - хо)п	C2.31)
называется ее рядом Тейлора в точке х0.
Согласно теоремам 4 и 5 всякая действительная аналитическая
в некоторой точке действительной оси функция C2.25) бесконечно
дифференцируема в этой точке и раскладывается в ее окрестности в
свой ряд Тейлора. Если же функция бесконечно дифференцируема в
какой-то точке, то может случиться, что она не равна сумме свое-
своего ряда Тейлора ни в какой окрестности этой точки (в этом случае
функция в силу сказанного выше заведомо не аналитическая в рас-
рассматриваемой точке).
Приведем пример такой функции.
Пример. Пусть
)| р Л- / X	РРТТТЛ f r^TL Г)
= <	'	^ '	C2.32)
[ 0,	если х = 0.
Если х/0, то
/// \	Z 	1 /т"	г 11 / \	О 	1 /т*	4 	1 /т»
вообще,
j ужj — гn i — i c-	,	^oz.ooj
где Pn(t) — некоторый многочлен от переменной t (n — его порядко-
порядковый номер, а не степень), т. е. f(n\x) имеет вид
^2^
k=ox

§ 32. Степенные ряды	379
Найдем предел
lim f^n\x).
х—>0
(Заметим, что поскольку здесь производные f(n\x), n = 1,2,..., опре-
определены пока только при х ф 0, то здесь и ниже предел берется по
х ф 0.) Сделав замену переменной t = 1/ж2, получим
1	-I/2	tm/2
lim —^- е 'х — lim —— =0, т G А/.
Отсюда в силу C2.33) имеем
lim /(n)(^) = lim Рп(-)е~1/х2 = 0.	C2.34)
Теперь, заметив, что lim е~х'х — 0 = /@), т. е. что функция / непре-
непрерывна в точке х — 0, получим отсюда (см. следствие 2 теоремы 3 из
п. 12.2), что она и дифференцируема в этой точке и что (в силу C2.34)
при п = 1) /'(О) = 0. Следовательно, согласно C2.34) производная /;
также непрерывна при х = 0. Повторив аналогичное рассуждение для
производной /; вместо функции /, получим, что в точке х = 0 су-
существует вторая производная /", что /"@) = 0 и что /" непрерывна
при х = 0. Продолжая это процесс, докажем, что при любом п = 1, 2,...
имеет место равенство
/(п)@)=0.
Из него следует, что все члены ряда Тейлора функции C2.32) равны
нулю, т. е. указанный ряд имеет вид
0 + 0 + ... + 0 + ...,
а поскольку сама функция f(x) ф 0 при х ф 0, то она не равна сумме
своего ряда Тейлора ни в какой окрестности точки х = 0.
Функция C2.32) является примером бесконечно дифференцируе-
дифференцируемой функции, не являющейся аналитической в данной точке. То, что
она бесконечно дифференцируема в точке х = 0, только что было до-
доказано, а то, что она неаналитическая в данной точке (т. е. не рас-
раскладывается в степенной ряд), следует из того, что она ни в какой
окрестности нуля не является суммой своего ряда Тейлора в этой
точке.
Пусть / — бесконечно дифференцируемая в точке хо функция,
yl_^){x-xor	C2.35)
^^ п!
п=0
— ее ряд Тейлора,
sn(x) = ^2~
к=0

380	Гл. 3. Ряды
—	частичная сумма порядка п = 1,2,... ряда C2.35) и
rn(x) = f(x)-sn(x)	C2.37)
—	остаточный член формулы Тейлора для функции / (а не сумма
остатка ряда C2.35), так как сумма остатка ряда имеет смысл только
тогда, когда известно, что ряд сходится; относительно же ряда C2.35)
это не предполагалось. Кроме того, если он даже и сходится, то неиз-
неизвестно, равна его сумма /(ж) или нет). Таким образом,
/(ж) = sn(x)+rn(x)	C2.38)
—	формула Тейлора для функции /.
Отсюда видно, что для того чтобы функция / равнялась сумме
своего ряда Тейлора в некоторой точке ж, надо, чтобы в этой точ-
точке остаточный член формулы Тейлора C2.38) стремился к нулю
при п —> оо:
lim rn(x) = 0.	C2.39)
п—юо
В самом деле, если это имеет место, то из формулы C2.38) следует,
что
/(ж) = lim sn(x),
га-юо
т. е. /(ж) является суммой ряда C2.35).
Для исследования свойства C2.39) остаточного члена гп(х) уста-
установим некоторые новые виды его записи.
Напомним предварительно, что если точка ? принадлежит интер-
интервалу с концами в точках жо и ж, т. е. либо ж < ? < жо, либо жо < ? < ж,
и если <9=^^> то ? = жо+#(ж-жо), 0 < в < 1.
X Xq
Теорема 6. Если функция / п + 1 раз непрерывно дифференци-
дифференцируема на интервале (жо — /г, жо + /i), h > 0, то остаточный член гп(х)
ее формулы Тейлора C2.38) для всех ж G (ж0 - Д,ж0 + К) можно запи-
записать в каждом из следующих трех видов:
гп(х) = ±Jf(n+1Ht)(x-t)ndt, C2.40)
гп(х) = ^Щ(х-хо)п+1, C2.41)
где ? принадлежит интервалу с концами в точках жо и ж, т. е.
? = х0 +<9(ж-ж0), 0 < в < 1, и
где 0 < в < 1.

§32. Степенные ряды	381
Формула C2.40) называется остаточным членом формулы Тей-
Тейлора в интегральной форме, формула C2.41) — в форме Лагранжа,
а C2.42) — в форме Коши.
Число #, 0 < в < 1, участвующее в записи остаточного члена
гп(ж), зависит от ж и от п.
|> В силу формулы Ньютона-Лейбница имеем
X	X
/(ж) = /(а*) + //'(*) dt = /(а*) - //'(*) Ф - t).
XQ	XQ
Применив интегрирование по частям к интегралу в правой части это-
этого равенства, получим
f{x) = /Ы + (-f'(t)(x - Щ\Цо + ff"(t)(x -t)dt =
= /Оо) + f'(xo)(x - х0) + Jf"(t)(x - t) dt.
х0
Пусть для некоторого т ^ п уже доказано, что
/(ж)= \J ^р (х - хо)к + _	^ш\г){х-г)ш-Ыг.
к=о к'	(Ш }-/0
C2.43)
Эта формула уже доказана нами для т = 1 и m = 2.
Проинтегрируем по частям последнее слагаемое в правой части
равенства C2.43):
X	X
[ь)[х ъ j аъ — г
т\ ,
XQ	XQ
ml
t=x
ml
XQ
/(га)Ы
X
(x - xo)m + ^ ff{m+1) (t)(x - t)m dt.
m\
XQ
Подставим получившееся выражение в C2.43):
г1 (х - х°)к + Л ff(m+1)(t)(x -
К.	ТП. J
к=0	х0
В результате получилась формула C2.43), в которой m заменено
на m + 1.
Таким образом, формула Тейлора C2.43) доказана методом мате-
математической индукции для всех m ^ п. При m = n ее остаточный член
имеет вид C2.40).

382	Гл. 3. Ряды
Применим теперь интегральную теорему о среднем значении к
интегралу C2.40). Заметив, что функция (ж — t)n не меняет знака
(п, жо и ж фиксированы, a t изменяется между жо и ж), а функ-
функция /(n+1) непрерывна на промежутке интегрирования, вынесем за
знак интеграла "среднее значение" производной /(n+1) (см. следствие
из теоремы п. 24.2):
гп(х) = 1 //(-+1)(?)(ж - t)n dt = /(П+1)(е) /(ж - t)n dt =
Tl. J	Tl.	J
Xq	Xq
(™ ™ \n+l
[X — Xo)	,
где ? лежит на интервале с концами в точках жо и ж. Формула C2.41)
доказана.
Если применить интегральную теорему о среднем к интегра-
интегралу C2.40), вынося за знак интеграла среднее значение всей подын-
подынтегральной функции (см. п. 24.2), то получим
х	(п+1) /
гп(х) = 1 Jf(n+l){t){x - t)ndt = f J0 (x - Оп(х - х0), C2.44)
XQ
где ?, как и выше, лежит на интервале с концами в точках ж0 и ж,
т.е. ? = ж0 +<9(ж - ж0), 0 < в < 1. Отсюда
ж — ? = ж — жо— #(ж — жо) = (ж — жо)A — в).
Подставив это выражение ж —? в C2.44), получим форму-
формулу C2.42). <
Укажем теперь одно достаточное условие разложимости функции
в степенной ряд.
Теорема 7. Если функция в окрестности точки ж0 имеет все
производные, ограниченные в совокупности на этой окрестности, то
функция раскладывается в степенной ряд в некоторой окрестности
точки хо-
\> Пусть функция / имеет на интервале (жо — h, хо + h) производ-
производные всех порядков и они ограничены в совокупности на этом ин-
интервале, т. е. существует такая постоянная с > 0, что для всех
ж е (ж0 - h, хо + h) и всех п = 0,1, 2,... выполняется неравенство
I i(n)/Vll < r	(V) 4^
Заметим, что
in
lim ^-=0.	C2.46)

§ 32. Степенные ряды
383
Это следует из того, что ряд \. ~ сходится при любом z Е С (при-
п=0 П'
мер 1 из п. 31.1), в частности, он сходится при z = ft, а равенст-
равенство C2.46) выражает собой необходимое условие сходимости этого ря-
ряда: последовательность членов сходящегося ряда стремится к нулю.
Для того чтобы доказать, что функция / раскладывается в сте-
степенной ряд, т. е. в ряд Тейлора:
fix) =
х -
n=0
достаточно убедиться в том, что (см. C2.39))
lim rn(x) = 0,
C2.47)
C2.48)
где гп(х) — остаточный член формулы Тейлора функции / в точке xq.
Возьмем гп(х) в форме Лагранжа (см. C2.41)). Из неравенства C2.45)
следует, что
hn+1
(х) =
где х и ? таковы, что
имеет место
1)! ^ '
е-^о|<
lim -
C2.49)
D1.45) К'К^Ч-
х — хо\ < ft. Так как согласно C2.46)
hn+1
1)!
= О,
то в силу неравенства C2.49) при \х — хо\ < h выполняется усло-
условие C2.48). <
Замечание. При доказательстве теоремы 7 было показано, что
остаток гп{х) ряда не только стремится к нулю, но и то, что это
стремление к нулю в силу оценки C2.49) происходит на интерва-
интервале (хо — h, xo + ft) равномерно. Поэтому если все производные функ-
функции / ограничены на интервале (жо — ft, жо + ft), то ряд Тейлора в точ-
точке хо сходится на этом интервале к самой функции f(x) равномерно.
32.4. Разложение элементарных функций в ряд Тейлора.
1. Разложение в ряд функции f(x) = ех. Поскольку
j(n)(x) = еж, п = 1,2,..., то для любого фиксированного а > 0, для
всех х G (—а, а) и всех п = 0,1, 2,... выполняется неравенство
0</(п)(х) <еа.
Таким образом, на интервале (—а, а) для функции ех выполнены усло-
условия теоремы 7 (хо = 0) и, следовательно, функция ех раскладывается
в ряд Тейлора на любом конечном интервале, а потому и на всей
числовой оси.

384	Гл. 3. Ряды
Заметив, что в данном случае /^п^@) = 1, получим (см. C2.47))
п=0
Напомним, что в п. 31.1 было установлено, что ряд V^ — абсолютно
сходится на всей комплексной плоскости (впрочем, это независимо от
предыдущего следует согласно первой теореме Абеля и из доказанной
здесь сходимости ряда C2.50) на всей действительной числовой оси).
В силу формулы C2.50) для действительных z = х его сумма рав-
равна ех. В случае существенно комплексных z его сумму по аналогии
обозначают ez. Таким образом, формула
* = Е ^	C2-51)
п=0
для существенно комплексных чисел z является определением функ-
функции ez.
Так определенная функция ez, z G С, не только совпадает для
действительных z = х с известной показательной функцией еж, но
и сохраняет в комплексной области ряд свойств показательной
функции действительного аргумента. Например,
eZleZ2 = eZl+z\ zx G С, z2 e С.	C2.52)
Действительно, ряды, полученные из C2.51) при z — z\ и z — z2, абсо-
абсолютно сходятся, поэтому их можно почленно перемножить; так как
получившийся при этом ряд также абсолютно сходится, то его чле-
члены можно располагать в произвольном порядке. Соберем все члены,
содержащие произведения степеней z\ и z2 с одинаковой суммой по-
показателей, равной п, расположим эти группы по возрастанию n, a
1
затем умножим и разделим их на —:
k\)\ m\) Z^ Z^ k\(n-k)\
т=0	п=0	п=0 к=0
bn!bjfe!(n-fc)! 12	Z^
n=0 k=0	n=0
Z2) = Zl
= Z
+Z2
2. Разложение в ряды sh x и ch x. Заменив в формуле C2.50)
x на —х (это означает просто изменение обозначения), получим
n=0

§ 32. Степенные ряды	385
Сложив и вычтя равенства C2.50) и C2.53), а затем деля их на 2,
C2-54)
получим	^
к=0
2k+l
BТТТ)!-	C2-55)
к=0
В правых частях этих формул в силу единственности разложений
функций в степенные ряды стоят ряды Тейлора соответственно функ-
функций спж и shx.
Поскольку функция ez определена для всех комплексных значе-
значений аргумента z, то на существенно комплексные значения аргумен-
аргумента можно распространить и гиперболические функции спж и впж,
положив
, def ez + e~z , def ez - e~z	^
ohz =	, shz =	, z E C.
Определенные таким образом функции chz и shz для комплекс-
комплексных z раскладываются в степенные ряды C2.54) и C2.55) (в которых
вместо ж надо написать z), сходящиеся на всей комплексной плос-
плоскости.
3. Разложение в ряды sin ж и cos ж. Формула Эйлера.
Если /(ж) = sin ж, то f^n\x) = sin (ж + п — ), п — 1, 2,... (см. п. 11.1),
поэтому |/(п)(ж)| ^ 1 для всех действительных ж. Согласно теореме 7
отсюда следует, что функция sin ж раскладывается в степенной ряд на
всей действительной числовой оси. Вспомнив формулу Тейлора для
синуса (см. п. 14.2), получим для него ряд Тейлора
к=0
Рассуждая аналогично для cos ж и вспоминая его формулу Тейлора,
получим	оо
к=0
В силу первой теоремы Абеля ряды, стоящие в правых частях фор-
формул C2.56) и C2.57), сходятся на всей комплексной плоскости. Это
позволяет распространить синус и косинус на комплексные значения
аргумента, положив для любого комплексного z
def^(S^	C2-58)
(-l)kZ2k
B
def ^ (-l)kZ
C08Z = 1
25 Л.Д.Кудрявцев, т.1

386	Гл. 3. Ряды
В комплексной области легко установить связь между показатель-
показательной и тригонометрическими функциями. Заменив z в ряде C2.51)
сначала на iz, а затем на —iz, получим
i y*z	e-iz = у (zlLlA..	C2.60)
y
п=0	п=0
Заметив, что г2к = (—1)к и, следовательно, i2/e+1 = (—l)ki, к =
= 0,1, 2,..., из C2.60) получим
= ?
(-l)kz2k+1
Сравнив эти формулы с C2.58) и C2.59), видим, что
cos2:=	, sin 2? =	, zeC.	C2.61)
В силу определения chz и shz для комплексных значений пере-
переменной z (см. выше) формулы C2.61) можно записать в виде
ch iz = cos z, sh iz = i sin z.
Таким образом, в комплексной области cosz может быть получен
из функции chz с помощью замены переменной z = г?, а функция
smz — из shz той же заменой и делением на г:
ch z = ch i( = cos C, sh г = sh г? = i sin ?.
Из формул C2.61) непосредственно следует также формула
cosz + isinz = eiz.	C2.62)
Формулы C2.61) и C2.62) называются формулами Эйлера. Они,
конечно, справедливы и для действительных значений z.
Если в формуле C2.62) z = ip — действительное число, то
cos cp + i sin <p = ei(/?.	C2.63)
Отсюда следует, что модуль комплексного числа вида ег(р, <р G /?,
равен 1:
= у cos2 у? + sin2 (^ = 1.
Из формулы C2.63) следует также, что комплексное число z с
модулем г и аргументом ср, т. е. z = r(cos(p + г sin у?), можно запи-
записать в виде
z = ret(p.
Положив здесь г = 1, ср = тт и, следовательно, z = —1, получим
ein = -1

§ 32. Степенные ряды	387
— удивительную формулу, открытую Эйлером, устанавливающую
связь между числами -1, тг, г и е. Удивительную потому, что эти чис-
числа были открыты математиками при изучении весьма далеких друг
от друга задач: число —1 появилось тогда, когда было понято, что
при введении отрицательных чисел операция вычитания приобрета-
приобретает смысл для любой упорядоченной пары натуральных чисел (кроме
того, отрицательные числа оказались удобными при сравнении тем-
температур тел с температурой замерзания воды, при измерении высот
и низин на земле относительно уровня моря и т. п.); число тг является
отношением длины окружности к диаметру, мнимая единица г дает
возможность решать любое квадратное уравнение с действительны-
действительными коэффициентами, а число е представляет собой такое основание
показательной функции, при котором с ней совпадает ее производная.
Поэтому не удивительно, что в городе Кингстоне в Канаде на фа-
фасаде главного здания Королевского университета можно увидеть ог-
огромную формулу Эйлера: е7™ = -1.
Из формулы C2.63) следует неожиданное, на первый взгляд,
свойство функции ez — она оказывается периодической на комп-
комплексной плоскости и ее период равен 2тгг. Действительно, так как
' = cos2tt + isin27r =
C2.63)
то для любого z имеем
= ez -e2ni = ez
Отсюда следует, что обратная к функции ez функция, обозначае-
обозначаемая \nz и определяемая равенством elnz = z, является в комплексной
области многозначной функцией.
Имея для комплексного переменного понятие экспоненциальной
функции ez и логарифмической функции lnz, можно для любых комп-
комплексных чисел z и w определить степень wz по формуле
wz =ez\nw^
Упражнение. Доказать, что все значения г1 являются действи-
действительными числами.
Из того, что функция ez имеет период 2тгг, вытекает, что функ-
функции cosz и s'mz остаются периодическими с периодом 2тг и для комп-
комплексных значений аргумента:
{	) C2eiJ^
Аналогично sinB: + 2тг) = sinz, z G С.
Замечание. Понятие функции комплексной переменной бывает
полезно использовать и при изучении функций действительного аргу-
аргумента, принимающих только действительные значения. Покажем это
25*

388	Гл. 3. Ряды
на примере вычисления интеграла еах sin Cxdx. Применив формулу
Э
sin/fo	,
получим
Геах sin Exdx = }-je^+iC)x dx - ^[е{а~^)х dx =
(a+iC)x	(a-iC)x
6	e
2i(a + ip) 2i(a - ip)
_ aeax{eiCx - e~iCx) - if3eax{eiCx + e~iCx) , n _
_ eax (a sin fix - f3 cos fix) n
— 	2	^2	"~
(ср. с вычислением этого интеграла в п. 22.4).
4. Разложение в ряд 1пA + ж). Согласно формуле Тейлора
1пA + х) = х - ^- + ^— - ... + (-l)n+1— +гп(ж), ж > -1.
2 3	п
Запишем остаточный член гп(х) этой формулы в виде Лагранжа.
Так как
то
(в, как всегда, зависит от х и от п).
Если 0^ж<1, то 0< 	— ^ 1. Поэтому гп(х)\ ^ 	 и,
1 + вх	п + 1
следовательно,
lim гп(ж) =0, 0 ^ х ^ 1.	C2.64)
п—>-оо
Если же — 1 < х < 0, то запишем остаточный член гп(х) в виде
Коши:
()"( )"
Здесь ж = — |ж| и поэтому
ибо в числителе дроби 	—— из 1 вычитается большее число, чем в
1 — и\х\
знаменателе: в\х\ < в. Кроме того,
1
1-в\х\
<

§ 32. Степенные ряды	389
ибо в\х\ < \х\. Поэтому при х е (-1,0) имеем
l-i
\1 п,\Х )\ —
и так как |ж| < 1, то и здесь
lim rn(x) =0, -К ж < 0.	C2.65)
п—>-оо
Из C2.64) и C2.65) следует, что для всех х Е (—1,1] справедливо раз-
разложение
п=1
При х = -1 этот ряд расходится, так как его члены только знаком
минус отличаются от членов гармонического ряда, который, как мы
знаем, расходится. Расходится ряд, стоящий в правой части форму-
формулы C2.66), и при всех ж, больших по абсолютной величине единицы,
так как в этом случае последовательность его членов не стремится к
нулю; более того,
(л\п+1 п
||
п-^оо	П
Если воспользоваться второй теоремой Абеля (п. 32.1), отмечен-
отмеченной звездочкой, как необязательной при сокращенной программе, то
разложение функции In A + х) в степенной ряд можно получить кос-
косвенным, но более коротким путем. Рассмотрим следующий ряд, пред-
представляющий собой сумму членов бесконечно убывающей геометри-
геометрической прогрессии:
!	1 + 2 х3
= 1 - х + х2 - х3 + ... + (-1)пхп + ..., \х\ < 1. C2.67)
± —|— X
Ряд в правой части равенства сходится равномерно на любом
отрезке [—q, q], 0 < q < 1. Это следует, например, из признака
Вейерштрасса, ибо при |ж| ^ q выполняются, очевидно, неравенст-
оо
2
ва \(—l)nxn\^qnJ n = 0,1,2,..., а числовой ряд 2_^ Qn сходится.
71=1
Из равномерной сходимости ряда C2.67) вытекает, что его можно
почленно интегрировать от 0 до х G (—1,1) (теорема 8 из п. 31.4).
Выполнив это интегрирование, получим
или, записав правую часть с помощью знака суммирования,
1пA + ж) = ^L_L2—хп.
п=1

390	Гл. 3. Ряды
При этом, согласно указанной теореме, ряд в правой части этого
равенства сходится на интервале (—1,1), а по признаку Лейбница
(теорема 9 из п. 30.5) он сходится и в точке х = 1. Следовательно,
согласно второй теореме Абеля (теорема 3* из п. 32.1), сумма ря-
v^ (-Dn+1
да 2_^ —	хП непрерывна на отрезке [0,1]. Но так как функция
71=1
1пA + ж) также непрерывна на этом отрезке, а на интервале (—1,1)
совпадает с суммой рассматриваемого ряда, то, устремив ж к 1, полу-
™ (-l)n+1
чим, что функция In A + х) и сумма ряда V^ -—	хп совпадают и
71=1
при х = 1. Таким образом, мы снова пришли к разложению функции
In A + х) в степенной ряд на промежутке (-1,1] (см. C2.66)).
5. Разложение в степенной ряд степени бинома
A + х)а. Формула Тейлора для функции A + х)а имеет вид
...+ а{а-1)-^-п + 1)хп + гп(х), х>-1. C2.68)
Соответствующий ряд, называемый биномиальным рядом с показате-
показателем а, имеет вид	^
71=1
Если а является натуральным числом, то этот ряд содержит лишь
конечное число членов, не равных 0, и превращается в известную фор-
формулу бинома Ньютона
n=0
Будем предполагать, что а не является натуральным числом и
что ж/0, тогда все члены ряда C2.69) не равны 0. Исследуем его
абсолютную сходимость с помощью признака Даламбера. Положив
_ а(а — 1)...(а — п + 1)
получим
Inn —— = Inn J	\x\ — \x\
yoo Un	n—yoo П + 1
Следовательно, ряд C2.69) абсолютно сходится при \х < 1 и, посколь-
поскольку этот ряд степенной, расходится при |ж| > 1.
Докажем, что суммой ряда C2.69) на интервале (—1,1) являет-
является функция A + х)а. Для этого исследуем остаточный член гп(х) в
формуле Тейлора C2.68), записав его в виде Коши. Поскольку
[A + x)a](n+1) = а(а - 1)...(а - п)A + х)а~п-\

§32. Степенные ряды	391
то
Гп(х) =	:	 A - в)ПХП+1, 0 < в < 1.
Положим
ап(х) =	—	х ,
Ьп(х) = ажA + вх)"-1, сп(х) =
тогда
^ (~.\ — п (ггЛи (гуЛг (гуЛ п — 10	(*?) 7П"|
Сомножитель ап(х) является членом биномиального ряда с показа-
показателем а - 1, и так как выше было показано, что любой биномиальный
ряд сходится на интервале (-1,1), то
lim an(x) =0.	C2.71)
п—>-оо
Далее, из неравенств
1 - \х\ < 1 - в\х\ ^ 1 + Ох ^ 1 + 0|ж| < 1 + |ж|,
где — 1 < х < 1, следует, что значения |ЬП(^)| заключены между
числами |аж|A — [ж])" и |аж|A + [ж])", не зависящими от п,
т. е. последовательность {Ьп(х)} ограничена при каждом ж G (—1,1).
Что же касается последовательности {сп(ж)}, то она ограничена
равномерно на всем интервале (-1,1):
В результате из C2.70) следует, что
lim rn(x) =0, -1 < ж < 1,
п—>-оо
а это означает, что на интервале (—1,1) имеет место разложение
оо
+ ж) = 1 + ^^ —^	—-}	 ж .	C2.72)
п=1
Сходимость ряда, стоящего в правой части равенства, в точках ж = — 1
и ж = 1 требует дополнительного исследования. Можно показать, что
в точке ж = 1 при а > — 1 биномиальный ряд сходится, а при а ^
^ — 1 расходится. В точке ж = — 1 при а^О он абсолютно сходится, а
при а < 0 расходится. При этом, согласно второй теореме Абеля,
всякий раз, когда биномиальный ряд C2.69) сходится, его сумма
равна A + х)а.
Иногда для получения разложения функции в степенной ряд вмес-
вместо оценки остаточного члена в формуле Тейлора проще воспользо-
воспользоваться каким-либо уже известным разложением и из него с помощью

392	Гл. 3. Ряды
общих теорем о функциональных рядах получить искомое разложе-
разложение. Поясним сказанное на нижеследующем примере.
6. Разложение arctgx. Найдем производную arctgx и разло-
разложим ее в степенной ряд по формуле для суммы бесконечно убываю-
убывающей геометрической прогрессии:
ОО
(arctgx)' = ^^ = ^(-1)-х2-.	C2.73)
Ряд, стоящий в правой части равенства, имеет радиус сходимос-
сходимости R = 1, и поэтому его можно почленно интегрировать на интерва-
оо
2п+1
-1)ntIn dt = 2^(~1)П^—p -К ж < 1.
6 n=o	n=o	n	C2.74)
Радиус сходимости получившегося ряда также равен 1 (см. тео-
теорему 3). Таким образом, функция arctgx оказалась разложенной в
степенной ряд с радиусом сходимости, равным единице. На первый
взгляд это представляется несколько неожиданным, так как arctgx
является бесконечно дифференцируемой на всей числовой оси функ-
функцией. Это связано с тем, что производная функции arctgx заведомо
не может быть разложена в степенной ряд с радиусом сходимости
больше единицы, так как функция	 обращается в бесконечность
при z = ±г.
Важно отметить, что разложение C2.74) справедливо и на концах
х = ±1 интервала сходимости (—1,1). Действительно, при х = ±1 ряд,
стоящий в правой части равенства C2.74), сходится в силу признака
Лейбница, а тогда его сумма s(x), согласно следствию из второй теоре-
теоремы Абеля (теорема 3* в п. 32.1), непрерывна на отрезке [-1,1]. Таким
образом, две непрерывные на отрезке [—1,1] функции arctgx и s(x)
совпадают в силу равенства C2.74) на интервале (—1,1), а тогда они
совпадают при х = ±1, т. е. и при этих значениях х функция arctgx
является суммой ряда, стоящего в правой части равенства C2.74):
°°	г2п+1
arctgx = 2^(-1)п	, -1 ^ х ^ 1.	C2.75)
п=0
При подстановке в разложение функции в ряд какого-либо фик-
фиксированного значения переменной получается формула для суммы
соответствующего числового ряда. Так, подставив в ряд C2.75) х = 1
и заметив, что arctgl = —, получим
2п-
п=0

§ 32. Степенные ряды	393
7. Разложение arcsinх. Заметив, что
(arcsin ж)' =	,
V1 — х2
разложим (arcsin ж)' в ряд по формуле разложения степени бинома
(см. 32.72)
оо
, dx	, v- Bn-l)!! x2n+1
агсятж = / y,	= ж + > /ts ' -——-
n=l
Радиус сходимости получившегося ряда, как для всякого биномиаль-
биномиального ряда, равен единице. Интегрируя получившийся ряд от нуля
до ж, |ж| < 1, получим
Г dx
sin ж = /	= ж
О	п=1
32.5. Формула Стирлинга. Разложение функции In A + ж) в
степенной ряд дает возможность легко получить асимптотическую
формулу для факториала п! при п ->• оо. Эта формула называется
формулой Стирлинга*)] она имеет вид
п! ~	, п ^ оо,	C2.76)
т. е. отношение п\ к выражению, стоящему в правой части этой
формулы, стремится к 1 при п —> оо.
> Действительно, если |ж| < 1, то
In iif = In A + ж) - In A - х) =
71=1	71=1
Положив ж =	-, п = 1,2,..., получим
2п + 1
In
l)=ln 2" + 1 =
п/	^ — 1
2 1
1 V + 3	+
2п + 1 V 3 Bп + 1K 5 Bп
откуда
Пропотенцировав и заметив, что функция In ж возрастает, а 1 = lne,
получим
/	1 ч п+1/2
A + -)	>е.	C2.77)
V п)
*) Д. Стирлинг A692-1770) — шотландский математик.

394	Гл. 3. Ряды
Положим
*п = ^-	C2.78)
Поскольку, согласно неравенству C2.77),
1/1 \™
жп+1 е V п)
жп+1
то последовательность {жп} убывает. Кроме того, она ограничена сни-
3У: хп ^ 0. Следовательно, она имеет конечный предел. Обозначим
его а:
lim xn = а.	C2.79)
Покажем, что а/0. Так как
11	11	1/1	1
1 1	1 /	:
5 Bn + lL '" < 3 \BтГ
3 Bп + 1J 5 Bп + 1L	3 VBn + 1J Bn +
1
_ 1 Bn + IJ	_ 	l_
~ 3 x _ 1	~ 12n(n ¦
Bn + IJ
TO
и, следовательно,
Поэтому
1/A2)	i/C^Cijj	C2.80)
Последовательность уп = Жпв^12^, п = 1,2,..., будучи произве-
произведением двух последовательностей {жп} и {е~1у/A2п)}, имеющих пре-
предел, также имеет предел, причем
Hm yn = lim xn lim e~1/A2n) = а.
п—>-оо	п—>-оо п—>-оо	C2.79)
Неравенство C2.80) означает, что последовательность {^/п} воз-
возрастает, поэтому 2/п < а, а так как ?/п > 0, то доказано, что а > 0.
Из равенства C2.79) следует, что
жп = аA+?п),	C2.81)
где lim en = 0. Подставив C2.81) в C2.78), получим
C2.82)

§ 32. Степенные ряды	395
Для того чтобы найти значение числа а, вспомним, что по формуле
Валлиса (см. B6.9) в п. 26.2)
1=Цш^-М2">!! У*.	C2.83)
2 n-юо 2п +1 \Bп- 1)!!/	v	J
Из формулы C2.82) следует, что
Bп)!! = (Bп)!!J = 22п(п!J =	/п A + enf
й V
=	=	=
Bп-1)!!	Bп)!	Bп)! C2.82) й V 2
Подставив это выражение в формулу Валлиса C2.83), получим
тг ,.	1 2п A + гпL 2
2 = Л ^ТТ а 2 (ГТ^
откуда а = л/2тг- Следовательно,
/— пп+1/2
n! = v^Ii_^(l + Sn), l
C2.82)	en	n
т. е. формула Стирлинга C2.76) доказана. <|
C2-84)

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Абсолютно интегрируемая функ-
функция 314, 319
—	сходящийся несобственный ин-
интеграл 313
	ряд 334
	на множестве 350
Алгебраическая форма записи комп-
комплексного числа 22
Аналитическая функция 374
Арифметическая разность (сумма)
числовых множеств 59
Арифметическое значение корня 18
Асимптота функции 198
Асимптотически равные функции
144
Астроида 232
Бесконечно большая последователь-
последовательность 69
—	малая более высокого порядка
145
	 последовательность 75
	функция 110, 205
Бесконечное множество 63
Биекция 13
Бином Ньютона 31
Биномиальный ряд 390
Вертикальная асимптота функции
199
Вектор, касательный к кривой в
точке 217
Вектор-функция (векторная функ-
функция) 201
Векторное представлением кривой
212
Величина мгновенной скорости
движения 155
—	средней скорости движения 155
Верхнее десятичное приближение
92
Верхний интеграл функции 258
Верхняя грань множества 56, 57
	 последовательности 80
	функции 115
—	сумма Дарбу функции 255
Внутренние точки промежутков 19
Внутренняя мера множества 283
Возрастающая последовательность
80
Возрастающая функция 115
Гармонический ряд 325
Гиперболический косинус 159
—	синус 159
Главная нормаль 227
—	часть функции в окрестности
точки 185
Гладкая кривая 217
График функции 33
Двусторонний предел 106
Действительная аналитическая
функция 376
Десятичная запись действитель-
действительных чисел 91
Дифференциал n-го порядка 164
—	функции 150, 206
Дифференциальный бином 246
Длина кривой 218
Допустимые бесконечные деся-
десятичные дроби 91
Замкнутая кривая 214
Знакочередующийся ряд 332
Изолированная точка множества
112
Интеграл Римана 252, 320
Интегральная сумма Римана 252
Интервал 19

Предметный указатель
397
Интервал строгой выпуклости вверх
(вниз) 195
—	сходимости степенного ряда 377
Инъекция 13
Иррациональные функции 34
Кардиоида 289
Касательная 216
—	к графику функции 153
Колебание функции на отрезке 130
Компактность 85
Композиция функций 15
Конечное множество 63
Конечный предел функции 96
Координатная плоскость 33
Координатные функции, отображе-
отображения 211
Корень многочлена 37
Кратная точка носителя кривой 213
Кратность корня многочлена 38
Кривая 211
—, п раз дифференцируемая 213
—,	непрерывно дифференци-
дифференцируемая 213
Кривизна кривой в точке 223
Критическая точка функции 188
Круг сходимости ряда 370, 372
Кусочно гладкая кривая 218
Линейная вектор-функция 206
Логарифм 50
Логарифмическая функция 51, 137
Мелкость разбиения 251
Мера множества 283
Метод математической индукции
17
Многочлен Тейлора порядка п 180
Множество действительных чисел
16
—	задания функции 13
—	значений функции 13
—	определения функции 13
—	пустое 11
—	числовое 15
—, ограниченное сверху 55
—, — снизу 56
Монотонная последовательность 81
Монотонные функции 115
Наибольшее значение функции 33
Наименьшее значение функции 33
Наклонная асимптота функции 199
Натуральный логарифм 137
Неограниченная последователь-
последовательность 74
—	сверху (снизу) последователь-
последовательность 74
Неограниченное множество 56
—	сверху (снизу) множество 56
Неособая точка 216
Непрерывная в точке функция 121
Непрерывность интеграла по верх-
верхнему (нижнему) пределу ин-
интегрирования 270
Несобственный интеграл 299,
301-303, 319
Неявное задание кривой 215
Нижнее десятичное приближение
92
Нижний интеграл функции 258
—	предел интегрирования 253
Нижняя грань множества 57
	 последовательности 80
	функции 115
—	сумма Дарбу функции 255
Нормаль к кривой 227
Носитель точки, кривой 213
Ограниченная на множестве
функция 121
—	последовательность 74, 95
—	сверху (снизу) последователь-
последовательность 74
—	функция 107
Ограниченное множество 56
Определитель Вандермонда 35
Ориентация кривой 214
Ориентированная кривая 214
Основные тригонометрические
функции 52
—	элементарные функции 33
Особая точка 216
Остаточный член формулы Тейло-
Тейлора в виде Пеано 180
	форме Коши 380
	Лагранжа 380
	интегральной форме
380
Отображение взаимно однознач-
однозначное 13
—	множества в множество 13
—	на множество 13
Парабола 46

398
Предметный указатель
Параметр кривой 212
Параметрически заданная непре-
непрерывная кривая 215
	функция 164
Переменная зависимая 13
—	независимая 13
Пересечение множеств 11
Перестановки элементов 29
Плоская кривая 214
Плоскость комплексная 22
Плотность действительных чисел
16
Площадь 283
—	поверхности вращения 291
Поверхность вращения 291
Подмножество 11
—	собственное 11
Подпоследовательность последо-
последовательности 83
Показательная функция 50, 134
Полукубическая парабола 50, 231
Последовательность 64
—	, ограниченная на множестве
349
—	, равномерно сходящаяся 351
—	, сходящаяся на множестве 349
Первообразная 233
Правило Лопиталя 176
Правильная рациональная дробь 40
Предел вектор-функции 202
—	последовательности 349
	комплексных чисел 94, 101
—	функции 95, 121, 258
	 слева 105
	 справа 105
—	числовой последовательности 68
Предельная точка множества 112
Преобразование Абеля 342
Преобразование параметра кривой
212
Произведение последовательностей
75
—	последовательности на число 75
—	числа на множество 59
Производная функции 149, 205
Проколотая ^-окрестность 99
Прообраз множества 14
Простой замкнутый контур 214
—	корень 38
Противоположная ориентация 215
Равномерно непрерывная функ-
функция 128
Равномерно сходящийся ряд 355
Равномощные множества 63
Радиус кривизны кривой 223
—	сходимости ряда 370
Радиус-вектор 202
Разбиение отрезка 218, 251
Разложение в ряд функции 350
Разность множеств 11
—	последовательностей 75
Расходящийся интеграл 299
—	несобственный интеграл 301
—	ряд 321
Расширенное множество действи-
действительных чисел 19
Рациональная функция от функ-
функций 245
Рациональные функции 34
Ряд 321, 349
—	Тейлора 378
Секущая 216
—	графика функции 152
Символ всеобщности 12
—	существования 12
Система вложенных отрезков 61
Скалярная функция 32
Скачок функции 114
Скорость вращения вектора 205
Собственный интеграл 300
Соприкасающаяся плоскость 227
Спрямляемая кривая 218
Стационарная последовательность
65
—	точка 188
Степенная функция 138
Степенной ряд 369
Строго возрастающая последова-
последовательность 80
	функция 115
—	монотонная последовательность
81
	функция 115
—	убывающая последовательность
80
	функция 115
Сужение функции на множество
14
Сумма последовательностей 75
Суперпозиция функций 15
Сходящаяся последовательность 68
Сходящийся интеграл 299
—	ряд 321

Предметный указатель
399
Счетное множество 65
Сюрьекция 13
Тело вращения 294
Теорема Безу 37
Теорема Больцано-Вейерштрасса 85
Точка возрастания функции, 188
—	изолированная 112
—	кривой 213
—	перегиба графика функции 196
	функции 196
—	предельная 112
—	прикосновения 96
—	разрыва второго рода 115
	первого рода 114
	функции 114
—	самопересечений кривой 213
—	строгого возрастания функции
188
	локального максимума 187
	минимума 187
	убывания функции 188
	экстремума 187
—	убывания функции 188
—	устранимого разрыва 114
Трансцендентные функции 34
Треугольник Паскаля 31
Тригонометрическая форма запи-
записи комплексного числа 24
Убывающая последовательность 80
—	функция 115
Угловая скорость вращения 230
Условие Коши 86
Условно сходящийся ряд 338
Формула Лейбница 162
—	Маклорена 180
—	Муавра 25
—	Стирлинга 393
—	Тейлора 180
—	Френе 226
—	замены переменной 238, 278
—	интегрирования по частям 241,
279
	 подстановкой 239
—	конечных приращений Лагран-
жа 169
Формулы Эйлера 386
Фундаментальная последователь-
последовательность 86
Функции одного порядка 144
Функция 13
—	Дирихле 99
—	Римана 369
—	многозначная 14
—	на множестве 14
—	обратная 14
—	однозначная 14
—	периодическая 33
—	сложная 15
—, аналитическая в точке 374
—, бесконечно малая относитель-
относительно функции 144
—, выпуклая вверх (вниз) на ин-
интервале 194
—, дифференцируемая в точке 150
—, интегрируемая по Риману на
отрезке 252
—, кусочно непрерывная на отрез-
отрезке 265
—, непрерывная в точке 101, 203
—, — на множестве, 122
—, — слева 106
—, — справа 106
—, ограниченная относительно
функции в окрестности точки
143
—, строго выпуклая вверх (вниз)
на интервале 194
Центр кривизны кривой 228
Частичная сумма ряда 321
Частичный предел последователь-
последовательности 85
Частное последовательностей 75
Численное значением скорости
вращения вектора 205
Число, ограничивающее сверху
множество 55
—, — снизу множество 56
Числовые функции 32
Член последовательности 64
—	ряда 321
Эволюта 229
Эквивалентные функции 144
Экспонента 134
Элементарная функция 33
Элементарные рациональные дро-
дроби 45
Явное представление кривой 214

Учебное издание
КУДРЯВЦЕВ Лев Дмитриевич
КРАТКИЙ КУРС МАТЕМАТИЧЕСКОГО АНАЛИЗА
ТОМ 1
ДИФФЕРЕНЦИАЛЬНОЕ И ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЯ
ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ.
РЯДЫ
Редактор Е.Ю. Ходан
Корректор Л. Т. Варьяги
Иллюстрации А.А. Логунова
Оформление переплета А.Ю. Алехиной
Оригинал-макет И.Л. Ивановой
ЛР №071930 от 06.07.99. Подписано в печать 15.12.04.
Формат 60x90/16. Бумага офсетная. Печать офсетная.
Усл. печ. л. 25. Уч.-изд. л. 28,6. Заказ №
Издательская фирма "Физико-математическая литература"
МАИК "Наука/Интерпериодика"
117997 Москва, Профсоюзная, 90
E-mail: fizmat@maik.ru; http://www.fml.ru
Отпечатано с готовых диапозитивов в ПФ «Полиграфист»
160001, г. Вологда, ул. Челюскинцев, 3
Тел.: (8172) 72-55-31, 72-61-75, факс (8172) 72-60-72
E-mail: form.pfp@votel.ru http://www.vologda/~pfpv
ISBN 5-9221-0184-6
9 78592201844