В С.НЕМЧИНОВ
ПОЛИНОМЫ
ЧЕБЫЫЕВА
ι г
МАТЕМАТИЧЕСКАЯ
СТАТИСТИКА
МОСКВА
1946

Институт экономики АН СССР
Московская ордена Ленина сельскохозяйственная академия
имени К. А. Тимирязева
Проф., д-р В. С. НЕМЧИНОВ
ПОЛИНОМЫ
ЧЕБЫШЕВА
МАТЕМАТИЧЕСКАЯ
СТАТИСТИКА
/ У 4 о
Издание Московской ордена Ленина сельскохозяйственной
академии имени К. А. Тимирязева

П. Л. Чебышев
(1821 -1894)

ПРЕДИСЛОВИЕ.
Настоящая монография является частью большой работы автора по
теории экономических расчетов. При изучении экономических процессов
весьма часто приходится иметь дело с разнообразными массовыми
явлениями. Объекты экономических исследований — это многомерные
совокупности различного рода событий и фактов, относящихся к множеству
объектов, характеризуемых многообразными признаками. Обобщение
фактов, относящихся к такого род многомерным совокупностям, требует
применения статистических методов исследования в виде
корреляционного и дисперсионного анализа и теории ошибок.
При планировании экономических явлений и при контроле за
выполнением плана неизбежен метод количественного измерения. Плановое
хозяйство требует создания теории экономических и планово-статистических
расчетов. Математический аппарат, с которым приходится иметь дело при
изучении планируемых экономических процессов, является своеобразной
экономометрикой, требующей большого количества уравнительных
вычислений при построении баланса народного хозяйства и при анализе
выполнения плана по такого рода явлениям как, например: урожайность, цены,
доходы колхозников, выработка агрегатов и т. д.
Русский математик П. Л. Чебышев ввел в науку ряд новых приемов
уравнительных вычислений но способу наименьших квадратов. Ему
принадлежит научный приоритет в отношении систематического применения
метода элиминационных средних, получивших в экономической статистике
название метода корректированных средних, а также приоритет в
отношении полиномов, получивших в дальнейшем название полиномов Эрмита и
Лагерра и так называемых обобщенных кривых Шарлье (тип «А» и «В»).
Основная задача настоящей работы — изложить математические идеи
П. Л. Чебышеза в приложении к практическим задачам, стоящим перед
етатистико-экономическим анализом.
Предлагаемые в работе новые схемы вычислений, связанные с
корреляционным и дисперсионным анализом, существенно облегчают вычисле-
тельную работу исследователя и обеспечивают ему всестороннюю
статистическую оценку полученных результатов.
В. С. НЕМЧИНОВ,
Действительный член Академии
наук БССР, Зав. сектором
экономической статистики Института
Экономики АН СССР, Зав.
кафедрой статистики
Сельскохозяйственной Академии имени Тимирязева.
S октября 194<3 года.
Москва.

ГЛАВА 1.
ПОЛИНОМЫ ЧЕБЫШЕВА
1. Ортогональные полиномы и интерполяционный ряд
Чебышева
В статистике имя знаменитого русского математика
Пафнутия Львовича Чебышева (1821—1894) известно
главным образом по так называемому неравенству
Чебышева, которое он предложил для распределения
вероятностей и которое имеет силу для любого статистического
распределения численностей.
Однако за последнее время в статистике все большее
значение приобретают ортогональные полиномы Чебышева,
которые имеют особое значение при определении
уравнений множественной и криволинейной регрессии и при
вычислении коэфициентов обобщенной функции нормального
распределения вероятностей.
Чебышев предложил общую интерполяционную
формулу, при помощи которой возможно интерполирование в
самых разнообразных случаях. Эта интерполяционная
формула удовлетворяет условиям метода наименьших
квадратов и выражена при помощи его ортогональных
полиномов. Общая интерполяционная формула или иначе
ряд Чебышева (1), предложен Чебышевым в 1855 году.
Этот ряд таков:
ПХ) и ^ο(*,·)β3 (*,№)) ψ {χ)
SlVmW-e4xdF(xd\ ψ , ν

Полиномы Чебышева
где /-"(л:)—искомая функция; Г(х{) — известные значения
искомой функции; Ѳ%х) — вес, например, — распределении
вероятностей (Частоты); Фт{Х) — полиномы Чебышева.
Эти полиномы получены Чебышевым при помощи
разложения некоторой функции F(x) в непрерывную дробь.
В зависимости от вида функции, которая преобразуется
в непрерывную дробь, полиномы Чебышева выражаются
различными уравнениями. Полиномы Чебышева (но его
собственному определению) суть знаменатели подходящих
дробей, полученные разложением данной функции в
соответствующую непрерывную дробь.
Чебышев предложил ряд формул для своих полиномов
в отношении частных случаев разложения в непрерывную
дробь различных функций, например:
а) ряда, характеризующего совокупность
равноотстоящих значений искомой функции (2);
б) функции параболического интерполирования (3);
в) функции нормального распределения вероятностей
(4, δ).
В своих работах Чебышев указывает, что разложение
Маклорена, а также разложение по косинусам и синусам
кратных дуг, разложение по функциям Лежандра — суть
также частные случаи его общей интерполяционной
формулы.
Рассмотрим сначала применение интерполяционной
формулы и полиномов Чебышева в отношении уравнений
множественной и криволинейной регрессии. Пусть
уравнение множественной регрессии дано в следующем виде:
у^а9 + ахxx+atxt + a3xs... атхл.
Искомая функция F(x) = У разлагается при помощи
интерполяционной формулы Чебышева в следующий ряд
(при Щх)^1):
У =■--· Α0Ψύ(χ) + At4\{x) + Λ,Ί·,(χ) AnWjx),
где A^jkl^h А^А^^У.
ο Γιι·» ι..\ 1 I- '
а в ооще.ч виде:
А = $0> *·«(*)
S[*«2(*)|
При этом полиномы Чебышева определяются
последовательно при помощи следующих уравнений, указанных
Чебышевым.

Полиномы с измененной последовательностью переменных V
Первая система полиномов Чебышева
(Система 7"):
ЧГ0(х) = 1
ЧГ1(л) = лх-7'1і)Ѵ0(х)
Ψ5(х) = л-„ - 7,0 Ч/0 (χ) - 7"„ ¥,(*) (3)
ΨΆ (χ) =-- л'3 - Ты У0 (х.) - Г31 ЧГ, (л-) - 732 ЗД
*„ W = *„ - ТѴо ^о (*) - 'Л,,·: *i (*) - rm.s V, (x) -
-■••^,...m-.,lm-iW.
Коэфициенты каждого из полиномов Чебышева в свою
очередь могут быть выражены через суммы произведений
и суммы квадратов полиномов Чебышева более низкого
порядка в виде аналогичных формул:
(4)
Л ОЛ~
20-
.<?[л-3ч-0(л-)] г _£[^Μί3_
а в общем виде:
т.к
Эти уравнения даны Чебышевым для случая
параболического интерполирования, т. е. для случая: Хі=х; хъ—х-;
.ѵ3=л8 и т. д.
Романовский (6) показал, что эти формулы Чебышева
применимы и для случая множественной регрессии.
Однако Романовский не указал наиболее удобного пути
вычисления этих полиномов и не рассмотрел возможные
различные системы этих полиномов.
Наша задача рассмотреть различные системы
полиномов Чебышева и на этой основе дать наиболее удобный
алогорифм их вычисления, а также установить их связь
с современными статистическими методами
дисперсионного и корреляционного анализа.
2. IIолиноиы с измененной: последовательностью
неременных.
От первой системы полиномов Чебышева (полиномы „Г")
легко перейти ко второй системе полиномов (полиномы пКи),
выраженных через первичные значения величин хт. Под-

JO
Полиномы Чебышева
(5)
ставляя в уравнение данного полинома соответствующие
значения предыдущих полиномов системы Т(х), имеем
новую их систему:
Вторая система полиномов Чебышева.
(Полиномы системы vk" — развернутые полиномы
последовательного элиминирования):
.Fj {X) — Xs κια «21Xj
3 \X)== -^з «So ft^X^ ■ #3jAj
<f m W— A'm ~ km.0X0 ~ km-l X\ ~ ^m-2 xo · ■ · km (m-\) Xm-\
Сопоставляя с первой системой, легко видеть, что
старший (последний) коэфициент каждого полинома второй
системы равен старшему коэфициенту соответствующего
полинома первой системы, т. е.: kl0 — T10; kiX = Ttx; £»,=
~ ■* »2» *лі. яі—1 m. m—V
Очевидно, что такого же рода равенства оудут иметь
место, если изменить порядок переменных, рассматривая
каждую данную переменную как последнюю. Это возможно
сделать, так как порядок включения переменных в
уравнение искомой функции вполне произволен. В случае
иной последовательности переменных, будем иметь
соответствующие уравнения для полиномов Чебышева с
измененной последовательностью переменных. Введем для
удобства письма новые обозначения полиномов Чебышева:
^ (*) = ·*!.<>
Ψ2(λ)-χ2.,
,Г» С*) - *3.21
η W == Xm.Vl...m-b
p-m W = Xp-\2...p-\.p+\...m
Здесь в подстрочном значке первая цифра (до точки)
обозначает номер переменной, для которой определяется
полином Чебышева (т. е., которая рассматривается как
.чависимая переменная), а цифры после точки — номера
элиминируемых переменных (включенных ранее в урав-

Полиномы с измененной последовательностью переменных II
Х3.21 = ХЛ-
Л2-13==Л'2~
Xl-23~Xl ~
_ Ь'"х k'"x -
кгйло кг\х\
- k'"x — k'" χ -
л20л0 К21ЛI
- k'"x — k'"x -
Л^оЛ.)
"" ^23Χ,ί
- k'"x
Л13Л3
нение;. Тогда отбирая из системы полиномов Чебышева
с измененной последовательностью переменных те
полиномы, в которых каждая данная переменная
рассматривается как зависимая переменная, имеем новую третью
систему полиномов Чебышева. Для случая трех
переменных эт:> система такова:
Третья система полиномов Чебышева
{Полиномы системы „с" —полного на данном этапе
элиминирования)
(6)
0-123 ге01)Л0 "OlAl Л02Л2 Лог\ѵ
где х0= 1.
в общем виде:
ΧρΊ2...ρ-1.ρ+1...πι ~ Хр ~ ^рОХи ~ *р\ Л1 "'"' &ρ2 ЛѴ · · -*pmXm
Здесь верхние значки * обозначают число
элиминированных переменных (считая и хй); первая цифра в
подстрочном значке — номер переменной, которая
рассматривается как зависимая переменная, а остальные цифры
(после точки) —номера остальных переменных.
Для полиномов Чебышева характерно, что частота,
т. е. число наблюдений (л:0), также рассматривается как
независимая переменная нулевого порядка. Это особенно
становится наглядным при рассмотрении 3-й системы
полиномов Чебышева.
Сравнивая систему полиномов последовательного
элиминирования (система 1) с системой развернутых
полиномов последовательного элиминирования (система 2), мы
установили, что для этих двух систем коэфициенты при
переменных, которые введены в уравнение последними,
равны между собой и могут быть выражены через суммы
произведений и суммы квадратов предыдущего полинома.
С другой стороны, из рассмотрения 3-й системы видим,
что осгальные коэфициенты 2-й системы полиномов равны
соответствующим последним коэфнциентам полиномов, с
измененной последовательностью переменных (см. систему
полиномов „с"), Это приводит нас к простому, но имею-

12
Полиномы Чебыіиева
щему оольшое практическое значение положению, что
коэфициенты системы „k" и „С полиномов Чебышев;>
определяются как следующие отношения:
Г,,, = k'L —
S(X3X,
s(4
кю—
м).
.)'
S(x3.
h"'
χο-νι)
П ч
S(Vi.i) .
S(xU)
В обшем виде: (7)
^{хтхр.\2.. p—U. р+1.... т—ϊ)
кт.р
S{xp.l2..p—l,p+l....m—\)
Уравнения регрессии вполне аналогичны
интерполяционному ряду Чебышева, а остаточные отклонения от
уравнения регрессии— полиномам Чебышева. Это верно
как для зависимых, так и независимых переменных
уравнения регрессии.
Легко поэтому показать, что коэфициенты
множественной регрессии у — а, + atxt -f- αζχ2 атхт
определяются при помощи аналогичных выражений, в которые
также входят полиномы полного на данном этапе
элиминирования (система „г" полиномов Чебышева)· В
частности, для у—ад—а^ + а^х^+а^ формулы для определения
(/. таковы:
В общем виде: (8)
"/; =
Ч^.^.-.р-!, р+1.../я)
S(-*7U2...,p-l.p+1...m)
Таким образом, зная те из полиномов Чебышева, в
которых каждая данная переменная рассматривается как
зависимая, легко определить все коэфициенты
множественной регрессии.

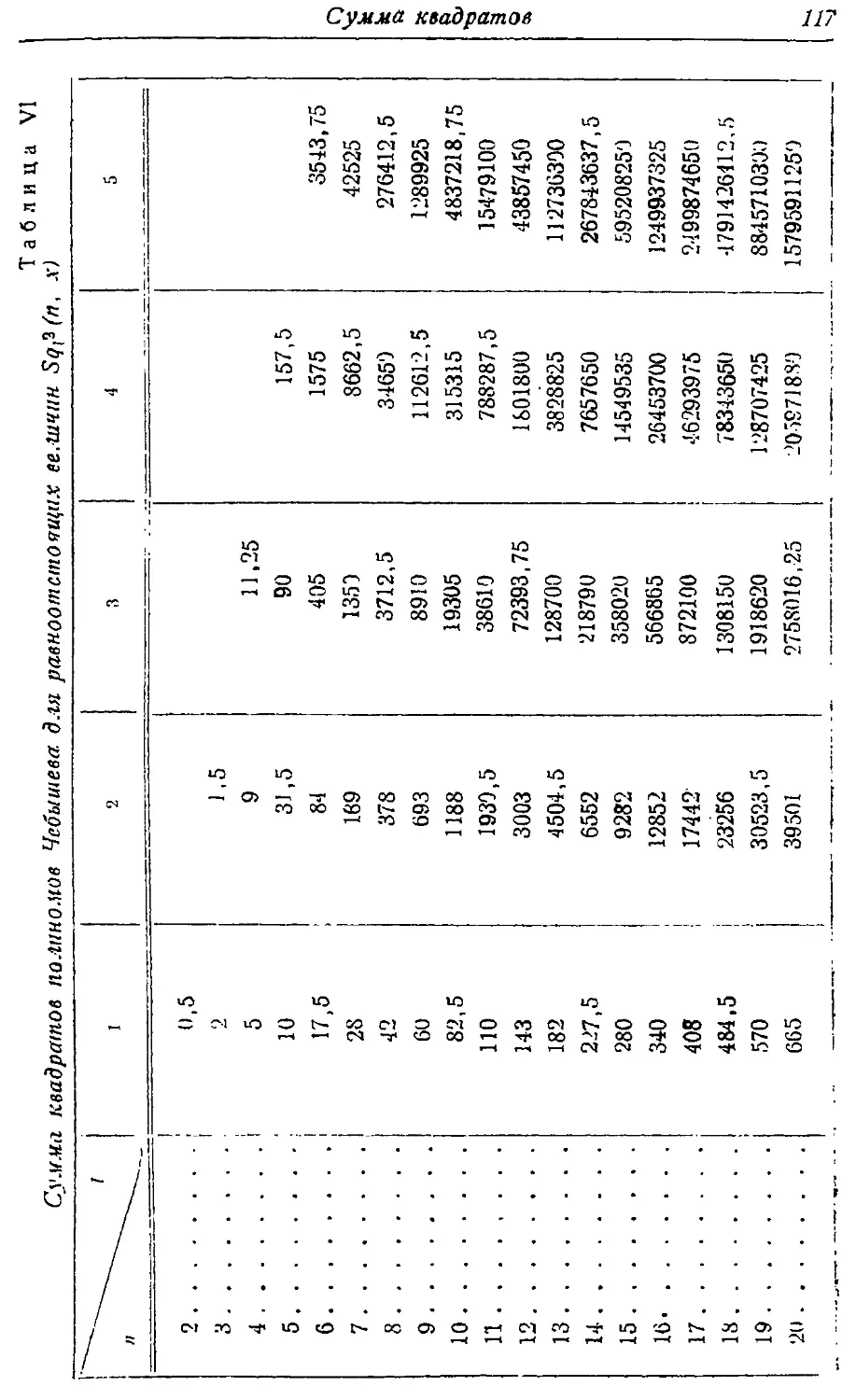
Суммы квадратов полиномов, сумма их произвед. и отношен, их сумм /3
3. Суммы квадратов нолиномов, сумма их произведений
и отношение их сумм.
Все полиномы Чебышева обладают свойствами
ортогональности, а именно:
!■ 5(-Vtw-i./.+i.»)=-°
2· 5(Ѵ-Л2...Р...П,_,)=°
В силу этих свойств ортогональности оказывается
возможным определить величины типа: S (yxm 123...ет_і);
S(Xp.m...p-l.p+l...my> S(XmXp.U...p-Up+U..m^ He ВЫЧИСЛЯЯ
индивидуальные значения каждого из полиномов
Чебышева. Следовательно, оказывается возможным определить
величины Гу и А;, а также Klf и ае. без определения
индивидуальных значений каждого из полиномов Чебышева.
В самом деле, пусть имеем систему „Т" полиномов
Чебышева, т. е. полиномов типа:
-Vm.l2..m-1== Xm * »ι·0Λ'ϋ·0— * тЛ Х\Л~
~ * т-2Х2Л - · ' ' т(т—1)Хда—1.12.т—2
а также уравнение множественной регрессии, выраженное
через полиномы Чебышева:
Уі2...ж~ ^0Х0.0+ АА'і.0~'~ ^■2Х2Л~>Г ^3Х3.21 +
+ .. ■А-тхтЛ-1,.т_х
На основе этих уравнений, имея в виду свойства
ортогональности полиномов, легко получить все необходимые
формулы для вычисления как коэфициентов регрессии,
так и коэфициентов соответствующих полиномов.
Для простоты письма покажем это на примере
уравнения множественной регрессии, выраженное в форме
интерполяционного ряда Чебышева:
Уш~ Α>ΑΌ.ο+ ΑΛΊ.ο"^" ^2λ"·2.ί+ Аіхял\
SI Ухт лаз....яі—l)
где Кг ~Ί(7 Г

и
Полиномы Чебышева
и на дримере системы полиномов ЯТ":
-Vq^1
ΧΊ ·0 Xl i
10
ν r=; 3f Τ" Τ V
2·1 2 20 21 1-0
■S-21 = д:з"- 'зо-' ':«·*ϊ·ο ' гчхі-ѵ
гпр Г — ^Γ"Λ'ρ-4·-Η,?·μ-'»-ι)
"·ρ " Si*2 ϊ
*\Χρ.\·>....ρ-\, р+l^..m-t)
На основе этой системы найдем формулы для
определения сумм: 1) S(xp,m^p__up+lm_l); 2) и сумм
S(yxm,i2..m~i)· Эти суммы легко получить если:
а) умножить каждый полином Чебышева на переменную
того же порядка, т. е. например, х3.21 на хг и затем
суммировать;
б) умножить каждый полином Чебышева на
следующую по порядку переменную, например, полином хгл на
переменную хг и затем суммировать.
В первом случае, подставляя значения Τ имеем:
SKo) = *
ЧХІ,)-ЧХЪ~ 7'.о *(*,) - 5(д?) - -[^^-
5(4,) -S(4 ) - Τχ5(χ2)~Τ21Ξ(χ2χ,.0) =-
ο/ν2\ ^(^^Ο-ο)·5^) ^(^г-^I-о) ς·/ ч„...
■"ίΚ) " "**? ^Γ ( 2 ,0)" ««
2 S(4o) «(*?.<>)
„ 5/ ^ _ Ηί?)]2 _ Н*з*ьо)]2 _ [£_(^)]2
* 3j 5(д£0) S(*2.0) S(4,)

Суммы квадратов полиномов, сумма их произвед. и отношен, их сумм /·>
Во втором случае (случай „б") соответственно будем
иметь:
5(*іА"о.о) = 5(*і)
5 ( Х2 Χ1·θ) = Ч Х2 Хі) - ТЮ S ( Х2) =
к ' } *Ш (іо)
5(*3*м) = 5(*8*2) - T^S{X,)-T2lS(XZXU0)-
-=S(x χ \ S ί*2*™}'S^ S (*2*i-o)'SС«з*ч>)
1 3 і} 5 (4ο) 5 (^о)
Аналогичным образом умножая полиномы системы
„Г" на у, а затем суммируя, имеем:
S(yx^) = S{y)
$(Ухы) = S{yx>) ~T20S(y)- ΤΆ S(yxuo)
3(Ухз.п) = *(Ухз) - Гзо 500 - Гзі 5(^ьо) -
- Г325(^2.і)·
Подставляя в эти уравнения значения „Г", имеем
окончательно:
с/ г с/ \ s(-*i*oo)·5^) МА ν
S(yXi*) = S(y*i) g / а ч (10"а)
ς/«г \-ѵѴ«И Д (*2*ОоН(-Ѵ) ^(^^1·θ)·^(^1·θ)
5(Ул2,)-^*2) _ ^—-
<?/«r Л <Уѵ.г\ 5(^00)·^) ^(*3^1.θ)^(^1.θ)
S(x3x2.{)-S(yx2.1)
S (Ji0
Наконец, умножая уравнение множественной регрессии
в полиномах Чебышева на У и суммируя имеем:
5(^23 )=4>5(У*Ьо) + А 5 (ух,.0) + Л25 (ух^) +А35 (ул-,,,)

16
Полиномы Чебышева
или,·иначе, подставляя значения Аш, имеем:
УУ l2:1 ) С ί 2 \ с/,2 \
5(Λό·ο) 5(;ѵьо)
, ft (J**-.)]2 , [5(^3-2l)]2
Η—■ ■ 1 —
S(-4l) S(-*3-2l)
Аналогичным образом находим S(y"); S(\r0) н
убеждаемся, что
4^123 / \>'l2'' o/J \
ύ \хг-і\)
Следовательно, Аи1 и Тт легко определить,
последовательно вычисляя суммы квадратов типа 5(л^„), «S (х|.Л,
-5'Сл·^.,,) и суммы проиагведений типа:
5(-У*1.о)> 5(>'ЛѴ0' 5(.У*3.2і)·
Несколько иначе обстоит дело с коэфициентами уравне-
нения регрессии обычного типа .Уи3—йо+^Л + а2-*а+
-і- <isx3. Эти коэфициенты могут быть определены, исходя
из коэфициентов Ли Г, следующим образом. Пусть имеем
систему уравнений регрессии:
ѴІ - Л„.+ Л,^., -- Л0 + Л1(х1 — Г]0) *= Лл + (і40 - AJ^) =■
= α':ΛΊ+α'0, так как .41 = л'1, то
„/ - 4 δ τ S(yx0.0).-a'iS (Λι-Χρ-ο)
s (4о.)
Затем пусть имеем: Д'і2-=Д + Α-*·ι.ο + ^г^г-і"
= α'0 + α\ 7J0 + α', (xj — 7'Jft) +
+ ά2'(χ2-- 720- ΤΆχ^ = α"2 x2 + (a\ -a\ T2[) Xj+-
+ («Ό-^ι^ιο-^ V)^ Ωο +Ωι ■*, +α2 χ2-

■ iifjcu.. l'uijLCa и полиномы Чсбышсии 17
Следовательно:
S(*lo) $(*&>) S^)
S|>?.0) 2 .ν(*?.0)
<V=
* (40
Аналогичным образом получаем значения α'ζ, aj", ο|" и
αο и уравнения для >Ί·>3·
Следовательно, через значения сумм квадратов и сумм
произведений могут быть определены также коэфициенты
акр. Приведя все эти формулы в систему, имеем известную
'эмпирическую схему американского геодезиста Дулитля (7),
предложенную им в 1878 г. (см. § 1, глава 2).
Полиномы Чебышева дают теоретическое обоснование
схемы Дулитля.
Несколько иные схемы решения нормальных уравнений
можно получить, основываясь на системе полиномов
Чебышева с измененной последовательностью переменных.
4-. „Веса," Гаусса и полиномы Чебышева
Теперь рассмотрим систему полиномов с измененной
последовательностью переменных (систему С). При
наличии переменных хІУ ха, имеем полиномы системы С,.
1.
2.
3.
ло.о=1
ν — χ — k!
-h-o Λι "ίο
Λ0·1 ~" Κ00Λ0 Λ01 Λ\
При наличии переменных хг, хг, и л\, имеем полиномы
системы С2:
I.
2.
3.
Χ2·\ — Х2
ЛѴ2 = χι -
Λ0·12 Λ00
ϊ Иилияпмгі Чебышѳші
k" —- k" χ
Λ20 Λ21Λ1
k" — k" Χ.
ν — h" v —

JS
Полиномы Чебышева
Умножая уравнения л'0.0, л"ь0, х2Л, первое на х0,
второе на л',, третье на л-, и суммируя, имеем;
$(*«,)= S(*0):
5(^) = 5(х?)-Л'105(Лі);
S(xl{) -5(4)- f^S(x3)- ^-S(¥l).
Аналогично умножая .r3.21 на Лі, и суммируя имеем:
Затем умножая систему Сг на .ѵ2, а систему С2 на .v.,
и суммируя каждое уравнение в отдельности, имеем:
и:і системы С}:
l- s(xsxo.o)==s{x2)
2. 5(х2лЬ0) = S(XjX2) - /е'10S(x2)
3. ^(дСуХо.,) ==*'„,5(л3) - -#01 5(-Ѵс,);
из системы С,:
1. S(x3x2.l) = S{xsx2)- ^(-"з)" ^і5(хзхі)
2. S(Vl.s) = 5(x3xI)- k"wS{x,)~ k';2S(x,x,2)
3. ο (·%ν'(Μ2) = "οα$(ΧχΧ-ο) — ^т^(хяхі)~ ^^M^rS)·
Разделим каждое из этих уравнений на сумму
квадратов соответствующего полинома, тогда будем иметь:
из системы ,,Cj":
5 Ко) " *Ко) 4*U)
9 S KvQ _ k го · ^(х2) 'уоі -5(-г2*і)
sK.)'~ «к,) ~ *К)
из системы ,,С2"
ι S(-*3*2-i) __S(*a*2) *20-3(*з) *я ·$(·«3·*ι)
5(40 5Ю s(40 5Ю

«Весил Гаусса и полиномы Чеоышева. 14
S(42) S(jc?.2) S(42) 5(42)
n S (-^з^о-іг) ^оо ' •^(•^0 ^оі '^{xixiJ ^02 '^\хзх-і)
5 \χ5·ΐ2) -' (Λ'ΰ·ι0 ^ (-^о-із) ^ (Λ'0·ΐ2)
В левой части уравнений но системе „С," имеем
величины &2j, Ari0, а по системе „С2", соответственно, &82,
^зі» -^зо-
Теперь введем обозначения:
1 , *
-г- 00
Ч*іо) J' s(40
Ь' h·
"10 , —κ ι
00 >
5 (40 5(40
и соответственно:
1 = с" ■ - = с" ■ ^— = с"
'"">» - - Ь11> „ / 9 ч Ь0Ч-
s(40 ~ 5(42» " 5(4I2)
— А,
5(40
к10
5 (42)
к0\
— k2l
s (4.1)
— k"
5(40
—а'
02
20 , . - _ .
20' „ / 9 \ 21»
~ С10>
г" ■ _ — г
— 01» „ / 9 \ 02"
5 (·*ό·ι2) 5 (-^о-іг)
Тогда имеем окончательно:
система „Q":
1. kii= (fu Sfojc,) + с\а S (xa)
2. /&= c'00 S(x2) + c'ai S (ед);
система ,,C2":
2. л3;'= ^5(^0 + <в*Ы + <2^(^0
3· *зо' = <о5Ы + <015(хЛ) + <25(х3а-2).
2*

20
Полиномы Чебышева
Из полиномов Чебышева легко получить систему
одновременно решаемых уравнений для определения
величин сі} и chr Так имеем: х2Л = х2 — к"10 — k"nxv Умножим
это уравнение последовательно, сначала на л'2, затем на
xL и" на л-0 и суммируем полученные произведения. В
результате имеем по свойству ортогональности:
Деля на 5 (-ν:?,.,) эти уравнения и вводя обозначения
с;! и сѴі имеем:
^^(¥0 + 4>5(*,) 4- 4 S(*J) =0. (12)
<25<Л*0) + <о5Ю + ^5(*Λ) =0·
Аналогичным образом получим систему одновременно
решаемых уравнений для определения с'[х, с"т, с'[2, (из
уравнения хи2~х1 — k"0 — k?2x2) и систему для
определения с2о, c'l)V c"Q2 (из уравнения хол2 = ££,*„ — A£, — A»*2)·
Известно, что c'i2 — c'2\; с^ — с^; с'21) ~ с"0) и т. д.
Эти системы уравнений предложил К. Гаѵсс (8) еще в
1823 г.
Таким образом „веса" Гаусса (си) есть ни что иное,
как обратные величины сумм квадратов чебышевских
полиномов с измененной последовательностью переменных.
Величины же с>7,суть ни что иное, как нормированные
коэфициенты соответствующих полиномов Чебышева fc
обратным знаком).
Величины скк и c{J получают в полиномах Чебышева
вполне определенный логический смысл.
Определение величин сц. и си по Гауссу, когда
совместно решается несколько систем уравнений, требует
много труда и сложно, хотя сам Гаусс (8) и писал, что
его метод не оставляет желать ничего лучшего.
Полиномы Чебышева с измененной последовательностью
переменных позволяют указать значительно более простой
путь определения скк и сіу
Из уравнения х1[0=х1 — Л']0 имеем указанным выше
способом: c'uS(xf) ·+- c'wS(xl) — 1.

«Веса» Гаусса и полиномы Чебышева. 21
Из уравнения х1.., = л1— k'llSx0—k'[2x2 имеем:
Вычитая из второго уравнения первое, имеем:
или иначе:
Сі ι ~~ С * ι . С ι п с'
с12 с12
С другой стороны, из уравнения х2.і~х2~~ Ко'~ Кіхі'
путем умножения на л^ и суммирования произведений, а
затем деления всех членов уравнения на ^(xj.,), имеем:
^5(^) + с»5(^)-=-ся5(ЛЛ).
или
с22 ^22
Сопоставляя это уравнение с предыдущим, имеем:
с о
ΰ22
Это равенство как доказал Cochran (9) может иметь
место, если:
а) во-первых:
" / "
СП~С11 С21 „ _ //
— или, так как с,„=с,.,,
6и==сіі"г — >
С22
б) во-вторых
или с,"'0 = с,10-г
20 „,, . . с20' С21
с,.,

22
Полиномы Чебышева
Аналогичные выражения будем иметь из других
полиномов Чебышева, например уравнения:
г'"-с" Л- Сз1'С*2 и с'" -с"' і 1ML-
c2i — с 21ч 7, и си--сіі
сзз сг>
получим из рассмотрения полиномов Чебышева л, й и
,tb,„ а также х.і-2У
Эти формулы имеют большое практическое значение.
Р. Фишер (10) без доказательств, но со ссылкой на
профессора Шульца из Чикаго, дал аналогичные формулы
для исключения одной переменной (в этом случае в
формуле знак плюс меняется на знак минус, так как
определяется, например, с'п, а не с'^. Отметим дополнительно,
что эти формулы легко могут быть выражены через коэ-
фициенты и суммы квадратов полиномов Чебышева. Так,
подставляя:
окончательно имеем:
k'"-к'" к"
аналогично:
ί Ο2 ι
сГі = сГг+· V ' Где С"= ~'
Следовательно, от одного этапа вычислений можно
переходить к следующему этапу, зная лишь коэфициенты
и суммы квадратов предыдущего и данного полинома. На
основе всех приведенных выше формул нами совместно
с В. Н. Перегудовым была выработана схема решения
уравнений множественной регрессии методом наименьших
квадратов в полиномах Чебышева. Эта схема
опубликована (11) в книге В. С. Немчинова
„Сельскохозяйственная статистика с основами общей теории" (стр. 325—344).
Однако в настоящее время могут быть предложены
новые, более удобные схемы решения нормальных
уравнений, основанные на иной системе полиномов Чебышева.

Нзаимооткошен. между коэфицисн. смежных полиномов Чебышева. _'·>'
5. Взаимоотношения между коэфнциснтамн смежных
полиномов Чебышева
Рассмотрим вопрос о взаимосвязи между коэфициен-
тами двух смежных полиномов, для чего отбираем из
всего многообразия полиномов Чебышева новую систему
толиномов (полиномы системы ,,№'), а именно, систему
полиномов для одной и той же переменной (например х,),
взятых для различных последовательных этапов
элиминирования (сначала от х0, затем от х, и х0, наконец от х,,
х,, х0). Тогда будем иметь:
Четвертая система полиномов Чебышева
(полиномы системы ,Ν'):
лл] —■■-х3— / ;і1д;ь0 --/;j0x(|_0--:X.j-0 ■* лі-Ν'ι .и (14)
ХЛ-Т, ~~ ХЯ ' 32·*:!· 1 * 31Х\-<> * ?.0Х0-Ь ~ Л,М ' 32"*2-1
Так как для старших коэфициснтов полиномов Чебы-
нева имеем:
Τ -— k'''
32 — 32
Τ — k"
1 30 ~ Λ30>
то, умножая на ху обе части предыдущих уравнений и
суммируя их, имеем: Sxfi-0 — Sx* —- ^05jc3-i,
ох3-] == ox.j 0 Γ;!1ώχΒχ]{) -— οχ30 «31<Sx3xM1 (15a)
cy2 _.. cv- „τ- 9г χ ■■— 9*-'" — £"" сх ν
3-21 — 3-1 32 3 2-1 — 3·1 32 3 2·1
Такой же характер имеют формулы при определении
суммы квадратов отклонений ііо уравнению
множественной регрессии. В самом деле, имея у0= Л0х0.0, находим
отклонения от уравнения этой горизонтальной линии:
ао=>У-Уо=У-Аохо.г
Умножая обе части этого уравнения на у и суммируя,
имеем: S(d0Y = SJy-y0f=-S (yf-AQS(yx0Q), 'так как
А, — я„. a Sy (у — у0) — 5 (у — Ѵо)г-

Полиномы Чебышева
Затем, имея уравнение прямой линии ух ~AqX00 -+-
Л'Аххх_0, а также отклонения di=y— yt =у — Айх0.0— А1х1_0
путем умножения на у и суммирования, получаем:
S(tf) = S(f-) ~A0S(yxJ -A, S{yxio) = 5Ю ~ ві^(у^і-о>
так как Ах — а\, a .Sy (_у — >Ί) — S(y —ух)' = SdJ .
Аналогичным образом имеем:
S(d22)^S(dl)- a'^Siyx^)
S(dl)==S{dl)-a;S(yx3.n).
Подобным же образом можем получить простые
формулы для определения сумм типа 8(хях2,) и S(yx^2:y
Так, исходя из уравнений:
ЛЫI '1 Id
Χ2·0 == Л2 20ΛΌ·ΰ
■Ѵ2-1~Д2 'гЛ-О ~ ' 2ff*0.0 ~ Λ2·0 '2Л.1І
и умножая их на л:а, а затем суммируя, получаем:
5«*3л:ь0 = oAr3A'j — ΤιοοχΆχΟΛ) = oXjXj ~ ^wSx-.i
Х'ЛХом — 3 2 20 3 0-0 ^^ 3 2 20 :j
З^г.I == 3Γ*2·0 21 ■*.Τ^1·ί) ~ *^3"*2·0 21 "**3"*|.ι>
Умножая те же уравнения на у и суммируя, имеем:
5(У*і.о) = S(yxi) - k'ioS(y)> затем ^г-о^ S (Ухм) - *»50')ι
а также 5(^2.,) = 5 (ул:2.0) — ^,5'(F|.0) т. к. Г10 =■- *10
и Tn — k2V
Все эти формулы позволяют определить старшие
коэфициенты смежных полиномов, так как эти коэфици-
S(x,xa(\ 5(j;,x .)
енты есть отношение типа: /г.==—ч . „ - —; д.. ---■>. ,. , ;
10 5(^o.o) 21 «(«/.о)
,'"„ 5('У3Х2-0
ЗЭ" " -5(4,) '

Взиимоотношен. между коэфициен. смежных гюлимшои Чсоыиіеаа 'і.~>
Они позволяют определить и старшие коэфйпйенты
регрессии, так как:
а^- 5(д-,.о); "ζ""' S(4,)~; "* ^К*)'
Наконец, из четвертой же системы полиномов Чебы-
шева легко вывести формулы, устанавливающие связь,
междѵ соответствующими коэфианентами данного и
.предыдущих полиномов. Так, из четвертой системы
полиномов „ЛЛ1 (смежные полиномы для одной и той же
переменной, но вычисленные на различных этапах
элиминирования) имеем следующие уравнения регрессии:
.св по хи; л':! no xt и х0; х, no xit хг, л'0.
Так как хм=^х.л — Т.ІОх^0, то
Так как Л,., = л3-7'31д:1.0-Ггодс0.0. то
,хя — ха — х.ІЛ —Τ31 хь0 + Τ::0-ѵ0.0=7 31 (х{ — й10)
"+" ^зо—^зіхі "*" (^го~^зі*ю)=:r; К\х\ 'г кж
Аналогично имеем
і2хз ~~хя χ3·ά~^ з&л г .;ιΛι·υ "г 'а>Ло-о ==-'зЛ-і s
-!- ^зГѴЬ0 ~~<~ ^30 ~~'32 (^ *21Χ1 ~~ *2θ) + *зЛ ~ % -*1 ~h .UV'l =
-τ^2 + κ, -Vii)^ + (Аю-Ѵм)=^+< *.. +■ *;»
Таким образом имеем окончательно:
^зо~ ^зо —"'зі^іо= зо — *чі^и> (1 7}
I*-?Я ~- ^30"~ *32^20 ~ ^ІIі" %>^20 " Т" "U
Ь"' Ь" _ Ь'" . Ъ"
К'Л — .І1 Л32 21*
Такого же рода формулы получаются для определения
коэфициентов множественной регрессии у по л:3, хъ, Xf
В самом деле, на основе интерполяционной формулы
Чебышева имеем:
у г «= Л*"о (χ) + Αψι (■*) = аа + Л (jcx - #,«) =-

2в Полиномы Чебышева
Следовательно, Аг -- α',; α'0 — α0 — Afl^-
Затем, так как ylt —уг Λ-Α^Υ-, (χ), то
У ι* = Αψ<? (л) + Л^ (λ-) + Л Д'а (л) = α'Λ + а'0 і-
- -43 (л? - Л" л-, - Л;'0) = Л2 л-2+ (а; - Л2 Л" ) хг+(а'а - - Л, £2'0) =,
— а, х2 -l· а1хг + а0.
Следовательно окончательно имеем:
β = α2; θ! = ^ - о2 · &2Ι; α0 = αη - - α,Α;2() и т. д.
Аналогичным образом имеем:
а£=Ая (18)
"Г=<-*;, «г
°С = ао — *!όαΓ·
Следовательно, все коэфициенты данного полинома
Чебышева и данного уравнения регрессии могут быть
определены исходя из соответствующих коэфициентов
предыдущих полиномов (или предыдущих уравнений
множественной регрессии) и старшего коэфициента данного
полинома (или соответственно старшего коэфициента
данного уравнения регрессии).
Данная система формул, полученная на основе системы
смежных полиномов Чебышева (полиномы системы „Ν"),
дает нам возможность предложить новую схему решения
нормальных уравнений в полиномах Чебышева.
Новая схема „Ν", как увидим в главе 3, одновременно
является своеобразной системой статистических
характеристик (средние арифметические, средние квадратические,
коэфициенты полиномов и коэфициенты регрессии,
критерии достоверности Фишера, коэфициенты и индексы
множественной и частной корреляции, ошибки коэфициентов
регрессии и средних и т. д.).
В новой схеме "Ν„ все эти характеристики даны в их
взаимной связи, как единая система метода средних чисел.

ГЛАВА 2
СХЕМЫ РЕШЕНИЯ НОРМАЛЬНЫХ
УРАВНЕНИЙ В ПОЛИНОМАХ ЧЕБЫШЕВА
1. Охоміі Дулитля
(Схема последовательного элиминирования)
Теория схемы Дулитля будет ясна, если эту схему
записать в полиномах Чебышева. Схема „D" представляет
собой схему Дулитля, записанную в общем виде в
полиномах Чебышева *).
Схема решения системы нормальных уравнений
Дулитля имеет дело с полиномами Чебышева последовательного
элиминирования (полиномы „Г"). В этих полиномах jci.o не
содержит в себе х0; дго-о не содержит в себе xti; х^л не
содержит в себе -ѵг и ха; х3.пщ не содержит в себе xt, хг
II -Ѵ0 И Т. Д.
В схеме »ΰ" записаны 4 типа уравнений, связанных с
полиномами Чебышева, необходимыми для решения данной
системы нормальных уравнений. Причем, коэфициенты
полиномов записаны в элиминационных строках. Уравнения,
характеризующие полиномы Чебышева (уравнения первого
типа), можно прочесть, если каждую колонку схемы
читать, начиная с заголовка по элиминационным строкам
сверху вниз. Так. например, имеем:
") Положения связанные с интерпретированием схемы Дулитля в
полиномах Чебышева впервые были высказаны автором в его докладе
Множественная корреляция , состоявшемся 15/1 1940 г. на заседании
Статистической секции Московского дома ученых.

Схемы решения нормальных, уравнении, в полиномах Чгбышеаа
Колонка:
d І.
ί'
Полиномы:
Л'.,
s(-*o-o)
Ц4.0)
X.
S(.V-2A-,.())
s'W.n)"
_ -s4-Vri-n)
^..„^
-Ч-I .1-21
Остаточные отклонения множественной регрессии:
5 (>>,») Л.
*(4>) "w" s(4o)
*(40
У12::
χ. , —
Следовательно, все эти уравнения имеют дело с
полиномами Чебышева последовательного элимнннроипнт:,
т. е. с первой системой ѵI'т(л").
В схеме „D" записаны также уравнения дли
определения сумм квадратов полиномов Чебышева (уравнения
второго типа). Эти уравнении можно прочесть в нижней
масти соответствующих колонок (между последней и
предпоследней элиминационными строками каждой колонки).
Колонка
h
Остаточная сумма квадратов.
S^) "■ '^(4оГ *(4«) -*1-
5(.ѵз) -
|£CVu?)J2. ΐ£ί^Νθ)ί2.. Н*:Л-і)\*
■5(4.іі)
Λ (Я..)

СХЕМА ДУЛИТЛЯ В ПОЛИНОМАХ ЧЕБЫШЕВА
СХЕМА <.,Т»
Значение линии
X Ξ
о <D
а я
первый
второіі
d
третий
Факторна льни іі
признак
Результатип-
ныіі признак
Варианты
I Х„„ = 1 !
Хі
X,
X,
Υ
f _
Су.мма

квадратов
откло-
пенпіі
SY-
а.
St
/'
S.,
//'
III
Сѵмма 1 п= Sx
Нулевая элпмина-
ционная строка
Сумма
произведений с X, ... 3
Поправка по
линии Sa .... 4
Сумма
произведений в
отклонениях от средней
(5-3+4) . . .
Элнмннаннопнан I
строка первая . О
Сумма
произведений с X.. . . .
Поправка но ;ш-
.іши S0 . . . .
Поправка по ли-'
пив 6", . . .: <і'
І !
Сумма 7;-8-;-У ~іч ці
Элпмппацпппная I j
строка вторам .'ц:
Сумма пронзве.и·- |
mi nit с Х3 . . .1 12
Последовательное элиминирование (А„,)
00
ІА'і х00 ~~ ^Х
Sx, χ.
00
Sx
00
Sx]
(S*i-W?.
S*oo
Sx2
Sx2 Y00 — '^γ2 $χ3 Χ00 ~~ $Χ3
-, i .Sx_2_x
Sx
=/ί χι
S(x,-x,)2! Sx, χ
Sx2 x00Sx, λ·.ι(, j sx3 x00Sx, χ
^xOo
Поправка по
липни S0 . . . .
Поправка по ли·
і мин 6\ . . . .
I
і Поправка по лп-
I нпн S.
13
і
14
ι
15
5 .Сумма 1С, = VI +■
" I 4 13 г 14 + 15 . |fi -
ΙΙΓι Ο.ίιι.μιιπ.ί.шинная j '
j строка третья .17 —
/у Сѵмма проіізреде-
■ 'unit с Υ . . . .! 1Η —
Коифнцнепты по элпмннаішопным ,
строкам I
Колонки результативного признака ί
Поправки по колонке признака Хя
то же, Х„
то же, Хх
ι .0
Sx,, χ
I .0
S*?.o~"
Sxl
(Sx,xmY- _,
——ч = nx:
ύ χοο
$хз χι.ο
Sx3 χι.ο
" Sv2
ώλ1.0
Sx3 x2
Sy*i.o
s>'xi.o
Д^у.ѵ,.' »
Sx
1.0
Syx-,
,1X3 X00 0X2 X0()
Sx-> Xno '■ SyXnnSx.' x
Sx,
,.2
00
00ол/ л00
Vv2
ών00
(£^2 x\. о)" : S xax1.0S.v.!x1., , Syx^ 0Sx2 χ, η
5χϊ.ο
с 2
Sx2.1
1
Sx1.0
$хз x2.l
(Sx3 χΟθ)2
Sv2
ώλ00
sx'i.o
syx-2.i
_^2.1 =
Sxl,'
Syx3
Syx00 Sx3 xm
' A.Svx
A, ■ ■
Sa'oo
(Sx3 xi .o)2 Syxx 0 Sx3 x, „
<fxz
ox1.0
(Sx3 X2.l)2
Sx
1.0
Syx2 , Sx3 x2 , j
Sx
Sx
2.1
.2
3.21
1
Sxl,
•S.W3.21
S>'X3.21
Sv2
ύΛ3.21
•Ц
i|-USxrr
(SVT
Полное элиминирование (ащ)
Ac
$хз xoo
ώλ00
Sx3 x1.0
a2
A-,
3 ^2. 1
Sx
1.0
Sx
2.1
Syx2:
2.31
!/·■ =
$X2 X00
^χόο
■·β2
Sx2
ον00
123
Syx
Sx0. 123
Sx?,.r
A3 ="3
S.VV., .,,
1.23

Схема Дулигля
29
Наконец, в колонке F аналогичным образом записаны
суммы квадратов отклонений по уравнению множественной
регрессии (если величины А заменить их значениями):
cf„, |sQ'-Wr ИО"ь»).Г К-^.і)? 0( - ν.
В схиме ,,/J" также записаны уравнения для
определения сумм произведений данной переменной на
соответствующие полиномы более низкого порядка (уравнения
третьего типа).
Эти уравнения записаны в соответствующих колонках
между строками сумм произведений. Так, имеем".
Колонка: Сумма произведений.
·4Λο·ο;
~· ·. ^ (^Д^О-о) · ^(.-ѵ2л"оэ) Ή Λ3ΛΊ·θ) ' $ (.·*2Λ"ΐ·ϋ)
= S(JC3*2.,)·
Наконец, в колонке „Ε" имеем аналогичные суммы для
уравнения регрессии:
S(y*,)-S(-^(?*'IO)°5(^-o>
^^ —-5(7з.0Г ^Ш (У 2·ι)
ідз 5(у^)·
В схеме „D", в-четвертых, записаны уравнения,
необходимые для вычисления коэфициентов множественной

■Hi Схемы решения нормальных уравнений в полиномах Чебышева
регрессии. Они записаны снизу схемы „D" (см. „Обратные
решения"). Эта уравнения таковы (если величины А
заменить их значениями из колонки „<?"):
5 (у*8-я)
" - SJS?3Ll ) _·_ 5 (Лз-ѵ2-і) ^Ο^.,η)
Д (■>'*·!-о) $(-*а*і.о) „ ^ s(*a-*i-o) д»_а'(-УЛ'і-а>
"'" 5(^.о) "' Α'(·*?-ο) ■■* " *(*Г-о)" ' *'(*?■*)
α" = ^ (·νΛο·ο) , s(*a-*b-o) α» + S (χ2χνο) α« + 5(-уі-ѵо-о) д,
5(·ϊο.ο) 5(-*ό·ο) s (*ο·ο) " ^(·*ο·ο)
Эти уравнения записаны в соответствующих колонках
обратного решения, если их читать также сверху вниз.
Схема Дулитля имеет дело только с полиномами
Чебышева, как функциями последовательного
элиминирования.
Если оказывается необходимым включить новую
переменную или исключить какую-либо из введенных ранее,
то необходимо заново проделать те вычисления, которые
предусмотрены уравнениями обратного решения. Кроме
того, тогда необходимо в схеме предусмотреть
дополнительную колонку для новой переменной, а также заново
решить уравнение, записанное в колонке „Зависимая
переменная". Если же бывает необходимо исключить какую-
либо из ранее включенных переменных, то становится
необходимым заново проделать все вычисления не только
обратного решения, но и по всем тем уравнениям,
которые записаны в колонках справа от исключенной
переменной.
Таким образом, если исключается первая переменная,
то необходимо заново сделать все вычисления.
2. Числовой пример решения нормальных уравнении
в полиномах Чебышева но схем»» Дулитля
Применение полиномов Чебышева для решения
нормальных уравнений по схеме Дулитля покажем на примере
Безенчукской опытной станции, проводившей
параллельные наблюдения над урожаем яровой пшеницы и
метеорологическими факторами за различные вегетационные
периоды в течение 25 лет.

Нахождение уравнении связи между урожаем и метеорологическими факторами по методу Чебыишна-Ду.шт.іч
(пшеница «Полтавка», Безенчукская опытная станция, 1901—1929 п\)
Τ а б л и !і а
ЛіПШіI
Отрока π способ
расчета
Нумерация граф
Нйзваипс гіпнпіі и строк
Кпцтро.-I.
'ѵ.ммі,і квадрант
отк: oiifiKUii
f
l. Последовательное э л и м и и и ρ о в а л и е
Si>
0
1
Si
1'
II
s2
11'
III
s8
III'
IV
1
2 = 1 :1a
3
4 = 1-26
5 = 3 + 4
6 = 5:5b
7
8 = 1.2c
9 = 5-6c
10 = 7 + 8 + 9
11 = 10 :10c
12
13 = l-2rf
14 = 5-6rf
15 = 10-11<ί
16=12+13+14+15
17=16:16d
18
Нулезая элиминационная
линия (средние с обратным
Суммы произведешй с χι . .
Поправка по линии 5Ό . . .
Суммы отклонений
(произведений C.t',.0)
Первая элиминацпоиная
линия (с обратным зчаком) .
Сумма произведений с χ·> . .
Поправка по линии S0 . . .
Поправка но линии Si . . .
Сумма произведений с х2.х ·
Вторая элиминационвая линия
(с обратным знаком) . . .
Сумма произведений с хй . .
Поправка по линии 50. . . .
Поправка по линич Si . . .
Поправка по линии S2 . . .
Суммы произведений с х3.2і
Третья элиминационная линия
(с обратным знаком) . . .
OS
1
—
—
—
Сумма п.>оизведении с ν . . —
і
714
—28,53
32116
- 20391,8!
11724,16
-1
—
—
—
1459
4857
-194,28
46766 i 121212 1., -w -,
-41669,84 --138 715,9.2 f^'4 xv w -ѵз>
5 095,96 '■ —17 503,92
-0,43474 j +1,492908
106111 \ o,„ rv.
-85 147,24f 5№-^)J
-2 215,85239
+ 18747,90761
— 1
—
—
251 79S
— 283454,52
+ 7 609,65418
— 24 046,86582
+ 1,282643
1 03 4 455
-943 617,96
—26131,741199!
-3)843,536651
+33 861,7613
-1
—
231,3
-9,252 = Л0
cot} д ч
- 6605,928P-V(-Vl—'Vl)
1618,072
-0,138112 = Ai
15 609.9
-13498,f68
—703,441621
+1407,791379
-0,075091 = A2
40 229,7
—44 936,964
2 475,632633
1 805,6932716
-485,9331
0,01435 =AS
—
7 286,3
-291,452
—2 139,9S76 = /i0S.Wo»
208318
-207382,728 : -223,313353 =
935,272 —-^lS.VJfj.o
-0,079844 j
373518,9.
—382100,428
+4 693,36117
—3 891,16683
+0,207552
1 074 684.7
-958 551,924
-23 716,1 9566
-29'i37,843:-8
33 375,8232
0,98565
—
-105,712462 =
= /43S_vjr2.1
-6,977693 =
= Aa Sv.v3.21
+ 2 512,29 = S\*
П. Полное элиминировав ие (горка):
л->.2 = 223,313+ 105,7125+ 6,9767 = 336,0022
1,44087
Строка 1 Справо налево
А3, А2, Ль А0
(с обратными знаками)
оѵ.ш —
9,252 = /5п 0,138012 = Λι 0,075091=л,> —0,01435 = А,
R
Строка 2 а3 умноженное на числа 2,7879
llrf, Qd, 2d
-0,0214277
-0.018409
0,056682= а-.
у-123г
У-
V-
36,0219
25
= 2512,29 - 2139,9836 = 372,2021
36,0219
■1
: 1-0,09726= 0,93274
nS'lm = 36,0219
С Т 9
'\'·123— '-
Λ'^,.,ο, ^0,950105
372,2024
: 6,10528 + 0,09194jk-i + 0,56682х, - 0,01435д-:і
= 9,252— "0,138012л-].0+0,07509Ц,.х — 0,01435х,.21 (в ортогональных многочленах).
Строка 3 я2 умноженное на числа —3,3079^15 —0.024641442
6с> 2с 0,09194 = βι
Строка 4 яі умноженное на 2Ь
-2,62666
(і, 10528= <іа
Примечания. 1. Знаки в элилинационных строках изменены на обратные.
2. Коэфициснты й2, «ι, (7,1 — алгебранческаи сумма чисм, стоящих в
столбцах «горки».
3. 'iSi.va— алгебраическая сумма чисел последней колонки, которые
η свою очередь, есть произведение двух последних чисел колонки е
(по разделу I, II, II! и т. д.).

2. Числовой пример решенач нормальных уравнений :sr
В качестве метеорологических факторов были взяты:
a'j—осадки в миллиметрах от начала сева до начала
кущения (от 3-й декады апреля по 2-ю декаду мая
включительно); х2 — осадки в миллиметрах за период от начала
кущения до начала цветения (от 3-й декады мая до 3-й
декады июня включительно); xt — испарения в
миллиметрах по эвапорометру Вильде за второй период. Результаты
обработки данных наблюдений приведены в таблице № 1.
Решение по схеме Дулитля дано в этой же таблице.
Решение по схеме Дулитля состоит в вычислениях,
основанных на приведенной в § 1, гл. 2 системе уравнений,
расположенных в соответствующих колонках схемы. Так,
в колонке b имеем первое уравнение данной системы:
5(Jci-o) = 5(jC?)-J£TiL = 32116--™= 11724,16 (1)
В колонке „с" сверху вниз расположены
последовательно одно за другим два следующих уравнения:
1) Между нулевой и первой элиминационными
строками размешены вычисления, основанные на следующем^
уравнении:
S(x2xuo) -S{xtxJ- SM-SM =
= 46766,0 1459.0-714,0 = 5096 9б ,2)
25
Между первой и второй элиминационными строками
сверху вниз расположены вычисления по уравнению:
*№)-*(4>-^--Е^-
^ 105111,0 - (Н59,0)2_ (5096,96)^ 187479076 (5)
25 11724,16
В колонке „d" аналогичным образом записаны
вычисления, основанные на трех следующих уравнениях:
1) Между нулевой и первыми элиминационными
строками п0 уравнению:
5(*8*ι.ο)β 5 *з*і -Sxa'SxX'= 121212 - -485^714-= 17503,92.

■?2 Схемы решения нормальных уравнений в полиномах Чебышева
2) Между первой и второй элиминационными строками
но уравнению:
S(.v,x,,) = 5(xx.S)- *(3№*)_Ц*&*)· *(*,*«) _
251798,0
" 5(*ы>)
4857,0-1459,0 (-17503,92) (5095,96)
25 11724 , 16
= 24046,86582.
3j Между второй и третьей элиминационными строками
•пи уравнению:
- 1034455 - - <l857'QV _ (=}7^92ρ _
25 11724,16
(-24046^2),
18747,9)76
В колонке „ί?" расположены последовательно
вычисления, основанные на следующих трех уравнениях:
1) Между нулевой и первой элиминационными
строками:
">Ч1 "Ϊ.7Η ί)
= 8224,0— —-■ — - 1618,072.
25
2) Между первой и второй элиминационными стро-
"""sin \-S(vx\ S(y)-S^ ^(-Ѵ^.о)^(-Ѵьо) „
,., 15609,9 - - 231'3·1459^ _ І«М72.«>9*М β 1407,791379.
25 11724,16
3) Между второй и третьей элпмипацнонпыми стро-
" ° V. -ч -о;
5 (yx.,.,).S ί'λ-,Λ·.,.,) 231,3-4857.')
1 -'; .Λ8 ' -= 40229,7 -
_ »'JUJ72_(-17503,92) _ (1407,791379) (-21046,8(5582)
11724,1(5 "" " 18747,9076
485,9331.

Числовой пример решгнич нормальных ураинений S3
В элиминационных строках записаны (с обратным
знаком) элиминационные средние, полученные путем деления
всех членов данной элиминационной строки на первый
слева член этой же строки. По каждому учтенному
признаку элиминационные средние записаны в колонках
соответствующих этому признаку. Нулевая элиминационная
строка есть не что иное, как обычные средние
арифметические факториальных и результативного признака* Во
второй элиминационной строке записаны выражения типа:
S(*t*i.o) S (*,■*,.„) S(yxu0)
«Ко) ' 5 Ко) ' Ч*1о) ЙТ*Д'
В колонке / по элиминационным строкам записаны
вычисления остаточной суммы квадратов отклонений по
данному уравнению множественной регрессии. Члены этого
уравнения последовательно равные: AuS(yx0); AyStyxi.o);
AaS(yx2.i); A^S (yx3.2i) есть не что иное, как произведение
значений каждой элиминационной строки по
результативному признаку (предпоследняя колонка) на
соответствующую сумму, стоящую над этим числом. Этим
исчерпывается первая часть схемы.
Вторая часть схемы Дулитля, так называемая „горка",
имеет обратный порядок вычислений по сравнению с
первой частью схемы.
В колонку „е" переносится (с обратным знаком) число,
стоящее в последней элиминационной строке колонки „е"
S ХЪ-1\)
md" записаны вычисления, основанные на следующем
уравнении:
,„ = S(yx3.v) = S(y*a.i) £(5β*?·0α-
5 (-*2-1з) 5 (Λ2·ΐ) 5 (·*2·ΐ)
1407,791379 (-24046,86582)
<" = : ι : (-0,01435) = 0,05бб82.
3 18747,9076 18747,9d76
В колонке „с" записано аналогичное вычисление,
основанное на уравнении:
в верхней части схемы т. е. о3 = ^—^—^'. В колонке
а, =
SQ'*i.») ^ $(Ухио) _ S(xzx\-o) ., s(xtxi-o)
S (*?.„) 5(4,) S(xl0) 3 S(xU)
1618,072 (—175u3,92) (-0,01435) 5C93.96-0.r5°682
2 11724,16 11724,16 11724,16
==0,09194.
2 Полиномы Чебышев".

34 Схемы решения нормальных уравнений в полиномах Чебышева
В колонке J)" записаны вычисления, основанные на
уравнении:
S(yxQ.Q) ,„ J_if^A.-.a"1 --^Vj -°·°)- - a"' S(x*Xq-^ __
= 9,252 - (0,03194) (2856) - (0,055682) (58,36) -
-(-0,01435) (194,28) = 5,10528.
Этим и заканчивается вычисление уравнений множест
венной регрессии по схеме Дулитля. Iаким образом в
полиномах" Чебышева каждое число, полученное в процессе
вычисления по схеме Дулитля, имеет свой логический
смысл. Эмпирическая схема Дулитля, таким образом,
получает свое теоретическое обоснование в свете полиномов
Чебышева.
3. Новые схемы решения нормальных уравнений в
полиномах Чебышева
На основе изучения полиномов Чебышева нами
выработана новая схема решения нормальных уравнений. Эта
новая схема основана на четвертой системе полиномов
Чебышева (полиномы системы N). Если отобрать из всех
разнообразных полиномов Чебышева те, которые
относятся к одной и той же переменной, т. е. напркмер,
полиномы х2ш0, хІЛ или х3.0, хъл, х3ш51 и т. д., то в нашем
распоряжении и будет четвертая система полиномов,
которая позволяет дать новую, весьма удобную схему решения
нормальных уравнений.
Удобства этой схемы проистекают из того, что
полиномы N в сущности идентичны отклонениям от
уравнения регрессии, но только вычислены для хт, а не дл;г у.
Преимущества новой схемы состоят в следующем:
1) Новая схема основана на легко запоминающихся
формулах одного и того же типа, имеющих характер
разностей; все коэфчциенты. данного полинома,
вычисленного по х„ (кроме стари его коэфициента этого полинома),
равны аналогичным коэфициентам предыдущего полинома
той же системы N минус произведение соответствующего
коэфициента полинома вычисленного по системе Ν для
предыдущей переменной Хт.\ и умноженного на старший
коэфициент данного полинома или данного уравнения
регрессии (см. схему Ν).
2) Новая схема позволяет расположить все важнейшие
статистические характеристики (п, хк, у, σ; a'j Δ-), коэфи-

Норые схімы решенаі нормальных уравнении 35
циенты (α, А, К, С) а также критерии (F, R, гтк и т. д.)
в стройную, логически законченную систему
статистических вычислений.
3) Новая схема позволяет легко вычислить, а также
статистически оценить с самых разнообразных точек
зрения, не только коэфициенты уравнения множественной
регрессии, например, у по xs, x2 хи но и всех других
промежуточных уравнений регрессии, а также коэфициен-
тов полиномов, например, хглѵ хІЛѴ xb23 и всех
промежуточных полиномов.
4) При этой схеме вычислений отпадает необходимость
повторять заново все вычисления, если подлежит
включению или исключению одна или несколько переменных.
При новой схеме, таким оэразом, полностью отпадает
Гауссовский способ совместного решения нескольких
уравнений, который до сих пор лежал в основе метода
наименьших квадратов. Все эти преимущества имеют
огромное практическое значение. Теоретическое же значение
новой схемы состоит в том, что:
1) она дает теоретическое обоснование методу
наименьших квадратов при помощи полиномов Чебышева. Метод
наименьших квадратов в связи с этим перестает быть
способом, стоящим несколько изолированно в современной
математике;
2) вскрывает в весьма наглядной форме статистическую
природу метода наименьших квадратов, как всестороннего
и глубоко развитого метода средних чисел.
В основе метода средних чисел, оказывается, лежат эли-
минационные (или иначе корректированные) средние типа:
SXm^k.lK.. m —t... ів + 1... (ft -1)
SX2/t.l2... т - 1, т + 1... (ft -1)
на которые указал еще Гаусс (12), как на наиболее
вероятные средние.
Основой всей новой схемы вычислений являются
старшие (на каждом данном этапе) коэфициенты полиномов
Чебышева, т. е. величины k 0, Kv tz™2 и т. д.
Эти коэфициенты вычисляются на основе сумм
нормальных уравнений и коэфициентов аналогичной системы
полиномов для предыдущей переменной. Таким образом,
если итти обратно, то доходим до полиномов Чебышева
нулевого порядка, причем в качестве исходной точки
всех вычислений оказывается нулевой полином Чебышева
Ψ0_ο'=1, а также S\4?liQ(x)\ = n (число наблюдений).
2*

36 Схемы решения нормальных уравнений в полиномах Чебышева
Таким образом повторность, число наблюдений («)
и объемы явлений (Sxk, Sy), определяют в конце концов
всю систему статистических величин, начиная с средних
арифметических, среднеквадратических и кончая кээ.рици-
ентами уравнения регрессии, коэфициентами полиномов
Чебышева и т. д.
Новая схема приведена на стр. 35.
По этой схеме ход вычисления таков:
I. Нулевой этап (вычисление средних
арифметических).
*о.0=1; S(xlo)^n> S(xixo.o) = s(xi)> S(yx0.0) = S(y).
ь· — 7 —Sxi- ν —7 —Sx*- b· — 7 5(*з)· η й S(y)
II. Первый этап (определение сумм квадратов
отклонений и коэфициентов полиномов Чебышева первого
порядка).
хио = х1 — к10; х.2.0 = х2 «20; ох,_0 = х.Л л;); d0=y a(j.
S«0) = S(*?)- А'105(^); 5(^.о) = 5(^)-^5(х2);
S(xU) = S(xl)-k'0S(x^
^)-·S(^-a05(y).
III. Второй этап (определение коэфициентов
уравнения прямолинейной регрессии и коэфициентов
полиномов второго порядка).
Центральным пунктом вычислений на этом этапе, как
и на предыдущем, является определение старшего коэфи-
циента полинома данного порядка. Для второго полинома
Чебышева хь 1 —х2 —k"M—к1\х\ старшим коэфициентом
S ( х2лГ] .0)
является к.,, ==—гт—,—ч—·
21 $ (-*?·<>)
Необходимая для определения старшего коэфициента
k"2X сумма квадратов S^xj^ нами уже вычислена на
первом этапе, остается определить S(x2xl \ Эта сумма равна:
Sfe.o) ^S(xSi) - KoS(x*)-
S ( κ χ \
Таким образом, к"Л= 21"°·-оказывается величиной,
5 ν. χϊ·ο)

Новые схемы решения нормальных уравнении 37
которую легко определить через величины уже известные:
5(хЛ); S(x2); S(xl); S(xJ); Uw
Младший коэфициент данного полинома Чебышева
также легко может быть определен по формуле:
k" —k' — h' -k"
для вычисления которого все величины уже определены.
Аналогичным же образом можно определитьвсе коэфи-
циенты второго полинома Чебышева для хѣ. а именно:
*=..і = кг - Ко - Кіхѵ 3Десь Кх — »У?\ . а сУмма
5(¥».)eS(¥i)-*'iosW·
Младший же коэфициент k"Q равен: к"ъа — &3о~^ю 'Κ\·
В результате имеем не только вторые полиномы
Чебышева хгл и х2л, но и уравнения прямолинейной
регрессии Х& ПО Хх И Xj ПО Хѵ
В самом деле, так как:
х2Л = х2 — й20 «31 хр то λχ2 — х2 л;2-1 = «20 + «гЛ·
Аналогично имеем: 1x3 = x3 — x31 — k'w + k3\xl.
Замечаем, что в уравнениях регрессии имеем такие же коэ-
фициенты, как и в чебышевских полиномах, но со знаком
плюс, а не минус. Затем определяем:
1
и вес величин х., в присутствии хх как с22=-~-,——у
Совершенно таким же образом определяем
прямолинейную регрессию у по χλ: ух = а'0 + а\хѵ Здесь
ві"(3«Ъ) ^*"' так как '11=="^R7)'
Затем 50/^.0)=--5(у^)-/г;05(д/).
Наконец, а'0 = а0 — k'10a\.
Следовательно, все величины, необходимые для
вычисления не только полиномов второго порядка, но и уравне-

3<1 Схемы решения нормальных уравнений в полиномах Чебышева
ний регрессии включая прямолинейную регрессию у по
хѵ а также х8 по ху> хг по х, и т. д., возможно легко
вычислить на основе величин, определенных на предыдущем
этапе.
Прежде чем перейти к следующему третьему этапу,
определим суммы квадратов для найденных полиномов и
для уравнения регрессии. Они также могут быть
определены на основе ранее полученных величин, а именно:
s(xi1)-s(xi0)-k;ls(x2xU0)
s(xil)=s(xi0)-k;1s(x3xV0).
S(d^ = S(d^-alS(yxUQ).
Для того, чтобы иметь возможность статистически
оценить полученные результаты, следует определить
величины, носящие название «весов» Гаусоі, т. е. вычислить
1
величину сп = . 2 . , а также нормированные коэфи-
s[xvo)
ь'
циенты первого полинома, т. е. величины: сю=---,—,!".
s(40)
_ -~^оо
Ст~ s(xl0y
Последняя величина определяется по уравнению:
Соо=1Г + 'о/ і \ или иначе соо-= соо + Косѵѵ
В результате оказывается возможным определить ту
часть вариации по уравнению регрессии, которая
воспроизводится при введении в уравнение регрессии
переменной хг. Эта величина нами уже определена как: a' S(yxx Л
(ЧУ
но она также может быть вычислена как ' , так как
с\\
= £j>bo) ar. а ■
Эта величина обычно называется суммой квадратов
коррелированной (или воспроизведенной) вариации. Дан-
ного типа формулы Ц--^ ^-У- будут использованы при
''и
статистической оценке коэфициеитов уравнений регрессии.

Строки Х0
S
S*oo *= "
1
X,
СХЕМА НВМЧИНОВА В ПОЛИНОМАХ ЧЕБЫШЕВА
х2 \ х3
СХЕМА «N»
—73
Sx,
Sx?
Sx2
SxzXl
sxi
Sx3
Sx3x,
Sx3x2
4
Sx?
Sy
Syx,
Syx2
syx3
Sy2
1. Вычисление уравнения регрессии У по Χ„ Χ2, Χ,
S[Pi]
С, —К, — а,
Μ
Ст—Кт -а,
C(D?)
S[P2]
Cs — K,— a,
Λί,
Λί,
Ст-Кт-а
Coo
Sx
00
Km =
Sx, Xq OXj
10 — c„2
ώχ00
Sx2
SX|_0= SX|— Kjo^xi
^10*^10
Coo*3 coo+^io cio
uxi.o
Cjo — A in С ι
Ч01"!!
"Sv2.0= 5X2—/C20^x2
Sx2Xj 0=SX2X1 — A",0 S.\2
,, *X2X1.0 ·
K2\ = ~^~2 ~Sx2x1.0Cll
ώΛΊ.Ο
Κ,η·Κ·
Ю"А21
a:
20
A'
20
К10-АГ2)
S.v2 ,'=Sx20—K2\Sx2x,_0
^зо =
*3.0 = ^Х3~
Sx„
«0 =
Sy
оХ^ ^—OJCq-—■ *Ѵдл oXq
S-x3x1.0=Sx3xl ~~ ^i0Sx3
Sx3xl.O
Sx3 X1.0'C11
^31 =
5xi.o
[Кі0-Кзі]
[^зо = А*зо —А'ю-Д'з,]
^x3.1 =Sx3.0 —^3! Sx3 X1.0
Sdl~Sy2-aQSy
Syxu0=Syxl-K\0Sy
a\ =syxi.o-c'u
K"'iofl'i
"о ~a0-I<\oa\
-i^.o-4^
КР
-00
Sd^SdZ—aySyXiQ
Κ·>η С
20 c20
'«
S(Dl)
C,-a,
Λί,
M2
Cm —am
s(dS)
^-00 "* ^00 + ^20 ^20
^21 C2]
[ΛΓ20 C2,J
CH "" Cll + ^21 C21
C\0 "" C10~^20 C2lJ
C22 — ov2"
^21 = K2i-C22
c2n = ^20c22
Sx3 x2 , =Sx3 x2—K21 Sx3 x, — K20Sx3 'syx2 i = Syx2—K'2\Syxi — K'2\tSy
^32 ~ ^X3X2. I "^22 ! a2 * SyX2.iC22 j
'22
^2 Γ ^32
^20 "^32
2ΓΑ32
^30 - Κ30 — Κ20·Κ32
^Χ3.21 ~^Χ3.1 —^32^Χ3Χ2.
Κ21·α3
ι'\ =α\ -^2і-аг
°0 =°0 — ^20 °2
κι
С'и
ΌΟ
Sd| == Srf? — α'2' Syx2. ι
Syx3.2i = Syx3 -K32 Syx2- K31' Syx,—K^yl
/Сол-С
зо^-зо
л-'" г'"
Λ31 u31
[^30 C3l]
С| 1 +К3I "С
^00 = ^оо+^ЗО^ЗО
ЗГ'-З! ι
^32 ^32
1^31 C32J
1^30 C32j
С22 = С22+К32-С32
\с2\ — ^2і ~^згсзг]
и33 сѵ2
с32 — ^зг'^зз
^31 = ^ЗI '^33
^30 ~ ^30 ' ^33
[С10= С10—К3о"сзи ! Iего = ^20 — К30-С32]
a3'=Syx3.2,-С зз
А'з2-"з
К'аі-а'з
^зо'аз
а" = а 2 — К32 ■ а3
а'\' жа\' — кз'\'а'з
ао =ао — кзо-аз
а3 -Syx3.2і
кт
И. Определение коэфициентов полиномов Х2.із и ^і-гз
К,
к'Г
22
[«=-£]
III. Исключение X! (определение регрессии V по Xs и Х3)
,С* и ,а*
I ісоо— соо~' ^ю cioJ
llC22= C22— ^12 ^21J
[іС33 = С33 — ^13'^31 I
,β3 =<г3 +β, -/C13]
[,а2 «ва'Ча',"·^]
ι «о ■= <Ό +α, ·Κ,ο]

Ноеые схемы peuiewi нормальных уравнений 39
Аналогичным образом может быть вычислена вариация.
/■л ——
«-вязанная с ха (частота), и она равна
Loo
На третьем этапе вычисляются коэфициенты полинома
третьего порядка и ураиение множественной
регрессии. Центральным пунктом и здесь остается
вычисление старшего коэфициента полином? Чебышева, т. е.:
к'" = ^ ( -VS-i)
Величина суммы квадратов S^.i) уже известна в
результате вычислений на втором этапе, остается
определить сумму S(k3x21}, которая равна
5 (-vs-i) = 5(^2) - b"xs(x3) - к;г s(xsXl).
Затем вычисляются остальные коэфициенты третьего
полинома по формулам:
Ь'" h" _ h" . h'"
Кгі — Кгі Кг\ Къі
k'" = k" — k" · k'"
K*.0 K30 K20 KZ2
Все величины, необходимые для вычисления, уже
известны в результате предыдущих вычислений.
Затем определяется 5(л:|-21)= 5(x|.j)~k'£2S(x^c2^. Таким
образом оказываются вычисленными все коэфициенты
третьего полинома Чебышева и суммы его квадратов.
Одновременно получаем уравнение регрессии х3 по х2
л\, т. е. аі*3 —^з^2+^з"А'і + ^'о> а также сумму квадратов
эа^ности х3 — ,[Х3, так как эта сумма квадратов равна
Таким же образом вычисляется уравнение
множественной регрессии у по хг и хѵ Для этого сначала
определяем: S{yx2^ = S{yx2^ — k'2\S{yx^) — Ка^(У)> а затем
вычисляем а"2 = -zy~TT ^ S (Ух<>-і) * c"ir Наконец,
Следовательно, все коэфициенты множественной
регрессии у — а"2 х2 + а"х1 + а"0 легко определяются на основе
величин, вычисленных ранее.

40 Схемы решения нормальных уравнений в полиномах Чебышева
Для оценки этих коэфициентов следует вычислить „вес"
и „нормированные коэфициенты" полиномов, а именно:
г" . г" — Ь" . г" · г" — k" с"
«-22— S(x2 V 21 21 22' *20ь22·
Для определения же величин с"г =
s(*U)
С00°а= /'2—Л* ИМеем·
г" — г 4- &" г"
ЬП ЬП ^ №21 °21
Г" — Г' 4- /fe" С"
•Ό) С00 ^ Л20 So*
Отсюда легко вычислить суммы квадратов
коррелированной вариации, необходимые для вычисления критериев
достоверности Фишера:
С22
2_W ,2_W
Л12 " ; Αθ2
С,
00
Наконец, имеем:
«У
'■п
На этом заканчивается третий этап вычислений. Если
в уравнение регрессии больше не вводятся независимые
переменные, то на четвертом этане вычисляются' лишь
уравнения множественной "регрессии у по xs x2 и хѵ
Сначала определяется числитель коэфициента άζ, а
именно: S(yx3.2i) - 5(ѵхя) - ££ S(yx2) - k^ 5(y.r,)- ft-^v).
j ,„ 5(-w;'··")
а затем сам коэфициент а = —V-^-—{-.
s(xln)
Остальные коэфициенты легко определяются но у
ранениям*.
а2 =а2-к^а.Л
,γ'" «" Χ.'" '

Новые схемы решенич нормальных уравнений 4-Г
в которых все величины уже известны. Для оценки этих
коэфициентов вычисляем „веса" переменных:
1
5(·*3·2ΐ) " 5(А'2-Зі) S {χί·23}
Эти .веса" определяются на основе следующих
уравнений
С22 С22 + Д32 ' С32
Cll Cll ' Я31 * С31
С'" — С' A- k'" . г'"
''oo ьоо ^ Лзо °го
После этого определяются и нормированные коэфици-
енты третьего полинома Чебышева:
к'" к!"
ш 32 * т -W. _w 31 ^ lw л»
С32 о /ѵ2 \ K32C33' С31 о / '? \— ЯЗГС33
ύ ^з-гі; ώ \хг-2\)
k'"
с'" = ^ — ь·" . г"'
сго о / ^2 \ №зо сіз·
В результате имеем все величины для вычисления суммы
квадратов коррелированной (воспроизведенной) вариации,
которые необходимы при вычислении критериев
достоверности Фишера.
К')2
Так, для оценки а3 имеем а% S (νχ3Λ=-—-„.-·
'33
а2 у
дли иценки а, имеем —,„-
С22
(iff \9
«1 )
J» » ,ί-() П " '
Наконец, для оценки всего уравнения множественной
регрессии у = а'3'х3 + а'2'х2 + а'1'х1 + а0" имеем сумму
квадратов отклонений S(d2) = S(di) — а3' 5(ул3.2і)·
В результате вычислены не только уравнения
множественной регрессии 2lx3 — k'32'x2 + k'3\'x1 + k^ и
у = а3"*з + а'2"х2 + а\"хг + а0",

42 Схемы решения нормальных уравнений в полиномах Чебышева
но и все величины, необходимые для оценки коэфициен-
тов этих уравнений с различных точек зрения, а именно,
дисперсионного и корреляционного анализа, а также
теории ошибок.
Кроме того, новая схема позволяет также определить
коэфициенты уравнений множественной регрессии ха по
х3 и хг, а также х1 по х2 и х3, т. е. коэфициенты
уравнений:
IЗ^ ~ ^23 Х3 + *21 Х\ "*" ^20
23Х1 ==Г ^13 Х3 ""*" *12 Л2 ~*~ *10
Эти коэфициенты получим, определив сначала
нормированные коэфициенты: с2'3 —- с^; с2'г'= с,2'; °ιΐ'"4ί', с^;
и с20·
На предыдущих этапах не были вычислены лишь
величины c2i', c20 и с',',,'. Остальные же величины были уже
определены. Указанные величины легко определить
последовательно на основе следующих формул:
СХ0= CW ~ ^20 С2I С2\ ~ С21 ^31 С32
СЮ ==С10 ^30 СЗI С20 ^ С20 ^ЗО С32 -
Все величины, входящие в эти формулы, уже
определены на предыдущих этапах. Вычислив нормированные
коэфициенты с"0, с10, с™ и г,0' и зная £\,2 и с,',' из
предыдущих вычислений, легко определить и коэфициенты
для нового полинома л:.мг
и затем коэфициенты полинома jcb2:! по формулам
Таким образом, оказываются определенными
коэфициенты полиномов Чебышева л1-23, *,мз и хл.2! и
уравнения множественной регрессии для определения ^Зс,, jr>e2,
Для полиномов Чебышева эти коэфициенты должны
Г)і.іть взяты с обратным знаком, а для уравнения регрессии

Новые схемы решенаі нормальных уравнений 43
с тем знаком, какой они будут иметь в результате
вычислений. Одновременно необходимо помнить, что если для
нормированных коэфициентов имеем равенство: el3 = cil,
си ~ сгі\ с32 = с23; то коэфициенты одного порядка
элиминирования, например, k"2l и k"2\ k"3 и k'^; k"i2 и k'^, a
также коэфициенты k'^ и КЦ, к^ и Iг^; k^_ и 'k'.^ и т. д.,
существенно отличны друг от друга.
Для оценки полученных коэфициентов полиномов
следует вычислить соответственно суммы квадратов
отклонений. Они вычисляются для х3.21 аналогично как и для
уравнения множественной регрессии у по ла и х, (но не
у по хй, х> и Χι). Соответственно имеем:
(*£)'. КТ. (JtoT
II J It J Hi
C22 cll c00
где'
^ 5(4,)' " «КО* °° 5(4i2)
Для оценки коэфициентов уравнения
2;Л~ Кз Х-г "*~ ^12 X2 "*" ^10
соответственно необходимо вычислить:
КТ. К,'У. ТО2
II 1 II У II J
С33 С22 С00
причем здесь:
с" . с" _ · с" = .
•Н-^з-г) s{xi-3) 5(-*o·»)
Эти величины нам пока неизвестны, но они могут быть
определены, если исключить из уравнения л3-2I
переменную хѵ
Наша схема позволяет в случае необходимости
исключать те переменные, по которым коэфициенты уравнения
регрессии оказались недостоверными, или по каким либо
другим соображениям ненужными.
Формулы, используемые при этом исключении
переменных, аналогичны формулам, применяемым при включении
новых переменных, только в них имеем дело с обратными
знаками. Так, при исключении хг необходимо определить
уравнение .ѵ 23 = ^X4- і^ + ιαό · в этом слУчае сначала

44 Схемы решения нормальных уравнений в полиномах Чебышева
определяем: , <£, = с^ — к^ с\'0; , с'22 = с2'2' - k'12 c'21; 1 c33 =
= c33 — fc13 c3j'. Это и есть „веса", которые необходимы в
случае оценки коэфициентов уравнения
Коэфициенты нового уравнения регрессии легко
вычисляются на основе формул:
!< = <'+4" #13'
ιαο=αο +αι *ιο·
Эти коэфициенты могут быть оценены, зная величины:
GO2. Ш. (^Г
с" ' с" ' г" *
ісзз і^г ι'όο
Сумма остаточных квадратов отклонений для нового
уравнения (с исключением переменной χ,) получается по
(α'Ύ
формуле: S(dj.,)= ЭД) + Мтг-·
Если необходимо было бы исключить х2 и определить
коэфициенты уравнения регрессии у = 2asx.i+2ulxl -\-2a0, то
следует исходить из коэфициентов полиномов хЪѴЛ, л
именно:
ь'"_.С*._. />"—^" · Ц"—-С'"
№20 -"" №21 /.·"> *23 у.·'-
""22 ^22 °33
При исключении ха „веса" определяются по уравнении)
г1 -_/."' k"'.r'"· г" —/■'" Ь'".г'"- г" —г"' Ь'".г"
2С0Э Ь0Э 20 С20 > 2t,U —tll Л2I fc21 ' 2 С33 .43 ^23 С2;і ·
Коэфициенты же нового уравнения но формулам:
.Х = «з" +«і"*я'; S<=flV, + <,-*ai'; Л = ао' +«2'*»'·
И, наконец, остаточная сумма квадратов отклонений:
С22
Таким образом, предлагаемая новая схема позволяет
легко вычислить все полиномы и все уравнения мнонсест-

Новые схемы решения нормальных уравнений 45
ценной регрессии, а также всесторонне оценить их коэ-
фициенты. В этом исключительное значение новой схемы
решения нормальных уравнений, составленной на основе
использования всех преимуществ, предоставляемых
полиномами Чебышева.
В схеме N все эти вычисления расположены в
стройную систему на основе формул, рассмотренных выше. Эта
<:хем.а обеспечивает последовательность, систематичность
и симметричность всех вычислений.
* *
Система N полиномов Чебышева лежит в основе новой
схемы решения нормальной системы уравнений,
предложенной автором.
Однако полиномы Чебышева позволяют расположить
вычисления несколько иначе.
В частности, В. Н. Перегудов предложил несколько
иную схему вычислений (схему Р). Эта схема приводится
на стр. 46—47.
Схема Ρ использует аналогичные, рассмотренные выше,
формулы.
Однако, если схема Немчинова построена на коэфи-
циентах системы полиномов ,,Ν", то схема Перегудова
основана на комбинации коэфициентов Τ и К.
Вся схема „Р" делится косой ступенчатой линией на
две части (как бы два треугольника —верхний и нижний).
Над косой ступенчатой линией, т. е. в верхнем
треугольнике, записаны коэфициенты полиномов системы К, под
косой линией в нижнем тр угольнике коэфициенты
уравнения регрессии, выраженные в полиномах системы Т.
При этом запись коэфициентов уравнений регрессии,
выраженных через полиномы Т, даны в нижнем треугольнике
по строкам, а запись коэфициентов полиномов системы К
дана в верхнем треугольнике по столбцам. Так, например,
в схеме на стр. 46 в третьем столбце треугольника снизу
вверх записаны коэфициенты полинома:
*2-1 = к"Л - КіХ1 - ΚΐΧ1 - k'LX0 ИЛИ< ТаК КЗК
к"12 — 1 и х0 = 1 то
х2Л —Х2~ ^гЛ — %)·

46 Схемы решения нормальных уравнении в полиномах Чеііышпга
СХЕМА ПЕРЕГУДОВА В
Sx2
Sx„xt
ч
Коо = '
Кх0 — —Тю-К
оо
К20—
■(т*кю+та1к\0)
13
Соо = 1/л = 1/Sx
Ч 43 ,, 46
' С10- K'l0/Sx?.0= C,0=K20/Sxiin=
00
— Kirfi
10^11
= Д'20С22
8
rio=S;lci xq/Sxoo-
=Sx, /л
Κ,, = 1
71 14
42
5*1*00 C'., = 1/SX?0
10
■^20~^*2 ΧθΰΙ$χϋ<
10,
12
=Sx. In \ 2i— 2 xio/ox\ .0
C21— K21/Sx2 ,—
= к21с22
/Co, = I
и I Sx2xt
00
9, 11
|5·χ2χ1.0-Κ105χ2λο +
ι 4" /Сц5х2 Xj
-22"
i/s*2.,
18
2
12
' 30 — ^x3 χθ/^χΟΟ~~
= Sx3/"
1 3i "охзЛі ,0'охі о
22
1 32 = SX3 ^2. l/^X2.1
13
Sx3x0
^-хз хі.о=*^іо^-хзxo+
+ /C'I1S.v3x,
14
2У
31
A0— SyxQ/Sx0Q
= Sy/n
A, =Syx, 0/Sx2 0
21
Sx3x2I = /v2oSx3x0+
+/C21Sx3x,+/<22Sx3x2
33
15
28
Syx00=Sy
Syx,.0-/CI0Syx0 +
+ /CnSyx,
32
Syx2_,=/C20Syx0H-
+ K2', Syx, t.K22Syx2
16
Sx;
00
ς*2 -
=K'ios*i Xo+K'nSx:
16
^X2. 1 ~^4 20^*2 X0+"
4-K2',Sx2Xi + /C22SX2

Новые схемы решена·: нэрмальных уравнений 47
СХЕМА «Р»
ПОЛИНОМАХ ЧЕБЫШЕВА
Sxsx,
5*3*г
Sxi
. 23
^ЗО = ~ V 30*4)0 +
+ ^зі^ю+^зг^го)
50
C30 = ^30/'Sjc3.21 = ^30C33
24
<ί="(Τ31*Π+Γ32Κ2ΐ)
49
С31=^3і/5*3.21=^31С33
Sy
Syx,
syx2
Syx3
Sy*
, 36
flo =—(ло^оо+
+ AjK'10+A2K20+A3/<3'0')
51
^-00 = ^00 ^00 +
+ ^1θ''10 + ·^20^-20+·^30<-30
. , 37
«ι =-(Αι*η +
+А2К'2\+ А3К'з[)
Сумма
квадратов
55
(п"'\2іг'" — )2 I
\aQ ) /С00 — Λ03
52 56
„ Да\ ) /(-и— ліз
+К2іС21+/<зі сзі 1
25 38
Κ32 = — ^32^22 Ι ΰ? ="~(А2^22 + Аз^32)
48
(-32='Кз2/5х3.2I=^32 ^-33
26
#33 = '
47
1-33='/^-ϊ3.21
Α3 = Syx3.2l/Sx|.21
йухъ.ы= K's0SyxQ+ 34
+K'i'lSyxi+K'^Syx2+
+Я33 Syx3
S*3 21 =^30 $x3 xo +
+Κ3Ί Sx3 x, + K32SX3X2+
'" 2
53
ί-22==^22^'22+·^32 ^32
57,
(α2 ) /С22 = ?'23
39
а3 = 43^33
54
^33=,/^Х3.21
58
(α3 ) /^33=λ33
40
1
1
—
Sd'i = ~(AQSyx00+ 41
+А, «ух, 0+А2ух2 ,+
+A3Syx3.2i)+Sy2

■ffi Схемы решения нормальных уравнений в полиномах Чебышева
В нижнем треугольнике по строке десятой (до косой
ступенчатой линии) записаны коэфициенты полинома
системы Τ
Х2Л ~ Х2 ' 2Г*1-0 20'
При этом запись дана в форме уравнения регрессии:
Л~ ^20 + Тпхі.«> причем гх2 = х2-х.,.ѵ
В связи с этим при записи уравнения регрессии для у
соответствующие коэфициенты (написанные в верхнем
треугольнике по столбцу) должны быть взяты с обратным
знаком. Это особенно необходимо помнить в отношении
коэфициентов аік, так как при записи уравнения
множественной регрессии знаки при этих коэфициентах должны
быть переменены на обратные.
Старшие коэфициенты полиномов системы Τ и системы
К равны друг другу, а именно:
МО= *;0' ' 21 == ™Л» ^32 ~ Ь&І И Т* Д·
В схеме Перегудова запись таких равновеликих
коэфициентов дана в двух смежных колонках (см. схему „Р")
При этом, так как в верхнем треугольнике записаны
коэфициенты полинома, а в нижнем коэфициенты уравнения
регрессии, и так как koa = ku = к^, = kl3 — 1, то связь
между этими двумя типами коэфициентов выражается в виде
следующих равенств:
ь — τ k' · ь" — τ ъ" ■ к"' τ k"
В схеме „Р", основанной на системе коэфициентов
полиномов Τ я К, коэфициенты Τ расположены по
строкам, а коэфициенты К— по столбцам схемы. В схеме „Ν",
основанной на коэфициентах системы Ν, коэфициенты
расположены по строкам схемы. Кроме того величины:
^χ1·2\> 3χί.ν Sxf,0 и т. д., а также величины типа:
■Syx3.2v Syx2-v Syxuo и величины типа*. 5х,х2#1; Sx2xU0
и т. д. вычисляются по схеме „Р" на основе сумм
произведений первичных данных (т. е. величина типа: Syxk,
Sx\, Sxkxk .,), а в схеме „Nu они вычисляются как суммы
произведений первичных величин нл соответствующие
значения полиномов.
В связи с этим в схеме „Р" все величины исчисляются
но формулам многочленов, а не двухчленов, как в схеме

Числовой пример решения трмальн. уравнений по норык схемам 49
Например 5л:|.21 по схеме Перегудова вычисляется по
уравнению:
•S*3-2i= ^ха ~ *зо Sx3 — кгуХгх1 — k^Sx3x2;
По схеме Немчинова они вычисляются по уравнению:
*->-х:з-2і=г ^з-і ~ ^32 Sx3xr
k.^ по схеме Перегудова вычисляется по уравнению:
По схеме же Немчинова:
Наконец, в схеме Перегудова ряд промежуточных
величин, важных для всестороннего анализа (например:
Sd\, Sd\, Sd'p а0, α*, а\, а", а"2, Sx.\_v Sx*.0, Sx\^ ся', с20'
c'j'j' и т.д.), отсутствует. Это, однако, делает схему более
экономной в отношении затрат труда на вычисления.
Схема „Р", как отмечает В. Н. Перегудов: „...была
построена на других теоретических основаниях, чем метод
Чебышева. Однако в своей окончагельнойформе она
вплотную подошла к методу Чебышева". Настоящая
интерпретация схемы „Р" в полиномах Чебышева принадлежит
лвтору.
§ 4. Числовой пример решения нормальных уравнении по
новым схемам в полиномах Чебышева
Схема „N"
Решение нормальных; уравнений в полиномах Чебышева
:ю новой схеме „N" состоит из нескольких этапов, причем
каждый этіш распадается на несколько стадий. Число
этапов определяется числом изучаемых переменных.
Переменные включаются в анализ последовательно одна за
другой, причем число наблюдений (частота) также
рассматривается как переменная только нулевого порядка.
Нулевой этап, имеющий дело с частотой наблюдений состоит
в получении сумм, входящих в систему нормальных
уравнений в качестве коэфицчентов ігри переменных. На нулевом
этапе получаются суммы типа:
« Полиномы Чебышева

30 Схемы решения нормальных уравнений в полиномах Чебышева
На последующих этапах прежде всего получаются
аналогичные суммы произведений изучаемых переменных
на соответствующий полином Чебышева.
На первом этапе такими полиномами будут величины
ль0, на втором — х2Л, на третьем — х3.2і и т- Д· Каждый
этап распадается на следующие пять стадий:
1) определение сумм произведений соответствующего
полинома Чебышева на числовое значение каждой дайной
переменной;
2) вычисление старших коэфициентов полиномов
Чебышева и старших коэфициентов уравнения регрессии;
3) вычисление поправок, необходимых для перехода к
младшим коэфициентам;
4) вычисление младших коэфициентов как для
полиномов Чебышева, так и для уравнений регрессии;
5) определение сумм квадратов.
Каждая стадия вычислений имеет в схеме одну строку,
за исключением вычисления поправок и вычисления
младших коэфициентов. Число строк для поправок и для
младших коэфициентов равно номеру этапа вычислений.
Таким образом, на нулевом этапе строчка поправок и
строчка младших коэфициентов отсутствуют. На первом
этапе этих строчек по одной, на втором — по две и т. д.
Ключом ко всей схеме „N" является определение
старших коэфициентов. В схеме имеем дело с определением
старших коэфициентов трех типов:
1) определение стгірших коэфициентов полинома
Чебышева, т. е. величины типа k0, k"n, /г32';
2) определение „весов переменных", или, иначе говоря,
старших коэфициентов нормированных полиномов
Чебышева, т. е. величин типи'. соу си, с"2, с.^\
3) определение старших коэфициентов уравнения
регрессии, т. е. величин типа: а0, аѵ а"г, а,".
В схеме двойной вертикальной чертой отделены
вычисления коэфициентов полиномов Чебышева от вычислений
нормированных коэфициентов этих же полиномов.
Вычисление первой строки поправок состоит в определении
произведения старших коэфициентов двух полиномов
(предыдущего и данного). Поправки, записанные во второй и
последующих строках, есть также произведение двух
величин, а именно, произведение млядишх коэфициентов
полиномов Чебышева предыдущего этапа вычисления на
соответствующий старший коафициент данного этапа.

Чаалояой пример решения, нормальн. уравнений по новым схемам SI
Следует запомнить следующие мнемонические правили,
облегчающие вычисление поправок:
а) каждая поправка есть произведение двух чисел;
б) для каждой данной строки поправок первое из этих
чисел (т. е. множимое) равно старшему коэфициенту
полинома Чебышева предыдущего этапа вычислений; для
каждой строки поправок это число одно и тоже;
в) вторые числа в произведении, определяющем
величину поправок, т. е. множители, равны старшему
коэфициенту данного этапа вычислений; эти числа в схеме
записаны над перЕОй строкой поправок; для всего столбца
поправок эти множители одинаковы по всему данному
столбцу;
г) если первые числа, входящие в произведение при
исчислении поправок, читать по столбцу сверху вниз, то
они равны числам предыдущего этапа, записанным
столбцом справа от двойной черты, отделяющей друг от друга
обычные и нормированные коэфициенты Чебышева.
Старшие коэфициенты получаем как отношение строки
суммы произведений данного этапа вычислений на строку
сумм квадратов, вычисленным на предыдущем этапе.
Младшие же коэфициенты определяются как разность
между аналогичным коэфициентом предыдущего этапа и
соответствующей поправкой. Сумма квадратов также есть
разность между суммой квадратов предыдущего этапа и
произведением старшего на данном этапе коэфициента и
S(Pk). Эта последняя сумма стоит в схеме над старшим
коэфициентом. Сумма произведений, т. е. величины S(Pk),
являются алгебраической суммой произведений двух чисел,
из которых второе число есть коэфициенты нормальных
уравнений по столбцу, соответствующему данной
переменной, а первое коэфициенты полинома Чебышева
предыдущего этапа вычислений (с обратным знаком).
Необходимо помнить, что в строке сумм произведений
и сумм квадратов имеются в виду алгебраические суммы,
причем коэфициенты полиномов Чебышева должны быть
взяты с обратным знаком. Следовательно, коэфициентам
придается тот знак, который они имеют в полиномах
Чебышева, а не в уравнениях регрессии.
В таблице на стр. 53 по схеме Немчинова (с соблюдением
указанных выше правил)- решен тот же пример, что и
ранее по схеме Дулитля. На нулевом этапе в качестве сумм
произведений записаны обычным порядком суммы,
представляющие собой коэфициенты системы нормальных
уравнений.
4*

Я'2 Схемы решения нормальных уравнений в полиномах Чебышева
Старшие коэфициенты нулевого этапа есть ни что иное
как обычные средние арифметические. В нашем примере
имеем:
iLflfsA -= lifU. = iii - 28 56·
S(jf0.o) " я 25 " ' '
Нр£=Ну)~™*=9&>2 и т. д.
S (-£0.о) л 25
Таким образом, k\0 = хг = 28,56; AJ,0-—х2 == 58,36; #,„ =
= х3=194'285 ао==3' = 9,252-
Сумма квадратов нулевого этапа есть сумма квадратов
отклонений от средней арифметической. В самом деле:
5 «о) = 5(*ϊ) - Ко S(хі) = 32116 - 28»56 · 714 = 11724,16
S(x2im0) = 105111 -58,36-1459 = 20963,76
5(dJ) = S(y2) - e05(j;) = 2512,29 - 9,252-231,3 = 372,30.
Аналогично вычисляется Sxj.0 = 90837,04.
Сумма произведений первого этапа вычисляется но
формулам:
S(x2xM)=-S(x2xl) - A"i0S(jc2) = 4676S - 28,56-1459 =5096,96
5(*Л.:>) = 5(*Л) - *іо5(* )= 121212 - 28,56-4857 =
=--17503,92
sO>xuo)'s=sO'xi)- KoS(y) =8224,1 -28,56-231,3 = 1618,17
Старшие коэфициенты первого этапа определяется но
формулам:
С'П== ^(ко) β ""^ =0,00008529,
* = lififlA. = A°^t β 0 434740
S«o) li724·16 U,*M/W'
^І-Ы,^. 0,138020.
5(4·ο) 11724,16

СХЕМА «Ν-
НОВАЯ СХЕМА РЕШЕНИЯ НО>МАЛЬНЫХ УРАВНЕНИЙ В ПОЛИНОМАХ ЧЕВЫШЕВА (числовой пример)
Строки
25
714
32116
*2
1459
46766
106111
*з
4857
121212
251798
1034455
s(pS>
s(p.)
Cs-Ks-a,
Μ
Cm — Km—am
Cs-Ks-a* Coo = 4000
3000
1. Вычисление уравнения регрессии
Υ
231,3
8224,1
15610,0
4229,0
! ι"
2512,29
Υ по λ', , Χ2, χ3
Κ10 = 28,56
Sx20 = 11724,16
Κ'20 = 58,36
κ\ 0 = 20963,76
λ'30 « 194,28
Sx'.
α0 = 9,252000
:§.ο = 90837,04
Ι
6956873
Cqo = Ю956873
C'n = 8529
С', 0 =243588
Sx
:2 хи о=5096,96 j Sx3 χ, 0 = -17503,92 Syx, ,„ = 1618,17
K2I =0,434740 ί Κ31 = - 1,492979 о', == 0ЛЗЯО2И ! ^)'
12,416174
I S</q = 372,30
K20 = 45,943826 j Κ'ή
Sx2, ι = 18747,91 . Sx2 , =64704
K31 = - 1,492979 a
— 42,639480
30= 230,919480 „0 = ό,?,10149 fe
I Crw
3,941851 I
■ v ' I = 093
І C'M
1
,34
\(ao)2
,06
I
257,35
^ on
Si/7 = 148,96
S(P2)
Μ
Μ,
''2
ί„— Km ·
*0>а)
s(p3)
Cj-α.
Μ,
Μ,
^m - α„
s (о?)
11259177
С0'0 = 22216050
1008
(106544)
С,', = 9537
С','0 = 137044
С 22 = 5334
С2', = 2319
С2'0 = 245064
Sx3 х2 ,= — 24040,87
Syx2_ , = 1407,85
1 .. '(а 'У
^32 == — 1,282661 ι «,=0,075095 —т,і—
г 2 г..
— 0,557624
— 58,930354
К3\ = —0,935355
0,032647
3,450152
, а',' = 0,105373
I
Кзо = 295,849834 I а'0 = 1,859997
5λ3.2ΐ =33860,56 | —
105,72
С22
К ΐ
., - 116,42
u 11
К)!
^ = ,5.57
SJ2
'\ = 43,24
2,58467432
<
2583
- 817137)
-ОО :
! C,'J = 12120
I
I
= 2,80683482J С'10 = 954181
ι
4857
(3542)
( — 1120383)
С22 = 10191
C2'J= —1223
С2'0 = 1365447
С33 = 2953
С 32 =—3787
Сзі = —2762
С3о = 873644
\syx3 2, =486.28
о3'' = —0,014360
0,018419
0,013432
— 4,248404
а2"= 0,056676
с," = 0,091941
й0" =6,108401
Κϊ
-7V,- = 6,98
L33
(jD:
к
II. Определение козфициентов полиномов
^-31
"-22
ίίιϊ
,523
,74
-Атт- = 69,
^00
Sd\ = 36,26
■^2.13 и ^1.23
^2'ό = 133,985670 |κ"2ΐ=—°
К,' К','о = 78,727806
.Саз- -0,378700
К р. - — 0.227888
, С
III. Исключение X, (определение регрессии 1' по Х2 и Х3)
,α" ,Соо= 2,05658323
j ,С22 = 10314
,С;,=~3341
я'з = -0,035312
, а2 = 0,047398
(ι аз)2
„- —37,52
1-зз
(ΐίΐϊ
-77-= 21,32
U22
(.О2
|(i0 = 13,346714 , 77-- =86,81
I иОО
'Sd\A =■ 106,00
Примечание: Величины Си и С^ даны в восьмизначных десятичны* дробях (Ю 8) и нули опущены при записи.

Числовой пример решения нормалън. уравнений по ноеым схемам .".:
Строка поправок заполняется умножением старшего
коэфициента предыдущего полинома Чебышева на строку
старших коэфициентов, только что вычисленных, а именно:
ст = к\0 сп= 28,56 · 0,00008529 = 0,00243588,
к'ю- с'10= 28,56-0,00243588 = 0,06956873,
*іо*и = 28,56-0,434740=12,416174,
Ко *зі= 28,56 ·( -1,492979) = -42,639480,
k'ma\ = 28,56-0,138020 = 3,941851.
Младшие коэфициенты получаются как разность между
соответствующими коэфициентами предыдущего (нулевого)
этапа и соответствующей поправкой. В нашем примере
имеем:
*£, = 58,36 - (28,56-0,434740) = 45,943826,
а0 = 9,252 - (28,56-0,138020) = 5,310149,
с;0 — 0,04 + 0,06956873 = 0,10956873.
Сумма квадратов равна разности между
соответствующими суммами квадратов предыдущего этапа и
произведением старших коэфициентов данного этапа на сумму
произведений, стоящую над ним. В нашем примере имеем".
5х|.!= 20963,76 - (0,434740-5096,96) = 18747,91,
Srf? = 372,30- (0,138020-1618,17)= 148,96-
Вычисление на следующем этапе вполне аналогично
вычислениям на первом этапе, с той лишь разницей, что
каждый раз увеличивается число строк поппавок и число
строк младших коэфициентов. Так, на втором этапе имеем
две строки поправок. Первая строка равна произведению
старшего коэфициента предыдущего этапа на
соответствующие старшие коэфициенты, вычисленные на данном
чтапе. В нашем примере для второго этапа имеем:
*ς 4=0,434740-0,00002319 = 0,00001008,
^'і^=0,434740-(-1,282661)= -0,557624,
ku2l a; "= 0,434740. (0.075095) = 0,032647.

54 Схемы решения нормальных уравнений в полиномах Чебышева
Вторая строка поправок есть произведение второго
коэфициента предыдущего полинома Чебышева на
соответствующий старший коэфициент данного этапа. В нашем
примере имеем:
k;0 с"п = 45,943826 · 0,00002319 = 0,00106544,
k"1Qk"a= 45,943826-(-1,282661) = - 58,930354,
kWal = 45,943826 · 0,075095 = 3,450152,
к'Л <£,= 45.943826.0,00245064 =. 0,11259177.
Необходимо в дальнейшем помнить, что поправки,
которые являются произведением величин ,,&" ж „с"
имеющих подстрочный значок одного и того же порядка, т. ѳ.
величины типа: k'i0. c10; k^c'^; /ζ"2οζ2; li'^c"Q, прибавляются,
а не вычитаются как все остальные.
Младшие коэфициенты получаются как разность между
соответствующими коэфициентами предыдущего этапа и
соответствующими поправками, например:
Щх = - 1,492979 - 0,434740· (- 1,282661) = - 0,935355,
а\ = 0,138020 - (0,434740 · 0,075095) = 0,105373.
В остальном вычисления как на этом, так и на
последующих этапах вполне аналогичны предыдущим.
Новая схема позволяет определить коэфициенты
полиномов с измененной последовательностью переменных.
Так, в нашем примере для полиномов х2лг имеем (см.
схему N):
0,01365447 ,„,пос™
Я20— О^СООЮIЭГ ~~ ld<J>S60D/u»
, и_ -0.0W1223 _ 019ПППо
.„ -0.003787 п О707ПЛ
Аналогично для полинома jci-23 имеем (см. схему N):
*ίόβ 'о!оооі2іію~ = 78>727806.
.,„_ —0.0С0Э1223 _ 0 .nnqf)8
Аі2— О.ООЛ2120 ~ ~ 0,100У08,
ь»_ -0,00002702 _ П997ооо
fti3- Т;0Э0Т2Т20 0,22/888.

Числовой пример решения ■норжалън. уравнений по новым схемам 5S
Новая схема позволяет и исключать переменные. При
исключении, например, хг определяем регрессию
следующего типа: у = ха"ъ хъ + ^а\хг + га"0
Коэфициент этого нового уравнения получается вполне
аналогично случаю включения новых переменных, но
только в случае исключения переменных знак поправки
меняется на обратный. В нашем примере при исключении
Хх имеем'.
ха"ъ = - 0,014360 + 0,091941 -(-0,227888)= - 0,035312,
,Oj = 0,056676 + (0 091941 · (- 0,100908) = 0,047398,
,oJ = 6,108401 + (0,091941 -78,727806) = 13,346714.
При исключении переменной остаточная сумма
квадратов уравнения регрессии также вычисляется аналогично,
но лишь с изменением знака поправки на обратный.
Вычисление сводится к прибавлению той поправки, которая
подлежала бы исключению из предыдущей суммы
квадратов отклонений, если бы данная переменная была
включена в анализ последней. В нашем примере имеем:
ЭД,)-ЭД)-Ь -ψ- = 36,26 + ^^ = Ю6,00.
В результате всех вычислений в разбираемом нами
примере оказались вычисленными следующие уравнения
регрессии:
у^ 5,310149 + 0,138020л:!,
у„= 1,859997 + 0,105373л:,. + 0,075095л:,,
уш= 6,108401 +0,091941xa + 0,056676л;3 - 0,014360л„
j/23= 13,346714 4- 0,047398л:2 - 0,035312*,.
Кроме того, в процессе вычисления определены_следую-
щие уравнения между величинами χ (где лг3.21 = 2^3):
x3.l2= 295,849834 - 0,0935355^- 1,282661.x,
^=133,985670 - 0,120008^ - 0,378700xs
^і-2з= 78,727806 - 0,100908/Г, - 0,227888л:!>.

56 Схемы решения нормальных уравнений в полиномах Чебышева
Одновременно вычислены и промежуточные уравнения:
х2>1= 0,043474^, + 45,943826,
χζλ= - 1,492979*!+ 236,919480.
Кроме того, вычислены все суммы квадратов
отклонений, которые необходимы для оценки всех коэфициентов
уравнения как с точки зрения дисперсионного и
корреляционного анализа, так и с точки зрения теории ошибок.
Статистическую оценку этих величин рассмотрим в
следующим параграфе.
Вычисления по новой схеме при достаточных навыкал
могут быть упрощены, если опускать запись поправок,
вычитая их сразу же после вычисления, не снимая с
каретки арифмометра.
Для уверенности в правильности полученных
результатов необходимо производить контрольную проверку
вычислений путем проверки выполнения следующих
равенств:
На первом этапе:
I. CnS(**)-CwS(Xiy=l
II. S(f) - a0S(y) - a; S(yXl) = S(dl).
На втором этапе:
і. c;2s(xf)-c;1s(x^x1)~c;0s(x2) = i
II. 5CV1) - al S[y)- a'l S{yx,) - a\ S(yx2) = S(dfy
На третьем этапе:
1· ^З(х^-С^(х^-С-З(х^-С^(х^^1.
II. 5 (У) - a;S(y) - a"; S{yxt) - αζ S(yx2) - < S(yx?;}
= S(d20) и т. д.
При выполнении этих контрольных равенств
вычисления произведены правильно, а в противном случае
необходимо искать ошибку.
Схема „Р"
Обработаем ту же систему нормальных уравнений ію
схеме „Я". Числовой пример вычисления по этой схеме
дан на стр. 57.

Схема „Р
НОВАЯ СХЕМА РЕШЕНИЯ НОРМАЛЬНЫХ УРАВНЕНИИ В ПОЛИНОМАХ ЧЕБЫШЕВА
(числовой пример)
Строка
1
2
3
4
5
6
7
8
9
10
И
12
13
14
15
16
25 714
1 32116
1
1==*оэ 1 —28,56000 = k\0
4000000 = сад ' — 243617 = с10
28.56С00 — Тт
714 = Sxi
58,ЗГО0О = 7-2О
1459 = 5 л-3
191,28300= 7Л0
4857 = 5xs
9,25200= А0
231,3 = S>
£,0 ΞΞΓ ΤΙ ^Ξί oJ^q л
1=*п
8530 = с'п
0,43475 = 7·2ι
5097 = Sjc2Jt;I,0
-1,49293 = 7·31
—17504=5^3^,.,)
0,1с8Э2 = Лі
1618,2 = 5;'л-і,0
11724 = 5л:^0
1459
467ο6
106111
-45,94354 =*2'0
— 245 63 = с"0
-0,43·.75 = /ί·2Ί
-2319 = 4
і = *і
5334 = с22
-1,28233 = Ті2
— 2iW = Sx2xl.0
0,075С9 = л2
1407,8 = 5 ѵд-2.1
18748 = 5^.,
4857
121212
251798
Ьс4455
-295,84807 = kl '0
—873639= cj0'
0.93536 = ^31
2762 = 4'/
1,2S263 = &32'
3787 = с32'
1 = кзз
2953 = С33
-0,01436 = Л3
-486,3 = 5_ѵлг3.21
33861 = 5 λγ^ι
231,3
8224,1
Ιδο'Ο,Ο
40229.0
2512,29
—6,10S63=.?y"
—2.80681175=^'
- 0.C9194 = «',''
12122 = α'ϊ'
—Ο,ΟδδΉ = a2 '
10191 =c22'
0,01436 = αϊ'
Л."ио :1::= С33
1
36,23 = 5 rff
Сумма
квадратов
13,79 = λ^
69,73 = л у..
3],52 = λ^}
6.93-λ*,
I
Все числа для коэфициентов сік и си. должны быть умножены на 10'

.).ς Схемы решения нормальных уравнений в полиномах Чебышева
Порядок вычислений по схеме ,,Р" показан на стр. 45
(схема Перегудова в полиномах Чебышева) порядковыми
числами, поставленными в верхнем правом углу каждой
клетки. Формулы, на основе которых вычисляются эти
коэфициенты, записаны в соответствующей клетке.
Если руководствоваться этой схемой, т. е.
записанными в ней формулами и порядковыми номерами
вычислений, то достаточно повторить все вычисления два раза
чтобы полностью овладеть всей схемой. В схеме „Р" так
же как и в схеме „Ν", можно различать этапы и стадии
вычислений. Включение каждой новой переменной дает
новой этап вычисления, причем, каждый этап раздаляется
на три стадии:
1) вычисление сумм квадратов;
2) вычисление коэфициентов Τ и А;
3) вычисление коэфициентов к.
Первая стадия состоит из определения сумм квадратов
предыдущего полинома, определяемого в виде
алгебраической суммы. Например, на третьем этапе эта сумма
равна:
Здесь коэфициенты к взяты с обратным знаком.
На второй стадии каждого этапа определяются
коэфициенты Τ и А. Эти числа записываются в клетках в
строках, расположенных влево . от вертикальной части косой
ступенчатой линии, разделяющей всю схему на верхний
и нижний треугольники, причем эта строка каждый раз
расположена влево от клетки, в которой стоит единица.
Третья стадия на каждом этапе состоит в определении
коэфициентов полиномов системы к. Поэтому эта стадия
включает в себя определение стольких чисел, сколько
коэфициентов в данном полиноме. Следовательно, для
полинома третьего порядка этих чисел будет четыре, для
полинома второго порядка — три, для полинома первого
порядка —два и для полинома нулевого порядка—одно.
Полезно запомнить мнемоническое правило, что числа,
определяемые на первой стадии, записываются в
соответствующей клетке самой нижней строки схемы, числа,
определяемые на второй стадии, записываются каждый раз
в двух строках, расположенных влево от косой
ступенчатой линии, т. е. в той прямоугольной полосе нижнего
треугольника, рядом с правым верхним углом которого стоит
единица, наконец, числа определяемые на третьей стадии

Числовой пример решениі нормальн. уравнений по но рым схемам 59
каждого этапа, записываются столбцом через одну клетку
в верхнем треугольнике.
Схема „Р". роме того, имеет заключительный этап,
состоящий в ипределениии чисел Сік и Скк, необходимых
для статистической оценки полученных коэфициентов
уравнения регрессии. Этот заключительный этап состоит
в заполнении тех клеток верхнего треугольни'ка, которые
оказались пропущенными при заполнении чисел,
полученных на третьей стадии каждого этапа. Следовательно,
заключительный этап состоит в заполнении тех клеток
схемы, которые в таблице на стр. 46 помечены порядковыми
номерами от 42-го до 58-го.
Покажем порядок вычислений по схеме „Р" на
примере второго этапа, имеющего дело с Хг. Эти
вычисления расположены в клетках, имеющих порядковый номер
с 8-го по 15-й В 8-й клетке записано число, полученное
но формуле:
o.xj.0 = κιύοχγκζ 4- ku Sx*,
Таким образом, сумма квадратов первого полинома
(записанная в 8-й клетке) является алгебраической суммой
произведений чисел, стоящих во 2-м столбце. Множимое
берется из самой верхней части схемы, где записаны
суммы типа SXiXk, составляющие систему нормальных
уравнений. Множителями являются числа, стоящие в верхнем
треугольнике того же второго столбца (т. е. коэфициенты
системы К полиномов Чебышева). Получением этой суммы
произведений заканчивается первая стадия третьего этапа
вычислений.
Вторая стадия этого же этапа вычислений состоит в
заполнении 9—12-й клеток. В 9-ю клетку переносятся из
верхней части схемы SXZ. В 10-ю клетку заносится число,
полученное в результате деления числа, стоящего в 9-й
клетке на число, стоящее во 2-й клетке. В 11-й клетке
определяется сумма SX2XX,Q, вычисляемая по формуле:
$х2х\-й ~*10 Sx2+kll Sx2xv
Таким образом, вычисление числа, стоящего в 11-й
клетке, состоит в умножении чисел, стоящих в 6-й строке
верхнего треугольника на число, стоящее в верхней части
схемы (в 1-й н во 2-й строках). Число, записанное в 12-й
клетке, получается путем деления числа, стоящего в 11-й
клетке на число, стоящее в 8- клетке.
Третья стадия вычислений состоит в определении
коэфициентов полиномов 2-го порядка- Результаты вычисле-

во Схемы решения нормальных уравнений в полиномах Чебышева
ний записываются в верхнем треугольнике, в клетках
13-й и 15-й. В клетке 13-й записываются k"lu. Этот коэфи-
циент получается по формуле'.
^20= "~ ( ^ 20 ^00 "^ * 21 ^іо)"
Таким образом, вычисление сводится к умножению
чисел, стоящих в строке 10-й нижнего треугольника, на
числа, стоящие в строке 6-й верхнего треугольника.
Полученная при этом алгебраическая сумма должна быть
взята с обратным знаком.
В клетке 14-й записываются коэфициенты к"ѵ Это
число получается путем умножения числа, стоящего в
12-й клетке, на число, стоящее в 7-й клетке. При этом
знак меняется на обратный.
В клетке 15-й записывается число к"іп т. е. единиц;і.
Этим и заканчивается вычисление, относящееся ко 2-му
этапу.
Совершенно аналогичным образом повторяются
вычисления, связанные с третьим и последующими этапами.
Заключительный этап состоит в вычислении коэфици-
ентов сік и скк (клетки с 42-й по 50-ю), путем деления
соответствующего коэфициента kn на сумму квадратов
отклонений.
Несколько иначе вычисляются коэфициенты сІЬ (клетки
с 51-й по 53-ю). Они получаются как алгебраическая
сумма произведений коэфициеитов k и с. Так, число,
стоящее в клетке 51-й, получается как сумма произведений
чисел строки 6-й на 7-ю. Число, стоящее в 52-й клетке,
получается как сумма произведений чисел, стоящих в 9-й
строке на число 8-ой строки (при этом берутся только числа,
записанные в клетках верхнего треугольника схемы).
Число, стоящее в клетке 53-й, получается также как
алгебраическая сумма произведений чисел 10-й строки на 11-ю
(берутся также только числа, записанные в клетках
верхнего треугольника). Число, стоящее в клетке 54-й,
является обратной величиной числа, записанного в 27-й
клетке.
Суммы квадратов, необходимые для оценки
коэфициеитов уравнения регрессии (клетки с 55-й по 57-ю),
получаются путем деления квадрата каждого коэфициента
уравнения регрессии на соответствующее скк.
Для контроля вычислений по схеме ,,Р" используются
равенства:

Числовой пример решения нормільн. уравнений по новым схемам 61
Для нашего числового примера для контроля
вычислений второго этапа имеем:
18748 + 0,43475-5097 + 58,36-1459=- 106111.
Аналогичным образом контролируются вычисления и на
остальных этапах, b частности, на этапе, где
определяются коэфициенты а^ имеем контрольное равенство:
Sd23 + Л8Sy.K3.21 + аі^Ух2-і + A2Syxuo + Л^У-Ѵ^ Sy*-
Как видим, схема ,,Ρ" является простой и легко
усваивается при небольшом опыте.

ГЛАВА 3
СИСТЕМА СТАТИСТИЧЕСКОГО АНАЛИЗА
И ПОЛИНОМЫ ЧЕБЫШЕВА
§ 1. Статистическая оцѳика коэфициентов уравнения
регрессии и полиномов Чебышева.
Новые схемы ,,Ν" и ,,Р" в процессе нахождения
коэфициентов уравнения множественной регрессии дают без
дополнительных вычислений все величины, необходимые
для всесторонней статистической оценки полученных
результатов. Статистическая наука знает три вида оценок:
а) определение достоверности полученных
статистических характеристик;
б) определение ошибок, сопутствующих в
стохастическом смысле каждой из полученных величин;
в) определение степени тесноты связи между
изучаемыми признаками.
Оценка полученных результатов с каждой из этих
точек зрения требует определения различного рода сумм
квадратов. Для целей статистической оценки со всех трех
указанных выше точек зрения оказывается достаточным
определить два рода сумм квадратов:
а) остаточные суммы квадратов отклонений типа:
S(xlQ); (Sxl,); S(^.n) и S(d$
б) суммы квадратов вариации, коррелированной с
элиминированными значениями факториальных признаков,
т. е., например, со значениями хі-21. Последнего рода
суммы квадратов определяются одним из следующих
способов (на примере х3.2і)'-
[$(УхЗ-ѵ)]2 _ т ςγ ч (°3 У _ , »,yj о / 2 \
* Кхзп) cj3

Статистичесгсаі оценка коэфіщиснпгов ураянгнпі регрессгш 6S
При этом по каждой переменной имеем дело с
элиминированными значениями, т. е. с величинами типа
х,
λ*2·13> •'1!'3·23'
ν1·23'
Следовательно, по каждой переменной коррелированная
вариация определяется так, что как бы каждая данная
переменная вводится в анализ последней. Полиномы Чебышева
обеспечивают это без дополнительных вычислений. Все
необходимые величины легко получить в процессе вычисления
уравнения регрессии в полиномах Чебышева. Вычисления,
связанные со статистическим анализом полученных
характеристик, удобнее расположить в виде особой схемы (стр. 65).
Из схемы решения нормальных уравнений в таблицу
статистического анализа переносятся веса переменных, а
также коэфициенты уравнения регрессии, остаточные
суммы квадратов по уравнению регрессии и суммы
квадратов коррелированной вариации.
Критерии статистической оценки целиком основаны на
этих величинах. Необходимо лишь предварительно
получить средние величины для сумм квадратов путем
деления соответствующих сумм квадратов на число степеней
свободы, определяемых обычным способом.
Критерий достоверности Фишера определяет как
отношение среднего квадрата коррелированной вариации к
среднему квадрату остаточной вариации, или иначе, как
отношение квадрата оцениваемого коэфициента к
квадрату его средней ошибки.
Так например, критерий достоверности коэфициентов
уравнения множественной регрессии у по хІУ хг, и хи в.
нашем случае равны:
Ко·ринневты
Средние квадрагы
Критерий достоверности Ρ
фактический
Ί'β,ί ЛВЧВЫЙ
<ζ= — 0,014360
<ζ =0,055676
а" = 0,091941
а" =6,103401
К)1
= 6,98
■"33
( III \ О
(«О
= 31,52
и22
= 69,74
:13,29
"5| = 1.73
К')1
= 4,04
"3 с33
К")2
_, Λ-=18,22
<VC22
. =40,31
а-ашСп
^-Λ- = 7,73
"з'соо
4,."7

64 Система статистического анализа и полиномы Чебышеея
Вычисленный таким образом критерий достоверности
сопоставляется по таблице Фишера с ожидаемыми
значениями этих критериев в условиях стохастической
вариации. Если величина критерия, вычисленного по данным
наблюдения, превышает ее табличное значение, то данный
коэфициент признается достоверным и наоборот.
Б нашем примере оказываются достовереными коэфи-
циенты регрессии при xt и л:, и недостоверными при хг.
Рассматривая данные статистического анализа (табл.
па стр. 65) видим, что вообще в статистическом смысле
наиболее удовлетворительным с точки зрения
достоверности полученных результатов оказывается уравнение:
у„= 1,859997 + 0,105373*!+ 0,0750Э5х2.
Статистическая оценка полученных результатов с
точки зрения теории ошибок требует вычисления средних
ошибок каждого из коэфициентов уравнения. Квадрат
средней ошибки есть отношение среднего квадрата
остаточных отклонений по уравнению регрессии к сумме
квадратов соответствующего полинома. Так, например,
квадрат ошибки коэфициентов уравнения регрессии у по
х,, х, и х3 определяется как отношение:
Δ\αζ) = IVS(xUi) = djc33 - 0,000051
Δ 2Ы=nil S(XL·) = dl on = °>000176
А2(в) = Й/^К.э.) = ^'?п =0,000210
Δ\%) = 111 S(x\.m) - d]^ = 4,855824
Ошибки коэфициентов уравнения множественной
регрессии, следовательно, в нашем примере равны'.
аз"±дОз")= -0,01336 + 0,00714
α2 '±Δ«') = 0,056676+0,013266
αΓ±ΔΚ')==°,031941+0,014491
β'ο"+ΔΚ") — 6,107401 +2,203400
Величина αχ превышает свою ошибку в шесть раз, а
коэфициент а2 почти в пять раз· Наименьшую
относительную ошибку имеет, таким образом, коэфициент ах, а
наибольшую — а% и а0.

Схема статистического анализа в полиномах чебышева
И
» я ι Iісса неизвестных (<»>
ЗБ
ратные величины сумм
квадратов полипомов)
5 га ι
Ч О ι
О со
£ _
га
ία я
Г О)
Ι Ε
<u я
э S
О-в·
3
Суммы квадратов по
уравнению регрессии
Lo.o
= '- = С
ύΛ0.0
00
ϊί'§
Средние
квадраты регрессии

Дисперсионный анализ
Ошибки коэфициентов ц-л»а, ,, , , „ „.
пегпессии I коэфииненш корреляции (множественной и частной)
регрессии
Критерий
достоверности F |
І!
Квадраты
(\-ф) и 0-г*)
( "о )f_ = /2
1.0
L0.1
X,
X
I .2
Ч). 12 |
</■>
X
3.21
X
2.зі
•1.23 !
'О.123
5ХІ.О
1
5λΌ.ι
= с
00
SX~
= с*.,.,
2.1
: -с,.
SA't ,
ДА(.I.I2
I
SX3.2\
1
sx2.:'ii
I
^0.123
- С
33
- C2'2
-00
("о)2
00
π ι
c Ου Ι Ι η — 1
—-. Ίι
~S
- ί "о-Соп=Л2(о0)
Δ ( ΰο )
г ч R
12
W = >
11
γ'\2
с;
-οο
С 11
л—2
-00
/z-2 '
"3.
й?.с'и = л2(в;)
5?-СОо-д2(°о)
л(«'і)
Δ («с
Ά = S(tf2)(/1-I)
^о [S(d2)+'T,]('^
1 —
1— r(YX)
> = i_^(VX)
r(VX)
(a2T _,2
-22
,"\2
12
K)2_,2
(«θ)2_,2
c00
S(d2)-№=S((,2)
ii—3
ш;-ъ
С 22
W2_72
^)2=^2
-00
£(rf2)_w2
1 гі
4
'12
Ik
4-с:2=±2(«д
~4-с'оо=±2(а'о)
л( „.;') ' '4 := ЧЧгЬЦ-гI
'("2
Λ(αό')
</; [s(rf|)+ ).у(н-3)
[S(rf2)](f;~2)
[S(</|)+'/?2].(n-3J
- ' ~" r("vx2.i)
= 1 -r2
d22
2 __ ι ρ 2
ψ~1 *(ΥΧ]2)
"о
'2.1
42
а..
{?'*)*. = ,?..
С,
33
"Л2
С',','
>?«
)2
'оз
5(.|)-(^0-2 = 5((/2)
сзз
п—4
(££-*
-33
,'"\2
С22
("•Т-7
С',','
(«θ")2 72
23
оз
-оо
s(4)
^_% = di
^ІЗ
'23
"4
' 13
72
^■Сзз=Аа(вз")
I ^2c2'2=i2(a2")
J
d§-cv;=A'(ai")
^ο'ο^Κ")
Δ(ΰ2")
НО
*з_ [s(rfg)]C-3) _,_r2
5i~[s(d!) + >I3]("-4) (1'Χ3·2''
[S(</2)]-(h-3) _,_f2
[s(di) + x223]-(»-4) (™2·3,)
S(rf2)-(n-3) = i _ ^
[S(-|)4A?8J.(«-4, (,'*'-M)
Я;
<VX,23)
3.21
'2.31
1.23
Й
123

Схема статистического анализа я полиномах
-ун а»
·* ъ
К*
8 * ~.
R л а
О О ■
1
ΑΌ·ο
</о
ΛΊ·ο
ΛΌ·ι
rft
*^2·1
Λ·1,2
ΑΌ·12
*β
ΧΆ·1\
ХІ-?Л
χ\ -23
χ0,\%
d*
Be·» огремиішых
(оСрлтиыо ве. и- 1 ицекпваѳыые
чины сумм ( ,.09тіIвпТЫ
квадратов
іюднно-мов „с·) j
2 I 3
с 00 = 1,04000000
en= 0,00003529
Cog = 0,10956873
—
с2',=.и,00 05334
Сц = 0,00009537
Сад = 0,22216050
—
Сзз = 0,00 0І953
^',==0,00010191
c*= 0,0.-012120
Сда = 2,80f 83-182
—
flof= 9,252
f?j = 0,138020
ΛΟ=5,3ΐυι-:9
—
4' = 0,075095
οί'=0,103373
ff0' = l,8;9997
—
ffg" = -0,014360
4" =0,0^6576
я" =0.09194-1
я0"=(Ѵ,1Ш01
—
Cjmmu квадрлгов
по уравнению
реіргссни
4
2140,00
S(^)= 372,30
223,34
257,35
S(d}) = 148 96
105,72
116,42
15,57
£(<*;) = 43,24
6,98
31,52
69,74
13,29
S(</|) = 36,26
!,
1!
5
1
24
1
.
23
22
21
1-
6
Чебытева (числовой іі
Диспер -лон-
ныіі анализ
Критерия доп-
тоиер.іоі-та F
фактн- тлб:.пч·
чесяшііі кы/I
7 1 8
2140,00137,97
15,51
223,34
257,35
6,48
105,72
116,42
15,57
1,97
6,98
31,52
69,74·
13,29
1,73
34,47
39,71
—
4,26
—
4,28
4,28
—
54,16' 4,30
59,10 4,30
7,90 4,30
- 1 -
4,04
■ 18,22
40,31
7,73
4,32
4,32
4,32
4,32
—
ρ и мер)
ОгапСкіі і:он-
фиіиеніоп
регрессии
явад-
pR-fU
Δ
9 1 )0
0,620100 0,788
- 1 -
0.0U0553JO.023
0,7100051,843
- 1 -
Коэфицвснти
корреляции (мноисеитвеккои
η частной)
ввад-
ра·/ ы
(і-А·)
и
(l-r·)
11
—
—
0,4178
—
0,4178
г η R
12
—
—
/-==0,64
—
—
0,0001050,0100,3040' ''2.i=°>S4
0,0 0188 0,014 0,2831
0,437653 0,662
—
- 1 — 0,1270
0,000051
0,000176
0.C00210
•1-, 855824
—
г, >2= 0,85
—
/?12= 0.93
0,0070,8782' /·3>21=0,35
0,0130,5604' r2.31=0,66
0,015 0,3584 /-,.^=0,80
2,204
—
—
0,1115 /?Ι2 = 0,94

66 Система статистического анализа и полиномы Чибышеви
Критериями, определяющими степень тесноты связи
между изучаемыми признаками, являются индексы
множественной корреляции и коэфициенты частной
корреляции. Квадрат индекса множественной корреляции является
дополнением до единицы отношения между средними
квадратами остаточных отклонений по данному уравнению
регрессии и средним квадратом отклонений от средней
арифметической. В нашем случае индекс множественной
корреляции у по xlt x2 и х, равен:
1 ~ЩуХ\=-^1 = -1·73- = о,Ш5.
Отсюда:
/?iffl = 0,8885: /?ш = 0,94.
Квадрат коэфициента частной корреляции является
дополнением до единицы отношения среднего квадрата
остаточных отклонений по данному и предшествующему
уравнению регрессии, т. е. определяется по формуле:
1 - Г* (J^.2))= ^" « ~7" ^ °-8782 ИЛИ ^> " °-35·
Средний квадрат отклонений для предыдущих
уравнений регрессии известен непосредственно только для
данного порядка включения перемени..іх в уравнение регрессии.
Однако, эти величины легко могут быть определены
для каждого случая, когда данная переменная включена
в уравнение регрессии последней. В этом случае сумма
квадратов остаточных отклонений, определенная для
Измененного порядка включения переменных в анализ,
вычисляется как следующая сумма:
для л'.і-21 имеем S(df) -f- Ц, - S(dh
м Xt«\ » ψ!) "Ι >■!;,
Здесь в подстрочном значке число перед точкой
обозначает номер переменной, включенной последней.
В таблице на стр. 65 приведены все необходимые
исчисления такого рода.

Статистический оценка коэфѵциеитов уравнения регрессии <і7
Таким образом, наивысший коэфициент частной
корреляции г,.23= 0,80 имеем между у и х, ,ч, наименьший -
г3.,2 = 0,35.
Аналогичным образом может быть произведена оценка
и коэфициентов полиномов Чебышева, т. е. уравнений
регрессии типа". ^хг = Щ^х2-¥ k'^'x, + Ц'0'.
В этом случае и качестве „весов" для определения
средних квадратов коэфициентов полинома имеем
обратные величины сумм квадратов предыдущего полинома. "Эти
„веса" в схеме „N" решения нормальных уравнений
.записаны на предыдущем этане вычислений в левой части
е;:емы, в колонках, соответствующих каждой данной
переменной и расположены по косой линии (слева направо и
снизу вверх). Эти величины и выписываются в таблицу
статистического анализа во вторую и третью колонки.
Следовательно, для к^ весом будет величина <„, дли
коэфициента k'.^' величина с'{ѵ а для k'^ величина c"w
В остальном же статистическая оценка коэфициентов
уравнения х^ по хх и xt вполне аналогична оценки
коэфициентов уравнения у по х3, xt, и хг.
Таким образом, новая схема решения нормальных
уравнений со сравнительно небольшой затратой труда дает:
а) всю систему статистических характеристик, начиная
со средних арифметических, „весов" переменных,
остаточных средних квадратов отклонений по уравнению
регрессии и по полиномам и кончая средними ошибками всех
коэфициентов, критериями достоверности Фишера,
индексами множественной и частной корреляции;
б) позволяет определить уравнение регрессии не
только у по х, но также и л:-ов между собой в самом
разнообразном их сочетании;
в) позволяет оценить коэфивденты всех уравнений
регрессии и всех полиномов с точки зрения
дисперсионного и корреляционного анализа, а также с точки зрения
теории ошибок.
В этом преимущества новой схемы „N" решения
нормальных уравнений.
Теоретическое значение новой схемы состоит в том,
что она через полиномы Чебышева и теорию квадратн-
ческих приближений тесно увязывает всю систему
статистического исчисления с основами современной математики.

6S Система статистического анализа: а поликоми Чебышева
§ 2. Система статистических характеристик и полиномы
Чебышева.
Полиномы Чебышева дают возможность представить
все основные статистические характеристики в виде
простой и стройной системы статистического исчисления.
Полиномы Чебышева позволяют связать в единую систему
теорию корреляционного, дисперсионного анализа и
теорию ошибок.
Согласно теории Чебышева, изложенной нами выше,
в основе системы статистических характеристик лежат не
арифметические, а элиминационные средние типа:
гг2 ,
Sy4r,(x)_ 'Γ/Ο) Λ '
SVJ(x) ~ S*}(x)
Необходимо отметить, что еще Гаусс (12) в своей
„Теорий движения небесных тел" указал, что наиболее
вероятным средними являются не арифметические средние,
а средние элиминационного типа. На стр. 266 Гаусс
пишет: „Наиболее вероятная средняя величина не будет
просто арифметической, но ——^тг/ут:,,,-^— ·
Здесь г = х ...3=—^—.
χρ·\ϊ...
Заслуга Чебышева в том, что он в развернутом и
систематичном виде использует этого типа средние в своих
работах.
В экономической статистике теория элиминационных
средних получила название корректированных средних.
Из предыдущего равенства ясно, что элиминационные
средние являются средней взвешенной из отношений двух
величин, из которых одна (знаменатель) —полином
Чебышева (х Л2 ), а другая (числитель) — изучаемая величина
(у), а вес —квадрат полинома. Следовательно,
элиминационные средние являются средними типа:
*3-21
*3·21 ЗУхя.о\
S4-n S.rj.8i
Таким образом в основе теории элиминационных
средних лежат полиномы Чебышева.

СИСТЕМА СТАТИСТИЧЕСКОГО ИСЧИСЛЕНИЯ В ПОЛИНОМАХ ЧЕБЫШЕВА
Этапы элиминирования | Суммы произведении
Элимииацноиные средине
Суммы квадратов отклонений
(кпадратические приближения)
Ошибки
Критерий
достоверности
Коэфициенты
корреляции
Нулевой этап
(вычисление средних
арифметических, средних квадратп-
ческпх и ошибок средних)
"У ^ "о
х,= Α·ιη
х2 = к'2П
S ( х2) - η
Syxm-;Sy
tSv'i voo ■-- Sx,
S.v, -v00 - S.\\
•5-ѵя xi>o =- S.v,
S.Vqq = η
_Sy__
S*So
Sx'L
- у ----- a0
xi = *ю
Sx,
- - -v, - K20
Sxoo
Sx3 _ -
- --.ѵ3-Я'30
ол00
Sd2 =S>·2 - a2, Syg0 ---- n-2 (y)
SX?.0 = SX2-(/C'10)2S.v020=nJ2(x1)
Sx·2.0 = Sx2 - (K20)2 Sx20 = n-? (-v..)
і-з ■ o's*3 - (^зо)2 5λ"00 = η-? (-v3)
С' - '
ОЛ1.0
SJ5
Л2 (у)
Sx:
- -'10, =л2(х,)
(;і —1) S.V5.0
Sxi
2 О
(«—l)S.vg_0
-А2(х2)
Sx
.2
Перішіі этап
(вычисление уравнения
прямолинейной регрессии и
статистическая оценка результатов)
у= а', х, + а0
1 *2 = /с21 х1 + Л20
1 х3 = ^31 Х1 + А'30
S.vx,_0- S.i'Л, - К,„Si
Syx0.
Sv'2 λΊ.Ο ·■- Sx2 X\
~!<\0Sx2
Sx2 X3.U - Sx3 X2
- K30 Sx2
Sx3 x,.0 = Sx3 Xi
6'>'ΛΊ.0
S-v2.0
_^o. 1 .
S-Vo..
Sx2 xb0
S.v
.2
""o-«i '<io
-A\„
Sd2 = Sii5 —(«1)2Sx2_„
1
Sx,"
1 Дк'.о)2
Sv2 S\2
Второй этап
(вычисление уравнений мио
жественной регрессии и ста"
тистнческая оценка
результатов)
У = "2 х2 + βί'χι +«о
21 х3 ~ Iс 32 х2 + А'зі Х1 + ''ЗО
A'u)Sx.j
s0'x2.\) SJ'X2 —
— К,', Syx, — A'2nSy
Sv:j x2.1 '-=Sv;i v2~
-K31 Sx3 x,-A'30Sx,
S.V, X0 . „
'4...= ", ' =K20-K2,.K10
bxo.i
Sx3 xi.o ,,"
- ---2-·- -Л31
Sx2, , - Sx?, 0 - (К,,)2 Sx2.,,
S.v'l.-Sxio-^a.fS.vr.o
S.v
1 .0
.. Sv3 x0 ,
'V in ^
S.v
- ^'.40 ~^3I' ^10
0. 1
Sv.<
2.1
S4.i
Svx. ,
S.v
SJj -.-, Sd2-(«2)?Sx?,
1 .2
11 " c,2
S-Vf .0 Sx2.1 Sx1.2
SJ'X0.12
Sx
---=«n~K,fw/,
0 ^20 "20
0.12
on - '-on
(><2оГ
.,. Sx, x
Sx2 ι Sxo.i2
K32-
i Λ 2 . 1
Sx2
2.1
... S.V., X, 2 ·. // ...
Л3 1- „ , K.)l *21 A32
Sxf.2
,„ SXg. X0 ,2 ., -/ ."
30-- -e„— --^30~Л20 л32
ΰχ0. 12
$*з\21==£х2л-(Кз'2)25х3 х2.,
Sx2.3 ~ Sv2.0 + (^2з)"5х2 Х3.0
^х2 Х3.0
где К23 =
$х3.о
Третий этап
(вычисление уравнений
множественной регрессии и
статистическая опенка
результатов)
У = а'з хз + а2 х2 +
+ α'," *ι + αό"
5yx3.2i=s);x3-
-K32Syx2-K3;Syx1
-K'30Sy
'_ ^Х3.21
flo =
Sv2
Sx2.31
«u2 —К32«з
Syx, ,, „ „. ...
«*?.23
Syx0.,23
S~x2"
S</2=Srfi-(a3")aSJc|.2,
r- 1 . (^'32)2 __»
с 22 _. - - -г . ... -
S.V2 ι й^3.21 *x2.13
r- r» . (^31? _ I_
cll --Lll 4- ,,"2 с„2
Sx3 2, Sx, 2;
23
'"\2
- = ίτ0 — ^зо аз
^оо -4)0 Ί"
(^зо)
ι0.123
Sx
Sx
2
3.2l ОЛ0.123
;!0 - = Л2(Х,)
(«-l)Sx2.0
(H-2)S.VT.0
("-2)S(.vg.,)
....^■> .»л2(к2·,)
(;i -2)Sx2 0
_.І(Аі) = Л2(К20)
(n-2)Sx2 ,
,._iib =л2(к;,)
(;l-2)Sxi 0
_sJuLl) = л2 (к30)
(n-ajsx2.,
(«-3)Sx2.i
(;i-?.)Sx2.2
Siio .2/ "\
(/;-S)Sx0 ,2
_.5іі_у =д2(/с32)
(n-3)Sx2,
_u'.-jl,_ = л2 (k;d
(n-?.) Sx2 2
(,i-3) S.v2 ,2
S^ ,2/ '"\
_J = A*( i73 )
(„_4)Sx221
SdL,_ = A2(.;")
(n -4)Sx231
Sd-3 =Δ2(«'Γ)
(n-4)Sx223
3 =A2("o)
(n-4)Sx2.I23
( «„)-
A2(y)
('<io)a _ (^>)2
A2(X,) "" A2(X,)
(^2)2
Α2(Λ,)
(^з)2
^(-V;i)
^2("Ί)
(«о)2
^2 («;,)
(«2?
(^2θ)2
^2 ^2П)
(к;;,)2
^з',)
(Кзо)2
(«2?_
л2КГ
(О2
^2(«;у
·ν·.ί2 (/ι - -1)
s.i27^7r
S(xl,)(" - ι)
s(xU(»~'-0
l — ^- (ух,)
1 — ;■- (л·., χ.)
S:/2 (/; — 2)
S.'/2 ;/i ■- :■!)
Sd'r, (n — 2j
s,2+'A"')2
ι -r\ , Pi.,)
-= l -^jvx, 2)
C,
:<»-3)
("o?
*3(«o)
(<2)2
a2(k3;)
(^зо)2
-^2 (^зо)
'(«3?
11 '
Sdj (n- I)
S'-, (,1 -'Λ)
5(χ2.2ΐ)(«-2)
! /?72(yx2x,)
--- -I -r2< x3x2.,)
(n 3)
5(хз.21)'."~'>
S (x2.0)("-3)
, 1-Λ'-(χ.(χ, χ,)
А2("з")
(«2?
Δ2(«Π
Λ2(α0'?
Scio(n—3) _, 2 ,,,.., ч
3J = ' — Γ3.21 (>λ3.2ΐ)
Sdl (η—A)
Sdj (n—3)
(«2'?
S</^ + 4-4.-, -
C22 j
1~'-2.3l(>'X2.3l)
(Π-4)
Sd? (n—3) , ·> / л
-4-W- = (- 4.23 (УХ1.23)
г.2^(й'Г)
sq +
(n-4)
Sd|(n—i) _ 2 f x .
= 1 — Κ123 (."■ X3 x: , Λ1 )
S^(«-4)

Система статистических характеристик и полиномы Чебышева 6У
Как видно из прилагаемой таблицы „Система
статистического исчисления в полиномах Чебышева" (стр. 68),
ортогональные полиномы Чебышева являются
непременными составными элементами всех основных статистических
характеристик.
В свете полиномов Чебышева очень удобно
представить всю систему статистического исчисления, как
отдельные этапы процесса элиминирования. Тогда на нулевом
этапе будем иметь систему средних арифметических,
средних квадратических и систему ошибок средних.
Характерно, что квадраты ошибок средних величин есть
отношение суммы квадратов первого полинома Чебышеза (3χ;..υ)
и суммы квадратов нулевого полинома (S*j;.0 = /i),
умноженной на число степеней свободы (п — 1).
Замечательно, что зависимая переменная в свете
полиномов Чебышева может рассматриваться как очередная
переменная, введенная в анализ в качестве некой новой
независимой переменной. При этом оказывается, что ква-
дратическое приближение по уравнению регрессии Sd-t, —
есть величина, вполне аналогичная сумме квадратов
соответствующего полинома Чебышева. Ошибки средней по у
поэтому также есть отношение суммы квадратов первого
долинома, но по зависимой переменной (Sdty к сумме
квадратов полинома нулевого порядка, умноженной на
я— 1, т. е. на число степеней свободы.
На первом этапе, состоящем в вычислении уравнения
прямолинейной регрессии, имеем коэфициенты регрессий,
как элиминационные средние типа'.
„ , ' ИЛИ ——5 ,
ол1-0 ол1.0
а квадратические приближения, как суммы квадратов
второго полинома Чебышева по очередной независимой
переменной (<Sa£j) или первого полинома по зависимой
переменной [Sd\^.
Ошибки коэфициентов прямолинейной и множественной
регрессии, так же, как и ошибки коэфициентов
последующих полиномов Чебышева, вычисляются аналогично
ошибкам средних. Так, ошибки коэфициентов полиномов
определяются как отношение суммы квадратов данного
полинома (для коэфициентов которого определяются ошибки)
к сумме квадратов предыдущего полинома, умноженного
на соответствующее число степеней свободы. При этом в
качестве предыдущих полиномов выбираются полиномы

7П Система статистического акытза а паланамах Че.бшие&а
для той- переменной, при которой стоит данный коэфи-
циент. Так, например, для коэфициента £,', ошибки
вычисляются как отношение:
Ολ,ι ι 4·91
• і-—5~; для &''►' как . г—=", а для К... как
(«-2)Sjcf.0 ■«* (я-;і)54і "
S'jt2
_ ύΛ3·21 _
Аналогичным образом вычисляются и ошибки коэфи-
циентов регрессии, только при этом для числителя сумма
квадратов берется но независимой неременной, т. е. Sa\y
Set* и т. д. (см. табл. на стр.69).
На нервом этапе появляются новые статистические
критерии \>. виде коэфициента корреляции и критерия
достоверности Фишера. Критерии достоверности Фишера
могут быть представлены как отношение квадратов коэфи-
циентов уравнения регрессии к квадрату ошибок каждого
из этих коэфициентов, как это показано в таблице на
стр. 65 и 69.
Коэфициенты линейной корреляции также могут быть
представлены как отношение средних квадратов первого
и нулевого полиномов, определенных для зависимых
переменных (у). При определении средних квадратов, суммы
квадратов делятся нп соответствующее число степеней
свободы. При этом необходимо помнить, что остаточные
суммы квадратов по уравнению регрессии имеют степень
свободы на единицу меньше, чем суммы квадратов,
аналогичных полиномов, так как порядок элиминирования для
уравнения регрессии на единицу выше, чем аналогичных
полиномов. Отношения средних квадратов, однако,
характеризуют не сами коэфициенты корреляции, а выражения
типа: 1 —г- (ул,.21).
Современные английские статистики специально
рассматривают величины такого типа, присваивая им
название „коэфициентов остаточной корреляции", или иначе,
the coefficient of поп determination. Такого рода величины
находим у Келли (13), Эзекиель (14), Девентропа и Экоса
(16).
Па втором, третьем и последующих этапах при
вычислении уравнений множественной регрессии и
статистической оценки полученных коэфициентов в качестве
новых статистических критериев появляются коэфициенты
частичной, частной и множественной корреляции.

Статистическая, оценка коэфицаентов уравнения регрессии 71
Коэфициенты множественной корреляции, при этом,
определяются как отношение среднего квадрата полинома
Чебышева данного порядка к среднему квадрату полинома
нулевого порядка. При этом полиномы должны быть взяты
по зависимой переменной, например'.
_Sd\{n-l)
l~R» S4(n-3)·
Коэфициенты частной корреляции определяются как
отношение средних квадратов данного полинома к
среднему квадрату предыдущего полинома например:
_ Sdj(n~3)
;i·21 S4(n—ij'
Если вычисляются частные коэфициенты корреляции
для переменных хк, то следует отметить, что при этом
берутся смежные полиномы системы „А/" для х-л, л-3, xlt в
зависимости от того, по какой из них вычисляется
частный коэфициент корреляции. Поэтому сумма квадратов
предыдущего полинома в этом случае определяется для
каждой переменной как выражение:
^'■*%.я ' " —Sj%-v τ· е· аналогично: Sd* + ѵ -?-/- == Sd'im
Характерно, что полиномы Чебышева и в случае
частной корреляции прямым образом определяют
коэфициенты остаточной корреляции, т. е. выражения типа:
1 — г2(ух3.21). Таким образом коэфициенты остаточной
корреляции, несомненно, являются основными величинами в
корреляционном анализе, что видно из простого
соотношения, которое существует между коэфициентами
множественной корреляции и коэфициентами частной
корреляции:
1 -Л*я= [1 - ^(^i-o)J ■ Π - '•'(ЗИ'мИ1 - 'в(У*..а)1-
Коэфициенты частичной (part,) корреляции, введенные
Эзекиелем (14) и относящиеся к так называемым чистым
линиям регрессии, также являются отношениями средних
квадратов двух смежных полиномов Чебышева. При этом
остаточная сумма квадратов для предыдущего полинома
определяется по чистой линии регрессии, т. е., по
уравнению множественной регрессии, где значения некоторого

72 Система статистического анализа и полиномы Чебышева
хк приняты равными его средней величине (*,,). Так,
например, пусть имеем уравнение множественной регрессии:
Ут^ао' + αϊ'χι + а2хг + °з"Ла·
Заменяя значения хг на их средние значения, имеем
уравнение чистой линии регрессии:
Β связи с этим переходом остаточная сумма квадратов
по уравнению J13.2 увеличивается на сумму (#2" )2 ·£*|·ο> τ· е·
будет равна: S(J.<) = Sd> +(u^ySx^.
Коэфициент же частичной (part) корреляции будет равен:
(<')^4.р
* 13 Saj+(a^Js4.o
Таким образом имеем:
Наконец, как уже было указано в начале работы,
полиномы Чебышева позволяют уяснить природу коэфициен-
тов множественной реірессии, которые являются
величинами, куда входят полиномы Чебышева с измененной
последовательностью переменных. Так, например, младшие
коэфициенты уравнения регрессии определяются по
формулам типа:
flVf = 2"——я/ - kj> aj" (см. „Систему статистиче-
ского исчисления в полиномах Чебышева" стр. 69).
По формулам такого же рода получаются не только
младшие коэфициенты уравнения регрессии, но и младшие
коэфициенты полиномов Чебышева, как системы „k", так
и системы „с*.
Внимательное рассмотрение „Системы статистического
исчисления в полиномах Чебышева", таким образом,
показывает, что статистическое исчисление в полиномах
Чебышева выражается в виде простой стройной и удобной
системы вычислений основных характеристик,
используемых в математической статистике.

ГЛАВА 4
ОБОБЩЕННЫЕ ПОЛИНОМЫ ЧЕБЫШЕВА
И СТАТИСТИЧЕСКОЕ ИСЧИСЛЕНИЕ
§ 1. Метод Чебьипева н свойства его иолннояои
В своих математических работах П. Л. Чебышев
создал общий метсд разложения различного рода функции к
ряды при помощи непрерывных дробей. Им показано
применение этого метода для целого ряда функций.
При решении задачи разложения данной функции в рял
он ставит одно общее условие, чтобы разность между
искомой функцией и ее разложением в ряд наименее
отличалась от некоторой функции ѵ. Характерно, что
П. Л. Чебышев не ставил условия, чтобы эта разность
стремилась к нулю, а удовлетворялся условием, чтобы
она наименее отличалась от функции ѵ, являющейся
функцией остаточных отклонений. Такое условие вполне
отвечает природе статистической науки, имеющей, как-
известно, дело с величинами, вариация которых всегда
отлична от нуля.
При решении задачи разложения функции в ряд при
помощи непрерывных дробей, П. Л. Чебышев (16)
рассуждает следующем образом: пусть F(у) — точное значение
функции, которая разлагается в непрерывную дробь, и пусть
■у—некоторое выражение, полученное при рэзложениѵ.
этих функций. Причем χ и у — полиномы, при которых
выражение F(y) —— наименее разнится от некоторой
функции ѵ. Чебышев рассматривал разность/7^—у,
собственно, имея дело с числителем этого выражения, ставя
условие, чтобы функция xF(y) — y в наибольшей сте-

74 Обобщенные полиномы Чебышева и статистическое исчисление
пени выражала некую функцию ѵ, иначе говоря, он ставит
условие, чтобы разность xF(y)—y —· ν наивозможно ближе
приближалась к нулю. При решении этой задачи он и
получает свои полиномы, связанные с сопровождающим их
зесом Ѳ2(х), зависящим от вида интерполируемой
функции. Чебышев показал, что для вычисления его
полиномов, связанных с данным весом в'г(х), достаточно искомую
функцию разложить путем последовательных делений в
непрерывную дробь таким образом, чтобы разность между
г (х) и от-нои подходящей дрооыо была порядка —t)fft_1 ■■.
Тогда знаменатели подходящих дробей будут отличаться
от полинома Чебышева только постоянным множителем.
Нел» знаменатель подходящих дробей разделить на этот
множитель, т. е их пронормировать, то будем иметь
полиномы Чебышева.
Пусть, например, имеем некоторую функцию F(y),
тогда путем последовательных делений получаем
следующую непрерывную дробь:
у -!- !jt — α2
у 4- fa - 4
,v+"«- -'Li
ν -- рл — an
",Ρ,-ιΟΟ
' f.Cv)
Если на основе этой непрерывной дроби составить
подходящие дроби-к'", то будем иметь в качестве числителя
(Ат) подходящей дроби выражения тина S\yWm(x)], т. е.
суммы произведений данной функции на соответствующий
иолином Чебышева. Знаменатель же (#„,) подходящей
дроби будет равен ^[^"^(х)], т. е. сумме квадратов данного
полинома Чебышева.
П. Л. Чебышев показал, что его полиномы обладают
рядом замечательных свойств, а именно:
1) нулевой полином всегда равен единице, т. е. Ч''п(х)=1;
2) полиномы обладают свойством ортогональности, а
именно: 5 [ЧГЖ (χ) Ψ, (*)] =.- 0, при т φ k, б) S[·Γ*(х)\ = В\,
3) смежные полиномы связаны единой рекуррентной
формулой:

Классификация полиномов Чебышева 7.7
4) полиномы обеспечивают квадратические приближения
к искомой функции на основе единого интерполяционного
рада Чебышева (при θ3 (χ) — 1):
У 8[ΨΙ(Χ)\ ΜΑ) · 8\Ψ>(Χ)\ ''W ■-
Такое приближение, как отмечает П. Л. Чебышев в
споем письме к проф. Н. Д. Брашману (17), составляет
необходимое и достаточное условие, чтобы полином Ψ(χ)
приводил суммы S[y — F(x)]2 и S[x—xV(x)Y к минимуму.
Полиномы Чебышева связывают теорию непрерывных
дробей с теорией квадратических приближений. Кроме того,
формулы для нахождения полиномов Ч;(х) являются
одновременно формулами для интерполирования по способу
наименьших квадратов.
В зависимости от вида функции F(y) Чебышев получал
различного рода ортогональные полиномы, связанные с
соответствующим весом Ѳ2(л;). Так как все они полностью
удовлетворяют четырем, формулированным выше условиям,
то они могут быть отнесены к одному классу полиномов,
который мы называем семейством полиномов Чебышева.
В зависимости от вида функции F(y) и, следовательно,
вида выражения В2(х), характеризующего вес полинома,
получаем полиномы различного рода как для линейных
функций многих неременных, так и для показательных,
тригонометрических, гипергеометрических и т. д. функций.
Все эти полиномы составляют одно семейство полиномов
Чебышева, удовлетворяя четырем вышеформулированным
условиям.
§ 2. Классификация полиномов Чебышева,.
П. Л. Чебышев впервые изложил свой оригинальный
метод наилучшего приближения функций в работе: „О
непрерывных дробях", относящейся к 1855 году.
В этой работе им дана общая формула
интерполяционного ряда (см. стр. 7 настоящей работы) в полиномах
Чебышева, члены которого составляются в виде суммы вы
ражений типа:
sm(x)-4^(x) 'λ

76 Обобщенные полиномы Чебышева и статистическое исчисление
Характерно, что в формуле для интерполяционного
ряда Чебышева вес входит в числитель и в знаменатель
коэфициентов. Особенно важен тот факт, что идея
Чебышева о весе, сопровождающем
ортогональные полиномы, открывает очень
широкие возможности для применения метода
наименьших квадратов к сложным
нелинейным функциям.
Идея Чебышева о весе, сопровождающем полиномы в
случае разложения в ряд сложных функций, дает
теоретическое обоснование для распространения метода
наименьших квадратов и на этот род функций.
β интерполяционной формуле Чебышева особое
значение имеют суммы квадратов полиномов Чебышева
5Ѳг(х) Ψ^ζχΥ являющиеся знаменателями как
коэфициентов интерполяционного ряда Чебышева, так и знаменате-.
лями коэфициентов самих полиномов Чебышева.
В этой же работе Чебышев впервые указал
рекуррентные соотношения, связывающие его полиномы. Исходя из.
общего правила составления подходящих дробей, он дал
(т. 1, стр. 216) для своих полиномов рекуррентную
формулу:
"'ЖИ= ^+і 4х) + ІГі-і(х) -- (Αι+ιχ+Βι»)4χ)+ Ψ>- ι (*)■
Исследование П. Л. Чебышева о непрерывных дробях
таким образом, закладывает основы его теории
приближенного представления функции, удовлетворяющего условиям,
метода наименьших квадратов.
В дальнейшем, делая различные частные
предположения о совокупности известных значений искомой функции.
II. Л. Чебышев получает различные ряды. Полиномы,
входящие в эти ряды, образуют семейство полиномов
Чебышева, удовлетворяющее четырем условиям, указанным
выше. Однако, сами полиномы Чебышева могут принимать
самый разнообразный вид в зависимости от вида искомой
функции.
В зависимости от вида искомой функции,
удовлетворяющей совокупность известных ее значений, получаются
различные полиномы, сопровождаемые различным весом
Ѳ2(х). При этом, в зависимости от вида искомой функции,
оказываются различными:
1) веса Ѳ2(х);
2) основная область суммирования;
3) значения сумм квадратов полиномов;

КЛАССИФИКАЦИЯ ПОЛИНОМОВ ЧЕБЫШЕВА
Функции Название полиномов
ι
Символ
полинома
Обобщенная
форма
I
Обобщенная система
полиномов Чебышева (1855 г.)
Фі(Х)
Вес,
сопутствующий полиному
Область

суммирования
Суммы квадратов полиномов
Коэфициенты
интерполяционного ряда
Рекуррентные формулы
Ѳ2
(X) : - со, + со
J [ ψ2(χ) Θ2 (χ) dx]
—■Χι
4 "О
| [Р(х)ф,(х)Ѳ2(х)<іх]
— со
|[ψ2(Χ)<)2(χ)<ϊχ]
*ι
«ίΨϊ(Χ) = ?ίΨί-1 (χ)-'(-1 Ψί_2 (χ)
Линейные
функции
многих
переменных
Чебышевские полиномы
множественной регрессии
ΝΗ(Χ)
где:
а) ί=/(123.../— 1)
б) і<і—1
Параболы
/—порядка
Полиномы
параболического
интерполирования
Чебышева
?і(х)

Показательные
Чебышева — Эрмита
(1859 г.) (1864 г.)
Чебышева — Лагерра
(1859 г.) (1879 г.)
Обобщенные Лагерра
Н,(х)
Ц(Х)
<?](Х)

Тригонометрические
Тригонометрические
полиномы Чебышева (1853 г.)
а) первого рода (косинусы
кратных дуг)
б) второго рода (синусы
кратных дуг)
Т,(х)
U,(x)
Гипергеоме-
трические
Лежянлра (1785 г.)
Якоби (1859 г.)
Р,(х)
J?,?(x>
Θ2(χ) = 1 I (
J ; SNji(x)^SN°J(i_l)(x)-kli-SxlNli(x)
Θ2(χ)=/ -co,+co,
(целые
положительные числа)
где: [ι—1]=(ί—1)(Ι23...ί—2)
SyNu(x) _
SNfox)
= <Чі ι Nli=-KuNi(x)+Nl(i_li(x)
Ѳ2
(X) = l
— CO, +CO
S-ff (x)=Sx'+' ?/_, (χί-β,δχ'φ,.,-β^ψ,
_Sf?-l (*) . ρ _ SX1 φ,_ι Χ _u'-|f,.1(l)
~δψ?_2(χ) ' ' S-ff_i(x) 5ψ2_2(χ)
S?2 (x)
a,
?I (x)=(X—?,) -f,_! (Χ)—α,ψ,_2 (Χ)
где βί=τι,ι-ι —ті_і,і-2
e2(x)=^/"|<!-fc3C*
Ѳа (χ)»**""*
θ2 (χ)=χ* ех
■ со, +со
О, со
О, со
+х>
Ι Θ2 (х) Н2(х) <іх=/! (2ft)
J02(x)L2(x)tfx=(/2)l
f θ2 (χ) [?ί (χ)]2 </χ=ί! Γ (S+1 + l)
ο
J уѲ2(х)Я{(х)<іх
—Οΰ .
Π (2ft)1
J уѲ2(х)Х-г(х)(іх
_o
(*2)!
J уѲ2 (χ) tf (x)
_0
11Г (S+l+l)
">l
= als
@2 _ 1
/l-x2
ft2 (x)^const
—l.+l
или (0, π)
-1, +1
ИЛИ (0, π)
+ 1
ί W(x)Tf(x)dx-
41
J θ2 (χ) ί;2(χ) dx =
-ι
? 2 Ί *
[ cos Ιφάφ\ = ν,'
b J
J sin2 / д5й0
о
2+1
-ι
2+1
^- I ye2(x)Tl(x)dx=Al
$yQ2(x)Ul(x)dx=Bl
Нг(х)=-2/схЯ/_](х)-
-2&(ί-1)Η:_2(χ)
L, (x) = -(ftx—2i+l) Lt-i(x) -
-(i-l)aLz_2
?!(χ)=?Γι(χ)+'τ!-ι(*)
T^x^/r^W-T^x)
Ul(x)=2lUl_l(x)-Ul_2(x)
И<Ѵ
:(1-.Χ)α(1+Χ)1
— Ι,+l
-I, -И
V 2 2
JP2(x)dx=27TT
— 1
-1
ie2(x)[j[xf)]2dx=
-1
23+ί>+1Γ(α+7 + 1)Γ(β+7+1)
(α+$+21 + 1)Γ(1 + 1)Γ(*+? + 1+1)
(1=0, 1,2...)
2ί + 1 "t1
-4- |ур((х)сгх=а!
" -1
)ly&2(x)J{?$dx
-1
+/е2(х)[^)]^х
- 1
at
(l+l)Pl+i (x)=(2i+l)xP,(x)-
--''i-iW
1
(2Ι+β+ρ+»)[(2ί+«+Ρ)·
(2ί+α+?+2) Х+(а'-?а)] Л(І)Р) -
- (I +«) С+?) (2ί+α+β+2) /,!:^ (Χ)

Классификация полиномов Чебышева 77
4) старшие коэфициенты полиномов;
5) коэфициенты интерполяционного ряда Чебышева;
6) значения коэфициентов γ„„ аг и β, рекуррентного
соотношения.
В скеме „Классификация полиномов Чебышева" (стр. 76)
приведены значения всех этих величин для различных
полиномов Чебышева. В таблице „Значения первых пяти
полиномов некоторых функций" (стр. 79) даны
алгебраические уравнения, определяющие эти полиномы.
Сам Чебышев неоднократно указывал, что известный
ряд Лежандра есть частный случай его ряда. Ряд Лежан-
дра получается, если разлагать в непрерывную дробь
Ѳ2 (χ)
выражение Ѣ^—, где Ѳ-(х)~х2 — лг = const, а значения
χ даны бесконечно близкими и равноотстоящими,
изменяющимися от Xj — — 1 до х„= + I. В результате
разложения такого выражения в непрерывную дробь
знаменатели подходящих дробей будут представлять собой
полиномы Лежандра.
В более ранней работе: „Об одном новом ряде" П. Л.
Чебышев, рассматривая ряд конечных разностей
указывает, что в случае, когда разность ряда h=-~ и η
бесконечно велико, ряд Чебышева сводится к ряду,
расположенному по полиномам Лежандра. Если же А=-^- и га
бесконечно велико, то этот ряд сводится к ряду Макло-
рена.
Если предположить, что известные значения искомой
функции даны равноотстоящими и бесконечно близкими
между собой, изменяющимися в пределах от —1 до +1,
то, разлагая выражение Σ—\~, где Ѳ-(х)= ' -, в
■* ■** у 1—xfi
непрерывную дробь, получим знаменатели подходящих
дробей, которые соответствуют разложению Фурье по
косинусам кратных дуг costs, cos2-f, cos За, где (s=arc cos x,
т. е. но неполным тригонометрическим полиномам.
В математической литературе широко известны эти
тригонометрические полиномы благодаря работам акад.
С. Н. Бернштейн. Тригонометрические полиномы Чебышева
имеют большое значение в статистике, составляя основу
для метода периодограмм и гармонического анализа
временных рядов.
Тригонометрические полиномы Чебышева первого и
второго рода являются неполными тригонометрическими

78 Обобщенные полиномы Чебышева и статистическое исчисление
полиномами. Ряд Фурье есть сумма неполных
тригонометрических полиномов. Приближение, получаемое с помощью
полиномов Т(х), учитывает в большей степени значение
приближаемой функции F(x) у конца отрезка (—1, +1).
Приближение, получаемое с помощью полиномов второго
рода Ut(x), учитывает в большей степени значение этой
функции в средине отрезка (—1, +1)- Ряд Фурье, являясь
суммой этих полиномов, поэтому дает лучшее
приближение.
В своей изумительной работе: „О разложении функции
одной переменной" (т. 1, стр. 501-508, 1859 г.) Чебышев
рассматривает:
а) различные значения переменной х, изменяющиеся от
— ου до 4- оъ и имеющей вероятность
б) значения переменной х, заключающейся между О и-f- ■·.
при законе их вероятностей Ле~*Л .
Исходя из этих предположений, он находит свои
полиномы, которые получили в математике название:
а) полиномы Эрмита;
б) полиномы Лагерра.
Полиномы Эрмита и Лагерра, собственно, частный
случай полиномов Чебышева, когда k = (—!)' или k—1. Эрмит
получил свои полиномы в 1864 году, (18) а Лаггер —
в 1879 году, (19) в то время как Чебышев дал их в более
общем виде в 1859 году. Полиномы Эрмита связаны с
обобщенными полиномами Лагерра следующими
соотношениями:
#„(*)-(- 1/ 2* φ/-'^(^) И
Яй..,(л:) = (-1У 2-*-*'ti-rJ(x*).
Обобщенные полиномы Лагерра очень схожи с гииер-
геометрическими рядами.
Полиномы Эрмита, если k~-co, дают ряд Маклорена.
Полиномы Эрмита и Лагерра имеют существенное
значение в статистике, являясь основой для обобщенного
закона распределения вероятностей и распределения
статистических численностей.
При обработке данных о распределении редких событий
в статистике приходится иметь дело с распределением
Пуассона и полиномами G. Эти полиномы являются
дальнейшим обобщением полиномов Лагерра.
|/т-«*

Классификация полиномов Чебышева ?%
Значение первых пяти полиномов некоторых функций
I. Показательные функции
1. Полиномы Чебышева-Эрми-
та функции e~kx'
Hl(x)=>-'2kxHl_.i{x)-Jl{l-l)M1^
Я„(*) = 1
Ηλ(χ) = — 2kxli^x) = — Ikx
Щ.ѵ) = - 2kxHl(x) — 2Ш0(л-) =
= 4*2*2 - 2k
Я3(л-) = -2Α·*/7,(α)-2·2· Ш,(*)=
= —ЬАз**>+12А2*
Ht(x) = 16А*д* — 48йЗл-2 -ι- 12*2
Нъ(х) = -32А5*5+160А**3—ША»*
Полиномы Эрмита есть
частный случай полиномов
Чебышева. когда А = (—1/.
2. Поликомы Чебышева-Лагар-
ра фунщии e~kx
Ц{х) = -(kx-2l + l)Lul (x) -
-(/-1)2£,_2(х)
І!(л;)= _ (kx - 1) і0(д}= -Α-α+1
Ι2(*)= - (kx-З) Ц (χ) - Ц (χ) =
= №x2 — 4kx+2
Ц{х)= - (kx-5) L2 (x) -4іі(а-)=
A»** -t- 9А-2да — 18 Ад: -|- б
Ζ.4(α)= А*д* — lPAW + 72Α2λ^ —
— 96Α*+24
/.5α-)= — А>Б*5+ 25Α***- 200ΑϋΛ·»_ι.
+ 60 jА2д2 _ 600Ад -ι- 120
Полиномы Лагерра есть
частный слу іаи полиномов Чебышева,
когда А= 1.
3.
G(х) функции
= ?(*)
Полиномы
х\
Ol+l (x)=01(x)-Gl(x)+DGl(x)
где DGi(x) есть производная от
Gj(*) по от и где χ принимает
лишь значения 0, 1, 2
Ge(*) = l
G2 (д) = Gi(*) Оі(дс) 4- DGj(*) -
2! ( х{х~ 1) /я _* л»2
от2 L
G* (χ) = Gj(x) G2(*) + DG2{x) =
_·*\| ■*(*— *) lx~2)_ m ХІХ~Ц
~~тЦ_ 31 ~" 1 2!
+ 2! Τ _ 31 J
r ( \ 4!ГА(д-I)(л--2) (*~3)
m x(x~l) (χ—2)
~ Τ 3!
яіз χ (χ—1)
/η>·* ж·*
2! 3!ll 4! |
δ1 ' ms[ 5!
m *-(д—!)(*—2)(д—3)
~ 1 ' 4! +
та-д(д-I)
3! 2!
СТ2*(*— !)(*—2)
2! 3!
от4· л'
4! ϋ"
Сумм;і квадратов полиномов Gj(.v)
равна:
S?(*)G?(*) = 4
2!
1 1
II. Тригонометрические функции
4. Полиномы Чесышева 1 рода
(синусы кратных дуг)
У"((а)=2а7 ι_λ(χ) 7;_2(*),где *=cos<*
Cos ΖΘ = 2cos «cos (/-1) θ -cos (1-2) β
7'ο(*) = 1
7! (д) = cos arc cos* = χ
73 (д) = cos 2 arc co<x = 2*2—-ί
Уз (χ) = cos 3:ггс cos χ = 4*3—3*
7'4 (д) = cos 4йгс cos χ = 8д*— 8*'<+ 1
7 5 (д) ==cos5'j:rc Cosa=16*5—20*3+5.ϊγ
5. Полиномы Чебышева 2 рода
(синусы кратных дуг)
Ul+l (*) = 2*ί/,(*)- ί/,_ι (χ). где
S;u(/ -j- 1) arc cos*
[/,(*) = 2*
ί/2(*) = 4*2-1
(7.,(а-) = 8дЗ — 4д
СД (а) = Ida* — 12*+I.
t/r, (χ) = 32*5 — 32дЗ + 6л-

>>'.') Обобщенные полиномы Чебышева и статистическое исчисление
т е
Полиномы G связаны с функцией .__.._ В математиче-
скую статистику эти полиномы введены Жорданом (20) и
Романовским (21). Более подробно о применении полиномов
:-}рмита и полиномов G в математической статистике см.
$ 6". „Распределение Пуассона и полиномы Чебышева".
Чебышев определил полиномы также для случая
параболического интерполирования. В его работе „Об интер-
•лолировании по способу наименьших квадратов" (т. 1,
стр. 473—498, 1859 г.) дан числовой пример
параболического интерполирования и даны:
а) рекуррентное соотношение, связывающее при
параболическом интерполировании смежные полиномы;
б) формула для определения сумм квадратов этих
полиномов;
в) формула дли определения коэфициентов
интерполяционного ряда.
Все эти формулы даны нами в схеме. „Классификация
полиномов Чебышева"
Чебышев определил значения сумм квадратов
полиномов для всех рассматриваемых нами полиномов, кроме
полиномов функций многих переменных и обобщенных
полиномов Лагерра. В таблице: „Классификация полиномов
Чебышева" нами даны все рекуррентные формулы и все
величины для сумм квадратов полиномов.
Как видим, полиномы Чебышева являются широким
обобщением, дающим новый оригинальный метод
приближенного представления функций самого разнообразного
вида.
§ 3. 'Рекуррентные формулы.
Для теории полиномов Чебышева имеет большое
значение закон образования коэфициентов рекуррентной
формулы, который он впервые формулировал в статье „О
непрерывных дробях".
Основная, наиболее общая рекуррентная формула,
связывающая смежные полиномы Чебышева, имеет
следующий вид:
ад=(ъ*;-Рі)χιΊ-ι(χ) -α/1Γ/-2(4
Для отдельных функций некоторые коэфициенты
рекуррентной формулы могут быть равны нулю или едини-

Рекуррентные формулы
SI
цс. Особенно часто равен нулю коэфициент β„ а
единице — коэфициент γ£.
Коэфициенты рекуррентного соотношения подчинены
определенному закону их образования. При этом
приходится различать нормированные и ненормированные
полиномы Чебышева. Нормированными называются полиномы,
у которых все коэфициенты разделены на коэфициент
ііри переменной χ наиболее высокой степени (для
уравнений множественной регрессии при независимой
переменной, введенной в анализ последней).
Таким образом в нормированных полиномах коэфициент
при старшей переменной равен единице.
Закон образования коэфициентов заключается в том,
что:
а) коэфициент ссг есть отношение сумм квадратов двух
смежных нормированных полиномов;
б) коэфициент γ, есть отношение старших
коэфициентов смежных ненормированных полиномов Чебышева;
в) коэфициенты β2 есть разность старших
коэфициентов двух смежных нормированных полиномов.
Все полиномы, приведенные нами в таблице
„Классификация полиномов Чебышева", удовлетворяют этим
условиям. Между прочим, для случая параболического
интерполирования Чебышев показал в статье „Об
интерполировании по способу наименьших квадратов" (т. 1, стр. 491),
что коэфициент £, (при γζ= 1) определяется как разность
старших коэфициентов двух смежных предыдущих
полиномов, а именно:
Sx2Vt(x) Sx^x)
β.,— - — I... — / ,.., аналогично:
Pi S*\{x) S*0{x) A W
&t = Tn—Tu, Ъ—Та—Тп и т. д.
Как известно, Чебышев не определил полиномы для
функций многих переменных. Так как такого рода
полиномы являются основными в математической статистике,
то приведем рекуррентные соотношения для полиномов
множественной регрессии. Напишем систему полиномов
N я Τ (для случая х2):
6 Нолшіохіі Чебышева

82 Обобщенные полиномы Чебышееа и статистическое исчисление
Система N
*з
χζ·ο~ хз го ■"•о.о
^з-иР" хзГ~ ^зі хі-о~ ^зо -^о-о
ΧΖ.2\0~ΧΖ~~ ^32Χ2Λ~ 7*31ΛΊ·0~
— ^зо^о-о
Система 7"
•^о-о—1
ΑΊ·ο== х\~ ^іо-^о-о
Х2Л~ Х2 ~21 Х\-й~ ^20 х0-й
А'з-2і— хг ^32 χ2·\ ' зі хі
~ ^30 А0-0
Отсюда имеем рекуррентные соотношения:
■^з-о ^ ^зо-^о-о"'-^
хз-іо= ~ ^зі-^ьо+^з.о
"3-210
^ 32Х2-1~^~Х3-Ѵ
Введем новые обозначения для полиномов системы Ν:
Система N
Система 7'
*з-о ■
■ Ми где / = 3, і = 0
-^з-іо— Nu гДе ' = 3< і=Ю
х3-210=Лгг,· где ί = 3, ί = 21()
*ο·ο
Χ1-0~Ν' ГДС '=г"-·1·»
= Л/< где / = 2.10
^2-10-
Таким образом і^.1—1 и символ г обозначает
комбинацию элиминированных переменных: і = 0, і=Ь0, t = 2-1
и вообще г = (/—1). [0.12 (/—2)1. Кроме того,
г — 1 == (£ — 1). [0-12 (/—2)].
Заметим, что порядок чисел после точки не имеет
значения. Тсгда вышеуказанные рекуррентные
соотношения могут быть записаны в общем виде:
ибо старшие коэфициенты Th=kti, как известно, равны друг
другу.
Таким образом, в случае многих переменных имеем
рекуррентную формулу, где:
а) полином системы N данного порядка равен разности
двух полиномов предыдущего порядка, из них первый (со
знаком минус) системы Т, а второй (со знаком плюс)
системы N;

Рекуррентные формулы 83
б) коэфициент при первом полиноме равен старшему
коэфициенту полинома для последнего (при данном числе
переменных) этапа элиминирования;
в) при втором полиноме коэфициент равен единице,
т. к. для данного числа переменных отношение сумм
квадратов последних полиномов высшего порядка, взятых
яз системы N и Τ равно единице. Как известно, для
данного числа переменных, последние полиномы системы
N и Τ равны друг другу.
Как видим, и в случае многих переменных рекуррентные
соотношения полиномов соответствуют общей
рекуррентной формуле, выведенной Чебышевым из свойств
подходящих дробей.
Старшие коэфициенты полиномов Чебышева для
функций многих неременных могут быть определены
различным способом. В предыдущем изложении мы их опреде-
SxfY^Jx)
ляли как отношение —-. Однако, если умножить
рекуррентные соотношения для полиномов системы N на
значения старшей переменной, а затем суммировать, то
будем иметь".
5Ко) = -Ѵ(*Л-о)+ ·*(*£)
ад.о=-ѵ(^л.о) + 5к^
ад.«)=-зд*л.і)+5ко
Отсюда:
КЛ2 32—
ΚΆ1 ■* 31
5 ( хз хіл )
^ V, -^З-О ) ^ ( ΧΆ·\ ).
S ( *3·*ι.ο)
ύ {хз χο·ο;
Так как коэфициент T.,„ = k^n, то отсюда имеем
общем виде:
£да(^(*)]-**Ц«) ,к
S ( xtNt )

84 Обобщенные полиномы Чебышева и статистическое исчисление
В этом случае суммы произведений 5 [xt Ν((χ)]
должны определятся, исходя из формулы, в которую входят
суммы системы нормальных уравнений и коэфициенты
полиномов предыдущего порядка системы „7"".
Если умножить обе части последней формулы на
значения старшего коэфициента, определяемого обычным
S ( дг3 х.2, )
способом, то-есть например, на —^— '-, то будем иметь
5(4і)
новую формулу для вычисления старшего коэфициента
полиномов множественной регрессии:
S(^, )-S ( х\ ,, )
или в общем виде:
г/.а у. *Кі-.(*)НКЛ*)1
Следовательно, старший коэфициент может быть
определен через соотношения сумм квадратов полиномов Че-
бышева. Однако, эта последняя формула не имеет
самостоятельного значения и удобна лишь для контрольной
проверки правяльности вычислений. Для полиномов
различных функций рекуррентные формулы даны в таблице на
стр. 77.
В работах П. Л. Чебышева находим рекуррентные
формулы для всех полиномов семейства Чебышева, кроме
полиномов функций многих неременных и обобщенных
полиномов Лагерра.
§ 4. Полиномы для функций с равноотстоящими
значениями.
Интерполированию величин равноотстоящих П. Л. Че-
бышев посвятил много работ, к которым относятся:
1. „Об одном новом ряде", 1858 г. (т. 1, стр. 381—384);
2. „Об интерполировании в случае большого числа
данных доставляемых наблюдением", 1858 г. (т. 1, стр. 387—469);
3. „Об интерполировании", 1864 г. (т. 1 стр. 514—560);
4. „Об интерполировании величин равноотстоящих",
1875 г. (т. II, стр. 219-242);
5. „О функциях, подобных функциям Лежандра", 1869 г.,
(т. II, стр. 61-68).

Полиномы для функций е равноотстоящими значениями So
При интерполировании равноотстоящих величин
П. Л. Чебышев вводит новую переменную:
В этом случае он получает свои полиномы, связанные
сіедующей рекуррентной формулой:
Ψ,(ζ) -= 2(2/ - 1)ζΨ,_, (ζ) - (/ - I)2 [/г3- [I - 1)3J Ч',_і (г>
Здесь /г — число членов ряда, а .ѵ,—a'j есть разность
членов ряда.
В статистической практике обычно эта разность равна
единице. В этом последнем случае, следовательно,
приходится иметь дело с натуральным рядом чисел: 1, 2,
З-.../ί. Тогда вспомогательная неременная упрощается и
оказывается равной:
пли
Ч\=х—-(?.~У-., если η -0, 1, 2, 3..
Для этого частного случая интерполирования
равноотстоящих величин легко получить таблицы,
определяющие числовое значение как полиномов Чебышева, так и
сумм их квадратов. Впервые эти таблицы были вычислены
в отделе научной методологии Центрального
Статистического Управления СССР и опубликованы в 1925 году (22).
Эти таблицы под названием: „Числа Чебышева"
перепечатаны в работе проф. А. К. Митропольского (23)
„Техника статистического исчисления" (М., 1931 г., стр. 598—
601).
В этих таблицах даны целые значения полиномов
Чебышева, для чего соответствующие значения полиномов
Чебышева умножены на коэфициенты ct, при помощи
которых осуществлен переход от дробных к целым числам.
При интерполировании равноотстоящих значении могут
быть использованы как ненормированные, так и
нормированные полиномы Чебышева. В последнем случае все
коэфициенты полинома разделены на коэфициент, стоящий
при старшей переменной.

86 Обобщенные полиномы Чебышепа а статистическое исчисление
Частные значения первых пяти полиномов Чебышева
для случая ненормированных полиномов таковы:
. ju+L
/„(*)-1
/,(г)-іѵ-и-1-2г
/s(z)=.-3(2*)2-/r+l
f,(z)^-15 (2г)г-3(3/і8- 7) 2г
/4 (г) = 105 (2г)4 - 30 (3«2- 13) (2zf + 9 (тіг- 1) (л=- 9)
/і (г) ----- 945 (2zf - 1050 (я1— 7) (2г)» +
-- 15(15я4-230л2+407)2г.
Эти полиномы связаны следующей рекуррентной
формулой:
/і+1 (г)-(2/+ 1)2гШ-Р(п*~ /2)/,_,ύ).
Старшие коэфициенты этих полиномов определяются
но формуле: γ,= (2/4-1)! В частности, при / = 5 имеем
ѵ.=3. 5. 7. 9 = 945. Легко видеть, что коэфициент в
рекуррентной формуле при 2zf((z) равен отношению старших
коэфишіентов двух смежных полиномов.
Что касается коэфициента рекуррентной формулы при
ft-ι (z)> то он равен отношению сумм квадратов двух
смежных полиномов, так как суммы квадратов этих
полиномов определяются по формуле:
с f> Г~ч._ (/!)-'η («·--!) (яа-23)....(яэ-/а)
■JJtKr) - ^7+1
Частные значения первых пяти нормированных
полиномов Чебышева для равноотстоящих величин таковы:
чг,(*Ь
ч\СФ=
i-,W-
-1
п+ 1
2
12
ψ,(χ)~^(χ)-*£=-7. Ψ,(χ)

Полакоми для функций с равноотстоящими значениями 87
Ψ4 (χ) = Ψ* (χ) - ± (3л« _ із) ψ* (χ) +
, 3(η2 —1) (η? — 9)
■ 560
Ψ6 (χ) = Ψ* (χ) - ± («2 - 7) Ψ» (л) +
+ Тою (15 η* ~ 23° η* + 407) Ψι (χ)-
Эти полиномы связаны друг с другом рекуррентной
формулой:
* ж W = ψι W ψι W - T^Elf ll ^ W-
Сумма квадратов этих полиномов равна;
5 ψ2 (χ) = (/ !)" П (^2 _ 1) (η3 _ 2) . .. . (»2 — /2)
' (21— 1)!·22ζ·(2/+1)
Легко видеть, что коэфициент при Ψ^ (χ) в вышена-
хіисанной рекуррентной формуле равен отношению сумм
квадратов двух смежных полиномов Чебышева.
В иностранной литературе полиномы Чебышева для
равноотстоящих величин использованы в работе Чарля
Жордана „Математическая статистика", 1927, (20).
Им введены полиномы qt, которые равны:
ql+1 = ~— ^г-н (ζ)· β работе Жордана используется
вспомогательная переменная 5Ί==χ— ~ . где га = 0, 1, 2,
3... Таким образом полиномы, использованные Жорданом,
соответствуют полиномам f{ (z), но для несколько
преобразованной переменной. В работе Жордана даны
числовые значения первых пяти полиномов и сумм их
квадратов для значения л от 2 до 20. В русских таблицах
„Числа Чебышева" эти значения вычислены для η от 5 до 50.
Таблицы Жорлана для полиномов ql вполне аналогичны
русским таблицам „Чисел Чебышева" (22), (23), только
материал систематизирован несколько иначе.
В русских таблицах эти числа даны отдельными
таблицами для пятичленных, шестичленных, семичленных и т. д.
статистических рядов. Каждая из этих таблиц
подразделена на колонки, отведенные каждому из пяти первых
полиномов Чебышева. Внизу каждой такой колонки в
русских таблицах дана сумма квадратов соответствующего
полинома Чебышева.

88 Обобщенные, полиномы. Чеоыше.иа и статистическое, исчисление
В таблицах Жордана для каждого полинома Чебышева
дана отдельная таблица, внутри которой приведены числа
Чебышева для статистического ряда с соответствующим
числом членов (я). Сумма квадратов полиномов Чебышева
у Жордана вынесена в самостоятельную таблицу.
От русских таблиц „Числа Чебышева "легко перейти к
таблицам Жордана» разделив числа Чебышева на коэфи-
циент Ск, стоящий при хі',(х) в заголовках русских таблиц
. (2/ -!-1)! ,
и умножив на коэфициент -—-.,——, где / — есть номер
полинома Чебышева, минус единица.
Таким образом в русских таблицах числа Чебышева
даны в виде целых чисел, а у Жордана — в виде целых и
дробных чисел.
Сѵмма квадратов полиномов qt равна".
" ' (2Н-1) 2->г
Числовые примеры параболического интерполирования
равноотстоящих величин при помощи полиномов
Чебышева, или иначе „Чисел Чебышева", можно найти в
работах, указанных в библиографии (22, см. стр. 64---66),
(23, см. стр. 453-461), (20, см. стр. 272-274).
Числами Чебышева легко пользоваться и для
статистических рядов, где интервал равен любому постоянному
числу. Следует только в этом случае перейти к новой
иеременной, так чтобы иметь натуральный ряд чисел.
Б приложении даны таблицы: „Числа Чебышева" в
интерпретации Чарля Жордана.
§ Г>. Кривые распределения чиеленностей и нолинояы
Чебышшіа.
Общеирнзнана роль II. Л. Чебышева в теоретическом
обосновании закона больших чисел. Работы Чебышева (24)
„О средних величинах" и „О двух теоремах относительно
вероятностей", несомненно, составили эпоху в истории
статистики в отношении обоснования закона больших
чисел и в развитии теории распределения вероятностей.
Однако, эта сторона вопроса в настоящей работе не
рассматривается, также как не рассматривается вопрос о
распределении Стюдента (25) и Р. Фишера (10). Не касаясь
вопроса о знаменитом „неравенстве Чебышева* и его
предельной теоремы нормального распределения вероятностей,
рассмотрим лишь вопрос о роли полиномов Чебышева
в теории кривых распределения численностей.

Кривые распределении часленностей. и полиномы Чсбыш*«а. S9
В работе „О разложении функции одной переменной·'
(1859), П. Л. Чебышев, опираясь на свою
интерполяционную формулу, разложил в ряд но ортогональным
полиномам функции распределения вероятностей т/-~ г-'■■'·'*
и ке~кх.
Первая функция имеет отношение к распределению
вероятностей Лапласа—Гаусса, (26), вторая—Пауссона (27).
Для первого случая Чебышев нашел полиномы,
приведенные нами на стр. 79 Эти полиномы сопровождаются весом
Ѳ2(л)—|/ — е-"х'. При £=--(—1)'имеем но. иномы Эомнтл,
полученные им позднее Чебышева (в 1864 году).
Для второй функции полиномы Чебышева (см. стр. 79)
сопровождаются весом θ2 (χ) =e~kx. Если положить в этих
формулах k—1, то будем иметь общеизвестные полиномы
Лагерра, полученные последним также позднее Чебышева
(1879 г.). Таким образом, приоритет в получении этих
полиномов принадлежит П. Л. Чебышеву.
Чебышевым установлено, что проивзодные от функций.
распределения вероятностей равны самой функции,
умноженной на соответствующий полином Чебышева, а суммы
квадратов его полиномов, сопровождаемые
соответствующим весом, оказались равны'.
а) в первом случае 1/ —е~кх' Ч f(x)dx — il{2k)'
Λ-f СО
б) во втором случае! ke "кх x¥f(x)dx — (/2)!
J — ел
Б качестве обобщенных законов распределения
вероятностей Чебышев предложил, в соответствии со свои*
интерполяционным рядом, новые ряды, являющиеся суммой
такого рода членов:
а) для первого случая'.
I л/ — *-**Ч-, (.*)/*<*) л*
/ К
У γ

.'Ю Обобщенные полиномы Чебышева и статистическое исчисление
б) для второго случая:
■·+ ее. ,·+ <х>
I ke-** Ъ№р(х>dx ke~kx \(х) F (χ)dx
'-*Дъ - Ф,(*) = -^ Φι W
ке~кх ί>? (χ) dx (/2)!
J + ее
В обоих случаях Z7 (л) — известные значения
интерполируемой функции.
Это исследование Чебышева оказало огромное влияние
на дальнейшее развитие статистической науки. Датский
математик А. Фишер (28) в своей работе:
„Математическая теория вероятностей" пишет, что знаменитые
исследования скандинавской школы математической статистики,
а именно, работы Грама (29), Тиле (30), и Шарлье (31)
основаны на исследованиях П. Л. Чебышева.
Грам в своих докторских тезисах, относящихся к
1879 году („Определение рядов посредством метода
наименьших квадратов"), рассмотрел вопрос о приложении
ортогональных полиномов к определению статистического
распределения численностей. Он первый показал, что
статистические распределения могут быть выражены черен
ряды ортогональных полиномов с весом, равным функции
нормального закона распределения вероятностей.
Датчанин Тиле, друг Грама, опубликовал в 1889 г. на
датском языке „Общую теорию наблюдений", где
разработал вопрос о характеристиках кривых распределения
численностей, которые он назвал «семиинварианты".
В сущности, работа Тиле является первой в статистике
работой по теории моментов, получивших свое
дальнейшее развитие в работах английского ученого Карла
Пирсона.
Датский ученый Шарлье в 1905 году развил идеи Грама
и дал в. окончательном виде (в двух формах) уравнения
кривых распределения, получивших в дальнейшем
название „кривые Грама-Шарлье" (тип „А") и „кривые Пуассона-
Шарлье" (тип „В").
Почти одновременно, в 1906 году, такого же рода ряды
дал немецкий ученый Брунс (32). В его работах уравнение
нормального распределения вероятностей выражено в так
называемых модулях, т. е.. в единицах а\г2 .
Следовательно, им в полиномах Чебышева положено &2—1/2з2.
Легко показать, что кривые Грама-Шарлье и Пуас-
сона-Шарлье есть лишь некоторая модификация
интерполяционного ряда Чебышева.

Кривые, распределения численностей а полиномы Чгоышыа 91
Если нормальному распределению вероятностей придать
_£І
k/r. е 2 > то-есть положить k=l/'t, χ~ζ—ζ, σ3=1,
N = 1, то полиномы Чебышева будут выражены в виде
зюлиномов Эрмита.
При этих условиях (при Ν=-Λ) имеем с одной стороны:
Г+ы ,1 _ "!
1 .ѵ г - е 2 dx-^-О (при / нечетном)
х1 г е idx = \. 3. 5... (/—1) (при / четном).
J _ о, V2π
С другой стороны при этих же условиях имеем:
х F (х) dx = 0
(A) J_a, KJ
Ι χ2 F (x) dx = \xs — 1
J — oo
■··+"'
χ*Ρ(χ) = μ3
J — oo
r+ л>
χ*Ρ(χ)^μ.. Где μ·2, μ3 и μ< -
J — CO
центральные моменты.
Полиномы Чебышева-Эрмита и производные
нормального распределения вероятностей могут быть
представлены в виде следующего ряда:
Производные от %(х); '^(х); <р2(*0; %(λ'); '·?*(Λ'): ЪІХ)
функции
полиномы Д>(л); ^iW; ^W; ДіИ; #4(·Ό; я, (λ).
Здесь φ, (.ν) = (— 1У а0 (X) ■ Η,(λ-J
1
&(χ)=4Α*) = \/—*''-
Μ, (*)-■!.

92 Обобщенные полиномы Чебышева в статистическое исчисление.
Грам и Шарлье, опираясь на ортогональные свойства
полиномов Чебышева, следующим образом преобразовали
члены интерполяционного ряда Чебышева:
| ?0(x)Hl{x)F(x)dx J Ht(x)F(x dx
K{x)H?{x)dx J и(л)//,з(.ѵ)Лѵ
J — CO . - C^
Где по прежнему ol(x) — (o0(x)Hi(x). Если иметь ввиду,
что при указанных условиях J w0(x)Hf(x)dx—ll, то
интерполяционный ряд Чебышева может быть представлен
окончательно как сумма членов ряда:
[ Hl{x)P{x)dx
"~'-п— __ '■?/(·*)—где / последовательно принимает
значения 0, 1, 2
Подставляя вместо полиномов Чебышева их значения
убеждаемся, что первый и второй члены
интерполяционного ряда исчезают.
В окончательном виде имеем ряд „А" Грама·Шарлье:
F (х) =. ί'() ш0 (л-)+е.». (.*) -!- r4 ot (а-)·
с0 = 1, сг =--■ О, Со = 0, с3 --= ^-, с4=-.-- ^ - ·
Следовательно, ряд Грама-Шарлье есть простое
преобразование интерполяционного ряда Чебышева, основанное
на ортогональных свойствах его полиномов.
Необходимо отметить, что интерполяционный ряд
Чебышева дает наилучшее приближение в смысле метода
наименьших квадратов, но не функции ^(.ѵ), а функции".
Грам в своей работе (29) доказал теорему, которую·
А. Фишер (28) формулирует следующим образом: ...„если
дана произвольная функция относительных частостей,
оплошная и конечная в интервале — со и + ^·-> и
исчезающая при л —4; со, следует определить константы сп, с,„
г, и т. д. таким образом, чтобы ряд:
со?о(*) + сі ?і (■*) + _£?.?2(fL + сз гз (■*) , ,ci.?iif)_
VtoW Vmx) Υ^ΰ) νζϊχ) ϊ1λχ~>

Кривые р ас пред еле кия численности и полиномы Чебышева S3
давал наилучшее приближение количеств -Р(^ в смысле
Ѵъ(х)
метода наименьших квадратов".
В. И. Романовский (21) также учитывает это
обстоятельство, определяя первый член квадратического прибли-
S+00
РЦх)
—7Т dx.
чо (χ)
Для функции φ,(Λ:) имеются готовые таблицы,
опубликованные первоначально Шарлье, затем Иоргенсеном (33),
и воспроизведенные у А. Фишера (28), Кэмпа (34), Ритца
(35). Митропольского (23), Эти же таблицы в модулях
(з]/Т) опубликованы у Чубера (36), Брунса (32) и Лахтина
(37).
Процедура Грама-Шарлье наиболее распространена в
мировой литературе.
При вычислении кривых распределения в
математической статистике пользуются определенной системой
статистических констант. Эти константы обычно излагаются
или в виде системы моментов Карла Пирсона (/и,, и μ(.) или
в виде семиинвариантов Тиле (λ,.).
Система семиинвариантов Тиле носит на себе более
явный отпечаток идей Чебышева, чем моменты Пирсона.
Можно показать, что статистические характеристики Тиле
легко получаются из полиномов Чебышева следующим
образом:
Система констант Тиле (λ4) и Пирсона (ц<) в полиномах
Чебышева
Константы Тиле (λ£) и Пирсона ((*,·)
Полиномы Чебышева
-Ѵо =!
ιΊ·ο = .νι — .χ
I
j SxQ.a—n
! 5λ:,-*0.0 , —
| ——-5 = A.1_.C]
I °-*o-o
(Первый
семиинвариант Тиле)
(Второй
семиинвариант Тиле)
іе (λ£) и

94 Обобщенные полиномы Чебышева и статистическое исчисление
Полиномы Чебышева
Ψ2(ί) = ί3_ι
Продолжение
Константы Тиле (λ,·) и Пирсова (|it)
5ΨΧ(0 F(x) = 0
При λ« = 1 и
При Ха=1 и 5Ч^.о= 1
имеем:
S^aW /г(д:) = —μ3=—λ3 (Третий и четвер-
SW, (/) F (дг) == μ,— 3=λ, тьій семиинварианты
4 * Тиле)
Система констант Тиле ближе к полиномам Чебышева
что особенно ясно видно при рассмотрении первого и
четвертого семиинвариантов Тиле, т. е., как раз тех его
констант, которые не совпадают с системой центральных
моментов Пирсона. Однако, константы Тиле сближаются
в своих принципиальных основах с системой полиномов
Чебышева, только если приравнять единице сумму
квадратов нулевых и первых полиномов Чебышева.
Таким образом константы Тиле, также как и моменты
Пирсона, являются слстемой средних арифметических, а
не элиминационных средних.
Характерно, однако, что ассиметрия и эксцесс К.
Пирсона приближаются к системе чебышевских полиномов.
Так можно показать, что для обычных статистических
рядов распределения относительных частостей, т. е. когда
единице равны суммы квадратов нулевых [Sx].o = n — l]> но
не первых полиномов Чебышева, имеем показатель
скошенности SxVu{x)F(x)=r-^- = Vfu а эксцесс 5ЧГ4(х) F(x)=
oil
= -*—3-£.
о*
Таким образом идея Чебышева о том, что коэфициенты
сто интерполяцлонного ряда есть элиминационные, а не
арифметрические средние, приводит к стройной системе
основных характеристик статистических распределений
численностей.
П. Л. Чебышев в работе: ,0 разложении функции
одной переменной" указал несколько иную процедуру вьі-

Кривые распределения численностей и полиномы Чедышева 9S
числения коэфициентов интерполяционного ряда, чем
Грама—Шарлье. Коэфициенты его интерполяционной
формулы равны:
Л_ J —оо ψ π
ι—— — ; ■*
' / ! {2k)1
Однако, процедура Грама—Шарлье, основная на
определении центральных моментов при вычислении
интерполяционной формулы, имеет некоторые преимущества, так
как в этом случае исчезают второй и третий члены
интерполяционного ряда.
Вычислительная процедура Грама-Шарлье наиболее
распространена в математической статистике при
выравнивании кривых распределения численностей.
§ 6. Распределение Пуассона и полиномы Чѳбышева.
В статистике большое значение, кроме нормального
распределения Лапласа-Гаусса, имеет распределение
Пуассона. Формальным признаком для распределения
Пуассона является приблизительное равенство средней
арифметической, среднего квадратического отклонения и третьего
центрального момента. Распределение редких событий
следует этому закону.
Русский статистик Борткевич (38) в 1896 году первый
открыл факт существования статистического
распределения, подобный распределению Пуассона. Он назвал этот
факт „законом малых чисел". В настоящее время известно
большое количество статистических распределений,
следующих закону Пуассона. Таковы распределения
численностей, встречающиеся в демографлческой статистике
(например: число рождений троен, число смертей от
редких причин и т. д.), в статистике телефонных станций
(например: занятость телефонных автоматических
аппаратов), в статистической физике (например: измерение
радиоактивных процессов и пр.), в биологической
статистике (наігр.ьѵер: счет бактерий под микроскопом на
единицу поля зрения и т. д.).
Распределение Пуассона имеет вид:

.W Обобщенные полиномы Чсбыше.на к статистическое, исчислении
где т.--— среднее арифметическое значение, ал: —число
::обытий- Распределение Пуассона может быть
представлено в виде следующего ряда'.
Каждый член вышеприведенного ряда легко получить
путем умножения предыдущего члена на —-—. Таблицы
для функции ψ (л)=- ■ -., · были впервые онуоликованы
Борткевичем в 1898 году в виде 4-значных таблиц для
значений т от 0,1 до 10. Более полные таблицы
опубликованы Н. Е. Soper (39) в 1914 году в „Biomeirika" (X, 25)
а виде 6-значных таблиц для т от 0,1 до 15 и для χ от
0 до 37. Эти таблицы даны в приложении в конце
настоящей работы (таб. VIII, стр. 127—131).
Чебышев в работе: „О разложении функции одной
переменной" показал, что функция ke~"xможет быть
разложена в ряд при помощи его интерполяционной
формулы, причем, Чебышевым определены и полиномы,
сопутствующие этой функции. Эти полиномы нами приведены
на стр. 79.
В дальнейшем были установлены так называемые
„обобщенные полиномы Лагерра" для функции тхе~т, а в
последнее время в работах Жордана (20) и Романовского
теет
(21) указаны полиномы О для функции —γ- при л-— 0, 1,
2, 3... Эти полиномы приведены на стр. 79.
Идеи Чебышева о разложении функции одной
переменной получили широкое практическое применение после
появления в 1905 году работ Шарлье (31). Предложенная
им формула для обобщенного распределения Пуассона
получила название „кривая Пуассона-Шарлье" (тин „В").
Кривая распределении Пуассона-Шарлье имеет вид:
F(x) --= В0 φ μ) 4- Вг Δ φ (χ) -\- В% Δ3 φ (χ) | ■....
где: Δ' φ(.ν) — конечные разности функции, а именно'.
Δφ(Λ:) = ψ(χ) —ф(лс—1),
Δ» φ (χ) := Δ φ (χ) — Δ φ (λ- - 1) и т. д.
ψ (.ν)

Распределение Пауссона и полиномы Чебышева 97
Если начало ряда перенести в точку равную средней
арифметической, то в интерполяционном ряде Пауссона-
Шарлье остаются лишь нулевой и второй члены, причем,
в этом случае Вй—1, B2 = 1jt(a2— х).
Обобщенный ряд распределения Пуассона широко
используется в статистической литературе, именно в виде
кривых Шарлье типа „В". Однако, вместо конечных
разностей при вычислении обобщенной кривой Пуассона
удобнее пользоваться полиномами G. В полиномах G функция
,, . тхе~т Л
ф(л:) = — может быть разложена в следующий ряд
при помощи интерполяционной формулы Чебышева:
Fix) = η [AtG0(x) + Α&(χ) 4- AtGt (χ) +...] φ (χ).
а«ь л- ^ЩР- - £ J ovmm, <*
χ!
так как SGf$(x) =—-·
от
Коэфициенты Аь могут быть выражены не только через
суммы произведений полиномов G{, но и через начальные
и центральные моменты распределения. Если параметр от
функции ф(л:) = j— выбрать равным средней арифме·
тической, тогда коэфициент А будет иметь следующие
значения:
Л0=1; Л, = 0; Л2 = -~- (μ, - от) = -±- (α' - *);
где μ — центральные моменты, а от —- средняя
арифметическая.
Таким образом обобщенное распределение Пуассона
может быть представлено в полиномах G в следующем
окончательном виде*.
F{x) = η φ (χ) [l + -i- (μ, - от) G2 (χ) +
+ (γμ3-γμ2+ \-m)G3(x)+... ].
7 Полнноиы ЧиСышева

9S Обобщенные полиномы Чебыіигся и стятастичееісое исчисление
Этот ряд, характеризующий кривую Пуассона-Шарлье
обычно применяется для выравнивания статистического
распределения численностеи в тех случаях, когда средняя
арифметическая приблизительно равна средней квадрати-
ческой, но третий центральный момент существенно
отличается от средней арифметической.
Квадратические приближения определяются для
обобщенной кривой Пуассона-Шарлье в полиномах G обычным
способом как Sty — ук) — Sd;;-
Если эта сумма квадратов оказывается достаточно
малой, то степень приближения по интерполяционной
формуле признается удовлетворительной.
§ 7. Выравнивание кривых распределения численностеи
(пример ы).
Пример нерв ы и. Параболическое интерполирование.
В качестве примера возьмем распределение рабочих по
дневной заработной плате в долларах, на основании
Сенатского отчета по США за 1893 год. Пример заимствован
из Боули „Элементы статистики" (изд. 5., стр. 97).
Обработаем эти данные в полиномах q. (Жордан.
„Математическая статистика" стр. 272—-275).
Исходные данные таковы (х — дневной заработок в
долларах, у — число рабочих):
Х\ — Хо
0,25-0.74
0,75-1,24
1,25—1,74
1,75-2,24
2,25-2,74
2,75—3,24
3,25-3,74
3,75-4,24
4,25-4,74
4,75-5,54
X
0,5
1,0
1.5
2,0
2.5
3,0
3,5
4,0
4,5
5,0
2
0
1
2
3
4
5
6
7
8
9
,
317
1472
1?97
970
506
198
254
9о
4
9
Sj' = 5123
У
100489
2165784
1682209
9409J3
256035
09204
64516
9J16
16
81
Sj« = 5259451
''«
3,54
-24,05
63,71
-67,15
— 6,29
79,99
—68,27
16,35
4,59
— 2,44
- 0,02
Здесь η—10, интервал А = 0,5.

Выравнивание кривых распределении численностеіі 99
Для перехода к натуральному ряду чисел введем
переменную -~^-°- = ζ. Затем имеем: а0 = -^ = 512,3, а
сумма кр,адратов отклонений равна: Sd% ~ Sy" — a0Sy =-
= 2634838.
Теперь воспользуемся полиномами q для
параболического интерполирования, (см. приложения таблицы I—VI,
стр. 112-117).
Так как эти полиномы симметричны, то можно вести
вычисление только для верхней части ряда, если частоты
преобразовать для нечетных полиномов (уі) путем
вычитания уй— j/9; Уі—у8; Уъ—Уч и τ· Д·, а Для четных
полиномов 0/2) путем суммирования: уй +уа; Уі+ув и т. д.
Затем, перенеся из таблиц полиномов q соответствующие
числа Чебышева для « = 10, можем вычислить
необходимые ak и Sdl ■
Определение а\ и S d%
г _Ѵі Ц\ „Μι
0 308 -4,5 -1386
1 1468 —3,5 -5138
2 1201 - 2,5 -3002,5
3 716 - 1,5 -1074
4 308 — 0,5 — 154
Отсюда имеем: ах = о 2 ==■ —^-^— = — 130,35/.
S ѵ?і = -10754,5
Syqi _ —10754,5
Sql ~ 82,5
Где S<7i=-'82,5 (Взято из таблицы VI, см. приложение стр. 117)
Sdl= Sd\—a1Sy1ql= + 1233015.
Вычисление β2 и Stfj
•ζ Уз <72 Уъіч
0. . . .
1. . . .
2. . . .
3. . . .
4. . .
Отсюда
ідратов
32ό
. . 1476
13РЗ
1224
704
имеем: а2 —
Sdt^Sdl-
18
6
- 3
- 9
—12
Syq0
/V =-7,51,
S<72
•a2Sy2^2= 11669S
5868
8856
— 4179
—11016
— 8448
Syq^— — 8919
остаточная с
и.
7*

100 Обобщенные полиномы Чебышева и статистическое исчисление
Вычисление па и S d^
Л Ч-і
308 —63
1468 21
1201 52,5
716 46,5
308 18
.Vl<7;i
—19404
318 28
630 Ѵ2.5
33294
5544
S,v1?3 = n3314,5
Отсюда a, = ^~ = 5,87, Sd\= 500879.
Вычисление і^ и Sd~b
і Уг Яі У\Ч*
О
1
2.· ....
3
4
Отсюда α4 =
— 98527.
г
О
1
2
3
4
S^6==612596,75
Отсюда «5 = 0,1268, Sdl^ 20850.
Таким образом для данного примера
интерполяционный ряд в полиномах q может быть написан:
у6 = 512,3 + 130 4 9і - 7,51 qt 4- 5,87?, - 1,13 q, + 0,127 <76.
Если вместо полиномов q подставить их значения,
выраженные в переменной ζ, то будем иметь следующие
уравнения для параболического интерполирования:
у = 320,54 4- 2144,76z- 1271,25za + 280,35z8^ 27,45z* 4- ζ5.
326
1476
1393
1224
704
1S9
-231
-178,5
31,5
189
-1,13, 54 =
Вычисление пь и Sd%
У\
308
14Р8
1201
716
308
Яь
- 472,5
1102,5
- 78,75
- 866,25
- 472,5
61614
-340955
—248650.5
38556
133056
5У2?4 = —35638Л5
Sd\ — a4 Sytq4 ■■
УіЧъ.
- 145530
1618470
- 94578.75
- 620235
- 145530

Выравнивание кривых распределения численнастеіг 101
Если сравнить число случаев, вычисленных по одному
из этих уравнений с фактическими данными, то будем
иметь ds. (См. таблицу исходных данных на стр. 98).
Квадратическое приближение в этом случае равно:
•5 <Й 90850 —
Ж = —- =■ — - = 5212,5 a 4,-72,2.
"6 η -6 4 '
I! ρ и м е ρ в τ ο ρ ο it. Вычисление обобщенной нормальной
кривой Лапласа-Шарлье.
В качестве примера возьмем данные о распределении
диаметра сосны (по Митропольскому „Техника
статистического исчисления1' стр. 316). Исходные данные для этого
примера, приведены в таблице на стр. 103.
Вычисление обобщенной нормальной кривой по этому
способу показано в той же таблице на стр. 103. Эти
вычисления основаны на применении функций <рг(л), которые
являются произведением полиномов Чебышева xi"t(x) на
1 х%
функцию -. - е~ 2" = φί)(.ν). Значения функции даны в таб-
γ'2π
лице IV (см. приложения). Вычисление коэфициентов
обобщенной кривой Лапласа-Шарлье удобно вести на
основе центральных моментов, так как в этом случае
исчезает второй и третий члены уравнения. Выражая
значения коэфициентов уравнения обобщенной нормальной
кривой через центральные моменты, имеем уравнение:
Вычисление центральных моментов производится
обычным способом на основе следующих формул:
«.-=9216; ^ = 0.025; ^ = 7,210; 5^=14.845;
η η η
•^ν-_:= 164,234.
η
Л Л2 '
α ==/,4 =2,673.
1А = № - 3(Syrf)-(Syx) ^ 2 [Syx\* = g 4б9
η л- п'1

102 Обобщенные полиномы Чедышева и статистическое исчисление
Syx* _ 4 (Syx3) · (Sух) 6 (Syjfi) ■ [S.vtp 3 (Syx)* __
η /i* tt-i я4
t*j η лаа.
= 152,081.
ѵт
=-- 0,496;
Ε = (-И- - 3) = ~ 0,0023;
/U
/Рі =
1 = 0,08267; /14 =
24
0,00096.
Подставляя эти значения имеем окончательно
следующее уравнение:
- 9216
Уъ "" 2,673
foo (*) τ 0,08267 φ3 (х) - 0,00096 φ4 (х)} --
= 3447,81 φ0 (χ) + 285,03 φ3 (л;) — 3,308 φ4(*).
Вычисленные по этому уравнению числа,
характеризующие распределение сосен по диаметру, даны в той же
таблице исходных данных.
Квадратическое приближение определяем по формуле:
&Й= S(y~ У*? = 41363,13.
л-5 = 11; 34 = 3760,2. а 54 = 61,3.
Полученное приближение вполне достаточно.
і Ι ρ и м е ρ τ ρ е τ и й. Вычисление обобщенной кривой
Пуассона-Шарлье.
Для примера обработаем данные о числе смертных
случаев для женщин в возрасте свыше 85 лет но
ежедневным данным за ]910—1912 гг. по Англии (Романовский,
„Математическая статистика" стр. 224—226). Исходные
данные и результаты обработки приведены в следующей
таблице:
Л'
о
1
2
3
4
5
IS
7
у
364
376
218
89
33
131
2} 16
1)
1096
Λ
336,2
397,3
234,7
92,4
27,3
6,5)
1,3} 8,1
о.зі
10Э6.0
-Ѵ2
366,5
372,5
214,5
94,2
31,4
1<>,5)
2,7^ 14.0
0.8І
1095,1
d.
-2,5
3,5
3,5
-5,2
—1,4
J 2,0
ί)

Вычисление кривых распределения численноетей
103
і *
о .з
4,5
%\ч
"5*3
а
г
іЛ
'?
то
X
Ξ! °
н-
ч^-ч^
^4
S!s
2
_^-^ч_
°?
1
яг
«
о-
о.
.
£
СО
О
ν
о
с?
• *
о
і7>
ΟΟ
Γ—
to
ч
£
ч
S
II
5
1
ч
О
S
|
»
\-
ю
Tf
σι
CM
00
■φ
■φ
СО
о
о
о
о
о
о
о
о
1
г-
СО
СМ
о
о
1
со
о
о
о
+
ю
η
то
■*
о"
^
СО
^ч
ел
то
<м

ΓΙ—*
—>
ю
о
о
то
см
о
О
С'
О
о

ίο?
•ч·
г-
со
■Ч"
о
ΓΝ
*—ч
о
СО
со
о
'-э
о
о
СЛ
СП
00
04
ю
00
ю
г-
о
г 1
<м
о
г-
сп
о
о
о
о
о
CM
-м
·—(
•fl
ю
о
ΓΝ
—Η
in
ΓΝ
со
о
о
ΓΝ
ΓΙ
о
о
о
44 4 4-
г—
о
оо
о
г>
1
ТО
Μ
о
о
ТО
о
1
СМ
СО
то
о
о
44
■*
СП
ю
СМ
о
о
I
1 00
со
ΓΝ
со
го
»Ν
I
ю
см
о
1
! со
1
га
то
1-
ΙΟ
О
о
-
СО
то
^
1
IГІ
ΟΙ
щ
I
t-
то
ГЛ
(О
о
о
о
■Ί<
ГО
CN
о
о
ю
СО
■^и
-φ
ο-
ο
ΓΝ
СО
СО
1—<

ΓΟΟ
,-ч
СП
СО
in
en
СО
С'
СО
о
о
о
о
1
оо
■ч4
оо
со
о
о
IО
о»
со
"*
со
со
со
СП
со
~
■ о
о
■ч<
о
(М
о
о
о
1
—Η
см
СП
05
о
о
4 4 + 44
СО
Ю
со
о
1
со
■ га
■*
ОС)
с>
о
1
о
Г-
IМ
^^
о
о
U5
ю
,_
1
см
—.
1
ОС
СО
то
о
С-
о
1
ю
СО
CN
СО
о
1
г-
о
СП
~*
о
СО
сч
г—1
1
ю
("N
С?
I
ТО
о
ΓΝ
о
ΓΝ
о
I

ΓΟΟ
en
со
из
о.
1
г—
on
ел
1 —
ΓΝ
о
СМ
оо
о
1
ю
см
С)
1
~
со
то
СП
»—1
CD
о
4
)Л
со
m
со
-а·
о
1
со
ю

ΓΙΟ
со
о
оо
со
-=f
о
1
CN
^
1
_
CD
■ч«
о
г-
r-t
»-4
4·
г—
СП
■—»
о
1
00
r-t
1 —
то
СО
о
-*
то
о
г;
1
•о
СМ
о
1
см
о со
со С"5
СМ СП
—*
ем ·*
-* о
Г— Ю
см ю
см то
1—1
СО
ΓΙΟ 1—
со см
о о
ГО СП
СП г-
и> со
о о
о —>
о о
1 !
СО СО
о оо
CD ^
ГМ ·&
о о
о о
I 1
00 to
t-ч со
г-1 СО
ι— СП
СП —
о о
4 4
Г- Γ-
Γ- о
·*}< СМ
СО Ю
о о
44
о см
Ю СП
со .-ι
ОО гч
со со
о о
— ю
СО Ю
см со
о о
44-
Ю "5
г- г-
О —■
-і- +
со т*
о· о
со г—
Ό ·*
см —
СМ г-·
СП Ю
с^ »о
чО *^
г- СМ
сп со
ι—1 1—4
о о
Ο —ι
Ю, г-
о о
с5 У
о о
»-■
ΟΙ
СО
Ю
о
го
05
см
IП
оо
о
о
г-
•Ή
о
о
о
о
+ + Н-
^- ю
СО го
со с—
го —-»
о о
о о
I 1
00 ТО
со 00
Tf Ό
CN CO
ю t>.
о о
1 1
Г-1
СО 00
СП .О
~о —
■ч< см
о о
+ 4-
со о
то —
■^ сп
СО ^г
см —<
о о
СП СО
см о
О -Ч"
<—< I-<
_^
СП
о
о
о
ч-
-^ь
ю
σ>
■*
о
1
ю
о
СО
см
о
о
1
г-
См
гм
00
о
о
г—
г-
г-
^,
ю
00
ι—1
■*
00
(П
г—
1—1
Ш
о
о
СО
о
^J
о
о
+
см
Ί"
«—4
о
о
+
ю
'^
см
со
»—(
о
1
СП
00
со
'-ι
сг
1
г-
-4-
то
СО
о
о
_
■о
сч
ю
то
ю
СП
СП
оо
ON
о
о
то
о
о
о
о
о
1
о
СП
о
о

-Ιοί
ι—
00
оо
о
о
4-
о
со
о
■*
о
1
со
--«
СО
о
о
in
см
ю
см
+ + + 4- +
ю ю
1- г-
CN СО
+ Jr
Ю со
1П
с-
■Гчн
ю

ΓΙΟ
ш
с-
со
г—
іП
см
00
■*
■ΊΪ*
со
о
о
со
о
8
о
1
СО
г—
г—
о
о
о
см
см
СП
со
о
СО
о
о
о
о
о
с·
о*
1
СО
СП
ТО
о
о
о
4- 4-
СО
IО
оо
со
г-і
%
СП
сЯ
то
о
о
1
г—
то
m
о
о
о
то
оо
см
4
ю
г—
I--
+ + + +
t—
эо
С7;
о
00
СО
со
о
о
4
СМ
ю
г-
■ф
о
о
1
оо
оо
о
о
о
со
г-
см
СО
4
ю
Γ-
00
4
СО
СМ
то
00
то
ю
гм
СП
со
со
см
1
1
1
1
■*
с—
СО
см
1
1
ее
S
υ

104 Оооощинпые полиномы ЧсОышееа и статистические исчисление.
Здесь л"— число смертных случаев в день, а у — число
дней с данным количеством случаев. Прежде всего найдем
начальные и центральные моменты· я—1096; Зѵл = 1295;
Svx 1295
т = χ = -γ- = — =1,1816; Syx-~-- · 3023; 5yjc3= 90305.
Отсюда:
Syx- (Syx)- . OCOf.
μ8 = —-— -■ · ■ — 1,3620;
η it1
Svx* 3Svx*-Syx , 2 (Svx)» Л11еп
μ = -ί— _ —^— J- -i---J- =--- 0,1160.
Для распределения Пуассона первый начальный момент,
второй и третий центральные моменты должны быть
приблизительно равны друг другу. В нашем примере третий
центральный момент значительно отличается от средней
арифметической и средней квадратической. Поэтому
необходимо применить обобщенную кривую Пуассона-Шарлье.
Приведенные данные могут быть выражены π , формуле
Пуассона в виде следующей функции:
(l,18?):,>-,-,Sj
у, = 1096· =.--·■■ 1096 ψ (.ν)
По таблицам функции ф(-ѵ), приведенным в
приложении для х— 1,182 находим значение уѵ Эти значения
приведены в колонке 3-й предыдущей таблицы.
Квадратическое приближение Sd\— S(y — y-tf— 1611,9.
(Л0 = 1). Следовательно, вычисленные данные недостаточно
согласуются с фактическими. Поэтому рычислим
обобщенную кривую Пуассона-Шарлье, используя полиномы 0.
Для этой кривой имеем интерполяционную формулу:
у~к ----- η φ (χ) [Л0О„ (χ) -f .4,0, (л-) н- Л2(72 (χ) + А.л03 (χ)}.
Так как при применении центральных моментов А1~0Г
то в качестве второго приближения имеем:
аі= Υ [ι*»— "**) = —γ— — 0,0902. Затем, так как
Уу = и-ф,(л;), то окончательно имеем:
у2 "-= у, [1 + AtG, (χ)) = у г {1 +0,0902 02 (*)].

Вычисление криеых распределения численностей. IО.у
Как видим, расчет удобнее вести исходя из первого
приближения.
2 Г х{х — 1) , тЗ]
Полином 0,(х) = -[-^—t-mx + T\^
^ χ (1-х) 1х j
«3 /71
Таким образом поправка к первому приближению равна:
_ гл-(лг —1) 2л- ί
Уг -0,0902 [7ГЩ^_ГГТ^+1Г
= 7іI°,0646х(х- 1)- 0,1527^+0,0902 j.
Вычисляя поправки по этой формуле для каждого члена
ряда и прибавляя их к ранее вычисленным значениям у±
имеем второе приближение у2. Вычисление значения у^
приведены в предыдущей таблице в последней колонке.
Квадратическое приближение вычисляем по формуле:
Sd* = s (у-у~3* = 63,75.
Вычисленные данные по обобщенной кривой Пуассона-
Шарлье дают вполне удовлетворительные результаты.
ВЫВОДЫ
П. Л. Чебышев получил свой знаменитый
интерполяционный ряд для случая параболического
интерполирования (1855 г.) и при разложении функции одной переменной
(1859). Его интерполяционный ряд может быть
распространен и на функции многих переменных. В этом случае
интерполяционный ряд Чебышева вполне аналогичен
уравнению множественной регрессии, а полиномы Чебышева —
остаточным отклонениям d=y—упз и -Кз-гю —Хг — гі-^з-
Для функций многих переменных полиномы Чебышева
могут быть представлены в виде различных систем:
1) система Τ полиномов Чебышева, при которой
полиномы вычисляются в следующем порядке: ха, хьо, *2.10,
хз-2іо· ^Ри этом> каждый последующий полином выражен
через предыдущий;
2) система К полиномов Чебышева имеет ту же
последовательность полиномов, только каждый из них выражен
через начальное значение хк;
3) система С имеет дело с полиномами: *3-2I0, х2.31ф.
-^ьззо' -ro-m (для слУчая трех независимых переменных);

10ti Обобщенные полиномы Чебышева и статистическое исчисление
4) система N имеет дело со следующей
последовательностью полиномов: х3, x.h0, χΆ.ιο, хя.го-
Полиномы системы С и N выражены в первичных
переменных х,..
В полиномах Чебышева получают вполне определенный
смысл коэфициенты множественной регрессии:
. _ $(УхтЛ2.......т~}). , __ (УхрЛ-1...р-\, /)+!.. .т)
/\ · f Ир — --
5(A'2m-12 m-l) 5(Α'2ρ·12...Λ - 1. p+). ..m)
■а также .веса" Гаусса:
r 1 . r __ — k,„b
" ****.12...*-і' *·* S*Vl2.*-l '
Коэфициенты полиномов связаны друг с другом
простыми соотношениями, что позволяет предложить
несколько схем вычислений по метолу наименьших
квадратов.
Схема Дулитля основана на системе полиномов Τ
(стр. 29). Новая схема N основана на системе полиномов
N (стр. 35). Схема Ρ основана на совместном применении
системы полиномов 7* и К (стр.47).
Новые схемы имеют ряд существенных преимуществ,
так как в этом случае отпадает необходимость
совместного одновременного решения нескольких уравнений.
В результате при включении новых независимых
переменных или их исключении, все предыдущие вычисления,
полученные по схемам N и Р, остаются в силе.
Прн схеме N я Ρ оказывается вычисленной целая
система уравнений регрессии как у по различным хк, так
и х,. по различным хь~\ в их разнообразном сочетании.
Основные статистические константы и критерии, как-то:
средние арифметические, средние квадратические,
коэфициенты уравнения множественной регрессии, коэфициенты
полиномов, индексы множественной, частной, частичной
корреляции, критерии достоверности Фишера, ошибки
коэфициентов регрессии и ошибки коэфициентов
полиномов— легко могут быть выражены в полиномах
Чебышева.
При вычислении уравнений регрессии по схемам Ν&Ρ
нее основные статистические константы и критерии легко
получить при весьма небольших дополнительных
вычислениях (стр. 65 и 69).
Идея Чебышева о весе Ѳ2(х), сопровождающем
ортогональные полиномы, оказалась весьма плодотворной при

Вычисление кривых распределения численностеи 107
разложении в ряд различных сложных функций. При
разложении функции одной переменной Чебышев получил
полиномы, частным случаем которых являются полиномы
Эрмита и Лагерра. Обобщенные кривые Грама—Шарлье
(тип <Л>) и Пуассона—Шарлье (тип «θ>) являются
несколько преобразованным интерполяционным рядом
Чебышева, полученным им при разложении функции одной
переменной.
Чебышеву принадлежит научный приоритет как в
отношении полиномов Эрмита и Лагерра, так и в
отношении обобщенных нормальных кривых (тип <Л» и тип «5»).
Идеи Чебышева, несомненно, имели большое влияние
на скандинавскую школу математической статистики
(Грам, Тиле).
П. Л. Чебышев указал также полиномы при
интерполировании равноотстоящих величин. Русскими
статистиками в 1925 г. эти полиномы вычислены и получили
название «чисе.і Чебышева> (22) (23). Таблицы q Жордана,
появившиеся в 1927 году, являются несколько
преобразованными таблицами чисел Чебышева (стр. 87).
Чебышев для большинства своих полиномов указал
вес, сопутствующий его полиномам, область суммирования,
а также рекуррентные формулы для перехода от
полиномов одного порядка к полиномом другого порядка (стр. 77).
Интерполяционный ряд Чебышева и его полиномы
имеют широкое применение в статистике при
корреляционном, дисперсионном и гармоническом анализе, а также
при оценке статистических параметров с точки зрения
теории ошибок. В свете идей Чебышева уравнительные
вычисления по методу наименьших квадратов являются
дальнейшим углублением и развитием метода средних
чисел, использующего систему элиминационных средних.

SUMMARY
P. L. TCHEBYCHEF received his distinguished
interpellating series for parabolical interpellation in 1855, and for
analysis of function of one variety in 1859.
His interpellating series can be extended for functions of
many varieties. In this case the interpellating series is quite
analogical to equation of multiple regression and the
orthogonal polynomials of Tchebychef equal to the residual of
d=y-~yV2i, and X,.a,0 = *8 - „x3.
The orthogonal polynomials can be represented for the
function of many varieties in different systems:
1) A system Τ gives his orthogonal polynomials in the
following order:
■\> Λ1·0> Λ2·10» Л3.21Гі''
and every the following polynomial is expressed by the
preceding one.
2) A system К has the same succession of polynomials
but each of them is expressed by the original quantity xk.
3) A system С uses the polynomials: x3.m, х2.ш> х\-ш<
xn.m (in the case of three independent varieties)
4) A system ./V uses the following succession of
polynomials: xv x3_0, xx.l0, -^.210·
The polynomials of the system С and N are expressed in
original varieties xk.
The coefficients of multiple regression get a quite definite
meaning in the polynomials of Tchebychef:
л __ $ {Ухт-12...т-і) . , {Ухр-1?...р-1, p+l...m)
<?*2 Six* \
ύ xm-Vl...m-\ ύ\χρΑ2...ρ—1, p+l...m/

SUMMARY
109
and also .Weight" of Gauss:
p 1 . ρ ~~Kmk ^
U'~ <?,-2 ' C«'*~ Cv-2
OAft-12...ft-l ύχ k-2-l...k-l
The coefficients of polynomials are connected one with
лпоШег by simple formulas and this allows to offer some
schemes for calculations by the method of least squares.
The scheme of Doolittle is based on the system of
polynomials Τ (page 29).
A new scheme N is based on the system of polynomials N
(page 35).
A scheme Ρ is based on a joint application of the system
of polynomials Τ and К (page 47).
The new schemes have many essential advantages and in
this case there is no need for joint and simultaneous solving
of some equations. Consequently, all the preceding,
calculations received by the schemes Λ/ and Ρ are active in addi-
tioning some new independent varieties or omissioning them.
A whole system of regression equations as Υ by various
Xk as well as Xh by various a'a_, in their various
"combination are determined by schemes N and P.
In the polynomials of Tchebychef, one can easily express
the primery statistical constancy and criterions as: mean,
mean square deviation, coefficients of equation of multiple
regression, coefficients of polynomials, indexes of multiple
correlation, partial correlations, part correlations, Fisher's
tests, errors of coefficients of regression and errors of
coefficients of polynomials (page 65 и 69).
When calculated eguations of regression by the schemes
Μ and P, all the principal statistical constancy and criterions
яге easy to get by a quite small additional calculations.
The idea of Tchebychef about weight θ2 (γ), accompanying
orthogonal polynomials was quite effective in case of
developing different complicated functions in series.
The polynomials of Hermite and Lagger are particular
cases of Tchebychef's polynomials wich he got in 1859 by
developing the function of one variety.
Generating Gram-Charlier curves (tape „A") and
Generating Poisson-Charlier curves (tape „β") are rather reformative
interpellating series of Tchebychef which he received by
developing the function of one variety.
The scientific priority of Tchebychef belongs both to
polynomials of Hermite and Lagger and generating normal
curves (tape „A" and „B").

■no
SUMMARY
The ideas of Tchebychef had absolulely a great influence
upon the Scandinavian school of mathematical statistics
(Gram, Thiele).
P. L. Tchebychef also indicated the polynomials by
interpellating equaldistant values.
These polynomials were calculated by Russian
statisticians in 1925, and they got the name of Tchebychef's numbers
(22) (23).
Tables q. of Jordan which appeared in 1927 were rather
reformative tables of Tchebychef's numbers (page 87).
Tchebychef indicated the weight attending to his many
polynomials and also recurrence formulas to pass from
polynomials of one order to polinomials of other order (page 77),
The interpellating series of Tchebychef and his
polynomials have a wide application in statistics, in analysis of
correlation, analysis of variance and periodogram analysis
and also in estimation of statistical constants from the theory
of errors point of view.
The method of least squares expressed in Tchebychef's
polynomials is the further development of the metnod of
averaging that uses the system of eliminating average.

ПРИЛОЖЕНИЯ

J12
Числг Чгбыиісва
«J
из
I
Η
a
о
о
с:
а.
,3
"о
..!-
4,5 !
•о
ч-
5,5
-
ь~
"*"
3.5 \
ю
~!"
СО
ю
ю
со
2,5 .
·*·
.-
СО
>ϊ
3,5
1С
~"
'".
со Γ-ί
1Г5
ΟΊ —ι
i.O
. .
Ό
~ О
ю
г
*
о
IЛ Ю Ю >Л in иО
•*согоечс«1-<«ово—1«
I I I
іО Ю Ю Ю Ю іО Ю
СО СО N W н н О О О - н W N
! I I I I
«О Ю Ю »С Ю Ю Ю
ГС £М ΤΙ —ι - О С Г н м Ν Μ СО П
I I ! I I I !
ЮЮХСЮЮЮіОіО
^~ Tl _ _ OO О і-н -м (Ν CI fO CO* П< V
I I ! I ! I I I I
<M —<" ■— О ~ О — t-< tTX <M CO CO -4» -О" Ю Ю
I I I I I I I I I I I
О Ю Ю Ю Ю «О iO Ю iO
~ч ~« О* О О —iHfNCNiOCO'ti'OiOtOco
I I I I I I ! I I I ! I I
^OOo'^'—C^CiCOro'-^^iOiC'OOt^t^
I I I I i I I I I I I I I I I
1С ΙΟ «0 Ό 1С: i.O Ю Ю Ю Ю
о" о o~ —ι *-* cn о· -"о со -г« -г* ю ю со со ("^ і- оо со
° I I I I I I I і II I I I I I I
ю ю и> ю о хс іс ю to ю
I i I I I I I 1 I I I I I I I I I I I
счсоч<ю<ог^<»епсг>^счсо-*іоОі^=ослг--

Числа Чебышева
113
0,5
■—С
1
0,5
! :
" ГС
іі
ю
•С
1
ю
·—<
1
ю
τ—ί
-
СО
1С
1
со
1
1
СО
1С
ю
I—,
1
-*·
1
1
1
1С
7,5
о
-4,5
СО
і
- 4,5
о
7,5

ΓΙΟ
о"
,—1
1С
г-ί
-4,5
-7,5
-7,5
-4,5
ιΟ
10,5
со
-*
τ—,
1С
со"
**<
I
- 8,5
о
1
-8,5
■φ
1
3,5
»—<
СП
00
to
со
1
σ>
1
ч—t
1
CN
1
σι
I
СО
1
СО
со
о
22,5
ел
ю
*-<
1
О»
I
Ю
СО
»-ч
1
1С
1
-13,5
(Л
1
1С
I
оз
22,5
СМ г-<
о» со
г-Ч
ю ю
сГ г-"
1
ю
оо ю
г*
I 1
-17,5 -14,5
-21 | -19,5
-17,5
-19,5
1 1
ю ю
00 С~
1 1
ю
о го
12.5
16,5
1С
г-Г оо
CN СО
сч го
со
to
1
1С
I
CN
I
CN
1
CN
1
CM
1
1С
1
CO
1
to
CN
02
CO
■*
1
-14,5
-22
—26,5
00
1
-26,5
-22
-14,5
1
9,5
CO
CM
45,5
Ю
-13,
-22,5
-28,5
ю
CO
1
Ю
r—t
CO
1
-28,5
-22,5
-13,5
1С
7
13,5
31,5
52,5
о
-22,
-30
-34,5
CD
CO
1
1С
1
f
-22,5
Μ
I—<
37,5
о
CO
f-
1
1
Τ
1
τ
7
-22
ο
Ι
Ю
СО
CN
■Χ·
оо
CO
00
-49
-43,5
-45
-39 > -43,5
-31,5
Ι
-7,5
en
28,5
76,5
α·.
-46,
-49,5
Ю
Ι
■C
CO
•Χ"
Ι
1С
ο"
ι
-31,5
-19,5
-4,5
13,5
34,5
58,5
85,5
ο
CN
S Полиномы Чсііыщчв»

ш
Числа Чебышвва
О i-ί О Г~ СО 00 Ю
ffl W β) * Ю О) О)
см см
<*- со
СО О N
Г- СМ
-ΠΙΟ
CM
ю гъ о
о to
"С
-5
<0
о
·—< СО СО Ю О
СМ СО СП О О
г- о о см ю
ТР ίΟ ΙΌ ι-·
t-· СМ
СМ СЛ
о го
1111
г- г. Μ S5
С— Ю СМ
оо σ> со см со
н W ■? * cj
СМ
«3 N (О
оі о га
і—' CM СО
ю
I^.
ю
1
Ю
См
СП
см
1
С--
CN
1
сооог^ооююоосо
см со о ч1 ο «э —ι г- -#
rt Η н Сч (О СО -,'
со О Ю
о со
+ I
О со Μ
—■ t— со ся со о t— ί< о ю t~ г- еч
ι—I СМ -V СО ОЭ СМ туі Г-* О СМ -V ОТ UO
f-і *—ι τ—( CM CM CM CM CM
СМОСОЮСОС&СЧСОСО
ι r-i CM Μ Ю CJ C—
О CD Ю t- ΙΟ
σ> сл. о о о
Ю CO η т-t CO —<
rt i-i СЧ СЧ ч н
СО О) 00 ΙΟ О Ч* С-
*—I СО СО С - IО CZ СО
і-ч —■ О» СЧ
ю ю ю ю
ю см с- ю см с—
г-оіомю^таіяіітиооміо
ПСЧ^ЩОIСЧО-1 I* 'ί1 N rt rt
.-l—iCMCNCOTPlOcOt--
! I I I I I I I 1 ! I I I I I I I
о со
-l*iOCOr-000>Or-icMC043<iOOt*-00<7SO
Ю
о
Щ
CM
■·- *
1 I
t~-
co ю
00 см
" ГЧ
ri
r-
CM
us
t—»
CO
о
о
со
Ю
CM
о

Числа Чебышева
115
ю ю со ю
ю
о
1
о
CN
1
■о
а>
Ί
СО
г—
со
1
CS
t-
^
rs
CD
«5
ΟΙ
со

Γι—I
о
«-
8
СП
со
со
ю ю ю ю
Ю іО іО г- O^t^O
ill!
со с» со со σ> ю
и IN И 1С
СО Ю СО СО
СО ,—f СО СО θί CS r-! ьГ О О О
О СО
г-і СМ СО
СП СО N.
СО —< ОТ —< .
ет ** оо со со
н и η Я
Ю со СО СО
СО СМ О О О "*■
N Ю Ю Я т-· СО
7 , «**д
со со Ю СО
ю со ю ю
S N fi СЧ Οι
—I CS СО О О
■Ψ Си NN 1С
со со со Ю
CS N
CS СП
CS—iOOOO,-iN-CN>CSlO,-<
озг0нсЧ(ОнпЗ'ОО>с0нМ
IП Ю СО Ю
t-." cs cs" ι-~ σι со о о
СО ΟΊ СО 00 у-* СМ СО
ι I .-ι СО ■* Τ
Ю Ю со со
CS «3 CN
1-. с- Ν-
Tt П н
sill
I I
Ю Ю tO iO
cs
CN
1
CO

ΝΙΟ
·*
N.
CO
67,5
а
67,5
en
00
31,5
со со Ю CO
о о ci n to s
—< CO 00 OJ Г— CO
CN — ι CO -
I I
О <-> CO
со Oi Ю
CS CO CO
rt ■-· CS
I I I
со со CO iO
CS со Ю О CO N
со О) О -С» со <г
i-i ■* со О со
lilt
ε— σ>
со со
О _ - .
cs cs со
I I I
со со со со
iO to со со
CO со О ·—
σ> cs e»
со n-
CO "ч« C~- СП CO CO
n- t- о
■4" CO r->
■' 4· oi
cs cs cs
I I I I II
CO Ю Ю Ю
CS CS N. N-
CS Ю Oi CO
CO со Ю CO
1 I
CO CO CO t— CO CS
— © o> r» ·* -eo
CO Tf* м< со CO CO
CM c-> О
CO CO τ-
со cv CO
I I I I I 1
CO CO CO CO
Ю Ю IO CO
CSCSlrtcniOCO'NeSr-iN-·—< Ο β -*
CSCOOOOv-C7l-*t— <~-*t«CON.cnr-.
r-(,—IC0^4N.010'->N-COCOOO
н н « η го * ю
woNioOiSHCifo^iotoNcomc

Числа Чебышева
»о
с-
сс
tO
г-
CO
_L
ю
r-
со
ю
г—
СО
|
1
ю
С—
со
to

ΓΟΟ
_..!.
to
to
CM
CM
I
о
со
ю
см
о
to
СМ
|
1
Г-;
со
to
Гм"
см
1

γιο
г-
со

ΓΙΟ"
Γ-
со
ΙΟ
CM
I
•о
CN
—Η
σι
ю

ΓΟΟ
~Ю~
Γ-
οο
СО
ι
οι
■—<
СГІ
ι
ι
ΙΟ
t—
SS
CM
ю

ΙΛΟ
ι-
.1
00
.—ι
CM
Ю
Γ-
г-
ю
о
О)
ю
см"
г—
·*
с—
ю
СМ
t-
-sf
i
о
ι—Ι
CM
t
I
Ю
Г-
Г—
Ю
r^
i-H
CM
1
СЛ
Ю
CM
t^
■*
wo
cm
о
>—Ϊ
7
UO
ι-
οο"
l-
CM
to"
со
CO
Ю
CM
Г-
-Ф
l-T
CN
t—
•Ψ
i
to"
CM
<o
CO
CO
1
Ю

ΓΟΟ

ΓΙ
I
CM
о
,—<
1-4
Ю
cm"
Г-
**r
.1.
о
ΙΟ
d)
о
со
oo
7
Ю
~-t
CO
1
о
to
CM
c—■
CO
CM
о
(->
CO
CM
1
о
CO
CM
1
Ю
CO
<-»
со
OO
1—4
Ю
■f
σ>
1
1—<
lO
см
CO
CO
CM
I
Ю
CM
о
.-.
to
CM
*M
to
T~4
о
CO
CM
o
tp
r^i
о
ΰ
I
о
f-Ч
CO
CM
I
Ю
CM
CM
Ю
ι—1
Ю
CM
о
Ю
CM
en
CO
CM
"0
cm"
00
Г-
7
CM
о
CO
-5·
CM
1
CO
°P
о
Ю
CO
,-.
ό
t-
CM
о
о
CM
1
о
Ю
CO
1.
tO
CO
-4<
T-H
1
о
CO
-4<
CM
tO
Ю
■4-
-T1
f~t
Г-
o>
CM
...1.
CO
to
-^"
OS
to
CM
y-Z
σ>
CO
"to
CM
CO
со
00
■*
CO
CM
о
CM
Ю
CM
о
CM
1
CO
CM
oo"
σ>
CO
7
>o
CM
r—«
CO
CO
!
Ю
■»-й
О)
1
ю
to
■φ
■ч*
to
CM
■ 1
CO
CO
lO
a
CO
CM
CO
·*
■*
Ю
cm"
CO
to
to
о
С-ϊ
Ю
Г-
Ю
CM
CO
о
ю
о
Ю
CM
CO
io
1
a
о
to
Г-
1
Ю
CM
CO
CO
to
1
о
CO
CO
Ю
CM
ТГ
CO
Г-
'—«
CO
ю
CO
LO
r-
^>
to
1
to
Ю
CM
CO
»—<
1
to
CM
to"
Ю
о
Oi
■о

ΓΟΟ
■*
to
CO
Ю
Γ-
oo"
*v
to
CO
1.
Ю
CM
to"
Ю
О)
I
Ю
CM
со"
1
1
to
Г-
co
«o
о
CO
1
Ю

ΓΟΟ
СЛ
Ό
CM
to
t—(
CO
CM
r—*
t—1
8'
f-·
CO
CM
»—(
to
CN_
CO
CM
1
to
о
to
CO
CO
to
см
CO
CO
00
о
to
CM
CO
to
CO
.1.
■—13860
to
! -13072,
о
г—
со
to
I
to"
l>
CM
T1
t—<
CO
i—1
OO
CO
CO
t—t
Ю
CM
CO
CO
-4·
о
00
со
CO
r-4
J.
г^-
Ю
Г-
CO
о
CO
Ю
to
Г-
l^
Ю
to
t—

ΓΙΟ
!
Ю

ΓΟΟ"
5!-153"
см
; · 19241.
to
CO
"3*
Ю
7
to
CO
о
t
1
CO
CM
r—t
CO
см
^
ю

ΓΟΟ
CO
oo
CM
CM
to
■4·
t—

Γι—*
Ю
CO
CM
CO
CM
1
CO
о
со
00
CO
о
о
to
CO
CO
7
о
ΐ-2331
1-24885
о
о
г—
1
ю
σ>
1
о
1—
см
со
T-t
о
t~.
СО
СО
о
см
■ф
СМ
о
со
»-ч
см
СО
1
со
со
00
о
со
00
і
о
1—<
см
•ф
см
1
ю
см"
см
СМ
СО
ю
Г-"
О)
ср
СО
1
ю
-17347,
to
г-
с~>
СЧ
■ф
to
OS
-φ
г-
CN
to
г*1
to
с
■*
to
s*
^ϊ
to
Ю
о
CO
со
•φ
I
CM

©Cni-WW^OCOOO^OiW^CuW
от сл >£■
сл ~j go
сл О tfc-
Д W и ω
Ο t- » >ν
Oq о О -J
OO >fc-
to Co
Co о
>£- to —
to со -i
о сл to с:
t
Go Ю ►— >-· _
о со -~j to со от λ.
сл ю >*- со to сл сл
to сл *- сл оо сл о
со от to to to to φ-
сл
сл
ω " н
о со >— от
CD CO 00 СО
Co o> со со
"сл
si cc α со
Co to ·£- '— to ^
2>
a
Ι Ό
! -ι
1 СЛ
CO
j ОТ
i to
! СЛ
I ■
CO
Co
<T>
to
о
) ι
CO
О
00
СЛ
c:
CO
—J
to
b-J
О
О
Сл
ОТ
от
со
от
сл
со
сл
00
о
to
с;
ГС
ОО
-0
to
с
1—*
to
ОО
-J
о
CJ
~-t
to
Со
to
со
-J
Сл
со
00
от
о
to
Со
с
Сл
00
to
о
Сд:
S)
t—*
to
сд
Го
Сл
о
*-
о
Сл
to ■—
о —
to
Сл
X
о
о
о
■ч
в
to -1 ·'- tO
οα οο от от
о
4*. _.
to сл
сл с;
сл
Со to tfc.
>λί tu Сл А
со со со to
от со -~і --
-~1 О
Сл О
-Ι Со
ОТ ОО СП
сл ю о
_ ~J —
Сл ОТ ОО 00
Сл о Сл
со сл ю й- со
to со от от от
00 ь-* t-* Сл ОТ
Со
Сл
to
СЛ
СО
to
сл
о
со
со
Сл
•^і

ΙΟ
СО
<_;
С-
-о
«5

■ΔΙΟ
ОТ
х^
to
to
со
со
00
-~j
Λ.
от
сл
~
to
>f^
CO
со
Go
-J
Co
to
СП
СЧ
CO
СЛ
to
о
<Vl
to
Сл
о
«о
ОТ
-~4
ОО
#-
СО
ОТ
Со
-J
>_,
to
S)
Со
от
00
о
о
ψ.
ОО
0О
СЛ
—I
*.
Сл
О
СЛ
.£.
~4
ГО
о
о
^
ОС
СО
—J
to
>—*
00
ι—1
t.-,
ОО
tf>
<£>
κν
сл
to
St
от
φ.
to
(Ъ.
to
СЛ
to
Сл
r, τ
Сл
it-
Co
о.
III
eoiuvdQVtx ѵтгнчСо

//ν
Распределение Лапласа—Гаусса
Τ а 6 л и да VII
1 ..
П.ишпОь кринои ν = ρη(ί)=—m <' · Фѵнкцтг -;,(fi и нторт/,
Ϋ2τ
треть» и :е пеер-пая производные.
f ϊο(0 *
" 0
Tu(0 j Уа(') I -,-<(» I ?4(0
/■
.00
.01
02
.03
.01
.05
.06
.07
.08
.09
.10
.11
.12
лз :
.14 ,
.15 ;
.16
.17 i
.18
.19
.21
.21 і
.22
.23
24
.2.5 ;
.2І i
.27 I
28
.29
.30
.31
.32
.33 :
34 ι
..35 І
.30 !
.37
~ ""Л " " * ' '
.000400
. 013989
.007978
.011936
.015955
.01S938
.023922
.0279'3
.031881
.035853
.039328
.'4379")
.047758
.051717
.055670
.0.59318
063500
.Ί67-195
.07 14 2"!
075345
.07926')
.0831'6
.087034
.09)954
.',94835
.'937)6
.1025:8
.106120
.110261
.114092
.117911
.121720
125516
.1293):)
. 133J72
.13*831
. 140576
.1443)9
.39894
.39S92
.39886
.39876
39862
.39844
.39822
39797
.39767
.39733
.39695
.39 Л1
.39380
.39559
.39505
39448
c93S7
.39322
.3)253
.39:81
.39104
.39)24
.38Л-0
.3SS53
.38762
.38667
.33568
.38466
.38361
.33251
.38139
.38023
.37903
.37780
.37654
.37524
.37391
.37255
...... ..
— .39894
—.3988S
— .39S70
— .39340
— .39799
-.39745
— .396^9
— .39602
-.39512
--.39411
- 39293
— .39174
—. 3') '38
— .3889.)
— .38731
— 385Л>0
— .3837 J
— .38186
— .37931
-.37766
— .37540
— .37803
-.37056
— .36798
-.36529
-.36250
— .35961
-.3566?
— .35353
— .35035
-.34706
— .34369
-.34012
— .33666
— .33301
-.32927
-.32545
-.32155
.o:)0o:i
."1197
.02393
.03588
.04781
.05472
.07159
.083 Μ
.' 9 І2-!
.10699
.11869
J 31)33
.1419 ι
.15341
.16484
.17618
.18744
.19861
.20968
.2206·!
.23150
.24224
. 252·4>
.26336
.27373
.28396
.29405
.30101
.31381
.32346
.33295
.34228
.35145
.36045
36927
.37791
.38638
.39466
1.19683
1.19653
1 1Γ533
1.19414
1.19204
1.18936
1.18608
1.18221
1.17775
1.17271
1.16703
1. HiOSS
1.15410
1.14676
1.13885
1.13038
1.12137
1.11180
1.10170
1.09106
1.07990
1 .06823
1.0560!
1.04335
1.03018
1.01651
1.00238
0 98778
0.97273
0.95723
0.94130
0.92 -i 95
0.90819
0.89103
0.87348
0.85555
0.83726
0.81862
;
.00
.01
! .02
! .03
ί .04
! .05
.06
.07
.OS
.'9
.10
.11
1 -12
1 .13
ι 14
.15
.16
.17
.18
.19
.20
.21
.22
.23
.24
.25
.26
.27
.28
..9
30
.31
.32
.33
.34
.35
.36
.37

Распределение Лаплас.
.148027
.151732
.155422
.159097
.1(52757
.1664-02
.170031
.173645
.177242
.180822
.184386
.187982
.191442
.194974
198468
.2 49 J 4
.205402
.208S40
.212260
.215661
.219043
.222405
.225747
.2290:9
.232371
.2?5'553
.231,914
.242154
.245373
.248571
.251748
.25,903
.254036
.261148
.264258
.267305
.27035)
273373
.27^373
.279350
.2825)5
.285236
Ѵо (t)
.37115
.36973
-3G827
.3f678
.ЗР526
.36371
.36213
.36053
.35889
.35723
.35553
35581
.35207
.35и:;э
.34849
.34667
.34482
.3429І-
.34105
.34912
.33718
.33521
.33322
.33121
.32918
.32713
.325)6
.32297
.32086
31874
.31659
.31443
.31225
.31006
.3078?
.3t5fi3
.30339
.30114
.29887
.29οΰ9
.29431
.29200
?s<>)
— .31756
— .31349
—.30935
-.30586
-.30053
-.29646
-.29203
— .28752
-.28295
-.27831
- 27362
-.26886
-.264^5
-.25918
— 25426
-.24929
-.24427
— .23920
— .234'9
—.22Γ94
—.22375
-.21853
— .21326
— .20797
— .20265
—. 197Ί9
-.19192
-.ты
— .ШЮ
-.17566
-.17020
-.16473
-.15925
— .15376
-.14826
-.14276
— .13725
-.13175
-.12624
— .12074
.11525
— .К/976
п.—Гаусса цу
Продолжение табл. Vtt
-';,·< 0
.4'"275
.41065
.41885
.42586
.43317
.44027
.44717
.45486
.46034
.46560
.47265
.47848
.48409
.4ί948
.494Р5
.49959
.50431
.5^880
.51306
.5171)
.52091
.52448
.52783
.55 94
.53383
.53648
.53891
.54110
.54306
.54480
.54630
.54758
.54863
.54945
.55015
.55043
.55)58
.55052
.55 '23
.54973
.54901
.54808
ЧііП
0.79953
0.78032
0.76070
0.74077
.0.-/2056
0.7)0)7
0.67932
0 65832
О.Р3709
0.61564
0.59398
0 57213
.55010
.52791
.50556
.48308
.46048
.•13777
.41497
.39203
36913
.34613
.32309
.300)3
.27693
.25,90
.23085
.20783
18486
.16195
.13912
.11636
09371
.07116
.04874
.0?о46
.00433
-.01754
- 03944
-.06106
-.08248
— ЛООоЭ
—
/ '
.38
39
.40
.41
JO I
'Л 1
.44 !
.45 і
.46 f
.47
.48
.49 ;
ι
.50 ;
• 51
.52 ί
.53
.54
.55
.56
.57 ;
.58 ;
.59
.60
.61
.62
.63
.64 !
.65
.66 :
.67
.68
.69 ί
.70 Ι
.71 Ι
.72 І
.73 ί
.74 ι
.75 ;
.76 :
.77
.78
.79 '

Распределение Лап.іас.а—Гаусса
Продолэісение табл. Ylt
.288145
.291030
.293892
.29ό731
.299546
.302338
.305106
.307850
.310570
.313267
.315940
.318589
.321214
.S3
.94
.95
,96
.97
.98
.99
1.00
1.01
1.02
1.03
1.04
1.05
1,06
1.07
1 08
1.09
1.10
1.11
].12
1.13
1.
ΜΙ.15
1.16
1.17
1.18
1.19
1.2J
1.21
1.22
1.23
1.24
.'323814
.326391
.328944
.331472
.333977
.336457
.3389ι3
.341345
.343752
.346136
.348495
.350830
.353141
.355428
.357ο90
.359929
.362143
.364334
366500
.368643
.370762
.372857
.374928
.37697ο
.379000
.3810 Ю
.382977
.384930
.386861
.388769
.390351
.392512
.28969
.28737
.28501
28269
.28034
.27798
.275b2
.27324
.27086
.26848
.26609
.26369
.26129
.25888
.25647
.25406
.25164
.24923
.24681
.24439
.24197
.23955
.23713
.23471
2323 J
.22988
.22747
.225 '6
.22265
.22025
.21785
.21546
.213 ·7
.21069
.20831
.20591
.20357
.20121
.198S6
.19ο52
.19419
.19186
.18954
.18724
.18494
— .10429
— .09883
— .09338
— .08795
— .08253
— .07714
-.07177
— .00643
— .06111
— .05582
— .05056
-.04533
-.04013
— .03497
-.02985
-.02477
— .01973
-.01473
— 00977
-.00486
.00000
. 00483
.00958
.01429
.01896
.02356
.02812
.03261
.03705
.04143
.04575
.05001
.06420
.05834
.06241
.06641
.07035
.07423
.078 3
.08177
.08544
.089 4
.09257
.09603
.09942
.54694
.54559
.54403
.54227
.54031
.53814
.53579
.53324
.5349
.52757
.52445
52116
.51769
.51404
.51023
.50624
.5^210
.49779
.49332
.48871
.48394
.47903
.47398
■46879
.46346
.45801
.45243
.44673
.44'92
.43499
.42895
.42281
.41657
.41023
.40380
.39728
.39067
.38399
.37724
.37041
.36352
.35656
.34955
.34248
.33536
.124681
.14545:
.16597!
.18621]
.20626!
.22600 І
.24546 Ι
.26464 Ι
.28351
.30208І
.32034 '
.33827
.35587
.3731!
.39005
.4^662ί
.42283
.43867
.45414 j
.46923
.48391
.49827
.51220
.5'>573
.53887
.551601
.56393 ί
.57584 Ι
.53731 j
59S43!
.609 ·9
.61934
62917
63857
.64755
.65611
.66425
.67196
.67924
.68610
.69255
.69857
.70417
.70935
.71411
.κι ι
.81
.Si
.83
.84
.85
.86
.87
.88
.S9

I ^
s.
"-.
—*
-ι
*«
s
s:
Ό
Ό
О
fc:
■*-
с
it-
^2,
ό":
о
с.
1С iC t - ос ОС ccc — ?i .^ -^ iri to t-, oc C73
олмсісчсі со со со со со со со со со sz
іл о ι~ κ Ο)
•п4 »f -ψ тр т<
lsr-ι ^· t—o
"*· "ΐ"ΟίΟΟΟ
ООСМ IОСП г-н
■чмеч см со
ts Is <sts ts
СО to о to СО
MOtOMQ
CO COCO CO ft
ts ts r- Cs t-ч
0)10^0** CI Ο ΰ CI Ό Is w ^ iCj Ю in =0 CO -н -^ —< -г* СО СП СО UJ I- 00 -—ι Ю -—< '-' ~I< СО Ό
СП СЛСО СО GO чу«СОІр*-«сО СМОО'—іг-чсо CMCOCMCO'-t NOCOOJh ONOKDS С-Ю·—'iDO)
£S Si Ж Ζ? Ex ;£ 31 £3 S fa Я Ρ с- "э °° 4O)ioora ts г-ч ■* ts ,-< π< ·ο σ> ^-t со insr9JGc!
CO CO CO CO CO CO CO CO CO CM ОСЧННО О СП О ОС CO Is ts to ΙΟ Ю <S« CO CM CM .— О CO 00 00 ts
ts ts, cs ts ts c^tsbSN ts ts ts ts ts ^ЩЮчЗ^ CO to CO to to to to CO tO CO СОЮЮЮЮ
III! Μ Μ Ι Ι Μ Μ Ι Ι Μ I II
I I
с-* со іл go ts
со о со to со
iNMrtC-Ol
CO CO CO CO CM
-*· ОТ CN ~г «Э
00 *r -H ts СО
^гг«г-СЛ(М
cooo r— so to
СЧ CM CM CM CM
io ю ю cc i-
CO Ю ·~ι Is CO
ю -^ ■**< со см
CM CM CM CM CN
OIOOJCS
oo сэ со to oo
tHHO0)50
CM CM CM г- i?
ЮС0 ■* ос ts
>-< **< ts со см
«StOiOiO
r-H p-4 r—* f-ч r-4
r- Co CM ;-< ю
ts О Is GO CO
tO 00 r-t ^ Cs
-гг4 CO CO CS ·-»
-i<0 CM —< CO
ι—! TJ* Г- r-< "°Г
rHCOlOlOO
г-lr-lO OO
ОIОСЮОСI
C- CO CO ~* CO
COhio(3)CS
tsts to ЮЮ
о ^>оо о
CM — Is CO CO
00 00G0 OCM
tOO^ttTJCO
·<* ■* CO СЧ CM
ooooo
^i< CO CO CO CO
is со —· CM см
<м ю со см ю
OOO—i г-.
•*PCOrotsrO rMcOtscOCN "φ CC Ю Ю ts СМСЭгчт^СГ' GNMOIN
<м .-< со со со оі^яию ts со ст> со оо ts ιο cm 00 ·* от со со со —<
00 —· CO CO CO η·*<0 3)γη ct)inSO>rH MlOSCOO ι-н CO ·* Ю Is
r-« CM CN CN CN CO CO CO CO >* τί· -7> -»« -=J< Ю ЮЮЮЮЮ to CO CO со СО
CO CO ^· со CM
OOCO O—<<N
lOtONNr-
ЗСП C-CJi Ю
Is ·φ О О
Cs Is ts ts ts
r-t ίο σ> cn ю
to to to cs cs
ts ts TSts
ΓΙΟ ts Ο ΙΟ Ο (s ιο ■** *=F tO
OCO^COtO COr-<C0CsiO
см - оо ю со —ι en to ·Ψ см
30 00 ts ts ts ts CO CO CO CO
cc сч со ю со
CO CM О CO OO
оооазеоч
ςΟ ιο ιο lO to
со^игмо
Cs to ЮЮ-Ф
a> tsuocor-i
•q" -^ ^г *ф *ίΓ*
CO Г-) CM ■*< ts
^ct1 ""i1 ^ί1 ^ϊ1 ^
gj is ю со
coco со CO
•^1 00 CO CO CO
Ю vO to Cs 00
σι is юго —<
CI CM C-l <M C)
r-i to CI i~- О
О —іСО Ю is
О 00 to "Г CM
C-l Η Η in Η
ОЮ- I- Ό СЗ ОТ, COCO ■£
occntsioco c-ioootsij
СГ LO cc Is ιο
ιΟΌΏΟΝ
CO —ι Ct) ts ,j4
gi to is οϊ r-i
СЛ ΟΪ OCJ) О
CO CO CO CO -^
Ο Π Μ r-< Is
OO CO ■* rs
см о> «о см oo
«■VOtOffl
Ο Ο Ο Ο -Ρ
■tr* *тн ~t -i1 —!*
C-l Ю О Is CO
cneonoro
TJO to CM cs
HCCS'CIS
Ι—ί Γ—ί r—( I—Ч I—I
-C -Φ -Γ1 -i· ·+
И О to CI (О
—;< со о -n< to
CN ts i-t CO О
σϊ -"' cn со «л
—t CM CM CM СЧ
—< ГС CD CO О
tslO r-ι tOtO
-^* OO CM lO OO
tOtsOO —ι
c-i см см со со
-r -r-T-v-v
со oo ■* см о
СЛ ts 454 CJ> ТЧ
>-■ 'u'tstTXM
CO *ФЮ to 00
COCOCOCOCO
"ΐ· *& -t -гр -гИ
СП О CM ts CO
ΟΪ CM СП -r* CO
·* tots ОС O
аонеч'"
CO ^ ^i< *t* "^
•Ч< Ч· -Ч< ТГ -Г
3§?Ь?сл
0 ^· см о?
CM CO CO ■* 3P ЮЮ«Й .
ю о ts op en c2 -2 су со -r
i????
ю^ьсссТі ^γ-,μ^^ Ю'оьосо; © — .ν <0 -*< ю tc ^ ос а> .
<МС-1(М(М7Ч COCQCOiOC- СОСОООСОСО -тГ-Т,,ч*<'Тч-Г* ^Т^Ф^^Т* ЮЮЮ
О '-I сМ СО тЦ
Ю '-С (^- -^С Сі " .
Ю Ю Ю Ю Ю "~ ;
«^Й-?-?
I- СС 1- X J.

«О СО Ю Κ> ΙΟ 1С tO W (О Μ tO to to to to
■—' t— "—»·—· >—· о"-'е' - QOCSOO (ОСОсОСОсО сОСОсОсОсО OOOOOc'cc'co осСОООСосс Ljt^LjL)^., «-J-»<t—l^-J
*ь tii U< >-Ό CO ОС »4 О) СЛ if» CO (.,. ι-Ό Ю » Μ Οι W >t» Сл) Μ ►— _j cw Co —t СП Сл *.WKbO CO CO —J О^ Сл *.W^i-c
»& »Ь. *ІЭ* i£l £ь
CcOOCcCOOO
CO it». СОСЛ >—
Μ <— CO —1 CO
CO >*>· *Ί ■— СП
4* 4> i^k 4* 4».
00 00 00 CO -}
>— ►-* — о со
CRfcO-lCcOO
CO v- —4 О ·—■
4* if». 4> 4> 4>>
CC 00 00 -J -I
CO00 CO—" to
(О in- С 09 Cl
4». 4»- 4> 4=>. 4*
•J-4 —1—> —1
σ> σ. о. ел j»
—1 ►— СПО ■£»
о*· вин
4* 00 у-* і^ S3
4»· 4» 4* 4» 4* £»»£^>£»>^і£>.
чч^чч -j сп ей с» сн
CoCotO·—>— OCCCOOO-l
со»— ot *o to c^tO'.-слээ
ι—CC-JCOOO Ю-<-СлСЛ4=»
O-Ji—COCO ь-СИОО—1СО
СИ СП СП СИ СП
-4 СП W* 4*
ι-» CO СП Co J>
ь- -ι to ІП -4
Ol Cl О К О
4». 4h> ι£ι 4^ 4b.
Sen o> спел
Ю —· JO
tN- ** Ol S Ό
•-4 en ча; ео 4*
со to 3-. ς-, ι—
4>. 4» A. 4*. 4*.
Сл гл сл спел
to ее -4 σι en
■— r— to CO 4*
-4 со оо σ> со
Ocn4*Nj^i
ооос о
Сн ЮСсСО
4* »0 ь- _ цр
ι—oo-i —jco
4* 4* 4* 4ь 4*
4>.сп-і сою
С» О Со J: СО
*· _> VI—I 00
1 1 I I 1
со со со Со со
С» Οι СО ►- С?
СЛі— ^..COtO
СО Со СО о. 4*.
111!!
' |£1 |+* lS Ц^ ΰ
>с Сл σ> *^ι со
COOoucOcM
>— Οϊ W w <£>
Сл ОіСл Сл СЛ
*-* Ю Со Сл Оі
00 Сл ί-* »ί*. ОЭ
Μ Ι Μ
do en*- too
·£ слеплю
COCOrfa. СЛ 00
Mill
О - i С О
АОИлчСл
CO _, ι— Ю ι
се со ос со со
о to ст. to ср
Сл СлСл О) СП
-4 00 СО О —'
if- СП —JO0 СО
СП (О СП 00 —1
1 Ι Ι Μ
сослСоо -5
ооі^э-о
ь-1 Сл COCO СО
Mil!
ρ о ρ о ^
Сл СЛ СЛ СЛ 'Л
Сл σ> --» со to
О »— СО »*>. сл
00 00О ·£» С£>
Оі Оі Οϊ С/· CTi
СО ►£* О* СТі --4
О о _ о
■Ψ* 00 (О Μ ►—
ι м ι ι
о о со со со
Οϊ ΪΟ СО СИ- СО
WCO I- 4ЧО
СО СОЛ. ОСП
1 II I 1
— о ; о ^
ОТ СП C75 СЛ СП
_ ι— СО 4* СЛ
—ι *-о >—* Со сп
-4 Сл со ос к>
сп о- о. -4 -4
—1 00 СО „ ι—
со ос а>>ь- м
СО 1— С~. 00 СИ
ι ! : м
QOOOO
СО 00 СО — < —4
О 7) COCO СЛ
>-»05N3C. _Э
tO-IСОСОСЛ
I I I I 1
о -г; о z> о
С» СП о: -4 -4
0.05(0010
сс^- — -J о
-4 ■*>■ Со 4- С7>
—> —1 —1-J. -4
to to со ct л-
■_ -J Со СС СЛ
ссмссс»
: ι ι ι ι
О о О ^г О
—J en оэ сп Сл
Ю ОО .A* Ls СП
СО#· СЛ А. СО
<-■ с. ^ч, —ι со
I I I I 1
О ^ J 2 О
444SS
Сч->^СП>1 СО
4^ —Д ν-* Οι Ό
>-■ ~J Λ. ,£. ОI
СЛ СЛ СП С, О
ι— СТ. О л^ 00
to to -ι ос сл
Mill
с о эоо
сп^ л coco
to —ι со со Φ.
Ο -J ΙΟ —4 Ι—
оо ^. СОСл >-*
Mill
оро о с
00 00 00 ОС 00
_ ►-· С0*-О5
СО СО (О —4 .-О
00 COCO 00 СО
>—*. сл ас со
-J*. СЛ СОСЛ
Μ Ι Μ
ОО О О ~J
to to >— ·-· 2
(OJ»to>b-(0
СоСл СП сл ^.
--) COCO 55^
Mill
о - oo ^
00 05 CO CO CO
-O.CO ^Ю Л-
00 ч>5 00 ^а. О
■^ CO со СП СЛ
00 00 -4—> -4
С ч_!С0 CO "J
to со cc Sin
ο ο ο j о
ΟΟΟ — ϋ
*. ι-ΌΙ Ю*4
to *-* en ο οι
to о о о со
Mil!
■ζ»
3
if
1
■ί
Λ СЛ СП СП-4
і—ос»~чсп
СП »-* ίο сл 4>
Ю-4СО*. СП
нмьію tO
cocoo>--to
СЛ »t- СО to (О
Фк ^. СП 00 to
to oo со—ι j
totoMto to
CO >£>. СЛСП СП
СП ОСП Ю CO
OtOi-4 01
to to to Co со
—4 ОС СО М
CO Ό CO CO CO
—I СЛ Goto · *
с оа сл со
to Co -' 7-1 en
со со со со со
·— ·— ·— to to
СП СП 00 Co Co
COCO Corf* ·Ρ>
CO CO Си СО СО
СО *~ ^ СП СП
АОСі JCO
hik rfi* h^ t^- >>.
κι со ^. en en
CO CO CO CO CO
О. СЛ -1- <Му-
Co — Co to сл
,ί. ^і^СЛСЛ
-4 00CO o>-;
CO 00 CO —1 •■J
CO СП to COCO
Сл} VOI CO СЛ CO
ЧЛСЛСЛ СЛСЛ
iOW>^01J>
СП . ι СП w^. CO
—) CO f—to J—'
>— со 3>toen
to to to to to to >o to to to to ι
и^ I—· -^ >—» ι—· J: О О О О
4к со to ι-> осооо-~»о;*л
ООООО СОСОСОСОСО (О СО Ό СО СО CO 00 ОС 00 00 СОООССОООО
>i».COtOi-O COOo-jCntn *■ СО Ю >— О СОСО-4СПСЛ .f.COtO'-O
—1-4 -J —I -J
СО 00 —I СП СП
>^ СО tOI-Ό

JtCtOtCtO ICtOtCl-iC МММЫМ tOMtOtOtO ЫЮММЮ tOlOIOtCtO IClOIOtClO tC 1С 1С 1С 1С tO 1С tO 1С 1С
Сл Пл СЛ СП СЛ
CO ОС -4 СГ. in
О101СЛО1СД
*<■ Ы tC ·— —:
^"^ifcn feiftA^ifc cococococo cococococo ιοίοίοίοιο tototoioto
oo »-t от en aiwto>-o cooo—іотсл Ж-coto·—.-; <о»часл »ωκ;>-Ό
<o oo -о. от сл
,:^ .Λ*. Js. φ., vt,
со со со so со
Οι ^ »ΐ- »*a -^
<_ O; >— C. ·;-
>— — Сл v~. .'-
hU *■* -Ь. -Ь. **.. ,.^. Λ^Λ A ►£*. н^ КО >fc» J^ *—.£*>£- -^ JU
CO CO CO CO CO CO CO CO CO CO CO CO CO C0 CO CO CO CO CO CO
><- »~ ~- t-^» U Ctf Ju Cu iv tv Cv Cv-f tC >— »— ■— f~u -^
.fc. ro >-* CO ^I OT*«tO 00 OT*-tOc;00 Cn"CO"i-*coOT
Сл CO Co oj CO >— соАСлСл Сл чл >&■ to „j kjac a*-J
S^WMS Wh^lOS ОТ ·—Ό 'Ϊ* to СП 4* ОТ Ю CO
►it» к** >£■. »£*■ >& с> ,£* „fcfc ^ >£ь
CO CO 0O "■ 00 0000000000
COCOCOIO O-OOOCOC^J
C^OwOtc^ ЮГСООЧ
OiCBWulS CKOCOCOS
ooncoSo: со en ς., со ς»
^ i£« ^ »** >f».
00 00 00 00 00
«■» >—» -~ϊ ^ СГ>
СЛ tC CO A. to
4*- >^ bj^ 4*. >t-
О0 00 ОС 00 00
СЛ Сл »+*■ ** t£*
-J OS СО ОТ СО
Си —t со ι— to
ОС ь— -*J 4*. СО
О О О О О © 15 _> О О © Ο Ο Ο Ο
со ^ ·** сл :л
СО СО ОТ -- £*
J- — 00 СТ. Сл
Сл ОТ ОТ -J -О
00 1С СГ. О СЛ
СЛ ѵі -4 СО СО
-J Эо 00 СО -О
СО 4*· 00 СО СО
■ѵі ts> СО СП ^
О© О ЗО
ty tC СО СО СО
Со со со ос со
СО СО Й* Оі СО
оое оо
Ю 1С 1С 1С (С
Ю СО ib- ^ СП
со -і* с ст. to
ѵ-ССФЫЮ
озаоо
tototo toto
СЛ СП ~J ~-4 00
СО к^. _ ОТ СО
юсоелл» со
Q so ;о оооо^
ююсососо сососососо
СХ СО н^ .-» tO СО Со ч~ Сл
СО от СО О -4 Λ ι- СО -^ —
00 сл ί>. Со Ψ» ОТ СО ч- О -4
О С! О О О
СО СО СО Со Со
О: --1 -о. СО СО
ГѵОКМСл
ОТ С; 00 >— СЛ
ос© оо
- 1 ОС СУ 00 00
СО О tO Сл: СЛ
о- со to ей о
-*1 tC ~-J *» *-
о о о ■= о
ОС Об ^I СО СО
СП --Д СО ^ (С
Со -~J J-* ОТ О
со со со о to
оо с- о о
со _сосо ста
со *ΐ* от -о со
via. СГ: СО -О, (ѵ
Сл СО Со Со ^.
OOG ,~о
О Ю СО СЛ ОТ
о ч*-мо
О О >-» »—1 ь-»
00 СО >-* 1С ►&.
СИОСлО
00 -~) ОТ О. СЛ
I-* )—< н- tC СО
Сл -J 00 С >—
CnO^ioOl
4w 4- -ί* Со Ю
to to to to ю
Co ·** wi --1 oo
О СЛ СГ ■£- CO
>— с_- СО-О »<-
СОСОСОСОСО CCOi^^Ja.
*_- >—' СО ►.'* ОТ StOOMCo
**■ 00 ІО ~-1 tC Οι ^ 00 1С
*- ooccootc сл^сосо^
Mill Mill Mill II II I IMM Mill Μ I I
CO CO CO CC CO
CO «- СЯ -q ^1
00 СП CD W· CO
со о·! и** ^ *
»U Oi (Л О W
F*i. ^ φ» Ji, Ι-ϊί.
CO О >(ъ. СЛ СЛ
Ο ί& к^ -* CO
»^ ίΑ 1^· ^ »ΐ^-
стз*-а--д-аоо
Сл О Сл СО СО
Ο Со t^ Сл ►■>·
»ί*. 1+i. ^ ^ *b.
OO Cn со CO CO
Οι CO Co**
W. U.» CO ^ CO
·+* ·*" ^ -i ^i
ее о to со уэ
спел слео ю
СЛ Оі <-> СО ч^>
^ ^ bU. »*i. pfb.
00 00 00--1 -^
со σι ts^ со to
слииоі»— со
.Ax *ii. ,£». >^. t-ii.
Οι СП СЛ >uw CO
-J О СО >**■ C7i
►Λ. Ji. »f^ C-- CO
σι сл «и ю to
CO tO CT) CT. -^
1
I I
Mill I I 1 II Mill
;oo«3'0
00 СЛ tC COOT
о -·- о. оо оо
кС* tO OO 1С CO
о о о о о
C'J СО 00 г» ^!
СО О -4 W СО
-4 -!^ >— Οι СО
to·-) о с -J
ООО DO
-^t ^ ОТ ОТ Сл
О) Сѵ СО »**. СО
to со іс і—оо
ниОонн
о - оо j
сл Сл >*>. .с», со
СЛ ОТ *—' Л
Со ~4 _ Ю (С
чсооо toco
оооо -
CotOtOi-Ό
МОIОЛСО
О 00>f» СО>-·
cote осл Сл
о о ооо
о -Sir-to
WtCOeCTlH-.
1С СЛ —1 1С ι—
oo о оо
to со J**^ сл
st-^t-'cecn
COOT J^ CO?»
4* H- hj СЛ tC
С О О О О
ОТ СП -4 00 СО
toioscn to
~ СО *»■ О ^I
ОТСО to*.
Sc
О О*-1 1С СО
■^ ΟΙ ОТ 4*. СО
СЛ -1 "^ 00 ►-'
СО СГ. Сл ОТ 00
lotototcto iciotctoto юкзююю ююміоіс мюююю tctcKStcto tctotctoic totototcto
слслслслсл ріслслспсл »i*4^4^4^V ^>>>λ.κ^4^ сососососо сососососо totototcto
СРСЛ-^ОТСЛ 4^00(0»—^- СОООМОТСЛ ^COtCi—O СООО^ОТСЛ ^СОIС—О СОСО<ІОТСЛ
to ю to to to
*» Co tci— о
to to to to to
cooo--lOTOt

124
Распределение Лапjaca—Гаусса
Продо.гясение таб.і. \"ll
τ
2.60
2.61
2.62
2.63
2.64
2.65
2.66
2.67
2.68
2.69
2.70
2.71
2.72
2.73
2 74
2.75 j
2.76 !
2.77
2.78
2.79 1
1
2.80 ι
2.81 '■
2.82 |
2.83 1
2.84 '.
2.85 :
2.86 1
2.87 !
2.88 |
2.89 |
2.90 i
2.91
2.92 |
2.93 |
2.91 |
2-ё 1
2.96 |
~-tl i
2.98 !
2 99 |
3.00 !
3.01 ι
3.02 ;
3.03 ;
3.04 i
~ (ι
.495339
.495473
.49560·!
.495731
.495855
.495975
.496093
.496207
.49o319
.496427
.496533
.496636
.496736
.496833
.49o928
.497020
.497110
.497197
.497282
.497365
.497445
.497523
.497599
.497673
.497744
.497814
.497882
.497948
.498012
.498074
.498134
.498193
.498250
498305
.498359
.498411
498462
.498511
.498559
.498605
.498650
.498691
498736
.498777
.498817
Vo (<\)
j .01358
.01323
.0)289
.01256
.0122:;
.01191
.01160
.01130
.01100
.01071
.01042
.01014
.00987
, 00961
.00935
.00909
.00885
.00861
00837
.00814
.00792
.00770
.00748
.00727
.00707
.00P87
.00668
.00649
00631
.00613
.00595
.00578
.00562
,00545
00530
.00514
.00499
.00485
.00471
.00457
.00443
.00430
.00417
.00405
.00393
Ъ(П
.07824
.07692
.07560
.07431
.07302
.07174
.07048
.06923
.06799
.06676
.06555
.06435
.06316
.06199
.06082
.05938
.05854
.05742
.05631
.05522
.05414
.05308
.05202
.05099
.04996
.04895
.04795
.04697
.04600
.04505
.04411
.04318
.04227
.04137
.04048
.03961
.03875
.03791
.03708
.03626
.03545
.03466
033fc9
.03312
.03237
?:: (/)
-.13279
-.13167
— .13053
-.12937
-.12818
-.12698
— .12576
— .12452
-.12326
— Л2199
— .12071
-.11941
— .11810
-.11677
— .11544
— .11410
— .11274
- 11139
— .11002
--.10865
— 10727
—.10589
— .10450
— .10312
— .10173
— .10034
~.09895
— .09755
-.09616
- .09478
— .09339
-.09201
— 09063
— .08925
— .08788
-.08651
— .08515
— .08380
-.08245
— .08111
— .07977
— .07845
--.07713
-.07582
— .07452
•4 (0
.11053
.11291
.11517
.1173?
.11935
.12127
.12308
.12479
.12638
.12787
.12926
.13055
.13174
.13283
.13383
.13473
.13555
.13627
.13691
.13746
.13793
Л 3832
.13863
.13886
.13902
.13910
.13912 1
.13906 !
.13894
.13875 '
.13850 i
.13819 i
.13782
.13739
.13691
.13638
13579 :
.13515 I
.13346 !
.13373 !
.13296 j
.13214 !
.13128 I
.13038 !
.imi
i
| 2.60
2.61
2.62
2.63
2.64
i 2.65
2.66
2.67
2.68
2.69
2.70
2.71
2.72
2.73
2.74
2.75
2.76
2.77
2.78
2.79
2.80
2.81
2.82
2.83
2.84
2,85
2.86
2.87
2.88
2.S9
2.90
2.91
2.92
2.93
2.9!
2.95
2.96
2.У7
2.98
2.99
3.00
3.01
3.02
3 03
3.04

: ее Со с; со со Со С- со со со со со
СлСлСЛ****·»*1'·*--'^ J*. Ja. 4^ **ь ·**
ιο»— ч^ «о ее -ι с сл о- ео ;о —* ·
ws^wvww-COCOCoCOCoCO Со СО С: СО СО СО СО СО СО СО СО СО СО СО СО СО СО С-; СО Со СО СО СО СО Сс
^СаХХСОСоСОСОСоСОСоСО tO ΙΟ ΙΟ tO tO Ю tO Ю to Ю μ μ ►-· t-» ь-· ϊ—* »—» —■ ι—· ι—» ОООСС
с iOccsjQui t^ccio'-'w «о oo "^ О; ci ^ w to н о со ос ~-i ел Сл >-.- Co' с >—* о со ос *<і ет ot
"fc>. Jb. ІАи U*. »^ »ΐ- >£>■ ►£* ^- ^ "^* ***■ ►** ^- **^ ***■ »**■ ·**■ »£* &* ^· ^ &* *** «^ '— *-*■ ^ *** *^ »^ *** »$*■ ^Atfc^e 4* И- 4- я— *>-
SuStOtOtOtOtOcOCOtO^COCOCDCOtOCOtOcOtOCOCOtO CO CO '-O CO CO CO CO CO CO Ю CQ CO CO CO CO CO CO CD CO CO
cotOtD (0(DtC(i)iO COtOtOO^CO (ьи.СОЮЮ (DlOlCtO^O CO CO CO CO CO «j CO CU CO CO CO CO CO CO CO CO CD CO CO CO
Cj2jC4 -~g ~u -4 *■*! -О ЧС СЛ CP С£ ФО)Оі<Э)Сл Ol Сл СЛ СЛ СЛ ^*-*"^·^ »£ OJ CO CO Co К.Ю(0»Ом »—<—' Ο Ο Ο
^■^o>u^^^^toc«?oo*-4cncncoto»--«3 0oa--c^cot-- to oo m »**■ to о оо ел оо ^ оо ст> со >-- оо сяіесооы
£оі^соссоОосссо^слсосоо4*осл»-'СЛі_-(а>.^і сс >— to со со to r- со сл со со **■ оо ь-* rf> сл Οι os сл ю
СО СО CD СО tO
со оо со оѵ се
COCO CO 00 CO
CD C7) СО СО См
СО СЛ О СО Οι
seS8ggg§§§§SS§8gggsec^
о о С; с; о о о <
соооо
О QO О О О О О О О
О О С? С О (_>СООС
to to to to to ю to to to to
OcOOQOtCtOCOOOO*— t— H-tOtOCOCO>*>>4^C7. Сл CTl C7i ---l 4 00COCDQ *— ►— fcO Co Co і^СлСЧЧ CO CO О <—' . _
Х-£^О»^^О^^>-еЛС0С0^10С7і>— О; *-*ς7ϊί--··-0.10 CO ^ О СП СО Ο 0"ϊ 4* ί— CO C7) ι*». ГО ·— CO CO 00 --1 "^-l --J -^ССООС
■ о о о оооооооооо о о о о о ооооо ооооо
r;CLJC-i ►—■ ι— М-» *—· к—· '— I—* (—»»—* I—« )—ι Η-» i_j j_ )—ι i_t (__ι ,_j >__. _* м.— МММ
tOCOCO OOO^*»-4 ►"* ►— Ю ЬЭ Со Co Co 4^ **. 4*. СлСлОэО-^ -«*1 "<1 CO CO CO
tO СЛ OO m^sOCo ОіСОСоЛО CO -g ι-* СЛСО CO*^1muiO 4*- CO ff>- JJ· 4=>-
-*i 4*- CO О О О О tO *i^*-J — СЛн- СССЛСО»—м- tO CO СЛ СО 4* СО СЛ СО ь-Ό
ооооо ооооо ооооо ооооо
<—· Ю tO tO fcO ЮМЮЮЮ tOtsjtOtOtO Ю tO СО СО СО
CDCOi-ΊΟ toCOCO^A СЛ СТз СЙ -4 00 Со СС О О—
СО 4»- СО 4=»- О Сл >-» -^ СО СО СЛ t—· 00>Ь. ι—» ОО ^ ^ ω О)
»— to ел оо со со ел 4> со со сл -^ *-* ел со о со со о со
\ \ \ I J I J J I I .1 I \ \ 1 I I ! I I і I ! ! 1
ebb bbob'o ρ ρ о Ό о ο ο Ό о о Ъ>Ъ>Ъ>Ъ>Ъ> о о b p b
tOtOrOlOtOCoCAiCOCOOOCuCoCOCOOJCoC04^4^4*4^4*.4*. ^ 4^ 4^- J&. μ-
a4COOO(OJt~*h- ЮСО^ОіСлОIЧООСОО Ь-^ОЮСО^ СЛСЛ-^ООСО
ОЗСЯЮ t£>0)4^>-00 CD^MOOO "^СЛ^ЬЭ»-· CO^COOOO CO O0 Ou CO CO чі^ ч^ i_< — і^ uw"f*w/^tv«
iO^Ol СЛЧО^О Oi^COifO) ОСП-· CO Co CO >—' 4* CO СЛ CO tO tO 4*. ---1 tO CO Сл CO CO UiOMSCO
ооооо ооооо ооооо о
слелслслсл слслслслог с» σ> σ> en σι σι
с_; ►— Со 4> Сл OJ-^COtOO Μ СО 4> Сл CTl 00
tO СО Ο »-ι tO Co4>C7>-^CO J—' 00 СЛ--О. СО ь-*
►. ·. ЛѴ-ι ί* π Γ·Ί Г.ч Гп *^Л t_l в.1 Г.-, 1_1 *-*-·. ί—> >—■ JS. ΛΛ
$c о о о
О) -*J *J "--Ι
\*s >rwiui ww CO Ο •~J CO
СОСЛ'-О.СО ь- 4*. en CO tO
ООн-4х ООСОСОСЛСО
о ооооо ооооо
ΪΟΟΟΟ OOOOO Ο О»—ч-4 >— м-»— —
сл0^от*^^'^^'^^^оососооососооососох)ср?осо cocdooo оооо*-· »—і-*і-*і-.н- ниюмьз toto»ototo
СЛС0Ю<ОIОС04^0^^00О>-''О4і.СЛ,*^00<0»--'IО»^СЛС7і OOCOJ-'tOCo СЛСЛ*^1СОО ►-'СОі^Сл-4 ООСООн-СО ^СлСЛ*-ЛСО
COH-»4^fc-40CO'--JOti^'4»-'OTCOtOa50»*»'OOt005C5t^cO С0-^ь-*4^00 tOCTitOCOOJ COtOCT)00»— СО СТ. 00 СО J—* toCO^^-к^-
^cn^corf^cnoot—icjiv-1-^^»—'е?09чмччосоо(0(оо oooco-a слюсосоел tooooo*. cooo»ooco ct:cj:co-vj-j
cocococococococococococoeococococococococococo cococococo cococoeoco cococococo cococococo cocococoeo
*СЛСЛСЛ)^»^>^^»^*^4^Ѵ^4^^СОСОСОСОСОСОСОСОСССО N3 Ю Ю ίθ tO tsjtOtOtOlO ·—«»—»»—·»—· »—' ι—' >-* м-> ►— м- ООООО
^о^-ососс-^слсл^оо^он-оссоо-^елсл^сс^ь-о сосо-^слсл ►** со to ►— w- сооо-^слел ѵ^ со кэ »-· о сооо^іо;сл

j Co Co CO Co Co COCOCOCOCO Co Co Co Co Co Co Co Co Co Co COCOCOCOCO COCOCOCOCO COCCC0C0CO Co Co CO Co CO CO CO CO CO CO COCO
! <r> to to'tO CO CO CO CO CO <0 000000200 0000000000 »-0. «-^ -0. ^J ^o *-a^4*^4^4^j oao. О": О C- cr Οι СЛ СГ> Сл'слслслсл Слог
I to CO "-* w. Οι ^СОЫі-О CD OS —ΙΟ. СЛ *ttuj>-U CO CX -4 О": Сл >*>■ Co Μ >— о CO 00 -J σ: Сл J»OJK3»-0 CC 00 -О. СЯ Сл *. Со
ѵі^ >t>. φ* >** Φ» ^ .£- »ι> >ί> ^. ф-ti^Ji^»^
, ν- се с» со со со со -о со со ее со со сг со
I Ut ~ CO CO u CL* CO CC CO CO CO CO ~>
I c_, CO Ό ·· < CO tO'Off (С'П СО CO '.O — CO
O". C~ CT> 35 Oi СЛСлОіСЛСл Си >ί- »£* Φ- и^
. -J СП &■ CO ·— COOOOlifeb- О 00 О CO ι-1
*&· »**■ »fc- >i* i^·
со с со cr ti
CI COCOCOCO
CO CO CO a- CO
0*.0-CoCO ι
00 O. Co c_ CO
^ φ. Λ ^ ^
CO —> CO CO со
CO CO CO CO CO
CO t*. CC CO CO
U W t- Μ κ-
Сл Μ ОС СЛ ΙΟ
*C\* >t* r{^ />. |^
со со со со со
CC CO CO CD CO
CC CO -O cr CO
с <„ с со со
05 «- C5.M
vfc* 4^ *fc" »£■ vb.
CO —* со ■·-■ со
CO CO CO CO CO
CO О. О ■ ОС 00
00 ОС —1^3 О.
СССОСС φ. СО
>^' 00 ио -^ >"
£±^>*~ Jb* Л*. ѵС^ ►**.
СОСОСОСОСО COCO
со ·<- со со со со си
θα 00 00 ОС 00 СЮ --.1
CuhjMWO О СО
Сл 00 tsj СЛ ~4 О tO
'оооос с—сое соосо
ѴѴО^^ с~ О С _ О CyOCCU
■_> о _ О С CttOo с с с, о
luMw^-i — ._. ь- , ю to [\. Ю Μ Ю
>**■ >г* сл σ> сл —jooocco-' t-^^-iocooo
оооос
о о оос_;
о о с с
О о о о о
С С С ОО
О С О с* С
со coot со со
CJ н- СО ^ СЛ
О С О О О
ссссу
с_- _ о о _)
СО Со Сс *. .'-
—» ос со ·— и
о с с о о
, С CJCU
о оооо
KU ►£* Jb. i.U СЛ
соосо
о - со о
CPCLO
Сп CtCn Сл СП
сосл -ч со —
с о о оо σο
О с; о с_; о СО
О с о с о о о
СП СТ. СП -J —J -~і -^)
со ст-оо ►-* со осе
ОС- Q ОО
о ~ ооо
ооооо с ~ о с о о 2 о о о ооооо соосо о о о о ^ о coco о о о с о сс
__ с о ο ο о ооооо оо со с ο ο ο с сюсо з с о с о о о с - с_; о соосо оо
К/ tO Ю Ю -Э Ю tO Ό tO tO Ю СО СО СО СО СО Со Со СО СО »і~ >£- >^ А- ·£*· >ь^>-^СЛСЛСЛ СЛ СЛ СЛ С/. О DiO.O^^J »-0 -~} 00 00 00 OOO
_ — кэ со со Ф.сло^-іэо сос^юсо Ф-слотоссо о— с·-· »μ. σ> S'-o_mco ςη --α со >— ю .!·· σ os ι- со оі^оюа чо
оо Сл со с оо -о en >t- со ю і^місюа *■ σι го о to сл сс to σ> ѵ- сл ι— сл to ее о. ф. t^ о ".о со со со с ю >сѵ ^з о >*» со ><=■ с
SOCCO
Ч ~4 ^ · -1 00
_ *. с-, оо —
00 1—*-ОС CO
OCCOQ --©CO —
0000 COCO СООрЭС
с^ о, со *— -ΐ» <-t _; со 2 <о
00 »i*. ь-· 00 СО Сл -ί* Сл О ОС
3 ООООО ООООС
о с _э-о о о'- Ό с Ό
•—: ^ ^ ^ т^ — -— — — — — ^ ^ ^ >—' *-^ —' ^^ «~ ^—·
и-' ^— »-· ГО :о СоСОСО-іхнь. СлСлСлЗ^СЛ ^-1·<10000Ο
COGi-OCOOi С4^^ЮЗІ С^СОСООС bO*^lO»vjrO
οί-ooco'-o o»r-cotoco ^чсоіо *-i.t.cocoCo
ог-ооо ооооо о о
ь— СО Ю Ю Ю ΓΟΪΟΙ^ΙΟΙΟ tOtO
со о о»— — to со со S-* >?і. сл съ
-4 Ю 00 г·"» со СЛ »-* -0 СО Ю Сл 1С
Cnootooo.^ toootorf» ooco
I
о:осо
■ч. (ОIч^ЬЭЮ
Ю — СО*· йі
А. О J) ■" со
ГО t~ О ОСл
О Г ООО
ι., to tote ' ■
СЛО: О: ^і 0о
СТ. СО Ό ^) А·
to о со с to
о scop
to t-.Coc^ Co
СС Ό Ο *— Ю
к-· со 5: *■ to
СО^- 00 05 0
оозоо оозео ооооэ со'о'о'о
Со Со со со со t со со ij^. ^. *ί^ к- ^^· -"- ^*. ь^ -: кЬ· сл сл
СОСО^СЛ^5 «*а ЭС СО О >—' tO'^COs-Сл ^ІССССО^
. ГО ^о СЛ -ί>- Со Ю >·- -J - О СО О СО СО О CD — Гч^ СО
^сососссъ >fc»^-c;coco с;-^о:^)со сосослсосо
СпСлСЛСЛСЛ СлСЛС7>СЛ_
ЮСО^СЛ~1 ОО СО О — СО
Ф-СЛ-JCpO Ю^'СПОО
^ ^J ~ С. СО *— t-* to і-— CO
оо
О. СЛ
^ Сл
СОСл
to сс
со Со Со Со Со Со Со Сс со I
СОСОСОСОСО СОСОСОСОСО СОСОСОСОСО СОСОСССОСО СОСОСОСОСО СОСОСОСОСО СОСОСОСОСО COCO
СО СО (О СО Ό
о о·- ^t σ. сл
СО СО СОЮ СО
^. со t» — о
00 СО 00 ОО ОС
Ό *j. ^і С5 СЛ
-.- со ю *- о со м ^ σ; сл
4S-J4-J CjCUOO-JJ
*· Со К "' w СССС'-ЮТСл
О СТ. СГ σ; О СЛ С" Сл СЛ СЛ
-^ СО Ю « О c-j 0; Μ СП СЛ
Сл СП
■>■ СО

Распределение Пуассона
Г-'7
я·
К
«1
Si
о
о
а.
«s
с:
*
I:
<3
ΐ
о
О ~» СМ СО *? lO"ONuC^)
00 00-f .-ι СО
СО 00 СО со οι
C-~t-. .Or-ilO
CO tO 00 CO —'
со t.j н о о
о юоо
coooo
OOOO
OOOO
t icoocn
ЮС0СС ""J"r-<
О coco ^ r-i
ѴИНОО
OMO
MOO
ooo
ooo
COCO OO-sf t~
CO CO CO ОО I--
■*03"0 О
00 ,-icOCOt-.
Ю CO CO V} GO
О)*мімо
TtCnOO
CO CO CM
<N-iO
—ι OO ι
Ooo I
ooo
oajrt
t~oo
ooo
ooo
ooo
.-"CO CO CO CO
00 CM l— !*·. CO
00 CO 00 CO CN
• ЧОІГ-.0
jeeooo
ase
CO Tf
CO О
Ί. °
о о
о о
00 Γ~'Μ·4>00
Ю CN СО СО Ю
СОСОЮСЧ —I
О О< t- fH О
СО COO ОО
СМООСОЮсМ
С" ^-ί СО —ί Г*
Ooo со с~о
ЬСОіООО
COCNOOO
со *-*
--· о
оо
о о
оо
0^<"МСО-Ч<
ΙΟ СО Г-. со
-3· г- с-- ю -м сТісо-^со
СО СО СО ·=*" ГМ OO'tOO
l/^OOOO CO CM CO О
00 t— b^OOCO
—· СМ<М—.0
- . . . OO
OOOO
t4» 00 I~- no CM
CO ~* CO OJ O»
CO τ*· С О *-»
4- 00 :0 t~- CO
" <MCN ,-Ό
nooc
oooc
PJ-^tUCOCO CM
00 CM CO .Ό CM Ο
о ·>· со со о о
^м .оо о
MNOOO О
ι ι ί
СО ιβ t·^ COCO
С- t» CO —ι Ο
00 CO ^ •-Ю
HCOwnO
ИнООО
•rf 00 СЧЮ
g§gg
1 1
Ο -?Ό0 Г-О
CO—<~1Ю
OOOO-·
CO t — OJO
i~·· О О О
oooo
CO CC CO CO CO
сиіослюй
гч о >.ссо о
CO r-t со -ѵг со·
—I ГО CN »-< О
CNCN СОС-I
со-« ч- со
гчСОгчП
«ООП
ОООО
о со сет со
СООтОО·-·
*· < СО 00 ι- Ю
остючю
СМ СО СМ—<0
■^ооосм
СО t— О CN
Iч^нО
OOOO
ГООИ-IN
,-f Г-- О Ю О
СО-ЧГ " IОГ^
см оо ιο см ■·*
СМ СО СМ г-< О
СЧС0 СО·*·
—I 1/»^-<
τ* ОС О О
нООС
ОООО
О -*- СО 00 с—
СО CN СО I- -*
со »л ,-< см со
ту! -ч- ·**·-, СО
СМСОСМ — О
Ю 00 IN СО
ою«ас^
—KNOO
r-ιΟΟΟ
ОООО
со со со со со
гч τ О СО 2J
f- ЮСО СО СО
СМС0СЧОО
•^•СО -ФСО
оооосоо
00 ·-< О О
О О О о
ОООО
О —I СМ СО -ф Ю СО С~- ОС СО
О) COCO -#(М
,-н -4t« 00 1-» О
τ—I *-Ч СО СО СО
О СО ·-< 00 Сч
СО СО СМ ОО
іОіО*ч со
см с ι см о
СО ·-· О О
ОООО
ОООО
г--со со-*»-;
00 ^-СО 00 СО
CJ СО ^ ». О
oocoot-~CN
COCOCNOO
t- СчОООі
•tCOrtO
■*ооо
ОООО
ОООО

/J,S'
Распределение Пуассона
^*
ч
~
с
S
<»
*
«>
о
<r«
.-,
4-
"~ч
^
с
гл
'-.
^
t=.
.
'-
"
С1
~
У
35 ~ —< CN
■—< ι Ι ι—Ι
СП -fi-с
-<оо
. ooo ι
I ooo 1
j ooo
ί
COIN
~o
oo ι ι
■ oo 1 1
■ о о
I
, СОСЧ
Ι ο ο
! 88 I I
co-<
1 oo
oo ι ι
■ о о
I
! *~
1 OO
; °° ι ι
1 oo 1 1
:
! i1 ! ι
!
! о
ι ο ι ι ι
'gill
1 -4
ι Ο
ο ι ι ι
, ο 1 1 1
; о
ι
' 1 I ! I
III!
!
| HrtH
Η
О
OD
:·
CI
{M
/ u·
О — :s ГО ■*
04979
14936
22404
22404
16803
CNf-t—СОЮ
onmiOrt
ко к» —«со ν
Ю lO CO rsl CD
О —ι CN С* —ι
— г-- OOOO·*
00 СЧ СО ■"*· t—
OOOOCNlO
COt-cONlO
CrtlNCi-
MucONM
(Ν-'ΤΌ ·*00
CO 00 -ί" Ο» "φ
OrtCSCJH
07427
19311
25104
21757
14142
0820S
20521
25652
21376
13360
•M CN t- 1 ~*
bISCNOT
OJ^CDOM
О CNOXM—·
гссоно
[МСОгчсОСЛ
ООЮСО О
OWiOCrH
О Г~ -4*"*f< Ю
OON^-( CO-H
oco oococo
r-i -Ф CO CD О
О COO — CO
-l< —ι О О СЧ
(NNOCSOl
СМЮГ-* OO СЛ
r-* Ol CN ■—* О
О —(СП CO -tf*
Ю О Г~ OO 05
«"OOO
oo ^fco — г--
OO-MN
О юс»о о
— oooo
lO О ГО го о
очгооооо*
-ФЮООсоО)
слѵ-оо
ооооо
—ι OOOO t-
CNP-IМГ-Р-
NOtOU3i-l
»«-oo
ooooo
Ώ О Ю г-1 r-ι
со —'Coh-'*
о со со·* —·
οΟΓΟ—ιΟ Ο
ооооо
-* Г-■* "0—«
Ю0О0О 00—.
СО — ·—'CO—I
t- СО—IО О
ООООО
О CO-fr-i СО
00 00 05 —IОО
со t—со coco
(ОГIООО
ООООО
О COCO 00 СО
CNOCN -ч<сО
о -*< оосмо
(DDOOO
ооооо
со^мпо
г*~сО с--05Ю
СО ОСО — О
IOCNOOO
ооооо
оэ іооо—f t^
ю -^^ toco
Г-счЮ—іО
τί· —( О О О
ооооо
cocooouot—
СО "0 00—· CM
—. Tj* ТГ 1-4 О
'ίπΟΟΟ
ООООО
Ю СО С- OO C5
О —' CN го -^
00081
00022
00006
00001
00064
00017
00004
00001
о го со —
IО —«OO I
oooo I
оооо
оооо
00038
00009
00002
00029
00007
00002
00022
00005
00001
00016
00004
00001
00011
00002
00008
0Э002
00006
00001
О—ГМГО -*

Распределение Пуассона
129
3
знммч ю се с- оо от о — см го -
* Iі
(Ν СО CMf»t--
со СМ ιΟ со со
SO CO CO Ό Ю
— r—«!ί·σ>σ>
OO— ——ι
·* ■*■ -*■ CM СЧ
CM OJ CO — —
0ИПО1Ч
СМг- ЮОС0
О О — <M —
I- — CM CO CD
«jocoooi
CM 00 CO CM t~
t-.-sPOJf-O
4j« — CO Э0 CO
<MO>tSOO>
OOr-<CM>-i
OiO^NCfl
CNStlflt^f)
CO «i- OS CO CO
—< —о 00
- _ _ IN
СЧ О) Щ IN О О
Ю- OOO О
с о ооо о
о oooo с
СО CM CM r~ ч^
— СЯ —< coco
СМ СОЮСО —
Ю СЛ со ι. м г-н
— о о о о
—* Ю СО <М 00
Г-- IАГ-» — —
t— со о -ч*©
-ςτ CO iO CM —ι
-sooo
00 — Ю ΙΟ СО
СМ, 00 СО — СО
■ч*« 00 *чг* ΟΙ О
— ооо©
-ςπ — CM CO ·** —
ю со ю — о о
*-ооо о
ооо оо о
ооо оо о
-#0> CN t-· C-.
!' I-- СО СМ.С0 -Ф
СО с-, тр.ГТ> to
о со 00 ^cf г-?
ооо — ·-»
Г--«<СМ ОМ СО —ι
00 СО "=Г>—'О О
со —■ о о о о
о оо оо о
о о ооо о
ООО -*0 со —
см — со —< о о
генооо о
о о о оо о
ооооо о
СМ СО СО t— СМ
СОЙО-ФСМ
Γ-ΟΟί-'Ν —
смел г- —05
ОО·— CN —
СО — 00 СМ »Л
coco ■* — со
г~ CM СМ СО
ΓΟΟ 00 -ф — О
— ООО©
IОО С4· СО СМ
t— со см о о
СМ О О ОО
ооооо
ооооо
О СП СО 00 —
СМ СОС7> С- 00
ОЮ^іОСО
ГОООО—'СО
© —— СМ —
I-ОЮСОСО
— — ΙΟ 00 ιΛ
СМ Г- 00 СО СО
СО Г- Го г-« О
«ОООО
сог-смо©
So о оо
оооо
ооооо
t~ t-o см ем
СО Ч.СП СО ОО
СО СО IN СОЮ
СО—СО — CO
О—с — СМ —
ж
)0 00 00 СО
О СО г- t^- ίΛ
со — ^ ·Φ uj
СМ С* СО —« О
— ОООО
СО іО — ОО
?<<5огао
ооооо
ооооо
оо — со—«ю
00 Г- 00 СО СМ
СО—ι О ОСМ
СО СМ О СМ 00
О — СМСМ-
СОСОСОСССМ
СМ — —< 00 Г-
ОсО—ι СМ ■*
— ОООО
со »-то
coin ·* — оо
— ОО О О
ООООО
ООООО
ssgsi
00 СО СО СМСЯ
СО с- С4· —ι сО
СОг-О
2S?
§.2<£ЙЗ »§Б^Й ЦЗоо
-Фсоосме~
О — СЧ СМ —
-СО СМ— О
-ОО ОО
llssi
to Ю COCO Ю
<~* со -г* со со
ЮО5СОС0С0
■ч* со —< см t—
О —СМ СМ —
со со со со оо
•*Ю Л'ОСМ
С-1Л-ФСДСО
оюсм оо
— оооо
см си г- См
О см О О
г- о о о
ОООО
ОООО
юсо-о —1~,
'Ч'ч'^ОСС
Г- Си ОТ СО 00
о со оо ^ г-і
о© о — —
COO —COM
о іо оо со о
оо со ■* -- ем
О со ОО Лео
000 — —
оіссо соем
— (Л -=г СС СО
СО CM Oh -ч*
о -sOiftoo
00 — ——
to^lO г-СО
О СМ ГО О Ю
о со со со с*·
— ■ч'осооо
— СО 00 CN —
— СО -ψ г-00
— СО см 00 О)
— т»« — СО -О
о о —·«—' —
СМ© ОС СО I4-
См *** СО -Ч* —
— іО —^Г-СО
оо — — —
Ь-ті«-фО00
СО »ЮС0СО
^- \гь СМ ι- О
о о — —· —*
О00 CD CO CM
005СМ — 5;
юсмемюз*
— СО і-О 0О Оі
оо — — —
іО СО I- ЭС СТ» О —* СМ СО τ
/
О — СМ ГО "*·
И Появшінм ЧяЯншовн

130
Распределение Пуассона
lOtCt-0005 О —СЧСО-Ч* ЮСОР-
t»tM^i«COr-> 00 ■"■* СО CN t»· com —
■С с» ·* СЧ CN — CN -τ СО -У --(OO
lOCO^TUSCO XCOCOt-tO OOO
ntoiopj — о о о о ооо
— -ч—ОО OOOOO OOO
СИЛ-00CN t-05000)<3> ίΟ-*ι-ι
CN — Тм СО ·<3« СО CM Oi — СО —· О О
10ΜΟ«Μ СО Г- 1.4 >-· Ο OOO
г-^ос«і ноооо ооо
——ι —OO ООООО ООО
ioococnoo смсмг~іасч оп«
I^ 00 ЭС UO СО I^-^.ГОІСО -ч О О
тгОіЮГ-О -ίΟΜΟΟ ООО
^ЯОЮМ — ОООО OOO
— — ООО ООООО ООО
СОИ-ОС—'Ю 00СО —ΌΝ ООСМ —
СО — -^ Г— Ч W-Д СЧ СО W ООО
СО «О — ЧЭ 00 C01OCNOO ООО
Г-* 00 £Л Ю -м —■ ^ <~> О О ООО
—• — ООО ООООО ООО
<мг~<м"ОЮ ю-нооі^~і г-е*
юечслслю t~c»«.tocM oo
' . <М _ СЛ Ю н jhOO О Ο
t-· СО °0 ·* <N — ОООО OO
— — OOO OOOOO OO
млояш счшоюга юсч
00 — сосо-ч -+cmcoo — OO
О 90 CM .О CO О·*—OO OO
t~<MCO-*i(M —lOOOO OO
r-ι — OOO OOOOO OO
COCOOOCO —1 ОООIЛСО^· ч*1 —«
Г— г- Г- с- СЛ CM CO CO -4« — OO
00 CO P- CN Ο Olt'.r-tOO OO»
CO CS P- -*H СП OOOOO OO
— --ооо ooooo oo
00 CD00t~CN CO—<
-_. О — Η,ΤΗ ΟΟ
соелсоелоо соеОіноо со
СО — f4- t·- — ООПОГ) OO
—,—OOO OOOOO OO
СЧСЧСЛ — О (DO-«001 СО—·
сооооооо ог-ел^со oo
CO -^ CO CO CO Г-. CN» .~Э О О О О
CO—HOtOrt OODOO OO
—,—,ΟΟΟ OOOOO OO
о^ч^ечю neoceiots о
О0СО00СЛ —cCNNN"> Ο
oaviN* сосчооо о
cco'oro—* onnoo о
нмООО OOOOO О
ЮСОГ-ООв» О —СЧС0-Ф U5tOr-
4
O'GI
14,0
13,0
12,0
11,0
n'oi
9,0
8,0
о
β,ο
s /
О — СЧ 00 ч*4 lODK-aoi
CO Г-- -^ -st* ^ Γ~· ^4 —
1 ΙΟ —ICO СЛ CO CO Tr· Tp
1 looo — *♦· о ел οι
OOO О О —i — Χ)
OOO ООООО
—IООООСО ПЗОСЛ·*'*
іоососо t-г— со -w< со
looo—ι со со t— о t-
ОООО ПОнМ^
ОООО ООООО
СОСЛСОСЛ СЛі/О^ССЮ
IО —чэЭсЬ СЛ— —it-O
Iооом июхюю
ОООО О — (NTCO
ОООО ООООО
— г--*г- —< -φοοοοοίΐο
OOtft>« NV1010P3
OOO —Ю CNUJICUJS
ООПОО — СМ-Ч<сО00
ООООО ООООО
00002
00Э18
00101
00370
01019
02242
04110
06458
08879
10853
•*i/it-.f~c4 соерсоо —,
о-фт^ілсл eoooto —
о о ex ι» oo t^ со -э сч Ό
о о о о — со со ел — CN
ооооо ооо—і —
CN — η ел ·* СО СЛ CN Ό СО
HHOuiN NOHNf>
О—«Ю-ГСО О — f- —ι —t
ооо —со ссел—<сосо
ООООО ОО ———
■^оя-^соіо отсслелоо
ООСОГ~СОСЧ CD — іОЮО
осмосов —· (Ν ел с» tji
оо—γνιο елсмсосооі
OOOOO О—* —— ^
— 00-.7<!50CO NOOOOO
СЛСОС»С —< ГЧ ts- О-~> CO Th
о со ~""чт -< t*. ел ел о —<
OOtNinO) (N*~1-COO
OOOOO — — — —i —
oo r» tN ··*< ю iN"»a<0"*
тг 30 CO ^Ч 00 COCO"-Pico
oj-* ■* ел со ocn oeo
О — ··*« CO CO COCOCOOCO
О О О О —· —ч—< — — О
о—ісчсо·* «зсос~еоел

Распределение Пуассона
131
3
1
"5"
Ч
15,0
14,0
υ'ει
12,0
ч
8,0
^
/
ΟΗΝΜ-*
— COCO — -ЧР
СО СМ 00 -О ТК
С0вО11П<М
-* СО 00 COO
оооо —
оосо см со со
сч со ті< со со
СО "* 00 чі О
сооо хоо
ооо ——
г— со -* -**> о
00 -ςρ Со СЛ О
Ю —ι . о. СМ
ооооо о
О — »—<«—* ·—·
-# г-·■—Г—СП
00 СО 00 іЛ г>
·& -ч4 "^ ЮО
Отн^оО)
мнгінО
t-ooco о ю
СО со τί* ςο I^
σ. со з> см о»
HrtOCON
— — — OO
—-Фоо — оо
— f-t«-C0O
U3 .о Tf -м CM
см —соо-ю
— — ООО
CO CM CO OOOO
IflONCOiO
OOf-CM ON
— CO!— Ό CO
— OOOO
CO CO CO CM CM
~4 — — OCT)
со ем оо en -a
CO Г- -«f CN —
OOOOO
00 MOOS CO
со—<co —ο
о iC CO -ЧГ1 t>.
f-^CM — О
OOOOO
о coco о со
СОЮСМСМСМ
- CM ι—ilOCM
■*И-ОГ1
OOOOO
о —см
cootie CO t— 00 <3>
■*οο·4< — Ю
4Or~CON
CM CO **0 U5
OOlOONiO
— OOOO
CM CO 00 ·*©
со ю cs ·* uj
СО(0-ЛО
CO oo t— Ю Tf«
OOOOO
00 CO г—О CO
T-0OC0 Ι-.—ι
00 —■ τ CO г-ч
oo t-- ч-і со см
OOOOO
епсосмю-*
гасчпюгч
см·* оою со
t^-Ю CO CM —
ооооо
юоосооо
СОчіі с— Ю-*
со со со ■* оо
«О СО »М НС
ооооо
01943 I 03472
01093 і 02170
00579 ■' 01276
00289 ! 03709
00137 ! 00373
СО —CM4O
О ΙΟ — СО "*t*
СО -7-СМ ОО
ооооо
ооооо
«юогасо
СОті· СОСМО
со .-«ооо
ооооо
ооооо
СО СО CM Tf —
COCO —OO
ооооо
noon о
ооооо
Ю со г- оо со
О —· СМ со чі<
CM CM CM CM !N
г-н CO СО 00 О
00 00 СО СМ СО
— СО О .О 00
•φ См СМ —О
ооооо
02860
01936
01213
00738
00431
со со со ю -о
ее со ■* со со
С— О СО L-, г-I
— — ооо
ооооо
00 ГО СМ 20 СО
COlOOlON
со .о со — о
ооооо
ооооо
00062 і 03187 00462
00026 : 03389 00242
00011 00.140 0Л21
00304 03318 00058
03002 і 00037 00026
со со см —
HOOD I
oooo I
О ооо
oooo
І§ Ι Ν
о о
оо
1 і 1 I I
о —см со ч·
см см см см см
"ОСО г—COCO
см см см см см
OONO'lt
а. оо со оо τ
-5fCM — О О
ооооо
ООООО
т-<о Г-·* СО
-*сосо со —
см — (ооо
ооооо
ооооо
со — ілемю
OUjCJhO
— OOOO
ооооо
ооооо
00 С- СО ГО —
«нООО
ооооо
ооооо
ооооо
емюем —
— О ОО 1
оо оо 1
оо оо
оооо
SS Μ 1
оо
оо
8 I 1 II
о
о
1 1 t I 1
Mill
Mill
1Г2СО t-00C0
см см см см см.
Ο — *"ΜΓΟ·^«
00 CO СО СО СО
СМ — О (О О
ооооо
ооооо
ооооо
00 СО СМ.-·
oooo t
оооо 1
ОООО
ОООО
tocco
SC00O
МИ!
Mill
Mill
Ι Μ Μ
Mill
Mill
Μ Μ 1
о — ем со чр
со coco со со
-

ЛИТЕРАТУРА
А. ЦИТИРОВАННАЯ ЛИТЕРАТУРА
1. Чебышев П. Л. «О непрерывных дробях» (Соч. τ Ι, стр.
Ж—230, 1855).
2. Чебышев II. Л. «Об одном новом ряде» (Соч. т. I. стр.
381—384, 1858).
3. Чебышев П. Л. «Об шітерполиронании и случае большого
числа данных доставленных наблюдениями» (Соч. т. 1, стр. 387—469,
1858).
Чебышев II. Л. «Об интерполировании величин
равноотстоящих». (Соч. т. И. стр. 219—242, 1875)
Чебышев П. Л. «О функциях, подобных функциям Лежандра».
(Соч. том II, стр. 61—68, 1869).
Чебышев П. Л. «Об интерполировании ко способу
наименьших квадратен». (Соч. т. I., стр. 473—498, 1859).
і. Чебышев II. Л. «О разложении функции одной
переменной». (Соч. г. I, стр. 501—508, 1859).
5. Чебышев П. Л. «О двух теоремах относительно
вероятностей». (Сэч. том II, стр. 481—492, 1887).
6. V. Romano ν sk,v. Статья в Оіогпніе dell'1st It degll Atiuari.
Ашто 11 п2 (1931). pp. 161-171.
7. Doollttle M. H. Статья η «U. S. Coast and Geodetic
Survey. Report for (1878) Appendix 8, 115.
8. Gauss. Methode des mcindres сапчЧ·. (Parts, 1855, перевод с
немецкого Bertrand'a.)
9 Cochran The Omisson or Addition of an independent variate
in mlltlple lineal regression. Supplement to the .louniale ot the Royal Stat.
Soc, vol. 2. 1938.
10. Fisher R. Statistical Methods for Research Workers. (1-ое Изд.
J925r,, 8 изд., 1941).
11. Немчинов В. С. «Сельссохозяііственнаи статистика с осно-
нами ебщей теории» (М, 1945).
12. Гаусс. «Движение небесных тел» 1861 (на латинском—1809 г.).
13. Kellev. Statistical MethoJ.. Ν —1. (1929).

Литература
IЗЛ
14. lozeklel M. Method of correlation analyses. (N.—I., 1 oil..
15H0, 2 ed., 1941.)
15. Davenport and Ekas. «Statistical method* (1 ed., 889.
4 ed. 1936.)
16. Чебышев II. Л. «Об определении функций по значеіиям,
которые они имеют при некоторых величинах переменной» (Соч т. II,
стр. 71-82, Г870).
17. Чебышев II. Л. «Разложение в ряды при помощи
непрерывных дробей» (Соч т. I. стр. 611—614, 1865).
18. Hermlte Ch. Stir ші nouveau developpemerit e:i serie di· fo c-
Hons (1864).
ι-00 β x
14. Laguerre K. Sur ('Integrate dx (1879).
J x
2··. С. J or gan. Statlstique rmthematique Paris (1927).
21. В. И. Романовский. «Математическая статистика». (М.,
19J8).
22. Хотимский. «Выравнивание статистических рядов по
методу наименьших квадратов (способ Чебышева)». (М 1925).
23. Митроподьский. «Техника статистического исчислении».
(М. 1931).
24. Ч е б ы ш е в II. Л. «О средних величинах» (Соч. т. 1,сір. 687—
Ь94. 1866).
25. Student. The probable Error of a Mean (Biometritca, VI, i,
1908).
26. La place. Theorle aiialytiqite des probabilites, 1872.
27. Polsson. Recherches sur la Probabillte des Iugements (1827).
28. Fisher Агне. The Mathematical Theory of Probabilities. (N.—1.
1923,, 2 ed.)
29. Oram, J. P. Om Kaekketidvlklin^er, bestemte ved Hfaelp af de
rnindsjtef Kvadwters Methode (1879).
30. Thlele T. N. Theory of Observation. I (tS03) (на датском
«зыке 1884 г.).
21. Charller С. V. Uberdus Fehlergesetz (1905)
32. В runs Μ. WahrschelnHchkeltsrechnung und Koll ktlvmass-
lehfe (19G6).
33. J δ r g e π s e и N Undersogelser over Frequensflader og Korrela-
tiot) (іэіе).
31. Camp. The mathematical part of elementary statistics, L. (1S34).
35. Ритц. «Математические методы в статистике». (Μ. 19?7 на
анг. 1924).
36. Czuber В. Wahrschethlichkeitsrechnung (1958).
37. Л ахт ин Е. «Кривые распределения и построение для них
интерполяционных формул». (М., 1922).
38. Bortktewlcz L. Das Gesetz der kWinen Zahl3;i (1898).

J 34
Литература
39. Soper Η. Ε. Tablss of Polsso:i's exponential binomial Hmlt
Blometrika, (X, 1914.)
40. Charlier. Die zweite Form des Fehlergesetzes (19Э5).
В. ДОПОЛНИТЕЛЬНАЯ ЛИТЕРДТУРА
■ .Чебышев П Л. «О функциях наименее уклоняющихся от
нуля». (Соч. т. II, стр. 189-215, 1873).
2. Чебышев П. Л. «Об одном новом ряде, доставляющем
предельные величины интегралов цри разложении подиніегральной
функции на множители». (Соч. т. II, стр. 405—417, 1883).
3. Чебышев П. Л. «О суммах, составленных из значений
простейших одночленов, умноженных на фув*цию, которая остается
положительной». (Соч. т. II, стр. 561—610, 1890).
4. Чебышев П. Л. «О функциях, зависящих от положительных
значений какой-либо функции». (Соч. т. И, стр. 613—666, )893).
5. Bernoulli J. Ars Conjectandi (1713). (на русском —IV часті.
1913)
6. Lexis W. Zur Theorie der Massenerscheinunge:i in der men-
schlichen Gesellschafi (1877).
7. Bernstein S. Sur un precede de summation des series frlgono-
metrlques.—Comptes Rendus Ac. Sc, t. 191 (1930).
8. Чупров А. А. «Основные проблемы теории корреляции».
(Μ. 1932).
9. Марков А. «Исчисление вероятностей». (Л-д. 1924).
10. Бернштейи С. Н. «Теория вероятностей». (М. 1934).
П. Kolmagoroff A. Grundbegriffe der Wahrschelnlichkeitsrecli-
HUllg (1933).
12. Слуцкий Е. «Теория корреляции и элементы учелия о
кривых распределения». (Киев, 1912).
13. Slutzky Ε. The Summation of Random Causes as the Source
of Cyclic Processes Econom trlca—5, (1937) (на русском языке, 1927).
14. Идельсон. Н. И. «Способ наименьших квадратов» (изд. II.
Л-д, 1932). .Уравнительные вычисления по способу наименьших
квадратов" (1927 г.)
15. Ait ken. Statistical Mathematics (1942).
16. Гончаров В. Л. «Теория интерполирования и приближении
фуикций». (М., 1934).
17. Научное наследие П. Л. Чебышева, т. I «Математика*. (М.і
J945).
18. Лагунов Б. И. К практике выравнивания статистических
рядов* (Киев, 1927).
19. Крылов А. И. „Лзкцик о приближенных вычислениях
{2-ое изд. 1Θ33 г)

ПРЕДМЕТНЫЙ И ИМЕННОЙ УКАЗАТЕЛЬ
Ассиметрия—94, 102
Бернулли—134
Бернштейн — 77, 134
Борткевич — 95, 97, 133
Боули — 98
Брунс —90, 93, 133
Вариация коррелированная 3S,
62, 63
«Вес» Гаусса—17, 18, 38, 40, 41;
50, 67, 77, 106
«Вес» Чебышева — 7, 8, 74—76.
89, 106, 107, 109
Веса переменных — 19, 40, 41, 50,
65
Гармонический анализ — 77. 107,
ПО
Гаусс— 18, 35, 68, 95, 106, 132
Гончаров —134
Грам —90, 92, 95, 107, 109, НО.
133
Девентроп — 70, 133
Дисперсионный анализ — 5, 9, 42,
56, 67, 107, ПО
Дулитль — 17, 27, 29, 30, 132
Жордан —80, 87, 88, 97, 98, 107,
ПО, 133
Закон больших чисел — 88
Закон малых чисел — 95
Идельсон — 134
Интерполяционная формула — 7, 8,
25. 75, 76
Иоргенсен — 93, 133
Исключение переменных — 22, 30.
35, 43, 53, 55, 106
Келли —70, 132
Кемп —93, 133
Колмогоров— 134
Контроль вычислений — 56, 60, 61
Корреляционный анализ — 5, 9,
42, 56, 67, 107, ПО
Корреляция:
множественная — 26, 65, 66,
69—71, 106, 109,
остаточная — 70, 71
частичная —70, 71, 106, 109
частная —26, 65, 66, 69—72, 106.
109
Кочран —21, 132
Кривые Шарлье —5, 90, 101
Критерий Фишера — 26, 35, 40, 41,
63, 65, 67—70, 106, 109
Коэфициенты корреляции — 35, 65,
70
Коэфициенты кривой
распределения—92, 95, 98, 101
Коэфициенты полинома:
младшие —37, 50, 51, 72
старшие—10, 24, 26, 35, 36, 39.
48, 50—52, 77, 83—86
Коэфициенты ряда Чебышева —
8, 75, 77
Коэфициенты рекуррентной
формулы — 81
Коэфициенты полиномов:
«К»—10, 13, 17—20, 23—26, 35—
40, 42—54, 57—60, 67, 69, 83

136 Предметный и именной у*-.мшг.и,
жС» — 19—22, 35, 37, 38, 40-47,
50—57, 65, 67, 69, 106, 109
«Т» — 9, 10, 13—17, 23, 25, 28, 40,
47—49, 57—60. 82, 83
Коэфицнеиты регрессии:
«А» —8, 13, 15, 16, 23, 25, 26,
28, 3!, 46, 47, 57, 58, 61
«а» — 12, 13, 16, 17, 25, 26, 30—
35, 38—49, 50, 52—57. 65. 99,
100. 106, 108
Крылов —134
Лагерр — 5, 78, 97. 107, !09, 133
Лагунов— 134
Лаплас— 89, 95, 101, ,133
Лахтин —93, 133
Лежаядр — 8, 77. 84
Лексис — 134
Маклорен — 8, 78
Марков — 134
Митропольский — 85, 93, 101, 133
Модуль— 90
Моменты —90, 93, 96
Наименьшие квадраты - 5, 7, 35
Натуральный ряд чисел — 85
Немчинов— 22, 132
Непрерывная дробь--8. 73 75,
77, 80
Неравенство Чебышева — 7, 88
Нормальное распределение н<>-
роятностей — 8, 118— 126
Нормальные уравнения — 26, 27.
30, 49, 67
Нормированные:
коэфшщенты — 20, 38, 40. -VZ, ">и
полиномы — 74, 81, 85
Обобщенные:
нормальные кривые—103
полином Чебышева — 73
Ортогональность — 13, 74, 92
Остаточная сумма квадратов — 28.
44
Отклонения — 23, 24, 105
Ошибки —5, 26, 42, 63—65, 67,
69, 106
Параболическое
интерполирование—8, 9, 77, 88, 98. 100, 105,
108
Перегудов— 22, 49
Переменная:
нспомогэтельная — 85, 87, 99
зависимая— 10, 12, 69
элиминированная—10, 27
Приближения квадратические —
67, 69, 75, 92, 93, 102, 104, 105
Пирсон —93, 94
Подходящая дробь —8, 74, 77
I Iоказательные функции — 77, 79
Полиномы Лагерра — 5, 77, 79,
39
1 Iолиномы Лежандра — 77
Полиномы N — 23. 35, 82, 84.
I Iолиномы q — 87, 88, 99, 100
Полиномы равноотстоящих
величин — 86
1 Iолиномы Эрмита — 5, 77. 79, 89
Полиномы G —78—80, 97, 98,104,
105
1 Iолиномы Якоби — 77
Гіолірномы Чебышева;
свойства — 74—76
семейство — 77, 84
система —9—11, 23
Поправки — 50, 51
Последовательность переменных—
9, 17, 49, 66, 72
Пуассон —78, 80, 89, 90. 95—98,
104, 107, 109, 133
Равноотстоящие величины -8.
84
Распределение численностей — 7.
88—91, 127—131
Регрессия:
криволинейная — 7, 8
множественная—7, 8, 12, 13,
55, 56, 63, 67, 69, 72, 105, 106
прямолинейная — 36, 37. 55, 69
чистая — 71
Рекуррентная формула — 74, 77,
80, 82—87, 107, ПО
Ритц— 93, 133

Предметный и именной указатель 137
Романовский — 9, 80, 93, 97, 132,
133
Ряд Чебышева ~-7, 75, 89, 92, 94,
105, 107
Свойства полиномов— 13, 74—75
Система полиномов Чебышева: —
первая («Т») — 9, 14, 15, 28, 48,
81. 82—84, 105, 106, 108
пторая («К»)—9, 10, 48, 59, 105,
106, 108
третья («с») —И, 17, 18, 19, 105,
108
четвертая («N») —23, 25, 26, 48,
50, 71, 82—84, 106, 108
Сканданавскаа школа — 90, ПО
Слуцкий— 134
Сопер —97, 134
Средние:
арифметически* — 36, 52, 69, 94
квадратичѳскне—52, 104
корректированные — 5, 35, 68
злиминационные— 5, 33, 35, 36,
68, 69, 94, 107, НО
Статистические величины — 26,
35, 36
Статистическая оценка — 5, 35,
38, 40, 41, 56, 62, 63, 67, 69,
107, ПО
Статистические характеристики -■■-
26, 31, 38, 69, 72
Степени свободы — 63, 65, 69, 70
Стюдент — 88, 133
Сумма квадрата (λ'-> — 31, 38—41,
11, 47, 52, 53, 57, 62, 63, 66
Сумма квадрата (Sd2) — 35, 36,
38, 40, 41. 44, 47, 49, 53, 55,
57, 63, 66, 69, 71, 99, 100, 102
Суммы квадратов полиномов —-
9, 13, 14, 16, 18, 24, 31, 35—38.
46, 47, 52, 53, 57, 67. 69. 76, 77:
87, 88, 94, 117
Суммы произведений полиномов—
9, 13, 15, 16, 18, 20, 22, 24, 29;
31, 32, 35—37, 69
Схемы вычислений:
Дулитля (Д) — 29, 31—34, 51,
106, 109
Немчинова (N) — 26, 34—36,
42—45, 48—51, 53, 58, 62, 67,
106, 109
Перегудова (Р) — 45—49, 56,
58, 62, 106, 109
Тиле—90, 93, 94, 107, ПО, 133
Тригонометрические полиномы
Чебышева — 7, 8, 77, 79
Уравнительные вычисления — 5,
107
Фишер А —90, 92, 93, 133
Фишер Р —22, 88, 133
Функции остаточных отклонений—
73
Фурье — 77, 78
Чебышев — 5, 7, 9, 68, 73—75,
105—107, 132, 133, 134
Число наблюдений—11, 39
Числа Чебышева — 85, 87. 88, 99.
107, ПО. 112, 117
Чубер — 93, 133
Чупров — 134
Эзеюіэль—70, 71. 133
Экономическая статистика -■- 5, 68
Элиминирование:
полное— 11, 29
последовательное—10, II, 28,
29
Экое —70. 133
Эксцесс —94, 102
Эрмит—5, 78, 91. 107. 109. Ш
Эйткен — 134
',ΙκοΓ,π - 77

ОГЛАВЛЕНИЕ
Предисловие
Глава I. Полиномы Чеоышеаа
1. Ортогональные полиномы и интерполяционный ряд Чебы-
шева
Ί. Полиномы с измененной последовательностью
переменных
і. Суммы квадратов полиномов, сумма их произведений и
отношение их сумм
4. .Веса' Гаусса и полиномы Чебышев;і
5. Взаимоотношения между коэфициентами смежных
полиномов Чебышева
Глава 11. Схемы решении нормальных уравнении и полиномах
Чебышева
1. Схема Дулитля
2. Числовой пример решения вормальных уравнений в
полиномах Чебышева
0. Новые схемы решения нормальных уравнепий в
полиномах Чебышева
4. Числовой пример решения нормальных уравнений по
новым схемам в полидомах Чебышева
Г л и a a 111. Система статистического анализа и полиномы
Чебышева
1. Статистическая оценка коэфициентов уравнения регрессии
и полиномов Чебышева
Ί. Система статистических характеристик и полиномы Чебы-
шеаа

Оглавление j:H'·
Глава IV. Обобщенные полиномы Чебышева и
статистическое исчисление
1. Метод Чебышева и свойства его полиномов . ".'!
2. Классификация иоляномог Чебышека 75
Ч. Рекуррентные формулы N0
4. Полиномы для функций с рашюотсюящііми значениями. . St
5. Кривые распределения численвостзй и полиномы
Чебышева НИ
6. Распределение Пуассона и полиномы Чебышева 9ό
7. Выравнивание кривых распределения численностей
(примеры) tis
Выводы 105·
Summary ]i.)S
Вклейки:
Схема „Д\ Схема Дулитля в полиномах Чебышева J9
Таблица 1. Нахождение связи между урожаем и
метеорологическими факторами по методу Чебышева
—Дулитля 31
Схема ,/Ѵ". Схема Немчинова в полиномах Чебышева .... ,Ί&
Схема ,№. Новая схема решения нормальных уравнений в
полиномах Чгбышева (числовой пример) .... 5S
Схема статистического анализа в полиномах
Чебышева (й
Система статистического исчисления в полиномах
Чебышева 69
Классификация полиномов Чебышева 77
Приложения:
Таблицы I —V. Полиномы Чебышева для равноотстоящих
величин ql (л, х) —Числа Чебышева. . . . 112
Таблица VI. Сумма квадратоз Sg^ (η, χ) 117
Таблица VII. Функция щ (г), вторая, третья и четвертая
производные lift
Таблица ѴЩ. Распределение Пуассона 127
Литература 132
Предметный и именной указатель 135
Ѵедакхор А. А. Конюс.
Технический редактор М. Б. Петрова.
Л146197. Сдано в naiop 12IIX 19-16 г. Пода. кдеч. 11|ХI 1916 г. Тиране 3.009. 8ак&8 1976.
Типографии «Квасное знамя» изд-ва ЦК ВЛКСМ «Молодая гвардия».
Мпсква. Сущевская, 21.