Текст
В С.НЕМЧИНОВ
ПОЛИНОМЫ
ЧЕБЫШЕВА
II
МАТЕМАТИЧЕСКАЯ
СТАТИСТИКА
МОСК'ПА
1046
Институт экономики АН СССР
Московская ордена Ленина сельскохозяйственная академия
имени К. А. Тимирязева
Проф., д-р В. С. НЕМЧИНОВ
ПОЛИНОМЫ
ЧЕБЫШЕВА
МАТЕМАТИЧЕС КАЯ
СТАТИСТИКА
I 'J 4 п
Издание Московской ордена Ленина сельскохозяйственной
академии имени К. А. Тимирязева
Э5 "najvK» нэзледие России"
П. Л. Чебышев
(1821 -1894)
ПРЕДИСЛОВИЕ.
Настоящий монография является частью большой работы автора по
теории экономических расчетов. При изучении экономических процессов
весьма часто приходится иметь дело с разнообразными массовыми явле*
няямк. Объекты экономических исследований — это многомерные сово¬
купности различного рода событий и фактов, относящихся к множеству
объектов, характеризуемых многообразными признаками. Обобщение фак¬
тов. относящихся к такого род многомерным совокупностям, требует
применения статистических методов исследования в виде корреляцион¬
ного н дисперсионного анализа н теории ошибок.
При планировании экономических явлений и при контроле за выпол¬
нением плана неизбежен метод количественного измерения. Плановое хо¬
зяйство требует создания теории экономических и планово-статистических
расчетов. Математический аппарат» с которым приходится иметь дело при
изучении планируемых экономических процессов, является своеобразной
жоыомометрикой, требующей большого количества уравнительных вычис¬
лений при построении баланса народного хозяйства и при анализе выпол¬
нения плана по такого рода явлениям как. например: урожайность, цены,
доходы колхозников, выработка агрегатов и т. д.
Русский математик П. Л. Чебышев ввел в науку ряд новых приемов
уравнительных вычислений по способу наименьших квадратов. Ему при¬
надлежит научный приоритет в отношении систематического применения
метола элнминацнонных средних, получивших в экономической статистике
название метода корректированных средних, а также приоритет в отноше¬
ния полиномов, получивших в дальнейшем название полиномов Эрмита и
Лагерра н так называемых обобщенных кривых Шарлье (тип «А» и «В»).
Основная задача настоящей работы — изложить математические идеи
П. Л. Чебышева п приложении к практическим задачам, стоящим перед
статистико-экономическим анализом.
Предлагаемые в работе новые схемы вычислений, связанные с корре¬
ляционным и дисперсионным анализом, существенно облегчают вычнеле-
тельную работу исследователя и обеспечивают ему всестороннюю стати¬
стическую оценку полученных результатов.
В. С. НЕМЧИНОВ,
Действительный член Академии
наук БССР, Зав. сектором эконо¬
мической статистики Института
Экономики АН СССР, Зав. кафед¬
рой статистики Сельскохозяйст¬
венной Академии имени Тимирязева.
S октября 1946 года,
Москва.
ГЛАВА 1.
ПОЛИНОМЫ ЧЕБЫШЕВА
I. Ортогональные полиномы и интерполяционный ряд
Чебышева
В статистике имя знаменитого русского математика
Пафнутвя Львовича Чебышева (1821 —1894) известно
главным образом по так называемому неравенству Чебы¬
шева, которое он предложил для распределения вероят¬
ностей и которое имеет силу для любого статистического
распределения численностей.
Однако за последнее время в статистике все большее
значение приобретают ортогональные полиномы Чебышева,
которые имеют особое значение при определении уравне¬
ний множественной и криволинейной регрессии и при вы¬
числении коэфициентов обобщенной функции нормального
распределения вероятностей.
Чебышев предложил общую интерполяционную форму¬
лу, при помощи которой возможно интерполирование в
самых разнообразных случаях. Эта интерполяционная
формула удовлетворяет условиям метода наименьших
квадратов и выражена при помощи его ортогональных
полиномов. Общая интерполяционная формула или иначе
ряд Чебышева (1), предложен Чебышевым в 1855 году.
Этот ряд таков:
f(X) = s ea ^ чг. (х) +
' S [Ч^о (*,)«*(*,)] 01 '
SjWMVlxjHW] + (1
u SlVJM-BHKdFixtl 4; , .
Sf*m{x{).enxf)
Полиномы Чебышсоа
где /■'(х)—искомая функция; /-'(.vj—- известные значении
искомой функции; 03(х) — вес, например, — распределение
вероятностей (Частоты); ll‘w(A’) — полиномы Чебышева.
Эти полиномы получены Чебышевым при помощи раз¬
ложения некоторой функции F(x) в непрерывную дробь.
В зависимости от вида функции, которая преобразуется
в непрерывную дробь, полиномы Чебышева выражаются
различными уравнениями. Полиномы Чебышева (но его
собственному определению) суть знаменатели подходящих
дробей, полученные разложением данной функции в соот¬
ветствующую непрерывную дробь.
Чебышев предложил ряд формул для своих полиномов
в отношении частных случаев разложения в непрерывную
дробь различных функций, например:
а) ряда, характеризующего совокупность равноотстоя¬
щих значений искомой функции (2);
б) функции параболического интерполирования (3);
в) функции нормального распределения вероятностей
(4, 5).
В своих работах Чебышев указывает, что разложение
Маклорена, а также разложение по косинусам и синусам
кратных дуг, разложение по функциям Лежандра — суть
также частные случаи его общей интерполяционной фор¬
мулы.
Рассмотрим сначала применение интерполяционной
формулы и полиномов Чебышева в отношении уравнений
множественной и криволинейной регрессии. Пусть уравне¬
ние множественной регрессии дано в следующем виде:
у «= ав + а, хх + а9х% 4- а,х,... а„,хя.
Искомая функция F(x) = У разлагается при помощи
интерполяционной формулы Чебышева в следующий ряд
(при W*(jc)=-1):
У .ДЧ^х) + -ViM + Д'1’,М AJTJx),
где д.- •■'[у1; .4,-.. Ф'-.О)!.
s [< ( V)] * К (О]
Д- iLiliWL.
* об",е>| тм: А _ svr.M
При зтим полиномы Чебышева определяются последо¬
вательно при помощи следующих уравнений, указанных
Чебышевым.
Полиномы с измененной последовательностью переменных ь
Первая система полиномов Чебышева
(Сггстемп Т):
*,(*) = 1
У1(л-) = л'1- 7\0 У4(х)
Уа (*),= л» — Ti0 У0 (х) — Тп У,(х> (3>
^)М=-' Л, - Tia У0(х) - 7*м V, (A-) - 7Siy,(jg
У„ W- x»-Tm.„У,(л) -Г„.а У, (А) - Гт.8Уаи> -
• • • Т'гн...'» -I ^ т -t W*
Коэфициенты каждого и:, полиномов Чебышева в свою
очередь могут быть выражены через суммы произведений
и суммы квадратов полиномов Чебышева более низкого
порядка в виде аналогичных формул:
7* _ 5[д:,Ч-о(л)| ^ $[л»
10 ” -S' К (А)]
■J' __ чЧл )] . Т — ^[ л»Ч>з(-с)]
5[4-:(,)j • s'TcwT
а в общем виде:
Т — ^ f'*’"* '^1^)1
S [<(*)]
(4)
т.к
Эти уравнения даны Чебышевым для случая параболи¬
ческого интерполирования, т. е. для случая: л,—х; xs=x'-';
а9=а8 и т. д.
Романовский (6) показал, что эти формулы Чебышева
применимы и для случая множественной регрессии. Одна¬
ко Романовский не указал наиболее удобного пути вы¬
числения этих полиномов и не рассмотрел возможные
различные системы этих полиномов.
Наша задача рассмотреть различные системы полино¬
мов Чебышева и на этой основе дать наиболее удобный
алогорифм их вычисления, а также установить их связь
с современными статистическими методами дисперсион¬
ного и корреляционного анализа.
2. Полиномы с измененной последовательностью
переменных.
От первой системы полиномов Чебышева (полиномы ,7'“)
легко перейти ко второй системе полиномов (полиномы ,К“),
выраженных через первичные значения величин хп. Под¬
JO
Полиномы. Чебышева
ставляя в уравнение данного полинома соответствующие
значения предыдущих полиномов системы Т(х), имеем
новую их систему:
Вторая система полиномов Чебышева.
(Полиномы системы — развернутые полиномы по¬
следовательного элиминирования):
*•(*)-1
^10 /с\
*,(*) = *,-- Л,Л {ь)
'v> (х)=хг - kn - /г,,*, -
»(Х)— Хт ^л.ОаО ' ^«-1 ■*! Ь/П‘1 Х> • • • (в_,)
Сопоставляя с первой системой, легко видеть, что
старший (последний) коэфициент каждого полинома второй
системы равен старшему коэфициенту соответствующего
полинома первой системы, т. е.: kl0— T1Cl; кц = Тгх; k»»=
~ Ги; km, m—1
Очевидно, что такого же родя равенства будут иметь
место, если изменить порядок переменных, рассматривая
каждую данную переменную как последнюю. Это возможно
сделать, так как порядок включения переменных в урав¬
нение искомой функции вполне произволен. В случае
иной последовательности переменных, будем иметь соот¬
ветствующие уравнения для полиномов Чебышева с из¬
мененной последовательностью переменных. Введем для
удобства письма новые обозначения полиномов Чебышева:
V, (X) - Л,.,,
‘F2 (л) — х9Л
,,г3 (*) =-
(х) —
^ •Р-Я1 ХрАЪ. ,.р—I. р+l...m
Здесь в подстрочном значке первая цифра (до точки)
обозначает номер переменной, для которой определяется
полином Чебышева (т. е., которая рассматривается как
зависимая переменная), а цифры после точки — номера
элиминируемых переменных (включенных ранее в урав¬
Полиномы с измененной последовательностью переменных //
нение). Тогда отбирая из системы полиномов Чебышева
с измененной последовательностью переменных те поли¬
номы, в которых каждая данная переменная рассматри¬
вается как зависимая переменная, имеем новую третью
систему полиномов Чебышева. Для случая трех перемен¬
ных эта система такова*.
Третья система полиномов Чебышева
(Полиномы системы „с*—полного на данном этапе
элиминирования)
•*3-21 ~ *ч ^20Х0 ^31*1 “
'*2-13 хг ^21*1 (6)
-^1 -23 ~ Xi ^10*0 ^12*2 ^13*3
•''0-123 ” ^01Л1 ^ОГ*2 ^1ПЛ3*
где х0= 1.
в общем виде:
х
р-12...р-\.р+\...т Хр VVo ^>1 А1 ^/>2 Л2* ' ' 'ЬрягКт
Здесь верхние значки * обозначают число элиминиро¬
ванных переменных (считая и xj; первая цифра в под¬
строчном значке—номер переменной, которая рассматри¬
вается как зависимая переменная, а остальные цифры
(после точки) — номера остальных переменных.
Для полиномов Чебышева характерно, что частота,
т. е. число наблюдений (х0), также рассматривается как
независимая переменная нулевого порядка. Это особенно
становится наглядным при рассмотрении 3-й системы по¬
линомов Чебышева.
Сравнивая систему полиномов последовательного эли¬
минирования (система 1) с системой развернутых полино
мов последовательного элиминирования (система 2), мы
установили, что для этих двух систем коэфициенты при
переменных, которые введены в уравнение последними,
равны между собой и могут быть выражены через суммы
произведений и суммы квадратов предыдущего полинома.
С другой стороны, из рассмотрения 3-й системы видим,
что остальные коэфициенты 2-й системы полиномов равны
соответствующим последним коэфициентам полиномов, с
измененной последовательностью переменных (см. систему
полиномов „с"), Это приводит нас к простому, но имею-
12
Полиномы Чебышева
тему большое практическое значение положению, что
коэфициенты системы яки и яси полиномов Чебышева
определяются как следующие отношения:
т- 5(Vl-j.
" ЩГ’ “ ФЬГ'
£«_ хзхо-1 •>)
10 %4.и) '
Б обшем виде*. (7)
_ р— 1.. />+!.... т—l)
к.
т.р
Хр. 12. .р— I. р+-\.... ///—1)
Уравнения регрессии вполне аналогичны интерполя¬
ционному ряду Чебышева, а остаточные отклонения от
уравнения регрессии — полиномам Чебышева. Это верно
как для зависимых, так и независимых переменных уравне¬
ния регрессии.
Легко поэтому показать, что коэфициенты множес¬
твенной регрессии у — а, + аххх -f а—аяхя определя¬
ются при помощи аналогичных выражений, в которые
также входят полиномы полного на данном этапе элими¬
нирования (система яс-* полиномов Чебышева). В частно¬
сти, для ^=rt0J-rt1x1-|-rts.Tt4-a1,xJ формулы для определения
I/,. таковы:
. 50’ЛЛ-2|) . _ ■S(',U2 «l) .
1 1 9
, s(yx^) 0.щ)
•^(дсь2з) •^(•'о-т)
В общем виде: (8;
а — s(?xp-u-- л-|. р+i...w)
S(-*T.t2...p-1j»+1...ir»)
Таким образом, зная те из полиномов Чебышева, в
которых каждая данная переменная рассматривается как
зависимая, легко определить все коэфициенты множес¬
твенной регрессии.
Суммы квадратов полиномов, сумма их произвед. и отношен, их сумм J'i
3. Оуяны квадратов нолвножов, сужаа их произведений
к отношение их суяж.
Все полиномы Чебышева обладают свойствами ортого¬
нальности, а именно:
!• (Л’р.1_>..у|-1./>+1. ,я) = 0
2- ^ iXpXm.V2 ... р...т—\)
3. S (ХрХрл-у ..р-\,р+\ ...т)~ ^{Хр.\>..р-1.р+1 ..ж)
В силу этих свойств ортогональности оказывается воз¬
можным определить величины типа: 5 (ухт ш);
не вычисляя
индивидуальные значения каждого из полиномов Чебы¬
шева. Следовательно, оказывается возможным определить
величины Т(} и At, а также K,f и а. без определения ин¬
дивидуальных значений каждого из полиномов Чебышева.
В самом деле, пусть имеем систему „Г* полиномов
Чебышева, т. е. полиномов типа:
Xm.l?..m~l~ Xm ^m-0X00~ ^m lX\-0~
Tm-2Xt.l • * • Xm— 1.12.Ж—1
а также уравнение множественной регрессии, выраженное
через полиномы Чебышева:
Уц.-.ж” A>*0.0^1Х1.0~^~ ^2Xt.\Jr ^3JC3.41**‘
4-. • -АтхтЛг
На основе этих уравнений, имея в виду свойства орто¬
гональности полиномов, легко получить все необходимые
формулы для вычисления как коэфициентов регрессии,
так и коэфициентов соответствующих полиномов.
Для простоты письма покажем это на примере урав¬
нения множественной регрессии, выраженное в форме
интерполяционного ряда Чебышева:
14
Полиномы Чебышева
и на примере системы полиномов „Г‘:
Vo — 1
Vo = *i- Гю
Vl = Xi ^20 ^2\Х1-0
Vjl ~ Х± Гт Г,, Хг 0 7 3.,
mp—к? Г'
На основе этой системы найдем формулы для опреде¬
ления сумм: 1) 5(х*.ш2) и сумм
Эти СУММЫ легко получить если:
а) умножить каждый полином Чебышева на переменную
того же порядка, т. е. например, -*3.я на х3 и затем сум¬
мировать;
б) умножить каждый полином Чебышева на следую¬
щую по порядку переменную, например, полином х2., на
переменную jc, в затем суммировать.
В первом случае, подставляя значения Т имеем:
5(*о.о)“л
■*<*;.„>Ту. «<*,) - s(^)-
S( *?.l) ” S( А ) ~Т» S ( v) - Г21 5 ( V*1-0 ) =
S{x2x0 <d’S(Xi) S(X2Xl-b> с/ ~ v
ч*Г ( "л) .я
с Г «.2 \ __ (*2)]2 _ [$ (*2*1-о)] 2
■ К * S(4.о) SW
jcj-2i)“=^(jcs) “ ^зо^(хз)— ^(*3Vo) — Vi)
= с/ Х2\ _ _ И (-*з-*1-о)Р [£_(jfaVi)]*
Суммы, квадратов полиномов, сумма их произвед. и отношен, их сумм 1Л
Во втором случае (случай ,б“) соответственно будем
иметь:
•£( х\ Л‘о-о)= *l)
•S (-*2 ль0) — S( х2 Г10 S (=
_ С/ х х \ _ 5 (jriJt)o),'s (*2)
*(*.„) • „о,
<S(-X3jc2.i)as=^(‘f3jca) — ^ао^^з) ~ ^21 ^(хзх1-о) ~
-= 5 ( X X 1 ^ (•г2хО-о)‘^(д:з) _ $ (х2х1-о) 'S (жЗж1-о)
$(-*0-о) ^(-*14))
Аналогичным образом умножая полиномы системы
,ТЯ на у, а затем суммируя, имеем:
s(yxw) = s(y)
•^(V-^1.0) ~ ^(^t) ^*10 *^00
^(^м) = %-*а)-T2oS(y)-Tn S(Vxi.o)
5(УХз.я) — $(УХз) гж <S(y) Гя 5(j/xl>0)
Подставляя в эти уравнения значения „Г*, имеем
окончательно:
s(y,(.0-.,
*,1ГГ ^-с/1ГГч S(^)^0?) 5(л2ж^).5(^1Ц>)
гщ-
С/,,* N S (ъхсо) ^) S(x3xb0ys(yxl.0)
S(yx,»)-S{y*>) s(40 s(x?.o)
^ ( x3*a-i) ( УЪа)
Наконец, умножая уравнение множественной регрессии
в полиномах Чебышева на У и суммируя имеем:
^(Ут )s=AoS(yjcoo) + А ^ (Vх!-о) + ^4<S (У*;*») "^з^ (^жз у|)
16
Полиномы Чебышева
или, иначе, подставляя значения Ат, имеем:
S(7,- 0' vi«)]" _j_ (^д'|1|||"
>,Г' $ (л’о-о) ' S(:<о)
44,) s(4«)
Аналогичным образом находим S(y-); 5(у*„) и убеж¬
даемся, что
Следовательно, Ам и Тт легко определить, последова¬
тельно вычисляя суммы квадратов типа S(xf.0), 5 (x|.s).
-SYAlUi) и суммы проиагведеннй типа:
(А2А1 о)’ ,^(АлА’м)
s(yxi.*)> 5(ух2,\), s(y*З.п)-
Несколько иначе обстоит дело с коэфицнентами уравне-
нения регрессии обычного типа Уцг=&ь+а1х1 + в**«+
•a- Эти коэфициенты могут быть определены, исходя
из коэфициентов Ли Г, следующим образом. Пусть имеем
систему уравнений регрессии:
Vi **=• *Л(, 4- A,jCj.0=- j40 -|- At(x} — TJU) — Atxt 4- (A0 — A^T^) =
—a'jA’j+a'j, так как A1—a’lt to
A л т $ ( Ухи о) ~ a'* $ (-*iAo-o)
at,— л0—л,/,0—
(aS.o)
Затем пусть имеем: y&~A0 + Aai-o + ^гАм=
= £ о 4” ^ i ^jo 4” л11 (хj I л») 4*
4- <i2(x2 720 7*2i x,) = a2 x2 + (a t — a2 ^21) •S4*
4- ia\-a\T\b—ai T*>)=aо 4-a',' x, 4-a; x2.
Н*л и / aytcu и полиномы Чсоытсаа
17
С ледовлтельно:
о.=*гж - < г„- *-Ща. —■*£&>> - „• *±*ы.
° ‘ ” s(4) «(О !
.'-Г _ (Ух\ -о) S(*2*l. о)
в, =*<1,-0, 7^, С2
. _ * (?*м)
2" -440
) \ ( х:-о)
Аналогичным образом получаем значения ал\ а2. а " и
ао и уравнении для у|23-
Следовательно, через значения сумм квадратов и сумм
произведений могут быть определены также коэфициенты
aif. Приведя все эти формулы в систему, имеем известную
эмпирическую схему американского геодезиста Дул и тля (7),
предложенную им в 1878 г. (см. § 1, глава 2).
Полиномы Чебышева дают теоретическое обоснованно
схемы Дулитля.
Несколько иные схемы решения нормальных уравнений
можно получить, основываясь на системе полиномов Че¬
бышева с измененной последовательностью переменных.
4. „Веса** Гаусс» и полиномы Чебышев»
Теперь рассмотрим систему полиномов с измененной
последовательностью переменных (систему С). При нали¬
чии переменных а-,, а*0, имеем полиномы системы С,.
1 • Ао.о = 1
-• -Vo ~ Х1 ^ло
3* А(М =~ ^сохо ^OJ'V
При наличии переменных а,, а-,, и д„ имеем полиномы
системы С9:
т * — х к" — k" х
I. -v2-l — 2 20 "21 I
'^1-2 ^ Xt ^10 ^12'^2
3- *о-12 “ ^00 Х<> ^01А1 ^05 Х3 И Т‘
*1 Нмэяяпип Чебишйпа
Полиномы Чебышева
Умножая уравнения *0>0, л‘ьи, х2л, первое на х1г вто¬
рое на л*,, третье на л*2 и суммируя, имеем;
•^(•X2-l) ~ _ *20 ^ (*?) ~ *21 '^(*V2Al)‘
Аналогично умножая х,.2, на л*.», и суммируя имеем:
Ч*ид=5И)~ *Го Six,) - к s(Vl) - k;2 s(х(ж,,.
Затем умножая систему С, на хг, а систему С* на л»
и суммируя каждое уравнение в отдельности, имеем:
и:» системы С,:
1. 6' (хтк0-0) = 5 (х2)
2. S (*2*1 -о) ~ ^ (*1*2) ' * ю^' (*2)
3- ,S'(*2*0-l) (*о) ‘ & 01 ^(*?*i)’
из системы С2:
1. S(*3*2>1) = S(*3*2) - ^20^(*3) ■ ■ ^..j ^(*3*1)
-• (*3*) .2) ~ ^ (*з*0 ^ю^(*з) *i? ■"* (*3*2)
3. (*1*0.12) ~ ^00 ^(*3*o) *01 "^(*3*1) ^02^(*i*n)•
Разделим каждое из этих уравнений на сумму квадра¬
тов соответствующего полинома, тогда будем иметь:
из системы „С,“:
j S (х2*1-о) 6Ч (_ *>
^ (*i-o) ^(*?-о) •<'(-vi o)
2 ^ (*2*0-1) _ *оо "^(*2) *01 '^(*2*1)
(Ло-1) ^(*оа) (^O l)
из системы „С4‘*
уВеса^ Гаусса и полиномы Чебышева. 19
\> ^ (*зл’|«а) e _ *10 '^(^з) __ *12 * $(*3*2)
5 (л‘Г-2) ^ (-4*2) ^ (ХЬ'}) $ (-KJ.j)
2 (*3-vo-i2) *00 * ^('Ч0 *01 *^(*з-у|) *02 * S(x,x2)
S (-*Т0«1>) ^ (ли-!2) ^(-*0.12) ^(^012)
В левой части уравнений но системе ,ЛУ‘ имеем вели¬
чины Л2а. Art0, а но системе ,,CV‘, соответственно, кьс%
^ао*
Теперь введем обозначения:
1 ь*
• Ki
00
~ 00»
=- г • w ,
5(4о) Л’ S(40~
' , ““ *01
s(4.) *«..)
и соответствевно:
1 . = *"•
l
— /»v •
*00
5(41) *’
5 (4г.|
и»
1
5 (4ia)
-4
-4
— ru •
5(40
— С20‘
5(40
— «-л»
--*5»
/»* .
-4
==
5(40
ет С10»
5(40
--4
, /»0 •
-4
— С*
5 (412)
С01»
5 (-*0.12)
02*
Тогда имеем окончательно:
система „С^*:
1. kjri— dл 5(х^|) + c’jq .S (jtj)
2. k-x)= doq S(xt) + d01 ^ (-^s^i)>
система
1- ^32 ~ ^22 (^з^) ■** с20^(-*э) "b cji^('Vci)'
2- == C]J -|- Cj0<S(jC3) + Cj2 *^(^3^2)
3- *jo = 4 5(л3) + c' 5(*,*,) + cTnS{x^y
2*
20
Полиномы Чебышева
Из полиномов Чебышева легко получить систему одно¬
временно решаемых уравнений для определения вели¬
чин cti и си.. Так имеем: x3.l — x.,—k20 — k3lxr Умножим
это уравнение последовательно, сначала на л#2> затем на
хх и на л*0 и суммируем полученные произведения. В ре¬
зультате имеем по свойству ортогональности:
*^(•*•].|) = '■^(•*'2) ^20 ^21
5(дС,Л211) ^20*^(Ai) ^21 ^(Л|) ~
5(X(IA'L>10) -- SfX^X^ -S('To) ^21 S (•'"Л) ~
Деля на <S(^.,) эти уравнения и вводя обозначения
с;; и ск: имеем:
c"nS(x$ + c"mS(x3) у с.” S(x2xt) - 1.
С2-2^(Х3Хj) — CW^(Xl) C2I ^(Al)
с»51¥») + VO*;») + <;,-Wo) =°-
Аналогичным образом получим систему одновременно
решаемых уравнений для определения с,",, ^ с3(Р с'2, (из
уравнения х,.2 = х, — А"0 —■ k33x3) и систему для определе¬
ния <£,, с", с", (из уравнения х0.12 = £"эх0 - /г" - к^х2).
Известно, что с"г = с"; с” = с"; c*№*=cvoiu т. д.
Эти системы уравнений предложил К. Гаусс (8) еще в
1823 г.
Таким образом „веса“ Гаусса (са.) есть ни что иное,
как обратные величины сумм квадратов чебышевских по¬
линомов с измененной последовательностью переменных.
Величины же с^.суть ни что иное, как нормированные
коэфиниенты соответствующих полиномов Чебышева (с
обратным знаком).
Величины сц и c{j получают в полиномах Чебышева
вполне определенный логический смысл.
Определение величин ru. и ci} но Гауссу, когда сов¬
местно решается несколько систем уравнений, требует
много труда и сложно, хотя сам Гаусс (8) и писал, что
его метод не оставляет желать ничего лучшего.
Полиномы Чебышева с измененной последовательностью
переменных позволяют указать значительно более простой
путь определения сп н с1у
Из уравнения л*,.0=а, — k'Xlt имеем указанным выше
способом: -+- с',05(а-,) = 1.
«Веса» Гаусса и полиномы Чебышева. 21
Из уравнения = —Л"2х2 имеем:
Г,, •$(•*?) + 1 10^(А1) г С12 *^(ДГ2Л|) 53 1 •
Вычитая из второго уравнения первое, имеем:
(«:. - - ^ч*,) - - <^(лЛ).
или иначе:
«и- «и
(*,) = -W>>
С12 c,2
С другой стороны, из уравнения хгЛ —хг—k^-k^xv
путем умножения на xt и суммирования произведений, а
затем деления всех членов уравнения на £(х£.,), имеем:
С.п + Сху S (•*)) ' - C22'^(‘KlXt)t
ИЛИ
е1\ - с
С.
22
Сопоставляя это уравнение с предыдущим, имеем:
K^n) 5(л;) + %|)„4_sW)^
с12 сХ2 сп
+ - Ч*г>
С1!
Это равенство как доказал Cochran (9) может иметь
место, если:
а) во-первых:
с|| с,|1 С21 >•
— --- или, так как cXi—с ,гх,
?12 ^2
,, • (*»)* . ПЗ)
1 II I! * * >
С>2
6) по-вторых:
22
Полиномы Чебышева
Аналогичные выражения будем иметь из других поли¬
номов Чебышева, например уравнения:
м ш / 'V 4 0
см — с * I Cjl с,й и с" *-= ст •- ~—;
С21 — п И И *11
еХХ с :В
иолучнм из рассмотрения полиномов Чебышева и
л,..„ а также х3.21.
Эти формулы имеют большое практическое значение.
Р. Фишер (10) без доказательств, но со ссылкой на про¬
фессора Шульца из Чикаго, дал аналогичные формулы
для исключения одной переменной (в этом случае в фор¬
муле знак плюс меняется на знак минус, так как опре¬
деляется, например, с'п, а не с",). Отметим дополнительно,
что эти формулы легко могут быть выражены через коэ-
фициенты и суммы квадратов полиномов Чебышева. Так,
подставляя:
Ьт Ь*
v» >31 w 32 v 1
м~ S(4*)’ Ч2_ *(4.*У г,~ 4-й)*
окончательно имеем:
аналогично:
443|/ ' ■" 44.) ,13*^
С1\ — С11+ л / о \> Г'^е
44,,)’ ' " 440
Следовательно, от одного этана вычислений можно
переходить к следующему этапу, зная лишь коэфициенты
и суммы квадратов предыдущего и данного полинома. На
основе всех приведенных выше формул нами совместно
с В. Н. Перегудовым была выработана схема решения
уравнений множественной регрессии методом наименьших
квадратов в полиномах Чебышева. Эта схема опублико¬
вана (11) в книге В. С. Немчинова „Сельскохозяйствен¬
ная статистика с основами обшей теории** (стр. 325—344).
Однако в настоящее время могут быть предложены
новые, более удобные схемы решения нормальных уравне¬
ний, основанные на иной системе полиномов Чебышева.
Нзиимоотношен. между козфицисн. смежных полиномов Чебышева. 21
5. Взаимоотношения между коэфнцпснтахп смежных
полиномов Чебышева
Рассмотрим вопрос о взаимосвязи между коэфиииен-
тами двух смежных полиномов, для чего отбираем из
ясего многообразия полиномов Чебышева новую систему
полиномов (полиномы системы ,,N-‘), а именно, систему
полиномов для одной и той же переменной (например xt),
язятых для различных последовательных этапов элимини¬
рования (сначала от х0, затем от х, и х0, наконец от хг,
хх, х0). Тогда будем иметь:
Четвертая система полиномов Чебышева
(полиномы системы ,N‘):
•v iJi *"
ХЯ '7;«-*4i.O г~ -Ч?.0 rVl.il 114)
•Чт-Я ~ 'Чч ^ЗгЧм ^ЗГ*Ы» ^"0Х()-0 ~ Л,М
'Гак как для старших коэфициентов полиномов Чебы-
нова имеем:
тя
т
1 .41
* .41
т
1 эо
^эо>
то, умножая на ха обе части предыдущих уравнений и
суммируя их, имеем: Sx:u() = Sxi; —
•^•Чз.] ~~ *^*Ч(.п *^Чи» •!' * 15а)
■^Я-21 = ^Яг'^'ЧгЧм *£Ч».1 ^32 ^*уЧы
Такой же характер имеют формулы при определении
суммы квадратов отклонений по уравнению множествен¬
ной регрессии. В самом деле, имея y0==i40x0 0, находим от¬
клонения от уравнения этой горизонтальной линии:
d0 - У —У0 = v —Л0хо.о-
Умножая обе части этого уравнения на у и суммируя,
имеем: S(d0)* = S(У ~ Уе)2 = $ (У)2 так кяк
Полиномы Чебышева
Затем, имея уравнение нрямой_линии V\ —;40Jte0 н-
1-у4,х,.0, а также отклоневия dt=y— у, ==у — /vc0.0— -4,л|0,
путем умножения на у и суммирования, получаем:
S(dj) — S(y2) —A0S(yx0t) —At S(yxl0) = S(d{) — a, 5(yx,.0).
так как At — a\, a Syfy — Уу) — 5(y — ух)г = Sd*.
Аналогичным образом имеем:
S(<$) — S(d?) - аг 5Сух.м)
5(dj) = 5(rf2) -- аз S(ухз.п).
Подобным же образом можем получить простые фор¬
мулы для определения сумм типа 5(хлх,м) и S(yx12tj_
Так, исходя из уравнений:
•'ьо ~ •'*! ^"|И
•'■2-0 ~Х2 ^ зЛ-О
2.1 ~~ -* 2 ^21*1*0 ^ 20rVO.O ‘ О ^ПХ> .<•
и умножая их на хл, а затем суммируя, получаем:
Sx.j-*!.,) — 5x^1 Tl0Sx^ — SX-jX^ kwSx-.к
Sx.jX^.q — •SXyX.j -- r^Sx^ — Sx^,, Sx:i
Sx^Xj ! -= SXyXj fl Tj 1 Sx^Xi ,f — SXtfX^Q •— fe2| w>A.jA'(-1)
Умножая те же уравнения на у и суммируя, имеем:
s (Ух 1.0) = 5 (Ухх) - k'io S<У)> затем $V**o ^ 5 (Ухг) - k»SO').
а также ^ S (yx?0) - Л;,5(ух,.0) т. к. Г10 • *10
и 7\, =■• Ла1.
Все эти формулы позволяют определить старшие
коэфициенты смежных полиномов, так как эти коэфиии-
-5(АаА,.у)
енты есть отношение типа: ь v ~ • ь - - '■
ь. _ Х(л-,л0.0) fc„ Л(АаА,.„)
,0~ ’ 21
*и 5(4.)
8:шимоотношсн. межОу коэфициен. смежных полиномов Чсбкаишх* У*
Они позволяют определить и стнршие коэфикиентм
регрессии, так как:
,S (Тл J.1) %s> (УХ3-2\)
*'s(»h.); s(4,); ~ Ч4*)‘
Наконец, из четвертой же системы полиномов Чебы¬
шева легко вывести формулы, устанавливающие связь
между соответствующими коэфиинентами данного и пре¬
дыдущих полиномов. Так, из четвертой системы полино¬
мов „АЛ* (смежные иолиномы для одной и той же пере¬
менной, но вычисленные на различных этапах элиминиро¬
вания) имеем следующие уравнения регрессии:
л*, по х, по х, и х0; х, по х„ х„.
Так как x^-x^-T^x^ то
о*з = *3 *з-0 = ^З0*о-о *»>■
Так как то
«*3 = *0 *Ы = 73! *1-0 ^ ^0*0.0 ~ ^ 31 (Л1 *ю)
*зо“^з!*1 (*го ^:п*ю) *ii*i h *ж>*
Аналогично имеем
12*3 ~ ~*3 *3-21 = ^32*2-1 Г ^1Л1-У г ^0*0-0 = ^32*2-1 V
^31*1-О *30 ^32 (*2 *21*1 *2о) *31*1 *31*1 **“ *;иЛ’| "
*=^32*2 (*31 ^32*2l)*l (*20 ^?2*Jо) ~ *Л>*> *И *' *У»
Такмм образом имеем окончательно:
*30 “ *30 ^31*10 = *ло *31 *л» < 1 7)
£*•' Ь" Т Ъ* — fc* Jbw V' п т ,
.-'О *30 4 32*20— .#> 32 20 *
Ь* — Ьп _ bw . Ь"
*31 32 21*
Такого же рода формулы получаются для определении
коэфициентов множественной регрессии jf по xt.
В самом деле, на основе интерполяционной формулы
Чебышева имеем:
K,“^tWeflo
у > ~ (*) + AiVi (х) = «,»-г Ai (xi ~ X ю) "-•
•— А^х1-^г(%<1п—А^iti)~= а ixi ‘Ь л о-
Полиномы Чебышева
Следовательно, А1--а\\ а'0 — ав — AtKXb.
Затем, так как y,» = 3'i — xl,4rt C-v), то
У и ~ Л0ЧГ, W A j't 1 (■*>) *Ь i4 jH11 (л) = rt jA'j f- а ф т
" ‘\(х! **i ^20) ~А2х.,-{- (at Ai^ix) *,ct^”(ao ~~
t=o£x2j-
следовательно окончательно имеем:
.4, = а;; а' = а\ - а* - £*; а" — а0 - а",Л2'0 и т. д.
Аналогичным образом имеем:
_ т
-4»
а.Г
*йа»
"Г
кма:<
к
- а; -
.,0UА
Следовательно, все коэфициенты данного полинома
Чебышева и данного уравнения регрессии могут быть
определены исходя из соответствующих коэфициентов
предыдущих полиномов (или предыдущих уравнений мно¬
жественной регрессии) и старшего коэфициента данного
полинома (или соответственно старшего коэфициента дан¬
ного уравнения регрессии).
Давная система формул, полученная на основе системы
смежных полиномов Чебышева (полиномы системы *№*),
дает нам возможность предложить новую схему решения
нормальных уравнений в полиномах Чебышева.
Новая схема „N*, как увидим в главе 3, одновременно
является своеобразной системой статистических характе¬
ристик (средние арифметические, средние квадратические,
коэфициенты полиномов н коэфициенты регрессии, крите¬
рии достоверности Фишера, коэфициенты и индексы мно¬
жественной и частной корреляции, ошибки коэфициентов
регрессии и средних и т. д.).
В новой схеме все эти характеристики даны в их
взаимной связи, как единая система метода средних чисел.
ГЛАВА 2
СХЕМЫ РЕШЕНИЯ НОРМАЛЬНЫХ
УРАВНЕНИЙ В ПОЛИНОМАХ ЧЕБЫШЕВА
1. Ох см и Дулитля
(Схема последовательного элиминирования)
Теория схемы Дулитля будет ясна, если эту схему
записать в полиномах Чебышева. Схема ,D' представляет
собой схему Дулитля, записанную в общем виде в поли¬
номах Чебышева*).
Схема решения системы нормальных уравнений Дулит-
лн имеет дело с полиномами Чебышева последовательного
элиминирования (полиномы „Г"). В этих полиномах Х\.о не
содержит в себе х0; х2о не содержит в себе х„; хм не
содержит в себе л*, и х0; *3.210 не содержит в себе *,
и л*0 и т. д.
В схеме „D" записаны 4 типа уравнений, связанных с
полиномами Чебышева, необходимыми для решения данной
системы вормальных уравнений. Прячем, коэфициенты по¬
линомов записаны в элиминационных строках. Уравнения,
характеризующие полиномы Чебышева (уравнения первого
типа), можно прочесть, если каждую колонку схемы чи¬
тать, начиная с заголовка по элиминационным строкам
сверху вниз. Так. например, имеем:
:!) Положения связанные с интерпретированием схемы Дулитля в
полиномах Чебышева впервые были высказаны автором в его докладе
Множественная корреляция , состоявшемся 15/1 1940 г. на заседании
Статистической секции Московского дома ученых.
v.S Схемы решения норлмлоных уравнении в полиномах Чебышева
Колонка:
•vi -
-V..
■S(~vl'w)
5(4о)
5 (Л2Л0Ч|)
Полиномы:
- • Л*
^'(■*0.0)
*^( -Vv*n. о)
Л:! “5(4оГ
S (.УдЛ,^
44.,У
Л ( Л;{.Г| .о)
5 (4п)
1 *о
S(.v.,.v2.,)
' 5(4.)"
'*2-1 ~ Л*1.д
Остаточные отклонения множественной регрессии:
5(^м)
», _ ^ 0'Аао) 5(j’.e,.u) ^
• ЦЖ Ч4.о)
ЛЫ)
5(4.)
5(.^:;,>.)
5(^2.)
Следовательно, все эти уравнения HAieioT дели с поли¬
номами Чебышева последовательного элимнннрононт..
т. е. с первой системой *rm(,v).
В схеме ,D* записаны также уравнения для определе¬
нии сумм квадратов полиномов Чебышева (уравнения вто¬
рого типа). Эти уравнения можно прочесть в ннжнеи
части соответствующих колонок (между последней н пред¬
последней элиминационнымн строками каждой колонки).
Колонка:
Остаточная сумма квадратов.
S ( к V’ |5 ^ -<| А|||))1 с / „2 \
( f) ( ,о)
-/ ... (S(.ir\ulj|- |S(JV,-,„)|- .
S{»> x(;q -i‘>"
с/ .- I [5 (лУГ<й)1~ j5(A3 v|.u)j' (S(-r.; V2 l )Y
5(4,|) 5(4л) 5(.v-:.j
*(4*,)
СХЕМА ДУЛИТЛЯ В ПОЛИНОМАХ ЧЕБЫШЕВА
СХЕМА «Л*
Значение линии
«О в
X S
о 5
Ч е*
= Я
То
первый
второй
d
третий
Факториальным
признак
Результатив¬
ный признак
Варианты I | Х*о =■ 1 1
*i
Х>
X,
У
Последовательное элиминирование (Ат)
Сумма
Нулевая элимина-
циониая строка
Сумма про наведе¬
ний с л, . . .
Поправка по ли¬
нии Sd ....
Сумма произведе¬
ний в отклоне¬
ниях пт средней
<5 =3+4) . . .
Э.шминл ннпиип и
строка порван .
Сумма произведе¬
ний с .V ., . . ,
1 /1= Sx%о
2 —1
3
4
5»
I
j -
iJrl T00 — ^A'l
Sx2 x00 = Sx,
| I
1
Sx j Xqq = Sx3
Sxt *00-_ x
S*oo
_ 5*2 -v00 Y 1
5voo
! 5x3 x00
3
“00
Sx-
Sx2 v, i
Sx3 x,
(SXpXfH,)1 -2
A ** *—1 /1 A I
Sx2 x00S.v, x 1(l :
' 5*3 *oo 5*i *oo
s4 о 1 |
| Cv2 1
i *>oo ;
5*oo
5xT.o =
[
I
\
1
* 5 ( xi — *,)’ '
1 Sx, x,_0
5*3 *i.o
00
.N'v
Syx,
5У*оо _ , |
$А‘оо
Syx,
5УХoo$xi *on
/ _
Сумма
квадра¬
тов
откло¬
нении
SY*~'
= ySy
<9
3*
О.
С
Sx
— 1
_ Sx2 *1 .0 S*3 *1.0 j
7:
S-
rr
III
Попытка ип ли-
| .Ifllll S0 . . . .
Поправка пи ли-’
nun S, • . . м
i i
Сумма 7 :-8-гУ in
Элпмниатшниан | j
строка вторая .* \\
\
Sxl о
Sx*
(SXf Хр+)*
Sx
,2
1.0
Sx3 х2
00
S>’Yl. о
Syx1.0 .
Syx2
| Sy A’j ^ j 9
= HAT.
ят3 Xqq Sx2 a*(>u Si'Xqq Sx ^ x,m j
5*00
(£*2*,.
5*?. о
5*2.1
I
Sx,
00
5*00
S Xa a I -0 Sx* X|t , (1^X2 Л*1 .0
S*1.0
S*3 *2.1
Sa
1.0
Сумма ирпизведе-
* iniii с Х3 . . .
Поправка по ли¬
нии S0 , . .
I1 Поправка по ли¬
нии S, . . .
12
I
13
1
Sx, x
2.1
14 —
5*1.,
Sxl
(S*3 *oo)2
Sx00
($x3 *l.o)2
Syx2l
Sy*2. I
"" S*2.1
Syx3
Syx00 Sx3 x^,,
:[
: \ .vS'r.v,
•4- I
S-Voo
Syx, 0Sx3 x
I .0
i Поправка no :iii-| •
ниц S.x 45
Sx
1.0
5*?.o
I (S*3 *2.l)2 | Sy*2. | SA-3 Xo j j
I
5 Сумма 1C* — 12 +
5 I -i 13 14 + 15 . If,
y//'J D.iii.Miiiia.iimiiuavi j '
, строка третья . 17
IV Сумма проашчглс-1
iniii с Y . . . J IX
s*b
Sx2
°*3.2|
—1
\
Sx$ ,
Sr-Vj.2i
Sy-v3.2i
Sx
,2
V*
3.2»
j ^ -4д5л'Г. :l
iSY?
Полное элиминирование (*ч)
Коэфициенты по зли.мкнациониым;
строкам I
Колонки результативного признака
Понрапкн по колонке признака Хя
тп же, Xа .
то же, Хш
ао
^0
S*3 *оо
voo
Sxf
Sx3 *1.0_
Sa?.o
a2
Л •»
Sa*3 Xo ]
* • ' • "a
Sxl, J
•b ~":t
Syv:j. i* i
Sa j ^ i
Sa2 *oo
Sxl
00
Sa, -Vqo
Sy2
ox00
Syx
= Sx
123
0. 123
Sv2 X,
SaJ . a i
Sxl
Syx,
23
23
Схема Дулитля
_'V
Наконец, в колонке F аналогичным образом записаны
суммы квадратов отклонений по уравнению множественной
регрессии (если величины А заменить их значениями):
SVv-i 1^(-,1д.''п)1 l5( vvi-»)J' М-,-Л'г|)|' t>r. г у
1 *(4„) s(4.) -44.) } y,Tj
В схеме „D* также записаны уравнения для определе¬
ния сумм произведений данной переменной на соответст¬
вующие полиномы более низкого порядка (уравнения тре¬
тьего типа).
Эти уравнения записаны в соответствующих колонках
между строками сумм произведений. Так, имеем:
Колонка: Сумма произведений.
o(Jf0.o)
^(•*ГЛДО и) ■ $(Х2Х0о) S( *3*1-о) • $(-*2Л1-п)
^ s(*U) ‘ s(*l0) -
= 5(дсдл20).
Наконец, в колонке ,£* имеем аналогичные суммы для
уравнения регрессии:
S(yx,) - S(yx,.,,
с/..„ Ч s(y*м) * 5(¥w) Ф*ьо) • S(x3x,.0)
(yi)
S(p-x2.1).S(x3x2.1)_ с/ _ ч
В схеме «О*, в-четвертых, записаны уравнения, необ¬
ходимые для вычисления коэфициеатов множественной
,)V> Схемы решения нормальных уравнений о полиномах- Чебыии ва
регрессии. Они записаны снизу схемы „D* (см. .Обратные
решения*). Эта уравнения таковы (если величины А заме¬
нить их значениями из колонки „е*):
„ ^ (w3.2i)
44.-.,)
... _ ^0^2-1 ) ^ (A3-v2-l) д" _ ^(•УХа-'Я)
5(д^.,) •<'(Л2.1 ) 3 $(л2~,и)
^(-l’Aio) •^(jr3jri-o) ^(Л2х1.о) я )
*•” *«.) " *W,) * " s(4.) * *К»)
. _ s(."'о ») , S(>rt<1) , s(^-%«) ...
*«») ’ ’ s(4.) 1 Ч4„) "
Эти уравнения записаны в соответствующих колонках
обратного решения, если их читать также сверху вниз.
Схема Дулитля имеет дело только с полиномами Че¬
бышева, как функциями последовательного элиминирова¬
ния.
Если оказывается необходимым включить новую пере¬
менную или исключить какую-либо из введенных ранее,
то необходимо заново проделать те вычисления, которые
предусмотрены уравнениями обратного решения. Кроме
того, тогда необходимо в схеме предусмотреть дополни¬
тельную колонку для новой переменной, а также заново
решить уравнение, записанное в колонке .Зависимая пе¬
ременная*. Если же бывает необходимо исключить какую-
либо из ранее включенных переменных, то становится
необходимым заново проделать все вычисления не только
обратного решения, но и по всем тем уравнениям, кото¬
рые записаны в колонках справа от исключенной перемен¬
ной.
Таким образом, если исключается первая переменная,
то необходимо заново сделать все вычисления.
2. Числовой пример решения нормальных уравнении
в полиномах Чебышева по схеме Дулитля
Применение полиномов Чебышева для решения нор¬
мальных уравнений по схеме Дулитля покажем на пример»
Безенчукской опытной станции, проводившей параллель¬
ные наблюдения над урожаем яровой пшеницы и метео¬
рологическими факторами за различные вегетациомньн
периоды в течение 25 лет.
Т «I Л .1 И II л 1
Похождение уравнении c$yju между урожаем и метеорологическими факторами по методу Чебышева-Ду.тт.1ч
(пшеница «Полтавка*, Везенчукосая опытная станция, 1901—19J9 гг.)
Л кип и
Строка л onocoG
расчета
1
И.глщмне линя А п еорои
//
•14 j
i
Нумерация граф
I н
—| —•
/» 1
1
1
а»
K'Mirpo.'i.
л
• '«■ими каалрмип
A?** OHOHIIli
f
I. Последовательное элиминирование
%•
1
2 = 1:1я
Суммы
Нулевая элнмннационная ли¬
ния (средние с обратпым
знаком)
25
1
71!
—28,53
1459
4857
-194,28
231.3
—9,252 = А„
7286,3 |
-291,452 j
-2 139,9376 = A0SyxOl,
1
Si
i'
3
4 = 1*26
5 = 3 + 4
6 = 5:56
Суммы произвело тип с a*i . .
Поправка по линии So • • •
Суммы отклонений (произве-
дений с л,.0 )
Первая элиминацгонная ли¬
ния (с обратным этаком) .
—
32116
-20391,8!
11724,16
-1
46 766
-41 669,84
5G9S.96
-0,43471 |
—138715,92 }S(-Vi-*i) (a-j—,v3)
—17 503,92
+ 1,492908
-6605,
1618,072
-0.138012 = /5i
208318
-207382.728
1
935.272
-0.079344
-223.313353=
— >4iS v.tj.o
п
7
Сумма произведений с л* . .
106111 \ s(xt—xt\i
251 798
15609 9
373518.9.
8 = Ь2е
Поправка по линии 50 / . .
—
—
-8514-7,24 f ' 1 Хх>
-28315-4.52
-13498.668
—382 100,428
9 cat 5"6C
Поправка но линии Si . . .
—
—
-2215,85239
+ 7619.65418
-703,440621
+4693,36117
— 105,712462 =
S,
10 = 7 + 8 + 9
Сумма произведений с х2Л .
—
—
+18747,90761
-24 046,86582
+1407,791379
-3891,16683
= i4aS.vje>.i
11'
11 = 10:10c
Вторая эдимннационпэя линия
(с обратным знаком) . . .
—
—
— 1
+ 1,282643
-0,075091 = At
+0,207552
HI
12
Сумма произведений с *, . ♦
_
1031455
40 229,7
1 074 684.7
13 = l»2rf
Поправка по линии 5а . . . .
—
—
-943617.96
-44936,964
-938 554.9 >4
14 = 5-Ы
Поправка по линпч 51 . . .
—
—
—
—26131.741199!
2 475,632633
-23716,1 9566
-0,977695 =
15 = l0.]ld
Поправка по линии S% . . .
—
—
—
-3)843.536651
1805,6932716
—29 -037,843^-8
. Л Ciiv
Ss
16=12+13+14+15
Суммы произведений с дг3.21
—
—
+33861.7613
-485,9331
33375.8232
— /J3Oy.r3.21
Ш'
17= 16:16rf
Третья элиминационная линия
(с обратвым знаком) . * .
—
—
-1
0,01-135 — Ал
0,98565
IV
18
Сумма произведений су , .
1
i
—
—
—
—
—
+2 512,29 = S;«
II. Полное элиыилировэвие (горка):
Строка 1 Справо вале во
«ji А,, A\t Ао
(с обратными знаками)
9,252=/о 0,138012 = i4i 0,075091=А* —0,01435 — А3
Строка 2 а. умвожонное на числа 2,7879
lid, 6d, 2d
-0,0214277 —0,018109
0,056682=*.
Строка 3 а: \ множенное на числа —3,3079515 —0,024641442
2е 0,09194 = Я!
Строка 4 а\ умноженное на 2b —2.62666
П, 10528 = я„
л /.2 = 223,313 +105.7125 + 6,9767 = 336,0022
е2 .
.v-UV
n»5f.a =
0')
Ку.т~
у -
V-.
36,0219
—^ - =1.41087
= 2512,29 - 2139,9836 = 372,2021
36,0219
1 -
= 1 - 0.09726 = 0,9)27!
hS*.123 = 36,0219
С то
1(-
372,2024
С, 10528 -4-0.09194^4 + 0,56682*, - 0,01435*,
:9,252 —t). 138012-^^-1-0,075091^^ — 0,01435а3.21 (в ортогональных многочленах).
Примечания. 1. Знаки в элнмниационяых строках изменены па обратные.
2. Коэфициснты flj, tf(l — алгебраическая с>мма чиеэл. стоящих в
столбцах «горки*.
3. алгебраическая сумма чисел последней колонки, которые
п свою очередь, есть произведение двух последних чисел колонки е
(по разделу I. II, III и т. д.).
2. Числовой пример решении нормальных уравнений >Г
В качестве метеорологических факторов были взяты:
X,—осадки в миллиметрах от начала сева до начала ку¬
щения (от 3-й декады апреля по 2-ю декаду мая включи¬
тельно); х, —осадки в миллиметрах за период от начала
кущения до начала цветения (от З-й декады мая до 3-й
декады июня включительно); х, — испарения в миллимет¬
рах по эвапорометру Вильде за второй период. Результаты
обработки данных наблюдений приведены в таблице № I.
Решение по схеме Дулитля дано в этой же таблице.
Решение по схеме Дулитля состоит в вычислениях,
основанных на приведенной в § 1, гл. 2 системе уравнений,
расположенных в соответствующих колонках схемы. Так.
в колонке Ъ имеем первое уравнение данной системы:
s( Ato) = 5 (*0 - = 32116 - = 11724,16 (1)
В колонке ясы сверху вннз расположены последова¬
тельно одно за другим два следующих уравнения:
1) Между нулевой и первой элиминационными стро¬
ками размещены вычисления, основанные на следующем
уравнении:
•Ь'(л2*,.о) -SU,*,)- =
/I
46766,0 Ц».0;7»4.0 _ 509696 (2)
25
Между первой и второй элиминационными строками
сверху вниз расположены вычисления по уравнению:
S(jfi ч - - lS(Xi)]2
106111,0 — (145?,0)3 -(-50^;—^ = 18747,9076. (5)
•25 11724,16
В колонке Kd* аналогичным образом записаны вычи¬
сления, основанные на трех следующих уравнениях:
1) Между нулевой и первыми элиминационными стро¬
ками по уравнению:
s(x9Kt^)asS *3*1 121212 - _^?5LZii_e= 17503,92.
32 Схемы решения нормальных уравнений в полиномах Чебышева
2) Между первой и второй элиминационными строками
но уравнению:
-О, . r v С/ г г \ S(X^S(^) S(AVvl-0 ) • А*|.0 )
Ь( Л, - О ( хях,) — - -
... 7о8 0 _ 4857,0-14-59,0 _ (-17503,92) (5095,95)
25 11724,16 ^
24046,86582.
3) Между второй и третьей элиминационными строками
•пи уравнению:
о/ ... ч С/гП— 1MVi.o )1~
( ' ( V s(^.„) "
„ Ю34455 ■<;^-0)= _ Ы75°Ш: _
25 11724,16
В колонке *ев расположены последовательно вычисле¬
ния, основанные на следующих трех уравнениях:
1) Между нулевой и первой элиминационнмми стро¬
ками:
s<y*,.a)-s(yx,)-
= 8224,0 — ——3‘7—— г_- 1618,072.
25
2) Между первой и второй элиминационными стро-
ними:
<Г/rr \-S(vx\ S(-V)'S(V;) .
'4vx,.i)-S(3^) if&J
-- 15609,9 - ^3-I-,3^59-°= 1407,791379.
3) Между второй и третьей элпмипационпымм гтро-
кями:
- Чу я -
^(-Vxg-i).5(A-a.va-i) __ 4Q229 7 — 731,3-1857,*1 ^
S(.v^.,) ‘-’5
_ ПИК.072 (—17503,92) (1-107,791.379) (-21016.86582)
11724,15 “ 18747,9076
485,9331.
Числовой пример решение нормальных уравнений
33
В элиминационных строках записаны (с обратным зна¬
ком) элиминационные средние, полученные путем деления
зсех членов данной элиминационной строки на первый
слева член этой же строки. По каждому учтенному приз¬
наку элиминационные средние записаны в колонках соот¬
ветствующих этому признаку. Нулевая элиминационная
строка есть не что иное, как обычные средние арифмети¬
ческие факториальных и результативного признака. Во
второй элиминационной строке записаны выражения типа:
S(*t*l.o) . ^ -о) S(.V*,.0)
SOW ' SOW' sow”-*
В колонке / по элиминационным строкам записаны вы¬
числения остаточной суммы квадратов отклонений по дан¬
ному уравнению множественной регрессии. Члены этого
уравнения последовательно равные: A^S(ух0); S(yjci.o);
i4,5(yjC2.i);i4sS(yx3.2i) есть не что иное, как произведение
значений каждой элиминационной строки по результатив¬
ному признаку (предпоследняя колонка) на соответствую¬
щую сумму, стоящую над этим числом. Этим исчерпы¬
вается первая часть схемы.
Вторая часть схемы Дулитля, так называемая .горка*,
имеет обратный порядок вычислений по сравнению с пер¬
вой частью схемы.
В колонку яел переносится (с обратным знаком) число,
стоящее в последней элиминационной строке колонки ,е*
. ^(-V-Xa.oi) п
в верхней части схемы т. е. а3 = ■ - -у. В колонке
,4* записаны вычисления, основанные на следующем ура¬
внении:
£CV2-t) *
2 5 (xj.,3) S (д2-0 ^ 3
1407.7913Т9 (—24^6,86582)
а" =1(-0,01435) = 0,056682.
^ 18747.9076 18747,9i>76 v
В колонке ,с* записано аналогичное вычисление, осно¬
ванное на уравнении:
»» SQ'-*i.gQ ^ Q’xi -о) -S $(*,*,-о)
* ^(-*1.27) ^(-*2.1) ^(jr?-o) 3 ет
. 1618.072 (—175иЗ,92) (-0,01435)
< = — “
2 11724,16 11724,16 11724,16
= 0,09194.
J Пол «НОМЫ Чвбышв»*»
34 Схемы решения нормальных уравнений в полиномах Чебышева
В колонке ,6* записаны вычисления, основанные на
уравнении:
=• 9,252 — (0,03194) (2856) - (0,055682) (58,36)-
-(-0,01435) (194,28) — 6,10528.
Этим и заканчивается вычисление уравнений множест
венной регрессии по схеме Дулитля. 1аким образом в по¬
линомах* Чебышева каждое число, полученное в процессе
вычисления по схеме Дулитля, имеет свой логический
смысл. Эмпирическая схема Дулитля, таким образом, полу¬
чает свое теоретическое обоснование в свете полиномов
Чебышева.
3. Новые схемы решения норнальных уравнений в иолнио-
иах Чебышева
На основе изучения полиномов Чебышева нами выра¬
ботана новая схема решения нормальных уравнений. Эта
новая схема основана на четвертой системе полиномов
Чебышева (полиномы системы N). Если отобрать из всех
разнообразных полиномов Чебышева те, которые отно¬
сятся к одной и той же переменной, т. е. например,
полиномы х2.0, х2., или х3.0, л-.,, х...2] и т. д., то в нашем
распоряжении и будет четвертая система полиномов, ко¬
торая позволяет дать новую, весьма удобную схему решения
нормальных уравнений.
Удобства этой схемы проистекают из того, что поли¬
номы N в сущности идентичны отклонениям от уравне¬
ния регрессии, но только вычислены для хв, а не для у.
Преимущества новой схемы состоят в следующем:
1) Новая схема основана на легко запоминающихся
формулах одного и того же типа, имеющих характер
разностей; все коэфчциенты данного полинома, вычислен¬
ного по хя (кроме стари его коэфкциента этого полинома),
равны аналогичным коэфициентам предыдущего полинома
той же системы N минус произведение соответствующего
коэфициента полинома вычисленного по системе N для
предыдущей переменной Хт-i и умноженного на старший
коэфициент данного полинома или данного уравнения ре¬
грессии (см. схему N).
2) Новая схема позволяет расположить все важнейшие
статистические характеристики (я, xlt у, с; Д-'), коэфи-
$(.™0.о)
S«o) 1 5(дг0.0
-sV - я
' а
Hofue схемы решена'l нормальных уравнении
35
циенты (а. А, К, С) а также критерии (F, R, гтк и т. д.)
в стройную, логически законченную систему статисти¬
ческих вычислений.
3) Новая схема позволяет легко вычислить, а также
статистически оценить с самых разнообразных точек зре¬
ния, не только коэфициенты уравнения множественной
регрессии, например, у по xt, хг хх, но и всех других
промежуточных уравнений регрессии, а также коэфициен-
тов полиномов, например, Xj.21, х1ЛУ хь73 и всех промежу¬
точных полиномов.
4) При этой схеме вычислений отпадает необходимость
повторять заново все вычисления, если подлежит включе¬
нию или исключению одна или несколько переменных.
При новой схеме, таким образом, полностью отпадает
Гауссовский способ совместного решения нескольких урав¬
нений, который до сих пор лежал в основе метода наи¬
меньших квадратов. Все эти преимущества имеют огром¬
ное практическое значение. Теоретическое же значение
новой схемы состоит в том, что:
1) она дает теоретическое обоснование методу наимень¬
ших квадратов при помощи полиномов Чебышева. Метод
наименьших квадратов в связи с этим перестает быть
способом, стоящим несколько изолированно в современной
математике;
2) вскрывает в весьма наглядной форме статистическую
природу метода наименьших квадратов, как всестороннего
и глубоко развитого метода средних чисел.
В основе метода средних чисел, оказывается, лежат эли-
минационные (или иначе корректированные) средние типа:
т — 1... СТ + 1... (А-1)
5Л*А.12... т - 1. т + 1... (А -1)
на которые указал еще Гаусс (12), как на наиболее веро¬
ятные средние.
Основой всей новой схемы вычислений являются стар¬
шие (на каждом данном этапе) коэфициенты полиномов
Чебышева, т. е. величины А 0, Л21, kZ, и т. д.
Эти коэфициенты вычисляются на основе сумм нор¬
мальных уравнений и коэфициентов аналогичной системы
полиномов для предыдущей переменной. Таким образом,
если итти обратно, то доходим до полиномов Чебышева
нулевого порядка, причем в качестве исходной точки
всех вычислений оказывается нулевой полином Чебышева
1, а также •SpTjUpc)] — п (число наблюдений).
v
3t> Схемы решения нормальных уравнений в полиномах Чебышева
Таким образом повторность, число наблюдений (л)
и объемы явлений (S*t, Sy), определяют в конце концов
всю систему статистических величин, начиная с средних
арифметических, среднеквадратических и кончая кээфици-
ентами уравнения регрессии, коэфициентами полиномов
Чебышева и т. д.
Новая схема приведена на стр. 35.
По этой схеме ход вычисления таков:
1. Нулевой этап (вычисление средних арифмети¬
ческих).
II. Первый этап (определение сумм квадратов от¬
клонений и коэфициентов полиномов Чебышева первого
порядка).
III. Второй этан (определение коэфициентов урав¬
нения прямолинейной регрессии и коэфициентов полино¬
мов второго порядка).
Центральным пунктом вычислений на этом этапе, как
и на предыдущем, является определение старшего коэфи-
циента полинома данного порядка. Для второго полинома
Чебышева хгл —х.г — А"0—старшим коэфициентоы
Необходимая для определения старшего коэфициента
Л я сумма квадратов <S(*f.0) нами уже вычислена на пер¬
вом этапе, остается определить 5(лг2дсЬ0). Эта сумма равна:
является к
Таким образом, к".. — о)
S{*U)
оказывается величиной,
Новые схемы решенич нормальных уравнений
которую легко определить через величины уже известные:
•S(x2x,); <S(x2); .S(x|); •$(•*?); AJ0-
Младший коэфициент данного полинома Чебышева
также легко может быть определен по формуле:
к” =k' — к •к*
*20 20 *10 21 *
для вычисления которого все величины уже определены.
Аналогичным же образом можно определитьвсе коэфи¬
циенты второго полинома Чебышева для х,. а именно:
*зо “ Кхг Здесь к;, =
^(Х9Х1Л>)~ ^{Х3Х\) ~ *10^(Хз)'
Младший же коэфициент k"0 равен: Аз0 — ^зо~ *io‘*If
В результате имеем не только вторые полиномы Че¬
бышева хгл и хм, но и уравнения прямолинейной регрес¬
сии X* ПО Хх и X, ПО Ху
В самом деле, так как:
•*2*1 = Х2 *20 *21 XV 1*^2 *■' Х2 ~~ Х2-1 ~ *20 *21^1*
Аналогично имеем: ,х3 = х3 — х3>1 = + А31х,. Заме¬
чаем, что в уравнениях регрессии имеем такие же коэ¬
фициенты, как и в чебышевских полиномах, но со знаком
плюс, а не минус. Затем определяем:
5(*?-о):= ад..)
1
и вес величин х2 в присутствии х, как с.^— -, , v
Совершенно таким же образом определяем прямоли¬
нейную регрессию у по х,: у, — а'0 + а',хг Здесь
Затем 5(ух,.0) = 5(ух,) - к\й S(у).
Наконец, ~ £,3а,.
Следовательно, все величины, необходимые для вычис¬
ления не только полиномов второго порядка, но и уравне-
, а сумма
3$ Схемы решения нормальных уравнений в полиномах Чебышева
ний регрессии включая прямолинейную регрессию у по
xv а также хг по хг по х, и т. д., возможно легко вы¬
числить на основе величин, определенных на предыдущем
этапе.
Прежде чем перейти к следующему третьему этапу,
определим суммы квадратов для найденных полиномов и
для уравнения регрессии. Они также могут быть опреде¬
лены на основе ранее полученных величин, а именно:
^(■*2-l) ~ '^(Л2-о) ^21 •^(*>С2ДС1-о)
Для того, чтобы иметь возможность статистически
оценить полученные результаты, следует определить ве¬
личины. носящие название «весов» Гаусс-*, т. е. вычислить
величину с'„ =—/ТТ» а также нормированные коэфи-
5 (а:, ,0)
£
циенты первого полинома, т. е. величины: Сш= - ^°v
~*оо
<no== s(*UY
Последняя величина определяется по уравнению:
1 W
<ч»= Т + s(~^~) ИЛИ ИНаче coo^cno + *.octo-
В результате оказывается возможным определить ту
часть вариации по уравнению регрессии, которая воспро¬
изводится при введении в уравнение регрессии перемеп-
ной xv Эта величина нами уже определена как: a'
(</,)-
но она также может быть вычислена как , так как
1 II
_£_(^ыд . |
‘ S(xU)’ ar" S(xloy
Эта величина обычно называется суммой квадратов
коррелированной (или воснрои.звгденной) вариации. Дан-
, («У
ного типа формулы будут использованы при
'и
статистической оценке коэфициентов уравнений регрессии.
СХЕМА НЕМЧИНОВА В ПОЛИНОМАХ ЧЕБЫШЕВА
СХЕМА *N*
Строки
*0
1
х2 |
^3
Y
_Г"»я-
5
5хрр » л
«х. ;
Sx2 1
Sx3
1 Sy
I
1
Sx*
Sx2X| i
Sx3xl
! Syx,
1
Sx*
Sx3jc2
i sy*i
.. .
« i
s*l
1 8Ухз
N
£
1
1
1
I. Вычисление уравнения регрессии Y по Х„ X,, X,
s{ol)
slPi]
С,-К.-а.
М
“ а*
с (о?)
SlP2)
с,-К. -а,
Мх
м2
Сщ *т — 0|
«KJ
G, — at
Мх
М2
М,
С»-а*
к
Sx, х0 _ Sx|
л
Sx,
10 “ с у2
ОХоо
20 П
SXj o*3 —К|0^х| j vS v2.0* *20^*2
. Sxз
^30- л
*3.0“S*3“
a0-
fteaSX^— УС30 SXj
Sdl-Sy2 — a0Sy
1
C,‘ “ *i.«
•10
K.oC
10 ^ 11
Sjt2xI.O=*SX2X,-iC|0S.V2
^X2*I.O »
-Sx2x1>0-C,,
k2l
5x?.o
^10*^21
KM ”* A'jp Kio'K])
Sx| , “Sxj q—K21Sx2 x j 0
KnCZ
99 99
Cpo “ Cpp +Kjp Cjp
K2X c"
Ко C2l)
Cn “ C'„ + K2X C21
[Cjo ■* C|p — K20 C21] '
с
** ®4.
c" -Kor c"
21 ^21 ^22
Coo • ^ao’C22
"*x3 xi .о-5хз *i — *10 ®x3
Sx3x1-0
*31 - 7? S*3*I.0-C,,
*x1.0
Ko*3l]
К*-«’зо-<о«’з\]
SxI , «aSxf 0 — K3, Sx3x, 0
$Ух1.о=5Ух|-*ю5У
«i-5yx,.0.c;,
*IOel
a0 ■= fl0-/c',pO,
I-'tP
11
Sx3 x2 , ~Sx3x2—K2l Sx3x, — K^>Sx3 lsyx2 ,~Syx2-K2l Syx,~K^Sv
К32 “ Sx3 x2 ,-C22
*21*32
*20‘*32
*« -*а.-**,*Г
^21 ''ЗЗ
*м “*»-*»•*£
^*3.21 = ®Х3.1 — *32®X3X2.I
а2 » Syx2i | С22
«* *#
*2Гв2
К20-л2
*• * I/" "
в, =о, — К2Ха2
•• 9 is"
°0 ^ аО — *20*^2
Ы!
с«°.
SdJ н Sdp — OjSyx | р
КТ
«25УХ2.1 -"7я""
с22
КТ
C'u
КТ
Cpp
Sd2 — Sd* — a2 Syx2.,
1
^Ф9Ф
Кор С
ЗО'^ЗО
<«' <s;
Ко c3I)
999 999
C|i = Cn+K3j-C3, |
<зСз2
к; c32]
[*£ c;2]
c22 - C22+K32.C32
fc2;-c21-K3;.c3'i
C33
5x3.2I
9Ф9
32 “
к'\
*32
г
c33
999
*31 “
tc"' >
*31
шг-
c33
999
30 —
999
^30
'^33
*/» >* »**
C0o “ Соо + *зо'^зо
Ко- cVo-K^C-] i Ко - С^-к£.Сз2]
Sy*3 21в^УХ3 —^32 Syx2— K31 SyX| K^Sy
ITT^r: = KT
fl3 в ^Ух3.21 *^33
a3 Syx 32l
33
*32’tf3
I
999 999
^31 *a3
999 999
Кзо'аз
—
99 #« •••
1 «2 I2
** a2 — K33-a3
c22
99 ..»/* ел»
(«;т
■ о, — K3,*e3
; cx;
I-of
* tf0 — *30 * a3
r'r#
00...
—
Sd3—Sd2 — e3 Syx3 2,
И. Определение коэфнциентов полиномов *2.13 и *1-23
K2‘
Г|Г- C“1
L ” cj;J
К'Г
и-а i
[*-fl
Kf]
[-■а
[<>|]
HI. Исключение X, (определение регрессии У по X, и X,)
,С' и
[,ср0-с--к;рс;р1
(.с22-с22-к;2с21']
[.Сэз-с£-к;3<;|
ftt 999 999 г.999%
1^3 efl3 +fll ^|з|
[** *99 999 ##♦»
I а3 ™в2 +а1 '^I2j
Г " . ••• ,.#«1
[I ао “ ^0 +а% /С,о]
Мз'Г
.Сзз
[.«'Л2
1^22
J.-0?
»Сро
Новые схемы решение нормальных уравнений
Аналогичным образом может быть вычислена вариация.
(a'V
.-вязанная с х0 (частота), и она равна
соо
На третьем этапе вычисляются коэфициенты полинома
третьего порядка и ураиение множественной ре¬
грессии. Центральным пунктом и здесь остается вычисле¬
ние старшего коэфициента полином? Чебышева, т. е.:
km ^
Величина суммы квадратов 5(<х2.,) уже известна в ре¬
зультате вычислений на втором этапе, остается опреде¬
лить сумму 5(x3xJ.1), которая равна
(Vm) ~ (Х3*2) “ ^20 ^(*з) ~ ^21 ^(*3*l)'
Затем вычисляются остальные коэфициенты третьего
полинома по формулам:
ьт — Ь" ь" . ьт
кг\ — кл 21 *32
ьт £>" ь" . Ьт
КШ Л20 *32
Все величины, необходимые для вычисления, уже из¬
вестны в результате предыдущих вычислений.
Затем определяется 5(л^г,)=5(х|.1)—Л^5(ХзХ2.1). Таким
образом оказываются вычисленными все коэфициенты тре¬
тьего полинома Чебышева и суммы его квадратов.
Одновременно получаем уравнение регрессии хг по л,
л,, т. е. 91*3 — +^3ix i+Ko> а та*<же сумму квадратов
разности jc3 — 21-^3» так как эта сУмма квадратов равна
’•^(*3-2l)-
Таким же образом вычисляется уравнение множествен¬
ной регрессии у по хг и xv Для этого сначала опреде¬
ляем: S(yx.i.x) = S(yxi') — k^StyXi')—-££>«£(у), а затем вы¬
числяем a" =5 (ухм) • с:п. Наконец,
5 (. Х1Л)
а1 — С1х~~ » ** ^0 == а0 ^20% ■
Следовательно, все коэфициенты множественной регрес¬
сии у = а2 л2 4-«" хх ч- а"й легко определяются на основе
величин, вычисленных ранее-
40 Схемы решения нормальных уравнений в полиномах Чебышева
Для оценки этих коэфициентов следует вычислить .нес*
н .нормированные коэфициенты* полиномов, а именно:
)
22 — S (*2 ,) ’ 21 21" 22> 20 ~ 20 22
Для определения же величин й
имеем:
СИ = С11 ^21 С21
С00 = С00 + ^20 С20*
Отсюда легко вычислить суммы квадратов коррелиро¬
ванной вариации, необходимые для вычисления критериев
достоверности Фишера:
)« = < 5(^2.1)= ^-
С22
.-(О1 ,,-MI
*12 * , *02 * '
*11 *00
Наконец, имеем:
S(<£) = 5(d?) - a; Syx= S (<*?)- Ы-
cii
На этом заканчивается третий этап вычислений. Если
в уравнение регрессии больше не вводятся независимые
переменные, то на четвертом этапе вычисляются' лишь
уравнения множественной регрессии у но х3 хг и xv
Сначала определяется числитель коэфициента ая, а
именно: S(ух^) =■, S(yx,) ~ ^ S(yXl)-k^S(y).
а затем сам коэфициент а” =
5 «2.)
Остальные коэфициенты легко определяются но урав¬
нениям:
-.Ш м
2 2 а,
Новые схемы решения нормальных уравнений
*Г
в которых все величины уже известны. Для оценки этих
коэфициентов вычисляем „веса* переменных:
с"~ч^йу
Эти „веса* определяются на основе следующих урав¬
нений
ст =*= с’ 4- km • сю
*’22 22 т *32 ь32
»г . ■ W .И»
СИ ~ Сп + *31 ’ С31
-А* V I
соо — соо + *зо ‘ сго
После этого определяются и нормированные коэфици-
енты третьего полинома Чебышева:
к" kZ
лт 32 Ьт г"• гт 31 h” . г-м
" s«„)~ “ 31
*;о
сго о / „а \ зо ‘ i3-
* ИЗ-я)
В результате имеем все величины для вычисления суммы
квадратов коррелированной (воспроизведенной) вариации,
которые необходимы при вычислении критериев достовер¬
ности Фишера.
(О2
Так, для оценки а3 имеем л^5(ух3>21)=
83
(аГУ
Для оценки а? имеем —
".
%
С,
22
«у
41
(-о )’
«-00
Наконец, для оценки всего уравнения множественной
регрессии у = а3‘х3 -+■ а3'х2 + aj'*, + а0" имеем сумму
квадратов отклонений S(d’) = $(<$) — a'a S(yxe-r)-
В результате вычислены не только уравнения множе¬
ственной регрессии 2г*з —*32*2 + *31*1+ *го и
У = ^3 "Ь ■’‘з ■)" *
42 Схемы решения нормальных уравнений в полиномах Чебышева
но и все величины, необходимые для оценки коэфициен-
тов этих уравнений с различных точек зрения, а именно,
дисперсионного и корреляционного анализа, а также тео¬
рии ошибок.
Кроме того, новая схема позволяет также определить
коэфициенты уравнений множественной регрессии х, по
х3 и х„ а также хг по хг и х3, т. е. коэфициенты уравне¬
ний:
13*2 ~ ^23 *3 ^21 *1 ^20
Г _ Ь"• х 4- к "л 4- Ы"
23 1 — К13 3 “ 12 2 ' ""10
Эти коэфициенты получим, определив сначала норми¬
рованные коэфициенты: с&~сЦ\ с21 = ci2; с13' — ^31'; с10‘;
и сю‘.
На предыдущих этапах не были вычислены лишь вели¬
чины Сд, с20 и с','0'. Остальные же величины были уже
определены. Указанные величины легко определить после¬
довательно на основе следующих формул:
<40 ~ С10 ■“ С21 С21 ~ С21 ^31 С32
С10 — с10 ^30 С31 СХ> ~С20 ^30 С32 •
Все величины, входящие в эти формулы, уже опреде¬
лены на предыдущих этапах. Вычислив нормированные
коэфициенты с”0, с10‘, и гД|' и зная с22 и с,',' из пре¬
дыдущих вычислений, легко определить и коэфициенты
для нового полинома x3t|r
C.rf, ^-ji С-»*,
ь,#г fe " . . ь'" — лг
«20 — , , К2Х — .7 г , — ..
22 22
и зятем коэфициенты полинома хигл по формулам
-ter m •••
С\ л С<1|
J/'» О , 21 . h’ * * _ •»*
*10 гш » *!2 — ev > *13 — —
‘'и и
Таким образом, оказываются определенными коэфи¬
циенты полиномов Чебышева х,.й, х2>п и х,.,, и уравне¬
ния множественной регрессии для определения ^х,, пх,,
.•1*3'
Для полиномов Чебышева эти коэфициенты должны
Г>ыть взяты с обратным знаком, а для уравнения регрессии
Ноше схемы решении нормальных уравнений
*3
с тем знаком, каков они будут иметь в результате вычи¬
слений. Одновременно необходимо помнить, что если для
нормированных коэфициентов имеем равенство: С|» = с„,
то коэфициенты одного порядка эли¬
минирования, например, А21 и А",; А"3 и А31; А32 и А^, а
также коэфициенты А21‘ и Ajj', Аи’ и А ”; АЛ' и А'а’ и т. д..
существенно отличны друг от друга.
Для оценки полученных коэфициентов полиномов сле¬
дует вычислить соответственно суммы квадратов отклоне¬
ний. Они вычисляются для Хз.21 аналогично как и для
уравнения множественной регрессии у по х9 и xt (но не
у по X*. х2 и х,). Соответственно имеем:
Эти величины нам пока неизвестны, но они могут быть
определены, если исключить из уравнения х3>21 перемен¬
ную Ху
Наша схема позволяет в случае необходимости исклю¬
чать те переменные, по которым коэфициенты уравнения
регрессии оказались недостоверными, или по каким либо
другим соображениям ненужными.
Формулы, используемые при этом исключении перемен¬
ных, аналогичны формулам, применяемым при включении
новых переменных, только в них имеем дело с обратными
знаками. Так, при исключении хх необходимо определить
уравнение у ,а"Х;,-f ® 9Т0М слУчае сначала
Я У Я У N у
с22 СИ с00
где:
Для оценки коэфициентов уравнения
соответственно необходимо вычислить:
ft > я у я у
сзз сп соо
причем здесь:
1 . _ 1.... . ^ I
44 Схемы решения нормальных уравнений в полиномах Чебышева
определяем. t ^ k]0 (?]0; , с 22 = сп kv2 с.п ; , ~
— с'х — Л,, cj','. Это и есть „веса", которые необходимы r
случае оценки коэфициентов уравнения
У2з~ iai •*•3"^’ i®2 1^0-
Коэфициенты нового уравнения регрессии легко вычи¬
сляются на основе формул:
_м# , ./W LMI
13 3 +а1 *13
Л“* I 11 и* **
1Л2 —«2 + а1 Л,2
у*" л’ I л" * и" '
1*0 = О I *10'
Эти коэфициенты могут быть оценены, зная величины:
(а7. (а7
г > ТТ5 4
1С33 1^22 1^00
Сумма остаточных квадратов отклонений для нового
уравнения (с исключением переменной х,) получается по
формуле: S(<*].,)= S(d*) + ЦтД-
cii
Если необходимо было бы исключить л*9 и определить
коэфициенты уравнения регрессии <y = 2<Vc:»+2ar,ci x'tao> Ги
следует исходить из коэфициентов полиномов ха.1н, а
именно:
У ‘—С*> • ■ к"’— С*‘
*20 >•”* *21 /-■'» *23 г • '
22 *'22 33
При исключении х, „веса" определяются по уравнении-
к’’.с"'- о" =.с"‘— к” • с"' с" = г"*— fe‘"
2 С010Э 20 20 * 2 11 611 *21 Si* 2 Si .13 *2:1 St-
Коэфициенты же нового уравнения но формулам:
е *ч , L»»r. „л I L»'*. V* ( А ’»
•/*3 — a3 *1" 2 ^2* ’ 2 1 ai <Z2 * 21 * 2 0 a0 ^ Л2 ^20 *
И, наконец, остаточная сумма квадратов отклонений:
Ч<Ч,)~Ч<$ с
S2
Таким образом, предлагаемая новая схема позволяет
легко вычислить все полиномы и все уравнения множест-
Новые схемы решения нормальных уравнении
пенной регрессии, а также всесторонне оценить их коэ-
фициенты. В этом исключительное значение новой схемы
решения нормальных уравнений, составленной на основе
использования всех преимуществ, предоставляемых поли¬
номами Чебышева.
В схеме N все эти вычисления расположены в строй¬
ную систему на основе формул, рассмотренных выше. Эта
схема обесиечивает последовательность, систематичность
и симметричность всех вычислений.
• *
*
Система N полиномов Чебышева лежит в основе новой
схемы решения нормальной системы уравнений, предло¬
женной автором.
Однако полиномы Чебышева позволяют расположить
вычисления несколько иначе.
В частности, В. Н. Перегудов предложил несколько
иную схему вычислений (схему Р). Эта схема приводится
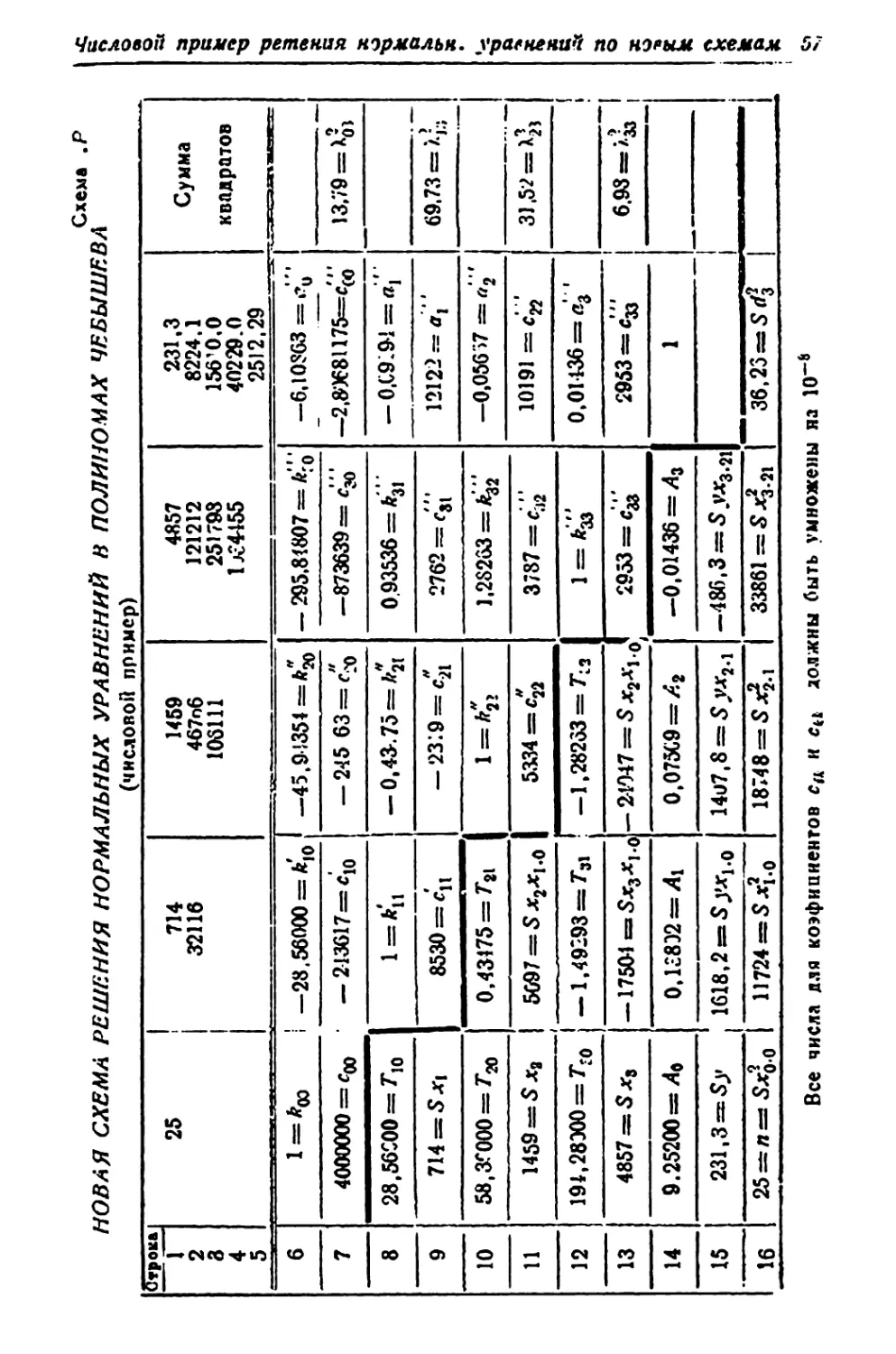
на стр. 46—47.
Схема Р использует аналогичные, рассмотренные выше,
формулы.
Однако, если схема Немчинова построена на коэфи-
циентах системы полиномов »Л/“, то схема Перегудова
основана на комбинации коэфициентов Т и К.
Вся схема ,Ри делится косой ступенчатой линией на
две части (как бы два треугольника — верхний и нижний).
Над косой ступенчатой линией, т. е. в верхнем треуголь¬
нике, записаны коэфициенты полиномов системы К, под
косой линией в нижнем тр угольнике коэфициенты урав¬
нения регрессии, выраженные в полиномах системы Т.
При этом запись коэфициентов уравнений регрессии, вы¬
раженных через полиномы Г, даны в нижнем треугольнике
по строкам, а запись коэфициентов полиномов системы К
дана в верхнем треугольнике по столбцам. Так, например,
в схеме на стр. 46 в третьем столбце треугольника снизу
вверх записаны коэфициенты полинома:
х2-1 = а ~ K\xi ~ Kix\ ““ Кохо или' так как
=■ 1 и х0 = 1 то
Г —— г — k!* X — k"
*2.1 Л2 21 1 20*
46 Схемы решение нормальных уравнении с полчнолтх Чсоыш*га
СХЕМА ПЕРЕГУДОВА В
Коо —1
! «10 * — rio‘«
I
ю,/чоо
«20=
— ^ | о)
Соо *■ 1/Л я 1/S*00 •
С'ю- K,o/Sxf .0= 4J| C.;o=K2o/S.vj. 10=
46
»К1ПС
10^11
-/v,oC
20u22
^ 10е ^X1 xo /5хоо=
—Sx, /л
42
7| „ U
K2l**— ^2Г «11
“45
S*i*oo С'„ - l/Sx?.0
10
т с Гг"^!
/•го^охгхоо/^оо" т _eY Y /0*2
«Sx^/л '21-**2 X!.o/*Xl.
1!
Sx~x{
2*00
9 И
;Sx 2 л, о -К, 0Sx2 xQ+
• + К11$*2 Х1
18
12
13
Г 30=Sx3 x^Sxq0«
- 5ч3/Л
*.•0
Г31 ^5х3х, 0/Sxf о
С2| = ^2 l/^x2 I
Я К2\С22
К22 и *
15
44
22
^32 = ^Х3 Х2. l/^X2.1
17
5хзхо
1У
S*3 Xj 0-/<ю^з хо*
4- /См5х3х,
21
$х3 Х2| я К20^Х3 х0 +
+^21^X3 х 1 4"'^22^Х3 Х2
14
Aq= 5yXQ/5XQQ Я
-Sy/n
2V
31
А1 »5yXj ф/Sx^ Q
зз
^2 “ ^УХ2. |/^Х2. I
15
Syx00-Sy
28 ^ 30
$У*1 ,0-К ю5Ухо +
+ Кп Syx,
32
^Ух2.1 —«20 $УХ0 +
+ К2| Syx, <-К22$ух2
16
Су2
оХоо
сх2
^х1.0 1
—«io*xi *o*^«ii^xi
16
^х2.1*"«20^Х2 х0 +
"Ь^21^х2 Х1 « 22^х2
Ноше схемы решение нормальных ура?нений
47
СХЕМА «Р»
ПОЛИНОМАХ ЧЕБЫШЕВА
Sx,
$***>
Sxtxt
5х3
Sy
$ух,
Syx,
Syx,
sys
Сумма
квадратов
, 23
*30 “ ~ (гзо*оо+
+ 7*3, К ю+ Т32К20)
„ »«
“ — vao*m>o+
+ ^1^10 + ^2^20 ^“^з^зо)
50
с 30 л 3<У ^х3.21 ** л 30е 33
31 55
coo=*oo coo+ !/ л'"\а/л'~«>2
+к;/„+кй+ед o) 00 03
24
*31~-(73l«11 + r32«2l)
37
о, = — (A,Ktl +
+A2K2j + A3K31)
49
^31e^3l/^x3.2! “^31^33
' /*' 52 56l
CU-K|,CU+ Vd'/V/cVi-x*,
+*;,с21+кз:сз;
25 38
Кз2=— ?32 К22 j а7 *=*'“■(^2^22+^3^32)
48
^32"^32/^х3.21"^32 ^33
53
c22—k22c22+k32 c32
51
(*3 12IC 22a=? 23
25
K3Z — 1
30
*3 e Л3^33
47
C33=1/SX3.21
54
£зз**1/5хз#21
58
(*зУ/с£-*!з
35
А3 5ух3 2i/5x| 21
40
1
I
^х3.21в/<30^Хо+ 34
+Кз! 5yx, + /<32 Syx2+
+Кзз5ух3
—
$х3 21 “^30 ^Х3 х0+ 27
-fK3| Sx3 х| + К325Х3Х2+
+Я33 х\
5<*з1=5 — (^0 ^У*оо+ 41
+A| Syx J .о+А2УХ2. 1 +
+^з ^Ухз.21) +$У2
4Н Схемы решения нормальных уравнений в полиномах Чебышева
В нижнем треугольнике по строке десятой (до косой
ступенчатой линии) записаны коэфициенты полинома си¬
стемы Т
Х2А ~ Х2 -о ^20'
При этом запись дана в форме уравнения регрессии:
Л» 7'ао+ т21хы» причем ,*2 —
В связи с этим при записи уравнения регрессии для у
соответствующие коэфициенты (написанные в верхнем треу¬
гольнике по столбцу) должны быть взяты с обратным
знаком. Это особенно необходимо помнить в отношении
коэфициентов aik, так как при записи уравнения множест¬
венной регрессии знаки при этих коэфициентах должны
быть перемевены на обратные.
Старшие коэфициенты полиномов системы Т и системы
К равны друг другу, а именно:
Т10 = Л.0; Тп = кл\ Тй2 = ki2 и т. д.
В схеме Перегудова запись таких равновеликих коэ-
фициентов дана в двух смежных колонках (см. схему ,РЯ)
При этом, так как в верхнем треугольнике записаны коэ¬
фициенты полинома, а в нижнем коэфициенты уравнения
регрессии и так как =££,*= Л.3’ = 1, то связь меж¬
ду этими двумя типами коэфициентов выражается в виде
•следующих равенств:
Ь Т k' • k" Т к" • к'" Т k"
10— 1 10 11’ 21 — 21 21’ \l-> 1 •
В схеме пРя. основанной на системе коэфициентов
полиномов Т и К, коэфициенты Т расположены по стро¬
кам, а коэфициенты К— по столбцам схемы. В схеме „ЛЛ,
основанной на коэфициентах системы N, коэфициенты
расположены по строкам схемы. Кроме того величины:
Sxl.jj Sxf'0 и т. д., а также величины тина:
Syx3'2l; Syx2Syxl0 и величины типа: Sxjc,#
и т. д. вычисляются по схеме „Р* на основе сумм произ¬
ведений первичных данных (т. е. величины типа: Syxlt
Sxl, Sxkxkjy а в схеме они вычисляются как суммы
произведений первичных величин на соответствующие зна¬
чения полиномов.
В связи с этим в схеме яРа все величины исчисляются
по формулам многочленов, а не двухчлеиов, как в схеме
. N".
Числовой пример решения нормальн. уравнений по новым схемам 49
Например 5дс|.2, по схеме Перегудова вычисляется по
уравнению:
*^*3-21 = *3 ^30 ^Х3 *31 XSXl *32 *^3^2»
По схеме Немчинова они вычисляются по уравнению:
^З-г! = ^3-1 *32 ^Х3Х2‘
по схеме Перегудова вычисляется по уравнению:
*30 = (^го^оо + ^31*10 + ^З2*я)-
По схеме же Немчинова:
к" = к" — к" к"’
КЛ *<А Л20 32 *
Наконец, в схеме Перегудова ряд промежуточных ве¬
личин, важных для всестороннего анализа (например:
Sd},, Sd\, Sd0, а0, а0, av о. , а2, «Sjc*.*Sxj 0, ^з-о» сп » cw
c\\‘ и т.д.), отсутствует. Это, однако, делает схему более
экономной в отношении затрат труда на вычисления.
Схема „Р“, как отмечает В. Н. Перегудов: «...была
построена на других теоретических основаниях, чем метод
Чебышева. Однако в своей окончагельнойформе она вплот¬
ную подошла к методу Чебышева*. Настоящая интерпре¬
тация схемы „Р* в полиномах Чебышева принадлежит
автору.
§ 4. Числовой пример решения нориадьных уравнений но
новыя схелам в полннолах Чебышева
Схема nN‘
Решение нормальных уравнений в полиномах Чебышева
:ю новой схеме „АЛ состоит из нескольких этапов, причем
каждый этап распадается на несколько стадий. Число
этапов определяется числом изучаемых переменных. Пе¬
ременные включаются в анализ последовательно одна за
другой, причем число наблюдений (частота) также рассма¬
тривается как переменная только нулевого порядка. Нуле¬
вой этан, имеющий дело с частотой наблюдений состоит
в получении сумм, входящих в систему нормальных уравне¬
ний в качестве коэфицчентов »гри переменных. На нулевом
этапе получаются суммы типа:
S(x,), S(V„). S(y*,), 5(>ф.
t Полвяомы Чебышева
SO Схемы решения нормальных уравнений в полиномах Чебышева
На последующих этапах прежде всего получаются
аналогичные суммы произведений изучаемых переменных
на соответствующий полином Чебышева.
На первом этапе такими полиномами будут величины
л,.0, на втором — х2Л, на третьем — х^21 и т. д. Каждый
этап распадается на следующие пять стадий:
1) определение сумм произведений соответствующею
полинома Чебышева на числовое значение каждой дайной
переменной;
2) вычисление старших коэфициентов полиномов Чебы¬
шева и старших коэфициентов уравнения регрессии;
3) вычисление поправок, необходимых для перехода к
младшим коэфициентам;
4) вычисление младших коэфициентов как для полино-
мов Чебышева, так и для уравнений регрессии;
5) определение сумм квадратов.
Каждая стадия вычислений имеет в схеме одну строку,
за исключением вычисления поправок и вычисления млад¬
ших коэфициентов. Число строк для поправок и для
младших коэфициентов равно номеру этапа вычислений.
Таким образом, на нулевом этапе строчка поправок и
строчка младших коэфициентов отсутствуют. На первом
этапе этих строчек по одной, на втором — по две п т. д.
Ключом ко всей схеме является определение стар¬
ших коэфициентов. В схеме имеем дело с определением
старших коэфициентов трех типов:
1) определение старших коэфициентов полинома Чебы¬
шева, т. е. величины типа k0, k"lx, кЛ2\
2) определение „весов переменных", или, иначе говоря,
старших коэфициентов нормированных полиномов Чебы¬
шева, т. е. величин типа: с0}, сп, с”;
3) определение старших коэфициентов уравнения ре¬
грессии, т. е. величин типа: а0. а\, а", а.".
В схеме двойной вертикальной чертой отделены вычи¬
сления коэфициентов полиномов Чебышева от вычислений
нормированных коэфициентов этих же полиномов. Вычи¬
сление первой строки поправок состоит в определении
произведения старших коэфициентов двух полиномов (пре¬
дыдущего и данного). Поправки, записанные во второй н
последующих строках, есть также произведение двух ве¬
личин, а именно, произведение младших коэфициентов
полиномов Чебышева предыдущего этана вычисления на
соответствующий старший коэфициент данного этапа.
Числовой пример решении нормален, уравнений по новым схемам 51
Следует запомнить следующие мнемонические правила,
«блегчающие вычисление поправок:
а) каждая поправка есть произведение двух чисел;
б) для каждой данной строки поправок первое из этих
чисел (т. е. множимое) равно старшему коэфициенту по¬
линома Чебышева предыдущего этапа вычислений; для
каждой строки поправок это число одно и тоже;
в) вторые числа в произведении, определяющем вели¬
чину поправок, т. е. множители, равны старшему коэфи-
циенту данного этапа вычислений; эти числа в схеме за¬
писаны над перЕОй строкой поправок; для всего столбца
поправок эти множители одинаковы по всему данному
столбцу;
г) если первые числа, входящие в произведение при
исчислении поправок, читать по столбцу сверху вниз, то
они равны числам предыдущего этапа, записанным столб¬
цом справа от двойной черты, отделяющей друг от друга
обычные и нормированные коэфициенты Чебышева.
Старшие коэфициенты получаем как отношение строки
суммы произведений данного этапа вычислений на строку
сумм квадратов, вычисленным на предыдущем этапе-
Младшие же коэфициенты определяются как разность
между аналогичным коэфициентом предыдущего этапа и
соответствующей поправкой. Сумма квадратов также есть
разность между суммой квадратов предыдущего этапа и
произведением старшего на данном этапе коэфициента к
S(PJ. Эта последняя сумма стоит в схеме над старшим
коэфициентом. Сумма произведений, т. е. величины о(РА).
являются алгебраической суммой произведений двух чисел,
из которых второе число есть коэфициенты нормальных
уравнений по столбцу, соответствующему данной перемен¬
ной, а первое коэфициенты полинома Чебышева предыду¬
щего этапа вычислений (с обратным знаком).
Необходимо помнить, что в строке сумм произведений
и сумм квадратов имеются в виду алгебраические суммы,
причем коэфициенты полиномов Чебышева должны быть
взяты с обратным знаком. Следовательно, коэфициентам
придается тот знак, который они имеют в полиномах Че¬
бышева, а не в уравнениях регрессии.
В таблице на стр. 53 по схеме Немчинова (с соблюдением
указанных выше правил) решен тот же пример, что и ра¬
нее по схеме Дулитля. На нулевом этапе в качестве сумм
произведений записаны обычным порядком суммы, пред¬
ставляющие собой коэфициенты системы нормальных
уравнений.
Л2 Схемы решения нормальных уравнений в полиномах Чебышева
Старшие коэфициенты нулевого этапа есть ни что иное
как обычные средние арифметические. В нашем примере
имеем:
S(*»*b.o) S(xi)_7H
5 (*0-0) n 25
5 О^о-о) S(;) 231-3
T7Z—\ nr~ = У>Л- и т. д.
( о*о) л 2о
Таким образом, fe*0=*,=-. 28,56; к'л — х2 = 58,36; k'M =
— хг = 194,28; а0 =у = 9,252.
Сумма квадратов нулевого этапа есть сумма квадратов
отклонений от средней арифметической. В самом деле:
5(*?-о) = - KoS(xi) = 32116 - 28,56-714 = 11724,16
^(х*.о) = Ю3111 - 58,36-1459 = 20963,76
-S(<ty = S(y2)- а05(у) = 2512,29 - 9,252-231,3 = 372,30.
Аналогично вычисляется •£*].„= 90837,04.
Сумма произведений первого этапа вычисляется но
формулам:
5(xaxi.o) = S “ #ю S(xj) = 46765 - 28,56-1459 =5096,96
5(¥10) = 5(*Л) - КоS(x ) = 121212 - 28,56-4857 =
= -17503,92
5(Ухio) = S(?xi) - КоS(y) — 8224,1 - 28,56-231,3 = 1618,17
Старшие коэфициенты первого этана определяется но
формулам:
СГ,1~ ^ (*?.<>) ~ 11724.16 ~ 0,00008529,
Г —--(X/X,-°) — 5093*96 Л ЛОА7ЛП
зХы'-птйм-°-И474°-
а', = JSlflA. = 1618,17 _
1 5 (х?.0) ТШ4ЛС ~ 0,13802°.
СХЕМА *N’
Строки
| *0
*1
*2
! x
л3
1'
—
25
j 714
J 32116
i :
1459
46766
106111
! 4857
I 121212
1 251798
1034455
1
i 231.3
8224,1
15610.0
4229.0
1. Вычисление уравнения регрессии У по Л', . Х2. Х3
C<-Kt-at
S (°о)
С00 - 4 000000
Kl0 = 28.56
Sx*q — 11724,16
К'го - 58.36
Sxf о - 20963,76
К30 19^.28
Sxlo - 90837,04
| a0- 9,252000
1 -
Чр>)
С, "" 0#
м
Cm — Кщ—ат
6956873
С оо - 10956873
1
С J t — 8529
Cj0 = 243588
Sx2 x, ^ q ■ 5096,96
K2l =0,434740
12,416174
Kj0 B 45,943826
jSx3x, 0 = -17503,92
1 K31 = - 1,492979
- 42,639480
j Кад - 236,919480
S>-x, 0=ICI8,I7
0. - ii.I3.4i2h
1 1
3,911851
1 Ло-5.310149
s К)
—
—
Sx| , =» 18747,91
S.V3 , a 64704,00
i “ __
S(P2)
—
|
i С 22 - 5334
Sx3 x2 |=—24046.87
Syx, , = |.Ю7.Я5
С>~К,~а,
М,
М2
11259177
1
1
1008
(106544)
j C2X = 2319
! C20 - 245064
K32 = — 1,282661
— 0,557624
— 58.930354
1 <12 — 0,(>75Uifl
0.032647
3.450152
Кт
—
С',', = 9537
—
X"j . —0,935355
, a,' = 0,105373
i
о
Сад « 22216050
C,'0 = 137044
—
Кад = 295,849834
1
! «0 - 1,859997
6‘ (Dj)
—
—
—
Sxl j, =33860,5G
—
ЧР з)
—
— 1
—
1
Syx3 j, — 486.28
С,-в.
-
...
—
Сад-2953
a3 = -4).01436(i
|*
и
Л4,
м3
2.58467432
2583
( - 817137)
~ j
4857
(3542)
(-1120383)
Сад-—3787
C3J = -2762
j Сад - 873644
0,018419
0,013432
— 4,248404
Cm - в.
—
1
i
1
C22 - 10191
—
a2 - 0.056676
•1
I
с*;; = 12120
i
C21'=—1223
—
ej" = 0,091941
И
6 (°з)
Сад = 2.80683482,'
CJo - 951181
Сад =» 1365447
eg' -6,108401
I
II. Определение коэфициентов полиномов X2I3 H ^1.23
К2
*Г
РСго в 133.965670 К'21 = —0.120008
К',© = 73.727806 j - J
К J 2 =,—0,100908
Хад • 0,378700 :
X," 0.227888 j
—
III.
Исключение X,
(определение регрессии )' no X2 и X
3*
, с - , в"
,Co0= 2.05658323
--
(C22 - 10314
|C\,j •'-3341 j,
i
, 03 == - 0,035312
|
1
I
1
i
1
1
, u2 = 0.047398
, 0O = 13,346711
2512.20
| s4~
372,30
; c'n
I
:ы2
> 223.34
■ 257.35
' c oo
Stl'i ■= 148,06
<-p-' -* 105.72
C22
-л- * Ilf),
c„
.42
(fov:
^00
SJ| 43.24
I *
- .4- =. 15,57
coo
K')2
•7^- = 0,98
сзз
(«ГУ ,
'-777- ~ 31.523
22
(«ГУ
-и
■ 69.74
coo
S<f| - 36.26
(1 аз)2
<•«
(jii)2
-.-37.52
L33
7* 21.32
22
Примечание: Величины Ca и Сц, даны в восьмизначных десятичны^- дробях (М"8) и нули опущены при записи.
Числовой пример решения нормален, уравнений по новым схемам
Строка поправок заполняется умножением старшего
коэфициента предыдущего полинома Чебышева на строку
старших коэфициентов, только что вычисленных, а именно:
tfioe к\осп= 28,56-0,00008529 = 0,00243588,
л;0- С10= 28.56-0,00243588 = 0,06956873,
k\0 к;х = 28,56-0,434740= 12,416174,
*;0 = 28,56 •( -1,492979) = -42,639480,
k[0(i\ = 28,56-0,138020 =-- 3,941851.
Младшие коэфициенты получаются как разность между
соответствующими коэфициентамн предыдущего (нулевого)
этапа и соответствующей поправкой. В нашем примере
имеем:
”58,36 - (28,56-0,434740) = 45,943826.
а0 = 9,252 - (28,56-0,138020) = 5,310149,
Сда = 0,04 4- 0,06956873 = 0,10956873.
Сумма квадратов равна разности между соответствую-
|цими суммами квадратов предыдущего этапа и произве¬
дением старших коэфициентов данного этапа на сумму
произведений, стоящую над ним. В нашем примере имеем:
Sjс|.,= 20963,76 - (0,434740-5096,96) =--18747,91,
5 d\ = 372,30- (0,138020-1618,17)= 148,96-
Вычисление на следующем этапе вполне аналогично
вычислениям на первом этапе, с той лишь разницей, что
каждый раз увеличивается число строк лоппавок и число
строк младших коэфициентов. Так, на втором этапе имеем
две строки поправок. Первая строка равна произведению
старшего коэфициента предыдущего этапа на соответ¬
ствующие старшие коэфициенты, вычисленные на данном
чтапе. В нашем примере для второго этапа имеем:
k\x с21— 0,434740-0,00002319 = 0,00001008,
к^к;,= 0,434740 •(—1,282661) = - 0,557624.
/г' а' = 0,434740.(0.075095) = 0,032647.
U Схемы решения нормальных уравнений в полиномах Чебышева
Вторая строка поправок есть произведение второго
коэфициента предыдущего полинома Чебышева на соот¬
ветствующий старший коэфициент данного этапа. В нашем
примере имеем:
Ко c2i = 45,943826 • 0,00002319 = 0,00106544,
Ко 45,943826 • (-1,282661) = - 58,930354,
кл'К = 45,943826-0,075035 = 3,450152,
Ко 45.943826.0,00245064 = 0,11259177.
Необходимо в дальнейшем помнить, что поправки, ко¬
торые являются произведением величин я „с“ имею¬
щих подстрочный значок одного и того же порядка, т. е.
величины типа: k'l0. с10; K\cli> KiKv ksiclо» прибавляются,
а не вычитаются как все остальные.
Младшие коэфициенты получаются как разность между
соответствующими коэфнциентами предыдущего этапа н
соответствующими поправками, например:
k” = - 1,492979 - 0,434740-( - 1,282661) - - 0,935355.
о; = 0,138020 - (0,434740-0,075095) -=0,105373.
В остальном вычисления как на этом, так и на после¬
дующих этапах вполне аналогичны предыдущим.
Новая схема позволяет определить коэфициенты поли¬
номов с измененной последовательностью переменных.
Так, в нашем примере для полиномов х3.,3 имеем (см.
схему N):
*»- «Я- -133>985670’
ft^»f = -°-120008'
г = -0,378700,
Аналогично для полинома х1ш73 имеем (см. схему N):
Л!о“ -Хйяй- =78,727806,
Ь™ —0.0C0D1223 Q 1 AQQAO
*12~ 0.C0J12120 —
—0,00002702 л 997000
ТМШ20 <>,227888.
Числовой пример решении нормальн. уравнений по новым схемам 53
Новая схема позволяет и исключать переменные. При
исключении, например, л, определяем регрессию следую
-него типа: у — ,а3 л3 + ,а"л2 + ,аГ0
Коэфиаиент этого нового уравнения получается вполне
аналогично случаю включения новых переменных, но
только в случае исключения переменных знак поправки
меняется на обратный. В нашем примере при исключении
*, имеем:
ха; = - 0,014360 4- 0,091941 -(-0,227888)= - 0,035312.
= 0,056676 + (0 091941 •(- 0,100908) = 0,047398,
,а' = 6,108401 + (0,091941-78,727806)= 13,346714.
При исключении переменной остаточная сумма квадра¬
тов уравнения регрессии также вычисляется аналогично,
но лишь с изменением знака поправки на обратный. Вы¬
числение сводится к прибавлению той поправки, которая
подлежала бы исключению из предыдущей суммы квадра¬
тов отклонений, если бы данная переменная была вклю-
чена в анализ последней. В нашем примере имеем:
•?№.) - ЭД)+ = 36.26 + 4ZZ “ 106.00-
с,,
В результате всех вычислений в разбираемом нами
примере оказались вычисленными следующие уравнения
регрессии:
у,= 5,310149 + 0,138020.x,,
у„= 1,859997 + 0,105373л, + 0,075095л,,
у,„= 6,108401 +0,091941л, + 0,056676л, - 0,014360л,,
у„= 13,346714 + 0,047398л, - 0,035312л,.
Кроме того, в процессе вычисления определены_следую¬
щие уравнения между величинами л (где л3.5, = ах^:
*3.12= 295,849834 - 0,0935355*,- 1,282661л,
х2.31=133,985670 - 0,120008*, - 0,378700л,
.<!.»“ 78,727806 - 0,100908*, - 0,227888л,.
56 Схемы решения нормальных уравнений в полиномах Чебышева
Одновременно вычислены и промежуточные уравнения:
x2.i= 0,043474*, + 45,943826,
— 1,492979*,+ 236,919480.
Кроме того, вычислены все суммы квадратов отклоне¬
ний, которые необходимы для оценки всех коэфициентов
уравнения как с точки зрения дисперсионного и корреля¬
ционного анализа, так и с точки зрения теории ошибок.
Статистическую оценку этих величин рассмотрим к
следующим параграфе.
Вычисления по новой схеме при достаточных навыках
могут быть упрощены, если опускать запись поправок,
вычитая их сразу же после вычисления, не снимая с ка¬
ретки арифмометра.
Для уверенности в правильности полученных резуль¬
татов необходимо производить контрольную проверку
вычислений путем проверки выполнения следующих ра¬
венств:
На первом этапе:
'• С„ад)-С* *(*,)“»
II. S(f)-a0S(y)-a\S(yx,) = S(dj).
На втором этане:
I. Cjj«S(-*2) “ ^21 '~>(XSXl) ~ ^*20*^(**2) “ 1
И. 5 Су*) — ад S(y) — a, S(ух,) — a"S (ух.) «= S(d-).
На третьем этапе:
«• CxS(xl) ~ С” 5(хЛ) - С” S(xзх.) - СГ0 S(x3) = 1.
II. S(y2) - а; S(y) - < S(yx,) - < S(yxs) - а; $(ухл)
= S(d%) и т. д.
При выполнении этих контрольных равенств вычисле¬
ния произведены правильно, а в противном случае необ¬
ходимо искать ошибку.
Схема „Р“
Обработаем ту же систему нормальных уравнений ни
схеме „Я“. Числовой пример вычисления по этой схеме
дан на стр. 57.
Числовой пример решения нормален. уравнений по новым схемам 57
«о
X
3
0
о
н
сЗ
О.
■*
СЗ
СП
CO^OCW
и! Л
Й22Й
253‘4
8*83
=§§
4*0
8
О
С*
я?
еб
ю
*•3
•ч
и
г
о
3
О
СО
I
со
£
6Ь
СМ
- О
00
lO
8
г
* сГ
II
' <Г
I еч
II
: В
о
-
е
II
3
1!
II
О)
о
см
8
О
о»
1
о'
н
О
о
о
1
1
о
* <ч
:Ч?
* «о
I N
II
«о
II
СМ
«о
II
3
см
* 0?
II
й
?<р
II
3
CI
со
см
I'-»
со
о
=*
СО
<2
*8
«Се
§
о
со
со
о
-*
СМ
к
$
о
со
сч
*Г
о
VT
О
н
’«Г
II
ь-
Щ.
1
JI
09
я
СМ
1
1
*3
о J—*CSC0 ^юп со
со
С1
ь;'
5.
со
со
S
4*
I
о
_
н
4*
ем
ч;
с
«0
II
Со
II
оо
g
II
со
3
Oe
г-“
С*
1
о*
*э
т—1
н
со
з
**•
е*сг>
Со
ецо
со
пт
со
о
о
ь
V
со
со
II
II
см
см
00
*•
•-Ч
о
V—<
к*
н
со
о>
о
о
с
оо
см
S'
<о
I!
5
00
S
й
см
С?
оо
см
О)
о —
о
С"©
Со
I
о
п
к
0
*
о
S
3
a
о
a
х
*
с;
О
«ч
«и
•4#
V)
Г
X
0
X
а
s
«©•
1Т»
О
X
о
X
X
4>
О
CQ
~>s Схемы решения нормальных уравнений в полиномах Чебышева
Порядок вычислений по схеме „Р" показан на стр. 46
^схема Перегудова в полиномах Чебышева) порядковыми
числами, поставленными в верхнем правом углу каждой
клетки. Формулы, на основе которых вычисляются эти
коэфициенты, записаны в соответствующей клетке.
Если руководствоваться этой схемой, т. е. записан¬
ными в ней формулами и порядковыми номерами вычисле¬
ний, то достаточно повторить все вычисления два раза
чтобы полностью овладеть всей схемой. В схеме „Р“ так
же как и в схеме „ЛЛ‘, можно различать этапы и стадии
вычислений. Включение каждой новой переменной дает
новой этап вычисления, причем, каждый этап раздаляется
на три стадии:
1) вычисление сумм квадратов;
2) вычисление коэфициентов Т и А;
3) вычисление коэфициентов k.
Первая стадия состоит из определения сумм квадратов
предыдущего полинома, определяемого в виде алгебраи¬
ческой суммы. Например, на третьем этапе эта сумма
равна:
, = k",0Sx2 + k”n Sx^ 4- k^Sx-.
Здесь коэфициенты k взяты с обратным знаком.
На второй стадии каждого этапа определяются коэфи¬
циенты Т и А. Эти числа записываются в клетках в стро¬
ках, расположенных влево . от вертикальной части косой
ступенчатой линии, разделяющей всю схему на верхний
и нижний треугольники, причем эта строка каждый раз
расположена влево от клетки, в которой стоит единица.
Третья стадия на каждом этапе состоит в определении
коэфициентов полиномов системы к. Поэтому эта стадия
включает в себя определение стольких чисел, сколько
коэфициентов в данном полиноме. Следовательно, для
полинома третьего порядка этих чисел будет четыре, для
полинома второго порядка — три, для полинома первого
порядка —два и для полинома нулевого порядка—одно.
Полезно запомнить мнемоническое правило, что числа,
определяемые на первой стадии, записываются в соответ¬
ствующей клетке самой нижней строки схемы, числа, оп¬
ределяемые на второй стадии, записываются каждый раз
в двух строках, расположенных влево от косой ступенча¬
той линии, т. е. в той прямоугольной полосе нижнего
треугольника, рядом с правым верхним углом которого стоит
единица, наконец, числа определяемые на третьей стадии
Числовой пример решении нормален, уравнений по новым схемам 59
каждого этапа, записываются столбцом через одну клетку
я верхнем треугольнике.
Схема „Р“. роме того, имеет заключительный этап,
состоящий в определениии чисел Cik и Си, необходимых
для статистической оценки полученных коэфициентов
уравнения регрессии. Этот заключительный этап состоит
в заполнении тех клеток верхнего треугольника, которые
оказались пропущенными при заполнении чисел, получен¬
ных на третьей стадии каждого этапа. Следовательно, за¬
ключительный этап состоит в заполнении тех клеток
схемы, которые в таблице ка стр. 46 помечены порядковыми
номерами от 42-го до 58-го.
Покажем порядок вычислений по схеме »Р“ на при¬
мере второго этапа, имеющего дело с *,. Эти вычисле¬
ния расположены в клетках, имеющих порядковый номер
с 8-го по 15-й В 8-й клетке записано число, полученное
по формуле:
•Sxio=^o5'cix3+
Таким образом, сумма квадратов первого полинома
(записанная в 8-й клетке) является алгебраической суммой
произведений чисел, стоящих во 2-м столбце. Множимое
берется из самой верхней части схемы, где записаны сум¬
мы типа SXtXkt составляющие систему нормальных урав¬
нений. Множителями являются числа, стоящие в верхнем
треугольнике того же второго столбца (т. е. коэфициенты
системы К полиномов Чебышева). Получением этой суммы
произведений заканчивается первая стадия третьего этапа
вычислений.
Вторая стадия этого же этапа вычислений состоит в
*аполнении 9—12-й клеток. В 9-ю клетку переносятся из
верхней части схемы SXr В 10-ю клетку заносится число,
полученное в результате деления числа, стоящего в 9-й
клетке на число, стоящее во 2-й клетке. В 11-й клетке
определяется сумма SXiXl,a, вычисляемая по формуле:
^Х2Х\.0 ^х2 4" .SjCjJCj.
Таким образом, вычисление числа, стоящего в 11-й
клетке, состоит в умножении чисел, стоящих в 6-й строке
верхнего треугольника на число, стоящее в верхней части
схемы (в 1-й и во 2-й строках). Число, записанное в 12-й
клетке, получается путем деления числа, стоящего в 11-й
клетке на число, стоящее в 8- клетке.
Третья стадия вычислений состоит в определении коэ¬
фициентов полиномов 2-го порядка. Результаты вычисле¬
во Схемы решения нормальных уравнений в полиномах Чебышева
ний записываются в верхнем треугольнике, в клетках
13-й и 15-й. В клетке 13-й записываются k"w Этот коэфи-
ииент получается по формуле’.
4о~ ( ^20 ^00 ^21 ^ю)‘
Таким образом, вычисление сводится к умножению чи¬
сел, стоящих в строке 10-й нижнего треугольника, на
числа, стоящие в строке 6-й верхнего треугольника. По¬
лученная при этом алгебраическая сумма должна быть
взята с обратным знаком.
В клетке 14-й записываются коэфициенты k\v Это
число получается путем умножения числа, стоящего в
12-й клетке, на число, стоящее в 7-й клетке. При этом
знак меняется на обратный.
В клетке 15-й записывается число т. е. единица.
Этим и заканчивается вычисление, относящееся ко 2-м\
этапу.
Совершенно аналогичным образом повторяются вычис¬
ления, связанные с третьим и последующими этапами.
Заключительный этап состоит в вычислении коэфици¬
ентов с1к и скк (клетки с 42-й по 50-ю), путем деления
соответствующего коэфициента на сумму квадратов
отклонений.
Несколько иначе вычисляются коэфициенты скк (клетки
с 51-й по 53-ю). Они получаются как алгебраическая сум¬
ма произведений коэфициентов k и с. Так, число, стоя¬
щее в клетке 51-й, получается как сумма произведений
чисел строки 6-й на 7-ю. Число, стоящее в 52-й клетке,
получается как сумма произведений чисел, стоящих в 9-й
строке на число 8-ой строки (при этом берутся только числа,
записанные в клетках верхнего треугольника схемы). Чис¬
ло, стоящее в клетке 53-й, получается также как алгеб¬
раическая сумма произведений чисел 10-й строки на 11-т
(берутся также только числа, записанные в клетках верх¬
него треугольника). Число, стоящее в клетке 54-й,
является обратной величиной числа, записанного в 27-й
клетке.
Суммы квадратов, необходимые для оценки коэфициен¬
тов уравнения регрессии (клетки с 55-й по 57-ю), получа¬
ются путем деления квадрата каждого коэфициента урав¬
нения регрессии на соответствующее ск1.
Для контроля вычислений по схеме „Р“ используются
равенства:
54-1 + TnSxtXU9 + T7bSjC1~' 54
Числовой промер решения нормален. уравнений по новым схемам в1
Для нашего числового примера для контроля вычисле¬
ний второго этапа имеем:
18748 + 0,43475-5097 + 58,36-1459=- 106111.
Аналогичным образом контролируются вычисления и на
остальных этапах, tt частности, на этапе, где определя¬
ются коэфициенты ait имеем контрольное равенство:
Sd* + AtSyx3^ + A, Syxbi + Ай Syxi 0 + AgSyx^^-- Sy*.
Как видим, схема „Р“ является простой и легко усваи¬
вается при небольшом опыте.
ГЛАВА 3
СИСТЕМА СТАТИСТИЧЕСКОГО АНАЛИЗА
И ПОЛИНОМЫ ЧЕБЫШЕВА
§ 1. Отатнстичсекая оценка коэфициентов уравнения
регрессии в полпнонов Чебышева.
Новые схемы ,,N“ и „Р“ в процессе нахождения коэ¬
фициентов уравнения множественной регрессии дают без
дополнительных вычислений все величины, необходимые
для всесторонней статистической оценки полученных ре¬
зультатов. Статистическая наука знает три вида оценок:
а) определение достоверности полученных статистичес¬
ких характеристик;
б) определение ошибок, сопутствующих в стохастичес¬
ком смысле каждой из полученных величин;
в) определение степени тесноты связи между изучае¬
мыми признаками.
Оценка полученных результатов с каждой из этих то¬
чек зрения требует определения различного рода сумм
квадратов. Для целей статистической оценки со всех трех
указанных выше точек зрения оказывается достаточным
определить два рода сумы квадратов:
а) остаточные суммы квадратов отклонений типа:
*^('Х1-о)> *^6*3-21) и
б) суммы квадратов вариации, коррелированной с эли¬
минированными значениями факториальных признаков,
т. е., например, со значениями х,.21. Последнего рода
суммы квадратов определяются одним из следующих спо¬
собов (на примере ^З.я):
* {.-*3-21/ СЛ
Статистичесхаи оценка коэфхцаентов уралнети регрессии tf.f
При этом по каждой переменной имеем дело с элими¬
нированными значениями, т. е. с величинами типа
Следовательно, по каждой переменной коррелированная
вариация определяется так, что как бы каждая данная пере¬
менная вводится в анализ последней. Полиномы Чебышева
обеспечивают это без дополнительных вычислений. Все необ¬
ходимые величины легко получить в процессе вычисления
уравнения регрессии в полиномах Чебышева. Вычисления,
связанвые со статистическим анализом полученных характе¬
ристик, удобнее расположить в виде особой схемы (стр. 65).
Из схемы решения нормальных уравнений в таблицу
статистического анализа переносятся веса переменных, *а
также коэфициенты уравнения регрессии, остаточные
суммы квадратов по уравнению регрессии и суммы квадра¬
тов коррелированной вариации.
Критерии статистической оценки целиком основаны на
этих величинах. Необходимо лишь предварительно полу¬
чить средние величины для сумм квадратов путем деле¬
ния соответствующих сумм квадратов на число степеней
свободы, определяемых обычным способом.
Критерий достоверности Фишера определяет как отно¬
шение среднего квадрата коррелированной вариации к
среднему квадрату остаточной вариации, или иначе, как
отношение квадрата оцениваемого коэфициента к квад¬
рату его средней ошибки.
Так например, критерий достоверности коэфициентов
уравнения множественной регрессии у по х„ л„ их,, в
нашем случае равны:
Ео»>«а*е«ты Средни# кяддрлш
<—0,056676
«Г—0,091941
<-6,103401
0,014360
4.3Т
(И Система статистического анализа и полиномы Чебышева
Вычисленный таким образом критерий достоверности
сопоставляется по таблице Фишера с ожидаемыми значе¬
ниями этих критериев в условиях стохастической вариа¬
ции. Если величина критерия, вычисленного по данным
наблюдения, превышает ее табличное значение, то данный
коэфициент признается достоверным и наоборот.
В нашем примере оказываются достовереными коэфи-
циенгы регрессии при *, и х, и недостоверными при *,.
Рассматривая данные статистического анализа (табл.
на стр. 65) видим, что вообще в статистическом смысле
наиболее удовлетворительным с точки зрения достовер¬
ности полученных результатов оказывается уравнение:
= 1,859937 + 0,105373*,+ 0,075035*,.
Статистическая оценка полученных результатов с точ¬
ки зрения теории ошибок требует вычисления средних
ошибок каждого из коэфициентов уравнения. Квадрат
средней ошибки есть отношение среднего квадрага оста¬
точных отклонений по уравнению регрессии к сумме
квадратов соответствующего полинома. Так, например,
квадрат ошибки коэфициентов уравнения регрессии у по
*,, *, и *, определяется как отношение:
А2(^) = 5}/ад.21)= 5]*»- 0,000051
д 2Ю - dll S(xlK) = 2] c'n = 0,000176
д Ча ) “ WS(XU) “ 0,000210
д Као) = dllS(xlm) -2}с'” = 4,855824
Ошибки коэфициентов уравнения множественной рег¬
рессии, следовательно, в нашем примере равны:
<£'±^0*')“* - 0,01336 + 0,00714
a7±W) — 0,056676 +0,013266
ai' d:^(aV') ~ 0,031941 +0,014491
*0’±д«') *= 6,107401 +2,203400
Величина а, превышает свою ошибку в шесть раз, а
коэфициент а, почти в пять раз. Наименьшую относитель¬
ную ошибку имеет, таким образом, коэфициент аи а наи¬
большую— а% и а0.
Схема статистического анализа в полиномах чебышева
*
zV
А
©
£
Дисперсион¬
ный анализ
Ошибки коэфициентов
регрессии
Коэфиииенгы корреляции (множественной и частной)
\J .х
i
1 G
BtC.I ИеН.Н/СОТНЫХ (<и'|-
ратиые величины сумм
о
i 3
5z
•х i-
а =
= ©
I*
о-в-
Суммы квадратов по урав¬
£
3
3
м
Средине квад¬
Критерий до¬
стоверности Р
i
i
|
25 S
s*
I§ ;
O 4»
С = !
кппдрптоя полиномов)
нению регрессии
°з
S3
sS
тЗ
раты регрессии
А«
Е*
5 о
&»
У
31
С i
Квадраты
: д
i
i
1
0-ft*) ч 0-г*)
1
г и R
2
:ч
4
5
7
8
0
10
i м • • 1
\ 12
1
^0.0
1 _ 1 -с
S*o.o " °°
1
"о
(«о)1’ 2
'<*00 °
1
(«о)-' „ ;2
> - " '0
<- оо
'о
i
)
: о * C0n ^2(
I
4(«o)
I
i _
|
—
*<> !
SO'1)-'?’”- -П-Э
с Он
л-1
S(do) _ *2
/1—1 d°
—
—
—
.
—
—
*1.0
тк~с"
• в* 'и
111
1
(d,V -?
..... - /,,
111
*1
-
i
I ^("i)
I
1 _ S(«/2)(/l —lj _f r2
\ ~ili i4A)+'2n](»~* 1УХ)
r[YX)
*'o.i
' с-
ЩГ т
4
("о)2 _,2
"^'оо ~
1
(°оГ _72
Соо " 01
70!
df
—
i
■ C>00 “ д2 ( ao)
*(ао'>
—
—
rf,
~
—
5(</о)-(^--5(^)
С,|
л_2
£(*?) =--?
«-2 ‘
—
—
—
—
i = | -r*lV-V)
1 4
t
—
V 1
2.1
s.vL
«а
с'22 2-
1 !
С "2
.2
22
d|T
1
i
1
1
A ( «2 )
1 (t>f Si/»>) (Л 2) ^ 2
7f ” :i) “ ~'(KX2-,)
r2.1
Х|2 i
1
о г "С | |
SA’b
«V
1
К)2-/*
.. =/,2
Ч|
1
с П
~ 12
rf*
—
3|.C”-A* (•'.')
*(«;*>
[S(rf2)](/»-2) = 2
(S(rf|) zf2J (rt—3) (>'A,-2)
r« 2
i
*0.12
*2
1 - с'"
SV2
(•. 12
Йо
1
(“ОТ _,2
• Г* «*
с00
*(.?)-<#-,(«
22 !
1
л-3
КТ_7*
/м
S(rf2)=-rf2
~п-Л а>
tf2
I
i
d22-C0'0=i2(Oo)
I
k
M-o')
1
1 Tl <V'X|2)
P, 2
*3.21
~ .. • ** L зз
ол3.21
1 i
^3
КУ_,2
сзз
1
г*,
с33
*•33
*3
-
. //*\
д(“з )
n (s(rf|))(«-3) ,2
п [в(4) + '1з]<«-4> ОАз-2''
r3.2l
*2.:u
1 Г'"
« С22
S*Li
1 ффф
! "2
(^,2
с22 "
1
(вП2ж72
— . . , * 23
с22
*23
“ i
1
A(fl2')
[s(rf2)l-(n-3) _,_г
I«(4) + 4.J-‘«--*> <V'X23,)
Г2.31
■*1.23
1 _ С"
SV* 11
; ол 1.2.4
*00
"1
(■'•"У-,*
л"' ' i*
4l
1
(-Г)2. 72
с1|
V.
I
(•;")
S(dl)-(n-3) , r2
rl.23
•*0.124
; 1 _г"'
-С00
ОЛ0.123
1 “о*
|
... - *03 !
С0<> |
.
(«оТ_72
^00
—
—
*!<o^2K")
д(<1о )
—
—
e3
i
1
к
1
1
s(‘»D-^£-s(j§)
L33
л—4
f- 5J
n—4 J
—
—
—
—
1 - *(2vxi23>
"0
^123
Схема статистического анализа а полиномах Чебышева (числовой пример)
Статистическая оценка коэфициентов* уравнения регрессии во
о*
?|
*?*
:• э
1*5
л *
5S
с
Of
►? ajv С
:st“i
К W
е\
1 1
3
° 1 1
II
3 S 8
о о сГ
111 1
•-Г С CSS
S8 8 at
О о о* о*
L II II, 1 в
<М СО е5
с5 с* с ^
1 1
ОС СО
г** г^.
? 1 ?
о о
Or; о
8 i 1 2
о о* о
О ^ см
3 о 8 I
_о_. о о
1/5 00 п
О 00 ю
•Н р- (О
8 ° Й !
О О чр
ООО
Й 3! ^
S 1 3 1 5
о* о о о*
5??
'iii
о
о
о
$ ,
t- 1
О
8
О 1
см 1
<о
о
ГО СО
Ц 3 1
О*
ь- СО ю 2* ,
8 ©381
о о о см"
3
2 S
* О*
3 8
р 1
О С-
о о*
Д © О ^
*40 ts. СМ
^ g ^
о о о -е
• о
я В
?s
f!
Р
4*-
п ■
= о
о* г
Z *•
2 *
0-0
*-
г
НС
»* I
40 X
с *
ь
► 3
Я
«0
»*%
3 '
а s ,
"d* f
<3 8 8 |
^ V
2“2f 8“
оГ гчГ |
Ю U0
CM c-t СМ СМ
со 00 со СО |
'Т t т
1М.
04
I
со
8 й
о ю"
*У -С
оЗ
0» —*
Ч* t'-
3 8 1
3 8 S К
V 00 О N 1
жсэээДюД па
•vdi’*43i •нпГ%4;)
СО
** Ю 00
СО СО МГ
ГО N Ф
см ю
см см
N W N N
ю о
W0 о й
О *—1
•н
00 <N V 0> ГО
Ю 04
* 3 8 s ^
rnro9^ao
1|*НАГ1»Х.1 OlfOKT^
*о
~ S
~ S3
м W м (V)
см
^ ГЧ
см
ж
о
ж
ft
ж
т
м
3
я
зс
V*
&
ft
в =
* в
• С/
S «,
•? е*
g; •
4 Oi
о
в
8
8 3
§ п
•-* У—N
CN «£р
'to
•t W ср
со с*. 35
СО Г^* 2
см см •-*
1^
'со
СМ СМ г- -f.
t' T UJ w
g со »о со
~ ~ ~ 1
sr
ч-^
СО
00 Л* ^ 05 О
CD 1Л N CN см
S 8 2 8
II
з г
г г
2 в-
2 л.
s. •
В о
о в
со
«ч
01
ю
СМ
оГ
1
о а>
о «—»
со о
2 ц 1
о* >Л
Н 11
■<г *«?
«о со гм
8 <5 8
ю от»
S | у I
О о —
(1 II 11
S
^ 2 2
•" ‘.о 05 •*
о о -j 00
о ь4 05 w
? <* О. 1
1 о о ^
1) 11 11 я
с й ^
и 1
I “ 1 2 *
■ * ® ? S "
1 :Ш!
О £ 3
еэ
со
о
С->
о
с
II
8
о
я> 2
8 s
о «О
8 1 1
о о
II II
■с*#
S й S
со »0 О
Ю О) о
8 1 1 Г
о о‘ с
0 II II
s \ 8
v> о о
со — о см
ю О см 00
о см о^
о i « 00
8 1 ь 1 1
О О г СМ
II II II II
*«?»<? \r*J
; [
шмадли-О ишаш I —
1 *П9ЭК мкоянкоц (
о
.О цр
ч ^
О *7
•-г ■*? ^
«
С» У-
с’| .О •!
ч ч ч ъ
?J о S 3
СУ ЧГ* — о* я
Ч Ч Ч ^
•'* И о ли шоп и Чобищоич
66 Система статистического анализа и полиномы Чебышева
Критериями, определяющими степень тесноты связи
между изучаемыми признаками, являются индексы мно¬
жественной корреляции и коэфициенты частной корреля¬
ции. Квадрат индекса множественной корреляции является
дополнением до единицы отношения между средними
квадратами остаточных отклонений по данному уравнению
регрессии и средним квадратом отклонений от средней
арифметической. В нашем случае индекс множественной
корреляции у по хи хг и х, равен:
«о
Отсюда:
= 0,8885: Яш<=0,94.
Квадрат коэфициента частной корреляции является до¬
полнением до единицы отношения среднего квадрата оста¬
точных отклонений по данному и предшествующему урав¬
нению регрессии, т. е. определяется по формуле:
1 - г*(ух. „Л= — = -Ы? = 0 8782 или г..~ 0 35.
Средний квадрат отклонений для предыдущих уравне¬
ний регрессии известен непосредственно только для дан¬
ного порядка включения переменных в уравнение регрессии.
Однако, эти величины легко могут быть определены
для каждого случая, когда данная переменная включена
в уравнение регрессии последней. В этом случае сумма
квадратов остаточных отклонений, определенная для изме¬
ненного порядка включения переменных в анализ, вычи¬
сляется как следующая сумма:
для хаимеем S(d-) -f /.j. • S(d\)
" >> '^(^.) * 'л
" Л| Aj..
Здесь в подстрочном значке число перед точкой обо¬
значает номер переменной, включенной последней.
В таблице на стр. 65 приведены нее необходимые вы¬
числения такого рода.
Статистическая оценка коэфициентов уравнения регрессии ь7
Таким образом, наивысший коэфициент частной корре¬
ляции г,.я= 0,80 имеем между у и хи.я, наименьший —
r3.i, —0,35.
Аналогичным образом может быть произведена оценка
и коэфициентов полиномов Чебышева, т. е. уравнений
регрессии типа: ,,*.< =+• k'^'x, -ь А'у‘.
В этом случае в качестве .весов" для определения
средних квадратов коэфициентов полинома имеем обрат¬
ные величины сумм квадратов предыдущего полинома. Эти
„веса* в схеме „N“ решения нормальных уравнении запи¬
саны на предыдущем этаис вычислений в левой части
с: смы, в колонках, соответствующих каждой данной пере¬
менной и расположены по косой линии (слева направо и
снизу вверх). Эти величины и выписываются в таблицу
статистического анализа во вторую и третью колонки.
Следовательно, для ^32 весом будет величина е£_„ для
коэфшшента величина с", а для величина c"w.
В остальном же статистическая оценка коэфициентов
уравнения Хз но х, и xt вполне аналогична оценки коэф¬
фициентов уравнения у по хэ, xt, и я,.
Таким образом, новая схема решения нормальных \ ран-
нений со сравнительно небольшой затратой труда дает:
а) всю систему статистических характеристик, начиная
со средних арифметических, .весов" переменных, остаточ¬
ных средних квадратов отклонений но уравнению регрес¬
сии и но полиномам и кончая средними ошибками всех
коэфициентов, критериями достоверности Фишера, индек¬
сами множественной и частной корреляции;
б) позволяет определить уравнение регрессии не толь¬
ко у но х, но также и х-ов между собой в самом разнооб¬
разном их сочетании;
в) позволяет оценить коэфициенты всех уравнении
регрессии и всех полиномов с точки зрения дисперсион¬
ного и корреляционного анализа, а также с точки зрения
теории ошибок.
В этом преимущества новой схемы „Л/“ решения нор¬
мальных уравнений.
Теоретическое значение новой схемы состоит в том,
что она через полиномы Чебышева и теорию квадрати¬
ческих приближений тесно увязывает всю систему статис¬
тического исчисления с основами современной математики.
6S Система статистического анализа и полиномы Чебьииееа
§ 2. Оистояа статистических характеристик и полиномы
Чебышева.
Полиномы Чебышева дают возможность представить
все основные статистические характеристики в виде про¬
стой и стройной системы статистического исчисления.
Полиномы Чебышева позволяют связать в единую систему
теорию корреляционного, дисперсионного анализа и тео¬
рию ошибок.
Согласно теории Чебышева, изложенной нами выше,
в основе системы статистических характеристик лежат не
арифметические, а элиминационные средние типа:
Sv Ч'| (х) ч/(-*) V
Svj(x) ” SV-(x)
Необходимо отметить, что еще Гаусс (12) в своей .Тео¬
рии движения небесных тел“ указал, что наиболее веро¬
ятным средними являются не арифметические средние,
а средние элиминационного типа. На стр. 266 Гаусс пи¬
шет: .Наиболее вероятная средняя величина не будет
. м3 -4- £'г V -f-
просто арифметической, но —г* + г'?+>£"— •
Здесь е=,Хр-п Ь=—^—.
хрА0...
Заслуга Чебышева в том, что он в развернутом и систе¬
матичном виде использует этого типа средние в своих
работах.
В экономической статистике теория элимииационных
средних получила название корректированных средних.
Из предыдущего равенства ясно, что элиминационные
средние являются средней взвешенной из отношений двух
величин, из которых одна (знаменатель) — нолином Чебы¬
шева (.х 12штш), а другая (числитель) — изучаемая величина
(у), а вес —квадрат полинома. Следовательно, элимина¬
ционные средние являются средними типа:
о У
-*3-21 ' 321 _ S-VX*-U
^•*3-21 $-r].2l
Таким образом в основе теории элимииационных сред¬
них лежат иолиномы Чебышева.
СИСТЕМА СТАТИСТИЧЕСКОГО ИСЧИСЛЕНИЯ В ПОЛИНОМАХ ЧЕБЫШЕВА
Этапы элиминирования
Нулевой этап
(вычисление средних а рифм*.*
пгческнх, средних квадрати¬
ческих и ошибок средних)
| Суммы произведений
!
S ( Х§) - N
j 5ухш) ■ ; Sy
'SI *00 S.v,
Элпмннацнонные средние
Суммы квадратов отклонений
(квадратические приближения)
Ошибки
Критерий
достоверности
S.Yq0 = п
Jii.
Svu<j
У ltQ
У ~
^0
xl^
* in
X.v2
•vi>o - Sx^
x2 ^
*20
хз -
*:»n
' Sx3
xim Sx,
s*t _
SXT " *1
**00
к
10
S.t
Sx?»
2 ^ *2 - K'20
Sx.j -
sJ-= **
^X00
A,
30
Sdl = Sy2 -4S.v2)-«:2<y)
Sv2>0 *= Sx] - (K\0)2 Sx*0=n-.4 x,)
S*l.0- S*l - {K20Y S-'oo - «;2 ( ** >
Ц.о‘^3 — (К30)” 5*oo = ,,s2 ^ л’3^
1
. = Л2(у>
oo
<n - I) S.v,
5v?o ;
(« -ijSx-J.o
x2 0
(n —1)Sx^ о
[>
(и —I)Sxqi0
a2(*,)
A2(v2)
< «.»)3
A2(y)
(K'io)2 _ (*.)2
Л'(Л',) ' A2(V,)
См =
l,~s^
1 .0
Первый этан
^)'xt.o: *>УХ 1 ~ A,<, Sy
Sy.v0.,
^•vvi .0
5*f.o
sV*o.i
--^o.
(вычисление уравнения пря- j
молипейпой регрессии ii стати-
стпческаяоценка результатов) ^'2 х».о S.v2Ai~"
Sx;
-а0 — «1 К к,
о. I
у* о, X, + а0
•• 0» *0
1 х2 — *21 Х1 + *20
1 *3 *31 *1 + *30
Второй этап
(вычисление уравнений ми<»
жествепиой регрессии к ста*
тистическля оценка резуль¬
татов)
у-02 х2 +а\' хг +а’о
21 х3 “ * 32 Х2 + *31 Х1 + *30
— /ч Ю ^*Yi*
SXn *3.|> •— Sx^ Л ^
— К зо S.\*2
^•V3 *Yi.0 "* *хз .v, —
— /\ j о -V.Vj
-S0’A2.l) Sy.V2-
— А 21 Sy.v j —A20
Sv, x2.1 *‘Sv3 v2-
— A3l S.y3 xl — A30S.v3
Sx2 x, 0
"Sv7‘ 21
ЭЛ1 .0
'• Sx>} л'л I / ,, ,
2,1 “ с .2 ^ ^20 ““^21*^1
o.V,
10 <
40.1
*1,6
5*1 .0
= K
31
// . _5*3 *0.1 L' I/ I/
'Vw - *j •- - - ляо Лд| • л к,
ivo. 1
" SyxI
5-4.,
Syx 1 2 * **
- —0 \ —K2\ a2
**T. 2
оу.Хл 12 ' rs" "
a0 =» —— — «0 “^20 a20
►
S.v. л 0
Sx0.12
K32*
2.1
о 2
4S.V5 ,
Sv.f л, L, ## -
^3 1 л '> Л31 21 л32
S.\
1 .2
... Sx3. x0 l2 _ I/ ' . к
*30~e *cv" -^30 л20 a32
ЪХ0.12
Третий этап
(вычисление уравнений мно¬
жественной регрессии и ста¬
тистическая опенка резуль¬
татов)
/**
У ша3 х3 + с2 х2 +
*t/ »•*
-fa! хг + а0
^Ух3.21в^УХ3
—^32^х2 — *3, ^Ух1
-К305у
^УХ3.21
Sx2
эх3.1
^Ух2.31
2
2.31
• О/А} «| ./
в, = —.-3 - г. а2—К32аз
Sx?
".
^*1.23 " ir'"
~~z~$ » u, — Л31 03
5tI.J3
Syx0 ,23
0 '« '2 ” °0 ” *30 °3
5*0.123
Sd2 = SiIq — (<*.)” 5-vT .0
(K.o)2
I 1 , V
_ r=» . . f -
^00 ** 0 о - ^ c 2 1 C-V2
5.V.V, 5x00 Sxl.O
5a’2 i ■ S.\2 0 — (^21 )*^,VT.0
S.vj 1 =• S.v3iQ — (A3l)2S.v2 0
SJ2 Sd2{ -(«2)?Sv2.i
(к=')г _..1
~n ‘ Sx2 Sx2 ,
^Л1.0 ^*X2.1 1 • 2
c” r‘ I (^2o)2 = 1
соп *-00 ^—
5.x2 I ^x0.12
5*3.21 r’ 5*з. 1 “ (*32)25*3 *2.)
5*2.3 ™ Sv2.0 + (*23)25*2 *3.0
5*2 *3.0
Sit]
(и - - 2) S.v2 u
Sd'y
(»-2) S (.*«!,)
5*1,
(/» - 2) S.v2 u
_ :
<ii-2)Sx£7
Sx2
1
(n— 2j S.v2 0
: 5 (xi..)
(».—2)Sx2.i
Sd2
{и - 3) Sx2.x
Sd?
- - - ** — .
(n — ?•) Sx2 о
j Sd2
j (/. - A)S.Vq_ |2
_ _
(a- j)Sx% ,
a2(-.*) ;
A*(0
A3(**2i)
A2(K2o) j
a3(k;,) j
1 A2 (K3o) 1
■A2 (4) !
)
.a*(.;•) j
1
i1 < > j
где К 2з —
5*lo
. +(K»)J !_
... .. . (Кз,*)2 I
Cll c"Cll + -*2*" “ct2
^X3.21 dX1.23
... .. (k;0)2 _ 1
*• 00 l00 ^ - -k * Г“о
1 («-?■) Sxf 2
—i!«o)
/1 — 3) Sxq
a2("D
Sd2
(« — 4)Sx3 21
Srfi . 2/ "4
= Д2(а2)
(n — 4)Sx3 j]
Sd2
)2
43.2i
Sx? Sx2
0. 123
(It — 4) Sxf 23
Sd2
(/»—4)Sxq_ 123
д2( ei )
= A2(«o')
S(x2)
(*:.)-
A-'(.V,)
(".)2
("«)2
(*2.)2
-•4*2,)
(*2o)'
'a2 (K'20)
'а2(Кз',)
(*3o)'
_А2(Клп)
,.(4)2_
i2(«2)
("V)2
д21«'.У
("о)2
'дГ("о)
(Кз'з)2
(*;;)2
А2(КЯ1)
(*зо)2
А2 (Кзо)
~К)2
д2("з)
("г")2
A*VO“
_(fD2
д2("Г)
("il>2
д2("0?
Коэфицпенты
корреляции
S.t2 (// 1»
s (II -ъ
^(x3.i)(/f ~ О
5 ( *1г.) ( « - -')
1 - Г* (.V. V.)
Sd? (/. - >)
Sit] in Hj
Sdi (11 —• 2j
1 -г2,(У*у.,)
Si<2 + ^U\} - ! l;, — •<)
= 1 — rf . O'* 1 2 )
1
liU(ys2xx)
S ';, (n - H)
С 22
(n 3)
S ( x? оЛ ‘и — U . •»
■ \ , • I--«-( •*:. *2 *.)
5 ( *?.o) ^
Stfii2z:iL = 1-4.2, <У*3.2.)
Sd| (и—4)
Sd| (r:-3)
1 — r2.31 (Ух2.31)
££3j£zg ^l-r2.23 (У*. .2з)
*s+w:?V>
. cn J
St/3 (n 1) p2 (v x x x, \
- ; = 1 “*^123 (У1 хз »xi)
Srfg(/i-4)
Система статистических характеристик и полиномы Чебышева ЬУ
Как видно на прилагаемой таблицы .Система статисти¬
ческого исчисления в полиномах Чебышева* (стр. 68),
ортогональные полиномы Чебышева являются непременны¬
ми составными элементами всех основных статистических
характеристик.
В свете полиномов Чебышева очень удобно предста¬
вить всю систему статистического исчисления, как отдель¬
ные этапы процесса элиминирования. Тогда на нулевом
этапе будем иметь систему средних арифметических, сред¬
них квадратических и систему ошибок средних. Характер¬
но, что квадраты ошибок средних величин есть отноше¬
ние суммы квадратов первого полинома Чебышева (^-.0)
и суммы квадратов нулевого полинома (Sx^ — n), умно¬
женной на число степеней свободы (л — 1).
Замечательно, что зависимая переменная в свете поли¬
номов Чебышева может рассматриваться как очередная
переменная, введенная в анализ в качестве некой новой
независимой переменной. При этом оказывается, что ква¬
дратическое приближение по уравнению регрессии Sd- —
есть величина, вполне аналогичная сумме квадратов соот¬
ветствующего полинома Чебышева. Ошибки средней ио у
поэтому также есть отношение суммы квадратов первого
полинома, но по зависимой иеременной (Sd*) к сумме
квадратов полинома нулевого порядка, умноженной но
п— 1, т. е. на число степеней свободы.
На первом этапе, состоящем в вычислении уравнения
прямолинейной регрессии, имеем коэфициенты регрессии,
как элиминационные средние типа:
Syx j .q
или
Sxl0 Sxf
ьо
а квадратические приближения, как суммы квадратов вто¬
рого полинома Чебышева по очередной независимой пе¬
ременной (Sa§.,) или первого полинома по зависимой пере¬
менной
Ошибки коэфициентов прямолинейной и множественной
регрессии, так же, как и ошибки коэфициентов последую¬
щих полиномов Чебышева, вычисляются аналогично ошиб¬
кам средних. Так, ошибки коэфициентов полиномов опре¬
деляются как отношение суммы квадратов данного поли¬
нома (для коэфициентов которого определяются ошибки)
к сумме квадратов предыдущего полинома, умноженной;
на соответствующее число степеней свободы. При этом в
качестве предыдущих полиномов выбираются полиномы
70 Система статистическоео виалчза а полиномах Чебишеса
для той- переменной, при которой стоит данный коэфн-
циент. 'Гак, например, для коэфициента £/, ошибки вычи¬
сляются как отношение:
-м* *« кш * *“ как
_ ^Лз-и _
(/«-3)Sx?.2
Аналогичным образом вычисляются и ошибки коэфн-
цпснтов регрессии, только при этом для числителя сумма
квадратов берется по независимой переменной, т. е. Sd-t
Sit* и т. д. (см. табл. на стр.69).
На нервом этапе появляются новые статистические
критерии » виде коэфициента корреляции и критерия до¬
стоверности Фишера. Критерии достоверности Фишера
могут быть представлены как отношение квадратов коэфи¬
циентов уравнения регрессии к квадрату ошибок каждого
из этих коэфициентов, как это показано в таблице на
стр. 65 и 69.
Коэфициенты линейной корреляции также могут быть
представлены как отношение средних квадратов первого
и нулевого полиномов, определенных для зависимых пере¬
менных (у). При определении средних квадратов, суммы
квадратов делятся ни соответствующее число степеней
свободы. При этом необходимо помнить, что остаточные
суммы квадратов по уравнению регрессии имеют степень
свободы на единицу меньше, чем суммы квадратов, анало¬
гичных полиномов, так как порядок элиминирования для
уравнения регрессии на единицу выше, чем аналогичных
полиномов. Отношения средних квадратов, однако, харак¬
теризуют не сами коэфициенты корреляции, а выражения
типа: 1 — г= (ух,.21).
Современные английские статистики специально рас¬
сматривают величины такого типа, присваивая нм назва¬
ние „коэфициентов остаточной корреляции", или иначе,
the coefficient of non determination. Такого рода величины
находим у Келли (13), Эзекиель (14), Девентрона и Экосл
Пб).
На втором, третьем и последующих этапах при вычи¬
слении уравнений множественной регрессии и статисти¬
ческой оценки полученных коэфициентов в качестве но¬
вых статистических критериев появляются коэфициенты
частичной, частной и множественной корреляции.
Статистическая оценка коэфициентов уравнения регрессии 71
Коэфициенты множественной корреляции, при этом,
определяются как отношение среднего квадрата полинома
Чебышева данного порядка к среднему квадрату полинома
нулевого порядка. При этом полиномы должны быть взяты
по зависимой переменной, например:
1 ~Н,‘ Sd$(»-a)
Коэфициенты мастной корреляции определяются как
отношение средних квадратов данного полинома к сред¬
нему квадрату предыдущего полинома например:
1 гч SrfI(n~3)
Если вычисляются частные коэфициенты корреляции
д 1я переменных хк, то следует отметить, что при этом
берутся смежные полиномы системы „N“ для хг, л3, xv в
зависимости от того, по какой из них вычисляется част¬
ный коэфициент корреляции. Поэтому сумма квалратов
предыдущего полинома в этом случае определяется для
каждой переменной как выражение:
S ,.4- » = т. е. аналогично: Sd* +v -- Stfj.
' сз$
Характерно, что полиномы Чебышева и в случае ча¬
стной корреляции прямым образом определяют коэфи-
циенты остаточной корреляции, т. е. выражения типа:
1 — Таким образом коэфициенты остаточной кор¬
реляции, несомненно, являются основными величинами в
корреляционном анализе, что видно из простого соотно¬
шения, которое существует между коэфициентами множе¬
ственной корреляции и коэфициентами частной корре¬
ляции:
1 - *?»“ П - • [1 ~ г> (3**01 ‘I1 “ '*0*^)1'
Коэфициенты частичной (part> корреляции, введенные
Эзекиелем (14) и относящиеся к так называемым чистым
линиям регрессии, также являются отношениями средних
квадратов двух смежных полиномов Чебышева. При этом
остаточная сумма квадратов для предыдущего полинома
определяется по чистой линии регрессии, т. е., по уравне¬
нию множественной регрессии, где значения некоторого
72 Система статистического анализа и полинома Чебышева
xt приняты равными его средней величине (хЛ.). Так, на¬
пример, пусть имеем уравнение множественной регрессии:
yt23 ~ "Ь 2
Заменяя значения х, на их средние значения, имеем урав¬
нение чистой линии регрессии:
V13-2 ~ а0 ■*: ~ а2 *'':»*
В связи с этим переходом остаточная сумма квадратов
по уравнению у13г2 увеличивается на сумму («г’)* т. е.
будет равна: 5(.^) = Sd* + (a'j' f Sxl0.
Козфициент же частичной (part) корреляции будет равен:
«. (а2 У^г-о
-* S^+(^'ys*U'
Таким образом имеем:
2 _ s4
Наконец, как уже было указано в начале работы, по¬
линомы Чебышева позволяют уяснить природу коэфициен-
тов множественной рецессии, которые являются величи¬
нами, куда входят полиномы Чебышева с измененной по¬
следовательностью переменных. Так, например, младшие
коэфициенты уравнения регрессии определяются по фор¬
мулам типа:
С
аУ" = — =- g,' — k'” а”' (см. «Систему статистиче-
Sx2-*l
ского исчисления в полиномах Чебышева* стр. 69).
По формулам такого же рода получаются не только
младшие коэфициенты уравнения регрессии, но и младшие
коэфнциенты полиномов Чебышева, как системы так
и системы «с*.
Внимательное рассмотрение .Системы статистического
исчисления в полиномах Чебышева*, таким образом, пока¬
зывает, что статистическое исчисление в полиномах Че¬
бышева выражается в виде простой стройной и удобной
системы вычислений основных характеристик, используе¬
мых в математической статистике.
ГЛАВА 4
ОБОБЩЕННЫЕ ПОЛИНОМЫ ЧЕБЫШЕВА
И СТАТИСТИЧЕСКОЕ ИСЧИСЛЕНИЕ
§ 1. Метод Чебышева к свойства его иолинояов
В своих математических работах Г1. Л. Чебышев соз¬
дал общий метод разложения различного рода функций г.
ряды при помощи непрерывных дробей. Им показано при¬
менение этого метода для целого ряда функций.
При решении задачи разложения данной функции в ряд
он ставит одно общее условие, чтобы разность между
искомой функцией и ее разложением в ряд наименее
отличалась от некоторой функции v. Характерно, что
П. Л. Чебышев не ставил условия, чтобы эта разность
стремилась к нулю, а удовлетворялся условием, чтобы
она наименее отличалась от функции v, являющейся
функцией остаточных отклонений. Такое условие вполне
отвечает природе статистической науки, имеющей, как
известно, дело с величинами, вариация которых всегда
отлична от нуля.
При решении задачи разложения функции в ряд прй
помощи непрерывных дробей, П. Л. Чебышев (16) рассужда¬
ет следующем образом: пусть F[y)— точное значение функ¬
ции, которая разлагается в непрерывную дробь, и пусть
— некоторое выражение, полученное при разложен»!,
этих функций. Причем хну — полиномы, при которых
выражение F(y) —наименее разнится от некоторой
функции V. Чебышев рассматривал разность/7 (у)—соб¬
ственно, нмея дело с числителем этого выражения, ставя
условие, чтобы функция xF(y) — y в наибольшей сте¬
74 Обобщенные полиномы Чебышева и статистическое исчисление
пени выражала некую функцию т\ иначе говоря, он ставит
условие, чтобы разность xF (у) —у — <о наявозможно ближе
приближалась к нулю. При решении этой задачи он и по¬
лучает свои полиномы, связанные с сопровождающим их
зесом в*(*Л зависящим от вида интерполируемой функ¬
ции. Чебышев показал, что для вычисления его полино¬
мов, связанных с данным весом в*(х), достаточно искомую
функцию разложить путем последовательных делений в
непрерывную дробь таким образом, чтобы разность между
F(x) и /л-ной подходящей дробью была порядка ■ •
Тогда знаменатели подходящих дробей будут отличаться
от полинома Чебышева только постоянным множителем.
Кслн знаменатель подходящих дробей разделить на этот
множитель, т. е их пронормировать, то будем иметь
полиномы Чебышева.
Пусть, например, имеем некоторую функцию F(y),
•огда путем последовательных делений иолучаем следую¬
щую непрерывную дробь:
*
у+Ь- *-■
J-Нз- a3
y + h-
V — (1/1 ая
*Sn-x(y)
F.(v)
Вели на основе этой непрерывной дроби составить под¬
ходящие дроби -4м, то будем иметь в качестве числителя
О ЮА
•Мв) подходящей дроби выражения типа S\уЧг„(х)), т. е.
суммы произведений данной функции на соответствующий
полином Чебышева. Знаменатель же (£м) подходящей дро¬
би будет равен ^['^(х)], т. е. сумме квадратов данного
полинома Чебышева.
П. JI. Чебышев показал, что его полиномы обладают
рядом замечательных свойств, а именно:
1) нулевой полином всегда равен единице, т. е. «1>‘0(х)=1;
2) полиномы обладают свойством ортогональности, а
именно: S [Vm (х) (х)] 0, при т * k, б) S[V|(x)J = В\;
3) смежные кол ином м связаны единой рекуррентной
•формулой:
Классификация полиномов Чебышева
4) полиномы обеспечивают квадратические приближения
к искомой функции на основе единого интерполяционного
ряда Чебышева (при в2 (х) 1):
• S|4W] •' } sP'fWI 1' ' •"
■ s t|- /vv
S KWI -( >
Такое приближение, как отмечает П. Л. Чебышев в
своем письме к проф. Н. Д. Брашману (17), составляет
необходимое и достаточное условие, чтобы полином Ч;(х)
приводил суммы 5[у — 7’(х)]8 и 5[х- -Ч. (х))! к минимуму.
Полиномы Чебышева связывают теорию непрерывных дро¬
бей с теорией квадратических приближений. Кроме того,
формулы для нахождения полиномов ’Г(х) являются одно¬
временно формулами для интерполирования по способу
наименьших квадратов.
В зависимости от вида функции F(y) Чебышев получал
различного рода ортогональные полиномы, связанные с
соответствующим весом Н2(х). Так как все они полностью
удовлетворяют четырем, формулированным выше условиям,
то они могут быть отнесены к одному классу полиномов,
который мы называем семейством полиномов Чебышева.
В зависимости от вида функции F(y) и, следовательно,
вида выражения в2(х). характеризующего вес полинома,
получаем полиномы различного рода как для линейных
функций многих переменных, так и для показательных,
тригонометрических, гипергеометрических и т. д. функций.
Все эти полиномы составляют одно семейство полиномов
Чебышева, удовлетворяя четырем вышеформулированным
условиям.
§ 2. Классификация полиномов Чебышева.
II. Л. Чебышев впервые изложил свой оригинальный
метод наилучшего приближения функций в работе: .О не¬
прерывных дробях", относящейся к 1855 году.
В этой работе им дана общая формула интерполяцион¬
ного ряда (см. стр. 7 настоящей работы) в иолиномах Че¬
бышева, члены которого составляются в виде суммы вы
ражений типа:
s/>(*). е2(х). *’,(*)
76 Обобщенные полиномы Чебышева и статистическое исчисление
Характерно, что н формуле для интерполяционного
ряда Чебышева вес входит в числитель и в знаменатель
коэфициентов. Особенно важен тот факт, что идея
Чебышева о весе, сопровождающем ортого¬
нальные полиномы, открывает очень широ¬
кие возможности для применения метода
наименьших квадратов к сложным нелиней¬
ным функциям.
Идея Чебышева о весе, сопровождающем полиномы в
случае разложения в ряд сложных функций, дает теоре¬
тическое обоснование для распространения метода наи¬
меньших квадратов и на этот род функций.
В интерполяционной формуле Чебышева особое зна¬
чение имеют суммы квадратов полиномов Чебышева
5в*(л) являющиеся знаменателями как коэфициен¬
тов интерполяционного ряда Чебышева, так и знаменате¬
лями коэфициентов самих полиномов Чебышева.
В этой же работе Чебышев впервые указал рекуррент¬
ные соотношения, связывающие его полиномы. Исходя из.
общего правила составления подходящих дробей, он дал
(т. 1, стр. 216) для своих полиномов рекуррентную фор¬
мулу:
^'/-iC*) ~ ! )'* /(Х)‘Г^Г/- i(A)-
Исследование II. Л. Чебышева о непрерывных дробях
таким образом, закладывает основы его теории приближен¬
ного представления функции, удовлетворяющего условиям
метода наименьших квадратов.
В дальнейшем, делая различные частные предположе¬
ния о совокупности известных значений искомой функции.
II. Л. Чебышев получает различные ряды. Полиномы,
входящие в эти ряды, образуют семейство полиномов Че¬
бышева, удовлетворяющее четырем условиям, указанным
выше. Однако, сами полиномы Чебышева могут принимать
самый разнообразный вид в зависимости от вида искомой
функции.
В зависимости от вида искомой функции, удовлетво¬
ряющей совокупность известных ее значений, получаются
различные полиномы, сопровождаемые различным весом
6*(х). При этом, в зависимости от вида искомой функции,
оказываются различными:
1) веса в4(х);
2) основная область суммирования;
3) значения сумм квадратов полиномов;
КЛАССИФИКАЦИЯ ПОЛИНОМОВ ЧЕБЫШЕВА
Функции
Название полиномов
i
Символ поли¬
нома
Вес, сопутствую¬
щий полиному
Область
суммиро¬
вания
Суммы квадратов полиномов
t
Коэфициенты интерполя¬
ционного ряда
Рекуррентные формулы
0
Обобщенная
Обобщенная система по¬
4-i (X)
1
1
1
й2 (X)
-со, + со
\
J [Ф2(*) в2 (X) </х]
—Л>
!
f [р(х)ф,(х)^(х)</х1
-»» = .7.
OO-M-i-i W-*i-14-1-2 (*>
1
форма
линомов Чебышева (1855 г.)
+ ^ :
П*1 (x)'-,a(x)rfxl ;
1
1
Линейные
функции
МНОГИХ
переменных
Чсбышевскме полиномы
множественной регрессии
NH(X)
где:
а) *-/(123.../— 1)
б) /</—1
1
e2(x)-i
ИЛИ
в2<Х)-/
(целые положи-
тельные числа)
j
— со, + со:
SNц(х) — (х)—кц-SXf Nn (х)
где: (/—1|—(|—I) (I23...I— 2)
Wi,Wmeu
SWfj(x) |
)
—KuNj(x)+Nt (i_|)(x)
2
Параболы
f—порядка
Полиномы
параболического
интерполирования
?1 <*>
в*(х)=1
-со, + со
S?2 (x)=»Sx,+ I о(_, (X)—PlSx1?!-!—«jSxty, !
„ (x) p_Sx‘?l_,x Sxl~l ?,_2(x) |
Itnj* L -
S?f(x)
ft (X)-(X—T| —I 00—al4-1—2 00
где |_| — T,_,# |_2
Чебышева
1 S«j.f_2(x) ' ‘ s?2_,(x) 5+2_2(X)
3
Чебышева — Эрмита
(1859 г.) (1864 г.)
Н,(х)
в* (х)= l/Te-**1
-СО, + СО
+x>
I 62 (x) H2(x) </x—/! (2k)
-Л)
+CO
1 y92 (x) Ht (x) dx
-®? , - a,
/1 (2*)'
Н,(х)--2^хЯ;_, (x)-
-2k(l~l)Hl_2(x)
4
Показа¬
тельные
Чебышева — Л а герра
(1859 г.) (1879 г.)
Ц(х)
в1 (х)-ке~кх
0. СО
J ©2 (x)L? (x) </x- (/2 )l
0
+л>
J ув2 (x) L,(X) dx
(/*)! '
Ц (x) - — (Лгх—2/+I) Ll-l(x) -
“(i-1)’ ^i—2
5
Обобщенные Л а герра
9* (*)
в2 (х)—х* ех
0. СО
J в2 <*) [ ?! <*)]2 <»*-« Г (5+/+D
0
+ПО
J ув2 (X) <f*, (X)
_Я я ais
/!Г(5+/+1)
?! (x)-?!~‘ (x) + ,?!-i <*>
6
7
Тригономет¬
рические
Тригонометрические поли¬
номы Чебышева (1853 г.)
а) первого рода (косинусы
кратных дуг)
б) второго рода (синусы
кратных дуг)
Т,(х)
<
| и,(х)
\
! в«--тЧ
V 1—X
^Ос>“|/1—ж2
—1.+1
или (0, п)
—1» +1
или (0, х)
+» г* 1 *
J в» (X) Г,2 (x) dx — 1J cos21фйф I - 2
+» Гп 1 x
J e2 (x) U*(x) dx - If sin* / фйф\ - 2
2 **
- J yb2 (x) Tt(x) dx=A,
f IW <*> Ui(x)dx=8,
-1
Г|(х)-2/Т<_1<х)-Г1„2(х)
t/j (X)“2/(/j_| (x)—</|_2 (*)
8
Лежандра <1785 г.)
Р, (X)
й2(х)«сол*1
—1,-f 1
+ 1 2
J (x) dx— 2/ + 1
2/ 4-1 +1
—J" J Vpi <*>
O+OPj+i (x)-(2/+l)xP,(x)-
-pi-i0O
9
Гипергсоме-
трическис
Якоби (1859 г.)
' Ji,:'<x)
1
•
1
1
1
’ Н<*>”
1 =(1—х)в(Ц-х)-!
1
1 —1, 4-1
!
i
1
i
/в2(х)[^“,’Р)Г^=
-1
2в+И-,Г(а+/+1) Г<Н<+1)
(в+р+2/+1)Г(/+1)Г(а+У+/+»)
(/=0, 1.2...1
+jyeawjfe5)<,x
“! ^ <Kj
Ye2 (x)!^^]2^
-1
(/+l)(l+*+HO(2l+e+P)jftP "
= .1. (2/+в+Ж)1(И+«+Р)-
(2/+a+?+2) x+(a*-?*)iy}“^> -
- (/ +<*) (*+?) (2/+e+p+2) j}iP (X)
Классификацич полиномов Чебышева 77
4) старшие коэфициенты полиномов;
5) коэфициенты интерполяционного ряда Чебышева;
6) значения коэфициентов и р, рекуррентного соот¬
ношения.
В схеме „Классификация полиномов Чебышева* (стр. 76)
приведены значения всех этих величин для различных по¬
линомов Чебышева. В таблице „Значения первых пяти по¬
линомов некоторых функций" (стр. 79) даны алгебраи¬
ческие уравнения, определяющие эти полиномы.
Сам Чебышев неоднократно указывал, что известный
ряд Лежандра есть частный случай его ряда. Ряд Лежан¬
дра получается, если разлагать в непрерывную дробь
6-
выражение £ jz'JT* где ^ ~ *vs ~ xi~ cons^ а значения
х даны бесконечно близкими и равноотстоящими, изме¬
няющимися от X/— — 1 до хш = 4-1. В результате разло¬
жения такого выражения в непрерывную дробь знамена¬
тели подходящих дробей будут представлять собой поли¬
номы Лежандра.
В более ранней работе: „Об одном новом ряде" П. Л. Че¬
бышев, рассматривая ряд конечных разностей указы¬
вает, что в случае, когда разность ряда А=-^- и п беско¬
нечно велико, ряд Чебышева сводится к ряду, располо¬
женному по иолиномам Лежандра. Если же л
бесконечно велико, то этот ряд сводится к ряду Макло-
рена.
Если предположить, что известные значения искомой
функции даны равноотстоящими и бесконечно близкими
между собой, изменяющимися в пределах от —1 до +1.
то, разлагая выражение S где ©*(*) = -Тг"**-’ И
непрерывную дробь, получим знаменатели подходящих
дробей, которые соответствуют разложению Фурье по
косинусам кратных дуг cos ®, cos 2®, cos 3®, где <?=arc cos x,
т. e. по неполным тригонометрическим полиномам.
В математической литературе широко известны эти
тригонометрические полиномы благодаря работам акад.
С. Н. Бернштейн. Тригонометрические полиномы Чебышева
имеют большое значение в статистике, составляя основу
для метода периодограмм и гармонического анализа вре¬
менных рядов.
Тригонометрические полиномы Чебышева первого и
второго рода являются неполными тригонометрическими
78 Обобщенные полиномы Чебышева и статистическое исчисление
полиномами. Ряд Фурье есть сумма неполных тригономе¬
трических полиномов. Приближение, получаемое с помощью
полиномов Т(х), учитывает в большей степени значение
приближаемой функции F(x) у конца отрезка (—1, +1).
Приближение, получаемое с помощью полиномов второго
рода Ut(x), учитывает в большей степени значение этой
функции в средине отрезка (—1, +1). Ряд Фурье, являясь
суммой этих полиномов, поэтому дает лучшее прибли¬
жение.
В своей изумительной работе: .О разложении функции
одной переменной* (т. 1, стр. 501- 508, 1859 г.) Чебышев
рассматривает:
а) различные значения переменной х, изменяющиеся от
— оо до -f и имеющей вероятность
б) значения переменной х, заключающейся между О н+ ..
при законе их вероятностей ke~lLX.
Исходя из этих предположений, он находит свои поли¬
номы, которые получили в математике название:
а) полиномы Эрмита;
б) полиномы Лагерра.
Полиномы Эрмита и Лагерра, собственно, частный слу¬
чай полиномов Чебышева, когда k — (— 1)' или k—1. Эрмит
получил свои полиномы в 1864 году, (18) а Лаггер —
в 1879 году, (19) в то время как Чебышев дал их в более
общем виде в 1859 году. Полиномы Эрмита связаны с
обобщенными полиномами Лагерра следую.цнми соотноше¬
ниями:
(— 1/ 2* <?/ '■>(.'•-"•) и
Htr \ (х) = (~1)' 2V: 1 'f,( ■' '' (х-).
Обобщенные полиномы Лагерра очень схожи с гииер-
геометрическими рядами.
Полиномы Эрмита, если к — ь~, дают ряд Маклорена.
Полиномы Эрмита и Лагерра имеют существенное зна¬
чение в статистике, являясь основой для обобщенного
закона распределения вероятностей и распределения ста¬
тистических численностей.
При обработке данных о распределении редких событий
в статистике приходится иметь дело с распределением
Пуассона и полиномами G. Эти полиномы являются даль¬
нейшим обобщением полиномов Лагерра.
Классификации полиномов Чебышева
7*
Значение первых пяти полиномов некоторых функций
I. Показательные функции
1. Полиномы Чебышева-Эрми-
та функция е~кх*
Я,(х) --2*х//,_,(х) 2(1- 1 )**,_,
Нфх) = 1
Н\(х) = — 2 кхН^х) = — 2Ах
Я*(х) = - 2кхН\(х) — 2кН^х) —
= 4Aiv2-2A
Я,(лг) = -2кхЩх)-2 ■ 2 ■ кН\(х)—
— — Ък*х*+12к1х
Я4(х) = 16А4х* - 48А»л2 +12*2
Н6(х) = -32А*л»*Н60А«хЗ—120А*х
Полиномы Эрмита есть част¬
ный случай полвиомов Чебыик-
»д. когда А = (—1/.
2. Полнкомы Чебышева-Лаггр-
ра фун* цин е~‘**
6,(ж) = - (Ах - 2/ + 1) L,., (.V) -
-(/-1)*1,_,(х)
*i(x)= — (Ах — 1) io(x)= — Ах+1
ij(x)= - (Ax-3) 1, (x) — io (x) —
= A2x2 —4Ax + 2
/-з(х)= - (Ax-5) I, (x) —4li (x)=
А»х»-*-9А«х*-18Ах+(»
Z.i(x)= A«x< — 10*2.13 + 72Аздз —
-96Ax + 24
Ux)= — A»x»-|- 25A<x4— 200A*.v*-J-
+ 60vA2jc2 _ (iooAx — 12)
Полиномы Лагерра **сть част¬
ный слу iqh полиномов Чсбышенн,
когда А = 1.
G(х) функции
= ?(*)
Полиномы
т*'е~х
Ф (х) = 0,(х) GJx) + DGt(x) =
3! I х (х — 1) (х—2) от х(х—1)
— т*1 3! _ 1 ?!~
xl
0/+1 (х) = GiW-GiW-t-DG^x)
где DG\(x) есть пронзеодпая от
Gi(x) по т и где х принимает
лишь значения 0, 1, 2
Ов(х) = 1
“■м-тгО—)
<Jj (х) = <?i(x) О i(x) DGi(x) ~-
2! j х (х—1) от х от? 1
^'otsI 2! “ 1 * 1 2! I
m- х mz I
+ ¥T~" з7J
4! fx(x-l) (x—2) (x—Л)
С4(х) = -|^ -
m x(x—1) (x—2)
_ Y 3! +
ОТ2 X (x—1) OT*-X . W< j
4! I
_ X<X-V
21 ' 21
3111
u.Sl I x(x-i)(x-2)(x-3)(x-4)
* } m»L 5!
m jc«(jc— 1) (x—’2) (x—3)
1 4!
rrtix(x~\) (x—2)
2? ,3?
m*-x
+
m*-x(x— 1)
3f 2!
тН-x m51
4! 1! 5Tj
Сумма квадратов полииомов Gt(.vi
равиа:
ST(x)Oif(x) = ~
II. Тригонометрические функции
4. Полиномы Чесышева 1 рода
(синусы кратных дуг)
7'1(jc)=2jc7 /_l (jc) Т^х), где x*=cos*
Cos /в = 2cos вс os (/-1) в -cos (/-2) в
7 I (JC) = cos ore со>х = дг
73(х) =cos2<.rcco*x = 2x*—i
7 u (х) = cos 3-irc cos х я= 4х$—Зх
74 (jc) — cos 4arc cos x = 8x4— 8x*+ i
7 & (x) =cos5'i/x cosxeltix5—20xa+5.tc
5. Полиномы Чебышева 2 рода
(синусы крапшх дуг)
Ut+х (x) = 2xUl(x)-Ul_l (х). где
S;n(/*Ь l)arccosx
1/,(х) = 1
(Д(х) = 2х
(Д(х) = 4х« — 1
(/а(х) = 8хЗ —4х
(Д (х) = ltjx< — Г2х + I
СД (х) = 32хь — 32дЗ + 6х
syv Обобщенные полиномы Чебышева и статистическое исчисление
/я е
Полиномы G связаны с функцией . _ В матеыатиче-
Л-!
%.кую статистику эти полиномы введены Жорданом (20) и
Романовским (21). Более подробно о применении полиномов
Зрмпта и полиномов G в математической статистике см.
$ 6*. „Распределение Пуассона и полиномы Чебышева".
Чебышев определил полиномы также для случая пара¬
болического интерполирования. В его работе „Об интер¬
полировании по способу наименьших квадратов" (т. 1,
стр. 473—498, 1859 г.) дан числовой пример параболиче¬
ского интерполирования и даны:
а) рекуррентное соотношение, связывающее при пара-
'-одическом интерполировании смежные полиномы;
б) формула для определения сумм квадратов этих по¬
линомов;
в) формула для определения коэфициентов интерполя¬
ционного ряда.
Все эти формулы даны нами в схеме „Классификация
полиномов Чебышева*
Чебышев определил значения сумм квадратов полино¬
мов для всех рассматриваемых нами полиномов, кроме поли¬
номов функций многих переменных и обобщенных поли¬
номов Лагерра. В таблице: „Классификация полиномов
Чебышева* нами даны все рекуррентные формулы и все
величины для сумм квадратов полиномов.
Как видим, полиномы Чебышева являются широким
обобщением, дающим новый оригинальный метод прибли¬
женного представления функций самого разнообразного
вида.
§ 3. Рекуррентные формулы.
Для теории полиномов Чебышева имеет большое зна¬
чение закон образования коэфициентов рекуррентной фор¬
мулы, который он впервые формулировал в статье „О не¬
прерывных дробях*.
Основная, наиболее общая рекуррентная формула, свя¬
зывающая смежные иол ином ы Чебышева, имеет следую-
:иий вид:
4x)Hw -й) Vi(-v) -«,v2(4
Для отдельных функций некоторые коэфициенты ре¬
куррентной формулы могут быть равны нулю или едини-
Рекуррентные формулы
SI
цс. Особенно часто равен нулю коэфициент ft, а едини¬
це — коэфициент у,.
Коэфициенты рекуррентного соотношения подчинены
определенному закону их образования. При этом прихо¬
дится различать нормированные и ненормированные поли¬
номы Чебышева. Нормированными называются полиномы,
у которых все коэфициенты разделены на коэфициент
ной переменной х наиболее высокой степени (для урав¬
нений множественной регрессии при независимой пере¬
менной, введенной в анализ последней).
Таким образом в нормированных полиномах коэфициент
при старшей переменной равен единице.
Закон образования коэфициентов заключается в том,
что:
а) коэфициент а, есть отношение сумм квадратов двух
смежных нормированных полиномов;
б) коэфициент у, есть отношение старших коэфици¬
ентов смежных ненормированных полиномов Чебышева;
в) коэфициенты ft есть разность старших коэфициен¬
тов двух смежных нормированных полиномов.
Все полиномы, приведенные нами в таблице .Класси¬
фикация полиномов Чебышева", удовлетворяют этим усло¬
виям. Между прочим, для случая параболического интер¬
полирования Чебышев показал в статье .Об интерполиро¬
вании по способу наименьших квадратов* (т. 1, стр. 491),
что коэфициент ft (при У;=1) определяется как разность
старших коэфициентов двух смежных предыдущих поли¬
номов, а именно:
ft
_ s*Mx) Т
^ / \ Н>*
SVl(x)
SxJVt( х) $ Jt,4*,/jc)
ft= : - — — Т.,. — Г,и, аналогично:
5*J(.r) ЗчЦх) л
ft ~Тп 7*21; ft ~ j 7*32 и т. д.
Как известно, Чебышев не определил полиномы для
функций многих переменных. Так как такого рода поли¬
номы являются основными в математической статистике,
то приведем рекуррентные соотношения для полиномов
множественной регрессии. Напишем систему полиномов
N и Т (дли случая х9):
6 II од и кожи Чобмпсиа
82 Обобщенные полиномы Чебышева а статистическое исчисление
Система N
Система Г
Хз-0~хз Тго хо.о
xZ'Vr* "*3— тг\ х\ о- 7зо -*0 0
■*З.Я0в*Э— ^32^-l ^ xi о
Xj.(|p= х,— Гю Xq.q
Xj.i= х2 хь0 7*20 •го-о
•*3-ЭТ~ -*3“ ^32 ^
Отсюда имеем рекуррентные соотношения:
Введем новые обозначения для полиномов системы N:
Таким образом t</—1 и символ i обозначает комби¬
нацию элиминированных переменных: i = 0, i = 1 -0, i = 2*1
и вообще / = (/—1). [0.12 (/—2)]. Кроме того.
* — 1 = (i — 1). [0-12 (/—2)].
Заметим, что порядок чисел после точки не имеет
значения. Тогда вышеуказанные рекуррентные соотноше¬
ния могут быть записаны в общем виде:
ибо старшие коэфициенты Tb=k{i, как известно, равны друг
Таким образом, в случае многих переменных имеем
рекуррентную формулу, где:
а) полином системы N данного порядка равен разности
двух полиномов предыдущего порядка, из них первый (со
знаком минус) системы Т, а второй (со знаком плюс) сис¬
темы N;
Система N
Система Т
-*з-о = Nu где/ = 3. <=0 х0.0 = 1
ж3 ]0=Л/,( где 1 = 3. /=10 А-1>0 = ЛГ,- где /~1.»
x3.m=Nti где / = 3. /=2Ю xb]0=Nt где / = ‘2.10
Nu(x)=-khNi(x)+Nt[_l(x)
Другу.
Рекуррентные формулы
83
б) коэфициент при первом полиноме равен старшему
коэфициенту полинома для последнего (при данном числе
переменных) этапа элиминирования;
в) при втором полиноме коэфициент равен единице,
т. к. для данного числа переменных отношение сумм
квадратов последних полиномов высшего порядка, взятых
из системы W и Г равно единице. Как известно, для дан¬
ного числа переменных, последние полиномы системы
N vi Т равны друг другу.
Как видим, и в случае многих переменных рекуррентные
соотношения полиномов соответствуют общей рекуррент¬
ной формуле, выведенной Чебышевым из свойств подхо¬
дящих дробей.
Старшие коэфициенты полиномов Чебышева для функ¬
ций многих переменных могут быть определены различ¬
ным способом. В предыдущем изложении мы их опреде¬
ляли как отношение Однако, если умножить
рекуррентные соотношения для полиномов системы N на
значения старшей переменной, а затем суммировать, то
будем иметь:
Так как коэфициент Т.„~И''2Х, то отсюда имеем в
общем виде:
S(4.o) = ~ r-oWo.o) (^.i)
■^(•*3-3l) = — ^32^(Х3Гм) ^ (xf l)
Отсюда:
_ 5 (-*3-1) —'s( *3-2i).
•I!
)]-**!(*)
5 ( )
, где- i ^ / 1.
r
Х4 Обобщенные полиномы Чебышева и статистическое исчисление
В этом случае суммы произведений S [л*, N((jc)] долж¬
ны определятся, исходя пз формулы, в которую входят
суммы системы нормальных уравнении п коэфициенты
полиномов предыдущего порядка системы ,Г*.
Если умножить обе части последней формулы па зна¬
чения старшего коэфициента, определяемого обычным
S ( х» | j
способом, то-есть например, на —= % то будем иметь
новую формулу для вычисления старшего коэфициента
полиномов множественной регрессии!
(^)2=
или в общем виде:
(kh?=
S ( ^-1 )~$ ( -*3-21 ) •
s(4t)
s x )]~s •*)]
S[JV*(A-)J
Следовательно, старший коэфициент может быть опре¬
делен через соотношения сумм квадратов полиномов Че¬
бышева. Однако, эта последняя формула не имеет само¬
стоятельного значения и удобна лишь для контрольной
проверки правильности вычислений. Для полиномов различ¬
ных функций рекуррентные формулы даны в таблице на
стр. 77.
В работах П. Л. Чебышева находим рекуррентные фор¬
мулы для всех полиномов семейства Чебышева, кроме по¬
линомов функций многих переменных и обобщенных поли¬
номов Лагерра.
§ 4. Полиномы дли функций с равноотстоящими
значениями.
Интерполированию величин равноотстоящих П. Л. Че¬
бышев посвятил много работ, к которым относятся:
1. ,06 одном новом рядс“, 1858 г. (т. 1, стр. 381—-384);
2. ,06 интерполировании в случае большого числа дан¬
ных доставляемых наблюдением*, 1858 г. (т. 1, стр. 387—469);
3. ,06 интерполировании*, 1864 г. (т. 1 стр. 514—560);
4. ,06 интерполировании величин равноотстоящих*,
1875 г. (т. II, стр. 219-242);
5. >0 функциях, подобных функциям Лежандра*, 1869 г.,
(т. II, стр. 61—68).
Полиномы для функций с равноотстоящими значениями 6V5
При интерполировании равноотстоящих величин
П. Л. Чебышев вводит новую переменную:
.и—Х\
В этом случае он иолучаот свои полиномы, связанные
следующей рекуррентной формулой:
ад- 2(2/- l)zV,_t (г, - (/--1)2 [л3- (/- ])■]
Здесь п — число членов ряди, а .V,—л1, ость разность
членов ряда.
В статистической практике обычно эта разность равна
единице. В этом последнем случае, следовательно, при¬
ходится иметь дело с натуральным рядом чисел: 1, 2.
З....П. Тогда вспомогательная переменная упрощается и
оказывается равной:
M'j — х если « = 1, 2, 3...
или
^ ... если п — 0, 1, 2, 3..
Для этого частного случая интерполирования равно-
отстоящих величин легко получить таблицы, определяю¬
щие числовое значение как полиномов Чебышева, так и
сумм их квадратов. Впервые эти таблицы были вычислены
н отделе научной методологии Центрального Статисти¬
ческого Управления СССР и опубликованы в 1925 году (22).
Эти таблицы под названием: «Числа Чебышева*1 перепе¬
чатаны в работе проф. А. К. Митропольского (23) «Тех¬
ника статистического исчисления11 (М., 1931 г., стр. 598—
601).
В этих таблицах даны целые значения полиномов Че¬
бышева, для чего соответствующие значения полиномов
Чебышева умножены на коэфициенты ск, при помощи ко¬
торых осуществлен переход от дробных к целым числам.
При интерполировании равноотстоящих значений могут
быть использованы как ненормированные, так и нормиро¬
ванные полиномы Чебышева. В последнем случае все коэ-
фициентм полинома разделены на коэфициент, стоящий
при старшей переменной.
86 Обобщенные полиномы Чебышена и статистическое исчисление
Частные значения первых пяти полиномов Чебышева
для случая ненормированных полиномов таковы:
/, (г) ----- '2х - ■ // — 1 = 2г
/,(*!---3(2г)5-я34-1
f.(z)- 15 (22/— 3 (3«2— 7) 2z
ft (2) = 105 (2zY - 30 (3ns— 13) (2z)- + 9 (n*- lj (n1 - 9)
/j(2)945(22/ - 1050(л*— 7)(2z)s f
-• 15(15л«-230я* 4-407)22.
Эти полиномы связаны следующей рекуррентной фор¬
мулой:
/,+, (*) - (2/ + 1) 22/, (2) - Г- (Я* - />)/,_, (2).
Старшие коэфициенты этих полиномов определяются
но формуле: Y/— (2/+1)1 В частности, при / = 5 имеем
Y-=3. 5. 7. 9 = 945. Легко видеть, что коэфициент в ре¬
куррентной формуле при 22ft (г) равен отношению старших
коэфициентов двух смежных полиномов.
Что касается коэфициента рекуррентной формулы при
ft-1 (г)> то он равен отношению сумм квадратов двух
смежных полиномов, так как суммы квадратов этих поли¬
номов определяются по формуле:
(/!JS«(MS-1) (Я3-23)....(Я3_/3)
‘Vi W 27+1
Частные значения первых пяти нормированных полино¬
мов Чебышева для равноотстоящих величин таковы:
Чго(*) •- 1
*,(•*)
Полакоми для функций с равно отстоящими знаке на яма 87
ЧГ4 (х) = V*(x) - ± (3л* — 13)'FJ (X) +
■ 3(п> — 1) (п»-9)
• 560
ч-,(х)= 'r;w--^('‘,“7)'r;w +
+ Т<Ю8 (I5'»‘-230'>,+<e7),‘.W-
Эти полиномы связаны друг с другом рекуррентной
формулой:
v. w ■- 'r.W w - *•-> <*>•
Сумма квадратов этих полиномов равна;
5ijrc/х\в (Л)2«(/>»-1) (из —2)....(»* — /*)
' (21 — 1)!-2и.(2/+1)
Легко видеть, что коэфициент при Ч^, (х) в вышена-
иисанной рекуррентной формуле равен отношению сумм
квадратов двух смежных полиномов Чебышева.
В иностранной литературе полиномы Чебышева для
равноотстоящих величин использованы в работе Чарля
Жордана „Математическая статистика*, 1927, (20).
Им введены полиномы д„ которые равны:
<7Ж = + (г). В работе Жордана используется
вспомогательная переменная д{=х — где я = 0, 1, 2,
3... Таким образом полиномы, использованные Жорданом,
соответствуют полиномам /, (z), но для несколько прео¬
бразованной переменной. В работе Жордана даны число¬
вые значения первых пяти полиномов и сумм их квадра¬
тов для значения л от 2 до 20. В русских таблицах „Чи¬
сла Чебышева* эти значения вычислены для п от 5 до 50.
Таблицы Жордана для полиномов qx вполне аналогичны
русским таблицам „Чисел Чебышева* (22), (23), только
материал систематизирован несколько иначе.
В русских таблицах эти числа даны отдельными табли¬
цами для пятичленных, шестичленных, семичленных и т. д.
статистических рядов. Каждая из этих таблиц подразде¬
лена на колонки, отведенные каждому из пяти первых
полиномов Чебышева. Внизу каждой такой колонки в
русских таблицах дана сумма квадратов соответствующего
полинома Чебышева.
ЯД Обибирнние полипами Чебышева и статистическое исчисление
В таблицах Жордана для каждого полинома Чебышева
дана отдельная таблица, внутри которой приведены числа
Чебышева для статистического ряда с соответствующим
числом членов (я). Сумма квадратов полиномов Чебышева
у Жордана вынесена в самостоятельную таблицу.
От русских таблиц «Числа Чебышева “легко перейти к
таблицам Жордана, разделив числа Чебышева на коэфи¬
циент Ct, стоящий при Ч',(.х) в заголовках русских таблиц
и умножив на коэфициент где /—есть помер по¬
линома Чебышева, минус единица.
Таким образом в русских таблицах числа Чебышева
даны в виде целых чисел, а у Жордана — в виде целых ц
дробных чисел.
Сумма квадратов полиномов qt равна:
" ' (21 ■+■ 1) 2Л
Числовые примеры параболического интерполирования
равноотстоящих величии при помощи полиномов Чебы¬
шева, пли иначе .Чисел Чебышева-, можно найти в рабо¬
тах, указанных в библиографии (22. см. стр. 64 66),
(23. см. стр. 453—461), (20, см. стр. 272 -274).
Числами Чебышева легко пользоваться и для статисти¬
ческих рядов, где интервал равен любому постоянному
числу. Следует только в этом случае перейти к новой
иеременной, так чтобы иметь натуральный ряд чисел.
Б приложении дани таблицы: .Числа Чебышева* в интер¬
претации Чарля Жордана.
$ 5. Крпвме распределения численностей н полиномы
Чебышнпя.
Общепрнзнана роль II. Л. Чебышева в теоретическом
обосновании закона больших чисел. Работы Чебышева (24)
.О средних величинах* и .О двух теоремах относительно
нероятностей", несомненно, составили эпоху в истории
статистики в отношении обоснования закона больших чи¬
сел и в развитии теории распределения вероятностей.
Однако, эта сторона вопроса в настоящей работе не
рассматривается, также как не рассматривается вопрос о
распределении Стюдента (25) и Р. Фишера (10). Не касаясь
вопроса о знаменитом .неравенстве Чебышева* и его пре¬
дельной теоремы нормального распределения вероятностей,
рассмотрим лишь вопрос о роля полиномов Чебышева
в теории кривых распределения численностей.
Кривые распределении численностей и полиномы Чебышева .Sзг
В работе „О разложении функции одной переменной *
(1859), П. Л. Чебышев, опираясь на свою интерполяцион¬
ную формулу, разложил в ряд но ортогональным полино¬
мам функции распределения вероятностей
и !ie~lx •
Первая функция имеет отношение к распределению ве¬
роятностей Лапласа—Гаусса, (26), вторая — Пауссона (27;.
Для первого случая Чебышев нашел полиномы, приведен¬
ные нами на стр. 79 Эти полиномы сопровождаются весом
Нг(х)—у/ — е~кх\ При k--- (— 1)' имеем по. иномы Эрмита,
полученные нм позднее Чебышева (в 1864 году).
Для второй функции полиномы Чебышева (см. стр. 79;
сопровождаются весом В2(х)~е~кх. Если положить в этих
формулах k~\, то будем иметь общеизвестные полиномы
Лагерра, полученные последним также позднее Чебышева
(1879 г.). Таким образом, приоритет в получении этих по¬
линомов принадлежит П. Л. Чебышеву.
Чебышевым установлено, что проивзодныс от функций,
распределения вероятностей равны самой функции, умно¬
женной на соответствующий полином Чебышева, а суммы
квадратов его полиномов, сопровождаемые соответствую¬
щим весом, оказались равны:
+VA “ Л {'2k,i
— ОО V ”
Н-ео
б) во втором случае! ke kxXlfit(x)dx — (J1)\
J — сл
В качестве обобщенных законов распределения вероят¬
ностей Чебышев предложил, в соответствии со своим
интерполяционным рядом, новые ряды, являющиеся суммой
такого рода членов:
а) для первого случая:
а) в первом случае Г
Ю Обобщенные полиномы Чебышева и статистическое исчисление
| ke-kxb(x)P(x)dx
б) для второго случая:
•+ “•
| ''"кг-** b(x)F(x)dx
ke-^bfixydx
(/*)!
В обоих случаях /•'(д) — известные значения интерпо¬
лируемой функции.
Это исследование Чебышева оказало огромное влияние
на дальнейшее развитие статистической наукш Датский
математик А. Фишер (28) в своей работе: „Математиче¬
ская теория вероятностей* пишет, что знаменитые иссле¬
дования скандинавской школы математической статистики,
а именно, работы Грама (29), Тиле (30), и Шарлье (31)
основаны на исследованиях П. Л. Чебышева.
Грам в своих докторских тезисах, относящихся к
1879 году („Определение рядов посредством метода наи¬
меньших квадратов*), рассмотрел вопрос о приложении
ортогональных полиномов к определению статистического
распределения численностей. Он первый показал, что ста¬
тистические распределения могут быть выражены через
ояды ортогональных полиномов с весом, равным функции
нормального закона распределения вероятностей.
Датчанин Тнле. друг Грима, опубликовал в 1889 г. на
датском языке „Общую теорию наблюдений*, где разра¬
ботал вопрос о характеристиках кривых распределения
численностей, которые он назвал „семиинварианты*.
В сущности, работа Тнле является первой в статистике
работой по теории моментов, получивших свое дальней¬
шее развитие в работах английского ученого Карла Пир¬
сона.
Датский ученый Шарлье в 1905 году развил идеи Грана
и дал в окончательном виде (в двух формах) уравнения
кривых распределения, получивших в дальнейшем назва¬
ние „кривые Грама-Шарльс* (тип „А*) и „кривые Пуассона-
Шарлье* (тип „В").
Почти одновременно, в 1906 году, такого же рода ряды
дал немецкий ученый Брунс (32). В его работах уравнение
нормального распределения вероятностей выражено в так
называемых модулях, т. с..в единицах о\г2 . Следователь-
no, им в полиномах Чебышева положено /е3 = 1 /2з*.
Легко показать, что кривые Грама-Шарлье и Пуас-
сона-Шарлье есть лишь некоторая модификация интерпо¬
ляционного ряда Чебышева.
Кривые распределения численностей а полиномы Чебмаыа 91
Нели нормальному распределению вероятностей придать
форму yf k/K е~Т, то-есть положить £=7*> x—z—z, а*=1,
N=1, то полиномы Чебышева будут выражены в виде
полиномов Эрмита.
При этих условиях (при N--1) имеем с одной стороны:
(•+<о 1 X*
■ ■ _ с~ г =-=.О (при / нечетном)
— cl l' 2п
J-hrr; 1 X*
ot — • :е~dx — 1. 3. 5... (/—1) (при / четном).
— о> У 2tz
С другой стороны при этих же условиях имеем:
(А)
f+es
х F (х) dx = О
*j — Ом
| д:* F(x)dx = jis — 1
J — ОЭ
/•+
x>F (х) = ъ
J — oo
I
4*00
a4 F (л) — ji4. Где jtf. H }14-
—
центральные моменты.
Полиномы Чебышева-Эрмита и производные нормаль¬
ного распределения вероятностей могут быть представ¬
лены в виде следующего ряда:
Производные от ?„(**); 'Рз(•*)'• 'Рз (ХУ> (ХУ Ь(х)
функции
полиномы Д>(Л‘); Н\(х): Hj(л-); Н4(х); Н,(х).
Здесь У/(.у)(—1У у0{х)-Н,(х)
1
К5Г
1
»4v)~ е -
92 Обобщенные полиномы Чебышева и статистическое исчисление
Грам п Шарлье, стираясь на ортогональные свойства
полиномов Чебышева, следующим образом преобразовали
члены интерполяционного ряда Чебышева’.
С+те?о (X) Я, (x)F (x)dx I + Я, (х) F (х dx
7*2 Ъ(Х).
•о (K)H?(x)dx I ?0 (х) Я,з (х) dx
— СО
Где по прежнему ?, (^) == <? 0 (*) Н( (х). Если иметь ввиду,
J-f СО
<р,(х)H?(x)dx — /!, то ин-
• гя
териоляционный ряд Чебышева может быть представлен
окончательно как сумма членов ряда:
j+'°я1(а-)/>(*)</*
~ " Ъ(х)—гДе / последовательно принимает
значения 0, 1, 2
Подставляя вместо полиномов Чебышева их значения
убеждаемся, что первый п второй члены интерполяцион¬
ного ряда исчезают.
В окончательном виде имеем ряд ,А“ Грама-Шарлье:
F (х) - сл % (л)+csf. (х) г с4 <?4 (л*).
ГДС* с — 1 с -- 0 г — О с — JiL с -
— I, Cj—• и, г.—-о, с-л——, с4-• ^ •
Следовательно, ряд Грама-Шарлье есть простое преоб¬
разование интерполяционного ряда Чебышева, основанное
на ортогональных свойствах его полиномов.
Необходимо отметить, что интерполяционный ряд Че¬
бышева дает наилучшее приближение в смысле метода
наименьших квадратов, но не функции F(x), а функции:
F(x)_
V'vo (х)'
Грам в своей работе (29) доказал теорему, которую-
А. Фишер (28) формулирует следующим образом: ....если
дана произвольная функция относительных частостей,
сплошная и конечная в интервале -- со и +.. > н исчезаю¬
щая при А-"^;оо, следует определить константы с0, с,,
г, и т. д. таким образом, чтобы ряд:
со то (*) + с» ?1 (-у) + + c9t3(x) с, ?| (f)_
У *0 (х) V ?0 (х) V 9о (х) V *0 (дг) \' Т0 (X)
Кривые распределения численностей и полиномы Чебышева 93
давал наилучшее приближение количеств ^ в смысле
VwW
метода наименьших квадратов*.
В. И. Романовский (21) также учитывает это обстоя¬
тельство, определяя первый член квадратического прибли-
. Г + ”^
j »Wdx'
жения Sdi в виде
Для функции имеются готовые таблицы, опубли¬
кованные первоначально Шарлье, затем Йоргенсеном (33),
и воспроизведенные у А. Фишера (28), Кэмпа (34), Ритца
(35). Митропольского (23), Эти же таблицы в модулях
(зуТ) опубликованы у Чубера (36), Брунса (32) и Лахтина
(37).
Процедура Грама-Шарлье наиболее распространена в ми¬
ровой литературе.
При вычислении кривых распределения в математиче¬
ской статистике пользуются определенной системой ста¬
тистических констант. Эти константы обычно излагаются
или в виде системы моментов Карла Пирсона (/п. н у.,) или
н виде семиинвариантов Тиле (XJ.
Система семиинвариантов Тиле носит на себе более
явный отпечаток идей Чебышева, чем моменты Пирсона.
Можно показать, что статистические характеристики Тиле
легко получаются из полиномов Чебышева следующим
образом:
Система ковстаяг Тиле (ХЛ н Пирсона (ft) в полиномах
Чефышева
Полиномы Чебышева
Константы Тиле (Х<) и Пирсона (ft)
-го-о — 1
S*6.o = п
5*1*л л , — (Первый сеинянва-
= Хч = *, = М рианг тиле)
5*о.о
*1.0 = д-i — * I S*? лоз
1-0'
сг2 (Второй семиинва-
1‘° ^ ft =: Xj рнант Тнле)
5*о.о
94 Обобщенные полиномы Чебышева и статистическое исчисление
Продолжение
Полиномы Чебышева Константы Тиле (X*) и Пнрсова (^)
(х-х) SVi(0 F(X) = 0
svt (0
При Xj = 1 и
s4o=^=i
При ^=1 n S4'‘^.0= I имеем:
4r4(f) = /< —6/i-f 3
SVs(f) f(x) — —i»v=—X9 (Третий Ii четвер-
SVt (<) F (x) = j»*- 3=X* тый семиинварианты
Система констант Тиле ближе к полиномам Чебышева
что особенно ясно видно при рассмотрении первого и чет¬
вертого семиинвариантов Тиле, т. е., как раз тех его
констант, которые не совпадают с системой центральных
моментов Пирсона. Однако, константы Тиле сближаются
в своих принципиальных основах с системой полиномов
Чебышева, только если приравнять единице сумму квад¬
ратов нулевых и первых полиномов Чебышева.
Таким образом константы Тиле, также как и моменты
Пирсона, являются системой средних арифметических, а
не элиминационных средних.
Характерно, однако, что ассиметрпя и эксцесс К. Пир¬
сона приближаются к системе чебышевских полиномов.
Так можно показать, что для обычных статистических
рядов распределения относительных частостей, т. е. когда
единице равны суммы квадратов нулевых [Sxj.o = rt= lj> но
не первых полиномов Чебышева, имеем показатель ско¬
шенности SVt{x)F(x)=*V$i, а эксцесс З'У*(х) F(x}=
Таким образом идея Чебышева о том, что коэфициенты
его интерполяционного ряда есть элиминацконные, а не
арифметрические средние, приводит к стройной системе
основных характеристик статистических распределений
численностей.
П. Л. Чебышев в работе: ,0 разложении функция
одной переменной* указал несколько иную процедуру вы-
Кривые распределения численностей и полиномы Чедышева 95
числения коэфициентов интерполяционного ряда, чем
Грама—Шарлье. Коэфициенты его интерполяционной фор¬
мулы равны:
Однако, процедура Грама—Шарлье, основная на опре¬
делении центральных моментов при вычислении интерпо¬
ляционной формулы, имеет некоторые преимущества, так
как в этом случае исчезают второй и третий члены ин¬
терполяционного ряда.
Вычислительная процедура Грама-Шарлье наиболее
распространена в математической статистике при вырав¬
нивании кривых распределения численностей.
§ в. Распределение Пуассона и полнножы Чебышева.
В статистике большое значение, кроме нормального
распределения Лапласа-Гаусса, имеет распределение
Пуассона. Формальным признаком для распределения Пуас¬
сона является приблизительное равенство средней арифме¬
тической, среднего квадратического отклонения и третьего
центрального момента. Распределение редких событий
следует этому закону.
Русский статистик Борткевич (38) в 1896 году первый
открыл факт существования статистического распределе¬
ния, подобный распределению Пуассона. Он назвал этот
факт «законом малых чисел*. В настоящее время известно
большое количество статистических распределений, сле¬
дующих закону Пуассона. Таковы распределения числен¬
ностей, встречающиеся в демографической статистике
(например: число рождений троен, число смертей от ред¬
ких причин и т. д.), в статистике телефонных станций
(например*, занятость телефонных автоматических аппа¬
ратов), в статистической физике (например*, измерение
радиоактивных процессов и пр.), в биологической статис¬
тике (напрлкер: счет бактерий под микроскопом на еди¬
ницу поля зрения и т. д.).
Распределение Пуассона имеет вид*.
ИСЩ1
Vr; (м',оСщснные полиномы Члбыше.тг н етатистическое исчисмниг.
где т — среднее арифметическое значение, ал —число
событий. Распределение Пуассона может быть представ¬
лено в виде следующего ряда:
! г | 0 j 1 2 i :: I ' J;' ■ J *
1 * !
/И*
!
tn\
f 1
1
2. г"
! 2.3.^"
"•Гз
Каждый член вышеприведенного ряда легко получить
путем умножения предыдущего члена на . Таблицы
X
для функции 4» (х) ■ - ”'\г~т Лыли «первые опубликованы
Борткевичем в 1898 году в виде 4-значных таблиц для
значений т от 0,1 до 10. Более полные таблицы опубли¬
кованы Н. Е. Soper (39) в 1914 году в .Blometrika* (X, 25)
а виде 6-значных таблиц для т от 0,1 до 15 и для х от
О до 37. Эти таблицы даны в приложении в конце насто¬
ящей работы (таб. VIII, стр. 127—131).
Чебышев в работе: „О разложении функции одной
переменной" показал, что функция ke~*xможет быть раз¬
ложена в ряд при помощи его интерполяционной форму¬
лы, причем, Чебышевым определены и полиномы, сопут¬
ствующие этой функции. Эти полиномы нами приведены
па стр. 79.
В дальнейшем были установлены так называемые .об¬
общенные полиномы Лагерра" для функции тхе~т, а в
последнее время в работах Жордана (20) и Романовского
ч mf еы
<21) указаны полиномы (/для функции при .v- = 0, 1,
3... Эти полиномы приведены на стр. 79.
Идеи Чебышева о разложении функции одной пере¬
менной получили широкое практическое применение после
появления в 1905 году работ Шарлье (31). Предложенная
им формула для обобщенного распределения Пуассона
получила название «кривая Пулссона-Шарльс" (тин »Вв).
Кривая распределения Пуассона-Шарлье имеет вид:
F(x)~ В0Ь(х) + Bt\’l(x) -!- В,ЛЦ(х) К...
где: A‘d»t.v) — конечные разности функции, а именно:
Дф(л) = ф(л)-ф(л-1),
Д*ф(х) = Дф(л) —Дф(л* — 1) и т. д.
Распределение Пауссона и полиномы Чебышева
97
Если начало ряда перевести в точку равную средней
арифметической, то в интерполяционном ряде Пауссона*
Шарлье остаются лишь нулевой и второй члены, причем,
в этом случае В9— 1, В, —*1,(0? — х).
Обобщенный ряд распределения Пуассона широко ис¬
пользуется в статистической литературе, именно в виде
кривых Шарлье типа „В*. Однако, вместо конечных раз¬
ностей при вычислении обобщенной кривой Пуассона удоб¬
нее пользоваться полиномами G. В полиномах G функция
^ /Я
ф(х)=—— может быть разложена в следующий ряд
при помощи интерполяционной формулы Чебышева:
F(x) — n [ДО0(х) 4- А&{х) + A,G,(*) + ...] ф(х).
Здесь А-—°УШПх), dx
так как 50,'ф(л)=-^-
от
Коэфициенты Д могут быть выражены не только через
суммы произведений полиномов G„ но и через начальные
и центральные моменты распределения. Если параметр от
функции ф (х) *= —— выбрать равным средней арифме¬
тической, тогда коэфициент А будет иметь следующие
значения:
Д — 1; Л, = 0; А3 — — (р2 от) — — (о* х);
1 1,1
где р—центральные моменты, а от —средняя арифмети¬
ческая.
Таким образом обобщенное распределение Пуассона
может быть представлено в полиномах О в следующем
окончательном виде:
В(х) = пф(л) |^1 + -у (р,— т)<?,(*) +
+ (у Р»- y Ps+ j- т ) 0,{х) + ... j*
7 Потоки ЧоСиям»
4W Обобщенные полиномы Чебышгсл и етятиетичеехое исчисление
Этот ряд, характеризующий кривую Пуассона-Шарлы,-
обычно применяется для выравнивания статистического
распределения численностей в тех случаях, когда средняя
арифметическая приблизительно равна средней квадрати¬
ческой, но третий центральный момент существенно от¬
личается от средней арифметической.
Квадратические приближения определяются для обоб¬
щенной кривой Пуассона-Шарлье в полиномах G обычным
способом как S(y —ук) — Sd/r
Если эта сумма квадратов оказывается достаточно ма¬
лой, то степень приближения по интерполяционной фор¬
муле признается удовлетворительной.
§ 7. Выравнивание кривых распределения численностей
(пример ы).
Пример первый. Параболическое интерполирование.
В качестве примера возьмем распределение рабочих ио
дневной заработной плате в долларах, на основании Сенат¬
ского отчета по США за 1893 год. Пример заимствован
из Боули .Элементы статистики- (изд. 5., стр. 97). Обра¬
ботаем эти данные в полиномах q. (Жордан. .Математи¬
ческая статистика- стр. 272— 275).
Исходные данные таковы (х — дневной заработок в
долларах, у — число рабочих):
А| — Jtj
X
Z
<U :
0,25-0.74
0.5
0
317
100489
3.54 !
0,75-1,24
1.0
1
1472
2165784
-24,05 1
1,25-1,74
1.5
2
1797
1682209
63,71
1.75-2.24
2.0
3
970
9409JO
-67,15
2,25-2.74
2.5
4
506
256036
— 6.29
2,75-3,24
3,0
5
198
£9204
79,99
3,25—3.74
3.5
6
254
64516
—68,27
3,75-4,24
4,0
7
93
9J16
16,35
4,25-4,74
4.5
8
4
16
4,59
4,75-5,54
5,0
9
9
81
- 2.44
Sy = 5123
Syt«= 5259451
- 0,02
!
Здесь л «10, интервал А = 0,5.
Выравнивание кривых распределении численностей 99
Для перехода к натуральному ряду чисел введем
переменную _ z. Затем имеем: = 512,3, а
сумма квадратов отклонений равна: Sd?\ ™Sy‘ — u0Sy =
« 2634833.
Теперь воспользуемся полиномами </ для параболичес¬
кого интерполирования, (см. приложения таблицы I— VI,
стр. 112-117).
Так как эти полиномы симметричны, то можно вести
вычисление только для верхней части ряда, если частоты
преобразовать для нечетных полиномов (у,) путем вычи¬
тания у в—у», У1—У6 Уг—Уч и т. д., а для четных поли¬
номов (у2) путем суммирования: Уг+У8 и т. д.
Затем, перенеся из таблиц полиномов q соответствующие
числа Чебышева для п = 10, можем вычислить необходи¬
мые ак и Sdl-
Определение <ц и 5 d\
.Vi q\ У\Ч\
0 308 -4.5 -1386
1 1468 —3.5 -5138
2 1201 — 2.5 -3002.5
3 716 - 1.5 -1074
4 308 - 0.5 - 154
S yqk = —10754.5
Sygi -10754.5 ,оП ЯЧ7
Отсюда имеем: а, = 0 2 = — — *= — 130,357.
Где S??=82,5 (Взято из таблицы VI, см. приложение стр. 117)
S<$= 5d?- alSylql = + 1233015.
Вычисление
<*2 и <S
2
Л
<h
ЛЛ
0. . . .
326
18
5868
1
1476
6
8856
2
1393
- 3
- 4179
3. . . . .
1224
- 9
-11016
4. . .
7(Vt
—12
- 8448
Syqt = — 8919
Syqt
Отсюда имеем: at = —= — 7,51, остаточная сумма
S
квадратов Sdl~ Sd*,— ajSy,^9= 1166981.
7»
100 Обобщенные полиномы Чебышева и статистическое исчисление
Вычисление ггг и Srf;
* .<’1 Чг УхЯз
0 3J8 -63 -1940*
1 1468 21 31828
2 1201 52.5 630V2.5
3 715 45.5 33294
4 308 18 5544
Syiq9 = 113314.5
Отсюда а, 5,87, S d\ =500879.
5 я\
Вычисление </4 и Sd\
i Уг Я4 .ЪЧ*
0 3>6 139 616И
1 1476 -231 -340956
2.- .... 1593 -178,5 -248650.5
3 1224 31,5 38556
4 704 189 133056
$Л<?4 = —356383,5
Отсюда а, — —г ^ ] ,13, Sdb--r S<tf - а« Sy.q< ~
о д4
— 98527.
Вычисление аь и .9<у|
* .‘’I 4i У\Яь
0 308 — 472.5 - 145530
1 1468 1102,5 1618470
2 1201 - 78.75 - 94578,75
3 716 — 866,25 - 620235
4 308 - 472,5 - 145530
Syqt=612596.75
Отсюда и» = 0,1268, Sd$ — 20850.
Такиы образом для данного примера интерполяцион¬
ный ряд в полиномах q может быть написан:
У( — 512,3 41130 4qt — 7,51 q^ 4- 5,87 q^ — 1,13 q^ ■(■ 0,127 qj.
Если вместо полиномов q подставить их значения, вы¬
раженные в переменной z, то будем иметь следующие
уравнения для параболического интерполирования:
320,54 + 2144,762— 1271,252» + 280,35г»- 27,452» 4- г».
Выравнивание кривых распределении численностей 101
Если сравнить число случаев, вычисленных по одному
из этих уравнений с фактическими данными, то будем
иметь dt. (См. таблицу исходных даниых на стр. 98).
Квадратическое приближение в этом случае равио:
$ ~ ~ ~ 5212,5 а 72.2.
Пример в т о р о й. Вычисление обобщенной нормальной
кривой Лапласк'Шарлье.
В качестве примера возьмем данные о распределении
диаметра сосны (по Митропольскому „Техника статисти¬
ческого исчисления* стр. 316). Исходные данные для этого
примера, приведены в таблице на стр. 103-
Вычисление обобщенной нормальной кривой по этому
способу показано в той же таблице на стр. 103. Эти вычис¬
ления основаны на применении функций <р4(х), которые
являются произведением полиномов Чебышева '^(х) на
1 **
функцию - • £'- = tpe(.v). Значения функции даны в таб-
У2*
лице IV (см. приложения). Вычисление коэфициентов
обобщенной кривой Лапласа-Шарлье удобно вести на
основе центральных моментов, так как в этом случае
исчезает второй и третий члены уравнения. Выражая зна¬
чения коэфициентов уравнения обобщенной нормальной
кривой через центральные моменты, имеем уравнение:
Вычисление центральных моментов производится обыч¬
ным способом на основе следующих формул:
п — 9216; — 0.025; Sy* = 7,210; ^«14.845;
И .. -
Sv.x*
п
п
-- - 164,234.
7,147.
п Т&
0=/^- 2,673.
,. e ~ 3($ул») • (S.v*) ^ lJSyx\l м 9 4б9
/1 /Г- п'Л
102 Обобщенные полиномы Чебышева и статистическое исчисление
Sj-jc* 4 (5уд*). (Syx) } 6 (Syx*) • |S,v-*]2 ii£Hli = i5O08l
*** ' ft It* Iti n*
Vb = g =-' 0,496; £ = (g - 3j = - 0,0023;
. Ж = 0,08267; Л _ 0,00096.
Подставляя эти значения имеем окончательно следую¬
щее уравнение:
.V» “ ££ Ifo (*) -г 0,08267 <?, (л; - 0,00096 (*))
2,673
= 3447,81 <f0 (х) + 285,03 <fs (л*) - 3,308 tp4 (л).
Вычисленные по этому уравнению числа, характери¬
зующие распределение сосен по диаметру, даны в той же
таблице исходных данных.
Квадратическое приближение определяем по формуле:
Sd?-SO-.V«>4 = 41363,13.
«-5 = 11; = 3760,2. a d4 -61,3.
Полученное приближение вполне достаточно.
Пример третий. Вычисление обобщенной кривой
Пуассона-Шарлье.
Для примера обработаем данные о числе смертных
случаев для женщин в возрасте свыше 85 лет по ежед¬
невным данным за 1910—1912 гг. по Англии (Романовский,
„Математическая статистика* стр. 224— 226). Исходные
данные и результаты обработки приведены в следующей
таблице:
Вычисление кривых распределения численностей 103
1 ч
з.н
?5»
О
X
1*1
I
о> 2 о
со f'*
со
о
-ч
Й«з со о
о n w
со CM Oi О
Н 1Л N
см оо О) *о
со •—<
г> О) Т
со го N
О 00 СО ’С О О! ^ О ОО Ю 90 ю
..0O5WiOt4iOO>N
со со о
ю см
с-
++
s 8 я а
о — см го
со
я.
о о о о* о
8
»о »о <о . _.
ф О 4 ь О) г)
со СО СМ —i
о ©' о
^ со со о
Л CN н О
о о о о
о о о о о о о
Ыа1
2 !
=и о
г4 cs О 0> О ^ с*
<л X* ^ — Л г*». ^
г> ~ 5» о о о о
о о 3 о <5 ©
О О О со О О
со
со О
о о о о
I I I
о о
о o’ о о
+ + + +
о
С.
о о
I I
^DObNgC0OiN(COSN<0^»
CSlO-^»'-iftOJOO(NWTOO(0*-00
8
OOOOOOOOOOOOOOOO
© © ~ ~ гм CO tO
CQ CM •—* о о о о
со a. <0 Cl со Т о с< СО О ^ h и lO со W
-N Р,* и О О с О О 7 ci N N с0
I I I I |Т I + “Т- + + + + ++ +
to ю
СМ СМ
«О Ю -г
I 1 I
iO ю ю «о ю
СМ ™ СМ см см
Ю to ю
t*- t** ь»
VO Ю Ю Ю VO to
С* N С4» С» С* I4
I I I
O*-CNf*3-*iCON00
"I I—I" -Ь + т пг + +
со
см
о>
Р0
о>
ю*
^■м
о»
о>
со
со
см
•ф
см
-т to W ^ С* О — |
It
91
9с
>%
и
104 Оо^Ощенпыс полиномы Чеоышее-а и статистическое исчисление
Здесь л — число смертных случаев в день, а у — число
дней с данным количеством случаев. Прежде всего найдем
начальные и центральные моменты* я—1096; Syx = 1295;
Svjc 1295
т х 1,1816; Syx- 3023; Syx*— 90305.
Отсюда:
11,= ^-- 1,3620;
п п*
Si>a« 3Syjfi • Syx , 2 (Syx)3 r. л
jl — — U,1 IbU.
n n* II-'
Для распределения Пуассона первый начальный момент,
второй и третий центральные моменты должны быть при¬
близительно равны друг другу. В нашем примере третий
центральный момент значительно отличается от средней
арифметической и средней квадратической. Поэтому необ¬
ходимо применить обобщенную кривую Пуассона-Шарлье.
Приведенные данные могут быть выражены и , формуле
Пуассона в виде следующей функции:
(1.18!Угл_м8*
у, = 1096* — - 1096ф(л)
По таблицам функции ф(х), приведенным н приложе¬
нии для х — 1,182 находим значение уг Эти значения при¬
ведены в колонке 3-й предыдущей таблицы.
Квадратическое приближение Sd? = S(y — ух)г= 1611,9.
(,40 1). Следовательно, вычисленные данные недостаточно
согласуются с фактическими. Поэтому рычислим обобщен¬
ную кривую Пуассона-Шарлье, используя полиномы С.
Для этой кривой имеем интерполяционную формулу:
4 A&ix) -ь .4.0. (х) 4- А,0,(х)|.
Так как при применении центральных моментов Ах— О,
то в качестве второго приближения имеем:
у, - л<!>(*)[А> +
1 al—~P
А„= *2* (у,- - яг*) = —^ = 0,0902. Затем, так как
у, *= я-ф,(х), то окончательно имеем:
Вычисление ьриеых распределении численностей.
105
Как видим, расчет удобнее вести исходя из первого при¬
ближения.
Ч Г х(х— 1) „ , «П
Полином (/,(*) = — [ ^ Т]~"
_л(1 —-г) 2х
да3 т
Таким образом поправка к первому приближению равна:
_ гл-(л—1) 2х 1
у, -0,0902 [ (1 Пу2 — J ,82 +1 J—
=у210,0646л: (*- 1) — 0,1527л+0,09021.
Вычисляя поправки по этой формуле для каждого члена
ряда и прибавляя их к ранее вычисленным значениям у,
имеем второе приближение yt. Вычисление значения у»
приведены в предыдущей таблице в последней колонке.
Квадратическое приближение вычисляем по формуле:
ЯЗ-5(у-й)»-63,75.
Вычисленные данные по обобщенной кривой Пуассона-
Шарлье дают вполне удовлетворительные результаты.
выводы
П. Л. Чебышев получил свой знаменитый интерполя¬
ционный ряд для случая параболического интерполирова¬
ния (1855 г.) и при разложении функции одной переменной
(1859). Его интерполяционный ряд может быть распростра¬
нен и на функции многих переменных. В этом случае ин¬
терполяционный ряд Чебышева вполне аналогичен урав¬
нению множественной регрессии, а_полиномы Чебышева —
остаточным отклонениям d=y —ую и х3.яо =хг — 21X3.
Для функций многих переменных полиномы Чебышева
могут быть представлены в виде различных систем:
1) система Т полиномов Чебышева, при которой поли¬
номы вычисляются в следующем порядке: ха> хьо, х2.„„
*3.210- ПРИ этом, каждый последующий полином выражен
через предыдущий;
2) система К полиномов Чебышева имеет ту же после¬
довательность полиномов, только каждый из них выражен
через начальное значение хк;
3) система С имеет дело с полиномами: лс3.2]0, л^.з,^.
-*1-2зо» -го.ш (для случая трех независимых переменных);
106 Обобщенные полиномы Чебышева и статистическое исчисление
4) система N имеет дело со следующей последователь¬
ностью полиномов: xjy л‘<|0, л': ГЛ.
Полиномы системы С и Л' выражены в первичных пе¬
ро менных хк.
В полиномах Чебышева получают вполне определенный
смысл коэфициенты множественной регрессии:
А S(-VXm-V2 «т-1». />+!...т)
я»-|) ^ (А’3р.15.../> -I. р+1...»я)
также ,веса“ Гаусса:
с -з ! • с = ~*
Коэфициенты полиномов связаны друг с другом про¬
стыми соотношениями, что позволяет предложить не¬
сколько схем вычислений по методу наименьших квадра¬
тов.
Схема Дулитля основана на системе полиномов Т
(стр. 29). Новая схема N основана на системе полиномов
N (стр. 35). Схема Р основана на совместном применении
системы полиномов Т я К (стр.47).
Новые схемы имеют ряд существенных преимуществ,
так как в этом случае отпадает необходимость совмест¬
ного одновременного решения нескольких уравнений.
В результате при включении новых независимых перемен¬
ных или их исключении, все предыдущие вычисления,
полученные по схемам N к Р, остаются в силе.
Прн схеме N я Р оказывается вычисленной целая
система уравнений регрессии как у по различным хк, так
и хк по различным .«*_i в их разнообразном сочетании.
Основные статистические константы и критерии, как-то:
средние арифметические, средние квадратические, коэфи¬
циенты уравнения множественной регрессии, коэфициенты
полиномов, индексы множественной, частной, частичной
корреляции, критерии достоверности Фишера, ошибки
коэфициеятов регрессии и ошибки коэфициентов полино¬
мов— легко могут быть выражены в полиномах Чебы¬
шева.
При вычислении уравнений регрессии по схемам ЫяР
нее основные статистические константы и критерии легко
получить при весьма небольших дополнительных вычисле¬
ниях (стр. 65 и 69).
Идея Чебышева о весе в3(а-), сопровождающем ортого¬
нальные полиномы, оказалась весьма плодотворной при
Вычисление кривых распределения численностей
107
разложении в ряд различных сложных функций. При раз¬
ложении функции одной переменной Чебышев получил
полиномы, частным случаем которых являются полиномы
Эрмита и Лагерра. Обобщенные кривые Грама—Шарлье
(тип <А>) и Пуассона—Шарлье (тип «В») являются не¬
сколько преобразованным интерполяционным рядом Чебы¬
шева, полученным им при разложении функции одной
переменной.
Чебышеву принадлежит научный приоритет как в от¬
ношении полиномов Эрмита и Лагерра, так и в отноше¬
нии обобщенных нормальных кривых (тип <А> и тип <£>).
Идеи Чебышева, несомненно, имели большое влияние
на скандинавскую школу математической статистики
(Грам, Тиле).
П. Л. Чебышев указал также полиномы при интерпо¬
лировании равноотстоящих величин. Русскими статисти¬
ками в 1925 г. эти полиномы вычислены и получили наз¬
вание «чисе.г. Чебышева» (22) (23). Таблицы q Жордана,
появившиеся в 1927 году, являются несколько преобра¬
зованными таблицами чисел Чебышева (стр. 87).
Чебышев для большинства своих полиномов указал
вес, сопутствующий его полиномам, область суммирования,
а также рекуррентные формулы для перехода от полино¬
мов одного порядка к полиномом другого порядка (стр. 77).
Интерполяционный ряд Чебышева и его полиномы
имеют широкое применение в статистике при корреля¬
ционном, дисперсионном и гармоническом анализе, а также
при оценке статистических параметров с точки зрения
теории ошибок. В свете идей Чебышева уравнительные
вычисления по методу наименьших квадратов являются
дальнейшим углублением и развитием метода средних
чисел, использующего систему элиминацнонных средних.
SUMMARY
P. L. TCHEBYCHEF received his distinguished interpella¬
ting series for parabolical interpellation in 1855, and for ana¬
lysis of function of one variety in 1859.
His interpellating series can be extended for functions oi
many varieties. In this case the interpellating series is quite
analogical to equation of multiple regression and the orthogo¬
nal polynomials of Tchebychef equal to the residual of
The orthogonal polynomials can be represented for the
iunction of many varieties in different syslems:
I) A system T gives his orthogonal polynomials in the
following order:
and every the following polynomial is expressed by the
preceding one.
2) A system К has the same succession of polynomials
but each of them is expressed by the original quantity xk.
3) A system С uses the polynomials: x3.2l0,
'*o.i23 (in the case °* t,uee independent varieties)
4) A system N uses the following succession of polyno¬
mials. Xj, -^з-о» -*3.10» '*3.210*
The polynomials of the system С and N are expressed tn
original varieties xt.
The coefficients of multiple regression get a quite definite
meaning in the polynomials of Tchebychef:
d—y — yvs , and x,.al0 = -v3 -
..л»—I
l) . ю (УхрЛ1...р-1. p+l...m)
SUMMARY №
and also .Weight' of Gauss:
/-» 1 r*
Ttf ’ №l~ ~s*i
The coefficients of polynomials are connected one with
another by simple formulas and this allows to offer some
schemes for calculations by the method of least squares.
The scheme of Doolittle is based on the system of poly¬
nomials T (page 29).
A new scheme N is based on the system of polynomials N
(page 35).
A scheme P is based on a Joint application of the system
of polynomials T and К (page 47).
The new schemes have many essential advantages and in
this case there is no need for joint and simultaneous solving
of some equations. Consequently, all the preceding calcula¬
tions received by the schemes N and P are active in addi-
tioning some new Independent varieties or omissloning them.
A whole system of regression equations as Y by various
Xk as well as Xk by various xk_x in their various ’combina¬
tion are determined by schemes N and P.
In the polynomials of Tchebychef, one can easily express
the primery statistical constancy and criterions as: mean,
mean square deviation, coefficients of equation of multiple
regression, coefficients of polynomials, indexes of multiple
correlation, partial correlations, part correlations, Fisher’s
tests, errors of coefficients of regression and errors of coef¬
ficients of polynomials (page 65 и 69).
Wnen calculated eguations of regression by the schemes
N and P, all the principal statistical constancy and criterions
ire easy to get by a quite small additional calculations.
The idea of Tchebychef about weight 0* (y), accompanying
orthogonal polynomials was quite effective in case of develo¬
ping different complicated functions in series.
The polynomials of Hermite and Lagger are particular
cases of Tchebvchef’s polynomials wich he got in 1859 by
developing the function of one variety.
Generating Gram-Charlier curves (tape ,A') and Genera¬
ting Polsson-Charlier curves (tape .5') are rather reformative
interpellating series of Tchebychef which he received by
developing the function oi one variety.
The scientific priority of Tchebychei belongs both to
polynomials of Hermite and Lagger nnd generating normal
curves (tape .A* nnd „£“).
SUMMARY
The ideas oi Tchebychef had absoluiely a great influence
upon the Scandinavian school of mathematical statistics
(Gram, Thiele).
P. L. Tchebychet also indicated the polynomials by inter¬
pellating equaldistant values.
These polynomials were calculated by Russian statistici¬
ans In 1925, and they got the name of Tcnebychef’s numbers
(22) (23).
Tables q. of Jordan which appeared in 1927 were rather
reformative tables of Tchebychef's numbers (page 87).
Tchebychef indicated the weight attending to his many
polynomials and also recurrence formulas to pass front po¬
lynomials of one order to polinomials of other order (page 77),
The interpellating series of Tchebychef and his polyno¬
mials have a wide application in statistics, in analysis oi
correlation, analysis of variance and periodogram analysis
and also in estimation of statistical constants from the theory
of errors point of view.
The method of least squares expressed in Tchebychef’s
polynomials is the further development of the metnod of
averaging that uses the system of eliminating average.
ПРИЛОЖЕНИЯ
Полиномы Чебышева д.гя равноотстоящих величин q\ (п, х) — ЧИСЛА ЧЕБЫШЕВА
112
Числг Чебышева
Полиномы q% (п, х) - ЧИСЛА ЧЕБЫШЕВА
Числа Чебышева
а
а
с
к
о
о
ю ю
rs- О
ем
го
со
Ю
I I !
•О
<6
**•
I
«о »о
22
IN г-I
<0
I
Ю Ю
2 Я
I I
*?
гО
СО
т
Ю
О?
гО «О
00 » о N
I I I I
3 5 3?
lill
гО го
^ to -4 со го
I I 7
гО
Я
го Ю го Ю
О со СО О) V о»
м •—<
1111
ssasis
I
гО
СО
гО
to
I I
го
o'
?тт
гО гО
го го
IIIIII
го
8
I
со
I
го го «О гО
Ю О V ОО « И N о» -
Н гЦ f-ч СМ
II I II I I
гО
8
I
Ш
го го го го го Ю го го
« ^ V N О N СО V Ю го V СО М О N V
*Н «—ч *Ц ^4 f-ч РИ рЦ
I II II II II II *ll II
ю «О
го го
гО го
го
II I II I М I I I I
ЮЮ 4 U) Ю 4 4 4 4 4
О « » Ч1 ^ V «С <9 •" О М <в «" СО «9 «J й S
II II I II I
4 4 4 4 4 4 4 4 4
_ _ о - «о о » cj « - 8 ~ ? 3 g
I I I
4 4 US «О U> Ю us Ю lO tO
• О - 4 4 N О 2 4 g 5 8 g 4 g g g JO |g
ft
I
I
>
f «: «
; li
Ю O N OO О) о —• CM
o«oiPCtiooN«Oiq
f4 *"“< И rH рч p-ч i—€ м pH CM
S Полиномы Чо*мпив%
flo.viMOMu <7з (п, .v)—ЧИСЛА ЧЕБЫШЕВА
Ш
Числа Чебышева
см
ю
ю
см
Г%
я
О-нОГ»«0срЮСМСМ
н н »н *-«
I I I I I
£
to
Ю Ю
см см
СО
О
00 00
*н N
120
см*
*т
-г
3 8 2 ° s’
|M
• I .1 I I I i 1
СМ
-Г см
$
to
ю
см
СО
to
3
105
о —«
О 00
•-Н
N
МГ
S82
СМ
1)11111
to
СМ
to
см
Ю
О
СМ
50 ^ N О) н
CM CM IO С**
1111
8
I
to
см
IO
SCM CD
N \г
»— •— См
Ю
С**
СО
С».
со
ю
с*
ю
см
1р
см
to
о
ю 00 О! (О м <о
« Н СО »5Г ^ С4
I I I 1 I
ою-н-гюсмо-г
со оо О) С ГО
—• —' CM C*J -V
со О
ю
ю
СМ
о
см
ю
ю
tp
С4!
N
ю
т
со
С*
1
Sm
J_.
оо
7
о
со
см
S
8
I 147
00
о*
ю
to
см
12
сЗ
378
со
Mi*
to
ю
см
ю
l'-
ю
to
с-
о
см
О
7
*о
7
i
о
00
см
ЧЕГ
с»
8
см
183
IO
Й
270
3)5
360
s
ю
I*»
to
см
to
Ю
t**
Ю
cm
to
Ю
о
+
(О
1
to
1
о
=
r*-
CM
о
€9
CO
o>
120
t*-
*v»
174
s'
CM
225
N
Я
c-
tr
CM
см
wo
Cl
ю
я
to
to
tp
CM
tO
to
CM
1
о
to
to
1-н
e5
39
CM
Ю
C6
00
90
s.
105
о
105
s
u>
*0*
30
CO
ti:
to
см
с! о
*2
to
СМ
о Ю оо И н 00
и n ^ « CI ^ «
ю
to см
О О) со
-* «о <о
I I I
to
ю
с**
to
ю
см
Ю СО см
• см
s
ю
*•* со
О CI
to
см
to
I I 1 I I I I I
СО ^ CV о сч с
•■м Г*. м-« СМ —4 •—I ■*
I I I I I I I I I
Полиномы (ft(п. х)—ЧИСЛА ЧЕБЫШЕВА
Числа Чебышева
"С
с
гз
h
Полиномы qb(nxx) —ЧИСЛА ЧЕБЫШЕВА
ли
Числа Чебышева
Сумма квадратов помшомов Чебышева, для равноотсточицих ее.шчин Sq{*(n% .v)
Сумма квадратов и?
//V
Распределение Лаплиса—Гa tccu
Т л б л и ц а VII
1
П.ищнОь кривой г =э j>0(f) г_х—^2 с /*,f . Функцич ?,/// // nmopifu,
\г2к
третьи и ке песр-пая производные.
г
f *о(0tf/
*/ г»
«оЮ
| ?Л()
*<(0
t
.00
.000')»')
.3989-1
-.39891
1
,»:)0it:i i
1
1.19681
! .oi*
.01
.')»3989
.39S92
-.39883
.'•1197 j
1.19651
j .01
02
.007978
.39886
— .39*70
.02193
l 1Г533
! .'*2
.03
.011956
.39876
— .39340
/‘3588 j
1.19114
1 .<*3
.01
.01595*
39862
-.39799
.01781 i
i
1.19204
! •<>*
.05
.019938
.3981-1
-.39745
05^72 i
1.18936! .05
.06
.023922
.39822
— .39619
.07159 ;
; 1.18608
.06
.07
. > 279 3
39797
—.39602
.08314
1.18221
1 .07 1
.'Ж
.Ч31Я«*
.39767
-.39512
/9 >2! 1
I 1.17775
1 .0,4 <
.09
.03583.»
.39733
— .39111
.10609
; 1.17271
; .• 9 *
• i
10
.039328
.39695
- 3939-3
.11869 :
1 1.16701
! .10 !
.11
.'4379»
.39.51
-.39174
. 13ВД I
j 1.16088
.11
.12
.047758
.39380
~.3‘-*'38
.1419» I
1.15110
1 .12
.13
.051717
.39559
— .38S9)
.15341 1
' 1.14676
.13
.14
.055670
.39505
-.38731
.16184 ;
1.13385
U
.15 :
<•39318
39-148
- 38500
.17618 I
1.13038 • .15
.16
0835* >0
£9487
—.38379
.18741 1
1.12137 !
! .10
.17 ;
.'•67J95
.39322
— .38186
.19861 1
1.1118:* 1
1 .17
.18
.07142-4
.3*253
— .37951
.2*968 J
1.10170
.IX
.19
0753-15
.39181
-.37766
.2206! I
1
1.03105 ,
19
•2»
.07926»
.39104
-.37510
.23150 !
1.07991* :
.20
.21 •
.'•831' 6
.39)24
— .37803
.2*22-1 i
1.05823 i
! .21
.2?
.'W70J4
.389:0
-.37056
.2524» •
1.0560! 1
.22
.23
.09195-1
.33^53
— .36798
.26336 I 1.01335
.23
.24
.'»94835
..38762
- 36529
.27373
1 .'03018
.21
.25 :
.'•987 «
.38667
-.36250
.28396 i
1.01651
25
.25
.1025:8
.33568
—.35961
.29105 1
1.0:*238 I
.26
.27 •
.106120
.38466
-.3566?
.30Ю1 ;
0 98778 |
.27
28
. 11**261
.38.361
-.35353
.31381
0.97273
/2Н
29
.114092
.33251
— ..>5035
.82346
9.95723 :
..9
..30
.117911
.38139
-.31706
.33295 ;
0.91139 |
:n
.31
.121720
.38023
-.34369
.34228 ;
M.92.95 i
.31
.32
125516
.137903
-.34012
.35145 i
9.90819 1
.32
.33
. 1293»
.37780
—.33666
.36945 1
0.89103 i
.33
34 ,
.133J72
.ты
-.33301
36927 ;
0.873-18 j
.31
.35 1
.13р831
.37524
-.32927
.37791 j
0.85555 !
.35
.33
. 140576
.37391
-.32545
.38638
0.83726
.36
.37
.1443)9
.37255
-.32155
,;i9i66 1
0.81862 1
.37
_
•
Расгр'деление Лапласа—Гаусса НУ
Продолжение табл. Vtf
1
' 1
1
У*л ?о (0 Л
!
■:АП i
1
V4(0
/
1
.38 .
.148027
.37115
— .31756
.4')2T5
0.79953
.36 1
.39 !
.151732
.36973
— .31349
.41065
0.78032
39
4»
.155422
•36827
—.30935
.11885
0.76070
.40 |
.41 .
.159>97
.3f678
-.30586
.42586
0.74077
.41
.42 |
.152777
.3P526
-.30033
.43317
0/-2056
■>2
.43
.166402
.36371
-.29646
.44027
0.7)0 >7
.43 j
.44 |
.170031
.36213
-.292)3
.44717
9.67932
.44 ;
.45 !
.173645
.36053
-.28752
.45386
0 65832
.45 ;
.46
.177212
.35469
-.28295
.46034
O.f3709
.46
.47 1
.180822
.35723
-.27811
.46360
0.61564
.47
.4*
. 1.84386
.35553
- 27362
.47265
0.59398
.48
\9
.187932
35581
-.26886
.17848
0 57213
.49
1
.50
.191462
.35207
—.264°5
.48409
.55010
.50
.5!
.194974
.35u-9
-.25918
.4-* 948
.52791
.51
.52
198463
.34849
— 25426
.49*5
.50556
.52
.53
.2 4914
.34667
-.24929
.9959
.48308
.53
.54
.205402
.34482
- .24427
.50431 I
t
.46948
.54
.55
.238810
.34294
-,2'920
.5'880
.13777
.55
.Л6
.212260
.34105
— .23-1'9
.513)6
.41497
.56
.57 i
! .215661
.34912
-.22694
.5171)
.39208
.57
.58
1 .2)9343
.33718
-.22375
.52091
3t913
.58
.59
222405
.33521
— .21853
.52448
.34613
.59
.(П
.225747
.33322
— .21326
.52783
.32309
.60
.Ы
i .2290.9
.33121
— .20797
.5) 94
.31» >3
.61
.62
| .232371
.32918
-.20265
.53383
.27693
.62
.63
.2.-5N53
.32713
—. 19719
.53648
.25.93
.63
64
.238914
.325)6
-.19192
.53891
.23085
.64
.65
i .242154
.32297
-.18652
.5411)
.20783
.65
.66
' .245373
.32086
—.181Ю
.54306
18486
.66
.67
.248571
31874
-.17566
.54480
.16195
.67
.68
.251748
.31659
-.17020
.54630
.13912
.68
.69
i .25.933
.31413
— .16473
.51758
.11636
.69
.7»
.254036
.31225
-.15925
.54863
09371
.70
.71
.261U8
.31006
— .15376
.54945
.07116
.71
.72
.264238
.30787
-.14826
.550'5
.04874
.72
73
, .26730.5
.3 56.3
-.14276
.55043
.02346
.73
.7!
.27035)
.30339
-.13725
.55)58
.03433
.74
.75
273-37.3
.30114
-.13175
.55052
-.>1754
.75
.76
.27г>373
.29887
- .12624
.55 23
- 03944
.76
.77
.279350
.29359
-.12074
.54973
-.06106
.77
.78
.2823)5
.294-31
.11525
.549»!
-.03218
.78
79
j .285230
.29201
~.1\976
- .54808
—.100u9
.79
JJO
Распределение. Лапласа—Гаугса
Продомсение табл. \ It
1
г
!....
1 уо(Г)/У/
м. (О
is(f)
Vil'J
t
.8)
.288145
.28969
-.10429
.54694
- 12468,
.80
.81
.291030
.28737
— .09883
.54559
— .14545
.81
.82
.293892
.28501
— .09338
.54403
-.16597:
.8.5
.296731
28269
-.08795
.54227
—.18621!
.83
.84
.299546
.28034
-.08253
.54031
—.20626'
.84
.85
.302338
.27798
— .07714
.53814
—.22600i
j .35
.86
.305106
.27562
—.07177
.53579
-.245461
i .so
.87
.307850
.27324
— .05643
.53324
—.26464 I
! .87
.88
.310570
.27086
—.06111
.53 49
—.283511 .88
.89
.313267
.-26818
-.05582
.52757
- .30208 i
i .89
.9.»
.315940
.26609
-.05056
.52445
-.32034
.90
.91
.318569
.26369
— .04533
52116
-.33827
.91
.92
.321214
.26129
, -.04013
.51769
-.35587
.92
.93
.323814
.25888
! —.03497
.51404
-.37311
.93
.91
.326391
.25647
1 -.02985
.51023
— 39005
.94
.95
.3-28944
.25406
- .02477
.50624
— .4'Ч562
.95
.96
.331472
.25164
— .01973
.5^210
— .42283
.96
.97
.333977
.24923
-.01473
.49779
— .43867
.97
98
.336457
.24681
— 00977
.49332
— .45414
.98
.99
.338913
.24439
-.00486
.48871
—.46923;
»
1 .Oil
.341345
.24197
.00000
.48394
—.48391
1.00
1.01
.343752
.23955
.00483
.47903
—.49827
1.01
1.02
.346136
.23713
.00958
.47398
— .51220
1.02
] .03
.348493
.23471
.01429
•46879
— .5’573
1.03
1.04
.350830
2323)
.01896
.46346
— .53887
1.04
• 1.05
.353141
.22988
.02356
.45801
— .5516“)
1.05
1,08
.355428
.22747
.02812
.45243
— .56393
l.lb
: 1.07
.357о90
.225 *6
.03261
.44673
-.57584
1 1.07
1 08
.359929
.22265
.03705
.44-" 92
— .53731
| 1.0<S
1.09
.362143
.22)25
.04143
.43499
- 59S43
• i .00
i
1.10
.364334
.21785
.04575
.42895
-.609 9
j 1.1')
1.11
366500
.21546
.05001
.42281
— .61934
l.li
«' 1.12
.368643
.213 7
.05420
.41657
— 62917
1.12
1.13
.370762
.21069
.05834
.41023
- 63857
i .13
1.14
.372857
.20831
.06241
.40380
— .64755
1.14
» 1.15
.374928
.20594
.06641
.39728
— .65611
I 15
1.16
.37697о
.20357
.07035
.39067
—.66425
1.1<>
1.17
.379000
.20121
.07423
.38399
— .67196
1.17
1.18
.3810 >0
.19886
078 3
.37724
— .67924
1.18
■ 1Л9
.382977
.19о52
.08177
.37041
—.68610|
1.19
1
1 21
.384930
.19419
.0854-1
.36352
—.69255
1.2)
• 1.21
.386861
.19186
.069 4
.35656
—.69857
1.21
1.22
.388769
.18954
.(•9257
.34955
—.70417
1.22
1 1.23
.590051
.18724
.09603
.34248
—.7o935
1.23
i 1.24
.392512
1
.18494
1
.09942
.33536
— .71411
1.24
Распределение. Лапласа—Гаусса
' 1
1
/ УоЮ >1' !
1
• (.(f)
1.25
.394350
.18265
1.26
.396165
.18*37
1.27
.397958
.17810
1.28
.399727
.17585
1.29
.401475
.17360
1.3l>
.403200
.17137
1.3)
.104902
.16915
1.32
.406582 {
.16694
1.33
.408241 I
.16474
1.34
.469877 i
.16256
1.35
.411492
.16038
1.36
.413085
.15822 ]
1.37
.414656
.15608
1 38
.416207
.15395
1.39
.417736
.15183
1.40
.419243
.14973
j 1.41
.42)730
.14764
! 1.42
422196
.14556
. 1.43
.423642
.14351
! 1.44
.425066
14146
1.45
.426471
.13943
: 1.46
.427855
.13742
' 1.47
.429219
.13542
' 1.48
.430563
.13344
1.49
.431889
.13147
! 1.50
.433193
.12952
• 1.51
.434478
.12758
1.52
.435744
.12566
1 53
436992
.12376
j 1 54
.438220
.12188
i 1.55
.439429
.12001
1.56
.440620
.11816
1.57
.441792
.11632 1
1.58
! .442947
.1145) 1
1.59
.444083 :
.11270 j
1 .<><1
.445201
Л1092 1
l.ftl
.446301
.10915 ]
1.62
.447384
.10741 |
1.63
448449
11*567
1.64
.449497
.103%
1.6Л
1 .450528
.10220
J .(*»
.451543
.10059
. 1 .(.7
г .152540
.09893
1
! .453521
.09728
1.09
1 .451!36
.09566
Продолжение табл. VII
ч(0 \
_._i
.10274
.32820
-.71847
1.25 i
.10599
.32009
-.72241
1.2ft ’
.10916
.31375
-.72594
1 27 *
.11226
.34648
-.72907
1.2.4 i
.11529
.29917
-.73180
1.29 1
.11824
.29184
-.73413
1.30 ;
.12113
.28449
-.73606
1.31 f
.12393
.27712
-.73760
1.32 1
.12667
.26974
-.73876
1.33 ;
.12933
.26235
-.739631
1.3; 1
i i
.13192
.25495
-.73993
1.35
.13443
.24755
- 73995!
! 1.35
Л3687
.24015
-.73961;
i i.37 :
.13923
.23276
-.73890
1 1.3*
.14152
|
.22537
|
— .73781
• 1.39 '
.14374
.21800
-.73642
• 1.40 •
.14588
.21065
-.73466
‘ 1.41 I
.14795
.20331
-.73256
i 1 42 1
.14995
.19600
-.73012
: 1.43
Л 5187
.18871
-.72736
| 1.44
.15372
18145
-.72427,
j 1.45 ,
Л5550
.17423
—.72087!
! 1.4* ;
.15721
.16704
— .71716
1.47
.15884
.15988
-.71315
1.48 -
.16040
.15277
-.70885
1.49
Л 6190
.14571
— .70425!
I 1.50
.16332
.13869 1
: -.69938:
! 1.51 ‘
.16467
.13172 j
; —.69423
1.52 !
.16595
.12481
-.68881:
> 1.53 j
.16717
.11795
-.68314
1 1.54 J
.16831
.11114
—.67721!
| 1.55 }
.16939
.10440
- 671041
1.5ft
.1704')
.09772
— .66463:
I 1.57 i
Л7135
.09111
-.65799
‘ 1.5* •
.17222
.08456
-.65113
1.59
.17304
.07809
— .64405
• 1.60
17379
.07168
— .63677
, i-*1 !
.17447
.06535
- 62928
j 1.62
.17509
.05910
-.62161
1.53 !
.17565
.05292
-.61375. 1.64 ;
.17615
.04682
-.60571
! 1.55 !
.17659
.04081
- 5975)1 1.66 1
.17697
.03487
-.58914
j 1.67 !
.17729
.02933
| -.58)63
! 1 63 »
.17755
.02326
— .57195
i 1.69 s
Распределение Лапласа—Гаусса
Продолжение табл. VH
"П
/ у«(0^
>«(')
1
Ы0 j
4(4)
t
1.70
.455434
.*■9405
.17775 !
.017.-9
-.55316
1.70
1.71
.456367
.09246
. 1779« j
.8120)
-.55422
1.71
1.72
.457284
.09 «9
.17799 1
00650
— .54516
1.72
1 73
.458185
.<'8933
.178 )3 i
.00110
-.53*99
1.73
1.74
.459 >70
.0878)
.17802 |
.00422
-.52671
1.74
1.75
.459941
08628
.17795
-.Г 944
-.51733
1 75
1.76
.46'793
.<>8478
.17783
—.01458
— .50785
1.76
1.77
.461616
.08329
.17765
—.01959
— 49329
1.77
1.78
.462462
.08183
.17744
— .02453
-.18865
1.78
1.79
.463273
.08 -38
.17717
— .02937
— .47893
1.79
1.80
.464070
.07875
Д7о85
-.03411
— .46915
1.80
1.81
.464852
.<'7754
.17648
- 03875
-.15932
1.81
1.82
.465620
.<‘7614
.17607
- .n4329
— .44943
1 82
1.83
466.175
.'•7477
.17562
- .01774
-.4395)
1.83
1.84
.467116
.07341
.17512
-.052)8
- .42933
1.84
1.85
,467843
.07206
.17458
— .05633
-.41953
1.85
1.86
.468557
.«707+
.17399
— .86 47
— .4095'
1.86
1.87
.469258
.05913
.17337
— .06452
- 39.446
1,87
1.83
.469916
.<'6814
. 17270
; -.06846
— .3f.9l0
1.88
1.89
.470521
.06387
. 172 JO j
.07231
-.37934
1.89
1 91
.471283
.06562
.17126
— 07605
-.36928
1.90
1.91
.471933
.06438
.17 48
—.07939
-.3*923
1 91
1.92
.472571
.'>6313
. 16С66
.08323
-.3-918
1.92
1.93
.473197
.06195
.1о881
— .08667
-.33916
r.93
1;94
.473810
. >6*77
.16793
— 090)2
-.32916
1 94
1.95
.474412
.■'5959
.16701
—.C9326
-.319:9
1.95
1.93
475W2
.05.844
.166 <7
— .0964)
-.3 925
1.96
1.97
.475581
.05730
.16309
- .09944
-.29936
1 97
1.93
476148
.05618
.164 8
— .10239
— 28950
1.93
1.99
.476704
055'.*8
.16304
-.10623
- 27970
1 99
2.00
.477251
.05-99
.16197
— .P798
-.26996
2 00
2.01
.477784
.05292
.16088
-.11063
—.26)27
2.01
2.01
.478308
.45186
.15976
-.11319
—.25064
2.02
2.03
.478822
.'5 >82
.15862
— .11565
-.24109
2.03
2.04
.479325
.04980
15745
— .11801
--.23160
2 04
2.'*5
.479818
.01879
.15626
-.11028
— .2222>
2.05
2. 6
.480331
.0478)
.15504
- .12245
-.21287
2.06
2.07
.48 >774
.04682
.15381
-.12454
-.20363
2.07
2."8
.481217
.04586
.15235
— .12653
— .19148
2.08
2.09
.481691
04У91
.15128
-.12843
-.18542
2.'9
2.10
2.10
.482136
.04398
.14998
-.13024
-.17646
2.11
.482571
.043 >7
.148H7
— 13193
-.16754
2.11
2.1 г
.482997
.04217
.14735
— .133)9
— .15883
2.12
2.13
.481414
.04128
•1460»
—.13513
-.15017
2.13
2.14
.483823
.04)41
.14464
-.13659
-.14162
2.14
Распределение Лапласа—Гаусса }2.i
Продолжение табл. VN
t
f VO (') dt
•' f*
'o<0 |
'3(0
?j(0
MO |
/
' ''л “
— . -v
—- —
— —. --
2 15
484222 !
.03955
.14327
-.13797
-.13318
2.15
2.16
.434614 :
03871
. 1418.8
—. i:-.£ 2b
-.12486
2.16
2.17
.484997
.03788
.14049
—.14046
— .11W5
2.17
2.18
.485371
.03703
.139 7
-.14159
-.103 Ъ
2.18
2.19
.485738
.03626
.13765
-.14263
—.)0>59
2.19
2.20
.4861.97
.л35!7
.13622
— .14360
-.09274
2.20
2.21
.486-147
.03470
.13478
-.14449
— .08502
2.21
2.22
.486791
.0339)
133.ЧН
—. 14531
-.07743
2.22
2.23
.487126
.03319
.13188
—.14604
-.06996
2.23
2.24
.48745-1
.03246
.13К1
—.14670
-.06263
2.24
2.25
.487776
.03174
.1-2891
-.14729
—.05542
2.25
2.26
.488089
. »3103
.127*7
— .14781
— .04835
2.26
2.27
.488393
.03 34
. 12)99
-.14826
-.04141
2.27
2.28
.488696
.'’2935
.1215)
— .14864
—.03161
2.28
2.29
.485989
.02898
12301
-.14895
-.02794
2.29
2.3)
.489276
02833
.12152
-.14920
-.02141
2.30
2.31
.479536
.'1276.»
.12003
-Л-938
-.015)2
2.31
2.32
.489038
.027 '5
.11854
— .14950
-.00877
2.32
2.33
490097
.n2613
.11704
— .Г4(Ч56
— .0)265
2.33
2.34
.49JJ58
.02582
11554
-.14955
— .003)2
2.34
2.35
.491613
.02522
.11405
— .14949
— J0915
2.35
236
.490362
.02463
.11256
— .14937
-.01485
2.36
2.37
.491106
-U2406
.11106
— .149 9
— .02040
2.37
2.38
.4913-14
.023-19
.10957
-.14893
— .02582
2.38
2 39
.191576
.02291
.10808
— .14863
— .03109
2.39
2.40
.4918 '2
.02239
.10660
-.14834
— .'’3623
2.40
2.41
.492024
.''гш
l'SU
-.14795
—.04122
2.41
2.42
.292240
.02134
.10364
-.14752
-.046 8
2.42
2.43
.492451
. 02-183
.10217
— .14703
-.’>5 79
2.43
2.46
.492656
.02)33
.10070
- 1465J
-.05537
2 44
2.45
.491857
.01984
.05924
-.14593
- .05981
2.45
2 46
.493 53
.01936
09778
-.14531
— .'45411
2.46
2.47
.490244
.01889
.«-9633
-.14464
— .06828
2.47
2.48
.493431
.01842
.0H89
-.14*94
— .07231
2.48
; 2.49
.493613
.01797
.09315
-.14320
- .07621
2.49
j 2.5)
.19379:1
1 .01753
.09202
— .11242
.07997
2 5)
! 2.51
.49 933 1
1 .01709
.09)69
-.14160
.08360
2.51
1 2.52
.491132
.01667
.07919
-.14075
.08710
2.52
2.53
.191297
.'U«2>
.08779
— .13916
.C9047
2.53
2.54
.191457
.01585
.08639
-.13894
.0Э372
2.54
2.55
.49 4614
.01.545
.08501
-.13793
.09683
2.55
2.56
.49475)
.015 «6
.08361
-.1370)
,<)9982
2.56
2.57
491415
.01468
.Ой227
- 13599
.10268
2.57
2.58
.49)03)
.11431
.0X092
-.13195
.10512
2.58
2.59
.4952)1
.01391
.07967
- .13388
.1080»
2.59
/2V
Распределение Лапласа—Гaver а
Продолжение табл.
/ voW'^ Vo (О
2.60
2.61
2.62
2.63
2.64
2.65
2.66
2.67
2.68
2.69
2.70
2.71
2.72
2.73
2 74
2.75
2.76
2.77
2.73
2.79
2.80
2.81
2.82
2.83
2.84
2.85
2.86
2.87
2.88
2.89
2.90
2.91
2.92
2.93
2.91
2.95
2.96
2.97
2.98
2 99
3.00
3.01
3.02
3.03
3.04
.495339
.495473
.49560!
.495731
.495855
.495975
.496093
.496207
.49о319
.496427
.496533
.496636
.496736
.496833
.49о926
.497020
.497110
.497197
.497282
.497365
.497445
.497523
.497599
.497673
.497741
.497814
.497882
.497918
.498012
.498074
.49813!
.196193
.498250
498305
498359
.498411
498462
.498511
.498559
.498605
.198650
.498694
498730
.498777
.498817
.01358
.01323
.01289
.01256
.01223
.01191
.01160
.01130
.01100
.01071
.01042
.01014
.00987
.00961
.00935
.00909
.00885
.00861
00837
.00814
.00792
.00770
.00748
.00727
.00707
.OOF87
.00668
.00649
00631
.00613
.00595
.00578
.00562
,00545
00530
.00514
.00499
.00485
.00471
.00457
.00443
.00430
.00417
.00405
.00393
.07824
.07692
.07560
.07431
.07302
.07171
.07018
.06923
.06799
.06676
.06555
.06435
.06316
.06199
.06082
.05958
.05854
.05742
.05631
.05522
.05414
.05308
.05202
.05099
.04996
.04895
.04795
.04697
.04600
.04505
.04411
.04318
.04227
.04137
.04048
.03961
.03875
.03791
.03708
,03626
.03545
.03466
03389
.03312
.03237
-.13279
-.13167
-.13053
-.12937
-.12818
-.12698
-.12576
-.12452
-.12326
-.12199
-.12071
-.11941
-.11810
-.11677
-.11514
-.11410
-.11274
- 11139
-.11002
.10865
■ 10727
-.10569
.10450
-.10312
.10173
.10034
.09895
09755
.09616
.09478
.09339
.09201
09063
.08925
.08788
.08651
.08515
.08380
.08245
.08111
.07977
.07845
.07713
.07582
.07452
.11053
.11291 )
.11517 1
.1173? |
.11935 j
.12)27 j
.12308 '
.12479 I
.12638 !
.12787 j
.12926 1
.13055 j
.13174 ;
.13283 I
.13383 :
.1347.4
.13555 |
.13627 I
.13691 |
.13746 :
.13793
.13832
.13863
.13886
.13902
.13910
.13912
.13906
.13894
.13875
.13850
.13819
.13782
.13739
.13691
.13638
13579
.13515
.13346
.13373
.13296
13214
.13128
.13038
.1294!
i
2.60
2.61
2.62
2.64
2.64
2.65
2.66
2.67
2.68
2.69
2.7U
2.71
2.72
2.74
2.74
2.75
2.76
2.77
2.78
2.79
2.80
2.81
2.82
2.83
2.84
2.85
2.86
2.87
2.88
2.89
2.90
2.91
2.92
2.94
2.9!
2.95
2.96
2.97
2.98
2.99
3.00
3.01
3.02
3 03
3.04
Par пред с ас нпе . 7апл гс /—Гаусса
Продолжение табл. 17/
f
/ VO (О Л
• (1
Vo (0
?s W
j t/>
| i
1
з.оз
.198856
.0)381
.03163
—.07323
, .12847
3.05
3.06
.195893
.00370
.03090
—.07195
. 12747
3.06
3.07
.198930
.00358
.03019
-.07068
.12643
3.07
3.0t>
.498965
.00348
.02949
— .05943
.12536
3.08
3.09
.198999
.00337
.02880
—.06818
12426
3.09
3.11
.499032
.00327
.02813
-.06694
.12313
3.10
3.11
.499065
.00317
02746
—.06571
.12198
3.11
3.11*
.499096
.00307
.02681
— .06450
.12080
3.12
3.13
.199126
.00298
.02617
— .06330
.11960
3.13
3.11
.499155
.00288
.02555
— .06211
.11838
3.14
3.15
.199184
.00279
.02493
-.06093
.11714
3.15 j
3.16
.199211
.00271
.02433
— 05977
.11588
3.16 ;
3:i7
.499238
.00202
.02374
— .05861
.11460
3 17
3.18
.499264
.00254
.02316
— .05747
.11330
3.18
3.19
.499289
-0)246
.02259
—.05635
.11199
3.19 !
3.2.)
.499313
.00238
.02203
— .05523
.11066
3.2J ;
3.21
.499336
.O'>231
.02148
-.05413
.10933
3.21 !
3.22
.499359
.00224
.02)95
— .05305
10798
3.22
3.23
.499381
.00216
.02042
— .05198
.10662
3.23
3.24
.499402
.00210
.01991
—.05)92
.10525
3.24
3.25 !
.499423
.00203
.01940
-.04987
.10387
3.25
3.26 ;
.499443
.00196
.01841
-.04884
.10249
3.26
3.27 :
.499462
0019)
.01843
-.04782
.10110
3 27
3.28
.499481
.00184
.01795
-.04682
.09970
3.28
3.29
.499499 !
! .ОЛ78
.01749
-.01583
.09830
3 29
3.3)
.499517
.00172
.01704
-.04485
.09690
3.30
3.31
.499534
.00167
.01659
-.04389
.09549
3.31 !
3.32
.49955)
.0)161
.01616
-.04294
.09409
3.32
3.33 '
.499566
.00155
.01573
— .04201
.09268
3.33
3.34 |
.499581
.00151
.01532
—.041)9
.09128
3.34
3.35 1
.499596
.00146
.01491
-.04018
.08987
3.35
З.36
.499510
.00141
.01451
-.03929
.08847
3.36 i
3.37 j
.499624
.00136
.01413
—.03841
.08707
3.37
3.38 i
.499638
.00132
.01375
— .03755
.08567
3.38
3.39 i
.499650
.00127
.01338
-.03670
.08428
3.39
3.4')
.499663
00123
.01301
-.03586
•.08290
3.40
3.41
.499675
.00119
.01266
-.03504
.08151
3.41
3.4:.’
.499687
.00115
.01231
-.03423
.08014
3.42
3.43
.499j98
.00111
.01197
—.03344
07877
3.43
3.44
.4997o9
.001)7
.01164
-.03266
.07741
3.44
3.45
.499720
.00104
.01132
-.03189
.07606
3.45
::.40
,4997o0
.00100
.01100
-.03114
.07471
3.46
3.47 :
.499740
.00097
.01070
-.03)40
.07388
3.47
3.4s
.499749
.00094
.01040
-.02967
.07205
3.48
3.49
.499758 j
00090
.01010
-.02895
.07074
3.49
3.5')
.499767 :
! .00087
.0)982
.02825
—.05943
3.50
3 51
.499776
.00)84
.0)954
.02757
— .06814
3.51
3.52
.499784
1 .00)81
.0)927
.02689
— .06685
3.52
Распределение Лапласа—Гаусса
Продолжение табл. Vlf
(
7%о (о м
:оО) ;
1
Ъ(‘) j
*л (0 !
1
V4(<) I
/
\
1
-
1
3.53
.499792
.00079
.оо°оо
.02623
— .06558
3.53
3 54
.499800
.000/6
.00874
.02568
— .06432
3.54
3.55
.499807
.00073
00849
.02494
— .063 8
3.55
3.56
.499815
.00071
.'»и824
.02-132
-.0618-!
3.56
3 57
.499822
.00068
.00800
.02370
— 06062
3.57
3.58
.49*828
.00066
.00777
.02310
— .< 59-.1
3.58
3.59
.499835
.00063
.0075-1
.02252
—.05821
3.5!'
3.60
.499841
.00061
.00732
.02194
— .05703
3.60
3 61
.499847
.00*59
.ОЛЮ
.02К-8
—.05586
3.61
3.62
.499'53
.00057
»ч>89
.02382
-.05471
3.62
З.сЗ
.499858
.0 4)55
,(»06о9
>,'2028
-.05357
3.63
3.64
.499864
.00053
.006*. 9
.01975
- 05244
3.64
3.65
.499869
.00051
.Л0629
.01923
-.05133
3.65
3.66
.4?9874
.03049
.00310
.01873
— .05023
3.66
3.67
.499679
.03047
.00592
.01823
— .049)5
3.67
3.68
.419363
.0и046
.00574
.'*1774
— .0.8С8
3.68
3.09
.499888
.0 044
.00556
.01727
-.04703
3.69
3.70
499892
. 00*4 2
.00539
.01680
—."4599
3.7)
3.71
.499i>S6
.00041
.00522
.01635
— 0-.Ч97
3.71
3.72
.499900
.00039
.005 'б
.01591)
— .0!3°<>
3.72
3.73
.4999Л
.00 '38
.03-191
.(И547
— .04197
3.73
3.74
.49*938
.00037
.03475
.01501
-.0420)
3.74
3.75
.499912
.00335
.00461
.01463
- .041 ‘3
3.75
3.76
.499915
.00334
.03446
.01422
— .040^
3.76
3.77
.499918
.03063
. 03432
.013/3
- ."39’.6
3.77
3.78
.419*22
.00331
,00419
.01341
—.03«24
3.77
3.79
.499925
.03030
.03405
.01305
— .0.734
3.79
3.8Э
.4399.8
.00329
.00392
.01269
-.03646
3.80
3.81
.499*33
.00028
.03380
.01233
— 03559
3.81
3.82
.499933
.000^7
.0 368
.01198
— .<'3473
3.82
3.83
.4V9935
.00 26
.'»0356
.01164
—.033/9
3.8,4
3.84
.49э938
.0001.5
.00344
.01130
—.033 -7
3.81
3.85
.49г941
.00023
.00333
.’>1098
-.03226
3.85
З.ы>
.499)43
.00 23
.00322
.0lOf6
—.о.)1*:в
3.86
3.87
.493946
.00322
.00312
.01035
-.03068
3.8/
3.88
.49 948
.00021
.'0302
.OWM
—Ю2991
3.83
3.89
.499950
.00021
.00292
.'9975
— .02*16
3.89
3.90
.499952
.0002»
.00282
.(Г946
— .0.842
3.90
3.91
.499954
.0 0.9
.03273
.009)8
— .02770
3.91
3.92
.499956
.00018
.00264
.03 91
—.02699
3.92
3.93
.493158
.00018
.00255
.00814
—.'■2630
3.93
3.94
.49*959
.03017
.00247
00838
— .02562
3.91
3.95
.499961
.00016
.00^38
.00813
—.02495
3.95
3.91
.499162
.03016
.00230
.(>0788
— .024.0
3.96
3.97
.49 9*64
.00 ‘15
.00223
.00764
— .0235о
3.97
3 98
,4У936
.00014
.6(215
.0-741
-.02 01
3.93
3.99
.499367
00314
.002)8
.07718
-.04242
1 3.90
Распределение Пуассона
G~4‘MC04f «OtOr^CO
t^COt^CQCM о ь»
sssasss ss
V обЪ N op со о О cr
~смсмс-© OOOC
O-r*00b-O
ОooО -J
lCN|4flN о
«О О) Ю 'О ^ л*ООГ
«—• оа см —• © о о о о
со© со О) с
см см 05 см
«иосьюю <о —< •» со
r-lO^W О
СОСМ О О О
:о см о ооос
23SS2 SSSft
©SSSS £3—
см to см—* о © о
r-f О
О О
оо
COOCM^N CM СО СО
—г о ю о
Гч<Н»ОСЧ^» мЛОС
Ncocm-*© о о о о
O^CDOOt^
СО CM © I**»
со »л -«см с
см to см —• с
СО 05 05 05 «О
о CN «-> *1?
5 СО
ю
05 СОСО ч? CM »0»0r!S2
<-)<-<Ос0(0 о —
ОСО^НООСМ ропо
СО со см О О ООО»
щш ши
sisss l§ss
о •—• см со **г
Иродолжшние табл. УШ
Распределение Пуассона
51 = — СЧ
V; |; ~ I
i 2S
>с^
I I
11
с-. с-нем
*
3 —• CM СО -**
3 30 О
О ~ СЧ ГС
о
04979
14936
22401
22404
16803
: 10082
05041
02160
00810
00270
00081
00022
00006
00001
г.
1
05502
15957
23137
22356
16215 j
09405 ;
04546
01883
00683
00220
00064
00017
00004
00001
'л.
"
i
06081
17027
23838
! 22248
I 15574
08721
04070
01628
00570
00177
00050
00013
00003
00001
1-»
06721
18146
24496
1 22047 !
14882 :
08036
03616
01395
00471
00141
00038
00009
00002
,
г*
1 сч -н £> uo ^
1 Т 00 •
1^ О) tO *9*
3 — CM CM —
о о о о о
00029
00007
00007.
08208
20521
25652
21376 |
13360
06680
02783
0099-1
00311
00086
00022
00005
00001
1
Гг j
09072
1 21772
1 26127
1 20901
12541
06020
02408
00826
00248
00066
00016
00004
00001
1
г- !:
еТ !i
I
! §523§
! OrtSg-
•ч CMCICM^
05378
02061
00677 ;
00195
00050
00011
00002
^ 1
»
t
11089
24377
26814
19664
10815
04759
01745
00548
00151
00037
00008 !
ОЭ002
i
cl
! 12246
25716
27002
18901
09923
04168
01459
00438
00115
00027
10000
I 9СС00
■ /
/
С -ч СЧ СО УГ
О •—•см 00 -f*
—< —Ч т-^
Продолжений нибл. УШ
Распределение Пуассона
129
-л ИОЛЯП»'*и
Продолжение табл. VIII
130
Распределение Пуассона
Ю tO tv 00 О) О ^ СЧ 00 ’Ч" ЮСОГ^
rv сч ч*оо tv со сосч tv tD VQ —
тгсчЗ*сЧсч — сч-г со -г — оо
ОС 00 qo — о ООО
Ь1«офо »-Лйао ооо
нниОО ООООО ООО
S55S832 82g£?§ 2S3
tO 00 О — 00 О f4» чч — О ООО
==28g S00S8 888
ю о <g сч С
оо х со
счеч tvtoc
Г- '■
28-
N “ ф I/O СО — О О О О О
— г-ООО ООООО О
к
чг
17383
13617
09*43
05371
028j5
01318
00563
00221
00080
00027
00008
00002
00 301
17.52
13227
08*92
04993
02555
01175
00*91
001Я8
00367
00022
00037
00002
*о
чГ
17083
12812
08236
04633
02316
01042
00426
00160
03055
00018
60000
SC000
V
СО СОСО 00 —
nnnn®
00 со tv сч 0
<OWN4*Cl
«—* •-« 0 0 0
00920
00.-68
00135
00046
00014
00004
00001
со
ч*
16622
11913
07318
0.-933
01879
00808
00316
03113
00037
03012
03303
03301
«
V
16332
11432
068.9
03601
01680
SpSI
0 лооо
ООООО
IOCCO
ессоо
V
16000
10934
03404
03282
0К95
СО 00 ОС to tv.
— Сч NOI
(ОМООО
ООООО
ООООО
00002
*/
00 в>
О —СЧСО'Ф
JOtDJ^
/«I
— — — — —«
о — сч со ч*
1
«оао ос с&!
0
0
1 ii§S
1 §®s
^ ч* tv ^ ~
о> СО СО ТГ ЧГ
-iociw
80000
о
ч»
1111
«OO^S
tv 1^. СО чр со
СО СО tv О tv
СЧ О — СО **
ООООО
13,0
,8232
J оооеЗ
о о о о
5ооо
22228
изоюоо
О — СЧ чгф
ООООО
о
7Я
iiiil
Я°° ®йс§
©©<£©§
11.0
сч 00-00
SoSSs
08880
сч©ооо)ео|
ч« —uotv^o 1
SsSill
э
о
3*tON.tv£*
OjNlfla
О 0 Cl i*» 00
ОЛОО —
00000
8882=
liiSS
о
О»
СЧ'-Пф'ф
— — О Ur £v
83828
ООООО
со Ф СЧ 'О to
NO*-* NN
о8^22
о
00
*4*» ОО Ч*« СО 1Л
со со tv со сч
OCNOCOrv
80000
ОН* 0)0 00
O-iOiOO
— СЧО)ОЬ
О) сч СО со СЧ
О — — —* Г-Н
о
г«^
58223
О (Л 'ч» —
олсиоа
ООООО
счоовоо
tvObOO —
сч ^ >г соо
^4 PH ^ ^
о
«г
00tvC4 v£U0
S2223
©ООО —
3SS8S
So^oS
— — — — 0
«/
/
0 — счсоч-
to (О tv 00 со
/ч
Продолжение табл. УШ
Распределение Пуассона
131
и
О«-*СМС0<чГ
v-4 •— р-4 1—1 ~т
Ю 01"» ООО
О -« СМ СО т*
см см см см см
юср £-оо а>
см см см см см
«5558*3 <5
о
i/Г
04861
06629
08286
09561
10244
10244
09603
08474
07061
05575
04181
02986
02036
01 (>28
00830
004Р8
00287
00160
00085
00044
1
ICOOO
7ГССОО
SCCOO
песо
ггссо
св
V
06628
08436
09842
10699
10699
09892
08656
07128
05544
040Е0
02860
01916
01213
00738
00431
00241
00130
00167
00034
00016
10000
госоо
есосо
8С000
С
«о
SS?g|
сооооЪ
О ^ м •—< м
в02'4® со
SoSSS
«О со со 45 “©
с£»'ФОО»
NOttii' *-•
^ — О О О
ооооо
00103
00051
00025
00012
00005
tOCOO
SC000
j 2
10484
11437
11437
10557
090i9
07239
05429
03832
02555
01614
00 со С) эооз
«ООО Ю
о5ооо
00038
00017
OU008
00003
00011
1 1 11 1
О'И
I ЬООСООО
1 C0«O5<PN
1 о. а> 2> см см
1 HnOttN
05335
03668
02373
01450
0.1840
00462
00242
01121
00058
00026
2Я85 ,
ОПОЛ |
лоло
0500
И II 1
^ -г оо — оо см о со® со с& о оо г- «2 л .
—MsSON оооо^-.о Л Q 111 II
1Л .С *4' СМ ^ см t*- со ^-1 о о СО £ I I I I I I »
СО <Nr-f гмг5 о о о о о оо
И^ООО ООО оо оосоо оо
зри пт liiii |
•— 03 г^“ *5 Ф r+ О О о хЗхЯа о
I I I I (till
оооос
«ОСПА п-
Is О Is
во
ООО
I II М I I I И I
ооt-иэ05д> гГ^ФЙ!? S32 . .
32S8S So I I
ssiss
)О^ПО
50000
IS
1 I I I I I
I I
?§§§§ f?3s£I i i : i i iиii ii11 i
ss; *
r? OOOOO
> о о о ooooo
о — смео-ч- ooNooa З — смсо;* 5GS6E:5&S5
и*чрч«нс< MMNCNC4 CM CM CM CM CM. со со со со со
ЛИТЕРАТУРА
А. ЦИТИРОВАННАЯ ЛИТЕРАТУРА
1. Чебышев П. Л. «О непрерывных дробях» (Соч. т I. стр.
*13-230, 1855).
2. Чебышев П. Л. «Об одно* новом ряде» (Соч. т. I. стр.
.481-384, 1858).
3. Чебышеи П. Л. «Об интерполиропаыип в случае большого
числа данных доставленных наблюдениям к» (Соч. т. I. стр. 387—469,
1858).
Чебышев (1. Л. «Об интерполировании величин равноотстоя¬
щих». (Соч. т. 1J. стр. 219-242, 1875)
Чебышев П. Л. «О функциях, подобных функциям Лежандра».
(Соч. том II. стр. 61—68, 1869).
Чебышев 11. Л. «Об интерполировании но способу наимень¬
ших квадратом». (Соч. т. I., стр. 473—498, 1859).
I. Чебышеи U. Л. «О разложении функции одной перемен*
ной». (Соч. т. I, стр. 501—508, 1859).
5. Чебышев П. Л. «О двух теоремах относительно вероятно¬
стей». (Соч. том II, стр. *181—492, 1887).
6. V. Romunovskv. Статья в Giorii.'le deil* 1st It degll Aiiuari.
Anno 11 п2 (1931), pp. 161-171.
7. Doolittle М. H. Статья n S. Coast ami Geodetic Sur¬
vey. Report for (1878) Appendix 8. 115.
8. Gauss. M6thodc des molndfes earn-*. (Paris, 1855. перевод с не¬
мецкого Bettrand'a.)
9 Cochran The Omb»oii or Addition of an iiidepence/it variaie
In mtltlple lineal regression. Supplement to the Joumale ot the Royal Stat.
Soc., vol. 2, 1938.
10. Fisher R. Stailstlcal Methods for Research Workers, (l-oe Иад.
1925г,, 8 изд., 1941).
II. Немчинов И. С. «Сельскохозяйственная статистика с осно¬
вами общей теории» (М, 1945).
12. Гаусс. *Двйжение небесных тел» 1861 (на латинском—1809 г.).
13. К е 11 е v. Statistical Method.. N —I. (1929).
Литература
Ш
14. I&zeklel М. Method of correlation analyses. (N.—■i.. 1 od..
1950. 2 ed.. 1941.)
15. Davenport and Ekas. «Statistical methods (1 ed., 889.
4 ed. 1936.)
16. Чебышеи II. Л. «Об определении фу акций по зпачешнм.
которые они имеют при некоторых величинах переменной» (Соч т.н.
стр. 71-82, 1870).
17. Чебышев II. Л. «Разложение в ряды при помощи непре¬
рывных дробей» (Соч т. I. стр. 611—614, 1865).
18. Hermlte Ch. Siir u.t nouveau developpemert e:i s6rfe dc fo c-
tlons (1864).
/00 £ *
19. L а g u e г г e К. Sur I'lntegrale 1 dx (1879).
X mJ
2К С. Jorgaii. Statlstlque mithematlque Paris (1927).
21. В. И. Романовский. «Математическая статистика». (М..
1938).
22. Хотимский. «Выравнивание статистических рядов ло ме¬
тоду наименьших квадратов (способ Чебышева)». (М 1925).
23. Митропоаьский. «Техника статистического исчислении».
(М. 1931).
24. Чебышев II. Л. «О средних величинах» (Соч. т. 1. стр. 687—
Ь94. 1866).
25. Scudeut. The probable Error ot a Mean (Btometxlka. VI. I,
1908).
26. Laplace. Theorle analytlque des probability, 1872.
27. Polsson. Recherche* sur la Probabllltfe des lugements (1827).
28. Plsher Arue. The Mathematical Theory of Probabilities. (N.— l.
1923.. 2 ed.)
29. Oram, J. P. Om KaekkendvlkllnRcr. bestemte ved Hfaelp af de
rnindile Кvadcaters Method* (1879).
30 Thiele T. N. Theory of Observation. I <fS03) (на датском
языке 1884 г.).
21. Charller С. V. Uberdus Pehlergesetz (1905)
32. Bruns M WahrschelnHchkeUsrechnung und К oil ktivmass-
lehfe (1906).
33. J6r g e :i s e и N Undersogeiser over Frequensflader or Korrela-
tiOti (1916).
34. Camp. The mathematical part of elementary statistics, L. (1934).
35. Риги. «Математические методы в статистике». (М. 1977 на
анг. 1924).
36. Czuber В. W&hrschelhllchkeitsrechnung (19Э8).
37. Лахтин Е. «Кривые распределения и построение для них
интерполяционных формул». (М., 1922).
38. Bortklewlcz L. Das Oesetz der klcinen Zahlen (1898).
134 Литература
39. Soper Н. Е. Tables of Polsso.i's exponential binomial limit
Blometrika, (X, 1914.)
40. Chari ier. Die zwelte Form des Fehlergesetzes (1905).
В. ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА
1. Чебышев П Л. «О функциях наименее уклоняющихся от
нуля». (Соя. т. II, стр. 189—215, 1873).
2. Чебышев П. Л. «Об одном новом ряде, доставляющем пре-
делыые величины интегралов при разложении под интегральной функ¬
ция на множители». (Соч. т II, стр. 405—417, 1883).
3. Чебышев П. Л. «О суммах, составленных из значений про¬
стейших одночленов, умноженных на функцию, которая остается поло¬
жительной». (Соч. т. II, стр. 561—610, 189Э).
4. Чебышев П. Л. «О функциях, зависящих от положительных
значений какой-либо функции». (Соч. т. II, стр. 613—666, 1890).
5. Bernoulli J. Ars Conjectaudt (1713). (на русском —IV часть
1913)
6. Lexis W. Zur Theorie der Massenerschelnungei in der men-
<chllchen Oesellschaft (1877).
7. Bernstein S. Sur un procede de somnntion des series rrfgono-
m£trlques.—Comptes Rendus Ac. Sc., t. 191 (1930).
8. Чупров А. А. «Основные проблемы теории корреляции».
(М. 1932).
9. Марков А. «Исчисление вероятностей». (Л-д. 1924).
10. Бернштейн С Н. «Теория вероятностей». (М. 1934).
11. Kolmagoroff A. Grundbegriffe der Wahrschelnllchkeitsrecli-
uung (1933).
12. Слуцкий E. «Теория корреляции и элементы учелия о кри¬
вых распределения». (Киев, 1912).
13. Slutzky Е. The Summation of Random Causes as the Source
of Cyclic Processes Econom trlca—5. (1937) (на русском языке, 1927).
14. Идельсон. Н. И. «Способ наименьших квадратов» (изд. II.
Л-д, 1932). .Уравнительные вычисления по способу наименьших квад¬
ратов* (1927 г.)
15. Ait ken. Statistical Mathematics (1942).
16. Гончаров В. Л. «Теория интерполирования и приближения
функций». (М., 1934).
17. Научное наследне П. Л. Чебышева, т. I «Математика». (M.t
1945).
18. Лагунов Б. И. К практике выравнивания статистических
рядов* (Киев, 1927).
19. Крылов А. И. „Л«кики о приближенных вычислениях
(2-эе изд. 1933 г)
ПРЕДМЕТНЫЙ И ИМЕННОЙ УКАЗАТЕЛЬ
Ассиметрия — 94, 102
Бернулли—134
Бернштейн — 77, 134
Борткевич —95, 97, 133
Боулн — 98
Брунс—90, 93, 133
Вариация коррелированиях 38.
62, 63
«Вес» Гаусса —17, 18, 38, 40, 41;
50, 67, 77, 106
«Вес» Чебышева — 7, 8, 74—76.
89. 106. 107, 109
Веса переменных — 19, 40. 41, 50.
65
Гарнонический анализ —77. 107,
110
Гаусс — 18. 35. 68. 95. 106, 132
Гончаров —134
Грам —90. 92, 95, 107, 109, ПО.
133
Девентрон—70, 133
Дисперсионный анализ —5, 9, 42,
56, 67, 107, 110
Дулитль—17, 27, 29, 30, 132
Жордан —80. 87, 88, 97. 98. 107.
110, 133
Закон больших чисел —88
Закон малых чисел — 95
И дел ьс он — 134
Интерполяционная формула — 7, 8.
25. 75. 76
Йоргенсен — 93, 133
Исключение переменных — 22. 30
35, 43, 53, 55. 106
Келли—70. 132
Кемп—93, 133
Колмогоров —134
Контроль вычислений — 56, 60. 61
Корреляционный анализ — 5. 9.
42, 56, 67, 107, 110
Корреляция;
множественная — 26. 65, 66.
69-71, 106, 109,
остаточная—70, 71
частичная —70, 71, 106, 109
частная —26. 65, 66. 69—72, 106.
109
Кочран —21, 132
Кривые Шарлье —5, 90, 101
Критерий Фишера — 26. 35, 40, 41.
63, 65. 67—70, 106, 109
Коэфициенты корреляции — 35,65,
70
Коэфициенты кривой распреде¬
ления — 92, 95. 98, 101
Коэфициенты полинома:
младшие —37, 50, 51, 72
старшие—10, 24, 26, 35, 36. 39.
48, 50—52, 77, 83-86
Коэфициенты ряда Чебышева —
8, 75, 77
Коэфициенты рекуррентной фор¬
мулы— 81
Коэфициенты полиномов:
«К*—10, 13, 17—20, 23—26, 35—
40, 42—54. 57—60. 67, 69, 83
136
Предметный и именной у*
«С> - 19—22, 35, 37, 38, 40-47,
50—57, 65, 67. 69, 106, 109
«Т* — 9. 10, 13—17, 23, 25. 28, 40,
47—49, 57—60. 82, 83
Коэфициенты регрессии:
«А>-8. 13, 15, 16. 23, 25, 26.
28. 31. 46, 47, 57, 58. 61
«а» — 12, 13. 16, 17, 25. 26, 30-
35 38—49, 50, 52—57. 65. 99,
100. 106, 108
Крылов —131
Лагерр — 5, 78, 97. 107, 109. 133
Лагунов — 134
Лаплас —89, 95, 101* .133
Лахтин — 93, 133
Лежандр — 8, 77, 84
Лексис — 134
Маклорен — 8, 78
Марков — 134
Митропольский — 85, 93, 101, 133
Модуль — 90
Моменты — 90, 93. 96
Наименьшие квадраты- 5. 7. 35
Натуральный ряд чисел — 85
Немчинов—22, 132
Непрерывная дробь — 8. 73 75.
77, 80
Неравенство Чебышева — 7, 88
Нормальное распределение не-
роятаостей — 8, 118—126
Нормальные уравнении26. 27.
30. 49. 67
Нормированные:
коэфициенты — 20, 38, 40. 42. Ги»
полиномы—74, 81. 85
Обобщенные:
нормальные кривые—103
полином Чебышева —73
Ортогональность — 13, 74, 92
Остаточная сумма квадратов — 28.
44
Отклонения — 23, 24, 105
Ошибки —Б, 26. 42. 63-65, 67.
69, 106
Параболическое интерполирова¬
ние—8. 9, 77, 88. 98. 100. 105.
108
1 (ерегудов— 22, 49
Переменная:
вспомогательная — 85. 87. 99
зависимая— 10, 12, 69
элиминированная—10. 27
Приближения квадратические -
67, 69, 75, 92, 93, 102, 104, 105
Пирсон — 93, 94
Подходящая дробь —8, 74, 77
Показательные функции — 77, 79
Полиномы Лагерра — 5. 77. 79,
89
1 [одиномы Лежандра — 77
Полиномы N — 23, 35, 82, 84.
11олииомы q — 87, 88, 99, 100
Полиномы равноотстоящих вели¬
чин— 86
11олиномы Эрмкта — 5, 77. 79. 89
Полиномы G — 78—80, 97, 98.104,
105
11олиномы Якоби — 77
Полиномы Чебышева:
свойства — 74—76
семейство — 77. 84
система—9—11, 23
Поправки — 50, 51
Последовательность переменных —
9, 17, 49, 66, 72
Пуассон —78, 80, 89. 90. 95-98.
104, 107, 109, 133
Равноотстоящие величины -Н,
81
Распределение численностей - 7.
88—91. 127—131
Регрессия:
криволинейная — 7, 8
множественная — 7, 8. 12. 13.
55. 56, 63, 67. 69. 72, 105, 106
прямолинейная — 36, 37. 55, 69
чистая — 71
Рекуррентная формула — 74. 77.
80. 82-87, 107, ПО
Рнтц — 93, 133
Предметный и именной указатель
Романовский — 9, 80, 93, 97, 132,
133
Ряд Чебышева - 7, 75, 89, 92, 94,
105, 107
Свойства лал ил омов — 13, 74—75
Система полиномов Чебышева: —
первая («Т») — 9. 14, 15, 28, 48,
81, 82—84, 105, 106, 108
вторая («К») — 9, 10, 48, 59, 105,
106, 108
третья («с») —11. 17, 18, 19, 105,
108
четвертая («N») — 23, 25, 26. 48,
50. 71, 82-84, 106, 108
Скандинавская школя- 90, ПО
Слуцкий—134
Сопер —97. 134
('.редкие:
арифметические—36, 52, 69, 94
квадратические— 52, 104
корректированные — 5, 35, 68
элкмикацнонкые — 5, 33, 35. 36.
68, 69, 94. 107. 110
Статистические величины — 26,
35, 36
Статистическая оценка — 5, 35,
38. 40, 41, 56, 62, 63, 67. 69.
107, 110
Статистические характеристики -
26, 31, 38, 69, 72
Степени свободы — 63. 65, 69. 7и
Стюдент — 88, 133
Сумма квадрата (W) —31, 38—41.
14. 47. 52, 53, 57, 62, 63, 66
Сумма квадратп (Sd‘) — 35, 36.
38. 41). 41, 44. 47, 49, 53, 55.
57. 63. 66. 69. 71, 99, 100, 102
Суммы квадратов полиномов - -
9, 13. 14. 16, 18, 24, 31, 35—38.
46, 47, 52, 53, 57. 67. 69. 76, 77:
87. 88. 94, 117
Суммы произведений полиномов—
9. 13, 15, 16. 18. 20, 22. 24, 29;
31, 32. 35-37, 69
Схемы вычислений:
Дулитля (Д) —29, 31—34. 51,
106, 109
Немчинова (N) — 26, 34—36,
42-45, 48-51, 53, 58, 62, 67.
106, 109
Перегудова (Р) — 45—49, 56.
58, 62. 106. 109
Тиле—90, 93, 94, 107, НО, 133
Тригонометрические полиномы Че¬
бышева—7, 8, 77, 79
Уравнительные вычисления — 5.
107
Фишер А —90, 92, 93, 133
Фишер Р —22, 88, 133
Функции остаточных отклонений—
73
Фурье — 77, 78
Чебышев — 5, 7, 9, 68. 73—75.
105—107. 132, 133, 134
Число наблюдений — II. 39
Числа Чебышева — 85. 87. 88, 99
107, ПО. 112. 117
Чубер— 93, 133
Чупров—134
Эзскнэль—70. 71. 133
Экономическая статистика - \ п8
Элиминирование:
полное—11, 29
последовательное- 10. 11. 28,
29
Экое — 70, 133
Эксцесс — 94, 102
Эрмит— 5. 78. 91, 1*j7. 109. ! V.\
Эйткен — 131
Чкобп 77
ОГЛАВЛЕНИЕ
Стр.
Предисловие ь
I л j в а I. Полиномы Чебышева
I. Ортогональные полиномы и интерполяционным ряд Чебы¬
шева 7
Поднвомы с иэмевеввой последовательностью перемен¬
ных ч
3. Суммы квадратов полиномов, сумма их произведений и
отношение их сумм 1$
4. .Веса" Гаусса и полиномы Чебышева 17
5. Взаимоотношения между коэфнциевтами смежных полино¬
мов Чебышева 2.;
Глава П. Схемы решении нормальных уравнении л полиномах
Чебышева
1. Схема Дулнтдн >7
2. Числовой пример решения вормальвых уравнений в поли¬
номах Чебышева
3. Новые схемы решения нормальных уравневнй в полино¬
мах Чебышева ;я
4. Числовой пример решения нормальных уравнений по но¬
вым схемам в полиномах Чебышева 14
Глава 111. Система статистического анализа и полиномы
Чебышева
1. Статистическая оценка коэфициентов уравнения регрессии
и полиномов Чебышева 02
2. Система статистических характеристик и полиномы Чебы-
шеза б*
Оглавление
Глава IV. Обобщенные полиномы Чебышева и статистиче-
cjcoc исчисление
1. Метод Чебышева и свойства его полиномов ~Л
*2. Классификация полнномо* Чсбышеиа 75
3. Рекуррентные формулы ЯП
4. Полиномы для функций с равноотноящимк значениями. . St
5. Кривые распределения числен в остей к полиномы Чебы¬
шева як
6. Распределение Пуассона и полиномы Чебышева <*5
7. Выравнивание кривых распределения численностей (при¬
меры) рь
Выводы 105
Summary 1US
В клеи/си:
Схема «Д‘. Схема Дул и тля к полиномах Чебышева 29-
Таблица 1. Нахождение связи между урожаем и метеорологи¬
ческими факторами по методу Чебышева —Ду¬
литла 31
Схема 9N•. Схема Немчинова в полиномах Чебышева ....
Схема mN*. Новая схема решения нормальных уравнений к
полиномах Чебышева (числовой пример) .... 53
Схема статистического анализа в полиномах Че¬
бышева 65
Система статистического исчисления в полиномах
Чебышева 69
Классификация полиномов Чебышева 77
Приложении:
Таблицы! —V. Полиномы Чебышева для равноотстоящих
величин qx (л, х) — Числа Чебышева .... 112
Таблица VI. Сумма квадратоз Sqf (п, х) 117
Таблица VII. Функция то (0* вторая, третья и четвертая
производные 116
Таблица VIII. Распределение Пуассона 127
Литература 132
Предметный и именной v/сазателъ 135
еедыгор А. А. Конюс.
ТохкжчегххЯ радажгор if. Б. Петрова.
Л146197. Сдано в набор 12|JX 19»$ г. Пода, ж аоч. 141X11916 г. Тираж 3.000. 8ахав 1976.
Типография «Кмсао* знамя» юд-м ЦК ВЛКСМ «Молода* гнардюь.
Мпскаа. Сушеаская. 21.