Н. И. БЕЗУХОВ
ТЕОРИЯ
УПРУГОСТИ
И ПЛАСТИЧНОСТИ
Допущено Министерством высшего
образования СССР в качестве учебника
для высших технических учебных
заведений
ГОСУДАРСТВЕННОЕ ИЗДАТЕЛЬСТВО
ТЕХНИКО-ТЕОРЕТИЧЕСКОЙ ЛИТЕРАТУРЫ
МОСКВА • 1 953

12-5-2
Редактор И. К.
Техн. редактор Н. Я- Мурашова.
Подписано к печати 28/11 1953 г. Бумага 60x92Vir,-
41 661 ткп. зн. в печ. л. T-0jO2O. Тираж 15 000
Заказ № I
Снитко.
Ксрректср О. А. Сигал.
13,125 бум. л. 26,25 печ. л. 27,6 уч.-изд. л.
жз. LUha книги ъ р. 30 к. Переплет 1 р.
4-я типография им. Евг. Соколовой Союзполиграфпрома Главиздата Министерства Культуры СССР.
Ленинград, Измайловский пр., 29.

ОГЛАВЛЕНИЕ
Предисловие 8
Глава I. Введение 11
§ 1. Теория упругости и смежные науки И
§ 2. Основные гипотезы и принципы классической теории
упругости 21
§ 3. Замечания о принципе локальности эффекта
самоуравновешенных сил 28
§ 4. Обозначение составляющих напряжений. Тензор напряжений 34
§ 5. Обозначение компонентов перемещения и вращения .... 40
§ 6. Обозначение компонентов деформации. Тензор деформации 42
§ 7. Разложение деформации на «чисто объемную» и на
«деформацию формы» 48
§ 8. Обозначения компонентов скоростей смещения,
напряжений и деформации : . 51
§ 9. Другие обозначения компонентов напряжений, деформации
и производных от них 52
§ 10. Постановка задач в теории упругости и пластичности . '. . 54
§ 11. Еще о методе сопротивления материалов. Метод теории
упругости 56
§ 12. Основные этапы в развитии теории упругости в XIX и
начале XX в 65
Глава П. Общие уравнения механики сплошной среды 71
А. Теория напряженного состояния (статические уравнения]... 71
§ 13. Обозначения компонентов напряжений вблизи заданной точки 71
§ 14. Дифференциальные уравнения равновесия и движения
(статическое обследование) 74
§ 15. Условия на контуре (продолжение статического
обследования) 78
§ 16. Исследование напряженного состояния в данной точке тела.
Главные напряжения 81
§ 17. Инварианты тензора напряжений 85
§ 18. Октаэдрические напряжения 87
§ 19. Наибольшие касательные напряжения 90
§ 20. Некоторые итоги по теории напряжений 92
15. Геометрическая теория деформаций (геометрические уравнения) 96
§ 21. Обозначения компонентов смещения вблизи заданной точки 96
§ 22. Дифференциальные зависимости компонентов деформации
от компонентов смещения (геометрические уравнения) . . 97
§ 23. Уравнения неразрывности деформаций 100
§ 24. Исследование деформаций в окрестности заданной точки . 104
§ 25. Оценка точности уравнений (2.25) с позиций нелинейной
теории упругости 107
1*

4
ОГЛАВЛЕНИЕ
Г л а в а III. Основные уравнения теории упругости 109
A. Связь напряжений с компонентами деформации {физические
уравнения теории упругости) 109
§ 26. Закон упругости 109
§ 27. Различные записи обобщенного закона упругости 112
§ 28. Продолжение: закон изменения объема и закон изменения
формы 114
§ 29. Удельная потенциальная энергия 117
Б. Синтезирующие уравнения 122
§ 30. Основные уравнения теории упругости и возможные методы
их решения 122
§ 31. Решение задач теории упругости в перемещениях .... 125
§ 32. Решение задач теории упругости в напряжениях 127
B. Частный случай — плоская задача 129
§ 33. Плоское напряженное состояние 129
§ 34. Дальнейшие упрощения 131
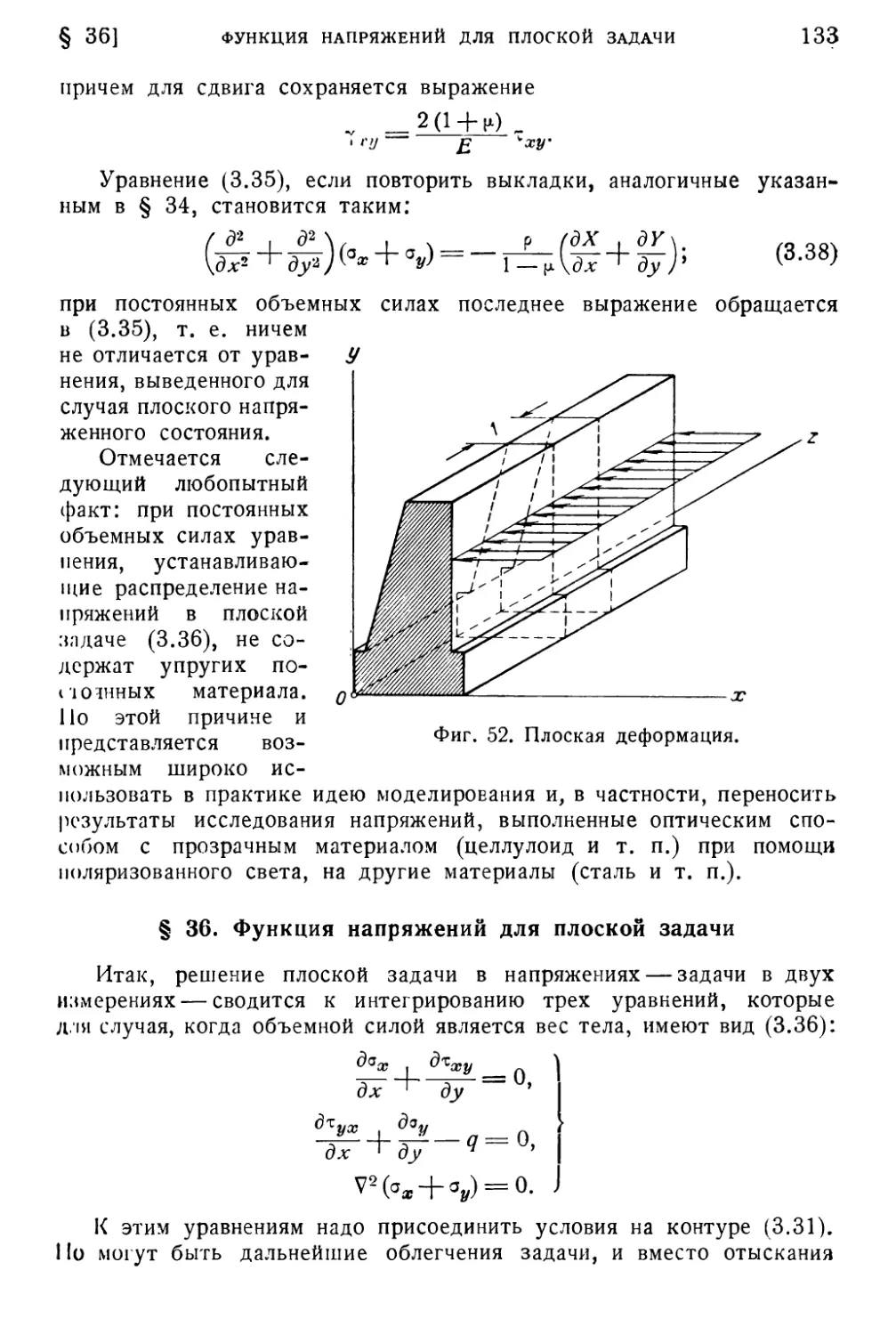
§ 35. Плоская деформация 132
§ 36. Функция напряжений для плоской задачи 133
§ 37. Плоская задача в полярных координатах 136
§ 38. Симметричное относительно оси распределение напряжений 138
§ 39. Сведения о развитии плоской задачи теории упругости за
советский период 139
Г. Другой частный случай — тела вращения с симметричным
относительно оси распределением напряжений 141
§ 40. Основные уравнения 141
§ 41. Решение задачи в перемещениях 143
§ 42. Решение задачи в напряжениях 144
§ 43. Функция напряжений при осесимметричной деформации . . 145
§ 44. Исторические замечания, касающиеся функций напряжений
в трехмерной задаче теории упругости 146
Глава IV. Простейшие задачи теории упругости 149
§ 45. Задачи о чистом изгибе и чистом кручении 149
§ 46. Пример решения задачи способом смягчения граничных
условий (изгиб консоли равномерно распределенной нагрузкой) 152
§ 47. Примеры для самостоятельных упражнений 158
§ 48. Пример решения задачи обратным методом 165
§ 49. Примеры для самостоятельных упражнений на
использование функций напряжений 167
§ 50. Другой вариант решения задачи об изгибе консоли .... 167
§ 51. Использование тригонометрических рядов для функций
напряжений 172
§ 52. Основные результаты исследований некоторых частных
случаев нагружения балок-стенок 173
§ 53. Примеры решений задач в полярных координатах. Задача
X. С. Головина 178
§ 54. Задачи А. В. Гадолина и Б. Г. Галеркина 182
§ 55. Примеры для самостоятельных упражнений 185
§ 56. Примеры для самостоятельных упражнений на
использование функции напряжений (в полярных координатах) .... 185
§ 57. Полярно-симметричная деформация толстостенного
сферического сосуда 194

ОГЛАВЛЕНИЕ
5
Глава V. Классические задачи теории упругости (упругая
полуплоскость, упругое полупространство) 198
§ 58. Сила, действующая на острие клина 198
§ 59. Сосредоточенная сила, приложенная к точке прямолинейного
края полубесконечной пластинки 200
§ 60. Деформация полубесконечной пластинки от
сосредоточенной силы 203
§ 61. Прогибы прямолинейного края полубесконечной пластинки
при частных видах загружения 204
§ 62. Влияние круглого отверстия (ослабления) на распределение
напряжений в растягиваемой пластинке 207
§ 63. Сосредоточенная сила, действующая на плоскость,
ограничивающую полубесконечное тело 210
§ 64. Частные случаи загрузки «упругого полупространства» . . 214
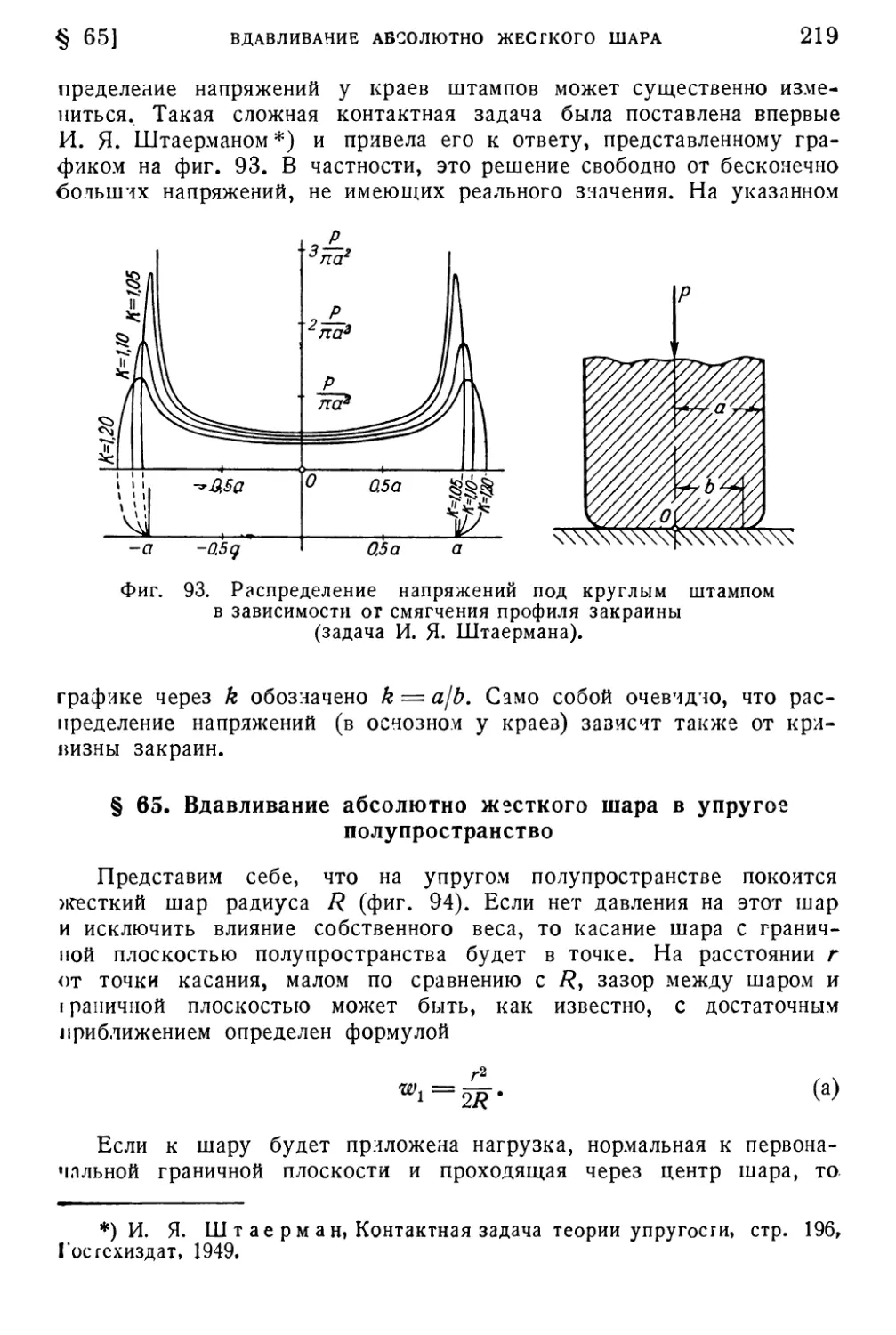
§ 65. Вдавливание абсолютно жесткого шара в упругое
полупространство 219
§ 66. Взаимное давление двух соприкасающихся сферических
тел (упругое смятие шаров) 222
Глава VI. Продолжение (задачи упругого кручения, вариацион-
ные методы в теории упругости) 225
§ 67. Кручение некруглых сечений. Задача Сен-Венана 225
§ 68. Кручение эллиптического сечения 230
§ 69. Депланация эллиптического сечения при его кручении . . . 231
§ 70. Кручение сечения в виде узкого прямоугольника 233
§ 71. Депланация при кручении сечения в виде узкого
прямоугольника и тонкостенного сечения открытого профиля . . 234
§ 72. Кручение тонкостенного замкнутого сечения 236
§ 73. Понятие о стесненном кручении 239
§ 74. Разложение тензорного поля напряжений на основное и
корректирующее (метод П. Ф. Папковича) 243
§ 75. Напряженное состояние упругого параллелепипеда при
заданных нагрузках на его гранях (задача М. М. Филоненко-
Бородича) 246
§ 76. Замечания по состоянию динамической теории упругости . 253
Глава VII. Некоторые задачи прикладной теории упругости . . 255
§ 77. Общая характеристика решения задач в прикладной теории
упругости и пластичности 255
§ 78. Изгиб плоской пластинки. Основные определения и гипотезы 257
§ 79. Вывод дифференциального уравнения упругой поверхности
пластинки 260
§ 80. План решения задачи по исследованию изгиба пластинок.
Условия на опорном контуре 265
§ 81. Пример—эллиптическая пластинка, защемленная по контуру 267
§ 82. Пример—свободно-опертая прямоугольная пластинка. . . 269
§ 83. Другая форма записи для напряжений и граничных
условий (приведение напряжений, параллельных срединной
плоскости, к статически эквивалентным им изгибающим и
крутящим моментам) 274
§ 84. Общее решение для прямоугольной пластинки 277
§ 85. Замечания о других решениях 278
§ 86. Круглая пластинка 279
§ 87. Изгиб пластинки под совместным действием поперечных
нагрузок и сил в ее срединной плоскости 281

6
ОГЛАВЛЕНИЕ
§ 88. Устойчивость прямоугольной пластинки,
свободно-опертой по четырем сторонам и сжатой в одном направлении . 286
§ 89. Всестороннее сжатие прямоугольной пластинки 287
§ 90. Исторические сведения о развитии теории пластинок . . . 288
§ 91. Стесненное кручение стержня эллиптического сечения . . . 290
§ 92. Сложное сопротивление тонких и тонкостенных стержней 293
§ 93. Продолжение: определение координат центра жесткости . . 297
§ 94. Основные результаты . теории стесненного кручения по
В. 3. Власову 298
§ 95. Аналогия задачи о стесненном кручении тонкостенного
стержня с продольно-поперечным изгибом балки 301
§ 96. Сведения о состоянии теории тонкостенных стержней . . 302
Глава VIII Основные уравнения теории пластичности 304
§ 97. Активная и пассивная деформации. Нелинейное упругое
тело и пластическое тело 304
§ 98. Связь напряжений с компонентами деформации за пределом
упругости при активной деформации 307
§ 99. Различные варианты начертания связи обобщенного
напряжения с обобщенной деформацией 311
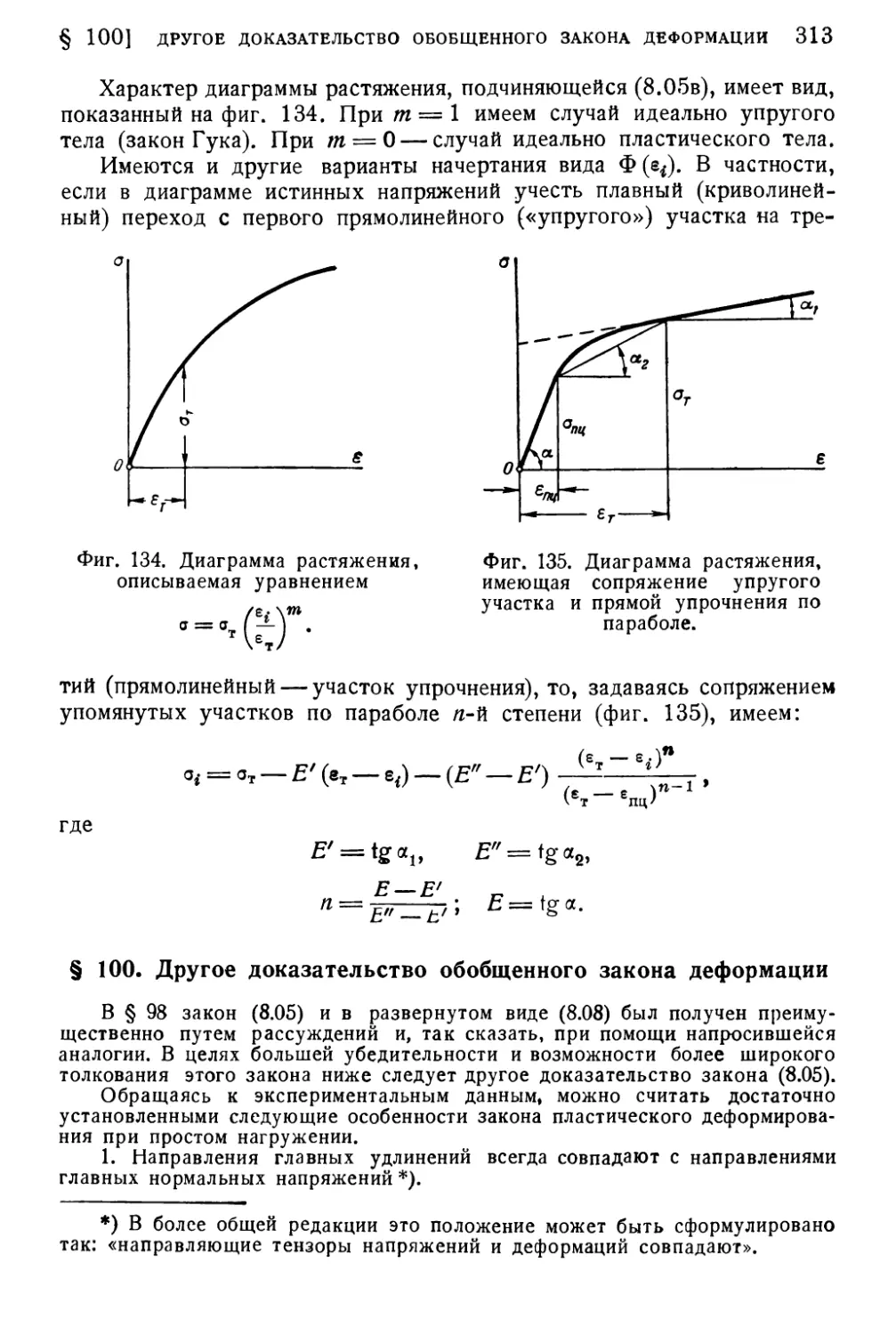
§ 100. Другое доказательство обобщенного закона деформации . 313
§ 101. Теорема А. А. Ильюшина о простом нагружении 315
§ 102. Теорема о разгрузке 316
§ 103. Иная редакция законов упруго-пластических деформаций 317
§ 104. Частный случай — идеально пластическое тело 320
§ 105. Основные уравнения механики упруго-пластических
деформаций твердого тела 322
§ 106. Частный случай — плоская задача, идеально пластический
материал 324
§ 107. Замечания, касающиеся установления связи между
напряжениями и деформациями в нелинейной теории упругости
и в теории пластичности 325
Глава IX. Простейшие задачи теории пластичности 328
§ 108. Чистый изгиб 328
§ 109. Чистое кручение 332
§ 110. Осесимметричное упруго-пластическое состояние
толстостенной трубы 334
§ 111. Продолжение: учет упрочнения материала 336
§ 112. Осесимметричные пластические деформации равномерно
вращающегося диска 340
§ 113. Полярно-симметричное упруго-пластическое состояние
шарового сосуда 342
§ 114. Примеры решения задач полуобратным методом 344
§ 115. Состояние теории пластичности в СССР 347
Глава X. Основные результаты решения некоторых згдач
прикладной теории пластичности 355
§ 116. Сбщие замечания по главе. Несущая способность сечения.
Несущая способность системы 355
§ 117. Несущая способность круглого цилиндрического стержня,
подверженного растяжению и кручению 358
§ 118. Несущая способность сечения в виде узкого
прямоугольника 362
§ 119. Пластическое состояние при нестесненном кручении
некруглых сечений 363

ОГЛАВЛЕНИЕ
7
§ 120. Осесимметричный упруго-пластический изгиб круговой
пластинки. Задачи В. В. Соколовского 367
§ 121. Изгиб и кручение (стесненное) тонкостенных стержней за
пределом упругости 369
§ 122. Давление пластической среды на жесткий штамп 373
§ 123. Условия предельного равновесия сыпучей среды. Задачи
В. В. Соколовского 374
§ 124. Замечания к теории пластического течения 378
§ 125. К истории зарождения динамической теории пластичности 381
Глава XI. Сближение теории упругости, строительной
механики, теории пластичности и реологии 382
§ 126. Общие соображения 382
§ 127. Синтез методов теории упругости и строительной механики.
Задачи В. 3. Власова, М. М. Филоненко-Бородича и др. . . 383
§ 128. Синтез методов теории пластичности и строительной
механики. Задачи А. А. Гвоздева и др 394
§ 129. Синтез методов теории упругости и пластичности (по
А. А. Ильюшину) 398
§ 130. Процесс деформации во времени (понятие о реологическом
уравнении состояния) 401
§ 131. Послесловие 406
Цитированная литература и источники 409
Именной указатель 415
Предметный указатель 418

ПРЕДИСЛОВИЕ
В советских условиях механика деформируемого тела развивалась,
как и все другие науки, в тесной связи с практикой. Это
обстоятельство имело своим следствием исключительные успехи в области теории
упругости, теории пластичности и строительной механики. Из
практики грандиозного строительства в СССР эти отрасли механики
деформируемого тела черпали источники для своего развития, в практику
несли они свои достижения и там, на практике, имели возможность
проверять достоверность своих открытий.
В этом смысле практика социалистического строительства для
механики деформируемого тела была и остается грандиозной лабораторией.
Научные достижения последних лет нашли отражение в
обширной научной и учебной литературе, выделяющейся принципиальностью,
глубиной анализа и широкими горизонтами использования науки
в различных областях нашего строительства.
Достаточно указать на отмеченные Сталинскими премиями
выдающиеся исследования в различных областях механики деформируемого
тела, а именно: по вопросам теории упругости — акад. Б. Г. Галер-
кина, акад. Л. С. Лейбензона, акад. Н. И. Мусхелишвили, члена-
корреспондента АН СССР, проф. П. Ф. Папковича; по вопросам
теории пластичности — члена-корреспондента АН СССР, проф. А. А.
Ильюшина, члена-корреспондента АН СССР, проф. В. В.
Соколовского, действительного члена АН Узбекской ССР, проф. X. А. Рахма-
тулина; по специальным вопросам теории упругости—проф. В. 3.
Власова, проф. С. Г. Лехницкого, и на многие другие, чтобы иметь
представление о большом идейном богатстве и практическом значении
советской науки в указанных выше областях.
В приобщении студенческих и инженерных масс к теории
упругости большое значение имели и продолжают иметь замечательные
учебники и монографии заслуженного деятеля науки и техники,
проф. М. М. Филоненко-Бородича, действительного члена АН УССР,
проф. С. В. Серенсена, действительного члена АА СССР, проф.
Б. Н. Жемочкина, проф. А. И. Лурье, члена-корреспондента
АН УССР, проф. И. Я. Штаермана; монографии по нелинейным
проблемам теории упругости и пластичности проф. В. В. Новожилова,
проф. Л. М. Качанова и др.

ПРЕДИСЛОВИЕ
9
В трудах перечисленных и многих других ученых *), обогативших
советскую механику деформируемого тела, читатель найдет
исчерпывающие ответы по многим вопросам, которые у него возникнут
в его практической инженерной деятельности.
Задачи предлагаемой вниманию читателя книги сравнительно
скромны. Настоящая книга является учебным пособием, составленным
применительно к утвержденной МВО СССР программе курса «Теория
упругости и пластичности» для тех втузов, где на преподавание
указанного курса в настоящее время отводится 50—70 часов.
Этот курс изучается студентами втузов на старших курсах и
в некотором смысле является для них завершающим в цикле
технических дисциплин (сопротивление материалов, строительная механика,
детали машин), затрагивающих вообще вопросы расчета на прочность
и вычисления деформаций различных инженерных конструкций.
Естественно, что при изучении теории упругости студенты втузов
обычно проявляют большой интерес не только к методам и
принципам этой науки, но и к таким вопросам, как оценка в свете
строгих решений теории упругости тех результатов, которые им известны
ранее из курса сопротивления материалов; их интересуют также новые
результаты для тех задач, постановка которых в элементарных
теориях вообще исключается; они заинтересованы в возможностях
эффективного кооперирования теории упругости с известными им ранее
дисциплинами, родственными с теорией упругости (строительная
механика и др.), наконец, они заинтересованы в правильной ориентации
в достижениях механики деформируемого тела, касающихся и тех
вопросов, которые лежат за пределами учебных программ (возможно
и за пределами их математической подготовки в настоящее время), но с
которыми они могут встретиться в будущем; в этом случае им
необходима библиография или указание на источники, где последняя имеется.
В равной степени указанные сейчас вопросы интересуют
инженеров, которые в свое время на школьной скамье курса теории
упругости не изучали (в учебных планах многих втузов до последнего
времени теория упругости значилась в числе факультативных
дисциплин или полностью отсутствовала).
Вообще претензии указанного круга читателей к курсу теории
упругости, а также и к теории пластичности большие и далеко не
соответствуют времени, предоставляемому на эти дисциплины
современными учебными планами. Вместе с тем требуется освещение
основ теории упругости и пластичности в наиболее простой и
доходчивой форме, не отягченной сложными математическими выкладками.
Удовлетворить всем перечисленным целям в небольшой книге,
конечно, невозможно, но в значительной степени эта задача
облегчается, если такая книга сможет подготовить читателя к
самостоятельному изучению капитальных сочинений и специальных исследований
*) Точное наименование трудов указано в конце книги.

10
ПРЕДИСЛОВИЕ
по теории упругости и пластичности, но не будет затрагивать
последние, когда исследования выходят далеко за пределы программы
краткого курса. Эта основная методическая мысль и руководила
автором при подборе материала книги.
Для расширения кругозора читателя (не обременяемого, однако,
необходимостью следить за всеми выводами) в настоящем учебном
пособии сообщаются также основные результаты решений некоторых
специальных задач с краткой характеристикой метода и идей, принятых
авторами решений; это относится к ряду ценных решений последнего
периода, полученных в СССР.
Тем же целям расширения кругозора служат и помещенные
в книге краткие обзоры современного состояния отдельных вопросов
теории упругости и пластичности, которые, конечно, не претендуют
на полноту.
Приведенные в книге параграфы с заголовком «Примеры для
самостоятельных упражнений» могут дать студентам условия задач
для практических занятий по теории упругости (в аудитории) или
темы их домашних заданий.
В книге приняты те обозначения, которые известны читателю по
курсам сопротивления материалов и строительной механики; они
соответствуют стандарту. Так как в теории упругости наиболее
компактными оказываются записи при других обозначениях, то они
также применяются для сопоставления с обозначениями, привычными
читателю.
Материал, набранный петитом, может быть при первом чтении,
а также и при очень сжатом курсе опущен без нарушения связности
изложения всего остального материала.
Ссылки в тексте на литературу, приведенную в конце книги,
отмечаются номером, стоящим в квадратных скобках.
При подготовке к печати настоящей книги автор после
существенной переработки использовал свою книгу «Введение в теорию
упругости и пластичности» (Стройиздат, 1950), значительно пополнив
ее новым материалом. Другие цели, поставленные при составлении
настоящей книги, побудили автора дать ей иное название.
Автор выражает глубокую признательность И. И. Гольденблату,
1^. С. Завриеву, В. В. Соколовскому, М. М. Филоненко-Бородичу
и И. Я. Штаерману за сделанные ими по предыдущему изданию или
по рукописи настоящего издания книги ценные замечания, учтенные
автором.
Автор

ГЛАВА I
ВВЕДЕНИЕ
§ 1. Теория упругости и смежные науки
Теория упругости является ветвью современной механики
твердого деформируемого тела, которую в свою очередь можно
рассматривать как один из разделов механики в широком смысле этого слова
и классической — в частности*
Понятие о классической теоретической механике обычно связы-
иают с аналитически оформленной наукой, рассматривающей одну из
простейших форм движения материи — механическое движение
материальных точек, их систем, абсолютно твердого тела, равно как и
идеальной жидкости и газа, но в рамках классических концепций и
абстракций.
Абстракции и понятия классической механики (материальная
точка, абсолютно твердое тело, идеальная жидкость и газ) не являются,
конечно, формальными изобретениями человеческой мысли. В период,
когда создавались эти абстракции (конец XVII и начало XVIII века),
они определенным образом, достаточным для практических задач того
мремени, отражали простейшие, наиболее элементарные свойства
реальных материальных тел. Но и в настоящее время эти абстракции
полностью сохранили свое значение для большого круга задач.
«Мышление, восходя от конкретного к абстрактному, не отходит —
если оно правильное,.,—от истины, а подходит к ней.
Абстракция материи, закона природы, абстракция стоимости и т. д.,
одним словом, все научные (правильные, серьезные, не вздорные)
пбстракции отражают природу глубже, вернее, полнее» (В. И. Ленин,
Философские тетради) *).
Под давлением запросов технической практики и естествознания
и результате тесной связи с экспериментом в течение XIX века по-
лучмют мощное развитие специальные разделы механики, которые
/I in с коих нужд требовали новых абстрактных моделей, но более
насыщенных реальными свойствами твердых тел, жидкостей (например,
i "'фидимамика вязкой жидкости) и газов и потому более пригодных дая
*) Госполитиздат, 1947, стр. 146.

12
ВВЕДЕНИЕ
[ГЛ. I
теоретического охвата объективных законов движения реальных тел
в тех новых условиях, которые были специфичны для новой техники.
Методология всех разделов механики, как и всякой науки,
базируется на гениальном положении, высказанном В. И. Лениным:
«От живого созерцания к абстрактному мышлению и от него к
практике— таков диалектический путь познания истины, познания
объективной реальности» (В. И. Ленин, Философские тетради)*).
Механика в современном состоянии представляет широкий
комплекс научных дисциплин, многие из которых фактически выделились
из общей механики.
Более того, для некоторых новых разделов механики, развитие
которых относится к последнему периоду и связано в основном с
работами советских ученых и инженеров (теория пластичности и др.),
прежняя граница между механикой в узком смысле и физикой
становится условной.
Эти отпочковавшиеся от классической механики отрасли знаний
получили наименование «механических дисциплин», их совокупность
иногда именуют практической, или прикладной, механикой, желая
этим названием подчеркнуть их прикладной характер в связи с
обслуживанием определенной практической отрасли.
Рассмотрим комплекс механических дисциплин практической
механики, имеющих отношение к расчету сооружений и машин на
прочность, и определим в этом комплексе место теории упругости и
пластичности.
а) О реологии. Наукой, устанавливающей общие законы
образования и развития во времени деформации любого вещества от
различных причин в различных термодинамических и физико-химических
условиях, является реология**) (наука о течении вещества).
В указанной выше формулировке вещество понимается именно
любым: оно может быть твердым или жидким, упругим, пластичным,
вязким и т. п. Причины для деформации также предполагаются
самыми разнообразными, как то: статические или динамические
нагрузки; изменения, происходящие в параметрах, характеризующих
как внешнюю среду (температурное поле), так и самое вещество,
и т. д. и т. п.
Инженера могут интересовать деформации также в разное время,
как то: вслед за приложением нагрузки или продолжительное время
спустя, когда полностью или частично удалены внешние причины, как
в состоянии равновесия, так и в случае движения, и т. д.
Иначе говоря, реология должна отвечать на вопрос: каковы
деформации и напряжения в данной точке заданного тела
*) Госполитиздат, 1947, стр. 146—147.
**) Перемещениями, при которых деформации тела отсутствуют
(например, переносом из одного положения в другое как абсолютно твердого тела
и т. п.), в реологии не интересуются.

§ 1]
ТЕОРИЯ УПРУГОСТИ И СМЕЖНЫЕ НАУКИ
13
в определенный момент времена при известных параметрах
внешнего воздействия и известной для последнего истории его в прошлом.
По существу перечисленных выше задач реология есть но-
ный отдел механики (см. § 130), рассматривающий движение
к относительно широком смысле. Сложность решения задач в
указанной выше общей формулировке должна быть очевидна нашему
читателю, знакомому с современными «прочностными» расчетами
сооружений, излагаемыми в курсах сопротивления материалов, где
также рассматривались напряжения и деформации твердых тел.
В этих расчетах на прочность принимались различные
идеализированные схемы самого сооружения; многие обстоятельства,
влияющие на напряжения или деформацию материала, исключались при этом
вовсе (отступление от закона Гука, явление ползучести, релаксации
и т. п.), и все же расчет часто оставался трудоемким. По этой
причине на данном этапе развития реологии представляется
целесообразным несколько отступить от указанной выше слишком общей
формулировки проблем этой науки, т. е. сузить задачи, схематизировать
изучаемую картину и т. д. Поэтому в собственно реологии, если
считать эту ветвь механики оформившейся в самостоятельную науку,
получены пока немногие, но важные результаты. Пока сделаны лишь
попытки установить взаимно однозначные зависимости между
напряжениями и деформациями для системы классических тел
(идеально пластическое, идеально вязкое и т. п.), играющие в этой
науке ту же важную роль, как, например, в сопротивлении материалов
закон Гука.
Некоторое абстрагирование реального тела применительно к данным
конкретным условиям, т. е. сознательное отбрасывание его
второстепенных свойств и сохранение за ним лишь основных качеств, вполне
допустимо для целей инженерной практики. Иначе говоря, в
практических расчетах неизбежно прибегают к тем или иным допущениям
или гипотезам, если в общем они подтверждаются опытом.
Более того, метод абстрагирования в указанном выше смысле
совершенно необходим и, как показывает история науки и техники, он
является одним из условий прогресса научного познания.
Но это, конечно, не означает культивирования в реологии
упрощенного взгляда на природу, на материю.
Метод абстрагирования должен учитывать бесконечную сложность
природы, ее неисчерпаемость. Познание никогда с абсолютной
полнотой не сможет исчерпать объекта природы, хотя оно будет все
более и более приближаться к этому.
«Мысль человека бесконечно углубляется от явления к сущности,
от сущности первого, так сказать, порядка к сущности второго
порядка и т. д. без конца» *).
*) В. И» Л е н и н, Философские тетради, стр. 237, Госполитиздат, 1947.

14
ВВЕДЕНИЕ
[ГЛ. I
Именно так, по мере накопления опытных данных и результатов
теоретических исследований, должно быть и в реологии. Важно
установить границы для практического применения той или иной
идеализированной схемы, того или иного комплекса гипотез.
б) Теория упругости. Одной из таких идеализации твердого тела
является приписываемое ему свойство идеальной упругости. Это
свойство и лежит в основе той ветви механики твердого деформируемого
тела, которая носит название теории упругости.
Идеальная упругость, как известно читателю, есть способность
тела, получившего деформацию, после устранения причин, ее
вызвавших, полностью восстановить свою первоначальную форму. Иначе
говоря, работа, затраченная внешними силами на перемещениях точек
их приложения, принимается телом в обратимой форме, а именно,
в форме накопления в теле упругой энергии^ равной по величине
работе внешних сил.
Таким образом, идеально упругое тело осуществляет первый
закон термодинамики о сохранении энергии в изолированной
системе.
Способность идеально упругого тела не оставлять на себе
никакого следа от его прошлых нагружений («забывать все пережитое
им ранее») приводит к тому, что такое тело всегда имеет форму,
зависящую лишь от тех нагрузок, которые в данный момент
действуют на тело, и не зависящую от того, как эти нагрузки
постепенно «росли от нуля», т. е. каковы были нагрузки в
предшествующие моменты времени *).
Вполне очевидно, какие существенные облегчения вносит в
расчеты предположение об идеальной упругости тела: отпадают вопросы
влияния «наследственности» (т. е. влияния на деформацию в данное
мгновение помимо действующих сил также и тех нагрузок, которые
когда-то в прошлом оказывали свое влияние на деформации и
напряжения), влияния последействия (временного отставания деформаций
от изменений нагрузки), релаксации (непрерывного спадания
напряжений при постоянной деформации) и т. д.
Упругое состояние твердого тела характеризуется
тем, что для каждой температуры тела независимо от
времени существует взаимно однозначная
зависимость между напряжениями и деформациями. Эта
зависимость обычно является линейкой и, как указывалось в курсе
сопротивления материалов, носит название закона Гука.
*) Если фактор времени (имеется в виду длительное время)j—
основное в реологии, то е г о отсутствие — основное в классической
теории упругости. Случаи быстрого нарастания нагрузки, связанные с
приобретением частицами тела существенных ускорений, в теории упругости
также изучаются и составляют так называемые динамические задачи теории
упругости; эти задачи в настоящей книге не рассматриваются.

§ и
ТЕОРИЯ УПРУГОСТИ И СМЕЖНЫЕ НАУКИ
15
Все строительные материалы в известной степени обладают
свойством упругости; если внешние силы, вызывающие деформацию
элемента конструкции, не превосходят определенной границы, то в
указанных границах можно описывать законы деформации материала и
конструкции в целом, исходя из предпосылки об упругом теле, чем
и занимается теория упругости.
Свойством упругости обладают не только строительные материалы,
им обладают жидкие тела и газы. Упругость есть основное свойство
мсех тел природы или во всяком случае их большинства.
Теория упругости обычно считается отделом математической
физики, ко она может рассматриваться и как ветвь реологии, самая
простая, но вместе с тем и основная.
Итак, теория упругости изучает действие сил на
упругие тела и определяет возникающие при этом
напряжения и деформации как в состоянии
равновесия, так и в состоянии движения*).
Как известно читателю, те же задачи стоят и в науке о
сопротивлении материалов, но имеется существенное и принципиальное
различие. Различие прежде всего заключается в исходных
предпосылках, в методах решения задач и в диапазоне последних.
Исходные предпосылки в теории сопротивления материалов
(например, так называемый закон плоских сечений) более или менее
оправдываются опытом в том случае, когда исследуемое тело имеет
форму стержня, бруса.
Поэтому сопротивление материалов не может решать задачи на
отыскание напряженного и деформированного состояний тела, если
(то форма отлична от обычного стержня и представляет собой,
например, пластинку, оболочку, массив и т. п.
Последняя задача (о напряженном состоянии массива) и ей подоо-
пые вообще не разрешены методами сопротивления материалов ни
точно, ни приближенно. Такие задачи (см. § 63) могут быть решены
только с позиций теории упругости, основные предпосылки которой
отличаются достаточной широтой и не ограничиваются такой формой
тола, как стержень.
Принятию более общих предпосылок в теории упругости соот-
истствуют и более общие методы решения задач и относительная
строгость решения по сравнению с методами сопротивления
материалом. Теория упругости ставит своей целью по возможности точное
решение поставленной задачи, хотя это не исключает в теории упру-
юсти наличия различных приближенных методов решения задачи.
*) Здесь движение понимается в узком — механическом — смысле,
ни пример, в смысле упругих колебаний и подобных малых перемещений,
■'миющихся во времени, но меняющихся, конечно, не «реологически». Иначе
iопори, при этих движениях физические и прочие свойства материала во
мремсни не изменяются.

16
ВВЕДЕНИЕ
[ГЛ. I
Выводы теории упругости широко используются в
многочисленных областях техники. В сейсмологии по результатам изучения
распространения упругих волн в земной коре вычисляют координаты
очага землетрясения. Инженеры-строители используют выводы и
методы теории упругости для вычисления напряжений и деформаций
в инженерных сооружениях. Инженеры-механики занимаются теми же
вопросами в машиностроении. Геологи используют теорию упругости
для определения давления горных пород. Физики широко
использовали теорию упругости при разработке волновой теории света
и т. д. и т. п.
Наконец, решение целого ряда задач газодинамики и
аэродинамики, не имеющих прямого отношения к расчету на прочность,
сводится к рассмотрению уравнений, общих с уравнениями теории
упругости.
Инженеру любой специальности предоставляется широкое поле
для применения теории упругости. Следует, однако, заменить, что
точное решение многих задач методами теории упругости
наталкивается на чрезвычайно сложные препятствия чисто математического
порядка.
в) Математическая и прикладная теории упругости.
Сопротивление материалов. По этой причине наряду с развитием
математической теории упругости, занимающейся изысканием способов
точного решения задач механики деформируемого тела, параллельно
идет развитие прикладной теории упругости, в которой, кроме
предпосылки об идеальной упругости материала, вводятся некоторые
дополнительные гипотезы и упрощения относительно характера
перемещений, что позволяет при решении многих задач исходить не из
полной системы уравнений теории упругости *).
Так, при расчете на изгиб тонких плит и оболочек (см. § 77),
т. е. в так называемых двухмерных задачах теории упругости (здесь
объектом изучения является тело, у которого два размера одного
порядка, а третий размер — толщина — мал по сравнению с первыми),
вводят гипотезу о прямолинейном элементе пластинки (или оболочки),
нормальном к срединной плоскости (или срединной поверхности) до
деформации, который остается прямым и нормальным к искривленной
*) Заметим, что граница между классической и прикладной теориями
упругости весьма условна, так как в ряде задач практики исключительные
трудности непосредственного интегрирования уравнений теории упругости
(т. е. получения точного решения) вынуждают часто обращаться к
различным приближенным методам.
Если эти приближенные методы относятся к решению только самих
уравнений классической теории упругости, т. е. при этом не привлекаются
какие-либо новые физические или геометрические гипотезы, то такие методы
обычно относят к классической теории упругости (см. §§ 74, 75).
Если же приближенное решение задачи связано с принятием
специальных для данной задачи допущений геометрического характера, то такое
решение относят к прикладной теории упругости (см. главу VII).

§ 1]
ТЕОРИЯ УПРУГОСТИ И СМЕЖНЫЕ НАУКИ
17
плоскости (поверхности) после деформации (аналогично гипотезе
плоских сечений в курсе сопротивления материалов).
Характерным представителем такого прикладного направления
теории упругости является сопротивление материалов] в этой науке,
как правило, рассматриваются одномерные задачи прикладной
теории упругости. (Изучаемые в сопротивлении материалов тела —
стержни — ивдеют два размера: высоту и ширину поперечного
сечения, малые по сравнению с третьим, т. е. длиной.)
Заметим, однако, что одномерные задачи прикладной теории
упругости, исследуемые в сопротивлении материалов, изучаются также
и в математической теории упругости, где приводятся более строгие
решения без привлечения тех геометрических гипотез (закон
плоскости и др.), которые иногда оказываются и слишком грубыми
(например, в случае высоких балок).
Указанные выше наименования «одномерные и двухмерные задачи» не
обязательно связывать с соотношениями в размерах тела по трем
характерным направлениям. Чаще всего эти наименования связываются или с
количеством тех основных (определяющих) функций в данной задаче,
посредством которых легко определить все интересующие нас величины в той же
задаче (напряжения, деформации и т. п.), или с количеством
аргументов, от которых зависят эти функции.
Так, например, в случае обычной балки, изучаемой в сопротивлении
материалов (когда ее длина в пять и более раз превышает высоту),
достаточно знать только уравнение изогнутой оси стержня (функция одного
аргумента — размера вдоль оси стержня), чтобы затем путем
дифференцирования найти все остальные величины (девиации, изгибающие моменты,
поперечные силы).
Именно в этом смысле задачи о брусе и вообще о стержневых системах
в теории упругости называются одномерными задачами. По тем же
соображениям пластинка, для которой такой определяющей функцией окажется
уравнение ее изогнутой срединной поверхности (см. § 79), являющееся
функцией от двух аргументов, считается двухмерной задачей теории
упругости.
г) Линейная и нелинейная теории упругости. Теория
пластичности. В основе классической теории упругости лежит представление
об упругом и линейно деформируемом теле. Такое тело наделяется
наиболее простой, а именно, линейной зависимостью между
слагающими деформации и возникающими при этом напряжениями
(обобщенный закон Гука). Последнее в свою очередь означает, что
если внешние силы, одновременно и статически прикладываемые
к упругому телу, возрастают или убывают в каком-либо известном
отношении, то в той же пропорции возрастают или убывают
напряжения, деформации и перемещения (прогибы, девиации и т. п.)
и .мобой точке тела. Диаграмма растяжения—сжатия для такого
материала в обычных координатах «напряжение — деформация» пред-
ст.чиляется прямой наклонной линией, выходящей из начала координат.
В теории упругости (см. § 6) под слагающими деформации в точке тела
понимают относительные удлинения и относительные сдвиги в окрестности
2 Зак. 3880. Н. И. Безухов

18
ВВЕДЕНИЕ
[гл. i
этой точки. Иначе говоря, удлинения и сдвиги являются характеристиками
деформации в бесконечно малом объеме тела.
Однако в инженерной практике прогибы и девиации тела также
называют деформацией; эти последние (линейные и угловые перемещения)
будем считать характеристиками деформации тела в
целом [74].
Если материал не подчиняется закону Гука (даже при малых
напряжениях) или рассматриваемое состояние деформации перешло за
предельное упругое и, стало быть, в изучаемом диапазоне
деформаций диаграмма растяжения материала представляется явно
выраженным отрезком кривой ОАВ (фиг. 1, я), то в этих случаях в качестве
физического закона надлежит принять уравнение упомянутой кривой*
т. е. о=/(е).
Фиг. 1. Диаграмма растяжения для упругого материала, но не
подчиняющегося закону Гука (слева). Диаграмма растяжения
для неупругого материала (справа).
Представим себе, что процесс медленной разгрузки происходит,
следуя той же кривой ВАО> причем в обратном порядке проходятся
те же состояния, какие осуществлялись при нагрузке по ОАВ. Если
график процесса вернется в начальную точку О, и мы не сможем
указать никаких изменений, т. е. процесс ОАВ оказывается
обратимым, то такое тело будем называть нелинейно-упругим.
Теория, устанавливающая законы образования деформаций в таком
теле, может быть названа нелинейной теорией упругости *).
Однако снятию нагрузки, как известно, для большинства
строительных материалов соответствует так называемая «прямая раз*
грузки» ВС (фиг. 1, <5), в результате чего тело не приходит в
исходное положение: имеют место остаточные, иначе говоря, пластине*
ские деформации.
*) К кругу задач нелинейной теории упругости относят также и те
задачи, в которых перемещения тела не могут считаться малыми, хотя в фи*
зическом отношении материал может являться и линейно-упругим, т. е.
подчиняться закону Гука.

§ 1] ТЕОРИЯ УПРУГОСТИ И СМЕЖНЫЕ НАУКИ 19
Известно, что при последующем нагружении того же материала
по деформации практически будут в начале следовать линейному
млкону (если игнорировать образование петли упругого гистерезиса),
и отступление от этого закона произойдет лишь при напряжениях,
превышающих те, которые были в теле при первом нагружении.
Вообще при пластическом состоянии в каждый
данный момент времени и для данной температуры
связь между напряжениями и деформациями стан о-
пится взаимно однозначной, если известны все пред*
шествующие (в крайнем случае одно — последнее)
напряженные и деформированные его состояния и
соответствующие значения температуры.
Наукой, устанавливающей общие законы образования пластических
деформаций и возникающих на всех стадиях пластического
деформирования напряжений, является теория пластичности, имеющая
тесную связь с нелинейной теорией упругости. Эта связь, как будет
показано в § 97, заключается в том, что законы деформаций упруго-
пластического тела при так называемом «простом нагружении» могут
Ныть описаны с помощью уравнений нелинейного упругого тела
с идентичной диаграммой растяжения.
Процесс нагружения тела считается простым, когда внешние
силы (если их несколько) от начала их приложения (непременно все)
возрастают, сохраняя между собой постоянное отношение, т. е.
изменяются пропорционально их общему параметру (подробно о простом
нагружении см. в § 101).
д) Математическая и прикладная теории пластичности. Как
п в теории упругости наряду со строгой теорией пластических
деформаций— назовем ее математической теорией пластичности —
параллельно идет разработка упрощенных методов расчета путем
ниедения дополнительных гипотез геометрического (например, закона
плоскости) или физического характера (например, наделение тела
смойствами идеальной пластичности). Круг задач по вопросам
пластичности, решаемых в последнем направлении, составляет прикладную
теорию пластичности.
Простейшие задачи теории пластических деформаций, изучаемые
обычно в курсе сопротивления материалов (упруго-пластический изгиб,
пластическое кручение бруса круглого сечения), характерны дляэ того
прикладного направления.
е) Теория упругости и строительная механика. Если
строительную механику, иначе называемую теорией сооружений,
понимать в широком смысле как комплекс всех технических дисциплин,
предназначенных для определения напряжений и деформаций во всех
сооружениях, создаваемых инженером (здания, мосты, машины,
механизмы и т. д.) независимо от их конструктивной формы (брус,
пластинка, оболочка, неограниченный упругий массив и т. п.), то
Теорию упругости вместе с сопротивлением материалов и строительной
2*

20
ВВЕДЕНИЕ
[ГЛ. I

§ 2] ОСНОВНЫЕ ГИПОТЕЗЫ И ПРИНЦИПЫ ТЕОРИИ УПРУГОСТИ 21
механикой в узком смысле (т. е. строительной механикой стержневых
систем, иначе — статикой и динамикой сооружений) можно отнести
именно к такой теории сооружений. Впрочем,
инженеры-строители давно считают, что теория упругости составляет один из
разделов самой популярной для них науки—именно строительной
механики.
Но суть дела не в том, куда формально отнести ту или другую
область знания, а в-том, что за последнее время отмечено сближение
теории упругости и строительной механики по существу, т. е.
проникновение методов, специфических для одной науки, в другую,
и наоборот.
Заметим, что перенесение в теорию упругости (см. § 127)
классических методов строительной механики (теории статически неопределимых
систем и др.) значительно расширило круг задач теории упругости,
оказавшихся при таком кооперировании теперь решенными, хотя и
с известной степенью приближения. От сближения с теорией
упругости обогатилась и строительная механика, получив уточненные
решения тех задач, для которых она раньше имела сравнительно
грубые ответы.
В заключение отметим, что в связи с общим развитием
сопротивления материалов, теории упругости и строительной механики в
дальнейшем, повидимому, будут стираться грани между ними. Имеется ряд
задач, которые и теперь с равным успехом можно отнести к
любой из перечисленных дисциплин (пластинки, оболочки). Даже
прежде принятые отличительные конструктивные формы изучаемых
в строительной механике объектов, как то: стержень и системы
стержней, уже не являются теперь специфическими для строительной
механики.
Строительная механика должна давать не только правила для
расчета сооружений (анализ), но и устанавливать эффективные новые
схемы сооружений любых конструктивных форм (синтез). Такие
задачи, конечно, могут быть решены только наукой, включающей весь
комплекс перечисленных выше технических дисциплин.
На фиг. 2 показаны связь и отчасти соподчинение между собой
всех названных выше технических дисциплин, имеющих отношение
к прочностному расчету инженерных сооружений.
§ 2. Основные гипотезы и принципы классической
теории упругости
Теория упругости, отличаясь от сопротивления материалов
большей строгостью в решении задач, вынуждена также прибегать к
некоторой схематизации явления, обращаться к гипотезам, хотя число
последних сводится к минимуму.
Основной предпосылкой в теории упругости, общей с
сопротивлением материалов, является так называемая гипотеза о сплош-

22
ВВЕДЕНИЕ
[гл. i
поста строения упругого тела, т. е. здесь не принимается во
внимание дискретная, атомистическая структура вещества и, тем более,
движение отдельных молекул, составляющих тело.
Совершенно очевидно, что предположение о непрерывном строении
материала, строго говоря, противоречит действительности, так как
реальные материалы всегда обладают характерной структурой, для
обнаружения которой даже не требуется микроскопа большого
увеличения (фиг. 3). Однако, так же очевидно, что попытки
математической интерпретации структуры материала в теории могут привести
Фиг. 3. Микроструктура стали и чугуна (масштаб
увеличения—100 и 200).
к результатам, слишком сложным для обычного употребления, если
такая интерпретация вообще окажется возможной (см. стр. 353).
Первые исследования по теории упругости строились, исходя из
предположения о существовании индивидуальных частиц, отделенных
друг от друга некоторым расстоянием и связанных друг с другом
силами взаимного притяжения и отталкивания, действующими даже
и при нормальной температуре и давлении и лишь изменяющими свое
значение при изменении температуры и давления. Такую теорию
упругости можно назвать дискретной теорией упругости.
Исключительные математические трудности такого изучения
вынудили отказаться впоследствии от принятия в исследованиях дискретной
схемы строения твердого тела и перейти к гипотезе *) о сплошной,
*) Из приведенных выше соображений по поводу предпосылки о
непрерывности среды совершенно очевидно, что ее трактовка как гипотезы
не совсем удачна, так как не соответствует представлению о гипотезе,
принятому в философии, физике и т. д. В дальнейшем изложении за
указанной предпосылкой и другими, ей аналогичными, сохраняется (в
условном смысле) название гипотезы.

§ 2 ОСНОВНЫЕ ГИПОТЕЗЫ И ПРИНЦИПЫ ТЕОРИИ УПРУГОСТИ 23
т. е. непрерывной среде (механика континуума). К этому также
побудило отсутствие (незнание) по тому времени многих физических
постоянных, без которых теоретическое исследование невозможно.
Следует заметить, что в теории упругости, оперируя с
непрерывной средой, мы все же для целей анализа мысленно делим тело на
частицы; однако они берутся достаточно и произвольно малыми (в
пределе бесконечно малыми), вырезаются произвольно, соседние частицы
исегда предполагаются плотно прилегающими друг к другу, и вообще
частицы лишены в известном смысле
индивидуальности.
Имеются попытки оценить степень точности результатов по
гипотезе непрерывности в зависимости от поперечных размеров зерен и
промежутков между ними. Эти попытки в конечном счете утверждают
практическую пригодность гипотезы сплошности.
Второй гипотезой, в некотором смысле примыкающей к первой,
является гипотеза о естественном ненапряженном состоянии тела;
согласно ей начальные напряжения в теле, существующие до
приложения поверхностных нагрузок, характер и величина которых зависят
от истории возникновения тела, полагаются равными нулю. Иначе
говоря, определяемые в теории упругости напряжения не являются
фактическими напряжениями в теле, а составляют лишь прирост
напряжений в рассматриваемых точках над начальными (неизвестными)
напряжениями в тех же точках.
Хотя и имеются способы экспериментального определения
упомянутых начальных напряжений методами современной теории упругости,
однако строгое решение этой задачи могла бы дать (если бы была
разработана) дискретная теория упругости, так как начальные
напряжения, будучи уравновешенными по любому произвольному сечению
тела, в пределах любого конечного объема, представляют собой
уравновешенную систему напряжений уже в пределах ничтожно малых
объемов, захватывающих небольшое число элементарных частиц
(микрообъемы).
В этом смысле дискретную теорию упругости можно
характеризовать как теорию микронапряжений^ а современную механику
континуума— как теорию макронапряжений.
Заметим, что игнорирование в технических расчетах начальных
напряжений, равно как и неучет отступлений в структуре материалов
от идеальной сплошности отчасти компенсируются тем, что
установление основных механических характеристик материала (предел упру-
тсти, предел текучести и т. д.) и связанное с ними определение
нормы допускаемых напряжений экспериментально выполняются также
6vi\ учета начальных напряжений и без учета неравномерности
заполнении веществом всего геометрического объема испытуемого образца.
Например, в опытах с простым растяжением характерное напряжение
i iходит делением характерной силы на площадь сечения,
подсчитанную в предположении сплошного, без пустот, заполнения веществом.

24
ВВЕДЕНИЕ
[ГЛ. I
Компенсация, конечно, будет неполной, так как начальные
напряжения в теле (деталь конструкции и т. п.) не будут такими же, как
в лабораторном образце, и т. п.
Следующими предпосылками классической *) теории упругости
являются наделение материала свойствами идеальной упругости,
шаровой изотропии, совершенной однородности и принятие линейной
зависимости между деформациями и напряжениями. О первом и
последнем из указанных допущений разъяснено в § 1.
Здесь лишь заметим, что пропорциональность между компонентами
напряжений и компонентами деформации (иначе говоря, обобщенный
закон Гука) не обязательно приводит к заключению о существовании
прямой пропорциональности между величиной внешних нагрузок и
приобретаемых телом перемещений, а следовательно, и вытекающему
отсюда закону сложения отдельных действий — принципу
независимости действия сил. В отдельных случаях (например, в так
называемых контактных задачах, см. § 66) линейная связь между
компонентами напряжений и компонентами деформаций приводит к
нелинейной зависимости между силами (например, нагрузка на шар) и
перемещениями (смятие шара и т. п.).
Шаровая изотропия материала понимается в том смысле, что физико-
механические свойства одинаковы по всем направлениям, проведенным
из данной точки материала, — любая плоскость, проходящая через
частицу, может рассматриваться как плоскость симметрии для нее.
Полагая, что этим свойством и в тех же числовых выражениях
обладают все частицы материала, приходим к понятию однородного
изотропного тела.
Для мельчайшего кристалла стали (для микрообъема) и вообще
для технических сплавов, конечно, упругие свойства не одинаковы
по разным направлениям, но беспорядочное расположение мелких
кристаллов в частице создает так называемую квазиизотропию
материала; таким образом, применительно к объему, включающему
большое количество частиц (для макрообъема), во всех
направлениях материал обладает одинаковыми свойствами в смысле среднего
статистического эффекта, создаваемого деформацией отдельных
кристаллов.
В этом смысле можно считать, что все величины, характеризующие
напряжения и деформации, определяемые в теории упругости, вообще
являются статистическими средними действительного их распределения
в конгломерате зерен металлов и подобных им технических материалов.
К гипотезам теории упругости, а впрочем, и всех ветвей
реологии следует также отнести предположение, что напряженное
*) В дальнейшем под классической теорией упругости будем понимать
только линейную теорию упругости однородного изотропного тела.
Случай анизотропии будем относить к области специальных задач теории
упругости.

§ 2] ОСНОВНЫЕ ГИПОТЕЗЫ И ПРИНЦИПЫ ТЕОРИИ УПРУГОСТИ 25
состояние в данной точке, необходимое для суждения о прочности
материала в окрестности этой точки, определяется состоянием
информации в этой же точке, а не в некоторой области возле
рассматриваемой точки.
Иначе говоря, принадлежит ли рассматриваемая точка однородно-
напряженной среде.(т. е. во всех соседних точках имеются одинако-
иые напряжения и деформации) или неоднородно-напряженной среде
(соседние точки имеют другие деформации, например меньшие, чем
рассматриваемая точка), — это не должно приблизить или
отдалить момент разрушения материала в данной точке, если и в том
и в другом случаях состояния деформации в рассматриваемых точках
одинаковы.
В математическом смысле это означает, что градиент
напряжений (величина, характеризующая изменение напряжения от точки
к точке) не влияет на прочность материала в данной точке.
Указанное сейчас допущение может и оспариваться, но надлежит
иметь в виду следующее обстоятельство, позволяющее все же такой
принцип автономной прочности в точке использовать.
Во-первых, при вычислении напряжений в данной точке методом
теории упругости степень неоднородности напряженного состояния
и теле будет сказываться на величине напряжений в данной точке,
т. е. косвенно градиент напряжений будет учитываться.
Во-вторых, теория упругости имеет дело с упругим состоянием
материала, достаточно отдаленным от момента разрушения, и потому
влияние упомянутого градиента напряжений для данной точки
имело бы смысл учитывать при рассмотрении вообще состояния
разрушения как в данной точке, так и в ее окрестности, что не
входит в задачу теории упругости, а ближе отвечает задачам теории
пластичности.
Большое количество задач теории упругости решается с
использованием принципа локальности эффекта самоуравновешенных внешних
нагрузок] в литературе он носит название принципа Се н-В е н а н а.
(1огласно этому принципу, если в како й-л ибо части тела
приложена уравновешенная система сил, то она вызовет
п теле напряжения, очень быстро убывающие по мере
удаления от этой части (экспоненциальный характер затухания
напряжений).
Примером может быть случай с клещами, которыми сминают малую
область тела (например, проволоку при ее перерезании). В этом слу-
чле клещи осуществляют уравновешенную систему сил, и как бы ни
целики были эти силы, они почти не вызывают напряжений в
остальных частях проволоки, вне малой области возле места нажатия
клещи ми (фиг. 4).
'Гак как по правилам механики абсолютно твердого тела операция
vimhili одной системы сил статически ей эквивалентной другой
(например, перенос силы с верхней поверхности балки на нижнюю или

Ull ВВЕДЕНИЕ [ГЛ. I
:i:imi*ii;i сосредоточенной силы, приложенной к концу балки, на группу
распределенных сил, имеющих ту же равнодействующую, или наоборот)
связана с использованием (добавлением и т. п.) дополнительных
самоуравновешенных сил, то представляется возможным принцип
локальности прочитать и в другой редакции, а именно: в точках твердого
тела, достаточно удаленных от мест приложения внешних
нагрузок, напряжения весьма мало зависят от детального способа
осуществления этих нагрузок.
Изучение же закона распределения напряжений в месте
приложения самих нагрузок составляет особые задачи теории упругости
(контактные задачи, исследование местных напряжений), точные решения
которых (см. §§ 62, 66) только и могут установить те расстояния от
нагрузок, на которых практически можно пользоваться принципом
локальности. В инженерной практике применительно к стержневым
системам часто полагают, что
упомянутые расстояния составляют
два-три наибольших размера
поперечного сечения стержня.
Наконец, в классической
теории упругости (т. е. в линейной)
принимается, что:
а) перемещения тела
(применительно к стержням в
строительной механике они
назывались прогибами) малы по
сравнению с линейными
размерами тела; для
полноты картины следует оговорить
Фиг. 4. Система взаимно
уравновешенных сил, приложенных в какой-
либо части тела, вызывает в теле
напряжения, очень быстро убывающие
по мере удаления от этой части.
еще два допущения линейной теории упругости [хотя они обычно
и вытекают как следствия из а); необходимость их сформулировать
показана в § 25];
б) относительные удлинения, а также и
относительные сдвиги, т. е. углы сдвига в материале
пренебрежимо малы по сравнению с единицей;
в) углы поворота (т. е. девиации) малы по сравнению
с единицей, а квадраты углов поворота пренебрежимо
малы по сравнению с относительными удлинениями и
сдвигами.
Указанные сейчас допущения а) и в) очевидны, а читателю известны
также из курсов сопротивления материалов или строительной
механики, так как только при соблюдении таких условий возможна
нормальная эксплуатация конструкции, машины и т. п.
Удачной иллюстрацией к возможности согласиться с допущением
б) является типичная диаграмма растяжения стали как наиболее
употребительного материала в современных конструкциях и характерного
по масштабу деформаций.

§ 2] ОСНОВНЫЕ ГИПОТЕЗЫ И ПРИНЦИПЫ ТЕОРИИ УПРУГОСТИ 27
На фиг. 5*) приведены результаты испытания на растяжение
образца, изготовленного из стали, применяемой в судостроении. По
оси абсцисс отложены относительные удлинения, а по оси ординат —
напряжения. На этой диаграмме участок ОВ соответствует упругой
стадии работы стали, участок ВС—пластической стадии (площадке
текучести) и наиболее длинный участок CD — стадии упрочнения.
Длина упругого участка (отрезок ОВ) в данном частном случае равна
1,15 • Ю-8, длина.площадки текучести около Ю-2 и лишь длина участка
упрочнения (до максимума кривой) около 0,17.
Указанные цифры типичны для сталей; в них область упругих
деформаций ограничивается относительными удлинениями порядка
10~3-5 • 10"3, что пренебрежимо мало по сравнению с единицей.
Фиг. 5. Характерная диаграмма растяжения для стали.
Аналогичный порядок для тех же сталей имеет предельная величина
упругих сдвигов.
Для теории конечных (немалых) деформаций (в нелинейной теории
упругости) упомянутые допущения, конечно, снимаются.
В связи с указанными выше допущениями в классической теории
упругости из круга ведения последней в силу ее ограниченности
выпадают все так называемые нелинейные проблемы (задача о потере
устойчивости упругого равновесия, задача изгиба брусьев, пластин,
оболочек при прогибах, сравнимых с толщиной, и т. п.). Эти
нелинейные задачи могут быть решены только с позиций нелинейной
теории упругости.
Перечисленные выше гипотезы **), применяемые или одновременно
псе или частично (если это достаточно), позволяют решать широкий
круг задач «прочностного расчета»; по окончательным результатам
п большинстве случаев они в общем удовлетворительно согласуются
С данными практики.
*) График заимствован из книги В. В. Новожилова, Основы
нелинейной теории упругости, М. — Л., 1948.
**) Их иногда называют «рабочими» гипотезами, подчеркивая этим удоб-
гтпо, вносимое ими в расчеты.

28
ВВЕДЕНИЕ
[ГЛ. I
Не исключаются, конечно, случаи (более того, они непременно
будут), когда именно опыт (но в отдельных, преимущественно новых
по своему характеру примерах) покажет неприменимость того или
иного предположения, укажет целесообразность замены его каким-то
иным, т. е. выявится необходимость введения новой гипотезы.
Последнее однако не должно означать, что надо отложить теоретические
исследования и всякие «прочностные расчеты» до получения более
совершенных схем, «точных» законов и т. п., так как
совершенствование расчетных схем в науке может быть получено в результате
практической работы с современными, хотя и не всегда
совершенными схемами и моделями.
«Если бы мы захотели ждать, пока материал будет готов в
чистом виде для закона, то это значило бы приостановить до тех пор
мыслящее исследование, и уже по одному этому мы никогда не
получили бы закона» *).
§ 3. Замечания о принципе локальности эффекта
самоуравновешенных сил
Указанный принцип занимает особое место во всех ветвях
механики деформируемого тела и на нем следует остановиться подробнее.
Более того, если бы этот принцип не был сформулирован, то
теория упругости не располагала бы многими решениями, которые
в настоящее время широко используются на практике.
Этот принцип, как сказано выше, устанавливает, что если силы,
действующие на малую площадку, заменить статически
эквивалентной системой на той же площадке, то'при новой системе сил
произойдет изменение в напряженном состоянии лишь в
непосредственной близости к прилагаемой нагрузке; в точках же упругого тела,
удаленных от места приложения упомянутых усилий на расстояния,
достаточно большие по сравнению с линейными размерами той
поверхности, ка которой они приложены, влияние перераспределения
усилий будет ничтожно.
Этот принцип иногда называют принципом упругой
равнозначности статически эквивалентных систем сил.
На фиг. 6 показаны четыре статически эквивалентные системы
сил, равнодействующая которых во всех случаях равна Р и
направлена вертикально. На известном удалении от места приложения
указанных сил напряжения и деформации тела можно считать во всех
четырех случаях практически одинаковыми.
На фиг. 7 показано несколько случаев нагружения консольной
балки, в которой, исключая небольшую область возле левого конца
балки, напряженное состояние практически одинаково.
*) Ф. Энгельс, Диалектика природы, стр. 191, Госполитиздат, М.,
1949.

§ 3]
ЗАМЕЧАНИЯ О ПРИНЦИПЕ ЛОКАЛЬНОСТИ
29
Фиг. 7. Области балки,
напряженное состояние в которых
существенно зависит от
способа приложения нагрузки,
заштрихованы. Вне этих
областей напряженное состояние
практически не зависит от
способа осуществления нагрузки.
Фиг. 6. Если диаметр канавки d весьма мал
относительно размеров пластинки, то во всех
указанных четырех случаях нагружения пластинки
напряженное состояние в точках с одинаковыми
координатами (/*, 0), находящихся на достаточном
отдалении от канавки (т. е. когда r^>d), прак-
тически^одинаково.

30
ВВЕДЕНИЕ
[ГЛ. I
На фиг. 8 показаны так называемые картины полос, полученные
экспериментальным путем с помощью поляризационно-оптического
метода. Эти полосы, иначе говоря — изохромы, т. е. линии равных
касательных напряжений, получены при сжатии осевой силой трех
коротких брусков. Там, где нет полос, надо считать однородное
сжатие, каковое было бы во всем объеме брусков, если нагрузка была
осуществлена равномерной по торцам.
На фиг. 9 верхней *) показана картина полос в диске,
опирающемся на плоский брус и сжатом сверху с помощью ролика.
Фиг, 8. В сечениях, более удаленных от тех, где приложены
внешние воздействия, напряжения выравниваются.
Результирующие силы, очевидно, равны, распределение же
напряжений у вершины отлично от распределения сил .у основания
(теоретические решения этой задачи см. в § 66).
На фиг. 9 нижней показана в увеличенном масштабе картина полос
в нижней и верхней частях диска. Из этих фигур следует, что
у ролика имеется резко выраженная концентрированная пластическая
зона, в то время как у плоского основания эта зона значительно
меньше и более расплывчата.
На фиг. 10 показано распределение напряжений (обозначения см.
§ 4) по различным сечениям прямоугольной пластинки, сжатой по
торцам неравномерно распределенной нагрузкой. Исследования
проведены теоретически М. М. Филоненко-Бородичем (см. § 75).
Выше (стр. 25—26) были указаны две формулировки принципа
Сен-Венана. Приводим еще одну, хотя она имеет смысл первой
*) Фиг. 9 заимствована из книги М. М. Ф р о х т а, Фотоупругость, т. II,
М., 1950.

§ 3]
ЗАМЕЧАНИЯ О ПРИНЦИПЕ ЛОКАЛЬНОСТИ
31
Фиг. 9. Картина полос в диске, опирающемся на плоский брус, сжатом
i iii'pxy с помощью ролика. Внизу показана в увеличенном масштабе картина
полос в верхней и нижней частях диска.

32
ВВЕДЕНИЕ
[ГЛ. I
формулировки: напряжение, производимое в теле путем приложения
к малой части его поверхности системы сил, статически
эквивалентной нулевой силе и нулевому
моменту, пренебрежимо мало на
расстояниях, значительных по
сравнению с линейными размерами
площадки, на которую эти силы действуют.
Теоретического доказательства
принципа Сен-Венана не имеется, однако
справедливость его доказать не сложно,
если исходить из принципа наименьшей
работы деформации *),
устанавливающего, что локальность эффекта
самоуравновешенных сил соответствует
минимуму потенциальной энергии
деформации.
Приведенные выше достаточно
разнообразные случаи подтверждают этот
принцип и исключают надобность
строгого общего доказательства его.
Значение указанного принципа для
теории упругости велико, так как он
позволяет в случае необходимости одну
систему сил (приложенных, например,
на каком-либо конце стержня) заменить
статически эквивалентной другой, но
такой, при которой решение постав-
1енной задачи (расчет стержня и т. п.)
будет значительно проще. Короче
говоря, согласно этому принципу можно
одни граничные условия в смысле сил
заменять другими, лишь бы
равнодействующая й момент новой заданной
системы сил были равны.
Таким Образом, этот принцип
практически разрешает ограничиться
приближенным решением, когда граничные
условия будут удовлетворены только
в интегральной форме. (В связи с
указанным принцип Сен-Венана иногда
называют, следуя Лейбензону Л. С. [56], смягчением граничных
условий на концах бруса **).
Фиг. 10. Распределение
напряжений по различным сечениям
прямоугольной пластинки,
сжатой по торцам распределенной
нагрузкой (по М. М. Филонен-
ко-Бородичу).
*) Понятие о работе деформации, или иначе потенциальной энергии
деформации, дано в § 29.
**) Интегральная форма граничных условий, вообще говоря, является
одной из форм идеи смягчения граничных условий, понимаемой в широком

§ 3]
ЗАМЕЧАНИЯ О ПРИНЦИПЕ ЛОКАЛЬНОСТИ
33
Фиг. 11. Пример неприменимости принципа
Сен-Венана.
Следует отметить, что применительно к тонкостенным стержням
и оболочкам этот принцип необходимо применять осторожно и именно
в смысле установления протяженности зоны существенного влияния
взаимно уравновешенной системы сил. На это обстоятельство
указывали В. 3. Власов и В. Э. Новодворские
Примером может явиться явление кручения двутавра,
закрепленного одним концом в
стену, при нагрузке его на
другом конце бипарой,
т. е. двумя равными, но
разного знака парами
(равнодействующий
момент равен нулю), из
которых одна действует в
плоскости одной полки,
я другая — в плоскости
другой (фиг. 11). Каждая
из полок будет изгибаться
и своей- плоскости, но,
кроме того, очевидно, по
условию жесткого соединения стенки двутавра с полками изгиб
полок в противоположных направлениях неизбежно вызовет
закручивание поперечных сечений двутавра.
В этом примере нагрузка, статически эквивалентная нулю, вызы-
iwot, следовательно, сложную деформацию стержня (изгиб с
кручением), причем, как
показывают
теоретические и
экспериментальные исследования,
убывание напряжений
иногда не носит
экспоненциального
характера, и они
продолжаются на значительное
расстояние от места
приложения бипары.
Последнее
рассматривают иногда, как
нарушение принципа
Сен-Венана.
И аналогичных условиях находится явление, представленное на
hi, 12, когда две равные и разнонаправленные силы (бисила) при-
"»»кнп>1 к полкам швеллера (или двутавра).
12. Пример неприменимости (при обычном
толковании) принципа Сен-Венана.
пиле. Так, в ряде задач (§ 127) оказывается успешным метод точечного
иодсппя граничных условий, сущность которого в том, что эти условия
■ ■■итворяются только в некоторых точках границы упругого тела.
J 3.IK. 3880. Н. И. Безухоа

34
ВВЕДЕНИЕ
[гл. i
Примеры, отрицающие экспоненциальный характер развития
напряжений, можно, однако, привести не столько для иллюстрации нарушения
принципа локальности эффекта самоуравновешенных сил, сколько для
разъяснения недопустимости его экстраполяции на систему тел
(двутавр можно рассматривать как систему трех пластинок).
Если в указанной на стр. 32 формулировке этого принципа иметь
в виду (или специально оговорить), что уравновешенная система сил
приложена к части тела, малой по сравнению с
наименьшим размером тела в области нагружения (применительно
к двутавру это означает, что бипара или бисила приложена к одной
только полке, а плечо бипары меньше толщины полки), то принцип
локальности эффекта самоуравновешенных сил и в этом случае
сохраняет свою силу *).
§ 4. Обозначение составляющих напряжений.
Тензор напряжений
Величины всяких усилий (внешних, т. е. поверхностных, нагрузок>
а также внутренних сил) характеризуются их интенсивностью, т. е*
величиной усилия, приходящегося на единицу площади поверхности,
на которую они действуют.
При рассмотрении внутренних усилий эта интенсивность
называется напряжением] впрочем, последнее наименование можно
сохранить и для внешних нагрузок, если они распределены на
рассматриваемой области сплошным образом.
Для дальнейшего условимся называть «волокном тела»
совокупность его точек, расположенных вдоль некоторой линии, а
«линейным элементом тела» — дифференциально малый отрезок какого-либо
волокна.
«Слоем тела» будем называть совокупность его точек,
располагающихся на некоторой поверхности, а «элементарной площадкой
тела» — бесконечно малый элемент какого-либо слоя.
Для обозначений интенсивностей сил удобно применить
следующую систему. Если в заданном теле, некоторым образом
ориентированном в прямоугольной системе координат (х> у, z)y рассматриваемая
нами точка лежит на какой-либо элементарной площадке, например
взятой на наружной поверхности тела (фиг. 13), внешняя нормаль
к которой у той же точки обозначена через v и не параллельна ни
одной из координатных осей х, уу z, то интенсивность усилия, или
иначе полное напряжение для данной точки, будем обозначать /?v.
Направление вектора рч совпадает с направлением усилия.
Если через Д/\ обозначим усилие, приходящееся на
рассматриваемую элементарную площадку Д/7, то указанное выше напряжение*
*) Уточнение редакции принципа Сен-Венана принадлежит М. М. Фило-
ненко-Бородичу.

* 4]
ОБОЗНАЧЕНИЕ СОСТАВЛЯЮЩИХ НАПРЯЖЕНИЙ
35
иначе говоря, плотность силы, вычисляется как предел
отношения
при А/7, устремляющемся к нулю.
Заметим, что такая формулировка понятия напряжения непременно
предполагает тело сплошным, непрерывным.
Для материалов, имеющих молекулярную структуру, невозможно
снизать элемент площадки с силой, действующей на этом элементе.
Фиг. 13. Обозначение полного напряжения в точке
на площадке с заданной нормалью v.
Иначе говоря, для дискретной теории упругости указанная выше
формулировка напряжения неприемлема.
Проекции полного напряжения на координатные оси х, у, z соот-
нстственно будем обозначать рх^ руч, ргч, причем, очевидно, имеет
место равенство
P^Pl + Pl+Pl- (1-01)
Если обозначение напряжения имеет два индекса, первый отмечает
ту ось, параллельно которой направлена составляющая напряжения,
а второй—нормаль к той площадке, на которой действует
рассматриваемая составляющая (т. е. второй индекс означает адрес
напряжения). Наличие у обозначения напряжения одного только индекса,
указывающего нормаль к площадке, на которой оно действует,
определяет полное напряжение в точке.
Если провести внутри тела какую-либо площадку, то для
обозначения как полного напряжения на этой площадке, так и его соста-
нляющих можно сохранить ту же систему. В частности, если в
рассматриваемом нами теле через произвольную его точку (х, у, г) про-
модем три плоскости, параллельные координатным, и, пересекая их
3*

36
ВВЕДЕНИЕ
[ГЛ. 1
одной наклонной плоскостью, достаточно близкой к точке (л:, ул <г),
вырежем элемент в виде тетраэдра (фиг. 14), то обозначения
действующих по его граням полных напряжений, представляющих
взаимодействие этого тетраэдра с остальным телом, должны иметь
начертания рх, ру, рг и рч.
Составляющие напряжений, параллельные координатным осям и
действующие по трем взаимно перпендикулярным площадкам,
параллельным координатным плоскостям (эти грани тетраэдра принято на-
Фиг. 14. Обозначения полных напряжений на всех четырех
гранях тетраэдра, вырезанного возле заданной точки.
зывать основными площадками), должны получить такие
обозначения:
от рх—составляющие рхх, рух, ргх,
от ру — составляющие рхуу pyyi ргу\
от /7, —составляющие рх&, руг, pzz.
Заметим, что составляющие рхх> руу, pzzy как нормальные к
соответствующим площадкам, представляют нормальные напряжения,
остальные же — рхуу руг и т. д.— касательные напряжения. Сохраняя
систему обозначений, известную читателю из курсов сопротивления
материалов, нормальные напряжения будем обозначать буквой о с
приданием ей индекса, указывающего ту ось, параллельно которой
направлено это напряжение, одновременно это будет и обозначением
нормали к площадке, па которой рассматривается нормальное напряжение;
для обозначения касательных напряжений примем букву т с
приданием ей двух индексов в соответствии с указанным выше правилом.
Так, например, ixy есть касательное напряжение, имеющее
направление, параллельное оси х и действующее на площадке, нормаль
к которой параллельна оси у.
Нормальное напряжение принято считать положительным, когда
оно вызывает растяжение (в этом случае оно направлено по внешней

§ 4]
ОБОЗНАЧЕНИЕ СОСТАВЛЯЮЩИХ НАПРЯЖЕНИЙ
37
нормали к площадке, принадлежащей рассматриваемой части тела),
и отрицательным, когда оно вызывает сжатие (в последнем случае
шю направлено для данной части тела по внутренней нормали).
За положительные направления составляющих касательного
напряжения, действующего на любой основной площадке, принимаются
положительные направления осей координат, если растягивающее
нормальное напряжение по той же площадке имеет направление,
сонм лдающее с положительным направлением той оси, параллельно
Фиг. 15. Обозначения компонентов напряжений по граням
бесконечно малого параллелепипеда, вырезанного возле
заданной точки М.
ко юрой действует упомянутое нормальное напряжение. Если растя-
i икающее напряжение на рассматриваемой площадке имеет
направление» противоположное положительному направлению соответствующей,
I, е. параллельной ему, координатной оси, то за положительные напра-
и.'К'мия составляющих касательного напряжения на той же площадке
с.К'чует взять отрицательные направления соответствующих им осей.
На фиг. 15 указаны обозначения всех составляющих (компонентов)
напряжений по граням бесконечно малого параллелепипеда, который
мысленно вырезан из заданного тела, причем предположительно все
напряжения назначены положительными.
1:сли размеры изучаемого параллелепипеда будут в самом деле
Лосконечно малыми, то одноименные и параллельные напряжения для
каждой пары параллельных граней разнятся между собой на
бесконечно малую величину, т. е. будут практически одинаковыми, что и
показано на фиг. 15. Бесконечно малый параллелепипед з дальнейшем
• »удем называть элементарным объемом или элементарным п а -
р л л л е л е пипе дом.

38
ВВЕДЕНИЕ
[ГЛ. I
Элементарный параллелепипед является одним из основных
.объектов изучения в теории упругости и родственных ей науках *).
Вполне очевидно, что когда возникнет задача нахождения закона
распределения напряжений в определенной области тела, то, переходя
от одного элементарного объема к другому, конечно, придется
учитывать упомянутые выше бесконечно малые разности в величинах
напряжений по параллельным граням (см. § 14).
Приступая к исследованию напряженного состояния элементарного
параллелепипеда, мы имеем, следовательно, неизвестными по три
компонента на каждой паре параллельных граней, а всего девять
величин— три нормальных и шесть касательных составляющих напряжений.
Впрочем, знакомый читателю из сопротивления материалов закон
о парности касательных напряжений остается в силе и в данном
случае пространственного напряженного состояния. В общем виде этот
закон взаимности доказывается в § 14; здесь лишь отметим, что
в принятых выше обозначениях следующие составляющие касательных
напряжений равны между собой:
Таким образом, всего неизвестных компонентов напряжений
будет шесть.
Все указанные выше составляющие напряжений вполне определяют
напряженное состояние рассматриваемого элементарного объема. Зная
напряжения по трем ортогональным площадкам, проведенным возле
рассматриваемой точки, без затруднений, как это показано в § 16,
можно вычислить напряжения по любой площадке, произвольно
наклоненной к основным взаимно перпендикулярным плоскостям.
Равным образом не составит затруднений перейти от напряжений
к деформациям ввиду простой линейной связи, существующей между
первыми и вторыми (см. § 26). Если затем деформированные
элементарные объемы сложить вместе, то, очевидно, получим в целом
деформированное тело..
Расположим все напряжения, определяющие собой напряженное
состояние в рассматриваемой точке, в виде следующей наглядной
таблички (матрицы):
(1.03)
*) Отметим, что в рассматриваемой прямоугольной координатной системе
элементарный объем имеет форму именно прямоугольного параллелепипеда.
В случае использования других координатных систем (цилиндрические и т. д.)
параллелепипед, очевидно, будет иным (криволинейный параллелепипед и т. п.),
так как грани его будут определяться направлением (и формой) принятых
координатных плоскостей (или поверхностей).

§ 4] ОБОЗНАЧЕНИЕ СОСТАВЛЯЮЩИХ НАПРЯЖЕНИЙ 39
В первой строке расположились все компоненты напряжений,
имеющие направление, параллельное оси х, во второй строке —
параллельное оси у и в третьей строке — параллельное оси z. Кроме того,
в первом столбце сгруппировались напряжения, действующие на
площадке, нормаль к которой параллельна оси х, во втором столбце —
все напряжения на площадке с нормалью, параллельной оси у *), и
и третьем столбце — на площадке с нормалью, параллельной оси z.
В связи с этим первый индекс у напряжений, расположенных
в первой строке, является общим, а именно х; у второй строки у,
а у третьей z. Вторые индексы (а для нормального напряжения —
тот же единственный индекс) оказываются общими по вертикали.
Так, у первого столбца — обозначение оси х, у второго — оси у и
у третьего — оси z.
Нормальные напряжения при таком способе построения таблички
расположились по главной диагонали, а одинаковые по величине
касательные напряжения расположились симметрично относительно этой
диагонали. По этой причине табличку будем для краткости письма
записывать также в виде
Тк:
(1.04)
Точки указывают, что члены, вместо которых они стоят, равны
симметрично расположенным.
Написанную выше симметричную квадратную матрицу называют
тензором напряжений. Впрочем, каких-либо специальных сведений
из тензорного анализа для дальнейшего изложения от читателя не
требуется и можно вообще обойтись без указанного понятия и
наименования**). Однако по ходу изложения будут выясняться некоторые
замечательные свойства написанной матрицы, расширяющие
представление о напряженном состоянии в точке.
В частности, если условно истолковать тензор как определитель
и подсчитать значение такого определителя, то (это показано далее
и § 17) полученное таким образОхМ числовое значение будет, как говорят,
инвариантно к ортогональному преобразованию координат. Последнее
надо истолковать в том смысле, что если возле той же
рассматриваемой точки вырезать новый элементарный параллелепипед,
*) Возможно поменять местами указания адреса и направления, т. е. вместо
обозначения txy принять zyx. Как показано далее (§ 14), такая перестановка
индексов ничего в дальнейшем не изменит; вместе с тем первая система
обозначений имеет некоторое преимущество (см. §§ 9, 24).
**) Название тензор впервые было введено в науку именно для обозна-
•1Г11ИИ совокупности всех векторов напряжений, действующих на площадках,
проходящих через одну и ту же точку в деформируемом теле. Определение
понятия тензора напряжений см. § 16 (стр. 84).

40
ВВЕДЕНИЕ
{1Л. I
но иным способом, т. е. иначе его ориентировать в пространстве
(по-другому направить координатные оси и т. п.), то, несмотря на то,
что компоненты напряжений у этого другого параллелепипеда будут
иными (так как напряжения для данной точки зависят от направления
плоскости, проходящей через эту точку), определитель, составленный
из новых компонентов, даст то же числовое значение, что и у
первого элементарного параллелепипеда. Еще несколькими важными
свойствами, характеризующими напряженное состояние точки, будет
обладать та же матрица напряжений. Вообще напряженное состояние
в точке вполне определено, если задан тензор напряжений для
этой точки *).
§ 5. Обозначение компонентов перемещения и вращения
Представим себе сплошное твердое тело, прикрепленное к земле,
к опорам и т. п., причем таким образом, что оно не может
перемещаться как тело абсолютно твердое. Тогда перемещения любой
точки этого тела могут произойти только за счет деформации (упругой
или пластической) самого тела.
Рассмотрим некоторую точку М (фиг. 16) с координатами
(первоначальными, т. е. до деформации тела) л:, у, z и пусть Mt есть новое
Фиг. 16. Обозначение компонентов перемещений. Параллелепипед до
деформации и после нее.
положение этой точки. Обозначим проекции полного перемещения ММ1
на оси координат л:, у, z через и, v и w и будем их называть
компонентами перемещения или проекциями вектора смещения.
*) Если бы мы располагали знанием тензора напряжений для каждой
точки тела, иначе говоря, было бы задано «тензорное поле напряжений»,
то последним определялось бы напряженное состояние всего.тела.

§ 3] ОБОЗНАЧЕНИЕ КОМПОНЕНТОВ ПЕРЕМЕЩЕНИЯ И ВРАЩЕНИЯ 41
Для совокупности трех величин
и
V
W
(1.05)
w целях краткости языка удобно в дальнейшем принять название
матрица — столбец смещения.
Компоненты перемещения различных точек различны и будут
функциями координат точки, т. е.
и=/1(х, у, г),
v=U{x>y> г), (1.06)
Около рассмотренной точки М можно построить бесконечно малый
параллелепипед с гранями, параллельными координатным плоскостям
(фиг. 16 справа). Если временно предположить, что этот
элементарный параллелепипед не претерпевает деформации (т. е. его объем и
форма остаются неизменными), то, для того чтобы определить его
новое положение в связи с общей деформацией всего тела, трех
компонентов смещения точки М, очевидно, недостаточно, так как
параллелепипед на пути Л4М1 может также еще и повернуться относительно
ребра М—1 (параллельного оси х) или относительно ребра М — 2
(параллельного оси у) или относительно ребра М—3 (параллельного
оси z) или относительно произвольной оси, не параллельной ни одной
\\\ координатных осей. В последнем случае надо говорить о трех
доставляющих угла вращения. Эги составляющие, называемые
компонентами жесткого вращения, обозначим <лх (поворот относительно
оси х), и>у и шг (то же относительно осей у и z) *).
Зная смещения точки М и повороты, можно без затруднений
in простейших соображений составить выражения для перемещения
но бой другой точки, например для вершины N того же
параллелепипеда. Однако действительные координаты вершины Мг в смещенном
положении будут иными, так как на пути ММ1 рассматриваемый
нами элемент сам претерпевал деформации — происходили изменения
члип ребер, могли исказиться его первоначально прямые углы.
На фиг,- 17 показана одна из проекций элементарного
параллелепипеда и в первоначальном его положении (М 12), и в смещенном,
но без учета собственных деформаций (М11/2/)у и в действительной
полиции (А11 1"2").
*) Частный случай, когда шх = юу = <ог == 0, т. е. при отсутствии поворота
и окрестности рассматриваемой точки, принято иногда называть чистой
• '■ формацией.

42
ВВЕДЕНИЕ
[ГЛ. I
Заметим, что упомянутые выше компоненты жесткого вращения
также являются функциями координат (т. е. изменяются при переходе
от одной точки к другой), тесно связаны с компонентами перемеще-
Фиг. 17. Проекция параллелепипеда до и после деформации.
ния (см. § 22), а в общем для теории упругости и вообще для
реологии интереса не представляют, так как их наличие не вызывает
напряжений и деформаций элементарного параллелепипеда *).
§ 6. Обозначение компонентов деформации. Тензор деформации
Деформация любого элементарного объема тела, имевшего,
например, до деформации вид бесконечно малого параллелепипеда, может
быть представлена состоящей из ряда отдельных простейших
деформаций, т. е. разложена на составляющие.
Так, в случае элементарного параллелепипеда можно говорить
о шести составляющих деформации: о трех ее линейных
составляющих {удлинениях ребер) и о трех угловых {сдвигах) **).
На фиг. 18 изображены эти составляющие деформации и указаны
их обозначения, в основном известные читателю из курсов
сопротивления материалов.
Относительные удлинения ребер (деформации первого рода)
будем обозначать буквой е с индексом, указывающим направление
удлинения, или, что все равно, ту ось, параллельно которой получило
*) Также, очевидно, не вызывают напряжений в элементарном
параллелепипеде и компоненты жесткого перемещения (случай поступательного
смещения элемента без его деформации).
**) Шесть простейших составляющих деформации элементарного
параллелепипеда, о которых идет повествование ниже, характеризуют
одновременно и полную деформацию в точке, в которую стягивается
рассматриваемый параллелепипед, если полагать длины его ребер устремляющимися
к нулю.

§ 6] ОБОЗНАЧЕНИЕ КОМПОНЕНТОВ ДЕФОРМАЦИИ 43
удлинение ребро. Положительными линейными деформациями считаем
удлинения, отрицательными — укорочения.
При указанных на фиг. 18 элементарных деформациях первого
рода изменяются объем параллелепипеда и его форма; так, если
Фиг. 18. Обозначения компонентов деформаций.
первоначальная форма была кубом, то после деформации формой
будет параллелепипед.
Считается, что положительному сдвигу (деформации
второго рода) соответствует уменьшение угла между положительными
исправлениями осей; отрицательному—увеличение тех же углов. Углы
сдвига (относительные сдвиги), проектирующиеся на плоскость лгу,
обозначаем ^ху (или "\yx)\ соответственно для остальных плоскостей
[уг и zx) углы сдвига обозначаем:
Туг (или ъу) и Тзд (или Та?2).
При углах сдвига, пренебрежимо малых по сравнению с единицей
(а такие именно углы сдвига и предполагаются в классической
теории упругости), можно считать, что объем параллелепипеда,
получившего деформации сдвига, не изменился, а ребра не получили
удлинений *).
*) Если исходить из фиг. 18, т. е. предполагать, что высота элемента
остается неизменной, то получающиеся при этом удлинения наклоненных
ребер будут составлять величины более высокого порядка малости, чем сами
умы сдвига.

44
ВВЕДЕНИЕ
(ГЛ. 1
Таким образом, при деформациях сдвига объем в окрестности
рассматриваемой точки остается неизменным, меняется лишь
форма.
Объемная же деформация приобретается лишь наличием
удлинений ребер.
При анализе возможностей для более строгого описания
деформации элементарного параллелепипеда может возникнуть мысль об
искривлении его граней, т. е. о превращении их в поверхности, каждая
из которых имеет свою
характеристику. По этому
поводу следует заметить,
что дополнительные
параметры, характеризующие
такие искривления (радиусы
кривизны
поверхностей и т. п.), будут
представляться по результатам
своего влияния на
деформацию тела в целом малыми
высших порядков малости
относительно влияния ранее
указанных шести
компонентов деформации. По этой
причине в классической
теории упругости и в современной теории пластичности деформация
элементарного параллелепипеда предполагается вполне определяющейся
только перечисленными шестью составляющими.
Если первоначальный размер каждой грани параллелепипеда принять
равным единице (значит, объем такого кубика равен единице) и
предположить одновременное наличие всех трех линейных составляющих
деформации (фиг. 19), то приращение объема куба вследствие такой
деформации (это будет вообще относительное изменение объема в
окрестности рассматриваемой точки), составит:
Если считать удлинения пренебрежимо малыми по сравнению с
единицей (а это и предполагается в классической теории упругости), то,
развертывая указанное выше произведение и отбрасывая малые
второго и третьего порядков, имеем:
« = ««»+«,+ •«, (1.07)
т. е. относительная объемная деформация в точке равна сумме
относительных удлинений по трем ортогональным направлениям,
проведенным через заданную точку *).
Фиг. 19. Объемная деформация определяется
суммой относительных удлинений по трем
ортогональным направлениям.
*) Полученный результат не зависит от того, какой формы элемент
выделяется из тела в окрестности рассматриваемой точки (прямоугольный парал-

§ 6]
ОБОЗНАЧЕНИЕ КОМПОНЕНТОВ ДЕФОРМАЦИИ
45
Вводя обозначение еср = — (e^-j-e^-j-e^) (в дальнейшем
именуемое средняя деформация), выражение (1.07) записывают так:
О = Згср.
(1.08)
Следует остановиться на относительности расположения
очередности индексов при обозначении углов сдвига. Так, если ребро,
первоначально параллельное оси лг, повернулось в направлении к ребру,;
первоначально параллельному оси у, то происходящее при этом
уменьшение угла можно обозначить ^ху (фиг. 20, а). Если на тот же угол
повернется второе ребро (параллельное оси у) по направлению к иер-
Фиг. 20. Эквивалентные сдвиги (взаимность сдвигов).
пому (параллельному оси лг), то угол сдвига можно обозначить через
Т„,г (фиг. 20, б).
Однако в обоих рассмотренных сейчас случаях деформация (~[ху
И.1И 1ух) и связанное с ней напряженное состояние по существу со-
иершенно одинаковы, так как из случая а) легко получить случай
б) путем жесткого поворота (следовательно, без всякого усилия и
деформации элементарного параллелепипеда) на угол ^ху.
Далее, тем же случаям а) и б) совершенно эквивалентен случай,
м.юораженный на фиг. 20, в. Впрочем, картин, подобных и равно-
цепных в смысле деформации сдвига, можно предложить
неограниченное число, лишь бы во всех таких случаях уменьшения (или
увеличения) первоначально прямого угла были бы одинаковы.
Таким образом, условливаясь в тождественности обозначений
(1.09)
[взаимность сдвигов), мы допускаем, что теряет значение тот или
иной способ изображения деформации сдвига. Для дальнейшего будет
Удобнее деформацию сдвига изображать именно по схеме фиг. 20, в.
и- '1ГШШСД, превращающийся при деформации в косоугольный, или сфера
п|н'1Ф<-|щающаяся при деформации в эллипсоид, или какая-либо иная геометри-
••i-t кал фигура).

46
ВВЕДЕНИЕ
[ГЛ. I
Итак, вследствие деформации сдвига, фактические углы поворота
ребер параллелепипеда, составлявших между собой до деформации
прямой угол, будут различны. Так, при обозначениях, принятых на
фиг. 21, для ребра Ml поворот составит:
хуу
(1.10)
, 1
а для ребра М2 поворот будет:
1
«.—J Ту*-
Все перечисленные выше компоненты деформации вполне
определяют деформацию элементарного параллелепипеда, так как путем
Фиг. 21. Углы поворота ребер параллелепипеда,
выраженные через «жесткий поворот» и
относительный сдвиг.
наложения всех упомянутых составляющих можно построить модель
деформированного элемента. Более того, как показано далее (§ 24),
через указанные компоненты деформации без затруднений можно
вычислить удлинение внутри параллелепипеда по любому направлению,
не совпадающему с направлениями координатных осей.
Расположим все компоненты, определяющие собой
деформированное состояние в рассматриваемой точке, в виде следующей таблицы,
которую сознательно построим подобной тензору напряжений, для
чего, поделив углы сдвигов пополам, повторим их половинки в
табличке два раза с перестановкой индексов:
Лдеф —
1
"2 ^ V
1 1
~2~ 7за?> 2 *гУ*
1
2 ^хг
1
2 Чу*
е*
(1.11)

§ 6]
ОБОЗНАЧЕНИЕ КОМПОНЕНТОВ ДЕФОРМАЦИИ
47
Эту матрицу будем называть тензором деформации. Здесь можно
повторить сказанное о тензоре напряжений, т. е. что для
дальнейшего от читателя не требуется каких-либо сведений из тензорного
анализа, что эту табличку не следует смешивать с определителем и
что, наконец, эта таблица обладает рядом замечательных свойств,
которые разбираются позднее (§ 24) *).
Впрочем, одно из свойств очевидно и сейчас. Так, если сложить
все члены по главной диагонали, то получим гх -)- &у + *z = в, т. е.
относительную объемную деформацию. А так как относительная
объемная деформация в окрестности данной точки не зависит от
ориентации элементарного параллелепипеда относительно координатных осей
и даже не зависит от формы элементарного объема (будь то
параллелепипед, сфера и др.), то, следовательно, указанная сумма
диагональных членов (ее в дальнейшем будем называть первым
инвариантом тензора деформации) инвариантна к ортогональному
преобразованию координатной системы.
Так как тензор деформации оказался симметричным (что мы
сделали преднамеренно), то для простоты записи его можно представить
н виде
^Деф= . в lv \- (1-12)
•> Ч/> 2 *Уг \
I •, •, *г J
И дальнейшем (§ 26) будет показано, что при некоторых частных
значениях упругих характеристик материала (это будет, когда
коэффициент Пуассона для рассматриваемого материала равен нулю) любой
компонент напряжений, взятый из таблички, названной тензором
напряжений, прямо пропорционален соответствующему компоненту
деформации из таблички, названной тензором деформации, который
располагается аналогично первому (в той же строке, в том же столбце);
коэффициент пропорциональности в этом случае оказывается для всех
компонентов одинаковым. Во всяком случае слагающие деформации
и компоненты напряжений, наиболее зависимые друг от друга,
занимают одинаковые позиции в тензоре деформации и в тензоре
напряжений.
Итак, деформированное состояние в точке вполне определено,
пли задан тензор деформации для этой точки.
'*) При изложении теории немалых, т. е. конечных, деформаций
применение тензорного анализа, ввиду общности этого анализа, его ясной и красно-
|н'чи»ой краткости, становится уже совершенно необходимым; отказ от него
нрннодит к очень громоздким и длинным формулам (см. Д. И. К у т и л и н,
Теория конечных деформаций, 1947).

48
ВВЕДЕНИЕ
[ГЛ. I
§ 7. Разложение деформации на «чисто объемную»
и на «деформацию формы»
Наблюдения показывают, что прочность материала зависит не только
от величины компонентов напряжений, но и от характера
напряженного состояния.
Так, большинство твердых тел противостоит без разрушения
действию одинакового всестороннего очень высокого давления. Только
в некоторых, менее плотных телах наблюдались случаи разрушения,
причину чего можно усмотреть в наличии внутри тела мелких щелей
и трещин, куда проникала жидкость, в которую были погружены
испытуемые тела.
И наоборот, те же тела иногда разрушаются при сравнительно
невысоких напряжениях, если последние в основном изменяют форму
тела (например, в случае сдвига или наличия разных по знаку
нормальных давлений, действующих на грани параллелепипеда).
В связи с этим для суждения о прочности представляется
необходимым из общей деформации тела выделить особо те компоненты,
которые связаны с изменением объема, и отдельно рассмотреть
компоненты деформации, имеющие отношение к изменению формы.
Уместным будет в том же смысле разделить и компоненты напряжений.
Хотя в случае всестороннего равномерного растяжения (случай
«чисто объемной» деформации) материал не обладает способностью
противостоять высоким напряжениям, однако и и этом случае, как
выяснится позднее, упомянутое разделение на чисто объемную
деформацию и на «деформацию формы» (иначе называемую
«скашивающей» или «девиаторной» деформацией) оказывается целесообразным.
Помимо того, что это удобно для решения в дальнейшем вопросов
прочности, то же самое разделение оказывается необходимым и для
наглядного описания законов деформации сложно напряженного тела.
В случае чисто объемной деформации независимо от знака
приращения объема материал практически подчиняется закону Гука даже
при очень высоких напряжениях (в случае гидростатического сжатия;
в случае равномерного растяжения — почти вплоть до разрушения);
в обычных же условиях испытания, например в опытах на чистое
сжатие или растяжение, отступления от закона прямой
пропорциональности между нагрузкой и деформацией наблюдаются при
сравнительно малых величинах напряжений.
На фиг. 22 показано разложение сложной деформации кубика на
чисто объемную (фиг. 22, а) и чисто девиаторную (фиг. 22, б). То,
что в первом случае происходит только изменение объема, а форма
остается без изменения (т. е. кубик до деформации остается
кубиком после деформации, хотя и с другим объемом), является
очевидным. То, что во втором случае изменяется только форма, а объем
остается прежним, можно проверить суммированием всех компонентов
удлинений. Как известно (§ 6), эта сумма должна дать относитель-

§ 7] РАЗЛОЖЕНИЕ ДЕФОРМАЦИИ 49
ное изменение объема. Имеем:
G = (sa, — еср) + (е2/ — £ср) + (е* — *сТ) = гх+*у + ег — Зеср = 0.
Табличка, аналогичная тензору полных деформаций, но
составленная из компонентов деформации, показанных на фиг. 22, я, очевидно,
примет вид
{ Sep, 0, 0 ]
^деф=] 0, еср, 0 1. (ЫЗ)
\ 0, 0, e0I, J
Такую табличку называют шаровым тензором деформации.
Фиг. 22. Разложение сложной деформации кубика на «чисто-объемную»
и «чисто-девиаторную».
Тензор деформации, составленный из компонентов деформации,
показанных на фиг. 22, б, т. е. из компонентов, связанных с
изменением формы, запишется так:
^деф —
(1.14)
Такой тензор деформации называют для отличия от других девиа-
тором деформации.
Сумма компонентов шарового тензора и девиатора деформации,
пчеиидно, даст полные компоненты деформации, т. е. составляющие
м-июра деформации; поэтому сделанное выше особое выделение
. ы'мной деформации и отделение компонентов формоизменения
можно рассматривать как разложение тензора деформации на шаро-
i ill тензор и на девиатор деформации.
4 Зак. 3880. Н. И. Безухов

50
ВВЕДЕНИЕ
[ГЛ. 1
Действительно, складывая (1.13) и (1.14), имеем:
^деф + ^деф = ^деф * (1.15)
Соответственно сделанному разложению полной деформации
элементарного параллелепипеда можно разложить и компоненты тецзора
напряжений. Введем обозначение
Jcp
= т(^ + 02/ + °г).
(1.16)
в дальнейшем именуемое средним напряжением. На фиг. 23, а
указаны составляющие напряжений, при которых будет только
объемная деформация, соответствующая фиг. 22, а. (То, что при
действии напряжений, равных аср, удлинения ребер будут равны именно
°г-°ср
Фиг. 23. Разложение компонентов тензора напряжений на составляющие,
связанные с изменением объема, и на составляющие компоненты,
обусловливающие изменение формы.
еср, доказывается в § 28.) На фиг. 23, б указаны составляющие
напряжений, связанные с изменением формы (аналогично фиг. 22, б).
Соответственно шаровой тензор напряжений записывается так:
а™, 0, 0
0
уо
н
'-'ср
0, аср,
I 0, 0, о,
а девиатор напряжений имеет вид
ср
(1.17)
£>„ =
-'срэ
ху>
ух*
Jcp>
Контролем правильности написанного служит равенство
(1.18)
(1.19>

§ 8] ОБОЗНАЧЕНИЯ КОМПОНЕНТОВ СКОРОСТЕЙ СМЕЩЕНИЯ 51
Итак, шаровые тензоры напряжений и деформации
характеризуют объемную деформацию в точке. Девиаторы напряжений и
деформации характеризуют формоизменение в окрестности той же
точки.
В дальнейшем (§ 28) будет показано, что все составляющие
девиатора напряжений прямо пропорциональны соответствующим по
положению, т. е. находящимся в той же строке и в том же столбце,
составляющим девиатора деформации; то же относится и к шаровым
тензорам.
Как и тензоры напряжений и деформации, девиаторы не в
меньшей, а еще в большей степени обладают замечательными свойствами,
раскрывающими характер ожидаемой деформации (упругая или
пластическая, момент наступления разрушения и т. д.; см. §§ 28, 98).
Помимо указанного здесь разложения тензора напряжений на
шаровой и девиатор иногда, по чисто вычислительным соображениям,
применяются и другие способы разложения (см. § 74).
§ 8. Обозначения компонентов скоростей смещения,
напряжений и деформации
При решении динамических задач теории упругости и теории
пластичности приходится иметь дело со скоростями перемещений отдельных точек
деформируемого тела; впрочем, с ними приходится встречаться и в таких
задачах, которые в обычном представлении относят к категории статических
ладач.
Если компоненты смещения, т. е. проекции полного перемещения
исследуемой точки на координатные оси, обозначить через и, v и w, то для
компонентов скоростей введем следующее: проекцию вектора скорости на ось
х% т. е. —тт , обозначим и (точка над и означает дифференцирование
функции по времени); аналогично и для остальных проекций. Таким образом:
du dv dw ,л _ЛЧ
Представляется целесообразным вводить в расчет и скорости
напряжении и скорости деформации. Для них введем такие обозначения:
*- • ^Ш=1 ит.д.,
~df ~ и*' ~Й ху
dt *' dt
= Чху и т. д.,
^арт> ' rfem ' d(ex — ега)
dt ot" IF cp' dt
(1.21)
Введение последних понятий оказывается целесообразным еще и потому,
что такие привычные определения, как хрупкий, пластичный материал,
деформация, течение материала и даже деление веществ на твердые и на
жидкости, являются весьма относительными и далеко неполными, если при
изучении деформации совершенно опустить такие параметры, как скорость
4*

52
ВВЕДЕНИЕ
[ГЛ. I
деформации и т. п. Как показывают опыты, в таком пластичном веществе,
как мягкая сталь, можно наблюдать хрупкое разрушение структуры,
нагружая его очень быстро. Кроме того, такой хрупкий материал, как
природный камень, не обнаруживает хрупкости, если одновременно подвергать
его высокому гидростатическому давлению.
Для правильного описания процесса деформации, особенно при быстром
нагружении и в аналогичных примерах, оказывается удобным ввести понятие
о девиаторе скоростей напряжений и о девиаторе скоростей деформации.
Девиатор скоростей напряжений включает в себя все компоненты
скоростей напряжений, связанных со скоростью изменения формы. Девиатор
скоростей деформации включает в себя все компоненты скоростей
деформации, определяющих указанную выше скорость формоизменения.
Табличная запись девиаторов скоростей представляется в виде
4< = <
Ядеф = '
°а> — аср»
У*
хгх*
Е Е
х ср'
1 •
2 1 ух*
1 •
i 2 ^вх*
txV*
аг/—аог,
т »
гу
1 •
2 ^ху>
еУ ~~ еср'
1 •
2 ^zw
XZ
т 1
Уг j
az— асР J
1 . \
2 ^хг
1 •
2" Ту* |
z ср )
(девиатор скоростей (1.22)
напряжений).
(девиатор
] скоростей
деформации).
(1.23)
Если бы для рассматриваемой точки твердого деформируемого тела мы
знали девиаторы напряжений и деформации, девиаторы скоростей
напряжений и деформации, то, как это показано далее (§ 130), тем самым нам была
бы известна полная динамическая картина состояния исследуемой точки *).
§ 9. Другие обозначения компонентов напряжений, деформации
и производных от них
Указанные ранее (§§ 4, 6) обозначения компонентов напряжений
и деформации широко применяются в учебниках и монографиях по
сопротивлению материалов и строительной механике.
Ниже приводятся, в сопоставлении с далее принятыми, для
ознакомления и другие обозначения.
Обозначения, приведенные в колонке II, широко используются
в капитальных сочинениях по теории упругости. Особо отметим
обозначения компонентов деформации, указанные в колонке III. Здесь
действительные углы сдвига (fxy, Чуг и т- Д-) обозначаются через
*) Термин «полная картина» надо понимать, конечно, не в смысле
абсолютного исчерпания всех сторон явления, что невозможно по бесконечной
сложности, неисчерпаемости природы, а в смысле их достаточности на
данном этапе для определенных технических целей и в соответствии с
принятыми ранее гипотезами и предположениями.

§9]
ДРУГИЕ ОБОЗНАЧЕНИЯ КОМПОНЕНТОВ НАПРЯЖЕНИЙ
5а
/1 1
удвоенные значения их половинок, причем для последних \-к1ху> "о" Чу*
и т. д.) принимают специальные обозначения (гху, гуз и т. д.)
I
°х
°У
°z
zxy
zyz
zzx
Напряжения
II
Xx
уу
zz
*v
yz
zx
III
xxx
zvv
*zz
zxy
zyz
xzx
I
*x
гУ
*z
Ixy
tyz
4zx
Деформации
II
exx
eyy
ezz
exy
eyz
ezx
III
%xx
*vv
*zz
*xy
*yz
2s*e
Эти обозначения, пока не распространенные, имеют ряд преимуществ
по сравнению с указанными в колонках I и П.
Так, тензор напряжений и тензор деформации в этой системе
обозначений представляются совершенно аналогичными матрицами, а именно:
( %хх> Т'ху zxz \ ( ъхх> ехуу exz \
[ = { # • ZVV* ТУ* [ ; Гдеф = { # ' *№ *У* \ ;
I • , • , *zz i I * * » zzz i
.шалогично девиаторы напряжений и девиаторы деформации записываются
и виде
.vv тср'
D„ =
УУ
ху>
X
ср'
Уг Г
-хср I
^деф -
ср»
ху*
' Zyy £cp» *yz
ср
и соответственно тензоры скоростей напряжений и деформации:
zxx>
1 # *
1 • J
хху*
zyy>
•
zxz
Zyz
zzz *
\\ f — *
Двф ""
exx>
•
L • .
ea>#»
e2/2/'
•
sxz
*yz 1
» zzz '

54 ВВЕДЕНИЕ [ГЛ. I
Применяются иногда другие обозначения и для координатных
осей и слагающих смещений вдоль них, как это указано в
приводимой табличке;
I
II
X
*1
У
Х2
Z
XS
и
«1
V
«2
W
И8 J
В соответствии с такими обозначениями осей индексы у слагающих
напряжений и деформаций применяются согласно следующей табличке:
т11
е11
*m
822
т33
езз
т12
е12
Х23
623
Т31
е31
§10. Постановка задач в теории упругости и пластичности
Принципиальная постановка задач в теории упругости и
пластичности относительно их постановки в курсе сопротивления материалов
отличается исключительной общностью.
Если объектом внимания в курсе сопротивления материалов был
преимущественно стержень или система стержней, то теория
упругости и пластичности рассматривает тело любой конфигурации и
в общем случае, как говорят, «тело трех измерений».
Обычно тело задается уравнением своей первоначальной (до
деформации) наружной поверхности (граничной поверхности)
Ф(*, Уъ *) —0
и законом распределения по поверхности тела внешней нагрузки,
чаще — уравнением ее компонентов, т. е.
Py. = h(x>y> ~~ZX ! (матрица-столбец),
Ршч = Ч(*> U z)> I
где х, у, z — координаты точек, лежащих на наружной поверхности
заданного тела; v — нормаль к поверхности, проведенная в
рассматриваемой точке; направляющие косинусы этой нормали по
отношению к координатным осям являются известными функциями координат
тех же точек (х, уу г), т. е.
cos (*v) = с?! (л:, у, z\
cosCyv) = <P2(Ar, ~У* z\
COS (2V) = cp3 (X, У, Z),

§10] ПОСТАНОВКА ЗАДАЧ В ТЕОРИИ УПРУГОСТИ 55
причем для каждой точки поверхности очевидно соотношение
cos2 (at/) + cos2 (yv) -|- cos2 (zv) = 1.
Впрочем, силы могут быть заданы также переменными во времени
(динамические силы), т. е.
Ра» = ei (*> У у *> 0 и т- п-
Наконец, силы могут задаваться приложенными и внутри тела; таковы
объемные силы, например силы тяжести, инерционные нагрузки
и т. п. Проекции объемных сил на координатные оси, отнесенные
к единице массы около рассматриваемой точки (л:, у, z), в
состоянии равновесия тела будут задаваться и обозначаться так:
Х=^г(х9 у, 2),
2 = ЫХ> У* *)•
Во всех приведенных записях имелась в виду ортогональная
прямолинейная система координат. Изучение теории упругости проще
начинать, используя именно декартову систему координат. Заметим,
однако, что в некоторых задачах уместнее применять другие системы
отсчета (полярные, цилиндрические, сферические, биполярные и т. д.).
Физические свойства тела в классической теории упругости
задаются известными читателю из курса сопротивления материалов
двумя упругими характеристиками: модулями продольной или
поперечной упругости и коэффициентом поперечного расширения,
постоянными для всех точек изотропного тела. Впрочем, в случае
неоднородного, анизотропного тела упругие характеристики, изменяющиеся
при переходе от одной точки и оси к другой, могут быть функциями
координат точки.
В теории пластичности также полагаются известными некоторые
величины, характеризующие пластические свойства рассматриваемого
тела (предел текучести и т. п.).
Искомыми будут преимущественно компоненты смещения и
компоненты напряжений для любой точки заданного тела, т. е.
«=/i(*> У, *) и т- Д-э
°ш =^Л 0*> У у *) И Т- Д->
хшк=М*> У> z) и т- д->
Иногда нас могут интересовать также компоненты деформации:
8a> = /io(*» У* г) и т. д.,
•и = Лб(*. У' г)-

56
ВВЕДЕНИЕ
[ГЛ. t
Таким образом, нас могут интересовать в каждой точке 15
компонентов: три компонента смещения, шесть компонентов напряжений,
шесть компонентов деформации.
Для решения такой общей задачи, очевидно, теория упругости
должна располагать 15 уравнениями, которые можно применить
к каждой точке внутри тела, и особыми уравнениями
(граничные условия) — для любой точки, расположенной у
наружной поверхности тела (граничные точки). Именно этим
комплексом уравнений располагает теория упругости, как это и
показано ниже (§ 30).
Впрочем, в некоторых задачах теории упругости и особенно
в теории пластичности нас могут интересовать также и
составляющие скоростей напряжений, деформации и смещения.
Наряду с указанной выше, так называемой прямой задачей может
встретиться и обратная задача, когда задается смещение наружной
поверхности тела (известны составляющие и, v и w) и определяются
поверхностные силы (составляющие рх^ ру^ ргч), вызвавшие такую
деформацию граничной поверхности, а также и напряжения,
возникшие внутри тела *).
Может быть и смешанная задача, когда частью заданы
поверхностные нагрузки, а частью — перемещения граничной поверхности.
Указанная общность постановки задач в теории упругости и
пластичности и определяет широкое использование этой науки в самых
разнообразных областях инженерной практики.
Применяя понятия о тензорах напряжений и деформаций, можно
прямую задачу теории упругости и пластичности сформулировать
коротко так: по заданным силам на граничной поверхности тела
определить тензоры напряжений {и деформации) в любой точке
тела (тензорное поле напряжений и деформаций) и
поле перемещений граничных и внутренних точек.
Соответственная обратная задача может быть сформулирована так:
по заданным смещениям граничной поверхности тела определить
тензорное поле напряжений (и деформаций).
§ 11. Еще о методе сопротивления материалов.
Метод теории упругости
Для решения сформулированных в § 10 широких задач теория
упругости располагает достаточным количеством уравнений,
получаемых в результате рассмотрения любой задачи с трех разных точек
зрения. В соответствии с этим уравнения разбиваются на три группы,
*) Обратной иногда называют также ту сравнительно простую задачу»
когда по назначаемым формулам (функциям) для напряжений (для всех или
некоторых) внутри тела определяют внешние нагрузки (граничные условия)
на контуре тела, вызвавшие упомянутые напряжения.

§ 11] ЕЩЕ О МЕТОДЕ СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ 57
Фиг. 24. Распределение
нормальных напряжений в поперечном се*
чении изгибаемой балки,
полученное в сопротивлении материалов.
а именно: статические уравнения, геометрические соотношения и
физические зависимости.
В смысле наименования указанных и совершенно необходимых
трех сторон обследования теория упругости не отличается от
сопротивления материалов, но существенно расходится в смысле строгости
исследования (особенно по
составлению статических и геометрических
уравнений), в результате чего
уравнения теории упругости совершенно
или значительно более свободны от
противоречий, имеющихся в ряде
задач сопротивления материалов.
Поясним это отдельными
примерами. При определении нормальных
напряжений в поперечном сечении
изгибаемого бруса в сопротивлении
материалов делалось допущение о их
линейном распределении по высоте
сечения (фиг. 24), что вытекало из
еще ранее принятой гипотезы о не-
искривляемости поперечных сечений (закон плоских сечений). Такая
предпосылка позволяла очень просто составить уравнение равновесия
между внутренними силами рассматриваемого сечения и внешними
силами, односторонне от него расположенными. Приравняв момент
внутренних сил внешнему, иначе
говоря, изгибающему моменту,,
получают известную формулу:
М
Далее, как помнит читатель,,
используя последнюю формулу,,
применяя ее при составлении
уравнений равновесия отдельной
элементарной отсеченной части
Фиг. 25. Схема вывода в сопротивле- балки выводят формулу Журав-
ими материалов формулы Журав- ^ * J J J r
ского. ского для касательных
напряжений, действующих в том же,
рамсе обследованном, поперечном сечении (фиг. 25), а именно:
QS_
Jb '
Не имея в виду умалить большого практического значения
приведенных выше формул технической теории изгиба, отметим лишь
формальные противоречия, допущенные при их выводе. Применяя
;i.'ikoh плоских сечений, мы считали, что в поперечном сечении нет

58
ВВЕДЕНИЕ
[ГЛ. I
причин для его искривления, т. е. нет касательных напряжений
(чистый изгиб); полученный при этом предположении результат
использовали для определения касательных напряжений, признавая
(и это правильно) их существование.
Таким образом, геометрическая (деформационная)
гипотеза оказалась в противоречии с законами
равновесия. Указанное формальное противоречие, конечно, осознавалось
создателями технической теории изгиба, и их заслуга, помимо всего
прочего, также заключалась в том, что они считали допустимым для
Фиг. 26. Распределение нормальных на- Фиг. 27. Напряженное состоя-
пряжений в поперечном и продольном ние бруса равного сопротив-
сечениях изгибаемых высоких балок по ления согласно сопротивлению
вычислениям в теории упругости. материалов.
практических расчетов обычных балок (с отношением высоты балки
к ее пролету менее 1 :5) примириться с упомянутой
противоречивостью. Строгие методы расчета теории упругости, выполненные много
позднее, исключающие искусственную гипотезу плоских сечений,
показали практическую допустимость для упомянутых балок, именно,
технической теории изгиба. Для сопоставления с фиг. 25 на фиг. 26
изображен эскиз распределения напряжений при изгибе высоких
балок, так называемых балок-стенок.
Возьмем другой, с точки зрения сопротивления материалов
элементарный пример бруса переменного сечения, например бруса
равного сопротивления, подверженного растяжению (фиг. 27).
Сопротивление материалов решало эту задачу просто: исходило из
условия равномерного распределения нормальных напряжений по поперечным
сечениям, считая их главными площадками, т. е. полагая, что
касательных напряжений в поперечном сечении бруса нет; нажатие про-

§ 11] ЕЩЕ О МЕТОДЕ СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ 59
дольных волокон одного на другое исключалось. Схема напряженного
состояния элементарного параллелепипеда при указанных
предположениях показана на фиг. 27.
Однако в действительности картина напряженного состояния
сложнее, а указанная выше находится в противоречии с законами
равновесия и с другими формулами того же курса сопротивления
материалов. В самом деле, при одноосном напряженном состоянии в площадке,
наклоненной под углом а к главной, должно действовать
касательное напряжение:
т = у о sin 2а;
такое же касательное напряжение по закону парности действует
и в плоскости, перпендикулярной к названной.
Если же мы рассмотрим площадку, совпадающую с нормалью
к внешней поверхности бруса (фиг. 27 и 28, а), то придем к
абсурдному выводу о
существовании касательных
напряжений по упомянутой
наружной поверхности. Но
так как внешняя
поверхность тела свободна от
напряжений, то,
следовательно, неверны
исходные
предпосылки о линейном
напряженном состоянии. К тому
же выводу можно прийти,
рассмотрев равновесие
элементарной призмочки,
выделенной возле
наружной поверхности тела
(фиг. 28,(5). Если
предположить, что в
поперечном сечении бруса имеются только нормальные напряжения (фиг. 27),
то надо заключить, что равновесие указанной призмочки невозможно.
Для предотвращения поступательного вертикального перемещения
необходимо существование касательного напряжения хгх (фиг. 28, б).
Однако по закону парности тогда должно иметься и ixz (фиг. 28, я);
последнее в свою очередь потребует для обеспечения равновесия
появление нормального напряжения ах (фиг. 28, г).
Конечно, при малой кривизне внешней поверхности тела можно
пренебречь компонентами аХ9 zzx, xxz, но станет задачей дать критерий
дли отнесения кривизны к малой, допускающей право пренебрегать
указанными дополнительными компонентами, или к большой, при
которой их учет необходим.
Фиг. 28. Доказательство существования в
поперечном сечении бруса «равного
сопротивления» касательных напряжений, не
учитываемых формулами сопротивления материалов.

60
ВВЕДЕНИЕ
[ГЛ. I
Кстати заметим, что наличие касательных напряжений в
поперечном сечении рассматриваемого растянутого бруса повлечет искривление
этого сечения, т. е. в данном случае гипотеза плоских сечений
принципиально неприменима.
На фиг. 29, б показаны траектории главных напряжений для
рассмотренного бруса, как это следует по точной теории, а на фиг. 29, а
для сопоставления указаны траектории с точки зрения
элементарной теории.
Для того чтобы избежать указанных выше и аналогичных проти*
воречий между деформационной гипотезой (относящейся ко всему
поперечному сечению в целом) и условиями равновесия отдельных
частей тела, в классической теории упругости, во-первых,
гипотеза плоских сечений и другие им подобные, вообще не
Фиг. 29. Траектории главных напряжений по
элементарной теории (слева) и по точной (справа).
принимаются, а во-вторых, уравнения равновесия составляются
чаще всего применительно не ко всему сечению (т. е. не в
интегральной форме), что было бы затруднительно, если не делать
сомнительных допущений о законе распределения внутренних сил по
сечению, а применительно к бесконечно малым элементарным объемам;
уравнения тогда будут выражаться в дифференциальной форме, что,
конечно, проще и может быть выполнено относительно точно.
Однако одних только статических уравнений в теории упругости
недостаточно. В самом деле, было указано (§ 4), что напряженное
состояние элементарного параллелепипеда определяется девятью
компонентами напряжений, в то время как независимых уравнений
равновесия статики можно написать для того же элементарного объема
только шесть. В этом смысле задача теории упругости
является статически неопределимой; помимо
статических уравнений приходится составлять также геометрические и
физические.

§ И] ЕЩЕ О МЕТОДЕ СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ 61
Исключая из рассмотрения гипотезы, аналогичные закону плоских
сечений, теория упругости свои геометрические уравнения составляет,
исходя из другой, более правдоподобной и во всяком случае
носящей общий характер гипотезы, а именно, из идеи непрерывности
деформаций *).
Последнее надо понимать в том смысле, что сплошное, т. е.
непрерывное тело до деформации остается непрерывным (без пустот,
•без разрывов непрерывности) и после деформации; непрерывным
останется любой объем тела и элементарный (микрообъем) в том
числе. В связи с этим деформации и перемещения точек тела
считаются непрерывными функциями координат.
Математическое оформление этой идеи связано с необходимостью
рассмотреть подробно все обстоятельства, сопутствующие деформации
элементарного объема, и потому она окажется записанной также
в дифференциальной форме (§ 22).
В курсе сопротивления материалов имелись также противоречия
между записью статических уравнений и физических уравнений. Так,
возвращаясь к изгибаемой балке,
напомним, что при вычислении
нормальных напряжений в поперечном
сечении, помимо ранее указанной
гипотезы плоских сечений, вносилось
предположение об отсутствии
надавливания продольных
волокон друг на друга, т. е.
применялся закон Гука в простейшей
записи, справедливой для линейного
напряженного состояния. Вместе с тем фиг- 30. К вычислению усилий
в дальнейшем вычислялись нормаль- надавливания продольных воло-
иые напряжения в поперечном напра- кон друг на друга,
влении (фиг. 30), т. е. усилия
надавливания (смятия) продольных волокон друг на
друга; при этом использовались уравнения равновесия и формулы
для нормальных (продольных) и касательных напряжений, выведенные
ранее в предположении отсутствия взаимного
надавливания волокон.
В теории упругости при написании физических уравнений
предполагается общий случай напряженного состояния, т. е. используется
обобщенный закон упругости, и таким образом упомянутые выше
противоречия, свойственные теории сопротлвления материалов,
отсутствуют. В теории пластичности взамен условий упругости
используются так называемые условия пластичности, которые также
записываются в достаточно общей форме (§ 98).
,:) Гипотеза непрерывности деформаций есть частное выражение
гипотезы о сплошном строении тела вообще (см. § 2).

62
ВВЕДЕНИЕ
[ГЛ. I
Выше было указано, что в теории упругости не имеет большого
применения интегральная форма записи уравнений равновесия, столь
широко и почти исключительно распространенная в сопротивлении
материалов. Но как же тогда в теории упругости устанавливается
связь между напряжениями внутри тела и внешними силами,
действующими на тело? Эта связь будет осуществляться при помощи так
называемых граничных условий (иначе условий на
контуре), представляющих собой уравнения равновесия, написанные для
элементарных объемов, мысленно выделенных из тела у его
наружной поверхности.
Эти элементарные объемы, с одной стороны, подвержены внешним
воздействиям (одна из граней таких частиц совпадает с наружной
поверхностью тела), а с другой стороны — действию внутренних на-1
пряжений (воздействие на рассматриваемый элементарный объем
среды), уравновешивающих первые.
На фиг. 31 представлены отличительные стороны в методах
теории упругости, сопротивления материалов и теории
пластичности.
Исключительное изящество методов теории упругости ввиду
совершенно общей в ней постановки задачи (любая конфигурация тела и
т. п.) и необычной для технических расчетов строгости их решения
обеспечило этой науке широкое использование в практике прошлого
и, несомненно, определяет еще большие перспективы ее применения
в будущем.
Но было бы неправильно переоценивать значение и диапазон
применения классической теории упругости. Ввиду бесконечной сложно-*
сти природы и ее неисчерпаемости познание не может исчерпать
своего объекта полностью, хотя оно все более приближается к
наиболее полному и глубокому раскрытию его.
Исходным пунктом наших знаний о мире является опыт. Однако
«самая простая истина, самым простым, индуктивным путем
полученная, всегда неполна, ибо опыт всегда незакончен»*).
Тем более «истина неполна» в нашем случае, если учесть наличие
ряда гипотез, упрощающих реальную схему материала, хотя такое
огрубление, как было указано выше (стр. 28), с практической точки
зрения на данном этапе и необходимо. Таким образом, самый
процесс исследования напряженного состояния тела не может совершаться
без известного огрубления, упрощения и расчленения. Более того,
такое огрубление содержится и в самом первом этапе познания —
ощущении.
«Мы не можем представить, выразить, смерить, изобразить
движения, не прервав непрерывного, не упростив, угрубив, не разделив,
не омертвив живого. Изображение движения мыслью есть всегда
огрубление, омертвление, — и не только мыслью, но и ощущением.
*) В.И.Ленин, Философские тетради, стр. 154, Госполитиздат, 1947.

§11 ЕЩЕ О МЕТОДЕ СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ 63
Условные обозначения:
(ТУ) —применяется в теории упругости
(Т.П.) — применяется в теории пластичности
(СМ) — применяется в сопротивлении материалов
(П.ТУ.)—применяется в прикладной теории упругости и пластичности
Фиг. 31. Связь и различие в методах теории упругости, теории пластичности и сопротивления материалов.

64
ВВЕДЕНИЕ
[ГЛ.
и не только движения, но и всякого понятия. И в этом суть
диалектики» *).
В этой связи от классической теории упругости нельзя получить
ответа на вопросы, постановка которых принципиально исключается
принятыми в этой науке гипотезами, упрощенными моделями. Это
в первую очередь относится к напряжениям, зависящим от истории
возникновения тела, от особенностей структуры последнего, т. е.
к так называемым структурным напряжениям.
Ранее (§ 2) было упомянуто о попытках в прошлом построения
дискретной теории упругости, в основу которой должна быть
положена модель молекулярного строения исследуемого тела. Именно
такая схема позволила бы проникнуть в особенности «микрообъема»
и вычислить структурные напряжения.
Надо полагать, что время от времени такие попытки будут
повторяться, хотя, конечно, не в форме простого поворота истории науки
назад, а с учетом экспериментального и теоретического материала,
вновь накопленного всей историей прошлого развития науки (как
в отношении дискретной, так и континуальной теории
упругости).
Тем самым будут конкретнее очерчиваться как диапазон
практического использования того или иного направления, так и
целесообразные в них коррективы.
Если история развития физики наглядно свидетельствует о
непрестанной борьбе старых и новых теорий, коренной ломке понятий,
то та же история доставляет доказательства и прочной
преемственности и взаимосвязи классических и новых теорий.
Так например, механика быстрых движений, так называемая
релятивистская механика, превращается в механику Ньютона при малых
скоростях движения.
Применительно к механике деформируемого тела это означает, что
дискретная и континуальная теории упругости, каждая в отдельности,
должны сохранять свое значение в надлежащих пределах.
Законы науки, установленные при определенных условиях
(применительно к макрообъемам в классической теории упругости и
применительно к микрообъемам в дискретной теории упругости) являются
относительно истинными, дающими нам объективные знания о
явлениях и вещах природы.
Новые законы поэтому не отменяют прежних законов, а включают
их, так как они имеют значение в известных условиях и границах.
В этом выражается диалектический характер процесса познания,
который дает нам объективную истину, приближение к абсолютной
истине, но не сразу, а в процессе развития «живого, плодотворного,
истинного, могучего, всесильного, объективного, абсолютного
человеческого познания» (В. И. Ленин, Философские тетради, стр. 330).
*) В. И. Ленин, Философские тетради, стр. 243, Госполитиздат, 1947.

§12] ОСНОВНЫЕ ЭТАПЫ В РАЗВИТИИ ТЕОРИИ УПРУГОСТИ 65
§ 12. Основные этапы в развитии теории упругости
в XIX и начале XX в.
Излагаемый ниже исторический экскурс отнюдь не претендует на
полноту п ставит целью отметить лишь основные этапы в развитии теории
упругости, которые имеют отношение к инженерной практике и ознакомление
с которыми для читателя может оказаться поучительным.
В этом параграфе мы ограничимся описанием лишь тех этапов развития
теории упругости, которые главным образом касаются развития взглядов на
физические принципы, лежащие в основании теории (эти этапы относятся
к XIX и началу XX в.)
Советскому периоду развития теории упругости, а также частичному
освещению других сторон истории посвящены §§ 25, 39, 44, 76, 90, 96, 107,
115, 125, 127—130.
Начала учения о прочности материалов, как связанные с потребностями
практики, уходят в глубь веков. История древнего мира знает таких ученых
механиков и строителей, как Архит (430—365 гг. до н. э.), Архимед (287—
212 гг. до н. э.), Витрувий (I в. н. э.) и других, пытавшихся выработать
приемы расчета сооружений. Все эти приемы основывались лишь на
умозрительных соображениях, часто весьма остроумных, но не имевших
объективной ценности, ибо они не были подтверждены опытом (например,
геометрический закон подобия), и потому на развитие учения о прочности материалов
п сооружений не оказали- влияния.
Несомненно также, что строители древнейших сооружений умели как-то,
иовпдимому на базе опыта ранее возведенных сооружений, назначать
размеры сооружений так, что они оказывались достаточно прочными. В этом
смысле большой интерес и в настоящее время представляют некоторые
постройки XV—XVI вв., как, например, изумительные по красоте и искусству
творения русских зодчих, а именно: башни, палаты и гидротехнические
сооружения Московского Кремля и таких старинных городов, как Новгород,
Киев, Псков, Владимир, Углич и др. В письменном виде расчетов таких
сооружений до наших дней не сохранилось.
Интерес представляют сооружения и более раннего периода,
принадлежащие талантливым мастерам, как-то некоторые храмы и здания в Закавказье
(Мцхети) и на юге нашей страны, относящиеся еще к V в.
Сооружения этих, а также и еще более ранних эпох поистине достойны
удивления современника и ожидают специальных исторических исследований,
которые помогли бы пролить свет и разгадать секреты производившихся
р.шес расчетов на прочность.
Условно связывая начало истории теории упругости и учения о
прочности материалов с первыми опубликованными и сохранившимися до наших
лиги печатными документами, историк должен начать повествование с
великою ученого своей эпохи Галилея (1564—1642 гг.), который впервые описал
прицеленные им в Венецианском арсенале опыты над изгибаемыми балками.
• им выводы из этих опытов, сделанные Галилеем, были ошибочными и ис-
полыусмая теперь так называемая техническая теория изгиба балок (1856 г.),
fli.i.ii;i создана в трудах нашего соотечественника Д. И. Журавского (1821 —
IMH 1т.)У но именно с Галилея начинается эра опытных исследований. Мысли
I ллплся через посредство печатных его произведений и при содействии
многочисленных его учеников скоро получили распространение.
Справедливость требует отметить, что вопросами прочности материалов
- «с* :i;i 150 лет до эпохи Галилея интересовался Леонардо да Винчи (1452—.
I »1!) п*.), кого Ф. Энгельс назвал одним из титанов по силе мысли,
страстно» гп и характеру, по многосторонности и учёности. Однако рукописи,
• цсржапшис исследования Леонардо да Винчи по вопросам прочности,
Омли утеряны и частично обнаружены сравнительно недавно. Известное
J Зик. 3880. Н. И. Безухо!

66
ВВЕДЕНИЕ
[ГЛ. I
высказывание, принадлежащее Леонардо да Винчи, «Практика — последний
критерий научной теории... Мне кажется» что те науки суетны и полны
ошибок, которые не рождаются из опыта—матери всякой достоверности
и которые не заканчиваются на опыте» полностью отвечает и современному
в механике деформируемого тела методологическому принципу.
Основной закон деформирования упругих тел в его простейшей,
линейной форме, но к тому времени еще без объяснения физической
сущности явления упругости, был в 1678 г. сформулирован Р. Гуком
(1635—1702 гг.).
Первая попытка рассмотрения нелинейной связи между напряжениями
и деформациями, т. е. в форме, отличной от закона Гука, была сделана
Бюльфингером и опубликована в трудах Российской Академии наук
в 1729 г.
Первые существенные вклады в дело создания математической теории
изгиба упругого стержня принадлежат русским академикам Л. Эйлеру (1707—
1783 гг.) и Д. Бернулли (1700—1782 гг.) и опубликованы в 40—70 гг. XVIII
века. Эйлеру принадлежат первые исследования упругой устойчивости (задача
о продольном изгибе). Эйлер и Бернулли занимались также проблемой
поперечных колебаний упругого стержня.
По вопросу о причинах упругости и о содержании самого понятия
упругости ценные мысли были высказаны нашим великим соотечественником
М. В. Ломоносовым (1711—1765 гг.) в его знаменитом трактате «Попытка
теории упругой силы воздуха», представленной им в 1748 г. в Российскую
Академию наук. В этом трактате Ломоносов решительно осуждал тенденции
призывать «по обычаю века» на помощь для отыскания причины упругости
воздуха «невесомую материю упругости». Ломоносов писал: «Мы
довольствуемся тонкостью и подвижностью самого воздуха и ищем причину
упругости в самой материи его». Материалистической корпускулярной
философии Ломоносова было органически чуждо представление о
невесомых материях *).
Попутно отметим, что Ломоносову принадлежит и введение в
употребление на русском языке самого слова «упругость».
Первым исследователем, занявшимся построением общих уравнений
равновесия и колебания упругих тел, был Навье (1785 — 1836 гг.).
Он исходил из концепции Ньютона о строении вещества и считал, что
упругие реакции возникают вследствие тех изменений
интрамолекулярных сил, которые являются результатом перемен во взаимном
расположении молекул.
В этом смысле исследования Навье примыкают к дискретной теории
упругости**).
*) Ломоносов рядом убедительных рассуждений показывает, что
упругость газов можно объяснить движением частиц газа, почему сжатый газ
будет оказывать уже большее сопротивление дальнейшему сжатию, чем газ
несжатый.
**) Заметим, что упомянутая «молекулярная» теория Навье, как и
родственные ей последующие попытки в том же направлении Пуассона и Коши,
имеют мало общего с современными в физике представлениями о поведении
молекул. Изыскания, проводимые в настоящее время и относящиеся к
дискретной теории упругости, не представляют, конечно, возврата к
элементарным концепциям Навье.
Попутно заметим, что для практических расчетов того времени Навье»
повидимому, считал возможным исходить из гипотезы сплошности и
отсутствия начальных напряжений в теле. Последнее можно усмотреть из
характера изложения его курса сопротивления материалов, относящегося к тому
зремешь

§ 12] ОСНОВНЫЕ ЭТАПЫ В РАЗБИТИИ ТЕОРИИ УПРУГОСТИ 67
Полученные им дифференциальные уравнения были выражены в
смещениях молекулы и содержали одну постоянную, выражающую упругие свойства
тела. Его мемуар был прочитан в Парижской Академии наук в 1821 г.
Однако примененный Навье ход рассуждений не встретил общего признания.
Были выдвинуты возражения против принятого Навье выражения для силы
взаимодействия двух молекул; оспаривалась также законность примененного
Навье способа интеграции взамен трехкратного суммирования при подсчете
сил, действующих на отдельную молекулу.
Относящиеся к тому же периоду открытия в теории распространения
света (гипотеза поперечных колебаний) тесно связали дальнейшее развитие
теории упругости с проблемой распространения света. Проблема
распространения волн в упругой среде привлекла тогда внимание трех выдающихся
математиков: М. В. Остроградского (1801—1861 гг.), Коши (1789—1857 гг.)
и Пуассона (1781—1840 гг.).
Русский академик М. В. Остроградский внес существенный вклад
в развитие динамической теории упругости своими работчми о
распространении деформации в упругой изотропной среде, опубликованными
в период 1829—1832 гг. С именем Остроградского связываются не только
его работы по динамической теории упругости, но и целая школа
в области механики в широком смысле слова, получившая мировое
признание*).
Коши в 1822 г. ввел современное в теории упругости понятие о
напряжении в точке, выразил деформацию в окрестности данной точки через шесть
компонентов деформации и вывел уравнения движения (или равновесия),
которые связывают компоненты напряжений с силами, распределенными
по объему, и с силами инерции. Соотношения между напряжениями и
деформациями Коши построил на допущениях, что эти соотношения линейны и
что главные напряжения в данной точке совпадают по направлению с
главными осями деформации. Остается неясным, почему Коши для
оправдания последних допущений не указал на экспериментальный закон Гука.
Полученные им уравнения — именно те, которые приняты ныне для
изотропных тел.
Методы первоначальных**) исследований Коши отличны от методов
исследования Навье; гипотеза материальных точек, связанных действием
центральных сил (через пустоту), Коши не применялась. Есть важные
различия и в уравнениях: уравнения Навье содержат одну постоянную,
выражающую упругие свойства тела, тогда как в уравнения Коши входят
две такие постоянные.
В начале XIX столетия указанными выше трудами Навье, Коши,
Остроградского, Пуассона и др. были положены основы той ветви механики,
которую теперь называют математической теорией упругости. Однако методы
теории упругости оставались в стороне от инженерной практики. Предста-
нптели математической теории упругости того времени занимались главным
образом такими физическими проблемами, как объяснение явлений
распространения света, исходя из представления об эфире как об упругом теле,
исследовали напряжения в земной коре вследствие тяготения и охлаждения
;юмли и т. д.
Теория упругости оставалась наукой, достаточно далекой от
конкретных технических приложений, и инженеры ею не пользовались. Такой отрыв
теории упругости от требований инженерной практики, с одной стороны,
рампитие строительства железных дорог, металлических для них мостов,
машиностроения, железного судостроения и связанная с этим необходи-
*) См. Н. Д. Моисеев, Общий очерк развития механики в СССР,
Сборник «Механика в СССР за тридцать лет», М—Л., 1950.
**) В последующем он распространил свою теорию и на случай
кристаллического тела, воспользовавшись гипотезой о материальных точках.
5*

68
ВЬЕДЕНИЕ
[ГЛ. I
мость производить расчеты на прочность машин и сооружений — с
другой, вызвали к жизни учение о сопротивлении материалов как чисто
практическую дисциплину, основанную на наглядных гипотезах и
элементарных математических приемах, широко использующих
экспериментальный материал, как полученный в результате специально поставленных
опытов, так и накапливающийся в процессе эксплуатации тех или иных
объектов.
Таким образом, дальнейшее развитие механики деформируемого тела
разветвляется на два русла. Одно, отправляющееся от методов,
введенных Л. Эйлером и Д. Бернулли, связанное в дальнейшем со славными
именами наших соотечественников Д. И. Журавского (1821—1891 гг.).
Ф. С. Ясинского (1856—1899 гг.). В. Л. Кирпичсва (1845—1913 гг.) и др.,
получает название теории сопротивления материалов, и другое,
именуемое математической теорией упругости, является продолжением
теории Навье.
В связи с первым направлением, впоследствии определившим
строительную механику, следует упомянуть также о современнике Л. Эйлера
выдающемся русском изобретателе И. П. Кулибине (1735"—1818 гг.), получившем
мировую известность за изобретение автоматов. В 1776 г. И. П. Кулибин
составил проект арочного деревянного моста пролетом 300 м через р. Неву
в Петербурге и изготовил, а затем испытал его модель в 1/ю
натуральной величины. Этот проект, будучи по тому времени дерзким вызовом
мировой технике, содержал достоверные суждения об упругой работе арок.
Расчеты арок были проверены Л. Эйлером и признаны правильными.
«На ней печать гения», — писал Д. И. Журавский по поводу арки
Кулибина.
Далее следует отметить плодотворную работу в Петербургском
институте инженеров путей сообщения французских инженеров Ляме (1795—1870 гг.)
и Клапейрона (1799—1864 гг.), которые развивали теорию Навье
применительно к строительному делу.
Плодотворное развитие известной задачи Ляме об осесимметричной
деформации толстостенной трубы было сделано русским академиком
А. В. Гадолиным (1828—1892 гг.); метод расчета скрепленных стволов,
разработанный Гадолиным, получил всеобщее признание и широкое
использование во всех странах.
Не касаясь освещения причин крушений гигантских железнодорожных
мостов, гибели некоторых пассажирских быстроходных пароходов и др.
{исследования которых давали большой толчок к развитию методов расчета
на прочность), интересующимся связью прогресса в теории упругости
и катастрофами рекомендуем обратиться к сочинениям В. Л. Кирпичева [51],
Ф. Д. Дмитриева [35] и к источникам, указанным в этих произведениях.
Возвращаясь к вопросу о развитии взглядов на физические принципы
в теории упругости, отметим большие споры о количестве упругих
постоянных (одна или две или больше) и о значении некоторых констант. Причиной
споров являлось расхождение опытных данных с результатами теории,
вытекающей из гипотезы центральных сил. Заметим, что опыты
приверженцев одних взглядов не всегда были достаточно убедительными для
сторонников других воззрений вследствие ограниченности методики испытаний и
специфики в выборе самого материала для экспериментирования (пробка,
желатин, каучук), что было характерно для многих участников спора того
времени, фактически оторванных от нужд практической жизни. Они, по
выражению А. Лява *), «интересовались скорее натуральной
философией, чем материальным прогрессом, стрем и^лись
скорее познать мир, чем сделать его более удобным».
*) А. Л я в, Математическая теория, упругости, М.—Л., 1935.

§ 12] ОСНОВНЫЕ ЭТАПЫ В РАЗВИТИИ ТЕОРИИ УПРУГОСТИ 69
Вместе с тем эти споры не прошли для науки без пользы; они пролили свет
на самые недоступные вопросы о природе молекул и характере их
взаимодействия (оказалась несостоятельной гипотеза упругой светоносной среды
и т. д. и т. п.).
Одновременно происходившая эволюция в физических воззрениях на
строение материи, развитие атомистической теории в химии, статистической
молекулярной теории в физике, на распространение энергетических
принципов и т. п. окончательно подорвали доверие, которым ранее пользовалась
гипотеза материальных точек, связанных действием центральных сил
через пустоту.
Эта гипотеза, отражающая дискретную схему строения материи, в
последующем была оставлена и уступила место гипотезе о сплошности,
т. е. механике континуума, с которой и связываются наиболее
выдающиеся произведения по теории упругости конца XIX в. и
современности *).
К таким выдающимся произведениям следует отнести работы Сен-Ве-
нана (1797—1886 гг.), связанные со строгой разработкой проблемы изгиба
и особенно кручения призматических тел (1855 г.; см. § 67),
исследования Герца (1882 г.; см. § 66) в области передачи силы (смятие
шаров) и др.
Исследования Сен-Венана по изгибу показали, что элементарная теория
изгиба, созданная Бернулли и Эйлером, обладает весьма большой точностью
и совершенно достаточна для практических целей. Его исследования по
теории кручения показали ошибочность предложения Навье рассчитывать
стержень любого профиля по тем формулам, которые еще в 1784 г. были
выведены Кулоном для стержней круглого сечения и основаны на гипотезе
плоских сечений [9]. Так, по теории Навье цельная и разрезанная по
образующей трубы обладают одинаковой жесткостью на кручение; стержень
круглого профиля и стержень узкого прямоугольного профиля при
одинаковых площадях сечений якобы также обладают равными жесткостями на
кручение и др. Авторитет Навье обеспечил этим ошибочным результатам
распространение в течение многих лет даже после опубликования в 1855 г.
работ Сен-Венана по теории кручения призматических тел.
В области так называемой плоской задачи теории упругости следует
особо отметить работы Г. В. Колосова (1909 г.), изложившего впервые
метод, основанный на применении теории функций комплексного переменного.
Метод Колосова был впоследствии развит и обобщен нашим талантливым
современником Н. И. Мусхелишвили.
Из ученых дореволюционной России, труды которых были
основополагающими, надо назвать И. Г. Бубнова (1872—1919 гг.) (теория пластинок
с цепными напряжениями), Б. Г. Галеркина (1871—1945 гг.) (приближенные
методы решения статических задач о расчете пластинок, впоследствии
использованные в других задачах теории упругости, в аэродинамике,
гидродинамике и т. п.), Л. С. Лейбензона (1879—1950 гг.) (расчет безбалочных
перекрытий), В. Л. Кирпичева (по сближению математической теории
упругости со строительной механикой), X. С. Головина (1844—1904 гг.) (теория
изгиба кривых брусьев), П. Ф. Папковича (1887—1946 гг.) и А. Н. Крылова
(IN63—1945 гг.) (строительная механика корабля).
Отрыв ученых от практики, характерный для науки в прошлом и
особенно для зарубежной, и вытекающее из этого отрыва определенное
умонастроение, по справедливому выражению А. Лява**), привели к тому, что
*) Гипотеза сплошности, иначе говоря, сознательное пренебрежение
дискретностью в строении тела и дискретностью в характере деформации,
и последнее время также подвергалась резкой критике (см. § 115), но
сохраняет свое значение и для настоящего времени.
!"•*) А. Л я в, Математическая теория упругости, стр. 42.

70
ВВЕДЕНИЕ
[ГЛ. I
«теория в меньшей степени, чем она могла бы,
содействовала материальному прогрессу человечества».
Великая Октябрьская социалистическая революция коренным образом
изменила развитие науки в нашей стране. Характерными особенностями
советской механики деформируемого тела являются ее тесная связь с
практикой строительства, принципиальность, научность и глубина анализа.
Организация мощных научно-исследовательских институтов, оснащенных
современным оборудованием, разработка проблем прочности не только
отдельными талантливыми учеными, а большими коллективами, участие всей
армии советских механиков в решении неотложных задач, выдвигаемых
грандиозными Стройками Коммунизма, все эти обстоятельства, вместе взятые,
определили столь значительный перелом в развитии науки, что новый этап
в развитии теории упругости следует считать с Великой Октябрьской
социалистической революции. Отдельным описаниям этого нового и
значительного для науки этапа посвящены §§ 39, 90, 96 и др.

ГЛАВА II
ОБЩИЕ УРАВНЕНИЯ МЕХАНИКИ СПЛОШНОЙ СРЕДЫ
А. ТЕОРИЯ НАПРЯЖЕННОГО СОСТОЯНИЯ
(СТАТИЧЕСКИЕ УРАВНЕНИЯ)
§ 13. Обозначения компонентов напряжений вблизи
заданной точки
Представим себе сплошное тело (упругое или неупругое,
находящееся в равновесии или в движении) и внутри этого тела через
точку УН с координатами х% у, z проведем какую-либо плоскость,
например, нормальную к оси х (фиг. 32). Тогда компоненты напряжений
для точки М указанной плоскости должны быть обозначены ат, хух, тгг.
Фиг. 32. Напряжения в двух бесконечно близких друг к^другу
точках, принадлежащих сплошному телу, в общем не равны и
отличаются между собою на бесконечно малые величины.
Если в бесконечной близости от заданной точки М рассмотреть
другую точку N с координатами x-\-dx, y-\-dy, z-\-dz и через
>ту точку также провести плоскость, нормальную к оси лг, то
компоненты напряжений для этой второй точки должны отличаться от
одноименных напряжений у точки М на бесконечно малые величины;
)\л разница тем меньше, чем ближе точка N к точке Ж.
Последнее утверждение вытекает из того положения, что
напряжения являются непрерывными функциями координат, т. е.
°х = F\ (х> У> z\ ~ух = F2 (*> У у Z) И *• Д-

72 ОБЩИЕ УРАВНЕНИЯ МЕХАНИКИ СПЛОШНОЙ. СРЕДЫ [ГЛ. II
Компоненты напряжений для точки N могут быть с достаточной
точностью записаны через компоненты напряжений в точке М в виде:
(2.01)
Смысл последних записей таков: мы допускаем функции
напряжений разложимыми в ряд Тейлора, но отбрасываем члены второго
и высших порядков малости *).
Фиг. 33. Обозначения нормальных напряжений по всем
граням элементарного параллелепипеда.
В случае, если обе рассматриваемые точки лежат на прямой,
параллельной одной из координатных осей, выражения (2.01) упро-
*) Эта же идея лежит в основе всех приложений дифференциального
исчисления: сложные зависимости становятся в бесконечно малом линейными,
неравномерные процессы — равномерными и т. д., если пренебречь бесконечно
малыми высших порядков. Но не только эти приложения, но и само
создание анализа бесконечно малых стало возможным только потому, что
материальные процессы имеют тенденцию в малых размерах приобретать
равномерный характер (пока, разумеется, не начинает сказываться атомное строение
вещества). Эту тенденцию в присущей ему форме и отражает
дифференциальное исчисление.

§13] ОБОЗНАЧЕНИЯ КОМПОНЕНТОВ НАПРЯЖЕНИЙ 73
щаются. Так, если прямая MN параллельна оси х и, следовательно,
dy = dz = О, то
°х = °х ~\~~d~^dx,
J _L. ^Еяз? dr
hjx — ^ух ^Г $х ал*
т' — т -L-dJh*dx
^ZX Т2Ж Ч^ fix UX-
Так как производная функции по какому-либо аргументу
представляет собой интенсивность изменения функции с приростом этого
аргумента, иначе говоря, величину прироста значения функции на
«единицу» длины аргумента, то отношение -^, умноженное на аху
Фиг. 34. Обозначения компонентов касательных
напряжений по всем граням элементарного параллелепипеда.
составляет прирост функции ох на длине dx. Аналогично -^ dx—
прирост zyx на длине dx и т. д.
В качестве иллюстрации применения приведенной выше записи
па фиг. 33 показаны обозначения нормальных напряжений по трем
и.члимно перпендикулярным граням, видимым наблюдателю, через
компоненты напряжений по соответственным им параллельным
остальным граням того же бесконечно малого параллелепипеда. Эти послед-
пне плоскости (закрытые от наблюдателя первыми тремя гранями),
примыкающие к точке Му приняты как бы за основные, и

74 ОБЩИЕ УРАВНЕНИЯ МЕХАНИКИ СПЛОШНОЙ СРЕДЫ [ГЛ. II
потому напряжения, действующие по плоскостям, отстоящим от
основных в положительном направлении соответствующих осей, будут иметь
в своем начертании указанные выше дифференциальные приращения
(с положительным знаком).
Для того чтобы не затемнять чертежа, обозначения касательных
напряжений даны отдельно на фиг. 34.
Заметим, что как бы ни были малы размеры граней элементарного
параллелепипеда, однако и в пределах каждой грани напряжения,
конечно, могут распределяться неравномерно. В свете этого замечания
следует считать, что указанные на фиг. 33—34 обозначения
компонентов напряжений имеют осредненные значения напряжений для
каждой грани в отдельности.
§ 14. Дифференциальные уравнения равновесия и движения
(статическое обследование)
Предположим, что данное тело находится в равновесии. Из этого
тела около некоторой точки М мысленно вырежем бесконечно малый
параллелепипед; для него должны удовлетворяться шесть условий
равновесия:
2^ = 0, 2^=0, | (а)
2z = o, 2^=°- I
Если тело находится в движении, то правые части уравнений
проекций (2 ^, 2^, 2 Z) не обращаются в нули, а согласно
второму закону Ньютона должны быть равны произведениям массы
элемента на соответствующую проекцию его ускорения *) (проекция
инерционных сил).
Пусть для рассматриваемой точки М (ее можно считать,
например, центром тяжести элементарного параллелепипеда) проекции пути
(перемещения) на оси координат будут соответственно равны: и
(на ось л;), ?/(на ось у) и w(na ось z). Смещения w, t/, w полагаем
очень малыми; проекции ускорения запишутся так:
д2и d2v d2w
W* ~дР' ~W'
Аналогично должны измениться и правые части уравнений
моментов, где вместо нулей должны быть проекции моментов от тех же
инерционных сил.
*) Можно, конечно, правые части равенств оставить равными нулю, если
указанное произведение массы на ускорение, но с обратным знаком (далам-
беровы силы инерции) подразумевать в составе объемной силы (А\ К, Z).

§14] ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ РАВНОВЕСИЯ И ДВИЖЕНИЯ 75
Подробно раскроем первое уравнение динамического равновесия
(строго говоря, уравнение движения), т. е.
У v д2и
(б)
Проекцию на ось Ох будут давать нормальные и касательные
напряжения, параллельные оси Ох. Раскрывая условие равновесия (б),
имеем (фиг. 33 и 34):
Г* + ~Ш dx\ dy dz~~ °* йУ dz + [~*у + T}f Лу\ dx dz ~ ~*y dxdz +"
+ Txz'-\~-jr1^z dy dx—zxzdy dx-\-Xpdxdy dz =
= p dx dy dz
d*u
(в)
где p— плотность вещества и X—проекция на ось х объемной силы
(например, силы тяжести), отнесенной к единице массы.
Таким же путем надлежит раскрыть и следующие два уравнения
динамического равновесия. После раскрытия скобок и выполнения
сокращений уравнения проекций напишутся так:
даг
"zyx
дх
fasx
dx
_L_
+
1
1
д~ху
ду~
ССу
dy
д~гу
ду
i
+
1
1
d^xz
dz
dxyz
dz.
dc2
dz
+
+
i
1
Xp
Y?
z?
d*u
d-w
= '¥'
(2.02)
Замечание 1. Уравнения (2.02) для удобства запоминания могут быть
представлены следующей таблицей (после переноса членов с объемными
силами в правые части):
Уравнения
2К=°
2^=°
Левая часть уравнений
с операциями
d
дх
Gx
1уХ
zzx
д
dy
хху
аУ
тгг/
d
dz
zxz
zyz
°z
Множители
Правая часть уравнений
без
операций
X
Y
Z
с операцией
и
V
W
— Р Р

76 ОБЩИЕ УРАВНЕНИЯ МЕХАНИКИ СПЛОШНОЙ СРЕДЫ [ГЛ. 11
Ксадратная матрица компонентов левой части уравнений, над которыми
должны быть произведены соответствующие операции по указанной в таблице
схеме, составляет тензор напряжений. Правая часть уравнений
представляет собой матрицу-столбец из объемных сил и вторые производные от
матрицы-столбца смещений.
Замечание 2. В большей части задач теории упругости и теории
пластичности массовые силы оказывают очень небольшое влияние, и поэтому
при расчетах ими можно пренебречь. В таком случае в уравнениях (2.02)
пропадают члены, содержащие X, К, Z. Если к тому же рассмотреть случай
покоя (статическая теория упругости), то уравнения равновесия (2.02)
оказываются однородными дифференциальными уравнениями. Если при
написании этих уравнений применить обозначения напряжений и
координатных осей, указанных на стр. 53, то такие однородные статические уравнения
запишутся исключительно кратко:
< = 1
дх£
-to
= 0 (k= 1, 2, 3).
В случае использования другой (не декартовой) координатной системы
уравнения равновесия записываются в виде, отличном от (2.02) (см. § 37).
Замечание 3. При выводе (2.02) не делалось различия между
величиной и положением до и после деформации тех площадок, на которых
действуют напряжения. В случае больших деформаций (круг задач нелинейной
теории упругости) необходимо учитывать упомянутое различие между
первоначальной и деформированной формами параллелепипеда, однако заметим
(см. [74]), что по внешнему виду
уравнения (2.02) сохраняются и в таком
случае, если под координатами дг, у, z.
по которым выполняется
дифференцирование в (2.02), понимать не
координаты точек до деформации, а
координаты окончательного положения точек.
Переходим ко второй группе
уравнений — сумме моментов.
Начнем, например, с условия 2^ = 0,
причем для простоты выкладок
начало координат примем в центре
параллелепипеда. Моменты
относительно этой оси у0у0 (фиг. 35)
будут давать только касательные силы,
нормальные к ней, которые только
и указаны на фиг. 35. Нормальные
силы, как не имеющие плеча
относительно выбранной оси УоуСУ не будут
давать моментов и на фиг. 35
потому не указаны. По тем же
причинам не будут давать момента компоненты силы тяжести.
Предполагая общий случай движения, когда в данный момент
времени рассматриваемый элемент имеет проекции угловых
перемещений на оси координат ш^, шуу сог, в правой части уравнений
Фиг. 35. К доказательству закона
о сопряженности касательных
напряжений.

§14] ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ РАВНОВЕСИЯ И. ДВИЖЕНИЯ 77
моментов (а) вместо нулей должны быть записаны произведения
момента инерции массы элемента на соответствующую проекцию
углового ускорения, т. е.
My = J
у
df*
(г)
Раскрываем условие (г):
di7
dz
'■dzs)dxdy-?-\-'zxzdxdy -± — >zgxdydz-£ —
dz
zx
dx
\ dx d2 со,
dx)dydz-2=J—=^
В последнем уравнении не все члены одинакового порядка
малости; так члены ixzdxdy dz, zzxdxdy dz— бесконечно малые третьего
порядка, а остальные: -*—dxdy-
di9
'dy dz-
dx*
J-
dc
У
■беско-
dzzdxdy 2 , -j^-^^ 2 ,. dt2
печно малые четвертого и пятого порядков, которые надлежит
исключить из уравнения ввиду соседства их с малыми низших порядков.
В итоге из выражения (г) определяем:
~хг = *zx- (Д)
Это есть известный читателю из сопротивления материалов закон
сопряженности касательных напряжений; соответствен-
то ему же два других уравнения дают:
^ху == ~ух'у 'zzy=='zyz' \^)
Выражения (д) и (е) могут быть прочитаны в такой объединенной
редакции: в каждых двух взаимно перпендикулярных плоскостях
компоненты касательных напряжений, направленные
перпендикулярно к линии пересечения этих плоскостей, равны между собой
и при этом направлены либо оба к линии пересечения, либо оба
от линии пересечения *).
Итак, к трем дифференциальным уравнениям (2.02), содержащим
девять функций от координат рассматриваемой точки (ах, ауу аг, ixy,
ТУ-С> Т£'2> ~zy> ^zxf ~xz
,), условие сопряженности дает еще три условия:
хху
~yz
^гх
=
=
=
zyx>
zzy>
^OTZ'
(2.03)
*) Заметим, что закон взаимности (сопряженности) касательных
напряжений является частным случаем общего закона взаимности напряжений,
гласящего: если при одной и той же точке напряженного тела построены
яме площадки, то проекция полного напряжения, отвечающего одной из этих
проекций, на нормаль ко второй равна проекции напряжения, отвечающего
нторой площадке, на нормаль к первой.

78 ОБЩИЕ УРАВНЕНИЯ МЕХАНИКИ СПЛОШНОЙ СРЕДЫ (ГЛ. II
Таким образом, использовав (2.03) в (2.02), число неизвестных
функций уменьшаем до шести.
Так как число неизвестных функций (шесть) превышает число
уравнений (три), то, следовательно, одного статического
рассмотрения задачи недостаточно для решения поставленной задачи о
нахождении упомянутых выше шести функций. Иначе говоря, всякая задача
теории упругости статически неопределима. Недостающие
уравнения получим, изучая происходящие в теле деформации и их связь
с напряжениями (т. е. физические свойства данного тела).
Эти геометрические и физические соотношения будут установлены
ниже (§ 22 и глава III), и в итоге число уравнений будет
соответствовать числу неизвестных функций. Интегрирование
дифференциальных уравнений в конечном счете раскроет вид искомых функций»
но, как и всякое интегрирование уравнений, повлечет появление
произвольных постоянных и неопределенных функций интегрирования,
для нахождения которых надлежит обратиться к использованию
граничных условий, иначе называемых поверхностными условиями
(условия на контуре)) эти условия устанавливают связь внутренних
сил (напряжений) с внешними силами, приложенными к наружной
поверхности исследуемого тела (§ 15).
§ 15. Условия на контуре
(продолжение статического обследования)
Если все сплошное тело будем мысленно разбивать на элементы
плоскостями, параллельными координатным, то в общем случае тела
любой формы выделить элементы в виде параллелепипеда у его
поверхности не представится возможным (фиг. 36). По имеющимся у
поверхности граням, очевидно, будут действовать внешние силы (нагрузки),
приложенные к данному телу.
Установление зависимостей между этими поверхностными силами
(например, по наружной грани ас) и внутренними силами
(напряжениями) по плоскостям (например, be, ba), параллельным координатным
и расположенным возле наклонной, и приведет к упомянутым выше
условиям на контуре.
Для общности можем предполагать, что форма изучаемого тела
не призматическая и поперечное сечение (фиг. 36) по длине тела
не постоянно, а потому заштрихованные на фиг. 36 элементы,
примыкающие . к наружной поверхности, могут представляться не
треугольными призмами, а тетраэдрами.
В курсе сопротивления материалов читатель изучал напряжения
в так называемых «косых» плоскостях, когда по известным
напряжениям по прямоугольным граням параллелепипеда устанавливались
выражения для компонентов напряжений в косых плоскостях,
проведенных внутри того же параллелепипеда. Очевидно, те же формулы

§ 15]
условия на контуре
79
могут быть использованы и сейчас, причем роль напряжений в
косых плоскостях здесь должны исполнять заданные внешние нагрузки.
Впрочем, выведем эти
формулы.
На фиг. 37, а отдельно
указаны усилия по трем взаимно
перпендикулярным граням, т. е.
внутренние силы этого тела, из
которого вырезан тетраэдр, а на
фиг. 37, б отдельно показаны
внешние силы, т. е. усилия,
действующие на наклонную грань
тетраэдра и уравновешивающие
ранее упомянутые внутренние
силы.
Обозначим площадь грани
тетраэдра, нормальной к оси х,
через Fx, аналогично другие,
ортогональные к ней грани, через Fy,
Fz. Наружную грань (четвертую)
тетраэдра, в общем случае не
параллельную ни одной из координатных осей, обозначим через /\
Фиг. 36. В общем случае тела его
нельзя разбить только на
«кирпичики», у поверхности тела окажутся
элементарные тетраэдры.
Pxv .
Фиг. 37. К написанию поверхностных условий.
(фиг. 37, е)\ одновременно через v обозначим нормаль к этой
«трижды» косой грани.

so
ОБЩИЕ УРАВНЕНИЯ МЕХАНИКИ СПЛОШНОЙ СРЕДЫ
[ГЛ. II
Условие равновесия в проекции на ось v запишется в виде
Px,F, = axFx + *xyFy + *xzFz- (a)
Так как отношение площади любой из трех ортогональных граней
к площади наклонной грани составляет, как известно, косинус угла
наклона между нормалями к тем же граням, т. е.
-f=cos(x, v), -^= cos Су, v), 7^ = cos(z9 v),
гч rv •rv
то из уравнения (а) следует:
Рхч = ахс°*(*> v) + T^cos(^, v) + t^cos(^, v). (2.04)
По правилу круговой подстановки можно записать сразу и два
других уравнения.
Вводя для направляющих косинусов обозначения:
cos (лг, v) = /, cos (у, v) = т, cos (г, v) = п>
интересующие нас три условия на контуре (иначе «граничные условия»)
запишем в виде
(2.05)
Указанные соотношения (2.05) и будут служить перекидным
мостиком от внутренних сил возле границы твердого тела (axi <zy и т. д.)
к внешним силам (рх„ рун, р^), действующим на наружной поверхности
того же тела. Поэтому уравнения (2.02) и условия (2.05) в
дальнейшем будут рассматриваться совместно, так как уравнения (2.02)
не могут иметь определенного решения, если не даны условия (2.05),
заключающие в себе внешние силы.
В уравнения (2.05) не вошли объемные силы и инерционные члены
не потому, что мы решили ими пренебречь, а потому, что они будут
бесконечно малыми третьего порядка, тогда как все члены уравнения (а) в его
первоначальном виде — второго порядка.
В самом деле, например, равнодействующая нормальных сил с площади Fx
составляет vxFx ~ бесконечно малую второго порядка, а проекция объемной
силы на ось Ох составит рХ =£— , т. е. бесконечно малую третьего порядка.
Аналогично обстоит дело и с инерционным членом, если тело пребывает
в движении. По тем же соображениям при написании (2.05) мы не вводили
никаких приращений напряжений.
Для удобства запоминания условий (2.05) можно представить их в виде
следующей таблички:

§ 16]
ИССЛЕДОВАНИЕ НАПРЯЖЕННОГО СОСТОЯНИЯ
81
Поверхностные
компоненты нагрузки
Pz* =
Множители
1 т п
°х
zyx
zzx
zay
'У
zzy
ZXZ i
zyz
°z
Квадратная матрица составляет попрежнему тензор напряжений.
§ 16. Исследование напряженного состояния в данной точке тела.
Главные напряжения*)
Формулами (2.05) можно воспользоваться для исследования
напряженного состояния в любой точке внутри тела и по любой площадке,
проведенной через нее. В самом деле, если нам заданы все
компоненты тензора напряжений для
данной точки, т. е. известны
нормальные и касательные
напряжения по трем
ортогональным граням бесконечно малого
параллелепипеда, вырезанного
возле данной точки, и
требовалось бы определить
напряжения в какой-либо наклонной
(по отношению к граням
параллелепипеда), иначе говоря,
«косой» площадке, проходящей
внутри параллелепипеда (фиг.
38), то нам пришлось бы
повторить все рассуждения
предыдущего параграфа. Разница была лишь в том, что составляющие
Ли» Pyv Pzvi которые были в § 15 известными (внешние силы),
в данной задаче были бы неизвестными—определяемыми внутренними
силами.
Итак, при обозначениях на фиг. 38 для наклонной площадки,
имеющей направляющие косинусы /, т и я, компоненты напряжений,
Фиг. 38. К вычислению напряжений по
«косой» площадке.
*) В §§ 16—19 содержатся сведения, обычно излагаемые в курсах
сопротивления материалов для суждения о прочности материала в точке (близость
I».крушения или состояния пластичности) по известным данным о
компонентах напряжений для этой точки. Эти сведения особенно необходимы для
пор ни пластичности.
() Зак. 3880. Н. И. Безухов

82 ОБЩИЕ УРАВНЕНИЯ МЕХАНИКИ СПЛОШНОЙ СРЕДЫ [ГЛ. II
параллельные координатным осям, записываются в виде
/V^W + V + V/2> (a)
Полное напряжение, действующее по рассматриваемой наклонной
площадке, определится из выражения
Указанные компоненты (рхп ру^ р^), вообще говоря, не являются
ни нормальными, ни касательными напряжениями и потому для суждения
о прочности не совсем удобны.
Вычислим нормальное и касательное напряжения, действующие
по рассматриваемой площадке, для чего вектор полного напряжения
разложим на составляющие по нормали к площадке и по касательной
к последней.
Проектируя компоненты рх^ ру.п ргч на нормаль v, имеем
нормальное напряжение для наклонной площадки:
°, = Pxv C0S (X> V) + Руч C0S CV» V) + Pa C0S (Z> V)»
или, используя (а), получаем:
*v = °xP + tyrt1 + V'2 + 2~x9lm + 2zyzmn + 2zaxnl. (2.06)
Касательное напряжение по той же площадке определится из
уравнения
02-|_т2 = р2в (2.07)
Если проведенная наклонная площадка является главной, то,
следовательно, для нее т = 0 и потому ov = /?v, т. е. полное
напряжение и нормальное напряжение для главной
площадки совпадают по величине и по направлению.
Из этого условия определим главные напряжения и положения
площадок, на которых они имеются. Обозначив искомое главное
напряжение временно через а и проектируя его на оси х, у, г, имеем:
ocos(v, x) = pxn
ccos(v, у) = ру,,
ocos(v, z)=pzn
а с помощью (а) записываем:
™ = W Л- Wn + V*-

§ 16]
ИССЛЕДОВАНИЕ НАПРЯЖЕННОГО СОСТОЯНИЯ
83
Кроме того, имеем известное из аналитической геометрии условие
Р-+-ГП*-\-П*=1. (б)
Последние четыре уравнения содержат четыре неизвестных
(главное напряжение и три его направляющих косинуса). На время оставим
последнее уравнение и перепишем первые три уравнения в виде
(Gx — °)l + iabm + W* = °>
W+ (Зу — °) т + V = °>
W + W^ + O3*-0)Аг==0- J
(в)
Так как написанные уравнения однородны, а кроме того, /, т и п
одновременно не могут быть нулями, то, следовательно, определитель
системы уравнений (в) должен быть равен нулю, т. е.
(2.08)
Раскрывая этот определитель, получаем кубическое уравнение
(2.09)
Решение уравнения (2.09) доставит три корня (о15 о2, о3), и все
они будут действительными *).
Расположим эти корни, т. е. значения трех главных напряжений,
в таком порядке:
°1 > °2 > °3>
т. е. Oj — максимальное, а ов — минимальное напряжение.
Внося какое-либо из этих значений о{ (/=1, 2, 3) в уравнения (в)
и пользуясь двумя из них [так как третье будет следствием
остальных двух вследствие условия (б)], присоединяем к этим двум
уравнение (б); из совместного решения трех уравнений найдем величины
направляющих косинусов для ait т. е. /г-, т{ и nt (/=1, 2, 3).
Исследования указанных направляющих косинусов показывают
(доказательства опускаем), что главные площадки, соответствующие
*) Доказательство действительности всех трех корней такого уравнения,
к.'ис (2.09), можно найти в любом курсе аналитической геометрии (см.
теорию поверхностей второго порядка). Основанием для такого утверждения
иилштся симметрия элементов определителя (2.08) относительно его главной
дн,!1 опали.
6*

84 ОБЩИЕ УРАВНЕНИЯ МЕХАНИКИ СПЛОШНОЙ СРЕДЫ [ГЛ. II
значениям аи а2 и а3, друг по отношению к другу оказываются взаимно
перпендикулярными.
Кроме того, исследование (2.06) показывает, что при подстановке
в него на место направляющих косинусов значений 11у //г1 и пх
(отвечающих главной площадке с напряжением <3j) определяется именно
наибольшее а< из всех возможных для данной точки нормальных
напряжений. Подстановка в то же выражение другой группы значений
направляющих косинусов /3, /я3, пъ (отвечающих главной площадке
с напряжением а3) определяет именно наименьшее Gi из всех
нормальных напряжений, действующих в различных плоскостях, проходящих
через заданную точку.
Итак, в общем случае пространственно напряженного состояния
тела через каждую его точку всегда можно провести три взаимно
перпендикулярные плоскости, на которых касательные напряжения
отсутствуют, причем действующие на них нормальные напряжения имеют
стационарные значения (максимум, минимум и минимакс)*)
для рассматриваемой точки.
Применим для компонентов напряжений систему обозначений,
указанную на стр. 53, т. е. нормальные и касательные напряжения по
всем трем ортогональным площадкам будем обозначать символом zik,
где / и k принимают последовательно значения 1, 2, 3.
Соответственно для нормального напряжения, действующего на
наклонной площадке (с внешней нормалью v), применим обозначение t.,v,
а для направляющих косинусов примем обозначения:
cos (л^) = /ь, cos Q/v) = /2.„ cos (zv) = /3v;
тогда выражение (2.06) запишется исключительно кратко в такой
форме:
i=lк=1
Аналогично (можно предложить читателю самостоятельно проделать
надлежащие преобразования) доказывается, что на той же наклонной
площадке (с нормалью v) любая другая составляющая напряжения
(например, касательное напряжение, параллельное некоторой оси Г|)
запишется в виде
1 г=1Л=1
*) Минимаксом напряжения будем называть промежуточное между
максимумом и минимумом значение напряжения, по площадке действия которого
сохраняются некоторые свойства, присущие площадкам с максимальным или
минимальным напряжением [в данном случае отсутствие касательных
напряжений и независимость величин главных напряжений (стационарность
значений) от способа их вычисления (см. § 17)].

§ 17]
ИНВАРИАНТЫ ТЕНЗСРА НАПРЯЖЕНИЙ
85
Формулы преобразования (2.06а) и (2.066) являются характерными
для преобразования составляющих всякого тензора. Именно поэтому-то
матрицы (1.04), (1.12) и т. п. и называются тензорами (точнее,
аффинными ортогональными тензорами второго ранга, но никаких других
тензоров в классической теории упругости и теории пластичности не
рассматривается).
Всякие другие матрицы, не позволяющие к их
компонентам применить формулы преобразования типа
(2.066), не могут называться тензорами.
§ 17. Инварианты тензора напряжений
Если около данной точки мысленно вырезать несколько бесконечно
малых параллелепипедов, грани которых различным образом
ориентированы по отношению к осям координат, то, очевидно, компоненты
напряжений для одного такого элементарного параллелепипеда будут
отличными от компонентов для другого, так как напряжения зависят
от направления рассматриваемой площадки, проходящей через
заданную точку. Однако также очевидно, что независимо от способа
вырезания элемента около заданной точки подстановка значений его
компонентов напряжений в уравнение (2.09) должна дать в итоге одни и
те же значения главных напряжений для всех таких элементарных
параллелепипедов. Главные напряжения в данной точке
существуют, и величины их независимы от метода их
нахождения, т. е. они инвариантны по отношению к
преобразованию координатной системы.
Следовательно, корни кубического уравнения (2.09) не должны
зависеть от системы координат х, у, z, а коэффициенты этого
уравнения также не зависят от выбора координатной
системы. Иначе говоря, эти коэффициенты являются
инвариантами преобразования координат.
В связи с указанным уравнение (2.09) перепишем в виде
0з _ 020i _|_ азн _ 0ш = 0> (2.09а)
где о1, о11, о111—инвариантные соотношения, иначе называемые пер-
uым, вторым и третьим инвариантами тензора напряжений. Итак:
о1 = ах + зу + oz = const,
q1 = 0ж°2/+0Л+^0ж — tly — Ъ* — т&» = const,
III I 0 2 2 2 .
0 = ах3уаш + **ху*уг*гх — °*ТУ* — °у*8х ~ Gzzxy = Const.
(2.10)
Заметим, что первый (или линейный) инвариант представляет
соГюй сумму членов, расположенных на главной диагонали в тензоре
илнрижеиий, которая, как показано далее (см. § 28), пропорциональна

86 ОБЩИЕ УРАВНЕНИЯ МЕХАНИКИ СПЛОШНОЙ СРЕДЫ [ГЛ. II
относительной объемной деформации у рассматриваемой точки, т. е.
о] = Ео0. (2.11)
Объемная же деформация 0, т. е. относительное изменение объема
в окрестности данной точки, как явление физического порядка, конечно,
не зависит от способа ее вычисления. Контролем правильности
решения кубического уравнения (2.09) может служить равенство
? + °2/+0s=°l+°.2 + S8-
(2.12)
Третий (иначе кубический) инвариант, между прочим,
представляет собой развернутый в строку определитель, составленный из
компонентов тензора напряжений, т. е.
i"i =
"хуу
"•уху "уу
~zx> ^zyy
^xz
^yz
(2.13)
Контролем правильности решения уравнения (2.09) может также
служить равенство, составленное применительно к параллелепипеду,
гранями которого являются главные площадки возле данной точки:
ли =
0, 0
0
0, о2>
0, 0, о8
= °1°2°3-
(2.14)
Второй (или квадратичный) инвариант, между прочим,
представляет сумму миноров определителя (2.13), если произвести
разложение его по главной диагонали, т. е.
(2.15)
Контролем правильности решения уравнения (2.09) может, очевидно,
служить равенство
~уху °у
+
°ХУ ZXZ
+
°у> ~yz
^zyy °z
3j, 0
0, о0
+
°1, 0
о,
+
о
о,
= а132 + а20з + 0з^1- (2.15а)
Написа! ные выше контрольные соотношения (2.13) — (2.15а) могут
быть использованы и для непосредственного вычисления корней
кубического уравнения (2.09). Так, если один из корней был найден
непосредственно из (2.09), то остальные могут быть подсчитаны с помощью
(2.12) —(2.15).
Заметим, что в теории напряжений, а также в теории
деформаций инварианты следует рассматривать как основные
характеристики напряженного и деформированного состояний в точке)

§ 18]
ОКТАЭДРИЧЕСКИЕ НАПРЯЖЕНИЯ
87
компоненты же напряжений и деформаций, как связанные с осями
координат, являются вспомогательными.
Указанные выше три инварианта напряжений (2.10) не исчерпывают
всех возможных комбинаций из компонентов напряжений, которые
были бы также инвариантны к ортогональному преобразованию координат.
Так, ниже, в § 29, приводятся еще другие инварианты (3.24), а вообще
инвариантов имеется бесконечное множество. Приведенные же
ранее инварианты (2.10) следует рассматривать как базисные, потому
что все другие могут быть выражены как функции трех базисных
инвариантов. Именно по этой причине условия пластичности, как это
будет своевременно показано, всегда можно выразить в виде
некоторой функциональной зависимости между тремя инвариантами тензора
напряжений и абсолютной температурой.
§ 18. Октаэдрические напряжения
Рассмотрим в некотором отношении замечательную площадку,
которая равно наклонена к главным плоскостям (фиг. 39). Вычислим
нормальное и касательное напряжения по такой площадке, называемой
октаэдрической или площадкой результирующих
напряжений в д а н н о й точке.
Оси координат направим по
нормалям главных площадок, т. е.
вдоль главных напряжений.
Направляющие косинусы для
октаэдрической площадки относительно
упомянутых осей координат, очевидно,
равны между собой и составляют
, 1
Уз
Согласно формуле (2.05) в дан-
пом случае находим:
Рп = °i/» Р2, = <уи, P3v = V*.
Для полного напряжения на октаэдрической площадке имеем
уравнение
-2 * / 2 i 2 i 2\
р*' = "3" (0l + °2 + °8^
т. е. квадрат полного напряжения на октаэдрической
площадке равняется среднему из квадратов главных
напряжений.
По формуле (2.06) для нормального напряжения на той же
площадке получаем:
Зокт = у О7! + °о -j- Зо),
Фиг. 39. Октаэдрическая
площадка.

88 ОБЩИЕ УРАВНЕНИЯ МЕХАНИКИ СПЛОШНОЙ СРЕДЫ [ГЛ. II
или согласно обозначению (1.16)
Сокт = °ср, (2Л6)
т. е. нормальное напряжение на октаэдрической
площадке равняется среднему нормальному
напряжению для данной точки.
Для касательного напряжения на октаэдрической площадке имеем
из уравнения (2.07):
2 2 ^2
^окт — V> gokt>
которое в данном случае переписывается в виде
^ОКТ = з" 0l + °2 + 4) — -g- fa + <J2 + ЧТ-
По раскрытии скобок имеем:
"окт :
2 , 2 , 2 | 2
— (0Х -j- 02 -~\- 03 ^iO-2 '
■ о0а,
2^3-
■°3°l)f
откуда
Обозначая
Токт = Т V(°l — °д2 + fa — аз)2 + fa" °1)
(2.17)
Ql — &2
Ч2>
^23>
и называя указанные полуразности главными касательными
напряжениями (см. § 19), выражение (2.17)
можем записать и так:
токт = |^2 + -22з + 4, (2.17а)
т. е. квадрат касательного
напряжения на октаэдрической
4
площадке равняется -^-(т. е.
немного меньше половины) суммы
квадратов главных
касательных напряжений.
Указанные выше нормальное и
касательное напряжения на октаэдриче-
ских площадках, иначе, так
называемые октаэдрические напряжения,
одинаковы для всех восьми площадок,
которые можно провести во всех
октантах; если отрезки, отсекаемые
площадками на главных осях /, 2, 3,
одинаковы во всех октантах, то
совокупность таких равнонаклоненных площадок образует замкнутую
восьмигранную фигуру — октаэдр (фиг. 40).
Фиг. 40. По всем восьми
граням октаэдра действуют
одинаковые нормальные и
одинаковые касательные напряжения.

§ 18)
ОКТАЭДРИЧЕСКИЕ НАПРЯЖЕНИЯ
89
В теории пластичности октаэдрическое касательное напряжение
является основным, определяющим характер развития пластических
деформаций.
Для октаэдрического касательного напряжения можно дать и
другие начертания. Так, из (2.17) на основании записи инвариантов
тензора напряжений (2.12) — (2.15), выраженных через главные
напряжения, следует:
^« = -|[(а1)а —Зо"]. (2.18)
Принимая для инвариантов записи через компоненты напряжений,
действующих по случайным (не главным) ортогональным площадкам,
на основании (2.10) имеем:
W = у Vi^-ty? + (V-*.)a + («,-'J9 + б (х^ + tJ. + ^). (2.19)
Из курса сопротивления материалов для суждения о прочности,
т. е. для выяснения вопроса о том, насколько состояние материала
в окрестности данной точки близко к предельному упругому или
к начальному состоянию пластичности, в числе многих теорий
прочности читателю известна так называемая «пятая теория прочности»,
или «теория энергии формоизменения». Расчетное (приведенное,
фиктивное) напряжение по указанной теории, как известно, записывалось
так:
апр=W^(01—°'2)"+(а'2 ~~ чТ'+(°3~~°l)2' (2'2Q)
Сопоставляя (2.17) и (2.20), заключаем, что октаэдрическое
касательное напряжение прямо пропорционально расчетному напряжению
но пятой теории прочности, т. е.
^окт=-^— Зпр- (2.21)
В теории пластичности апр, устанавливаемое независимо от тех
соображений, которые были в сопротивлении материалов, называется
интенсивностью напряжения (лучше было бы назвать обобщенным
напряжением) и обозначается через о4. Таким образом, в дальнейшем
применяем запись*)
а, = -^=токт. (2.21а)
*) Удобство введения в теорию пластичности аг- взамен т0кт объясняется
ггм, что в случае одноосного растяжения (или сжатия), когда существует
отличное от нуля только одно главное напряжение, например сь а два других
отсутствуют, интенсивность напряжений согласно (2.20) становится равной
жому единственному напряжению cj.

90 ОБЩИЕ УРАВНЕНИЯ МЕХАНИКИ СПЛОШНОЙ СРЕДЫ [ГЛ. II
Заметим, что если, подобно тому как на стр. 86 мы
записывали второй инвариант тензора напряжений, теперь записать второй
инвариант девиатора напряжений (1.18), т. е. составить сумму
миноров такого определителя:
loj — оор, О, О I
О, о3 — ос,э 0 i
I 0, 0, °.д — °0]> I
то получим (после преобразований):
в" = -1 [(о, - в,? + (з2 - о3)2 + (а8-3]?],
что оказывается пропорциональным квадрату октаэдрического
касательного напряжения:
т. е. квадрат октаэдрического касательного
напряжения с точностью до числового множителя равен
второму инварианту девиатора напряжений.
Позднее (§ 29) будет дана еще одна интерпретация этого же
напряжения.
Исследования показывают *), что октаэдрическое напряжение близко
по величине к наибольшему касательному напряжению (см. § 19) для
той же точки и находится в пределах
0,941 > — >0,816.
max
§ 19. Наибольшие касательные напряжения
Примем для заданной точки направления главных напряжений а1У
а2 и о3 за направления координатных осей х, у, z. Тогда для любой
«косой» площадки по отношению к упомянутым главным
направлениям нормальное и касательное напряжения запишутся согласно (2.06),
(2.07) в виде
оч = Oj/'2 -[- z.jii1 -(- a3AZQ, (а)
т2 = р2, — а2 = а\I1 -j- oim2 -\- ъ\п~ — (а2/2 -j- a2m -j- о3я2)2. (б)
Исключим теперь из уравнения (б) один из косинусов, например я,
при помощи зависимости
pJi-m<1-{-rP = \y
*) А. А. Ильюшин, Пластичность, стр. 29, Гостехиздат, 1948.

§ 19] НАИБОЛЬШИЕ КАСАТЕЛЬНЫЕ НАПРЯЖЕНИЯ 91
после чего определим косинусы / и т таким образом, чтобы
касательное напряжение т получило максимальное значение.
После подстановки п2 = 1 — /2 — т2 в выражение (б) составим
производные последнего по / и т и приравняем эти производные нулю.
Получим следующие два уравнения для направляющих косинусов / и
т, определяющие положение площадок, по которым напряжение т
получает максимальное или минимальное значение:
I [0>i - о8) /2 + (ст2 — о8) т2 — | (а, - а8)] = 0, ]
Г 1 1 \ (В)
т ^(oj — о8) /2 + (о2 — о8) т2 — у (а2 — а8)J = 0. j
Одно из решений этих уравнений получится, если приравнять /
и т нулю. Можно получить и решения, отличные от нуля. Так,
приняв /=0, найдем по второму из уравнений (в)
а приняв т равным нулю, найдем по первому из уравнений (в)
Повторяя приведенные выше выкладки, при исключении из
выражения (б) сначала косинуса т, а затем косинуса /, в конечном итоге
получим следующую таблицу шести значений косинусов углов, при
которых напряжение т получает максимальное или минимальное
значение:
/
т
п
0
0
ztl
0
0
zt 1
0
0 0
0
*V1
--i\
±/i
0
*/?
-v\\
*/Tj
0
Первые три столбца дают площадки, совпадающие с плоскостями
координат, которые, как это было принято вначале, являются
главными площадками. По этим площадкам касательные напряжения
обращаются в нуль, т. е. выражение (б) для квадрата т получает
минимальное значение.
Три последних столбца дают площадки, проходящие через одну
из трех главных осей и делящие угол между двумя другими главными
осями пополам. Подставив направляющие косинусы, определяющие
положения этих трех площадок, в выражение (б), найдем следующие

92 ОБЩИЕ УРАВНЕНИЯ МЕХАНИКИ СПЛОШНОЙ СРЕДЫ [ГЛ. II
значения касательных напряжений (иногда называемых главными
касательными) по этим трем плоскостям:
Т12
Т23
Т31
=
=
=
±=
±
-4-
2
1
2
1
2
(°1-
(*2"
(°3-
~ 02) ,
-°в),
-а,).
)
(2.22)
;
Это показывает, что наибольшее касательное напряжение действует
по площадке, делящей пополам угол между наибольшим и
наименьшим главными напряжениями, и что оно равно половине разности между
этими двумя главными напряжениями.
На площадках, на которых касательные напряжения принимают
значения (2.22), действуют также нормальные напряжения, которые
согласно (а) оказываются равными полусуммам соответствующих
главных напряжений:
у ('! + «*), у(^ + «зЬ у(*3 + '!). (2-23)
Из (2.22) следует, что если величины главных напряжений
подчинены неравенствам о1 > о2 > оа, то наибольшее касательное
напряжение равно -Ц>—-, т. е. полуразности наибольшего и
наименьшего главных напряжений.
§ 20. Некоторые итоги по теории напряжений
Подведем итог изложенному в §§ 16, 18, 19. Через каждую
пространственно напряженную точку можно провести несколько
замечательных плоскостей. Действующие на этих плоскостях (площадках)
напряжения являются в том или ином смысле характерными.
Так, три взаимно перпендикулярные главные площадки не имеют
касательных напряжений, а действующие на них нормальные
напряжения имеют стационарные для данной точки значения (максимум,
минимум, минимакс). Обозначим эти площадки номерами 1, 2 и 3 и
назовем их главными площадками для нормальных
напряжений.
Три пары площадок, которые делят пополам двугранные углы между
главными площадками, испытывают стационарные значения
касательных напряжений. Обозначим эти пары плоскостей номерами 4 и 5,
6 и 7, 8 и 9 и назовем их главными площадками для
касательных напряжений.
Значения этих касательных напряжений равны полуразностям
нормальных напряжений тех главных площадок, по отношению к
которым равнонаклоненными являются рассматриваемые две (из них одна

20] НЕКОТОРЫЕ ИТОГИ ПО ТЕОРИИ НАПРЯЖЕНИЙ 93
биссекторная) главные для касательных напряжений площадки.
Нормальные напряжения на этих плоскостях равняются соответственно
полусуммам тех же главных напряжений.
Далее, через ту же напряженную точку можно провести еще четыре
замечательные плоскости, названные в § 18 октаэдрическими.
Обозначим эти плоскости номерами 10, 11, 12, 13.
Нормальные напряжения, действующие на каждой из последних
площадок, равны между собой и равняются среднему значению из
нормальных напряжений для той же
точки. Касательные же напряжения на
таких площадках, равные между собой
по величине, принимают значения,
характерные для суждения о прочности
материала в окрестности
рассматриваемой точки в свете энергетической
теории прочности.
Итак, в общей сложности через
всякую пространственно напряженную
точку можно провести 13
замечательных плоскостей.
Возле рассматриваемой точки можно
построить замкнутые геометрические
фигуры, грани которых будут состоять
лишь из плоскостей первой или
второй, или третьей группы.
Так можно построить куб, грани которого совпадают с
плоскостями главных нормальных напряжений (фиг. 41). Назовем его
главным кубом у данной точки.
Сечения с главными касательными напряжениями (при а1 > а2 >о3)
образуют ромбический додэкаэдр, окружающий или вписанный в куб
(фиг. 42). Назовем его главным додэкаэдром у данной точки.
Сечения с октаэдрическими напряжениями, как это уже
указывалось ранее (§ 18), образуют октаэдр (фиг. 43). Назовем его главным
октаэдром у данной точки.
Можно попытаться построить геометрическую фигуру, включающую
нее указанные выше замечательные плоскости. Такую фигуру (26-гран-
иик) нужно назвать главным гексаикосаэдром у данной точки (фиг. 44).
Наконегц если около заданной точки построить сферу, то все
точки на этой сфере, испытывающие те или иные характерные
напряжения (фиг. 45), представляются точками касания сферы с
указанными выше геометрическими фигурами, если для последних
укапанная сфера будет вписанной в них.
Важным выводом в теории напряжений является установление
трех инвариантных соотношений (2.10). Именно они — инварианты,
как не зависящие от способа исследования напряжений в данной
точке (независимо от «каприза» исследователя), могут объективно
Фиг. 41. «Главный куб»,
построенный возле заданной
точки напряженного тела.

94 обдие уравнения мехакики сплошной среды [гл. и
Фиг. 42. «Главный додекаэдр», построенный
возле заданной точки.
Фиг. 43. «Главный октаэдр», построенный
возле заданной точки.

§ 20] НЕКОТОРЫЕ ИТОГИ ПО ТЕОРИИ НАПРЯЖЕНИЙ 95
характеризовать напряженное состояние в данной точке. Как будет
показано далее (§ 28), первый инвариант тензора
напряжений характеризует изменение объема материала
в окрестности данной точки при деформации. Второй
Фиг. 44 и 45. Геометрическая замкнутая фигура,
построенная возле заданной точки тела и
включающая в себя замечательные плоскости для этой
точки (вверху). Если возле заданной точки
построить сферу бесконечно малого радиуса, то на
поверхности этой сферы обнаружим 26
замечательных точек (внизу).
инвариант девиатора напряжений характеризует масштаб
формоизменения в окрестности данной точки при деформации и часто
оказывается тесно связанным с напряжением, ответственным за
разрушение материала в данной точке.

95 ОБЩИЕ УРАВНЕНИЯ МЕХАНИКИ СПЛОШНОЙ СРЕДЫ [ГЛ. II
Б. ГЕОМЕТРИЧЕСКАЯ ТЕОРИЯ ДЕФОРМАЦИИ
(ГЕОМЕТРИЧЕСКИЕ УРАВНЕНИЯ)
§ 21. Обозначения компонентов смещения вблизи
заданной точки
Для компонентов смещения точки М (х, у> г), находящейся внутри
заданного сплошного тела, были приняты (§ 5) обозначения и> v и
w (фиг. 46). Если в бесконечной близости от заданной точки М
рассмотреть другую точку N, координаты которой до деформации были
x-\-dx, \-\-dy, z-\-dz> то компоненты смещения указанной сосед-
Фиг. 46. Компоненты смещений двух бесконечно близких
точек, принадлежащих непрерывному телу.
ней точки, обозначенные на фиг. 46 через и\ vf и w\ могут быть
с достаточной точностью записаны в виде
(2.24)
Аналитическая интерпретация написанного такова, что мы полагаем
функцию смещения, а следовательно, и компонентов смещения
непрерывной, раскладываемой в ряд Тейлора, но отбрасываем члены
второго и высших порядков малости.
Последнее допущение находится в соответствии с предпосылками
классической теории упругости (см. стр. 26), но, очевидно, не
может быть принято в тех случаях, когда ожлдаемые смещения точек
тела не являются малыми.
Если обе рассматриваемые точки находятся в плоскости,
параллельной одной из координатных, и, тем более, лежат на прямой,
параллельной любой оси, то запись компонентов смещения соседней
точки упрощается. Так, если точки М и N находятся в плоскости,
параллельной координатной плоскости х — z> и прямая MN парал-

§ 22] ДИФФЕРЕНЦИАЛЬНЫЕ ЗАВИСИМОСТИ 97
лельна оси х, то dy = dz = 0, и потому
и = u-j-jr— dx, v = v -\- -3— dxf w = w -j- -g- dx.
Отношение -т— может быть истолковано как интенсивность
развития в горизонтальном направлении горизонтальной компоненты и;
Фиг. 47. Обозначение компонентов смещений концов
отрезка прямой в частном случае расположения в
пространстве соседних точек.
будучи умножено на dx (т. е. на длину отрезка MN в
рассматриваемом сейчас частном случае), оно представит приращение
горизонтального перемещения на длине dx. Аналогично могут быть истолкованы
вторые слагаемые в записях остальных компонентов.
В качестве иллюстрации на применение указанной выше записи
на фиг. 47 (масштаб искажен) показаны приращения компонентов
смещения для двух точек А и В, находящихся в бесконечной
близости с точкой М, для которой компоненты смещения иу v заданы;
псе три названные точки лежат в плоскости хуу а отрезки MB и
МЛ параллельны осям х и у.
§ 22. Дифференциальные зависимости компонентов деформации
от компонентов смещения (геометрические уравнения)
Около заданной точки М внутри сплошного тела выделим
плоскостями, параллельными координатным, бесконечно малый
параллелепипед с ребрами dx, dy, dz (фиг. 48).
Такой элементарный объем в статическом отношении рассмотрен в
§ 14. При деформации тела он переместится и сам продеформируется,
7 Зак. 3880. Н. И. Безухов

98
ОБ ДИЕ УРАВНЕНИЯ МЕХАНИКИ СПЛОШНОЙ СРЕДЫ
[ГЛ. II
причем изменятся длины его ребер и исказятся первоначально
прямые углы между гранями.
Для дальнейшего достаточно изучить удлинения ребер Ml, M2,
МЗ (линейные деформации) и изменения углов /—М — 2, /—М — 3
и 2 — М — 3 (сдвиги, т. е. угловые деформации).
Фиг. 48. Параллелепипед и его проекции до деформации.
Фиг. 49. Одна из проекций параллелепипеда до
деформации и при деформации.
Пусть фиг. 49 изображает проекцию рассматриваемого
параллелепипеда на плоскость ху {abed—проекция до перемещения и
деформации, a1b1c1d1— проекция после перемещения и деформации).
Компоненты смещения для точки а в прежних обозначениях
будут и и v. Компоненты смещения точек b и с на фиг. 49
записаны согласно указаниям в § 21 для случая весьма малых
деформаций.

§ 22]
ДИФФЕРЕНЦИАЛЬНЫЕ ЗАВИСИМОСТИ
99
Из рассмотрения фиг. 49 следует, что относительное удлинение
ребра ас (по фиг. 48 — М /), первоначальная длина которого была dx>
записывается (с точностью до бесконечно малых первого порядка) так:
'* + %dx + dx-u)-dx ди
~дх*
e„ =
axc<i — ас
ас dx
Аналогично для относительного удлинения вдоль оси Оу имеем:
~ду-
ахЬ2 — ab у ' ду
ab dy
Для угла поворота ребра ab в плоскости Оху имеем
„ ду .
tgOC:
i ди
v + jjdy + dy — v
dv
i +
dv
отбрасывая в знаменателе -ч- = еу как весьма малую величину по
сравнению с единицей, переписываем:
ди
Аналогично для угла поворота ребра ас в плоскости Оху:
р dx'
Итак, относительный сдвиг, т. е. искажение прямого угла Ьас
(его уменьшение), записывается так:
,о ди , dv
При помощи круговой подстановки, не делая специальных
выкладок, можем записать выражения сдвигов и в других координатных
плоскостях. Таким образом, располагаем следующими
дифференциальными зависимостями:
Относительные удлинения:
Относительные сдвиги:
ех =
еу =
ez =
Тагу =
ь
*\zx ~
ди
dv
dw
~~dz~'
ди ,
dv ,
dz ~+~
dw ,
" dx~T~
dv
Jx~y
dw
du
~dz~'
(2.25)
7*

100 ОБЩИЕ УРАВНЕНИЯ МЕХАНИКИ СПЛОШНОЙ СРЕДЫ [ГЛ. II
Указанные уравнения иногда называются уравнениями Кош и.
Дифференциальные уравнения равновесия и геометрические
уравнения, составляя в совокупности девять уравнений, содержат в общей
сложности 15 неизвестных (а^, <зуу а£> -zxy, тугУ тгл, еж, еу, ег, fxy4
Чуг> 1гх> и> v> w)* Следовательно, для полного решения поставленной
задачи к полученным пока двум группам уравнений необходимо
добавить еще шесть уравнений, но при условии, что эти новые
уравнения не будут содержать новых неизвестных. Такими уравнениями
являются условия упругости для упругого тела, условия пластичности
для тела, ^пребывающего в пластическом состоянии, т. е. это должны
быть физические уравнения, форма записи которых должна быть
в каждом отдельном случае своей, в зависимости от свойств тела и
его состояния (§§ 26, 98).
Уравнениями (2.02) и (2.25) определяются уравнения механики
сплошной среды, одинаковые для теории упругости и для теории
пластичности как для твердых тел (строительные конструкции), так
и для тел, находящихся в других состояниях (жидкости,
рассматриваемые в гидравлике, и т. п.).
Прежде чем покончить с общими уравнениями механики сплошной
среды, осветим весьма важное свойство деформации сплошного
непрерывного тела, известное под названием «условия
неразрывности деформаций» (§23).
Если применить необычные обозначения компонентов деформации,
указанные в колонке III на стр. 53, а также принять приведенные на стр. 54
обозначения координатных осей (хь х2, *з) и составляющих смещения
(#!, и2, м3), то уравнения (2.25) предстанут в виде
_\ (дщ диЛ __ 1 (дих ,ди2\л
__ 1 (ди2 ,ди2\ __ 1 (ди2 ,диЛ.
е22-^Кдх-2 + Щ)> ш*-Т\д7л + д^)'
£з3- J\d^ + Wj9 4l^^[dx~ + dx-J'
Отмечая полную аналогию во внешнем начертании всех шести
зависимостей, можно для краткости письма запись любого компонента
деформации дать в форме
_ 1 (Ьщ , дин\
§ 23. Уравнения неразрывности деформаций
Перемещение любой точки сплошного тела определяется тремя
функциями:
и, vy w, (а)
деформация же данной точки определяется шестью функциями:
ех> е//> ezf txyy tyz* Y*ar (б)

§ 23] УРАВНЕНИЯ НЕРАЗРЫВНОСТИ ДЕФОРМАЦИЙ 101
Уравнения (2.25) показывают, что если заданы три функции и,
v, wy то этим самым будут определены все шесть составляющих
деформации (б), так как они выражаются через первые производные
от составляющих перемещения *).
Таким образом, очевидно, все шесть функций для компонентов
деформации (б) произвольно задать нельзя, между ними должны
существовать какие-то зависимости, которые ниже и
устанавливаются.
Число таких зависимостей равно шести, и они делятся на две
группы: I группа — зависимости между составляющими деформации
в одной плоскости и II группа — зависимости между составляющими
деформации в разных плоскостях.
Начнем с I группы. Продифференцируем первые два из
уравнений (2.25) следующим образом:
дЧх д*и . д*ву d*v
~ду* = дхду* ' ~дх* ~ ду дх* '
Складываем эти уравнения почленно:
д2*х . дЧу д*и d*v д2 [да dvl
Ту* ~+~ ~дл? ~ дхду2 ' ду дх1 ~ дхду \_~ду ' ~дх\ '
и замечаем, что выражение, заключенное в скобках, есть
деформация сдвига Чху
Таким образом, для каждой точки существует зависимость между
удлинениями и углом сдвига в каждой плоскости вида
дЧт . дЧу _ д^ху
ду* "+" дх* ~ дхду' ^
Итак, если заданы своими уравнениями две линейные
деформации, то этим самым уже предопределяется и угол сдвига:
Аналогично зависимости (в), установленной для плоскости хуу
можно установить зависимости для деформации в других плоскостях,
как это выписано ниже в сводной таблице (2.26).
*) В (2.25) входят девять неизвестных, и потому для самостоятельного
их решения необходимо задаться любыми тремя неизвестными. Так,
задавшись тремя компонентами перемещения из (2.25), найдем шесть
составляющих деформации; задавшись тремя линейными деформациями, найдем три
перемещения и три угловые деформации; возможны и другие комбинации.

102 ОБЩИЕ УРАВНЕНИЯ МЕХАНИКИ СПЛОШНОЙ СРЕДЫ [ГЛ. II
Для вывода зависимостей II группы дифференцируем (2.25)
следующим образом:
дЪ
Ml
d2w
дх
dfzx
ду ■
д1*у
дхду
д*и
д*у
dzdx y
d2w
ду dz
дхду у
d2u
dz dz dx ] dy dz '
Сложим первые две написанные строки и вычтем третью; получим:
dx * dy dz dx dy '
Это уравнение еще раз дифференцируем по z и, замечая, что
d'6w д2е2
получим:
_d_
dz
dx
dx dy dz dx dy '
d'lxy~] 0
°4zx
d4z
(r)
dy dz J dx dy '
Это—одна из зависимостей II группы; она определяет тот факт,
что если заданы три деформации сдвига (чху, 4yz, Хг»)> т- е- известны
для них уравнения, то этим самым вполне определяется (и не может
быть задано произвольно) удлинение ег, т. е.
г_ 2 J J dz[
dr
Уг
dU
дг
ху
dx
dy
dz
дх ду.
Делая в уравнении (г) круговую подстановку, получим еще два
уравнения такого же вида, как (г). Итак, имеем следующую систему
уравнений:
(2.26)

§ 23] УРАВНЕНИЯ НЕРАЗРЫВНОСТИ ДЕФОРМАЦИЙ 103
Написанные уравнения называются уравнениями совместности
или неразрывности деформаций] выведены они С е н-В е н а н о м.
Физический смысл этих уравнений таков. Если мы,
задаваясь деформацией, их не учтем и каждому из параллелепипедов, на
которые мысленно разбили все тело, назначим шесть независимых
составляющих деформации, то из отдельных таких деформированных
параллелепипедов мы не сложим непрерывного, деформированного
тела, так как между ними могут, например, оказаться бесконечно
малые разрывы (пустоты).
Иначе говоря, заданное тело, сплошное и непрерывное до
деформации, остается сплошным и непрерывным после
деформации *).
Таков физический смысл уравнений (2.26).
Если бы нам удалось по заданным нагрузкам точно найти
перемещения точек тела (и, v, w\ то после этого деформации можно
вычислить по формулам (2.25); в этом случае условия неразрывности
будут удовлетворены сами по себе, так как они выведены из
уравнений (2.25) и являются их следствием.
Если же по заданным нагрузкам будем искать напряжения и
затем деформации, то при этом необходимо одновременно
удовлетворить и уравнениям неразрывности (2.26); в противном случае
деформации будут несовместны, и мы не будем в состоянии найти
перемещения из уравнений (2.25), так как в них будут взаимные
противоречия.
Энергетический смысл тех же уравнений, как показал
Л. С. Лейбензон, таков, что осуществлению указанного принципа
неразрывности деформаций соответствует в упругом теле
минимальное значение накапливаемой телом потенциальной энергии
деформации **).
Таким образом, для упругого тела принцип наименьшей работы
деформации и уравнения совместности деформаций тождественны
между собой (хотя в теории и расчетах они не могут полностью
заменять друг друга).
В несколько иной, но близкой по идее форме указанный
минималистский принцип и его тождественность уравнениям нераз-
*) Весьма наглядно условие совместности деформации представляется на
примере фермы (стержневой системы с жесткими или шарнирными узлами),
стержни которой после своего удлинения (или укорочения), вызванного
нагрузкой, должны образовать попрежнему замкнутую фигуру вида, сходного
с первоначальной фигурой фермы.
**) Впрочем, то положение, что нарушение условий неразрывности
(например, образование трещин в сплошном теле, разрыв стержня в ферме и
т. п.) должно именно увеличить работу внешних сил (сумма, составленная
мл произведений внешних сил на соответствующие им перемещения),
очевидно само по себе, так как такой факт связан с увеличением перемещений
тела (прогибы ферм и т. п.) против того случая, когда соблюдаются уело-
ими неразрывности.

104 ОБЩИЕ СРАВНЕНИЯ МЕХАНИКИ СПЛОШНОЙ СРЕДЫ [ГЛ. II
рывности деформаций сохраняются и в случае пластических
деформаций.
Уравнения (2.26) установлены для трехмерной задачи, в других
случаях число независимых уравнений неразрывности будет другое*).
§ 24. Исследование деформаций в окрестности заданной точки
Исследуем удлинение по произвольному направлению, проходящему
через заданную точку твердого тела.
Пусть прямая MN (фиг. 46) соединяет две точки, находящиеся
в бесконечной близости друг к другу до деформации заданного тела.
Прямая M1N1 соединяет те же точки в деформированном состоянии.
Обозначим первоначальную длину отрезка MN через Z,, причем
очевидно:
L* = d** + dy* + dz*. (a)
Направляющие косинусы отрезка MN в недеформированной
конфигурации будут:
1 dx dy dz /ггч
/==Т; т==Т; п = Т' (б)
Обозначим длину M1N1 через Lv причем согласно фиг. 46, очевидно,
имеем:
L\ = (dx-\-uf — u)*+(dy + v' — v)* + (dz + w' — wf\ (в)
кроме того, эту же длину можно записать через первоначальную
длину и относительное удлинение ее следующим образом:
^ = 1(1 + 6).
Раскрывая скобки в (в), имеем:
L\ = dx^-\-df^dz^+2dx{uf — u)-\-2dy(v' — v)-{-
+ 2dz (w' — w) -f (u' — uf + (*>' — vf -f («;' — wf\ (r)
с другой стороны,
L2 = L2(1 + 2e4-e2). (д)
Вычитая (а) из (г) и пренебрегая квадратами приращений, имеем:
L\ — L? = 2 dx {и' — и) + 2dy {vf — v) + %dz (wf — w).
*) В. З. Власов (см. его «Общую теорию оболочек», 1949) установил,
что в общем случае евклидова пространства, имеющего п измерений, число
независимых уравнений неразрывности определяется формулой
. _ п*(п*—\)
1 ~ 12 '
при п = 2 (плоское напряженное состояние) / = 1; при п = 1 (линейное
напряженное состояние) i = 0; при п = 4 (например, четвертое измерение —
время) / = 20.

§ 24] ИССЛЕДОВАНИЕ ДЕФОРМАЦИЙ В ОКРЕСТНОСТИ ЗАДАННОЙ ТОЧКИ 105
Пренебрегая также членом е2 по сравнению с е, из (д) имеем:
L\ — L* = 2L4.
Сопоставляя последние две записи, заключаем:
L4 = dx (и' — и)-\- dy (V — v)-\-dz (w' — w),
или
dx и' — и , dy v/ — v , dz wf — w
На основании (2.24) и (б) последнее переписываем:
, / ди dx , ди dy ,ди dz\, (dv dx _,dv dy \dv dz\ j
B — l{teT^iyT^dz-i;)^m{teT^djT~^dz~T)-^
, (dw dx [ dw dy , dw dz\
+ " \teT~r'dyTi~~dz~T)'
или, перегруппировывая члены, имеем:
ди ,о i dv о , dw о , (ди , dv\ , ,
На основании (2.25) окончательно получаем:
е = еа/2+ е^2+ V*2+T*ff'* + Ty. «** + Т«*'- (2'27)
Таким образом, удлинение какого-нибудь отрезка,
проходящего через данную точку, может быть
выражено через шесть компонентов деформации той же
точ к и.
Заметим, что выражение для удлинения в произвольном
направлении в окрестности данной точки оказалось сходным в отношении
множителей при компонентах деформации с выражением (2.06) для
нормального напряжения по произвольной площадке, проходящей через
ту же точку. Множители «двойки», которые были в (2.06) при
касательных напряжениях, здесь [в (2.27)] отсутствуют, но надо также
отметить, что в тензоре деформации преднамеренно углы сдвигов
были записаны с коэффициентом 0,5 (стр. 47).
Вообще можно доказать, что между теорией напряжений и
деформаций имеется полная аналогия. Все необходимые формулы
м теории деформаций можно записать по аналогии,
с соответствующими формулами в теории напряже-
п и й. Так, можно утверждать, что в каждой точке тела существует
iри взаимно перпендикулярных направления, называемых главными
осями деформации, которые обладают тем свойством, что волокна,
шшравленные по ним, испытывают только изменения длин, но не по-
морачиваются, т. е. сдвиги в главных осях деформации равны нулю.

106 ОБЩИЕ УРАВНЕНИЯ МЕХАНИКИ СПЛОШНОЙ СРЕДЫ [ГЛ. II
Кубическое уравнение для определения главных удлинений
запишется аналогично (2.09) с заменой компонентов тензора напряжений
на компоненты тензора деформации, т. е. ох на exi zxy на -^ Чху
и т. д. В результате получим уравнение
ез _ е2Л _j_ eaii _ еш = о, (2.28)
где инварианты тензора деформации записываются таким образом:
eI = *х + гу + *г = COnst,
*п = 8*8, + eyez + szex — I {fxy + T2^+ T*J = const,
•ш = W* +T Т^ТиТ»—г(«вТ^+%Т^+в.тУ=сопй. (2.29)*)
Значения главных удлинений будем обозначать и располагать в
таком порядке: ег > е2 > s3.
Очевидно, в материале, свойства которого не связаны с
направлением (т. е. изотропное тело), направления главных напряжений и
главных деформаций должны совпадать. В самом деле, нет ведь никаких
причин для того, чтобы симметричная система только нормальных
напряжений вызвала несимметричную деформацию.
Итак, каково бы ни было в данной точке деформированное со-
стояние, всегда можно найти три взаимно перпендикулярные
прямые, проходящие через эту точку, которые были взаимно
перпендикулярными также и до деформации. Эти прямые являются
направлениями, для которых удлинения имеют характерные
(стационарные) значения (максимум, минимум или минимакс).
Продолжая аналогию, запишем, что удлинения в направлении,
нормальном к октаэдрическим площадкам, выражаются так:
еокт = ~з" (е1 Н~ е2 ~Т 8з)-
Для сдвига в октаэдрических плоскостях можем по аналогии
с (2.17) записать:
Т<™ = 4 V(h - е2)2 + (е.2 - .„)* -+- (зь - в,)8 (2.30)
или в виде
Токх =4/"(.,-.,)»+ (Sy-ef+(*-sxf+ | (Ъ+Ъ+ТУ- (2-ЗОа)
*) Если применить обозначения компонентов деформации, указанные
в колонке III на стр. 53, то инварианты тензора деформации запишутся
совершенно аналогично инвариантам тензора напряжений, а именно:
еП == е е 4-е е 4- е е — (е2 4- е2 4- е2 ),
хх уу ' уу zz* гг хх у осу i *yz « гх> ♦
еШ = s е е 4-2s ее — (е е2 4-е е2 4-е е2 ).
хх уу гг * * ху *уг zx у хх У* ' уу zx~ Zz xy>

§ 25] ОЦЕНКА ТОЧНОСТИ УРАВНЕНИЙ 107
Для наибольшего сдвига по аналогии с (2.22) имеем:
В теории пластичности имеет большое применение величина,
пропорциональная октаэдрическому сдвигу, а именно:
именуемая интенсивностью деформации (удачнее было бы ее назвать
обобщенной деформацией). Итак, под интенсивностью деформации
будем понимать выражение *)
Y2
У(«1 —«Л*+(^ — «вР +(■» — «!>*. (2.32)
1 2(1+ц)
где [1 — коэффициент Пуассона.
В пределах упругих деформаций, как это доказывается в § 27,
между обобщенными напряжением и деформацией существует
исключительно простая зависимость, а именно:
а< = £в„ (2.33)
где Е — обычный модуль упругости рассматриваемого материала.
§ 25. Оценка точности уравнений (2.25) с позиций нелинейной
теории упругости
При выводе геометрических уравнений механики сплошной среды (2.25)
фактически были сделаны допущения, о которых указывалось на стр. 26
(пункты а, б, в), надобность в которых, возможно, была для читателя не
совсем очевидна. Приведем дополнительное пояснение.
Если не делать указанных на стр. 26 допущений, то окончательные
выражения для компонентов деформации значительно осложнились бы.
Приведем без вывода из книги В. В. Новожилова «Основы нелинейной теории
упругости» (1946, стр. 21 и 55—58) выражения для относительного
удлинения и сдвига:
"<*** = *ау + Вх (у txy - wt) + гу (г" Та* + *•) +
+ ("2" Та* — w2/) ("2 Ъ* + Шя) , (2.34)
I де через гх и -\ху (со звездочкой) обозначены точные значения
компонентов деформации и через е<т, ^ху и т« Д» (без звездочек) — приближенные
записи для них согласно (2.25).
:) Удобство введения понятия об интенсивности деформации е^ помимо
прочего также выгодно тем, что для случая одноосного растяжения (или
сжатия) б$ становится равным главному удлинению е1#
Для случая одноосного растяжения (или сжатия) указанный ниже
закон (2.33) обращается, т аким образом, в простейший закон Гука.

108 ОБЩИЕ УРАВНЕНИЯ МЕХАНИКИ СПЛОШНОЙ СРЕДЫ [ГЛ. II
Рассматривая случай, когда малы по сравнению с единицей не только
компоненты деформации, но и углы поворота, В. В. Новожилов приходит
к такой упрощенной записи:
C««.+t(-S+-». | (2.35)
* I
*ху ~ *Ху х у J
Если, наконец, предположить, что квадратами и произведениями углов
поворота в формулах (2.34) можно пренебречь, то приходим к формулам
классической линейной теории упругости, т. е.
* ди
* ^ _ дп dv
Чху ^^xy — ~dy^dx
и т. д.
Таким образом, использование линейных выражений для компонентов
деформации [формулы (2.25)] возможно лишь при соблюдении следующих
условий:
а) удлинения, сдвиги и углы поворота должны быть малы по сравнению
с единицей;
б) квадратичные комбинации углов поворота, входящие в формулы (2.35),
должны быть малы по сравнению с соответствующими компонентами
деформации.
Последнее условие приблизительно может быть сформулировано как
требование, чтобы квадраты углов поворота были пренебрежимо малы по
сравнению с удлинениями и сдвигами.
Если тело массивно, т. е. имеет одинакового порядка протяженность
во всех своих трех измерениях, то соблюдение условия а) влечет за собой
и соблюдение условия б).
Иначе будет, если тело является гибким. В этом случае углы поворота
могут значительно превосходить удлинения и сдвиги.
Итак, очевидно, что областью применения линейных формул (2.25)
являются деформации массивных тел, а областью применения нелинейных
формул (2.34) и (2.35) — деформации гибких тел.
В. В. Новожилов в указанной выше книге проводит обстоятельный
анализ условий применимости линейных формул (2.25). Им, в частности,
показано, что нелинейная и классическая теории упругости занимаются
фактически конечными деформациями и притом одного порядка малости.
Разница в подходе этих двух теорий к определению деформаций
заключается в том, что линейная теория пренебрегает влиянием поворотов на
удлинения и сдвиги, а нелинейная как раз его учитывает.
В соответствии с этим повышается не только точность решения задачи,
но оказывается возможным нелинейной теорией охватить более широкий
класс задач (проблемы упругой устойчивости и т. д.), чем линейной теорией.

ГЛАВА HI
ОСНОВНЫЕ УРАВНЕНИЯ ТЕОРИИ УПРУГОСТИ
А. СВЯЗЬ НАПРЯЖЕНИЙ С КОМПОНЕНТАМИ ДЕФОРМАЦИИ
(ФИЗИЧЕСКИЕ УРАВНЕНИЯ ТЕОРИИ УПРУГОСТИ)
§ 26. Закон упругости
В предыдущей главе установлены общие уравнения механики
сплошной среды, которые сами по себе еще не могут решить задачи
о напряжениях и деформациях в твердом теле: статическое и
геометрическое обследования задачи должны быть дополнены специальными
уравнениями, связывающими разнообразные признаки изучаемого
явления, т. е. силы и деформации. Эти зависимости, очевидно,
определяются физическими свойствами твердого тела и, как связанные с
особенностями микроструктуры тела, должны быть предметом изучения
в физике.
Теоретическое выяснение упомянутых зависимостей требует
проникновения в природу межмолекулярных сил, стремящихся удержать
частицы твердого тела на определенных расстояниях друг от друга *).
Отсутствие в настоящее время законченных всесторонних
исследований по упомянутым физическим зависимостям (применительно к
микрообъемам), которые были бы одновременно и удобными для
технических расчетов, вынуждает инженерную практику оперировать такими
осредненными статистическими образами, как напряжение,
составляющие деформации и т. п. Поэтому в настоящей главе в полном
соответствии с предпосылками § 2 твердое тело предполагается
наделенным свойствами упругости и изотропности. Свойство сплошности,
подразумеваемое при выводе уравнений глав I и II, переносится
полностью и сюда.
Рассмотрим вновь частицу твердого тела в форме бесконечно
малого параллелепипеда, находящегося в общем случае пространственного
напряженного состояния (фиг. 15). Зависимость между напряжениями
и деформациями для объемного напряженного состояния может быть
*) Интересующихся попытками построения дискретной теории упругости
можно отослать к [93].

ПО ОСНОВНЫЕ УРАВНЕНИЯ ТЕОРИИ УПРУГОСТИ [ГЛ. Ш
легко записана путем распространения на этот случай известных
читателю законов Гука для чистого растяжения-сжатия и чистого сдвига.
Практическая возможность такой экстраполяции оправдывается опытом
для большинства материалов, применяемых в технике, при соблюдении
следующих условий:
а) одновременное наличие всех компонентов напряжений, а равно
их действие порознь (если таковое возможно) не переводят материал
в пластическое состояние, т. е. материал пребывает в рамках упругих
деформаций;
б) материал практически можно считать изотропным *);
в) деформации ничтожно малы по сравнению с размерами
изучаемого тела;
г) процесс деформации изотермичен**).
Перечисленные условия, делают практически возможными
применение принципа независимости действия сил и приложение указанных
элементарных законов (для одноосного растяжения и для сдвига)
к вычислению деформаций по любому направлению внутри
рассматриваемого параллелепипеда.
Полагая вначале действие одних только напряжений cxi т. е.
линейное напряженное состояние, мы должны признать, что
элементарный параллелепипед получит следующие относительные удлинения:
в направлении оси х согласно первому закону Гука
в' =22.
х е *
а в направлении осей у и г, являющихся поперечными по отношению
к направлению действующего усилия:
где Е—модуль упругости, постоянный для изотропного материала
(в пределах упругости), и ja — коэффициент Пуассона***).
Полагая далее действие одних только напряжений ау1
аналогичными рассуждениями получим:
~" °у *» о"— .. °у
У Е ' » г » Е
*) Случай анизотропных материалов входит, вообще говоря, в сферу
теории упругости, но обычно составляет специальный раздел (см., например,
[59], [60]). В настоящей книге эти случаи не рассматриваются.
**) В круг ведения классической теории упругости относятся не только
изотермические, но и адиабатические процессы, а также и другие возможные
обратимые процессы деформации, связанные с изменением температуры.
Однако последние задачи составляют специальный раздел теории упругости
и не затрагиваются в настоящей книге.
***) Этот коэффициент в случае конечных деформаций не будет
величиной постоянной, а будет функцией величины самой деформации (хотя
рассматривается упругий процесс); при малых же деформациях, изучаемых
в линейной теории упругости, он может приниматься постоянным.

§ 26]
ЗАКОН УПРУГОСТИ
111
Наконец, рассматривая действие напряжений о2, имеем:
е = -
= —И-
тт
Во всех трех порознь рассмотренных случаях действия нормальных
напряжений отсутствует перекашивание прямых углов (углы сдвига)
на гранях элементарного параллелепипеда. Касательные напряжения,
наоборот, как известно, влекут за собой искажение формы
параллелепипеда, удлинения же ребер отсутствуют; точнее, эти удлинения
пренебрежимо малы по сравнению с деформациями сдвига *).
Совокупность касательных напряжений 1ху = 1ух будет вызывать
перекашивание граней, параллельных плоскости лгОу, и оставлять без
искажения другие грани параллелепипеда. Согласно второму закону
Гука имеем:
/
"for
"•ху
где, как известно:
G '
G =
Ту* — Т«а?:
Е
О,
2(1+1*)
Аналогично от действия системы zyz = zgy имеем:
1уг
о
7yz — "7Т~» 7ЗХ — Чху — О,
а от касательных напряжений тЛВ = та.г должны получить:
'" _ *zx -/" — т"' = о.
\гх— ~~G~' ху yz
Таким образом, наличие всех компонентов напряжений определяет
следующие составляющие деформации:
e* = ~F[0*~~*1K+ °*)ь
*у = ~Ё^у — Ke« + °Л>
еа=-^г[ов — K^r+S))'
_ *ху ш
Лху ^ >
Туг = ~£~ \
v Tz.-r
1-га? q •
(3.01)
*) Указанную независимость касательных деформаций или напряжений
ит нормальных напряжений или удлинений можно мотивировать также из-
нсппым в строительной механике законом прямой и обратной симметрии:
при ирямосимметричном воздействии (наличие только нормальных, равномерно
распределенных по параллельным граням напряжений) нет
антисимметричных компонентов деформаций, т. е. сдвигов; при антисимметричном воздей-
стппи (наличие касательных напряжений) отсутствуют прямосимметричные
компоненты деформации, т. е. удлинения ребер.

112 ОСНОВНЫЕ УРАВНЕНИЯ ТЕОРИИ УПРУГОСТИ [ГЛ. III
В этом виде закон упругости обычно и записывается для
изотропного тела. Выражения (3.01) можно зачитать в такой редакции: ком-
поненты тензора деформации в данной точке тела находятся
в линейной зависимости от компонентов тензора напряжений,
относящихся к той же точке.
При р. = 0 обнаруживается, что любой компонент тензора
напряжений прямо пропорционален соответствующему компоненту тензора
деформации (см. замечание на стр. 47).
§ 27. Различные записи обобщенного закона упругости
В формулах (3.01) составляющие деформации выражены через
составляющие напряжения. Часто бывает необходимо иметь обратные
зависимости, т. е. напряжения, выраженные через деформации. Для
этой цели решим уравнения (3.01) относительно ах, ау и т. д.
Опуская преобразования, сообщаем окончательные результаты:
°1хУ;
зх = 2G [ел+ f^^ sop] , Ч
°у = 2 G [Qy + Г=^ 8°г]' V = °Ъш>
ог = 2G [t, + —^ sop J , хгх = Gisx,
(3.02)
где обозначено:
(средняя деформация).
Уравнения (3.02) для нормальных напряжений записывают и в таком
виде:
ay=2Gzy-\-kb, \ (3.02а)
о,=20в,+Хв, J
где
„о 1 _ 2f-g
U_deop, л— j—^.
Из (3.02) вытекают следующие любопытные зависимости:
°х — o„ = 2G(ee— «„),
з,—о,=20(.
у
■ч)>
и далее:
г *х гу "у 'г
(а)
ПГ

§ 27] РАЗЛИЧНЫЕ ЗАПИСИ ОБОБЩЕННОГО ЗАКОНА УПРУГОСТИ 113
эти же пропорции определяют собой геометрическое подобие круга
Мора для деформации (в координатах е, f) кругу — для напряжений
(в координатах а, т).
Применительно к «главному кубу», построенному около данной
точки, выражения (а) запишутся так:
°i — o2 = 2G(el — е2), а2 — а3 = 2G(s2 — s3), а3 —^ = 2G (s3—Sj). (б)
Замечая, что на основании (2.22) можно записать:
а1 °2= 2т12> а2 а8 = 2t23 И °3 а1 = 2т31 >
а согласно (2.31)
sl— S2=Tl2> £2 —S3=T23 И е3—el=T31»
соотношения (б) перепишем так:
*1« = GTl2, *28 = GT23 И Х31 = ОТМ- (В)
Последние записи, очевидно, можно было получить и
непосредственно, рассмотрев около заданной точки параллелепипед, для
которого по двум его парам параллельных граней действуют
касательные напряжения т12 = т21 или ъ2з=:Хз<2» или ^31 === xis (т- е- две паРы
граней такого параллелепипеда принадлежат граням «главного
додекаэдра») *).
Применяя к такой схеме напряженного состояния непосредственно
иторой закон Гука, придем к соотношениям (в).
Построим у той же рассматриваемой точки куб, ориентированный
относительно главных площадок так, что по двум парам параллельных
граней такого куба действуют касательные напряжения, по величине
раиные октаэдрическому касательному напряжению токт (т. е. эта
пара граней куба принадлежит граням главного октаэдра)*); если т0Кт
имеет направление действия, параллельное какой-либо стороне этой
грани, то применительно к такой схеме напряженного состояния можем
но второму закону Гука записать:
^ОКТ = GfoKT. (3.03)
Через главные нормальные напряжения выражение (3.03) на осно-
иаиии (2.17) и (2.30) запишется так:
W = "з V{°l — °2)2 + (°2 — °з)2 + (а3 — al)2 =
= О 4 V("i - *2)2 + (Ч - гз)2 + («в - si)2- (3-°3а)
Вводя обозначения:
3 _ 3 _
*) См. стр. 94.
8 Зак. 3880. Н. И. Безухое

114 ОСНОВНЫЕ УРАВНЕНИЯ ТЕОРИИ УПРУГОСТИ [ГЛ. 111
называя первое, т. е. ог«, обобщенным напряжением и второе, ег-,
обобщенной деформацией у и принимая во внимание зависимость
G= 9 , равенство (3.03) записываем в исключительно простой
форме:
о, = Ее,.
(3.04)
В справедливости (3.04) также можно убедиться, не исходя из
физического уравнения (3.03), а проделав с выражением обобщенного
напряжения (2.20) следующие формальные преобразования. Вначале
запишем (2.20) через составляющие напряжений (с помощью
инвариантов тензора напряжений) в виде
а. = Х^У(? —° )2+(° — о )2+(° —а )2 + 6(т2 -f т2 + т2 ).
* 2 v v * yJ * к У z' * ^ г х> I ^ ху \ yz \ zx>
(3.05)
Заменим теперь разности компонентов нормальных напряжений
через разности относительных удлинений [согласно (а)] и
составляющие касательных напряжений — через углы сдвига [согласно (3.02)];
тогда после вынесения за знак радикала 2G правая часть (3.05)
представится в точности правой частью (3.04), где, очевидно,
\£i=
Y2
2(1+1»
) V <•--
-V+(v
Z' 1 V Z
(v2 _Lv2 J-
т«)
(3.06)
является прежним (2.32), но записанным через иные компоненты
деформации [см. (2.30) и (2.30а)].
При наличии шести условий (3.02) выражение (3.04) в теории
упругости можно рассматривать как контрольное. В теории
пластичности, где будет неизвестным также и коэффициент Е (это уже не
будет модуль упругости), уравнение (3.04) [или варианты его записи,
например, (3.03)] будет присоединяться к системе (3.02) как
полноправное и притом как одно из важнейших условий.
§ 28. Продолжение: закон изменения объема и закон
изменения формы
Сложим левые части первых трех строк в выражениях (3.01) и
приравняем сумме правых частей тех же строк. Имеем:
еж + *у + *z = l~^ (°х+°у + <Ъ). (а)
Так как
j(Qx + ey + ez) = soP и -(ош + оу4- аг) = аор

§ 28]
ПРОДОЛЖЕНИЕ
115
составляют так называемые средние деформацию и напряжение, то
из (а) следует:
Е (3.07)
уор ■
1 —2р.
»ор»
Таким образом, среднее напряжение пропорционально средней
деформации. Так как сумма относительных удлинений по трем
взаимно перпендикулярным направлениям составляет объемную
деформацию, т. е. Зеор==Ь, то (3.07) можно записать также в виде
°°1 = 31ГЬЩ», (3.07а)
т. е. среднее напряжение в точке пропорционально объемной
деформации в окрестности той же точки.
Выражения (3.07), а также (3.07а) носят название закона
упругого изменения объема. Опыт показывает, что этот закон
оказывается справедливым и при высоких значениях среднего
напряжения, .значительно превышающих обычный предел упругости
материала (т. е. установленный в лабораторных условиях при испытании
на одноосное растяжение или сжатие). В связи с этим объемная
деформация, вычисляемая по выражению
й=3(1-2ц).
иоГ>
(3.076)
практически всегда оказывается исчезающей по удалении вызвавших
ее причин.
Обратимся вновь к (3.02) й от левых и правых частей первой
строки отнимем по оор, причем для правой части последнее выразим
через еор на основании (3.07). Тогда получим:
; —оср = 2о[еж+г=^еср] —Г=
2ц
"ср«
Заменяя Е = 2 (1 -|- jx) G, имеем:
°х — Оор = 20(8^ — вор).
Аналогичное проделаем со второй и третьей строками и перепишем
систему (3.02) в виде
°ж —°ср = 20(ел —еср),
ср;
°2/ —°cp = 2G(ey —еср),
°«—°оР = 20(в, —вор),
1
^ = 20
2 Тяу»
%уг — 2G~2 4y8>
^гх 9 Тгаг
(3.08)
8*

116 ОСНОВНЫЕ УРАВНЕНИЯ ТЕОРИИ УПРУГОСТИ [ГЛ. III
Последняя запись (3.08) пользуется особым вниманием в теории
пластических деформаций.
Если систему напряжений (ож— оср), (зу— оср), (а^— аор), хху,
zyz, tzx назвать компонентами напряжений, соответствующими
изменению формы, а систему деформаций (гх— еср), (е^ — еср), (ег — еср),
Y^' ~2~Т*/г» ТТгж назвать компонентами деформации, отвечающими
изменению формы, то обобщенный закон упругости (3.08),
являющийся законом изменения формы, может быть прочитан в
следующей простой редакции: компоненты напряжений и деформации,
соответствующие изменению формы, пропорциональны друг
другу; первые равняются вторым, умноженным на двойной
модуль сдвига.
Систему зависимостей (3.08) можно записать в виде следующей
таблицы:
JCP)
'°ср, 1уг
> аг — °ср.
1 1 1
" сср> 2 Та?#> 2 ^хг I
. _е Iv , (3.08a)
• ,s2- ecpJ
m которой левые и правые части уравнений (3.08), пропорциональные
друг другу, располагаются соответственно одинаково.
Так, например, выражению (ру— оср) из второй строки второго
Столбца левой матрицы соответствует в правой матрице и также во
второй строке и во втором. столбце выражение (гу— еср), которое,
как известно, пропорционально первому.
Как установлено в § 7, левую матрицу, составленную из
компонентов напряжений, влияющих на изменение формы, называют де-
виатором напряжений (1.18), а правую матрицу — соответственно
девиатором деформации (1.14).
В связи с этим обобщенный закон упругости можно
символически записать в виде
Оя = 20Олеф (3.09)
и прочитать в такой изящной редакции: девиатор напряжений прямо
пропорционален девиатору деформации.
Выражения (3.08а), а также и (3.09) носят название закона
изменения формы.
Возвращаясь к закону изменения объема и используя цонятия
о шаровых тензорах (§ 7), можно (3.07) записать так:
Тп = ЕоГдеф, (3.10)
т. е. шаровой тензор напряжений пропорционален шаровому тен-

§ 29]
УДЕЛЬНАЯ ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ
117
зору деформации*). Коэффициент пропорциональности (объемный
модуль упругости) записывается в виде
и, заметим, при jj, = 0,5 обращается в бесконечность.
Из четырех упругих постоянных Е, ji, G, Е0> очевидно,
независимы только два. В связи с наличием указанных двух характерных
законов деформации упругого тела и входящих в эт,и законы
модулей Е0 и G логично в качестве двух основных, т. е. независимых
физических характеристик упруюго тела, считать именно Е0 и G.
Объемный модуль Е0 измеряет сопротивление материала
изменению объема, которое не сопровождается изменением формы (случай
гидростатического давления). Модуль сдвига G (иначе, модуль
упругого формоизменения), наоборот, измеряет сопротивление материала
изменению его формы, которое не сопровождается изменением объема-
§ 29. Удельная потенциальная энергия
Под действием внешних сил упругое тело испытывает
деформацию, при которой силы совершают некоторое количество работы.
Эта работа превращается в потенциальную энергию и в последующем,
при удалении внешних сил, расходуется на восстановление
первоначальной (недеформированной) формы тела.
Энергия, накапливаемая при деформации в единичном объеме
материала, выделенном около данной точки, называется удельной
потенциальной энергией или эластическим потенциалом в
окрестности рассматриваемой точки **).
Для подсчета эластического потенциала необходимо составить
сумму произведений цз компонентов напряжений (компонентов
тензора напряжений) на соответствующие им компоненты деформации
(компоненты тензора деформации). Половинное значение такой суммы
и составит искомую удельную энергию, обозначаемую в дальнейшем Э.
Представим себе около заданной точки кубик с единичным
объемом: следовательно, площадь каждой его грани равна единице.
11риходящаяся на нее упругая сила будет количественно равна
самому напряжению, действующему на эту грань. Так, в случае
одноосного растяжения вдоль оси х эта сила будет ах на одной грани
*) Очевидно, возможна и такая редакция: первые инварианты тензоров
напряжений и деформации пропорциональны друг другу, т. е.
а = Е0г .
**) Выражения для потенциальной энергии деформации упругого тела
широко используются в различных методах решения сложных задач, в
частности, в вариационных методах теории упругости (см. §§ 74, 75).

118 ОСНОВНЫЕ УРАВНЕНИЯ ТЕОРИИ УПРУГОСТИ [ГЛ. III
и такая же (если пренебречь приращением ож), но противоположно
направленная, на другой грани, параллельной первой.
Система двух противоположно направленных сил {обобщенная
сила) совершает работу, зависящую от изменения расстояния между
точками приложения упомянутых сил, т. е. на деформации удлинения
кубика (на обобщенном перемещении); и так как в упругом теле
зависимость между напряжением и деформацией линейна, то работа
внутренних сил запишется как половина произведения из обобщенной
силы на обобщенное перемещение.
Деформация удлинения ребра с первоначальной длиной в единицу
количественно будет равна относительному удлинению того же ребра.
Таким образом, при одноосном растяжении энергия запишется так:
\_
аналогично составятся выражения работы и для других
составляющих напряжений.
Таким образом, в общем случае пространственно напряженного
состояния для подсчета эластического потенциала имеем:
23 = °х*х + °угу + °ггг "Ь *ху1яу + *уг1уг + WW (3.12а)
На основании (3.01) выражение (3.12а) может быть переписано
в виде
Е (2Э) = а* + о* + °1 - 2^ (охоу + V, + <,*„) +
+ 2 (1 + ц) (~1у + V + ■£.)• (3.126)
Если напряжения выразить через деформации, т. е.
использовать (3.02), то (3.12а) перепишется в виде
^.(23)-2(ei + ^4-; + TzV0,) + ^ + T^ + U. (3.12b)
Как известно, количество потенциальной энергии деформации,
накопленной в единице объема материала, иногда принимается за
основу для определения того «приведенного напряжения», при
котором наступает предельное упругое состояние (энергетическая теория
прочности). Но так как изотропные материалы могут выдержать
очень большие гидростатические давления без появления текучести,
то в целях лучшего согласования теории с опытом подсчитанную
выше энергию (3.12а) делят на две части: одну, происходящую от
изменения объема тела, и другую — от искажения формы тела, и
рассматривают для определения прочного сопротивления только эту
вторую часть. Таким образом, записывают:
С/ С/о —у- £7ф,
(3.13)

§ 29]
УДЕЛЬНАЯ ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ
119
где Э0— энергия, расходуемая на изменение объема у данной точки,
и Эф — энергия, расходуемая на формоизменение (удельная энергия
формоизменения).
Для подсчета Э0 исходим из рассмотрения фиг. 23, а, где
представлены те компоненты напряжений, наличие которых связано
с объемной деформацией в точке.
Таким образом,
Эо = (•£ acpecpJ -3, (3.14)
или на основании (3.07)
Э0:
з о-ад 2
Jcp»
(3.15)
Удельная энергия формоизменения определится тогда вычитанием из
полной энергии (3.126) той части энергии, которая затрачивается на
совершение объемной деформации (3.15), т. е.
£/ф С/ — С/фу
или после преобразований имеем:
ЭФ = 4G [(°ж — °ср)2 + (°* — °ср)2 + (°« ~~ 0ср^2 +
+ 2(^ + ^ + ^)1- (3-16)
При написании (3.16) использованы зависимости (3.08).
Выражение (3.16) после замены оср через компоненты может быть
представлено в виде
эф = ш К3* - °.)2+(°* - °*)2+К - °*? 4-
+ 6(^ + ^ + ^)1- (3-!7)
ху
Все указанные выше формулы можно получить наглядно использованием
понятий о тензорах напряжений и деформации.
Так из самого определения удельной потенциальной энергии следует,
что ее можно записать в виде
2Э=ГнГдвф*).
(3.18)
Подставляя в (3.18) известные обозначения для тензоров (1.03), (1.12),
имеем:
_1_ \_
23 =
"yz
1
2 V
(3.19)
Использовав примечание к (3.18) и развернув (3.19), приходим к (3.12а).
*) Произведение, стоящее в правой части, следует понимать
символически и рассматривать его как сумму произведений одноименных
компонентов напряжений и деформации.

120 ОСНОВНЫЕ УРАВНЕНИЯ ТЕОРИИ УПРУГОСТИ [ГЛ. III
Для указанных ранее слагающих энергии Э0
следующие символические выражения:
*3х можно составить
23ф = ОнОдвф.
(3.20)
(3.21)
Здесь учтено, что составляющие чисто объемной деформации (составляющие
шаровых тензоров) связаны лишь с изменением объема и независимы от
составляющих, оценивающих только изменение формы (компонентов де-
виаторов).
Выражения (3.20)—(3.21) можно получить также из следующих
формальных преобразований над (3.18):
ЧЭ = (7-2 + Da) (Гдеф + />деф) = Г°Гдеф + ОнЯдеф + Г°Одеф + ЯнГдеф.
Но легко показать (если произвести надлежащее перемножение), что
работа составляющих шарового тензора напряжений на компонентах девиа-
тора деформаций (Т'н^деф)» а также работа составляющих девиатора
напряжений на компонентах шарового тензора деформации (DKT^e*)
равны нулю.
Таким образом, получается, что работа составляющих
шарового тензора напряжений на компонентах шарового
тензора деформации представляет собой удвоенную
упругую работу внутренних сил, идущую на изменение объема.
И далее, работа составляющих девиатора напряжений на
компонентах девиатора деформации составляет
удвоенную работу внутренних сил, затрачиваемую на
изменение формы (без изменения объема). Итак:
1 Q
(3.22)
Ф 2
х ср' ху
{
а — g . т
у ор» уг
' * cpj
еср' 2 "*ХУЧ
2 ^хг
еср' 2 Чуг
ср J
. (3.23)
Развертывание последней записи в строку с использованием (3.08)
приводит к (3.16).
Можно доказать, что
внутри упругого тела в
энергии деформируемого
вается весьма успешным
Так как количество
как и упомянутых выше
соба вычисления, т. е
действительному распределению напряжений
сегда соответствует минимум потенциальной
тела. Этот минималистский принцип оказы-
при решении сложных задач (см. § 74).
потенциальной энергии деформации, равно
ее слагающих, не должно зависеть от спо-
. энергия инвариантна к ортого-

§ 29]
УДЕЛЬНАЯ ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ
121
нальному преобразованию координатной системы,
то следующие выражения, входящие в (3.12 6, в), (3.16) и (3.17),
составляют инварианты:
°1 + 4 + 4 — Ч (ах°у + ay°z + *г°х) +
+ 2 (1 + р) (&, + 4. + ■&) = const>
2 (ej + 4 + в! + j-^; 92) + 7**/ + Tfi» + Т« = const,
(аж —аср)2 + (^—аср)2 + (аг—aop)2 + 2(42/+4« + T^)=const>
К—а^/)2+(аг/—az)2+K — аа/+6 (4y+V+TL) = Const.
Сопоставляя (3.17) с (2.19) и с замечанием на стр. 90 по поводу
второго инварианта девиатора напряжений, замечаем, что квадрат
касательного октаэдрического напряжения, второй инвариант
девиатора напряжений и удельная энергия формоизменения
пропорциональны друг другу.
Таким образом, октаэдрическое напряжение, а также обобщенное
напряжение (2.21а) с точностью до постоянных множителей равны
квадратному корню из второго инварианта девиатора напряжения или
квадратному корню из удельной энергии формоизменения.
Составим теперь полупроизведение из обобщенного напряжения
па обобщенную деформацию, т. -е. -^ orfe<# Используя (3.05) и (3.06),
получаем:
2" °*е* = ~Ш [(°* ~~ °У)2 + ^у ~" а*)2 +(а* ~~ °*? +
+ 6С4, + Ч. + ТУ]' (3.25)
т. е. упругая работа обобщенного напряжения в
данной точке на обобщенной деформации составляет
м точности количество удельной энергии
формоизменения у той же точки.
Таким образом, оперирование с понятиями обобщенных
напряжения и деформации позволяет при рассмотрении любого сложного
объемного напряженного состояния как бы отвлечься от всей
сложной совокупности компонентов, вообразив случай чистого растяжения
или сжатия с единственным действующим напряжением, равным по
исличине <з4. В частности, каким бы сложным ни было задано объемное
напряженное состояние для рассматриваемой точки, зависимость между
обобщенным напряжением и соответствующей ему деформацией будет
такой же, как в случае одноосного напряженного состояния того же
упругого материала, т. е. линейной зависимостью.
(3.24)

122 ОСНОВНЫЕ УРАВНЕНИЯ ТЕОРИИ УПРУГОСТИ [ГЛ. III
Б. СИНТЕЗИРУЮЩИЕ УРАВНЕНИЯ
§ 30. Основные уравнения теории упругости и возможные
методы их решения
Выпишем еще раз все три группы уравнений теории упругости.
А. Статические или динамические уравнения:
да~
дт
ху
дъ~
дх
дт
ух
ду
до„
dz
dz,
yz
дх
ду
dz
zy
dz
д*г
( д2и \
-f-pA'=0 ^или p-^rj,
/ d2v \
+ 9Y=0 ^или p-^rj,
/ d2xt
+ ?Z = 0 (^или p -^
дх ' ду ' dz
Б. Геометрические уравнения:
ди dv , ди .
» Чху "^ * ф7 у
d2w\
w)m
(А)
dv
\ху— дх
dw
гУ ~ду* ^yz "gyi"^^'
dw ди , dw
ez ~X7» Тга? "яТ "г" ~л~7 •
dw
dz ' »** — d*
Б. Физические уравнения:
a* = 2Gex 4- *6> T^ = °т»*;
oe=2Gee-J-XG, тот=Отад.
(Б)
(В)
В написанных 15 уравнениях являются неизвестными: шесть
компонентов напряжений (аж, а^, аг, т , туг, тгя?), шесть компонентов
деформации (еж, е^, ег, fxy9 чуг, fzx) и три компонента перемещения
(и, v, w\ т. е. всего 15 неизвестных. Таким образом, с
математической точки зрения задача может быть разрешена и сводится к
нахождению 15 функций, удовлетворяющих 15 уравнениям (Л), (Б), (В),
я также условиям на контуре:
Рхч = °* cos (v*) + *ау cos (vy) + тто cos (У), ]
Яг/v = V C0S (VA:) + °2/ C0S (ЧУ) + V C0S (VZ\
Pzi = *« COS (VAT) -f- T^ COS (vy) + Gz COS (v*).
(0

§ 30] ОСНОВНЫЕ УРАВНЕНИЯ ТЕОРИИ УПРУГОСТИ 123
При прямом решении задачи [когда в решении участвуют все
15 уравнений (А), (Б), (В)] уравнения неразрывности деформаций:
ду2 ~ дх* дх ду '
dz* * ду* ду dz 9
д2Ч | дчт, _ д2Ьх
дх* ~r dz* dzdx y I
dz\dx ' ду dz ) дхду '
д (дугх | д^у d-jyz \=o дЧх
дх \ ду ■" dz дх ) ду dz ' \
_а_ /d-jry , дчуг _ дчгя. \ _ 2 а2еу
д_у \ д.г •" дл: ду / dz dx ' )
сами по себе [как вытекающие из (Б)] не нужны и могут исполнять
роль контрольных уравнений.
Однако, если решается статическая задача теории упругости
[следовательно, правая часть уравнений (А) обращается в нуль] и притом
отыскиваются только напряжения и деформации (значит, неизвестных
будет 12), целесообразно уравнения (Б) подменить тремя (из шести)
уравнениями (Д) (проще принять первую группу уравнений
неразрывности).
При. такой комбинации будет, следовательно, три уравнения
равновесия (А), шесть физических уравнений (В) и три уравнения
неразрывности из группы (Д). Задача сводится к нахождению 12 неиз-
пестных функций, удовлетворяющих в каждой точке упругого тела
12 уравнениям, на поверхности тела также удовлетворяющих
граничным уравнениям (Г).
Далее, если это потребуется, по найденным деформациям из (Б)
можно вычислить оставленные временно без рассмотрения компоненты
перемещений.
Решение указанных выше трех групп уравнений можно вести
рапными путями в зависимости от того, что нас интересует в пер-
ную очередь. В связи с этим можно отметить три основных
направления.
1. Принять за основные неизвестные перемещения точек упругого
тела; тогда в каждой точке тела (с координатами лг, у, z) имеем три
неизвестных:
«=/i(*> У у г\ v=f2(x, у, z), w=fs(x, у, г). (а)
Для получения уравнений (а), очевидно, надлежит в физические
уравнения (В) подставить геометрические соотношения (Б), т. е. выра-
нить напряжения через перемещения и затем полученные для них

124 ОСНОВНЫЕ УРАВНЕНИЯ ТЕОРИИ УПРУГОСТИ [ГЛ. III
выражения подставить в три уравнения равновесия, в результате чего
и получим три уравнения типа (а).
Таким образом, природа уравнений (а) будет, как в группе (А),
статическая. Назовем этот метод методом перемещений. Указанные
операции выполнены в § 31.
2. Принять за неизвестные напряжения; тогда в каждой точке
тела будет шесть неизвестных:
°* = *l(*> У у *)> a2/ = $2<X У> *). °.= *8(*» У> г\ I /бч
Так как напряжения из уравнений равновесия непосредственно не
определяются, надо обратиться к уравнениям деформаций. Используя,
например, уравнения неразрывности деформаций (Д), с помощью (В)
и (А) можно получить уравнения типа (б).
Назовем этот метод методом сил. Указанный метод разобран
в § 32. Возможны и некоторые разнообразия указанных двух
основных методов.
3. Очевидно, возможен смешанный метод, когда за основные
неизвестные приняты некоторые из перемещений и некоторые из
напряжений.
Вообще в выборе основных неизвестных и метода получения уравнений
для них можно провести аналогию с теорией расчета статически
неопределимых систем в строительной механике стержневых систем.
Там есть три основных метода: метод сил, метод деформаций и
смешанный метод. Неизвестные силы определяются, как известно читателю, из
уравнений деформаций (канонические уравнения в методе сил), неизвестные
перемещения (углы поворота и смещения узлов рам) определяются из
уравнений равновесия.
Итак, в смысле выбора основных неизвестных в теории
упругости имеется три указанных метода.
Что касается способов математического решения полученной по
предыдущему системы уравнений, то и здесь можно указать
следующие три основные направления.
а) Прямой способ, или иначе способ непосредственного
интегрирования уравнений теории упругости.
б) Возможен и обратный способ, когда, например, задаются
перемещениями как функциями координат точки (лг, у, z) и
разыскивают на основании условий (Б) деформации, а по ним с помощью (В)
напряжения; знание же последних дает возможность с помощью (Г)
установить поверхностные условия, т. е. те внешние нагрузки,
которым соответствуют заданные перемещения.
в) Оказался вполне плодотворным полуобратный способ Сен-
Венана, согласно которому задают часть внешних сил и часть
перемещений и разыскивают остальные факторы из условия
удовлетворения соответствующих уравнений указанных выше групп.

§31] РЕШЕНИЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ В ПЕРЕМЕЩЕНИЯХ 125
Для облегчения техники решения некоторых уравнений теории
упругости оказывается целесообразным способ
последовательных приближений, в основном опирающийся на идеи
обратного способа.
Одной из эффективных разновидностей такого способа
оказывается использование в некоторых задачах вначале тех решений,
которые доставляются каким-либо элементарным решением, например,
найденным в курсе сопротивления материалов. Подстановка этих
решений в уравнения теории упругости приводит к некоторым
несоответствиям (противоречиям), из анализа которых можно найти
путь корректировки предварительного решения, если и не дающий
и итоге точного решения задачи, то приводящий к
удовлетворительному для практики приближенному решению (более строгому, чем
исходное элементарное решение).
Указанный способ последовательных приближений можно
использовать и в методе сил, и в методе перемещений, и в случае прямого
или обратного решения исходных уравнений.
§ 31. Решение задачи теории упругости в перемещениях*)
Перейдем к преобразованию основных уравнений (§ 30), выражая
псе неизвестные через три перемещения: #, v, w, которые здесь
принимаются за основные.
Из уравнений (В) с помощью (Б) имеем:
..-*»£ + М; ^_0(£+£). ,__<,(£+*.),(.)
где
f) = ЗгСр
Дифференцируя (а), получаем:
дох __ г &и_\г &Ь_\\ _^_
дх —и дх* "+" дх* "+"Л дх '
дъху _ q d2v . Q д2и
ду дх ду *"Т~ дуг '
dixz __ £ d2w , ^ д2и
dz дхdz "* dzL
*) При первом ознакомлении с курсом теории упругости читателю можно
пгкомендовать §§ 31 и 32 вначале опустить и вернуться к ним после § 36.
Попутно заметим, что для решения частных задач, разбираемых в настоящей
!♦ миге, общие уравнения, указанные в §§ 31 и 32, не имеют широкого
применения.

126
ОСНОВНЫЕ УРАВНЕНИЯ ТЕОРИИ УПРУГОСТИ
[ГЛ. III
Внося это в первое уравнение группы (А), имеем:
, дЬ , ~(д2и , d2v , d2w
дх
+ о(-
дх2
-)+
дх ду ' дх дг
+°(-р+w+~^) +Ар==р-^--
(б>
Выражение, заключенное в первой скобке, может быть короче
записано так:
д2и
d2v
d2w
д ( ди
дх*
дх ду
дх дг
— (
дх\
dv
dw
дх
ду
дг
)-
(^+^+6,)=-^.
дх
дх9
Введем для краткости письма обозначение гармонической
операции:
d2U ' d2U ' d2U :ФЦ (3.26)
дх2
ду2
дг2
(читается «набла два»), называемое также лапласовым оператором
второго порядка над функцией u=f(x9 у, z). Тогда уравнение (б)
перепишется так:
(X+0)|i+OV2M + ^P = p-a2M
дР
(в)
Аналогично можно преобразовать и другие два уравнения группы (А),
но можно и сразу написать результат, сделав в (в) круговую
подстановку букв (лг, у, z) и (и, v, w).
Итак, приходим к следующей системе основных уравнений метода
перемещений теории упругости:
(X+O^+OVa + Jrp-p*".
дх
dt2
(М-0)$+о**+Гр=р-Й-.
<Э8
(* + O)-S7 + 0V»W + Zp = p
дР
d2w
~д¥~
(3.27)
Эти уравнения носят название уравнений Ламе. Они являются
синтезом статического, геометрического и
физического обследований задачи, каждое из которых было ранее
выполнено в отдельности.
Поверхностные условия (Г) также можно преобразовать, выразив
напряжения через перемещения.

§ 32]
РЕШЕНИЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ В НАПРЯЖЕНИЯХ
127
Подставив в первое уравнение группы (Г) на место напряжений
выражения для них в форме (а), имеем:
P..-[" + 20^.]cos(»*) + o[||- + ^.]cos(^) +
Аналогично преобразуются и два других уравнения группы (Г)»
В итоге условия на контуре запишутся в виде
рхН = Х8 cos (vx) -+-
+ G [If cos ^+17cos ^+17 cos (v^] +
+ G ["57 cos (V^ +17 cos ^ + IF cos ^J ;
/V = x6 cos M +
+ G ["57 cos ^ + "57 cos ^ + 17 cos ^] + } (3.28)
+ G ["§7 cos ^ + 17 cos W + 17 cos (v^];
Рмч = M cos (v,e) -f-
+ G [l7 cos (v^ + ly~ cos M +17 cos ^ J +
+ G [l7 cos (v^ +17 cos № +17 cos (v^] • j
Уравнения (3.27) совместно с условиями на поверхности (3.28)
позволяют перейти непосредственно к решению задач теории
упругости в перемещениях.
§ 32. Решение задачи теории упругости в напряжениях
В противоположность приему, принятому в предыдущем параграфе,
когда во всех преобразованиях мы преследовали цель выразить неиз-
псчтные через перемещения, можно поставить другой: все выражать
через напряжения.
Освобождая внимание читателя от необходимых для этой цели
ииюшдок, сообщим окончательные результаты и ограничимся лишь
случаем статического равновесия тела при условии отсутствия
объемных сил или постоянства их.

128 ОСНОВНЫЕ УРАВНЕНИЯ ТЕОРИИ УПРУГОСТИ [ГЛ. III
Трех условий равновесия:
до-
дт;
ху
д*я
дх
ух
ду
до,.
дг
дх
di„
ду
дг
да.
+ *> = <>,
aF+^ + iH^0'
(АО
оказывается недостаточно, и надо обратиться к условиям
неразрывности деформаций (Д). Так как в последние входят деформации еж,
гу> 8г> Т<г*/> Т#г> 4zx> т0 их необходимо выразить через напряжения
с помощью закона упругости (В). Выполнив эту подстановку и
пользуясь одновременно уравнениями равновесия (А7), уравнения
неразрывности преобразуют к следующему виду (уравнения Бельтрами):
(1 + ^4,4-^ = 0,
(l+!x)V^ + g = 0,
(i+n)V4-fS = o,
дЬ
(l+t*)V4
ху
(i+t*)v2v+
дх ду
ду dz
д^
= 0,
-О,
где
(3.29)
:3а(
ср ■
Таким образом, для решения задачи придется проинтегрировать
девять уравнений (А7), (3.29), а входящие в общие решения этих
уравнений произвольные функции определить из условий на
поверхности:
Рх, = Gx C0S (v*) + хху COS (4V) + *хг cos (v*)>
Руч = *уя COS (VA0 + Gy COS М + V «>S (V*),
P* = Zzx COS (v*) + ^zy COS (vy) + o, COS (vz).
При решении задач теории упругости в напряжениях или в
перемещениях может возникнуть вопрос о том, является ли полученное
в итоге решение однозначным? Не могут ли заданным на
поверхности упругого тела силам соответствовать внутри тела не одна,
а несколько систем напряжений? Или: заданным смещениям или

§ 33]
ПЛОСКОЕ НАПРЯЖЕННОЕ СОСТОЯНИЕ
129
напряжениям внутри тела не могут ли соответствовать различные
контурные условия?
Если исключить случай начальных напряжений в теле, то ответ
на указанные выше вопросы с позиций классической теории
упругости должен быть дан только отрицательным. Для естественно
ненапряженного тела (т. е. при отсутствии внешних сил в теле
нет напряжений) решения теории упругости однозначны.
Доказательство упомянутой однозначности можно найти в книге
проф. М. М. Филоненко-Бородича «Теория упругости» (Гостехиздат,
1947, стр. 105—108).
Однако указанное категорическое заключение справедливо только
в линейной теории упругости и, следовательно, только для задач,
входящих в сферу ее ведения. С позиций нелинейной теории
упругости такой вывод считается неправильным и объясняется
недостаточной точностью формул классической теории упругости.
При рассмотрении теории устойчивости упругого равновесия
в нелинейной теории упругости показывается, что при увеличении
до известного предела действующей на тело нагрузки (критическое
значение) решение классической теории упругости действительно
является единственным решением, однако по достижении такого
критического значения оказывается возможным раздвоение ре-
тения задачи (см. В. В. Новожилов, Основы нелинейной теории
упругости, М. —Л., 1948, стр. 147—169).
В. ЧАСТНЫЙ СЛУЧАЙ —ПЛОСКАЯ ЗАДАЧА
§ 33. Плоское напряженное состояние
Все уравнения теории упругости значительно упрощаются, если
пи пряжения параллельны одной плоскости, например, в случае тонкой
пластинки (брус, стер-
1
жепь), подверженной
действию сил, приложенных
к ее контуру,
параллельных плоскости пластинки
и равномерно
распределенных по ее толщине
<фиг. 50).
В этом случае
составляющие напряжений
eft ххг и zyz равны нулю
на обеих поверхностях
пластинки, и можно
полагать, что они отсут-
И
Фиг. 50. Плоское напряженное состояние.
стиуют и по всей толщине пластинки, т. е. распределение
напряжений является плоским.
9 Зак. 3880. Н. И. Безухов

130
ОСНОВНЫЕ УРАВНЕНИЯ ТЕОРИИ УПРУГОСТИ
[гл. ш
Естественно предположить, что другие три компонента
напряжений Од,, ау и zxy не зависят от координаты z, т. е. остаются
постоянными по всей толщине пластинки *).
Будем полагать, что объемной силой, как это чаще всего и
бывает, является только сила тяжести, т. е. Z = Х= 0; Yp = — д
(д— объемный вес).
Уравнения равновесия принимают вид
до*
дт.
х у
дх
dzyx ,д°у
дх "i" ду '
ду
■д = 0.
)
Условия на контуре:
Рх, = °х cos (vx) + ixy cos (vy),
Py, — *xy COS (VX) -+- Oy COS (vy).
Геометрические уравнения:
Физические уравнения:
dv
&*~dy' Ti
xy
du_j,dv
dy*dx'
*x = £ (°* — I10*)» e2/ = -£ К — I40*)'
1. _ 2(1+rt
*a?ir
(3.30)
(3.31)
(3.32)
(3.33)
Из уравнений неразрывности деформаций остается одно:
дЧ
д2««
д*г
ху
ду'* ' дх2 " дхду
(3.34)
Уравнения (3.30), (3.32), (3.33) общим количеством 8 содержат
восемь неизвестных и потому могут быть разрешены по методу сил
или по методу перемещений, или, наконец, по смешанному методу. Для
метода сил (три неизвестных) надлежит из (3.32) исключить переме-
*) Деформации и перемещения, происходящие в направлении
координаты z, не имеют практического интереса и вообще легко определяются
при известных компонентах напряжений и деформации, параллельных пло-
и,
скости пластинки; так, fyz = чгх = 0 и гг == — J_ (s^ -)- е^); последнее
получается из известного выражения ег = ^ [°г — Iх (°х + су)] подстановкой
cz = 0, а Од. и ау по уравнениям (3.33).

§ 34]
ДАЛЬНЕЙШИЕ УПРОЩЕНИЯ
131
тения и и v> что даст (3.34); далее, заменяя в (3.34) деформации
через силы по (3.33), получаем дополнительное уравнение к прежним
двум статическим уравнениям (3.30). В итоге получим три
уравнения с неизвестными от, оу, txy\ эти уравнения устанавливаются в § 34ч
Для метода перемещений (два неизвестных) надлежит через два;
статических уравнения (3.30) использовать замены, как в § 31, т. е,
исключить силы. В итоге получим два уравнения с неизвестными и и V,
§ 34. Дальнейшие упрощения
Уравнение неразрывности (3.34), выраженное с помощью (3.33)
через напряжения, записывается в следующем виде:
дуЛ°х — Р°у) + м(°у — ^) = 2(1 + Ю-^
ху
ду'
(3.34а)
Написанное уравнение (3.34а) совместно с уравнениями
равновесия (3.30) составляет систему трех уравнений с тремя неизвестными.
Если объемной силой является только вес тела (Х= 0, Yp = —q)y
то с помощью уравнений равновесия (3.30) выражение (3.34а)
переписывается проще. Так, дифференцируя первое из уравнений (3.30)
но х и второе — по у и затем складывая их, найдем:
дх ду ~ дх* ду* ' w
Подстановка (а) в (3.34а) приводит уравнение совместности
виду, выраженному только через нормальные напряжения
(уравнение Леви):
&<?* + °») + фК + °у) = 0- (3.35) •)
Итак, для плоского напряженного состояния, когда объемной
силой является сила тяжести, совокупность основных уравнений
теории упругости может быть приведена к следующим трем уравнениям:
(3.36)
') Для общего случая объемных сил уравнение (3.35) приняло бы вид
/ <Эа , д2\, . ч /1,ч (дХ,дГ\
te+^)(^+ay)=""(1+ll)fc+^;-
9*

132 ОСНОВНЫЕ УРАВНЕНИЯ ТЕОРИИ УПРУГОСТИ [ГЛ. III
где для краткости письма обозначена, как и ранее в § 31, операция
v \дх* «^ дуУ'
которая читается «набла два» и именуется гармонической операцией.
§ 35. Плоская деформация
Если при каком-либо напряженном состоянии тела перемещения
всех его точек могут происходить только в двух направлениях, т. е.
только в одной плоскости, то такая деформация называется плоской.
Примером может служить
тело, помещенное между
двумя абсолютно твердыми
плитами (фиг. 51),
расстояние между которыми остается
неизменным, и сжимаемое
силами, параллельными
плоскостям плит.
В таких же условиях
фактически оказывается тело,
размеры которого в одном
направлении, например, в
направлении оси .г, очень
велики; если такое длинное призматическое тело нагружено силами, не
меняющимися по длине тела и перпендикулярными к этому
направлению, то часть его, находящаяся на значительном расстоянии от
концов, фактически будет подвергаться плоской деформации;
перемещения всех точек деформированного тела в таком случае происходят
в плоскостях, перпендикулярных к длине тела (фиг. 52), т. е.
Const
Фиг. 51. Плоская деформация.
ег=0,
Из выражения
О, Т*. = 0,
~xz — V — 0.
имеем:
0« = t*(0a>H-°J-
(а)
Уравнения равновесия имеют прежний вид (3.30), также остаются
без изменения геометрические уравнения (3.32).
Физические уравнения (3.01) благодаря ог, определяемому по
выражению (а), принимают для относительных удлинений другой вид:
(3.£7)

§ 36] ФУНКЦИЯ НАПРЯЖЕНИЙ ДЛЯ ПЛОСКОЙ ЗАДАЧИ 133
причем для сдвига сохраняется выражение
„ _2(1 + Е)
, ГЦ
*ху
{д^ + д^)^ + ауУ-
Уравнение (3.35), если повторить выкладки, аналогичные
указанным в § 34, становится таким:
при постоянных объемных силах последнее выражение обращается
в (3.35), т. е. ничем
не отличается от
уравнения, выведенного для
случая плоского
напряженного состояния.
Отмечается
следующий любопытный
факт: при постоянных
объемных силах
уравнения,
устанавливающие распределение
напряжений в плоской
задаче (3.36), не
содержат упругих
попоенных материала.
Но этой причине и
представляется
возможным широко
использовать в практике идею моделирования и, в частности, переносить
результаты исследования напряжений, выполненные оптическим
способом с прозрачным материалом (целлулоид и т. п.) при помощи
поляризованного света, на другие материалы (сталь и т. п.).
Фиг. 52. Плоская деформация.
§ 36. Функция напряжений для плоской задачи
Итак, решение плоской задачи в напряжениях — задачи в двух
измерениях— сводится к интегрированию трех уравнений, которые
дли случая, когда объемной силой является вес тела, имеют вид (3.36):
^ху
дх
дт.
ух
дх
ду
= 0,
V2(o. + a,) = 0.
К этим уравнениям надо присоединить условия на контуре (3.31).
11о могут быть дальнейшие облегчения задачи, и вместо отыскания

134 ОСНОВНЫЕ УРАВНЕНИЯ ТЕОРИИ УПРУГОСТИ [ГЛ. III
трех функций (од., ау, zxy) достаточно определить одну, так
называемую функцию напряжений, посредством которой дальше уже не
интегрированием, а дифференцированием определяются все искомые
функции.
В самом деле, представим себе, что имеется такая функция <р от
координат х и у, при помощи которой напряжения определяются
следующим образом:
Легко проверить, что такая функция существует, так как если
подставить (3.39) в уравнения равновесия (3.30), то получим
тождества. Действительно,
дх * ду дх ду2 дх ду2 '
ду "I дх q~dx*dy dx*dy~T~q q~~ '
т. е. уравнения удовлетворяются тождественно».
Для отыскания вида самой функции о подставим (3.39) в
уравнение (3.35), откуда получим, что функция напряжений (иначе говоря,
«разрешающая ф у н к ц и я») должна удовлетворять уравнению
дх* t~ * дх* ду* "^ ду4 '
(3.40)
Уравнение (3.40) можно для краткости письма записать в виде
V4c? = 0,
где под операцией V4 (читается «набла четыре»), называемой бигар-
моническойу понимается следующая:
V*( ) = Va[Va( )].
В случае плоской задачи *)
Таким образом, решение плоской задачи в том случае, когда
объемной силой является вес тела, сводится к нахождению решения
бигармонического уравнения (3.40), которое удовлетворяло бы и
условиям на контуре.
*) В общем случае (в трехмерной задаче), очевидно,
V ( ' ~\дх*^ ду** дз*)\дх*~Т- ду*~т~ д*){ )и

§ 36] ФУНКЦИЯ НАПРЯЖЕНИЙ ДЛЯ ПЛОСКОЙ ЗАДАЧИ 135
Обращаться к услугам функции напряжений, называемой в
литературе функцией Эри, оказывается весьма плодотворным при
решении задач обратным или полуобратным способом. В самом деле,
если бы мы пожелали задаться какой-либо системой
напряжений (ож, <зу9 ъху) и найти им соответствующие внешние нагрузки
(поверхностные условия), то вначале надо проверить, может ли вообще
существовать задаваемая система напряжений (удовлетворяются ли
при этом уравнения равновесия и неразрывности), тогда как,
задаваясь функцией напряжений, удовлетворяющей только одному
уравнению (3.40)*), мы уже уверены в том, что все вышеперечисленное
удовлетворится автоматически.
Примеры на использование функции . напряжений приведены
в §§ 48 и 49.
Примечание 1. Функция напряжений не обязательно должна
толковаться как некоторая отвлеченная аналитическая функция (абстракция),
с помощью которой (учиняя над ней элементарные операции
дифференцирования) просто получаются выражения (функции) для самих конкретных
напряжений. Каждой «разрешающей» функции при желании всегда можно
подобрать некоторый геометрический образ, иначе говоря, конкретную
модель. Так, на стр. 267 (в § 80 о поперечном изгибе тонких пластинок)
показано, что функция напряжений (3.40) для заданной плоско-напряженной
пластинки может быть истолкована и как уравнение искривленной
срединной поверхности той же пластинки, если последнюю изгибать специально
подобранными силами (стр. 267). Эти силы должны мыслиться приложенными
на граничной линии пластинки (на опорном контуре) и действующими в
плоскости, нормальной к плоскости заданной пластинки. Такая аналогия
открывает возможность экспериментально проверять или, наоборот, находить
«разрешающие» функции в плоской задаче теории упругости.
Примечание 2. Вообще гармонические и бигармонические функции
имеют в теории упругости исключительно важное значение. Это вытекает
хотя бы из указанных ниже выводов, которые предлагается проделать
читателю в порядке самостоятельного упражнения.
Если положить отсутствие массовых сил, состояние покоя и
продифференцировать первое уравнение равновесия Ляме (3.27) по лг, второе по у%
третье — по г, а затем результаты сложить, то получим:
vV = o,
т. е. объемное расширение е1 есть гармоническая функция.
Если, далее, сделать операцию V2( ) над каждым из уравнений Ляме,
то получим:
V4a = 0,
V*v = 0,
V%> = 0,
т. е. компоненты упругого перемещения суть бигармонические функции*
*) Если для ср задаться любым полиномом не выше третьей степени
относительно х и у, то уравнение (3.40) удовлетворится и при любых
коэффициентах полинома. Однако во всяком случае коэффициенты полинома
должны удовлетворять граничным условиям, если только решение оказы-
иастся пригодным (см. § 48).

136 ОСНОВНЫЕ УРАВНЕНИЯ ТЕОРИИ УПРУГОСТИ [ГЛ. III
Если проделать бигармоническую операцию над обеими частями шести
формул обобщенного закона упругости (3.01), то получим:
*Ч* = *% = V4 = Ч^ХУ = V %* = V4r = 0,
т. е. компоненты напряженного состояния суть бигармонические
функции.
^ Выводы, полученные для трехмерной задачи, естественно, остаются
действительными и для плоского напряженного состояния.
§ 37. Плоская задача в полярных координатах
При исследовании напряжений в круглых кольцах, дисках и т. п.
удобно пользоваться полярными координатами. Ниже приводятся без
вывода соответствующие уравнения, доказательство которых не
должно теперь встретить затруднений у читателя, что и рекомендуется
выполнить в порядке самостоятельного упражнения.
Положение точки на срединной плоскости пластинки определяется
расстоянием г от начала координат О (фиг. 53) и углом 6 между
Фиг. 53. Обозначение напряжений в полярных
координатах.
этим направлением г и некоторой осью Оаг, занимающей
определенное положение на плоскости.
Взамен параллелепипеда с прямоугольной формой граней теперь
выделим малый элемент abed, вырезанный из пластинки двумя
радиальными сечениями Ос и Ob, перпендикулярными к пластинке, и
двумя нормальными к пластинке цилиндрическими поверхностями ad
и be, радиусы кривизны которых равны г и г -\- dr. Составляющие
нормальных напряжений в радиальном направлении обозначим
через ог, а в тангенциальном — через ан. Для касательного напряжения
примем обозначения тг9. Прочие обозначения указаны на фиг. 53.

§ 37J ПЛОСКАЯ ЗАДАЧА В ПОЛЯРНЫХ КООРДИНАТАХ 137
Если спроектировать все силы на направление радиуса и на
перпендикулярное к нему направление, то после отбрасывания
бесконечно малых высших порядков получим аналогично дифференциальным
уравнениям равновесия в декартовых координатах (3.30) следующие
выражения:
(3.41)
где R — объемная сила, отнесенная к единице объема и
предположенная действующей только в радиальном направлении.
Если составляющие перемещения точки в радиальном и
тангенциальном направлениях обозначить через и и vy то соответствующие
этим направлениям деформации запишутся следующим образом:
относительное удлинение в радиальном направлении
ди
е„ =
дг
(3.42)
то же в тангенциальном направлении
и , dv
Sfi = —
гдЬ
деформация сдвига
ди | dv
(3.43)
(3.44)
Функцию напряжений, удовлетворяющую условию (3.40):
д*у
д*ч?
д^ г
дх*
дх*ду* ' д*у
можно применять и при таком координатном исчислении.
Так как между декартовыми и полярными координатами имеются
зависимости
г2==х2^гу2
и
6 = arctg^-,
то, учитывая их и подставляя в (3.40) вытекающие из них
соотношения, после ряда преобразований придем к следующему уравнению-
неразрывности деформаций в полярных координатах:
Г д* , 1 а . 1 дП (дЦ
[дг* * г дг ' г* д№ J V dr*
1 ду
1 д^
дг
г* д№
= 0.
(3.45)

138 ОСНОВНЫЕ УРАВНЕНИЯ ТЕОРИИ УПРУГОСТИ [ГЛ. Ill
Зависимости же напряжений от функции напряжений имеют вид
(при отсутствии объемной силы)
1 дер . 1 дЦ дЦ д /1 д?\ /о ла\
ar = TW+lt-W °9 = -^"J Tre = — -fr[T~W)- (ЗЛ6)
В справедливости (3.46) можно легко убедиться подстановкой (3.46)
и (3.41), которые удовлетворяются. Примеры на использование
функции напряжений приведены в § 56.
§ 38. Симметричное относительно оси распределение напряжений
Если распределение напряжений симметрично относительно оси,
проходящей через точку О и перпендикулярной к плоскости деформации,
то компоненты напряжений не зависят от угла Ь и являются
функциями одного лишь г. Из условий симметрии вытекает,.что
касательное напряжение т^ = 0. В таком случае из (3.41) остается только
первое уравнение равновесия:
£ + ^Р + * = 0. (3.47)
Если объемная сила R отсутствует, то можем воспользоваться
функцией напряжений ©, уравнение для которой вследствие симметрии
получается таким:
\дг* "г" г дг) \дг* I г дг)~ дг* ~г г дг* г* дг*"»" г» дг — * ^ ;
Дифференциальное уравнение (3.48) — обыкновенное, линейное,
общим интегралом которого будет:
9 = Л1пг + Б^1пг + С/-2 + Д (3.49)
в справедливости чего легко убедиться подстановкой (3.49) в (3.48)
Компоненты напряжений определяются формулами:
°r=j£ = £ + B(l+21nr) + 2C, |
°9 = ^ = -^+5(3+21пг) + 2С. j
Постоянные интегрирования в каждой конкретной задаче будут свои
в зависимости от поверхностных условий, которым должна
удовлетворять функция ср, а следовательно, и компоненты напряжений (оп ое).
Указанное выше решение было дано в напряжениях, но можно,
конечно, дать его и в перемещениях.
Выпишем еще раз полную совокупность уравнений при осесим-
метричной деформации в полярных координатах (объемную силу
исключим). Статическое уравнение:

§ 39] СВЕДЕНИЯ О РАЗВИТИИ ПЛОСКОЙ ЗАДАЧИ 139
Геометрические уравнения:
и du
е, = —, гг = -г~. (б)
Г
Физические (для плоского напряженного состояния) уравнения:
Е «
Подставляя (б) в (в) и далее в (а), получаем дифференциальное
уравнение:
&+7£-*-* <3-51>
общий интеграл которого записывается так:
и = Аг + -у. (3.52)
§ 39. Сведения о развитии плоской задачи теории упругости
за советский период
Исследования русских и советских ученых по плоской задаче
теории упругости являются ведущими во всей мировой литературе.
Отметим лишь наиболее значительные работы в смысле использования
их результатов в инженерной практике.
К 1882 г. относится опубликование X. С. Головиным
замечательного решения для половины кольца с заданными на концах моментами
или радиальными силами. Это решение было в советский период
широко развито [131] и обобщено на расчет круговых арок с
защемленными пятами, подверженных действию гидростатической нагрузки
и температуры.
В 1909 г. Г. В. Колосов [53] дал впервые применение теории
функций комплексного переменного к плоской задаче теории
упругости. Ему удалось в весьма простом и удобном виде выразить
компоненты тензора напряжений и вектора смещения через две функции
комплексного переменного, аналитические в области, занимаемой
упругой средой. В дальнейшем Н. И. Мусхелишвили (1922 г.) строго
обосновал эти формулы для более общего случая многосвязной
области (конечной и бесконечной) и исчерпывающим образом
сформулировал проблемы теории функций комплексного переменного, к которым
сводятся основные и некоторые смешанные (контактные) задачи теории
упругости.
Н. И. Мусхелишвили удалось решить много практических задач
(бесконечная пластинка, ослабленная эллиптическим отверстием,
изгибаемая полоса с эллиптическим отверстием и др.). Его монография

140 ОСНОВНЫЕ УРАВНЕНИЯ ТЕОРИИ УПРУГОСТИ [ГЛ. III
«Некоторые основные задачи математической теории упругости»
(М., 1935) была отмечена Сталинской премией.
Метод Н. И. Мусхелишвили нашел широкое применение у разных
авторов и в различных задачах, таких, например, как изгиб тонкой
плиты с отверстиями в форме правильных криволинейных
многоугольников (М. М. Фридман), изгиб пластин с опертыми краями
(А. И. Лурье) и др.
Ряд важных для инженерной практики задач (в 1936 г. и
позже) рассмотрел Г. Н. Савин [91]: растяжение пластинки,
ослабленной отверстием, имеющим форму криволинейного многоугольника,
близкого к квадрату, прямоугольнику, треугольнику; влияние
закругления углов отверстий на картину напряженного состояния вблизи
последних и др. Его монография «Концентрация напряжений около
отверстия» удостоена Сталинской премии за 1951 г.
К 1940 г. относится опубликование П. Ф. Папковичем его
исследований напряженного состояния прямоугольной полосы под действием-
произвольной системы сил, приложенных к ее поперечным кромкам
и взаимно уравновешивающихся порознь на каждой из них.
В основу своего метода П. Ф. Папкович принял разложение
функций напряжений в ряды по некоторым, специального вида
элементарным функциям, весьма оригинально подобранным.
К 1946 г. относится работа М. М. Филоненко-Бородича,
содержащая решение основных задач для прямоугольника [119]. В ней автор,
комбинируя тригонометрические функции определенным образом,
получает почти ортогональную систему, благодаря которой точно
удовлетворяет граничным условиям, а в пределе — и бигармоническому
уравнению.
К 1921 г. относится работа Б. Г. Галеркина о напряженном
состоянии в плотинах и подпорных стенках трапецоидального профиля
при различного рода типичных нагрузках.
Эффективное применение метода интегральных уравнений в
задачах теории упругости связано с именем С. Г. Михлина (с 1934 г.
и далее), в одной из задач которого разобран случай изотропной
неоднородной среды, состоящей из нескольких однородных тел с
различными упругими свойствами. В той же области опубликовано много
исследований Д. И. Шерманом.
Практически важная задача о деформации эксцентричного
кругового кольца под действием равномерного внутреннего давления
решена С. А. Чаплыгиным [127] и Н. С. Аржанниковым (1933 г.).
Большое количество исследований посвящено изучению
термических напряжений. Укажем некоторые практически важные задачи,,
имеющие решения: полый цилиндр, нагреваемый стационарным
потоком тепла (Н. И. Мусхелишвили), термические напряжения в
пластинках (Б. Г. Галеркин), термические напряжения в бетонных
сооружениях (Г. Н. Маслов), термические напряжения в облицовке тоннеля
(Н. Я. Панарин), использование теории функций комплексного

S 40]
ОСНОВНЫЕ УРАВНЕНИЯ
141
переменного при изучении неустановившегося теплового потока
(Н. Н. Лебедев) и др.
Продолжая и талантливо развивая направления Г. В. Колосова и
Н. И. Мусхелишвили по применению теории функции комплексного
переменного, С. Г. Лехницкий [59, 60] решил широкий класс задач
по анизотропной среде. Вот далеко не полный перечень его работ
в указанном направлении: влияние сосредоточенных сил на
распределение напряжений в бесконечной анизотропной среде; задача о
бесконечном клине и полуплоскости при любых внешних силах для
полуплоскости, если заполняющая ее среда имеет три взаимно перпендикулярные
плоскости упругой симметрии (иначе говоря, является ортотропной);
пластинка, ослабленная эллиптическим отверстием; задача о
напряженном состоянии в анизотропной толстостенной трубе, подверженной
действию наружного и внутреннего давлений, при условии, что
материал является ортотропным.
Ряд задач о деформациях анизотропной среды решен П. П. Куфа-
ревым, В. М. Абрамовым и др. Н. Г. Ченцов обследовал фанеру
как ортотропную пластинку.
К исследованиям в области плоской задачи можно отнести и
большой круг так называемых коьтактных смешанных задач, простейшие
яз которых рассмотрены в § 66.
Выдающиеся работы в этой сложной области связаны с именами
Н. И. Мусхелишзили, Н. М. Беляева, С. Г. Михлима, Г. Н. Савина,
Л. А. Галина, И. Я. Штаермана, М. И. Горбунова-Посадова,
О. Я. Шехтер, Д. В. Вайнберга и др.
Обстоятельный разбор достижений советских ученых в области
.плоской и контактной смешанных задач статической теории упругости
имеется под одноименным названием в статье Д. И. Шермана,
опубликованной в сборнике «Механика в СССР за тридцать лет/> (М. —Л.,
1950), где приведена также и обширная библиография по затронутому
вопросу.
Г. ДРУГОЙ ЧАСТНЫЙ СЛУЧАЙ —ТЕЛА ВРАЩЕНИЯ
С СИММЕТРИЧНЫМ ОТНОСИТЕЛЬНО ОСИ РАСПРЕДЕЛЕНИЕМ
НАПРЯЖЕНИЙ
§ 40. Основные уравнения
Представим себе тело вращения, к которому приложены силы,
расположенные симметрично относительно оси этого тела (фиг. 54).
Примерами могут быть круглый цилиндр, усеченный конус, деформирующийся
под действием равномерного внутреннего или наружного давления или
сил, равномерно приложенных по торцевым сечениям, и подобные тела.
За ось вращения примем ось г, ось же, перпендикулярную к
первой, обозначим через г. Двух координат z и г вполне достаточно,
так как все точки с одинаковыми такими координатами находятся
\\ одинаковых условиях.

142 ОСНОВНЫЕ УРАВНЕНИЯ ТЕОРИИ УПРУГОСТИ [ГЛ. ИГ
№£{
У
L.
Так как каждая меридиональная плоскость zOr представляет
плоскость симметрии как в отношении формы, так и в отношении
нагрузки тела, то в меридиональных плоскостях касательных
напряжений быть не может. Поэтому для каждой точки тела, расположенной,
на меридиональной плоскости, площадка, в ней взятая, является
главной площадкой рассматриваемого*
напряженного состояния. Главное
напряжение, действующее по этой площадке,
обозначим через о9.
Кроме меридионального сечения, чере'з^
точку с координатами г, г проведем еще
второе сечение, перпендикулярное к оси
.г, и третье сечение, перпендикулярное
к двум первым. Следы этих двух новых:
секущих плоскостей ка меридиональной,
плоскости будут параллельны
соответственно осям гиг.
Вследствие симметрии в обеих
секущих плоскостях, в точке «г, г могут
действовать лишь такие касательные
напряжения, которые параллельны
меридиональной плоскости. Нормальные
напряжения, действующие в секущих плоскостях,
обозначим через ог и ог, касательные —
через irz и xzr. Эти напряжения, очевидно,
надо считать функциями от г и г.
Указанные выше условия задачи характеризуют случай, когда-
основные уравнения упругого равновесия можно представить в такой
же простой форме, как и в случае плоской задачи, и потому можем*
ограничиться рассмотрением соотношений, имеющих место для точек.
одной и той же плоскости.
Собственный вес и другие массовые силы в дальнейшем из
рассмотрения исключаем.
Проектируя все усилия, принадлежащие элементарному объему,,
показанному на фиг. 55, на оси z и г> имеем уравнения равновесия
в виде
^rdbdzdr — 4zrrd<)dz + (^zr + ^dr){r + dr)dbdz = 0,
—згЫЪ dz+(or +^- dr\ (r + dr)db dz+ ^-dz r d) dr—^ dr dz d6=0.
После сокращения на общего множителя drdzdb имеем:
Фиг. 54. Тело вращения
с симметричным
относительно оси распределением
напряжений.
dz
rr dr ' dz
= 0,
dr
— o9 = 0#

§ 41]
РЕШЕНИЕ ЗАДАЧИ В ПЕРЕМЕЩЕНИЯХ
на
Более компактно статические уравнения запишутся:
о
'^ + -^v) = o,
дг
(гаг) — а9 + г
дтг
dz
(3.53)
Обозначая, как и ранее в
плоской задаче (§ 35), упругие
перемещения точки (z, r) в
направлении оси г через w, в на-
правлениирадиуса через и (в
тангенциальном направлении
перемещение отсутствует),
геометрические уравнения для
данного случая можем
представить в виде
е.=
dw
ди
' дг
и dw , ди
(3.54)
Фиг. 55. Проекции элемента в ци>.
линдрических координатах.
дг «^ dz * J
Наконец, физические уравнения представятся согласно (3.02а)
где обозначено
dz
cr = 2G-^- + X6,
oe = 2G-£-.fA6f
i
(3.55)
§ 41. Решение задачи в перемещениях,
Объемное расширение
л dw . ди , и
может быть переписано иначе; или в виде:
a dw * ( д , 1 \

144 ОСНОВНЫЕ УРАВНЕНИЯ ТЕОРИИ УПРУГОСТИ [ГЛ. III
или так:
6 = |^ + £>и> (3.56)
где под D надо понимать обозначение следующей операции:
Подставляя (3.56) в физические уравнения (3.55), а далее в уравнения
равновесия (3.53), придаем последним вид
d*w , 1—S> n dw , 1 д
-a^+2(l-(x)D^7+2(l-ix)a7DM = 0' <3'57)
/D„ + l^^+_^^_ = 0. (3.58)
д/* 2(1 — /ul) д^ 2(1— fx) drd* v '
Таким образом, задача определения напряжений в теле вращения,
загруженном симметрично относительно оси, сводится к нахождению двух
функций w и н, которые должны удовлетворять в каждой точке уравнениям
(3.57) и (3.58) и одновременно граничным условиям на поверхности тела.
Если, кроме того, ввести оператор D2, положив
дг дг\дг^ г)~\дг*\ г дг г*)'
то из уравнений (3.57) и (3.58), исключая из них w, т. е. дифференцируя
d^w
(3.57) по г и г, и подставляя . из (3.58), получим:
l± + 2D*^- + D4*u = 0, (3.59)
что можно записать короче:
[~+D^Ju = 0. (3.59а)
Аналогично можно составить дифференциальное уравнение четвертого
яорядка, которому должно удовлетворять перемещение w, если к
уравнению (3.58) сначала применить операцию ~^- D, а затем вставить -^- Du из
уравнения (3.57). После простых вычислений это даст:
dAw
4<t(4b' <т
dz*
§ 42. Решение задачи в напряжениях
Установленные в § 32 синтезирующие уравнения теории упругости
в напряжениях (иначе говоря, уравнения неразрывности деформаций,
выраженные через напряжения), написанные в декартовых
координатах, можно преобразовать к цилиндрическим координатам.

§ 43] ФУНКЦИЯ НАПРЯЖЕНИЙ ПРИ ОСЕСИММЕТРИЧНОЙ ДЕФОРМАЦИИ 145
Для этой цели, очевидно, надлежит выразить напряжения ог и ав
через ох и <зу по известным формулам перехода:
ох = <зг cos2 0 -\- а6 sin2 6, оу = ar sin2 9 —|— oe cos2 6,
заменив запись суммы другой:
°х + °у + °г = °,- + ае + зг = а»
но учесть, что ог и з9 не зависят от угла 9, тогда как ож и ау
являются функциями 0.
Опуская преобразования *), запишем окончательные результаты
для уравнений совместности, которых ввиду осесимметричного
характера деформаций останется четыре:
V4_4(*,-*e) +
1
дЬ
О,
1 + ц дг*
чч
где введен символ
>'* г* "т" 1 + (х дг аг ~~ '
(3.61)
дг*
г дг
д&
(3.62)
Заметим, что одновременно с уравнениями неразрывности должны
fibiTb удовлетворены уравнения равновесия (3.53) и условия на контуре.
§ 43. Функция напряжений при осесимметричной деформации
Подобно тому как в плоской задаче теории упругости удалось
псе компоненты напряжений выразить через одну функцию
напряжений, так и в разбираемом осесимметричном пространственном случае
имеется такая же возможность.
В самом деле, если задаться:
--i[d-rt^-S].J
(3.63)
*) Они подробно приведены в книге проф. Б. Н. Ж е моч к ин а, Теория
упругости, стр. 128—132, Стройвоенмориздат, М., 1948.
Ю Зак.
0. Н. И. Безухов

146 ОСНОВНЫЕ УРАВНЕНИЯ ТЕОРИИ УПРУГОСТИ [ГЛ. III
где о — произвольная функция, и подставить (3.63) в первое
уравнение равновесия (3.53), то оно обратится в тождество. Второе
уравнение равновесия и все уравнения неразрывности будут
удовлетворены, если принять <р согласно уравнению
или короче
V2(Va?) = 0. (3.64а)
Можно подобрать много решений уравнения (3.64). Вот
некоторые из них:
<? = С2 In г + С2г In г 4- С8г2 In г + САг* In r; (3.65)
? = <V + С2г2 + С3г2 + С4г2г + <V3 (3.66)
[так как эти значения о удовлетворяют уравнению (3.64) при любых
значениях коэффициентов С, следовательно, любой член их также
удовлетворяет уравнению (3.64)];
? = С(г3+г2)н, (3.67)
где
где
__± 1 _L±
п— 2' ' ' 2
? = С(г2 +**)"*. (3.68)
2 ' 2 '
— _i_ _1 1.
? = с[(г» + г9)"»^—1(г«+^Г2]; (3.69)
?=--С(Зг4 — 8г4); (3.70)
? = С(3/'2 —222)22; (3.71)
? = С(г2 —4г2)г2; (3.72)
г 2 +z* — Z
* + 20 + *
(3.73)
§ 44. Исторические замечания, касающиеся функций напряжений
в трехмерной задаче теории упругости
При решении плоской задачи было доказано существование
специальной функции напряжений (3.40), посредством которой (путем надлежащего
ее дифференцирования) весьма престо определяются самые функции (т. е.
формулы) напряжений.
Аналогично может быть поставлен вспрос и для трехмерной задачи, но
в этом случае таких разрешающих функций должно быть» повидимому, не
лгенее трех. Последнее утверждение вытекает из того условия, что в каж-

§ 44]
ИСТОРИЧЕСКИЕ ЗАМЕЧАНИЯ
147
дой точке тела имеется шесть независимых величин (компоненты
напряжений), связанных между собой тремя уравнениями равновесия (2.02), а потому
их (шесть компонентов) можно выразить как функции трех специально
подобранных и независимых функций координат точки. Было предложено
несколько систем таких функций *).
Система Максвелла (1870 г.) в случае отсутствия массовых сил имела вид
"-ху '
д2п , д2?2
(3.74)
дхду'
Выражения для прочих компонентов напишутся по правилу круговой
подстановки:
Система Морера (1892 г.):
Ьг)
(3.75)
х дудг' *ХУ 2дг\дхп~ду
и т. п.
Заметим, что условия, которым должны были бы удовлетворять сами
разрешающие функции, их авторами не были сформулированы.
Р. О. Кузьмин показал, что формулы Максвелла действительно дают
общее решение уравнений равновесия (2.02), тогда как формулы Морера
этому условию удовлетворяют, если компоненты напряжений удовлетворяют
некоторым условиям интегрируемости.
Указанные выше решения Максвелла и Морера отличаются тем
существенным недостатком, что содержащиеся в них функции связаны мало
удобными дифференциальными соотношениями, резко снижающими их прак-
тческую значимость (помимо того, что не записано условий или
ограничений для самих функций).
В этом смысле выгодно от них отличается предложенная в 1930 г.
В. Г. Галеркиным замечательная по изяществу форма представления
решения уравнений теории упругости, содержащая три бигармонические
скалярные функции Ф1? Ф2 и Ф3.
Формулы Галеркина имеют вид (для компонентов смещений):
и = В з- -f У2ф1;
дх ' J
ду
со = Б ^ + У2Ф
dz ~ s
(3.76)
■!:) Указанные ниже формы решений, а также и методы их нахождения
представляют большой интерес, но по существу, как замечает Л. С. Лейбен-
.loii [56J, «переносят трудности от одной системы уравнений к другой, пови-
/тмому, более простой».
10*

148 ОСНОВНЫЕ УРАВНЕНИЯ ТЕОРИИ УПРУГОСТИ [ГЛ. III
где
^ф, дф_3 дф* 1_ (ЗЩ
дх ^ ду ^ dz > 2(1—»х) '
а функции напряжений удовлетворяют условию У4Ф = уа^2Ф = 0.
В 1932 г. Г. Д. Гродским (частично) и П. Ф. Папковичем (полностью)
было предложено решение в виде
■«£+<■
(3.77)
причем
w = wo + y(^+Uy + ^)» в = 2(\—р)'
П. Ф. Папкович показал, что четыре независимые функции 6, yj, С и <о0
являются гармоническими, т. е. удовлетворяют условию V2S = V2yj = V2C =
= v2o30 = 0; функция oj при этом оказывается бигармонической, т. е.
удовлетворяет условию V2F2o> = 0.
Указанные выше функции П. Ф. Папковича в 1934 г. были предложены
немецким ученым Нейбером (без ссылки на первого).
Полное исследование вопроса об общности представления интегралов
уравнений статической теории упругости, данных Б. Г. Галеркиным и
П. Ф. Папковичем, принадлежит Л. Н. Тер-Мкртичьяну (1947 г.).
В. И. Блох (1936 г.) видоизменил решение Б. Г. Галеркина и установил
связь его с решениями Максвелла и Морера.
М. Г. Слободянский (1938 г.) дал представление интеграла уравнений
теории упругости в трех вариантах: с помощью одной тригармонической
функции, с помощью одной бигармонической и одной гармонической и,
наконец, с помощью трех гармонических функций.
Функции напряжений были использованы рядом исследователей при
решении практических задач, как то: С. Г. Гутманом — в задаче об изгибе
толстых плит (1940 г.), В. Г. Короткиным — в задаче об осадке изотропного
упругого основания при нагружении последнего трапецоидальной нагрузкой
(1938 г.), Г. Н. Масловым — в связи с задачей определения температурных
напряжений при твердении бетонных массивов (1938 г.), Г. С. Шапиро —
в задаче о деформации полого конуса, эллипсоида вращения (1944 г.),
Д. И. Шерманом — в задаче о двух сопряженных между собой
полупространствах с различными упругими свойствами (1943 г.) и др. [129].
Интересующихся более подробными сведениями о функциях напряжений
отсылаем к оригинальному сочинению Ю. А. Пруткова «Тензор функций
напряжений и общие решения в статике теории упругости», Изд-во АН СССР,
М.—Л., 1949. Известные функции напряжений получаются из предложенного
им всеобъемлющего (так его называет Ю. А. Прутков) тензора функций
напряжений.

ГЛАВА IV
ПРОСТЕЙШИЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
§ 45. Задачи о чистом изгибе и чистом кручении
К числу задач сопротивления материалов, оправдываемых точным
решением теории упругости, помимо очевидной задачи о чистом, т. е.
одноосном растяжении — сжатии, относятся также задачи о
сопротивлении чистому изгибу и чистому кручению.
1. Чистый изгиб. Для случая пластинки, имеющей узкое
прямоугольное сечение и изгибаемой двумя парами с моментами Му
приложенными к торцевым сечениям и
(фиг. 56), сопротивление
материалов дает следующие решения:
М
a2/==Vv==0-
(а)
О*
"Т
i
Фиг. 56. Случай чистого изгиба.
Так как выражения для
напряжений—- линейные относительно
координат, то'уравнение неразрывности
деформации (3.35) удовлетворяется
независимо от коэффициентов, стоящих при координатах, и потому
достаточно проверить только уравнения равновесия и условия на
контуре. Подставляя (а) в (3.30) и полагая собственный вес
равным нулю (иначе рассматриваемый случай не был бы задачей о
чистом изгибе), имеем тождества:
дх^~ ду '
да
ду ' ох п
На верхней и нижней гранях (при у = ±-^\
°у = ~ху = °'>
па боковых гранях (при х—±-?А
М п
°х = -7У'> Хху=°>

150 ПРОСТЕЙШИЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ [ГЛ. IV
т. е. по торцам бруса действуют нормальные усилия, распределенные
по линейному закону, равнодействующая которых
М
J
N
О,
т. е. равна нулю, и потому указанные усилия приводятся к паре
\У
по
\р
4
о
■t—
^
l
Фиг. 57. Поперечный изгиб
консоли.
Итак, известный из курса сопротивления материалов закон
распределения напряжений при чистом изгибе оправдывается полностью
при условии, что указанные в задаче концевые моменты
представлены силами, распределенными по
торцевым сечениям именно по линейному закону.
Если приложение этих пар будет
осуществлено как-либо иначе, то распределение
напряжений будет другим, более сложным
и переменным по длине бруса. Но, как
показывает опыт, а также и точное
решение задачи для других возможных
случаев приложения внешних воздействий по
торцам, перераспределение напряжений
в отличие от (а) будет наблюдаться только в непосредственной
близости от концов балки, а во всем остальном закон
распределения напряжений практически будет согласен с формулами (а).
Предлагается читателю самостоятельно убедиться в соответствии
уравнениям теории упругости также известных формул
сопротивления материалов для случая изгиба
консоли сосредоточенной силой Р на
конце (фиг. 57). Как известно,
сопротивление материалов для этого
случая дает решение
Фиг. 58. Распределение касатель-
= 0. ных сил по торцевому сечению,
' " при котором напряжения в
консоли точно следуют элементарной
теории*).
хху "
°х
QS
Jb
М
0(Ла —
8J
Р-ху
~ J
4.У2) .
>
Для полного соответствия
уравнениям теории упругости
необходимо, чтобы на левом торцевом сечении сила Р была распределена
по закону касательных напряжений (фиг. 58).
*) Исключая небольшую область вблизи от закрепленного конца,
вследствие стеснения деформации поперечного сечения (см. стр. 165).

§ 451 задачи о чистом изгибе и чистом кручении 151
2. Чистое кручение (фиг. 59). Для этого случая
сопротивление материалов дает выражение
J П
(б).
причем касательное напряжение, действующее в поперечном сечении,
имеет направление, нормальное к радиусу. Прочие составляющие
напряжений отсутствуют.
Разлагая напряжения (б) на слагающие, параллельные осям Ох
и Оу, находим (фиг. 59,
справа):
zxz = — т sin ос,
"z
где
ту8 = т cos a,
УЛ
sin а =
cos а =
г
X
Таким образом,
**. = —*V.
где
*У*
= kx,
k =
М,
p
(в)
(О
2
Фиг. 59. Случай чистого кручения.
Так как
напряжения (в) являются
функциями не выле первой
степени от координат
тчки, то данная задача
относится к
простейшим, т. е. уравнения неразрывности деформаций (2.26) удовлетворяются
сами собой; поэтому придется удовлетворить только уравнениям
равновесия (2.02) и контурным условиям. Подставляя (в) в (2.02),
находим:
^=r=z = o,
т. е. напряжения (в) возможны при условии отсутствия объемных сил
(например, собственного веса стержня).
Переходим к условиям на поверхности стержня. Легко видеть>
что на боковой поверхности всюду cos(v,e)==0, далее:
cos (vat) = cos a = — ;
cos (vy) = sin a = 2-,

152 ПРОСТЕЙШИЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ [ГЛ. IV
Подставляя (в) в (2.05), имеем:
/^ =/V» = А* = °>
т. е. боковая поверхность свободна от нагрузки.
На концевом поперечном сечении имеем:
cos (vat) = cos (vy) = 0, cos (vz) = 1;
таким образом,
Pm = *хг= — *У> Py> = ?уг = kx> Pzh = °'>
следовательно, здесь приложены только касательные напряжения.
Равнодействующая концевых усилий равна нулю, в чем легко
убедиться, если проинтегрировать выражения
/ *xzdF, J zyzdF
F F
и принять во внимание, что равны нулю статические моменты
f xdF = f ydF = 0y
F F
так как начало координат помещено в центре тяжести сечения.
Момент крутящей пары вокруг оси О г равен:
MM = f( — W + zyix)dF=kf(y* + x*)dF = kJp,
F
что согласуется с (г).
Предлагается читателю самостоятельно продолжить с помощью
остальных уравнений теории упругости рассматриваемую задачу и
показать, что при кручении круглого бруса любое его поперечное
сечение остается при деформации плоским, не выходит из своей
первоначальной плоскости (как иногда говорят в технике, не
деплани рует), а поворачивается, как одно целое (иначе говоря, контур
сечения недеформируется).
§ 46. Пример решения задачи способом смягчения граничных
условий (изгиб консоли [равномерно распределенной нагрузкой)
Пусть балка узкого прямоугольного сечения с шириной, равной
единице, закрепленная одним концом в стену, изгибается равномерно
распределенной нагрузкой интенсивности q, как показано на фиг. 60.
Данный случай относится к плоскому напряженному состоянию.
В качестве первой попытки решения такой задачи примем
результаты, известные из сопротивления материалов, а именно:
М qx* л
Т = 01 z=z 3- {(Л V2^ x
ХУ Jb 2.Л y > '
(а)

§ 46] РЕШЕНИЕ ЗАДАЧИ СПОСОБОМ СМЯГЧЕНИЯ ГРАНИЧНЫХ УСЛОВИЙ 153
в основе которых лежала так называемая гипотеза плоских
сечений.
Фиг. 60. Пример поперечного изгиба.
Выпишем еще раз группу уравнений, которым должно
удовлетворять точное решение (собственный вес исключаем):
1 ду '
дх
д
д<г„
(б)
Записываем частные производные, входящие в (б), используя для
этой цели временно (а):
qxy
' J '
^ху
дах
дх J ' ду ~ J
д^Ж^1.(с2_у2) ^ = 0
—дух |
дх
2Jy
ду
(в)
Подставляя (в) в (б), устанавливаем, что первое уравнение
удовлетворяется, так как
д°х _ dtg.y
дх ~ ду *
хотя отсюда не следует непременно, что функции ах и хху,
заимствованные из (а), точны; это лишь указывает, что производные от
них, участвующие в (б), удовлетворяют первому уравнению равно-
нссия, ко сама функция ох может иметь, например, такой вид:
ae=^;+/iW,
(г)
где fx(y) — неизвестная нам пока функция от у.
В дальнейшем показано, что такая функция для данной задачи
существует и она является следствием того, что поперечное сечение

154
ПРОСТЕЙШИЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
[ГЛ. IV
бруса при изгибе искривляется — выходит из плоскости (т. е., как
говорят, сечение депланирует).
Второе уравнение, очевидно, не удовлетворяется, так как в
элементарном решении пренебрегали надавливанием продольных волокон
друг на друга, но из этого же второго уравнения вытекает
следующее соотношение:
ду
__ _д*ху
дх
и если надеяться, что функция для ixy выбрана правильно, то
ду 2/ V у )т
Интегрируя (е), имеем:
(д)
(е)
(ж)
где Д (лг) — неизвестная нам функция координаты х.
Постараемся определить вид функции/2 (лг). Для этой цели
используем граничные условия по горизонтальным (верхней и нижней)
кромкам, а именно: при любом значении х и при у = с имеем ъу = — q,
а при^у = — с имеем оу = 0. Подставляя эти граничные условия, получим:
(«л=-с=-§(-'»+5)+/а(*)в°.
4)+/.ю-?. !
(°Л=с = — £j(c*-
(з)
Из (з) с очевидностью вытекает, что ДО*:) не может заключать
координаты х и, следовательно, Д(лг) = С. Из первого и второго
выражений (з) следует одно и то же значение постоянной С (что является
правильностью указанных выше суждений о том, что ДО*:) есть
постоянное число), именно:
С=— £.
(и)
Используем третье уравнение (б), принимая для о.г начертание
более полное (г) и для чу — обнаруженное (ж):
дЧс _ ЧУ
дл*~ J '
№3L_qy
ду* ~~* J '
i=sy
ЧУ
ve(^+^)=^+/i(y) + ^=o.
(к)

§ 46] РЕШЕНИЕ ЗАДАЧИ СПОСОБОМ СМЯГЧЕНИЯ ГРАНИЧНЫХ УСЛОВИЙ 155
откуда
Из последнего уравнения (к) следует:
J '
ду2
/ГО)=-
/iO) = -
ду
Чг+Ъ + с*
(л)
Итак, имеем следующую прокорректированную запись для
компонента о •
_^1У
£У
2У
^ + ^ + 0,
(м)
Для определения постоянных Сг и Q, входящих в формулу для <зх9
заметим следующее: по записанному выше выражению (м) при лг=0
(т. е. на левом конце) нормальные напряжения не обращаются в нуль,
как это должно быть (в действительности на левом конце
продольных усилий не приложено). Согласно (м) имеем:
Однако, если эти напряжения (<зх) на левом торце будут сводиться
к взаимно уравновешивающейся системе сил, то согласно принципу
Сен-Венана (локальности) наличие таких сил практически не изменит
закона распределения напряжений в балке против случая отсутствия
таких сил (за исключением области балки в непосредственной близости
от левого конца). Итак, поставим условием, что при лг = 0
faxdF=0 и forydF=0,
F F
т. е. равнодействующая продольных усилий на левом торце и их
момент равны нулю. Иначе говоря, смягчим граничные условия на
свободном торце бруса. Итак, имеем:
—с
(")
Интегрируя, получим:
2С2с = О,
и таким образом,
15/ +Cl 3 U>
г„ = о с — — i-

156
ПРОСТЕЙШИЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
[ГЛ. IV
Окончательно, имеем:
_q^L_S_\l V3_! С2 у1 )
а*~ 2J 2У [3 -У 5 C^J' |
°v— 2 V ^ 2 с 2сУ'
ХУ
(4.01)
В полученном нами решении касательное напряжение ixy оказалось
в точности соответствующим элементарной теории изгиба.
Напряжения ох отличаются от даваемых элементарной теорией поправочным
членом
(4.01а)
Член этот мал по сравнению с величиной ах, если только с мало
по сравнению с /. Характер распределения напряжений ах по высоте
балки согласно (4.01) указан на фиг. 61. Эпюру оу см. фиг. 60, справа.
Сечение дг=с
Сечение х= Юс
Фиг. 61. Характер распределения по высоте сечения нормальных
напряжений ах согласно теории упругости. Пунктиром показано распределение
нормальных напряжений согласно элементарной теории сопротивления
материалов. Разница в эпюрах показана на фиг. 65.
В сечении балки, совпадающем с ее свободным концом,
касательные напряжения отсутствуют, нормальные напряжения в сечении х= 0,
как это было указано выше, нулю не равны, но нулю равны их
главный вектор и момент.

§ 46] РЕШЕНИЕ ЗАДАЧИ СПОСОБОМ СМЯГЧЕНИЯ ГРАНИЧНЫХ УСЛОВИЙ 157
Точное решение для рассмотренной балки должно поэтому
отличаться от найденного (4.01), но за счет принципа локальности, т. е.
ценой пренебрежения местными напряжениями в районе нагрузки,
иполне уравновешиваемыми в пределах малой части исследуемого тела,
решение (4.01), а при невысоких балках и более простое решение (а)
практически могут бцть приемлемы.
Представляет интерес проследить определение перемещений разобранной
выше консольной балки после того, как найдены напряжения. В частности,
пусть нас интересует уравнение изогнутой оси консоли (или, иначе, по
терминологии в курсе сопротивления материалов — «упругой кривой»).
Для этой цели надлежит вначале на основании уравнений (3.33) от
составляющих напряжений перейти к составляющим деформации. Имеем:
Еа? = £г (C*~~^G2/)'
1 /
еу = £- (ау — ^.г);
_ 2 (1 + [J-)
ЧХУ "~ £ zxy-
Далее на основании геометрических соотношений (3.32)
__ ди __dv __ да , dv
'х~д^с; sv-~dj; Y^~ay + ^
можем записать:
и = J ех дх + cf»! (у); v = j ву ду + ?2 (х);
"Ь* = ду / е" дх + *i О) +Ш J Ву ду + f2 W'
где <f>t (у) и ср2 (л*) — произвольные функции (первая зависит только от
координаты у, вторая — только от координаты jc), для определения которых
надлежит использовать кинематические условия, а именно, закрепление правого
конца консоли, т. е. при х = /. В этом закреплении должно быть и = 0
и v = 0 для любых значений у.
К сожалению, найденное ранее решение для напряжений не сможет
удовлетворить этому, казалось бы, очевидному условию, так как условий
оказывается больше (по числу точек в опорном сечении, т. е. бесконечности),
чем число параметров разыскиваемых функций.
Поэтому приходится ограничиться требованием, чтобы оставалась
неподвижной одна точка поперечного сечения, например, лежащая на оси
пруса, т. е.
(я)а,яj, у=о = 0, (v)Xssh у=0 = 0,
и далее обусловить, чтобы горизонтальный элемент оси, примыкающий к этой
точке, был неподвижен и не поворачивался (фиг. 62, а), т. е.
(зг) =°- <">
\oxjx=l% y=o
Впрочем, можно потребовать (и это более строго), чтобы не поворачи-
1ылся вертикальный элемент в той же точке (фиг. 62, б), т. е.
1г) = °- <р>
ду)х = 1, у=о

158
ПРОСТЕЙШИЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
[ГЛ. IV
Принятие условия (р) взамен (п), конечно, изменит окончательный
результат. Таким образом, перемещения будут различными на всем протяжении
бруса в зависимости от того, примем ли условие (п) или (р).
Однако упомянутые сейчас различия в окончательных результатах в
зависимости от принимаемого условия закрепления точки на оси бруса
представляют скорее теоретический интерес. Для обычных (низких) балок разница
между решением по условию (п) или по (р) оказывается пренебрежимо малой
вообще; в смысле прогиба эти решения мало отличаются от того, что дается
в.курсах сопротивления материалов. Разница в основном ложится на учет
влияния сдвигов (влияние поперечной силы), которым по сравнению с влия-
Фиг. 62. Два варианта закрепления опорного сечения
в теории упругости.
нием изгибающих моментов на прогиб обычно пренебрегают в
сопротивлении материалов.
Из рассмотрения фиг. 62 следует, что для получения полного
закрепления опорного сечения (а не только неподвижного закрепления от смещения
и поворота одной точки на оси бруса) потребуется приложение к этому
сечению особых добавочных усилий. Иначе говоря, в месте полного
защемления балки в стену и в непосредственной близости от этого сечения
действительные напряжения должны описываться иными, более сложными
законами, чем это записано в (4.01). Однако влияние упомянутых
дополнительных усилий должно сказаться лишь на небольшом участке около
защемления балки; на всем остальном протяжении вполне пригодны будут
уравнения (4.01).
§ 47. Примеры для самостоятельных упражнений
Ниже (таблица 1) дается несколько решенных в теории упругости
задач (плоское напряженное состояние); выписаны формулы для
напряжений.
Читателю предлагается:
а) проверить, удовлетворяют ли написанные формулы для
напряжений уравнениям теории упругости;
б) проверить, точно ли удовлетворяются краевые (поверхностные)
условия;
в) сравнить характер распределения напряжений по формулам
теории упругости и по методу сопротивления материалов.

§ 47]
ПРИМЕРЫ ДЛЯ САМОСТОЯТЕЛЬНЫХ УПРАЖНЕНИЙ
159
ч
О*
С
05
аз
^» г-
+
>>
^Ьй
СО
So
.5 Р
' .*:
гГ
1
1
1
о
; <d
. X
I S
> CQ
1 5 *
s с s
НПДЧ
о^ л С
О . Ou
« н н о
К <U t<
QJ
\o и
я л
и ч
<T> <U t=-
S * s
:§

160
ПРОСТЕЙШИЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
[ГЛ. IV
X
ч
о
гз
н
<и
S
о
о
а,
я
X
о?
а,
с
аз
a
о?
ч
а,
PQ
кф^:
7
-,-4-,г
1 1
| !
Lm
t
»-«•
Jl
+
IOQ-
Н
i

§ 47]
ПРИМЕРЫ ДЛЯ САМОСТОЯТЕЛЬНЫХ УПРАЖНЕНИЙ
161
3
я*
я
ч
VO
со
н
О)
я
я
CD
*
Ч
О
О
Си
С
эЯ
я
CD
Си
с
СО
Я
«
Я
я
си
X
со
Си
3
0Q
СО
S
си
и
S
о
X
X
СО
(Я
g о N
1 " сф
н а 1
Ё II II
* И
5 II
« р И
£ II *|а
ж ^ д.
§ I i
II ^
'-Ц
° а.
- S И ||
J3 CD с. II
со ^ ° 3
Доказ
случае и\
1
.-^ .J
_ ч =£
1 1 1
1 1^ о -,
1 * ъ"
■
£- '
' 1
1
Н
_
тх"""! I—J—"
1 Х^
i—-*Л \ Ji
** v-*\\ «
\ \
Ъ* V
•М } i
х/ r^Sh.ч s'^K^
V^V 4г ^. ~~ "" ^г\ь \
о
>-> о
s я
о си
J \ « О
Z \ n >» =
то Я
3 я ь>
Н-i ТО
янной толи
►льного оче
давлением
посто
оизвс
жата
w 7 _ Си о
^s^ / ^ Я
v Г Я >^
Пласти
контур
5Я
Я
я
CD
я'
CD
S
о
н
о
я
ё *
2 ь
я о
CD ex,
CUo
а п
ТО о
CD g
^g
CD S
ST
О
E-
Я
H
Я
CD
CD
4
Злк.
3880. H. И. Безухов

162
ПРОСТЕЙШИЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
[ГЛ. IV
*—■
Я
а
я
ч
о
с«
н
CU
в
должен]
Про
ряжений
со
5
S
Я
а;
СО
а-
3
1 «
гз
5
и
ев; С
1
+
со
54
«Г
1
XJ
*^
~Т«
^i
II
t>
-
5
1 1
о
«г
1
ОО
♦Si
v—'
-КГ
+
I
6
ъ*
•*-*?
8
.е:
«о
£
{Z
*> П
i Л~\
х2
^ь»
„
ч
a
'55
| т
1 "
54
- 1
1 1
1 ^
1 "-'
XJ 1
<-> 1
^
—' [^3
1
II
3»
И
Н 1
—•у
^7
о
^
*-я-Ч-*д-*
^
+
?
XJ
о
1
i
>>
XJ
3
ч
О
и
хз
ел
5S
а^у— а
ХЗ
о
«J
+
1 ГН
^ 1^3
i
|
II
е
П^
-*-^
^
СО
«1-
II
0
г~|
•
Т
^ 1 ,
\
1
Н 1
о
Я
О)
со
Я
ГО
о
\о
о
0)
ЕС
с
II
о
X!
1
ХЗ
о
в
^
Q
II
в
хз
в
«г
II
ч
в
хз
00
в
*Ь
II
5Я
аз
3
<v
*
со
н
н
О)
Он
н
о
S
о
а.
II
XJ
00
+
в
XJ
II
XJ
1
в
XJ
со
в
43
II
<^>
в
1
^»
в |
•С
00
II
+
СМ
•в
«л
■5»
II
ХЗ
+
<->
в
хз
СП
в

§ 47] ПРИМЕРЫ ДЛЯ САМОСТОЯТЕЛЬНЫХ УПРАЖНЕНИЙ 163
2
а-
я
VO
(«
н
4)
X
X
а>
о
t=C
О
Q.
С
«
я
я
CU
*
пря
со
Я
05
5
05
Я
Я
О)
СО
CU
2
0Q
СО
S
1 <L>
,©• с
*в-
«л
О
?
|
N«^
S
1
*)
8
Ы
е
^
см
1
1
II
<?
N
»
W
*
^
1
1
в
25
8 Ч К L
,—, » SP
&1 1 II
+ о в
^
С^ в
Г Г
1 1
л *> ^
8^-.-< 8 -,-•
| 11^» iWl
в g 8 g 8
О- ^i
CN CN
1 1
1 1
II II
1 >*о
1 ^
1 ^
1 *•
1 ^
I S*
Г Ч'
j ;
ъ»
5&—
—:
с
V—-
^
Г
ч
i
ъ«
1 ь»
t^
'аГ
Я"
Я
стз
CU
9
^
а;
о
Я
|
|
О)
я
О)
£
^
CU
II*

164 ПРОСТЕЙШИЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ [ГЛ. IV
ч
о
со
н
<L>
S
К
<и
а
ч
о
сС
О
Си
а
Я
К
«
а.
с
аз
К
«
§
а,
PQ
7<?=</
?=Z
« я
е; со
е* Я
Ч
(Я VO
О m
1=4
« к^
о; J л
ч- г; I—
«5 га
— Л «з
£§*
ч ь °*
« rd С
2 «з
О О
а«н
н
о m
Я vj
О) Г*5
ЕГ «
о си
с
5я
§ я
о я
И а;
о ч
-я ^
« с
Он о
5 "з
° си
° я
vo g
И vo
О)
QJ со
s я
я я
си
За
я ^
ч
сз
из
ч
VO ь
О
^-а.
Я
х с
Я ет»
Я
еС S
<и <и
си я
О)
ОТ) Я
Я «з
Си
VO
Я О
Я м
с=С Я
Т:
н о
Си Си

§ 48] ПРИМЕР РЕШЕНИЯ ЗАДАЧИ ОБРАТНЫМ МЕТОДОМ 165
Примечание к примерам 1 и 4. Приведенные формулы, если они
и удовлетворяют основным уравнениям теории упругости, могут
рассматриваться как точные в том случае, если по подошве действуют усилия,
распределенные таким же образом, как напряжения ах и ixy в указанном
решении. В действительности подошва плотины связана с фундаментом, и
условия отличаются от тех, которые выражаются написанными уравнениями.
Однако на основании принципа локальности можно утверждать, что влиянием
особенностей закрепления по подошве на достаточных расстояниях от
последней можно пренебречь.
Настоящее замечание относится и к примеру 3 в § 55.
При проработке примера 7 читателю рекомендуется вначале ознакомиться
с § 51.
Общие замечания к примерам, приведенным в
таблице 1.
а) Схемы нагружений, показанные в таблице, в основном соответствуют
приведенным там же выражениям для напряжений, но не в точности. Так,
для примеров 1—3 в торцевых сечениях, т. е. при х = О в примере 1 и при
х = г£ / в примерах 2, 3, из формул для ах вытекает, что эти напряжения
в упомянутых торцевых сечениях существуют (на чертежах не указаны), хотя
к сумме и составляют силы, статически эквивалентные нулю. На основании
принципа локальности эффекта самоуравновешенных сил эффект их быстро
затухает и не скажется существенно на распределении напряжений вне
области их непосредственного действия. Но принципиально для схем нагру-
жения, показанных в таблице, точные формулы для напряжений должны
иметь более сложный вид.
б) Указанные в таблице формулы для напряжений отличаются от
известных для таких же в задачах сопротивления материалов, и это отличие
тем больше, чем больше высота полоски.
В примерах 1—3 первые слагаемые формулы для ах в точности
соответствуют элементарному решению, принятому в курсе сопротивления
материалов.
Формулы для Gy, приведенные в таблице 1, в элементарном решении
сопротивления материалов вообще отсутствовали.
в) Существенно отличные результаты от данных сопротивления
материалов дает теория упругости в примере 4. Так, касательные напряжения
в «поперечном» сечении, понимая его перпендикулярным к вертикальной
грани (и, следовательно, параллельным «поперечной» нагрузке), по точному
решению оказываются распределенными по линейному закону с наибольшим
.шачением этих напряжений у тыльной поверхности пластинки.
г) Насколько в высоких балках, иначе называемых
балками-стенками, действительное распределение напряжений не следует ни в
количественном ни в качественном отношении тем эпюрам, какие доставляет
элементарное решение сопротивления материалов, служит пример 7, для которого
специально приведены эпюры распределения напряжений в поперечных^и
продольных сечениях, показанные в конце таблицы 1.
§ 48. Примэр ргшгния задачи обратным методом
В разбираемом ниже примере с пластинкой (плоское напряженное
состояние) произвольно задаемся [законами распределения напряжений
ииутри тела и определяем, каким внешним воздействиям соответствуют
принятые законы для напряжений. Так как можно задаваться не со-
иершенно произвольными законами для напряжений, а такими, чтобы
они удовлетворяли уравнениям равновесия и неразрывности, то лучше
задаться функцией напряжений.

166
ПРОСТЕЙШИЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
[ГЛ. IV
Зададимся в качестве примера функцией напряжений в виде
полинома пятой степени, например:
<р =
ах^ , Ьх^у , сх*у2 , dxly
5-4 ■ 4.3
• 2 * 3.
e;cy4
3-2
fyb
3-2
4.3 ~5.4e
(a)
Подставив (а) в уравнение неразрывности (3.34), заключаем, что
это уравнение будет удовлетворено, если:
е = — (2с-\-Ъа)\
Соответствующие компоненты напряжений (собственный вес
исключается) будут:
^ = ^-j^ + ^yd-(2c+Sa)xy^-\(b + 2d)y^
* — —?- = — \bx* — слРу — dxy*+\(2c-{-3a)y*.
ху
дхду
Здесь коэффициенты а, £, с, d произвольны, и подбирая их, мы
получим решения для различных условий нагружения пластинки.
Так, если все коэффициенты за исключением d принять равными
нулю, то найдем:
>~а{*У-ТУ*)> °y = Jdy*> ^v = -dxy\
(б)
Такой закон распределения напряжений соответствует внешним
воздействиям, приложенным к пластинке и показанным на фиг. 63,
а)
imiimn
б)
-+- ■-£■
±
ттттттттт
—i .
24 d
7
/
Фиг. 63. Случай плоского напряжения состояния.
т. е. нормальные усилия равномерно распределены по продольным
сторонам пластинки (фиг. 63, а). По стороне лг=/ нормальные уси-

§ 50] ДРУГОЙ ВАРИАНТ РЕШЕНИЯ ЗАДАЧИ ОБ ИЗГИБЕ КОНСОЛИ 167
лия состоят из двух частей: одной — следующей линейному закону,
другой — изменяющейся по закону кубической параболы.
Касательные усилия пропорциональны абсциссе х на продольных
сторонах пластинки и следуют параболическому закону на стороне
х=1. Распределение этих напряжений показано на фиг. 63, tf.
Решение при помощи полиномов для функций напряжений
представляет практический интерес потому, что легко доставляет точные
решения для многих, хотя и искусственно назначенных задач; однако
комбинация из таких решений (путем сложений или вычитаний) и
подобных им отдельных известных результатов может позволить
получить непосредственно решения и для реальных поверхностных условий.
§ 49. Примеры для самостоятельных упражнений
на использование функций напряжений
В указанных ниже случаях (таблица 2) предполагается заданной
тонкая прямоугольная пластинка длиной /, высотой h и толщиной
в единицу.
Внешние силы, приложенные по кромкам пластинки и равномерно
распределенные по их толщине, создают обобщенное плоское
напряженное состояние пластинки.
Положительные направления осей указаны на фигурах в таблице.
Задаются различные начертания для функций напряжений. Читателю
предлагается:
1) проверить возможность существования таких функций
напряжений, используя (3.40);
2) по функции напряжений найти выражения для компонентов
напряжений на основании (3.39);
3) используя контурные условия (3.31), выяснить характер внешних
нагрузок, при которых будет иметь место найденная система
напряжений.
В таблице рядом с задаваемой функцией напряжений изображен
чскиз контурных условий, в правильности которого и надлежит
читателю удостовериться.
§ 50. Другой вариант решения задачи об изгибе консоли
В § 46 задача об изгибе консоли была решена использованием
ипачале элементарного решения из курса сопротивления материалов,
латем благодаря применению уравнений теории упругости упомянутое
приближенное решение мы уточнили.
Решим ту же задачу, используя функцию напряжений.
Из рассмотрения различных вариантов (таблица 2) начертания
функций напряжений и соответствующих им контурных условий можно
заключить, что для случая консоли с равномерно распределенной
нагрузкой по верхней кромке не может подойти ни одна из указанных

168 ПРОСТЕЙШИЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ [ГЛ. IV
Таблица 2.
Вид функций
напряжений
Контурные условия
Л-
ф^ах2
9<=Щ
<р=ая/
*ч t м i м н н и
тттттттттт
X т
:2а
>а
p=t7J7J
, - ■ •
. • 1 4 « 4 t
• • ♦ t м ♦
(jfaJ
'
Ф=ах*у
У -птГГГГТТТТТТТТТТТТТТ^^
g^-J-4 J- Ы- ♦ J-i. LJ-L. ^ _ Г^г
if^aZ —
~а7к
ум
<p=axt/
<р=ау3
г
У&==-^
'ал
ah
ah
,2al
LyX
■^3ah
ГГ~ ^o/?
p = azy
styah2
^3/4ah<
там функций; не удовлетворит также и их комбинация (например,
случаи 5 и 3, так как это не избавляет от касательных сил по
левому торцу).
Однако, если комбинировать случаи 5, 1 и разобранный на
стр. 166, то при надлежащем подборе коэффициентов у функций

§ 50]
ДРУГОЙ ВАРИАНТ РЕШЕНИЯ ЗАДАЧИ ОБ ИЗГИБЕ КОНСОЛИ
169
напряжений можно получить нижнюю кромку пластинки свободной
от вертикальной нагрузки (соединяя случаи 1 и 5), а обе
горизонтальные кромки — свободными от касательных сил (соединяя случаи 5
и разобранный ранее на стр. 166).
Итак, примем для функции напряжений начертание
<р = ах>- + Ъх*у + сл?у* + df.
Принимая во внимание, что
^=о
0 = 120 «у,
2W==24c-v'
и используя (3.40), заключаем:
теперь функция напряжений имеет вид
© = ах- -f- bx-y -j- с (х"*уь — ^U J.
Напряжения в этом случае будут:
(а)
(б)
= Ц=с(6х*у-4у%
х ду
^ = S==2a + 2*-y + 2c-J'3'
Для соблюдения условий по верхнему и нижнему краям должны
быть справедливы уравнения:
Ьху) = ь = — Ibx— -н- слг/г2 = 0,
("от) л = — 2*лг — 4 схУР = 0,
»=—;
(о,) _n = 2a-\-bh-\--\-ch* = — q,
Ю
h = 2a — bh — -^-с№ = 0.
(в)

170 ПРОСТЕЙШИЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ [ГЛ. IV
Первое и второе уравнения оказались тождественными (но в нашем
случае для определения постоянных множителей достаточно именно
трех условий). Решая систему (в), имеем:
Я
4> °— 4 Л'
с =
h*
Напряжения теперь запишутся так:
ав = -£-(6*«у-4у»),
°v=-t-wy+wy°
"ay
= ±±Х — ^
ху*
(г)
2 А
2 h ~ Л»
Однако, прежде чем на указанных формулах остановиться
окончательно, надо прове-
Ц УЛ рить еще контурные усло-
I V \ I I I I I I I I I I Ц вия на левом торце, где
I
I
согласно заданию в любой
точке хху = ах = 0.
Подставляя в (г) л: = 0, имеем
X fl3 J
(л)
График изменения напря-
Фиг. 64 Схема нагружения балки, отвечаю- жения согласно (д) показан
щая функции напряжении (а) со стр. 169. Ж fi4
Очевидно, сумма усилий
от а'х для всего левого торца равна нулю, так как
h
2
i<
h
2
,dy =
— 4-i
h
2
\у*
h
" 2
dy =
= 0
Но эти усилия составляют пару с моментом
h h
М,
,- \<aydy—i£ J>4v = -§.
Так как такого внешнего момента в действительности на левом
торце не было, то для получения правильного решения рассматри-

§ 50] ДРУГОЙ ВАРИАНТ РЕШЕНИЯ ЗАДАЧИ ОВ ИЗГИБЕ КОНСОЛИ 171
ваемой задачи необходимо на левом торце консоли приложить момент
такого же значения, но противоположного направления. Наличие
такого момента (случай чистого изгиба) не вызовет в балке напряжений
xxyy а напряжения а" могут быть подсчитаны по известной фор-
°у и
муле сопротивления материалов (которая в случае чистого изгиба
оправдывается и уравнениями теории
упругости), а именно:
$,,
; = --=*, = о,б,.
_^-г=^
0.200
0.094
0.016
f="_L. :
^=+^ЕЕ^
: Z'^*^
0.039
0.072
0.087
0.088
0.076
0.066
0.030
0
Таким образом, окончательными
формулами дпя напряжений можно
принять:
о. = -£(6*^ —4ув + 0,6уАв);
что соответствует прежней записи
(4.01).
Как это уже отмечалось ранее,
формулы (4.01) не являются
совершенно точными, так как
соответствуют несколько иным условиям
загружения, а именно, помимо
заданных сил на левом торце также
действуют напряжения,
получающиеся в результате наложения эпюры
фиг. 64 на эпюру напряжений от чистого изгиба (фиг. 56). Но так
как в результате такого наложения равнодействующая указанной
разности сил и их момент равны нулю (фиг. 65), то согласно принципу
локальности эффекта самоуравновешивающихся сил их эффект не будет
иметь существенного значения вне области их непосредственного
действия.
К тому же и напряжения, получившиеся у нас на левом торце,
оказываются обычно несущественными и для самого сечения, где они
приложены. В самом деле, эти напряжения определяются формулой:
* —4*£ + 0,6*£.
Наибольшего значения эти напряжения достигают при
Фиг. 65. Эпюра распределения по
высоте взаимно уравновешенных
напряжений, получаемых в
результате наложения решения (д) на
решение чистого изгиба (фиг. 56).
j/ = ±y и составляют z±z0f2q.

172 ПРОСТЕЙШИЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ [ГЛ. IV
При длинных балках указанная величина напряжений во много раз
меньше обычных напряжений в опасном сечении балки, но для
высоких балок (балки-стенки) напряжения могут оказаться соразмерными
и потому при расчете высоких балок пользование функциями
напряжений в полиномах оказывается неэффективным.
§ 51. Использование тригонометрических рядов
для функций напряжений
Заслуживают внимания решения задач через функции напряжений,
сводящиеся к тригонометрическим функциям и рядам. Возьмем,
например, функцию
<р =/ (у) sin алг, (4.02)
где f(y)— функция одной только ординаты у> а =-у-, / — длина
бруса, т — любое целое число.
Подставляя (4.02) в (3.40), найдем следующее уравнение для
определения f(y):
а4/ СУ) - 2а2/" О) +/IV (.у) = О. (4.03)
Общий интеграл этого линейного дифференциального уравнения
с постоянными коэффициентами записывается так:
f(y) = C1 ch ay-\-C2sh *y-\-C.6y ch ay -f- Cky sh ay. (4.04)
Зная функцию напряжений <p, можно определить напряжения аш,
°у и хху-> a п0 ним выяснить поверхностные условия. Задаваясь
различными значениями а, получим решения для всевозможных случаев
нагружения балки по верхней и нижней горизонтальным кромкам
распределенной сплошной нагрузкой, график изменения интенсивности
которой изменяется по длине балки по синусоиде (с числом волн
в зависимости от задаваемого значения ос). Одна из таких задач
рассмотрена в § 47. Подобного рода метод оказывается успешным
в приложении к случаям прерывных нагрузок, если применять для
этой цели ряды Фурье.
При решении задачи в полярных координатах аналогично
указанному выше часто будет удобным положить функцию напряжений в виде
<р =/(г) sin 6, (4.05)
где f (г) — функция только радиуса г.
Подставляя (4.05) в (3.45), находим для f (f) выражение
/ (г) = Лг3 + Яг In r+Cr + Z) у. (4.06)
Представляет также интерес такое начертание функции
напряжений:
ср = Л^г cosO, (4.06а)
удовлетворяющей (3.45).

§ 52] РЕЗУЛЬТАТЫ ИССЛЕДОВАНИЙ НЕКОТОРЫХ ЧАСТНЫХ СЛУЧАЕВ 173
Зная функцию напряжений, при помощи (3.46) найдем выражения
для самих компонентов напряжений. Так, объединяя (4.05) и (4.06а),
получим:
/ол . В 2D\ . ft 2АХ . ft 1
ог = (2Лг-| r)sin^ -sin 8,
aQ = (6^ + 4 + ^)sin8,
:г9 = -(2Лг + 4-^)з1п6-
(4.07)
Несколько задач на использование последних формул
рассмотрено в § 55.
Успешное применение тригонометрических рядов к расчету
неразрезных балок-стенок и рандбалок читатель может найти в книге
проф. Б. Н. Жемочкина «Теория упругости» (Стройвоенмориздат,
стр. 58—71, 1948).
Наряду с (4.02), очевидно, можно принять начертание функции
напряжений в виде
<Р =/00 cos ах,
где для f(y), конечно, остается прежнее выражение (4.04).
Так как т, входящее в формулу (4.02), — произвольное целое число, то,
давая ему различные значения, получим бесчисленное множество функций ср.
Общее решение представится таким бесконечным рядом:
М = оо
<f = 2d |CishT-V+ 2C h~y + С*У shT-V + 643/ch— sin —x +
n = l
w=oo
+ 2 [c«sh r-? + c«ch т-у+c'^9h т -^ + c^ch т-5']cos т *• <404a>
w = l
Использованием (4.04а) решается пример 7 в таблице 1, причем ввиду
симметричности деформации (а следовательно, и симметричности напряжений ах)
относительно оси у достаточно было принять вторую часть ряда I при мно-
пк \
жителе cos — x), но для возможности удовлетворить всем условиям на
контуре пришлось добавить еще полином второй степени в виде
D^ + D^y + Dsy2.
§ 52. Основные результаты исследований некоторых
частных случаев нагружения балок-стенок
Из примеров, разобранных в §§ 46—48, 50, следует, что
элементарная теория изгиба, изучаемая в сопротивлении материалов, дает
результаты, отклоняющиеся от действительности, и в тем большей
степени, чем высота балки больше. Попутно еще раз заметим, что и

174 ПРОСТЕЙШИЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ [ГЛ. IV
5q
У
,4
ifllHlllit
решение, найденное в §§ 46, 50 с помощью уравнений теории
упругости, будучи уточнением элементарной теории сопротивления
материалов, само по себе еще не является совершенно точным, так как
граничные условия на торцевых сечениях балки были удовлетворены
лишь в интегральной форме (в смысле Сен-Венана).
Для дальнейшего уточнения задачи (а для очень высоких балок
это обязательно) надлежало бы на решение (4.01) наложить
специальное решение для случая, когда на левом торце ранее разобранной
балки действуют взаимно уравновешенные силы (4.01а). Эта
последняя задача (самоуравновешенное
нагружение) оказывается не
простой и не всегда может быть решена
точно, а чаще решается с
привлечением специальных приближенных
способов, например с помощью
вариационных методов (см. §§ 74 и 75).
Однако степень приближения таких
методов обычно является вполне
достаточной и даже в том случае,
когда балки очень высоки, т. е.
представляют собой так называемые балки-
стенка.
Если напряжения, получаемые по
элементарной теории изгиба, называть
(в терминах вариационного метода
теории упругости) приближением нулевого
порядка, то прежнее решение, полученное
в § 46 (когда граничные условия были
удовлетворены лишь в интегральной форме), уместно назвать
приближением первого порядка, а дальнейшие уточнения (наложение
самоуравновешенного нагружения бипарой) следует уже считать
приближением второго или (если выполняется несколько последовательных
нагружений) высших порядков.
Ниже сообщаются результаты расчетов для некоторых частных
случаев загрузки высоких балок, обследованных Я. А. Пратусевичем *)
(идея расчета изложена в §§ 74 и 75). Исследования показали, что
вполне можно ограничиться расчетами второго приближения.
Для балки-стенки с отношением -г = 1, нагруженной (фиг. 66)
по верхней кромке равномерной нагрузкой интенсивностью q, а по
нижней кромке уравновешивающей нагрузкой, изменяющейся вдоль
х4
кромки по закону q1 = 5q -j, на фиг. 67, а— в изображены эпюры
шп.
Фиг.
66. К примеру расчета
балки-стенки.
*) Я. А. Пратусевич, Вариационные методы в строительной
механике, Гостехиздат, 1948.

1>иг. 67. Эпюры аХУ ау, zxy для балки-стенки с нагрузкой,
показанной на фиг. 66, при отношении — = 1.

176 ПРОСТЕЙШИЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ [ГЛ. IV
напряжений qx, oy и хху в различных вертикальных сечениях: х=0>
а а 3 ( ^ , Ь\
x=-r-yX=-^,x = -^aiA горизонтальных сечениях (у = О, у = ± -^ ).
На фиг.
Um Q »-
b
— а •-.
8,028q
=^
i»
8.254 q
f-<
б)
а)
Фиг. 68. Эпюры ох по среднему сечению
для балки-стенки при отношении а/b = 1/4
(слева) и при отношении а\Ь = 4
(справа).
данные второго при-
Использованы
ближения.
На фиг. 67, а по сечению х=0
показана пунктиром эпюра
напряжений для ох согласно
элементарной теории; разница между точным
и элементарным решениями для
нижней кромки (х = 0, у = — Ь)
составляет 232°/0. Эпюра напряжений для оу
(фиг. 67,6), как известно,
элементарной теорией вообще не раскрывалась.
показаны эпюры ох по
среднему вертикальному сечению (л;=0)
для двух относительно крайних случаев:
для высокой балки-стенки с отношением
а
Т
= J/4 (фиг. 68, а) и для балки сред-
когда отношение
*-<
it
Aq-
ТгтТПТ
Шгк
V
кх -q
ней высоты,
(фиг. 68, б), а нагрузка прежняя.
Во втором случае характер эпюры ох
сходен с тем законом, который доставляет
элементарное решение (расхождение в
крайней нижней ординате составляет всего
лишь 3,17%). В первом же случае
(фиг. 68, а) эпюра ох не имеет общего
с элементарным решением и в
качественном отношении (три «нейтральных» слоя);
в ординатах точная теория для нижнего
дает результат, отличный от элементарного решения, в 1298%.
Ч
Фиг. 69. К примеру расчета
балки-стенки на действие
нагрузки,взаимно
уравновешенной по одной кромке.
волокна (х = 0, у = — Ь)

§ 52] РЕЗУЛЬТАТЫ ИССЛЕДОВАНИЙ НЕКОТОРЫХ ЧАСТНЫХ СЛУЧАЕВ 177
ц
а)
«^вшШШШШППы
^тттттттМТТЫ
б)
Фиг. 70. Эпюры ад,, <jy и txy при нагрузке балки-стенки, показанной
на фиг. 69.
12 3.IK. 3880. Н. И. Безухов

78
ПРОСТЕЙШИЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
[ГЛ. IV
Проведенные Я. А. Пратусевичем и другими авторами (А. С. Малиев,
М. В. Николаева, И. И. Гольденблат и др.) исследования приводят к
практическому выводу, что в балках с отношением — = 4 и больше
можно пользоваться элементарной теорией сопротивления материалов.
В качестве иллюстрации того, в какой степени убывают
напряжения от сечения, где приложены самоуравновешенные нагрузки, приводим
пример балки-стенки, загруженной по нижней кромке нагрузкой
q[x) = q(\—5^jJ, уравновешивающейся в пределах той же кромки
(фиг. 69). Для такого нагружения на фиг. 70 показаны эпюры ах> <зу
и ixy в нескольких вертикальных и горизонтальных сечениях для
случая, когда балка-стенка имеет отношение — =1.
§ 53, Примеры решений задач в полярных координатах.
Задача X. С. Головина
а) Чистый изгиб кривого бруса. Рассмотрим кривой брус с
постоянным сечением в виде узкого прямоугольника и круговой осевой
линией, изгибаемый в плоскости своей кривизны парами сил Af,
приложенными по концам (фиг. 71).
Так как изгибающий момент
по всей длине постоянен, то>
очевидно, напряжения не зависят
от полярного угла 6 и возможно
использовать (3.50).
Условия, утверждающие, что
выпуклая и вогнутая
поверхности бруса свободны от
нормальных усилий, записываются
так:
(°г)г=о = °'> Ыг=ь = 0. (а)
Условие на контуре (включая и торцевые сечения), где отсутствуют
касательные усилия, записывается следующим образом:
Фиг. 71. Изгиб кривого бруса.
тгЗ
= 0.
(б)
Граничные условия по торцам, выраженные в интегральной форме,
будут:
ъ ъ\
fo3tfr = 0; fc9rtfr =—М. (в)

§ 53] ПРИМЕРЫ РЕШЕНИЙ ЗАДАЧ В ПОЛЯРНЫХ КООРДИНАТАХ 179
Используя первое уравнение (3.50) и подставляя в него
последовательно г = а и г = ду имеем:
^ + Я(1 + 21пя) + 2С=0, ]
А (г>
£-\-B(l + 2\nb)-\-2C=0. J
Первое из условий (в) оказывается после подстановки в него
выражения для а6 тождественным с (г). Последнее условие имеет вид
ь ъ
J oe r dr = J j$ r dr = — М,
а
или после интегрирования
Л\п^ — B(b*\nb — а*\па) — (В + С)(Ь* — а*) = М. (д)
Решение уравнений (г) — (д) доставляет:
л AM о.о 1 Ь
лг
N=(P — a°-f — 4e»*« (in А\2
Окончательно формулы для напряжений запишутся в форме
°" = -^(-T?Inl+*2Ini+a2InT+^-«2)' ^-°-
М
С = ^- [Ь2 — а* + 2 (U1 In * — я2 In a)],
где обозначено
6\2
(4.08)
Эти выражения дают распределение напряжений, удовлетворяющее
псом условиям на контуре для чистого изгиба, и представляют собой
точное решение задачи, если только распределение нормальных усилий
но концам бруса следует выражению для о9.
Однако, как это уже неоднократно отмечалось ранее, если усилия,
образующие изгибающую пару, распределены по концам бруса каким-
либо иным образом, то на основании принципа локальности можно
исключить, что отклонения от решения (4.08) будут очень невелики
и ими можно пренебречь на расстояниях от концов, больших, чем
высота сечения бруса.
12'

180
ПРОСТЕЙШИЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
[ГЛ. IV
В курсах сопротивления материалов также разбирается задача об
изгибе кривого бруса, исходя из гипотезы, что поперечные сечения
бруса остаются при изгибе плоскими^ откуда вытекало, что
нормальные напряжения в сечении распределяются по гиперболическому закону.
Сравнение точного решения (4.08) с гиперболическим законом
показывает относительно малую разницу между этими двумя решениями.
Точные решения задач о чистом, а также и о поперечном изгибе
кривого бруса (см. § 54) были впервые даны русским ученым
X. С. Головиным в 1881 г.
б) Осесимметричная деформация толстостенного цилиндра или
диска. Рассмотрим полый цилиндр, подвергающийся равномерно
распределенному давлению с внешней и внутренней сторон (фиг. 72).
Условия на контуре запишутся так:
(°г)г=а = —Ра\ (*г)г=Ъ = — Pb-
В связи с тем, что условий меньше, чем постоянных
интегрирования, в формулах (3.50) примем постоянную В равной нулю. Тогда
получим:
°г = ~л + 2^ °е:
~^ + 2С.
Использование граничных условий
доставляет уравнения:
а-
откуда
2С
окончательно
Ра*-Ръ*
= —a2b-(pa—pb)
о* — а1 '
Ра#—РъР.
а9:
Ь*-
(Pn-ph)*W
Фиг. 72. Осесимметричная
деформация толстостенного
цилиндра.
Рд*-РЬ»
(Рп-Рь)*»
[(4.09)
Заметим, что сумма (а9-|~°г) для всех точек диска оказывается
постоянной.
Эпюры напряжений для частных случаев одного внутреннего или
одного наружного давлений показаны на фиг. 73. Наибольшие
тангенциальные напряжения в обоих случаях оказываются на внутренней
поверхности диска. В первом случае
Ф + Ь*

§ 53] ПРИМЕРЫ РЕШЕНИЙ ЗАДАЧ В ПОЛЯРНЫХ КООРДИНАТАХ 181
а во втором
maxaG = —2/;ь^^.
При h, достаточно большом по сравнению с а, указанные напряжения
стремятся: первые к ра, а вторые к 2ръ.
Заметим, что если бы в диске, равномерно обжимаемом снаружи,
внутреннего отверстия не было, то в диске по всем направлениям
возникали бы напряжения ръ. Таким образом, для сплошного диска,
подверженного снаружи равномерному давлению, «булавочный прокол
увеличивает напряжение у
поверхности прокола вдвое» против случая
отсутствия такого ослабления.
Разобранное выше решение
принадлежит Ляме. Первое практическое
приложение этого решения и
значительное его развитие получено в
России в трудах А. В. Гадолина
в связи с расчетом на прочность
стволов артиллерийских орудий.
При решении этой задачи было
сделано допущение, что
постоянная В = 0. Можно доказать, что Фиг. 73. Распределение
напряжено допущение соответствует дей- ний в толстостенном диске,
ствительности.
Особенность этой задачи заключается в том, что мы здесь
встречаемся с двухсвязным контуром, так как сечение трубы
ограничено двумя замкнутыми кривыми, не пересекающимися между
собой. При наличии двухсвязного или многосвязного контура
решение задачи вообще осложняется и возможна многозначность
решения.
Условию В=£0 физически соответствует случай наличия начальных
напряжений в диске, вызванных, например, тем, что небольшая часть
кольца между двумя смежными сечениями была вырезана, а затем
концы диска сведены и спаяны *). В данной задаче затруднение
можно обайти, выбрав решение задачи не в напряжениях, а в
перемещениях.
Используя (б) и (в) стр. 139, имеем:
Е (и , du\
Е fdu . и \
*) См. М. М. Ф и л о н е н к о-Б о р о д и ч, Теория упругости, Гостехиздат,
П)47, стр. 62.

182
ПРОСТЕЙШИЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
[ГЛ. IV
После подстановки (3.52) записываем:
/г в | (4Л°)
Использование граничных условий
(аг)г=а = — ра и (аг)г=& = — ръ
определит постоянные Л и В, которые, будучи поставлены в (4.10),
дадут в точности (4.09).
§ 54. Задачи А. В. Гадолина и Б. Г. Галеркина
Рассмотрим бесконечно длинный толстостенный цилиндр (или диск),
подверженный равномерно распределенному по всей внутренней поверхности
радиальному давлению р.
Радиусы внутренней и наружной поверхностей цилиндра соответственно
будут а и Ь. Цилиндр заключен снаружи в линейно-деформируемую среду
с коэффициентом постели k. Таким образом, при смещении наружной
поверхности цилиндра в направлении радиуса на величину и (при радиальной
деформации цилиндра) упругая среда порождает сопротивление, равное — ku.
Такая задача была решена Б. Г. Галеркиным методом сил (т. е. в
напряжениях).
Выполним решение этой задачи (случай плоской деформации) в
перемещениях и при этом повторим все рассуждения аналогично сделанным
на стр. 139 для плоского напряженного состояния. Для точки, находящейся
вначале от центра трубы на расстоянии г, смещение вдоль радиуса обозначим
через и. Так как деформация осесимметричная, то другого компонента
смещения (тангенциального) не будет; иначе говоря, в данном случае
задача — одномерная.
Для тангенциальной и радиальной относительных деформаций, как и
и прежде (стр. 139), имеем:
и du , ч
£* = 7' г* = Тг- (а)
Для рассматриваемого случая плоской осесимметричной деформации
остаются без изменения, как и в плоском напряженном состоянии, уравнения
равновесия (3.47), полученные в результате проектирования всех сил,
приложенных к элементарному параллелепипеду, на направление радиуса, т. е.
da~
<*r — a0
dr
= 0.
(б)
Физические уравнения согласно (3.37) примут вид
ег = IT [(1 — !*2) <V — !* (1 + V) ffel.
(в)

§ 54] ЗАДАЧИ А. В. ГАДОЛИНА И Б. Г. ГАЛЕРКИНА
или в обратной записи
"е = АМ1 —l*) + *rMl + iO].
иг = Ех [е6[х (1 + [х) + ьг у
где
■rMl + iO]. \
183
(г)
Подставляя геометрические уравнения (а) в физические (г) и далее
в статическое (б), получаем исходное дифференциальное уравнение
d2u 1 du и __ п
(4.11)
т. е. в точности то же, как и в случае плоского напряженного состояния.
Общий интеграл записывается так:
и = Аг-\-
В
(4.12)
Подставляя (4.12) в той же последовательности, как и раньше, сначала
в (а), а затем в (г), имеем выражения для напряжений
Л(1+10+£(1-Р-2^)],
°8 = Ег [^
аг = Е^А (1 + v) -J(1 ~ V- -2^2)] • j
(Д)
где
(е)
Используем граничные условия:
при г = а аг = —р,
при г = by ar = —k (u)r = ь,
Таким образом, для определения постоянных А к В получаем уравнения:
£i[^(i+K>-§(i-n -w]=-p.
^[л(1+|*)-|(1-^-2|»»)]=-*[л* + |
решая которые, имеем:
Л =
£ =
/>*»(l-bP- + *J^)
Mdj-5d0 ' j
(ж)

184
ПРОСТЕЙШИЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ [ГЛ. IV
где
d2 = (l-^-2^2)(l + ^+^).
При k = О получаем известное решение Ляме (для отдельной
толстостенной трубы).
При k = оо имеем случай, когда труба заключена в абсолютно жесткую
среду, т. е. деформации наружной поверхности исключаются. В этом случае
А = -
и потому
£l[l + ^-^(l-^-2^)]
(u)r=b = Ab + j = 0.
; B = Ab2t
(з)
Рассмотренную выше упругую среду, в которую заключена труба, можно*
представить в виде другой трубы (случай составной трубы), которая надета
на первую или свободно или с натягом.
Не представит затруднений определить в этом случае коэффициент
постели k по отношению к внутренней трубе. Для этого надлежит
рассмотреть самостоятельно наружную трубу под действием внутреннего (по-
отношению к наружной трубе) давления #, при котором радиальная
деформация внутренней поверхности радиуса Ь окажется равной единице (таков
смысл коэффициента постели).
Можно воспользоваться результатами первой, задачи, сделав следующие
замены в формулах (ж): внутренний радиус вместо а положить равным Ьу
внутреннее давление вместо р положить равным k; наружное давление,
отраженное в формулах (ж) через коэффициент k, считать отсутствующим
(т. е. положить k = 0). Наружный радиус второй трубы примем г. Модуль
упругости материала второй трубы и коэффициент Пуассона примем Eq и
[i^. Прежнее Е1 запишется так:
ft- *-
В таком случае из формулы (4.12) имеем:
где мы должны принять:
(и)г=ь = АЬ + -^ = \,
_ft(l-|i0-2pjj)
*('-а
_Ас»(1+Но)
В =
Использование (к) в (и) приводит к результату
(и)
(к)
k =
[i -н-Ъ%
+£о + к.)

§ 56] ПРИМЕРЫ ДЛЯ САМОСТОЯТЕЛЬНЫХ УПРАЖНЕНИЙ 185
При с = оо имеем предельное значение коэффициента упругой постели
к = ЙП^У (4ЛЗ>
Рассмотренное выше решение для составной трубы имеет широкое
практическое приложение. Случаи, когда наружная труба надевается на
внутреннюю с предварительным натяжением, а также случаи многослойных
труб были рассмотрены русским академиком А. В. Гадолиным (1861 г.),
именем которого и называются формулы для расчета так называемых
скрепленных стволов.
Предельный случай (4.13) используется широко в практике
туннелестроения.
§ 55. Примеры для самостоятельных упражнений
Как и в § 47, читателю рекомендуется для указанных ниже
примеров (таблица 3, стр. 186—189) плоского напряженного
состояния при известных выражениях для напряжений, выписанных
н полярных координатах, выполнить следующее:
а) проверить, удовлетворяют ли написанные формулы уравнениям
теории упругости (применить полярные координаты);
б) проверить, точно ли удовлетворяются граничные условия;
в) вычислить недостающие коэффициенты;
г) сравнить эпюры распределения напряжений по данному
решению с теми формулами, которые известны для подобных примеров,
из курса сопротивления материалов.
§ 56. Примеры для самостоятельных упражнений
на использование функции напряжений
(в полярных координатах)
В случаях 1 — 3 (таблица 4, стр. 19Э—193) предполагается
обобщенное плоское напряженное состояние, а в случаях
А —7 — плоская деформация. Задаются различные начертания
дли функций напряжений. Читателю рекомендуется:
1) проверить возможность существования таких функций,
используя (3.45);
2) по функции напряжений найти выражения для компонентов
напряжений на основании (3.46);
3) используя граничные условия, выяснить характер
распределении внешних нагрузок, при которых будет справедлива найденная си-
сп'ма напряжений;
4) проверить, соответствуют ли найденные расчетом контурные
условия тому характеру распределения внешних воздействий, эскиз
мморых показан в таблице.

186
ПРОСТЕЙШИЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
[ГЛ. IV
иин
ля напряже
жения д,
га
Выр
eg
1 X
О
^» я
проектируя на
п; он окажется
«6
= 0.
нове
азреа
и о, 0
II « О
я g
да О S
kP .
cos I
ть из у
цилиндр
8
CN
В
*сл
1
«
1
Я ,s
1 J3 cj
с <->
циент & о
льную ось
|ффи
тика
ным
g о,ю
О О) сз
Ь£ а О,
4—7^
/^
V^
ejA
*А\
eg/
^tem
УИдДсг
:ШЖ^
~
ние к таблице 1.
сз
си
. при
условий см,
торных
о
чных
я
тношении гран
о
PQ
о
II
in 26
ел
'в4
CN
(Л
О
о
в
CN
1
1
а
CN
В
'ел
*!?
W.
V
1 с
cos 2a)
1
CN
СЛ
О
О
^—•
5=
!а COS 2а)
in 2а — 2
СЛ
1 ^
II
<ъ
ч
Ъ\ \
U\ \
4—
CN

§ 56]
ПРИМЕРЫ ДЛЯ САМОСТОЯТЕЛЬНЫХ УПРАЖНЕНИЙ
187
Я*
Я
О
О
эй
Я
пряжен
со
Я
к
ения
1 «в
о.
3
0Q
1 —
1 ^
5S
Cxei
J
.~
^-^ со
да^ CN
(М сл
С °
? 8
Н<* ьл
+ H<N
S (N се»
00 со О
~|<* Ч<" ^(сч |
1 1 1 в
1 1 55 *~
1 i в II
rt о JX
So ьо » •*
Z? "- 8
т-н |(N '-' |<N £Д
+ + H<N
I | '
1 1 H<N
ed»«s Ci, Ui ed^
II II II
ев К <х>
t> t> ^
P
<D
II ^
^^^
llTHHIfHH1
«^
£
^
jjfc
v-
00
о *
^я
ю о
т—1 С
. о
у5«
**§
= g §
<D 5 Ч
я S °
сО
<и s
IS s
я ?
^я
с я
. о
а
ения
сО
а.
3
са
J3
с0
CJ
я
я
сО
X
2 о
2 ^
fe 5
^я
&'§
2 Я
at
-1
•9-эя
я
я я
Я <L>
я ^
2 R
si
СО «
i§
^
О
\SW \
^

188 ПРОСТЕЙШИЕ ЗАДАЧ
ИТЕОРИИ УПРУГОСТИ [ГЛ. IV
ю
<£>
t^

§ 56]
ПРИМЕРЫ ДЛЯ САМОСТОЯТЕЛЬНЫХ УПРАЖНЕНИЙ
189
о
m
X
U
^
| oq|v. ^
+
+
"41
О
1^
Q,
CN
+
С£
£
а
^ 1
+ с,
С£ CN
В 1
1
1 1
+
CN
^
1
1
й
Я
1
1!
CN
1

190
ПРОСТЕЙШИЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
[ГЛ. IV
НИИ
нап]
я
£
я
жения для функ
Выра
СС
1 •—^ч
VO Я
о а
«а £
2 н
1=3 ч 1
<d'§ II
я £ *
3£ и
СО ^ «=>
* § §|В
<D С csj
в 25 05 и
«? я я
9Я || СО «
5 II 2 *
* *3 «1«
с 5 ^ и
s 1 § «_
Я "^ Q«
« a; S 2 о'Ги
я 5^^ ог
•& £• я й II
£ ° = 2
я лс=[
i
»
-J1
—>
^
^ -J
Vj
Jk/T
1
-
Я ' ' Л О)
n U О) £-. ч
точке ЛГ nj
юмерно ра
ользуя реш
представи
, показаннь
n « S « я
со н >■» ав
я s °Q ^ S
8Г Э
К Я <U Jco
UH Я g со
суя £
ражения для на
бесконечной плс
сгрузкой на дл
его случая (1).
заданную нагр
на два частных
авить вы]
узке полу
еленной i
преды дущ
этой цели
оженной
) и б)
,°. Й a s ^ со га
О со с я Чая
|*£"
<*>
^
* 1
i
i
i
i
'Т J
?
3
/**
1 -*
) з
-v
С>
CS
| [
\ -t
3
3
-*
5
о 1
' 1
/ \|
/ 1
/ |
/
/ 1
1 1
^ \
-^ 1
<>

§ 56]
ПРИМЕРЫ ДЛЯ САМОСТОЯТЕЛЬНЫХ УПРАЖНЕНИЙ
191
3
QJ
ч
о
^1
о
о-|
С
о»
5 о
а
PQ

192 ПРОСТЕЙШИЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ [ГЛ. IV
Я
О)
О,
Я
я
я
«
я
5
я
я
PQ
сз Я
СО ^
i- СО
2 сх
я о
2i <и
я а
>-> о
К н
2 g
& cd
ч
[И1
о
и

§ 56] ПРИМЕРЫ ДЛЯ САМОСТОЯТЕЛЬНЫХ УПРАЖНЕНИЙ 193
я*
PQ
CD
сх
CD
прим
в
О)
Я
Я
ден
ий, приве
жен
«
сх
я
03
X
DC
ч
к
J3
ормул
•У*
что
J3
н
Показа
сх
я
в
о
я
я
CD
*,
03
сх
О
о
СП
Я
of
03
ч
о
о
и
CD
О
DC
ч
1=1
я
я
2
Я
м
я
CD
в
03
СХ
я
о
DC
и
я
ъ
в
3
СП
рЗ
О
О
о
8
•
•
^
О
».
О
н
О
CD
S
рЗ
Я
ч
5*
сх
о
•в-
я
н
СО
в
CD
tf
в
о
я
рЗ
н
fcf
о
я
я
сх
я
CD
СХ
CD
S
DC*
га
я
CD
СХ
(->
03
СО
о
о
я
сх
CD
S
О
Я
03
03
СХ
CD
Я
Я
03
Р4
>>
ч
>->
CD
3
\о
о
я
9
РЗ
э«
CD
Н
О
эЯ
га
я
CD
03
Я
СО
/^Ч
(Л
П
Я
о
о
я
ч
CD
н
я
о
о
я
н
о
о
о
я
Н4
я
СХ
н
CD
я
о
н
о
сх
+
Я DC w
оз Я*
О я
К CD
сх«
Я «=;
CD CJ
* Н
§|
*1
Я ^
ч
&§
S ^
+
CM
CM
+
II 5^1 II
+
!wt
+
d-l
CD
CD
и
13 Зак. 3880. H. И. Безухов

194 ПРОСТЕЙШИЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ [ГЛ. IV
§ 57. Полярно-симметричная деформация толстостенного
сферического сосуда
При решении некоторых простейших задач, когда многие
компоненты напряжений и деформаций отсутствуют, можно не прибегать
к общим уравнениям теории упругости (в перемещениях или в
напряжениях), которые, конечно, должны значительно упроститься, а
все три необходимые стороны исследования (геометрическую,
физическую и статическую) выполнить непосредственно применительно
к рассматриваемому частному случаю. К такому случаю можно
отнести задачу об упругом равновесии сферического сосуда.
Представим себе шаровой сосуд, подвергающийся действию
внутреннего и внешнего равномерных давлений. Пусть а и b обо-
Фиг. 74. Полярно-симметричная деформация толстостенного
сферического сосуда.
значают соответственно внутренний и наружный радиусы шара
(фиг. 74), а ра и ръ — внутреннее и наружное давления газов.
Начнем со статического обследования. Вырежем для
исследования бесконечно малый элемент двумя парами взаимно
перпендикулярных меридиональных сечений и двумя концентрическими
сферическими поверхностями. Действие отброшенных частей сосуда заменим
тангенциальными (af, ог) и радиальными (ог) напряжениями. Так как
в рассматриваемом случае, как в аналогичной задаче о равновесии

§ 57] ПОЛЯРНО-СИММЕТРИЧНАЯ ДЕФОРМАЦИЯ СФЕРИЧЕСКОГО СОСУДА 195
толстостенной трубы, известной читателю из курса сопротивления
материалов, напряжения зависят только от текущего радиуса г, то
напряжения по двум бесконечно близким друг к другу
концентрическим поверхностям будут отличаться на величину -r1dr = dor и не
будут зависеть от угла 0—другого параметра, определяющего
местоположение рассматриваемого элем-ента. Проектируя все силы на
нормаль к элементу, имеем уравнение равновесия в виде
— °г (г %) (г dvz) — (or + dor) (r + drf dyt doz —
— ot (r dr doz) dvt — qz (r dot dr) dyz = 0,
Имея в виду равенство ot = oz и производя сокращения,
получаем уравнения равновесия:
2(о,-о,) + г^ = 0. (4.14)
Переходим к геометрическому обследованию. Из
рассмотрения перемещения и формоизменения, выделенного для
детального исследования элемента, заключаем, что относительное
тангенциальное удлинение выражается так:
_ _ (r + u)d4t — rd'it _ и
а относительное радиальное удлинение
(4.15)
g _ (u + du) — (u) ^du (4 16)
r dr dr* ^ ' '
Переходим к физическому обследованию. Зависимость
напряжений от деформаций при помощи закона упругости в данном,
случае имеет вид
Напряжения через деформации выражаются (принимая во
внимание равенство ot = oz) так:
°*= 1-tf_2^(^+^). )
Е \ (4Л7)
«г=-1_Д2^[2^+(1-^)«г1. j
Переходим теперь к обобщению полученных с разных точек
зрения результатов. Данные геометрического обследования используем
13*

196 ПРОСТЕЙШИЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ [ГЛ. IV
для преобразования полученных физических зависимостей, т. е.
подставляем (4.15) и (4.16) в (4.17). Имеем:
Е [и , du\ /лч
°«= ^-^[т + ^аф (a)
Выражения (а) и (б) подставляем в уравнение статики (4.14), но
для этого предварительно запишем -j^, входящее в (4.14).
Дифференцируя (б), имеем:
du
"57
г- d#
(в)
Подставляя (а), (б), (в) в (4.14), получим:
+ 2Рё-2^+(1-,)^}-0,
или после надлежащих сокращений
d2u i 2 du п и ~ /л т\
что представляет собой уравнение, объединяющее в себе все три
стороны исследования (геометрическую, физическую и статическую).
Общий интеграл дифференциального уравнения (4.18) имеет вид
и = ±+Вг. (4.19)
Действительно, дифференцируя (4.19), находим:
du 2Л_ , д. d2u 6А /\
dr гз г > $гъ ri
и, подставляя (4.19) и (г) в (4.18), имеем тождество
6Л
+Я-"+вЬМ*+*]-л
Подставляя (4.19) и (г) в (а) и (б), получаем вместо
дифференциальной формы выражения для напряжений в алгебраической форме:
««= i-Д^ [^(1-2^)+Д(1 + ^)]; (д)
^1-Д»> [-^(1-2,) + Д(1+1х)]. (е)

§ 57] ПОЛЯРНО-СИММЕТРИЧНАЯ ДЕФОРМАЦИЯ СФЕРИЧЕСКОГО СОСУДА 197
Постоянные интегрирования Л и В определим из поверхностных
условий, а именно:
Ыг=а =—Ра и (аг)г= Ъ = —РЪ-
Подставляя указанное в (е), имеем:
i-£-2^-y(1-2rt+*(1+|t)}~~p"
1^r^{-^(i_2(i)+5(i+[A)}=_P6(
откуда
л ^(Ра-Рь)^ЬЦ1-^-2^)
2Е(1—2у.)(Ь* — а*)
R_(Paa*-pblfi)(l-*-W)
£(1+[х)(^ — я3)
Подставляя (ж) в (д) и (е), имеем окончательно:
(ж)
дз (2гз -f ft3)
:^° 2л3(63 — я3)
■Рь
б3 (2г3 + а3)
°г = Ра
,-3(бЗ__дЗ)_
■Рь
2г3(^ —а3) '
£3 (Я3 — Г3)
Г3(^__в3)-
(4.20)
Для случая одного внутреннего давления ра наибольшее
растягивающее тангенциальное напряжение будет на внутренней поверхности
сосуда (при г = а):
2я3 + б3
а минимальное на наружной поверхности (при r = b):
За3
тта, = р02(^3_дЗГ
Неравномерность распределения напряжений характеризуется
отношением
maxa# _2+ E8
7] =
где обозначено
Мри р = 3 имеем:
mm at
b_
а
7] = 9,67.
По существу приведенное здесь решение задачи теории упругости
получено применением метода перемещений.

ГЛАВА V
КЛАССИЧЕСКИЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
(УПРУГАЯ ПОЛУПЛОСКОСТЬ, УПРУГОЕ ПОЛУПРОСТРАНСТВО)
§ 58. Сила, действующая на острие клина
В настоящей главе рассмотрено несколько характерных задач, для
решения которых совершенно исключаются возможности (хотя бы даже
в качестве попытки первого приближения) применения к ним каких-
либо элементарных решений из теории сопротивления материалов.
В этом смысле прлводимые ниже задачи и названы классическими
в теории упругости.
Рассмотрим симметричный клин, показанный на фиг. 75. Толщину
клина в направлении, перпендикулярном к плоскости ху, примем
равным единице. В направлении оси х протяженность клина бесконечна.
На острие клина приложена сила Р, равномерно распределенная по
толщине острия *). Случай потери упругой устойчивости исключаем
из рассмотрения.
В этой задаче представляются абстракциями как «сила на острие»,
так и бесконечная протяженность клина. Однако, как это показано
позднее (§ 61), пользуясь формальным решением такой абстрактной
задачи, не представит затруднений перейти к реальным задачам о
действии непрерывно распределенных нагрузок и притом на тело с
реальными граничными условиями (без острия, с конечной протяженностью
и т. д.).
В рассматриваемой сейчас задаче, характерной для использования
уравнений плоской задачи в полярных координатах, выясняется также
неприменимость элементарного решения сопротивления материалов.
Сделаем вначале (но это окажется и окончательным)
предположение о простом радиальном распределении напряжений, а именно,
допустим, что элемент С на расстоянии г от точки приложения груза
испытывает простое радиальное сжатие в радиальном направлении, но
тем меньшее, чем дальше удалена рассматриваемая точка С от острия
*) Это так называемая «погонная сила»; ее размерность — сила на
единицу длины.

§ 58]
СИЛА, ДЕЙСТВУЮЩАЯ НА ОСТРИЕ КЛИНА
199
и чем больше определяющий ее радиус отклонен от линии действия
силы. Иначе говоря, сделаем предположение:
or = — kP^y (5.01)
где k — коэффициент, подлежащий определению.
Тангенциальное напряжение о6 и касательное тг6 в этом случае для
упомянутого выше элемента С равны нулю.
Докажем, что решение (5.01) является
точным и что оно может быть выведено
при помощи следующей функции
напряжений:
kP
ср = ~~r0sin6.
Действительно,
имеем:
2
на
г2 д№ '
основании (3.46)
kP cos 8
ГГПтгт^ггтТГР
ПЕР*
^rrrm
■•чг
Это совпадает с (5.01), чем
доказывается, что уравнения равновесия и
неразрывности удовлетворены. Проверим
граничные условия: при 0 = ±а, т. е. на
внешних наклонных гранях клина,
никакие внешние силы не действуют.
Действительно,
Остается подобрать постоянную k так,
чтобы удовлетворить условиям равновесия
между внешней силой Р и внутренними
силами по какому-либо сечению клина. Для
этой цели сделаем сечение по
цилиндрической поверхности радиуса г (фиг. 75). Равнодействующая усилий,
действующих по этой поверхности, должна уравновешивать силу Р.
»'-)та равнодействующая получается суммированием вертикальных
составляющих:
or {ab • 1) cos 6 = orr db cos 6,
действующих на каждый элемент ab по поверхности. Имеем:
а
_2[^-s2-i^6 = -AP(a + Isin2a) = -P,
Фиг. 75. Случай нагрузки
бесконечного клина силой
на острие.

200 КЛАССИЧЕСКИЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ [ГЛ. V
откуда
a -f- -у sin 2а
Таким образом, окончательно
(5.02)
Для поперечного сечения тп имеем следующие компоненты
напряжений, отнесенных к прямоугольным осям;
оу = or sin2 6,
ъху — у^ sin 20.
Распределение указанных напряжений по сечению тп изображено
на фиг. 75 внизу.
§ 59. Сосредоточенная сила, приложенная к точке
прямолинейного края полубесконечной пластинки
Представим себе сосредоточенную вертикальную погонную силу
интенсивностью Р, действующую на горизонтальный прямолинейный
Фиг. 76. Полубесконечная пластинка, нагруженная
сосредоточенной силой.
край пластинки (фиг. 76), бесконечно простирающейся вниз, влево,
вправо. Такую пластинку называют полубесконечной или иначе
упругой полуплоскостью.

§ 59] СОСРЕДОТОЧЕННАЯ СИЛА 201
Распределение груза Р по толщине пластинки предполагается
равномерным. Толщину пластинки примем равной единице. Для отыскания
закона распределения напряжений возможно использовать решение
задачи о клине (§ 58), полагая угол растворения клина 2а = тт. В таком-
случае
-J+o я
и потому
2PCOS6 /г AQV
ог = — — -у-. (5.03)
Проведя горизонтальную плоскость тп на расстоянии х от
прямолинейного края пластинки, определим нормальные и касательные
напряжения для любой точки в этой плоскости по формулам перехода,,
а именно:
2Р cos3 0 2Р х*
°х = °r cos ° = —
9Р
ол = or sin2 8 = — — sin2 6 cos2 8;
» г ъх '
те (^2+^2)2'
• а п 2Р . L «л 2Р Х2у
ixv = or sin 8 cos 0 = sin 8 cos3 8 = . , / ,,.,..
Ha фиг. 76 показано распределение напряжений <зх и тву по
горизонтальной плоскости тп.
В точке приложения груза напряжения оказываются бесконечна
большими, а потому под силой и в непосредственной близости от нее
неизбежны пластические деформации. Однако на некотором удалении
от силы согласно известному читателю принципу локальности
приведенные выше формулы «упругого» решения практически пригодны.
В порядке самостоятельного упражнения рекомендуется читателю дока-
зать, что если провести окружность произвольного диаметра d, касающуюся,
верхнего края в точке приложения внешней- силы (фиг. 77, я), то для всех.
точек этой окружности радиальные напряжения будут одинаковы и равны:
"' —5Г (5-03а>
Равны также для этих точек и наибольшие касательные напряжения:
W = ^-. (5.03б>
Если обозначить через тх наибольшие касательные напряжения на
окружности диаметра db то на окружности диаметра d2 = -~- d1 касательные
напряжения будут иметь удвоенную величину, утроенную величину на
окружности диаметра ds = -^-d и т. д. (фиг. 77,6).
о
Напомним, что геометрическое место точек, для которых наибольшие
касательные напряжения равны, называются изохромами, а в случае просве-
•пшлпия модели из прозрачного материала на поляризационной установке

202 КЛАССИЧЕСКИЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ [ГЛ. V
при монохроматическом источнике изохромы представляются черно-белой
картиной полос. На фиг. 78 дано сравнение теоретической и
экспериментальной картин полос, из которого видно, что результаты теории упругости
совпадают с экспериментальными данными (в данном случае с результатами
лоляризационно — оптического исследования).
а) б)
Фиг. 77. Для всех точек окружности, касающейся
верхнего края в точке приложения внешней силы, радиальные
напряжения одинаковы.
Фиг. 78. Сравнение теоретической и экспериментальной картин полос»
подтверждающее совпадение результатов теории упругости с опытом.
Также в порядке самостоятельного упражнения рекомендуется читателю
убедиться в справедливости показанных на фиг. 79 для рассматриваемого
случая нагружения полуплоскости изоклин (а), траекторий главных
напряжений (б) и траекторий наибольших касательных напряжений (в).

§ 60] ДЕФОРМАЦИЯ ПОЛУБЕСКОНЕЧНОЙ ПЛАСТИНКИ 203
Напомним, что изоклины представляют собой геометрическое место
точек, направления главных напряжений в которых параллельны;
траекториями главных напряжений (изостаты) называются кривые, касательные
Траектории
'касательных
напряжений
Фиг. 79. Изоклины (а), траектории главных напряжений (б)
и траектории наибольших касательных напряжений (в).
к которым совпадают с направлениями соответствующего главного
напряжения, действующего в точках касания.
§ 60. Деформация полубесконечной пластинки
от сосредоточенной силы
Продолжим решение предыдущей задачи в смысле определения
перемещений. Используем формулы (3.42)—(3.44) и закон Гука.
Подставляя в них (5.03), имеем:
ди _ 2Р cos 6
___ti\dv 2Я cos 6
ди , dv v п
Интегрируя первое из этих уравнений, находим:
и = ?g cos 6 in r+/(6),
(а)
(б)

204
КЛАССИЧЕСКИЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
[ГЛ. V
(г>
где /(0) является функцией только одного угла 6. Подставляя
полученное во второе уравнение (а) и интегрируя, имеем:
v = 2-£ sin 6 + g In r sin 6 - J/ (0) db +/(r), (в>
где /(г) — функция одного только г.
Подставляя (б) и (в) в третье уравнение (а), придем к
заключению, что
/ (б) = — (1 ~^} P 8 sin 6 -f Л sin 6 -f В cos 6, |
/M = o, J
где Л, В и С—постоянные интегрирования, которые подлежат
определению из уравнений связи.
Пусть связи полуплоскости таковы (фиг. 76), что точки,
лежащие на оси лг, не имеют бокового перемещения, т. е. v = 0; тогда
найдем А = С=д> и вертикальное перемещение точек, лежащих на
оси лг, будет:
(«)e=0 = -glnr + B. (5.04а)
Чтобы найти постоянную В, допустим, что некоторая точка,
лежащая на оси х в расстоянии d от начала координат, не имеет
вертикального перемещения. Тогда найдем:
B = ^\nd.
Для вертикальных перемещений по горизонтальному
прямолинейному краю будем иметь выражение
^Ё ' (5-046)
/ \ 2Р. d
Оо) те = —77 1П —-
2
§ 61. Прогибы прямолинейного края полубесконечной пластинки
при частных видах загружения
Прогибы прямолинейного края пластинки легко найти для любого
распределения нагрузки при помощи формул (5.04а, б), выведенных
l^mrnimJ
"•w
WxAo
Фиг. 80. Загружение граничной пноскости полубесконечной пластинки.
для случая сосредоточенной силы., Если q — интенсивность
вертикальной нагрузки (фиг. 80, слева), то прогиб, возникающий в точке О

§ 61] ПРОГИБЫ ПРЯМОЛИНЕЙНОГО КРАЯ ПОЛУБЕСКОНЕЧНОЙ ПЛАСТИНКИ 205
на расстоянии г от заштрихованного элемента qdr нагрузки, согласно
(5.046) запишется так:
■кЕ г
1-1*
%Е
qdr.
Полный прогиб в точке О:
1+х
1+х
^Ы 4XnTdr-4i-\ ^r.
(5.05)
а) Действие равномерно распределенной нагрузки. В этом
случае q постоянно, и потому
Для точки, находящейся в пределах нагруженной части (фиг. 80 справа),
получим:
б) Обратная задача. Если задается уравнение прогиба
прямолинейного края пластинки, то из (5.05) можно найти закон распределения
нагрузки, вызвавшей такой прогиб.
Так, в случае, когда прогиб v постоянен по длине загруженной
части прямолинейного края (фиг. 81), то решение (5.05) (которое будет
уже интегральным уравнением, так
как неизвестная функция q входит
под знак интеграла) доставляет
следующий закон:
Я= v f 8- (5-06)
те У я2 — х%
Наименьшее значение давления будет
при х= 0:
<7min лл »
Фиг. 81. Задача о жестком штампе.
я по краям жесткого штампа
давление теоретически обращается в
бесконечность.
Фактически бесконечно больших напряжений не будет, так как
материал пластинки у краев штампа придет в пластическое состояние,
или в этом надобности не будет, если края штампа будут закруглены.
в) Задача И. Я. Штаермана. В предыдущей контактной задаче
граничный край пластинки предполагается идеально прямым. Однако
и действительности, даже при очень тщательной отделке пластинки,
последняя всегда имеет мельчайшие неровности, которые могут
окапать существенное влияние на последующее распределение напряжений
под штампом.

206 КЛАССИЧЕСКИЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ [ГЛ. V
Фиг. 82. Задача И. Я. Штаермана.
Таким образом, при решении контактной задачи
следовало бы учитывать микроструктуру поверхности
сминаемых тел.
f^ffffffffl ?friUilliLfTX ^aK как совРеменная
физика пока не дает
какой-либо законченной
теории поверхностной
структуры твердого
тела, то И. Я. Штаерман*)
предложил оригиналь-
ноерешение, основанное
на том, что при нормальном давлении на поверхность упругого тела
в нем возникают два рода перемещений. Одни получаются вследствие
деформации всего упругого тела
(в данном случае «упругой
полуплоскости»), другие предопределяются
поверхностной структурой данного
тела.
Первые определяются
дифференциальными уравнениями теории
упругости, в частности уравнением (5.05).
В отношении вторых делается
предположение о том, что они в данной
точке линейно связаны с местным
давлением в той же точке.
Иначе говоря, граница упругой
плоскости представляется схемой,
указанной на фиг. 82. Тогда эти
вторые перемещения могут быть
описаны зависимостью kqy где
k—некоторый коэффициент, зависящий от
поверхностной структуры упругого
тела (исполняющий в данном случае
роль коэффициента постели в извест-
механики задаче о балке на упругом
Фиг. 83. Распределение
напряжений под плоским жестким
штампом при различных упругих
характеристиках тонкого
подстилающего слоя (по Штаерману).
ной читателю из строительной
основании).
Прогиб граничного края для такой модели тела запишется так:
I-
1-х 1-х
(5.07)
Если вернуться к задаче о вдавливании плоского штампа, то в
написанном уравнении следует v0 считать постоянным, a q разыскиваемым.
*) И. Я. Штаерман, Контактная задача теории упругости, стр. 162,
Гостехиздат, 1949.

§ 62] ВЛИЯНИЕ КРУГЛОГО ОТВЕРСТИЯ НА РАСПРЕДЕЛЕНИЕ НАПРЯЖЕНИЙ 207
Исследование этой задачи привело Штаермана к интересным и
важным в практическом отношении выводам, представленным на фиг. 83,
На этой фигуре показаны графики давления q под штампом для
следующих значений параметров с
2я(1 —ц2)
= Ь 1—(— • п —- П п —-
kE
0, £ = 0,1, <•=!,
с =10 и £ = оо. Случай с = оо соответствует общепринятой теории
штампа, в соответствии с которой при х =± а давление q обращается
в бесконечность; при конечных значениях с давление q остается
ограниченным, и в предельном случае при с = 0 получается равномерна
распределенное давление под штампом.
§ 62. Влияние круглого отверстия (ослабления)
на распределение напряжений в растягиваемой пластинке
Пусть имеем пластинку (фиг. 84), подвергающуюся действию
растягивающего усилия, равномерно распределенного по торцам пластинки, так что-
р
с = —. На оси Ох пластинка имеет небольшое круглое отверстие. Наличие
последнего повлияет на распределение напряжений около ослабления, и
в частности, по сечению т\п± напряжения будут распределяться неравномерно*
с резко выраженной концентрацией около ослабления (точки т и п).
0 ■*
т,
Ur*—
7*
\
~У^Г
^
—
(о
г\ \х <
/
2
f
а
/
/
У
>
J
Фиг. 84. Растягиваемая пластинка, ослабленная отверстием.
К решению этой задачи подойдем таким искусственным способом.
Вырежем из заданной пластинки концентрической окружностью радиуса Ь
ч;1сть и рассмотрим ее отдельно от остальной части пластинки. Если раз-
мор b значительно превышает размер а, то согласно принципу локальности
напряжения по окружности радиуса Ь по существу будут мало отличаться
от случая, если бы выреза в пластинке не было совсем.
Таким образом, взамен расчета пластинки задачу сводим к расчету
толстостенного кольца,, изображенного на фиг. 85, я, где согласно известной
формуле сопротивления материалов (напряжения в косых плоскостях при чистом,
растяжении) р = a cos 6.
Воздействие по фиг. 85, а может быть разложено на компоненты,
покачанные на фиг. 85, б, где
(ar)r=ft =p cos 6 = с cos2 6 = — a (1 + cos 28),
(Vo)r=b = — P sin 6 = — у * sin 26.
(a>

208 КЛАССИЧЕСКИЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ [ГЛ. V
В свою очередь эти компоненты можно между собой
перегруппировывать, т. е. считать состоящими из двух частей. Первая — от действия
постоянной по всему наружному периметру (фиг. 86) составляющей, равной половине
нормальных напряжений. Напряжения, возникающие под действием этой
составляющей, можно определить при
помощи выражений, полученных для задачи . i 1 * IQ
§ 53, т. е. воспользоваться известным у\*^""^ЧУ0<?
решением (4.09).
Вторая часть (фиг. 86, а, б),
состоящая из нормальных составляющих
1°г)„
1 ! ой
(б)
вместе с касательными
— -^-с sin 26
вызывает напряжения, которые над-
Фиг. 85. Схема усилий,
действующих на круговую пластинку
(полных усилий и ее
компонентов).
Фиг. 86. Три группы
напряжений, эквивалентные
схеме усилий,
показанных на фиг. 85, б.
лежит сейчас специально определить. Но и для этой группы внешних
воздействий возможно воспользоваться готовым решением задачи § 56,
«случай 3, а именно:
аг = — г + тж = -о-1 +3-Г —4"т cos26,
Tr3 = -|(l-3^ + 2^)sin26.
(в)

§ 62] ВЛИЯНИЕ КРУГЛОГО ОТВЕРСТИЯ НА РАСПРЕДЕЛЕНИЕ НАПРЯЖЕНИЙ 209
Присоединяя к ним напряжения от первой группы (фиг. 86),
окончательно получим:
*-7(1-тК(1+8£-*$)"»а1' )
i=auifi+^-
дг*
('+М'+£Ь2'.
V9
--тО-'я+'д)-*
(5.08)
Напряжение а0 будет наибольшим по концам диаметра тп и будет
равно*):
(се) =3а.
v И'тят
Располагая знанием компонентов напряжений в каждой точке (5.08),
можно составить выражения для главных напряжений и для наибольших
а) б)
Фиг. 87. ^Изостаты (справа) и изохромы (слева), построенные по
теоретическим исследованиям.
касательных напряжений в тех же точках. Рекомендуется читателю
проделать эту часть исследования самостоятельно и провести анализ формул для
главных напряжений.
На фиг. 87, б показаны траектории главных напряжений (изостаты) и
на фиг. 87, я — линии равных ттах (изохромы). На фиг. 88 изображены
•) Приведенный здесь вывод можно рассматривать точным при —
Ь
устремляющимся к нулю. В таком случае по отношению к размерам ослаб-
лппш пластинка является бесконечно большой, иначе говоря, пластинка
иилястся упругой плоскостью.
14 Зак. 3880. Н. И. Безухов

210
КЛАССИЧЕСКИЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
[ГЛ. V
интерференционные полосы, сопоставление которых с фиг. 87, а показывает
совпадение вычислений в теории упругости с действительностью.
Большое количество задач,
связанных с вычислением местных
напряжений, имеется в обстоятельной
монографии Г. Н. Савина «Концентрация
напряжений около отверстий» (Гостех-
издат, 1950), удостоенной Сталинской
премии за 1951 г. Там разобраны случаи
отверстий в форме эллипса,
прямоугольника, правильного многоугольника,
исследованы случаи изгиба плит со
всевозможными отверстиями в плане и т. д.
§ 63. Сосредоточенная сила,
действующая на плоскость,
ограничивающую полубесконечное
тело
В § 59 была рассмотрена задача
о распределении напряжений в
полубесконечной пластинке от
сосредоточенной силы, приложенной на
внешнем крае. Аналогично упомянутой
плоской задаче решена и трехмерная
задача.
Пусть плоскость z = 0 является
гранью полубесконечного сплошного
тела (т. е. это тело имеет безгра-
ничное простирание вниз в глубину
Фиг. 88. Картина полос, получен- и бесконечное же простирание в
ная экспериментальным путем. ч л/,„,
r J ширину); пусть на эту плоскость
действует сосредоточенная сила Р на оси z (фиг. 89). В литературе
эта задача именуется задачей Буссинеска.
Очевидно, в таком полубесконечном теле, иначе называемом
упругим полупространством, напряжения в теле должны по мере
удаления от силы Р убывать быстрее, чем в полубесконечной пластинке.
Напрашивается для радиального напряжения принять в качестве
первой попытки такое начертание:
Переходя к цилиндрическим координатам, по формулам перехода
должны тогда получить:
°г = Од COS2 0, ]
1 • ои \ (5Л())
••1

§ 63]
СОСРЕДОТОЧЕННАЯ СИЛА
211
Заменяя cos6 =-i; sinO = f; i-sin26 = 2 и P = г2 + r2,
■ cos3e_ ьр£!-
,2V
o2 = — kP-
P
T„ = -lfeP^sin20 = -feP^.
имеем:
(5.11)
(5.12)
Для определения входящего в последние формулы коэффициента k
\Р
Фиг. 89. Сосредоточенная сила, действующая на
плоскость, ограничивающую полубесконечное тело.
составим уравнение равновесия по какому-либо горизонтальному
сечению z = a *).
Для элементарной площадки в виде бесконечно тонкого кольца
шириной dr и радиусом г имеем элементарную внутреннюю силу:
ог dF = 2nozr dr.
Со всех таких элементарных площадок, т. е. со всего сечения
г = а, имеем сумму внутренних усилий:
2к | <jzrdr = — 2v:kPz* | Г-^.
(а)
*) Можно, конечно, определить указанный коэффициент и аналогично
тому, как это было сделано на стр. 199, если собирать давления с полу-
гфгры, вырезанной около точки приложения силы.
14*

212 КЛАССИЧЕСКИЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ [ГЛ. V
Так как /2 = (z2 -\- г2), то, дифференцируя, имеем: 2ldl=2r dr.
Таким образом, (а) перепишется:
№—■
— 2itkPz* | -£ = — 2itkPz*!-^ =
2 --? 2
=4*ft^*8(*2+/'2) 2 =—4 «*л
3 v- I / | з
о
Уравнение равновесия по сечению z = а (сумма проекций на
ось z) приводит к выражению
—-JitftP-[-/> = °»
откуда
То, что выражения (5.11) и (5.12) дают точное решение задачи,
можно доказать путем использования функции напряжений.
Выполнение этой операции позволит определить нам также и другие
компоненты напряжений (oq, or).
На основании (3.65), (3.67), (3.73) примем для функции напряжений
следующее начертание:
9 = C1z\nr + C2(r* + z*)2 +С3*1п\чу^=— )> <а/)
удовлетворяющее условиям неразрывности и равновесия, что было доказано
ранее (§ 43). Используя (3.63) и (а'), имеем:
+ С.Л —4{i.r(A-2+^2) 2 +6^e2 + 22) 21; (60
-— _JL
ал=сЛ-(1-2{х)г(А'2+^) 2-ЗгЗ(г2+^) 2] +
Так как на поверхности, т. е. при z = О, тгг = 0, то из (60 следует:
Сз = -Ц^С, (ГО
Условие (a2)z=i0 = 0 согласно (в/) удовлетворяется. Ранее указанное
условие равновесия по сечению z = а даст значение
С2 = ^~, (дО
и на основании (г') получим:

§ 63]
СОСРЕДОТОЧЕННАЯ СИЛА
213
Подстановка (д') и (е7) в (б7) и (в7) приводит после сокращений к (5.11) и
(5.12), чем и доказывается, что эти выражения являются окончательными.
На основании (3.63) далее имеем:
_3_ 5^ _J_
'r = ^ + C2[(l-2rt*(,e + *2) 2^-3^(r2+^) 2]+C3[^(A-2+^) 2 +
+ 4(l+ix)z(r2+^) 2 _2$(а* + **) 2 -6*з(г2 + ^) 2J.
Для бесконечно удаленных точек (внизу) при г = оо должно быть
аг = 0. Это уравнение приводит к соотношению
С1 = -2Сз = Ц^Я.
Аналогично можно найти выражение и для aQ.
Окончательно формулы для напряжений примут вид
___3/>£3
°*— 2* /&'
__ Р Г 1 - 2[х ЗггЭ I
°г~~ 2л [/(/+*) /5 J»
(5.13)
*,.« = •
" 2« /5 '
Для определения перемещения используем (3.54). Компонент
смещения вдоль радиуса г равен:
и = еьг = -^- [ее — p(<v+ oj].
(б)
После подстановки в (б) выражений (5.13) и преобразований
получаем:
При /=^оо, как и следует ожидать, и = 0. На основании (3.54)
dw 1
IF ~ *г — ~Ё
W'= *г = -р\*г— Р(°г + °в)Ь
откуда
хе;
= Т j [3г-^(°Г+'в)]^+/(г).
(в)
После подстановки в (в) выражений (5.13) и интегрирования,
принимая также очевидное положение, что wr=oo=0i получаем из (в): _

214 КЛАССИЧЕСКИЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ [ГЛ. V
Для вертикальных перемещений точек на граничной плоскости
г = 0 для так называемой «дневной поверхности» получим выражение
Р(1_ ц2)
(5.15)
У начала координат, как это было и в птоской задаче,
перемещения и напряжения становятся бесконечно большими *), и потому,
чтобы избежать принципиальных затруднений при применении
указанных выше выражений, необходимо представить, что у начала
координат в области пластических деформаций материал вырезан
полусферической поверхностью малою
радиуса, а сосредоточенная сила Р
заменена статически эквивалентными
усилиями, распределенными по этой
поверхности.
Для самостоятельного упражнения
можно предложить читателю доказать
следующие особенности распределения
напряжений в упругом
полупространстве от сосредоточенной силы.
Полное напряжение в любой точке
горизонтальной площадки (т. е.
равнодействующая напряжений аг и ъгг, см.
фиг. 90) направляется к началу
координат и равно:
ЗР cos2 6
Фиг. 90. К вычислению полного
напряжения на горизонтальной
площадке.
Если, далее, очертить произвольным диаметром d сферу, касающуюся
граничной плоскости в той же точке О, то по всем горизонтальным
площадкам, размещенным на поверхности этой сферы, полные напряжения
одинаковы и равны:
р-ш- (5Л6)
§ 64. Частные случаи загрузки «упругого полупространства»
а) Равномерная загрузка по площади круга. Имея решение
для сосредоточенной силы, действующей на плоскую грань упругого
полупространства, мы не встретим затруднений найти перемещения и
напряжения, возникающие под действием распределенной нагрузки,
если применим принцип сложения действия сил.
*) Если, однако, площадку действия силы Р считать не равной нулю
(см. § 64), то бесконечно больших давлений и перемещений не получим.

§ 64] ЧАСТНЫЕ СЛУЧАИ ЗАГРУЗКИ «УПРУГОГО ПОЛУПРОСТРАНСТВА» 215
Пусть нагрузка общим весом Р равномерно распределена на
«дневной поверхности» полубесконечного тела по площади круга радиуса а.
р
Интенсивность нагрузки будет равна: д = -^-.
Составим выражения для перемещения точки С, находящейся на
дневной «поверхности», но в пределах загруженного круга (фиг. 91).
Проведем через точку С секущую МС, а в бесконечной близости
другую — МгС и рассмотрим влияние на «прогиб» точки С нагрузки,
расположенной на
элементарной площадке, заштрихован- Я
ной на фиг. 91. Эта площадка
равна dF = sd?ds, а на- wwwwA(/№W»>sM,
грузка, на нее приходящаяся,
будет:
dP= q dF= qs dv ds.
От такой нагрузки точка С
должна опуститься согласно
(5.15) на
vEs '
т. е.
1 — и з
dw •
Полное перемещение
точки С от всей нагрузки
представится интегралом
Фиг. 91. Равномерная загрузка упругого
W-
1 „ /» л ФИ1. У1. гаиномернаи ddi рус$ка упруи
1 У" д fa d^t (ач полупространства по площади круга.
Из фиг. 91 ясно, что взятый по всей длине секущей интеграл
составит:
J ds = s = 2 У а*- —г-sin2?;
(б)
тогда окончательно
w
= 4q(±=p. J* ya*_r2sin*?
dt>.
(5.17)
Для «прогиба» в центре круга, т. е. при г=0, имеем:
Е *~ каЕ ' '
Таким образом, зная а, избавимся от бесконечности, получаемой по
формуле (5.15).

216 КЛАССИЧЕСКИЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ [ГЛ. V
Для «прогиба» точек, лежащих на контуре загруженного круга,
т. е. при г = а, получим:
4(1 — р-2)
wa = —^qa.
Отношение перемещений двух характерных точек составляет:
»!о = " 1,57.
Перемещения точек, лежащих внутри загруженного круга, но не
в центре его, могут быть вычислены на основании (5.17) с помощью
таблиц эллиптических интегралов.
б) Загрузка на площади круга по «полушару». Рассмотрим
случай, когда на площади круга радиуса а расположена нагрузка в виде
шапки (фиг. 92) таким образом, что в любой точке загруженной
__ территории интенсивность нагрузки
пропорциональна ординате полусферы,
имеющей радиус а и основанием
которой служит упомянутая площадь круга.
Иначе говоря, интенсивность
нагрузки в любой точке согласно
обозначениям фиг. 92 записывается так:
q = *УкР;
здесь yKV — ордината круга, имеющего
радиус ау к — коэффициент
нагрузки, т. е.
«■**;
л = 29,
а
(в)
Фиг. 92. Загрузка упругого
полупространства по
«полушару».
а д0 — наибольшая интенсивность
нагрузки (т. е. в центре загруженной
территории); q0 может быть выражена через
общий вес:
Р
Для вычисления перемещения точки С, поступая аналогично
предыдущему примеру, имеем:
w
^Чяг j d* j «ds'
В данном случае интенсивность qy очевидно, нельзя вынести за
знак интеграла.
Выясним геометрический смысл последнего интеграла. Из
рассмотрения фиг. 92 следует, что
fqds = Q9

§ 64] ЧАСТНЫЕ СЛУЧАИ ЗАГРУЗКИ «УПРУГОГО ПОЛУПРОСТРАНСТВА» 217
где Q — площадь эпюры нагрузки на длине 5. Но так как, рассекая
сферу любой плоскостью, мы всегда в разрезе будем получать круг,
то и в данном случае, рассекая нагрузку, в общем изображаемую
«полушаром», мы всегда в разрезе должны получить «полукруг»
(собственно говоря, этой фигурой в разрезе будет полуэллипс). Таким
образом, можем записать:
где к — коэффициент, позволяющий перейти от геометрического
полукруга к «полукругу» в кавычках, т. е. к нагрузке q [см. (в)]. Итак,
/
, us2 q0
^ = 17-
или на основании (б)
qds = ~(ai — r2sin2u)i». (г)
Теперь для полного перемещения точки с имеем:
j
w = 2 1=£ ( Si £ (а°- — г2 sin2 ?) d?.
пЕ J a 2 К iJ '
о
После интегрирования получаем:
w = Wo — рг2} (5.18)
где обозначено
w0=lk1^qtia*)i (5.19)
Р=-^-^о; (5-20)
*х—Ц/. (5.21)
Если радиус изогнутой поверхности граничной плоскости будет
иелик по сравнению с радиусом загруженного круга (а это так обычно и.
*) Выражению (5.19) можно дать такое начертание:
.3(1-^)D
Wq:
\Еа
Сличая последнее выражение с (5.17а), заключаем, что замена нагрузки
«по полу шару» на равномерно распределенную нагрузку по площади того
же круга мало изменяет окончательный результат для прогиба в центре
3 2
пагружения, уменьшая его в —: — ад 1,19 раза.

218 КЛАССИЧЕСКИЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ [ГЛ. V
бывает), то выражение (5.18) можно практически считать уравнением
некоторой сферической поверхности.
в) Обратная задача. Очевидно, можно решать и обратные задачи,
когда задано уравнение изогнутой «дневной поверхности» и требуется
найти уравнение нагрузки, вызвавшей такую деформацию.
Возьмем, например, абсолютно жесткий штамп в виде круглого
цилиндра, вдавливаемого в плоскую грань упругого полупространства.
В этом случае перемещение w для всех точек будет постоянным
по круглой подошве штампа; распределение же давлений не будет
постоянным и должно определиться в результате решения
интегрального уравнения
—~ qdsd's> = w0 = const.
^ату
(5.22)
Решение такого уравнения приводит к результату
Р
2па Y"2 — '2'
где Р—полная нагрузка на штамп, а — радиус штампа и г — радиус
круга, на который действует давление q. Это распределение
неравномерно и наименьшее его значение в центре {г = 0), где
<7mm = ^> (5-23)
т. е. наименьшее давление равно половине среднего давления по
круговой площади подошвы штампа.
На контуре этой площади {г = а) давление становится бесконечно
•большим. В действительности на контуре мы в таком случае штампа
всегда должны иметь явления текучести. Однако эта текучесть будет
иметь местный характер и не будет оказывать существенного влияния
на распределение напряжений в точках, находящихся на некотором
расстоянии от контура круга.
Перемещение штампа выразится формулой
Между прочим заметим, что если подсчитать среднюю величину
деформации в случае равномерного распределения давлений, то
получим величину, мало отличающуюся от перемещения абсолютно
жесткого штампа, а именно:
а
Г w2nr dr
р ъа1 ' аЕ
Еслч предположить, и это более вероятно, что края штампа имеют
некоторое закругление краев, как это показано на фиг. 93, то рас-

§ 65] ВДАВЛИВАНИЕ АБСОЛЮТНО ЖЕСТКОГО ШАРА 219
пределение напряжений у краев штампов может существенно
измениться. Такая сложная контактная задача была поставлена впервые
И. Я. Штаерманом *) и привела его к ответу, представленному
графиком на фиг. 93. В частности, это решение свободно от бесконечно
больших напряжений, не имеющих реального значения. На указанном
Фиг. 93. Распределение напряжений под круглым штампом
в зависимости ог смягчения профиля закраины
(задача И. Я. Штаермана).
графике через k обозначено k = ajb. Само собой очевздчо, что
распределение напряжений (в осчозном у краев) зависит также от
кривизны закраин.
§ 65. Вдавливание абсолютно жесткого шара в упругое
полупространство
Представим себе, что на упругом полупространстве покоится
жесткий шар радиуса R (фиг. 94). Если нет давления на этот шар
и исключить влияние собственного веса, то касание шара с
граничной плоскостью полупространства будет в точке. На расстоянии г
от точки касания, малом по сравнению с /?, зазор между шаром и
i раничной плоскостью может быть, как известно, с достаточным
приближением определен формулой
^1 = 27р (а)
Если к шару будет приложена нагрузка, нормальная к
первоначальной граничной плоскости и проходящая через центр шара, то
*) И. Я. Ш т ае рм ан, Контактная задача теории упругости, стр. 196,
Госгсхиздат, 1949.

220 КЛАССИЧЕСКИЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ [ГЛ. V
вследствие упругости полупространства граничная плоскость
изогнется и шар опустится, как это показано на фиг. 94 (внизу).
Ввиду симметрии деформации относительно оси, совпадающей
с направлением силы, площадка контакта шара с деформированной
граничной поверхностью упругого полупространства будет, очевидно*
представлять в плане круг некоторого радиуса а; закон распределения
давления под шаром не известен, подлежит определению.
Очевидно, эпюра этого давления должна представлять фигуру,,
симметричную относительно оси, совпадающей с силой.
Для вычисления прогиба какой-либо точки с упругого
полупространства, лежащей в пределах площадки контакта, можно провести
рассуждения, аналогичные описанным
в предыдущем параграфе (см. фиг. 92).
Так, проведя через точку с в плане
бесконечно близкие секущие сп и сп1У
вычислим нагрузку, приходящуюся на
бесконечно малую площадку dF,
отстоящую на расстоянии б' от точки с. Если
напряжение смятия у этой площадки
обозначим через #, то элементарная сила
на площадке dF (стр. 215) составит:
dP= qdF = qs dy ds. (6)
Влияние этой элементарной силы на
опускание точки с определится согласно
(5.15) так:
dP(\ — [л2)
nEs '
Фиг. 94. Вдазливание абсолютно
жесткого шара в упругое
полупространство.
или после подстановки (б)
qdVds~^ET-
Влияние на прогиб рассматриваемой
точки с всех элементарных давлений
со всей площади контакта шара и упругого полупространства оце-
нится интегралом
w = kx Г Г q dy ds, (в)
где попргжнему
В выражении (в) неизвестными являются w и функция
распределения давления q. С другой стороны, из чисто геометрических
соображений, поскольку шар не деформируется, следует (фиг. 94),
что
w = w0 — wv (г)

§ 65] ВДАВЛИВАНИЕ АБСОЛЮТНО ЖЕСТКОГО ШАРА 221
где w0 — опускание шара (и одновременно «прогиб» полупространства)
в центре касания, a wt — первоначальный зазор между шаром и
граничной плоскостью. На основании (а) имеем:
w = w0 — р/2, (д)
где обозначено
Pi — 2ЛГ (е)
Уравнение (д) выражает условие, что «упругая поверхность»
полупространства представляет под шаром часть поверхности этого
шара. Объединяя (в) и (д), имеем:
kx j J qdyds = w0 — ^r2. (5.25)
В выражении (5.25) неизвестная функция q входит под знак
интеграла и, следовательно, (5.25) является интегральным уравнением.
Но именно такое же уравнение имелось в предыдущем параграфе,
где, наоборот, была известна нагрузка (она была задана по
«полушару»), а определялся характер изгиба граничной плоскости.
На основании сходства правых частей (5.25) и (5.18) заключаем,
что эпюра распределения давления по площади контакта представляет
«полушар». Таким образом, если давление в центре контакта
обозначим через <7с> т0 на расстоянии г от этого центра давление составляет
«7 = ?o|/l—J. (5-26)
а при г = а (на контуре круга касания) обращается в нуль.
Все выражения предыдущего параграфа (§ 64) целиком относятся
и к данной задаче, т. е.
P=j™»-q0. j
Решая (5.27) относительно a, q0 и w0, имеем:
(5.27)
(5.28)
(5.29)
(5.30)

222 КЛАССИЧЕСКИЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ [ГЛ. V
§ 66. Взаимное давление двух соприкасающихся сферических
тел (упругое смятие шаров)
Представим, что абсолютно жесткий шар радиуса /?j покоится
на упругом теле сферической формы, имеющей очень большой
радиус R2y и в дальнейшем подвергается
действию силы Р (фиг. 95). При
вычислении глубины вдавливания, радиуса
площадки контакта и наибольшего
напряжения смятия под указанным шаром можно
использовать формулы (5.28) — (5.30),
введя вместо прежнего j3j новое
значение (32, определяемое выражением
2/?t ' 2tf2
8, = -^--L ——
Г2 О/?, ' Of?.'
(5.31)
Фиг. 95. Вдавливание
абсолютно жесткого шара
в упругую «почти
бесконечную» сферу.
Последнее выражение вытекает из
зависимости, составляемой для выбираемого
первоначального зазора wt в случае
касания двух сферических тел (фиг. 95):
а именно, в данном случае имеем:
w< =
/-2
_Г2_
2Яа
^— 4- J— — 8 г2
2Rt ^ 9А>. — Р2Г
Таким образом, при вдавливании жесткого шара в «почти
бесконечную» сферу получаем:
а~ V 4 R, + R2И>
(5.32)
%'■
(5.33)
If 6 (/?д + /?2)« л.
У л; /??/?; '
Указанные формулы (5.32) — (5.34) практически могут
употребляться лишь в случае, если радиус площадки смятия а будет весьма
малым по сравнению с радиусом сферы /?2, вследствие чего
последнюю можно при небольших размерах вдавливаемого шара считать
«полубесконечным» телом, закон деформации которого был положен
в основание вывода формул (5.28) — (5.30).
Если теперь представить случай двух упругих «почти
бесконечных» сфер, взаимно надавливаемых силами Р (фиг. 96), т. е. верхнюю-
сферу считать не абсолютно жесткой, а способной деформироваться,,
то в этом случае можно воспользоваться выводами предыдущей

§ 66] ВЗАИМНОЕ ДАВЛЕНИЕ ДВУХ СОПРИКАСАЮЩИХСЯ ТЕЛ 223
задачи (5.32) — (5.34), если ввести изменение в коэффициент,
зависящий от упругих свойств материалов, т. е. вместо kx подставить
где
К &j -f- #2,
(5.35)
*,=
1 2
ъ£л
kn
тг£9 '
Et и pt — упругие характеристики материала верхней сферы; Е2 и
р2 — то же нижней сферы.
Возможность такого простого перехода от формул (5.32) — (5.34)
вытекает из тех соображений, что в данной задаче ввиду
деформаций обеих сфер исходное уравнение деформации (5.25) должно быть
записано в виде
kx \ I qd<?ds-{-k2\ jqdvds = w0— р/-2.
(5.36)
Последнее после введения обозначения (5.35) приводится к виду
(5.25) с заменой kt на k.
Так как при сжатии упругих шаров радиус площадки смятия
оказывается очень малым по сравнению с радиусами самих шаров,
то рассмотренная сейчас задача о
сжатии двух «почти бесконечных» сфер может
быть практически использована и в задаче
об упругом сжатии шаров (задача Герца).
Итак, при сжатии шаров имеем:
а— V 4 * /?, + /?2 ^'
% у кЧ^ + ъ?
/?г/?2
W,
(5.37)
(5.38)
(5.39)
16 /?i/?2
Зная закон распределения давления по
поверхности контакта, можно перейти к
вычислению напряжений внутри шаров,
используя для этой цели (5.13) и применяя принцип
наложения.
Большой практический интерес предста-
иляет нахождение внутри сжимаемых шаров
точек, имеющих большие касательные напряжения.
Исследование этого вопроса *) приводит к выводу, что точка, где
касательное напряжение является наибольшим, лежит на оси z на
мубине, равной примерно половине радиуса поверхности касания.
Фиг. 96. Упругое смятие
шаров.
*) Н. М. Беляев, Сопротивление материалов, стр. 151, Гостехиздат, 1950.

224 КЛАССИЧЕСКИЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ [ГЛ. V
Такую точку и следует рассматривать как самую опасную (в свете
третьей теории прочности) для таких пластичных материалов, как
сталь. Наибольшее касательное напряжение в этой точке (при jx = 0,3)
составляет примерно 0,31 q0.
Из (5.37) — (5.39) следует, что радиус площадки смятия, взаимное
вдавливание и напряжения смятия не находятся в линейной
зависимости от силы Р. При увеличении силы Р напряжения и деформации
шаров возрастают медленнее, чем возрастает сила.
Таким образом, в контактной задаче принятие в основу
исследования линейной связи между компонентами напряжений и
компонентами деформации в каждой точке упругого тела (обобщенный
законом Гука) повлекло за собой нелинейную зависимость между
силой и перемещениями.
Более сложные контактные задачи теории упругости (общий
случай касания поверхностей второго порядка, учет сил трения по
площадке контакта и т. д.) решены в ряде работ советских ученых:
Н. И. Мусхелишвили, А. Н. Динника, Н. М. Беляева, А. И. Лурье,
Л. А. Галина, Д. В. Вайнберга*) и др.
Интересующихся теорией контактных задач отсылаем к капиталь-
кому сочинению чл.-корр. АН УССР проф. И. Я. Штаермана
«Контактная задача теории упругости» (1949), содержащему также много
новых и важных решений, принадлежащих автору.
*) См. его обширную монографию «Напряженное состояние составных
дисков и пластин», Изд-во АН УССР, Киев, 1952 г., где рассмотрено много
важных для машиностроительной практики задач.

ГЛАВА VI
ПРОДОЛЖЕНИЕ (ЗАДАЧИ УПРУГОГО КРУЧЕНИЯ,
ВАРИАЦИОННЫЕ МЕТОДЫ В ТЕОРИИ УПРУГОСТИ)
§ 67. Кручение некруглых сечений. Задача Сен-Венана
При рассмотрении кручения круглого сечения (§ 45) оказалось,
что поперечные сечения поворачиваются как одно целое и при этом
остаются плоскими. При кручении некруглых сечений опыт
показывает, что поперечные сечения стержня непременно искривляются.
Нетрудно было бы показать, что предположение о неискривляемости
таких сечений находится в противоречии с законом о взаимности
касательных напряжений*).
Неприменимость гипотезы плоских сечений в задаче о кручении
некруглого сечения оставалась незамеченной несколько десятков лет
и приводила к явно нелепым результатам (см. стр. 69). Ниже
излагается решение Сен-Венана (1855 г.), которое допускает, что
поперечные сечения при кручении искривляются, но предполагает,
что перемещения точек, лежащих в плоскости поперечных сечений,
происходят так, что каждое поперечное сечение поворачивается как
(дно целое. Нормальные напряжения в поперечном сечении стержня
попрежнему, как и в теории чистого кручения, примем равными нулю.
Применительно к тонкостенным профилям сформулированные выше
предпосылки отвечают экспериментально подтвержденной теории сложного сопро-
швления тонкостенных стержней, разработанной В. 3. Власовым. В теории
R. 3. Власова предполагается неизменяемость контура поперечного
сечения. Неизменяемость понимается лишь в смысле недеформируемости контура
и плоскости поперечного сечения (жесткий контур); перемещения же
отдельных точек контура, а следовательно, и деформация его из плоскости попе-
*) Если боковая поверхность стержня свободна от нагрузки (а это
соблюдается во всех задачах на кручение, где усилия прикладываются в виде
крутящих пар по торцам стержня), то касательные напряжения в поперечном
еечении в точках, примыкающих к контуру сечения, не могут пересекать
гмободную от нагрузки поверхность тела. Иначе говоря, они имеют напра-
и.'к-пие по касательной к соответствующим точкам контура. Таким образом,
ммления, когда касательные напряжения перпендикулярны к вектору, нро-
иедешюму из центра кручения, как это было в случае круглого сечения (как
следствие закона плоских сечений), при кручении некруглых сечений не
ПМссТСЯ.
15 Зак. 3380. Н. И. Безухов

226
ПРОДОЛЖЕНИЕ
|ГЛ. VI
речного сечения, т. е. так называемая депланация сечения, полагаются
возможными. В отличие от теории Сен-Венана, предполагающей
беспрепятственную депланацию сечений (свободное кручение), в теории В. 3. Власова
(см. § 94) изучаются случаи ограниченной (стесненной) депланации,
следствием чего задача осложняется появлением нормальных напряжений в
поперечном сечении.
Совместим ось z с осью кручения (т. е. осью, которая при
кручении остается на месте), а оси х и у расположим пока совершенно
произвольно в плоскости по-
У перечного сечения.
Указанным выше предположениям
о характере смещений при
кручении будет
соответствовать смещение точки М
в направлении,
перпендикулярном к радиусу (фиг. 97):
'^ии^
Фиг. 97. Смещение точки М при кручении
в случае недеформируемости контура
сечения.
?Af, /J'
Х^^Х ММ1 = аг,
'До деформации где а _ угол закручивание
рассматриваемого сечения.
Если стержень имеет
постоянное сечение на всей
длине и подвержен действию
крутящих моментов,
приложенных только по его
концам, то естественно считать, что касательные напряжения во всех
поперечных сечениях распределяются по одному и тому же закону.
Также естественно считать, что угол закручивания сечения будет
пропорционален расстоянию этого сечения от того сечения, по
отношению к которому исчисляются а. Проще всего считать, что один
из концов стержня не закручивается; тогда а = ду, где /—длина
стержня, z — расстояние рассматриваемого сечения от закреплений,
а 0 — угол закручивания одною (свободного) конца стержня
относительно другого (закрепленного). Очевидно, что 0 и / должны в
дальнейшем расчете выступать на правах постоянных величин.
Компоненты смещения и и v запишутся так:
: = — MMj sin a = — & —у,
ч)= ММ
a z
1 cos а = &у-лг.
(6.01)
Компоненты смещения той же точки М вдоль оси г,
характеризующие выход точки М из первоначальной позиции сечения
(депланация точки), нам не известны, и логично предположить, что каждой

§ 67]
КРУЧЕНИЕ НЕКРУГЛЫХ СЕЧЕНИЙ. ЗАДАЧА СЕН-ВЕНАНА
227
точке в поперечном сечении соответствует своя депланация, т. е.
w = f(x,y). (6.02)
Удобно для последующих преобразований переписать (6.02) в виде
да = уф(лг, у), (6.03)
где ф есть неизвестная функция от х и уу учитывающая искривление
(депланацию) поперечного сечения.
С помощью геометрических уравнений теории упругости (2.25)
получаем:
Tw = -g7 + ^ = T(* + ^J, | (6.04)
1*х~~дх"^ oz ~ I \ У * дх)'
Соответственно касательные напряжения запишутся так:
*уг
(6.05)
Все компоненты нормальных напряжений в площадках,
параллельных координатным, как это сказано выше, примем равными нулю, т. е.
оя = ау = ож=0. (6.06)
Подставим (6.05) и (6.06) в статические уравнения (2.02). В
первом и втором уравнениях пропадут все члены, а в третьем останутся
только два члена и уравнение примет вид
дт,;
дх
ду — / L дх* ~^ дуЧ~~ U'
или
дХ* ~^ <^>2
дЦ___{
ду*
(6.07)
Функция, удовлетворяющая условию (6.07), как известно, назы-
нается гармонической, а в данном случае — функцией кручения
Сгн-Венана. В символической записи, указанной ранее (3.26), она
имеет вид
V*cp = 0. (6.08)
Для полного определения функции ср необходимо задание её
граничных значений, т. е. значений на контуре поперечного сечения.
15*

228
ПРОДОЛЖЕНИЕ
[ГЛ. VI
Так как на контуре поперечного сечения, иначе говоря, на внешней
поверхности стержня (исключая торцевые сечения стержня), никаких
внешних сил нет, то касательные напряжения в поперечном сечении
контура сечения должны быть
направлены по касательной к кон-
ТУРУ (фиг. 98). Последнее
требование приводит к соотношению
t а = ЛУ = V
или
iyzdx-
\^<0' = 0>
(а)
Фиг. 98. К написанию граничных
условий при кручении.
ничное условие (а), получим
на контуре уравнение
для
где dx и dy означают
проекции элемента дуги
контура поперечного сечения па
оси х и у.
Подставляя выражения
касательных напряжений (6.05) в гра-
определения значений функции ср
д<р
д<р
j%dy + djdx+xdx+ydy = 0'
(6.09)
Дальнейшие вычисления значительно упрощаются, если взамен
гармонической функции ср ввести так называемую сопряженную
ей (и также гармоническую) функцию <]/, связанную с функцией ср
зависимостями:
ду д<1> ду дф
дх ду ' Ъу дх '
При такой замене (6.10) уравнение (6.09) переписывается так:
(6.10)
-^-dx-\--^-dy — х dx -
-ydy = 0.
Интеграл этого уравнения может быть записан *) в виде
(6.И)
(6.12)
Таким образом, задача о кручении стержня с произвольным
поперечным сечением может считаться решенной, если для
рассматриваемого сечения определена функция ф (или ср), которая внутри
сечения удовлетворяет уравнению Лапласа V26 = 0, а на контуре сечения
х*+у*
принимает значения ^—•
*) В случае многосвязного контура, т. е. имеющего внутренние полости
(которого мы здесь не рассматриваем), пришлось бы включить в (6.12)
еще постоянную интегрирования С.

§ 67) КРУЧЕНИЕ НЕКРУГЛЫХ СЕЧЕНИЙ. ЗАДАЧА СЕН-ВЕНАНА 229
Зная^, можно далее найти функцию <р, определяющую согласно (6.03)
форму поверхности, которую принимает первоначально плоское
сечение после кручения (форму депланации). Вместо функции ф можно ввести
так называемую функцию напряжений Прандтля F (х, у),
связанную с <Ь соотношением
r2 _L v2
F = ^— х у . (6.13)
Удобство введения такой функции заключается в том, что на
контуре функция F = 0, что с очевидностью следует, если подставить
в (6.13) условие (6.12). Внутри контура поперечного сечения
функция F удовлетворяет дифференциальному уравнению
V2F=V2'} — V2(*2+y2W — 2. (6.14)
При пользовании функцией F упрощаются также выражения для
касательных напряжений. Последние взамен (6.05) принимают
начертание:
г Ь dF . rb dF (R л ^
через функцию F крутящий момент Мк записывается так:
Дважды интегрируя (6.16) по частям и имея в виду граничное
условие для F (на контуре F = 0), получаем:
М,
= 2G~ f ( Fdxdy. (6.17)
Эта важная формула принадлежит Прандтлю. Интеграл в правой
чисти (6.17) есть не что иное, как объем, ограниченный
поверхностью F и плоскостью хуу причем пересечением поверхности F с
плоскостью ху является контур поперечного сечения (так как согласно
i раничному условию функция F принимает значение F = 0 именно
па контуре). Следовательно, поверхность F(x, у) возвышается над
поперечным сечением стержня в виде бугра и поэтому называется
бугром напряжений.
Таким образом, выражение (6.17) показывает, что крутящий мо-
мспт Мк равен объему бугра напряжений, увеличенному в 2Gy-pa3.
Из выражения (6.15) следует, что касательное напряжение
м каждой точке поперечного сечения
пропорционально уклону бугра напряжений.

230 ПРОДОЛЖЕНИЕ [ГЛ. VI
Выражение (6.17) иногда записывают в форме
где
Л/К = с|, (6.18)
С=20 Г [Fdxdy, (6.19)
называется жесткостью при кручении.
Выражения для напряжений (6.15) и крутящего момента (6.17)
послужили основанием для так называемой мембранной аналогии Прандтля.
Суть аналогии заключается в следующем: пусть однородная мембрана
постоянной толщины оперта по контуру такого же очертания, как и
поперечное сечение скручиваемого стержня, и нагружена равномерной нагрузкой q,
а по контуру подвергнута постоянному натяжению Т. Оказывается, что
теоретически подсчитанная при указанных условиях нагружения и закрепления
поверхность прогиба такой мембраны будет подобна функции
напряжений при кручении.
На контуре мембраны прогиб равен нулю, так же как на контуре
поперечного сечения функция напряжений F=0.
Исходные дифференциальные уравнения для прогиба мембраны и для
функции напряжений F совпадут полностью, если назначить
4-2G-
Простое доказательство сходства дифференциальных уравнений для
функции F и прогиба мембраны имеется в книге М. М. Филоненко-Бородича
«Теория упругости» (стр. 205—211, М., 1947). В указанной книге имеется много
примеров использования этой аналогии для различных случаев поперечных
сечений стержня, в том числе и для многосвязных.
§ 68. Кручение эллиптического сечения
Пусть поперечное сечение стержня представляет эллипс с
полуосями а и Ь. Так как на контуре эллипса, где ^-j-^== 1, функция
напряжений F должна быть равна нулю, то, очевидно, ее можно взять
в виде , з va \
/7=Л6Н-1)- (6-20)
Коэффициент А определим из условия, что внутри контура
согласно (6.14) должно быть: V2/7 = — 2. Подставляя (6.20) в (6.14),
получаем:
Располагая теперь формулой для Z7, с помощью зависимостей (6.15),
(6.16) получаем:
^=/(Д»+У); (6-22»
2Af„ 2M.
Х«*=-Щ»У> ~>У* = ^ГЬХ- ^23)

§ 69] ДЕПЛАНАЦИЯ ЭЛЛИПТИЧЕСКОГО СЕЧЕНИЯ ПРИ ЕГО КРУЧЕНИИ 231
Полное касательное напряжение равно:
l/"~2 Г Ш* Г** А У'1
и достигает наибольшего значения в концах малой оси (т. е. при
а > bt при v = ± Ь):
2AL
Так как площадь эллиптического сечения Q = тгд£, а полярный
момент инерции того же сечения
то (6.22) можно переписать в виде
M« = G\Srp <6-25>
Эта формула, принципиально применимая только для
эллиптического сечения, широко используется в практике при вычислении
крутящего момента при заданном угле кручения (или наоборот) для
любого плавно очерченного поперечного сечения стержня с учетом
в этой формуле соответственных значений Q и Jp.
§ 69. Депланация эллиптического сечения при его кручении
Подставляя функцию напряжений F для эллиптического сечения (6.20)
в формулу (6.13) и используя (6.21), имеем для функции ф выражение
* = 2 (*« + *») [2а2Ь2 ~ (а2 "" Ь2) (Х2 ~3,2)1- (3)
Из выражений (6.10), связывающих сопряженные функции ср и ф, имеем:
или
* — !&'у+м*)-
Дифференцируя (а) по х и по у, имеем:
дх Ф + Ь*
дЬ а2 — b'z
v.
ду а* + & "
Таким образом,

232
ПРОДОЛЖЕНИЕ
[ГЛ. VI
<р =
а? — №
а* + Ъ*
fdy+f2(x).
(в)
Из сопоставления (б) и (в) заключаем, чю ДО') =h(x) = С, и потому
<р=.
fl2 — b'i
& + V
ху + С.
(г)
Формула (6.03) дает:
w
+£*■"+*)•
Так как депланацией одной из точек поперечного сечения можем
распорядиться по своему усмотрению (в зависимости от граничных
кинематических условий, не стесняющих
деформации кручения
стержня), то, полагая, что центр
кручения (х =у = 0) не депла-
нирует {w =0), получаем, что
С = 0.
Таким образом,
окончательно для смещения вдоль оси z,
т. е. для депланации сечения
имеем выражение
д д2_ ь*
w = — ■ _., , I.) ху.
I a* + b*
(6.26)
Фиг. 99. Депланация эллиптического
сечения при кручении.
Для круглого поперечного
сечения (а = Ь) из (6.26)
вытекает w = 0, т. е. депланации не
происходит (см. § 45).
Используя (6.22),
перепишем выражение для
депланации сечения:
w= mLw ху-(6Л7)
Из (6.27) вытекает, что при кручении эллиптическое
поперечное сечение искривляется, принимая форму
гиперболического параболоида. На фиг. 99 показан эскиз депланации
сечения. Отмечаются следующие любопытные особенности искривления
сечения: точки, расположенные на осях симметрии сечения, не депланируют; если
в первом и третьем квадрантах — депланации положительны, то во втором
и четвертом квадрантах они отрицательны.
Если алгебраическую сумму объемов фигуры, заключенной между
искривленной поверхностью сечения и его первоначальной позицией, назвать
объемом депланации сечения, то объем этот равняется нулю.
Заметим, что равенство нулю объема депланации оказывается
справедливым при закручивании поперечного сечения любой формы. В
аналитической записи последнее утверждение записывается так:
w dF = 0.

§ 70] КРУЧЕНИЕ СЕЧЕНИЯ В ВИДЕ УЗКОГО ПРЯМОУГОЛЬНИКА 233
§ 70. Кручение сечения в виде узкого прямоугольника
Для прямоугольного сечения точное решение в конечной форме
невозможно, и его приходится решать в форме бесконечных рядов
(см. М.М. Фи л оненк о-Бо родич, Теория упругости, стр. 199—205,
М., 1947; Л. С. Лейбензон, Курс теории упругости, стр. 256—259,
М., 1947).
Ограничимся рассмотрением кручения узкой прямоугольной полосы.
В этом случае можно пренебречь влиянием ее.узких сторон на рас-
Фиг. 100. Сечение в виде узкого прямоугольника с
изображением траекторий касательных напряжений (справа) и
«бугра напряжений» (слева).
пределение касательных напряжений и принять, что траектории
касательных напряжений параллельны длинным сторонам прямоугольника
на всем их протяжении (это равносильно принятию бугра напряжений
в форме цилиндра с образующей, параллельной длинным сторонам
прямоугольника) (фиг. 100).
Функцию напряжений примем в виде
Г = л(* + -|)(дг—|). (6-28)
Эта функция на длинных сторонах прямоугольника, уравнения
которых х=--~ и х= — -н-, удовлетворяют условию /7=0 (условия на
коротких сторонах, конечно, при сделанном допущении, не
удовлетворяются, но это несущественно ввиду малой протяженности
коротких сторон в общем периметре сечения).

234 ПРОДОЛЖЕНИЕ [ГЛ. VI
Постоянную Л найдем из условия, что V2/7 = — 2. Это нам даст
Л== — 1. На основании (6.15) получаем:
— __ г 0 dF_2G$
V — U l дх — I Х' )
(6.29)
Наибольшее касательное напряжение будет в серединах длинных
сторон и равно:
*max=Gf£. (6.30)
Из выражения (6.17) имеем:
. = 20 j | Г Fdxdy = 2Gj Г Fhdy = -I О -J-ЬЧ. (6.31)
4
Жк
Подставляя (6.31) в (6.29), получим:
ЗЛ1
к
§ 71. Депланация при кручении сечения в виде узкого
прямоугольника и тонкостенного сечения открытого профиля
Подставляя функцию напряжений (6.28) в (6.13), имеем для
функции <|* выражение
♦--И-тХ— 1)+^- <•>
Выполняя операции, аналогичные указанным в § 69, и
распоряжаясь постоянным интегрирования (принимая ее равной нулю),
получаем:
<? = ху. (6.33)
Соответственно для депланации, согласно (6.03), имеем:
w=rxy. (6.34)
Эскиз депланации согласно (6.34) показан на фиг. 101. Точки,
принадлежащие осям симметрии сечения, не депланируют {w = 0).
Для точек, лежащих на контуре сечения (у= — J, функция кручения
имеет значение
Ь

§ 71]
ДЕПЛАНАЦИЯ ПРИ КРУЧЕНИИ СЕЧЕНИЯ
235
и может быть для этих точек истолкована (фиг. 102) как удвоенная
площадь {векториальная площадь) треугольника АМ0М, образованная
Фиг. 101. Характер депланации при кручении
сечения в виде узкого прямоугольника.
начальным радиусом ЛМ0 (совмещенным с осью симметрии сечения),
подвижным радиусом AM (соединяющим центр сечения с рассматри-
Фиг. 102. К истолкованию функции кручения через
векториальную площадь.
ваемой точкой на контуре) и наружным контуром сечения. Обозначая
такую удвоенную площадь через ш, имеем:
© = О).
В случае тонкостенного сечения открытого профиля (фиг. 103) можно
получить приближенное выражение для функции кручения, если
рассматривать тонкостенный стержень как совокупность прямолинейных. Такая
задача была решена Г. Ю. Джанелидзе [31], показавшего, что при такой
постановке задачи функция кручения совпадает с
векториальной площадью В. 3. Власова, т. е.
ср (5, П) = со (S).
(6.35)
\\ записи (6.35) стержень отнесен к координатам s, n (где 5 — координата,
отсчитываемая вдоль срединной линии профиля, а п — по нормали к ней).

236 ПРОДОЛЖЕНИЕ [ГЛ. VI
Указанное совпадение, строго говоря, имеет место в том случае, если
пренеоречь при вычислении ср членом— по сравнению с единицей (о — радиус
срединной линии).
Напомним читателю из курса сопротивления материалов определение
секториальной площади, или, иначе, секториальной координаты: это есть
удвоенная площадь сектора АМ0М (фиг. 104), образованного начальным,
Фиг. 103. Тонкостенное сече- Фиг. 104. Главная секториальная координата
ние открытого профиля. Оси (со), начальный радиус (ЛМ0), центр изгиба
Ох и Оу — главные централь- (А). Оси Ах и Ау параллельны главным
ные. центральным осям инерции.
подвижным радиусами и срединной линией сечения. Заметим, что направление
начального радиуса AMq выбирается так, чтобы
£ц>= Г <»dF=0. (6.36)
F
Положение полюса А (это, оказывается, так называемый центр изгиба)
выбирается так, чтобы
Г усо dF = 0; Г хм dF = 0. (6.37)
F F
§ 72. Кручение тонкостенного замкнутого сечения
Пусть поперечное сечение закручиваемого стержня представляет
собой замкнутое сечение, толщина стенок которого может быть
переменной, меняющейся плавно, но остающейся всюду достаточно малой
(фиг. 105). Строгое решение для такого двухсвязного контура весьма
сложно, однако благодаря тонкостенности сечения оно может быть
выполнено чрезвычайно просто и достаточно точно.
Для решения удобно использовать представление функции
кручения F как «бугра напряжений», а касательные напряжения
интерпретировать как уклоны такого бугра. Но так как в пределах внутренней

§ 72] КРУЧЕНИЕ ТОНКОСТЕННОГО ЗАМКНУТОГО СЕЧЕНИЯ 237
полости, не заполненной материалом, напряжения отсутствуют, то
в «бугре напряжений» над пространством внутренней полости должна
быть плоскость, параллельная плоскости сечения. Именно при этом
условии уклоны бугра напряжений в упомянутой области будут равны
нулю (а следовательно, нулю будут
равны и касательные напряжения).
Иначе говоря, «бугор напряжений»
должен иметь вид, указанный на
фиг. 106, а.
Если бугор напряжений
истолковать в смысле мембранной аналогии,
то по жесткому контуру,
совпадающему по очертанию с наружным
контуром заданного сечения, надо
прикрепить мембрану, которая по Фиг. 105. Тонкостенное замкнутое
другому контуру, совпадающему по сечение,
очертанию с внутренним контуром
заданного сечения, должна быть соединена с абсолютно жесткой
пластиной (в плане такая пластина будет в точности повторять
внутреннюю полость заданного сечения). Далее, надлежит подвергнуть
мембрану равномерному давлению, однако для того чтобы жесткая
Фиг. 106. «Бугор напряжений» при кручении
тонкостенного замкнутого сечения (я), траектории касательных
напряжений (б).
пластина могла перемещаться лишь поступательно, к ней надлежит
приложить также специальные моменты (или упомянутое выше
давление осуществить специально неравномерно в пределах пластины), чтобы
воспрепятствовать повороту.

238
ПРОДОЛЖЕНИЕ
[ГЛ. VI
Так как искривление мембраны будет незначительным, то можно
считать, что уклон мембраны в пределах каждого размера 8 (т. е.
в пределах толщины стенки заданного сечения) не меняется.
Ввиду того что толщина 8 мала, пренебрегая искривлением
поверхности «бугра напряжений», в пределах каждого размера 8 и обозначая
в пределах внутренней полости сечения ординату функции напряжений
через Л, принимаем постоянным уклон этой функции в направлении к
(нормальном к срединной линии профиля сечения); он составит:
А
но согласно (6.15) это одновременно есть величина касательного
напряжения, т. е.
^п^Ш^Т* (6-38)
которое также надлежит принять постоянным в направлении п в
пределах рассматриваемой толщины 8. Выражение (6.38) можно переписать
и так:
tS23 = A = const. (a)
Левую часть равенства (а) можно истолковать как сумму
касательных усилий с площади прямоугольника, один размер которого (в
направлении п) равен толщине стенки сече шя 8, а другой размер (в
направлении s) вдоль средней линии контура равен единице. Обозначая эту
сумму через Т и называя потоком касательных напряжений,
выражение (а) можем записать в виде
T=iszo = const. (6.39)
и прочитать в такой редакции: поток касательных напряжений при
кручении тонкостенного плавного замкнутого профиля, отнесенный
к средней линии контура, является величиной постоянной для всех
точек этого контура.
Так как толщина стенок 8, если она переменная, изменяется по
условию задачи плавно вдоль средней линии контура сечения, то уклон
бугра напряжений в направлении 5 будет пренебрежимо мал, и потому
dF
т- = -^ = 0-
Таким образом, при кручении тонкостенного замкнутого профиля
в сечении возникают касательные напряжения, которые для всей
совокупности точек, лежащих на направлении я, параллельны касательной
к средней линии контура в том месте, где проведена нормаль п
(см. фиг. 106, 5, в).
Наибольшее касательное напряжение будет в самом «узком горле»
сечения (т. е. там, где толщина стенки сечения наименьшая) и

§ 73]
ПОНЯТИЕ О СТЕСНЕННОМ КРУЧЕНИИ
239
должно вычисляться по формуле
(6.40)
Срединная
линия
Для вычисления потока Т составим уравнение равновесия между
внешними и внутренними силами. Для этой цели возьмем произвольную
точку О (фиг. 107) (не обязательно центр кручения, и для
дальнейшего не имеет значения, взять ли ее внутри сечения или вне его),
относительно которой и составим сумму
моментов.
На элементарную площадку
сечения 8 ds приходится касательная сила
7^8 ds — Tds, которая относительно
точки О дает момент Tdsp, где р—длина
перпендикуляра, опущенного из точки О
на направление касательной s.
Обозначая произведение рds
(очевидно, представляющее удвоенное
значение секториальной площади, дважды
заштрихованной на фиг. 107) через 2^ш,
можем уравнение равновесия между крутящим моментом и внутренними
силами записать в виде
AJK = J Tpds==2T Г rf<o.
Фиг. 107. К выводу
формулы (6.43).
Очевидно, что интеграл, взятый по всей замкнутой средней линии
контура, составит фигуру ограниченную той же средней линией, т. е.
do* •
(6.41)
Эга площадь на фиг. 107 заштрихована. Таким образом,
Г =
и на основании (6.40) имеем:
2<о '
Mv
2<о5„
(6.42)
(6.43)
§ 73. Понятие о стесненном кручении
В §§ 67—71 были рассмотрены задачи о кручении стержня
постоянного сечения, причем предполагалось, что во всех поперечных
сечениях стержня возникают только касательные напряжения, что
закон распределения их во всех сечениях одинаков; наконец, было
сделано предположение (вытекающее, впрочем, из предыдущих), что
нее поперечные сечения беспрепятственно и притом одинаково депла-
ипруют, так как в выражении (6.03) координата z отсутствует. Этот

240
ПРОДОЛЖЕНИЕ
[ГЛ. VI
случай кручения называют кручением по Сен-Венану; будем его в
дальнейшем именовать случаем нестесненного кручения.
В практике имеется много случаев, когда свободной депланации
сечений оказывается противодействие, полное или частичное.
Примером может служить стержень, один из концов которого
наглухо закреплен в стене, а к другому свободному концу приложена
крутящая пара (фиг. 108). В этом случае поперечное сечение,
совпадающее с опорным
закреплением депланировать не может
. {абсолютное стеснение искри-
* влению плоскости сечения).
Поэтому в таком сечении
непременно возникнут нормальные
напряжения, благодаря которым
сечение и может остаться
плоским. Сечение, совпадающее со
свободным концом, наоборот,
находится в условиях
нестесненной депланации. В этом сече-
Фиг. 108. Пример стесненного кручения. нии н0Рмальных напряжений
нет, имеются только
касательные напряжения, распределенные согласно (6.05) или (6.15) и в
совокупности составляющие крутящую пару.
Все прочие поперечные сечения находятся в промежуточных
условиях относительного стеснения, и в них также появятся нормальные
напряжения, которые по длине стержня будут убывать от опорного
сечения к свободному.
Нормальные напряжения в поперечных сечениях при стесненном
кручении имеют важную особенность: они в каждом сечении
составляют систему взаимно уравновешенных сил. Это
очевидное утверждение вытекает из условий равновесия, так как по
одну сторону от любого поперечного сечения из внешних воздействий
имеется только крутящая пара, которая вполне уравновешивается
касательными напряжениями в рассматриваемом сечении.
Самоуравновешенность нормальных напряжений при стесненном
кручении является также следствием развитого в § 68 положения, что
объем депланации сечения равен нулю. В самом деле, в задачу
нормальных напряжений, возникающих, например, в опорном поперечном
сечении, входит ликвидация депланации сечения, которая была бы при
отсутствии стеснения. Это означает, что тем точкам сечения, которые
стремятся выйти из плоскости сечения в ту или другую сторону,
нормальные напряжения должны оказать сопротивление. Поясним это
на примере закручивания эллиптического сечения.
Так как вся площадь эллиптического сечения при его
депланации (§ 69) делится на четыре одинаковых по площади части, из которых
две части депланируют в одном направлении, а две остальные — в дру-

§ 73] ПОНЯТИЕ О СТЕСНЕННОМ КРУЧЕНИИ 241
гом, то отсюда вытекает, что сумма нормальных усилий, возникающих
в сечении и направленных в одну сторону, должна равняться сумме
нормальных усилий, направленных в другую сторону.
Примерный характер распределения нормальных напряжений,
возникающих в прямоугольном сечении при стесненном кручении, показан
на фиг. 109 и сводится, таким образом, к «четверке сил» (Я, —Я,
а) б)
Фиг. 109. Характер распределения нормальных
напряжений в поперечном сечении в случае стесненного
кручения (а), статически эквивалентная нормальным
напряжениям четверка сил (б) или бипары (в и г).
Я, —Я), которую можно истолковать или как две взаимно
уравновешенные «бисилы» (Я, Я и — Я, —Я) или как две взаимно
уравновешенные пары {Рсх, —Рсх или Рсуу —Pcp)i составляющие «бипару»
и вбобще ее можно рассматривать как обобщенную продольную силу,
статически эквивалентную нулю. Такую обобщенную силу, по
терминологии В. 3. Власова, называют бимоментом *).
Случай стесненного кручения не обязательно связывать с наличием
опорных закреплений, препятствующих свободному искривлению
сечений. Рассмотрим случай, когда стержень с двумя свободными концами
подвержен на этих концах действию двух одинаковых по направлению
и величине скручивающих моментов, уравновешенных в среднем сечении
*) Для указанного бимомента можно ввести условную количественную
характеристику, а именно перемножить момент пары Рсх (или Рсу) на
расстояние между плоскостями действия этих пар, т. е. на су (или сх). Тогда
> помянутый бимомент запишется так: В = Рсхсу. Очевидно, что чем больше
указанный бимомент, тем больше будут и самые нормальные напряжения
и поперечном сечении.
16 Зак. 3880. Н. И. Безухо*

242
ПРОДОЛЖЕНИЕ
[ГЛ. VI
скручивающим моментом противоположного направления удвоенной
величины (фиг. ПО). В этом случае ввиду симметрии, очевидно,
среднее поперечное сечение искривляться не может. Таким образом,
каждая половина рассматриваемого сейчас стержня будет находиться
в условиях, сходных с рассмотренным ранее (фиг. 108). Заметим
попутно, что эпюра крутящих моментов для случая, показанного
на фиг. 110, должна иметь уступ в средней части. Это означает,
что депланации левой и правой частей бруса, если бы они были
разделены в среднем сечении, протекали бы в разных направлениях;
условие же неразрывности деформаций бруса вынуждает левую и
2М правую части пойти на ограниче-
М ^—^ м ние (стеснение) депланации в
среднем сечении бруса.
QaUA-
Вообще при неравномерном
кручении (когда крутящие моменты
по длине стержня меняются) бруса
постоянного сечения (исключая
Фиг. ПО. Среднее сечение стеснено пР°стейший случай—круглое по-
к проявлению депланации. перечное сечение) всегда будет
некоторая стесненность в
депланации сечения, всегда будут в поперечных сечениях возникать
нормальные, взаимно уравновешенные напряжения.
Нормальные напряжения, статически эквивалентные нулю, возникнут
и в случае постоянного по всей длине стержня крутящего момента,
но если сам стержень будет иметь по длине переменное (и отличное
от круглого) сечение. В последнем случае тенденции каждого сечения
к свободной депланации были бы различны, но благодаря требованию
совместности деформаций, сечения вынуждены иметь согласованные
между собою депланации.
Точное решение задачи о стесненном кручении должно быть весьма
сложным. Ниже, в § 91, излагается приближенное решение задачи
о стесненном кручении стержня эллиптического сечения.
Большую практическую важность расчет стесненного кручения
имеет главным образом для тонкостенных стержней так называемого
открытого профиля (швеллер, двутавр, уголковое сечение и т. п.) и
в меньшей степени для замкнутых профилей (коробчатое сечение,
трубчатое).
Теория сложного сопротивления (стесненное кручение, изгиб с
кручением и т. п.) тонкостенных стержней открытого профиля была
с исчерпывающей полнотой разработана в СССР В. 3. Власовым,
удостоенным Сталинской премии.
Применительно к замкнутым профилям теория была разработана
A. А. Уманским. Ниже, в § 92, даны основные результаты прикладной
теории сложного сопротивления тонкостенных стержней в изложении
Г. Ю. Джанелидзе, из которой легко получить результаты теории
B. 3. Власова и теории А. А. Уманского.

§ 74] РАЗЛОЖЕНИЕ ТЕНЗОРНОГО ПОЛЯ НАПРЯЖЕНИЙ 243
§ 74 *). Разложение тензорного поля напряжений
на основное и корректирующее (метод П. Ф. Папковича)
Подобно тому как общий интеграл неоднородного
дифференциального уравнения может быть представлен в виде суммы двух решений:
общего интеграла однородного уравнения (т. е. когда правая часть
уравнения, характерная для данной конкретной задачи, отсутствует)
и любого частного решения заданного неоднородного уравнения, так
и общий интеграл дифференциальных уравнений теории упругости
может быть представлен аналогичной суммой частного и общего
решений.
Пусть на поверхности тела заданы компоненты внешних сил рХНУ
Руч и Pzv Желая разыскать соответствующие этой внешней
нагрузке тела напряжения внутри тела, разыщем вначале какое-нибудь
частное решение уравнений равновесия:
дз~
d*xij , foxz
дх
dz
Ьг+^+^=°>
ух
ду
да,
di
дх
dtz~
ду
dz
zy
дг
до.
дх
ду
уг ' гР = о, \
dz
00
удовлетворяющее на поверхности тела граничным условиям:
Пусть это решение есть
0<°>, а<°>. т(°).
(б)
а<°),
у '
(в)
Если указанная система напряжений случайно удовлетворит также
и уравнениям неразрывности деформаций, то найденное частное
решение уравнений (а) и (б) и будет искомым точным решением задачи.
Если совокупность функций о<£), о<°), ..., т^ не удовлетворит
условиям неразрывности деформации, то для нахождения истинного
решения задачи необходимо найти ряд таких частных решений
*) В §§ 74 и 75 излагается один из приближенных методов решения
.♦лдач теории упругости и потому формально здесь нет классической задачи
•ичфии упругости, но в группе различных приближенных методов этот
метод может считаться классическим.
16*

244
ПРОДОЛЖЕНИЕ
[ГЛ. VI
однородных уравнений:
да,
Тх
д*„
"1" fy "1" Яг ~"и».
ух
до„
dz
dz
yz
дх
ду
dz.
•zy
дх
ду
dz
dcz
Jz
= 0,
(г)
)
которые удовлетворяют на поверхности тела отсутствию внешних
нагрузок, т. е.
W+ v/*~bv = °>
Пусть такими решениями являются *):
з«>.
zx'
где /= 1, 2, 3,
(Д)
И
Тогда истинное решение задачи можно представить в форме
0 =а<°>-|-У1Л.а<')
2/ У 1 Л г у >
— т(о) 4-УЛ т<1'>
за; ' ^J t газ'
(6.44)
где At — некоторые, пока неопределенные константы.
Варьируя значения величин Аь получаем возможность изменять
напряженное состояние тела, не нарушая условий равновесия (а), (б).
Для определения этих констант подставим (6.44) в выражение
потенциальной энергии деформации
и заметим, что так как действительному напряженному
состоянию в упругом теле соответствует минимум
потенциальной энергии деформации, то искомую
комбинацию параметров Аь при которой будут удовлетворены условия
сплошности, можно разыскать из системы уравнений
Ц-=0 при 1=1, 2, 3, ..., п. (6.45)
*) Очевидно, что каждое такое частное решение соответствует
самоуравновешенному напряженному состоянию (т. е. возбужденному без
участия внешних поверхностных нагрузок).

§ 74} РАЗЛОЖЕНИЕ ТЕНЗОРНОГО ПОЛЯ НАПРЯЖЕНИЙ
245
Таких уравнений (6.45) можно выписать столько, сколько
неизвестных А4 будет сохранено в решении (6.44). Так как точное
решение потребует составления и решения бесконечного множества
уравнений (6.45), что практически невозможно, то приходится
ограничиться небольшим количеством членов ряда в (6.44).
Степень точности такого «укороченного» решения зависит
от того, насколько удачно выбрано частное решение (в) и насколько
удачно выбраны из всего множества решений (6.44),
соответствующих различным Аь те несколько, которые удержаны в (6.44).
Иногда может оказаться достаточным в (6.44) сохранить только
первый член. Компоненты напряжений, составляющие частное
решение (в) и входящие первыми слагаемыми в правую часть (6.44),
будем называть компонентами основного тензора напряжений
в данной точке; компоненты же напряжений, составляющие общее
решение (е) и входящие вторыми слагаемыми в правую часть (6.44),
по терминологии М. М. Филоненко-Бородича будем называть
компонентами корректирующего тензора напряжений в той же точке.
В символической записи выражения (6.44) можно кратко записать
так:
* напр === 'напр "Г" *напр« (0.4О)
Так как совокупность тензора напряжений для всех точек тела
составляет тензорное поле напряжений, последнее, по
П. Ф. Папковичу, представляется составленным из
основного тензорного поля напряжений и
корректирующего тензорного поля напряжений.
Примечание. Читателю, знакомому со строительной механикой,
указанное выше изложение в какой-то степени напоминает классическое построение
расчета статически неопределимых стержневых систем по так называемому
«методу сил», энергетическое обоснование которого также сводилось
к отысканию именно таких значений «лишних неизвестных», при которых
потенциальная энергия деформации системы оказывается минимальной.
Сходство еще более усиливается, если представить себе расчет статически
неопределимой системы (например, фермы), где за «лишние»
неизвестные взяты внутренние усилия (например, усилия в стержнях), иначе говоря,
если «основную», т. е. статически определимую, систему получать из
заданной не путем отбрасывания элементов, связей и т. п., а путем
перерезания их и т. д.
В этом случае применяемые в строительной механике так называемые
«единичные состояния» представляют обычно в з а и м н о
уравновешенную систему усилий (т. е. для их существования не требуется
наличия внешних сил на контуре системы, например, опорных реакций и т.п.).
Далее, не исключается и такая возможность выбора «основной» системы,
при которой напряженное состояние последней от заданной внешней
нагрузки, даже без участия «лишних» неизвестных, будет состоянием
действительной (не основной, не преобразованной, а именно — заданной) системы.
Это будет тогда, когда за «лишние» неизвестные приняты усилия в тех
связях, которые в заданной системе случайно оказываются неработающими.
В последнем случае расчет статически неопределимой системы
ограничивается только расчетом статически определимой, т. е. «основной» системы.

246
ПРОДОЛЖЕНИЕ
[ГЛ. VI
Такому счастливому случаю в теории упругости соответствует, очевидно,
назначение такого частного (основного) решения (в), при котором оно
случайно оказывается и действительным решением задачи.
Указанные выше для строительной механики «единичные»
самоуравновешенные состояния соответствуют в методе П. Ф. Папковича
самоуравновешенному корректирующему тензорному полю.
После ссылок на такие аналогии читатель, естественно, поставит
вопрос: не возможно ли в таком случае перенести в теорию упругости,
именно в метод П. Ф. Папковича, все наиболее эффективные современные
методы расчета статически неопределимых систем (канонические
уравнения деформаций, способ ортогонализации взаимно нулевых эпюр и т. п.).
Ответ на этот вопрос может быть дан только положительный. Горизонты
использования указанной аналогии чрезвычайно широкие и
увлекательные [18], [81].
§ 75. Напряженное состояние упругого параллелепипеда
при заданных нагрузках на его гранях
(задача М. М. Филоненко-Бородича)
Указанная в заглавии задача, когда нагрузки, приложенные на
гранях параллелепипеда, предполагаются любыми (но
уравновешенными по всем граням, вместе взятым), представляется особо трудной;
наличие же общего ее решения открывало бы весьма широкие
практические приложения. В частности, была бы тем самым
аналитически решена задача о практической границе локальности эффекта
самоуравновешенных сил (принцип Сен-Венана и др.). Не безинте-
ресно отметить, что Ляме, придававший этой теме большое
значение, сравнил ее значимость с классической проблемой в астрономии
о трех мировых телах, а французская Академия наук в 1846 г. и
затем в 1858 г. объявляла премию за решение указанной выше
задачи. Однако полное решение ее не было известно до
последнего времени.
Ниже излагается оригинальное решение задачи, принадлежащее
М. М. Филоненко-Бородичу *), позволяющее получить результаты,
сколь угодно близкие к точным.
Следуя П. Ф. Папковичу, тензор напряжений строим в виде
суммы двух тензоров: частного тензора и корректирующего тензора,
т. е.
'напр== ' напр |~ ' напп* (Ь.47)
Первому тензору ставим требование, чтобы его компоненты
удовлетворяли всюду в области тела уравнениям равновесия (2.02) и
удовлетворяли граничным условиям (2.05). Компонентам
корректирующего тензора ставим условия, чтобы они удовлетворяли
дифференциальным уравнениям равновесия, а во всех точках поверхности
тела давали отсутствие нагрузки.
*) М. М. Филоненк о-Б ородич, Об одной системе функций и ее
приложениях в теории упругости, ПММ, т. X, вып. 1, 1946.

§ 75] НАПРЯЖЕННОЕ СОСТОЯНИЕ УПРУГОГО ПАРАЛЛЕЛЕПИПЕДА 247
Частный тензор (автор его называет «основной тензора)
приходится выбирать особо для каждой категории задач в зависимости от
характера заданных нагрузок. Корректирующий тензор для
параллелепипеда можно построить один раз навсегда с помощью
специальных функций М. М. Филоненко-Бородича, названных им функциями
косинус-биномов, именно:
,. тпх (т + 2) кх . л 1 п
P.»(*\=cos—; cosv—Ц-^ (т = 0, I, 2,
т (х)
э
п (у)
1 Р(г) — cos ~й COS й
1?)
^^=cos^_cos^L±2Kv (Л = 0э 1, 2,
(Р = 0, 1, 2, .
.),}(6.48>
I
где dy k, h — длины ребер заданного параллелепипеда (фиг. 111),
параллельных осям лг, у, z.
Эти функции обладают следующими важными свойствами.
ГГ,
,i!'\|i
Фиг. 111. К задаче М. М. Филоненко-Бородича.
а)" Функции эти вместе со своими производными обращаются
в нуль на концах соответствующих интервалов (0, d), (О, k) и (0, /г).
б) Системы функций (6.48) являются полными и замкнутыми на
соответствующих интервалах (0, d), (О, k) и (0, h).
Таким образом, если компоненты напряжений будут выражаться
суммой произведений из указанных выше функций или из
произведений их производных, то такие выражения будут для точек,
принадлежащих граням параллелепипеда, давать нулевые значения. Иначе

248
ПРОДОЛЖЕНИЕ
[r;i. vi
говоря, это будут компоненты именно корректирующего тензора
напряжений, при котором все шесть граней параллелепипеда
свободны от нагрузок.
Для построения основного и корректирующего тензоров автор
использует функции напряжений Максвелла ov «a и ср3 (3.74),
согласно которым
==d%i , дЦ2 _ д2ул
1+
дуз г ^2 > *ху— дхду э
2 dxt'T'dy*' с**~~ dzdx* J
Для функций напряжений принимаются выражения:
ь = 2 2 2 4-.Л (•*) р« (у) р* (*). )
?*=2 2 2 л»<«*р- W p» Cv) pp (*)«
% = 2 2 2 с™прр«> (*) р« Cv) />, (*)•
(6.49)
(6.50)
Компоненты корректирующего тензора напряжений запишутся при
этом так (для краткости письма аргумеьты лг, у, z в обозначениях
функций Р опускаем):
о =VVV(C Р Р"Р А-В Р Р Р")
х JZj Za £а V wmjo w п р ' w«;; ш п р>>
т п р
а = \* \^ Wi4 PP Р " —I— С Р "Р Р )
у Zl 2* Z*y тпр ш п р* тпр т п р'у
т п р
а* = 2 2 2 (ВмнрРтРпРр + АтпрРтРпРр^ \ (6.51)
тпр •
VVVC Р' РгР т = VVV^l Р Р'рг
*ху £dZl£i тпр тпр' yz jL* £J jL* тпр m п р>
т п р т п р
~ w v я рг р рг
^zx jL± jL± jL* тпр тпр'
т п р
В силу граничных свойств косинус-биномов все компоненты (6.51)
на поверхности тела дают отсутствие нагрузки.
Число произвольных коэффициентов в формулах (6.51) в три раза
превосходит число постоянных А{ в формулах (6.44) П. Ф. Папко-
вича, и в этом смысле они являются более общими; однако в
практических расчетах М. М. Филоненко-Бородич рекомендует положить
Л — R
**тпр ^тпр '
■'тпр

§ 75} НАПРЯЖЕННОЕ СОСТОЯНИЕ УПРУГОГО ПАРАЛЛЕЛЕПИПЕДА 249
и за этот счет взять большее число членов в суммах (6.51),
увеличивая порядок вводимых биномов.
В статье автора*) дана иллюстрация указанного метода на
нескольких примерах, в том числе рассмотрен параллелепипед, к
которому на грани z = О и z = h приложены равные и
противоположно направленные нормальные нагрузки, распределенные по закону
q = F(x, у). Тогда основной тензор может быть построен весьма
просто: достаточно положить <з° = F(х, у), а остальные компоненты
приравнять нулю; уравнения равновесия при этом тождественно
удовлетворены.
Общий тензор получим, складывая основной тензор с
корректирующим тензором (6.51); все компоненты его совпадут с (6.51) за
исключением ог, для которого получим:
°з== ' \ху У) I 2j 2j 2j {ВтпрРтРпРр "Г ^тпр РтРпРр)'
т п р
Общий тензор будет удовлетворять дифференциальным уравнениям
и всем граничным условиям задачи при отсутствии объемных сил;
кроме того, в зависимости от числа взятых членов в суммах (6.51)
он содержит желаемое число свободных параметров Amnpi Bmnp, Стпр.
Согласно началу наименьшей работы эти параметры определятся из
условия
дЭ дЭ
vAmnp v"mnp v^mnp
где потенциальная энергия Э определяется согласно (3.17).
В цитируемой выше статье М. М. Филоненко-Бородича дано
числовое решение для случая, когда по верхней и нижней граням действует
нагрузка, распределенная по закону
ч = F(х'У^ = ж0_cos пг)i1 -cos nr)•
Поверхность нагрузки имеет колоколообразную форму (фиг. 1124
Выполнен числовой подсчет для случая d=l, k=l, /г =2, Р=1;
подсчитаны напряжения в сечении z=\. Эпюра напряжений для этого
сечения показана на фиг. 113 в первом приближении (когда в
формулах корректирующих функций были приняты и
ограничились /я = п== р = 0), а на фиг. 114 — во втором приближении,
когда в формулах (6.51) была добавлена следующая пара косинус-
биномов.
*) См. [119].

250
ПРОДОЛЖЕНИЕ
[ГЛ. VI
Примечание. Изложенный выше метод по своей идее может найти
применение и в том случае, когда заданное тело будет иметь другую форму,
отличную от параллелепипеда (цилиндр и т. д.), и даже тогда, когда это тело
Фиг. 112—114. Распределение напряжений в сечении z = 1 в первом (фиг. 113)
и втором (фиг. 114) приближениях (задача М. М. Филоненко-Бородича).
будет не сплошное, а имеет внутреннюю полость. Очевидно в зависимости
от формы тела необходимо в каждом случае подыскать надлежащее
начертание функций косинус-биномов, которые для наружных и внутренних
границ тела давали бы нулевые значения этих функций и их производных.
Замечания о других методах приближенного решения
уравнений теории упругости. Понятие о методе
Галеркина
В предыдущих параграфах (§§ 74 и 75) основными неизвестными
являлись напряжения и потому вспомогательными были коэффициенты при
варьируемых функциях для напряжений. В этом смысле такой приближенный
(вариационный) метод может быть отнесен к разновидности метода сил.
Очевидно, основными неизвестными можно принять и перемещения,
тогда вспомогательными неизвестными будут коэффициенты при
варьируемых функциях для компонентов перемещений.

§ 75] НАПРЯЖЕННОЕ СОСТОЯНИЕ УПРУГОГО ПАРАЛЛЕЛЕПИПЕДА 251
Например, можно для компонентов упругого перемещения принять
выражения:
i — m
и = и0 + 2 a*fi (*> -У. *).
г = 1
t = l
г-т
(6.52)
где
-произвольные постоянные;
< = i
Л|, rt-2, . . ., #ир
clt г2, ..., ст —
/i. /s. •••./«,.
ft. ?2 «Си.
'r-t. +2 ^m
(6.53)
— известные (назначаемые) функции координат х, у, z; u0 (x,y, z), v0 (x,yy z),
W()(xi У> z) — также известные функции координат, но не содержащие
произвольных постоянных.
Вид функций fb /2, ..., cph <р2, ..., ф,, ф21 ..., очевидно, надо выбрать
так, чтобы согласно (6.52) были удовлетворены геометрические связи
(граничные условия в перемещениях).
Дальнейший ход рассуждений должен быть сходен с изложенным
в §§ 74 и 75, т. е. надлежит использовать начало наименьшей работы.
Начертание для потенциальной энергии в таком случае следует принять
выраженным не через компоненты напряжения, а через компоненты деформации (3.12в),
а последние в свою очередь выразить через компоненты смещений согласно
известным геометрическим уравнениям (2.25). Такой способ приближенного
решения може-т быть отнесен к разновидности метода перемещений.
Совершенно очевидна возможность смешанного метода, когда
назначаются приближенные начертания для некоторых (не всех) компонентов
перемещения и некоторых компонентов напряжений.
Не раскрывая содержания этих методов (обстоятельное изложение
читатель может найти в интересной книге Л. С. Лейбензона «Вариационные
методы решения задач теории упругости», М. — Л., 1943), остановимся кратко на
одной форме приближенного метода, известного в литературе как «метод
Галеркина», нашедшей широкое применение в различных областях техники
(теория упругости, строительная механика, гидро- и аэромеханика).
Исходными уравнениями этого метода являются следующие:

252
ПРОДОЛЖЕНИЕ
[ГЛ. VI
где /= 1, 2, 3, ..., т\ /г-, cpt-, ^. — определяются согласно (6.53), а
интегрирование распространяется на весь объем упругого тела.
При пользовании (6.54) необходимо компоненты напряжений выразить
согласно (3.02) через компоненты деформаций, а последние согласно (2.25)—
через компоненты смещения, которые в свою очередь принимаются
согласно (6.52).
Подставляя в (6.54) поочередно /=1, 2, 3, ..., т, в итоге получим
систему линейных уравнений для определения постоянных коэффициентов
(аь аъ ..., Ьь Ь2, ..., clt с2» • ••); число таких уравнений будет равно числу
постоянных.
Если функции /lf /2, ..., cp1t cp2, ..., фь ф2> ... выбраны так, чтобы были
удовлетворены не только геометрические связи, но и статические граничные
условия (хотя условия неразрывности и не удовлетворяются), то метод Га-
леркина становится самым эффективным вариационным методом; для него
положительно разрешается вопрос о сходимости решения, т. е. при
увеличении числа варьируемых функций до бесконечности получаем точное
решение задачи.
Доказательство (6.54) можно дать очень простое; выражения,
заключенные в скобки, как известно, представляют левые части уравнений
равновесия (2.02) и сами по себе уже равны нулю (если, конечно, начертания для
напряжений приняты точными). По этой причине умножение таких скобок
на любую функцию, например на fjdxdydz и т. п., и последующее
интегрирование по любому объему не должны изменить результата, т. е. в правой
части останутся нули.
Если функции и, v и w выбраны так, что они оказались (случайно или
преднамеренно) интегралами уравнений Ляме (3.27), хотя граничные условия
и не удовлетворяются, то согласно предложению Трефца может оказаться
удобной следующая система уравнений для нахождения коэффициентов:
J J (°xl + ~хУ™ + ^xz*1 — PxJfi d* = 0,
J J (*yaf + *y™ + tyzn —PyJ cp?: dz = 0,
J J (W + V + °*л — p„) b{ dz = 0,
где также /=1, 2, 3, ..., т.
Интегрирование выполняется по всей поверхности упругого тела (de —
элемент поверхности тела).
Выражения, заключенные в скобки левых частей уравнений (6.55),
представляют собой перенесенные в левую часть граничные условия (2.05), и
потому эти выражения равны нулю.
В некоторых задачах (кручение и изгиб авиационных профилей и т. п.)
оказался эффективным своеобразный смешанный метод, разработанный
Л. С. Лейбензоном, М. Конторовичем и др. Он состоит в том, что искомые
функции представляют в виде произведения двух функций, из которых одна—
известная, причем подбираемая так, чтобы частично удовлетворить граничные
условия; другая же функция — неизвестная — должна зависеть от меньшего
числа переменных и подлежит определению при помощи вариационного
уравнения.
Упомянем также о существовании оригинального вариационного метода,
состоящего в требовании, чтобы взятый по всей поверхности упругого тела
интеграл от квадратичной ошибки при удовлетворении граничных условий
имел наименьшее значение, либо чтобы взятый по всему объему упругого-
тела интеграл от квадратичной ошибки при удовлетворении уравнений
упругого равновесия (Ляме) тоже имел наименьшее значение.
(6.55)

§ 76] ЗАМЕЧАНИЯ ПО СОСТОЯНИЮ ДИНАМИЧЕСКОЙ ТЕОРИИ УПРУГОСТИ 253
§ 76. Замечания по состоянию динамической теории
упругости
В настоящей книге рассмотрены только статические задачи теории
упругости. Читателю будет, однако, не безинтересно иметь хотя бы краткое
представление о современном состоянии динамической теории упругости;
этой цели и посвящено содержание данного параграфа.
Теория распространения упругих волн имеет большое приложение в
практике благодаря широкому распространению в природе волнового движения,
изучаемого указанной теорией. Сюда следует отнести задачи
сейсмологии, изучающей упругие колебания земной коры при землетрясении,
геофизические вопросы, связанные с исследованием строения земли, и
многочисленные технические проблемы (ударные, взрывные, акустические
волны и т. п.).
Изучение всяких возмущений и особенно сейсмических составляет задачу
динамической теории упругости с определенными начальными (в смысле
времени) и граничными (в смысле положения, позиций) условиями. Согласно
этой теории в упругой среде, не ограниченной во всех направлениях,
распространяются два вида волн: волны продольные и волны поперечные,
распространяющиеся независимо друг от друга с различными скоростями.
Продольные волны характеризуются тем, что при их прохождении в среде
наблюдаются сжатия, растяжения, но при этом частицы среды не
испытывают поворотов. Поперечные волны вызывают сдвиги и повороты, не
создавая сжатия и растяжения.
О первых исследованиях по динамической теории упругости, связанных
с именами Остроградского, Коши и Пуассона, было указано ранее в § 12.
К тому же периоду можно отнести также исследования Ламба, которым была
решена динамическая задача колебания полупространства под влиянием сил,
действующих на границе полупространства, причем были получены формулы
для компонентов смещений на границе полупространства; в дальнейшем
у нас Д. И. Шерман (1946) изучил поле смещений и в глубине
полупространства.
В 1930 г. С. Л. Соболев исследовал распространение волн в
неоднородной среде, неоднородность которой меняется непрерывно, и обобщил
формулу Кирхгофа, представляющую решение волнового уравнения. Согласно
формуле Соболева в неоднородной среде не только каждый элемент
поверхности посылает возмущение, но во все время движения волны каждая точка
возмущенного объема порождает дополнительные возмущения.
Исследование волн в неоднородной и анизотропной среде было сделано
B. Г. Гоголадзе в 1934 г.
Развивая свой метод, С. Л. Соболев создал новую теорию
интегрирования линейных дифференциальных уравнений в частных производных
гиперболического типа, представляющую важный вклад в теорию этих уравнений.
C. А. Христианович обобщил теорию С. Л. Соболева для широкого класса
уравнений, решив задачу Коши для нелинейных дифференциальных
уравнений гиперболического типа.
Указанные примеры являются хорошей иллюстрацией тезиса,
характеризующего взаимное влияние математики на физику и физики на
математику.
В 1932 г. В. И. Смирнов и С. Л. Соболев разработали важный метод
решения динамических задач теории упругости, основанный на теории
функций комплексного переменного.
В 1934 г. Е. А. Нарышкина решила фундаментальную задачу всей
теории— трехмерную задачу колебаний полупространства при произвольных
начальных условиях.
Уместно будет также отметить работу Л. С. Лейбензона «Деформация
упругой сферы в связи с вопросом о строении земли», опубликованную еще

254
ПРОДОЛЖЕНИЕ
[ГЛ. VI
в 1912 г., в которой автор на основе методов статической теории упругости,
теории упругих приливов и на данных распространения сейсмических волн
исследовал структуру земли (модуль твердости, толщину земной коры,
вопрос о существовании жидкого слоя между корой и внутренним ядром земли
и многие другие геофизические проблемы).
Распространению волн в области с криволинейной границей посвящены
работы С. Г. Михлина и Г. И. Мюнтца (1934—1947).
Указанные выше исследования по динамической теории упругости,
принадлежащие В. И. Смирнову и С. Л. Соболеву и их ученикам, определили
значительные успехи в этой области и широкое использование их
результатов в практике.

ГЛАВА VII
НЕКОТОРЫЕ ЗАДАЧИ ПРИКЛАДНОЙ ТЕОРИИ УПРУГОСТИ
§ 77. Общая характеристика решения задач в прикладной
теории упругости и пластичности
К небольшому количеству задач, содержащихся в предыдущих
главах IV — VI, для которых приведенные в этих главах решения
полностью удовлетворяли основным уравнениям теории упругости,
можно было бы добавить еще немного практически важных задач,
для которых также имеются точные решения, полученные в
результате преодоления немалых трудностей математического характера.
Для преобладающего количества задач, выдвигаемых инженерной
практикой, точных решений теорий упругости пока не имеется и
приходится обращаться к различным приближенным теориям
деформаций. Эти различные теории и составляют современную так
называемую прикладную теорию упругости.
Не останавливаясь на том, что наименование «прикладная»,
конечно, неудачное, но сохраняя в дальнейшем для приближенных
теорий такое же название-, отметим некоторые характерные
особенности для всех излагаемых в этой главе решений.
Прежде всего заметим, что во всех прикладных (лучше было
бы назвать приближенных) теориях все напряжения и им
соответствующие деформации четко разделяются на основные и второстепенные.
Под второстепенными напряжениями и деформациями понимаются те,
которые по сравнению с остальными, относимыми к группе основных,
настолько малы, что можно пренебречь влиянием таких
второстепенных напряжений на деформации в направлении основных
напряжений. Это, конечно, не означает, что второстепенные напряжения
и деформации вообще из расчета снимаются: исключается лишь
взаимное влияние одних на другие. Иначе говоря, принимается
гипотеза о связи основных напряжений только с
основными деформациями. Такова первая частная, так называемая
статическая «гипотеза», характерная для прикладкой теории
упругости и пластичности. Одним из примеров использования такой
гипотезы может служить известная читателю из курсов сопротивления
материалов задача о поперечном изгибе балки. В этой задаче при исчисле-

256 НЕКОТОРЫЕ ЗАДАЧИ ПРИКЛАДНОЙ ТЕОРИИ УПРУГОСТИ [ГЛ. VII
нии деформаций продольных волокон не принималась во внимание
роль нормальных напряжений, перпендикулярных к оси балки (силы
надавливания продольных волокон друг на друга). Впрочем, такая
предпосылка не исключала возможности в дальнейшем вычислить
указанные «поперечно-нормальные» напряжения.
К категории второстепенных напряжений часто относят не только
те напряжения, которые весьма малы по сравнению с другими или,
как это сказано выше, влияние которых на деформацию по
направлению других, основных напряжений, незначительно, но также и те,
которыми можно пренебречь при вычислении потенциальной энергии
рассматриваемой системы *). Последнее условие значительно
расширяет круг второстепенных напряжений и деформаций. При этом сами
напряжения, относимые к второстепенным, по величине могут и не
быть значительно меньше основных. Такова вторая частная (назовем
ее условно энергетической «гипотезой», используемая в некоторых
прикладных теориях.
Напомним читателю известные примеры из сопротивления
материалов и строительной механики на вычисление прогибов, девиаций,
а также расчеты статически неопределимых стержневых систем; во
всех этих случаях при исчислении потенциальной энергии изгиба
совершенно исключалась деформация сдвига, а также продольная
деформация оси стержней и т. п.
Наконец, третьей и, пожалуй, наиболее сильной (по своему
влиянию на упрощение метода расчета) гипотезой в прикладных теориях
является определенное предположение о характере перемещений или
деформаций исследуемого тела. В этих предположениях сознательно
пренебрегается второстепенными особенностями в картине смещений
или деформации, иначе говоря, кинематическая картина
упрощается. В каждой характерной задаче такая кинематическая
«гипотеза» формулируется особо.
Примером кинематической гипотезы, известной читателю по
курсам сопротивления материалов, являлась гипотеза плоских
сечений, принимаемая в теории изгиба тонкого стержня с массивным
профилем поперечного сечения (круг, прямоугольник и т. п.). В
случае изгиба пластинок, как показано ниже (§ 78), упомянутая
гипотеза вырождается в особую гипотезу плоских нормалей.
В случае изгиба и кручения стержня с тонкостенным профилем
гипотеза плоских сечений оказывается слишком жестким ограничением:
она качественно искажает картину деформации и потому совершенно
неприемлема, как это показано в § 92; тогда она заменяется менее
жестким условием, а именно гипотезой о
недеформируемости контура поперечного сечения.
Упомянутые частные гипотезы (статическая, энергетическая,
кинематическая), если не между собой (но и это возможно), то по от-
*) См. [31].

§ 78]
ИЗГИБ ПЛОСКОЙ ПЛАСТИНКИ
257
ношению к некоторым уравнениям классической теории упругости
могут оказаться в несоответствии. Более того, результаты,
получаемые в прикладных теориях, обычно находятся в противоречии
с уравнениями неразрывности деформации.
Наличие таких противоречий не должно рассматриваться как
недостаток прикладных теорий; построение внутренне непротиворечивой
приближенной теории принципиально невозможно. Важно лишь то,
чтобы полный комплекс «гипотез», несмотря на некоторые
несогласованности между собой в частностях, общую картину напряжений и
деформаций обследуемого объекта обрисовал качественно правильно
и окончательные результаты были достаточно близкими к
действительности. В связи с указанным значение опыта как критерия теории
для прикладных теорий исключительно велико. Иначе говоря, никакая
вновь предлагаемая прикладная теория не может быть принята прежде,
чем ее результаты не получат практического подтверждения.
Решения, полученные в прикладных теориях, могут быть при
надобности уточнены и доведены по степени точности сколь угодно
близко к точному результату. В § 74 был изложен метод П. Ф. Пап-
ковича, в котором искомое напряженное состояние (точное решение)
представляется суммой двух решений, из которых первое — неточное
решение (с точки зрения полной системы уравнений классической
теории упругости) и второе — дополнительное, уточняющее первое
(корректирующее). Чем ближе к действительности первое решение
(оно может быть получено именно методами прикладной теории
упругости), тем легче получить второе — корректирующее, а
следовательно, придти к точному решению.
§ 78. Изгиб плоской пластинки. Основные определения
и гипотезы
Плоской пластинкой средней толщины или тонкой плитой
принято называть упругое тело призматической или цилиндрической
формы с малой по сравнению с размерами основания высотой (фиг. 115).
Практическое применение технической теории изгиба плит,
которая излагается в настоящей главе, как показали исследования
академика Б. Г. Галеркина, должно ограничиваться следующими
пределами:
а) отношение толщины к наименьшему другому размеру плиты
должно быть меньше 1/КУ хотя теория остается все же применимой,
когда это отношение доходит до 1/б;
б) ожидаемые прогибы плиты малы по сравнению с толщиной.
Отдельные авторы *) называют верхний предел для указанного
прогиба в */б толщины плиты.
*) См. [46].
17 Зак. 3880. Н. И. Безухое

258 НЕКОТОРЫЕ ЗАДАЧИ ПРИКЛАДНОЙ ТЕОРИИ УПРУГОСТИ [ГЛ. VII
Если соотношение в размерах плиты не отвечает условию а), то
такая плита считается толстой. Систематически разработанной теории
толстых плит в литературе не имеется. Одна из классических задач
этой сложной области теории упругости показана в § 75 (задача
М. М. Филоненко-Бородича).
Если не выдерживается условие б), то задача усложняется как
по причине конечных деформаций (а не весьма малых, как то
предполагается в технической теории изгиба), так и по причине влияния
на прогиб пластинки тех составляющих реакций опорного контура,
которые действуют в плоскости пластинки.
Последние возникают в том случае, когда смещению в плоскости
пластинки точек, принадлежащих опорному контуру, препятствуют
Фиг. 115. К определению пластинки. Срединный слой.
опорные связи. Пластинки, не удовлетворяющие условию б), иногда
называют пластинками малой толщины или малой жесткости (типа
мембраны).
Плоскость, параллельную основанию пластинки и делящую
пополам ее высоту, называют срединной плоскостью, а поверхность,
в которую она обращается при изгибе, —упругой поверхностью
или изогнутой срединной поверхностью. Линия пересечения срединной
плоскости с боковой поверхностью пластинки называется контуром
(опорным) пластинки.
Считая пластинку горизонтальной, направим ось Oz вертикально
вниз, а оси Ох и Оу расположим в срединной плоскости.
При изучении изгиба пластинок внешними нагрузками считаем
поперечные (перпендикулярные к срединной плоскости) и исключаем
силы, параллельные или находящиеся в срединной плоскости. Случай
нагружения пластинки силами в срединной плоскости составлял бы
известную из главы III плоскую задачу теории упругости.

§ 78]
ИЗГИБ ПЛОСКОЙ ПЛАСТИНКИ
259
Техническая теория изгиба пластинок построена на следующих
двух допущениях, существенно упрощающих исследования.
а) Кинематическая «гипотеза». Совокупность точек, лежавших
до деформации пластинки на какой-либо прямой, перпендикулярной
к срединной плоскости, остается на прямой, нормальной к упругой
поверхности деформированной пластинки.
Это допущение, аналогичное гипотезе плоских сечений в
технической теории изгиба балок, носит обычно название гипотезы
прямолинейного элемента или гипотезы плоских нормалей.
Считается, что упомянутый прямолинейный элемент при
перемещениях сохраняет свою длину.
б) Статическая «гипотеза». Как и в элементарной теории изгиба
балок (в курсе сопротивления материалов), будем пренебрегать
нормальными напряжениями (cz) на площадках, параллельных срединной
-х
Фиг. 116. Обозначение компонентов напряжений
в сечениях, параллельных координатным. К
составлению упрощенной физической зависимости (7,1).
плоскости, возникающими вследствие взаимного нажатия
горизонтальных слоев пластинки друг на друга. Таким образом, каждый
бесконечно тонкий слой пластинки, взятый параллельно срединной
плоскости, может быть рассматриваем в условиях плоского напряженного
состояния.
Кинематическая «гипотеза» позволяет трехмерную задачу теории
упругости свести к более простой двухмерной задаче, а именно
к задаче об определении усилий и перемещений, относящихся
к точке на срединной плоскости (функции от двух координат).
Вторая «гипотеза» будет использована лишь в части упрощения
записи обобщенного закона упругости, а именно, применительно
к обозначениям компонентов напряжений, показанным на фиг. 116„
17*

260
НЕКОТОРЫЕ ЗАДАЧИ ПРИКЛАДНОЙ ТЕОРИИ УПРУГОСТИ [ГЛ. VII
будем ограничиваться такой формой записи:
е»=£-(а* — Р°у)>
Вместе с тем ниже будет получено выражение и для а2 с
помощью дифференциальных уравнений равновесия трехмерной задачи
теории упругости. В этом смысле вторая гипотеза может
рассматриваться не столько как статическое допущение, сколько как
математическое упрощение (игнорирование ввиду малости членами — \кзя
в формуле (3.01) для ея и еу); иначе говоря, напряжение oz
относится к числу второстепенных.
§ 79. Вывод дифференциального уравнения упругой
поверхности пластинки
Пластинка будет предполагаться постоянной толщины и
загруженной поперечной нагрузкой р(х, у), распределенной любым образом
по верхней поверхности пластинки (для краткости письма она в
дальнейшем обозначается просто р); объемные силы (собственный вес
и т. п.) из рассмотрения исключаем.
Будем исходить из уравнений общей трехмерной задачи теории
упругости с внесением в них тех упрощений, которые доставляют
перечисленные в предыдущем параграфе гипотезы.
Начнем с использования кинематической гипотезы. Обозначим
через w прогиб срединной поверхности, т. е. вертикальное
расстояние между точкой, взятой на срединной плоскости, до деформации
и положением той же точки на упругой поверхности. В связи с
допущением о том, что прямолинейный нормальный элемент сохраняет
свою длину, перемещение w будет (с точностью до малых высших
порядков) общим для всех точек, принадлежащих упомянутому
прямолинейному элементу. Иначе говоря, уравнение перемещений
точек пластинки, параллельных оси Oz, которое в случае толстой
плиты есть функция трех координат, т. е. w(x,y, z), в данном
случае тонкой плиты принимается функцией двух координат. Ввиду
предположения о малых деформациях пластинки по сравнению
с толщиной плиты и исключением из рассмотрения внешних сил,
действующих в срединной плоскости пластинки, можно считать, что
все точки, принадлежащие срединной плоскости, получают только
вертикальные смещения (w). Впрочем, принятие во внимание
горизонтальных смещений этих точек (составляющие малых высших
порядков по сравнению с величиной w) не изменит окончательных
выводов данного параграфа, но пренебрежение ими, конечно, упростит
последующие выкладки.

§ 79] ВЫВОД ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ УПРУГОЙ ПОВЕРХНОСТИ 261
Горизонтальные смещения точек (не принадлежащих срединной
плоскости), параллельные осям х и у, обозначим соответственно
через и и v.
Из рассмотрения фиг. 117 следует:
и = — z
dw
дх
v = •
Так как на основании (2.25)
dw
ду
(7.02)
ди
*х~~ дх
dv
\ху
ди , dv
~ty~^~dx~'
то с помощью (7.02) переписываем их следующим образом:
d*w
е*— Z дх*
гу = -
d2w
~ду^
, — 2z
d2w
(7.03)
Чху— «* бхду
Выражения (7.03) — геометрические уравнения данной задачи.
JX
^
_Жу
дх
Ь i
ЕЬ
Фиг. 117. «Гипотеза» плоских нормалей.
Физическими уравнениями будут (7.01) или в обратной записи
Е
1
7r(8* + l"y)»"
Е
zxy— 2(1 + р.) Тя?*'

262 НЕКОТОРЫЕ ЗАДАЧИ ПРИКЛАДНОЙ ТЕОРИИ УПРУГОСТИ [ГЛ. VII
Последние уравнения с помощью (7.03) переписываются так:
Ez (d2w . d2w\
dx2 "+"^ ду* )у
Ez /d2w _j_ |t d2w^
r 1 — p.2 \ дл:2
°» = -
ижг/:
(7.04)
1 + fx d* dj/
Законы изменения ол, оу и т^ = -zyx по толщине плиты
оказываются линейными и представлены на фиг. 118.
Фиг. 118. Распределение напряжений ах, <jv, z.
и zyx по толщине пластинки.
"ху
Статическими уравнениями будут (2.02). Из уравнений равновесия
dx
dz
dz
ху
dz„
ух
ду
да»
dz
dz,
= 0;
дх
ду
М- = 0
dz
имеем:
dz
д^уг
dz
Ez
_d_/_d2
W
1 — p.2 dx V дх2
Ez d ( d2w
d2w \ u
~dy*~)>
d*ws
\ — \#dy
Интегрируя эти уравнения, получаем:
Ez2 d ( d2w
f d*w | d2w \
\dx* "Г ~dy*)'
d2w\
Xxz ~ 2 (1 — fj*) dx \ dx2 + dy* ) + ?1 ^' ^;
V — 2 (1 — p.2) dy V dx2 ^ dy* J ' ?2 ^' -^
Используя граничные условия на верхней и нижней поверхностях
пластинки, а именно, что при г = ± -^ имеем ххг = zyz = 0, совер-

§ 79] ВЫВОД ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ УПРУГОЙ ПОВЕРХНОСТИ 263
шенно очевидно получаем:
?i № У)— 8 (1 _ ^ а;с ^ ^ ■+■ ау, J,
, \_ £^а а /a2w . d2w\
?2 i*. -W — — 8(i-ji») ay да+ a^J•
Таким образом,
_ E(/fc2_4*a) а /а»ш ■ d*w\. ,
^ — 8 (1 _ ^2) дх { дх2 -Г ду2 J > V 'К3°)
^я 8(1 — р.2) ау V, ал:2 »~ ay*/* t'-u°J
Законы изменения ххг = izx и т^ = zzx по толщине пластинки
оказываются параболическими.
Обращается внимание на то, что все полученные формулы для
напряжений (7.04)—(7.06) выражены через прогиб срединной
поверхности. Уравнение этой упругой поверхности является в данном случае
как бы «разрешающей» функцией, т. е. аналогично функции
напряжений в плоской задаче теории упругости.
Осталось найти это уравнение. Для этой цели надлежит
обратиться к еще неиспользованным граничным условиям, а именно, что
при г = у имеем ог =— /?, а при z = — у имеем as = 0.
Предполагаем случай поперечной нагрузки, приложенной к верхней
поверхности пластинки; между прочим, если предположить нагрузку на
нижней поверхности или на срединной поверхности, то это изменит
формулу для аг, но не изменит вида окончательного уравнения упругой
поверхности плиты (7.11).
Для поставленной цели надлежит найти выражение для ag.
Из третьего уравнения равновесия (2.02)
+ ^ = о
дх ' ду * dz
имеем:
да- дт,,ж ах:
'*!L
dz дх ду
На основании (7.05), (7.06) получим:
д*ех Е (№ — 4г2) а2 / d2w , d*w\
дх ~~ 8(1 — р.2) дх2 V дх2 ~"~ ду* )
и
д*гу _ _ Е (h* — 4г2) а2 fd*w , d*w\
ду' ~ 8(1- ц2) ду2 [ дх* ~"~ ду* )'
Таким образом, имеем:
д<*8 __ E(h* — 4z*) ( д* , d*\fd*w , d*w \
а* ~ 8(i — р.а) va*2 "^ ауу v а^2 "^ ду2;*

264 НЕКОТОРЫЕ ЗАДАЧИ ПРИКЛАДНОЙ ТЕОРИИ УПРУГОСТИ
интегрируя, получим:
[ГЛ. VII
Fz (hi —эй\
Используем граничные условия:
(•л--* =
/ а2 , д2 \ / d*w . 9*w \ , . , . ,_ _ .
2Ч1-Щ\Ш + д^)\д^ + ^^Г^{Х'У) = ~Р' (7-7а)
Произведя сложение последних выражений, получаем:
откуда *)
2ф(*, J0 = —р,
tK*>jO = —у/К*, дО-
(7.08)
Согласно (7.07) напряжения ог по толщине плиты (т. е. по длине
нормального элемента, для всех точек которого х = const и #y=const)
изменяются по закону кубической параболы.
Фиг. 119. Распределение напряжения аг по толщине пластинки
в зависимости от плоскости, в которой находится внешняя
нагрузка.
Эпюра gz имеет вид, показанный на фиг. 119 в зависимости от
того, к какой поверхности (верхней, срединной или нижней)
непосредственно приложена нагрузка.
Подставляя (7.08) в (7.7а) или (7.76), получаем искомое
дифференциальное уравнение упругой поверхности (изогнутой срединной
поверхности первоначально плоской пластинки)
12
Eh* ( д2 , _д*\ /d*w , d*w_\ _ _ (7 ос.ч
(1 — ц2) V дх* "Т~ ду*) \ дх* + ду* )~ Р' ^ }
*) В случае приложения нагрузки к нижней поверхности плиты,
очевидно, ty(x, у)= —р.

§ 80] ПЛАН РЕШЕНИЯ ЗАДАЧИ ПО ИССЛЕДОВАНИЮ ИЗГИБА ПЛАСТИНОК 265
Вводя обозначение
ЕНЪ =D (7.10)
12(1-^)
(так называемая цилиндрическая жесткость при изгибе
ч / а2 . в2 \
пластинки) и раскрывая операцию (тгт~Ь -у^) наД выражением
/ д2хе) , d2w \
\дх* + ду*)'
окончательно имеем:
(7.11)
d4w
Тх^~
. 9 d*w
' дх* ду*
^"аТ""""
1
Это есть основное уравнение теории изгиба плоской пластинки
средней толщины при отсутствии сил в срединной плоскости
или параллельных ей. Уравнение (7.11) иногда называют уравнением
Софи Жермен.
§ 80. План решения задачи по исследованию изгиба пластинок»
Условия на опорном контуре
Если удастся для данной конкретной задачи проинтегрировать
уравнение (7.11), то по найденному конечному уравнению упругой
поверхности w=f(x, у) получим из выражений (7.04)—(7.07) все
интересующие нас компоненты напряжения в любой площадке,
проходящей через исследуемую точку.
Задача интегрирования уравнения (7.11) заключается, очевидно,
не только в том, чтобы найти функцию w=f(xy у), подстановка
которой в (7.11) удовлетворяла бы последнее уравнение тождественно,
но также, чтобы эта функция удовлетворяла условиям на опорном
контуре.
Выясним, как составляются эти условия на контуре пластинки,
рассмотрев случай прямоугольной пластинки (фиг. 120) с различными
опорными связями. Для левого защемленного конца имеем следующие
очевидные условия: при л:=0 и при у любом должно быть w = 0
(отсутствие прогиба) и -^— = 0 (отсутствие угла наклона срединной
плоскости по отношению к оси Ох).
Для шарнирно-опертого контура, т. е. при ^ = 0 и при х любом,
следует потребовать отсутствия прогиба и нормальных напряжений
(Оу) по опорному сечению и касательных напряжений (?ху), имеющих
направление, параллельное оси Ох (касательные напряжения,
параллельные оси Oz, могут и должны быть, так как именно ими осуще-
стнляется поддержание пластинки).

266 НЕКОТОРЫЕ ЗАДАЧИ ПРИКЛАДНОЙ ТЕОРИИ УПРУГОСТИ [ГЛ. VII
На основании формул (7.04) следует, что эти граничные условия
аналитически представляются так: при у = 0 и w = 0
d2w , d°-w ~
ду2 * г дх2
d2w
дхду
= 0.
Впрочем, как это было в случае балки-стенки, рассмотренной
в § 46, если трудно подобрать уравнение w=f(x, у),
удовлетворяющее всем без исключения граничным условиям, то можно н е-
сколько смягчить граничные условия, например,
отказавшись от непременного условия хху = 0, потребовать лишь, чтобы
0 Шарнирное закрепление
Фиг. 120. К составлению граничных условий для
пластинки.
сумма этих напряжений по толщине пластинки сводилась к системе
.взаимно уравновешенных усилий. Иначе говоря, граничным условиям
удовлетворить только в интегральной форме.
На правом, свободном крае должны отсутствовать все напряжения,
т. е. а9 = хух = хгх = 0.
На основании (7.04) заключаем, что в этом случае, т. е. при
х=а, должно быть:
d2w , d2w n
d2w п д (d2w . d2w \ 0
IxTj И дх \ дх'2 ~+~ ду2 J •
В связи с тем что удовлетворить граничным условиям в
интегральной форме легче, чем в каждой точке опорного контура, в таких
случаях представляется целесообразным перестроить формулы (7.04) —
(7.07) для напряжений, выразив последние через интегралы
напряжений (через интенсивность поперечных сил, изгибающих, крутящих
моментов), что и выполнено в § 83.

§ 81] ПРИМЕР ЭЛЛИПТИЧЕСКАЯ ПЛАСТИНКА, ЗАЩЕМЛЕННАЯ ПО КОНТУРУ 267
Выше было указано, что уравнение упругой поверхности в теории
изгиба плоской пластинки играет такую же важную роль, какую в плоской
задаче теории упругости исполняет функция напряжений. Действительно, как
там, в плоской задаче, зная функцию напряжений, можно было просто
получить выражения для всех компонентов напряжений, так и здесь, в теории
изгиба пластинок, зная уравнение изогнутой поверхности, легко получить
выражения для всех компонентов напряжений, а также (это показано
в § 83) и для компонентов усилий.
Из сопоставления (7.11) и (3.40) заключаем, что и по внешней форме
бигармоническое уравнение для функции напряжений в плоской задаче
в точности совпадает с однородным бигармоническим уравнением (без
правой части) изогнутой поверхности пластинки.
Таким образом, функцию напряжений в плоской задаче можно при
желании истолковать как уравнение упругой поверхности той же пластинки,
поперечный изгиб которой осуществляется поперечными нагрузками (силами
и моментами), приложенными по опорному контуру пластинки. Об этой
аналогии и упоминалось на стр. 135.
Существует интересная аналогия и в граничных условиях для
упомянутых двух сходственных в математическом отношении задач, а именно: чисто
статическим граничным условиям плоской задачи соответствуют чисто
кинематические граничные условия фиктивного поперечного изгиба пластинки;
чисто кинематическим граничным условиям плоской задачи соответствуют
чисто статические граничные условия фиктивного поперечного изгиба
пластинки. Интересующихся указанными аналогиями и их использованием
отсылаем к книге А. С. Калманок «Строительная механика пластинок» (1950).
§ 81. Пример—эллиптическая пластинка, защемленная по контуру
Пусть эллиптическая в плане пластинка с защемлением по кон-
ТУРУ (фиг. 121) имеет равномерно распределенную нагрузку, т. е.
Р(х> JO = P = const>
по всей поверхности пластинки. Выбирая оси Ох и Оу проходящими
через центр пластинки,
имеем уравнение контура
0, (7.12)
где х и у— координаты
точек на опорном контуре.
Решаем задачу обратным
методом. Зададимся
выражением прогиба в форме
да=дао(5 + |—1)2-(7.13)
Фиг. 121. Эллиптическая пластинка с
защемленным контуром.
Вполне очевидно, что на
эллиптическом контуре, т. е.
при х = х ку=у, согласно (7.12) прогиб обращается в нуль.
Уравнение (7.13) отвечает и другому граничному условию о том, что
опорный контур защемлен, т. е. изогнутая срединная поверхность на

268 НЕКОТОРЫЕ ЗАДАЧИ ПРИКЛАДНОЙ ТЕОРИИ УПРУГОСТИ [ГЛ. VII
контуре остается горизонтальной. В самом деле, дифференцируя,
имеем:
dw
dw „ /лгз , у* \ 2у
и при х = х и у=у указанные производные обращаются в нуль.
Итак, выбранное уравнение упругой поверхности удовлетворяет
граничным условиям. Удовлетворяет ли оно исходному
дифференциальному уравнению (7.11)? Для этой цели выполним ряд
дифференцирований. Опуская промежуточные, приводим четвертые производные:
^Е — 94 ^ • — — 94 ^ • d*W — R ™±.
дх* ~~ а* ' ду* — Ь*> дх* ду* ~~~ ° аЧ* *
Подставляя эти производные в (7.11), имеем:
/24 , 16 . 24\ р /71А
"*\7Г* + т + ¥) = Т>> <7Л4>
откуда заключаем (так как левая часть равенства представляет
постоянную величину), что принятая форма изгиба пластинки возможна>
если р = const, т. е. если нагрузка сплошная и притом равномерная,.
Из (7.14) получаем прогиб при х — у = 0, т. е. в центре
пластинки:
Р
(7.15)
Зная w = f(x, у), не представит затруднений вычислить
напряжения. Так, например, на основании (7.4) и (7.5)
Ez d2w Ez SwQxy e
*ту— Г+"? # дх ду ~ 1 + {jl "a2p~;
zxz — 8 (1 _ ^2) ^ $xi i~ дх дуг) "—
8(1 — p-2) | a4 ' a*b~ J
После преобразований последняя формула принимает вид
** (За4 + <2aW + З^4) Л» * ^ ** '"
Предлагается читателю продолжить исследование —
самостоятельно вывести формулы для нормальных напряжений, и показать,,

§ 82] ПРИМЕР СВОБОДНО-ОПЕРТАЯ ПРЯМОУГОЛЬНАЯ ПЛАСТИНКА 269
что в центре пластинки (х = у = 0)
4Ew0 /J_ , \хЛ
°у— l — ^^T-aV'
а на концах малой полуоси эллипса (л:=0, у = Ь) напряжение изгиба
_ SEwp
Это напряжение оказывается для пластинки наибольшим.
В случае круглой пластинки, полагая b = а, получаем упрощение.
Так, например:
^г = -ЦгХ^-Аг% (7.15а)
где заменено х2-\-у2 = г2, а для точек срединной поверхности еще
проще, именно:
, ч _3_ X
\~хг)г=0 2 P h *
В случае бесконечно вытянутой пластинки (а = оо) имеем так
называемый цилиндрический изгиб пластинки:
w = wo(^ — 1J
и
что соответствует случаю изгиба обычной балки с теми же
граничными условиями и нагружением с заменой в формулах для прогиба
изгибной жесткости балки (EJ) на цилиндрическую жесткость
(*-&>)■
§ 82. Пример — свободно-опертая прямоугольная пластинка
Рассмотрим случай, когда прямоугольная в плане пластинка со
сторонами а и b свободно подвешена по контуру (статически
эквивалентно шарнирному опиранию) и имеет нагрузку по уравнению
. пх . пу
Графически такая нагрузка представляется «горкой», показанной
на фиг. 122. В качестве первой попытки примем уравнение упругой

270 некоторые задачи прикладной теории упругости [гл. vii
поверхности подобное уравнению нагрузки, т. е.
(7.16)
Нетрудно доказать, что уравнение (7.16) удовлетворяет дифферен-
^ . кх . пу
w = С sin —sin-^-.
а о
Фиг. 122. Пример прямоугольной пластинки с
нагрузкой в виде «горки».
циальному уравнению (7.11) и граничным условиям в перемещениях.
Начнем с последнего. Действительно,
при х = 0 <ш = 0, при#у = 0 w==Q-i
при х = a w = 0, при у = b w = 0.
Выпишем последовательные производные от w:
d4v
ду2'
я2 dAw rc4
: — — *W\ -=г-7 = — W)
а2
b2
dAw
w:
дх* ~~ я*
d4w и4
"dy*~¥w'
дх2 ду2 а2Ь2
w.
Подставляя написанные производные в (7.11), имеем тождество
(функции от х и у сокращаются)
А ( 1 I 1 \2 г> • К* • %У 1 . ТХ . ПУ
откуда
С =
Ро
1 \2Ш
">(*+£)

§ 82] ПРИМЕР СВОБОДНО-ОПЕРТАЯ ПРЯМОУГОЛЬНАЯ ПЛАСТИНКА 271
Величина С согласно (7.16) представляет прогиб в центре плиты,
т. е. при х = -у и у = ~ .
По кромкам пластинки могут действовать вертикальные
касательные напряжения izx (на сторонах, параллельных оси у) и zzy (н^
сторонах, параллельных оси х). На основании (7.05)
f(/z2 —4z2) (d*w , d*w
Так как
Е (№ — 4z2) (d*w . д3ш \
d3o>
тел: . теу
TO
3—5- = С -f cos — sin . .
d3a> ^ it3 itjc . ity
, -, 9 = С —гг. COS Sin -77-,
_ £(Д2-4*«)*в /1 l\un
6 "
По сторонам длиной b касательные напряжения распределяются
по закону, изображенному на фиг. 123.
Аналогично может быть получено выражение для %гу. Очевидно,
что система напряжений хгх и г действующая по кромкам пластинки,
тахт г
1—\
£
Ё
1 1
1 2
.гихй
г
З.ТШ11
L 1
1
)
LLrcoJ
1
LT^>
f
Фиг. 123. Распределение касательных напряжений zzx по стороне длиной К
Заштрихован характер распределения ъгх по толщине пластинки.
в своей совокупности должна уравновесить внешнюю нагрузку,
действующую на пластинку (поддержать пластинку).
Для нормальных напряжений на основании (7.04) соответственно-
имеем:
х (1— \&)сРЬ*"
_ £п2 (д2 4- 62 [А)
дог,
_______ , (7.17)
"2/ (1—f**)flW
Наибольших значений нормальные напряжения по толщине плиты
достигают на периферии (при z = zt -у)» и эпюра таких максимальных.

272
НЕКОТОРЫЕ ЗАДАЧИ ПРИКЛАДНОЙ ТЕОРИИ УПРУГОСТИ [ГЛ. VII
напряжений согласно (7.17) подобна упругой поверхности
пластинки. Из (7.17) следует, что кромки пластинки от нормальных
напряжений свободны.
Переходим к вычислению напряжений zxy на основании (7.04):
Ez d2w
Так как
то
d2w
дхду
ху'
= С
1 + Iх дх ду'
2 пх пу
— cos —cos -^r
^ху ''
dW
Ez ~ 7i2 nx к у
-1—- С —гп, COS — COS -f1.
По кромкам пластинки соответственно имеем
\хху)у=о== \хху)у=ъ ==
\^ух)х=0 \zyx)x=a
Ez ~ я2 т.х
-Г-: С —^ж COS —,
Ez * т& ку
ТТ7 S2p"C0ST-
(7.18)
Характер распределения указанных напряжений показан на фиг. 124.
Очевидно, что в пределах каждой кромки х=0, х=а, у = 0,у = Ь
Фиг. 124. Распределение касательных напряжений ixy
по кромкам у = 0 и у = Ь.
такие «наружные» касательные напряжения имеют главный вектор и
главный момент, равные нулю, т. е. они статически эквивалентны
нулю.
Является ли уравнение (7.16) решением поставленной задачи?
Строго говоря, — нет, так как согласно заданию пластинка «свободно
подвешена по контуру». Это означает, что по контуру могут
действовать только вертикальные касательные напряжения, имитирующие
вертикальные реакции опорного контура. Никаких других напряжений
по опорному контуру не должно быть.

§ 82]
ПРИМЕР СВОБОДНО-ОПЕРТАЯ ПРЯМОУГОЛЬНАЯ ПЛАСТИНКА
273
Однако уравнению (7.18) соответствует наличие на опорном
контуре также горизонтальных касательных напряжений. Вместе с тем,
поскольку эти напряжения в пределах каждой кромки статически
эквивалентны нулю, можно в практических целях остановиться н$
решении (7.16) и не искать точного и, конечно, значительно более
сложного решения.
Может возникнуть сомнение в последнем утверждении, так как
правильное использование принципа Сен-Венана предусматривает размеры
территории, на которой действует взаимно уравновешенная нагрузка» очень малыми
по сравнению с наименьшим размером тела.
Само собой очевидно, что этого нельзя сказать относительно площадей
опорных поверхностей {ah или bh). Однако в данном случае применение
принципа Сен-Венана все же возможно и именно потому, что
рассматриваемые касательные напряжения в пределах толщины пластинки меняют
направление, т. е. они двухзначные.
В самом деле, рассмотрим элемент опорной поверхности, например,
hdx (или hdy)\ приходящиеся на такой элемент горизонтальные
касательные напряжения составляют пару, имеющую некоторый элементарный
момент mdx (через т обозначены момент на единицу длины, т. е.
интенсивность момента касательных сил по опорному контуру). Если толщина
пластинки мала, то замена элементарного момента mdx от горизонтально
направленных сил на такой же по величине момент, но от вертикально
В—=ъ—>-i-*—^—0
H--
! Idbo
Фиг. 125. К доказательству практической возможности
остановиться на решении (7.16).
направленных сил (фиг. 125), не скажется существенно в области, вне
опорной плоскости. Новые же, фиктивные, силы — обозначим их ~ъгу (на кромках
у = 0 и у = Ь) или izx (на кромках лг = 0 и х = а) — можно присоединить
к прежним zzy и izx. Очевидно, что условия равновесия пластинки от такого
присовокупления к прежним силам еще новых сил, но статически
эквивалентных нулю в целом, не нарушатся.
Примечание. Если закон синусоидального распределения нагрузки
задан уравнением
ткх , пку
v = ро sin sin —r^y
(7.19)
18 Зак. 3880. Н. И. Безухов.

274 НЕКОТОРЫЕ ЗАДАЧИ ПРИКЛАДНОЙ ТЕОРИИ УПРУГОСТИ [ГЛ, VII
где т и п — целые числа, то, поступая аналогично предыдущему, получим
для изогнутой поверхности следующее выражение:
w = -Г^- 2ТГ sin sin —и • (7-2°)
-°&+ij a b
§ 83. Другая форма записи для напряжений и граничных условий
(приведение напряжений, параллельных срединной плоскости,
к статически эквивалентным им изгибающим и крутящим
моментам)
Так как согласно (7.04) нормальные напряжения ах и о?/, а также
касательные напряжения хху, изменяются по толщине пластинки по
линейному закону, то если суммировать указанные напряжения на
элементарных прямоугольниках высотою h и основаниями dx и dyy
приходим к статически эквивалентным им моментам (фиг. 126)»
Фиг, 126. Приведение напряжений, параллельных средин
ной плоскости к статически эквивалентным им изгибаю
щим и крутящим моментам.
Нормальные напряжения сх и ау приводятся к изгибающим
моментам, действующим на элемент пластинки по двум взаимно
перпендикулярным направлениям. Касательные напряжения txy и zyx приводятся
к крутящим моментам. Эти крутящие моменты для двух взаимно
перпендикулярных сечений в силу парности касательных напряжений
равны между собой и противоположны по знаку.
Если обозначить интенсивность изгибающих моментов по сечениям
х = const и у = const соответственно через Мх и Му, а интенсивность
крутящих моментов на тех же сечениях через Мху и Мух, то для

§ 83] ДРУГАЯ ФОРМА ЗАПИСИ ДЛЯ НАПРЯЖЕНИЙ И ГРАНИЧНЫХ УСЛОВИЙ 275
них получим выражения:
2
Mx=faafzdz,
2
2
м
У= 5' °yzdz>
МХу =
м
ух
-!
ixyzdz.
(7.21)
Подставляя в (7.21) выражения для напряжений (7.04), имеем:
.. ~ fd^w , d2w\ \
м =-D(l-,x)
d2w
(7.22)
*ху— -V- V) дхду' ,
Напряжения же через интенсивность моментов представятся в виде
J
М*
М.
где обозначено J =
Л*
*э
Ж2/
va?2/ '
^»
(7.23)
12'
Формулы (7.23) могли бы быть написаны и сразу, по аналогии
с известными формулами сопротивления материалов, построенными на
пшотезе линейного распределения напряжений.
Заметим, что размерность величин МХУ Му и Мху — это
размерность силы, а размерность J (погонного момента инерции) — длина
м третьей степени.
Так как запись (7.23) привычна для инженерных расчетов, то все
табличные данные и графики, составленные для расчета пластинок,
обычно содержат именно указанные выше погонные изгибающие и
крутящие моменты.
Диалогично можно ввести понятие об интенсивности поперечных
i'ili по тем же двум взаимно перпендикулярным площадкам, а именно:
А А
2 2
Az и Qy = f?Mydz. (7.24)
h _A
Qx= j4,

276 НЕКОТОРЫЕ ЗАДАЧИ ПРИКЛАДНОЙ ТЕОРИИ УПРУГОСТИ [ГЛ. VII
Подставляя в (7.24) формулы для касательных напряжений,
соответственно получим:
(7.25)
О — — D±-(^+^\
wy~~ ду\дх*^ dy*J
Размерность Qx и Qy — сила, поделенная на длину (погонная
поперечная сила). Очевидно, для самих касательных напряжений,
входящих в (7.24), согласно (7.05), (7.06) можно дать также привычную
в инженерных расчетах запись:
ъ-^; ^-^, (7-26)
где J — прежнее, а^ и Sy — статические моменты относительно
осей у и х той части площади сечения пластинки на единицу длины,
которая расположена выше того горизонта, на уровне которого
вычисляются касательные напряжения.
В заключение уместно будет ввести еще одно понятие о так
называемой приведенной погонной поперечной силе. На стр. 273 было
показано, что касательные напряжения на опорном контуре пластинки,
например, при x = d (или при y = b) izx (или xzy) могут быть путем
использования принципа Сен-Венана условно объединены с
касательными напряжениями от кручения, т. е. с ixy (или zyx). Тогда,
очевидно, получаем представление о приведенной (условной) силе
V* = Q* + (^f)x=a- (7-27)
На основании (7.24) и (7.22) можем записать по краю лг= const
".—"[fc+p-rt^] см
и по краю у = const соответственно
v. — oiip+*-*>&]■ <"»»
В связи с введением указанных выше понятий граничные условии
для свободного края лг = а могут быть записаны в виде уИж = (),
Vx = 0 или

§ 84] ОБЩЕЕ РЕШЕНИЕ ДЛЯ ПРЯМОУГОЛЬНОЙ ПЛАСТИНКИ 277
Таким образом, оперируя понятием приведенной поперечной силы,
на свободном крае пластинки вместо прежних (§ 82) трех граничных
условий можно решать поставленную задачу при условии
удовлетворения лишь двум условиям типа (7.28), (7.29), что вполне достаточно
для полного решения задачи.
§ 84. Общее решение для прямоугольной пластинки
Рассмотренными выше примерами (§§ 81 и 82) и осесимметрич-
ными случаями изгиба круглых пластинок (§ 86) почти
исчерпываются те случаи изгиба пластинок, где окончательные формулы
могут быть даны в замкнутой форме. В большинстве случаев это не
удается и остается решение исходного уравнения разыскивать в форме
бесконечного тригонометрического ряда или использовать для
решения теорию функций комплексного переменного, или, наконец,
обратиться к различным приближенным методам. В качестве примера на
использование решения в рядах рассмотрим пластинку с шарнирно-
закрепленными краями, загруженную произвольной нагрузкой
4=f{x> У)- (а)
Представим функцию /(лг, у) в виде двойного тригонометрического
ряда:
оо оо
/ С*, у) — 2 2 а»'»sin ^Гsin ^Г' №
w = l п = 1
где коэффициенты ряда *)
amn=±[(f(x,y)sin^sinn-f. (7.30)
о о
Произведя согласно (7.30) интегрирование для заданного
распределения нагрузки, т. е. для заданной /(лг, у), найдем коэффициенты
ряда (б) и таким образом представим заданную нам нагрузку как
сумму синусоидальных нагрузок.
Прогиб, производимый каждой такой синусоидальной нагрузкой,
был обследован в § 82, полный же прогиб будет определяться путем
суммирования членов, аналогичных (7.16). Итак,
оо оо
™=4п S S, атп *,*« — sinT- (7-31>
tc4D AJ AU (m1 , n*\2 a b v '
Для частного случая равномерной сплошной нагрузки/(лг, у) =
в q0 = const вычисление коэффициентов ряда упрощается.
*) См., например, Ю. А. Ш и м а н с к и й, Изгиб пластин, М. — Л.,
Главная редакция судостроительной литературы, 1934.

278 НЕКОТОРЫЕ ЗАДАЧИ ПРИКЛАДНОЙ ТЕОРИИ УПРУГОСТИ [ГЛ. VII
Рекомендуется читателю проделать указанные выше операции для
случая q = const и показать, что в этом случае прогиб пластинки
имеет вид
w
_ityo V V
х . у
оо оо Sin НТК —Sltl ЛЯ ^т-
а b
SS
= 1п = 1 \а* Т №.
где /ю = 1, 3, 5,,.. и п = 1, 3, 5,..., а прогиб в центре
т-\-п
оо оо — 1
= }&fo у У ( — 1) 2
Этот ряд быстро сходится, и удовлетворительное приближение
достигается уже одним лишь его первым членом. Так, для квадратной
пластинки первый член дает:
max пЬ£) »
что отличается от точного примерно на 2,5%.
Указанным выше методом и другими приемами (§ 85) решено
большое количество задач по изгибу пластинок, а результаты
представлены преимущественно в таблицах и графиках.
Все наиболее характерные случаи пластинок в смысле граничных
условий и характера загружения собраны в капитальном труде акад.
Б. Г. Галеркина «Упругие тонкие плиты» (Госстройиздат, 1933).
§ 85. Замечания о других решениях
Помимо решений в двойных тригонометрических рядах (§ 84) возможны
решения и в одинарных рядах. Так, в случае, если два противоположных
края пластинки (х = 0, х = а) свободно оперты, можно взять решение в виде
ряда
w
Fmsm-^-, (a)
где Ym — функция одного лишь у.
Каждый член ряда (а) удовлетворяет граничным условиям, т. е. при х = О
и х = а имеем oi = 0h МХ = 0. В дальнейшем остается определить Ym так,
чтобы удовлетворялись граничные условия на краях у = zt —, а также
уравнение изогнутой поверхности (7.11).

§ 86]
КРУГЛАЯ ПЛАСТИНКА
279
В общем случае, когда граничные условия отличны от случая свободного
опирания, взамен (а) надлежит принять:
оо
w = J] YmXm, (б)
где Хт — функция одного лишь х и подбирается в соответствии с
граничными условиями пластинки на сторонах х = О и х = а.
Если направление пластинки, совпадающее с осью Ох, назвать
поперечным, а совпадающее с направлением Оу — продольным, то, следуя В. 3. Власову,
функции Ym называют обобщенными прогибами, а функции Хт — функциями
поперечного распределения прогибов.
Представление поверхности прогибов в виде разложения (б) при
конечном числе т означает сведение пластинки к системе с конечным числом
степеней свободы в поперечном направлении при сохранении бесконечного
числа степеней свободы в продольном направлении.
Это означает также приведение двухмерной задачи теории упругости
к одномерной, так как после разыскания всех т функций Ym (функций
одного переменного) значения прогибов w (xy у) будут определены с
известной степенью точности.
Функции поперечного распределения прогиба Хт, аппроксимирующие
деформированное состояние произвольной поперечной полоски, вырезанной
из пластинки, могут быть выбраны различными способами, лишь бы эти
функции удовлетворяли геометрическим условиям пластинки на продольных
краях и были линейно независимыми.
Можно принять за функции Хт фундаментальные функции поперечных
колебаний балки постоянного сечения или функции потери устойчивости
стержня, или в случае шарнирного опирания пластинки на продольных
краях — тригонометрические функции.
Из числа приближенных методов решения задачи отметим так
называемый «метод сеток», «энергетические» и «вариационные методы». В
методе сеток интегрирование выполняется численным путем при помощи
исчисления конечных разностей. (См. работы А. П. Синицына, П. М. Варвака,
А. Ф. Смотрова и др.). Энергетические и вариационные методы в основном
исходят из положения, что истинному решению задачи соответствует
минимум потенциальной энергии изгиба пластинок.
Кооперирование методов теории упругости с методами строительной
механики за последнее время составило специальное отраслевое
направление в механике, а именно, «строительную механику пластинок» (см § 90).
§ 86. Круглая пластинка
Для случая круглой пластинки, защемленной по контуру и
имеющей равномерно распределенную нагрузку, решение просто
получается из задачи с эллиптической пластинкой. В общем случае на-
гружения круглой пластинки весьма удобно пользоваться полярными
координатами г и 6; поэтому все основные уравнения изгиба
пластинки преобразуем к полярным координатам по формулам
x = rcosb; #v=rsin8.
Впрочем, необходимый результат может быть получен сразу.
Дело в том, что левая часть уравнения (7.11) по своей конструкции
сходна с левой частью уравнения (3.40) для функции напряжений

280 НЕКОТОРЫЕ ЗАДАЧИ ПРИКЛАДНОЙ ТЕОРИИ УПРУГОСТИ [ГЛ. VII
(и то и другое уравнения написаны в декартовых координатах).
Поэтому для перевода уравнения (7.11) в полярные координаты
необходимо использовать (3.45) с заменой в нем ср на w.
Основное уравнение изогнутой поверхности (7.11) примет вид
д2 , 1 д , 1 d2\/d2w . 1 дда , 1 d2w\ 1 , (i, n QQ,
В случае, когда нагрузка не зависит от в, т. е. когда она по
всем направлениям от центра пластинки распределена равномерно
(полярно-симметричное нагружение), уравнение упругой поверхности
принимает вид
D(dF + 7^-Wl?*+-?*-dF) = «- (7'34)
Общий интеграл этого уравнения составится из общего интеграла
w1 однородного уравнения без правой части, т. е. если q = 0 [здесь
можно по аналогии воспользоваться уравнением (3.49)], и какого-либо
частного интеграла w2. Последний зависит от характера нагрузки, и
если q постоянно (случай сплошной равномерной нагрузки), для него
можно взять выражение
~2 64D '
Таким образом, общим решением для круговой пластинки при
сплошной равномерной нагрузке будет:
^ = ^lnr + £^lnr + Cr2+D + J^. (7.35)
Для сплошной пластинки, т. е. без выреза в средней части, из
условий, что при г = 0 прогиб w и производные должны быть
конечными, заключаем: А = В = 0. Остальные постоянные найдем из
граничных условий. Этими условиями будут:
а) если пластинка защемлена по контуру, то при г = a, w = О
dw л
-— = 0; используя эти граничные условия, получим выражение
(7.15а);
б) если пластинка оперта по контуру, то граничные условия
запишутся: при r = a, w = 0, ог = 0, т. е. при г = а
d2w , (х dw
рекомендуется читателю использовать указанные граничные условия
и убедиться в справедливости для такого случая следующего
уравнения изогнутой поверхности:
W
-Ы^-^+^ттг*]'' (7-36)

§ 87]
ИЗГИБ ПЛАСТИНКИ
281
в) для случая пластинки с шарнирно-опертым краем при отсут*
ствии нагрузки (q = 0), но под действием равномерно
распределенного момента МГ = М, граничные условия запишутся: при г = а>
w = 0
для такой краевой задачи в итоге получим:
• = 5ЩГЙ0(^-/Л)- (7-37)
Некоторые особенности представляют задачи для случая
сосредоточенной силы Я, приложенной в центре пластинки. Приводим без
доказательства решения. Если пластинка защемлена по контуру, то
w=8^[W'-r^-r2lnTl (7-38>
Если пластинка оперта по контуру, то
™ = М^3т^(а2-г2)-г2]пт1 (7-39>
Для случая пластинки, опертой по контуру и в центре и
нагруженной сплошной равномерной нагрузкой, необходимое решение
получим, надлежаще комбинируя указанные выше.
§ 87. Изгиб пластинки под совместным действием поперечных:
нагрузок и сил в ее срединной плоскости
В предшествующем изложении предполагалось, что пластинка
изгибается одними лишь поперечными нагрузками. Если кроме по*
перечных нагрузок будут еще и силы, действующие в срединной
плоскости пластинки (для краткости будем их называть
«продольными») (фиг. 127), то они могут оказать значительное влияние на
изгиб пластинки и потому при выводе дифференциального уравнения
изогнутой поверхности их необходимо учесть. Очевидно, что сами
по себе «продольные» силы *), т. е. при отсутствии поперечных
нагрузок, поперечного изгиба пластинки не вызвали бы, и по терминологии
теории упругости это составляло бы задачу на плоское напряженное
состояние. Также очевидно, что при наличии поперечных нагрузок
эти «продольные» силы окажут влияние на прогиб (уменьшат, если
«продольные» силы — растягивающие, и увеличат, если они — сжиг
мающие).
Если , при поперечном изгибе пластинки напряжения ох> оу и
тг//, взятые со всей толщины пластинки, приводились (см. § 83) к
*) Если, конечно, они не превышают критических значений, при которых
теряется устойчивость плоской формы пластинки (см. § 88).

282 НЕКОТОРЫЕ ЗАДАЧИ ПРИКЛАДНОЙ ТЕОРИИ УПРУГОСТИ [ГЛ. VII
изгибающим моментам (МХУ Му) и крутящим (Мху)у иначе говоря, к
парам, то при наличии сил, параллельных срединной плоскости,
указанные выше напряжения будут приводиться не только к парам, но и
к силам.
В дальнейшем вводятся следующие обозначения внутренних
усилий на единицу длины:
f axdz = Nxi
faydz=Ny,
h_
2
'Xydz — Nxyl
(7.40)
называемые интенсивностями сил, действующих в
срединной плоскости (размерность их — сила, деленная на длину).
Для опорного контура пластинки, очевидно, Nx, Ny и Nxy
составляют внешние силы, приходящиеся на единицу длины контура.
Если задачу решать в духе классической теории упругости и,
в частности, при написании дифференциальных уравнений равновесия
исходить из первоначальной, т. е. недеформированной формы
элементарного параллелепипеда, то мы потеряем взаимосвязь во влиянии
поперечных нагрузок на деформации от продольных, и наоборот.
Иначе говоря, решение разобьется на два независимых решения: от
продольных сил (это будет плоско-напряженное состояние) и от
поперечных сил (решение, изложенное в §§ 78—82).
Рассматриваемая задача характерна именно для нелинейной теории
упругости (нелинейность понимается в смысле геометрическом) и в этом
плане только может быть решена. Не будем приводить всего комплекса
исходных уравнений нелинейной теории упругости, так как, имея
целью получить решение, приемлемое для практических целей
(следовательно, не претендующее на абсолютную точность), будет достаточно
внести поправки только в дифференциальные уравнения равновесия (2.02).
Эти последние должны быть написаны, исходя из деформированной
формы элементарного параллелепипеда. Последовательность
исследования должна быть сходной с изложенной ранее в § 79.
На фиг. 127 (внизу) показаны две проекции элементарного
параллелепипеда с учетом того, что компоненты напряжений, первоначально

§ 87] изгиб пластинки 283
параллельные срединной плоскости пластинки, в связи с ее изгибом
оказываются уже не параллельными друг другу.
Выдерживая характер исследования, свойственный прикладной
теории, логично допустить, что все параллелепипеды, принадлежащие
одной нормали (т. е. имеющие общие координаты х и у), «искри-
Фиг. 127. Изгиб пластинки под совместным действием поперечных нагрузок
и сил в ее срединной плоскости.
вляются» одинаково. Иначе говоря, их срединная плоскость при
искривлении оказывается параллельной искривленной срединной
поверхности пластинки.
Если при составлении уравнений равновесия пренебречь малыми
величинами выше третьего порядка малости, то первые два
дифференциальных уравнения равновесия (^Х=0, ^Y=0) после упрощений
ничем не будут отличаться от прежних (2.02). Существенные
изменения претерпит третье уравнение y^Z = 0).

284 НЕКОТОРЫЕ ЗАДАЧИ ПРИКЛАДНОЙ ТЕОРИИ УПРУГОСТИ [ГЛ. VII
В результате изгиба пластинки между направлениями компонентов
Од,, оу, тху, действующих на противоположные грани элемента,
образуются малые углы. Так, проекция напряжений ох на ось Oz дает:
После упрощения, если пренебречь малыми величинами выше
третьего порядка малости, эта проекция получает такое выражение:
°* Ш2 dX dy dz + ~д§ Jx~ dX dy dz' (a)
Аналогично запишется проекция напряжений ау на ось Oz:
d2w dcydw
Gvdj*dxdydz + 'dj-dydxdydz- (б)
Что касается проекции касательных напряжений zxy на ось Oz, то
заметим, что уклон изогнутой срединной поверхности элементарного
параллелепипеда в направлении Оу на двух противоположных гранях
dw „ (dw , d2w , \
элемента выразится производными -^— на одной грани и Ы г а ' a dx)
на другой грани. В результате проекция на ось Oz запишется так:
d2w dixv dw
х^Шд^ dxd»dz^^T-dj dx йУ dz-
Аналогично запишется проекция на ось Oz и напряжений zyx.
Окончательное выражение для проекции напряжений zxy и zyx на
ось Oz представится в виде
d2w дтху dw dixy dw
2z*vWdjdxdSdz + ^r^dxdydz + -bT^dxdSdz- (в>
Проекции на ось Oz остальных напряжений (на фиг. 127 не
показанных): izx, >z az можно записать без изменений относительно
прежнего (2.02). Таким образом, окончательное уравнение равновесия
на ось Oz после сокращения у всех членов уравнения множителя
dxdydz будет:
d2w dcx dw d2w day dw d2w
^xI^^JxJ^^^y~dy2^~~dy'dy^~ 2z*y Jx~dy ""J"
4.f^i^!^l__n (\
"^ dx dy ~T~ dy dx "" L dx "^ dy ~^ dz J ~~ u* ^
Выражение, написанное в скобках, есть прежнее уравнение
равновесия (2.02).
Если повторить все выкладки, указанные на стр. 263, то, очевидно,
diay dw dzxy dw

§ 87]
ИЗГИБ ПЛАСТИНКИ
285
в отличие от (7.07) должны получить:
Ez (№ - 3 z*) д2 д d2w д
Лш + ш )\ш+7пя ) + *(*• у)—
г~ 8(1— \>?) \дх* ^дуУ \дх* ^дуУ
-дх-*)а*аг--дх-1]Шс1*+ )l)y-d2\-
-W) a*dz-Ty [J HJ** + J TF*J -2 a^J ^- <*>
В последнем выражении интегралы можно взять по всей толщине
h h ,
пластинки, т. е. от z = -9- Д° ^ === — "о" (эт0 отразится на постоянной
интегрирования, завуалированно присутствующей в ф (лг, у)). Далее
придем к заключению, что попрежнему
Ф(*> ^) = ^/?-
Принимая во внимание обозначения (7.40), а также учитывая, что
следующие интегралы, взятые по всей толщине пластинки, очевидно,
равны нулю *):
h Л^
*) В этом легко убедиться, если вырезать во всю толщину пластинки
о
'Ki
г 3
А<*У
%1_
&dy
1
v*a?*
f Чг+^^
£*
Фиг. 127а. К доказательству формул (е).
элемент с размерами граней dx, dy и h и к нему применить уравнения
равновесия (3.30) 2*=0, 2 Г= ° (*иг- 127а)*

286
НЕКОТОРЫЕ ЗАДАЧИ ПРИКЛАДНОЙ ТЕОРИИ УПРУГОСТИ [ГЛ. VII
взамен (7.11) мы получим из (д) следующее окончательное
дифференциальное уравнение изогнутой поверхности пластинки:
d^w
дх* ду* ' ду* D \и ^ х дх* ^
(7.41)
Этим уравнением и следует пользоваться вместо уравнения (7.11)
при определении прогиба пластинки, если кроме поперечных нагрузок
она подвергается еще и действию сил в ее срединной плоскости.
§ 88. Устойчивость прямоугольной пластинки, свободно-
опертой по четырем сторонам и сжатой в одном направлении
Пусть пластинка свободно оперта по сторонам л: = О, х= я, у = О
и у = Ь, причем а > Ь> и подвергается действию продольных
сжимающих сил по коротким сторонам (фиг. 128). Вычислим, при каких зна-
Мкр
*1
I
т I
mi
j
1
— а -А
"нр
Фиг. 128. К задаче по упругой устойчивости пластинки.
чениях сжимающих сил пластинка потеряет устойчивость. Предположим,
что выпучивание пластинки происходит по уравнению
^ . тпх . пу
w = Csm sin -f1,
a b '
(7.42)
т. е. в направлении длинных сторон имеем синусоиду с т
полуволнами {т — целое и пока неизвестное число), а в направлении
короткой стороны — то же с одной полуволной.
Уравнение (7.42) удовлетворяет граничным условиям, так как
при лг=0, х=а, у = 0, у = д перемещение w обращается в нуль.
Удовлетворяет (7.42) и исходному дифференциальному уравнению
изогнутой поверхности (7.41). В самом деле, дифференцируя (7.42),

§ 89] ВСЕСТОРОННЕЕ СЖАТИЕ ПРЯМОУГОЛЬНОЙ ПЛАСТИНКИ 287
имеем:
d*w тс4 # d*w т2ъ*
Jyi — b*™' dx* dy2 ~~ ~tf¥ W'
(a)
Подставляя (а) в (7.41) и принимая во внимание, что в данном
случае Ny = Nxy = 0, a NX= — iVKr, видим, что уравнение (7.41)
удовлетворяется, так как функция w в уравнении сокращается.
Итак, получаем следующее тождество:
/га4*4 , 9 /я2*4 , п4 1 т2п2
откуда
или в краткой записи
(7.43)
N9p = ^kt (7.44)
где fe = m2+2_+_.
Остается обследовать выражение (7.44) на минимум, учтя, что
по смыслу задачи (граничные условия) m может принимать только
целые положительные значения. Для квадратной пластинки (а = Ь)
минимум (7.44) получается при m = 1, и таким образом, в этом случае
ЛГкр = 4^, (7.45)
и соответственно критическое напряжение в пластинке, переход через
которое влечет выпучивание пластинки,
Л/кр &Е fh\2
jkp— h — 3(1—и*)
У
§ 89. Всестороннее сжатие прямоугольной пластинки
Пусть пластинка, обследованная в предыдущем параграфе на
устойчивость, подвергается сжатию в двух направлениях силами, величина
которых на единицу длины опорной кромки соответственно Nx и Ny
(фиг. 129). Пусть между последними сохраняется соотношение Ny = aNx.
Положим a>b и а<1. В качестве попытки примем уравнение
выпучившейся пластинки в виде
~ . ткх . пъу ,м ла^
w = Cs\n sin —^- , (7.46)
где т и п — целые, пока неизвестные числа. Уравнение (7.46)
удовлетворяет граничным условиям; так как при лг=0, лг=а, у = О,
у = #, по (7.46) получаем w — 0.

288 НЕКОТОРЫЕ ЗАДАЧИ ПРИКЛАДНОЙ ТЕОРИИ УПРУГОСТИ [ГЛ. VII
Удовлетворяет (7.46) и исходному уравнению, так как,
дифференцируя его и подставляя производные в (7.41), имеем тождество
т*к* . 0т*п*к* , nW 1 Г.. mW . лг nW
откуда
N Ю"Щ-
х ab
т b , па
Ьа г
па т b
(7.47)
цшшии
Для случая квадратной пластинки и одинаковых в двух
направлениях сжимающих усилий
последнее выражение упрощается и
принимает вид
наименьшее значение для NKV имеем,
очевидно, при /и = 1, т. е.
окончательно
гптгттгп1~
"у
Фиг. 129. Всестороннее сжатие
прямоугольной пластинки.
Мср = 2*2§'
(7.48)
§ 90. Исторические сведения о развитии теории пластинок
Пластинка, будучи, как и стержень, сравнительно простым
конструктивным элементом сооружения, являлась в некотором смысле пробным камнем
для проверки эффективности многих предлагаемых методов решения
уравнений теории упругости. В этом смысле на истории развития теории
пластинок отчасти можно проследить и эволюцию отдельных методов и частных
подходов к решению задач теории упругости.
Вместе с тем можно отметить и обратное, а именно: достижения в
области расчета пластинок оказывали благоприятное влияние на разработку
практических методов, главным образом в прикладной теории упругости.
Обстоятельный обзор работ по теории упругого изгиба толстых и
тонких плит имеется в интересной статье Г. Ю. Джанелидзе,
опубликованной в томе XII журнала «Прикладная математика и механика» за 1948 г.
В указанной статье читатель найдет также подробную библиографию по
математической теории пластинок, работающих в пределах упругости. Ниже
ограничимся сжатым обзором исследований, главным образом в прикладной
теории упругости и пластичности.
Помимо исследований, положивших начало развитию теории пластинок
и отмеченных выше в §§ 79, 84, в числе фундаментальных работ,
опубликованных до Великой Октябрьской социалистической революции, следует
в первую очередь назвать исследования И. Г. Бубнова в его труде
«Строительная механика корабля» (1914 г.) и С. П. Тимошенко в труде «Теория
упругости» (1916 г.).
После Революции первые исследования по теории толстых плит были
выполнены акад. Б. Г. Галеркиным, применившим при изучении задачи об
изгибе толстой плиты развитый им ранее метод решения пространственной
задачи теории упругости с помощью трех бигармонических функций.
Гипотеза прямых нормалей, конечно, в теории толстых плит неприменима.

§ 90] ИСТОРИЧЕСКИЕ СВЕДЕНИЯ О РАЗВИТИИ ТЕОРИИ ПЛАСТИНОК 289
Б. Г. Галеркиным были получены решения в двойных
тригонометрических рядах для случая свободно-опертой прямоугольной и треугольной
толстых плит, а затем в одинарных рядах для прямоугольной толстой плиты.
Доведенные до численных результатов и сопоставленные с вычислениями по
формулам теории тонких плит исследования Б. Г. Галеркина установили,
что обычная теория тонких плит пригодна даже для плит с отношением
толщины к наименьшему другому размеру, равным 1/3.
Оригинальные исследования в теории толстых плит были проведены
проф. А. И. Лурье (1936 г.), разработавшим новый метод решения задач
математической физики для тел, ограниченных двумя параллельными
плоскостями. Им же было выведено уравнение равновесия плиты переменной
толщины. Задача изгиба толстых плит, нагруженных гармонической нагрузкой
(т. е. нагрузкой, удовлетворяющей уравнению Лапласа), была решена
С. Г. Гутманом.
Исследования А. И. Лурье были обобщены П. Г. Шулежко на случай
плит из анизотропного и неоднородного материала.
К числу оригинальных, практических методов расчета толстых плит
следует отнести исследования М. М. Филоненко-Бородича (§ 75).
В СССР имеется обширная литература по теории тонких плит. Здесь
в .первую очередь следует опять упомянуть акад. Б. Г. Галеркина,
подытожившего свои многочисленные исследования в капитальной монографии
«Упругие тонкие плиты» (1933 г.).
Как справедливо отмечает Г. Ю.Джанелидзе в упомянутой выше статье,
«без преувеличений можно сказать, что классическая теория плит, бывшая
до выхода работ Б. Г. Галеркина достоянием математиков, стала после
появления его книги действенным орудием в руках инженеров». Здесь под
классическим направлением понимается использование метода Фурье при
интегрировании неоднородного бигармонического уравнения и представление
решения в виде двойных или одинарных рядов.
Значительное развитие упомянутое классическое направление получило
в обширной монографии П. Ф. Папковича «Строительная механика
корабля» (1941 г.), удостоенной Сталинской премии, второй том которой
посвящен вопросам расчета пластин.
К тому же направлению примыкает монография Ю. А. Шиманского
«Изгиб пластин» (1935—1937 гг.).
С именем В. 3. Власова связано начало успешного применения методов
строительной механики к задачам о равновесии тонких упругих плит. Такой
синтез методов теории упругости и строительной механики был применен
В. 3. Власовым (еще ранее) к более сложной задаче о равновесии оболочек
и складчатых покрытий (1933 г.). К этому же направлению примыкают
исследования А. С. Калманок, изложенные в монографии «Строительная механика
пластинок» (1950 г.).
Выше было указано о том, что достижения в области расчета плит,
явившиеся результатом создания новых эффективных методов решения задач
теории упругости, сами затем оказывались плодотворными в решении более
общих и сложных задач теории упругости. Примером может являться
монография В. 3. Власова «Строительная механика тонкостенных
пространственных систем» (1949 г.), в которой отдельные решения задач по пластинкам
успешно используются при расчете целых пластинчатых систем,
призматических оболочек и т. п. Указанная монография вместе с другой книгой
В. 3. Власова «Общая теория оболочек» (1949 г.) была удостоена
Сталинской премии.
Ряд сложных задач об изгибе, колебаниях и устойчивости
прямоугольных пластинок, подкрепленных ребрами жесткости, были решены А. С. Лок-
шиным и А. Н. Филипповым (1935—1937 гг.).
Ценные исследования по расчету плит, лежащих на упругом основании
В смысле гипотезы Фусса (иногда называемой гипотезой Винклера-Циммер-
19 Зак. 3880. Н. И. Безухов

290 НЕКОТОРЫЕ ЗАДАЧИ ПРИКЛАДНОЙ ТЕОРИИ УПРУГОСТИ [ГЛ. VII
мана, хотя русский академик Николай Иванович Фусс ее высказал еще
в 1801 г., т. е. намного раньше Винклера), были выполнены Н. М. Герсева-
новым (1933 г.) с помощью специального разработанного им метода
функциональных прерывателей. В этом направлении работы были продолжены
О. Я. Шехтер, А. В. Винокуровой, Г. С. Шапиро, А. С. Малиевым.
По теории расчета плит, лежащих на упругом основании (трактуемом
как упругое полупространство; см. § 127), в первую очередь следует
отметить М. И. Горбунова-Посадова (1940 г.).
Приближенный метод расчета круглой плиты на упругом основании,
связанный с применением методов строительной механики (см. § 127), был
дан Б. Н. Жемочкиным (1938 г.).
Использование функций комплексной переменной, аналогичное
предложенному для плоской задачи Н. И. Мусхелишвили, было сделано А. И. Лурье
(1928 г.).
Изящное обобщение метода комплексного переменного на случай изгиба
анизотропных плит было дано С. Г. Лехницким, обширные исследования
которого по названному вопросу и по устойчивости плит были собраны
в монографии «Анизотропные пластинки» (1947 г.), а также в монографии
«Теория упругости анизотропного тела» (1950 г.); первая была удостоена
Сталинской премии.
Оригинальные решения по расчету упругих плит были предложены
Ю. Б. Репман, Б. Г. Кореневым, С. С. Голушкевичем, Я. Л. Лунц, С. А. Герш-
гориным, Г. Ю. Джанелидзе и др.
Упруго-пластические деформации изгиба плит были обследованы В. В.
Соколовским (1944 г.) и А. С. Григорьевым.
Упруго-пластическая устойчивость пластинок была изучена А. А.
Ильюшиным (1946 г.) и изложена в его монографии «Пластичность» (1948 г.).
Отметим исследования на ту же тему С. Н. Никифорова и А. С. Вольмира.
Ряд исследований по пластическим деформациям плит, сложных в плане
очертаний, выполнены А. А. Гвоздевым, положившим начало синтеза теории
пластичности и строительной механики; его исследования были продолжены
А. Р. Ржаницыным (см. § 128).
Из приведенного выше краткого и далеко не полного обзора читатель
может все же составить представление о том, что советская наука в
развитии методов расчета пластинок обогатилась рядом ценных идей и
практических методов. Последнее, впрочем, следует отнести и ко многим другим
разделам теории упругости и пластичности, большая группа ученых в
области которых удостоена за свои исследования Сталинских премий.
§ 91. Стесненное кручение стержня эллиптического сечения
Рассмотрим стержень эллиптического сечения, левый конец которого
закреплен против дспланации (например, защемлен наглухо в стену), а на
правом — свободном конце приложен крутящий момент. Примем, что
последний осуществляется только касательными усилиями, распределенными по
сечению согласно (6.23). Как было показано в § 73, в данном случае имеем
стесненное кручение, и поэтому найденный ранее для случая нестесненного*
кручения (§ 69) закон дспланации сечения (6.27)
Мк(а2 — №)
W= G**» ХУ
совершенно неприменим в области стержня, расположенной близко к левому
опорному сечению.
В поперечных сечениях помимо касательных напряжений,
уравновешивающих крутящий момент, должны появиться, как об этом было разъяснено
в § 73, также и нормальные напряжения, которые статически взаимно»

§ 91] СТЕСНЕННОЕ КРУЧЕНИЕ СТЕРЖНЯ ЭЛЛИПТИЧЕСКОГО СЕЧЕНИЯ 291
уравновешены. Наибольшие значения упомянутые нормальные напряжения,
естественно, будут иметь в опорном сечении стержня, где оказывается
наибольшее сопротивление депланации.
В соответствии с высказанным следует предположить, что эффект
стеснения должен иметь местный характер, быстро убывающий от опорного
сечения.
Направим ось z по оси стержня, начало координат примем на левом
конце стержня и напишем, предположительно, для депланации любого
сечения, находящегося на расстоянии z от закрепленного сечения, следующее
выражение:
w = чш& м*ху <! - е~п^ <7-49>
Выражение (7.49) при z = О определяет w = 0 (что соответствует
полному закреплению сечения против депланации) и переходит в формулу
свободной депланации (6.27) только при z = оо. В этом смысле выражение (7.49)
формально не удовлетворяет тому условию, что при z = / (на свободном
конце) можно практически ожидать именно свободной депланации. Но, как
это видно из последующего рассмотрения, показательная функция (7.49)
такова, что уже при небольшом z она определяет депланацию, практически
не отличимую от свободной депланации.
Для определения значения неизвестного множителя п в дальнейшем
используем принцип минимума потенциальной энергии. Сейчас внесем
уточнения в напряжения, полученные ранее для эллиптического сечения при его
чистом (не стесненном) кручении. Можно сохранить прежние допущения, что
ах = а = 0. Тогда для осевых напряжений az можно записать:
или на основании (7.49)
°я = Е*г
z dz ita*bs G K ^
E
а заменяя G = n ,. ,—г-, имеем:
2(1+P)
°* = n 4Йг 2 (1 + 10 Mjye-™. (7.50)
Наличие в поперечных сечениях нормальных напряжений (и к тому же
неравномерно распределенных по сечению) должно изменить прежние
касательные напряжения zxz и т^, подсчитанные для нестесненного
кручения (при отсутствии qz)9 и естественно предположить наличие касательных
напряжений ixy.
Примем для этих последних (это будет новое допущение) следующее
начертание:
t^y = k (cPb* — Лк*— я2у2) *-**• (7.51)
Это выражение удовлетворяет следующим условиям: при z = со, ixy
обращается в нуль, т. е. закон для zxy связан с законом стесненной
депланации (7.49).
Далее на контуре сечения, т. е. для точек, удовлетворяющих уравне-
х2 у2
пню —2" + "Т2~=1» имеем ^^ = 0, что при наличии ох = ау = 0
соответствует случаю отсутствия нагрузки на боковой поверхности стержня. Под k
необходимо понимать постоянную величину, зависящую от крутящего
момента, которую определим в дальнейшем.

292 НЕКОТОРЫЕ ЗАДАЧИ. ПРИКЛАДНОЙ ТЕОРИИ УПРУГОСТИ [ГЛ. VII
Обратимся теперь к дифференциальным
которые при Сд. = Су = о примут вид
уравнениям равновесия (2.02),
dz.
ху
дт„
ду
<^ух_
дх
dz
dz.
■ = 0,
yz
dz
:0. \
dzz
dz.
дх
zy_
ду
dz
= 0.
(7.52)
Для принятого выражения zxy из первых двух уравнений (7.52) путем
интегрирования получаем:
— e-nz 4ka*y (аЧ2— bW — а*у*) + ^%_
— L е- nz 4Шх (аЧ2—№х* — а?у2) -
2МК
ncfib
(7.53)
Оба последних члена являются независимыми от z произвольными
функциями (исполняют роль постоянных интегрирования) и имеют такой же вид
(преднамеренно принято), как и соответствующие выражения в теории
нестесненного кручения эллиптического сечения.
Граничным условиям формулы (7.53) удовлетворяют, так как на боковой
поверхности стержня первые члены формул zxz и zyz обращаются в нуль,
а вторые их члены, вместе взятые, удовлетворяют граничному условию
(см. стр. 291).
При подстановке значений для аг, zxz и %yz из формул (7.50) и (7.53)
в последнее уравнение (7.52) заключаем, что оно будет тождественно
удовлетворено, если для k принять значение
* = л3та?(1+^в- (7-54>
Установленные выше формулы для напряжений (7.50), (7.51) и (7.53)
удовлетворяют дифференциальным уравнениям равновесия и статическим
граничным условиям, так как и те и другие были использованы. Но, к
сожалению, вследствие произвольности принятого выражения для депланации w
и для касательного напряжения zxy (хотя с качественной стороны и
соответствующих характеру задачи) упомянутые выражения не удовлетворяют
условиям неразрывности деформации. В последнем можно легко убедиться
путем надлежащих подстановок принятых формул для напряжений в
уравнения совместности деформации, например, в (3.29).
Однако мы можем получить приближенные значения для напряжений,
которые будут мало отличаться от действительных, если оставшийся пока
неопределенный коэффициент п определим из условия, чтобы работа
деформации имела минимум. Для этой цели надлежит выполнить следующие
вычисления. На основании (3.126) удельная потенциальная энергия в
рассматриваемом случае (ах = ау = 0) запишется так:
3 = ^О Ьп + е) G* + **У + "& + ****] • <7'55)
2(1 + |0
Для получения полной потенциальной энергии надлежит выражение (7.55)
проинтегрировать по всему объему стержня, т. е.
Э = I I I ddzdx dy.
(7.56)

§ 92] СЛОЖНОЕ СОПРОТИВЛЕНИЕ ТОНКИХ И ТОНКОСТЕННЫХ СТЕРЖНЕЙ 293
Подставляя (7.50), (7.51) и (7.53) в (7.56), имеем (опуская громоздкие
хотя и элементарные операции):
о -1 /1 , 49 пл2 а* — Ь* Г . аЧ* . ч (£ + № 1 .
1 <(*2 + *2)
+ 20 ^^— '' (7'57)
где / — длина стержня.
Выражение (7.57) дифференцируем по п и производную приравниваем
нулю, что соответствует условию минимума потенциальной энергии. Таким
образом, для п получаем выражение
9- 1 / Д2+62 /~(д2+£2)2 , 16 \
П ab\ ab — V аЧ* ~*~ 1 + у. f'
Перед радикалом мы должны взять лишь один знак (именно плюс), так как
согласно условиям задачи п должно быть действительным и положительным.
Интересно проследить на частных случаях результаты изложенной выше
приближенной теории стесненного кручения эллиптического сечения. Так,
при а = Ь (сечение — круг) имеем п = 1,45 —; при таком п по формуле (7.54)
получаем k = 0, и таким образом, обращаются в нуль все те члены в
выражениях напряжений, в которые входит п\ остается лишь решение,
полученное ранее для нестесненного кручения. Иначе говоря, закрепление от депла-
нации круглого сечения ничего не меняет, так как в круглом сечении при
его закручивании вообще не происходит депланации.
Для случая а = 106 (сильно сплюснутый эллипс) наибольшее по
абсолютной величине нормальное напряжение получается в защемленном сечении
и на 65% больше самого касательного напряжения в том же сечении.
Для случая, когда а по сравнению с Ь можно считать бесконечно
большим (практически соответствует прямоугольному сечению с таким же
отношением сторон), наибольшее нормальное напряжение в опорном сечении
оказывается в 1,58 раза больше ттах для того же сечения, если последнее
подсчитать по формулам нестесненного кручения.
§ 92. Сложное сопротивление тонких и тонкостенных стержней
В дальнейшем изложении предполагается тонкий стержень,
подвергаемый действию осевых сил, поперечных нагрузок и
скручивающих моментов.
Ось Oz совмещаем с осью стержня, оси Ох и Оу отнесем к
главным осям сечения. Для рассматриваемого в дальнейшем поперечного
сечения компоненты равнодействующей внешних сил, расположенных
по одну сторону от этого сечения, обозначим: Nz — продольная сила;
Мх и Му — изгибающие моменты относительно главных осей сечения.
Примем следующие предположения *), оправдание которым дано ниже;
в» = ву = Та>у = °; (7-58)
™д = ?(*, У)*, (7.60)
*) Изложение по Г. Ю. Джанелидзе [32].

294 НЕКОТОРЫЕ ЗАДАЧИ ПРИКЛАДНОЙ ТЕОРИИ УПРУГОСТИ [ГЛ. VII
где т = т(г) — угол закручивания на единицу длины; <р = ср(лг, у)—
функция кручения — иначе функция свободной депланации,
удовлетворяющая (6.07), о)д — стесненная депланация.
И, наконец, напряжения ода, ъу и zxyi хотя и не отрицаются, но
считаются в дальнейшем второстепенными. Основными напряжениями
принимаются ог, хуг и zzx.
Условие (7.58) соответствует предположению о недеформируемости
контура поперечного сечения. Условия (7.59), соответствующие (6.05),
целиком взяты из теории простого (нестесненного) кручения.
Условие (7.60) выражает гипотезу о том, что фактическая, т. е.
стесненная, депланация ставится в зависимость от изменения вдоль оси
стержня относительного угла закручивания.
Из (7.60) следует, что относительное удлинение за счет
депланации равно
('.)ж = -Л? = ?{х,У)ч, (7.61)
При сделанном разделении напряжений на основные и
второстепенные, пренебрегая влиянием второстепенных напряжений (например,
ож, оу) на деформации в направлениях основных (например, в
направлении ог), можем записать для напряжения ag9 вызванного только
за счет стеснения депланации:
(а,)д = Егй = Е.о (*, у) х. (7.62)
Из (7.62) следует, что если по всей длине стержня
относительный угол закручивания одинаков, т. е. никакого стеснения чистому
закручиванию нет, то о2 = 0 (так как х = 0), а депланация ничем не
отличается от свободной.
Таким образом, нормальные напряжения в поперечном сечении
закручиваемого стержня появляются лишь при наличии стеснения
депланации. Таков смысл кинематического условия (7.60) или (7.61),
С качественной стороны соответствующего действительности.
Наличие в рассматриваемой задаче продольного усилия Nzi а также
изгибающих моментов Мх и Му заставляет взамен выражения (7.61)
принять более общее:
Ч = е + V — *2*+ (е*)д> (7.63)
где первые три слагаемые, обычные в элементарной теории изгиба
стержней, изображают закон плоских сечений. В (7.63) обозначено:
е — относительное удлинение оси стержня в рассматриваемом сечении;
Xj (z) и х2(г) — кривизны деформированной оси стержня для того же
сечения.
Четвертое слагаемое в (7.63) выражает отступление от закона
плоских сечений. Итак, взамен (7.61) принимаем более общее:
% = в + ЧУ — ха*+ в (*, У) т. (7.64)

§ 92] СЛОЖНОЕ СОПРОТИВЛЕНИЕ ТОНКИХ И ТОНКОСТЕННЫХ СТЕРЖНЕЙ 295
Используем вначале следующие три уравнения равновесия:
EZ=0; mx = 0; )1Му = 0. (а)
По одну сторону от сечения согласно условиям задачи проекция
внешних сил на ось Oz составляет Nz\ относительно главных осей
сечения те же силы составляют изгибающие моменты Мх и Му*
Таким образом, уравнения (а) записываются так:
F
[ ozydF = Mx1
F
Г ozxdF = Му.
(б)
F
Подставляя в (б) взамен ае выражение
ая = Еег = Е [г -f %гу — х2*+ <р (а:, у) х],
имеем:
EJX*1 -f EJ^Jz = МХУ \
EJy*-2 EJ<?y T == My,
(7.65)
(7.66)
где характеристики рассматриваемого сечения обозначены следующим
образом:
F F F
sv = j?(*> y)dF\ J<tx = f y-<?(x, y)dF; i ^^
F F
Некоторые интегралы обращаются в нуль, так как оси Ох и Оу—
главные оси сечения:
j* xdF=: j у dF= f xydF=0.
F F F
В соответствии с четырехчленной формулой (7.65) для а3 к трем
уравнениям равновесия (б) необходимо еще добавить одно. Для этой
цели можно обратиться к остальным еще не использованным
уравнениям равновесия, однако оказывается проще обратиться к энергети-

296 НЕКОТОРЫЕ ЗАДАЧИ ПРИКЛАДНОЙ ТЕОРИИ УПРУГОСТИ [ГЛ. VIF
ческому уравнению: работу внешних сил приравнять потенциальной
энергии или, это удобнее, элементарную работу обобщенных сил
приравнять вариации потенциальной энергии:
8Л = 8Э. (7.68)
Принимая за «обобщенные силы» в рассматриваемом сечении Nz>
Mxi My, Мг, а за соответствующие им «обобщенные координаты»
е, х1? х2, т, запишем элементарную работу обобщенных сил:
L
8Л = J [/V> + МхЬъ, + Лух2 + Mfr] dz, (в)
о
где L — длина стержня.
Формула, определяющая потенциальную энергию стержня, после
отбрасывания членов, содержащих второстепенные напряжения aXi зу>
zxyi записывается в виде
6 F
Освобождая внимание читателя от дальнейших и относительно
кропотливых преобразований, укажем лишь схему этих
преобразований и сообщим окончательные результаты. В выражение (г) взамен ог
надлежит подставить (7.65), а вместо касательных напряжений
согласно (7.59) следующие формулы:
1д 1 * (7-69)
Получив развернутое выражение для энергии, надлежит составить
выражение для вариации потенциальной энергии, т. е. для 8Э. Далее,
составив ЬЛ = 8Э, заметим, что в левой и правой частях уравнений
окажутся по четыре произведения при одинаковых множителях Ne, МХУ
Му и Мг.
Сравнивая коэффициенты при вариациях, приходим к четырем
соотношениям, три из которых были уже получены ранее (7.66)
с помощью уравнений равновесия, а четвертое имеет вид
Мш= GJd>z — EJjt — EJ^ + EJ^ — ES9*t (7.70)
- •• d2z • d%i • dv*o • de r
где обозначено т = ^2; *i = -^ ; *2 =-£ , e = ^; /d
—геометрическая жесткость сечения при свободном кручении и дополнительно
A=JV(*, y)dF. (7.71)

§ 93] продолжение: определение координат центра жесткости 297
Четыре соотношения (7.66) и (7.70) в случае известной функции
ср(лг, у) полностью решают задачу о сложном сопротивлении тонкого-
стержня.
Прежде чем перейти к частным случаям разобранной теории,
отметим важные следствия, вытекающие из формул (7.66) и (7.70),
наблюдаемые у стержней с несимметричным профилем:
1) неравномерное закручивание вызывает изгиб;
2) неравномерный изгиб вызывает закручивание;
3) неравномерное удлинение вызывает кручение;
4) неравномерное кручение вызывает изгиб.
В самом деле, если имеется т (неравномерное кручение), то иа
(7.66) вытекает, что будут %г или х2 (изгиб). Если имеется Xj или х^
(неравномерный изгиб), то из (7.70) вытекает, что будет т
(кручение). Если имеется е (неравномерное удлинение оси стержня), то из-
(7.70) вытекает, что будет т. Если имеется т, то из (7.66) следует,,
что будет хj или х2.
Заметим, что первое и второе следствия друг по отношению
к другу находятся во взаимности. То же можно сказать относительно
следствий третьего и четвертого. Собственно говоря, здесь мы имеем-
дело с известным читателю из строительной механики принципом
взаимности перемещений, своеобразно трансформируемым для стержня.
с несимметричным сечением.
§ 93. Продолжение: определение координат центра жесткости
Рассмотрим изгиб консольного призматического стержня силами Q^
и Qyy приложенными в точке свободного торца х = хх) и у=у0.
Для сечения на расстоянии z от торца имеем изгибающие и
крутящий моменты:
Mx = — Qvz, My = Qxz, Mt = x0Qy—y0Qx. (a>
Подставляя (а) в соотношения (7.66), (7.70), принимая во
внимание, что в данном случае 7VS = 0, находим:
EJX*X + Я/фа/с = — Qyz; EJy%i — EJ^i = Qxz\ (6>
OJdz — EJ^z — EJ9Xv.t + EJ^2 = x0Qy —y0Qx. (b>
Разрешая уравнения (б), (в) относительно Xj и х2 и подставляя
значения Xj и х2 в соотношение (7.70), получим дифференциальное
уравнение для определения угла закручивания на единицу длины:
^-£(/f-^-^)x"-(^ + ^)^-(v.-^)<?..(7.72>

298 НЕКОТОРЫЕ ЗАДАЧИ ПРИКЛАДНОЙ ТЕОРИИ УПРУГОСТИ [ГЛ. VII
Правая часть уравнения (7.72) обращается в нуль, если силы Qx
и Qy приложены в точке с координатами
*с = -^; Л = ^. (7-73)
В этом случае силы Qx и Qy не вызывают закручивания стержня,
так как из (7.72) следует, что т = 0. Точка с координатами (хс и ус)
является, следовательно, цеьтром жесткости сечения.
Точное решение задачи об отыскании центра жесткости читатель
может найти в книге Л. С. Лейбензона «Курс теории упругости»
(1947, стр. 295—304). Упомянутое точное решение связано с
необходимостью знать полное решение задачи об изгибе стержня вообще,
что значительно сложнее, чем изложенное в настоящем параграфе.
§ 94. Основные результаты теории стесненного кручэния
по В. 3. Власову
Не останавливаясь на выводе основных соотношений теории
В. 3. Власова, включенной теперь в учебные программы курса
сопротивления материалов *), сообщим лишь основные результаты этой
теории, увязав последние с разобранной в предыдущем параграфе
общей теорией сложного сопротивления тонких стержней.
Если использовать приближенное выражение функции кручения
для тонкостенных стержней, рассматривая криволинейный профиль
как совокупность прямолинейных, то, как показано в § 71, эта
функция кручения тогда совпадает с секториальной площадью В. 3.
Власова, т. е.
<p(s, /z) = co(s). (7.74
В записи (7.74) стержень отнесен к координатам s, n (где 5 —
координата, отсчитываемая вдоль срединной линии профиля, ал — по
нормали к ней).
Заметим еще раз, что секториальная площадь — это удвоенная
площадь сектора АМ0М (фиг. 130), образованная начальным и
подвижным радиусами и срединной линией сечения. Направление
начального радиуса ЛМ0 выбирается из условия
S„ = fudF = 0t
F
«а положение полюса А (центра изгиба) — из условий
J*w=fy*>dF=0 и Jiay=fxa>dF=0.
*) См. общеизвестный «Курс сопротивления материалов» под ред. проф»
М. М. Филоненко-Бородича, т. II, 1949, главу XI.

§ 94]
ОСНОВНЫЕ РЕЗУЛЬТАТЫ ТЕОРИИ СТЕСНЕННОГО КРУЧЕНИЯ
299
Из последних условий, между прочим, вытекают формулы для
.координат такого полюса:
С и>0у dF С щх dF
п _F . Р
ах — / » ау — / >
где ш0 — секториальная площадь при первоначальном полюсе в центре
тяжести поперечного сечения.
Рассматривая случай кручения, т. е. полагая Nz = Mx = My = Oy
и заменяя в формулах предыдущего параграфа обозначение о всюду
Фиг. 130. Секториальная площадь в теории
стесненного кручения сечения открытого профиля по
В. 3. Власову.
на ш, а элементарную площадку ввиду тонкостенности стержня
записывая в виде dF = bds, будем иметь:
[ ш2 (s) Ь ds\
(7.75)
Е(а (s)'
(7.76)
Из уравнений (7.66) вытекает е = х1=х2 = 0, а выражение
(7.70) записывается так:
MM=QJ# — EjJi. (7.77)

300 НЕКОТОРЫЕ ЗАДАЧИ ПРИКЛАДНОЙ ТЕОРИИ УПРУГОСТИ [ГЛ. VII
Выражение (7.77) и есть исходное дифференциальное уравнение
при стесненном кручении.
Формулу (7.76) в целях подражания обычной формуле для
напряжений при изгибе переписывают (опуская знак s) в виде
(7.78)
где обозначено £тУи) = £10. Величину В^ В. 3. Власов назвал изгибно-
крутящим бимоментом.
Введение понятия о бимоменте, как видно из всего указанного-
выше, не является абсолютно необходимым, но все же желательным.
Этому бимоменту можно дать и статическую трактовку. В самом:
деле, составим для всего сечения следующее выражение:
/■
оо) dF, (a)
F
т. е. каждую элементарную внутреннюю силу odF умножим на
своеобразное «плечо», а именно на секториальную координату, и затем
проинтегрируем по всему сечению. Имеем, по подстановке в (а)
выражения (7.76):
j оо) dF = Ex [ о)5 dF,
а это последнее и есть названный выше бимомент.
Не представит также затруднений доказать, что указанный
бимомент и есть условный момент бипары, о котором было рассказано
в § 73. Иначе говоря, бимомент дает количественную
характеристику взаимно уравновешенных в сечении
нормальных напряжений, возникающих от
стесненности кручению.
Само вычисление бимомента, как связанное с характером
стеснения кручения, должно производиться с учетом граничных условий
(характера закреплений концов и т. п.) стержня. Подобную задачу
уместно отнести к статике тонкостенных конструкций (строительная
механика).
В заключение без доказательства приведем формулу для дополни-
ельных напряжений, возникающих в поперечном сечении вследствие
наличия в нем нормальных напряжений:
— MaS°J° .. dBa
Тц> = j-j , где Мф = — Я/ц/с = -^ = В„. (7.79)
Величину М^ принято называть изгибно-крутящим моментом*
Помимо указанных касательных напряжений в сечении,
обусловленных присутствием ог, в сечении будут действовать обычные каса-

§ 95] АНАЛОГИЯ ЗАДАЧИ 301
тельные напряжения от кручения, для которых, как для узких
прямоугольников, можно принять приближенную формулу
=Г- 8, (7.80)
>d
где, очевидно, под Мк, ч (частью крутящего момента) следует
понимать
(Мц — общий, т. е. заданный крутящий момент; в прежних
обозначениях это будет Mz).
Примечание 1. Исходное дифференциальное уравнение
стесненного кручения (7.77) можно записать иначе, если ввести в (7.77)
полный угол закручивания 8 для рассматриваемого сечения. Очевидно,
т = — и т = — = 6'"
dz c dz*
Если, кроме того, продифференцировать (7.77) еще раз по z
и ввести обозначение
Ук=*т{г), (7.81)
представляющее собой интенсивность распределенного крутящего
момента по длине стержня, то взамен (7.77) будем иметь:
в" _*V = --£-, (7.82)
где обозначено
£2 = _g±. (7.83)
Примечание 2. В случае, если на стержень оказывает также
влияние Л/г, Мх, Муу то взамен (7.78) получим четырехчленную
^формулу В. 3. Власова:
Nz Mx Му В^
o=. — ^—y—-JLx + -r<s>. (7.84)
§ 95. Аналогия задачи о стесненном кручении тонкостенного
стержня с продольно-поперечным изгибом балки
Исходное дифференциальное уравнение стесненного кручения
т
Ж
eIV_fc2e" = _-^- (7.82)
при k2 = -p-p- оказывается по своей структуре совпадающим с
«известным дифференциальным уравнением упругой линии стержня,
нагруженного сплошной поперечной нагрузкой q и продольной

302 НЕКОТОРЫЕ ЗАДАЧИ ПРИКЛАДНОЙ ТЕОРИИ УПРУГОСТИ [ГЛ. VII
растягивающей силой TV*):
v™-k\v"=-±, (7.82')
2 N
где&! = -ру, v — прогиб. Напомним, что полная поперечная сила
в сечении растянуто-изогнутого стержня определялась выражением
Q = Nx/ — EJv'". (7.85)
Решение уравнения (7.82') в форме метода начальных параметров
имеется в ряде пособий **).
Итак, для возможности решить задачу о стесненном кручении
посредством известных формул продольно-поперечного изгиба
необходимо в последних формулах сделать замены N на GJd, EJ на EJ^V
а нагрузку q на /я, где m = qe (e — эксцентриситет скручивающей
нагрузки по отношению к центру жесткости).
Тогда изгибно-крутящий бимомент В определится как изгибающий
момент в сечении растянуто-изогнутого стержня (при фиктивной
продольной силе N=GJd и фиктивной поперечной нагрузке m~qe).
Изгибно-крутящий момент определится перерезывающей силой в
сечении того же стержня.
Много ранее разобранной аналогии В. 3. Власов установил
сходную с ней для следующего частного случая. Если возможно
пренебречь жесткостью сечения на кручение, т. е. положить GJd = 0\
то исходное дифференциальное уравнение упрощается и принимает вид,
сходный с дифференциальным уравнением упругой линии обычной
балки:
v" = —§j. (7.86')
Отсюда получаем простое правило расчета на кручение тонкостенного
стержня: необходимо изучаемый брус загрузить интенсивностью
внешних скручивающих моментов т и принять ее за интенсивность-
фиктивных поперечных нагрузок q. Значения поперечной
силы и изгибающего момента от такой фиктивной
нагрузки дадут действительные значения
разыскиваемых бимомента и изгибно-крутящего момент а,.
т. е. В^ = Мф, АГШ = <2Ф.
§ 96. Сведения о состоянии теории тонкостенных стержней
Для описания деформации стесненного кручения стержней имеется
несколько приближенных теорий. Различие между теориями заключается в
различии кинематических гипотез, лежащих в основании таких теорий. В § 91
*) См. ВИТ, № 3, 1948.
**) М. М. Ф и л он е н к о-Б ор од и ч и др., Курс сопротивления
материалов, т. II, 1949.

§ 96J СВЕДЕНИЯ О СОСТОЯНИИ ТЕОРИИ ТОНКОСТЕННЫХ СТЕРЖНЕЙ 303
была рассмотрена теория стесненного кручения эллиптического сечения,
принадлежащая А. А. Фепплю [116], где в основу был положен
экспоненциальный характер стеснения депланации, т. е. принималось, что стеснение
депланации существенно лишь в небольшой части стержня, примыкающей
к тому сечению, которое наглухо закреплено против депланации.
Основатель современной теории сложного сопротивления (включающей и
стесненное кручение) тонкостенных стержней так называемого открытого»
профиля (уголок, швеллер, двутавр и т. д.), В. 3. Власов (1941 г.) исходил
в своих исследованиях из представлений современной теории оболочек,
наделяя последнюю специальной гипотезой о недеформируемости контура
поперечного сечения и об отсутствии сдвигов в так называемой срединной
поверхности оболочки-стержня.
Эта теория А. А. Уманским [114] была распространена на тонкостенные
стержни замкнутого профиля. Применение вариационных принципов для
нахождения закона изменения стесненной депланации сечений вдоль оса
стержня было сделано Н. В. Зволинским.
В последнее время А. Р. Ададуров *) разработал теорию расчета
цилиндрических оболочек, поперечный контур которых не может деформироваться
вследствие большого количества диафрагм. В указанной работе была
отброшена одна из гипотез Власова, а именно гипотеза об отсутствии сдвигов
в срединной поверхности оболочки, и потому в некотором смысле теорию*
A. Р. Ададурова можно рассматривать [33] как обобщение теории.
B. 3. Власова.
Обстоятельный разбор различных гипотез, вскрытие некоторых
несоответствий внутри известных теорий, имеется в работе А. Л. Гольденвейзера
[28] (1949), предложившего также свою систему уравнений для
тонкостенных стержней, которая является уточнением к ранее имевшимся
предложениям других авторов.
Г. Ю. Джанелидзе (1949) в своей работе [32] в отличие от А. А. Феппля
исходил из гипотезы, что стесненная депланация пропорциональна
произведению из свободной депланации (при отсутствии стеснения) на фактический
относительный угол закручивания (угол закручивания на единицу длины).
При такой постановке задачи частными случаями теории оказываются
некоторые известные теории.
Учитывая методические достоинства такого построения, выше, в § 92„
было дано соответствующее изложение теории тонкостенных стержней.
Рассмотрение упруго-пластического состояния в тонкостенных стержнях
выполнено Г. Ю. Джанелидзе [43], Р. А. Межлумяном [65, 66], В. С.
Медведевым (см. также § 121).
Более подробные сведения о развитии- упругой теории тонкостенных
стержней читатель найдет в статье Я. Г. Пановко**).
Для подробного ознакомления с основополагающими работами В. 3.
Власова читателю рекомендуем обратиться к первоисточникам, а именно к
книгам В. 3. Власова «Упругие тонкостенные стержни» (1941), «Строительная
механика пространственных систем» (1949) и «Общая теория оболочек» (1949)*
Поиски дальнейших уточнений и вместе с тем упрощений в современной
теории тонкостенных стержней интенсивно продолжаются.
*) См. [32] и [47].
**) Я. Г. Пановко, Развитие прикладной теории тонкостенных
конструкций за последние годы, Труды Ленинградской Краснознаменной:
военно-воздушной инженерной академии, вып. XI, 1947.

ГЛАВА VIII
ОСНОВНЫЕ УРАВНЕНИЯ ТЕОРИИ ПЛАСТИЧНОСТИ
§ 97. Активная и пассивная деформации. Нелинейное упругое
тело и пластическое тело
Явление чистого (одноосного) растяжения, при котором нагрузка,
удлиняющая стержень, непрерывно растет, условимся назыйать
активной деформацией. Явление растяжения, наблюдаемое при разгрузке
того же стержня, назовем пассивной деформацией.
При сложном напряженном состоянии в точке или в элементе
тела (т. е. когда все три главных напряжения для рассматриваемой
точки отличны от нуля) деформацию будем считать, следуя А. А.
Ильюшину, активной в том. случае, если обобщенное напряжение oi
для этой точки (или элемента) в данный момент нагружения имеет
значение, превышающее все предшествующие его значения. Если
обобщенное напряжение будет меньше хотя бы одного из
предшествующих значений, деформацию в этом случае будем считать
пассивной.
Для идеально упругого тела (см. фиг. 1, слева), хотя бы и не
подчиняющегося линейному закону Гука (нелинейное упругое тело),
уравнения, описывающие активную или пассивную деформацию,
должны быть, конечно, общими, так как именно упругое состояние
характеризуется существованием взаимно однозначной зависимости
между напряжениями и деформацией (см. стр. 14).
Для реального тела, нагружение которого вызвало в нем
напряжения выше предела упругости, законы активной и пассивной
деформаций должны быть разными (фиг. 1, справа), так как одному и тому
же значению силы может отвечать много разных значений
деформации в зависимости от того, впервые ли приложена упомянутая сила
или она оказалась данным значением в результате частичного
уменьшения предшествующего ее значения, или, наконец, она приложена
вторично и т. п.
При чистом растяжении пластическим состоянием элемента обычно
считают то, при котором нормальное напряжение в поперечном
сечении (в данном случае — главное напряжение) превышает предел
упругости материала, из которого выполнен данный элемент.

§ 97]
АКТИВНАЯ И ПАССИВНАЯ ДЕФОРМАЦИИ
305
Если придерживаться энергетической точки зрения на причину
наступления в материале предельного упругого состояния, то при
сложном напряженном состоянии рассматриваемого элемента (или точки)
пластические деформации следует ожидать для него тогда, когда
обобщенное напряжение для этого элемента (или точки) превышает
обычный предел упругости.
В технике с понятием пластичность часто связывают тот этап
в напряженном состоянии тела, когда его деформации значительно
возрастают без заметного при этом увеличения нагрузки.
В случае чистого растяжения мягкой стали этот этап на
индикаторной диаграмме соответствует площадке текучести и отвечает
определенным значениям нормального и касательного напряжений,
характерным для данного материала, которые могут при активной
деформации возрастать лишь после получения материалом иногда
значительных пластических деформаций, а до приобретения таковых (на
индикаторной диаграмме — до конца площадки текучести) сохраняют
постоянные значения.
Аналогичное явление текучести может начаться и в случае
сложного напряженного состояния элемента, когда в процессе активной
деформации наибольшее касательное напряжение (в свете так
называемой «третьей» теории прочности) или удельная энергия
формоизменения (в свете «пятой» теории прочности) достигли вполне
определенных для данного материала значений (предельные упругие константы).
Вслед за площадкой текучести, как известно, в диаграмме
растяжения мягкой стали имеется значительная область «упрочнения»,
почему и состояние материала,
отвечающее этому этапу
работы или испытания, иногда
называют «состоянием
упрочнения»»
При большой протяженно- \1 у^ ' | •**
о
X
]—
к.
Li 6z
сти площадки текучести, а тем
более тогда, когда известно,
что материал при его
расчетных нагружениях не достигает фиг 13L Индикаторные диаграммы
состояния упрочнения, возможно (диаграмма растяжения и" диаграмма
при теоретических расчетах сдвига) для идеально-пластического тела,
упомянутую выше диаграмму
растяжения упростить, положив безграничное протяжение площадки
текучести. Так приходим к понятию об идеально пластическом теле,
диаграммы растяжения и сдвига для которого представлены на фиг. 131.
Большинство теоретических исследований в теории пластичности
выполнено в предположении, что рассматриваемое тело обладает
указанным свойством идеальной пластичности.
Ниже при составлении физических уравнений теории
пластичности мы не будем особо выделять состояние текучести и состояние
20 Зак. 3880. Н. И. Беаухов

306 ОСНОВНЫЕ УРАВНЕНИЯ ТЕОРИИ ПЛАСТИЧНОСТИ [ГЛ. VIII
упрочнения. Более того, никаких ограничений или особенностей на
диаграмму растяжения — сжатия накладывать не будем. Можно считать,
что уравнения будут составляться как бы для третьего участка
(состояние начавшегося упрочнения), частными случаями которого легко
представить второй участок (идеальная пластичность) и даже
первоначальный участок (идеальная упругость).
Для описания связи, существующей между напряжениями и
компонентами деформации при пластических деформациях, было предложено
большое количество теорий (правильнее сказать, гипотез)
пластичности, но почти всегда после появления новой теории ее вскоре
опровергали на основании новых экспериментов.
Все известные теории пластичности, имеющие своей целью определение
пространственного деформирования твердых тел, могут быть разделены на
два вида, в зависимести от того, лежат ли в их основе уравнения,
связывающие напряжения и деформации, или уравнения, связывающие
напряжения и скорости деформации.
В первом случае имеем так называемые теории упруго-пластических
деформаций, а во втором — теории пластического течения. Ниже в
основном рассматривается первый вид теорий.
В настоящей книге не будем касаться изложения многих
известных и противоречивых точек зрения на механизм образования
пластических деформаций. Заметим лишь, что сложный клубок этих
противоречий был распутан в советских исследованиях, главным
образом в работах А. А. Ильюшина, к книге которого «Пластичность»
(Гостехиздат, 1948) и отсылаем интересующихся читателей. Им было,
в частности, установлено, что в случае активной деформации,
совершающейся при простом нагружении *), все известные теории
пластичности являются частными случаями общей, т. е. существует
одна единая теория пластичности, достаточно достоверно
описывающая свойства твердых тел при малых упругих и пластических
деформациях.
Эта теория и будет излагаться ниже.
Для описания напряженного и деформированного процесса при
так называемом сложном нагружении, когда главные оси
деформации в каждой точке тела существенно меняют свою ориентацию
с течением времени, в настоящее время теорий пластичности не
существует.
Строение вещества в этой главе будет, как и в теории упругости,
полагаться сплошным, непрерывным **), а деформации весьма малыми,
и потому все выводы и уравнения механики сплошной среды (глава II)
полностью используются и здесь. Из рассмотрения исключаем все
*) Определение простого нагружения см, в § 101.
**) О дискуссии по поводу отправных положений современной
теории пластичности и их значении в настоящее время кратко сообщено
ь § 115.

§ 98] СВЯЗЬ НАПРЯЖЕНИЙ С КОМПОНЕНТАМИ ДЕФОРМАЦИИ 307
явления и свойства (ползучесть, релаксация, вязкость и т. д.),
зависящие от времени протекания деформации (об этом кратко сказано
в § 130), т. е. ниже рассматривается равновесный (в смысле
независимости от времени) необратимый процесс деформирования.
§ 98. Связь напряжений с компонентами деформации
за пределом упругости при активной деформации
В случае активной деформации уравнения, описывающие пластик
ческое состояние тела (напряжения, деформации, перемещения и связи
между ними), ничем не должны отличаться от уравнений, написанных
для нелинейного упругого тела с идентичной диаграммой растяжения *).
Лишь в случае разгрузки тела, т. е. при пассивной деформации,
нелинейное упругое тело отличается
от пластического.
Устанавливаемые в этом
параграфе физические уравнения в
одинаковой степени приложимы как
к деформациям нелинейного
упругого тела, так и к активной
пластической деформации. Для простоты
рассуждений при изучении активной
деформации удобнее исходить из
представления именно о нелинейном
упругом теле.
Исходное физическое уравнение
нелинейной теории упругости,
которое одновременно является
уравнением теории пластичности при
активной деформации, можно установить
различными способами, надлежаще
используя те или другие
экспериментальные данные. Самое простое
доказательство упомянутого
уравнения, но содержащее элемент
гипотетичности, можно получить путем следующих логических соображений.
Пусть для данного материала известна диаграмма истинных
напряжений, полученная экспериментальным путем при опыте с чистым
растяжением (фиг. 132). Пока относительное удлинение не
превосходит значения еупр (предельное упругое удлинение), зависимость между
напряжением и деформацией линейна:
о = Ее. (8.01)
*) Строгое доказательство этого положения сделано Л. М. Качановыад
па основе термодинамического анализа активной пластической деформации
(см. «Прикладная механика и математика», т. 5, вып. 3, 1941).
Фиг. 132. Характерная диаграмма
истинных напряжений при чистом
растяжении для мягкой стали. Та
же диаграмма принимается и при
сложном напряженном состоянии
элемента, но в качестве связи
обобщенного напряжения с
обобщенной деформацией.
20*

308 ОСНОВНЫЕ УРАВНЕНИЯ ТЕОРИИ ПЛАСТИЧНОСТИ [ГЛ. VIII
При е > 8уПр связь напряжений и деформаций оказывается
сложной, нелинейной и в общем виде представляется некоторой функцией,
зависящей только от свойств материала*):
о= Ф(е). (8.02)
В целях аналогии с (8.01) можно записать (8.02) в форме
o = E'et (8.03)
где, очевидно, коэффициент Е' (по фиг. 132) равен:
и потому для каждой точки диаграммы (для каждого мгновения
пластической деформации тела) будет иметь особое значение и
изменяться при переходе от одной точки диаграммы к другой (от
состояния с одним напряжением к другому состоянию — с другим значением
напряжения). Из фиг. 132 следует, что
значит,
Е/=Ф£1в(Ив)| (8>04)
т. е. Е' есть некоторая функция деформации, нам известная,
поскольку диаграмма растяжения (фиг. 132) задана. Назовем величину Е'
приведенным модулем деформации первого рода.
Возникает вопрос, как записать связь напряжений с деформацией,
если элемент из того же материала, что был обследован на чистое
растяжение — сжатие, будет находиться в условиях объемного
(пространственного) напряженного состояния и притом такого, когда
отдельные компоненты напряжений заведомо перешли предел упругости?
Не может ли оказаться полезным в этом случае известный закон (8.02)
или (8.03)?
Вспомним, что для такого объемного напряженного состояния
в пределах упругости существовало несколько вариантов начертания
зависимости (3.01), (3.02) и в том числе такая изящная запись (3.04):
совершенно сходная по форме с (8.01), справедливой для случая
линейного напряженного состояния (чистое растяжение). Разница лишь
в том, что место обычного напряжения заняло обобщенное
напряжение, а место обычного удлинения — обобщенная
деформация.
*) Строго говоря, Ф (е) — функция не только свойств материала
(существа), но и формы; однако последнее обстоятельство (влияние формы
образца на диаграмму растяжения и т. п.) не имеет практического значения
для применяемых в практике размеров (относительно больших деталей).

§ 98] СВЯЗЬ НАПРЯЖЕНИЙ С КОМПОНЕНТАМИ ДЕФОРМАЦИИ 309
Естественно напрашивается мысчь о том, нельзя ли и в случае
деформации за пределами упругости при изучении объемного
напряженного состояния воспользоваться аналогичной формой связи, придав
коэффициенту пропорциональности, как и в (8.03), смысл
переменного коэффициента, зависящего от масштаба происходящих в
рассматриваемой точке деформаций и именно в рассматриваемый момент?
Таким образом, возникает предложение записать закон деформаций
при е^>еупр в форме
о4 = Е%. (8.05)
Ьполне очевидно, что формальных препятствий такому начертанию
зависимости между обобщенными напряжением и деформацией за
пределами упругости нет и не может быть, но надлежит выяснить,
сохраняется ли за коэффициентом пропорциональности та же
зависимость от деформаций (в данном случае от обобщенной деформации),
как это имеет место при чистом растяжении того же материала?
Короче говоря, возможно ли для приведенного модуля
деформации Е' исходить из представления и отождествления:
£/=Ф(**)=Ф(е)?
Ч е
Ответ на этот вопрос может дать только опыт. Многочисленные
опыты крупнейших экспериментаторов в области изучения
пластических деформаций, проведенные в условиях простого нагружения,
равно как и теоретические исследования*), подтверждают
практическую пригодность указанной гипотезы в большом числе случаев, тем
самым доказывая, что вид Ф(е<) зависит в основном от материала.
Исключительное значение закона (8.05) для механики упругих и
пластических деформаций, а следовательно, и важность понятий
обобщенного напряжения и обобщенной деформации заключаются
прежде всего в том, что при помощи этого закона сколь угодно
сложное объемное напряженное состояние и притом независимо от
того, находится ли рассматриваемая область в состоянии упругих или
неупругих деформаций, как бы сводится к простому растяжению или
сжатию стержня. В самом деле, так как вид Ф(е^) зависит только
от материала тела, то не требуется производства специальных
опытов со сложным напряженным состоянием, если под руками имеется
диаграмма Ф(е) для чистого растяжения.
Так как (3.04) было получено в результате формальных
преобразований с (3.01), (3.02) и (3.03), то очевидно, поскольку в области
пластических деформаций существует зависимость (8.05), по форме
аналогичная (3.04) с заменой лишь Е на Е\ существуют в области
*) Описание опытов и анализ результатов см. в ранее цитированной
книге А. А. Ильюшина «Пластичность».

310
ОСНОВНЫЕ УРАВНЕНИЯ ТЕОРИИ ПЛАСТИЧНОСТИ
[ГЛ. VIII
пластических деформаций и зависимости, аналогичные (3.01) — (3.03)
и, более того, аналогичные (3.08), (3.09), но также с заменой в
указанных формулах Е на Е'.
Итак, можно для описания деформации за пределом упругости
предложить следующие уравнения:
°х — <3cp = 2G/(ea, — scp), ]
°у — аср = 2G' (гу — scp),
°z — °сР = 2 G' (еж — еср);
zxy = G Чху*
*-yz — w lyzy
~zx == ^ Tzo?>
где, очевидно,
G' =
^ (1 И- к-0 *
(8.06)
(8.07)
Так как в области пластических деформаций объем материала
практически не изменяется, то в (8.07) следует положить [х/ = -^-,
и тогда
G' = ±E>.
(8.07а)
Из (8.05) следует Е' = -^ и, следовательно,
G' =
3s, '
(8.076)
Подставляя (8.076) в (8.06), имеем такой, наиболее
употребительный вариант записи физических уравнений при активной пластической
деформации:
ах °ср — "з^Г \гх есг;»
— 2а* ( \
ау °°р — ~з7Т \sy S(w>
3.<
— аср= з£(«. — £ср);
ха?г/ = "з^Т" Та?2/>
ZV* — Зб2. Чу**
(8.08)

§ 99J РАЗЛИЧНЫЕ ВАРИАНТЫ. 311
где попрежнему согласно (3.05) и (3.06) соответственно:
** = -it/"(•» -•*>' + (ev- е->2+& -**>*+т (& + ?**+т«).
§ 99. Различные варианты начертания связи обобщенного
напряжения с обобщенной деформацией
В (8.05), как в обычном законе Гука, множителем непосредственно
входит Е'. Можно, и это бывает иногда удобно, сохранить
множителем Е (обычный модуль упругости), изменив при этом сомножитель.
Так, если на фиг. 132 продолжить начальную прямую до пересечения
с вертикалью, проходящей через точку с рассматриваемым
напряжением oit то можно записать:
at. = zitga — ас. (а)
Очевидно, что отрезок ас зависит от е^ и, как правило,
увеличивается при возрастании е£. Пусть функциональная связь ас с е^ нам
известна; обозначим ее так:
ас = <р (е<). (б)
Тогда, принимая во внимание, что tga = £, выражение (а)
перепишем таким образом:
<*< — £«< — ?0<)
или
Обозначим:
^-»W; (в)
тогда
oi = Ezi[\— о>(е<)], (8.05а)
где функция со (е^) является прерывной и определяется из условий:
для е, < еупр со (е<) = 0;
для е< > еупр со (е<) = -*М,
Начертанием (8.05а) мы выделяем множителем «упругую» часть,
т. е. Ег{. Сопоставляя (8.05а) с (8.05), имеем следующее начертание
для переменного модуля деформации:
£' = £[1_ш(в,)],

312
ОСНОВНЫЕ УРАВНЕНИЯ ТЕОРиИ ПЛАСТИЧНОСТИ
ГЛ. VII
или в более короткой записи
Е' = Е(1 — со). (г)
В дальнейшем придется встретиться с применением переменного
модуля деформации второго рода, под которым будем понимать
выражение
G'=G[1 — в(е«)],
или короче
G'=G(1—ш). (д)
Весьма часто, и это для целей практики вполне достаточно,
диаграмму растяжения — сжатия материала условно заменяют
полигональной. Так, если аппроксимировать диаграмму двумя наклонными
участками, показанными на фиг. 133, то при е<>еудр = ет имеем:
ас = ab — cd — db =
= Ее{—(S< — еупр) tg р — £еупр.
Вводя обозначения tg [3 = Et
(модуль упрочнения), \=-Ly—-
(параметр упрочнения) и
отождествляя в данном случае
обозначение еупр с ет, записываем:
ас = к {1 — -^-) Ее4\
таким образом,
Фиг. 133. Спрямленная диаграмма — е ч
растяжения. м (в<) = _ в Я ^ __l).
Окончательно для случая диаграммы из двух наклонных участков
(фиг. 183) имеем:
o, = £e,[l—x(l—-£)]. (8.056)
В этом случае разрывная функция co(ef) определяется так:
для е,< ег (0(6^ = 0;
для е^>ег <в(е<) = Х^1 ^fj.
Для некоторых материалов удается иногда аппроксимировать
функцию Ф (г^) при помощи степенной зависимости:
<*
«J-
I
0
1
Act
— f,
i
/
i
1
"ZT-'
£
rf
_fc
■ ? "
Г
it
где
0<от<1.
(8.05в)

§ 100] ДРУГОЕ ДОКАЗАТЕЛЬСТВО ОБОБЩЕННОГО ЗАКОНА ДЕФОРМАЦИИ 313
Характер диаграммы растяжения, подчиняющейся (8.05в), имеет вид,
показанный на фиг. 134. При т = \ имеем случай идеально упругого
тела (закон Гука). При т = 0 — случай идеально пластического тела.
Имеются и другие варианты начертания вида Ф (е^). В частности,
если в диаграмме истинных напряжений учесть плавный
(криволинейный) переход с первого прямолинейного («упругого») участка на тре-
Фиг. 134. Диаграмма растяжения,
описываемая уравнением
'=•*©'
Фиг. 135. Диаграмма растяжения,
имеющая сопряжение упругого
участка и прямой упрочнения по
параболе.
тий (прямолинейный — участок упрочнения), то, задаваясь сопряжением
упомянутых участков по параболе /z-й степени (фиг. 135), имеем:
з< = °т — Е' (ет — е<) — (£" — £')
К-£г)*
Се — е )n_1 '
где
Е Е'
n = E« — t'* E=^a-
§ 100. Другое доказательство обобщенного закона деформации
В § 98 закон (8.05) и в развернутом виде (8.08) был получен
преимущественно путем рассуждений и, так сказать, при помощи напросившейся
аналогии. В целях большей убедительности и возможности более широкого
толкования этого закона ниже следует другое доказательство закона (8.05).
Обращаясь к экспериментальным данным, можно считать достаточно
установленными следующие особенности закона пластического
деформирования при простом нагружении.
1. Направления главных удлинений всегда совпадают с направлениями
главных нормальных напряжений *).
*) В более общей редакции это положение может быть сформулировано
так: «направляющие тензоры напряжений и деформаций совпадают».

314 ОСНОВНЫЕ УРАВНЕНИЯ ТЕОРИИ ПЛАСТИЧНОСТИ [ГЛ. VIII
2. Плотность или объем массы заметно не изменяется.
3. Диаграмма Мора для деформаций (в координатах е, у) всегда
геометрически подобна такой же диаграмме для напряжений (в координатах а, т).
Первый закон представляет собой лишь другую формулировку
экспериментального факта, заключающегося в том, что направления наибольших
сдвигов совпадают с направлением наибольших касательных напряжений.
Второй закон экспериментально устанавливается просто, хотя следует
заметить, что очень точные измерения удлинения при значительных
пластических деформациях показывают незначительные изменения объема, но эти
изменения при пластической деформации такого же порядка, как и упругие
деформации, так что ими можно пренебречь. Записывается второй закон
в виде:
Ч+Ч + Ч = 0< (8.09)
где et, e2, е3 — главные удлинения*).
Правильность третьего закона была подтверждена специально
поставленными опытами **). Математически этот закон подобия может быть записан,
например, в виде следующих пропорций (их может быть много, но избираем
наиболее удобные для последующих преобразований):
а1— а2_£1— Ч ^ а2 — а3 __ £2 — Н /ач
а1 — а3 е1 — е3 ' а3 — а1 е3 — е1 "
Объединение (8.09) и (а) приводит к возможности записать следующие
зависимости:
е1 = С К — у (а, + ог3) , е2 = с а2 — — (а3 + *i) ,
Ч = С^ав — — (а1 + а2)\
(8.10)
где с — некоторая величина, общая во всех трех приведенных выражениях.
Действительно, если сложить написанные зависимости, то имеем:
ei + Н + Ч = с U + Ч + °з — ~2 (а2 + сз + аз + ai + °i + аг) = 0,
что соответствует второму закону.
Далее, подстановка (8.10) в правые части (а) приводит к тождествам.
Например:
1 3
ei~e2 (*i — аг)— -2"[(а2 + аз) — (4 + °i)] ~2 [а1 — а2] а1~а2
= j = __ =
е1 —е3 (»1— аз)— Y [(а2-Ь аз) — (b+Ч)] 2-[Jl — аз] »1— *3
И Т. П.
Формулы (8.10) сходны по форме с законом Гука для линейно
деформируемого упругого тела (3.01); роль прежнего коэффициента (л исполняет
в (8.10) величина -=-, а модуль Е заменяется —. Таким образом, устанавли-
л с
ваем, что в теории пластичности при «простом нагружении» и, конечно, при
условии небольших деформаций имеют место по внешней форме записи
такие же уравнения, как и в теории упругости.
*) Учет сжимаемости материала выполняется по закону изменения объема
(стр. 318).
**) А. А. Ильюшин, Пластичность, стр. 57—96.

§101] ТЕОРЕМА А. А. ИЛЬЮШИНА О ПРОСТОМ НАГРУЖЕНИИ 315
Поскольку установлена аналогия во внешней записи законов упругой
и пластической деформации, то, применяя к (8.10) известные из главы III
формальные преобразования, очевидно, придем к возможности и такой записи
обобщенного закона пластической деформации:
1
* С %
или, обозначая — = £', получаем (8.05) аг- = Е%.
Так же можно доказать, что
4 = 0%; (8.11)
^i2=^23=^3i = G/> (812)
712 Т23 Т31
где при р- = "о" имеем:
°'=т£/-
Физический смысл законов (8.08), (8.12) можно истолковать так: для
каждой точки деформируемого тела напряжения по различным
направлениям (площадкам) являются линейными функциями
соответствующих компонентов деформации. В частности, площадкам,
претерпевающим наибольшие сдвиги, соответствуют
наибольшие касательные напряжения, пропорциональные
указанным сдвигам.
При упругой деформации коэффициент пропорциональности (модуль
упругости) постоянен для всех точек упругой области тела, тогда как при
пластической деформации этот коэффициент (модуль деформации) изменяется
от точки к точке и уменьшается тем сильнее, чем больше деформация в
новой рассматриваемой точке по сравнению с ранее обследованной.
§ 101. Теорема А. А. Ильюшина о простом нагружении
Выше (§§ 98, 109) было подчеркнуто, что закон (8.05)
справедлив для случая так называемой активной пластической деформации
элемента, когда обобщенное напряжение представляет монотонно
возрастающую функцию. Из соотношений (8.12), связанных с (8.05),
вытекает также, что отношение главных касательных напряжений
к соответствующим главным сдвигам для данного элемента тела
оказывается постоянным (но различным для разных точек тела).
Возникает вопрос о том, как должны изменяться во времени
нагрузки, действующие на неоднородно напряженное тело любой формы,
чтобы каждый элемент такого тела оказался в состоянии именно
активной деформации, и в частности, чтобы в каждой точке тела
обеспечивалось постоянство направлений главных осей напряжений,
и чтобы сохранялось упомянутое в § 100 постоянство отношений
касательных напряжений к сдвигам? Не может ли при этом
непрерывный рост нагрузок, вызывая в одной, хотя бы и значительной
части тела, возрастание обобщенного напряжения, вызвать в другой
части уменьшение напряжений?

316 ОСНОВНЫЕ УРАВНЕНИЯ ТЕОРИИ ПЛАСТИЧНОСТИ [ГЛ. VIII
Короче говоря, существует ли в общем случае неоднородно
напряженного тела любой формы такая нагрузка, при которой все
элементы тела оказываются в состоянии активной деформации?
Введем понятие о «простом нагружении», понимая под ним такой
процесс нагружения, когда все внешние силы от начала их
приложения возрастают пропорционально общему параметру.
Оказывается, что закон (8.05) и вытекающие из него следствия
возможно применять ко всему объему тела, если процесс его
нагружения будет именно простым. Этот постулат носит название теоремы
А. А. Ильюшина о простом нагружении*), гласящей: теория малых
упруго-пластических деформаций дает правильные (согласные с
опытом) результаты по крайней мере в том случае, когда процесс
нагружения тела является простым.
Доказательство теоремы предполагает степенную зависимость между
обобщенными напряжением и деформацией, т. е. случай, когда ai = Ae™9
но на основании анализа экспериментов А. А. Ильюшин заключает
о возможности применения теоремы и в случае любого другого
начертания зависимости о{— е<#
В последнее время В. В. Соколовский [104] вывел
сформулированные условия с помощью предложенной им тригонометрической
формы представления компонентов напряжения и деформации.
§ 102. Теорема о разгрузке
Пусть стержень предварительно растянут на величину ви что
соответствует в нем напряжению о1э причем ох > о (фиг. 136). Если
частично (или полностью) разгрузить
стержень, т. е. оставить в нем
напряжение а^^а^ то, как это видно
из диаграммы растяжения,
остаточная деформация запишется так:
ео = е1— е2- (а)
В записи (а) обозначено:
et—деформация, полученная при первом
нагружении и определяемая упруго-
пластическими свойствами
материала; е2 — упругая часть
деформации, для вычисления которой, оче-
зависимость
о
да
— е,
*
с
с^
\
е
Фиг. 136. Случай разгрузки.
видно, можно использовать
в2 —
а'
7Г'
*) А. А. Ильюшин, Пластичность, стр. 115—118.

§ 103] ИНАЯ РЕДАКЦИЯ ЗАКОНОВ УПРУГО-ПЛАСТИЧЕСКИХ ДЕФОРМАЦИЙ 317
где о' = а1 — а2 и Е — тангенс угла наклона к горизонту прямой
разгрузки, или, что все равно, тангенс угла наклона первого «упругого»
участка диаграммы растяжения.
Таким образом, для вычисления остаточной деформации стержня
необходимо из приобретенной им ранее деформации, т. е.
соответствующей действию первоначальной силы, вычесть упругую
деформацию, соответствующую значению той силы (или напряжения), на
величину которой уменьшилась первоначальная сила.
Это положение, совершенно очевидное на примере с растянутым
(или сжатым) стержнем, остается справедливым и в общем случае
формы тела и при неоднородном напряженном состоянии, лишь бы
разгружение было простым (§ 101), т. е. когда все внешние силы
в стадии пассивной деформации изменяются (уменьшаются)
пропорционально их общему параметру *).
Таким образом, перемещения точки в некоторый момент стадии
простой разгрузки отличаются от их значений в момент начала
разгрузки на величины упругих перемещений, которые возникли бы
в теле, если бы в естественном (недеформированном)
состоянии к нему были приложены внешние силы, равные
разностям внешних сил, действующих на тело, в
указанные моменты. То же положение сохраняется как для
деформаций, так и для напряжений.
Само собой разумеется, что такой принцип простого вычитания
из полных первоначальных значений перемещений, деформаций и
напряжений тех их значений, которые соответствуют указанным выше
фиктивным силам (и должны быть подсчитаны в предположении
линейного деформируемого упругого тела), имеет ограничения. Он теряет
смысл тогда, когда при разгрузке с последующим переходом
нагрузки через нуль обобщенное напряжение (оно уже будет другого
знака, чем при первом нагружении) достигнет или превысит значения
предела упругости. Следует указать, что с учетом эффекта Баушин-
гера этот новый предел может оказаться .меньшим обычного предела
упругости.
§ 103. Иная редакция законов упруго-пластических деформаций
Подведем итог соображениям и выводам, касающимся физических
уравнений теории малых упруго-пластических деформаций,
изложенных в § 97—100, и дополним их законом изменения объема,
доказанного ранее в § 28 и, как известно (см. стр. 115), справедливого
при упругих и пластических деформациях.
Кроме того, выписывая еще раз известные зависимости, как то:
(8.06) или (8.08), для краткости письма используем понятие
*) Строгое доказательство теоремы разгрузки см. А. А. Ильюшин,
Пластичность, стр. 118—120.

318 ОСНОВНЫЕ УРАВНЕНИЯ ТЕОРИИ ПЛАСТИЧНОСТИ [ГЛ. VIII
о девиаторах напряжений и деформации [см. (3.09) и (3.08а) и
аналогичные (8.06)].
1. Первый основной закон — закон изменения объема. «При
упругих и пластических, при активных и пассивных деформациях
твердого тела относительное изменение объема элемента этого
тела прямо пропорционально среднему напряжению, причем модуль
объемной деформации остается постоянной величиной как в
пределах, так и за пределами упругости» (3.07):
Е
ср I — 2[Х ор»
где Е — модуль упругости и \i — коэффициент Пуассона.
2. Второй основной закон — закон изменения формы при
активной деформации. «При упругих и пластических
деформациях, соответствующих случаю простого нагружения для
каждой точки тела, девиатор напряжений прямо пропорционален
девиатору деформации», т. е.
DH = 2G^e*, (8.13)
где G' — модуль деформации второго рода, имеющий для каждой
точки изотропного тела в общем случае напряженного состояния свое
собственное значение, зависящее от значения обобщенного напряжения
для этой точки. В скалярной форме закон (8.13) записывается
согласно (8.06) или (8.08).
Только что изложенный закон назван законом изменения формы
п отому, что в девиаторе напряжений и в девиаторе деформации
исключены среднее напряжение и среднее удлинение, как связанные
с изменением объема элемента, и поэтому оба девиатора
характеризуют работу, затрачиваемую только на изменение формы.
3. Третий основной закон — закон связи обобщенного
напряжения с обобщенной деформацией при активном нагружении*
Обобщенное напряжение, возникающее в теле при любой
активной деформации (упругой или пластической), для каждого-
материала есть определенная функция обобщенной деформации^
т. е.
а, = Ф(е«). (8.05а)
Вид функции Ф зависит только от материала тела и не зависит
от того, при каких составляющих (при простом — одноосном или
сложном — объемном напряженных состояниях) интенсивность
деформации достигла данного значения; величина интенсивности напряжения
будет зависеть только от величины достигнутой интенсивности
деформации и, конечно, от физических свойств данного материала.
Зависимость о{ от г{ должна определяться опытом, но в силу
указанного сейчас ее проще установить из опытов с чистым
растяжением.

§ 103] ИНАЯ РЕДАКЦИЯ ЗАКОНОВ УПРУГО-ПЛАСТИЧЕСКИХ ДЕФОРМАЦИЙ 319
Итак, третий закон устанавливает единство природы деформации
изотропных тел в сложных и простых случаях напряженных
состояний в пределах и за пределами упругости.
4. Четвертый основной закон — закон пассивной деформации.
При простой (полной или частичной) разгрузке тела, находившегося
в момент начала пассивной деформации в пластическом состоянии,
во все последующие моменты девиатор напряжений зависит от
девиатора деформации, соответствующего моменту начала
разгрузки, и от девиатора деформации, подсчитанного в
предположении нагружения ненапряженного и линейно деформируемого
тела фиктивными силами', значения фиктивных сил равны
превышению первоначальных значений сил (отвечающих моменту начала
разгрузки) над фактическим их значением в рассматриваемый
момент.
В символической записи этот закон можно представить так:
£>„ = 207)двф — 207)деф, (8.14)
где £>Деф — девиатор деформации, соответствующий моменту начала
разгрузки; £)деф— «упругий» девиатор деформации, подсчитанный
в предположении идеально упругого тела от указанных выше
фиктивных сил; DE — девиатор напряжений (остаточных),
соответствующий рассматриваемому моменту нагружения; О'— модуль деформации
второго рода для рассматриваемой точки, соответствующий моменту
начала разгрузки, в общем случае различный для разных точек
изотропного тела; G — общий модуль сдвига, постоянный для всех точек
изотропного материала.
В проекциях на оси Ox, Oy, Oz равенство (8.14) дает:
°х — °оР = 20' (ех — еор) — 20 (гх — еог),
^ху == ^ То?г/ ^Чху>
И Т. Д.,
(8.15)
где ох, оор, ixy, ... — остаточные напряжения в рассматриваемой точке;
еа?> еор> Тжт/» •• • — компоненты деформации той же точки в момент
полного нагружения (т. е. в момент начала разгрузки); гх, еор, ^ху, . ..—
компоненты деформации той же точки от упомянутых выше
фиктивных сил, найденные по законам классической (линейной) теории
упругости.
Далее (в § 107) показано, что приведенные в этом параграфе
основные законы не являются независимыми друг от друга и что число
независимых законов связано с тем, какие предпосылки и допущения
явно или неявно приняты.

320 ОСНОВНЫЕ УРАВНЕНИЯ ТЕОРИИ ПЛАСТИЧНОСТИ [ГЛ. VIII
В § 124 дана еще одна редакция основных законов теории упруго-
пластических деформаций, эквивалентная по существу изложенным
здесь, хотя и в несколько отличной форме.
§ 104. Частный случай —идеально пластическое тело
Если диаграмма растяжения — сжатия материала имеет ясно
выраженную и притом большого протяжения площадку текучести (фиг. 131),
то обобщенный закон деформации (8.05), соответствующий
протеканию явлений текучести, запишется проще, а именно:
или
•^ ^(°.~V+t0»-'.)' + (°*-°*f+6 (<,+<.+т2*) = °т, (8Л6)
что представляет известное читателю из общего курса сопротивления
материалов так называемое условие пластичности по Губер-Мизесу.
Левая часть (8.16) в курсе сопротивления материалов называлась
приведенным напряжением по так называемой энергетической теории
прочности (теория энергии формоизменения).
Наиболее простые теории пластичности и исходят из указанного
представления об условии пластичности, утверждающем, что при
пластическом состоянии вещества приведенное напряжение в
любой точке остается постоянным.
Так как приведенное напряжение, определяемое формулой (8.16),
будучи возведено в квадрат и поделено на удвоенный модуль
упругости, представляет собой удельную энергию формоизменения (т. е. ту
часть потенциальной энергии элементарного «единичного» объема,
которая расходуется только на изменение формы), то условие (8.16)
может быть прочитано и так: при пластическом состоянии вещества
удельная энергия формоизменения для любой точки остается
постоянной.
Еще проще должен быть математический аппарат теории
пластичности, если исходить из теории наибольших касательных напряжений
(в духе так называемой третьей теории прочности), базирующейся
на тех опытах, которые обнаружили, что при пластическом
состоянии вещества максимальное скалывающее напряжение в любой
точке остается постоянный. Запись последнего условия через
главные напряжения может быть сделана в виде
ai—аз = а*; (8-17)
для плоского напряженного состояния, пользуясь в этом случае
компонентами напряжений, имеем соотношение
V(°*-°yf + ±~*v = °T (8.18)

§ 104] ЧАСТНЫЙ СЛУЧАЙ ИДЕАЛЬНО ПЛАСТИЧЕСКОЕ ТЕЛО 321
Условие постоянства касательного напряжения (условие Сен-Ве-
нана) в общем удовлетворительно характеризует состояние текучести
материала и согласуется с наблюдениями над линиями Д. К. Чернова *).
Однако более тщательные экспериментальные исследования
обнаруживают систематические отклонения поведения ковких металлов
в состоянии текучести от условия (8.17).
Через главные напряжения, если положить хху = хуг = izx = 0,
а Од., Су, сг — соответственно равными главным напряжениям о1э о2, а3,
условие (8.16) запишется таким образом:
Y2
У (°i — "a)" + (°а — °3)2 + К - °i)2 = °т. (8Л6а)
Для случая, когда c2z=zc1 или с2 = о.д, условие (8.16а) получается,
как и (8.17):
"У "К(а1 — а2)2 + (а2 — аз)2 + (а3 — al)2 = а1 — а3 = ат-
Для случая плоской деформации, когда а2 = -^- (at -\- а3), левая
часть условия (8.16а) примет вид
^\/~(^-^Щ°1-\^Мч-^=^(°1-°ъ) (8-19)
и, следовательно, для такого случая условие пластичности (8.16)
запишется аналогично теории наибольших касательных напряжений (8.17)
с заменой лишь коэффициента в правой части перед пределом
текучести, а именно:
«1-^ = ^^.. (8.20)
Для случая плоского напряженного состояния, когда а3 = 0,
условие (8.16а) становится таким:
0?+02_ал = 02. (8.21)
Случай, описанный в (8.19), имеет место, например, в
толстостенной трубе, подверженной равномерным внутреннему и внешнему
давлениям, и когда осевое напряжение можно приблизительно полагать
равным полусумме двух других главных напряжений, так как труба
*) В литературе, по недоразумению, именуемыми линиями Людерса.
21 Зак. 3880. Н. И. Безухов

322 ОСНОВНЫЕ УРАВНЕНИЯ ТЕОРИИ ПЛАСТИЧНОСТИ [ГЛ. VIII
в осевом направлении не удлиняется. В таком случае, действительно,
°г = Р (°ш + °у) = Iх (31 + °2) =^= "2 (°1 + °2>>
так как при пластической деформации коэффициент [х следует поло-
1
жить равным -тт.
§ 105. Основные уравнения механики упруго-пластических
деформаций твердого тела
После того как установлен обобщенный закон деформации и
доказана возможность записи связей между напряжениями и компонентами
деформации в форме, сходной с принятой в теории упругости,
математический аппарат теории пластичности можно представить
совокупностью: трех статических уравнений (2.02), шести геометрических
соотношений (2.25), шести физических уравнений, написанных через
компоненты напряжений и деформации (8.06) или (8.08), выражений
для обобщенного напряжения и обобщенной деформации (3.05) и (3.06)
и уравнения (8.05), связывающего последние между собой. Всего,
таким образом, имеем 18 уравнений, куда входят 18 неизвестных.
Решением задачи теории пластичности, следовательно, явится такое,
которое для каждой точки деформируемого тела удовлетворяет
упомянутым выше 18 уравнениям и, кроме того, на границе тела
удовлетворяет контурным условиям (2.05).
Если рассматривать состояние равновесия (упруго-пластический
равновесный процесс) и не интересоваться компонентами смещения,
то задачу можно свести.к меньшему числу уравнений, а именно:
взамен шести геометрических уравнений (2.25) принять первую группу
уравнений неразрывности (2.26). Тогда имеем следующую совокупность
уравнений.
Уравнения равновесия:
дсл
дт;
ху
dz„
дх
дъ
ух
ду
да,,
дг
д%
V*
дх
дх
ду
дг
-fpK=0,
+ -^T + 17 + PZ = 0-
(А)
Уравнения сплошности:
д**«
дЧ
ху
ду*
дЧ
дх*
дхду
дЧ
1<д^= _
дг* ~^ ду* ду дг '
уг
д*ч . дЧ-
дх* * дг*
Г Д~2
&Ъх
дгдх
(Б)

§ 105] ОСНОВНЫЕ УРАВНЕНИЯ УПРУГО-ПЛАСТИЧЕСКИХ ДЕФОРМАЦИЙ 323
Уравнения зависимости компонентов напряжений от компонентов
деформации:
Qx~°oP = 2G'(sa,— ecp), \
°у— acP = 2G,(e2/ —еор),
аг — Оор = 2G' (е, — еср),
*ху
*уг
ху>
= G'y
(В)
Выражение для обобщенного модуля деформации
G' = G[1— ш(в,)1. (Г)
Выражение для обобщенной деформации
•*-:!г|/"(в.-в/+(«»-0' + («.-О,Н-|-(^+т5»+т«)- (Д)
Приведенные 14 уравнений (А) — (Д) содержат 14 неизвестных
(шесть компонентов напряжений, шесть компонентов деформаций, два
обобщенных параметра — деформация и модуль), и таким образом,
с математической точки зрения задача может быть разрешена без
обращения к помощи каких-либо новых уравнений, гипотез и т. п.
С практической точки зрения прямое решение указанных уравнений
почти невозможно из-за большого количества уравнений в частных
производных и нелинейности самих уравнений.
Для плоского напряженного состояния количество уравнений
уменьшается до восьми, а именно:
д**
дъ
ху
дх
<Эт,
ух
ду
да,.
дх
34.
ду
+-рК=0,
ду2 ' дх» дхду *
°а> — °ор = 20' (ех — еор),
°у — °ог = 20' (zy — еор),
тЖ|/=:= ^ fxy>
G'=G[l-a>(et.)].
(8.22)
21*

324 ОСНОВНЫЕ УРАВНЕНИЯ ТЕОРИИ ПЛАСТИЧНОСТИ [ГЛ. VIII
Для упругого процесса, очевидно, о> (ej = 0, обобщенный модуль
деформации равен обычному модулю сдвига и постоянен для каждой
точки; в таком случае уравнение (Г) отпадает, надобность в
уравнении (Д) исключается, а оставшиеся уравнения (А), (Б), (В) переходят
в известные уравнения линейной теории упругости.
§ 106. Частный случай — плоская задача, идеально
пластический материал
1. Уравнения в декартовых координатах. В случае плоской
деформации и идеально пластического материала написанное в
предыдущем параграфе число уравнений для напряжений может быть
уменьшено до трех, а задача разрешена без привлечения уравнений,
содержащих компоненты деформации, т. е. задача оказывается статически
определимой *).
Уравнения будут следующими (полагаем отсутствие объемных сил).
Условия равновесия:
доя
дх.
ху
дх
ух
ду
да,.
0,
= 0;
(8.23)
дх ' ду
условие пластичности (без эффекта упрочнения)
4 х У 1 яу
где & = -о-от, если придерживаться гипотезы Сен-Венана [см. (8.13)],
(8.24)
или
, 1
Я = -7= От,
если исходить из энергетических представлений
[см. (8.20)].
Из уравнений (8.23)—(8.24) можно получить решение путем
непосредственного интегрирования. Продифференцировав уравнения (8.23)
соответственно по у и х и произведя вычитание, получим:-
<ЭЧ,
дН
ху
дхду
д*
ду*
= 0;
д%„
дН
ху
ду дх
дх*
= 0,
<°х — °у)-'
дН
ху
дН.
ху
(8.25)
дхду ^х ~vJ~ дх* ду*
Подставляя в (8.25) значение (ош — оу) из (8.24), т. е.
У ¥ ху*
*) Применяемое в таких случаях название «статически определимая»
следует понимать условно» так как помимо статических уравнений
приходится для решения задачи привлекать и физическое уравнение (уравнение
состояния).

§ 107]
ЗАМЕЧАНИЯ
325
имеем для касательного напряжения тху следующее дифференциальное
уравнение в частных производных:
д2 д2т t „
~н 2 V k2 ■ т* — У
дхду у ху дх2
^ху 1
ду* '
(8.26)
2. Уравнения в полярных координатах.
в полярных координатах имеют вид
ду)_
о,
о,
Уравнения равновесия
(8.27)
а условие пластичности [без эффекта упрочнения, см. (8.24)]
(ог — о9)2 + 4^8 = 4&2. (8.28)
По исключении ог и о9 дифференциальное уравнение для касательного
напряжения тгд принимает вид
^ae ir|/ * тг9/—г ^7г + ^г аг
ав*
(8.29)
Примечание. Приведенными выше уравнениями полностью
определяется напряженное состояние тела, но не его деформация.
Более того, при известных напряжениях в данном случае идеально
пластического материала компоненты деформации не могут быть определены
однозначно, и это положение будет не только в случае плоской деформации,
но и при пространственной деформации. Указанное положение есть результат
выпадения в системе уравнений, приведенных на стр. 323, одного уравнения
в случае материала без упрочнения (связь обобщенного напряжения с
обобщенной деформацией).
Таким образом, в отличие от упругого состояния материала, где имело
место однозначное соответствие между шестью компонентами деформации
и шестью компонентами напряжения, при пластическом состоянии материала
без упрочнения, если шесть компонентов напряжений даны, один из
компонентов деформации может быть взят произвольно, а пять остальных тогда
определятся однозначно. При пластическом состоянии материала с
упрочнением, как и при упругом состоянии материала, все шесть компонентов
деформации полностью определяются шестью компонентами напряжений.
В телах, находящихся в упруго-пластическом равновесии, т. е. когда
наряду с пластическими зонами существуют также упругие зоны, никакой
неопределенности в отношении пластических деформаций нет даже в случае
материала без упрочнения. Возрастание деформаций сопровождается
изменением форм'границы, разделяющей указанные зоны.
§ 107. Замечания, касающиеся установления связи между
напряжениями и деформациями в нелинейной теории упругости
и в теории пластичности
В § 103 были сформулированы основные четыре закона в теории малых
упруго-пластических деформаций. Заметим, что не все упомянутые законы
являются совершенно независимыми друг от друга, и более того, само
количество независимых законов упруго-пластической деформации зависит от того,

326 ОСНОВНЫЕ УРАВНЕНИЯ ТЕОРИИ ПЛАСТИЧНОСТИ [ГЛ. VIII
в какой степени, в явной или завуалированной, оговорены предпосылки и
допущения. Так, в процессе выкладок в §§ 98—106 всюду предполагался,
выражаясь в терминах термодинамики, равновесный процесс, т. е. состояние
материала, характеризуемое напряжением сг- и деформацией ц, не изменялось во
времени. Далее, подразумевалось то, само по себе очевидное положение для
изотропного тела, что направления главных нормальных напряжений и
направления главных удлинений совпадают.
Можно доказать, что если первой и основной предпосылкой теории
принять идеальную изотропность материала (как при упругой, так и при
пластической деформации), а второй предпосылкой принять равновесный процесс,
то в качестве следствия получаем закон изменения формы (иначе закон
подобия девиаторов). Далее, приняв закон упругого изменения объема, в качестве
следствия получаем закон связи обобщенного напряжения с обобщенной
деформацией.
Интересующихся этим вопросом отсылаем к интересной работе И. И. Голь-
денблата «Некоторые вопросы теории упругих и пластических деформаций»
(Стройиздат, 1950). В этой книге дано доказательство того положения, что
в случае малых деформаций связь между компонентами напряжений и
деформаций полностью определяется при задании первого и второго инвариантов
тензора напряжений как функций первого и второго инвариантов тензора
деформаций.
Иначе будет в случае немалых, т. е. конечных деформаций. Связи между
компонентами тензора напряжений и тензора конечной деформации
полностью определяются заданием трех уравнений состояния, связывающих три
инварианта тензора напряжений с тремя инвариантами тензора деформации.
Для хрупких сталей и специальных сплавов, как показывают опыты, даже
при простом нагружении на момент наступления пластичности может оказать
влияние среднее нормальное напряжение. В частности, закон упрочнения при
простом нагружении должен для хрупких сталей иметь более сложный вид
°4 = Ф (V еср)-
Но для основной массы металлов, как отмечает А. А. Ильюшин [40], при зср
порядка не более ст влиянием а можно пренебречь, а в тех случаях, когда
это влияние становится существенным, требуются дополнительные
специальные опыты.
Заслуживают внимания также и такие связи между напряжениями и
деформациями, введение которых в основные уравнения теории
упруго-пластических деформаций облегчает решение самих уравнений. Само собой
очевидно, что речь идет о таких искусственных связях, которые с качественной
стороны более или менее правдоподобны, и расхождение их с
действительностью оказывается в пределах допустимой точности расчетов. Упомянем
о степенном законе связи обобщенного напряжения с обобщенной
деформацией в форме (предложено В. В. Соколовским)
где k и т — связанные между собой константы для данного материала.
Благодаря применению в теории пластичности функций комплексного
переменного В. В. Соколовскому удалось при наличии указанного выше
закона получить решение ряда новых задач теории пластичности и, в
частности, тех задач, для которых имеется решение в теории упругости *) (при
тех же граничных условиях).
*) Доложено В. В. Соколовским на общем собрании Отделения техни»
ческих наук АН СССР 15/V 1950 г.

§ 107]
ЗАМЕЧАНИЯ
327
По поводу последних приближенных зависимостей между напряжениями
и деформациями следует заметить, что и основные положения теории
пластичности являются в некоторой степени приближенными и потому логично
допустить и решение задачи в той же мере приближенное.
Иначе говоря, нет смысла теорию формулировать в виде замкнутой
системы дифференциальных уравнений со строгими граничными условиями,
а, напротив, в виде системы, имеющей класс решений, лежащих в более или
менее (соответственно с точностью экспериментальных законов) узкой полосе.
Во многих случаях это обстоятельство, не уменьшая физической точности
решения, позволит находить его гораздо более простыми средствами [40J.
Выше предполагалось, что среда является изотропной. Опыты, однако,
свидетельствуют о том, что с развитием пластической деформации материал
приобретает известную анизотропию и, следовательно, только в первом
приближении может быть рассматриваем как изотропный. Иначе говоря, опыты
свидетельствуют о некотором отклонении от условия подобия девиаторов.
В связи с этим делалась попытка начертания более сложных связей
между девиаторами, например, типа
DX9t=AEt + BDu + CT°, (a)
где D* — квадрат девиатора напряжений; Т^ — единичный тензор (шаровой,
при единичном среднем напряжении), Л, В и С — некоторые функции
второго и третьего инвариантов девиаторов напряжений.
Практического применения связи (а) не получили как по причине
сложности оперирования с ними, так и потому, что новые и более тщательные
эксперименты приводили к некоторому несоответствию действительности
с записью (а).
В последнее время В. В. Новожиловым [73] предложена новая форма
соотношения между напряжениями и деформациями для произвольного
нелинейно-упругого изотропного тела. В эти соотношения входят три
подлежащие определению из опыта функции инвариантов деформации:
обобщенный модуль объемного расширения, обобщенный
модуль сдвига и (по терминологии автора) фаза подобия
девиаторов. Если фаза подобия девиаторов равна нулю, то вышеуказанные
соотношения превращаются в формулы современной теории малых упруго-
пластических деформаций. К этой работе примыкают исследования Г. А. Смир-
нова-Аляева, который для описания законов пластического
деформирования ввел понятия об углах вида деформации и вида напряженного
состояния [95].
Исследования В. В. Новожилова показали, что даже значительные
отклонения фазы подобия девиаторов от нуля относительно мало влияют на закон,
связывающий обобщенные напряжения и деформации. Таким образом, им
доказано, что:
а) современная теория малых пластических деформаций не нуждается
в уточнении в сторону учета фазы подобия девиаторов;
б) связь между напряжениями и деформациями для произвольного
нелинейно-упругого тела следует искать в форме, аналогичной
соответствующим соотношениям теории пластичности.

ГЛАВА IX
ПРОСТЕЙШИЕ ЗАДАЧИ ТЕОРИИ ПЛАСТИЧНОСТИ
§ 108. Чистый изгиб
К числу простейших задач теории пластичности, для решения
которых нет необходимости иметь дело со всей совокупностью основных
уравнений теории пластичности, так как многие из них удовлетворяются
тождественно, а к оставшимся уравнениям оказывается достаточным
приложение элементарного математического анализа, принадлежат задачи
о чистом растяжении, чистом кручении, чистом изгибе и о
пластическом равновесии толстостенного кольца и сферического сосуда.
Переходим к рассмотрению чистого изгиба. В этом случае точно
оправдывается «гипотеза плоских сечений» как в области упругих
деформаций, так и за пределом упругости.
Таким образом, известное читателю из
общего курса сопротивления материалов
положение, что при изгибе удлинения
продольных волокон прямо
пропорциональны расстояниям их от нейтрального слоя,
в достаточной степени справедливо по
самый момент разрушения сечения. Как
известно, этот результат записывался так:
ex = jy> 00
Фиг. 137. Чистый изгиб „
(в средней части бруса). где ^— расстояние изучаемой точки
поперечного сечения от нейтрального слоя,
коэффициент пропорциональности, являющийся одновременно
кривизной при изгибе (фиг. 137).
Так как при чистом изгибе в поперечном сечении отсутствуют
касательные напряжения, а при малых деформациях изгиба
практически равно нулю и давление продольных волокон друг на друга
(оу = 0), надо считать, что каждое продольное волокно находится
в условиях одноосного напряженного состояния (обобщенное
напряжение о{ = Од., обобщенная деформация е^ = ех). В этом случае все

§ 108]
ЧИСТЫЙ ИЗГИБ
329
основные уравнения теории пластичности удовлетворяются при таких
значениях напряжений, которые должны быть увязаны только с
законами деформации.
Закон распределения нормальных напряжений в поперечном
сечении бруса для верхней и нижней его половин будет сходен с обычной
диаграммой растяжения при чистом растяжении — сжатии. Если для
этого последнего случая известна диаграмма
°* = *(«*)>
то можно найти положение нейтрального слоя и радиус кривизны
оси бруса по известному моменту.
Фиг. 138. Распределение по высоте сечения
относительных удлинений и нормальных напряжений при
упруго-пластическом изгибе.
Два уравнения равновесия между внешними я внутренними силами
данного сечения (2^=0, ^М = 0) запишутся так:
foxdF = 0- fo^dF^M. (б)
Элемент площади dF = bdy (фиг. 138); в общем случае при b=f{y)
и заменяя у = ер, имеем dF = /(ep)pde, тогда выражения (б)
перепишутся:
р§ <$>{s)f{zp)d*
р2 f Ф(е)е/(ер)^е
где 6j и е2 — удлинения (отрицательное и положительное) в крайних
волокнах.
:0,
:М9
(в)

330 ПРОСТЕЙШИЕ ЗАДАЧИ ТЕОРИИ ПЛАСТИЧНОСТИ [ГЛ. IX
При постоянной ширине сечения b выражения (в) упрощаются:
J* ф (8) rfe = 0,
Ь? f Ф (е)
е de = М.
(0
Г Ф(е)^е представляет собой площадь диаграммы напряжений, и так
как в пределах от гх до е2 согласно первому уравнению (г) она должна
быть равна нулю, то это означает, что площадь диаграммы,
соответствующая растянутой зоне, равна площади диаграммы,
соответствующей сжатой зоне. Если диаграммы растяжения и сжатия данного
материала при одноосном напряженном состоянии одинаковы (и отли-.
чаются лишь знаками удлинения и напряжения), то указанная выше
необходимость равенства площадей диаграмм влечет за собой и равенство
соответствующих частей площади поперечного сечения, т. е. F1 = F2.
I Ф (е) е йг представляет собой, очевидно, статический момент
площади диаграммы относительно нейтральной оси и как для верхней,
так и для нижней половины сечения берется со знаком плюс.
Если аппроксимировать диаграмму растяжения при помощи
степенной функции вида (фиг. 134)
—■$••
где 0<т< 1, а сечение бруса полагать с двумя осями симметрии
и материал с одинаковыми свойствами на растяжение и сжатие, то
второе уравнение равновесия в раскрытом виде запишется так:
заменяя
Уо „ в Л
имеем:
., = _ и е1==^,
М = т— . (9.01)
Если т = 1 (упругий процесс) и положить
_ /г _
Л — ~2> °max — jti
ТО
^ = 0,*^. (9.02)

§ 108] чистый изгиб 331
Если т = 0 (идеально пластическое состояние, фиг. 131), то
Жт = ат^-. (9.03)
Первый (предел упругого сопротивления при изгибе
стержня прямоугольного сечения) и второй (предел
пластического сопротивления) результаты известны
читателю из сопротивления материалов.
Из второго выражения (г) при заданном изгибающем моменте Л1, значение
которого лежит в промежутке Мупр < М < jVfT, можно получить формулу
для )>о, т. е. для расстояния от нейтрального слоя сечения до того волокна,
относительное удлинение и величина напряжения в котором имеют
характерные значения ет и ат.
Для частного случая, когда диаграмма растяжения аппроксимируется
степенной функцией, выражение для у0 непосредственно следует из (9.01).
В случае, когда диаграмма растяжения имеет вид фиг. 131, т. е.
ат
ф (е) = — * при е < ет
ет
И
Ф (е) = <jt при е > ет,
использование (г) приводит к выражению
Высота упругого слоя сечения в этом случае равна 2_у0. Если по длине
бруса изгибающий момент изменяется (случай поперечного изгиба), то
согласно (9.04) меняется и высота упругого слоя балки.
Строго говоря, на высоту упругого слоя (в смысле его уменьшения) при
поперечном изгибе оказывает влияние также поперечная сила (см. § 118),
но указанное влияние оказывается невысоким, если состояние балки (хотя
и перешедшей за предельное упругое) все же отстоит далеко от предельного
пластического.
Может представить интерес изучение прогиба оси балки при упруго-
пластическом поперечном изгибе. Эта задача сводится к интегрированию
дифференциального уравнения изогнутой оси балки, которое для участков
балки, где изгибающий момент меньше предельного упругого, т. е. M<^MJupf
имеет обычный вид (ось х направлена по оси балки)
а для упруго-пластических участков
EJ-j^ = ^=== • (9-05)
8/ff/l -£
Последнему уравнению можно придать внешний вид обычного уравнения
«упругой оси», если ввести в употребление понятие о приведенном моменте
инерции:
j«p=j^1V1-w> (9-06)

332
ПРОСТЕЙШИЕ ЗАДАЧИ ТЕОРИИ ПЛАСТИЧНОСТИ [ГЛ. IX
причем, очевидно, ^упр<С^ Эта приведенная характеристика не является
чисто геометрической, а зависит также от внешних сил (входят в М) и от
пластических свойств материала (входят в ЛГТ).
Иначе говоря, задачу определения прогибов балки постоянного
сечения, находящейся в упруго-пластическом состоянии,
можно заменить *) задачей определения прогибов балки некоторого
переменного сечения, находящейся якобы в упругом состоянии. В последнем
случае можно использовать широко известные эффективные приемы,
разработанные в сопротивлении материалов. За последнее время эта мысль находит
применение в задачах об упруго-пластическом стесненном кручении (см. §121).
§ 109. Чистое кручение
При кручении бруса круглого поперечного сечения в последнем
возбуждаются только касательные напряжения, направленные
перпендикулярно к радиусу. Радиусы
в поперечном сечении и за
пределами упругости при
кручении круглого бруса
можно считать неискривляю-
щимися (фиг. 139, справа).
В таком случае, как и
при рассмотрении подобной
задачи в упругом состоянии,
уравнения равновесия и
уравнения неразрывности
деформации удовлетворяются при
значениях напряжений,
которые должны быть увязаны
только с законами
деформации.
Фиг. 139. Распределение касательных
напряжений и схема сдвигов в поперечном
сечении при чистом кручении.
Читателю известна геометрическая сторона деформации, т. е.
7 = «Р>
(а)
где а — угол, на который поворачиваются друг относительно друга
два поперечных сечения, находящихся одно от другого на расстоянии,
равном единице; р — расстояние от оси бруса до рассматриваемой
точки; f — угол сдвига для этой точки.
Касательное напряжение т представляет собой функцию угла
сдвига 7- Кривую, имеющую уравнение
*=/(т).
(б)
называют кривой деформации для чистого сдвига.
Будем полагать, что такая кривая нам известна.
*) См. статьи автора [4, 5].

§ 109]
ЧИСТОЕ КРУЧЕНИЕ
333
Уравнение равновесия между внешними силами (крутящий момент)
и внутренними силами сечения запишется так:
М
заменяя здесь по (а)
p-±s
= j x9dF;
F
dF = 2itp dp = 2ir \ d-i,
(в)
имеем:
•о
(г)
В выражении (г) через *(а обозначен предельный угол сдвига,
который имеют периферийные точки сечения.
Если, как это было сделано выше при изгибе, аппроксимировать
диаграмму сдвига при помощи степенной функции вида (фиг. 140)
где
0</и<1,
то будем иметь:
М
_2я
а*
п Г (ТУ
2/*y —
72rff
о vW+3
2'ЛТт «О
a8Tm (т + 3)
(д)
Имея возможность заменить
Та = «П Тт = «/"о,
где г0 — радиус «упругого» ядра, выражение (д) переписываем так:
М = 2итт
-W + 3
С (т + 3)
Полагая m = 1 (упругое состояние)
и г0 = г, получаем известное из курса
сопротивления материалов выражение
для предела упругого сопротивления
при кручении бруса круглого сечения:
-Мупр — 2 ^°*
-о1'8- (9.07)
г*-7т^
Фиг. 140. Диаграмма сдвигов,
описываемая уравнением
Полагая тп = 0, получаем
выражение для предела пластического
сопротивления при кручении круглого бруса
для случая идеальной диаграммы сдвига (идеально пластическое тело):
-№■
М т = у ii-CtA
(9.08)

334 ПРОСТЕЙШИЕ ЗАДАЧИ ТЕОРИИ ПЛАСТИЧНОСТИ [ГЛ. IX
Если имеем трубку малой, толщины 8, находящуюся в состоянии
пластического кручения, то соответствующий этому состоянию момент
приближенно запишется (через наружный радиус г) таким образом:
АТТ = (2тсг8) тг = 2тгг28тт, (е)
что соответствует в данном случае Муцр для той же трубки.
§ ПО. Осесимметричное упруго-пластическое
состояние толстостенной трубы
Рассмотрим толстостенную трубу, находящуюся под осесимме-
тричным внутренним и внешним давлениями (плоская задача); материал
полагаем идеально пластическим (фиг. 141)»
Будем полагать, что ра > рь.
Так как в этом случае распределение
напряжений симметрично относительно оси-
трубы (зависит только от одной
координаты— от радиуса), а тангенциальное ,и
радиальное напряжения (ое и сг) суть
главные напряжения, то следует
удовлетворить лишь одному уравнению равновесия
(3.47), которое принимает вид
«г—> + /^~0.
Присоединяем сюда условие
пластичности, которое по теории наибольших
касательных напряжений, а также и по
энергетической теории, если только осевая
деформация ег=0, запишется (полагаем,
что внутреннее давление значительно преобладает над наружным,
поэтому тангенциальное напряжение — растягивающее) так:
ое — ог=2£,
где k—пластическая постоянная (£ = 0,5от по теории касательных
напряжений и k = 0,57от по энергетическим представлениям). Сравнивая
полученные уравнения, имеем:
dr
Интегрируя, получаем:
а, = 2ft In r + С. (a)
На наружной поверхности (при r = b) ог = — ръ> а потому из (а)
следует:
C = — pb — 2k\nb. (б)
Фиг. 141. К задаче о
пластическом равновесии
толстостенной трубы.

§ 110] ОСЕСИММЕТРИЧНОЕ УПРУГО-ПЛАСТИЧЕСКОЕ СОСТОЯНИЕ ТРУБЫ 335
На внутренней поверхности (при г = а) ог = — ра, и поэтому из (а),
учитывая (б), имеем:
— ра = 2k In a — рь — 2k In by
или в окончательном виде
Ра — Ръ = Ы\п--.
(9.09)
Выражение (9.09) есть условие пластичности для трубы,
подверженной одновременно наружному и внутреннему давлениям.
Для того чтобы вся труба пришла в пластическое состояние,
необходимо, чтобы внутреннее давление превышало наружное
согласно (9.09). При /?ь = 0 имеем так называемый предел
пластического сопротивления трубы (предельное внутреннее
давление), подверженной одному внутреннему давлению:
2&1п-.
а
(9.10)
Рассмотрим теперь случай, когда давление в трубе меньше
предела пластического. сопротивления, но больше предела упругого со-
Упругая
зона
Пластическая
зона
Фиг. 142. Упруго-пластическое состояние толстостенной трубы.
противления. В этом случае в поперечном сечении трубы будем
иметь две зоны: внутреннюю — пластическую и наружную —
упругую.
Обозначим давление пластической среды на упругую через q
(фиг. 142). Тогда применительно к пластической зоне можем
написать условие пластичности, например, при А = 0,5от по (9.09):
/V
? = °т!п-;
(в)

336 ПРОСТЕЙШИЕ ЗАДАЧИ ТЕОРИИ ПЛАСТИЧНОСТИ [ГЛ. IX
обозначаем:
—■ Рпл)
тогда
Ра ? = От In рдл.
Применительно к упругой зоне можем написать условие
предельного состояния (например, по теории наибольших касательных
напряжений). Отождеставляя для простоты вычислений предел упругости
с пределом текучести, получаем:
Я — Рб = 3НЬ—» (г)
Щ
где
Р7~
вычитая (г) из (в), имеем:
Ра — Рь = От[|пЭ„л — ^i- + ^J-
(9.11)
Для случая, когда осевая деформация трубы егфО (имеется осевая
сила Р), и приняв допущение о несжимаемости материала, В. В.
Соколовский (104) установил, что чисто пластическое состояние наступает при
соблюдении условий
Ра— Ръ = к\п ^ ^
Ф (i 4- yi -f щ
Ybk
{b2yi + x* - yS*+ >№ + n(paa*-pbb*),
(9.12)
где параметр Х находится из уравнения
J. J/ k
к*
3 \Gt,
)'-'■
В. В. Соколовский обследовал вопрос о применимости к решению задачи
об упруго-пластическом равновесии трубы допущения о несжимаемости
материала. Это допущение не позволяет (если jj. ф 0,5) полностью
удовлетворить условию непрерывности всех компонентов напряжения и смещения на
общей границе упругой и пластической зон, поэтому применение его, строго
говоря, возможно лишь в чисто пластических задачах, когда упругая зона
отсутствует.
В. В. Соколовским было показано, что значения компонентов ог и а9,
найденные с учетом или без учета сжимаемости материала, все же довольно
близки. Вычисление компонента напряжений qz и радиального компонента
смещения без учета сжимаемости недопустимо.
§ 111. Продолжение: учет упрочнения материала
Для случая осесимметричной и притом плоской деформации
(е^ = 0) толстостенной трубы напряжения и деформации в ней
определяются также просто и при наличии упрочнения материала.

§ 111) продолжение: учет упрочнения материала 337
Будем полагать известной из опытов (например, из опыта на
кручение) зависимость
*=/(T). (а)
Наибольшее касательное напряжение в любой точке
рассматриваемой трубы может быть, как известно, выражено через главные
нормальные напряжения:
x = io^ (б)
Кроме того, для случая е., = 0 и несжимаемости материала имеем
с помощью соотношений, приведенных на стр. 107 и 139:
2В . .
Ч = ч — гг=—. (в)
Уравнение равновесия элемента трубы записываем без
изменения (3.47):
Интегрируя уравнение (г) в пределах от г до г = Ь, имеем:
ь ъ
dr_
г
о о
J d<3r = J (о, —а,.)
Г Г
или, принимая граничные условия (при r = b, ог = 0), переписываем)
ъ
— °г = J Об — *,.) -у- . (Д)
г
Дифференцируя (в), имеем:
__i^ d 2В 2dr
или, принимая во внимание (в), записываем:
rfY = -2-^4 (e)
Подставляя в (д) зависимость (б) и (е), имеем:
Ч
т
или
Ч
22 Зак. 3880. Н. И. Безухов
т
Ч
>•= //(т)-^-, сиз)

338 ПРОСТЕЙШИЕ ЗАДАЧИ ТЕОРИИ ПЛАСТИЧНОСТИ [ГЛ. IX
где верхний предел в этом интеграле обозначает значение f при
г = Ь.
Для тангенциального напряжения с помощью (а) и (б) имеем:
Ч
зе = 2/(т)+//(т)у-. (ж)
т
Так как при г = а радиальное напряжение ог = — /?, то при по-
"мощи (9.13) можем вычислить давление р, при котором на
внутренней поверхности трубы деформация сдвига равна fa:
^//(T)-f. (9-14)
Ч
Пределы интегрирования ^а и уь между собой связаны
зависимостями (в):
_ 2В _ 2В
То — а> > Т& — bi у
и потому
_ ii
Та Tb а2 •
При наличии сколь угодно сложного графика т=/(т) решение
интеграла (9.14) может быть раскрыто графически или методом
численного интегрирования, но если аппроксимировать кривую
деформации для чистого сдвига при помощи степенной зависимости
'-£)"•
то выражение (9.14) может быть легко проинтегрировано. Так, для
внутреннего давления р имеем:
«,2m i'
v /7,а
■'■ (9.15)
{a ъ*
Так как диаграмму истинных напряжений при испытании материала
на чистое растяжение (в координатах а и е) можно считать условно
подобной диаграмме напряжений при сдвиге и кручении (в
координатах т и ч), то указанному выше результату (9.15) можно придать
другое начертание, заменив т=/(«у) через функцию о=/(е).
Вспомним, что предел текучести при чистом сдвиге связан (по
энергетической теории) с пределом текучести при растяжении
зависимостью
_ ат
"-"TV

§ 111] продолжение: учет упрочнения материала 339
а при пластической деформации удлинение образца ег в два раза
больше поперечного сужения е2 (т. е. коэффициент ja =-у J, и потому
максимальный относительный сдвиг при одноосном пластическом
растяжении:
3
T = si —е2 = "2-е1-
Заменяя в (9.15)
_3 _ с*
Тт__ет, *,—^=,
имеем:
При т = 1 (упругий процесс), когда график о=/(е) —
прямолинейный, из (9.16) получаем известное читателю выражение для предела
упругого сопротивления трубы (считая, что га достигло предела ет):
При т = О (идеально пластический материал), что равносильно
т =/(?) = const,
Q
и полагая попрежнему тт = —-?=, из (9.14) имеем:
',eTJTeWeT,n^ (9Л7)
ч
Последнее соответствует полученному ранее известному
выражению (9.10) для предела пластического сопротивления, записываемому
иногда в виде
р= 1,15от1пр,
где
r a
Предлагается читателю в порядке самостоятельного упражнения
продолжить рассматриваемую задачу и доказать справедливость следующих
формул:
радиальное напряжение
а2т (ffim г2т\
аг = Р г2т (рш а2т) *
тангенциальное напряжение
__ Д2ж [ь2т (2т — 1) + г2™] в
а& ~~ Р fim (film фт) '
22*

340
ПРОСТЕЙШИЕ ЗАДАЧИ ТЕОРИИ ПЛАСТИЧНОСТИ
[ГЛ. IX
увеличение внутреннего радиуса (компонент смещения)
1
«—
а
7т
;— I m ,
.'■О-©
увеличение наружного радиуса
Если трубу, подвергнутую внутреннему давлению, которому отвечал
наибольший относительный сдвиг 7а, далее освободить от давления, то,
применяя закон пассивной деформации (§ 102), мы должны получить для
остаточной деформации по внутреннему радиусу выражение
(и ) =_1т I" ЕЕ "]«_.„ 11+•*> b"'a
Уиг=а> ост 2 ''' I / я8'»\ ^ I
(62 — Я2)
§ 112. Осесимметричные пластические деформации
равномерно вращающегося диска
Если диск имеет небольшую толщину и равномерно вращается
относительно центральной оси, нормальной к плоскости диска, с угловой
скоростью со, то условие пластичности по теории наибольших касательных
напряжений может быть записано
исключительно просто в виде
°о = V (а)
Эта возможность вытекает из того
факта, что при быстром, но равномерном
вращении диска радиальные напряжения
сг—растягивающие, а осевые а3 ввиду
малой толщины диска практически
отсутствуют.
В связи с указанным определение
угловой скорости вращения диска, при
которой весь материал диска переходит в
пластическое состояние, выполнится
непосредственно из условия равновесия по
диаметральному сечению между
внутренними силами по такому сечению и
центробежными силами инерции мысленно
отсекаемой половины диска. При обозначениях
фиг. 143 имеем:
Фиг. 143. Распределение
тангенциальных нормальных
напряжений во вращающемся
диске при пластическом
состоянии материала диска.
и с
2<тт (Ь — а) = 2 (1 ©2Л (rd-i dr) sin <р,
откуда для критической скорости имеем выражение
3?т (b — a) g
где 7 — удельный вес материала диска.
■iT-
(9.18)

§ 112] ОСЕСИММЕТРИЧНЫЕ ПЛАСТИЧЕСКИЕ ДЕФОРМАЦИИ ДИСКА
341
Для случая вращающегося кольца, когда его толщина
Ь = Ь — а
очень мала по сравнению с размером Ь (или д), выражение (9.18)
упрощенно записывается так:
о-Т У у '
b
и наоборот, для сплошного диска, когда а = 0, имеем:
= /1 лГ ?*
Ь ' -I
Уз
оз0.
(9.19)
(9.20)
Если исходить из теории постоянства интенсивности напряжения, то для
той же задачи, как показал В. В. Соколовский [104], выражение для
критической скорости мало отличается от (9.20)
и имеет вид
с»!^ 1,79(о0.
Для вычисления радиальных
напряжений <зг составим уравнение равновесия
части сектора диска, показанного на
фиг. 144:
г
2aQSin-^-= (— со2/-] r dy dr-\-orrdy,
Фиг. 144. Определение
радиальных напряжений в быстро
вращающемся диске.
rfcp dy
где после замены sin -—- на ~- и
использования (9.18), имеем:
г— а Г Ь— а г*— сРЛ
*r=** — [l-T=^-W=¥\' (б)
что при любом г в пределах Ь^> г> а определяет положительное
(растягивающее) значение, чем и оправдывается принятая выше запись условия
пластичности в форме aQ = от, а не в форме а8 — а = ат.
В случае вращающейся трубы, одновременно испытывающей
продольное растяжение (а2 не равно нулю), может оказаться более неблагоприятным,
а значит, и действительным, условие пластичности в виде
°Н — ar = ffr (B)
В таком случае задача несколько усложняется, но в общем остается
простой. К уравнению (в) присоединяем уравнение равновесия бесконечно
малого элемента (с учетом массовой силы)
dar
ан — ar = г -7+ + — <oV2.
dr g
Подставляя (в) в (г) и интегрируя, имеем:
,г = а, 1П г—!«»-£ + £
Используя граничные условия (при г=а и r=b, ar = Q), находим:
■aTln я,
(г)
Г 7 9 й
g

342 ПРОСТЕЙШИЕ ЗАДАЧИ ТЕОРИИ ПЛАСТИЧНОСТИ \ГЛ. IX
после чего критическая скорость
а?) •
При Ь, стремящемся к а% по раскрытии неопределенности получаем, как
н выше:
V*--
-■ »■ 1
Случай ступенчатого диска (фиг. 145) был рассмотрен В. В. Соко-
*Ъ k
1_"
jp.
Фиг. 145. К задаче о предельной угловой скорости
для ступенчатого диска.
ловским [104], который для критической скорости такого диска получил
выражение
,/-о- и-шГ b + d(m — l)
где
В. В. Соколовским рассмотрена также задача о напряженном состоянии
диска при степенном условии пластичности с учетом упрочнения.
§ 113. Полярно-симметричное упруго-пластическое
состояние шарового сосуда
Пусть шаровой сосуд, имеющий радиус внутренней поверхности
а и наружный Ь, давлением газа приведен по всей толщине своих
стенок в идеально пластическое состояние. Давление газов изнутри
обозначим через ра> а снаружи /?6. Будем полагать, что ра > рь.
Вырежем для исследования из шарового сосуда бесконечно малый
элемент двумя парами взаимно перпендикулярных меридиональных
сечений и двумя концентрическими сферическими поверхностями
(фиг. 74). Действие отброшенных частей сосуда заменим
тангенциальными (о*, аг) и радиальными (аг) напряжениями.
Проектируя все силы на нормаль к элементу, имеем уравнение
равновесия в виде (см. подробнее в § 57, так как уравнения
равновесия не зависят от того, в каком состоянии находится материал,

§ ИЗ] ПОЛЯРНО-СИММЕТРИЧНОЕ СОСТОЯНИЕ ШАРОВОГО СОСУДА 343
упругом или пластическом)
2(ar-a,)+rg? = 0. (а)
Условие пластичности примем по условию (8.16а) (предполагаем
материал способным к идеальной пластичности и не имеющим
эффекта упрочнения):
у= V("r - **? + К - °*)2 + (<v - з*)2 = ст.
Это уравнение в данном случае принимает вид
at — ar==zi=aT. (б)
Объединяя (а) и (б) и производя разделение переменных, имеем
дифференциальное уравнение
г г
Интегрируя последнее, находим:
<зг = ±2о?\пг-\-С. (в)
Используем граничные условия: при г = я, ar= — ра\ при r = b
zr= — ph. Из (в) находим:
— pa = ±:2aTlna + C,
— рь = ± 2aT In b + С.
Производя вычитание первой строки из второй, имеем:
Pa — p* = ±2aTln- (г)
или, обозначая
получаем окончательно:
(9.21)
Ра — Ръ = ±2°Г\П$.
Выражение (9.21) и есть условие пластичности шарового сосуда
(предел пластического сопротивления сосуда). Знак (-f-), очевидно,
надо брать в случае, когда ра > рь> знак (—) в обратном случае.
Рассмотрим теперь упруго-пластическое состояние шарового
сосуда, когда в пластическом состоянии находится часть сферы от
г = а до г = с, причем а < £ < £. Обозначим интенсивность
давления пластического слоя (толщиной с — а) на упругую часть
шарового сосуда (толщиной b — с) через д.

344 ПРОСТЕЙШИЕ ЗАДАЧИ ТЕОРИИ ПЛАСТИЧНОСТИ [ГЛ. IX
Тогда условие пластичности для внутренней части сферы с
радиусами г = а и г = с запишется с помощью (г):
Ра — ? = :±:2зт1п|Злл, (д)
где
Условие предельного упругого состояния наружной оболочки
запишется (если отождествлять для простоты расчетов предел
упругости с пределом текучести) так:
Wr=c- (°г)г=с = Ъ> (е)
где (or)r=e = — q, а для тангенциального напряжения согласно
известным формулам из теории упругости
. g(2c»+6») 3/7Ь&з
^t)r=c 2(b* — c*) 2(63 — сз) •
Таким образом, условие (е) становится таким:
д(2е* + Ь*) 3pbb*
2 (b* — с*) 2 (Ь9 — с*)
f q = ± от. (ж)
Обозначим — = ру; тогда условие (ж) примет вид
,r1+j+S_l_„_£—^,. (з,
Ч T2(^-l)J /fr2(^—1) V '
Объединяя (д) и (з), имеем уравнение упруго-пластического
равновесия шарового сосуда
рв —ft = =t2a,[lnpna + l-^]. (9.22)
§ 114. Примеры решения задач полуобратным методом
Ниже приводится решение некоторых задач, когда по известному закону
распределения отдельных компонентов напряжений внутри пластически
деформируемого тела выявляются остальные компоненты напряжений, а также
внешние поверхностные условия задачи. Материал во всех задачах
настоящего параграфа подразумевается идеально пластическим, деформация плоская.
1. Одним из решений уравнения (8.26) является z=f(y)y т. е.
касательные напряжения в плоскостях, параллельных осям х и у, зависят только
от координаты у. Тогда из (8.26) вытекает:
^ = 0
откуда х = С± — С?у.

§ 114] ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ ПОЛУОБРАТНЫМ МЕТОДОМ
345
Далее, из уравнений равновесия имеем:
и потому
а следовательно,
дх ~ ду * ~'
<jx = C2x+f1(y);
ду дх
'«=/2(4
Обе произвольные функции следует определить таким образом, чтобы
условие пластичности удовлетворялось тождественно:
С*х +Л (у) -ft {x) = ±2 yv-iC^-C^K
Из последней записи заключаем:
Д (у) = ± 2 У*» — (С, - C2j/)2 + С3;
/2(лг) = С2дг+Са.
Таким образом, окончательно:
^ = С3 + С2х ± 2 V» - (С! - С2>)*,
а2/ = ^ ~Т" ^2-**>
Т = Q — CoJ/.
(9.23)
Варьируя значениями постоянных Сь С2 и С3, зависящих от характера
поверхностных условий, получим различные случаи внешнего воздействия
ГГГПТГГТТТТтттг^т^
Фиг. 146. Схема усилий, воздействующих на
пластическую массу, сжатую между двумя
шероховатыми параллельными плитами.
на пластическую массу, сжатую между двумя шероховатыми параллельными
плитами (изображено на фиг. 146).

346 ПРОСТЕЙШИЕ ЗАДАЧИ ТЕОРИИ ПЛАСТИЧНОСТИ {ГЛ. IX
2. Предполагаем, что в круговом секторе касательное напряжение не
зависит от 6. В гаком случае дифференциальное уравнение (8.29)
запишется так:
д2т дт
г ;Г^> + 3 Т = °-
Ьг1 ' дг
Интегрируя, получаем:
Из второго уравнения (3.41) имеем:
Интегрируя, почучаем:
,9 = _2С28+С8+/(г),
где /(г) — функция г (способ определения ее аналогичен выполненному
в следующем примере). Из условия пластичности
имеем:
ar = <jQ zt 2 у^ — т*. (а)
3. Предполагаем, что в круговом секторе касательное напряжение не
зависит от г. В таком случае уравнение (8.29) упрощается и принимает вид
4J- = =F 2 У& — + + С; (9.24)
при С = О интегрирование дает:
х = it A? sin (Ct + 26).
Из уравнений равновесия имеем:
-^• = -x-lr(rl) = -2t = ±2ftsln(C1 + 2e),
откуда
а6 = + £ cos (d + 26) +/(/-),
где/(г) — произвольная функция г; далее,
аг == ае + 2 У"А;2 —х2 = + 3k cos (Cx + 26) +/(г),
или
■г = 3*в —2/(г);
при /(г) = 0 имеем:
*r = 3jq.
Неизвестную функцию /(г) определим, используя первое уравнение
равновесия (3.41). Так как
d6
щ 2k cos (Ct + 26), ffr _ afJ = =р 2 Y& — ^

§ 115] СОСТОЯНИЕ ТЕОРИИ ПЛАСТИЧНОСТИ В СССР 347
то первое уравнение (3.41) запишется следующим образом:
но из (а) следует, что
т2/^+г^ + £-0.
(6)
даг дзц
дг
дг
-Г (г),
а потому (б) перепишется так:
зр 4 у^/р2 — Х2 4- rf (г) = О,
откуда, принимая во внимание, что % есть функция только угла 6, находим:
4
Г (г)-.
yw
Интегрируя, имеем:
f(r) = ±4 у& — т:Ппг+С.
Итак, окончательно имеем следующую систему напряжений:
а9 = + k cos (Ct + 26) ± 4 У^ — х^ 1п г + С,
(7Г = + 3k cos (Ct + 26) it 4 /£^=1* In г + С,
Tr9 = 4=*sin(C1 + 2e).
Ha фиг. 147 показаны внешние силы, вычисленные по (9.17); они соот-
(9.25)
Фиг. 147. Схема усилий, воздействующих на
пластическую массу, сжатую между двумя шероховатыми
жесткими плитами.
ветствуют случаю пластической массы, сжатой между двумя наклонными
жесткими плитами.
§ 115. Состояние теории пластичности в СССР
Теория пластичности свое настоящее и богатое содержание
получила именно в СССР. Для читателя составит несомненный интерес
знать хотя бы краткий перечень задач теории пластичности и
методов их решения, предложенных советскими учеными, помимо,
конечно, тех задач, которые разобраны в главах IX и X.
Для случая плоской деформации, как это было показано в § 106,
определение напряжений в пластической области при отсутствии

348 ПРОСТЕЙШИЕ ЗАДАЧИ ТЕОРИИ ПЛАСТИЧНОСТИ [ГЛ. IX
упрочнения является статически определимой задачей. С. А. Христиа-
нович показал, что в таком случае решение задачи теории
пластичности сводится к решению классических задач на построение
характеристик уравнений гиперболического типа, и исследовал ряд общих
относящихся сюда закономерностей.
В. В. Соколовский [104] широко развил применение метода Хриг
стиановича к конкретным задачам определения напряженного
состояния в областях, перешедших в пластическое состояние (без
упрочнения). В частности, В. В. Соколовский произвел построение
характеристик вокруг произвольного отверстия в предположении, что
пластическая область это отверстие полностью окружает.
Статически определимыми задачами оказались задачи об обжатии,
раздаче и волочении труб. Эти задачи были обстоятельно изучены
А. А. Ильюшиным [42].
Статика сыпучей среды в предельном состоянии оказалась
аналогичной (в математическом отношении) теории пластичности без
упрочнения, т. е. статически определимой задачей. В. В. Соколовский дал
общую теорию статики сыпучей среды и решил ряд интересных задач
о давлении на подпорные стенки, о форме откосов, об устойчивости
фундаментов и др. Его монография «Статика сыпучей среды» (1942)
была удостоена Сталинской премии. Выводы из этой теории нашли
широкое применение на Великих Стройках Коммунизма в части
решения задач об устойчивости оснований под грандиозные
гидротехнические сооружения. Некоторые результаты этой теории указаны
в § 123.
Статике сыпучей среды посвящены также работы В. И. Новотор-
цева, С. С. Голушкевича, В. Г. Березанцева и др. [100].
Точно так же статически определимой оказывается задача об
определении напряжений в пластической области, образующейся при
кручении за пределом упругости стержней и валов переменного сечения.
Л. А. Галину принадлежит аналитическое решение
упруго-пластической задачи о кручении стержней, сечение которых представляет
собой многоугольник. Ему же принадлежит установление интересной
аналогии между упруго-пластической задачей о распределении
напряжений в плоской пластинке с отверстием, ограниченным круговым
контуром, растягиваемой силами, действующими на бесконечности и
специально подобранной упругой пластинкой, изгибаемой
надлежащими моментами на бесконечности [104].
Эта аналогия похожа на известную аналогию для кручения
стержней (§ 119) и позволяет экспериментальным путем решать некоторые
упруго-пластические задачи.
Для случая, когда при кручении все сечение стержня переходит
в пластическое состояние, аналитическое решение дал В. В.
Соколовский.
Для статически определимой задачи остается пока открытым
вопрос об определении перемещений в пластической области (упроч-

§ 115] СОСТОЯНИЕ ТЕОРИИ ПЛАСТИЧНОСТИ В СССР 349
пение отсутствует) за исключением случая осевой симметрии; этот
случай был исследован С. Л. Соболевым [44].
Так как при монотонном изменении гг законы пластического
деформирования имеют сходство с законами деформирования нели«-
нейного упругого тела, то вследствие этого А. А. Ильюшину и
Л. М. Качанову [49] удалось установить в теории пластичности ряд
теорем вариационного характера, аналогичных некоторым общим
теоремам теории упругости. Использование этих теорем при решении
задач приводит по существу к так называемому методу упругих
решений, кратко изложенному в § 129.
Из задач, имеющих широкое практическое использование,
отметим решение А. А. Ильюшиным задачи по обжатию бесконечной
трубы распределенным кольцевым усилием по внешней окружности
какого-либо сечения. Ему же принадлежат многие задачи об
определении несущей способности, т. е. предельной нагрузки пластин и
оболочек. Большим вкладом в советскую науку явилась созданная
А. А. Ильюшиным теория устойчивости пластин и оболочек за
пределом упругости. Большой круг практически важных задач, помимо
ранее отмеченных, принадлежит В. В. Соколовскому. Им обстоятельно
исследовано постепенное распространение пластического состояния
по мере увеличения нагрузки в круглой пластинке (сплошной и с
отверстием), решена задача о пластических деформациях растягиваемой
пластинки с отверстием.
Большое количество задач решено В. В. Соколовским для случая
степенного условия пластичнооти с упрочнением (изгиб пластинок,
кручение конического стержня, упруго-пластическое равновесие
полуплоскости и т. д.). Им же рассмотрено плоское деформированное
состояние при условии пластичности, определяемом кривой
произвольной формы. Показано, что особенно простые результаты могут
быть получены, когда предельной кривой является циклоида. Им же
сформулирован закон механического подобия для двух пластических
напряженных состояний [104] аналогично известной теореме подобия
в теории упругости, принадлежащей В. Л. Кирпичеву. В последнее
время А. А. Ильюшин установил закон механического подобия
в теории пластичности для случая больших скоростей
деформирования и высокого температурного поля.
Отметим также исследования В. В. Соколовского по теории
вдавливания в пластическую среду штампов всевозможных очертаний,
гладких и шероховатых. Задача о вдавливании осесимметричного
штампа (в частности, шарика) была решена А. Ю. Ишлинским.
Применительно к технологическим задачам (ковка, штамповка и т. п.) ряд
оригинальных исследований выполнен Г. А. Смирновым-Аляевым.
Общие идеи о несущей способности (предельное пластическое
состояние) конструкций и методы расчета их по предельным
нагрузкам были даны А. А. Гвоздевым [23]. Некоторые результаты его
теории показаны в § 128.

350 ПРОСТЕЙШИЕ ЗАДАЧИ ТЕОРИИ ПЛАСТИЧНОСТИ [ГЛ. IX
Наряду с ценными теоретическими исследованиями имеются
большие достижения в экспериментальном изучении законов пластического
деформирования.
По вопросам экспериментального изучения ползучести и
релаксации жаропрочных сплавов следует отметить работы
И. А. Одинга [78].
Большое количество исследований по физике твердого тела,
выводы из которых ждут своего приложения в теории пластичности,
принадлежит В. Д. Кузнецову (Томск) и его школе, акад. А. Ф. Иоффе
и его многочисленным ученикам.
Создан ряд новых оригинальных испытательных машин
(пневматический копер А. А. Ильюшина, машина для исследования сложного
нагружения С. В. Малашенко и др.).
Большую часть указанных выше и другие интересные задачи
читатель может найти в ранее указанной книге А. А. Ильюшина
«Пластичность» и в новом издании книги В. В. Соколовского
«Теория пластичности» (М.—Л., 1950). Упомянутые книги являются
большим вкладом в теорию пластичности.
Выше (§ 12), характеризуя основные этапы развития теории
упругости и смену одной фундаментальной гипотезы —
гипотезы отдельных материальных точек — другой, а
именно, гипотезой о сплошности, было упомянуто о том,
что и эта последняя гипотеза время от времени также подвергалась
критике *).
В 1950 г. при Академии наук СССР под председательством
акад. А. А. Благонравова было проведено дискуссионное Всесоюзное
совещание по вопросу о путях дальнейшего развития теории
пластичности. Поводом для дискуссии явилась статья А. А. Ильюшина
«Некоторые основные задачи теории пластичности» (Известия АН
СССР, Отделение технических наук, № 12, 1949).
В указанной статье с позиций механиков были сформулированы
ближайшие задачи развития теории пластичности. Большое внимание на
дискуссии было уделено критике основных положений современной
теории пластичности и особенно тому месту и значению, которые
*) Более того, спор об этих гипотезах вообще уходит в глубь веков и
связан с философскими проблемами мироздания вообще. В этом споре
участвовали и убежденные сторонники гипотезы непрерывности материи
(Анаксагор, Аристотель), и талантливые провозвестники современной
атомистической теории (Демокрит, Эпикур).
Поэтическое изложение этого спора древних философов Греции и
наивные, по теперешнему состоянию вопроса, мотивы, которыми каждый из
сторонников оправдывал свои воззрения, читатель может найти в известной
книге Тита Лукреция Кара (95—55 до Р. X.) «О природе вещей». Русский
перевод — в из ании АН СССР под общей редакцией академика С. И.
Вавилова, 1945.

§ 115] СОСТОЯНИЕ ТЕОРИИ ПЛАСТИЧНОСТИ В СССР 351
должны занимать в ней гипотезы о сплошном, непрерывном строении
материи (см. [77]).
Некоторые участники дискуссии считали, что если эта гипотеза
практически и приемлема в теории упругости, то того же нельзя
сказать применительно к теории, которая должна описывать процесс
пластической деформации материалов и металлов — в частности. Они
полагали, что на ход развития пластических деформаций металлов
должны оказать существенное влияние особенности микроструктуры
того или иного сплава.
Указывалось, что гипотеза о сплошности, как игнорирующая
роль природы металла и его структуры в вопросах прочности и
пластичности, несовместима якобы с материалистическим пониманием
процесса деформации твердых тел.
Конечно, гипотеза о сплошности является наиболее уязвимой
предпосылкой в современной механике твердого деформируемого тела.
Однако не безупречными явились бы и различные попытки (если бы
они были) построения дискретной теории пластичности, коль скоро
они будут использовать обычные представления классической
механики. Впрочем, на данном этапе состояния физической науки
последнее (использование образов и методов современной механики) пока
неизбежно. «Мы твердо уверены в ошибочности мнения механистов *),
но так же, как и они, все же вынуждены пользоваться при изучении
мира атомов всем арсеналом классической физики, т. е. понятием
о частице — теле, скорости, силе и т. д. Делать это приходится
потому, что у нас нет еще понятий, адэкватных новому миру явлений
и вместе с тем привычных для нас» (С. И. Вавилов [12]).
Сторонники удержать исходные предпосылки современной
механики сплошной среды, наоборот, отмечали большую значимость и
положительные результаты, достигнутые при использовании этих
предпосылок в различных юбластях техники (аэро- и гидромеханика).
Указанные споры по существу натолкнулись на противоречивую
сущность предметов природы.
«В собственном смысле диалектика есть изучение противоречия
в самой сущности предметов» (В. И. Ленин, Философские
тетради, 1947, стр. 237).
Попутно заметим, что критики по адресу советской школы
теории пластичности со своей стороны не предлагали взамен современной
теории пластичности каких-либо новых теорий для установления
новых категорий, понятий, совместимых с представлением о дискретной
теории пластичности, о «квантовости» пластической деформации.
По конкретному вопросу о степени точности законов
современной теории пластичности было констатировано, что в условиях
простого нагружения многочисленные эксперименты именно хорошо под-
*) Имеется в виду намерение механистов с привычными образами обы
денных явлений и выводами проникнуть в мир.атомов.

352 ПРОСТЕЙШИЕ ЗАДАЧИ ТЕОРИИ ПЛАСТИЧНОСТИ [ГЛ. IX
тверждают указанные законы для обширного класса материалов.
Имевшиеся по этому вопросу сомнения, базировавшиеся на
некоторых опубликованных в печати экспериментальных данных, оказывались
часто результатом недоразумения (несоблюдение при опытах условий
«простого нагружения» и т. п.).
Итак, в ходе свободной дискуссии совещание, отмечая
существование большого разрыва в понимании проблемы прочности между
физиками и механиками, в итоге констатировало, что советская
школа теории пластичности находится на правильном пути и, в
частности, отказ на данном этапе науки от гипотезы сплошности не был
бы оправданным и оказался бы неподготовленным. Иначе говоря,
такой отказ на данном этапе состояния вопроса не был бы для науки
прогрессирующим началом.
Решение совещания отнюдь не следует рассматривать в том
смысле, что признаются нецелесообразными всякие попытки
построения теории пластичности, освобожденной полностью или частично от
гипотезы сплошности.
Ни в какой другой стране не созданы, как в СССР, большие
предпосылки для глубоких научных изысканий. Эта возможность
определяется наличием правильных диалектико-материалистических
позиций, занимаемых советскими учеными. С этих позиций возможно
наметить правильный путь разрешения возникающих в науке
противоречий; более того, рядом работ советских ученых уже были
сделаны попытки построения некоторых механических теорий, в которых
идея о сплошности отнюдь не абсолютируется. Достаточно указать
на общеизвестные работы по механике трехкомпонентных сред
Н. М. Герсеванова (по механике грунтовой массы), по теории
движения природных жидкостей, в слегка пористой и деформируемой
среде, начало которой (теории) было положено Л. С. Лейбензоном,
и на ряд других исследований.
В последнее время Н. А. Слезкин [95] рассмотрел некоторые
задачи газодинамики и теории пластичности, в которых гипотеза
сплошности не абсолютируется, представление об элементарном
объеме частицы расширено (элементарная частица представлена из
двух компонентов, обладающих существенно различными качествами).
Н. К. Снитко в ряде известных работ [97] путем синтеза условий
текучести отдельных монокристаллов, применяя статистический метод,
нашел предел текучести поликристалла для любого сложного
напряженного состояния как среднее арифметическое из частных пределов
текучести. На основе учета кристаллической структуры Н. К. Снитко
получает аналитическую зависимость между напряжением и
деформацией в пластической области и, далее, величины начальных
напряжений микроструктуры.
Были проведены опыты по установлению некоторых
статистических закономерностей в поликристаллических металлах в зависимости
от степени пластической деформации [14]. Эти опыты, в частности,

§ 115] СОСТОЯНИЕ ТЕОРИИ ПЛАСТИЧНОСТИ В СССР 353
позволяют установить тот характерный линейный размер тела при
данной поликристаллической структуре (он оказался существенно
больше размера отдельного зерна) или величину площади сечения,
или элементарный объем тела, являющиеся в определенном смысле
граничными. Последнее надо понимать так, что если фактические
размеры заданного тела (или площадь сечения или объем изделия)
или конструктивные детали в этом теле (выточка, ослабление и т. п.)
существенно превышают эти характерные величины, то применение
положений механики континуума не должно вызывать сомнений и
в противоположном случае, наоборот, для описания процесса
деформации, для расчета на прочность использование выводов
современной теории упругости и пластичности должно быть признано
неправильным.
Уместно отметить ценные работы советских физиков (А. Ф. Иоффе,
Я. М. Френкель), рассмотревших пластическую деформацию как
прерывную в пространстве и во времени, обследовавшие
своеобразную «квантовость» пластической деформации монокристаллов.
Оригинальная попытка построения дискретной теории упругости,
исходя из кристаллической решетки, дана в работе В. В.
Синельникова [93]. Им, в частности, дается способ аналитического построения
диаграммы растяжения, т. е. функции а=/(е), если известны
система кристаллографической решетки и данные, к ней относящиеся.
Ценны и для механиков экспериментальные исследования
выдающихся металловедов, как то: А. А. Бочвара — по изучению природы
и ползучести жаропрочных сплавов, С. И. Губкина — по
исследованию течения металла, С. Т. Кишкина — по исследованию
диффузионных процессов, протекающих в напряженной высокопрочной стали,
и других советских ученых; помимо того большого значения,
которое эти исследования сыграли в решении важных металловедческих
задач (проектирование новых сплавов и т. п.), они дают также
богатый отправной материал для построения уточненной теории
пластичности. Эта последняя, если и будет по внешней форме (что удобно
для инженерной практики) носить макроскопический характер, то
косвенно может отразить особенности структуры металла, ориентацию
при наличии текстуры и т. д.
В этом смысле такую теорию пластичности можно именовать
механикой пластической дискретно-континуальной среды. Упоминание
о дискретности среды здесь надо понимать в том смысле, что такая
теория будет отражать наиболее важные стороны микроструктуры
(при описании, например, момента наступления пластического
состояния в окрестности данной точки). Одновременное же упоминание
о континуальной среде здесь понимается в том смысле, что всякая
техническая теория деформации при описании деформации в
конечном объеме будет, конечно, исходить из представления об
осредненных механических характеристиках материала, а уравнениям,
написанным для малого объема (например, уравнениям равновесия
23 Зак. 3880. Н. И. Безухов

354 ПРОСТЕЙШИЕ ЗАДАЧИ ТЕОРИИ ПЛАСТИЧНОСТИ [ГЛ. IX
применительно к элементарному объему, включающему ограниченное
количество зерен, и т. п.), преднамеренно будет подыскиваться
возможность толкования их в смысле дифференциальных уравнений
с правом их интегрирования в конечном объеме тела.
Указанные суждения находятся в соответствии со взглядами
современной физики, которая «рассматривает строение материи, как
диалектическое единство непрерывности среды и ее дискретности» . ..
«жесткие антитезы старой физики — прерывное и непрерывное, кор-
пусколы и волны ...предстали перед физиками в неоспоримом
единстве» (С. И. Вавилов в статье «Ленин и современная физика», из
книги «Современные проблемы науки и техники», из-во «Молодая
Гвардия», 1949 г.).
Можно не сомневаться, что механика пластической дискретно-
континуальной среды будет создана советскими учеными, и в
механике отдельных твердых сред гипотеза сплошности уступит место
(надо полагать — не без борьбы различных мнений) другим, более
глубоким гипотезам, но произойдет это тогда, когда полностью будет
подготовлена почва для такой замены.
«Общепризнано, что никакая наука не может развиваться и
преуспевать без борьбы мнений, без свободы критики». (И. Сталин,
Марксизм и вопросы языкознания. Издательство «Правда», 1950 г.,
стр. 26).

ГЛАВА X
ОСНОВНЫЕ РЕЗУЛЬТАТЫ РЕШЕНИЯ НЕКОТОРЫХ ЗАДАЧ
ПРИКЛАДНОЙ ТЕОРИИ ПЛАСТИЧНОСТИ
§ 116. Общие замечания по главе. Несущая способность сечения.
Несущая способность системы
В настоящей главе, ограничиваясь лишь изложением основных
идей, сообщаем без подробного вывода результаты решения
некоторых характерных задач теории пластичности, имеющих
практическое значение при определении так называемой несущей способности
системы, иначе говоря, для расчета предельной (разрушающей)
нагрузки для данного сооружения.
Исключительные трудности точного вычисления предельной
нагрузки вынуждают на данном этапе состояния теории исходить из
допущения, что материал конструкции обладает сильно выраженными
свойствами пластичности, что позволяет условно его считать
идеально пластическим. Экспериментальные исследования, выполненные
в СССР целым рядом научно-исследовательских институтов, показали,
что для металлических конструкций имеем достаточно хорошее
совпадение действительной разрушающей нагрузки с теоретической,
вычисленной из указанного выше допущения об идеально пластическом
материале.
Для дальнейшего условимся в следующих Определениях.
Пределом упругого сопротивления сечения назовем то значение
характеристики нагрузки (или величину самой нагрузки), при которой
в рассматриваемом сечении наступает предельное упругое состояние.
Предельное упругое состояние понимается в том смысле, что в одной
более напряженной точке сечения (или в нескольких точках
одновременно) напряжение (приведенное, отвечающее принятой теории
прочности, например, обобщенное напряжение) достигло предела упругости
материала, из которого выполнено рассматриваемое сечение.
Характеристикой или, иначе, параметром нагрузки может
быть выбрана при чистом изгибе балок величина изгибающего
момента, для закручиваемых стержней — крутящий момент, для ствола
орудия — давление газов в канале и т. д. и т. п.
23*

356 ОСНОВНЫЕ РЕЗУЛЬТАТЫ РЕШЕНИЯ НЕКОТОРЫХ ЗАДАЧ [ГЛ. X
В случае нагружения системы группой различных сил, однако
связанных между собой какой-либо постоянной зависимостью
(находящихся между собой всегда, на любом этапе нагружения системы,
в определенном отношении), за параметр нагрузки может быть
принято значение любой из сил, выбираемой как бы за эталон для
сравнения с ней других сил. Параметром нагрузки при специальном
оговаривании могут считаться и другие величины, связанные с
нагрузкой и зависящие от нее. Так, при поперечном изгибе балки, характер
нагружений которой однообразен, за предел упругого сопротивления
рассматриваемого поперечного се
Область пластических
деформаций
\
А
,
lirf-
2
^ МУПР
i
*" 6 "*"
..._
1
2
Фиг. 148. Распределение пластических
и упругих зон в двухопорной балке
в момент исчерпания ее несущей
способности.
чения может быть принята
величина изгибающего момента в этом
сечении, при котором хотя бы в
одной точке сечения (или в
нескольких, но одновременно)
приведенное напряжение достигло предела
упругости материала балки.
При изгибе вала с кручением
его за предел упругого
сопротивления сечения можно принять
изгибающий момент или крутящий
момент в отдельности, если они между
собой находятся всегда в
определенном отношении; в противном
случае за предел упругого
сопротивления следует принять величину результирующего момента (т. е.
приведенного момента в свете принятой теории прочности).
Пределом пластического сопротивления сечения назовем то
значение параметра нагрузки, при котором наступает исчерпание
несущей способности сечения, т. е. пластические деформации^
захватывают всю область рассматриваемого сечения, и притом обобщенное
напряжение в любой точке его достигает предела текучести
материала. Так как в идеально пластическом теле значение предела
текучести есть предельная величина обобщенного напряжения, то
упомянутому выше исчерпанию несущей способности сечения отвечает тот
факт, что все точки рассматриваемого сечения оказываются в
состоянии иметь (а при соблюдении определенных условий и будут иметь)
возможность неограниченного роста деформаций.
При простейшей, однородной деформации бруса постоянного
сечения, как то: при чистом изгибе, чистом кручении и т. п.,
исчерпание несущей способности одного сечения означает одновременно такое
же исчерпание и всех остальных, т. е. исчерпание несущей
способности всего бруса (так как внутренние усилия сечения, т. е.
изгибающий или крутящий момент, во всех сечениях одинаковы). При
поперечном изгибе (фиг. 148) статически определимого бруса,
когда изгибающие моменты в сечениях не одинаковы, исчерпание

§ 116]
ОБЩИЕ ЗАМЕЧАНИЯ ПО ГЛАВЕ
357
несущей способности одним лишь сечением (на фиг. 148 это
будет сечение под грузом) уже означает потерю несущей способности
балки в целом.
В самом деле, наличие в двухопорной балке одного сечения в
пролете, способного к неограниченному росту деформаций, означает
превращение балки в геометрически изменяемую систему. Среднее
сечение балки, показанной на фиг. 148, как бы уподобляется
некоторому; шарниру, позволяющему сходящиеся в нем левую и правую
части балки свободно взаимно поворачиваться друг относительно
друга. Появление в балке такого «шарнира» равносильно
приобретению балкой одной степени свободы (или, что все равно, потере
одной внутренней связи). Подобный кинематический образ
оказывается весьма удобным- при расчетах сооружений по предельным
нагрузкам.
Принято называть такой воображаемый шарнир шарниром
текучести (или пластическим шарниром). Однако шарнир текучести
имеет существенные отличия от обыкновенного шарнира. Во-первых,
изгибающий момент в сечении, проходящем через шарнир текучести,
не равен нулю, а равен пределу пластического сопротивления изгибу
сечения. Во-вторых, шарнир текучести является односторонним
шарниром, так как он исчезает при перемене направления действующих
сил или при разгрузке.
Для статически неопределимых балок и рам образование в одном
сечении «шарнира» текучести не означает потери несущей
способности системы в целом, так как потеря одной связи не
превращает обычно такую систему в геометрически изменяемую
кинематическую цепь.
Так, система, п раз статически неопределимая, превращается при
образовании шарнира в систему п—1 раз статически
неопределимую. Поэтому в статически неопределимых системах следует
отличать предел пластического сопротивления сечения от предела
пластического сопротивления системы в целом.
Как показал И. Я. Штаерман*), расчет в этом случае имеет
тесную связь с замечательной теорией П. Л. Чебышева о функциях,
наименее уклоняющихся от нуля.
Пределом пластического сопротивления статически
неопределимой системы будем называть то значение параметра нагрузки,
при котором рассматриваемая система превращается в
геометрически изменяемую систему с одной кинематической степенью
свободы.
Превращение сооружения в механизм возможно и частичное, в
какой-либо одной области или части, тогда как другие части могут
продолжать оставаться в условиях геометрически неизменяемых систем.
*) См. «Современные методы аппроксимации функций», Известия
отделения технических наук АН СССР, 1939.

358 ОСНОВНЫЕ РЕЗУЛЬТАТЫ РЕШЕНИЯ НЕКОТОРЫХ ЗАДАЧ | ГЛ. X
Примером может служить многопролетная неразрезная балка (фиг. 149),
несущую способность которой следует, конечно, считать
исчерпанной, если в каком-либо одном (обычно в самом большом или
загруженном более других) пролете образуется три пластических шарнира
(например, один шарнир
в средней части, в том
сечении, где изгибающий
момент оказывается
наибольшим, т. е.
предельным, и два других
пластических шарнира — в
опорных сечениях, где
опорные моменты также
достигли предельных
значений для этих сечений).
Образование трех
пластических шарниров в одном
пролете исключает
эксплуатацию такого
пролета, тогда как другие
пролеты оказываются способными к дальнейшему нагружению.
Примеры вычисления несущей способности статически
неопределимой системы (плиты) имеются в §§ 120 и 128.
§ 117. Несущая способность круглого цилиндрического стержня,
подверженного растяжению и кручгнию *)
Считая стержень достаточно длинным, полагая, что напряженное
состояние одинаково для всех сечений стержня (фиг. 150) и
учитывая условие симметрии нагрузки, мы должны принять для
продольных деформаций закон плоских сечений; более того, следует считать,
что деформации (осевые удлинения) должны быть одинаковы во всех
точках стержня. В противном случае искривления сечений после
деформации, будучи неодинаковыми для различных точек стержня,
накапливаясь по длине стержня, привели бы к слишком большим
искривлениям торцевых плоскостей, чего в действительности не наблюдается.
Итак, принимаем ег = const.
При малых деформациях естественно предположить, что контур
поперечного сечения в своей плоскости не деформируется, а
поворачивается как жесткий диск, что равносильно наложению условий,
°х = Gtj = *ху = °-
*) Подробное освещение этого вопроса имеется в книге проф. А. Р. Ржа-
ницына (см. [89]).
Фиг. 149. Случай исчерпания несущей
способности многопролетной неразрезной балки
вследствие образования лишь трех
пластических шарниров в одном пролете; прочие
пролеты могут при этом не быть в
предельном равновесии.

§ 117] НЕСУЩАЯ СПОСОБНОСТЬ КРУГЛОГО ЦИЛИНДРИЧЕСКОГО СТЕРЖНЯ 359
Выпишем все уравнения теории пластичности применительно к
данной задаче и примем во внимание, что материал стержня идеально
а) ^"""4^^
4-;
о
шМ
Эпюра
г
ш
и
z
Ufl 4L—AL4L.
Фиг. 150. Одновременное кручение и растяжение.
Распределение пластических напряжений по
диаметру (а). Область предельных значений М и М (б).
пластичен. Из трех дифференциальных уравнений равновесия остается
только одно (остальные обращаются в тождество):
di~
дт
уг
до~
дх ' ду * dz
Из физических уравнений остаются:
1
= 0.
3G'°zi
О'Ча
*хг ^ \хг> хуг ^ Т#г*
Условием пластичности будет:
00
(б)
(в)
(О
где &0 = 3 в случае справедливости условий текучести по
уравнению (8.20) и 60 = 4 в случае применимости уравнения (8.16).
Геометрические соотношения для сдвигов в данной задаче, ввиду
отсутствия депланации поперечного сечения (искривление из
плоскости), запишутся, как и в случае чистого кручения:
Та* = *У; Чу* = ах>
(Д)
где а — относительный угол закручивания сечения. Присоединим сюда
уже принятое условие:
ег = const, (e)
Используя (д) и (в), имеем:
,= G'zyy т =G'ax
(ж)

360 ОСНОВНЫЕ РЕЗУЛЬТАТЫ РЕШЕНИЯ НЕКОТОРЫХ ЗАДАЧ
Из (б) и (ж) следует:
откуда
г 4-х2 ~(-)*^г*
где г — расстояние от центра круга до рассматриваемой точки.
Введем обозначение:
= <!\
тогда из (и) имеем:
2 | 2 19
*х* + 1уг = Г
[гл. х
(з)
(и)
(к)
(л)
Подставляя (л) в (г), получаем:
(i + V
•2 =nf.
откуда
j/~l+|f2/-2
(10.01)
Из (3) следует:
W
wys •
31/ 1+^ф2г2
атфлг
" XZ • W2
а:г ' уг
»jA + ^
(10.02)
(10.03)
График изменения напряжений <зг и напряжений т, направленных
перпендикулярно к радиусам сечения, в зависимости от радиуса г,
показан на фиг. 150, а.
Дифференциальное уравнение равновесия (а), очевидно,
удовлетворяется. Контурные условия также, очевидно, выполняются, так как
касательные напряжения у контура имеют направление вдоль линии
контура.

§ 117] НЕСУЩАЯ СПОСОБНОСТЬ КРУГЛОГО ЦИЛИНДРИЧЕСКОГО СТЕРЖНЯ 361
По напряжениям вг и х вычислим предельные значения
нормальной силы и крутящего момента. Интегрируя по сечению, имеем:
М= j ozdF = j* oe2icr dr%
F 0
R
M = f xr dF = [ т2тгг2 dr.
(м)
J* 0
По подстановке в (м) выражений (10.01) и (10.03) имеем:
Из (10.04) следует:
*-*Уъ N • (10-06>
Подставляя (10.06) в (10.05), после преобразований получаем
уравнение, связывающее продольную силу и крутящий момент в
предельном состоянии:
№ + ^&- + ^Г = ^, (10.07)*)
где обозначено
3*и 9*V* ko
{Wf — пластический момент сопротивления при чистом кручении
круглого стержня).
Область предельных значений М и N очерчивается на основании
(10.07) кривой третьего порядка, изображенной на фиг. 150, б
(наружная кривая).
Область предельных значений для упругой стадии работы сечения
найдется путем подстановки в условие пластичности (при
отождествлении предела текучести материала с пределом упругости — это
будет одновременно условием предельного упругого состояния)
i+V2 = ^
*) Если вначале прикладывается продольная сила, а затем добавляется
крутящий момент, доводящий сечение до потери несущей способности, то
взамен (10.07) получаем:
4 №R* Glwl

362
ОСНОВНЫЕ РЕЗУЛЬТАТЫ РЕШЕНИЯ НЕКОТОРЫХ ЗАДАЧ
[ГЛ. X
краевых напряжений, вычисляемых по формулам теории упругости, т. е.
В результате подстановки получаем уравнение эллипса (на фиг. 150, б
внутренняя кривая):
__№_ , 4М^ (1008)
\*7~- — 2 ** ^ *" "^—*- Г *" - "у "il
§ 118. Несущая способность сечения в виде узкого прямоугольника
а) Кручение с растяжением. Рассуждениями, аналогичными
изложенным в предыдущем параграфе, можно просто получить решение
для тонкой пластинки,
для которой, пренебрегая
участками закругления
линий касательных
напряжений вблизи кромок
пластинки, можно считать,
что касательные
напряжения в сечении везде
параллельны длинным
сторонам сечения (фиг. 151).
Связь между крутящим моментом и продольной силой для
предельного состояния имеет вид (см. [89]):
ШИШ»'
Фиг. 151. Направления потока касательных
напряжений при кручении прямоугольного
сечения.
1 Л„6
"J-^/i+3**;
(10.09)
k0
величина ^ определяется при заданном N из трансцендентного
уравнения:
6 т 6ba.
Yk^N
(10.10)
где h—толщина; b—ширина пластинки.
б) Изгиб и кручение пластинки.
В этом случае эпюры нормальных и
касательных напряжений по толщине
пластинки образуют два
прямоугольника (фиг. 152), причем величины
нормальных и касательных напряжений
связаны условием текучести:
Фиг. 152. Распределение
нормальных и касательных
напряжений по высоте узкой
пластинки при ее изгибе и
кручении.
Так как изгибающий момент Мк и крутящий момент Мк будут при
прямоугольных эпюрах соответственно равны:

§ 119] ПЛАСТИЧЕСКОЕ СОСТОЯНИЕ ПРИ НЕСТЕСНЕННОМ КРУЧЕНИИ 363
то, подставляя эти выражения в условия текучести, имеем
зависимость между Ми и М& в предельном состоянии:
16Ми + Ak0M2K = &2h\ (ЮЛ 1)
в) Изгиб с растяжением и сдвигом. Для случая, когда в
поперечном прямоугольном сечении имеются одновременно изгибающий
момент Му продольная N и поперечная сила Q, может быть
предложено сравнительно простое решение *), устанавливающее связь между
перечисленными выше компонентами внутренних усилий в предельном
состоянии; оно имеет вид
, 1 л/2 , Q О2
где
Решение (10.12) является приближенным, так как исходит из
предположения, что предельное состояние текучести достигается лишь
в крайних зонах и только в одной точке в средней части на
нейтральной оси.
Уточнение (10.12), но в условиях «простого нагружения», дано
А. Р. Ржаницыным |89], где показано, что действительная область
предельного состояния несколько шире, чем это следует из (10.12),
и особенно при больших значениях Q. Расчетные формулы,
естественно, оказались очень сложными. Им же в этом труде дано
графическое изображение действительной области предельного состояния
и условной, определяемой из (10.12).
§ 119. Пластическое состояние при нестесненном кручении
некруглых сечений
Обозначая ось призматического стержня через г, при свободном
кручении (когда нет препятствий к депланации, т. е. к искривлению
поперечных сечений из плоскости сечений) будем иметь о2 = 0.
Аналогично по соображениям, изложенным в § 117, примем ox=Gy=zxy=0.
*) См. [3]. Задача решалась в предположении, что вначале на
сечение действует продольная сила и изгибающий момент, достигающий
такого значения, при котором сечение оказывается в упруго-пластическом
состоянии; средняя область сечения при этом находится еще в упругом
состоянии. Затем, не снимая указанных продольной силы и изгибающего
момента, начинаем на сечение оказывать действие поперечной силой, которая
ловлекает в пластическое состояние и среднюю область сечения.
В рассматриваемом случае нагружение сечения моментом, продольной
и поперечной силой, очевидно, не является простым (в смысле Ильюшина),
.1 представляет частный случай сложного нагружения.

364 ОСНОВНЫЕ РЕЗУЛЬТАТЫ РЕШЕНИЯ НЕКОТОРЫХ ЗАДАЧ [ГЛ, X
Из дифференциальных уравнений равновесия в этом случае
останется только третье:
fczx , дчгу , дог _^
переписываемое в виде
dx * ду * dz
= 0. (10.13)
uzzx , v^zy
дх ' ду
Условие пластичности в данном случае запишется так
Y2
i-Jr/6(i + ^)e.T
или в виде
где
^ + ^ = ^> (10-!4)
l/3
Совокупность уравнений (10.13) и (10.14) полностью решает
задачу. Аналогично функции напряжений в теории упругости (§ 36)
и здесь можно подобрать так называемую функцию пластических
напряжений F (л;, у).
Действительно, (10.13) удовлетворяется, если принять:
та* = -^-> V = —aj- (10Л5>
Функция напряжений на основании (10.14) и (10.15) должна
удовлетворять следующему уравнению:
Выражение, стоящее в левой части этого уравнения, представляет
собой квадрат величины наибольшего уклона поверхности F
(градиента F). Следовательно, во всех точках поперечного сечения,
в которых получается пластическая деформация, должно иметь места
следующее равенство:
(grad) F = тт = const. (10.17)
На основании этого свойства, а также и того очевидного условия,
что касательное напряжение т у наружного контура сечения
направлено по касательной к этому контуру, функция пластических
напряжений для данного поперечного сечения определяется вполне.
Указанные свойства функции F показывают, что поверхность
пластических напряжений представляет собой поверхность с по-
стоянным углом ската (поверхность естественного откоса), которую
можно построить на контуре поперечного сечения. Если вырезай*

§ 119] ПЛАСТИЧЕСКОЕ СОСТОЯНИЕ ПРИ НЕСТЕСНЕННОМ КРУЧЕНИИ 365,
из куска жесткого картона шаблон поперечного сечения, положить
его горизонтально и посыпать песком, то получится куча,
естественные откосы которой и дадут представление о поверхности F.
Поверхность равного ската легко построить для любого контура
поперечного сечения. В частности, для круга это будет конус, а для
прямоугольника — поверхность в виде крыши (фиг. 153, а).
Опыты по кручению железных стержней дают хорошее
подтверждение теории. Наблюдения показывают, что в поперечных сечениях
стержней получаются довольно правильные слои скольжения. Их
можно обнаружить методом травления, в котором слои скольжения
становятся темными полосами или линиями. Ряд травленых шлифов
стержней из мягкого железа, подвергнутых кручению, показан на
фиг. 153, tf (заимствовано из книги В. В. Соколовского [104]).
а) б)
Фиг. 153. а) поверхность равного ската для прямоугольного сечения; б) фото
травленых шлифов стержней из мягкого железа, подвергнутых кручению
(при травлении); слои скольжения становятся темными линиями или
полосами.
Предельный крутящий момент, определяющий несущую
способность сечения на чистое кручение, определяется удвоенным объемом
тела, ограниченного поверхностью равного ската. Так, для круглого
сечения (радиус сечения R)
ЛГ = |-1с/?*ст. (10.18)
Для эллиптического сечения с полуосями а и И, В.
Соколовский [104] нашел предельный момент:
Af = yica»(l—у<^+4аЗ)т„ (10.19)
Ъ\ , а — Ь а-\- Ь
где «=^5 *i=-2-, ах = ~Г'
Для квадрата
M=-£zr. (10.20)

366 ОСНОВНЫЕ РЕЗУЛЬТАТЫ РЕШЕНИЯ НЕКОТОРЫХ ЗАДАЧ [ГЛ. X
Для прямоугольника со сторонами а и b (b < a)
М = ^(3а — Ь)ъ. (10.21)
Для тонкой полосы (фиг. 154) условие (10.21) можно упрощенно
записать в виде
Af = yfl*V (10.22)
Теория упругости для предела упругого сопротивления при
кручении круглого сечения даёт:
ал —nR3
для эллиптического
для квадрата
для тонкой полосы
., *ab2 ^ .
Afynp = 0,208a3v,
м?щ = "з"аЬ<1^-
Таким образом, отношения предела пластического сопротивления
сечения при кручении к пределу
1 упругого сопротивления
составляют:
Фиг. 154. Сечение в виде узкого
прямоугольника.
для круга 1,33
для эллипса при Ь = -^а ... 1,4&
для тонкой полосы 1,50
для квадрата 1,60
В литературе [104] можно найти следующую интерпретацию упруго-
пластического кручения.
Если на контур поперечного сечения с построенной на нем поверхностью
равных скатов, перевернутой вниз (для наглядности), натянуть тонкую
пленку и нагружать ее равномерно распределенной нагрузкой,
пропорциональной относительному углу закручивания стержня, то при постепенном
деформировании такой пленки она начнет частично ложиться на поверх-
ность равного ската, местами не доходя до нее.
Свободные участки пленки будут соответствовать упругой зоне сечения*
а примыкающие к поверхности равного ската — пластической.
В пределе, при бесконечно большом значении относительного угла
кручения, пленка полностью должна заполнить поверхность равного ската со
всеми ее двухгранными и пространственными углами. Это и будет
соответствовать предельному состоянию сечения, которое, конечно, можно^лишь
представить теоретически; фактически разрушение должно произойти раньше
вследствие ограниченной деформации сдвига (отсутствие в природе идеально
пластического тела), но действительный предельный момент обычно мало>
отличается от определяемого из условия идеально пластического материала.

§ 1201 осесимметричный упруго-пластический изгиб 367
§ 120. Осесимметричный упруго-пластический изгиб
круговой пластинки. Задачи В. В, Соколовского.
Круговая пластинка, находящаяся под действием произвольной
нагрузки р, распределенной осесимметрично, была рассмотрена в ряде
работ В. В. Соколовского [104]. К некоторым из его результатов
довольно близко подходят приближенные решения, основанные на
слиянии методов теории
пластичности и
строительной механики, о чем
подробно рассказано в § 128,
а потому здесь сообщим
без вывода лишь формулы,
полученные В. В.
Соколовским, относящиеся к
несущей способности пла
стинки.
В случае равномерно-
распределенной нагрузки
на пластинку, свободно-
опертую по контуру _£_
(фиг. 155), пластичность
впервые возникает в
центрах граничных плоскостей
пластинки (при z = ±тг),
если
Разрез по 1—1
Пластическое
состояние
Упругое
состояние
Упруго-
пластическая
зона
Чисто упругая
зона
8x^2
Рупр ;
/3(3 +|i) ft*
7> (а)
Фиг. 155. Упруго пластическое состояние
круговой пластинки.
а с возрастанием нагрузки р упруго-пластическая зона заполняет
некоторый круг радиуса с\ кольцевая зона вне этого круга остается
в чисто упругом состоянии. При дальнейшем увеличении нагрузки р
чисто упругая кольцевая зона уменьшается, вырождается в
окружность г = £, а затем и вовсе пропадает, так что вся пластинка
переходит в упруго-пластическое состояние. Исследования показали,,
что одновременно с появлением чисто пластического состояния в центре
вся пластинка переходит в чисто пластическое состояние. В этом
состоит существенное отличие задачи об изгибе круговой пластинки
от задачи изгиба балки; образование чисто пластического состояния:
в одной точке балки (и даже в целом сечении) вовсе не влечет
появления чисто пластического состояния во всей балке.
Если исходить из условия пластичности Сен-Венана и записать
его в данном случае упрощенно в виде

368 ОСНОВНЫЕ РЕЗУЛЬТАТЫ РЕШЕНИЯ НЕКОТОРЫХ ЗАДАЧ [ГЛ. X
то чисто пластическое состояние пластинки наступает при
Рю = 4°т-£. (Ю.23)
Для приближения этих результатов к соответствующим
результатам, получаемым на основе условия постоянства интенсивности
касательных напряжений (обобщенного напряжения), следует в (10.23)
заменить предел текучести аг на
2+VT
2 Y3
Для свободно-опертой по контуру и находящейся под действием
нагрузки /? = const, равномерно распределенной по площади круга
радиуса d<b, предельная нагрузка (предел пластического
сопротивления пластинки) оказывается равной
3 о,Ь№
Для случая сосредоточенной силы в центре предельное ее
значение составляет:
Несущая способность кольцевых пластин (с вырезом) исследована
А. С. Григорьевым [30].
Для случая степенного условия пластичности с упрочнением
для круговой пластинки, свободно-опертой по контуру при нагрузке
р = const, равномерно распределенной по всей площади, В. В. Соколовский
нашел прогиб в центре
•b=W.».(2g?)Tf
где
в *®
В= 2 + г] '
причем Wo и а — коэффициенты, которые определяются численным
интегрированием надлежащих уравнений для каждого yj, но годятся для любых /?,
Ь и В. Так, для TQ = -o" имеем: а = 0,21, Wq = 0,094,
w0 =s 0,094^2 Л),21 Р-^\
или
Понятие о несущей способности, указанной в § 116, где имелся в виду
случай материала без упрочнения, очевидно, к данной задаче со степенным

§ 121] изгиб и кручение (стесненное) тонкостенных стержней 369
упрочнением неприменимо. Уместно в таком случае несущую способность
связывать с нагрузкой, при которой обобщенное напряжение достигает
предельного значения (предел прочности) или прогиб w0 достигает такого
значения, при котором исключается возможность дальнейшей
эксплуатации пластинки.
§ 121* Изгиб и кручение (стесненное) тонкостенных стержней
за пределом упругости
В § 108 была показана возможность замены исследования
упруго-пластических деформаций прямого стержня (поперечное сечение которого
предполагалось имеющим массивную форму) другой задачей, но с
эквивалентными окончательными результатами, а именно, замены задачей вычисления
упругих деформаций в стержне, имеющем особое так называемое
приведенное сечение, отличное от заданного (жесткость приведенного сечения меньше
жесткости заданного и тем меньше, чем пластические деформации захватили
большую территорию заданного сечения).
Аналогичная идея, хотя и значительно сложнее реализуемая, оказалась
возможной в задаче исследования изгибного кручения тонкостенных стержней
и цилиндрических оболочек.
Ниже излагаются основные результаты, полученные Р. А. Межлумяном [65]
в развитие работ В. 3. Власова и А. А. Уманского.
Материал оболочки предполагается обладающим упрочнением, т. е.
принимается связь между обобщенными напряжениями и деформацией в виде
а, = 30 [1-« (*)]•,; (а)
объемная деформация считается упругой, следовательно,
Помимо заданной функции со (ег-), определяемой по опытным данным
(для краткости письма в дальнейшем обозначается to), P. А. Межлумян
вводит в рассмотрение две вспомогательные функции:
м /еч ■ [2Н1+»0 + (1-2|*)(2-ю + М1<».
0)2 (Ч)- l + «i + 2(l+,0(l-»)' ()
o,3(ei) = <o2(e<)+^l)Ej, (Г)
В дальнейшем изложении эти вспомогательные функции обозначаются ю2
и <о3 и поэтому (г) будем записывать так:
Щ = °>2 + -^Г- е* (Д)
Далее предположим, что каким-либо образом, хотя бы приближенно, нам
известно местоположение пластических зон в сечении (фиг. 156). Для такого
приближенного метода можно принять обычное упругое решение задачи
и те области сечения, в которых обобщенное напряжение превышает предел
упругости, принять за пластические области.
Построим два следующих вспомогательных «приведенных» сечения.
Одно сечение (элементарную площадку его будем обозначать через dH")
будет определяться следующим соотношением с заданным сечением (для
которого элементарную площадку обозначаем просто dF):
dF" = dF (1 — to2) (e)
24 Зак. 3880. H. И. Безухов

370 ОСНОВНЫЕ РЕЗУЛЬТАТЫ РЕШЕНИЯ НЕКОТОРЫХ ЗАДАЧ [ГЛ X
или иначе
f"= Г(1— <»2)dF.
Другое приведенное сечение будет определяться соотношением
dF'" = dF(\ — cog) (ж)
или иначе
/™ = J* (1 — (о3) dF.
Наконец, примем для
дальнейшего две вспомогательные
системы отсчета. Одна,
названная автором главной
кинетической системой отсчета,
определяется, как и в упругой
теории тонкостенных стержней
В. 3. Власова, но исходя из
приведенного сечения F3. Иначе
говоря, главная кинетическая
система отсчета удовлетворяет
условиям
Фиг. 156. Упруго-пластическое состояние
тонкостенного стержня и две
вспомогательные системы отсчета.
*.«*;
... __ ... _
Jxy — °<о —
__ С'" _ С" .
= 0; (з)
знак «"'» означает, что указанные статические моменты площади,
центробежный момент инерции, секториальный статический момент и секториально-
линейные статические моменты относятся именно к приведенной площади Fm'.
Так как условие S^ = 0 по аналогии с теорией В. 3. Власова определит
положение нулевой точки на срединной линии контура сечения F,n', то эту
точку в данном случае можно назвать кинетической секториальной
нулевой точкой.
Так как условия SX(li = S'" = 0 определят в плоскости поперечного
сечения положение полюса для отсчета секториальных площадей, то эту точку
в отличие от обычного центра изгиба Р. А. Межлумян назвал кинетическим
центром. Таким образом, под главными кинетическими «центральными»
осями инерции, под кинетическим центром, под кинетической
секториальной нулевой точкой подразумеваются главные центральные оси инерции,
центр изгиба, секториальная нулевая точка приведенной фигуры F"r. У
тонкостенного стержня несимметричного профиля кинетический центр не
совпадает с центром изгиба и потому за пределом упругости стержень может
закручиваться, если внешняя поперечная нагрузка всюду пересекает ось
центров изгиба.
Вторая вспомогательная система, названная автором главной
приведенной системой, определяется из условия
Qff ^f jll
ъх — ъу — Jxy ''
. с" _ о" _ с" _ о
(И)
Знак «"» означает, что указанные моменты относятся именно к приведенной
площади F".

§ 121] ИЗГИБ И КРУЧЕНИЕ (СТЕСНЕННОЕ) ТОНКОСТЕННЫХ СТЕРЖНЕЙ 371
Введя указанные выше понятия о двух приведенных фигурах и двух
вспомогательных системах отсчета, автор получает формулы для напряжений,
сходные с общеупотребительными в теории изгибного кручения
тонкостенных стержней и внешне отличные от них только наличием множителя,
меньшего единицы. Так, для нормального напряжения получаем:
n m„ м„ в
[14 му тх в л
~^ + ~7Г х ~~ ~7^у + "Т7"03 •
F Jy Jx Jw J
Для касательного напряжения соответственно
1 \Qx с"'/о ч. Qv с'"/о ч хМ<* с'"/о чЛ
ъ \S) L Л, Jx Jш J
(10.25)
(10.25a)
где Sx (s, et-)» Sy (s> н) — кинетические статические моменты
рассматриваемой части поперечного сечения относительно главных кинетических осей,
•S'd (5» ц) — кинетический секториальный статический момент той же части
сечения относительно кинетического центра; В и М^ — бимомент и изгибно-
крутильный момент; о (s) — толщина стенки профиля в общем случае
переменна по длине S.
Для установления конечного соотношения между силами и моментами
с учетом упрочнения материала надлежит, очевидно, обобщенное
напряжение приравнять пределу прочности материала (^п<1). Это приводит к сле^
дующей зависимости:
• / N Мх Mv В V
ЬЦ8)
\®х о'", ч . ®У о'"/ ч , М<» о'"/ v-l 2
угг Sy (s, ъ) + -утг$>х (* Ч) + -77Г 5Ш (* в,) = <£,, (Ю.26)
где
Р*(*<) = «2 (*/)-«(**)+ 15
д/сч = (1+>*) + (1-21х)[1-со*(в<)]
Ki) 2(l+(x) + (l+2t,)[l-co*(s/)]t
а о* (ег-) — значение о (е4-) при ег-, соответствующем сг- = сП1Г То же
относится и к оз2.
Пользование (10.26), конечно, предполагает, что на контуре сечения
найдена наиболее напряженная точка, по сравнению с которой в других точках
сечений обобщенное напряжение меньше предела прочности. Таким
образом, вычисление разрушающей нагрузки должно выполняться методом
попыток.
Заметим также, что и оперирование формулами для компонентов
напряжений (10.25), (10.25а) также требует прибегнуть к методу попыток, так
как в основе этих формул лежат представления о приведенных площадях
F" и Fm, которые можно знать точно, располагая данными о точной
границе между упругой и пластической зонами в поперечном сечении.
Из уравнения (10.26) как частный вариант получается конечное
соотношение между силами и моментами для случая, когда материал не обладает
упрочнением. В таком случае надлежит положить а{ = ar = const, где ат —
предел текучести материала.
24*

372 ОСНОВНЫЕ РЕЗУЛЬТАТЫ РЕШЕНИЯ НЕКОТОРЫХ ЗАДАЧ [ГЛ. X
Для частных видов поперечных сечений, и особенно обладающих двумя
осями симметрии (в этом случае кинетический центр совпадает с обычным
центром изгиба, а последний с центром тяжести сечения), задача упрощается,
решение может быть дано в замкнутой форме, не придется прибегать к
методу последовательных приближений.
Для двутаврового профиля при стесненном кручении А. И. Стрельбицкая
108], исходя из эпюр нормальных и касательных напряжений в предельном
(В)
&
'А
+
(МШ,М)
+ \°
Ei^3=K
г
г
Фиг, 157. Эпюра нормальных и касательных напряжений
в предельном состоянии для двутаврового сечения.
состоянии, как это показано на фиг. 157, получила следующее соотношение
между бимоментом В, изгибно-крутящим моментом М^ и крутящим
моментом М:
М2
О)
5~=1. (К)
& (Af-Af,tCT) / В*
вГ *W V в\
где £т = ст&п-^— и ЛТШТ— предельный бимомент и предельный изгибно-кру-
тящий момент, вызывающие потерю несущей способности каждый в
отдельности, а
"..««"Т*»2* и
^.«=тАа«-
- предельные крутящие моменты полок
и стенки при свободном кручении.
При выводе (к) условие пластичности принималось в форме
! + 3*2 = °*
YT
Вопрос о кручении и изгибе замкнутых цилиндрических оболочек за
пределом упругости был решен В. С. Медведевым методом, аналогичным
предложенному Р. А. Межлумяном для тонкостенных стержней открытого
профиля и разобранному в настоящем параграфе.
По вопросу о влиянии на несущую способность стержня эффекта
стеснения при кручении имеются разные мнения. Так, С. Н. Кан и Я. Г. Па-
новко [47], подчеркивая существенную разницу в поведении систем с
открытым и закрытым профилями, указывают, что по мере приближения зам-

§ 122] ДАВЛЕНИЕ ПЛАСТИЧЕСКОЙ СРЕДЫ НА ЖЕСТКИЙ ШТАМП 373
кнутого сечения к состоянию предельного равновесия (исчерпание несущей
способности) нормальные напряжения прн стесненном кручении такого
замкнутого профиля (в противоположность случаю открытого профиля)
постепенно исчезают и поведение системы приближается к свободному
кручению.
В упомянутом выше исследовании В. С. Медведева, наоборот, показано,
что рост нормальных напряжений, возникающих при стесненном к.ручении
замкнутых оболочек, за пределом упругости не только не ослабевает, но и
усиливается; нормальные напряжения увеличиваются по мере увеличения
крутящего момента, и различие в кручении открытых и закрытых оболочек
за пределом упругости сглаживается.
§ 122. Давление пластической среды на жесткий штамп
При вдавливании жесткого штампа вначале происходит местное смятие
среды в упругом ее состоянии.
Сопротивление среды вдавливанию на этом этапе может быть
подсчитано с помощью формул, приведенных в §§ 65 и 66. При дальнейшем
вдавливании вблизи контактной поверхности возникает пластическая зона.
Подобного рода задачи решались Прандтлем, Соколовским и др.; ниже указаны
результаты исследований
Соколовского, опубликованные в журнале
«Прикладная математика и механика»,
т. IV, вып. 5—6, 1940.
Пластические смещения
предполагаются достаточно малыми, задача
рассматривается плоской, исходными
уравнениями являются (8.23), штамп
считается абсолютно твердым, так
что форма линии контакта штампа
и среды известна. Задается
уравнение кривой, ограничивающей штамп
(фиг. 158):
х = х{Ъ) — Ь; у=у{Ъ), (а)
а также уравнение кривой,
ограничивающей свободную поверхность
пластической среды:
х = х(Ь)у у=у(р)у (б) Фиг. 158. Давление пластической
причем кривые (а) и (б) симметричны сРеды на жесткий штамп,
относительно оси х.
Здесь через 6 и 6 обозначены углы между нормалями соответственно
к кривым (а) и (б) и осью х; через о — глубина вдавливания штампа; б и 6t
показывают значения 6 в точках ЛТ, М{} 0О — значение 6 в точке ЛТ2; р и
р — радиусы кривизны кривых (а) и (б). Кривая (а) — выпуклая, кривая
(б) может иметь точки перегиба. В точке Mt кривая (а) может иметь
перелом.
Задача решается для трех разных условий вдоль линии контакта:
znt = 0 (гладкий штамп);
xnt = const (постоянное трение)
и
^nt = a?i tg И-.

374 ОСНОВНЫЕ РЕЗУЛЬТАТЫ РЕШЕНИЯ НЕКОТОРЫХ ЗАДАЧ [ГЛ. X
Граница пластической среды рассматривается прямолинейной и
криволинейной. Для прямолинейной границы пластической среды и для гладкого
штампа (int = 0) В. В. Соколовским получено следующее выражение для
равнодействующей давления штампа, взятой на единицу длины вдоль оси z:
/>=-2[pr(60) + s(* + 2)] f pcosO
d0-
— 2? Г х (6) p cos 0 dti + 4тт Г 6 p cos 0 db. (10.27)
Если штамп круглый, то
х = — R (cos 0 — cos 0O); у = — R sin 6^
л: (0) = R (1 — cos 0); 5 = R (1 — cos 60); 6 = — R sin 60
и вместо (10.27) имеем:
p = _T#2 ^e0 —I-sin 20o) +4<cTtf (1-0O sin 0O — cos 60) +
+ 2tt# (ti+2) sin 60, (10.28)
где i — удельный вес среды (влияние членов, содержащих ?, незначительно).
Если пренебречь членами с т, то формула запишется так:
р = 4тт/?| 1 — 00 sin 60 — cos 0О + (~ + 1\ sin 601 . (10.29)
В целях ориентировочного представления о величинах, определяемых по
(10.29), приводим некоторые численные результаты; задаваясь величинами bjR,
имеем для p/iTR:
А = 0,01, 4 = « ^ = 0,2, ^=1,976;
А = о,1, 4 = 1'008: 1 = од ^ = 2-904:
1 = 0,4, ^ = 3,789.
Для углового штампа В. В. Соколовским [104] получено выражение
р = 2ъЬ(к + 2 — 2й0у (10.30)
Для прочих условий контакта (негладкий штамп, криволинейная граница
пластической среды) выражения для давлений, приведенные в указанной
работе, естественно, становятся значительно более сложными.
§ 123* Условия предельного равновесия сыпучей среды.
Задачи В. В. Соколовского
Сыпучей средой принято считать среду, состоящую из весьма
мелких твердых однородных частиц, между которыми имеет место
трение (внутреннее трение) и некоторое небольшое сцепление.
Величина внутреннего трения сыпучей среды измеряется углом
внутреннего трения р, а величина сцепления — коэффициентом сцеп-

§ 123] УСЛОВИЯ ПРЕДЕЛЬНОГО РАВНОВЕСИЯ СЫПУЧЕЙ СРЕДЫ 375
ления k, отнесенным к единице площади. В случае отсутствия
сцепления (k = 0) тело называется идеально сыпучим (сухой песок, бисер,
горох и т. п.).
Равновесие сыпучей среды возможно, если в каждой точке ее
будет соблюдаться неравенство
l*„|<ontgp+fe, (10.31)
т. е. если касательное напряжение (усилие), способствующее
соскальзыванию частиц по любой площадке (с нормалью /г), будет менее
суммы сил трения и сцепления по той же площадке.
Условие предельного равновесия запишется так:
KI = °»tgP + ft; (10.32)
соответствующие площадки, удовлетворяющие условию (10.32), носят
название площадок скольжения.
Условие (10.32) может быть наглядно представлено с помощью
круга Мора (фиг. 159), а именно, нормальное и касательное напря-
Фиг. 159. Круги напряжений для трехмерной задачи.
жёния, определяющие в общем случае точку N (внутри
криволинейного треугольника PQR, ограниченного тремя полукругами), таковы,
что указанная точка N лежит ниже прямой ОхА с уравнением
* + °п*гр- (а)
Условие (а) отвечает случаю касания прямой ОхА большого
круга (фиг. 160).
Из рассмотрения фиг. 160 вытекает, что
- | gt — стз
„ _ gi + стз
cosp;
gt-
-я— 2 2 'Sinp'
Таким образом (10.32) записывается так:
at — аз ffi Ч~ аз + fft — аз
fcosp =
2 cosp
sin2 p -
К

376 ОСНОВНЫЕ РЕЗУЛЬТАТЫ РЕШЕНИЯ НЕКОТОРЫХ ЗАДАЧ [ГЛ. X
или окончательно:
а1 — а3 1
2 cos p
ai + G3t?o — k
2 TsP —*• |
(10.33)
Для плоского напряженного состояния условие (10.33) может
быть несложно записано через компоненты напряжений, так как
ах + ау
-1— 2~"
°х + °у
8 2 У \ 9 У ~Г '«У
В результате условие (10.33) приводится к следующему:
i?m — °*/)2 + 4^ = (о. + °« + 2^ ctg p)2 Sin2 р
(10.34)
Для среды с идеальным сцеплением, т. е. при отсутствии
внутреннего трения (р = 0), условие (10.34) имеет простой вид:
К-^)2 + 4х^ = 4^,
что совпадает с условием пластичности по (8.18).
Если к условию (10.34) добавить два известных дифференциальных
уравнения равновесия, то получим все основные уравнения так
называемой статики сыпучей среды — той ветви механики, которая позво-
Фиг. 160. Изображение на круге напряжений
предельного равновесия сыпучей среды.
ляет решить широкий круг вопросов, связанных с предельным
равновесием земляных масс (давление земли на подпорные стенки,
распределение напряжений внутри земляного массива при заданных нагрузках
на поверхности, давление сыпучей массы на стенки бункеров и т. п.),
а равно и тех масс, которые по своим физическим свойствам, и
именно в момент предельного равновесия, близко соответствуют
сыпучим средам.

§ 123]
УСЛОВИЯ ПРЕДЕЛЬНОГО РАВНОВЕСИЯ СЫПУЧЕЙ СРЕДЫ
377
Итак, основными уравнениями механики сыпучей среды,
пребывающей в предельном равновесии, являются следующие:
до~
<Н
а у
дх
ду
= 0,
\
ьху
к
(°х — VS + *£jf= (a» + eif+2*ctgp)2sin2p, J
(10.35)
где f, р, /г — объемный вес, угол трения и удельное сцепление
сыпучей массы (ось у направлена по отвесу вверх).
Исходя из системы уравнений (10.35), В. В. Соколовский решает
широкий круг упомянутых выше вопросов в своей монографии
«Статика сыпучей среды» (Изд-во Академии наук СССР, 1942),
удостоенной Сталинской премии.
Приведем результаты некоторых задач, представляющих интерес
для строителя.
Для минимальной величины заглубления h (фиг. 161), при которой
сыпучая среда сохраняет предельное равновесие (не выпирается), если
gywfeH^wy
Фиг. 161. К задаче о необходимом
заглублении фундамента против
его выпирания.
Фиг. 162. К задаче о
давлении земли на
ограждающие стенки.
известно значение нормального напряжения вдоль основания р0 = р (х)%
имеем выражение
А = -
.gt , Яо 1 —ship ^tgP_^c /x _ 1 —sinpgTCtgp
Y ' Y 1 H- sin p y V 1 + sin p
'), (Ю.36)
что, между прочим, сильно расходится [в сторону преуменьшения
для (10.36)] с известной в инженерной практике формулой Паукера:
k = Pof-l~- sinP.V
Y \ 1 —|— sin p
(10.37)
которая по данным опыта обычно дает завышенные значения для
глубины заложения фундаментов.
Для вертикальной гладкой подпорной стенки (фиг. 162) при
наличии на поверхности временной нагрузки интенсивностью pQ имеем

378 ОСНОВНЫЕ РЕЗУЛЬТАТЫ РЕШЕНИЯ НЕКОТОРЫХ ЗАДАЧ [ГЛ. X
следующие поверхностные условия: при х = 0 н при любому имеем
znt = О (давление земли нормально к стенке), а при у = 0 для
любого х имеем ъу — —Ро»
Использование их при интегрировании (10.37) приводит к
известной формуле для давления земли:
, , ч 1 — sin о 2k cos р /1лоо\
9 = (_^ + ^о)__^_п_£. (Ю.38)
§ 124. Замечания к теории пластического течения
В § 97 было упомянуто, что для описания пространственного
деформирования твердых тел за пределом упругости в разное время предлагалось
много различных теорий (гипотез) пластичности, но наиболее «устойчивой»
оказалась именно теория малых упруго-пластических деформаций,
разработанная нашими современниками: А. А. Ильюшиным, Г. А. Смирновым-
Аляевым, В. В. Соколовским и др. В основу этой теории были положены
уравнения, связывающие напряжения и деформации.
Теории пластичности, в основу которых были положены уравнения,
связывающие напряжения и скорости деформации, составили так называемые
теории пластического течения. По смыслу своего названия эти теории,
конечно, рассматривают пластическую деформацию твердого тела как состояние
движения. В случае медленного и непродолжительного течения пластических
деформаций, когда можно пренебрегать так называемым вязким
сопротивлением материала, т. е. сопротивлением, зависящим от скоростей деформации,
уравнения теории малых упруго-пластических деформаций и теории
пластического течения оказываются, как показал А. А. Ильюшин, тождественными.
Отделение проблемы течения от проблемы малых упруго-пластических
деформаций является более или менее формальным, хотя и необходимым по
причине различия методов их исследования. Уравнения теории пластического
течения могут быть написаны аналогично уравнениям теории малых упруго-
пластических деформаций. Проследим указанную аналогию.
Если обозначить через и, z/, w — компоненты скорости частицы,
находящейся в момент времени t в точке (лг, у% z)y т. е.
то компоненты скорости самой деформации можно записать по формулам,
аналогичным (2.25), а именно, скорость относительных удлинений:
• _ *** _
dt
_dsy_
у dt
;_*.._
г dt -
d
dt
d
dt
d
dt
du du \
dx dx ' \
dv dv 1
ду dy ' 1
dw dw I
dz ~ dz ' j

§ 124]
ЗАМЕЧАНИЯ К ТЕОРИИ ПЛАСТИЧЕСКОГО ТЕЧЕНИЯ
37У
Скорость относительных сдвигов соответственно:
• * _ dv dw i
_ dw , ди
(б)
Ввиду указанной аналогии не представляет затруднений доказать и ряд
других зависимостей, аналогичных статической задаче теории упругости и
пластичности, но содержащих компоненты скоростей деформаций. Приводим их
без вывода. Средняя скорость пластической деформации
ср
= "о" (£а> + гу + вг) = -г (£1 + е2 + ез)
где е1$ е2» ез — главные скорости пластической деформации. Главные скорости
деформации сдвигов:
TI2 = е1 — 62» Т23 = е2 — е3» Т31 = е3 — е1-
Обобщенная скорость деформации (интенсивность скорости деформации)
Н = ^ >/" (i*- */ + ("•„ - ^8+(i.-«'e)9+ 4 (Т^ + Т& + &). (Ю.39)
Зависимость компонентов напряжений от компонентов скоростей
деформации аналогично (8.06):
воР=:ЯЙ(«л-«вр);
СР .
тг/г = ^ "2" *fy«'
(10.40)
где Ш — модуль — величина переменная, подлежащая определению. Этот
модуль аналогично (8.05) связывает обобщенное напряжение с обобщенной
скоростью деформации:
а< = 9Ле,. (10.41)
Предполагается далее, что из опыта известна зависимость
9Й =/(•",). (10.42)
Приведенные уравнения вместе с уравнениями динамического
равновесия (2.02) при соблюдении граничных и начальных условий (по силам,
смещениям и скоростям) позволяют решать задачи динамики в области пласти-

380 ОСНОВНЫЕ РЕЗУЛЬТАТЫ РЕШЕНИЯ НЕКОТОРЫХ ЗАДАЧ [ГЛ. X
ческих деформаций в случае отсутствия сил вязкого сопротивления (см. § 130);
в задачах статики эти уравнения тождественны уравнениям теории малых
упруго-пластических деформаций.
Приведем в заключение параллельное сопоставление (сводку) основных
законов теории упругих деформаций, теории упруго-пластических деформаций
и теории пластического течения (в редакции В. В. Соколовского).
1 №
п/п.
1
2
3
4
В теории упругости
Направления главных
нормальных
напряжений и направления
главных удлинений
совпадают
Объемная деформация
пропорциональна
среднему нормальному
напряжению
Главные касательные
напряжения
пропорциональны главным
сдвигам
Интенсивность
касательных напряжений
пропорциональна
интенсивности сдвига
В теории
пластических деформаций
То же (как и в
теории упругости)
То же (как и в
теории упругости)
То же (как и в
теории упругости)
Интенсивность
касательных
напряжений постоянна
(идеально пластическое
тело) или есть
вполне определенная для
каждого материала
функция
интенсивности деформации
сдвига
В теории пластического
течения
Направления главных
нормальных
напряжений и направление
главных скоростей
удлинений совпадают
Материал в
пластическом состоянии
несжимаем
Главные касательные
напряжения
пропорциональны главным
скоростям сдвигов
Интенсивность
касательных напряжений
постоянна (идеально
пластическое тело) или
есть вполне
определенная для каждого
материала функция
интенсивности скоростей
деформации сдвига
При пластическом деформировании, происходящем с большими
скоростями, способность материала сопротивляться внешним воздействиям, как
показывает опыт, возрастает. На основании результатов исследований
предлагались различные эмпирические формулы (логарифмические, линейные
зависимости и т. д.) для повышенных пределов текучести, прочности и т. д.
Законченное построение системы уравнений, описывающих
вязко-пластическую деформацию для плоской задачи, было выполнено А. А. Ильюшиным.
К двум обычным гипотезам теории пластического течения о том, что:
а) направление максимальной скорости скольжения совпадает в
каждой точке с направлением максимального касательного напряжения и
б) материал в пластической деформации несжимаем,
А. А. Ильюшин в отличие от предположения постоянства наибольшего
касательного напряжения (идеально пластическое тело по Сен-Венану) принимает
гипотезу
*max = * + PW. (Ю.43)
т. е.
в) максимальное касательное напряжение ттах при течении тела
всегда больше некоторой постоянной k и является линейной функцией
максимальной скорости скольжения 7тах-

§ 125] К ИСТОРИИ ЗАРОЖДЕНИЯ ДИНАМИЧЕСКОЙ ТЕОРИИ ПЛАСТИЧНОСТИ 381
В компонентах напряжений и скоростей деформации третья гипотеза для
случая плоской деформации аналитически записывается так:
yV('* ~°yf + Ky = к + ?У('а,~ *у? + Л-ху ■ <1а44>
Из приближенных методов решения задач теории пластического течения
отмстим разработанный в последнее время А. А. Ильюшиным и П. М. Оги-
баловым «Метод вязких решений», в котором в первом приближении
принимается решение гидродинамической задачи со сходственными граничными
условиями.
§ 125. К истории зарождения динамической теории пластичности
Из-за трудностей математического анализа и ввиду сложности
экспериментирования при быстро протекающих процессах пластического
деформирования динамическая теория пластичности до самого последнего времени
оставалась не раскрытой. Первый толчок, вызванный необходимостью решать
ряд важных задач, исходит из советской машиностроительной практики, и
первые полученные результаты принадлежат советской науке.
X. А. Рахматулиным [88, 89] впервые был рассмотрен ряд важных
динамических задач из теории малых упруго-пластических деформаций. Ему
принадлежат фундаментальные результаты о распространении в стержне
пластических волн разных скоростей и о существовании особого типа волн — волн
разгрузки.
Задачи подобного рода весьма осложняются тем обстоятельством, что
после прохождения пластических волн материал упрочняется, и следовательно,
при прохождении повторных волн они распространяются в теле с переменным
пределом упругости в разных его точках. За указанные исследования
X. А. Рахматулин был удостоен в 1949 г. Сталинской премии.
Ряд задач по распространению пластических волн рассмотрели: Г. С.
Шапиро [44], В. С. Ленский [58], Ф. А. Бахшиян [2] (продольные колебания
стержней, упруго-пластическая сферическая волна нагружения), В. В.
Соколовский [105] (распространение прерывных волн сдвига и цилиндрических,
вызванных граничными возмущениями).
Уравнения вязко-пластического течения несжимаемого вещества для
случая плоской деформации были предложены в 1940 г. А. А. Ильюшиным.
Задачи об устойчивости вязко-пластических течений круглого прута и
круглой плиты были решены в 1943 г. А. Ю. Ишлинским [44]. Учет инер-
дионных членов при вязко-пластическом течении произвел П. М. Огибалов [75],
рассмотревший удар по балке малой длины. Удар по круглой плите и
крутящий удар по границе круглого отверстия бесконечной среды рассмотрел
в 1948 г. Ф. А. Бахшиян.
Деформации не вполне упругих тел с учетом свойств упругого
последействия, ползучести, релаксации и гистерезиса изучены в ряде работ:
Д. Ю. Панова, А. П. Бронского, В. Г. Гоголадзе [25], Ю. Н. Работнова [87],
А. Ю. Ишлинского, Н. М. Беляева [7], Н. Н. Малинина, Л. М. Качанова [49],
Н. X. Арутюняна [1] и других в период 1938—1948 гг.
Значение упомянутых выше исследований по динамической теории
пластичности и примыкающей в известном смысле к ней теории пластического
течения, принадлежащих X. А. Рахматулину, А. А. Ильюшину, В. В.
Соколовскому, А. Ю. Ишлинскому и их ученикам, исключительно большое. Теперь
на очередь дня можно ставить не решенные и труднейшие проблемы упругих
и упруго-пластических колебаний слоистых сред, теорию удара с учетом
неизбежных при этом пластических волн и волн разгрузки и т. п.

ГЛАВА XI
СБЛИЖЕНИЕ ТЕОРИИ УПРУГОСТИ,
СТРОИТЕЛЬНОЙ МЕХАНИКИ, ТЕОРИИ ПЛАСТИЧНОСТИ
И РЕОЛОГИИ
§ 126. Общие соображения
Во введении (§ 1) указывалось, что в настоящее время не удается
четко разграничивать круг задач теории упругости, сопротивления
материалов, строительной механики. Некоторые задачи почти с равным
успехом могут быть предметом рассмотрения в любой из отмеченных
отраслей механики. Более того, такое разграничение, будучи
естественным в прошлом, являлось бы ненужным в настоящее время при
сильно развитом состоянии указанных выше научных дисциплин.
Наконец, одна и та же конструктивная форма может интересовать
конструктора с разных точек зрения, вследствие чего он может по*-
дойти к ее расчету с позиций математической теории упругости или
же прикладной теории пластичности, или рассчитывать методами
сопротивления материалов.
Так, при определении жесткости или напряжений в пластинке,
являющейся элементом в конструкции точного измерительного прибора,
естественно обратиться к помощи математической теории упругости.
При расчете на жесткость пластинки, являющейся фундаментной
плитой сооружения, лежащей на податливом основании, точные
физические характеристики которого отсутствуют, достаточно будет для
инженерной практики воспользоваться подходящими формулами прикладной
теории упругости или сопротивления материалов. Для суждения же
только о запасе прочности той же плиты уместно исходить из теории
предельного равновесия (см. § 128), т. е. использовать приемы
прикладной теории пластичности.
Но, как это отмечалось ранее (§ 1), за последнее время
наметилось сближение между упомянутыми выше ветвями механики по
существу, т. е. проникновение методов, ранее популярных в одной ветви
механики, в задачи другой ветви. Такое проникновение оказывается
исключительно плодотворным для практики, так как представляется
возможным быстрее получать необходимые результаты расчетов,
с одной стороны, и это содействует расширению круга задач, охва-

§127] СИНТЕЗ МЕТОДОВ ТЕОРИИ УПРУГОСТИ И СТРОИТЕЛЬНОЙ МЕХАНИКИ 383
тываемых той или иной ветвью механики, и обогащает последние, —
с другой стороны.
Научное и практическое значение указанного синтеза методов и,
тем более, перспектив его дальнейшего развития, трудно переоценить,
хотя на данном этапе еще и не полностью отработаны формы такого
синтеза для отдельных конструктивных схем.
«Для диалектического метода важно прежде всего не то, что
кажется в данный момент прочным, но начинает уже отмирать, а то,
что возникает и развивается, если даже выглядит оно в данный
момент непрочным, ибо для него неодолимо только то, что возникает
и развивается» (И. В. Сталин, О диалектическом и историческом
материализме. Госполитиздат, 1949, стр. 5).
Указанное кооперирование методов, получившее в методическом
и практическом отношениях изящные формы, обязано трудам
советских исследователей (В. 3. Власов, Б. Н. Жемочкин, А. А. Гвоздев,
М. М. Филоненко-Бородич и др.).
Начало синтеза методов теории упругости и строительной
механики было положено В. 3. Власовым в его выдающихся работах по
теории строительных оболочек и тонкостенных стержней. Разработка
форм решения задач пластичности с использованием методов теории
упругости принадлежит А. А. Ильюшину.
В настоящей главе мы даем лишь краткое изложение некоторых
основных идей расчета, которые можно отнести к тому или иному
синтезу, отсылая читателя за подробностями к первоисточникам, ниже
указанным.
§ 127. Синтез методов теории упругости и строительной
механики. Задачи В, 3. Власова, М. М. Филоненко-Бородича и др.
а) О расчете призматических складчатых покрытий и оболочек
(задачи В. 3. Власова). Оболочку, состоящую из конечного числа
тонких прямоугольных
пластинок и имеющую по- *"~/
перечное сечение,
очерченное по некоторой
произвольно заданной линии
(фиг. 163), будем называть
призматической
оболочкой. Прямоугольные
пластинки, составляющие
оболочку, жестко
соединены между собой на узло- _ 1СО _
,,тл Фиг* 163. Призматическая оболочка,
вых линиях, так что в г
каждой точке узловой
(контактной) линии устранена всякого рода подвижность одной
пластинки относительно другой, соседней с ней.

384 СБЛИЖЕНИЕ ТЕОРИИ УПРУГОСТИ И СТРОИТЕЛЬНОЙ МЕХАНИКИ [ГЛ. XI
В результате своих теоретических и экспериментальных
исследований В. 3. Власов показал возможности для целей статического
расчета разделить призматические, а также и цилиндрические оболочки
на три класса: длинные, средние и короткие.
К длинным оболочкам отнесены им те, у которых отношение пролета
к длине оболочки, т.
е. у- < -д-; для расчета
их практически можно
л-/
принять гипотезу о неизменяемости формы поперечного сечения
(см. § 94). Теория изгиба таких оболочек, иначе называемых
тонкостенными стержнями, изложена в его книге «Тонкостенные упругие
стержни» (Стройиздат, 1940), удостоенной Сталинской премии в 1941 г,
К оболочкам средней длины относятся оболочки, обладающие
деформируемым профилем, но сопротивляющиеся изгибу только в одном
поперечном направлении. Это означает, что такая оболочка может
рассматриваться как
тонкостенная непрерывная
пространственная система
[15J, отдельные пластинки
которой в поперечных се-
/7 чениях испытывают одни
только нормальные и
сдвигающие усилия,
действующие в средней плоскости
пластинки (фиг. 164).
Продольные изгибающие
и крутящие моменты как
факторы, мало влияющие
на основные напряжения
и деформации оболочки,
принимаются равными
нулю. Из внутренних сил оболочки удерживаются, следовательно, только
осевые нормальные и сдвигающие силы Tv Г, *S, а также поперечные
изгибающие моменты G вместе с сопутствующими им поперечными
силами Q. Критерием для отнесения оболочек к этой категории служит усло-
Ь ^ 1
Фиг. 164. Внутренние усилия по продольному
и поперечному сечениям призматической
оболочки средней длины.
вие
4>,
>
8
Это — наиболее распространенный в строительной
практике тип оболочки.
Кроме указанной выше статической гипотезы (исключение
продольных изгибающих и крутящих моментов) В. 3. Власов на основании
исследований принимает для таких оболочек также следующую
геометрическую гипотезу: деформация оболочки происходит так, что
поперечные удлинения и сдвиги отдельных пластинок равны нулю. Согласно
этой гипотезе призматическая оболочка рассматривается как
тонкостенная пространственная непрерывная система, для которой,
во-первых, линейный элемент срединной поверхности, расположенный на
контурной линии, сохраняет свою длину и, во-вторых, прямые углы

§ 127] СИНТЕЗ МЕТОДОВ ТЕОРИИ УПРУГОСТИ И СТРОИТЕЛЬНОЙ МЕХАНИКИ 385
между линиями z = const м = const, лежащими в срединной
поверхности, после деформации остаются прямыми. Деформация срединной
призматической поверхности может происходить вследствие
растяжений этой поверхности в одном только продольном направлении и
вследствие изгиба и кручения составляющих поверхность плоских
прямоугольных полос.
Принятыми выше гипотезами определяется расчетная модель
оболочки. Если разделить оболочку на ряд поперечных элементарных
полосок, то каждую из этих полосок можно рассматривать как
плоский ломаный стержень, состоящий из нерастяжимых элементов, изги-
Фиг. 165. Расчетная модель В. 3. Власова для расчета
призматических оболочек средней длины.
баемых в плоскости поперечного сечения оболочки. Отдельные
элементы этой плоскости при жестком соединении их в узловых точках
контурной линии (на ребрах призматической поверхности) образуют
стержневую систему рамного типа, сопротивляющуюся растяжению
(сжатию) и изгибу в своей плоскости и сдвигу в направлении,
перпендикулярном к этой плоскости. Так как в поперечных сечениях
оболочки согласно статическим допущениям могут возникать одни
только нормальные и сдвигающие силы, действующие в средней
поверхности, то между двумя соседними элементарными рамами следует
предположить существование связей, передающих от одной рамы
к другой продольные нормальные и сдвигающие силы. Эти связи на
фиг. 165 изображены схематически в виде стерженьков,
расположенных в средней поверхности.
Иначе говоря, оболочка средней длины рассматривается В. 3.
Власовым как тонкостенная непрерывная пространственная система,
состоящая из бесконечного множества изгибаемых элементарных рам
и обладающая в продольном направлении безмоментной структурой.
25 Зак. 3880. Н. И. Безухов

386 СБЛИЖЕНИЕ ТЕОРИИ УЦРУГОСТИ И СТРОИТЕЛЬНОЙ МЕХАНИКИ [ГЛ. XI
у?-;
Основную систему (по терминологии строительной механики)
В. 3. Власов получает путем постановки цилиндрических шарниров
в п — 3 промежуточных ребрах складки; на крайних же ребрах 1
и п — 1 соседние пластинки в основной системе будут иметь между
собой жесткое соединение. Такая основная шарнирно-складчатая
система с нерастлжимыми продольными ребрами показана на
фиг. 166.
За основные неизвестные (статически неопределимые параметры)
принимаются продольные нормальные напряжения ак ^ в /г -|— 1 основ-
I ных точках поперечного сечения
(& == 0, 1, 2, ..., п) и изгибающие
моменты Gk (г) {к = 2, 3, ..., п — 2)
в /г — 3 промежуточных ребрах.
Моменты G0 (s) и Gn (г) на продольных
краях и G1 {e) и G{n_1) {г) в ребрах
1 и п — 1 определяются статическими
граничными условиями (условиями
равновесия крайних пластинок
оболочки).
Так же как в обычном расчете
рам в строительной механике,
приходится и здесь рассматривать
различные элементарные состояния
основной системы, в которой взамен
стержня как элемента обычной рамы
выступает пластинка как элемент
оболочки.
Упомянутые неизвестные (<зг и G2)
в отличие от неизвестных в
расчетах обычных рамных систем, где
они являются числами, подлежащими
определению, здесь, в расчете
оболочки, оказываются функциональными неизвестными, так как
значения их изменяются по длине ребра складки (т. е. они являются
функциями координаты z).
Потребовав, чтобы на ребрах оболочки в каждой точке
соблюдались как условия равновесия, так и условия деформации, В. 3.
Власов после надлежащего дифференцирования таких уравнений приходит
к системе восьмичленных дифференциальных уравнений.
Для решения указанных уравнений применяется метод
фундаментальных функций. В случае однопролетной оболочки, имеющей
шарнирное опирание на концах, фундаментальными функциями могут быть
'тригонометрические функции. При этом разложенными в
тригонометрические ряды представляются как внешняя нагрузка на оболочку,
так и основные искомые функции ak ^ и Gk^. Система
восьмичленных дифференциальных уравнений для каждого члена разложения
Фиг. 166. Основная система для
расчета призматической оболочки
по методу В. 3. Власова.

§ 127] СИНТЕЗ МЕТОДОВ ТЕОРИИ УПРУГОСТИ И СТРОИТЕЛЬНОЙ МЕХАНИКИ 387-
переходит далее в систему алгебраических уравнений относительно
коэффициентов разложения окп и Gkn.
Теория расчета оболочек средней длины изложена в ряде работ
В. 3. Власова, начиная с 1931 г., ив капитальном труде
«Строительная механика тонкостенных пространственных систем» (Строй-
издат, 1949).
Цилиндрическая оболочка для расчета может быть заменена
вписанной в нее семигранной складкой.
Оболочки, для которых у>1, относятся к категории коротких
оболочек, и для них пренебрегать продольными изгибающими и
крутящими моментами нельзя. Для таких оболочек автор дает строгое
решение, примыкающее по характеру к классической теории
упругости (см. В. 3. Власов, Общая теория оболочек, Гостехиздат, 1949).
Упомянутыми здесь, работами В. 3. Власов намного опередил
зарубежную науку и содействовал прогрессу нашей отечественной
техники (строительная промышленность, авиация, машиностроение).
Из работ, следующих идеям синтеза методов, отметим
исследования П. Л. Пастернака*), А. Ф. Смотрова.
Под влиянием указанных выше работ В. 3. Власова за последнее время
в области синтеза методов теории упругости и строительной механики было
выполнено большое количество специальных исследований как применительно
к оболочкам промышленных зданий (случаи многопролетных оболочек,
наличие затяжек [55] и т. п.), так и к специальным типам сооружений (плову-
чие доки [20], кораблестроение, самолетостроение и т. п.); проведены
обследования степени погрешности принятых в теории Власова рабочих гипотез
как самим автором, так и другими исследователями [28, 111], показавшие
возможность широкого диапазона практического применения его теории.
К указанному выше синтезу методов теории упругости и строительной
механики можно также отнести сформировавшуюся за последнее время
строительную механику пластинок. Хотя пластинка и представляет собой значительно
более простой тип сооружения, чем оболочка, однако исключительное
разнообразие пластинок как по форме (многопролетные, различного очертания
в плане, усиление ребрами и т. п.), так и по нагружению и опиранию делает
возможным выделение их расчета в специальнуюобласть строительной
механики (см. § 90).
б) О расчете балок и плит, лежащих на упругом
полупространстве или полуплоскости (задачи Б. Н. Жемочкина,
М. М. Филоненко-Бородича). К тому же направлению, что и работы
В. 3. Власова, ведущие к сближению теории упругости и
строительной механики, следует отнести начатые в 1937 г. исследования проф.
Б. Н. Жемочкина, касающиеся вопросов расчета балок и плит,
лежащих на упругом полупространстве.
Широко применяемая для расчета балок, лежащих на грунте и
вообще на упругом основании, так называемая гипотеза Винклера
(точнее Н. И. Фусса), по которой сопротивление основания в данной
*) Информационный бюллетень НКТП, 1932, а также «Проект и
стандарт» № 2, 1933.
25*

388 СБЛИЖЕНИЕ ТЕОРИИ УПРУГОСТИ И СТРОИТЕЛЬНОЙ МЕХАНИКИ [ГЛ. XI
точке пропорционально осадке основания только в этой точке,
практически ке подтверждается.
Так, осадку грунта можно наблюдать и за пределами балки или
фундамента, т. е. там, где непосредственно нагрузки на основание
не прикладываются. Ближе к действительности получают решение,
если рассматривают основание как упругое полупространство; в таком
WJWfJi.fftUKwiy^
ibi
iluu^LL
tjmt^wjww
п
Фиг. 167. Осадки упругого основания.
случае осадка основания в точке зависит не только от нагрузки,
приложенной непосредственно у этой точки, но и от загружения в
соседних точках (фиг. 167). Впервые такая задача была поставлена у нас
в 1922 г. Г. Э. Проктором; ее решение сводилось к интегральному
уравнению, разрешение которого в ряде случаев представляет
большие математические трудности.
Б. Н. Жемочкин [35] значительно упростил задачу применением
следующего приема, практическую пригодность которого он доказал
специальными
исследованиями. Непрерывную связь
балки с основанием он
заменяет точечным контактом,
воображая, что между
балкой и основанием помещен
ряд абсолютно жестких
связей— стержней (фиг. 168).
Прогибы балки и осадки
оснований в местах
установки стержней будут
одинаковыми.
За неизвестные можно принять усилия в условных связях, после
чего расчет балки будет составлять элементарную задачу. Так как
балка с упругим основанием связана только в некоторых точках, то
решение, конечно, будет приближенным. Однако, как показали
исследования Б. Н. Жемочкина, для практических целей достаточно
поставить 6 —10 стержней.
Автор показал, что решать статически неопределимую систему
(фиг. 168) удобнее не методом сил (хотя число уравнений и будет
Фиг. 168. Расчетная схема балки, лежащей
на упругом полупространстве, по Б. Н. Же-
мочкину.

§127] СИНТЕЗ МЕТОДОВ ТЕОРИИ УПРУГОСТИ И СТРОИТЕЛЬНОЙ МЕХАНИКИ 389
Т" ? ? ? } } Г
н^ Ч41 *Р *Г й° *? Ч4
наименьшим) или методом деформаций, а смешанным методом. Хотя
этот метод и требует большего числа уравнений, чем метод сил, но
сами уравнения оказываются проще.
Основная система выбирается путем разрезания всех стержней и
добавления в каком-либо сечении балки, например у левого конца,
закреплений, препятствующих вертикальному смещению и повороту
(фиг. 169). Промежуточное
каноническое уравнение,
выражающее условие, что
суммарное обобщенное
перемещение по направлению Хк
равно нулю, запишется так:
+ Хк\и + • •. + X,ihn —
—Л-?«*+Д«р = 0.(11.01)
Таких уравнений придется составить по числу стержней. Кроме
того, добавятся два уравнения равновесия: проекция всех сил на
вертикальную ось равна нулю, и сумма моментов сил относительно
закрепления также равна нулю:
— 2 **+1Я = о,
к = 1
к = п
Элементарное перемещение ьк1 (т. е. перемещение по
направлению ХкУ но вызванное действием Х{=\) слагается из двух частей:
Фиг. 169. Основная система в расчете балки
на упругом полупространстве по Б. Н. Же-
мочкину.
(11.02)
ХГ1
*T**TWT&YumFT№W?W'1&1XBy&Yi!py!P
j : щ,
Фиг. 170. Составляющие перемещения Ьк{.
из осадки основания в точке k от единичной силы, приложенной
в точке / (обозначим это перемещение через (wki) и из прогиба
балки zki, т. е.
8н = wu + *ы-
Прогиб балки можно определить по правилам сопротивления
материалов (фиг. 170). Для осадки wu следует использовать результаты
теории упругого полупространства.

390 СБЛИЖЕНИЕ ТЕОРИИ УПРУГОСТИ И СТРОИТЕЛЬНОЙ МЕХАНИКИ [ГЛ. XI
Так как единичную силу предполагать сосредоточенной нельзя,
иначе получим перемещения wki бесконечно большими, то ее
распределяем равномерно по прямоугольнику с размерами в плане
ЬХс (фиг. 171), где b — ширина балки, а с — расстояние между
условными стержнями.
Исходя из основной формулы (5.15)
W:
пЕг
и произведя интегрирование по площади b X £> получим для осадки
J L
Фиг. 171. Распределение
условной сосредоточенной силы.
Фиг. 172. Условная и действительная эпюра
реакций упругого основания.
в точке от загружения единичной силой, распределенной по площадке,
в центре которой расположена точка /, такое выражение:
™ы =
1—И-2
пЕс
кг*
(11.03)
Здесь Fu — некоторая функция, зависящая только от
отношения — и от расстояния между точками к и /, выраженными в целых
числах с. Таблицы таких функций приведены Б. Н. Жемочкиным в его
книге [36].
Для гы по формулам сопротивления материалов имеем:
*н=^(*)Ъ*-*)- а1-04)
б^б
После определения всех усилий Xv X2} ... надлежит каждую из
сил поделить на площадку £ X £> чтобы получить интенсивность
реакций.
Эпюра реакций будет ступенчатой (фиг. 172) и при достаточном
числе фиктивных стержней (6—10) мало будет отличаться от
действительной плавной эпюры (на фиг. 172 пунктиром указана
криволинейная эпюра).
В недавнее время [36] Б. Н. Жемочкиным применен его способ
к расчету упругой заделки стержня в стену или грунт (фиг. 173).
В последнем случае приходится вычислять перемещения wki, исходя
не из полупространства, а из рассмотрения бесконечной среды.

§127] СИНТЕЗ МЕТОДОВ ТЕОРИИ УПРУГОСТИ И СТРОИТЕЛЬНОЙ МЕХАНИКИ 391
Описанная выше идея замены сплошного основания дискретным
контактом была несколько ранее использована А. А. Поповым в
расчете кривого бруса.
Оригинальным решением задач о расчете балок, лежащих на
упругом полупространстве или полуплоскости, является также метод
М. М. Филоненко-Бородича [120].
В отличие от модели упругого основания по Винклеру, которую
можно представить в виде ряда пружин (фиг. 174, справа) М. М. Фи-
лоненко-Бородич в своей расчетной схеме соединяет пружины поверху
горизонтальной нерастяжимой нитью с постоянной горизонтальной
проекцией натяжения Н (фиг. 174, слева).
Такая модель упругого основания освобождена от недостатков
винклеровского основания, так как способна «распределять нагрузку»
и вызывать оседание поверхности и вне непосред-
ственного приложения нагрузки (что соответствует "
действительности).
Обозначая через у вертикальное перемещение
точки от начального уровня, дифференциальное ^^Ш^
уравнение равновесия нити напишем в виде
d*y
dx*'
где
•a°-v — — 4-
ау — н
Я*
(а)
Общим решением уравнения (а) будет:
у = Сг ch ах -f-
Фиг. 173.
Расчетная схема шпунто-
. _ 1 (* . _ вой стенки или
-\-C2shax—-^ q(t)sha(x — f)dt. (11.05) Сваи по Б. Н.
J Жемочкину.
Постоянные интегрирования определяются из условия, что при
х—> оо перемещение у исчезает. Предполагая, что в сторону
положительной оси Ох нагрузки распространяются лишь на конечном
отрезке х0, найдем при х > х0
у" — а*у = 0;
у = С1 ch ax-\-C2 sh ax,
и следовательно, С2 = — С1У а потому
у = ct (ch ах— sh ах) = Се-<*х. (б)
Таким образом, согласно (б) оседание поверхности асимптотически
и весьма быстро стремится к нулю. Для дальнейших уточнений
М. М. Филоненко-Бородич принимает модель, включающую множество
горизонтальных нитей, расставленных на одинаковых расстояниях

392 СБЛИЖЕНИЕ ТЕОРИИ УПРУГОСТИ И СТРОИТЕЛЬНОЙ МЕХАНИКИ [ГЛ. X]
и одинаково натянутых. Пространства между нитями заполняются
упругой средой, подчиняющейся гипотезе Винклера.
Для получения пространственной модели автор заменяет нити
нерастяжимыми мембранами (получается своеобразная «мембранная
модель»). Еще лучшие результаты Филоненко-Бородич получает,
Фиг. 174. Расчетная схема балки на упругом
полупространстве по М. М. Филоненко-Бородичу. Справа
для сопоставления показана модель основания по
Винклеру.
заменяя в плоской задаче нити тонкими упругими стержнями, а в
пространственной задаче заменяя мембраны тонкими упругими пластинками
(переход к «ламинарной модели»),
в) Плоская балка или арка на упругом основании как
расчетный элемент при исследовании пространственных систем
(задача И. Я. Штаермана и др.)» Если изучение теории расчета
балок на упругом (винклеровском) основании только теперь относят
к строительной механике стержневых систем (что соответствует
современным программам по строительной механике и инженерному
характеру отработанности этой теории в настоящее время), надо все
же заметить, что синтез методов теории упругости и строительной
механики имеет давнюю историю.
Достаточно указать на известную (частично уже проникшую
в учебные пособия по сопротивлению материалов) задачу теории
упругости по определению изгибных напряжений в тонких стенках
цилиндрической оболочки, возникающих от действия приложенной
к ней осесимметричной радиальной нагрузки с неравномерным
распределением вдоль образующей. Широкое обобщение этой идеи
имеется в прекрасной монографии А. И. Лурье «Статика
тонкостенных упругих оболочек», 1947 (глава III).
Как известно, в этом случае из цилиндрической оболочки
выделяется вдоль образующей полоска и рассматривается ее изгиб под
действием как заданных внешних сил, так и упругих реакций со
стороны соседних полосок. Эти реакции оказываются
пропорциональными прогибу «полоски», и таким образом, действительные ус :овия
работы упомянутой полоски сходны по характеру с работой балки,
уложенной на некотором воображаемом упругом основании.
Дальнейшим развитием этой плодотворной для инженерной
практики идеи явилась известная задача И. Я. Штаермана по расчету
тонкостенных куполов на действие осесадметричного нагружения.

§127] СИНТЕЗ МЕТОДОВ ТЕОРИИ УПРУГОСТИ И СТРОИТЕЛЬНОЙ МЕХАНИКИ 393
В общем случае распределения нагрузки вдоль меридиана (но при
одинаковом законе нагружения для всех меридианов), когда возможен
изгиб последнего, И. Я. Штаерман [133) сводит расчет купола
к расчету арки, лежащей на упругом основании. Роль арки у него
исполняет «полоска», вырезаемая из купола по меридиану, а роль
упругого основания исполняют, следовательно, кольца, пересекающие
эти арки.
Если в указанных до сих пор примерах этого параграфа в сферу
задач упругости вводились образы строительной механики стержневых
систем, то будет уместным указать и пример, в некотором смысле
обратный.
А. А. Уманский в своей книге «Пространственные системы»
(Стройиздат, 1949) разработал приближенный расчет
пространственных конструкций, составленных из двух (или нескольких)
параллельных плоских систем. Сущность предлагаемого им приближенного
расчета таких «биконструкций» состоит в замене сосредоточенных
усилий, передающихся от связей к плоской конструкции, силами,
непрерывно распределенными, т. е. в замене решетчатых связей
тонкой стенкой. Таким образом, автор нашел упрощение решения задачи
путем частичной замены стержневой системы оболочкой, а не
наоборот.
В связи с упомянутыми методами аналогии в расчете оболочек и в
расчете специально подобранной модели балки на упругом основании следует
заметить, что вообще идея аналогий (в широком смысле метод
моделирования) доставляет большие возможности для исследований в области теории
упругости и строительной механики.
Напомним читателю аналогию с кучей песка при исчислении несущей
способности сечения при пластическом кручении (стр. 365), о
гидродинамической аналогии, широко используемой при исследовании концентрации
напряжений у выточек *).
Однако в первую очередь здесь следует отметить метод электрического
моделирования, необозримым возможностям которого исследователи посвятят
в будущем не одну книгу; здесь мы его коснемся исключительно кратко.
Сущность возможности такого моделирования заключается в том, что
дифференциальные уравнения строительной механики и теории упругости
сопоставляются с соответствующими идентичными им дифференциальными
уравнениями электродинамического поля, а электродинамические величины,
входящие в эти последние, легко измеряются приборами. Наиболее
совершенные для этой цели аппараты, так называемые электроинтеграторы,
изобретены советским ученым Л. Г. Гутенмахером [31].
Так можно легко установить аналогию между балкой, нагруженной
силами, и электропроводником с подводимыми перпендикулярно к нему
токами. В результате оказывается, что эпюре поперечных сил в балке
соответствует эпюра накопления силы токов в электропроводнике. Эпюре
изгибающих моментов соответствует эпюра напряжений в
электропроводнике, которые легко могут быть замерены измерительным прибором.
В отдельных исследованиях устанавливается аналогия между пластинкой,
нагруженной силами, и электрической сеткой, составленной из сопротивлений,
*) С. А. Бернштейн, Сопротивление материалов, М., 1946, стр. 112—
113.

394 СБЛИЖЕНИЕ ТЕОРИИ УПРУГОСТИ И СТРОИТЕЛЬНОЙ МЕХАНИКИ [ГЛ. XI
к узловым точкам которой подводятся источники тока, соответственно
пропорциональные и так же расположенные, как силы, действующие на
пластинку [21].
Основной конструктивной частью упомянутого выше
электроинтегратора и является сетка сопротивлений. Имеется возможность подводить
в узлы сетки дополнительные токи, или «истоки» по терминологии Гутенма-
хера, посредством особо сконструированных конденсаторов и делителей
напряжений.
Процесс расчета пластинок на электроинтеграторе сводится, таким
образом, к замерам напряжений в отдельных узловых точках сетки, которая
покрывает поле пластинки, т. е. по существу проводится механическое
решение системы уравнений (в данном случае для пластинки — системы пяти-
членных или тринадцатичленных уравнений) численного метода.
§ 128. Синтез методов теории пластичности и строительной
механики. Задачи А. А. Гвоздева и др.
Большим событием для инженерной практики будет повсеместный
переход на расчет сооружений по предельным нагрузкам, т. е.
вычисление допускаемой нагрузки как некоторой доли от разрушающей.
Такая идея расчета требует предварительного выяснения несущей
способности сооружения. Для сооружения, выполняемого из
пластичного материала, несущая способность отождествляется с так
называемым «пределом пластического сопротивления».
Впервые идея расчета по предельным нагрузкам была изложена
проф. К. С. Завриевым в 1913 г. в его книге «Расчетные формулы
в сложных случаях изгиба», последнее переиздание которой было
в 1935 г. В этой замечательной книге автор предлагал новую
методику расчета стержней на прочность при продольно-поперечном
изгибе, по существу являющуюся именно расчетом по предельному
состоянию.
Идея расчета по предельным нагрузкам нашла уже в СССР
достаточно полное выражение в ныне действующих у нас нормах
расчета металлических и железобетонных конструкций. Эти нормы,
особенно по железобетону, значительно опередили европейскую
и американскую практику расчета конструкций. Создание этих
норм в большой степени обязано работам проф. А. А. Гвоздева,
проф. М. Я. Штаермана и проф. А. Ф. Лолейта.
Ниже рассматривается идея решения некоторых характерных
задач, выполненных А. А. Гвоздевым [23] и его учениками.
Так как в этом решении не используется весь комплекс
уравнений математической теории пластичности (да это и не привело бы
на данном этапе состояния теории пластичгости к удобным для
практики результатам) и А. А. Гвоздев вводит ряд оригинальных
гипотез (последнее вообще характерно для прикладной теории
упругости и строительной механики), а в математическом оформлении
своих идей применяет аппарат, популярный в строительной механике,
то его направление расчета можно отнести именно к синтезу теории
пластичности и строительной механики.

§128] СИНТЕЗ МЕТОДОВ ТЕОРИИ ПЛАСТИЧНОСТИ И СТРОИТЕЛЬНОЙ МЕХАНИКИ 395
а) Несущая способность полигональной плиты. Рассмотрим
полигональную плиту, шарнирно-опертую по периметру и
нагруженную в точке О сосредоточенной силой Р (фиг. 175,\
Форму разрушения такой плиты, отвечающую превращению ее
при достижении несущей способности в геометрически изменяемую
систему, можно представить себе в виде пирамиды с вершиной
в точке О и с ребрами — цилиндрическими шарнирами текучести,
идущими в вершины опорного контура (фиг. 175). Высота пирамиды,
т. е. прогиб под силой Р в
состоянии текучести, является неопределен- ,-
ной величиной, и ее можно принять
условно за единицу. Вместо
составления уравнений предельного
равновесия для указанной формы
разрушения плиты изящнее применить
кинематический метод, т. е. написать
условие равенства нулю работы всех
сил системы на возможном ее
перемещении.
В качестве возможных
(виртуальных) перемещений примем
перемещения системы в момент исчерпания
несущей способности, т. е. согласно
фиг. 175. Виртуальная работа
составится из работы силы Р на
назначенном по ее направлению единичном
перемещении, из работы предельных
моментов тг на двугранных углах
перелома в цилиндрических
шарнирах текучести и, наконец, из работы внутренних усилий,
возникающих в тех треугольных пластинках (ограниченных двумя смежными
цилиндрическими шарнирами текучести и частью опорного контура),
на которые к моменту начала разрушения разбивается заданная плита.
Однако последней работой пренебрегают.
Таким образом, для определения разрушающей силы Р следует
интенсивность предельных моментов тг помножить на сумму
произведений двугранных углов перелома в шарнирах текучести на длины
этих шарниров. В результате имеем уравнение
я = тт2 о А- (II-06)
Не представляет затруднений [23, 89] установить следующие со-
Фиг. 175. К расчету несущей
способности полигональной плиты по
А. А. Гвоздеву.
отношения:
где
«.-4г+'
а = 1Лк <*i
Ь '

396 СБЛИЖЕНИЕ ТЕОРИИ УПРУГОСТИ И СТРОИТЕЛЬНОЙ МЕХАНИКИ [ГЛ. XI
Таким образом, окончательно:
P = mlS(ctga< + ctgP<)> (11.07)
где ог^ и $i — углы, образуемые линиями перелома со сторонами
периметра пластинки.
В частности, если пластинка имеет форму правильного
многоугольника, а сила Р приложена в центре, то
P = 2*yitg-J, (11.08)
где п — число сторон многоугольника.
Для круглой пластинки, загруженной в центре и шарнирно-опер-
той по контуру, из (11.08) при п -> оо получаем:
Р = 2ътг (11.09)
Поверхность пластинки в предельном состоянии здесь образует
конус. Его сплошь заполняют цилиндрические шарниры текучести,
направленные по радиусам.
В указанных выше формулах (11.07), (11.09) под тТ следует
понимать значение
/ят = ст|, (11.10)
где h — толщина пластинки.
Для прямоугольной пластинки, загруженной в центре, согласно
(11.07) имеем:
р = 4«т (£ + -!), (11.11)
где а и 0 — размеры сторон пластинки.
Любопытно заметить, что для круглой пластинки, обследованной
проф. В. В. Соколовским [104] точными методами теории
пластичности, получено то же решение (11.09) (см. также § 120).
б) Другие случаи плит. Исходя из указанной выше идеи
А. А. Гвоздева, А. Р. Ржаницыным *) [89] исследовано несколько
случаев.
Так, для эллиптической пластинки, нагруженной силой Р в
фокусе (фиг. 176), им получено выражение для предельной силы в виде
P = 2iu-J/ht. (И.12)
При нагружении той же пластинки в центре эллипса (фиг. 177)
*) Проф. А. Р. Р ж а н и ц ы н, Расчет сооружений с учетом
пластических свойств материала, Стройвоенмориздат, 1949, стр. 130—164.

§ 128] СИНТЕЗ МЕТОДОВ ТЕОРИИ ПЛАСТИЧНОСТИ И СТРОИТЕЛЬНОЙ МЕХАНИКИ 397
Для круглой пластинки, загруженной сосредоточенной силой Р с
эксцентриситетом с (фиг. 178):
Р = 2* , * /ит. (ПЛ4)
А. Р. Ржаницыным показано, что в формулу (11.07) разрушающей
силы для полигональной — шарнирко-опертой плиты приходится
^
N1
Ь- а —
а —
Г
i
•О
1
•о
1
Фиг. 176. Эллиптическая
пластинка, опертая по контуру и
загруженная сосредоточенной силой в
фокусе. Линии, сходящиеся в
фокусе, — цилиндрические
шарниры текучести (задача А. Р. Ржа-
ницына).
Фиг. 177. Эллиптическая
пластинка при загрузке в центре.
вносить поправки (если какая-либо
вершина контура имеет угол
меньше 90°) вследствие
возможности появления краевых
шарниров (фиг. 179). Оказывается, что необходимо вводить поправки
также и в формулы для эллиптической пластинки в случае
вытянутого эллипса.
Фиг. 178. Круглая
пластинка при
эксцентричном загружении.
Фиг. 179. Образование «краевых»
шарниров текучести в плитах с
острыми углами.
Так, формула (11.13) будет уже неприменима при наличии
значительных углов наклона (фиг. 180) касательных контура к радиусу-

398 СБЛИЖЕНИЕ ТЕОРИИ УПРУГОСТИ И СТРОИТЕЛЬНОЙ МЕХАНИКИ [ГЛ. XI
вектору, а именно больших 135°. В таком случае образуются краевые
шарниры текучести. Точно так же формула (11.14) применима при
Фиг. 180. Образование Фиг. 181. Образование краевых
«краевых» шарниров те- шарниров в круглой пластинке
кучести в эллиптической при наличии большего эксцен-
пластинке, вытянутой в триситета в приложении сосре-
плане. доточенной силы.
а < 0,707 /?, иначе разрушение будет происходить по форме (фиг. 181)>
отличной от представленной на фиг. 178.
§ 129. Синтез методов теории упругости и пластичности
(по А. А. Ильюшину)
Выражения для напряжений при пластической деформации через
компоненты последней, как известно, могут быть записаны по форме
(8.06), аналогичной записи в теории упругости (3.08) с заменой
в последних постоянного модуля сдвига G на переменный G',
определяемый (стр. 312) так:
G/ = G/(1— со). (а)
В свою очередь можем записать, сопоставляя (8.07 6) с (а):
ш=1_з^. (11.15)
Подставляя (а) в (8.06), для касательного напряжения хху получаем:
*ху = О (1 — «О Лху = °Чху — <Ь>Т*йг
Замечая, что слагаемое G^xy представляет согласно С3.08) величину
касательного напряжения при той же деформации сдвига (^ху)у но
в случае идеально упругого процесса, и обозначая такое фиктивное
напряжение
имеем:
zxy — zxy " ^^Чху

§ 129] СИНТЕЗ МЕТОДОВ ТЕОРИИ УПРУГОСТИ И ПЛАСТИЧНОСТИ 399
Аналогичное выражение можно записать и для остальных
компонентов. Таким образом, имеем возможность закон деформации
записать в форме
°х = *х — 2Gco (ех — еср)>
где
(11.16)
аа?' °г/' °г> ~ху> ^уг* ^гх
— фиктивные упругие напряжения, которые могли бы быть в
действительности, если бы тело было идеально упругим, т. е. при ш = 0.
Подставляя (11.16) в дифференциальные уравнения равновесия
(2.02), используя (2.25) и выполняя преобразования, аналогичные
приведенным в § 31, получим решение задачи теории пластичности в
перемещениях. Проделаем указанное с первым уравнением группы (2.02).
Рассмотрим случай равновесия, т. е. положим равным нулю
инерционный член в правой части (2.02). Итак, имеем:
Как известно [§ 31г уравнения (3.27)]:
где
у2=^ + - + -.
дх2 ' ду2 dz2
Обозначим в (11.17) через Rx сумму всех членов, которые
обращаются в нуль вместе с <о, т. е.
D 0 д<*> , ч , дм _,ди> ,
На основании (2.25) последнее выражение можно записать в виде
. до> (ди , dv\ , да/ди , dw\ ,лл 1 пч

400 СБЛИЖЕНИЕ ТЕОРИИ УПРУГОСТИ И СТРОИТЕЛЬНОЙ МЕХАНИКИ [ГЛ. XI
Итак, уравнение (11.17) и аналогичные два следующие могут быть
представлены в виде
(A-f 0)g+av*t> + pK = fl,0, [ (11.20)
(*+G)S + GV*«>-|-PZ = fl.a. j
Уравнения (11.20) аналогичны уравнениям (3.27) теории упругости.
В (11.20) выражения для Ry и Rz составляются на основании (11.19)
по правилу круговой подстановки.
Аналогично на основании (3.28) можно записать поверхностные
условия, выраженные через перемещения. Так, первое уравнение из
группы (3.28) записывается так:
\iit i ^/1 ,\ди , , ди . ди , ди , , dv . dw ~|
или в виде
Pxv ~ Pxv~\~ ^RX^
где рхч соответствует в точности (3.28), а
>» /п ди , . ди . ди , ди . dw \ /лл П1Ч
Л»»=--Ч2д1/ + 3£'я + ^Я+^,И + ^Я); (1L21>
последнее обращается в нуль вместе с ш.
Итак, поверхностные условия запишутся в виде
рх* = р.» + оя»»; /V =7v -Н <"V, ^ = а* + g/?„, (ii .22)
где /7^, /?yv, p^, — поверхностные нагрузки, отвечающие
действительным смещениям на границе тела, если бы последнее находилось
в идеально упругом состоянии. Выражения для Ry4 и Rz^
записываются по аналогии с (11.21) по правилу круговой подстановки.
Для решения задач пластичности А. А. Ильюшин применяет
следующий общий метод, названный им методом упругих решений.
В первом приближении полагает ш = 0 и, следовательно,
Rx = Ry= Rz = Rxv= Ry*= #*v = °-
Тогда из (11.20) имеем уравнения теории упругости в форме Ляме
и граничные условия в напряжениях, т. е. в первом приближении
имеем обычную задачу теории упругости; предположим, что для
данных массовых (X, К, Z) и поверхностных сил (pXs, ру^ рг.) она
решена и найдены компоненты перемещения #, v, w.
Далее, по формулам (2.25) и (3.06) находим деформации и по
формулам (11.16) или (3.02 а) — напряжения в первом приближении:

§ 130]
ПРОЦЕСС ДЕФОРМАЦИИ ВО ВРЕМЕНИ
401
й » еаЛ Чху, е(/\ <4П , ..., ч£у, а по значению е(/} из (11.15)
находим ш(°).
Формулы (11.19) и (11.21) позволяют теперь найти второе
приближение для Rxy Ry, Rz и для Rx„ Ry„ R&, они являются
известными функциями координат и потому в (11.20) величину рХ—RXG
** т. п. можно рассматривать как массовую силу, а в (11.22)
Pxv-j-GRxv и т- п- как поверхностную силу, т. е. можно принять:
PXW = pX—RxG,
Pxi = Px,+ QR^.
Решая задачу теории упругости для этих сил, мы найдем новые
значения компонентов смещений и<2\ v^\ w{2> во втором приближении,
после чего, повторяя все вычисления по формулам (11.19) и (11.21)>
найдем третье приближение величин ша>, R&\ ..., /?(2>, ... и,
следовательно, новые значения рХ<2\ . . . pxl> ... Таким образом, из (11.20)
и (11.22) получаем задачу теории упругости для новых внешних сил
и т. д. Процесс такого решения задач теории упругости может быть
закончен, как только разница между последовательными
приближениями окажется в пределах допустимой точности вычислений.
Вычисления по указанному способу показывают очень быструю сходимость
приближений. В ряде выполненных решений сложных задач
пластичности оказалось вполне достаточным третье, а иногда и второе
приближение.
Читатель, хорошо знакомый со строительной механикой, может провести
аналогию между указанным выше методом упругих решений и способом
последовательных приближений, применяемым при расчете сложных
каркасных пространственных рамных конструкций. В последнем способе в
качестве первого приближения принимают, например, плоское решение, т. е.
из пространственного каркаса выделяют для рассмотрения стержневую
систему из элементов, расположенных в одной (обычно в вертикальной)
плоскости, полагая отсутствующими все элементы, примыкающие к выделенному
отсеку и имеющие направления, перпендикулярные к нему («аксиальные»
элементы). Определив девиации и смещения сечений, где примыкают
аксиальные элементы, вычисляют силы сопротивления этих элементов указанным
смещениям.
Найденные силы вводят далее в состав внешних сил плоской системы,
вновь выполняют расчет и вычисляют девиации и смещения узлов, а по ним
силы сопротивления аксиальных элементов и т. д. до тех пор, пока новое
приближение будет давать результаты, мало отличные от предыдущего.
§ 130. Процесс деформации во времени
(понятие о реологическом уравнении состояния)
В теории малых упруго-пластических деформаций, рассмотренной
в настоящей книге, время как независимая переменная исключалось
из законов деформирования. Так, в теории упругости деформация
однозначно определялась действующими в данный момент силами
независимо от истории всех предыдущих нагружений.
26 Зак. 3880. Н. И. Безухов

402 СБЛИЖЕНИЕ ТЕОРИИ УПРУГОСТИ И СТРОИТЕЛЬНОЙ МЕХАНИКИ [ГЛ. XI
В теории пластичности уже требовалось знать напряженное и
деформированное состояния, приобретенные телом от предыдущего на-
гружения. Но и в этом случае найденная новая деформация
полагалась в будущем сохраняющейся без изменения, если не будет
изменения в самой нагрузке.
Однако пластическая деформация твердого тела по своей
природе, вообще говоря, является состоянием движения и потому
явление текучести должно было бы исследоваться как некоторое
движение непрерывной среды. Изменения во времени деформаций, а
следовательно, и напряжений, в одних случаях могут быть уже ощутимы
на протяжении сравнительно небольшого отрезка времени, например
в течение нескольких месяцев или лет (случай падения напряжений
в натянутом болте, сохраняющем постоянную деформацию, т. е. так
называехмое явление релаксации).
В других случаях, наоборот, существенные изменения могут
произойти лишь в течение нескольких веков. Примером последнего
Фиг. 182. Течение пластов горных пород как результат многовекового
действия сил.
является случай изгиба пластов горных пород (фиг. 182);
своеобразное течение указанных пород происходит в результате исключительно
большой продолжительности действия сил.
Природа таких явлений, как релаксация (падение напряжений
при неизменной деформации), ползучесть (рост деформаций при
постоянных нагрузках), не может быть объяснена с точки зрения
идеально упругого тела или идеально пластического. Частичное
объяснение указанных явлений можно получить, если исходить из предста-

§ 130]
ПРОЦЕСС ДЕФОРМАЦИИ ВО ВРЕМЕНИ
40»
вления об упруго-вязком или вязко-пластическом телах, понимая
под последними такие тела, в которых при деформации возникают
напряжения, зависящие не только от размеров деформаций, но также
и от скоростей, с которыми развиваются эти деформации. В этом
смысле всякое реальное тело уподобляется конгломерату, состоящему
из твердого (упругого или пластического) скелета и полужидкого,
жидкого или газообразного вещества, которым заполнены промежутки
между твердыми элементами. Ярким примером последнего является
грунт, в котором влага заполняет пространство между твердыми
частицами песка и глины.
С известным приближением аналогичную картину можно встретить
в бетонах и растворах, где даже чисто упругие деформации
обусловливаются не только деформацией твердых зерен, но и растяжимостью
поверхностных пленок жидкости в капиллярных порах между зернами.
В древесине можно найти упругие волокна — фибриллы — и в
промежутках между ними — влагу, пары и воздух. Будучи
деформированы, волокна давят на окружающую их жидкость и заставляют
перетекать ее в менее напряженные зоны, а также во внутренние
полости. Вполне очевидно, что сопротивление, которое окажет
упомянутая жидкость при ее перемещениях выдавливанию, будет
зависеть от скорости, с которой должно произойти такое смещение
(известное положение из гидродинамики).
Терминология реологии и содержание, вкладываемое в отдельные
понятия, не являются окончательно установившимися.
А. А. Ильюшин считает удобным называть релаксацией в широком
смысле слова ослабление материала (имеется в виду главным образом металл),
длительное время находящегося в постоянном или меняющемся во времени
напряженном и деформированном состояниях и, вообще говоря, переменном
тепловом режиме. Таким образом, к релаксации А. А. Ильюшин относит и
явления ползучести (которое в технике именуют также крипом), после
действия и релаксации в узком смысле, вязкости (являющейся причиной
затухания собственных колебаний упругих систем) и нарастания усталости.
Объединение одним словом указанных выше и на первый взгляд различных
явлений удобно потому, что они управляются общими законами, дальнейшее
отыскание которых является важной и благодарной задачей для теоретиков
и экспериментаторов [40].
Вообще расширенное толкование понятия пластичности оправдывается
тем, что, как это показал А. А. Ильюшин в своих последних работах,
построение в теории пластичности так называемой теории сложного нагру-
жения переплетается с «теорией наследственных сред», а эта в свою
очередь смыкается с теорией ползучести.
Было предложено много различных моделей, имитирующих
указанные явления, и различные математические зависимости, их
отражающие (см. в перечне литературы труды А. Р. Ржаницына, Л. М.
Кабанова, А. Ю. Ишлинского, Ю. Н. Рабогнова, И. И. Гольденблата *).
В случае, малых нагрузок имеем линейные законы деформации, в
*) См. также его «Введение в теорию ползучести строительных
материалов», 1952.
26*

404 СБЛИЖЕНИЕ ТЕОРИИ УПРУГОСТИ И СТРОИТЕЛЬНОЙ МЕХАНИКИ {ГЛ. ХГ
случае больших нагрузок, т. е. за границей упругой текучести,—
нелинейные законы деформации.
Для случая растяжения (вообще для одноосного напряженного
состояния) линейный закон деформации можно принять в такой форме:
a -f па = Ее + mi. (11.23)
При п = т = 0 имеем обычный закон Гука:
а = Е в; (а)
тело, подчиняющееся закону (а), т. е. идеально упругое, не
способно к релаксации и ползучести.
Если положить п = 0, т. е. принять закон деформаций в виде
q = E* + me, (11.24)
будем иметь случай у пру го-вязк ого, но не ре л а ксирую щега
тела. Явление ползучести уравнением (11.24) описывается вполне.
Так, в случае постоянной нагрузки а=const и при условии, чта
при / = 0 деформация равна нулю, решением (11.24) будет:
—И1-«
(11.25)
Движение происходит по показательному закону, причем
асимптотически приближается к величине -=- (фиг. 183).
Фиг. 183. Развитие деформаций во Фиг. 184. Падение напряжений во*
времени при а = const (ползучесть), времени при е = const (релаксация
по Максвеллу).
£
Дробь — можно рассматривать как коэффициент затухания. Для
дальнейшего удобно величину Е именовать модулем длительного
сопротивления.
При е = const из (11.24) следует, что и а = const.
Следовательно, уравнение (11.24) не способно отразить явления релаксации.
Если положить Е = 0, т. е. принять закон деформации в виде
(уравнение Максвелла)
а-{- по= теу (11.26)
то будем иметь случай релаксирующего тела. Так, при
е== const из (11.26) имеем:
а = а.А. (11-27)

§ 130] ПРОЦЕСС ДЕФОРМАЦИИ ВО ВРЕМЕНИ 405
где о0 — напряжение при /=0. Графически (11.27) представлено на
фиг. 184. Величина п представляет собой постоянный коэффициент,
имеющий размерность времени и называемый временем релаксации.
При постоянной нагрузке о = const и уравнение (11.26) дает
постоянную скорость деформаций, что не соответствует
действительности, так как дчя большинства материалов при относительно
небольшой величине нагрузки деформации затухают во времени, приближаясь
к некоторой постоянной величине.
Из решения (11.23) при e = a = const следует:
о = £а+(о0 — Еа)е~. <1L28)
График, построенный по (11.28) и показанный на фиг. 185, отвечает
действительности: падение напряжений во времени есть, но не до нуля.
При постоянной нагрузке, т. е. при а= const, решение (11.23)
имеет вид
'• = i+a{rx-i)
1 \ -:
е
Et
(11.29)
где обозначено — =EV Уравнению (11.29) соответствует график на
фиг. 186. Характерным является в этом графике то, что в момент
e=a=const
Фиг. 185. Релаксация
согласно уравнению (11.28).
о=const
Фиг. 186. Ползучесть при
а = const согласно (11.29).
приложения о имеется мгновенный скачок деформации на величину^- .
Поэтому величину —■ можно назвать мгновенным модулем
упругости. При деформировании за пределом упругости (текучести),
очевидно., следует в (11.23) линейный член Ее заменить нелинейной
зависимостью, т. е..считать модуль длительного сопротивления переменным и
зависящим от деформации.
Повидимому, аналогичное можно сказать и относительно
мгновенного модуля упругости. Тогда взамен (11.23) должны записать:
° + w==/i(«)«+/2(e)i. (11.30)
На основании (11.30), переходя к сложному напряженному
состоянию для каждой точки, можно записать в символической форме,

406 СБЛИЖЕНИЕ ТЕОРИИ УПРУГОСТИ И СТРОИТЕЛЬНОЙ МЕХАНИКИ [ГЛ. XI
аналогично (3.09) в теории малых упруго-пластических деформаций,
закон нелинейного деформирования в виде
£>п + nDH = 20'£>деф + гС'Ьдеф, (11.31)
где Da и /)деф—девиаторы напряжений и деформаций; Dn и /)деф—
девиаторы скоростей напряжений и скоростей деформации; & —
переменный модуль длительного сопротивления; G" — величина,
пропорциональная переменному модулю мгновенного сопротивления.
Запись (11.31) можно считать реологическим уравнением
состояния тела. Решение такого уравнения, равно как и
экспериментальное определение всех физических констант, входящих в него,
составляет по существу задачу теоретической реологии, с понятием о
которой встретился читатель на первой странице этой книги.
В задачу настоящей книги не входило касаться интересных
вопросов этой важной области науки. Здесь лишь заметим, что
теоретическая реология как новая ветвь механики, вырастающая ныне на
границах термодинамики, кристаллографии, геологии, физической
химии, учения о прочности материалов, учения об обработке
металлов давлением и т. д., представляет широкое поле для исследований
во всех областях инженерной практики (машиностроение,
строительство, транспорт и т. д.) с многообещающими результатами в части
регулирования процесса деформирования твердых тел во времени.
§ 131. Послесловие
Итак, читатель дошел до последней страницы книги, но прежде
чем он ее закроет, подведем некоторые итоги.
Теория упругости, выделившаяся из общей механики в
самостоятельную научную дисциплину, призвана решать в числе прочих главным
образом сложные «прочностные» задачи инженерной практики.
Многое из того, что не укладывается в формы современной
строительной механики и сопротивления материалов, может найти ответ
именно в теории упругости (расчет балок-стенок, деформации и
напряжения в массивах, контактные задачи, изгибное кручение
тонкостенных стержней и т. д.).
В настоящей книге были изложены основы теории упругости и
пластичности. Краткое изложение их не может создать у читателя
полного, представления о больших усилиях, затраченных
основоположниками механики твердого деформируемого тела на создание
упомянутых основ.
Еще большие усилия были затрачены на доведение теории
упругости и пластичности до их современного состояния, которое в
полной мере не отражено в настоящей книжке. Вместе с тем
приведенные в книге обзоры и исторические очерки все же помогут читателю
составить правильное представление об итогах, о. достижениях в
теории упругости и пластичности за последнее время. А. итог, несо-

§ 131]
ПОСЛЕСЛОВИЕ
407
мненно, такой: развитие механики твердого деформируемого тела
за советский период составляет одну из ярких страниц в
истории развития советской и мировой науки.
Было решено много важных и сложных задач. Еще больше задач
поставлено перед теорией упругости и пластичности Великими
Стройками Коммунизма и всей практикой нашего грандиозного строительства.
Исторические задачи перед советской наукой и, в частности, перед
наукой о прочности поставил XIX съезд Коммунистической партии
Советского Союза.
Для решения многих из этих задач потребуются объединенные
усилия инженеров-специалистов по прочности материалов, механиков,
математиков, физиков, металловедов и других специалистов. Да и
самые границы между некоторыми отраслями знаний становятся услов-
ными» Стираются прежние границы между теорией упругости и
строительной механикой, сглаживаются границы между задачами теории
пластичности (в узком смысле) и задачами реологии (в широком смысле).
Для облегчения математического решения задач теории упругости
начинают все шире использовать средства других наук.
Несомненно, что такое кооперирование методов и средств в
решении задач из разных областей, но описываемых сходственными
уравнениями, и дальнейшие изыскания в области синтеза методов
различных ветвей механики являются прогрессивный направлением в науке.
Споры, которые имели место и продолжаются по отправным
положениям теории пластичности, в применении ее к особым случаям
(сплавы с метастабильной структурой, особые термодинамические условия
среды и др.), вынуждают искать новую конституционную форму теории
пластичности, в которой гипотеза сплошности не была бы
абсолютизирована, не исключены коррективы или отказ от некоторых концепций
классической механики.
Поле, для теоретических исследований необозримо, возможности
для этого неограниченны.
Нет границ для «живого, плодотворного, истинного, могучего,
всесильного, объективного, абсолютного человеческого познания» *).
В условиях нашей советской действительности, когда, в
частности, к проблемам прочности привлечено внимание большого
коллектива исследователей, располагающих многочисленными
лабораториями, оснащенными советской техникой, и когда сама практика
строительства в СССР является в этом смысле грандиозной
лабораторией,— в таких условиях естественно ожидать и в области
механики твердого деформируемого тела творений, достойных
переживаемой нами Великой Эпохи.
*) В. И. Ленин, Философские тетради, 1947, стр. 330.

ЦИТИРОВАННАЯ ЛИТЕРАТУРА И ИСТОЧНИКИ*),
1. Арутюнян Н. X., Некоторые проблемы напряженного состояния
бетона и железобетона. Автореферат. Ереван, 1949.
2. Б а х ш и я н Ф. А., Вращение жесткого цилиндра в вязко-пластической
среде, ПММ т. XII, вып. 6, 1948. Упруго-сферическая волна нагруже-
ния, т. XII, вып. 3, 1948.
3. Безухов Н. И., Теория пластического расчета на изгиб, Вестник
инженеров и техников, № до, 1936.
4. Безухов Н. И., Основы теории сооружений, материал которых не
следует закону Гука, Труды Московского автодорожного института, вып.
IV, 1936.
5. Безухов. Н. И., Универсальные формулы для определения упруго-
пластических перемещений в балках переменного сечения, Труды
МАДИ, вып. 6, 1936.
6. Б е з у х о в Н. И., Общие начала теории упругости и пластичности, изд.
Арт. акад., 1943 и 1944.
7. Беляев Н. М., Применение теории пластических деформаций к
расчетам на ползучесть деталей при высоких температурах, Известия
ОТН АН СССР, № 7, 1943.
8. Бернштейн С. А., Сопротивление материалов, изд. Военной
академии БТ и MB CA, М., 1946.
9. Вавилов С. И., Исаак Ньютон, Изд-во АН СССР, М.—Л., 1943.
10. Вавилов С. И., Ленин и философские проблемы современной физики.
Статья в сборнике «Великая сила идей ленинизма», Гос. изд-во
политической литературы, 1950.
11. Вайнберг Д. В., Развитие методов теории упругости применительно
к расчету частей машин и сооружений (обобщенная бигармоническая
задача для составных тел), изд. АН УССР, Киев, 1949.
12. Вайнберг Д. В., Сжатие диска с ободом сосредоточенными силами,
Сборник трудов Киевского инженерно-строительного института,
вып. VIII, Гостехиздат Украины, 1948.
13. Вайнберг Д. В., Местные напряжения в плоском кольцевом диске от
двух сосредоточенных сил, Прикладная математика и механика, т. XIII,
вып. 2, 1949.
14. Вестник Московского университета № 50, 1953. Сборник статей по
теории пластичности (под редакцией А. А. Ильюшина).
15. Власов В. 3., Новый метод расчета тонкостенных призматических
складчатых покрытий и оболочек, Госстройиздат, М.—Л., 1933.
*) Порядковый номер соответствует номеру ссылки в тексте, указанному
там в квадратных скобках.
Звездочкой отмечены работы, где имеется обширная библиография по
вопросу, одноименному с названием самого источника.

ЦИТИРОВАННАЯ ЛИТЕРАТУРА И ИСТОЧНИКИ
409
16. Власов В. 3., Строительная механика тонких упругих пластинок, ПММ,
т. X, вып. 1, 1946.
17. Власов В. 3., Тонкостенные упругие стержни (прочность, устойчивость,
колебания), Госстройиздат, М.—Л., 1940.
18. Власов В. 3., Строительная механика тонкостенных пространственных
систем, Стройиздат, 1949.
19. Власов В. 3., Общая теория оболочек, Гостехиздат, 1949.
20. Вы рб а нов X. П., Анализ напряженного и деформированного
состояния пространственных тонкостенных конструкций типа пловучего дока
на основе теории проф. В. 3. Власова. Автореферат диссертации,
изд. МИСИ, 1950.
21. Гагарина А. А., Инженерные методы расчета пластинок, опертых
по контуру. Биб-ка Моск. инженерно-строительного института, М.,
1949.
22. Г а лерки н Б. Г., Упругие тонкие плиты, Госстройиздат, М.—Л., 1933.
23. Гвоздев А. А., Определение величины разрушающей нагрузки для
статически неопределимых систем, претерпевающих пластические
деформации, Изд-во АН СССР, Труды конференции по пластическим
деформациям, 1938.
24. Г л ушков Г. С, Определение напряжений во вращающемся диске при
различных упругих свойствах материала в двух направлениях, Труды
Моск. станко-строит. института, сб. 3, 1939.
25. Г о г о л а д з е В. Г., Упругие волны, статья в сборнике «Механика в СССР
за тридцать лет», Гостехиздат, 1950.
26. Г о л ь д е н б л а т И. И., Некоторые вопросы теории упругих и
пластических деформаций, Стройиздат, 1950.
27. Г о л ь д е н б л а т И. И., Расчет и конструирование железобетонных балок-
стенок, Стройиздат, 1940.
28. Г о л ь д е н в е й з е р А. Л., О теории тонкостенных стержней, ПММ,
т. XIII, вып. 6, М.—Л., 1949.
29. Г о р б у н о в-П о с а д о в М. И., Плиты на упругом полупространстве,
Госстройиздат, 1941.
30. Григорьев А. С, Об изгибе круглой плиты за пределом упругости,
ПММ, т. XVI, вып. I, 1952.
31. Г у т е н м а х е р Л. Г., Электрическое моделирование, М., 1951.
32. Д ж а н е л и дз е Г. Ю., К теории тонких и тонкостенных стержней,
ПММ, т. ХШ, вып. 6., М.—Л., 1949.
33. Джанелидзе Г. Ю. и П а и о в к о Я. Г., Статика упругих
тонкостенных стч^ржней, серия «Современные проблемы механики»,
Гостехиздат, 1948.
34. Д ж а н е л и д з е Г. Ю., Обзор работ по теории изгиба толстых и
тонких плит, опубликованных в СССР, Прикладная математика и
механика, т. XII, вып. 1, 1948.
35. Дмитриев Ф. Д., Крушения инженерных сооружений, анализ их
причин и уроки, вытекающие из них. Автореферат докторской
диссертации, изд. МИСИ, 1948.
36. Ж е м о ч к и н Б. Н., Расчет балок на упругом полупространстве, изд.
Военно-инж. академии, Москва, 1937.
Жемочкин Б. Н., Расчет упругой заделки стержня, Стройиздат,
1948.
37. Жемочкин Б. Н., Теория упругости, Стройвоенмориздат, 1948.
38. Жодзишский И., Л., Практические способы расчета некоторых
комбинированных пространственных систем. Автореферат диссертации, изд.
МИСИ, 1950.
39. 3 а в р и е в К. С, Расчетные формулы прочности в особых случаях, ОНТИ,
1935 (впервые эти формулы опубликованы автором в 1913 г. в
«Вестнике общества технологов»).

410
ЦИТИРОВАННАЯ ЛИТЕРАТУРА И ИСТОЧНИКИ
40. И л ь ю ш и н А. А., Некоторые основные задачи теории пластичности,
Известия АН СССР, отделение технических наук, № 12, 1949.
41. Ильюшин А. А., Проблема пластичности в машиностроении и
строительном деле, Известия АН СССР, отделение технических на\'к, № 4—5,
1945.
42. Ильюшин А. А., Пластичность, Гостехиздат, М.—Л., 1948.
43. Институт механики АН СССР, Тезисы докладов на Всесоюзном
совещании по теории упругости, строительной механике и теории
пластичности. 7—10 декабря 1950 г. Изд-во АН СССР, М.—Л., 1950.
44. И ш л и н с к и й А. Ю. *, Пластичность, статья в сборнике «Механика
в СССР за тридцать лет», Гостехиздат, 1950.
45. И ш л и н с к и й А. Ю., Линейные законы деформирования не вполне
упругих тел, Доклады АН СССР, т. XX.VI, № 1, 1948.
46. К ал манок А. С, Строительная механика пластинок, Машстройиздат,
1950.
47. Кан С. Н. и Па нов к о Я. Г., Элементы строительной механики
тонкостенных конструкций, Оборонгиз, 1949.
48. Карякин Н. И., Кручение тонкостенных стержней и рам, изд.
МЭМИИТ, Москва, 1950.
49. К а ч а н о в Л. М., Механика пластических сред, Гостехиздат, 1948.
50. К а ч а н о в Л. М., Некоторые вопросы теории ползучести, Гостехиздат,
1949.
51. К и р п и ч е в В. Л., Учение о прочности построек и машин, Киев,
1905.
52. Кокер Э. Г. и Ф а й л он Л. Г.*, Оптический метод исследования
напряжений, ОНТИ, 1936.
53. Колосов Г. В., О некоторых приложениях комплексного
преобразования уравнений математической теории упругости к отысканию общих
типов решения этих уравнений, Известия Ленинградского элекгр.
института, 1928.
54. К ути лин Д. И., Теория конечных деформаций, Гостехиздат, 1947.
55. Л евитская Н. Д., Пространственная работа цилиндрической оболочки,
опертой на колонны и усиленной затяжками, М., 1949. (Библиотека
МИСИ.)
56. Л е й б е н з о н Л. С, Курс теории упругости, изд. 2-е, Гостехиздат, 1947.
57. Ленин В. И., Философские тетради, Госполитиздат, 1947.
58. Л е н с к и й В. С, Метод построения динамической зависимости между
напряжениями и деформациями по распределению остаточных
деформаций, Вестник Моск. университета, № 5, 1951.
59. Лехницкий С. Г., Анизотропные пластинки, Гостехиздат, 1947.
60. Л е х н и ц к и й С. Г. *, Теория упругости анизотропного тела,
Гостехиздат, М.—Л., 1950.
61. Лурье А. И.*, Статика тонкостенных упругих оболочек, 1948.
62. Л у р ь е А. И., Концентрация напряжений в области отверстия на
поверхности кругового цилиндра, ПММ, т. X, вып. 3, 1946.
63. Л я в А., Математическая теория упругости, ОНТИ, М.—Л., 1935.
64. Межлумян Р. А., Граничные условия при изгибе и кручении
тонкостенных оболочек за пределом упругости, ПММ, т. XIV, вып. 5,
1950 г.
65. Межлумян Р. А., Изгиб и кручение оболочек за пределом упругости,
статья в журнале ПММ, т. XIV, вып. 3, 1950.
66. Межлумян Р. А., Определение несущей способности тонкостенных
конструкций с учетом упрочнения материала, ПММ, т. XV, вып. 2,
1951.
67. Михлин С. Г., Теория пластичности, Изд-во АН СССР, 1934.
68. Михлин С. Г., Основные уравнения математической теории
пластичности, Изд-во АН СССР, 1934.

ЦИТИРОВАННАЯ ЛИТЕРАТУРА И ИСТОЧНИКИ
411
69. Моисеев Н. Д.*, Общий очерк развития механики в России и в СССР,
статья в сб. «Механика в СССР за тридцать лет», Гостехиздат, 1950.
70. М у с х ел и ш в и л и Н. И., Некоторые основные задачи математической
теории упругости, изд. 2-е, Изд-во АН СССР, М., 1935.
71. М у с х е л и ш в и л и Н. И., Некоторые задачи теории упругости, Гостех-
издат, 1937.
72. Н а д а и А., Пластичность, ОНТИ НКТП, 1936.
73. Новожилов В. В., О связи между напряжениями и деформациями
в нелинейно-упругой среде, ПММ, т. XV, вып. 2, 1951.
74. Новожилов В. В.*, Основы нелинейной теории упругости, Гостех-
издат, 1948.
75. О г и б а л о в П. М., О распространении вязко-пластического течения
с учетом упрочнения для случаев вращения и сдвига, ПММ, т. V,
вып. 1, 1947.
76. Одинг И. А., Проблема прочности в машиностроении, Известия
АН СССР, отделение технических наук, № 12, 1949.
77. Одинг И. А., За материалистические принципы в теории прочности и
пластичности металлов, Вестник машиностроения, № 2, 1950.
78. Одинг И. А., Релаксация и ползучесть металлов, Вестник
машиностроения, № 5—6, № 7—8, № 9—10, 1946.
79. Орлов С. А., Статический расчет круговой обделки тоннеля на
линейно-деформируемом основании (без гипотезы Винклера).
Автореферат диссертации, изд. МИИТ, 1951.
80. Папкович П. Ф., Теория упругости, Оборонгиз, 1939.
81. П р ату с е в и ч Я. А., Вариационные методы в строительной механике,
М.—Л., 1940.
82. Прокофьев И. П., Теория сооружений, т. 2 и 3, Трансжелдориздат,
1949.
83. Рабинович И. М. *, Достижения строительной механики в СССР,
краткий обзор, Стройиздат, 1949.
Рабинович И. М., Строительная механика стержневых систем,
Стройиздат, 1946.
84. Р а б о т н о в Ю. Н., Сопротивление материалов, изд. Моск. университета,
1950.
85. Р а б о т н о в Ю. Н., Пластинки и оболочки, статья в сборнике
«Механика в СССР за тридцать лет», Гостехиздат, 1950.
Ра бот нов Ю. Н., Приближенная техническая теория
упруго-пластических оболочек, ПММ, т. XV, вып. 2, 1951.
86. Ра бот но в Ю. Н., Расчет деталей машин на ползучесть, Известия
АН СССР, отделение технических наук, № 6, 1948.
87. Р а х м а ту л и н X. А., Упруго-пластические волны, ПММ, т. IX, вып. 1,
1945.
88. Р а х м а т у л и н X. А., Об ударе по гибкой нити, ПММ, т. XI, вып. 3, 1947.
89. Ржаницын А. Р., Расчет сооружений с учетом пластических свойств
материала, Стройвоенмориздат, 1949.
90. Савин Т. Н.*, Концентрация напряжений около отверстий,
Гостехиздат, М.—Л., 1950.
91. Саверин М. М., Контактная прочность материала в условиях
одновременного действия нормальной и касательной нагрузок, Машгиз,
М.—Л., 1946.
92. С е р е н с е н С. В., Основы технической теории упругости
(применительно к расчетам прочносии в самолетостроении), X. — К., 1934.
93. С и н е л ь н и к о в В. В., О природе упругости и прочности твердых
тел. Диссертация, 1947. Библиотека Моск. института инженеров
транспорта.
94. Слезкин Н. А., Основные уравнения движения деформируемой среды,
ДАН, № 1, 1951.

412
ЦИТИРОВАННАЯ ЛИТЕРАТУРА И ИСТОЧНИКИ
95. Смирно в-А л я е в Г. А., Сопротивление материалов пластическим
деформациям, Машгиз, 1949.
96. С м и р н о в В. И. и Соболев С. Л., О применении нового метода
к изучению упругих колебаний в пространстве при наличии осевой
симметрии, Труды Сейсмического института АН СССР, № 2, 1930.
97. С н и т к о Н. К., Теории прочности металлов с учетом внутрикристал-
лической структуры, изд. Военно-транспортной академии, Л., 1946.
98. С н итк о Н. К., К теории упруго-пластического состояния
квазиизотропных тел и методы вычисления скрытно-упругих напряжений,
Изв. АН СССР, 1942, № 7—8.
99. Соболев С. Л. и К у п р а дз е В. Д., К вопросу о распространении
упругих волн на границе двух сред с различными упругими
свойствами, Труды Сейсмического института АН СССР, № 10, 1930.
100. Совещание по контактным напряжениям и усталости рабочих
поверхностей 23—25 мая 1941 г. Тезисы докладов, издание Института
машиноведения АН СССР, М., 1941.
101. Соколовский В. В.*, О некоторых работах по теории пластичности,
ПММ, т. IX, вып. 6, 1945.
102. С о к о л о в с к и й В. В., Теория пластичности, Изд-во АН СССР, 1946.
103. Соколовский В. В., Статика сыпучей среды, Изд-во АН СССР, 1942.
104. Соколовский В. В., Теория пластичности, Гостехиздат, 1951.
105. Соколовский В. В., Распространение упруго-вязко-пластических
волн в стержнях, ПММ, т. XII, вып. 3, 1948.
106. Сталин И. В., Марксизм и вопросы языкознания, Изд-во «Правда»,
1950.
107. Сталин И. В., О диалектическом и историческом материализме
(сентябрь 1938 г.), Гос. изд-во политической литературы, 1949.
108. Стрел ьбицкая А. И., Предельное состояние двутаврового профиля
при стесненном кручении, статья в Сборнике трудов Института
строительной механики, № 14, Киев, 1950, изд. АН УССР.
109. Тезисы совещания по теории упругости, строительной механике и
теории пластичности 25—28 марта 1946 г., Изд. Института механики
АН СССР, М., 1946.
ПО. Тезисы докладов на конференции по пластическим деформациям, Изд.
АН СССР, М., 1936.
111. Тихонова Л. Г., Анализ различных теорий цилиндрических оболочек.
Автореферат диссертации, изд. Института механики АН СССР, 1949.
112. Теория пластичности*, Сборник статей под редакцией Ю. Н. Работнова,
Гос. изд. иностранной литературы, М., 1948.
113. У майский А. А., Пространственные системы, Стройиздат, 1949.
114. Ума некий А. А., Кручение и изгиб тонкостенных конструкций, М.,
1939.
115. Урбан И. В., Теория изгпбного кручения тонкостенных конструкций
открытого и закрытого профиля, изд. МЭМИИТ, М., 1950.
116. Ф е ппл ь А. и Ф е пп л ь Л., Сила и деформация, т. Н,ОНТИ,М.—Л., 1936.
117. Ф и л он е н к о-Б оро ди ч М. М., Теория упругости, Гостехиздат, 1947.
118. Ф и л он е н ко-Б о ро д и ч М. М., Новые вопросы строительной
механики, статья в сборнике «Механика в СССР за тридцать лет»,
Гостехиздат, 1950.
119. Ф и л о не н к о-Б о р од и ч М. М., Задача о равновесии упругого
параллелепипеда при заданных нагрузках на его гранях, ПММ, т. XV,
вып. 2, 1951.
120. Ф ил он е н ко-Б о р од и ч М. М., Некоторые приближенные теории
упругого основания, Ученые записки Моск. государственного
университета, Механика, вып. 46, 1940.
121. Фридман М. М. *, Математическая теория упругости анизотропных
сред, ПММ, т. XIV, вып. 3, 1950.

ЦИТИРОВАННАЯ ЛИТЕРАТУРА И ИСТОЧНИКИ
413
122. Фрохт М. *, Фотоупругость, т. I, Гостехиздат, 1948.
123. Холмянский М. М., Некоторые задачи изгиба тонких пластинок.
Автореферат диссертации, издание Моск. инженерно-строительного
института, М., 1950.
124. X р и с т и а н о в и ч С. А., Плоская задача математической теории
пластичности при внешних силах, заданных на замкнутом контуре,
Математический сборник, нов. серия, т. 1 (43), вып. 4, 1938.
125. Цейтлин Ш. Ю., Расчет пологих оболочек, прямоугольных в плане
на основе теории В. 3. Власова. Автореферат диссертации, изд. МИСИ,
1951.
126. Чау сов Н. С, Применение теории проф. В. 3. Власова к расчету
эллиптических и сферических куполов, М„ 1949 (Библиотека МИСИ),
1951.
127. Чаплыгин С. А., К вопросу о деформации трубы, ограниченной
двумя эксцентрическими цилиндрами и сжатой постоянным давлением,
Полное собрание сочинений, т. III, Изд-во АН СССР, 1935.
128. Ченцов Н. Г., Исследование фанеры как ортотропной пластинки,
Труды ЦАГИ, вып. 383, 1938.
129. Шапиро Г. С.*, Пространственные задачи теории упругости, статья
в сборнике «Механика в СССР за тридцать лет», Гостехиздат, 1950.
130. Шапиро Г. С, Напряжения у отверстия в бесконечном клине, Труды
Ленинградского политехнического института им. М. И. Калинина, № 3,
1941.
131. Шерман Д. И.*, Основные плоские и контактные (смешанные)
задачи статической теории упругости, статья в сборнике «Механика в
СССР за тридцать лет», Гостехиздат, 1950.
132. III им а некий Ю. А., Изгиб пластин, ОНТИ, 1934.
133. Штаерман И. Я.» Теория расчета купола как арки на упругом
основании, журнал «Проект и стандарт», 1933.
134. Штаерман И. Я., Контактная задача теории упругости, Гостехиздат,
1949.
135. Энгельс Ф., Диалектика природы, Гос. изд-во политической
литературы, 1948.
136. Энгельс Ф., Анти-Дюринг, Гос. изд-во политической литературы,
1948.

ИМЕННОЙ УКАЗАТЕЛЬ
Абрамов В. М. 141
Ададуров А. Р. 303
Анаксагор 350
Аржанников Н. С. 140
Аристотель 350
Арутюнян Н. X. 381, 408
Архимед 65
Архит 65
Бахшиян Ф. А. 381, 408
Безухов Н. И. 363, 408
Беляев Н. М. 141, 223, 224, 381, 408
Березанцев В. Г. 348
Бернулли Д. 66, 68
Бернштейн С. А. 393, 408
Благонравов А. А. 350
Блох В. И. 148
Бочвар А. А. 353
Бронский А. П. 381
Бубнов И. Г. 70, 288
Бюльфингер 66
Вавилов С. И. 351, 407, 408
Вайнберг Д. В. 141, 224, 408
Варвак П. М. 279
Винокурова А. В. 206
Витрувий 65
Власов В. 3. 8, 104, 226, 235, 241, 242,
279, 289, 298, 300, 302, 303, 360,
370, 383, 384, 387, 408, 409
Вольмир А. С. 290
Вырбанов X. П. 409
Гагарина А. А. 409
Гадолин А. В. 68, 181, 182
Галеркин Б. Г. 8, 70, 140, 147, 148,
182, 251, 257, 278, 288, 289, 409
Галилей 66
Галин Л. А. 141, 224, 348
Гвоздев А. А. 290, 349, 383, 394, 409
Герсеванов Н. М. 290, 352
Гершгорин А. С. 290
Глушков Г. С. 409
Гоголадзе В. Г. 253, 381, 409
Головин X. С. 70, 130, 178, 180
Голушкевич С. С. 290, 348
Гольденблат И. И. 10, 409
Гольденвейзер А. Л. 303, 409
Горбунов-Посадов М. И. 141, 290, 409
Григорьев А. С. 368, 409
Гродский Г. Д. 148
Губкин С. И. 353
Гук Р. 66
Гутенмахер Л. Г. 393, 409
Гутман С. Г. 148, 2S9
Демокрит 350
Джанелидзе Г. Ю. 235, 242, 288, 289,
290, 303, 409
Динник А. Н. 224
Дмитриев Ф. Д. 69, 409
Дюпре А. 67
Жемочкин Б. Н. 8, 145, 290, 387, 388,
390, 409
Жодзишский И. Л. 409
Журавский Д. И. 57, 66, 68
Завриев К- С. 10, 394, 409
Зволинский Н. В. 303
Ильюшин А. А. 8, 90, 290, 306, 309,
314, 315, 316, 317, 326, 348, 349,
350, 378, 380, 383, 385, 398, 403,
410
Иоффе А. Ф. 350
Ишлинский А. Ю. 349, 381, 403, 410
Калманок А. С. 267, 289, 410
Кан С. Н. 372, 410
Карякин Н. И. 302, 410
Качанов Л. М. 8, 307, 381, 403, 410
Кирпичев В. Л. 68, 69, 70, 349, 410
Кишкин С. Т. 353

ИМЕННОЙ УКАЗАТЕЛЬ
415
Клапейрон 68
Кокер Э. Г. 410
Колосов Г. В. 70, 139, 141, 410
Конторович М. 252
Коренев Б. Г. 290
Короткий В. Г. 148
Коши 67, 68, 253
Крутков Ю. А. 148
Крылов А. Н. 15, 70
Кузнецов В. Д. 350
Кузнецов И. В. 64
Кузьмин Р. О. 147
Кулибин И. П. 68
Кулон 69
Купрадзе В. Д. 412
Кутилин Д. И. 410
Куфарев П. П. 141
Лебедев Н. Н. 141
Левитская Н. Д. 410
Лейбензон Л. С. 8, 32, 70, 103, 233,
251, 252, 25Э, 298, 352, 410
Ленин В. И. 11, 12, 13, 62, 351, 408,
410
Ленский В. С. 381, 410
Леонардо да Винчи 66
Лехницкий С. Г. 141, 290, 410
Лолейт А. Ф. 394
Ломоносов М. В. 66
Лунц Я. Л. 290
Лурье А. И. 8, 140, 224, 289, 290, G92,
410
Ляв А 69, 410
Ляме 68, 181
Малашенко С. В. 350
Малиев А. С. 178, 290
Малинин Н. Н. 381
Маслов Г. Н. 140, 148
Максвелл 147
Медведев В. С. 303, 372, 373
Межлумян Р. А. 33, 369, 370, 410
Менделеев Д. И. 21
Михлин С. Г. 140, 141, 254, 410
Моисеев Н. Д. 67, 411
Морер 147
Мусхелишвили Н. И. 8, 15, 70, 139,
141, 224, 290, 411
Мюнтц Г. И. 254
Навье 67, 68
Надаи А. 411
Нарышкина Е. А. 253
Нейбер 148
Никифоров С. Н. 290
Николаева М. В. 178
Новожилов В. В. 8, 27, 107, 108, 129
327, 411
Новоторцев В. И. 348
Ньютон 67
Огибалов П. М. 381, 401, 411
Одинг И. А. 350, 351, 411
Орлов С. А. 411
Остроградский М. В. 67, 253
Панарин Н. Я. 140
Панов Д. Ю. 381
Пановко Я. Г. 303, 372, 409
Папкович П. Ф. 8, 70, 140, 148, 243,
245, 246, 257, 289, 411
Пастернак П. Л. 387
Попов А. А. 391.
Прандтль 229, 373
Пратусевич Я. А. 174, 178. 411
Прокофьев И. П. 411
Пуассон 67, 68, 253
Рабинович И. М. 411
Работнов Ю. Н. 381, 403, 411
Рахматулин X. А. 8, 381, 411
Репман Ю. Б. 290
Ржаницын А. Р. 290, 358, 362, 363,
396, 403, 411
Саверин М. М. 411
Савин Г. Н. 140, 141, 210, 411
Сен-Венан 69, 103, 226
Серенсен С. В. 8, 411
Синельников В. В. 353, 411
Синицын А. П. 279
Слезкин Н. А. 352, 411
Слободянский М. Г. 148
Смирнов В. И. 253, 254, 327, 412
Смирнов-Аляев Г. А. 378, 412
Смотров А. Ф. 279, 387
Снитко Н. К. 352, 412
Соболев С. Л. 253, 254, 349, 412
Соколовский В. В. 8, 10, 290, 316,326,
327, 336, 348, 349, 363, 365, 366,
373, 374, 377, 378, 381, 412
Сталин И. В. 354, 383, 412
Стрельбицкая А. И. 412
Тер-Мкртичьян Л. Н. 148
Тимошенко С. П. 70, 2&8
Тихонова Л. Г. 412
Трефц 252
Уманский А. А. 242, 303, 369, 393, 412
Урбан И. В. 412

416
ИМЕННОЙ УКАЗАТЕЛЬ
Файлон Л. Г. 410
Феппль А. 242, 303, 412
Феппль Л. 303, 412
Филоненко-Бородич М. М. 8, 10, 30,
34, 129, 140, 181, 233, 245, 246, 258,
289, 298, 302, 383, 387, 391, 412
Френкель Я. М. 353
Фридман М. М. 140, 412
Фрохт М. М. 30, 413
Фусс Н. И. 290
ХоЛмянский М. М. 413
Христиаиович С. А. 253, 348, 413
Чаплыгин С. А. 140, 413
Чебышев П. Л. 357
Ченцов Н. Г. 141, 413
Аналогия Прандтля мембранная 230
Арка на упругом основании 392
Балка на упругом полупространстве
или полуплоскости 387 и д.
Балка-стенка 165, 173 и д.
Бимомент 241, 300
£ипара 33
Бисила 33
Брус равного сопротивления 58
Бугор напряжений 229
Вдавливание абсолютно жесткого
шара в упругое полупространство 219
в упругую почти
бесконечную сферу 222
Взаимность сдвигов 45
Вектор смещения 40
Волокно тела 34
Время релаксации 404
Гексаикосаэдр главный 93
Гипотеза кинематическая 256, 259
— материальных точек 350
— непрерывности деформаций 61
— о естественном напряженном
состоянии тела 23
— о недеформируемости контура
поперечного сечения 256
— о сплошности строения упругого
тела 22, 350
— плоских нормалей 256, 259
сечений 60, 153, 256, 328
— рабочая 27
— статическая 255
— элемента прямолинейного 259
— энергетическая 256
Шапиро Г. С. 148, 290, 381, 413
Шахтер О. Я. 141, 290
Шерман Д. И. 140, 141, 148, 253, 413
Шиманский Ю. А. 277, 289, 413
Штаерман И. Я- 8, 10, 141. 205,
206, 219, 224, 357, 392, 393, 394,
413
Штаерман М. Я. 393
Шулежко П. Г. 289
Эпикур 350
Эйлер Л. 66, 68
Энгельс Ф. 28, 66, 413
Ясинский Ф. С. 68
Давление пластической среды на
жесткий штамп 373
Девиатор деформаций 49, 116
— напряжений 50, 116
— скоростей деформаций 52
напряжений 52
Депланация сечения 226
в виде узкого прямоугольника
234
эллиптического 231
Деформация активная 304, 307
— второго рода 43
— обобщенная 107, 114, 308, 311
— объемная 49, 51, 86, 115
— осесимметричная 145, 180 и д.
пластическая равномерно
вращающегося диска 340
— относительная объемная 44
— пассивная 304
— первого рода 42
— пластическая (остаточная) 18
— плоская 132
— полярно-симметричная
толстостенного сферического сосуда 194
— скашивающая (девиаторная) 148
— средняя 45, 112, 115
— формы 48
— чистая 41
— чисто объемная 48
Диаграмма растяжения для стали
27
Диск равномерно вращающийся,
осесимметричная пластическая
деформация 340
— толстостенный 180 и д.
Додекаэдр главный 93
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
417
Жесткость при кручении 230
— цилиндрическая при изгибе
пластинки 265
Зависимость между деформациями и
напряжениями линейная 24
Задача Власова 383
— Гадолина 182, 185
— Галеркина 182
— Герца 223
— Головина 178
— Гвоздева 394
— двухмерная теории упругости 17
— обратная 56
— одномерная 17
— плоская 129 и д.
в полярных координатах 136
, идеально пластический
материал 324
— прямая 56
— Сен-Венана 225
— смешанная 56
— Соколовского 363
— Штаермана 205, 392
— Филоненко-Бородича 246
Задачи теории упругости
классические 198 и д.
Закон взаимности (сопряженности)
напряжений 11
касательных 38, 77
— Гука 13, 14, НО, 111
— изменения объема 318
формы 116
при активной деформации
318
— пассивной деформации 319
— плоских сечений 57
— связи обобщенного напряжения с
обобщенной деформацией при
активном нагружении 318
— упругого изменения объема 115
— упругости обобщенный 112
Изгиб консоли 132, 167
— пластинки 257
круглой и кольцевой осесим-
метричный упруго-пластический 367
под совместным действием по-
' перечных нагрузок и сил в ее
срединной плоскости 281
— тонкостенных стержней и
цилиндрических оболочек за пределом
упругости 369
— чистый 149
кривого бруса 178
, пластичность 328
Изоклина 203
Изостата 203
Изотропия шаровая 24
Изохрома 202
Инвариант тензора напряжений
второй (квадратичный) 86
первый (линейный) 85, 95
— третий (кубический) 86
Интенсивность деформации 107
— напряжения 89
— сил, действующих в срединной
плоскости 282
Картина полос 30
Клин под действием силы,
действующей на его острие 198
Компоненты жесткого вращения 41
— напряжений касательных 73
— — нормальных 72
— перемещения 40
— скоростей смещения, напряжений,
деформации 51
— тензора напряжений
корректирующего 245
основного 245
Контур (опорный) пластинки 258
Косинус-бином 247
Коэффициент Пуассона 107, ПО
— сцепления 374
Кривая деформации для чистого
сдвига 332
Кручение некруглых сечений 225
нестесненное 363
— нестесненное 240
— сечения в виде узкого
прямоугольника 233
— стесненное 239, 298
стержня эллиптического
сечения 290 и д.
■— тонкостенных стержней и
цилиндрических оболочек за пределом
упругости 369
— чистое 150
, пластичность 332
— эллиптического сечения 230, 290
и д.
Куб главный 93
Купол тонкостенный 392
Линии Чернова 321
Локальность эффекта
самоуравновешенных внешних нагрузок 25
Матрица напряжений 40
Матрица-столбец смещения 4J
Метод вариационный 252
— вязких решений 381
— Галеркина 251
— моделирования 393
— ■— электрического 393
27 Злк. 3880. Н. И. Безухое

418
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Метод обратный 165
— перемещений 124, 251
— полуобратный 344
— сил 124, 250
— смешанный 124, 250
— упругих решений 400
Механика 11
— континуума 23
— практическая (прикладная) 12
— строительная 19, 382 и д.
пластинок 279
Модуль длительного сопротивления
404
— объемный 117
— приведенный деформации первого
рода 308
— сдвига 117
— упругости 107, ПО
мгновенный 405
Момент изгибно-крутящий 300
Нагружение простое 19, 306, 315,316
Напряжение 34
— главное 81, 85
касательное SS
— касательное 36
наибольшее 90
— начальное 23
— нормальное 36, 72
— обобщенное 89, 114, 121, 308, 311
— октаэдрическое 88, 121
— приведенное 320
— среднее 50, 115
— структурное 64
Наследственность 14
Непрерывность деформации 61
Оболочка призматическая 383
Объем элементарный 37
Однородность совершенная 24
Операция бигармоническая 134
— гармоническая 132
Ось деформации главная 105
Отверстие круглое, влияние при
растяжении пластинки 207
Параллелепипед упругий при
заданных нагрузках на его гранях 246
— элементарный 37
Параметр нагрузки 355
Перемещение обобщенное 118
Пластинка круглая, изгиб 279
, — осесимметричный упруго-
пластический 367
— плоская средней толщины 257
— под совместным действием
поперечных нагрузок и сил в ее
срединной плоскости 281
Пластинка полубесконечная 200 и д.
— прямоугольная, всестороннее
сжатие 287
свободно-опертая, нагрузка в
виде «горки» 269
1 сжатая в одном
направлении, устойчивость 286
с шарнирно-закрепленными
краями 277
— эллиптическая, защемленная по
контуру 267
Пластичность 304 и д.
— идеальная 305
Плита на упругом полупространстве
или полуплоскости 387 и д.
— полигональная, шарнирно-опертая
по периметру и нагруженная
сосредоточенной силой 395
— толстая 258
— тонкая 257
Плоскость срединная 258
Площадка главная 82
для напряжений касательных
92
нормальных 92
— октаэдрическая 87, 93
— основная 36
— результирующих напряжений в
данной точке 87
— тела элементарная 34
Площадь секториальная 235
Поверхность естественного откоса 364
— упругая 258
Покрытие призматическое складчатое
383
Поле напряжений тензорное 245
корректирующее 245
■ основное 245
Ползучесть 402
Полуплоскость упругая 200
Полупространство упругое 210, 214,
219
Последействие. 14
Потенциал эластический 117
Поток касательных напряжений 238
Предел пластического сопротивления
394
сечения 356
статически неопределимой
системы 357
. трубы 335
■— упругого сопротивления сечения
355
Принцип автономной прочности в
точке 25
—взаимности перемещений 297
— Сен-Венана 25

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
419
Принцип упругой равнозначности
статически эквивалентных систем сил
28
Прогиб обобщенный 279
Процесс нагружения простой 19
Прочность автономная в точке 25
Разгрузка 316
Релаксация 14, 402
Реология 12, 382 и д., 406
Связь обобщенного напряжения с
обобщенной деформацией при
активном нагружении 318
Сдвиг относительный 17, 99
Сейсмология 253
Сечение в виде узкого
прямоугольника 362
— некруглое, пластическое состояние
при нестесненном кручении 363
Сжатие всестороннее прямоугольной
пластинки 287
Сила, действующая на острие клина
198
— обобщенная 118
—, приложенная к точке
прямолинейного края полубесконечной
пластинки 200 и д.
— сосредоточенная, действующая на
плоскость, ограничивающую
полубесконечное тело 210
Синтез 21
Система главная приведенная 370
— отсчета главная кинетическая 370
Скорости смещений, напряжений и
деформации 51
Слой тела 34
Смягчение граничных условий на
концах бруса 32
Смятие шаров упругое 222
Сопротивление материалов 13, 15, 17,
56 и д., 68
— сложное тонких и тонкостенных
стержней 293
Сопряженность касательных
напряжений 77
Состояние осесимметричное упруго-
пластическое толстостенной трубы
> 334
— пластическое 19
при нестесненном кручении
некруглых сечений 363
— плоское напряженное 120 и д.
— полярно-симметричное
упруго-пластическое шарового сосуда 342
— упрочнения 305
Сосуд сферический 194, 342
Способ обратный 124
— полуобратный 124
— последовательных приближений
125
— прямой 124
— смягчения граничных условий 132
Способность несущая 355
круглого цилиндрического
стержня, подверженного
растяжению и кручению 358
Среда непрерывная 23
— сыпучая 374 и д.
Стационарность нормальных
напряжений 85
Стержень круглый цилиндрический,
подверженный растяжению и
кручению 358
— тонкостенный 293, 384
— эллиптического сечения,
стесненное кручение, 290 и д.
Стеснение относительное 240
Тело вращения с симметричным
относительно оси распределением
напряжений 141 и д.
— вязко-пластическое 402
— идеально пластическое 305, 320
сыпучее 375
упругое 404
— нелинейно-упругое 18, 304
— однородное изотропное 24
— релаксирующее 404
— упруго-вязкое 402
— упруго-вязкое, но не
релаксирующее 404
Тензор 85
— деформации 47
шаровой 49, 117
— напряжений 39
корректирующий 245
основной 2, 45
шаровой 50, 117
— функций напряжений 148
Теорема Ильюшина о простом
нагружении 315
— о разгрузке 316
Теория макронапряжений 23
— микронапряжений 23
— наследственных сред 403
— пластического течения 306, 378
— пластичности 19, 304 и д., 382 и д.
динамическая 381
— прочности математическая 19
прикладная 19
пятая 89
— сложного нагружения 403
— сооружений 18
27*

420
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Теория стесненного кручения по
Власову 298
— упруго-пластических деформаций
306
— упругости 11 ид., 14, 382 и д.
динамическая 253
дискретная 22, 64, 109
классическая 24
— — математическая 16, 68
нелинейная 18, 107, 325
прикладная 16, 255 и д.
— энергии формоизменения 89
Течение пластическое 378
Точка кинетическая секториальная
нулевая 370
Трение внутреннее сыпучей среды
374
Труба толстостенная,
упруго-пластическое осесимметричное состояние
334
Угол внутреннего, трения 374
Удлинение относительное 17, 42, 99
Упрочнение 305, 336
Упругость идеальная 24
Уравнение дифференциальное
упругой поверхности пластинки 264
— Коши 100
— Ламе 126
— Леви 131
— неразрывности деформаций в
полярных координатах 137
— реологическое состояние тела 406
— совместности или неразрывности
деформаций 103
Условие граничное 56, 62
— на контуре 78
— неразрывности деформации 100
Условие пластичности по Губер-Мизе-
су 320
— поверхностное 78
Устойчивость прямоугольной
пластинки, свободно опертой по
четырем сторонам и сжатой в одном
направлении 286
Фаза подобия девиаторов 327
Формоизменения 49, 51
Формула Журавского 57
Функция напряжений 137
для плоской задачи 133, 137
— — для трехмерной задачи 147
пластических 364
Прандтля 229
при осесимметричной
деформации 145
, сводящаяся к
тригонометрическим функциям и рядам 172
— поперечного распределения
прогибов 279
— Эри 135
Центр жесткости 297
— кинетический 370
Цилиндр толстостенный, осесимме-
тричная деформация 180 и д.
Шарнир пластический 357
— текучести 357
цилиндрический 395
Штамп жесткий, давление на него
пластической среды 373
Элемент тела линейный 34
Энергия удельная потенциальная 117
формоизменения 119
— упругая 14