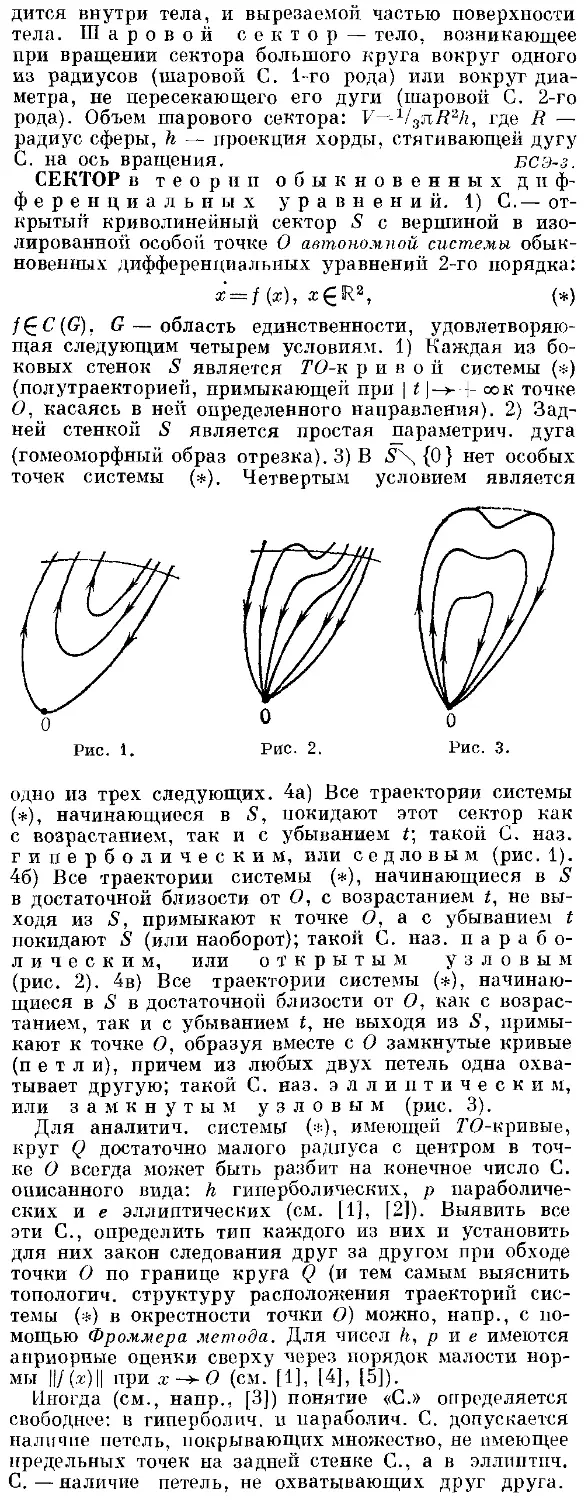
Текст
ОКА ТЕОРЕМЫ — теоремы о классич. проблемах
теории функций многих комплексных переменных, впер-
впервые доказанные К. Ока в 1930—50 (см. [1]).
1) О. т. о Кузена проблемах: первая проблема Кузена
разрешима в любой области голоморфности в С";
вторая проблема Кузена разрешима в любой области
голоморфности ЯсгС", гомеоморфной DiX...XDn,
где все области Dvc:C, кроме, возможно, одной, од-
носвязньт. ¦
2) О. т. о Леей проблеме: всякая пеевдовынуклая ри-
манова область является областью голоморфности.
Первоначально эта теорема была доказана К. Ока
для размерности «=-2; в случае произвольной размер-
размерности она доказана К. Ока и др. математиками.
3) Ока — Re и ля те о р е м а: пусть D — об-
область в С" и компакт KczD совпадает со своей обо-
оболочкой относительно алгебры Q(D) всех голоморфных
в D функций; тогда для любом функции /, голоморфной
в окрестпости К, и любого е>0 найдется функция
^'€6№) такая, что
шах | / — F | < 8.
К
Эта фундаментальная теорема теории голоморфных
приближений широко применяется в комплексном и
функциональном анализе.
4) О. т. о к о г е р е н т н о с т и: пусть Q — пучок
голоморфных функций на иомблсксноммногообразии X;
тогда для любого натурального числа р любой локально
конечно порожденный подпучок пучка QP=6X- • -Х0
(р раз) является когерентным аналитически.» пучком.
Это одна из основных теорем т. н. теории Ока --
Картина, к-рая существенно используется при доказа-
доказательстве Нартапа теорем Л и В.
Лит.: Г1] Ока К., Sur k's fourh'ons analitiques plusieurs
variables, Tokyo, 1961; Г2] X c|i м а и д с р Л., Введение в тео-
теорию функций несколько помп.н'коных переменных, пер. с англ.,
М., 1908; ПИ Г ;] п м и и г Р., I1 о с с и X., Аналитические функ-
функции многих комплексных переменных, пер. с англ., М., 1969.
Е. М. Чирка.
ОКАЙМЛЕНИЕ ПРОСТРАНСТВА X в биком-
бикомпактном р а с ти и р е н и и ЬХ— конечное семей-
семейство {?/,, . . ., Uk} открытых в X множеств такое, что
множество K\Ui[) . . . (J Uk бикомпактно и ЪХ~
= if|Jt/iU • • -Ut^fei гДе Uk—наибольшее открытое
в ЬХ множество, высекающее на X множество [/,- (X
предполагается вполне регулярным). Понятие О. и. X в
ЬХ совпадает с понятием близостного продолжаемого
окаймления пространства близости А' (близость на X
индуцирована расширением ЬХ), формулируемом в
близостных терминах: кроме бикомпактности К тре-
требуется, чтобы для любой окрестности (^ семейство
{Ьк-1 Uu ¦ ¦ ., Uk} было равномерным покрытием прост-
пространства X. Просто окаймлением пространства
X наз. его окаймление в бикомпактном расширении
Стоуна --- Чеха. На языке окаймлений формулируется
ряд теорем о размерности наростов бикомпактных рас-
расширении топологических и близостных пространств.
Лит.: [1J I', м п |i и о в Ю. М., «Матсм. сб.», 19В(>, т. 71, JN» 4,
с. 454—82. В. В. Федорчук.
ОКАЙМЛЕНИЯ МЕТОД — метод решения системы
линейных алгобраич. уравнений Ах~ Ь с невырожденной
матрицей, обращения матрицы и вычисления опреде-
определителя, основанный на рекуррентном переходе от ре-
решения задачи с матрицей
... ai,fc-i
i ••• ak-i,k~ll\
к решению задачи с матрицей А^, рассматриваемой
как результат окаймления A^-i-
Вычислительная схема О. м. для обращения матриц
такова. Пусть А)г^1 — невырожденная матрица. Для
обращения матрицы А^ используется представление
Ak-i "-к
Vk Ofefe
где
, ft» a2, k>
Тогда
»Oft + i
Ak-iukvkAk\
vkAk-i
A)
> Oft, *-i).
B)
Последовательное обращение матриц At, A 2, ¦ ¦ ., А„
по этой схеме дает матрицу А~г.
Описанная схема О. м. пригодна лишь для матриц
с отличными от нуля главными минорами. В общем слу-
случае следует принять схему О. м. с выбором главного
элемента. В этой схеме в качестве окаймляющих стро-
строки и столбца берутся тс, для к-рых a.k=akk—v^A^-iU^
будет максимальным по модулю. Тогда вычисленная
матрица будет отличаться от Л лишь перестановкой
строк и столбцов [1].
По быстродействию О. м. не уступает самым быстро-
быстродействующим из прямых методов обращения матрицы.
О. м. позволяет эффективно обращать треугольные
матрицы. Если A^-i— правая треугольная матрица,
то в A)
= 0 и А\1 =
О —
akk
Об'ьем вычислений в этом случае уменьшается в 6 раз.
Особенно эффективен О. м. при обращении эрмитовых
положительно определенных матриц. Для этих матриц
не нужно применять схему выбора главного элемента.
Кроме того, они могут быть заданы лишь половиной
своих элементов. Вычислительная схема в этом слу-
случае упрощается:
"¦к
i't
Вычислительная схема О. м. для решения системы
состоит н следующем. Пусть b'-*Pi--(aip, а.1р, . . ., а^,,O,
к=\, 2, . . .,' п\ й1". « + !) = _Ь. Если Л6_х —невы-
—невырожденная матрица и х{/г~1^Р)— решение системы
A^-ix^-1* /"+61*^ 1' Р]-О, то решение x{kP] системы
AkX*-kP)-rbikP)— -0 находится из представления
C)
и из B) следующим образом:
х 'Р п! о о!
1 +
«а-!| —z
x(k-x,p)
О
Таким образом, по решениям х(*-1- ^'и х1*' *' систем
с одной и той же матрицей A j_t и разными правыми ча-
частями легко получить решение системы с окаймленной
матрицей Ak. Решение исходной системы: хш'п + 1).
Оно может быть получено рекуррентным применением
соотношения D). Это сводится к последовательному
вычислению совокупности векторов х{кР\ А;- -1,2,
...,«, р>А, то есть
х(п-\,п)
По объему вычислительной работы приведенная схе-
схема О. м. равносильна Гаусса методу, одному из самых
быстродействующих прямых методов решения систем.
О. м. позволяет решать системы повышенного поряд-
порядка за счет эффективного использования памяти ЭВМ.
Это обусловлено тем, что для вычисления векторов
x(ft, p)^ р>к, требуется запоминание только векторов
x(k-i,p)t p>(k—\), и коэффициентов А-го уравнения
системы, т. е. массива чисел длины f(k)=k(n—&+1)+
+ (га+1). Поэтому для решения системы «,-го порядка
достаточно иметь рабочее поле длины (я+1) (ii+5)/4«
«(т?/2)а. При этом элементы матрицы и правой части
можно вводить в память ЭВМ не сразу, а последова-
последовательно — по строкам.
О. м. целесообразно использовать при решении
системы, для к-рой уже ранее решена усеченная систе-
система. Тогда соотношение D) сразу дает искомое решение.
Описанная схема О. м. может быть использована для
вычисления определителя. Из представления A) следует,
что
Рекуррентное применение этого соотношения дает \А\.
Так же, как и обращение матрицы, решение систолы
и вычисление определителя по О. м. возмогкно лишь
для матриц с ненулевыми главными минорами. В общем
случае здесь также необходимо использовать схему
выбора главного элемента.
Лит. 11] В о с и один В. В., Численные методы алгебры,
М., l!)Uii; [2] Ф а д д о е в Д. К., Фаддеева В. Н., Вычисли-
Вычислительные методы линейной алгебры, 2 изд., М,—Л., 1903.
Г. Д. Ким.
ОКАТЫВАНИЕ — см. Симметризация.
ОКЕАНОЛОГИИ МАТЕМАТИЧЕСКИЕ ЗАДАЧИ —
математические задачи и области физики, химии, гео-
геологии и биологии океана. В физике океана это прежде
всего задачи геофизич. гидродинамики (определяемой
как гидродинамика природных течений вращающихся
бароклмнных стратифицированных жидкостей). Вра
щенио Земли, существенно влияющее на крупномасш-
крупномасштабные течения (глобальных и синоптич. масштабов),
и стратификация, т. е. изменение плотности среды по
направлению силы тяжести (вертикали), создают спе-
цифич. анизотропию индивидуальных гидродинамич.
полей в океане или их статистич. характеристик, к-рую
необходимо учитывать, напр., при выборе базисных фун-
функций для описания этих полей по методу Галеркина, при
объективном анализе (интерполяции, экстраполяции,
сглаживании) эмпирич. данных об этих полях и выбо-
выборе статистич. моделей для вертикально-неоднородных
случайных полей турбулентности и внутренних волн.
Аналитич. описание собственных колебаний океана
при помощи линеаризированных уравнений гидроди-
гидродинамики затрудняется из-за неправильной формы его
границ — дна и берегов, что делает невозможным ис-
использование решений с разделяющимися переменными.
Поэтому в теории приливов, в к-рой существенна воз-
возможность резонансных реакций океана на приливообра-
приливообразующие силы, имеются аналитич. расчеты лишь для
модельных океанов правильной формы (напр., ограни
ченных отрезками меридианов и параллелей). В реаль-
реальной же геометрии последовательные (возрастающие) соб-
собственные частоты должны определяться как экстремумы
квадратичных интегральных функционалов, родствен-
родственных энергии, на экстремалях, подбираемых по методу
Галеркина; такой подход полностью еще не реализован.
В теории приливов заметна не только линейная, но и
нелинейная реакция океана на приливообразующие си-
силы, к-рая может быть описана при представлении вы-
высоты прилива в виде функционального степенного ряд»
по нриливообразующим силам; функциональные коэф-
коэффициенты такого ряда описывают свойства океана как
резонансной системы.
Для океана специфично наличие среди решений урав-
уравнений гидродинамики нескольких классов волн — акус-
акустических, поверхностных (капиллярных и гравитацион
ных), внутренних гравитационных, инерционных (вклю-
(включая баротропные и бароклинные волны Росби —
Блиновой, образующиеся вследствие изменения с ши-
широтой вертикальной проекции угловой скорости вра-
вращения Земли) и, наконец, гидромагнитных, возникаю-
возникающих при движениях электропроводной жидкости (со-
(соленой морской воды) в геомагнитном поле. Построение
отдельных классов волновых решений (и динамич. урав-
уравнений для них) осуществляется при помощи асимпто-
тич. методов нелинейной механики, родственных ме-
методу Ван дер Поля, в виде асимптотич. рядов по сте
пеням малых параметров, стоящих при «лишних» про
ипводных по времени. Примером служит т. н. квазигео
строфич. разложение, отфильтровывающее из числи
решений уравнений гидродинамики быстрые волны и
выделяющее класс волн Росби—Блиновой.
Волны в океане, как правило, нелинейны. Для длин-
длинных нелинейных волн, поверхностных и внутренних,
удается вывести уравнение Кортевега—де фрига и ис-
использовать его солитонные и периодические (кноидаль-
пые) решения. Для коротких волн сколько-нибудь общих
методов нахождения солитонных и периодич. решений
еще не построено, и существуют лишь отдельные приме-
примеры (капиллярные полны Сле.чкина — Краипера, гравита-
гравитационные волны Герстнера и Стокса, баротропные и ба-
бароклинные солитоны Росби). Недостаточно развиты
и статистич. теории нелинейных волновых полей, осо-
особенно актуальные для описания поверхностных и вну-
внутренних гравитационных волн (для внутренних волн —
с генерацией ими турбулентных пятен и расплываниом
последних в смой вертикальной микроструктуры) и
волн Росби (с эволюцией квазидвумерной турбулент-
турбулентности в нелинейное волновое поле).
Одной из важнейших проблем гидродинамики океана
является математич. моделирование его циркуляции
(в наиболее общей постановке — в его взаимодействии
с атмосферой через т. н. верхний перемешанный слон
океана и пограничный слой атмосферы), причем вслед-
вследствие большой ширины спектра масштабов пространст-
пространственных неоднородностей (от миллиметров до 10' кило-
километров) моделируемая система здесь имеет огромное
число степеней свободы (при миллиметровых элементар-
элементарных объемах порядка 1028), и неизбежно возникает
необходимость их аггрегирования, напр, методом пара-
параметризации мелкомасштабных процессов.
При аппроксимации континуальных гидродинамич.
уравнений разностными возникают вопросы о порядке
аппроксимации, сходимости и устойчивости разностной
схемы. В современных т. п. вихреразрешающих моде-
моделях циркуляции океана используются пространствен-
пространственные сетки с горизонтальными тагами порядка немно-
немногих десятков километров. Конкурирующими могут быть
схемы, использующие спектральные (в том числе галер-
кинские) разложения пространственных гидродинамич.
полей.
Основные задачи математич. обработки данных изме-
измерений в гидродинамике океана делятся на задачи зон-
зондирования (функции от глубины, их разложения на мо-
моды, спектры), буксировки (горизонтальные и прост-
пространственно-временные спектры с доплеровскими эффек-
эффектами) и полигонных измерений (временные ряды на
трехмерной сетке точек, их спектры и взаимные спект-
спектры, объективный анализ, синхронные пространствен-
пространственные картины, четырехмерный анализ волновых полей).
В акустике океана рассматриваются типичные зада-
задачи распространения волн в слоистых средах; для ана-
литич. описания вертикальной структуры волновых по-
полей в ряде случаев используется приближение ВКБ
(см. ВКВ-метод). В оптике океана сиецифич. процес-
процессом является многократное рассеяние света, для опи-
описания к-рого используются численные решения уравне-
уравнения переноса излучения, получаемые методами Монте-
Карло, и асимптотические аналитич. решения. В химии
океана важной математич. задачей является расчет
конвективной диффузии неконсервативных примесей со
специфич. источниками и стоками.
В геологии океана в связи с развитием мобилистской
геотектоники (т. н. тектоники литосферных плит)
возникли задачи кинематич. расчетов движения жест-
жестких плит на поверхности сферы и их генетич. объясне-
объяснения при помощи математич. моделирования процессов
плотностной конвекции в земной мантии (возникаю-
(возникающей вследствие перехода тяжелых веществ из мантии в
ядро). Одной из важных частных задач геологии явля-
является биостратиграфия, т. е. распознавание возрастов
слоев осадочных пород по содержащимся в них микро-
па леонтологич. ассамблеям при помощи программ с са-
самообучением (пока что в большинстве работ эта задача
решается приближенно без использования ЭВМ).
Весьма объемные вычислительные задачи оценки ста-
тистич. характеристик сигналов, фильтрации шумов и
распознавания образов возникают при регистрации и
обработке данных морского многоканального непрерыв-
непрерывного глубинного сейсмопрофилирования и вибропросве-
вибропросвечивания океанского дна, причем в ряде случаев и при
постановке измерений (пространственные распределе-
распределения излучателей и приемников сигналов), и при их
регистрации перспективны голографпч. методы, ис-
использующие преобразования Фурье.
В биологии океана в проблеме управления биологич.
продуктивностью океана важное значение приобретает
математич. моделирование структуры и функциониро-
функционирования экологич. систем и, в частности, динамики попу-
популяции. Примером служит задача об эволюции со вре-
временем t вертикальных распределений g,(z, t) компонент
q; экологич. системы (включающих концентрации ряда
видов фито- и зоопланктона, кислорода, углекислого
газа, фосфорных и азотных солей, температуру и соле-
соленость воды, освещенность фотосинтетическн-активной
радиацией), описываемой уравнениями вида
где Aia. Bia\i — биологич. и биофизич. параметры;
здесь представляют интерес как численные решения
задачи Коши с конкретными начальными данными, так
и выводы качественной теории дифференциальных урав-
уравнений о поведении решений в целом и об их зависимости
от имеющихся в уравнениях параметре!!.
Лит.: [1] Биология океана, т. 1—2, М., 1977; [2] Физика
океана, т. 1, М,, 1978; [3] Геофизика океана, т. 1—2, М., 197!'
[4] Химия океана, т. 1—2, М., 11O9; [5] Геология океана, т. 1
М., 1979. А. С, Монин
ОКОЛЬЦОВАННОЕ ПРОСТРАНСТВО — топологиче-
топологическое пространство X, снабженное пучком колец Qx-
Пучок Qx наз- структурным пучком О. п.
(^> Qx)- Обычно предполагается, что Qx есть пучок
ассоциативных и коммутативных колец с единицей.
М орфизмом О. п. (X, Qx) в О. п. (У, Qy) наз.
пара (/, /*), где / : X^>-Y ¦— непрерывное отображение
и /*: j*Qy—f.Qx— гомоморфизм пучков колец над Y,
переводящий единицы слоев в единицы. О. п. п их
морфизмы составляют категорию. Задание гомомор-
гомоморфизма /* равносильно заданию гомоморфизма
переводящего единицы в единицы-
Окольцованное пространство (A', Qx) наз. л о-
кально окольцованным, если Qx — пучоь
локальных колец. В определении морфизма (/, /#)
локально О. п. (X, Qx)-+{Y, Qy) дополнительно
предполагается, что для любого х?Х гомоморфизм
является локальным. Локально О. п. составляют под-
подкатегорию в категории всех О. н. Другую важную под-
подкатегорию составляют О. п. над (фиксированным) полем
к, то есть О. п. (X, Qx), где Qx — пучок алгебр над
к, а морфизмы согласованы со структурой алгебр.
Примеры О. п. 1) Каждому топологич. простран-
пространству X соответствует О. п, (X, Сх), где Сх— пучок
ростков непрерывных функций на X.
2) Каждому дифференцируемому многообразии!
(напр., класса С°°) X соответствует О. п. (X, Ох), где
О^~ пучок ростков функций класса 6"° на X; при
этом категория дифференцируемых многообразий вкла-
вкладывается в категорию О. п. над R в качестве полной
подкатегории.
3) А налитические многообразия и аналитические
пространства над полем к составляют полные подка-
подкатегории в категории О. п. над к.
4) Схемы составляют полную подкатегорию в кате-
категории локально О. п.
Лит.: [1] Шафарспич И. Р., Основы алгебраическом
геометрии, М., 1972; [2] Хартсхорн Р., Алгебраически,;
геометрия, пер. с англ., М., 198]. А. Л. Онищш;.
ОКРЕСТНОСТЬ точки х (подмножества
А) топологического пространства —любое открытое
подмножество этого пространства, содержащее точку
х (множество А). Иногда под О. точки х (множества А)
понимается любое такое подмножество топологич.
пространства, к-рое содержит точку х (множества А)
В своей внутренности. Б. А. Пасынков
ОКРУГЛЕНИЕ числа — приближенное пред
ставленне числа в нек-рой системе счисления с помощью
конечного количества цифр. Необходимость О. дикту-
диктуется потребностями вычислении, в к-рых, как правило,
окончательный результат не может быть получен аб-
абсолютно точно и следует избегать бесполезного выписы-
выписывания лишних цифр, ограничивая все числа лишь
нужным количеством знаков.
При О. числа оно заменяется другим числом (/-раз-
(/-разрядным, т. е. имеющим t цифр), представляющим его
приближенно. Возникающую при этом погрешность
наз. погрешностью округления, или
ошибкой округления.
Применяются различные способы О. числа. Простей-
Простейший из них состоит в отбрасывании младших разрядов
числа, выходящих за t разрядов. Абсолютная погреш-
погрешность О. при этом не превосходит единицы t-то раз-
разряда числа. Способ О., обычно применяемый в ручных
вычислениях, состоит в О. числа до ближайшего /-раз-
/-разрядного числа. Абсолютная ошибка О. при этом не пре-
превосходит половины «-го разряда округляемого числа.
Этот способ дает минимально возможную ошибку среди
всех способов О., использующих t разрядов.
Способы О., реализуемые на вычислительной маши-
машине, определяются ее назначением, технич. возможностя-
возможностями п, как правило, уступают по точности О. до бли-
ближайшего f-разрядного числа. В ЭВМ наиболее приня-
приняты два режима арифметич. вычислении: т. н. режим с
плавающей запятой и режим с фиксированной занятом.
В режиме с плавающей запятой результат О. числа име-
имеет определенное количество значащих цифр; в режиме
с фиксированной запятой — определенное количество
цифр после запятой. В первом случае принято гово-
говорить об О. д о ( разрядов, во втором — об О. д о
t разрядов после запятой. При этом в
первом случае контролируется относительная погреш-
погрешность О., во втором — абсолютная погрешность.
В связи с использованием вычислительных машин
развились исследования накопления ошибок О. в
больших вычислениях. Анализ накопления ошибок в
численных методах позволяет характеризовать методы
по чувствительности их к ошибкам О., строить страте-
стратегии реализации их в вычислительной практике, учи-
учитывающие ошибки О., и оценить точность окончатель-
окончательного результата.
Лит.: [1] К рыло и А. Н., Лекции о приближенных вы-
вычислениях, 5 изд., М.— Л., 1950; 12] Б е р с з и в И. С, Ж и д-
ков Н. П., Методы вычислений, 3 изд., т. 1, М., 19'i6; [3] Б а х-
в а л о в Н. С, Численные методы, 2 изд., М., 1975; [4] В о е в о-
д и н В. В., Вычислительные основы линейной алгебры, М.,
1977. Г. Д. Ким.
ОКРУГЛЕНИЯ ТОЧКА — эллиптическая точка по-
поверхности, в к-poii соприкасающийся параболоид вы-
вырождается в параболоид вращения. В О. т. нормальные
кривизны по всем направлениям равны, Дюпена инди-
индикатриса является окружностью. О. т. иногда наз.
омбилической точкой, шаровой т о ч-
к о й, или круговой точкой. Д- Д. Соколов.
ОКРУЖНОСТЬ — замкнутая плоская кривая, все
точки к-рой одинаково удалены от данной точки (ц е н т-
р а О.), лежащей в той же плоскости, что и кривая. О.
с общим центром наз. концентрическими.
Отрезок R, соединяющий центр О. с какой-либо ее
точкой (а также длина этого отрезка), наз. ради у-
с о м О. Уравнение О. в прямоугольных декартовых
координатах:
(*-«.)*+(у-6)«= Л»,
где а и Ь — координаты центра.
Прямая, проходящая через две точки О., наз. с е-
кущей; отрезок ее, лежащий внутри О.,— х о р-
д о й. Хорды, равноотстоящие от центра, равны. Хорда,
проходящая через центр О., наз. ее диаметром.
Диаметр, перпендикулярный к хорде, делит ее попо-
пополам.
Каждая из двух частей, на к-рые две точки О. де-
делят ее, наз. дугой.
Угол, образованный двумя радиусами О., соединяю-
соединяющими ее центр с концами дуги, наз. центральным
у г л о м, а соответствующая дуга — дугой, на к-рую
он опирается. Угол, образованный двумя хордами с
общим концом, наз. вписанным углом. Впи-
Вписанный угол равен половине центрального угла, опи-
опирающегося на дугу, заключенную между концами впи-
вписанного угла. Длина окружности С=2яД, длина дуги
г=ГБ7гг-=-~Ла- где а0— величина (в градусах) соответст-
вующего центрального угла, а — его радианная мера.
Если через какую-либо точку плоскости провести
к О. несколько секущих, то произведение расстояний
от точки до обеих точек пересечения каждой секущей
с О. есть постоянное число (для данной точки), в част-
частности, оно равно квадрату длины отрезка касательной
к О. из этой точки (степень точки). Совокупность
всех точек плоскости, относительно к-рых данная точка
имеет одинаковую степень, составляет связку О. Сово-
Совокупность всех общих О. двух связок, лежащих в одной
плоскости, наз. пучком О.
Часть плоскости, ограниченная О. и содержащая ее
центр, наз. кругом. Сектором наз. часть кру-
круга, ограниченная дугой О. и радиусами, проведенны-
проведенными в концы этой дуги. С с г м с н т о м наз. часть кру-
круга, заключенная между дугой и ее хордой.
Площадь круга S — nR2, площадь сектора Sx=
, где а —градусная мера соответствующего
центрального угла, площадь сегмента 52=я/?2,{|,(I1 ±
±S/±, где 5д—площадь треугольника с вершинами в
центре круга и в концах радиусов, ограничивающих
соответствующий сектор, знак «—» берется, если
а°<180°, и знак «+», если а°>180°.
О. на выпуклой поверхности локально почти изоме-
трична границе выпуклой поверхности конуса (т е о-
рема Залгаллера). О. в многообразии огра-
ограниченной кривизны может иметь достаточно сложное
строение (т. е. могут существовать угловые и кратные
точки, О. может состоять из нескольких компонент и
т. п.). Тем не менее точки О. в многообразиях ограни-
ограниченной кривизны можно естественно упорядочить,
превратив ее тем самым в циклически упорядоченное
множество (см. [1]).
Об О. в более общих пространствах — банаховых,
финелеровых и т. п. см. в ст. Сфера.
Лит.: Ш Энциклопедия элементарной математики, кн. 4,
М., 1963; [2] «Тр. Матем. ин-та АН СССР», 1065, т. 7(i, с. 88—114.
А. Б. Иванов.
ОКТАНТ — любая из восьми областей, на к-рые про-
пространство делится тремя взаимно перпендикулярными
координатными плоскостями.
ОКТАЭДР — один из пяти типов правильных много-
многогранников. О. имеет 8 граней (треугольных), 12 ребер,
6 вершин (в каждой вершине
сходятся 4 ребра). Если а —
длина ребра О., то его объем
БСЭ-3.
ОКТАЭДРА ПРОСТРАНСТ-
ПРОСТРАНСТВО — пространство, получаю-
получающееся из октаэдра при отожде-
отождествлении противоположных его
граней — треугольников, по-
повернутых друг относительно друга на угол я/3. О. п. —
трехмерное многообразие, являющееся пространством
орбит действия бинарной группы октаэдра на трехмер-
трехмерной сфере. Оио может быть отождествлено с и р о с т-
ранством куба, получающимся аналогичным
образом. Одномерная группа Бетти О. п. является груп-
группой третьего Порядка. М. И. Войцехоеспий-
ОМБИЛИЧЕСКАЯ ТОЧКА — то же, что округлении
точка.
«ОМЕГА-КВАДРАТ» РАСПРЕДЕЛЕНИЕ — рас-
распределение вероятностей случайной величины
где Z(t) — условный винеровскии процесс. Характерп-
стич. функция «О.-к.» р. выражается формулой
В математической статистике «О.-к.» р. часто встре-
встречается в связи со следующим обстоятельством. Пусть
Х1, . . ., Хп— независимые случайные величины, рав-
равномерно распределенные на [0, 1], по к-рым построе-
построена функция эмпирич. распределения Fn(-). В этом
случае процесс
слабо сходится К условному винеровскому процессу,
откуда следует, что
Игл Р { J о Z«О dt<\.}=P {со2 < \} =
^Ldt,x>o.
x Bt-l)n V-t sin t
См. также Крамера — Мизеса критерий.
Лит.: [1] С м и р н о в Н. В., «Матем. сб.», 1937, т. 2, с. 973 —
993; [2] Anderson Т. W., D а г 1 i n g D. A., «Ann. Math.
Statist.», 1952, v. 23, p. 193 — 212. M. С. Никулин.
ОМЕГА-НЕПРОТИВОРЕЧИВОСТЬ — свойство фор-
формальных арифметич. систем, означающее невозможность
получения омега-противоречия. Омега-противо-
Омега-противоречием наз. такая ситуация, когда для нек-
некрой формулы А (х) доказуема каждая формула из бес-
бесконечной последовательности формул А (П;П), А (Г1~1),
. . ., А A~мЛ), ... и формула ~\УхА (х), где ' 0 ' --
константа формальной системы, обозначающая число О
а константы Г~п ' определяются рекурсивно через терм
(а:)', обозначающий число, непосредственно следующее
за х: Гп + 1-| = (Г«П)'.
Понятие О.-н. появилось в свяяи с Гёде.чя теоремой
а неполноте арифметики. Именно в предположении
О.-н. формальной арифметики К. Гёдель (К. Godel)
доказал ее неполноту. Свойство О.-н. сильнее свойства
просто» непротиворечивости. Простая непротиворе-
непротиворечивость получится, если взять в качестве А (х) формулу,
не содержащую х. Из теоремы Гёделя о неполноте
вытекает существование непротиворечивых, но омега-
иротиворечивых систем.
Лит.: [1] К л и н и С. К., Введение в метаматематику, пер.
с англ., М., 1957. В. Н. Гришин.
ОМЕГА-ПОЛНОТА — свойство формальных ариф-
арифметич. систем, состоящее в том, что для всякой формулы
А (х) из выводимости формул А (ПЗ^), А (ГО), . . .
.. .,А (f~ri~l), . . . следует выводимость формулы УхЛ (х),
где 1~и~1 — константа, обозначающая натуральное число
п или 0. В противном случае система наз. омега-
неполной. К. Гёдель в своей теореме о неполноте
формальной арифметики фактически установил ее оме-
омега-неполноту. Если в качестве аксиом взять множество
всех формул, истинных в стандартной модели арифме-
арифметики, то получится омега-полная акскоматнч. система.
Наоборот, во всяком омега-полном расширении ариф-
арифметики Пеано выводима всякая истинная в стандарт-
стандартной модели формула.
Лит.: tl] К лини С. К.-, Введение в метаматематику,
пер. с англ., М., 1957. В. Н. Гришин.
ОПЕРАНД в языках программирова-
программирования — аргумент операции; грамматич. конструкция,
обозначающая выражение, задающее значение аргу-
аргумента операции; иногда О. наз. место, позиция в тек-
тексте, где должен стоять аргумент операции. Отсюда
понятие местности, или арности, операции,
т. е. числа аргументов операции.
В зависимости от положения О. относительно знака
операции различают префиксные (напр., sin ,r),
инфиксные (напр., а+fo) и нос т ф и к с н ы с.
(напр., х2) о п е р а ц и и. В зависимости от числа 0.
различают одноместные (унарные, или м о-
надические) операции; двуместные
(бинарные, или диадические) опера-
операции; многоместные (или полиадиче-
полиадические) операции.
В связи с различением операнда-позиции и операн-
операнда как фактического аргумента возникает понятие
приведения О. к виду, требуемому операцией. Напр.,
если действительный аргумент находится в позиции
целого О., правила языка могут подразумевать тот
или иной способ округления действительного числа
до подходящего целого. Другим примером приведения
является изменение формы представления объекта,
напр. скаляр приводится к вектору, состоящему из
одной компоненты. А. п. Ершов.
ОПЕРАТОР в программировании —
грамматическая конструкция в языках программирова-
программирования, выражающая нек-рое законченное действие при
выполнении программы на ЭВМ. В императивных язы-
языках программирования (напр., алгол, фортран) О.
является командой, предписывающей выполнить вы-
выражаемое им действие. В апликативных языках
(напр., лисп) О. является обозначением результата
выполнения выражаемого им действия. В нек-рых язы-
языках (напр., алгол-68) императивные и аплнкативные
свойства О. объединяются: каждый О. вырабатывает
нек-рое значение, может быть пустое, и выполняет
(в качестве побочного эффекта) предписываемое им
действие. Обычно действие О. состоит из двух частей:
информационной и логической.
Инфор маг; ионная часть О. состоит в
выработке нек-рого значения как функции состояния
памяти или, более общо, в отображении состояния па-
памяти на другое состояние.
Логическая часть О. состоит в выборе пз
программы другого О., выполняемого вслед за данным.
В зависимости от однозначности выбора имеет место
детерминированность или недетерминированность вы-
выполнения программы.
См. также Алгоритмический язык. а. п. Ершов.
ОПЕРАТОР — отображение одного множества на
другое, каждое из к-рых наделено нек-рой структурой
(алгебраич. операциями, топологией, отношением по
рядка). Общее определение О. совпадает с определением
отображения пли функции: пусть X и У — два мно-
множества ; оператором А из множества X во мно-
множество Y наз. правило или соответствие, к-рое каждому
алементу х из нек-рого подмножества DaX сопостав-
сопоставляет однозначно определенный элемент A (x)?Y; мно-
множество D наз. областью определения опе-
оператора А и обозначается D (А); множество {А (х),
х? D} наз. областью значений опера-
оператора Ли обозначается R(A). Часто пишут Ах вме-
вместо А (х). Термин «О.» используется чаще всего в слу-
случае, когда X и Y — векторные пространства. Если
А — оператор из X в Y, где Y ^Х, то А наз. о и е-
ратором в X. Если D(A)-=X, то А наз. всюду
определенным оператором. Если Alt
А 2— операторы из Х± в Yx и из Хг в У2 с областями
определения D (Ay) и D {A 2) соответственно и такяр, что
D (A-^aD (A 2) и А-ух-А.2х при всох jf O(i,), то при
Xy— X 2, У1"- У2 оператор Лг называется сужен нем,
или ограничение м, оператора А 2, а оператор
А2~ р асширением оператора 4j; при XiCTX2,
Л 2 называется расширением оператора Аг с выходом
из Хь
Многие уравнения в функциональных или абстракт-
абстрактных пространствах можно представить в виде Ах---у,
гДе !l?Y, .т?Х, у — задан, х — неизвестен, /4 — опе-
оператор из X в У. Утверждение о существовании реше-
решения такого уравнения при любой правой части y?Y
равносильно утверждению, что область значении опе-
оператора А есть все иространство У; утверждение, что
уравнение А (х)= у имеет при любом y?R(A) единст-
единственное решение, означает, что А взаимно однозначно
отображает D (А) на Я (А).
Если X и У — векторные пространства, то в множе-
множестве всех О. из X в У можно выделить класс линейных
операторов; остальные О. из .Y в У на:!, н е л и н е й-
н ы м и операторами. Если X и У — тополо-
топологические векторные пространства, то в множестве 0.
из X в У естественно выделяется класс непрерывных
операторов, а также класс ограниченных ли-
линейных операторов Л (таких операторов А,
что образ любого ограниченного множества в X огра-
ограничен в Y) п класс линейных компактных операторов
(т. е. таких О., что образ любого ограниченного мно-
множества в X предкомпактен в У). Если X и У — локаль-
локально выпуклые пространства, то в X и У естественно рас-
рассматривать различные топологии; О. наз. п о л у н е-
1т р е р ы в н ы м, если он определяет непрерывное
отображение пространства X (в исходной топологии)
в пространство У в слабой топологии (понятие полуне-
полунепрерывности используется главным образом в теории
нелинейных О.); О. наз. усиленно непрерыв-
н ы м, если он непрерывен как отображение простран-
пространства X в ограниченно слабой топологии в пространство
У; О. наз. слабо непрерывным, если он
определяет непрерывное отображение X в У, где X и
Y наделены слабой топологией. Часто компактные О.
наз. вполне непрерывным и. Иногда тер-
термин «вполне непрерывный О.» используется вместо
термина «усиленно непрерывный О.» или для обозна-
обозначения О., переводящего любую слабо сходящуюся после-
последовательность в сильно сходящуюся; если X и У —
рефлексивные банаховы пространства, то эти условия
эквивалентны компактности О. Если О. усиленно не-
непрерывен или компактен, то он непрерывен; если О.
непрерывен, то он слабо непрерывен.
Графиком оператора А наз. множество
Г(/1)сгХХУ, определенное соотношением
Г (А) = {{х, Ах}, x?D (A)}.
Пусть X и У — топологические векторные простран-
пространства; оператор Л из X в У наз. замкнутым оператором,
если его график замкнут. Понятие замкнутого О. осо-
особенно плодотворно в случае линейных О. с плотной
областью определения.
Понятие графика позволяет обобщить понятие О.:
многозначным оператором из X в У
наз. любое подмножество А в XX К; если X и У —
векторные пространства, то многозначным линейным
О. наз. линейное подпространство X >, У; областью
определения многозначного О. наз. множество
V (А) = {х?Х: существует y?Y такой, что {х, у}?А).
Если X — векторное пространство над полем к
и У=/с, то всюду определенный О. из X в к наз. функ-
функционалом на X.
Если X и У — локально выпуклые пространства,
то оператор А из X в У с плотной в X областью опре-
деления имеет сопряженный оператор Л * с ило-тои п
У* в ослабленном топологии областью омрею.ченин
тогда и только тогда, когда А — .(амкпу ii.ni О,
Примеры операторов. I) О. сопоставля
ющий любому элементу х?Х элемент 0?V (н у л о
вой оператор).
2) О., сопоставляющий любому элементу ,r?.Y ятот
же элемент х ? X (единичный опер а т о р is
X обозначается id^ или 1#).
3) Пусть X — векторное пространство функции на
нек-ром множестве М и / — функция на М; О. в X
с областью определения
действующий по правилу
при <f?D {А), нал. о п е р а т о р о м \ м о о '.к с н и я
на функцию; А — линейный О.
4) Пусть X — векторное пространство функции на
множестве М и F — отображение множества М в себя;
О. в X с областью определения
действующий по правилу
Лф = ф о /•'
при ф?О(Л), будет линейным О.
5) П X Y
р ф?()
5) Пусть X, Y — векторные пространства дейстип
тельных измеримых функций на пространствах с мерог
(М, ~щ, и) и (N, 2дг, v) соответственно, if — функция
на Л/ХЛгхК, измеримая относительно произведения
мор [tXvXUoi гДе N— мера Лебега на R. и непрерыв-
непрерывная по t?R при любых фиксированных т?М, n?N;
О. из X в У с областью определения
D(A)-=\q>eX:f.(x)=[ К (х, y,<p(y))dy),
1 •> М I
существующий для почти всех x?N n f?Y, дс1'|ствую-
щий по правилу Лф=/ при ц>?и(А), наз. интег-
интегральным оператором; если
К(х, у, z) = K(x, y)z, x?M, y?\, z?R,
то А линейный О.
6) Пусть X — векторное пространство функций на
дифференцируемом многообразии М, 2; — векторное
ноле на М; оператор Л в X с областью определения
U (Л) = {/?Х: производная D^f
функции / вдоль поля | определена всюду и D*f?X},
действующий по правилу Af—Dt,f при f?D(A), hh:i.
оператором дифференцирования;/! —
линейный О.
7) Пусть X — векторное пространство функций на
множестве М; всюду определенный О., сопоставляющий
функции ф?Х значение этой функции в точке а?М.
есть линейный функционал на X; он наз. 6-ф у н к ц н-
е и в т о ч к е а и обозначается ба.
8) Пусть G — коммутативная локально компактная
группа, G — группа характеров группы G; dg, dii
меры Хаара на G, G соответственно; пусть
X=L2(G, d,a). Y=L-(G, dj>);
лине]'шый оператор А из X в У, сопоставляющий Функ-
Функции /?Х функцию /?У, определяемую формулой
/ Q) = \ I (g) g (g) dg
всюду определен, если сходимость интеграла пони-
понимается как сходимость г; среднем.
Еслн X и Y — топологические векторные простран-
пространства, то О. в примерах 1) и 2) непрерывны; если в при-
примере 3) пространство X есть L2(M, 2ЛЬ и), где jx —
мера на X, то О. умножения на ограниченную измери-
измеримую функцию замкнут и имеет плотную область опре-
определения; если в примере 5) пространство X=F есть
гильбертово пространство L2(M, 2^, |х) и К (х, у, z) =
= АГ(х, у) z, где К (х, у) принадлежит L2{MxM,
2д|X 2^ц, цХ |х), то А компактен; если в примере 8) про-
пространства X и У рассматриваются как гильбертовы
пространства, то А непрерывен.
Если А — О. из X в Y такой, что АхфАц при хфу,
x,y(zD{A), то можно определить обратный оператор
A~J к А; вопрос о существовании обратного О. и его
свойствах связан с теоремой существования и единст-
единственности решения уравнения Ax=f\ если А~л сущест-
существует, то х—A~1f при f?R(A).
Для О. в векторных пространствах можно опреде-
определить сумму, произведение на число и произведение О.
Если А . В — операторы из X в Y с областями опреде-
определения D (Л) и D (В) соответственно, то сум м о и
операторов А л В наз. О., обозначаемый А-\-В,
с областью определения
= D (A)[\D (В),
действующий по правилу
(А + В) х = Ах-\-Вх
при x?D D+B). Произведением опера-
оператора Л на число X наз. О., обозначаемый ХА,
с областью определения
D (ХА) = D (А),
действующей по правилу
(ХА) х~Х (Ах)
при х ? D (КА). Произведение операто-
операторов определяется как композиция отображении:
если А оператор из X в Y, В — оператор из Y в Z.
то произведением В и А наз. оператор ВЛ с областью
определения
(В)},
действующий по правилу
(ВА)х = В (Ах)
при ?(
Если Р — всюду определенный О. в X такой, что
РР=Р, то Р наз. проектором в X; если / —
всюду определенный О. в X такой, что //— idx, то /
наз. инволюцией в X.
Теория О. составляет важнейшую часть линейного
и нелинейного функционального анализа, являясь, и
частности, основным аппаратом теории динамич. сис-
систем, представлений групп и алгебр и важнейшим мате-
матич. инструментом математич. физики и квантовой
механики.
Лит.: Г1] Л ю с т с р н и к Л. А., Соболев В. И., Эле-
Элементы функционального анализа, 2 изд., М., 1965; [2] Коли о-
г о р о в А. Н., Фомин С. В., Элементы теории функций и
функционального анализа, й изд., М., 1981; [3] К а н т о р о-
в и ч Л. В., А к и л о в Г. П., Функциональный анализ, 2 изд.,
М., 1977; [4] Д а н ф о р д Н., Шварц Дж. Т., Линейные опе-
операторы, пер. с англ., ч. 1—3, М.,,1962—74;[5] Э д в а р д с Р. -Э.,
Функциональный анализ, пер. с англ., М., 1969; [6] И о с и д а
К., Функциональный аналиа, пер. с англ., М., 1967.
М. А. Нпймарк, А. П. Штерн.
ОПЕРАТОРНАЯ ГРУППА — 1) О. г.— однопарамет-
рическая группа операторов в банаховом пространст-
пространстве Е, т. е. семейство линейных ограниченных опера-
операторов f/f, -<x <(<<», такое, что UB—I, Us + t=Us-Ut
и b't непрерывно зависит от t (в равномерной, сильной
или слабой топологии). Если Е — гильбертово про-
пространство и \\Ui\\ равномерно ограничены, то группа
{подобна группе унитарных операторов (теоре-
(теорема Надя).
Лит.: [1] S г.- N a g у В., «Acta Univ. szeged. Sec. scient.
Math.», 1947, t. 11, p. 152 — 57; [2] X и л л е Э., Фи л л и не Р.,
Функциональный анализ и полугруппы, пер. о англ., 2 изд.,
М., 1962. В. И.Ломоносов.
2) О. г., группа с областью операто-
операторов 2,— такая группа G, что всякому элементу a?G
н всякому о?2, где 2 —нек-рое множество символов,
поставлен в соответствие элемент aa?G, причем
(ab)a=aa-ba при любых a, b?G. Пусть G и G'— группы
с одной и той же областью операторов 2; изоморфное
(гомоморфное) отображение ф группы G на G' наз. опе-
операторным изоморфизмом (гомомор-
(гомоморфизмом), если (аа)ф—(яф)о для любых a?G, а? 2.
Подгруппа (нормальный делитель) Я группы G с об-
областью операторов 2 наз. допустимой под-
подгруппой (допустимым нормальным
делителем), если На^Н при всяком а?2. Пе-
Пересечение всех допустимых подгрупп, содержащих
данное подмножество М группы G, наз. д ои уст и-
м о й подгруппой, порожденной мно-
множеством М. Группа, не имеющая допустимых
нормальных делителей, кроме себя и единичной под-
подгруппы, наз. простой (относительно заданной
области операторов). Всякая факторгруппа О. г. по
допустимому нормальному делителю является группой
с той же областью операторов.
Группа G наз. группой с полугруппой
операторов 2, если G — группа с областью опе-
операторов 2,2 — полугруппа и а(ах)=(аа) т. для любых
a?G, а, т?2. Если 2 —полугруппа с единицей ё,
то считается, что ае~ а при всяком a?G. Всякая груп-
группа с произвольной областью операторов 20 есть группа
с полугруппой операторов 2 , где 2 — свободная полу-
полугруппа, порожденная множеством 20. Группа F с полу-
полугруппой операторов 2, обладающей единицей, наз.
2 — свободной, если она порождается такой
системой элементов X, что элементы ха, где х? X, а? 2 ,
составляют для F (как группы без операторов) систему
свободных образующих. Пусть F есть Г-свободная
группа (Г— группа операторов), Д — подгруппа груп-
группы Г, f?F и Af, \ — допустимая подгруппа группы F,
порожденная всеми элементами вида f-'1(fa), где <х?Д.
Тогда всякая допустимая подгруппа группы F явля-
является операторным свободным произведением групп типа
Af, д и нек-рой Г-свободной группы (см. [2]). Если
2 — свободная полугруппа операторов, то при аф\.
допустимая подгруппа 2 -свободной группы F, порож-
порожденная элементом а, сама является 2-свободной груп-
группой со свободным образующим а (см. также [3]).
Абелева группа с ассоциативным кольцом операторов
К — это модуль над К.
Лит.: [1] К у р о ш А. Г., Теория групп, 3 изд., М., 1967;
[2] 3 а в а л о С. Т., «Матем. сб.», 1953, т. 33, с. 399—432; [3]
его же, «Укр. матем. ж.», 1964, т. 16, К» 5, с. 593—В02; № 6,
с. 730—51. А. П. Митина.
ОПЕРАТОРНАЯ ТОПОЛОГИЯ — топология в прост-
пространстве Л (A1, F) непрерывных линейных отображений
одного топологического векторного пространства Е
в другое топологич. пространство F, превращающая
пространство L(E,F) в топологическое векторное
пространство. Пусть F — локально выпуклое простран-
пространство и © — такое семейство ограниченных подмножеств
пространства К, что линейная оболочка объединения
множеств этого семейства плотна в Е\ пусть 33 — ба-
базис окрестностей нуля в F. Семейство
М (S, V) = {f:f€L(E, F), f(S)t=V},
где S пробегает 3, а V пробегает ^, является базисом
окрестностей нуля для единственной инвариантной
относительно сдвигов топологии, к-рая является О. т.
и превращает пространство L(E, F) в локально вьшук-
лое пространство; эта топология наз. @-т о п о л о-
г и е й на L(E, F).
П р и-м е р ы. I. Пусть Е, F — локально выпуклые
пространства; 1) пусть S - семейство всех конечных
подмножеств в Е, соответствующая <2-топология (в
L (E, F)) наз. топологией простой (или п о-
точечной) сходимости; 2) пусть @ — се-
семейство всех выпуклых закругленных компактных под-
подмножеств Е, соответствующая топология наз. топо-
топологией выпуклой закругленной
компактной сходимости; 3) пусть <2> —
семейство всех цредкомпактных подмножеств Е, соот-
соответствующая S-топология наз. топологией пред-
предком п а к т н о и сходимости; 4) пусть <3 —
семейство всех ограниченных подмножеств, соответ-
соответствующая топология наз. топологией ограни-
ограниченной сходимости.
II. Если Е, F — банаховы пространства, рассматри-
рассматриваемые одновременно в слабой или сильной (норми-
(нормированной) топологии, то соответствующие простран-
пространства L(E, F) алгебраически совпадают; соответствую-
соответствующие топологии простой сходимости наз. слабой и
сильно й О. т. в L(E, F). Сильная О. т. мажорирует
слабую О. т.; обе они согласуются с двойственностью
между L(E,F) и пространством функционалов на
L(E.F) вида /D)=2<р,-(Л %¦), где ?,-??, ср,-^*,
?L )
III. Пусть Е, F — гильбертовы пространства и Е,
F — счетные прямые суммы гильбертовых пространств
Еп, Fn соответственно, где Еп~Е, Fn=F для всех
натуральных «;_ пусть if> — вложение пространства
L(E, F) в L(E, F), определенное условием: для любого
оператора A?L(E, F) ограничение оператора ty(A) на
подпространство Еп переводит Еп в Р„ и совпадает на
Еп с оператором А. Тогда полный прообраз в L(E, F)
слабой (сильной) О. т. в L(E, F) наз. ультрасла-
б о й (соответственно ультрасильной) О. т. в
L(E, /•'). Ультраслабая (ультрасильная) топология ма-
мажорирует слабую (сильную) О. т. Симметричная под-
подалгебра Ж алгебры L(E) всех ограниченных линей-
линейных операторов в гильбертовом пространстве Е, со-
содержащая единичный оператор, тогда и только тогда
совпадает с множеством всех операторов из Ь(Е), пере-
перестановочных с каждым оператором из L(E), переста-
перестановочным со всеми операторами из 9Г, когда Й зам-
замкнута в слабой (или сильной, или ультраслабой, или
ультрасильной) О. т., то есть является Неймана
алгеброй.
Лит.: [11 Шеф ер X., Топологические векторные прост-
пространства, пер. с англ., М., 1971; [2] Д а н ф о р д Н., Шварц
Д ж., Линейные операторы. Общая теория, пер. с англ., М.,
1ЭВ2; 13] Н а й м а р к М. А., Нормированные кольца, 2 изд.,
М., 1968; Ш S a k a i S., C*-algebras and W*-algebras, В., 1971.
А. И. Штерн.
ОПЕРАТОРНАЯ ЭРГОДИЧЕСКАЯ ТЕОРЕМА — об
щее название теорем о пределе средних по неограниченно
удлиняющемуся «промежутку времени» ге=0, 1, . . .,N
или 0<?<Г для степеней {Ап} линейного оператора
А , действующего в банаховом (или даже топологическом
векторном, см. [5]) пространстве Е, либо для действую-
действующей в Е однопараметрич. полугруппы линейных опе-
операторов {Af}. В последнем случае можно рассматривать
также предел средних по неограниченно уменьшающе-
уменьшающемуся промежутку времени (локальные э р г о-
д и ч е с к и е теоремы, см. [5], |6J; говорят также
об «эргодичности в нуле», см. [1]). Средние могут по-
пониматься в различных смыслах, аналогично тому, как
это делается в теории суммирования рядов. Чаще всего
используются средние Чезаро
J42
или средние Абеля
Условия эргодич. теорем заведомо обеспечивают сходи-
сходимость подобных бесконечных рядов или интегралов;
при этом, хотя абелевы средние образуются с участием
всех Ап или Af, главную роль играют значения А"
или Af на конечном отрезке времени, неограниченно
возрастающем при 0->-1 (или ?->-0). Предел средних
(limAjv и т. д.) тоже может пониматься в различных
N-><c
смыслах — в сильно)! или слабой операторной
топологии (статистические э р г о д и-
ч е с к и е теоремы, т. с. Неймана теорема эрго-
дическая -- исторически первая О. э. т.— и ее обобще-
обобщения), в равномерной операторной топологии (р н в н о-
мерные оргодические теоремы, см. 111,
[2], [3]), а если Е реализовано как нек-рое простран-
пространство функций ва пек-ром пространстве с мерой, то п
в смысле сходимости почти всюду средних А^ ср и т. п.
при Ц>?Е (индивидуальные эргодиче-
с к и е теоремы, т. о. Яиркгофа ,>ргодическая те-
теорема и ее обобщения, см., напр., Орнстейна—Чекона
эргодическая теорема; их, впрочем, не всегда относят
к О. э. т.). Нек-рые из О. э. т. как бы сравнивают силу
различных упомянутых выше вариантов, устанавливая,
что из существования пределов средних в одном смысле
следует существование пределов в другом смысле.
В нек-рых теоремах речь идет не о пределе средних,
а о пределе отношения двух средних (такова теорема
Орнстейна — Чекона).
Имеются также О. о. т. для ге-нараметричеоких и даже
более общих полугрупп.
Лит.: El] X и л л е Э., Ф и л л и п с Р., Функциональный
анализ и полугруппы, пер. с англ., М., 1962; [2] Д а н ф о р д Н.,
ШварцДж., Линейные операторы. Общая теория, пер. с англ.,
М., 1962; 13] Неве Ж., Математические основы теории вероят-
вероятностей, пер. с франц., М., 1969; [4] Вершин А. М., Ю з в и п-
с к и й С. А., в кн.; Итоги науки, в. 15 — Математический ана-
анализ. 1967, М., 1969, с. 133—87; [5] Каток А. Б., С и н а Н
Я. Г., С т е п и н А. М., в кн.: Итоги науки и техники. Сер.
Математический анализ, т. 13, М., 1975, с. 129—262; [6] К г е п-
g e I U., «Asterisque», 1977, t. 50, p. 151—92. Д. В. Аносов.
ОПЕРАТОРНО НЕПРИВОДИМОЕ ПРЕДСТАВЛЕ-
ПРЕДСТАВЛЕНИЕ — представление я группы (алгебры, кольца,
полугруппы) X в (топологическом) векторнодг простран-
пространстве Е такое, что любой (непрерывный) линейный опе-
оператор в пространстве Е, перестановочный со всеми опе-
операторами я (.г), х?Х, кратен единичному оператору в Е.
Если я — вполне неприводимое представление (в ча-
частности, если я — конечномерное неприводимое пред-
представление), то я — О. н. п.; обратное, вообще говоря,
неверно. Если л — унитарное представление группы
или симметричное представление симметричной алгеб
ры, то я тогда и только тогда является О. н. п., когда
я — неприводимое представление. а. И. Штерн.
ОПЕРАТОРНОЕ КОЛЬЦО, кольцо с обла-
областью операторов 2,-- кольцо, в к-ром опре-
определено умножение элементов кольца на элементы n;s
нек-рого фиксированного множества 2 (внешний за-
закон композиции), удовлетворяющее следующим ак-
аксиомам:
A)
), B)
где а — элемент множества 2, а а, Ь, а<х, Ъа—элементы
кольца- Операторы, таким образом, действуют как
эндоморфизмы аддитивном группы, перестановочные с
умно?кением на элемент кольца. Кольцо с областью
операторов 2, или короче 2-о ператорное
кольцо, можно трактовать и как универсальную
алгебру с двумя бинарными операциями (сложением
и умножением) и множеством 2 унарных операций,
связанных обычными кольцевыми тождествами, а так-
также тождествами A) и B). Понятия 2-д опусти-
мого подкольца, 2-допусти мог о иде-
идеала, 2-о ператорного изоморфизма и
2 -операторного гомоморфизма мо-
могут быть определены подобно тому, как вто делается
для операторных групп. Если 2-онераторное кольцо
Я обладает единицей, то все идеалы и все односто-
односторонние идеалы кольца R 2-допустимы.
Кольцо R наз. кольцом с кольцом опе-
операторов 2, если оно есть 2-операторное кольцо,
область операторов 2 к-рого сама является ассоциатив-
ассоциативным кольцом, причем для любых а, р"?2 и»?Д спра-
справедливы равенства
а (оф) = (аа) р\
Кольцо с кольцом операторов можно определить так же,
как кольцо являющееся одновременно 2-модулем и
удовлетворяющее аксиоме B). Всякое кольцо можно
естественным образом считать операторным над коль-
кольцом целых чисел.
Для всех а из Я и a, (J из 2 элемент a{af> — Ра) яв-
является аннулятором кольца R. Поэтому, если R —
кольцо без аннуляторов, то его кольцо операторов 2
непременно коммутативно.
Наиболее часто рассматриваются кольца с ассоциа-
ассоциативно-коммутативным кольцом операторов, обладаю-
обладающим единицей. Такое О. к. наз. обычно алгеброй над
коммутативным кольцом, а также линейной алгеброй.
Наиболее изучены линейные алгебры над полями, их
теория развивается параллельно общей теории колец
(без операторов).
Лит.: [1] К у р о ш А. Г., Лекции по общей алгебре, 2 изд.,
М., 1973. К. А. Жевлаков.
ОПЕРАТОРНЫЙ ГОМОМОРФИЗМ — гомоморфизм
алгебраической системы, перестановочный с каждым
оператором из нек-рого фиксированного множества,
действующим на этой системе, т. е. гомоморфизм опе-
операторной группы, операторного кольца и т. д.
ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ — один из мето
дов математич. анализа, позволяющий в ряде случаев
сводить исследование дифференциальных операторов,
псеедодифференциалъных операторов и нек-рых типов
интегральных операторов и решение уравнений, содер-
содержащих яти операторы, к рассмотрению более простых
алгебраич. задач. Развитие и систематич. применение
О. и. началось с работ О. Хевисайда (О. Heaviside,
1892), к-рый предложил формальные правила обраще-
обращения с оператором дифференцирования j^~ и решил ряд
прикладных задач. Однако О. и. не получило у него
математич. обоснования: оно было дано с помощью
Лапласа преобразования; Я. Микусиньский (J. Miku-
siiiski, 1953) алгебраизировал О. и., опираясь на поня-
понятие функционального кольца; наиболее общая кон-
концепция О. и. получается с помощью обобщенных
функций.
Простейший вариант О. и. строится следующим обра-
образом. Пусть К — совокупность функций (с действитель-
действительными или комплексными значениями), заданных в об-
области 0</<оо и абсолютно интегрируемых в любом
конечном интервале. Ивер т к о й функций /,
наз. интеграл
h = f:t.g=\^uf(t — T)g(x) dr.
Относительно обычного сложения и операции свертки К
становится кольцом без делителей нуля (теорема Тит-
чмарша, 1924). Элементы поля частных Р
этого кольца наз. операторами и обозначаются
?- ; невыполнимость деления в К как раз и есть источ-
источник нового понятия оператора, обобщающего понятие
функции. Для выявления необходимого в О. и. разли-
различия между понятиями функции и ее значения в точке
введены следующие обозначении:
{/(*)} — функция f(t);
I (t) — значение / (t) в точке (.
Примеры и II с р л т о р о в.
1) е--~{1} — о п е> |i а т up ннтегриров а-
н и я:
при этом
и, в частности,
Jo Jo
= r
0 (n-DI
п раз
/ (т) dx;
это — формула Кошп, обобщение к-poii на случай про-
произвольного (нецелого) показателя служит для опреде-
определения дробного интегрирования.
2) [a]=|jj (где a — функция-константа) — ч и с-
ловой оператор; поскольку [a] [fl] =
-[а, рЧ, [а] {/}={а/}, в то время как {a} {$}={a$t},
то числовые операторы ведут себя как обычные числа.
Таким образом, оператор является обобщением не
только функции, но и числа; единицей кольца К явля-
является [1].
3) s---— — оператор дифференциро-
н а н и я, обратный оператору интегрирования. Так,
если функция a(t)= {a{t)} имеет производную a (t), то
«{«} = {«'} +[« @)]
и
{а<">} —s" {«} — S"'1 [а @)] — ... — [а"'1 @)];
отсюда, напр.,
На оператор дифференцирования s можно умножать
не только дифференцируемые функции, однако резуль-
результат есть уже, вообще говоря, оператор.
4) ?>{/}= {—*/(')} — алгебраическая про-
производная, она распространяется на произволь-
произвольные операторы обычным способом, при этом оказыва-
оказывается, что действие этого оператора на функции от s
совпадают с дифференцированием no s.
О. и. дает удобные способы решения линейных диф-
дифференциальных уравнений как обыкновенных, так и с
частными производными. Напр., решение уравнения
а„г<">-f ...-j-а„г = /, а/= const, г = 0, 1, ..., п,
удовлетворяющее начальным условиям ж@) = у0, ¦ • •-
,r(" J)@)—\n_l автоматически приводится к алгебраич.
уравнению и символически выражается формулой
решение в обычном виде получается разложением на
элементарные дроби от переменной s с последующим
обратным переходом по соответствующим таблицам к
функциям.
Для применения О. и. к уравнениям с частными про-
производными (а также к более общим псевдодифферен-
псевдодифференциальным уравнениям) строятся дифференциальное и
интегральное исчисления операторных функ-
ц и ii, т. е. функций, значениями к-рых являются опе-
операторы: вводятся понятия непрерывности, производ-
Hoii, сходимости ряда, интеграла и т.д.
Пусть f (к, t) — нек-рая функция, определенная для
<>0 и к?\а, Ь]. Параметрическая опера-
операторная функция / (к) определяется формулой
/(А.)= {f(k, t)}\ она ставит в соответствие рассматривае-
рассматриваемым значениям к операторы частного вида — функции
от /. Операторная функция наз. непрерывной при
к?1а, Ь], если она представима как произведениенек-
рого оператора д и такой параметрич. функции /i(^) —
— {/i(^> t)}, что ft (к, t) непрерывна в обычном смысле.
П р и м е р ы. 1) С помощью параметрич. функции
А (Я)= {*<*,<)}:
@ дляО<г<Я,
; V — к для
определяется функция X е в и с а й д а
H{k)=s{h(k, «)};
значения гиперболической показатель-
показательной ф у н к ц и и
e-}-s^sH(k)=s°-{h(k, 0}
наз. операторами сдвига, поскольку умно-
умножение данной функции на e~^s вызывает смещение ее
графика на длину к в положительном направлении оси t.
2) Решение уравнения теплопроводности
at — a dv
выражается через параболическую пока-
показательную функцию (являющуюся также
параметрической операторной функцией):
\2Vnt'
3) Периодич. функция /(/) с периодом 2кп имеет пред-
представление
4) Если f(k) принимает числовые значения в интер-
интервале [А,, Я2], то
т. е. умножение данной функции {/} на (?"*•' с после-
последующим интегрированием вызывает усечение ее
графика. В частности,
о
таким образом, каждой функции / (t), для к-рой рассмат-
риваемыи интеграл сходится, ставится в соответствие
аналптич. функция
F („) =
— ее преобразование Лапласа. Благодаря этому обстоя-
обстоятельству довольно обширный класс операторов описы-
описывается функциями одного параметра s, более того,
это формальное сходство уточняется математически
установлением определенного изоморфизма.
Имеются различные обобщения О. и.; таково О. и.
дифференциальных операторов, отличных от s= щ,
напр. Ь=—( t-тт ), к-рое основывается на функци-
ональных кольцах с надлежащим образом определен-
определенным произведением.
Лит.: [1] Д и т к и н В. А., II р у д н и к о в А. П., Справоч-
ник по операционному исчислению, М., ПЮ5; [21 М и к у с и н-
ский Я., Операторное исчисление, пор. с полъск., М., 1950.
М. 11. Войцеховский.
А -ОПЕРАЦИЯ, операция А ,— теоретико-мно-
теоретико-множественная операция, открытая П. С. Александровым
[1) (см. также [2] с. 39 и [3]). Пусть {?„_..„ }-
система множеств, заиндексированных всеми конечны-
конечными последовательностями натуральных чисел. Мно-
Множество
= U П
kl
k
где суммирование распространяется на все бесконечные
последовательности натуральных чисел, наз. результа-
результатом А -О., примененной к системе {Еп п }.
Применение А-О. к системе интервалов числовой
прямой дает множества (названные А-множествами в
честь П. С. Александрова), к-рые могут не быть боре-
левскими (см. Дескриптивная теория множеств). А-О.
сильнее операций счетного объединения и счетного пе-
пересечения и является идемпотентной. Относительно
А-О. инвариантны Бэра свойство (подмножеств про-
произвольного топологич. пространства) и измеримость
по Лебегу.
Лит.: [1] Александров П. С, «С. г. Acad. sci», 191B,
t. 162, p. 323—25; 12] е г о же, Теория функций действитель-
действительного прременного и теория топологических пространств, М.,
1978; [31 Колмогоров А. Н., «Успехи матем. наук», 1966,
т. 21, в. 4, с. 275—78; [4] Суслив М. Я., «С. г. Acad. sci.»,
1917, t. 1A4, p. 88—91; [5] Л у л и п Н. Н., Собр. соч., т. 2, М.,
1958, с. 284; [6] К у р а т о в с к и й К., Топология, пер. Lc
англ.], т. 1, М., 1966. А. Г. Елъкии.
6«-ОПЕРАЦИЯ — теоретико-множественная опера-
операция, результат применения к-рой к последовательности
(Еп) множеств может быть записан в виде
Ф(Я„)= U П Еп,
г 6 Л' п е г
где N — система множеств положительных целых чисел,
наз. б а з о й 8s = 0. См. Дескриптивная теория мно-
множеств.
Лит.: [1] К о л м о г о р о в А. Н., «Матем. сб.», 1928, т. 35,
Л1» 3—4, с. 415—22; [2] X а у с д о р ф Ф., Теория множеств, пер.
с нем., М.— Л., 1937; [3] Александров П. С, Теория функ-
функций действительного переменного и теория топологических
пространств, М., 1978, с. 35—40, 53—58; [4] О ч а н Ю. С, «Ус-
«Успехи матем. наук», 1955, т. 10, в. 3, с. 71 —128; [5J К о л м о г о-
р о в А. Н., там же, 1966, т. 21, в. 4, с. 275 — 78. А. Г. Елъкин.
ОПЕРЕНИЕ пространства — счетное семей-
семейство Р покрытий пространства X множествами, от-
открытыми в нек-ром объемлющем пространстве У,
такое, что
для каждой точки х?Х (здесь Sty (x) означает звезду
точки х относительно у, т. е. объединение всех эле-
элементов из у, содержащих точку х).
Понятие О. лежит в основе определения т. н. р-
пространства (в смысле А. В. Архангельского). Про-
странство X нал. р-пространством, если оно имеет О.
в своем Стоуна — Чеха бикомпактном расширении или
Уолмрнп бикомпактном расширении. Каждое полное п
емысче Чехи пространство является /^-пространством.
Каждое //-пространство имеет точечно-счетный тип.
В р-простраистве справедливы аддиционная теорема
для веса, и сетевой вес совпадает с весом. Параком-
пактные р-пространства — это в точности совершенные
прообразы метрич. пространств. Паракомнактные р-
пространства с точечно-счетной базой метризуемы, рав-
равно как метризуемы и пространства этого вида с диаго-
диагональю Се . Совершенный образ и совершенный прооб-
прообраз паракомпактного р-пространства — также параком-
ПаКТНые р-пространства. В. И. Пономарев.
ОПОРНАЯ ГИПЕРПЛОСКОСТЬ множества
А/ в «-мерном векторном н р о с т р а н с т-
в е — (п — 1)-морная плоскость, к-рая содержит точки
замыкания М и оставляет М в одном замкнутом про-
пространстве. При п~ О. г. наз. опорной пло-
плоскостью, а при п"-2 — опорной прямо й.
Граничную точку множества М, через к-рую прохо-
проходит хотя бы одна О. г., наз. опорной т о ч к о ii M.
У выпуклого множества М все его граничные точки —
опорные. Последнее свойство Архимед использовал
как определение выпуклости М. Граничные точки
выпуклого множества М, через к-рые проходит един-
единственная О. г., наз. гладкими.
В общих векторных пространствах, где гиперплос-
гиперплоскость определяется как область постоянства значе-
значений линейного функционала, также вводится понятие
О. г. как гиперплоскости, экстремальной по значению
этого функционала среди гиперплоскостей, оставляю-
оставляющих М В ОДНОМ полупространстве. В. А. Залгаллер.
ОПОРНАЯ ФУНКЦИЯ, опорный функцио-
функционал, множества А, лежащего в векторном простран-
пространстве X,— функция sA, задаваемая в находящемся с
ним в двойственности векторном пространстве Y соот-
соотношением
(sA) (у) = sup <я, у>.
У€А
Напр., О. ф. единичного шара в нормированном прост-
пространстве, рассматриваемом в двойственности со своим
сопряженным пространством,— это норма в последнем.
U. ф. всегда выпуклая, замкнутая и положительно
однородная (первой степени). Оператор *¦ : A—>-sA вза-
взаимно однозначно отображает совокупность выпуклых
замкнутых множеств в X на совокупность выпуклых
замкнутых однородных функций, обратный оператор —
не что иное, как субдифференциал (в нуле) опорной
функции. Именно, если А — выпуклое замкнутое под-
подмножество в X, то d(sA) = A, и если р — выпуклая
замкнутая однородная функция на Y, то s(dp(O))=p.
.')ти два соотношения (являющиеся следствием теоремы
Фенхеля — Моро, см. Сопряженная функция) и выра-
выражают двойственность между замкнутыми выпуклыми
множествами и выпуклыми замкнутыми однородными
функциями.
Примеры соотношений, связывающих оператор s с
алгебраическими и теоретико-множественными опе-
операциями:
ЬС, Я > 0; s(A1-\~Ai)=s
s (conv (A1\jAi)) (ж)=тах [sAx {x), sA2(x)).
Лит.: h] Pq. кафе л л ар Р., Выпуклый анализ, пер. с
атм., М., 1973-12] Miokowski H., Geometrie der Zahlen
Lpz, — В., 1910; 1,3] его же, Gesammelte Abhandlungen, Bd 2
Lpz.— В., 1911; [i] F e n с h e 1 W.,«Canad. J. Math.», 1949 v. 1,
p. 73—77; L5J e г о же, Convex cones, sets and funktlons, Prin-
Princeton, 1953; [6] H б T m a n d e r L., «Ark. for Mat.», 1955, bd 3
p. 181—80. В. М. Тихомиров.
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ — см. Интеграл.
ОПРЕДЕЛИТЕЛЬ, детерминант, квадратной
матрицы А \\а;j\\ порядка п над ассоциатпнно-комму-
тативным кольцом А' с единице]! 1 — элемент кольца
А', равный сумме всех членов вида
<-*>ч<, •••«„<„.
где i1, . . ., in— перестановка чисел 1, . . ., п, a t —
число инверсий перестановки it, . . ., in. О. матрицы
A-j
1 "nl ¦ ¦ ¦ ann
обозначается
an .. -a,,,
ii.-iii dot Л.
¦inl. ..а,
О. матрицы А содержит п\ членов; при и- 1 det Л =
- ап, при n=-2 det А -~апа22—«2iai2- Наиболее важ-
важные для приложений случаи: А* — поле (в частности,
числовое поле), К — кольцо функций (в частности,
кольцо многочленов), К — кольцо целых чисел.
Всюду ниже К — ассоциативно-коммутативное коль-
кольцо с 1, Мп(К) — совокупность всех квадратных мат-
матриц порядка п над А", Еп— единичная матрица над К.
Пусть А ?Мп(К), а а1: . . ., ап— строки матрицы А
(все далее изложенное справедливо и для столбцов
матрицы А). О. матрицы А удобно рассматривать как
функцию от ее строк:
det А= Г) (а,, . .., ап).
Отображение
d:Mn-^ К (Ль-*-det A)
подчинено следующим трем условиям:
1) d(A) —линейная функция любой строки матри-
матрицы А:
D (аи ..., Xai + цЬ,-, ..., ап)—
= lD[au ..., a,-, ..., ап)+цО (а,, . .., bh ап),
где X, |х?А';
2) если матрица В получена \\л А :\а\\(чнп\ строки а;
строкой ai-j-af, Хф'1, то fi(A)=d{B);
3) d(?n)=l.
Условия 1) — 3) однозначно определяют отображение
d, т. с. если отображение /; : Мп(К)-^~К удовлетворя-
удовлетворяет условиям 1) —3), то h(A) = det A . Таким обра.чом
получается аксиоматнч. построение теории О.
Пусть отображение / : Мп(К)—уК удовлетворяет ус-
условию:
1а) если В получается u.s матрицы Л умножением од-
нон строки на К? К, то j (B) = Xf (А ). Очевидно, 1) ^> 1а).
В случае, когда К — поле, совокупность условий
1) — 3) оказывается равносильной условиям 1а), 2), 3).
О. диагональной матрицы равен произведению ее
диагональных алементов. Отсюда вытекает сюръектив-
ность отображения d. Мп(К)-+К. О. треугольной
матрицы также равен произведению ее диагональных
элементов. Для матрицы А — ^ р , где В и С —
квадратные матрицы,
det A =-. det В det С.
Из свойств перестановок вытекает, что det Л7"--- det A ,
где 7— знак транспонирования. Если матрица А имеет
две одинаковые строки, то ее определитель равен 0:
если поменять местами две строки матрицы А , то ее О.
изменит знак;
D («J, ..., at + laj я„) =?>(«!, ..., ah , ,., ап)
при ijbj,, 'k^K; для А и В из Мп{К)
det ЛЯ = det A det 5.
Таким образом, отображение d есть эпиморфизм муль-
мультипликативных полугрупп Л'/„(Л) и Л.
Пусть m<n, А — \\aij\\ есть (т , п) матрица, S = II6//||
есть (пХ /н)-матрнца над А", а С=АВ Тогда верна
формула Вине — Кош»:
det C = '
/i < ¦ • ¦ < im < п
11т
/ml' ' ' /mm
Пусть .4 = |а//| ? Afn(AT), a ^4/y—алгебраич. донолне-
ние элемента а/у. Тогда верны формулы
V a- A, —I
где bij— символ Кронекера. Для ны'шслений О. часто
используются разложение его по элементам строки или
столбца, т. е. формулы A), теорема Лапласа (см. Ал-
Алгебраическое дополнение) и преобразования матрицы А ,
не меняющие О. Для матрицы А из Мп(К) тогда и
только тогда существует обратная матрица А ~2 в
М„(К), когда в К имеется элемент, обратный элементу
det A. Следовательно, отображение
GL (га, А')—>К* (А >—». det A),
где GL (га, К) — группа всех обратимых матриц в
Мп(К), т. е. полная линейная группа, а К*— группа
обратимых элементов А", есть эпиморфизм этих групп.
Квадратная матрица над поле\г обратима тогда и
только тогда, когда ее О. отличен от нуля, п-мерные
векторы alt . . ., ап над полем /¦' линейно зависимы
тогда и только тогда, когда
D(ai, ..., о„)=0.
О. матрицы А порядка ге>1 над полем равен 1 тогда
и только тогда, когда А есть произведение элементар-
элементарных матриц вида
где гф'1, а >ч/ — матрица, единственный ненулевой
элемент к-рой равен 1 и расположен на позиции (г, /).
Теория О. возникла в связи с задачей решения систем
линейных уравнений:
. ..+а1па:п=Ь],
•,
B,
anlx1-\- . . .
где a[j, by— элементы нек-рого поля F. Если det A #0,
где /4~||а,-у|| — матрица системы B), то эта система
имеет единственное решение, вычисляемое по формулам
Крамера (см. Крамера правило). В случае, когда сис-
система B) задана над кольцом К и det А обратим в А",
система также имеет единственное решение, определяе-
определяемое теми же формулами Крамера.
Теория О. построена также и для матриц над не-
некоммутативным ассоциативным телом. О. матрицы над
телом к (определитель Д \, ё д о н н е) вво-
вводится следующим образом. Тело />¦ рассматривается
как полугруппа и строится ее коммутативный гомоморф-
гомоморфный образ к. к — группа к* с внешне присоединенным
нулем 0, а в качестве к берется также группа к* с
внешне присоединенным нулем U, где к* — фактор-
факторгруппа группы к* по коммутанту. Эпиморфизм к-*-к,
h—>-Л, задается канонич. эпиморфизмом групп к*->-к*
и условием 0—>-0. Очевидно, 1 — единица полугруп-
полугруппы /,-.
Теория О. над телом основана на следующей теореме.
Существует единственное отображение
Ь:Мп (к) I—>F,
удовлетворяющее следующим трем аксиомам:
I) если матрица В получена из матрицы А умноже-
умножением слева одной строки на к?к, то 6(В) — ^Ь(А);
II) если В получена из А заменой строки а, строкой
я,4-а/, где ЬФ)± то Ь(В) — Ь{Ау,
III) «(?„) = !.
Элемент 6 (А) наз. определителем матрицы А
и обозначается det A. Для коммутативного тела ак
сиомы I), II), III) совпадают с условиями 1а), 2), 3)
соответственно, и, следовательно, в этом случае полу-
получаются обычные О. над полем. Если ^4 = diag [an, . . .,
апп], то det ^4=a_n . . . апп; таким образом, отображе-
отображение 6 : Мп(к)-+к сюръективно. Матрица А из М„(к)
обратима тогда и только тогда, когда det АфО. Спра-
Справедливо равенство det AB~det A -det В. Как и в ком-
коммутативном случае, det А не изменится, если строку
о,- матрицы А заменить строкой ai-^Xaj, где 1ф], %?к.
При «>'! det 4 = 1 тогда и только тогда, когда А иро-
ir.чвслеша1 мемеятарных матриц вида t(j (Я)=~ ?n~h^eiji
'^/ h?k Если а^О то
Если a-j±0, то
a h
, —ad — aca~1b,
с d
О Ъ
с d
В отличие от коммутативного случая, det AT может и
не совпадать с det А. Напр., для матрицы А —- К ^
над телом кватернионов det Л — ¦—2i, a det И Т- 0.
Бесконечные О., то есть О. бесконечных матриц, оп-
определяются как предел, к к-рому стремится О- конеч-
конечной подматрицы при бесконечном возрастании ее по-
порядка. Если этот предел существует, то О. наз. сходя-
сходящимся, в противном случае — расходящимся.
Понятие «О.» восходит к Г. Лейбницу (G. Leibnitz,
1678); первая публикация принадлежит Г. Крамеру
(G. Cramer, 1750). Теория О. создана трудами А. Ван-
дермонда (A. Vandermonde), П. Лапласа (P. Laplace),
О. Коши (Л. Cauchy) и К. Якоби (С. Jacobi). Термин
«О.» встречается впервые у К. Гаусса (С. Gauss. 1801).
Современное обозначение введено А. Кэли (A. Cayley,
1841).
Лит.: [ll К у р о ш А. Г., Курс высшей алгебры, 11 изд.,
М., 1975; [2] К о с т р и к и н А. И., Введение в алгебру, М.,
1977; [3] К ф и м о в Н. В., Розендорн Э. Р., Линейная
алгебра и многомерная геометрия, М., 1970; [4] Тышке-
Тышкевич Р. И., Ф е д е н к о А. С, Линейная алгебра и аналити-
аналитическая геометрия, 2 изд., Минск, 1976;[5] А р т и н Э., Геометри-
Геометрическая алгебра, пер. с англ., М., 1969; [Н] Бурбаки Н.,
Алгебра. Алгебраические структуры. Линейная и полилинейная
алгебра, пер. с франц., М., 19«2; [7] Kara н В. Ф., Основания
теории определителей Одесса, 1922. Д. А. Супрунечко.
ОПРЕДЕЛЯЮЩАЯ СИСТЕМА ОКРЕСТНОСТЕЙ
множества А в т о п о л о г и ч е с к о м про-
пространстве X — любое семейство % подмножеств
пространства X, подчиненное следующим двум усло-
условиям: а) для каждого О? | найдется открытое множество
Г пространства X такое, что ОгэПэЛ, б) каково бы
ни было открытое в X множество W, содержащее А ,
найдется адемент U семейства 1, содержащийся в W.
Иногда дополнительно предполагают, что все элементы
семейства % открытые множества. Определяющей сис-
системой окрестностей точки х?Х в топологич. простран-
пространстве X нал. О. с. о. в X одноточечного множества {х}.
Лит.: Ill Архангельский А. В., II о н о м а-
р е в В. И игкикы ибщей топологии в задачах и упражнениях,
М . 1H7'i. А. В, Архангельский.
ОПРЕДЕЛЯЮЩЕЕ УРАВНЕНИЕ — уравнение, ас-
ассоциированное с регулярной особой точкой z — a обык-
обыкновенного линейного дифференциального уравнения
Pl) (z) ii-ci-t-p! (z) ц.(«-1)+ ... +рп (г) н,- = 0. A)
Пусть
функции qj(z) голоморфны в точке z а и г/„(«)^0.
Определяющее уравнение имеет вид
X (Х-1). ..{к-п +1) д„ (а) + ... + Un-\ («) -!- 'In (а)--О.
B)
Если корни Xj, 1 <:;<:«, уравнения B) таковы, что все
разности Xj—%к при )фк не являются целыми числами,
то уравнение (I) имеет фундаментальную систему ре-
тении вида
wJ(z)^(z-a)'Kj<fj(z)% 1</<», C)
где функции фу (г) голоморфны в точке z=a. В против-
противном случае решения уравнения A) могут быть много-
многочленами от In (z—а) с коэффициентами, голоморфными
в точке z=a.
О. у. для системы из п уравнений
(z — a)w' = A(z)w, D)
отвечающее регулярной особой точке 2= я, имеет вид
detflU — Л (а) || = О,
где A (z) — матрица-функция порядка пХп, голоморф-
голоморфная в точке z-~a, и А (а)фО. Если все разности "kj—к^
при }фк не являются целыми числами, где Xj— соб-
собственные значения матрицы А, то система D) имеет
фундаментальную систему решений вида C), где ф/(г) —
вектор-функции, голоморфные в точке г—а; в проти-
противоположном случае вектор-функции фу- (z) могут быть
многочленами от ln(z—а) с коэффициентами, кото-
которые являются голоморфными в точке z = a вектор-функ-
вектор-функциями.
В ином смысле термин «О. у.» употребляется при
исследовании групп преобразований, допускаемых
обыкновенными дифференциальными уравнениями и
уравнениями с частными производными (см. [3]).
Лит.: [1] Коддингтон Э. А., Левин сон Н., Тео-
Теория обыкновенных дифференциальных уравнений, пер. с англ.,
М., 1958; [2] К а м к е Э., Справочник по обыкновенным диффе-
дифференциальным уравнениям, пер. с нем., 5 изд., М., 1976; [3] О в-
с я н н и к о в Л. В., Групповой анализ дифференциальных
уравнений, М., 1978. ' М. В. Федорюп.
ОПРЕДЕЛЯЮЩИЕ СООТНОШЕНИЯ универ-
универсальной алгебры G относительно системы
{g;, '?/} ее порождающих элементов — соотношения
вида
u/(gn, gin, ¦¦¦,gin)=i>j(gn, gn, •¦•,?,•„), i?J,
между порождающими (где uj, vj—термы в сигнатуре
рассматриваемой алгебры) такие, что все остальные
соотношения этого вида являются следствиями данных
и тождеств многообразия, в к-ром рассматривается
алгебра G. Обычно, когда говорят о задании алгебры
порождающими и О. с, имеют в виду факторалгебру
свободной алгебры многообразия с теми же порождаю-
порождающими по конгруэнции, определяемой всеми парами
(и/, vj), j?J. В случае мультиоператорных групп
(в частности, групп, алгебр, колец, модулей) вид О. с.
упрощается: их можно записать либо как wj=(), либо
как Wj~l (в группах).
О. с. выбираются неоднозначно даже при одной и
той же системе порождающих. Напр., циклическая
группа второго порядка с порождающим элементом а
может быть задана одним О. с. а2--1, а также двумя
О. с. а('=1 и а4=1. Существуют специальные преобра-
преобразования (преобразования Тице в группах,
см. [2], и их аналоги в различных многообразиях ал-
алгебр), позволяющие по одному заданию алгебры по-
порождающими и О. с. строить другие задания тон же ал
гебры. При этом для конечно определенных
групп (или алгебр), то есть задаваемых конеч-
конечной системой образующих и конечной системой О. с,
можно конечным числом преобразовании Тице перептп
от любого такого задания к любому другому ее (конеч-
(конечному) заданию порождающими и О. с. Если алгебра
конечно порождена, то из любой системы ее порождаю-
порождающих можно выбрать конечную подсистему порождаю-
порождающих; если алгебра в нек-рой конечной системе порож
дающих задается конечным числом О. с, то в любом
другой конечной системе порождающих из любой сие
темы О. с. можно выбрать конечную подсистему О. с.
Изучение конечно определенных алгебр породило
целый ряд проблем алгоритмического характера, таких,
как проблема равенства (тождества), проблема изомор
физма и др. (см. Алгоритмическая проблема). Ряд ре
зультатов получен для алгебр с одним О. с. Напр., и
группах с одним О. с. разрешима проблема равенства,
описаны элементы конечного порядка, центр и все
подгруппы с нетривиальными тождествами (см. также
Групповое исчисление).
Лит.: Ell Кон П., Универсальная алгебра, пер. с англ.,
М., 1968; [2] К у р о ш А. Г., Теория групп, 3 изд., М., 19В7;
[3] Магнус В., К а р р а с А., С о л и т э р д., Комбина-
Комбинаторная теория групп, пер. с англ., М., 1974.
А. Л. Шлгелъки 11.
ОПРОВЕРЖИМАЯ ФОРМУЛА, формально
опровержимая в данной системе
формул а,— замкнутая формула данной системы,
отрицание к-рой выводимо в этой системе.
В. Н. Гришин.
ОПТИМАЛЬНАЯ ГАРАНТИРУЮЩАЯ СТРАТЕ
ГИЯ — стратегия, к-рая имеет в данном операции оцен
ку эффективности, равную наилучшему гарантирован
ному результату (см. Наибольшего гарантированного ре-
результата принцип). Если, напр., в операции с крите-
критерием эффективности /(г, у) неопределенный фактор у
принимает значения из множества Y, то О. г. с. х* оп-
определяется из равенства
sup inf f (х, у)--- inf / (х*, у).
Если верхняя грань по х не достигается, то вводится
понятие е-о птимальноп гарантирующей
стратегии xs, для к-рой
inf f{xs, yK=sup inf f (x, y) — E,
ysY ~x уе y
где f>0. В зависимости от множества стратегий ,т=
= х(у) и информации о неопределенном факторе (об-
(обстановке проведения операции) запись О. г. с. кон-
конкретизируется (см. [1]). Так, если множество стратегий
х состоит из всех функций х(у) и в операции имеется
полная информация об у, то О. г. с. х* (у) наз. аб-
абсолютно оптимальной стратегией и
определяется из условия
sup/(.г, у) = / (х* (у), у) при всех y?Y.
х
Изучаются также оптимальные стратегии, соответ-
соответствующие иным принципам оптимальности (см., напр.,
[2], 13]).
Лит.: [1] Г е р м е й е р Ю. Б., Введение в теорию исследо-
исследования операций, М., 1971; [2J е г о же, Игры с непротивопо
ложными интересами, М., 1976; [3] В о р о б ь е в Н. Н., в кн.
Теория игр Ер. 1973 с. 5 — 57. Ф. И. Ерешко, В. В. Федорш;
ОПТИМАЛЬНАЯ КВАДРАТУРА — квадратурная
формула, дающая наилучшее приближение интегралу
на классе F подинтегралышх функций. Если
то
наз. погрешностью квадратуры при
вычислении интеграла от данной функции, а
rN(F)=si:v\RN(f)\
feF
наз. погрешностью квадратуры на клас-
классе F. Если существует такая квадратура, что для соот
ветствующей рй гл\{Р) выполняется равенство
i-n(F)= inf rN(F),
то :>ту квадратуру наз. оптимальной на этом
к ласе е.
О. к. построены лишь для нек-рых классов функции
в основном одного переменного (см. [1] — [3]). О. к.
наз. также и а и л у ч ш ими квадратурны м и
ф о р м у л а м и, пли экстремальными квад-
квадратурными формулами.
Лит.: Ll] H и к о л ь с it и й С. М., Квадратурные формулы,
3 изд., М., 1979; [2] Б а х в а л о в Н. С, в кн.: Численные ме-
методы решения дифференциальных и интегральных уравнений и
квадратурные формулы, М., 1964, с. 5—03; [3J С о б о л е в С. Л.,
Введение в теорию кубатурных формул, М., 1974.
Н. С. Бахвалов.
ОПТИМАЛЬНАЯ ТРАЕКТОРИЯ — кривая x(t) в
0г4-1)-мерном пространстве переменных t, хх, ... ,х",
по к-рой точка x(t)=(xl (t), . . ., x"(t)), движение к-рой
описывается векторным дифференциальным уравнением
x = f(t, х, и), /:RxRnXR/> — R", A)
переводится из начального состояния
.r(to)=xo B)
в конечное состояние
x(t1) = xl C)
под воздействием оптимального управления u(t). до-
доставляющего минимальное значение заданному функ-
функционалу
'f°(t, х, и) <lt, /°:RxR"\Rr —> R. D)
На выбор оптимальном) упр.шлеппя накладывается
ограничение
u?U, E)
где U — замкнутое множество допустимых управлений,
U(ZRP. Начальный и конечный моменты времени
t0 и tx для определенности предполагаются соответ-
соответственно фиксированным и свободным.
Аналогичным образом О. т. определяется для вариа-
вариационных задач более общего вида по сравнению с
A) — E), напр, для задач с подвижными концами и
с ограничениями на фазовые координаты. О методах
отыскания О. т. см. Вариационное исчисление; численные
методы.
Для автономных задач, в к-рых функции /°, / не
зависят явно от времени V.
/» = /"(*, и), J = f(r, и),
бодее удобным для теории и приложений оказывается
понятие фазовой оптимальной траектории. Фазовая
оптимальная траектория есть п роекцпя
О. т. на «-мерное подпространство фазовых переменных
^л, . . ., х". Для автономных задач фазовая О. т. не
зависит от выбора начального момента времени ta.
Исследование множества фазовых О. т., переводя-
переводящих систему из произвольного начального состояния
в заданное конечное состояние (или, наоборот, из задан-
заданного начального состояния в произвольное конечное),
позволяет решить многие качественные вопросы для
рассматриваемой вариационной .задачи. Построение
множества фазовых О. т. является обязательным этапом
построения синтеза оптимальных управлении
обеспечивающего движение по О. т. в любой точке
фазового пространства.
Лит.: [1] Пои т р и г и н Л, С, Б о л т я н с к и й В. Г.,
Г а м к р е л и д з е Р. В., М и щ е н к о К. Ф., Математическая
теория оптимальных процессов, 3 изд., М., 1976; [2] Д е р у с-
с а II., Рой Р., К л о у з Ч., Пространство состояний в тео-
теории управления, пер. с англ., М., 1970. И. В. Вапнярский,
ОПТИМАЛЬНОГО БЫСТРОДЕЙСТВИЯ ЗАДАЧА —
одна из задач оптимального управления математиче-
математической теории, состоящая в определении минимального
времени
•/(")=*!, A)
за к-рое управляемый объект, движение к-рого описы-
описывается системой обыкновенных дифференциальных урав-
уравнении
j--f(r, и), u?U, f:RnxRp~*R",
можно перевести из заданного начального состояния
,г@)--.г(| в заданное конечное состояние x(t{) xx. Здесь
x~x(t) есть и-мерный вектор фазовых координат, а
u,— u,{t) есть р-мерный вектор управляющих парамет-
параметров (управлений), принадлежащий при любом / за-
заданной замкнутой допустимой области управлении U.
Искомое минимальное время tx является функциона-
функционалом A), зависящим от выбираемого управления u{t).
В качестве класса допустимых управлений, среди к-рых
разыскивается управление, оптимальное по быстро-
быстродействию, для большинства приложений достаточно
рассматривать кусочно непрерывные управления u(t),
т. е. функции, непрерывные для всех рассматриваемых
t, за исключением конечного числа моментов времени, в
к-рых они могут терпеть разрывы 1-го рода. Теорети-
Теоретически, строго говоря, следует рассматривать более об-
общий класс функций u(t), 0<?<«j, измеримых по Лебегу.
О. б. з. можно рассматривать как частный случай
Волъца задачи и Майера задачи, рассматриваемых в
вариационном исчислении, получающийся из этих
задач при специальном задании оптимизируемого функ-
функционала. Оптимальное по быстродействию управление
и (t) должно удовлетворять принципу максимума Пон-
трягнна, являющемуся необходимым условием, обоб-
обобщающим необходимые условия Ойлера, Клебша и Вейер-
штрасса, используемые в классическом вариационном
исчислении.
Для линейных О. б. з. из необходимых условий можно
получить нек-рые выводы о качественной структуре
оптимального управления. Л и н е й и ы м и О. б. з.
(см. [1], [2]) наз. такие задачи, в к-рых выполнены сле-
следующие три условия:
1) уравнения движения объекта линейны по ,т п и:
х = Ах -1- Ви,
где А и В — постоянные матрицы размерности пХп
и пХр соответственно;
2) конечное состояние хх совпадает с. началом коор-
координат, являющимся состоянием равновесия объекта
при м=0;
3) область управления U является /(-мерным выпук-
выпуклым многогранником таким, что начало координат
пространства и принадлежит U, но не является его вер-
вершиной.
Пусть выполнено условие общности положения, со-
состоящее в линейной независимости векторов
Bw, ABw, A2Bw, ..., A"-xBw,
где w — произвольный р-мернын вектор, параллельный
ребру многогранника Г. Тогда для оптимальности по
быстродействию управления u(t), 0</<гь переводя-
переводящего объект из заданного начального состояния х0 в
положение равновесия (начало координат в простран-
пространстве х), необходимо и достаточно, чтобы оно удовлет-
удовлетворяло принципу максимума Понтрягина. Дален,
оптимальное управление u'(t) в линейной задаче оп-
оптимального быстродействия кусочно постоянно, п его
значениями являются лишь вершины многогранника U.
В общем случае число переключений u(t) хотя п
конечно, но может быть произвольным. В следующем
важном случае число переключений допускает точную
оценку сверху.
Если многогранник U является р-мерным параллеле-
параллелепипедом
(Is< IIs S^bs, S~-i, . . ., р,
и все собственные значения матрицы А действительны,
то каждая из компонент us(t), s---l, . . ., />, оптималь-
оптимального управления u(t) является кусочно постоянной
функцией, принимающей только значения as и bs
и имеющей не более п— 1 переключении, т. е. не более
п интервалов постоянства.
О. б. з. может рассматриваться и для неавтономных
систем, т. о. для систем, у к-рых правая часть / зависит
еще п от нремени t.
В тех случаях, когда это удается, полезно рассма-
рассматривать О. б. з. не только в программной постановке,
как это описано выше, но и в позиционной постановке
в форме задачи синтеза (см. Оптимальное управление
позиционное). Решение задачи синтеза позволяет полу-
получить качественное представление о структуре оптималь-
оптимального по быстродействию управления, переводящего
систему из любой точки, находящейся в нек-рой окрест-
окрестности исходной начальной точки х0, в заданное конеч-
конечное состояние х\.
Лит.: [1] Понтрягин Л. С, Болтянский В. Г.,
Г а ы к р с л и д з е Р. В., Мищенко Е. Ф-, Математический
теория оптимальных процессов, 3 изд., М., 197С; [2] Б о л т я н-
с к и й В. Г., Математические методы оптимального управления,
М., I960. И. В. Вапнярский.
ОПТИМАЛЬНОГО УПРАВЛЕНИЯ МАТЕМАТИ-
МАТЕМАТИЧЕСКАЯ ТЕОРИЯ — раздел математики, в к-ром
изучаются способы формализации и методы решения
задач о выборе наилучшего в заранее предписанном
смысле способа осуществления управляемого динамич.
процесса. Этот динамический процесс мо-
может быть, как правило, описан при помощи диффе-
дифференциальных, интегральных, функциональных, конеч-
норазностных уравнений (или иных формализованных
эволюционных соотношений), зависящих от системы
функций или параметров, нал. управлениями
и подлежащих определению. Искомые управления, а
также реализации самого процесса следует в общем
случае выбирать с учетом ограничений, предписанных
постановкой задачи.
В более специальном смысле термином «О. у. м. т.»
принято называть математич. теорию, в к-рой изу-
изучаются методы решения неклассических вариационных
задач оптимального управления (как правило, с диф-
дифференциальными связями), допускающих рассмотрение
негладких функционалов и произвольных ограничений
на параметры управления или иные зависимые нере-
неременные (обычно рассматривают ограничения, задавае-
задаваемые нестрогими неравенствами). Термину «О. у. м. т.»
иногда придают более широкий смысл, имея в виду
теорию, изучающую математич. методы исследования
задач, решения к-рых включают какой-либо процесс
статической или динамич. оптимизации, а соответ-
соответствующие модельные ситуации допускают интерпрета-
интерпретацию в терминах той или иной прикладной процедуры
принятия наилучшего решения. В таком толковании
О. у. м. т. содержит элементы исследования операций,
математического программирования и игр теории.
Задачи, рассматриваемые в О. у. м. т., возникли из
практич. потребностей, прежде всего в области меха-
механики космич. полета и автоматического управления
теории (см. также Вариационное исчисление). Формали-
Формализация и решение этих задач поставили новые вопросы,
напр, в теории обыкновенных дифферонциалтзных урав-
пений, как в области обобщения понятия решения н
вывода соответствующих условий существования, так п
в изучении динамических и экстремальных свойств три
екторин управляемых дифференциальных систем; it
частности, О. у. м. т. стимулировала изучение свойств
дифференциальных включений. Соответствующие направ-
направления О. у. м. т. поэтому часто рассматриваются как
раздел теории обыкновенных дифференциальных урав-
уравнений. В О. у. м. т. содержатся математич. основы тео-
теории управления движением — нового раздела общей
механики, в к-ром исследуются законы формирования
управляемых механич. движений и смежные математич.
вопросы. По методам исследования и но своим прило-
приложениям О. у. м. т. тесно связана с аналитич. механи-
механикой, в особенности с разделами, относящимися к ва-
вариационным принципам классической механики.
Хотя частные задачи оптимального управления и
неклассические вариационные задачи встречались и ра-
ранее, основы общей О. у. м. т. были заложены в 1950—
1961. Ключевым пунктом этой теории послужил Пон-
трягина принцип максимума, сформулированный Л. С.
Понтрягиным в 1956 (см. [1]). Важными стимулами со-
создания О. у. м. т. были открытие метода динамического
программирования, выяснение роли функционального
анализа в теории оптимальных систем, открытие свя-
связей решении задач оптимального управления с резуль
татами теории устойчивости по Ляпунову, появление
работ, связанных с понятиями управляемости и наблю-
наблюдаемости динамич. систем (см. [2]—[5]). В последую-
последующие годы были развиты основы теории стохастич. управ-
управления и стохастич. фильтрации динамич. систем,
построены общие методы решения неклассических ва-
вариационных задач, получены обобщения основных по-
положений О. у. м. т. на более сложные классы динамич.
систем, изучены связи с классическим вариационным
исчислением (см. [6]—[11]). О. у. м. т. интенсивно раз-
развивается, в частности, в направлении изучения игро-
игровых задач динамики (см. Дифференциальные игры),
задач управления в условиях неполной или неопреде-
неопределенной информации, систем с распределенными пара-
параметрами, уравнений на многообразиях и т. д.
Результаты О. у. м. т. нашли широкие приложе-
приложения в формировании процессов управления, относя-
относящихся к самым разным областям современной техники,
в изучении зкономич. динамики, в решении ряда задач
из области биологии, медицины, экологии, демогра-
демографии и т. д.
Задача оптимального управления
в общем виде может быть описана следующим образом.
1) Дана управляемая система S, состояние к-рой
в момент времени t изображается величиной х (напр.,
вектором обобщенных координат и обобщенных им-
импульсов механнч. системы, функцией от пространствен-
пространственных координат в распределенной системе, вероятност-
вероятностным распределением, характеризующим текущее со-
состояние стохастич. системы, вектором выпуска продук-
продукции в динамич. модели экономики и т. д.). Предполага-
Предполагается, что к системе S приложены управляющие воздей-
воздействия и, оказывающие влияние на ее динамику. Они
могут, напр., иметь смысл механич. сил, температурных
или электрич. потенциалов, программы капиталовло-
капиталовложений и т. д.
2) Дано уравнение, связывающее переменные х,
и, t и описывающие динамику системы. Указан про-
межуток времени, на к-ром рассматривается уравнение.
В типичном случае это может быть обыкновенное диффе-
дифференциальное уравнение вида
x = f(t, х, и), <o*S'<'i. *€к"> u?RP, A)
с заранее оговоренными свойствами функции / (часто
требуют, напр., непрерывности / по t, х, и и непрерыв-
непрерывной дифференцируемое™ по х).
3) Известен характер информации, к-рая может быть
использована для формирования управляющих воздей-
воздействий (напр., в каждый момент времени или в заранее
предписанные моменты становятся известными доступ-
доступные измерению величины — значения фазовых коорди-
координат системы A) или функций от этих координат). Огово-
Оговорен класс функций, описывающих управления, допу-
допускаемые к рассмотрению: множество кусочно непре-
непрерывных функций вида u=u(t), множество линейных по
х функций вида u=«(/, x) = P'(t)x с непрерывными
коэффициентами и т. д.
4) Установлены ограничения на процесс, подлежа-
подлежащий реализации. Сюда прежде всего входят условия,
определяющие цель управления (напр., для системы
A) — попадание в заданную точку или на заданное
множество фазового пространства R", требование ста-
стабилизации решений около заданного движения и т. д.).
Кроме того, ограничения могут быть наложены на ве-
величины управляющих воздействий и или координат
состояния х, на функции от этих величин, на функцио-
функционалы от их реализации и т. д. В системе A), напр.,
возможны ограничения на параметры управления
u?U ^ Rp или ф (и)<0, y:Rp —* R*, B)
и на координаты
igX?R" или if (*) < 0, if: R" —* R'; C)
здесь U, X — замкнутые множества, ф, if — дифферен-
дифференцируемые функции. Могут рассматриваться и более
сложные ситуации, когда множество U зависит от t,
х или задано неравенство вида g(t, x, ;/)<:() (случай
смешанных ограничений) и т. д.
5) Задан показатель (критерий) качества процесса,
подлежащего реализации, представимый в виде функ-
функционала J (х{-), «(•)) от реализации переменных х, и
на рассматриваемом отрезке времени. Условия 1)—4)
теперь дополняются требованием оптимальности про-
процесса — минимума, максимума, минимакса и т. д. по-
показателя J(x(-), и(-)).
Таким образом, в заданном классе управлений для
заданной системы требуется выбрать управление и,
оптимизирующее показатель /(.г(-), и(-)) (при условии
достижения цели управления и при выполнении нало-
наложенных ограничений). Функция (напр., вида u=u(t)
или u-—u(t, х) и т. д.), решающая задачу оптимального
управления, наз. оптимальным управле-
управлением (пример формулировки типичной задачи опти-
оптимального управления см. в ст. Понтрягина принцип
максимума).
Среди динамич. объектов, охватываемых задачами
О. у. м. т., принято отличать конечномерные от беско-
бесконечномерных — в зависимости от размерности фазового
пространства соответствующих систем дифференциаль-
дифференциальных уравнений, описывающих их, или от вида ограниче-
ограничений, наложенных на фазовые переменные.
Различают задачи оптимального управления про-
программного и оптимального управления позиционного.
В первом случае воздействие и формируется в виде
функции времени. Во втором случае воздействие и
формируется в виде стратегии управления по принципу
обратной связи, как функция от доступных значений
текущих параметров процесса.
В изучении задач О. у. м. т. выделяют вопросы суще-
существования решений, вывод необходимых условий экс-
тремума (оптимальности управления), исследование
достаточных условии, построение численных алгорит-
алгоритмов. Рассматриваются также соотношения между ре-
решениями задач О. у. м. т., полученных в классе про-
программных и позиционных управлений.
Описанные варианты постановок задач оптимального
управления предполагают существование корректной
математич. модели процесса и рассчитаны на полную
априорную или даже на полную текущую информацию о
соответствующей системе. Однако в прикладных по-
постановках доступной информации о системе (напр.,
сведений о начальных и конечных условиях, о коэффи-
коэффициентах соответствующих уравнений, о значениях до-
дополнительных параметров пли доступных измерению
координат и т. д.) часто оказывается недостаточно для
прямого применения отмеченной выше теории. Послед-
Последнее приводит к задачам оптимального управления,
сформулированным в иных информационных предпо-
предположениях. Большой раздел О. у. м. т. посвящен зада-
задачам, где описание недостающих величин носит стати-
стич. характер (т. н. теория стохастического
оптимального управления). Если ка-
какая-либо статистич. информация о недостающих ве-
величинах отсутствует, но заданы лишь допустимые
области их изменения, то соответствующие задачи
рассматриваются в рамках теории оптимального
управления в условиях неопреде-
неопределенности. К решению этих задач тогда привле-
привлекают методы минимакса и теории игр. Задачи стоха-
стохастического оптимального управления и оптимального
управления в условиях неопределенности особенно
содержательны, когда речь идет о позиционном опти-
оптимальном управлении.
Хотя формализованное описание управляемых систем
может принимать достаточно абстрактную форму (см.
[И]), простейшая классификация допускает также де-
деление их на системы с непрерывным вре-
временем (описываемые, напр., дифференциальными
уравнениялш — обыкновенными пли с частными про-
производными, уравнениями с отклоняющимся аргумен-
аргументом, уравнениями в банаховом пространстве, а также
дифференциальными включениями, интегральными,
интегро-дифференциальными уравнениями и т. д.) и
многошаговые (дискретные) свете-
м ы, описываемые рекуррентными разностными урав-
уравнениями и рассматриваемые лишь в изолированные
(дискретные) моменты времени.
Дискретные системы управления, помимо самостоя-
самостоятельного интереса, имеют серьезное значение как ко-
конечно-разностные модели непрерывных систем. По-
Последнее важно для построения численных методо» реше-
решения задач оптимального управления (см. [12], |13J),
в особенности в тех случаях, когда исходная задача
подвергается дискретизации, начиная с самой поста-
постановки. К дискретным системам применимы основные
указанные выше постановки задач. Хотя теоретико-
функциональная сторона исследования здесь оказы-
оказывается проще, перенесение основных фактов теории
оптимального управления для непрерывных систем и
изложение их в компактной форме связано со специ-
фич. трудностями и не всегда возможно (см. [14], [15]).
Теория оптимальных линейных дискретных систем
управления с ограничениями, задаваемыми выпуклыми
функциями, разработана достаточно полно (см. [15]).
Она смыкается с методами линейного и выпуклого про-
программирования (особенно с соответствующими «дина-
«динамическими» или «нестационарными» вариантами) (см.
[161). Важное значение в этой теории приобретают ре-
решения, позволяющие соединять в рекуррентном
процессе оптимизацию дискретной динамической си-
системы с реализацией адекватного численного дискрет-
дискретного алгоритма.
Отдельный круг проблем О. у. м. т. образуют вопро-
вопросы аппроксимации решений задач оптимального управ-
управления для непрерывных систем дискретными, тесно
связанные с проблемой регуляризации некорректно
поставленных задач (см. 117]).
Лит.: [1] П о н т р я г и н Л. С, Болтянский В. Г.,
ГамкрелидзеР. В., Мищенко Е. Ф., Математическая
теория оптимальных процессов, 3 изд., М., 1970; [21 Бел л-
ман Р., Динамическое программирование, пер. с англ., М.,
1960; [3] К р а с о в с к и й Н. Н., Теория управления движе-
движением, М., 1968; [4] е г о ж е, в сб.; Механика в СССР за 50 лет,
т. 1, М., 1968, с. 179—244; [5] К а л и а н Р., в кн.: Труды 1 Меж-
Международного конгресса Международной федерации по автомати-
автоматическому управлению, т. 2, М., 1961, с. 521—47; [6] Фле-
Флеминг У., Р и ш е л Р., Оптимальное управление детермини-
детерминированными и стохастическими системами, пер. с англ., М., 1У78;
[7] Алексеев В. М., Тихомиров В. М.,Фомин С. В.,
Оптимальное управление, М., 1979; [8] В а р г а Дж., Оптималь-
Оптимальное управление дифференциальными и функциональными урав-
уравнениями, пер. с англ., М., 1977; [9] HcstenesM. , Calculus
of variations and optimal control theory, N. Y., 1966; [10] Я н г Л.,
Лекции по вариационному исчислению и теории оптимального
управления, пер. с англ., М., 1974; til] К а л м а н Р., Фа л б П.,
Ар б и б М., Очерки по математической теории систем, пер. с
англ., М., 1971; [12] Моисеевы. Н., Элементы теории опти-
оптимальных систем, М., 1975; [13] Ч е р н о у с ь к о Ф. Л., К о л-
м а н о в с к и й В. Б., в кн.: Итоги науки и техники. Сер. Мате-
Математический анализ, т. 14, М., 1977, с. 101—66; [14] Болтян-
Болтянский В. Г., Оптимальное управление дискретными системами,
М., 1973; 115] Canon M. D., С и 1 1 и m С. D., Р о 1 a k E.,
Theory of optimal control and mathematical programming, N. Y.,
1970; [lti] II p о п о й А. И., Элементы теории оптимальных дис-
дискретных процессов, М., 1973; [17] Тихонов А. Н., А р с е-
нин В. Я., Методы решения некорректных задач, 2 изд., М.,
1979. А. Б. Нуржанский.
ОПТИМАЛЬНОЕ ДЕКОДИРОВАНИЕ — декодирова-
декодирование, к-рое максимизирует сообщений точность воспро-
воспроизведения для заданных источников сообщений, канала
связи и метода кодирования. В случае, когда точность
воспроизведения сообщений характеризуется средней
ошибочного декодирования вероятностью, О. д. миними-
минимизирует оту вероятность. Пусть, напр., для передачи М
сообщений, занумерованных числами 1, . . ., Л?, вероят-
вероятности появления к-рых равны р1? . . ., рм соответст-
соответственно, используется дискретный канал с конечным чис-
числом значений сигналов на входе и выходе и переходной
функцией, задаваемой матрицей
_Я(У, У)=Р{Ц = У\Ц = У]
где Y, Y — множества значений сигналов т] на входе
и т] на выходе соответственно, а кодирование задается
функцией /(•) такой, что f{m) = ym, m—1, . . ., М,
гДе Vm€iY, m=l, . . ., М,— код, т. е. нек-рый набор М
возможных значений сигнала на входе канала. Тогда
О. д. задается функцией g(-) такой, что g(y) = m' для
любого y?Y, где т' удовлетворяет неравенству
Рт-Ч (Ут', УMгРт<}(Ут, У)
для всех тфт. В частности, если все сообщения рав-
равновероятны, т. е. Pi=. . . = pm=i/M, то описанное
О. д. является в то же время декодированием по методу
«максимального правдоподобия» (к-рое в общем случае
оптимальным не является): полученный на выходе ка-
канала сигнал у следует декодировать в сообщение т',
для к-рого
Ч(Ут-, y)Szq(ym, У) при тфт'.
Лит.: [1] Г а л л а г е р Р., Теория информации и надежная
связь, пер. с англ., М., 1974; [2] Возенкрафт Дж., Дже-
Джекобе И., Теоретические основы техники связи, пер. с англ.,
М., 1969. Р. Л. Добрушип, В. В. Прелое.
ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ —решение неклас-
неклассической вариационной задачи оптимально-
оптимального управления (см. Оптимального управления
математическая теория). В типичном случае О. у.
дает решение задачи об экстремуме заданного функцио-
функционала вдоль траекторий обыкновенного дифференциаль-
дифференциального уравнения, зависящего от параметров-«управле-
ний» (при наличии дополнительных ограничений,
предписанных постановкой задачи). Здесь, в аависи-
ногти от рассматриваемого класса управлений, О. у.
может принимать форму функции времени
(в задаче оптимального управления программного) или
функции времени и текущего сос-
состояния (позиций) системы (в задаче синтеза опти-
оптимального управления позиционного).
В более сложных или более специальных задачах
О. у. может принимать форму обобщенного
управления — функции времени со значениями
во множестве мер, функционала от отрезка траектории
или от нек-рого множества в фазовом пространстве,
краевого условия для уравнения с частными производ-
производными, многозначного отображения, последовательности
экстремальных элементов нестационарной задачи мате-
матич. программирования и т. д. а. б. Нуржанский.
ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ ПОЗИЦИОН-
ПОЗИЦИОННОЕ — решение задачи оптимального управления ма-
математической теории, состоящей в синтезе оп-
оптимального управления в виде страте-
стратегии управления по принципу обратной связи, как
функции текущего состояния (позиции) процесса (см.
[1] — [3]). Последнее определяется, помимо текущего
момента t, также доступными значениями текущих пара-
параметров. Таким образом, введение позиционной страте-
стратегии позволяет формировать реализацию управления и
апостериорно, корректируя его на основе дополнитель-
дополнительной информации, получаемой по ходу процесса.
Простейшая задача синтеза, напр, для системы
x — f{t, х, и), «„<«<?!, x?Rn, u?Rp, A)
с ограничениями
u^W=RP или if И «5 0, ,|, ; RP—+ R*, B)
и заданным «терминальным» показателем
предполагает поиск решения и'\ минимизирующего
функционал 1(х(-), «(•)) среди функций вида u(t, х)
для произвольной исходной позиции {т, х}. Естест-
Естественный путь состоит в решении для каждой позиции
{т, х} соответствующей задачи о построении оптималь-
оптимального управления программного
ц°[<|т, х], х = х(х),
на минимум того же функционала /(.г(-), «(•)) и при
тех же самых ограничениях. Далее полагается, что
u°(t, x) = u°\t\t, х]
и если функция u°(t, x) корректно определена, а урав-
уравнение
i = / (t, х, и0 (t, x)), х (т)=ж, т«5<</ь C)
имеет единственное решение, то задача синтеза реше-
решена, причем оптимальные значения показателя /, най-
найденные в классах программных и позиционных управ-
управлений, совпадают (в общем случае выделяют условия,
обеспечивающие существование в определенном содер-
содержательном смысле решений уравнения C), и условия,
гарантирующие оптимальность всех траекторий этого
уравнения).
Синтезированная функция u°(t, x), являющаяся
О. у. п., позволяет построить оптимальное в смысле
минимума функционала / решение задачи оптимального
управления для любой исходной позиции {т, х),
в отличие от программного оптимального управления,
зависящего, вообще говоря, от фиксированного началь-
начального состояния {tu, xa) процесса. Решение задачи
оптимального управления в форме синтеза оптимального
управления находит большие приложения, в частности
в связи с тем, что реальные процедуры построения
управления осуществляются, как правило, на фоне ин-
формацпонных помех пли возмущений процедуры счета.
В указанных ситуациях позиционное управление пред-
предпочтительней программного.
Нахождение u°(t, x) сразу в виде функции текущего
состояния связано с использованием метода динамиче-
динамического программирования (см. [2]). Вводимая в рассмот-
рассмотрение функция действия (функция
Б е л л м а н a) V(i, x), имеющая смысл минимума
(максимума) оптимизируемой величины (напр., функ-
функционала
/(*(¦). «(¦))= ^'/"V, -г', И) Л -Ьф (*!,*(*!» D)
для системы A) при х(х) = х, t^[x, ij), должна удовлет-
удовлетворять дифференциальному уравнению Беллмана с
частными производными и с краевыми условиями, за-
зависящими от цели управления и показателя /. Для
системы A), B), D) яти уравнение имеет вид
где
^т, f (/, x, u)j-f-/''(/, ,r, u)\u?r\ (fi)
— функция Гамильтона. Оно связано с уравнениями,
фигурирующими в условиях Понтрягииа принципа мак-
максимума, подобно тому, как уравнение Гамильтона —
Якоби для функции действия связано в аналитнч.
механике с обыкновенным дифференциальным уравне-
уравнением Гамильтона (см. Вариационные принципы клас-
классической механики).
Вывод уравнения E) для задачи синтеза опирается
на принцип оптимальности, утверждаю-
утверждающий, что отрезок оптимальной траектории есть снова
оптимальная траектория (см. [2]). Правомерность та-
такого подхода зависит от корректного определения ин-
информационных свойств процесса и, в частности, поня-
понятия позиции (текущего состояния, см. [5]).
В задаче быстродействия — о мини-
минимальном времени Т (х) попадания траектории автоном-
автономной системы A) из положения х на множество М —
функцию Г(т, х)=У (х) можно рассматривать как свое-
своего рода потенциал V (х)— Т (х) относительно множества
М. Выбор оптимального управления un(t.x) и.ч усло-
условий E), (G), приобретающих здесь вид
V (ж)=0 при х?М,
тогда означает, что u°(t, ?) — u°(x) осуществляет спуск
оптимальной траектории .t" (/) относительно поверхно-
поверхностей уровня функции V (х) наискорейшим из способов,
допускаемых условием u(-U.
Применение метода дннамич. программирования (как
достаточного условия оптимальности) будет обосновано,
если функция V(x, а) всюду удовлетворяет определен-
определенным условиям гладкости (напр., в задаче C) —F) функ-
функция V (т, х) должна быть непрерывно дифференцируе-
дифференцируемой) или если условия гладкости выполняются всюду,
за исключением нек-рого «особого» множества JV. При
выполнении нек-рых специальных «условий регуляр-
регулярного синтеза» метод динамич. программирования ока-
оказывается эквивалентным принципу Понтрягина, к-рый
тогда выступает как необходимое и достаточное усло-
условие оптимальности (см. [8]). Трудности, связанные с
априорной проверкой применимости метода динамич.
программирования и с необходимостью решать диффе-
дифференциальное уравнение Беллмана с частными произ-
производными, усложняют использование этого метода. Me-
тод динамического программирования нашел распро-
распространение, в задачах синтеза оптимального управле-
управления для дискретных (многошаговых) систем, где соот-
соответствующее уравнение Беллмана конечно-разностное
(см. [2], [9]). '
В задачах оптимального управления с дифференци-
дифференциальными связями метод динамич. программирования
дает эффективное решение задачи синтеза в замкнутой
форме для класса задач, охватываемых линейными си-
системами с квадратичным показателем D) (функции /°, ф
суть положительно определенные квадратичные формы
соответственно по х, и и по х). Эта задача об а н а л и-
т и ч е с к о м конструировании опти-
оптимального регулятора при <р (t, .r)=«0, /,= оо
переходит в задачу об оптимальной г та б н-
л и з а г; и и с и с т е м ы (из существования допу-
допустимого управления здесь сразу вытекает свойство
асимптотич. устойчивости положения равновесия син-
синтезированной системы) (см. [10], [4]). Существование
решения в данном случае обеспечивается свойством ста-
билизируемостп системы (см. [4]). Для линейных ста-
стационарных и периоднч. систем оно эквивалентно свой-
свойству управляемости системы по неустойчивым собст-
собственным координатам (см. Оптимальное управление
программное).
Решение задачи оптимальной стабилизации показа-
показало, что соответствующая функция Беллмана является
в то же время «оптимальной» функцией Ляпунова для
исходной системы с найденным оптимальным управле-
управлением. Отмеченные обстоятельства позволили получить
эффективные условия стабилизируемое™ и построить
для задач стабилизации полный аналог теории устой-
устойчивости по Ляпунову (по первому приближению и в
критич. случаях), охватывающий обыкновенные ква-
квазилинейные и периодич. системы, а также сдетемы с за-
запаздыванием. В последнем случае роль функции Белл-
Беллмана играют «оптимальные» функционалы Ляпунова —
Красовского, заданные на отрезках траектории, соот-
соответствующих величине запаздывания в системе (см.
[4], [5]). Теория линейно-квадратичных задач оптималь-
оптимального управления хорошо развита и для дифференциаль-
дифференциальных уравнений с частными производными (см. [11]).
В прикладных задачах синтеза оптимального управ-
управления измерение всех фазовых координат системы
доступно далеко не всегда. Поэтому возникает следую-
следующая задача наблюдения, допускающая мно-
многочисленные обобщения: зная на промежутке a^.t^.b
реализацию y\t]?Rm доступной измерению функции
¦' -g{t,x) координат системы A) (при известном м(/),
напр. при u(*)=eO, и 7Ж?г), найти вектор z(Q)?Rn в
заданный момент О. Системы, позволяющие по реали-
реализации y[t] однозначным образом восстанавливать
х(§), каким бы он ни был, наз. вполне наблюда-
наблюдаемым и.
Свойство полной наблюдаемости, как и построение
соответствующих аналитич. операций, выделяющих
х(д), а также оптимизация этих операций хорошо
изучены для линейных систем. Здесь известен п р и н-
ц и п дуальности, состоящий в том, что каждой
задаче наблюдения может быть поставлена в соответ-
соответствие эквивалентная двухточечная краевая задача уп-
управления для дуальном системы. Вследствие этого ока-
оказывается, что свойство полной наблюдаемости линейной
системы совпадает со свойством полной управляемости
дуальной системы с управлением. Более того, оказыва-
оказывается, что и соответствующие дуальные экстремальные
задачи об оптимальном наблюдении и оптимальном
управлении могут быть составлены так, что их решения
совпадут (см. [3]). Свойства управляемости и наблюдае-
наблюдаемости линейных систем допускают весьма разнообраз-
разнообразие обобщения на линейные бесконечномерные объек-
объекты (уравнения в банаховом пространстве, системы с
отклоняющимся аргументом, дифференциальные урав-
уравнения с частными производными). Имеется и ряд ре-
результатов, характеризующих соответствующие свой-
свойства. Для нелинейных систем известен лишь ряд ло-
локальных теорем о наблюдаемости. Решения проблемы
наблюдения нашли многочисленные применения в зада-
задачах синтеза в условиях' неполной информации о коор-
координатах, в том числе в задачах оптимальной стабили-
стабилизации (см. [3]-[5], [14], [15]).
Задача синтеза становится особенно содержательной,
когда информация об уравнениях управляемого про-
процесса, исходных начальных условиях и текущих пара-
параметрах искажена возмущениями. Если описание воз-
возмущений носит статистпч. характер, то задачи опти-
оптимального управления рассматривают в рамках тео-
теории стохастического оптимального
управления. Эта теория, начатая с решения
стохастических программных задач [16], в наибольшей
степени разработана для систем вида
*¦=/(/, х, u)-i-g(t, х, и) л, x(tti)=x°, G)
со случайными возмущениями r\(t), описываемыми
гауссовскими диффузионными процессами или более
общими классами марковских процессов (начальный
вектор обычно также считают случайным). При этом,
как правило, предполагается, что заданы нек-рые ве
роятностпые характеристики величин п (напр., све-
сведения о моментах соответствующих распределений или
о параметрах стохастич. уравнений, описывающих
эволюцию процесса r\(t)).
В общем случае применение программных и синте-
синтезирующих управлений здесь дает существенно различ-
различные значения оптимальных показателей / качества
(роль таких показателей могут играть, напр., те или
иные средние оценки неотрицательных функционалов,
заданных на траекториях процесса). Задача синтеза
стохастического оптимального управления теперь имеет
очевидные преимущества, т. к. непрерывное измерение
координат системы позволяет корректировать движе-
движение с учетом реального хода случайного процесса, не-
непредсказуемого заранее. Здесь было обнаружено, что
метод динамич. программирования совершенно естест-
естественным образом сопрягается с теорией бесконечно ма-
малых производящих операторов для полугрупп преобра-
преобразований, генерируемых марковскими случайными про-
процессами. Эти обстоятельства позволили построить и
строго обосновать серию достаточных условий опти-
оптимальности, приведших к решению на конечном и бес-
бесконечном интервале времени ряда задач о синтезе сто-
стохастического оптимального управления с полной и
неполной информацией о текущих координатах, сто-
стохастич. задач преследования и т. д. При этом сущест-
существенно, что для справедливости принципа оптимальностп
управление и здесь должно строиться в каждый момент
времени t как функция «достаточных координат» z
процесса, для к-рых будет обеспечено свойство мар-
марковости (см. [5], [6], [17], [18]).
Таким путем, в частности, была разработана тео-
теория оптимальной стохастической
стабилизации, связанная с соответствующей
теорией устойчивости по Липупонх. развитой для сто-
стохастич. систем [19].
Для формирования синтезирующего оптимального
управления, а также для иных целей управления целе-
целесообразно оценивать состояние стохастич. системы
по результатам измерения. Решению этого вопроса
гтрп условии, что процесс измерения искажается веро-
вероятностными «шумами» (т. е. решению задачи наблюде-
наблюдения в условиях случайных- возмущений), посвящена
теория с т о х а с т и ч е с к о и фильтрации.
Наиболее полные решения здесь известны для линей-
линейных систем с квадратичными критериями оптимума
(т. н. фильтр К а л м а н а -Б ь то с п, см. [13]).
В применении этой теории к задаче синтеза стохасти-
стохастического оптимального управления были выявлены усло-
условия, обеспечивающие справедливость принципа раз-
разделения, позволяющего решать собственно задачу
управления независимо от задачи оценивания текущих
позиции на основе достаточных координат процесса
(см. [20]; более общим закономерностям стохастич.
фильтрации, а также задачам стохастич. оптимального
управления, когда само управление выбирается в клас-
классе марковских процессов диффузионного типа, посвя-
посвящены работы [18], [21]).
Строго формализованное решение задачи стохасти-
стохастического оптимального управления неизбежно соприка-
соприкасается с проблемой корректного обоснования вопро-
вопросов существования решении соответствующих стохасти-
стохастических дифференциальных уравнений. Последнее об-
обстоятельство порождает определенные трудности в
решении задач стохастического оптимального управ-
управления при наличии неклассич. ограничении.
Содержательньп'г процесс динамич. оптимизации воз-
возникает в задачах синтеза оптимального управления
в условиях неопределенности (см. Оптимальное управ-
управление программное). Позиционные решения в общем
случае позволяют и здесь улучшить показатели каче-
качества процесса по сравнению с программными, представ-
представляющими собой все-таки результат статпч. оптимиза-
оптимизации (проводимой, правда, в пространстве дпнампч.
систем и функций-управлений). К решению задач тогда
привлекают понятия и методы теории игр.
Пусть имеется система
x = f(t, х, и, !/¦), /0*S'<-'i, (S)
при ограничениях
на начальный вектор х°, управление и и возмущения
w. В отличие от игрока-союзника, представляющего
исходное управление и, подлежащее определению, воз-
воздействия w здесь трактуют как управление игрока-
противника и допускают к рассмотрению любые целе-
целенаправленные стратегии w, формируемые на основе
любой допустимой информации. При этом цели управ-
управления могут быть сформулированы с точки зрения
каждого из игроков в отдельности. Если названные
цели противоположны, то возникает задача к о н-
фликтного управления. Исследование за-
задач позиционного управления в условиях конфликта
или неопределенности составляет предмет теории диф-
дифференциальных игр.
Процесс формирования позиционного оптимального
управления в условиях неопределенности может быть
осложнен неполнотой информации о текущем состоя-
состоянии. Так, в системе (8) могут быть доступны лишь ре-
результаты косвенных измерений фазового вектора х —
реализации y[t] функции
y(t)=g(t, х, |), (9)
где неопределенные параметры | стеснены известным
априорным ограничением 1?Е. Знание y[t\, /„</<(>
(при заданном u(t)), позволяет построить в фановом
пространстве информационную область
X {$, у(-)) состояний системы (8), совместимых с реа-
реализацией у [t], уравнением (9) и ограничениями на и>,
|. Среди элементов X (О, у()) --- X (&, •) будет содержать-
содержаться и неизвестное истинное состояние системы (8), к-рое
может быть оценено выбором нек-рой точки .г*(§,-)
из Х(9,-) (напр., «центра тяжести» или «чебышевского
центра» X (ft, •) ). Изучение эволюции областей Х("&, •)
и динамики векторов х* (ft, •) составляет содержание
теории минимаксной фильтрации.
Наиболее полные решения здесь известны для лпней-
ных систем и выпуклых ограничении (см. [22]).
В общем случае выбор позиционной стратегии опти-
оптимального управления в условиях неопределенности
(напр., в виде функционала u=u(t,X(t, •))) должен
быть нацелен на управление эволюцией областей
X(fly-) (т.е. на изменение их конфигурации и пере-
перемещение их в пространстве) в соответствии с предписан-
предписанными критериями. Для указанной задачи известен ряд
общих качественных результатов, а также конструк-
конструктивных решений в классе специальных линейно-выпук-
линейно-выпуклых задач (см. [7], [22]). При этом информация, достав-
доставляемая измерениями (напр., функцией y[t] в системе
(8), (9)), позволяет по ходу процесса апостериорным
образом переоценивать области допустимых значений
неопределенных параметров в направлении их суже-
сужения. Таким образом попутно решается задача
идентификации математич. модели процесса
(напр., параметров w уравнения (8)). Сказанное позво-
позволяет трактовать решения задачи о синтезе оптимально-
оптимального управления в условиях неопределенности как про-
процедуру адаптивного оптимального уп-
управления, в к-ром уточнение свойств модели
процесса переплетается с выбором управляющего воз-
воздействия как такового. Вопросы идентификации моде-
моделей динамич. процессов и задачи адаптивного опти-
оптимального управления подробно изучены в предположе-
предположениях о существовании того или иного вероятностного
описания неопределенных параметров (см. {23], [24]).
Если в задачах синтеза оптимального управления
в условиях неопределенности трактовать параметры м>,
S как «управления» фиктивного игрока-противника,
то цели управлений и и {w, §} могут быть различными.
Последнее обстоятельство приводит к нескалярному
показателю качества процесса, вследствие чего соот-
соответствующие задачи могут рассматриваться в рамках
понятий о равновесных ситуациях, свойственных мно-
многокритериальным задачам теории неантагонистич. игр
или их обобщениям.
Лит.: [1] П о н т р я г и н Л. С, Болтянский В. Г.,
Г а м к р е л и д з е Р. В., М и щ е н к о К. Ф., Математическая
теория оптимальных процессов, з изд., М., 1976; L2] Б е л л-
ман Р., Динамическое программирование, пер. с англ., М.,
I960; [3] К р а с о в с к и й Н. Н., Теория управления движе-
движением, М., 1968; [4] его ;к е, «Дифференциальные уравнения»,
1965, т. 1, № 1, с. 5—16; [5] его ж е, в сб.: Механика в СССР за
50 лет, т. 1, М., 1968, с. 179—244; [6] e г о же «Прикл. матем.
и мех.», 1961, т. 25, .14» 5, с. 806—17; [7 j Красовский Н. Н.,
Субботин А. И., Позиционные дифференциальные игры,
М., 1974; [8] Болтянский В. Г., Математические методы
оптимального управления, М., 1966; [9] е г о ж е, Оптимальное
управление дискретными системами, М., 1973; [10] Лето в
А. М., Математическая теория процессов управления, М., 1981;
til] Лионе Ж., Оптимальное управление системами, описы-
описываемыми уравнениями с частными производными, пер. с франц.,
М., 1972; 112] Калман Р., в кн.: Труды 1 Международного
конгресса Международной федерации по автоматическому управ-
управлению, т. 2, М., 1961, с. 521—47; [13] К а л м а н Р., Б ь го-
си Р., «Труды Амер. об-ва инженеров-механиков. Сер. 1, Д.»,
1961, т. 83, с. 123; [14] Ли Э.-Б., Маркус Л., Основы теории
оптимального управления, пер. с англ., М., 1972; [15] Б у т-
ковский А. Г., Структурная теория распределенных сис-
систем, М., 1977; [16] Колмогорова. Н., Мищенко Е. Ф.,
П о н т р я г и н Л. С, «Докл. АН СССР», 1962, т. 145, .№ 5, с.
993—95; [17] Л и и ц е р Р. Ш., Ширяев А.Н., Статистика
случайных процессов, М., 1974; L18] Острей К. Ю., Введе-
Введение в стохастическую теорию управления, пер. с англ.,М., 1973;
[19] К а ц И. Я., К j) а с о в с к и й Н. Н., «Прикл. матем. и
мех.», I960, т. 24, № 5, с. 809—23; [20] Won ham W. M.,
«SIAM J. Contr.», 1968, v. 6, p. 312—26; [21] К р ы л о в Н. В.,
Управляемые процессы диффузионного типа, М., 1977; [22]
КуржанскийА. Б., Управление и наблюдение в условиях
неопределенности, М., 1977; [23] Цыпки н Я. 3., Основы теории
обучающихся систем, М., 1970; [24} Эйкхофф П., Основы
идентификации систем управления, пер. с англ., М., 1975.
А. Б. Нуржанский.
ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ ПРОГРАММ-
ПРОГРАММНОЕ — решение задачи оптимального управления
математической теории, в к-рои управляющее воздей-
воздействие и=и(<) формируется в виде функции времени
(тем самым предполагается, что по ходу процесса ни-
какой информации, кроме заданной в самом начале,
в систему не поступает). Таким образом, О. у. п. фор-
формируется по априорным сведениям о системе и уже не
может быть скорректировано, в отличие от оптималь-
оптимального управления позиционного.
Проблема существования решении задачи О. у. п.
разбивается на два вопроса: выяснение осуществимости
цели управления при заданных ограничениях (сущест-
(существование допустимого управления, реа-
реализующего цель управления) и установление разреши-
разрешимости экстремальной задачи — достижимость экстре-
экстремума (как правило, относительного) — в упомянутом
выше классе допустимых управлений (существование
оптимального управления).
В связи с первым вопросом весьма важно изучение
свойства управляемости системы.
Для системы
^-=/(<, х, и)
оно означает существование в заданном классе U=
~ {"(¦)} функций, допускаемых к рассмотрению,
управлений u(t), переводящих фазовую точку (см.
Понтрягина принцип максимума) из любого заданного
начального положения x(i0)—x°?R" в любое задан-
заданное конечное положение x(t1) = x1?R" (за фиксиро-
фиксированное или свободное время T=t1—tn, в зависимости
от постановки задачи). Необходимые и достаточные
условия управляемости (или, как еще принято гово-
говорить, полной управляемости) известны
в конструктивной форме для линейных систем
) и, x?R", u?RP, A)
с аналитическими или периодич. коэффициентами
(они наиболее просты при /1 "const, B=const). Для
линейных систем общего вида полностью решается и
вопрос, о разрешимости задачи попадания с одного
выпуклого множества на другое (при выпуклых огра-
ограничениях на и, х). В нелинейном случае известны
лишь локальные условия управляемости (справедли-
(справедливые в малой окрестности заданного движения) или
условия для частных классов систем (см. [2], [4], [5]).
Свойство управляемости изучают и в рамках много-
многочисленных обобщений, связанных, в частности, с рас-
рассмотрением специальных классов U (напр., множества
U всех ограниченных кусочно непрерывных управле-
управлений u(t)), задач управляемости по части, координат или
изучением более общих классов систем, и том числе
бесконечномерных.
Вопрос о существовании оптимального управления
в общем случае связан со свойством компактности в
той или иной топологии минимизирующих последова-
последовательностей управлений или траекторий и свойством
полунепрерывности по соответствующим переменным
минимизируемых функционалов. Первое из этих
свойств тесно связано для системы
x = f (t, х, и), /„</</,. .r?R", u?RP, B)
при ограничениях
„ ? U <= RP C)
с выпуклостью множества
f(t, х, U) = {f(t, x, u)\u?U},
а второе (для интегральных функционалов) — с вы-
выпуклостью по соответствующим переменным J (х{-),
"{¦)). Отсутствие этих свойств возмещают путем рас-
расширения исходных вариационных задач. Так, невы-
невыпуклость f(t, х, и) можно возместить путем введения
скользящих режим о в — обобщенных реше-
решений обыкновенных дифференциальных уравнений, по-
порожденных управлениями-мерами, заданными на U и
создающими эффект «овыпукления» (см. 16], 17]). От-
Отсутствие выпуклости у интегральных функционалов
J(x( ¦), «¦( ¦)) возмещают путем погружения задачи в
более общую, с новым функционалом, являющимся вы-
выпуклой минорантой прежнего, и решения новой задачи
в более широком классе управлений (см. [8]). В отме-
отмеченных случаях существование оптимального управле-
управления часто вытекает из существования допустимого уп-
управления.
Теория необходимых условий экстремума наиболее
развита в задачах О. у. п. Основополагающим резуль-
результатом здесь послужил принцип максимума Понтрягина,
содержащий необходимые условия сильного экстре-
экстремума в задаче оптимального управления.
Следует отметить создание общих приемов получе-
получения необходимых условий в экстремальных задачах, эф-
эффективно использованных для задач О. у. п. с более
сложными ограничениями (фазовыми, функциональны-
функциональными, минимаксными, смешанными и т. д.) и основанных,
так или иначе, на теоремах об отделимости выпуклых
конусов (см. [9], [10]). Пусть, напр., Е — векторное
пространство, 1(х), х?Е,— заданный функционал,
Ql— множества из Е,
Q = r\Qh * = L ¦••• ».
— точка, в к-рой f(x) достигает минимума на Q,
Суть распространенного общего метода состоит в том,
что каждое из множеств (?,-, г —0, 1, . . ., п, аппрок-
аппроксимируется в окрестности точки х° нек-рым выпуклым
конусом К; с вершиной в точке х° (конус «убывания»
для <?„; конус «допустимых направлений» для ограни-
ограничений, изображаемых неравенствами; конус «касатель-
«касательных направлений» для ограничений типа равенства, в
том числе для дифференциальных связей, и т. д.).
Необходимое условие минимума теперь состоит в том,
чтобы х° была единственной точкой, общей для всех
A;, t—0, 1, . . ., п, и, следовательно, чтобы конусы
были «отделимы» (см. [8]). Последнему «геометриче-
«геометрическому» условию далее придают аналитич. форму и по
возможности преобразуют к удобному виду, напр, при
помощи функции Гамильтона. В зависимости от ис-
исходных ограничении, а также от класса используемых
вариаций, необходимые условия могут принимать как
форму, аналогичную принципу Понтрягина, так и
форму локального (линеаризованного) принципа мак-
максимума (условия слабого экстремума по и). Реализа-
Реализация отмеченного пути, таким образом, зависит от воз-
возможности аналитически описывать конусы А/. Эф-
Эффективное их описание достигается для множеств (?,-,
задаваемых гладкими функциями, удовлетворяющими
нек-рым дополнительным условиям регулярности в рас-
рассматриваемой точке, или выпуклыми функциями (см.
|9], [10]). В принципе отмеченный путь допускает обоб-
обобщения и на случай негладких ограничений, в том числе
дифференциальных. Здесь, напр., может быть исполь-
использовано понятие субдифференциала выпуклой функции
или его обобщения, когда выпуклость отсутствует
(см. [11], [12]).
Условия 1-го порядка, аналогичные принципу Понт-
Понтрягина, известны для решений в классе обобщенных
функций-мер (т. н. интегральный прин-
принцип максимума), для управляемых систем,
описываемых дифференциальными уравнениями с от-
отклоняющимся аргументом, дифференциальными урав-
уравнениями с частными производными, эволюционными
уравнениями в банаховом пространстве, дифференци-
дифференциальными ураэнениями на многообразиях, рекуррент-
рекуррентными разностными уравнениями и т. д. (см. [1], [6],
[7], [13] -Ц6]).
Из указанных необходимых условий экстремума в
задаче оптимального управления вытекают известные
необходимые условия 1-го порядка классического ва-
вариационного исчисления. В частности, в двухточечной
краевой задаче для системы B), C), где U — открытое
множество, J(x(-), и{-)) — стандартны» интегральный
функционал, из принципа Понтрягина вытекает не-
необходимое условие экстремума Вейерштрасса в класси-
классическом вариационном исчислении.
В теории оптимального управления развиваются ме-
методы получения необходимых условий высших поряд-
порядков (особенно 2-го порядка) для неклассических ва-
вариационных задач (см. [19]). Интерес к условиям вы-
высших порядков в значительной степени был связан с
изучением вырожденных задач оптимального управле-
управления, приводящих к т. н. о с о б ы м управ л е н и-
я м и не имеющих адекватных аналогов в классич. те-
теории. Напр., в принципе Понтрягина функция H(t,\p,
х, и) либо может приводить к целому семейству управ-
управлений, каждое из к-рых удовлетворяет принципу мак-
максимума, либо вообще не зависит от и (тогда любое из
допустимых значений и удовлетворяет принципу Понт-
Понтрягина). Эта ситуация оказалась весьма характерной
для целого ряда прикладных задач управления в про-
пространстве. В данном случае выделение оптимального
управления уже требует перебора экстремалей 1-го
порядка (т. н. экстремалей Понтрягина)
и применения к ним необходимых условий оптимально-
оптимальности 2-го или, в общем случае, более высокого порядка.
Здесь разные по форме необходимые условия были полу-
получены путем использования специальных классов «не-
«неклассических» вариаций (напр., «связок» игольчатых
вариаций и т. д.). Реализация особых управлений ча-
часто связана снова с использованием скользящих ре-
режимов (см. [17], [18]).
Теория достаточных условий оптимальности разра-
разработана в меньшей степени. Известны результаты, отно-
относящиеся к условиям локальной оптимальности и со-
содержащие, в числе прочих требований, условия невы-
невырожденности системы в вариациях и ограничения на
свойства гессиана правых частей, вычисленного вдоль
исследуемой траектории для соответствующего обык-
обыкновенного дифференциального уравнения. Другая груп-
группа достаточных условий опирается на метод динамич.
программирования и его связь с теорией принципа
максимума (см. [8]). Имеются и формализмы, приво-
приводящие к достаточным условиям абсолютного мини-
минимума, основанные на идее расширения вариацион-
вариационных задач. Область их реальной применимости охва-
охватывает специальные классы задач с выпуклыми крите-
критериями и вырожденных задач оптимального управления
(см. [18]).
Полное решение задачи О. у. п. (необходимые ц до-
достаточные условия оптимальности) известно для ли-
линейных систем A), когда рассматриваемые функциона-
функционалы и ограничения на и, х выпуклы (в ряде случаев
здесь требуется выполнение нек-рых дополнительных
условий). Привлечение идей двойственности, исполь-
используемых в выпуклом анализе, выявило особое экстре-
экстремальное свойство траекторий системы, описывающей
сопряженные переменные принципа
максимума Понтрягина. Это позволило свести крае-
краевую задачу, возникающую при использовании необ-
необходимых условий общего вида, к решению более про-
простой двойственной экстремальной задачи. В рамках
названного подхода получила развитие теория линей-
линейных систем с импульсными управления-
м и, моделирующих объекты, подверженные мгновен-
мгновенным воздействиям (ударным, взрывным, импульсным),
и формализуемых при помощи дифференциальных урав-
уравнений в обобщенных функциях соответствующих по-
порядков сингулярности. Эффективное применение, осо-
особенно в теории игровых систем, нашел метод облас-
областей достижимости (см. [2], [3]).
В отсутствии полной априорной информации о систе-
системе (и в том числе статистич. описания недостающих
величин) рассматривают задачу О. у. и. в условиях
неопределенности. Пусть в системе (to <)
*'-/(/, т, и, w), z(ta)=x*?X\ w?W, D)
параметр a-^R17, реализующийся в виде функции вре-
времени w~w(t), и вектор х° неизвестны, но заданы'лишь
множества X'fcR", W^lR4 . Тогда, предполагая су-
существование и продолжаемость на [t0, tH решений
x(t\x\ и(-), w(-)), x(to\x\ м(-), w(-))=xB
уравнения D) (при заданных .г", г<(т), ц-(т), to<T<?i),
можно построить пучок (ансамбль) траекторий
Х(*|и(-)) =
-=U{*(*I*°. u(-), w(-))\x*?X\ w(t)?W.
Выбирая программное управление u(t) (одно и то же
для всех траекторий пучка), можно управлять поло-
положением X(t\u(-)) в фазовом пространстве. Типичная
задача О. у. и. в условиях неопределенности теперь
состоит в оптимизации и (t) в силу функционала Ф
типа максимума
Ф (X (ti I и (¦))) -max {ф (х) [х?Х (^ [ и (¦))} E)
(тогда решение н° (/) задачи будет обеспечивать нек-рып
гарантированный результат) или интегрального функ-
функционала
5(ми())/о(.г)^. F)
Применение техники вывода необходимых условий
оптимальности или ее модификаций позволило сформу-
сформулировать требования, обеспечивающие существование
аналогов принципа Понтрягина для задач E), F) (в
первом случае он принимает форму нек-рого условия
минимакса). Для линейных систем эти задачи допуска-
допускают столь же детальное решение, как п в случае полной
информации (см. [3], [20], [21]).
Лит.: [И Понтрпгин Л. С, Б о л т я и с к и И В. Г.,
Г а м к р с л и д з с Р. В., Мищенко Е. Ф., Математичес-
Математическая теория оптимальных процессов, 3 изд., М., 197Ц; [2] К р а-
со некий Н. Н., Теория управления движением, М., 1968;
[31 К р а е о в с к и й Н. Н., Субботин А. И., Позицион-
Позиционные дифференциальные игры, М., 1974; [4] К а л м а н Р., в кн.:
Труды 1 Международного конгресса Международной федерации
по автоматическому управлению, т. 2, М., 1961, с, 521—47; [5]
Л и Э.- Б., М а р к у с Л., Основы теории оптимального управ-
управления, пер. с англ., М,, 1972; [б] Г а м к р е л и д з е Р. В., Ос-
Основы оптимального управления, Тбилиси, 1977; [7] В а р г а Дя;.,
Оптимальное управление дифференциальными и функциональ-
функциональными уравнениями, пер. с англ., М., 1977; [8] Иоффе А. Д.,
Тихомиров В. М., «Успехи матем. наук», 1968, т. 23, в. 0,
с. 51—116; [9] Д у б о в и ц к и и А. Я., М и л ю т и н А. Д.,
«Журн. вычисл, матем. и матем. физики», 1965, т. 5, № 3, с. 39Г> -
453; [10] Neustadt L. W., Optimizations. A theory of neces-
necessary conditions, Princeton, 1974; [11] Пшеничный Г>. Н.,
Необходимые условия экстремума, М., 1969;[12] Clark e Р. П.,
«Trans. Amer. Math. Soc», 1975, v. 205, p. 247—62; [13] S u s s-
mann H. J., «Math. Syst. Theory», 1977, v. 10, X» 3, p.263 -
284; [14] Лион с Ж., Оптимальное управление системами, опи-
описываемыми уравнениями с частными производными, пер. с
франц., М., 1972; [15] Болтянский В. Г., Матс51атические
методы оптимального управления, М., 1966; [16] его же,
Оптимальное управление дискретными системами, М., 1973;
[17] Габасов Р., Кириллова Ф. М., Особые оптималь-
оптимальные управления, М., 1973; L18] Кротов В. Ф., Б у к р е-
е в В. 3., Г у р м а н В. И., Новые методы вариационного ис-
исчисления в динамике полета, М., 1969; 119] Левитин Е. С,
М и л ю т и н А. А., О с м о л о в с к и й Н. Л., «Успехи матем.
наук», 1978, т. 33, в. 6, с. 85—148; [20] К у р ж а н с к и й А. В.,
Управление и наблюдение в условиях неопределенности, М.,
1977; [21] Демьянов В. Ф., Малоземов В. Н., Введе-
Введение в мипимакс, М., 1972. А. В. Куржанский.
ОПТИМАЛЬНОСТИ ДОСТАТОЧНЫЕ УСЛОВИЯ —
условия, обеспечивающие оптимальность данного ре-
шения задачи вариационного исчисления в выбранном
классе кривых сравнения.
О. д. у. с л а б о г о м ц н и м у м а (см. [11): для
того чтобы кривая у (х) доставляла слабый минимум
функционалу
¦/"(</)= ['иР(х, У, y')dx A)
при граничных условиях
достаточно, чтобы выполнялись следующие условия.
1) Кривая у (х) должна быть экстремалью, т. е. удов-
удовлетворять Эйлера уравнению
2) Вдоль кривой у (.г), включая ее концы, должно
выполняться усиленное Лежандра условие
Руу (ж. У, У') > 0.
3) Кривая у (х) должна удовлетворять усиленному
Якоби условию, требующему, чтобы решение уравнения
Якобн
с начальными условиями
1W=O, r)'(xo) = l
не обращалось в нуль в точках замкнутого справа ин-
интервала .r,,<a:<;zj.
Коэффициенты уравнения Якобп B), представляю-
представляющего собой линейное дифференциальное уравнение 2-го
порядка, вычисляются вдоль экстремали у(х) и пред-
представляют известные функции от х.
Для сильного минимума достаточно, что-
чтобы дополнительно, помимо перечисленных выше, вы-
выполнялось следующее условно.
4) Существует окрестность кривой у(х), в каждой
точке (г, у) к-рой при любом у' выполняется неравен-
неравенство
? (х, у, и(х, у), у')^0, C)
где
?(х, у, и, y')---F(x, у, y') — F(x, у, и) —
— (у — u)Fy. (x, у, и)
— функция Вейерштрасса, а м (х, //) — наклон поля
экстремалей, окружающего у(х).
На самой экстремали у (х.) условие C) принимает вид
? (х, у, у', у') —
~—F(x, У, У')-*'(х, 7, 7') — (у'—'у'I'у{.х, 7, г/)йзО.
D)
Условие D) является необходимым для сильного мини-
минимума; оно наз. необходимым условием
Вейерштрасса. Таким образом, в отличие от
достаточных условий слабого минимума, к-рые требуют
выполнения нек-рых усиленных необходимых условий
в точках самой экстремали, в достаточных условиях
сильного минимума требуется выполнение необходи-
необходимого условия Вейерштрасса в нек-рой окрестности
экстремали. В общем случае нельзя ослабить формули-
формулировку достаточных условий сильного минимума, заме-
заменив требование выполнения условия Вейерштрасса
в окрестности экстремали на усиленное условие Вейер-
Вейерштрасса (условие D) со знаком строгого неравенства)
в точках экстремали (см. [1]).
Для неклассических вариационных задач, рассмат-
рассматриваемых в оптимального управления мате мимической
теории, существует несколько подходов к установле-
установлению О. д. у. абсолютного экстремума.
Пусть поставлена задача оптимального управления,
в к-рой требуется определить минимум функционала
^ /»<*, u)dt, E)
/°: ^"<ЛР —-R,
при условиях
i = /(z, м), /: R"xR/'—*R". F)
*@)=r0, x(h)=xl, G)
«€#, (8)
где U — заданное замкнутое множество р-мерного
пространства.
При использовании метода динамического програм-
программирования [3] О. д. у. формулируются следующим
образом. Для того чтобы управление u(t) было опти-
оптимальным управлением в задаче E)—(8), достаточно,
чтобы:
1) существовала такая непрерывная функция S(x),
края имеет непрерывные частные производные при
ниех х, ;)а исключением, быть может, нек-рого кусочно
гладкого множества размерности меньше п, равна нулю
в конечпой точке хг, 6'(х1) = 0, и удовлетворяет урав-
уравнению Веллмана
max (fxf(x, »)-Н«,»А-0; (9)
ueU \ x У
2) и (t) — v(x(t)), при O^.t^.tl, где v(x) — синтези-
синтезирующая функция, определяемая из уравнения Белл-
мана:
— fix, v(x))-j*(x, „(*)) =
D§-/(s, u)-f(x, и))=0.
В действительности при использовании метода дина-
мич. программирования получается более сильный
результат: О. д. у. для множества различных управ-
управлений, переводящих фазовую точку из произвольного
начального состояния в заданное конечное состояние х1.
В более общем случае, когда рассматривается неавто-
неавтономная система, т. с. подинтегральная функция и век-
вектор-функция правых частей зависят еще и от времени t,
функция S должна зависеть от г и к левой части урав-
уравнения (9) следует добавить слагаемое -j, . Имеется до-
доказательство (см. [4]), в к-ром удалось снять весьма
стеснительпое и не выполняющееся в большинстве
задач, но обычно предполагаемое условие непрерывной
дифференцпруемости функции S (х) для всех х.
О. д. у. могут быть построены на основе принципа
максимума Понтрягина. Если в нек-рой области G
фазового пространства осуществлен регулярный син-
синтез, то все траектории, полученные с помощью прин-
принципа максимума при построении регулярного синтеза,
являются оптимальными в области G.
Определение регулярного синтеза хотя и является
довольно громоздким, но по существу не накладывает
особых ограничений на задачу E)—(8).
Существует другой подход к установлению О. д. у.
(см. |5]). Пусть ф(а) — функция, непрерывная вместе
со своими частными производными при всех допусти-
допустимых х, принадлежащих заданной области G, и
Л(х, и)-^ух1(х2 и)-Р(х, и). A0)
Для того чтобы пара u(t), x(t) доставляла абсолютный
минимум в задаче E)--(8), достаточно существование
такой функции <р(у), что
R(x, п)= max R(x,u). A1)
xs a, ue и
Допускаются соответствующие изменения приведенной
формулировки О. д. у. для более общих случаев неав-
неавтономной системы, задач с функционалами типа Майера
и Больца (см. Болъца задача), а также для скользящих
оптимальных режимов (см. 15|).
Исследовались вариационные задачи с функционала-
функционалами в виде кратных интегралов и дифференциальными
связями в форме уравнений с частными производными,
в к-рых рассматриваются функции нескольких пере-
переменных (см. [6]).
Лит.: [1] Лаврентьев М, А., Л ю с т е р н и к Л. А..
Курс вариационного исчисления, 2 изд., М.— Л., 1950; [21
Б л и с с Г. А. Лекции по вариационному исчислению, пер. с
англ., М., 1950; [3] Б е л л м а н Р., Динамическое программи-
программирование, пер. с англ., М., 1960; [4] Болтянский В. Г.,
Математические методы оптимального управления, М,, 1966;
[5] К р о т о в В. Ф., «Автоматика и телемеханика», 19В2, т. 2U,
№ 12, с. 1571—83; 19611, т. 24, .V» 5, с. 581—98; [6] Bjikoj-
ский А. Г., Теория оптимального управления системами с
распределенными параметрами, М., 1965. И. Б. Вапнярский.
ОПТИМАЛЬНОСТИ ПРИНЦИПЫ — формальные
описания различных представлений об оптимальном.
Обычно О. п. отражают те или иные черты интуитив-
интуитивного понимания устойчивости, выгодности и справед-
справедливости. Существенно, что одновременная реализация
исех (или хотя бы достаточно большого числа) таких
черт часто оказывается невозможной ввиду их формаль-
формальной несовместности. По мере того как теория О. п. при-
приобретает аксиоматич. характер, создаются новые О. п.,
уже не всегда обладающие интуитивной прозрачностью.
Проблемы О. п. возникают, напр., в тех случаях,
когда ищется значение переменного, одновременно эк-
стремизирующее несколько заданных функций (т. н.
многокритериальные экстремальные задачи). Задачи,
требующие для своего решения привлечения нетриви-
нетривиальных О. п., фактически относятся к игр теории.
Одним из наиболее простых теоретико-игровых О. п.
является минимакса принцип. Другие О. п. реализуют-
реализуются в виде с-ядра решения по Нейману—Моргснштерну,
Шепли вектора и т. д.
О принципе оптимальности Беллмана см. Динамиче-
Динамическое программирование. Н. II. Воробьев.
ОПТИМАЛЬНЫЙ РЕЖИМ ОСОБЫЙ, особое
оптимальное у п р а в л е н и е,— оптимальное
управление, для к-рого на нек-ром учапьт времени
одновременно выполняются условия
^--0, A;
где // — Гамильтона функция. В векторном случае,
когда О. р. о. имеет место по к, &>1, компонентам уп-
управления, условие A) заменяется на к условий
^- = 0, « = 1, ...,*, C)
а вместо равенства B) требуется обращение в нуль оп-
определителя
д'Н
dus дир
=-0, р, * = 1, ..., к. D)
На О. р. о. функция Гамильтона // стационарна, но
ее второй дифференциал не является отрицательно
определенным, т. е. максимум // но и (при и, изменяю-
изменяющемся внутри допустимой области) оказывается «раз-
«размытым».
Наиболее типичными задачами, в к-рых может иметь
место О. р. о., являются задачи оптимального управле-
управления, в к-рых подннтегральная функция и правые части
линейно зависят от управления.
Ниже рассматриваются задачи такого рода сначала
со скалярным особым управлением.
Пусть требуется определить минимум функционала
' (Р(х) + иФ {x))dl E)
при условиях связи
i' = /' (л)+ мф'(ж), i = l, ..., га, F)
граничных условиях
ж@)=го, ж(^)=ж, ; ', • G)
и ограничениях на управление i ;
Ы<1. (8)
Необходимые условия, к-рым должен удовлетворять
О. р. о., позволяют'заранее последовать задачу E)—(8)
ц выделить многообразия особых участков, на к-рых
оптимальное управление лежит внутри допустимой об-
области: |м|<1. Пристраивая к ним неособые участки,
удовлетворяющие граничным условиям G), с управле-
управлением |в| = 1, определяемым из Понтрягина принципа
максимума, можно получить оптимальное решение за-
задачи E)—(8).
Согласно принципу максимума" оптимальное управ-
управление при любом f?[0,/J должно доставлять максимум
функции Гамильтона
Я (г|) (t), x(t), u(t))= шах Н (\!p(t), x(t), и), (9)
где
#(ф, ж, и)=—(
а г|)=(г|I, .-. , t|)rt) — нек-рая не обращающаяся в нуль
сопряженная вектор-функция, удовлетворяющая сис-
системе уравнений
^-ЭД(Ф''"", « = 1, .... «. A0)
дх1
Условие B) выполняется для любого управления, а
не только для О. р. о.
На тех участках времени, на к-рых г—?=0, условие (9)
определяет неособое оптимальное управление, прини-
принимающее граничные значения
дН . .
±l
Таким образом, участки [т0, тх] с оптимальным особым
управлением
могут появиться лишь при выполнении условия A):
дН (ф (f), х (<), u(t))_Q < ; <; (\U
при к-ром функция Гамильтона перестает явно зави-
зависеть от управления и. Следовательно, для задач, ли-
линейных ио управлению, условие (9) не позволяет непо-
непосредственно определить оптимальное особое управле-
управление u(t).
Пусть функция -^- дифференцируется по t в силу
систем F), A0) до тех пор, пока управление и не войдет
с ненулевым коэффициентом в очередную производную.
Доказывается (см. [1]—[3]), что управление и может
войти с ненулевым коэффициентом лишь в четную про-
производную, т. е.
— ( UL ( дн
ди \dt* \ ,iu
-~П { -з— ) —а (Ф, &)-\-u-b (ii), jc), Ь (ф (t) x(t)) :
dt ч V au '
A2)
и что необходимым условием оптимальности особого
управления является выполнение неравенства
<_,)^,,, = <_!>,(А (?!(-?))<<>. A3,
Если b(ty(t), x(t)O=0 на всем отрезке, то оптимальное
особое управление
Поскольку условия A2) получены в результате по-
последовательного дифференцирования A1), то на участке
особого режима, в частности в точках сопряжения т0
и т1 особого и неособого участков, помимо равенства
A1), выполняется 2q — 1 равенств
lit*
Анализ условии A1), A4) показывает, что для слу-
случаев четного п нечетного q характер сопряжения осо-
особого и неособого участков траектории различен (см.
[4]).
При четном q оптимальное управление на неособом
участке не может быть кусочно непрерывным. Разрывы
управления (точки переключения) сгущаются к точке
сопряжения с особым участком, так что оптимальное
управление оказывается измеримой по Лебегу функци-
функцией со счетным множеством точек разрыва.
При нечетном q только две кусочно гладкие опти-
оптимальные траектории могут входить в точку, лежащую
на особом участке (или исходить из нее). Пусть размер-
размерность многообразия особых участков в ?г-мерном прост-
пространстве фазовых координат равна к. Тогда в рассмат-
рассматриваемом случае нечетного q оптимальные траектории
с кусочно непрерывным управлением заполняют в фа-
фазовом пространстве лишь нек-рую поверхность размер-
размерности fe+1. Поэтому при к<.п—2 почти все оптималь-
оптимальные траектории будут иметь управление с бесконечным
числом точек переключения.
Сформулировано предположение (см. [4]), что ft—
-—re—q. Если это так, то при q^2 сгущение точек пере-
переключения перед выходом на особый участок (или сходом
с него) является типичным явлением для задач типа
Пример сопряжения неособого и особого участков
оптимального управления с бесконечным числом пере-
переключений приведен в [5].
При четном q, q^2, оптимальное особое управление
на неособом участке, примыкающем к особому, не мо-
может быть кусочно непрерывным, а имеет бесконечное
число точек переключения, сгущающихся к точке входа
т0, т. е. не существует е>0 такого, что в промежутке
[т0—е, т0] оптимальное управление постоянно.
В наиболее часто встречающемся О. р. о. величина
q = i. Для этого случая сопряжение неособого и особого
участков осуществляется с помощью кусочно непрерыв-
непрерывного оптимального управления.
В более общем случае О. р. о., в к-ром рассматри-
рассматривается к, /с>1, управлений:
(*)+2*_ ,мм*))л. A5)
(как и в скалярном случае) условие D), в силу линей-
линейности, выполняется для любого управления. На участ-
участке [т0, xj О. р. о. по к компонентам с |its|<l должны
выполняться к условий C):
a—\,
и,ф,(х))
где
а ф,- определяются из A0).
Дальнейшие необходимые условия оптимальности
для О. р. о. по нескольким компонентам отличаются
от рассмотренного выше случая О. р. о. по одной ком-
компоненте следующими особенностями. На участке О. р. о.
должны выполняться необходимые условия двух видов.
Одно из них, типа неравенства, является аналогом ус-
условия A3). Другие необходимые условия являются ус-
условиями типа равенства и не имеют более ранних ана-
аналогий (см. [6]).
Дифференцируя A7) полным образом по t, получают
систему к линейных уравнений относительно к неиз-
неизвестных Щ, ... , Uk-
dMsW,x)_r,k „ f v," (эМзс дМР
di - Zj,,= 1 "p I A=i V эк' Yp—aJ
+ 2 \~~*?f /(Ps)=O, s—i, ..., k. (
Матрица коэффициентов системы A8)
, s, p = l, ..., к,
является кососимметричной: aSp=:—aps- Отсюда, в чавт-
ности, следует, что элементы ass, стоящие на главной
диагонали матрицы (asp), равны нулю. Остальные
элементы asp, s?=p, в системе A8) в общем случае на
произвольной траектории, соответствующей нек-рому
неоптимальному управлению, отличны от нуля. На
О. р. о. по к компонентам должны выполняться необхо-
необходимые условия, требующие обращения в нуль всех
—5— коэффициентов системы A8) (см. 16)):
VI « /дМ, : дМр Л
A9)
Кроме этих условий должно выполняться условие
типа неравенства (являющееся аналогом условия A3)
для О. р. о. по одной компоненте при q—i):
Условия A3), B0) можно рассматривать как обобще-
обобщение Лежандра условия и Клебша условия на случаи
О. р. о., поэтому указанные неравенства наз. иногда
обобщенным условием Лежандра —
Клебша.
Важность выявления и исследования О. р. о. в зада-
задачах оптимального управления объясняется следующим
свойством О. р. о. (см. [4]): если оптимальная траекто-
траектория, исходящая из нек-роп точки, содержит участок
О. р. о., то этим же свойством обладают все оптималь-
оптимальные траектории, исходящие из близких точек.
Исследованы нек-рые вопросы, связанные с опреде-
определением порядка О. р. о. для линейных и нелинейных по
управлению задач (см. [8]).
Все приведенные выше результаты по О. р. о. полу-
получены из рассмотрения второй вариации функционала.
Оказывается, что можно получить дополнительные не-
необходимые условия оптимальности особого режима из
рассмотрения третьей и четвертой вариаций функцио-
функционала (см. [9]).
Лит.: [1] К е л л и Г., «Ракетная техника и космонавтика»,
1964, Л- 8, с. 26—29; [2] Р о б б и н с Г., тан же, L965, № 6, с.
139—45; [3] К о п п Р., М о й е р Г., там же, 1965, № 8, с. 84—
90; [4] Б с р щ а н с к и Й Я. М., «Автоматика и телемеханика»,
1979, Л5 3, с. 5—11; 15] Ф у л л е р А. Т., в кн.: Тр. 1 Междуна-
Международного конгресса Международной федерации по автоматичес-
автоматическому управлению. Теория дискретных оптимальных и самонаст-
самонастраивающихся систем, М., 1961, с. 584—605; [6] В а п н я р-
ский И. Б., «Ж. вычисл. матем. и матем. физ.», 1967, т. 7,
№ 2, с. 259—83; [7] К reneT A., «SIAM J. Contr. and Opti-
miz.», 1977, v. 15, Xs 2, p. 256—93; [8] L e w i s R. M., там же,
1980, v. 18, Ms 1, p. 21 — 32; [9] С к о p о д и н с к и й И. Т.,
«Ж. вычисл. матем. и матем. физ.», 1979, т. 19, Ы 5, с. 1134—40;
[10] ГаОасов Р., Кириллова Ф. М., Особые оптималь-
оптимальные управления, М., 1973. И. В. Вапнярский.
ОПТИМАЛЬНЫЙ РЕЖИМ СКОЛЬЗЯЩИЙ — тер-
термин, используемый в теории оптимального управления
для описания оптимального способа управления систе-
системой в случае, когда минимизирующая последователь-
последовательность управляющих функций не имеет предела в классе
измеримых по Лебегу функций.
Пусть, напр., требуется найти минимум функционала
yo(x"-u2)dt A)
при условиях
х = и , B)
я@)=1, жC)=1, C)
|и|<1. D)
Для получения минимума функционала A) желательно
иметь при каждом t как можно меньшее значение \x(t)\
и кат\ можно большее значение \u(t)\. Первому требо-
требованию, с учетом условия связи B), граничных условий
C) и ограничений на управление D), удовлетворяет
траектория
( l-t, 0</<1,
] 0, 1 < t < 2, E)
t—2,
Если бы траекторию E) можно было построить при
нек-ром управлении, принимающем при всех t гранич-
граничные значения
u(l)=-\-l или иA) = —1, F)
был бы получен абсолютный минимум функционала A)
Однако «идеальная» траектория E) не может быть
построена ни при какой управляющей функции u(t),
удовлетворяющей F), поскольку при 1<^<2 и(г)=О.
Тем не менее можно, используя управляющие функции
»„(<)> реализующие при п -> оо и 1<<<2 все более
частые переключения с 1 на —1 и обратно:
и» С) -
,«-1,
|
-i,
I
I -\-\. 2 <
( п = 1, 2, ...,
О)
построить минимизирующую последовательность уп-
управлений {un(t)}, удовлетворяющую F), и минимизи-
минимизирующую последовательность траекторий {xn(t)}, схо-
сходящуюся к «идеальной» траектории E).
Каждая из траекторий xn(t) отличается от E) только
на интервале A, 2), на к-ром вместо точного движения
по оси х она обеспечивает «пилообразное» движение с п
одинаковыми «зубьями», расположенными над осью х.
«Зубья пилы» становятся все мельче при л-^-оо, так
что lim xn(t)=0, I </<2. Таким образом, минимизирую-
П->-00
щая последовательность траектории {xn(t)} сходится
к E), но минимизирующая последовательность управ-
управлений {un{t)}, реализующих при п —»- оо и 1<<<2 все
более частые переключения с 1 на —1 и обратно, не
имеет предела в классе измеримых (а тем более в классе
кусочно непрерывных) функций. Это означает, что на
участке A, 2) имеет место О. р. с.
Используя не очень строгие рассуждения, можно опи-
описать полученный О. р. с. следующим образом: опти-
оптимальное управление в каждой точке интервала A, 2)
«скользит», т. е. перескакивает со значения -)-1 на —1
и обратно так, что для любого, сколь угодно малого,
интервала времени мера множества точек t, в к-рых
м=-г 1, равна мере множества точек t, в к-рых и=—1,
что обеспечивает, в силу уравнения B), точное движе-
движение по оси х. Приведенное описание характера изме-
изменения оптимального управления на участке скользя-
скользящего режима является нестрогим, ибо оно не удовлет-
удовлетворяет обычному определению функции.
Можно дать строгое определение О. р. с, если наря-
наряду с исходной задачей A)—D) ввести в рассмотрение
вспомогательную, расщепленную задачу: найти мини-
минимум функционала
1 (х, а, и) = ^ {х- — auMJj— aiu\) dt (8)
прп условиях
a;=^a0"o-v«iMi, " (П)
*@) = 1, *C) = 1, A0)
|uo|<l, )«i]<l, ao + aj = l, a0S=0, «i^O. A1)
Расщепленная задача (8)—A1) отличается от исход-
исходной тем, что: вместо одной управляющей функции
u(t) вводятся две независимые управляющие функции
uo(t) и Mj(/); подинтегральная функция и функция, стоя-
стоящая в правой части уравнения B) исходной задачи,
заменяются линейной выпуклой комбинацией соответст-
соответствующих функций, взятых при различных управлениях
uo(t) и ui(t) с коэффициентами ao(i), a^t), к-рые также
рассматриваются как управляющие функции.
Таким образом, в задаче (8)—A1) имеется 4 управ-
управления м0, ult a0, аг. Поскольку а0 и ах связаны условием
типа равенства ao-|-ai=l, то от одного из управлении
а0 или ах можно избавиться, выразив его через другое.
Однако для удобства последующего анализа целесооб-
целесообразно оставить оба эти управления в явном виде.
В отличие, от исходной задачи оптимальное управле-
управление в расщепленной задаче (8) — A1) существует. На
участке О. р. с. исходной задачи оптимальное управле-
управление расщепленной задачи имеет вид
«„ (<)=«! (О-у, М0--1. "i@ — 4-l, 1</ч2,
а на участках входа и выхода
а„ {l) — \, uo(/) ——1, п, (п 0. uj (/) -любая,
0<2 < 1,
ai(/)--l, MO^-rl, «oU)^O, щ (t)— любая,
На участке О. р. с. управления сс0 и аь линейно вхо-
входящие в правую часть и подинтегральную функцию,
принимают значения, лежащие внутри допустимой об-
области. Это означает, что О. р. с. исходной задачи A) —
D) есть особый оптимальный режим, пли особое опти-
оптимальное управление, для вспомогательной, расщеплен-
расщепленной задачи (8)—A1).
Аналогичные результаты для О. р. с. имеют место
в общем случае задачи оптимального управления. Пусть
требуется найти минимум функционала
У (.*, ,л = ^'/" С, х, u)dt, A2;
f»(t, х, и) ;R/sRnX.Rm—>R,
при условиях
:г =,= /(/, .г, и), f(t, х, и): RxR"xRm-^R", A3)
x(to)=xo, x(t1)=xu A4)
u?U. A5)
О. р. с. характеризуется неединственностью максимума
по и функции Гамильтона
H(t, х, г|>, ")--2Г=0Ч'//''С, х, и),
где г|)| -- сопряженные переменные (см. [2]). При этом
на участке [т,, т2] «скольжения» но к-\-\, к~>1, максиму-
максимумам и0, //,...., I//; исходная задача расщепляется и при-
принимает вид
1(х, а, и) = $?2*=оа*/П (/' х' Us)dl' A6)
j^Z'^^Jit, х, us), A7)
''*(<)=*•„, ж(^)=л:1, A8)
"^' Х* „^ = 1,^5=0,5 = 0, 1, ...,?. A9)
Функцию Гамильтона для задачи AВ)—A9)
H(t, х, г|>, a, »)-=2,1o! )
после исключения а„ и перегруппировки слагаемых
можно привести к виду
Н (I, х, я|>, a, и) =
Поскольку все II (t, x,\|', "s), s=0, 1, ... , к, ость равные
между собой максимумы И по к на множестве U, то на
участке [т^ т2) О. р. с. с fc + 1 максимумами коэффици-
коэффициенты при i независимых линейных управлениях alt ...
... , aft функции Гамильтона расщепленной задачи
A2)—A5) равны нулю. О. р. с. со «скольжением» по
fc-j-1 максимумам есть особый оптимальный режим но к
компонентам для расщепленной задачи A6)—A9). Мак-
Максимально возможное значение к, к-рое целесообразно
брать при исследовании скользящих режимов, опреде-
определяется из условия выпуклости множества значений
вектора правых частей и выпуклости вниз точной ниж-
нижней границы множества значений иодинтегральной.
функции расщепленной системы, получающихся, когда
вектор управления (-zs, us), s=0, 1, ... , к пробегает
всю допустимую область значений. Таким образом,
к<.п — оценка сверху для к. В самом общем случае
все О. р. с. исходной задачи могут быть получены как
особые оптимальные управления расщепленной задачи,
записанной при к—п. В частности, в рассмотренном
выше примере расщепленная задача рассматривалась
при к — \, поскольку условия связи содержали только
одно уравнение; исследование расщепленной задачи
(8)—A1) было достаточно для исследования О. р. с.
исходной задачи A)—D).
Если известны к-\-\ управлений uo(t), Uj(t), ... , Uk(t),
доставляющих равные между собой абсолютные максп
мумы функции Гамильтона Н (t, x, тр, и) в допустимой
области U, то анализ О. р. с. сводится к исследовании'
особого оптимального режима по к компонентам. Эт<.
исследование может быть проведено с использованием
необходимых условий оптимальности особого управле
ния (см. Оптимальный режим особый).
Исследовались О. р. с. с помощью достаточных ус-
условий оптимальности (см. [4]).
Лит.: [1] Г а мире .1 и д з о Р. В., «Дикл. АН СССР», 11)В^,
т. 143, № 6, с. 1243 — 45; 12] II о н г р я г и и Л. С, Б о л т я и-
с к п й В. Г., Г а м к р е л и д з е Р. В,., М и щ с и к о Е. Ф.,
Математическая теория оптимальных процессов, 2 изд., М., ИШЯ;
[3] В а п в я |1 с к и й И. В., <'Ж. вычислит, матем. и матсм. физ.»,
1967, т. 7, Л» 2, с. 259—83; [4] К р о т о в В. Ф., «Автоматика и
телемеханика», 1963, т. 24, № 5, с. 581—98.
И. Б. Вапнярский.
ОПТИМИЗАЦИЯ ВЫЧИСЛИТЕЛЬНОГО МЕТОДА —
обычно то же, что оптимизация вычислительных алго-
алгоритмов. Иногда, однако, эти понятия трактуются раз-
различно. Напр., можно говорить об оптимальности кон-
конкретного сеточного метода решения краевой задачи на
нек-ром классе задач, имея в виду, что он требует вы-
вычисления право» части в минимальном числе точек.
При рассмотрении вопросов об оптимизации вычисли-
вычислительного алгоритма изучается дополнительно ряд дру-
других моментов: способы решения возникающей системы
сеточных уравнений, программная реализация этих
способов И Т. П. Н. С. Бахвалов.
ОПТИМИЗАЦИЯ ВЫЧИСЛИТЕЛЬНЫХ АЛГОРИТ-
АЛГОРИТМОВ — выбор оптимального вычислительного алгорит-
алгоритма при решении прикладных задач пли при разработке
гнетем стандартных программ. При решении конкрет-
конкретной задачи оптимальная тактика поведения может со-
состоять в том, чтобы не оптимизировать метод решения,
а подключиться к стандартной программе или восполь-
воспользоваться простейшим методом, составление программы
для к-рого не потребует много усилий.
Теоретич. постановка вопроса об О. в. а. имеет сле-
следующее основание. При выборе метода решения задачи
исследователь ориентируется на нек-рые ее свойства
и выбирает алгоритм решения в зависимости от них,
причем алгоритм будет применимым и при решении
других задач, обладающих этими свойствами. Поэтому
при теоретич. исследовании алгоритмов вводят в рас-
рассмотрение нек-рый класс задач Р, обладающих опреде-
определенными свойствами. При выборе метода решения ис-
исследователь располагает нек-рым множеством М мето-
методов решения. При применении метода т к решению за-
задачи р решение будет получено с нек-рон погрешностью
ь(р, п). Величина
Е (Р, m) = sup |e (р, т) \
реР
нал. и о 1 р с ш и о с 1 ь ш метода т на к л а с-
с и задач Р, а
Е (Р, М)— inf E (Р, т)
тйМ
— оптимальной на классе Р оценкой
погрешности методов из множества М. Если
существует метод такой, что
Е(Р, щ) = Е (Р, М),
то этот метод наз. оптимальны м. Такая схема
рассмотрения проблемы О. в. а., восходящая к
А. Н. Колмогорову [2], изучает множество задач вы-
вычисления интеграла
при условии |/(л))<Л, М — множество всевозможных
квадратур
каждая квадратура задается совокупностью 2N чисел
С] и xj . Задача о минимальном количестве информации
(см. [2], [3]), необходимой для запоминания функции
из данного класса с требуемой точностью, также может
быть уложена в эту схему. Рассматривается [4] более
сложная постановка проблемы, где трудоемкость реали-
реализации алгоритма в определенном смысле увязывается с
объемом используемой памяти. Оптимальные алгорит-
алгоритмы построены для незначительного числа задач типа 11].
Однако для большого числа вычислительных задач по-
построены методы, но своим асимитотич. характеристикам
близкие к оптимальным (см. [5]—18]).
Исследование характеристик оптимальных па клас-
классах вычислительных алгоритмов решения задач (см. [5],
[7]) складывается из двух частей: построение конкрет-
конкретных методов решения с возможно лучшими характери-
характеристиками и получение оценок снизу характеристик вы-
вычислительных алгоритмов (см. [2]—[4], [9]). По сущест
ну первая часть вопроса является основной проблемой
теории численных методов и в большинстве случаев
рассматривается независимо от проблемы оптимизации.
Получение оценок снизу обычно сводится к оценке
снизу е-энтропии или поперечников соответствующих
пространств; иногда оно проводится независимо, но с
использованием техники, аналогичной технике получе-
получения указанных оценок.
Вычислительные алгоритмы условно делят на ц а с-
сивныо и активные. В первом случае алго-
алгоритм решения задачи не зависит от получаемой в ходе
решения задачи информации, а во втором — зависит.
При вычислении интеграла используемая информация
о функции есть обычно информация о ее значениях в .V
точках. В случае пассивного алгоритма интеграл вы-
вычисляется по формуле
где веса С/ и Рj из области И определения / задаются
заранее. Активные алгоритмы вычисления интеграла
укладываются в следующую схему: задается точка
Pi ? Q и функции
Qq--=Q>q(Ql, ¦••> Qq-U Vu ¦•¦, Уо-l), 2-2, ..., Лг,
sn(Qu ..., <?,v; Hi, ¦¦¦, vn),
ГД° !//, ^'лт— числа, Qj?Q- Последовательно вычисляют
/(/>!), Ра = Фа(/'ь f(Pj)), f.(Pl),
Р3 = Ф3(Ри Р,; /1РХ), /(Р,)), ..., f(PA)
и полагают
/ (/) « SA- (Pi, ..., PN\ f (Pi), ..., f (PN)).
В случае выпуклых классов иодинтегралъных функ-
функций, центрально симметричных относительно функции
/=ъО, оптимальная оценка на классе пассивных алго-
алгоритмов совпадает с оптимальной оценкой на классе
активных алгоритмов (см. [10], [11]).
В практике численного интегрирования активные
алгоритмы тина алгоритмов интегрирования с автома-
тич. выбором шага (см. [10]) показали свое превосход-
превосходство над пассивными алгоритмами. Это подтверждает
общепринятую точку зрения о том, что формальная схе-
схема О. в. а. зачастую не охватывает специфики реаль-
реальных задач. При решении задач оптимизации (в частно-
частности, задач минимизации) пассивные алгоритмы практи-
практически не употребляются (см. [12], [13]). Выше за единицу
трудоемкости алгоритма неявно принимается трудоем-
трудоемкость вычисления одного значения функции из нек-рого
класса F. Возможны и другие подходы к оценке опти-
оптимальности характеристик алгоритма. Напр., за единицу
трудоемкости принимается трудоемкость вычисления
нек-рого функционала I (/) из множества функционалов
L (/). В этом случае оценка снизу трудоемкости алго-
алгоритмов производится с помощью теории поперечников
(см. [14], [15]). Трудоемкость алгоритма складывается
не только из трудоемкости получения информации об
исходных данных, но и из трудоемкости обработки по-
полученной информации. В настоящее время, по-видимо-
по-видимому, нельзя привести примеров классов реальных вычис-
вычислительных задач, где бы были получены оценки снизу
трудоемкости алгоритмов, отличные от информационных
оценок рассматриваемого типа. Однако для ряда задач
невычислительного характера такого типа оценки из-
известны (см. Алгоритма сложность).
В случае, когда исследование проблемы О. в. а.
имеет своей целью решение задач на ЭВМ, проблема
О. в. а. приобретает дополнительные оттенки, связан-
связанные с устойчивостью алгоритма к вычислительной по-
погрешности, с ограничением на объем разных видов ис-
используемой памяти (см. Вычислительный алгоритм).
Выше задача О. в. а. рассматривалась как задача О. в. а.
на классах задач. Существенный интерес для практи-
практики представляет задача О. в. а. на конкретной задаче
(см. [10], 116]). Постановка проблемы оптимизации (см.
A6]) заключается в следующем. Дифференциальное
уравнение интегрируется методом Рунге — Кутта с
переменным шагом. Производится оценка главного
члена оценки погрешности. Затем эта оценка оптимизи-
оптимизируется по распределению узлов интегрирования (при
общем заданном числе узлов). Такой подход к проблеме
оптимизации оказал существенное влияние на развитие
теории и практики активных алгоритмов численного
интегрирования.
Лит.: Н] Ник о л ь с к и й С. М., Квадратурные формулы,
3 изд., М., 1979; [2] Колмогоров А. Н., «Докл. АН СССР»,
1956, т. 108, MS 3, с. 385—88;[3] Колмогорова. Н., Т и-
х о миро в В. М., «Успехи матем. наук», 1951), т. 14, в. 2,
с. 3—86; [4] В и т у ш к и н А. Г., Оценка сложности задачи
табулирования, М., 1959; [5] Б а б у ш к а И. Соболеве. Л.,
«Aplikace mat.», 1»(>5, t. 10, s. 96—29; [6] Б а х в а л о в Н. С,
гам же, J9BS, I. J3, s. 27—ЗН; 17) е г о же, вин.: Международ-
Международный конгресс математиков а Ницце. 1970. Доклады советских
математиков, М., 1972, с. 27—33; 18) е г о ж е, в кн.: Числен-
Численные методы решения дифференциальных и интегральных урав-
уравнений и квадратурные формулы, М., 1964, с. 3—63; [9] е г о же,
«Матем. заметки», 1972, т. 12, в. 6, с. 655—64; [10] его же,
Численные методы, 2 изд., М., 1975; [11] его же, «Ж. вычис-
вычислит, матем. и матем. физ.», 1971, т. 11, № 4, с. 1014—18; [12]
У а й л д Д.- Д ж ., Методы поиска экстремума, пер. с англ.,
М., 1967; [13] Васильев Ф. П., Численные методы решения
экстремальных задач, М., 1980; [14] Оганесян Л. А., Р у-
ховец Л. А., Вариационно-разностные методы решения эл-
эллиптических уравнений, Ер., 1979; [15] Тихомиров В. М.,
Некоторые вопросы теории приближений, М., 1976; [16] Тихо-
Тихонов А. Н., Горбунов А. Д., «Ж. вычислит, матем. и ма-
матем. физ.», 1964, т. 4, Ли 2, с. 232—41. Н. С. Бахвалов.
ОПЦИОНАЛЬНАЯ ff-АЛГЕБРА — наименьшая а-ал-
гебра 6=6(F) множеств из ЙХЙ + ={(ш, t) : w?Q,
i^=0}, порожденная всеми отображениями (ш, i)~-*-
/(ш, t) множества ЯхВ+ в R, к-рые (для каждого
фиксированного w?Q) являются (по t) непрерывными
справа, имеют пределы слева и F-согласованы с неубы-
неубывающим семейством F = (A"t)i>0 под-а-алгебр Ft*~F,
t^:0, где (Q, F) — измеримое пространство. О. ст-а.
совпадает с наименьшей а-алгеброй, порожденной сто-
хастич. интервалами [о, т|= {(ш, t) : 0<:/<т(<о)}, где
т=т(ш) — марковские моменты (относительно F=
~№)г>о)- МежЛУ опциональными и предсказуемыми
а-алгебрами имеет место соотношение ?7()g^Q()
Лит.: [1] Дел л,а ш е р и К., Емкости и случайные процес-
процессы, пер. с франц., М., 1975. А. Н. Ширяев.
опциональный случайный процесс -
стохастический процесс Х— (Xf((o), Ff)(>0, являющийся
измеримым (как отображение (ш, <)~^-Х(со, t)=
= Xt (ш)) относительно опциональной а-алгебры Q=
= 6(П- А. Н. Ширяев.
ОРБИТ МЕТОД — метод изучения унитарных пред-
представлений групп Ли. С помощью О. м. была построена
теория унитарных представлений нилыютентных групп
Ли, а также указана возможность его применения к
другим группам [1].
О. м. основан на следующем «экспериментальном»
факте: существует глубокая связь между унитарными
неприводимыми представлениями группы Ли G и ор-
орбитами этой группы в коприсоединенном представлении.
Решение основных задач теории представлений с по-
помощью О. м. осуществляется следующим образом (см.
12».
I. Конструкция и классификация
неприводимых унитарных представ-
представлений. Пусть Q — орбита действительной группы
Ли G в коприсоединенном представлении, F — точка
этой орбиты (являющаяся линейным функционалом
на алгебре Ли g группы G), G(F) — стабилизатор точки
F, #(F) — алгебра Ли группы G(F). Поляриза-
Поляризацией точки F наз. комплексная подалгебра I) в Дл ,
где cJjn— ко.чпленсификация алгебры Ли с;, обладающая
свойствами:
1) diin(Qf) = dim д—— dim Q;
2) [t), ft] содержится в ядре функционала F на д;
3) [) инвариантна относительно Ad G(F).
Пусть Д°=схр@Пд) и H=G(F)-H". Поляризация fi
наз. действительной, если 1)— (), и чисто
комплексной, если ()C\li=#(F). Функционал F
определяет характер (одномерное унитарное представ-
представление) xF группы На по формуле
ехр X —>¦ ехр 2л j <F, X>.
Пусть %°р продолжается до характера %F группы И.
Если f) — действительная поляризация, то пусть
rf (Л — индуцированное характером %р подгруппы
// представление группы G (см. Индуцированное пред-
представление). Если {) — чисто комплексная поляризация,
то пусть Тр (п х — голоморфно индуцированное пред-
представление, действующее в пространство голоморфных
функций на GIH.
Первая основная гипотеза состоит в
том, что представление Tf ь % непРив°Дим0 и его
класс эквивалентности зависит только от орбиты Q и от
выбора продолжения %F характера %р. Эта гипотеза
доказана для нильпотентных групп [1] и для разреши-
разрешимых групп Ли [5]. Для нек-рых орбит простой особой
группы <32 гипотеза неверна [7]. Возможность продол-
продолжения и степень его неоднозначности зависят от топо-
логич. свойств орбиты: препятствием к продолжению
служат двумерные когомологии орбиты, а в качестве
параметра, нумерующего различные продолжения, мож-
можно взять одномерные когомологии орбиты. Более точно,
пусть B(j — каноническая 2-форма на орбите О. Для
существования продолжения необходимо и достаточно,
чтобы форма Ви принадлежала целочисленному классу
(т. е. интеграл ее по любому двумерному циклу был це-
целым числом); если это условие выполнено, то множество
продолжений параметризуется характерами фунда-
фундаментальной группы орбиты.
Вторая основная гипотеза состоит
в том, что указанным способом получаются все унитар-
унитарные неприводимые представления рассматриваемой
группы G. Единственным A983) противоречащим этой
гипотезе примером являются т. н. дополнительные се-
серии представлений полуиростых групп Ли.
II. Функтор и альные свойства соот-
соответствия между орбитами и пред-
представлениями. Значительное место в теории
представлении занимают вопросы о разложении на не-
неприводимые компоненты представления, получаемого
ограничением на подгруппу // неприводимого представ-
представления группы G и индуцированием с помощью непри-
неприводимого представления подгруппы HczG. О. м. дает
ответ на эти вопросы в терминах естественной проек-
проекции р : з* —»¦ Ь* (* означает переход к сопряженному
пространству; проекция р состоит в ограничении функ-
функционала с g на Г)). А именно, пусть С — экспоненци-
экспоненциальная группа Ли (для таких групп соответствие между
орбитами и представлениями взаимно однозначно).
Тогда неприводимое представление группы G, соответ-
соответствующее орбите QcZfl*, при ограничении на Н разла-
разлагается на неприводимые компоненты, соответствующие
тем орбитам <о?()*, к-рые лежат в р (Q), а представление
группы G, индуцированное неприводимым представле-
представлением группы Н, соответствующим орбите coczf)*, раз-
разлагается на неприводимые компоненты, соответствую-
соответствующие тем орбитам Qczc}*, к-рые имеют непустое пересе-
пересечение с прообразом р~1(ю). Из этих результатов выте-
вытекают два следствия: если неприводимые представления
Т( соответствуют орбитам Q,-, г=1, 2, то тензорное про-
произведение Тг@Т2 разлагается на неприводимые компо-
компоненты, соответствующие тем орбитам Q, к-рые лежат в
арифметич. сумме fiiH-Q2"> квазирегулярное представле-
представление группы G в пространстве функций на G/H разла-
разлагается на неприводимые компоненты, соответствующие
тем орбитам Qcz<}*, для к-рых образ p(Q)crf)* содер-
содержит нуль.
III. Теория характеров. Для характеров
неприводимых представлении (как обобщенных функции
на группе) предложена [2] следующая универсальная
формула:
где ехр : д —>- G — экспоненциальное отображение ал-
алгебры Ли (\ в группу G, р(Х) — квадратный корень из
плотности инвариантной меры Хаара на G в канонич.
координатах, Р — форма объема на орбите Я, связан-
связанная с канонической 2-формой Ва соотношением E=
а 1
=-гг , к~— dim ^- Эта формула справедлива для
нильпотентных групп, разрешимых групп типа 1,
компактных групп, дискретной серии представлений
полупростых действительных групп и основной серии
представлений комплексных полупростых групп. Для
нек-рых вырожденных серий представлений SLC, R)
формула неверна. Из формулы (*) получается простая
формула для вычисления пнфинитезнмального харак-
характера неприводимого представления Та, соответствую-
соответствующего орбите Q, а именно: каждому оператору Лапласа Д
на G может быть сопоставлен А й*С-инвариантный мно-
многочлен Р\ на g* так, что значение инфинитезимального
характера представления Гй на элементе Д в точности
равно значению Ра на Q.
IV. Конструкцию неприводимого унитарного
представления группы G по ее орбите Q в конрисоеди-
ненном представлении можно рассматривать как опе-
операцию квантования нек-рой гамильтоновой системы,
для к-рой Q играет роль фазового пространства, a G —
роль многомерного некоммутативного времени (или
группы симметрии). При этом (J-орбиты в коприсоеди-
ненном представлении — это все С-однородные симп-
лектич. многообразия, допускающие квантование. Та-
Таким образом, вторую основную гипотезу можно пере-
переформулировать так: каждая элементарная квантовая
система с временем (или группой симметрии) G полу-
получается квантованием из соответствующей классич. сис-
системы (см. [2]).
Обнаружена также связь О. м. с теорией вполне ин-
интегрируемых гамильтоновых систем (см. [11]).
Лит.: [1] К и р и л л о в А. А., «Успехи матем. наук», 1962,
т. 17, в. 4, с. 57—110; [2] е г о же, Элементы теории представ-
представлений, 2 изд., М., 1978; [3] Д и к с м ь е Ж., Универсальные обер-
обертывающие алгебры, пер. с франц., М., 1978; [4] S i m m s D. J.,
Woodhouse N. M. J. , Lectures on geometric quantization,
В.— Hdlb.— N. Y., 1976; [5] A u s 1 a n d e г L., К о s t a n t B.
«Invent, math.», 1971. v. 14, p. 255—354; [6] Moore C.C.,
«Arm. Matli.», 1965, v. 82, № 1, p. 14B —82; [7] Rothschild
L. P. , Wolf J. A.. «Ann. Sci. Ecolc norm, super. Stir.4»,1974,
v. 7, № 2, p. 15a—74; Is] Representations des groupes d« Lie re-
solubles P., 1U72; [9] Г и н а б у р г В. А., «Докл. АН СССР»,
1979, т. 24», № 3, с. 525—28; И0] К i r i 1 1 о v A. A., Infinite
dimensional groups, their representations, orbits, invariants,
в сб.: Proc. Int. Congr. Math., Helsinki, -1978; [11] Hey-
man A. G., S e m e n о v - T i a n - S h a n s к у М. A., «In-
«Invent, math.», 1979, v. 54, № 1, p. 81 — 100. .4. А. Кириллов.
ОРБИТА точки х относительно группы G, действую-
действующей на множестве X (слона),— множество
Множество
является подгруппой в G и наз. стабилизато-
р о м, или стационарной подгруппой
точки х относительно G. Отображение
g\-^ g(x), g?G, индуцирует биекцию между G/Gx и орби-
орбитой G(x). О. любых двух точек из X либо не пересека-
пересекаются, либо совпадают; иначе говоря, О. определяют раз-
разбиение множества X. Фактормножество по отношению
эквивалентности, определенному этим разбиением, наз.
пространством орбит, или фактор-
фактормножеством X по G, и обозначается X/G. Сопо-
Сопоставление каждой точке ее О. определяет канонич. ото-
отображение пх, а '¦ X —>¦ XlG. Стабилизаторы точек из
одной О. сопряжены в G, точнее Gg(x) = gGxg~1. Если
в X имеется только одна О., то X ~ о д н о р о д н о е
пространство группы <?; говорят также, что
G д е й с т в у е т на X т р а н з и т и в н о. Если G —
топологич. группа, X — топологич. пространство и
действие непрерывно, то XlG обычно снабжается топо-
топологией, в к-poii множество UaXlG открыто в XlG тогда
и только тогда, когда множество я (U) открыто в X.
X, и
Примеры. 1) Пусть G — группа поворотов пло-
плоскости X вокруг фиксированной точки а. Тогда О.—
это всевозможные окружности с центром в в (в том числе
и сама точка а). 2) Пусть G — группа всех невырож-
невырожденных линейных преобразований конечномерного дей-
действительного векторного пространства V, X — множест-
множество всех симметрич. билинейных форм на V, а действие G
на X определено формулой {gf)(u, v)=f{g~1(u), g-1(u))
для любых и, v? V. Тогда О. группы G на X — множест-
множество форм, имеющих фиксированный ранг и сигнатуру.
Пусть G — вещественная группа Ли, гладко дейст
вующая на дифференцируемом многообразии X (см.
Ли группа преобразований). Для любой точки х?Х
орбита G(x) является погруженным подмногообразием
в X, диффеоморфным GlGx (диффеоморфизм индуциро-
индуцирован отображением gн» g(x), g?G). Это подмногообразие
не обязательно замкнуто в X (не обязательно вложено)
Классич. примером служит «обмотка тора», то есть О.
действия аддитивной группы R на торе
заданного формулой
t(zu 22) = (ЛЬ e"*tz2)
где а — иррациональное действительное число; зам^т-
канио такой О. совпадает с Г2. Если G компактна, то
все О. являются вложенными подмногообразиями.
Если G — алгебраич. группа, X — алгебраич. мно-
многообразие над алгебраически замкнутым полем к, а
действие регулярно (см. Алгебраическая группа преоб-
преобразований), то любая орбита G{x) является гладким ал-
алгебраич. многообразием, открытым в своем замыкании
G(x) (в топологии Зарнского), причем в G(x) всегда со-
содержится замкнутая О. группы G (см. [5]). В этом случае
морфизм G-^-G(x), gH>g(r), индуцирует изоморфизм
алгебраич. многообразии G/Gx и G(x) тогда и только тог-
тогда, когда он сепарабелен (это условие всегда выполнено,
если к — поле нулевой характеристики). О. макси-
максимальной размерности образуют открытое в X множе-
множество.
Описание структуры О. для данного действия обычно
сводится к указанию в каждой О. нек-рего единствен-
ного представителя х, к нахождению стабилизатора Gx
и к описанию какого-либо — по возможности обозри-
обозримого — класса функций, постоянных на О. (инвариан-
(инвариантов) и разделяющих разные О.; эти функции позволяют
описать «расположение» О. в -Y (О. являются пересече-
пересечениями нх множеств уровня). Эта программа обычно наз.
задачей орбитального р а и л о ж е н и я.
К такой задаче часто сводятся многие задачи классифи-
классификации. Так, в примере 2) ото — задача классификации
билинейных симметрпч. форм с точностью до эквива-
эквивалентности; инварианты в этом случае «дискретны» —
¦ото ранг и сигнатура, а стабилизатор G/, где / невы-
невырождена, является соответствующей псевдоортого-
нальной группой. Классич. теория жордановой формы
матриц (также, как п теории других нормальных форм
матриц) тоже укладывается в эту схему: жорданова
форма — это канонич. представитель (определенный,
правда, с точностью до порядка жордановых клеток)
в О. полной линейной группы GLrt(C) па пространстве
всех комплексных (вХи)-матриц при действии, задан-
заданном формулой У—*¦ AYA~1', среди инвариантов важное
место занимают коэффициенты характеристпч. много-
многочлена матрицы У (к-рые не разделяют, однако, любые
две О.). Идея рассмотрения эквивалентных объектов
как О. нек-рой группы активно используется в различ-
различных задачах классификации, напр, в алгебранч. моду-
модулей теории (теория Мамфорда, см. [10]), в теории пере
числения графов (см. [2]) и др.
Если G и X конечны, то
где \Y\ — число элементов множества Y, а
Если G — компактная группа Ли, гладко действую-
действующая на связном гладком многообразии X, то структура
О. па X локально копечна, т. е. у любой точки х?Х
существует такая окрестность U, что число различных
стабилизаторов Gy, y? U, с точностью до сопряженности
в G конечно. В частности, если X компактно, то конечно
число различных (с точностью до сопряженности в G)
стабилизаторов G,r у?Х. При этом для любой подгруп-
подгруппы Н в G каждое пз множеств
Х{Н) — [х?X | Gx сопряжена Н в G}
является пересечением открытого и замкнутого инвари-
инвариантных подмножеств в X. Исследование Х^/у, приводит
в этом случае к классификации действий (см. [1]). Ана-
Аналоги этих результатов получены в геометрич. инвари-
инвариантов теории (см. [3]). А именно, пусть G — редуктнв-
ная алгебраич. группа, регулярно действующая на
аффинном алгебрапч. многообразии X (основное поле к
алгебраически замкнуто и имеет характеристику 0).
В замыкании любой О. содержится единственная замк-
замкнутая О. Существует разбиение X в объединение коноч-
коночного числа локально замкнутых инвариантных непере-
непересекающихся подмножеств X—\]аХа, обладающее свой-
свойствами: а) если х, у?Ха и G(x) замкнута, то стабилиза-
стабилизатор Gy сопряжен в G подгруппе в Gx, а если замкнута
ц G(i/),to Gy сопряжен с Gx\ б) еслих?Ха, г/?Хр , а?=р\
a G(x) и G(y) замкнуты, то Gx и Gy не сопряжены в G.
Если X — гладкое алгебраич. многообразие (папр.,
в важном случае, когда рассматривается рациональное
линейное представление G в векторном пространстве
V—X), то существует такое непустое открытое подмно-
подмножество Q в X, что Gx и Gy сопряжены в G для любых
х, !/?Q. Последний результат является утверждением о
свойстве точек общего положения в X,
т. е. точек, заполняющих непустое открытое подмпоже-
ство; имеется и ряд других утверждений такого типа.
Напр., для рационального линейного представления
полу прост ой группы G в векторном пространстве V О.
точек общего положения замкнуты тогда и только тогда.
когда их стабилизаторы редуктивны (см. [7]); в случае,
когда С ненрпводима, найден явный вид стабилизаторов
точек общего положения (см. [8], [9]). Вопрос о замк-
путости О. является специфическим и важным в этой
теории. Так, множество тех точек х?_ V, О. к-рых содер-
содержит в своем замыкании нуль пространства V, совпадает
с многообразием нулей непостоянных инвариантных
многочленов на V; во многих случаях, и в частности в
применениях теории инвариантов к теории модулей,
это многообразие играет существенную роль (см. [10]).
Любые две различные замкнутые О. разделяются инва-
инвариантными многочленами. Орбита G(x) замкнута тогда
и только тогда, когда замкнута О. точки х относительно
нормализатора G(x) в С (см. D]). Появление незамкну-
незамкнутых О. связано со свойствами G; если G унипотентна
(а X аффинно), то любая О. замкнута (см. [6]). Одним ни
направлений теории инвариантов является изучение
орбитальных разложений различных конкретных дей-
действий (в особенности линейных представлений). Одно и:>
mix — присоединенное представление редуктивной
группы G — подробно исследовалось (см., напр., [11]).
Его изучение свя.чапо с теорией представлений группы
С; см. Орбит метод.
Лит.: [1] Palais (!., The classification of G-spnccs, Provi-
ice, 1960 (Mem. Amer. Math. Soc, № 36); [2J X a p a p и Ф.,
Теории графов, пер. с англ., Ы., 1973; [3] Luna D., «Bull. Soc.
Matti. France. Mem. S3», ii)T3, p. St —105; Ш е г о же, «Invent,
math.», 1975, v. 29, .Nj 3, p. 231—38; [5] Б о р е л ь А., Линейные
алгебраические группы, пер. с англ., М., 1972; [6] Stein-
Steinberg R., Conjugacy classes in algebraic groups, В.—Hdlb.—
N. Y., 1974; [7] И о п о в В. Л., «Изв. АН СССР. Сер. матем.»,
1970, т. 34, с. 523—31; [8] П о п о в А. М., «Ф\ш;ц. анализ и его
прилож.», 1978, т. 12, Jvft 2, с. 91—Я2; [9] Элашвили А. Г.,
там же, 1972, т. и, № 2, с. 65—78; [10] MumtordD., Geo-
Geometric invariant theory, В.—Hdlb.—N. Y., 1965; [11] К о s-
t a n t В., «Amer. J. Math.», 1963, v. 85, № 3, p. 327—404; [12]
Хамфри Дж., Линейные алгебраические группы, пер. с англ.,
М., 1980. В. Л. Попов.
ОРБИТАЛЬНАЯ УСТОЙЧИВОСТЬ — свойство тра-
траектории | (решения x(t)) автономной системы обыкно-
обыкновенных дифференциальных уравнений
x = f (x), x?Rn, (*)
состоящее в следующем: для всякого р>0 существует
6>0 такое, что всякая положительная полутраектория,
начинающаяся в б-окрестности траектории |, содержит-
содержится в е-окрестности траектории §. Здесь под траект о-
р и е й понимается множество значений решения
x(t), i?R, системы (*), а под положительной
полутраекторпен--- множество значений ре-
решения x(t) при ?5=0. Если решение х(t) устойчиво по
Ляпунову, то его траектория орбитально устойчива.
Траектория ? наз. асимптотически орби-
орбитально устойчивой, если она орбитально
устойчива и, кроме того, найдется бо>0 такое, что
траектория всякого решения x(t) системы (*), начинаю-
начинающегося в 6,,-окрестиости траектории ? (т. е. d(x@), 5) <
<6„), стремится при г —*- -f- oo к траектории |, то есть
lim <l(x(t), |)-0,
<-> + »
где
d (х, I) = inf d (x, y)
— расстояние от точки х до множества \ (d(.r, у) — рас-
расстояние между точками х и у).
Роль понятия асимптотической орбитальной устой-
устойчивости основана на следующих фактах. Периодич.
решение системы (*) никогда не бывает асимптотически
устойчивым. Но сслп у периодич. решения такой сис-
системы модули всех .мультипликаторов, кроме одного,
меньше единицы, то траектория этого иериодич. реше-
решения асимптотически орбитально устойчива (А н д р о-
нова — Витта теорема). Имеет место также
более общая теорема Д е м и д о в и ч а (см. C|):
пусть xo{t) — ограниченное решение системы (*), при-
причем
inf | х0 (t) | > О,
о
и пусть система уравнении в вариациях вдоль xo(t)
правильная (см. Правильная линейная система), при
чем все ее Ляпунова характеристические показатели,
кроме одного, отрицательны; тогда траектория решения
жо(/) асимптотически орбитально устойчива.
Лит.: [1] Андронов А. А., Собр. трудов, М., 1956; [2]
Андронов А. Л., В и т т А. А., X а й к и и С. У., Теория
колебаний, 2 изд., М., 1959; [Я] Демидов и ч Б. II., «Диффе-
ренц. уравнения», 1968, т. 4, № 4, с. 575—88; № 8, с. 1359—7:1
В. М. Миллионщиков.
ОРДИНАЛЬНОЕ ЧИСЛО, о р д и н а л,— то же, что
порядковое число.
ОРДИНАТА — одна из декартовых координат точки.
ОРИЕНТАЦИЯ — формализация и далеко идущее
обобщение понятия направления обхода. Определяется
О. нек-рых специальных классов пространств (многооб-
(многообразий, векторных расслоений, Пуанкаре комплексов
и т. д.). Современный взгляд на О. дается в рамках
обобщенных теорий когомологий.
В класенч. случае ориентация — выбор одного
класса систем координат, связанных между собой по-
положительно в нек-ром определенном смысле. Каждая
система задает О., определяя класс, к к-рому она при-
принадлежит.
В случае векторного пространства R" конечной раз-
размерности две системы координат связаны положитель-
положительно, если положителен определитель матрицы перехода
от одной из них к другой. Здесь имеется два класса.
В комплексном пространстве С" комплексный репер
е(, ... , еп определяет действительный репер ех, ... , еп,
гв], ... , ien в том же пространстве, рассматриваемом как
R2", и все такие реперы связаны попарно положитель-
положительными переходами (т. е. комплексная структура задает
О. в R3").
На прямой, плоскости и вообще в действительном
аффинном пространстве Е" системы координат состоят
из точки (начала 0) и репера е, переход определяется
вектором переноса начала и заменой репера. Этот
переход положителен, если положителен определитель
матрицы замены (напр., при четной перестановке
векторов репера). Две системы координат определяют
одну и ту же О., если одну из них можно переве-
перевести в другую непрерывно, т. е. существует непрерыв-
непрерывно зависящее от параметра t?\0, 1] семейство коор-
координатных систем Oi, ef, связывающее данные систе-
системы О0, еп и О1, ех. При отражении в плоскости (раз-
(размерности п—1) системы двух классов переходят друг в
друга.
Классы систем координат можно задавать различны-
различными геометрич. фигурами. Если какая-либо фигура X по
определенному закону связывается с системой коорди-
координат, то зеркально симметричная eit фигура будет по
тому же закону связана с системой координат из дру-
другого класса. Тем самым X (вместе с данным законом)
определит О. Напр., на плоскости Ег окружность с
фиксированным направлением обхода задает системы
координат из одного класса по правилу: начало лежит
в ее центре, первый вектор берется произвольно, а вто-
второй так, чтобы вращение от первого ко второму через
меньший угол происходило в направлении, заданном
на окружности. В Е3 репер можно связать с винтом с
точностью до непрерывного вращения и растяжения
пространства: первый вектор идет по направлению ввин-
ввинчивания, вращение от второго вектора к третьему сов-
совпадает с вращением при ввинчивании (предполагается
при этом, что все винты находятся в положительной
связи друг с другом). Репер может быть также задан
тремя первыми пальцами руки хорошо известным спо-
способом.
Если в Е" задана О., то каждоо полупространство
Е'1 определяет О. на граничной плоскости Еп~х. Напр.,
уславливаются, что если в репере последние и -\
векторов лежат в Еп~х, а первый смотрит наружу из
Е'1, то последние векторы задают О. в Е"-1. В Е" О.
может быть задана порядком вертБин n-мерного сим-
симплекса (треугольника в Ег, тетраэдра в Е3). Репер опр<
деляется условием: в первую вершину помещается и,\
чало, в остальные из первой направляются векторы ре-
репера. Два порядка задают одну О., если и только если
они отличаются на четную перестановку. Симплекс с
фиксированным с точностью до четной перестановки
порядком вершин наз. ориентированным.
Каждая (/I—1)-грань а"-1 ориентированного симплекса
получает индуцированную ориентацию: если первая
вершина не принадлежит о", то порядок остальных
принимается яа положительный для о".
В связном многообразии М системой координат слу-
служит атлас — набор карт, покрывающих М. Атлас наз.
ориентирующим, если координатные преобра-
преобразования все положительны. Это означает, что их сте-
степени равны +1, а в случае дифференцируемого много-
многообразия, положительны якобианы преобразования во
всех точках. Если ориентирующий атлас существует,
то многообразие М наз. ориентируемым.
В этом случае все ориентирующие атласы распадаются
на два класса, так что переход от карт одного атласа к
картам другого положителен, если и только если атласы
принадлежат одному классу. Выбор такого класса наз.
ориентацией многообразия. Этот выбор
может быть сделан указанием одной карты или локаль-
локальной О. в точке х0 (связные карты, содержащие ,г0, ес-
естественным образом распадаются на два класса). В слу-
случае дифференцируемого многообразия локальную О.
можно задать указанием репера в касательной плоско-
плоскости в точке х0 (напр., вращение на окружности можно
задать указанием одного касательного вектора). Если
М имеет край и ориентировано, то край также ориенти-
ориентируем, напр, по правилу: в точке края берется репер,
ориентирующий М, первый пектор к-рого направлен из
дМ, а остальные векторы лежат в касательной плоско-
плоскости края", эти последние и принимаются за ориентирую-
ориентирующий репер края.
Вдоль любого пути q: [0, 1] ->¦ М можно выбрать це-
цепочку карт так, что две соседние карты связаны положи-
положительно. Тем самым О. в точке q@) определяет О. в точ-
точке q(i), и эта связь зависит от пути q лишь с точностью
до его непрерывной деформации при фиксированных
концах. Если q — петля, т. е. q@) = q(i)==x0, то q наз.
дезориентирующим путем, если эти О.
противоположны. Возникает гомоморфизм фундамен-
фундаментальной группы л,(Л/, х0) в группу порядка 2: дезориен-
дезориентирующие петли переходят в —1, а остальные в +1.
По этому гомоморфизму строится накрытие, являющее-
являющееся двулистным в случае неориентируемого многообра-
многообразия. Оно наз. ориентирующим (т. к. накры-
накрывающее пространство будет ориентируемым). Этот же
гомоморфизм определяет над М одномерное расслое-
расслоение, тривиальное, если и только если М ориентируемо.
Для дифференцируемого М оно может быть определено
как расслоение Л"{М) дифференциальных форм поряд-
порядка п. Ненулевое сечение в нем существует лишь в ориен-
ориентируемом случае и задает форму объема на М и одно-
одновременно О. Классифицирующим отображением этого
расслоения служит отображение к: М ->¦ R/5". Многооб-
Многообразие М ориентируемо. сс:\и н только если не равен
нулю класс yi^Hn~i{M, й)-сл\жаший образом классн.
двойственного к Rpn-*c:RPn. Он двойствен циклу,
носителем к-рого служит многообразие, являющееся
прообразом КР"-1 при отображении к, приведенным
в общее положение. Этот цикл наз. ориентирую-
ориентирующим, т. к. дополнение к нему ориентируемо: если по
нему М разрезать, то получится ориентируемое много-
многообразие. Само М ориентируемо (неориентируемо), если
ц только если после разреза получится несвязное мно-
многообразие (это дополнение связно). Напр., в RP~
ориентирующим циклом служит проективная пря-
прямая Ri».
Триангулированное многообразие М (или псевдомно-
гоооразие) ориентируемо, если можно ориентировать
все л-мерныо симплексы так, что два симплекса с общей
(п—1)-мерной гранью индуцируют на ней противопо-
противоположные О. Замкнутая цепочка п-мерных симплексов,
каждые два соседа в к-рой имеют общую (п—1)-грань,
наз. дезориентирующей, если оти симплексы
могут быть ориентированы так, что первый и послед-
последний симплексы индуцируют на общей грани совпадаю-
совпадающие О., а остальные соседи — противоположные.
О. может быть определена на гомологич. языке: для
связного ориентируемого многообразия без края гомо-
гомологии группа Нп(М; '?) (с замкнутыми носителями)
изоморфна Ъ, и выбор одной из двух образующих за-
задает О.— отбираются карты с положительными степе-
степенями отображений. Для связного многообразия с краем
то же верно и для Нп{М, дМ; %}. В первом случае
ориентируемость есть гомотопич. инвариант Л/, а во
втором — пары (М, дМ). Так, лист Мёбиуса и кольцо
имеют один и тот же абсолютный гомотонич. тип, но
разный — относительно края. Локальная О. многооб-
многообразия может быть также задана выбором образующей в
группе Нп(М, М\х0; %), изоморфной '?¦ Гомологич.
интерпретация О. позволяет перенести это понятие на
обобщенные гомологические многообразия.
Пусть над пространством X задано расслоение /;:
Е —>- X со стандартным слоем Fa. Если О. всех слоев
можно выбрать так, что любое (собственное) отображе-
отображение р~1(у(О)) -*¦ P~x(yA))> определенное путем у:
(О, I)—*- X однозначно с точностью до собственной гомо-
топии, сохраняет О., то расслоение наз. ориентиро-
ориентированным, а указанный выбор О. слоев — ориен-
ориентацией расслоения. Напр., лист Мёбиуса,
рассматриваемый как векторное расслоение над окруж-
окружностью, не обладает О., в то время как боковая поверх-
поверхность цилиндра — обладает.
Понятие О. допускает естественное обобщение и для
случая бесконечномерного многообразия, моделиро-
моделированного при помощи бесконечномерного банахова или
топологического векторного пространства. При этом
необходимы ограничения на линейные операторы, яв-
являющиеся дифференциалами функций перехода от кар-
карты к карте: они должны не просто принадлежать общей
линейной группе всех изоморфизмов моделирующего
пространства, к-рая гомотопическп тривиальна (в рав-
равномерной топологии) для большинства классических
векторных пространств, а содержаться в нек-рой линей-
линейно несвязной подгруппе общей линейной группы. Тогда
компонента связности данной подгруппы и будет зада-
задавать «знак» О. В качестве такой подгруппы обычно вы-
выбирается фредгольмова группа, состоящая из тех изо-
изоморфизмов моделирующего пространства, для к-рых
разность с тождественным изоморфизмом есть вполне
непрерывный оператор.
О р и инт а ц и я в о б о б ще ин ы х теориях
к о г о м о л о г и ii. Пусть Е* — мультипликативная
обобщенная теория когомологий (ниже — просто теория).
Имеется единица l?E°(Sa), и при изоморфизме над-
надстройки E"(S")zaEn(Sn) ей отвечает элемент Xa?E"(Sn),
рде Sn есть га-ыерная сфера.
Пусть | есть гс-мерное векторное расслоение над ли-
линейно связным пространством X и пусть Т\ — Тома
пространство расслоения ?. Пусть i: Sn —*¦ Т% — стан-
стандартное вложение, т. е. гомеоморфизм на «слой» над не-
к-рой точкой хи?Х. Элемент u?E~n(TQ наз. ориен-
ориентацией или Тома классом расслоения |,
если i*(u)~ гуп, где е?Я°E°)— некоторый обратимый
элемент (напр., 6—1). Расслоение, обладающее О.,
наз. ориентируемым в теории Е*, или про-
просто Е-о риентируемым, а расслоение с выбран-
выбранной ^-ориентацией наз. Е-о риентированным.
Изоморфизм Тома E*(TQ^E*(X) (см. [6]). Множество
О. данного ^-ориентированного расслоения % над X
находится во взаимно однозначном соответствии с
элементами группы 2?°(Х)ф(?°Eи))*, где ( )* — груп-
группа обратимых элементов кольца ( ).
Тривиальное n-мерное расслоение 0" обладает О.
в любой теории Е", и если два из трех расслое-
расслоений |, т), ?фт) Я-ориентируемы, то Я-ориентируемо
и третье (см. [7]). В частности, Я-ориентируемость
асслоения § влечет Я-ориентируемость расслоения
©в
Понятие л-ориентируемости вводится и для любого
расслоения в смысле Гуревича р: Е —у В, слой к-рого
гомотопически эквивалентен сфере. Пространст-
Пространством Тома такого расслоения наз. конус отображе-
отображении р; в остальном определение аналогично. Определе-
Определение О. векторного расслоения | сводится к этому, если
в качестве Е взять расслоение на единичные (в нек-рой
римановой метрике на |) сферы, ассоциированное с %.
^-ориентируемость есть инвариант стационарного по-
послойного гомотопического типа векторного (сфериче-
(сферического) расслоения. Расслоение, ориентируемое в од-
одной теории, не обязано быть ориентируемым в дру-
другой, но при наличии кольцевого гомоморфияма теорий
Е* —*¦ F* из Я-ориентируемости следует /•'-ориенти-
/•'-ориентируемость.
Примеры. 1) В теории #*( —; Z2) ориентируемо
любое векторное (сферическое) расслоение. 2) В теории
//*( —; '?) ориентируемы в точности те расслоения |,
для к-рых характеристич. класс Штифеля u^d) — 0, т. е.
ориентируемы те расслоения, к-рые ориентируемы в
классич. смысле. 3) Ориентируемость векторного рас-
расслоения | в вещественной К-meopuu эквивалентна тому,
что !?>!(!)= и>2(?,)=0, а в комплексной А'-теории — тому,
что ш1(|) = 0 и к>2(|) — целочисленный элемент [8].
При этом для А'-ориентируемости сферич. расслоений
это условие необходимо, но не достаточно. 4) Ориенти-
Ориентируемость в теории унитарных кобордизмов U* не оха-
охарактеризована A983); комплексные расслоения fZ-ори-
ентируемы, но это явно не необходимо. 5) В теории П*
стабильных когомотопич. групп ориентируемы лишь
расслоения тривиального стационарного послойного
гомотопич. типа.
В задаче описания класса расслоений, ориентируемых
в данной теории, имеется следующий общий результат.
Пусть топологич. группа G действует на R" и пусть
Е* — нек-рая теория. Существует (см. [7], где дана яв-
явная конструкция) пространство В (G, Е) с универсаль-
универсальным ^-ориентированным расслоением над ним, класси-
классифицирующее ^'-ориентированные векторные расслое-
расслоения со структурной группой G, т. е. для любого (линей-
(линейно связного) пространства X множество ^-ориентиро-
ванных G-векторных расслоений над X находится в ес-
естественном взаимно однозначном соответствии с множе-
множеством \Х, В (G, Е)] гомотопич. классов отображений
X^>-B(G, E). Это же верно для сферич. расслоений и
«хороших» моноидов С
Обратная задача состоит в описании теории, где дан-
данное расслоение (или данный класс расслоений) орион-
тируемо. Известно, что если в теории Е* ориентируемы
все векторные расслоения, то
Е*{Х) « Я* (Л'; Ё (S»)),
причем 2E*(Sa) — 0. В этом контексте иногда ослабляют
условия на теорию Е*, напр, снимают условие комму-
коммутативности умножения Ti т. д. Для любой теории Е*,
в к-рой все комплексные расслоения ориентируемы,
имеется гомоморфизм теории U* —»-?*, где U* — тео-
теория унитарных кобордизмов, и этот гомоморфизм пол-
полностью задается Я-ориентацией канонич. расслоения г\
над СР°°. Аналогичное верно и для Л'^-расслоений (см.
Кобордизм). Построение для любого класса векторных
расслоений универсальной теории, отображающейся в
любую теорию, где ориентируем данный класс расслое-
расслоений, вше A983) не проведено.
Ориентацией (другое название — фунда-
фундаментальный класс) замкнутого «-мерного
многообразия (или, более общо, комплекса Пуанкаре
формальной размерности п) в теории Е* наз. такой эле-
элемент z?En{M), что гомоморфизм E'(M)-*-En-l(M) вида
!¦->¦ zf\x (см. [9]) есть изоморфизм; это — т. н. изомор-
изоморфизм двойственности Пуанкаре. Оказывается, что мно-
многообразие (комплекс Пуанкаре) ?'-ориентируемо тогда
и только тогда, когда й-ориентируемо его нормальное
расслоение. Определяется О. и для многообразий
(комплексов Пуанкаре) с краем.
Лит.: [11 Д у Г) р о в и н Б. А., Нови к о в С. П., Ф о м е н-
и о А. Т., Современная геометрия, М., 1979; [2] Введение в то-
топологию, М., 1980; [3] Р о х л и н В. А., Ф у к с Д. Б., Началь-
Начальный курс топологии. Геометрические главы, М., 1977; [4] X ью з-
м о л л е р Д., Расслоенные пространства, пер. с англ., М., 1970;
[5] Спеньер Э., Алгебраическая топология, пер. с англ.,
М., 1971; [К] Д о л ь д А., «Математика», 1965, т. 9, .№ 2, с. 8—
14; [7] May J., ?«, ring spaces and Е„ ring spectra, В.— N. Y.,
1977; [8] С т о н г Р., Заметки но теории кобордизмов, пер. с
англ., М., 1973; 19] -У а й т х е д Дж., Новейшие достижения в
теории гомотопий, пер. с англ., М., 1974.
Ю. В. Рудяк, А. В. Чериавский.
ОРИСФЕРА — поверхность пространства Лобачев-
Лобачевского, ортогональная к прямым, параллельным в не-
некотором направлении. О. можно рассматривать как сфе-
сферу с бесконечно удаленным центром. На О. реализу-
реализуется евклидова геометрия, если под прямыми понимать
орициклы, порядок точек определить через порядок
прямых в пучке параллелей, определяющих орицикл, а
движением называть такие движения в пространстве
Лобачевского, к-рые переводят О. в себя.
А. Б. Иванов.
ОРИЦИКЛ, предельная лини я,— ортого-
ортогональная траектория параллельных в нек-ром направ-
направлении прямых плоскости Лобачевского. О. можно рас-
рассматривать как окружность с бесконечно удаленным
центром. О., порожденные одним пучком параллельных
прямых, конгруэнтны, концентричны (т. е. высекают
на прямых пучка конгруэнтные отрезки), незамкнуты
и вогнуты в сторону параллельности прямых пучка.
Кривизна О. постоянна. В модели Пуанкаре О.— ок-
окружность, касающаяся изнутри абсолюта.
Прямая и О. либо не имеют общих точек, либо ка-
касаются, либо пересекаются в двух точках под равны-
равными углами, либо пересекаются в одной точке под
прямым углом.
Через две точки плоскости Лобачевского проходят
два и только два О.
Лит.: [1] Каган В. Ф., Основания геометрии, ч. 1—2,
М.— Л., 1049—56; [2] Н о р д е н А. П., Элементарное введение
и геометрию Лобачевского, М., 1953; [3'J E ф и м о в Н. В.,
Высшая геометрия, 6 изд., М., 1978. д g Иванов
ОРИЦИКЛИЧЕСКИЙ ПОТОК — поток в простран-
пространстве биэдров такого «-мерного риманова многообразия
Мп (обычно замкнутого), для к-рого определено понятие
орицикла; О. п. описывает движение биэдров вдоль оп-
определяемых ими орициклов.
Основные случаи, когда определено понятие орицик-
орицикла,— те, когда кривизна римановои метрики отрицатель-
отрицательна и либо п=2, либо кривизна постоянна. Б и э д р у,
т. е. ортонормированному 2-реперу (х, е,, е2) (,с?М'!;
ег, е2 — взаимно ортогональные единичные касатель-
касательные векторы в точке х), сопоставляется орицикл
h(x, е1,е2), к-рый проходит через х в направлении е2 и
расположен на проходящей через х орпсфере Н(х, ег),
являющейся (п—1)-мерным ортогональным многообра
зием семейства геодезич. линий, асимптотических (с.
положительном направлении) к геодезич. линии, про-
проходящей через х в направлении е1. Направление на А,
определяемое е2, принимается за положительное (при
п=-2 роль е2 только к этому и сводится; Huh могут
иметь самопересечения; простейший способ избежать
могущих возникнуть из-за этого неясностей состоит в
том, чтобы выполнить аналогичные построения не и
М", а в его универсальном накрывающем многообра
,чии — при постоянной кривизне это обычное ?г-мернос
пространство Лобачевского — и спроектировать полу-
полученный там орицикл в М"). Под действием О. п. бгодр
(х, ег, е2) за время t переходит в
(x(t), ei(t), e2(t)),
где x(t) с изменением / движется с единичной скоростью
по h(x, ex, е2) в положительном направлении, единич-
единичный вектор e^t) ортогонален II(х, ег) в точке x(t) (вы-
(выбор одного из двух возможных направлений для e-^t)
производится по непрерывности) и e2(t)=dx(t)/dt.
Изучение О. п. было начато в связи с тем, что он иг-
играл важную роль при исследовании геодезических пото-
потоков на многообразиях отрицательной кривизны [1].
Позднее эта роль перешла к нек-рым слоениям, возни-
возникающим в теории У-систем, а О. и. стал самостоятель-
самостоятельным объектом исследования. Свойства О. п. хорошо
изучены (см. [2]—[7], [11]). О нек-рых обобщениях см.
в [8]-[10].
Лит.: [1] Хопф Э., «Успехи матем. наук», 1949, т. 4, и. 2,
с. 129—70; [2] П а р а с ю к О. С, там же, 1953, т. 8, в. 3, с.
125—26; [3] Г у р е в и ч Б. М., «Докл. АН СССР», 19151, т. 13ti,
.Ni 4, с. 768—70; [4] Furstenberg H., в кн.: Recent advan-
advances in topological dynamics, В.— [u. a.]. 1973, p. 95—115; 15]
M а г с u s В., «Israel J. Math.», 1975, v. 21, № 2—3, p. 133—44:
[6] e г о же, «Ann. Math.», 1977, v. 105, JVs 1, p. 81 — 105; [7]
его же, «Invent, math.», 1978, v. 46, № 3, p. 201—09; [8] Gre-
Green L. W., «Duke math. J.», 1974, v. 41, .№ 1, p. 115 — 26; [9]
Bo wen R., «Israel ,1. Math.», 1976, v. 23, № 3—4, p. 267—
73; [10] Bovven R., Marcus В., там же, 1977, v. 26, № 1,
p. 43—67; [11] Katner M., «Ann. Math.», 1982, v. 115, №3,
p. 597—614. Д. В. Аносов.
ОРЛИЧА КЛАСС — множество функций LM, удов-
удовлетворяющее условию
М (х (t)) dt < оо,
где G — ограниченное замкнутое множество в R".
dt — мера Лебега, М(и) — четная выпуклая функция,
возрастающая при положительных и, и
lim u~iM(u)— lim и [М (и)]-1 ---U.
и -> 0 и -f со
Такие функции наз. N-ф у н к ц и я м и. Функция
М(и) допускает представление
U\(v) do,
где р(о) = М'(о) не убывает на полуоси,
р@)= Пш А'М=0,
v-+ о
p(O)>U при у>0. Функции М(и) и
где р~1{ь) —обратная к р(и) функция, наз. допол-
дополнительными ф у н к ц и я м и. Напр., если
М (и)=ир'1р\ \<р <оэ, то N(u)=up'lp', где рр
= 1. Для пары дополнительных функций справедливо
неравенство Юнга:
(ft).
Функция М (и) удовлетворяет Д2-у с л о-
в н ю, если существуют такно С н а0, что МBи)<:
<СЛ/(и) для всех и^.иа. О. к. линеен тогда и только
тогда, когда М(и) удовлетворяет Д2-условшо. Из Иен-
сена неравенства вытекает выпуклость Lm-
Пусть Mi(u) a M2(u) — две УУ-функции. Для того
чтобы Lfiitctj[i2, необходимо и достаточно, чтобы
Л/2(и)<:СЛГ1(м) для нек-рого С а достаточно больших и.
О. к. рассмотрены В. Орличсм и 3. Бпрнбаумом [1].
Лит.: [1] В i r n b a u m Z., О г ] i с г W-, «Studia math.»,
1931, v. 3, p. 1 —117; 12] Красносельский М. А.,
Рутицкий Я. Б., Вьшуклыс функции и пространства
Орлича, М., 1958. Е. М. Семенов.
ОРЛИЧА ПРОСТРАНСТВО — банахопо пространство
измеримых функций; введено В. Орлнчем [1]. Пусть
М(и) и N (и) — пара дополнительных Л'-функций (см.
Орлича класс) и G — ограниченное замкнутое множество
в К". Пространством Орлича Lm на:),
множество измеримых относительно меры Лебега функ-
функций ua G, на к-рых
О. п.— полное нормированное пространство относи-
относительно нормы |М|д1, к-рая наз. нормой Орлича.
Когда М(и)—иР, 1<р<оо, то Lm совпадает с Рисса
пространством Lp и с точностью до скалярного множи-
множителя \\х\\м совпадает с \\x\\Lp.
Если Mi(u) и М2(и) суть iV-функции, то вложение
^, имеет место тогда и только тогда, когда для
нек-рого С и всех достаточно больших и выполнено не-
неравенство il/2(;/)<:7l/j(C«). Для любого О. п. Lm спра-
справедливы вложения L^cL'mcLx. Всякая суммируемая
функция принадлежит нек-рому О. п.
Пространство Lm ссиарабельно тогда и только тогда,
когда М(и) удовлетворяет Д2-условию. В общем случае
1<„о не плотно в Lm и замыкание L^ в Lm обозначается
через f^j, оно всегда сепарабельно. Если x?Lm, to
lim sup ЦххЕ{\м — р{х, Ем),
х ->¦ 0 mes?-T
где
Если М (и) и Л'(и) — дополнительные Лт-функщш и
x?Lm, h?Ln, to справедлив аналог Гёлъдера нера-
неравенства
где IMIi/ti) — Люксембурга норма. Всякий непрерывный
линейный функционал / на Ещ представим в виде
/ (х) = [ х (t) у (t) dt,
где y^Lpr u !i/||= \\у\\(pj)•
Критерии компактности М. Pucca (M. Riesz) и
А. Н. Колмогорова для пространств Lp иереносятся на
Ещ- Следующие условия эквивалентны: 1) пространст-
пространство Lm рефлексивно; 2) М(и) и N {и) удовлетворяют
Д2-условию; 3) в Lm существует безусловный базис;
4) Хаара система образует безусловный базис в Лд1>
5) тригонометрич. система — базис в Lm- Система Ха-
Хаара — базис в Ем-
Аналогичным образом определяется пространство
последовательностей 1м, однако свойства пространства
1м зависят от асимптотики функции М(и) в 0. Изучены
[5] многие геометрич. свойства пространств Lm и 1м\
напр., для любой функции М (и) паходится множество
всех таких р, что 1р изоморфно вкладывается в 1*м-
О. п. применяются прп изучении свойств интеграль-
интегральных операторов, в теории дифференцируемых функций
многих переменных и в других разделах анализа.
Лит.: [1] Orlicz W. , «Bull, intern. Acad. Pol. Ser. A»,
1933 (annee 1932), p. 207—20; 12] К р а с н о с с л ь с к и ИМ. А.,
Рутицкий Я. Г>., Выпуклые функции и пространства Орли-
ча, М., 1938; [3] Галош к и н В. Ф., «функц. анализ и его
прилож.*, 1967, т. 1, As h, с. 2ti -32; [4) К р е й н С. Г., П е т у-
н и н Ю. И., Семенов К. М., Интерполяция линейных опе-
операторов, М., 1978; [зШ n d с л s t г а и s s J., T z а ( г i г i L.,
Classical Banach Space?, v. 1-2, В. - Hdlb.— N. V., 1977—79.
E. M. Семенов.
ОРНСТЕЙНА — ЧЕКОНА УРГОДИЧЕСКАЯ ТЕО-
ТЕОРЕМА: пусть (W, (д.) — пространство с ст-конечной ме-
мерой и Т — линейный положительный, оператор в Li(W,
ц), причем Ьгнорма ||7Ч|<1; если/, g^Li(W, \i) и >0
почти всюду, то предел
lim
существует почти всюду на том множестве, где знамена-
знаменатель при достаточно больших п отличен от нуля, т. е.
где хоть одно из чисел 7'*g(w)>0.
Эта теорема сформулирована и доказана Д. Орнстеи-
ном и Р. Чековом [\\ (см. также [2], [3]); позднее был
получен ее аналог для непрерывного времени (см. [4]).
Непосредственными следствиями О.—Ч. э. т. яв-
являются Виркгофа эргодическая теорема и нек-рые из
ранее предложенных обобщений последней, но имеется
также ряд эргодич. теорем, независимых от О.—Ч. э. т.,
а сама она подвергалась различным обобщениям (см.
[5], [6], а также лит. при ст. Операторная эргодическая
теорема). Вместе с тем из всех обобщений теоремы Бирк-
гофа, по-видимому, чаще всего используется О.—Ч. о. т.
В иностранной литературе О.—-Ч. э. т., как и вообще
теоремы, в к-рых речь идет о пределе отношения двух
временных средних, паз. i-alio ergodic theorem.
Лит.: 11] Chacon R. V., О г n s t с i u D. S., «111.
J. Matli.i), 1900, v. i, .4} 2, p. 153—60: [2] Л о п ф Э., «Математи-
«Математика», 1962, т. 6, № з, с. 29 36; [31 Ы е в ё Ж., Математические
основы теории вероятностей, пер. с франц., М., 1969; [4|
А к с о g 1 и М. А., С u n s о I о J., «Proc. Amer. Math. Soc»,
1970, v. 24, ЛЬ 1, р. НИ —70; [5] Chacon R. V., в i;h.: Ergo-
Ergodic theory. Proceedings of an International Symposium. New Or-
Orleans 1961, N. Y.— L., 1903, p. 89—120; [б] Т е г г e 1 1 Т. П.,
«Boll. Unionemat. ital.», 1972, v. й,Лв2,р. 175—80. Д.В.Аносов.
ОРНШТЕЙНА — УЛЕНБЕКА ПРОЦЕСС — гаус-
coBCKnii стационарный случайный процесс V(I) с нуле-
нулевым математич. ожиданием и экспоненциально затуха-
затухающей корреляционной функцией вида
fi(T)=-a-exp (~а|т|), а > 0.
О.- У. п. может быть также определен как стационар-
стационарное решение стохастич. уравнепия (уравнения Ланже-
вена) вида
md V (t)-Yf,V(t) dt = dW (t), (*)
где W(t) — винеровский процесс (так что dW(t)/dt—
— W'(t) — обобщенный случайный процесс белого шу-
шума), а т и Р — положительные постоянные, причем
p7m-a.
Уравнение (*) приближенно описывает одномерное
броуновское движение свободной частицы; при этом
V (t) интерпретируется как скорость частицы, т — ее
масса, —f>V (t) — пропорциональная скорости сила
«вязкого трения» (для сферич. частицы радиуса а коэф-
коэффициент р" равен о'лт]а, где г\ — коэффициент вязкости,
в силу гидродинамич. формулы Стокса), а белый шум
W'{t) — это «случайпая сила», порожденная хаотнч.
толчками молекул среды, находящихся в тепловом дви-
движении, и являющаяся основной причиной броуновско-
броуновского движения. В первоначальной теории броуновского
движения, развитой А. Эйнштейном (A. Einstein) и
М. Смолуховским (М. Smoluchowski) в 1905—06, пре-
небрегалось инерцией частицы, т. е. считалось, что
т—0; при атом уравнение (*) приводило к выводу, чт
координата броуновской частицы
равна $~г\?A), т. е. представляет собой винеровский
процесс. Таким образом, винеровскпй процесс описы-
описывает модель Эйнштейна — Смолуховского броуновского
движения (отсюда другое его название — процесс
броуновского движения); т. к. этот про-
процесс недифференцпруем, то в теории Эйнштейна — Смо-
Смолуховского частица, совершающая броуновское движе-
движение, не имеет конечной скорости. Уточненная теория
броуновского движения, опирающаяся на уравнение
(*), где тфО, была предложена Л. Орнштейном и Дж.
Уленбеком ([11; см. также [2]); позже та же теория была
выдвинута С. Н. Бернттейном [3] и А. Н. Колмогоро-
Колмогоровым [4]. В теории Орнттейна — Уленбека скорость
V(t) броуновской частицы является конечной, но ее
ускорение бесконечно (так как О.— У. п. недиффе-
недифференцируем); для того чтобы и ускорение оказалось
конечным, надо уточнить теорию, учтя отличие случай-
случайной силы от идеализированного белого шума W'(t).
Уравнение (*) можно использовать и для описания
одномерного броуновского движения гармонич. осцил-
осциллятора, если пренебречь его массой и считать, что
т/ / \ mdV
V{t) — это координата осциллятора, j-, сила
иязкого трения, —§V — регулярная упругая сила,
удерживающая осциллятор, a W(t) — случайная сила,
создаваемая молекулярными толчками. Таким обра-
образом, О.— У. п. доставляет также модель пульсаций
координаты гармонич. осциллятора, совершающего
броуновское движение, родственную модели Эйнштей-
Эйнштейна — Смолуховского броуновского движения свобод-
свободной частицы.
О.— У. п. является однородным но времени марков-
марковским процессом диффузионного типа (см. Диффузион-
Диффузионный процесс); наоборот, процесс V(t), являющийся
одновременно стационарным случайным процессом,
гауссовским процессом и марковским процессом, обя-
обязательно представляет собой О.— У. п. Как марков-
марковский процесс О.— У. п. удобно характеризовать его
переходной плотностью вероятности р (t, x, у), представ-
представляющей собой фундаментальное решение соответствую-
соответствующего уравнения Фоккера — Планка (т. е. прямого
Колмогорова уравнения) вида
п, следовательно, задаваемой формулой
Многие свойства О.— У. и. V(t) (включая и его мар-
марковость) можно вывести на известных свойств винеров-
ского процесса, воспользовавшись тем, что процесс
является стандартным винеровскнм процессом (см. [5]).
В частности, отсюда следует, что реализации О.— У. п.
непрерывны и нигде не дифференцируемы с вероят-
вероятностью \ и что
,— i v (о-т (Pi = 1; — JXA1U.. _ 4
_ , V'2o> In (
с вероятностью 1.
Лит.: [1] U h le nb ее к G. E., OrnstcinL. S., «Phys.
Rev.», 1930, v. 36, p. 823—41; [2] Ч а н д р а с e it a p C, Cto-
хастические проблемы в физике и астрономии, пер. с англ., М.,
1947; [3] Бернште й н С. Н., «Докл. АН СССР», 1934, т. 1,
.V, 1, с. 1—9; Л- 7, с. 361—65; [4] К о 1 m о g о г о v A. N., «Ann.
Math.», 1934 v. 35, p. 116—17; [5] D о о b J. L., «Ann.
Math.», 1942, v. 43, p. 351 — 69. A. M. Яглом.
OPPA — ЗОММЕРФЕЛЬДА УРАВНЕНИЕ — линей-
линейное обыкновенное дифференциальное уравнение
где R — число Рейнольдса, w(y) — заданная функция
(профиль скорости невозмущенного потока), к-рая
обычно предполагается голоморфной в окрестности
отрезка [ — 1, 1] в комплексной плоскости у, а>0 —
постоянная и с — спектральный параметр. Для О.—
3. у. исследуется краевая задача
Ф (-1) =Ф' (-1) =Ф A) =ф' A) =0. B)
О.— 3. у. возникло при исследовании У. Орром [1] и
А. Зоммерфельдом [2] устойчивости в линейном при-
приближении плоского течения Пуазёйля — течения вяз-
вязкой несжимаемой жидкости в слое —оо<а<оо, —1<
<;/<1 с твердыми границами; возмущение для функ-
функции тока берется в виде ср(у)е'а(-х~с1К
Собственные значения задачи A), B), вообще говоря,
комплексны; течение устойчиво, если 1тс<0 для всех
собственных значений, и неустойчиво, если Imc>0 для
нек-рого из них. Кривая Imc(a, Д) = 0 наз. нейтраль-
нейтральной кривой. Течение Пуазёйля устойчиво при
небольших числах Рейнольдса. В. Гейзенберг [6] впер-
впервые высказал предположение, что течение Пуазёйля
неустойчиво при больших числах Рейнольдса, и вычис-
вычислил 4 точки нейтральной кривой. Для квадратичного
профиля скорости установлено, что течение неустой-
неустойчиво при аЛ^>1.
Асимптотич. теория О.— 3. у. построена в предполо-
предположении, что (aR)~—»-0 — малый параметр. Точка уГ,
в к-poii w(yc) — 0, является точкой поворота (см. Малого
параметра .метод). В малой окрестности точки уФус
О.— 3. у. имеет фундаментальную систему решений вида
где ф?B/), 4>i(y) — фундаментальная система решений
невязкого (то ость аД=0) уравнения
(w — с) (ф" — а2ф) — и/'ф = 0.
Исследование задач A), B) связано, напр., со следую
пиши трудностями: 1) невязкос уравнение в окрестно-
окрестности точки у=ус имеет голоморфное в ней решение и ре-
решение с логарифмич. особенностью; 2) при малых \с\
(т. е. в наиболее важном случае) точки поворота сли-
сливаются с концами отрезка [—1, 1] (напр., для квадра-
квадратичного профиля скорости w—1—у2).
При аЯ^>1 получено строгое обоснование неустойчи-
неустойчивости (см. [3], [4]).
Лит.: Ц] О г г W. М с F., «Proa R. Irish. Acad. A», 1907,
v. 27 , р. 9—68, 6U —138; [2j Sommerfeld А., в кн.: АШ
del IV Congresso internazionale del matematici (Roma, 1908),
1909, p. 116—24; [3] Л и н ь Ц з я - Ц з я о, Теория гидродина-
гидродинамической устойчивости, пер. с англ., М., 1958; [4] Гидродинами-
Гидродинамическая неустойчивость. Сборник, пер. с англ., М., 1964; [5] Ссг-
sting J.M., Janowski D. F., «Internal;. J. Num. Meth.
in Eng.», 11G2, v. 4, p, 195—206; [6]Heisenberg W., «Ann.
Phys.», 1924, Bd 74, JVs 15, S. 577—627, M, В.Федорюп.
ОРТ, единичный вектор,— вектор, длина
к-рого равна единице выбранного масштаба.
ОРТОГОНАЛИЗАЦИИ МЕТОД — метод решения си-
системы линейных алгебрапч. уравнений Ах=-Ъ с невы-
невырожденной матрицей А, основанный на процессе Гра-
ма — Шмидта ортогонализации системы векторов.
Если
^4 = II «Г/ II; ж=-(*1 *г х)Т'>
..., 6В)Т;
—6,-), i =
n;
то исходная система уравнений может быть записана
в виде
(ai,y)=0, i = l, 2, ..., re.
Это значит, что решение системы равносильно нахож-
нахождению вектора у, имеющего единичную последнюю ком-
компоненту и ортогонального ко всем векторам а,-, г=1,
2, ... , п. Для этого к системе векторов alt аг, ¦¦¦ , ап,
Яц+it где an+i^@> 0, ... , 1), линейно независимой в си-
силу невырожденности матрицы А, применяется процесс
ортогонализации, состоящий в построении ортонорми-
рованноп относительно скалярного произведения (х,
i/)=xT(/ системы векторов?!, д2, ¦¦¦ , 'Jn+i по рекуррент-
рекуррентным соотношениям
vk).
'¦(
(¦*)
Коэффициенты с,- здесь находятся из условия ортого-
ортогональности vk векторам q1, q2, ... , q^-i- Векторы аг,
а2, ... , ап линейно выражаются через q1, q2, ... , qn,
поэтому вектор ?,i + i=(z1, z2, ... , zn + 1) ортогонален ко
всем векторам at, a2, ... , ап. При этом невырожденность
матрицы А обеспечивает выполнение zn+1?tO. Таким
образом,
(zi/zn + i, zt/zn+i, ..., zjzn + 1)
— искомое решение системы.
Описанная схема О. м. хорошо вписывается в общую
схему прямых методов решения системы: соотношения
(*) равносильны преобразованию матрицы системы в
матрицу LnLn-i- . .LtA, где
1
1
С\С.г ... Ck
1
и тем самым осуществляют факторизацию матрицы сис-
системы в виде A = LQ, где L — треугольная, Q — унитар-
унитарная матрицы.
Процесс факторизации матрицы А по О. м. устойчив
к ошибкам округления. Если в (*) при выполнении
операции скалярного произведения векторов использо-
использовать процедуру накопления с удвоенной точностью, то
для факторизации матрицы по О. м. имеет место одна
из лучших оценок точности в классе прямых методов.
При этом, однако, свойство ортогональности векторов
qx, q2, ... , <7,„ то есть унитарности матрицы Q, неустой-
неустойчиво по отношению к ошибкам округления. Поэтому
решение системы, полученное из рекуррентных соотно-
соотношения (*), может иметь большую погрешность. Для
устранения этого недостатка используются различные
методы переортогонализации (см. [1], [2J).
О. м. уступает многим прямым методам по быстро-
быстродействию.
Лит.: [1] Воеводин В. В., Вычислительные основы
линейной алгебры, М., 1977; [2] Б а х в а л о в Н. С, Числен-
Численные методы, 2 изд., М., 1975. Г. Д. Ким.
ОРТОГОНАЛИЗАЦИЯ, процесс ортогона-
л и з а ц и н,— алгоритм построения для данной ли-
линейно независимой системы векторов евклидова или
эрмитова пространства V ортогональной системы не-
ненулевых векторов, порождающих то же самое подпро-
подпространство в V. Наиболее известным является и р о-
ц е с с о р т о г о н а л и з а ц и и Шмидта (или
Г р а м а — Шмидта), при к-ром по линейно неза-
независимой системе аг, ... , а^ строится ортогональная
система Ьи ... , Ь^ такая, что каждый вектор 6,- (i—1,
... , к) линейно выражается через аг, ... , а,-, то ость 6,=
= 2y=-iViVa/' гДе С~ 11т//!! — верхняя треугольная мат-
матрица. При этом можно добиться того, чтобы система
{&,•} была ортонормированной и чтобы диагональные
элементы уи матрицы С были положительны; этими
условиями система {&; } и матрица С определяются одно-
однозначно.
Процесс Грама—Шмидта состоит в следующем. По-
Полагают 6j=aj; если уже построены векторы ftj, ... , ft;,
то
где
„ (ai+Vbj)
; = 1, ... , i, найдены из условия ортогональности век-
вектора b; + i к blt ... , 6;. Геометрпч. смысл описанного
процесса состоит в том, что на каждом шагу вектор
6, + t является перпендикуляром, восстановленным к
линейной оболочке векторов аь ... , а,- до конца вектора
а;+1. Произведение длин |61|. . .|6^| равно объему
параллелепипеда, построенного на векторах системы
{а;}, как на ребрах. Нормируя полученные векторы 6,-,
получают искомую ортонормированную систему. Явное
выражение векторов 6; через ах, ... , а^ дает формула
... (аь а,-_х) с
(а;, ох) ... (а;, а;_а)
(определитель в правой части следует формально раз-
разложить по последнему столбцу). Соответствующая ор-
тонормированная система имеет вид
где Г; — Грама определитель системы а:, ... , а/.
Этот процесс применим также и к счетной системе
векторов.
Процесс Грама—Шмидта может быть истолкован как
разложение невырожденной квадратной матрицы в про-
произведение ортогональной (или унитарной матрицы в
случае эрмитова пространства) и верхней треугольной
матрицы с положительными диагональными элемента-
элементами, что есть частный случай Иеасавы разложения.
Лит.: [1] Гантмахер Ф. Р., Теория матриц, 2 изд.,
М., 1966; [2] К у р о ш А. Г., Курс высшей алгебры, 11 изд.,
М., 1975. И. В. Проскуряков.
ОРТОГОНАЛИЗАЦИЯ СИСТЕМЫ ФУНКЦИИ — по-
построение для заданной системы функций {fn(x)}, интег-
интегрируемых с квадратом на отрезке [a, ft] функций орто-
ортогональной системы {<р„(х)} путем применения нек-рого
процесса ортогонализации пли же путем продолжения
функций fn(x) на более длинный интервал [с, d\,
<b<d.
Применение процесса ортогонализацпи Шмидта к
полным системам {/„(.г)} всегда приводит к полным ор-
тонормированным системам {ф„(.г)} и при соответствую-
соответствующем выборе последовательности {fn(x)} дает возмож-
возможность построения систем, обладающих теми или иными
хорошими свойствами. Таким путем построена, напр.,
система Франклина (см. Ортогональная система), яв-
являющаяся базисом в С [0, 1] и в Ьр[0, 1], р>1.
О. с. ф. путем продолжения на более длинный интер-
интервал впервые рассматривалась И. Шуром (см. [1] с. 84).
Он доказал, что для существования ортонормированной
В ЩО, 1] системы {(fn(x)}, <р„(.г)--/„(¦*), r?[a, ft], 0<я<
<Ь<1, необходимо и достаточно выполнение условия
где верхняя грань берется по всем {?,}, 2й 1- Найде-
Найдены также необходимые и достаточные условия, при вы-
выполнении к-рых можно путем такой ортогонализации
получить полную ортонормированную систему {ф„(з.)}
(см. [2]).
Нек-рые конструкции ортогонализации продолже-
продолжением функций даны Д. Е. Меньшовым [3]. Они исполь-
использовались при доказательстве теорем о точности условия
j^anln2re<oo для сходимости почти всюду ортогональ-
ортогональных рядов $]я„ф„(х).
Лит.: [1] На ч м а ж С, Щ т е й н г а у з Г., Теория орто-
ортогональных рядов, пер. с нем., М. 1958; 12] О л ев с к и й А. М.,
«Матем. заметки», 1969, т. 6, № 6 с. 737—47; [3] М е в ь-
ш о в Д. Е., «.Матом, сб.», 1938, т. 3, с. 103—20; [4] Frank-
Franklin Ph.,<,Math. Ann.», 1928, Bd 100, S. 522—29.
А. А. Толалян.
ОРТОГОНАЛЬНАЯ ГРУППА — группа всех линей-
линейных преобразований /г-мерного векторного пространст-
пространства V над полем к, сохраняющих фиксированную невы-
невырожденную квадратичную форму Q на V (т. е. таких
линейных преобразований ф, что Q (ф (v))~Q (v) для
любого у? V). О. г. принадлежит к числу классических
групп. Элементы О. г. наз. ортогональными
(относительно О) преобразованиями F, а
также автоморфизмами формы Q. Пусть,
далее, char/c?=2 (об О. г. над полями характеристики
2 см [I], {'}) и / — связанная с. Q невырожденная сим-
метрич. билинейная форма на V, определенная форму-
формулой
f(v, U)^±(Q (v + u)-Q (v)-Q (и)).
Тогда О. г. состоит в точности из тех линейных преоб-
преобразований пространства V, к-рые сохраняют /, и обоз-
обозначается через Оп(к, /) или (когда ясно о каком поле к
и форме / идет речь) просто через О„. Если В — матрица
/ в каком-либо базисе пространства V, то О. г. может
быть отождествлена с группой всех таких (пХя)-мат-
риц А с коэффициентами в к, чтоЛтВЛ=.б(т—транс-
чтоЛтВЛ=.б(т—транспонирование).
Описание алгебраич. строения О. г. составляет пред-
предмет классич. исследований. Определитель любого эле-
элемента из О„ равен 1 или —1. Элементы с определите-
определителем 1 наз. вращен и я м и; они образуют в О. г.
нормальный делитель О„*"(/с, /) (или просто О„) индек-
индекса 2, наз. группой вращений. Элементы из
Оп — On наз. переворачиваниями. Всякое
вращение (переворачивание) является произведением
четного (нечетного) числа отражений из Оп.
Пусть Zn — группа всех гомотетий фа: р(-* av,
а?&, а#0, пространства V. Тогда On(]Zn — это центр
О„; он состоит из двух элементов: фх и ф_1. Если я
нечетно, то Оп является прямым произведением своего
центра и Оп- Центр Оп при ге>3 тривиален, если п не-
нечетно, и совпадает с центром Оп, если п четно. Если же
га=2, то группа О,, коммутативна и изоморфна либо
мультипликативной группе к* поля к (в случае, когда
индекс Витта v формы / равен 1), либо группе элементов
с нормой 1 в поле к ( у —Д), где Д — дискриминант фор-
формы / (в случае, когда v—0). Коммутант группы Оп(к, /)
обозначается через Qn(k, /) или просто Q,,; он порож-
порождается квадратами элементов из Оп. При п^'Л комму-
коммутант группы On совпадает с Qn. Центр группы Яп имеет
вид Qnf\Zn.
Классич. группами, связанными с О. г., являются
также канонич. образы On и Й„ в проективной груп-
группе; они обозначаются РО„(к,/) и PQn(k, f) (или просто
POti и РЯп) и изоморфны соответственно Оп1{О*п[\2п)
и Qn/(QnnZn).
Основные классич. факты об алгебраич. структуре
О. г. относятся к описанию последовательных факторов
следующего ряда нормальных делителей в О. г.
Группа Оп/Оп имеет порядок 2. Всякий элемент в
On/Qn имеет порядок 2, ввиду чего строение этой
группы полностью определяется кардинальным числом
ее элементов, к-рое может быть либо бесконечным, либо
конечным вида 2а, а — целое. Описание остальных фак-
факторов существенно зависит от того, отличен ли от нуля
индекс Витта v формы /.
Пусть сначала v>l. Тогда Оп1Япя*к*/к*г при п>2.
Этот изоморфизм определен спинорной нормой, к-рая
задает эпиморфизм 0% на к*/к*2 с ядром QH. Группа
^пГ|2п нетривиальна (и состоит из преобразований
cf>! и ф-i) тогда и только тогда, когда п четно и Д?й2.
Если ге>5, то группа РЯп=~Qn/(Qnf\Zn) проста. Слу-
Случаи и = 3, 4 рассматриваются отдельно. А именно, PQ3~
= Q3 изоморфна PSL2(k) (см. Специальная линейная
группа) и также проста, если число элементов в к не
равно 3 (группа О? изоморфна проективной группе
PGL2{k)). При v=l группа PQi=Qi изоморфна группе
PSL2(k( ^Д)) и проста (в этом случае Д^&2), а при v=2
группа РЙ4 изоморфна PSL2(k)XPSL2(k) и не проста.
В частном случае, когда fc=R. и Q — форма сигнатуры
C, 1), группа PQi^Qi^iPSL^C) наз. группой
Лоренца.
В случае же, когда v=0 (т. е. Q — анизотропная фор-
форма), многие из указанных результатов не верны. Напр.,
если &=R, a Q — положительно определенная форма,
то Qn=On, хотя R.*/R.*? состоит из двух элементов;
при k=Q, ra=4, возможен случай, когда Д?А2, но
ср_!^Й4- Вообще при v=0 структура О. г. и связанных
с ней групп существенно зависит от fe. Напр., если &=
= R, то РОп, га>3, й#4, v=0, проста (a POt изоморф-
изоморфна прямому произведению OgXO% двух простых групп);
если же к — поле р-адических чисел, то при v=0 в Са
(и в О4) существует бесконечный ряд нормальных дели-
делителей с абелевыми факторами. Наиболее изучены слу-
случаи локально компактного поля и поля алгебраич. чи-
чисел. Если к — поле р-адических чисел, то случай v==0
невозможен при д^=5. Если же к — поле алгебраич.
чисел, то такого ограничения нет и один из основных
результатов состоит в том, что РЙП при v=0 и п^5
проста. В этом случае изучение О. г. тесно связано с
теорией эквивалентности квадратичных форм, к-рая
основывается на рассмотрении форм, полученных из Q
при расширении к до локальных полей, определенных
нормированиями /((принцип Хассе).
Если к — конечное поле F^ из q элементов, то О. г.
является конечной группой. Порядок On при нечетном
» равен
(9л-»_1) 9п-2(9л-з__1) qn-t ... (g2 —1) q.
а прп и=2?и равен
(g2m-i_er//»-i) (?2m-2_ 1) Ч2т-я . . . (^2 _<|) ^
где е=1 при (—l)mA?F,7 ие=-1 в противном случае.
Указанные формулы вместе с приведенными общими
фактами об О. г. при v^l позволяют вычислить также
и порядки Qa и PQn, так как v^l при п^З, а порядок
k*jk*% равен 2. Группа PQn, =5, является одной из
классических простых конечных групп (см. также Ше-
оалле группа).
Один ил основных результатов об автоморфизмах
О. г. состоит в следующем: если n^'i, то всякий авто-
морфпзм Ф группы Оп имеет вид ф(«)=х(и)§ад~1,
«б^и. ГЛ° % —фиксированный гомоморфизм О„ в ее
центр, a g — фиксированное биективное полулинейное
отображение Г в себя, удовлетворяющее условию
Q(g(v))=rgQa(v) для всех v?V, где rg?k*, а о — свя-
связанный с g автоморфизм к. Если v^l а гс^=6, то всякий
автоморфизм On индуцирован автоморфизмом О„ (см.
Ш, [31).
Так же, как и другие классич. группы, О. г. допуска-
допускает (при нек-рых предположениях) геометрия, характери-
зацию. А именно, пусть Q — такая анизотропная фор-
форма, что Q(v)?k'~ для любого v? V. В этом случае к —
пифагорово упорядочиваемое поле. При фиксированном
упорядочении поля к «-мерной цепью инцидент-
инцидентных полупространств в Г нал. любая по-
последовательность {Нs)\^^n> построенная ио линейно
независимой системе векторов (/1^I<8<п, где ITs — мно-
множество всех линейных комбгшаций вида 2/=jV*/' ^s^O.
Группа Оп обладает свойством свободной
подвижности, т. е. для любых двух п-мерных
цепей полупространств существует единственное преоб-
преобразование из Оп, переводящее первую цепь во вторую.
Это свойство характеризует О. г.: если L — любое
упорядоченное тело и G — подгруппа в GLn(L), ге^З,
обладающая свойством свободной подвижности, то L
является пифагоровым полем, a G~OJ.L,-f), где / —
такая анизотропная симметрия, билинейная форма, что
/(;;, v)?L2 для любого вектора v.
Пусть к — фиксированное алгебранч. замыкание
поля к. Форма / естественно продолжается до невы-
невырожденной симметрия, билинейной формы / на V®^/..
а О. г. Оп(к, f) является определенной над к линейной
алгебраической группой с группой /с-точек Оп(к, /). Опре-
Определяемые таким образом (для разных /) линейные ал-
гебрапч. группы изоморфны над к (но, вообще говоря,
не над к)', соответствующая линейная алгебраич. груп-
группа над к наз. ортогональной алгебра-
алгебраической группой Оп(к). Ее подгруппа 0},(?, /)
также является линейной алгебраич. группой над к
и наз. собственно ортогональной, или
специальной ортогональной, алгеб-
алгебраической группой (обозначение: SOn{k))\ она
является связной компонентой единицы группы Он(к).
Группа SOn(k) — почти простая алгебраич. группа (т. е.
не содержащая неиульмерных алгебраич. нормальных
делителей) типа Bs при n-—2s-\-i, s>l, и типа Ds при
«-—2*, s^3. Универсальной накрывающей группы SOn
является спинорная группа.
Если k=R, С или /j-адическое поле, то Оп(к, /)
естественно снабжается структурой вещественной, ком-
комплексной или ^-адической аналитической группы.
Группа Ли 0,,(R, /) определяется с точностью до изо-
изоморфизма сигнатурой формы /; если эта сигнатура име-
имеет вид (р, q), р+9=г», то On(R, f) обозначается через
О(р, q) и наз. псевдоортогональной груп-
группой. Ее можно отождествить с группой Ли всех деист-
вптельных (//X и)-матриц А, удовлетворяющих условию
ГГ, ,_г г -1? °
L<7
(через 1^ обозначена единичная («X.^-матрица); алгебра
Ли 3Toii группы отождествляется с алгеброй Ли всех
действительных (z?X и)-матриц X, удовлетворяющих ус-
условию Х~^1р, д=—Iy,(i X. В частном случае q=0 груп-
группа О(р, q) обозначается через О(п) и наз. вещест-
вещественной ортогональной группой; ее
алгебра Ли состоит из всех кососиммртричоеких дейст-
действительных (геХ п)-матриц. Группа Ли ()(/>, q) имеет че-
четыре компоненты связности при g?i() н две компоненты
связности при q = Q. Связной компонентой единицы яв-
является ее коммутант, к-рьш при д=0 совпадает с под-
подгруппой SO (и) в О (и), состоящей из всех преобразова-
преобразований с определителем, равным 1. Группа О(р, q) компакт-
компактна только при д==0. Инварианты SO(n) как топологич.
многообразия достаточно подробно изучены. Один из
классич. результатов в этом направлении — вычисле-
вычисление чисел Бетти многообразия SO(n): его полином Пу-
Пуанкаре имеет вид
JJ™_ (l-j-f^-i)
при н=т2ш + 1 и вид
при п —2т. Фундаментальная группа многообразия
SO(n) есть 22- Вычисление высших гомотопич. групп
ni(SO(n)) имеет непосредственное отношение к клас-
классификации локально тривиальных главных SO(n)-
расслоений над сферами. Важную роль в топологиче-
топологической К-теории играет теорема периодичности, согласно
к-рой при N^>n имеют место изоморфизмы
я„ + 8 (О (Л')) ~ пп(О (N)), лп(О (Л')) ~ Zi,
если ?г~ 0, 1;
если /1—3, 7, и
л„(О(Л-))=0,
если ге=2, 4, 5, 0. Изучение топологии группы О(р, q)
по существу сводится к предыдущему случаю, т. к.
связная компонента единицы группы О(р, q) диффео-
морфна произведению SO(p)xSO(q) на евклидово про-
пространство.
Лит.: [1] Д ь е д о и н е Ж., Геометрия классических групп,
пер. с франц., М., 1974; 12] А р т и н Э., Геометрическая алгеб-
алгебра, пер. с англ., М., 1969; [3] Автоморфизмы классических
групп, пер. с англ. и франц., М., 1976; [4] В е й л ь Г., Класси-
Классические группы, их инварианты и представления, пер. с англ., М.,
1947; [о] Ж с л о 0 е и к о Д. II., Компактные группы Ли и их
представления, М., 1970; [D] Б у р б а к и Н., Алгебра. Модули,
кольца, формы, пер. с франц., М., 1966; 17] О'М с а г л О. Т..
Introduction to quadratic forms, В.—Hdlb., 1963; [8] X ь ю з-
м о л л е р Д., Расслоенные пространства,'пер. с англ., М., 1970.
ОРТОГОНАЛЬНАЯ МАТРИЦА — матрица над ком-
коммутативным кольцом Н с единицей 1, для к-рой транс-
транспонированная матрица совпадает с обратной. Опреде-
Определитель О. м. равен ±1. Совокупность всех О. м. по-
порядка п над R образует подгруппу полной линейной
группы GLn (R). Для любой действительной О. м, а
существует такая действительная О. м. с, что
cac~1 = diag [±1, . .., ±1, Я], ..., at],
где
Sill фу
Невырожденная комплексная матрица а тогда и только
тогда подобна комплексной О. м., когда система ее
элементарных делителей обладает следующими свойст-
свойствами: 1) для Х#±1 элементарные делители (х—к)'" п
(i—к'1) повторяются одно и то же число раз; 2) каж-
каждый элементарный делитель вида (х±ЪJ1 повторяется
четное число раз.
Лит.: [1] Мальцев А. И., Основы линейной плгеСры,
4 ИЗД., М., 1975. Д. А. Супруненпо.
ОРТОГОНАЛЬНАЯ СЕТЬ — сеть, у к-рой касатель-
касательные в нек-рой точке к линиям различных семейств орто-
ортогональны. Примеры О. с: асимптотическая сеть на
минимальной поверхности, кривизны линий сеть.
ОРТОГОНАЛЬНАЯ СИСТЕМА — 1) О. с. в е кТо-
р о в — множество {ха} ненулевых векторов евклидова
(гильбертова) пространства со скалярным произведе-
произведением (• , •) такое, что (ха, ?р) = 0 при а?=р\ Если при
этом норма каждого вектора равна единице, то система
!ха} наз. о р т о н о р м п р о в а н н о й. Полная О, с.
ха} наз. о р т о г о н4а л ь н ы м (ортонорми-
р о в а н н ы м) базисом. и. И. Войцеховский.
2) О. с. координат — система координат, п
к-рой координатные линии (или поверхности) пересе-
пересекаются под прямым углом. О. с. координат существуют
в любом евклидовом пространстве, но, вообще говоря,
не существуют в произвольном пространстве. В двумер-
двумерном гладком аффинном пространстве О. с. всегда
можно ввести по крайней мере в достаточно малой ок-
окрестности каждой точки. Иногда возможно введение
О. с. координат в целом. В О. с. метрич. тензор #,-_,¦ диа-
гонален; диагональные компоненты #,-,• принято наз.
коэффициентами Ламе. Ламе коэффициент
О. с. в пространстве выражаются формулами
La= У(дх/ди)*-f (ду/ди)* + (dz/duf,
+ {dzjdv)\
J+ (dz/dwJ,
где x, у и г — декартовы прямоугольные координаты.
Через коэффициенты Ламе выражаются элемент длины:
ds = V' 1?и <*и2-Ь 'Л dv^-l- Lw dw2,
элемент площади поверхности:
da = y~(LuLv du Л>J+ (LULW du dwJ-]- (LVLU, dv dw)-,
элемент объема:
dV = LULVLW du dv dw,
векторные дифференциальные операции:
div а=т^ц
+ ±{awLaLv)];
. t ГЭ (LyLw ЭфЛ , Э fL,,Lw Эф
^ LULVLW \_3u V La Эй/ до \ Lv dv
~1 dw\ Lw
Наиболее часто используемые О. с. координат: на пло-
плоскости — декартовы, полярные, эллиптические, пара-
параболические; в пространстве — сферические, цилиндри-
цилиндрические, параболоидальные, бицилиндрические, бипо-
биполярные. Д. Д. Соколов.
3) О. с, ф у н к ц и й — конечная или счетная сис-
система {ф,-^)} функций, принадлежащих пространству
L2(X, S, \i) и удовлетворяющих условиям
Если hj—i для всех i, то система наз. о р т о н о р-
м и р о в а н н о й. При этом предполагается, что мера
(х(х), определенная на а-алгебре S подмножеств множе-
множества X, счетно аддитивна, полна и имеет счетную базу.
Это определение О. с. включает все рассматриваемые в
современном анализе О. с; они получаются при раз-
различных конкретных реализациях пространства с мерой
(X, S, ц).
Наибольший интерес представляют полные ортонор-
мированные системы {<fn(x)}, обладающие тем свойст-
свойством, что для любой функции f(x)?L2(X, S, \л) сущест-
существует единственный ряд $}сиФ«(х)' сходящийся к /(х)
в метрике пространства L2(X, S, (х), при этом коэффи-
коэффициенты с„ определяются формулами Фурье
Такие системы существуют в силу сепарабельности
пространства L2(X, S, р.). Универсальный способ по-
построения полных ортонормированных систем дает метод
ортогонализации Шмидта. Для этого достаточно при-
применить его к нек-рой полной в L2(S: X, \i) системе
линейно независимых функций.
В теории ортогональных рядов в основном рассматри-
рассматриваются О. с. пространства L2[a, b] (тот частный случай,
когда Х=\а, b], S — система множеств, измеримых по
Лебегу, и |х — мера Лебега). Многие теоремы о сходи-
сходимости или суммируемости рядов ?)anwn(x), 2Я"<°°> п0
общим О. с. {ф„(х)} пространства ?2[а, Ь] верны и для
рядов по ортонормированным системам пространства
L2(X, S, (х). Вместе с тем в этом частном случае по-
построены интересные конкретные О. с, обладающие
теми или иными хорошими свойствами. Таковы, на-
например, системы Хаара, Радемахера, Уолша—Пэли,
Франклина.
1) С и с- т е м а Хаара {Хп(г))Г=г ул(х) = 1
¦"' 11,
,/¦— ._ __^(Ы-2 2ft- 1
у 2" при
JL
2"+"
О в остальных точках отрезка [0, 1),
где т—2"-\-к, l<A-<2", m = 2, 3 Ряды по системе
Хаара представляют типичный пример мартингалов
и для них верны общие теоремы из теории мартингалов.
Кроме того, система {Хп(х)}"=1 является базисом в
//[О, 1], р>1, и ряд Фурье по системе Хаара любой
интегрируемой функции почти всюду сходится.
2) Система Радемахера {гп{х)}™=1:
1],
представляет собой важный пример О. с. независимых
функций и имеет применения как в теории вероятно-
вероятностей, так и в теории ортогональных и общих функцио-
функциональных рядов.
3) Система Уолша — Пэли {^в(х)}"=1
определяется через функция Радемахера:
»-„(*)=1, wB(*)=nr-o[r*(*)j**' х€[0'1Ь
где числа т и q^ определяются из двоичного разложения
числа п:
4) С ii с т е м а Франклин а{Ф„(.г)}^1 получа-
получается ортогонализацирй методом Шмидта последователь-
последовательности функций
Ш(х)=х, U2(.r)=l — х, и„(х)^
1].
Она является примером ортогонального базиса прост-
пространства С [О, 1] непрерывных функций.
В теории кратных ортогональных рядов рассматри-
рассматриваются системы функций вида
«,- = 1, 2, ...,
где {фп(^)}™=1 — ортонормированная система в L2\a, Ь].
Такие системы ортонормированы на m-мерном кубе
/т = |а, 6]х. . .Х|а, frjn полны, если полна система
Лит.: [1] К а ч м а ж С, ШтейнгаузГ., Теория орто-
ортогональных рядов, пер. с нем., М., 1958; [2] Итоги науки. Матема-
Математический анализ, 1970, М., 1971, с. 109—46; [3] там же, с. 147—
202; [4] Д у 0 Д ж., Вероятностные процессы, пер. с англ., М.,
195В; [5] Л о э в М., Теория вероятностей, пер. с англ., М., 1962;
[6] Зигмунд А., Тригонометрические ряды, пер. о англ., т.
1 — 2, М., 1965. А. А. Талалян.
ОРТОГОНАЛЬНАЯ ТАБЛИЦА, ортогональ-
ортогональный массив, ОА (JV, к, п, t, X) — матрица размера
kXN, элементы к-рой суть числа 1, 2, ... , я, обладаю-
обладающая тем свойством, что в каждой ее подматрице размера
tXN любой из и* возможных i-мерных векторов-столб-
векторов-столбцов, имеющих координатами эти числа, встречается в
качестве столбцов этой подматрицы точно X раз. Из опре-
определения О. т. следует, что N=Xnf. Иногда под О. т.
понимают ОА (N, к, п, t, X) с t=2 и к—l, и тогда эта
О. т. обозначается ОА (п, к). При &>3 О. т. ОА (п, к)
эквивалентна множеству из к—2 попарно ортогональ-
ортогональных латинских квадратов. При заданных п, t, Я макси-
максимальное значение параметра к определено лишь в не-
нескольких частных случаях. Так, напр., к^.(Хп2—1)/
1(п—1) при ?=2 или &тах=*+1 в случае нечетного X
при га=2.
Лит.: [1]! D ё п е s J., К е е d w e 1 1 A. D., Latin Squares
and their applications, Bdpst, 1974; [2] X о л л М., Комбинато-
Комбинаторика, пер. с англ., М., 1970. В. М. Михеев.
ОРТОГОНАЛЬНАЯ ТРАЕКТОРИЯ — см. Изого-
Изогональная траектория.
ОРТОГОНАЛЬНОЕ ПРЕОБРАЗОВАНИЕ — линейное
преобразование А евклидова пространства, сохраняю-
сохраняющее длины или (что эквивалентно этому) скалярное про-
произведение векторов. О. п. и только они переводят ор-
ортонормированный базис в ортонормированный. Необхо-
Необходимым и достаточным условием ортогональности яв-
является также равенство А*=А -1, где А* — сопряжен-
сопряженное, а А~х — обратное линейные преобразования.
В ортонормированном базисе О. п. (и только им)
соответствуют ортогональные матрицы. Собственные
значения О. п. равны ±1, а собственные векторы, отве-
отвечающие различным собственным значениям, ортого-
ортогональны. Определитель О. н. равен +1 (собствен-
(собственное О. п.) или —1 (несобственное О. п.).
В случае евклидовой плоскости всякое собственное
О. п. является поворотом, и его матрица в подходящем
ортонормированном базисе имеет вид
coscp —siii ф 1|
sin ф cos ф )|'
где ф — угол поворота, а всякое несобственное О. и.
является отражением относительно нек-рой прямой,
его матрица в подходящем ортонормированном базисе
имеет вид
1 °||
О -1 \
В трехмерном пространстве всякое собственное О- п.
есть поворот вокруг нек-poii оси, а всякое несобствен-
несобственное — произведение поворота вокруг оси и отражения
в перпендикулярной плоскости. В произвольном и-мер-
ном евклидовом пространстве О. п. также сводятся к
поворотам и отражениям (см. Вращение).
Множество всех О. п. евклидопа пространства обра-
образует группу относительно умножения преобразова-
преобразований — ортогональную группу данного евклидова прост-
пространства. Собственные О. п. образуют нормальную под-
подгруппу в этой группе (специальную ортогональную
группу). Т. С. Пигол-Kuva.
ОРТОГОНАЛЬНОЙ ПРОГОНКИ МЕТОД — вариант
метода прогонки, основанный на ортогональном преоб-
преобразовании неизвестных. Пусть при а<:х<:Ь рассмат-
рассматривается граничная задача для пары линейных обык-
обыкновенных дифференциальных уравнении
у' (*)=ai (х) у (*) + &! (х) г (x)+h (х), A)
г' (х) = а2 {х) у (х) + й2 (х) г (х) + /а (х) B)
с условиями вида
a,*/(ffl)-t-Piz(a)-Yi. o^-1-Pl-i, C)
<ЗД(Ь) + Р22(Ь) = у2. а'з-ЬР! = 1. D)
Пусть данные функции a,-(z), b[(x), fi(x), i = l,2, непре-
непрерывны на отрезке а<:ж<:й. Решение граничной задачи
A)—D) О. п. м. осуществляется следующим путем.
I. Решается вспомогательная задача Коти
s' (x) —с(х)г(х), с' (x)=—s (х) г (.г),
г (х) = .s2 (х) Ъх (х) +s{x)c [х) (b2 (х) —я, (х)) —
-с*(х)аг(х), E)
U' (X) ^ Я] (X) U (X) + /j (X) , F)
s(a)=ax, c(a) = pb u(a) = yu (")
где
в", (х) =- at (х) ,9° (х) + Ьг (х) с* (х) -I- (Ьх (х) + а2 (х)) s (x) с (х),
(прямой ход прогонки).
II. Проверяется условие A=-a.2c(b)—$2s(b)?=Q, и если
оно выполняется, то в направлении от точки :r=b к
точке ж=в решается задача Коши
v' (х) = а2 (х) и (х) + Ь~ (х) v (х) + J2 (x), (8)
v (Ь) = {у2~[а2.5 (Ь) + р2с (Ь)] « (Ь)}/Д, (9)
где
,72 (ж) == 2 (ei (ж) - Ъг (х)) s (х) с (х) -f
+ (bi (х) + а2(ж)) (с2 (ж)— s-(z)),
/Т2 (i) = л, (х) с2 (х) + 62 (х) s- (x) — (bj (x) -f- a2 (x)) s (г) с (х),
7а W=/i(x)c(x)-/2(x)s(x)
(обратный ход прогонки).
III. Искомые функции вычисляются но формулам
у (x)=s(x) и (ж) + с (ж) v (х),
г(х) = с (х) и (x) — s (х) v (х),
Если решение у(х), г(х) гранично!! задачи A)—D) су-
существует, единственно и устойчиво относительно малых
изменений коэффициентов и свободных членов, опреде-
определяющих ее, то Д#0 и рассмотренный метод также ус-
устойчив (см. [2]).
Система линейных алгебраических уравнений
l-k, (Ю)
1, ..., л-1, (И)
A2)
где AkDk^BkCk, ссо+Ро='1> ап+р„=1, ])егаается по
следующим правилам.
Я Используя формулы
— Dksk),'pk,
— Akck)/pk,
Pk = V{(Ckck
последовательно вычисляют Sfc + i, сЛ + 1, гг^ + 1 при к~0,
... , и—1 (прямой ход. прогонки).
2) Проверяется условие Д„=а„сп—-($„«„ ??0, и если
оно выполняется, то вычисляют
при А;—я—1, n— 2, ... , 1 (о б р а т н ы и ход про-
прогонки).
3) Значения искомого решения системы уравнении
A0)—A3) вычисляются по формулам
Если решение системы уравнений A0)—A3) сущест-
существует, единственно и устойчиво относительно малых из-
изменении коэффициентов и свободных членов, то и рас-
рассмотренный О. п. м. также устойчив (см. [2]).
Иногда ортогональной прогонкой наз.
методы, основанные на использовании фундаменталь-
фундаментальной системы решений однородной системы уравнений
для целен переноса граничных условий (см. [1], [3]).
Однако яти методы являются скорее вариантами при-
пристрелки метода.
Лит.: [1] Бахвалов Н. С., Численные методы, 2 изд.,
т. 1, М., 1A75; [2] К р ы л о в В. И., Б о б к о в В. В., М о п а с-
т ы р н ы й П. И., Вычислительные методы высшей математики,
т. 2, Минск, 1975; [3] Самарский А. А., Нико-
Николаев Е. С, Методы решения сеточных уравнений, М., 11178.
А. Ф. Шаттаин.
ОРТОГОНАЛЬНОСТЬ — обобщение понятия перпен-
перпендикулярности векторов евклидова пространства. Наи-
Наиболее естественное понятие О. введено в теории гиль-
гильбертовых пространств. Два элемента хну ил гильбер-
гильбертова пространства Н наз. ортогональными
(хХ_у), если их скалярное произведение равно нулю
{(х, у)=0). Это понятие О. в том частном случае, когда
Н — евклидово пространство, совпадает с понятием
перпендикулярности двух векторов. В терминах этого
понятия в любом гильбертовом пространстве верна
теорема Пифагора' если элемент х?Н равен
конечной пли счетной сумме попарно ортогональных
элементов я-,-, х,-? Н (счетная сумма 2"_ г' понимается
в смысле сходимости ряда в метрике пространства Н),
то i|.r||2=2^_ IMP (CM- Парсеваля равенство).
Полная счетная система {•?<} ортонормированных
векторов сепарабельного гильбертова пространства
представляет аналог полной системы попарно ортого-
ортогональных векторов конечномерного евклидова прост-
пространства: любой элемент х?Н единственным образом
представляется в виде суммы Z4i^\cixi^ причем е,-.г,-==
~(х, Х()х[ — проекция элемента х на х,-.
В случае функционального пространства L2[a, b]
такую роль играют полные ортонормированные системы
функций {ф*}: если/(.r)gL2[a, b], то
в метрике пространства L2\a, b], где
rb
ск=)аПх) Фа И йх-
В случае, когда ф&(т) — ограниченные функции, ко-
коэффициенты с? можно определить для любой интегри-
интегрируемой функции. При этом представляет интерес вопрос
о сходимости соответствующего разложения в том или
ином смысле (см. Тригонометрическая система, Хаара
система). Поэтому для функций термин «О.» употреб-
употребляется в более широком смысле: интегрируемые на от-
отрезке [а, Ь] функции /(.т) и g(x) наз. ортогональ-
ортогональными, если
(для существования интеграла обычно требуется, чтобы
f(x)?lP[a, b), 1<j«Eoo, g(x) = L9[a, b], l/p + l/g=l,
L°° [a, b] —
множество ограниченных функций).
Существуют также определения О. элементов произ-
произвольного действительного нормированного простран-
пространства. Одно из них (см. [4]) следующее: элемент х дейст-
действительного нормированного пространства В считается
ортогональным элементу у, если ||ж||<:||^+А:!/|| для лю-
любого действительного к. В терминах этого понятия
установлены нек-рые необходимые и достаточные усло-
условия, при к-рых может быть определено скалярное (вну-
(внутреннее) произведение элементов пространства В (см.
[5], [6]).
Лит.: L1J К а н т о р о в и ч Л. В., А к и л о в Г. П., функ-
функциональный анализ, 2 изд., М., 1977; [2J Д а н ф о р д Н.,
Шварц Дж,, Линейные операторы. ООщая теория, пер. с
англ., М., 19В2; [3] К а ч м а ж С, Ш т е й н г а у з Г., Теория
ортогональных рядов, пер. с нем., М., 1958; U] В irklioff G,,
«Duke Math. J.» 1935, v. l,p. 109—72; [5] James R., «Trans.
Amer. Math. Soc», 1947, v. 61, p. 285—92; [6] его же, «Bull.
Amer. Math. Soc», 1947, v. 53, p. 559—66. А. А. Талалян.
ОРТОГОНАЛЬНЫЕ ЛАТИНСКИЕ КВАДРАТЫ —
пара латинских квадратов А = ||а,-у||, В= \\Ьу\{ порядка п.
таких, что (о,у, bij)jb{akl, bkl) при (г, ])ф{к, I), г, /, к,
l?S= {1, ... , п }. Квадраты А и В наз. ортогональ-
ортогональными соквадратами. Матрица, получаемая
наложением А на В, наз. греко-латинским,
или эйлеровым, квадратом, ее элементы —
все rfl упорядоченных пар элементов S. Ортогональ-
Ортогональность А и В обозначается А^В. Пример пары О. л. к.
и их эйлерова квадрата для п=3:
12 3 12 3 11 22 33
2 3 1 3 12 23 31 12
3 12 2 3 1 32 13 21.
Латинский квадрат А порядка п имеет ортогональный
соквадрат тогда и только тогда, когда в А существует п
непересекающихся трансверсалей (см. Латинский квад-
квадрат). Если А — латинский квадрат порядка 4/+2 (или
4г+1) с подквадратом порядка 2t-\-i (соответственно 2t),
все клетки к-рого за исключением, быть может, t (соот-
(соответственно [(/—1)/2]) клеток заполнены не более чем
2г+1 (соответственно 2t) элементами, то для А не су-
существует ортогонального соквадрата. Для всех я>2,
ифЬ, имеются примеры пар О. л. к., а для д=6 путем
перебора всех возможностей доказано, что таких пар
нет [3|.
Несколько латинских квадратов одного порядка наз.
попарно ортогональными, если любые
два из них ортогональны. Если N (п) — максимальное
возможное число попарно О. л. к., то Л'(п)<:п—\. Для
Л'(п) получены следующие оценки снизу:
п» 7 52 53 63 90
N{n)> 2 3 4 5 6.
Кроме того, 7VA2Ks5, iV C3K*3, Л'C5)^4, Л'D0K=4,
JVD5)>4 и доказано, что N (и) -к оо при « -»- оо;
напр.. Л'(п)>«1/17 --2 П))И достаточно большом и
(см. [2]).
Множество из я—1 попарно О. л. к. порядка я наз.
полным. При га>4 множество из га—3 попарно О. л.
к. всегда может быть дополнено до полного. В настоя-
настоящее время A983) полные множества известны только в
случае п=рк, где к — натуральное, р — простое числа
(то есть N(pk)=pk—1). Если же nssl (mod 4) или
п~2 (mod 4) и свободная от квадрата часть числа п
содержит хотя бы один простой множитель р=3 (mod 4),
то по существует полного множества попарно О. л. к.
порядка п. Напр., не существует полных множеств при
п=2р, p=3(mod4).
Полные множества попарно О. л. к. находят прило-
приложение в статистике при построении симметрических
уравновешенных неполных блок-схем с параметрами
»=ns+re+l, k---n-\-i, Л=]. Полные множества могут
интерпретироваться и как конечные проективные пло-
плоскости (см. [2]).
Предложено много методов построения О. л. к. (см.
[2]). Все они созданы с целью получения как можно
большего множества попарно О. л. к. порядка п. Каж-
Каждый из методов может быть отнесен к одной из следую-
следующих двух групп. К первой группе принадлежат методы,
характерной особенностью к-рых является то, что они
дают способ построения «основного» латинского квад-
квадрата и указывают, как переставить в нем строки и столб-
столбцы, чтобы получить ортогональный соквадрат. Ко вто-
второй группе относятся методы, к-рые используют из-
известные приемы построения О. л. к. меньшего порядка
для построения О. л. к. заданного порядка.
Если Л = ||а/у || — латинский квадрат порядка п,
построенный на множестве S, то упорядоченный набор
перестановок a,-, i?S, определяемых равенствами а,-(/)=
= aij, однозначно определяет латинский квадрат А. Не
каждый упорядоченный набор перестановок соответст-
соответствует какому-либо латинскому квадрату. Если А -
= [аи ... , ап] и В—[тх, ... , т„] — два латинских квад-
квадрата, заданных указанным способом перестановками
о/ и т,- множества S, то А }_В тогда и только тогда, когда
[сгГЧц ... , Оп'т,,] — латинский квадрат. Если опреде-
определить произведения a.A = [ad\, ¦¦¦ , <ха„], Л|3 — [o"jp\ ... ,
... , о„р], где а и'Р — перестановки S, то, напр., А_\_аА
тогда и только тогда, когда [of'aOj, ... , o^aaj —
латинский квадрат.
Методы первой группы обычно используются в слу-
случае, когда А — таблица умножения конечной группы
G, то есть aij-gjgj, g;, gjgG, i, j?S; отличие одного
метода от другого заключается в выборе группы G, в
выборе взаимно однозначных отображений a, p группы
G на себя и в использовании произведений аА, А$,
<х~1А<х н т. д.
Если G — аддитивная группа, то условие А ]_а.А
сводится к тому, что a — ортоморфизм G, т. е.
такое взаимно однозначное отображение G на себя, что
если для glt gi?G выполняется равенство ct{g\)—gy--
=a{gi)—gi, то g!=--g2. Напр-, пять попарно О. л. к.
порядка 12 были найдены после определения четырех
нетривиальных ортоморфизмов абелевой группы, яв-
являющейся прямым произведением циклпч. групп 6-го
и 2-го порядков (см. [2], [6]).
Если G —¦ аддитивная группа коночного поля
GF(pr)={a-o=0, Я!=1, я2, ... , en_i}, n = pr, то все по-
построения значительно упрощаются п получается сле-
следующее полное множество попарно О. л. к.:
A^Ubl «?, = o,efc+o;-; *, /€@, 1 «-*},
2, ..., и-1}.
Следует отметить, что для п, удовлетворяющих ус-
условиям пф2 (mod 4), пфЪ (mod 9) и пфЪ (mod 9), ока-
оказалось возможным всегда построить такой латинский
квадрат А порядка п, что Л_1_ЛТ.
Использование прямого произведения латинских
квадратов составляет основу следующего метода, отно-
относящегося ко второй группе. Пусть А, и Bt - О. л. к.
порядка и, построенные на множестве X, а Л2 и 52 —
О. л. к. иорядка т, построенные на множестве У,
тогда прямые произведения матриц А1ХА2 и Z?,xB2
будут О. л. к. порядка inn, построенные на множестве
XxY. Если n—p^p^-. . .p ''t то указанный метод при-
приводит к оценке Л"(?i)^mii/(pf''—1).
В основе многих других методов второй группы ле-
лежит следующее построение. Пусть Аг, Blt C1 — попар-
попарно О. л. к. порядка m'^t'lii, построенные на Sx— {1,2,...,
... , m}, Л2, В2 — О. л. к. порядка и, построенные на
Л'2={т-И, ... , m-\~n}. Чтобы получить теперь два ла-
латинских квадрата А и В порядка /ге-Ьи, построенные на
S=SL\J S-2, добавляют к А строки и столбцы с номерами
то-f-l, ... , m-f-n с незаполненными клетками, в резуль-
результате чего получают частичный латинский квадрат по-
порядка m-\-n, содержащий Л] в верхнем левом углу.
Клетки А± и Ви имеющие те же номера, что и клетки С,,
содержащие элемент i, составляют общую для Ах и Вх
i-ю трансверсаль, i=l, 2, ... , m. Элементы i-ii транс-
версали в Л1 при 1=1, 2, ... , 7t помещают в (/re-fO-й
столбец (и в (m+0-ю строку) в том же порядке, в каком
они располагались в строках (соответственно столбцах)
A j, а на их место ставится число m-\-i. Остается в правый
нижний угол частичного квадрата поставить Л2, чтобы
завершить построение А.
Построение В проводится аналогичным образом из В±
и В2, но только с использованием трансверсалей с но-
номерами га-(-1, п-[-2, ... , 2п. Квадраты Л и В будут ла-
латинскими, но не обязательно ортогональными. Всегда
можно получить пару О. л. к. порядка m-\-n при /п—
= р*5"=13, где р — нечетное, и n=(m—1)/2; показано,
как, используя приведенное выше построение, получить
пару О. л. к. порядка п при n=2 (mod 4), га>6 (см. [2]).
Приложения О. л. к. в статистике, теории информа-
информации и в теории планирования эксперимента требуют по-
построения О. л. к. специального вида и перенесения по-
понятия ортогональности на другие объекты. Так, обоб-
обобщением О. л. к. являются ортогональные таблицы.
Два частичных латинских квадрата одного порядка
наз. ортогональны м и, если при наложении
их друг на друга получаемые в клетках упорядоченные
пары будут все различны. Говорят, что частичный
латинский квадрат А вложен в латинский квадрат В,
если Л совпадает с нек-рой подматрицей В (за исклю-
исключением пустых клеток Л). Каждый квадрат из множест-
множества попарно ортогональных частичных латинских квад-
квадратов может быть вложен в латинский квадрат таким
образом, что полученные латинские квадраты будут
О. л. к. (см. [6]).
Лит.: [1] Сачков В. Н., Комбинаторные методы дискрет-
дискретной математики, М., 1977; [ZlDene s J., Keedwell A. D.,
Latin Squares and their applications, Bdpst, 1974; [3] X о ллМ.,
Комбинаторика, пер. сангл., М., 1970; [4] Р а й з е р Г.- Д ж.,
Комбинаторная математика, пер. с англ., М., 19КС; (М Не-
d а у a t A., S e i d о n E., «Pacif. J. Math.», 1977, v. iH, Ai 2,
p. 85—113; [Я] Lindner С li., «Proc. Amer. Math. Soc», 1976,
v. 59, JNs 1, p. 184—8A В. М. Muxeee.
ОРТОГОНАЛЬНЫЕ МНОГОЧЛЕНЫ — система мно-
многочленов {Ри{х)}, удовлетворяющих условию ортого-
ортогональности
5д Р" W Рт (х) h (х) dx-O, n ф т,
причем степень каждого многочлена /'„ (.г) равна его
индексу и, а весовая функция (вес) h (.rJJaO на интер-
интервале (а, Ь) или (в случае конечности а н Ь) на отрез-
ке [а, Ь]. О. м. наз. ортонормированными
и обозначаются {Рп (х)}, если каждый многочлен
имеет положительный старший коэффициент и выпол-
выполняется условие нормпрованности
А если старший коэффициент каждого многочлена
равен 1, то система О. м. обозначается {Рп(х)}.
Система О. м. {Р„(х)} определяется однозначно,
если весовая функция (дифференциальным
вес) h(x) интегрируема по Лебегу на (а, Ь), не экви-
эквивалентна нулю и, в случае неограниченного интервала
(а, Ь), имеет конечные степенные моменты
xnh{x)dx.
Вместо дифференциального веса h (x) можно рассмат-
рассматривать интегральный в е- с do(x), где п(т)—
ограниченная неубывающая функция с бесконечным
множеством точек роста (ь этом случае в условии
ортогональности интеграл понимается в смысле Ле-
Лебега — Стилтьеса).
Для того чтобы многочлен Р„ (х) степени п входил
в систему О. м. {Рп(х)} с. носом h(x), необходимо и
достаточно, чтобы для любого многочлена Qm (.г) сте-
степени т<С>г выполнялось условие
Если интервал ортогональности (о, Ь) симметричен
относительно начала координат, а весовая функция
h(x) четна, то каждый многочлен Рп(х) содержит только
те степени х, к-рые имеют одинаковую с номером п
четность, т. е. имеет место тождество
Ра(-х)**(-\)"Ра(х)-
Нули О. м. в случае ортогональности по интервалу
(о, Ь) все действительны, различны и расположены
внутри (а, Ь), причем между двумя соседними нулями
многочлена Рп(х) есть один нуль многочлена Pn-i{x).
Нули О. м. часто применяются в качестве узлов ин-
интерполяционных и квадратурных формул.
Любые три последовательных многочлена системы
О. м. связаны рекуррентной формулой
Рп + 1[х)г^(апх + Ьп)Рп(х)-спРп_1(х), ге = 1, 2, ... ,
где Р0(х)-=-и0,
?! (Ж) =-:(.! iZ'-Vi, ... ,
Число dn1 — HopMiipyroinviii множитель многочлена
Р„(ж), так что система {dn~1Pn(.r)} ортонормирована,
т. е.
Для О. м. имеет место формула К р и с т о ф-
феля — Дарбу
2L Р()р«)
Чп
О. м. представляются через степенные моменты
весовой функции h (x) по формуле
где
ha Л] ... hn
111 h2 ... hп^
(x) ^
а определитель An_t получается из ^п(х) вычеркива-
вычеркиванием последних строки и столбца, Д„ определяется
аналогично.
На множестве многочленов Qп{х) степени п с еди-
единичным старшим коэффициентом минимум функцио-
функционала
F(Qn)=\ba Ql(x)h(x)dx
достигается тогда и только тогда, когда
причем этот минимум равен \\.п~ ¦
Если многочлены {Р~п(х)} ортонормированы с ве-
весом h{x) на отрезке [а, 6], то при р>0 многочлены
Qn(t) = VpPn(pt + <l), п=0, 1, 2, ...,
ортонормированы с весом h{pt-\-q) на отрезке [А, В],
к-рый переходит в отрезок [а, 6] в результате линей-
линейного преобразования я —pt-\-q. Поэтому при изучении
асимптотич. свойств ортогональных многочленов сна-
сначала рассматривается случай стандартного отрез-
отрезка [ —1, 1], а затем полученные результаты распрост-
распространяются на другие случаи-
Наиболее важный класс О. м., встречающихся при
решении краевых задач математич. физики, состав-
составляют т. н. классические ортогональные многочлены:
Лагерра многочлены {Ln(x\ а)} (для них h(x) = xae-x,
а>—1, интервал ортогональности @, со)); Эрмита
многочлены {Нп(х)} (для них fe(x) = exp(— хг), интер-
интервал ортогональности (—со, со)); Якоби многочлены
{Рп(х; а, р)} (для них /г(а-) = A—.т)а(Ц-аг)Р, а> —1,
р>—1, отрезок ортогональности [—1, 1]) и их част-
частные случаи: ультрасферичеспие многочлена, или мно-
многочлены Гегенбауэра {Рп(х, а)} (для них а=Р), Ле-
жандра многочлены {Рп(х)} (для них а=р = 0), Че-
бышева многочлены первого рода {Тп(х)} (для них
а^-р——Vo) и второго рода {Un(x)} (для них а,—
=-P=V2). "
Весовая функция h{x) классических О. м. {Кп(х)}
удовлетворяет дифференциальному ура-
уравнению Пирсона
Ь)
причем на концах интервала ортогональности выпол-
выполняются условия
lim h (х) В (х) — lim ft (x) В (х) =0.
х-»а + о ,v-»b-o
Многочлен у—Кп(х) удовлетворяет дифференциаль-
дифференциальному уравнению
В(х) у".'г[А(х) + В' (х)] у'-п [/>i + (n-M)?2] у = 0.
Для класснч. О. м. имеют место обобщенная
формула Ро д р и г а
где сп — нормировочный коэффициент, и формулы
дифференцирования
(-| Ln (х; а] = - ?„_, (х- а + 1), ^ Нп (х) = 2пНп-1 (х),
±Ра(х;а, ^^^-(a^p + n-'r^Pn-tix; o + l, р + 1).
Для частных случаев классических О. м. имеют место
представления через гипергеометрич. функцию
= f(-i», и; 4"! ^
-i», n + 2; 4
и через вырожденную гипергеометрич. функцию
Исторически первым примером О. м. были много-
многочлены Лежандра. Затем были введены многочлены
Чебышева, общие многочлены Якоби, многочлены
Эрмита и Лагерра. Все эти классич. О. м. играют
важную роль во многих прикладных вопросах.
Общая теория О. м. была построена П. Л. Чебыше-
вым. При этом в качестве основного аппарата иссле-
исследования применялось разложение интеграла
a x-t
в цепную дробь; знаменатели подходящих дробей этой
цепной дроби образуют систему О. м. на интервале
(а, Ь) с весом h(t).
При изучении О. м. большое внимание уделяется
их асимптотич. свойствам, ибо от этих свойств зависят
условия сходимости рядов Фурье по О. м.
Асимптотич. свойства классических О. м. впервые
исследовал В. А. Стеклов в 1907 (см. [8], с. 218). При
этом он применил и усовершенствовал метод Лиувилля,
к-рый ранее использовался для изучения решений
уравнения Штурма — Лиувилля. В дальнейшем ме-
метод Лиувилля — Стеклова применялся во многих
работах, в результате чего к настоящему времени
A983) подробно изучены асимптотич. свойства О. м.
Якоби, Эрмита, Лагерра.
В общем случае ортогональности на отрезке [—1, 1]
с произвольным весом, удовлетворяющим нек-рым
качественным условиям, асимптотич. формулы для
О. м. впервые получил Г. Сегё (G. Szego) в 1920—24.
При этом он ввел тиногочлены, ортогональные на ок-
окружности, изучил их основные свойства и нашел
весьма важную формулу, представляющую много-
многочлены, ортогональные на отрезке [—1, 1], через много-
многочлены, ортогональные ла окружности. А для исследо-
исследования асимптотич. свойств многочленов, ортогональ-
ортогональных на окружности, Г. Сегё разработал метод, осно-
основанный на специальном обобщении теоремы Фейера
о представлении неотрицательных тригонометрич. по-
полиномов с использованием методов и результатов
теории аналитич. фуккдий.
В 1930 С. Н. Бернштейн [2] для исследования асим-
асимптотич. свойств О. м. применил методы и результаты
теории приближения функций. Он рассмотрел случай
весовой функции вида
*(*) = ?§,, *€(-!, 1), A)
где функция h0(x), наз. тригонометриче-
тригонометрическим весом, удовлетворяет условию
Если функция ha(x) на всем отрезке [—1, 1]. удовлет-
удовлетворяет условию Дин и — Липшица по-
порядка у=1+е, где е>0, то есть
х, х + Ь?[-1, 1],
о(I<
I In I 6 | |
то для многочленов {Рп(х)}, ортонормированных
с весом A) на всем отрезке [—1, 1], имеет место асимп-
тотич. формула
где 0=arccos х, & q зависит от 8.
При исследовании сходимости рядов Фурье по О. м.
возникает вопрос об условиях ограниченности О. м.
либо в отдельной точке, либо на нек-ром множестве
/1с[—1, 1], либо на всем отрезке ортогональности
[—1, 1], т. е. рассматриваются условия, при к-рых
имеет место неравенство типа
\Рп(х)\<М, x^A^l-i, 1], B)
Впервые такой вопрос поставил В. А. Стеклов A921).
Если тригонометрич. вес ha(x) на множестве А ограни-
ограничен от нуля, т. е.
A0(z)Ssc3>0, x?A^[-i, 1], C)
и удовлетворяет нек-рым дополнительным условиям,
то неравенство B) имеет место. А в общем случае из
неравенства C) при А=[—\, i] без дополнительных
условий следует оценка
\Ра(х)\<е„Уп, е„—>0, *?[-*. М- D)
Нули весовой функции являются особыми точками
в том смысле, что свойства последовательности
{Р„(я-)} существенно различны в нулях и в других
точках интервала ортогональности. Пусть, напр.,
весовая функция имеет вид
Тогда если функция hx(x) положительна и удовлетво-
удовлетворяет условию Липшица на [—1, 1], то последователь-
последовательность {Рп(х)} ограничена на всяком отрезке [а, Ь]с
с\~i, 1], не содержащем точек {.rfe}, а в нулях вы-
выполняются неравенства
V
/
\ к = 1, 2, ..., т.
Случай, когда нули весовой функции расположены
на концах отрезка ортогональности, рассмотрел
С. Н. Бернштейн [2]. Один из его результатов заклю-
заключается в том, что если весовая функция имеет вид
h (x) = h1 (x) A— х)« A+ж)Р, х?[—1, 1],
где функция ^i(^) положительна и удовлетворяет ус-
условию Липшица, то при а>—1/2, р">—V2 О. м. до-
допускают весовую оценку
Рп(х)\<еь, *6[-1, 1],
а в точках л:=±1 возрастают со скоростью геа+1/'2 и
„р + '/г соответственно.
В теории О. м. часто рассматриваются т. н. теоремы
сравнения. Так, напр., теорема сравнения
К о р а у с а: если многочлен^ {ып(х)}, ортогональ-
ортогональные с весом р(х) на отрезке [а, Ь], равномерно огра-
ограничены на нек-ром множестве Ас[а, 6], то на этом
множестве ограничены также и многочлены {Рп(х)},
ортогональные свесом h(x)=p (x)g (х), где множитель
q (x) положителен и удовлетворяет на отрезке [а, Ь]
условию Липшица порядка а- I. Аналогично, при
нек-рых условиях на множитель ц (г) с системы
{шп(х)} на систему {Рп(,т)} переносятся асимптотич.
формулы или другие асимптотич. свойства. Более
того, если множитель q(x) есть неотрицательный нп
отрезке [я, Ь] многочлен степени т, то многочлены
{Рп(х)} представляются через многочлены {ш„(ж)}
с помощью определителей порядка m-f-1 (см. [8] с. 42).
Эффективные формулы для О. м. получены также в слу-
случае весовых функций вида
1 УТ^Т* ^Т^Г 1
Qm (х) У 1-х2 ' Qm (*) ' У l + xQrn(x)'
где Qm ix) — произвольный положительный на от-
отрезке [ — 1, 1] многочлен (см. [8J с. 44). А в большинстве
случаев вычисление О. м. произвольного веса при
больших номерах п затруднительно.
Лит.: [1] Ч с б ы ш е в II. Л., Поли. собр. соч., т. 2, М.—Л.,
1947, с. 103-211, 314—34, 335—41, 357—74; [2j Б е р н ш т е й и
С. Н., Собр. соч., т. 2, М., 1954, с. 7—106; [3] Г е р о н и м у с
Я. л.. Теория ортогональных многочленов, М.—Л., 1950; [41
Сует и п П. К., Классические ортогональные многочлены,
2 изд., М., 1979: [51 Н и к и ф о р о в А. Ф., Уваров В, Б.,
Специальные функции математической физики, М., 1978; [<>J
J3 е и т м е н Г., Эрдейи А., Высшие трансцендентные
функции, т. 2 — Функции Бесселя, функции параболического
цилиндра, ортогональные многочлены, пер. с англ., 2 изд., М.,
1974; [7] Д ж е к с о н Д., Ряды Фурье и ортогональные поли-
полиномы, нер. с англ., М., 1948; L8] Сеге Г., Ортогональные мно-
многочлены, пер. о англ., М., 19С2; [9] Справочник по специальным
функциям..., пер.с англ., М., 1979; [10] S h о h a t J. A., H i 1-
le E., Walsh J. L., A bibliography on orthogonal polyno-
polynomials, Wash., 1940. Л. К. Суетин
ОРТОГОНАЛЬНЫЕ МНОГОЧЛЕНЫ в ко м-
плексной области — общее название много-
многочленов, ортогональных на окружности, по контуру
или по площади. В отличие от случая ортогональ-
ортогональности в действительной области, многочлены ука-
указанных трех систем могут иметь мнимые коэффи-
коэффициенты и рассматриваются при всех комплексных
значениях независимого переменного. Характерной
особенностью случаев ортогональности в комплексной
области является тот факт, что в ряды Фурье по ука-
указанным системам разлагаются обычно аналитич. функ-
функции комплексного переменного, удовлетворяющие нек-
рым дополнительным условиям в окрестности границы
области аналитичности.
1H. м. на окружност и — система многочле-
многочленов {ф„(г)}, имеющих положительный старший коэф-
коэффициент и удовлетворяющих условию ортогональности
(обычно ортонорыированности):
2Я
('в)
где и(В) — ограниченная неубывающая на сегменте
[0,2я] функция с бесконечным числом точек роста,
наз. функцией распределения, а бпт —
символ Кронекера. Аналогично случаю ортогональ-
ортогональности на отрезке, для многочленов {<pn(z)} имеют место
рекуррентное соотношение и аналог формулы Крис-
тоффеля — Дарбу.
Асимптотич. свойства исследуются при условии
2Л1п ц,' F) dQ > —со.
Случай ортогональности на окружности как перио-
днч. случаи нлучен достаточно подробно, поскольку
здесь успешно применяются результаты о приближе-
приближении периодических функций тригонометрическими
полиномами.
Пусть многочлены {Рп(х)} ортонормированы на
сегменте 1—1, 1! с дифференциальным весом h(x), a
весовая функция на окружности имеет вид
ц' F) = h (cos 6) | sin 6 |.
Тогда при условии .r=-jz-)--j имеет место ф о р-
м у л а Сегё
где а2п — старший коэффициент многочлена ф2„(с).
Если аналитическая в круге |z|<l функция /(г)
имеет угловые граничные значения на окружности
|z|=l, то при нек-рых дополнительных предположи-
ниях справедливо разложение
коэффициенты к-poro определяются по формуле
e»=2F Jo /(«'в)ф«("'в)''и(в)-
Ряды вида A) являются непосредственным обобщением
рядов Тейлора: при ц.@)=8 будет q>n(z)sszn. При
нек-рых условиях на функцию распределения и.(в)
ряд A) в точках окружности \z\ -~1 сходится или рас-
расходится одновременно с рядом Тейлора этой же функ-
функции f(z), т. с. имеет место теорема о равносходимости
этих двух рядов.
2) О. м. по контуру — система многочленов
(Р„(г)}, имеющих положительный старшин коэффи-
коэффициент и удовлетворяющих условию
Рп М Р,п (г) h (z) | dz | = 6„,л,
где Г — спрямляемая жорданова (обычно замкнутая)
кривая в комплексном плоскости, а весовая функция
h(z) интегрируема по Лебегу и почти всюду положи-
положительна на Г.
Пусть в конечной односвязной области С, ограни-
ограниченной кривой Г, задана аналитич. функция /(г),
граничные значения к-рой на контуре Г интегрируемы
в квадрате с весом Л (г). Тогда с помощью формулы для
коэффициентов
а»^4г5г f A)Т\Ш HI) \'К\
этой функции ставится в соответствие ряд Фурье по
ортогональным многочленам:
Эти ряды являются естественным обобщением рядов
Тейлора по свойству ортогональности на случай одно-
связной области и служат для представления анали-
аналитич. функций. Если выполняется условие пол-
полноты
inf \rh(z)\f(z)-Qn(z)\*\dz\=O,
где нижняя грань берется по множеству всех много-
многочленов Qn(z), то ряд B) сходится к функции f(z) в
среднем по контуру Г с весом h(z), а при нек-рых допол-
дополнительных условиях и равномерно внутри области G.
3) О. м. п о нло щ а д и — система многочленов
{А'„(г)}, имеющих положительный старший коэффи-
коэффициент и удовлетворяющих условию
G A'B (z) /fm (z) A (z) Ar dy •=•-- 8nm,
где весовая функция /г (г) неотрицательна, интегрпруо-
ма по площади конечной области G и неэквивалентна
нулю. Если имеет место условие полноты
inf \\rh(z) \f(z)-Qn(z)\'d.rd;, = O,
{CJ rl}
где нижняя грань берется по множеству всех многочле-
нов Qn(z), то ряд Фурье по многочленам {Kn(z)} функ-
функции f(z), аналитической в односвязноп области G
сходится к этой функции в среднем по площади об-
области G с весом h(z), а при нек-рых дополнительных
условиях и равномерно внутри области G.
Лит.: [1] Szegfi G., «Math. Z.» 1920 Bd 6, S. 167 — 202;
1921, Bd 9, S. 167 — 90,218 — 70; 12] С a r 1 e m a n Т., «Ark. for
mat., astr. oclifys.», 1922—23, Bd 17, J\s 9, S. 1—30; [3] Cere Г.,
Ортогональные многочлены, пер. с англ., М., 1962; [4] Г е р о-
н в м у с Я. Л., Многочлены, ортогональные на окружности и
на отрезке, М., 1958; [5] Смирнов В. И., «Журнал Ле-
Ленинградского физико-матем. об-ва», 1928, т. 2, в. 1, с. 105—79;
16] К о р о в к 1Гн П. П., «Матем. сб.», 1941, т. 9, № 3, с. 469—
'i8">; [7] С уетин П. К., «Успехи матем. наук», 1966, т. 21, в. 2,
с. 41—88; [8] е г о ж е, «Тр. Матем. ин-та АН СССР», 1971, т.
100, с. 1—96. П. К. Суетип.
ОРТОГОНАЛЬНЫЙ БАЗИС — система попарно ор-
ортогональных элементов elt е2, . . ., еп, . . . гильбертова
пространства X такая, что любой элемент х?Х одно-
однозначно представим в виде сходящегося по норме ряда
наз. рядом Фурье элемента х по сис-
системе {е,}. Обычно базис {е,} выбирается так, что
Ik/I! ~ 1, п тогда он наз. о р т о н о р м и р о в а н н ы м
базисом. В этом случае числа С,-, наз. коэффи-
коэффициентами Фурье элемента х по о р-
тонормпрованному базису {<?,}, имеют
вид г,-—(.г, е,). Необходимым и достаточным условием
того, чтобы ортонормпрованная система {«/} была ба-
базисом, является равенство Парсеваля —
Стек лова
для любого ,г?Х. Гильбертово пространство, име-
имеющее ортонорммрованньга базис, является сепарабель-
ным, н обратно, во всяком сепарабельном гильбертовом
пространстве существует ортонормированный базис.
Если задана произвольная система чисел {с,} такая,
что 2,|с;|2<оо, то в случае гильбертова пространства
с базисом {<?,} ряд 2,с,е,- сходится по норме к нек-ро-
му элементу х?Х. Этим устанавливается изоморфизм
любого сепарабельного гильбертова пространства про-
пространству 1.2 (теорема Р и с с а — Фишера).
Лит.: [1] Л ю с т е р н и к Л. А., Соболев В. И., Эле-
Элементы функционального анализа, 2 изд., М., 1965; [2] К о л м о-
г о р о в А. Н., Фомин СВ., Элементы теории функций и
функционального анализа, о изд., М., 1981; [3] А х и е-
;! е р Н. И., Г л а з м а н И. М., Теория линейных операторов в
гильбертовом пространстве 2 изд. М., 1966. В. И. Соболев.
ОРТОГОНАЛЬНЫЙ ПРОЕКТОР, ортопроек-
т о р,— отображение Pi гильбертова пространства Н
на его подпространство L такое, что х—Pix ортого-
ортогонально Р[\ x—Pix\J>Lx. О. п. есть ограниченный
самосопряженный оператор, действующий в гильбер-
гильбертовом пространстве Н, п такой, что P\—-Pi и ||Р?||—1.
Обратно, если дан ограниченный самосопряженный
оператор, действующий в гильбертовом пространстве
Н, я такой, что Р2—Р, то Lp= {Px\x?H} является
подпространством и Р есть О. п. на Lp. Два О. п.
Pjt, Р[_а наз. ортогональными, если Р^Р/,,—
~Pi_,Pli=Q'i 9Т0 эквивалентно условию, что Ьх\_1г.
Свойства О. п.: 1) для того чтобы сумма Pl^YPl-,
двух О. п. была О. п., необходимо и достаточно, чтобы
РцР1,= 0, в этом случае Р;.,+Ри= РL^ u; 2) для
того чтобы композиция Pl,Pli была О. п., необхо-
необходимо и достаточно, чтобы Рl^Pu~PL,Pi.v B этом
случае PLlPr^-PLinL2.
О. п. Pj, нал. частью О. п. Л/, если V есть
подпространство L. При этом Pi—PL, является О. п.
на L—tj'— ортогональное дополнение к L' в L. В част-
частности, /—Pi есть О. п. на H—L.
Лит.: [1] Л ю с т е р н и к Л. А., Соболев В. И., Оле-
менты функционального анализа, 2 изд., М., 1965; [2] Ахи i-
з е р Н. И., Г л а з м а н И. М., Теория линейных операторов в
Ф/ (x) Ф (x) = S
гильбертовом пространстве, 2 изд., М., 19Gf3; [3] Рисе Ф.,
Сёкефальви-Надь В., Лекции но функциональному
анализу пер. с франц., 2 изд., М., 1979. В. И. Соболев.
ОРТОГОНАЛЬНЫЙ РЯД — ряд вида
где {tyn(x)} — ортонормированная система функций
(онс) относительно меры u,(i):
f 0 при I Ф U
при i — j.
Начиная с 18 в. при изучении различных вопросов
математики, астрономии, механики и физики (движе-
(движение планет, колебание струн, мембран и др.) в иссле-
исследованиях Л. Эйлера (L. Euler), Д. Бернулли (D. Ber-
Bernoulli), А. Лежандра (A. Legendre), П. Лапласа (Р.
Laplace), Ф. Бесселя (F. Bessel) и др. эпизодически
появляются нек-рые специальные онс и разложения
функций по ним. Определяющее же влияние на ста-
становление теории О. р. оказали:
а) исследования Ж. Фурье (J. Fourier, 1807—22)
(Фурье метод решения краевых задач уравнений мате-
матич. физики) и в связи с ними работы Ж. Штурма
и Ж. Лиувилля (J. Sturm, J. Liouville, 1837—41);
б) исследовании ГГ. Л. Чебышева по интерполиро-
интерполированию и проблеме моментов (сер. 19 в.), повлекшие за
собой создание им общей теории ортогональных много-
многочленов',
в) исследования Д. Гильберта (D. Hilbert, нач.
20 в.) по интегральным уравнениям, где, в частности,
были установлены общие теоремы о разложении функ-
функций в ряд по онс;
г) создание А. Лебегом (Н. Lebesgue) теории меры
п интеграла Лебега, придавшие теории О. р. совре-
современный вид.
Активному развитию теории О. р. в 20 в. способст-
способствует применение онс функций и рядов по ним в самых
разнообразных разделах науки (математич. физика,
вычислительная математика, функциональный ана-
анализ, квантовая механика, математич. статистика, опе-
операционное исчисление; автоматпч. регулирование и
управление, различные технич. задачи и т. п.).
Характерные результаты и направления исследований
в теории О. р.
1) Пусть Х~\а, Ь], d\i (x) = dx — мера Лебега п
{фп} — онс- Тогда если /?La(a, Ь), то числа
наз. коэффициентами Фурье, а ряд A)
с ап ¦«„(/) — рядом Фурье функции / по сис-
системе {ф„}.
Система {ф„} замкнута относительно прост-
пространства L2, если для любой функции /?/-а и любого
числа е>0 найдется полином
такой, что норма \\1—Ф\\.,<у. Система {ф„} полна
относительно L2, если ии условий /?/>'- и а„(/) = 0 при
всех гс>0 следует, что /(?)=(; щиип всюду, т.е. / —
пулевой элемент пространства L?.
Если для нек-рой функции f?L'2 выполняется ра-
равенство
то говорят, что функция / удовлетворяет у с л о в и то
замкнутости Ляпунова — Стеклова
(или равенству Парсеваля). Это условие
эквивалентно сходимости частных сумм ряда Фурье
от / по норме пространства L2 к функции /.
Аналогично даются определения замкнутости, пол-
полноты и условия замкнутости для более общих прост-
пространств и пер.
Одним из важнейших вопросов теории О. р. явля-
является вопрос однозначного определения функции по
ее коэффициентам Фурье. Для пространств L2 он са-
самым тесным образом связан с выполнением равенстпа
B) для всех функций /??2.
Для случая тригонометрич. системы равенство B)
в 1805 было приведено (фактически без доказательства)
М. Парсевалем (М. Parseval), а в 1828 Ф. Бессель уста-
установил, что
неравенство Вессоля). В 1896 А. М. Ля-
Ляпунов доказал равенство B) для интегрируемых по
Риману функций, а потом П. Фату (P. Fatou) для слу-
случая /?L2.
В. А. Стекловым A898—1901) был поставлен воп-
вопрос о замкнутости общих онс и положительно решен
для многих ортогональных систем (сферим. функции,
собственные функции оператора Штурма — Лиувилля,
системы ортогональных многочленов Ормита, Лагер-
ра, функции Ламе и др.).
Что касается неравенства C), то оно оказалось
справедливым для произвольных онс и функций /?/А
В 1907 Ф. Рисе (F. Biesz) и Э. Фишер (Е. Fischer)
доказали, что для любой онс {фп} и любой последо-
последовательности чисел {ап}6^2 найдется функция f?L2,
для к-рой ап(/)^=(/, ф„)=о„ и выполнено равенство B).
Из этой теоремы и неравенства Бесселя вытекает, что
для любых онс полнота и замкнутость эквивалентны
в пространство L2; замкнутость в пространствах I?
с 1</><оо эквивалентна полноте в пространстве Lp',
где 1/р' + 1/р=1 (С. Банах, S. Baiiach, 1931).
Неравенство Бесселя и теорема Рисса — Фишера
были распространены ]'. Харди (G. Hardy), Дж. Литл-
вудом (J. Littlewood) и Р. Пэли (R. Paiey) на прост-
пространства W. Именно, пусть {ф„} — онс, [ф„(.г)|<Л/
и 1<р<2. Тогда:
а) если f?LP, то
б) если дана последовательность {ап} с
то найдется функция f?Lp', для к-рой (/, ф,,) — я„
и ||/||р' <:Л /, где А зависит лишь от р и М.
2) Другой крупной проблемой теории О. р. является
вопрос разложения функции п ряд по простым функ-
функциям, сходящийся к ней по норме того или иного
пространства. Система элементов {ф„} ил Д-прост-
ранства Е нац. базисом (безусловным
б а з и с о м), если каждый элемент /?/? единственным
образом представляется в виде ряда
сходящегося (безусловно сходящегося) к / по норме
пространства Е.
Если {ф„} — базис, в Е, то а„(/) являются линей-
линейными непрерывными функционалами в пространстве Е
и в случае E—Lp@, 1) с \ <р<<» имеют вид
ГД° {фп} — базис пространства Lv' @, 1), {фн, г!1,,}""
биортонормированная система (С. Банах). В част-
частности, если фп^^л> то есть {ф„} — онс, то ортого-
пальный базис в Lp автоматически является базисом
во всех пространствах //, где г — любое число между
Р и р.
Исследования по указанной проблеме ведутся в двух
направлениях:
а) но заданной онс {ф„} находятся те пространства,
в к-рых {фп} является базисом;
б) для заданного пространства Е отыскиваются
в нем базисы или ортогональные базисы.
В обоих случаях исследуется взаимосвязь свойств
функции / и ее разложения.
Что касается тригонометрии, системы, то она не яв-
является базисом пространства непрерывных функций С
(П. Дюбуа-Реймон, P. Du Bois Reymond, 1876), но яв-
является базисом в пространствах W с 1<р<оо (М. Рисе,
М. Riesz, 1927). Результат П. Дюбуа-Реймона был рас-
распространенна любые ограниченные в совокупности онс.
Ортонормированная система многочленов Лежандрл
является базисом в пространствах //при р€0/з, 4)
и не является таковой в остальных пространствах L4
A946—52, X. Поллард, И. Pollard, Дж. Нейман,
J. Neumann, и В. Рудин, W. Rudin).
В 1910 была построена онс {%т}т=о такая, что вся-
всякая непрерывная функция /?С@, 1) единственным
образом раскладывается в равномерно сходящийся
ряд Фурье по этой системе (А. Хаар, А. Нааг). Однако
система Хаара {%т} не является базисом пространства
С@,1), т. к. функции %т разрывны при т>1. Проин-
Проинтегрировав систему {%т}, Г. Фабер (G. Faber, 1910)
установил, что система
является базисом в пространстве С @,1) п тем самым
был найден первый базис в пространстве непрерывных
функций. Этот результат Г. Фабера был переоткрыт
К). Шаудером (J. Schauder, 1927), к-рый указал также
класс базисов пространства С @,1) типа бааиса {/„};
в честь последнего и введен термин «базис Шаудера»,
хотя более справедливо было бы называть его «базис
Фабера — Шаудера».
Построенные Г. Фабером и Ю. Шаудером базисы не
являются ортогональными. Первый ортонормированный
базис {Fn} в пространстве С @,1) был найден Ф. Франк-
Франклином (Ph. Franklin, 1928), к-рый проортогонали-
зировал методом Шмидта систему Фабера — Шаудера
{/„} и получил {Fn}. На этом пути (ортогонализация
и интегрирование) был введен и изучен новый класс
базисов. Все ортонормированные базисы пространства
С @,1) автоматически являются базисами во всех про-
пространствах Lp с 1 <:;?<: оо.
Система Хаара {%„,} является безусловным базисом
но всех пространствах Lp с 1<р<оо A931—37, Р. Пэ-
ли, Ю. Марцинкевич, J. Marcinkiewicz). Аналогичный
результат имеет место и для системы {Fn} Франклина.
В пространствах С и L вообще нет безусловных бп-
зисов. Точно также не существует нормированных и
ограниченных в совокупности безусловных базисов
в пространствах Lp при 1<р<оо и р ф 2.
3) Большой цикл исследований проведен по пробле-
проблеме сходимости почти всюду тригонометрических п
ортогональных рядов.
В 1911 Н. Н. Лузин построил первый пример почти
всюду расходящегося тригонометрия, ряда, коэффи-
коэффициенты к-рого стремятся к нулю. Такого типа ряд
Фурье был построен А. Н. Колмогоровым A923). Ре-
Результат Н. Н. Лузина был распространен на произ-
произвольные полные онс, а результат А. Н. Колмогорова
обобщен на множества положительной меры для огра-
ограниченных в совокупности онс.
Неотрицательная последовательность {ш(ге)} г
со(ге„)>0 и со(и)| наз. множителем Вейля
для сходимости почти всюду рядов по системе {ф„},
если всякий ряд A) сходится почти всюду на Хз5[0,1],
как только
"V* * 2 ( \ s'
Если m(n)sEl является множителем Вейля, то {([¦„}
наз. системой сходимости почти вс ю-
д у. Последовательность {m(n)} наз. точным
множителем Вейля для сходимости почти
всюду рядов A), если {ш(гс)} — множитель Вейля,
а всякая т(п)=о(ш(п)) при п—voo уже не является
таковой. Аналогично даются определения множите-
множителей Вейля для тех или иных видов сходимости и сум-
суммируемости (по мере, безусловная сходимость почти
всюду и др.).
Множители Вейля были найдены для тех или иных
систем. В 1913 М. Планшерель (М. Plancherel) доказал,
что {log3n} является множителем Вейля для сходи-
сходимости почти всюду рядов по любым онс {ф„}, в 1922
Д. Е. Меньшов и X. Радемахер (Н. Rademacher) уста-
установили, что в качестве множителя Вейля можно взять
{log2n}. И что особенно важно, Д. Е. Меньшов доказал
неусиляемость этого результата во всем классе онс,
т. е. {log2n} является точным множителем Вейля для
нек-рых онс.
Впоследствии были найдены необходимые и доста-
достаточные условия того, чтобы {ы(п)} была множителем
Вейля для сходимости или (СД)-суммируемости почти
всюду (по мере и др.) О. р. Было показано, напр.,
что система {sign sin nnx) не является системой схо-
сходимости почти всюду. В 1975 была построена первая
полная онс {фп} строгой сходимости, т. е. ряд A)
сходится почти всюду на Х=[0,1] тогда и только тогда,
когда {ап}?12.
В 1927 установлено, что последовательность ш(д)=
=%(п) log2n является множителем Вейля для безус-
безусловной сходимости почти всюду любых О. р., если
Этот результат оказался неусиляемым.
В 1960 было показано, что система Хаара {%„} не
является системой безусловной сходимости почти
всюду. На основе этого результата было доказано,
что многие системы (базисы в L2, полные онс и др.)
не являются системами безусловной сходимости почти
всюду. Для системы {%т} последовательность {со(»)}
лишь тогда является множителем Вейля для безуслов-
безусловной сходимости почти всюду, когда
ч = п„па (п)
<ос.
Поэтому не всякая полная онс имеет точный множи-
множитель Вейля для безусловной сходимости почти всюду-
Много исследований было проведено по проблеме
представления функций рядами, сходящимися почти
всюду, по мере и др. Так, в 1957 было установлено, что
для любой полной онс {ф„} с з-?Х^=[0,1] и любой
измеримой функции f(x) найдется ряд вида A), к-рый
сходится по мере к / (х) (для случая тригонометрия,
системы это утверждение было получено в 1947 Д. Е.
Меньшовым). Этот результат теряет силу даже для
случая конечных измеримых функций, если вместо
сходимости по мере рассматривать сходимость почти
всюду.
Лит.: Ill Лузин Н. Н., Интеграл и тригонометрический
ряд, М,—Л., 1951; [2] Б а н а х С, Курс функщонального ана-
Л1зу, К., 1948; [3] Г е р о н и м у с Я. Л., Теория ортогональ-
ортогональных многочленов, М.— Л., 1950; [4] К а ч м а ж С, Ш т е й н-
г а у з Г., Теория ортогональных рядов, пер. с нем., М., 1958;
Ы Джексон Д., Ряды Фурье и ортогональные полиномы,
пер. с англ., М., 1948; f(i] С е г е Г., Ортогональные многочле-
многочлены, пер. с англ., М., 1 <)и2; L71 А л е к с и ч Г., Проблемы сходи-
сходимости ортогональных рядоп, пер. с англ., М. 19В,'!; [8] Т г i-
с о m i P. G., Vorlesungen iiber Orthogonalreihen, 2 Aufl., В.,
1970; [9] О 1 e v s k i T A. M.. Fourier series with respect to gene-
general orthogonal systems, В., 1975; [10] M e н ь ш о в Д. Е., У л ь-
я н о в ГГ. Л., О метрической теории функций в Московском уни-
университете за пятидесятилетие, «Вести. Моск. ун-та. Сер. 1. Ма-
Математика, механика», 1967, JMi 5, с. 24—36; [11] Тала-
л я н А. А., Представление измеримых функций рядами, «Успе-
«Успехи матем. наук», 1960, т. 15, в. 5, с. 77—141; [12] Ульянов
П. Л., Решенные и нерешенные проблемы теории тригонометри-
тригонометрических и ортогональных рядов, там же, 1964, т. 19, в. 1, с. 3—
69; [13] Итоги науки. Математический анализ. 1970, М., 1971,
с. 5—264; [14] БурбакиН., Очерки по истории математики,
пер. с франц., М., 1963; L15] П а п л а у с к а с А. Б., Тригоно-
Тригонометрические ряды от Эйлера до Лебега, М., 1966.
ОРТОМОДУЛЯРНАЯ РЕШЕТКА — решетка (^"ну-
(^"нулем @) и единицей A), в к-рой для любого элемента а
существует ортодополнение я-1-, т. е. такой
элемент, что
1) яуй1-!, яла-1 —0; а11-—а;
2) а<1> =» а1 3s6х,
п выполняется ортомодулярный закон:
3) о<6 =?> b — av{b/\a-1).
В О. р. исследовались в основном дистрибутивность
и перспективность, неприводимость, модулярность пар,
свойства центра и идеалов, коммутант и разрешимость,
приложения к логике квантовой механики (см. [1],
12]).
Если 31 — произвольная Неймана алгебра, то сово-
совокупность Р (91) всех ее проекций является полной
О. р. При этом, если 21 — фактор, то на множестве
Р (Ш) можно определить размерности функцию. В за-
зависимости от множества значений этой функции фак-
факторы делятся на типы In, [M, Пх, П^, III (классифика-
(классификация Муррея — Неймана, [4]). Было установлено, что
решетки проекций факторов типа 1„ и Их являются
непрерывными геометриями, т.е. пол-
полными дедекиндовыми решетками с дополнениями, удо-
удовлетворяющими следующим двум аксиомам непрерыв-
непрерывности:
1) Ъл(\/аа)— v (Ь/\аа) для любого направленного
а е D а б D
множества индексов D и такого множества элементов
Ыа, а ? D\, что а'<а" влечет °а,<°а»;
2) условие, двойственное к 1).
Возникла задача построения абстрактной теории
размерности в рамках такого класса решеток, к-рый
нключил бы в себя, кроме модулярных решеток про-
проекций факторов типов 1„ и IIlt и немодулярные ре-
решетки проекций факторов остальных типов. Доказано
(см. [5], [6]) существование функции размерности на
полной О. р. с отношением эквивалентности, удовлет-
удовлетворяющим нек-рым дополнительным условиям. Этот
класс решеток включает в себя и решетки проекций
факторов, и непрерывные геометрии.
О. р., являясь естественным обобщением решеток
проекций факторов, в то же время составляют сущест-
существенно более широкий класс, поскольку многие свой-
свойства решеток проекций неверны для произвольных
О. р. Подобно тому как непрерывные геометрии коор-
динатизируются регулярными кольцами (см. [1]), О. р.
могут быть координатизированы бэровскими *-полугруп-
пами. Если полная О. р. модулярна, то она непрерыв-
непрерывна (см. [7]). Существует модулярная решетка с орто-
ортодополнениями, пополнение сечениями к-рой не орто-
модулярно (в то время как пополнение сечениями
полумодулярной решетки с ортодополнениями полу-
модулярно, и решетка проекций алгебры Неймана
иолумодулярна).
Лит.: [1] С к о р н я к и в ."I. А., Дрдркиндовы структуры с
допи.ипениями и регулярные кольца, М., 1!Ш1; [2] Итоги науки.
Алгебра. Топология. Геометрия, 1968, М., 1970; [3] Ф о ф а'н о-
в а Т. С, в сО.: Упорядоченные множества и решетки, в. 3, [Са-
[Саратов], 1975, с. 28—40; [4] Murray F., Neumann J.,
«Arm. Math.», 1936, v. 37, № 1, p. 11C—229;45] LoomisL.H.
«Mem. Amer. Math. Soc», 1955, Ml 18 p. 1—36- [6] M a e d a S.
«J. Sci. Hiroshima Univ., Ser. A.», 1955, v. 19, № 2, p. 211 —37;
[7] К a p 1 a n s k у I., «Ann. Math.», 1955, v. 61, Л1 3, p. 524—
541. T.C. Фофанова.
ОРТОНОРМИРОВАННАЯ СИСТЕМА —1) О. с. в с к-
торов — множество {ха} ненулевых векторов евк-
евклидова (гильбертова) пространства со скалярным про-
произведением (• , •) такое, что (ха, хр) = 0 при афр (ор-
(ортогональность) и (ха, ла)~1 (нормируемость).
М. И. Войцеховский.
2) О. с. ф у н к ц и й — система {ф/(ж)} функции
пространства L2(X, S, и.), являющаяся одновременно
ортогональной и нормированной в L'2(X, S, (х), то
есть
\ ср.-Ы Ф,- (х) rfu. = < .
Jx^"'^1 ' ^ \ 1 при i = j
(см. Нормированная система, Ортогональная сис-
система). В математич. литературе часто термин «орто-
«ортогональная система» означает «ортонормированная сис-
система». При исследовании данной ортогональной сис-
системы ее нормированность не играет существенной
роли. Тем не менее нормированность систем дает воз-
возможность более ясной формулировки нек-рых теорем
о сходимости рядов
в терминах поведения козффициентов {с^}. Такой тео-
теоремой является, напр., теорема Р и с с а — Ф и-
¦ш ера: ряд
по ортонормированной в L2\a, b] системе {ф/г()}1
сходится в метрике пространства L2\a, b] тогда и только
тогда, когда
Лит.: [1] Колмогоров А. Н., Ф о м и н С. В., Эле-
Элементы теории функций и функционального анализа, 5 изд., М.,
1981; [2] Качмаж С, Штейн га уз Г., Теория ортого-
ортогональных рядов, пер. с нем., М., 1958. -4. А. Талаляп.
ОРТОЦЕНТР треугольника — точка пере-
пересечения трех высот треугольника. О. треугольника
лежит на Эйлера прямой. Середины трех сторон, се-
середины отрезков, соединяющих О. с тремя вершинами,
и основания высот треугольника лежат на одной ок-
окружности. О. является центром окружности, вписанной
в ортоцентр и чески й треугольник,
т. е. треугольник, вершинами к-рого являются основа-
основания ВЫСОТ данного. П. С. Моденов.
ОСВЕЩЕНИЯ ЗАДАЧА — задача определения ми-
минимального числа направлений пучков параллельных
лучей или числа источников, освещающих всю границу
выпуклого тела. Пусть К — выпуклое тело п-мерного
линейного пространства Rn, a bd К и int К — соот-
соответственно граница и внутренность его, причем bd КФ
Ф4>. Наиболее известны следующие О. з.
1) Пусть I — нек-рое направление в пространстве
R". Точка х?Ъй К наз. освещенной извне
направлением I, если прямая, проходящая
через х параллельно I, проходит через нек-рую точку
у ^int К и направление вектора ху совпадает с /.
Ищется минимальное число с (Л') направлений в прост-
пространстве R", достаточное для освещения в этом смысле
всего множества bd К.
2) Пусть z — нек-рая точка множества R"\?.
Точка 2-?bd К наз. освещенной извне точ-
к о it z, если прямая, определяемая точками z и х,
проходит через нек-рую точку y^int Л' и векторы ху
и zy одинаково направлены. Ищется минимальное
число с' (К) точек из R"\K, достаточное для освеще-
освещения в этом смысле всего множества bd К.
3) Пусть z — нек-рая точка множества bd К. Точка
.rgbd К наз. освещенной изнутри т о ч-
к о й гфх, если прямая, определяемая точками z и х,
проходит через нек-рую точку y?int К и векторы
ху и zy противоположно направлены. Ищется мини-
минимальное число р(К) точек из bd К, достаточное для
освещения изнутри всего множества bd К.
4) Система точек Z={z|z?bd К} наз. фиксиро-
фиксированной для К, если она обладает свойствами:
a) Z достаточна для освещения изнутри всего множества
bd К; б) Z не обладает никаким собственным подмно-
подмножеством, достаточным для освещения изнутри мно-
множества bd К. Ищется максимальное число р'{К) точек
фиксированной системы для тела KcR"-
Задача 1) была поставлена в связи с Хадвигера ги-
гипотезой (см. [1]): минимальное число тел Ь(К), гомо-
гомотетичных ограниченному К с коэффициентом гомоте-
гомотетии к, 0</с<1, достаточное для покрытия К, удов-
удовлетворяет неравенству ге-f-l <6(Л')<2", причем зна-
значение Ь(К)-~2п характеризует параллелепипед. Для
ограниченного К cr R"c(K)~Ъ(К). Если К неограни-
неограниченно, то с(К)<^.Ь(К) и существуют такие тела, что
с(К)<Ь(К) или с(К)-= Ь(К)=оэ (см. [1]).
Задача 2) поставлена в связи с задачей 1). Для ог-
ограниченного A'crR" верно равенство с(К)=с' (А*).
Если же К неограниченно, то е'(А')<6(А') и с(Л')<
<с'(Л'). Число с'(К) для любого неограниченного
A'cR3 принимает одно из значений: 1, 2, 3, 4, оо
(см. [1]).
Решение задачи 3) имеет вид: число р(К) определено
тогда и только тогда, когда К отлично от конуса.
В этом случае
причем р(К)~ п-\-1 характеризует n-мерный симплекс
пространства R" (см. [1]).
Для задачп 4) (см. [2]) предполагается, что при огра-
ограниченном KdR" верно неравенство
р'(К)<2а.
Каждая из О. з. тесно связана с нек-рым гттециал!.
ным покрытием тела К (см. [1]).
Лит.: [1] Б о л т я н с к и й В. Г., С о л т а н П. С, Ком-
Комбинаторная геометрия различных классов выпуклых множеств,
Киш., 1978; [2] GriinbaumB., «Acta math. Acad. sci~
hung.», 1964, v. 15, p. 161—63. П. С. Солтан.
ОСЕВОЙ ВЕКТОР, аксиальный вектор,
псевдовектор, вектор в ориентированном про-
пространстве, к-рый при изменении ориентации прост-
пространства на противоположную преобразуется в про-
противоположный вектор. Пример О. в.— векторное про-
произведение векторов. БСд-з.
ОСНАЩЕННОЕ ГИЛЬБЕРТОВО ПРОСТРАНСТВО —
гильбертово пространство Н с выделенным в нем ли-
линейным всюду плотным подмножеством ФсД, на
к-ром задана структура топологического векторного
пространства так, что вложение непрерывно. Это
вложение порождает непрерывное вложение сопря-
сопряженных пространств Ф'сЯ' и цепочку непрерывных
вложений ФсЯсФ' (с помощью стандартного отож-
отождествления Н'=Н). Наиболее содержательным яп-
ляется случай, когда оснащение Ф — ядерное прост
ранство. Здесь верно следующее усиление спектраль
ной теоремы для самосопряженных операторов, деп-
ствующих в Н: любой такой оператор А. непрерывно
(в топологии Ф) переводящий Ф в себя, обладает пол-
полной системой обобщенных собственных функции {1'а,
а?21} (Ж — нек-рое множество индексов), т. е. та-
таких элементов Fa^O', что для любого
причем множество значений функции а-*-Аа, а?21,
содержится в спектре оператора А и имеет полную
меру относительно спектральной меры в/(к), /?//,
A,?R, любого элемента /?//. Полнота системы озна-
означает, что ф/0, Fa (ф)т=0 для любого ф?Ф хотя бы
при одном а ?91. Кроме того, для любого элемента
фбФ существует его разложение по системе обобщен-
обобщенных собственных функций {Fa, а?Щ, обобщающее
известное разложение по базису собственных векторов
для оператора с дискретным спектром.
Приме р: разложение в интеграл Фурье
R ' 'ft 'il li I С J!l
[eisx, s?R}—система обобщенных собственных функ-
функций оператора дифференцирования, действующего в
LS(R), возникающая при естественном оснащении этого
пространства с помощью пространства Шварца S(R).
Аналогичные утверждения верны и для унитарных
операторов, действующих в О. г. п.
Лит.: [1] Г е л ь ф а н д И. М., Ш и л о в Г. Е., Некоторые
вопросы теории дифференциальных уравнений, М., 1958: [2]
Г е л ь ф а и д И. М., В и л е н к и и Н. Я., Некоторые приме-
применения гармонического анализа. Оснащенные гильбертовы про-
пространства, М., ИМИ; [Я] Б е р е э а н с к и й Ю. М., Разложение
по собственным функциям самосопряженных операторов, К.,
190Г1. Р. А. Минлос.
ОСНАЩЕННОЕ МНОГООБРАЗИЕ — гладкое много-
многообразие с фиксированной тривиализацией нормаль-
нормального расслоения. Более точно, пусть гладкое п-мерное
многообразие М вложено в Rn + ft и пусть (^-мерное)
нормальное расслоение v, отвечающее этому вложе-
вложению, тривиально. Оснащением многообразия М, от-
вечающпм этому вложению, нал. любая тривиализа-
ция расслоения v; при этом одному и тому же вложе-
вложению могут отвечать разные оснащения. О. м. введены
в 1937 (см. [11) для доказательства того, что группы
борОизмов О. м. размерности п, лежащих в Rn+ ,
изоморфны гомотопич. группе Пп+k (Sn)\ на этом пути
Пыли вычислены группы nn + 1(S") и яп + 2E").
Лут.: [11 If о п т р я г и н Л. С, Гладкие многообразия и
их применения в теории гомотопий, 2 изд., М., 1976.
Ю. Б. Рудяк.
ОСНОВАНИЕ ИЗГИБАНИЯ - сопряженная сеть
на поверхности F и ее изгибании /¦** вне точек их
конгруэнтности. О. п. характеризуется тем.
что и з г и б - - отношение нормальных кривизн к
и А;* в соответствующих по изометрии точках F и F*
вдоль соответствующих направлений — имеет окстре
мальные значения вдоль направлений О. и.
Лит.: A] К а г а н В. Ф., Основы теории поверхностей в
тензорном изложении, ч. 2, М.— Л., 1948. Ы. 11. Войцеховспий.
ОСНОВАНИЯ ГЕОМЕТРИИ — раздел геометрии, в
к-ром исследуются основные понятия геометрии, со-
соотношения между ними и связанные с ними вопросы.
Важная роль основных понятий и соотношений
между ними, на базе к-рых строятся определения фи-
фигур и доказываются геометрич. предложения, отме-
отмечается уже в работах античных геометров. Так, раз-
развивая дедуктивпый метод в геометрии, они указывали
на особую роль основных понятий, аксиом и постула-
постулатов, составляющих фундамент геометрии. В «Нача-
«Началах» Евклида C в. до н. э.) аксиомам и постулатам
предпослана день определений всех понятий, к-рые
используются в дальнейшем изложении. Среди этих
определений особое место принадлежит понятиям
«точка», «прямая», «плоскость», определения к-рых
не опираются на другие геомотрич. понятия. Сами
определения этих основных понятий с гео-
геометрия, точки зрения неудовлетворительны, т. к. они
выражают лишь характерное фнзич. свойство (напр.,
«точка есть то, что не имеет частей», т. е. под точкой
понимается малое физически неделимое тело). Поэтому
уже в трудах геометров, написанных почти одновре-
одновременно с «Началами», содержатся многочисленные
комментарии и критич. анализ определений основных
и других геометрич. понятий, аксиом и постулатов.
Но это были лишь уточнения, не затрагивающие ос-
основы определений. По существу, доказательства мно-
многих F-еометрич. теорем опирались в основном на на-
наглядность чертежа, на физич. осуществимость необхо-
необходимых геометрич. построений, а не выводились строго
логически из аксиом и постулатов. Только в 19 в.
и особенно в нач. 20 в. появляются работы, в к-рых
выясняется все глубокое значение основных понятий
и соотношений между ними для логически безупреч-
безупречного дедуктивного метода построения геометрии и ео
обоснования. Причем во многом этому углубленному
анализу основ геометрии способствовало открытие не-
неевклидовой геометрии Лобачевского A826). Резуль-
Результаты по обоснованию евклидовой геометрии на основе
тех же принципов и понятий, что и в «Началах» Евк-
Евклида, содержатся в работах Дж. Пеано (G. Реапо,
1894), М. Паша (М. Pasch, 1882), М. Пиери (М. Pieri,
1899), Д. Гильберта (D. Hilbert) и др. Наибольшую
известность получила Гильберта система аксиом евк-
евклидовой геометрии A899). Добиваясь логически удов-
удовлетворительного построения евклидовой геометрии,
Д. Гильберт выделил 5 групп аксиом, показал их не-
необходимость и достаточность для построения всей
евклидовой геометрии. Вместе с тем впервые была
проведена логич. обработка всей системы, выяснена
непротиворечивость системы с помощью построения
числовой модели, установлена независимость групп
аксиом, а также полнота системы. В отличие от кон-
концепции пространства как «места» для всех фигур, про-
проводимой в «Началах», Д. Гильберт рассматривает его
как множество всех «точек», «прямых», «плоскостей»
и фигур, построенных на основе этих понятий.
Набор основных понятий в системе Гильберта был
заимствован (н уточнен) из «Начал», однако эта система
является, по существу, чисто геометрич. схемой, сво-
свободной от ссылок на наглядность чертежа. Вместе с тем
язык геометрии, построенной на основе системы Гиль-
Гильберта, почти не отличается от языка «Начал».
Почти одновременно с системой Гильберта появи-
появились и др. системы аксиом евклидовой геометрии.
Так, в системе Ф. Шура (F. Schur, 1909) в качестве
основных понятий были «точка», «отрезок» и т. д.,
а вместо «конгруэнтности» фигур в этой системе вво-
вводилось понятие «движение». Введение понятия «дви-
«движение» позволило применить в геометрии групповой
подход к исследованию движений, алгебраизпровать
методы исследования. Упомянутые выше геометрич.
схемы не полностью удовлетворяют требованиям даль-
дальнейшего обобщения понятия пространства и др. поня-
понятий и, кроме того, недостаточно «алгебраичны».
Новые подходы к обоснованию евклидовой геомет-
геометрии потребовали выработки нового «языка», с помощью
к-рого оказывается возможным провести соответствую-
соответствующие дальнейшие обобщения понятий, алгебраизацию
доказательств, классификацию объектов и т. д. Одной
из распространенных схем основания евклидовой гео-
геометрии, в к-poii сконцентрированы возможности об-
обобщений, перевода на язык алгебры гоометрич. поня-
понятий, является система аксиом, предложенная Г. Вей-
лем (Н. Weil, 1916). Ниже приводится одна из тран-
транскрипций схемы Вейля.
Трехмерное евклидово пространство R;l определя-
определяется как множество, состоящее из элементов двух
родов — «точек» и «векторов», удовлетворяющих сле-
следующим 4 группам аксиом:
I группа — аксиомы, определяющие соотношения
между точками и векторами. 1г. Существует по мень
шей мере одна точка. 12- Каждой упорядоченной паре
точек поставлен в соответствие один и только один
вектор. 13. Для каждой точки А и каждого вектора а
существует одна п только одна точка В такая, что
АВ=а (АВ есть вектора). 14. Если AB = CD, то АС=
= BD.
На основе этой группы аксиом определяется сумма
векторов, к-рая удовлетворяет требованиям коммута-
коммутативности и ассоциативности. Существует нуль-вектор,
противоположный вектор. Векторы по сложению об-
образуют группу.
II группа — аксиомы, описывающие операцию ум-
умножения вектора на число. Пг. Каждому вектору а и
каждому к ? R поставлен в соответствие определен-
определенный вектор к» (ка наз. произведением вектора а на
число к). П2. Умножение вектора на 1 не изменяет
вектора. П3. Умножение вектора на число дистрибу-
дистрибутивно относительно сложения чисел (kl-\-k2)a=k1a-{~
-ffc2a. 114- Умножение вектора на число дистрибутив-
дистрибутивно относительно сложения векторов k(at -f- «2)=^et;i+
+fca2- Ib- Умножение вектора на число ассоциативно
1\(к1а)=(к1кг)а.
С помощью операций сложения и умножения на
число определяется линейная комбинация векторов,
их линейная зависимость.
III группа определяет размерность пространства,
Illf. Существуют три линейно независимых вектора,
но всякие четыре — линейно зависимы.
Эта аксиома имеет топологич. характер; из нее
вместе со второй группой аксиом следует, что R3
является топологич. пространством размерности 3.
Первые три группы аксиом определяют трехмерное
аффинное пространство.
IV группа определяет метрцч. свойства. IVл. Любым
двум векторам a ub поставлено в соответствие опреде-
определенное число (скалярное произведение) («, 6)=/,
l?R. IV2. Симметричность скалярного произведе-
произведения: (я, b)={b, a). IV3. Дистрибутивность скалярного
произведения (я, b-\-e)=(a, b)-\-(a, с). IV4. Для fc?R
имеет меето (я, kb)=k(a, Ь). IV5. Скалярный квадрат
вектора неотрицателен (я, а)^0, причем (я, я)—О
только для нуль-вектора.
На основе IV группы аксиом определяется расстоя-
расстояние между точками, угол между векторами и т. д.;
с помощью векторов — «отрезки», «прямые», «плос-
«плоскости» и т. д.
Схема Вейля допускает обобщение на случай любой
размерности, с помощью соответствующего изменения
аксиом в эту схему включаются гиперболич. и эллип-
тич. пространства и т. д.
Система аксиом Вейля евклидовой геометрии яв-
является непротиворечивой, независимой и удовлетво-
удовлетворяет требованию полноты (категоричности, или мини-
минимальности). Непротиворечивость устанавливается с по-
помощью числовой модели: упорядоченным тройкам
чисел (х1, х2, xs), х1 ?R; ?=1, 2, 3, ставятся во взаимно
однозначное соответствие «точки» пространства R3.
Вектор с началом в (jc\, х\, х\) и концом в (х\, х\, xf)
определяется тройкой a—(a1, a2, a3), a' = x!i—х[; ?=
= 1, 2, 3. Сумма векторов (о1, а2, а3) и (Ь1, Ь2, Ь3) оп-
определяется тройкой (a^-1-fc1, а2+Ь2, а3-\-Ь3), произве-
произведение вектора (а1, а2, а3) на число fc?R есть тройка
(ка1, ка2, кая). Скалярное произведение векторов (о1,
а2, а3) и (б1, Ь2, Ь3) выражается числом Ej^a'b'. Ба-
зисныо векторы (тройка линейно независимых векто-
векторов) можно изображать тройками el=A,0,0), p2=
= @,1,0), е3= @,0,1). Для доказательства независи-
независимости аксиом друг от друга и независимости групп ак-
аксиом строится интерпретация системы, получающейся
из данной путем замены какой-либо ее аксиомы ее от-
отрицанием. Полнота системы выводится из полноты
множества действительных чисел.
В качестве основных понятий при создании схемы
евклидовой геометрии могут быть положены геомет-
рич. преобразования. Так, в системе аксиом Ф. Бах-
мана (P. Bachmann) в качестве такого понятия вво-
вводится преобразование симметрии. С помощью симмет-
симметрии, порождающих группу движений евклидовой
(метрической) плоскости, определяются «точки» и
«прямые» как инволютивные элементы этой группы.
Теоретико-групповые отношения являются основой
при определении понятий «инцидентность», «ортого-
«ортогональность» и т. п., геометрич. доказательства заме-
заменяются вычислениями, переводятся на язык алгебры.
Обоснование евклидовой геометрии влияло и на
разработку вопросов обоснования неевклидовых гео-
геометрий. В кон. 19 — нач. 20 вв. сформировались ос-
основные современные методы и подходы в О. г. Новые
подходы к понятиям, лежащим в основе геометрии,
были разработаны Б. Римаиом (В. Riemann), С. Лп
(S. Lie). Ф. Клейном (F. Klein), А. К эли (A. Cayley)
и др. В основу геометрич. понятий были положены
многомерные многообразия, группы преобразований,
действующих на многообразиях, инварианты групп
преобразований и т. п.
Групповой подход впервые был четко сформулиро-
сформулирован в эрлангенской программе Ф. Клейна: геометрич.
пространство определяется как множество Ф с фикси-
фиксированной группой Q его преобразований; объектом
геометрии является изучение Q-инвариантных свойств
пространства. (Напр., n-мерное аффинное простран-
пространство А" определяется как множество, на к-ром просто
транзитивно действует векторная группа размернос-
размерности п.) С. Ли, Ф. Клейн, А. Кэли провели исследование
групп преобразований, на основе к-рого возникают
новые возможности в классификации и обосновании
евклидовой и неевклидовых геометрий как геометрий
определенных групп преобразований. Геометрия ста-
становится учением об инвариантах групп преобразова-
преобразований, и О. г. опирается на теорию групп.
В работах Б. Римана был разработан метрич. под-
подход к О. г. Геометрич. пространство рассматривается
как множество, снабженное метрикой, к-рая удовлет-
удовлетворяет тем или иным аксиомам. Б. Риман показал, что
все внутренние свойства пространства определяются
заданной квадратичной дифференциальной формой
(кривизна, геодезич. линии и т. д.), тем самым были
открыты широкие классы различных метрич. геомет-
геометрий. Впервые классификация пространств и их гео-
геометрий была осуществлена на метрич. основе. Б. Ри-
Риман указал на особую роль выбора координат в точеч-
точечном многообразии для исследования самих квадратич-
квадратичных форм. Так, для пространства постоянной рпмано-
вой кривизны Б. Риман привел стандартный вид,
к к-рому может быть приведена квадратичная форма
путем соответствующего выбора координат.
Координатный метод евклидовой геометрии был
обобщен для различных пространств, а также нашел
развитие в дифференциальной геометрии; понятие
многообразий, опирающееся на выбор координатных
систем, получает многочисленные применения в гео-
геометрии. Групповой подход к исследованию преобра-
преобразований дифференциально-геометрич. объектов по-
позволил создать теорию инвариантов метрических (ква-
(квадратичных) форм. Эта теория инвариантов групп
преобразований явилась основой для построения и
логич. обоснования современно!! дифференциальное!
геометрии. В качестве одного п.ч основных понятий
выкристаллизовалось понятие геометрич. объекта, гео-
геометрия рассматривается как геометрических объектов
теория. Понятие дифференцируемого многообразия
позволяет дать строгие определения дифференцнально-
геометрич. объектам, в частности обосновать методы
анализа в геометрии и геометрич. методы в анализе.
Обоснование евклидовой (и, вообще, любой) гео-
геометрии, опирающееся на определенную систему ак-
аксиом, обнаруживает особую роль теоретико-множест-
теоретико-множественных принципов при логич. анализе систем аксиом.
Именно, независимость и непротиворечивость системы
аксиом может быть установлена путем построения
числовой модели, реализующей эту систему. Поэтому
теория множеств в О. г. является своего рода эталоном
безупречного логич. построения геометрич. теории.
Геометрич. аксиомы непрерывности (и полноты) по
существу являются нек-рыми эквивалентами теорети-
теоретико-множественных аксиом.
Построение геометрии над определенным полем
обосновывается путем применения попятим теоретико-
множественного характера. Начиная с создания дека-
декартовой аналитич. геометрии, идея отображения мно-
множества точек на множество действительных чисел
(или на произвольное числовое множество) приобре-
приобретает большое значение для О. г. Развитие этой идеи
позволяет определить и классифицировать геометрии по
тому числовому множеству, над к-рым они построены.
В О. г. широко применяются теоретико-множествен-
теоретико-множественные методы для изучения геометрич. преобразований.
Как уже отмечалось выше, инварианты групп преобра-
преобразований являются предметом изучения в определенной
этой группой геометрии. Важное применение теории
инвариантов (проективных) преобразований нашел Ф.
Клейн для интерпретации неевклидовых пространств
и доказательства непротиворечивости неевклидовых
геометрий. Углубленному анализу подверглись такие
понятия, как «угол», «ортогональность» и т. д. Исследо-
Исследования проективных комплексных пространств, раз-
различных проективных мероопределений имеют боль-
большое значение в классификации пространств с опреде-
определенной структурой.
В О. г. применяются также топологич. методы клас-
классификации многообразий, с помощью этих методов вы-
выявляются наиболее существенные различия между
классами и типами многообразий, исследуются гло-
глобальные их свойства.
Основные методы и подходы в О. г.— синтетический,
групповой и метрический — имеют значение и в со-
современных исследованиях в этой области геометрии.
Напр., обобщением идей Б. Римана в О. г. является
инфинитезимальный подход, при к-ром геометрич.
структура определяется заданием поля нек-рых инфи-
нитезимальных величин (напр., финслеровой мет-
метрики, связности и т. п.). Многие задачи физики и
механики при этом допускают геометрич. интерпре-
интерпретацию и при их решении используются геометрич.
соображения. Вообще, все современные системы ак-
аксиом евклидовой (и неевклидовой) геометрии исполь-
используют в различной степени все три подхода в О. г.
Изучение средств, используемых в доказательствах
теорем на основе данной системы аксиом, является
одной из важных проблем в О. г. В «Началах» Евкли-
Евклида для доказательств применялась классич. логика
Аристотеля. Много внимания уделил этим вопросам
Д. Гильберт, наметивший основные задачи математич.
логики. Непротиворечивость систем геометрич. ак-
спом устанавливается путем построения числовых
моделей этих систем и их логического исследования.
Значительное место в О. г. занимают вопросы изме-
измерения отрезков, плошадей, объемов. Понятия меры
отрезка, площади, объема основываются на опреде-
определенных группах аксиом. Так, напр., теория площадей
многоугольников на евклидовой плоскости в системе
аксиом Гильберта обосновывается аксиомами, относя-
относящимися только к плоскости и независимо от аксиом
непрерывности (см. Неархимедова геометрия, Иепас-
калева геометрия).
В О. г. исследуется проблема о материальных объек-
объективных истоках геометрич. понятий и систем аксиом.
Одним из принципов построения геометрич. систем
долгое время являлся принцип физич. осуществимости
системы на какой-либо материальной модели. Как
отмечалось выше, еще в «Началах» была сделана по-
попытка дать истолкование основных понятий с точки
зрения их физич. свойств. В кон. 19 в., после откры-
открытия геометрии Лобачевского, вновь возник вопрос
об объективной возможности других, отличных от
евклидовой, геометрий. Проблему объективного су-
существования неевклидовых геометрии многие геометры
решали путем построения физич. моделей, с помощью
к-рых пытались убедиться в независимости и непроти-
непротиворечивости геометрич. систем аксиом. Так, Н. И. Ло-
Лобачевский пытался обосновать непротиворечивость
выводов, вытекающих из его аксиомы о параллель-
параллельных, путем физич. измерений дефектов треугольников
гигантских размеров, вершины к-рых располагались
на удаленных от Земли космич. телах, чтобы убе-
убедиться в том, что дефекты различны для различных
треугольников и что сумма внутренних углов тре-
треугольников может быть меньше двух прямых углов.
Попытку обосновать существование различных метрич.
геометрий предпринял Г. Гельмгольц (Н. Helmholtz).
в работе, написанной вскоре после появления резуль-
результатов Б. Римана. Основным понятиям, к-рыми опе-
оперирует метрич. геометрия, Г. Гельмгольц дал физич.
истолкование, в основу геометрич. свойств простран
ства он положил нек-рые физич. законы, из к-рых вы-
вытекает возможность построения геометрии этого прост-
пространства. Эвристическим путем из основных физич.
законов Г. Гельмгольц получил метрику пространства
в виде дифференциальной формы, к-рая, как показал
Б. Риман, определяет все внутренние свойства прост-
пространства. Вместо гипотез, лежащих в О. г., предложен-
предложенных Б. Риманом, Г. Гельмгольц рассматривал факты,
из к-рых вытекали те же выводы в метрич. геометрии,
подчеркивая тем самым опытную проверку справед-
справедливости (непротиворечивости) этих выводов.
Объективно работы по опытной проверке геометрич.
систем служили распространению новых геометрич.
идей, способствовали появлению углубленного логич.
анализа геометрич. систем, выработке современных
основных требований к этим системам. Вместе с тем
попытки физич. обоснования геометрии способстно
вали проникновению геометрических идей и мето-
методов в различные области математики, физики и ме-
механики.
О. г. имеют большое значение в методологии гео-
геометрии. В процессе преподавания современных кур-
курсов геометрии в университетах и педагогич. вуза v
раздел О. г. занимает одно из центральных мест.
13 связи с этим все большую роль играет выбор системы
основных понятий и аксиом, чтобы «сократить» путь
от самих аксиом до выводимых из них содержатель-
содержательных теорем, находящих практич. применение (в част-
частности, в решении задач).
Лит.: [1] Начала Евклида, кн. 1 —15, пер. с греч., М.,
1948—50; 12] Гильберт Д., Основания геометрии, пер. с
нем., М.~ Л., 1948; [3] В е б л е н О., У а й т х е д Д ж., Ос-
Основания дифференциальной геометрии, пер. с англ., М., 1949;
[4] Об основаниях геометрии, М., 1956; [5] Каган В. Ф.,
Основания геометрии, ч. 1—2, М.— Л., 1949—56; [6] К а г а н
В. Ф., Очерки по геометрии, М., 19вЛ; [7J Б у я е м а н Г.,
Геометрия геодезических, пер. с англ., М., 1902; [8] Ефи-
Ефимов Н. В., Высшая геометрия, li изд., М., 1Н78; [9] Бах-
ман Ф., Построение геометрии на основе понятия симметрии,
пер. о нем., М., 1969; [10] РозенфельдБ. А., История не-
неевклидовой геометрии, М., 1976; til] Погорелов А. В.,
Элементарная геометрия, 2 изд., М., 1974; [12] Шоке Г., Гео-
Геометрия, пер. с франц., М., 1970; [13] Д о н е д д ю А., Евкли-
Евклидова планиметрия, пер. с франц., М., 1978; [14] К а р т е с и Ф.,
Введение в конечные геометрии, пер. с англ., М., 1980.
Л. А. Сидоров.
ОСНОВНОГО ТИПА АЛГЕБРАИЧЕСКАЯ ПОВЕРХ-
ПОВЕРХНОСТЬ, общего типа алгебраическая
поверхность,— поверхность одного из самых
обширных классов алгебраических поверхностей в клас-
классификации Энрикеса. А именно, гладкая проективная
поверхность X над алгебраически замкнутым полем к
наз. О. т. а. п., если
где К — Кодаиры размерность. 9то условие равно-
равносильно тому, что для нек-рого целого ге>0 линейная
система \пК\, где К — канонич. дивизор на X, опре-
определяет бирациональное отображение поверхности X
на ее образ в PN для нек-рого N. Всякая О. т. а. и.
обладает бирациональным морфизмом на свою мини-
минимальную модель.
Минимальные О. т. а. и. характеризуются (см. [1],
[3], [6]) каждым из следующих наборов свойств:
а) К*>0 и KD^O для любого эффективного диви-
дивизора D;
б) Яа>0 и Р2>2, где P2—dim\2K\ + \— двукратный
род X;
в) .Ка>0 и поверхность X не рациональна;
г) существует такое целое п0, что при любом п^п0
отображение Ф,,^, определяемое системой \пК\, яв-
является бирациональным морфизмом поверхности X на
ее образ в pdlmlnKl. для о. т. а. п. существуют (см.
[2], [3], [6], ?10]) соотношения (вида неравенств) между
численными характеристиками. Пусть pg — геомет-
рич. род и q — иррегулярность поверхности X, тогда
для минимальной О. т. а. п. имеют место следующие
неравенства:
1) <КРе'<
2) pg<— A!2-f 2, если К2 четно, pg<— К*-{-— , если
К- нечетно (эти два неравенства наз. неравенст-
неравенствами Н стера);
3) А'2<ЗС2, где С2 — второй класс Чжэня поверх-
поверхности X (или топологическая эйлерова характери-
характеристика).
Наиболее полный результат о кратноканонич. от-
отображениях ц>„к О. т. а. п. есть теорема Б о м-
бьери — Кодаиры: пусть X — минимальная
О. т. а. п. над алгебраически замкнутым полем харак-
характеристики 0, тогда отображение
является бирациональным морфизмом на свой образ
при всех п>5. Существуют (см. [5], [8], (9J) О. т. а. п.,
для к-рых ф4к уже не обладает этим свойством.
Лит.: Ш Алгебраические поверхности, М., 1965 (Тр. Матем.
ин-та АН СССР, т. 75); [2] Б о г о м о л о в Ф. А., «Изв. АН
СССР. Сер. матем.», 1978, т. 42, с. 1227—87; [3] Beauville
A., Surfaces algebriques complexes, P., 1978; [4] В о m b 1 e-
r i E., «Publ. Math. IHES», 1972, № 42, p. 171—219; [5] В о m-
bieri E., Cataneso F., The tricanonical map of surface
withK=2, pg=0, C. P. Ramanujam, Atribute, В.— [е. a.], 1978,
p. 279—90; [6]Bombieri E., H u s e m о 1 1 e г D., Classi-
Classification and embeddings of surfaces, Proceedings of Symposia in
Pure Math., .\l« 29, Algebraic geometry, 1974, p. 329—420; t7]
Horikawa E., «Ann. Math.», 1976, v. 104, p. 357—87; [8]
его же, «Invent, math.», 1976, v. 37, p. 121—55- 1978/79
v. 50, p. 103—28; [9] Kodaira K., «J. Math. Soc. Japan»;
1908, v. 20, p. 170—92; [10] Miyaoka Y., «Invent, math.»
1977, V. 42, p. 225 — 37. ' В. А. Псковских.
ОСОБАЯ ТОЧКА —1) О. т. аналитической
функции /(г) — препятствие для аналитического
продолжения элемента функции j(z) комплексного
переменного z вдоль какого-либо пути на плоскости
этого переменного.
Пусть аналитическая функция f(z) определена не-
некоторым вейерштрассовым элементом
(?/(?, Я),/*), состоящим из степенного ряда
и его круга сходимости _
U a, R) = {z?C:\z-S,\<R}
с центроги J^oo и радиусом сходимости Д>0. Рассмот-
Рассмотрим всевозможные пути L : [0,1]—»-С, т. е. непрерыв-
непрерывные отображения L : z~<p(<) отрезка^ 0<г<1 в рас-
расширенную комплексную плоскость С, начинающиеся
в центре этого элемента ?, ?=ф@). Если аналитич.
продолжение данного элемента возможно вдоль лю-
любого такого пути в любую точку z?C, то получаю-
получающаяся при этом полная аналитич. функция /(г) сво-
сводится к константе: /(z)=const. Для нетривиальных же
аналитич. функций f(z) Ф const характерно существо-
существование препятствий для аналитич. продолжения вдоль
нек-рых путей L.
Пусть точка а расширенной плоскости С располо-
расположена на пути Li : z— q>i(f). а=ф1.(т1), 0<Ti<l,
4>i@)^?, и на пути L2 ¦ z—ф2(*), а=ф2(т2), 0<т2<1,
Фа(О)—S. причем аналитич. продолжение вдоль if
и L2 осуществимо во все предшествующие точки z=
---«Pi(/), 0<*<Тц и z—<рг(*Ь 0<г<т2. Два таких пути
Li и ?2 наз. эквивалентными по отношению
к аналитич. продолжению данного элемента (U(?, R),
/>) в точку а, если для любой окрестности V(a) точки а
в С существует такое число е>0, что вейерштрассов
элемент, получаемый из ({/(?, R), /j) посредством
аналитич. продолжения вдоль if до какой-либо точки
г'-=ф1(т'), Tj—е<т'<Т], может быть продолжен вдоль
нек-рого пути, расположенного в V(a), в элемент,
получаемый посредством продолжения вдоль L2 из
(U(t,, R), U) до какой-либо точки г"=ф2(т"), т2—8<
<т"<т2.
Если аналитич. продолжение в точку а осущест-
осуществимо вдоль нек-рого пути L, то оно возможно и вдоль
всех путей класса эквивалентности {i}, содержащего L.
В этом случае пара (а, {?}) наз. регулярной,
или правильной; она определяет однозначную
регулярную ветвь аналитич. функции f(z) в окрест-
окрестности точки V(a).
Если же аналитич. продолжение вдоль нек-рого
пути L : г=ф(г), 0<i<l, ф(О)=Е;, проходящего через
а, а^ф(т), 0<т<1, осуществимо во все точки ф@>
0<?<т, предшествующие а, но не осуществимо в точ-
точку а=ф (т), то а есть особая точка при ана-
аналитическом продолжении элемента
({/(?, R), /j) вдоль пути L. В этом случае она
будет особой и при продолжении вдоль всех проходя-
проходящих через а путей класса эквивалентности {?}. Пара
(а, {?}), состоящая из точки а?С и класса эквива-
эквивалентности {L} путей L, проходящих через а, для каж-
каждого из к-рых точка а особая, наз. особой точ-
точкой аналитической функции f(z), опре-
определяемой элементом ({/(?, R), f^). Две О. т. (a, {L})
и (Ь, {М}) считаются совпадающими, если а=Ъ и со-
совпадают классы{L} и {М}. При этом точка а расширен-
расширенной комплексной плоскости С наз-. проекцией,
или z-к о о р д и н а т о й, О. т. (а, {?}); говорят
также, что О. т. (a, {L}) расположена над точкой
а?С. В общем случае над одной и той же точкой' а?0
могут располагаться несколько и даже счетное мно-
множество различных особых и регулярных пар (а, {?}),
получающихся при апалитич. продолжении одного и
того же элемента (?/(?, R), fr).
Если радиус сходимости исходного ряда A) Л<оо,
то на окружности Г= {z?C : |z—?|—Л} круга схо-
димости U(t,, R) непременно имеется хотя бы одна
особая точка а элемента (U(?, Л), /»),
то есть О. т. аналитич. функции f(z) при продолжении
вдоль путей г=ф((), 0<:<<:1, класса {L} таких, что
-=ф@€^(?' ^) ПРИ 0<*<1, а=фA). Иначе говоря,
О. т. элемента (U(?, Л), /g) — это такая точка а?Г,
что непосредственное аналитич. продолжение элемента
(?/¦(?, ДЬ/g) из круга t/(?, Л) в любую окрестность
V(a) невозможно. В этой ситуации и вообще во всех
случаях, когда отсутствие явного описания класса
путей {L} не может повести к недоразумениям, огра-
ограничиваются обычно только указанием z-координаты
О. т. а. Изучение расположения О. т. аналитич. функ-
функции в зависимости от свойств последовательности
коэффициентов {cfc}?L0 исходного элемента (U(С, Л),
/») является одним из важных направлений исследо-
исследований в теории функций (см. Адамара теорема муль-
мультипликационная, Звезда элемента функции, а также
[1J, [3], [5]). Известно, напр., что О. т. ряда
где Ь?С, |Ь[<1, й>2 — натуральное число, запол-
заполняют всю границу Г={г?С : |z|^=l} его круга схо-
сходимости U(О, 1), хотя сумма этого ряда непрерывна
всюду в замкнутом круге U@, i)={z?C: fz|<l}.
Здесь окружность Г есть естественная граница ана-
аналитич. функции /0(z), аналитич. продолжение /0(z) за
пределы круга {7@, 1) невозможно.
Пусть в достаточно малой окрестности V(a)— {z?C :
\z—a\<R} точки афоо (или F(oo)={z?C : \z\ >Л})
аналитич. продолжение элементов, получаемых вдоль
путей определенного класса {L}, возможно во все
точки, отличные от а, т. е. по всем путям, рас-
расположенным в проколотой окрестности V' (а) =
= {z?C : 0<|z—а|<Л} (соответственно V'(<х>)=
= {zgC: Л<|г|<оо}); тогда О. т. (a, {L}) наз. изо-
изолированной особой точкой. Если при этом аналитич.
продолжение элементов, получаемых вдоль путей
класса {L}, по всевозможным замкнутым путям, рас-
расположенным в V (а), не изменяет этих элементов, то
изолированная О. т. (а, {?}) наз. особой точ-
точкой однозначного характера. Такая
О. т. может быть полюсом или существенно особой
точкой: если существует бесконечный предел lim f{z)—
= оо при стремлении z-^-a вдоль путей класса {?}, то
О. т. однозначного характера (а, {?}) наз. полюсом;
если не существует никакого конечного или бесконеч-
бесконечного предела lim f(z) при стремлении z-+-a вдоль путей
класса {?}, то (а, {?}) — существенно особая точка;
случай конечного предела соответствует регулярной
паре (в, {?}). Если же аналитич. продолжение эле-
элементов, получаемых вдоль путей класса {?}, по зам-
замкнутым путям, окружающим в V (а) точку а, изменяет
эти элементы, то изолированная О. т. (а, {?}) наз.
ветвления течкой, или особой точкой мно-
многозначного характера. Класс точек вет-
ветвления, в свою очередь, подразделяется на алгебраи-
алгебраические точки ветвления и трансцендентные точки
ветвления (включая логарифмические точки ветвле-
ветвления). Если после нек-рого конечного числа rn^'l
однократных обходов точки а в одном п том же направ-
направлении в V' (а) элементы, получаемые вдоль путей клас-
класса {L}, принимают исходный вид, то ({а, {?}) есть
алгебраич. точка ветвления и число т — 1 наз. ее п о-
рядком. В противном случае, когда обходы точки а
дают все новые и новые элементы, (а, {?}) есть транс-
трансцендентная точка ветвления.
Напр., для функции
точки а=0, оо (для всех путей) являются алгебраич.
точками ветвления порядка 5. Как однозначную функ-
функцию точки /(z) можно представить только на соответ-
соответствующей римановой поверхности S, состоящей из
6 листов над С, определенным образом соединенных
над точками 0, оо. Кроме того, над точкой а=1 рас-
расположены три правильные ветви f(z), однозначные
на трех соответствующих листах S; на одном лирте S
расположен полюс второго порядка и на двух листах
S — полюсы первого порядка. Вообще, привлечение
понятия римановой поверхности оказывается весьма
удобным и плодотворным при изучении характера
О. т.
Если радиус сходимости исходного ряда A) Д=оо,
то он представляет целую функцию /(г), голоморфную
во всей конечной плоскости С. Такая функция в слу-
случае /(г)Фconst имеет единственную изолированную
О. т. а— оо однозначного характера; если при этом
а— оо — полюс, то f(z) есть целая рациональ-
рациональная функция, или многочлен; если же
а— оо —существенно особая точка, то /(z) есть це-
целая трансцендентная функция.
Мероморфная функция /(z) в конечной плоскости С
получается, когда аналитич. продолжение ряда A) при-
приводит к однозначной аналитич. функции /(z) в С,
имеющей в С в качестве О. т. только полюсы. Если
при этом и а=оо есть полюс или регулярная точка,
то общее число всех полюсов /(z) в расширенной пло-
плоскости С конечно и /(z) есть рациональная
функция. Для трансцендентной мероморфной
функции / (z) в С бесконечно удаленная точка а— оо
может оказаться предельной точкой полюсов — это
простейший пример неизолированной О. т. однознач-
однозначной аналитич. функции. Мероморфная функция в про-
произвольной области DdC определяется аналогично-
Вообще говоря, проекции неизолированных О. т.
могут образовывать различные множества точек рас-
расширенной комплексной плоскости С. В частности,
какова бы ни была область DdC, существует анали-
аналитич. функция /д (z) в D, для к-роп Ь является ее ес-
естественной областью существования, а граница Г--
= 9Д — естественной границей, так что аналитич.
продолжение функции /д(г) за пределы области D
невозможно. При этом естественная граница Г со-
состоит из достижимых и недостижимых точек (см. Гра-
Граничные элементы). Если точка а?Г достижима вдоль
путей класса {L} (таких классов может быть и не-
несколько), расположенных целиком, кроме конечной
точки а, в области D, то над ней необходимо располо-
расположены только О. т. функции fp(z), т. к. в противном
случае было бы возможно аналитич. продолжение
/jr>{z) за пределы области D через иек-рую часть Г
в окрестности точки а; достижимые точки образуют
плотное множество на Г.
В качестве определяющего элемента аналитич.
функции /(z) многих комплексных переменных z=
r-(zj, . . ., zn), п>1, можно принять, напр., в е и с р-
штрассов элемент (Un(t,, R), f-) в виде
кратного степенного ряда
h =>с <*>=2ГЬ.... *„=0 %... *>- ^kl ¦ ¦ ¦ ^~ukn
B)
и поликруга сходимости этого ряда
п},
имеющего центр ?=(?1, . . ., ?„)?СЧ и радиус сходи-
сходимости Я={Лг>0, . . ., Я„>0}. Полагая в основу
процесс аналитич. продолжения элемента B) вдоле.
всевозможных путей L : [О, 1]->С", отображающих
отрезок 0<:<<:1 в комплексное пространство С",
получают общее определение О. т. (a, {?}), а?С",
функции /(z), формально вполне аналогичное приве-
приведенному выше для случая п=1.
Однако вследствие переопределенности Коши — Ри-
жана условий при »>1 и проистекающей отсюда «боль-
«большей силы» аналитич. продолжения случай к>1 ко-
коренным образом отличается, по существу, от случая
ге=1. В частности, при «>1 существуют такие об-
области DdCn, к-рые не могут быть естественными об-
областями существования никакой однозначной анали-
аналитической, или голоморфной, функции. Иначе говоря,
определенные участки границы dD такой области сво-
свободны от О. т. любой голоморфной функции /(г),
заданном и D, и через них возможно аналитич. про-
мшженио. Напр., справедлива теорема О с-
• уда — Брауна: если компакт К расположен
и ограниченной области DdCn, причем D\K яв-
является также областью, и функция f(z) голоморфна
в D\K, то она голоморфно продолжается на всю об-
область D (см. также Устранимое множество). Естест-
Естественные области существования голоморфных функ-
функций наз. иначе голоморфности областями, они харак-
характеризуются определенными геометрия, свойствами.
Аналитически продолжая голоморфную функцию /(z).
заданную первоначально в области DdC", и желая
сохранить ее однозначность, приходят к необходи-
необходимости введения, вообще говоря, многолистных над С"
областей голоморфности на риманоеых областях
аналогах римановых поверхностей. В этой трактовке
оказывается, что О. т. голоморфной функции /(z) —
.по точки гравицы Г — dD ее области голоморфности ?>•
Георема Осгуда — Брауна показывает, что связные
компоненты Г не могут образовывать компактных
множеств К таких, чтов/}\/<Г функция /(z) голоморф-
голоморфна- В частности, при ге>1 не существует изолирован-
изолированных О. т. голоморфных функции.
Простейшие типы О. т. аналитич. функций многих
комплексных переменных доставляют мероморфные
функции f(z) в области DdC", n^i, характеризую-
характеризующиеся следующими свойствами: 1) j(z) голоморфна
всюду J й, за исключением полярного множества Р,
состоящего из О. т.; 2) для любой точки а?Р сущест-
существуют окрестность V (а) и голоморфная в V(a) функция
i|)a(z) такие, что функция (f>a(z)—\р„ (z)f(z) голоморфно
продолжается в V(a). При этом О. т. а?Р делятся
на полюсы, в к-рых сра (а)фО, и точки н е о п р е-
Л елейности, в к-рых ср0 (а)=0. В случае полюса
Jim/(z)=oo при стремлении z-»-a, z?D\P; в любой
окрестности точки неопределенности /(z) принимает
все значения w?C. Напр., мероморфная функция
/(z)=z1/z2 в С2 имеет в качестве полярного множества
прямую /•--= {s=(zj, z2)?C2: z2 = 0}, все точки к-рой
суть полюсы, за исключением одной точки неопреде-
неопределенности @,0). Мероморфная функция /(z) в своей об-
области голоморфности D представима глобально в D
в виде отношения двух голоморфных функций, т. е.
ее полярное множество Р есть аналитическое мно-
множество.
Точка а?С" наз. точкой мероморфно-
мероморфности фз'нкции /(z), если /(z) мероморфна в нек-рой
ее окрестности; таким образом, если О. т. есть точка
мероморфности, то она либо полюс, либо точка неопре-
неопределенности. Все остальные О. т. аналитич. функции
/(з), не являющиеся точками мероморфности, иногда
наз. существенно особыми точками.
К ним относятся, напр., точки ветвления i{:).. т.е.
точки ветвления ее (многолистной) области голоморф-
голоморфности D. Размерность множества всех О. т. голоморф-
голоморфной функции /(г) в общем случае равна 2/г — 1. При
нек-рых дополнительных ограничениях на /(г) это
множество оказывается аналитическим (и, следова-
следовательно, имеющим меньшую размерность; см. [2]).
Лит.: [1] М а р к у ш е в п ч А. II., Теория аналитических
функций, 2 изд., т. 1—2, М., 19(J7—68; [2] Ш а б а т Б. В., Вве-
Введение в комплексный анализ, 2 изд., ч. 1—2, М., 1976; [3] С т о-
и л о в С, Теория функций комплексного переменного, пер. с
рум., т. 1 — 2, М., 1962; Е4] Г у р в и ц А., К у р а н т Р., Теория
функций, пер. с нем., М., 196S; [5] Б и б е р б а х Л., Аналити-
Аналитическое продолжение, пер. снем.,М., 1967; [6] В i e b e rb а с h
L., Lehrbuch der Funktionentheorie, 3 Aufl., Bd 1, Lpz,—В., 1931),
Bd 2, Lpz.— В., 1927; [7] В л а д и м и р о в В. С, Методы тео-
теории функций многих комплексных переменных, М., 1964; [8]
Фукс Б. А., Введение в теорию аналитических функций мно-
многих комплексных переменных, 2 изд., М., 1962; [9] Г а и-
н и н г Р., Р о с с и X., Аналитические функции многих комплекс-
комплексных переменных, пер. с англ., М., 1969; [10] В е h n k с II.,
Thullen P., Theorie der Fimktionen mehrcrer komjilexer
Veranderlichen, В., 1934. E. Д. Соломенцеч.
2) О. т., особенность, алгебраического мно-
многообразия — точка, в к-рой нарушается гладкость.
Точнее, пусть X —- алгебраич. многообразие или схе-
схема конечного типа над полем к, тогда тонка х?Х
наз. особой, если соответствующее локальное коль-
кольцо Qx, х но регулярно (регулярность локаль-
локального нётерова кольца А с максимальным идеалом m
означает равенство dim m/m-=dim А). Множество
О. т. алгебрапч. многообразия X замкнуто в тополо-
топологии Зариского и обозначается Sing X. Если X—
приведенное многообразие, то Siug X нигде не плотно
в X. Если х является изолированной точкой в Sing X,
то х наз. изолированном О. т. Для про-
проверки того, будет ли точка х?Х особой пли неособой,
используется якобиев критерий (см. Гладкая схема).
Разрешением особенности (д е с и н-
гуляризацией) алгебраич. многообразия X наз.
собственный бирациональный морфизм я : X—>-.Y, где
X — гладкое многообразие. Существование разре-
разрешения особенностей доказано для широкого класса
многообразий, в частности для всех многообразии
над полем характеристики 0 (см. [13]); как правило,
оно не единственно. Разрешение особенностей исполь-
используется для введения различных инвариантов много-
многообразия X; примером служат пространства когомоло-
гий Н'{Х, 0-у)- Нормальное многообразие X, для
к-рого Н'(Х, Q—)—0 при всех i>0, нал. много-
многообразием с рациональными особен-
особенностям и. Рациональными являются тороидальные
особенности [6] и особенности многообразий Шубер-
Шуберта [3]. Размерность пространства Нп~1(Х, E^) для
«-мерного многообразия X наз. г е о м е т р и ч е-
с к и м р о д о м X. См. также Разрешение особенно-
особенностей.
Теория деформаций особенностей, т. е.
многообразий с О. т., строится параллельно теории
деформаций (гладких) алгебраич. многообразий. Д е-
формацией многообразия Х„ наз. плоский мор-
морфизм/: X-+S такой, что /~x(s0)=X0 для нек-рой so?^
многообразие S при этом наз. базой деформн
и, и и. Для многообразия Хо с изолированной О. 'i
существует нереальная деформация, содержащая в<ч
деформации многообразия Ха. Может оказаться, что
особенность жесткая, т. е. база нереальной де-
деформации ее состоит из одной точки и все ее деформа-
деформации тривиальны [4]. Противоположными к жестким
являются сглаживаемые О. т., в базе S
версальной деформации к-рых есть такие точки, что
Xs =/~1(s) неособы. Множество D точек s?S с осо-
особыми Xs наз. д и с к р и м и н а н т н ы м и о д-
М II О Ж С С Т И о М.
При изучении деформаций большую роль играет
действие группы монодромии яг (S\D) на когомологиях
слоев X.
Одновременным разрешением осо-
особенностей семейства X—>S наз. собственный морфизм
л : Х^>-Х такой, что X — гладкая 5-схема и для лю-
любого s?S морфизм Xs—*-Xs является разрешением
особенностей. Версальная деформация простых О. т.
(см. ниже) допускает одновременное разрешение после
нек-рого конченого накрытия ее базы, причем группой
Галуа этого накрытия служит группа Вейля соответ-
соответствующей корневой системы (см. [5], с. 179—203).
Особые точки комплексной гипер-
гиперповерхности. Пусть гиперповерхность X за-
задана в Cn + I одним уравнением f(x0, . . ., хп)=0, где
/ — многочлен (или росток аналитич. функции в точ-
точке 0). Якобиевым идеалом многочлена /
наз. идеал J (f) = (df/dx0, . . ., df/dxn) в кольце С {х0,
. . ., х„}; изолированность О. т. 0 эквивалентна ко-
конечномерности пространства С{х0, . . ., xn}/J(f). Раз-
Размерность ^ этого пространства наз. числом Мил-
н о р а многочлена / и совпадает с рангом свободной
абелевой группы Hn{Xs, g), где Хг задается уравне-
уравнением f(x0, . . ., ?„)—е, при малых ет=О. Более точно,
многообразие Хг гомотопически эквивалентно букету
\i сфер размерности п (см. [12]). База ве'рсальной де-
деформации этой особенности неособая и также имеет
размерность ух (см. \%). Простейшим примером яв-
является невырожденная квадратичная особенность го+
+ . . . + х„=-0, для нее ii=l.
Простой О. т. гиперповерхности наз. особенность,
при деформации к-рой появляется лишь конечное
число других особенностей [9]; гиперповерхность при
этом задается одним из следующих уравнений:
А»: 4+1 + 4+ ¦ ¦ ¦ +4 = 0, |iS&l,
? 4+ ... +4 = 0, (AS&4,
Д.:
?7:
Et:
Жо -f- Xi -4- X-i -|-
Х^1+Ж? + Х2-
4-1 4 + ^2 +
...+x^O,
]-...+4=
...+4=o.
Нижний индекс (х здесь — число Милнора особенности.
В случае поверхностей («==2) эти особенности наа.
особенностями дю Валя, или двой-
двойными рациональными О. т. Эти О. т. можно
также охарактеризовать тем, что форма пересечения на
пространстве Нп(Х& , R) является определенной. Име-
Имеется классификация следующих по сложности, унимо-
унимодальных особенностей [9]. Изучается вещественный
аналог этих понятий, а также их связь с теорией ка-
катастроф [10]. Многие теоремы об О. т. гиперповерх-
гиперповерхностей распространяются на О. т. полных пересечений.
Особые точки кривых. Пусть А —
локальное кольцо О. т. х кривой, а Л — его нор-
нормализация; главным инвариантом О. т. является
6x=dim А/А. Для неприводимой кривой X ее ариф-
метич. род равен геометрич. роду плюс 2хбх (сумми-
(суммирование по всем О. т. кривой X). Причем для плос-
плоской кривой 26x=|i+r—1, где ^ — число Милнора, а
г — число ветвей кривой в точке х.
Пусть ХсС*— плоская неприводимая кривая, име-
имеющая в точке 0 особенность кратности п (см. Крат-
Кратность особой точки). Тогда X допускает параметриза-
параметризацию х— t", j/=2i>na,i', к-рая записывается в виде
(разложение П ю и з ё). Характеристич. пока-
показателями этого разложения наз. числа
_т, тг ^ mg mg
III И,Я, ^ ' " П, . . . ng П '
где — — первый нецелый показатель в разложении
Пюизё, — первый показатель некратный — и т. д.
Последовательность {п, Pi, . . ., Рг), где $v = -——
наз. характеристикой особенности.
Плоские одномерные особенности топологически экви-
эквивалентны тогда и только тогда, когда их характери-
характеристики совпадают (см. [8]).
Особые точки поверхностей. Среди
разрешений особенностей нормальных поверхностей
однозначно выделяются минимальные разрешения я :
X—*-Х, через к-рые пропускаются все остальные раз-
разрешения. Если х — О. т. поверхности X, то кривая
4 = л~1(х) наз. исключительной. Комбинаторным инва-
инвариантом О. т. х является взвешенный граф
Г кривой А, вершины которого соответствуют непри-
неприводимым компонентам Л,- кривой А, точки пересече-
пересечения компонент At и Aj изображаются ребрами меж-
между соответствующими вершинами, вершине припи-
приписывается вес, равный роду кривой А;, а иногда еще
и индекс самопересечения {А\). Матрица 11D/, Aj)\\
пересечений компонент кривой А отрицательно опре-
определена, граф Г связен. Наименьший положительный
дивизор Z=4Zr/Aj такой, что (Z, Л;)<0 для всех г,
наз. фундаментальным циклом осо-
особенности. Он всегда существует, и его арифметик.
род
= 1 — dimff°(Z, 0z) + dim ШA, QZ)
неотрицателен. О. т. рациональна тогда и только
тогда, когда p(Z)=0; в этом случае кратность ее равна
—(Z2), а размерность касательного пространства За-
риского на единицу больше [1]. Исследуются также [71
эллиптические особенности (то есть О. т. с p(Z)=i).
Лит.: [1] Artin M., «Amer. J.Math.», 1966,v. 68, p. 129—36;
12] Groupes de monodromie en geometrie algebrique, B.—
Hdlb.—N. Y., 1972; [3] Kempf G., «Invent, math.», 1976,
v. 37, p. 229—39; [4] S с h 1 e s s i n g e r M., «Invent, math.»,
1971, v. 14, p. 17—26; [5] Seminaire sur les singularites des sur-
surfaces, В.—Hdlb.—N. Y., 1980; [6] Toroidal embeddings, fv. 1],
В.—Hdlb.—N. Y., 1973; [7] Yau S. S.-Т., «Trans. Amer.
Math. Soc», 1980, v. 257, p. 269—329; [8] Z a r i s k i O.,
«Amer. J. Math.», 1968, v. 90, p. 961 — 1023; [9] A p н о л ь д
В. И., «Успехи матсм. наук», 1975, т. 30, в. 5, с. 3—65; A0]
Голубиц кий М., ГийеминВ., Устойчивые отображе-
отображения и их особенности, пер. с англ., М., 1977; [11] Гриффите
Ф., X а р р и с Дж., Принципы алгебраической геометрии, пер.
г англ., т. 1—2, М., 1982; [12] Милнор Дж., Особые точки
комплексных гиперповерхностей, пер. с англ., М., 1971; [13]
Хиронак а X., «Математика», 1965, т. 9, №6, с. 2—70;
1966, т. 10, № 1, с. 3—89. В. И. Данилов.
3) О. т. векторного поля X — точка а,
для к-рой Х(а):-0. О. т. наз. изолированной,
если X не обращается в нуль в отличных от а точках
достаточно малой окрестности точки а. О. т. наз. н е-
вырождена,ой, если
j l Эх'
det
Невырожденная О. т. всегда изолирована.
М. И. Войцеховский.
4) О. т. дифференциального уравне-
уравнения
X (х, у) dy = Y (х, у) их A)
— любая точка (х0, yo)?G, удовлетворяющая условию
-*'(*<), !/о)=у(?(ъ г/о)=^и; B)
здесь X, Y : G—»-R — непрерывные в нек-рой области
GcR2 функции. Точки области G, не удовлетворяющие
условию B), наи. обыкновенными точка-
м и уравнения A). Иногда точку (,г„, </„)(; G низ. О. т.
уравнения A) и в том случае, когда условие B) не вы-
полняется, но задача Копт для уравнения A) с на-
начальными данными (sn, ;/„) пмеет более одного реше-
решения.
Уравнение A) — частный случай системы диффе-
дифференциальных уравнений в симметричной форме:
dxt _ dxn /Ч)
Xi{x) ~="'~ Хп{х) ' { >
где п>2, х— (хь . . ., хп), функции X/ : G->R, i—
= 1, 2, .... га, непрерывны в нек-рой области GcR".
Точка xv?G наз. особой точкой системы
C), если Xi(rtt) — 0, I -1, . . ., га. В противном случае
ха — обыкновенная точка этой системы.
Пусть Н — множество О. т. системы C) в области С.
Если xo?G\H, то существуют индекс го?{1, . • •, «}
и окрестность V точки х0 такие, что в U система C)
представима в нормальной форме:
/() /6Cf/ ф
Таким образом, поведение интегральных кривых сис-
системы C) в окрестности обыкновенной точки описы-
описывается теоремами общей теории обыкновенных диф-
дифференциальных уравнений. В частности, справедлива
следующая теорема о выпрямлении: если
через любую точку х0 множества G\H проходит един-
единственная интегральная кривая системы C), то каждая
точка атого множества имеет окрестность V такую,
что семейство дуг интегральных кривых системы C),
заполняющих V, гомеоморфно (а если X,-^C1(G),
j=l, . . ., п, то диффеоморфно) семейству параллель-
параллельных прямых.
Если же х„^Н, то пары (t0, U), обладающей указан-
указанным выше свойством, не существует, и интегральные
кривые системы C) могут образовывать вблизи х0
различные конфигурации. Так, для уравнения
(ax-\-by) dy = (cx + ey) dx,
где а, Ь, с, e?R, а матрица А =- —невырожден-
II с е II
наи, расположении интегральных кривых в окрест-
окрестности точки @, 0) может относиться к типу седло,
узел, центр или фокус. Соответствующее название за-
закрепляется при этом и за самой точкой @, 0).
Систему C) можно рассматривать как результат
исключения времени / из автономной системы диффе-
дифференциальных уравнений
х = Х[х), х g R», Х = (Хи ..., Хп). D)
Если D) -— система класса (С, единственность)
в G, то есть X?C(G), и через каждую точку области G
проходит единственная траектория системы, что да-
далее и предполагается, то точки множества Н будут
для нее точками покоя (равновесия положениями).
Часто их наз. О. т. и для этой системы, поскольку они
являются таковыми (по определению) для векторного
поля X. Интегральные кривые системы C), располо-
расположенные в G^H, представляют собою траектории си-
системы D), отличные от состояний покоя.
Таким образом, задачи о поведении интегральных
кривых системы C) в окрестности О. т. и о расположе-
расположении траекторий системы D) в окрестности положений
равновесия эквивалентны. Исследования этих задач
ведутся по двум основным направлениям.
Одно направление, берущее свое начало в трудах
А. Пуанкаре [1], ставит своей целью выяснение воз-
возможных топологич. типов расположения траекторий
системы D) в окрестности изолированной точки покоя
(к-рую всегда можно считать совпадающей с началом
координат О(.с-0)) и отыскание аналнтпч. крптерщч!
их различения. Наиболее законченные рюч.ил'аты
получены здесь для того случая, когда система D)
представила в виде
), E)
где А — постоянная невырожденная матрица, /(я)=
= оAМ0 при IU-[|->-0. В этом случае точка О наз. про-
просто й, или невырожденной, особой
тонко й системы D). Для системы E) установлена
следующая теорема о топологической
эквивалентности: если матрица А не имеет
чисто мнимых собственных значений, а функция
/?СХ(С), то существует гомеоморфизм h окрестности
U точки О на окрестность V той же точки, переводящий
траектории системы E) в траектории линейной системы
х = Ах. F)
Гомеоморфизм h : U—*-V, осуществляющий топологич.
соответствие между траекториями систем E) и F),
в общем случае но является (и не может быть заменен)
диффеоморфизмом.
При условиях этой теоремы точка покоя О системы
E) относится к тому же топологич, типу, что и точка
покоя О системы F). В частности, для системы 2-го
порядка она будет при этом седлом, если собст-
собственные значения Xt, Хг матрицы А удовлетворяют усло-
условию ЯД2 <0, топологическим узлом
(узлом или ф о к у с о м), если Х1Х2'>0 (при чисто
мнимых Х1у Х.2 точка О для системы F) — ц е н т р,
а для системы E) — центр, фокус или центро-фокус).
Если матрица Л имеет чисто мнимые или нулевые
собственные значения, то топологич. эквивалентности
между системами E) и F) в окрестности точки О В об-
общем случае нет. При этих условиях поведение траек-
траекторий системы E) в окрестности точки О весьма де-
детально изучено в тех случаях, когда матрица А имеет
не более двух собственных значений с нулевыми дей-
действительными частями, а функция / — аналитическая.
В частности, для системы 2-го порядка с ненулевой
матрицей А выяснены все возможные топологич. типы
расположения траекторий в окрестности точки О
и даны коэффициентные критерии их различения с точ-
точностью до различения центра и фокуса [9]. Здесь, кроме
седла, топологич. узла и центра, точка О может быть:
двухсеиаратрисным седлом, седло-узлом (нек-
(некрая окрестность U точки О разбивается тремя примы-
примыкающими к О траекториями (сепаратрисами) на три
сектора: два гиперболических, заполненных траекто-
траекториями, к-рые обоими концами покидают U, и один
параболический, заполненный траекториями, к-рые
одним концом покидают U, а другим примыкают к О)
и точкой (нек-рая ее окрестность U разбивается сепа-
сепаратрисами на 4 сектора: один гиперболический, два
параболических и один эллиптический, заполненный
траекториями, к-рые обоими концами примыкают к О,
охватывая друг друга). Для системы 2-го порядка
с нулевой матрицей А разработаны алгоритмы расщеп-
расщепления особенности (см., напр., Фроммера метод),
позволяющие с помощью конечного числа шагов про-
процесса расщепления выяснить топологич. тип точки О
с точностью до решения задачи о различении центра
и фокуса. Последняя задача (см. Центра и фокуса
проблема) возникает для системы 2-го порядка вида E)
в случае, когда матрица .4 имеет чисто мнимые собст-
собственные значения, и может возникать в случае двух
нулевых собственных значений этой матрицы. Она ре-
решена для частных классов таких систем.
Важной характеристикой изолированной точки по-
покоя О системы D) является ее индекс П у а н-
к а р е. Для д—2 он определяется как вращение век-
векторного поля X при обходе точки О по окружности
IU]|--p достаточно малого радиуса р в положительном
направлении, измеренное в единицах полного оборота.
Напр., индекс простого седла равен —1, индекс узла,
фокуса и центра равен 1. При произвольном п индекс-
точки О определяется как степень отображения h
сферы |Ь||=р достаточно малого радиуса р на себя,
определенного формулой:
h /-' — рХ (ж)
Это направление развилось в обширную качествен-
качественную теорию дифференциальных уравнений, а центр
тяжести исследований переместился с локальных проб-
проблем на глобальные — изучение поведения траекторий
системы D) во всей области задания G, к-рая все чаще
предполагается гладким многообразием той или иной
природы.
Другое направление, заложенное трудами А. М. Ля-
Ляпунова [2], занимается исследованием решений (в ча-
частности, состояний равновесия) систем вида D), а
также неавтономных систем дифференциальных урав-
уравнений на устойчивость. Оно представляет собою раз-
разветвленную теорию устойчивости движения (см. Устой-
Устойчивости теория).
В комплексном анализе вводится понятие О. т. диф-
дифференциального уравнения
w m
а также системы дифференциальных уравнений
¦g-=P <«,«>), (8)
где z — комплексная переменная, Р — рациональная
функция от w, w', . . ., w{n~1) или от компонент w
ш2, • . ., и>п вектора w, »^1, коэффициенты к-рой —
известные аналитич. функции от г. Особой для урав-
уравнения G) (системы (8)) наз. любая точка z0 комплекс-
комплексной плоскости, к-рая является О. т. хотя бы одного
из коэффициентов функции Р (см. Особая точка ана-
аналитической функции). О. т. уравнения или системы,
как правило, являются особыми и для их решений как
аналитич. функций от z. Они наз. неподвижными осо-
особыми ^точками решений. Кроме того, решения урав-
уравнения G) (системы (8)) могут иметь подвижные особые
точки, положение к-рых определяется начальными
данными решений. Исследование различных классов
уравнений вида G), (8) с целью изучения аналитич.
природы решений в окрестное™ особых точек урав-
уравнений и с целью выяснения вопроса о наличии у реше-
решений этих уравнений подвижных О. т. различных ти-
типов составляет предмет аналитической теории диффе-
дифференциальных уравнений.
Лит.: [1] Poincare H., Sur les courbes definies par une
equation differentielle, Oeuvres, t. 1, P., 1892; рус. пер.— П у-
a it к а р е А., О кривых, определяемых дифференциальными
уравнениями, М.— Л., 1947; [2] Л я п у н о в А., Общая задача
об устойчивости движения, М.— Л., 1950; [3] Н е м ы ц-
к и й В. В., Степанов В. В., Качественная теория диф-
дифференциальных уравнений, 2 изд., М.— Л., 1949; [4] К о д-
дингтон Э. А., Левинсон Н., Теория обыкновенных
дифференциальных уравнений, пер. с англ., М., 1958; [5] Л е ф-
шецС, Геометрическая теория дифференциальных уравнений,
пер. с англ., М., 1961; [6] Sansone G., ContiR., Non-li-
Non-linear differential equations, Oxf., 1964; [7] Хартман Ф.,
Обыкновенные дифференциальные уравнения, пер. с англ., М.,
1970; [8] А р н о л ь д В. И., Обыкновенные дифференциальные
уравнения, М.,1971;[9]БаутинН. Н.,Леонтович Е.А.,
Методы и приемы качественного исследования динамических
систем на плоскости, М., 1976; [10] Голубев В. В. Лекции
по аналитической теории дифференциальных уравнений, 2 изд.,
М.— Л., 1950; [11] Е р у г и и Н. П., Книга для чтения по об-
общему курсу дифференциальных уравнений, 2 изд., Минск, 1972;
[12]БрюноА.Д., Локальный метод нелинейного анализа диф-
дифференциальных уравнений, М., 1979; [13] Андреев А. Ф.,
Особые точки дифференциальных уравнений, Минск, 1979.
А. Ф. Андреев.
5) О. т. дифференцируемого отобра-
отображения / — точка, к-рая является для / нерегуляр-
ной (критической) и неправильной одновременно. Точ-
Точнее, пусть Мт и Nn— два дифференцируемых много-
многообразия размерностей тип соответственно, а / : Л/т->-
ЛТп - дифференцируемое отображение первого во
, х' и yl'=f(xJ) — локальные координаты в них.
-Л—
второе
Если ранг матрицы
-^11 в точке а?Мт равен го,
дх'
дх! .
то отображение / наз. регулярным в точке
г * I
Если ранг матрицы
равен п в точке
дх-' |.
то отображение / наз. правильным в точке а.
В О. т. / ранг этой матрицы меньше обоих чисел m
и га. См. также Особенности дифференцируемых от-
отображений. М. И. Войцеховский.
6) О. т. действительной кривой
F{x,y)=0 —точка (х0, у0), в к-рой первые частные про-
производные равны нулю (FxH=0, (FyH=0. О. т. наз.
двойной точкой, если по крайней мере одна
из вторых частных производных функции F(x, у) не
равна нулю. При исследовании строения кривой в
окрестности О. т. рассматривают знак выражения
— К*хх)о \г уу!в — К?ху/о-
Если Д>0, то О. т. является изолированной
точкой (см. рис. , а); узловой т о ч к о й
(или точкой самопересечения), если
Д<0 (см. рис. , б); если Д=0, то О. т. является либо
изолированной точкой, либо характеризуется тем, что
различные ветви кривой имеют в этой точке общую
касательную. Если ветви кривой расположены по
разные стороны от общей касательной и по одну сто-
сторону от общей нормали, то О. т. наз. точкой
возврата 1-го рода (см. рис. , в); если
ветви кривой расположены по одну сторону от общей
касательной и по одну сторону от общей нормали,
то О. т. наз. точкой возврата 2-го рода
(см. рис. , г); если ветви расположены по разные сто-
стороны от общей нормали и по разные стороны от общей
касательной (см. рис. , д) или по одну сторону от
общей касательной и по разные стороны от общей нор-
нормали (см. рис. , е), то О. т. наз. точкой само-
самоприкосновения. См. также Двойная точка.
Если в нек-рой точке все частные производные от
функции F(x, у) до (к—1)-го порядка включительно
обращаются в нуль, а среди производных /с-го порядка
по крайней мере одна отлична от нуля, то эта точка
наз. особой точкой к - т о порядка
(кратной точкой).
Иногда О. т. наз. точки, отличающиеся каким-либо
свойством от других точек кривой; см., напр., Пере-
Перегиба точка. Прекращения точка, Излома точка, Спрям-
Спрямления точка, Уплощения точка.
О. т. пространственной кривой, за-
заданной уравнениями F(x, у, z) = 0, G{x, у, z) = 0 —
точка, в окрестности к-рой ранг матрицы
\Fx F'y F'z
1 Gx by bz
меньше двух.
Лит.: [1] Р а ш с в с к и й П. К., Курс дифференциальной
геометрии, 4 изд., М., 1956; L2] Б ю ш г е н с С. С, Дифферен-
Дифференциальная геометрия, т. 1, М.— Л., 1940; [3] Ф и х т е н-
г о л ь ц Г. М., Курс дифференциального и интегрального ис-
исчисления, 7 изд., т. 1, М.— Л., 1969. А. Б. Иванов.
7) О. т. действительной поверхно-
с т и — точка поверхности х=х(и, v), y=y(u, v),
z=z(u, v), в к-рой ранг матрицы
Уи z
Уь *"v II
меньше двух. Если иоверхность определяется как
множество точек, координаты к-рых удовлетворяют
уравнению F(x, у, г)=0, то О. т. наз. точку (х0, у0, zq)
поверхности, в к-рой первые частные производные
функции F(x, у, г) равны нулю:
Если в О. т. не все вторые частные производные
функции F(x, у, г) обращаются в нуль, то касательные
к поверхности в О. т. образуют конус. Если конус
касательных невырожденный, то О. т. наз. кони-
конической точкой; если конус вырождается в две
а
ния и др.
о г о р е л о в А. В., Дифференциальная гео-
гео., 1969; [2] Н о р д е н А. П., Краткий курс
й геометрии, 2 изд., М., 1958; [3] Иль-
ИльЭ Г О
действительные плоскости, то О. т. является точ-
точкой самопересечения поверхности! если
конус мнимый, то| О. т.— изолированная
точка поверхности.
О. т. могут составлять т. н. особые линии
поверхности: возврата ребро, линии самопересечения,
самоприкосновения и др.
Лит.: [1] П о г о е
метрия, 5 изд., М.
дифференциальной р, зд, М, 8; [3]
ин В, А., П о з н я к Э. Г., Основы математического анализа,
2 изд., ч. 2, М., 1980. А. Б. Иванов.
ОСОБЕННОСТИ ДИФФЕРЕНЦИРУЕМЫХ ОТОБ-
ОТОБРАЖЕНИЙ — раздел математич. анализа и дифферен-
дифференциальной геометрии, в к-ром изучаются свойства
отображений, сохраняющихся при заменах координат
в образе и прообразе отображения (или при заменах,
сохраняющих нек-рые дополнительные структуры);
предлагается общий подход к решению различных за-
задач о вырождениях отображений, функций, векторных
полей и т. д.; дается классификация наиболее часто
встречающихся вырождений, указываются их нормаль-
нормальные формы и алгоритмы приведения к нормальным
формам.
Точка области определения дифференцируемого от-
отображения (т. е. отображения класса С*, см. Диффе-
Дифференцируемое многообразие) наз. регулярной, если
в этой точке матрица Якоби имеет максимальный ранг,
и критической в противном случае.
Строение отображения в окрестности регулярной
точки описывает классич. теорема о неявной функции,
в окрестности такой точки и в окрестности ее образа
существуют координаты, в к-рых отображение ли-
линейно.
Во многих случаях ограничиться рассмотрением
лишь регулярных точек недостаточно, поэтому ес-
естественны вопросы:
а) описания отображения в окрестности каждой
критич. точки;
б) описания строения множества критич. точек.
Ответы на а) и б) для произвольного отображения
отсутствуют по двум причинам: при попытке охватить
все отображения нет надежды на получение обозри-
обозримых ответов (например, множество критических точек
локально может быть произвольным замкнутым мно-
множеством), и для приложений достаточно знать ответы
лишь для достаточно обширного множества отобра-
отображении.
Вопросы а), б) и многие другие в теории особенностей
исследуются по следующей схеме:
1) из рассмотрения исключается множество «нети-
«нетипичных», «патологических» отображений,
2) указывается критерий «типичности» отображения,
3) проверяется, что всякое отображение аппроксими-
аппроксимируется «типичными»,
4) изучаются «типичные» отображения.
Выбор множества типичных отображений зависит от
решаемой задачи и не однозначен: чем меньше отобра-
отображений отнесено к типичным, тем легче задача их из-
изучения, однако 2) и 3) требуют, чтобы множество ти-
типичных отображений было достаточно широким и до-
достаточно конструктивно определяемым.
Эту схему иллюстрирует следующая теорема
У и т н и: всякое дифференцируемое отображение
R2_».R2 можно аппроксимировать таким отображе-
отображением /, что для любой точки а ? R2 в окрестностях то-
точек а и /(а) можно выбрать координаты, в к-рых отоб-
отображение / записывается в одной из трех нормальных
форм:
/
уг—х\\ | y2 = x
(критерий типичности см. в [3] или [4]). Работа X. Уит-
ни (Н. Whitney, 1955), в к-рой была доказана эта тео-
теорема, считается началом теории О. д. о., хотя ряд
отдельных результатов появился гораздо раньше (тео-
(теория Морса критических точек функций, теоремы Уитни
об особенностях вложений, работы Л. С. Понтрягина
о связи особенностей с характеристическими клас-
классами).
Основные понятия теории особенностей дифферен-
дифференциальных отображений.
Ростки дифференцируемых отоб-
отображений. Пусть X, У — гладкие многообразия,
р?Х> ?€^- (Всюду ниже термин «гладкий» будет
употребляться как синоним термина бесконечно диф-
дифференцируемый.) Ростком в точке р наз.
класс эквивалентности отображений Х-»-У, совпа-
совпадающих в некоторой окрестности точки р; множество
ростков отображений, переводящих р в q, обозна-
обозначается С°°(Х, Y)pq. Группа ростков гладких замен
переменных в X, сохраняющих точку р, обозначается
Dili» {X)p.
Важная локальная задача теории О. д. о.— изуче-
изучение естественного действия группы
Dili" (X^XDifr (У), на С° (X, У),,,.
Решение этой и многих подобных задач обычно начи-
начинается с аппроксимации функциональных пространств
и бесконечномерных групп, действующих на них, ко-
конечномерными многообразиями и действиями на них
групп Ли. Полученные результаты затем переносятся
в исходную бесконечномерную ситуацию.
Расслоения струй. Пусть /, g : Х-»-У —
гладкие отображения и f(p)=g(p)=q', отображения /
и g имеют, по определению, касание порядка
к в точке р, если их ряды Тейлора в этой точке совпа-
совпадают до порядка к. Класс эквивалентности отображе-
отображений, имеющих в точке р касание порядка к, наз. к-
струей. Множество всех fc-струй отображении,
переводящих р в q, наделяется естественной структу-
структурой гладкого многообразия и обозначается Jk(X, У)^ г
Определена естественная проекция
p,q( )я,,
Класс эквивалентности гладких замен переменных
в X, сохраняющих точку р и имеющих в этой точке
касание порядка А:, наз. обратимой А:-с т р у е й
в точке р. Обратимые А-струи образуют группу Ли
Lk(X)r. Группа Ли L'i(X)pxLlt(Y).l действует на
Jb(X У)р, ц, аппроксимируя действие
Diff- (Х)р X Dill" (У), на С- (X, У)^ц.
Пусть Jk(X, У) = {дизъюнктное объединение (,
У)Р,д по всем (р, q)?XxY). Множество J*(X, Y)
наделяется естественной структурой гладкого рас-
расслоения над X ;< Y со слоем
У*(К">, R«H,0W(m, n)
и структурно!! группой
Lk (RmH X Lft(R"H — Lft(m, re),
где m~Aim X, n = dim Y.
Особенности и классы особенно-
особенностей. Орбита действия Ьк(т, п) на ./*(/«, n) наз.
/с-о соб«нностьк>; любое подмножество в /*(т,
«). инвариантное относительно Lk(m, re), наз. клас-
классом /с-особенностей. Пусть S такой класс.
Поскольку/*(т, п) можно отождествить с Jk(X, Y)ptt[,
в Jk(X, Y)pjq определяется подмножество S(X, Y)p'itl,
не зависящее от способа отождествления. Множество
S(X, Y) = {объединение S[X, Y)pjll но всем (р, q)?
XxY) наз. универсальным классом
особенностей (или универсальной
особенностью, если S — особенность). Универ-
Универсальная особенность S{X, Y) является подмногообра-
подмногообразием в Jk{X, Y), коразмерность этого подмногообра-
подмногообразия равна коразмерности S в Jk(m, n).
Пусть / : X—>-У — гладкое отображение. Сопостав-
Сопоставлением каждой точке р?Х /с-струи отображения /
в точке р получается гладкое отображение ;'*/ : X—>-
-+Jk(X, Y), наз. It-струйным р а с ш и р е-
н и е м /. Отображение / : X-+Y имеет, по определе-
определению, в точке р особенность типа S, если
ikf(p)(z.S(X, Y). Множество S(/) всех точек, в к-рых /
имеет особенность типа 5, есть не что иное, как
(jkf)~1S(X, Y). Поэтому изучение множества S (/)
разбивается на два этапа: изучение универсального
множества S(X, Y) в Jk(X, У), сводящееся к изуче-
изучению S в Jk(m, n)\ изучение взаимного расположения
S (X, Y) и jkf(X). На втором этапе обычно приме-
применяется теорема трансверсальности Тома.
Трансверсальность. Гладкое отображение
гладких многообразий / : А—уВ трансверсально под-
подмногообразию СаВ (обозначается f^C), если для
любой точки а?А либо f(a)?C, либо (df)a(TaA)Q-
(?iTf(a)C=T/(a)B. Если f^C, то множество f~'(C)
либо пусто, либо является подмногообразием в А,
коразмерность к-рого равна коразмерности С в В.
Теорема трансверсальности Тома:
пусть X, Y — гладкие многообразия и С — подмного-
подмногообразие в Jk(X, Y); тогда множество тех /, для к-рых
/*/^С, является массивным подмножеством в С°°{Х,
Y) в С°°-топологии Уитни. (Множество наз. м а с-
с и в н ы м, если оно является пересечением счетного
числа открытых плотных подмножеств.)
Топология У и т н и. Пусть /с>0 и U — от-
открытое множество в Jk(X, Y). Пусть
M(U)~{I 6C-(A", Y):jkf(X)c:U}.
Множества М(U) образуют базис нек-рой топологии,
наз. С°°-т о п о л о г и е й Уитни на С°°(Х, Y).
В этой топологии С°°(Х, Y) является Бэра простран-
пространством, т. е. каждое массивное подмножество плотно.
Мультиструи. При изучении самопересече-
самопересечений образа гладкого отображения используется поня-
понятие мультиструи. Пусть a: Jk(X, Y)^-X — естест-
естественная проекция. Пусть
Х<*> = {(хи ..., xs)?X X ... XX: лу ф xit i ф /}
и as=aX...xa (s раз). Множество Jg(X ,Y) = (as)-1(X<s))
может быть наделено естественной структурой глад-
гладкого многообразия и наз. s-к ратным рас-
расслоен и е м к-с т р у и. Для s-кратных струй опре-
определяются ^-струйное расширение отображения /,
А--особенности, универсальные особенности и т. д. и
доказывается аналог теоремы трансверсальности Тима.
Устойчивые дифференцируемые
отображения. Центральной проблемой теории
О. д. о. в период ее возникновения была задача из-
изучения устойчивых дифференцируемых отображений.
Гладкое отображение / : Xm-^-Y" гладких многообра-
многообразий наз. устойчивым, если для любого достаточ-
достаточно близкого к / отображения / найдутся диффеоморфиз-
диффеоморфизмы h : X'"-+Xm и к : Yn-+Yn такие, что [^ hofok.
При небольших т, п(т, п<4), а также при га —1
и любом т устойчивые дифференцируемые отображе-
отображения плотны в пространстве всех собственных дифферен-
дифференцируемых отображений [3]. В пространстве отображе-
отображений X9-+Y9 устойчивые отображения не составляют
всюду плотного множества (см. [1]). Для нек-рых пар
многообразий (напр., для Х=К/9, У=^К1!)) вообще нет
ни одного устойчивого отображения X в Y. Найдены
[14], [15) все «устойчивые размерности» (/и, п) : для
любых гладких многообразий Хт и Y" устойчивые
отображения X в Y" плотны в пространстве собст-
собственных дифференцируемых отображений Xя1—>-Уп,
снабженном 6Т°°-топологией Уитни, тогда и только
тогда, когда пара (т, п) удовлетворяет хотя бы одному
из следующих условий (q—n — т) : а) и<7<у-г8 и q^'t,
б) п<7</+9 и 3>9>0; в) ге<8 ид^—1; г) п<6 и q 2;
д) и<7 и <?<3.
При доказательстве этой теоремы, а также во многих
других вопросах оказываются полезными следующие
два понятия: отображение /0 : Xm-+Yn наз. г о м о-
топи чески устойчивым, если для любой
гладкой гомотопии ft отображения /0 найдутся гладкие
гомотопии hf и kt тождественных диффеоморфизмов
X'" и У" такие, 4To/f=/i(j/0o/ct для достаточно малых (;
отображение / : Xm-+Y" наз. инфинитези-
мально устойчивым, если всякое бесконечно
близкое к /0 отображение / может быть получено из /„
«бесконечно близкими к тождественным» диффео-
диффеоморфизмами Хт и Y". Для собственного отображения
понятие устойчивости, гомотопич. устойчивости и ин-
финитезимальной устойчивости совпадают [3]. Задача
нахождения локальных нормальных форм устойчивых
отображений сводится к задаче классификации нек-
рых конечномерных локальных алгебр [14], [15]. Для
фиксированных т, п число таких нормальных форм
конечно.
Если в определении устойчивого отображения в ка-
качестве h и к взять вместо диффеоморфизмов гомеомор-
гомеоморфизмы, то получится определение топологиче-
топологически устойчивого отображения. До-
Доказана теорема (см. [8]) о плотности множества топо-
топологических устойчивых отображении в нространстве
всех отображений любого компактного многообразия
Хт в любое многообразие Y" (при любых т, п).
Конечно определенные ростки.
Пусть ~ — нек-рое отношение эквивалентности на
множестве C°°(Rm, R")o, о ростков отображений Rm —>-
—>- R™, переводящих 0' в 0. /с-струя любого такого
ростка — это его отрезок ряда Тейлора порядка к.
Росток / наз. к-о пределенным, если любой
другой росток g, имеющий ту же fc-струю, удовлетво-
удовлетворяет соотношению /~g. Росток наз. конечно
определенным, если он fc-определен при нек-
ром к. Достаточной наз. такая /с-струя а, что
любые два ростка /, g, имеющие а в качестве А--струи,
удовлетворяют соотношению /~g. Наиболее часто
встречающиеся эквивалентности носят специальные
названия:
r-'з квивалентность — принадлежность од-
одной орбите группы Difl'°° (RmH «правых» замен коор-
координат; rl-'j квивалентность — принадлеж-
принадлежность одной орбите группы Dif?°° (RmHX Diff°° (R")o-
Топологическая эквивалент-
эквивалентность — принадлежность одной орбите группы
Diff0(RmHX Diff°(R™H. Изучение ^-определенного ростка
сводится к изучению отображения, заданного много-
многочленами степени <:&.
Решение вопроса о том, является ли росток /
^-определенным относительно rZ-эквивалентности, сво-
сводится к задаче о разрешимости нек-рой явно выписы-
выписываемой системы конечного числа линейных уравнений.
Множество конечно определенных относительно
^-эквивалентности ростков открыто в С°° (Rm, R™)o,o-
однако плотно не для любых т, п. Естественно рас-
рассмотреть более грубое отношение топологич. экви-
эквивалентности. После выбрасывания из С°° (Rm, R™H, о
подмножества бесконечной коразмерности остается
счетное число классов топологич. эквивалептности,
каждый из к-рых является полуалгебраич. множест-
множеством. Отсюда следует, что открытое плотное множество
в С°°(Х, У) (Хт—компактно) составляют отображе-
отображения, ростки к-рых топологически эквивалентны поли-
полиномиальным [13].
Деформации. Если отображение зависит от
параметров, то говорят, что задано семейство отобра-
отображений. Если семейство отображений изучается ло-
локально, то при малом изменении параметров в окрест-
окрестности фиксированных значений говорят о деформации
отображения, соответствующего этим значениям пара-
параметров. Оказывается, во многих случаях изучение
всевозможных деформаций сводится к изучению одной
единственной, из к-рой получаются все остальные.
Такая деформация, в нек-ром смысле самая большая,
содержит в себе все существенно разные деформации
данного отображения. Она наз. нереальной
деформацией (см. [11], [12], [13]).
Критические точки функций. Критич. точка функции
наз. невырожденной, если второй дифферен-
дифференциал — невырожденная квадратичная форма. Функция
общего положения имеет лишь невырожденные критич.
точки, а в окрестности каждой из них она может быть
приведена к стандартной форме. Вырожденные критич.
точки приходится рассматривать в тех случаях, когда
эти функции зависят от параметров, и чем больше
число этих параметров, тем более сложные критич.
точки будут встречаться неустранимым (малым шеве-
шевелением) образом при нек-рых значениях параметров.
Семейство функций, зависящее от любого числа па-
параметров, можно превратить малым шевелением в се-
семейство, в к-ром при каждом значении параметра
в окрестности любой точки области определения функ-
функция представляется многочленом в нек-рой локальной
системе координат. Это позволяет при локальном изу-
изучении функций рассматривать только многочлены и
использовать комплексный анализ.
Классификация критических то-
точек функций. Естественно начать с классифика-
классификации ростков в 0 голоморфных функций в С™, бчитая
два ростка эквивалентными, если один пере-
переводится в другой ростком голоморфной замены коор-
координат в С", сохраняющей 0. Струя (многочлен Тей-
Тейлора) голоморфной функции в 0 достаточна, если она
определяет функцию с точностью до эквивалентности.
Росток, у к-рого критич. точка 0 изолирована, всегда
имеет достаточную струю и, следовательно, эквива-
эквивалентен многочлену. Кратностью (или чис-
числом Милнора) |я критич. точки 0 наз. число не-
невырожденных критич. точек, на к-рые распадается
критич. точка 0 при малой шевелении функции. Если
кратность критич. точки функции / равна и,, то(и,+ 1)-
струя достаточна. Т. к. кратность [i при малом изме-
изменении / не может увеличиваться, то классификация
функций, близких к функции с изолированной кри-
критич. точкой, сводится к изучению действия группы Ли
&-струп замен переменных на пространстве &-струй
при достаточно большом к. В пространстве А-струй
функций / таких, что /@) —0, <//@) —0, коразмерность
орбиты / равна (д, —1, поэтому критич. точки крат-
кратности [i встречаются неустранимым образом в семей-
семействах функций, зависящих от (и,—1) параметров.
Получены классификация (см. [10]) всех критич. то-
точек кратности (х<16 и алгоритм приведения любой
такой функции к нормальной форме. Сложность кри-
критич. точки определяется не только ее кратностью и,,
но и ее модальностью т (числом модулей).
Критич. точка наз. простой (или 0-м одаль-
н о и), если среди всех близких критич. точек най-
найдется не более чем конечное число попарно неэквива-
неэквивалентных. Два ростка функций наз. стабильно
эквивалентными, если они становятся экви-
эквивалентными после прямого сложения с невырожден-
невырожденными квадратичными формами от подходящего числа
неременных (для ростков функций от одинакового
числа неременных стабильная эквивалентность не от-
отличается от обычной).
С точностью до стабильной эквивалентности простые
ростки исчерпываются следующим списком:
Dk:f(x, y)=x*
М одальностью точки х?Х при действии
группы Ли G на многообразии X наз. наименьшее
число ш такое, что достаточно малая окрестность
точки х покрыта конечным числом т-параметрич.
семейств орбит.
Получена также классификация ростков функций
модальности 1 и 2 (см. [10]). Классификация простых
особенностей и особенностей малой модальности ока-
оказывается связанной с группами Ли, Кокстера и Вейля
серий A, D, Е, с теорией Кос Артина, классификацией
правильных многогранников в трехмерном прост-
пространстве, классификацией Кодаиры вырождений эл-
липтич. кривых, классификацией треугольников на
плоскости Лобачевского (см. [10], [11]).
Краевые особенности. Ряд геометрич.
задач требует изучения критич. точек функций на
многообразии с краем.
В комплексном случае эта ситуация соответствует
изучению ростка функции, заданной в пространстве
С™ с выделенным подпространством С". Такие
ростки изучаются с точностью до замен переменных
в С", переводящих С" в себя. В этой Ситуации
также получена классификация всех простых ростков,
ростков модальностей 1 и 2. Классификация простых
краевых особенностей оказывается связанной с прос-
простыми алгебрами Ли В, С, F^.
Топологические характеристики
ростка голоморфной функции. Пусть
/ : (С, 0)->-(С, 0) — функция, голоморфная в ок-
окрестности нуля и имеющая в нуле критич. точку крат-
кратности и,. Пусть т), е — положительные числа,
BczC— шар |ж]12+. . .+|xn|2<e2, S — его граница,
ТаС — диск |i| <i), Т'— проколотый диск Т\0.
Пусть X(t)--f~l(t)[\B, X=f-L(T')r\B. Для подхо-
подходящих вит) (е достаточно малого и п достаточно
малого по сравнению с е) отображение / : Х^>-Т'—
гладкое локально тривиальное расслоение. Слой X (t)
этого расслоения — Bге—2)-мерное многообразие с
краем, гомотопичееки эквивалентное букету ц, (п.—1)-
мерных сфер. Край X (t) есть 2ге—3-мерное многооб-
многообразие, диффеоморфное f~1(O)f\S. Даже для сравни-
сравнительно простых / это многообразие может быть не-
нетривиальным. Напр., 28 многообразий
4"-* + 4 + х1 + х1 + 4 = 0,
28,
суть 28 сфер Милнора (к-рые все гомеоморфны обыч-
обычной семимерной сфере, но попарно не диффеоморфны).
Группа приведенных гомологии Hn-i\X(t), *, %)
изоморфна Z1* ¦ Индекс пересечения определяет на
//„_! целочисленную билинейную форму. Перенос
слоев расслоения / : Х^>-Т' над кривыми в Т' опреде-
определяет действие фундаментальной группы Л1(Г') в (ге—1)-
мерных гомологиях слоя. Образующей л1(Т') отве-
отвечает автоморфизм группы гомологии, наз. опера-
оператором м о н о д р о м и и. Оператор монодромии
сохраняет форму пересечений. Собственные значения
оператора монодромии несут информацию об асимпто-
асимптотиках различных интегралов, связанных с функ-
функцией /.
Лит.: [1] Арнольд В. И., Варченко А. Н., Г у-
сейн-Заде СМ., Особенности дифференцируемых отобра-
отображений, М., 1И82; [2] Арнольд В. И., Математические методы
классической механики, М., 1074; [3] Голубицкий М.,
Гийемин В., Устойчивые отображения и их особенности,
пер. о англ., М., 1977; [4] Б р с к е р Т., Л а и д е р Л., Диф-
Дифференцируемые ростки и катастрофы, пер. с англ., М., 1977;
[5] ПостонТ., Стюарт И., Теория катастроф и ее прило-
приложения, пер. с англ., М., 1980; [6] Ми л нор Д ж., Особые точки
комплексных гиперповерхностей, пер. с англ., М., 1971; [7]
Особенности дифференцируемых отображений, Сб. ст., пер. с
англ. и франц., М., 1968; [8] Topological stability of smooth map-
mappings, В.— Hdlb.— N. Y., 1976; [9] T h о m R., Stabilite struc-
turelle et morphogenesc, N. Y., 1972; [10] A p н о л ь д В. И.,
«Функц. анализ и его приложения», 1972, т. й, J\T« 4, с. 3—25;
[11] его же, «Успехи матем. наук», 1972, т. 27, в. 5, с. 119—
184; 1973, т. 28, в. 5, с. 17—44; 1974, т. 29, в. 2, с. 11—49;
1975, tr. 30, в. 5, с. 3—65; [12] Т о м Р., там же, 1972, т. 27,
в. 5, с. 51—57; [13] Варченко А. Н., «Изв. АН СССР.
Сер. матем.», 1974, т. 38, № 5, с. 1037—90; 1975, т. 39, № 2, с.
294—314; [14] Мааср Д., «Математика», 1970, т. 14, JVi 1, с.
145—75; 115] его же, «Успехи матем. наук», 1973, т. 28, в. 6,
с. 165 — 90; 1974, т. 29, в. 1, с. 99 — 158.
А. Н. Варченко, А. Г. Нушниренко.
ОСОБЕННОСТЬ аналитической ф у н к-
ц н и — 1) Множество особых точек аналитич. функции
f(z) комплексных переменных z— (zlt . . ., zn), re^l,
выделяемое теми или иными дополнительными усло-
условиями. В частности, изолированные особые точки иногда
наз. изолированными О.
2) Множество ЯсС" такое, что в нек-рой области
D, примыкающей к К, определена одпозначная ана-
лптич. функция /(z) и для к-рого ставится вопрос
о возможности аналитич. продолжения /(z) на К.
Напр., пусть D — область пространства С™, К —
компакт, содержащийся в D, и /(z) голоморфна на
D\K. Тогда К — потенциальная О. функции /(z),
ц ставится вопрос об аналитич. продолжении (быть
может, при нек-рых дополнительных условиях) /(z)
на всю область D, иначе говоря, вопрос об «устране-
«устранению, или «стирании», особенности К.
См. также Устранимое множество.
Е. Д. Соломепцсв.
ОСОБОЕ РЕШЕНИЕ обыкновенного диф-
дифференциального уравнения — реше-
решение, в каждой точке к-рого нарушается единственность
решения задачи Коши для этого уравнения. Напр.,
для уравнения 1-го порядка
!/=/(*, У) (*)
с непрерывной правой частью, всюду имеющей конеч-
конечную или бесконечную частную производную по у, О. р.
может лежать только во множестве
М = {(х, у)\\1у{х, У)\=<*>].
Кривая усМ есть О. р. уравнения (*), если у являет-
является интегрально!! кривой уравнения (*) и через каждую
точку кривой у проходит по крайней мере еще одна
интегральная кривая уравнения (*). Пусть уравне-
уравнение (*) имеет в нек-рой области G общий интеграл
Ф(х,у, С)=0; если это семейство кривых имеет огиба-
огибающую, то она является О. р. уравнения (*). Для диффе-
дифференциального уравнения
F(x, у, jO =0
О. р. находится исследованием дискриминантной кри-
кривой.
Лит.: [1] Степ а н о в В. В., Курс дифференциальных урав-
уравнений, 7 изд., М., 1958; [2] Сан со не Дш., Обыкновенные
дифференциальные уравнения, пер. с итал., т. 2, М., 1954.
Я. X. Розов.
ОСОБОЙ ТОЧКИ ИНДЕКС — одна из основных
характеристик изолированной особой точки векторного
поля. Пусть векторное поле X определено в Rn, Q —
сфера малого радиуса, окружающая особую точку х0,
такая, что X\q^0. Тогда индексом indAl)(-Y) осо-
особой точки х0 векторного ноля X наз. степень
отображения deg /, где
Если х0 невырождена, то
ind^0 (X) = sign det
О. т. и. не зависит от направления поля.
М. И. Войцеховский.
ОСОБЫЕ ПОКАЗАТЕЛИ линейной системы обык-
обыкновенных дифференциальных уравнений — величины,
определяемые формулой:
й» (А) = TTui g-^- In |! X F, т) |!
(верхний особый показатель) или
формулой
шОD)= Ит _1-In || А'(г, 6) |j
О —т -> + со
(нижний особый показатель), где
Х(в, т) — Коши оператор системы
x = A(t)x, i e R". A)
где А (•) — отображение R+->Hom(R", R"), суммируе-
суммируемое на каждом отрезке.
О. п. могут равняться ± оо; если для нек-рого Г>0
sup V || А (т) || йт < + оо,
то О. п. суть числа.
Для системы A) с постоянными коэффициентами
(A (t)=A @)) О. п. Q°(A) и а>°(А) равны соответственно
максимуму и минимуму действительных частей собст-
собственных значений оператора А @). Для системы A) с
периодич. коэффициентами (A (t-\- T)—A (t) при всех
/?R для нек-рого 7>0) О. п. Q°(A) и (а°(А) равны соот-
соответственно максимуму и минимуму логарифмов модулей
мультипликаторов, деленных на период Т. Иногда О. п.
наз. иначе, напр, генеральными показа-
показателями (см. [4]).
Следующие определения эквивалентны приведен-
приведенным выше: О. п. п°(А) равен точной нижней грани мно-
жества тех чисел а, для каждого из к-рых найдется чис-
число С«>0 такое, что для всякого решения x(t)?=0 систе-
системы A) выполнено неравенство
I х F) К Саеа iQ"x) \х(т)\ для всех 6 Эз т S& 0;
О. п. ы°(А) равен точной верхней грани множества тех
чисел р, для каждого из к-рых найдется число Ср >0
такое, что для всякого решения x(t)^=O системы A) вы-
выполнено неравенство
I х F) | Ss Cji еР <0~т) | х (т) | для всех ОЗэ т > 0.
Для О. п. и Ляпунова характеристических показате-
показателей имеют место неравенства:
sup ¦+r
...^skn(A)^a<>(A)^ — sup 4-
te R+ J
Для линейных систем с постоянными или с нериодич.
коэффициентами
но существуют системы, для к-рых соответствующие не-
неравенства — строгие (см. Равномерная устойчивость).
О. п. О°(Л) (соответственно шй{А)) как функция на
пространстве систем A) с ограниченными непрерывны-
непрерывными коэффициентами (отображение А (¦) непрерывно и
sup \\A (/)||<+оо), наделенном метрикой
<6 R +
d(A, B)=s. sup \\A (l) — B(t)\\,
полунепрерывна сверху (соответственно снизу), но но
всюду непрерывна.
Если отображение А (•) : R->- Hom(R", R") равно-
равномерно непрерывно и
вирИ(()||< + оо,
ti R
то сдвигов динамическая система (S— Hom(R™, R"))
имеет инвариантные нормированные меры ut и ц2)
сосредоточенные на замыкании траектории точки А,
такие, что для почти всех А (в смысле меры ц^) верхний
О. п. системы
х = А (t) х B)
равен ее наибольшему (старшему) характористич. пока-
показателю Ляпунова
и для почти всех А (в смысле меры (х2) нижний О. п.
системы B) равен ее наименьшему характористич. по-
показателю Ляпунова
Для почти периодич. отображения А (•) (см. Линейная
система дифференциальных уравнений с почти перио-
периодическими коэффициентами) меры [Xj и [х2 идентичны и
совпадают с той единственной нормированной инвари-
инвариантной мерой, сосредоточенной на сужении динамич.
системы сдвигов на замыкание траектории точки А,
к-рая в этом случае имеется.
Пусть динамич. система на гладком замкнутом п-
морном многообразии V задана гладким векторным
полем. Тогда у этой системы найдутся нормированные
инвариантные меры [хх и [х2 такие, что для почти всякой
(в смысле меры Цх) точки x?V* совпадают верхний О. п.
и старший характеристич. показатель Ляпунова сис-
системы уравнений в вариациях вдоль траектории точки х
и для почти всякой (в смысле меры (х2) точки a?F"
совпадают нижний О. и. и наименьший характеристич.
показатель Ляпунова системы уравнений в вариациях
вдоль траектории точки х. Определения О. п., харак-
теристич. показателей Ляпунова и т. п. сохраняют
смысл для систем уравнений в вариациях гладких дина-
мич. систем, заданных на любых гладких многообра-
многообразиях. Система уравнений в вариациях такой динамич.
системы вдоль траектории точки х может быть записана
в виде A), напр, с помощью задания в касательном про-
пространстве к V" в каждой точке траектории точки х ба-
базиса, полученного параллельным перенесением вдоль
траектории точки х (в смысле римановой связности, ин-
индуцированной какой-либо гладкой римановой метри-
метрикой) нек-рого базиса касательного пространства к V"
в точке х.
Лит.: [1] В о h I P., i<J. reine und angew. Math.», 1913, Bd
144, S. 284—318; [2] Персидский К., «Матем. сб.», 1933,
т. 40, № 3, с. 284—93; [3J Б ы л о в Б. Ф., Виноград Р. Э.,
Гробманд. М., Немыцкий В- В., Теория показателей
Ляпунова и ее приложения к вопросам устойчивости, М., 1966;
[4]Далецкий Ю. Л., К р е й н М. Г., Устойчивость решений
дифференциальных уравнений в банаховом пространстве, М.,
1970; [5] И з о бо в Н. А., в кн.: Итоги науки и техники. Матсм.
анализ, т. 12, М., 1974, с. 71—146. В. М. Миллионщиков.
ОСРЕДНЕНИЕ, усреднени с,— операция вы-
вычисления средних значений функций, входящих в
структуру дифференциальных уравнений, описываю-
описывающих периодические, почти периодические ц, вообще,
колебательные процессы. Операция О. может рассмат-
рассматриваться как нек-рый сглаживающий оператор. Ме-
Методы О. впервые стали применяться в небесной механи-
механике при исследовании движения планет вокруг Солнца.
Позже они получили распространение в самых разно-
разнообразных областях: в теории нелинейных колебаний, в
физике, в теории автоматич. регулирования, астро-
астродинамике и др. Методы О. часто позволяют находить
приближенные решения для исходных уравнений.
Наиболее типичные классы дифференциальных урав-
уравнений, к к-рым применяются методы О., следующие.
1) Стандартные системы в смысле Н. Н. Боголюбова
где х, X — векторы, / — время, [х — малый положи-
положительный параметр.
2) Многочастотные автономные 2я-перподические
системы
dx v , .
f (х, У), )
где х, у, X, Y — векторы, причем
X (х, у+Bп))=тХ(х, у), Y(x, р.]-Bл)) == У (х, у),
ш(х) — вектор частот.
3) Многочастотные неавтономные системы
¦~ = цХ (х, у, t),
$- = ео(я, У, t)-\iiY(x, у, 0. C)
Вместо систем A) — C) рассматриваются «более прос-
простые» осреднвнные системы 1-го приближения:
^- = ^Х0(х) (Г)
^- = цХ2(ж, х„, 1/0, t), ~]
dii , .,
-^-^(i)(a>, у, I),
где
JT0 (x) = lim -\r\TX (x, t, O)dt, D)
T -* <E 1 JO
E)
X2(a>, x0, y0, <„) =
= lira -М!0 + Г Х(а5,ф(а;0) ;,„, t0, t),t)dt. F)
Г ->• CO J >O
Формулы D) —F) выражают наиболее распространен-
распространенные схемы О.
Формула F) выражает схему О. «вдоль порождающего
решения». В функции Х(х, у, t) вектор у сначала заме-
заменяется порождающим решением системы
dx/dt = O,
dijldt—ю (х, у, t),
после чего вычисляется интегральное среднее F).
Принципиальный вопрос, к-рый возникает при заме-
замене систем A)—C), состоит в том, чтобы построить е-
оценки для норм
\\x(i, \i)-x(t, u.)||, \\y(t, \i)-y(t, ц,)|]
на возможно большем (порядка 1/|л) промежутке вре-
времени, если
а; @, м) = ж@, |i), у @, ц) = //((), ц).
В этом состоит проблема обоснования методов О. Для
систем A) проблема обоснования методов О. была по-
поставлена и решена Н. Н. Боголюбовым, результаты
к-рого заложили основы современной алгоритмич. тео-
теории обыкновенных дифференциальных уравнений.
Лит.: П] Боголюбов Н. Н., Митрополь-
с к и й IO. Л., Асимптотические методы в теории нелинейных ко-
колебаний, 4 изд., М., 1974; [2] М и т р о п о л ь с к и й Ю. А.,
Метод усреднения в нелинейной механике, К., 1971; [3J В о л о-
сои В.М., Моргунов Б. И., Метод осреднения в теории
нелинейных колебательных систем, М., 1071; [4] Г р е б е н и-
к о в Е. А., Рябов Ю. А., Конструктивные методы анализа
нелинейных систем, М., 1979. Е. А. Гребеников.
ОСТАТОЧНЫЙ ЧЛЕН разложения функ-
функции — аддитивное слагаемое в формуле, задающей ап-
аппроксимацию функции с помощью другой, в каком-то
смысле более простой. О. ч. равен разности между за-
заданной функцией и функцией ее аппроксимирующей,
тем самым его оценка является оценкой точности рас-
рассматриваемой аппроксимации.
К указанным формулам относятся формулы типа Тей-
Тейлора формулы, интерполяционных формул, асимпто-
тич. формул, формул дли приближенного вычисления
тех или иных величин и т. п. Так, в формуле Тейлора
/(¦*) = А = 0 ft! (г-*о)" + »((*-*о)"), *—-*,,
О. ч. (в виде Пеано) наз. слагаемое О((х — хо)п). При
аснмптотич. разложении функции
О. ч. является о( п + Л , х ->оо. В частности, в Стир-
линга формуле, дающей асимптотич. разложение гамма-
функции Унлсра
г (,+1) = УШ* (т)' + о Vе"ss$~ Т)' s -*¦+ ю'
О. Ч. является O(e-lSss~"'i'!). Л. Д. -Кудрявцев.
ОСТРОГРАДСКОГО МЕТОД — метод выделения ал-
гебраич. части у неопределенных интегралов от рацио-
рациональных функций. Пусть Р (х) и Q(x) — многочлены с
действительными коэффициентами, причем степень Р(г
меньше степени Q(x) и, следовательно, ^~ —правиль-
—правильная дробь,
1, A)
ah Pji <lj — действительные числа, pj/4—<?y<0, щ и
P,- — натуральные числа, s=l, 2, . . ., r, /=i, 2, . . ., s,
Тогда существуют такие действительные многочлены
Р\(х) и Р%{х), степени к-рых меньше соответственно чем
степени пх и n2=r-\-2s многочленов Qi(x) и Q-i(x), что
Важным является то обстоятельство, что многочлены
Qi(x) и Q2(x) можно найти без знания разложения A)
многочлена Q(x) на неприводимые множители: много-
многочлен Q\(x) является наибольшим общим делителем мно-
многочлена Q (х) и его производной Q'(x) и может быть полу-
получен с помощью алгоритма Евклида, а Q2(z)=Q(x)/Qi(x).
Коэффициенты многочленов Р\(х) и Рг(х) можно вычис-
вычислить с помощью неопределенных коэффициентов метода.
О. м. сводит, в частности, задачу интегрирования пра-
правильной рациональной дроби к задаче интегрирования
правильной рациональной дроби, знаменатель к-рой
имеет простые корни; интеграл от такой функции вы-
выражается через трансцендентные функции: логарифмы
и арктангенсы. Следовательно, рациональная дробь
1'' в формуле C) является алгебраич. частью неоп-
неопределенного интеграла \ х dx.
О. м. впервые опубликован М. В. Остроградским в
1845 (см. [1]).
Лит.: [1] О с т р о г р а д с к и й М. В., «Bull, scient. Acad.
Sci. St.-Pitershourg», 1845, t. 4, JVt 10—11, p. 145—67; № 18—19,
p. 2S6—300. Л. Д. Кудрявцев.
ОСТРОГРАДСКОГО ФОРМУЛА — формула интег-
интегрального исчисления функций многих переменных, уста-
устанавливающая связь между и-кратным интегралом по
области и (п—1)-кратным интегралом по ее границе.
Пусть функции X{—Xi(x1,x.z, ..., хп) вместе со своими
частными производными dXf/dxj, (=1, 2, . . ., п, ин-
интегрируемы по Лебегу в ограниченной области GdRn,
граница dG к-рой является объединением конечного
множества кусочно гладких (п—1)-мерных гиперповерх-
гиперповерхностей, ориентированных с помощью внешней нормали
V. Тогда О. ф. имеет вид
Если cos a,-, i==l, 2, . . ., n,— направляющие ко-
косинусы внешних нормален V гиперповерхностей, со-
составляющих границу dG области G, то формула A)
может быть записана в виде
я дХ1
где dv=dxi . . . dxn— элемент re-мерного объема в Rn,
a do — элемент (и—1)-мерного объема на dG.
В терминах векторного ноля ге— (Хг, . . ., Хп) фор-
формулы A) и B) означают равенство интеграла от дивер-
дивергенции этого поля по области G его потоку (см. Потоп
векторного поля) через границу области G:
Для гладких функций О. ф. была впервые получена
в трехмерном случае М. В. Остроградским в 1828
(опубл. в 1831, см. fl]). На re-кратные интегралы в слу-
случае произвольного натурального п О.ф. была обобщена
им в 1834 (опубл. в 1838, см. [2]). С помощью этой фор-
формулы М. В. Остроградский нашел выражение произ-
производной по параметру от re-кратного интеграла с пере-
переменными пределами и получил формулу для вариации
м-кратного интеграла; при ге=3 для одного частного
случая О. ф. была получена К. Гауссом (С. Gauss)
в 1813 , поэтому иногда О. ф. наз. также формулой
Остроградского — Гаусса. Обобщением
О. ф. является Стокса формула для многообразий с
краем.
Лит-: [1] ОстроградскийМ: В., «Memoires de Г Aca-
Academic des Sciences de St. Petersbourg. Ser. 6 — Sciences mathe-
matiques, physiques et naturelles», 1831, t. 1, p. 117—22; [2]
его же, там ше, 1838, t. 1, p. 35—58. Л. Д. Кудрявцев.
ОСТРОГРАДСКОГО — ЛИУВИЛЛЯ ФОРМУЛА —
см. Лиувилля — Остроградского формула.
ОСЦИЛЛИРУЮЩЕЕ РЕШЕНИЕ — то же, что ко-
колеблющееся решение обыкновенного дифференциального
уравнения.
ОСЦИЛЛЯТОР ГАРМОНИЧЕСКИЙ — система с
одной степенью свободы, колебания к-рой описываются
уравнением вида
Фазовые траектории — окружности, период колеба-
колебаний Г=2я/со не зависит от амплитуды. Потенциальная
энергия О- г. квадратично зависит от х:
Примеры О. г.: малые колебания маятника, колебания
материальной точки, закрепленной на пружине с пос-
постоянной жесткостью, простейший электрический коле-
колебательный контур. Термины «гармонический осцилля-
осциллятор» и «линейный осциллятор» часто употребляются
как синонимы.
Колебания квантовомеханичеокого линейного осцил-
осциллятора описываются уравнением Шрёдингера
b-Q
Здесь т — масса частицы, Е — се энергия, h — посто-
постоянная Планка, со — частота. Квантовомеханический
линейный осциллятор имеет дискретный спектр уров-
уровней энергии ?1„=(п+1/2)йA), ге=0, 1, 2; соответствую-
соответствующие сооственные функции выражаются через Эрмита
функции.
Термин «осциллятор» употребляется по отношению
к системам (механическим или физическим) с конечным
числом степеней свободы, движение к-рых носит коле-
колебательный характер (напр., многомерный линейный
осциллятор — колебания материальной точки, на-
находящейся в потенциальном ноле сил с потенциалом,
к-рый является положительно определенной квадра-
квадратичной формой от координат, нелинейный осциллятор
Ван дер Поля, см. Ван дер Поля уравнение). По-види-
По-видимому, не существует однозначного толкования термина
«осциллятор» или даже «линейный осциллятор».
Лит.: [1] Мандельштам Л. И., Лекции по теории
колебаний, М., 1972; [2] Ландау Л. Д., Л и в ш и и Е. М.,
Квантовая механика. Нерелятивистская теория, а изд., М.,
11O4 (Теоретическая физика, т. 3). М. В. Федирюк.
ОСЦИЛЛЯЦИОННАЯ МАТРИЦА — вполне неот-
неотрицательная матрица А такая, что существует целое
положительное число %, для к-рого А"*-—вполне поло-
положительная матрица; при этом матрица А наз. в п о л-
не неотрицательной (вполне поло-
положите л ь н о й), если все ее миноры любого порядка
неотрицательны (положительны). Наименьший ил по-
показателей % наз. показателем О. м. Если А —
О. м. с показателем %, то при любом целом к~^% мат-
матрица Ак вполне положительна; натуральная степень
О. м. и матрица D+)-1—также О. м. Для того чтобы
вполне неотрицательная матрица А = ||e,-fc||i была О. м.,
необходимо и достаточно, чтобы: 1) А была неособенной
матрицей, 2) при г = 1, . . ., ге было выполнено а,', , + 1>0,
а/ + 1,,->0.
Основная теорема для О. м.: О. м. А=ЬчЛ\ всегда
имеет п различных положительных собственных зна-
значений; у собственного вектора и1, отвечающего наи-
наибольшему собственному значению Xlt все координаты
отличны от нуля и одного знака; у собственного век-
вектора us, соответствующего s-му по величине собствен-
собственному значению %s, имеется точно s— 1 перемен знака;
при любых действительных числах cg, cg + i,. . ., с^, 1«:
_ в ряду координат вектора
и~ 2jk=ifn число перемен знака заключается между
1Г-1 и fc-1.
Лит.: [1] Г а н т м а х е р Ф. Р., К р е й н М. Г., Осцилля-
ционные матрицы и ядра и малые колебания механических сис-
систем, 2 изд., М.— Л., 1950. В. И. Ломоносов.
ОСЦИЛЛЯЦИОННОЕ ДИФФЕРЕНЦИАЛЬНОЕ
УРАВНЕНИЕ — обыкновенное дифференциальное
уравнение, обладающее хотя бы одним осцилляцион-
ным (колеблющимся) решением. Имеются различные
понятия осцилляционности решения. Наиболее рас-
распространены следующие: осцилляционность в точке
(в качестве к-рой, как правило, берется + оо) и осцил-
осцилляционность в промежутке. Ненулевое решение урав-
уравнения
«<»> = /(*, к, и', ..., m<"-]»), «Sa 2, A)
где f(t, 0', , . ., ()) —0, наз. исцилляц ионным в
точке + оо (в промежутке /), если оно имеет
последовательность нулей, сходящуюся к +00 (соот-
(соответственно имеет в / не менее п нулей с учетом их.крат-
ности). Осцилляционность уравнения A) в -Ь оо или
в промежутке / понимается в соответствующем смысле.
Среди осцилляционных в + оо уравнений выделяют
уравнения, обладающие т. н. свойствами А или В,
т. е. в определенном смысле сходные с одним из урав-
уравнений
и(я> = — и или и(л) = и.
При этом уравнение A) обладает свойством
А, если каждое его решение, заданное в окрестности
+ оо, при четном « является осцилляционным, а при
нечетном п — либо осцилляционным, либо удовлетво-
удовлетворяющим условию
lim it('-D (t)=0, i = l, ..., п. B)
Если же каждое решение уравнения A), заданное в ок-
окрестности + оо, при четном п является либо осцилля-
осцилляционным, либо удовлетворяющим условию B) или
lim | мС'-1' (t)\= + оо, j = l, ...,re, C)
t->- + <х
а при нечетном и — либо осцилляционным, либо удов-
удовлетворяющим условию C), то оно обладает свой-
свойством В.
Линейное уравнение
u,w=-a(t)u D)
с локально суммируемым коэффициентом а : [tn, -(-»)
—>-R обладает свойством А (свойством В), если
a(t)<0 [а(<MзО] при t Ss /0.
^ + " гч-1-е j а (?) 1 ^ == + »,
пли
при t^t0, где е>0, a цп— наименьший (vn— наи-
наибольший) из локальных минимумов (максимумов) мно-
многочлена х(х—1). . .(х—ге+1) (см. [1] — [5]).
Уравнение типа Омдсна — Фаулера
и<"> = a (*) | и 1 *" sign и (X > О, X Ф 1) E)
с локально суммируемым неположительным (неотри-
(неотрицательным) коэффициентом а : [<0, -j-oo)—>-R обладает
свойством А (свойством В) тогда и только тогда, когда
где ц=тш{ге—1, (re— 1)Х} (см. [4], [6], [7J).
В ряде случаев вопрос об осцилляционности урав-
уравнения A) можно свести к аналогичному вопросу для
эталонных уравнении вида D) ц E) с помощью теорем
сравнения (см. [11]).
При изучении осцилляционных свойств уравнений с
отклоняющимся аргументом проявляются нск-рые спе-
цифич. особенности. Напр., если п нечетно, Д>0 и для
больших / соблюдается неравенство
то все ненулевые решения уравнения
и(п) (t)=a (t) и («—Д)
ЯВЛЯЮТСЯ ОСЦПЛЛЯЦИОННЫМИ В -1-00 (СМ. [10], [11]).
В то же время при неположительном а и нечетном п
уравнение без запаздывания D) всегда имеет неосцил-
ляционное решение.
Понятия осцилляционности и неосцилляционности
в промежутке изучаются в основном для линейных од-
однородных уравнений. Они имеют фундаментальное
значение для теории краевых задач (см. [12]).
Лит.: [1] К n e s е г A., «Math. Ann.», 18B3, Bd 42, S. 409—
435; [2] Mikusinski J. G-, «Golloq. Math.», 1949, v. 2, p.
34—39; [3j Кондратьев J3. А., «Тр. Моск. матсм. об-ва»,
1961, т. 10, с. 419—36; [4] К и г у р а д з е И. Т., «Матем. сб.»,
1964, т. 65, № 2, с. 172—87; [5] Ч а н т у р и я Т. А., «Изв. АН
СССР. Сер. матем.», 1976 т 40, № 5, с. 1128—42; [6] L i С к о I,,
S v е с М., «Чсхосл. матем. ж.», 1963, т. 13, с. 481—91; [7] К и-
гурадзе И. Т., «Arch. Math.», 1978, v. 14, № 1, p. 21—44;
[8] S w a n s о n С. A., Comparison and oscillation theory of li-
linear differential equations, N. Y.— L., 1968; [9] X a p т-
ман Ф., Обыкновенные дифференциальные уравнения, пер. с
англ., М., 1970; [10] М ы ш к и с А. Д., Линейные дифференци-
дифференциальные уравнения с запаздывающим аргументом, 2 изд., М.,
1972; [11JK о п л а т а д з е Р. Г., Ч а н т у р и я Т. А., Об ос-
осцилляционных свойствах дифференциальных уравнений с откло-
отклоняющимся аргументом, Тб., 1977; [12] Л е в и н А. Ю., «Успехи
матем. наук», 1969, т. 24, и. 2, с. 43—96. И. Т. Кигурадзе.
ОСЦИЛЛЯЦИОННОЕ ЯДРО — функция К{х, s),
, s<:6, такая, что для любых точек х1} . . ., ,г„?
[а, Ь], среди к-рых (при ге—2) имеется по крайней
мере одна внутренняя, матрица \\К(х^, ж^Ц" является
осцилляционной матрицей. В. И. Ломоносов.
я-ОТДЕЛИМАЯ ГРУППА — группа, у к-рой среди
различных простых делителей каждого индекса ее ком-
композиционного ряда содержится не более одного просто-
простого числа из я (я — нек-рое множество простых чисел).
Класс я-О. г. содержит класс п-разрешимых групп.
Для конечных я-О. г. установлена справедливость
л-силовских свойств (см. [1]). Именно, для любого
множества Я)С=я коиечная я-О. г. G содержит Я!-
холловскую подгруппу н любые две Я1-холловские
подгруппы сопряжены в G. Любая ni-подгруппа я-О. г.
G содержится в нек-рой Я1-холловской подгруппе
группы G (см. [2]).
Лит.: [1] Ч у н и х и н С. А., «Докл. АН СССР», 1948, т. 59,
JV» 3, с. 443—45; [2] Н а 11 Р., «Ргос. London Math. Soc», 1956,
v. 6, Х« 22, p. 286—304. С. П. Струнков.
ОТДЕЛИМОЕ ПОПОЛНЕНИЕ КОЛЬЦА — попол-
пополнение топология, кольца А/о, где А — топологич.
кольцо, а о — замыкание в А нулевого идеала о.
О. п. к. снова является топологич. кольцом и обозна-
обозначается обычно А. Всякий непрерывный гомоморфизм
кольца А в полное отделимое кольцо В единственным
образом продолжается до непрерывного гомоморфизма
А-уВ.
В наиболее важном случае, когда топология кольца
А линейна и задается фундаментальной системой идеа-
идеалов (ЭГх)^€д, отделимое пополнение А канонически
отождествляется с проективным пределом lim (Л/31х)
ЯбЛ
дискретных колец А/Жх. Аналогично устроено отде-
отделимое пополнение модулей. В. И. Данилов.
ОТДЕЛИМОСТИ АКСИОМА — условие, налагаемое
на топологич. пространство и выражающее требование,
чтобы те или иные дизъюнктные, т. е. не имеющие
общих точек, множества были в нек-ром определенном
смысле топологически отделены друг от друга. Про-
Простейшие, т. е. самые слабые из этих аксиом, касаются
лишь одноточечных множеств, т. е. точек пространства.
Это т. н. аксиомы То (аксиом а Колмогорова)
и Tf. Дальнейшие суть Г2 (а к с и о м а X а у с д о р-
ф а), Та (а к с и о м а р е г у л я р н о с т и) и ^(ак-
^(аксиома нормальности), требующие, соответствен-
соответственно, чтобы всякие две различные точки (аксиома Т2),
всякая точка и всякое не содержащее ее замкнутое мно-
жество(аксиома Г3), всякие два дизъюнктные замкнутые
множества (аксиома Г4) были отделимы окрестностями,
т. е. содержались в дизъюнктных открытых множест-
множествах данного пространства.
Топологич. пространство, удовлетворяющее аксиоме
Г,-,i=2, 3, 4, наз. Tj-n ространством, Га-про-
Га-пространство наз. хаусдорфовым, а 7"з-простран-
ство — регулярным; хаусдорфово ^-простран-
^-пространство всегда регулярно и наз. нормальным.
Особое место занимает т. н. функциональная
отделимость. Два множества А и В в данном
топологич. пространстве X наз. функциональ-
функционально отделимыми в X, если существует такая
определенная во всем пространстве действительная
ограниченная непрерывная функция /, к-рая прини-
принимает во всех точках множества А одно значение a, a
во всех точках множества В — нек-рое отличное от а
значение 6. При этом всегда можно предположить, что
а=0, 6=1, 0</(ж)<1 во всех точках х?Х.
Два функционально отделимых множества всегда
отделимы и окрестностями, обратное утверждение
верно не всегда. Однако имеет место лемма У р ы-
с о н а: в нормальном пространстве всякие два дизъюн-
дизъюнктные замкнутые множества функционально отделимы.
Пространство, в к-ром всякая точка функционально от-
отделима от всякого не содержащего ее замкнутого мно-
множества, наз. вполне регулярным. Вполне
регулярное Гг-пространство наз. тихоновским.
Лит.: [1] А л е к с а н д р о в П. С, Введение в теорию мно-
множеств и общую топологию, М., 1977. В. И. Зайцев.
ОТДЕЛИМОСТЬ МНОЖЕСТВ — одно из основных
понятий дескриптивной теории множеств (введенное
Н. Н. Лузиным [1]). Служит важным инструментом
для исследования дескриптивной природы множеств.
Говорят, что множества А и А' отделимы при
помощи множеств, обладающих свойствами Р, если
существуют обладающие свойством Р множества В и
В' такие, что АаВ, А'сВ', ВГ\В'-ф.
Основополагающие результаты по отделимости при-
принадлежат Н. Н. Лузину и П. С. Новикову. В дальней-
дальнейшем не только появились многочисленные варианты
теорем отделимости, но и само понятие О. м. было обоб-
обобщено и получило новые формы. Одно из таких обобще-
обобщений связано со следующей теоремой Новик о-
в a [2J: пусть {Ап} — последовательность А-множеств
полного сепарабельного метрич. пространства такая,
что П п^лА „= ф, тогда существует последователь-
последовательность {Вп} борелееских множеств такая, что A^CZBn,
и^1, и (]n-iBn=<p. Эта теорема и различные ее ва-
варианты и обобщения получили название теорем
кратной (или обобщенной) отделимо-
отделимости.
Классич. результаты относятся к множествам, ле-
лежащим в полных сепарабельных метрич. пространствах.
В хаусдорфовом пространстве X: 1) два непересекаю-
непересекающихся аналитич. множества отделимы борелевскими
множествами, порожденными системой G открытых
множеств этого пространства [3] (если X — Урысона
пространство, то «G открытых» можно заменить на «F
замкнутых»; в хаусдорфовом пространстве этого сде-
сделать, вообще говоря, нельзя [4]); 2) пусть $?С — нек-рая
система Л-множеств, порожденных системой F; если
Л есть А -множество, порожденное системой ^f, и
В — аналитич. множество, A f\B= ф, то существует
борелевское множество С, порожденное системой jffl,
такое, что ACZC, СГ\В — ф (еж. [5]).
В отличие от этих (и других) вариантов первого прин-
принципа отделимости многие формулировки второго прин-
принципа отделимости не зависят от топологии простран-
пространства, в к-ром лежат рассматриваемые множества. Одна
из них [6г. пусть система Sft подмножеств данного мно-
множества замкнута относительно операций перехода к
дополнению и содержит ф; пусть {Ап} — произвольная
последовательность СА-множеств, порожденных систе-
системой ffl; тогда существует последовательность {Сп}
попарно непересекающихся С А -множеств, порожден-
порожденных системой Ж, такая, что С„сЛ„, п^1, и (J™=iCi —
— Un=iA п (более точно, это — одна из формулировок
принципа редукции, см. [7]).
Лит.: [1ГЛ у з и н Н. Н., Собр. соч., т. 2, М., 1858; [2] Н о-
в и к о в II. С, «Докл. АН СССР», 1934, т. 3 [т. 4], № 3, с. 145—
148; [3] F roli k Z., «Czechosl. Matli. J.», 1970, v. 20, p. 406—67;
[4] OstaszewskiA. I., «Proc. London Math. Soc», 1973,
v. 27, № 4, p. 649—66; [5] Rogers С A., «J. London Math.
Soc», 1971, v. 3, № 1, p. 103—08; [6] e г о же, там же, 1973,
v. в, Mi 3, p. 491—503; [71 К у р а т о в с к и й К., Топология,
[пер. с англ.], т. 1, М,, 1966. А. Г. Елъкип.
ОТКОСА ЛИНИЯ — кривая, касательная к к-рой
образует постоянный угол с нек-рым неизменным на-
направлением. Пример: винтовая линия. Отношение кру-
кручения О. л. к кривизне О. л. постоянно. Сферич. инди-
индикатриса касательных к О. л. является окружностью.
Если r=r(s) — естественная параметризация О. л.,
то (г", г1", />lv)=0 (см. [2]). Эволюты плоской кривой у
являются О. л., касательные к к-рым наклонены к
плоскости кривой у под постоянным углом (см. [1]).
Дйя всякой О. л. существует неподвижно связанный с
ее сопутствующим триэдром конус, вершина к-рого
лежит на кривой, а образующие описывают разверты-
развертывающиеся поверхности.
Лит.: [1] Б л я ш к е В., Дифференциальная геометрия и
геометрические основы теории относительности Эйнштейна, пер.
с нем., т. 1, М.— Л., 1935; [2] F о г s у t h A. R., Lectures on
the differential geometry of curves and surfaces, Camb., 1912; [3]
A p p e 1 1 P., «Arch. Math. Phys.», 1879, Bd 64, № 1, S. 19—23.
E. В. Шикин.
ОТКРЫТОЕ МНОГООБРАЗИЕ — многообразие, не
имеющее компактных компонент, т. е. не являющееся
замкнутым многообразием. м. И. Войцеховспий.
ОТКРЫТОЕ МНОЖЕСТВО топологического
пространства — элемент топологии этого про-
пространства. Подробнее, пусть топология т топологич.
пространства (X, т) определяется как такая система
т подмножеств множества X, что: 1) Х?т, ф ?т,
2) если 0,?т, г=1, 2, то О^О^х, 3) если0а€т, а€».
то U {0а, а?91}(;т> тогда открытыми мно-
множествами в пространстве (X, т) считаются эле-
элементы топологии т и только они. Б. А. Пасынка.
ОТКРЫТОЕ ОТОБРАЖЕНИЕ — отображение од-
одного топологич. пространства в другое, при к-ром образ
каждого открытого множества открыт.
Проектирование топологич. произведений на со-
сомножители— О. о. Открытость отображения можно тол-
толковать как вид непрерывности обратного к нему мно-
многозначного отображения. Взаимно однозначное непреры-
непрерывное О. о. на — гомеоморфизм. В общей топологий О. о.
применяются при классификации пространств. ВаЖен
вопрос о поведении топологич. инвариантов при не-
непрерывных О. о. Все пространства с первой аксиомой
счетности и только они являются образами метрич.
пространств при непрерывных О. о. Метризуемое про-
пространство, являющееся образом полного метрич. про-
пространства при непрерывном О. о., метризуемо полной
метрикой. Если паракомпакт является образом пол-
полного метрич. пространства при непрерывном О. о.,
то он метризуем. Счетнократное непрорывное О. о.
компактов не повышает размерности. Но трехмер-
трехмерный куб можно непрерывно и открыто отобразить на
куб любой большей размерности. Каждый бикомпакт
является образом некоего одномерного бикомпакта
при непрерывном О. о. с нульмерными прообразами
точек.
Самостоятельное значение имеют непрерывные О. о.,
при к-рых прообразы всех точек бикомпактны,— т. н.
открытые бикомпактные отображе-
отображения. Пространства с равномерной базой и только
они являются образами метрич. пространств при би-
бикомпактных О. о. Важны замкнутые непрерывные О. о.
Таковы все непрерывные О. о. бикомпактов в хаусдор-
фовы пространства. Непрерывные замкнутые О. о.
сохраняют метризуемость. О. о. с дискретными прооб-
прообразами точек играют существенную роль в теории
функций одного комплексного переменного: таковы
все голоморфные в области функции. Теорема об от-
открытости голоморфных функций играет центральную
роль при доказательстве принципа максимума модуля,
при доказательстве фундаментальной теоремы о су-
существовании корня у произвольного непостоянного
многочлена над полем комплексных чисел.
Лит.: [1]Куратовский К., Топология, [пер. с англ.],
т. 1—2, М., 1966—69; [2] К е л Д ы ш Л. В., в кн.: Тр. 3 Всесо-
Всесоюзного математического съезда, т. 3, М., 1958, с. 368—72; [3]
С т о и л о в С, Теория функций комплексного переменного,
пер. с рум., т. 1, М., 1962. А. В. Архангельский.
ОТКРЫТОЕ ОТОБРАЖЕНИЕ, теорема об от-
открытом отображении: линейный непрерыв-
непрерывный оператор А , отображающий банахово пространство
X на все банахово пространство У, является открытым
отображением, т. е. A (G) открыто в У для любого G,
открытого в X; доказана С. Банахом (S. Banach). В
частности, непрерывный линейный оператор А, отобра-
отображающий взаимно однозначно банахово пространство X
на банахово пространство У, является гомеоморфизмом,
т.е. А~х—также линейный непрерывный оператор
(теорема Банаха о гомеоморфизме).
Условиям теоремы об О. о. удовлетворяет, на-
например, всякий ненулевой линейный непрерывный
функционал, определенный на вещественном (ком-
(комплексном) банаховом пространстве X со значениями
в R (в С).
Теорема об О. о. допускает следующее обобщение:
непрерывный линейный оператор, отображающий со-
совершенно полное топологич. векторное пространство
X на бочечное пространство Y, есть открытое отображе-
отображение. К теореме об О. о. примыкает теорема о замкнутом
графике (см. Замкнутый график, теорема о замкнутом
графике).
Лит.: [1] И о си да К., Функциональный анализ, пер. с
англ., М., 1967; [2] РоОертсон A.-IL, Робертсон В,-
Д ж., Топологические векторные пространства, пер, с англ., М.,
10E7. В. И. Соболев.
ОТКРЫТОЕ ЯДРО - множество всех точек х под-
подмножества А топологич. пространства X, для к-рых
существует такое открытое в X множество Ux, что
x?UxCzA. О. я. множества А обозначается обычно
Int А и представляет собой максимальное открытое в
X множество, содержащееся в А. Имеет место равенст-
равенство Int А =-X — \Х—А], где [ ] обозначает замыкание
в пространстве X. О. я. множества топологич. простран-
пространства X есть открытое регулярное, или канони-
каноническое множество. Пространства, в к-рых открытые ка-
нонич. множества образуют базу топологии, наз. п о-
лурегулярными. Всякое регулярное про-
пространство полурегулярно. Иногда О. я. наз. внут-
внутренностью множества. В. И. Пономарев.
ОТКРЫТО-ЗАМКНУТОЕ МНОЖЕСТВО — подмно-
подмножество топологич. пространства, одновременно откры-
открытое и замкнутое в нем. Топологич. пространство X
несвязно тогда и только тогда, когда в нем имеется от-
отличное от X и от ф О.-з. м. Если семейство всех
О.-з. м. тонологич. пространства является базой его
топологии, то это пространство наз. индуктивно
нульмерным. Всякая булева алгебра изоморф-
изоморфна булевой алгебре всех О.-з. м. подходящего индук-
индуктивно нульмерного бикомпакта. Особый класс нуль-
нульмерных бикомпактов образуют т. н. экстремально
несвязные бикомпакты, характеризую-
характеризующиеся тем, что в них замыкание любого открытого мно-
множества также открыто (и замкнуто). Всякая полная бу-
булева алгебра изоморфна булевой алгебре всех О.-з. м.
подходящего экстремально несвязного бикомпакта.
В. И. Пономарев.
ОТНОСИТЕЛЬНАЯ ГОМОЛОГИЧЕСКАЯ АЛГЕБ-
АЛГЕБРА — гомологическая алгебра, ассоциированная с па-
парой абелевых категорий C1, Ш) и фиксированным
функтором Д : 21 —v 5CR. Функтор Д предполагается
аддитивным, точным и полным. Короткая точная после-
последовательность объектов категории 3(
U — -> А —>¦ В —> С —^ О
наз. допустимой, если точная последователь-
последовательность
О —г АА —* АВ -->¦ АС —¦> О
расщепляется в категории 2R. Посредством класса ^
допустимых точных последовательностей определяется
класс ^-проективных (соответственно ^-инъектив-
ных) объектов как класс таких объектов Р (соответ-
(соответственно Q), для к-рых функтор Homs( (P, —) (соот-
(соответственно Нопь( (—, Q)) точен на допустимых корот-
коротких точных последовательностях.
Любой проективный объект Р категории 31 яв-
является (^проективным, это не означает, однако, что
в категории 21 достаточно много относительно проек-
проективных объектов (т. е. что для любого объекта А из
21 существует допустимый эпиморфизм P^r-А нек-рого
^-проективного объекта категории 2Г). Если в ка^
тегории % достаточно много ^-проективных или
4^-пнъектнвных объектов, то обычные конструкции
гомологич. алгебры позволяют строить в этой кате-
категории производные функторы, наз. относитель-
относительными производными функторами.
Прим е р ы. Пусть Щ. — категория Д-модулей над
ассоциативным кольцом/? с единицей, 2R — категория
множеств, Д : 31 —>- Ш1 — функтор, «забывающий»
структуру модуля. В этом случае все точные последо-
последовательности допустимы, и в результате получается «аб-
«абсолютная» (т. е. обычная) гомологич. алгебра.
Если G — группа, то каждый G-модуль является, в
частности, абеловой группой. Если R является алгеб-
алгеброй над коммутативным кольцом к, то каждый if-мо-
дуль является А;-модулем. Если R и S — кольца и
RZlS, то каждый Я-модуль является S-модулем. Во
всех этих случаях имеется функтор из одной абелевой
категории в другую, определяющий относительные про-
производные функторы.
Лит.: [1] М а к л е й н С, Гомология, пер. сангл., М., 196В;
[2] Е i I enberg S. , Moore J. С, Foundations of relative
homological algebra, Providence, 1965.
В. Е. Говоров, А. В. Михалев.
ОТНОСИТЕЛЬНАЯ МЕТРИКА — ограничение мет-
метрики р на подмножество А метрич. пространства X,
т. е. ограничение отображения р квадрата XXX на
квадрат АХАсХХ X. Это понятие позволяет рассма-
рассматривать как метрич. пространство любое его подмно-
подмножество. Б. А. Пасынков.
ОТНОСИТЕЛЬНАЯ СИСТЕМА КОРНЕЙ связ-
связной редуктивной алгебраической
г р у п пы G, определенной над полем к,— система
Ф(;E, G) ненулевых весов присоединенного представ-
представления максимального /с-расщенимого тора S группы G
в алгебре Ли д этой группы. Сами веса наз. корня-
корнями G о т н о с и т е л ь н о ?. О. с. к. Ф&E, G), рас-
рассматриваемая как подмножество своей линейной обо-
оболочки L в пространстве X(S)@gR, где X(S) —груп-
—группа рациональных характеров тора S, является корне-
корневой, системой. Пусть N (S) — нормализатор, a Z{S) —
централизатор S в G. Тогда Z(S) является связной
компонентой единицы группы N(S); конечная группа
Wk(S, G) = N(S)/Z(S) наз. группой Вейля
группы G над к, или относительной
группой Вейля (о. г. В.). Присоединенное
представление N(S) в С} определяет линейное пред-
представление Wk(S\ G) в L. Это представление является
точным и его образ есть Вейля группа системы корней
Ф^E, G), что позволяет отождествить эти две группы.
Ввиду сопряженности над к максимальных /с-расщени-
мых торов bG О. с. к. Ф&E, G) и о. г. В. Wk{S, G) не
зависят, с точностью до изоморфизма, от выбора тора S
и часто обозначаются простоФА(в) и W&(G). В случае,
когда G расщепима над к, О. с. к. и о. г. В. совпадают
соответственно с обычной (абсолютной) системой кор-
корней и группой Вейля группы G. Пусть ga — весовое
относительно S подпространство в д, отвечающее кор-
корню а^Ф^E, G). Если G расщепима над к, то dim #«—-1
для любого а и Ofc(G) — приведенная система корней;
в общем случае это не так: Ф&(в) может быть неириве-
денной, a dim ga может быть больше 1. О. с. к. Ф*(в)
неприводима, если G проста над к.
О. с. к. играет важную роль в описании структуры и
в классификации полупростых алгебраич. групп над к.
Пусть G — нолупроста и Т — максимальный тор, опре-
определенный над А; и содержащий S. Пусть X(S) и X {Т) —
группы рациональных характеров торов S и Т с
фиксированными согласованными отношениями по-
порядка, Д — соответствующая система простых корней
группы G относительно Т и Ло— подсистема в Д, сос-
состоящая из характеров, тривиальных на S. Пусть так-
также Afe— система простых корней в О. с. к. Ф&E, G),
определенная выбранным в X (S) отношением порядка;
она состоит из сужений на S характеров системы Д.
Группа Галуа F==Gal (ks/k) естественно действует на
Д, и набор данных {Д, До, действие Г на Д} наз. к-
индексом полупростой группы G.
Роль fe-индекса объясняется следующей теоремой: вся-
всякая нолупростая группа над к однозначно с точностью
до /с-изоморфизма определяется своим классом отно-
относительно изоморфизма над ks, своим /с-индексом и
своим анизотропным ядром. О. с. к. ®fe(G) полностью
определяется системой Д& и набором таких натураль-
натуральных чисел лк. «6 Д(г (равных 1 или 2), что ма?Ф(С)
)^й(б). В свою очередь, Д(, и »«,
^;, могут быть восстановлены по ^-индексу. В ча-
частности, два элемента из Д\А0 имеют одно и то же огра-
ограничение на S тогда и только тогда, когда они лежат в
одной орбите группы Г; это определяет биекцию между
Aj и множеством орбит группы Г в Д\Д0.
Если у?Д/г, О сД\/\о—соответствующая орбита и
А (у) — любая связная компонента в A0\JO , не все
вершины к-poii лежат в До, то ге есть сумма коэффициен-
коэффициентов при корнях а? А (у) f\O^ в разложении старшего
корня системы Д(у) по простым корням.
Если k--R, к —С, то это О. с. к. естественно отож-
отождествляется с системой корней, а о. г. В.— с группой
Вейля соответствующего симметрич. пространства.
Лит.: [1] Т и т с Ж., «Математика», 1968, т. 12, № 2, с. 110—
143; [2] Б о р е л ь А., Т и т с Ж., там те, 19A7, т. 11, Л"> 1, с.
43—111; № 2, с. 3—31; [3] Tits J., «Proc. of Symposia in pure
math.», 1966, v. 9 p. 33—62 (AMS). В. Л. Попов.
ОТНОСИТЕЛЬНАЯ ТОПОЛОГИЯ подмножества А
тошлогич. пространства (X, т) — система пересече-
пересечений всевозможных открытых подмножеств простран-
пространства (X, т) (т. е. элементов топологии т) с множеством
А- Часто О. т. наз. индуцированной то-
топологией.
Подмножество топологич. пространства (X, т), снаб-
снабженное О. т., наз. подпространством пространства
(X, т). Подпространство ^/-пространства является Т,-
пространством, 1=0, 1, 2, 3, 31/2. Подпространство ме-
тризуемого пространства метризуемо. Любое тихонов-
тихоновское пространство веса <Э гомеоморфно подпростран-
подпространству бикомпакта веса <:Э (теорема Тихонова).
ОТНОСИТЕЛЬНО БИКОМПАКТНОЕ МНОЖЕСТВО—
подмножество М топологич. пространства X такое,
что его замыкание М бикомпактно, м. и. Войцеховский.
ОТНОСИТЕЛЬНО ОТКРЫТОЕ (ЗАМКНУТОЕ)
МНОЖЕСТВО, множество, открытое (з а-
мкнутое) относительно нек-рого множества
/?,— множество М топологич. пространства X такое,
что
М — Е\(Е\М) (МШ
(черта сверху означает операцию замыкания). Для того
чтобы нек-рое множество было открытым (замкнутым)
относительно Е, необходимо и достаточно, чтобы оно
было пересечением М с нек-рым открытым (замкну-
(замкнутым) множеством. М. И. Войцеховский.
ОТНОСИТЕЛЬНОСТИ ПРИНЦИП — один из наибо-
наиболее фундаментальных фиаич. законов, согласно к-рому
любой процесс протекает одинаково в изолированно!!
материальной системе, находящейся в состоянии покоя,
и в такой же системе, находящейся в состоянии рав-
равномерного прямолинейного движения. Состояние дви-
движения или покоя определяется здесь по отношению к
произвольно выбранной ииерциальной системе отсчета;
физически эти состояния полностью равноправны.
Эквивалентная формулировка О. п.: законы физики
имеют одинаковую форму во всех инерциальных систе-
системах отсчета. О. п. вместе с постулатом о независимости
скорости света в вакууме от движения источника света
легли в основу специальной (частной) относительности
теории. ВСЭ-Я.
ОТНОСИТЕЛЬНОСТИ ТЕОРИЯ — физическая тео-
теория, рассматривающая пространственно-временные
свойства физич. процессов. Эти свойства являются
общими для всех физич. процессов, поэтому их часто
наз. просто свойствами пространства-времени. Свой-
Свойства пространства-времени зависят от полей тяготения,
действующих в данной его области. Свойства про-
пространства-времени при наличии полей тяготения иссле-
исследуются в о б щ е и О. т., наз. также теорией тя-
тяготения. В частной (специальной)
О. т. рассматриваются свойства пространства-времени
в том приближении, в к-ром эффектами, связанными с
полями тяготения, можно пренебречь. Ниже излага-
излагается частная О. т., об общей О. т. см. Тяготения теория.
О. т. часто наз. также теорией относитель-
относительности Эйнштейна по имени ее создателя
А. Эйнштейна (см. [1], [2]).
Основные черты теории относительности. Снецифн
ческие (релятивистские) эффекты, описываемые О. i.
и отличающие ее от предшествующих физич. теорий,
проявляются при скоростях движения тел, близких к
скорости света в вакууме с« 3 -10го см/сек. При таких
скоростях, наз. релятивистскими, зависи-
зависимость энергии Е тела массы т от его скорости v опи-
описывается формулой
р тс2
Е = ^=^Г ¦ A)
При скоростях v, много меньших с, формула A) при-
приобретает вид
E^mc* + 2f. B)
второй член справа в формуле B) совпадает с формулой
для кинетич. анергии в классич. механике, а первый
член показывает, что покоящееся тело обладает энер-
энергией Е-=тс2, наз. анергией покоя. В ядерных
реакциях и процессах превращения элементарных
частиц энергия покоя может переходить в кинетич.
анергию частиц. Из формулы A) вытекает, что энергия
тел с ненулевой массой стремится к бесконечности при
v—>-c. Если тфО, то скорость тела всегда меньше с.
Частицы с га=0 (фотоны и нейтрино) всегда движутся
со скоростью света. Иногда говорят, что при реляти-
релятивистских скоростях масса тела начинает зависеть от
его скорости, и величину
У
i -
(газ. массой движения тела, am — его м а с-
с о й п о к о я. Из формул 1,1 A) следует, что
Скорость света в вакууме в О. т. является предель-
предельной скоростью, т. е. передача любых взаимодействий
и сигналов из одной точки в другую происходит со
скоростью, не превышающей скорости света.
Существование предельной скорости несовместимо с
представлениями классич. механики и вызывает необ-
необходимость глубокой перестройки классич. пространст-
пространственно-временных представлений.
Принцип относительности Эйнштейна и другие прин-
принципы инвариантности. В основе О. т. лежит принцип
относительности, согласно к-рому любой физич. про-
процесс протекает одинаково (при одинаковых начальных
условиях) в изолированной материальной системе, на-
находящейся в состоянии покоя по отношению к нек-рой
произвольно выбранной инерциальпой системе отсчета,
и в такой же системе, находящейся в состоянии рав-
равномерного и прямолинейного движения относительно
этой же инерциальной системы отсчета.
Справедливость принципа относительности означает,
что различие между состоянием покоя и равномерного
и прямолинейного движения не имеет физич. смысла.
Говорят, что движущаяся система отсчета получается
из системы отсчета, условно считающейся покоящей-
покоящейся, с помощью преобразования движения. Из принципа
относительности вытекает, что физич. законы инвари-
инвариантны относительно преобразований движения и име-
ют один и тот же вид во всех инерциальных системах
отсчета.
Кроме принципа относительности, известны еще три
типа преобразований, к-рые оставляют неизменным ход
протекания фиаич. процессов: перенос (сдвиг) в прост-
пространстве, вращение в пространстве, перенос (сдвиг) во
времени. Симметрии физич. законов относительно этих
преобразований выполняются точно только в изоли-
изолированных системах или им отвечают соответственно за-
законы сохранения импульса, момента импульса и энер-
энергии.
Инерциальные системы отсчета и преобразования
Лоренца. Инерциальные системы отсчета образуют
в О. т. выделенный класс систем отсчета, в к-рых эффек-
эффекты О. т. имеют наиболее простое описание.
Первичными понятиями О. т. являются понятия
точечного события и светового сигнала. В данной инер-
циальной системе отсчета точечное событие можно ха-
характеризовать тремя пространственными координатами
х, у, z в нек-рой декартовой системе координат и вре-
временной координатой t. Системы координат х, у, z, t
в разных инерциальных системах отсчета связаны Ло-
Лоренца преобразованиями. Из принципа относительно-
относительности, условий симметрии и требования того, чтобы ука-
указанные преобразования образовывали группу, можно
получить вид преобразований Лоренца. Если инерци-
альная система отсчета L' движется относительно инер-
циальной системы отсчета L со скоростью V так, что
оси х и х' совмещены и направлены по V, оси у и у'
и z и г' соответственно параллельны, начала коорди-
координат в L и L' совпадают в момент *=0 и часы в системе V
в начале координат показывают при <=0 время t' — 0,
то преобразования Лоренца имеют вид
, x-Vt , ,
У =У, z' = 2,
Vx
C)
Для получения всех преобразований Лоренца к пре-
преобразованиям C) нужно добавить пространственные
вращения вокруг начала координат. Преобразования
Лоренца образуют группу, наз. группой Лорен-
ц а. Свойство инвариантности фияич. законов при пре-
преобразованиях Лоренца наз. лоренц-инвари-
лоренц-инвариантностью или релятивистской инвариантно-
инвариантностью.
Из преобразований Лоренца вытекает релятивистский
закон сложения скоростей. Если частица движется в
инерциальной системе отсчета L со скоростью v вдоль
оси х, то скорость этой частицы в системе V равна
<4>
Формула D) показывает, что скорость света не зависит
от скорости D) движения источника света.
Из преобразований Лоренца вытекают также основ-
основные эффекты О. т.: относительность одновременности,
памедление времени п сокращение продольных разме-
размеров тел. Так, события А и В, одновременные в системе L
Ьа~*в) и происходящие в разных точках (xi, щ, zx)
и (¦r2t i/21 zi)i оказываются неодновременными в V:
Далее, когда часы, покоящиеся в системе L в точке
(О, 0, 0), показывают время t, то время t' по часам в
U, пространственно совпадающим с часами в L в этот
момент, равно
Таким образом, с точки зрения наблюдателя в L' ча-
часы в ? отстают. Однако в, силу принципа относитель-
относительности с точки зрения наблюдателя в L часы в ?' также
отстают. Размеры тел, покоящихся в L (т. н. с о б с т -
венная длина), при измерении в L' оказывают-
оказываются уменьшенными в "|/Ч — V2/c2 раз в направлении ско-
скорости V сравнительно с размерами в L:
При малых скоростях v преобразования Лоренца C)
с точностью до величин, стремящихся к нулю при
Vic—»-0, совпадают с преобразованиями Галилея:
x'=x—Vt, у' = у, z' = z, t' = t. E)
Эти преобразования соответствуют повседневному опы-
опыту, в к-ром не встречаются движения тел с релятивист-
релятивистскими скоростями. В частности, преобразования Га-
Галилея сохраняют пространственные размеры тел и дли-
длительности физич. процессов. Преобразования E) и
различные их комбинации с пространственными пово-
поворотами образуют т. н. группу Галилея. Важ-
Важным отличием преобразований Лоренца от преобразо-
преобразований Галилея является то, что в формулу преобразо-
преобразования временной координаты t входит пространствен-
пространственная координата х. В связи с этим в О. т. сформирова-
сформировалось представление, согласно к-рому пространствен-
пространственные и временные свойства физич. процессов нельзя
рассматривать изолированно друг от друга. Это при-
привело к возникновению понятия пространства-
времени, т. е. объекта, геометрич. свойства к-рого
определяют пространственные и временные свойства
физич. процессов. В классич. механике Ньютона про-
пространственные свойства физич. процессов определяются
геометрич. свойствами трехмерного евклидова простран-
пространства, а временная переменная входит в уравнения как
параметр. В частной О. т. адекватной моделью про-
пространства-времени является четырехмерное псевдоев-
псевдоевклидово пространство Е*г^ 3)> наз. пространст-
пространством Минковского. Формирование понятия
пространства-времени открыло путь к геометризации
аппарата О. т., значительно развитой при разработке
общей О. т.
Математический аппарат теории относительности и
геометрия пространства Минковского. При аксиома-
тич. описании О. т. аксиомы, фиксирующие свойства
первичных понятий О. т. (точечного события и светового
сигнала), удается вычленить из приведенного выше не-
неформального описания основных положений О. т. Эта
система аксиом дополняется естественными с физич.
точки зрения аксиомами, гарантирующими существова-
существование достаточно большого числа событий и световых сиг-
сигналов, а также нек-рыми аксиомами непрерывности
на множестве световых сигналов и точечных событий.
Иными словами, эти аксиомы гарантируют, что каждый
набор чисел (t, x, у, z) определяет точечное событие.
Получающаяся при таком расширении система аксиом
О. т. оказывается эквивалентной системе аксиом про-
пространства Минковского. Таким образом, пространство
Минковского может служить моделью пространства-
времени частной О. т. Точечное событие интерпрети-
интерпретируется в рассматриваемой модели пространства-вре-
пространства-времени как точка в пространстве Минковского, в связи
с чем точка последнего принято наз. мировыми
точками. Каждая прямоугольная система коор-
координат (t, х, у, z) в пространстве Минковского определя-
определяет нек-рую инерциальную систему отсчета, в связи о
чем сами прямоугольные системы координат в О. т. при-
принято наз. галилеевыми. Плоскость (= const
пространства Минковского наз. пространствен"
ным сечением, соответствующим данной систе-
системе координат. Линейный элемент пространства Мин-
Минковского в прямоугольной системе координат (t, х, у, z)
может быть представлен в виде
Величину ds наз. элементом интервала, а
величину
s2 = с2 (МJ - (Д*J - (ДуJ — (Д»)«
— квадратом интервала. (В качестве модели про'
странства-времени частной О. т. можно использовать
и псевдоевклидово пространство Я^з, j, с линейным
элементом
Преобразования, образующие общую группу Ло-
Лоренца, в рассматриваемой модели являются преобразо--
ваниями, связывающими две галилеевы системы коор-
динат в пространстве Минковского. Эти преобразова-
преобразования сохраняют интервал и являются аналогом орто-
ортогональных преобразований в евклидовой геометрии,
В частности, преобразованиям Лоренца можно при-
придать вид
z'= chip + с? shi|>,
ct' —x' ah\p-\-ct chi|>,
где W — угол поворота в плоскости (ct, x), имеющей
индефинитную метрику
¦<|)=arcsh- —
По знаку квадрата интервала происходит классифи-
классификация векторов в пространстве Минковского. Векторы,
для к-рых s2>0, наз. в р е м е н и п о д о б н ы м и;
векторы, для к-рых s2<0,— пространстве н-
ноподобными; векторы, для к-рых «2=0,— с в е-
топодобными. Если в пространстве Минков-
Минковского выделена нек-рая точка (напр., начало коорди-
координат), то его можно разбить на три области. Две из них,
составленные из точек, соединенных с точкой 0 вре-
мениподобными векторами, наз. областями аб-
абсолютного будущего и абсолютного
прошлого. Эти названия связаны с тем, что при
любом преобразовании из полной группы Лоренца,
связывающей данную галилееву систему координат о
другой галилеевой системой координат (<', х', у', z'),
событие А, лежащее в области абсолютного будущего,
по-лреяшему будет иметь большее значение временной
координаты t', чем событие 0. Область, точки А к-рой
соединяются с 0 пространственноподобными векторами,
наз. областью абсолютного удаления.
Эта область характеризуется тем, что не существует
такого преобразования Лоренца, в результате к-рого
точки Л и 0 получают одинаковые пространственные
координаты. Точки, лежащие на границе этих облас-
областей, образуют световой конус точки 0. Точки этого
конуса соединены с 0 нулевыми векторами. Простран-
Пространственно-временной истории всякой точечной частицы
(материальной точки) соответствует нек-рая линия в
пространстве Мпнковского, наз. мировой л и н и-
е й этой частицы. Точки этой линии определяют коор-
динаты частицы во все моменты времени. То, что ско-
скорости всех частиц не превосходят с, означает, что (в ес-
естественном предположении гладкости) все касательные
векторы мировой линии являются либо времениподоб-
ными, либо иаотропными. Первые из них соответству-
соответствуют частицам с ненулевой, а вторые — с нулевой мас-
массой покоя. Натуральный параметр на мировой линии
наз. собственным временем частицы. Фи-
Физич. смысл собственного времени состоит в том, что
оно является временем, отсчитываемым часами, к-рые
движутся вместе с частицей.
Выражением закона инерции в рассматриваемой мо-
модели О. т. является то, что свободные, т. е. не подвер-
подверженные действию сил, частицы имеют в качестве сво-
своих мировых линий времениподобные и изотропные
прямые (т. е. геодезические) пространства Минков-
Минковского. В частности, частицы с нулевой массой покоя
имеют мировые линии, лежащие на нек-ром световом
конусе, с чем и связано название последнего. В общей
О. т. выражением закона инерции является т. н. геоде-
геодезических гипотеза, согласно к-рой частица, не испыты-
испытывающая действия иных сил, кроме гравитационных,
движется по геодезической соответствующего простран-
пространства-времени. Световой сигнал, соединяющий данные
точечные события, интерпретируется в рассматривае-
рассматриваемой модели как отрезок изотропной геодезической,
соединяющей соответствующие мировые точки.
Времениподобная геодезическая в пространстве Мин-
Минковского, соединяющая данные мировые точки А и В,
является кривой наибольшей длины среди всех време-
ниподобных мировых линий, соединяющих эти точки.
Это вытекает из обратного неравенства треугольника,
согласно к-рому времениподобная наклонная короче
своей времениподобной геодезической. С точки зрения
О. т. максимальность длины времениподобной геоде-
геодезической означает, что собственное время частицы, сво-
свободно движущейся от мировой точки А к мировой точке
В, больше, чем собственное время любой другой части-
частицы, мировая линия к-рой соединяет эти мировые точки.
Это обстоятельство принято называть парадок-
парадоксом близнецов.
При построении тензорных величин, выражающих
физич. величины, как правило, в один тензорный объект
в пространстве Минковского объединяются несколько
соответствующих тензорных объектов классич. физики.
Напр:, вектор энергии-импульса составляется следую-
следующим образом: первой его компонентой в галилеевой
системе координат является величина <§1с, а остальны-
остальными тремя — компоненты вектора импульса (обозначе-
(обозначение этой операции ($1с, р)). Для того чтобы отличить
тензоры пространства Минковского от тензоров на его
пространственных сечениях, к-рые рассматривались в
классич. физике, принято говорить о четырехмерных,
или 4-тензорах. Примеры нек-рых физич. величин,
являющихся 4-тензорами: 4-вектор
и' = / r i .; ?==\, '=0, 1, 2, 3,
наз. 4-скоростью. Этот вектор является касательным
единичным вектором к траектории мировой частицы.
Вектор
Fv F
где F — сила, является вектором 4-силы. Основные
уравнения релятивистской динамики с использованием
этих векторов могут быть переписаны в виде
dp1' du'
gi =т s= тс —— .
S ds <*s
Роль теории относительности в современной физике.
О. т. с высокой точностью подтверждена обширной сово-
совокупностью фактов и лежит в основе всех современных
теорий, рассматривающих явления при релятивистских
скоростях. Уже последовательная теория электромаг-
электромагнетизма — классич. электродинамика — возможна
только на основе О. т. (исторически анализ основ
классич. электродинамики, и в частности оптики дви-
движущихся тел, привел к построению О. т.). О. т. лежит
в основе квантовой электродинамики, теорий сильного
и слабого взаимодействия элементарных частиц. Кван-
Квантовые законы движения и взаимопревращения элемен-
элементарных частиц рассматриваются в квантовой теории
поля.
Лит.: [1J Э й н ш т е й н А., Собр. научных трудов, т. 1— 4,
М., 1985 — 67; [2] Einstein A., «Ann. Phys.», 1905, Bd 17,
S. 891—921; [Л] MinkowskiH., «Phys. Z.», 1909, Bd 10,
S. 104—11; U] Ландау Л. Д., Л и ф ш и п Е. М., Теория
поля, 6 изд., М., 1973 (Теоретич. физика, т. 2); [5] Ф е й н-
манР.,ЛейтонР., СэндсМ., Фейнмановские лекции по
физике, пер. с англ., в. 2, М., 1905; [6] П а у л и В., Теория от-
относительности, пер с нем., М.— Л., 1047; 17] Ф о к В. А., Теория
пространства, времени и тяготения, 2 изд., М., 1961; [8] П е н-
роуз Р., Структура пространства-времени, пер. с англ., М.,
1Я72; [9] Р а ш е в с к и й П. К., Риманова геометрия и тензор-
тензорный анализ, 3 изд., М., 1967; [10] Александров А. Д.,
«Вопросы философии», 1953, Л1 5, с. 225—45. Д. Д. Соколов.
ОТНОСИТЕЛЬНЫЕ ГОМОЛОГИИ — группы гомоло
гий НСр(Х, A; G) пары пространств (X, А). Они опре-
определяются факторкомплексом комплекса цепей X с ко-
коэффициентами в группе G по подкомплексу, состоящему
на всех цепей с носителями в А. Эти группы обычно не
изменяются при «вырезании», т. е. при замене пары
(Х,А) парой (X\U, A\U), где U — содержащееся
в А открытое подмножество X. Относительные
Когомологии Нр (X, А \ G) определяются под-
подкомплексом комплекса цепей X, состоящим из всех
коцепей с носителями в Х\А, в то время как фактор-
комплекс обычно определяет когомологии подмноже-
подмножества AczX.
Лит.: [1] Скляренко Е. Г., «Успехи матем. наук»,
1979, т. 34, в. в, с. 90 — 118. Е. Г. Скляренко.
ОТНОШЕНИЕ — подмножество конечной декарто-
декартовой степени А" ~АХАХ. . .ХА данного множества А,
т. е. подмножество систем (а±, а2, . . ., о„) из п элемен-
элементов множества А.
Подмножество RczA" наз. и-м е с т н ы м, или п-
арным, отношением в множестве А. Число
п наз. рангом, или типом, отношения R. Под-
Подмножество Rcz.A" наз. также га-м е с т н ы м, или
и-й р н ы м, предикатом на множестве А. За-
Запись Я(аг, . . ., а„) означает, что (аг, . . ., а„)?Я.
Одноместные О. наз. свойствами. Двумест-
Двуместные О. наз. бинарными, трехместные О.— т е р-
н а р н ы м и и т. д.
Множество А" и пустое подмножество ф в А" наз.
соответственно универсальным отноше-
отношением и н у л ь - о т н о m е н и е м ранга п в
множестве А. Диагональ множества Ап, т. е. множество
Д = {(а, а, ..., а)\а?А},
наз. отношением равенства в множест-
множестве А .
Если R и S суть n-местные О. в множестве А, то
«-местными О. в А будут также следующие подмноже-
ггна в А":
Множество всех n-арных О. в множестве А относитель-
относительно операций U* П' является булевой алгеброй, (п+1)-
местное отношение F в А Hart, функциональным,
если для любых элементов <zj, . . ., ап, a, b из А из
того, что ((?!, . . ., ап, a)?F и (alt ... ,а„, b) g f, следует
а=Ь.
См. также Бинарное отношение, Соответствие.
Д. Ы. Смирнов.
ОТНОШЕНИЯ ПРАВДОПОДОБИЯ КРИТЕРИИ —
статистический критерии, статистика к-рого есть от-
отношение наибольших значений функций правдоподо-
правдоподобия, отвечающих проверяемой и множеству всех допу-
допустимых гипотез. Пусть случайная величина X прини-
принимает значения в выборочном пространстве {?, 3&, Ре },
8?6, а семейство мер ^ - {Ре , 9?6} абсолютно не-
непрерывно относительно нек-рой о-конечной меры [i
и Р$(х)=с1Рб (x)/du, (x). Пусть по реализации случай-
случайной величины X необходимо проверить сложную гипо-
гипотезу Но, согласно к-рой неизвестное истинное значение
00 параметра 6 принадлежит множеству в(,с:в, против
сложной альтернативы Н1 : Й0?6] = в^в0. Сог-
Согласно О. п. к. с уровнем значимости а, 0<а<'/2-
гипотезу Но следует отвергнуть, если в результате ак-
сперимента окажется, что Я(х)<Ха, где Я(Х) — ста-
статистика О. п. к., определяемая следующим образом:
sup рв (X)
б8
Х(Х)~ sup рв(ЛГ) '
666
а Ха— критич. уровень, к-рыи находится из того усло-
условия, что размер критерия
равен а. В частности, если множество в содержит лишь
две точки в = {Ро, Pi}, а конкурирующим гипотезам,
к-рые в данном случае являются простыми, отвечают,
напр., плотности р0 (•) и Pi (•) соответственно, то в атом
случае статистика О. п. к. выражается формулой
Л <Л) - max {Ра (X), р, IX)} ~ тт X1' ЪТхТ] •
Согласно О. п. к. с уровнем значимости а, гипотезу
//о следует отвергнуть, если fn(X)/ Pt(X)<Xa, где
число Ка, 0<Ха<1, определяется из условия
Р{Х(Х) <Ха\ Яо} =
{х: р„ (х) < р, (х) Ха) Ро (х) |i W = а.
О. п. к. предложен Ю. Нейманом it Э. Пирсоном
(J. Neyman, E. Pearson, 1928). Ими же было доказано
A933), что среди всех критериев уровня, предназна-
предназначенных для проверки простых гипотез, О. п. к. явля-
является наиболее мощным (см. Неймана — Пирсона лемма).
Лит.: [1] Neyman J., Pearson E. S., Joint statisti-
statistical papers, Camb., 1967; [2] Л е м а н Э., Проверка статистиче-
статистических гипотез, пер. с англ., 2 изд., М., 1979. М. С. Никулин.
ОТОБРАЖЕНИЕ однозначное — закон, но к-рому
каждому элементу нек-рого заданного множества X
ставится в соответствие вполне определенный элемент
другого заданного множества Y (при этом X может
совпадать с Y). Такое соотношение между элементами
х?Х и y?Y записывается в виде y~j(x), y — jx или
у~у(х). Пишут также / : X—>-У и говорят, что отобра-
отображение /действует из X в Y. Множество X наи.
областью определения отображе-
отображения, а множество {y=f(x), x?X}cY наз. мно-
множеством значений отображения. Ото-
Отображение / : X—yY наз. также отображением
множества Хво множество Y (или н а
множество Y, если {y~f(x), ж?Х}-У). Ло-
Логически понятие «О.» совпадает с понятиями функция,
опера тор, преобразован ие.
Отображение / : X —>- Y порождает множество Giy=
= {х, / (.г) \х ? X} с X х У, наз. графиком о т о б р а-
ження. Обратно, множество М а X><У определяет
однозначное О. если и только если для всех и ? X'
существует V ? У, притом только один такой, что
(и, v)cM, тогда /л(и) = 1>.
Два отображения fag наз. равными, если об-
области их определения совпадают и f(x)—g(x) для лю-
любого х? X. В этом случае совпадают и области значений
этих О. Отображение / на X наз. постоянным,
если f(x)=a для любого х?Х. Сужением отоб-
отображения / : Х-»-У на подмножество AdX наз.
отображение <г, заданное на множестве А равенством
<p(x)=f(x), х?А; это сужение обозначается /л- Рас-
Расширением отображения (или продол-
продолжением) на множество ЯЗХ наз. отображение F,
определенное на Е и удовлетворяющее равенству
F(x)=f(x) для всех х^ Х- Если заданы три множества
X, У, Z, на X определено отображение / со значениями
в У, а на У задано отображение g со значениями bZ,
то существует отображение h с областью определения
X, принимающее значения в Z и определяемое равен-
равенством h(x)=g\j(x)]. Это О. наз. композицией
отображений /и g. а /и j соответству-
соответствующими отображениями, и обозначается g°/,
причем порядок записи играет существенную роль (для
функций действительного переменного принят термин
суперпозиция). Отображение h наз. также
сложным отображением, составленным из
внутреннего отображения / и внешнего отображения g.
Понятие сложного О. обобщается на любое конечное
число составляющих О.
Отображение /, определенное на X и принимающее
значения в У, порождает новое О., заданное на под-
подмножествах множества X и имеющее в качестве значе-
значений подмножества множества У. Именно, если ACZX, то
def
f(A)={y = f(x),
Множество j(A) наз. образом множества .4.
Если положить А— {./}, то получится исходное отоб-
отображение f(x), так что f(A) есть расширение отображе-
отображения / (х) с множества X на множество 5K (X) всех под-
подмножеств множества А', если отождествлять одноэле-
одноэлементное множество с элементом, его составляющим.
В случае У=Х множество А наз. инвариант-
инвариантным подмножеством отображения /, если
1 (А)СА, а точка х наз. неподвижным эле-
элементом отображения /, если f(x) = x. Инвариант-
Инвариантные множества и неподвижные элементы играют важ-
важную роль при решении функциональных уравнений
вида f(x)-=a или x~f{x)~a.
Каждое отображение / : Х->-У порождает О., задан-
заданное на подмножествах множества /(X) и имеющее в ка-
качестве значений подмножества множества X. Именно,
для каждого Вс/(Х) через f~1(B) обозначается мно-
множество {х, f(z)(zB}, называемое полным про-
прообразом множества iS. Если /"'(.'/) Для любого
y?f{%) состоит из единственного элемента, то /~'
есть О. элемента, определенное на f(X), принимаю-
принимающее значения в X и называемое обратным от-
отображением к /. Существование обратного О.
эквивалентно разрешимости уравнения f(x) — y,
Если множества X и У наделены нек-рыми свойства-
свойствами, то во множестве /'(X, У) всех О. на X в У могут
быть выделены содержательные классы. Так, для ча-
частично упорядоченных множеств X и У отображение /
наз. изотопным, если х<у влечет /(ж)</(/у).
Для комплексных плоскостей X п Y выделяется класс
голоморфных О. Для топологии, пространств X и У
естественным образом выделяется класс непрерывных О.
лтих пространств; строится развернутая теория диф-
дифференцирования отображений. Для О. скалярного ар-
аргумента и, в более общем случае, для О., определен-
определенных на пространстве с мерой, может быть введено по-
нятие (сильной или слабой) измеримости и могут быть
построены различные интегралы лебеговского типа
(напр., Бохнера интеграл, Даниеля интеграл).
О. наз. многозначным отображением,
если нек-рым значениям х соответствуют подмножества
YXCY, состоящие более чем из одного элемента. Та-
Таковы, напр., многолистные функции комплексного
переменного, многозначные О. топологических про-
пространств и др.
Лит.: [1] Б у р б а к и Н., Теория множеств, пер. с франц.,
М., 1965; [2] е г о же, Общая топология. Основные структуры,
пер. с франц., 2 изд., М., 1968; [3] К е л л и Д ж. Л., Общая то-
топология, пер. с англ., 2 изд., М., 1981. В. И. Соболев.
ОТОБРАЖЕНИЕ ПЕРИОДОВ — отображение, сопо-
сопоставляющее точке s базы S семейства {Xs} алгебраич.
многообразий над полем С комплексных чисел когомо-
логии //* (Xs) слоя над этой точкой, снабженные Ходжа
структурой. Полученная при этом структура Ходжа
рассматривается как точка в многообразии модулей
структур Ходжа данного типа.
Изучение О. п. восходит к исследованиям Н. Абеля
(N. Abel) и К. Якоби (С. Jacobi) интегралов алгебраич.
функций (см. А белев дифференциал). Однако до недав-
недавнего времени глубоко были изучены лишь О. п., отве-
отвечающие семействам кривых.
Пусть {Xs} есть семейство слоев AV^/^fs) гладкого
проективного морфизма / : X-+S, где S -— гладкое
многообразие. Тогда когомологии H*(XS, Z)=F_
ал
снабжены чистой, поляризованной структурой Ходжа,
к-рая задается гомоморфизмом вещественных алгебра-
алгебраических групп h : С*—»-GR, где С* — мультипликатив-
мультипликативная группа С* поля комплексных чисел, рассматри-
рассматриваемая как вещественная алгебраич. группа, а
G = {g?GL(V), $(gz, gy) = k(g)$(x, у)}
— алгебраич. группа линейных преобразований про-
пространства V, умножающих невырожденную (симме-
(симметрическую или кососимметрическую) билинейную форму
г|з на скалярный множитель; причем автоморфизм Ad h(i)
группы GR является инволюцией Картана и h (R*)
лежит в центре группы GR. Множество Xq гомомор-
гомоморфизмов fe:C*—>-GR, обладающих указанными свойст-
свойствами, естественным образом снабжено Gjj-ннварпант-
ной структурой однородного кэлерова многообразия и
наз. многообразием Гриффите а, а фак-
фактор Mq—Xq/G^ является пространством модулей
структур Ходжа. Гомоморфизм h задает разложение
Ходжа
©c=e©Pi ~p
алгебры Ли © группы G, где &Р< ~Р — подпрост-
подпространство в (SV на к-ром А<1 h (г) действует умноже-
умножением на zPz~p. Сопоставление h-+P(h), где Р(К) —
параболнч. подгруппа в Gq, алгебра Ли к-рои есть
0 >(|(й''1 ~р, задает открытое плотное вложение мно-
многообразия Xq в компактное G^-однородное многооб-
многообразие флагов Xq. В касательном пространстве
к Xq в точке h выделено горизонтальное
подпространство
Голоморфное отображение в Xq или Mq наз. гори-
горизонтальным, если образ его касательного отоб-
отображения лежит в горизонтальном подрнсслоенин.
Установлено, что О. п. Ф : S-*-Mq горизонтально
(см. [1], [3]). Особенности О. п. описываются теоре-
теоремой Шмида о нильпотентной орбите,
к-рая в случае, когда 5=5\{0} — кривая с выколо-
выколотой точкой, утверждает, что если z — локальная коор-
координата на S, z@) —0, то при z->-0 Ф (г) асимптотически
близко к
где й?Х(з, a -/V^6'q —нильпотентный элемент (см.
[4]). Относительно группы монодромпп
Ф, (лх (S,
известно, что ее образ полупрост во всяком рациональ-
рациональном представлении группы G, а преобразования об-
обхода Т вокруг дивизора с нормальными пересечения-
пересечениями 6'\5 в гладкой компактификации S многообразия S
порождают к в а з и у н и л о т е н т н ы е (т. е. име-
имеющие в качестве собственных значений корни из 1)
элементы Ф*(Г)?С„. Важность группы монодромии
([л
подчеркивает теорема жесткости (см. [1],
12], [41): если над S имеются два семейства алгебраич.
многообразий, то соответствующие О. и. ©i и Ф2 Из S
в Мо совпадают тогда и только тогда, когда ®i(so)~:
-~Ф2(.'о) в нек-рой точке so?S и гомоморфизмы Ф/* :
.Tj (S, s0) -»- G , г=1, 2, совпадают.
Законченные результаты о строении ядра и образа
О. п. относятся в основном к случаям кривых и R3-
пивер.гпостей. Если {Xs} — семейство многообразий
указанного тина иф («)~Ф (s'), то XS^XS, (теорема
Т о р е л л и), а для /{-поверхностей максимально
возможный образ О. п. совпадает с Mq (cm. [7]). В слу-
случае кривых образ О. гг. частично описан (соотношения
Шоттки — Юнга, см. [6], [8]). Существует гипотеза
Гриффитса о том, что многообразие модулей
допускает частичную аналитич. компактификацию,
т. о. открытое вложение в такое аналитич. простран-
пространство Mgi что О. п. S—>-Мд продолжается до голоморф-
голоморфного отображения SZ)S для всякой гладкой компакти-
компактификации 5з5. Такая компактификация известна A983)
лишь для случая, когда Xq~ симметрическая об-
область [9].
Лит.: 11] Г р и ф ф и т с Ф. А., «Успехи матем. наук», 1970,
¦г. 25, в. 3, е. 175—234; [2] Griffiths Ph. А., в кн.: Actes du
Hoiigies international des mathematiciens (Nice), 1970, t. 1 P.,
1971, p. 113—19; [3] Deligne P., Travaux de Griffiths, в кн.:
Sominaire Bourbaki. 1969/70, В.— N. Y.— Hdlb., 1971, p. 213—35;
14] S с li m i d W., «Invent, math.», 1973, v. 22, p. 211—319;
15] С a t t a n i E. H., К a p 1 a n A. G., «Duke Math. J.», 1977,
v. 44, Xt 1, p. 1—43; [6] Д у б р о в и н Б. А., «Успехи матем.
наук», 1981, т. 36, в. 2, с. 11—80; [7] К у л и к о в В. А., там же,
1977, т. 32, в. 4, с. 257—58; [8] М а м ф о р д Д. «Математика»,
1У73, т. 17, № 4, с. 34—42; [9] В a i 1 у W., В о г е 1 A. «Ann.
Math.», 1966, v. 84, p. 442—528. А. И. Овсеевич.
ОТОБРАЖЕНИИ КЛАССЫ — важнейшие классы не-
непрерывных отображений, рассматриваемые в общей
топологии и ее приложениях. К ним относятся: о т-
крытые отображения — такие, что образ
любого открытого множества является открытым мно-
множеством; замкнутые отображения — та-
такие, при к-рых образ каждого замкнутого множества
замкнут; бикомпактные отображения —
для них прообраз любой точки является бикомпакт-
бикомпактным множеством; совершенные отобра-
ж е п и я — замкнутые бикомпактные отображения.
Факторные отображения определяются
требованием: множество в образе открыто в том и
только в том случае, если его полный прообраз открыт.
П.икньг также открытые бикомпактные отображения,
и i ¦ (? в д о о т к р ы т ы е о т о б р a Ht e н и я и
уплотнения — последние определяются как
взаимно однозначные непрерывные отображения на.
Таким образом, при классификации отображении в об-
общей топологии ограничения накладываются либо на
поведение (при переходе к образу) открытых или
замкнутых множеств, либо на свойства прообразов
множеств. Второй подход приводит, в частности, к сле-
следующим О. к. Монотонные отображе-
отображения— те, при к-рых прообраз каждой точки нульме-
нульмерен. Конечно к ратные отображения
характеризуются конечностью всех прообразов точек.
Отображения, при к-рых прообраз каждого биком-
бикомпактного множества бикомпактен, наз. к-о т о б р а-
ж е н и я м и. Соединением ограничении первого и
второго типа выделяются основные классы непрерыв-
непрерывных отображений в общей топологии. Самими опреде-
определениями О. к. естественно организуются в нек-рую
иерархию, к-рая может быть положена в основу систе-
матпч. классификации топологич. пространств [1].
Эта классификация строится Как результат решения
вопросов следующих двух типов. Дан класс прост-
пространств с</, целесообразность выделения к-рого нр
вызывает сомнений, и пусть &3 — нек-рый класс отоб-
отображений из нашей исходной иерархии. Требуется оха-
охарактеризовать посредством внутренних топологич. ин-
инвариантов образы пространств из класса jl при все-
всевозможных отображениях из класса <Й. Вопросы вто-
второго тина аналогичны — требуется охарактеризовать
прообразы пространств из класса ,Л при отображе-
отображениях из класса <®.
При решении вопросов указанных двух типов полу-
получаются совсем не очевидные теоремы общего харак-
характера. Напр., пространства с первой аксиомой счет-
ности — это в точности образы метрич. пространств
при непрерывных открытых отображениях. Прост-
Пространства с равномерной базой и только они — образы
метрич. пространств при открытых бикомпактных
отображениях. Пространства Фреше — Урысона ха-
характеризуются как псевдооткрытые образы метрич.
пространств, а секвенциальные пространства — :>то
факторпространетва метрич. пространств. Далее, про-
прообразы метрич. пространств при совершенных отобра-
отображениях — это в точности паракомпактные перистые
пространства, а прообразами полных метрич. прост-
пространств являются паракомпактные пространства, пол-
полные по Чеху. Непрерывные образы пространств со
счетной базой — пространства со счетной сетью. При
систематич. следовании указанному пути получается
единая взаимная классификация нрострапств и отоб-
отображений.
Особую роль среди различных классов непрерыв-
непрерывных отображении занимает класс факторных отобра-
отображений. Важнейшей особенностью факторных отобра-
отображений является то, что они могут служить средством
для построения новых топологич. пространств. Л
именно, если дано отображение / топологич. прост-
пространства X на иск-рое множество У (напр., если рас-
рассматривается естественное отображение я прост-
пространства X на множество всех элементов нек-рого раз-
разбиения этого пространства), то на множестве У всегда
можно ввести естественную топологию требованием,
чтобы отображение / было факторным: множество
VaY объявляется открытым в том и только в том сл5г-
чао, если его полный прообраз /~1(V) открыт в прост-
пространстве X. Помимо уже названных, весьма важны
неприводимые отображения, напр. в теории абсолю-
абсолютов. См. также Бифакторное отображение, Много-
Многозначное отображение.
Лит.: |1] Архангельский А. В., «Успехи матем.
наук», 1906, т. 21, в. 4, с. 131!—84. А. В. Архангельский.
ОТОБРАЖЕНИЙ МЕТОД — то же, что изображе-
изображений метод.
ОТОБРАЖЕНИЯ ГЛАВНАЯ СЕТЬ, основание
от о б р а и; е н п я,—ортогональная сеть в областп
G n-мерного многообразия М (в частности, М может
иыть евклидовым пространством), к-рая переходит
в сеть, также ортогональную, при диффеоморфизме
/ : G-yG' области G на область G' того же или другого
риманова многообразия М'. Направления, касатель-
касательные к линиям О. г. с. в точке x(^G, являются главными
направлениями эллипсоида деформации индуцирован-
индуцированного отображения /„ : Тх-+Т'цХ) касательного прост-
пространства Тх на касательное пространство Tf(X). При
/i>2 О. г. с, вообще говоря, не является голономной.
Еглп отображение / — конформное, то любая ортого-
ортогональная сеть в области G служит О. г. с.
him.: Рыжков В. В., в сб.: Итоги науки, Серия Матема-
,„.,а, в. 3— Геометрия. 1963, М., 1965. В. Т. Базылее.
ОТРАЖЕНИЕ — движение <т я-мерного односвяз-
ного пространства постоянной кривизны X" (т. о.
евклидова аффинного пространства Е", сферы S" или
пространства Лобачевского Л"), множество непод-
нижных точек Г к-рого является п—1 мерной гипер-
гиперплоскостью. Множество Г наз. зеркалом о т о б-
j) а ж е н и я а; говорят также, что а есть О. относи-
относительно Г. Всякое О. однозначно определяется своим
зеркалом. Порядок О. в группе всех движений X"
равен 2, то есть a'2=id^n.
Пусть Х"~Е" и х?Г. Выбор х в качестве начала
координат позволяет отождествить евклидово аффин-
аффинное пространство Еп с линейным евклидовым прост-
пространством Г" ого параллельных переносов. Тогда от-
отражение a — линейное ортогональное преобразова-
преобразование пространства V", имеющее а пек-ром ортонорми-
ортонормированием базисе матрицу
О 1-
и наоборот, всякое ортогональное преобразование
пространства Г", имеющее в нек-ром ортонормпро-
ианном. базисе такую матрицу, является О. в Е".
Солее общо: линейное преобразование ф произволь-
произвольного векторного пространства W над полем к характе-
характеристики, отличной от 2, наз. линейным о т р а-
,к е н и е м, если tp2-~id^ и ранг преобразования 1 — ср
равен 1. В этом случае подпространство W\ непод-
неподвижных относительно ср векторов имеет в W коразмер-
коразмерность 1, а подпространство W_j собственных векторов
( собственным значепнем —1 имеет размерность 1 и
W=:WiQ)W-.-i. Если a — такая линейная форма на
W, что ос(ы>)--О при w^W1, а h?W~i — такой эле-
элемент, что а (А)---2, то <р задается формулой
(f>w=w — a(w)h, w(^W.
Описание О. в произвольном односвязном прост-
пространстве X" постоянной кривизны может быть сведено
к описанию линейных О. следующим способом. Вся-
Всякое такое пространство Хп вкладывается в виде ги-
гиперповерхности в действительное (п-(--1)-мерное век-
векторное пространство V" + 1 таким образом, что движе-
движения X" продолжаются до линейных преобразований
Vn + 1, причем в подходящей системе координат в V"+ 1
уравнения указапнон гиперповерхности записываются
ледующим образом:
4 г*!+•¦•+4 = 1 Для S";
хо = 1 дляЯ";
s
*о —-Г1— ¦ ¦ ¦ ~xn~i и хй > 0 для Л".
При этом вложении всякая гиперплоскость в X" есть
пересечение с Л'" нек-рого ;г-мерного подпространства
в Vn+l, а всякое О. в -Y" индуцировано линейным О.
в V+1.
Если в определении линейного О. отказаться от
требования qj2=id^, то получается более общее по-
понятие псевдоотражения. Если к — поле ком-
комплексных чисел, а ф — псевдоотражение конечного
порядка (не обязательно равного 2), то ф наз. к о м-
п л е к с н ы м отражение м. Комплексным О.
наз. также всякий биголоморфным автоморфизм ко-
конечного порядка ограниченной снмметрич. области
в комплексном пространстве, множество неподвижных
точек к-рого имеет комплексную коразмерность 1.
См. также Отражений группа.
Лит.: [1] Бурбаки Н., Группы и алгебры Ли, пер. с
франц., М., 1972; [2] В и я б е р г Э. Б., «Изв. АН СССР. Сер.
матем.», 1971, т. 35, №5, с. 1072—112; [3] Gottschling E..
«Comm. Pure and Appl. Math.», 19G9, v. 22, p. 693—714; [4]
Ровенфепьд Б. А., Неевклидовы пространства, М., 1969.
В. Л. Попои.
ОТРАЖЕНИЙ ГРУППА — дискретная группа пре-
преобразовании, порождаемая отражениями относительно
гиперплоскостей. Наиболее часто рассматриваются
О. г., состоящие из движений односвязного полного
риманова многообразия постоянной кривизны, т. е.
евклидова пространства Еп, сферы S" или прост
ранства Лобачевского L".
Истоками теории О. г. являются исследования пра
вильных многогранников и правильных разбиении
евклидовой плоскости и сферы («орнаментов»). Во 2-й
пол. 19 в. эти исследования были распространены па
n-мерный случай и, в связи с задачами теории функций
комплексного переменного, на плоскость Лобачев-
Лобачевского; были также описаны правильные разбиения
пространства //' на правильные многогранники. Грум
па симметрии любого правильного многогранника, а
также группа симметрии правильного разбиения при
странства на правильные многогранники являются
О. г. В 1934 были перечислены (см. [1]) все О. г. в F"
и ^"(последние можно рассматривать как частный слу
чай О. г. в E'i + 1). Еще в 1925—27 в работах Г. Вейля (Н.
Weyl) и Э. Картана (Е. Cartan) О. г. появились как
Вейля группы, полупростых групп Ли. Позднее было
установлено, что группы Вейля — это в точности
те О. г. в Еп, к-рые имеют единственную неподвижную
точку и записываются в нек-ром базисе целочисленны-
целочисленными матрицами, а аффинные группы Вейля — это все
О. г. в Еп с ограниченным фундаментальным много-
многогранником (см. Дискретная группа преобразований).
Основные результаты теории
групп отражений. Пусть X"—S", En или
//'. Всякая О. г. в X" допускает в качестве образую-
образующих отражения rt относительно гиперплоскостей #,-,
i?/, ограничивающих фундаментальный многогран-
многогранник Р. Относительно этой системы образующих она
является Кокстера группой с определяющими соотно-
соотношениями (г^гу)"//— 1, где числа пц находятся следую-
следующим образом: если грани Н,-{\1' н Hjf\P смежны и
угол между ними равен гс,-у-, то «,•/""—- ; если они не
смежны, то ге,у—со (и тогда гиперплоскости Я,- и Н;
но пересекаются). Обратно, любой выпуклый много
гранник в пространстве X", все двугранные углы
к-рого суть целые части я, является фундаментальны-м
многогранником группы, порожденной отражениями
относительно ограничивающих его гиперплоскостей.
Всякая О. г. в Е" является (как группа движений)
прямым произведением тривиальной группы, дейст-
действующей в евклидовом пространстве нек-рой размер
ности, и групп движений следующих двух типов:
(I) конечная О. г., фундаментальный многогранник
к-рой есть симшшциальный конус, и (II) бесконечная
О. г., фундаментальный многогранник к-рой есть сим-
плекс. Группа типа (I) может рассматриваться как
О. г. на сфере с центром в вершине фундаментального
конуса; ее фундаментальным многогранником будет
тогда сферич. симплекс. О. г. типа (I) однозначно
определяется своей матрицей Кокстера, поэтому клас-
классификация таких групп совпадает с классификацией
конечных групп Кокстера. О. г. типа (II) определя-
определяется своей матрицей Кокстера с точностью до гомо-
гомотетии. Классификация таких групп с точностью до
гомотетии совпадает с классификацией неразложимых
параболич. групп Кокстера. Всякая О. г. в Е", имею-
имеющая ограниченный фундаментальный многогранник,
является (как группа движений) прямым произведе-
произведением групп типа (II).
О. г. в Еп изучены значительно хуже. По многим
причинам естественно выделить те из них, фундамен-
фундаментальный многогранник к-рых ограничен или выходит
на абсолют лишь в конечном числе точек (это равно-
равносильно конечности объема). Ниже рассматриваются
только такие группы. Они описаны более или менее
яино только при п =2, 3.
О. г. в L- определяются ^-угольником с углами
(семи вершина бесконечно удаленная, то считается,
что угол при ней равен нулю). Многоугольник с за-
заданными углами вгегдд существует и аависит от к—3
параметров.
При гс^З фундаментальный многогранник О. г.
и //' однозначно определяется своим комбинаторным
строением и двугранными углами. Для п=3 получено
исчерпывающее описание таких многогранников [5]
н, тем самым, О. г. Для ге^4 известны лить примеры
и нек-рые общие способы построения О. г. в L" (см.
[0], [7]). Неизвестно A983), существуют ли О. г. в L"
с ограниченным фундаментальным многогранником
при п^8 и с фундаментальным многогранником конеч-
конечного объема при л^20.
Наряду с О. г. в пространствах постоянной кри-
кривизны рассматриваются линейные О. г., действующие
дискретно в открытом выпуклом конусе действитель-
действительного векторного пространства. Это позволяет дать
геометрич. реализацию всех групп Кокстера с конеч-
конечным числом образующих (см. [3], [4]).
Всякую конечную О. г. можно рассматривать как
линейную группу. Конечные О. г. характеризуются
среди всех конечных линейных групп тем, что алгебры
инвариантных многочленов этих групп обладают ал-
алгебраически независимыми системами образующих [4].
Напр., для группы всех перестановок базисных век-
векторов такими образующими будут элементарные сим-
метрпч. многочлены. Пусть mx+l, . . ., тл+1 — сте-
степени образующих инвариантов конечной О. г. G (п —
размерность пространства); числа ти . . ., тп наз.
и о к а :! а т е л я м и группы G. Имеет место
ф
A+//1,0...(
1,чг г/; — число элементов группы G, для к-рых прост-
пространство неподвижных точек имеет размерность п—к.
\'> частности, 7/1, + . . ¦-\-тп равно числу отражений
в группе G; (mt + l). . .(/ге„+1) равно порядку группы.
Если группа G неприводима, то собственные значения
ее элемента Киллинга — Кокстера (см. Кокстера
группа) равны exp JI'"tfe, где h — число Кок-
Кокстера:
Утверждения предыдущего абзаца, за исключением
гле;нег<>, сохраняют силу для линейных групп над
произвольным полем нулевой характеристики (см. [4|).
Отражением в этом случае следует называть линейное
преобразование, пространство неподвижных точек
к-рого имеет размерность ?г—1. Перечислены [8] все ко-
конечные линейные О. г. над полем комплексных чисел.
Найдены [9] конечные линейные О. г. над полями не-
ненулевой характеристики.
Лит.: [1] С о х е t e r H. S. M., «Ann. Math.», 1934, v. 35,
p. 588—621; [2] К о к с е т е р Г. С. М., М озер У. О. Дж., По-
Порождающие элементы и определяющие соотношения дискретных
групп, пер. с англ., М., 1980; [3j Tits J., в кн.: Proceedings of
the International Congress of Mathematicians. 1962, Dursholm,
[1963], p. 197—221; [4] Б у р б а к и Н., Группы и алгебры Ли,
пер. с франц. М., 1972 гл. 4—В; [5] А н д р е е в Е. М., «Матем.
сб.», 1970, т. 81, с. 445—78; т. 83, с. 256—60; F] Мака-
р о в В. С, в кн.: Исследования по общей алгебре, в. 1, Киш.,
1968, с. 120—29; [7] Винбсрг Э. Б., «Матем. сб.», 1967, т. 72,
с. 471—88; 1972, т. 87, с. 18—36; [8] S h e p h а г d G. С, Т о d d
J. A., «Canad. J. Math.», 1954, v. 6 p. 274—304; [9] С е р е ж-
к и и В. Н., «Докл. АН СССР», 1976, т. 227, с. 574—75.
3. Б. Винберг.
ОТРАЖЕНИЯ ПРИНЦИП — обобщение симметрии
принципа для гармонич. функций на гармонич. функ-
функции от произвольного числа независимых переменных.
Формулировки О. п. таковы.
1) Пусть G — область fc-мерного евклидова прост-
пространства (fc>l), ограниченная жордановон поверх-
поверхностью Г (в частности, гладкой или кусочно гладкой
поверхностью Г без самопересечений), в состав K-poii
входит (к—1)-мерная подобласть о (к—1)-мернон ги-
гиперплоскости L. Если функция U(хг, . . ., х^) гармо-
гармонична в G, непрерывна на G\Ja и всюду на о равна нулю,
то U(xlt . . ., хь) продолжается как гармонич. функция
сквозь 0 в область G*, симметричную с G относительно
L, с помощью равенства
U{xi, .. ., x*k) = — U (xu ...,xk),
где точки (х[, . . ., ,r*k)€.G* и (хи . . ., xk)?G симмет-
симметричны относительно L.
2) Пусть G — область fc-мерного евклидова прост-
пространства (fc^l), ограниченная жордановой поверхно-
поверхностью Г, в состав к-рой входит (к—1)-мерная подобласть
а (к—1)-мерной сферы 2 нек-рого радиуса i?>0 с цент-
центром в нек-рой точке M°=(xl, . . ., xt). Если V(хи
. . ., Xk) гармонична в G, непрерывна на G\Ja и всюду
на а равна нулю, то U(xlt . . ., т^) продолжается как
гармонич. функция сквозь о в область G*, симметрич-
симметричную с G относительно 2 (т. е. полученную из G по-
посредством преобразования обратных радиусов — ин-
инверсии — относительно сферы 2). Это продолжение
осуществляется посредством взятого с обратным зна-
знаком Кельвина преобразования функции U относительно
сферы 2, именно:
и(х\, ..., 4) =
где (х{ )g, () + {ilf
При преобразовании обратных радиусов относительно
упомянутой сферы 2 точка М* = (х\, . . ., хи) перехо-
переходит в точку М (х1, . . ., X),) в соответствии с равенствами
так что если M*?_G*, то М принадлежит области G
(где U задана), и если М* ?ст, то М--М*.
Лит.: [1] Курант Р., Уравнения с частными производ-
производными, пер. с англ., М., 1964, с. 272. Е. П. Долженпо.
ОТРЕЗОК, сегмент, — множество точек на
прямой, расположенных между двумя данными точ-
точками а, Ь и удовлетворяющих условию вида a<^..r*g.b;
обозначают [а, Ь]. См. также Интервал и сегмент.
ОТРИЦАНИЕ — логическая операция, в результате
к-рой из данного высказывания А получается новое
высказывание «не А». В формализованных языках вы-
высказывание, получающееся в результате О. высказы-
высказывания А, обозначается ~]А, ~А, А, —А, А' (читается:
«не А», «неверно, что А», «А не имеет места»). Семанти-
Семантически О. высказывания А означает, что допущение А
приводит к противоречию. В классической двузнач-
двузначной логике операции О. соответствует следующая
истинностная таблица:
А\~\А
Л
И
В. Е. Плиско.
ОТРИЦАТЕЛЬНАЯ ВАРИАЦИЯ ФУНКЦИИ, о т-
рицательное изменение функци и,—
одно из двух слагаемых, сумма к-рых есть полное из-
изменение или вариация функции на данном отрезке.
Пусть /(j) — функция действительного переменного,
заданная на отрезке fa, b] и принимающая конечные
значения.
Пусть П— {а=хо<.х1<^. . .<хп~Ъ} — произвольное
разбиение отрезка [я, 6] и
где суммирование производится по тем номерам ;,
для к-рых разность f(xj)—/(?,•_,) неположительна.
Величина
N(f)=N(f. [a, b])=supWn(/)
наз. отрицательной вариацией (отри-
(отрицательным изменением) функции /
на отрезке [а, Ь]. Всегда О <ЛГ (/)<:+<». См. также
Положительная вариация функции.
Лит.: [1] Л е б е г А., Интегрирование и отыскание прими-
примитивных функций, пер. с франц., М.— Л., 1934. Б. И. Голубое.
ОТРИЦАТЕЛЬНАЯ КОРРЕЛЯЦИЯ — вид корре-
корреляционной зависимости между случайными величи-
величинами, при к-рой условные средние значения одной из
них уменьшаются при возрастании значений другой
величины. Об О. к. между величинами с корреляции
коэффициентом р говорят в том случае, когда р<0.
См. Корреляция. А. В. Прохоров.
ОТРИЦАТЕЛЬНОЕ БИНОМИАЛЬНОЕ РАСПРЕДЕ-
РАСПРЕДЕЛЕНИЕ — распределение вероятностей случайной ве-
величины X, принимающей целые неотрицательные зна-
значения к -0, 1, 2, ... в соответствии с формулой
при любых действительных значениях параметров
0</9<1 и г>0. Производящая функция и характерис-
тич. функция О. б. р. задаются формулами
где г/—1—/>. Матпматич. ожидание и дисперсия равны
соответственно rq/p и rqlp2. Функция распределения
О. б. р. для значений к -0, 1, 2, ... определяется через
значения функции бета-распределения в точке р сле-
следующим соотношением:
F (fc)-P {X < к} = В(г'л + 1) [I S-* (l-*)*d*,
где В (г, /fc-j-1) — бета-функция.
Происхождение термина «О. б. р.» объясняется тем,
что :>то распределение порождается биномом с отрица-
отрицательным показателем, а именно, вероятности (*) яв-
являются коэффициентами разложения рг A—qz)~r по
степеням л.
О. б. р. встречается во многих приложениях тео-
теории вероятностей. При целом />0 О. б. р. интерпре-
интерпретируется как распределение времени ожидания г-го
«успеха» в схеме Бернулли испытаний с вероятностью
«успеха» р; в такой форме оно наз. обычно Паскаля рас-
распределением и является дискретным аналогом гамма-
распределения. При г=1 О. б. р. совпадает с геометри-
геометрическим распределением. Часто О. б. р. появляется в за-
задачах, связанных с рандомизацией параметров рас-
распределений, напр, если Y случайная величина, име-
имеющая Пуассона распределение со случайным парамет-
параметром %., к-рый в свою очередь имеет гамма-распределе-
гамма-распределение с плотностью
*-^е-ах, *>0,ц>0,
то распределение Y будет О. б. р. с параметрами r—>\i
и р—а/A+ос). О. б. р. служит предельной формой
Пойа распределения.
Сумма независимых случайных величин Хг, . . .,
Хп, имеющих О. б. р. с параметрами р и гх, . . ., гп,
соответственно, имеет О. б. р. с параметрами р и
г1-\-. . .-\-г„. При больших г и малых </, когда rq~"k,
О. б. р. приближается распределением Пуассона с
параметром Я. Многие свойства О. G. р. определяются
тем фактом, что оно представляет собой обобщенное
распределение Пуассона.
Лит.: [1] Ф ел л ер В., Введение в теорию вероятностей и
ее приложения, пер. с англ., 2 изд., т. 1—2, М., 1967.
Л. В. Прохоров.
ОТРИЦАТЕЛЬНОЕ ГИПЕРГЕОМЕТРИЧЕСКОЕ
РАСПРЕДЕЛЕНИЕ — распределение вероятностен
случайной величины X с целыми неотрицательными
значениями, заданное формулой
? {Хк}^ ^ |
CN
параметры N, М, т — целые неотрицательные числа,
удовлетворяющие условию т<Л?<Л-. О. г. р. обычно
возникает в схеме выбора 6e:i возвращения. Если
в нек-рой генеральной совокупности объема Лт име-
имеется М «отмеченных» и N—М «неотмеченных» элемен-
элементов и если выбор (без возвращения) производится до
тех пор, пока число «отмеченных» элементов в выборке
не достигает фиксированного числа т, то случайная
величина X — число «неотмеченных» элементов в та-
такой выборке — подчиняется О. г. р. (*). Случайная
величина Х-\-т — объем выборки — также имеет
О. г. р. Распределение (*) названо по аналогии с от-
отрицательным биномиальным распределением, к-рое воз-
возникает подобным образом при выборе с возвращением.
Математич. ожидание и дисперсия О. г. р. равны
соответственно
N-M
т-
М+1
(iV+l)(iV-M) Г,
М JV М
При N—*-od, 7W—>-оо, N—М—>-оо, так что -^-—>-р, —-^ >-
—>-'/> P+V==li О. г. р. стремится к отрицательному би-
биномиальному распределению с параметрами тир.
Функция распределения F(п) О. г. р. с параметрами
Лг, М, т связана с функцией гипергеометрического
распределения G(m) с параметрами N, М, п соотноше-
соотношением
F (и) = 1 —б (лг —1).
!1то позволяет при решении задач в математич. ста-
статистике, связанных с О. г. р., пользоваться табли-
таблицами гипергеометрич. распределения. О. л. р. приме-
няется, например, при статистическом контроле ка-
качества.
Лит.: [1] Б е л я е в Ю. К., Вериятнистныр методы выбороч-
выборочного контроля, М., 1975; [2] Большее Л. Н., Смирнов
Н. В., Таблицы математической статистики, 2 изд., М., 1968.
А. В. Прохоров.
ОТРИЦАТЕЛЬНОЕ ПОКАЗАТЕЛЬНОЕ РАСПРЕДЕ-
РАСПРЕДЕЛЕНИЕ — то же. что показательное распределение.
ОТРИЦАТЕЛЬНОЕ ПОЛИНОМИАЛЬНОЕ РАСПРЕ-
РАСПРЕДЕЛЕНИЕ — совместное распределение вероятностей
случайных величин Xj, . . ., Х&, принимающих не-
неотрицательные целые значения т=0, 1, 2, . . ., за-
заданное формулой
= Г(г)т,1 ... mk\
где r>0, p0, . . ., Pk @<Pi<i, i=-0, ...,*; Pn+. . .+
-f-p/e=l) — параметры. О. п. р. является многомер-
многомерным дискретным распределением — распределением
случайного вектора (Xf, . . ., Х#) с неотрицательными
целочисленными компонентами.
Производящая функция О. п.р. с параметрами г,
/>„, . . ., Pk имеет вид
Р (zu ..., zfe) = pS(l —2*=,1z,-p/)-r.
О. п. р. возникает в следующей полиномиальной
схеме. Производятся последовательные независимые
испытания, и в каждом исшлтанм возможны fe+l раз-
различных исходов с индексами 0, 1, . . ., к, к-рым соот-
соответствуют вероятности р0, р]? . . ., р^. Испытания про-
продолжаются до r-го появления исхода с индексом О
(здесь г — целое). Если X,-— число появлений исхода
с индексом i, i— 1, . . ., к, ва время до конца испыта-
испытаний, то формула (*) выражает вероятность появления
исходов с индексами 1, . . ., к, соответственно, равно
т1, . . ., mk раз до r-то появления исхода 0. О. п. р.
в указанном смысле служит обобщением отрицательно-
отрицательного биномиального распределения, совпадая с последним
при к—Л.
Если случайный вектор (Хо, . . ., Х^,) имеет поли-
полиномиальное распределение с параметрами л>1, р0,
...,/)? и параметр п сам является случайной величи-
величиной, имеющей отрицательное биномиальное распреде-
распределение с параметрами г>0, 0<я<1, то распределение
вектора (Х1ч . . ., Xj,) при условии Х0=г является
О.п. р. с параметрами г, роA— я), . . .,р^A— я).
А. В. Прохоров.
ОТРИЦАТЕЛЬНОЕ РАССЛОЕНИЕ — голоморфное
векторное расслоение Е над комплексным пространст-
пространством X, обладающее такой эрмитовой метрикой h, что
функция v-*-k(v, v) на Е строго псевдовыпукла вне
нулевого сечения (обозначается ?<0). Расслоение Е
отрицательно тогда и только тогда, когда сопряженное
расслоение ?"*>() (см. Положительное расслоение).
Если X — многообразие, то условие отрицательности
можно выразить в терминах кривизны метрики h.
Любое подрасслоение О. р. отрицательно. Расслоение
Е над комплексным многообразием наз. отрица-
отрицательным в смысле Накано, если Е* поло-
положительно в смысле Накано. Голоморфное векторное
расслоение Е над компактным комплексным простран-
пространством X наз. слабо отрицательным, если
его нулевое сечение обладает строго псевдовыпуклой
окрестностью в Е, т. е. если Е* слабо положительно.
Всякое О. р. над X слабо отрицательно. Аналогично оп-
определяются также отрицательные и слабо отрицательные
линейные пространства над пространством X.
Лит. см. при ст. Положительное расслоение. А. Л. Онищик.
ОТРИЦАТЕЛЬНОЙ КРИВИЗНЫ ПОВЕРХНОСТЬ в
непосредственном понимании — дву-
двумерная поверхность трехмерного евклидова простран-
пространства, к-рая в каждой своей точке имеет отрицательную
гауссову кривизну К<0. Простейшие примеры: одно-
полостный гиперболоид (рис. 1, а), гиперболический
параболоид (рис. 1, б), катеноид.
Непосредственное понимание
О. к. и. можно обобщать, напр.,
но размерности самой поверхно-
поверхности или по размерности и по
структуре объемлющего простран-
пространства.
Рис. 1, а.
Рис. 1, б.
Локально О. к. п. имеют седловое строение. Это зна-
значит, что в достаточно малой окрестности любой своей
точки О. к. п. похожа на седло (см. рис. 1, б, не интере-
интересуясь поведением поверхности вне изображенной ее
части). Локальный седловой характер поверхности
ясно усматривается на этом рисунке, где показаны глав-
главные сечения поверхности в произвольной точке О.
Пусть — , -J их нормальные кривизны, т. е. глав-
ные кривизны в точке О. По классич. определению, га-
гауссова кривизна в точке О есть число Я=д-д~ . Так
как ЛГ<0, то главные кривизны имеют разные знаки,
поэтому главные сечения имеют противоположные на-
направления выпуклости; на рис. 1, б выпуклость сечения
02 направлена по нормали п, выпуклость другого —
против нормали, что и соответствует седловому харак-
характеру поверхности. Топологич. строение О. к. п. в це-
целом («глобальное») может быть весьма разнообразным.
Напр., гиперболич. параболоид (рис. 1, б) топо-
топологически эквивалентен плоскости, однополостный ги-
гиперболоид (рис. 1, а) — цилиндрич. трубке. Пусть
два однополостных гиперболоида с параллельными ося-
осями пересекаются по гиперболе (рис. 2, а). Пусть эти
Рис. 2.
гиперболоиды не прозрачны и их невидимые части
(т. о. части любого пи них, лежащие внутри другого)
отброшены. Получившаяся поверхность имеет отрица-
отрицательную кривизну всюду, кроме точек указанной гипер-
гиперболы. В точках этой гиперболы кривизны вообще нот
(в классическом понимании), т. к. гипербола является
ребром поверхности. Но поверхность вблизи ребра в
данном случае можно загладить >(см. [7]) так, чтобы по-
получилась поверхность, к-рая имеет кривизну во всех
точках, причем отрицательную (см. рис. 2, б). Она то-
топологически эквивалентна тору с двумя проколами.
Включая в конструкцию большее число однополостных
гиперболоидов, можно построить О. к. п. сколь угодно
сложного топологич. строения.
Поверхность наз. полной, если она является
полным метрич. пространством с расстоянием в смысле
ее внутренней геометрии. Во всех указанных примерах
рассматривались полные поверхности. Идея построе-
построения полных О. к. п. разнообразных тонологич. типов,
исходя из нек-рых простейших (как изложено выше),
принадлежит Ж. Адамару (J. Hadamard, [1]). Предло-
Предложен принципиально другой пример (рис. 3) полной
О.к. п. (см. [6] — [7]). Эта поверхность имеет всюду
отрицательную кривизну и вся заключена внутри нек-
рого шара. Она бесконечно ветвится, причем перемен-
переменная ее точка, двигаясь по ветвям, может сколь угодно
близко подойти к граничной сфере шара, но нигде не
достигает этой сферы. Поверхность построена так, что
при указанном движе-
движении переменная точка
всегда проходит путь
бесконечной длины. Тем
самым обеспечивается
полнота поверхности в
смысле ее внутренней мет-
метрики. Этот пример пока-
показывает, что внутренне
полная О. к. п. не обяза-
обязательно уходит в беско-
бесконечность в пространстве,
подобно поверхностям и
примерах Адамара.
В приведенном при-
Рвс- 3- мере повсеместное со-
соблюдение условия К <0
удается обеспечить, допуская хотя бы слабую
нерегулярность поверхности. Это значит, что по-
поверхность предполагается гладкой (всюду класса С),
но допускается, что в нек-рых изолированных точках
она но принадлежит С2; в таких точках требуется су-
существование предельного значения кривизны. После
дополнения предельными значениями кривизна всюду
определена и непрерывна. Вопрос о протяженности
поверхности и связь его с условием регулярности су-
существенно дополняется следующими теоремами [8].
Если гауссова кривизна К полной поверхности
класса С2 удовлетворяет неравенству — a2</f<0, где
a—const, то поверхность не может содержаться в шаре,
^ /~~2~~
радиус к-рого меньше 71/ у-
Если на полной поверхности класса С2, неограничен-
неограниченной во внутреннем смысле, гауссова кривизна A'—>-U
на бесконечности, то поверхность не ограничена в
пространстве (в этой теореме допускается перемена зна-
знака кривизны).
Особое внимание привлекали (и привлекают) по-
постоянной О. к. п., к-рые имеют гауссову кривизну с
одним и тем же численным значением во всех точках.
Они замечательны уже тем, что их внутренняя геометрия
локально совпадает с геометрией на плоскости Лоба-
Лобачевского (см. Лобачевского геометрия). Это значит, что
для фигур, лежащих на постоянной О. к. п., осущест-
осуществляются в точности те же соотношения, какие имеют
место в планиметрии Лобачевского (при этом роль пря-
прямых играют геодезич. линии); напр., тригонометрич.
формулы для треугольников на постоянной О. к. п.
и соответствующие формулы в неевклидовой геометрии
Лобачевского точно совпадают. Тем самым на постоян-
постоянной О. к. п. получается локальная модель геометрии
Лобачевского. Такая модель была построена Э. Бель-
трами (Е. Beltrami, 1868), что существенно содейство-
содействовало признанию геометрии Лобачевского. Э. Бельтра-
ми указал также важный пример О. к. п.; она наз.
псевдосферой (рис. 4) и образована вращением
трактрисы вокруг ее асимптоты (рис. 5). Характери-
стич. свойство трактрисы — отрезок касательной от
точки прикосновения до асимптоты постоянно равен
нек-рому числу а. Оказывается, что гауссова кривизна
псевдосферы А — —j-. Еще раньше, чем Э. Бельтрами,
поверхности вращения отрицательной кривизны изу-
изучал Ф. Миндинг (F. Minding,
1839). Он нашел два вида перио-
периодических постоянной О. к. п. вра-
вращения (рис. 6), к-рые вместе с
псевдосферой исчерпывают все
Рис. 4.
Рис. 5.
Рис. 6.
возможные постоянной О. к. п. (уравнения их см. в
131 и [5]).
Построение глобальной модели планиметрии Лоба-
Лобачевского на какой-нибудь постоянной О. к. п. враще-
вращения, напр, на псевдосфере, невозможно по двум причи-
причинам. Во-первых, на псевдосфе-
псевдосфере имеются нерегулярные точ-
точки; они составляют ребро возв-
возврата (рис. 4). Во-вторых, псевдо-
псевдосфера топологически эквива-
эквивалентна трубке и значит даже
с топологич. точки зрения отли-
отличается от плоскости Лобачевс-
Лобачевского. Но можно построить на ре-
регулярной О. к. п. вращения мо-
модель бесконечной части плоско-
плоскости Лобачевского. С этой целью
отсекается от псевдосферы
плоскостью, перпендикулярной
оси, бесконечная (сужающаяся) область U. Плоскость
проводится так, чтобы она не содержала ребра возвра-
возврата. В качестве U берется та часть псевдосферы, где
ребра возврата нет. Далее рассматривается только
U, к-рую для простоты также наз. псевдосферой; на
ней нет особых точек. Пусть V — универсальная накры-
накрывающая псевдосферу U поверхность. Это понятие
можно наглядно ввести следующим образом. Берется
бесконечно много одинаковых и совмещенных экзем-
экземпляров псевдосферы U, к-рые различаются введением
нумерации: . . ., С7_2, U-t, UQ, Uu . . . Затем все они
разрезаются по какому-нибудь общему меридиану, а
на каждой из них устанавливается левый и правый бе-
берег разреза так, чтобы все левые берега были совмеще-
совмещены (также — правые). Теперь для любого номера
к, — оо</с<оо, левый берег U\ соединяется с правым
берегом Ufr + i (следовательно, правый берег Uи с левым
берегом Uk-i). Так получится связная поверхность U',
к-рая и является универсальной накрывающей поверх-
поверхности U, она иногда наз. односвязной оберткой
поверхности U. Универсальную накрывающую можно
построить для любой поверхности, но наглядное описа-
описание ее конструкции будет далеко не так просто, как
для псевдосферы. Существенно, что универсальная на-
накрывающая всегда односвязна. Важно также, что на
универсальную накрывающую можно перенести ло-
локальную внутреннюю геометрию накрываемой по-
поверхности. Для этого достаточно учесть, что каждая
точка р накрываемой поверхности имеет выпуклую
окрестность V(p), к-рая однолистно накрывается ок-
окрестностью V'(p') накрывающей (здесь р'— точка,
к-рая накрывает точку р; соответствие р—>-/>' биектив-
биективно). Геометрия V (р) переносится на Г' (/>') тождест-
тождественно, т.е. расстояние между точками pi, ря?У
принимается равным расстоянию между их прообраза-
прообразами. Вместе с тем определяется глобальная геометрия
универсальной накрывающей, но она, как правило,
будет совершенно отличаться от глобальной геометрии
накрываемой.
На псевдосфере U меридианы, уходя в бесконеч-
бесконечность, сближаются; кроме того, они ортогональны краю
(/. Поэтому край универсальной накрывающей есть
кривая в плоскости Лобачевского, к-рая является орто-
ортогональной траекторией пучка параллельных по Лоба-
Лобачевскому (сближающихся) прямых. Эта кривая в гео-
геометрии Лобачевского наз. орициклом. Таким
образом, с точки зрения своей внутренней геометрии
универсальная накрывающая псевдосферы U есть вну-
внутренняя область орицикла в плоскости Лобачевского.
Универсальная накрывающая U' псевдосферы U удоб-
удобнее для построения модели геометрии Лобачевского,
чем сама псевдосфера U. Напр., сколь угодно большой
круг можно расположить на U', но в U слишком боль-
большой круг без перекрытий может не уместиться. Но даже
U' недостаточно обширна, чтобы вместить любой объект
геометрии Лобачевского, напр, полная прямая в V
не умещается. Иначе говоря, построить с помощью U'
модель всей плоскости Лобачевского нельзя.
Д. Гильбертом A900) был поставлен вопрос: но су-
существует ли поверхности, внутренняя геометрия к-рой
в целом совпадает с геометрией плоскости Лобачевско-
Лобачевского? Из простых соображений следует, что если такая
поверхность есть, то она должна иметь постоянную
отрицательную кривизну и быть полной. Далее, она
должна быть односвязной, поскольку односвязна пло-
плоскость Лобачевского. Но на самом деле достаточно бы-
было бы найти любую полную поверхность постоянной от-
отрицательной кривизны (согласно изложенному выше,
универсальная накрывающая такой поверхности полна
и односвязна). При этом имеются в виду только регу-
регулярные поверхности (хотя бы дважды непрерывно диф -
ференцируемые в любой точке, т. е. класса С2).
Уже в 1901 Д. Гильберт решил свою проблему (см.
[2]), причем в отрицательном смысле: в трехмерном ев-
евклидовом пространстве не существует полной регуляр-
регулярной поверхности постоянной отрицательной кривизны.
Эта теорема привлекала внимание геометров на протяже-
протяжении ряда десятилетий и привлекает внимание до сих пор.
Дело л том, что с ней и с ее доказательством связано
много интересных вопросов (см. ниже). При этом нали
чие особых линий у поверхностей вращения постоянной
отрицательной кривизны (см. рис. 4, 6) не случайно.
Оно соответствует теореме Гильберта.
Доказательство теоремы Гильберта о поверхностях
любого топология, строения прежде всего интересно
тем, что в нем существенно использовано понятие уни-
универсальной накрывающей поверхности. Оно сводит
дело к поверхности с простейшей топологией, именно,
к односвязной поверхности. По-видимому, теорема
Гильберта была одним из ранних предложений мате-
математики, где это понятие уяснилось. После публикации
первой статьи Д. Гильберта с доказательством его те-
теоремы выражалось сомнение в справедливости этого
доказательства. Замечания относились к необозримо-
необозримости поведения асимптотич. линий, к-рые по ходу дела
рассматривались на поверхности ввиду сложности ее
топологии. Предполагалось даже, что Д. Гильберт
перерабатывал свое доказательство, чтобы уточнить
его. Между тем доказательство Д. Гильберта с самого
начала было безупречным. Вероятно, этих замечаний
не было бы, если бы Д. Гильберт отчетливо сказал,
что исследуется полное односвязное многообразие по-
постоянной отрицательной кривизны, т. е. сама плоскость
Лобачевского, в предположении, что она изометрнчно
и регулярно погружена в трехмерное евклидово про-
пространство.
Интересным является также то, что в доказательстве
Д. Гильберта неожиданно появляются ч е б ы m e в-
с к и е сети: так называется
сеть, в каждом сетевом четырех-
четырехугольнике к-poii противоположные
стороны имеют равные длины (см.
рис. 7). И вот оказывается, что
асимптотич. сеть (к-рая определена
и невырождена во всех точках на
любой О. к. п.) в случае постоян-
постоянной О. к. и.— чебышевская. Эту
сеть можно принять в качестве
координатной: к —const, г const..
Тогда линейный элемент получает Рис. 7.
чебышевский вид
s w du dv-ydv-, A)
где со — сетевой угол. Предполагая, что поверхность
регулярна, полна я односвязна, и, пользуясь чебышев-
ским характером сети, можно доказать, что и, v при-
принимают все значения: —оо<ы<оо, —oo<i><oo и
этим исчерпывают сеть; иначе говоря, асимптотич.
сеть в целом гомеоморфна декартовой сети на евклидо-
евклидовой координатной плоскости (см. [9]). С другой сторо-
стороны, в предположении, что гауссова кривизна постоян-
постоянна, напр. А'——1, из A) получается уравнение
-^- - sin ш, B)
rtu dv '
при атом из геометрич. соображений следуют ограниче-
ограничения
О < ш < я. C)
Д. Гильберт показал, что уравнение B) не может иметь
регулярного на всей координатной плоскости решения
№=ш(н, v), подчиненного условию C), и тем самым
полная плоскость Лобачевского не может быть регу-
регулярно и изометрично погружена в трехмерное евклидо-
евклидово пространство. Отсюда, как объяснялось выше, выте-
вытекает более общая формулировка зтой теоремы: в трех-
трехмерном евклидовом пространстве невозможна полная
регулярная постоянно]! О. к. п. (никакой топологии,
структуры).
Во многих разделах математики случалось, что ка-
какое-нибудь утверждение или какой-нибудь вопрос игра-
играли особую роль в развитии всего раздела. В дифферен-
дифференциальной геометрии одним из таких утверждений была
(и еще остается) теорема Гильберта. Ей посвящено
много публикаций. Интерес к ятой теореме вызван
прежде всего сочетанием в ее доказательстве разнооб-
разнообразных идет! и понятий (универсального накрытия,
чебыпгевской сети). Позднее обнаружилась ее связь
с физикой.
Оказалось, что уравнение B), написанное в несколь-
несколько ином виде и без ограничения C), выражает условие
на потенциал в т. н. эффекте Джозефсона из теории
сверхпроводимости. Физики дали уравнению B) наз-
название «синус-Гордона». Используя связь уравнения B)
с теорией О. к. п. (см. [13], [141), находят в конечном
виде нек-рые его решения, регулярные на всей пло-
плоскости.
С. Э. Кон-Фоссен высказал (см. [15]) предположение,
что имеет место гораздо более общая теорема, чем тео-
теорема Гильберта, именно, что условие на гауссову кри-
кривизну К—const<0 можно заменить условием А<:
<const<0. Однако до нач. 60-х гг. 20 в. не было най-
найдено ни одной теоремы, к-рая включала бы теорему
Гильберта как частный случай. Только в 1961 (см. [16])
была ^доказана корректность теоремы Гильберта, т.е.
пыла установлена теорема о переменной О. к. п., для
к-рой теорема Гильберта является предельным случа-
случаем. Иначе говоря, те свойства постоянной О. к. п.,
к-рые вызывают эффект теоремы Гильберта (наруше-
(нарушение регулярности), и сам эффект возможно понимать
в приближенном смысле. Для доказательства было
найдено уравнение в случае переменной кривизны,
к-рое обобщает уравнение B). Именно,
1} sin ш, D)
где со имеет прежний смысл, k2=—К, дифференциро-
дифференцирование ведется по дугам асимптотич. линий, А и а —
величины, модули к-рых допускают внутреннюю оцен-
оценку, т. е. оценку в зависимости только от погружаемой
метрики. При A'—const получается А—0, а~0 и урав-
уравнение D) превращается в уравнение B).
И случае переменной кривизны найдено (см. [17])
уравнение
LS!L* (со) — М sin со, E)
где Ls —линейный оператор, пропорциональный опе-
оператору дифференцирования по дуге асимптотич. ли-
линий второго семейства, L* — квазилинейный опера-
оператор похожей структуры. Существенно, что функция М
при нек-рых условиях на метрику допускает внутрен-
внутреннюю оценку снизу положительным числом, благодаря
чему и благодаря строению левой части уравнение E)
сходно с уравнением B). Поэтому при таких условиях на
метрику можно провести рассуждения, сходные с рас-
рассуждениями Д. Гильберта (хотя гораздо более слож-
сложные), и получить сходный результат. Таким путем впер-
впервые было получено обобщение теоремы Гильберта (см.
[18]). Что касается условий на метрику, о к-рых только
что говорилось, то они заключаются в требовании, что-
чтобы гауссова кривизна К была отгорожена от нуля и
медленно изменялась. Если предположить, что А*<—1,
то медленное изменение кривизны нужно понимать в
том смысле, что первые и вторые производные от К
по дуге любой геодезической достаточно малы. Доста-
Достаточные оценки устанавливаются с таким расчетом, что-
чтобы к уравнению E) были применены указанные выше
рассуждения, идущие от Д. Гильберта. Эти оценки (см.
[19]) выражены с помощью положительных постоянных,
обозначаемых h и Д. Соответственно, получаемые ме-
метрики с медленно изменяющейся отрицательной кри-
кривизной наз. (h, Д)-м е т р и к а м и (определение см.
в [18] или в [19]); при этом метрики постоянной кри-
кривизны получаются при Д= + °°- Таким образом, полная
(h, Д)-метрика не допускает регулярного изометрич.
погружения в трехмерное евклидово пространство.
Вопрос о возможности обобщения теоремы Гильберта
в том виде, как он ставился в 30-е гг. (без ограничений
характера поведения кривизны, см. [12]), на указан-
указанных сейчас путях, т. е. с помощью дифференциальных
уравнений теории поверхностей, завершить не уда-
удалось. Но решение этого вопроса получилось совсем
на другом пути, именно, с помощью тщательного ис-
исследования граничных свойств сферич. образа О. к. п.
Таким способом доказано (см. [19], [20]), что полная ме-
метрика с гауссовой кривизной A*<xonst<0 не допускает
регулярного изометрич. погружения в Е3. Тем самым
вопрос решен точно в классич. постановке. Одновре-
Одновременно доказана теорема: в Е3 на всякой полной регу-
регулярной поверхности отрицательной гауссовой кривиз-
кривизны К имеет место равенство
suptf = 0. F)
Здесь достаточна регулярность С2. Но в случае Сл* ' есть
(см. [7]) контрпример (в виде слабо нерегулярной по-
поверхности).
Кроме ((i) получены также (см. [21]) другие равенст-
равенства и оценки, универсальные в том смысле, что они от-
относятся ко всем О. к. и. в Е3. Кроме того, метод до-
доказательства F) позволил получить теоремы, к-рые
дают достаточные признаки, когда отображение пло-
плоскости в плоскость с отрицательным якобианом явля-
является не только локальным, но и глобальным диффео-
диффеоморфизмом.
Несмотря на изложенные сейчас результаты, иссле-
исследование (h, Л)-метрик и других метрик с медленно
изменяющейся кривизной (напр., g-метрик; см. [9])
не потеряло смысла. Дело в том, что в задачах погру-
погружения метрик с медленно изменяющейся отрицательной
кривизной возникают эффекты, к-рые не имеют места в
случае более общих метрик отрицательной кривизны
(см., напр., теорему о простой зоне в [9]). Образно мож-
можно сказать, что чем медленнее изменяется кривизна,
тем «труднее» метрике отрицательной кривизны быть
погруженной в Е3. Для метрики постоянной кривизны
это «явление» проявляется особенно заметно (см. уси-
усиленную теорему Гильберта в [9]). Что касается диффе-
дифференциальных уравнений, к-рые отмечались в связи г
вопросом о погружении (h, Д)-метрик, то они сущест-
существенно использовались и в других вопросах. Так, с их
помощью установлен [7] ряд сильных теорем о связи
между внутренними и внешними свойствами О. к. п.;
в частности, теоремы о зависимости внешней регуляр-
регулярности кривизны О. к. п. от регулярности ее метрики
(см. [7]).
Влияние регулярности метрики на внешнюю регу-
регулярность О. к. п. представляется особенно интерес-
интересным, так как О. к. п. входят в нек-рый специальный
класс поверхностей, к-рый может быть определен чисто
геометрически (интересно, что чисто геометрич. опре-
определение допускает и класс выпуклых поверхностей).
Поверхности этого класса наз. Серовыми. Седло-
вые поверхности в нек-ром смысле — антиподы вы-
выпуклых (см. [22] — [25]).
Теорема о невозможности в евклидовом пространстве
полной О. к. п. X<:const<0 получает весьма усилен-
усиленную форму в случае поверхности, к-рая однолистно
проектируется на плоскость, т. е. может быть представ-
представлена как график функции z—/(ж, у). В этом случае
существуют универсальные оценки протяженности по-
поверхности, и полнота ее становится несущественной.
Доказаны теоремы (см. 126]): 1) если на прямоуголь-
прямоугольник со сторонами а, Ь регулярно проектируется по-
поверхность с гауссовой кривизной Х<:—a2=con.4t<0,
то неравенство j/'a^Cx+e, e>0 влечет а]/"а<С]+—'
где Cj, С2— универсальные постоянные (напр., С5=4я,
(?2=12я); 2) если а, Ь и (для простоты) а=1, то а<18,9.
Пусть дана метрика ds2 с отрицательной гауссовой
кривизной К и k-¦- У~К. Пусть метрика ds2 погружена
в Е3 и I, m, n — приведенные коэффициенты получив-
получившейся второй квадратичной формы (приведенные —
значит удовлетворяющие уравнению In—то2=—К). В за-
задаче о погружении I, m, n — неизвестные функции.
В качестве новых неизвестных функций вводятся т. н.
инварианты Римана:
т+ь in—h
Тогда основная система уравнений теории поверхно-
поверхностей примет симметричный вид
rx-\-sr,J — An-{-A1r-{-AzS + A3r2-\-A4rs-\-Abr2s, I
где Ао, . . ., А:-, выражаются только через метрику ds2.
Выше указывалось, что полная О. к. п. с X<:const<0
не допускает иаометричного регулярного погружения в
Ео. Поэтому полученпые результаты о возможности
ызометрич. погружения двумерных многообразий от-
рицательной кривизны в ?3 по необходимости отно-
относятся к частям нолных многообразии. Само многообра-
многообразие предполагается односвязным. Так, доказано (см.
[29], [30]), что каждый геодезич. круг на произволь-
произвольном регулярном многообразии отрицательней кривиз-
кривизны A'<const<0 может быть регулярно изометрически
погружен в Яд. .'(та теорема получена как следствие
более общей теоремы: при нек-рых естественных усло-
ннях регулярности на метрику полной О. к. п. с if<
<const<0 каждая бесконечная эквидистантная полоса
на этом многообразии может быть изометрично и ре-
регулярно погружена в Ея. Эта теорема в свою очередь
получена как следствие теоремы о существовании
II целом решений гиперболич. систем квазилинейных
уравнений вида G), причем rj±s.
Построен пример односвязного многообразия знакопе-
знакопеременной кривизны, на к-ром есть геодезич. круг, не
допускающий изометрич. погружения в Е3 (см. [10]).
Доказано [31] при нек-рых ограничениях на полную
метрику односвязной О. к. и. /C<const<0, что внут-
внутренняя область произвольного орицикла такого много-
многообразия может быть изометрично погружена в Е3.
Таким образом, для полных односвязных многообра-
многообразий отрицательной кривизны К <const<0 доказана воз-
возможность изометрич. погружения в Е^ всех компакт-
компактных и некомпактных его частей, к-рые сходны с частя-
частями плоскости Лобачевского, изометрич. погружения
к-рых известны из работ Ф. Миндинга и Э. Вельтрами.
Изучаются погружения метрики с гауссовой кривиз-
кривизной К=const <0, т. е. погружения частей плоскости Ло-
Лобачевского. Так, доказано, что каждый, даже бесконеч-
бесконечно протяженный, многоугольник плоскости Лобачев-
Лобачевского, может быть изометрически погружен в Еа.
Разнообразие топологич. типов полных О. к. п. в Ея
приводит к необходимости рассматривать различные
подклассы этого слишком широкого класса, удовлетво-
удовлетворяющие тем или иным дополнительным условиям.
Весьма естественным является подкласс полных О. к.п.,
имеющих взаимно однозначное сферическое («о дно-
лес т н о е») отображение (см. [33]). Если поверх-
поверхность F из этого класса не имеет самопересечений, то
она односвязна или двусвязна. Если такая поверх-
поверхность F имеет рог, то, используя неограниченность
седлового рога (см. [34]), можно получить ряд внешне-
геометрич. свойств этой поверхности: F допускает
задание уравнением z=f(x, у) над областью, получен-
полученной из плоскости .г, у удалением компактного выпук-
выпуклого множества; F имеет предельный конус A (F),
состоящий из луча, соответствующего рогу, и выпукло-
выпуклого конуса, соответствующего чаше поверхности; за-
замыкание F* сферич. образа поверхности /' имеет своим
дополнением до сферы открытую по-
полусферу и открытое выпуклое мно-
множество (рис. 8 —10). Ряд аналогичных '
рог
Рис. 0.
Рис. 10.
вопросов изучен и для других типов полных О. к. п.
со взаимно однозначным сферич. отображением.
Другим интересным по своим свойствам и свойствам
своего сферич. отображения классом является класс
сужающихся О. к. п. (см. [361, [37]). Такой
поверхностью, напр., является поверхность, заданная
уравнением т2у2-\-у2г2-]-??х2~-а2. По ряду своих свойств
сужающиеся 6. к. и. напоминают замкнутые поверх-
поверхности. Их сферич. образ можно рассматривать как ри-
манову поверхность с краем, каждая компонента к-рого
является сферич. ломаной, лежащей на одной из боль-
больших окружностей.
Иначе выглядит теория О. к. п. в псевдоевклидовом
пространстве ?"! д. В этом пространстве О. к. п. явля-
являются выпуклыми; при этом кривизна понимается обыч-
обычным образом, как кривизна метрики, индуцированной
объемлющим пространством. Именно она предполага-
предполагается отрицательной.
Единичная сфера пространства -?г, i состоит из трех
связных компонент Lb L2, L3 (рис. И). Компоненты
Ьл и L2 являются выпуклыми по- ^________^
верхностями, на к-рых индуцирует-
индуцируется положительно определенная
метрика постоянной отрицательной
кривизны; эти поверхности дают
известную интерпретацию геомет-
геометрии Лобачевского. Поверхность L3
седлообразная, на ней индуцирует-
индуцируется индефинитная метрика посто-
постоянной положительной кривизны;
метрика этой поверхности известна Рис. и.
как двумерная метрика де Ситтера.
О. к. п. с дефинитной метрикой образуют в Е%> i ши-
широкий и естественный класс поверхностей, обобщаю-
обобщающих свойства поверхностей Li и L2 так же, как по-
поверхности положительной кривизны образуют в ев-
евклидовом пространстве класс, обобщающий сферу
(см. [38]).
Исчерпывающим образом изучены свойства поверх-
поверхностей с дефинитной метрикой и отрицательной кри-
кривизной, полная интегральная кривизна к-рых кончена.
Свойства этих поверхностей аналогичны свойствам вы-
выпуклых поверхностей с кривизной, меньшей 2я, в ев-
евклидовом пространстве (класс поверхностей Оловяштш-
никова). Именно, полная дефинитная метрика отри-
отрицательной кривизны и конечной интегральной кривиз-
кривизны К и геодезич. луч у на многообразии, несущем эту
метрику, определяют единственным образом выпуклую
поверхность с данным выпуклым предельным конусом
полной кривизны К без изотропных образующих и с
данной образующей, к-рая является предельной для
луча у. Регулярность получаемых поверхностей опре-
определяется регулярностью метрики.
Полные О. к. п. с индефинитной метрикой также
являются выпуклыми. Но свойства их отчасти сходны
со свойствами седлообразных поверхностей в евкли-
евклидовом пространстве. В частности, для них справедлива
оценка sup К— 0. Такие поверхности должны были
бы соответствовать компоненте Ls единичной сферы
пространства E\t г, однако она не выпукла. Здесь иг-
играет определяющую роль не только знак гауссовой
кривизны, но и знак определителя метрич. формы по-
поверхности.
Лит.: [1] Н a d a m a r d J., «.I. math, pures et appl.», 1898,
v. 4, p. 27—73; [2] H i 1 b e r t D., «Trans. Amer. Math. Soc»,
1901, v. 2, p. 87—99; [3j В i a n с h i L., Lezioni di georaetria
differentiate, 3 ed., v. 1, pt 1, Bologna, 1927; L4] E ф и м о в Н. В.,
Высшая геометрия, 6 изд., М., 1978; [5] Н о р д е и А. П., Тео-
Теория поверхностей, М., 1956; [6] Р о з е н д о р н Э. Р., «Успехи
матем. наук», 1961, т. 16, в. 2, с. 149—56; [7] е г о те, там же,
1966, т. 21, в. 5, с. 59—116; [8] А м и н о и Ю. А., «Укр. геометр.
сб.», 197:!, п. 13, с. 3-Я; [9] Е ф и м о в Н. В., «Успехи матем.
наук», 191Ш, т. 21, в. 5, с. 3—58; [10] П о з н я к Э. Г., там же.
1973, т. 28, в. 4, с. 47—76; 111] Позня к I). Г., ШнкннЕ. В.,
и кн.: Итоги науки и техники. Сер. Алгебра. Топология Геомет-
Геометрия, т. 12, М., 1974, с. 171—207; [12] П о л н я к Э. Г., в кн.:
Итоги науки и техники. Сер. Проблемы геометрии т. 8, М., 1977
с. 225—41; [13] Грибков И. В., «Вестн. Моск. ун-та. Сер.
Математика. Механика», 1977, Ms 4, с. 78—83; [14] его же
«Успехи матем. наук», 1978, т. 33, в. 2, с. 191—92; [15] Коп-
Фоссен С. Э., там же, 1936, в. 1 с. 33—76- [16] Ефи-
Ефимов Н. В., «Докл. АН СССР», 1961, т. 136, № 6, с. 1283—8С5;
[17] Ефимов Н. В., П о з к я к Э. Г., там же, т. 137, J* 1
с. 25—27; [18] их же, там же, № 3, с. 509—12; [19] Е ф и-
м о в Н. В., там же, 1963, т. 150, № 6, с. 1206—09; [20] его
ж е, «Матем. сб.», 1964, т. 64, К» 2 с. 286—320; [21] его же
там же, 1968, т. 76, MS 4, с. 499 — 512; [22] Ш е ф е л ь С. 3., Ис-
Исследования по геометрии седловых поверхностей, Новосиб., 1963;
[23] е г о же, «Сиб. матем. ж.», 1964, т. S, К 6, с. 1382—96;
[24] его же, там же, 1967, т. 8, Ml 3, с. 705—14; [25] е г о
же, «Докл. АН СССР», 1965, т. 162, № 2, с. 294 — 96; [26] Е ф и-
мо вН. В., «Матем. сб.», 1976, т. 100, Mi 3, с. 356—63; [27] е г о
же, «Докл. АН СССР», 1953 т. 93, М 4, с. 609—11- [28] Н е i n z
Е., «Math. Ann.», 1955, Bd 129, Н. 5, p. 451—54; [29] По з-
н я к Э. Г., «Докл. АН СССР», 1966, т. 170, Mi> 4, с. 786 — 89; [30]
его же, «Укр. геометр, сб.», 1966, в. 3, с. 78—92; [31] Ш и-
ч и н В. В., «Докл. АН СССР», 1974, т. 215, М° 1, с. 61—63; [321
" 1 ж д е с т в е п с к и и Б. Я., там же, 1962, т. 143, № 1, с.
S0 — Г>2; [33] В е р н е р А. л. «Матем. сб.» 1967 т. 74, JV° 2, с.
2.S —40; 1968, т. 75, № 1, с. 112—39, т. 77, Me 1, с. 136; [34] его
ж е, «Сип. матем. ж.», 1970, т. 11, Л» 1, с. 20—29; М» 4, с. 750 —
7<ifl; [35] его ж е, «Матем. заметки», 1972, т. 12, М5 3, с.
281 -86; [36] Соколов Д. Д., «Успехи матем. наук», 1975,
т. :ц, в. 1, с. 261 — 62; 1978, т. 33, в. 4, с. 227 — 28; 1979, т. 34,
в. .(, с. 213—14; [37] Александров А. Д., Внутренняя ге-
«лгфин выпуклых поверхностей, М. -- л., 1948; [38] Л о г о-
релин А. В., Внешняя геометрия выпуклых поверхностей,
М., 1969. Н. В. Ефимов.
ОТСЧЕТА СИСТЕМА — совокупность системы коор-
координат и часов, связанных с телом, по отношению к к-ро-
му изучается движение (или равновесие) каких-нибудь
других материальных точек или тел. Любое движение
является относительным, и движение тела следует
рассматривать лишь по отношению к какому-либо
другому телу (телу отсчета) или системе тел. Нельзя
указать, напр., как движется Луна вообще, можно лишь
определить ее движение по отношению к Земле или Солн-
Солнцу и звездам и т. д.
Математически движение тела (или материальной
точки) по отношению к выбранной О. с. описывается
уравнениями, к-рые устанавливают, как изменяются
с течением времени / координаты, определяющие поло-
положение тела (точки) п этой О. с. Напр., в декартовых
координатах .г, ;/, z движение точки определяется
уравнениями
наз. уравнениями движения.
Выбор О. с. зависит от целей исследования. При кине-
матич. исследованиях все О. с. равноправны. В зада-
задачах динамики преимущественную роль играют инерци-
алъные системы отсчета, по отношению к которым
дифференциальные уравнения имеют обычно более
простой вид.
По материалам статьи Система отсчета из БСЭ-з.
ОЦЕНКА СТАТИСТИЧЕСКАЯ — функция от слу-
случайных величин, применяемая для оценки неизвестных
параметров теоретич. распределения вероятностей. Ме-
Методы теории О. с. служат основой современной теории
ошибок; обычно в качестве неизвестных параметров
выступают измеряемые физич. постоянные, а в качестве
случайных величин — результаты непосредственных
измерений, подверженные случайным ошибкам. Напр.,
если Xj, Ж2,. . ., Хп — независимые одинаково нор-
нормально распределенные случайные величины (резуль-
(результаты ранноточных измерений, подверженных независи-
независимым нормально распределенным случайным ошибкам),
то в качестве О. с. для неизвестного среднего значения а
(приближенного значения измеряемой физич. постоян-
постоянной) применяется среднее арифметическое
X=±(Xi-\-Xt+...+Xn)- И)
О. с. как функция от случайных величин чаще всего
задается теми пли иными формулами, выбор к-рых опре-
определяется требованиями практики. При этом различают
оценки точечные и оценки интервальные.
Точечные оценки. Точечной оценкой наз.
такая О. с, значение к-рой представимо геометрически
в виде точки в том же пространстве, что и значения
неизвестных параметров (размерность пространства
равна числу оцениваемых параметров). Именно точеч-
точечные О. с. и исиользуются как приближенные значения
для неизвестных физич. величин. В дальнейшем для
простоты предполагается, что оценке подлежит один
единственный параметр; в этом случае точечная О, с.
представляет coooii функцию от результатов наблюде-
наблюдений, принимающую числовые значения.
Точечную О. с. наз. несмещенной, если ее ма-
тематич. ожидание совпадает с оцениваемой величиной,
т. е. если О. с. лишена систематич. ошибки. Среднее
арифметическое A) несмещенная О. с. для математич.
ожидания одинаково распределенных случайных вели-
величин Xt (не обязательно нормальных). В то же время вы-
выборочная дисперсия
B)
является смещенной О. с. для дисперсии о-—ОХ;, так
как Es2= ( 1—— 1 о2; в качестве несмещенной О. с. для
о2 обычно берут функцию
См. также Несмещенная оценка.
За меру точности несмещенной О. с. а для параметра
а чаще всего принимают дисперсию Da.
О. с. с наименьшей дисперсией наз. наилучшей.
В приведенном примере среднее арифметическое A) —
наилучшая О. с. Однако если распределение вероятно
етей случайных величин Xt отлично от нормального, тч
О. с. A) может и не быть наилучшей. Напр., если ре-
результаты наблюдений X/ распределены равномерно в
интервале (Ь, с), то наилучшей О. с. для математич.
ожидания аг~ (Ь-\-с)B будет полусумма крайних зна-
значений
min X, + max X-
« = ?- L . C)
В качестве характеристики для сравнения точности
различных О. с. применяют эффективность —
отношение дисперсий наилучшей оценки и данной
несмещенной оценки. Напр., если результаты наблю-
наблюдений Xi распределены равномерно, то дисперсии оценок
A) и C) выражаются формулами
D)
(п + 2) '
Так как оценка C) наилучшая, то эффективность
оценки A) в данном случае есть
еп (X) = %nj(n + \) (п + 2) ~ 6/д.
При большом количестве наблюдений п обычно требуют,
чтобы выбранная О. с. стремилась по вероятности к ис-
истинному значению параметра а, т. е. чтобы для всякого
г >0
lim Р {|а—а\ > е}^0;
такие О. с. паз. с о с т о ц г <> л ь н ьг м и рр
состоятельной О. с.— любая несмещенная оценка,
дисперсия к-рой при » -^- оо стремится к нулю; см. так-
также Состоятельная оценка). Поскольку важную роль
при этом играет порядок стремления к пределу, то асим-
асимптотически наилучшими являются асимптоти-
асимптотически эффективные О.с, то есть такие
О. с, для к-рых при п —у оо
е (а-а) „ , . ,
\ ¦' —>0и е„ ос —>!.
VE (а-аJ
Напр., если Хг, Х2,. . ., Хп распределены одинаково
нормально, то О. с. B) представляет собой асимптоти-
асимптотически эффективную оценку для неизвестного параметра
о2 — DXh так как при п -> оо дисперсия оценки s2
и дисперсия наилучшей оценки s2n/(п—1) асимптоти-
чнски эквивалентны:
,2 „ о„4
и, кроме того,
Е (s2 — о2) = — о2/ге.
Фундаментальное значение для теории О. с. и ее при-
приложений имеет тот факт, что квадратичное отклонение
О. с. для параметра а ограничено снизу нек-рой вели-
величиной (этой величиной Р. Фишер (R. Fischer) предло-
предложил характеризовать количество информации относи-
относительно неизвестного параметра а, содержащийся в ре-
результатах наблюдений). Напр., если Хи X2,- . ., Хп
независимы и одинаково распределены с плотностью
вероятности р(х\ а) и если а=ф(А\, Х2,- ¦ -, Хп) —
О. с. для нек-рой функции g(a) от параметра а, то в
широком классе случаев
, У+Ь(аI' , E)
где
6 («) = Е [«-*(«)! и /(a)=-
Функцию i(a) наз. смещением, а величину, обрат-
обратную правой части неравенства E), наз. количест-
количеством информации (по Фишеру) относительно
функции g{a), содержащейся в результате наблюдений.
В частности, если a — несмещенная О. с. параметра а,
то
E[a — g(a)]2 = DaSal/n/(a), F)
причем количество информации nla в этом случае про-
пропорционально количеству наблюдений (функцию I (а)
наз. количеством информации, содержа-
содержащейся в одном наблюдении).
Основные условия, при к-рых справедливы неравен-
неравенства E) и F), — гладкость оценки а как функции от
Х(, а также независимость от параметра а множества
тех точек х, где р(х, а)--0. Последнее условие не вы-
выполняется, напр., в случае равномерного распределе-
распределения, и поэтому дисперсия О. с. C) не удовлетворяет
неравенству F) [согласно D) эта дисперсия ость вели-
величина порядка п~2, в то время как по неравенству F)
она не может иметь порядок малости выше, чем п~1\.
Неравенства E) и F) справедливы и для дискретно
распределенных случайных величин Xf. нужно лишь
в определении информации I (а) плотность р(:г; а)
заменить вероятностью события {А'^-.г}.
Если дисперсия несмещенной О. с. а* для параметра
а совпадает с правой частью неравенства F), то а* —
наилучшая оценка. Обратное утверждение, вообще
говоря, неверно: дисперсия наилучшей О. с. может
превышать [и/(а)]~]. Однако если п —*¦ оо, то дисперсия
наилучшей оценки Da* асимптотически .эквивалентна
правой части F), т. p. uDa* -+¦ Ml (а). Таким образом,
с помощью количества информации (по Фишеру) можно
определить асимптотич. эффективность несмещенной
О. с. а, полагая
Особенно плодотворным информационный подход к
теории О. с. сказывается тогда, когда плотность (в
дискретном случае — вероятность) совместного рас-
распределения случайных величин Хи Х2,- . ., Хп пред-
ставима в виде произведения двух функций к(хг, .г2,. . .,
xn)i[y(^i, Х2,- ¦ ¦! хп)'' ah из к-рых первая не зависит
от а, а вторая представляет собой плотность распреде-
деления нек-рой случайной величины Z=y(Xlt X2,. . .,
Хп), наз. достаточной статистикой,или исчерпы-
исчерпывающей статистикой.
Один из наиболее распространенных методов нахож-
нахождения точечных О. с.— моментов метод. Согласно это-
этому методу, теоретич. распределению, зависящему от
неизвестных параметров, ставят в соответствие дискрет-
дискретное выборочное распределение, к-рое определяется ре-
результатами наблюдений X; и представляет собой рмс -
пределение вероятностей воображаемой случайной ве-
величины, принимающей значения Xj, X2,. . ., Хп с
одинаковыми вероятностями, равными Ма (выборочное
распределение можно рассматривать как точечную
О. с. для теоретич. распределения). В качестве О. с.
для моментов теоретич. распределения принимают
соответствующие моменты выборочного распределения;
напр., для математич. ожидания а и дисперсии о2 метод
моментов дает следующие О. с: выборочное среднее A)
и выборочную дисперсию B). Неизвестные параметры
обычно выражаются (точно или приближенно) в виде
функций от нескольких моментов теоретич. распределе-
распределения. Заменяя в этих функциях теоретич. моменты вы-
выборочными, получают искомые О. с. Этот метод, ча-
часто приводящий на практике к сравнительно про-
простым вычислениям, дает, как правило, О. с. невы-
невысокой асимптотической эффективности (см. выше при-
пример оценки математического ожидания равномерного
распределения).
Другой метод нахождения О. с, более совершенный
с теоретич. точки зрения,— максимального правдоподо-
правдоподобия метод, или наибольшего правдопо-
правдоподобия метод. Согласно этому методу, рассматри-
рассматривают функцию правдоподобия//(а), к-рая
представляет собой функцию неизвестного параметра а
и получается в результате замены в плотности совмест-
совместного распределения р(хи х2,. . ., хп; п) аргументов х,-
самими случайными величинами X,¦; если X; независимы
и одинаково распределены с плотностью вероятности
р(х; а), то
L(a)=p (Xi; а) р (Хг; а) ... р (Хп; а)
(если X; распределены дискретно, то в определении
функции правдоподобия L следует плотности заменить
вероятностями событий {Xj=xj}). В качестве О. с.
максимального правдоподобия для неизвестного пара-
параметра а принимают такую величину а, для к-рой L (а)
достигает наибольшего значения (при этом часто вме-
вместо L рассматривают т. н. логарифмическую функцию
правдоподобия l(a)~~In/, (а); в силу монотонности
логарифма точки максимумов функций L(a) и 1{а)
совпадают). Примерами О. с. максимального правдо-
правдоподобия являются оценки по наименьших квадратов
методу.
Основное достоинство О. с. максимального правдо-
правдоподобия заключается в том, что при нек-рых общих
условиях эти оценки состоятельны, асимптотически
эффективны и распределены приближенно нормально.
Перечисленные свойства означают, что если а есть
О. с. максимального правдоподобия, то при п -*¦ оо
Еа — а и Е (а — «)- ~ Da ~ а,, (а) =-
(если .Y независимы, то о„(а) = [и/(а)]-1). Таким обра-
лом, для функции распределения нормированной О. с.
(a-«)'<j,,(a) имеет место предельное соотношение
e-'3/adt^a>(x). (8)
Преимущества О. с. максимального правдоподобия
оправдывают вычислительную работу но отысканию
максимума функции L (или I). В нек-рых случаях
вычислительная работа существенно сокращается бла-
благодаря следующим свойствам: во-первых, если а* — та-
такая О. с, для к-рой неравенство F) обращается в ра-
равенство, то О. с. максимального иравдоподобия един-
единственна и совпадает с а*, во-вторых, если существует
достаточная статистика Z, то О. с. максимального
правдоподобия есть функция Z.
Пусть, напр., X-i, Хг,. . •, Хп независимы и рас-
распределены одинаково нормально так, что
поэтому
I (a, a) = lnL (a, a) —
=--|-In Bл)-re In a-т^^]" (Xi-af.
Координаты а—а0 и а--а„ точки максимума функции
I (a, a) удовлетворяют системе уравнений
1аким образом, au-X=ZXi!n, a§=s2=2 (Х;—ХJ/п
п, значит, в данном случае О. с. A) и B) — оценки мак-
максимального правдоподобия, причем X — наилучшая
0. с. параметра а, распределенная нормально (ВХ=а,
DX=a2/n), а s'2 — асимптотически эффективная О. с.
параметра о2, распределенная при больших п прибли-
приближенно нормально (Es2 ~ a2, Ds2 ~ 2ailn). Обе оценки
представляют собой независимые достаточные статис-
статистики.
Еще один пример, в к-ром
р(х; а)^={л[1 + (х-а)*]}.
Эта плотность удовлетворительно описывает распреде-
распределение одной из координат частиц, достигших плоского
экрана и вылетевших n;s точки, расположенной вые
экрана (а — координата проекции источника на экран —
предполагается неизвестной). Для указанного распре-
распределения матоматич. ожидание не существует, т. к.
соответствующий интеграл расходится. Поэтому отыс-
отыскание О. с. для а методом моментов невозможно. Фор-
Формальное применение в качестве О. с. среднего арифме-
арифметического A) лишено смысла, т. к. .Y распределено в
данном случае с той же плотностью/; (.г; а), что и каж-
каждый единичный результат наблюдений. Для оценки а
можно воспользоваться тем обстоятельством, что рас-
рассматриваемое распределение симметрично относительно
точки х=а и, значит, а — медиана теоретич. распреде-
распределения. Несколько видоизменяя метод моментов, в ка-
качестве О. с. для а принимают т. н. ныборочную медиа-
медиану и, к-рая при и >: 3 является несмещенной О. с.
для a, причем1 если к велико, то ц. распределена при-
приближенно нормально с дисперсией
Do. — л2 /in.
В то же время
I (а) = - в In я + 2 "= 1 1" [1 + (Xt -аП,
поэтому nl(a)=n!2 и, значит, согласие) G) аецмптотич.
эффективность е„((л) равна 8/я2 « 0,811. Таким обра-
образом, для того чтобы выборочная медиана ц. была столь
же точной О. с. для а, как и оценка наибольшего прав-
правдоподобия а, нужно количество наблюдений увеличить
на 25%. Если затраты на эксперимент велики, то для
определения а следует воспользоваться О. с. а, к-рая
в данном случае определяется как корень уравнения
Sl_ о V " Xj-a ..
В качестве первого приближения выбирают an= u и
далее решают это уравнение последовательными приб-
приближениями по формуле
4 -v-i n Xi~ ak
См. также Точечная оценка.
Интервальные оценки. Интервальной оцен-
оценкой наз. такая О. с, к-рая геометрически представи-
ма в вид« множества точек, принадлежащих простран-
пространству параметров. Интервальную О. с. можно рассмат-
рассматривать как множество точечных О. с. Это множество
зависит от результатов наблюдений и, следовательно,
оно случайно; поэтому каждой интервальной О. с.
ставится в соответствие вероятность, в к-рой эта оценка
«накроет» неизвестную параметрич. точку. Такая ве-
вероятность, вообще говоря, зависит от неизвестных па-
параметров; поэтому в качестве характеристики досто-
достоверности интервальной О. с. принимают коэффи-
коэффициент доверия — наименьшее возможное зна-
значение указанной вероятности. Содержательные стати-
стич. выводы позволяют получать лишь те интервальные
О. с, коэффициент доверия к-рых близок к единице.
Если оценивается один параметр а, то интервальной
О. с. обычно является нек-рый интервал (f5, 7) (т. н.
доверительный интервал), конечные
точки к-рого Р и 7 представляют собой функции от
результатов наблюдений; коэффициент доверия со в
данном случае определяется как нижняя грань вероят-
вероятности одновременного осуществления двух событий
{р < а} и {7 > а}, вычисляемая но всем возможным
значениям параметра а:
co^inf Р {р < а < 7}.
а
Если середину такого интервала (р -\- у)'2 принять
па точечную О. с. для параметра а, то с вероятностью
не менее чем со можно утверждать, что абсолютная
погрешность этой О. с. не превышает половины длины
интервала G — Р)/2. Иными словами, если руководст-
руководствоваться указанным правилом оценки абсолютной
погрешности, то ошибочное заключение будет полу-
получаться в среднем менее чем в 100 A — ш)% случаев. При
фиксированном коэффициенте доверия о) наиболее вы-
выгодны кратчайшие доверительные интервалы, для к-рых
математич. ожидание длины ЕG—Р) достигает наимень-
наименьшего значения.
Если распределение случайных величин X; зависит
только от одного неизвестного параметра а, то построе-
построение доверительного интервала обычно осуществляется с
помощью какой-либо точечной О. с. а. Для большин-
большинства практически интересных случаев функция распре-
распределения P{a < ,r}—F(x; а) разумно выбранной О. с. a
монотонно зависит от параметра а. В этих условиях для
отыскания интервальной О. с. следует в F(x; а) под-
подставить х=а и определить корни al~a1{a, со) и а2^
— а.2(а, со) уравнений
где
/¦(ж + 0; а)= Jim F (г + Д2; а)
[для непрерывных распределений Р(ж+0; «)=F(,r; a)].
Точки с координатами ах (ее; со) и а2 (а; со) ограничи-
ограничивают доверительный интервал с коэффициентом дове-
доверия со. Разумеется, интервал, построенный столь
простым способом, во многих случаях может отличаться
от оптимального (кратчайшего). Однако если a --
асимптотически эффективная О. с. для а, то при доста-
достаточно большом количестве наблюдений такая интер-
интервальная О. с. практически несущественно отличается
от оптимальной. В частности, это верно для О. с. наи-
наибольшего правдоподобия, т. к. она распределена асимп-
асимптотически нормально (см. (8)). В тех случаях, когда
решение уравнений (9) затруднительно, интервальную
О. с. вычисляют приближенно с помощью точечной О. с.
максимального правдоподобия и соотношения (8):
Р w P* = a —жо„(а) и 7 ~ у* — а4-ха„ (от),
где х — корень уравнения Ф (х)— A+ш)/2.
Если и-*- ов, то истинный коэффициент доверия
интервальной оценки (Р*, у*) стремится к ш. В более
общем случае распределение результатов наблюдений
Xi зависит от нескольких параметров а, Ь,. ... В этих
условиях указанные выше правила построения довери-
доверительных интервалов часто оказываются неприменимыми,
т. к. распределение точечной О. с. а зависит, как пра-
правило, не только от а, но и от остальных параметров.
Однако в практически интересных случаях О. с. a
можно заменить такой функцией от результатов наблю-
наблюдений Xj и неизвестного параметра а, распределение
к-рой не зависит (или «почти не зависит») от всех неиз-
неизвестных параметров. Примером такой функции может
служить нормированная О. с. максимального правдо-
правдоподобия (а—а)/ап(а, Ь,. . .); если в знаменателе аргу-
аргументы а, Ь,. . . заменить их оценками максимального
правдоподобия а, Р,. . . , то предельное распределение
останется тем же самым, что и в формуле (8). Поэтому
приближенные доверительные интервалы для каждого
параметра в отдельности можно строить так же, как и в
случае одного параметра.
Как уже отмечалось выше, если Хъ Х3, . . ., Xп,
... — независимые и одинаково формально распреде-
распределенные случайные величины, то X и s2 — наилучшие
О. с. для параметров а и гга соотпетственно. Функция
распределения О. с. выражается формулой
и, следовательно, она зависит пе только от а, но
также и от ст. В то же время распределение т. Н. о т-
н о in с в и я С т ь ю д е н т а
Уп Сх- а)
" " i , • i %
S
не зависит ни от я, ни от о, причем
где постоянная C',,_i выбирается так, чтобы выполнялось
равенство con_i(oo) = l. Таким образом, доверитель-
доверительному интервалу
X — stiV"n < а < X -\-stlV~n
соответствует коэффициент доверия шг[_ i (г1).
Распределение оценки s2 зависит лишь от о2, причем
функция распределения О. с. s3 задается формулой
Р {*а < Щ =С„_! {х) =/>„_! \ хо „(«-»)/а c-«/2rfu,
где постоянная ?>„_ t определяется условием С„_] (оо)— 1
(так наз. Ха-расиределением с н— 1 степенями свободы).
Так как с ростом о вероятность Р{«2 < о2х1(п—1)}
монотонно возрастает, то для построения интервальной
О. с. применимо правило (9). Таким образом, если хх и
,т2 — корни уравнений 6'„_, (jrt) — (i —ш)/2 и GH.-j (г2)--
—(l-fco)/2, то доверительному интервалу
(л—1) s2/z2 < а2 < (га —1) s2/n
соответствует коэффициент доверия <о. Отсюда, в част-
частности, следует, что доверительный интервал для отно-
относительной ошибки задается неравенствами
Подробные таблицы функций распределения Стьюдента
о)„_,(<) и Х2-распределения Gn-1(x) имеются в боль-
большинстве руководств но математич. статистике.
До сих пор предполагалось, что функция распределе-
распределения результатов наблюдений известна с точностью до
значений нескольких параметров. Однако в приложе-
приложениях часто встречается случай, когда вид функции
распределения неизвестен. В этой обстановке для оцен-
оценки параметров могут оказаться полезными т. в. непара-
непараметрические методы статистики (т. е. такие методы,
к-рые не зависят от исходного распределения вероят-
вероятностей). Пусть, напр., требуется оценить медиану т
теоретич. непрерывного распределения независимых
случайных величин Х1, Х2,. . ., Хп (для симметричных
распределений медиана совпадает с математич. ожида-
ожиданием, если, конечно, оно существует). Пусть У, <
<: У2 ¦<¦ . . -<Yn — те же величины X,-, но распо-
расположенные в порядке возрастания. Тогда, если к --
целое число, удовлетворяющее неравенствам 1 < к <
<« '2, то
Р {Yk < т < У„_й + 1} =
Таким образом, (У^, У„„^+1) — интервальная О. с.
для т с коэффициентом доверия ш— ш,,, ^. Этот вывод
верен при любом непрерывном распределении случай-
случайных величин X/.
Выше отмечалось, что выборочное распределение —
точечная О. с. для неизвестного теоретич. распределе-
распределения. Более того, функция выборочного распределения
/'„(х) - несмещенная О. с. для функции теоретич.
распределения F(x). При этом, как показал А. Н. Кол-
Колмогоров, распределение статистики
K=Yn max \Fn{x)-F(x)\
— 00 < X СО
не зависит от неизвестного теоретич. распределения
и при п —>- оо стремится к предельному распределению
А' (у), к-рое наз. распределением Колмо-
Колмогорова. Таким образом, если у — решение уравне-
уравнения if(y)~co, то с вероятностью со можно утверждать,
что график функции теоретич. распределения F (у)
целиком «покрывается» полосой, заключенной между
графиками функций Fn(.r)±yl Yn (при п ~^ 20 различие
допредельного и предельного распределений статисти-
статистики Хп практически несущественно). Такую интерваль-
интервальную О. с. наз. доверительной зоной.
См. также Интервальная оценка.
Статистические оценки в теории ошибок. Теория
ошибок - раздел математич. статистики, посвященный
численному определению неизвестных величин но ре-
зультатам измерений. В силу случайного характера
ошибок измерений и, быть может, случайной природы
самого изучаемого явления не все такие результаты
равноправны: при повторных измерениях нек-рые из них
встречаются чаще, другие — реже.
В основе теории ошибок лежит математмч. модель.
согласно к-роп до опыта совокупность всех мыслимых
результатов измерения трактуется как множество зна-
значений нек-рой случайной величины. Поэтому важную
роль приобретает теория О. с. Выводы теории ошибок
носят статистич. характер. Смысл и содержание таких
выводов (как, впрочем, и выводов теории О.с.) прояв-
проявляются лишь в свете закона больших чисел (пример
такого подхода — статистич. толкование смысла коэф-
коэффициента доверия, указанпого выше).
Полагая результат измерения X случайной величи-
величиной, различают три основных типа ошибок измерений:
систематические, случайные и грубые (качественные
описания таких ошибок даны в ст. Ошибок теория).
При этом ошибкой измерения неизвестной величи-
величины а наз. разность X—а, математич. ожидание этой
разности Е (X—а)— Ь наз. систематической
ошибкой (если Ь = 0, то говорят, что измерения
лишены систематич. ошибок), а разность ё — Х—а—b
наз. случайной ошибкой (Еб—0). Таким
образом, если приведено п независимых измерений
величины а, то их результаты можно записать в виде
равенств
Xi = a + b-\-8h i = l, 2, ..., re, A0)
где а и 6 — постоянные, a б,- — случайные величины.
В более общем случае
Х1 = а-\-(Ъ+Ь) + 8{, г = 1, 2, .... и, A1)
где Р,- — не зависящие от 6,- случайные величины,
к-рые равны нулю с вероятностью, весьма близкой к
единице (поэтому всякое другое значение Р,-?= 0 мало-
маловероятно). Величину р,- наз. грубой ошибкой.
Задача оценки (и устранения) систематич. ошибки
обычно выходит за рамки математич. статистики. Иск-
Исключения составляют т. н. метод эталонов,
согласно к-рому для оценки b производят серию изме-
измерений известной величины а (в этом методе b — оце-
оцениваемая величина и а — известная систематич. ошиб-
ошибка), а также дисперсионный анализ, поз-
позволяющий оценивать систематич. расхождения между
несколькими сериями измерений.
Основная задача теории ошибок — отыскивание О. с.
для неизвестной величины а и оценка точности из-
измерений. Если систематич. ошибка устранена (Ъ- 0)
и наблюдения грубых ошибок не содержат, то согласно
A0) Xi = a-\-b( и, значит, в этом случае задача оценки а
сводится к отысканию в том или ином смысле оптималь-
оптимальной О. с. для математич. ожидания одинаково распре-
распределенных случайных величин X;. Как было показано в
предыдущих разделах, вид такой О. с. (точечной или
интервальной) существенно зависит от закона распре-
распределения случайных ошибок. Если этот закон известен с
точностью до нескольких неизвестных параметров, то
для оценки, а также для оценки а можно применять,
напр., метод максимального правдоподобия; в против-
противном случае следует сначала по результатам наблюде-
наблюдений X,- найти О. с. для неизвестной функции распреде-
распределения случайных ошибок б,- («непараметрическая»
интервальная О. с. такой функции указана выше).
В практич. работе часто довольствуются двумя О. с.
I к а и s2 яг D6,- (см. A) и B)). Если б,- распределены
одинаково нормально, то эти О. с. наилучшие; в дру-
других случаях эти оценки могут оказаться малоэффектив-
малоэффективными.
Наличие грубых ошибок усложняет задачу оценки
параметра а. Обычно доля наблюдений, в к-рых р(/-0
бывает невелика, а математил. ожидание ненулевых
1Р,| значительно превышает У~йЬ; (грубые ошибки
возникают в результате случайного просчета, непра-
неправильного чтения показаний измерительного прибора и
т. п.). Результаты измерений, содержащие грубые ошиб-
ошибки, часто бывают хорошо заметны, т. к. они сильно
отличаются от других результатов измерений. В этих
условиях наиболее целесообразный способ выявления
(и устранения) грубых ошибок — непосредственный
анализ измерений, тщательная проверка неизменности
условий всех экспериментов, запись результатов «в
две руки» и т. д. Статистич. методы выявления грубых
ошибок следует применять лишь в сомнительных слу-
случаях.
Простейший пример таких методов — статистпч. вы-
выявление одного резко выделяющегося наблюдения, ког-
когда подозрительным может оказаться либо Yl=minXx,
либо Yn — maxX; (предполагается, что в равенствах
A1) i=0 и закон распределения величин б,- известен).
Для того чтобы выяснить, обосновано ли предположе-
предположение о наличии одной грубой ошибки, для пары У,, У„
вычисляют совместную интервальную О. с. (дове-
(доверительную область), полагая все р1,- равными нулю.
Если эта О. с. «накрывает» точку с координатами
(Уь У„), то подозрение о наличии грубой ошибки
следует считать статистически необоснованным; в про-
противном случае гипотезу о присутствии грубой ошибкп
надо признать подтвердившейся (при этом обычно
забракованное наблюдение отбрасывают, т. к. сколько-
нибудь надежно оценить величину грубой ошибки по
одному наблюдению статистически не представляется
возможным).
Пусть, напр., а неизвестно, Ь^=0 и б,- независимы и
распределены одинаково нормально (дисперсия неиз-
неизвестна). Если все Р,-^0, то распределение случайной
величины _
_ max | Xi — X |
s
не зависит от неизвестных параметров (О. с. X и s
вычисляются но всем п наблюдениям согласно форму-
формулам A) и B)). Для больших значений
где (ог@ — функция распределения Стьюдента, oupe-
деленная выше. Таким образом, с коэффициентом дове-
A2)
рия можно утверждать, что при отсутствии грубой
ошибки выполняется неравенство Z < z или, что то
же самое,
X—zs<Y1<Yn<X + zs.
(Погрешность оценки коэффициента доверия по формуле
A2) не превышает со'2/2.) Поэтому если все результаты
измерений X; лежат в пределах X ±zs, то нет оснований
считать какое-нибудь измерение содержащим грубую
ошибку.
Лит.: ШКрамерГ., Математические методы статистики,
пер. с англ., 2 изд., М., 1975, гл. 33, 34; [2] Д у н и н - Б а р-
к о в с к и й И. В., Смирнов Н. В., Теория вероятностей и
математическая статистика в технике. (Общая часть), М., 19S5;
[3] Линник Ю. В., Метод наименьших квадратов и основы
математико-статистической теории обработки наблюдений, 2
изд., М., 1962; [4] В а н дер В а р ден Б. Л,, Математичес-
Математическая статистика, пер. снем., М., 1960;L5] А р л е й Н., Б у х К. Р.,
Введение в теорию вероятностей и математическую статистику,
пер. с англ., М., 1951; [6] Колмогоров Л. Н., «Изв. АН
СССР. Сер. матем.», 1942, т. в, .N5 1—2, с. 3-32.
.7. П. Нолыиев.
ОЧЕРЕДЕЙ ТЕОРИЯ - - раздел массового обслужива-
обслуживания теории. О. т. изучает системы, в к-рых требования,
застающие систему занятой, не теряются, а ожидают
ее освобождения и затем обслуживаются в том или
ином порядке (часто с предоставлением приоритета
определенным категориям требований). Выводы О. т.
используют для рационального планирования систем
массового обслуживания. С математич. точки зрения
задачи О. т. могут быть включены в теорию случайных
процессов, а ответы часто бывают выражены в терми-
терминах преобразований Лапласа искомых характеристик.
Применение методов О. т. необходимо даже в простей-
простейших случаях для правильного понимания статистич.
закономерностей, возникающих в системах массового
обслуживания.
Лит.: 11] Г н е д е я к о Б. В., К о в а л е н к о И. Н., Вве-
Введение в теорию массового обслуживания, М., 1966; [2] Приори-
Приоритетные системы обслуживания, М., 1973. Ю. В. Прохоров.
ОШИБОК ТЕОРИЯ — раздел математпч. статистики,
посвященный построению уточненных выводов о
численных значениях приближенно измеренных ве-
величин, а также об ошибках (погрешностях) измерений.
Повторные измерения одной и той же постоянной ве-
величины дают, как правило, различные результаты, т.к.
каждое измерение содержит нек-рую ошибку. Разли-
Различают три основных вида ошибок: систематические, гру-
грубые и случайные. Систематические ошибки
все время либо преувеличивают, либо преуменьшают
результаты измерений и происходят от определенных
причин (неправильной установки измерительных при-
приборов, влияния окружающей среды и т. д.), системати-
систематически влияющих на измерения и изменяющих их в одном
направлении. Оценка систематич. ошибок производится
с помощью методов, выходящих за пределы математич.
статистики (см. Наблюдений обработка). Грубые
ошибки возникают в результате просчета, непра-
неправильного чтения показаний измерительного прибора и
т. п. Результаты измерений, содержащие грубые ошиб-
ошибки, сильно отличаются от других результатов измере-
измерений и поэтому часто бывают хорошо заметны. Слу-
Случайные ошибки происходят от различных слу-
случайных причин, действующих при каждом из отдель-
отдельных измерений непредвиденным образом то в сторону
уменьшения, то в сторону увеличения результатов.
О. т. занимается изучением лишь грубых и случай-
случайных ошибок. Основные задачи О. т.: разыскание зако-
законов распределения случайных ошибок, разыскание оце-
оценок (см. Оценка статистическая) неизвестных измеряе-
измеряемых величин по результатам измерений, установление
погрешностей таких оценок и установление грубых
ошибок. Пусть в результате п независимых равно-
равноточных измерений нек-рон неизвестной величины ц
получены значения Уь >'„,. . ., Уп. Разности
наз. истинными ошибками. В терминах
вероятностной О. т. все б,- трактуются как случайные
величины; независимость измерений понимается как
взаимная независимость случайных величин би. . ., б„.
Равноточность измерений в широком смысле истолко-
истолковывается как одинаковая распределенность: истинные
ошибки равноточных измерений суть одинаково распре-
распределенные случайные величины. При этом математич.
ожидание истинных ошибок Ъ~Еб\—. . . = Ебп наз-
систематической ошибкой, а разности
Ь1—Ь, . . ., б„—Ъ — случайными о ш и 6 к а-
м и. Таким образом, отсутствие систематич. ошибки
означает, что 6=0 и в этой ситуации 6], . . ., б„ суть
случайные ошибки. Величину ИаУ~2, где а — квадра-
квадратичное отклонение, наз. мерой точности (при
наличии систематич. ошибки мера точности выражается
отношением \1У~2 (Ь2 \-а-)). Равноточность измерений в
узком смысле понимается как одинаковость меры точ-
точности всех результатов измерений. Наличие грубых
ошибок означает нарушение равноточности (как в ши-
широком, так и в узком смысле) для нек-рых отдельных
измерений. В качестве оценки неизвестной величины и
обычно берут арифмитич. среднее из результатов изме-
измерений
а разности Д1=У1- У, . . ., А„-гУ„ — У наз. кажу-
кажущимися ошибками. Выбор У в качестве оцен-
оценки для \\. основан на том, что при достаточно большом
числе п равноточных измерений, лишенных система-
тич. ошибки, оценки У с вероятностью, сколь угодно
близкой к единице, сколь угодно мало отличается от
неизвестной величины ц. (см. Нолъших чисел закон);
оценка У лишена систематич. ошибки (оценки с таким
свойством наз. несмещенными), дисперсии
оценки есть
Опыт показывает, что практически очень часто случай-
случайные ошибки б,- подчиняются распределениям, близким
к нормальному (причины этого вскрыты т. н. предель-
предельными теоремами теории вероятностей). В атом случае
величина У имеет мало отличающееся от нормального
распределение с математич. ожиданием ц. и дисперсией
а2/«. Если распределения б,- в точности нормальны, то
дисперсия всякой другой несмещенной оценки для ц,,
напр. медианы, не меньше DY. Если же распределение
б,- отлично от нормального, то последнее свойство мо-
может не иметь места (см. пример в ст. Рао — Крамера
неравенство).
Если дисперсия о- отдельных измерений заранее не-
неизвестна, то для ее оценки пользуются величиной
(Es2=a2, то есть s2 — несмещенная оценка для а2).
Если случайные ошибки 6,- имеют нормальное распре-
распределение, то отношение
подчиняется Стьюдента распределению с п — 1 сте-
степенями свободы. Этим можно воспользоваться для оцен-
оценки погрешности приближенного равенства ц. « У (см.
Наименьших квадратов метод).
Величина {п—I)s2/o2 при тех же предположениях
имеет «хи-квадрат» распределение с п—1 степенями
свободы. Это позволяет оценить погрешность прибли-
приближенного равенства а » s. Можно показать, что отно-
относительная погрешность не будет превышать числа q
с вероятностью
co = F(z2, п — 1) —1; (i\, и — 1),
где F(z, п—1) — функция %а-РаспРеДелешш
Если нек-рые измерения содержат грубые ошибки,
то предыдущие правила оценки \i и о дадут искажен-
искаженные результаты. Поэтому очень важно уметь отличать
измерения, содержащие грубые ошибки, от измерений,
подверженных лишь случайным ошибкам б,-. Для слу-
случая, когда б, независимы и имеют одинаковое нормаль-
нормальное распределение, наиболее совершенный способ
выявления измерений, содержащих грубые ошибки,
предложен II. В. Смирновым [3].
Лит.: [II ,1 и и и и к Ю. В., Метод наименьших киадратов и
оенопы математико-стмтистичесь'ои теории обработки наблю-
наблюдений, 2 4X1.. М.. 1!НJ; [2] Г> о л ь ш к в Л. Н., Г, м и р-
нив II. В., Таблицы математической статистики, 2 изд., М.
19ti8; l.;ij Смирнов Н. В., «Докл. АН СССР», 11L1, т. 33, № о,
с. 34(j — 49. Л. Н. Большее.
ОШИБОЧНОГО ДЕКОДИРОВАНИЯ ВЕРОЯТНОСТЬ
— одна из возможных мер характеризации точности
воспроизведения сообщений, передаваемых по каналу
связи (см. также Сообщений точность воспроизведения).
Пусть для передачи сообщения |, вырабатываемого
источником сообщений и принимающего М различных
возможных значений 1,. . ., М с распределением веро-
вероятностей р,л = Р{|=т), т—\, . . ., Л/, используется
нек-рый канал связи. Тогда для фиксированных мето-
методов кодирования и декодирования (см. также Информа-
Информации передача) О. д. в. Ре^т, m—i, . . ., М, определяется
равенством
где \ — декодированное сообщение на выходе ка-
канала.
Средней О. д. в. Ре наа. величина
Особый интерес представляет изучение оптималь-
оптимальной О. д. в. P°v , определяемой равенством
Pgpt =- inf Ре,
где нижняя грань берется по всевозможным методам
кодирования и декодирования. Ввиду трудностей по-
получения точного выражения для Рер , связанных с
тем обстоятельством, что в общем случае неизвестны
оптимальные методы кодирования, интерес представля-
представляет изучение асишиотич. поведения P°pt при возраста-
возрастании длительности передачи по каналу. Точнее, рас-
рассматривается следующая ситуация. Пусть для передачи
используется отрезок длины N канала связи с дискрет-
дискретным временем и Л=Aп M)!N. Требуется изучить
асимптотич. поведение P°pi при N -+ оо и Д—const
(это означает, что длительность передачи возрастает,
а ее скорость остается постоянной). Если рассматривае-
рассматриваемый отрезок канала является отрезком однородного
канала без памяти с дискретным временем и конечны-
конечными пространствами У и У значений компонент сигналов
на входе и выходе, то пзвестны следующие верхние и
нижние оценки P°pt^P°p\N, Я):
ехр {- N [Esp (Я-а (Л')) + р1 (N))}<
< Pept (N, Л)<ехр {— NEr (Д)}, A)
где a(N) и p"(./V) стремятся к нулю с ростом JV, a функ-
функции Er(R) и Esp(R) определяются следующим образом:
Er(R)= max шах [?„ (р, g (¦)) — рД], B)
О < р < 1 q (¦)
Esp(R)= sup шах [?0(р, g(-))— рД], C)
Р > о ?(¦)
где
Здесь ?(•)—{?(i/)i г/?У} — произвольное распределе-
распределение вероятностей на Y, д(у, у) — р{т]й—//|r]ft=0},
y?Y, y?Y, a r\k и rjfe, ft=l, . . ., TV,—компоненты
сигналов на входе и выходе рассматриваемого канала
без памяти. Известно, что Er(R) и Esp(R), определяе-
определяемые формулами B) и C), являются положительными,
выпуклыми вниз, монотонно убывающими функциями
от Д при 0 <: Д < С, где С — канала пропускная
способность, причем Er(R) = Esp(R) при R^Rcr,
здесь Rcr — величина, определяемая переходной мат-
матрицей канала и называемая критической ско-
скоростью для данного канала без памяти. Таким обра-
образом, для значений R, АСГ<Д < С, главные члены
верхней и нижней оценок A) для P°pt асимптотически
совпадают, откуда следует, что для этого диапазона
изменения R известно точное значение функции
надежности канала Е (Л), определяемой ра-
равенством
-inP?pi(N, Я)
Е (Л) = lim ~п .
N -*¦ х
Для значений Д, 0 <: Д < Rcr, точное значение Е(Д)
для произвольных каналов без памяти неизвестно
A983), хотя оценки A) и могут быть улучшены. Экспо-
Экспоненциальный характер убывания Pept(N, R) доказан
для весьма широкого класса каналов.
Лит.: [1] Г а л л а г е р Р., Теория информации и надежная
свямь, иер. с англ., М., 1974; |2] Файнстейн А., Основы
теории информации, пер, о англ., М., 1960.
Р. Л. Добрушии, В. В. Прелое.
ПАДЕ АППРОКСИМАЦИЯ — наилучшая рацио-
рациональная аппроксимация степенного ряда. Пусть
— произвольный степенной ряд (формальный или схо-
сходящийся), п, т^О — целые числа, Rn,m — класс
всех, рациональных функций вида p/q, где р и q —
многочлены от z, deg q <: т, dog р < н, q ф 0. Ап-
Аппроксимацией Падо типа (га, т) ряда A)
(функции /) наа. рациональная функция яВ1 т?./?П) т,
имеющая максимально возможный в классе Л'П1 -, поря-
порядок касания с рядом A) в точке г—0. Точнее, функция
я,(] т определяется условием
о(/ — п„, m) -max{a(/— г), г ? «„,,„},
где о(ф) — индекс первого из отличных от нуля ко-
коэффициентов ряда
2
Функцию я„ т можно определить также как отно-
отношение nth m--plq любых многочленов р, q(q^kO),
удовлетворяющих соотношениям
При фиксированных п, m существует единственная
П. а. я„, ffi ряда A). Таблица {я,,, ,„}п,т=о наз. табли-
таблицей Паде ряда A). Последовательности вида
{яп, т }п=о наз. строками таблицы Паде
(нулевая строка совпадает с последовательностью много-
многочленов Тейлора для/); {п„, и}т-о — столбцами таб-
таблицы Паде; {nn+j, n}/=o — диагоналями таблицы
Паде. Наиболее важный частный случай /—О — глав-
главная диагональ.
Вычисление функции яп> ,Л сводится к решению
системы линейных уравнений, коэффициенты к-рых
выражаются через коэффициенты /^, fc=0,l,. . ., п-\-т,
заданного ряда. Если отличен от нуля определи-
определитель Ганкеля
'n
fti-m + 2 ¦•¦ In
In
fny
то знаменатель </„_ m функции пп> т определяется по
формуле
fn+i
'In
I n
1
(нормировка qn^ m@)=l; явная формула может быть
наиисана и для числителя функции лп%т). При этом
\! —яп, т) \ъ) — А п, mz : . . . .
Последнее соотношение иногда принимают за опре-
определение П. а.; в этом случае П. а. могут не существо-
вать для нек-рых (п, т.). Для обозначения П. а. типа
(и, т) заданного ряда / часто употребляется символ
[п/т] = \njm\j.
Для эффективного вычисления П. а. удобнее пользо-
пользоваться не явными формулами, а рекурентными соотно-
соотношениями, существующими в таблице Паде. Разработано
большое количество алгоритмов для машинного вычис-
вычисления П. а.; эти вопросы имеют особенно важное зна-
значение в связи с приложениями (см. [17], [18]).
Впервые общую задачу об интерполяции заданных
значений функции в и-f-m-f-l различных точках по-
посредством рациональной функции класса Вп т рас-
рассмотрел О. Коти [1]; К. Якоби [2] распространил ре-
результаты О. Коши на случай кратных узлов интерполя-
интерполяции. Случай одного (п+т+1)-кратного узла интерпо-
интерполяции соответствует П. а. Понятие П. а. сформирова-
сформировалось в кон. 19 в. в рамках классич. теории непрерывных
дробей (Г. Фробениус |3], А. Паде [4]). Фундаменталь-
Фундаментальные результаты о диагональных П. а. были получены
II. Л. Чебышевым, А. А. Марковым, Т. Стильтьесом
(Т. Stieltjes) в терминах непрерывных дробей; ими
были обнаружены и исследованы связи диагональных
П. а. с ортогональными многочленами, квадратурными
формулами, проблемой моментов и другими вопросами
классич. анализа (см. [7] — [9]). Начало изучению
строк таблицы Паде было положено работами о радиусах
мероморфности функции, заданной степенным рядом,
и о сходимости строк таблицы Паде в кругах мероморф-
мероморфности (см. [5], [6]).
С нач. 20 в. П. а. становятся самостоятельным объек-
объектом анализа и составляют важную главу теории рацио-
рациональных приближений аналитич. функций. Используя
для своего построения локальные данные (коэффици-
(коэффициенты степенного ряда), они позволяют изучать глобаль-
глобальные свойства соответствующей аналитич. функции
(аналитич. продолжение, характер и расположение
особенностей и т. п.) и вычислять значение функции
за пределами круга сходимости степенного ряда.
Наряду с классическими П. а. рассматриваются
различные их обобщения: общие процессы интерполя-
интерполяции посредством рациональных функций со свободными
полюсами (многоточечные аппроксимации Паде); ра-
рациональные аппроксимации рядов по заданной системе
многочленов (напр., по ортогональным многочленам);
совместные П. а. (аппроксимации Паде — Эрмита);
рациональные аппроксимации (типа П. а.) степенных
рядов от нескольких переменных и др.
Лит.: [1] С а и с h у A.-L., Cours d'analyse de l'EcoIe ro-
yalc polyteclmique, pt. 1— Analyse algebrique, P., 1821; [2]
.1 а с о b i С G. J., «J. reine und angew. Math.», 184ti, Bd 30,
S. 127—56; [3] P г о b e n i u s G., там же, 1881, Bd 90, S. 1 —
17; [4] P a d ё Н., «Ann. scient. Ecole norm, super.», 1892, t. 9,
p. 1—93; [5] H a d a m a r d J., «J. math, pures et appl.», 1892,
t. 8, p. 101—86; MMontessus deBalloreB.de, «Bull.
Soo. math. Prance», 1902, t. 30, p. 28—36; [7] Чебыш е в П. Л.,
Полн. собр. соч., т. 3, М.— Л., 1948; [8] М а р к о в А. А., Избр.
труды по теории непрерывных дробей и теории функций, наиме-
наименее уклоняющихся от нуля, М.— Л., 1948; [9] Стилтьес Т.,
Исследования о непрерывных дробях, пер. с франц., Хар.—
К., 1936; [10] W а 1 1 Н. S., Analytic theory of continued fracti-
fractions, Toronto — N. Y.— L., 1948; [11] P e г г о и О., Die Lehre
von den Kcttcnbruchen, 3 Aufl., Bd 2, Stuttg., 1957: [12] The Рн-
de approximant in theoretical physics, N. Y.— L., 1970; [13] Pa-
de approximants and their applications, L.— N. Y-, 1973; [14]
Fade approximants method and Us applications to mechanics,
В.— Hdlb.— N. Y., 1976; [15] BakrrC. A., Essentials of Pade
approximants, N. Y.— San Franc.— L., 1975; [16] Pade and ra-
1iona\ approximation, N. Y.— la. o.l, W7; [\TS GHcwiti
.Т., Approximants de Pade, В.— Hdlb.— N. Y., 1978; 118] Pade
approximation and its applications, B.— Hdlb.— N. Y., 1070.
E. А. Рахманон.
ПАППА АКСИОМА: если 1ж1' — две различные пря-
прямые, А, В, С и А', В', С — тройки различных точек
прямых I и Г соответственно, отличных от точки пере-
пересечения прямых / и V, то точки пересечения прямых
АВ' и А'В, ВС' и В'С, АС и Л'С лежат на одной пря-
прямой. Выполнение П. а. эквивалентно коммутативности
тела, соответствующего рассматриваемой проективной
геометрии. Дезарга предложение является следствием
П, а. (т е о р е м а X с с с е н б е р г а), в то же время
П. а. представляет собой вырожденный случай Паскаля
теоремы. П. а. предложена Паппом C в.).
Я. С. Моденов, А. С. Пархоменко.
ПАППЕРИЦА УРАВНЕНИЕ — линейное обыкно-
обыкновенное дифференциальное уравнение 2-го порядка
класса Фукса, имеющее ровно три особые точки:
z-а Т z-Ь ' г-с
аа'(а-Ь) (а-с) pg' (Ь-с) (Ь-а) уу' (с-а) (с-Ь)"
x
здесь а, Ь, с — попарно различные комплексные числа,
а, а.' (Р, Р' и у, у') — характеристич. показатели в
особой точке z—a (соответственно z—b и z—c). П. у.
однозначно определяется заданием особых точек и ха-
характеристич. показателей. Для решений П. у. A) ис-
используется обозначение Римана:
(а
w - Р
4 •
Б. Риман исследовал [11 задачу: найти все много-
многозначные аналитические в расширенной комплексной
плоскости функции w(z) со следующими свойствами:
1) функция w(z) имеет ровно три особые точки а, Ь, с;
2) любые три ее ветви связаны линейным соотношением
A1wl (г) -f- A2w2 (г) -f- Aaw3 (z) — 0
с постоянными коэффициентами; 3) функция w (z)
имеет простейшие особенности в точках а, Ъ, с, а имен-
именно: в окрестности точки z— а существуют две ее ветви
w1(z), w.2(z) такие, что
щ (z) = (z — а)ащ (г), щ (г) = (г —а)а'ф2 (г),
где <Py(z), /=1, 2,— голоморфные в точке z—a функции;
и аналогично для точек Ь, с.
Б. Риман при нек-рых дополнительных предположе-
предположениях относительно чисел a, a', . . ., у' показал, что
все такие функции выражаются через гипергеометрич.
функции и что w(z) удовлетворяет линейному диффе-
дифференциальному уравнению 2-го порядка с рациональ-
ными коэффициентами, но явно его не выписал (см.
[1]). Это уравнение (уравнение A)) было приведено
У. Папперицем [2]. Оно наз. также Р-уравнени-
е м Р и м а в а, уравнением Римана в
форме JI а и и е р и ц а, уравнением Р и м а-
н а, а его решения наз. Р-функциями.
Основные свойства решений П. у.
1) П. у. инвариантно относительно дробно-линей-
дробно-линейных преобразований: если z1—(Az-\-B)/(Cz-\-D) отобра-
отображает точки а, Ъ, с ъ точки а^, Ь1; Cf, то
p U р v ч\ •
W Р' г' )
2) Преобразование
переводит П. у. в П. у. с теми же особыми точками, но
с другими характеристич. показателями:
**) Г, I I 'Г
{<х Р 7 /
(а Ь с
Р -—А; — г y-\-l z
Р'-*-« y' + i
3) Гипергеометрическое уравнение
z (I — z) <«"-]- [С —(i4-f Я + 1) г] ш'-
есть частный случай П. у. и ему соответствует обозна-
обозначение Римана
( 0 оо 1 Ч
Р | О Л 0 z\ .
11 —С В С —А —В )
4) Всякое решение П. у. выражается через гипергео-
метрич. функции:
B)
в предположении, что а—а' не естг> целое отрицательное
число. Если все разности а—а', Р—Р', 7—У' — неце-
нецелые числа, то, переставляя в B) местами а и а' или 7
и у', получают четыре решения П. у. Кроме того, П. у.
не меняется, если переставлять мостами тройки (т,
а' 1 а), (Р, Р, Ь), (у, у', с); все эти перестановки
приводят к 24 частным решениям П. у. A), к-рые впер-
впервые были получены Э. Куммером [5].
Лит.: [11 Р и м а н Б., Соч., пер. с нем., М.-—Л., 1948, с.
15В—75; [2] Р а рр er i t zE.,«Math. Ann.», 1885, Bd 25, S. 212—
21; [3] У и т т е к е р Э. Т., В а т с о н Д ж. II., Курс современ-
современного анализа, пер. с англ., 2 изд., т. 1—2, М., 1962—63; L4] Г о-
л у б е в В. В., Лекции по аналитипвской теории дифференци-
дифференциальных уравнений, 2 изд., М Л., 1950; [5] К u m m е г Б.,
«J. reine und angew. Math.», 1836, Вя 15, S. 39—83, 127—72.
M. В. Федорюк.
ПАРАБОЛ МЕТОД — метой вычисления корней мно-
многочлена
с комплексными коэффициентами, основанный на интер-
интерполяции многочленами 2-й степени. П. м. позволяет
найти все корни многочлена без предварительной инфор-
информации о начальном приближении. Сходимость П. м.
установлена лишь эмпирически. Бблмзл простого корня
скорость сходимости близка к квадратичной.
Вычислительная схема П. м. состоит в следующем.
По произвольным комплексным числам г„, zlt z2 как
узлам интерполяции строится интерполяционный
многочлен Лагранжа для Pn(z). Это будет нек-рый
многочлен 2-й степени. Находятся оба его корня и за
z3 берется ближайший к z«. После этого вместо точек
z0, Zj, z2 берутся точки zt, z2, z3 и процесс повторяется.
Эмпирически установлено, что последовательность
~о> zi> г2. 2з>- • ч построенная таким образом, сходится
к корню многочлена. Вычисленный корень выделяется,
и далее метод применяется к многочлену меньшей
степени.
Расчетные формулы П. м.: если z,_2, z,-_j, z; — ис-
исходная тройка чисел г'-го шага, то в обозначениях
h = z — z,-, hi = Z( — Z[-i, hi_i — zi_± — z,-_2,
К = h/ ht, Kt = hi/hi _!, 6,- = 1 -|- Ki
интерполяционный многочлен Лагранжа имеет вид
?"¦> (Х)=Х26Г1 [Рп (zi-г) ti-Pn (zi-i) Ь
Корни L(" (к) находятся по формуле
где
11.) двух возможных значений X берется наименьший
но модулю и далее вычисляется
При реализации описанного процесса на ЭВМ возмож-
возможно переполнение сверху и снизу при вычислении значе-
значения многочлена в точке. Появление больших чисел
возможно также при вычислении корней многочлена
2-й степени. Существует ряд приемов, имеющих целью
избежать это явление (см. [1], [3]).
Лит.: [1] Воеводин В. В., Численные методы алгебры,
М., 1966; И У и л к и н с о н Д ж. X., Алгебраическая проб-
проблема собственных значений, пер. с англ., М., 1970; [3] Бах-
Бахвалов Н. С, «Ж. вычисл. матем. и матем. физ.», 1971, т. 11,
К 6, с. 1568—74. Г. Д. Ним.
ПАРАБОЛА — плоская кривая, получающаяся в
пересечении кругового конуса с плоскостью, не прохо-
проходящей через вершину конуса и
параллельной его образующей.
П. есть множество точек М плоско-
плоскости, для каждой из к-рых рассто-
расстояние до данной точки F (фоку-
(фокуса П.) равно расстоянию до нек-
некрой данной прямой d (дирек-
(директрисы). Расстояние р от фоку-
фокуса П. до директрисы наз. па-
параметром. П.—симметричная
кривая; точка пересечения П. с
осью ее симметрии наз. верши-
вершиной П., а ось симметрии —
осью П. Эксцентриситет равен
единице. Диаметр П.— лю-
любая прямая, параллельная ее оси,
и сама ось. Диаметр П. может
быть определен как прямая, про-
проходящая через середины параллельных хорд.
П. есть нецентральная линия второго порядна. Ее
канонич. уравнение имеет вид
'/г о
Уравнение касательной к П. в точке (,г0, уа):
УУоР( + о)
Уравнение П. в полярных координатах р, ср:
р — -.—-— , где 0 < ш < 2я.
1 1—cos q> ' " т
П. обладает следующим оптическим свойст-
в о м: световые лучи, исходящие из фокуса, после
зеркального отражения от П. пойдут параллельно оси.
А. ?>. Иванов.
ПАРАБОЛИЧЕСКАЯ ПОДАЛГЕБРА — подалгебра
конечномерной алгебры Ли g над алгебраически замк-
замкнутым полем, содержащая какую-либо подалгебру
Б о р е л я, т. е. максимальную разрешимую подалгеб-
подалгебру алгебры д. Если g — конечномерная алгебра Ли
над произвольным полем к, то ее подалгебра р наз.
II. п., если р®кк — П. п. в 3®fcfc, где к — алгеб-
ранч. замыкание поля к. Если G — неприводимая
линейная алгебраич. группа над нолем характеристики
О и g — ее алгебра Ли, то подалгебра peg, тогда и
только тогда является П. п. в д, когда она совпадает с
алгеброй Ли нек-рой параболической подгруппы груп-
группы G.
Примерами П. п. в алгебре Ли всех квадратных мат-
матриц порядка п над полем к являются подалгебры вида
р(|х)(и.= (т1, т.2, . . ., ms) — произвольный набор
натуральных чисел, сумма к-рых равна п), где алгебра
р(ц) состоит из всех верхних треугольных блочных
матриц, у к-рых диагональные блоки являются квад-
квадратными матрицами порядков ть т2, ¦ ¦ ¦ , ms.
Пусть g — редуктивная конечномерная алгебра
Ли над полем к характеристики 0, f — максимальная
диагонализируемая над к подалгебра в g, R — система
fc-корней алгебры Ли q относительно f, Д — базис
(множество простых корней) системы R и Auteg —
группа элементарных автоморфиз-
автоморфизмов алгебры Ли д, т. е. группа, порожденная авто-
автоморфизмами вида exp ad х, где х — нильпотентный эле-
элемент алгебры д. Тогда всякая П. п. алгебры Ли g
переводится нек-рым автоморфизмом из группы Aut,,g
в одну из стандартных параболиче-
параболических подалгебр вида
где д° — централизатор подалгебры f в д, да —
корневое подпространство алгебры Ли д, отвечаю-
отвечающее корню af й, Ф — некоторое произвольное под-
подмножество множества Д, а П(Ф) — множество тех кор-
корней из В, в разложении которых по простым корням
из базиса Д корни, принадлежащие множеству Ф, вхо-
входят только с неотрицательными коэффициентами.
Таким образом, число классов П. п., сопряженных от-
относительно Auteg, равно 2Г, где г~!Д| есть /с-ранг
полупростой алгебры Ли [д, д]. При этом если Ф^Ф,,
то !|рф1э?ф,- В частности, ^=д, а рД — минимальная
П. п. в д.
Максимальными П. п. исчерпываются все нередук-
тивные максимальные подалгебры конечномерных
редуктивных алгебр Ли над полем характеристики О
(см. [2], [3], [5]).
Лит.: [1] Б у р б а к и Н., Группы и алгебры Ли. Подалгеб-
Подалгебры Картана, регулярные элементы, расщепляемые полупростые
алгебры Ли, пер. с франц., М., 1978; [2] К а р п е л е в и ч Ф. И.,
«Докл. АН СССР», 1951, т. 7В, Л 6, с. 775—78; [3] Моро-
Морозов В. В., «Успехи матем. наук», 1956, т. 11, в. 5, с. 191—94;
[4] М о s t о w G. D., «Ann. Math.», 1961, v. 74, № 3, p. 503 — 17;
[5] Б о ре ль А., Тите Ж., «Математика», 1972, т. 16,
Л'> 3, с. 3 — 12. В. Л. Попов.
ПАРАБОЛИЧЕСКАЯ ПОДГРУППА — 1) П. п. ли-
линейной алгебраич. группы G, определенной над полем
к,— замкнутая в Зариского типологии подгруппа РсО
такая, что факторпространство G/P является проектив-
ным алгебраич. многообразием. Подгруппа Р czG тогда
и только тогда является П. п., когда она содержит
какую-нибудь Бореля подгруппу группы G. Пар а-
болической подгруппой группы С^ к-
рациональных точек группы G наз.
подгруппа PfcdGfe, являющаяся группой А-рациональ-
ных точек нек-рой П. п. Р в G и плотная в Р в топо-
топологии Зариского. Если char7e=0 ид — алгебра Ли
группы G, то замкнутая подгруппа PczG тогда и только
тогда является П. п., когда ее алгебра Ли является
параболической подалгеброй в д.
Пусть G — связная редуктивная линейная алгебраич.
группа. Минимальные ^-замкнутые (т. е. определенные
над к) П. п. играют в теории таких групп для произ-
произвольного основного поля к ту же роль, что подгруппы
Бореля для алгебраически замкнутого поля к (см. [1]).
В частности, любые две минимальные /с-замкнутые
П. п. группы G сопряжены над к. Если две ^-замкнутые
П. п. группы G сопряжены над каким-нибудь расшире-
расширением поля к, то они сопряжены и над к. Множество
классов сопряженных П. п. (соответственно множество
классов сопряженных /г-замкнутых П. п.) группы G
состоит из 2Г (соответственно 2 к) элементов, где г —
ранг коммутанта (G, G) группы G, а г^ — его /с-ранг,
равный размерности максимального расщеиимого над к
тора в (G, G). Точнее, каждый такой класс определя-
определяется нек-рым произвольным подмножеством множества
простых корней (соответственно простых А:-корней)
группы G аналогично тому, как каждая иараболич.
подалгебра редуктивной алгебры Ли сопряжена одной
из стандартных подалгебр (см. [2], [4]).
Всякая П. п. Р группы G связна, совпадает со
своим нормализатором и допускает разложение
Л е в и, т. е. может быть представлена в виде нолу-
прямого произведения своего унипотентного радикала и
нек-рой fe-замкнутой редуктивной подгруппы, нау.
подгруппой Леви группы Р. Любые две под-
подгруппы Леви в П. п. Р сопряжены посредством рацио-
рационального над к элемента группы Р. Две П. п. группы G
наз. противоположными, если их пересече-
пересечение является подгруппой Леви в каждой из них. Замк-
Замкнутая подгруппа группы G тогда и только тогда явля-
является П. п., когда она совпадает с нормализатором
своего унипотентного радикала. Всякая максимальная
замкнутая подгруппа группы G либо является П. и.,
либо имеет редуктивную связную компоненту единицы
(см. [2], [4ft.
П. п. в группе GLn(k) невырожденных линейных
преобразований re-мерного векторного пространства
V над полем к исчерпываются подгруппами P(v),
состоящими из всех автоморфизмов пространства
V, которые сохраняют фиксированный флаг типа
v= (щ, п2, . . ., rif) в V. При этом факторпростран-
ство GLn(k)/P (v) совпадает с многообразием всех
флагов типа v в пространстве V.
В случае, когда k—R, R-замкнутые П. п. допускают
следующую геометрич. интерпретацию (см. [5]). Пусть
GR — некомпактная иолупростая вещественная группа
Ли, совпадающая с группой вещественных точек полу-
полупростой алгебраич. группы G. Подгруппа группы GR
тогда и только тогда является П. п., когда она совпа-
совпадает с группой движений соответствующего некомпакт-
некомпактного симметрич. пространства М, сохраняющих нек-рый
к-иучок геодезич. лучей в М (два геодезич. луча в М
считаются принадлежащими одному Л-пучку, если рас-
расстояние между двумя точками, движущимися с одина-
одинаковыми постоянными скоростями вдоль этих лучей в
бесконечность, стремится к конечному пределу).
2) П. и. с и с т е м ы Т и т с a (G, В, N, S) — под-
подгруппа группы G, сопряженная подгруппе, содержащей
В. Каждая П. п. совпадает со своим нормализатором.
Пересечение любых двух П. п. содержит подгруппу
группы G, сопряженную с Т— Bf\N. В частности,
П. п. системы Титса, связанной с редуктивнои линейной
алгебраич. группой G,— это то же, что П. и. группы G
(см. ГЗ], [4]).
Лит.: [1] Бор ель А., Тите Ж., «Математика», 1967,
т. 11, JVi 1, с. 43—111; [2] их же, там же, 1972, т. 16, № 3,
с. 3—12; [3] Б у р б а к и Н., Группы и алгебры Ли. Подал-
Подалгебры Картава, регулярные элементы, расщепляемые пплупро-
стые алгебры Ли, пер. с франц., М., 1978; [4] Хамфри Д ж.,
Линейные алгебраические группы, пер. с англ., М., 1980; [5]
Карпелевич Ф. И., «Труды Моск. матем. об-ва», 1965,
т. 14, с. 48—185. В. Л. Попов.
ПАРАБОЛИЧЕСКАЯ РЕГРЕССИЯ, полиноми-
полиномиальная регресс и я,— модель регрессии, в
к-рой функции регрессии суть многочлены. Точнее,
пусть Х= (Хх, . . ., Хт)Т и Y-— (Yj, . . ., Yn)T — слу-
случайные векторы, принимающие значения х= (х1, . . .,
xm)T€^-m и У~ (Уи • ¦ •> г/п)г€^П! и пусть существует
Е{У|А'}=/(Х) = (/1(Х), ..., fn(X))T
(т. е. существуют e{Y1|X}=/1(X), . . ., E{Yn|X}=
--/„(X)). Регрессия наз. параболической,
если компоненты вектора Е{У|Х}=/(Х) суть много-
многочлены от компонент вектора X. Напр., в простейшем
случае, когда У и X — обычные случайные величины,
уравнение П. р. имеет вид
где р\,, . . ., $р — коэффициенты регрессии. Частный
случай П. р.— линейная регрессия. Добавлением к
вектору X новых компонент можно всегда свести П. р.
к линейной. См. Регрессия, Регрессионный анализ.
Лит.: [1] Крамер Г., Математические методы статисти-
статистики, пер. с англ., 2 изд., М., 1975; [2] С е б е р Д ж., Линей-
Линейный регрессионный анализ, пер. с англ., М., 1980.
Ы. С. Никулин.
ПАРАБОЛИЧЕСКАЯ СПИРАЛЬ — плоская транс-
трансцендентная кривая, уравнение к-рой в полярных
координатах имеет вид
I >0.
Каждому значению ф со-
соответствуют два значения
У<р — положительное и отри-
отрицательное. Кривая имеет бес-
бесконечно много двойных точек
и одну точку перегиба (см.
рис.). Если 2=0, то кривая наз. Ферма спиралью.
П. с. относится к т. н. алгебраич. спиралям (см. Спи-
Спирали).
Лит.: [1] С а в е л о в А. А., Плоские кривые, М., 1960.
Д. Д. Соколов.
ПАРАБОЛИЧЕСКАЯ ТОЧКА — точка регулярной
поверхности, в к-рой соприкасающийся параболоид
вырождается в параболич. цилиндр. В П. т. Дюпена
индикатриса является парой параллельных прямых,
гауссова кривизна равна нулю, одна из главных кри-
кривизн обращается в нуль, а для коэффициентов второй
квадратичной формы справедливо равенство
LN— М1 — 0.
ПАРАБОЛИЧЕСКИЕ КООРДИНА-
КООРДИНАТЫ — числа и и v, связанные с пря- *"<
моугольными координатами х и у
формулами
где — оо < и < оо, 0 <:у<оо. Ко-
Координатные линии; две системы вза-
взаимно ортогональных парабол с проти-
противоположно направленными осями.
Коэффициенты Ламе:
Элемент площади:
da = 4(u2 + T>2) dudv.
Векторные дифференциальные операции:
a/
dn a~—± (aJiM
Уравнение Лапласа допускает в П. к. разделение пере-
переленных. Д.Д.Соколов.
ПАРАБОЛИЧЕСКИЙ ЦИЛИНДР — цилиндриче-
цилиндрическая поверхность второго порядка, для к-рой направ-
направляющей служит парабола. Каноническое уравнение
П. ц.:
у» = 2р*.
Л. Ь. Иванов.
ПАРАБОЛИЧЕСКОГО ТИПА УРАВНЕНИЕ — урав-
уравнение вида
— а(х, t)u^f(x, t),
где 2а'Д'^/ ~ положительно определенная квадра-
квадратичная форма. Переменная t выделена и играет роль
времени. Типичным примером П. т. у. является урав-
уравнение теплопроводности
Л. II. Силдатов.
ПАРАБОЛИЧЕСКОГО ТИПА УРАВНЕНИЕ; ч и с-
ленные методы решения — методы реше-
решения уравнений параболич. типа на основе вычислитель-
вычислительных алгоритмов. Для решения П. т. у. часто приме-
применяются приближенные численные методы, рассчитанные
на использование быстродействующих ЭВМ. Наиболее
универсальным является метод с с т о к (к о н е ч-
н о разностный метод).
Ниже рассмотрен метод соток на примере уравнения
теплопроводности
%^, + fU, t), t>0, 0<x<l, A)
с краевыми условиями 1-го рода
и (О, 0-=М«). " С 0^=1^2 @. и (*, О) = ио(*).
Вводится равномерная сетка узлов (х,-, („),
xr~ih, i—0, 1, . . ., Л', hN~l, tn — n%, n — 0, 1, . . .;
и обозначения
Метод сеток состоит в том, что уравнение A) прибли-
приближенно заменяется системой линейных алгебранч. урав-
уравнений (разностной схемой)
У'!, i = «J?\+V-°) УЪ,- 1+Ф?,* = 1,2, • • ., N-1,)
ljn0--lh(tn), y'lN = V2(tn), Jj = M0(*l). J
где о — числовой параметр и tf" — сеточная аппрокси-
аппроксимация функции/(a1, t), напр. <р?=/(л7> /„+0,5т).
Система уравнений B) решается по слоям, т. е.
для каждого ге=0, 1, ... по известным значениям у",
ф" находятся новые значения y" + 1, j—1, 2, . . ., N—1.
Если С7=О (явная схема), то у1 выражаются явным
образом через у?, ф". Если же а#0 (неявные схемы),
то относительно y"?1, i—i, 2, . . ., JV—1, возникает
система уравнений, имеющая трехдиагональную матри-
матрицу. Эта система уравнений решается прогонки методом.
Недостатком явной схемы является сильное ограничении
на шаг т, возникающее из условия устойчивости, а
именно т < 0,5 А2. Неявные схемы при о > 0,5 абсо-
абсолютно устойчивы, т. е. устойчивы при любых шагах h
и т. Известны и другие разностные схемы для уравне-
уравнения A) (см. [1], [2]).
Если схема B) устойчива и ф" аппроксимирует
/(.г, t), то при h, х —>- 0 решение у'1 разностной задачи
сходится к решению и(х/, tn) исходной задачи (см.
[1]). Порядок точности зависит от параметра а. Так,
симметричная схема (о—0,5, ф" -/(л-,-, <„-|-0,5т)) имеет
второй порядок точности по т и по h, т. е. для каждого
и выполняется оценка
max | уп — и {xit tn) К Л/ (т2 + Л2)
0<i<N
с константой М, не зависящей от h и т. При а—О,5—
—А2/A2т) и специальном выборе ф" схема B) име-
имеет точность О(т2~)-Л4). Для остальных а — точность
О(+Л2)
()
При решении П. т. у. на больших отрезках вредюни
существеннее значение имеет асимптотич. устойчивость
разностной схемы. Решение уравнения A) с f(x, ?)=0,
u,1(i)=(x2@ —0 ведет себя при ( —*¦ оо как е~ ',
А^я2Л2. Этим свойством обладает не всякая разност-
разностная схема, аппроксимирующая уравнение A). Напр.,
симметричная схема (а—0,5) асимптотически устойчива
при условии %-^.lhln. Построены схемы 2-го порядка
точности, асимптотически устойчивые при любых т,
h, однако они но входят в семейство B) (см. [3])^
Краевые условия 3-го рода
¦?@, О-МО, 0-=И(«)
аппроксимируются с порядком О (/г) разностными
уравнениями
Для уравнения теплопроводности в цилиндрич. и
сферич. координатах
dt г™ с
вводятся сетки (г,-, tn), где tn~nx, re—0, 1, . . .,
и рассматриваются разностные уравнения (см. [4])
где
г,-= 0,5 (г,-+ г,-+х) при т=^1, г,- — Vriri-i ЦРИ — 2,
i = l, 2, . .., .V —1.
Для решения П. т. у. с переменными коэффициента-
коэффициентами применяются однородные консервативные разност-
разностные схемы, выражающие на сетке законы сохранения,
присущие исходному дифференциальному уравнению
(см. [1], [5]). При построении разностных схем для
П. т. у. с переменными коэффициентами применяются
методы: баланса, вариационный, конечных элементов.
Напр., для уравнения
§7 = 4 (* (*, 0 з?)-И(*. О, 0 < * < I, * > О,
используются разностные схемы с весами
т. /=(а(аг/« + 1 + A-а)у'')й)Х1(' + ф?,
где
а = а" = к (*,• — 0,5Л, г„ + О,5т).
Доказана сходимость и получены оценки погрешно-
погрешности однородных консервативных разностных схем
для П. т. у. как в случае непрерывных, так и в слу-
случае разрывных коэффициентов (см. [1]).
Для решения систем уравнений нараболич. типа,
содержащих одну пространственную переменную, при-
применяются те же разностные схемы, что и для одного
уравнения. Вектор j/" + 1 решения на новом слое нахо-
находится матричной факторизации методом.
При решении квазилинейного П. т. у. используются
неявные абсолютно устойчивые разностные схемы.
Решение уп + 1 разностного уравнения находится итера-
итерационным методом с использованием прогонки. Напр.,
для уравнения
применяют чисто неявную разностную схему
*?..• = (а (УГ1)!^1),,,,
к-рую решают с помощью итерационного метода (*¦
номер итерации):
((Г)<^),1, s = 0, 1 т,
Решение ;/i-shl) на каждой итерации находится методом
прогонки. При решении нелинейного П. т. у. нашли
также применение схемы, основанные на идее Рунге —
Кутта метода. Так, для уравнения C) используется
двухитаиный метод
УГ1 = У1 + 0,5т (а (уГ1'2) (»» + > + »»)*)*. /•
Тестирование и проверка качества разностных схем
для нелинейного П. т. у. проводится путем сравнения
с точными автомодельными решениями, такими, напр.,
как решение типа температурной волны (см. [6]).
При решении многомерного П. т. у. используются
переменных направлений методы, к-рые позволяют
свести решение многомерной задачи к решению последо-
последовательности одномерных задач (см. [1], [7] — [10]).
Предложено и исследовано значительное число абсо-
абсолютно устойчивых алгоритмов переменных направле-
направлений. Эти алгоритмы являются экономичными в том
смысле, что число арифметич. действий, необходимых
для вычисления решения на новом временном слое <„., i,
имеет порядок числа узлов пространственной сетки.
Ниже рассмотрен пример схемы переменных направле-
направлений для уравнения
в прямоугольнике G{0 < хл < la, сс=1, 2}. Вводится
сетка
xtj=(/i\ 4"),4"=^ь i=0, 1, . . ., Nlt h1N1 = l1,
и обозначения
yli = V(Xij, in), y"l+llt = y(*ij, <„ + 0,
Aiy"i = (y"i-i.i -2ylj +y"-u )/fe'i,
Уравнение D) решается с помощью следующей разност-
разностной схемы
=ЛС7 ЛУЦ
Эти уравнения записываются при г—1, . . ., N± — 1,
/ = 1, . . ., Na—1 и доопределяются соответствующими
граничными условиями. Из первого уравнения прогон-
прогонкой по направлению хх для каждого 7 = 1, 2, . . ., jV2—1
находится j///+1/2, а затем из второго уравнения про-
прогонкой но направлению х.г для каждого i—1, 2, . . .,
N1— 1 находится j/?/+1. Таким образом, вычислительный
алгоритм состоит в последовательном применении
одномерных прогонок.
Теоретич. основой построения и исследонания эко-
экономичных разностных схем для многомерного П. т. у.
является метод суммарной аппроксимации (см. [1], [8|,
[9]). Обобщением методов переменных направлений яви-
явились аддитивные экономичные схемы с уравнениями на
графах и векторные схемы (см. [11]).
В случае нерегулярных пространственных сеток раз-
разностные схемы для П. т. у. строятся методом конечных
олементов и методом баланса (см. [12]).
Для решения сеточных уравнений, возникающих при
аппроксимации многомерного П. т. у. неявными разпо-
стными схемами, применяются эффективные прямые и
итерационные методы, разработанные для эллиптичес-
эллиптических разностных краевых задач: метод разделения пе-
переменных, использующий алгоритм быстрого дискрет-
дискретного преобразования Фурье, метод цнклич. редук-
редукции, попеременно-треугольный итерационный метод и
др. (см. [13]).
Лит.: [1] Самарский А. А., Теория рииноитныл схем,
М., 1977; [2] С а у л ь е в В. К., Интегрирование уравнений
параболического типа методом сеток, М., 1960; [3] Самар-
Самарский А. А., Г у лин А. В., Устойчивость разностных
схем, М., 1973; [4] Ф р я з и н о в И. В., «Ж. вычислит, ма-
тем. и матем. физ.», 1971, т. 11, № 5, с. 1219—28; Г5] Map-
ч у к Г. И., Методы вычислительной математики, 2 изд., М.,
1980; [6] Самарский А. А., Соболь И. М., «Ж. вы-
вычислит, матем. и матем. физ.», 1963, т. 3, № 4, с. 702—19; L7I
Я н е н к о Н. Н., Метод дробных шагов решения многомер-
многомерных задач математической физики, Нопосиб., 1967; [8] Сама р-
ский А. А., «Ж. вычислит, матем. и матем. физ.», 1962,
т. 2, К 1, с. 25—56; [9] Я йен к о Н. II., «СиП. матем. ж.»
1964, т. 5, № 6, с. 1431 — 34; [10] Дьяконов К. Г., «Ж. вы-
вычислит, матем. и матем. физ.», 1962, т. 2, Л« 4, с. 549—68; L11J
Самарский А. А., Ф р я э и п о в И. В., «Успехи матем.
наук», 1976, т. 31, в. в, с. 167—96; [12] Ф р я и и н о в И. В.,
«Дифференц. уравнения», 1980, т. 16, Я« 7, с. 1332—43; [13]
Самарский А. А., Николаев Е. С, Методы ре-
решения сеточных уравнений, М., 1978. А. В. Гулип.
ПАРАБОЛИЧЕСКОГО УРАВНЕНИЯ МЕТОД —
метод приближенного решения высокочастотных диф-
дифракционных задач (см. Дифракции математическая
теория). Как правило, к П. у. м. приходится прибегать
для нахождения волнового поля в тех областях, где
лучевой метод применять нельзя из-за того, что ноле
лучей теряет в том или ином смысли регулярность.
Пусть, напр., ииставлена ааднчи о падении плоской
волны на идеально отражающее выпуклое тело. Вол-
Волновой процесс описывается уравнением Гельмгольца
Здесь точка (х, у) пробегает внешность ограниченной
выпуклой области Q, на границе к-рой выполняется
краевое условие Дирихле u|s=0. Предполагается, что
ай=5?С°°и имеет всюду положительную кривизну.
Решение и представимо в виде г'**+и°, где ии удовлет-
удовлетворяет излучения условиям. Решение такой задачи
существует и единственно.
В высокочастотном случае (к «велико») важно по-
построить формальное коротковолновое решение этой за-
задачи (т. е., грубо говоря, разложение, формально
удовлетворяющее всем условиям задачи, достаточно
далекие члены к-рого имеют сколь угодно высокий
порядок малости при к —>. оо). Можно показать, что в
рассматриваемом случав формальное решение будет
асимитотич. разложением классич. решения.
Лучевой метод позволяет построить искомое корот-
коротковолновое разложение всюду, кроме области тени
(см. рис.). Выраже-
\У Полутень ние для волнового но-
_ля, построенное с ио-
х мощью лучевого ме-
метода, теряет гладкость
на границе тень—
свет (полупрямые
-{-—О А и О'А' на рис.).
j i В окрестности О А (и
Полутень О'А') коротковолно-
коротковолновая асимптотика вол-
волнового поля уже не выражается лучевыми формулами.
Окрестности ОА (и О'А') наз. обычно полутенью.
Ключевым моментом при построении формального
решения поставленной выше задачи является рассмотре-
рассмотрение окрестности точек касания О и О' лучей падающей
волны и кривой S=dQ. Точка О принята за начало
координат, положительная часть оси Ох отделяет
область тени от освещенной области.
Пусть в окрестности О введены новые координаты
s, п. Точка M(?S характеризуется ее расстоянием
вдоль S от О. Считается, что s > 0 (соответственно
s < 0) и области тени (соответственно в освещенной
области). Если M?Q, то точка М характеризуется ее
расстоянием п от S и координатой s проекции М на 5.
В координатах s, n уравнение Гельмгольца имеет вид
.21VTA
B)
(p=p(s) > 0 — радиус кривизны S в точке s).
Используя ряд Маклорена для —:
можно заменить все коэффициенты уравнения B) их
формальными разложениями по степеням s и п. В ра-
растянутых координатах
полагая в уравнении B)
и ~ e'ks („0 (Oi v) +Л-1'8 vr (a, v) + . . .) C)
и приравнивая нулю коэффициенты при последователь-
последовательных степенях k~4'J, приходят к типичной для метода
пограничного слоя цепочке рекуррентных уравнений
= 0, Lovl-irL1va=i),
Здесь первое уравнение и есть «параболическое» урав-
уравнение, давшее название П. у. м.:
По существу уравнение D) является уравнением типа
Шрёдингера. В операторах Lj коэффициенты —
полиномы от а и v. Для формального выполнения
краевого условия и\$— 0 достаточно потребовать, что-
чтобы Uj-\s=0. Роль других краевых условий играет
требование, чтобы при больших |а|, а < О, ряд C)
формально переходил бы в разложение лучевого метода.
Для ии можно вывести явную формулу (т. н. ф о р м у-
л у Фока), имеющую вид интеграла Фурье
J
где Ф сравнительно просто выражается через функции
Эйри. Методика склеивания (сращивания) асимптотич.
разложений дает возможность получить формулы
для волнового поля по всей области тени и полутени.
В случае волн соскальзывания и шепчущей галереи
выводятся соответствующие «параболические» уравне-
уравнения и их решения выражаются через функции Эйри.
Развитие теории лазеров привело к необходимости
рассматривать волны, сосредоточенные в окрестности
изолированных лучей. Выделяя соответствующий фазо-
фазовый множитель и прииоди далее построения, аналогич-
аналогичные построениям метода пограничного слоя, приходят
к «параболическому» уравнению, через решение к-рого
выражается в первом приближении волновое поле.
В этом случае «параболическое» уравнение будет урав-
уравнением Шрёдингера с квадратичным потенциалом.
П. у. м. находит применение также при расчете вол-
волнового поля в световодах, в статистически неоднородных
средах и во многих др. задачах. Аналоги П. у. м. ис-
используются в теории нелинейных волн.
Лит.: [1] Фок В. А., Проблемы дифракции и распро-
распространения электромагнитных полн, М., 1970; \'i] Бабич
В. М., Булдырев В. С, Асимптотические методы к зада-
задачах дифракции коротких волн, М., 1972; [3] Бабич В. М.,
К и р п и ч н и к о в а Н. Я., Метод пограничного слоя в за-
задачах дифракции, Л., 1974. В. М. Бабич.
ПАРАБОЛИЧЕСКОГО ЦИЛИНДРА ФУНКЦИИ,
В е б ч р а функции, В е б е р а — Э р м и т а
ф у н к ц ии,— решения дифференциального уравнения
к-рое получается в результате разделения переменных
в волновом уравнении Ди=/сги в параболических ци-
линдрич. координатах. Наиболее часто используется
решение
1
где "Р (a, b; z) — вырожденная гипергеометрич. функ-
функция. Уравнению (*) удовлетворяют также Dv (—z),
D-v-i{±iz). Функции Dv (z) и D_v-i(±iz) линейно
независимы при любых v, Dv (z) и Dv (—z) при v?=0,
±1, ±2 ... П. ц. ф.— целые функции от z. Функция
Dv (z) действительна при действительных v и z.
Формулы дифференцирования (ге=1, 2, . . .):
Рекуррентные формулы:
Dv ц (;) — zDv (г) + vBv-i W = 0,
Асимптотика: при фиксированном v largzl < Зя/4 и
при ограниченном U|, |arg(—v)|<:n/2 и lv| -»- оо
Dv(z) =7Tex
V У\ vi
П. ц. ф. связана с др. функциями следующими соотно-
соотношениями. С многочленами Эрмита:
fleW = 2-"/2r«7<I,(z/^), 7г=-=0, 1, 2, . . .;
с интегралом вероятности:
-^?1(^2 erf ?
ге = О, 1, 2, . . .;
с функциями Бесселя:
Пит.: [1] Б е й т м е н Г., Э р д е й и А., Высшие транс-
трансцендентные функции. Функции Бесселя, функции параболи-
параболического цилиндра, ортогональные многочлены, пер. с англ.,
t изд., М., 1974; [2] Миллер Д Ш.-Ч.-П., Таблицы функ-
функций Вебера (функций параболического цилиндра), пер. с англ.,
М., 1968. Ю. А. Брычков, А. П. Прудников.
ПАРАБОЛОИД — незамкнутая нецентральная по-
поверхность второго порядка. Канонич. уравнения П.:
— эллиптический, параболоид (при p — q называется П.
вращения) и
f-'-^&.p, ,>0,
— гиперболический параболоид. А. Б. Пеанов.
ПАРАБОЛОИДАЛЬНЫЕ КООРДИНАТЫ — числа
и, v и w, связанные с прямоугольными координатами х,
у и г формулами:
x = 2,uw cos v, y = 2uwsii\v, z —u2—w2,
где 0<:u<oo,0<;y< 2я, 0 <; w < оо. Координат-
Координатные поверхности: две системы параболоидов вращения
с противоположно направленными осями (ц--const и
w— const) и полуплоскости (v= const). Система П. к.—
ортогональная.
Коэффициенты Ламе:
La^Lw^2V~u*+w*, Lv = 2uw.
Элемент площади поверхности:
da = 4 \r(u<i^rwi) u2w2 (du2-^dw*) dv2+(u2 + w2){du dwJ.
Элемент объема:
dV = Ъ (uiJrW2) uwdu dv dw.
Векторные дифференциальные операции:
div re = ^===== [wau Bu2 -^ w2) -{- uaw (u'-i-\-2w'i)\-<r
2uw V (u2 + «)s)'
_j 1 / da u j daw \ . 1_ 9«a ,
rot.,, a = (шаи — aw) -\-
,
Лш= 1 Г9'" | | u?
т 4 (ua + tu* [9u'Tu 8ttT^u' Гюг J dv*
I Й'Ф I 1 Эф "I
Д. Д. Соколов.
ПАРАДОКС — то же, что антиномия.
ПАРАКОМПАКТНОЕ ПРОСТРАНСТВО — тополо-
топологическое пространство, в любое открытое покрытие
к-рого можно вписать локально конечное открытое
покрытие. (Семейство у множеств, лежащих в топологич.
пространстве X, наз. локально конечным в
X, если у каждой точки х?Х существует окрестность
в X, пересекающаяся лишь с конечным множеством
алементов семейства у; семейство у множеств в п и с а-
в о в семейство X множеств, если каждый элемент се-
семейства у содержится в нек-ром элементе семейства X.)
Паракомпактом наз. паракомпактное хаусдор-
хаусдорфово пространство. Класс паракомпактов весьма ши-
широк — он включает все метрич. пространства (теорема
Стоуна) и все бикомпакты. Однако не каждое локально
бикомпактное хаусдорфово пространство паракомпакт-
но.
Значение паракомпактности определяется отмечен-
отмеченной общностью этого понятия и рядом замечательных
свойств паракомпактов. Прежде всего, каждое хаусдор-
хаусдорфово П. и. нормально. Это позволяет строить на пара-
компактах разбиения единицы, подчиненные
произвольному заданному открытому покрытию у.
Так называются семейства действительных неотрица-
неотрицательных непрерывных функций на пространстве, под-
подчиненные следующим условиям: а) семейство носите-
носителей этих функций локально конечно и вписано в 7",
б) в каждой точке пространства сумма значений всех
тех функций семейства, к-рые отличны в ней от нуля (а
таких функций конечное число), равна 1. Разбиения
единицы являются основным средством построения
погружений пространств в стандартные пространства.
В частности, они используются для вложений многооб-
многообразий в евклидовы пространства и при доказательстве
теоремы о метризуемости каждого тихоновского про-
пространства с сг-локально конечной базой. Кроме того, на
разбиениях единицы в теории многообразий основаны
методы, с помощью к-рых осуществляется единовремен-
единовременный синтез локальных построений, производимых в
пределах отдельных карт (в частности, тех или иных
некторных. и тензорных полей). Поэтому одним из тре-
требований исходных в теории многообразий является
требование паракомпактности, не являющееся лишним,
т. к. существуют непаракомпактные связные хаусдорфо-
вы многообразия.
В присутствии паракомпактности нек-рые локальные
свойства пространства синтезируются и выполняются
глобально. В частности, если паракомпакт локально
метризуем, то он метризуем; если хаусдорфово простран-
пространство локально полно по Чеху и паракомпактно, то оно
полно по Чеху. В размерности теории для параком-
паракомпактов удается получить ряд важных соотношений, не
распространяющихся даже на нормальные простран-
пространства. Это не удивительно, т. к. одно из основных опре-
определений размерности — по Лебегу — связано с рассмот-
рассмотрением кратности открытых покрытий, что, несомненно,
родственно идее локальной конечности, на к-рой осно-
основано определение паракомпактности.
Паракомпактность не наследуется произвольными
подпространствами (в отличие от метризуемости), ина-
иначе, напр., все тихоновские пространства, как подпро-
подпространства бикомпактных, оказались бы паракомпактами.
По каждое замкнутое подпространство паракомпакта
есть паракомпакт. Большим недостатком паракомпакт-
паракомпактности является отсутствие мультипликативности:
произведение двух паракомпактов может паракомпактом
не быть. С другой стороны, в классе хаусдорфовых
пространств прообраз наракомпакта при совершенном
отображении является паракомпактом, и образ пара-
компакта при непрерывном замкнутом отображении
является паракомпактом. К числу паракомпактов от-
относятся, в частности, Линделёфа пространства. Дли
пространства всех неирерывных действительных функ-
функций на произвольном тихоновском пространстве, наде-
наделенном топологией поточечной сходимости, паракомпакт-
паракомпактность равносильна линдолёфовости. Если банахово
пространство в слабой топологии топологически порож-
порождается нек-рым лежащим в нем бикомпактом, то оно
паракомиактно. Важный пример паракомпактов —
полиэдры, стоящие на C'W-комплексами.
В классе паракомнактов упрощаются критерии мет-
метризуемости. В частности, паракомиакт метризуем н том
и только в том случае, если он обладает базой счетного
порядка, т. v. базой, любая убывающая последова-
последовательность элементов к-рой, содержащих какую-либо
точку х?Х, непременно образует базу в этой точке.
Многообразны паракомпактности критерии. В ча-
частности, для тихоновского пространства X равносиль-
равносильны условия: а) X пара компактно, б) в любое открытое
покрытие пространства X можно вписать локально
конечное покрытие, в) в каждое открытое покрытие
пространства X можно вписать о-локально конечное
открытое покрытие, г) в любое открытое покрытие
пространства X можно вписать консерватив-
консервативное замкнутое покрытие, т. е. покрытие,
объединение любого подсемейства к-рого замкнуто в X.
Важным является следующий критерий: тихоновское
пространство X паракомиактно в том и только в том
случае, если в каждое его открытое покрытие 7 можно
вписать нек-рое открытое покрытие к звездно;
последнее означает, что для каждой точки л?Х объеди-
объединение всех элементов покрытия X, содержащих х,
содержится в нек-ром элементе покрытия у. Понятие
звездной вписанности служит выражением идеи не-
неограниченной дробимости пространства и может вос-
восприниматься как наиболее общая теоретико-множест-
теоретико-множественная форма аксиомы треугольника.
Лит.; ll\ К о л л я Д т., Общая топология, пер. с англ.,
2 изд., М., 1981; [2] Архангельский А. В., Поно-
Пономарев В. И., Основы общей топологии в задачах и упраж-
упражнениях, М., 1974; [3] Архангельский А., «Докл. АН
СССР», 19В1, т. 141, № 1, с. 13—15. А. В. Архангельский.
ПАРАКОМПАКТНОСТИ КРИТЕРИИ — следующие
утверждения, равносильные для произвольного вполне
регулярного хаусдорфова пространства X. 1) X па-
ракомпактно. 2) В каждое открытое покрытие про-
пространства X можно вписать локально конечное от-
открытое покрытие. 3) В каждое открытое покрытие
пространства X можно вписать а-л окал ь но ко-
конечное открытое покрытие, т. е. от-
открытое покрытие, распадающееся на счетное множество
локально конечных в X семейств множеств. 4) В каж-
каждое открытое покрытие пространства X можно вписать
локально конечное покрытие (о строении элементов
к-рого не предполагается ничего). 5) Каково бы ни
было открытое покрытие у пространства X, существует
открытое покрытие этого пространства, звездно впи-
вписанное в у. 6) В каждое открытое покрытии простран-
пространства X можно вписать консервативное покрытие.
7) Каково бы ни было открытое покрытие у простран-
пространства X, существует счетное семейство кх, Я2, . . . от-
открытых покрытий этого пространства такое, что для
каждой точки х ? X и каждой ее окрестности Ох най-
найдутся U?y и номер г, удовлетворяющие условию:
каждый элемент покрытия к,-, пересекающийся с Ох,
содержится в U (т. е. вся звезда множества Ох отно-
относительно А,- лежит в U). 8) Каково бы ни было открытое
покрытие со пространства X, существует непрерывное
отображение / пространства X на нек-рое метрич.
пространство У, подчиненное условию: у каждой
точки пространства У существует окрестность, про-
прообраз к-рой при / содержится в элементе покрытия ш.
9) Пространство X коллективно нормально и слабо
паракомпактно. А. В. Архангельский.
ПАРАЛЛЕЛЕПИПЕД — шестигранник, противопо-
противоположные грани к-рого попарно параллельны. П. имеет
8 вершин, 12 ребер; его грани представляют собой
попарно равные параллелограммы.
П. наз. прямым, если его боко- /-L.
вые реора перпендикулярны к пло- / /
скости основания (в этом случае 4 / /
боковые грани — прямоугольники); //L~
прямоугольным, если этот
П. прямой и основанием служит прямоугольник (следо-
(следовательно, 6 граней — прямоугольники); П., все грани
к-рого квадраты, ваз. кубом. Объем П. равен про-
произведению площади его основания на высоту, всэ-з.
ПАРАЛЛЕЛИЗМ АБСОЛЮТНЫЙ — поле реперов
е= («j, . . ., <¦„) на многообразии. П. а. определяет
изоморфизм всех касательных пространств многооб-
многообразия М, при к-ром отождествляются векторы каса-
касательных пространств ТрМ и ТЧМ, имеющие одина-
одинаковые координаты относительно реперов ер и е?. Это
задает на многообразии линейную связность Vе с ну-
нулевой кривизной. Параллельными полями относи-
относительно этой связности являются тензорные ноля, име-
имеющие постоянные координаты относительно поля ре-
реперов е (в частности, векторные поля еъ . . ., еп па-
параллельны), а операция ковариантного дифференци-
дифференцирования тензорного поля Т по направлению вектор-
векторного поля X сводится к дифференцированию по на-
направлению поля X координат поля Т относительно е.
Обратно, линейная связность v c нулевой кривизной
на односвязном многообразии М определяет П. а. е,
если задан дополнительно репер ер нек-рого касатель-
касательного пространства ТрМ. П. а. е получается из репера
е„ разнесением с помощью параллельного переноса
связности v (параллельный перенос не зависит от
выбора пути, соединяющего две данные точки мно-
многообразия, если связность имеет нулевую кривизну,
а многообразие односвязно).
С точки зрения теории С-структур П. а. является
{1} — структурой, где {1} — группа, состоящая из
одной единицы. Интегрируемость такой структуры
означает, что в окрестности любой точки многооб-
многообразия существует система координат х1, для к-рой
е,-=д/дх1, г=1, . . ., п. Для этого необходимо и до-
достаточно, чтобы векторные поля ег, . . ., еп иоиарно
коммутировали или, иначе говоря, чтобы тензор кру-
кручения C=-C)k связности v?, задаваемый формулой
Iеji ек\~^1^1, был тождественно равен нулю. П. а.
наз. полным, если все векторные поля, имеющие
постоянные координаты относительно доля реперов,
полны или, что эквивалентно, если связность \е гео-
геодезически полна. В интегрируемом случае для этого
достаточно полноты векторных полей ег, . . ., е„
Полный интегрируемый П. а. на односвязном много-
многообразии М задает на М структуру аффинного про-
пространства. Более обще, полный П. а. с ковариантно
постоянным тензором кручения С F'yft—const) яа одно-
связном многообразии М с отмеченной точкой задает
на М структуру группы Ли со структурными кон-
константами Cljk, для к-рой ноля е/ образуют базис про-
пространства левоинвариантных полей.
Группа автоморфизмов П. а. есть группа Ли, сно-
бодно действующая на М. Известны необходимые и
достаточные условия того, чтобы две П. а. были ло-
локально изоморфны (см. [31). Они выражаются в тер-
терминах тензора кручения и его ковариантных произ-
производных .
Лит.: ll] V а ш е в с к и й П. К., РимаНова геометрия И
тенворный анализ, 3 изд., М., 1U67; L2] Н о м и д з у К., Груп-
Группы Ли и дифференциальная геометрия, пер. с англ., М., 1960;
[3] Стернберг С, Лекции по дифференциальной геомет-
геометрии пер. с англ., М., 1970. Д. В. Але-ксеевс-кий.
ПАРАЛЛЕЛИЗУЕМОЕ МНОГООБРАЗИЕ — много-
многообразие М размерности п, допускающее поле реперов
е= (et, . . ., еп), то есть п линейно независимых в каж-
каждой точке векторных полей el7 . . ., еп. Поле е задает
изоморфизм касательного расслоения т: ТМ —>- М
на тривиальное расслоение е: R"xM-+M, сопостав-
сопоставляющий касательному вектору v?TpM его коорди-
координаты относительно репера е\р и его начало. Поэтому
П. м. можно также определить как многообразие,
имеющее тривиальное касательное расслоение. При-
Примерами П. м. являются открытые подмногообразия
евклидова пространства, все трехмерные многообра-
многообразия, пространство произвольной группы Ли, много-
многообразие реперов произвольного многообразия. Сфера
Sn является П. м. только при ге=1, 3, 7. Для паралле-
параллелизуемости 4-мерного многообразия необходимо и
достаточно обращение в нуль его второго характерп-
стич. класса Штифеля — Уитни. В общем случае
равенство нулю всех характеристич. классов Штифе-
Штифеля — Уитни, Чжэня и Понтрягина является необхо-
необходимым, но недостаточным условием для того, чтобы
многообразие М было П. М. /f- В. Алексеевский-
ПАРАЛЛЕЛОГРАММ — четырехугольник, у к-рого
стороны попарно параллельны (см. рис., а — г).
П. может быть также охарактеризован как выпуклый
\z\uz\o
четырехугольник при любом m.i следующих нрн.ша
ков: 1) та и другая пара противоположных сторон
состоит из равных отрезков; 2) одна пара противопо-
противоположных сторон состоит из равных и параллельных
отрезков; 3) при противоположных вершинах той и
другой пары углы равны; 4) точка пересечения диаго-
диагоналей делит каждую из них пополам. Различные
виды П.: прямоугольник (б) — П., все углы к-рого
прямые; ромб (в) — П., все стороны к-рого равны;
квадрат (?) — равносторонний прямоугольник.
г.с.'}-!
ПАРАЛЛЕЛОТОП, и а р а л л р ,ч о i |. и и и м к.
множество точек, радиус-векторы i;-pi.is имени нп.ч
со всевозможными значениями 0<:х'<:1, 1 <:<<:/>.
Здесь «х, а2, ¦ ¦ ¦, dp — фиксированные векторы н-мер-
ного аффинного пространства А. Они наз. образу-
образующими параллелотопа и совпадают с
нек-рыми ребрами IF. Все остальные ребра П. им па-
параллельны. Если образующие П. линейно независимы
(зависимы), то П. наз. р-м е р н ы м, или невырож-
невырожденным (вырожденным). Вырожденный П.
является параллельной проекцией нек-рого /(-мерного
П. на плоскость размерности /с<р—1. Невырожденный
П. определяет несущую его р-мерную плоскость. Такой
П. при р—2 является параллелограммом, при р--3—
параллелепипедом.
Два невырожденных П. на;1. пара л л е л ь н ы м и,
если параллельны несущие их плоскости. У параллель-
параллельных П. можно сравнивать их р-мерные «объемы» (хотя
в пространстве А может и не быть метрики). Количе-
Количественной характеристикой отношения р-мерного «объ-
«объема» П. с образующими %, а2, . . ., ар к р-мерному
«объему» параллельного П. с образующими bt, Ь,г,
. . ., Ьр служит скаляр det (.!¦}), где (¦?¦}) — (р Х;>)-мат-
рица перехода от (Ьи Ь2, . . ., Ьр) к (аи as, . . ., а,р), т. е.
« 2L ** 1<''S^
Если в пространстве А определено скалярное ироинве-
денио, то квадрат р-мерного объема П. с образующими
Я], . . ., пр равен определителю (рХр)-матрицы Грама
с элементами (a,, aj).
Понятие П. тесно связано с понятием поливектора.
Лит.: [1] Широков II. А., Тензорное исчисление,
Казань, 1961; [2] Беклемишев Д. В., Курс аналитиче-
аналитической геометрии и линейной алгебры, 3 изд., М., 1978; 1.1] П и-
ао Ш., Зама некий М., Курс математики. Алгебра
и анализ, пер. с франц., М., 1971. Л. П. Купцов.
ПАРАЛЛЕЛОЭДР — многогранник, параллельным
перенесением к-рого можно заполнить пространстве
так, чтобы многогранники не входили друг в друга
и не оставляли пустот между собой, т. е. образовать
разбиение пространства. П. является, напр., куб или
правильная 6-угольная призма. Топологически раз-
различных сеток ребер П. пять (см. рис.). Число их
граней: 6, 8, 12, 12, 14. Для того чтобы многогранник
был П., необходимо н достаточно, чтобы он был вы-
выпуклым многогранником одного из пяти указанных
топологич. типов и чтобы все его грани имели центры
симметрии. Центры П. образуют точечную решетку
(см. Воропиги типы, решеток). А. Б. Иванов.
ПАРАЛЛЕЛЬНОЕ ПЕРЕНЕСЕНИЕ — изоморфизм
слоев над концами х0 и хх кусочно гладкой кривой
L{xa, хх) базы М гладкого расслоенного пространства
Е, определяемый нек-рой заданной в Е связностью;
в частности, линейный изоморфизм касательных про-
пространств ТХп(М) и TXt(M), определяемый вдоль
кривой L?M нек-рой заданно)! на М аффинной связ-
связностью. Развитие понятия П. п. началось с обычного
параллелизма на евклидовой плоскости Еъ для к-рой
Ф. Миндинг (F. Minding, 1837) указал возможность
обобщить ее на случай поверхности М ъ Е3 с помощью
введенного им понятия развертывания кривой L?M
на плоскость Е2. Это указание Миндинга послужило
отправным пунктом для Т. Леви-Чивита [1], к-рый,
оформляя аналитически П. п. касательного вектора
на поверхности, обнаружил зависимость его только от
метрики поверхности и на этой основе обобщил его
сразу на случай «-мерного риманова пространства (см.
Леви-Чивита свявноетъ). Г. Вейль [2] положил понятие
П. п. касательного вектора в основу определения аф-
финной связности на гладком многообразии Л/. Даль-
Дальнейшие обобщения этого понятия связаны с развитием
общей теории свянностей.
Пусть на гладком многообразии М задана аффинная
связность с помощью матрицы локальных форм связ-
связности:
со' = Т{ (х) dx*, со} = Г}„ (х) со*, dot |
0.
Говорят, что вектор Х„?ТХо{М) получен парал-
параллельным перенесением из вектора
X1^LTX^(M) вдоль гладкой кривой L(x0, xs) ?M, если
на L существует гладкое векторное поле X, соединя-
соединяющее Хо и Xt, такое, что \yX-~0, где У — ноле ка-
касательного вектора кривой L, а \уХ — ковариантная
производная поля X относительно У, определяемая
формулой
ш' (\}уХ) = Усо^ (X) + ы[ (Y) со* (X).
Таким образом, координаты ?'=со''(Л') поля X должны
удовлетворять вдоль L системе дифференциальных
уравнений
II:) линейности этой системы следует, что П. и. вдоль
Л определяет нек-рый изоморфизм между ТХа(М) и
7\.ЛМ). П. п. вдоль кусочно гладкой кривой опреде-
определяется как суперпозиция П. п. вдоль ее гладких кус-
кусков.
Автоморфизмы пространства ТХ(М), определяемые
П. п. вдоль замкнутых кусочно гладких кривых L (х, х),
образуют линейную голопомии группу Фх; при этом ФЛ.
н ФХ' всегда сопряжены между собой. Если ФА. дис-
дискретна, т. е. ее компонента единицы одноэлементна, то
говорят об аффинной связности с (локальным) абсо-
абсолютным параллелизмом векторов, или о (локально)
плоской связности. Тогда П. п. при любых
г,, п хх но зависит от выбора линии L(x0, х±) из одного
класса гомотонии; для атого необходимо и достаточно
равенство нулю тензора кривизны связности.
Па основе П. п. вектора определяется П. п. ковектори
м, вообще, тензора. Говорят, что поле ковектора 0
на L совершает параллельное переносе-
н н е, если для любого векторного поля А' на L, совер-
совершающего П. п., функция 0(Х) постоянна вдоль L.
Нообще, говорят, что ноле тензора Т, напр, тина B, 1),
совершает параллельное перенесение
вдоль L, если для любых X, У и 6, совершающих
П. п., фгункция Т(Х, У, 0) постоянна вдоль L. Для
этою необходимо и достаточно, чтобы компоненты
T)k удовлетворяли вдоль L системе дифференциальных
уравнений
После введения Э. Картаном |3| пространств про-
проективной и конформной связностей в 1920-х гг. и
общей концепции связности на многообразии понятие
П. п. получило более общее содержание. В наиболее
общим смысле оно понимается теперь при рассмот-
рассмотрении связностей в главных расслоенных простран-
пространствах или присоединенных к ним пространствах. Су-
Существует способ определения самого понятия связ-
связности с помощью понятия П. п., к-рое тогда опреде-
определяется аксиоматически. Связность, однако, может быть
задана горизонтальным распределением или нек-рым
другим эквивалентным способом, напр, связности
формой. Тогда для каждой кривой L(x0, xj базы М
определяются ее горизонтальные поднятия как инте-
интегральные кривые горизонтального распределения над
L. П. п. наз. тогда отображение, к-рое концам этих
понятии в слое над хх ставит в соответствие их другие
кшщы в слое над х0. Аналогично определяются понятия
группы голономип u (локально) плоской связности;
последняя также характеризуется равенством нулю
кривизны формы.
Лит.: [1] Lcvi-Civita Т., «Kend. Circolo mat. Pa-
Palermo», 11I7, t. 42 p. 178—205; [2] Weyl H., Raum, Zeit,
Materie, 5 Aufl., В., 1923; [3] G a r t a n E., «Acta math.», 1928,
t. 48, p. 1—42; [4] H о м и д з у К., Группы Ли и дифферен-
дифференциальная геометрия, пер. о англ., М., I960; [5] Р а ш е в-
с к и й П. К., Риманова геометрия и тензорный анализ, 3 изд.,
М., 1967. Ю. Г. Лумисте.
ПАРАЛЛЕЛЬНОЕ ПОЛЕ, к о в а р и а н т н о по-
постоянное пол е,— поле тензоров А на много-
многообразии М с л-инейной связностью у, инвариантное
относительно параллельного перенесения вдоль кривых
на М. Это означает, что для любых точек р, q?M тензор
А у (значение тензорного поля А в точке р) при парал-
параллельном перенесении в точку q вдоль любой гладкой
кривой, соединяющей точки р и q, переходит в тензор
Л„.
Поле тензоров А будет параллельным тогда л только
тогда, когда его ковариантная производная по на-
направлению любого векторного ноля X тождественно
равна нулю: vx^~0 или, иначе, когда ковариантный
дифференциал DA поля А равен нулю.
Множество П(М, v) параллельных полей образует
подалгебру алгебры всех тензорных полей на много-
многообразии М, инвариантную относительно сперто к тен-
тензорных полей и перестановок их индексов. Алгебра
П(М, v) естественным образом изоморфна алгебре
тензоров в фиксировалной точке р многообразия М,
инвариантных относительно однородной группы голо-
номии Г^, связности v B точке р. Для связности с
полной группой голономии r=GL(/i, R), где га—
-d\mM, алгебра П(М, у) порождается символом
Кронекера &f, для римановой связности с группой
голономии О (и) — метрич. тензором g— (g/j) и об-
обратным к нему тензором g~l~ {g'J), а для римановой
связности с группой голономии 8О(«) — тензорами
g, g~x и /(-формой объема. Описаны также образующие
алгебры параллельных дифференциальных форм на
произвольном пространстве линейной связности без
кручения с любой неприводимой группой голономип
15].
Особый интерес представляют П. п. дифференци-
дифференциальных форм в римановом многообразии со связностью
Леви-Чивиты. С каждой такой формой со ассоциируется
(с помощью операции свертки) ряд линейных опера-
операторов в пространстве дифференциальных форм, пере-
перестановочных с оператором Бельтрами — Лапласа Д,
напр, операторы внутреннего и внешнего умножения
на форму со или операторы ортогонального проекти-
проектирования на инвариантные относительно группы го-
голономии подпространства пространства дифференци-
дифференциальных форм. Изучение этих операторов позволяет
получить оценки для размерностей пространств гар-
монич. форм различных степеней, т. е. (н компактном
случае) для чисел Бетти многообразия М (см. [4]).
Наиболее содержательная теория (см. Ходжа теорема)
развита для кэлеровых и кватернионных римановых
пространств, в к-рых всегда имеется П. п. 2-форм и,
соответственно, 4-форм. Любая параллельная диффе-
дифференциальная форма в римановом пространстве гармо-
гармонична. В компактном симметрическом римановом
пространстве верно и обратное: любая гармонич.
форма параллельна. Поэтому кольцо вещественных
когомологий компактного симметрич. пространства
изоморфно кольцу параллельных дифференциальных
форм.
Поле тензоров А является П. и. относительно нек-рой
линейной связности v тогда и только тогда, когда
оно инфинитезимально однородно, т. е.
когда в каждой точке р многообразия М существует
репер, относительно к-рого тензор А ;1 имеет фикси-
рованныр координаты Аг^ "• г-к, ае зависящие от
точки р. В этом случае множество реперов, относи-
относительно к-рых тензоры Ар, р?М, имеют координаты
а)\ '" )к, образует G-структуру, т. е. главное подрас-
слоение Р (А) расслоения реперов со структурной
группой G, являющейся стабилизатором точки Ар при
действии группы GL(n, R) в пространстве тензоров.
Поле А параллельно относительно любой связности
в G-структуре Р(А). В частности, любое сечение рас-
расслоения Р (А) (если оно существует) задает связность
с нулевой кривизной, относительно к-рой поле А
параллельно.
Более сложным является вопрос о существовании
связности без кручения, относительно к-рой данное
пнфинитезимальпо однородное иоле параллельно. Если
поле А является псевдоримановой метрикой, то такая
связность (связность Лев и-Ч и в и т а) всегда
существует и единственна. Оказывается, что этот слу-
случай является исключительным: если для нек-рого
тензорного поля А существует единственная связность
оез кручения, относительно к-рон оно параллельно,
то структурная группа G G-структуры Р(А) является
псевдоортогональной группой и, следовательно, с
полем А канонич. образом ассоциируется псевдорима-
яова метрика [7]. Для широкого класса инфинитези-
мально однородных тензорных полей А наличие связ-
связности без кручения, относительно к-рой поле парал-
параллельно, влечет за собой интегрируемость поля А, т. е.
существование локальной системы координат, в к-рой
координаты поля А постоянны. Это верно, напр., для
почти комплексной структуры, почти симплектич.
структуры и для любого поля А, для к-рого струк-
структурная группа G расслоения Р (А) неприводима и не
принадлежит известному списку неприводимых групп
голономии пространств линейной связности без пру
чения [5].
Лит.: [1] Кобаяеи Ш., Номидзу К., Основы диф-
дифференциальной геометрии, пер. с англ., т. 1—2, М., 1981; [2]
Л и х н е р о в и ч А., Теория связностей в целом и группы
голономии, пер. с франц., М., I960: [3] Чжэнь Ш э н-
ш з н ь. Комплексные многообразия, пер. с англ., М., 19E1;
14] С hern S. S., в кн.: Algebraic geometry and topology.
A symposium in honor of S. Lefschetz, N. Y., 1957, p. 103—21;
15) В e r g e r M., «Bull. Soc. math. France», 1955, t. 8.4, p. 279- -
330; [6] Kobayashi S., Transformation groups in differen-
differential geometry, В.— Hdlb.—N. Y., 1972; [7] Kobayashi S.,
Nagano Т., «J. Math. Soc. Japan», 1905, v. 17, № 1, p. 84--
101. Д. В. Алепсеейспий.
ПАРАЛЛЕЛЬНОСТИ АКСИОМА — аксиома, опре-
определяющая соотношение параллельности в различных
геометриях. См. Параллельные прямые, Пятый по-
постулат.
ПАРАЛЛЕЛЬНЫЕ ЛИНИИ — диффеоморфные глад-
гладкие линии в пространстве, имеющие в соответству-
соответствующих точках параллельные касательные. Таковы,
напр., гладкие компоненты эквидистантных линий на
плоскости (см. Эквидистанта) — они характеризу-
характеризуются тем, что расстояние между соответствующими
точками равно расстоянию между соответствующими
касательными. Пример П. л. в трехмерном простран-
пространстве: если две поверхности находятся в Петерсона
соответствии и имеют общую сопряженную сеть,
то линии этой сети имеют параллельные касательные.
П. л. пространства Е", имеющие параллельные нор-
нормали до порядка m<:nO, расположены в нек-ром
подпространстве Е"~т.
Для линейного семейства плоских выпуклых П. л.
(т. е. выпуклых линий, радиус-вектор к-рых линейно
зависит от параметра е.) справедлива теорема
Брунна-М инков с кого: площадь области,
ими ограниченная, является вогнутой функцией пара-
параметра е.
Обобщенно понятия параллельности на случай ли-
линий, расположенных в группах Ли, получается с
помощью понятия эквиполлентности векторов.
Д. Д. Соколов.
ПАРАЛЛЕЛЬНЫЕ ПОВЕРХНОСТИ — диффеоморф-
ные, одинаково ориентированные поверхности F1 и F2,
к-рые имеют в соответствующих точках параллельные
касательные плоскости, причем расстояние h между
соответствующими точками Ь\ и 1<\ постоянно и равно
расстоянию между соответствующими касательными
плоскостями. Радиус-векторы га и г, П. п. F1 и F2
связаны соотношением: г2—r-l = hn, где п — единичный
вектор нормали, один и тот же для РЛ и F2,
Таким образом, можно определить однопараметрич.
семейство /<'ft поверхностей, параллельных данной
F=F0, причем регулярность F^ имеет место для до-
достаточно малых значений /;, удовлетворяющих нера-
неравенству
w(h)—i—2Hh + Kh2 > 0.
Значениям корней fej и h2 уравнения w(h)~0 соот-
соответствуют поверхности Fhx и F^, являющиеся яво-
лютами поверхности /•', так что П. п. имеют общую
иволюту. Средняя Н^ и гауссова К^ кривизны поверх-
поверхности F/i, параллельной F, связаны с соответствую-
соответствующими величинами Н и К для F соотношениями
линии кривизны П. п. соответствуют друг другу, так
что между ними имеется соответствие Комбескгора,
являющееся частным случаем Петерсона соответствия.
И. X. Си битов.
ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ в евклидово й
геометрии — прямые, к-рые лежат в одной пло-
плоскости и не пересекаются. В абсолютной геометрии
через точку, не лежащую на данной прямой, проходит
хотя бы одна прямая, не пересекающая данную. В ев-
евклидовой геометрии существует только одна такая
прямая. Этот факт рав-
равносилен пятому посту-
постулату Евклида (о парал-
параллельных). В Лобачевско-
Лобачевского геометрии в плоскости
через точку С (см. рис.)
вне данной прямой А В
проходит бесконечное
множество прямых, не
пересекающих АВ. Из них параллельными
к АВ наз. только две. Прямая СЕ паз. параллельной
прямой А В в направлении от Л к В, рели 1) точки В
и Е лежат но одну сторону от прямой А С; 2) прямая
СЕ не пересекает прямую АВ; всякий луч, проходя-
проходящий внутри угла АСЕ, пересекает луч АВ. Анало-
Аналогично определяется прямая CF, параллельная к А В
в направлении от В к А. всэ-з.
ПАРАЛЛЕЛЬНЫЙ ПЕРЕНОС — частный случай
движения, при к-ром все точки пространства переме-
перемещаются в одном и том же направлении на одно и то же
расстояние. Иначе, если М — первоначальное, а М' —
смещенное положение точки, то вектор ММ' — один
и тот же для всех пар точек, соответствующих друг
другу в данном преобразовании.
На плоскости П. п. выражается аналитически в
прямоугольной системе координат (х, у) при помощи
формул
где вектор МЛ/'—(я, 6).
Совокупность всех П. п. образует группу, к-рая в
евклидовом пространстве является подгруппой группы
движений, а в аффинном — подгруппой группы аф-
аффинных преобразований. А. В. Иванов.
ПАРАМЕТРА ВАРИАЦИИ МЕТОД — метод прибли-
приближенного решения нелинейных (и линейных) функцио-
функциональных и операторных уравнений в банаховых про-
пространствах у=Р (х), х?Х, у?У, а также для качествен-
качественных исследований. П. в. м. состоит в том, что урав-
уравнение Р(х)=0, где оператор Р (х) непрерывно диффе-
дифференцируем по Фрете до нужного порядка, или нек-рый
нелинейный функционал Ф(х), связанный с решением
этого уравнения, обобщаются путем введения вспо-
вспомогательного числового (или общего функциональ-
функционального) параметра А, принимающего значения на ко-
конечном или бесконечном промежутке А0<:А<:А*, так:
/¦'(г, А)—0, где f (тД), х?Х, А0<:А<:А*,— оператор
со значениями в У, так что Р(х)~0 получается при
А=А* : F(x, X*)—P(x), а уравнение F(x, Л„)=0 лег-
легко разрешается или известно его решение х0. При этом
предполагается, что оператор F(x, А) непрерывно
дифференцируем (в смысле Фрете) по х и А, т. е. су-
существуют непрерывные частные производные F'x(x, A)
и F\{x, А), и что существует непрерывный оператор
У (or, K)=[Fx(x, А)]-1 пз У в X. Для построения решо-
ннн .г(к) уравнения F(r, А)—0 на всем интервале Ао<:
<a<jA* строится соответствующая дифференциальная
задача (задача Копта) в предположении, что .г (А) не-
непрерывно дифференцируемая функция со значениями
и X, определяемая этим уравнением:
F'x(x, k)§ + Fi(x, а)-0, х(к0)^х0, A)
^--V(x,k)FK(x,k), х(ко)^хй. B)
Интервал [А, А*] разбивается точками Я0<Л!<Аг<
<. . . <А„—А* на более мелкие подинтервалы длины
Лц—Aft—Afc-x, fc—1, 2, . . ., п, и к задаче Коши B)
(или A)) применяются методы численного интегри-
интегрирования обыкновенных дифференциальных уравнений
с шагом кь (или несколько таких методов). В резуль-
результате для построения решения „г (А) уравнения F (х, к) О
получаются П. в. м. соответствующих типов. Построен-
Построенное значение х(к*) будет решением уравнения Р(х)---0.
„ dx
Решение на каждом шаге линейных относительно ^
задач вида A) пли обращение линейных операторов
F'x(x, А) в B), или последовательная аппроксимация
обратного оператора Г (х, к) проводятся различными
методами или опять-таки П. в. м.
Шаги hk выбираются различными способами, напр,
из условия минимума нормы невязки \\Р(х^ + \)\\ как
функции многих, вообще говоря, переменных. При
итом эффективным является также совместный выбор
Aft и свободных параметров метода численного инте-
интегрирования, напр. Рунге — Кутта метода s-ro по-
порядка точности, использование корней полиномов
Чебышова и близких к ним и др.
Задача Коши B) служит не только средством для
определения ириближенного решения рассматрива-
рассматриваемого уравнения, но и для доказательства существо-
существования самого решения. Изучен ряд различных спо-
способов введения параметра А. В качестве числового
параметра А может быть использован также и один из
естественных параметров, содержащихся и рассмат-
рассматриваемой задаче.
В зависимости от способа введения параметра А
П. в. м. является прямым или итерационным методом.
Совместное применение прямого и итерационного
методов ная. комбинированным П. в. м. Напр., ите-
итерационный метод тина усовершенствованного метода
Эйлера — Коши с тагом h^-\ (при F(x, Х)~Р(х)—
— A—Х)Р(.га), Я0~0 it Я* 1) является методом 3-го
порядка точности it имеет следующий вид:
zi + i =xi-^ lr (xi)-i- Г (*,—Г (*/) Р fa))] P (Xi),
i = 0, I, 2, ...; V(x) = [P' (x)]~\
Каждый метод численного интегрирования порождает
свой итерационный П. в. м. высокого порядка точ-
точности, причем без привлечения производных Р (.г)
порядка выше первой.
Использование методов численного интегрирования
в прямом П. в. м. совместно с корректировкой резуль-
результатов после каждого шага с помощью итерационного
П. н. м. (комбинированный П. в. м.) представляет
собой один из наиболее эффективных методов решения
нелинейных задач.
П. в. м. достаточно хорошо разработан и исследован
для широкого класса задач. Первоначально он был
предложен для систем алгебраич. и трансцендентных
уравнений, интегральных уравнений, дифференциаль-
дифференциальных уравнений обыкновенных и с частными производ-
производными, а затем для решения более общих нелинейных
и операторных уравнений. Изучены условия, при
к-рых гарантируется разрешимость уравнения Р(х)~О
и возможность построения его решения интегриро-
интегрированием задачи Коши B) на интервале |Я0) X*] и уста-
установления области его расположения. Изучены условия
сходимости и даны оценки погрешности. Исследованы
также вопросы применения П. в. м. для обращения
и псевдообращения линейных операторов, построения
псевдорешений (и решений) линейных функциональ-
функциональных уравнений с минимальным уклонением по норме
(в заданном подпространстве) от начального значения,
суммирования операторных рядов и построения нек-рых
классов проекторов, определения начальных прибли-
приближений для итерационных процессов, решения опера-
операторных дифференциальных уравнений н задач линей-
линейной алгебры, для доказательства разрешимости нели-
нелинейных систем, связанных с вариационными задачами,
и построения их решений, минимизации функционалов
и многих других. Изучены обширные классы эффек-
эффективных модификаций П. в. м,, в том числе и с последо-
последовательной аппроксимацией обратного оператора Г (х, X)
или Г (я). Изучены также широкие классы задач
ветвления и нелинейные задачи на собственные зна-
значения. (Впрочем, случай ветвления может быть бло-
блокирован другим способом введения параметра X или
путем введения дополнительного параметра т.) П. в. м.
исследован также как метод «градиентного» типа, а
также без предположения существования Г (.г).
См. также Продолжения пи параметру метод.
Лит.: [1] Д а в и д е н к о Д. Ф., «Докл. АН СССР», 1953,
т. 88, .N» 4, с. 601 — 02; [2] его же, «Укр. матем. ж.», 1955,
т. 7, с. 18—28; [3] Гавурин М. К., «Изв. ВУЗов. Мате-
Математика», 1958, N5 5, с. 18 — 31; [4] Поляк Б. Т., «Ж. вычисл.
матем. и матем. физ.», 19G4, т. 4, JVS в, с. 995 — 1005; [5] Дав и-
д е н к о Д. Ф., «Докл. АН СССР», 1965, т. 162, .№ 3, с. 499—
502; [6] М и х л и н С. Г., Численная реализация вариацион-
вариационных методов, М., 196В; [7] Kleinmichel H., «Mat.li.
Nachr.», 1968, Bd 37, Н. 5/6, S. 313 — 43; [8] К р а с и о с о л ь-
с к и й М. А. [ид р.]. Приближенное решение операторных
уравнений, М., 1969; [91 Лика Д. К., Ш а фи ев V. А.,
«Изв. АН Молд. ССР. Сер. физ.-техн. в матем. наук», 1970,
Л6 2, с. 13—18; [10] Жидков Е. П. [и др.], «Физика эле-
элементарных частиц и атомного ядра», 1973, т. 4, в. 1, с. 127 — 66;
[11] Д а в и д е н к о Д. Ф., «Ж. вычисл. матем. и матем. физ.»,
1975, т. 15, .№ 1, с. 30—47; [12] О рте га Д ж., Р е и н-
болдт В., Итерационные методы решения нелинейных систем
уравнений со многими неизвестными, пер. с англ., М., 1975;
[13] Келлер Г., в кн.: Методы вычислительной и приклад-
прикладной математики, в. 2, Новосиб., 1977, с. 6—30; [14] Д а в и-
денко Д. Ф., в кн.; Математическое программирование и
смежные вопросы. Вычислительные методы, М., 1976, с. 187—
212; [15] Коляда 10. В., Сигорский В. П., «Кибер-
«Кибернетика», 1980, № 3, с. 24—28. Д. Ф. Давиденкч.
ПАРАМЕТРИКСА МЕТОД — один из методов изу-
изучения краевых задач: для дифференциальных урав-
нений с переменными коэффициентами с помощью ин-
интегральных уравнений.
Пусть в какой-либо области G гг-мерного евклидова
пространства R" рассматривается эллиптич. диффе-
дифференциальный оператор порядка т
В равенстве A) символом а обозначен мультииндекс
а= (ах, а2, . . ., ап), где ау — неотрицательные целые
числа, |а[-аН-. . .+«„,?>"=?>?'. . .D*», Dj=-i-?r .
Каждому оператору A) сопоставляется однородный
эллиптич. оператор
10(х0, />)=-• 2, „. aa(x0)Da
с постоянными коэффициентами, где xo?G — произ-
произвольная фиксированная точка. Пусть е(.т, га) обозна-
обозначает фундаментальное решение оператора L0(x(l, D), па-
параметрически зависящее от ,г0, тогда функция е, (х, х0)
ная. параметриксом оператора A) с особен-
особенностью в точке ,г0.
В частности, для эллиптич. оператора 2-го порядка
в качестве параметрикса с особенностью в точке у
может быть взята функция Лев и:
{ ' [Л (х, y)f-», n > 2,
-2>-^<»> B)
В равенстве B) ш„—2яп-/2/Г(н/2), А (у)— определи-
определитель матрицы \\aij(y)\\,
AiAv) — элементы матрицы, обратной к матрице \\aij{y)\\.
Пусть Sx — интегральный оператор
(SXo(f) (х) = ^ G г (х—у, х0) ф (у) dy, C)
действующий на функциях ив Co°(G), и
TXt = SXB\Lb(x0, D)-Hx, D)\.
Поскольку, в силу определения фундаментального
решения,
Lo (x0, D) SXa = SXoLo (x0, Д)=/,
где / — тождественный оператор, то
Это равенство означает, что для каждой достаточно
гладкой и финитной в области G функции ц> справед-
справедливо представление
<p = SX0L(z, D)<p + Txjp D)
и, кроме того, если
то ф является решением уравнения
L (x, /J)q> = /.
Таким образом, вопрос о локальной разрешимости
уравнения Лф=-/ сводится к вопросу об обратимости
оператора /— ТХа.
Ксли применять оператор Тха к функциям ф, к-рые
обращаются в нуль вне шара радиуса К с центром в
точке х0, то при достаточно малом R норма оператора
Тх может быть сделана меньше единицы. Тогда будет
существовать оператор (/—Г^) и, следовательно,
оператор Е= (I— TXo)-1SX(l, к-рый является обратным
к оператору L(x, D). Оператор Е является интеграль-
интегральным оператором, ядро к-рого представляет собой фун-
фундаментальное решение оператора L(x, D).
Параметриксом иногда наз. не только функцию
8 {х, х0), но и интегральный оператор SXg с ядром
8(х, х0), определенный равенством C).
В теории псевдодифференциальных операторов вме-
вместо оператора SXq параметриксом оператора L(x, D)
наз, оператор 5 такой, что I—L(x, D)S и I—SL(x, D)
являются интегральными операторами с бесконечно
дифференцируемыми ядрами. Если же таким опера-
оператором является лишь оператор I—SL (или /—LS),
то S наз. левым (соответственно правым) параметрик-
оом оператора L(х, D). Иначе говоря, оператор SХи
в равенстве D) является левым параметриксом, если
оператор ТХа в этом равенстве имеет бесконечно диф-
дифференцируемое ядро. Если у оператора L(x, D) сущест-
существуют левый параметрикс S п правый парамотрикс S",
то каждый из этих операторов является параметрик-
параметриксом. Существование параметрикса доказано для гипо-
эдлиптических псевдодифференциальных операторов
(см. [3]).
Лит.: [1] Б ер с Л., Джон Ф., Ш е х т е р М., Урав-
Уравнения с частными производными, пер. с англ., М., 1960; [2]
Миранда К., Уравнения с частными производными эл-
эллиптического типа, пер. с итал., М., 1957; [3] X 6 р м а н-
дер Л., в сб.: Псевдодифференциальные операторы, М., 1967.
Ш. А. Алимов.
ПАРАМЕТРИЧЕСКИХ ИНТЕГРАЛЬНЫХ ПРЕД-
ПРЕДСТАВЛЕНИЙ МЕТОД — метод в геометрич. теории
функций комплексного переменного, использующий
для решения экстремальных задач в классах функций
представление этих классов с помощью интегралов,
зависящих от параметров.
К таким классам относятся Каратеодори класс,
класс однолистных звездообразных в круге функций,
класс типично вещественных функций. Функции этих
классов имеют парамотрич. представление, содержащее
интеграл Стилтьеса
**(«, t)d[i(t)
с заданными действительными числами а, Ь и функцией
g(z, t) (ядро класса), ц(«)?Ма ь, где Ма,ь —класс
функций, не убывающих на промежутке (a, b\, [i(b) —
—ц(о) = 1 (ц — параметр класса).
Для классов функций, имеющих параметрич. пред-
представление с помощью интегралов Стилтьеса, получены
вариационные формулы, к-рые при решении экстре-
экстремальных задач в этих классах показывают, что экс-
экстремальная функция имеет вид
где 'ь?[я, Ь] причем указывается значение т (см. fl]
гл. 11; [3]).
При нахождении областей значений функционалов
и систем функционалов на таких классах иногда по-
полезны следующие теоремы.
1) Множество В точек х~ (х,, хг, . . ., хп) я-мерного
евклидова пространства R", допускающих представ-
представление
xk^^auk(i)d\x(t), A=-l, 2, ... п,
где uk{l) — фиксированные непрерывные на [a, ft|
действительные функции и [д. (<) gJWд_ ь, совпадает с
замкнутой выпуклой оболочкой R{U) множества U
точек
хк^икA)< * = 1, 2, ..., п, a<t<b
(теорема Рисе а).
2) Каждая точка х= (хи х2, . . .,
может быть представлена в виде
где ?iy>0, /—-1, 2, . . ., m, 2fLi\j=i, m<re+l, а если
x?dR(U), то го<ге (теорема Каратеодори).
3) Для того чтобы существовала, но крайней мере,
одна неубывающая функция [i(t), а<:г<Л, такая, что
Wfc (t) d^i (t) =^ Yfe, к~ 1, 2, ..., л,
где
1(),k()k() + k();k(),tt(), ,, ,,
— заданные действительные непрерывные на [а, Ъ]
функции, Yi>0, Yfc — заданные комплексные числа,
необходимо и достаточно, чтобы всякий раз, когда при
нек-рых комплексных числах а3, а2, . . ., сс„ выпол-
выполняется неравенство
2L: @] =&0, a
имело место также и неравенство
(теорема Р и с с а).
Приведенные теоремы позволили дать геометрич.
и алгебраич. характеристики областей значений си-
систем коэффициентов и отдельных коэффициентов на
классах функций, регулярных и имеющих положи-
положительную действительную часть в круге (кольце), регу-
регулярных и типично вещественных в круге (кольце) и на
нек-рых других классах (см. [1] Добавление; [4], [5]).
Лит.: И] Г о л у а и н Г. М., Геометрическая теория функ-
функций комплексного переменного, 2 изд., М., 1966; [2] К р е йн
М. Г., «Успехи матем. наук», 1951, т. 6, в. 4, с. 3—120; [3]
Лебедев Н. А., Александров И. А., «Тр. Матем.
ин-та АН СССР», 1968, т. 94, с. 79—89; 14] Г о л у з и н а Е. Г.,
там же, с. 33—46; Ы ее ж е, «Зап. науч. семинаров Ленингр.
отделения Матем. ин-та АН СССР», 1972, т. 24, с. 29—62; 1974,
т. 44, с. 17—40; 1980, т. 100, с. 17 — 25. Е. Г. Голузина.
ПАРАМЕТРИЧЕСКИХ ПРЕДСТАВЛЕНИЙ МЕ-
МЕТОД — метод теории функций комплексного пере-
переменного, возникший из параметрического представле-
представления однолистных функций и базирующийся большей
частью на Лёвнера уравнении и его обобщениях (см.
[1]). Самим К. Лёвнером (К. Lowner) П. п. м. исполь-
использовался на классе S всех регулярных однолистных
в единичном круге функций ш=/(г), /@) —0, /'@)=1,
для оценки коэффициентов разложений
+ • ¦ • -\-bnwn~\-...
(см. Бибербаха гипотеза). Затем П. п. м. систематиче-
систематически применял Г. М. Голузин при решении проблем
искажения, вращения, взаимного роста и других
геометрич. характеристик отображения w—f(z), свя-
связанных со значениями / (z0) и /' (z0) при фиксированном
%, Ь„1<1.
П. п. м. связан с теорией оптимальных процессов.
Эта связь базируется на том факте, что аналитически
все упомянутые выше задачи формулируются как эк-
экстремальные задачи для управляемой системы обыкно-
обыкновенных дифференциальных уравнений, получаемой из
уравнения Лёвнера. Использование принципа мак-
максимума Понтрягина (см. Понтрягина принцип макси-
максимума) и изучение свойств функции Понтрягина по-
зволяют изучить ряд новых задач на классе S и его
подклассах вплоть до их полного решения либо по-
получить результаты, сравнимые (напр., в проблеме
Бибербаха) с результатами, найденными другими
методами (см. [1] п. 74).
Лит.: [1] Александров И. А., Параметрические
продолжения в теории однолистных функций, М., 1976.
В. И. Попов.
ПАРАМЕТРИЧЕСКОГО РЕЗОНАНСА МАТЕМАТИ-
МАТЕМАТИЧЕСКАЯ ТЕОРИЯ — раздел теории обыкновенных
дифференциальных уравнений, изучающий явление па-
параметрич. резонанса.
Пусть S — нек-рая динамич. система, способная
совершать лишь колебательные движения и описыва-
описываемая гамильтоновои системой линейной (вевоэмущев-
нмм уравнением)
О -/*
/* о
с постоянным действительным гамильтонианом ff0.
Таким образом, BkX 2Л:)-матрица J~1Hn приводится
к диагональному виду с чисто мнимыми злементами
| o)v | — собственные частоты системы. Пусть нек-рые
параметры системы S начинают периодически изме-
изменяться с частотой г*^>0 и малыми амплитудами, зна-
значения к-рых определяются малым параметром е>0.
Если возбуждения не выводят из класса линейных га-
мильтоновых систем, то движение системы S будет
описываться возмущенным уравнением
Jx— [Яо + effj (Щ-\-г2П2 (Ы)-\- ¦ ¦ -\х, A)
где Hj(s+2n)=Hj(s) — Hj(s)*, /=1, 2, . . ., суть ку-
кусочно непрерывные, интегрируемые в @,2я) Bкх2к)~
матрицы-функции, и ряд в правой части A) сходится
при е<г0, где г0 не зависит от t.
Возникновение неограниченно возрастающих коле-
колебаний системы S при сколь угодно малом периодич.
возмущении нек-рых ее параметров наз. парамет-
параметрическим резонансом. Параметрич. резо-
резонанс имеет две существенные особенности: 1) спектр
частот, при к-рых возникают неограниченно возраста-
возрастающие колебания, не является точечным, а состоит из
совокупности малых интервалов, длины к-рых зависят
от амплитуды возмущений (т. е. от е) и к-рые стяги-
стягиваются в точку при е —>- 0; значения частот, к к-рым
стягиваются эти интервалы, наз. критическими;
2) колебания нарастают не по степенному, а по экспо-
экспоненциальному закону. Этим параметрич. резонанс
намного «опаснее» (или «полезнее», в зависимости от
задачи) обычного резонанса.
Пусть 1Щ, . . ., гш? — собственные значения 1-го
рода, перенумерованные так, что сог<со2<:. . .<:ш^.
Тогда критическими могут быть лишь частоты вида
¦&/й)=-^-|Шу-|-шА|, /, h~i,..., к; т^-Л, 2, ... B)
Пусть собственные векторы /v матрицы J~lHa, для
к-рых J-^-HJv — itih/fv , v= T1 Т/с, нормированы
у р /v рц п, д
рых /-YHufv — !G>V/v , v=T 1, . . ., ^k, нормированы
так, что
v, v,
где 6V|x — символ Кронекера, а
Тогда области неустойчивости в первом приближении
по е определяются неравенствами
..., C)
где
Х_,_ ,
Если j—h, то область неустойчивости отвечает основ-
основному резонансу, при }ФЪ — комбина-
комбинационно м у резонансу. Величина 1х-/л'1 ха~
растеризует «степень опасности» критич. частоты
#(Д"'- чем больше эта величина, тем шире «клинышек»
неустойчивости C) с острием в точке ¦&'$ . Установ-
Установлена аналитнт. зависимость границ областей неустой-
неустойчивости от параметра е и получены эффективные фор-
формулы для вычисления областей C) во втором при-
приближении (см. [3], [4]).
Li часто встречающемся в приложениях случав,
когда возмущенная система S описывается векторным
уравнением 2-го порядка
,Н-[Л> + рР1 {Щ + е2Р2 (#/)+...] у=0, E)
где Р„*-Р0>0иЯ/(«)*-Ру(«)=Яу-(«+2л),/=1,2, . . .,
собственные векторы и собственные значения (квадраты
частот невозмущенной системы) матрицы Ро определяют
формулами
Пусть
Тогда формулы B) и D) примут вид
соответственно. В частности, в базисе еи . . ., ек,
где Ро диагональна:
i, ..., рк)
имеет место:
и, следовательно (см. [5]):
л-у-У 2@^. J7/ • ЛЛА - 2o)ft ^ '
Рассмотрен случай нелинейной зависимости коэф-
коэффициентов уравнений A) и E) от параметра 1/f> (см.
[А]). Изучен параметрич. резонанс в линейных систе-
системах, близких к гамильтоновым (см. [6]). Здесь обла-
областям основного резонанса предшествуют области глав-
главного резонанса, а наряду с областями комбинацион-
комбинационного резонанса появляются области комбинационно-
разностного резонанса. Для параметрич. резонанса в
линейных распределенных системах (см. [7]) получен
ряд аналогичных результатов для операторных урав-
уравнений A) в гильбертовом пространстве. Исследовался
параметрич. резонанс для нек-рых классов систем с
конечным числом степеней свободы, описываемых нели-
нелинейными дифференциальными уравнениями (см. [8\).
Лит.: Ц] К р е й н М. Г., в кн.: Памяти Александра Алек-
Александровича Андронова, М., 1955, с. 413—98; [2] Якубо-
Якубович В. А., «Докл. АН СССР», 1958, т. 121, J41 4, с. 002—05;
[3] его ж е, в кн.: Методы вычислений, в. 3, Л., 1966, с. 51 —
69; [4] Якубович В. А., Старшинский В. М., Ли-
Линейные дифференциальные уравнения с периодическими коэф-
коэффициентами и их приложения, М., 1972; 15] М а л к и н И. Г.,
Некоторые задачи теории нелинейных колебаний, М., 195ц;
[6] С т а р ж и н с к и й В. М., «Инженерный ж. Механ.
тверд, тела», 1967, т. 3, с. 174—80; 17] Фомин В. Н., Мате-
Математическая теория параметрического резонанса в линейных
распределенных системах, Л., 1972; [8] Шмидт Г., Парамет-
Параметрические колебания, пер. с нем., М., 1978.
В. М. Старжипский.
ПАРАМЕТРИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ в тео-
теории однолистных функций — представ-
представление однолистных функций, осуществляющих кон-
конформное отображение плоских областей на области
канонич. вида (напр., на круг с концентрич. разре-
.чами); оно возникает обычно следующим образом.
Выбирается однопараметрич. семейство областей Qi,
()«<?', вложенных друг в друга, <?(,с<?(, 0«7'<t<7\
Для области Qu предполагается известным ее кон-
конформное отображение /„ на нек-рую канонич. область
fi0. По известному отображению /( области (?| на об-
область канонич. вида строится такое же отображение
fi+e для области Qt + e, где е>0 и мало. При непре-
непрерывном изменении параметра t на этом пути возни-
возникают дифференциальные уравнения, наиболее извест-
известными из к-рых являются Лёвнера уравнение и урав-
уравнение Лёвнера — Куфарева. В дискретном случае —
для сеточных областей Qf и натурального параметра
t — переход от отображения // K отображению ft+e,
r— 1, осуществляется по рекуррентным формулам.
Источником упомянутых формул и уравнений служит
обычно формула Шварца (см. [1] с. 92) и ее обобщения
(см. [2]). Не менее важным источником П. п. служат
вариации Адамара (см. [3], [4]) для функций Грина
G/(z, г'), г, z' ?<?/, указанного выше семейства обла-
областей. Метод Адамара наз. также методом инва-
инвариантного погружения (см. [5]) для эл-
эллиптических дифференциальных уравнений. Ниже по-
показана связь П. п., вариаций Адамара и инвариантного
погружения в простейшем (дискретном) случае.
Пусть Q — нек-рый набор целых комплексных чи-
чисел (сеточная область) и функция Грина
Gf (г, г') — экстремаль функционала Дирих-
Дирихле — Дугласа
It (g)^2g (*') + 2Lo 2ге Qo Р* W I ^^ (*) |2
в классе Др всех действительных на Q функции g(z).
Здесь Q0-={z\z, z-\, z-i, z-\-i?Q),
Vo? («)—g (z) — g (г — 1 — i), Vxg («) = <? (z — 1) — g (г — i),
(i)
N — натуральное число, b\ — символ Кронекера и
St= (kti zl)i t=0, 1, . . ., Г—1,—нек-рый набор пар
чисел; {zf\t—i, . . ., Т] — граница области Qt, /c/ = 0
или 1. Нахождение экстремума функционала /;(#) —
задача квадратичного программирования. Сравнение
ее решений при t и t-\-i дает основную фор-
формулу инвариантного погружения
(вариацию Адамара):
Gt + 1( z, z')=-Gt (z, z') i- V^G, (zt, z) sskGt (zt, z'),
B)
где Cf—N-1— V/, VftG((r.;, z<)>0, символ v^ означает
разностные операторы A) по второму аргументу функ-
функции Грина. Зная функцию G0(z, z'), можно шаг за шагом
(рекуррентно) получить по формуле B) все функции
Gt(z, z'), t—\, . . ., Т. Достроив функцию Грина до
сеточно аналитич. функции jT(z)~GT(z, z')-LiHT(z, z')
согласно уравнениям типа Коши — Римана
получают однолистное сеточно-квазиконформное ото-
отображение w~ exp[2n/7-(z)) области Q-p в единичный
круг. Ближайшим к началу координат будет образ
точки z'. В пределе при N -*¦ оо отображение сеточно-
ко'нформно и образом области QT служит круг с кон-
центрич. разрезами. Получен непрерывный аналог
формулы B) (см. [6]). В случав, когда все области Gf
односвязны и канонич. областью служит единичный
круг В, удается, используя дробно-линейные автомор-
автоморфизмы круга В, представить функцию Грина в явном
виде
Gt (z, z') = ln | 1-ft (z) /TFTl-ln | ft (z)-h (O I
через функцию ft (г), отображающую Qt на В с норми-
нормировкой /@)=0, O?Qt Для всех <€№, т)-
В терминах отображения w~ft(z) вариация Ада-
мара сводится к обыкновенному дифференциальному
уравнению (Лёвнера). По сравнению с вариацией Ада-
мара dto уравнение значительно проще, однако ин-
информация о границе области Qt представлена в нем
неявно —• через управляющий параметр a(<)=arg/j(zt)i
поскольку функция ft(z) заранее неизвестна. Тем не
менее уравнение Лёвнера — основной инструмент П. п.
Были рассмотрены более общие однопараметрич.
семейства областей Qt, Q<.t<_T, не обязательно вло-
вложенных друг в друга (см. [7]). Возникающие при таких
П. п. уравнения наз. уравнениями К у ф а-
рова — Лёвнера. Существуют также модифика-
модификации уравнений Лёвнера и Куфарева — Лёвнера на те
случаи, когда области Qt обладают различного рода сим-
метриями или иными геометрич. особенностями (см. [1]).
Лит.: [1] Го л у зин Г. М., Геометрическая теория
функций комплексного переменного, 2 изд., М., 1906; [2] Аде к-
о, а н Д Р о Bi И. А., С о р о к и н А. С, «Сиб. матем. ж.», 1972,
т. 13, N, 5, с. 971 — 1001; [3] Н а й a m a T d J., Memoire sur le
probleme d'analyse relatif к l'equilibri des plaques elastiques en-
cnstrees, P., 1908; [4] его >к e, Lecons sur le ealcul des varia-
variations, v. 1, P., 1910; [5] Беллман Р.,Энджел Э., Дина-
Динамическое программирование и уравнения в частных производ-
производных, пер. с англ., М., 1974; [б] П о п о в В. И., «Докл. АН
СССР», 1972, т. 207, К. 5, с. 1048—50; [7] К у ф а р е в П. П.,
«Матем. сб.», 1943, т. 13, № 1, с. 87—118. В. И. Попов.
ПАРАМЕТРИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ функ-
функции — эадание функции y—f(x), определенной, напр.,
на отрезке [а, Ь] с помощью пары функций а--— ср(/),
2/=i|)(i), t?[a, f$], таких, что у функции ср : [а, [5]-у
—>- [а, Ь\ существует такая однозначная обратная
функция ср : [а, Ъ] —у [а, р], что /=г|зоф-') т. е.
для любого х?[а, Ь] имеет место
/(«)=!)) [ф-1 (Ж)].
П р и м е р. Пара функций x~cost, j/=sinf, 0<*<я,
является П. ц. функции у=\г\—х2, —1<х<1.
Если и точке tu?[a, b] П. и. функции/ дифференци-
дифференцируемо, т. е. функции фи\|) дифференцируемы, и ф' (t0) ф
Ф0, то параметрически представленная функция / диф-
дифференцируема в точке xo=4>(to) и /' (io)=i|)' (@)/ф' (t0).
Если, кроме того, у функций ipaifB точке t0 сущест-
существуют производные порядка п, н—2, 3, . . ., то и у
функции / в точке х0 существует производная порядка
п, причем она является дробно-рациональной функ-
функцией от производных функций ф и г)} порядков к, к^ 1,
2, . . ., п, в знаменателе к-рой стоит Bге—1)-я степень
значения производной ф'(<0), напр.,
' (х°> - 1ф'('о)]3 ~~ •
Л. Д. Кудрявцев.
ПАРАМЕТРИЧЕСКОЕ ПРОГРАММИРОВАНИЕ —
раздел математического программирования, посвящен-
ный исследованию задач оптимизации, в к-рых ус-
условия допустимости и (или) целевая функция зависят
от нек-рых детерминированных параметров. (Задачи,
в к-рых эти параметры являются случайными, состав-
составляют предмет стохастического программирования.)
В общем виде задача П. п. заключается в максими-
максимизации целевой функции f(x, X) по всем х= (xlt . . .,
¦rn) € "^"i удовлетворяющим ограничениям
gt(x, %Xbi(k), i=l, ..., т, A)
где X — врктор параметров, принадлежащий нек-рому
заданному множеству параметров ЛсК^. При любом
фиксированном X эта задача представляет собой обыч-
обычную задачу математич. программирования. Пусть
Л'сЛ — множество тех значений X, при к-рых эта
задача разрешима (множество разрешимо-
разрешимости). Оптимальное решение х* = х\ естественным
образом является функцией от X. Под решением
задачи П. п. понимается семейство {х%} при всех
Х'
Источники задач П. п. довольно разнообразны. Это
прежде всего стремление отразить определенный про-
произвол, с к-рым нередко бывают определены все или
нек-рые исходные данные практической оптимизаци-
оптимизационной задачи, либо охватить единой формулировкой
несколько связанных между собой вариантов задачи
(или целое семейство задач, напр., зависящих от вре-
времени). П. п. является наиболее адекватным способом
постановки важной проблемы устойчивости решений за-
задач оптимизации относительно вариаций тех или иных
исходных данных. Наконец, с задачами П. п. тесно
связана проблема нахождения множества оптимумов
Парето в задачах многокритериальной оптимизации.
Если при любом фиксированном X задача П. п. пред-
представляет собой задачу линейного программирования
(выпуклого программирования и т. п.), то говорят о за-
задаче линейного (соответственно выпуклого
и т.п.) параметрического программи-
программирования. В общем виде проблематику П. п. мож-
можно охарактеризовать следующим образом. 1) Нахож-
Нахождение и выяснение свойств множеств разрешимости Л'.
2) Нахождение областей устойчивости решений, харак-
теризация их строения; анализ поведения неустойчи-
неустойчивых задач. 3) Характеризация зависимости оптималь-
оптимального значения целевой функции от вектора параметров.
В полном своем объеме (т. е. для произвольных це-
целевых функций, ограничений и областей изменения
параметров Л) эти задачи весьма трудны. Достаточно
продвинуты в теоретическом и вычислительном отно-
отношении лишь нек-рые частные их классы. В основном
эго касается задач линейного П. п., в к-рых: либо
а) целевая функция линейно зависит от одного скаляр-
скалярного (Л=К1) параметра, либо б) правые части огра-
ограничений линейно зависят от одного параметра, либо
в) целевая функция и правые части ограничений ли-
линейно зависят от двух независимых скалярных пара-
параметров или от одного и того же параметра, г) целевая
функция линейно зависит от векторного параметра,
д) правые части ограничений линейно зависят от
векторного параметра. Случай зависимости от пара-
параметров матрицы ограничений задачи линейного про
граммирования весьма сложен и пока A983) иссле-
исследован недостаточно. Для случая а), напр., решение
указанных проблем 1) — 3) характеризуется следую-
следующим образом. Пусть требуется максимизировать
при условиях
I',-, i- {,..., т; xjZ-0, i - 1,..., п,
где Я?Л~ R1. Тогда существует такое разбиение Л
на коночное число открытых слова интервалов: Л-~
= Ui=i-^* (гДе интервал Л1 неограничен слева, AQ не-
неограничен справа, причем возможен случай совпа-
совпадения одного из них с Л), что при всех X?Ak соответ-
соответствующая задача линейного П. и. разрешима, причем
на каждом интервале Л*, к—А, . . ., q, она имеет один
и тот же базис. Исключение могут составлять лишь
интервалы Л1 и А9, на к-рых целевая функция B)
может быть неограниченна. Таким образом, в данной
задаче множество разрешимости Л' представляет
собой объединение всех Л* за возможным исключением
Л1 и (или) Ач. Далее, оптимальное значение целевой
функции на каждом ЛА, к=\, . . ., ц, является выпук-
выпуклой кусочно линейной функцией параметра X.
Численные методы решения однопараметрических
(Л=Ка) задач линейного П. п. представляют собой
модификации симплексного метода; в случае много-
многомерного пространства параметров приходится привле-
привлекать более сложные соображения.
Лит.: [1] Г о л ь ш т е й н Е. Г., К) д и н Д. Б., Новые
направления в линейном программировании, М., 1966; [2] Theo-
rie der linearen parametrischen Optimierung, В., 1974.
А. А. Корбут.
ПАРАМЕТРИЧЕСКОЕ УРАВНЕНИЕ множест-
множества точек пространства — задание точек
этого множества или их координат в виде лначений
функций нек-рых переменных, называемых пара-
параметрами.
Параметрич. задание прямой в n-мерном векторном
пространстве R" имеет вид
, a?R", — со < t < + со, A)
где xw и а — фиксированные векторы, z<0> — началь-
начальный вектор, а а?=0 — направляющий вектор, парал-
параллельный прямой. Если и R" задан базис и координаты
вектора х обозначаются через xlt . . ., хп, то уравнение
A) в координатной форме имеет вид
*fc= 40>-гв*|*. —оо < t < + со, /с=т1, 2, ..., п.
Параметрич. задание да-мерной гиперплоскости п
R" имеет вид
B)
a</)g/?n, _«,< *y. <-f со, ; = 1, 2, ..., m,
гдр г<0) — начальный вектор, соответствующий нуле-
нулевым значениям параметров tj, а аA), . . ., а{т) - ли-
линейно независимая система т векторов, параллельных
рассматриваемой гиперплоскости. В координатной фор-
форме уравнение B) имеет вид
/ = 1, 2, ..., т, к=-А, 2, ..., п.
Параметрич. задание m-мерной поверхности в R"
имеет вид
r=x(t)=-..r(tu ..., tj, t = (tlt..., g^cR»,C)
где Е — напр., замыкание нек-рой области т-мерного
пространства R"', а х :?'—>. R" — отображение не-
к-рого класса: непрорывное, дифференцируемое, не-
непрерывно дифференцируемое, дважды дифференциру-
дифференцируемое и т. д., в зависимости от чего рассматриваемая
т-мерная поверхность также паз. соответственно не-
непрерывной, дифференцируемой и т. д. В случае т=4
множество Е является отрезком: Е—\а, Ь] и П. у. C)
превращается в П. у. кривой: x~x(t), a<:i<:6, в про-
пространстве К". Напр., ^!==cos t, z2=sin t, 0<г<2я,
является П. у. на плоскости окружности единичного
радиуса с центром в начале координат.
В качество множества К, на к-ром задано рассмат-
рассматриваемое параметрич. представление, иногда вместо
замыкания m-мерной области берутся подмножества
пространства Rm другой природы. л. Д. Кудрявцев
ПАРЕТО РАСПРЕДЕЛЕНИЕ — непрерывное распре-
распределение вероятностей с плотностью
У 0,
зависящей от параметров жо>О и а>0. В такой «усе-
«усеченной» трактовке П. р. выделяется как самостоя-
самостоятельное распределение из семейства бета-распределе-
бета-распределений 2-го рода с плотностью
при н = 1. Для любого фиксированного х„ П. р. сио
дится преобразованием ,т= -i-2 к бета-распределению
1-го рода. В системе Пирсона кривых П. р. принад-
принадлежит к распределениям «типа VI» и «типа XI». Мате-
Математическое ожидание П. р. конечно при а>1 нравно
а.го/(сс—1); дисперсия конечна при а>2 и равна
а.го/(а—1JХ (а.—2); медиана равна 21/а.г0.Функция рас-
распределения П. р. определена формулой
Р{Х <x} = i-(^-Y , х>хй,а>0.
П. р. получило широкое распространение в различ-
различных задачах экономич. статистики начиная с работ
В. Парето (W. Pareto, 1897) о распределении доходов.
Считалось, что П. р. достаточно хорошо описывает
распределение доходов, превышающих нрк-рый уро-
уровень, в том смысле, что ато распределение должно
иметь хвост порядка 1/ха, при х —*- оо.
Лит.: [1] Крамер Г., Математические методы статис-
статистики, пер. с англ., 2 изд., М., 1975. Л, В. Прохоров.
ПАРИКМАХЕРА ПАРАДОКС — то же, что анти-
антиномия «деревенский парикмахер».
ПАРСЕВАЛЯ РАВЕНСТВО — равенство, выражаю-
выражающее квадрат нормы элемента в векторном пространство
со скалярным произведением через квадраты модулей
коэффициентов Фурье этого ялемента по нек-рой ор-
ортогональной системе элементов; так, если X — норми-
нормированное сепарабельное векторное пространство со
скалярным произведением (¦), || • || — соответствующая
ему норма и {«„} — ортогональная и X система, е„#0,
л=1, 2, ..., то равенством Парсеваля
для элемента х?Х наз. равенство
2 "
2 "=
где ап— ' , п~ 1, 2, . . .,— коэффициенты Фурье
элемента х по системе {<?„}• Если эта система {еп}
ортонормирования, то П. р. имеет вид
Выполнение П. р. для. данного элемента .г?Х явля-
является необходимым и достаточным условием того, чтобы
ряд Фурье этого элемента но ортогональной системе
{еп} сходился к самому элементу .г по норме про-
пространства X. Выполнение П. р. для любого элемента
х^Х является необходимым и достаточным условием
для того, чтобы ортогональная система {е„} была пол-
полной системой в X. Отсюда следует, в частности:
если X — сепарабельное гильбертово пространство
11 {еп} — его ортонормированный базис, то П. р. по
системе {еп} выполняется для каждого элемента х?Х;
если X — сепарабельное гильбертово пространство,
xf-Х, у?Х, {еп} — ортонормированный базис в X,
о„= (х, е„) и Ьп-= (у, еп) — коэффициенты Фурье
соответственно элементов х и ;/, то справедливо ра-
равенство
наз. обобщенным равенством Парсе-
в а л я. В достаточно законченном виде вопрос о
полноте систем функций, являющихся собственными
функциями дифференциальных операторов, был изу-
изучен В. А. Стендовым [1].
П. р. обобщается и на случай несепарабельных
гильбертовых пространств: если {еа}, а?Ж (Ж нек-рое
множество индексов), является полной ортонормиро-
ванной системой гильбертова пространства X, то для
любого элемента х?Х справедливо П. р.
(г, ж)=2а6,(|(*, еа)\",
причем сумма в правой части равенства понимается как
где верхняя грань берется по всевозможным конечным
подмножествам Шп множеств;) 3L
В случае, когда X~-L2\—я, я] состоит из действи-
действительных функций, квадрат к-рых интегрируем но Лебе-
Лебегу на отрезке [—я, я], /?i-2l—Л1 л]> в качестве полной
ортогональной системы взята тригонометрич. система
функций и
равенство A) имеет вид
и наз. классическим равенством Пар-
Парсе в а л я; оно было указано М. Парсевалем
(М. Parseval, 1805).
Если #?12[—я, я) и
g ~ — + Zin= i ап f0S " z + lin si» nr,
то равенство, аналогичное формуле B), выглядит сле-
следующим образом:
2Г=1 (Wn + bM- C)
Классы К я К' действительных функций, опреде-
определенных на отрезке [—я, я], такие, что для всех f?K
и g?K имеет место обобщенное П. р. C), наз. допол-
дополнительными. Примером дополнительных классов яв-
являются пространства Lp\—я, я] и
Lp,[—n, я], J- + J^ = l, 1<р< + оо.
Лит.: [1] С текло в В. А., «Записки физико-математич.
общества», сер. 8, 1904, т. 1.1, М 7, с. 1—32; [2] Никол г,-
с к и Й С. М., Куре математического анализа, 2 изд., т. 2, М.,
1У75; 13] Ильин В. А., II о з н я к Э. Г., Основы математи-
математического анализа, 2 изд., ч. 2, М., 1980; ['il Бари Н. К.,
Тригонометрические ряды, М., 1961; 15] Зигмунд А.,
Тригонометрические ряды, пер. с англ., т. 1, М., 19К5; [ti]
Кириллов А. А., Г в в ш и а н и А. Д., Теоремы и за-
задачи функционального анализа, М., 1979. Л. Д. Кудрявцев.
ПАРСЕВАЛЯ — ПЛАНШЕРЕЛЯ ФОРМУЛА — см.
Планшереля теорема,
ПАСКАЛЕВА ГЕОМЕТРИЯ — геометрия плоскости,
построенной над полем (коммутативным телом). На-
Название этой геометрии связано с тем, что в этой гео-
геометрии на плоскости выполняется конфигурационное
предложение Пап па — Паскаля: если
точки 1, а, 5 н 2, 4, 0 соответственно лежат на прямых
(коллинеарны), то точки пересечения пар прямых
A, 2) и D, 5), B, 3) и E, 6), C, 4) и F, 1) — точки 9, 7,
8 — также лежат на одной прямой при любом выборе
системы образующих
точек 1, 3, 5 на од-
одной прямой и 2, 4,
в — на другой пря-
прямой, отличной от пер-
первой (см. рис.). Важней-
Важнейший частный случай
этого предложения (в
аффинной плоскости)
утверждает: из того, J в 2
что прямая D, 3) па-
параллельна F, 5) и прямая F, 1) параллельна B, 3),
следует параллельность прямых B, 5) и D, 1).
П. г. плоскости может быть построена над беско-
бесконечными или конечными полями, соответственно этому
плоскость наз. бесконечной или конечной паска-
левой плоскостью.
Впервые важную роль предложения Паскаля в
построении геометрич. систем над бесконечными по-
полями исследовал Д. Гильберт (D. Hilbert, см. [1]),
к-рый устанавливал доказуемость предложения Па-
Паскаля при различных наборах аксиом из системы
аксиом евклидова пространства. Д. Гильберт показал,
что Паскаля теорему в бесконечной плоскости можно
доказать с помощью плоскостных акеиом инцидент-
инцидентности, порядка, конгруэнтности, параллельности и
непрерывности, причем было установлено, что без
аксиом непрерывности в этом случае теорему Паскаля
доказать нельзя.
Опираясь же на пространственные аксиомы системы
Гильберта, теорему Паскаля можно доказать без
аксиом конгруэнтности, но обязательно с применением
аксиом непрерывности (исключение аксиом непрерыв-
непрерывности в бесконечной плоскости приводит к непасна-
левой геометрии). Возможность доказательства тео-
теоремы Паскаля аналогична в указанном смысле воз-
возможности доказательства Дезарга предложения с ис-
использованием пространственных аксиом, однако в
доказательстве теоремы Паскаля проявляется особая
роль аксиом непрерывности Архимеда в бесконечных
плоскостях (см. Неархимедова геометрия).
Предложение Паппа — Паскаля проективно выпол-
выполняется в нек-рой плоскости тогда и только тогда, когда
умножение во всех натуральных телах этой плоско-
плоскости обладает коммутативным свойством, или иначе:
натуральное тело всякой паскалевой плоскости яв-
является полем и, наоборот, плоскость, построенная над
полем, обладает П. г. Поэтому П. г. иногда наа. гео-
геометрией с коммутативным умноже-
п и е м. Таким образом, в паскалевой плоскости кон-
конфигурационное предложение Паппа — Паскаля имеет
алгебраич. инвариант, выражающий коммутативное
свойство умножения в множестве, над к-рым построена
эта плоскость.
В любой проективной плоскости теорема Паппа —
Паскаля влечет за собой предложение Дезарга.
Конечная цаскалова плоскость как конечная про-
проективная плоскость существует только в случае,
если число точек, лежащих на каждой прямой этой
плоскости, есть ps+l, где р — простое, s — нату-
натуральное число. Так как всякое конечное альтерна-
альтернативное тело является полем, то в конечной плоскости
предложение Дезарга влечет за собой теорему Пап-
Паппа — Паскаля, причем последняя является следствием
т. н. малой теоремы Дезарга. Вместе с тем существуют
конечные проективные плоскости, являющиеся не-
паскалевыми. Паскалева плоскость изоморфна двойст-
двойственной себе плоскости.
Значение П. г. определяется ее ролью при исследо-
исследовании независимости системы аксиом, в частности
системы аксиом Гильберта евклидовой геометрии. При
построении бесконечной плоскости на основе групп
аксиом инцидентности, порядка и параллельности
предложение Паппа — Паскаля должно рассматри-
рассматриваться как дополнительная аксиома. С другой стороны,
с помощью комбинаций конечного числа конфигураций
Паппа — Паскаля оказывается возможным решить
задачи на построение, в к-рых используется лить
ионятие инцидентности и, может быть, параллель-
параллельности.
Лит.: 11] Гильберт Д., Основания геометрии, пер.
с нем., М.— Л., 1948; [2] Bieberbacb. L., Einleitung in
die hohere Geometric, Lpz., 1933; [3] Скорняков Л. А.,
«Успехи матем. наук», 1951, т. 6, в. 6, с. 112—54; [4] D e m-
bowiki P., Finite geometries, В.— [и. а.], 1968; [5] Rei-
demeister К., Grrnidlagen der Geometrie, В., 1930; [(>]
Ар тин 3., Геометрическая алгебра, пер. с англ., М., 19В'.).
ПАСКАЛЯ РАСПРЕДЕЛЕНИЕ — дискретное рас-
распределение вероятностей случайной величины X, при-
принимающей целые неотрицательные значения к—О, 1,
2, ... в соответствии с формулой
где 0<р<1 и целое г>0 — параметры.
Производящая функция и характеристич. функция
П. р. равны соответственно
f(t)=pr(i — qeit)-ry <7=-1— Р-
Математич. ожидание и дисперсия суть rg/р и rq/p2.
П. р. с параметрами г и р возникает естественным
образом в схеме Бернулли испытаний с вероятностью
«успеха» р и вероятностью «неудачи» </=1—р как
распределение числа «неудач» до наступления г-го
«успеха». При г—1 П. р. совпадает с геометрическим
распределением с параметром р, а при г>1 — с рас-
распределением суммы независимых случайных величин,
имеющих одинаковое геометрич. распределение с па-
параметром р. В соответствии с этим сумма независимых
случайных величин Хг, . . ., Хп, имеющих П. р. с
параметрами р и гь . . ., гп соответственно, имеет П. р.
с параметрами р и гг-\-. . .+г„.
Функция распределения П. р. при fe=0, 1, 2, ...
задается формулой
р (ь\ —
\ р Тг -11\ т
jo'T A x
\
В (г, ft+1) jo'
где в правой части стоит значение функции бета-рас-
бета-распределения в точке p(B(r, k-\-i) — бета-функция).
Используя это соотношение, можно доопределить
F (к) для всех действительных г>0. В таком обобщен-
обобщенном смысле П. р. наз. отрицательным биномиальным
распределением.
Лит.: [1] Феллер в.. Введение в теорию вероятностей
и ее приложения, пер. с англ., 2 изд., т. 1, М., 1967.
А. В. Прохоров.
ПАСКАЛЯ ТЕОРЕМА: противоположные стороны
шестиугольника, вписанного в линию 2-го порядка,
Рис. 1.
пересекаются в трех точках, лежащих на одной прямой
(на прямой Паскаля, см. рис. 1). П. т. верна
и в том случае, когда две или даже три соседних вер-
Рис. 3.
Рис. 4.
типы совпадают (но
не более чем но две в
одной точке). В этом
случае в качестве
прямой, проходящей
через две совпадаю-
совпадающие вершины, при-
принимается касательная
к линии в этой точке. Касательная к линии 2-го по-
порядка, проведенная в одной из вершин вписанного
пятиугольника, пересекается со стороной, противо-
противоположной этой вершине, в точке, к-рая лежит на
прямой, проходящей через
точки пересечения остальных
пар несмежных сторон этого
пятиугольника (см. рис. 2).
Если ABCD — четырех-
четырехугольник, вписанный в ли-
линию 2-го порядка, то точки
пересечения касательных в
вершинах С и D соответст-
соответственно со сторонами AD и ВС
и точка пересечения прямых
А В и CD лежат на одной пря-
прямой (см. рис. 3).
Точки пересечения каса-
касательных в вершинах тре-
треугольника, вписанного в линию 2-го порядка, с про-
противоположными сторонами лежат на одной прямой
(см. рис. 4).
П. т. двойственна Бриаплиона теореме.
П. т. установлена Б. Паскалем (В. Pascal, 1639).
Частный случай П. т. для линии 2-го порядка, вырож-
вырождающейся в пару прямых, был известен еще в древ-
древности (см. Паппа аксиома).
Лит.: [11 Глаголев Н. А., Проективная геометрия,
2 изд., М., 1963; [2] Ефимов Н. В., Высшая геометрия,
6 изд., М., 1978. П. С. Моденов, А. С. Пархоменко.
ПАСКАЛЯ ТРЕУГОЛЬНИК — таблица чисел, яв-
являющихся биномиальными коэффициентами. В этой
таблице по боковым сторонам равнобедренного тре-
треугольника стоят единицы, а каждое из остальных
чисел равно сумме двух чисел, стоящих над ним слева
и справа:
I 1
1 2 1
13 3 1
14 6 4 1
1 5 10 10 5 1
1 1
В строке с номером и+1 выписаны коэффициенты раз-
разложения бинома (а+й)л. Треугольная таблица, пред-
предложенная Б. Паскалем в «Трактате об арифметическом
треугольнике» A654), отличается от выписанной здесь
поворотом на 45°. Таблицы для изображения бино-
биномиальных коэффициентов были известны и ранее.
Лит.: [11 Успенский В. А., Треугольник Паскаля,
2 изд., М., 1979; [2] История математики с древнейших времен
до начала' XIX столетия, т. 2, М., 1970. В. И. Нечаев.
ПАСКАЛЯ УЛИТКА — плоская алгебранч. кривая
4-го порядка; конхоида ок-
окружности диаметра а (см.
рис.). Уравнение в пря-
прямоугольных координатах:
в полярных координатах:
р — а cosy + l.
Начало координат —
двойная точка, изолиро-
изолированная при а<С1, узловая
при а>/, точка возврата
a<L
при а=1 (в атом случае П. у.— кардиоида). Длина
дуги выражается мдпптич. интегралом 2-го рода.
Площадь, ограниченная П. у.:
s = —г- + яг;
при а>2 площадь внутренней петли при вычислении
по этой формуле считается дважды. П. у.— частный
случай Декартова овала, она является эпитрохоидой
(см. Трохоида).
П. у. названа по имени Э. Паскаля (Е. Pascal, 1-я
пол. 17 в.), впервые рассмотревшего ее.
Лит.: [lj С а в е л о в А. А., Плоские кривые, М., i960.
Д. Д. Соколов.
ПАУЛИ МАТРИЦЫ — двурядпые комплексные по-
постоянные эрмитовы матрицы коэффициентов. Введены
В. Паули (W. Pauli, 1927) для описания спинового
механич. момента (спина s= — а) и магнитного момента
(|д,= 2^-с а) электрона, .-Jto уравнение корректным
образом в нерелятивистском случае описывает частицы
со сшшом — (в единицах Й-) и может быть получено
из Дирака уравнения при условии —<^1. В явном
виде П. м. можно записать следующим образом:
0
1
11
о|
; а2 —
0
i
—i
0
; о3=
1
0
0
1
Их собственные значения равны ±1. П. м. удовлетво-
удовлетворяют следующим алгебраич. соотношениям:
Вместе
единичной матрицей о„
„ ^
П. м.
образуют полную систему матриц второго ранга, по
к-рой может быть разложен произвольный линейный
оператор (матрица) размерности 2. П. м. действуют
на двухкомионентные функции-спиноры tyA, Л—1, 2,
преобразующиеся при вращении системы координат
по линейному двузначному представлению группы
вращений. При повороте на бесконечно малый угол
вокруг оси с единичным направляющим вектором п,
спинор г))^ преобразуется по формуле
= |аЛ/?-г 4" Ш
Из П. м. можно образовать Дирака матрицы уа, а=0,
1, 2, 3:
а0 0 1
О — а01
0 at
— оч О
с = 1, 2, 3.
П. м. изоморфны системе простейших гинсркомплокс-
ных чисел — кватернионов. Они используются всегда,
когда элементарная частица имеет дискретный параметр,
принимающий лишь два значения, напр, при описании
изосшша нуклопа (протон — нейтрон). Вообще П. м.
используются не только для описания изотопич. прост-
пространства, но и в формализме группы внутренней сим-
симметрии SU B). В этом случае П. м. являются генера-
генераторами двузначного представления группы SU B)
и обозначаются как Т], т2, т3. Иногда удобно пользо-
пользоваться линейными комбинациями
1 , 0 0
т =t(Ti-it2)= i о
10 1
О О
В нек-рых случаях для релятивистски ковариантного
описания двукомпонентных спинорных функций вме-
сто П. м. вводятся связанные с ними матрицы Sa с
помощью следующего изоморфизма:
SoSo+ao = O- S,-So=c/, i = l, 2, 3, A)
где знак (*) обозначает комплексное сопряжение. Мат-
Матрицы So. удовлетворяют перестановочным соотноше-
соотношениям:
5а5р + 5р5« = 2г|а> р, B)
где т)а, з — компоненты метрич. тензора пространства
Минковского с сигнатурой +2. Формулы A) п B)
позволяют ковариантным образом обобщить П. м.
па произвольное искривленное пространство
где gafj — компоненты метрич. тензора искривленного
пространства.
Лит.: [1] II а у ли В., Труды по квантовой теории, [пер.
о нем., т. 1—2], М., 1975—77; [2] Не ли па Н. Ф., Физика
элементарных частиц, М., 1977; [3] Б р и л ь Д., У и л е р
Д ж., в кн.: Новейшие проблемы гравитации, М., 19В1, о. 381 —
'i27. В. Г. Кречет.
ПАША АКСИОМА — одна из аксиом порядка в
Гильберта системе аксиом евклидовой геометрии.
Формулировка аксиомы использует понятие «лежать
внутри отрезка», причем отрезок здесь рассматривается
как система двух различных точек А и В, принадле-
принадлежащих одной прямой; точки, лежащие «между» точ-
точками А и В, наз. точками отрезка (или внутренними
точками отрезка). Понятие «между» (лежать между)
описывается группой аксиом порядка, куда входит
и П. а., к-рая формулируется следующим образом:
пусть А, В, С — три точки, не лежащие на одной
прямой, и а — прямая в плоскости (ABC) этих трех
точек, пе проходящая ни через одну из точек А , В, С\
если при этом прямая проходит через одну из точек
отрезка АВ, то она должна пройти через одну из точек
отрезка АС пли через одну из точек отрезка ВС.
П. а. является аксиомой абсолютной геометрии.
С помощью других гильбертовых аксиом порядка
.можно доказать, что прямая а не может пересечь оба
отрезка АС и ВС. Аксиома сформулирована М. Па-
Пашем [1].
Лит..- [1] Pasch M., Vorlesurigen iiber neuere Geometric,
Lpz., 1882; [2] Гильберт Д., Основания геометрии, пер.
с нем., М.— Л., 1918. Л. А. Сидоров.
ПЕАНО АКСИОМЫ — система из пяти аксиом для
натурального ряда N и функции S (прибавление 1)
па нем, введенная Дж. Пеано (G. Реапо, 1889):
A)
B)
C) х?А —+ Sx ф 0;
D) x?Nf\y^Nr\Sx = Sy—yx=y;
E) 0?MAVs (s?M —+Sx?M)—>-N^M для лю-
любого свойства М (а к с и о м а индукции).
В первом варианте вместо 0 использовалась 1. Сход-
Сходные аксиомы независимо предложил Р. Дедекинд
(R. Dedekind, 1888). П. а. категоричны, т. о. любые
две системы (TV, S, 0) и (N', S', 0'), удовлетворяющие
П. а., изоморфны. Изоморфизм определяется функ-
функцией f(x, x), где
/ @, 0) = 0', / (Sx, Sx)=S'f (x, х);
1 (z, sy) = f (х, У)\ / {х, у)=0 для у < х.
Существование f(x, у) для всех пар (х, у) и взаимная
однозначность при т<:;/ доказываются по индукции.
П. а. позволяют развить теорию чисел, в частности
ввести обычные арифметич. функции и доказать их
свойства. Все аксиомы независимы, однако C) и D)
можно объединить в одну:
Ax < у —I- х ф у,
229
если определить х<у как
V-1/ [M (Sx)AVz(M (z)
ПЕАНО
230
¦M(Sz))-+M(y)].
Независимость доказывается предъявлением модели,
в к-рой верны все аксиомы, кроме рассматриваемой.
Для A) такая модель — натуральный ряд, начиная с
единицы; для B) — множество N\J {1/2}, где 50=1/2,
S A/2) =1; для C) — множество {0}; для D) — множе-
множество {0, 1} с i90 = i91='l; для E) —множество N\J
iH-i}-
Иногда под арифметикой Пеано пони-
понимают систему в языке 1-го порядка с функциональ-
функциональными символами S, -\ -, •, состоящую из аксиом
Sx ф 0, Sx = Sy—*x = y,
определяющих равенств для + , • и схемы индукции
А @) Л Vz (А (х) —* A {Sx)) —> VxA (x)
(см. Арифметика формальная).
Лит.: [1] К л и и и С. К., Введение в метаматематику,
пер. с англ., М., 1957. Г. Е. Мипц.
ПЕЛНО КРИВАЯ — непрерывный образ отрезка,
заполняющий внутренность квадрата (или треуголь-
служить пепроницаемой для дождя крышей, однако
она вовсе не есть непрерывная поверхность.
Известный интерес представляют т. н. правил ь-
п ы е замкнутые кривые типа П е а-
Рис. 2.
Рис. з.
Рис. 1.
ника). Открыта Дж. Пеапо [1]. П. к., рассматривае-
рассматриваемая как плоская фигура, не есть множество, ни-
нигде не плотное на плоскости; она является жордано-
вой, но не канторовой кривой, а потому не являет-
является линией. Построение П. к., заполняющей квадрат,
см. в ст. Линия; оно принадлежит Д. Гильберту
(D. Hilbci't). На рис. 1 приведен аналог его построения
для треугольника (первые шесть шагов) (другие кон-
конструкции см. в [2] и 13]).
Всякая П. к. имеет кратные точки — это «пред-
«предложение имеет огромную принципиальную важность
для геометрии, так как оно показывает, в чем имен-
именно кроется самая геометрическая сущность различия
числа измерений плоскости и прямой» (Н. Н. Лузин).
Не существует П. к., всякая точка к-рой была бы
простои или двукратной, но существует П. к., имею-
имеющая самое большое лишь трехкратные точки (в счетном
числе),— такова, напр., кривая, построенная самим
Дж. Пеаио; конструкция Д. Гильберта содержит
четырехкратные точки (также в счетном числе).
С понятием П. к. связан любопытпый факт сущест-
существования пространственных простых дуг, проектирую-
проектирующихся на плоскость в виде сплошных площадей,—
такова, напр., кривая x=(f(t), y~ty{t), z—t, где пер-
первые две функции задают П. к. Хотя эта дуга и может
но — пределы последовательностей симметричных
замкнутых кривых, соответствующих последовательно-
последовательностям триангуляции произвольного правильного мно
гоугольника, каждая из к-рых является правильным
(т. е. полученным делением на две равные части) под
разделением предыдущей (при-
(пример — на рис. 2). При этом по-
последовательность кривых можно
выбрать так, чтобы предел пло-
площадей областей, ими ограничен-
ограниченных, был равен заданной вели-
величине (даже нулю или площади
всей подразделяемой фигуры)
(рис. 3). Кажется вероятным, что
подобные картинки могут быть
полезны при исследовании роста
кристаллич. структур. Анало-
Аналогично с помощью последователь-
последовательностей триангуляции можно стро-
строить отображения прямой в пло-
плоскость, в частности «периодиче-
«периодические» кривые типа Пеано.
Существует аналог П. к., за-
заполняющий многомерный и даже
счртноморный куб (см. [3]).
6 Далеко идущее обобщение со-
содержит теорема Мазур-
Мазурке в и ч а : если X — контину-
континуум, то эквивалентны условия:
а) пространство X локально связно, б) X — непре-
непрерывный образ интервала.
Лит.: [1] Peano G., «Math. Ann.», 1890, Bd 36, S. 157;
1.2] Александров П. С, Введение в теорию множеств
и общую топологию, М., 1977; [3] Лупи н Н. Н., Теория функ-
функций действительного переменного, 2 изд., М., 1948.
М. И. Войцеховспий.
ПЕАНО ПРОИЗВОДНАЯ — одно из обобщений по-
понятия производной. Пусть существует 6>0 такое, что
для всех t с |i|<6 имеет место
f(*o + t)=ao + alt+...+??¦ С+ y(t)t>;
где а0, . . ., аг — постоянные и y{t) —у 0 при t -*¦ 0.
Пусть \{0)= 0. Тогда число аг наз. обобщенной
производной Пеано порядка г функции
/ в точке х0. Обозначение: jr(xQ)~ar, в частности
ao=/(;rc). ai = /'(-то)- Если существует /(г,(ж0), то су-
существует и /(r_i)(.rn), т\>1. Если существует конеч-
конечная обычная двусторонняя производная f-r)(x0), то
f(r){x0)—fin{x0). Обратное неверно при г>1: для
функции
( е'*2, грО и рационально,
I 0, х = 0 или иррационально,
1
229 пеано
если определить х<.у как
\/М [М (Sx)AVz (M (z) —* М (Sz)) —»¦ М (у)].
Независимость доказывается предъявлением модели,
в к-рой верны все аксиомы, кроме рассматриваемой.
Для A) такая модель — натуральный ряд, начиная с
единицы; для B) — множество N\J {1/2}, где 50=1/2,
S A/2) =1; для C) — множество {0}; для D) — множе-
множество {0, 1} с .90 = i91='l; для E) — множество N\J
Иногда под арифметикой Пеано пони-
понимают систему в языке 1-го порядка с функциональ-
функциональными символами S, -\-, • , состоящую из аксиом
Sx ф 0, Sx — Sy—>х = у,
определяющих равенств для +, -и схемы индукции
А @) Л \fx (А (х) —у A (Sx)) —> ух А (х)
(см. Арифметика формальная).
Лит.: [1] К л и н и С. К., Введение в метаматематику,
пер. с англ., М., 1957. Г. Е. Минц.
ПЕЛНО КРИВАЯ — непрерывный образ отрезка,
заполняющий внутренность квадрата (или треуголь-
230
служить пепроницаемой для дождя крышей, однако
она вовсе не есть непрерывная поверхность.
Известный интерес представляют т. н. правил ь-
п ы е замкнутые кривые типа Пеа-
Пеаж
X
X
щ
i-
и
щ
X
X
Щ
щ
X
х
Рис. 2.
Рис. 3.
Рис. 1.
ника). Открыта Дж. Пеапо [1]. П. к., рассматривае-
рассматриваемая как плоская фигура, не есть множество, ни-
нигде не плотное на плоскости; она является жордано-
вой, но не канторовой кривой, а потому не являет-
является линией. Построение П. к., заполняющей квадрат,
см. в ст. Линия; оно принадлежит Д. Гильберту
(D. Hilbcrt). На рпс. 1 приведен аналог его построения
для треугольника (первые шесть шагов) (другие кон-
конструкции см. в [2] и 13]).
Всякая П. к. имеет кратные точки — это «пред-
«предложение имеет огромную принципиальную важность
для геометрии, так как оно показывает, в чем имен-
именно кроется самая геометрическая сущность различия
числа измерений плоскости и прямой» (Н. Н. Лузин).
Не существует П. к., всякая точка к-рой была бы
простой или двукратной, но существует П. к., имею-
имеющая самое большое лишь трехкратные точки (в счетном
числе),— такова, напр., кривая, построенная самим
Дж. Пеаио; конструкция Д. Гильберта содержит
четырехкратные точки (также в счетном числе).
С понятием П. к. связан любопытпый факт сущест-
существования пространствепных простых дуг, проектирую-
проектирующихся на плоскость в виде сплошных площадей,—
такова, напр., кривая x=(f(t), y~ty(t), z—t, где пер-
первые две функции задают П. к. Хотя эта дуга и может
но— пределы последовательностей симметричных
замкнутых кривых, соответствующих последовательно-
последовательностям триангуляции произвольного правильного мно
гоуголыгака, каждая из к-рых является правильным
(т. е. полученным делением на две равные части) под
разделением предыдущей (при-
(пример — на рис. 2). При этом по-
последовательность кривых можно
выбрать так, чтобы предел пло-
площадей областей, ими ограничен-
ограниченных, был равен заданной вели-
величине (даже нулю или площади
всей подразделяемой фигуры)
(рис. 3). Кажется вероятным, что
подобные картинки могут быть
полезны при исследовании роста
кристаллич. структур. Анало-
Аналогично с помощью последователь-
последовательностей триангуляции можно стро-
строить отображения прямой в пло-
плоскость, в частности «периодиче-
«периодические» кривые типа Пеано.
Существует аналог П. к., за-
заполняющий многомерный и даже
счртноморный куб (см. [3]).
6 Далеко идущее обобщение со-
содержит теорема Мазур-
Мазурке в и ч а : если X — контину-
континуум, то эквивалентны условия:
а) пространство X локально связно, б) X — непре-
непрерывный образ интервала.
Лит.: [1] Peano G., «Math. Ann.», 1890, Bd 36, S. 157;
L2J Александров П. С., Введение в теорию множеств
и общую топологию, М., 1977; [3] Лупи н Н. Н., Теория функ-
функций действительного переменного, 2 изд., М., 1948.
М. И. Войцеховспий.
ПЕАНО ПРОИЗВОДНАЯ — одно из обобщений по-
понятия производной. Пусть существует 6>0 такое, что
для всех t с |zj<6 имеет место
где а0, . . ., аг — постоянные и у(() ->- 0 при t -*¦ 0.
Пусть у@) = -0. Тогда число аг наз. обобщенной
производной Пеано порядка г функции
/ в точке х0. Обозначение: jr(xQ)~ar, в частности
ao=/(;rc). ai = /'(-To)- Если существует /(г,(ж0), то су-
существует и /(,._])(.г0), т\>1. Если существует конеч-
конечная обычная двусторонняя производная f-r)(x0), то
f(r)(x0)—f(r)(x0). Обратное неверно при г>1: для
функции
[ е/*2, грО и рационально,
0, х = 0 или иррационально,
имеет место /(п@) = 0, г=1, 2, . . ., но не существует
f(-i)(x)--f' (.т) при ,т?=0 (ийо /(.т) разрывна при ?=?0).
Следовательно, не существует обычная производная
/С)@) при 7->1.
Вводятся также и бесконечные обобщенные
производные Пеано. Пусть для всех t с
\t\ <б имеет место
/ (хо-Н) =ao + ait+ . .. -r~fjr гг-1 + -^- *г,
где а0, . • ., аг_! — постоянные и ar(t) —у аг при t—>-0
(аг — число или символ со). Тогда аг также наз. П. п.
порядка г функции / в точке ,т0. Введена Дж. Пеано
(G. Реапо). а. а. нонюшков.
ПЕАНО ТЕОРЕМА — одна пз теорем существования
решения обыкновенного дифференциального уравне-
уравнения, установленная Дж. Пеано [1] и состоящая в
следующем. Пусть дано дифференциальное уравнение
*/' = /(*, У)- (*)
Тогда если функция / ограничена и непрерывна в
области G, то через каждую внутреннюю точку (.г„,
;/0) этой области проходит, по крайней мере, одна ин-
интегральная кривая уравнения (*). Может оказаться,
что через нек-рую точку проходит более одной инте-
интегральной кривой, напр, для уравнения у' = 2Уу су-
существует бесконечное множество интегральных кри-
кривых, проходящих через точку @, 0):
у @), —
у — (х— aJ,
где а, Ь — произвольные постоянные.
Имеются обобщения (в том числе многомерные)
П. т. (см. [2], [3]).
Лит.: [1] Peano G., «Math. Ann.», 1890, Bd 37, S. 182—
228; [2] Петровский И. Г., Лекции по теории обыкно-
обыкновенных дифференциальных уравнений, 6 изд., М., 1970; [3]
X а р т м а н Ф., Обыкновенные дифференциальные уравнения,
пер. с англ., М., 1970. М. И. Войцеховский,
ПЕЙДЖА ТЕОРЕМА — 1) П. т. о нулях
/.-ф у н к ц и и Дирихле: пусть L (s, у)— Ди-
Дирихле L-функция, s=a-\-it, % — Дирихле характер по
mod d, d^3; существуют абсолютные положительные
постоянные с1, . . ., с8 такие, что
а) L (s, %) Ф 0 при а > i—c1/\ogdt, гЗэЗ;
б) L (s, %) Ф 0 при а > 1 — c2/logd, 0 < t < 5;
в) для комплексного % mod d,
L (s, x) Ф 0 при а > 1 —c3/log d,
г) для действительного примитивного у_ mod d,
L (а, х) Ф 0 ПРИ о" > 1 — CJV d log2 d;
д) для 2<d<:Z) существует не более одного d~d0,
d0>c5log2 ?»/(log log/))8 и не более одного действи-
действительного примитивного уЛ mod d0, для к-рого L{s, ул)
может иметь действительный нуль Р]>1 — ce/log D,
причем р] является однократным нулем п для всех f)
таких, что L(f>, x) = 0i P>1—c6/log ?» с действитель-
действительным -/ mod d имеют d=0 (mod rf0).
2) П. т. о я (ж; d, I) — числе простых чисел p<z,
p^^Z(modd), при 0<^<:d, I и d — взаимно простых.
В обозначениях и при условиях п. 1 вследствие а) —
в) и д) справедливо равенство
я fa- d I)- lix E 7jl) V nP'~x .
Jogn
где ?=1 или Е—-0, смотря по тому, существует р\
или нет для данного d, и вследствие 2), для любого
d<(log.xI-6 при фиксированном 6>0
Этот результат является единственным A983), к-рый
эффективен в том смысле, что, если значение б задано,
можно указать численные значения с8 и постоянной,
входящей в символ 0. Замена оценки 2) оценкой Зи-
геля: L(a, ж)?=0 при а>1—c{e)d~e, s>0 распростра-
распространяет действие формулы (чО на существенно большие
d, d*c(logx)A, с любым фиксированным А, но при
этом утрачивается эффективность оценок в формуле
(*) — но заданному е>0 невозможно оценить е8—с8(е)
и O=OZ.
П. т. установлены Г). Пейджем [1].
Лит.: Ш Page A., «Proc. London Math. Soc. Ser. 2»,
1935, v. .19, Л» 2, ]). 116—41; [2] К а р а ц у 0 а А. А., Основы
аналитической теории чисел, М., 1975; [3] П р а х а р К.,
Распределение простых чисел, пер. с нем., М., 1967.
А. Ф. Лаврик.
ПЕКЛЕ ЧИСЛО — один из критериев подобия для
процессов конвективного теплообмена. П. ч. харак-
характеризует соотношение между конвективным и моле-
молекулярным процессами переноса тепла в потоке жид-
жидкости. П. ч.
где I — характерный линейный размер поверхности
теплообмена, и — скорость потока жидкости относи-
относительно поверхности теплообмена, а — коэффициент
температуропроводности, Ср — теплоемкость при по-
постоянном давлении, р — плотность и X — коэффици-
коэффициент теплопроводности жидкости.
П. ч. связано с Рейнольдса числом Re и Ирандтля
числом Рг соотношением Pe™Re-Pr.
П. ч. названо по имени Ж. Пекле (J. Peclet).
17 о материалам одноименной статьи из БСЭ-3.
ПЕЛЛЯ УРАВНЕНИЕ — дпофантово уравнение
вида
ar2-dir=1, A)
а также более общее уравнение
где d — натуральное, ]/~d — иррациональное число,
с — целое, неизвестные х и у — целые числа.
Если PSIQS, s — Q, 1, 2, . . .,— подходящие дроби
разложения Y~d в цепную дробь с периодом к, то поло-
положительные решения уравнения A) имеют вид
* = Pkn-l, V=Qkn-U
где п — любое натуральное число такое, что кп четно.
Все решения уравнения A) получаются из формулы
x+yV~d=± (xt + UoV"d)n,
где п — любое целое, а (х0, у0) решение с наимень-
наименьшими положительными значениями неизвестных. Общее
уравнение B) либо совсем не имеет решений, либо —
бесконечно много. При с——1 решения существуют
тогда и только тогда, когда к нечетно. При с—4 урав-
уравнение B) всегда имеет решения. С помощью решений
П. у. при с—-±1, ±4 находятся единицы квадратич-
квадратичного поля R(y^d). Решения П. у. используются при
нахождении автоморфизмов бинарных квадратичных
форм Ахг-\-Вху-\~Су2; они позволяют по одному ре-
решению диофантова уравнения Ах2-{-Вху-\~Су2=п по-
получить бесконечное множество решений.
Уравнение A) изучалось У. Броункером (W. Broun-
cker, 1657), П. Ферма (P. Fennat) и Дж. Валлисом
(J. Wallis). Л. Эйлер (L. Euler) но недоразумению
связал его с именем Дж. Пелля (J. Pell).
Лит.: [1] Вальфиш А. 3., Уравнение Пелля, Тб.,
195:!; [2] Гельфонд А. О., Решение уравнений в целых
чипах, 3 изд., М., 1978; [31 he Vcque W. J., Topics in
number theory, L., 1ЯВ1. А. А. Бухштаб.
ПЕНЛЕВЕ ПРОБЛЕМА — проблема характериза-
ции устранимых множеств для класса ограниченных
однозначных аналитич. функций комплексного пере-
переменного z. Пусть Е — компактное множество на ком-
комплексной плоскости С такое, что дополнение СЕ —
= С\Е есть область. Каковы минимальные условия на
Е, при выполнении к-рых любая ограниченная одно-
однозначная аналитич. функция в СЕ продолжается ана-
аналитически на Е и, следовательно, является констан-
константой? П. Пенлеве [1] указал достаточное условие: ли-
линейная мера Хаусдорфа множества Е (такие множества
иногда наз. множествами Пенлеве) должна
обращаться в нуль; однако его рассуждения содержали
ряд неточностей (см. [2|, |3]). Необходимое и достаточ-
достаточное условие на Е состоит в том, чтобы аналитическая
емкость Е обращалась в нуль (теорема Аль-
фор с а). Построен пример множества нулевой ана-
аналитической емкости, но положительной линейной
меры [5].
Лит.: [1] Р a i п 1 е v 6 P., Lecons sur la theorie analytique
des equations differentidies professees a Stockholm, [1895] P.
1897; [2] Zoretti I,., «J. math, pure appl.», 1905, t. 1, p.
1—51; [3] его же, Lemons sur le prolongement analytique, P.,
1911; [4] Ahlfors L., «Duke Math. J.», 1947, v. 14', p. 1 — 11;
[5] В и т у ш к и н А. Г., «Докл. АН СССР», 1959, т. 127, № 2,
с. 246—49. Е. Д. Солимепцев.
ПЕНЛЕВЕ ТЕОРЕМА — 1) П. т. о решениях
аналитических дифференциальны х
уравнений: решения дифференциального урав-
уравнения Р (wJ, w, г)~ 0, где Р --- многочлен относительно
неизвестной функции w и ее производной w' и w —
аналитич. функция относительно независимого пере-
переменного z, не могут иметь подвижных (т. е. зависящих
от произвольной постоянной) существенно особых
точек и трансцендентных точек ветвления.
2) П. т. об аналитическом продолже-
н и и: если Г — спрямляемая жорданова кривая,
расположенная в области D на плоскости комплекс-
комплексного переменного z, и функция /(z) непрерывна в D
и аналитична на ?>\Г, то /(z) — аналитич. функция
и во всей области D (см. [1], [2]).
Лит.: [1] Р a i п 1 е v ё P., Sur les lignes singulieres des fon-
ctions analytiques, P., 1887; [2] его же, Lecons sur la theorie
analytique des Equations differentielles professees a Stockholm,
[1895], P., 1897; [3] Голубев В. В., Лекции по аналитиче-
аналитической теории дифференциальных уравнений, 2 изд., М.— Л., 1950.
Е. Д. Соломенцев.
ПЕНЛЕВЕ УРАВНЕНИЕ — общее название груп-
группы из шести специальных обыкновенных дифферен-
дифференциальных уравнений типа
w" = R (u/, w, z),
где R — рациональная функция от w' и w и аналитич.
функция от z. Любое такое уравнение, имеющее лишь
неподвижные критич. точки, может быть приведено к
одному из 50 канонич. уравнений. Среди этих урав-
уравнений имеются линейные уравнения, уравнения Рик-
кати и др. известные уравнения, а также 6 уравнений,
называемые уравнениями Пенлеве и име-
имеющие своими решениями трансцендентные
функции Пенлеве — специальные функции,
не сводящиеся к другим известным функциям. Распо-
Расположенные в общепринятом порядке, П. у. имеют сле-
следующий вид (а, Ь, с, d?C — константы):
2) w" = 2vfi ^ z
3) w»=^ + ez
4) u/' = |^+4
О) "> — —
i ™(h>-1)(m-z) Г | f z z-1 rfz (z-l)"l
^ Z'(Z-1)! L ' lO*^ (№-1J I " (w-zY J •
Указанные результаты впервые получены в иссле-
исследованиях П. Пенлеве (см. [1], [2]), к-рые были про-
продолжены, уточнены и дополнены Б. Гамбьо [3].
Лит.: [1] Painleve P., «Bull. Soc. math. France»,
1900, t. 28, p. 201 — 61; L2] его же, «Acta math.», 1902, t. 25,
p. 1—85; [3] Gam bier В., там же, 1910, t. 33, p. 1 — 55;
[4] Голубев В. В., Лекции по аналитической теории диф-
дифференциальных уравнений, 2 изд., М.— Л., 1950; [5] Айне
Э. Л., Обыкновенные дифференциальные уравнении, пер. с
англ., Хар., 1939. Н. X. Рояов.
ПЕНТАСФЕРИЧЕСКИЕ КООРДИНАТЫ — вид од-
однородных координат, связанных с декартовыми пря-
прямоугольными координатами формулами:
П. к. точки в 3-мерном евклидовом пространстве
связаны соотношением
Zl — NZi^O. (*)
С помощью П. к. можно пополнить 3-мерное евклидово
пространство до сферического, допуская элемент N=0.
При этом соотношение (*) описывает положение этого
3-мерного сферич. пространства в 4-мерном проек-
проективном пространство.
Существует 2-мерный аналог П. к.— тетрацик-
лические координаты. Именно, пусть
— уравнение сферы в однородных координатах, где
тг — радиус сферы. Числа хл, х2, х3, хл являются
П. к. той точки плоскости, к-рая соответствует точке
сферы при стереографич. проекции сферы на пло-
CKOCTF,.
Вполне аналогичные построения могут быть прове-
проведены в пространствах более высокой размерности, в
результате чего получаются полисферические
координаты. В 4-мерном случае они наз. г е к-
сасферическими координатами. По-
лисферич. координаты используются в конформной
геометрии, при изучении многообразий фигур.
Лит.: Ш Клейн Ф., Высшая геометрия, пер. с нем.,
М,— Л., 1939; [21 Бушманова Г. В., Н о р д е н А. П.,
Элементы конформной геометрии, Казань, 1972. Д.Д. Соколов.
ПЕРВАЯ АКСИОМА СЧЕТНОСТИ — понятие теоре-
теоретико-множественной топологии. Топологич. простран-
пространство удовлетворяет первой аксиоме счет-
счетно с т и, если система окрестностей всякой его точки
обладает счетной базой. Класс пространств, удовле-
удовлетворяющих П. а. с, выделен Ф. Хаусдорфом (F. Haus-
dorff, 1914); к атому классу принадлежат, напр., все
метрич. пространства, пространство непрерывных функ-
функций на отрезке и др. Пространства, удовлетворяющие
второй аксиоме счетности, удовлетворяют и П. а. с.
Обратное неверно, напр, всякое несчетное простран-
пространство с дискретной топологией не удовлетворяет П. а. с.
М. И. Войцеховский.
ПЕРВАЯ ВАРИАЦИЯ — см. Вариация функционала.
ПЕРВАЯ КВАДРАТИЧНАЯ ФОРМА, метрич е-
ская форма, поверхности — квадратичная форма
от дифференциалов координат на поверхности, к-рая
определяет внутреннюю геометрию поверхности в
окрестности данной точки.
Пусть поверхность задана уравнением
Г = Г (U, V),
где « it v — внутренние координаты иа поверхности;
dr — ru du -\- rv dv
— дифференциал радиус-вектора г вдоль выбранного
направления du : dv смещения ггз точки М в беско-
бесконечно близкую точку М' (см.
рис. 1). Квадрат главной ли-
линейной части приращения
длины дуги ММ' выража-
выражается квадратом дифференци-
дифференциала dr:
Рис. 1. -j- 2rarv du dv -p r'v dv2
и наз. первой основной квадратичной
формой поверхности. Коэффициенты П. к. ф.
обычно обозначают через
E = rl, F = (ra, rv), G = r%
или в тензорных символах
dr~ = gu du2 -f- 2#ij du dv-{- g22 dv2.
Тензор gjj наз. основным, или метрическим,
тензором поверхности. П. к. ф. является положи-
положительно определенной формой в обыкновенных топках
поверхности:
EG — F > 0.
П. к. ф. характеризует метрич. свойства поверхности1
знание П. к. ф. позволяет вычислять длины дуг на
поверхности:
E(dt)
dv
~dt
02-Ydt,
где t — параметр на кривой; углы между кривыми
на поверхности:
Е du
cos (dr (V) =
F (du 6v + iiv6u
йг,
YE rf«2+2F dudv + G dr"- 1 E «u2 i-'lF du fir + G 6r' '
где du : dv п би : 8у — направления векторов, каса-
касательных к кривым (см. рис.
2); площади областей на по-
поверхности:
г — I' du dv.
Вид коэффициентов П.
к. ф. существенно зависит
от выбора координат на поверхности. П. к. ф. имеет
т. н. ортогональный вид:
Е (и, v) du2jrG (и, v)dv*
в ортогональных координатах; канонический
в и д
du2 + G2 dv2
в полугеодезич. координатах; изотермический
(изометрический) вид в изотсрмич. коорди-
координатах
Иногда поверхности характеризуются специальными
видами П. к. ф. Напр., Лиувилля поверхности ха-
характеризуются следующим видом П. к. ф.:
П. к. ф. является инвариантом изгибания поверх-
поверхности: полная кривизна поверхности в данной точке
может быть вычислена через коэффициенты только
П. к. ф. и их производные (теоремы Гаусса).
О связи П. к. ф. с другими квадратичными формами
поверхности и лит. см. в ст. Квадратичные формы по-
поверхности. А. Б. Иванов.
ПЕРВАЯ КРАЕВАЯ ЗАДАЧА — краевая задача
специального вида; заключается в отыскании в области
D переменных х= (.г'], . . ., хп) решения дифференци-
дифференциального уравнения
Lu=f A)
четного порядка 2то по заданным значениям всех
производных порядка не выше т на границе S об-
области I) (или ее части). Эти условия обычно задаются
в виде
фй, 0<&<т —1, B)
О
3
где jj^ — производная по направлению внешней
нормали к 3D. Функции ф#, 0«:/с<т — 1, паз. дан-
данными Дирихле, а сама задача A), B), если
S = dD,— Дирихле задачей.
Для обыкновенного дифференциального уравнения
Lu = и"-\ а^и' Arau = f C)
в области D= (.ro<;E<a;i) П. к. з. определяется кра-
краевым условием
Для линейного равномерно эллиптич. уравнения
LuГ^Ж, /= ! aHuxixj + 2"=! а'\ + «»^/ D)
П. к. з. (задача Дирихле) состоит в нахож-
нахождении решений этого уравнепия при условии
Если функции а,-/, а,-, а, /, ф и (п—1)-мерное много-
многообразие dD достаточно гладки, то эта задача фред-
)ольмова. В частности, когда мора D достаточно мала
или когда а«:0 в D, П. к. з. однозначно разрешима.
Условия гладкости могут быть значительно ослаблены
как в отношении коэффициентов уравнения и данных
Дирихле, так и в отношении границы dD.
Если A) является системой 7V>i уравнений отно-
относительно неизвестного ТУ-компонентного вектора и,
то П. к. з. ставится аналогичным образом. В этом
случае между задачами Дирихле для систем C) и D)
имеется существенное различие: если задача C), B)
(S=dD) всегда фредгольмова, то фредгольмовость
задачи D), B) может нарушаться. Напр., однородная
задача Дирихле для равномерно эллиптич. системы
Бицадзе (см. [11)
в круге ,г2+у3</?2 имеет бесконечное число линейно
независимых решений. Этот пример послужил отправ-
отправным пунктом различных дополнительных условий на L
(правильная эллиптичность, сильная эллиптичность),
обеспечивающих фредгольмовость задачи Дирихле.
Для линейных параболич. уравнений П. к. з. ста-
ставится в цилиндре и носителем данных Дирихле служит
его основание и боковая поверхность. Напр., для
уравнения теплопроводности
решение ищется в области
D = {0< t < Г, х-.(хи .... xn)?G)
и носителем данных Дирихле <$=и\$ служит
Если граница dG — гладкое (и—1)-мерное многооб-
многообразие, функция ф гладкая и выполнено условие согла-
согласования на {(=0, r?dG}, то II. к. :s. однозначно раз-
разрешима.
Лит.: [1] Б и ц а д з е А. В., Некоторые классы уравне-
уравнений в частных производных, М., 1981; [2] Б е р с Л., Джон
Ф., Ш е х т ер М., Уравнения с частными производными, пер.
с англ., М., 196В; [3] Курант Р., Уравнения с частными
производными, пер. с англ., М., 19E4; [4] Миранда К.,
Уравнения с частными производными эллиптического типа, пер.
с итал., М., 1957; [5] Петровский И. Г., Лекции об урав-
уравнениях с частными производными, 3 изд., М., 1961; 1E] Б и-
цадзе А. В., Уравнения математической физики, М., 1976;
[7] X е р м а н д е р Л., Линейные дифференциальные опера-
операторы с частными производными, пер. с англ., М., 1965.
А. П. Солдатов.
ПЕРВИЧНОЕ КОЛЬЦО — кольцо Л, в к-ром про-
произведение любых двусторонних идеалов Р и Q равно
нулевому идеалу в том и только в том случае, когда
либо Р, либо Q является нулевым идеалом. Другими
словами, идеалы П. к. по умножению образуют полу-
полугруппу без делителей нуля. Кольцо R является П. к.
тогда и только тогда, когда правый (левый) аннулятор
любого ого ненулевого правого (соответственно левого)
идеала равен @), а также тогда и только тогда, когда
alibjr-Q для любых ненулевых a, b?R. Центр П. к.
является областью целостности. Любое примитивное
ко.и,но первично. Если кольцо R не содержит ненуле-
ненулевых шшьидеалов, то R — подпрямая сумма первичных
колец. Класс П. к. играет важную роль в теории ради-
радикалов колец (см. [1]).
Существует следующее обобщение понятия П. к.
Кольцо R наз. полупервичным, если оно не
имеет ненулевых нильпотентных идеалов.
Лит.: [1] А н д р у н а к и е в и ч В. А., Р я б у х и п
Ю. М., Радикалы алгебр и структурная теория, М., 1979; I.2J
Джекобсон Н., Строение колец, пер. с англ., М., 1961;
[3] X е р с т е й и И., Некоммутативные кольца, пер. с англ.,
М., 1972. К. А. Жевлаков.
ПЕРВИЧНЫЙ ИДЕАЛ — такой двусторонний идеал
/ кольца А, что из включения PQc^T для любых
двусторонних идеалов Р и Q кольца А следует, что
либо Рс=/, либо Q<^zl. Для первичности идеала 1
кольца R необходимо и достаточно, чтобы множество
Д\ I было т-с и с т е м о и, т. е. чтобы для любых
a, b?R\I существовал x?R такой, что axb?R\I.
Идеал/ кольца Л первичен тогда и только тогда, когда
факторкольцо по нему является первичным кольцом.
К. А. Жеалаков.
ПЕРВООБРАЗНАЯ, первообразная (при-
(примитивная) ф у н к ц и я, для конечной функции
1(х) — такая функция V(x), что всюду F'(x) = f(r).
Это определение является наиболее распространенным,
но встречаются и другие, в к-рых ослаблены требования
существования всюду коночной F' и выполнения всюду
равенства F'—f; иногда в определении используют
обобщения производной. Большинство теорем о П.
касается их существования, нахождения и единствен-
единственности. Достаточным условием для существования П.
у задаппой на отрезке функции / является непрерыв-
непрерывность /; необходимыми условиями являются принад-
принадлежность функции / первому Бэра классу и выполнение
для нее Дарбу свойства. У заданной на отрезке функции
любые две П. отличаются на постоянную. Задачу
нахождения F по F' для непрерывных F' решает Ри-
мана интеграл, для ограниченных F — Лебега инте-
интеграл, для любой F' — узкий (а тем более широкий)
Данжуа интеграл и Перрона интеграл.
Лит.: [1] Кудрявцев Л. Д., Курс математического
анализа, т. 1, М., 1981; [2] Н и к о л ь с к и й С. М., Курс мате-
математического анализа, 2 изд., т. 1, М., 1975. Т. П. Лукашенко.
ПЕРВООБРАЗНЫЙ КОРЕНЬ — 1) П. к., п'р и м и-
тивный корень, из единицы в поле К степени
т — элемент ? поля К такой, что ?т = 1 и X/тЛ для
любого натурального r<m. Элемент ?, порождает
циклит, группу ц(т) корней из единицы порядка т.
Если d поле К существует П. к. степени т, то т
взаимно просто с характеристикой поля К. Алгебраи-
Алгебраически '.замкнутое ноле содержит П. к. любой степени
взаимно простой с характеристикой поля. Если Z, —
И. к. степени п. то для любого к взаимно простого с п
элемент ?* также является П. к. Число всех П. к. сте-
степени т равно значению функции Эйлера ф(т).
В поло комплексных чисел П. к. степени т имеют вид
2лА , . . 2як
cos г-1 sm — ,
т ' т '
где 0<fc<ro и к взаимно просто с т.
2) П. к. по модулюто — целое число g такое, что
gf т) se I (mod т) и gv^l(modra)
при 1<:у<сГ(т) —1> гДе ф(га) — функция Эйлера.
Для П. к. g ого степепп gOr=i, g, . . ., g<t>(m)-i несрав-
несравнимы между собой по модулю т и образуют приве-
приведенную систему вычетов по модулю т. Таким образом,
для каждого числа а, взаимно простого с т, найдется
показатель у @<:у<ср (т) — 1), для к-рого a5=gV (mod m).
П. к. существуют не для всех модулей, а только для
модулей т вида т—2, 4, ра, 2ра, где р>2 — простое
число. В этих случаях мультипликативные группы
приведенных классов вычетов по модулю т устроены
наиболее просто: они являются циклич. группами
порядка ф(т). С понятном П. к. по модулю га тесно
связано понятие индекса числа по модулю га.
П. к. для простых модулой р были введены Л. Эйле-
Эйлером (L. Enler), по существование П. к. для любых
простых модулей /> было доказано лишь К. Гауссом
(С. Gauss, 1801).
Лит.: Лен г С, Алгебра, пор. с англ., М., 1968; [2] Г а-
усс К. Ф., Труды по теории чпсс.1], пер. с лат. и нем., М., 1959;
[3J Виноградов И. М., Основы теории чисел, 8 изд., М.,
1972. Л. В. Кузьмин С. А. Степанов.
ПЕРВЫЙ ИНТЕГРАЛ обыкновенного
дифференциального уравнения — от-
отличная от постоянной и непрерывно дифференциру-
дифференцируемая функция, производная к-рой вдоль решений
данного уравнения тождественно равна нулю. Для
скалярного уравнения
y'=f (х, у) (*)
П. и. есть функция F(x, у), находящаяся в левой части
общего решения F(x, у)-=С, где С — произвольная
постоянная. Таким образом, F(x, у) удовлетворяет
линейному уравнению
dF(x,y) dFjx, у)
дх "Г 0у 1{Х' У)-Ю
с частными производными 1-го порядка. П. и. может
но существовать во всей области задания уравнения
(*), однако в малой окрестности точки, в к-рой функция
f(x, у) непрерывно дифференцируема, он всегда су-
существует. П. и. определяется не единственным обра-
образом. Так, для уравнения у'=—х/у П. и. является как
функция х2-\-у2, так, напр., и функция exp(z2+y2).
Знание П. и. нормальной системы
x = f(x,t), x?Rn,
позволяет понизить порядок этой системы на единицу,
а отыскание п функционально независимых П. и. рав-
равносильно отысканию общего решения в неявном виде.
Если F1(x, t), . . ., Fn(x, t) — функционально неза-
независимые П. и., то всякий другой П. и. F(x, t) можно
представить в виде
F(x, t)=O(Fi(x, t), ..., Fn{x, t)),
где Ф — нек-рая дифференцируемая функция.
Лит.: [1] П о п т р я г и н Л. С, Обыкновенные дифферен-
дифференциальные уравнения, 4 изд., М., 1974. Н. Я. Ладис.
ПЕРЕВАЛА МЕТОД — метод вычисления асимпто-
асимптотики интегралов вида
где Х>0, Я-> +оэ — большой параметр, 7 — контур
п комплексной плоскости z, функции f(z) и S (z) голо-
голоморфны в области D, содерягащей 7- Нули функции
S' (z) наз. точками перевала функции S (с);
точка перевала — седловая точка поверхности U —
— Re S (x-\~iy). Суть П. м. состоит в следующем. Кон-
Контур 7 Деформируется в коптур 7 c теми же концами,
лежащий в fl u такой, что max Re S (z) достигается
zev"
только в точках перевала или на концах 7 (пере-
(перевальный контур). Асимптотика интеграла (*¦)
по перевальному контуру вычисляется с помощью
Лапласа метода и равна сумме вкладов от указанных
точек максимума. Вклад Г2,(Х) от точки z0 —
это интеграл нида (*), взятый по малой дуге контура у,
содержащей точку z0. Если z0 — внутренняя точка
контура 7, го — точка перевала и 5"(лоM=О, то
Перевальный контур обладает минимаксным свойст-
свойством: на нем достигается
min max Re S (z),
где минимум берется по всем контурам 7', лежащим
в D и имеющим те же концы, что и 7- Основная труд-
трудность при применении П. м.— отбор точек перевала,
т. е. выбор перевального контура у, отвечающего 7-
П. м. восходит к П. Дебаю [1|; идеи этого метода
были высказаны ранее Б. Риманом (см. [2]). Вычис-
Вычисление вкладов от точек перевала и от концов контура
см. в [3] - [9].
П. м.— по существу единственный метод, позволя-
позволяющий вычислять асимптотику интегралов вида (*).
С его помощью вычислены асимптотики преобразований
Лапласа, Фурье, Меллина, экспоненты от полинома,
многих специальных функций.
Пусть z?C", 7 — ограниченное многообразие с краем
размерности п и класса С°°, функции /(z), S (z) голо-
голоморфны в нек-рой области D, содержащей у, и dz—
= dzr . . . dzn. Пусть max Re S (z) достигается только
zsv ..
в одной точке z , к-рая является внутренней точкой 7
и невырожденной точкой перевала функции S (z),
т. е. As(z°)=uet,S"(zo)^0. Тогда вклад от z° равен
F (X) = (f У" (- AS (*»))-V.^ <z°> [/ (zo) .;- О (Х-
Лит.: [1] D е Ь у е P., «Math. Ann.», 1909, Bd 67, S. 535—f>8;
[2] Рима и Б., Сочинения, пер. с нем., М.— Л., 1948; [3J
Эрдейи А., Асимптотические разложения, пер. с англ., М.,
19В2; [4] Г. р е й н Н. Г., Асимптотические методы в анализе,
пер. с англ., М., 1961; [5] Е в г р а ф о в М. А., Асимптотические
оценки и целые функции, 2 изд., М., 1962; [6] К о п с о н Э.-Т.,
Асимптотические разложения, пер. с англ., М., 19G6; [7j О 1-
v e r F. W. J., Asymptotics and special functions, N. Y.— [a. o.],
1974; [8] Рис к с т ы п ь ш Э. Я., Асимптотические разложения
интегралов, т. 1 — 2, Рига, 1974—77; [9] Ф е д о р ю к М. В.,
Метод перевала, М., 1977. М. В. Федорюк.
ПЕРЕГИБА ТОЧКА — точка М
плоской кривой, обладающая сле-
следующими свойствами: в точке М
кривая имеет единственную ка-
касательную, в достаточно малой
окрестности точки М кривая рас-
расположена внутри одпой пары вер-
вертикальных углов, образуемых ка-
Рис. 1. V\ сательной и нормалью (см. рис. 1).
Пусть функция /(х) определена в нек-рой окрест-
окрестности точки х0 и непрерывна в этой точке. Точка хи
наз. точкой перегиба функции }(х), если она
является одновременно концом интервала строгой
выпуклости вверх и концом интервала строгой выпук-
выпуклости вниз. В этом случае точка (х0; f(xu)) наз. точкой
перегиба графика
функции, т. е. график /
функции j (х) в точке
(хп\ f(xo)) «перегиба-
«перегибается» через касатель-
касательную к нему в этой
точке: при z<z0 ка-
касательная лежит под
графиком f(x), а при
х>х0 — над графиком
!{х) (или наоборот)
(см. рис. 2). Необходимое условие
существования П. т.: если функция f(x),
дважды дифференцируемая в нек-рой окрестности
точки хй, имеет в ,г0 П. т., то f" (х№)- 0. Достаточ-
Достаточное условие существования П. т.:
если функция /(ж) в нек-рой окрестности точки х
к раз непрерывно дифференцируема, причем к нечетно
и А->3, и /(">(:г0)^0пригс-2, 3, . . .,А:—1,а/<*>(.то)^О,
то функция /(.г) имеет в хп П. т.
Лит.: [1] И л ь и и В. А., 11 о я н я к О. Г., Основы мате-
математического анализа. 2 изд., ч. 2, М., 1080; [2] К у д р я fi-
fine я л. Д., Курс математического анализа, т. 1, М., 1981.
ПЕРЕГОРОДКА — замкнутое множество Е топо-
логич. пространства X, разбивающее X между дан-
данными множествами Р и Q (или, др. словами, отделяю-
отделяющее Р и Q в X), т. е. такое, что Х'\Е---Их \]Н%, где Н1
Н Е РН QH
рис 2.
Q ) \
и Н2 дизъюнктны и открыты в Х\Е,
(
QdHa
X)
2 д р , г, Qa
(при этом оказывается, что Р и Q открыты во всем X).
П. наз. тонкой, если ее внутренность пуста. Всякое
бинарное (т. е. состоящее из двух элементов) разбиение
а= (А1, А2) пространства X определяет в X тонкую
П.: Д—граница А]=граница А2, причем X ^В=01{}02,
где О,- — открытое ядро А/, г=1, 2. Верно и обратное.
По существу понятие П. между множествами сводится
к понятию связности. Но и обратно, пространство X
несвязно, если 0 есть П. между непустыми множе-
множествами. М. И. Войцехоаский.
ПЕРЕДАТОЧНАЯ ФУНКЦИЯ линейной
стационарной системы управления
(системы автоматич. регулирования) — Лапласа пре-
преобразование отклика системы на воздействие единич-
единичной импульсной функции (дельта-функ-
(дельта-функции) b(t) при нулевых условиях в момент t—О (сам
этот отклик наз. функцией в е с а, и м п у л ь с-
ной переходной функцией или импульс-
импульсной характеристикой системы). Экви-
Эквивалентное определение: П. ф. есть отношение изобра-
изображений по Лапласу (см. Операционное исчисление)
выходного и входного сигналов с нулевыми начальными
данными. П. ф. представляет собой дробно-рациональ-
дробно-рациональную функцию W(р) комплексного переменного р; она
является коэффициентом в линейном соотношении
Y(p) = W(p)U (Р), A)
связывающем изображение по Лапласу U(р) входа
системы (воздействия, управления) u(t) и изображение
по Лапласу У (р) выхода системы (отклика, реакции)
у (t) с нулевыми начальными значениями. В теории
управления соотношение A) принято изображать
графически (см. рис.).
Пусть, напр., система управления описывается ли-
линейным обыкновенным дифференциальным уравнени-
ем с постоянными коэффициентами
(в реальных системах, как правило, га<:п). Тогда
Это же выражение можно получить, если, используя
операторную форму записи уравнения B) с помощью
оператора дифференцирования р
А(р)у=^В (р)и,
определить П. ф. как отношение входного опе-
оператора системы В (р) к собственному опе-
оператору системы А (р). П. ф. C) системы B) допу-
допускает следующее толкование: если выбрать управ-
управление u=est, где s — комплексное число такое, что
,
()ф, то линейное неоднородное уравнение B) имеет
частное решение у= W(s)est.
П. ф. не следует путать с переходной функ-
ц и е и, к-рая представляет собой отклик системы на
воздействие единичной с т у п е н ч а т о и
ф у н к ц и и
( О, Z<0,
B(Hl.l>0
при нулевых начальных условиях.
П. ф. является одним из основных понятий теории
линейных стационарных систем управления. Она не
зависит от характера приложенных к системе управ-
управляющих воздействий, а определяется лишь парамет-
параметрами самой системы и дает тем самым ее динамич.
характеристику. Особую роль в теории управления
играет функция W(ia) чисто мнимого аргумента, наз.
амплитудно-фазовой, или частотной,
характеристикой системы. Понятие П. ф. обобщается
и на линейные системы управления иных типов (мат-
(матричные, нестационарные, дискретные, с распределен-
распределенными параметрами и др.).
Лит.: [1] Р о й т е н б е р г Я. Н., Автоматическое управле-
управление, 2 изд., М., 1978; [2] Математические основы теории автома-
автоматического регулирования, М., 1971; [3] К а л;м а и 1>.,Фалб П.,
Арби б М., Очерки по математической теории систем, пер.
с англ., М., 1971; [4] Б у т к о в с к и й А. Г., Характеристики
систем с распределенными параметрами. Справочное пособие,
М., 1979. Я. X. Розов.
ПЕРЕМЕННЫХ НАПРАВЛЕНИИ МЕТОД — итера-
итерационный метод решения систем линейных или нели-
нелинейных уравнений, возникающих в разностных или
проекционно-разностных методах при приближенном
решении, напр., краевых задач для уравнений с част-
частными производными эллиптич. типа.
Пусть, напр., имеются две пространственные пере-
переменные и последовательности квадратных сеток coft
с шагом &>0 и узлами ;г,= (гуг, i2h), где i=(ii, t2) —
вектор с целочисленными компонентами. Пусть ?2Л —
множество узлов co/j, в к-рых ищется решение разност-
разностной или ироекционно-разностной задачи, записанной
в виде операторного уравнения
в евклидовом пространстве Н^, отождествляемом с
пространством функций, заданных в узлах Q/,; раз-
размерность lift совпадает с числом точек Nh из Q/j.
Пусть
Ahuh (xi) =2а-(. .€Gft°(V"A (*? + ./), Щ € ^A. (!)
— линейные операторы, отображающие Hh в Hh.
Среди операторов A) имеются операторы, у к-рых
ненулевые коэффициенты a,- j в A) соответствуют лишь
векторам сдвига ;=(/j, /2)' с /2=0. Такие операторы
наз. одномерными операторами, дейст-
вующими по Xf, и обозначаются Ah, л.2; аналогично
для векторов сдвига с /V—0 определяются и одномер-
одномерные операторы Ah^x^ действующие по г2.
Системы уравнений
Л/1,хгиП = ёп, г = 1, 2,
расщепляются на отдельные подсистемы, каждая из
к-рых связывает лишь значения иГг(х1) в узлах, лежа-
лежащих на отдельных горизонтальных (для ЛЙ,Х1) или
вертикальных (для Ah<Xl) линиях сетки. Для II. н. м.
характерно использование расщепляющихся опора-
торов Ah, имеющих вид
Решение системы
Ah,XlAh,Xiuh=gh B)
toj да сводится к последовательному решению двух
систем
Afl,X>l'fl=g/z> C)
Ah,X2uit^"h, D)
в к-рых вначале решаются отдельные подсистемы на
горизонтальных линиях сотки (в случае C)), а затем
осуществляется перемена направлений и решаются
подсистемы на вертикальных линиях сетки (в случае
D)). При этом обычно операторы Rh выбираются
такими, что на решение систем C), D), а следовательно,
и B), уходит только O(Nfl) арифметич. действий.
Поэтому и каждая итерация в П. н. м. вида
ЛМ+1) = Л^4П)-(^DП))-/А), «-0, 1, .-., E)
где верхний индекс п соответствует номеру итерации,
обычно осуществляется с затратой O(jVft) арифметич.
действий.
Наиболее эффективные результаты для П. н. м.
получаются для т. н. коммутативного случая, когда
оператор Ь/г является самосопряженным положительно
определенным оператором, а операторы Яд" — са-
самосопряженные и перестановочные с Lh. В этом случае
для любого 8>0 погрешность начального приближения
можно уменьшить но норме в е-1 раз за число итера-
итераций Л?=ОAпе||1пА|). Коммутативный случай может
встретиться только для краевых задач, в к-рых можно
произвести разделение переменных, и, следовательно,
область должна быть прямоугольником. Наиболее
частым случаем метода E) для уравнения
является метод
где Eh — тождественный оператор.
Наряду с подходом, в к-ром за счет выбора итера-
итерационных параметров стремятся минимизировать норму
оператора перехода от нулевой итерации к итерации
с фиксированным номером, используются и подходы,
основанные на различных вариационных принципах.
П. н. м. часто используется в качестве внутреннего
итерационного процесса в двухступенчатых итераци-
итерационных методах, использующих операторы, эквивалент-
эквивалентные по спектру и пригодные в случае переменных
коэффициентов и нелинейных задач.
Лит.: [1] Р е а С е га a n D. W., Rachford H. H., «J.
Soc. Industr. Appl. Math.», 1955, v. 3, Л1 1, p. 28—41; L2] Д ь я-
к о и о в Е. Г., Итерационные методы решения разностных ана-
аналогов краевых задач для уравнений эллиптического типа, К.,
1970; [3] Я н е н к о Н. Н., Метод дробных шагов решения мно-
многомерных задач математической физики, Новосио., 1967; Ш
Самарский А. А., Введение в теорию разностных схем, Ы.,
1971; [5] М а р ч у к Г. И., Методы вычислительной матема-
математики, 2 илд., М., 1980. Е. Г. Дьяконов,
ПЕРЕМЕШИВАНИЕ — свойство динамич. системы
(каскада {Sn} или потока {Sf}) с конечной инвари~
антной мерой ц., состоящее в том, что для любых
двух измеримых подмножеств Л, В фазового про-
странства W мера
соответственно
стремится к
(я (А) и (В)/ц (W)
при ге—>-оо, соответственно при i —>- со. Если преоб-
преобразования S, Sf обратимы, то в определении П. вместо
прообразов множества А относительно этих преобра-
преобразований можно брать образы S"A, StA, что более
наглядно. При наличии свойства II. говорят также,
что система перемешивает, а в случае перемешивающего
каскада {$"} о порождающем его эндоморфизме ?
пространства с мерой (W, и) тоже говорят, что S пере-
перемешивает (обладает свойством П.; впрочем, в послед-
последнем случае под II. часто понимают не свойство объ-
объекта, а сам этот объект, то есть S).
В аргоднч. теории наряду с П. рассматривают род-
родственные свойства — кратное перемеши-
перемешивание и слабое перемешивание (см.
[1]; последнее в старой литературе часто называли
П. в широком смысле, или короче — просто П., а о
П. говорили как о П. в сильном смысле). Рассматри-
Рассматривают также свойство, промежуточное между П. и
слабым П. (см. [2]). Все эти снойстиа сильнее эргодич-
эргодичности.
Имеется аналог П. для систем с бесконечной инва-
инвариантной мерой (см. [3]).
Лит.: [II X а л м о ш II. Р., Лекции по эргодической теории,
пер. с англ., М., 1959; l2j F u r s t e n b e r g H., Weiss В.,
в кн.: The structure of attractors in dynamical systems, В.— Hdlb—.
N. Y., 1978, p. 127—aa (Lecture Notes in Math., № 668); [3]
К r e n g e 1 П., Sucheston L., «Z. Wahrscheinlichkeitsthe-
or. und verw. Geb.», 1989, Bd 13, Jsn. 2, S. 150—64. Д. В. Аноаов.
ПЕРЕНОРМИРОВКА — процедура устранения рас-
ходимостей, присущих теории возмущений в лагран-
жевой формулировке квантовой теории поля. При
построении формальных рядов теории возмущений
в квантовой теории поля появляются выражения,
не имеющие однозначного матоматич. смысла, связан-
связанные с т. н. ультрафиолетовыми расходимостямп. Такие
расходимости возникают из-за того, что коэффициенты
этих рядов являются произведениями обобщенных
функций, т. е. объектом, вообще говоря, не опреде-
определенным корректно.
Удобно начинать рассмотрение с регулярпзованной
теории, в к-рой обобщенные функции заменены доста-
достаточно гладкими. Регуляризация вводит в теорию
дополнительные параметры, не имеющие прямого
физич. содержания. Но в регуляризованной теории
уже возможно выделить нз каждой коэффициентной
функции ту ее часть, к-рая при снятии регуляризации
порождает ультрафиолетовые расходимости. Собствен-
но П. состоит в отбрасывании расходящихся вкладов п
коэффициентные функции. После П. регуляризация
снимается, т. е. регуляризующий параметр исключа-
исключается соответствующим предельным переходом.
Идея П., предложенная X. Бете (см. [!]), состой*
в том, что отбрасывание расходимостой должно произ-
производиться таким способом, чтобы оно сводилось к пере-
переопределению (П.) параметров исходного лагранжиана,
т. е. затравочных масс, констант связи и нормировки
полей. Точная формулировка перонормировочной про-
процедуры в квантовой теории ноля (Л-операция) была
дана Н. Н. Боголюбовым и О. С. Парасюком (см. [2J).
Ими была доказана теорема (теорема Боголю-
бова — Парасюка) о конечности в смысле
обобщенных функций из Sr перенормированных выра-
выражений в каждом порядке теории возмущений. При
этом П. сводится к добавлению к лагранжиану до-
дополнительных членов — «контрчленов». Каждый контр-
члеп представляет собой нек-рую локальную оператор-
операторную структуру с числовым коэффициентом, являющим-
являющимся, вообще говоря, бесконечным рядом по затравочным
константам связи. Эти коэффициенты конечны лишь
при наличии регуляризации и обращаются в беско-
бесконечность при снятии ее. Таким образом, II. демонст-
демонстрирует вспомогательный характер исходного лагран-
лагранжиана. Физнч. смысл придается лишь лагранжиану
перснормиропанному. Его параметры, т. е. перенор-
мпрованные массы, константы связи и т. д., к-рые
конечны, можно идентифицировать с наблюдаемыми
величинами.
Лагранжева формулировка теории возмущений воз-
возможна лишь для теорий, в к-рых число контрчленов,
отличающихся по своей операторной структуре, ко-
конечно. Такие теории делятся на два класса — супер-
нормируемые и перенормируемые. В сунернормиру-
емых теориях коэффициенты при контрчленах явля-
являются конечными рядами по константам связи, а в
перенормируемых — эти ряды бесконечны. В этих
теориях операторная структура контрчленов, как
правило, та же, что и отдельных членов исходного
лагранжиана. Их объединение и приводит к П. затра-
затравочных констант.
В классич. варианте П. ость Д-онерация Боголю-
Боголюбова — Парасюка (устранение расходимостей из каж-
каждой диаграммы, возникающей, напр., в разложении
5-матрицы) и сводится к переопределению коэффищь
ентноц функции этой диаграммы следующим образом.
Пусть Л/у — оператор, сопоставляющий коэффици-
коэффициентной функции диаграммы у начальный отрезок ее
разложения в ряд Маклорена по импульсам. Тогда
коэффициентная функция RGr [plt . . ., р^) перенор-
перенормированной диаграммы Г запишется как
RGv(Pu ..., pN)^
где {у,} — совокупность всех расходящихся поддиа-
поддиаграмм диаграммы Г, а символ ¦ . . . ; означает, во-
первых, отбрасывание в получающемся из (*) при
раскрытии скобок выражении всех членов, содержащих
произведения My.My., отвечающие паре поддиаграмм,
для к-рых но выполняется ни одно из условий YiCTV/i
y,OYy, Y/DVy ~ 0, н, во-вторых, упорядочивание
операторов My. таким образом, что My. стоит правее
My., если Y/CYy
Ограничения, накладываемые на процедуру П., не
фиксируют ее полностью. Остающийся произвол имеет
двоякий характер. Во-первых, требование конечности
перенормиронанных выражений определяет лишь не-
к-рое минимальное число «вычитаний» в каждой рас-
расходящейся поддиаграмме, т. е. минимальное число
выделяемых членов ряда Маклорена. П. будет по-
прежнему приводить к конечным результатам, если
число вычитаний увеличивать, соблюдая нек-рые ус-
условия согласования для вычитаний в различных под-
поддиаграммах церенормируемой диаграммы. Во-вторых,
вместо отрезка ряда Маклорена можно вычитать выра-
выражение, отличающееся от него многочленом но импуль-
импульсам той же степени с конечными коэффициентами.
Указанный произвол приводит к эквивалентности
различных процедур П., отличающихся по своей
формулировке от /^-операции. Их конкретный выбор
обычно диктуется рассматриваемой задачей. Так, для
теорий с калибровочной инвариантностью, была пред-
логкена П., получившая название размерной. Она бази-
базируется на регуляризации, использующей в качестве
параметра отклонение размерности пространства-вре-
пространства-времени, в к-ром производятся вычисления, от физич.
значения. Устранение расходимостей производится пу-
путем отбрасывания выражений, сингулярных по этому
отклонению.
В других задачах пользуются аналитич. П. В ее
основе лежит регуляризация, состоящая в замене
пропагатора частицы, имеющего вид тина (р2— m2-[-i0)~1
на (р2—m2-\-i0) . Продолжение в комплексную область
по параметрам к осуществляет регуляризацию теории,
а ультрафиолетовые расходимости выделяются как
полюса по нек-рым линейным комбинациям этих
параметров. Согласованное отбрасывание таких полю-
полюсов устраняет все расходимости.
В приложениях используются и другие схемы П.
(см. [3]).
Лит.: [1] В е t h e H. A., «Phys. Rev.», 1947, v. 72, p. 339—
341; [2] Боголюбовы. Н., П а р а с ю к О. С, «Докл.
АН СССР», 1955, в. 100, № 1, с. 25; М 3, с. 429; [3] Завья-
Завьялове И., Перенормированные диаграммы Фейнмана, М.,
1979. С. А. Анипин.
ПЕРЕНОСА ИЗЛУЧЕНИЯ ТЕОРИЯ — исследова-
исследование прохождения электромагнитного излучения, гамма-
квантов, нейтронов и др. элементарных частиц че-
через вещество с помощью линейного кинетического
уравнения, или уравнения переноса (см. Кинетическое
уравнение).
Задача определения поля излучения в атмосфере,
рассеивающей свет по известным физич. законам,
возникла в 80-е гг. 19 в. в связи с исследованиями
по освещенности дневного неба. Кинетич. уравнение
переноса излучения было найдено в нач. 20 в. для
задачи о лучистом равновесии в звездных атмосферах.
Фнзич. смысл уравнения переноса — баланс энергии,
числа квантов, числа частиц в элементе фазового
пространства координат и скоростей частиц:
йФ __ ( дФ \ s ,
dt ~\ dt /столки."' ' [ >
где Ф (г, v, t)— функция распределения частиц в
d
точке г, v — скорость, t — момент времени, ~dj —
полная производная по траектории движения ча-
/8Ф\ «
стицы, ( -jj- 1 ст,,лкн. — скорость изменения функции
распределения за счет столкновения частиц с веществом
(нейтронов с ядрами или квантов с атомами вещества),
5 — мощность источника частиц. Для электромагнит-
электромагнитного излучения в качестве независимых переменных
функции распределения, определяющей среднюю интен-
интенсивность излучения, входят вектор направления из-
излучения и его частота. Одни и те же уравнения для
описания распространения частиц и квантов получают-
получаются вследствие одинакового физич. смысла этих кинетич.
уравнений — баланс энергии в фазовом пространстве.
Член, описывающий столкновения, является инте-
интегральным:
Л [ 2с (г, »'— +v)<$(r, v', t)dv' —
столки. J д ч ' /vi I /
— 2 (Г, V) Ф (Г, V, t),
а само уравнение переноса (кинетическое
уравнение) — интогро-дифференциальным урав-
уравнением. Здесь 2 — полное сечение взаимодействия
частиц с веществом в элементарном акте столкновения,
25(г, «'_>.»') — сечение перехода (вероятность пере-
перехода) из скорости v' до рассеяния в скорость v после
рассеяния (с учетом вероятности, что столкновение
произойдет). Для свободного движения частиц полная
производная от функции распределения по траектории
движения имеет вид
<М> 6Ф .
Для полного определения решения необходимо задать
начальное условие
Ф|/=0=/(Г, V)
н граничное условие. На границе тела (области про-
пространства, внутри к-рой решается уравнение переноса)
могут быть заданы, напр., условия абсолютного по-
поглощения частиц
Ф {г, v, t) ---0 при (v-n) < О,
где п — внешняя нормаль к поверхности (границе)
тела. Возможны п более общие граничные условия,
описывающие отражение частиц от границы или «про-
«прострел» частиц через вакуум (для невыиуклого тела,
граничащего с вакуумом — областью, где нот столк-
столкновении). Мате.матич. исследование уравнений перепо-
са в односкоростном случае, т. о. в предположении, что
изменяется лишь направление распространения излуче-
излучения или частиц при постоянной энергии кванта или
частицы, было проведено B.C. Владимировым [1] для
случая -gj- =0. При изотропном рассеянии задача сводит-
сводится к интегральному уравнению с положительным ядром,
к к-рому применима теория вполне непрерывных опе-
операторов, оставляющих инвариантным конус в банахо-
банаховом пространстве. При этом однородная задача имеет
положительное собственное значение (стоящее множи-
множителем при интеграле столкновений), к-рое не больше
модуля всякого другого собственного значения X,-, и
ему отвечает, по крайней мере, одна неотрицательная
собственная функция (соответствующая ?м). Эта тео-
теорема обобщается на случай анизотропного рассеяния.
В широком классе случаев первое собственное значение
задачи оказывается простым, а собственная функция,
соответствующая ему,— положительной почти всюду
в фазовом пространстве координат и направлений.
Таков, напр., случай, когда ?$(/•, v' —у v)>0 поч-
почти всюду. Найдены условия, при к-рых для уравне-
уравнения переноса с анизотропным рассеянием справедлива
теория Гильберта — Шмидта, построен новый вариа-
вариационный функционал для уравнений переноса с чет-
пой вероятностью перехода относительно переменной
цо= («•;/). С помощью нового вариационного метода
последовательно исследованы уравнения метода сферич.
гармоник, к-рыс вместе с краевыми условиями полу-
получаются применением прямого вариационного метода
Галеркина к уравнению переноса, если в качестве
пробных функций взять линейные комбинации сферич.
функций, зависящих от направления распространения,
умноженных на неизвестные функции пространствен-
пространственных координат. Вариационный принцип позволил
отобрать наилучшие граничные условия для метода
сферич. гармоник, ранее найденные эмпирически, из
вдвое большего количества возможных линейно неза-
независимых условий на границе тела (для плоской гео-
геометрии) (см. [I]).
В нестационарном случае (см. [2]) при исследовании
спектра собственное значение при переходе к интег-
интегральному уравнению (для изотропного рассеяния) нели-
нелинейно входит в ядро интегрального уравнения. .Что
обстоятельство приводит в конечном счете к тому, что
число точек дискретного спектра оказывается конеч-
конечным (а в некоторых случаях — нестационарная задача
для тепловых нейтронов в малом блоке замедлителя —
их вообще нет), кроме того, появляется сплошной
спектр собственных значений.
В ряде случаев удается получить аналитическое
решение уравнения переноса. Например, методом Ви-
Винера — Хопфа решается задача Милна; метод разло-
разложения по сингулярным собственным функциям опера-
оператора переноса позволяет решить ряд одномерных за-
задач [3].
В связи с потребностями инженерной практики были
развиты оперативные численные методы решения урав-
уравнения переноса нейтронов для расчета критич. режима
ядерного реактора (задача на собственные значения
для уравнения (¦!¦) при 5Ф/9(- = 0). Одним из основ-
основных методов решения является метод сферич. гармо-
гармоник, к-рый, однако, сложен для реализации на ЭВМ
и, как, впрочем, и другие методы, медленно сходится
(это объясняется наличием особенности в ядре интег-
интегрального уравнения переноса). См. Переноса уравне-
уравнения; численные методы решения.
Лит.: [1] Владимиров В. С, «Тр. Матем. ин-та АН
СССР», 1961, т. 61; 12] III и х о в С. В., Вопросы математичес-
математической теории реакторов. Линейный анализ, М., 1973; [3] К е й а К.,
Ц в а й ф е л ь П. Ф., Линейная теория переноса, пер. с англ.,
М., 1972; U] Соболев В. В., Перенос лучистой энергии
в атмосферах звезд и планет, М., 1956. В. А. Чуянов.
ПЕРЕНОСА ПОВЕРХНОСТЬ — поверхность, обра-
образованная параллельным переносом кривой Lx так, что
нек-рая ее точка М0?Ьл скользит но кривой L2. Если
г1{и) и r2(v) — радиус-векторы кривых L1 и L2 соот-
соответственно, то радиус-вектор П. п. есть
r = rl (u) + r2(y) — r2 К),
где r1(ug) = r2(v0) — радиус-вектор точки
u=-const и y=const образуют переноса сеть. Каждая
линейчатая поверхность имеет со1 сетей переноса
(Рейде мейстера теорема), развертываю-
развертывающаяся П. п. может быть только цилиндром или пло-
плоскостью. Если поверхность имеет две сети переноса,
то несобственные точки касательных к линиям этих
сетей лежат на алгебраич. кривой 4-го порядка. Ин-
Инвариантным признаком П. п. является существование
сопряженной чебышевской сети (сети
переноса). Напр., изотропная сеть на минимальной
поверхности есть сеть переноса, так что эта поверх-
поверхность есть П. п. Можно также П. п. охарактеризовать
тем, что одна из ее кривых (линия переноса) переходит
в линию, лежащую на той же поверхности, под воз-
воздействием однопараметрич. группы параллельных пе-
переносов. Замена этой группы произвольной одноиара-
метрич. группой G приводит к обобщенным
поверхностям переноса (см. [1]).
Лит.: [1] Ш у л и к о в с к и й В. И., Классическая диф-
ферепциа.чьнал геометрия в тензорном изложении, М., 1963.
И. X. Сабитов.
ПЕРЕНОСА СЕТЬ — сопряженная чебышевская сеть
на двумерной поверхности аффинного (или евклидова)
пространства. Поверхность, несущая П. с, наз. пере-
переноса поверхностью.
В расширенном пространстве имеет место теорема
Л и: если поверхность несет две П. с, то касательные
к лшпшм этих сетей высекают на несобственной пло-
плоскости кривую 4-го порядка (см. [1]).
Лит.: [1] ШуликовскийВ. И., Классическая диф-
дифференциальная геометрия в тензорном изложении, М., 1963.
В. Т. Базылев.
ПЕРЕНОСА ТЕОРЕМА в теории д и о ф а н-
товых приближений — утверждение о связи
разрешимости в целых числах одной системы нера-
неравенств с разрешимостью другой системы, определенным
образом связанной с первой. Классич. примером ли-
линейных П. т. является принцип переноса Хинчина (см.
Дипфантовы приближения). Более общие линейные
П. т. касаются связи между решениями в целых числах
системы однородных линейных неравенств с неособой
квадратной матрицей и решениями соответствующей
системы с обратной транспонированной матрицей:
существование нетривиального решения одной си-
системы гарантирует существование нетривиального ре-
решения другой, и наоборот. Подобные связи существуют
между линейными однородными и неоднородными
системами неравенств, при этом отсутствие нетриви-
нетривиальных решений однородной системы неравенств га-
гарантирует существование решений соответствующих
неоднородных систем, и наоборот. Известны такого
рода связи и в случае нелинейных задач, но они менее
определенно выражены и мало изучены. Принципи-
Принципиальные основы П. т. теории диофантовых приближений
проясняются II. т. геометрии чисел: для выпуклых
множеств устанавливаются связи между наличием
целых точек в данном и взаимном к данному множе-
множествах.
Лит.: [1] К а с с е л с Дж. В. С, Введение к теорию дио-
диофантовых приближений, пер. с англ., М., 1961; 12] его же,
Введение в геометрию чисел, пер. с англ., М., 19U5.
В. Г. Спринджук.
ПЕРЕНОСА УРАВНЕНИЯ; численные ме-
методы решения — методы решения интегро-диф-
ференциальных уравнений, описывающих перенос ча-
частиц или излучения. Для стационарных задач уран-
нения имеют вид
Q
=; [ dv' [ dii' <fw(x, Q, Q', v,
где x= (x, y, z), Q= (Qx, Q2, fi3) — единичный вектор,
ф--ср(а", Q, v) — поток частиц в точке х, летящих со
скоростью vil; положительные функции 2, w описы-
описывают взаимодействие частиц с веществом, а / — источ-
источник. Рассматривают две основные задачи: 1) найти
решение уравнения A) в (выпуклой) области D (х, у, z)
такое, что на ее границе Г
<р(лг, Q, v)-^Q при (Q, п)<0, B)
где п — внешняя нормаль к Г; 2) найти наибольшее
собственное значение X, и соответствующую собствен-
собственную функцию задачи A) — B), в к-рой
/ =-1- f
dv' [ dSl' (fwi (ж, Q, Q', v, v'). C)
Уравнение A) содержит шесть независимых перемен-
переменных; из-за существенной многомерности его сводят
к более простым уравнениям. Заменяя в A), C) инте-
интеграл по v квадратурной формулой с jV членами и
предполагая изотропность рассеяния, получают си-
систему т. н. многоскоростных уравне-
уравнений
2/I1 »'=!. 2, ..., N, D)
где
ф,- = ф,- (х, Q), ф,-0 ^ ^ \ ф,- dQ'
— нулевые моменты, а коэффициенты S,-, 2 s', /,• полу-
получены применением методов усреднения с использова-
использованием решений сопряженных задач. Для задачи 2)
аналогично получают, что
//=r^(T) = f^2r=1Vyo- E)
Для N= 1 получают односкоростное урав-
уравнение
F)
для функции ф=ф(х, Q). Уравнение F) для плоского
слоя 0 <:?<:.//, когда решение зависит только от одной
координаты х и одной угловой переменной |х, )ц|<:1,
имеет вид
±[1l(f(x, ^dp' + hlz, ц), G)
где 1=1/2, с=2$/2,/i=//2 . Характеристиками левой
части F) являются все прямые x=xo-\-t,Q, xo?D; вдоль
каждой из них уравнение F) принимает вид
g + 2q> = Zj4H + /. (8)
Если в F) сделать замену и= (<р(х, Q)-\-($(x, —й))/2,
то оно принимает вид
[— IQ S7]2u + it=-cu0 + F. (У)
Решение уравнения (9) минимизирует квадратичный
функционал Владимирова:
G(u) = (lQ\Ju, Шу ")+(", и)-(си0, и) +
, u)\u*dQdr-2(u,F), A0)
гха
где
("'"HdSq1
dx dQ.
Пусть краевые задачи записаны в операторной
форме
Z<P = S<P + /. A1?
Характерным свойством задач переноса, использу-
используемым в численных алгоритмах, является то, что зна-
значение L-1^ находится по заданному ip прямым мето-
методом иутем интегрирования (8) вдоль характеристик.
Учитывая это, из A1) получают т. н. интеграль-
интегральное уравнение Пайерлса
) A2)
для нулевого момента Sep.
Для решения задач переноса существенное развитие
получил метод сферических гармоник
(являющийся вариантом метода Галеркина). Прибли-
Приближенное решение (Р„-приближение) находят в виде
Ф1«>(х, Q) = y2nk=fiBk + i)^i=_k^ki(x)Yki(Q), A3)
где <fki(x)— неизвестные функции, a Ykj(Q) — сфе-
рич. гармоники /с-го порядка. Подставляя A3) в F),
умножая результат на Yk[ и интегрируя uo Q, полу-
получают систему уравнений с частными производными
для определения <ffc/(:r). В /^-приближении система
имеет вид
div<p!-{-2cpo=/o, ~ Уфо + фо + 2фг = /1,
2(Фь «)-фо|Г^°. (!4)
где Фо=Фоо' 4i'-= (Фп. Ф12, ф]з)- При /i=0 из A4) полу-
получают диффузионное приближение
где Д = 1/C2). Это — эллиптич. задача, решение
к-рой находят, применяя вариационные или сеточные
методы.
Для решения одномерных задач развиты аналитич.
методы, основанные на разложении решения по обоб-
обобщенным собственным функциям. Для нахождения зна-
значений функционалов от решений сложных многомер-
многомерных задач применяют Монте-Карло метод.
Широкое распространение получили методы конеч-
норазностных аппроксимаций уравнения переноса.
Так, используя квадратурную формулу для области
D, заменяют интегральное уравнение A2) системой
линейных уравнений. В уравнениях D), E), F), (8)
для аппроксимации интегрального оператора приме-
применяют квадратурные формулы для сферы. Известны
Гаусса квадратурные формулы для сферы до 35-го
алгебраич. порядка точности. В методе характеристик
через каждую точку пространственной сетки проводят
семейство характеристик по направлениям, соответ-
соответствующим узлам квадратуры для сферы, и заменяют
дифференциальный оператор L в (8) разностным. Раз-
Разностные уравнения 5„-м е т о д а получают интегри-
интегрированием уравнения F) по сеточной ячейке фазового
пространства, предполагая линейность решения в
пределах ячейки по независимым переменным. В м е-
тоде Галеркина решение ищут в виде
Если <рп(х) заданы, то для определения gn(Q) полу-
получают систему вырожденных интегральных уравнений;
если ф„(х) — финитные функции, то получают м е-
тод конечных элементов; если gn(Q) —
заданные финитные функции и выражение A6) миними-
минимизирует функционал A0), то получают так наз. Рду-
уравнения.
Итерационные методы решения разностных задач
переноса обладают своей спецификой; она заключается
в том, что сходимость итерационных методов, как пра-
правило, замедляется при с —>- 1 (е<1), а для нахождения
следующего приближения tpft + 1 используют только
часть информации о предыдущем приближении фй
существенно меньшей размерности — запоминают и
используют лишь значения ф0. В итерационных ме-
методах в качестве промежуточной операции (операции К)
часто входит решение следующей задачи
A7)
Тогда ошибка ф—Ф* удовлетворяет (И) с независящим
от Q источником S (Ф*—фА) и невязка тоже не зависит
от Q. Это свойство позволяет ускорить сходимость
итераций. Пусть задана периодич. задача для урав-
уравнения G) с постоянными коэффициентами, четным по
A источником и Н=2я, Применительно к этой задаче
нише рассмотрены следующие итерационные методы.
Для уравнения G) строится сетка с N узлами по х
и М угловыми направлениями по ц.. Пусть
!| ft 'I 1*1
[| eo||=max | е„ |.
п
Для сходящихся итерационных методов ||бо+1||<:д||во1|,
где 0<:<7<1. Пусть Цо — цена (количество действий)
операции К, Ц — цена полной итерации, а Д=Ц —¦ Ц„.
Для различных методов имеют место следующие со-
соотношения.
1) П р о с т а я итерация: фо + 1—Фо; для нее
Д^О, q=c.
2) Метод Люстерника: для нек-рых к
полагают в простой итерации
где ^j>1 — наибольшее собственное значение задачи
Lq>~Я5ф; тогда A=0(N), q= cr(I) {q ->- 1 при с ->¦ 1,
<-*0).
3) Метод оценки итерационных от-
отклонений: фо+1—Фо+И7^, где Wk — решение
уравнения
'И1й-+A-с)И"=^(Фо-фо);
тогда
Д =. О (NM), q = шах (сг (I), ^
(д ~> 1 при с —>¦ 1, I _>. 0).
4) Метод с балансовыми множите-
множителями: фо + 1=6*Фо, где
" (\—c)<b%dx
о
для него h~-O(N), q=cr(l) (q —>- 1 при с—у I, I—у 0).
5) Метод средних потоков (метод
ребаланса):
функцию у* выбирают, чтобы минимизировать функ-
функционал A0) или чтобы минимизировать его на нек-ром
конечномерном подпространстве: и*—S,-a,-t|),-, тогда а,-
удовлетворяют определенной системе уравнений.
6) Метод к в а з и д и ф ф у з и и:
гдо
тогда A-O(NM).
7) Мотоды расщепления:
(/ + тЛ2) (/ + гЛ1)ср*+1 =
= (/-|-тЛ2)(/-тЛ1)<р* + 2т
где
Методы 4) — С) — нелинейные, их сходимость мо-
может замедляться при с—v 1, I -у 0; метод 7) требует
запоминания ср*(я, u)(g—>- 1 при с_>1, /—>-0).
8) ffP-методы: поправку Wk определяют как
решение в D краевой задачи
<?nW* = /V(Wa»S-er.S), A8)
где Qn, Pn — линейные дифференциальные операторы
2-го порядка, и полагают фо11 —Фо+W*- В одном из
вариантов ^СУ'-мотода уравнение A8) имеет вид
Для уравнения A9) A=O(N); g=0, 186е нри ^fc=0,843,
а при gk= (l-)-;/fe).'2, где i/д, — корни многочлена Якоби
р(— V». 2(JV + P)—*Js)(y^ p>0, среднегеометрическое за
7V итераций значение g близко к 0,15с. В Л"Р-методе
сходимость итераций не замедляется при с—у i, 1-+0.
Для решения многоскоростной задачи D) применяют
итерационный метод Зейделя:
=Zi/-i2s^° +А=,+1^ч>/о-г-л
i = l, 2, ..., Л', B0)
а решение ф»+1 в каждом уравнении B0) находят
итерационным методом для одпоскоростного урав-
уравнения.
Для решения многоскоростных задач на собствен-
собственные значения D), E) к описанным двум итерационным
циклам добавляют еще один внешний для нахождения
максимального значения Л=Х1 и соответствующей
собственной функции ф. Если х= Q (ф), A = Q(L—S)/.,
то задача D), E) преобразуется в задачу
Ax = U. B1)
Для нахождения X, и <р применяют итерационные
методы с чебышевскими параметрами
u" + i), B2)
где
| m)cosjTG)fe), B3)
o)ft€t0, 1], М, m — параметры. Предполагая неотри-
неотрицательность спектра, сначала находят л, и Х2 — наи-
наибольшие собственные значения B1), считая, что т--0,
М=а, где я^О — оценка снизу для Xlt и беря за со^
Г-последовательность (см. ниже). Значения Xt, X.,
определяют т. п. обобщенным методом
Э и т к е н а, учитывающим сдвиги pft. После нахож-
нахождения к1у к2 функцию ф находят по формулам B2),
B3), полагая М~к2. Бесконечная Т-и о с л е д о в а-
тельность образована, соответственно, из спе-
специальным образом упорядоченных корней многочленов
Чебышева 1-го рода Га-з" (cos я со); начальный отрезок
^-последовательности длины 2-3" состоит из всех
чисел вида B/ft—1)/4-3", 1</А<2-3",
1
4 '
3
Т'
1
12 '
11
12 '
12 '
7
12 '
1
36
Любой отрезок ^-последовательности длины 2-3"
обеспечивает оптимальное в нек-ром смысле подав-
подавление ошибки и устойчивость в итерационном методе
B2), B3).
Для решения нестационарных аадач
1 dtp i г о 1
применимы: метод характеристик в пространстве (.г, t),
метод Галеркина и конечноразностные методы, сво-
сводящиеся к явным и неявным по разностным схемам
или к методам расщепления оператора. В случае
неявных схем для нахождения решения на верхнем
слое может быть применен /СР-метод.
Лит.: [1] Владимиров В. С, «Тр. Матем. пн-та АН
СССР», 1961, т. 61, с. 1 — 158; L2J М арчу к Г. И., Лебе-
Лебедев В. И., Численные методы в теории перенооа нейтронов,
2 изд., М., 1981; [3] Л е б е д е в В. И., Ф и н о г е н о в С. А.,
«Ж. вычисл. матем. и матем. физ.», 1976, т. 16, № 4, с. 895 —11A7;
[4] Л е б е д с в В. И., там же, 1977, т. 17, № 1, с. 100—108.
В. И. Лебедев.
ПЕРЕОПРЕДЕЛЕННАЯ СИСТЕМА — система, чис-
число уравнений к-рой больше числа неизвестных. В ли-
линейном случае такие системы задаются прямоугольной
(тХ п)-матрицей, ,т<п, где т — число уравнений,
are — число неизвестных. Для П. с. первоочередным
является вопрос ее разрешимости, выражаемый в ус-
условиях совместности.
Напр., П. с. линейных алгебраич. уравнений
разрешима тогда и только тогда, когда ранги основ-
основной матрицы Л—||а(-у|| и расширенной матрицы, по-
полученной приписыванием к А столбца свободных
членов, совпадают.
Для П. с. линейных дифференциальных уравнений
с постоянными коэффициентами
У"_ pij (D) uj = fh 1< i < m, A)
^¦¦v — i
где pij — многочлен от одного (обыкновенное урав-
уравнение) или нескольких (уравнение с частными произ-
производными) переменных, a D — символ дифференци-
дифференцирования, условие совместности выражается в виде
однородной системы уравнений с постоянными коэф-
коэффициентами
где матрица q находится по матрице р с помощью ал-
алгебраич. соображений.
Для П- с. A) дифференциальных уравнений с част-
частными производными с переменными коэффициентами
Pij=Pij(x, D) отыскание условий совместности, имею-
имеющих вид B) с 4ki—4ki(x' D)< является значительно
более трудной задачей.
Простейшим примером П. с. служит система диффе-
дифференциальных уравнений
Условия совместности для этой системы, необходимые
и достаточные для ее разрешимости, имеют вид
Аналитич. функции многих комплексных перемен-
переменных «(zj, . . ., zm) можно также рассматривать как
решения П. с. уравнений
ди 1 / ди , . ди
где zj=Xj-\-iyj.
Лит.: [1] М а л ь ц е в А. И., Основы линейной алгебры,
3 изд., М., 1970; [2] П а л а м о д о в В. В., в сб.: Итоги науки.
Математический анализ. 1968, М., 19В9, с. 5—37.
А. П. Солдатов.
ПЕРЕСЕЧЕНИЕ множеств — одна из основных
операций над множествами. Пусть имеется нек-рая (ко-
(конечная или бесконечная) совокупность множеств {Аа}
(индексы а служат для различения элементов данной
совокупности). Тогда множество тех элементов, к-рые
содержатся во всех данных множествах (множество
элементов, общих всем множествам Аа) наз. пере-
пересечением этих множеств.
П. множеств обозначается A=f\Aa.
М. И. Войцеховский.
ПЕРЕСЕЧЕНИЙ ТЕОРИЯ на алгебраиче-
алгебраическом многообразии — теория пересечений
алгебраич. подмногообразий и циклов. Пусть X —
гладкое алгебраич. многообразие размерности п над
полем к, a У и Z — подмногообразия X коразмерности
i и / соответственно. Если У и Z пересекаются транс-
версально, то Yf\Z является гладким подмногооб-
подмногообразием коразмерности i-\-j, к-рое обозначается Y-Z.
В общем случае паре (У, X) сопоставляется алгебраи-
алгебраический цикл Y-Z коразмерности i-\-j. Идея его опре-
определения состоит в том, чтобы заменить Y и Z на эк-
эквивалентные в каком-то смысле циклы У и Z'", нахо-
находящиеся уже в общем положении, и взять затем пере-
пересечение У н Z'; конечно, при этом цикл У -Z' также
определен с точностью до эквивалентности.
Пусть А'(Х) — группа классов алгебраич. циклов
коразмерности i на X по модулю рациональной экви-
эквивалентности; А (Х)= ф А' (X). Теория пересечений
Чжоу состоит из построения трех частей:
а) структуры градуированного коммутативного коль-
кольца на А (X) для каждого гладкого квазипроективного
многообразия X;
б) гомоморфизма градуированных колец /* : А (У) ->
-v А (X) для каждого морфизма / : X ->- Y (обратный
образ);
в) гомоморфизма групп /„. : А {X) -»- A (Y) степени
сЦтУ—dimX для каждого собственного морфизма
/ : X —>- У (прямой образ).
При этом структуры а), б), в) связаны рядом соотно-
соотношений, важнейшими из к-рых являются:
формула проекции: для собственного мор-
морфизма / : X -»- У и циклов а?А (X) и $?А (У)
редукция к диагонали: если Д : „Y —>-
+ХхХ — диагональный морфизм, а а, р?4 (X), то
.?у=Д*(аХР)
Кроме того, существует естественный гомоморфизм
сх : Pic (А') — ¦* А1 (X),
что позволяет построить теорию Чжэня классов со
значениями в кольце Чжоу, и в частности характер
Чжэня
ch : К (X) —* А (X) ® Q,
являющийся гомоморфизмом колец.
Проще всего определяется гомоморфизм прямого
образа /». Пусть ZczX — неприводимое подмногооб-
подмногообразие; если dim/(Z)<dim Z,to/,. (Z)=0, если dim f(Z)—
= dimZ,TO f*(Z)^d-f(Z), где d — степень Z над f(Z).
По линейности определение продолжается на циклы
и классы циклов. Гомоморфизм обратного образа /*
сводится к умножению циклов по формуле
где р : XXY -+ X — проекция, a Г/ClXX У — график
/. Определение умножения циклов делается в два
этапа. Пусть сначала У и Z — неприводимые подмно-
подмногообразия и X, к-рые пересекаются собственно
(т. е. коразмерность Yf\Z равна сумме коразмерностей
У и Z). Каждой компоненте W пересечения Y[\Z
приписывается пек-рое целое положительное число
i (У, Z; W) — локальная кратность пе-
пересечения. Есть несколько определении числа
г (У, Z\ W), напр. Tor-формула Серра:
i(Y, Z; И0 = 2л>0(-1)*НТог?(Л/а, А/Ъ)),
где А — локальное кольцо C,v, w> flub — идеалы }
и Z, а I — длина Л-модуля. После этого полагают
где W пробегает неприводимые компоненты Yf[Z.
Второй этап — лемма Чжоу о сдвиге —
состоит и утверждении, что для произвольных циклов
У, Z на квазипроективном многообразии X сущест-
существует цикл Z', рационально эквивалентный Z, к-рый
пересекается собственно с У; более того, класс рацио-
рациональной эквивалентности У -Z' не зависит от Z'.
Наиболее интересен случай проективного многооб-
многообразия X; применяя функтор прямого образа к струк-
структурному морфизму X —»¦ Spec k, получают отображение
степени deg : А (X) -*¦ %. По существу, степень цик-
цикла — это число точек в нульмерной компоненте цикла.
Композиция умножения со степенью позволяет чис-
численно измерять пересечение. Напр., если У и Z имеют
дополнительные размерности, то получается пересе-
пересечения индекс (число) У и Z. Аналогично, получа-
получается индекс пересечения ге дивизоров Dlt . . ., Dп:
(?>!, .... Dn) = dag(Dv .... Dn).
Напр., кольцо Чжоу проективного пространства
Р.™ порождается классом гиперплоскости //, причем
(//")-=(//, . . ., Н)=\. Поэтому если Du . . ., Dn-
гинорповерхиости степени dx, . . ., dn, то (?>,, . . .,
?>n) = di- ¦ ¦ ¦¦ dn (теорема Везу). Степень
проективного многообразия УсР" размерности к
определяется как индекс пересечения У с линейным
подпространством \>п-к дополнительной размерности;
если многообразия У и Z пересекаются трансверсально.
то степень Yf\Z есть произведение степеней У и Z.
Для собственно пересекающихся эффективных дл-
визоров (?*,, . . ., ?)„)>0, но в общем случае это уже
неверно. Напр., для исключительной кривой Е на
поверхности (Е, Е)=-—1.
Многими формальными свойствами теории колец
Чжоу обладают другие теории: циклы но модулю
алгебраической или численной эквивалентности, К-
теория, теория сингулярных когомологий Н* ( , г?)
(в случае к=С), теория l-адических кого.чологий (см.
также Вейля когомологии). Это приводит к аксиоматич.
построению теории пересечения как сопоставления
каждому многообразию X (из нек-рой категории)
кольца С (X) и гомоморфизмов /* и /*, связанных
рядом аксиом типа формулы проекции или редукции
к диагонали (см. [1]). Сравнение различных П. т.
приводит к полезным соотношениям. Напр., в ком-
комплексном случае понятие фундаментального цикла
позволяет определить гомоморфизм теорий пересе-
пересечений А(Х)^>~Н*(Х, Z), что позволяет использовать
трансцендентные методы. Сравнение X-теории и теории
Чжоу приводит к теореме Римана — Роха — Гротен-
дика. Важную роль при этом играет поведение П. т.
при моноидальном преобразовании (см. [2]). Другое
применение П. т. относится к обоснованию исчисли-
тельной геометрии Шуберта (см. [3]). Эту ветвь гео-
геометрии можно рассматривать как теорию колец Чжоу
различных многообразий, классифицирующих гео-
метрич. объекты — многообразия Грассмана, много-
многообразия флагов и т. д.
Лит.: [I] Anneaux de Chow et Applications, Seminaire Cheval-
ley, Seer. Math., P., 1A58; Vl] Мании Ю. И., Лекции по алгеб-
алгебраической геометрии, ч. 2, М., 1971; [3J Проблемы Гильберта,
М., 19К!1, с. 175—81; [4] Бальдассари М., Алгебраиче-
Алгебраические многообразия, пер. с англ., Ы., КИИ; Г51 Серр Ж.-П.,
«Математика», 1963, т. 7, с. 3—93; Lti] Theorie des intersections
et theoreme de Riemann — Roch, B. - Hdlb.—N. Y., 1971; [7]
Algebraic geometry, Arcata 1974, Providence, 1975; X a p т c-
x о р н Р., Алгебраическая геометрия, пер. с англ., М., 1981.
В. II. Данилов.
ПЕРЕСЕЧЕНИЯ ИНДЕКС — число точек пересече-
пересечения ге дивизоров на re-мерном алгебраич. многообразии
с учетом кратностей этих точек. Точнее, пусть X есть
и-мерное неособое алгебраич. многообразие над полем
к, а ?»!, . . ., Dn — эффективные дивизоры на X, пере-
пересекающиеся в конечном числе точек. Локальным
индексом (или кратностью) пересечения
этих дивизоров в точке х ?Х наз. целое число
(Оъ ..., Dn)x = dmikA'(u1, ..., и„),
где U[ — локальные уравнения дивизора/),• в локальном
кольце А = 0х, х- В комплексном случае локаль-
dtii du,i
ный индекс совпадает с вычетом формы — Л... Л -j— ,
а также со степенью ростка отображения
(щ, ..., ип): (X, *)—>(?", 0).
Глобальный индекс пересечения
(?>!, . . ., D„) есть сумма локальных индексов по
всем точкам пересечения D1(]- . -ftDn. Если это пе-
пересечение не пусто, то (D1, . . ., ?>„)>0.
См. также Пересечении теория. в. И. Данилов
ПЕРЕСЕЧЕНИЯ ИНДЕКС — гомологический инва-
инвариант, характеризующий алгебраическое (т. е. учиты-
учитывающее ориентацию) число точек пересечения двух
подмножеств дополнительных размерностей в евкли-
евклидовом пространстве или ориентированном многооб-
многообразии (находящихся в общем положении). В случае
неориентируемого многообразия в качестве кольца
коэффициентов i? для гомологии рассматривается г?2.
Пусть Х^эА , YZ3B — такие пары подмножеств евкли-
евклидова пространства R™, что A flY—0=--Х()В, и пусть
d:(XX.Y, (А ХУ)и (XX В)) ->¦ (R«. R"\0) — отобра-
отображение, для к-рою d(x, y)=x—у. Индексом пе-
пересечения |ог| классов гомологии !?#„_,-(Х, А),
ц?Нп(У, В) наз. элемент (~1)'й»(|хт)). Здесь
A% — индуцированное отображение гомологии, а
tX4?Hn(XxY, (А XY)(J (X{)В)) — внешнее гомо-
логнч. пропзведенпе элементов | и г\.
II. и. §jt) зависит лишь от тех частей классов |
и ц, носители к-рых попадают в произвольно малую
окрестность V замыкания множества Xf\Y. В част-
ности, 5оГ1=0, если X()Y—0. Кроме того, если F=
= Ui'//. ^|П'//=0ири '5=/. то определены соответ-
соответствующие каждому открытому множеству F,- локаль-
локальные П. и. | и г), сумма к-рых совпадает с с,ог\. Инва-
Инвариант got] не меняется при гомеоморфизмах R". Вместе
с предшествующим свойством локальности это позво-
позволяет определить П. и. |от] для компактных подмножеств
ориентированного многообразия. Имеет место следу-
следующее соотношение антикоммутативности:
Если X и Y — векторные подпространства общего
положения, А=-Х\0, B = Y\0, a \ и т) — образующие
Л = Я„_,(Х, Л) = #,(У, В), то |oi| — образующая
Hn(Rn, К"\0) = Д. Так как выбор указанных образу-
образующих равносилен выбору ориентации в соответству-
соответствующих евклидовых пространствах, ото дает возмож-
возможность определить П. и. сое' двух цеией дополнительных
размерностей (в том числе сингулярных), для к-рых
Н П 1^с' ! = 0^1С'1 П \дс\ (!с —носитель, а дс— грани-
граница цени с). При этом сос'==|ог| для определяемых цепя-
цепями с, с'классов гомологии ?,?Hn-j(X, А), цСПЛУ, В),
\c\cX, \dc\cA, \c'\cY, \дс'\сВ.
П. и. применяется для описания нек-рых соотноше-
соотношений двойственности в многообразиях.
Лит.: [1] Дольд А., Лекции по алгебраический типоло-
типологии, пер. с англ., М., 1976. К. Г. Склярепко.
ПЕРЕСТАНОВКА из п элементов — конечная по-
последовательность длины п, все элементы к-рой раз-
различны, т. е. П.— это размещение без повторения из ге
элементов по п. Число перестановок равно л!
Обычно в качестве элементов П. берут элементы
множества Z,,—{1, 2, . . ., «}; взаимно однозначное
отображение л множества Z,, на себя определяет пере-
перестановку ji=(jiA), лB), . . ., л(»))- Отображение л
наз. подстановкой Zn. Многие задачи, связан-
связанные с перечислением П., формулируются в терминах
подстановок, как, напр., задачи о перечислении П.
с различными ограничениями на позиции перестав-
переставляемых элементов (см., напр., [1], [2]). Перестановка я
может рассматриваться как упорядоченное
множество, состоящее из п элементов, если считать,
что элемент n(i) предшествует элементу л(/+1),
т—12 п
Примеры. 1) Пара {л(г), л(/)} образует в я
инверсию, если л(г)>л(у) при г</. Если аг —
число П. из п элементов с г инверсиями, то
V1 г A-*)A-*г). . .A-х")
2) Если bn — число таких перестановок л из п эле-
элементов, что я(;)>л(?— 1) при i четном и я(г)<я(г — 1)
при i нечетном, то
„со хп
Иногда П. наз. отображения в себя конечного мно-
множества, т. е. подстановки.
Лит.: [1] Сачков В. П., Комбинаторные методы дискрет-
дискретной математики, М., 1977; [2] РиорданД ж., Введение
в комбинаторный анализ, пер. с англ., М., 1963. В. М. Михеев.
ПЕРЕСТАНОВОК КРИТЕРИЙ — статистический
критерий, предназначенный для проверки гипотезы
//*, согласно к-рой плотность вероятности наблюда-
наблюдаемого случайного вектора X— (Xj, . . ., Х„) принад-
принадлежит семейству всех re-мерных плотностей, симмет-
симметричных относительно перестановок аргументов.
Пусть по реализации случайного вектора Х= (Х1?
. . ., Х„), принимающего значения х= (хи . . ., хп)
в ;г-мерном евклидовом пространстве R", надлежит
проворить гипотезу #„. о принадлежности плотности
вероятности р (х) случайного вектора X семейству
Hf.= {p(x)} всех n-мерных плотностей р (z)=p (zj,
. . ., хп), симметричных относительно перестановок
аргументов х1: . . ., хп, то есть
где г= (Г], r2, . . ., г„) — произвольный вектор пз
пространства № всех перестановок (гь г2, . . ., г„)
вектора A, 2, . . ., п). Пространство *R является мно-
множеством всех реализаций вектора рангов R= (Rit R2,
. . ., Rn), естественным образом возникающим при
построении вектора порядковых статистик X(i), при-
принимающего значения ж('' в множестве 3?<oc:R".
II[in справедливости гипотезы Н% статистики X1'' и В
стохастически независимы, при этом
а плотность вероятности вектора порядковых стати-
статистик Х(-> равна п\р(хи)), x(->gj(i).
Свойство (*) равномерно!! распределенное™ стати-
статистики R при справедливости гипотезы Н* и лежит в
основе построения П. к.
Если V (х(->, г) — функция, определенная на J@X2ft
таким образом, что O^Y^gl, и для любого г?Э{ она яв-
является измеримой относительно борелевской о-алгебры
пространства ЭЕ(-) и, кроме того, для нек-рого а? @,1)
~nT*?ir ж^г(х<0' '')^а почти всюду,
то статнетич. критерий для проверки Нх, имеющий
критич. функцию
ф(х) = ф(ж1, хг, ..., хп)=Ч (*<¦>, г),
наз. критерием перестановок. Если П. к.
не является рандомизированным, то а следует выби-
выбирать кратным 1/ге!.
Наиболее мощный критерий для проверки Н^ про-
против простой альтернативы q(x) (д (х) — произвольная
н-мерная плотность, не принадлежащая семейству
Н*) может быть найден в семействе П. к.
Семейство П. к. и семейство критериев, инвариантных
относительно изменения параметров сдвига и мас-
масштаба, играют большую роль при построении ранговых
критериев. И, наконец, следует отметить, что в лите-
литературе по математич. статистике вместо термина П. к.
часто употребляют термин «рандомизации критерий».
См. Порядковая статистика, Инвариантный кри-
критерий, Критическая функция.
Лит.: Ш Гаек Я., Шивав 3., Теория ранговых кри-
критериев, лср. с англ., М., 1971; [2] Л с м а н Э., Проверка ста-
статистических гипотез, пер. с англ., 2 изд., М., 1979.
М. С. Никулин.
ПЕРЕСТАНОВОЧНОСТИ СООТНОШЕНИЯ — пра-
правила перестановки произведения двух операторов рож-
рождения или уничтожения. Именно, для уничтожения
операторов {«(/), /?Н} и сопряженных к ним рождения
операторов {а* (/), f?H}, где Н — нек-рое гильбертово
пространство, действующих в симметричном Фока
пространстве Р (Я) над пространством Н, эти соот-
соотношения имеют вид
aUi)a(J2)-a(f2)a(fl)= Л
= a*l/1)a*(/2)-a*(/2)a*(/i)=0, j. A)
а (М а* (/2)~о* (/2) « (/!) = -(/!, П) Е, /ь h?H, )
где (•, •) — скалярное произведение в Н, а Е — еди-
единичный оператор, действующий в Р(Н). Соотношения
A) наз. также коммутационными соот-
соотношениями. В случае антисимметричного про-
пространства Фока операторы рождения и уничтожения
переставляются согласно правилам:
[ B)
a (/1) a* (/2) + a* (/2) a (t1) = (fi, h) E, flt
к-рые наз. ант и ком мутационными соот-
соотношениям и.
В случае бесконечномерного пространства // кроме
операторов рождения и уничтожения, действующих
в пространствах Фока над Н, существуют и другие,
не эквивалентные им, неприводимые представления
коммутациопных и антикоммутационных соотношений,
т. е. другие семейства операторов, действующих в
каком-нибудь гильбертовом пространстве и удовлет-
удовлетворяющих правилам перестановки A) или B) (см.
[11, [2]). В случае конечномерного гильбертова про-
пространства Н все неприводимые представления как
соотношений A), так и соотношений B) унитарно
эквивалентны.
Лит.: [1] Березин Ф. А., Метод вторичного квантова-
квантования, М., 1905; [2] GJrding L., Wightman А., «Ргоо.
Nat. Acad. Sci. USA», 1954, v. 70, № 7, p. 617—26.
P. A. Mwuioc.
ПЕРЕСТАНОВОЧНЫЕ ОПЕРАТОРЫ — линейные
операторы В и Т, из к-рых Т — общего вида, а В —-
ограничен, такие, что
ВТ^ТВ A)
(запись TczT' означает, что Т' является расширением
Т). Отношение перестановочности обозначается В\]Т
и подчиняется следующим правилам:
1) если В(]Тг, В(]Т2, то ВЦ(Т, 2
2) если ВуЦТ, B2\JT, то (В^В^ЦТ, t2j
3) если Т~х существует, то из В U Т следует В[]Т~1,
4) если B\JTn, ге^-1, 2, . . ., то B\J\imTn;
5) если Bn\JT, л=1, 2, . . ., то Iim5n(j7 при ус-
условии, что lira Вп ограничен, а Т замкнут.
Если оба оператора определены на всем простран-
пространстве, то условие A) сводится к обычному:
ВТ=-ТВ, B)
причем ограниченность 5 не требуется. Обобщение
условия B) оправдано тем, что, напр., даже ограни-
ограниченный оператор В но будет перестановочным со своим
обратным -В, если этот последний определен не на
всем пространстве.
Лит.: [1] Люстерник Л. А., Соболев В. И., Эле-
Элементы функционального анализа, 2 изд., М., 1965; [2] Р и с с Ф.,
Сёкефальви-Надь Б., Лекции по функциональному
анализу пер. с франц. 2 изд., М. 1979. М. И. Войцеховский.
ПЕРЕСТРОЙКА, сферическая пере-
перестройка, на многообразии типа (X, п—%) — переход
от одного (я—1)-мерного многообразия Мх к другому
многообразию М2, состоящий в изъятии вложенной
в Мл сферы размерности I.— 1 и замене ее вложенной
сферой размерности п—Я—1. Подробнее см. Ручек
теория. м- -И. Войцеховский.
ПЕРЕХОД С ЗАПРЕЩЕНИЯМИ для цепиМар-
к о в а — множество траекторий Маркова цепи, к-рые
па рассматриваемом отрезке времени ни разу не по-
попадают в фиксированное множество состояний. Пусть,
напр., \(t) — цепь Маркова с дискретным временем
и множеством состояний S, а II — «запрещенное» мно-
множество состояний. Тогда вероятности пере-
переходов с запрещениями яРг'у W СУТЬ
Свойства вероятностей П. с з. //р,у@ во многом ана-
аналогичны свойствам обычных переходных вероятностей
Pi/(t), так как семейства матриц Р (t)= ||р,у (г)|]4 jeS
и Рн^)=\\нРц{Щ, j6s\H> f>0' образуют полугруппы
по умножению; однако если ^\ р,у (i)=l, то
2jeS//P;7@<l- К изучению тех или иных свойств
вероятностей П. с з. фактически сводятся исследо-
исследование распределения момента первого попадания цени
Маркова в фиксированное множество, доказательство
предельных теорем для ветвящихся процессов при
условии невырождения и т. п.
Лит.: [11 Ч ж j е К а в • л а в, Однородные цепи Маркова,
пер. с англ., М., 1964. А. М. Зубков.
ПЕРЕХОДНАЯ ФУНКЦИЯ, вероятность
переход а,— семейство мер, используемых в тео-
теории марковских процессов для определения распреде-
распределения процесса в будущие моменты времени по из-
известным состояниям в предшествующие моменты. Пусть
измеримое пространство (Е, 33) таково, что а-алгебра
33 содержит все одноточечные подмножества из Е,
и пусть Т — подмножество действительной прямой R.
Функция P(s, x;t,B), заданная при s, t?T, s*?t, x?E
и В ?33, наз. переходной ф у н к ц лей в из-
измеримом пространстве (Е, 93), если: а) при фиксиро-
фиксированных s, х, t она является мерой на 93, причем P(s,
х; t, 5)<:1; б) при фиксированных *, t, В она является
^-измеримой функцией точки х; в) Р (s, х; s, {x})^si
и для всех s, предельных для Т в правой топологии
прямой R,
lim P (s, x; t, E) = l;
sit, teT
г) при всех х?Е, В?33 и s<:i<:u пз Т выполняется
уравнение Колмогорова — Чей мен а:
Р (s, х; и, Щ=\ЕР К х; t, dy) P (t, у; и, В) (*)
(в нек-рых случаях требование в) опускают или ос-
ослабляют). П. ф. наз. марковской переход-
переходной ф у и к ц и е и, если Р (s, x; /, Е)^\, и суб-
субмарковской переходной функцией
в противоположном случае. Если Е не более чем счетно,
П. ф. задают с помощью матрицы вероятностей перс-
хода
*"'=II/>»„<«' О В
(см. Переходные вероятности, Переходных вероятно-
вероятностей матрица). Нередко оказывается, что при любых
допустимых s, х и t мера P(s, x; t, ¦) обладает плот-
плотностью р (s. x; t, ¦) относительно нек-рой моры. Если
при этом выполнен следующий вариант уравнения (*):
г-
р (s, х; и, z)—\P(s, x; t, dy)p(t, у; и, z)
для любых х, z из Е и s<;i<;u из Т, то функцию p(s,
х; t, у) паз. переходной плотностью.
При широких условиях (см. [1], |2]) с П. ф. Р (s, x;
t, В) можно связать марковский процесс X— (xf, ?,
<FJ. ps, *), Для к-рого PSiX{xt?B}=P(s, x; t, В) (в
случае марковской П. ф. этот процесс но обрывает-
обрывается). Наоборот, марковское свойство случайного про-
процесса, как правило, позволяет сопоставить ему П. ф.
(см. [3]).
Пусть Т однородно в том смысле, что совокупность
значений t—s при s<i из Т образует полугруппу t в
R относительно сложения (напр., T~R, T-~{t?R : R :
i>0}, Т= {0, 1, 2, . . .}). Если при этом П. ф. Р (s, x\
t, В) зависит лишь от разности t—s, т. е. если Р (s, x;
t, B)--=P(t—s, x, В), где P(t,ji,B) — функция от t?T,
х?Е, В ?33, подчиненная соответствующему варианту
условии а) — г), то Р (*-, ,r; t, В) наз. однородной
переходной функцией. Последнее назва-
название присваивается и функции Р (t, x, В), для к-рой (*)
принимает форму
P(t + s, х, В)=[Е P(t, х, dy)P (s, у, В),
Для нек-рых целен (напр., при регуляризации П. ф.)
оказывается необходимым расширить определение П. ф.
Напр., считают заданным семейство измеримых про-
странств (Ef,ffif),t?T, а П. ф. относительно этого
семейства определяют как функцию Р (s, x; t, В), где
s, t?T, 6-«, x^F,s, В ?33t, удовлетворяющую подходя-
подходящей модификации условий а) — г).
Лит.: [1] Неве Ж., Математические основы теории вероят-
вероятностей, пер. с франц., М., 1969; [2] Г и х м а н И. И., Скоро-
Скороход А. В., Теория случайных процессов, т. 2, М., 1973; [3]
Кузнецове. Е., «Теория вероятн. и ее примен.», 1980, т. 25,
•N; 2, с. 389—93. М. Г. Шур.
ПЕРЕХОДНЫЕ ВЕРОЯТНОСТИ — вероятности пере-
перехода Маркова цепи \{t) на отрезке времени [s, t] из
состояния i в состояние /:
Нвиду основного свойства цепи Маркова для любых
состояний г, j?S (где S — множество всех состояний
цепи) и любых s<Ct<Cu
Plj(s, u) = '?k^spik(s, t)pkJ{t, и).
Обычно рассматриваются однородные цепи Маркова,
для к-рых П. в. p,j(s, t) зависят от длины отрезка
[s, t], но не от его положения на оси времени:
Для любых состояний I, j однородной цепи Маркова
с дискретным временем последовательность рц(п)
сходится по Чезаро, т. е. существует
lim n~1'S\ Pi/ W 2э= 0.
П -> оо «—1
При нек-рых дополнительных условиях (а также для
цепей с непрерывным временем) пределы существуют
и в обычном смысле. См. Маркова цепь эргодическая,
Маркова цепи положительный класс состояний.
П. в. Pij(t) цепи Маркова с дискретным временем
определяются значениями р,уA), i, j (zS; для любых
В случае цепей Маркова с непрерывным временем
обычно предполагается, что П. в. удовлетворяют до-
дополнительным условиям: все Pij(t) измеримы как
функции i?@, oo),
P{j)j) P, €
При этих предположениях существуют плотности
вероятностей перехода
X!j = \\mt--4pij (t)-ptj ф)Х<х, i, j?S; A)
если все ?.,у конечны и \*. Х,,-у=О, i?S, то П. в. p,-j(t)
удовлетворяют системам дифференциальных уравнений
Колмогорова — Чепмена
с начальными условиями р,-(-@)=1, /j,/@)=0, i^j, i,
j?S (см. также Колмогорова уравнение, Колмогорова —
Чепмена уравнение).
При задании цепи Маркова плотностями перехода
A) ее П. в. Pij(t) удовлетворяют условиям
Pi/@ 3s°. ^jeSPij(O<l, I, )?S, t>0;
цепи, для к-рых \\. р,-у(<)<1 при нек-рых i?S и
t>0, наз. нерегулярными (тогда имеет место
неединственность решения систем B)); если VV „P[j{t)=
= 1 для всех i?S и ?>0, то цепь па-ч. регулярно п.
Пример. Цепь .Маркова ?(<) с множеством со-
состояний {0, 1, . . .} и плотностями перехода
h, i + i = — hi = ^i > °. *.// = 0, 1 * 1 Г1 i + 1
(т. н. процесс чистого ра а м н о ж е в и я)
нерегулярна тогда в только тогда, когда
Пусть
тОн =- inf {i > О : | (t) =
т^ Iim x0
п -> ср
тогда
и при Ет<оо имеет место Р{т<оо}=1, т. е. траек-
траектория цени |(<) «о вероятностью 1 за конечное время
уходит в бесконечность» (см. также Ветвящихся про-
процессов регулярность).
Лит.: [1]Чжун Кай-лай, Однородные цепи Маркова,
пер. с англ., М., 1964. А. М. Зубков.
ПЕРЕХОДНЫХ ВЕРОЯТНОСТЕЙ МАТРИЦА —
матрица Pf= \\Pij(t)\\, элементами к-рой являются
переходные вероятности за время t однородной Мар-
Маркова цепи |B) с не более чем счетным множеством со-
состояний S:
П. в. м. ||р,у(*)!1 Цепей Маркова с дискретным временем
и регулярных цепей Маркова (см. Переходные вероят-
вероятности) с непрерывным временем при любых ?>0, i, j^S
удовлетворяют условиям
т. е. являются стохастическими матрицами, для нере-
нерегулярных цепей
2
такие матрицы наз. полустохастическими.
В силу основного свойства однородной цепи Мар-
Маркова:
Pij (s +') = 23* е SPik (s) PhJ (f)'
семейство матриц {Pi, 00} образует полугруппу по
умножению; в случае, когда время дискретно, эта
полугруппа однозначно определяется матрицей Рх.
А. М. Зубков.
ПЕРЕХОДНЫХ ОПЕРАТОРОВ ПОЛУГРУППА —
полугруппа операторов, порождаемых переходной функ-
функцией марковского процесса. По переходной функции
P(t, х, А) однородного марковского процесса Х= (x-f,
?, Ifi, Рх) в фазовом пространстве (Е, ЗВ) можно по-
построить нек-рые полугруппы линейных операторов Pt,
действующих в том или ином банаховом пространстве В
(см., напр., [1]). Чаще всего в роли В берут простран-
пространство В (Я) ограниченных действительных функций f
на Е с равномерной нормой (а для феллеровского
процесса X — пространство С (Е) непрерывных функ-
функций с той же нормой) или пространство ~V(E) конечных
счетно аддитивных функций ф на Si с полной вариа-
вариацией в качестве нормы. В первых двух случаях пола-
полагают
P4{x)=\Ef(\))P(t, х, dy)\
в третьем
Мр(Л)=$? P(t, у, A)<p(dy)
(здесь / и Ф принадлежат соответствующим простран-
пространствам, х?Е, A <zS3). Во всех этих случаях выполнено
полугрупповое свойство: ptps—pt+s^ S) t~^zO, и любая
из трех полугрупп {/"} наз. полугруппой
переходных операторов.
В дальнейшем речь идет только о первом случае.
Инфинитезимальный оператор А по-
полугруппы {Р*} (он же — инфинитезималь-
инфинитезимальный оператор процесса) определяется обыч-
обычным образом:
/
НО
для всех тех /?[В(Я), для к-рых указанный предел
существует как предел в В (Я). Предполагая, что P(t,
х, А) при А ?3$ является измеримой функцией пары
переменных (t, х), вводят рваольвенту R& процесса
X, а>-0;
Если ||i>*/—/[I _». О при t\0, то Ag=ag—/, где g=Ra.t.
При определенных предположениях интеграл (*) су-
существует и при сс=О, причем #==Д°/ удовлетворяет
«уравнению Пуассона»
(по этой причине, в частности, R°f наа. потенциа-
потенциалом функции f\.
Знание ивфинвтезимального оператора позволяет
найти важные характеристики исходного процесса;
более того, вопросы классификации марковских про-
процессов сводятся к описанию соответствующих им ин-
финитезимальных операторов (см. [2], [3]). Немало-
Немаловажно и то обстоятельство, что инфинитезимальный
оператор входит в уравнения, позволяющие находить
средние значения различных функционалов от про-
процесса. Так, при нек-рых предположениях функция
v(t, x) = Ex [exp
является единственным не слишком быстро растущим
по t решением задачи v\=A u+cv, у@, x)=f (x), где Вх —
математич. ожидание, отвечающее Рх, а «а?=щт(г, ?),
Оператор А родственен характеристическому опе-
оператору 91 (см. [2]). Пусть X •— непрерывный справа
марковский процесс в топологии, пространстве Е,
Для борелевскай функции / полагают
если предел существует для всех х?Е, где U пробегает
систему окрестностей точки х, стягивающихся к х,
и где т — момент первого выхода X из U (при Елт= оэ
дробь, стоящую под знаком предела, приравнивают
нулю). Во многих случаях вычисление Af сводится
к вычислению 91/.
Лит.: [1] Feller W., «Ann. Math.», 1952, V. 55, p. 468 —
519; МДыикинЕ. Б., Оонования теорци адарвдвскцх про-
процессов, St., 1959; [3] Г и х м а н И. И., Скороход А. В.,
Теория елучайныч процессов, т. 2, М., 1973. М. Г. Шур.
ПЕРЕЧИСЛЕНИЯ ОПЕРАТОР — отображение мно-
множества всех множеств натуральных чисел в себя (т. е.
отображение 2 в 2 , где N — множество натураль*-
ных чисел), определяемое следующим образом. Пусть
Wz — рекурсивно перечислимое множество с гёделе-
вым номером 2, Du — конечное множество натуральных
чисел с канонич. индексом и (то есть Du={x1, х2, . . .,
х„), где хг<х2<. . .<ха и 2*i+2*»+. . . + 2х»=и),
<х, иу — номер упорядоченной пары, состоящей из
чисел х та. и, при нек-ром фиксированном взаимно
однозначном рекурсивном иодировании пар. С каждым
рекурсивно перечислимым множеством Wz свявана
процедура, преобразующая любое множество нату-
натуральных чисел В в нек-рое множество натуральных
чисел А. А именно, если число <х, и} принадлежит
множеству Wz и конечное множество Du содержится
в множестве В, то х относится к множеству А. Иными
словами,
Эта процедура позволяет из любого пересчета множе-
множества 5 эффективно получить пересчет множества А.
Она наз. П. о. и обозначается Ф2. Если для нек-рого
П. о. W имеет место ХР(В) = А, то говорят, что Дово-
Доводится по перечислимости к В (Л<е5).
Если Фв1 суть П. о., то их композиция ФЧ также
есть П. о. Если ? — П. о. и А<=В, то "У {А)^?(В).
Еслиж^'Р(Л), то x?^?(D) для нек-рого коночного
множества Ds^A. Каждый П. о. W имеет неподвижную
точку, а именно, существует такое рекурсивно пере-
перечислимое множество А, что У(А)=А, и если VFE)=5,
то А^В.
Лит.: [1] Роджерс X,, Теория рекурсивных функций и
эффективная вычислимость, пер. с англ., М., 1972. В, Е. Плиско.
ПЕРЕЧИСЛЕНИЯ ПРОБЛЕМА — алгоритмическая
проблема, в к-рой для заданного множества А требу-
требуется построить алгоритм, перечисляющий А, т. е.
такой алгоритм 31, к-рый применим ко всякому на-
натуральному числу и перерабатывает его в элемент
из А, причем любой элемент из А получается в резуль-
результате применения Э( к нек-рому натуральному числу;
иными словами, А = (J^,0{3t{0}- П. п. для множества
А разрешима тогда и только тогда, когда А — непустое
перечислимое множество. в Е Плиско
ПЕРЕЧИСЛЕНИЯ ТЕОРИЯ — раздел комбинатор-
комбинаторного анализа, в к-ром изучаются и разрабатываются
методы решения перечислительных задач. Эти задачи,
как правило, сводятся к подсчету числа элементов
конечного множества, обладающих определенными
свойствами, или их классов эквивалентности. К таким
методам относятся, напр., включения и исключения
принцип и различные его обобщения. Теория пере-
перечисления Пойа (см. Попа теорема) часто позволяет
преодолевать трудности при подсчете разных объек-
объектов, когда их приходится рассматривать как нераз-
неразличимые. Основным инструментом при решении пере-
перечислительных задач являются нроизводящие функции;
они также играют существенную роль при получении
асшштотич. соотношений (см. [1] — [3]).
Для получения производящих функций в комбина-
комбинаторике широко применяются алгебры формальных
степенных рядов и различные символич. методы (см.
[1], [2], [4]). В основе общего подхода к разработке
методов получения производящих функций лежит
тот факт, что многие дискретные объекты обладают
естественной упорядоченностью (см. [1], [5]). Ниже
в качестве примера даны построения алгебр инцидент-
инцидентности и показано, как с их помощью решаются нек-рые
перечислительные задачи.
Пусть задано частично упорядоченное множество X
с отношением порядка <: и пусть X локально конечно,
т. е. любой его сегмент
[х, y] = {z:x^z^y; x, у, z?X}
конечен.
Алгеброй инцидентности / (А') наз.
совокупность функций f(x, у), х, у?Х, принимающих
действительные значения и таких, что j(x, y)~=0 при
?=?</• Сумма двух таких функций и умножение на
число определяются обычным образом, а произведе-
произведение f-*g=h вводится соотношением
h(x, V) = ^x<t<yf(x, Z)S(Z> У)-
Умножение оказывается ассоциативным и дистрибутив-
дистрибутивным относительно сложения. Алгебра 1(X) обладает
единицей
б ==6 (х, у) = < v
7 @ при х Ф у.
В алгебре I (X) выделяют два элемента: дзета-функцию
t,= t,(x, у) (?(х, !/)=1 при ж<.у) и обратную ей функцию
Мёбиуса [i=?~1- Справедливо утверждение: если ло-
локально конечное частично упорядоченное множество
X содержит свою наибольшую нижнюю грань, функция
/(.г) определена для всех х?Х и g(x)= V f(y)
для всех х?Х, то для всех х?Х
(теорема обращения Мёбиуса).
Если Х=5 — множество всех конечных подмножеств
нек-рого счетного множества, а х<^у означает, что х<^у,
то при хс^у
а обращение Мёбиуса есть не что иное, как принцип
включения и исключения.
Если X=D — множество натуральных чисел и z<i/
означает, что х делит у, то при ж<:г/ имеем Цд(ж, ;/) =
= [j/— J, где ц(п) — теоретико-числовая Мёбиуса
функция.
Редуцированной алгеброй инци-
инцидентности II (X) наз. подалгебра I (X), к-рой при-
принадлежат все функции 1[Х), принимающие равные
значения на эквивалентных сегментах. При этом от-
отношение эквивалентности сегментов обладает тем
свойством, что если f(x, y) = j{u, v) и g(x, y)~g(u, v)
для [x, у] ~ [и, v], то и
(f*g)(x, y) = (f*g)(u, v).
Это будет, напр., выполняться, если эквивалентными
считать изоморфные сегменты. К алгебре R(X) всегда
принадлежат дзета-функция и функция Мёбиуса.
Если X = JV0={0, 1, 2, . . .} с естественной упорядо-
упорядоченностью чисел, то алгебра /(^Vo) изоморфна алгебре
верхнетреугольных бесконечных матриц. Если к R (No)
отнести все такие функции /?/GV0),4TO f(m, n) = f(m', п)
при п—т=п'—т' = к, то имеет место взаимно одно-
однозначное соответствие
где ak — j(m, n), g^-- (m, п) при п — т~к, так что
Таким образом, алгебра R(N0) изоморфна алгебре
формальных степенных рядов и
б-<-> A --х)-1, ц«->1— х.
Если Х = В, то алгебра R {В) изоморфна алгебре
экспоненциальных степенных рядов
^k-й я h !
и s<r->ex, [i4-»e~-v, где \х, у]~[и, v] цри Iу\х\ — ;1'\м|.
Если X=D и рассматриваются j(m, n)=f(m', n')
при — —-^ , то алгебра R(D) оказывается изоморф-
изоморфной алгебре рядов Дирихле и
При м е р. Пусть с(х, у) — число цепей вида х<
<.гг<. . .</(_!<} в X, тогда (?—б)*(ж, ;/) — число
таких цепей длины к (то есть 1=к). Поэтому
с(х, У) = ^=оа-Ь)"(х, у) =
Рассмотрим эту формулу в R (X) при X = N0, В, D.
В случае X=JV0 и у—г—и число с (.г, у) = сп есть число
упорядоченных разбиений (композиций) п. В R (No)
полученная формула имеет вид
V00 1
следовательно сп=2Гг~1, п>0.
В случае Х—В число с(х, у)--сп есть число упорядо-
упорядоченных разбиений га-элементного множества, |ж\у| = п и
В случае X = D число с(х, у)=сп есть число упорядо-
упорядоченных разложении на множители п=у/х. Следова-
Следовательно,
2 х ?2_= '
п = 1 п' 2-Е
Лит.: [1] С а ч к о в В. Н., Комбинаторные методы дискрет-
дискретной математики, М., 1977; [2] Риордан Д ж., Введение в
комбинаторный анализ, пер. с англ., М., 1963; 13] Перечисли-
Перечислительные задачи комбинаторного анализа. Сб. переводов, М., 1979;
[4] К о t a G.-C, M u I I i n К., в кн.: Graph theory and il*
applications, N. Y.— L., 1970, p. 167—213; [5] Rota G.-C.
«Z. Wahrscheirilichkeitstheor. xind verw. Gen.», 1964, Bd 2, H. 4J
S. 340—68; [li] X ол л М., Комбинаторика, пер. с англ., М.
1970. В. М. Михеев.
ПЕРЕЧИСЛИМОЕ МНОЖЕСТВО — множество, воз-
возникающее в результате развертывания "какого-либо
конструктивного порождающего процесса. Такой про-
процесс можно мыслить как процесс вычисления значений
нек-рого алгоритма с исходными данными в виде на-
натуральных чисел, и потому, напр., определению П. м.
натуральных чисел можно придать следующий точный
вид: множество натуральных чисел наз. перечне-
л и м ы м, если существует такая частично рекурсивная
функция, что это множество является множеством ее
значений.
Всякое разрешимое множество натуральных чисел
является П. м. Обратное неверно: можно указать при-
пример неразрешимого П. м. Этот факт, установленный в
1936 Л. Че'рчем (A. Church), является одним из фунда-
фундаментальных результатов общей алгоритмов теории.
На нем основаны (или могут быть основаны) все из-
известные отрицательные решения алгоритмических про-
проблем. Если какое-либо множество и его дополнение
суть П. л., то это множество разрешимо (теорема
Пост а). Изучение и классификация П. м. являются
предметом исследований алгоритмич. теории множеств.
Лит.: Ш Успенский В. А., Лекции о вычислимых
функциях, М., 1960. Я. М. Нагорный.
ПЕРИМЕТР — 1) П. п л о с к о й области, ог-
ограниченной спрямляемой криво й,—
полная длина границы области.
2) П. измеримого множества А в га-
мерном евклидовом (или римановом) пространстве —
нижний предел (л—1)-мерной площади границы много-
многогранников Рi (или множеств Pt с б^-гладкой границей),
сходящихся к А по объему, т. е. так, что Vol ((A \P,) (j
U {Pj\A )) -> 0 при i ->- со.
Лит.: [1] С а с с о р р о 1 i R., «Rand. Accad. naz. Lincei.
Ser. 8» 1952, № 1, p. 3 — 11, № 2, p. 137—46; [2] GorgiE.
de, там же, Ser. 1, 1958, 5, № 2, p. 33—34. В. А. Залгаллер.
ПЕРИОД группы — наименьшее общее кратное
порядков элементов данной группы (предполагается,
что группа периодическая и порядки всех ее элементов
ограничены в совокупности). П. группы наз. также
показателем группы. О. А. Иванова.
ПЕРИОД функции /(х) — число Г#0 такое,
что при любом ;r?XcR (или ХсС) числа х—Т и
х-\- Т также принадлежат множеству X и выпол-
выполняется равенство
J(x + T)=f(x).
Числа ±пТ, где п — любое натуральное число, также
являются П. функции /(ж). У функции /= const на
оси или на плоскости любое число Т?=0 будет П.;
для функции Дирихле
f 1, если х — рациональное,
\ О, если х — иррациональное,
любое, рациональное число Ту=0 будет П. Если функ-
функция f(x) имеет период Т, то функция ty(x)=f(az+b),
где а и Ъ — постоянные и а^О, имеет период — . Если
действительная функция f(x) с действительным аргу-
аргументом непрерывна на X (и не равна тождественно
постоянной), то она имеет наименьший период Г0>0
и всякий другой действительный П. кратен То. Сущест-
Существуют функции с комплексным аргументом, у к-рых
имеются два некратных с мнимым частным П.; таковы,
напр., эллиптические функции.
Аналогично определяется П. функции, определен-
определенной на нек-рой абелевой группе. а. а. Конюшков.
ПЕРИОДИЧЕСКАЯ ГРУППА — группа, каждый
элемент к-рой имеет конечный порядок. Всякая перио-
дич. абелева группа разлагается в прямую сумму
примерных групп по различным простым числам.
Об условиях конечности П. г. см. Бёрнсайда проблема
о периодических группах. О. А. Иванова.
ПЕРИОДИЧЕСКАЯ ПОЛУГРУППА — полугруппа,
в к-рой каждая моногенная подполугруппа конечна
(другими словами, каждый элемент имеет конечный
порядок). Всякая П. п. имеет идемпотенты. Множество
Ке всех элементов П. ц., нек-рая (зависящая от эле-
элемента) степень к-рых равна данному идемпотенту е,
наз. классом кручения, соответствующим
этому идемпотенту. Множество Ge всех элементов из
Ке, для к-рых е служит единицей, является ^-классом
(см. Грина отношения эквивалентности), наибольшей
подгруппой в Ке и идеалом в подполугруппе <.Ке>,
порожденной Ке; таким образом <Afe> будет гомогруп-
гомогруппой (см. Минимальный идеал). П. п. с единственным
идемиотентом наз. унипотентной. Унипотентность П. п.
S эквивалентна каждому из следующих условий: S
ость идеальное расширение группы при помощи нилъ-
полугруппы, S есть подпрямое произведение группы
п нильполугруппы.
Разбиение Й. п. на классы кручения играет опре-
определяющую роль при изучении многих вопросов для
периодич. полугрупп. Произвольный класс кручения
не обязательно является подполугруппой: минималь-
минимальный контрпример — пятиэлемонтная Брапдта полу-
полугруппа В2, изоморфная рисовской полугруппе матрич-
матричного типа над единичной группой с единичной сэндвич-
матрицей 2-го порядка. В П. и. S все классы кручения
будут подполугруппами тогда и только тогда, когда S
не содержит подполугруппы, являющейся идеальным
расширением унипотентной полугруппы при помощи
В2; в этом случае разбиение S на классы кручения
не обязательно будет связкой. Известны различные (в
том числе необходимые и достаточные) условия, при
к-рых П. п. есть связка классов кручения; это, оче-
очевидно, имеет место для коммутативных полугрупп,
это верно для П. п. с двумя идемпотентами [3].
В любой II. п. отпошения Грина Щ и ^ совпадают;
О-простая П. п. будет вполне О-простой. Для П. п.
S следующие условия эквивалентны: 1) S — архиме-
архимедова полугруппа, 2) все идемпотенты из S попарно
не сравнимы относительно естественного частичного
порядка (см. Идемпотепт), 3) S есть идеальное рас-
расширение вполне простой полугруппы при помощи
нильполугруппы. Известно много условий, эквива-
эквивалентных тому, что П. п. S разлагается в связку (а
тогда и в цолурешетку) архимедовых полугрупп;
среди них: 1) для любого а^5идля любого идемпо-
тента e?S, если e?SaS, то e?Sa2S (см. [5]); 2) в 6' каж-
каждый регулярный ??)-клаес есть подполугруппа; 3) каж-
каждый регулярный элемент из S является групповым.
Пусть S — бесконечная П. п., Е$ — множество
всех ее идемпотентов. Если Es конечно, то S содержит
бесконечную ущшотентную подполугруппу, если Es
бесконечно, то S содержит бесконечную подполугруппу,
являющуюся нилъпотентной полугруппой или полу-
полугруппой идемпотентов [4].
Важный подкласс П. п. составляют локально конеч-
конечные полугруппы. Более широкий класс составляют
квазипериодич. полугруппы (S наз. квази перио-
периодической, если нек-рая степень каждого ее эле-
элемента лежит в подгруппе GcS). Многие свойства И. и.
переносятся на квазипериодич. полугруппы.
Лит.: [1] К л и ф ф о р д А., П р е с т о н Г., Алгебраиче-
Алгебраическая теория полугрупп, пер. с англ., т. 1, М., 1972; [2] Ля-
пин Е. С, Полугруппы, М., 1960; [3] П р о с в и р о и А. С.
«Матем. зап. Уральск- ун-та», 1971, т. 8, № 1, с. 77—94; [4] Ш е н-
р и н Л. Н., «Изв. вузов. Математика», 1974, К« 5, о. 205—15-
[5] Putcha M., «Semigroup Forum», 1973, v. 6, № 1, p. 12—34;
[6] Schwa г г St., «Чехосл. матем. ж.», 1953, т. 3, с. 7—21.
Л. Н. Шеврин.
ПЕРИОДИЧЕСКАЯ ТОЧКА динамической
системы — точка траектории периодич. движония
динамич. системы /* (i?R или *?й), заданной на про-
пространстве S, т. е. такая точка х ?S, что найдется число
Т>0, для к-poro fTx=x, но рхфх при t? @, Т). Это
число Т наз. периодом точки (иногда перио-
периодами наз. также все целые кратные числа Т).
Траектория П. т. наз. замкнутой траекто-
р п е и, или циклом. При употреблении последних
терминов часто отвлекаются от конкретной парамет-
параметризации множества точек траектории параметром t,
рассматривая тот или иной класс эквивалентных пара-
параметризаций: если /' — непрерывное действие группы
R на топологич. пространстве S, то цикл рассматри-
рассматривают как окружность, топологически вложенную в
S; если /* — дифференцируемое действие группы R
на дифференцируемом многообразии S, то цикл рас-
рассматривают как окружность, гладко вложенную u S.
Если х — П. т. (a S — метрич. пространство), то
ее а-предельное множество Ах и со-нредельное множе-
множество iix совпадают с ее траекторией (понимаемой как
множество точек). Это свойство в определенной мере
выделяет П. т. среди всех точек, не являющихся не-
неподвижными. А именно, если пространство, на к-ром
задана динамич. система /', является полным метри-
метрическим и точка х такова, что Qx= {/*z}46 R, то х —
неподвижная или нериодич. точка динамич. системы /'.
Лит.: [1] Н е м ы ц к и й В. В., С т е и а и о в В. В., Качест-
Качественная теория дифференциальных уравнений, 2 изд., М.— Л.,
1949. В. М. Миллионщиков.
ПЕРИОДИЧЕСКАЯ ТРАЕКТОРИЯ автоном-
автономной системы обыкновенных диффе-
дифференциальных уравнений — траектория
периодического решения этой системы; обычно подра-
подразумевается, что это решение не сводится к константе,
т. е. траектория не сводится к одной точке (равновесия,
положению). Синоним П. т.— замкнутая тра-
траектория (поскольку она является замкнутой
Кривой). Д. В. Аносов.
ПЕРИОДИЧЕСКАЯ ФУНКЦИЯ — функция, имею-
имеющая период.
1) Пусть функция f(x) определена на X?R и имеет
период Т. Для получения графика f(,r) достаточно
график функции /(.г) на [а, а+Т](~)Х, где а — нек-рое
число, переместить вдоль R на ±Т, ±2Т, .... Если
П. ф. f(x) с периодом Т имеет конечную производную
f (х), то /' (х) является П. ф. с тем же периодом. Пусть
f(x) интегрируема на любом отрезке и имеет период Т.
Первообразная F= \ f{t)dt имеет период Т, если
\ f(t)dt=-O, в противном случае первообразная П. ф.
непериодическая, такова, напр., первообразная функ-
функции /(я) —COS ж+1. А. А. Конюшков.
2) II. ф. комплексного переменного
z — однозначная аналитич. функция /(г), имеющая
только изолированные особые точки во всей плоскости
комплексного переменного С, для к-рой существует
число рФО, называемое периодом функции
/(z), такое, что
Любая линейная комбинация периодов данной П. ф.
/(z) с целочисленными коэффициентами также явля-
является периодом /(г). Все периоды данной П. ф. /(г)#
¦х: const составляют дискретную абелеву группу но
сложению, называемую группой периодов
функции /(г). Если базис этой группы состоит из
одного единственного основного, или прим и-
т и в н о г о, периода 2ш=;2@]?=0, т. е. если любой
период р есть целое кратное 2со, то /(z) ыаз. одноперио-
Оической функцией. В случае базиса, состоящего из
двух основных периодов 2@^ 2ш3, Im (щ/а>3)ф0, имеем
двоякопериодическую функцию. Если П. ф. /(z) отлична
от константы, то базис ее группы периодов не может
состоять более чем из двух основных независимых
периодов (теорема Якоб и).
Любая полоса вида
2ш: — oo < т < со, 0< г < 1, 0 < а <; л/2},
где 2ш — один из основных периодов П. ф. /(г), или
ой конгруэнтная, наз. полосой периодов
функции /(z); обычно принимают а=я/2, т. е. рас-
рассматривают полосу периодов, стороны к-рой перпенди-
перпендикулярны основному периоду 2со. В каждой полосе
периодов П. ф. принимает любое свое значение и при-
притом одинаково часто.
Любая целая П. ф. /(z) во всей плоскости С разлага-
разлагается в ряд Фурье
nik
/(z) = 2ft=_co «fee <° ,
- я!к .
к-рьга сходится равномерно и абсолютно на прямой
{z=/co: —оо<«<оо} и вообще на любой сколь угодно
широкой полосе конечной ширины, параллельной
этой прямой. Случай, когда целая П. ф. /(z) стремится
к определенному конечному пли бесконечному пределу
в каждом из двух концов полосы периодов, характери-
характеризуется тем, что ряд (¦¦;¦¦) содержит лишь конечное число
членов, то есть /(г) есть тригонометрич. полином.
Любая мероморфная П. ф. /(z) во всей плоскости С
с основным периодом 2со иредставима в виде отношения
двух целых П. ф. с тем же периодом, т. е. в виде от-
отношения двух рядов вида (*). В частности, класс всех
тригонометрич. функций можно описать как класс
таких мероморфных П. ф. с периодом 2я, к-рые в каж-
каждой полосе периодов имеют лишь конечное число по-
полюсов и стремятся к определенному пределу в каждом
конце полосы периодов.
Лит.: Ш Маркушевич А. И., Теория аналитических
функций, 2 изд., т. 2, М., 1968. Е. Д. Соломенцсв.
ПЕРИОДИЧЕСКОЕ РЕШЕНИЕ обыкновенно-
обыкновенного дифференциального уравнения
или системы — решение, периодически зависящее
от независимого переменного t. Для П. p. x(i) (в случае
системы х — вектор) имеется такое число Т^О, что
x(t-\-T)=x(t) при всех J?R.
Всевозможные такие Т наз. периодами данного
П. р.; при этом из непрерывности х(t) следует, что
либо хA) не зависит от /, либо всевозможные периоды
являются целочисленными кратными одного из них —
м и и и м а л ь и о г о периода 7'0>0. Говоря о
П. ])., часто подразумевают, что имеет место второй
случаи, а о То говорят просто как о периоде.
П. р. рассматривают обычно для систем обыкновен-
обыкновенные дифференциальных уравнений, правые части к-рых
либо не зависят от t (автономная система):
x^-f(x), x?U. A)
где U -- область в R", либо зависят от t периодически:
* = /(«, х), f(t-.-Tx, *)=/(*, х), x?U. B)
(У систем с иным характером зависимости правых ча-
частей от t чаще всего нет П. р.) В случае системы B)
период То П. р. обычно совпадает с периодом Тг правой
части или является целочисленным кратным Тх\ дру-
другие То возможны лишь в исключительных случаях.
П. р. с периодом Т0-кТх, fc>l, описывают субгармо-
нич. колебания (см. Вынужденные колебания) и потому
сами иногда наз. субгармоническими П. р.
(или с у б г а р м о н и к а м и).
Система B) определяет наследования отображение
F (зависящее от выбора начального момента tQ): если
x(t, %) — решение системы B) с начальным значением
хЬо, 1) = ?, то
F(l) = x(to-'VTU I).
Свойства системы B) тесно связаны со свойствами /';
в частности, значение при t~ta П. р. с периодом кТг
является при к— 1 неподвижной точкой отображения
F, а при fc>l — его периодич. точкой периода к, т. е.
неподвижной точкой для итерации Fk. Изучение П. р.
в значительной степени сводится к исследованию со-
соответствующей неподвижной (или периодической) точки
отображения последования.
Для автономной системы A) используется следующая
модификация этой конструкции: в фазовом простран-
пространстве в какой-либо точке траектории рассматриваемого
П. р. (она является замкнутой кривой) берут какое-
нибудь локальное сечение, т. е. гладкую площадку
П коразмерности 1, трансверсальную к этой траек-
траектории, и рассматривают отображение, переводящее
точку |?П в первую но времени точку пересечения с II
исходящей из ? траектории системы A).
Поведение решении, близких к данному П. р., опи-
описывается в линейном приближении соответствующей
системой уравнений в вариациях. Коэффициенты этой
линейной системы и данном случае периодически за-
зависят от t, и поэтому можно говорить о соответст-
соответствующих монодромии операторе и мультипликаторах.
О последних говорят как о мультипликато-
мультипликаторах данного П. р. Линейное приближение
определяет свойства П. р. (устойчивость, инвариант-
инвариантные многообразия) примерно в той же степени, как
и для равновесия положений.
П. р. автономной системы A) имеют нек-рые специфич.
особенности: один из мультипликаторов всегда равен
единице (если П. р. не сводится к константе), что при-
приходится, в частности, учитывать при исследовании
устойчивости этих П. р. (см. Андронова — Витта тео-
теорема); период может измениться при малом возму-
возмущении, что приходится учитывать в возмущений теории.
Отыскание II. р. и исследование их свойств пред-
представляет интерес по только с чисто математич. точки
зрения, но и потому, что при математич. описании
реальных фнзич. систем их периодич. режимы обычно
соответствуют II. р. (см. Автоколебания, Вынужде}тые
колебания, Колебаний теория, Нелинейные колебания,
Релаксационное колебание). Однако эта задача очень
трудна — так, не имеется пикаких общих методов,
к-рые позволили бы устанавливать, существуют ли
П. р. у конкретной системы. В различных случаях
используются различные соображения и методы. Мно-
Многие из них относятся к возмущений теории (гармони-
(гармонического баланса метод, Крылова — Боголюбова, метод
усреднения, Малого параметра метод), к к-рой при-
примыкает также исследование бифуркаций; другие —
к качественной теории дифференциальных уравнений.
Последняя, в частности, устанавливает особую роль
П. р. для системы A) при ге=2: в этом случае П. р.
вместе с нек-рыми другими типами решений полностью
определяют поведение всех решений вообще (см.
также Предельный цикл). В связи с этим имеется ряд
специальных результатов о П. р. таких систем (напр.,
о П. р. Ван дер Ноля урав}1ения и его обобщений или
модификаций — Лъенара уравнения, Рэлея уравнения).
Д. В. Аносов.
ПЕРИОДОГРАММА — функция IN(l), —оэ<Х<оо,
N — целое положительное, определяемая по выборке
ХA), . , ., X (N) стационарного случайного процесса
X(t), i==0, ±1, . . ., следующим образом:
где
(X) vVv
П. является периодической по Я функцией с периодом
2я. Дифференцируемая спектральная плотность f(k)
стационарного процесса X (/) со средним с==ЕХ (t)
может быть оценена с помощью П. при Я#0 (mod 2я)
. .. ЛЯ
I? то же время П. не является состоятельной оценкой
f('k) (см. [1]). Состоятельные спектральной плотности
оценки могут быть получены на основе нек-рых даль-
дальнейших построений, использующих асимптотическую
некоррелированность П. разных частот ХлФ'к2, так
что осреднение 1 n(x) по близким к К частотам может
привести к асимптотически состоятельной оценке. В слу-
случае re-мерного случайного процесса X (t)— {Xk(t)}k==^-yl
матрица периодограммы /дг(-Я) определяется своими
элементами
Наряду с периодограммой 1^{к), к-рую еще паз. П.
2-го порядка, иногда рассматривают П. m-го порядка
=1
к-рые используют для построения оценок спектральных
плотностей m-ro порядка (см. Спектральный семиин-
семиинвариант).
Лит.: Ill Бриллинджер Д., Временные ряды. Обра-
Обработка данных и теория, пер. с англ., М., 1980; [2] X е и н а н 3.,
Многомерные временные ряды, пер. с, англ., М., 1974.
И. Г. Шурбенна.
ПЕРИСТОЕ ПРОСТРАНСТВО — вполно регулярное
хаусдорфово пространство, обладающее оперением в
нек-ром своем хаусдорфовом бикомпактном расшире-
расширении. Оперением подпространства X топологич.
пространства У в У наз. счетная система $> семейств
открытых множеств в Y такая, что для каждой точки
х ? X пересечение ео звезд Stv (x) относительно семейств
y^ZP но всем у ?'/3 содержится в X. При этом з в е я д а
Stv (x) точки х относительно семейств множеств у
есть объединение всех элементов семейства у, содер-
жащих х. Если пространство X обладает оперением в
нек-ром своем бикомпактном расширении, то оно
имеет оперение и в каждом бикомпактном хаусдорфо-
вом расширении. Если множество X является пересе-
пересечением убывающей последовательности U1, U2, . . ,
множеств, открытых в объемлющем X пространстве F,
то система {t/j}, {U.,}, . . . составляет оперение под-
подпространства X в Y. В частности, если пространство
полно п о Ч е х у, т. е. является множеством типа
Gs в нек-ром своем бикомпактно хаусдорфовом расши-
расширении, то это — П. п. Все метрич. пространства яв-
являются перистыми. Таким образом, понятие П. п.
является одновременным обобщением понятий локально
бикомпактного пространства и метрич. пространства.
Класс П. п. устойчив относительно операций: произ-
ведение (в счетном числе) П. п. является П. п., пери-
стость сохраняется при переходах к замкнутому под-
подпространству и к подпространству типа Gg. Прообраз
П. п. при совершенном отображении является П. п.
(в классе тихоновских пространств). Предположение
пространства перистым обеспечивает его правильное
поведение во многих существенных отношениях. Вся-
Всякое П. п. является А-пространством. Каждое счетное
П. п. обладает счетной базой. Более того, если в П. п.
есть счетная сеть, то в нем есть и счетная база (и это
пространство метризуемо). При непрерывном отобра-
отображении на П. п. вес не может увеличиваться. Важно,
что в присутствии перистости принципиально меня-
меняется поведение нек-рых других фундаментальных
свойств. В частности, произведение паракомпактных
П. п. является паракомпактным П. п., хотя параком-
паракомпактность сама по себе не мультипликативна. Далее,
произведение финально компактных П. п. является
финально компактным П. п., хотя финальная компакт-
компактность не мультипликативна. Понятие перистости по-
позволило охарактеризовать те пространства, к-рые
могут быть совершенно отображены на метрич. про-
пространства. А именно, для того чтобы существовало
совершенное отображение тихоновского пространства
V на нек-рое метрич. пространство, необходимо и
достаточно, чтобы X было паракомпактным П. п.
(теорема Архангельского). Образ пара-
компактного П. и. при совершенном отображении
является паракомнактнБШ П.п. (теорем а Филип-
Филиппов а); однако известен пример совершенного ото-
отображения П. п. на нснеристое тихоновское простран-
пространство. Важными примерами непаракомпактных П. п.
служат непаракомпактные локально бикомпактные
пространства и нсметризуемые м о р о в с к и е про-
пространства — тихоновские пространства со счет-
счетной измельчающейся последовательностью открытых
покрытий. Для пространств тоиологич. групп из
пористости следует паракомпактность. Для групп
справедлив простой критерий пористости: пространство
топологич. группы является перистым в том и только
в том случае, если в нем имеется непустой бикомпакт,
обладающий счетной определяющей системой окрест-
окрестностей (теорема П а с ы н к о в а). В присут-
присутствии перистости существенно упрощаются критерии
метризуемости. В частности, если паракомпактнос
П. п. X взаимно однозначно и непрерывно отображается
на метрич. пространство, то X метризуемо. На этой
основе доказывается, что тихоновское пространство X
метризуемо в том и только в том случае, если оно
является паракомпактным П. п. с диагональю типа
Ge,; последнее условие означает, что множество Д--
= {(х, х) : х?Х} представимо как пересечение счет-
счетного семейства открытых в пространстве XX X мно-
множеств. Приведенные и другие результаты позволяют
считать перистость одним из основных общих свойств
метрич. пространств и бикомпактов наряду с параком-
паракомпактностью. I
Лит.: Ш Архангельский А. В., П о н о м а-
р е в В. И., Основы общей топологии в задачах и упражнениях,
М. 1974; [2] Архангельский А. В., «Матем. сб.», 1965,
т. 67, № 1, с. 55—88; [3] Ф и л и п п о в В. В., «Докл. АН СССР»,
1967, т. 176, № 3, с. 533—35; [4] П а с ы н к о в Б. А., там же,
1965, т. 161, № 2, с. 281—84. А. В. Архангельский.
ПЕРИФЕРИЧЕСКИ БИКОМПАКТНОЕ ПРОСТРАН-
ПРОСТРАНСТВО — топологическое пространство, обладающее
базой открытых множеств с бикомпактными границами.
Вполне регулярное П. б. п. X имеет бикомпактные
расширения с нульмерными (в смысле размерности
ind) наростами. Если всякий бикомпакт АаХ допу-
допускает вложение в другой бикомпакт ВаХ, для к-рого
в X имеется счетная фундаментальная система окрест-
окрестностей (напр., когда X метризуемо), периферия, би-
компактность X равносильна существованию у X
бикомпактных расширений с нульмерными наростами.
Е. Г. Скляренко.
ПЕРМАНЕНТ (тХге)-матрицы А = \\ац\\ — функция
где aij — элементы из коммутативного кольца, сум-
суммирование производится по всем взаимно однозначным
отображениям а из {1, 2, . . ., т} в {\, 2, . . ., п}.
Если т=п, то а — всевозможные подстановки, и II.
представляет собой частный случай матричной
функции Шура
при H—Sn, %=1, где % — характер степени 1 на
подгруппе Н симметрической группы Sn (при H = Sn,
Х(о")=±1, в зависимости от четности а, получается
определитель).
П. применяется в линейной алгебре, теории веро-
вероятностей и комбинаторике. В комбинаторике П. можно
интерпретировать следующим образом: число систем
различных представителей для заданного семейства
подмножеств конечного множества есть П. матрицы
инцидентности для инцидентности системы, связан-
связанной с этим семейством.
Наибольший интерес представляют П. матриц из
нулей и единиц ((ОД)-матриц), матриц с неотрицатель-
неотрицательными действительными элементами, в частности дваж-
дважды стохастических матриц (у к-рых
суммы элементов по любой строке и любому столбцу
равны 1) и комплексных эрмитовых матриц. Из ос-
основных свойств П. следует отметить теорему о раз-
разложении (аналог теоремы Лапласа для определителей)
и теорему Бине — Коши, дающую представление П.
произведения двух матриц через сумму произведений
П., образованных из сомножителей. Для П. комплекс-
комплексных матриц полезно представление их в виде скаляр-
скалярного произведения на классах симметрии вполне сим-
симметричных тензоров (см., напр., [3]). Один из наиболее
эффективных способов вычисления П. дает формула
Р а й з е р а:
где Л(, — совокупность подматриц размера тХк
квадратной матрицы А, г,-=г?-(Х) — сумма элементов
в i-й строке X, i, /r-1, . . ., т. Ввиду сложности
вычисления П. важны его оценки. Ниже приведены
нек-рые из оценок снизу.
а) Если А есть @, 1)-матрица с г,(Л)>г, г—1, . . .,
т, то
per A^t \/(t — m) !
при t^m,
рл' 4 3s t !,
если Z</ra и per A >0.
б) Если А есть @, 1)-матрица порядка п, то
per -4 Зг JJ. _ {М -И — п\,
где гх^гъ^. . -~^гп — суммы элементов в строках А,
расположенные в порядке невозрастания, {rj-|-i— п}—
= max@, r,- + i — re).
в) Если А — положительно полуопределенная эр-
эрмитова матрица порядка ге, то
где s(A)^-2. .djj, если s(A)?=0.
Оценки П! сверху:
1) для @, 1)-матрицы порядка п
2) для вполне неразложимой матрицы порядка п
с неотрицательными целыми элементами
per (,4)<2sM)-2n-)_i;
3) для комплексной нормальной матрицы с собст-
собственными значениями к±, ...,%.„
Наиболее известной проблемой в теории П. являлась
гипотеза Ван дер Вардева: П. дважды
стохастич. матрицы порядка п ограничен снизу ве-
величиной п\/п", и это значение достигается лишь для
матрицы, составленной из дробей 1/ге. Положительное
решение этой проблемы было получено в 1980 (см. [4]).
Из применений П. следует отметить связь с извест-
известными комбинаторными задачами о встречах, об ис-
исполнителях, с Фибоначчи числами, с перечислением
латинских квадратов и троек Штейнера, с нахож-
нахождением числа 1-факторов и линейных подграфов в
графе; дважды стохастич. матрицы связаны с нек-рыми
вероятностными моделями. Интересны физич. приме-
применения П., среди к-рых наиболее важна проблема ди-
меров, возникающая при изучении адсорбции двухатом-
двухатомных молекул поверхностного слоя: через П. @, 1)-
матрицы простого строения выражается число спо-
способов объединения атомов вещества в двухатомные
молекулы. Известны также применения П. в стати-
стич. физике, теории кристаллов, физич. химии.
Лит.: [1] Райзер Г. Д т,, Комбинаторная математика,
пер. с англ., М., 1966; [2] С а ч к о в В. Н., Комбинаторные ме-
методы дискретной математики, М., 1977; [3] Минн X., Перма-
Перманенты, пер. с англ.,М., 1982; [4] Е г о р ычев Г. II., Решение
проблемы Ван дер Вардена для перманентов, Красноярск, 1980;
[5] Ф а л и к м а н Д. И., «Матем. заметки», 1981, т. 29, в. 6,
с. 931 — 38. В. Е. Тарапапов.
ПЕРМУТАТОР — собственное значение X стохастич.
ядра такое, что оно отлично от единицы и \X\ = i. Не-
Неотрицательная непрерывная функция К(х, у), заданная
на компактном множестве Q конечномерного про-
пространства, наз. стохастическим ядром,
если
Собственные значения такого ядра удовлетворяют ус-
условию |Х|<:1. В теории операторов П. наз. оператор
А : Е -> Е, если область его значений А (Е) конечно-
конечномерна и в этой области существует такой базис еи
¦ • -, е„, что Aej—ek, ; = 1, . . ., п.
Лит.: [1] Интегральные уравнения, М., 1968.
Б. В. Хведелидзе.
ПЕРПЕНДИКУЛЯР к данной прямой (плоскости) —
прямая, пересекающая данную прямую (плоскость)
под прямым углом.
ПЕРПЕНДИКУЛЯРНЫЕ ПРЯМЫЕ — прямые, со-
составляющие прямой угол (в пространстве такие пря-
прямые не должны обязательно пересекаться). Прямая I
и плоскость а наз. взаимно перпендикулярными,
если I перпендикулярна ко всякой прямой, лежащей
на ос. Об обобщении понятия перпендикулярности см.
ст. Ортогональность.
ПЕРРОНА ИНТЕГРАЛ — обобщение понятия ин-
интеграла Лебега. Функция /(.г) наз. интегриру-
интегрируемой на [а, Ь] в с м ы с л е Перрона, если су-
существуют функции М (х) (мажоранта) и т (х) (мино-
(миноранта) такие, что
М (а) - О, DM (х) 2э / (х), DM (х) ф — оо,
т (а) = 0, Dm (х) < / (х), Dm (х) ф + оо
(D и D — нижняя и верхняя производные) для х?[а, Ь]
и нижняя грань значений М(Ь) мажорант М(х) равна
верхней грани зпачешш т(Ь) минорант т(х)\ их общее
значение нал. интегралом Перрона от f(x)
на [я, 6] и обозначается
~\i(x)dx.
П. и. восстанавливает функцию по ее точной конеч-
конечной производной; он эквивалентен Данжуа интегралу
узкому. П. и. для ограниченных функций ввел О. Пер-
Перрон [1], окончательное определение дал X. Бауэр [2].
Лит.: [1] Perron О., «Sitzungsber. Heidelberg. Acad.
Wiss.», 1914, Bd V A., S. 1 — 16; [2] В a u e r H., «Monatsh. Math,
und Phys.», 1915, Bd 26, S. 153—98; [3] Сакс С, Теория ин-
интеграла, пор. с англ., М., 1949; [4] Виноградова И. А.,
Скворцов В. А. Итоги науки. Математический анализ,
1970, М., 1971. ' Т.П.Лукашенко.
ПЕРРОНА МЕТОД — метод решения Дирихле за-
задачи для Лапласа уравнения, основанный на свойствах
субгармонических функций (и супергармонич. функций).
Первоначальное изложение этого метода было дано О.
Перроном [1], существенное развитие получено в
работах Н. Винера [3] i M. В. Келдыша [4].
Пусть Q — конечная область евклидова простран-
пространства R", л^:2, с границей Г=ЗЙ, /=/(у) — дейст-
действительная функция на Г, —оо <:/((/)<:+ оо. Пусть Ф —
(непустое) семейство всех супергармонич. функций
и(х), x?Q, в широком смысле (т. е. функция v(x)=-{-co
принадлежит Ф), ограниченных снизу и таких, что
Jim infi' (x)Ssf(y), y?T,
и пусть
— нижняя огибающая семейства Ф. Наряду с Ф рас-
рассматривается (непустое) семейство Ч' всех субгармонпч.
функций и{х), x?Q, в широком смысле (функция ц(г) =
==—oo^4f), ограниченных сверху и таких, что
lim snp и (аг)</ (у),
и пусть
Hf(x)~-Uf(x; Q) = sup{« (x):
— верхняя огибающая семейства У.
Относительно функции Нf (и Hf) имеются только
три возможности: 11 f(x) j^+oo, Hj-(x)^s—оо, Нf(x) —
гармонич. функция, причем всегда
H_f{x) <Hf{x), x?Q.
Функция /(у), ?/?Г, наз. разрешимой, если обе
огибающие Нf и IIf конечны и совпадают. В этом
случае гармонич. функция Л^(х)~Н^(х)=Н^(х) есть
обобщенное решение задачи Дирихле
для функции /(у), </?Г (в смысле Винера — Перрона).
Для того чтобы функция /(у), г/?Г, была разрешимой,
необходимо и достаточно, чтобы опа была интегрируе-
интегрируемой по гармошм/. мерс на Г (т с о р с м а Брел о).
Любая непрерывная конечная функция /(г/), у?Г, раз-
разрешима (теорема Винера).
Точка уд ? Г паз. регулярной граничной
точкой, если для любой непрерывной конечной
функции f(y), 1/?Г, выполняется предельное соот-
соотношение
lim
Регулярность всех точек у?Г равносильна сущест-
существованию классич. решения Wj(x) задачи Дирихле для
любой непрерывной конечной функции f(y), у?Г,
причем в этом случае Hf{x)z=wj(x); область Q, все
граничные точки к-рой регулярны, иногда наз. также
регулярной. Для того чтобы точка г/п?Г была
регулярной, необходимо и достаточно, чтобы сущест-
существовал барьер в уп.
Точки ;/о?Т\ не являющиеся регулярными, наз.
иррегулярными граничными точка-
м и. Напр., иррегулярными граничными точками яв-
являются изолированные точки и при ге^З вершины
юстаточно сильно заостренных входящих в область Q
острий (пример Лебега). Множество всех ирре-
иррегулярных точек Г есть множество типа Fa емкости
нуль.
Пусть имеется последовательность областей Qj,,
Q/idQ/i + u такая, что Q— (J*==i^*i п непрерывная
конечная функция 1(у), ?/?Г, продолжена непрерывно
на окрестность Г. Тогда
lim ПАх; Qk)—Hf(x; Q), x?Q,
равномерно внутри Q; в случае регулярных областей
Q/i здесь получается конструкция обобщенного решения
задачи Дирихле по Винеру. Рассмотрим теперь для
области Q без внутренней границы произвольную
последовательность областей G/,, dGk ->¦ Г, GkZ2&-
1! этом случае, вообще говоря,
lim IIf(x; Gk) ф II,(х; Q).
Задача Дирихле устойчива в области Q или в замкпу-
той области Q, если
lim П/(х; Gk)=H,(x; Q)
k -> со
соответственно для всех x^Q или для всех x?Q. Для
устойчивости задачи Дирихле в области Q необходимо
и достаточно, чтобы множества всех иррегулярных
точек дополнений СО. и CQ совпадали; для устойчи-
устойчивости в замкнутой области — чтобы дополнение CQ
не имело иррегулярных точек (теоремы Кел-
Келдыша, см. [4], где построен также пример регулярной
области Q, внутри к-рой задача Дирихле неустойчива).
См. также Верхних и нижних функций метод.
Лит.: [1] Р е г го п О., «Math. Z.», 1923, Bd 18, S. 42—54;
[2] Петровский И. Г., «Успехи матем. наук», 1941 [1940],
в. 8, с. 107—14; L3J WienerH., «J. Math, and Phys.», 1924,
v. 3, p. 24—51, 127 — 46; 1925, v. 4, p, 21 — 32; [4] К е л-
ды ш М. В., «Успехи матем. наук», 1941 [1940], в. 8, с. 171 —
2.41; [5] Брело М., Основы классической теории потенциала,
пер. с франц., М., 1964. Е. Д. Соломенцев.
ПЕРРОНА ПРЕОБРАЗОВАНИЕ — ортогональное
(унитарное) преобразование
гладко зависящее от t и преобразующее линейную си-
систему обыкновенных дифференциальных уравнений
в систему треугольного вида
Введено О. Перроном [1]. Справедлива теорема
Перрона : для всякой линейной системы B) с
непрерывными коэффициентами a) (t) сущестпует II. п.
П. п. строится с помощью процесса ортогоналпяа-
ции Грама — Шмидта (при каждом I) системы векторов
xL(t), . . ., xn(t), где xl(t), ¦ . ., xn(t) — какая-либо
фундаментальная система решений системы B), при-
причем различные фундаментальные системы дают, вообще
говоря, различные П. н. (см. [1J, [2]). Для систем B)
с ограниченными непрерывными коэффициентами исе
П. п. являются Ляпунова преобразованиями.
Если матричнозначная функция ||a/(i)||, i, /=1; • • •>
п, является рекуррентной функцией, то найдется
рекуррентная матричнозначная функция ||и)@ |. г',/=1,
..., п, такая, что A) есть П. п., приводящее систему
B) к треугольному виду C), причем функция
\р) О ' '' ' ~ ^' "' '' п'
рекуррентна.
Лит.: [1] Р р г ro n О., «Math. Z.», 1930, Bd 32, S. 465—73;
[2J D i 1 i b e r to S. P., «Ann. Math. Studies», 1950, v. 20, p.
1—38; [3] Билон Б. Ф., В и н о гран Р. Э., Г р о б м а и
Д. М., Немыцкий В. В., Теория показателей Ляпунова и
ее приложения к вопросам устойчивости, М., 19(i(i; [4] И з о-
б о в Н. А., п со.; Итоги науки и техники. Математический ана-
анализ, т. 12, М., 1974, с. 71 —146. В. М. Миллионщиков.
ПЕРРОНА — СТИЛТЬЕСА ИНТЕГРАЛ — обобщенно
понятия Перрона интеграла от функции одного дей-
действительного переменного. Конечная функция f (х)
наз. интегрируемой в смысле Перрона — Стилтьеса
относительно конечной функции G (х) на [а, Ь], если
на [а, Ь) существуют мажоранта М (х) и миноранта
т (х) функции / (х) относительно G {х) па [а, Ъ\ с М (х) -¦
—~-т (в) = 0 такие, что в каждой точке х?[а, Ь]
М (х+$)—М(х — a)^sf(x) (G(x-]-$)-С, (х-а)).
т (х -[ Р) — т (х - а)< / (z) (G (.г -[ |3) - С, (х - а))
при всех достаточно малых aS?0 и fS^O, кроме того,
нижняя грань чисел М(Ь), где М (х) — произвольная
мажоранта / (.т) относительно G (х), и верхняя грань чи-
чисел т(Ь), где т (х) —произвольная миноранта / (х)
относительно G (х), равны между собой. Общее значение
лтих двух граней наз. П.—С. и. от / (х) относительно
G(x) на [а, Ь\ и обозначается
(P-S)\lbaf(x)dG(x).
Такое обобщение интеграла Перрона ввел О. Уорд
[1].
Лит.: [1] W a rd A. J., «Math. Z.», 1036, Bd 4J, S. 578 —
604; 12] Сакс С, Теория интеграла, пер. с англ., М., 1949;
[3] В и н о г р а д о в а И. А., С к в о р ц о ц В. Д., в кн.: Мате-
Математический анализ. 1970, М., 1971, с. 65—107. Т. П. Лукашенко.
ПЕРРОНА — ФРОБЕНИУСА ТЕОРЕМА: пусть
действительная квадратная (пХ п)-матрица А, рас-
рассматриваемая как оператор в пространстве R", не
имеет инвариантных координатных подпространств
(такая матрица наз. неразложимой) и неотри-
неотрицательна (т. е. все ее элементы неотрицательны).
И пусть Ху, . . ., Я„ — ее собственные значения, зану-
занумерованные так, что
Тогда:
1) число г~- |Xj| — простой положительный корень
характеристпч. многочлена матрицы А;
2) существует собственный вектор матрицы А с
положительными координатами, соответствующий г\
3) числа >„!, . . ., 'kh совпадают с точностью до нуме-
нумерации с числами г, изг, . . ., u>fl~1r, где ы-=е2Я'< ';
4) произведение любого собственного значения мат-
матрицы А па m есть собственное значение матрицы А;
5) при /г>1 найдется перестановка строк и столб-
столбцов, приводящая матрицу А к виду
О Ах 0...0 О
О О
О
О 0 0 .. .0 Л/,
40 о ...о о
где A j — матрицы порядка nh~x.
О. Перрон доказал в [1] утверждения 1) и 2) для
положительных матриц, а в полном объеме приведен-
приведенную теорему доказал Ф. Фробениус в [2].
Лит.: [1] Perron О., «Malh. Ann.», 1907, Bd (H, S. 2Л8 —
263; 12] P г о b e n i u s G., «Sitzungsber. der Kgl. Prouss. Akad.
Wiss.», 1912, S. /,5П — 77; [3] Гантмахсрф. Р.. Теория
матриц, 3 изд., М., 1ЯВ7. Д. А. Супруиенпо.
ПЕРСЕЯ КРИВАЯ, сппрпческая крива я,—
плоская алгебраич. кривая 4-го порядка; является
линией пересечения поверхности тора плоскостью,
параллельной его оси (см. рис.). Уравнение в прямо-
прямоугольных координатах:
где г — радиус окружности, описывающей тор, d —
расстояние от начала координат до ее центра, р —
расстояние от оси тора до секущей плоскости. К П. к.
d>r
d=r
d<r
етаэеэ
р-о р-о
p>d-r
p>r
p>d
относятся: Бута лемниската, Кассини овал и Ьер-
нулли лемниската.
П. к. названа по имени древнегреч. геометра Персея
B в. до н. э.), исследовавшего ее в связи с изучением
различных способов задания кривых.
Лит.: [Ц С а в е л о в А. А., Плоские кривые, М., 1960.
Д. Д. Соколов.
ПЕРСПЕКТИВА с центром S — отображение
плоскости я в плоскость л', при к-ром каждой точке
М плоскости я ставится в соответствие точка М' пере-
пересечения прямой SM с плоскостью я' (если прямая SM
не параллельна плоскости я'; см. рис.).
В проективной геометрии П. опре-
определяется следующим образом: пусть
К и V — собственные подпростран-
подпространства одинаковой размерности проек-
проективного пространства Q, Т — под-
подпространство максимальной размер-
размерности, не имеющее общих точек нн
с V, ни с V. Пусть U — подпрост-
подпространство, содержащееся в V, и W —
подпространство минимальной раз-
размерности, содержащее U и Т, а V —
пересечение W и Г'. Соответствие,
при к-ром каждому подпространству
U, содержащемуся в V, ставится в соответствие подпро-
подпространство U', содержащееся в V, наз. перспек-
перспективным отображением пространства V
на пространство V с центром перспективы Т.
П. есть коллинеация. Если подпространства У и У
пересекаются, то каждая точка подпространства Vf\V
сама себе соответствует.
Если в пространствах V и V введены проективные
координаты, то перспективное соответствие может
Г>ыть задано линейным отображением.
Лит.: [1] А р т и и Э., Геометрическая алгебра, пер. с англ.,
М., 1909; [2] Глаголев Н. А., Проективная геометрия'
2 изд., М., 11H3. П. С. Моденов.
ПЕРЦЕНТИЛЬ — одна пз числовых характеристик
распределения вероятностей; частный случай квантили.
Именно, П. определяется как квантиль Кр, соответст-
соответствующая значениям р, равным //100 для / = 0, 1,2,.. .,
99. Для непрерывной строго монотонной функции
распределения F (х) /-я перцентиль представляет собой
решение уравнения
F(x) =
з
100 ¦'
7~0, 1, 2, . . ., 99. В математич. статистике П. дают
хорошее представление о виде функции распределения.
П. также наз. п р о ц о н т и л я м и, или цент и-
Л Я М И. А. П. Прохоров.
ПЕТЕЛЬ ПРОСТРАНСТВО — снабженное компакт
но открытой топологией пространство QX всех петель
в точке * топологич. пространства X с отмеченной
точкой *. П. п. является слоем Серра расслоения
(Е, р, X) над пространством X (здесь Е — путей
пространство). А. Ф. Харшиладзе.
ПЕТЕРА — ВЕЙЛЯ ТЕОРЕМА — теорема об ап-
аппроксимации функций на компактной топологич. груп-
группе представляющими функциями. Пусть я пробегает
семейство 2 представителей всех классов эквивалент-
эквивалентности неприводимых непрерывных унитарных пред-
представлений компактной группы G. Пусть dim я — раз-
мерпость представления я и к'.1?1 — ого матричные эле-
элементы в нек-ром ортонормированном базисе. П. — В. т.
утверждает, что функции вида
образуют ортонормированный базис в пространстве
X2(G) суммируемых с квадратом функций относи-
относительно меры Хаара на G (мера всей группы считается
равной 1). Алгебра всех нредставляющих комплексных
функций на G, совпадающая с множеством конечных
линейных комбинаций функций uffi (я ?2), равномерно
плотна в пространстве всех непрерывных комплексных
функций на G.
В случае, когда G= T — группа вращений плоско-
плоскости,— это утверждение совпадает с элементарной тео-
теоремой об аппроксимации периодических непрерывных
функций тригонометрич. многочленами.
В качестве следствия из П.— В. т. выводится, что
совокупность линейных комбинаций характеров не-
неприводимых представлений группы G плотна в алгебре
всех непрерывных функций на G, построенных на
классах сопряженных элементов. Другое следствие
состоит в том, что для любого элемента a?G, афе,
найдется такое неприводимое непрерывное представ-
представление ф группы G, что (р(а)т&Е; если же G — компакт-
компактная группа Ли, то G допускает точное линейное пред-
представление.
Из П.— В. т. вытекает также следующее, более
общее, утверждение (см. [5], |6]). Пусть дано непре-
непрерывное линейное представление ф компактной группы
G в пространстве Фреше Е, тогда подпространство
представляющих элементов пространства Е плотно
в Е. При этом элемент v?E наз. представляю-
щ и м, или сферическим, или почти инва-
инвариантным, если орбита <p(G)i> порождает в Е
конечномерное подпространство. Это, в частности,
применимо к случаю, когда Е — пространство сечений
нек-рого класса гладкости гладкого векторного G-
расслоения, напр, пространство тензорных полей
определенного типа и заданного класса гладкости на
гладком многообразии с гладким действием компактной
группы Ли G.
П.— В. т. была доказана в 1927 Ф. Петером (F. Peter)
и Г. Вейлсм (Н. Weyl) (см. [1]).
Лит.: [1] Петер Ф., В е й л ь Г., «Успехи матем. наук»,
1930, в. 2, с. 144—60; 12] П о н т р я г и н Л. С, Непрерывные
группы, 3 изд., М., 1973; [3] ХьюиттЭ., Р о с с К., Абст-
Абстрактный гармонический анализ, пер. с англ., т. 1, М., 1975; [4]
Ш е в а л л е К., Теория групп Ли, пер. с англ., т. 1, М., 1948;
[")] Р al a i s R. S. , Stewart Т.Е., «Amer. J, Math.», 1961,
v. 83, № 4, p. 623—44; [6] MostowG.D., «Ann. Math.», 1961,
v. 73, Ni 1, p. 20—48. А. Л. Онищик, А. И. Штерн.
ПЕТЕРСОНА ПОВЕРХНОСТЬ — поверхность, обла-
обладающая сопряженной сетью конических или цилинд-
рич. линий, являющейся главным основанием изги-
изгибания (см. Изгибание на главном основании). Напр.,
П. п. является капаловая поверхность, переноса поверх-
поверхность, вращения поверхность. Вращений индикатриса
П. п. есть прямой коноид (в частности, для каналовой
поверхности ею является геликоид, для поверхности
переноса — гиперболич. параболоид). Впервые рас-
рассмотрена К. М. Петерсоном как пример поверхности,
допускающей изгибание на главном основании.
И. X. Сабитов.
ПЕТЕРСОНА СООТВЕТСТВИЕ — соответствие двух
поверхностей, при к-ром их касательные плоскости
в соответствующих точках параллельны. В общем
виде рассмотрено К. М. Петерсоном [1] в связи с за-
задачей изгибания на главном основании. Напр., в П. с.
находятся поверхность и ее сферич. обра:!, поверх-
поверхность и ее индикатриса вращения, присоединенные
минимальные поверхности.
Если поверхности S и S* имеют общую параметри-
параметризацию, то их третьи квадратичные формы равны. Глав-
Главная сеть асимптотич. сетей 5 и S* сопряжена на каж-
каждой из них. Эта сеть определяется однозначно, если
асимптотич. сети не имеют общих семейств линий;
вырождается, если эти сети связанные; становится
неопределенной, если эти сети соответствуют друг
другу. Соответствующие касательные к линиям глав-
главной сети на 5 и S* параллельны.
Если главную сеть принять за координатную (и, и),
то радиус-векторы х и х* поверхностей S и S* связаны
уравнениями
причем функции р, о удовлетворяют системе урав-
уравнений
то есть р, о зависят только от метрики F (?\ F, G —
коэффициенты ее первой квадратичной формы). Ес-
Естественно поэтому применение П. с. к паре изометрич-
ных поверхностей S, S: оно дает другую пару изомет-
ричных поверхностей S*, S* с теми же нормалями
п=п*, п—-п соответственно. Кроме того, оказывается,
что диаграммы поворота этих поверхностей одни и
те же и что основание изометрии новых поверхностей
имеет то же сферич. изображение, как и первоначаль-
первоначальных. Напр., сфере и изометричной ей поверхности
положительной постоянной кривизны отвечают при
П. с. изометричные поверхности с соответствующими
линиями кривизны — т. н. поверхности Бонне.
В частности, если основание изометрии S и S* было
главным основанием, то оно и остается таковым.
Это — т. н. преобразование Петерсона
поверхности, изгибаемой на главном основании в
поверхность того же типа. Имеется обобщение итого
преобразования на случай семейства сетей (см. [2]).
Специальный случай П. с, при к-ром главная сеть
является сетью кривизны одновременно на 5 и на S*,
паз. соответствием Ком беек юр а.
Если П. с. является конформным, то либо одна из
поверхностей минимальная, а другая — сфера (то
есть П. с.— сферич. отображение), либо обе поверх-
поверхности минимальные, а вектор конформного отображения
удовлетворяет уравнению Лапласа, либо поверхности
подобны, либо обе поверхности изотермические и на-
находятся в соответствии Комбескюра.
Имеется многомерное обобщение П. с. (см. [4]).
Лит.: [1] П е т е р с о н К. М., «Матем. сб.», 1866, т. 1, с.
391 — 438; МШуликовскийВ. И., Классическая диффе-
дифференциальная геометрия в тензорном изложении, М., 1963;
[3] Ф и и и к о в С. П., Изгибание на главном основании и свя-
связанные с ним геометрические задачи, М.— Л., 1937; [4] Широ-
Широков П. А., Широков А. П., Аффинная дифференциальная
геометрия, М., 1959. М. И. Войцеховский.
ПЕТЕРСОНА — КОДАЦЦИ УРАВНЕНИЯ — урав-
уравнения, составляющие вместе с уравнением Гаусса (см.
Гаусса теорема) необходимые и достаточные условия
интегрируемости системы, к к-рой сводится задача
восстановления поверхности по ее первой и второй
квадратичным формам (см. Бонне теорема). П. — К. у.
имеют вид
где b(j— коэффициенты второй квадратичной формы,
Тц— символы Кристоффеля 2-го рода.
Уравнения впервые найдены К. М. Петерсоном в
1853, переоткрыты Г. Майнарди (G. Mainardi, 1856)
и Д. Кодацци (D. Codazzi, 1867).
Лит.: [1] Рашевский П. К., Курс дифференциальной
геометрии, М., 1956. А. Б. Иванов.
ПЕТЛЯ — замкнутый путь. Подробнее, петля / —
непрерывное отображение отрезка [О, 1] в топологич.
пространство X такое, что /@) = /A). Совокупность
всех П. пространства X с отмеченной точкой * таких,
что /@) = /A)=*, образует петель пространство.
М. И. Войцеховский.
ПЕТРИ СЕТЬ — математическая модель дискретных
динамич. систем, в том числе информационных систем
(параллельных программ, операционных систем, ЭВМ
и их устройств, сетей ЭВМ), ориентированная на ка-
качественный анализ и синтез таких систем (обнаруже-
(обнаружение блокировок, тупиковых ситуаций и узких мест,
автоматич. синтез параллельных программ и компо-
компонентов ЭВМ и др.). Введена К. Петри (С. Petri) в 60-х
гг. 20 в. П. с— это набор N= (Т, Р, F, Мо), где Т —
конечное множество символов, паз. переходами,
Р — конечное множество символов, паз. местами,
Р[)Т=ф, F — функция инцидентности:
F: TXP{JPXT~^{O, 1},
Мо — начальная разметка мест:
Мо: Р-^{0, 1, 2, ...}.
Неформально П. с. представляют размеченным ори-
ориентированным графом со множеством вершин Т[)Р
(см. рис.). Из вершины-места р?Р, изображаемой круж-
кружком, ведет дуга в вершину-переход f ? Т, изображаемую
прямоугольником, тогда и только тогда, когда
F(p, t) = l
(р—входное место перехода t; на рис. Р={рг, р2, Р.;},
Г={в, Ъ, с, d}). Из вершины-перехода t ведет дуга
в вершину-место р тогда и только тогда, когда
F(t, p) = l
(p — выходное место перехода t). Место р помечается
разметкой Mo(p)jr0, часто изображаемой соответст-
соответствующим числом точек (фишек).
Динамика поведения моделируемой системы описы-
описывается в терминах функционирования П. с. Сеть функ-
функционирует в дискретном
времени, переходя от
разметки к разметке.
Каждая разметка — это
функция М : Р ->- {О,
1, 2, . . .}; смена раз-
разметок (начиная с Мо)
происходит в резуль-
результате срабатывания пе-
переходов сети. Переход
t?T может сработать
при разметке М, если для любого р?Р
M(p)—F(p, 0 SsО,
т. е. если каждое его входное место имеет хотя бы одну
фишку. В результате срабатывания t при разметке .1/
последняя сменяется разметкой М' по правилу: для
любого ?Р
(t, p),
т. е. переход t изымает по фишке из каждого своего
входного места и посылает по фишке в каждое свое
выходное место. Если может сработать несколько пере-
переходов, то срабатывает один, любой из них. Сеть ос-
останавливается, если при нек-рой разметке (тупиковая
разметка) ни один из ее переходов не может сработать.
При одной и той же начальной разметке П. с. может
порождать, в силу недетерминированности ее функцио-
функционирования, различные последовательности срабаты-
срабатываний ее переходов. Эти последовательности образуют
слова в алфавите Т, а множество всевозможных слов,
порождаемых П. с, наз. ее языком. Две П. с.
эквивалентны, если они порождают один и тот же
язык.
Исследования по П. с. развиваются в двух направ-
направлениях. Математич. теория сетей разрабатывает методы
формального анализа их свойств. Среди наиболее ин-
интересных проблем следует отметить задачи распозна-
распознавания тупиковых ситуаций в сетях, задачи распозна-
распознавания эквивалентности сетей по порождаемым языкам,
оценки сложности анализа сетей, сравнение вырази-
выразительной мощности различных подклассов П. с. и их
обобщений. Установлено, что проблема тупиковых
ситуаций разрешима, изучены свойства класса языков,
порождаемых П. с. Этот класс строго содержится в
классе рекурсивно перечислимых языков, строго вклю-
включает класс регулярных языков и частично пересека-
пересекается с классом контекстно свободных языков. Второе
направление — применение П. с. как основы приклад-
прикладных моделей дискретных динамич. систем в инфор-
информатике, экономике, цифровой технике и т. п.
В отличие от автоматов конечных, в терминах к-рых
описываются глобальные изменения состояний систем,
П. с. концентрирует внимание на локальных собы-
событиях (им соответствуют переходы), локальных усло-
условиях (им соответствуют места) и на локальных связях
между событиями и условиями. Поэтому в терминах
П. с. более адекватно, чем с помощью автоматов, мо-
моделируется поведение распределенных асинхронных
систем.
Лит.: [)] Peterson J. L., Petri net theory and the
modeling of systems, Englewood-Cliffs, 1981; [2] К о т о в В. Е.,
«Кибернетика», 1980, № 5, с. 10—18; [3] Апериодические авто-
автоматы, М., 1976; [4] Net theory and applications, В., 1980.
В. Е. Нотов.
ПЕТТИСА ИНТЕГРАЛ — интеграл от векторнознач-
ной функции по скалярной мере, являющийся т. н.
слабым интегралом. Введен Б. Петтисом [1].
Пусть F(X, E, 55, ji) — векторное пространство
функций x(i), l(zE, со значениями в банаховом про-
пространстве X, заданных на множестве (Е, SB, ц) со
счетно аддитивной мерой а. на ст-алгебре 33 подмно-
подмножеств Е. функция х (t) наз. слабо и з м е р и м о й,
если для любого f?X* измерима скалярная функция
/[.г(?)]. Функция x(t) интегрируема по Пет-
т и с у на измеримом подмножестве МаЕ, если для
любого f?X* интегрируема на М функция f[x(t)) и
существует элемент х(М)?Х такой, что
Тогда
def
r*@fy =x(M)
и наз. интегралом Петтиса. Такой интеграл
для случая Е~ (а, 6) с обычной мерой Лебега был
впервые введен И. М. Гельфандом [2].
Лит.: [1] Petti s В., «Trans. Amer. Math. Soc», 1938,
v. 44, № 2, p. 277 — 304; 12] Г е л ь ф а н д И. М., «Зап. Науково-
досл. шст. матем. и мех. Харк1В. матем. тов.», 1930, т. 13, в. 1,
с. 35—40; [3] Н i I d e b г a n d t Т., «Bull. Amer. Math. Soc»,
1953, v. 59, p. 111—39; [4] X и л л е Э., Ф и л л и п с Р., Функ-
Функциональный анализ и полугруппы, пер. с англ., М., 1962.
В. И. Соболев.
ПИ, число я,— отношение длины окружности к
диаметру; представляется бесконечной непериодиче-
непериодической десятичной дробью
я = 3,141 592 653 589 793...
Разыскание пределов нек-рых арифметич. последо-
последовательностей, составляемых по простым законам, часто
приводило к числу я. Примером может служить ряд
Л е и б н и ц а
я _. 1,1 11
4 ~х з + 5 7 +1 •••'
к-рый, однако, очень медленно сходится. Существуют
значительно быстрее сходящиеся ряды, пригодные для
вычисления я.
Возможность чисто аналитич. определения числа я
имеет принципиальное значение и для геометрии.
Так, в неевклидовой геометрии я также участвует в
нек-рых формулах, но уже не как отношение длины
окружности к диаметру (это отношение в неевкли-
неевклидовой геометрии не является постоянным). Средствами
анализа, среди к-рых решающую роль сыграла фор-
формула Эйлера
была окончательно выяснена и арифметич. природа
числа я. В кон. 18 в. И. Ламберт (J. Lambert) и А. Ле-
жандр (A. Legendre) установили, что л — иррацио-
иррациональное число, а в 19 в. Ф. Линдеман (F. Lindemann)
доказал, что л является трансцендентным числом.
По материалам одноименной статьи из БСЭ-3.
ПИКА ТЕОРЕМА, инвариантная форма
леммы Шварц а,— обобщение Шварца леммы,
состоящее в следующем. Пусть w—f(z) — ограничен-
ограниченная регулярная аналитич. функция в единичном круге
Q={z?C: |z|<l}, |/(z)|<1, |z|<l. Тогда дйя любых
точек z-i и z2 круга Q неевклидово расстояние d(w1, ш2)
их образов Ш]-~/(гх) и м>2—/(z2) не превосходит неев-
неевклидова расстояния d(zj, z2), то есть
d(™i, м>2) <й (zj, 22), | zx | < \, | z21 < 1. A)
Кроме того, имеет место неравенство
между элементами неевклидовой длины (дифференци-
(дифференциальная форма П. т., или леммы Шварца). Знаки ра-
венства в A) и B) имеют место только в том случае,
когда w~f (z) есть дробно-лштойная функция, ото-
отображающая круг Q на себя.
Неевклидово, или гиперболическое,
расстояние d(zx, z^} есть расстояние в геометрии
Лобачевского между точками z1 и z2, когда круг Q
принимается в качестве плоскости Лобачевского, а
прямыми Лобачевского служат дуги окружностей,
ортогональных единичной окружности (м о д е л ь П у-
а н к а р е); при этом
<ZBi, z2)=--4-ln (a, р, z,, z2) =
— J_ In 1 1-Г|г2| + |г,-гг|
- | 1-Г,г2|- (г,-гИ
где (а, р, zt, z2) — двойное отношение точек zb c2
и определяемых этими точками точек пересечения а, р1
прямой Лобачевского, про-
проходящей через zj и z2, с еди-
единичной окружностью (см.
рис.).
Неевклидова длина образа
/(L) любой спрямляемой
кривой LcQ при отображе-
отображении w^--f(z) не превосходит
неевклидовой длины L.
П. т. была установлена Г.
Пином (см. [i]); дальней-
дальнейшим ее обобщением являет-
является гиперболической метрики
принцип. В геометрич. теории функции из этих теорем
выводятся оценки различных функционалов, связан-
связанных с отображающей функцией (см. [2], [3]).
Лит.: [1] Р i с k G., «Math. Ann.», 1316, Bd 77, S. 1—6; [2]
Г о л у з и н Г. М., Геометрическая теория функций комплекс-
комплексного переменного, 2 изд., М., 1966; [3] К а р а т е о д о р и К.,
Конформное отоЛражепие, пер. с англ., М.— Л-, 1934.
Е. Д. Соломенцев.
ПИКАРА ГРУППА — группа классов обратимых
пучков (или линейных расслоений). Более точно,
пусть (Аг, 0х) — окольцованное пространство. Пучок
(9х-модулей X на:!, обратимы м, если он ло-
локально изоморфен структурному пучку Qx- Множе-
Множество классов изоморфных обратимых пучков на А'
обозначается Pic (X). Тензорное произведение X®
®6х-%' определяет на множестве Pic(X) операцию,
превращающую его в абелеву группу, наз. группой
И и к а р а пространства X. Группа Pic (X) естест-
естественно изоморфна группе когомологий ИХ{Х, Qx),
где Eх— пучок обратимых элементов в Qx-
Для коммутативною кольца А группой Пикара
Р]'сЛ паз. группа классов обратимых А -модулей;
Picyl sePjc (Spec А). Для кольца Крулля А группа
Pic^4 тесно связана с классов дивизоров группой этого
кольца.
П. г. полного нормального алгебраич. многообразия
обладает естественной алгебраич. структурой (см.
Пикара схема). Связная компонента нуля группы Pic (X)
обозначается Pic°(X) и наз. многообразием Пикара
для X; это — алгебраич. группа (абелево многооб-
многообразие, если многообразие X гладко). Факторгруппа
Pic (X)/Pic° (X) нпз. группой Н е р о н а — С е-
в е р п и имеет конечное число образующих; ранг ее
наз. числом Пикара. В комплексном случае,
когда X — гладкое проективное многообразие над С.
группа Pic" (X) изоморфна факторгруппе пространства
Л"(Х, Qx) голоморфных 1-форм на X по решетке
ЯХ(Х, '?).
Лит.: [1] М а м ф о р д Д., Лекции о кривых на алгебраи-
алгебраической поверхности, пер. с англ., М., 1968. В. И. Данилов.
ПИКАРА МНОГООБРАЗИЕ полного гладкого ал-
алгебраического многообразия X над алгебраически
замкнутым полем — абслево многообразие 5р(Х), па-
параметризующее факторгруппу Diva(X)IP (X) группы
D\va(X) дивизоров, алгебраически эквивалентных ну-
нулю, по группе главных дивизоров ^(Х), т. е. дивизоров
рациональных функций. С точки зрения теории пучков
П. м. параметризует множество классов изоморфных
обратимых пучков с нулевым классом Чжэня, т. е.
^s (X) совпадает со связной компонентой единицы
Pic°(X) Пикара группы Pic(X) многообразия X.
Структура абелева многообразия на группе ty (Х) =
—Diva (X)/P (X) однозначно характеризуется следу-
следующим свойством: для любого алгебраич. семейства
дивизоров СнаХс базой 5 существует такое регуляр-
регулярное отображение ср: S1 ~> 5р (.У), для к-рого О (s) —
—D (•%) ?ф («), где s0 — нек-рая фиксированная точка из
S{) (см. 12]). Размерность g-=dim^(X) наз. upper y-
л я р н о с т ь ю многообразия X.
Классической пример П. м.— Якоби многообразие
гладкой проективной кривой. Другим примером
может служить двойственное абелево многообразие
(см. [3]).
В случае, когда X — гладкое проективное ком-
комплексное многообразие, §р(Х) можно отождествить с
группой обратимых аналитич. пучков на X, имеющих
нулевой класс Чжуня [4]. Более того, многообразие
Пикара 5Р(Х) в этом случае изоморфно факторгруппе
пространства Н1 (X, Qx) по решетке ЯХ(Х, 1J)c:H1 (X,
Qx)- В частности, иррегулярность q многообразия X
совпадает с dim Я1 (A', 0x)=-dim//n (X, Q*), где Об-
Облучок регулярных 1-форм. Последний результат верен
также в случае нсособых проективных кривых над
любым алгебраически замкнутым полем и в случае
полных гладких многообразий над алгебраически замк-
замкнутым полем характеристики 0; для произвольной
характеристики имеет место лишь неравенство
И г у з ы : dim/71 (X, Qx)^1 (известен пример глад-
гладкой алгебраич. поверхности F иррегулярности 1 с
dim//1 (F, Qp) - 2; см. [6]). Как видно отсюда, П. м.
тесно связано с теорией одномерных дифференциаль-
дифференциальных форм. Начало исследования таких форм на рима-
повых поверхностях положил Э. Пикар [1]; оп доказал
конечномерность пространства IIй (X, 12^) всюду регу-
регулярных форм.
Понятие П. м. может быть обобщено на случай
полного нормального многообразия X. Изучалось
также многообразие Пикара $рс(Х), соответствующее
дивизорам Картье и обладающее, в отличие от ^ (X),
хорошими функториальными свойствами |9]. Много-
Многообразие Ц$с (X) было построено для полных нормаль-
нормальных многообразий X (см. [5]), а также для произволь-
произвольных проективных многообразий [8|.
Лит.: [1] Р i с а г d В., «С. г. Acad. Sci.», 1884, t. 99, р. П(И —
963: [2] Ш а ф ар е в и ч И. Р., Основы алгебраической геомет-
геометрии, М., 1972; [3] М а м ф о р д Д., Абелепы многообразия, пер.
с англ., М., 1971; [4] Гриффите Ф., Харрис Дж.,
Принципы алгебраической геометрии, пер. с англ., т. 1—2,
М., 1982; Ы С h e v а 1 1 е у С «Amcr. J. Math.», 19(iO, v. 82,
p. 435—90; [6] I g u s a J.-I.,' «Proc. Nat. Acad. Sr.i. USA», 1У.Г>5,
v. 41, № 11, p. 964—67; [7] M a t s u s a k а Т., «Jap. J. Math.»,
1951, v. 21, M 2, p. 217 — 30; 18] Seshadri C, «Ann. mat.
pura cd appl.», 1962, v. 57, p, 117—42; l!)J его же, «Math.
Ann.», 1905, Bd 158, ,N» 3, S. 293 — 96. В. В. Шокуров,
ПИКАРА СХЕМА — естественное обобщение в рам-
рамках теории схем понятия Пикара многообразия % (X)
гладкого алгебраич. многообразия X. Для определения
П. с. произвольной 5-схемы X рассматривается отно-
относительный функтор II и кар a Pic^ /й на
категории Sch/S схем над схемой S. Значение этого
функтора на S-схеме S' есть группа
где /' : XXs$' -*¦ S' есть морфизм замены базы,
Rfpqcf* (Рт, X') — пучок на топологии Гротендика
Sfpqc строго плоских квазикомпактных морфнямов,
ассоциированный с иредпучком
Т-+Ю(Т,рчс, Gm)=W(Tet. Gm),
a Gm обозначает стандартный мультипликативный
пучок. Если функтор Пикара Pic^,s представим на
(Sch/5), то представляющая его 5-схема наз. отно-
относительной схемой Пикара iS-схемы X
и обозначается Pic^-zg. В случае, когда X — алге-
браич. схема над нек-рым полем к, имеющая рацио-
рациональную fe-точку,
Pic-X/k (s>) = Pic (X X kS')/Pic (Sr)
для любой /с-с.чемы S' (см. [3]); в частности, Pic^-^A(ft)=
= Pic(Ar) отождествляется с группой /с-рациональных
точек Picx/ft (к) схемы Picx/s, если таковая сущест-
существует.
Если f : X -+ S — проективный морфпям с геомет-
геометрически целостными слоями, то схема IJicx/s СУ~
шествует и является локально конечно представленной
отделимой групповой 5-схемой. Если S=Spec(/c), то
связная компонента единицы Picx^ схемы PicY/h
является алгебраической /с-схемой и соответствующая
приведенная А;-схема (Pic",/ft)re(] есть в точности
многообразие Пикара 5).v(A) (см. [4]). Нильпотентные
элементы в локальных кольцах схемы Pic^.,ft дают
много дополнительной информации о П. с. и позволяют
объяснить ряд паталогий в алгсбраич. геометрии над
полем характеристики /-»>(). С другой стороны, над
полем характеристики 0 схема Pic^,(l всегда при-
приведена (см. [6]). Известно также, что схема Picf/,ft
приведена, если F — гладкая алгебраич. поверхность
n№(F,QF) = 0 (см. [5]).
Для любого собственного плоского морфизма /:
X -»- S (конечно представленного, если база S нёте-
рова), для к-рого f',(Qx')~6<-i ПРИ любой замене
базы /' : X' =-- ХУ.$ S' —>¦ S функтор PicY/s является
алгебраич. пространством над S (см. [1]). В частности,
функтор Pic^,g представим, если базисная схема S
есть спектр локального артинова кольца.
Лит.: [1] А г t i n M., в сб.: Global analysis. Papers in Ho-
Honor of K. Kodaira, Tokyo, 19G9, p. 21—77; [2] G h e v a 1 1 e у С,
«Amer. J. Math.», 1960, v. 82, p. 435—90; [3] G г о t h e n d i-
eck А., в кн.: Seminaire Bourbaki 1961 — 19G2, annee 14, [P.,
1962], p. 232/01—232/19; [4] e г о же, «Publ. math. Inst. hautes
etudes scient.», I960, .Ys 4, p. 1 —1B8; [5] M а м ф о р д Д., Лек-
Лекции о кривых на алгебраических поверхностях, пер. с англ.,
М., 1968; [6] О о г t P., «Invent, math.», 1906, v. 2, jvft 1, p. 79 —
80; 17] Итоги науки и техники. Алгебра. Топология. Геометрия,
т. 10, М., 1972, с. 47 — 112. В.В.Шокуров,
ПИКАРА ТЕОРЕМА — 1) П. т. о поведении анали-
аналитической функции /(г) комплексного переменного z
в окрестности существенно особой точки а — название
результата классич. теории функций, явившегося
отправным пунктом многочисленных глубоких ис-
исследований и состоящего из двух частей, а) Малая
теорема Пикара: всякая целая функция /(z) Ф
Фconst принимает любое конечное комплексное зна-
значение, за исключением, быть может, одного, б) Бол ь-
шая теорема Пикара: всякая однозначная
аналитич. функция /(z) в произвольной окрестности
изолированной существенно особой точки а прини-
принимает любое конечное комплексное значение, за исклю-
исключением, быть может, одного.
Впервые эта теорема опубликовала Э. Пнкаром [1],
[2]. Она существенно дополняет Сохоцкого теорему.
Малая П. т. есть следствие большой П. т. Из большой
П. т. непосредственно следует, что любое конечное ком-
комплексное значение, за исключением, быть может,
одного, принимается в произвольной окрестности
существенно особой точки бесконечно часто. Для
мероморфпой функции в конечной плоскости С : |г|<оо
П. т. принимает вид: если точка а— оо — существенно
особая для мероморфной в С функции F(z), то в про-
произвольной окрестности точки а функция F(z) прини-
принимает любое комплексное значение из расширенной
комплексной плоскости С : |г|<:оэ, за исключением,
быть может, двух, и притом бесконечно часто. Как
покалывают примеры целой функции егФ0 и меро-
мероморфной функции tg гф-i, —i, все эти утверждения
точные. Фигурирующие в П. т. исключительные зна-
значения паз. пикаровскими исключитель-
исключительными значениями.
П. т. существенно дополняется Иверсена теоремой
и Жюлиа теоремой, к-рые покалывают соответственно,
что пикаровские исключительные значения являются
асимптотическими значениями и что существуют лучи
Жюлиа Л, исходящие из существенно особой точки а
и такие, что неисключительные значения принимаются
бесконечно часто даже в любом сколь угодно малом
секторе с вершиной а и осью симметрии L.
Для современных исследований, связанных с П. т.,
характерны следующие два направления. Пусть Е —
множество существенно особых точек мероморфной
функции F(z), то есть F(z) — мероморфная функция
в пек-рой окрестности любой точки zo(?E, и предельное
множество С(г0; F) функции F(z) в точке zo(zE не сво-
сводится к одному значению. Пусть R (a; F), а(-Е,— мно-
множество тех значений w?C, к-рые в любой окрестности
точки а принимаются бесконечно часто. Тогда П. т.
утверждает, что если а — изолированная точка Е,
то дополнение
CR(a; F)^=€\R(a; F)
обладает свойством Пи кар а, т. е. состоит
не более чем из двух точек. В. В. Голубев в 1910 ус-
установил, что если емкость множества Е равна нулю,
cap E — 0, то CR(a\ F) имеет емкость нуль для всех
а?Е. Вопрос о том, каковы минимальные условия на
Е, чтобы множество CR(a; F) для всех а?Е обладало
свойством Пикара, пока A983) полностью не решен.
Примеры показывают, что, с одной стороны, условие
сар?'=0 не является достаточным, а с другой — что
имеется множество Е, cap ?>0, вне к-рого не сущест-
существует мероморфпых трансцендентных функции, выпу-
выпускающих четыре значения (см. [4], |5], [8]).
Второе направление связано с обобщениями П. т.
для аналитич. функций / (z) многих комплексных
переменных z— (zb . . ., zn), rc^sl. При ге=1 П. т. можно
формулировать и так: любое голоморфное отображение
/ : С —>- С, выпускающее по крайней мере две точки,
постоянно. Однако в 1922 П. Фату (P. Faton) пост-
построил пример невырожденного голоморфного (и даже
биголоморфного) отображения / : С2 —>- С2, для к-рого
множество исключительных значений С2\/(С2) содержит
непустое открытое множество. Это означает, что П. т.
(и даже теорему Сохоцкого) непосредственно нельзя
распространить на случай ге>1. Обобщения П. т. все
же возможны, если отправляться, напр., от другой ее
формулировки, несколько искусственной при ге-=1:
любое голоморфное отображение F : С —>¦ СР в ком-
комплексную проективную плоскость СР--=С, выпуска-
выпускающее по крайней мере три гиперплоскости (т. е. точки
при ге=1), постоянно. Верна, в частности, такая тео-
теорема Грина: любое голоморфное отображение
F : Ст —>¦ СРп, выпускающее по крайней мере 2re-j-l
гиперплоскостей в общем положении, постоянно (см.
[3]. [6], [8].
2) П. т. об униформизации алгебраических кривых:
если алгебранч. кривая Ф (z, w) = 0 имеет род g>i,
то не существует пи одной пары мероморфных функций
z — j(t), w = h(t) таких, что Ф(/(г), h(t))ss=.(). Иными
словами, упиформизацпя алгебраич. кривых рода g>l
при помощи мероморфных функций невозможна. На-
Напротив, в случае g=l униформизация всегда осущест-
осуществима при помощи (мероморфных) эллиптич. функций.
Установлена 0. Пикаром [7].
Лит.: [1] Р i С а г d Е., «С. г. Acad. sci.», 1879, t. 88, p. 1024 —
1027; t. 89, p. 662—65; [2] с г о же, «Ann. Ecole norm, super.»,
1880, t. 9, p. 145—66; [3] Ш а б а т Б. В., Введение в комплекс-
комплексный анализ, 2 изд., ч. 1—2, М., 1976; [4] К о л л и н г в у д Э.,
Л о в а т е р А., Теория предельных множеств, пер. с англ., М.,
1971; [5] Л о в а т е р А., в кн.: Итоги науки и техники. Матема-
Математический анализ, т. 10, М., 1973 с. 99—259; [6] Гриф-
Гриффите Ф., Кинг Дж., Теория Неванлинны и голоморфные
отображения алгебраических многообразий, пор. с англ. М.,
1976; [7] Р i с а г d E., «Acta math.», 1887—88, v. 11, p. 1 — 12;
[81 HI а б ат Б. В., Распределение значений голоморфных отоб-
отображений, М., 1982. Е. Д. Соломепцев.
ПИРАМИДА — многогранник, одной из граней
к-рого служит многоугольник (основание П.), а ос-
остальные грани (боковые) суть треугольники с общей
вершиной (вершина П.) (см. рис. 1, 2). В зависимости
от числа боковых граней П. делятся на треугольные,
Рис. 1.
Рис. 2.
четырехугольные и т. д. Отрезок перпендикуляра,
опущенного из вершины П. на плоскость ее основания
(а такнч-е его длина), наз. высотой П. Объем П. вычис-
вычисляется по формуле
где // — высота, S — площадь основания, П. наз.
правильной (см. рис. 2), если п основании ее лежит
правильный многоугольник и высота 11. проходит
через центр основания. Боковые грани правильной
И. суть равные между собой равнобедренные треуголь-
треугольники; высота каждого из отих треугольников наз.
апофемой правильной П. (апофема основания П.
служит проекцией апофемы П. на плоскость основания).
Рассекая П. плоскостью, параллельной ее основа-
основанию, получают две части: П., подобную данной, и
т. в. усеченную П. (см. рис. 3).
Многоугольник, полученный от пере-
пересечения П. и секущей плоскости, наз.
верхним основанием, осно-
основание П.— нижним основа-
основанием усеченной П. Расстояние
между секущей плоскостью и нижним
основанием наз. в ы с о т о й усеченной
П. Объем усеченной П. вычисляется по формуле
рпс
где h — высота, s, S — площади основа-
оснований. БСЭ-З.
ПИРСА СТРЕЛКА — двуместная логи-
логическая операция, обычно обозначаемая J
и задаваемая следующей истинностной
таблицей'.
Таким образом, высказывание А \В озна-
означает «пи А, ни JS». II. с. обладает тем
свойством, что через нее выражаются все другие ло-
А
И
II
Л
л
в
и
л
и
л
А\В
Л
Л
Л
и
гическне операции. Например, высказывание ~\А (от-
(отрицание А) эквивалентно высказыванию А ,А , конъ-
конъюнкция А &В высказываний А и В выражается так:
(А^А)\(В\В), дизъюнкция А\/В оквпвалентна
{а\В)\(А\В). П. с. была введена в рассмотрение
Ч. Пирсом (С. Peirs). в. Е. плиспо.
ПИРСОВСКОЕ РАЗЛОЖЕНИЕ — представление
кольца в виде прямой суммы подколец, связанное с
данным идемпотентом е. Для кольца В, содержащего
идемпотент е, существуют левое, правое и двустороннее
П. р., определяемые равенствами
R=Re-\-R A-е),
R=eR + (i — e) R,
R = eRe-j-eR (I — е) + A — е) /?е + A — е) R A-е)
соответственно. При этом в случае отсутствия в R
единицы полагают, по определению,
R (\ — е) = {х — xe\
A — е) Re={xe — exe\x?R},
A-е) R A — e) = {z — ex — xe + exe\x?R}.
Множества A— e)R и eR(i-e) определяются анало-
аналогично. Таким образом, при двустороннем П. р. элемент
x?R представляется в виде
х = ехе-\- (ех — ехе) -|- (хе — ехе)-\- (х — ех —хе-\-ехе),
при левом — в виде
х-=хе-\- (х—хе)
и при правом — в виде
х — ех-\-(х — ех).
Рассматривается также П. р. относительно ортого-
ортогональной системы идемпотентов {ех, . . ., еп}, где 2,-е;=1,
а именно:
П. р. было предложено Б. Пирсом (см. [1]).
Лит.: Ш Р е i г с е В., «Amer. J. Math.», 1881, v. 4, p. 97.
Л. А. Скорняков.
ПИРСОНА КРИВЫЕ — название семейства непре-
непрерывных распределений вероятностей (распреде-
(распределений Пирсона), плотности к-рых р (х) удов-
удовлетворяют дифференциальному уравнению
dp (х) х —а . . , .
~~dbT== Ьа + Ь,х + Ъ,х' Р (Х)' W
где параметры а, Ьо, Ьг, Ь2 — действительные числа.
Более точно, кривыми Пирсона наз. гра-
графики зависимости р (х) от х. Распределения, являю-
являющиеся решениями уравнения (*), совпадают с предель-
предельными формами гипергеометрического распределения.
П. к. классифицируются в зависимости от характера
корней уравнения
Семейство П. к. составляют 12 типов и нормальное
распределение. Многие важнейшие распределения в
математич. статистике могут быть получены с помощью
преобразований из уравнения (*).
Систематич. описание типов П. к. дано У. Элдерто-
ном (W. Elderton, 1938). В упрощенном виде класси-
классификация по типам такова.
Тип I:
частный случай — бета-распределение 1-го рода.
Тип II:
(вариант П. к. типа I); частный случай — равномерное
распределение.
Тип III:
^а «, ц > 0, а > О;
частные случаи — гамма-распределение, «хи-кеадрат»-
распределение.
Тип IV:
— оо s?zs? oo, а > О, (Я > О.
Г и и V:
_iL
р (х) = кх-Че х,0<ж<оо,а>0, д>1
(сводится преобразованием к типу III).
Тип VI:
р (x) = kx~Ql (x — a)q\ as^x < ж, q±> q2 — 1;
частные случаи — бета-распределение 2-го рода, Фи-
Фишера F-распределение.
Тип VII:
р{х) = к ^i+^т
частный случай — Стъюдента распределение.
Тип VIII:
3, o<;w<;l.
Тип IX:
Тип X:
*— m
p(x) = ke ° , от«?ж < oo, о > О
показательное распределение.
Тип XI:
р (x)~kx~m, 6<а:< оо, тге > 0;
частный случай — Парето распределение.
Тип XII:
(вариант типа I).
Наиболее важны в приложениях типы I, III, VI, VII.
Всякая П. к. однозначно определяется своими пер-
первыми четырьмя моментами
если они конечны. Это свойство семейства П. к. ис-
аользуется для приближенного описания эмпирических
распределений.
Метод подгонки П. к. к нек-рому эмпирич. распре-
распределению состоит в следующем. По независимым ре-
результатам наблюдений вычисляют первые четыре вы-
выборочных момента, затем определяется тип подходящей
П. к. и методом моментов находятся значения неиз-
неизвестных параметров искомой П. к. В общем случае
метод моментов не является эффективным методом
получения оценок П. к. Проблема более точной ап-
аппроксимации распределений с помощью П. к. получила
новое решение в работах Л. Н. Болынева A963) по
асимптотич. преобразованиям.
П. к. были введены К. Пирсоном (К. Pearson, 1894).
Лит.: [1] Elderton W. P., Frequency curves and corre-
correlation, 4 ed., Camb., 1953; [2] К е н д а л л М., С т ь ю а р т А.,
Теория распределений, пер. с англ., М., 1966; [3] Крамер Г.,
Математические методы статистики, пер. с англ., 2 изд., М., 197"i;
Ш В о л ь ш е в л. Н., «Теория вероятн. и ее примен.», 1963,
т. 8, № 2, с. 129 — 55. А. В. Прохоров.
ПИРСОНА РАСПРЕДЕЛЕНИЕ — см. Пирсона кри-
кривые.
ПИТМЕНА ОЦЕНКА — эквивариантная статистич.
оценка параметра сдвига относительно группы ве-
вещественных сдвигов, имеющая минимальный риск при
квадратичной функции потерь.
Пусть компоненты Х1г Х2, . . ., Хп случайного
вектора Х= (Хг, Х2, . . ., Хп) суть независимые слу-
случайные величины, подчиняющиеся одному и тому же
вероятностному закону, плотность вероятности к-рого
принадлежит семейству
{/(г — 6), \х\ < оо,
причем
для любого 0?в. Далее, пусть G~ {g} — группа ве-
вещественных сдвигов, действующая в пространстве
реализаций R1—(—со, + оо) случайной величины X,-
(i=l, 2, . . ., п):
G = {g:gXi = Xi + g, \g\> a>}.
В таком случае задача оценивания параметра 0 будет
инвариантной относительно квадратичной функции
потерь L(9, 9)= (Э—вJ, если в качестве в=§(Х)
выбрать эквивариантную оценку. Э. Питмен [1] по-
показал, что эквивариантная оценка @(Х) параметра
сдвига 6 относительно группы G, имеющая минималь-
минимальный риск при квадратпчпои функции потерь, имеет вид
где Yi~Xini)—Z(nl), А'(„,-, есть г-я порядковая ста-
статистика, построенная но вектору наблюдений X.
П. о.— несмещенная оценка, она является минимакс-
минимаксной в классе всех оценок параметра сдвига 6 при
квадратичной функции потерь, если все эквивариапт-
ные оценки параметра 9 имеют коночные функции
риска [2].
Пример 1. Если
то есть Х{, t=l, 2, . . ., п, подчиняется показатель-
показательному закону с неизвестным параметром сдвига Э, то
П. о. в{Х) для 9 выражается формулой
причем ее дисперсия равна 1/ге2.
П р и м е р 2. Если
(х- ОJ
/(яг —в) = гр==-в 2 , |*|<оо,
то есть X;, i=l, 2, . . ., п, подчиняется нормальному
N F, 1) закону с неизвестным математич. ожиданием 9,
то в этом случае среднее арифметическое
является П. о.
Лит.: lllPitmanE. J., «Biometrika», 1939, v. 30, p. 391 —
421; [2] G i r s li i с k M. A., S a v a g e L. J., «Proc. Second Ber-
Berkeley Symp. Math. Statist. Prob.», 1951, p. 53—73; [3] 3 а к с ГЛ.,
Теория статистических выводов, пер. с англ., М., 1975.
М. С. Никулин.
ПИФАГОРА ТЕОРЕМА — теорема геометрии, уста-
устанавливающая связь между сторонами прямоугольного
треугольника. П. т. была, по-видимому, известна до
Пифагора F в. до п. э.), но ему приписывается ее до-
доказательство в общем виде. Первоначально теорема
устанавливала соотношения между площадями квад-
квадратов, построенных на гипотенузе и катетах прямо-
прямоугольного треугольника: квадрат, построенный на
гипотенузе, равновелик сумме квадратов, построенных
на катетах. Обычно П. т. принято кратко формулиро-
формулировать так: квадрат гипотенузы прямоуголыгого треуголь-
треугольника равен сумме квадратов катетов. Верна и теорема,
обратная П. т.: если квадрат стороны треугольника
равен сумме квадратов двух других его сторон, то
этот треугольник прямоугольный. бсэ-з.
ПИФАГОРОВЫ ЧИСЛА — тройки целых положи-
положительных чисел х, у, z, удовлетворяющих уравнению
ж2_|_2/2=22 gce решения этого уравнения, а следова-
следовательно, и все П. ч. выражаются формулами х~а2— б2,
y=2ab, 2=о2+Ь2, где а, Ъ — произвольные целые
положительные числа (а>6). П. ч. могут быть истол-
истолкованы как длины сторон прямоугольного треуголь-
треугольника.. БСЭ-З.
ПЛ/1 — универсальный алгоритмический язык (со-
(сокращение от Programming Language One), разработан-
разработанный в 1963—64 фирмой по производству вычисли-
вычислительных машин ИБМ (International Business Machines).
В языке ПЛ/I нашли свое отражение как опыт пред-
предшествующих ему языков алгол, фортран, кобол, так
и многие новые идеи программирования, появившиеся
к моменту создания ПЛ/1. На язык также оказали
заметное влияние особенности вычислительных машин
фирмы ИБМ и их операционной системы.
ПЛ/1 устроен таким образом, чтобы из него можно
было выделять подмножества, удовлетворяющие нуж-
нуждам конкретного приложепия. Программа на ПЛ/1
составляется из независимо транслируемых модулей,
называемых внешними процедурами, к-рые имеют
алголоподобную блочную структуру и включают про-
процедуры (возможно, многовходовые и рекурсивные)
и блоки.
Наибольшее значение для диапазона применения
ПЛ/1 имеет разнообразие типов данных. Язык имеет
дело с данными арифметическими (действительными
и комплексными, с фиксированной и плавающей за-
запятой, двоичными и десятичными), строковыми (ли-
(литерными и битовыми), данными с шаблоном (аналогич-
(аналогичными шаблонам в коболе) и данными для управления
программой (метка передачи управления, вход, ука-
указатель, файл, ветвь и событие).
Язык ПЛ/1 обеспечивает возможность объединения
данных в агрегаты — массивы и структуры. М а с-
с и в ы представляют собой упорядоченный набор од-
однородных элементов (скаляров или структур). Струк-
Структурами в ПЛ/1 нал. иерархически упорядоченный
набор элементов, каждый из к-рых имеет свое имя
и может иметь свой тип данных и организацию.
Правила вычисления выражений позволяют выраба-
вырабатывать произвольные значения. В случае несоответст-
несоответствия типов данных при их вычислении осуществляется
автоматич. преобразование к типу, требуемому опера-
операциями или конкретным контекстом.
Существенной особенностью ПЛ/1 являются пра-
правила умолчания, позволяющие программисту
указывать, напр., не все свойства данных, не все
компоненты операторов, не все параметры встроенных
функций. То, что не указано явно программистом,
понимается нек-рым заранее определенным образом
пли же исходя из контекста.
ПЛ/1 обладает развитыми средствами управления
работой с памятью. Эти средства позволяют програм-
программисту самому определять момент размещения перемен-
переменных в памяти, объем требуемой памяти, скорость вы-
выборки элементов данных, повторно использовать уже
выделенную память под другим именем и, возможно,
с другой интерпретацией содержащихся в ней зна-
чений без переразмещения. Память может быть выде-
выделена статически (до исполнения программы) или ди-
динамически (при входе в блок или при исполнении
оператора размещения). Выделенная для нек-рой пере-
переменной память может быть организована по типу стека
с соответствующими правилами доступа или может
быть связана с нек-рым указателем.
Наряду с обычными операторами присваивания,
перехода, итеративного исполнения, вызова процедур,
условными операторами, ПЛ/I включает средства для
синхронизации параллельно исполняемых процедур,
для исполнения нек-рых операторов во время компи-
компиляции, а также для выполнения нек-рых действий
(системных или определенных программистом) при
возникновении ситуаций (стандартных или определен-
определенных программистом), вызывающих прерывание при
исполнении программы. В ПЛ/I представлены разно-
разнообразные средства для обмена данными с внешними
устройствами (посредством записей, посимвольно и с
редактированием). В язык ПЛ/I встроено большое
количество стандартных функций, к-рые существенно
облегчают программирование.
Стандарт ПЛ/I, опубликованный в 1976, дает более
формальную и точную спецификацию языка, обобщает
понятие типа и правила вычисления выражений и
вычисляемых функциями значений. В то же время в
стандарт языка не включены средства для параллель-
параллельного исполнения и средства организации вычислений
в период трансляции.
Лит.: [1] Универсальный язык программирования PL/1,
пер. с англ., М., 1968; [2] С к о т т Р., С о н д а к Н., ПЛ/1 для
программистов, пер. с англ., М., 1977; [3] Программирование на
ПЛ/1 ОС ЕС, М., 1979; [4] Бухтияров A.M., Ф р 0-
л о в Г. Д., О л ю н и н В. Ю., Сборник задач по программиро-
программированию на языке ПЛ/1, М., 1978; [5] American National Standard
programming language PL/1, ANSI, X 3.53 —1976. Л. А. Иорнева.
ПЛАНИГОН — выпуклый мпогоугольник правиль-
правильного разбиения плоскости на равные многоугольники,
т. е. такого разбиения, что существует группа движе-
движений плоскости, совмещающая разбиение с собой, к-рая
действует транзитивно на совокупности многоуголь-
многоугольников разбиения. Нп евклидовой плоскости существует
11 комбинаторных типоп разбиения — т. н. сет и
Шубникова — Лавеса (см. рис.). Однако груп-
группа симметрии для одного комбинаторного типа может
действовать по-разному. Взаимосвязь комбинаторного
типа и группы симметрии характеризуется т. н. с и м-
в о л о м с м е ж н о с т и. На евклидовой плоскости
существует 46 общих правильных разбиений с раз-
различным символом смежности.
Нп плоскости Лобачевского планигонами являются
правильные многоугольники с любым числом к сторон
и любым данным числом а сходящихся в каждой вер-
вершине П. Для числа сторон &=3, 4, 5, 6,>6 можно
выбрать такой размер П., что а>7, >5, >4, >4, >3.
Многомерным аналогом П. является стереоэдр.
Лит.: [1] Делоне Б. Н.. «Изв. АН СССР. Сер. матем.»,
1959, т. 23, № 3, с. 365—86; [2] Делоне Б. Н., Долби-
л и н Н. П., Ш т о г р и н М. И., «Тр. Матем. ин-та АН СССР»,
1978, т. 148, с. 109—40; [3] Узоры симметрии, пер. с англ., М.,
1980. А. Б. Иванов.
ПЛАНИРОВАНИЕ ЭКСПЕРИМЕНТА — раздел ма-
математической статистики, изучающий рациональную
организацию измерений, подверженных случайным
ошибкам. Обычно рассматривается следующая схема
П. э. Со случайными ошибками измеряется функция
/ @, х), зависящая от неизвестных параметров (век-
(вектора 9) и от неременных х, к-рые по выбору экспери-
экспериментатора могут принимать значения из нек-рого
допустимого множества X. Целью эксперимента яв-
является обычно либо оценка всех или нек-рых пара-
параметров В или их функций, либо проверка нек-рых
гипотез о параметрах 0. Исходя из цели эксперимента,
формулируется критерий оптимальности плана экс-
эксперимента. Под планом эксперимента понимается
совокупность значений, задаваемых переменным х
в эксперименте.
Лит.: [1] Налимов В. В..Чернова Н. А., Статисти-
Статистические методы планирования экстремальных эксперименте в,
М., 1965; [2] Федоров В. В., Теория оптимального экспери-
эксперимента, М., 1971; Ш X и к с Ч., Основные принципы планирова-
планирования эксперимента, пер. с англ., М., 1907; [4] Ф и н н и Д., Вве-
Введение в теорию планирования экспериментов, пер. с англ., М.,
1970.
ПЛАНКА ПОСТОЯННАЯ — одна из абсолютных
физич. копстант, имеющая размерность действия (энер-
(энергия X время); в системе CGS П. п. h равна
F,62377 ± 0,00018)-Ю-27 эргХсек
(±0,00018 — возможная погрешность в измерении).
Впервые была введена М. Планком (М. Planck, 1900)
в работе по световому излучению, в к-рой он пред-
предположил, что энергия е фотона (электромагнитной
волны) равна e=hv, где v — частота волны. Позднее,
с возникновением квантовой механики, П. п. была
использована в определении важнейших квантовоме-
ханич. величин (оператора импульса, энергии и т. д.)
и вошла почти во все уравнения и соотношения кван-
квантовой механики.
П. п. в нек-ром смысле характеризует границы при-
применения классич. механики: оказывается, что законы
квантовой механики существенно отклоняются от за-
законов классич. механики лишь для тех физич. систем,
для к-рых характерные расстояния, скорости и массы
таковы, что соответствующая характерная величина
действия сравнима по порядку с величиной h. При
формальном математическом рассмотрении это озна-
означает, что при h —>• 0 соотношения квантовой механи-
механики переходят в соответствующие классич. соот-
соотношения .
Наряду с постоянной h используют константу %=
= 2я, к-рую при этом также наз. П. п. р. а. минлос.
ПЛАНШЕРЕЛЯ ТЕОРЕМА: для каждой квадратич-
квадратично суммируемой функции /??2(—оо, +оо) интеграл
1 С 1 оо
;=- \ / (у) е~'хУ dy
У 2л; J -оо
f со (г)"~ "
сходится в L2k нек-рой функции f(x)?L2 при ш —>-сл,
то есть
lim \ I / (х)—] (х) \2 dx = 0.
щ^.00 J -СО
При этом сама функция f(x) представляется как предел
в Ьг при ti —>-оо интегралов
Ц7(у)е
у '±п j -ri
то есть
/ (.i)= lim /т) (ж).
Кроме того, справедливо соотношение
(формула Парсеваля — Планшереля).
Функция
7 (ж) = lim -4=- [ + <?> f (у) е-'Ух dy,
со->сс I 2л J - со
где предел понимается в смысле сходимости в L2l наз.
преобразованием Фурье функции / и
обозначается обычным символом
"/(y)e-'*J'dy, A)
при этом интеграл A) понимается в смысле главного
значения на оо в метрике L2. Аналогично истолковы-
истолковывается равенство
[ + Xl(y)ei*ydy. B)
Для функций f?L2 интегралы A) и B) существуют в
смысле главного значения почти при всех х.
Функции /и / удовлетворяют почти при всех х также
соотношениям
~, , . d \ 1 Г+а - , \ е~'хУ - 1 , 1
"х ^ > 2 J оо — l^ J
' dx \ 1 2Я J -
/ (у)
,\
Если обозначить 7 преобразование Фурье, 7 — его
обращение, то П. т. перефразируется так: f и /-1 —
взаимно обратные унитарные операторы в L2.
П. т. установлена М. Планшерелем (М. Plancherel,
1910).
Лит.: [1] Зигмунд А., Тригонометрические ряды, пер.
с англ., т. 2, М., 1965; [2] Титчмарш Е., Введение в тео-
теорию интегралов Фурье, пер. с англ., М.~ Л., 1948; [3] Б о х-
нер С., Лекции об интегралах Фурье, пер. с англ., М.,
1962. П. И. Ливоркин.
ПЛАНШЕРЕЛЯ ФОРМУЛА — формула, выражаю-
выражающая инвариантность скалярного произведения при
преобразовании Фурье в пространстве L2(X):
Н(х) j2(x) Jn (х).
В классич. случае, когда X=Y=Rn есть п-мерное
евклидово пространство, \i (x) и [л (у) суть гс-мерные
меры Лебега, преобразование Фурье
на пространстве ?2(^")Э/ является непрерывным
продолжением классич. преобразования Фурье
x=(xu ...,xn), y = (yu ..., yn),
(x, у) — скалярное произведение в R", с множества
Lx (R")n^2(R") на пространство L2(Rn).
П. ф. справедлива также, когда X — локально ком-
компактная коммутативная топологич. группа, Y — ее
группа характеров, х?Х, y?Y, ц(х) и и (г/) —соот-
—соответствующим образом нормированные инвариантные
меры в группах X и Y, а преобразование Фурье / (х) н>
Н> Ну) на пространстве L2(X)^f является непрерывным
продолжением отображения
defp
g (х) ь-» g (у) = \ g (х) у (х) dp (х),
с множества L1(X)[\L2(X) на пространство L2(X).
П. ф. обобщается на некоммутативные топологич.
группы. Пусть, напр., G — бикомпактная группа,
|х — инвариантная на ней мера, |х(С)=1, g н» C/gra>—
неприводимое конечномерное размерности ла унитар-
унитарное представление группы G в гильбертовом простран-
пространстве, g?G, a=l, 2, . . ., x(g)?L2(G),
def ,.
)=\ax{g)U^dll(g)
(* — переход к сопряженному оператору), S (Г^'Г^00*)
— след оператора Т'?1>Т'ха)*¦ Тогда обобщенная П. ф.
имеет вид
Лит.: Ш Колмогоров А. Н.,Фомин С. В., Элементы
теории функций и функционального анализа, 5 изд., М., 1981;
[2] Н а й м а р к М. А., Нормированные кольца, 2 изд., М., 1968.
Л. Д. Кудрявцев.
ПЛАСТИЧНОСТИ МАТЕМАТИЧЕСКАЯ ТЕОРИЯ —
теория деформируемого пластичного твердого тела, в
к-рой исследуются задачи, состоящие в определении
полей вектора перемещений и (х, t) или вектора скоро-
скоростей v(x,t), тензора деформации е,у (х, t) или скоростей
деформации v;j(x, t) и тензора напряжений otj(x,t),
к-рые возникают в теле, занимающем область Q с
границей 5, под действием массовых К(х, t) и поверх-
поверхностных F (x, t) сил при заданных начальных и гра-
граничных условиях, а также в определении тех нагрузок
и процессов, при к-рых равновесие (движение) тела
является неустойчивым. Особенности П. м. т. состоят
в том, что
а) соотношения a(y~6,-y нелинейны и необратимы и
описываются, вообще говоря, функционалами; следо-
следовательно, задачи П. м. т. существенно нелинейны;
б) конфигурации искомых квазистатич. полей опре-
определяются процессом изменения заданных функций па
промежутке [0, t], а не их мгновенными значениями в
момент t;
в) в процессе изменения функций К, F возникают
области упругой деформации, активной пластич. де-
деформации (нагрузки) и пассивной деформации (раз-
(разгрузки), в к-рых соотношения а//~е,-у- различны; эти
области должны быть определены при решении задачи;
г) уравнения краевой задачи могут, вообще говоря,
оказаться разных типов (эллиптического или гипербо-
гиперболического) в разных областях тела.
При произвольном сложном процессе известны лишь
весьма общие свойства функционалов пластичности,
их япная аналитич. структура не установлена. Кон-
Конкретные соотношения ст,/~е,у, не содержащие явно
функционалов, построены и экспериментально обо-
обоснованы для ряда типичных процессов деформации.
Иногда рассматриваются также нек-рые искусствен-
искусственные «модели» соотношений о,у~Ё,у-, к-рые лишь ча-
частично отражают упругопластич. свойства материалов.
Статические краевые задачи. В теории упруго-
упругопластич. процессов (см. [1]) согласно постулату изо-
изотропии А. А. Ильюшина соотношения а,/~Р,-/ можно
представить в виде
а,7=Л*е*, A)
(суммирование по ft от 1 до 6), где е,-/— базис, по-
построенный на основе тензора малой деформации,
Л k — функционалы от инвариантов тензора дефор-
деформации, давления р, температуры Т и, возможно, дру-
j гих инвариантных величин немеханич. природы. Ис-
Искомые функции Uj(x, t), &ij(x, t), atj(x, t) при равно-
равновесии удовлетворяют уравнениям
, B)
< C)
, D)
И; = (р,-, x?Sa, Sa\}Sa = S, Sar\Su = 0 F)
при заданных функциях Kj(x, t), F{{x, t), ф,-(ж, t) и
областях Q, So, Sa. Здесь /;- — направляющие коси-
пусы внешней нормали к граничной поверхности S;
t — параметр процесса (напр., истинное или условное
время); р — плотность материала; B) — дифференци-
дифференциальные уравнения равновесия, C) — кинематич. со-
соотношения между малыми деформациями и перемеще-
перемещениями, E) и F) — граничные условия в напряжениях
и перемещениях соответственно. Равенства B) — F),
строго говоря, не реализуют постановку краевой
задачи, поскольку при неизвестной структуре функ-
функционалов пластичности нельзя решить вопрос о су-
существовании решения.
С учетом этой неопределенности для решения зада-
задачи B) — F), допуская его существование при произ-
произвольном сложном нагружении (СН), предложен и в ча-
частных задачах реализован следующий метод СН-ЭВМ.
Ниже система равенств B), C), E), F) будет наз.
неполной системой (В). В связи с использованием ко-
нечноразностной процедуры область Q разбивается
на N ячеек (элементов), в каждой из к-рых искомые
функции имеют постоянные (средние) значения, за-
зависящие от параметра t (интересующий интервал вре-
времени [0, t] разбивается на М шагов), и в v-й ячейке
заменяются соотношения D) аппроксимирующими со-
соотношениями вида
°w/ = cv*e*f/l G)
где CVk — функции t, такими, что решение задачи
(В), G) существует. Пусть в первом приближении с
конкретно заданными (по возможности — наиболее
простым способом, напр, в соответствии с обобщенным
законом Гука) функциями Cvk
решение задачи (В), G) есть ulv\-(t), еЩ,
Определяемый по нему набор инвариантов I(^} (t)
вместе с pv(t) и Tv(t) рассматривается как совокуп-
совокупность программ испытаний N образцов в однородном
напряженном состоянии. Проведение их на испыта-
испытательном комбайне класса СН дает истинные зависи-
зависимости о,-у~е,,у в процессах Iy(t), Pv(l), T\(t), что
определяет уточненные аппроксимирующие соотно-
соотношения
к-рые используются для численного решения задачи
(В), G2) во втором приближении. Аналогично строятся
последующие приближения. Сходимость оценивается
по нормам разностей двух последующих приближений.
В отличие от применяемых вариантов теоретико-
экспериментальных методов решения краевых задач
с известными соотношениями D), здесь используется
испытание стандартных образцов в одномерном напря-
напряженном состоянии по стандартной методике, а не на-
натурного объекта или его модели в сложном напряжен-
напряженном состоянии.
Предложен апостериорный критерий существования
(см. [2]): если указанный процесс итераций сходится,
то решение задачи B) — F) (с неизвестной структурой
функционалов Ак) существует и с заданной степенью
точности определяется в ге-м приближении.
Если соотношения D) известны, но сложны, то этот
метод также применим с использованием D) вместо
испытательного комбайна СН.
Сложности постановки и решения краевой задачи тео-
теории пластичности в общем случае существенно уменьша-
уменьшаются при рассмотрении конкретных классов процессов.
Степень сложности процесса деформации в точке
тела определяется сопоставлением кривизн траектории
деформации, к-рая в 5-мерном евклидовом простран-
пространстве изображает процесс изменения девиатора дефор-
деформации 9ij—e.jj—ebij Ce=e,-,-), с типичной для каждого
материала величиной следа запаздывания h, опреде-
определяемой экспериментально. На этой основе выделяются
частные классы процессов, для к-рых соотношения D)
конкретизируются и не содержат явно функционалов.
Для каждого такого класса процессов постановка
краевой задачи B) — F) становится определенной,
допускающей доказательство теорем существования и
единственности и построение общих методов решения.
При этом, однако, возникает проблема физич. досто-
достоверности решения, поскольку при заданных функциях
К[(х, t), F[(x, t), <fi(x, t) процессы, определяемые
решением, могут не соответствовать области достовер-
достоверности частного вида соотношения D), принятого при
постановке задачи. Эту проблему можно поставить
как задачу об определении класса заданных функций
Hi, F[, (p[ и, может быть, ограничений на соотношения
D) частного вида, при к-рых система уравнений B) —
F), дополненная соотношениями, определяющими со-
соответствующий класс процессов, совместна.
В теории малых упругопластич. деформаций (см.
[3]), относящейся к процессам простой деформации
(нулевой кривизны), соотношения D) имеют вид
2Ф (г 1
(в) + ЗЯб (8)
где Еи=Г-д-3,уЗ,у j — интенсивность деформации,© —
экспериментально определяемая функция упрочнения,
К — константа (модуль объемной упругости), Зе— е,-,-.
При ограничениях
(9)
— число), приемлемых для конструкционных
материалов, установлена эллиптич. природа краевой
задачи (В), (8), доказаны теоремы существования
и единственности решения, установлены минимальные
принципы и даны соответствующие вариационные
постановки задач. Доказана теорема о простом на-
гружении, определяющая класс функций К[, F;, ср,-
(однопараметрич. нагрузки), при к-ром решение задачи
физически достоверно. Для решения краевой задачи
(В), (8) в принципе применимы методы Ритца и Буб-
Бубнова — Галоркина, к-рые, вследствие нелинейности
задачи, малоэффективны. Широко используется метод
упругих решений, сходящийся при условиях (9): в
каждом последовательном приближении решается более
простая краевая задача линейной теории упругости
(см. [3]). При этом в ходе решения определяются об-
области упругих деформаций, в к-рых имеет место обоб-
обобщенный закон Гука. Применяется также метод пере-
переменных параметров упругости (см. [4]).
Постановка задачи (В), (8) и указанные методы
решения применяются также к задачам термопластич-
термопластичности. При этом при температурном поле Т(х, t),
определяемом решением задачи теплопроводности, в
соотношениях (8) полагается Ф^Ф (ец, Т) и член
3Ke,f>ij заменяется выражением ЗАГ(е—aT)bij. Ввиду
функциональной природы соотношений 0,у~е,-у ис-
использование функции Ф (еи, Т) ограничено нек-рым
классом тепловых процессов. Специальный интерес
представляют задачи о циклич. нагружении тела
(см. [5]), сопровождающемся периодич. возникнове-
возникновением областей разгрузки и нагрузки обратного знака.
В теории упругопластич. процессов малой кривизны
(наибольшая кривизна значительно меньше h-1) с
соотношениями
"в
где
/ 2 \ 1/2
vu = {tV'JVu) > Vij = Vij-vbij, 3v = vmm,
udt — длина дуги траектории деформации, и с
кинематич. уравнениями
2vij = Vi,j-\-Vjti, A1)
где vi(x, t) — координаты вектора скорости частицы
среды, ставится краевая задача B), A0), A1), E), F),
для к-рой доказаны теоремы существования и единст-
единственности, сформулированы вариационные принципы
и предложен метод последовательных приближений.
Условия физич. достоверности решения не выяснены.
Эта задача формулируется, в частности, примени-
применительно к расчету установившегося пластич. течения
упрочняющегося металла в технологич. процессах
обработки давлением (прессование, прокатка и т. п.).
Аналогично ставится краевая задача для упруго-
упругопластич. процессов средней кривизны (главная кри-
кривизна траектории деформации меньше или порядка
Для теории двухзвенных процессов (траектория де-
деформации — ломаная с углом излома 0 при s=s0),
типичных для двухпараметрич. нагружении тела, с
соотношениями (8) при s<:s0 и соотношениями
A2)
при s>s0, где аа, ¦& — известные функции от s0, 0, s,
дана постановка краевой задачи (В), A2) при s>s0
и (В), (8) при s<s0 с доказательством теорем сущест-
существования и единственности. Доказана локальная тео-
теорема физич. достоверности, определяющая достаточные
условия, налагаемые на функции A",-, F,-, ср,-, при к-рых
почти всюду в области Q происходят изломы траек-
траекторий деформации. Свойства решений и материальных
функций в окрестности точки излома существенны
для решения задач об устойчивости равновесия при
упругопластич. деформациях.
В современной теории течения для пластич. части
тензора деформации ef/ из постулатов пластичности
энергетич. типа выводятся соотношения пида
а для упругой части принимается обобщенный лакон
Гука
где к, |л — постоянные Ламе, причем функция нагру-
нагружения / является функционалом процесса нагружения
G;/(t), а функция упрочнения //, кроме того, зависит
от приращений Да,-/. Чаще всего предполагается, что
Н не зависит от Да,-/. При этом линеаризованные по
приращениям соотношения A3) позволяют строго
формулировать краевую задачу типа (В), A3) с дока-
доказательством ряда общих теорем и минимальных прин-
принципов (см. [6]); разработаны процедуры численно-
аналитич. решения. Преимущество простоты, даваемое
линеаризацией соотношений A3), серьезно ослабля-
ослабляется ограниченностью области, в к-рой линеаризо-
линеаризованные соотношения физически достоверны.
В П. м. т. часто используется постановка краевой
задачи на основе теории пластичности Прандтля —
Рейса, к-рая описывается соотношениями
2Gsu = 6ij - ad;, + R (°ij — aS'V) + 17f °8и'<
где G, К — константы упругости, R — функция от
ои~ (-Tj-stj-sijA . Область достоверности этих соот-
соотношений ограничена (точно не определена).
Развита теория идеально пластич. тел (см. [7],
[8]), основанная на физич. соотношениях Сен-Венана —
Леви — Мизеса. Эти соотношения формально полу-
получаются из соотношений малой кривизны A0), если в
них положить Ф (s)=a,s=const (as — предел текучести
материала) и принять условие несжимаемости:
а0— а6,7 = 4^ <-•;/, * = 0. A4)
Понятие идеальной пластичности подразумевает, кроме
того, соблюдение в области активных пластич. дефор-
деформаций условия текучести вида
*>//) = 0, A5)
напр, условия Генки — Мизеса 3/.2$,7$,-/---
=¦ as, s,y= °7/—об,-/, или условия Треска —
Сен-Венана ттах=т.5, где ттах—наибольшее
касательное напряжение, as, xs — константы мате-
материала.
Краевая задача вида (В), A4), A5) с заменой C) на
A1) обычно гиперболического (иногда эллиптиче-
эллиптического) типа. Полная задача теории идеальной пла-
пластичности состоит в решении уравнений B), A1), A4),
A5) в части области Qlt в к-рой имеют место пластич.
деформации, и уравнений B), C) с соотношениями
обобщенного закона Гука в области упругих деформа-
деформаций Q2 с соответствующими граничными условиями
и кинематич. и динамич. условиями сопряжения ре-
решений на неизвестной границе областей Qx и Q2 (уп-
ругопластич. задача).
Часто практически полезные результаты дает жестко-
пластич. анализ, в к-ром упругие деформации игно-
игнорируются и части тела вне области пластичности
считаются недеформируемыми. При этом, как пра-
правило, возникают стационарные поверхности разрыва
скоростей частиц, что несовместимо с классич. положе-
положениями механики сплошной среды. В нек-рых задачах
при задании граничных условий в напряжениях урав-
нения равновесия вместе с условиями типа A5) можно
рассматривать как автономную систему гиперболич.
типа. При этом возникает возможность неоднозначного
определения области нластич. деформаций и напря-
напряжений в этой области, к-рую часто разрешают на ос-
основе нек-рых эвристич. соображений. Многозначность
не возникает при решении упругопластич. задачи.
Среди задач, решаемых методами теории идеальной
пластичности, специального упоминания заслуживают
задачи об установившемся пластич. течении неунроч-
няющегося металла в «каналах» с определением ско-
скоростей и напряжений, включая контактные, примени-
применительно к технологпч. задачам обработки давлением
(ковка, штамповка, прессование).
Для ряда инженерных приложений особый интерес
представляет теория пластич. течения тонких слоев
металла, основанная на ряде рациональных гипотез
кинематич. и физич. характера. При этом определяются
условия, необходимые для поддержания пластич. те-
течения (напр., мощность пресса), и распределение ско-
скоростей, позволяющее предвидеть форму изделия.
Прикладные задачи П. м. т. (напр., о равновесии
оболочек) приводят к краевым задачам с нелинейными
дифференциальными уравнениями с частными произ-
производными высокого порядка (напр., четвертого).
Для задач об устойчивости равновесия при пластич.
деформациях характерно бифуркационное изменение
типа процесса деформации в момент потери устойчи-
устойчивости с образованием точек излома па траекториях
деформации. Напр., при простом нагружении тела в
момент потери устойчивости возникает сложное на-
гружение, и для решения задачи об устойчивости
необходимо привлекать соотношения, описывающие
бесконечно малый процесс после точки излома траек-
траектории (см. [1]).
Динамические задачи теорий пластичности. Общая
постановка динамич. задачи получается, если B)
заменить уравнением движения
п к B) — F) добавить начальные условия, напр, вида
щ(х, 0)=%И, uht(x, Q)=%i(x), x?Q.
При этом возникают трудности двоякого характера:
1) вследствие возникновения разных типов волн с
различными скоростями распространения, зависящими
от величин деформаций, процессы деформации в разных
точках тела (и в каждой точке в разные промежутки
времени) имеют разную степень сложности даже при
простейших типах прилагаемых нагрузок, и априори
нельзя установить возможность использования соот-
соотношений 0,у~е,у частного вида;
2) необходимо использовать динамич. соотношения
a,y~s,-y с учетом зависимости от развития процесса
деформации во времени.
Динамич. функционал пластичности изучен не пол-
полностью даже для одномерного процесса, т. е. при про-
простой деформации. Информация о динамич. характери-
характеристиках материалов в сложном папряженном состоянии
при сложных процессах деформации чрезвычайно
скудна и не позволяет судить хотя бы о качественных
свойствах динамич. функционалов пластичности. В свя-
связи с этим динамич. задачи теории пластичности ста-
ставятся с использованием статич. соотношений теории
пластичности, что позволяет отрабатывать методы
решения, выяснять специфические для динамики ме-
ханич. эффекты и получать решения, полезные для
практики в качестве оценок. Такой подход в качестве
этапа исследования оправдывается чрезвычайной важ-
важностью изучения динамич. процессов в конструкциях,
сооружениях и массивах.
Анализ распространения активных нелинейных де-
деформаций в сложном напряженном состоянии обна-
обнаруживает возникновение комбинированных разрывов
разных типов, характерных только для нелинейных
.i.iдач. Насколько можно судить по имеющимся ре-
результатам, наиболее сложные процессы протекают в
областях, примыкающих к поверхностям разрыва,
тогда как в основной области движения сложность
процесса по кривизнам траекторий и по времени ог-
ограничена. Поэтому представляется возможным решать
динамич. задачи теории пластичности для сложных
случаев путем комбинированного использования со-
соотношений частного вида (напр., для процессов сред-
средней кривизны) в основной области и соотношений для
окрестности точки излома (или для двухзвенных про-
процессов) в областях, примыкающих к поверхностям
разрыва. Нетривиальной и специфической для динамич.
задач теории пластичности является задача о нахож-
нахождении поверхности разгрузки, разделяющей области
активных и пассивных деформаций.
Наиболее детально изучены задачи о распростране-
распространении одномерных упругопластич. волн (см. [9]). Иссле-
Исследована задача о распространении волны разгрузки
в стержне при растяжении-сжатии (см., напр., [9]).
В дальнейшем распространение и взаимодействие уп-
упругопластич. продольных волн в стержне исследовано
с учетом различных типов зависимости механич. на-
нагрузок от скорости деформации. В свою очередь, полу-
полученные решения используются в качестве теории экспе-
эксперимента (базисного или контрольного) для изучения
динамич. свойств материалов (см. [10]).
Математические задачи теории уравнений состояния.
Явлепие пластичности настолько сложно, что постро-
построить уравнения состояния (соотношения а,-_/~в,у) путем
прямого обобщения опытных данных не удается. В свя-
связи с этим доминирует тенденция к созданию общей
теории, к-рая, в частности, определит и теорию экс-
эксперимента. На этом пути ведется математич. исследо-
исследование допустимых форм уравнений состояний, не про-
противоречащих законам механики и термодинамики,
изучение свойств кривых и поверхностей в гс-мерном
пространстве в связи с исследованием процессов и
предельных конфигураций, формулирование опреде-
определяющих принципов, относящихся к нек-рым классам
(так или иначе идеализированных) материалов, ука-
указывающих выбор независимых параметров состояния
и уточняющих (в достаточно общем виде) структуру
соотношений Oij~?j/, аналитич. исследование свойств
функционалов пластичности, выяснение классов про-
процессов, допускающих более простое математич. опи-
описание в рамках общих соотношений (см. [1], [11]).
Большое значение для теории и экспериментального
исследования имеет развитие теории представления
функционалов. Результаты этой теории позволяют,
в частности, устанавливать физич. достоверность урав-
уравнения состояния сложной функциональной структуры
ио анализу явлений, сравнительно легко воспроизво-
воспроизводимых в натуре.
Лит.: [1] И л ь ю ш и н А. А., Пластичность. Основы общей
математической теории, М., 1963; [2] И л ь ю ш и н А. А., Л е н-
с к и й В. С, Модель и алгоритм, «Прикладные проблемы
прочности и пластичности», 1975, К» 1 (Горький); [3] Илью-
Ильюшин А. А., Пластичность, ч. 1— Упруго-пластические де-
деформации, М.— Л., 1948; [4] Б и р г е р И. А., «Прикл. матем.
имехан.», 1951, т. 15, № 6, с. 765—70; [5] М о с к в и т и н В. В.,
Пластичность при переменных нагружениях, М., 1965; [6] К о й-
т е р В. Т., Общие теоремы теории упруго-пластических сред,
пер. с англ., М., 19(И; [7] Соколовский В. В., Теория
пластичности, 3 изд., М., 1969; [8] X и л л Р., Математическая
теория пластичности, пер. с англ., М., 1956; [9] Р а х м а т у-
л и н X. А., Демьянов Ю. А., Прочность при интенсивных
кратковременных нагрузках, М., 1961; [10] Васин Р. А.,
Л е н с к и й TS. С. ,т| е н с к и й Э. В., Динамические зависимос-
зависимости между напряжениями и деформациями, в кн.: Проблемы ди-
динамики упруго-пластических сред, М., 1975; [11] Т р у с-
д е л л К., Первоначальный курс рациональной механики сплош-
сплошных open. iiRi). с, англ.. Ы.. 1975. В. С. Ленский.
ПЛАТО ЗАДАЧА — задача нахождения минималь-
минимальной поверхности (м. п.) с заранее заданной границей Г.
Впервые такая задача была поставлена Ж. Лагранжем
(J. Lagrange, 1760), к-рый свел ее в классе поверхно-
поверхностей вида z=z{x, у) к решению уравнения Эйлера —
Лагранжа м. п. После опытов Ж. Плато (J. Plateau,
1849), в к-рых он показал, что м. н. могут быть полу-
получены в виде мыльных пленок, натянутых на проволоч-
проволочные каркасы (см. [1]), эту задачу стали называть зада-
задачей Плато.
В строгой постановке П. з. требует ряд дополни-
дополнительных уточнений, относящихся к искомой м. п. и к
ее границе. Напр., должно ли искомое решение быть
регулярной м. п. или же его можно искать среди обоб-
обобщенных минимальных поверхностей (о. м. п.); обяза-
обязательно ли искомая поверхность должна реализовать
абсолютный минимум площади; каков должен быть
конформный или топологич. тип поверхности; в каком
смысле понимать границу поверхности, и т. п. В за-
зависимости от постановки задачи, ее решения и свой-
свойства этих решений (существование, единственность,
регулярность и т. д.) могут быть существенно раз-
различными.
В течение 19 в. П. з. была решена для нек-рых част-
частных видов заданной границы Г, главным образом для
различных полигональных контуров. В 1928 было
доказано существование решения П. з. для о. м. п.
типа круга, представляемой формулами Вейерштрасса
и ограниченной заданной незаузленной жордановой
кривой. В 1931 дано решение П. з. в следующей фор-
формулировке: пусть Г— жорданова кривая в R™, ге^2,
тогда в R" существует о. м. п., заданная в изотермич.
координатах (и, v) радиус-вектором r—r(u, v), непре-
непрерывным в круге |ш|<:1, w=u-\-iv, и гомеоморфно ото-
отображающим окружность \w{=l на Г; при этом пло-
площадь этой о. м. п. оказывается наименьшей среди всех
непрерывных поверхностей типа круга, натянутых на
контур Г, в предположении, что на Г можно натянуть
хотя бы одну такую поверхность конечной площади.
После решения П. з. в 1931 для односвязной поверх-
поверхности Дж. Дуглас (J. Douglas) поставил вопрос (т. н.
задача Дугласа) о существовании в R",
п^2, м. п., имеющем заданный топологич. тип (т. е.
заданную эйлерову характеристику и характер ори-
ориентируемости) и ограниченной заданным контуром Г.
состоящим из объединения к~^\ жордановых кривых
1\, . . ., 1\. В 1936—40 были даны достаточные
условия разрешимости этой задачи, одно из к-рых
заключается в возможности натянуть на Г какую-
нибудь поверхность данного топологич. типа, площадь
к-рой была бы меньше, чем площадь любой поверх-
поверхности с меньшей эйлеровой характеристикой, натяну-
натянутой на тот же контур. В такой постановке П. з. была
рассмотрена и решена также в римановом пространстве.
В нач. 60-х гг. 20 в. было достигнуто большое про-
продвижение и в решении П. з. для А-мерных поверхно-
поверхностей, к^З. Было предложено несколько обобщений
П. з., основанных на новых определениях понятий
поверхности, границы и площади. Одно из обобщений
исходит из следующего определения понятия поверх-
поверхности X и ее границы L в Кп. Пусть имеются компакт
XdRn и компакт А^Х, G — абелева группа и fc=:l —
целое число; тогда определены группы гомологии Че-
Чеха—Александрова Я^._,(Л, G) и Hk_1(X, G); ядро
гомоморфизма ?*: Я^_1(Л, G) —>- Hfl_1(X, G), индуци-
индуцированного вложением i : А —>- X, наз. алгебраич. гра-
границей компакта X (в размерности к) по отношению к А .
Если L — подгруппа группы Я^_г (А, G), то X является
поверхностью с границей ZDf*, если L принадлежит ал-
алгебраич. границе компакта X; под площадью компак-
компакта X в R" понимается его ^-мерная хаусдорфова (сфери-
(сферическая) мера Л*. При таких определениях доказаны
существование и регулярность почти всюду (топологи-
(топологическая локально евклидовость и аналитичность) ком-
компакта Хо, реализующего минимум меры Ак по всем
компактам X с заданной границей L. Впоследствии
эти теоремы были распространены на случай поверх-
поверхностей X в римановом пространстве.
Другие предложенные обобщения П. з., в частности
обобщение в терминах интегральных потоков, явля-
являются в нек-ром смысле эквивалентными постановке
П. з. в терминах гомологии.
В классич. постановке Плато многомерная задача
решена в 1969; а именно, доказана теорема: если в
римановом пространстве V" задано (к—1)-мерное под-
подмногообразие Г, А^З, то существует поверхность,
реализующая минимум хаусдорфовой меры А* среди
всех параметризуемых поверхностей X, являющихся
в V" непрерывными /-образами А-мерных гладких
многообразий М с краем, гомеоморфным Г при ото-
отображении / : М ->- Vn.
Наряду с вопросами разрешимости П. з. интерес-
интересными являются также вопросы единственности и ре-
регулярности ее решения. Наиболее продвинуто иссле-
исследование вопроса о регулярности решения. Показано,
что решение П. з., данное Дугласом в R3, не содер-
содержит внутренних точек ветвления. Для случая мно-
многомерной П. з. доказана регулярность решения поч-
почти всюду, причем возможность наличия нерегуляр-
нерегулярных точек подтверждается примерами. Что касается
единственности решения П. з., то здесь известны лишь
нек-рые достаточные признаки единственности (напр.,
решение П. з. единственно, если заданный контур Г
имеет однозначную выпуклую проекцию при централь-
центральном или параллельном проектировании па нек-рую
плоскость). Чтобы подчеркнуть сложпость этого во-
вопроса, достаточно сказать, что есть основания ожи-
ожидать существование спрямляемых контуров, стягива-
стягивающих континуум м. п. типа круга.
Лит.: [1] EncyklopSdie der mathematischen Wissenschaften,
Bd 3, H. 2/3, Lpz., 1903;[2J Darboux G., Lemons sur la the-
orie generale des surfaces..., 2 ed., pt. 1, P., 1914; l:'<] В i a ri-
rich i L., Vorlesungen iiber Differentialgeometrie, 2 Aufl., Lpz.—
В., 1910; [4] К ур ант Р., Принцип Дирихле, конформные отоб-
отображения и минимальные поверхности, пер. с англ., М., 1953;
15] Моггеу С, «Ann. Math.», 1948, v. 49, № 4, p. 807—51;
[6] R a d о Т., On the problem of Plateau, В., 1933; [7] H и ч е
И. С. С, «Математика», 1967, т. И, № 3, с. 37—100; [8] О с с е р-
м а н Р., там же, 1971, т. 15, Я» 2, с. 104—25; [9] Ф о м е н-
к о А. Т., «Изв. АН СССР. Сер. матем.», 1972, т. ,36, с. 1049—
1079; [11] NitscheJ.C.C, «Invent, math.». 1969, v. 8, N 4,
p. 313—33; [12] О с с ер м а н Р., «Успехи матем. наук», 1967,
т. 22, в. 4, с. 55—136; [13] Federer H., Geometric measure
theory, В.— [u. a.], 1969; [14] М о г г е у С, Multiple integrals
in the calculus of variations, B.— [u. a.], 1966. И. Х. Сабитов.
ПЛАТО МНОГОМЕРНАЯ ЗАДАЧА — термин, обо-
обозначающий серию задач, связанных с изучением экс-
экстремалей и глобальных минимумов функционала ft-мер-
ного объема volfe, определенного на ft-мерных обоб-
обобщенных поверхностях, вложенных в re-мерное риманово
пространство М" и удовлетворяющих тем или иным
граничным условиям.
В истории развития указанной вариационной задачи
(см. Плато задача) выделяются несколько периодов,
характеризующихся различными подходами к поня-
понятиям «поверхности», «границы», «минимизации» и,
соответственно, методами получения минимального
решения. Многомерная задача Плато
формулируется так. Пусть Ак~1аМп — фиксирован-
фиксированное замкнутое гладкое (к—1)-мерное подмногообразие
в римановом пространстве М" и пусть X (А) — класс
всех таких пленок (поверхностей) ХаМ", имеющих
i раницей многообразие А, причем каждая пленка
X ? X (А) допускает непрерывную параметризацию (пред-
ставима в виде образа нек-рого многообразия с краем),
т. е. X=f(W), где W — нек-рое А-мерное многооб-
многообразие с краем д W, гомеоморфным А , а / : W —*¦ М" —
непрерывное отображение, совпадающее с фиксиро-
фиксированным гомеоморфизмом на крае д W, то есть / : д W—A.
Вопрос: можно ли найти в классе X (А) пленку Хо,
к-рая была бы в каком-либо разумном смысле мини-
минимальной, напр, чтобы ее й-мерный объем был наимень-
наименьшим по сравнению с /с-мерными объемами других
пленок X из этого же класса? Оказалось, что перене-
перенесение классич. «двумерных» методов на многомерный
случай наталкивается на серьезные трудности. Это
привело к тому, что классич. постановка П. м. з. была
на время оставлена и задача была сформулировапа
в иных (гомологических) терминах. Если отбросить
понятие многообразия-пленки с краем dW ~ А и сильно
расширить понятие пленки и ее границы, ослабив
связь пленки с ее границей (в частности, если рас-
рассматривать непараметризованные пленки), отбросив
условие X=f(W), то П. м. з. может быть сформулиро-
сформулирована на языке обычных целочисленных гомологии Н^:
найти минимальную пленку Хо, аннулирующую фун-
фундаментальный цикл [А]?Нь-\(А) многообразия Л (в
предположении, что А ориентируемо), т. е. 1*[Л] = 0,
i)f:Hk-1(A) ->- lfk_1(X), где г* — гомоморфизм, ин-
индуцированный вложением i : А -+ X. Для решения
П. м. з. в этой новой расширенной постановке был
разработан (см. [1], [2]) геометрич. подход, при к-ром
минимизировался функционал А-мерной хаусдорфовой
меры (объема), определенный на А-мерных измеримых
компактах (поверхностях) в Мп, и развита (см. [3],
[4]) теория интегральных потоков и варифолдов, но-
носителями к-рых являются ^-спрямляемые подмноже-
подмножества в М". Однако указанное расширение понятия
границы пленки в терминах гомологии Н* (то есть
к—1-мерное многообразие А считается границей к-
мерной пленки W, если при вложении А —>- W фунда-
фундаментальный цикл [А] аннулируется) означает отход
классич. постановки П. м. з., так как, располагая
теоремой существования минимального решения в
гомологич. классе Х(А), uo-прежнему ничего нельзя
сказать о существовании минимального решения в
классе всех пленок, являющихся непрерывными об-
образами многообразий с краем, т. е. допускающих
параметризацию. Дело в том, что если многообразие А
гомологично нулю (как цикл) в пленке Хо, то Х„ не
обязательно допускает представление в виде X0=f(Wa),
где WQ — нек-рое /с-мерное многообразие с краем.
В классич. постановке, т. е. в терминах пленок вида
X=f(W), где W суть А-мерные многообразия с краем
А, П. м. з. была решена (см. |5], [6]). При этом было
замечено, что классическая П. м. з. допускает экви-
эквивалентную формулировку на языке бордизмов. Пусть
V есть (к—1)-мерное компактное ориентированное
замкнутое многообразие, / : V -*- Мп — непрерывное
отображение; пара (F, /) наз. сингулярным
бордизмом Мп. Два бордизма (F:, Д) и (F2, /2)
наз. эквивалентными, если существует /г-
мерное ориентированное многообразие W с краем
dW=V1[] (—F2) (где— F2 означает F2 с обратной
ориентацией) и непрерывное отображение F : W —*¦ Мп
такое, что F\Vl=fl, F\Vl)~f2. Бордизм (V, f) эквива-
эквивалентен нулю, если V—dW=V1, F2=0. Классы экви-
эквивалентности сингулярных бордизмов образуют абелсвы
группы, к-рые после выполнения процесса стабилиза-
стабилизации образуют одну из обобщенных теории гомологии
(теорию бордизмов). П. м. з. формулируется (на этом
языке) так: а) можно ли среди всех пленок XczM, А сХ
и обладающих тем свойством, что сингулярный бор-
бордизм (А, i) (где i : А —>- X — вложение) эквивалентен
нулю в X, найти Хо с наименьшим объемом vol^X,,?
б) Можно ли среди всех сингулярных бордизмов (V, g)
(где g : V -v Mn), эквивалентных данному бордизму
(F', g'), найти такой бордизм (Fo, g-0), чтобы объем
пленки gl>(Xl))czMn был бы наименьшим? Положи-
Положительный ответ на эти вопросы см. в [5], [6], [13].
Классическая П. м. з. значительно отличается от
ее гомологич. варианта. На рис. 1 показаны контур
A = S1 и пленка X, стремящаяся занять в R3 поло-
положение, соответствующее наименьшей площади. В нек-
рый момент наступит склейка, схлопывание пленки,
d
Рис. 1.
в результате чего вместо двумерной трубки Т появится
одномерный отрезок Р. В двумерном случае отрезок Р
может быть непрерывно отображен в двумерный диск,
заклеивающий А. В многомерном случае описанный
;>ффект появления у минимальной пленки зон мень-
меньших разномерностей присутствует еще в большей
степени, причем если в двумерном случае все такие
куски Р, dim Р-кк—1, можно было отобразить без
потери параметризующих свойств пленки Хо в /с-мер-
ную (двумерную) часть этой пленки, то при /с>2 эти
зоны меньшей размерности, в общем случае, неуст-
неустранимы (если мы хотим сохранить топологич. свой-
свойство пленки Хо, аннулирующей бордизм (А, г))- В силу
тех же причин зоны меньшей размерности не могут
быть отброшены, так как ^-мерная часть Х(*> пленки
X может вообще не допускать непрерывной парамет-
параметризации и, тем самым, вообще говоря, не аннулирует
бордизм (A, i). Это показывает необходимость вве-
введения стратифицированного объема пленки X, состав-
составленного из объемов всех ее зон Х<<>, то есть (volfcX1**,
volfe-jX**-1). . .). Теорема, являющаяся решением
П. м. з., формулируется так (см. [5], [6]): существует
глобально минимальная поверхность, минимизирую-
минимизирующая стратифицированный объем.
Следствие: для любого фиксированного (к—1)-мер-
ного ориентированного гладкого замкнутого подмного-
подмногообразия А в римановом пространстве М" (в том слу-
случае, когда Х(А)Фф) существует глобально минималь-
минимальная поверхность X0=fg(W0), аннулирующая бордизм
(А, г) (в частности, А-мерный объем пленки Хо не
больше /с-мерного объема любой пленки вида X=f(W)),
см. [5], [13]. Более того, пленка Хо минимальна в
каждой своей размерности s<&; если Х<*> — часть
пленки X, имеющая размерность s, то Х<л> содержит
подмножество Z<s\ s-мерный объем к-рого равен нулю,
а дополнение X<S>\Z<S) является открытым s-мерным
всюду плотным в А"*5' аналптич. подмногообразием в
Мп. Здесь Z(i) — множество сингулярных точек в
размерности .v.
Этот результат является частным случаем общей
теоремы существования и почти всюду регулярности
глобально минимальной поверхности, доказанной (см.
[5], [6], [13] для любой обобщенной теории (ко)гомоло-
гией и для любого набора краевых условий. Кроме
того, такая поверхность существует и в каждом ста-
стабильном гомотопич. классе. Вот пример вариацион-
вариационной задачи, сформулированной и получившей решение
в когомологич. терминах. Пусть 5 — стабильно нетри-
нетривиальное векторное расслоение на компактном рима-
римановом пространстве Мп\ пусть X (|) — класс всех
таких поверхностей ХсМ", что ограничение \\%
расслоения \ на X стабильно нетривиально (т. е. X —
носитель \). Тогда всегда существует глобально ми-
минимальная поверхность Х0?Х(?,), имеющая наимень-
ший объем в классе Х(?). Общая теорема существо-
существования может быть сформулирована и доказана также
и на языке интегральных потоков, для чего следует
ввести фильтрованные потоки, состоящие из потоков
различных размерностей. На этом пути было затем
получено решение П. м. з. в классах гомотопий [14].
В сфере задач, окружающих П. м. з., выделяются
исследования конкретных аналитич. и топологич.
свойств глобально минимальных поверхностей. Напр.,
актуальна задача предъявления конкретных поверхно-
поверхностей в римановых пространствах. Так, напр., известно
(см. [3]), что комплексные алгебраич. подмногообразия
в С" и СРп — глобально минимальные поверхности.
Этот результат носит ярко выраженный комплексный
характер. В случае вещественных подмногообразий
долгое время отсутствовали какие-либо методики об-
обнаружения конкретных глобально минимальных по-
поверхностей. Первым результатом (см. [6]) в этом на-
направлении, учитывающим их топологию, была мето-
методика, применение к-рой позволило доказать, что
каждому компактному риманову пространству Мп
можно сопоставить универсальную функцию Qx(k),
где х?Мп, к — целое число, 1<&<:п. Если Хо — гло-
глобально минимальная поверхность, реализующая не-
нетривиальный (ко)цикл в Нь(Мп), то volftX0^Qx(fe)
для любой точки х?Х0. Если M=GlH — однородное
пространство, то Qx(k)^=Q (к) не зависит от точки х.
Функция &х(к) вычисляется в явном виде и дает об-
общую оценку снизу на объемы всех А-мерных (ко)циклов
в Мп. Оценка эта в общем случае неулучшаема, т. е.
существуют бесконечные серии глобально минималь-
минимальных Хо, для к-рых volftZ0=Q (к). Для симметрич.
пространств получено (см. [6], [13], [15]) полное опи-
описание всех таких поверхностей, для к-рых volfcX0=fi (к).
Разработаны (см. [11], [12], [14], [15]) дальнейшие
методики получения конкретных глобально минималь-
минимальных поверхностей. В различных задачах вариационного
исчисления, топологии, алгебраич. геометрии,комплекс-
геометрии,комплексного анализа возникает следующая ситуация: а) дано
многообразие Мп и его «исчерпание» га-мерными обла-
областями Dг, расширяющимися с ростом параметра г;
б) в Мп фиксирована глобально минимальная поверх-
поверхность Хк\ в) ставится вопрос: с какой скоростью растет
volfe(X*nDr), рассматриваемый как функция от г?
К этому вопросу сводятся, напр., задачи о вычислении
Qx(k), задачи о структуре базисов в пространствах
целых функций, теоремы типа Штолля (см. [11]) и
т. д. Оказывается (см. [6], [15]), существует универ-
универсальная точная эффективно вычислимая оценка снизу
на скорость роста volk(Xkf]Dr), из к-рой, как частные
случаи, получаются явные формулы для vol^X*,
где Хк — глобально минимальная поверхность. Напр.,
объем такой поверхности, заключенной в шаре S^czR™
и проходящей через центр шара (и имеющей границу
на границе шара), всегда не меньше стандартного к-
мерного шара Вк (плоского сечения), проходящего
через центр В" (см. [13], [15]).
В особое направление выделилась П. м. з. «кораз-
«коразмерности один»: рассматриваются глобально мини-
минимальные поверхности коразмерности 1 в R". Так,
напр., решена (см. [7]) проблема Бернштей-
н а : пусть Vn~x~ гладкое полное локально мини-
минимальное подмногообразие в R", допускающее взаимно
однозначную проекцию на нек-рую гиперплоскость,
т. е. F" задается графиком функции /, определенной
на R"-1; верно ли, что / — линейная функция? При
3<:га<8 ответ положителен (см. [8]). Минимальность
таких гиперповерхностей тесно связана с минималь-
минимальностью конусов в R": из существования локально
минимальной поверхности следует существование ми-
минимального конуса СМ"~г, т. е. поверхности, состав-
составленной из точек радиусов, идущих из точки O?R™ в
точки х?Мп~2, где Мп~г— локально минимальная
поверхность в сфере Sn~x. Установлено (см. [8]), что
если Мп~2 — замкнутое локально минимальное под-
подмногообразие (т. е. обращающее в нуль оператор Эй-
Эйлера) вЛ1", но являющееся экватором Sn~2cSn~1,
то при гс<7 конус СМп~2 (с основанием Мп~2 и вер-
вершиной в центре сферы) не минимизирует (п—1)-мерный
объем vol,,-! (при фиксированной границе Мп~2),
т. е. существует вариация (носитель к-рой сосредоточен
около цептра сферы), уменьшающая объем конуса.
Отсюда и выводится линейность функции / при га<8.
При ге>9 ответ на вопрос отрицателен: существуют
(см. [7] локально (it даже глобально) минимальные
поверхности K^'crR", задаваемые как графики не-
нелинейных функций. Построение осуществляется явно;
при этом обнаружилось, что конусы, задаваемые в
R2m уравнением
х*\ +Х Х +
являются глобально минимальными поверхностями
при фиксированной границе V= Sm~1XSm~1, m^4.
Эти конусы — частный случай конусов более общего
вида, являющихся глобально минимальными поверх-
поверхностями (см. [10]).
Развивается новое направление в П. м. з. — так
наз. экв и вариантные многомерные
задачи Плато. Среди глобально минимальных
поверхностей естественно выделен класс пленок, пере-
переходящих в себя при действии нек-рой группы симмет-
симметрии (см. [9], [10]). Пусть G — компактная связная
группа Ли, гладко действующая на Мп изометриями
и расслаивающая его на орбиты G(x), x^Mn. Тогда для
нахождения глобально минимальных поверхностей
Xh в Мп, инвариантных относительно G, достаточно
перейти к факторпространству P=Mn/G и снабдить Р
римановой метрикой вида
p
где v=vo\G(x), a
p = dim X*—dim G (x) = k—dimG (x)
(здесь через A\mG(x) обозначена размерность орбиты
общего положения в Мп), ds — естественная метрика-
проекция, возникающая на Р при изометрич. действии
G. Для нахождения гло-
глобально минимальных по-
поверхностей в Мп, инвари-
инвариантных относительно G,
достаточно описать тако-
таковые в Mn/G, снабженном
метрикой dip (см. [9]), так
что получается редукция
П. м. з. на М" к П. м. з.
на MnlG меньшей размер-
размерности. Эта методика поз-
позволила получить серии
конкретных глобально ми-
минимальных поверхностей,
Рис. 2. обладающих большими
группами симметрии (см.
[13]). В частности, «конусы Саймонса», задаваемые
уравнением (*), изображаются отрезком ОД (см. рис. 2)
на двумерном факторе
снабженном метрикой
и являющемся первым квадрантом К на плоскости
R2 (см. [13]). Для нахождения глобально минимальной
поверхности с границей
достаточно найти геодезические, идущие из D на гра-
границу К и имеющие наименьшую длину. На рис. 2
показан пучок геодезических, исходящих из точки D;
этот пучок можно понимать как пучок световых лучей,
распространяющихся из источника D в прозрачной
среде, заполняющей К с показателем преломления
(хуJ™-2. При m<-|—f|/ наряду с поверхностью OD
существует еще одно минимальное решение меньшей
длины, изображаемое геодезической OQ; это означает,
что конус Саймонса — не глобально минимальная
поверхность. С ростом т точка Q стремится к О, и при
т>—-{-У2 существует единственная геодезическая,
соединяющая D с границей квадранта, т. е. конус
Саймонса — глобально минимальная поверхность (см.
[13]).
Лит.: [1] Моггеу Ch., Multiple integrals in the calculus
of variations, В., 1966; [2] R e i f e n b e г g E., «Acta Math.»,
1960, t. 104 X>. 1/2, p. 1—92; [3] FedererE, Geometric mea-
measure theory, В., 1969; [4] A 1 m g г e n E. J., «Ann. Math.», 1968,
v. 87, Л» 2, p. 321—91; [5] Фоме н к о А. Т., «Матем. сб.», 1972,
т. 89, № 3, с. 475—519; [6] е г о же, «Изв. АН СССР. Сер. ма-
матем.», 1972, т. 36, N» 5, с. 1049—79; [7] В о ш b i е г i E., D с
Giorgi E.,GiustiE., «Invent. Math.», 1969, v. 7, fasc. 3, p.
243—268; [8] Simons J., «Ann. Math.», 1968, v. 88, Ki l,p. 62—
105; [9] L a w s о n H., «Trans. Amer. Math. Soc», 1972, v. 173,
№ 446, p. 231—49; [10] L a w s о n H., Simons J., «Ann.
Math.», 1973, v. 98, № 3, p. 427—50; [11] Фоменко А. Т.,
«Изв. АН СССР. Сер. матем.», 1971, т. 35, N, 3, с. 667—81; [12]
Дао ЧонгТхи, там же, 1980, т. 44, № 5, с. 1031—65; [13]
Фоменко А. Т., «Тр. Семинара по вект. и тенз. анализу...»,
1974, в. 17, с. 3—176; 1978, в. 18, с. 4—93; [14] Дао Чонг
Т х и, «Изв. АН СССР. Сер. матем.», 1978, т. 42, в. 3, с. 500—05;
[15] Фоменко А. Т., там же, 1981, т. 45, № 1, с. 187—213.
А. Т. Фоменко.
ПЛАТОНА ТЕЛА — названия пяти выпуклых
правильных многогранников: тетраэдр, куб, октаэдр,
додекаэдр и икосаэдр. Многогранники названы по
имени Платона, к-рый в соч. «Тимей» D в. до н. о.)
придавал им мистич. смысл; были известны до Пла-
Платона.
ПЛЕСНЕРА ТЕОРЕМА — один из основных резуль-
результатов в теории граничных свойств аналитических
функций. Пусть /(z) — мероморфная функция в еди-
единичном круге JD= {z?C: |z|<l}, Д=Д(е'В) — открытый
угол с вершиной е»8 на окружности Г— {z?C: \z\ — 1},
образованный двумя хордами круга D, проходящими
через eiC. Точка е'8 наз. точкой Плеснера
(или е<8 обладает свойством Плеснера),
если в любом сколь угодно малом угле А для любого
значения w из расширенной комплексной плоскости С
существует последовательность {z^JczA такая, что
lim Zfc=e'B, lim /(zfc) = u\
k -*¦ CO k -*¦ GO
Точка е'9 наз. точкой Фату для f(z), если су-
существует один единственный предел
lim f(z) = A,
ie
г -> е
когда z стремится к е'9 внутри любого угла А. Тео-
Теорема Плеснера: почти все точки окружности
Г но мере Лебега на Г являются либо точками Фату,
либо точками Плеснера. Доказана А. И. Плеснером
(см. [1]).
Известно также, что множество Р (/) всех точек
Плеснера имеет тип Go на Г. Построены примеры ана-
литич. функций в D, для к-рых множество Р (/) плотно
на Г и имеет любую наперед заданную меру Лебега
mes P(f) = m, 0<т<2я (см. [3]). П. т. верна для меро-
морфных функций /(z) в любой односвязной области D
со спрямляемой границей Г. В атом случае ??Г есть
точка Фату, если существует предел
Нт/(г) = Л, z?D,
при стремлении z-*¦ % по любому некасательному
пути; определение точки Плеснера ? ? Г нужно изме-
изменить так, чтобы рассматривались углы А с вершиной ?
и сторонами, образующими углы, меньшие я/2, с
нормалью к Г в точке ? (см. [2]).
Аналогом П. т. в терминах категории множеств яв-
является Мейера теорема.
Лит.: [1] П л е с н е р А. И., «Успехи матем. наук», 1967,
т. 22, в. 1, с. 125—36; [2] Привалов И. И., Граничные свой-
свойства аналитических функций, 2 изд., М. —Л., 1950; [3] Л о-
ватер Д ж., в кн.: Итоги науки и техники. Математический
анализ, т. 10, М., 1973, с. 99—259. Е. Д. Соломенцсе.
ПЛОСКАЯ ДЕЙСТВИТЕЛЬНАЯ АЛГЕБРАИЧЕС-
АЛГЕБРАИЧЕСКАЯ КРИВАЯ — множество точек L действительной
аффинной плоскости, координаты к-рых удовлетворяют
уравнению
/(*, У)=0, A)
где / (х, у) — многочлен степени п от координат х, у;
число п наз. порядком кривой L. Если многочлен /
приводим, т. е. разлагается на множители /1; . . ., /&,
то определяемая уравнением A) кривая L наз. при-
приводимой и является объединением кривых Lu
. . ., L), (компонент L), задаваемых соответст-
соответственно уравнениями
/1=0, ..., /„ = 0.
Если же многочлен / неприводим, то кривая L наз.
неприводимой. Две неприводимые П. д. а. к.,
одна из к-рых имеет порядок п, а другая — порядок т,
пересекаются не более чем в тп точках (теорема
Без у).
Одна и та же П. д. а. к. L может определяться раз-
различными уравнениями. Пусть 1^— совокупность мно-
многочленов, обращающихся в нуль во всех точках кривой
L. Если L неприводима, то из того, что fg=O на L,
следует равенство нулю / или g; в этом случае фактор-
кольцо K(L) = KlIi (здесь К — кольцо всех много-
многочленов) не имеет делителей нуля и наз. кольцом
многочленов на//.
С неприводимой П. д. а. к. L ассоциируется также
нек-рое поле К (L), наз. нолем рациональных
функций на L. Оно состоит из рациональных
функции -^—Ц-, причем q не делится на /, рас-
рассматриваемых с точностью до равенства на if — и ¦=¦
V q (I
паз. равными на кривой L, заданной уравнением A),
если многочлен pq—pq делится на /). Поле K(L) яв-
мется полем частных кольца K(L).
Отображение F : (х, у) -> ф(х, у), г]з(х, у) плоскости
is себя наз. регулярным на П. д. а. к. L, если
Ф, ty?K(L). Кривые L и М наз. изоморфными,
если существуют регулярные (соответственно на L
и на М) отображения F : L —>- М и G : М -> L, обрат-
обратные друг другу; при этом кольца K(L) и К(М) изо-
изоморфны. В частности, изоморфны аффинно эквивалент-
эквивалентные кривые.
Более общим является рациональное ото-
отображение кривой L в кривую М, осуществляемое
рациональными функциями. Оно устанавливает соот-
соответствие между всеми точками кривых, кроме конеч-
конечного их числа, и определяется так. Пусть /=0 и ?=0—
уравнения кривых L и М соответственно, тогда рацио-
рациональное отображение /' задается такой парой рацио-
рациональных функций ф и г]з, определенных на L, что #(ф,
i|') = 0 на М. Кривые L и М наз. бирациональ-
но эквивалентными, если существуют ра-
рациональные отображения L в М и М в L, обратные
друг другу; при этом поля k(L) и k(M) оказываются
изоморфными. Такие рациональные отображения наз.
бирациональными, или к р е м о н о в ы м и,
преобразованиями. Все кремоновы преобразования на
плоскости могут быть осуществлены последовательным
проведением преобразовании вида х —>- •—, у —>- —.
Бирациональная эквивалентность — более грубое от-
отношение, чем изоморфизм, однако классификация
П. д. а. к. с этой точки зрения оказывается проще и
обозримее.
Простейшим примером рационального отображения
является проективное преобразование. Важную роль
играет дуальное отображение неприводи-
неприводимой кривой L, отличной от прямой, в кривую L*, ду-
дуальную L, определяемое формулами:
df df
T~x ex u ay T~x~dx~~v~Щ
где / — многочлен, определяющий L. Уравнение
g(u, v) = 0,
определяющее кривую L*, получается исключением
х, у из уравнений A), B). Вследствие связи дуального
отображения с касательным преобразованием саму
кривую L* в ряде случаев можно представлять как
огибающую семейства прямых, касательных к L.
Порядок L* наз. классом и* кривой L. Отноше-
Отношение дуальности взаимно, т. е. L** = L, и является
отражением двойственности принципа проективной
геометрии.
Точка х П. д. а. к. L, заданной уравнением A), наз.
особой точкой, если в ней grad /=0. Анализ
особенностей является необходимым элементом ис-
исследования кривой L, однако полная классификация
особенностей еще далека от завершения A983).
Если все производные многочлена / до (г—1)-го
порядка включительно в точке х равны нулю, а хотя
бы одна производная r-го порядка отлична от нуля в
х, то х наз. точкой кратности г и притом
обыкновенной, если в ней существуют г различных
касательных. Примеры особых точек:
1) х3—х2-\~у2=0; @, 0) — обыкновенная двойная
точка, точка самопересечения;
2) а-2+а;3+у2=0; @, 0) — изолированная точка;
3) ж3+!/2=0; @, 0) — точка заострения, возврата;
4) 2.z4—Зхгу+у2—2г/3+!/4=0; @, 0) — точка само-
самоприкосновения.
Неособая точка х П. д. а. к. L, заданной уравнением
A), наз. точкой перегиба, если в ней
Н(х, 2,) =
Эх2 дхву дх
a3/ d'f _a/
Вхду ду2 Ну
EL 1L О
дх ду
= 0. C)
Другими словами, точки перегиба — это точки пере-
пересечения кривой L и кривой Н, задаваемой уравнением
C) и называемой гессианой кривой L. Точкам
перегиба кривой L соответствуют на дуальной кривой
L* точки возврата.
Для всякой П. д. а. к. имеет место соотношение
(Ф. Клейн, F. Klein, 1876):
п + 1А + г = п* -f 2d* + г*,
где п — порядок L, п* — класс L, г* — число точек
перегиба L, d* — число изолированных двойных ка-
касательных к L (двойных точек L*), г — число точек
возврата L (точек перегиба L*), d — число двойных
точек L. См. также 11 люккера формулы.
Любая неприводимая плоская кривая L бирацио-
нально эквивалентна неприводимой кривой Lo, име-
имеющей лишь обыкновенные особенности.
311
ПЛОСКАЯ ДЕЙСТВИТЕЛЬНАЯ АЛГЕБРАИЧЕСКАЯ КРИВАЯ
312
Род (или жанр)П.д. а. к. L определяется числом
р, являющимся разностью между наибольшим числом
двойных точек, к-рые может иметь L, и их фактич.
числом. Род р и порядок п кривой L связаны соот-
соотношением
где суммирование распространяется на точки кратно-
кратности г,-.
Кривые нулевого рода (наз. также рациональ-
рациональными, уникурсальными) обладают важным
свойством, а именно: координаты точки, движущейся
по такой кривой, могут быть выражены рациональными
функциями ?, т] нек-рого параметра t. Другими сло-
словами, кривые рода нуль бирационально эквивалентны
прямой. Уникурсальные кривые имеют важные приме-
применения. Пусть, напр., уравнение такой кривой опреде-
Классификация Ньютона кривых 3-го порядка
Каноническая
форма А
2 s
Класс V
Каноническая
форма В
ху = oxs+bx2 +
+ cx + d
Трезубец
Класс VI
Каноническая
форма С
' » Ъ
Расходящаяся
парабола
Класс VII
Каноническая
форма D
y = uxa + bxz +
+ сх + d
Кубическая
парабола
I
5 типов
Класс I
(а > 0)
Гипербеличе-
ская гипербола
Класс II
(«< 0)
Дефективная
гипербола
Класс III
(о=0, ЬфО)
Параболическая
гипербола
(ефО)
Адиамет-
ральная
,„( )
Монодиа-
Монодиаметральная
6 типов
7 типов
(ефО)
Адиаметраль-
ная
I
7 типов
I
(О 0)
Гиперболизм
гиперболы
(с< 0)
Гиперболизм
эллипса
I
4 типа
3 типа
Адиаметраль-
ная
(е—0, Ъ2 Ф 4ас,
ЬФО)
Монодиамет-
Монодиаметральная
( , 4
ЬФО)
Тридиамет-
ральная
И типов
11- ТНПОИ
ляет у как алгебраич. функцию от х; тогда для любой
рациональной функции g {x, у) неопределенный инте-
интеграл
[*, V)dx
может быть выражен через элементарные функции.
Кривые рода 1, тесно связанные с эллиптическими
функциями, бирационально эквивалентны кривой 3-го
порядка без особенностей. Нек-рые кривые рода р>1
(т. н. гиперэллиптические) бирационально
эквивалентны кривой порядка р-\-2, имеющей един-
единственную особую точку кратности р.
Род р является бирациональным инвариантом, од-
однако две кривые, имеющие один и тот же род, не обя-
обязательно бирационально эквивалентны.
Полная классификация кривых порядка и>4 еще
A983) не получена. Неприводимая кри-
кривая 2-го порядка является либо пустым
множеством, либо эллипсом, либо ги-
гиперболой, либо параболой (см. Линия
второго порядка). Эти кривые неособен-
неособенны и уникурсальны.
Первая классификация кривых 3-го
порядка была предложена И. Ньюто-
Ньютоном (I. Newlon, 1704), к-рый поло-
положил тем самым начало систематич. ис-
исследованию П. д. а. к. В основе ее ле-
лежит подразделение кривых 3-го поряд-
порядка на классы в зависимости от коли-
количества и характера бесконечных ветвей.
Уравнение кривой надлежащим выбо-
выбором координатной системы приводит-
приводится к одной из четырех канонич. форм
А, В, С, D, которые затем разделяют-
разделяются на классы, подклассы и типы (см.
схему).
У каждой кривой 3-го порядка L
есть либо (единственная) двойная точ-
точка, и тогда L уникурсальна, либо
точка перегиба, быть может находя-
находящаяся на бесконечности; если есть три
точки перегиба, то они лежат на од-
одной прямой; более трех точек пере-
перегиба быть не может.
Пополнение аффинной плоскости не-
несобственными элементами приводит к
(е_0) проективной плоскости, на к-рой П.
Монодиамет- д. а. к. определяется уравнением
ральная р , г ^ ^.n^Q,
где F — однородный многочлен степе-
степени п от проективных координат х1,
х2, х3. Проективная классификация
кривых проще; напр., каждая кривая
3-го порядка может быть рассматри-
рассматриваема как сечение конуса, направля-
направляющей к-рого служит одна из пяти
т. н. дивергентных парабол, т. е. име-
имеется пять типов нроективно неэквива-
неэквивалентных кубич. кривых (теорема
Ньютона).
При исследовании П. д. а. к. полез-
полезным оказывается также и привлечение
мнимых элементов, и, далее, переход
в комплексную область. См. Алгебра-
Алгебраическая кривая.
Лит.: [1] У о к е р Р., Алгебраические
кривые, пер. с англ.. М., 1952; [2] С мог о р-
ж е в с к и й А. С, С т о л о в а Е. С, Спра-
Справочник по теории плоских кривых третьего
порядка, М., 19A1; [3] С а в е л о в А. А.,
Плоские кривые, М., 1960.
М. И. Войцеховский.
Класс IV
(а = Ь=О)
Гиперболизмы
конических
сечений
I
4 типа
(с=0)
Гиперболизм
параболы
I
2 типа
(Ь=0)
С асимпто-
асимптотами, пересе-
пересекающимися
в одной
точке
I
9 типон
311
ПЛОСКАЯ ДЕЙСТВИТЕЛЬНАЯ АЛГЕБРАИЧЕСКАЯ КРИВАЯ
312
Род (или жанр)П.д. а. к. L определяется числом
р, являющимся разностью между наибольшим числом
двойных точек, к-рые может иметь L, и их фактич.
числом. Род р и порядок п кривой L связаны соот-
соотношением
где суммирование распространяется на точки кратно-
кратности г,-.
Кривые нулевого рода (наз. также рациональ-
рациональными, уникурсальными) обладают важным
свойством, а именно: координаты точки, движущейся
по такой кривой, могут быть выражены рациональными
функциями ?, т] нек-рого параметра t. Другими сло-
словами, кривые рода нуль бирационально эквивалентны
прямой. Уникурсальные кривые имеют важные приме-
применения. Пусть, напр., уравнение такой кривой опреде-
Классификация Ньютона кривых 3-го порядка
Каноническая
форма А
2 s
Класс V
Каноническая
форма В
ху = oxs+bx2 +
+ cx + d
Трезубец
Класс VI
Каноническая
форма С
' » Ъ
Расходящаяся
парабола
Класс VII
Каноническая
форма D
' Ь2
Кубическая
парабола
I
5 типов
Класс I
(а > 0)
Гипербеличе-
ская гипербола
Класс II
(«< 0)
Дефективная
гипербола
Класс III
(о=0, ЬфО)
Параболическая
гипербола
(
Адиамет-
ральная
,„( )
Монодиа-
Монодиаметральная
6 типов
7 типов
(ефО)
Адиаметраль-
ная
I
7 типов
I
(О 0)
Гиперболизм
гиперболы
(с< 0)
Гиперболизм
эллипса
I
4 типа
3 типа
(ефО)
Адиаметраль-
ная
(е—0, Ъ2 Ф 4ас,
ЬФО)
Монодиамет-
Монодиаметральная
( , 4
ЬФО)
Тридиамет-
ральная
И типов
11- ТНПОИ
ляет у как алгебраич. функцию от х; тогда для любой
рациональной функции g {x, у) неопределенный инте-
интеграл
[*, V)dx
может быть выражен через элементарные функции.
Кривые рода 1, тесно связанные с эллиптическими
функциями, бирационально эквивалентны кривой 3-го
порядка без особенностей. Нек-рые кривые рода р>1
(т. н. гиперэллиптические) бирационально
эквивалентны кривой порядка р-\-2, имеющей един-
единственную особую точку кратности р.
Род р является бирациональным инвариантом, од-
однако две кривые, имеющие один и тот же род, не обя-
обязательно бирационально эквивалентны.
Полная классификация кривых порядка и>4 еще
A983) не получена. Неприводимая кри-
кривая 2-го порядка является либо пустым
множеством, либо эллипсом, либо ги-
гиперболой, либо параболой (см. Линия
второго порядка). Эти кривые неособен-
неособенны и уникурсальны.
Первая классификация кривых 3-го
порядка была предложена И. Ньюто-
Ньютоном (I. Newlon, 1704), к-рый поло-
положил тем самым начало систематич. ис-
исследованию П. д. а. к. В основе ее ле-
лежит подразделение кривых 3-го поряд-
порядка на классы в зависимости от коли-
количества и характера бесконечных ветвей.
Уравнение кривой надлежащим выбо-
выбором координатной системы приводит-
приводится к одной из четырех канонич. форм
А, В, С, D, которые затем разделяют-
разделяются на классы, подклассы и типы (см.
схему).
У каждой кривой 3-го порядка L
есть либо (единственная) двойная точ-
точка, и тогда L уникурсальна, либо
точка перегиба, быть может находя-
находящаяся на бесконечности; если есть три
точки перегиба, то они лежат на од-
одной прямой; более трех точек пере-
перегиба быть не может.
Пополнение аффинной плоскости не-
несобственными элементами приводит к
(е_0) проективной плоскости, на к-рой П.
Монодиамет- д. а. к. определяется уравнением
ральная р , г ^ ^.n^Q,
где F — однородный многочлен степе-
степени п от проективных координат х1,
х2, х3. Проективная классификация
кривых проще; напр., каждая кривая
3-го порядка может быть рассматри-
рассматриваема как сечение конуса, направля-
направляющей к-рого служит одна из пяти
т. н. дивергентных парабол, т. е. име-
имеется пять типов нроективно неэквива-
неэквивалентных кубич. кривых (теорема
Ньютона).
При исследовании П. д. а. к. полез-
полезным оказывается также и привлечение
мнимых элементов, и, далее, переход
в комплексную область. См. Алгебра-
Алгебраическая кривая.
Лит.: [1] У о к е р Р., Алгебраические
кривые, пер. с англ.. М., 1952; [2] С мог о р-
ж е в с к и й А. С, С т о л о в а Е. С, Спра-
Справочник по теории плоских кривых третьего
порядка, М., 19A1; [3] С а в е л о в А. А.,
Плоские кривые, М., 1960.
М. И. Войцеховский.
Класс IV
(а = Ь=О)
Гиперболизмы
конических
сечений
I
4 типа
(с=0)
Гиперболизм
параболы
I
2 типа
(Ь=0)
С асимпто-
асимптотами, пересе-
пересекающимися
в одной
точке
I
9 типон
ПЛОСКАЯ ЗАДАЧА теории упругости —
название типа задач, в к-рых картина изучаемого
явления в упругой среде одинакова во всех плоскостях,
параллельных нек-рой плоскости (напр., плоскости
0x^2 декартовой системы координат Охххгх3). Мате-
ыатич. теорией П. з. часто описываются и задачи,
к-рые по содержанию имеют пространственный харак-
характер (напр., изгиб тонких пластинок).
По П. з. теории упругости успехи достигнуты глав-
главным образом благодаря использованию формул, выра-
выражающих искомые решения через аналитич. функции
одного комплексного аргумента; впервые эти формулы
были выведены в 1909 Г. К. Колосовым (см. [1]), а
начиная с 20-х гг. 20 в. в работах Н. И. Мусхелишвили
они нашли полное обоснование, и на их базе развиты
методы решения широкого круга граничных (краевых)
и контактных П. з. теории упругости. Полученные по
П. з. теоретич. результаты используются при решении
практич. задач.
Комплексное представление полей смещений и напря-
напряжений. Говорят, что упругая среда находится в со-
состоянии плоской деформации, если существует такая
декартова система координат Ох1х2х3, относительно
к-рой компоненты вектора смещения имеют вид
ua = !ta(*i> x-i-> l)> « = 1,2, "з=0,
где t — время. Компоненты тензора напряжений таковы
*ар = М«аВ + 2^„р. Хаз=0, Xaa = M,
где X, fi — постоянные Ламе, Sap — символы Кроне-
i'i-ра, еа$ — компоненты тензора деформации: «ар=
=daufi +д$иа; в=еаа — даиа — дилатация (а, E=1, 2;
наличие в выражении двух одинаковых индексов озна-
означает суммирование).
Плоская деформация возможна в упругой среде,
к-рая заполняет цилиндр с образующими, перпенди-
перпендикулярными плоскости Охгх2, если при этом компоненты
объемных сил имеют вид Ха=Ха(х1, х2, t), Х3=0, а
боковые усилия не зависят от координаты х3 и распо-
расположены на плоскостях, перпендикулярных оси цилинд-
цилиндра. Для реализации плоской деформации упругого
цилиндра к его торцам необходимо приложить нор-
нормальные силы, равные ±Я,6.
При сделанных допущениях система уравнений дина-
динамики упругого тела относительно компонентов век-
вектора смещений имеет вид
a aQ + Xa =p"ia,a = l, 2,
где р — плотность распределения масс, рйа — силы
инерции, Д — оператор Лапласа. Если воспользо-
воспользоваться операциями комплексного дифференцирования:
2d-=d1+idi, 2dz=d1—id2i(da =д/дха), то при отсут-
отсутствии сил инерции (статич. задача) эту систему можно
записать в виде одного (комплексного) уравнения:
а--
Пусть область S, занятая упругой средой, пред-
представляет связную часть плоскости Охгх2, ограниченную
одним или несколькими контурами Lo, Llt . . ., Lm
без общих точек, L=L0+Ll+. . - + Lm — граница об-
области S; точка z=Q принадлежит S.
Искомое решение уравнения равновесия выражается
по формуле u=uQ+TX, где ТХ — нек-рое частное
решение, к-рое можно выразить в виде
ТХ = — у. (,ил A + х))-1 f [ X Q In \?, — zldZ,1dt,2 +
+ BцлA+*))-
a u, — общее решение однородного уравнения (Х=0),
к-рое выражается по формуле
цо = ^(ф> ¦»!>; х)=Хф (z) — 2ф' (z)— 1J3 (г),
где ф и г|з — произвольные аналитич. функции от
z-—zl-\-ix2 в области 6" (х=3—4а, где а — постоянная
Пуассона, 0<а<0,5). Если X — многочлен от х, у,
то ТХ можно выразить в явной форме.
Оператор К(ср, 1|з; х) не изменится, если функции
Ф и г|) подчинить условию ф@) = 0 или if>@) = 0. При
выполнении одного из этих условий всякому полю
смещений u=Uj+w2, заданному в области S, соот-
соответствует вполне определенная пара аналитич. функций
ф, if.
Если в предыдущих формулах постоянную х за-
заменить через х*~ C—о)/A + о), то получается фор-
формула для поля смещения обобщенного плосконапря-
зкенного состояния.
Комплексная запись
m ги + д-и), *u-22 + 12 f
компонентов тензора напряжений, в силу равенства
и = К(у, if; %)
принимает вид
где Ф = 2(хф', ? =
Пусть упругая среда подвергается непрерывной де-
деформации. Тогда можно считать, что компоненты тен-
тензора напряжений и смещений — непрерывные однознач-
однозначные функции в области S; Ф и ? голоморфны в S,
причем Ф можно подчинить условию Ф'@) = Ф'@).
Если область S ограничена и односвязна, а дефор-
деформация непрерывна, то функции ф и 1|з голоморфны в S.
В случае конечной многосвязной области ф и 1|з будут,
вообще говоря, многозначными функциями опреде-
определенного вида.
Основными задачами плоской теории упругости яв-
являются следующие задачи.
1) Первая основная задача: опреде-
определить упругое равновесие тела, когда на его границе
заданы внешние силы.
Сила напряжения (Хп, У„), действующая на эле-
элемент дуги ds контура L с нормалью п, может быть
записана в комплексной форме:
{Xп-\~iYn) ds = — 2i\xd (ф (z)-\-гф' (z)~r"if(z))»
и краевые условия первой задачи имеют вид
где
причем дуга s отсчитывается на каждом L^ от нек-рой
фиксированной точки z^^L/^ в положительном направ-
направлении; c(t) = Cfe=const на Lk. Всегда можно считать
со=О, остальные постоянные с^ определяются в ходе
решения задачи. Если т=0, то искомые функции ф
ит)з голоморфны в S. Тогда равенства ф@) = 0, 1тф' @)=
= 0 обеспечивают единственность решения задачи A),
а необходимые и достаточные условия существования
решения
s = O, 2ц JL (XlYn-xtXn) ds =
= Re
представляют собой условия статич. равновесия абсо-
абсолютно жесткого тела.
При то>0, как уже было отмечено, ф и г|) — много-
многозначные функции специального вида, причем они вы-
выражаются через новые искомые голоморфные в области
S функции ф* и г|5*.
2) Вторая основная задача: определить
упругое равновесие тела по заданным смещениям точек
его границы.
Эта задача приводит к граничному условию вида
где f=u1-\-iui — заданная на L функция.
3) Основная смешанная задача. Пусть
S — конечная односвязная область, ограниченная замк-
замкнутым контуром L; L=L'-\-L", где V состоит из конеч-
конечного числа дуг V, . . ., L'm контура L, к-рые попарно
не имеют общих точек; на L' заданы внешние напря-
напряжения, а на L" — смещения. Соответствующие кра-
краевые условия можно записать в виде
где / — заданная функция точки t?L\ y(t)=i, если
t?L', и y(t)——х, если t?L"; c(i) = Cfc=const, если
t^L'; c(t) = Q, если t?L". Постоянные с^ (кроме одной,
выбираемой как угодно) но задаются заранее и под-
подлежат определению в ходе решения задачи.
4) Третья основная задача. На границе
области задаются нормальная составляющая вектора
смещения и касательная составляющая вектора внеш-
внешнего напряжения.
Такая задача возникает, напр., в случае соприка-
соприкасания упругого тела с жестким профилем заданной
формы, когда контакт между упругим и жестким
телами осуществляется по всей границе. Рассматри-
Рассматриваются также другого рода контактные задачи. Все
эти задачи также приводятся к граничным задачам
для аналитич. функций.
5) Граничные задачи изгиба тонких
пластинок. К аналогичным граничным условиям
приводят задачи изгиба тонких пластинок. Прогиб w
серединной поверхности тонкой однородной упругой
пластинки, подверженной действию распределенной
по ее поверхности нормальной нагрузки интенсивно-
интенсивности q, удовлетворяет неоднородному бигармонич. урав-
уравнению
где D-=Eh3/i2(i — о2) — цилиндрич. жесткость; h —
толщина пластинки, Е — модуль Юнга. Общее реше-
решение этого уравнения имеет вид
w=w0 \-fq,
где Tq — частное решение, к-рое выражается фор-
формулой
Гд=(8кО)-1 J $<7(?)|?-4a14S-*Kid&2.
a w0 — общее решение
wu = -Re(lQ>(z)-\-V(z))
однородного бигармонич. уравнения
где Фи1? — произвольные аналитич. функции в S.
Если q — многочлен от х1 и х2, то Tq выражается в
явной форме. Если Ф@)==0, Чг@) = 0, Ф'@) = Ф'@),
то функции ФиТ выражаются однозначно посредством
заданной бигармонич. функции и-0.
Решение w уравнения AAw=q/D следует подчинить
граничным условиям, соответствующим тому или иному
характеру закрепления границы пластинки. В случае
заделанной по краям пластинки на границе L области
S, занятой серединной поверхностью пластинки, долж-
должны выполняться условия w=dw/dn=Q, где п — внеш-
внешняя нормаль к контуру L, Эти два условия можно
написать в виде одного комплексного равенства dzw~Q
(на L). Последнее приводится к виду A).
Решение этой задачи всегда существует, единст-
единственно и выражается по формуле
G (*!,*„?!,&) 5 (Si. &.)
где G — функция Грина. Для круга |z|<l:
В случае свободной пластинки граничные условия
имеют вид
аД w-{-(l —a) (wXlXicos2 v -f- wXlXjsin2 u+ \
+ ">*,*, sin 2y)=0, |
^-+а-")^ (т("'*.«-"'««) sin2p+ B)
+ ">*i*,cos2y)=0,
где у — угол, составляемый внешней нормалью п
с осью Ох1. Левые части равенств B) представляют
собой соответственно изгибающий момент и обобщен-
обобщенную перерезывающую силу, отнесенные к единице
длины и действующие на боковой элемент пластинки
с нормалью п. Граничные условия B) можно записать
в виде
d(C + a)/(l—а)Ф —2ф'—?') =g,
где g — заданная функция на L.
6) Плоские стационарные упругие ко-
колебания. Когда решения системы уравнений дина-
динамики упругой среды ищутся в виде
и =и (хи х2) eivt, и3 = 0,
где v — частота колебания, для v получается формула
v = d-(w1-\- iw.2)
(предполагается, что внешние силы равны нулю, Xа=
= 0), где w1 и w2 — произвольные решения уравнений:
Поле напряжений выражается по формулам
Общее решение уравнения
Дц>-)- k2w = 0, /c2 = const,
выражается в виде
ш = Ло/О (к | z | ) + 5 J, Be [гф (zt)] /0 (A-1 z ] ^Г^Т) <2г, C)
где Ло — произвольная действительная постоянная,
Ф — произвольная аналитич. функция, /0 — функция
Бесселя 1-го рода нулевого порядка. При помощи
формулы C) выводится комплексные представления
для полей смещений и напряжений при плоском ста-
стационарном колебании упругой среды; они могут быть
использованы для исследования граничных задач,
а также для построения различных полных систем
частных решений, к-рые позволяют аппроксимировать
любые поля смещений и напряжений. В частности,
эти полные системы можно использовать для построе-
построения приближенных решений краевых задач.
7) Задача определения концентра-
концентраций н а п ряжений около отверстий
в анизотропных и изотропных пла-
пластинах. Основу приближенных методов решения
таких задач также составляют введение функций ком-
комплексного переменного специальной структуры в виде
степенных рядов и различных модификаций теории
возмущений, а также использование теорем сложения
цплиндрич. и сферич. функций с последующим све-
сведением граничных задач к бесконечным системам алге-
браич. уравнений.
Методы решения граничных задач. Формулы пред-
представления полей смещений и напряжений через ана-
литич. функции используются для доказательства
существования и единственности решения общих гра-
граничных задач, а также для построения в явной форме
решений нек-рых классов задач частного вида.
Метод степенных рядов с применением конформного
отображения позволяет решать основные плоские
задачи для областей, конформно отображающихся на
круг посредством рациональных функций. Задача
редуцируется к линейной алгебраич. системе урав-
уравнений и квадратурам. Этим методом практически реша-
решаются основные граничные задачи для любой односвяз-
ной области с использованием приближенного конформ-
конформного отображения области на круг с помощью рацио-
рациональных функций. При использовании ЭВМ этот прием
является эффективным для построения решений ос-
основных граничных П. з. теории упругости и изгиба
пластинок.
На основе теории интеграла типа Коши исследо-
исследование П. з. редуцируется к хорошо изученным инте-
интегральным уравнениям.
Полезными являются также методы, сочетающие кон-
конформное отображение с применением аппарата инте-
интегралов типа Коти.
Существуют и другие способы приведения граничных
П. з. теории упругости к интегральным уравнениям,
к-рые дают возможность изучить вопросы существо-
существования и единственности решения.
Для редукции граничных П. з. теории упругости к
интегральным уравнениям используется также метод
потенциалов, не вводящий в рассмотрение комплекс-
комплексные аналитич. функции (ф и г|з).
Лит.: 11] К о л о с о в Г. В., Об одном приложении теории
функций комплексного переменного к плоской задаче математи-
математической теории упругости, Юрьев, 1909; [2] е г о же, Приме-
Применение комплексных диаграмм и теории функций комплексной
переменной к теории упругости, Л.— М., 1935; [3] М у с х е л и-
ш в и л и Н. И., Некоторые основные задачи математической тео-
теории упругости, 5 изд., М., 1968; [4] е г о же, Сингулярные ин-
интегральные уравнения, 3 изд., М., 1968; 15] Век у а И. Н.,
М у с х е л и ш в и л и Н. И., Методы теории аналитических
функций в теории упругости, в кн.; Тр. Всесоюзного съезда по
теоретической и прикладной механике (I960), М.— Л., 1962;
[6] В е к у а И. Н., Новые методы решения эллиптических урав-
уравнений, М.— Л., 1948; [7] С а в и н Г. Н., Концентрация напря-
напряжений около отверстий, М.— Л., 1951; [8] Г а л и н Л. А., Кон-
Контактные задачи теории упругости, М., 1953; [9] Ш т а е р-
м а и И. Я., Контактная задача теории упругости, М.— Л., 1949;
[10] К а л а н д и я А. И., Математические методы двумерной
упругости, М., 1973; [И] S о к о 1 n i к о f f I. S., Mathematical
theory of elasticity, N. Y.— L., 1946; [12] Трехмерные задачи ма-
математической теории упругости, Тб., 1968.
И. Н. Вепуа, Р. А. Кордзадзе.
ПЛОСКИЙ МОДУЛЬ — левый (или правый) модуль Р
над ассоциативным кольцом R такой, что функтор тен-
тензорного произведения — ®rP (соответственно -P(X)r —)
точен. Приведенное определение эквивалентно любому
из следующих: 1) функтор Torf (—, Р) = 0 (соответст-
(соответственно Toij (P, —) = 0); 2) модуль Р представим в виде
прямого (инъективного) предела спектра свободных
модулей; 3) модуль характеров P* = Homz (Р, Q/Z)
инъективен, где Q — группа рациональных чисел, а
Z — группа целых чисел; 4) для любого правого (со-
(соответственно левого) идеала / кольца R канонич.
гомоморфизм
является изоморфизмом.
Проективные модули и свободные модули являются
примерами П. м. Класс П. м. над кольцом целых чисел
совпадает с классом абелевых групп без кручения.
Все модули над кольцом R являются П. м. тогда и
только тогда, когда R регулярно в смысле Неймана
(см. Абсолютно плоское кольцо). Когерентное кольцо
может быть определено как кольцо, над к-рым прямое
произведение U.Ra любого числа экземпляров кольца В
является П. м. Операции локализации и пополнения
по степеням идеала кольца R приводят к П. м. над
этим кольцом (см. Адическая топология). Классич.
кольцо частных кольца R является П. м. над R.
Лит.: [1]КартанА.,ЭйленбергС, Гомологическая
алгебра, пер. с англ., М., 1960; [2] Ламбек И., Кольца и
модули, пер. с англ., М., 1971. В. Е. Говоров.
ПЛОСКИЙ МОРФИЗМ — морфизм схем f:X-+Y
такой, что для любой точки х?Х локальное кольцо
бх,х является плоским над QY, /u> (CM- Плоский
модуль). Вообще, пусть ff~— пучок (З^-модулей, он
наз. плоским над У в точке х?Х, если §~х—
плоский модуль над кольцом 6к,/<*>• При нек-рых
(довольно слабых) условиях конечности множество
точек, в к-рых когерентный (З^-модуль gr является
плоским, открыто в X. Если при этом схема Y целостна,
то существует открытое непустое подмножество UcY
такое, что JF— П. м. над Y во всех точках, лежащих
над U.
П. м. конечного тина соответствуют интуитивному
понятию непрерывного семейства многообразий. П. м.
открыт и равноразмерен (т. е. размерность слоев
f~1(y) локально постоянна по y?Y). Для многих гео-
метрич. свойств множество точек х?Х, в к-рых слой
/~1(/(х)) плоского морфизма / : X -> У обладает этим
свойством, открыто в X. Если П. м. / собственный, то
открытым является и множество точек г/?У, слои над
к-рыми обладают этим свойством (см. [1]).
П. м. применяются также в теории спуска. Морфизм
схем наз. строго плоским, если он плоский
и сюръективный. Тогда, как правило, для проверки
какого-либо свойства нек-рого объекта над У доста-
достаточно проверить это свойство для объекта, полученного
после строго плоской замены базы / : X -> У (см. [1]).
В связи с этим представляют интерес критерии пло-
плоскостности морфизма / : X —>• У (или (З^-модуля §f);
при этом У можно считать локальной схемой. Про-
Простейший критерий относится к случаю, когда база У
одномерна и регулярна: когерентный 0^-модуль |р
будет плоским тогда и только тогда, когда униформизл-
рующая на У имеет тривиальный аннулятор в §~. Об-
Общин случай в нек-ром смысле сводится к одномерному.
Пусть У — приведенная нётерова схема и для любого
морфизма Z -+Y, где Z — одномерная регулярная
схема, замена базы /^: XyXZ —>- Z является II. м.;
тогда / есть П. м. Другой критерий плоскостности
требует, чтобы / : X -> У был универсально открыт,
а У и геометрич. слои f~1(y) — приведены.
Лит.: [1] Grothendieck A., Dieudonne J.,
Elements de geometrie algebrique, 4, «Publ. math. IHES»,
1964, J>ft 24; 1966, № 28; [2] M а м ф о р д Д., Лекции о криных
на алгебраической поверхности, пер. с англ., М., 1968; [3] R а у-
n a u d M., Gruson L., «Invent, math.», 1971, v. 13, p. 1—89.
В. И. Данилов.
ПЛОСКОСТЬ — одно из основных понятий геомет-
геометрии; обычно косвенным образом определяется аксио-
мами геометрии. П. может рассматриваться как сово-
совокупность двух непересекающихся множеств — множе-
множества точек и множества прямых с симметричным отно-
отношением инцидентности, связывающим точку и прямую.
В зависимости от требований, к-рым удовлетворяет
отношение инцидентности, описываемое определенными
аксиомами, различают проективные, аффинные,
гиперболические, эллиптические П. и др.
П. можно классифицировать по группам коллинеа-
ций (см., напр., [7] гл. 3, где дана классификация
Ленца — Бартолоцци проективных и аффинных П.)
или по реализации в плоскости тех или иных конфи-
конфигураций (см., напр., Дезаргова геометрия, Паскалееа
геометрия).
П. наз. метрической, если кроме отношения инци-
инцидентности определено расстояние между любой парой
точек. Так, в Гильберта системе аксиом евклидовой
геометрии расстояние вводится на базе аксиом кон-
конгруэнтности и непрерывности, и П. в этом случае
паз. непрерывной (см. [1]). В случае невыполнения
для П. аксиом непрерывности П. наз. дискретной
(см., напр., Неархимедова геометрия), а П., состоящая
из конечного числа точек, а следовательно, и прямых,
паз. конечной (см. [7]).
Одним из путей изучения П. является введение в
ней координат и тернарной операции с последующим
ее изучением (см., напр., [7]), [8]).
В системе аксиом Вейля пространства Е3 П. является
производным понятием от понятий «вектор» и «точка».
Под П., проходящей через точку Л ??3 и векторы m и п,
понимается множество точек таких, что
AM = tm^\-%n, где ?, t?R.
В прямоугольной системе координат (х, у, ?) прост-
пространства Е3 П. задается линейным уравнением
коэффициенты А, Б, С определяют координаты нор-
нормального вектора этой П. В то-мерном пространство
n-мерные П. описываются системами линейных урав-
уравнений (см. [5]).
Взаимное расположение П. в различных т-мерных
пространствах определяется соответствующими ак-
аксиомами инцидентности так же, как и свойства инци-
инцидентности плоскостей и прямых.
Лит.: [1] Гильберт д., Основания геометрии, пер. с
нем., М.— Л., 1948; [2] Ефимов Н. В., Высшая геометрия,
6 изд., М., 1978; [3] Об основаниях геометрии, М., 1956; [4]
Батан Ф., Построение геометрии на основе понятия сим-
симметрии, пер. с нем., М., 1960; [5] Д о н е д д ю А., Евклидова
планиметрия, пер. с франц., М., 1978; [6] Розенфельд
Б. А., Многомерные пространства, М., 1966; [7] D e m Ъ о w s-
k i P., Finite geometries, В., 1968; [8] P i k e r t G., Projektive
Ebenen, В., 1955. В. В. Афанасьев, Л. А. Сидоров.
ПЛОТНОЕ МНОЖЕСТВО — то'же, что всюду плот-
плотное множество. Более общо, множество А наз. плот-
плотным в открытом множестве G простран-
пространства X, если G содержится в замыкании А или, что то
же самое, если A f\G всюду плотно в подпространстве
GaX. Если А не плотно ни в каком непустом открытом
множестве G, то оно является нигде не плотным мно-
множеством В X. М. И. Войцеховский.
ПЛОТНОСТИ МАТРИЦА состояния р, определен-
определенного на алгебре Щ (SK) ограниченных линейных опе-
операторов, действующих в гильбертовом пространстве
$С,— положительный ядерный оператор р^Щ,^) та-
такой, что
pD)=Sp4p, A&HSfg), A)
причем Spp=l. Обратно, всякое состояние р, т. е.
линейный положительный (р(А*А)~^0) нормированный
(p(E) = i) функционал на 2t {$%), пред ставимо в виде
A), т. е. имеет П. м. р и притом единственную.
Впервые понятие П. м. появилось в статистич. фи-
физике при определении квантового состояния Гиббса.
Пусть квантовая система, занимающая конечную об-
область V пространства R3, описывается векторами
нек-рого гильбертова пространства ,%V и гамильтониа-
гамильтонианом Hyii обладает, быть может, нек-рым набором ком-
коммутирующих друг с другом «первых интегралов» Ну,
. . ., Ну, /с=1, 2, ... . Состоянием Гиббса такой
системы паз. состояние на %{SKv), задаваемое П. м.:
р-2-1 с-хр {- р A1°У + 1цНЬ+ ... + ЦкНу)\, B)
где Z — нормирующий множитель, а E>0, fxx, . . .,
flfe — действительные параметры.
Наряду с П. м. B) состояние системы в квантовой
статистич. физике можно задавать с помощью т. н.
приведенной матрицы плотности.
В наиболее простом случае системы одинаковых частиц
(бозонов или фермионов), описываемых векторами
Фока пространства SfCvi приведенная П. м. р состоя-
состояния р представляет собой набор функций (вообще
говоря, обобщенных)
P={Pm,n(*l> ¦¦¦,Хт,У1, ••-,!/„), Xi&V
i = l, ..., то, / = 1, ..., и; т = 0, 1, ...}, C)
где
а а(х), а* (у), х, J/^R3,— рождения операторы, и уни-
уничтожения операторы соответственно, действующие в
SfCv- В случаях, когда в алгебре %.{$Ку) вместо опе-
операторов рождения и уничтожения выбрана какая-
нибудь другая система образующих {а^, л?<5?} (X—
нек-рое множество индексов), приведенная П. м. со-
состояния р определяется аналогично C) как совокуп-
совокупность значений состояния р на всевозможных мономах
вида
г = 1, ..., п, и = 1, 2, ... .
Приведенная П. м. оказывается особенно удобной при
определении предельного гиббсовского состояния на
С*-алгебре 9tre так наз. квазилокальных наблюдаемых:
3loo= U Щ^у) (черта означает замыкание в рав-
V6 R»
номерной топологии).
Лит.: [1] Л а н д а у Л. Д., Л и ф ш и ц Е. М., Статисти-
Статистическая физика, Зизд., М., 1976 (Теоретическая физика, т. 5);
t2j P ю я л ь Д., Статистическая механика. Строгие результаты,
пер. с англ., М., 1971. Р. А. Минлос.
ПЛОТНОСТИ ТОЧКА множества Е в ге-мерном
пространстве R"— точка х, в к-рой плотность .мно-
.множества Е равна единице. Если единице равна внешняя
плотность, то точка х наз. точкой внешней
плотности. П. т. множества является одновре-
одновременно точкой разрежения для дополнения этого мно-
множества. Почти все точки измеримого множества суть
его П. т. С помощью понятия П. т. вводится понятие
аппроксимативно непрерывной функции и аппрокси-
аппроксимативной производной. В. А. Скворцов.
ПЛОТНОСТНАЯ ГИПОТЕЗА — предполагаемое не-
неравенство, доставляющее оценку для числа N (а, Т)
нулей р = Р+гу дзота-функции Римана
где s---<5-]-it, в прямоугольнике 1/2<а<Р<1,
Наиболее точная формулировка П. г.:
N {а, Т)<сТ2A-а>\аАТ.
Более простой, но менее точный вид П. г.:
N (а, Г)<сГA-о)+е.
П. г. позволяет получать в теории простых чисел
результаты, сравнимые с теми, к-рые вытекают из
гипотезы Римана. Напр., из П. г. следует, что при
достаточно больших х в каждом сегменте [х, х-\-х '2+t]
содержится хотя бы одно простое число.
П. г. является следствием более сильной Линделёфа
гипотезы. В отличие от последней П. г. частично
доказана, т. к. содержится в плотностных теоремах,
начиная с нек-рых значений а^ао>1/2-
Для числа N(a, T, у) нулей L-функций Дирихле
где х(п, к) — характер по модулю к, имеет место
аналогичная П. г. В усредненной форме она имеет вид
2ft < Q 2х* mod k N (о, Т, Х) <
где х* — примитивный характер по модулю к.
П. г. для //-функций Дирихле применяется в теории
распределения простых чисел, принадлежащих ариф-
метич. прогрессиям.
Лит.: [1] М о н т г о м е р и Г., Мультипликативная теория
чисел, пер. с англ., М., 1974; [2] Л а в р и к А. Ф., «Успехи
матем. наук», 1980, т. 35, в. 2, с. 55—G5. Б. М. Бредихин.
ПЛОТНОСТНЫЕ ТЕОРЕМЫ — общее название тео-
теорем, к-рые дают оценку сверху для числа N (а, Т, у)
нулей p=P+jy /--функций Дирихле
где s=o+ii, i(n, к) — характер по модулю fc в прямо-
прямоугольнике 1/2<о<Р<1, IyI<7. В случае к=1 полу-
получают П. т. для числа нулей дзета-функции Римана
П. т. для L-функций при кф\ сложнее, чем соот-
соответствующие теоремы для дзета-функции Римана.
При растущих параметрах Т и к получаются оценки,
зависящие от этих параметров. В приложениях реша-
решающую роль играет параметр к.
Значение П. т. выясняется из соотношений, позво-
позволяющих оценивать остаточный член в формуле для
количества простых чисел р, принадлежащих ариф-
метич. прогрессии кт-\-1, 1«/</с, (I, к)=1, т=0, 1,
2, . . ., и не превосходящих х, в зависимости от
N(a, T, х).
Поскольку функция Л'(а, Г, %) не возрастает при
возрастании а и N A, Т, %)~0, целью П. т. является
получение оценок, наиболее быстро стремящихся к
нулю при о-> 1. В свою очередь эти оценки сущест-
существенно дополняются результатами об отсутствии нулей
у L-функций Дирихле в окрестности прямой 0=1,
к-рые получаются с помощью кругового метода Хар-
ди — Литлвуда — Виноградова. На этом пути уда-
удалось получить сильные оценки для количества четных
чисел n*g:x, возможно непредставимых в виде суммы
двух простых чисел.
Первые П. т., доставлявшие оценки N(a, T, %) для
индивидуального характера % и усредненные оценки
но всем характерам данного модуля к, были получены
Ю. В. Линником. Дальнейшее значительное улучше-
улучшение П. т. принадлежит А. И. Виноградову и Э. Бомбь-
ери (Е. Bombieri), к-рые использовали оценки N (а, Т,
X), усредненные по всем модулям /с«2 и по всем при-
примитивным характерам данного модуля к, для доказа-
доказательства теоремы о распределении простых чисел в
арифметич. прогрессиях в среднем (при Q—Ух/(In x)c).
Теорема Виноградова — Бомбьери позволяет в ряде
классич. задач аддитивной теории чисел заменять
расширенную гипотезу Римана. Имеется ряд других
улучшений П. т.
Лит.: [1] П р а х а р К., Распределение простых чисел, пер.
с нем., М., 1967; 12] Монтгомери Г., Мультипликативная
теория чисел, пер. с англ., М., 1974; [3] Л а в р и к А. Ф.,
«Успехи матем. наук», 1980, т. 35, в. 2, с. 55—65.
Б. М. Бредихин.
ПЛОТНОСТНЫЙ МЕТОД — один из методов анали-
тич. теории чисел, основанный на изучении статистики
распределения нулей дзета-функции Римана
и L-функции Дирихле
s=a+it — характер по модулю к. Многие теоретико-
числовые проблемы получают наиболее законченное
решение в предположении, что все нули p=P + 'V
функций ? (s) и L(s, %), находящиеся в полосе 0<о<1,
— оо<?<+оо, лежат на прямой а=1/2. Однако в
ряде случаев достаточно сильные результаты полу-
получаются, если удается показать, что нули указанных
функций с абсциссой Р^о>1/2 если и существуют,
то все же составляют множество, к-рое становится все
более редким при а —>- 1. Существует большое количе-
количество теорем, к-рые дают оценки сверху для числа
N (а, Т) нулей ? (s) и для числа N (а, Т, %) нулей L (s, у)
в прямоугольнике 1/2<а«Р<1, Ii>l<s7\ П. м. сущест-
существенно опирается на эти теоремы, получившие название
плотностных теорем.
Впервые П. м. с использованием плотностной тео-
теоремы для ?(s) применил Г. Хоайзель (G. Hoheisel,
1930) для оценки разности двух соседних простых чи-
чисел. Ему удалось доказать существование положитель-
положительной константы а<1 такой, что при х>хо=ха(а.) между
х и х-{-ха всегда находится простое число. 6 дальней-
дальнейшем всякое улучшение оценки для N (о, Т) приводило
к уточнению константы а. Для L-функции Дирихле
П. м. был разработан Ю. В. Линником A944 и после-
последующие годы). Ю. В. Линник впервые исследовал
распределение нулей L-функций при переменном к,
в частности получил результаты о «частоте» нулей
L(s, x) вблизи точки s=l, что позволило найти оценку
для наименьшего простого числа ро=Ро(^' 0> лежащего
в арифметич. прогрессии kx-\-l, (I, k)=i, 1</<;/с,
х=0, 1, 2, . . . ; ро</сс, где с — нек-рая абсолютная
константа. Улучшение оценок для N (а, Т, %) приводит
к уточнению константы с. Применяя плотностные тео-
теоремы для L-функций, Ю. В. Линник нашел новое
доказательство теоремы Виноградова о представлении
всякого достаточно большого нечетного числа суммой
трех простых чисел (см. Гольдбаха проблема).
П. м. в теории //-функций позволил получить силь-
сильный результат в направлении бинарной проблемы
Гольдбаха: всякое достаточно большое натуральное
число можно представить в виде суммы двух простых
чисел и ограниченного абсолютной константой нек-ро-
го числа степеней двоек.
Наиболее сильные результаты П. м. дает в сочетании
с др. методами, в частности с методом большого решета.
На этом пути была доказана теорема Виноградова —
Бомбьери A965), к-рая заменяет во многих случаях
Римана обобщенную гипотезу. Идеи и результаты П. м.
переносятся с поля рациональных чисел на поля алге-
браич. чисел.
Лит.: [1] П р а х а р К., Распределение простых чисел, пер.
с нем., М., 1967; [2] М о н т г о м е р и Г., Мультипликативная
теория чисел, пер. с англ., М., 1974; [3] Halberstam H.,
Richert H.- E., Sieve methods, L. —[а. о.], 1974.
Б. М. Бредихин.
ПЛОТНОСТЬ топологического пространства — одна
из его мощностных характеристик.
ПЛОТНОСТЬ ВЕРОЯТНОСТИ, плотность рас-
распределения вероятностей,— производ-
производная функции распределения, отвечающей абсолютно
непрерывной вероятностной мере.
Пусть X — случайный вектор, принимающий зна-
значения в re-мерном евклидовом пространстве R"(n^l),
Р(хг, . . ., хп) — его функция распределения и пусть
существует неотрицательная функция f(xlt . . ., хп)
такая, что
^* (*"м / К, ..., ип) &щ...пип
для любых действительных хх, . . ., хп. Тогда ] (хи . . .,
хп) наз. плотностью вероятности слу-
случайного вектора X и для любого борелевского мно-
множества ЛсК"
J J (щ,... ,ип) dux.. .dun.
Любая неотрицательная интегрируемая функция
f(xu . . ., хп), удовлетворяющая условию
f(xu...,xn)dxi...dxn = l,
00
является П. в. нек-рого случайного вектора.
Если случайные векторы X и У, принимающие зна-
значения в Rn, независимы и имеют П. в. f(xu . . ., хп)
и g(xlf . . ., хп) соответственно, то случайный вектор
ХЦ-Y имеет П. в. h(x1, . . ., xrt), к-рая является сверт-
сверткой функций fug:
h(xlt ...,хп) =^"ж ...^^fixi — uu ...,х„ — и„)Х
Xg(ult ...,un)du1...dun =
= \ ¦¦¦[Х) f ("ь • ••. un)g(x! — щ, ...,х„ — ип)Х
J - СО J - оо
Xdux...dun.
Пусть Х= (Xt , Хп) и Y= (Ylt . . ., Ym) - слу-
случайные векторы, принимающие значения в R" и Rm
(и, га>1) и имеющие П. в. f(xx, . . ., хп) ng(yt, . . ., ут)
соответственно, и пусть Z= (Хъ . . ., X„, У1? . . .,
Ут) ¦— случайный вектор в R« + m. Тогда если X и
У независимы, то Z имеет П. в. h(tr, . . ., tn+m), наз.
совместной плотностью распреде-
распределения вероятностей случайных векторов
X и У, причем
h(h, •¦¦,ta + m) = f(h, ...,tn)g(tn + i, ...,tn + m). A)
И обратно, если Z имеет П. в., удовлетворяющую
соотношению A), то X и У независимы.
Характеристич. функция q>(tlt . . ., tn) случайного
вектора X, имеющего П. в. /(%, . . ., хт), выражается
формулой
-СС J - СО
X/ to, ...,xn)dx1...dxn,
причем если ф(гх, . . ., tn) абсолютно интегрируема,
то f(xii ¦ ¦ ч хп) является ограниченной непрерывной
функцией и
!
Х<р(*1, ...,tn)dl1...dtn.
П. в. f(xlt . . ., хп) и соответствующая характеристич.
функция ф(<х, . . ., tn) связаны также следующим
соотношением (тождество Планшереля):
функция /?(#!, . . ., хп) интегрируема тогда п только
тогда, когда интегрируема функция \<p(tlt . . ., tn)\2
и в этом случае
Пусть (Q, Л) — измеримое пространство, v я ц
суть а-конечные меры на (Q, А), причем v абсолютно
непрерывна относительно ц, т. е. из равенства |х(Л)=0
следует равенство v(A)=0, А ?,/?. В этом случае на
(Q, Л) существует неотрицательная измеримая функ-
функция / такая, что
для любого Л ?с/?. Функция / наз. производной
Радона — Никодима меры v по мере fx, а в
случае, когда v — вероятностная мера, также П. в. v
по отношению к |х.
С понятием П. в. тесно связано понятие д о м и н и-
рованного семейства распределе-
н и й. Семейство вероятностных распределений ^У
на измеримом пространстве (Q, Jl) наз. доминирован-
ным, если на (ii, А) существует ст-конечная мера ц
такая, что каждая вероятностная мера из <J> имеет
П. в. по отношению к fx (или, что то же самое, каждая
мера из <у> абсолютно непрерывна относительно [х).
Предположение о доминированности является сущест-
существенным в нек-рых теоремах математич. статистики.
Лит.: [1] П р о х о р о в Ю. В., Р о з а н о в Ю. А., Теория
вероятностей, 2 изд., М., 1973; [2] Ф е л л е р В., Введение в тео-
теорию вероятностей и ее приложения, пер. с англ., 2 изд., т. 2,
М., 1967; [3] Леман Э., Проверка статистических гипотез,
пер. с англ., 2 изд., М., 1979. Н. Г. Ушаков.
ПЛОТНОСТЬ МНОЖЕСТВА Е, измеримого на
действительной прямой R, в точке х — предел (если
он существует) отношения
^Д|-^0, A)
где Д — произвольный отрезок, содержащий х, а |Д| —
его длина. Если вместо меры рассматривать внешнюю
меру, то получится определение внешней П. м.
Е в точке х. Аналогично вводится П. м. в ге-мерном
пространстве. При этом длины отрезков в R заменя-
заменяются объемами соответствующих re-мерных параллеле-
параллелепипедов с гранями, параллельными координатным
плоскостям, а предел рассматривается при стремлении
к нулю диаметра параллелепипеда. Для множеств
из R оказывается полезным понятие правой (левой)
П. м. Е в точке х, к-рое получается из общего опреде-
определения, если в нем рассматривать лишь отрезки Д,
имеющие левым (правым) концом точку х. Чаще всего
понятие П. м. применяется в случае, когда П. м. равна
единице (см. Плотности точка) или нулю (см. Раз-
Разреженность множества).
Лит.: [1] Н а т а н с о н И. П., Теория функций веществен-
вещественной переменной, 3 изд., М., 1974; [2] С а к с С, Теория интегра-
интеграла, пер. с англ., М., 1949. В. А. Скворцов.
ПЛОТНОСТЬ ПОСЛЕДОВАТЕЛЬНОСТИ — понятие
общей аддитивной теории чисел, изучающей законы
сложения последовательностей общего вида. П. п.
является мерой того, какая часть из последовательно-
последовательности всех натуральных чисел принадлежит данной
последовательности A={ak} целых чисел ао = О<1<:
<:а1<а2<. . .<«&. Под понятием П. п. имеется в виду
плотность d(A) (введенная в 1930 Л. Г. Шнирельманом)
последовательности А, а именно:
где
Плотность d(A) = l тогда и только тогда, когда А
совпадает с множеством No всех целых неотрицательных
чисел. Пусть А-\-В — арифметич. сумма последова-
последовательностей Л= {ак} и В= {6(}, т. е. множество А -\-В—-
= {aft+b(}, где числа ?&+?>; берутся без повторений.
Пни А=В полагают 2А=А-\-А, аналогично ЗЛ=Л +
-\-А-{-А и т. д. Если kA=N0, 10 А паз. базисом h-то
порядка. При исследовании структуры множеств,
получающихся в результате суммирования последова-
последовательностей, заданных лишь их плотностями, исполь-
используются теоремы о плотности суммы двух последова-
последовательностей:
d (А + В) Зз d (А) -|- d(B)~d (A) d (В)
— нера
в
d
в
е н с
\{А +
е н с
т
В
т
в
);
в
0
22 1
0
Ш
min
М
н и р
(d(A)
а н н
е л
+ d
а -
ь м
\(В)
- Д
а и
.1)
а й
а,
с о н а.
— нерав Д
Из неравенства Шнирельмана следует, что всякая
последовательность положительной плотности есть
базис конечного порядка. Применение этого факта к
аддитивным задачам, в к-рых часто суммируются
последовательности нулевой плотности, осуществля-
осуществляется посредством предварительного конструирования
из заданных последовательностей новых с положи-
положительной плотностью. Напр., с помощью методов решета
доказывается, что последовательность {р}-{-{р}, где р
пробегает простые числа, обладает положительной
плотностью. Отсюда следует теорема Шнирель-
Шнирельмана: существует такое целое число со>О) что любое
натуральное число есть сумма не более с0 простых
чисел. Эта теорема дает решение т. н. ослабленной
проблемы Гольдбаха (см. также Аддитивная теория
чисел).
Разновидностью понятия П. п. является понятие
асимптотической плотности, частным случаем к-рой
будет натуральная плотность. Понятие П. п. обобща-
обобщается на числовые последовательности, отличные от
натурального ряда, напр, на последовательности целых
чисел в полях алгебраич. чисел. В результате уда-
удается изучать базисы в алгебраич. полях.
Лит.: [1] Гельфонд А. О., Л и н н и к Ю. В., Элемен-
Элементарные методы в аналитической теории чисел, М., 1962; [2] О s t-
шаппН.- Н., Additive Zahlentheorie, Bd 1—2, В., 1956.
Б. М. Бредихин.
ПЛОЩАДЕЙ МЕТОД — способ решения различных
задач теории однолистных функций, использующий
теоремы площадей (см. Площадей принцип).
ПЛОЩАДЕЙ ПРИНЦИП: площадь дополнения к об-
образу области при ее отображении регулярной в ней
функцией неотрицательна. Впервые П. п. использовал
в 1914 Т. Гронуолл [1], к-рый доказал этим путем т. н.
внешнюю теорему площадей для функ-
функции класса 2 — функций
+
регулярных и однолистных в области Д'= {г : 1<Ы<
<оэ} (см. Однолистная функция). Площадь a{CF(A'))
дополнения для образа F(A') области А' при отобра-
отображении w=lA(z)?2 определяется формулой
e(CF(A')) = n (l-2"=1*|a*
и, следовательно,
С помощью неравенства A) получены первые резуль-
результаты для функций классов 2 и 5, где S — класс функ-
функций f(z) -~-z-\-I,'k=2ak z*t регулярных и однолистных в
круге Д— {г : |з|<1 } (см. Бибербаха гипотеза. Искаже-
Искажения теоремы). Доказана [2] более общая теорема пло-
щадей. Г. М. Голузин [3] распространил теорему пло-
площадей на р-листные функции в круге (см. Многолист-
ная функция).
Доказана следующая теорема площадей [4]: пусть
/r'?2, B = CF(A'), Q(w) — регулярная на В функция,
(?(jP(z)) = "V «fez~* ^ const;
тогда
и знак равенства имеет место только в том случае,
если площадь а (В) множества В равна нулю.
Под теоремой площадей в нек-ром классе
однолистных функций /(г), z?B, В — область (или в
классе систем однолистных функций {/^(z), z?.Bfc}?=0,
и=1, 2, . . ., Bk — области), понимают обычно всякое
неравенство, обладающее тем свойством, что знак
равенства в нем имеет место в том и только в том слу-
случае, если площадь дополнения G для f{B) (соответст-
(соответственно дополнения G для \i"k=sJk (Bk)) равна нулю.
Обычно такая теорема доказывается с помощью П. п.
Именно, рассматривается произвольная регулярная
функция Q (ш) (или, более общо, имеющая регулярную
производную) на G и вычисляется площадь a{Q(G))
образа G при отображении функцией Q. Таким образом,
неравенство B) есть нек-рая весьма общая теорема
площадей в классе 2.
Пусть F?2 и
, F(t)-F(z) ^,00
1п 2»t-pi-'l *€*'
Выбирая надлежащим образом функцию Q, регулярную
на С F (&.'), неравенство B) можно записать в виде
п=^Р'«ХР
¦Vю
C)
где хр — произвольные числа, не равные одновре-
одновременно нулю и такие, что
Получены и более общие теоремы площадей в классе
2 (см. [5]).
Теоремы площадей доказаны: для класса 2Л («i, . . .,
ап) систем {fk(z), /ft@) = aft, z^A}t=i функций /fc,
конформно и однолистно отображающих круг Д на
области, попарно не имеющие общих точек,— нена-
легающие области (см. [6]); в классе 2 (В) B (В),
В^оа,— класс функций F, регулярных и однолистных
в В\{оо} и таких, что ^(оо) = оо, lim ?lil = l,
2-»- 00 Z
см. [7]); для неналегающих многосвязных областей
(см. [6], а также [8], [9]). Все теоремы площадей для
многосвязных областей доказываются контурного ин-
интегрирования методом.
Под методом площадей понимают способы
решения различных задач теории однолистных функ-
функций, использующие теоремы площадей.
Напр., из C) с помощью неравенства Коши можно
получить:
X. q=, «я. «V* Г< Sp"», т I *Р i2 S,"= 1 т I ^ I1. <4>
где хр и .г^ такие, что ряды, стоящие в правой части,
сходятся. Если в неравенстве D), напр., xp=t~P,
Xq=z~i, U!>1, Ы>1, то получают теорему искажения
хорд:
lnF(t)-f(z)
t-z
Теоремы площадей, напр, в классе QJl(ai, • . ., »„),
дают необходимые и достаточные условия принадлеж-
принадлежности системы {/fe(z),/j@) = a^, г?Д}?=1 мероморфных
функций fk классу [&!(%, . . ., ап) (см. [6] с. 179).
Лит.: [1] G г о n w а 1 1 Т. Н., «Ann. Math. Ser. 2», 1914/
1915, v. 16, p. 72—76; [2] P r a w i t z H., «Arkiv mat., astron.,
fysik», 1927, Bd 20A, № 6, S. 1 — 12; [3] Г о л у з и н Г. М., «Ма-
тем. сб.», 1940, т. 8, № 2, с. 277—84; [4] Л с б е д е в Н. А., М и-
л и н И. М., там же, 1951, т. 28, № 2, с. 359—400; [5] N е h a-
r i г., «Arch. Ration. Mech. and Anal.», 1969, v. 34, № 4, p. 301 —
30; [6] Л е б е д е в Н. А., Принцип площадей в теории однолист-
однолистных функций, М., 1975; [7] М и л и н И. М., Однолистные функ-
функции и ортонормированные системы, М., 1971; [8] А л е н и-
цын Ю. Е., «Изв. АН СССР. Сер. матем.», 1973, т. 37, Ли 5,
с. 1132—54; [9] Г у т л я н с к и й В. Я. Щ е п е т о в В. А.,
«Докл. АН СССР», 1974, т. 218, ЛД 3, с. 509—12; [10] Gruns-
к у Н., «Math, г.», 1939, Bd 45, Н. 1, S. 29—61. Н. А. Лебедев.
ПЛОЩАДЬ — численная характеристика, приписы-
приписываемая плоским фигурам определенного класса (напр.,
многоугольникам) и обладающая следующими свой-
свойствами: 1) П. неотрицательна; 2) П. аддитивна (в
случае многоугольников это означает, что если фигура
P[]Q составлена из фигур Р и Q, не имеющих общих
внутренних точек, то пл. (P(jQ) = na. Р+пл. Q;
3) П. сохраняется при перемещениях; 4) П. единичпого
квадрата равна 1. Термин «П.» употребляется также
в более широком смысле как численная характери-
характеристика, сопоставляемая двумерным поверхностям в
трехмерном пространстве; А-мерным поверхностям в
и-мерном B<А<я) евклидовом или римановом прост-
пространстве; границам множеств и др. объектам, см. ниже.
Площадь плоской фигуры. Историче-
Исторически П. определялась сначала на классе многоуголь-
многоугольников (фигур, допускающих разбиение на конечное
число треугольников без общих внутренних точек).
Существенно, что на классе многоугольников П. со
свойствами 1) ¦— 4) существует и единственна (см. [1J,
[2]). Одним из следствий свойств 1) — 4) является то,
что П. всей фигуры не меньше П. ее части.
В древности существование и единственность П.
со свойствами 1) — 4) принимались без ясного опи-
описания класса рассматриваемых фигур; внимание со-
сосредоточивалось на приемах вычисления П. Формула
для П. прямоугольника, в том числе с иррациональ-
иррациональными сторонами, обосновывалась исчерпывания мето-
методом. П. треугольника и произвольных многоугольни-
многоугольников вычислялась как П. равносоставленного с ними
прямоугольника. Доказано, что любые многоуголь-
многоугольники равной П. равносоставлены (см. [2]).
Затем был выделен класс квадрируемых (измеримых
по Жордану) фигур. Фигура М на плоскости наз.
квадрируемой, если для любого s>0 сущест-
существуют такие многоугольные фигуры Р и Q, что
PdMczQ и (пл. Q — пл. .Р)<8. Класс квадрируемых
фигур весьма богат. Он включает, в частности, все
ограниченные плоские области с кусочно гладкими
границами. Но есть и пеквадрируемые плоские фи-
фигуры. На классе квадрируемых фигур также суще-
существует и единственна П. со свойствами 1) — 4) (см. [2]).
Исторически до рассмотрения класса квадрируемых
фигур умели вычислять П. нек-рых из них — круга,
кругового сектора и сегмента, различного рода лунок,
криволинейных трапеций. Эти вычисления обосновы-
обосновывались методом исчерпывания многоугольниками. В ря-
ряде случаев для обоснования таких вычислений привле-
привлекался Каеалъери принцип, состоящий в том, что если
две плоские фигуры указанного типа пересекаются
каждой прямой, параллельной фиксированной прямой,
по отрезкам одинаковой длины, то эти фигуры имеют
равную П. Средства интегрального исчисления (см.,
напр., [3]) дают удобные приемы для вычисления П.
любых плоских областей с кусочно гладкими грани-
границами. Эти средства обосновывают также принцип
Кавальери.
Стремление распространить понятие П. на более
общие плоские множества с сохранением свойств 1) —
4) ведет к теории меры, к выделению класса плоских
множеств, измеримых но Лебегу. Переход к еще более
общим классам множеств на плоскости приводит уже
к неединственным мерам со свойствами 1) — 4).
Ориентированная площадь. Если на
ориентированной плоскости расположена направлен-
направленная замкнутая кривая I, быть может с самопересече-
самопересечениями и налеганиями, то для каждой не лежащей на /
точки плоскости определена целочисленная функция
(положительная, отрицательная или нулевая), наз.
степенью точки относительно I. Она показывает сколь-
сколько раз и в какую сторону контур I обходит данную
точку. Интеграл по всей плоскости от этой функции,
если он существует, наз. охватываемой I ориентирован-
ориентированной П. Последняя, в отличие от обычной П., имеет
знак. О простейших свойствах ориентируемой П. см. [4].
Площадь поверхности. Проще всего опре-
определяется П. многогранных поверхностей: как сумма
П. плоских граней. Попытка ввести понятие П. кри-
кривых поверхностей как предела П. вписанных много-
многогранных поверхностей (подобно тому, как длина кри-
кривой определяется как предел вписанных ломаных)
встречает трудность. Даже для весьма простой кривой
поверхности П. вписанных в нее многогранников со
все более мелкими гранями может иметь разные пре-
пределы в зависимости от выбора последовательности
многогранников. Это наглядно демонстрирует извест-
известный пример Шварца, в к-ром последовательности впи-
вписанных многогранников с разными пределами П. стро-
строятся для боковой поверхности прямого кругового
цилиндра (см. [2]).
Чаще всего П. поверхности определяют для класса
кусочно гладких поверхностей с кусочно гладким краем
(или без края). Обычно это делают с помощью следу-
следующей конструкции. Поверхность разбивают на мелкие
части с кусочно гладкими границами: в каждой части
выбирают точку, в к-рой существует касательная пло-
плоскость, и ортогонально проектируют рассматриваемую
часть на касательную плоскость поверхности в вы-
выбранной точке; П. полученных плоских проекций
суммируют; наконец, переходят к пределу при все
более мелких разбиениях (таких, что наибольший из
диаметров частей разбиения стремится к нулю). На
указанном классе поверхностей этот предел всегда
существует, и если поверхность задана параметри-
параметрически кусочно б^-гладкой функцией г {и, и), где пара-
параметры и, и изменяются в области D на плоскости (и, v),
то площадь F выражается двойным интегралом
где gir=rl, g12=^rurv, g22=rl, a ra и rv — частные
производные по и и v. Доказательство см., напр., в
[3], [5]. В частности, если поверхность есть график
С^-гладкон функции z—f (х, у) над областью D на пло-
плоскости (х, у), то
\V B)
Здесь A+/a--(-/j/)~'''!=cos а, где а — острый угол
между нормалью к поверхности и осью Oz. На основе
формул A), B) выводятся известные формулы для П.
сферы и ее частей, обосновываются приемы для вы-
вычисления П. поверхностей вращения и т. п.
Для двумерных кусочно гладких поверхностей в
рнмановых многообразиях [6] формула A) служит
определением П., при этом роль gn, g12, g2z играют
составляющие метрич. тензора самой поверхности.
Существенно, что уже в случае двумерной поверх-
поверхности П. приписывается не множеству точек, а отобра-
отображению двумерного многообразия в пространство и
тем отличается от меры.
к-м ерная площадь. Для кусочно гладкого
погружения / : М —> R" /с-мерного многообразия (с
краем или без края) в n-мерное евклидово простран-
пространство, 2</с<п, П. определяют с помощью конструкции,
вполне аналогичной описанной выше для кусочно
гладких поверхностей. Разница состоит в том, что
проектирование ведется на /с-мерные касательные пло-
плоскости и суммируются й-мерные объемы проекций.
Если в области DC.M можно ввести координаты и1, .. .,
ик, то площадь F погружения (D, f\D) выражается
интегралом
F=^DVdet(gij)du\..duk, C)
где g;f — скалярные произведения /—4 , -^4\. Если
\du' du-7/
к=п—1 и D — область на координатной гиперпло-
гиперплоскости {xlt . . ., xn^j), а /допускает явное задание хп —
= z(xlt . . ., хп_1), то формула C) принимает вид
F =
Если отображение / гладкое, то g,y— коэффици-
коэффициенты метрич. тензора, индуцированного погружением,
и из C) следует, что П., определяемая внешней кон-
конструкцией, принадлежит внутренней геометрии по-
погруженного многообразия. Иногда равенство C) при-
принимают за определение П., напр, в случае погружения
не в R", а в риманово многообразие.
На классе кусочно гладких погруженных многооб-
многообразий П.: а) неотрицательна; б) равна 1 на k-мерном
единичном кубе в R"; в) не меняется при ортогональ-
ортогональных преобразованиях; г) аддитивна; д) полунепрерывна,
т. е. F (/) <limF (/,-) при равномерной сходимости
/,—у /; е) если <р : R" —>- R" есть нерастягивающее
отображение, то F(q>°f)<.F(f); ж) если {Р,} — набор
из Сп попарно ортогональных /с-мерных плоскостей
и р[— проектирование на Р{, то
F (pi о /) < F (/) < 2ji=i (р< ° ^' &)
Дальнейшие обобщения. Теория
площадей. Распространение функции F на более
общие объекты с сохранением хотя бы части их свойств
а) — ж) может осуществляться разными путями и
вести к разным результатам. Изучение таких обобще-
обобщений составляет предмет теории П. Обзор соотношений
разных понятий П. см. в [10].
Граница между теорией П. и теорией меры довольно
условна. По традиции к теории П. относят в первую
очередь изучение П. непрерывных отображений, где
учитывается кратность и меньшую роль играет сохра-
сохранение аддитивности. О /с-мерных мерах в ге-мерном
пространстве см., напр., Хаусдорфа мера, Фавара мера.
Ту или иную II. можно вводить на основе аппрок-
аппроксимативного, интегрально геометрического, функцио-
функционального подхода, либо — аксиоматически. Ниже при-
приведены наиболее распространенные понятия.
Площадь по Лебегу (см. [7], [9]) опреде-
определяется равенством
L (М, /) =lim F (//), F)
г -* оэ
где М — конечно триангулируемое /с-мерное многообра-
>ие; /; : М —у R"— всевозможные кусочно линейные от-
обряжения; /,¦-v/; F(f,) есть fc-мерная П. соответст-
соответствующей полиэдральной поверхности. П. по Лебегу
одинакова для эквивалентных по Фреше отображений
и потому является характеристикой Фреше поверхности.
В случае к=2 условие Ь(М, /)<оо влечет ряд по-
полезных свойств поверхности (напр., возможность вве-
введения изотермич. параметров); в этом случае П. по
Лебегу оказалась удобным инструментом, достаточным
для решения Плато задачи и более общих двумерных
задач вариационного исчисления. При fc>2 исследо-
исследование вариационных задач в классе непрерывных от-
отображений столкнулось с трудностями (в проблеме
компактности), что заставило обратиться к поиску
других объектов (потоки и вариобразия) и связанных
с ними характеристик типа П. Использование П. но
Лебегу ограничивается также сложностью, с к-рой
устанавливаются ее связи с другими понятиями П.
и нек-рые ее свойства (напр., правое пз неравенств
E)). Следует отметить две особенности L(M, /): во-
первых, при L(M, /) = 0 может оказаться, что объем
F(/(il#))>0; во-вторых, даже при к=2 для разбиения
М на Му и М2 с общей границей в виде кривой может
оказаться
L(M,f) >L(M1,f\Ml) + L(Mi,f\MJ. G)
Изучался вопрос о том, в какой мере соблюдение
нек-рых из свойств а) — ж) с заменой аддитивности на
полуаддитивность, т. е. допущением неравенства типа
G), приводит к П. по Лебегу. Вопросы этого типа ис-
исследованы A983) не до конца (см. [7]).
Интегрально геометрические пло-
площади [9]. Пусть N (М', ф, у) есть какая-либо функция
кратности для отображений ф : М —>- Rk в точке у? R*,
напр. N=ca.rd(p~1(y). Тогда для / : М —>- R" можно
образовать интегрально геометрическую П.
^N(M,Poof,y)dV(y)dv(a), (8)
где G(n, к) — Грассмана многообразие /с-мерных под-
подпространств R*cR", v — нормированная Хаара мера
на G(n, к), ра — ортогональное проектирование на
<j?G(n, к). Для разных функций кратности П. (8)
могут различаться. Весьма специальный выбор N (М, <р,
у) приводит для триангулируемых М к совпадению (8)
с П. но Лебегу при /с=2, а также при fo>0 в случае
равенства нулю меры Хаусдорфа Hk + 1(j(M)) (см. [9]).
Для случая &=2 различные интегрально геометриче-
геометрические П. вводились еще Пеано, Гецем, Банахом (см.
[7]).
Площадь границы множества. В свя-
связи с доказательством неравенства Брунна — Мин-
ковского и классического изопериметрич. неравенства
была введена П. по Минковскому. Она приписывается
множеству Acz^", но характеризует П. его границы
и определяется равенством
F(A)= \im \ (V (A+ hB)—V (A)), (9)
где В — единичный шар в R™, а V — объем. Для множеств
А с кусочно гладкой границей и для выпуклых А в (9)
существует обычный предел, совпадающий с (п—1)-
мерной П. границы. Определение (9) сохраняет смысл
для множеств в конечномерных нормированных про-
пространствах, где даже для выпуклых А значение П.
(9) может отличаться от меры Хаусдорфа Нп_х(дА).
Другой полезной характеристикой, аналогичной
П., к-рая сопоставляется множеству, но характеризует
л основном его границу, является периметр измери-
измеримого множества. Он является частным случаем по-
понятия массы потока.
Внутренняя площадь. Если М метризовано
и / : М -v R" — локально изометрич. отображе-
пие, то возникает вопрос о соотношении между L (М, /)
и мерой Хаусдорфа Н^(М). Когда М — двумерное
многообразие ограниченной кривизны, то L(M,f) —
= Яа(Л?). Вообще же непрерывное / : М —>- R" инду-
индуцирует на компонентах связности/-*(«), u?Rn, обоб-
обобщенную метрику р, отличающуюся возможностью
Р(я, 2/)=о°- Конструкция /с-мерной меры Хаусдорфа,
примененная к р, дает характеристику, к-рую можно
принять за внутреннюю П. погружения. Для липши-
цевых / она совпадает с L(M, f) (см. [11]).
Массы потоков и вариобразий. Ин-
Интегрирование /с-форм по /с-мерному кусочно гладко
вложенному в R" ориентированному многообразию
М приводит к потоку Тмц>=\ (<f(x), v(x))dF(x) —
линейному функционалу на /с-формах (р в R". Здесь
v — единичный касательный к М /с-вектор. Линейный
функционал ТЛ1 в существенном характеризует М.
Кроме того, определен (на этот раз и при неориенти-
неориентированном М) нелинейный функционал — вариобразие
|((p,v)|dF. Интегральные нормы (массы)
\\Тм\\ и Wm\\ совпадают с П., то есть с F{M). Включе-
Включение класса кусочно гладких подмногообразий про-
пространства R" в более общие классы потоков и вари-
вариобразий играет в вариационном исчислении такую же
роль, как обобщенные решения в теории уравнений в
частных производных.
Среди всех потоков и вариобразий выделяют широ-
широкие классы целочисленных потоков и вариобразий.
Последние сохраняют многие геометрич. свойства под-
подмногообразий. Напр., целочисленный поток есть по-
поток, допускающий представление T=?di^1mTM, где
ге,- — целые числа, a Af,- суть ^-гладкие подмногооб-
подмногообразия, при условии, что конечна масса (к—1)-мерного
потока dT, определяемого равенством а?Г(ф)= Г (акр).
Массы целочисленных потоков и вариобразий можно
рассматривать как обобщения понятия П. поверхно-
поверхности. И здесь есть связь с П. по Лебегу. Пусть кусочно
гладкие отображения /; : М -v R" равномерно схо-
сходятся fi~+f и L(M, f) = \imL(M, /,-). Тогда соответ-
?->со
ствующие вариобразия V/ слабо сходятся к нек-рому
целочисленному ьариобра.чию VV, причем \\V f\\— L (М, /).
Тем самым каждому / : М —>- IR" с L(M, /)<oo естест-
естественно сопоставляется вариобразие Vj с массой L(M, /);
на языке потоков об этом см. в [13].
Лит.: [1] Л е б е г А., Об измерении величин, пер. с франц.,
2 изд., М., 1960; [2] Энциклопедия элементарной математики, т. 5,
М., 1966; [3] И л ь и н В. А., П о з н я к Э. Г., Основы матема-
математического анализа, 3 изд., ч. 1, М., 1971; [4] Л о п ш и ц А. М.,
Вычисление площадей ориентированных фигур, М., 1956; [5]
И о г о р е л о в А. В., Дифференциальная геометрия, 5 изд.,
М., 1969; [6] Р а ш е в с к и й П. К., Риманова геометрия и тен-
тензорный анализ, 3 изд., М., 1967; [7] С е s a r i L., Surface area,
Princeton, 1956; [8] P e d e г e r H., Geometric measure theory,
В.—Hdlb.—N. Y., 1909; [9] PedererH., «Bull. Amer.
Math. Soc», 1952, v. 58, № 3, p. 306—78; [10] Б у р а г о Ю. Д.,
ЗалгаллерВ. А., Геометрические неравенства, Л., 1980;
[11] Busemann H., «Ann. Math. 2 ser.», 1947, v. 48,
p. 234—67; [12] A1 m g r e n P. J., The theory of varifolds, Prin-
Princeton, 1965; [13] Federer H., «Trans. Amer. Math. Soc», 1961,
v. 98, Jfi 2, p. 204—33.
Ю. Д. Бураго, В. А. Залгаллер, Л. Д. Кудрявцев.
ПЛЮККЕРА ИНТЕРПРЕТАЦИЯ — модель, реали-
реализующая геометрию трехмерного проективного про-
пространства Р3 в гиперболич. пространстве 3S6. П. и.
основана на специальном истолковании плюккеровых
координат прямой, определяемых для любой прямой
пространства Р3.
При проективных преобразованиях пространства
Р3 плюккеровы координаты преобразуются линейно.
С помощью плюккеровых координат прямых про-
странства Р3 устанавливается взаимно однозначное
соответствие между прямыми пространствами Р3 и
точками проективного пространства Рь, координаты
к-рых численно равны плюккеровым координатам
прямых пространства Р3.
Прямые пространства Р3 изображаются точками
невырожденной квадрики пространства Ръ, индекс
к-рой равен трем.
Если считать эту квадрику за абсолют и определить
в пространстве Ръ проективную (неевклидову) мет-
метрику, то получается пятимерное гиперболич. про-
пространство 355. При каждой коллинеации и корреляции
пространства Р3 происходит линейное преобразование
плюккеровых координат, т. е. каждая коллинеация
и корреляция изображаются коллинеацией простран-
пространства Ръ, переводящей в себя абсолют. Эти коллинеации
тем самым являются перемещениями пространства
3Sb. Перемещения пространства sSb изображают или
коллинеации или корреляции пространства Р3.
Каждому линейному комплексу пространства Р3
сопоставляется точка пространства 3Sb. Проективную
геометрию пространства Р3 можно рассматривать как
неевклидову геометрию гиперболич. пространства 355.
Именно эта интерпретация геометрии пространства Р3
в пространстве 3S5 наз. интерпретацией
Плюккера в связи с ролью плюккеровых коор-
координат.
Если в качестве основного образа пространства Р3
берется прямая, то геометрию этого пространства
можно рассматривать как геометрию на абсолюте
пространства 355.
Группа проективных преобразований пространства
Р3 изоморфна группе перемещений пространства 3Sb,
и всякому инволюционному проективному преобразо-
преобразованию пространства Р3 соответствует инволюционное
перемещение пространства 3Sb. Напр., нуль-системе
в пространстве Р3 соответствует отражение от точки
и от ее полярной гиперплоскости в пространстве 36'5;
инволюционной гомологии в пространстве Р3 соот-
соответствует гиперболический паратактич. сдвиг на полу-
полупрямую в пространстве 355 и т. д. Каждой связной
компоненте группы проективных преобразований нро-
нространства Р3 соответствует связная компонента группы
перемещений пространства 355.
1) Коллинеациям пространства Р3 с положительным
определителем, включая тождественное преобразова-
преобразование, отвечают перемещения пространства 3&5с опреде-
определителем, равным +1 (сюда включаются тождественные
преобразования).
2) Корреляциям пространства Р3 с положительным
определителем (включая нуль-систему) отвечают пе-
перемещения пространства 3S5 с определителем, равным
— 1, переводящие собственную и идеальную области
соответственно в себя (включая отражения от точки).
3) Коллинеациям пространства Р3 с отрицательным
определителем отвечают перемещения пространства
3S5 с определителем, равным +1, переводящие собст-
собственную область в идеальную и обратно, эта компо-
компонента содержит гиперболич. сдвиг на полупрямую.
4) Корреляциям пространства Р3 с отрицательным
определителем отвечают перемещения нространства
36'6 с определителем, равным —1, переводящие соб-
собственную область в идеальную и обратно.
Образам симметрии, соответствующим в простран-
пространствах -Р3 и 3>^5> сопоставляются числовые инварианты,
между к-рыми существуют определенные связи.
П. и. применяется в исследованиях групп переме-
перемещений трехмерных неевклидовых пространств S3,
'Sg, 2S3l к-рые изоморфны определенным подгруппам
группы перемещений пространства 3<S5. Устанавли-
Устанавливается также взаимосвязь групп движений этих трех-
трехмерных пространств (эллиптического, гинерболиче-
ского) с группами перемещений пространств низших
размерностей (см. Фубини интерпретация, Котелъ-
никоеа интерпретация). С помощью П. и. изучается
интерпретация трехмерного симплектич. пространства
Sp3 в пространстве 355.
П. и. предложена Ю. Плюккером [1].
Лит.: [1] Р 1 и с к е г J., Neue Geometrie des Raumes gegriin-
det auf die Betrachtung der geraden Linie als Raumelement, Lpz.,
1868—69; [2] Розенфельд Б. А., Неевклидовы прост-
пространства, M., 1969; [3] Клейн Ф., Высшая геометрия, пер. с
нем., М.— Л., 1939. Л. А. Сидоров.
ПЛЮККЕРА ФОРМУЛЫ — формулы, связывающие
внешние, т. е. отвечающие проективным вложениям,
и внутренние характеристики апгебраич. многооб-
многообразий. Наиболее старыми и известными среди числен-
численных формул алгебраич. геометрии являются П. ф.
для плоской приведенной и неприводимой кривой
ZaCP2, к-рая имеет лишь обыкновенные двойные
и каспидальные особые точки. Пусть d — степень
к р и в о й Z, т. е. число точек из Z на прямой общего
положения в СР2, a d* — класс кривой Z,
т. е. число прямых, касательных к Z в неособых точках
и проходящих через одну и ту же фиксированную
точку общего положения в СР2. Основные две формулы
Плюккера таковы:
A) d* = d(d-i)— 26 — 3k,
B) d* = 2d+Bg-2)-k,
где g — род разрешения X кривой 2, б — число обык-
обыкновенных двойных точек, а к — число каспидальных
точек. Формула A) сводится к виду d* = d(d—1), если
кривая Z неособа.
Другие классические П. ф. следуют из A) и B) по
двойственности. Если Z — не прямая, тогда двой-
двойственная кривая Z* к Z определяется как
замыкание множества касательных к Z, рассматрива-
рассматриваемых как точки двойственной плоскости СР2*. Теорема,
принадлежащая Ю. Плюккеру (J. Plucker, см. [3]),
состоит в том, что дважды двойственная кривая Z**
совпадает с Z. Предполагая, что Z* имеет лишь б*
обыкновенных двойных и к* каспидальных особых
точек, получают формулы
A*) d = d*(d* — 1) — 26* — ik*,
B*) d = 2d* + 2Bg—2) — 2к*.
Число 6* можно интерпретировать также как число
бикасательных к Z, т. е. прямых, к-рые ка-
касаются Z ровно в двух различных и неособых точках,
с порядком касания 2, а к* — как число точек перегиба.
Четыре формулы A), B), A)*, B)* не независимы:
из любых трех следует четвертая. Однако любые
три из них независимы. Из них вытекают также сле-
следующие соотношения:
C) k* = 3d(d—2)— 68 — 8к,
C*) k = 3d* (d*— 2)— 66*— 8к*.
Именно эти формулы были получены Ю. Плюккером
вместе с формулами A) и A)* в 1834—39.
В случае основного поля конечной характеристики
П. ф. и теорема двойственности не всегда справедливы.
Напр., в характеристике 2 все касательные к конике
проходят через одну определенную точку, наз. стран-
странной точкой коники, поэтому двойственная кривая
есть прямая. В характеристике 3 имеется неособая
кубика только с тремя точками перегиба и даже с
одной (по П. ф. их должно было бы быть девять). При
правильной интерпретации d* формулы A), B) ос-
остаются справедливыми во всех характеристиках ф2;
в характеристике 2 их нужно заменить на
A2) d* = d(d — 1)—26 — 4/с,
B„) d* = 2d+Bg-2)-2k.
Известно обобщение П. ф. на случай кривых в f в
произвольными особенностями (см. [2]), а также на
случай гиперповерхностей в Р".
Лит.: [1] В е г z о 1 а г j L., в кн.: Encyklopadie der mathe-
matischen Wissenschaften, Bd 32, Lpz., 190B; [2] Г р и ф-
фитс Ф.,Харрис Дж., Принципы алгебраической гео-
геометрии, т. 1—2, пер. с англ., М.. 1982; [3] Клейман С.Л.,
«Успехи матем. наук», 1980, т. 35, в. 6, с. 69—148.
В. В. Шокурое.
ПЛЮККЕРОВЫ КООРДИНАТЫ — координаты
прямой в трехмерном пространстве, шесть чисел р01,
Рог* Роз. Ро4> Ро5, Рое, из к-рых первые три являются
координатами направляющего вектора I прямой L,
а вторые три — моменты этого вектора относительно
начала координат. Пусть прямая L проходит через точ-
точки X и Y с проективными координатами (х0, xt, . . .,
хз) и (Уо> Ун ¦ ¦ ч Уз) соответственно П. к. этой пря-
прямой являются числа
П. к. применяют в линейчатой геометрии. Впервые
были рассмотрены Ю. Плюккером (J. Plucker, 1869).
Иногда вместо П. к. используют Клейна коор-
координаты (х0, . . ., хъ), связанные с П. к. формулами:
Естественно рассматривать П. к. как координаты в
р-мерном векторном подпространстве n-мерного век-
векторного пространства V. При этом они понимаются
как совокупность чисел, равных (рХр)-субдетерми-
нантам (геХр)-матрицы А (аи аг, . . ., ар), столбцы а,-,
1<:г<;р, к-рой являются столбцами координат (в
каком-либо базисе пространства V) базисных векторов
подпространства W. Если а[ — компоненты столбца
а,-, 1<г«?р, то П. к. (или грассмановы коор-
координаты) являются числа
4 4 ••• 4
ip=
4
[Pa\P ... a.
П. к. симметричны по всем индексам. Число сущест-
существенных П. к. равно (JJ).
При замене базиса W и фиксированном базисе V
П. к. умножаются на одно и то же ненулевое число.
При замене базиса V и фиксированном базисе W П. к.
преобразуются как координаты контравариантного
тензора валентности р (см. Поливектор). Два под-
подпространства совпадают тогда и только тогда, ког-
когда их П. к., вычисленные в одном и том же базисе
пространства F, отличаются лишь ненулевым мно-
множителем.
Принадлежность вектора х подпространству W
записывается в виде линейных уравнений
с коэффициентами, являющимися П. к. подпростран-
подпространства W. В этих уравнениях i1<i2<. . .<Cip — всевоз-
всевозможные наборы из чисел 1, 2, . . ., га. Л. П. Купцов.
ПЛЮРИГАРМОНИЧЕСКАЯ ФУНКЦИЯ — функ-
функция u=u(z) от п комплексных переменных л= (zl5 . . .,
zn) в области D комплексного пространства С", п^1,
имеющая в D непрерывные частные производные по
координатамxv , yv, zv—xv-{-iyv,v=l, . . ., п, до 2-го
порядка включительно и удовлетворяющая в D си-
системе п2 уравнений:
д'и дги л
X^uV __ W \ A)
|Я, V = l, . . . , Л.
Применяя формальные производные
ди 1 / ди . ди \ ди 1 / ди ди \
V
можно записать систему A) в более компактной форме:
Значение класса П. ф. определяется тем, что дейст-
действительная и мнимая части «=Re/, г;=1т/ любой голо-
голоморфной в области D функции f=u-\-iv являются
П. ф. в D; такие две (действительные) П. ф. наз. с о-
пряженными. Обратно, если дана П. ф. и в
окрестности V точки z<>=xajriy0?Cn, то в этой окрест-
окрестности существует голоморфная функция f—u-j-iv,
действительная часть к-рой равна и. Задача определе-
определения этой голоморфной функции / сводится к нахож-
нахождению сопряженной П. ф. v по формуле
где интеграл не зависит от пути в силу A).
Вообще говоря, рассматриваются сами по себе и
комплексные П. ф., определяемые как решения си-
системы A) или B). При п>1 П. ф. составляют правиль-
правильный подкласс класса кратиогармоиических функций,
к-рый, в свою очередь, есть правильный подкласс
класса гармонических функций: при и=1 все эти три
класса совпадают. С другой стороны, при re^l дей-
действительные П. ф. составляют правильный подкласс
класса плюрисубгармонических функций, к-рын, в
свою очередь, при п>1 является правильным под-
подклассом класса субгармонических функций.
Кроме общих свойств гармонич. функций, П. ф.
при ге>1 обладают характерными свойствами, обуслов-
обусловленными ь веновном переопределенностью системы A)
или B) в'етом случае. Пусть, напр., при к>1 П. ф.
и (z) в единичном поликруге
Un = {z?Cn:\zv\ < I, v=l, ...,«}
непрерывна в замкнутом поликруге Un. При этом
даже ее граничные значения на остове 2""={??Cn:
!?v 1 = 1, v=l, . . ., re}, являющемся правильной частью
всей границы dU", не могут быть заданы в виде про-
произвольной непрерывной функции U*(E,), t,?Tn,— они
удовлетворяют определенным дополнительным усло-
условиям. Таким образом, задача Дирихле в классе П. ф.
с данными на остове разрешима лишь при специально
подобранных граничных данных (см. [3]).
Лит.: El] Ш а б а т Б. В., Введение в комплексный анализ,
2 изд., ч. 2, М., 1976; [2] С о л о м е н ц е в Е. Д., в кн.: Итоги
науки. Математический анализ. Теория вероятностей. Регули-
Регулирование. 1962, М., 1964, с. 83—100; [3] Рудин У., Теория
функций в поликруге, пер. с англ., М., 1974. Е. Д. Соломенцев.
ПЛЮРИСУБГАРМОНИЧЕСКАЯ ФУНКЦИЯ —
действительная функция u=u(z), — oo<u<+°°, n
комплексных переменных z= (zlt . . ., zn) в области D
комплексного пространства С": п^1, удовлетворяю-
удовлетворяющая следующим условиям: 1) u(z) полунепрерывна
сверху всюду в D; 2) u(z°-\-Xa) есть субгармоническая
функция переменного Х^С в каждой связной компо-
компоненте открытого множества {X ? С: г°-]-^а ? D } для любых
фиксированных точек z°?D, а?Сп. Функция v(z) наз.
плюрисупергармоническойфункци-
о и, если — v(z) есть П. ф. Плюрисубгармонич. функ-
функции при и >1 составляют правильный подкласс класса
субгармонич. функций, а при п--\ эти два класса
совпадают. Наиболее важные примеры П. ф.: ln]/(z)|,
ln + |/(z)|, \i{z)V, p>0, где/(г) — голоморфная функция
в D.
Для того чтобы полунепрерывная сверху в области
DdCn функция u(z), u(z)<+оо, была П. ф., необхо-
необходимо и достаточно, чтобы для любых фиксированных
:?D, а?С", |а|=^1 существовало число б=о(г, а)>0
такое, что при 0<г<б выполняется неравенство
a)dcf.
Для функций u(z) класса C2(D) более удобен следую-
следующий критерий: и (г) есть П. ф. в D тогда и только тогда,
когда эрмитова форма (гессиан функции и)
#((*;»)«.«) = 2" h=1g^
неотрицательно определена в каждой точке z?D.
Помимо общих свойств субгармонич. функций, для
П. ф. справедливы следующие: 1) u(z) есть П. ф. в
области D тогда и только тогда, когда u(z) — П. ф.
в окрестности каждой точки z?D; 2) линейная комби-
комбинация П. ф. с положительными коэффициентами есть
П. ф.; 3) пределы равномерно сходящейся и монотонно
убывающей последовательностей П. ф. суть П. ф.;
4) для того чтобы u(z) была П. ф. в области D, необ-
необходимо и достаточно, чтобы ее можно было предста-
представить в виде предела убывающей последовательности
П. ф. {«/j(z)}ftLi соответственно классов C"(D^, где
области Ъь таковы, что D^aD^aD^ +1 и Uk=iDk=D;
5) для любой точки z°?D среднее значение
-^~ С
u(
по сфере радиуса г, где e-in— 2лп/(п—1)! — площадь
единичной сферы в R2", есть возрастающая функция
по г, выпуклая относительно Inr на отрезке 0<г«:й,
если шар
V(z°,R) = {z?Cn: \z — za\ <R}
расположен в D, причем и(zn)</(z°, г; и); 6) при го-
голоморфных отображениях П. ф. переходит в П. ф.;
7) если u(z) — непрерывная П. ф. в области D, Е —
замкнутое связное аналитич. подмножество D и суже-
сужение и\Е достигает максимума на Е, то u(z) = const
на Е.
Имеют значение для приложений также следующие
правильные подклассы класса П. ф. Функция и (z)
наз. сильно плюрисуб г ар ионической,
если существует выпуклая возрастающая функция
() +o,
lim ^ = + oo,
= e', то получают логарифмически плюри-
субгар ионические функции.
Класс П. ф. и только что названные его подклассы
важны для описания различных свойств голоморфных
функций и областей комплексного пространства С",
а также и более общих аналитич. пространств (см.
|1] — [4], [7]). Напр., класс функций Г а р т о г-
с а Н (D) определяется как наименьший класс дейст-
действительных функций в области D, содержащий все
функции 1п|/(-)|, где f(z) — голоморфная функция в D,
и замкнутый относительно следующих операций:
2) {uk?H (D), uk^M (D') для всякой подобласти
'cO'cO.t = l,2, ...}=> sup {«fe(z): к —I, 2, ...}?
H(D);
3) {uk<=-H (D), uk^uk + 1.k = l,2, ...}—> lira uk(z)?
k ->¦ CO
4) {«?#(/)),
_
5) {м?Я (?>') для всякой подобласти D' С D' С Щ =>
Полунепрерывные сверху функции Гартогса являются
П. ф., но не всякая П. ф. есть функция Гартогса. Если
D — область голоморфности, то классы полунепрерыв-
полунепрерывных сверху функций Гартогса u?H(D) и II. ф. в D
совпадают (см. [5], [6]).
Лит..: [1] Владимиров В. С, Методы теории функций
многих комплексных переменных, М., 1964; 12] Г а н н и и г Р.,
Р о с с и X., Аналитические функции многих комплексных пере-
переменных, пер. с англ., М., 1969; [3j L е 1 о n g P., в кн.: Colloque
sur les fonctions de plusieurs variables, Bruxelles, 1953, P., 1953,
p. 21—40- [4] Bremermann H. J., «Trans. Amer. Math
Soc», 1956, v. 82, p. 17—51; [5] его же, «Math. Ann.», 1956
Bd 131, p. 76—86; [6] e г о ж e, «Proc. Amer. Math. Soc», 1956
v. 7, p. 771—75; [7] С о л о м е н ц е в Е. Д., в кн.: Итоги науки
Математический анализ. Теория вероятностей. Регулирование,
1962, М., 1964, с. 83—100. Е. Д. Соломенцев
ПЛЮРИСУПЕРГАРМОНИЧЕСКЛЯ ФУНКЦИЯ —
см. Плюрисубгармоническая функция.
ПОВЕРХНОСТЕЙ ТЕОРИЯ — раздел дифференци-
дифференциальной геометрии, в к-ром изучаются поверхности.
В П. т. исследуются форма поверхности, ее искрив-
искривление, свойства различного рода линий на поверхности,
рассматриваются вопросы изгибания, вопросы суще-
существования поверхности с данными внутренними или
внешними свойствами и др.
В П. т. имеются две точки зрения: поверхность можно
рассматривать как метрич. пространство со своей
внутренней метрикой (т. н. внутренняя геометрия),
шбо поверхность рассматривается как фигура в про-
пространстве (т. н. внешняя геометрия). Многие направ-
направления в П. т. (вопросы изометрического погружения,
изгибания и др.) посвящены изучению связей между
внутренней и внешней геометриями. Для регулярных
поверхностей класса С2 эти связи довольно тесны.
См. также Погруженных многообразий геометрия.
Изучение поведения кривых на поверхностях (асимп-
(асимптотических линий, геодезических линий и др.), а также
пар их однопараметрич. семейств — т. н. сетей —
привело к выделению специальных классов поверхно-
поверхностей. Напр., переноса поверхность характеризуется
существованием на ней сети переноса, Фосса поверх-
поверхность — сетью Фосса, линейчатая поверхность — по-
полугеодезической асимптотич. сетью и т. д. Теория
с^тей тесно связана с вопросами отображений поверх-
поверхностей на поверхности. Наиболее важными классами
отображений являются: изометрическое отображение,
при к-ром сохраняются длины дуг, площади и углы
между двумя направлениями, исходящими из одной
точки; конформное отображение, при к-ром сохра-
сохраняются углы между всякими двумя направлениями,
выходящими из одной точки (напр., стереографическая
проекция); сферическое отображение, при к-ром каждой
точке поверхности по параллельности нормалей ста-
ставится в соответствии точка сферы; геодезическое от-
отображение, при котором геодезические линии одной
поверхности соответствуют геодезическим другой по-
поверхности; эквиа реальное отображение, при к-ром пло-
площади соответствующих фигур находятся в постоянном
отношении.
Исследования в П. т. сопровождались изучением
большого числа классов поверхностей, таких как
поверхности второго порядка, винтовые поверхности,
геликоиды, Каталана поверхности, коноиды, резные
поверхности, каналовые поверхности, Дюпена циклиды,
Эннепера поверхности, Вейнгартена поверхности и
др. Много внимания уделяется изучению минимальных
поверхностей. В связи с приложениями широко ис-
исследовались триортогоналъные системы поверхностей,
напр, конфокальные поверхности 2-го порядка.
Помимо изучения свойств поверхностей, неизменных
при любых изометрич. преобразованиях всего про-
пространства (относящихся к т. н. метрической
П. т.), изучаются свойства поверхностей, инвариант-
инвариантные по отношению к какой-либо другой группе пре-
преобразований, напр, группе аффинных или проективных
преобразований. Аффинная П. т. рассматривает свой-
свойства поверхностей, неизменные при эквиаффинных
преобразованиях (т. е. аффинных преобразованиях,
сохраняющих объем). Проективная П. т. рассматривает
прооктивно инвариантные свойства поверхностей. См.
также Аффинная дифференциальная геометрия, Про-
Проективная дифференциальная геометрия, Конформно*
дифференциальная геометрия.
Исследования П. т., изучение полей тех или иных
геометрич. объектов, связанных с поверхностями,
стимулировали развитие многих методов, нашедших
применение и в др. областях математики, физики и
механики (напр., тензорный анализ, Нартана метод
внешних форм и др.).
Для П. т. в том виде, в каком она сложилась в кон.
19 в., характерно рассмотрение только достаточно
регулярных для применения дифференциального ис-
исчисления поверхностей (или их частей). С нач. 20 в.
появились направления исследований П. т., в к-рых
отказ от требований дифференцируемости компенсиру-
компенсируется какими-то иными требованиями, гарантирующими
получение содержательных геометрич. результатов.
Такими требованиями были, напр., выпуклость изу-
изучаемой поверхности (см. Выпуклая поверхность), ло-
локальная единственность геодезической. Кроме того,
предметом изучения стали поверхности во всем их
протяжении (т. н. геометрия в целом), а не в достаточно
малом участке, как это имело место в классической
дифференциальной геометрии. При этом существенными
являются учет их топологич. строения (напр., род
поверхности), их полноты в том или ином смысле и
связи этих характеристик с распределением кривизны.
Исследования по дифференциальной геометрии мно-
многомерных пространств, эллиптического пространства
и пространства Лобачевского установили ряд геомет-
геометрич. фактов, относящихся к П. т. в этих пространствах.
Лит.: [1] Рашеяский П. К., Курс дифференциальной
геометрии, 4 изд., М., 1956; [2] Б л я ш к е В., Дифференциаль-
Дифференциальная геометрия..., пер. с нем., т. 1, М.— Л., 1935; [31 Н о р-
д е н А. II., Теория поверхностей, М., 1956; [4] К а г а н В. Ф.,
Основы теории поверхностей в тензорном изложении, ч. 1—2,
М.— Л., 1947—48; [5]Шуликовский В. И., Классическая
дифференциальная геометрия в тензорном изложении, М., 1963;
[6] А л е к с а н д р о в А. Д., Внутренняя геометрия выпуклых
поверхностей, М.— Л., 1948; [7] II о г о р е л о в А. В., Внешняя
геометрия выпуклых поверхностей, М., 1969; [8] D а г Ь о u x G.,
LeQons sur la thfiorie generale des surfaces, 2 ed., t. 1—4, P., 1914—
1925; [9] Bianchi L., Lezioni di geometria differenziale, 3
ed., t. 1—2, Bologna, 1937. Ю. А. Аминов.
ПОВЕРХНОСТНАЯ ФУНКЦИЯ — функция мно-
множества на сфере Q, равная площади S (Е) той части
выпуклой поверхности F, к-рая имеет своим сферич.
изображением EczQ. Она сохраняет смысл для общих
выпуклых поверхностей и является вполне аддитивной
на кольцо борелевских множеств.
Лит.: [1] Александров А. Д,, «Матем. сб.», 1938, т. 3,
JVi 1, с. 27—44; [2] Б у з е м а н Г., Выпуклые поверхности, пер.
с англ., М., 1964. М. И. Войцеховский.
ПОВЕРХНОСТНЫЙ ИНТЕГРАЛ — интеграл по по-
поверхности. Пусть поверхность S, расположенная в
трехмерном евклидовом пространстве R3 с декарто-
декартовыми координатами х, у, z и имеющая, быть может,
самопересечения, задана векторным представлением
Г = Г (tt, V),
где Г (и, v) = (х (и, v), у (и, v), z (и, v)) A)
— непрерывно дифференцируемая вектор-функция, оп-
определенная на замыкании G двумерной измеримой по
Жордану области G, расположенной на плоскости с
декартовыми координатами и, v. Пусть
/ дг \ 2 вг дг Г дг \ 2
) Z 8()
— коэффициенты первой квадратичной формы поверх-
поверхности S. Если через F(x, у, z) обозначить функцию,
определенную на поверхности S, т. е. функцию F(х {и, и),
у(и, v), z(u, v)), то Поверхностный инте-
интеграл первого рода (или интеграл по
площади поверхности) определяют ра-
иенством
s F (*> У, г) ds =
Это определение не зависит от выбора представления
поверхности. П. и. 1-го рода является пределом соот-
соответствующих интегральных сумм, к-рые могут быть
описаны в терминах, связанных с поверхностью. Напр.,
если функция F(x(u, v), у (и, v), z(u, v)) интегрируема
по Риману, т= {iS,}JZi— разбиение поверхности S
на части S,, являющиеся образами при отображении
A) множеста EjCG, образующих разбиение хо~ {?,};=i
множества G (см. Кратный интеграл), и
mes Si = S 5 в, ^^1^22- ей dudv
— площадь S(, то
Л ,F(x,y,z)dS =
Si,
! s
= lira УГ F (x (lh r\i), у (I;, r\i), z (I;, T),-)) mesS,-,
где бт — мелкость разбиения т0, а (?,-, Т|,-)?Е;. В случае
явного задания поверхности S в виде z~=f(x, у),
(х, y)?G, формула B) принимает вид
= SI
Если на поверхности 5 с векторным представлением
A) нет особых точек, т. е. ruX/v?=0, то ее можно ори-
ориентировать, выбрав на ней непрерывную единичную
нормаль п= (cos a, cos p\ cosy), напр. ¦*—г~7»П'>
Для ориентированной поверхности S+ определяют
поверхностные интегралы второго
рода по формулам
'1FC:, у, z) cosydS,
F(x, у, z)cosadS, > C)
У, z)dydz=\j'{jSF(x, у, *)c
где в правой части стоят П. и. 1-го рода. Если 5~ —
поверхность S с ориентацией, противоположной ори-
ориентации S h, то
^ _F(x, у, z)dxdy=-f\j<\)S+F(x, у, z)dxdy.
Аналогичные равенства имеют место в случае осталь-
остальных П. и. 2-го рода C). Как и П. и. 1-го рода, П. и.
2-го рода являются пределами интегральных сумм,
к-рые можно описать п терминах поверхности.
Если п= а " , то справедлива формула
1»\,Хг
И
s+ F (х, у, z) dxdy =
F (х (и, v), у (и, v), z (и, v)) -Q ' v) dudv.
Аналогичные формулы справедливы и для других
П. и. 2-го рода C).
В частности, для случая поверхности z=f(x, у),
(.г,
(x, у, f(x, y))dxdy,
x, у, z)dxdy= — ^GF (x, y, j(x, y))dxdy.
Первый из этих интегралов наз. интегралом по «верх-
«верхней» стороне поверхности S, а второй — по «нижней».
г Хг
Эта терминология связана с тем, что вектор »=- ~
'ги 'V
в случае явного задания поверхности S, т. е. когда
х~и, y=v, z=f(x, у), составляет острый угол с осью
z, т. е. направлен «вверх», а во втором случае — тупой
угол и, следовательно, направлен «вниз».
Если гладкая поверхность S является границей
ограниченной области и S+ обозначает ее ориентацию
с помощью внешней, а, значит, S~ с помощью внут-
внутренней, нормали по отношению к указанной области,
то П. и. 2-го рода по ориентированной поверхности S +
наз. П. и. по внешней стороне поверх-
поверхности, а по S~ — П. и. по внутренней
стороне.
П. и. по кусочно гладким поверхностям, к-рые
могут быть разбиты на конечное число частей, каждая
из к-рых имеет векторное представление A), опреде-
определяются как суммы П. и. по соответствующим частям.
Так, определенные П. и. по кусочно гладким поверх-
поверхностям не зависят от способа разбиения поверхности
на указанные части.
Остроградского формула устанавливает связь между
тройным интегралом по трехмерной ограниченной
области и П. и. по ее границе, а Стокса формула —
между П. и. и криволинейным интегралом по контуру,
являющимся ее краем.
П. и. \ I dS равен площади поверхности S. Если
на поверхности S распределена масса с плотностью
F(x, г/, z), то И. и. \ \ F(x, у, z)dS равен величине
всей этой массы. Если а^а (х, у, z) — векторная функ-
функция, заданная на ориентированной с помощью единич-
единичной нормали п поверхности S, то П. и.
И
an dS
S
наз. потоком векторного поля о через
поверхность S. Очевидно, он не зависит от выбора
системы координат в пространстве R3. С помощью
П. и. записывают двойного слоя потенциал и простого
слоя потенциал.
Если поверхность S является дифференцируемым
многообразием, непрерывно дифференцируемые не-
неотрицательные функции (fj (х, у, z), / = 1, 2, . . ., т,
образуют разбиение единицы на S, т. е.
носитель каждой функции содержится в пек-рой карте
многообразия S и ^,/!=1ф/(г, У, z)=l для каждой точки
(jo, y,z)?S,a функция F(x, у, z) определена на S, то,
по определению,
где каждый интеграл в правой части понимается в
смысле B). Если S+—ориентированное двумерное
многообразие, то
E)
Аналогично определяются П. и. 2-го рода других
типов C). Определения D) и E) не зависят от выбора
разбиения единицы на многообразии S.
Лит.: [!] И л ь и н В. А., П о з н я к Э. Г., Основы матема-
математического анализа, 2 изд., ч. 2, М., 1980; [2] Кудряв-
цев Л. Д., Курс математического анализа, т. 2, М., 1981; [3]
Никольский С. М., Курс математического анализа, 2 изд.,
т. 2, М., 1975; [4] Д у б р о в и н Б. А., Н о в и к о в С. П., Ф о-
менко А. Т., Современная геометрия, М., 1979; [5] Ми-
Мищенко А. С, Фоменко А. Т., Курс дифференциальной
геометрии и топологии, М., 1980. Л. Д. Кудрявцев.
ПОВЕРХНОСТНЫЙ ПОТЕНЦИАЛ — потенциал ме-
меры, сосредоточенной на нек-рой поверхности. При
решении основных граничных задач потенциала теории
применяются два вида П. п.: простого слоя потенциал
создаваемый распределенной по поверхности S мерой
с плотностью ц(у), у(Ц$; и двойного слоя потенциал
IV/ / х Г / ч 9 1 J с
w (х)= \ v (у) ^— гттт «л„,
создаваемый распределенной на S мерой с плотностью
v(y). Физически потенциал простого слоя интерпре-
интерпретируется как потенциал электрич. зарядов с плотно-
плотностью ц(у), а потенциал двойного слоя — как потенциал
диполей с плотностью v (у) (см. также Мультиполя
потенциал). Е- Я- Соломенцев.
ПОВЕРХНОСТЬ — одно из основных понятий гео-
геометрии. Определения П. в различных областях гео-
геометрии существенно отличаются друг от друга.
В элементарной геометрии рассматриваются плоско-
плоскости, многогранные П., а также нек-рые кривые П.
(напр., сфера). Каждая из кривых П. определяется
специальным способом, чаще всего как множество
точек или линий. Общее понятие П. в элементарной
геометрии лишь поясняется, а не определяется: го-
говорят, что П. есть граница тела или след движущейся
линии и т. п.
В аналитич. и алгебраич. геометрии П. рассматри-
рассматривается как множество точек, координаты к-рых удов-
удовлетворяют определенному виду уравнений (см., напр.,
Поверхность второго порядка, Алгебраическая поверх-
поверхность).
В 3-мерном евклидовом пространстве Е3 П. опреде-
определяется с помощью понятия простой П. как гомео-
гомеоморфизм квадрата в Е3. П. понимается как связное
множество простых П. (напр., сфера является объеди-
объединением двух полусфер — простых П.).
Обычно задание П. в Е3 осуществляется вектор-
функцией
r~r(x(u, v), у (и, v), z(u, v)),
где 0<м<:1, 0<:у<1, а
х = х(и, v), y = y{u, v), z = z(u, v)
— функции параметров и и и, удовлетворяющие нек-рым
условиям регулярности, напр. условию
*'» Уи z'J
гап? \~^
XV JJV "V I
(см. также Дифференциальная геометрия, Поверхно-
Поверхностей теория, 1'и.малоеа геометрия).
С точки зрения топологии П.— двумерное многооб-
многообразие. -Т. А. Сидоров.
КЗ-ПОВЕРХНОСТЬ — гладкая проективная алгебра-
ич. поверхность X, у к-рой канонич. класс тривиален
и размерность сИтЯ1(Х, Я1) пространства одномерных
дифференциальных форм на X равна 0. Для КЗ-П.
известны значения следующих инвариантов: геометрич.
род pg = Aim Я2 (X, Я2) = 1, эйлерова характеристика
структурного пучка х@)=2, этальные или (над полем
комплексных чисел) топологич. числа Бетти Ь0=Ь4=1,
&!—63:~0, ^2=22, характеристика Эйлера —Пуанка-
—Пуанкаре е(Х) — 24. Формула Римана — Роха для одномер-
одномерного обратимого пучка D на КЗ-П. приобретает вид
dim Я0 (X, D)+dim Н° (X, D-1)=-~+2+dimH1(X,D),
где (Z>J — индекс самопересечения класса дивизо-
дивизоров, соответствующего пучку D (см. Римана — Роха
теорема). Если пучку D соответствует эффективный
неприводимый дивизор, то НХ(Х, D) = 0.
Формула для вычисления арифметич. рода непри-
неприводимой кривой С на X тоже имеет простой вид:
Как следствие получается, что (CJJ>—2, а равенство
(СJ~—2 будет выполнено только для гладких рацио-
рациональных кривых. Отсюда также следует, что (DJ —
четное число для любого дивизора D. Пусть N (X) —
группа Нерона — Севери поверхности X, т. е. группа
классов дивизоров на X относительно алгебраич.
эквивалентности. Тогда N (X) —свободная абелева
группа ранга р, где 1«:р«:20, если характеристика
основного ноля к равна 0, и 1<:р<20 или р=22, если
char &>0. Индекс пересечения определяет на N (X)
целозначную билинейную форму, у к-рой квадрат
любого элемента четен. Поверхности с р=20 (при
char fc=0) наз. сингулярными, а с р=22 (при
char k>0) — суперсингулярными.
Еще один численный инвариант поверхности X —
это минимальный возможный индекс я самопересече-
самопересечения эффективного очень обильного дивизора на X,
т. е. минимальная возможная степень поляризации
на X. Если я=2п—2, то поверхность X можно вложить
в n-мсрное проективное пространство и нельзя вложить
в проективное пространство меньшей размерности.
Важный способ изучения КЗ-П.— представление их
в виде семейства (пучка) эллиптич. кривых. Поверх-
Поверхность X представлена в виде семейства эллиптич.
кривых, если задано регулярное отображение т : X —«-
—>- Р1, все слои к-рого, кроме конечного их числа,—
пеособые эллиптич. кривые. Поверхность X может
быть представлена в таком виде тогда и только тогда,
когда в группе N (X) есть ненулевой элемент с индек-
индексом самопересечения 0, причем всевозможные такие
представления соответствуют классам эффективных
дивизоров с индексом самопересечения 0. Если по-
поверхность, представленная в виде семейства эллиптич.
кривых, является КЗ-П., то у нее нет кратных слоев.
Построенное по такому семейству якобиево эллиптич.
семейство снова будет КЗ-П.
Важный класс КЗ-П.— Нуммера поверхности. Кум-
мерова поверхность — это неособая модель фактора
двумерного абелева многообразия А по подгруппе
автоморфизмов, порожденной отображением замены
знака. В частности, куммеровой будет поверхность,
задаваемая уравпепием хо+х*+.г2+л:з=О в Р3. Любая
гладкая поверхность 4-й степени в Р3 является КЗ-П.
Поверхностями КЗ будут гладкие поверхности, полу-
получаемые как пересечение трех гиперповерхностей 2-й
степени (квадрик) в Р5 и как двойное накрытие пло-
плоскости с кривой ветвления 6-й степени.
Все КЗ-П. над полем комплексных чисел диффео-
морфны, их многообразие модулей связно и имеет раз-
размерность 19. Строение этого многообразия модулей
и автоморфизмы КЗ-П. изучают при помощи отобра-
отображения периодов. Для КЗ-П. над полем комплексных
чисел отображение периодов биективно (теорема тина
Торелли) (см. [2]).
Если задано одномерное семейство КЗ-П. (над С)
с одним вырожденным слоем, то после накрытия базы
его можно перестроить, не меняя вне вырожденного
слоя, так что этот вырожденный слой либо станет
невырожденным, либо будет одного из двух типов: (а)
компоненты вырожденного слоя и кривые пересечений
рациональны, двойственный полиэдр вырожденного
слоя имеет топологич. тип двумерной сферы, (б) ком-
компоненты вырожденного слоя составляют цепочку,
непустое пересечение имеют только соседние поверх-
поверхности, крайние две поверхности рациональны, сред-
средние — эллиптические линейчатые, кривые пересече-
пересечения — эллиптические. Типы (а) или (б) возникают,
когда монодромия семейства нетривиальна (см. [2]).
КЗ-П. над алгебраически замкнутым полем положи-
положительной характеристики допускают подъем в характе-
характеристику нуль, модули их кристаллич. когомологий не
имеют кручения, а ранги этих модулей совпадают с
размерностями соответствующих этальных когомоло-
когомологий. Для суперингулярных поверхностей построен
аналог отображения периодов, и для него тоже дока-
доказана теорема типа Торелли. Многообразие периодов
здесь неприводимо, полно, имеет размерность 9 и
унирационально. Описаны все возможные для супер-
суперсингулярных поверхностей формы пересечений на
N(X), их 9 для каждого значения характеристики
основного поля (см. [4]).
Лит.: [1] Алгебраические поверхности, М., 1965 (Тр. Матем.
ин-та АН СССР, т. 75); [2] К у л и к о в В. С, «Изв. АН СССР.
Сер. матем.», 1977, т. 41, Хя 5, с. 1008—42; [31 Р у д а к о в А. Н.,
Ш а фаре вич И. Р., «Изв. АН СССР. Сер. матем.», 1981,
т. 45. № 3, с. 646—61; [4] Итоги науки и техники. Современ-
Современные проблемы математики, т. 18, М., 1981. А. Н. Рудаков.
ПОВЕРХНОСТЬ ВТОРОГО ПОРЯДКА — множество
точек 3-мерного действительного (или комплексного)
пространства, координаты к-рых в декартовой системе
удовлетворяют алгебраич. уравнению 2-й степени
а22г/2 -f a33z2 + 2ахгху + 2a13xz -j- 2ai3yz +
Уравнение (*) может и не определять действительного
геометрич. образа, в таких случаях говорят, что урав-
уравнение (*) определяет мнимую П. в. п. В зависимости
от значений коэффициентов общего уравнения (*)
оно может быть преобразовано с помощью параллель-
параллельного переноса и поворота системы координат на нек-рый
угол к одному из 17 приведенных ниже канонич.
видов, каждому из к-рых соответствует определенный
класс поверхностей. Именно,
невырождающиеся нераспадающие-
нераспадающиеся поверхности:
fr + "P" + -JT = '1 —эллипсоид,
хг у2 z2
¦^Г + "ьГ + "ЗГ = — 1 —мнимый эллипсоид,
х2 у2 z2
~^г-\-~ьГ — ~JT = 1 —однополостный гиперболоид,
х2 уг , z2 „
—-^г—"gr + ~ = ' —двуполостныи гиперболоид,
х2 у2
—+ —= 2z, р, q > 0 —эллиптический параболоид,
х2 у3
¦xj- — — = 2z, р, q > 0 —гиперболический параболоид;
вырождающиеся нераспадающиеся
поверхности:
цилиндрические поверхности —
— Iй 1
— эллиптический цилиндр,
—мнимый эллиптический
цилиндр,
~ _У Л
а2 Ь2 — L
— гиперболический цилиндр,
— 2рх —параболический цилиндр;
конические поверхности —
г + тг — 7Г=0 —коническая поверхность,
?1 , 11 , il_
а2 "Г 62 -f- C2 —
— мнимая коническая поверх-
поверхность;
вырождающиеся распадающиеся
поверхности:
¦—? — ~ьГ~ 0 —пара пересекающихся плос-
плоскостей,
—г 4- -jT" = 0 — пара мнимых пересекающихся
плоскостей,
х2
-^-=1 —пара параллельных плоскос-
плоскостей,
а:2-|-.а2 = 0 —пара мнимых параллельных
плоскостей.
х2 ==0 —пара совпадающих плоскостей.
П. в. п., имеющие единственный центр симметрии
(центр П. в. п.), наз. центральными по-
поверхностями. Координаты центра определя-
определяются решением системы:
— 0.
а21х
апх -+- а32у -)-
П. в. п. без центра симметрии или с неопределенным
центром наз. нецентральными поверх-
поверхностями.
Исследование П. в. п. может быть осуществлено без
приведения общего уравнения к канонич. виду. Это
достигается совместным рассмотрением значений т. н.
основных инвариантов П. в. п.— выраже-
выражений, составленных из коэффициентов уравнения (*),
значения к-рых не меняются при параллельном пере-
переносе и повороте системы координат:
а11я12а13а14
в31а32аЗЗа34
a41ai2ai3a44
, 6 =
а1Ха1г
а21а22
+
а22а23
а32аЗЗ
+
аЗЗа31
а13ац
Т =
и семиинвариантов (полуинвариан-
(полуинвариантов) Л' и Д", к-рые являются инвариантами относи-
относительно поворота системы координат:
где Д,7 — алгебраич. дополнение элемента а^, в Д;
Д" =
апаы
041^44
+
а22«24
а42а44
4-
аЗЗа34
ai3au
См. табл. 1 и 2.
Табл. 1.— Классификация поверхностей
второго порядна по инвариантам
В а
$i
§§+
Нецентраль-
Нецентральные поверх-
поверхности 6 = 0
6>.> 0,
Т> 0
6S< 0
и (или)
Т<0
Невырождающиеся
поверхности
Д > 0 | Д < 0
Мнимый эл-
эллипсоид
Однопол ост-
ный гипербо-
гиперболоид
Гиперболи-
Гиперболический пара-
параболоид
Эллипсоид
Двуполост-
ный гипербо-
гиперболоид
Эллиптиче-
Эллиптический пара-
параболоид
Вырождаю-
Вырождающиеся
поверхности
Л = 0
Мнимый ко-
конус
Действи-
Действительный ко-
конус
Цилиндриче-
Цилиндрические и рас-
распадающиеся
поверхности
(см. табл. 2)
Табл. 2.—Цилиндрические и распадающиеся
поверхности второго порядка (Д = 0, 6 = 0)
Т>0
Т<0
Г= 0
Цилиндрические по-
поверхности Д' ф 0
Эллиптический ци-
цилиндр
Мнимый
Д'в> 0
Действи-
Действительный
A'S< 0
Гиперболический ци-
цилиндр
Параболический ци-
цилиндр
Распадающиеся поверхности
Д' = 0
Пара мнимых
пересекающихся
плоскостей
Пара пересе-
пересекающихся пло-
плоскостей
Пара мнимых
параллельных
плоскостей
Д"> 0
Пара парал-
параллельных пло-
плоскостей Д" < 0
Пара совпа-
совпадающих пло-
плоскостей
Д" = 0
Инварианты в общем случае определяют П. в. п.
с точностью до движения евклидова пространства,
если соответствующие инварианты двух поверхностей
равны, то такие поверхности могут быть совмещены
движением. Иными словами, эти поверхности экви-
эквивалентны по отношению к группе движений простран-
пространства (метрически эквивалентны).
Существует классификация П. в. п. с точки зрения
других групп преобразований. Так, относительно
группы аффинных преобразований эквивалентными
являются любые две поверхности, определяемые урав-
уравнениями одного канонич. вида, напр, две подобные
П. в. п. являются эквивалентными.
Связи между различными аффинными классами
П. в. п. позволяет установить классификация с точки
зрения проективной геометрии. При этом эквивалент-
эквивалентными считаются поверхности, к-рые могут быть пе-
переведены друг в друга посредством проективного пре-
преобразования. Напр., эллипсоиды, эллиптич. параболо-
параболоиды и двуполостные гиперболоиды с точки зрения
проективной геометрии являются действительными
овальными поверхностями. Их проективная эквива-
эквивалентность проявляется в том, что существует нек-рая
система проективных координат, в к-рой уравнения
этих поверхностей имеют одинаковый вид:
Т = 0
2
2
Xl
2
Xl
2
2
Xl
2
+ ^2
+ *2
+ ^
+ 72
- 0
2 2
— Хэ — X\
+4=0
-*S=o
-0
0
т. е. соответствующие квадратичные формы Ф (xlt х2,
xs, ,r4) имеют одинаковые ранг D) и сигнатуру C).
Аффинное их различие проявляется в тине линии
пересечения с несобственной плоскостью: эллипсоиды
пересекаются с ней по мнимому овалу, гиперболоиды —
по действительному овалу, эллиптич. параболоиды —•
по паре мнимых пересекающихся прямых. Всего су-
существует 8 классов проективной эквивалентности
П. в. п.:
х\-\-х\-\-х\^гх\ — 0 —мнимая овальная поверхность,
э'1 + х\ + х\—х\-0 —действительная овальная по-
поверхность,
— кольцевидная поверхность,
— мнимая коническая поверхность,
— действительная коническая по-
поверхность,
— пара мнимых плоскостей,
— пара действительных плоскостей,
— пара совпадающих плоскостей.
Лит. см. при ст. Линия второго порядпа. А. Б. Иванов.
ПОВОРОТОВ ДИАГРАММА — поверхность в эллип-
эллиптическом пространстве Э3, определяемая изометрич-
ными гладкими поверхностями F и F* в евклидовом
пространстве Е3 аналогично тому, как определяется
вращений индикатриса для бесконечно малых изги-
изгибаний в Е3. О поверхности в эллиптич. пространстве,
совпадающей с П. д., впервые упомянул Л. Бианки
(L. Bianchi) при исследовании сферич. изображения
основания изгибания поверхностей, показавший, что
оно совпадает с изображением в смысле Клиффорда
асимптотич. линий П. д.
Пусть F и F* — изометричные гладкие одинаково
ориентированные поверхности. В соответствующих
по игюметрии точках М и М* триэдры, образованные
касательными векторами хи, xv и х.и, xv к соответст-
соответствующим по изометрии парам кривых и— const и и=
= const и нормалями п и и*, равны, т. е.
\Хи) == \ Хli) , \Х<у) ==~ \ Ху/ ,
(Н ) ::= уТ1) = 1, \Xq, Ху) = \ Хц, Xd) ,
(пхаJ = (п* xl) = (nxv) = (п* x*v) = 0,
и потому получаются один из другого поворотом вокруг
оси с направляющим ортом V на угол % (определяемый
с точностью до 2я). Пусть
X ° X
Q = cos ~2~+ V s'n~
— кватернион, по модулю равный 1 и определяемый
с точностью до знака, представляющий указанный
поворот. Совокупность таких кватернионов, парамет-
параметризованная точками M?F (или M*^F*), определяет
множество точек в эллиптич. пространстве, называемое
диаграммой поворота для изометричяых
поверхностей F и F*. Напр., если F и F* — изомет-
изометричные куски цилиндров, то П. д.— кусок поверх-
поверхности Клиффорда, причем круглым цилиндрам соот-
соответствует минимальная поверхность Клиффорда. Если
1x1 <я, то вне П. д. есть эллиптич. плоскость, и при
геодезич. отображении эллиптич. пространства в ев-
евклидово:
„ т°, . X , X • . X
Q =Fsm-2" + cos у -» у= Vtg — ,
образом П. д. является индикатриса вращений нек-рого
бесконечно малого изгибания срединной по-
поверхности, соответствующей F и ]¦'* (см. Кон-
Фоссеиа преобразование) (при условии |%|<я она регу-
регулярна).
Свойства П. д. для изометричных поверхностей
положительной гауссовой кривизны аналогичны свой-
свойствам индикатрисы вращений: напр., удельная внут-
внутренняя кривизна П. д. всюду отрицательна, и потому
она играет при исследовании изометрии выпуклых
поверхностей такую же роль, что и индикатриса вра-
вращений, м. И. Войцеховский.
ПОВТОРНОГО ЛОГАРИФМА ЗАКОН — предельная
теорема теории вероятностей, являющаяся уточнением
больших чисел усиленного закона. Пусть Х%, Х2, ¦ ¦ ¦ —
последовательность случайных величин и
Для простоты предполагается, что Sn для каждого п
имеет нуль своей медианой. В то время как теоремы
об усиленном законе больших чисел указывают ус-
условия, при к-рых ~- —>- 0 почти наверное (п. н.)
при n-v оо, где {ап} — числовая последовательность,
теоремы о П. л. з. имеют дело с числовыми последова-
последовательностями {сп} такими, что
limsup^i —1 п.н. A)
ИЛИ
limsupL5«J = l п.п. B)
п-+ оо сп
Соотношение A) равносильно тому, что
P{Sn> A + 8) С„ б.Ч.}=0
" P{Sn> A-е)спб.ч.} = 1
для любого е>0, где запись «б. ч.» означает бесконечное
число раз.
Соотношения вида A) и B) справедливы при более
ограничительных условиях, чем оценки, вытекающие
из усиленного закона больших чисел. Если {Хп} —
последовательность независимых случайных величин,
имеющих одинаковое распределение с математич.
ожиданием, равным нулю, то
'-^ ->0 п.н. при п ->¦ оо
(теорема Колмогорова); если выполнено
дополнительное условие 0<ЕХ]<оо, то имеет место
более сильное соотношение B), в к-ром
где 6= ЕХ^ (теорема Хартмана — Винт-
н е р а).
Первой теоремой общего типа о законе повторного
логарифма был следующий результат А. Н. Колмого-
Колмогорова [1]. Пусть {Хп} — последовательность незави-
независимых случайных величин с математич. ожиданиями,
равными нулю, конечными дисперсиями и пусть
s«=2Li
Если Вп -> оо при п —>-оо и существует последова-
последовательность положительных постоянных {Мп} такая, что
то выполнены соотношения A) и B) при
сп=BВпЫпВпу/К
В частном случае, когда {Хп} — последовательность
независимых случайных величин, имеющих одинако-
вое распределение с двумя значениями, это утвержде-
утверждение было гюлучено А. Я. Хинчшгым [2]. Ю. Марцин-
кевич и А. Зигмунд [3] показали, что в условиях тео-
теоремы Колмогорова нельзя заменить о на О. Обобщения
П. л. з. Колмогорова для последовательностей незави-
независимых ограниченных неодинаково распределенных слу-
случайных величин были исследованы В. Феллером [4].
Другие обобщения П. л. з. см. в [5]; имеется также
следующий результат (см. [6]), примыкающий к тео-
теореме Хартмана — Винтнера: если {Хп} — последова-
последовательность независимых случайных величин, имеющих
одинаковое распределение с бесконечной дисперсией, то
limsup !_E«J =00 пн
"-*¦" (п In п In n)V«
Результаты, полученные в области П. л. з. для
последовательностей независимых случайных величин,
послужили отправным пунктом для многочисленных
исследований применимости П. л. з. к последователь-
последовательностям зависимых случайных величин и векторов и к
случайным процессам.
Лит.: [1] Колмогоров А. II., «Math. Ann.», 1929, Bd
101, S. 12fi—35; [2] Хинчин А. Я., «Fundam. math.», 1924,
v. 6, p. 9—20; L:t] Marcinkiewicz J. Zygmund A.,
там же, 1937, v 29 p. 215—22; [4] Feller W.', «Trans. Amer.
Math. Soc», 1943, v. 54, p. 373—402; F5] S t r a s se n V., «Z. Wahr-
scheinlichkeitstheor. und verw. Geb.», 1964 Bd 3, S. 211—2«:
[6] e г о же, там же, 1965—66, Bd 4, S. 2155—68; [7] H а г t-
m a n P., W i n t n e г A., «Amer. J. Math.», 1941, v. 63, p. 169—
176; [8]Ламперти Д ж., Вероятность, пер. с англ., М., 1973;
[9] Петров В. В., Суммы независимых случайных величин,
М., 1972. В. В. Петров.
ПОВТОРНЫЙ ИНТЕГРАЛ — интеграл, в к-ром по-
последовательно выполняется интегрирование по разным
переменным, т. е. интеграл вида
A(y)t(x,y)dX]dy. A)
Функция /(.г, у) определена на множестве А, лежащем
в прямом произведении XXY пространств X и У, в
к-рых заданы 0-конечные меры цх и (х,у, обладающие
свойством полноты; множество А (у)= {.г: (х, у)?А }dX
(«сечение» множества А), измеримое относительно
меры и..,.; множество Ау (проекция множества А
в пространство Y), измеримое относительно меры \ху.
Интегрирование по А (у) производится по мере \хх, а
по А у — по мере \iy. Интеграл A) обозначают также
J^j, L J
К П. и. могут быть сведены кратные интегралы.
Пусть функция /(.г, у), интегрируемая по мере
и.= цлх Ну на множестве A CZXX Y, продолжена нулем
на все пространство XXY, тогда П. и.
х 1 (х, У) dx
существуют и равны между собой:
(см. Фубини теорема). В левом интеграле внешнее
интегрирование фактически производится по множе-
множеству А*у= {у : у?Ау, \ixA (у)>0). Таким образом, в
частности, для точек у?Ау множества А (у) измеримы
относительно меры цх. По всему множеству Ау брат),
этот интеграл, вообще говоря, нельзя, т. к. при изме-
измеримом относительно меры и, множества А множество
А у может оказаться неизмеримым относительно меры
Ну, так же, как и отдельные множества А (у), у?Ау,
могут быть неизмеримы относительно меры цх. Мно-
Множество же А у всегда измеримо относительно меры |i,r.
если только множество А измеримо относительно
меры (х.
Сформулированные условия возможности перемены
порядка интегрирования в П. и. являются лишь до-
достаточными, но не необходимыми: иногда перемена
порядка интегрирования в П. и. допустима, а соот-
соответствующий кратный интеграл не существует.
Напр., для функции f(x, у)={х,^у,у при х2+у2>0 и
/(О, 0) = 0 П. и.
S+1 Г+1 р+1 Г+1
ах \ / (.г у) dy—\ dy \ f (х, у) dx,
-1 J-l ' J-l J-1
а кратный интеграл
/ (х, у) dx dy
vij|.t|<l,|y|<l
не существует. Однако если существует хотя бы один
из интегралов
С С
тс, у) | dx или \ dx \ | / (х, у) \ dy,
то функция / интегрируема на множестве X X Y и
справедливо равенство B).
Для П. и. в случае, когда внутренний интеграл яв-
является интегралом Стилтьеса, а внешний — интегра-
интегралом Лебега, справедлива следующая теорема о перемене
порядка интегрирования: пусть функция g(x, у) сум-
суммируема по у на [с, d] для всех значений х из [а, Ь]
и является функцией ограниченной вариации по х
на [а, Ь] для почти всех значений у?\с, d]. Пусть, да-
далее, полная вариация функции g(x, у) по переменной х
на \а, Ь] при всех указанных значениях у не превы-
превышает нек-рой неотрицательной и суммируемой на [с, d]
функции. Тогда функция \ g(x, y)dy является функ-
функцией ограниченной вариации от переменной х на [а, Ъ\
и для любой непрерывной на [а, Ь] функции /(х) имеет
место формула
dy[b f (x) dxg (х, у) = \" / (х) dx Г \d g (x, у) dy~\ .
Лит.: [1] И л ыи В. А., П о з н я к Э. Г., Основы матема-
математического анализа, 2 изд., ч. 2, М., 1980; [2] Колмого-
Колмогорова. Н., Фомин С. В., Элементы теории функций и функ-
функционального анализа, 5 изд., М., 1981; [3] К у д р я в ц е в Л. Д.,
Курс математического анализа, т. 2, М., 1981; [4] Николь-
Никольский С. М., Курс математического анализа, 2 изд., т. 2, М.,
1975; [5] Смирнов В. И., Курс высшей математики, т.
5, М., 1959. Л. Д. Кудрявцев.
ПОВТОРНЫЙ ПРЕДЕЛ — предел функции несколь-
нескольких переменных, при к-ром предельный переход со-
совершают последовательно по различным переменным.
Пусть, напр., функция / двух переменных х и у опре-
определена на множестве вида XX Y, x?Xcz$lm, y? Y(zR",
и пусть хв, у0 — предельные точки соответственно
множеств X и У или символы оо (в случае, когда т — 1
пли п=1, х0 и соответственно у0 могут быть бес-
бесконечностями со знаком: +оо, —оо). Если при любом
фиксированном y?Y существует предел
<f(y) = limf(x, у) A)
и у функции ф (у) существует предел
lim <p (у),
У-*Уо
то этот предел наз. повторным пределом
lim lim / (x, у) .„.
функции f(x, у) в точке (х0, у0). Аналогично опреде-
определяется П. п.
lira lim / (х, у). C)
Если существует (конечный или бесконечный) двой-
двойной предел
lim / (х, у) ,..
(ж, у)->- (х0, у„) W
и при любом фиксированном у? Y существует конечный
предел A), то существует и П. п. B) и он равен двой-
двойному пределу D).
Если при каждом y?Y существует предел A),а при
каждом х? X существует предел
1|з (х) = lim / (х, у)
и если при i->-i, функция f(x, у) стремится на Y к
предельной функции ф (у) равномерно относительно у,
то оба П. п. B) и C) существуют и равны друг другу.
Если множества X и Y являются множествами на-
натуральных чисел, то функция / наз. в этом случае
двойной последовательностью и зна-
значения аргументов пишут в виде индексов:
f(m, n)=umn,
а П. п.
lim lim ~итп и lim lim umn
п~> ее т-*- со т-+ ее n-> x
паз. повторными пределами двойной
последовательности. Понятие П. п. обоб-
обобщается на случай, когда X, Y и множество значений
функции / являются подмножествами нек-рых тополо-
ГИЧ. пространств. Л. Д. Кудрявцев.
ПОВТОРНЫЙ РЯД — ряд, члены к-рого являются
также рядами
П. р. A) наз. сходящимся, если при любом
фиксированном и сходится ряд
и, кроме того, сходится ряд
Сумма последнего ряда и наз. суммой повтор-
повторного ряда A). Сумма
П. p. A) является повторным пределом его частичных
сумм
то есть
s = lim lim smn.
Если сходится двойной ряд
и при любом натуральном п сходятся ряды
ТО сходится и П. р. A), причем он имеет ту же сумму,
что и двойной ряд B). Условие этой теоремы выпол-
няется, в частности, если двойной ряд B) абсолютно
СХОДИТСЯ. Л. Д. Кудрявцев.
ПОГЛОЩАЮЩЕЕ СОСТОЯНИЕ цепи Марко-
Маркова | (t) — такое состояние г, что
р {I @ = г | ? (s) = i} = 1 при любых t^s.
Примером Маркова цепи с поглощающим состоянием О
является ветвящийся процесс.
Введение дополнительных поглощающих состоя-
состояний — удобный прием, к-рый помогает исследовать
свойетва траекторий цепи Маркова, связанные с до-
достижением того или иного множества.
П р и м е р. Пусть в множестве S состояний одно-
однородной цепи Маркова | (t) с дискретным временем в
переходными вероятностями
выделено подмножество Н и нужно найти вероятности
где -c(#)=min {«>0 : l(t)?H} — момент первого до-
достижения множества Я. Если ввести вспомогательную
цепь Маркова |* (t), отличающуюся от % (t) лишь
тем, что в ?* (t) все состояния h?H поглощающие, то
при k?H вероятности
монотонно не убывают при t \ со п
g,-ft = lim p*h(t), i?S,
В силу основного определения цепи Маркова
та('-т-1)=2,-еЧР.л,, @, *sso,
Phh{t) = i, h?H, p*h(t)=O, i,
Переход к пределу при t -*¦ оо с учетом (*) дает для
g,/j систему линейных уравнений:
Лит.: [1] Ф е л л е р В., Введение в теорию вероятностей и
ее приложения, пер. с англ., 2 изд., т. 1, М., 1967.
А. М. Зубков.
ПОГЛОЩЕНИЯ ЗАКОНЫ — тождества вида
х Л (х V у)~х, х V (х А у)=х,
где л и V — две двуместные операции на нек-ром
множестве L. Если, кроме П. з., эти операции удов-
удовлетворяют законам коммутативности и ассоциативно-
ассоциативности, то отношение х<.у, определяемое эквивалентно-
эквивалентностью
?<!/ HIV У = У (*)
(или равносильной эквивалентностью х<г/ <-> хЛу=х),
будет порядковым отношением таким, что хЛу — наи-
наибольшая нижняя грань, a xvy — наименьшая верхняя
грань элементов х и у. С другой стороны, если в упо-
упорядоченном множестве (?, <) существуют наибольшая
нижняя грань хЛу и наименьшая верхняя грань
xvу для любой пары элементов х, у, то для операций
V и Л выполняются законы поглощения, коммутатив-
коммутативности, ассоциативности и справедлива эквивалент-
эквивалентность (*).
Лит.: Ш Р а с ё в а Е., С и к о р с к и й Р., Математика ме-
метаматематики, Пер. с англ., М., 1972. В. Н. Гришин.
ПОГОНИ ЛИНИЯ — кривая, представляющая собой
решение задачи о «погоне», к-рая ставится следующим
образом. Пусть точка М равномерно движется по
нек-рой заданной кривой. Требуется найти траекто-
риго равномерного движения точки N такую, что
касательная, проведенная к траектории в любой мо-
момент движения, проходила бы через соответствующее
этому моменту положение точки М. В плоском слу-
случае система уравнений, к-рым должна удовлетворять
П. л., имеет вид
где — угловой коэффициент П. л., F(?, т))=0—
уравнение заданной кривой.
Задача о П. л. поставлена Леонардо да Винчи (Leo-
(Leonardo da Vinci), решена П. Буге (P. Bouguer, 1732).
Лит.: [1] С а в е л о в А. А., Плоские кривые, М., i960.
Д. Д. Соколов.
ПОГРАНИЧНОГО СЛОЯ ТЕОРИЯ — асимптотиче-
асимптотическое приближение решения граничных задач для
дифференциальных уравнений с малым параметром
при старших производных (сингулярных задач) в
подобластях с существенным влиянием членов со
старшими производными на решение. Явление погра-
пограничного слоя (п. с.) возникает в узких зонах вблизи
частей границы, на к-рых существует различие между
числом граничных условий исходной и вырожденной
(при нулевом значении параметра малости) задач, а
также вблизи поверхностей разрыва решения вырож-
вырожденной задачи.
Решение сингулярных задач представимо суммой
двух разложений. Внешнее разложение дает метод
малого параметра с частью Во граничных условий
В=В0-\-В1 задачи. Внутреннее разложение быстро
убывает вне п. с. и отыскивается, как правило, в виде
многочленов по степеням е. Для их определения диф-
дифференциальные уравнения преобразуются к неремен-
неременным, зависящим от е и растягивающим подобласти
пограничного слоя. Уравнения п. с. возникают в
результате приравнивания нулю коэффициентов при
различных степенях е после подстановки многочленов
в преобразованные уравнения. К ним добавляются
условия #!• Оценка погрешности внешнего разложения,
если она найдена, показывает необходимую замену
переменных. При решении сложных прикладных задач
необходимая замена переменных может быть выявлена
на основе физич. оценки величин членов исходных
уравнений и соответствующих им упрощений и должна
освободить старшие производные от е. Для решения
задачи необходимо определить, где расположены п. с.
и как условия В разделяются на 8, в Вг Своеобразие
такого решения заключается в том, что исходным
эллиптич. уравнением могут отвечать гшгерболич.
уравнения внешних разложений и параболические —
внутренних разложений.
В теории систем обыкновенных дифференциальных
уравнений
xt^f(x, у, t), eyt = g(x, у, t), 0<t<7\ A)
где х и / суть га-мерные, а у и g суть и-мерные век-
векторные функции, для задачи Коши с условиями х (О, е)=
=х°, у @, е)=у° и определенными свойствами fag
доказана теорема существования и единственности
решения и установлены свойства решения при е -> О
(см. [1]). В случае краевой задачи для уравнения A)
с условиями
х@, e)=i», У1@, B) = y°lt УАО, e) = yl
где сумма числа компонент векторов #, и у2 равна п,
существуют, вообще говоря, и. с. в окрестностях кон-
нов сегмента [О, 'Г]. Построен алгоритм нахождения
¦ имптотики решения этой задачи, при определенных
иойствах функций / и g доказано существование и
единственность решения и даны его оценки (см. [3]).
В случае неединственности решения предельного урав-
уравнения g~0 относительно у построен внутренний (в
окрестности т, 0<т<7') п. с, разделяющий области с
различными решениями предельного уравнения. Для
одного типа интегро-дифференциального уравнении
построен алгоритм асимптотич. разложения по е
задачи с начальными условиями и исследованы нек-рые
особенности поведения решений.
В случае линейных обыкновенных дифференциаль-
дифференциальных уравнений (L+sM)r--}(t), 0<г«1, где /, и М —
дифференциальные операторы, с граничными условия-
условиями fio4-5j выделен класс задач, решение к-рых содер-
содержит п. с, и введено понятие регулярного вырождения,
при к-ром решение предельного уравнения позволяет
удовлетворить условиям Во, а асимптотич. решение
для п. с.— условиям В1 (см. [4]). Построен итерацион-
итерационный процесс асимптотич. представления решения и
;>аньг оценки остаточных членов разложений.
В П. с. т. общего нелинейного обыкновенного диф-
дифференциального уравнения 2-го порядка при опреде-
определенных предположениях доказано (см. [5]), что реше-
решение 1-й краевой задачи складывается из внешнего
решения, п. си остаточного члена, имеющего с 1-й
производной порядок г на всем сегменте.
Изучено поведение решений красных" задач основ-
основных типов для линейного уравнения с частными про-
производными вида
еАи + А(х, у)их-\-В(х, у)иу-\ С (.г, у)и-](х, у),
где Д — оператор Лапласа, в области D с границей S.
Построены условия на функции А, В, С, /, границу S
и функции а, ср точки Р линии S, входящие в граничное
условие в„+» (Р) = <р(Р), при к-рых и п D-\S равно-
равномерно стремится к решению предельного уравнения с
приведенным граничным условием на определенной
части S (отсутствие п. с.) (см. [6]).
Для эллиптпч. уравнения 2-го порядка в области D
с границей S на примере двух независимых переменных
е [я (г, у)ихх-\2Ъ(х, у)иху + с(х, у)иуу +
+ d(x, 2/) "*"!-<¦ (*, y)uy + g(x, u)u]~\-ux —
— h(x, y)u = j(x, у), йЗза2>0,
построены итерационные процессы решения задачи с
условием и=0 на S, доказаны теоремы о структуре
разложения и по f и даны оценки остаточного члена
этого разложения (см. [4]). Аналогичные результаты
получены и для уравнений высших порядков.
Разработан (см. [7]) метод сращивания асимптотич.
разложений для уравнения
еДи — а (х, у) uy = f (х, у)
в прямоугольнике с заданным и на его границе.
Исследования II. с. т. для нелинейных уравнений с
частными производными связаны в основном с аэро-
аэрогидродинамикой и базируются на уравнениях Навье—
Стокса и их обобщениях. Запросы практики привели
как к развитию математич. теории, так и к возникно-
возникновению различных задач п методов их решения. Здесь
речь будет идти только о ламинарных течениях (см.
18] -- [10]).
Гидродинамика плоских (к—О) и осесимметричных
{к--\) течений несжимаемой жидкости с постоянным
коэффициентом вязкости v описывается уравнениями
Навье — Стокса
(Т]*н)| -bOlft'-)n =0, и% -,-uui-y-vUf]=i:-\u—pi ) \ 2
где е=Д~ '2, R--wXi\ — число Рейнолъдса, представ-
представленное через характерные величины скорости и> и
линейного размера Х- На замкнутой границе S области
D решения задаются краевые условия, причем на
обтекаемом контуре Г при т] = Я(|) задаются условия
м=0, i'—-vo{l, В (I)), где и, v — касательная и нор-
нормальная к Г составляющие вектора (и, v). В D^S
задаются начальные значения к, v. p.
При малом е асимптотам, решение задачи в первом
приближении составляется из решения уравнений B)
при е=0 с частью условий на S (на Г ставится только
условие v=v0) и решения уравнений п. с. Уравнения
динамического п. с. выводятся в предположении, что
условная толщина н. с. б и величина v имеют порядки
б ~ Хе, v ~ we, а члены левых частей последних
уравнений из B) имеют порядок членов с е2. Введение
переменных t=i, x=l, у~х\1г. V—v/e приводит при
е->0к уравнениям Прандтля
(r"u)x-\-(r4')}l=0, vt-\-uux + Vul/^UyV-px, ру---0, C)
0 < I < Г, 0 < .г < Л'„, 0 < (/ < оо ,
с условиями
и -->- W (t, х) при у ->¦ оо , рх— —WWх — Iff, и |х_о=0,
где г — расстояние от оси симметрии при к~1, W(х) —
известная функция. Эти уравнения и условия справед-
справедливы для любого криволинейного контура, радиус
кривизны к-рого много больше S. В последнем случае
.г, у — координаты вдоль контура и по нормали к
нему.
При постоянном W задача сводится к краевой для
обыкновенного дифференциального уравнения. Име-
Имеются и другие классы подобных решений.
Известны условия, при к-рых решения задач п. с.
существуют, исследованы вопросы единственности и
устойчивости решений и их выхода на решения стацио-
стационарных задач (см. [11]). Решения строятся по методу
прямых, доказана их сходимость.
Уравнения п. с. для сжимаемой жидкости выводятся
из уравнений для течений вязкого и теплопроводного
газа и значительно более сложны, чем C). Возрастает
и их количество. Имеется интегральное преобразо-
преобразование, упрощающее эти уравнения в общем случае
и сводящее их к C) при числе Прапдтля Pr=Cp/K—i,
ГД(" Ср — теплоемкость газа при постоянном давлении,
А' — коэффициент теплопроводности (см. [12]). Известен
ряд модификаций преобразования. В общем случае
уравнения п. с. описывают т. н. естественные конвек-
конвективные течения. Если v не зависит от температуры
и архимедова сила пренебрежимо мала, то уравнение
энергии отделяется от системы уравнений п. с. и гово-
говорят о вынужденных конвективных течениях. Урав-
Уравнение энергии определяет тепловой п. с. толщина
к-poro отличается от б.
П. с. возникают и в зоне раздела течений с различ-
пыми характерными скоростями. Ударные волны также
являются п. с.
Отдельный класс двумерных задач п. с. связан с тече-
течениями у вращающихся осесимметричных пластин и тел.
Вместе с развитием методов решения нестационар-
нестационарных задач решены задачи с периодическим W, при
движении скачком из состояния покоя, при ускорен-
ном движении, для п. о. за ударной волной, при пере-
переменной температуре обтекаемой поверхности.
В П. с. т. трехмерных течений развиты методы реше-
решения задач и рассмотрены случаи, приводящие к уп-
упрощению уравнений. Уравнения п. с. на скользящем
цилиндрич. крыле бесконечного размаха аналогичны
уравнениям двумерного п. с. В приближенной поста-
постановке решены задачи п. с. на вращающейся цилиндрич.
лопасти пропеллера и на вращающемся цилиндре в
косо набегающем потоке, а также задача п. с. вблизи
линии пересечения двух плоскостей.
Перечисленные исследования п. с. в аэрогидродина-
аэрогидродинамике относятся к первому приближению П. с. т. Выс-
Высшие приближения позволяют проводить исследования
взаимодействия п. с. с внешним потоком, а также
расчеты при умеренных числах R (см. [13]).
Устойчивость п. с. позволяет определить границы
применимости теории. Имеются исследования (см.
[14]) на основе метода малых возмущений с периоди-
периодическими и локальными начальными возмущениями.
В случае плоских течений анализ 3-мерных возмущений
в линейном приближении сводится на основании тео-
теоремы Сквайра к 2-морному с измененным значением v.
Нелинейный анализ при потере устойчивости обнару-
обнаруживает появление продольных вихрей.
Физич. обобщения задач П. с. т. (см. [15] — [17])
связаны с изучением многофазных течений, с исполь-
использованием реальных уравнений состояния и коэффици-
коэффициентов переноса (усложнение уравнений), с рассмот-
рассмотрением неравновесных течений с диффузией (расши-
(расширение системы уравнений и приобретение ею парабо-
лико-гиперболич. типа), с учетом абляции обтекаемой
поверхности (усложнение граничных условий и не-
необходимость расчета теплопроводности в теле), с уче-
учетом переноса излучения (интегро-дифференциальные
уравнения).
Дальнейшее развитие П. с. т. в аэрогидродинамике
получила при исследовании течений, не удовлетворя-
удовлетворяющих предположениям Прапдтля, с решениями в
виде многослойных асимптотич. разложений. Источ
пиком сложности структуры решения являются до-
дополнительные малые параметры в граничных условиях
(напр., из-за малого радиуса кривизны обтекаемого
контура), существования особых точек, линий пли
поверхностей в первом приближении П. с. т., а также
возможная бифуркация решения.
К этому классу относятся точения около точек от-
отрыва и присоединения п. с. к обтекаемому контуру и
около точек падения на п. с. ударных волн. Харак-
Характерные решения (см. [18] — [20]) имеют трехслойную
структуру. Внешнее решение определяет возмущенное
н. с. потенциальное течение и описывается уравне-
уравнениями в возмущениях. Средний слой толщины порядка
Хе описывается уравнениями невязких завихренных
течений с pv=0, и в него поступает газ из основной
части предшествующего п. с.
Уравнения 3-го, самого тонкого, пристеночного
слоя выводятся в предположении, что его длина и
толщина имеют соответственно порядки Хе,", Хе'• '¦
Введение в стационарном случае переменных
х~^г~'!\ у — Г|е~г'/4, Г/ = ме~''/4, V~x>s~'^4, P=pF~'/s
приводит при к —>. О снова к уравнениям C), в к-рых
следует и заменить на U, ар — на Р. Эта структура
решения задачи характерна для широкого класса
течений с малыми величинами возмущений.
Исследованы многие задачи динамики течений при
малых е, в к-рых на коротких расстояниях давление
во внешнем сверхзвуковом (Д/>1, M—w/с, где w —
скорость газа, с — скорость звука) потоке меняется
сильно. К ним относятся задачи расчета обтекания
контуров с большой локальной кривизной и присоеди-
нения потока к поверхности тела. В ятих случаях
при трехслойной схеме решения в среднем слое p^=cO.
Изучен класс задач, в к-рых возмущенное решение
занимает конечную область. Эти решения реализу-
реализуются на режимах умеренного и сильного взаимодей-
взаимодействия гг. с. с внешним гинерзвуковым (М —v oo) по-
потоком и при сверхзвуковом обтекании тел конечной
длины, через поверхность к-рых производится интен-
интенсивный вдув (уо>О) газа. В этих задачах величина
давления на всей внешней границе п. с. определяется
из решения полной задачи. Возмущение от задней
кромки тела распространяется вверх по потоку, что
определяется неединственностью решения в окрест-
окрестности передней кромки тела.
Лит.: [I] Тихонов А. Н., «Матем. сб.», 1952, т. 31,
Л» 3, с. 575—86; [2] Вазой В., Асимптотические разложе-
разложении решений обыкновенных дифференциальных уравнений, пер.
с англ., М., 1968; [3] Васильева А. Б., Бут у :i ив Й.
Ф., Асимптотические разложения решений сингулярно ио.ччу-
щенных уравнений, М., 1973; 14] В и ши к М. Й., .1 ю с г о \>-
ни к Л. А., «Успехи матем. наук», 1957, т. 12, в. 5, с. 3 - -122;
I960, т. 15, в. 3, с. 3—80; [5] К о у л Д ж., Методы возмущении
в прикладной математике, пер. с англ., Mi, 1972; [В] Оле й-
ник О. А., «Матем. сО.», 1952, т. 31, №1, с. 104—17; [7J
И л ь и н А. М., Леликова К. Ф., там же, 1975, т. 96, № 4,
с. 568 — 83; 18] К о ч и н Н. Е., К и б е л ь И. А., Розе
Н. В., Теоретическая гидромеханика, 4 изд., ч. 2, М., 1963;
[9] Л о й ц я н с к и й Л. Г., Ламинарный пограничный слой,
М., 1962; [10] Шлихтинг Г., Теория пограничного слоя,
пер. с нем., М., 1974; [11] О л е й н и к О. А., «Успехи матем.
наук», 1968, т. 23, в. 3, с. 3—65; [12] Дородна пы н А. А.,
«Прикл. матем. и механ.», 1942, т. 6, в. 6, с. 449—86; [13] В а н-
Д а й к М., Методы возмущений в механике жидкости, пер.
с англ., М., 1967; [14] Б е т ч о в Р., К р и si и и а л с В.,
Вопросы гидродинамической устойчивости, пер. санг.ч., М., 1971;
[15] С о у С., Гидродинамика многофазных систем, пер. с англ.,
М., 1971; [16] Дорренс У. X., Гинерзвуковые течения
вязкого газа, пер. с англ., М., 1966; [17] К з й с В. М., Конвек-
Конвективный тепло- и массообмеи, пер. с англ., М., 1972; [18] Не й-
л а н д В. Я., «Изв. АН СССР. Механ. жидк. и газа», 1ЯВ9,
.Ni 4, с. 53 — 57; 119] его же, «Тр. ЦЛГИ», 1!>74, в. 1529; [20]
Stewartson К., «Advances Appl. Mech.» 1974, v. 14,
p. 145—239. Ю. Д. Шмыглевспий.
ПОГРАНИЧНЫЙ СЛОЙ — область больших значе-
значений градиента функций, в частности в гидродинами-
гидродинамике, область течения вязкой жидкости (газа) с малок
по сравнению с продольными размерами поперечной
толщиной, образующаяся у поверхности обтекаемого
твердого тела или на границе раздела двух потоков
жидкостей с различными скоростями, температурами
или химич. составами. П. с. характеризуется резким
71зменснием в поперечном направлении скорости (д и-
н а м и ч е с к и и П. с.) или температуры (т е п л о-
в о и, и л и температурный, П. с), или ;ке
концентраций отдельных химич. компонентов (д и ф-
ф у з и о н н ы й, или концентрационный,
ТТ. с). Понятие И. си сам термин были введены J1.
Прандтлем (L. Prandll, 190'i) в связи с решением кра-
краевой задачи для нелинейных уравнений с частными
производными гидродинамики вязких жидкостей. Нуж-
Нужды развития авиации определили разработку теории
II. с. в аэрогидродинамике. В сер. 20 в. стала разви-
развиваться математическая пограничного слоя теория, а
также приложения в теории теплопередачи, диффузии,
ПрОЦеССОВ В ПОЛупрОВОДНИКаХ И Др. Ю. Д. Шмыглевский.
ПОГРЕШНОСТЬ — разность х — а, где а — дан-
данное число, к-рое рассматривается как приближенное
значение нек-рой величины, точное значение к-рой
равно х. Разность х — а наз. также абсолютной
П. Отношение х — а к а наз. относительной
П. числа а. Для характеристики П. обычно пользуются
указанием ее границ. Число Д (а) такое, что
|.г — а|<Д (а),
паз. границей абсолютной П. Число б (а)
такое, что
'Л (а),
наз. границей относительной П. Гра-
ницы относительной П. часто выражают в процентах.
В качестве Д («) и S (а) берутся по возможности мень-
меньшие числа.
Информацию о том, что число а является приближен-
приближенным значением числа х с границей абсолютной П.
Л (а), принято записывать в виде
х = а ± Д (а).
Аналогичпое соотношение для относительной П. за-
записывается в виде
z = a(l ± б (я)).
Границы абсолютной и относительной П. указывают
на максимально возможное расхождение х и а. Наряду
с ними часто употребляются характеристики П.,
учитывающие характер возникновения П. (напр.,
погрешность измерений) и частоту различных значений
разности х и а. При таком подходе к П. используются
методы теории вероятностей (см. Ошибок теория).
При численном решении задачи П. результата обус-
обуславливается неточностями, к-рые присущи формули-
формулировке задачи и способам ее решения. П., возникающую
вследствие неточности математич. описания реального
процесса, паз. П. математической модели;
возникающую вследствие неточности задания исход-
исходных данных — П. входных данных; возника-
возникающую вследствие неточности метода решения — П.
метода; возникающую вследствие неточности вы-
вычислений --вычислительной П. Иногда П.
математич. модели и П. входных данных объединяют
под одним названием — неустранимая П.
В процессе вычислений исходные П. последовательно
переходят от операции к операции, накапливаясь
и порождая новые П. Возникновение и распространение
П. в вычислениях являются предметом специальных
исследований (см. Вычислительная математика).
Лит.: [1] Б е р е з и н И. С, Жидков Н. П., Методы
вычислений, 3 изд., т. 1, М., 1966; [2J Бахвалов Н. С.,
Численные методы, 2 изд., М., 1975; [3] Воеводин В. В.,
Вычислительные основы линейной алгебры, М., 1977.
Г. Д. Ким.
ПОГРУЖАЮЩАЯ ОПЕРАЦИЯ — в математической
логике операция, переводящая выражения одного
логико-математич. языка в выражения другого с со-
сохранением тех или иных дедуктивных свойств. П. о.
широко используются для установления взаимосвязи
между различными логич. теориями, исчислениями.
Напр., если формуле А формальной арифметики со-
сопоставить формулу А* этого же языка, вставив два
отрицания перед ней и перед каждой ее подформулой
(напр., (А\/В)* есть ~| ~] (~) "]А* V 15*), а (jxA)*
есть i ~1зж~1 П^*> и т- Д-)> т0 из выводимости А в
классической формальной арифметике следует выво-
выводимость А* уже в интуиционистской формальной
арифметике. Отсюда вытекает, что непротиворечивость
интуиционистской формальной арифметики влечет не-
непротиворечивость и классической формальной ариф-
арифметики. Описанная негативная интерпре-
интерпретация Гё деля позволяет, следовательно, ука-
указать важное взаимоотношение между интуиционист-
интуиционистской и класенч. арифметиками.
Другой типичный пример П. о.— перевод Г ё-
деля — Тарского, позволяющий установить вза-
взаимосвязь модальных и интуиционистских логик. По-
Построение моделей в аксиоматич. теории множеств также
может быть обычно интерпретировано синтаксически
как построение нек-рой П. о.— внутренней модели
теории множеств.
Лит.: [1] Шенфилд Д ж. Р., Математическая логика,
пер. с англ., М., 1975; [2] Фейс Р., Модальная логика, пер.
с англ., М., 1974; [31 Д р а г а л и н А. Г., Математический
интуиционизм, М., 1979. А. Г, Драгалин.
ПОГРУЖЕНИЕ, п м мерс и я,— отображение
/ : X -v Y одного топологич. пространства в другое,
при к-ром каждая точка в X имеет окрестность U. к-рую
/ гомеоморфно отображарт на fU. Это понятие приме-
применяется главным образом к отображению многообразий,
где часто дополнительно требуется еще выполнение
условия локальной плоскости (такое же, как и для
локально плоского вложения). Последнее условие авто-
автоматически выполнено, если многообразия X и Y яв-
являются дифференцируемыми, и матрица Якоби ото-
отображения / имеет в каждой точке максимальный раиг,
равный размерности X. Задача классификации П.
одного многообразия в другое с точностью до т. н.
регулярной гомотопии сведена к чисто гомотопич.
задаче. Гомотопия ff. Xm —>¦ Y" наз. регуляр-
регулярной, если для каждой точки х?Х она может быть
продолжена до изотопии Ff : UXDk -> Y, где U —
окрестность х, Dk — диск размерности к— п—т, и Ff
совпадает с /; на Г/ХО, где 0 — центр диска. В диффе-
дифференцируемом случае достаточно потребовать, чтобы
матрица Якоби имела максимальный ранг при каждом
t и непрерывно зависела от t. Дифференциал Dj П.
определяет послойный мономорфизм касательного рас-
расслоения %Х в касательное расслоение %Y. Регулярная
гомотопия определяет гомотопию таких мономорфиз-
мономорфизмов. Оказывается, что этим устанавливается биекция
-Между классами регулярных гомотопии и гомотопич.
классами мономорфизмов расслоений.
Задача П. в евклидовы пространства сводится к
задаче гомотопич. классификации П. в Штифеля
многообразия Vn,m- Напр., так как я2СГЯ1 2)—О, то
имеется только один класс П. сферы S2 в R3, так что
стандартное вложение регулярно гомотопно своему
зеркальному отражению (сферу можно «регулярно
вывернуть наизнанку», см. рис.). Так как F2,i«S1,
то имеется счетное число классов П. окружности в
плоскость, а т. к. расслоение Штифеля над S2 гомео-
гомеоморфно проективному пространству R.P3 и n1(RP!i) =
— %г, то имеется только два класса погружений S1
В S^r и Т. Д. ^- #• Чернавский.
ПОГРУЖЕНИЕ многообразия — непрерыв-
непрерывное отображение F: Л/т->- N" т-мерного многообра-
многообразия Мт в гс-мерное многообразие N" такое, что для
каждой точки х?Мт существует окрестность Ux, для
к-poiiFecTb вложение, т. е. гомеоморфизм на F (Ux)czNn.
В частности, если F есть гомеоморфизм на F(Mm),
то он наз. вложением Мт в N". Погружение
F наз. С1- а-п о г р у ж е н и е м, если Мт и Nn суть
С', "-гладкие многообразия (^1, 0<а<1, т*сп)
и отображение F в соответствующих картах задается
функциями
!'' = /' (и1, . . ., Um), 1 = 1, . . ., П,
принадлежащими классу гладкости С1-а, а рант
матрицы "
—~ равен т в каждой точке xGMm{C -
гладкое многообразие — многообразие, наделенное Г-
структурой, где псевдогруппа состоит из I раз диффе-
дифференцируемых отображений, производные к-рых удов-
удовлетворяют условию Гёльдера с показателем а).
К понятию П. и С', «-гладкого II. непосредственно
примыкают понятия поверхности и С1- «-гладкой по-
поверхности. Погружения /' и G многообразия М в А
наз. эквивалентными, если существует такой гомео-
гомеоморфизм Ф : М —>- М, что F~-G($.
Погруженным многообразием наз.
пара, состоящая из многообразия М и его погруже-
погружения F. т-ш ерной поверхностью в га-мерном
многообразии N" наз. класс эквивалентных погружений
F : Мт ->- N"; каждое П. этого класса наз. пара-
параметризацией поверхности. Поверхность
наз. С а-г л а д к о й, если на многообразиях М
и N можно ввести С- "-структуры и если среди пара-
параметризаций поверхности найдется такая параметрп-
зация /', т:-рая в этих структурах оси, С1- «-погруже-
«-погружение.
Теория погруженных многообразий, как правило,
особенно в тех случаях, когда рассматриваются во-
вопросы, связанные с геометрией П., изучает свойства,
инвариантные относительно введенного выше понятия
эквивалентности, и по существу совпадает с теорией
поверхностей.
Пусть Мт есть С1- "-многообразие, />1, 0<а<1.
Всякое Мт допускает при m~^z\ вложение в евклидово
пространство R2m и С'"' "-погружение в R2m ~ :при
т^2. Если т положительно и не является степенью
двойки, то всякое Мт допускает (?'¦ "-вложение в
R2m~', в то же время при любом m=2s с sJsO сущест-
существуют замкнутые гладкие m-мерные многообразия, не
допускающие даже топологич. вложения в R2"-1
(таково, напр., проективное пространство). Если Мт
не имеет компактных компонент, то оно допускает
С1' «-вложение в R2™-1.
Ориентируемое /в-мерноо многообразие при тф\Л
допускает б1'-"-вложение в R2m->. Вопрос о воз-
возможности погружения /«-мерного многообразия в
R2m при п<2т — 1 связан с классами Уитни и Понтря-
гина классами этого многообразия. Известно также,
что каждое С1- "-гладкое /«-мерное многообразие с,
/5=1, 0<:а<1 допускает собственное (т. е. такое, что
прообраз каждого компактного множества компактен)
П. в К'1'" и собственное вложение в R2"» + I. Если на
Мт задана риманова метрика, то часто рассматривают
изометрическое погружение Мт в R" или другое
риманово пространство Л'". С- "-гладкое риманово
многообразие, 1=2, 0<а<1; />2, 0<:а<1, допускает
С1' "-гладкое изометрическое II. в нек-рое R". В слу-
случае компактного Мт число п= Bm-j-l) Fm + 14).
Наоборот, С/а-гладкое П. (/Ss2, 0 < а < 1) Мт в
К™ индуцирует на Мт С."-гладкую риманову мет-
метрику [4].
Лит.: 11] П it f л л С, «Успехи матем. наук», 1964, т. 19
в. 1, с. 12Г>—38; Vl\ Jacobowitz H., «Ann. Math.» 1972,
v. 95, № 2, p. 191 —22ft; [3] P о х л и н В. А., Фукс Д. Б.,
Начальный курс топологии. Геометрические главы, М., 1977;
[4] Сабитов И. X., Шефель С. 3., «СиГ>. матем. ж.»,
1976, т. 17, №4, с. 91 'i — '2о. С. 3. Шефелъ.
ПОГРУЖЕННЫХ МНОГООБРАЗИЙ ГЕОМЕТРИЯ —
теория, изучающая внешнюю геометрию и связь между
внешней и внутренней геометрией под-
подмногообразий евклидова или риманова пространства.
К. м. г. является обобщением классич. дифференци-
дифференциальной геометрии поверхностей в евклидовом про-
пространстве R3. Локально внутренняя и внешняя гео-
геометрии погружения многообразия обычно описываются
соответственно с помощью первой и второй квадра-
квадратичных форм. Для погружений m-мерного многооб-
многообразия Мт в многообразие N" существует понятие
.(Квивалентности (см. Погружение многообразия). В
П. м. г. изучаются свойства, одинаковые у эквива-
эквивалентных погружений, т. е. свойства поверхности Fm,
определяемой погружением /. В связи с этим в гео-
геометрических вопросах погружение и поверхность не
различаются. Погружение / индуцирует отображение
'II : ТМ'" —>- TN" касательных расслоений.
Первая квадратичная (фундамен-
(фундаментальная) форма f поверхности /¦' определяется
на ТМт равенством
иР(Х, У)-ё/1рАХ, Y),
р?т, X, V>c ТМ'". а ц — риманова метрика в Л"',
^десь и далее векторы Л" ? ТМт не различаются в обо-
обозначениях с их образом df(X). Квадратичная форма g
определяет на Мт структуру риманова пространства
Wg1; свойства М™ составляют предмет внутренней
геометрии поверхности F. Если {xk}, {(/"}, k—i, . . .,
т, а~1, . . ., п,— локальные координаты в Мт и
N", то погружение / задается параметрич. уравне-
уравнениями ya = fa(x1, . . ., хт). В локальных координатах
где {X'}, {У}— координаты векторов X, Y,
а {gafi} — компоненты метрич. тензора g риманова
пространства Л'".
К внутренней геометрии поверхности F принадлежат
такие понятия, как длина кривой, объем области, связ-
связность Леви-Чивита у^ внутренней метрики, ее преобра-
преобразования кривизны Я (X, Y)Z и т. д. Относящиеся сю-
сюда вычислит, формулы см. в ст. Риманова геометрия.
Вторая (фундаментальная) форма
// определяется равенством
н(х, >v=(vxy)P-(V)/;,
где V) V — связности Леви-Чивита на Л'", Мт соот-
соответственно. Фактически // зависит не от векторных
полей Л", У, а лишь от их значений в точке р и является
билинейным симметричным отображением
(ТМт)рх(ТМт)р > (хМ'»)р,
где \Мт — нормальное расслоение Мт в А". Для каж-
каждого единичного вектора ?? (vMm)f, равенства
<Н(Х, У), t}p = h?(X, Y)p <Л|(Д-), Y>p
определяют вторую квадратичную фор-
форму /ig и в т о р о й фундаментальный т е н-
з о р ~А\. В локальных координатах компоненты /г,-_,-(?.)
формы /г| имеют вид
u.x'dx)
где {|Р} — координаты вектора ?.
Для формы h^ обычным образом (т. о. так же, как
для поверхности в евклидовом пространстве R3)
определяют главные кривизны, главные направления
(зависящие от |) и другие связанные с ними понятия.
Исходя из элементарных симметрич. функций, можно
строить различные функции главных кривизн. Таковы,
напр., средняя кривизна
1 1/vim+n
я ^--
т
где {§,} — ортонормированный набор нормалей, а
Л",-(?) — главные кривизны формы h ,•; кривизна
Чжэня — Лашофа
А' =—
где щ — объем сферы S1; длина второй основной
формы
(см. [1] - [3]).
«Значение первой и второй квадратичных форм по-
поверхности в точке р определяет ее вблизи /) с точно-
точностью до бесконечно малых 2-го порядка. Каждому
?? (vMm)p, ||| = 1, соответствует соприкасающийся па-
параболоид. (Для поверхности в евклидовом простран-
пространстве — это соприкасающийся параболоид для про-
проекции поверхности на (то+1)-нлоскость, определяемую
(ТМт)р и |.) При то---;? — 1 (т. е. в случае гиперповерх-
гиперповерхности) форма hi единственна с точностью до знака.
В этом случае вторые фундаментальную и квадратичную
! формы не различают, и теория приобретает большое
i сходство с классич. теорией поверхностей в R3.
Основные уравнения. Коэффициенты пер-
uoi'i и кторой квадратичных форм не являются неза-
независимым!!. Они связаны уравнениями Гаусса и Петер-
comt — Кодацци — Майнарди.
Уравнения Гаусса
R(X, Y)Z = fi(X, Y)Z-H(X^xZ)-\-II(Y,\xZ)-^
+ #([*, У], Z) A)
выражают преобразование кривизны поверхности F
через преобразование кривизны N" и коэффициенты
квадратичных форм (здесь [• , ¦] — скобка Пуассона).
Инвариантная форма уравнений Петерсона — Ко-
Кодацци — Майнарди связана с понятием риманова рас-
расслоения над М™. Расслоение Е (I) Z-мерных плоско-
плоскостей над римановым многообразием М™ наз. р н м а-
н о в ы м, если в Е (I) задана риманова метрика < • , ¦>/?
и риманова (т. е. согласованная с метрикой) связность
U ; ТМ"Х Е —>- Е. Билинейное g-симметричное ото-
отображение
А\ : ТМ">хЕ -* ТМт
паз. вторым фундаментальным т е н з о-
р о м в Е; равенство
<Н(Х, Y), l>E^(AiX, Y>g
определяет вторую фундаментальную форму в Е, ас-
ассоциированную с А\. Уравнения
VXAtY— VyaIx^=ad Y—AdX, B)
Н(Х, Y)l = H(AiX, Y) — H(X, AiY), C)
где Я — форма кривизны связности D, наз. урав-
уравнениями Петерсона — Кодацци —М а й-
н а р д и. Уравнения C) часто наз. уравнениями
I' и ч ч и (координатную запись уравнений B) — C)
см. в [1]). Уравнения B) — C) всегда выполнены,
если Е (I) — нормальное расслоение М'п в N" и Dх%
равно проекции Vx? на (v^m)p-
Имеется следующее обобщение Бонне теоремы (см.
|2|). Пусть Е (I) — риманово расслоение над односвяз-
ным Л/у и пусть па Е (I) задан второй фундаментальный
тензор Л| . Если при этом выполняются соотношения
A) — C), то существует изометрич. погружение М™
в евклидово пространство R'" + l с нормальным рас-
расслоением ЕA). Такое погружение единственно в сле-
следующем смысле: если /, /' — изометрич. погружения
М™ в R'" + ' с нормальными расслоениями Е, Е', осна-
оснащенными, как и выше, и нек-рая изометрия (р: М™—>¦ М™
накрывается отображением (р: Е —>• Е', согласованным
с оснащенным, то существует такая изометрия Ф про-
пространства R'n+l, ЧТО Фо/=/'оф.
Классы погружений. Многомерная П. м. г.
возникла и долгое время развивалась как теория су-
существования изометрич. погружений римановых мно-
многообразий как правило в К", реже — в пространство
постоянной кривизны К (см. Изометрическое погру-
погружение). Что касается внешне геометрич. свойств и
связей между внешней и внутренней геометрией по-
поверхностей, то она подробно изучена только для дву-
двумерных поверхностей в R3. В этом случае существует
классификация точек поверхности, с помощью к-рой
двумерные поверхности разбиваются на классы: вы-
выпуклые поверхности, седловые поверхности и развер-
развертывающиеся поверхности. Именно эти классы явля-
являются основным объектом изучения в дифференциальной
геометрии в целом. В многомерном случае такая клас-
классификация точек поверхности неизвестна A983). Из-
Известны только нек-рые классы многомерных поверхно-
поверхностей: А--выпуклые, /с-седловые и ^-развертывающиеся.
к-в ы п у к л ы е поверхности. Поверхность
рт в ?к наз д._в ь[ и у к л о и, если д.!:i каждой точки
p?Fm существует нормаль |^? iyFm)p, ЛЛ'Л к-рой hp(\)
положительно определена, и для любого /с-мерного
направления о&? (TF'")p, 2<fe<m, найдется в ак дву-
двумерное направление а2 такое, что крA,)(Х, У)>0
(либо hp(l)(X, У)^=0) для каждого ?„? (чРт)р при
X, У?сг2, X, У7~0. 2-вьшуклая поверхность F'" в К"
есть выпуклая шпсрповерхность в Rm + LcR" (см.
[4]). Внутренняя метрика /с-выпуклой поверхности
обладает следующим свойством: в каждой точке /<
для каждого А:-мерного направления ст/г касательного
пространства найдется двумерное направление 02Са/г,
в к-ром риманова кривизна строго положительна.
к-с едловыо поверхности. Поверхность F"<
в R" наз. к-с в д л о в о й, если каждой ее точке р для
каждой нормали ?(z (vFm)p число собственных значе-
значений /г^(|) одного знака не превосходит (к—1), 2<&«:7?i.
Двумерная /с-седловая поверхность есть обычная сед-
ловая поверхность в R", от к-рой нельзя отсечь «гор-
«горбушку» гиперплоскостью. Внутренняя метрика /с-сед-
ловой поверхности обладает следующим свойством:
в каждой точке р для каждого Амперного направления
од. касательного пространства найдется двумерное
направление оСа/г> в к-ром риманова кривизна не
положительна. Если /с-седловая поверхность полна в
R", то ее гомологии Я,-(F'") = 0 при t>/c (cm.[4j, [5]).
Полная m-мерная fe-седловая поверхность F'" с неот-
неотрицательной кривизной Риччи есть цилиндр с(т--
—&+1)-мерной образующей.
к-р азвертывающиеся (А:-п а р а б о л и ч е-
ские) поверхности. Поверхность Fm в R"
наз. к-р азвертывающейся, если в каждой ео
точке р существует fc-мсрное направление a/cci(TJ<'m)p,
к-рое состоит из собственных векторов, принадлежа-
принадлежащих нулевому собственному значению матрицы второй
квадратичной формы относительно каждой нормали в
данной точке. Внутренняя метрика fc-развертывающей-
ся поверхности обладает следующим свойством: г,
каждой точке р найдется подпространство а/; касатель
ного пространства (TF'")p размерности к такое, что
Яху—У Для любого вектора X^-GkFi гДе ^€: {Т1'1т)р —
любой вектор касательного пространства, Иху—
оператор кривизны. Если ^-развертывающаяся по-
поверхность Fm полна в R™ и несет на себе внутреннюю
метрику неположительной кривизны Риччи, то она
является цилиндром с /с-мерной образующей [6'|.
Свободные погружения. Если обраи
Нр(Х, Y) в каждой точке p?Fm имеет максимально
возможную размерность та(т+1)/2, то погружение
наз. свободным. В этом случае первые и вторые
производные радиус-вектора погружения Fm образуют
линейно независимую систему. В классе свободных
погружений существует изометрич. погружение в
размерность n>m(m+l)/2+3m+5, но при этом пол-
полностью теряется связь между внутренней и внешней
геометрией. Напр., два свободных изометрич. погру-
погружения m-мерного многообразия Мт в R", п~>т(т-\-
+ l)/2-f Зт+5, можно соединить гомотопией, состоящей
из свободных изометрич. погружений Мт (см. [7]).
Погружения с малой коразмерно-
коразмерностью. Если коразмерность q погружения мала, то
из условий на внутреннюю метрику многообразия
вытекают условия на вторую квадратичную форму
поверхности. А из свойств второй квадратичной формы
далее выводятся топологические и внешне геометрич.
свойства поверхности. В частности, получаются тео-
теоремы непогружаемости. Так, если Мт с секционной
кривизной Ко <() изометрически погружено в Rm+?c
(?<m, то Мт есть (<?+1)-седловая поверхность и ее
гомологии (в случае полноты) Н^—О при k~^qA-\
(см. [5]). В частности, компактное Мт с Ка <0 не
может быть погружено в R-™-1 (см. [8], [9]). Если же
Ко <0, то Мт даже локально непогружаемо в R2"'-'2
(см. [9]). Аналогично, Мт с Л'о <1 неиогружаемо в
сферу 52т~2радиуса 1. Компактное Fm в S2m~1 имеет
нулевую эйлерову характеристику и компактное па-
раллелизуемое накрывающее многообразие, если Ко <1
(см. [10]). О поверхности Fm в Rm + 4 при q*g.m-;-2г— 2
и Ка <0 известно, что ео нормальные Ноптрягина
класса удовлетворяют условию
Если Хо >0, то из <?<т—1 следует, что 1'т есть (g
выпуклая иоверхность [9]. В частности, при q—i
это 2-выпуклая поверхность. Если Ка >0 и (?т-2, то
компактная поверхность Fm, т^З, имеет гомологии
сферы [llj. Если F в R |? имеет неположительную
секционную кривизну, то она — (т— </(д+1))-развер-
тываюшаяея и, в случае полноты, Fm есть цилиндр с
(m—q(q-\- 1))-мерной образующей [10]. Если же Мт—=
-=М*Х R'l~k и <7</г—2&, то погружение многообразия
Мт в Rm+? есть (т—2k—д)-развертывающаяся по-
поверхность [8] и, в случае полноты, Fm есть цилиндр с
(т—2k—д)-мерной образующей. При более общих,
предположениях компактная поверхность
М"' = МР'Х-..ХМ1'1 -- R" + 9, p/Sa2,
есть произведение гиперповерхностей [12].
,7шп.: [1] Эйзенхарт Л., Риманона геометрия, пер.
с англ., М,, 1948; [2] Chen В., Geometry of submanifolds,
N.Y., 1973; [3] С hern S.-s., Lisliol R. K., «Amer. J.
Math.», 1957, v. 79, p. 306—18; [4] Ш е ф е л ь С. 3., «Сиб. ма-
тем. ж.», 1969, т. 10, № 2, с. 459—66; [5] Г л а з ы р и п В. В.,
«Докл. АН СССР», 1977, т. 233, Л5 6, е. 1028 — 30; [С] Hart-
man P., oTrans. Amer. Ma1h. Soc.» 1965, v. 115 p. 94 — 109
1970, v. 147, p. 529 —40; 171 Громов М. Л., «Докл. АН СССР»,
1970, т. 192, Л 6 с. 1206 -09; [8] С h e r n S., К u i p e r N.
-Ann. of Math.», 1952, v. 56, № 3, p. 422—30; [9] Б о р о н-
i'bkII Ю. Е,, Ш е ф е л ь С, 3 ., «Сиб. матем. ж.», 1978, т. 19,
,N5 6, с. 1386—87; [10] Б о р и с е н к о А. А., «Матем. сб.»,
1977, т. 104, №4, с. 559—76; [II] Moore J., «Proc. Amer.
Math. Soc», 1978, v. 70, №1; [12J Gardner R. B. «Bull.
\mer. Math. Soc», 1977, v. 83, № 1, p. 1 — 35,
В. А. Тононогов, С. З. Шефель.
ПОДВИЖНАЯ ОСОБАЯ ТОЧКА — особая точка
z0 решения дифференциального уравнения /-'(г, w, iv')~0
(F — аналитпч. функция), рассматриваемого как функ-
функция w(z) комплексного переменного z, при условии,
что решения того же уравнения с близкими начальными
данными имеют близкие к z0 особые точки, не совпада-
совпадающие с zu. Классич. пример П. о. т. возникает при
рассмотрении уравнения
dw Р (г, w)
</z ~ Q (z, v) '
i де Р и Q — голоморфные функции в нек-рой области
пространства С2. Если поверхность {Q-=0} неприво-
дима и проектируется вдоль оси Uw на область QczOz,
то все точки области Q являются П. о. т.; для решения
с начальным условием (=(|, w0), где
Q - (z0, "•о)-О ф Р (z0, i/'o),
iочка z0 — алгебраическая точка ветвления.
Лит.: llj Голубев В. В., Лекции но аналитической
теории дифференциальных лравпений, 2 изд., М.— Л., 1950.
Ю. С. Ильягиенко.
ПОДВИЖНОГО РЕПЕРА МЕТОД — дифференциаль-
дифференциально-геометрический метод локального исследования под-
подмногообразий различных однородных пространств,
исходным моментом к-рого является отнесение самого
подмногообразия и всех его геометрич. объектов к
возможно более общему (подвижному) реперу. П. р. м.
включает в себя последующий процесс канонизации
репера — инвариантного присоединения к каждой точ-
точке подмногообразия единственного репера с целью
получения дифференциальных инвариантов, характе-
характеризующих подмногообразие с точностью до преобра-
преобразований вмрщлюггрго его однородного пространства.
В наиболее общей форме П. р. м. был предложен П. Кар-
таном (Е. Cartan, см. |1]), давшим разнообразные ofi-
раицы его применений. Позднее метод получил широкое
распространение и развитие (см. Продолжений и охва-
охватов метод). Аналитлч. основу П. р. м. составляют
инвариантные линейные дифференциальные формы
группы Ли и их структурные уравнения, а также теория
представлений групп Jin как групп преобразований.
В современной геометрии основные положения II. р. м.
потребовали уточнений и получили оформление в
терминах теории расслоенных пространств.
Пусть Хп есть «-мерное однородное пространство
и G есть r-мерная группа Ли его преобразований (G
действует слева). Пусть Xn—GIH — представление,
где HaG — группа изотропии (стационарности) нек-рои
точки х„?Хп; (е/г, еа), к—1, 2, . . ., п, а—/1+1, . . .,
г,— базис левоинвариантных векторных полей на G
такой, что на Я еа составляют также базис левоинваг-
риантных векторных полей подгруппы Ли Н. Базису
(Р*, «а) отвечает сопряженный базис левоинвариантных
линейных дифференциальных форм (9*, ()а) на группе
Ли G. Канонич. проекция л: G —>- Хп, сопоставляющая
точкам х?Хп левые классы смежности л(х)~ IIX?G
группы G по подгруппе Н-НХа, вносит в группу Лп С
структуру главного //-расслоения с базой Хп и струк-
структурной группой Н размерности г—п. При таком пред-
представлении G векторные поля еа составляют ба-
базис фундаментальных векторных полей расслоения
л: G —>- Х„, а векторные поля ek натягивают нек-
некрое трансверсальное к слоям расслоения я: G —>- Хп
re-распределение. В соответствии с этим линейные диф-
дифференциальные формы 0* являются иолубазовыми
формами расслоения я: G —>- А'„ и образуют вполне
интегрируемую подсистему форм в системе @*, 6а).
Слон HxdG являются интегральными многообразиями
максимальной размерности для системы уравнений
Пфаффа 6*=0.
Системой реперов в классической диффе-
дифференциальной геометрии (евклидовой, аффинной, про-
проективной и т. д.) наз. множество фигур пространства
Хп, находящееся в биективном соответствии с множе-
множеством преобразований пространства Xп (или, что то же
самое, с множеством элементов фундаментальной груп-
группы С данного пространства), при этом любой репер Я
из данной системы можно получить из нек-рого началь-
начального Яа с помощью только одного преобразования:
Lg:Xn **„, R=.Lg(R0),g?G.
Учитывая,что главная роль подвижного репера Lg(R0)~
= Rg по отношению к неподвижному Ео состоит в
том," чтобы определять произвольное преобразование
Lg однородного пространства Хп, можно отождествить
.множество реперов {Kg} с. множеством элементов
группового пространства С, приобретающих таким
образом смысл абстрактных реперов, обслуживающих
любое однородное пространство с данной фундамен-
фундаментальной группой G.
Пусть задано нек-роо г.чилное подмногообразие
MczXn размерности т. I' (.¦ мерами нулевого
порядка подмногообразия М наз. элементы огра-
ограничения С (я, М) = G \M cz G расслоения л: G —>- Хп
па М, как на новую базу. Это значит, что главное
расслоение б(я, М) —>- М вложено в G и определяется
в нем как полный прообраз л~1 (М) czG. Так как ле-
воинвариантные формы 9*, 9а на группе Ли G подчи-
подчиняются уравнениям Маурера — Картана
dQk = _L с'Ц)' А 9'" + CfaQi л 9* , 4j
a = -L cv9P л ev -[. cfeep л e* r 4- c%p л «, Г
к, I, m — 1, 2, . . ., n; a, f>, y = n-\ 1, .. ., r, )
где Cim. Ckia, Cpv, Cpft, Cfm — структурные константы
группы Ли, то ограничение форм б*, ба на подрас-
слоение G(n, M), т. е. формы ы", ша, будет подчиняться
таым же уравнениям, но, сверх того, среди форм со*
возникнут линейные зависимости
(йР--АРша,а = 1, 2, ...,т; р = т-\-1, ..., п, B)
где ша — формы, оставшиеся вместе с ша линейно
независимыми на главном расслоенном пространстве
б(я, М) —>- М, а Лд — функции, также определенные
на расслоении реперов нулевого порядка С(я, М)—>М.
Функции Л§ являются координатами касательной
плоскости Тх(М)аТХ(Х„) подмногообразия МсХ„,
зависящими от точки х?АТ и репера
Л ? л (х) ^---ЯА. cr G (я, А/).
Касательные плоскости х —>- ТХ(М) образуют сечение
/: Л/->-;§„, (А/) грассманова расслоения <$,п(М) -* М
m-плоскостей, проходящих через точки подмногооб-
подмногообразия МаХп. Расслоение $,Я(М)—>-М является
присоединенным к главному расслоению С (я, М) —>- М.
Структура функций Л„ характеризуется уравнениями
явный вид к-рых можно получить внешним диффе-
дифференцированием уравнений B) с помощью A) и по-
последующим применением леммы Картана. Функции
•Ла> Л{?й являются относительными координатами 1-
струи j\f сечения / по отношению к подвижному реперу
Н^л~1(а-) точки х?М. Геометрич. объект/1/ образует
также сечение fj: M -v gm(^) соответствующего
расслоенного пространства gj^(M) -v M, присоеди-
присоединенного к главному расслоению в(л, М) —>- М. Анало-
Аналогичным образом возникает сечение ;2/: М —>. gm (Л/) с
координатами Л^, Л^ь, Л^ьс образующего его гео-
метрпч. объекта, а также его последующие продолже-
продолжения /3/, . . ., jqf, к-рым соответствуют дифференциаль-
дифференциальные продолжения уравнений C).
До тех пор пока расслоение gm (М) -у- М, к-рому
принадлежит сечение j^f(M), является однородным,
возможна редукция G4'(я, М) главного расслоепия
С (л, М) —>- М реперов к нек-рой подгруппе liczff,
определяемая по Картану с помощью нек-рой фикса-
фиксации относительных координат л?, Agj,, . . ., Л?
'"' q + l
геометрпч. обт>екта fxf, не зависящей от точки х?М.
Так определяется частичная канонизация репера.
Реперы R ?Gq (л, М) наз. полуканоническн-
м и реперами порядка (?+1 данного подмного-
подмногообразия MczXn. Если же следующее продолжение
дает геометрнч. объекты, группа стационарности к-рых
содержит лишь тождественное преобразование, то
возможна фиксация лишь части координат геометрич.
объекта сечения jq + lj, не зависящая от точки х, после
чего оставшаяся часть координат Л геометрич. объекта
ji + 1f зависит только отх?М. Таким обрааом возникает
сечопие s: M -v G(n, M) расслоения реперов нулевого
порядка подмпогообразия МсХп. Репер R~s(x) этого
сечения наз. каноническим репером под-
подмногообразия МсХп, или сопровождающим
репером этого подмногообразия. Описанный выше
процесс продолжения уравнений C) и выбранный
способ фиксации функций Л приводит к уравнениям
шР = А^ша, со«=Л^ша, D)
связывающим линейные формы со*, ша на сечении s{M).
Поле канонич. репера строится не однозначно, а за-
зависит от произвола фиксации относительных коор-
динат геометрич. объекта /9 + 1/. Важно лишь то, что
часть коэффициентов уравнения D) имеет постоянные
(црп желании наиболее простые) числовые значения,
тогда как другая часть их образует дифференциальные
инварианты подмногообразия MczXn, определяющие
его с точностью до преобразования в Хп. Капонич.
реперы сечения s(M) являются аналогом клас.сич.
примера — сопровождающего репера Френе кривой
евклидова пространства, а уравнения D) соответствуют
уравнениям Френе кривой. На пути канонизации
репера могут возникать осложнения, связанные с
неоднородностью расслоений gm(M) и разнотипно-
разнотипностью в этом смысле различных подмногообразий М в
Хп и даже их отдельных кусков. На этом и основы-
основывается классификация различных типов точек и раз-
различных классов подмногообразии в Хп. Благодаря
этим особенностям П. р. м. сыграл плодотворную роль
в изучении подмногообразии в разнообразных одно-
однородных пространствах и, кроме того, указал путь к
развитию современных методов исследования самых
общих дифференциально-геометрич. структур на глад-
гладких многообразиях.
Лит.: [1] Киртан Э., Теория конечных непрерывных
групп и дифференциальная геометрия, изложенные методом под-
подвижного р: пера, пер. с франц., М., 1963; 12] Фа вар Ж.,
Курс локальной дифференциальной геометрии, пер. с франц.,
М., 1960; [3J Карта н А., Дифференциальное исчисление.
Дифференциальные формы, пер. с франц., М., 1971; L4J Фи-
Фиников СП., Метод внешних форм Картана в дифферен-
дифференциальной геометрии, М.— Л., 1948. Е. Л. Евтушик.
ПОДВИЖНЫХ СЕТОК МЕТОД — метод численного
решения задач математич. физики, где разностная
сотка, на к-рой осуществляется аппроксимация урав-
не. ИИ основной задачи, не остается фиксированной;
она прослеживает в процессе расчета изменение гра-
границ счетных областей. Простейшая разностная сетка,
получаемая точками пересечения прямых, параллель-
параллельных осям декартовой системы координат (прямоуголь-
(прямоугольная сетка), позволяет максимально упростить разност-
разностные уравнения, описывающие основную задачу. Од-
Однако адекватное представление на ней границ сложной
формы 1! задаваемых на них граничных условий свя-
связано со значительными трудностями, зачастую непре-
непреодолимыми при ограниченных ресурсах ЭВМ. Эти
трудности особенно возрастают при решении нестацио-
нестационарных задач математич. физики, когда границы рас-
расчетных областей подвижны и претерпевают зпачитель-
ную деформацию. Построение системы координат с
координатными линиями, совпадающими с границами,
становится существенной частью алгоритма решения
таких задач.
При применении П. с. м. в каждый фиксированный
момент времени счетная область разрезается па ко-
конечное число ячеек сетки, не налегающих друг на
друга и заполняющих всю область без зазоров. В слу-
случае двух пространственных переменных с точки зрения
практич. реализации наиболее удобно счетную область
двумя семействами линий разрезать на четырехуголь-
четырехугольные ячейки. Тогда становится простой нумерация
ячеек (аналогичная нумерации элементов матрицы по
строкам и столбцам).
Расчет координат узлов такой сетки можно тракто-
трактовать как разностный аналог задачи об отыскании функ-
функций х(%, т|), у(%, т|), обеспечивающих однолистное
отображение на область физич. плоскости (х, у), в
к-рой проводится расчет, нек-рой параметрич. области
на плоскости (|, т)), напр, единичного квадрата 0<;|<:1,
0<:i]<l. Граничные значения этих функций устанав-
устанавливают нек-рое взаимно однозначное соответствие меж-
между точками на сторонах параметрич. квадрата и на
границах физич. области. Это соответствие целесооб-
целесообразно оставлять в распоряжении вычислителя, к-рый
расставляет узлы сетки на границе счетной области,
исходя из конкретного содержания задачи и имеющих-
имеющихся ресурсов.
Для областей несложной формы координаты узлов
сетки можно вычислять но явным формулам, основан-
основанным на использовании интерполяции или конкретного
вида отображения. В случае сложных областей прихо-
приходится прибегать к итерационному процессу, в ходе
к-рого положение узла сетки на каждой итерации
пересчитывается в зависимости от положения его
соседей. Такие итерационные пюоцессы, как правило,
моделируют решение нек-рой системы дифференциаль-
дифференциальных уравнений с частными производными. При их
конструировании зачастую в той или иной форме
привлекаются конформные и квазиконформные ото-
отображения .
Структура решения задач математич. физики (напр.,
задач газовой динамики) может характеризоваться
наличием зон, в к-рых происходит резкое изменение
параметров потока. Размеры таких зон могут быть
существенно меньше характерного линейного размера
задачи, а их местонахождение заранее неизвестно и,
кроме того, может меняться в процессе расчета. В связи
с этим разрабатываются алгоритмы, к-рые позволяли
бы использовать в расчетах сетки, сгущающиеся в
таких зонах.
С целью создания надежных вычислительных алго-
алгоритмов задача построения сетки зачастую формули-
формулируется как задача минимизации нек-рого вариацион-
вариационного функционала. Функционал может содержать
управляющие параметры, изменение к-рых обеспечи-
обеспечивает определенную свободу и возможность приспосаб-
приспосабливать рассчитываемую сетку к особенностям кон-
конкретной задачи.
Лит.: И] Численное решение многомерных задач газовой
динамики, М., 1976; [2] Сидоров А. Ф., «Численные ме-
методы механики сплошной среды», 1977, т. 8, № 4, с. 149—5К;
[3] Мещеряков Ю. П., Ш а п е е в В. П., там же, 1978,
т. 9, .№ 2, с. 91 — 103; [4] Д а н а е в Н. Т., там же, 1979, т. 10,
№ 4, с. 60—74; [5] Томас П. Д., М и д д л к о ф ф Д. Ф.,
«Ракетная техника и космонавтика», 1980, т. 18, № 7, с. 55—61.
Г. П. Прокопов.
ПОДГРУПП РЯД — конечная цепочка вложенных
одна в другую подгрупп группы G:
Рассматриваются также бесконечные цепочки вложен-
вложенных подгрупп (убывающие и возрастающие), зануме-
занумерованные порядковыми числами или даже элементами
упорядоченного множества. Их чаще наз. подгрупп
системами.
Важную роль в теории групп играют субнормаль-
субнормальные, нормальные п центральные ряды. П. р. (*) наз.
субнормальным, если каждый его предыдущий
член есть нормальная подгруппа следующего члена.
Если, кроме того, каждая подгруппа G,-, i=0, 1, . . .,
?i, нормальна в G, то ряд (*) наз. нормальным
рядом в С. Существует и иная терминология, в
к-рой нормальным рядом наз. то, что здесь названо
субнормальным, а для второго определенного здесь
понятия используется термин «инвариантный
ряд» (преобладает, однако, первая терминология).
Факторгруппы Gi+jGj паз. факторами, а число
п — длине й субнормального ряда. Нормальный
ряд (*) наз. центральным, если все его факторы
центральны, т. е. Gi+l/G,- лежит в центре группы
GIG; для всех i или, что равносильно, взаимный ком-
коммутант Gl + 1 и G лежит в G,- для всех г. Если Gj + i/G,-
в точности совпадает с центром группы G/G/ (соответ-
(соответственно коммутант G;+l и G совпадает с Gj) для всех
г, то ряд (*) наз. верхним центральным
р я д о м (соответственно нижним централь-
н ы Л! р я л о м) группы G.
Пусть в группе С заданы субнормальный (соответ-
(соответственно нормальный или центральный) ряд и нек-рая
подгруппа //c=G и пусть IIi=Gif]H, ?' = •>, 1, . . ., п.
Тогда цепочка
К -Т10<=Н,<=: ....(= Нп = Н
является субнормальным (соответственно нормальным
или центральным) рядом в //, а факторы этого ряда
изоморфны подгруппам соответствующих факторов
ряда (*). Если G/.V — нек-рая факторгруппа группы
6', то цепочка
является субнормальным (соответственно нормальным
или центральным) рядом в GIN, а факторы этого ряда
суть гомоморфные образы соответствующих факторов
ряда (*).
Два субнормальных (в частности, нормальных)
ряда группы наа. изоморфным и, если они имеют
одинаковую длину и между их факторами существует
взаимно однозначное соответствие, при к-ром соответ-
соответствующие факторы изоморфны. Если всякая под-
подгруппа одного ряда совпадает с одной из подгрупп
другого, то нторой ряд на:), у п л о т н е п и е м пер
вого. Неуплотняемый далее нормальный ряд паз.
г л а в н ы м, а субнормальный — к о м п о з и ц и о н-
н ы м. Факторы этих рядов наз. соответственно глав-
главными и композиционными факто-
факторам и. Любые два субнормальных (соответственно
нормальных или центральных) ряда группы обладают
изоморфными субнормальными (соответственно нор-
нормальными или центральными) уплотнениями. В част-
частности, любые два главных (композиционных) ряда
изоморфны (см. Жордана — Гёльдера теорема).
Лит.: [1] Каргаполов М. И., М е р я л яков Ю. И.,
Основы теории группы, 3 изд., М., 1982; [2] Черников
С. Н., Группы с заданными свойствами системы подгрупп, М.,
15180. Н. С. Романовский.
ПОДГРУПП СИСТЕМА — множество 31 подгрупп
группы G, удовлетворяющее условиям: 1) 91 содержит
единичную подгруппу 1 и саму группу G, 2) 31 линейно
упорядочено по вложению, т. е. для всяких А, В из
9С либо А^В, либо В>=А . Говорят, что подгруппы А,
А' из 31 составляют скачок, если А' непосред-
непосредственно следует за А в 31. П. с, замкнутая относи-
относительно объединений и пересечений, наз. полной.
Полная П. с. наз. субнормальной, если для
всякого скачка А, А' отой системы А является нор-
нормальной подгруппой в А'. Факторгруппы А'/А наз.
факторами системы ЗГ. П. с, все члены к-рой
суть нормальные подгруппы группы G, наз. н о р мал ь-
н о к. В случае, когда одна субнормальная система
содержит (в теоретико-множественном смысле) другую,
первую из них наз. уплотнением второй. Нор-
Нормальная П. с. наз. центральной, если все ее
факторы центральны, т. е. А'/А содержится в центре
GIА для всякого скачка А, А'. Субнормальная П. с.
наз. разрешимой, если все ее факторы абелевы.
Наличие в группе тех или иных П. с. выделяет в
классе всех групп различные подклассы, наиболее упо-
употребительны из к-рых RN, ~RN*, ЯЙ~, ЯГ, RI*, Я~Г,
Z, ZA , ZD, Z, Л', N — класс ы К у р о m a —
Черникова:
-ffjV-групна — обладает разрешимой субнормальной
П. с;
#iV*-rpynna — обладает разрешимой субнормальной
П. с, вполне упорядоченной по возрастанию;
RN -группа — всякую субнормальную П. с. этой
группы можно уплотнить до разрешимой субнормаль-
субнормальной;
Л/-группа — обладает разрешимой нормальной П. с ;
Я/*-группа — обладает разрешимой нормальной
П. с, вполне упорядоченной по возрастанию;
ДУ-груцпа — всякую нормальную П. с. этой группы
можно уплотнить до разрешимой нормальной;
2-грунпа — обладает центральной П. с;
2Л-группа — обладает центральной П. с, вполне
упорядоченной по возрастанию;
ZZ)-rpynna — обладает центральной П. с, вполне
упорядоченной ни убыванию;
Z-группа всякую нормальную П. с. такой группы
можно уплотнить до центральной;
Л'-гругша — через всякую подгруппу такой группы
проходит субнормальная П. с;
Л'-rpyinia — через всякую подгруппу такой группы
проходит субнормальная П. с, вполне упорядоченная
по возрастанию.
Частный случай П. с.— подгрупп ряды.
Лит.: [1J К у р о ш А. Г., Теория групп, 3 изд., М., 1907;
12J Ч е р и и к о в С. Н., Группы с заданными свойствами сис-
системы подгрупп, М., 1980; [3] Каргаполов М. И., Мерз-
Мерзляков Ю. И., Основы теории групп, 3 изд., М., 1982.
Н. С. Романовский.
ПОДГРУППА — подмножество Я группы G, само
являющееся группой относительно операции, опреде-
определяющей G. Подмножество II группы G является ее
подгруппой тогда и только тогда, когда: A) // содер-
содержит произведение любых двух элементов из Я, B) 11
содержит вместе со всяким своим элементом h обрат-
обратный к нему элемент ft. В случае конечных и, вообще,
периодич. групп проверка условия B) является из-
излишней.
Подмножество группы G, состоящее из одного эле-
элемента 1, будет, очевидно, подгруппой, и эта П. на;!,
единичной П. группы G и обозначается обычно
символом Е. Сама G также является своей П. Всякая
П., отличная от всей группы, наз. истинной II.
этой группы. Истинная П. нек-рой бесконечной группы
может быть изоморфна самой группе. Сама группа G
и подгруппа Е наз. несобственными П. груп-
группы G, все остальные — собственны м и.
Теоретико-множественное пересечение любых двух
(и любого множества) П. группы G является П. груп-
группы G. Пересечение всех П. группы G, содержащих все
элементы нек-рого непустого множества М, наз. под-
подгруппой, порожденной множеством
М, и обозначается символом {М}. Если М состоит из
одного элемента а, то {а} наз. циклической I].
элемента а. Группа, совпадающая с одной из своих
циклических П., наз. циклической группой.
Теоретико-множественное объединение П., вообще
говоря, не обязано являться П. Объединением
подгрупп //,-, if I, паз. П., порожденная объеди-
объединением множеств IIj.
Произведение подмножеств Sx и 52 группы G есть
множество, состоящее из всевозможных (различных)
произведений s^, где s^dS^, s2?S2. Произведение
подгрупп НлДг есть П. тогда и только тогда, когда
Н1Н.2=Н2Н1, и в этом случае произведение Н^Н^ сов-
совпадает с объединением подгрупп Нх и II г.
Гомоморфный образ П.— подгруппа. Если группа
Gr изоморфна нек-рой подгруппе Н группы G, то го-
говорят, что группа Gl может быть вложена в группу G.
Если даны две группы п каждая из них изоморфна
нек-рой истинной П. другой, то отсюда еще не следует
изоморфизм самих ЭТИХ групп. О. А. Иванова.
ПОДГРУППЫ ИНДЕКС в группе G — число
смежных классов в каждом из разложений группы G
по этой подгруппе // (в бесконечном случае — мощ-
мощность множества этих классов). Если число смежных
классов конечно, то Л наз. подгруппой ко-
конечного индекса в G. Пересечение конечного
числа подгрупп конечного индекса само имеет конеч-
ный индекс (творила П у а н к а р о). Индекс
подгруппы // в группе G обычно обозначается \G : Н\.
Произведение порядка подгруппы Н на ее индекс
\G : Н\ равно порядку группы G (теорема Л а г-
р а н ж а). Это соотношение имеет место как для ко-
конечной группы G, так и в случае бесконечной G —
для соответствующих мощностей.
Л [11 К
ущ щ
Лит.: [11 К а р г а и о .;i о в
И О 4
М. П., Мерзляков
LJ
О. А. Ива-нова.
М
ит.: [11 К а р г а и .;i о в П, Мерзляков
IO. И., Основы теории групп, ,4 изд., М., 1У82; LliJ К урош
А. Г., Теории групп, 3 изд., М., I'-'M"
ПОДЕРА, и о д :) р а, крипом
I относительно точки О — мно-
множество оснований перпендику-
перпендикуляров, опущенных из точки
О на касательные к кривой
I. Напр., улитка Паскаля —
П. окружности относительно
точки О (см. рис.). П. плоской
линии x=x(t), y=y(t) относи-
относительно начала координат:
'"' +ии'
XX'+!"J'
V .. ' лл т.'Л/ v^ _ / -1л -гни
~x7JTl/i~ ' У—^ 'х7Г^~у7'
Уравнение И. пространственной линии x=x(t), y=
~y(t), z=z(i) относительно начала координат:
+ уц' л-zz'
X =х — j
Z~ z-
. л ' г
i XX' -\-Vll' И Z2'
I 2'2
X'" ¦
А н т и п о д о р о н линии / относительно точки О
наз. линия, П. к-рой относительно точки О есть ли-
линия I.
П. поверхности относительно точки О —
множество оснований перпендикуляров, опущенных
из точки О на касательные плоскости поверхности.
Уравнение П. поверхности F(x, у, z)=0 по отношению
к началу координат:
где
ПОДКАСАТЕЛЬНАЯ И ПОД-
ПОДНОРМАЛЬ — направленные от-
отрезки QT и <^ЛГ, являющиеся
проекциями на ось Ох отрез-
отрезков касательной МТ и норма-
нормали MN к нек-рой кривой в ее
точке М (см. рис.).
А. П. Иванов.
О N
Если кривая есть график функции ц=:/(.г), то зна-
значения величин И. и п. равны соотиетстиешш:
/ ix) s\ у _ f / _, f / /_,
QT = —
/' (х)
где х — абсцисса точки М. Если кривая задана пара-
параметрически:
() ty()
то тогда
где f — значение параметра, определяющее точку М
кривой. БСЭ-з.
ПОДКАТЕГОРИЯ — частный случай понятия под-
подструктуры математич. структуры. Категория $: наз.
подкатегорией категории Й\ если
(А, В)-=
$(А, В) П Мог «
для любых Л, BgOb^. и произведение морфизмов
из & совпадает с их произведением в Ш. Для каждого
подкласса ?' класса Obft существуют наименьшая п
наибольшая подкатегории ?х и ?2 категории &{, клас-
классы объектов к-рых совпадают с ?'; подкатегория .^
содержит только единичные морфизмы объектов из
€' и наз. дискретной П., порожденной
?'; подкатегория ?2 содержит все морфизмы из ST,
начала и концы к-рых лежат в ?' и наз. полной
П., порожденной ?'. Всякая подкатегория
? категории Я, для к-рой Л а {А, В) = Л&(А, В)
для любых А, б?ОЬ?, наз. полной П. катего-
категории ,4. Полными П. являются: II. непустых множеств
в категории всех множеств, II. абелевых групп в кате-
категории всех групп и т. д. Для малой категории 3) пол-
полная П. категории всех контравариантных функторов
из Х> в категорию множеств, порожденная основными
функторами, изоморфна категории jT. Этот результат
позволяет строить пополнение произвольной малой
категории пределами и копределами.
Произвольная II. категории Я' не наследует никаких
свойств этой категории. Однако существуют важные
классы П., наследующих многие свойства объемлю-
объемлющей категории, таковы, напр., рефлективные П., ко-
рефлективные П. м. ш. Цаленко.
ПОДМАТРИЦА матрицы А размера
тХ и — матрица размера kXl, где l<;it<:m, l<Z<:n,
образованная элементами, находящимися на пересе-
пересечении фиксированных к строк и I столбцов матрицы А
с сохранением прежнего порядка. Определитель квад-
квадратной П. порядка к матрицы А наз. минором
к-то порядка матрицы А. т. С. Пиголпина.
ПОДМНОГООБРАЗИЕ — 1) В узком смысле слова
топологическое и-мерное П. топологического /«-мер-
/«-мерного многообразия М — такое подмножество Л'С-М,
к-рое в индуцированной топологии является п-мерным
многообразием. Число m — n наз. коразмерно-
коразмерностью подмногообразия N. Наиболее часто встре-
встречаются локально плоские П., для к-рых тождествен-
тождественное вложение i: N—*-M является локально плоским
вложением. Подмножество NcM является локально
плоским П., если для каждой точки p?N имеются
такая окрестность U этой точки в М и такие локаль-
локальные координаты л,, тт в ней, что в терминах этих
координат ЛГП^ описывается уравнениями хп+1=
= . . . = *„ = <).
2) В широком смысле слова топологическое ге-мер-
иое П. топологического m-мерного многообразия М —
такое n-мерное многообразие N, к-рое как множе-
множество точек является подмножеством М (иными словами,
N — это подмножество М, снабженное структурой п-
мерного многообразия) и для к-рого тождественное
вложение /: N^>-M является погружением. П. в узком
смысле является П. в широком смысле, а последнее
является П. в узком смысле тогда и только тогда,
когда i есть вложение в топологич. смысле (т. е. у каж-
каждой точки р ?У имеется сколь угодно малые окрест-
окрестности в Лг, являющиеся пересечениями с N нек-рых
окрестностей в М).
3) Кусочно линейное, аналитиче-
аналитическое или дифференцируемое (класса
С1, Z<oo) П. кусочно линейного, аналитического или
дифференцируемою (класса Ck, i<:/c<:oo) многооб-
многообразия М в широком смысле (соответственно узком) —
;>то подмножество 1\ аМ, к-рое снабжено структурой
кусочно линейного, аналитического или дифференци-
дифференцируемого (класса С1) многообразия, причем i является
кусочно линейным, аналитическим или дифференци-
дифференцируемым (класса С1) погружением (соответственно вло-
вложением). Определение дифференцируемого П. класса
С1 годится и при 1--Q, совпадая в этом случае с опре-
определением топологического П. Обычно подразумевается,
что 1
В аналитическом и дифференцируемом случаях П.
всегда является локально плоским. Поэтому определе-
определение аналитического (дифференцируемого) II. в узком
смысле обычно с самого начала формулируется как
аналитический (дифференцируемый) вариант данного
в 1) определении локально плоского П. с помощью ло-
локальных координат, добавляя к сказанному там усло-
условию, чтобы локальные координаты хг, . . ., хт были
аналитическими (дифференцируемыми класса С1). Если
подмножество N удовлетворяет последнему определе-
определению, то оно естественным образом снабжается структу-
структурой аналитического (дифференцируемого класса С1)
многообразия и i оказывается вложением в смысле
соответствующей структуры.
Кусочно линейное П. в узком смысле локально пред-
представляется как нодполиэдр объемлющего многообра-
многообразия, кусочно линейно эквивалентный симплексу. Оно
не всегда является локально плоским (хотя это так при
т — я>2); кроме того, для таких П. свойство быть
локально плоским в топологич. смысле не совпадает
(по крайней мере непосредственно) со свойством быть
локально плоским в кусочно линейпом смысле.
4) Простой модификацией этих определений полу-
получаются определения: П. с краем; П. многообразия
с краем (при этом в ряде топологич. вопросов оказы-
оказывается целесообразным ограничить возможные рас-
расположения П. у края объемлющего многообразия, см.
[1]); П., различные компоненты к-рого могут иметь
различную размерность; П. бесконечномерного много-
многообразия [2]; комплексно аналитического П. комплексно
аналитического многообразия.
Понятие П. в узком смысле является непосредствен-
непосредственным обобщением понятия кривой и поверхности. П.
в широком смысле используются в теории групп Ли
(где это понятие и было впервые введено [3]), диффе-
дифференциальной геометрии [4] и теории слоений.
5) В алгебраической геометрии П.— замкнутое под-
подмножество алгебраич. многообразия в Зариского то-
топологии. Этим формализуется идея, что П. задается
алгебраич. уравнениями. Помимо перехода от R к дру-
другим полям, изменение понятия П. в этом случае сос-
состоит в том, что допускаются П. с особенностями.
Лит.: 11] Рохлин В. А., Ф у к с Д. Б., Начальный
курс топологии. Геометрические главы, М., 1977; [2] Л е н г С,
Введение в теорию дифференцируемых многообразий, пер.
с англ., М., 1967; L3] Ш е в а л л с К., Теория групп Ли, пер.
с англ., т. 1, М., 1948; [4] Стернберг С, Лекции по диф-
дифференциальной геометрии, пер. с англ., М., 1970. Д. Б. Аносов.
ПОДМОДУЛЬ — подмножество модуля, являющееся
подгруппой его аддитивной группы и замкнутое отно-
относительно умножения на элементы основного кольца.
В частности, левый (правый) идеал кольца В явля-
является П. левого (правого) Л-модуля R. П., отличный
от всего модуля, наз. собственным. Множество
П. данного модуля, упорядоченное по включению,
является полной дедекиндовой решеткой (см. Вполне
приводимый модуль). Если ф — гомоморфизм модуля
А в модуль В, то множество
оказывается П. модуля А и наз. ядром гомомор-
гомоморфизма ф. Каждый П. служит ядром некоторого
гомоморфизма. П. наз. большим (или суще-
существенны м), если он имеет ненулевое пересечение
с любым другим ненулевым П. Напр., целые числа
образуют большой TI. группы рациональных чисел.
Каждый модуль является большим П. своей инъектив-
ной оболочки (см. Ипъективный модуль). Подмодуль
А модуля В наз. малым (или косуществен-
н ы м), если для любого подмодуля А'с^В равенство
А~\А' = В влечет А' = В. Малым оказывается, напр.,
всякий собственный П. цепного модуля. Малый П.
образуют необратимые элементы локального кольца.
Сумма всех малых II. совпадает с пересечением всех
максимальных Li. Левый идеал 1 принадлежит ради-
радикалу Джекобсона тогда и только тогда, когда IM
мал л М для всякого конечно порожденного левого мо-
модуля М. Элементы малого П. являются необра-
необразу ю щ и м и, т. е. любая система образующих моду-
модуля остается таковой после удаления любого из этих
элементов (это, конечно, не означает, что их можно
удалить все сразу!). Радикал Джекобсона кольца эн-
эндоморфизмов модуля совпадает с множеством эндомор-
эндоморфизмов, имеющих малый образ.
Лит.: \\\ Каш Ф., Моду.ш и кольца, пор. с нем., М., 1981;
\'1\ Ф е й с К., A.ireopa: кольца, модули и категории, пер. с
лил., т. J - 2, М., 11O7-79. Л. А. Скорняков.
ПОДОБИЕ — преобразование евклидова простран-
пространства, при к-ром для любых двух точек А, В и их об-
образов А', В' имеет место соотношение \А'В'\---к\АВ\,
где к ~ положительное число, называемое к о э ф-
ф,и ц и е н т о м П.
: Каждая гомотетия является подобием. Каждое
движение (в том числе и тождественное) также можно
рассматривать как преобразование П. с коэффициен-
коэффициентом к, равным единице. Фигура F наз. и о д о б н о и
фигуре /•", если существует преобразование П., при
к-ром /'-W-". П. фигур является отношением эквива-
эквивалентности, т. с. обладает свойствами рефлексивности,
симметричное in it транзитивности. П. есть взаимно
однозначное отображение евклидова пространства на
себя; II. сохраняет порядок точек на прямой, т. с.
если точка В лежит между точками А, С и В', А',
С— соответствующие их образы при нек-ром П., то
В' также лежит между точками А' и С; точки, не ле-
лежащие иа прямой, при любом П. переходят в точки,
не лежащие на одной прямой. П. преобразует прямую
в прямую, отрезок в отрезок, луч в луч, угол в угол,
окружность в окружность. При П. угол сохраняет
величину.
IJ. с коэффициентом к^1, преобразующее каждую
прямую в параллельную ей прямую, является гомоте-
гомотетией с коэффициентом к или —к. Каждое II. можно
рассматривать как композицию движения D и нек-рой
гомотетии Г с положительным коэффициентом.
П. наз. собственным (несобствен-
н ы м), если движение D является собственным (не-
(несобственным). Собственное П. сохраняет ориентацию
фигур, а несобственное — изменяет ориентацию на
противоположную.
Аналогично определяется П. (с сохранением ука-
указанных выше свойств) в 3-мерном евклидовом прост-
пространстве, а также в л-мерном евклидовом и псевдоевк-
псевдоевклидовом пространствах.
В л-мерных римановых, псевдоримановых и фиисле-
ровых пространствах П. определяется как преобразо-
преобразование, переводящее метрику пространства в себя
с точностью до постоянного множителя.
Совокупность всех П. «-мерного евклидова, псевдо-
евклцдова, риманова, псевдориманова или финсле-
рова пространства составляет r-членную группу пре-
преобразований Ли, наз. группой подобных
(г о м о т е т и ч е с к и х) преобразований соответ-
соответствующего пространства. В каждом из пространств
указанных типов r-членная группа подобных преоб-
преобразований Ли содержит (/•—1)-членную нормальную
подгруппу движений.
Представляют интерес метрич. пространства вектор-
векторных плотностей с группами П. и изометрий, содержа-
содержащими бесконечномерные подгруппы и.чометрий с об-
общими траекториями. И. п. Егоров.
ПОДОБИЯ ТЕОРИЯ — учение об исследовании фи-
зич. явлений, основанное на понятии о физич. подобии.
Два физич. явления « о д о б ны, если но числен-
численным значениям характеристик одного явления можно
получип. численные значения характеристик другого
явления простым пересчетом, к-рыи аналогичен пере-
переходу от одной системы единиц измерения к другой.
Для всякой совокупности подобных явлений все соот-
соответствующие безразмерные характеристики (безраз-
(безразмерные комбинации из размерных величин) имеют оди-
одинаковое численное значение (см. Размерностей ана-
анализ). Обратное заключение тоже верно, т. е. если все
соответствующие безразмерные характеристики для
двух явлений одинаковы, то эти явления физически
подобны.
Анализ размерностей и II. т. тесно связаны между
собой и положены в основу экспериментов с моделями.
В таких экспериментах осуществляются замены
изучения нек-рого явления в натуре изучением ана-
аналогичного явления на модели меньшего или больше-
большего масштаба (обычно в специальных лабораторных
условиях).
После установления системы параметров, опреде-
определяющих выделенный класс явлений, устанавливаются
условия подобия двух явлений. Именно, пусть явле-
явление определяется я независимыми параметрами,
нек-рые из к-рых могут быть безразмерными. Пусть, да-
далее, размерности определяющих, переменных и физич.
постоянных выражены через размерности к из утих
параметров с независимыми размерностями (к^.п).
Тогда из п величин можно составить только /;—к не-
независимых безразмерных комбинаций. Все искомые
безразмерные характеристики явления можно рассмат-
рассматривать как функции от этих п—к независимых без-
безразмерных комбинаций, составленных из определяю-
определяющих параметров. Среди всех безразмерных величин,
составленных из определяющих характеристик явле-
явления, всегда можно указать нек-рую базу, т. е. систему
безразмерных величин, к-рые определяют собой все
остальные.
Определенный соответствующей постановкой задачи
класс явлений содержит явления, вообще неподобные
между собой. Выделение из него подкласса подобных
явлений осуществляется с помощью следующего ус-
условия.
Для подобия двух явлений необходимо и достаточно,
чтобы численные значения безразмерных комбинаций,
составленных из полного перечня определяющих пара-
параметров, образующих базу, в этих двух явлениях были
одинаковы. Условия о постоянстве базы отвлеченных
параметров, составленных из заданных величин, оп-
определяющих явление, наз. критериями подо-
подобия.
В гидродинамике важнейшими критериями подобия
являются Рейнолъдса число, характеризующее соотно-
соотношение между инерционными силами и силами вяз-
вязкости, Маха число, учитывающее сжимаемость газа, и
Фруда число, характеризующее соотношение между
инерционными силами и силами тяжести. Основными
критериями подобия процессов теплопередачи между
жидкостью (газом) ц обтекаемым телом являются:
Прандтля число, характеризующее термодинамич. со-
состояние среды; Нусселъта число, характеризующее
интенсивность конвективного теплообмена между по-
поверхностью тела и потоком жидкости (газа); Пекле
число, характеризующее соотношение между конвек-
конвективным и молекулярным процессами переноса тепла
в жидкости; Стэнтона число, характеризующее ин-
интенсивность диссипации энергии в потоке жидкости
или газа. Для распределения тепла в твердом теле
критериями подобия являются Фурье число, характе-
характеризующее скорость изменения тепловых условий в
окружающей среде и скорость перестройки поля темп-ры
внутри тела, и число Впо, определяющее характер
соответствия между температурными условиями среды
и распределением температуры внутри тела. В про-
цессах, изменяющихся с течением времени, основными
критериями подобия, характеризующими одинако-
одинаковость протекания процессов во времени, являются
критерии гомохронности. В задачах аэрогидромехаии-
ки этот критерий наз. Струхаля числом. Критерием
подобия мехапич. движения является Ньютона число.
При изучении упругих деформаций критерием подобия
является коэффициент Пуассона.
Если условия подобия выполнены, то для фактич.
расчета всех характеристик в натуре но данным о
размерных характеристиках на модели необходимо
знать переходные масштабы для всех соответствующих
величин. Если явление определяется п параметрами, из
к-рых к имеют независимые размерности, то для ве-
величин с независимыми размерностями переходные
масштабы могут быть произвольными и их нужно
задать с учетом условий задачи, а при эксперимен-
экспериментах — и с учетом условий опыта. Переходные мас-
масштабы для всех остальных размерных величин полу-
получаются из формул, выражающих размерности каждой
размерной величины через размерности к величин
с независимыми размерностями, для к-рых масштабы
подсказаны условиями опыта и постановки задачи.
Напр., в задаче об установившемся обтекании тела
несжимаемой вязкой жидкостью все безразмерные ве-
величины, характеризующие движение в целом, опреде-
определяются тремя параметрами: углами а, В (направление
поступательной скорости тела относительно его по-
поверхности) и числом Рейнольдса R. Условия физич.
подобия — критерии подобия — представляются со-
соотношениями:
a = const, В —const. R —- ^-^ = const.
Здесь подразумевается, что при моделировании явле-
явления результаты опытов с моделью можно переносить
на натуру только при одинаковых a, P и R. Первые два
условия всегда легко осуществить на практике, тре-
третье — труднее, особенно в тех случаях, когда модель
меньше обтекаемого тела, к-рое в натуре имеет большие
размеры, напр, крыло самолета. При уменьшении раз-
размеров для сохранения величины числа Рейнольдса
необходимо либо увеличивать скорость обтекаемого
потока, что практически обычно неосуществимо, либо
существенно изменять плотность и вязкость жидкости.
На практике эти обстоятельства приводят к большим
затруднениям при изучении аэродинамич. сопротивле-
сопротивления (напр., продувка самолетов в натуральную вели-
величину в аэродинамич. трубах, а также труб закрытого
типа, в к-рых циркулирует с большой скоростью сжа-
сжатый, т. е. более плотный, воздух).
Специальные теоретические и экспериментальные
исследования показывают, что в ряде случаев для тел
хорошо обтекаемой формы число Рейнольдса заметно
влияет только на безразмерный коэффициент лобового
сопротивления и иногда очень слабо влияет на безраз-
безразмерный коэффициент подъемной силы и на нек-рые др.
величины, играющие весьма важную роль в различных
нрактич. вопросах. Различие в значении числа Рей-
Рейнольдса на модели и в натуре в нек-рых вопросах не
является существенным.
Аналогичным образом при моделировании движения
тел в газе с большими скоростями необходимо иметь
одинаковые значения числа Маха на модели и в натуре.
При моделировании плавания кораблей по воде не-
необходимо обеспечивать равенство для натуры и моде-
модели чисел Фруда и Рейнольдса. Однако при уменьшении
линейных размеров и опытах в воде в лаборатории из
условия о постоянстве чисел Рейнольдса следует тре-
требование об увеличении скорости движения модели, а из
постоянства числа Фруда следует требование об умень-
уменьшении скорости движения модели, поэтому точное моде-
лированне (при испытании моделей кораблей в лабора-
лаборатории), вообще говоря, невозможно. Иногда такого
рода трудности можно обходить путем использования
различных жидкостей или путем искусственного изме-
изменения ускорения силы тяжести с помощью «центробеж-
«центробежного моделирования», располагая испытываемые объек-
объекты на вращающейся установке большого диаметра.
Детальное проникновение в сущность гидродинамич.
явлений показывает, что во многих случаях влияние
числа Рейнольдса можно учесть с помощью дополни-
дополнительных расчетов или с помощью простых опытов с
использованном данных по буксировке плоских пла-
пластинок. В гидродинамике обычных водоизмещающих су-
судов основное значение имеет число Фруда, и поэто-
поэтому моделирование проводится с соблюдением постоян-
постоянства числа Фруда.
Исследование с помощью моделей часто является
единственно возможным способом экспериментального
изучения и решения важнейших практич. задач. Так
обстоит дело при изучении натурных явлений, проте-
протекающих в течение десятков, сотен или даже тысяч лет;
в условиях модельных опытов подобное явление может
продолжаться несколько часов или дней (напр., при мо-
моделировании просачивания нефти). Могут встречаться
и обратные случаи, когда вместо исследования чрезвы-
чрезвычайно быстро протекающего в природе явления изу-
изучают подобное явление, происходящее на модели го-
гораздо медленнее.
Моделирование является исходной базой для задачи,
к-рая состоит в фактич. определении законов природы,
в отыскании общих свойств и характеристик различ-
различных классов явлений, в разработке эксперименталь-
экспериментальных и теоретич. методов исследования и разрешения
различных проблем, в получении систематич. материа-
материалов, приемов, правил и рекомендаций для решения
конкретных практич. задач.
Лит.: [1] Б р и д ж м е н II. В., Анализ размерностей,
пер. с англ., Л.— М., 1934; [2] С е д о в Л. И., Методы
подобия и размерности в механике, 9 изд., М., 1981.
Л. II. Седов.
ПОДОБНАЯ ОБЛАСТЬ — общепринятое сокращение
термина «критическая область, подобная выборочному
пространству», употребляемого в математич. статистике
по отношению к критич. области нерандомизирован-
нерандомизированного подобия статистич. критерия.
Пусть X — случайная величина, принимающая зна-
значения в выборочном пространстве (ЗЁ, S3, Ро), й?®,
и пусть проверяется сложная гипотеза //„ : 0?впс:в
против альтернативы Нх : 9^01=в\0о. Далее, пусть
для проверки На против Н1 построен нерандомизиро-
нерандомизированный подобный критерий уровня а@<а<1), кри-
критич. функция к-рого естг, <{>(.r), x??t'. Так как этот
критерий является нерандомизированным, то
где К — нек-рое множество из пространства Э?, наз.
критическим множеством критерия
(согласно этому критерию гипотеза //,, отклоняется
в пользу Я,, если в эксперименте наблюдается событие
{X ?К}). Кроме того, построенный критерий является
подобным, в силу чего
w (x) dPe =а при всех 8?G0. B)
Из A) и B) следует, что критич. область К нерандоми-
нерандомизированного подобного критерия обладает следующим
свойством:
Ре{Л"?А'}=^а при всех в?в0.
Именно, акцентируя внимание на последнем свойстве
критич. множества К нерандомизированного подобного
критерия, Дж. Нейман и Э. Пирсон назвали К «об-
«областью, подобной выборочному пространству ЭЕ» в том
смысле, что обе вероятности Pq {X ?К} и Ре {X ?ЭЕ}
не зависят от 8?вп.
Лит.: [1] Л е м а н Э., Проверка статистических гипотез,
пер. с англ., 2 изд., М., 1970; [2] Ван дер В а р д е и Б. Л.,
Математическая статистика, пер. с нем., М., 1960; [3] N е у-
m a n J., Р с а г н о n E. S., «Philos. Trans. Roy. Soc. Ser. A»,
1933, v. 231, p. 289—337; [4] Lehmann R.L., Scheffii
H., «Sankhya», 1950, v. 10, p. 305—40; [4] их же, там же,
1955, v. 15, p. 219—3E. М. С. Никулин.
ПОДОБНАЯ СТАТИСТИКА — статистика, имеющая
одно и то же распределение вероятностей при справед-
справедливости нек-рой сложной гипотезы.
Пусть статистика Т отображает выборочное прост-
пространство (¦?, 33Х , Ре), 9?0, в измеримое пространство
(л?, .53.))) и пусть рассматривается нек-рая сложная ги-
гипотеза i/0: 6^в0с^в. В таком случае, если для любого
события В ? 33Sg вероятность
Рд(Т~1{В)) не зависит от 8, когда 6?G0, (*)
то говорят, что Г является П. с. по отношению к гипо-
гипотезе На или просто П.с. Очевидно, что условие (*) равно-
равносильно тому, что распределение статистики Т не меня-
меняется, когда 6 пробегает 6„. Имея в виду это свойство,
часто о П. с. говорят, что она является свободной от-
относительно параметра 9, 8?в„. П. с. играют боль-
большую роль при построении подобных критериев, а
также при решении статистич. задач с мешающими
параметрами.
П р и м е р 1. Пусть А",, Х2 , . . ., Хп— независимые
одинаково нормально N1(a, а'2) распределенные слу-
случайные величины (|я|<оо, а>0). Тогда при любом
<х>0 статистика
где
является свободной относительно двумерного пара-
параметра (а, а2).
П р и м е р 2. Пусть Хи Х2, . . ., Хп + т — незави-
независимые одинаково распределенные случайные величины,
функция распределения к-рых принадлежит семейству
Jf-= {F (х)} всех непрерывных функций распределений
на (—оо, +оо). В этом случае, если Fn(x) и Fm(x) суть
функции эмпирич. распределений, построенные по
наблюдениям Х1, Х.л, . . ., Хп и А'„+1, Хп + 2, ¦ ¦ .,
Хц + т соответственно, то статистика Смир-
Смирнова
?„, т= sup \Fn(.r)-Fm(x)\
I X |<со
является подобной относительно семейства ff".
Лит.: [1] Соле Ж.-Л., Основные структуры математи-
математической статистики, пер. с франц., М., 1972; [2] Лин-
н п к Ю. В., Статистические задачи с мешающими параметрами,
М., 1966; [3] Барра Ж. - Р., Основные понятия математиче-
математической статистики, пер. с франц., Ы., 1974. М. С. Никулин.
ПОДОБНЫЕ МАТРИЦЫ — квадратные матрицы
А и В одного порядка, связанные соотношением 5 =
— S~1AS, где S —какая-либо невырожденная мат-
матрица того же порядка. П. м. имеют один и тот же ранг,
один и тот же определитель, один и тот же характе-
ристич. многочлен, одни и те же собственные значе-
значения. Часто бывает важно выбрать для данной матрицы
ей подобную, имеющую возможно более простую форму,
напр. диагональную пли жорданову (см. Жорданоеа
матрица). Т. С. Пиголпииа.
ПОДОБНЫЕ МНОЖЕСТВА — обобщение элемен-
тарно-геометрпч. понятия подобия. Множества А и В,
линейно упорядоченные отношениями Щ и if, наз.
подобными, если для них существует такое взаимно
однозначное отображение / : А^-В, что для любых
-г, у?А ИЗ хЭ\у следует f(x)tfl(y). М. П. Войуеховский.
ПОДОБНЫЕ ОПЕРАТОРЫ операторы S и Т в
банаховом пространстве X (не обязательно ограничен-
ограниченные) такие, что существует ограниченный оператор U
в X, обладающий ограниченным обратным, и выпол-
выполняется соотношение
S ^U~1TU.
Если U — унитарный оператор, то S и Т наз. у н и-
тарно эквивалентными.
Ото понятие — пример понятия т. н. подобных
отображений. Пусть fug — дна отображения
множества X в себя. Тогда если существует взаимно
однозначное отображение U : Х—>-Х такое, что Uf—
= gU, то эти отображения наз. подобны м и. Име-
Имеются попытки дать определение подобия для отобра-
отображений одного множества X на другое У; напр., отоб-
отображения наз. подобными, если существуют взаимно
однозначные отображения U и V множеств X и Y
на себя такие, что Vf-—gU. м. И. Войцехоеский.
ПОДОБНЫЙ КРИТЕРИЙ — статистический крите-
критерий для проверки сложной гипотезы Н„ : 6?в() против
сложной альтернативы Н1 : 8 ?в1(воПв1 = 0), функ-
функция мощности к-рого принимает на 0О одно и то же за-
заранее заданное значение из интервала @,1).
См. Неймана структура, Веренса — Фишера проб-
проблема, Подобная область.
Лит.: [1] Леман Э., Проверка статистических гипотез,
пер. с англ., 2 изд., М., 1979. М. С. Никулин.
ПОДОБЪЕКТ объекта категории — поня-
понятие, аналогичное понятию подструктуры математич.
структуры. Пусть it — произвольная категория и
А — фиксированный объект из Я'. В классе всех моно-
мономорфизмов из Я' с концом в А вводится отношение
иредпорядка (отношение делимости справа): и, : X—>А
предшествует а : Y—>-А или u,—ia, если ц = и/0 для
нек-рого li': X^~Y. В действительности, морфизм и/
однозначно определен, поскольку а — мономорфизм.
Отношение предпорядка индуцирует отношение эк-
эквивалентности между мономорфизмами с концом в А:
мономорфизмы и,: Х->А и а : Y^-A эквивалентны
тогда и только тогда, когда и—^0 и a—i\a. Класс экви-
эквивалентных мономорфизмов наз. подобъектом
объекта Л. П. с представителем [i : X~>Y иногда обоз-
обозначают (ц, : Х^-А] или (и]. Допускается также воз-
возможность с помощью т. н. символа т Гильберта произ-
произвести выбор представителей подобъектов объекта А
и рассматривать этих представителей в качестве под-
подобъектов. В категориях множеств, групп, абелевых
групп, векторных пространств П. любого объекта оп-
определяется канонич. вложением подмножества (под-
(подгруппы, подпространства) в объемлющее множество
(группу, пространство). Однако в категории тополо-
гич. пространств введенное понятие П. шире понятия
подмножества с индуцированной топологией.
Отношение предпорядка между мономорфизмами с
общим концом А индуцирует отношение порядка меж-
между П. объекта А : (u]<:(ai, если \х<Са. Это отношение
аналогично отношению включения подмножеств неко-
некоторого множества.
Если Мономорфизм ц регулярен, то любой эквива-
эквивалентный ему мономорфизм также регулярен. Поэтому
можно говорить о регулярных П. любого объекта А .
В частности, П. с представителем 1_4 регулярен. В ка-
категориях с нулевыми морфизмами аналогично вводятся
нормальные П. Если в категории Я существует бика-
тегорная структура (.*,?, (v, DJJ), то подобъект (п,: X—>-
—>-А] об'ьекта А наз. допустимым (относительно ука-
указанной бикатегорной структуры), если и,?ЭД1.
М. Ш. Цалечко.
ПОДПРЕДСТАВЛЕНИЕ ПРЕДСТАВЛЕНИЯ — ли-
линейное представление р в инвариантном подпростран-
стве FcE представления я группы (алгебры, кольца,
полугруппы) X в векторном (топологии, векторном)
пространстве Е, определяемое формулой р(,т)|— я(ж)|
для всех |?/\ x?X. Если я — непрерывное пред-
представление (топологич. группы, алгебры, кольца, полу-
полугруппы), то любое его П. п. также непрерывно.
А. И. Штерн.
ПОДПРЯМОЕ ПРОИЗВЕДЕНИЕ алгебраиче-
алгебраических систем — специальный тип подсистем пря-
прямого (декартова) произведения систем. Пусть Л,-, г?/,—
семейство однотипных алгебраич. систем и пусть А =
— ТТ. А; —прямое произведение этих систем с проек-
проекциями (¦>,-: А-*-А{, t^/. Алгебраич. система В того же
типа наз. п о д и р я м ы м произведением
систем А,-, если существует такое вложение т: В-^-А
что гомоморфизмы тар;, '?/, сюръективны. Иногда
под П. п. понимается любая система, изоморфная под-
подсистеме прямого произведения: тогда системы, удов-
удовлетворяющие сформулированному выше условию, наз.
специальными п о д п р я м ы м и произ-
произведениями. В теории колец и в теории модулей
П. п. наз. также подпрямой с у м м о и.
Подпрямое произведение (подпрямую сумму) обозна-
обозначают TJjg/^i Eji*6l-^i соответственно).
Следующие условия равносильны: а) система В
является П. н. систем Aj, i?I; б) существует раз-
разделяющее семейство сюръективных гомоморфизмов
/,¦: В—*-Л,-, i?/;b) существует такое семейство конгру-
конгруэнции р/, i ?1, системы В, что пересечение этих конгру-
энцип является единичной конгруэнцией и B/picaA/
для каждого t?/. Всякая универсальная алгебра яв-
является II. п. подпрямо неразложимых алгебр.
С теоретнко-категорной точки зрения понятие П. п.
двойственно понятию правильного произведения ал-
алгебраич. систем с нулевыми (одноэлементными) подсис-
подсистемами. М. Ш. Цаленко.
ПОДРАЗДЕЛЕНИЕ геометрического сим-
плициального комплекса К — такой
геометрический симшшциальный комплекс Кг, что
тело \Кг\ совпадает с телом \К\ и каждый симплекс
К1 содержится в нек-ром симплексе К. Практически
переход к П. производится с помощью разбиения сим-
симплексов комплекса А' на более мелкие симплексы так,
чтобы разбиение каждого симплекса было согласовано
с разбиением его граней. В частности, каждая вершина
К является вершиной Кг, Переход к П. обычно исполь-
используется для доказательства инвариантности комбина-
комбинаторно определяемых характеристик полиэдров (напр.,
эйлеровой характеристики, гомологии групп), а также
для получения триангуляции с пужными свойствами
(напр., достаточно мелких триангуляции). Звезд-
Звездное П. комплекса К с центром в точке а?|ЛГ| полу-
получается следующим образом. Замкнутые симплексы К,
не содержащие точку а, остаются без изменения. Каж-
Каждый замкнутый симплекс а, содержащий точку о,
разбивается на конусы с вершиной в точке а над теми
гранями о, к-рыо не содержат а. Для любых двух три-
триангуляции Тг, Т2 одного и того же полиэдра Р сущест-
существует триангуляция Т3 полиэдра Р, получающаяся как
из Тг, так и из Г2 последовательностью звездных ГГ.
Понятие звездного П. допускает формализацию на
языке абстрактных симплициальных комплексов (сим-
нлициальных схем). Любое звездное П. замкнутого
подкомплекса продолжается до авездного П. всего
комплекса. Производное подразделе-
подразделение К' комплекса К получается в результате после-
последовательных звездных П. с центрами во всех открытых
симплексах К в порядке убывания их размерностей.
Для произвольного замкнутого подкомплекса К ком-
комплекса L подкомплекс K'cL'— полный в следующем
смысле: из того, что все вершины нек-рого симплекса
a?L' лежат в К', следует, что а^К'. Если в качество
центров производного П. выбрать барицентры сим-
симплексов, то получится барицентрическое П.
Если диаметр каждого симплекса я-мерного комплек-
комплекса К не превосходит числа d, то диаметры симплексов
его барицентрического П. ограничены числом ?-^-j .
Диаметры симплексов тп-кратного барицентрического
П. комплекса К ограничены числом [ —~ уl d, т. е.
г ^ п +1 у '
могут быть сделаны сколь угодно малыми путем вы-
выбора достаточно большого т.
Лит.: 11] Александров П. С, Комбинаторная топо-
логия, М.— Л., 1947; 12] Хилтон П. - Д ж., У а й л и С,
Теория гомологии. Введение в алгебраическую топологию, пер.
с англ., М., 1966. С. В. Матвеев.
ПОДРЕШЕТКА — подмножество А элементов ре-
решетки, замкнутое относительно операций + и-, т.е.
такое подмножество, что а-\-Ь^А и ab?A для любых
а, Ь из А. Таким образом, П. является подалгеброй ре-
решетки, рассматриваемой как универсальная алгебра
с двумя бинарными операциями. Подрегастка А на;!,
выпукло й, если из а, Ь?А и а<^с<^.Ь вытекает,
что с?А. Примерами П. являются всякое одноэле-
одноэлементное подмножество решетки, идеал, фильтр, интер-
интервал. Все эти П. выпуклые. Любое подмножество эле-
элементов цепи является ее П. (не обязательно выпуклой).
Все П. данной решетки, упорядоченные отношением
включения, образуют решетку.
Лит.: [1] Биркгоф Г., Теория структур, пер. с англ.,
М., 1952; [2] Скорняков Л. А., Элементы теории струк-
структур, М., 1970; 13] Житомирский Г. И., в сб.: Упорядо-
Упорядоченные множества и решетки, в. 7, Саратов, 1981; [4] Г р е т-
цер Г., Общая теория решеток, пер. с англ., М.. 1982.
Т. С. Фофанова.
ПОДСТАНОВКА множества — взаимно одно-
однозначное отображение множества на себя. Термин «П.»
главным образом применяется для конечною множе-
множества А'. В атом случае удобно считать, что А'—A, . . .,
и}, и записывать П. в виде
/1 2 ...п\
Т= . . К (*)
Vi Ч ¦¦•in/
где iu i2, . . ., ln — нек-рая перестановка чисел 1, 2,
. . ., п (впрочем, иногда термин «перестановка» упот-
употребляется как синоним термина «П.», см., напр., [2]
с. 146). Запись (*) означает, что 7 переводит число
к в ifc, то есть y(k) = ik (пишут также A:V=z'fc) для i-=
= 1,2,..., п. Число всех различных П. множества X
при \Х[ = п равно числу всех перестановок этого мно-
множества, т. е. «!. Произведение подстановок аи Р мно-
множества X определяется как последовательное выпол-
выполнение отображении an f n задается формулой аР(ж) =
= а,(р(х)) для всех х?Х. Совокупность всех П. мно-
множества X образует группу относительно введенного
умножения, к-рая наз. симметрической группой. Лю-
Любая подгруппа спмметрич. группы паз. подстановок
группой.
Симметрич. группа П. множества X обозначается
S(X), она содержит в качестве подгруппы SF(X) —
группу, состоящую из таких подстановок у, к-рые пе-
перемещают лишь конечное подмножество элементов
(то есть у{х)^.г лишь для конечного множества эле-
элементов х^Х). Если X конечно и состоит из п элемен-
элементов, то еимметрпч. группа обозначается S,,.
Т р а н с п о з и ц и е й наз. такая П. множества X,
к-рая меняет местами только два элемента i w i; она
обозначается (г, ;). В ?„ имеется ровно п (п —1)/2 транс-
транспозиций. Любая подстановка у из SF(X) представима
в виде произведения транспозиций. В частности, каж-
каждая П. из Sn есть произведение транспозиций. П. может
разлагаться и произведение транспозиций многими спо-
способами. Однако для данной у характер четности числа
множителей в разложении на транспозиции не зависит
от способа разложения. П., представимая в виде про-
произведения четного числа транспозиций, наз. четной,
а разлагающаяся в произведение нечетного числа
транспозиций — нечетной. В Sn имеется и!/2
четных П. и столько же нечетных. Если П. y?Sn за-
записана в виде (:•¦), то ее четность совпадает с четностью
числа инверсий перестановки гъ . . ., („,
к-рос равно числу таких пар {;&, if}, что &</, iu>lj-
Транспозиция, очевидно, есть нечетная П. Примене-
Применение одной транспозиции к любой перестановке меняет
четность числа ее инверсий на противоположную. Про-
Произведение двух четных, а также двух нечетных II. есть
четная П., а четной и нечетной II. (в любом порядке) —
нечетная. Все четные П. составляют нормальную под-
подгруппу А (X) в группе SF(X), к-рая наз. знако-
знакопеременной. При \Х\— п подгруппа А (X) обо-
обозначается А п.
Циклом длины I наз. такая подстановка а конеч-
конечного множества У— {i/j, . . ., yt), что
о Ы - у-,, о {у2) — у3,..., a (</(_i) = у,, а (;/,) ---= уъ
Конечный цикл обозначается (ylt у.2, . . ., </,). В е с-
к О'н е ч н ы м ц и к л о м наз. такая П. счетного
множества
У = {..., !/_„, У-1,.Уо, У1, У 2, •••}.
что для любого целого i а (у,•)--</,¦., i- Обозначение бес-
бесконечного цикла таково:
Цикл длины 2 есть транспозиция. Группа Sn содер-
содержит (п — 1)! циклов длины п. Для любой подстановки
у из S (X) существует такое разбиение множества X
на непересекающиеся подмножества, что на каждом
из них у действует как цикл. Конечные подмножества
этого разбиения имеют вид
{х, у (.г), ..., y'-1 (.г)},
где у1 (х)=х, а бесконечные —
{..., у-^(х), у'1(х), х, у{х), у- (,с), ...},
где ук (х)фх при k?bQ. Циклы, индуцируемые подста-
подстановкой у на подмножествах разбиения, наз. н е з а в и-
с и м ы м и цикла м и подстановки у. Например,
A, 3, 4) и B, 5)— независимые циклы II.
12 3 4 5s
! 5 4 1 2,
у записывается в виде
A, 3, 4) B, 5)
¦и является произведением своих независимых циклов.
Вообще, если у нетождественная П., имеющая лишь
конечное число циклов неединнчной длины, то у —
произведение таких циклов. В частности, каждая не-
нетождественная II. va SF(X) является произведением
своих- независимых циклов неединичной длины. П о-
рядок подстановки у из SF(X), т. е. по-
порядок циклич. группы <7>, равен наименьшему общему
кратному длин ее независимых циклов.
Из независимых циклов данной П. можно получить
независимые циклы П., сопряженной с ней. Напр.,
если
произведение независимых циклов подстановки 7 из
Sn, а 6?5„ и б (а,) —6,-, i=l, . . ., п, то
— разложение подстановки буб ~1 в произведение не-
независимых циклов. Две II. группы ?'„ тогда и только
тогда сопряжены в Sn, когда они имеют одно и то же
число независимых циклов каждой длины.
Пусть s?Sn, к — число независимых циклов под-
подстановки s, включая и циклы длины 1. Тогда разность
п—к паз. д о к р е м е н т о м подстановки s. Наимень-
Наименьшее число множителей при разложении подстановки s
в произведение транспозиций совпадает с се декремен-
декрементом. Четность П. совпадает г, четностью ее декремента.
П. возникли впервые в комбинаторике 18 в. В кон.
18 в. Ж. Лагранж (J. Lagrange) применил их при ис-
исследовании разрешимости алгебраич. уравнений в ра-
радикалах. О. Коши (A. Cauchy) посвятил многочислен-
многочисленные исследования этому понятию. Ему, в частности,
принадлежит идея разложения П. в произведение цик-
циклов. Исследования групповых свойств П. восходит
к Н. Абелю (N. Abel) и особенно к Э. Галуа (Е. Ga-
Galois). См. Галуа теория, Подстановок группа.
Лит.: [1] Jordan С, Traite des substitutions et des equa-
equations algebriqucs, P., 1957; [2] Кострикин А. И., Введе-
Введение в алгебру, М., 1977; 13] К урош А. Г., Курс высшей
алгебры, II изд., М., 1975; [4] Холл М., Теория групп, пер.
с англ., М., 1962. Д. А. Супруненко.
ПОДСТАНОВКИ ПРАВИЛО — одно из вывода пра-
правил логико-математических исчислений. Под назва-
названием «П. п.» могут фигурировать различные виды пра-
правил. Напр., в высказываний исчислении это 11. п. фор-
формулы вместо всех вхождений пропозициональной пере-
переменной. Для предикатов исчисления: а) П. п. формулы
вместо предикатной переменной; при этом требуется
выполнение ряда ограничений на вхождения индивид-
индивидных переменных с тем, что ы избежать колли-
коллизии п е р е и е н н ы х, т. е. ситуации, когда пере-
переменная, свободная в подставляемой формуле, ока-
окажется связанной в результате подстановки; б) П. п.
терма вместо свободных вхождений индивидной пере-
переменной соответствующего сорта; при этом также не-
необходимо избегать коллизии переменных.
Лит.: Ш Новиков И. С, Элементы математической ло-
логики, 2 изд., М., 1973; [2] Ш е н Ф и л д Д ж. Р., Математи-
Математическая логика, пер. с англ., М., 1975; [3] Гильберт Д.,
Б ер на й с П., Основания математики. Логические исчисле-
исчисления и формализация арифметики, пер. с нем., 2 изд., М.,
1982. С. II. Артемов.
ПОДСТАНОВОК ГРУППА — совокупность под-
подстановок на нек-ром множестве X, образующих группу
относительно операции умножения подстановок. Ина-
Иначе, 11. г.— ято пара (G, X), где G — группа, X —
множество и каждому y?G соответствует подстановка
хн>хУ множества X такая, что 1) хаЬ=(ха)$ , х?Х,
a, P?G, и 2) ха~-х для любого х(~Х тогда и только
тогда, когда а=Е — единица группы G. Если выпол-
выполняется лишь условие 1), то говорят о действии
(или представлении) группы G на множестве
X. В этом случае подмножество Н элементов группы G,
оставляющих на месте все х?Х, будет нормальным
делителем в G (называемым ядром д е п с т в и я)
и факторгруппа GjH действует на X уже как П. г.
Если X — конечное множество, то П. г. (G. X) наз.
конечной, в противном случае — бесконеч-
бесконечной. Множество всех подстановок на X наз. с и м-
м е т р и ч. группой и обозначается S (X) или S,,, ес-
если Х=-- {1, 2, . . ., и}.
II о д о б и е м (или изоморфизмом) II. г.
(G, X) на П. г. (С, X') наз. пара (ф, т|;) отображений,
где ф — изоморфизм G на С, а ф — биекция X на
X', причем оба отображения согласованы в том смыс-
смысле, что для всех х?Х и a?G имеет место равенство
(xa)^=(x^)a(f. II. г., между к-рыми существует подобие,
наз. подобными. Если (G, X) — П. г., то на
множестве X естественно определена эквивалентность:
у~х, у, x?X<^zz$y=xa для нек-рого a?G; классы
эквивалентности 11. г. наз. орбита м и, или о б-
л а с т я м и транзитивное т н, группы (G, X).
П. г. т р а н з и т и в н а, если она имеет лишь одну ор-
биту, в противном случае она и н т р а н з и т и в н а
(см. ТраIзитивная группа).
Произвольная абстрактная группа G может быть
представлена как П. г. на подходящем множестве X
(теорема К э л и). При этом в качестве X можно
выбрать множество всех элементов группы G и сопо-
сопоставить каждому y?G отображение, получающееся
в результате умножения справа на элемент у : |v =
= !y- Полученное таким образом регулярное
представление группы G в виде П. г. не яв-
является единственно возможным. При исследовании
П. г. интересуются другими свойствами, чем при изу-
изучении абстрактных групп. Речь идет не только о строе-
строении группы, а в первую очередь о том, как группа
действует на множестве X', так, напр., свойство тран-
транзитивности есть свойство П. г., а не абстрактных
групп.
Пусть (G, X) — П. г., а М — подмножество в X.
Совокупность всех подстановок у ? G, переводящих М в
себя (то есть ж? M$$xv?M), образует подгруппу
0д1, называемую стабилизатором множества
М. Множество тех подстановок, к-рые оставляют все
у^М на месте, наз. фиксатором множества М
и обозначается G,My Фиксатор будет нормальным де-
делителем стабилизатора. Если М={а} — одноэлемент-
одноэлементное множество, то понятия стабилизатора и фиксатора
совпадают (он обозначается Ga). Группа наз. п о л у-
регулярной (или действующей сво-
свободно), если стабилизатор каждой точки является
единичной группой и регулярной (или прос-
просто транзит и вно и), если группа, кроме того,
транзитивна. Централизатором b(G) группы G наз.
ее централизатор в симметрии, группе S (X) — это
совокупность подстановок на X, поэлементно переста-
перестановочных со всеми элементами из G. Централизатор
транзитивной группы полурегулярен, и наоборот,
централизатор полурегулярной группы транзитивен.
Регулярная П. г. (С, X) подобна вышеприведенному
регулярному представлению группы G. Централиза-
Централизатором л (G) регулярного представления будет т. н.
левое регулярное представление
группы G, сопоставляющее элементу y?G подстанов-
подстановку Ге=.т-1|, ??G.
Существуют операции (см. [6]), позволяющие из за-
заданных П. г. строить новые.
а) С у м м а П. г. Пусть (G. X) и (Я, Y) — две П. г.,
причем пересечение X (]Y пусто. Сумма (G, X)-\-(H, Y)
определяется как 11. г. прямого произведения GXII
на объединении X[jY, причем для a?G, P?i/ ?
?XY
б) Произведением (G, X)X(H, Y) П. г.
(G, X) и (Я, Y) наз. группа (GxII, XXY), действую-
действующая на XXY согласно формуле (х, у)<-а- P>=(.ra, yP).
Обе операции ассоциативны и могут быть определены
для произвольного числа групп.
в) Сплетение. Пусть (G, X) и (Л, Y) — П. г. и
Р (') € НХ — отображение X в //. На множестве пар
fa, P (х)], называемых таблицами, определяется умно-
умножение:
[а, $(х)][а', Р'И] = [««'. РИР(*а)Ь
относительно к-рого они образуют группу G^H. Спле-
Сплетение П. г. (G, X) и (//, Y) есть П. г. (G~//, XXY),
причем действие определяется формулой
Сплетение также ассоциативно и может быть опреде-
определено даже для любого вполне упорядоченного семей-
ства П. г. Сплетение несдиничных П. г. будет импри-
митивной группой. Если G и Н рассматривать как их
регулярные представления, то это определение с точ-
точностью до порядка сомножителей совпадает с обычным
теоретико-групповым сплетением групп.
г) Экспонирова пи е. Группа таблиц, дей-
действующая на множестве Yx, приводит к П. г.
(Н, Y) 1 (С, A')-=(G=c H, YX).
Причем действие определяется следующим образом:
где / (х) ? Yx. Экспонирование не ассоциативно и при-
приводит обычно к примитивным группам. А именно,
(Н, Y) f (С, X) примитивна, если (Н, Y) — примитив-
примитивная нециклич. группа.
Группы подстановок возникают обычно как совокуп-
совокупность подстановок, сохраняющих нек-рые отношения
или операции на множестве X (см. также Преобразо-
Преобразований группа). Так, исходным для возникновения тео-
теории П. г. было понятие группы Галуа многочлена.
Если
/ (х) = апх" + . . . -]- я0
многочлен с коэффициентами а,- из нек-рого поля К,
а |г, . . ., ?„ — его корни в нек-ром надполе, то груп-
группой Галуа будет П. г. множества {?ь . . ., ?,г}, сохра-
сохраняющих рациональные отношения между корнями,
т. е. равенства вида
V1 г Р1 ?'»— О
где с,- и ; ?А". Как показал Э. Галуа (Е. Galois),
от свойств этой группы зависит разрешимость или не-
неразрешимость уравнения f(x)~0 в радикалах. Этот
результат привел к развитию теории П. г. в трудах
Э. Галуа, Ж. Серре (J . Serret), К. Жордана (С. Jordan)
и др. Дальнейшее развитие (кон. 19 — нач. 20 вв.)
эта теория нашла в работах У. Бёрнсайда (VV. Burnside),
У. Маннинга (W. Manning), Г. Фробениуса (G. Fro-
benius), О. Ю. Шмидта, И. Шура (J. Schur). П. г.
имеют многочисленные применения в дискретной мате-
математике, напр, при классификации булевых функций и
конечных автоматов, в теории кодов с исправлением
ошибок, при подсчете изомеров сложных органич.
соединений.
Лит.: [1] Passman D., Permutation groups, N.Y.—
Amst. 19ti8; [2] W i e 1 a n d t H., Finite permutation groups,
N. Y. — L., 19(U; [3] Burnside W., Theory of groups of fini-
finite order, N.Y., 1958; [4] Кал ужни н Л. А., Суща и-
с к и й В. И., Преобразования и перестановки, пер. с упр.,
М., 1979; [5] X о л л М., Теория групп, пер. с англ., М., 19В2;
[6] К а л у ж н и н Л. А., К л и н М. X., С у щ а н с к и и
В. И., «Известия вузои. Математика», 1979, № 8, с. 26—33.
Л. А. Иалужнин.
ПОДФОРМУЛЬНОСТИ СВОЙСТВО — свойство
нек-рых логических исчислений и логико-математических
исчислений, заключающееся в том, что посылки каж-
каждого правила исчисления состоят из подформул за-
заключения. П. с. позволяет организовать поиск вы-
вывода «снизу вверх» (см. Генцена формальная система).
С целью повышения эффективности такого поиска для
многих исчислений рассматриваются различные спе-
специализации и обобщения П. С. С. Ю. Маслив.
ПОДХОДЯЩАЯ ДРОБЬ — см. Цепная дробь.
ПОДЧИНЕНИЯ ПРИНЦИП — одна из форм Лии-
деле'фа принципа, использующая понятие подчинения
функций. Пусть со (z) — любая функция, регулярная
в круге |z| <1 и удовлетворяющая условию: со@)=0,
|co(z)|<l в |z|<l; пусть функция F(z) мероморфна
в |z|<1. Если функция f(z) имеет вид j (z) = F (m (z)),
то I (z) паз. п о д ч и и с н н о й функции F (z) в круге
I z\ < 1, a F (z) — н о д ч и и я ю щ е й ф у н к ц и е й.
Это отношение подчинения обозначается
через f(z)-4F(z). В простейшем случае, когда F (z) —
однолистная функция в |z|<l, указанное отношение
означает просто, что f(Q)—F(Q) и что функция /(z)
не принимает в круге |z|<l тех значений, к-рых в нем
не принимает функция F(z). Имеют место следующие
основные теоремы.
Теорема 1. Пусть функция w—F(z) мероморфна
в круге !z|<l и отображает его на римапову поверх-
поверхность G(F). Пусть Gr(F) — часть G(/*'), соответствую-
соответствующая |z|<r, г<1. Если f(z)-$F(z), то значения /(г)
в |z|<:r (при аналитическом продолжении из /@) =
= Р@)) лежат в Gr(F), причем граничные точки Gr(F)
достигаются только для / (z)=F (ez), |р|~1 (см. [2]).
Т е о р е м а 2. Если /(z)—ZF (z) и /•'(z) регулярна
в \z\ <r, л<1, то, полагая
имеем Mk(r, f)<.Mh(r, F), Л>0, 0<г<1 (см. [1]).
Теорема 3. Если f(z)-^l-'(z) и F (z) регуляр-
регулярна в z=0, то для коэффициентов разложении /(z)-
Xil^»l2. w=l, 2, ... (см. [2]).
Общая теория подчинения полезна при рассмотре-
рассмотрении вопроса о множестве значений, принимаемых (или
выпускаемых) аналитич. функцией. Отношение под-
подчинения можно использовать в двух различных на-
направлениях. Во-первых, можно исходить из заданной
функции F (z) и изучать свойства всех функций f(z),
подчиненных /¦'{'). Если при этом подчиняющая функ-
функция F (z) полностью известна, то известна и область
Gr(F), в к-рон лежат значения /(z) (теорема 1), и верх-
верхняя граница интегральных средних М^ (г, /) (теорема 2).
Если, кроме того, F(z) регулярна в z=0, то имеем
верхние границы для коэффициентов функции /(z) (те-
(теорема 3). Во-вторых, можно рассмотреть какую-либо
мероморфную в круге |z|<l функцию f(z), из свойств
к-рой следует невозможность со подчинения в \z\ <1
надлежащей функции F(z). Если при этом F(z), напр.,
однолистна, то f (z) необходимо принимает в |z| <1 зна-
значения вне G(F). Эти идеи использования отношения
подчинения и выражают П. и. II. п. можно распро-
распространять и на многосвязные области (см. [31).
Лчт.: [1] LittlewoodJ. Е., «Proc. Lond. Math. Soc. B)»,
1»2\ v. 23, ]). 48J — 519; [2] R о g о s i n s k i W., «Proc Camb.
Pliilos. Soc», 1939, v. 35, p. 1—26; [3] Аленицын Ю. E.,
«Тр. Матем. ин-та АН СССР», 1961, т. 60, с 5—21; 14]
Rogosinski W., «Schr. Konigs. Gelehrt. Gesellsch. Natur-
wiss. Kl.», 1931, Jr. 8, H. 1, S. 1—31; [5] HogosUski W.,
«J. Lond. Math. Soc», 1939, v. 14, M» 53, p. 4 — 11; [6] его же,
«Proc. Lond. Math. Soc», 1943, v. 48, p. 48—82; [7] Little-
wood J. E., Lectures on the theory of functions, L., 1944; [8]
Г о л у з и н Г. М., Геометрическая теория функций комплекс-
комплексного переменного, 2 изд., М., 1966, с. 356 — 57, 60В — 09.
Ю. Е. Аленицын.
ПОЗИТИВНАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ — после
довательность действительных чисел ц0, цх, р.2, . . .
на промежутке [а, Ь] такая, что для всякого многочлена
Р (х) — а„ -\- ахх+...-{- апхп,
нетождественного нулю и неотрицательного на [а, Ь]
выражение
Ф (Р) ^а0и0-!-я1Ц1+ . . . -f аиц„?э0.
Если же для всякого такого многочлена будет ф (Р) >0,
то последовательность наз. строго позитив-
н о й. Для того чтобы последовательность ц0, и,х,
ц2, . . . была позитивной на [а, Ь\, необходимо и до-
достаточно существование возрастающей на [а, Ь] функ-
функции g(x), для к-рон
^'а x"dg(x)=nn, u = l, 2, ... .
М. И. Войцеховскип.
ПОЗИТИВНОЕ ПРОПОЗИЦИОНАЛЬНОЕ ИСЧИС-
ИСЧИСЛЕНИЕ — исчисление высказываний в языке {&, V'
ZD}, задаваемое следующими 8 схемами аксиом:
4 3 (Я 3 A), (AZD (В Z) С)) Z3 ((A dB)DD3 6')),
А & В з А, А&ВГ) В, А Г) E з А&В),
А^А v В, BZ}A v В, (Аг>С) г> ((ДГ)С) Г> (А
и правилом вывода модус поненс. II. п. и. содержит ту
часть интуиционистского исчисления высказываний
I (см. Интуиционизм), к-рая не зависит от отрицания.
а именно: всякая пропозициональная формула, не
содержащая связки ~] (отрицания), выводима в П. п. и.
тогда и только тогда, когда она выводима в /. Если
к П. п. и. добавить две схемы аксиом:
1) ~\А^> (А^>В) (закон отрицания а н т е-
ц е д е н т а),
2) (Ar>B)Z2({AZ3~\B)r>~]A) (закон приве-
приведения к абсурду),
то получится исчисление /. Для получения / можно
вместо 2) взять и более слабую схему:
2') (А 3 П А ) з ~| А (закон частичного
приведения к абсурду).
См. также Импликатиепое пропозициональное ис-
исчисление.
Лит.: Ll] Ч ё р ч А., Введение в математическую логику,
пер. с англ., т. 1, М., 19В0; [2] Г и л ь G с р т Д., Б с р it а й с
П., Основания математики. Логические исчисления и формали-
формализация арифметики, пер. с нем., 2 изд., М., 1982. С. К. Соболев.
ПОЗИЦИОННАЯ ИГРА — игра, имеющая характер
развертывающегося в дискретном времени процесса на
древовидно упорядоченном множестве (наз. также де-
деревом). Конечной П. и. наз. система
Г </, X, Ж, {Рх}х€Ха. {%}i6l, {h,}i€ly,
где 1) / — множество игроков (\f\--n); 2) X — ко-
конечное дерево, вершины к-рого наз. позициями,
а корень — начальной позицией. Для по-
позиций естественно определяется отношение следова-
следования; позиции, непосредственно следующие за данной
;г? X, наз. альтернативами х; полиции, не
имеющие альтернатив, наз. окончательными,
а ведущие в них пути — п а р т и я ми; множество
окончательных позиции обозначается X*; 3) ;К —
разбиение множества Х\Х* на п-~\- множеств
очередности Хо, Ху, ¦ ¦ ., Хп. В позициях
из Х(, ?>(>, ход осуществляется игроком г, в позипиях
из Хп — случайно; 4) Рх — вероятностные распреде-
распределения на множествах альтернатив каждой позиции
х?Х0; 5) Ж;-={и1, г/г, • • •, Г/^.} — разбиение каж-
каждого Xj, i>0. Предполагается, что все позиции х из
данного и% имеют одинаковое число альтернатив и
никакие две из них не следуют друг за другом; мно-
множества U% наз. информационными. Между
альтернативами всех позиций одного информацион-
информационного множества установлено однозначное соответст-
соответствие, и каждый его класс наз. альтернативой
самого информационного .множества; 6) k,- — функция,
ставящая в соответствие каждой окончательной пози-
позиции выигрыш в ней игрока i.
Чистой стратегией игрока I в П. и. яв-
является функция, ставящая в соответствие каждому ин-
информационному множеству г/'ft нек-рую его альтерна-
альтернативу. Набор п чистых стратегий всех игроков состав-
составляет ситуацию. Процесс игры в условиях сложив-
сложившейся ситуации можно понимать как случайное блуж-
блуждание по множеству позиций от начальной позиции
к окончательной, причем в каждой позиции игрок, мно-
множеству очередности к-рого принадлежит ата позиция,
знает лишь содержащее ее информационное множество
и выбирает альтернативу в соответствии со своей стра-
тегией. В позициях из Хо выбор альтернативы случаен.
Это случайное блуждание определяет вероятностное
распределение на множестве окончательных позиций.
Принимая за выигрыш игрока математич. ожидание
его выигрыша на окончательных позициях, получают
бескоалиционную игру в нормальной форме.
П. и. наз. игрой с полной информа-
информацией, если информационные множества игроков со-
состоят из одной позиции каждое. В игре с полной ин-
информацией существует ситуация равновесия в чистых
стратегиях (теорема Ц о р м е л о — Н е й м а-
н а).
Важную роль в П. и. играют смешанные стратегии.
Две смешанные стратегии игрока наз. эквивалент-
эквивалентными, если в ситуациях, отличающихся только
этими стратегиями, вероятности каждой окончательной
позиции равны. Игрок имеет полную память,
если каждое его информационное множество следует
за единственной альтернативой всех предшествующих
информационных множеств этого игрока. Наличие
полной памяти у игрока означает, что в момент совер-
совершения хода он помнит все информационные .множества,
в к-рых он находился, и свои выборы в них. Стра-
Стратегией поведения наз. такая смешапная
стратегия, тфи к-рой случайные выборы альтернатив
информационных множеств стохастически независимы.
Каждая смешанная стратегия игрока эквивалентна
нек-рой стратегии поведения тогда и только тогда,
когда игрок имеет полную память (теорема К у-
н а).
Более общими являются П. и. с бесконечным мно-
множеством альтернатив в каждой позиции и с бесконечно
продолжающимися партиями, а также игры на графах.
Лит.: [1] Позиционные игры, М., 1967; [2] Б ер ж К.,
Общая теория игр нескольких лиц, пер. с франц., М., 1961;
[3] Кун Г. У., в сб.: Позиционные игры, М., 11N7, с. 13—40;
[4] Т h о rn ]) s о n G. L., в кн.: Contributions to the theory of
games, v. 2, Princeton, 1953, p. 267—77; [5] В op о б ьев Н. Н.,
«Проблемы кибернетики», 1962, в. 7, с. о—20; [6] Б у й
Конг К ы (I и г, «Вестник ЛГУ», 1969, №1, с. 49—59.
Н. Н. Воробьев, А. Н. Ляпунов.
ПОЙА РАСПРЕДЕЛЕНИЕ — распределение вероят-
вероятностей случайной величины Х„, принимающей целые
неотрицательные значения к, 0<:/с<:гс, в соответствии
с формулой
Р{Х„ = Л} =
- Гк b (b ±с). . . [Ь цк-1) с]г (,г + с) ... jr+(n-h- 1) с]
п (Ь t- r) (ft + r + c) ... [b + r + (n- 1) с] '
где целые »>0, 6>0, г>0, с~^ — \ — параметры, или
эквивалентной формулой
Р {*„=/,}
_ j-.ft р (р + у) ¦ ¦¦ [р Hft- 1) У] g (q + v) ..Л'/- (n-h- i) y |
~ л A+v) ••• [l+(n-l) 7] ™
ph pn~k Ism ,'
~~ (P/V) + *-l (<7/v) + n-ft-l/ °(l/y) + n-l' \^
где целое гс>0, действительные 0<р<1, д— 1—p,
y>0 — параметры. Связь между A) и B) устанавли-
устанавливается равенствами
_ h _ г _ с
/)=17Т7' '/="й77' "!~—~ьТ~г-
Математич. ожидание и дисперсия II. р. равны соот-
соответственно ЕА'„=пр и ОХп=прд т-р— • Специальные
случаи ГГ. р.: Хп имеет при с- 0 биномиальное распре-
распределение с параметрами п и р; Хп имеет при .?-=—1
гипергеометрическое распределение с параметрами М~ Ь.
N=b-\-r и п. При Ь—у<х, г—>-оо, когда p=b/(b-'t-r) по-
постоянно, и у—с/(Ь-\-г)—^{), П. р. стремится к биноми-
биномиальному распределению с параметрами п и р.
П. р. было рассмотрено Д. Пойа (G. Polya, 1923)
в связи с т. п. у р н о в о и схемой II о и а. Из
урны, содержащей Ь черных и г красных шаров, осу-
осуществляется выбор с возвращение.м при условии, что
каждый извлеченный шар возвращается в урну вместе
с с шарами того же цвета. Если Хп — полное число
черных шаров в выборке объема п, то распределение
X п задается формулами A) или B). Последовательность
Хп, и=1, 2, . . ., представляет собой дискретный
марковский процесс, причем состояния процесса опре-
определяются числом черных шаров в выборке в мо-
момент я, а условная вероятность перехода от состоя-
состояния А- в момент времени п в состояние /с+1 в момент
времени ге+1 равна
к j b + r + nc i + nf
(зависит от п).
Предельным переходом из урновой схемы Пойа мо-
может быть получен процесс Пойа — неодно-
неоднородный марковский процесс с непрерывным временем,
принадлежащий классу процессов «чистого размноже-
размножения». При условии, что за бесконечно малое время At
происходит лишь одно извлечение шара, при н—>-оо,
когда np~>t. ny—^at, выводится предельная условная
вероятность перехода из состояния к в состояние
за время At:
При переходе от урновой схемы Пойа к процессу Пойа
возникает важная предельная форма П. р. Именно,
вероятность Рь (t) в момент времени t пребывать в со-
состоянии к равна
и (,\—гп fat\n /_1 \1,гх
Л (<)<(l/) l( ^ J [ГГш)
Полученное предельное распределение является отри-
отрицательным биномиальным распределением с парамет-
параметрами 1/а и l/(l-|-ai) (соответствующее лштематич. ожи-
ожидание равно t, а дисперсия t(\-\-at).
Урновая модель и процесс Пойа, в к-рых возникает
П. р. и его предельная форма, являются моделями
с аффектом последействия (извлечение
шара определенного цвета из урны увеличивает вероят-
вероятность извлечения шара того же цвета при следующем
испытании).
При стремлении параметра а к нулю процесс Пойа
переходит в пуассоновский процесс, а П. р. при а->0
имеет своим пределом Пуассона распределение с пара-
параметром t.
Лит.: [1] Ф е л л е р Б., Введение в теорию вероятностей
и ее приложения, пер. с англ., 2 изд., т. 1—2, М., 1967.
А. В. Прохоров.
ПОЙА ТЕОРЕМА: пусть RD— множество отобра-
отображении коночного множества D, \D\--n. в множество
И и пусть G — группа подстановок множества D, по-
порождающая разбиение RD на классы эквивалентности,
при к-ром /l5 fi€.RD принадлежат одному и тому же
классу тогда и только тогда, когда найдется такое
g(zG, что fi(g(d))—f2(d) для всех d?D; если каждому
r?R сопоставлен вес /г(г) —элемент коммутативного
кольца (вес /полагается равным w(/) = TJ . w(f(d))
и вес w (F) класса FcRD определяется как вес любого
/€*'), то
где в левой части равенства сумма берется по всем
классам эквивалентности, а
Р (О; xltX,, •••,*«) = |G|IlL Ш
есть цикловой индекс С, при этом /\(G) —
число циклов длины к подстановки g в разложении
ее в произведение независимых циклов.
Теорема была опубликована в 1937 Д. Попа (G. Р6-
1уа, см. [3] с. 36—138), хотя фактически она была
известна раньше (см. [3] с. 9—35).
Если в качестве веса элементов И брать степени
независимой переменной х (или произведение степеней
нескольких переменных), то для ср (х)=2»k=-oakxk 'т' н'
«ряд. перечисляющий фигуры», где а% — число эле-
элементов R веса xh) и Ф (x) = ^dk_^obitxk (т. н. «ряд, пере-
перечисляющий конфигурации», где hf, — число классов
RD веса хк) согласно П. т. имеет место соотношение:
Ф (х) ---: Р (С; (р(х), ф (х-), . . ., ф (х")) =-- Р (С; ф (х)).
II р и -м с р ы. 1) Если | Я |-----m, u>(r)=l, то q>(x)- n,
и тогда Р (G; т, т, . . ., т) — число классов эквива
лентности.
¦2) Если i?--=-{0, 1}, w{r) = xr, то ф(.г)=1-1 ж, а /С
?BD с w(f) — .tk можно истолковать как подмножество
В- мощности к. Группа G индуцирует орбиты подмно-
подмножеств D, и коэффициент при хк в многочлене Р (G:
1+.г) есть число орбит, состоящих из подмножеств
мощности к.
3) Пусть R— {0, 1}, J9— V2 —все 2-подмножества
} F{1, 2, . . ., } ?ff°
ф
) у { }, д
{?, /} множества F={1, 2, . . ., р }, тогда /?-ff° пред-
представляет помеченный граф с вершинами из F, у к-рого
две вершины I и / смежны, если /({г, /})=1. Пусть
w{r)-=xr, тогда если w(j)=xk, то к — число робер
в графе, соответствующем отображению /. Если на Г
де)гствует симметрич. группа S;}, то, определив для
o^Sp подстановку ga на D соотношением go {i, i}—
= {a(i), a (;)}, получают парную группу G=5B'=
= {ga }. действующую на D~V^K
Для последовательности %ръ (чисел графов с р вер-
вершинами и к ребрами). &—1, 2, . . . , по П. т. получают
производящую функцию
Для единичной группы подстановок Еп, симметрич.
группы подстановок Sn и парной группы подстановок
Уп цикловоп индекс имеет соответственно вид
Р(Е„; хО-^х",
Г'ТТ L~2~ J
ххЧ2;д
Г«-П -,
/¦, s)
)
где (г, s) — наибольши!! общий делитель, {г, s] — наи-
наименьшее общее кратное чисел /¦ и s, а суммирование
2* проводится но frj, fe2> • • •> ^п иРи условии &!+
+ 2Л2+. • .-[-пк,;=п. Известны цикловые индексы для
знакопеременной, циклической и диэдральной групп,
а также формулы для получения цикловых индексов
для произведения, декартова произведения и сплете-
сплетения групп (см. [4]).
Имеются обобщения П. т. на случай иного определе-
определения как веса функции, так и классов эквивалентности
[1].
Лит.: [1] Д е Б р е й н Н. Д ж., в кн.: Прикладная ком-
комбинаторная математика, пер. с англ., М., 1968, с. 61 —106;
[2] С а ч к о 1! В. в., Комбинаторные методы дискретной ма-
математики, М., 1977; [3] Перечислительные задачи комбинатор-
комбинаторного анализа. Сб. переводов, М., 1979; [4] Харари Ф.,
Па л мер Э., Перечисление графов, пер. с англ., М., 1977.
В. М. Михеев.
ПОКАЗАТЕЛЬНАЯ ФУНКЦИЯ, экспонен-
экспоненциальная функция, экспонент а,—
функция
г/ = ег= exp z
(где е — основание натуральных логарифмов— непе-
рово число), для любого значения z (действительного
или комплексного) определяемая соотношением
ez = lim A-i- —V. A)
Она обладает следующими свойствами:
при любых значениях гл и z2.
При действительных х график П. ф. у=ех— экс-
экспоненциальная кривая — проходит через
точку @, 1) и асимптотически прибли-
приближается к оси Ох (см. рис.). У,
В курсе математич. анализа рассма-
рассматривается П. ф. у=ах при действитель-
действительных х и а>0, а?гЛ; она связана с (основ-
(основной) Л. ф. у =ех соотношением
,х In a
П. ф. у = ах определена при всех х,
положительна, монотонна (возрастает,
если а>1, и убывает, если 0<а<1), непрерывна,
бесконечно дифференцируема; при этом
(ах)' :-ах In a. \axdx — -
]i частности
(еху _-.exi
в окрестности каждой точки П. ф. может быть разло-
разложена в степенной ряд, напр.:
в* —14- —4- —-I- 4-—-L ^У"° — B)
График П. ф. у=ах симметричен графику П. ф.
г/=A/а)л относительно оси ординат. Если а>1, то
П. ф. ах при х~*--г-<х возрастает быстрее любой сте-
степени х, а при г—>-—оо стремится к пулю быстрее любой
степени IIх, т. е. при любом натуральном &>0
lim — = oo, lim |^|ьа*=0.
Обратной к П. ф. является логарифмическая функ-
функция.
При комплексных а и z П. ф. связана с (основной!
П. ф. w—ez формулой
где Ln a — логарифм комплексного числа а.
П. ф. w—ez— целая трансцендентная функция и
является аналитич. продолжением П. ф. у=ех с дейст-
действительной оси в комплексную плоскость.
Помимо формулы A), П. ф. може» быть определена
также с помощью ряда B), сходящегося во всей комп-
комплексной плоскости, или по формуле Эйлера
e* = e* + <> = e* (cos у + i sin у).
Если z=x-\-iy, то
| ez \ = ex, Argez = у-\-2лк, k — O,±i, ±2, ....
П. ф. ег— периодическая с периодом 2ni:
П. ф. ez принимает все комплексные значения, за ис-
исключением нуля: уравнение ег=а имеет бесконечное
число решений для любого комплексного числа
Эти решения находятся по формуле
z = Ln a = In \а \ - \- i Arg a.
П. ф. ег является одной из основных элементарных
функций. Через нее выражаются, напр., тригономет-
рич. функции и пшерболич. функции. ю. в. Сидоров.
ПОКАЗАТЕЛЬНОЕ РАСПРЕДЕЛЕНИЕ — непре-
непрерывное распределение вероятностей случайной вели-
величины X, задаваемое плотностью
е~л*, х 5й О,
A)
Плотность р (х) зависит от положительного масштабно-
масштабного параметра X. Формула для моментов: EXn = n\/kn,
в частности — для математич. ожидания ЕХ=1Л, и дис-
дисперсии DZ=1/X2; характеристич. функция: A—itl\)~i.
IJ. р. входит в семейство распределений, называемых
гамма-распределениями и задаваемых плотностью
и-кратная свертка распределения A) равна гамма-
распределению с тем же самым параметром к и с а=п.
П. р.— единственное распределение, обладающее
свойством отсутствия последействия: для любых х>0,
2/>0 выполняется равенство
?{Х >х+у\Х> у} = ?{Х>х), B)
где ?{Х>х^гу\Х>у} — условная вероятность собы-
события X ~>х-\-у при условии X >г/. Свойство B) называется
также марковским свойством.
В однородном пуассоповском процессе расстояние
между двумя последовательными скачками траектории
имеет П. р. Наоборот, процесс восстановления с по-
показательным временем жизни A) является пуассонов-
ским процессом восстановления. П. р. часто возни-
возникает как предельное при суперпозиции или разреже-
разрежении процессов восстановления, в задачах пересече-
пересечения высокого уровня в различных схемах блуждания,
в критических ветвящихся процессах и т. п.
Упомянутыми выше свойствами объясняется широ-
широкое применение П. р. при расчетах различных систем
в теории массового обслуживания и в теории надеж-
надежности. Предполагая времена занятости приборов слу-
случайными, независимыми друг от друга и распределен-
распределенными показательно, можно благодаря свойству B)
изучать системы массового обслуживания с помощью
конечных или счетных цепей Маркова с непрерывным
временем. Аналогичным образом используются цепи
Маркова и в теории надежности, где времена исправ-
исправной работы отдельных приборов часто можно предпола-
предполагать независимыми и распределенными показательно.
Лит.: [1] Ф е л л е р В., Введение в теорию вероятностей
и ее приложения, пер. с англ., 2 изд., т. 2, М., 1967.
Б. А. Севастьянов.
ПОКООРДИНАТНОГО СПУСКА МЕТОД — один из
методов минимизации функций многих переменных,
использующий лишь значения минимизируемой функ-
функции. П. с. м. применяется в тех случаях, когда мини-
минимизируемая функция недифференцируема или вычис-
вычисление ее производных требует большого объема ра-
работы. Ниже описан П. с. м. для задачи минимизации
функции F (х) на множестве
X — {ж = (х1, ..., хп) :а; s? х< < bit i-^-i, . .., п},
где a/, ft,- — заданные числа, a,<6,-; случаи, когда
все или нек-рые а,-= — оо, bj—-\-со, здесь не исклю-
исключаются. Пусть ei~@, . . ., 0, 1,0,.. ., 0) — коорди-
координатный вектор, у к-рого 1-я координата равна 1, ос-
остальные координаты равны нулю. Задают начальное
приближение хо?Х, ао>О. Пусть известно k-е при-
блшкение эго?Х, а^>0 при каком-либо fc^O. Полагают
Pk = ei > ГД° lk=k—п\ — + 1 (здесь [а] — целая часть
числа а). Таким образом,
po--=elt ..., 2>n-i---=tfn. Pn=ei. •••. P2n-i=en. />2«=Ci,...,
т. е. осуществляется циклич. перебор координатных
векторов elt . . ., еп. Сначала проверяют выполнение
условия
У (»*)• A)
Если A) выполняется, то полагают з"? + 1=:..г
aft + i=aft. Если A) не выполняется, то проверяют
условие
X, F (Xk —
В случае выполнения условия B) полагают fc
—-ж^—o-kPh-i aft + i = afe- Если оба условия A), B) не
выполняются, то полагают
( Xaft при гй = ге, aok--=xk_n+i, C)
( апри i#ra или хк ф as^_ni i, илиOs^/vsg// 1;
где Л, 0<Я<1,— параметр метода. Условия C) озна-
означают, что если за один цикл из п итераций при пере-
переборе всех координатных векторов «1? . . ., е„ с шагом
а/г выполнилось хотя бы одно из условий A) или B),
то длина шага а^ не дробится и сохраняется на про-
протяжении по крайней мере следующего цикла из и
итераций; если же на последних п итерациях оба
условия A), B) ни разу не выполнились, то шаг ад,
дробится.
Если функция F (ж) выпукла и непрерывно диффе-
дифференцируема на X, множество {ж?Х : F (x)s?F (ж0)}
ограничено, а0 — произвольное положительное чис-
число, то метод A) — C) сходится, т. е.
lim F (жк)= inf F (ж),
к-* ж же X
последовательность {ж^} сходится к множеству точек
минимума F (ж) на X. Если F (ж) недифференцируема
на X, то П. с. м. может не сходиться (см. [1], [2]).
Лит.: [1] Васильев Ф. II., Численные методы реше-
решения экстремальных задач, М., 1980; [2] Карманов в. Г.,
Математическое программирование, 2 изд., М., 1980.
Ф. П. Васильев.
ПОКРЫВАЮЩИЙ ЭЛЕМЕНТ в частично
упорядоченном множестве — элемент,
непосредственно следующий за другим элементом; точ-
точнее, выражение «а покрывает Ь в частично упорядо-
упорядоченном множестве Рь означает, что Ь<а и не сущест-
существует элемента х?Р, удовлетворяющего условию 6<
<?<а. Т. С. Фофанова.
ПОКРЫТИЕ множества X — любое семей-
семейство подмножеств этого множества, объединение к-рого
есть X.
1) Под П. топологического про-
пространства, равномерного пространства и вообще
какого-либо множества, наделенного тем или иным
строением, понимают произвольное П. этого мно-
множества. Однако в теории топологич. пространств осо-
особенно естественно рассматривать открытые по-
покрытия, то есть П., все элементы к-рых являются
открытыми множествами. Большое значение открытых
П. вызвано тем, что их элементы несут в себе полную
информацию о локальном строении пространства, а
свойства П. в целом (в частности, число элементов
в пом, кратность, комбинаторные свойства) отражают
существенно глобальные характеристики пространства.
Так, на языке открытых П. определяется размер-
размерность по Лебегу dim топологич. пространства: размер-
размерность нормального пространства X не превосходит
натурального числа п, если в каждое конечное откры-
открытое П. этого пространства можно вписать конечное
открытое П., кратность к-рого в каждой точке (т. е.
число элементов П., содержащих данную точку) не
превосходит ге-|-1. Отношение вписанности одного П.
в другое является основным общим элементарным от-
отношением между П. Семейство множеств у вписано
я семейство множеств Л, если каждый алемент се-
семейства у содержится в нек-ром элементе семейства X.
На языке открытых П. определяется класс параком-
паптных пространств.
Подпокрытием покрытия у множества X
наз. всякое подсемейство семейства у, само являю-
являющееся П. множества X. В терминах подпокрытий опре-
определяются фундаментальные понятия бикомпактно-
сти, счетной и финальной компактности. Простран-
Пространство бикомпактно, если из каждого его от-
открытого П. можно выделить конечное подпокрытие.
Пространство счетно компактно, если из
каждого его счетного открытого П. можно выделит],
коночное подпокрытие. Пространство финально
компактно, если из каждого его открытого II.
Можно выделить счетное подпокрытие. С помощью от-
открытых П. определяются абстрактные комбинаторные
объекты, открывающие дорогу применению алгебраич.
методов к исследованию топологич. пространств, более
общих, чем полиэдры. П. С. Александров определил
фундаментальное понятие нерва произвольного
покрытия у как абстрактного комплекса, вершины
к-рого поставлены во взаимно однозначное соответст-
соответствие с элементами покрытия у и конечный набор этих
вершин составляет абстрактный симплекс в том и
только в том случае, если пересечение отвечающих этим
элементам покрытий у не пусто. Системам открытых П.
пространства, взятых вместе с отношением вписан-
вписанности, отвечают системы абстрактных комплексов, свя-
связанных симплициальными отображениями,— т. н.
спектры комплексе в.
Заметную роль в топологии играют и замкну-
замкнутые покрытия — то есть II., все элементы к-рых
являются замкнутыми множествами. Если в топологич.
пространстве все одноточечные множества замкнуты,
то примером замкнутого П. этого пространства может
служить семейство всех его одноточечных подмно-
подмножеств. Но в таком П. не заключено никакой инфор-
информации о топологии рассматриваемого пространства,
кроме той, что в нем выполнена Г,-акеиома отдели-
отделимости. Поэтому требование замкнутости П. следует
соединять с другими существенными ограничениями.
В частности, полезно рассматривать замкнутые ло-
локально конечные П. Они существенны в теории раз-
размерности. Важным примером замкнутого П. является
П. полиэдра замкнутыми симплексами какого-нибудь
подразделяющего этот полиэдр комплекса.
Среди ограничений на П., связанные не с характе-
характером элементов, а с их расположением, наиболее часто
встречаются следующие. Мощность П.— число
элементов в нем, локальная конечность
(у каждой точки пространства есть окрестность, пере-
пересекающаяся с конечным множеством элементов се-
семейства подмножеств этого пространства), точеч-
точечная конечность (означающая, что множество
ялементов П., содержащих произвольно взятую точку,
конечно), звездная конечность (каждый
элемент П. пересекается лишь с конечным числом
элементов этого П.).
Семейство множеств в топологич. пространстве наз.
консервативным, если замыкание объедине-
объединения любого ого подсемейства равно объединению за-
замыканий элементов этого подсемейства. Каждое ло-
локально конечное семейство множеств консервативно.
Консервативные П. возникают при исследовании пара-
компактных пространств, при этом важны и не три-
тривиальны не только открытые, но и любые консерва-
консервативные П.
Важную роль играет понятие звезды точки
¦г относительно семейств множеств (в частности, по-
покрытий) у. Это — объединение всех элементов семей-
семейства у, содержащих х, обозначаемое обычно St-j,(^).
Аналогично определяется у в е з д a Sty (Л) м н о-
ж е с т в а А относительно семейства множеств 7-
На понятии звезды основано фундаментальное отно-
отношение звездной вписанности одного И. в другое, су-
существенно более тонкое, чем отношение вписанности.
Семейство множеств К наз. звездно вписан-
вписанным в семейство множеств у, если для каждой точки
найдется элемент семейства у, содержащий звезду этой
точки относительно X. Отношение звездной вписан-
вписанности открытых П. имеет важное значение в теории
размерности, на нем основаны нек-рые критерии мет-
метризуемости, оно является одним из основных элемен-
элементарных понятий, входящих в определение равномер-
равномерной структуры и равномерного пространства. Полезно
рассматривать семейства F открытых II. топологич.
пространства, направленные отношением звездной впи-
вписанности в следующем смысле: для любых у1 и у2 из
F найдется |я?/', звездно вписанное и в ух, и в у2.
Представляет ценность следующая характеристика
паракомпактности на языке звездной вписанности
(теорема Морит ы): хаусдорфово пространство
иаракомпактно в том if только в том случае, если в лю-
любое его открытое П. можно вписать открытое П. звезд-
звездно.
Звездная вписанность в случае произвольных (или
даже замкнутых) П. не столь содержательна. В част-
частности, это видно из того, что семейство всех одното-
одноточечных подмножеств пространства звездно вписано
п любое П. этого пространства.
Лит.: [1] К е л л и Д ж., Общая топология, пер. с англ.,
2 изд., М., 1981; [2] Архангельский А. В., П о н о м а-
р е в В. И., Основы общей топологии в задачах и упражнениях,
М., 11174. А. В, Архангельский.
2) В комбинаторной геометр и и име-
имеется ряд задач и предложений, относящихся к специ-
специальным 1Г., в основном выпуклых множеств. Пусть
К — выпуклое тело га-мерного векторного пространст-
пространства R", bd К и int К — соответственно граница и внут-
внутренность К. Наиболее известны следующие задачи
с П.
а) Ищется минимальное число t(K) транслятов (па-
(параллельных переносов) int К, при помощи к-рых можно
покрыть тело К.
б) Ищется минимальное число Ь(К) гомотетичных
К тел с коэффициентом гомотетии к, 0</с<1, при
помощи к-рых можно покрыть тело К.
в) Ищется минимальное число d(K) гомотетичных
К множеств с коэффициентом гомотетии /с>1 и цент-
центром гомотетии в R"\int X, при помощи к-рых можно
покрыть тело К.
При ограниченности К задачи а) и б) эквивалентны
между собой, эквивалентны освещения задаче (извне)
множества bd К и связаны с Хадвигера гипотезой.
Для неограниченного К задачи а) и б), вообще говоря,
различны, причем числа Ь(К) и t(K) могут быть бес-
бесконечными.
Лит.: [1] Данцер Л., Грюнбаум Б., К л и В.,
Теорема Хелли и ее применения, пер. с англ., М., 1968; [2]
Болтянский В. Г., Г о х б е р г И. Ц., Теоремы и за-
задачи комбинаторной геометрии, М., 1965; [3] и х ж е, Разбие-
Разбиение фигур на меньшие части, М., 1971; [4] X а д в и г е р Г.,
Дебруннер Г., Комбинаторная геометрия плоскости,
пер. с нем., М., 1905; [5] Роджерс К., Укладки и покры-
покрытия, пер. с, англ., М., 1968; [В] Болтянский В. Г., G о л-
тан П. С, Комбинаторная геометрия различных классов вы-
выпуклых множеств, Киш,, 1978. П. С. Сплтан,
ПОКРЫТИЯ И УПАКОВКИ — комбинаторные кон-
конфигурации, связанные с многозначным отображением
одного множества на другое. Пусть заданы множества
V и Е и многозначное отображение Г множества Е
на множество Г. Пусть Г (с) - образ элемента е?Е
при отображении Г и для литого С~_^Е пусть Г (С) -
— UeeE^(e)- Подмножество Ci~E наз. покрыти-
покрытием (для (Г, Е, Г)), если Г(С)=Г. Подмножество
Рд^Е наз. у и а к о в к о й, или укладкой (для
(V, Е, Г)), если для любых двух различных элемен-
элементов е,-, еу из Р множества Г(е,-) и Г(еу) пе пересекаются.
Подмножество Рс^Е наз. совершенной у п а к о в-
к о й, или совершенным покрытием,
если Р является одновременно и покрытием, и упаков-
упаковкой. Множество Е наз. покрывавши м, а мно-
множество I'' — н о к р и наем ы м. Если обратное от-
отображение Г таково, что Т~1(\т) — Е, то можно
рассматривать Г как покрывающее множество, а Е
как покрываемое. Отображение Г : E-+-V определяет
отношение инцидентности Т. мрп к-ром
v из V и е из Е инцидентны (обозначение г/с), если
6Г()
6
С понятиями упаковки и покрытия связаны экстре-
экстремальные задачи, заключающиеся и отыскании (по
произвольно заданной тройке (V, Е, Г)) П. и у., до-
доставляющих экстремум тех или иных функционалов.
Такой функционал можно, напр., задать с помощью
функции, сопоставляющей каждому элементу е из Е
неотрицательное действительное число w(e), наз. ве-
весом элемента е. Задача о минимальном покрытии заклю-
заключается в построении покрытия С, для к-рого 2eeCw(e)
принимает минимальное значение. Часто рассмат-
рассматривается случай, когда i»(c)=d; здесь речь идет о на-
нахождении покрытия минимальной мощности, или
т. н. к р а т ч а Й ш его по к |> ы i и я. Если тропка
(V, Е, Г) такова, что
max | Г (е) |< и, min | Г (v)\Ssw,
eiE v?V
то минимальная мощность х(Г, Е, Г) покрытия удо-
удовлетворяет неравенствам
В экстремальных задачах об упаковках чаще всего
требуется найти упаковки максимальной мощности.
Иногда на покрываемом множестве 1' задается функ-
функция к, принимающая целые неотрицательные значе-
значения, тогда Х-п скрытном (к-у паковкой) наз.
подмножество Рс^Е, удовлетворяющее условию: для
каждого v? V число а (с, Р) тех элементов е?Р, к-рые
инцидентны элементу г, подчиняется неравенству
a (v. Р)^Х (v)
(соответственно ст('\ /))<Я(г;)). Существует связь меж-
между Я-покрытиямп минимальной мощности и Х-упаков-
ками максимальной мощности. Именно, пусть заданы
множества V и Е, многозначное отображение Г : _?"—>-
—>V, а также функции % и X' на множестве V такие, что
для каждого г? Г:
Тогда, если множество С есть минимальное по мощ-
мощности Л-покрытие для (V, Е, Г), то множество Р —
— Е\С является максимальной но мощности V-yria-
ковкой, и наоборот: если Р — максимальная л'-уна-
ковка, то множество С--Е\Р есть Х-покрытпе мини-
минимальной мощности. К классу задач о П. и у. отно-
относятся, напр., следующие:
1) Пусть G — граф с множеством вершин Г и мно-
множеством ребер Е. Если рассматривать множество Г
в качестве покрываемого, множество Е — в качестве
покрывающего и отношение инцидентности вершин
и ребер — и качестве /, то покрытием является ребер-
реберное покрытие графа, упаковкой — паросочетание, со-
совершенной упаковкой — совершенное наросочетание.
Если в качестве и покрывающего, и покрываемого
взять множество вершин, а в качестве 1 — отношение
смежности вершин, то покрытием будет внешне устой-
устойчивое множество, а упаковкой — внутренне устойчи-
устойчивое множество; при утом минимальная мощность по-
покрытия наз. числом внешней устойчивости, а макси-
максимальная мощность упаковки — числом внутренней
устойчивости (см. Графив числовые характеристики).
2) Пусть Г — непустое множество в метрич. про-
пространстве Я. Система я множеств Uc^li на:!, е-и о к р ы-
т и е м множества V, если диаметр d(U) любого мно-
множества /*?л не превосходит 2в и Fcz|J Usnll. Мно-
Множество 4'cfl наз. р-с е т т, ю для множества V, если
любая точка множества Г находится на расстоянии,
не превышающем е, от нек-рой точки из S. Множество
Uc^li наз. р-р а з л и ч и м ы м, если любые две его раз-
различные точки лежат на расстоянии, большем е. Пусть
NF (Г) — минимальное число множеств в г -покрытии
множества V, а Ме (У) -- максимальное число точек
в Р-разлнчпмом подмножестве множества V. Число
log^Vu (V) на:*, е-э н т р о п и е й множества V, а
log2il/(. ([') нал. Р-е м к о с т ь ю множества I*. Поня-
Понятия к-;-штрошш и р.-омкости применяются в теории
приближения функции и в теории информации.
3) Пусть В" — единичный «-мерный куб с метри-
метрикой Хемминга и покрываемое множество есть множе-
множество его вершин, а покрывающее множество — мно-
множество шаров радиуса г в В". Тогда множество цент-
центров шаров упаковки есть код, исправляющий г оши-
ошибок. Если упаковка является совершенной, то код
на-ч. плотно упакованным, или с о в е р-
ш с н н ы м.
Если в качестве покрываемого множества взять под-
подмножество Nf вершин куба В", на к-ром нек-рая бу-
булева функция /(j'i, . . ., хп) принимает значение 1, а
в качестве покрывающего — множество граней (ин-
(интервалов), целиком содержащихся в Nf, то покрытие
наименьшей мощности будет соответствовать кратчай-
кратчайшей дизъюнктивной нормальной форме функции
/(.ть . . ., х„), а покрытие с наименьшей суммой ран-
рангов — минимальной дизъюнктивной нормальной фор-
форме функции /(.г,, . . ., ,г„) (см. Булевых функций нор-
нормальные формы).
В задачах о И. и у. оцениваются их мощности, ис-
исследуются вопросы существования, построения, пере-
перечисления совершенных упаковок, изучаются возмож-
возможности построения эффективных алгоритмов для реше-
решения этих задач.
Лит.: [И Роджерс К., Укладки и покрытия, пер. с
англ., М., ПN8; 121 Т от Л. Ф., Расположения на плоскости,
на сфере и и пространстве, пер. с нем., М., 1958; [3] Пите р-
с о и у., у о ядов Э., Коды, исправляющие ошибки, пер.
г англ., М., 1И7Н; [4] Дискретная математика и математические
вопросы кибернетики, т. 1, М., 1974; [5] X а р а р и Ф., Теория
графов, пер. с англ., М., 1973; [6] Б ер ж К., Теория графов
и ее применения, пер. с франц., М., 1962; ["J В и т у ш к и н
А. Г., Оценка сложности задачи табулирования, М., 1959: [8]
Колмогоров А. Н., Тихомиров В. М., «Успехи
матем. наук», 1959, т. 14, в. 2, с. 3—86; [9J Б а х в а -
л он Н. С., Численные методы, 2 изд.. М., ИO 5; [10] Я 0-
л о н с к и й С. В., Введение в дискретную математику, М., 1979.
Л. А . Сшюженко.
ПОКРЫТИЯ ТЕОРЕМЫ — теоремы для различных
классов регулярных функций, устанавливающие
нек-рые свойства таких множеств, к-рые целиком содер-
содержатся в множестве значений каждой функции соответ-
соответствующего класса. Ниже приведены нек-рые из основ-
основных П. т. (см. также |1]).
Теорема 1. Если функция w=f(z) = z-\-a2z2+
~г. . . регулярна и однолистна в круге Ы<1 (то есть
l(z)?S), то круг IH<J/4 целиком покрывается образом
круга ]г|<1 при отображении этой функцией. На
окружности |ii-|=V4 только в том случае имеются точки,
но принадлежащие образу, если
/ (z) = - , 0 < а < 2я.
Т '.¦ о р е м a 2. Если мероморфная функция w=
= /E)-^тао+ут. • ¦ однолистно отображает !?|>1,
то вся граница образа лежит в круге \w—ао|<2.
Теорема 3. Если f(z)?S, то но крайней мере
одна пз а плижашпнх к ш=0 точек границы образа
круга Ы<1 при отображении w=f(z), лежащих на п
любых лучах, исходящих из w=Q под равными уг-
углами, отстоит от ц7=0 не ближе чем на ^/1!i.
Теорема 4. Если /(z)??, то в образе круга
|:|<1 при отображении w — f(z) содержится множество,
состоящее из п открытых . прямолинейных отрезков
с,суммой длин, не меньшей п, исходящих из начала под
равными углами величины 2л.
Для /(")?5 и удовлетворяющих в круге Ы<1 нера-
неравенству |/(z)KM, M^l, имеют место И. т., анало-
аналогичные теоремам 1, 3 (с соответствующими постоян-
постоянными). П. т. 1 в 3 переносятся и на класс функций
w=f(z), регулярных и однолистных в кольце 1<Ы<г
и отображающих его на области, лежащие в |u;|>l, a
окружность Ы = 1 —на окружность |ц?|=1.
Для класса R функций w~ f(z)~z-\-aiziJ\-. . ., ре-
регулярных в круге |г|<1, но существует круга |и>|<р,
|>>0, целиком покрываемого значениями каждой пз
функций этого класса. Для функций
регулярных в |z|<l, каждый образ итого круга цели-
целиком покрывает нек-рый отрезок любого заданного на-
наклона, содержащий точку w- 0 внутри, длиной не мень-
меньше /1=8я2/Г*A/4) = 0,45. . ., причем число А нельзя
увеличить без дополнительных ограничений. В этом же
классе функций при условии, что /'(z)#0 в кольце
0<Ы<1, каждый образ круга |-|<1 целиком покры-
покрывает круг |tt'|<J/i6i но не всегда покрывает больший
круг с центром в ш—0.
В классе Sp регулярных в U|<1 функций /(:)¦-
= zP(i-}-a1z-1-a2z2-\-. . .) таких, что каждое свое значе-
значение w они принимают не более чем в /; точках круга
Ы<1, имеет место аналог П. т. 1с соответствующим
;.ругом \w\ <}l.iP + l. Если при этом аг~. . .=а^_1:=0или
«!=. . . =ар—0, то соответствующими кругами будут
|w|<1/4 или |№|<1/2- Аналогичные результаты имеют
место для функций, />-листных в среднем но окруж-
окружности, /j-листных в среднем по площади и др. На класс
Sp перенесена и П. т. 3.
См. также теорему Блоха в ст. Блоха константа.
Лит.: [1] Г о л у з и н Г. М., Геометрическая теория функ-
функций комплексного переменного, 2 изд., М., 1966.
Г. К. Антонюп.
ПОЛЕ — коммутативно-ассоциативное кольцо с еди-
единицей, множество ненулевых элементов к-рого не пусто
и образует группу относительно умножения. П. можно
охарактеризовать также как простые ненулевые ком-
коммутативно-ассоциативные кольца с единицей. П р и-
м е р ьг поле й: П. рациональных чисел С, П. дей-
действительных чисел R, II. комплексных чисел С, ко-
конечные П. (см. Га.и/а поле), П. частных областей цело-
целостности.
II о д и о л о м ноля К наз. подмножество MczK,
к-рое само является П. относительно операций сложе-
сложения и умножения, заданных в К. Напр.,если а—нек-рый
автоморфизм поля К, то множество
является подполем в К. Если М и Л' — подполя ноля
А', то их пересечение Mf[N будет подполем в К; кроме
того, существует наименьшее подполе MN ноля А,
содержащее М и N и называемое композитом
полей М и N (в А'). Каждой П. содержит единствен-
единственное простое (т. е. не содержащее подполей) подполе.
Любой гомоморфизм полей является вложением.
Для произвольного ноля К существует единственный
гомоморфизм ф: ?—*-К, переводящий единицу кольца
2 в единицу поля А'. Если кег <р~0, то К наз. полем
характеристики н у л ь. В этом случае про-
простое подполе ноля А* совпадает с П. частных кольца
ФB) и изоморфно нолю Q. Если ker<p?=O, то кег <р=
— рЖ Для нек-рого простого р. Это р наз. характе-
характеристикой поля А. Простое подполе поля К
совпадает в этом случае с «p(Z) = z//>Z-
Если к подполе поля А, то К наз. расширени-
расширением п о л я к. Пусть Y — нек-рое подмножество
в А', тогда определено ноле к(Y) — наименьшее под-
подполе поля К, содержащее Y и к. Говорят, что к(Y) по-
получено из к присоединением элементов множества У.
Основные задач» теории нолей — это описание всех
подполей данного П., всех П., содержащих данное П.,
то есть надполей (см. Расширение поля), изу-
изучение всех вложений П. в нек-рое другое П., класси-
классификация полей с точностью до изоморфизма и изучение
группы автоморфизмов данного П.
Поле К наз. конечно порожденным над
своим нодиолем fc, если существует конечное множество
YczK такое, что K-=k(Y). Любое такое П. можно ин-
интерпретировать как П. рациональных функций к(Х)
нек-рого неприводимого алгебраич. многообразия X,
определенного над к. Изучением таких П. занимается
алгебраическая геометрия. В частности, задача класси-
классификации таких II. эквивалентна задаче бирациональ-
ной классификации неприводимых алгебраич. много-
многообразий, а задача нахождения группы всех автомор-
автоморфизмов II. К-=*к(Х), оставляющих на месте все эле-
элементы поля к, эквивалентна задаче нахождения всех
бирацнональных автоморфизмов многообразия X, оп-
определенных над к.
Изучение конечных сепарабельных расширений про-
произвольных П. составляет предмет Галуа теории. В тео-
теории чисел важную роль играет рассмотрение конеч-
конечных расширений поля Q, называемых П. алгебраич.
чисел. Изучением этих П. занимается алгебраическая
теория чисел.
Теория полей изучает также П., несущие нек-рые
дополнительные структуры, напр, дифференциальные
П., топологические П., упорядоченные П., формально
вещественные и формально р-адические П. и др.
Зарождение теории П. (в рамках теории алгебраич.
уравнений) относится к сер. 19 в. После публикации
работ Э. Галуа (Е. Galois) и Ж. Лагранжа (J. La-
grange) в теории групп и К. Ф. Гаусса по теории чисел
стало очевидно, что нужно исследовать природу самих
числовых систем. Концепции П. появляются в работах
Л. Кронекера (L. Kronecker) и Р. Дедекинда (R. De-
dekind). 1'. Дедекинд ввел понятие П., к-рое он перво-
первоначально называл «рациональной областью». Теория
Р. Дедекинда опубликована в примечаниях и допол-
дополнениях к «Теории чисел» П. Дирихле (P. Dirichlet).
В них Р. Дедекинд существенно дополнил и развил
теорию чисел, теорию идеалов и теорию конечных
П. Термин «П.» впервые появился в издании этой
книги в 187:1.
Лит.: [1] Б у }> б а к и Н., Алгебра. Многочлены и поля.
Упорядоченные группы, пер. с франц., М., 1965; [2] В а н дер
Вар ден Г>. Л., Алгебра, пер. с нем., 2 изд., М., 1979; [3]
Л е н г С, Алгебра, пер. с англ., М., 1968; [41 Зарисский
О., С а « ю ¦) л ь П., Коммутативная алгебра, пер. с англ.,
т. 1, М., 1963, Л. В. Кузьмин.
ПОЛЕ РАЗЛОЖЕНИЯ многочлена — наимень-
наименьшое поле, содержащее все корни данного многочлена.
Точнее, расширение L поля К наз. полем разло-
ж е н и я многочлена / над полем К, если /
разлагается над полем L на линейные множители:
и L=K(a1, . . ., «„) (см. Расширение ноля). И. р. су-
существует для любого многочлена /?А"|.г] и определено
однозначно с точностью до изоморфизма, тождествен-
тождественного на К. II. р., по определению, является конечным
алгебраич. расширением поля А'.
Пример ы. Поле комплексных чисел С служит
П. р. многочлена х--\-1 над полом Ik действительных
чисел. Любое конечное ноле GF (<•/), где qr--}>", есть
II. р. многочлена хЧ—х над простым нодиолем GF(p)d
CGF (q). О. А, Иванова.
ПОЛЕЗНОСТИ ТЕОРИЯ — теория, изучающая пред-
предпочтение индивидов и его представление в виде число-
числовой функции. Предпочтением на множестве
альтернатив X наз. транзитивное бинарное отноше-
отношение Д на I; оно представляется функцией и(х) на X;
при этом и(х) наз. функцией полезности,
если для любых х, у^Х из xRу следует и(х)~^и(у) и
наоборот. Таким образом, в II. т. изучаются упорядо-
упорядоченные множества и их монотонные отображения в чис-
числовое пространство (обычно одномерное). П. т. воз-
возникла в работах экономистов 18 в.; начало современ-
современной E0-е гг. 20 в.) П. т. было положено Дж. Нейманом
(J. Neumann) и О. Моргенштсрном (О. Morgenstern)
(см. [1]).
Существование функции полезности в случае конеч-
конечного множества X является очевидным. В бесконечном
случае необходимым и достаточным условием существо-
существования функции полезности является существование
плотного по полезности счетного подмножества AczX,
т.е. для любых х, у?Х\А, xR*y, существует такое
z?A, что xR*z и zR*y, где Я*— строгое пред-
предпочтение (xR*y( У xRy и не yRx). Если X — вы-
выпуклое множество векторного пространства, R непре-
непрерывно на X и для любых х, у, z?X, xR*y, и любого
а, 0<а<1, верно |ou-f(l — a)z]R*[ay-\-(i—a)z\, то
существует единственная с точностью до положитель-
положительной линейной трансформации линейная функция по-
полезности (см. |3]). Различные комбинации более сла-
слабых условий приводят к нелинейной, разрывной или
в том же смысле неединственной функции полезности.
Напр., если X — векторное пространство и из xR*i/
следует (x-\-z)R* (j/+z) и axR*ay для всех z?X и а>0,
то функция оказывается однозначной, но кусочно
линейной.
В П. т. также рассматриваются стохастич. упорядо-
упорядочения и упорядочения сумм или разностей альтерна-
альтернатив (тогда функция полезности строится по нек-рому
кватернарному отношению на X), обобщения для и-
арного отношения вместо бинарного, построение функ-
функции полезности одновременно с субъективными веро-
вероятностями, связь между полезностью многокомпонент-
многокомпонентных альтернатив и полезностями их компонент и др.
(см. |3], [4]).
Лит.: [I] Нейман Д ж., Морген Штерн О., Тео-
Теория игр и экономическое доведение, пер. с англ., М., 1970; [2]
Б и р к г о ф Г., Теория структур, пер. с англ., М.. 1952; [8]
Фишберн П. С, Теория полезности для принятия реше-
решений, пер. с англ., М., 1978; [4] С у п п е с П., 3 и н е с Д ж.,
в кн.; Психологические измерения, пер. с англ., М., 1967.
д. Й. Вилкас.
ПОЛЕЙ КЛАССОВ ТЕОРИЯ — теория, дающая опи-
описание всех абелевых расширений (ко-
(конечных расширений Галуа с абелевой группой Галуа)
поля К, принадлежащего к одному из следующих
типов: \) К — поле алгебраич. чисел, т. е. конечное
расширение поля С; 2) К — конечное расширение
поля рациональных р-адических чисел Q^; 3) К — поле
алгебрапч. функций одной переменной над конечным
полем; 4) А — поле формальных степенных рядов над
конечным полем.
Основные теоремы П. к. т. были сформулированы и
доказаны в частных случаях Л. Кронекером (L. Кгопе-
скег), Г. Вебером (Н. Weber), Д. Гильбертом (D. Hil-
bert) и др. (см. также Алгебраическая теория чисел).
Поля типа 2) и 4) на з. локальными, а поля
типа 1) и 3) — глобальными. Соответственно
можно говорить о локальной и глобальной П.к. т.
В локальной П. к. т. каждому конечному абелеву
расширению L/K с группой Галуа G (L/К) ставится
в соответствие норменная подгруппа NL,K(L*) мульти-
мультипликативной группы А'* ноля К. Группа N L,K(L*) пол-
полностью определяет поле L, и существует канонич.
изоморфизм ф : G(LIK)~K*IN L,K (L*) (основной
изоморфизм П.к. т.). Явный вид этого изомор-
изоморфизма дает теория формального комплексного умноже-
умножения (см. [2] гл. 6). Наоборот, любая открытая подгруп-
подгруппа конечного индекса в К * реализуется как нормен-
ная подгруппа для нек-рого абелева расширения L
(теорема существования).
Если L и L1 — конечные абелевы расширения ноля
А', М— L[\L1 и Лг— L-L1: то справедливы соотношения
м*) =.nl,k(l*) nl,,'k (Ll), \
Nn/K [N*) = Nlik {L*) V\NLllK (Li). J
Включении LjzP.L выполняется тогда и только тогда,
когда
причем в этом случае диаграмма
где а получен ограничением автоморфизмов с Lt на
L, а Р индуцирован тождественным отображением
К*-*-К*, коммутативна. В частности, если КаЬ—
максимальное абелево расширение поля К, то группа
Галуа G(KablK) канонически изоморфна нроконеч-
ному пополнению группы К*.
Изоморфизм ср дает также описание последователь-
последовательности подгрупп ветвления в G(LlK). Так, расширение
ЫК не разветвлено тогда и только тогда, когда группа
единиц U(К) поля К содержится в группе NLjK(L*).
В этом случае изоморфизм ср полностью определяется
тем, что автоморфизм Фробениуса, порождающий
группу G(LlK), переходит в класс n-NL,K(L*), где
л — простой элемент поля К.
На языке когомологий групп изоморфизм ср интер-
интерпретируется как изоморфизм между группами когомо-
когомологий Тейта
До (G (LIК), L*)=K*/Nl,k (?*)•
Более того, пусть L/K — произвольное конечное
расширение Галуа локальных полей. Тогда для лю-
любого целого и определен канонич. изоморфизм ср„:
H"~2(G(L/K), z)^H"(G(L/K), L*).
Если задана башня иолей Галуа MiDL'ZiK, то ин-
инфляция
inf: E2(G(L/K), L*) —> IP(G(MJK), M*)
сохраняет инвариант (см. Браулра группа), а огра-
ограничение
res: H"(G(MjK), M*) —*- H2(G(M/L), M*)
умножает инвариант на [L : К]. Если К — сенарабель-
ное замыкание поля К, то инвариант определяет ка-
вонич. шоморфизм между группой Брауэра поля К
Br(A)~//2(G(A7A), А*)
В глобальной П. к. т. роль мультипликативной
группы поля играет группа классов иделей. Пусть
Ll К — конечное расширение Галуа глобальных по-
полей, и 11 — группа иделей поля L. Группа L* вкла-
вкладывается в 11 в качестве дискретной подгруппы (она
наз. группой главных иделей), а фактор-
факторгруппа Ci~I JL*, наделенная фактортонологией, наз.
группой классов иделей. Доказывается,
что №(G(L/K), CL)=i nH2(G(L/K), CL)~z/nZ, где
n=\L : К]. Существует канонич. вложение inv:
H2(G(L/K), CL)-+.QI'?. Как и в локальной П. к. т.,
для любого целого п определен изоморфизм (основной
изоморфизм глобальной П. к. т.)
1р„: II"-*(G{L/K), z)c±II»(G(L/K), CL).
Для абелева расширения Ll К изоморфизм г|эп сво-
сводится к изоморфизму^ : G (Li K)caC^/Nj ,K(Ci). Hop-
менная подгруппа NIIK(Ci) однозначно определяет
поле L, и наоборот, любая открытая подгруппа конеч-
конечного индекса в Сд- является норменной подгруппой
для нек-рого конечного абелева расширения L (г л о-
бальная теорема существования).
Соотношении, аналогичные A) и B), остаются справед-
справедливыми и для глобальных полей. Если КаЬ— макси-
максимальное абелсво расширение поля А', то в функцио-
функциональном случае группа G (КаЬ1 К) изоморфна проко-
нечному пополнению группы С^, а в числовом случае
группа G(KablK) изоморфна факторгруппе группы С к
по связной компоненте.
Изоморфизмы <р„ и 1|)„ согласованы. Если Ll К конеч-
конечное расширение Галуа глобальных полей, Lv — попол-
пополнение поля L относительно нек-рой точки v и Kv —
пополнение поля К относительно ограничения v на А",
то существует коммутативная диаграмма
Н*-°' (G (L/K), %) ^ Я" (G (LjK), CL),
!¦"))
L*),
где отображение / индуцировано вложением L* — Тi~>
¦+С] и коограничением cores. Для и —0 C) дает ком-
коммутативную диаграмму
у: G(LjK)l[G(LIK), G (L/K)]?*CK!XUK (С L)
: t (*)
ф: G(Lv/Kv)i\G(LJKv), G (Lv/Kv)] ^ A;/^^^).
Диаграмма D) позволяет получить закон разложе-
разложения простых дивизоров поля К в абелевом расширении
UК. Именно, дивизор с поля А" не разветвлен в L
(нполне распадается в L) тогда и только тогда, когда
l'(Kc)c:A'LIK(G[) (соответственно K*aNL/K(GL)).
Если с — нек-рый простой дивизор поля А', не раз-
нетвленный в L, и — точка поля Л', соответствующая с,
и л — простой элемент поля Кг„ то определен символ
Лртина ( -^-\-~ip~1 (я) ?G(L/K), зависящий только
от С. Элемент (—— j — ято автоморфизм Фробениуса
и подгруппе разложения точки v. Согласно теоре-
теореме плотности Чеботарева любой эле-
элемент группы G(LIK) имеет вид (~~-\ Для бесконеч-
бесконечного числа простых дивизоров с ноля А".
Напр., максимальное абелево неразветвленное рас-
расширение числового поля К (называемое гильбер-
гильбертовым полем классов) — ято поле, нормен-
j)
ная подгруппа к-рого совпадает с образом относитель-
относительно проекции /А~-э-СА- группы A"*xJJ U(KV), где v
пробегает все точки поля К. Группа 1^1 К* X TJ U (Kv)
канонически изоморфна группе классов дивизо-
дивизоров Cl^- поля К, что дает важный изоморфизм
G(FiK)~Clf(. В частности, над К нет неразветвленных
абеловых расширении тогда и только тогда, когда
поле К одноклассно.
Тип разложения простого дивизора с поля К в F
полностью определяется классом с в С1С . Вполне рас-
распадаются в F все главные дивизоры и только они.
Все дивизоры поля К становятся главными в F.
Подобно тому, как П. к. т. для абелевых неразвет-
неразветвленных расширений можно излагать на языке группы
классов дивизоров и ее подгрупп, можно дать харак-
теризацию любого конечного абелсва расширения поля
К в терминах группы лучевых классов по нек-рому
модулю (см. Алгебраическая теория чисел). Сущест-
Существуют также обобщения П. к. т. на случай бесконечных
расширении Галуа [4].
Хотя П. к. т. возникла как теория абелевых расши-
расширении, ее результаты дают важную информацию и для
неабелевых расширений Галуа. Напр., на теории по-
полей классов основано доказательство существования
бесконечных башен полей классов (см. Башня полей).
Лит.: [1] Алгебраическая теория чисел, пер. с англ., М.,
IPfii'; 12] В ей ль А., Основы теории чисел, пер. с англ., М.,
1972; [3] Кох X., Теория Галуа р-расширений, пер, с нем.,
М., 1973- [4] К у з ь м и н Л. В., «Изв. АН СССР. Сер. матем.»,
19E9, т. 33, в. 'В, с. 1220—54. Л. В. Кузьмин.
ПОЛИАНАЛИТИЧЕСКАЯ ФУНКЦИЯ поряд-
порядка т — комплексная функция w=u-\-iv действитель-
действительных переменных х и у или, что эквивалентно, незави-
независимых комплексных переменных z=,r-{-iy и z= x— iy
в плоско]] области D, представимая в виде
w = f(*,7)=2l™~*7*/k(z\, A)
где /fc(z), &=0, . . ., т — 1,— комплексные аналитич.
функции в D. Иначе, П. ф. w порядка т можно оп-
определить как функцию, имеющую в D непрерывные
частные производные по х и у или по г и г до порядка
т включительно и удовлетворяющую всюду в D обоб-
обобщенному условию Коши — Римана:
dmw „
dzm
При т=\ получаются аналитич. функции.
Для того чтобы функция и = и(х, у) была действитель-
действительной (или мнимой) частью нек-рой П. ф. w=u-\-iv в об-
области D, необходимо и достаточно, чтобы и была по-
полигармонической функцией в D. На П. ф. переносятся
с соответствующими изменениями нек-рые классич.
свойства аналитич. функций (см. [1]).
П. ф. мультипорядка щ— (тг, . . ., тп) от комплекс-
комплексных переменных zlt . . ., г„ и z1, . ¦ ., г„ в области D
комплексного пространства С", »^1, наз. функция
вида
lZ /** <zl Z>
где lh h — аналитич. функции переменных z1, ...,
zn в D.
Лит.: [1] Б а л к М. Б., 3 у е в М. Ф., «Успехи матем.
наук», 1970, т. 25, в. 5, с. 20IS—2G. Е. Д. Соломенцев.
ПОЛИВЕКТОР, р-в е к т о ]>, векторного простран-
пространства V* — злемент р-й внешней степени \PV простран-
пространства Г над полем к (см. Внешняя алгебра), р-вектор
может пониматься как кососимметризованный р раз
контравариантный тензор на V. Любая линейно неза-
независимая система векторов ,гь . . ., ,г„ из V определяет
ненулевой р-вектор хха ... Ахр; такие П. наз. р а з-
л о ж и м ы м и, или просты м и (часто — просто
П.). При этом линейно независимые системы хх, . . .,
х„ и г/х, . . ., Ур порождают одно и то же подпрост-
подпространство в V в том и только в том случае, когда ух А
. . .Ayp=cxtA. ¦ -Ахр, где с?К. Для любого шшу-
левого поливектора t?ApV его аннулятор
Ann t= {v? V\tAv=0} есть подпространство размер-
размерности <р, ирнчем поливектор t разложим тогда и
только тогда, когда dim Ami t=/>. Разложимые р-
векторы п-мерного пространства V образуют кониче-
коническое алгебраич. многообразие в \'JV\ соответствующее
проективное алгебранч. многообразие есть Грассмана
многообразие. Любой ненулевой «-вектор или (га—1)-
вектор в га-мерном пространстве Г разложим; бивек-
бивектор t разложим тогда и только тогда, когда tAt~O.
Если !>!, . . ., vn — базис пространства V и т,=
= У" xi.vi, то координатами поливектора t=xxA. • •
А*р в базисе {^ Л . ¦ . Лi); | 1Х<. ¦ -<ip} прост-
пространства APV являются миноры i!''"'/)~clet||zjfc||,
ij<. . .<ip, матрицы ||г{||. В частности, при р = п
х\ Л ... Л хп = det j| xi. '| l\ A ¦ ¦ ¦ Л vn.
Если фиксировать ненулевой п-вектор (o?AnF, то
возникает двойственность между р-векторами и
(ге—р)-векторами, т. е. естественный изоморфизм
л : \Р (V) —> (Л"""^^)* ?*А"-р (V*)
такой, что tAu—л (t) (и)ы для всех t?ApV я ц^Лп~^Т'.
Пусть k=R и в V задано скалярное произведение,
югда в APV индуцируется скалярное произведение,
обладающее следующим свойством: для любого орто-
нормированного базиса i'j, . . ., vn в V базис {i-; Л. . .
Avi |гх<. . •Kip} в APV также ортонормирован. Ска-
Скалярный квадрат
разложимого поливектора t~x1A- ¦ -Ахр совпадает
с квадратом объема параллелепипеда в V, натянутого
на векторы г1, . . ., х„. Если фиксировать в «-мерном
евклидовом пространстве V ориентацию (что равносиль-
равносильно выбору n-вектора ш, для к-рого (ш, ш)— 1), то ука-
указанная выше двойственность приводит к естественному
изоморфизму у : APV~*-A"~PV такому, что tAu--
= (y(t), и)ы для всех t?ApV, u?An~PV. В частности,
(ге—1)-вектору <=^]Л. . ¦Ахп_1 соответствует вектор
У tt) G ^> наз- векторным произведением
векторов х17 . . ., хп_х.
Лит.: [1] Бур баки Н., Алгебра. Алгебраические
структуры. Линейная и полилинейная алгебра, пер. с франц.,
М., 1962; [2] К о с т р и ь- и н A. IT., Манив Ю. И., Линей-
Линейная алгебра и геометрия, М., 1980; [3] Постников М. М.,
Линейная алгебра и дифференциальная геометрия, М., 1979.
ПОЛИГАРМОНИЧЕСКАЯ ФУНКЦИЯ, г и и е"р-
i ар ионическая функция, мета гар-
гармоническая функция, порядка т — функ-
функция и(х)^^и(х1, . . ., хп) действительных неременных,
определенная в области D евклидова пространства
R", ге^2, имеющая непрерывные частные производ-
производные до 2т-го порядка включительно и удовлетворяю-
удовлетворяющая всюду в D полигармоническому
уравнению
i де Д — оператор Лапласа. При т—Л получаются
гармонические функции, при т — '1 — бигармониче-
ские функции. Каждая П. ф. есть аналитич. функция
от координат .ту. Нек-рые другие свойства гармонпч.
функций также переносятся с соответствующими изме-
изменениями на П. ф.
Для П. ф. любого порядка w>l обобщаются пред-
представления при помощи гармонпч. функций, известные
для бпгармонич. функций (см. [1] — [5]). Напр., для
П. ф. и двух переменных справедливо представление
х.г),
2 __ r2 .1_ r2
где o)k, к—О, . . ., m—i — гармония, функции в об-
области Z). Для того чтобы функция и(х1, хг) двух пере-
переменных была П. ф., необходимо и достаточно, чтобы
она была действительной (или мнимой) частью поли-
полианалитической функции.
Основная краевая задача для П. ф. порядка т>1
состоит и следующем: найти П. ф. и=и(х) в области
U, непрерывную вместе с производными до (т — 1)-го
порядка включительно в замкнутой области D —
~- D U С и удовлетворяющую на границе С условиям:
где ди/дп — производная по нормали к С, а /0(у),
. . ., fm-i(y) — заданные достаточно гладкие функции
на достаточно гладкой границе С. Многие исследова-
исследования посвящены решению задачи (*) в шаре прост-
пространства R" (см. [1], [6]). Для решения задачи (*)
в случае произвольной области применялся метод ин-
интегральных уравнений, а также различные вариацион-
вариационные методы (см. [1], |6]).
Лит.: [1] Веку а И. Н.. Новые методы решения эллипти-
эллиптических уравнений, М.-- Д., 1948; l^J Привалов И. И.,
Пчелин Б. М., «Матем, сб.», 1937, т. 2, в. 4, с. 745—58;
[3] N i с о 1 е s с о М., Les foncfions polyharmoniques, P., 1936:
[4] его же, «Disq. Math. Phys.», 1940, v. 1, p. 43—56; [5]
T о 1 о 1 1, 1 С, <-Giorn. Math. Battaglini», 1947, v. 1, p. 61 — 117;
Ifi] Миранда К., Уравнения с частными производными
эдлиптического типа, пер. с итал., М., 1957. Е. Д. Соломенцев.
ПОЛИГОН над моноидом Я, Л-п о л и г о н, он с-
р а н д,— непустое множество с моноидом операторов.
Точнее, непустое множество А нал. левым П. над
моноидом Л, если для любых Х?Я и а?-А определено
произведение Ха^А, причем
и .
la —a
для любых 1, ц^fl, s^i.II равнй П. определяется
аналогично. Задание Я-полигона А равносильно зада-
заданию гомоморфизма ер моноида R в моноид отображений
множества А в себя, переводящего 1 в тождественное
отображение. При этом Ха-=Ь тогда и только тогда,
когда
ф(Я)(а) = Ь.
В частности, каждое непустое множество можно рас-
рассматривать как П. над моноидом его отображений
и себя. Таким образом, П. тесно связан с представле-
представлением полугруппы преобразованиями.
Если А — универсальная алгебра, сигнатура к-рои
И содержит лишь унарные операции, то А .можно пре-
превратить в П. над свободным моноидом F с системой
свободных образующих Q, положив
для любых /,?U, а?А . Если Q — множество входнь'
сигналов автомата с множеством состояний А, то ,,
аналогичным образом превращается в ^-полигон (ср.
Автоматов алгебраическая теория).
Отображение ф Л-полшона А в Я-полпгон В наз.
г о м о м о р ф и -л м о .м, если ц>Ом)=^/ q>(a\ сгя ио-
бых \?R и а?А. При А=^В получается определение
э н д о м о р ф » з м а. Псе эндоморфизмы полигона А
образуют моноид, и А можно рассматривать как П.
над ним.
Эквивалентность 0 на Я-полигоне А наз. кон-
конгруэнцией, если (я, ft) ?6 влечет (Ха, №)?в
для любого Л?Я. Множество классов конгруэнции О
естественным образом превращается в Я-полигон, на-
называемый факт ори оли г оном полигона Л и
обозначаемый через А/в. Если А — полигон над Я,
то на Я можно определить отношение Лип А, положив
(к, и.)?Аш1/1, если Xa=-[ia для всех а?А. Отноше-
Отношение Ann А оказывается конгруэнцией моноида Я,
и А естественным образом превращается в П. над
фактормоноидом Л/Ann А. Если полигон А возник из
нек-рого автомата, то описанный переход равносилен
«склеиванию» одинаковым образом действующих по-
последовательностей входных сигналов. Наряду с обыч-
обычными для универсальных алгебр конструкциями пря-
прямого и подпрямого произведения, в теории П. рассмат-
рассматривается важная для алгебраич. теории автоматов
конструкция сплетения. Свободное произведение (или
копроизведение) П. совпадает с их дизъюнктным
объединением.
На П. можно смотреть как на неаддитивный аналог
модуля над кольцом, что служит богатым источником
задач теории П. В частности, установлена связь П.
с радикалами в полугруппах и исследуются связи
свойств моноида со свойствами П. над ним. Напр.,
все левые R -полигоны проективны тогда и только
тогда, когда Я — одноэлементная группа, а инъектив-
ность всех П. над коммутативным моноидом R равно-
равносильна наличию в R нуля и порождаемое™ всех его
идеалов идемпотентами (ср. Гомологическая классифи-
классификация колец).
Если Я — моноид с нулем 0, то можно говорить об
Я-полигоне А с нулем как об Я-полигоне с отмеченной
точкой и, причем Оа=и для всех а?А . Теория П. с ну-
нулем имеет нек-рые особенности.
Каждый П. можно рассматривать как функтор из
однообъектной категории в категорию множеств.
Лит.: [1] Алгебраическая теория автоматов, языков и полу-
полугрупп, пер. с англ., М., 1975; [2] Клиффорд А., Прес-
Престон Г., Алгебраическая теория полугрупп, пер. с англ., т. 2,
М., 1972; [3] Скорняков Л. А., п ей.: Модули, в. 3, Но-
носиб., 1973, с. 22—27; [4] Итоги науки и техники, Алгебра.
Топология. Геометрия, т. 14, М., 1976, с. 57 — 190.
Л. А. Скорняков.
ПОЛИКРУГ, полицилиндр,— область
Д = Д(а = (аь ..., ап), г=(г1, ..., г„) =
= {2 = (zi, ..., zn) ? C»:|zv-ev|<rv, v = l, ..., n)
комплексного пространства С", «^1, являющаяся
топологич. произведением п кругов,
Д = Д1Х...ХД„,
Точка a=(aj, . . ., ап)?С" — центр поликруга Д,
с-~ (fj, . . ., /-„), ;\- >0, v=l, . . ., п,— его нули н-
радиус. При а~-0, г==A, . . ., 1) получается е д и-
н и ч н ы и п о л и к р у г. О с т о в о м п о л и к р у-
г а Д наз. часть
Т = Т(а, r)={2 g С": |sv-av| = rv, v = l, ..., п)
его полной топологпч. границы <9А. П. есть полная
кратно круговая область.
Естественным обобщением понятия П. является по-
полиобласть (поликруговая область,
обобщенный полицилиндр) Z) = ?IX
. . .XDn, являющаяся топологич. произведением п
(вообще говоря, многосвязных) областей jDvc:C, v-,
. . ., п. Граница T~dD полиобласти D состоит ил ге
множеств размерности 2 и — 1:
общая часть к-рых есть «-мерный остов поли-
полиобласти D:
T = dD1X...XdDn = {z ?C":zv ? dDy, v = l, ..., re}.
E. Д. Соломенцев.
ПОЛИЛИНЕЙНАЯ АЛГЕБРА — часть алгебры,
изучающая полилилейные отображения модулей (в ча-
частности, векторных пространств'). Первыми разделами
II. а. явились теория билинейных форм и квадратич-
квадратичных форм, теория определителей и развивающее ее
исчисление Грассмана (см. Внешняя алгебра). Основ-
Основную роль в П. а. играют понятия тензорного произве-
произведения, тензора, полилинейной формы. Приложения
П. а. к геометрии и анализу связаны главным обра-
образом с тензорным исчислением и дифференциальными
формами,. А. Л. Онищик.
ПОЛИЛИНЕЙНАЯ ФОРМА, га-линейная
форма, на унитарном Л-модуле Е — полилинейное
отображение Е"^тА (здесь А — ассоциативно-комму-
ассоциативно-коммутативное кольцо с единицей). П. ф. наз. также поли-
полилинейной функцией (п-л и н е й н о й ф у-
н к ц и е и). Поскольку П. ф.— частный случай поли-
полилинейных отображений, можно говорить о симметри-
симметрических, кососимметричсских, знакопеременных, сим-
симметризованных и кососимметризованных 11. ф. Напр.,
определитель квадратной матрицы порядка п над А —
это кососимметризованная (и тем самым знакоперемен-
знакопеременная) «-линейная форма на А", n-линейные формы на Е
образуют А -модуль Ln (Е, А), естественно изоморф-
п п
ный модулю {(/)Е)* всех линейных форм на (g)?. В слу-
случае п=2 (и~3) говорят о билинейных формах (трили-
(трилинейных формах).
re-линейные формы на Е тесно связаны с п раз ко-
вариантными тензорами, т. е. элементами модуля
Т"(?*)=(Я)"?*. Точнее, имеется линейное отображе-
отображение
yn:T»(E*)—+La(E, A)
такое, что
Уп(и1® ¦ ¦¦ ®и„) (*i. ¦ ¦ ¦, xn) — Ui (.Г]).. .ип (,г„)
для любых п/?Е*, Х[?Е. Если модуль Е свободен, то
у ннъективно, а если Е к тому же конечно порожден,
то и биективно. В частности, n-линейные формы на
конечномерном векторном пространстве над полем
отождествляются с п раз ковариантными тензорами.
Для любых форм u?Ln(E, A), v?Lm(E, А) опреде-
определяется их тензорное произведение u(^)v^-Ln+m(E, A)
формулой
u(g)v(xu . .., хп + т)--=и {хи .. .,х„) v (хп + 1, ...,хп + т).
Для симметризованных П. ф. определено также сим-
метрич. произведение
(апи) v (omv)=ani.m (u®v),
а для кососимметризованных. П. ф.— внешнее произве-
произведение
(а„и) Л (amv)=,an,m (u®v).
Эти операции распространяются на модуль Llf{E, A)*=
-^t??=oL(E, А), где L0(E, A) = A, L^E, A) = E*, мо-
модуль симметризованных форм La (E, А ) = фп°=оО;!¦?«(?,
А) и модуль кососимметризованных форм La(E, A) =
—-¦(^—^xnLn(E, А) соответственно, превращая их
в ассоциативные алгебры с единицами. Если Е — ко-
конечно порожденный свободный модуль, то отображе-
отображения уп определяют изоморфизм тензорной алгебры
Т(Е*) на Ь%{Е, А) и внешней алгебры А(Е*) на ал-
алгебру La{E, А), совпадающую в этом случае с алгеброй
знакопеременных форм. Если А --поле характерис-
характеристики 0, то имеется также изоморфизм симметрпч. ал-
алгебры S (Е*) на алгебру LO(E, А) симметрич. форм.
Всякой П. ф. u?Ln(E, А) соответствует функция
<?>п(и) : Е—*-А, заданная формулой
(Оп(и) (х) = и (.г, . . ., .;), ,г ? Е.
Функции вида ш„(м) наз. формами степени??
на Е; если Е — свободный модуль, то в координатах
относительно произвольного базиса они задаются одно-
однородными многочленами степени п. В случае ге—2
(ге=3) получаются квадратичные формы и кубические
формы на Е. Форма F=a(u) полностью определяет
симметризацию anit формы м ?/,„(/?, А), имеющую вид
апи (х1, . . ., ,гн) —
В частности, для и=2
(<т2и) (.г, y) = F (x^y)-F (x) — F (у).
Отображения уп и со„ определяют гомоморфизм алгеб-
алгебры S (Е*) на алгебру всех полиномиальных функций
Р(Е), к-рьгй является изоморфизмом, если Е — сво-
свободный конечно порожденный модуль над бесконечной
областью целостности А .
Лит.: [1] Бурбаки Н., Алгебра. Алгебраичесние
структуры. Линейная и полилинейная алгебра, пер. с франц.,
М., 1962; [2] Б у р б а к и Н., Алгебра. Многочлены и поля.
Упорядоченные группы, пер. с франц., М., 19В5; [3] Л е н г С,
Алгебра, пер. с англ., М., 1968. А. Л. Онищик.
ПОЛИЛИНЕЙНОЕ ОТОБРАЖЕНИЕ, ге-л и н е и и о е
отображение, полилинейный опера-
т о р,— отображение / прямого произведения ТТ Е; п
унитарных модуле!! Е,¦ над ассоциативно-коммутатив-
ассоциативно-коммутативным кольцом А с единицей в нек-рый Л-модуль F,
линейное по каждому аргументу, т. е. удовлетворяю-
удовлетворяющее условию
/(¦*•!, ¦•¦. *,•-!, ay + bz,xi + x, .....г„Ь--=
=-aj (хи ..., xi_lt у, xi + 1, ..., .<•„) +
-\-bf(x,-, ..., х/_ъ г, xi + i, ..., хп)
(а, Ь ? А; г/, z ? Е,-, i — i, . .., п).
В случае п = 2 (и = 3) говорят о билинейном отображе-
отображении (соответственно трилинейном). Каждое П. о.
определяет единственное линейное отображение / тен-
тензорного произведения ?p;'=iA',- в /' такое, что
Т(-Г1®---®Х„)=/ (X!, .-., Хп), Xi?El,
причем соответствие /)-»/ есть биекция множества П. о.
ТТ Ej-yF на множество всех линейных отображений
®1=\Е,i-^-F. П. о. ТТ Ef-^-F естественным образом
образуют А -модуль.
В А -модуле Ln(E, F) всех 7?-линейных отображений
/?"—>-/'¦ действует симметрич. группа Sn:
(.?/) (.rj. ..., xn)^f(xs{lh ..., xs(n)),
где s?SH, f?La(E, F), x^E. П. о. / наз. с и м м е т-
р и ч е с к и м, если sf=f для всех s?Sn, и кос о-
симметрическим, если */=¦--е (.?)/, где е (х) [1
в зависимости от четности подстановки s. li. о. наз.
знакопеременным (или альтерниро-
альтернирован н ы м), если f(x1: . . ., xn)=Q, как только x~Xj
для нек-рых 1Ф). Всякое знакопеременное П. о. косо-
симметрично, а если в F уравнение 2(/ = 0 имеет един-
ственное решение у- О, то верно и обратное. Симмет-
Симметрические II. о. образуют подмодуль в Ln(E, F), ес-
естественно изоморфный модулю линейных отображений
L(S"E, F), где S"E ость я-я симметрия, степень Е
(см. Симметрическая алгебра), знакопеременные П. о.—
подмодуль, естественно изоморфный L(AnE, F), где
Л"к есть н-я внешняя степень модуля Е (см. Внешняя
алгебра). П. о. вида а„/= V s/ наз. симметризо-
ванным и, а П. о. вида ст„/= > _ e(s)s/ — к о с о-
с и м м е т р и з о в а н н ы м и. Симметризованные (ко-
сосимметризованные) Л. о. симметричны (соответст-
(соответственно знакопеременны), а если в F уравнение п[у=с
имеет для каждого с?/' единственное решение, то
верно и обратное. Для того чтобы всякое знакоперемен-
знакопеременное П. о. было кососимметризованным, достаточно
также, чтобы модуль Е был свободным.
Лит. см. при ст. Полилинейная форма. А. Л. Оншцик.
ПОЛИНИЛЫ1ОТЕНТНАЯ ГРУППА — группа,
обладающая конечным нормальным рядом, факторы,
к-рого нильпотентны; такой ряд наз. полинильт
п о т е н т н ы м. Длина кратчайшего полинильпотентг
ного ряда П. г. наз. ее и о л и п и л ь ц о т е н т-
н о и д л и н о й. Класс всех П. г. совпадает с клас-
классом всех разрешимых групп; однако, вообще говоря,
нолинилыютентная длина меньше разрешимой. П. г.
длины 2 наз. метанильпотентными.
Все группы, обладающие (возрастающим) полиниль-
потентным рядом длины I, факторы к-рого (в порядке
возрастания ряда) имеют классы нильпотентности, не
превосходящие чисел сх, с2, . . ., ct соответственно, об-
образуют многообразие 2Л, являющееся произведением
нильпотентных многообразий:
(см. Групп многообразие). Свободные группы такого
многообразия наз. свободными полиниль-
потентными группами. Особый интерес
представляют многообразия 9tc3l и ШЯС- Первое
из них содержит все связные разрешимые группы Ли;
во втором все конечно порожденные группы конечно
аппроксимируемы и удовлетворяют условию макси-
максимальности для нормальных подгрупп.
Лит.: [1] К у р о ш А. Г., Теория групп, 3 изд., М., 1967:
12] Нейман X., Многообразия групп, пер. с англ., М..
НШ9. А. Л. Шмелъкин.
ПОЛИНОМ — то же, что многочлен.
ПОЛИНОМИАЛЬНАЯ ФУНКЦИЯ — обобщение
понятия целой рациональной функции (см. Много-
Многочлен). Пусть V — унитарный модуль над ассоциативно-
коммутативным кольцом С с единицей. Отображение ер :
V-+C наз. П. ф., если ср==фо+. . .-Ьфи, гДе ф< — форма
степени i на V, t=0, 1, . . ., т (см. Полилинейная фор-
форма). Наиболее часто П. ф. рассматриваются в случае,
когда V — свободный С-модуль (напр., векторное про
странство над нолем С) с конечным базисом vlt ....
vn. В этом случае отображение ф : V—*-C является
П. ф. тогда и только тогда, когда ff (x)= F{rlt . . ., хп),
где F^iC\X1, . . ., Xп] — многочлен над С и а-,,
. . ., х„ — координаты элемента х? V в базисе ь\, . . ., ;•„.
Если при этом С — бесконечная область целостности,
то многочлен F определяется однозначно.
П. ф. на модуле V образуют ассоциативно-коммута
тивную С-алгебру Р (V) с единицей относительно ес-
естественных операций. В случае, когда V — свобод-
свободный модуль с конечным базисом над бесконечной об-
областью целостности С, алгебра Р (V) канонически изо-
изоморфна симметрич. алгебре S (V*) сопряженного мо-
модуля V*, а если V — конечномерное векторное прост-
пространство над полем характеристики 0,— алгебре сим-
симметрических полилинейных форм на V. А. Л. Онищик.
ПОЛИНОМИАЛЬНОЕ РАСПРЕДЕЛЕНИЕ, м у л ь-
т л и о м п а л ь н о о р а с и р е д е л е н и е, — сов-
латное распределение случайных величии Х1, . . .,
Хк. к-рое задается для любого набора целых неотри-
неотрицательных чисел пг, . . ., пк, удовлетворяющих усло-
условию Л] + . . . + л^=н, /Су = О, 1, . . ., п, /—1, . . ., к,
формулой
l
^1
где п, pj, . . ., Pk(Pj~^"i ZdjPj~4 — параметры рас-
распределения. П. р. являотся многомерным дискретным
распределением — распределением случайного векто-
вектора {Хи . . ., Хк) с A'j-f-. - --гХ^—п (это распределение
ннляется по существу (к — 1)-мерным, т. к. в евклидо-
евклидовом пространстве к измерений оно вырождено). П. р.
естественным образом обобщает биномиальное распре-
распределение и совпадает с последним при к=2. Название
распределения объясняется тем, что вероятность (*)
является общим членом разложения многочлена (поли-
(полинома) (р! + . . .-\-PkV' 11- Р- появляется в следующей
вероятностной схеме. Каждая из случайных величин
JV,ecTb число появлений одного из взаимоисключающих
событий Aj, jT=\, . . ., к, при повторных независимых
испытаниях. Если при каждом испытании вероятность
появления события A j равна pj, /=1, . . ., к, то ве-
вероятность (*) равна вероятности того, что при п
испытаниях события Ах, . . ., A k появятся «j, . . ., nk
раз соответственно. Каждая из случайных величин X,-
имеет биномиальное распределение с математич. ожи-
ожиданием прj и дисперсией npj(\—pf).
Случайный вектор (Хи . . ., Xь) имеет математич.
ожидание (пр1, . . ., прк) и ковариационную матрицу
B—\\b;j\\, где
', ;=-!, -.., к
|ранг матрицы В равен к—1 в силу того, что ^V.=1»/ =
п). Характеристнч. функция П. р. равна
1 {>1, ¦¦¦: tk)-=\Ple +---+Pke k) ¦
При и—>-оо распределение вектора (У\, . . ., Yк) с нор-
нормированными компонентами
у. _.— ' ' —
фемптся к нек-рому многомерному нормальному рас-
"ределенит, а распределение суммы
(края используется в математич. статистике для пост-
построения «хн-квадрат» критерия) стремится к </хи-кеад-
рат» распределению с к—1 степенями свободы.
Лит.: L1J Крамер Г., Математические методы статис-
статистики, пер. г. англ., 2 изд., М., 1975. А. В. Прохоров.
ПОЛИНОМИАЛЬНЫЙ КОЭФФИЦИЕНТ — коэф-
коэффициент
n,!»/'. .nm\ ' n1+ni+...+nm=n,
iipH.r"'3- . . . х™™ в 1)а.чло?кснии многочлена (поли-
(полинома) (.г]+а"гН"- • ¦~i~?m)n- В комбинаторике П. к.
пыражает: а) число всевозможных перестановок из /t
элементов, из к-рых п1 элементов одного вида, п2 эле-
элементов другого вида, . . ., ит элементов нг-го вида; б)
число способов размещения п различных элементов
по т различным ячейкам, при к-ром в i-ю ячейку
помещается ni элементов, i—1, 2, . . ., /», без учета
порядка элементов в любой ячейке.
Частным случаем П. к. являются биномиальные
коэффициенты.
Лчт.\ [1] Холл Л., Комбинаторика, net), с англ,, М.,
1970; L2] Р и о р д а н Д ж., Введение и комбинаторный ана-
анализ, пер. о англ., М., 19A3. С. А. Рукова.
ПОЛИЦИКЛИЧЕСКАЯ ГРУППА — группа, об-
обладающая п о л и ц п к л и ч е с к и м ряд о м, т. е.
субнормальным рядом с циклич. факторами (см. Под-
Подгрупп ряд). Класс II. г. тождествен классу разреши-
разрешимых групп с условием максимальности рля подгрупп;
он замкнут относительно перехода к подгруппам, фак-
факторгруппам и расширениям. Число бесконечных фак-
факторов в любом нолициклич. ряде — инвариант П. г.
(п о л и и, и к л и ч е с к и й ран г). Голоморф П. г.
изоморфно вкладывается в группу матриц над кольцом
целых чисел; ато позволяет применять в теории II. г.
методы алгебпаич. геометрии, теории чисел и р-адичс-
ского анализа. Если к — алгебраич. расширение конеч-
конечного поля, G — конечное расширение П. г., то всякий
простой AG-модуль конечномерен над к. Во всякой
группе произнецение двух локально полициклич. нор-
нормальных подгрупп — локально полициклич. подгруппа.
Лит.: fl] Кяргаполов М. И., М с р з л я к о в Ю. И.,
Основы теории групп, 3 изд., М., 1882; L2] Three lectures on
polycyclic groups, L., 197.'!. Ю. И. Мерзляков.
ПОЛИЭДР — объединение локально конечного се-
семейства выпуклых многогранников в нек-ром R".
Под выпуклым многогранником по-
понимается пересечение коночного числа замкнутых
полупространств в случае, если это пересечение ог-
ограничено. Локальная конечность семей-
семейства означает, что каждая точка R" имеет окрест-
окрестность, пересекающуюся лишь с конечным числом мно-
многогранников. Компактный П. являете: объеди-
объединением конечного числа выпуклых многогранников.
Размерность П. определяется как максималь-
максимальная размерность составляющих его многогранников.
Любое открытое подмножество П., в частности любое
открытое подмножество евклидова пространства, есть
П. Полиэдрами являются также конус и надстройка
над компактным П. Простые примеры (конус над ин-
интервалом) показывают, что соединение компактного и
некомпактного П. может не быть П. Подпол из д-
р о м полиэдра Q ная. любой полиэдр Р, лежащий
в Q. Иногда ограничиваются рассмотрением только
замкнутых подполиэдров. Каждая точка а полиэдра
Р ?R» обладает в Р окрестностью, являющейся кону-
конусом в R." с вершиной а и с компактным основанием.
;1то свойство окаш.гпается характеристическим: любое
подмножество R.", каждая точка к-рого имеет конич.
окрестность с компактным основанием, является П.
Каждый компактный полппдр Р можно так разбить
на конечное число замкнутых симплексов, чтобы каж-
каждые два симплекса либо не пересекались, либо пере-
пересекались по их общей грани. В случае некомпактного
П. требуется, чтобы семейство симплексов было ло-
локально конечным. Такое разбиение наз. н р я м о л и-
н е й н о и триангуляцией П. Любые две
триангуляции одного н того же П. имеют общее под-
подразделение. Если Р — замкнутый подполиэдр поли-
полиэдра Q, то любая триангуляция К полиэдра Р продол-
продолжается до нек-рой триангуляции L полиэдра Q. В атом
случае говорят, что получающаяся пара {L, К) гео-
геометрических еимплициальных комплексов триангули-
триангулирует пару (Q, Р). Отображение / полиядра PcR"
и полиэдр QcR" наз. кусочно линейным,
или /^-отображением, если / является симшгациаль-
пым в нек-рых триангуляциях полиэдров Р и Q. Эк-
Эквивалентное определение: / кусочно линейно, если /
локально коническое, т.е. если каждая точка а?Р
имеет такую конич. окрестность A — atL, что / (ка-\-
f ц.г) — Kj (a)-\-\if(x) при любых ,г?/, и 'к, uJsO, h-\-fi—i.
Для тою чтобы отображение / было кусочно липей-
ным, необходимо и достаточно, чтобы его график
Г/СК."ХК" являлся П. Суперпозиция кусочно ли-
линейных отображений кусочно линейна. Обратное от-
отображение к обратимому кусочно линейному отобра-
отображению / кусочно линейно. В этом случае / наз. pl-
гомеоморфизмом.
Категория, объектами к-рой являются П. (и полиэд-
полиэдральные пары), а морфизмами являются pi-отображе-
pi-отображения, обозначается PL или fp (см. также Кусочно ли-
линейная топология). Категория PL является одним из
основных объектов и инструментов исследования в то-
топологии. Особенно велика роль категории J'L в ал-
алгебраической топологии и топологии многообразий.
.Это объясняется тем, что класс П. достаточно широк.
Напр., каждое дифференцируемое многообразие мож-
можно естественным образом представить в виде П. Каж-
Каждое непрерывное отображение одного П. в другой сколь
угодно точно аппроксимируется /^-отображением. По-
Поэтому категория PL является хорошим приближением
к категории всех тоиологич. пространств и непрерыв-
непрерывных отображений. С другой стороны, триангулируе-
триангулируемость II. позволяет использовать методы комбинатор-
комбинаторной топологии. Многие алгебраич. инварианты (напр.,
гомологии группы, когомологий кольцо) строятся и эф-
эффективно вычисляются с помощью разбиения на сим-
симплексы. Вопрос о том, всякие ли гомеоморфныо поли-
полиэдры pi-гомеоморфны, носит название основной
1ипотезы и решается отрицательно: для «J&5
существуют гомеоморфные, но не pi-гомеоморфныс
/г-мерные П. (см. [3]). При п<3 гомеоморфные п-мерные
полиэдры pZ-гомеоморфны, при п---4 вопрос остается
A983) открытым для компактных П. и решается отри-
отрицательно для некомпактных: существует нестандартная
/Л-структурана RA Полиэдр М наз. н-мерным р!-мн о-
г о о б р а з и е м, если каждая его точка имеет ок-
окрестность, pi-гомеоморфную R" или R.+ . Всякая пря-
прямолинейная триангуляция Т pi-многообразия М ком-
комбинаторна. Это означает, что звезда каждой ее
вершины комбинаторно эквивалентна симплексу. Ос-
Основная гипотеза для П., являющихся «-мерными то-
пологич. многообразиями, естественно распадается на
две гипотезы: гипотезу о комбинаторное™ всякой три-
триангуляции такого II. и основную гипотезу для pi-
многообразий. Одним из важнейших достижений совре-
современной топологии является отрицательный ответ на
обе гипотезы для п~^Ъ (см. [4], [5]). Для гс«:3 обе ги-
гипотезы справедливы.
Пусть Р — компактный подполиэдр полиэдра Q и
пусть пара геометрических симплицнальных комплек-
комплексов (L, К) триангулирует пару (Q, Р) так, что А' —
полный подкомплекс. Это означает, что
каждый симплекс комплекса L, вершины к-рого лежат
в К, лежит в К, и этого всегда можно добиться с по-
помощью перехода к производному подразделению. Поли-
Полиэдр N, состоящий из всех замкнутых симплексов про-
производного подразделения L', имеющих вершину в К, а
также его образ при любом неподвижном на Р pi-гомео-
pi-гомеоморфизме Q на себя, наз. регулярной окре-
окрестностью полиэдра Р в полиэдре Q. Для любых
тух регулярнык окрестностей Nx, N2 полиэдра Р су-
существует неподвижная на Р pi-изотошш hf : NXXJ—»-(),
переводящая N1 в N2, т. е. такая, что ho(N1)-=N1 и
А1(ЛГ1)=ЛГ2. Говорят, что полиэдр Р получается эле-
элементарным полиэдральным стяги-
стягиванием полиэдра PrZDP, если для нек-рого я^О
пара (Рг\Р, Р{\Р П!}) pZ-гомеоморфна паре AпХТ,
ТпХ {0}). Полиэдр Pj полиэдрально стягивается на
свой подполиэдр Р (обозначение (Р1\/>)), если от
/¦", к Р можно перейти конечной последовательностью
элементарных полиэдральных стягиваний. Если Р{\Р,
то в нек-рой триангуляции пары (Р,, Р) полиэдр Р
можно получить из Р1 последовательностью элементар-
элементарных комбинаторных стягиваний, каждое из к-рых
состоит в отбрасывании главного симплекса вместе
с его свободной гранью. Если Q является п-мерным
/^-многообразием, то любая регулярная окрестность
компактного подполиэдра PczQ является п-мерным
/^-многообразием и полиэдрально стягивается на Р.
Это свойство оказывается характеристическим: если
«-мерное /Я-многообразие NczQ таково, что V'clnt N
и N~\P, то N — регулярная окрестность Р. При этом
любая регулярная окрестность края дМ "компактного
р/-многообразия М р/-гомеоморфна дМ х /.
Пусть Р, Q — замкнутые пОдполиэдры «-.мерного
/(/-многообразия М, dim Р=р, dim Q—q. Говорят, что
Р и Q находятся в общем положении, если
dim (/>П<?)<р+?—"¦ Любые замкнутые подполиэдры
Р, Qczlnt M можно привести в общее положение-сколь
угодно малой изотопией М. Ото означает, что для лю-
любого е>0 существует такая (е — р/)-изотопия hf : М—у
-+М, что полиэдры Р и Qi'-hj^iQ) находятся в общем
положении. Иногда в определение общего положения
включают условия типа трансверсальности. Напр.,
если p-\-q~n, то можно добиться, чтобы для каждой
точки a?Pf)Qi и нек-рой окрестности V точки а в М
тройка (U, U(]P, С/ПCi) была р/-гомеоморфна тройке
(RfxRi, R'Jx{0}, {0}xR').
Криво й, или топологический, П.— то-
пологич. пространство X, снабженное гомеоморфизмом
/ : Р—>-Х, где Р есть П. Образы симплексов какой-либо
триангуляции Т полиэдра Р образуют к р и в о л и-
пенную триангуляцию X. Говорят также,
что гомеоморфизм / задает на X р/-с т р у к т у р у.
Две р/-структуры /,¦ : Р,—>-А', i- I, 2, совпадают, если
гомеоморфизм /^3/i К5тсочно линеен, изотопны, если
гомеоморфизм /2 Vi изотопен кусочно линейному, и
эквивалентны, если Рг и Р2 р/-гомеоморфны. Для лю-
любого дифференцируемого многообразия М существует
р/-структура / : Р-+М, согласованная с дифферен-
дифференцируемой структурой на М. Ото означает, что для
каждого замкнутого симплекса о нек-рой триангуля-
триангуляции полиэдра Р отображение /|0 : о^-М дифференци-
дифференцируемо и не имеет особых точек. Любые две такие pl-
структуры на М изотопны. Все понятия, определяемые
для П. (триангуляция, иодполиэдр, регулярная окрест-
окрестность, общее положение), переносятся с помощью
гомеоморфизма /: Р—>-Х на криволинейный полиэдр X.
Лит.: Ш Александров Д. С, Комбинаторная то-
топология, М. — Л., 1947; 12] Рур к К., Сан дер сон П.,
Введение в кусочно линейную топологию, М.. 1974; [3) М i 1-
п о Г .Т., «Ann. Main.», 1961, v. 74, № 3, р. Г>75; [4] К 1 г b у R.,
Siebenmann L., «Ann Math. Stud.», 1077, .V» 88; [5] E d-
wards R., «Notices A. M. S.», 1975, v. 22, Mb 2, p. А-З.Ч4.
С. В. Матвеев.
ПОЛИЭДРАЛЬНАЯ ЦЕПЬ — линейная форма
2j"!_ d'*i в о(")ЛасТ11 VczR", где V. суть г-мерные сим-
симплексы, лежащие в U. При этом под r-мерным симплек-
симплексом в U понимается упорядоченное множество из r-f-1
точки U, выпуклая оболочка к-рого лежит в U. Гра-
Граница П. ц. определяется обычным образом. Понятие
П. ц. занимает промежуточное положение между по-
понятиями симнлнцнальной цепи триангуляции U и син-
сингулярной цепи в U и отличается от последнего линей-
линейностью симплексов.
Лит.: [1] Александров П. С, Введение в гомоло-
гомологическую теорию размерности и общую комбинаторную тополо-
топологию, М., 1975. С. В. Матвеев.
ПОЛИЭДРАЛЬНЫЙ КОМПЛЕКС — коночное мно-
множество замкнутых выпуклых многогранников в нек-
ром R", к-рое вместе с каждым многогранником со-
содержит все его грани и такое, что пересечение различ-
различных многогранников либо пусто, либо является гранью
каждого из них. Примером П. к. может служить сово-
совокупность всех верганн, ребер и двумерных граней
стандартного трехмерного куба. Рассматриваются так-
также комплексы, состоянии1 и:> бесконечного, но локально
конечного ceMeiicTaa многогранников. Понятие П. к.
обобщает понятие геометрического симилшгиального
комплекса. Тело \Р\ П. к. Р представляет собой объеди-
объединение всех входящих в него многогранников и является
полиэдром. Число многогранников в Р, как правило,
меньше числа симплексов в триангуляции. П. к. Рх
наз. подразделением комплекса Р, если их тела совпа-
совпадают и каждый многогранник из Pt содержится в нек-
ром многограннике из /'. Звездное и о д р а л д е-
л е я и е комплекса Р с центром в точке а? |/'| полу-
получается с помощью разбиения замкнутых многогранни-
многогранников, содержащих а, на конусы с вершиной а над темп
их 1ранями, к-рьте не содержат а. Любой П. к. Р имеет
подразделение А', являющееся геометрическим симп-
лициальным комплексом. Такое подразделение можно
получить без добавления новых вершин. Достаточно,
напр., последовательно произвести звездные подразде-
подразделения Р с центрами во всех вершинах Р.
.'lum.: [1] Александров П. С, Комбинаторная то-
топология, М.— Л., 1947. С. В, Матвеев.
ПОЛИЭДРАЛЬНЫЙ ЦИКЛ — полиэдральная цепь,
граница к-рой равна нулю. с. в. Матвеев.
ПОЛНАЯ АНАЛИТИЧЕСКАЯ ФУНКЦИЯ — со-
совокупность всех элементов аналитич. функции, полу-
получающихся при всевозможных аналитических продол-
продолжениях исходной аналитич. функции / /(•) комплекс-
комплексного переменного г, заданной первоначально в нек-рой
области D расширенной комплексной плоскости С.
Пара (D, /), состоящая из области /JczC и заданной
в D однозначной аналитической, или голоморфной,
функции /, наз. элементом аналитиче-
аналитической функции, аналитическим эле-
элемент о м, или, короче, просто элементом.
Всегда возможно, в частности, при задании аналитич.
функции пользоваться вейерш трассовым, или
регулярным, элементом (U (а, /?), /а),
состоящим при а=^оо из степенного ряда
и круга сходимости С (a, R)-- {г?С : \z— a\ <Я} этого
ряда с центром а и радиусом сходимости й>0. В случае
а= со вейерштрассов элемент (?/(оо, В), /л,) состоит
из ряда
/- = /-(«) =2Г= о е*г~* .B)
и области сходимости этого ряда U(<x>, R)— --{z?C :
\z\>R), Я>0.
Пусть Ei — множество всех тех точек ??С, в к-рые
исходный элемент (U(a, R), /в) аналитически продол-
продолжается хотя бы по одному пути, связывающему в С
точки а и ?. Следует иметь в виду возможность такой
ситуации, когда в точку Z€.E/ аналитич. продолжение
возможно вдоль нек-рого класса путей Lx и невоз-
невозможно вдоль другого класса путей L2 (см. Особая точ-
точка аналитич. функции). Множество Е, есть область
плоскости С. Полной аналитической
функцией (в смысле В е и е р ш т р а с с а)
fw, порожденной элементом (V (а, В), fa), называ-
называется совокупность всех вейерштрассовых элементов
(U(?, Я), /j ), l,?Ej, получаемых при этом аналитич.
продолжении вдоль всевозможных путей LcC. Об-
Область Еi наз. (в е й е р ш т р а с с о в о й) обла-
областью существования П. а. ф. fw. Приме-
Применяя элементы общего вида (D,f), вместо веперштрассо-
вых на самом деле получают ту же самую П. а. ф. f^.
Элементы (D, /) П. а. ф. fw часто наз. ветвями анали-
аналитической функции /1V/. Любой элемент (D, /) П. а. ф.
/и/, будучи взят за исходный при аналитич. продол-
продолжении, приводит к той же самой П. а. ф. lw. Каждый
элемент (U(?, В), /j.) П. а. ф. fw может быть получен
из любого другого ее элемента (V(а, В), fa) посредст-
посредством апалптич. продолжения вдоль нек-рого пути,
связывающего в С точки а и ?..
Может оказаться, что исходный элемент (D, 1) не
допускает аналитич. продолжения ни в одну точку
?(?!). В этом случае D --Ej является естествен-
н о ri о б л а с т ь ю существования, или
областью голоморфности, функции /, а ее
граница Y—dD — естественной границей
функции /. Напр., для вейерштрассова элемента
(г/(о, 1), /о (*) = 2*= „**'•)
естественной границей является окружность Г={г?
?С : |z|=l} его круга сходимости ?/@, 1), т. к. этот
элемент нельзя продолжить аналитически ни в одну
точку 1; такую, что \t,\~^l. Какова бы ни была область
1>аС, можно построить аналитич. функцию /д(г),
для к-рой D есть естественная область существования
/o(z), а ее граница Г=<5/) — естественная граница
fo(z) (это следует, напр., из Миттаг-Леффлера тео-
теоремы).
II. а. ф. fyy в своей области существования Е^ во-
вообще говоря, не является функцией точки в обычном
смысле этого слова. Часто встречающаяся в теории
аналитич. функций ситуация такова, что П. а. ф.
fw есть многозначная функция: для каждой точки
???¦ f существует, вообще говоря, бесконечное мно-
множество элементов (?/(?, В), /j ) с центром в этой точке.
Однако это множество не более чем счетное (теоре-
(теорема Пуанкаре — Вольтерр а). В целом
П. а. ф. iw можно рассматривать как однозначную
аналитич. функцию только на соответствующей рима-
новой поверхности, являющейся многолистной накры-
накрывающей поверхностно над С. Напр., И. а. ф. /(z)=
---Ln з—-In \z\-\-i Arg z многозначна в своей области
сущеетвования E/~{z?C : 0<|z|<oo}; в каждой точ-
точке t,?Ej она принимает счетное множество значений
гш, s —0, ±1, .. .,
и каждой точке ??/^ соответствует счетное множество
элементов
(U (I, \l\), ft(z; .?)) =
с центром ?. Обычно используется однозначная ветвь
этой П. а. ф.— главное значение логарифма In z=
= ln U| + t arg z, являющееся голоморфной функцией
в области D - {z?С : 0<|z|<oo, —n<argz<jx}, не-
непрерывно продолжаемой на множество {Z?C : 0<
<|z|<oo, - .-i<arg?«jc}.
При обращении (см. Обращение ряда) вейергптрас-
совых элементов A), B) возникают элементы более
общей природы, определяемые соответственно р я-
д а м и II ю и з ё:
где и — целое число, v — натуральное число, и кру-
кругами сходимости этих рядов U(а, Я), U(ее, В). В част-
частности, при uJSsO, v=l ряды C) совпадают с рядами
A), B), определяющими регулярные элементы; в от-
отличие от них определяемые рядами C) элементы при
[|<0 или v>l наз. особыми. При v—1 и v>l ря-
ряды C) определяют соответственно неразветв-
ленные п (алгебраические) развет-
разветвленные элементы.
Допуская при продолжении исходного элемента
(U(a, В), ]а) и особые моменты с рядами вида C),
вообще говоря, многозначные (при v>l) и имеющие
особенности типа полюса (при и,<0), получают более
обширную, чем венерштрассова, р и м а н о в у об-
область существования Е$ и соответствую-
соответствующую более обширную совокупность элементов, опре-
определяемых рядами вида C), называемую аналитическим
обра.юм. Аналитич. образ отличается от П. а. ф. при-
присоединением всех особых элементов, получаемых при
продолжении данного регулярного элемента. После
введения соответствующей топологии аналитич. об-
образ превращается в риманопу поверхность данной
функции.
При описанном построении П. а. ф. /ц? можно поль-
пользоваться вместо элемента понятием ростка аналитич.
функции, смысл введения к-рого заключается в лока-
локализации понятия элемента, в отвлечении от не имею-
имеющей и данном случае существенного значения вели-
величины радиуса сходимости. Два элемента (D, /) и (G, А)
такие, что области D и G содержат общую точку а,
наз. эквивалентными в точке а, если
существует окрестность точки а, в к-рой f—h. Это от-
отношение эквивалентности обладает обычными свойст-
свойствами рефлексивности, симметрии и транзитивности.
Класс эквивалентности элементов в данной точке а?С
паз. ростком аналитической функ-
ци н t'o в точке а. Росток характеризует локальные
свойства функции в данной точке. Два ростка ia и ga
равны, если в нек-рой окрестности точки а совпадают
какие-либо представители классов эквивалентности.
Аналогично, при помощи представителей, определяются
арифметич. действия с ростками и их дифференциро-
дифференцирование. П. а. ф. jw есть совокупность всех ростков
аналитич. функций f^, l,?E/, получаемых из дан-
данного ростка ia аналитич. продолжением вдоль всевоз-
всевозможных путей в С. Равенство двух П. а. ф. /ц/, gw
п действия с П. а. ф. определяются как равенство
ростков fa, й,а в какой-либо точке а?Е^[)Е g и дейст-
действия с ростками.
Элементы (D, /), вейергатрассовы элементы (Un(a,
^)> /я) и ростки аналитич. функции многих комплекс-
комплексных неременных z=(z1, . . ., z,,), n^\, определяются
точно так же, как выше, но с помощью областей D
комплексного пространства С" или поликругов схо-
сходимости
U» (a, /?) = {z ? C:\zj —aj\ < /?,-, / = 1, ...,»};
Rj > 0, ; = 1, . . ., //; а ¦-- («, я„);
Л = (Д1, .... Л„),
кратных степенных рядов
Понятие П. а. ф. многих комплексных переменных
строится далее вполне аналогично случаю одного пере-
переменного.
Лит.: [1] М а р к У ш е в и ч А. И., Теория аналитических
функций, 2 изд., т. 2, М., 1968; [2] Ш а б а т Б. В., Введение
и комплексный анализ, 2 изд., ч. 1-2, М., 1976; [3J С п р и н-
гер Д ж., Введение в теорию римановых поверхностей, пер.
с англ., М., 1900; [4] Фукс Б. А., Введение в теорию анали-
аналитических функций многих комплексных переменных, М., 1962.
Е. Д. Соломенцев.
ПОЛНАЯ ВАРИАЦИЯ ф у н к ц и и — то же, что
вариация функции.
ПОЛНАЯ ГРУППА — группа, в к-рой для любого
го элемента g и любого целого числа пфО разрешимо
уравнение х"~ g. Абелева П. г. наз. также дели-
делимой группой. Важными примерами П. г. являются
аддитивная группа всех рациональных чисел и группа
всех комплексных корней из 1 степеней /;*, k=-i,
2, . . ., где р — простое число (к в а з и ц и к л и ч е-
с к а я группа). Всякая абелева П. г. разлагается
в прямую сумму групп, каждая из к-рых изоморфна
одной из указанных. О неабелевых П. г. известно зна-
значительно меньше. Всякая неединичная II. г. беско-
бесконечна. Всякая группа вложима в подходящую П. г.
Если в П. г. указанные в определении уравнения раз-
разрешимы однозначно, она наз. D-т р у п и о й. Таковы,
в частности, локально нильпотентные II. г. без круче-
кручения.
Лит.: [1] К у р о ш А. Г., Теория групп, .'1 изд., М,, 1967;
[2] К а р г а п о л о в М. И., Мерзли к о в Ю. И., Основы
теории групп 3 изд., М., 1982. А. Л. Шмелъкин.
ПОЛНАЯ КРИВИЗНА — 1) П. к. в точке по-
поверхности Ф в евклидовом пространстве IR:1—
скалярная величина К, равная произведению главных
(нормальных) кривизн к1 и к2, вычисляемых в точке
поверхности: К=к1к2; наз. также гауссовой кривизной
поверхности. Понятие П. к. обобщается для гиперпо-
гиперповерхности и евклидовом пространстве К" + г, т?>2.
П. к. в этом случае есть величина К = к±. . .кп, где fc;- —
главная нормальная кривизна в точке гиперповерх-
гиперповерхности в г-м главном направлении.
П. к. в точке двумерной поверхности в трехмерном
римановом пространстве равна разности внутренней
кривизны — римановой кривизны двумерной поверх-
поверхности, и внешней кривизны — римановой кривизны
объемлющего пространства в направлении бивектора,
касательного к поверхности в рассматриваемой точке.
2) П. к. о б л а с т и О на поверхности Ф в евкли-
евклидовом пространстве R3— величина \ \ Kda, где К —
гауссова кривизна поверхности в точке, da — элемент
площади поверхности. Аналогично определяется П. к.
области нек-рого рнманова многообразия, причем под
К понимается риманова кривизна многообразия, вы-
вычисляемая в точках многообразия в направлении ка-
касательных бивекторов, а интегрирование ведется по
площади (мере) области многообразия. л- А- Сидоров.
ПОЛНАЯ ЛИНЕЙНАЯ ГРУППА — группа всех
обратимых матриц степени п над ассоциативным
кольцом К с единицей; общепринятое обозначение:
Ghn(K) или GL(/(, К). П. л. г. GL(/(, А') может быть
также определена как группа автоморфизмов АиЦ-(Г)
свободного правого АГ-модуля [' с п образующими.
В исследовании группы GL(n, А') большой интерес
представляет вопрос о ее нормальном строении. Центр
Хп группы GL(«, А") состоит из скалярных матриц с
элементами из центра кольца К. В классич. случае,
когда К — поле, решающую ролр> играет исследова-
исследование нормального строения специальной линейной
группы SL(n, К), состоящей из матриц с определите-
определителем 1. А именно, коммутант группы ОЦц, К) совпа-
совпадает с SL(rc, К) (кроме случая п—2, |А'|- 2), и всякая
нормальная подгруппа группы GL(n, А") либо содер-
содержится в Z,,, либо содержит SL(/i, К). В частности,
специальная проективная группа
PSL(n, K) = SL(n, K)/SL(n, K)(]Zn
является простой (за исключением случаев л—2,
1*1=2,3).
Если К — тело и п>1, то всякая нормальная под-
подгруппа группы GLGi, А') либо содержится в Zn, либо
содержит коммутант SL+ (п, К) группы GL(», К),
причем коммутант SL+(tj, А') порождается транс-
векциями и факторгруппа SL+(«, A')/SLb(re, K)[)Zn
проста. Кроме того, существует естественный, изо-
изоморфизм
GL (л, AT)/SL+ (n, К)^К*/[К*, К*],
где А*— мультипликативная группа тела К. Если
К конечномерно над своим центром к, то роль группы
>SL(», А') играет группа псех матриц из GL(», Л') с при-
приведенной нормой \. Группы SL(n, A') n SLH (п, К) не
всегда совпадают, но если к — глобальное поле, то это
так (см. Кнезера — Титса гипотеза).
Исследование нормального строения П. л. г. над
произвольным кольцом К связано с развитием алгеб-
алгебраической К-теории. Над кольцами К общего типа
группа GL(n, К) может быть весьма насыщена нор-
нормальными подгруппами. Напр., если К — коммута-
коммутативное кольцо без делителей нуля и с конечным чис-
числом образующих, то группа GL(n, К) финитно аппрок-
аппроксимируема, т. е. для каждого ее элемента g существует
нормальная подгруппа Ng конечного индекса, не со-
содержащая g. В случае А'=- % задача описания нор-
нормальных подгрупп группы GL(n, z) фактически экви-
эквивалентна конгруэнц-проблеме для группы SL(n, Z),
поскольку
[CL(ra, Z):SL(n, Z)] = 2,
а всякая нескалярная нормальная подгруппа группы
SL (п, 2) при п>2 является конгруэнц-подгруппой.
Имеется глубокая аналогия между строением П. л. г.
и строением других классич. групп, к-рая прости-
простирается далее на простые алгебраические группы и
группы Ли.
Лит.: [1] Ар тин Э., Геометрическая алгебра, пер.
с англ., М., 1969; [2] Дьедонне Ж., Геометрия классиче-
классических групп, пер. с франц., М., 1974; [3] Басе X., Алгебраи-
Алгебраическая К-теория, пер. с англ., М,, 1973. В. П. Плато}шв.
ПОЛНАЯ МЕРА — мера [г на а-алгебре 2, для
к-рой равенство ||а|(Л) = 0 влечет за собой А"?2 для
всякого ЕсА. Здесь \\у\ —полная вариация ц (для
положительной Меры ||l] = U.). А. П. Терехин.
ПОЛНАЯ НЕУСТОЙЧИВОСТЬ — свойство дина-
динамической системы. Динамич. система наз. впол-
вполне неустойчивой, если все ее точки — блуж-
блуждающие (см. Блуждающая точка).
Для того чтобы динамич. система, заданная на R",
была глобально выпрямляемой (т. е.
чтобы существовал гомеоморфизм R"—>-R"X R, отобра-
отображающий каждую траекторию системы на нек-рую
прямую {a}xR, где точка a?R« зависит от траекто-
траектории), необходимо и достаточно, чтобы система была
вполне неустойчивой и не имела седла в бесконечности
(теорема Немыцкого, см. [1]).
Лит.: [1] Н е м ы ц к и й В. В., С т е п а н о в В. В., Ка-
Качественная теория дифференциальных уравнений, 2изд.,М.— Л.,
1949. В. М. Миллионщиков.
ПОЛНАЯ ПОДКАТЕГОРИЯ — подкатегория К ка-
категории ,й' такая, что для любых объектов А, В ни (§
выполняется равенство
На{А, B) = HR(A, В).
Таким образом, П. п. однозначно определяется клас-
классом своих объектов. Обратно, всякий подкласс класса
объектов категории Ж однозначно определяет П. п.,
для к-рой он служит классом объектов: в эту подкате-
подкатегорию входят те и только те морфизмы, начала и концы
к-рых принадлежат выделенному подклассу. В част-
частности, П. п., соответствующая единственному объекту
А, состоит из множества Н^(А, А).
Многие важные классы подкатегорий (рефлективные
и корефлективные подкатегории, многообразия и т. п.)
ЯВЛЯЮТСЯ П. П. М. Ш. Цаленко.
ПОЛНАЯ ПРОБЛЕМА собственных зна-
значений — задача вычисления всех (в отличие от
частичной проблемы) собственных значений квадрат-
квадратной матрицы, обычно действительной или комплекс-
комплексной. Часто помимо собственных значений требуется
еще и построение базиса из собственных или корне-
корневых векторов матрицы.
Решение П. п. собственных значений матрицы А
сводится к построению характеристич. многочлена
Фд этой матрицы и вычислению его корней, действи-
тельных или комплексных (последнее обусловливает
невозможность нахождения собственных значений ко-
коночным вычислительным процессом). Для каждого
собственного значения к соответствующие собственные
векторы могут быть определены из однородной системы
линейных уравнений (А —кЕ)х-=0 (E — единичная мат-
матрица). При вычислениях над полем комплексных чи-
чисел достаточным условием существования базиса из
собственных векторов является простота спектра, а
необходимое и достаточное условие состоит в том, чтобы
алгебраич. кратность каждого собственного значения
к (т. е. его кратность как корня характеристич. много-
многочлена ц>А) совпадала с его геометрич. кратностью, под
к-рой понимается дефект матрицы А—'КЕ. При необ-
необходимости вычисления корневых векторов высоты,
превосходящей единицу, приходится рассматривать
однородные системы вида
(А — ХЕ)*х = 0, к ? N, к > 1.
Примерно но этой схеме строились и численные ме-
методы решения П. п. собственных значений, практико-
практиковавшиеся до кон. 1940-х гг. В 1930-х гг. были разра-
разработаны высокоэффективные (по количеству арифметич.
операций) алгоритмы вычисления характеристич. мно-
многочлена матрицы по ее коэффициентам. Так, в методе
Данилевского построение характеристич. многочлена
матрицы порядка п выполняется с затратой ~«;! муль-
мультипликативных операций (см. [1], [2]).
Методы этой группы получили название прямых, или
точных, по той причине, что, проводимые в точной
арифметике, они дают точные значения коэффициентов
характеристич. многочлена. Их поведение в условиях
реальных вычислений, сопровождающихся ошибками
округлений, не могло быть проверено для задач сколь-
сколько-нибудь значительного порядка до появления циф-
цифровых ЭВМ. Такая проверка произошла в 1950-х гг.,
в результате чего прямые методы были полностью вы-
вытеснены и.ч численной практики. Катастрофич. неустой-
неустойчивость вычисления собственных значений, связанная
с этими методами, имеет две основные причины. Во-
первых, коэффициенты характеристич. многочлена в
большинстве точных методов прямо или косвенно оп-
определяются как компоненты решения системы линейных
уравнений, матрица к-рой составлена по столбцам из
векторов v, Av, A2v, . . ., A"-'v, где v — начальный
вектор метода. Такая матрица обычно очень плохо
обусловлена, что видно хотя бы из того, что длины ее
столбцов, как правило, весьма различны, причем тем
больше, чем больше п. Тем самым коэффициенты ха-
характеристич. многочлена в общем случае вычисляются
с очень большими ошибками. Во-вторых, сама по себе
задача вычисления корней многочлена зачастую оказы-
оказывается численно неустойчивой. В этом отношении по-
показателен пример (см. [3]): если у многочлена
р (х) = (х — 1)(х — 2). . . (я —19) (я —20) =.г30 —210;г19+ ...
изменить коэффициент при .г19 с —210 на —210+2-23,
то у возмущенного многочлена р (х) появится пять пар
комплексно сопряженных корней; у одной из этих пар
мнимые части достигают ±i-2, 81, ... .
Подобная чувствительность собственных значений
матрицы к изменениям коэффициентов характеристич.
многочлена обычно не сопровождается сравнимой чув-
чувствительностью в отношении элементов самой матрицы.
Так, если указанный многочлен р (х) является харак-
характеристич. многочленом симметрич. матрицы А, то
изменения порядка 2~2;l в любом элементе матрицы
приводят самое большее к изменениям того же порядка
в ее собственных значениях.
Современные численные методы решения П. п. соб-
собственных значений находят собственные значения без
предварительного вычисления характеристич. много-
члена (см. Итерационные методы решения проблемы
собственных значений матрицы). Трудоемкость луч-
лучших из этих методов составляет ~кп? мультипликатив-
мультипликативных операций, где п — порядок матрицы, к — кон-
константа, не зависящая от п и имеющая смысл среднего
числа итераций метода, приходящегося на вычисле-
вычисление одного собственного значения. В (?.й-алгоритме
значения к обычно заключены между 1,5 и 2.
Приближенные собственные значения (векторы)
(пХ п)-матрицы А, вычисленные ортогональным ме-
методом М ((?/?-алгоритмом для матриц общего вида,
методом Якоби или методами, основанными на деле-
делении спектра, в случае симметрических и эрмитовых
матриц), можно интерпретировать как точные собст-
собственные значения (векторы) возмущенной(ых) матрицы
(матриц) А-{-Р^. Здесь F^j—матрица .эквивалентного
возмущения метода М — допускает оценку вида
A)
где е — относительная точность машинной арифме-
арифметики, \\А ||?=B|e,-y|2) ^— евклидова матричная нор-
норма, j (п) — функция вида Скпа. Число к описано выше,
а точные значения константы С и показателя а зави-
зависят от таких деталей вычислительного процесса, как
способ округления, использование операции накоп-
накопления скалярных произведений и т. д. Обычное значе-
значение а равно 2.
Располагая априорной оценкой A), можно оценить
точность вычисления собственных значений (векторов),
достигаемую в методе М. Эта точность зависит от
обусловленности отдельных собственных значений
(собственных подпространств).
Пусть Я — простое собственное значение матрицы А,
х — соответствующий нормированный собственный
вектор, у — нормированный собственный вектор тран-
транспонированной матрицы .4 т для того же собственного
значения. При возмущении матрицы А на матрицу F
возмущение собственного значения Я с точностью до
малых 2-го порядка выражается величиной
B)
и оценивается как
I ЛЯ I *S II F У\ утх | C)
(II 1!г — спектральная норма). Таким образом, чувст-
чувствительность Я к возмущениям матрицы А характеризу-
характеризуется числом s(k)—\y~x\~1, паз. (индивидуальным)
числом обусловленности этого собствен-
собственного значения. В случае, когда оба вектора хну дейст-
действительные, число s~](X) имеет простой геометрич.
смысл: это — косинус угла между векторами .гиг/,
что объясняет другое наименование s(k) — коэф-
коэффициент перекоса, соответствующий К.
Если матрица А диагонализуема (т. е. имеет базис
из собственных векторов), то обусловленность ее соб-
собственных значений К; может быть охарактеризована
и интегрально. Пусть Р — матрица, составленная по
столбцам из собственных векторов Я,,- и имеющая среди
всех таких матриц наименьшее число обусловлен-
обусловленности. Справедлива теорема (см. [4]): все собственные
значения возмущенной матрицы А -\ F заключены
в области комплексной плоскости, являющейся объеди-
объединением кругов
\z — X; К cond P |] F ||, i = l, ...,п. D)
Если эта область распадается на связные компоненты,
то каждая из них содержит столько собственных зна-
значений возмущенной матрицы, сколько кругов ее сос-
составляют. (В качестве нормы в D) можно ваять спект-
спектральную норму и для Р -- спектральное число обус-
обусловленности.)
Число com! Р нал. числом обусловлен-
обусловленности матрицы А но отношению к П. п. собствен-
собственных значений. Выражаемой в спектральной норме,
оно связано с коэффициентами перекоса следующим
образом:
s (ki) ==? cond2 P ==? 2"_, s (^')-
Более сложно зависит от возмущения матрицы А
возмущение собственного вектора х, относящегося
к простому собственному значению X. Оно опреде-
определяется, вообще говоря, не только коэффициентом пере-
перекоса, соответствующим самому X, но и коэффициентами
перекоса для прочих собственных значений. Чувстви-
Чувствительность собственного вектора х возрастает и при на-
наличии собственных значений, близких к к. В предель-
предельном случае, когда X становится кратным, сама поста-
постановка вопроса о чувствительности отдельного собст-
собственного направления теряет смысл и нужно говорить
о чувствительности собственного (или инвариантного)
I] однространства.
Качественно оценки C) и D) означают, что величина
возмущения каждого собственного значения диагона-
лияуемой матрицы А пропорциональна величине воз-
возмущения /•', а множителями пропорциональности вы-
выступают числа обусловленности, индивидуальные либо
глобальные. Если жорданова форма А — недиаго-
недиагональная и собственному значению X отвечает элемен-
элементарный делитель (z—Х)т, то возмущение X в общем
случае пропорционально уже не \\F\\, а ||/г|| 'т.
Наиболее важным частным случаем П. п. собствен-
собственных значений является вычисление всех собственных
значений (собственных векторов) действительной сим-
симметрической либо комплексной эрмитовой матрицы А .
Коэффициенты перекоса такой матрицы равны еди-
единице, и приближенная оценка C) переходит в точное
неравенство
Матрицу Р в D) можно выбрать ортогональной либо
унитарной, и потому глобальное число обусловлен-
обусловленности в спектральной норме равно единице. Незави-
Независимо от кратности точек спектра А существует такое
упорядочение собственных значений 1, матрицы A-\-F,
что выполняются при всех I соотношения
Еще более точные оценки возможны, если не только
сама матрица А является симметрической (эрмито-
(эрмитовой), но и ее возмущение F (см. [5]).
Помимо указанных имеется еще ряд апостериорных
оценок точности вычисленных собственных значений
и векторов. Они наиболее эффективны для симметриче-
симметрических и эрмитовых матриц А.
Пусть х,- — приближенный, а .г,- — точный собст-
собственный вектор для простого собственного значения X
матрицы А . Оба вектора предполагаются нормирован-
нормированными. Наилучшую оценку А,,-, к-рую можно получить
посредством вектора х,-, дает значение функционала
Рэлея
ф(Л, z) = Dz, z)/(z, z),
соответствующее х;, т. е. число ц;=фD, ж,-) (этот факт
имеет силу для произвольной, не обязательно эрми-
эрмитовой матрицы А). Вектор г,=Лх,-—u,,-:r/ наз. в е к т о-
р о м н е в я з к и.
Пусть
e = ||r,-|!2, a= min \Xj — u,-|.
Оценку величины а легко получить по вычисленным
собственным значениям "Kj. Справедливы оценки:
I ^/— 14 I «? 42i'a, I sin /L (T;Vy) I < e/a-
Если 'h[ — кратное собственное значение или имеется
группа близких к X,- собственных значений, то нужно
оценивать суммарное возмущение всей этой группы и
возмущение соответствующего ей инвариантного под-
подпространства (см. [5]).
Наряду с описанной П. и. собственных значений
часто возникает необходимость в решении т. н.
обобщенной проблемы собственных
значений
Ах = \Вх. E)
В наиболее важном случае обобщенной проблемы соб-
собственных значений матрицы А и В являются симмет-
симметрическими (эрмитовыми), и одна из них положительно
определена. Теория и методы численного решения за-
задачи E) в этом случае параллельны теории и методам
для обычной симметрической (эрмитовой) проблемы
собственных значений.
Если ни одна из матриц А и В не является опреде-
определенной или хотя бы одна из них даже симметриче-
симметрической, то пользуются т. н. (^-алгоритмом (см. [6]),
своеобразным обобщением <?Д-алгоритма. Необходимо
отметить, что здесь возможны новые эффекты, нена-
ненаблюдаемые в обычной П. п. собственных значений: бес-
бесконечные собственные значения, непрерывный спектр.
Еще более сложны нелинейные задачи на собствен-
собственные значения
Такие задачи решают обычно путем сведения к ли-
линейным более высокого порядка (см. [7]).
Лит.: [1] Данилевский A.M., «Матем. сб.», 1937,
т. 2, № 1, с. 169—71; [2] Фаддеев Д. К., Ф а д д е е в а
В. Н., Вычислительные методы линейной алгебры, 2 изд., М.,
1963; [3] Wilkinson J. H., Rounding errors in algebraic
processes, Englewood cliffs (N.Y.), 1963; [4] Уилкинсон
Д ж. X., Алгебраическая проблема собственных значений, иер.
с англ., М., 1970; [5] П а р л е т т Б,, Симметричная проблема
собственных значений. Численные методы, пер. с ачгл., М.,
1983; [6] М о 1 е г СВ., Stewart G. W., «SIAM J. Num.
Anal.», 1973, v. 10, p. 241; [7] К у б л а н о в с к а я В. Н., в
сб.: Вычислительные методы линейной алгебры, Новосиб.,
1980, с. 37—53. X. Д. Икрамов.
ПОЛНАЯ ПРОИЗВОДНАЯ функции — произ-
производная по t от функции y = f(t, u, v, . . ., z), зависящей
от переменной t как непосредственно, так и через
промежуточные переменные u=u(t, хх, . . ., хп), у=*
— v(t, xu . . ., хп), . . ., z=z(t, xu . . ., х„), вычисляе-
вычисляемая по формуле
dy_ _<2f_ , df_ du . df_ Э?_, i^L2L
dl~dt'dudi ' dv dt ' ' " " ' dz dt '
Э/ df df du dz
где at ' ЬИ' ¦ ¦ ¦' ЪЧ • m ' ¦ ¦ •' m ~ частные пРоиз-
водные. е. Д. Соломенцев.
ПОЛНАЯ РЕШЕТКА, полная структу-
р а,— частично упорядоченное множество, в к-ром вся-
всякое непустое подмножество А имеет точную верхнюю
и точную нижнюю грань, называемые обычно объе-
объединением и пересечением элементов
подмножества А и обозначаемые \/ аа и Л аа
V аа 6 Л ' >оа6 А
(или просто W^ и Д^) соответственно. Если частично
упорядоченное множество имеет наибольший элемент
и каждое его непустое подмножество обладает точной
нижней гранью, то оно является П. р. Решетка L
тогда и только тогда является полной, когда для лю-
любого изотопного отображения ср этой решетки в себя
существует неподвижная точка, т. е. такой элемент
a?L, что а(( = а. Если Р (М) —упорядоченное вклю-
включением множество подмножеств множества Миф —
отношение замыкания на Р (М), то совокупность всех
ф-замкнутых подмножеств япляется П. р. Всякое час-
частично упорядоченное множество Р можно изоморфно
вложить в П. р., к-рая в этом случае наз. попол-
пополнением множества Р. Пополнение сечениями яв-
является наименьшим из всех пополнений данного час-
частично упорядоченного множества. П. р. образуют мно-
множество всех подалгебр универсальной алгебры, мно-
множество всех конгруэнции универсальной алгебры,
множество всех замкнутых подмножеств топологич.
пространства.
Лит.: [1J Б и р к г о ф Г., Теория структур, пер. с англ.,
М., 1052; 12] Скорняков Л. А., Элементы теории струк-
структур, М., 1970. Т. С. Фофанова.
ПОЛНАЯ СИСТЕМА, замкнутая система
(дифференциальных уравнений), —
система дифференциальных уравнений с частными про-
изиодными 1-го порядка
I''i(x, и, р) = 0, 1<«<т, A)
.г = (х\, ..., хп), и = и(хъ ..., хп),
ди ди \
j
со следующим свойством: для любого набора чисел
(.г, и, р), удовлетворяющего уравнениям A), справед-
справедливы равенства
FtJ (х, и, р) = 0, 1 < (, / < т,
где Fjj=[Fi, Fj] — Якоби скобки.
Для линейных однородных систем условие полноты
формулируется несколько иначе. Скобка Якоби в атом
случае линейна по переменным p^(plt . . ., р„), и
если система записана в виде
Pi (м) = 0, 1<г<от,
где Pj — линейные дифференциальные операторы 1-го
порядка, то этой скобке отвечает коммутатор [Р,-, Ру] =
=P,Pj—РjPi- Полнота системы заключается в предста-
представимости всех коммутаторов [/",-, Рj\ в виде линейных
комбинаций от Pj с колффициентами, зависящими
только от х= (г,, . . ., хп).
Если и = и(х) — совместное решение двух уравне-
уравнений
Fi(.r, и, р)=0, Fj(x, и, р) = 0,
то и является решением и уравнения
\Fit Fj\(x, и, p)=Q. B)
Произвольную систему вида A) обычно пытаются
расширить до полной добавлением к ней новых неза-
независимых уравнений, полученных из старых с помощью
операции образования скобок Якоби. При этом рас-
расширении в соответствии с B) ни одно из решений пере-
переходной системы не должно теряться, если она вообще
разрешима.
Свойство системы быть полной инвариантно относи-
относительно тех неособых преобразований переменных (х,
ui Р, F), Для к-рых сохраняется смысл дифференци-
дифференциальных уравнений. К таким преобразованиям отно-
относится, напр., замена независимых переменных х—
— g(y), У=(Уи ¦ ¦ -. i/«)i a также преобразование сле-
следующего типа. Пусть А : R2" + 1 + '"—^.R"'— такое глад-
гладкое отображение, что
У = х, q = p,
v = u, t~H(x, и, р, s),
* = («i sm), t = (h, ¦¦., tm)
есть диффеоморфизм R2n + i + m_^R2n + i + m_ Тогда рас-
рассматриваемое преобразование заключается в переходе
от системы A) к системе
Gi(x, и, р) = Н((х, и, р, F) = 0, l<i<m.
Лит.: [1] Камке Э., Справочник по дифференциальным
уравнениям в чнетных производных первого порядка, пер. с
кем., М., 19R6; [2] Гюнтер Н. М., Интегрирование уравне-
уравнений первого порядка в частных производных, Л.— М., 1934;
L3] С а г a I li (¦¦ о d о г у С, Variatiotisrechnimg und partielle
Different mltrluieliungen i-rster Ordnung, 2 Auft., Bd 1, Lpz., 1956;
[4] Gouts a t E., Lemons sur rintegration des equations aus
dSrivees partielles du premier ordre, P., 1891. А. П. Солдатов.
ПОЛНАЯ СИСТЕМА ВЫЧЕТОВ по модулю
т ¦— любой набор из т несравнимых между собой
по модулю т целых чисел. Обычно в качестве П. с. в.
по модулю т берутся наименьшие неотрицательные
кычеты 0, 1, . . ., m — 1 или абсолютно наименьшие вы-
вычеты, состоящие из чисел 0, ±i, . . ., ±—ir- B СЛ.У"
чае нечетного т. и чисел 0, ±\, . . ., т~~, 2- в случае.
четного т. С. А. Степанон.
ПОЛНАЯ СИСТЕМА ФУПКЦНШ—о р то нормиро-
нормированная система функций {ф (г)} нек-рого гильбертова
пространства Н такая, что в Н не существует функции,
ортогональной всем функциям данного семейства. Си-
Система функций, полная в одном пространстве, может
оказаться неполной в другом. Напр., система
:^tCosj?3->, л—0, 1, .... образует П. с. ф. в про-
I V л |
странстве L [0, л], но не образует П. с. ф. в про-
пространстве L[ — n, л]. Е. Д. Соломенцев.
ПОЛНОГО НАКОПЛЕНИЯ ТОЧКА—точках мно-
множества М в топологич. пространстве X такая, что
пересечение М с любой окрестностью х имеет мощ-
мощность ту же, что и все множество М.
М. И. Войцеховскип.
ПОЛНОЕ АЛГЕБРАИЧЕСКОЕ МНОГООБРАЗИЕ —
обобщение понятия компактного комплексного ал-
гебраич. многообразия. Многообразие X наз. п о л-
н ы м, если для любого многообразия Y проекция
XXY-+Y является замкнутым морфизмом, т. е. пере-
переводит замкнутые (в топологии Зариского) подмноже-
подмножества XX Y в замкнутые подмножества У. Имеется т. н.
валюативный критерий полноты: для
любого кольца дискретного нормирования А с полем
частных К и любого морфизма и : Spec К—*-Х должен
существовать единственный морфизм ч : Spec А^-Х,
продолжающий и. Это условие является аналогом тре-
требования того, чтобы любая последовательность в X
имела предельную точку.
Любое проективное многообразие является полным,
но не наоборот. Для любого П. а. м. X существует
проективное многообразие X' и проектинный бирацио-
нальный морфизм X'—*-Х (лемма Ч ж о у). Для
любого алгебраич. многообразия X существует откры-
открытое вложение в полное многообразие X (теорема
Н а г а т ы). Обобщением понятия П. а. м. на отно-
относительный случай служит собственный морфизм схем.
Лит.: [1] Хармсхорн Р., Алгебраическая геометрия,
пер. с англ.,М., 1981; [2] ГЯафаревич И. Р., Основы
алгебраической геометрии, М., 1972. В. И. Данилов.
ПОЛНОЕ ИЗМЕНЕНИЕ ФУНКЦИИ — то же, что
вариация функции одного переменного. П. и. ф. есть
сумма положительной вариации функции и отрица-
отрицательной вариации функции. Б. И. Голубое.
ПОЛНОЕ МЕТРИЧЕСКОЕ ПРОСТРАНСТВО — ме-
метрическое пространство, в к-ром каждая фундамен-
фундаментальная, или сводящаяся в себе, последовательность
сходится. П. м. и.— частный случай полного равно-
равномерного пространства. м. И. Войцеховский.
ПОЛНОЕ МНОЖЕСТВО в топологическом
векторном пространстве X над полем
К — множество А такое, что совокупность линейных
комбинаций элементов из А (всюду) плотна в X, т. е.
порожденное множеством А замкнутое подпростран-
подпространство, или замкнутая линейная оболочка А, совпадает
с X. Напр., в нормированном пространстве С неире-
рывных функций на [О, 1] со значениями в С множество
{хп} является П. м. Если К — недискретное норми-
нормированное поле, то каждое поглощатощое множество
(и в частности каждая окрестность пуля в X) является
П. м.
Для того чтобы А— {й(}, t?T было П. м. в ослаб-
ослабленной топологии а(Х, X*) пространства X, необхо-
необходимо и достаточно, чтобы для каждого »? X* сущест-
существовал индекс t такой, что <а(, ъ>=^0; это означает, что
никакая замкнутая гиперплоскость не содержит всех
элементов at, т. е. что А — тотальное мно-
множество. При этом если X — локально выпуклое
пространство, то П. м. в ослабленной топологии будет
ПОЛНЫМ И В ИСХОДНОН ТОПОЛОГИИ. М. И, Войцеховский.
ПОЛНОЕ ПРИРАЩЕНИЕ функции несколь-
нескольких переменных — приращение, приобретае-
приобретаемое функцией, когда все аргументы получают (вообще
говоря, ненулевые) приращения. Точнее, пусть функция
/ определена в окрестности точки ж(П)= (г(,0', . . ., х$])
и-мерного пространства R" переменных хг, . , ., хи.
Приращение
А/ = / (.z«»-fA;r) — / (л-(в))
функции / в точке х{П), где
Дж=(Дг1, .. ., Д.г„),
я«»+Дж ==(*(<» + Д*!, ..., .r<«>-f Д.г„),
нпз. полным приращением, если оно рас-
рассматривается как функция п всевозможных прираще-
приращений Д^, . . ., Дж„ аргументов хи . . ., хп, подчинен-
подчиненных только условию, что точка .г|(|'+Дг принадлежит
области определения функции /. Наряду с П. п. функ-
функции рассматриваются частные приращения
Джь/ функции / в точке ?@> по переменной х^, т. е.
такие приращения Д/, для к-рых Дау^-О, /, 2, . . .,
к— 1, к-\-\, . . ., ч, к -- фиксировано (к— 1, 2, . . ., п).
Л. Д. Кудрявцев.
ПОЛНОЕ ПРОСТРАНСТВО — термин, относящийся
к метрическому пространству, равномерному про-
пространству, топологическому пространству, близости
пространству, пространству топологической группы,
пространству с симметрикой, псевдометрическому про-
пространству; возможны употребления этого термина и
в других ситуациях. Все определения полноты осно-
основаны на одной общей идее, конкретное воплощение
к-рой зависит от рассматриваемого типа пространств.
Общее в определениях полноты состоит в требовании
сходимости достаточно широкого класса последователь-
последовательностей, направленностей или центрированных систем.
Метрич. пространство наз. полным, если каждая
фундаментальная последовательность в пем сходится.
В этом же смысле понимается полнота псевдометрич.
пространства и пространства с симметрикой. Равно-
Равномерное пространство наз. полным, если для каж-
каждой центрированной системы множеств в ном, содер-
содержащей сколь угодно мелкие по отношению к покры-
покрытиям из данной равномерной структуры множества,
пересечение элементов ятой системы не пусто. На то-
нологич. группе есть естественные правая и левая
равномерные структуры. Если пространство группы
в одной из этих равномерных структур полно, то оно
полно и в другой, и топологич. группа наз. тогда
полной п о Be ii л ю. Полнота по отношению
к двусторонней равномерной структуре на группе,
получаемой структурным объединением ее правой и
левой структур, наз. полной по Райкову.
Полнота метрич. пространства и полнота по Райкову
могут быть истолкованы как абсолютная замкнутость
по отношению к любым представлениям данного про-
пространства, как подпространства пространства того же
типа. В частности, метрич. пространство полно в том
и только в том случае, если оно замкнуто в любом
объемлющем его метрич. пространство. Топологнч.
группа полна по Райкову, если и только если она
замкнута в любой топология, группе, содержащей ее
в качестве тонологич. подгруппы. Это связано с фун-
фундаментальной конструкцией пополнения: каждому мет-
метрич. пространству канонич. образом сопоставляется
его пополнение — полное метрич. пространство, со-
содержащее исходное пространство в качестве всюду
плотного подпространства. Аналогично, каждая то-
пологич. группа пополняема по Райкову, но не каж-
каждая тонологич. группа пополняема по Вейлю.
Для топологич. пространств требование абсо-
абсолютной замкнутости — т.е. замкнутости
в любом объемлющем пространстве,— приводит, если
ограничиться классом вполне регулярных хаусдорфо-
вых пространств, к бикомпактным пространствам: та-
такие и только такие пространства обладают этим свой-
свойством. Однако есть другой полезный и естественный
подход к определению полноты тонологич. простран-
пространства. Вполне регулярное хаусдорфово пространство наз.
полным по Чеху, если оно представимо в виде
пересечения счетного семейства открытых множеств
в нек-ром своем бикомпактном хаусдорфовом расши-
расширении. Все такие пространства обладают свойством
Бэра: пересечение счетного семейства непустых от-
открытых всюду плотных множеств в них всегда не пусто.
Метризуемое пространство полно по Чеху в том и
только в том случае, если оно метризуемо полной мет-
метрикой (теорема Александрова — Хаус-
до р ф а). Полнота по Чеху обеспечивает правильное
поведение топологич. пространства во многих сущест-
существенных отношениях. Так, полное по Чеху счетное
пространство имеет счетную базу и метризуемо. Пара-
Паракомпактность сохраняется при операции произведения,
когда пространства полны по Чеху. Полнота но Чеху
сохраняется совершенными отображениями, а в клас-
классе метризуемых пространств она сохраняется в сторо-
сторону образа открытыми непрерывными отображениями.
Другой полезный подход к определению полноты
вполне регулярного хаусдорфова пространства связан
с рассмотрением максимальной равномерной струк-
структуры на нем: если такое равномерное пространство
полно, то топологич. пространство наз. полным
по Дьёдонне. Полны по Дьёдонне в точности те
пространства, к-рые гомеоморфны замкнутым под-
подпространствам топологич. произведений метризуемых
пространств. В присутствии полноты по Дьёдонне
в одно свойство сливаются псевдокомпактность, счет-
счетная компактность и бикомпактность. Все нараком-
пакты полны по Дьёдонне, в частности полны по
Дьёдонне все метрич. пространства. Отсюда видно,
что из полноты по Дьёдонне не следует наличие у про-
пространства свойства Бэра. Специальный случай пол-
полноты по Дьёдонне — полнота топологич. про-
пространства в смысле Хьюитта, означающая го-
гомеоморфность пространства замкнутому подпро-
подпространству топологич. произведения нек-рого семейства
действительных прямых.
Лит.: [1] Архангельский А. В., Пономарев
В. И., Основы общей топологии в задачах и упражнениях, М.,
1974. А. В. Архангельский.
ПОЛНОЕ РАВНОМЕРНОЕ ПРОСТРАНСТВО — рав-
равномерное пространство, в к-ром всякий Коши фильтр
сходится. Важнейший пример П. р. п.— полное мет-
метрическое пространство. Замкнутое подпространство
П. р. п. полно; полное подпространство отделимого
равномерного пространства замкнуто. Произведение
П. р. п. полно; обратно, если произведение непустых
равномерных пространств полно, то и все пространства
сомножители полны. Всякое равномерное простран-
пространство X равномерно непрерывно отображается на
нек-рое плотное подпространство П. р. п. X (см. По-
Пополнение).
Лит.: [1] Б у р 0 a i; и II., Общая топологии. Основные
структуры, пер. с франц., М., 19В8; I'Z] К е л л и Д ж., Общая
топология, пер. с англ., ;! изд., М., 1981. М. И. Воицехавский.
ПОЛНОЕ РИМАНОВО ПРОСТРАНСТВО — рима-
ново пространство с функцией расстояния р, полное
как метрич. пространство с метрикой р.
Пусть М — связное риманово пространство со связ-
связностью Леви-Чивита, тогда следующие три утвержде-
утверждения эквивалентны: а) М — полно; б) для каждой точки
р(^М экспоненциальное отображение ехр^ определено
на всем Мр (где Мр — касательное пространство и
Мир); в) каждое ограниченное по отношению к рас-
расстоянию р замкнутое множество А сМ компактно
(теорема Хопфа — Рино в а). Следствия:
любые две точки р, q?M П. р. п. можно соединить на
М геодезич. длины р(р, q); любая геодезическая не-
неограниченно продолжаема.
Имеется [2] обобщение этой теоремы на случай про-
пространства с несимметричной функцией расстояния.
Лит.: [1] Г р о м о л Д., КлингенОерг В., Мей-
ер В., Риманова геометрия в целом, пер. с нем., М., 1971; [2]
К о и - Ф о с с е н С. Э., Некоторые вопросы дифференциаль-
дифференциальной геометрии в целом, М., 1959. М. И. Воицехавский.
ПОЛНОЕ ТОПОЛОГИЧЕСКОЕ ПРОСТРАНСТВО —
см. Полное пространство.
ПОЛНОЙ ВЕРОЯТНОСТИ ФОРМУЛА — соотноше-
соотношение, позволяющее вычислять безусловную вероятность
события через его условные вероятности относительно
событии, образующих полную группу.
Точнее, пусть (Й, Л, Р) — вероятностное про-
пространство, Л, Л], . . ., Л п^_Л — события, причем
Ajf\Aj- 0 при 1ф}, i, у —1, 2, . . ., и,
и Р (А б)>0 для всех к. Тогда имеет место формула
полной вероятности:
Р (А)^^"к=1Р уА\ Ak) P (Ak).
П. в. ф. верна и в том случае, когда число событий
Л,, Л 2, ... бесконечно.
Имеет место П. в. ф. для математич. ожиданий.
Пусть X (ш), (o?Q —случайная величина на (Q, Л,
Р), ЕХ — ее математич. ожидание, а Е(Х|ЛА) —
условные математич. ожидания относительно событий
A k, образующих полную группу. Тогда
ЕХ^-^Е (Х\Ак)Р(Ак).
П. Г. Ушаков.
ПОЛНОТА в математической логике
— свойство, близкое к понятию максимального эле-
элемента в частично упорядоченном множестве. Термин
«П.» в математич. логике употребляется в контекстах
вида: полное исчисление, полная теория (или полное
множество аксиом), ш-полная теория, полная в смысле
Поста система аксиом, полное вложение одной модели
в другую, полная формула полной теории и др.
Одним из наиболее важных в гносеологич. отноше-
отношении является понятие П. исчисления относительно
данной семантики. Исчисление наз. полны м, если
всякая верная в семантич. смысле формула этого ис-
исчисления выводима в нем. При этом понятие выводи-
выводимости должно быть эффективным, т. е. имеются
набор правил и инструкция их применения, позволяю-
позволяющая строить выводы, причем есть алгоритм, отли-
отличающий выводы от невыводов. Понятие семанти-
семантически верной формулы, наоборот, форму-
формулируется, как правило, с использованием неэффектив-
неэффективных понятий, с помощью кванторов всеобщности по
бесконечным и даже несчетным совокупностям. В тео-
теоремах о полноте классического и интуиционистского
исчислений предикатов П. понимается в указанном
смысле. В случае классич. исчисления семантически
верными считаются те формулы языка узкого полис-
ления предикатов (УИП), к-рые истинны во всех мо-
моделях для рассматриваемого я:)ыка. В интуицпоинст-
ском случае семантически верными считаются формулы,
истинные во всех Крипке моделях. Понятие истинной
в данной модели формулы также использует кванторы
по бесконечным областям (если модель бесконечна)
как в классическом, так и в интуиционистском слу-
случаях. Иногда рассматривают исчисления, не удовлет-
удовлетворяющие требованию эффективности.
С понятием П. исчисления тесно связано понятие
полной теории. Теорией (точнее, элементарной
теорией) наз. произвольное множество Т замкнутых
формул языка УИП. Непротиворечивая теория Т наз.
полной, если множество, всех следствий из Т в клас-
сич. исчислении предикатов является максимальным
непротиворечивым множеством, т. е. добавление к Т
любой замкнутой невыводимой из Т формулы позво-
позволяет вывести любую формулу. В этом определении не
предполагается, что множество Т задано эффективно,
так что понятие вывода становится тоже неэффектив-
неэффективным. П. теории Т эквивалентна следующему условию:
для всякой замкнутой формулы ср имеет место в точ-
точности одно из двух утверждений — либо ф выводима
ив Т, либо ~]ф выводима из Т.
Если дана какая-то модель М языка УИП, то воз-
возникает семантич. понятие формулы, истинной в мо-
модели М. Теория Т наз. полной относится ь-
н о М, если в классич. исчислении предикатов, по-
пополненном формулами из Т, выводимы в точности все
истинные в М формулы. Между понятиями П. теории
и П. относительно М имеется следующая связь. Тео-
Теория Т полна тогда и только тогда, когда существует
модель М, относительно к-рой она полна. Модель М
наз. моделью теории Т, если все формулы
из Т истинны в М. Достаточный признак П. теории:
если все модели нек-рой мощности теории Т изоморф-
изоморфны, то теория Т полна. Обратное не всегда верно.
Понятие П. теории находит применение в вопросах
разрешимости теорий из-за следующего свойства пол-
полных теорий: если теория Т полна и множество Т ко-
конечно или даже рекурсивно иеречислимо, то существует
алгоритм, распознающий по любой формуле ф выво-
выводима она или нет. Если не требовать эффективного
задания множества Т, то всякую теорию можно по-
пополнить, т. е. расширить добавлением новых аксиом
до полной. При наличии требования эффективности
дело обстоит не так, как показывает теорема Гёделя
о неполноте арнфметич. исчислений. Теория 7" наз.
расширением теории ?', если всякая фор-
формула, выводимая из Т, будет выводима из Т. Пусть
Т — непротиворечивая рекурсивно перечислимая тео-
теория. Теория Т наз. эффективно непонол-
н и м о й, если по всякому рекурсивно перечислимому
непротиворечивому расширению Т' теории Т можно
эффективно найти формулу ф, формально неразреши-
неразрешимую в Г', т. е. такую, что ни ф, ни ~]ф не выводимы из
Т'. Теорема Гёделя о неполноте утверждает, что
нек-рая конкретная арнфметич. теория Q, имеющая
конечное число аксиом, эффективно не пополнима. Из
этой теоремы вытекает неполнота относительно стан-
стандартной модели натуральных чисел любого арифметич.
исчисления, удовлетворяющего требованию эффек-
эффективности.
Арифметич. теория Т наз. ш-п одной, если из
того, что в Т выводимы все формулы вида
ф@), ф A), фB), ..., (:•:)
следует выводимость в Т формулы V-r ф (¦*¦)¦ Из дока-
доказательства теоремы Гёделя о неполноте следует, что
существуют теории, не являющиеся ю-иолными, и
даже такие, в к-рых выводима бесконечная серия фор-
формул (*), а также формула Эх ~]Ц'(х), и тем не менее
противоречия вывести нельзя. Такая теория нап. to-
tori р о т н и о р о ч и в о п.
Непротиворечивая система аксиом нал. и одно и
в смысле Поста, если добавление к ней любой
схемы аксиом либо не расширяет запаса выводимых
формул, либо превращает систему в противоречивую.
Напр., аксиоматика классич. исчисления высказыва-
высказываний полна в смысле Поста, а интуиционистского исчис-
исчисления высказываний не полна.
Лит.: [II К л и н и С. К Введение в метаматематику, пер.
с англ., М., 1957; 1.2] К е й с л е р Г., Чан Ч. Ч., Теория
моделей, пер. с англ., М., 1977; [3] Ш е н ф и л д Д ж., Мате-
Математическая логика, пер. с англ., М., 1975; [4] Роджерс X.,
Теория рекурсивных функций и эффективная вычислимость,
пер. с англ., М., 1972; [5] Ф е й с Р., Модальная логика, пер.
с англ., М., 1974 (Дополнения). В. Я. Гришин.
ПОЛНОТА в топологии — свойство про-
пространства, заключающееся в сходимости последователь-
последовательностей, направленностей или семейств множеств, под-
подчиненных условию Коши или его обобщениям (см.
Полное пространство). А. В. Архангельский.
ПОЛНЫЙ ДИФФЕРЕНЦИАЛ функции п перемен-
переменных в точке xo(^Rn — то же самое, что дифференциал
функции в атой точке. Термин «П. д.» употребляется
с целью противопоставления его термину «частный
дифференциал». Понятие П. Д. функции п переменных
обобщается на случай отображения открытых множеств
линейных топологич. пространств в подобные же про-
пространства (см. Гато дифференциал, Фреше дифферен-
дифференциал, Дифференцирование отображения).
Л. Д. Кудрявцев.
ПОЛНЫЙ ИНТЕГРАЛ — решение и(х, а),
г~(хх, . . .. х„), а— (й), . . ., а„), дифференциального
уравнения с частными производными 1-го порядка
,, / ди ди \ ,, ,, .
/' (*1, -.., Х„, U, g^, ...,—j=0, A)
к-рое зависит от п параметров %, . . ,, а„ и в рассмат-
рассматриваемой области удовлетворяет условию
dell,,,. фО.
"х.а
Если и (х, а) рассматривать как п-параметрическое
семейство решений, то огибающая любого его (п—1)-
параметрического подсемейства, выделяемого условием
al~-aii(tl, . . ., tn_1), 1<:г«:я, является решением
уравнения A). При этом линии касания поверхностей,
задаваемых полным интегралом, и огибающей являются
характеристиками A). С помощью П. и. можно опи-
описать решения характеристич. системы обыкновенных
дифференциальных уравнений, отвечающей уравне-
уравнению A), и, следовательно, обратить метод Коши. к-рый
сводит решение уравнения A) к решению характерис-
характеристич. системы. Этот подход применяется в аналитич.
механике, где требуется найти решение канонич. сис-
системы обыкновенных дифференциальных уравнений
dx- вН dp. ОН
at —ер.' ~dT^dXi' i^is^n- i-;
Эта система является характеристической для уравне-
уравнения Якоби
. ди ди \ , ,„,
Если для уравнения C) II. и. и—-и(х1, . . . , х„, t.
ау, . . ., а„)-\-а0 известен, то 2м интегралов канонич.
системы B) даются равенствами и — Ь;, и —ph
i i
1<i<», где й/,Ь,- — произвольные постоянные.
А. П. Солдатов.
ПОЛНЫЙ ОПЕРАТОР — обобщенный волновой опе-
оператор, т. е. частично изометрич. оператор, определяе-
определяемый равенством
W v (A2, Ai)=s- lim е'1-\-"А,Ри
где Ai и А2 — самосопряженные операторы в сепара-
бельном гильбертовом пространстве //, Рг — орто-
проектор на Н^мс, и такой, что
{W+(A2, A1)x\\\W + (A2, A1)x\\ = \\x*} = ]Ji>ac.
Здесь Hi, ас- i=1, 2,— совокупность всех спектрально
м", олюпш непрерывных относительно А; элементом х,
т.е. таких, что спектральная .мера <? л (|i) x, х} мно-
множества .1/ абсолютно непрерывна относительно меры
Лебега ц,(х).
Если оператор W+ (А3, Aj) (или аналогично опреде-
определяемым оператор W~(A2, Лг)) существует и является
полным, то А,-, ас—части операторов А; на Я/. ас
унитарно эквивалентны. Если А1 и А 2 — самосопряжен-
самосопряженные операторы в // и Л2=Лг+е<-, />/, где /?# и с
вещественно, то W^(A2, Аг) и W±{A1, A2) сущест-
существуют и являются полными.
Лит.: [1] К а т о Т., Теория возмущений линейных опера-
операторов, пер. с англ., М., 1972. В. И. Соболев.
ПОЛОВИННОГО ДЕЛЕНИЯ МЕТОД, метод
дихотомии,— 1) Один из методов численного
решения уравнения с одним неизвестным. Пусть име-
имеется уравнение /(,/¦) = (_> с непрерывной на отрезке [а, Ь]
функцией f(x), принимающей на концах отрезка значе-
значения разных знаков и имеющей внутри [а, ft] единствен-
единственный кореш, х^. Для приближенного нахождения х*
отрезок [а, ft] делят пополам и вычисляют значение
f{xx) в средней точке х1=(а-\-Ь)/2. Если f(xx)?=O, то
из двух отрезков [а, х^\ и [ж-,, ft] для последующего де-
деления пополам выбирается тот, на концах к-рого зна-
значения функции различны по знаку. Возникающая в
процессе такого дробления последовательность сере-
середин отрезков хх, хг, . . . сходится к корню ж* со ско-
скоростью геометрич. прогрессии:
\xn-xt\<L(b-a)l2.", ге = 1, 2, ..., A)
причем в рассматриваемом классе функций оценка A)
неулучшаема. В случае, когда функция /(.г) имеет на
[я, ft] более одного корня, последовательность будет
сходиться к одному из них.
2) Один из методов минимизации функций одного
переменного. Пусть требуется найти минимум
/»= min / (х)
а < х < Ъ
унимодальной функции /(х) на отрезке [а, Ь] и указать
точку X*, в к-рой он достигается. Тогда отрезок [а, Ь]
делят пополам и вблизи его середины i1=(a+ft)/2
вычисляют значения функции f (х) в двух точках
г1 — х1~е/2 и хг--х1-\-ь12, где число 8>0, являющееся
параметром метода, достаточно мало. Затем значения
/(з^) и /(.г2) сравнивают и с учетом унимодальности
функции f(x) из двух отрезков [а, х2] и [.rx, ft] выбирают
тот, к-рый заведомо содержит точку х.%. Так, если
f (x1)<^f(x2), это будет отрезок [а, х?), в противном слу-
случае — отрезок [.г,, ft]. Выбранный отрезок вновь делят
пополам, вблизи его середины хг берут две точки хг—
= х2—е/2 и r2=.r2-i-e/2, сравнивают в них значения
функции и т. д. В результате возникает последователь-
последовательность срединных точек {хп}, для к-рой
\x~n — xt\<(b—a~-e)/2" + e/2, п = 1, 2, ... B)
За приближения к /„ принимают значения / (хп) при
достаточно больших п.
Название метода объясняется тем, что на каждом
следующем шаге описанного алгоритма отрезок, со-
содержащий точку минимума, становится примерно
вдвое короче. На классе унимодальных функций П. д. м.
не является наилучшим. Существуют более эффектив-
эффективные методы, позволяющие при том же количестве вы-
числений значений функции достигнуть лучшей по
сравнению с B) точности (см., напр., Фибоначчи ме-
метод).
Лит.: [1] Д е м и д о в и ч Б. П., Марон И. А., Основы
вычислительной математики, 3 изд., М., 196В; [2] У а й л д Д.-
Д ж., Методы поиска экстремума, пер. с англ., М., 1967.
М. М. Потапов.
ПОЛОЖИТЕЛЬНАЯ ВАРИАЦИЯ ФУНКЦИИ —
одно из двух слагаемых, сумма к-рых есть полное
изменение, или вариация функции, на данном отрезке.
Пусть f(x) — функция действительного переменного,
заданная на отрезке [а, Ь] и принимающая конечные
значения. Пусть П= {а—х()<х1< ... <хп=Ь)— произ-
произвольное разбиепие отрезка [а, Ь] и
где суммирование производится по тем номерам г,
для к-рых разность j(x{)—/(.t,_j) неотрицательна.
Величина
P{f) = P(f, К *>])•= sup Рп(/)
наз. положительным изменениемфун-
к ц и и /на отрезке [а, Ь]. Всегда 0 <:/*(/) <:-|-оо. Поня-
Понятие «П. и. ф.» введено К. Жорданом [1]. См. также От-
Отрицательная вариация функции.
Лит.: [1] Jordan С, «С. г. Acad. sci.», 1881, t. 92, p. 228—
230; [2] Л е б е г А., Интегрирование и отыскание примитив-
примитивных функций, пер. с франц., М.— Л., 1934. Б. И. Голубое.
ПОЛОЖИТЕЛЬНАЯ КОРРЕЛЯЦИЯ — вид кор-
корреляционной зависимости между случайными величи-
величинами, при к-рой условные средние значения одной из
них увеличиваются при возрастании значений другой
величины. О П. к. между величинами с корреляции
коэффициентом р говорят в том случае, когда р>0.
См. Корреляция. А.В.Прохоров.
ПОЛОЖИТЕЛЬНО ОПРЕДЕЛЕННАЯ ФОРМА —
выражение вида
2," *=,«'¦**'•'*¦
где aik-=aki, принимающее неотрицательные значения
при любых действительных значениях xlt х2, . . ., хп
и обращающееся в нуль лишь при хг=х2=. . .=ж„=0.
Т. о., П. о. ф. есть квадратичная форма специального
типа. Любая П. о. ф. приводится с помощью линей-
линейного преобразования к виду
A
i
Для того чтобы форма
была П. о. ф., необходимо и достаточно, чтобы
Ai>0, Д2>0, ..., Д„>0. где
••¦ alk
В любой аффинной системе координат расстояние точки
от начала координат выражается П. о. ф. от коорди-
координат точки.
Форма
/ = A. *=i "<**<**
такая, что aik=a^i и /^0 для всех значений
xlt х2, • ¦ ., хп и /--0 лишь при ж1=ж2=. . . = х„=0
наз. э р м и т о в о й П. о. ф.
С понятием П. о. ф. связаны также понятия:
1) положительно определенной мат-
р и ц ы l|rt,-fc|!" — такой лгатрицы, что ?. к=1ацгх^хк
есть эрмитова И. о. ф.; 2) положительно определенно-
определенного ядра — такой функции К{х, у)—К {у, х), что
для любой функции ф (ж) с интегрируемым квадратом;
3) положительно определенной функции — такой функ-
функции /(х), что ядро А" (ж, y)=f(x—y) является положи-
положительно определенным. Класс непрерывных положи-
положительно определенных функций / (х) с /@)=1 совпадает
с классом характеристических функций законов рас-
распределения случайных величин. всэ-з.
ПОЛОЖИТЕЛЬНО ОПРЕДЕЛЕННАЯ ФУНКЦИЯ—
комплекснозначная функция ф на группе G, удов-
удовлетворяющая неравенству
для любых наборов xlt . . ., xm?G, a,, . . ., ат?С.
Совокупность П. о. ф. на G образует конус в простран-
пространстве М (G) всех ограниченных функций на б, замкну-
замкнутый относительно операций умножения и комплекс-
комплексного сопряжения.
Причина выделения итого класса функций состоит
в том. что именно 11. о. ф. определяют положительные
функционалы на групповой алгебре CG и унитарные
представления группы G. Точнее, пусть ф : G—> С —
произвольная функция и lv : CG—y С — функционал,
заданный равенством
1<е Bg s aags) " 2g ? а Ф (S) agt,
тогда для положительности 1щ необходимо и доста-
достаточно, чтобы ц> была ГГ. о. ф. Далее, 1$ определяет
*-представление алгебры CG в гильбертовом прост-
пространстве У/ф и, следовательно, унитарное представле-
представление лф группы G, причем ф (^)-(яф (g)|, 5) для нек-рого
??#ф. Обратно, для любого представления л и лю-
любого вектора |^^ф функция #-»-(л (s)|, |) является
П. о. ф.
Если G — топологич. группа, то представление лф
слабо непрерывно тогда и только тогда, когда П. о. ф.
непрерывна. Если G локально компактна, то непре-
непрерывные П. о. ф. взаимно однозначно соответствуют
положительным функционалам на 1} (G).
Для коммутативных локально компактных групп
клаке П. о. ф. совпадает с классом преобразований
Фурье конечных положительных мер на двойственных
группах. Имеется аналог зтого утверждения для ком-
компактных групп: непрерывная функция ф на компакт-
компактной группе G является П. о. ф. тогда и только тогда,
когда ее преобразование Фурье /F) принимает поло-
положительные (операторные) значения на каждом эле-
элементе двойственного объекта, т. е.
для всякого представления о и всякого вектора
Лит.: [1] X ь ю и т т Э., Росс К., Абстрактный гармо-
гармонический ана.шз, пер. с англ., т. 2, М., 1375; [2] На им ар к
М. А., Нормированные кольца, 2 изд., М., 1968.
В. С. Шулъман.
ПОЛОЖИТЕЛЬНО ОПРЕДЕЛЕННОЕ ЯДРО —
комплекснозначная функция К на XXX, где X —
произвольное множество, удовлетворяющая условию
2 К (xit xj) kJkj-5sO
для любых i, /?ж, Я,-?С, t,QX. Измеримые П. о. я.
на пространстве с мерой (X, ц) соответствуют положи-
положительным интегральны,1» операторам в Т?(Х, [х); вклю-
включение в схему такого соответствия произвольных по-
ложительных операторов требует введения обобщен-
обобщенных П. о. я., ассоциированных с оснащенными гиль-
бортовыми пространствами (см. [11).
Теория П. о. я. обобщает теорию положительно
определенных функций на группе: для положительной
определенности функции / на группе G необходимо и
достаточно, чтобы функция К(х, y)=f(ху~1) на GxG
была П. о. я. В частности, на П. о. я. распростра-
распространяются нек-рые результаты теории положительно оп-
определенных функций. Напр., теорема Б о х н е-
р а о том, что всякая положительно определенная
функция есть преобразование Фурье положительной
меры (т. е. интегральная линейная комбинация харак-
характеров), обобщается следующим образом: всякое П. о. я.
(обобщенное) допускает интегральное представление
с помощью т. н. элементарных П. о. я. относительно
данного дифференциального выражения [1].
Лит.: [1] Б е р е з а н с к и й Ю. М., Разложение по соб-
собственным функциям самосопряженных операторов, К., 1965;
[2] К р е й н М. Г,, «Укр. матем. ж.», 1949, т. 1, № 4, с. 64—
98: 1950, т. 2, № 1, с. 10 — 59. В. С. Шулъмап.
ПОЛОЖИТЕЛЬНО ОПРЕДЕЛЕННЫЙ ОПЕРАТОР
— симметричный оператор А в гильбертовом про-
пространстве // такой, что
„ <Ах, х~>
f^ °
для любого х?Н,хфО. Всякий П. о. с. является поло-
положительным, оператором. М 11 Войцехавский.
ПОЛОЖИТЕЛЬНОЕ РАССЛОЕНИЕ — обобщение
понятия дивизора положительной степени на рпмано-
вой поверхности. Голоморфное векторное расслоение
Е над комплексным пространством X наз. положи-
положительным (обозначается Е>0), если в Е существует
такая эрмитова метрика h, что функция
v i—> —h (v, v)
на Е строго псевдовыпукла вне нулевого сечения.
Если X — многообразие, то условие положительности
выражается в терминах кривизны метрики h. А именно,
кривизны форме метрики h в расслоении Е отвечает
эрмитова квадратичная форма Й на X со значениями
в расслоении Негш Е эрмитовых эндоморфизмов рас-
расслоения Е. Условие положительности эквивалентно
тому, что Qx(u) — положительно определенный опе-
оператор в Ех для любого х?Х и любого ненулевого
случае, когда Е — расслоение на комплексные
прямые над многообразием X, условие положитель-
положительности равносильно положительной определенности мат-
матрицы
II д" 1ок Л
где z,, . . ., гп — локальные координаты на X, Л>0 —
функция, задающая эрмитову метрику при локальной
тривиализации расслоения. Если X компактно, то
расслоение на комплексные прямые Е над X положи-
положительно тогда и только тогда, когда Чжэня класс с1 (Е)
содержит замкнутую форму вида
где ЦфарН — положительно определенная эрмитова мат-
матрица. В частности, если X — риманова поверхность,
то расслоение над X, определяемое дивизором степени
d, положительно тогда и только тогда, когда d>0.
В случае, когда Е — расслоение ранга >1 над много-
многообразием X размерности >1, рассматривается также
следующий более узкий класс П. р.: расслоение Е-+Х
наз. положительным в смысле На-
к а н о. если на Е существует такая эрмитова метрика
h, что эрмитова квадратичная форма Н на расслоении
заданная формулой
Hx(v®u)=hx(v, ax(u) v),
тцех?Х, 1>?ЕХ, и?Тх, х' положительно определена.
Примеры: касательное расслоение Тр к проективному
пространству Рп положительно, но при ге>1 не яв-
является положительным в смысле Накано; расслоение
на комплексные прямые над Рп, определяемое гипер-
гиперплоскостью, положительно.
Любое факторрасслоение положительного векторного
расслоения положительно. Если Е', Е" — положи-
положительные (положительные в смысле Накано) расслое-
расслоения, то Е'Рг)Е" и Е'@Е" положительны (положи-
(положительны в смысле Накано).
Понятие «П. р.» было введено в связи с Кодаиры
теоремой об обращении в нуль для случая расслоений
на комплексные прямые, а затем обобщено на произ-
произвольные расслоения. Несколько позже, в связи с воп-
вопросом о существовании вложения в проективное прост-
пространство, были выделены понятия слабо положитель-
положительного и слабо отрицательного расслоений.
Голоморфное векторное расслоение Е над компакт-
компактным комплексным пространством X наз. слабо
отрицательным, если его нулевое сечение
обладает строго псевдовыпуклой окрестностью в Е,
т. е. является исключительным аналитич. множеством.
Расслоение Е наз. слабо положительным,
если сопряженное расслоение Е* слабо отрицательно.
В случае, когда X — риманова поверхность, понятия
слабо положительного и П. р. совпадают [5]. В общем
случае из положительности вытекает слабая положи-
положительность; примеров слабо положительных, но не
положительных расслоений пока A983) не известно.
Слабая положительность расслоения Е-+Х равно-
равносильна каждому из следующих свойств: для любого
когерентного аналитич. пучка f на X существует
такое то>О, что пучок ^"(ХMог^> при т^т0 порож-
порождается глобальными сечениями; для любого когерент-
когерентного аналитич. пучка Jf на X существует такое т>0,
что
НЧ(Х, «F ® ?"»<?)= О
для всех q^sl (см. [3], [4]). Через <§ здесь обозначается
пучок ростков голоморфных сечений расслоения Е.
Слабо положительные расслоения аналогичны, таким
образом, обильным векторным расслоениям из алгеб-
раич. геометрии и иногда наз. обильными
аналитическими расслоениями. Сла-
Слабо положительное расслоение над пространством X
естественным образом определяет вложение прост-
пространства X в многообразие Грассмана и тем самым в
проективное пространство.
Понятия положительного, отрицательного, слабо
положительного и слабо отрицательного расслоений
естественным образом обобщаются также на случай
линейных пространств над комплексным пространством
X (см. Векторное аналитическое расслоение).
См. также Отрицательное расслоение.
Лит.: [1] Уэллс Р., Дифференциальное исчисление на
комплексных многообразиях, пер. с англ., М., 1976; [2] Ч ж э н ь
Шэн-шэнь, Комплексные многообразия, пер. с англ.,
М., 1961; [3] Итоги науки и техники. Алгебра. Топология. Гео-
Геометрия, т. 15, М., 1977, с. 93—171; [4] Schneider M.,
«Abhandl. math. Semin. Univ. Hamburg», 1978, Bd 47, S. 150—
j 70; [5] U m e m u r a H., «Nagoya Math. J.», 1973, v. 52, p.
97—128. ^4. л Онищик.
ПОЛОЖИТЕЛЬНЫЙ КОНУС — подмножество К
действительного векторного пространства Е, удовле-
удовлетворяющее следующим условиям:
1) если х, у?К, a, ffeO, то ах+$у?К;
2) А'П(-Л')=0.
II. к. определяет полуупорядочение в Е: но опреде-
определению, х-$у, если у—х?К.
Пусть Е — банахово пространство. Если Е — замк-
замкнутый воспроизводящий П. к. (т. с. такой
П. к., каждый вектор z?E к-рого представим в виде
z=x—y, где х, у?К), то ||a:||+||y||<Af||z||, M не зави-
зависит от z. Телесный, т. е. имеющий внутренние
точки, П. к. является воспроизводящим.
Пусть Е*— сопряженное пространство к банахову
пространству Е. Если КаЕ — воспроизводящий П. к.,
то множество К*аЕ* положительных (относительно
П. к.) функционалов (т.е. таких /, что f(x)^0 при
х?К) является П. к. (это т. н. сопряженный
к о н у с). П. к. К восстанавливается на А *, а именно:
# = {*?? |/(*) Sa 0 при f?K*}.
Если К — телесный П. к., то его внутренность совпа-
совпадает с
{x?E\f(x) >0 при f?K*, f ФЩ.
Конус в банаховом пространстве Е наз. нормаль-
нормальным, если найдется такое 6>0, что Цг+г/Ц^б (||и||+
+ ||у||) при х, у?К. П. к. нормален тогда и только
тогда, когда сопряженный конус К* является воспро-
воспроизводящим. Если К — воспроизводящий конус, то
сопряженный конус К* нормален.
Конус К наз. миниэдральным, если каждая
пара элементов х, у?Е имеет точную верхнюю грань
z==sup(i, у) (то есть z^x, у и для любого z±^? из
z{^x, у вытекает z{^z). Если П. к. правилен и мини-
эдрален, то всякое счетное ограниченное подмножество
имеет точную верхнюю грань.
Лит.: [1] Красносельский М. А., Положитель-
Положительные решения операторных уравнений, М., 1962.
В. И. Ломоносов.
ПОЛОЖИТЕЛЬНЫЙ ОПЕРАТОР, положи-
положительное отображени е,— 1) П. о. в г и л ь-
бертовом пространстве — линейный опе-
оператор А, для к-рого соответствующая квадратичная
форма (Ах, х) неотрицательна. П. о. необходимо сим-
симметричен и допускает самосопряженное расширение,
также являющееся П. о. Самосопряженный оператор А
является П. о. тогда и только тогда, когда выпол
няется любое из следующих условий: а) А =В*В,
где В — замкнутый оператор; б) А=В2, где В — само-
самосопряженный оператор; в) спектр А содержится в
(О, оо). Совокупность ограниченных П. о. в гильбер-
гильбертовом пространстве образует конус в алгебре всех
ограниченных операторов.
2) П. о. в пространстве с конусом —
отображение векторного пространства X в себя, сох-
сохраняющее выделенный в X конус К. Интегральные
операторы с положительными ядрами в различных
функциональных пространствах с выделенными кону-
конусами положительных функций являются линейными
П. о. При нек-рых дополнительных условиях на гео-
геометрию конуса К и действие П. о. А удается устано-
установить существование Л-собственных векторов из X
(соответствующие собственные значения наз. пози-
позитивными, или ведущими, они превосходят
абсолютные величины всех остальных собственных
значений). Напр., доказано (см. [3]), что если А —
вполне непрерывный П. о. с ненулевым спектром, то
его спектральный радиус является позитивным собст-
собственным значением. Условие компактности можно за-
заменить условиями на поведение резольвенты (см. [4]).
В случае нелинейных П. о. исследуется вопрос о су-
существовании неподвижной точки оператора (т. е. ре-
решения уравнения Ах=х) и о возможности нахождения
этой точки как предела определенных рекуррентных
последователей.
Нек-рые результаты теории П. о. могут быть пере-
перенесены на операторы, оставляющие инвариантными
выделенные подмножества более общей природы, чем
конусы (см. [5]).
3) П. о. в инволютивной алгебре (¦¦¦*-
алгебре) — линейное отображение *-алгебры А в ин-
волютивную алгебру В, переводящее положительные
элементы в положительные. Наиболее изучены И.о.
С*-алгебр (являющиеся, поскольку положительные
элементы С*-алгебры образуют конус, частным случаем
П. о. пространств с конусом). Имеет место неравенство
Шварца для П. о. С*-алгебр: ф (а2)^(ф (а)J, еслия=я*.
Найдены крайние точки множества унитальных
(т. е. сохраняющих единичный элемент) П. о. Изуча-
Изучались вполне непрерывные положи-
положительные операторы (в. н. п. о.), то есть ли-
линейные отображения ср : А—*-В, для к-рых положи-
положительны все отображения
матричных С*-алгебр М (А) в М(В). Оказалось, что
для в. н. п. о. справедлив аналог теоремы о продол-
продолжении положительного функционала: в. н. п. о. С*-
алгебры А в нек-рую алгебру Неймана может быть
продолжен до в. н. п. о. любой С*-алгебры, содержа-
содержащей А. Если одна из С*-алгебр А, В коммутативна
(я только в этом случае), то всякий П. о. является
в. н. п. о.
4) П. о. в банаховом пространстве
Е — линейный оператор А такой, что АКаК, где
К — положительный конус в Е. Собственный вектор
А, лежащий в К, наз. положительным, а со-
соответствующее собственное значение — позитив-
н ы м. Если К — воспроизводящий конус, А — вполне
непрерывный положительный оператор и АРи^аи
для нек-рого вектора и, не принадлежащего конусу —
К, натурального р и а>0, то спектральный радиус гА
оператора А является позитивным собственным зна-
значением А, причем гд^а. '!> (теорема К р е й н а —
Р у т м а н а).
Лит.: [1] А х и е з е р Н. И., Г л а з м а н И. М., Теория
линейных операторов в гильбертовом пространстве, 2 изд.,
М., 1966; [2] Sherman S., «Amer. J. Math.», 1951, v. 73,
№ 1, p. 227—32; [3] Крейн М. Г., Р у т м а н М. А., «Ус-
«Успехи матем. наук», 1948, т. 3, в. 1, с. 3—95; [4] Ш е ф е р X.,
Топологические векторные пространства, пер. с англ., М., 1971;
[5] Красносельский М. А., Соболев А. В., «Докл.
АН СССР», 1975, т. 225, № 6, с. 1256—59; [6] Красносель-
Красносельский М. А. [и др.], Интегральные операторы в прост-
пространствах суммируемых функций, М., 1966; [7] Д и к с м ь е Ж,.
С*-алгебры и их представления, пер. с франц., М., 1974; [8]
Красносельский М.А Положительные решения
операторных уравнений, М., 1962.
В. С. Шулъман, В. И. Ломоносов.
ПОЛОЖИТЕЛЬНЫЙ ФУНКЦИОНАЛ на а л г е б-
ре с инволюцией * — линейный функцио-
функционал / на *-алгебре А, удовлетворяющий условию
f(x*x)^0 для всех х?А. Важность П. ф. и причина
их введения заключается, в частности, в том, что они
используются в так наз. ГНС-к онструкции—
одного из основных методов исследования структуры
банаховых * -алгебр. На ней (и на ее обобщениях,
напр, на веса на С*-алгебрах) основано доказательство
теоремы абстрактной характеризации равномерно зам-
замкнутых * -алгебр операторов в гильбертовом прост-
пространстве и теоремы о полноте системы неприводи-
неприводимых унитарных представлений локально компактной
группы.
ГНС-конструкция есть способ построения по произ-
произвольному П. ф. /на * -алгебре А с единицей такого
*-представления я^ алгебры А в гильбертовом прост-
пространстве IIf, что /(ж)=<лу(г) ?, ?> для всех х?А, где
ь?Н/ — нек-рый циклич. вектор, к-рый состоит в сле-
следующем. В А определяется полускалярное произве-
произведение <(х, y>=f(y*x); соответствующим нейтральпым
подпространством является левый идеал N/= {х ?
?А : f (х*х)~0}, поэтому в предгильбертовом прост-
пространстве AlNr корректно определены операторы левого
умножения La на элементы а?А (Lu(z-\-Nj) = t
операторы La непрерывны и продолжаются до непре-
непрерывных операторов La в пополнении Hf пространства
Alllf. Отображение л/, переводящее а?А в La, и
есть требуемое представление, причем в качестве ¦?
можно взять образ единицы при суперпозиции кано-
иич. отображении A-*-AlHf-+-Hj.
Лит.: [1] Г с л ь ф а и ц И. М., Н а й м а р к М. А.,
«Изв. АН СССР. Сер. матем.», 1948, т. 12, с. 445—80; [2] Se-
Segal I., «Bull. Amer. Math. Soc», 1947, v. 53; [3] H а й м а р к
M. А., Нормированные кольца, 2 изд., М., 1968. В. С. Шулъман.
ПОЛОЖИТЕЛЬНЫЙ ЭЛЕМЕНТ алгебры
с инволюцией * — элемент х * -алгебры А,
допускающий представление х=у*у, где у?А. Мно-
Множество Р {А) П. э. банаховой *-алгебры ,4 содержит
множество Q (А) квадратов эрмитовых элементов, со-
содержащее, в свою очередь, множество Р0(А)+ всех
эрмитовых элементов с положительным спектром, но,
вообще говоря, не содержит множества А+ всех эрми-
эрмитовых элементов с неотрицательным спектром. Усло-
Условием Р (А)аА + определяется класс вполне симмет-
симметричных (или эрмитовых) банаховых *-алгебр; для
того чтобы ^-алгебра была вполне симметричной,
необходимо и достаточно, чтобы все ее эрмитовы эле-
элементы имели действительный спектр. Равенство Р (А) =
= А + имеет место тогда и только тогда, когда А есть
С*-алгебра. В этом случае Р (А) — воспроизводящий
конус в пространстве всех эрмитовых элементов ал-
алгебры А .
Лит.: [1] Наймарк М. А., Нормированные кольца,
2 изд., М., 1968; 12] Д и к с м ь е Ж., С*-алгебры и их пред-
представления, пер. с франц., М., 1974; [3] Райков Д. А.,
«Докл. АН СССР», 1946, т. 54, М, 5, с. 391—94; [4] Р t a k V.,
«Bull. Lond. Math. Soc», 1970, v. 2, p. 327—34; [5] Palmer
I., «Bull. Amer. Math. Soc», 1972, v. 78, p. 522—24.
В. С. Шулъман.
ПОЛОС МЕТОД — метод в теории функций комплекс-
комплексного переменного, опирающийся на оценки, связываю-
связывающие длины нек-рого специального семейства кривых и
площадь области, заполняемой этим семейством. В ос-
основе П. м. лежат леммы Грётша (см. [1]). Одна из них
формулируется следующим образом.
Пусть в прямоугольнике со сторонами длины А и В
имеется конечное число не налегающих друг на друга
односвязных областей S^, к={, . . ., п, с жордан<м;ими
границами, содержащими на сторонах длины А по от-
отрезку, к-рые не вырождаются в точки (области S^ обра-
образуют полосы, идущие от одной стороны длины А к дру-
другой). Если область S^ конформно отображается на
прямоугольник со сторонами длины а& и Ъ^ так, что
упомянутые отрезки переходят в стороны длины аь, то
причем равенство достигается только в том случае,
если Sk, k=i, . . ., п,— прямоугольники со сторонами
длины а'к и В и 2jk^ia'k=A-
В качестве другой леммы служит Грётша принцип.
Леммы Грётша верны и для бесконечного множества
подобластей.
П. м. как метод теории однолистных конформных и
квазиконформных отображений был впервые исполь-
использован X. Гре'тшем [1], к-рый с помощью этого метода
систематически исследовал и решил большое коли-
количество экстремальных задач для однолистных функ-
функций, заданных в конечносвязных и бесконечносвязных
областях (см. [3]; о других применениях П. м. см. [2],
гл. 4, § 6).
П. м. лежит в основе экстремальной метрики метода.
Лит.: Ll] Grotzsch H., «Ber. Verhandl. Sachsisch. Akad.
Wiss. Leipzig. Math.-physische. Kl.», 1928, Bd 80, H. 6, S. 367—
7E; H. 7, S. 503—07: 1929, Bd 81, H. 1, S. 38—48; H. 2, S. 51 — 87;
[2] Голу зи н Г. М., Геометрическая теория функций ком-
комплексного переменного, 2 изд., М., 19G6; [3] Дженкинс
Д ж.. Однолистные функции и конформные отображения, пер.
с англ., М., 1962. Е. Г. Голузина.
ПОЛОС МЕТОД — метод приближенного решения
одномерных интегральных уравнений Фредгольма 2-го
рода, основанный на специальном способе замены ядра
на вырожденное, на получении резольвенты вырож-
вырожденного уравнения и последующем уточнении прибли-
приближенного решения с помощью быстросходящегося
итеративного алгоритма.
Пусть исходное интегральное уравнение записано
в виде
K(x, s)9(s)rfs = /(j-). (I)
Для построения вырожденного ядра в П. м. квадрат
разбивается на N полос
\ь — а ь — о , , .ч ,1
i = 0, 1, ..., .V—1.
В каждой полосе (г) функция К (х, s) приближается
в среднем квадратическом или равномерно функцией
вида
К{(х, s) = Ci
В простейшем случае
Ki(x, &•) = #(?<. s), l
При помощи функции Ki (x, s) можно образовать
вырожденное ядро:
s) = 2^~' С, (х) + Pi (х) Q i (s), B)
Pi(X) = io, «*\Чг'.Цг« +
Ь-а -\
*. -wit-1)]
Ь—а . Ь—а
Решение уравнения с вырожденным ядром B) ап-
аппроксимирует решение A), вообще говоря, тем лучше,
чем больше число полос N и чем лучше аппроксимация
К(х, s) в каждой полосе. Приближенное решение
tp0 (х) можно еще улучшить с помощью итеративного
алгоритма:
х, s)<pk(s)ds =
x, s)—KN(x, s)]<pk_L(s)ds. C)
Итерация C) сходится к решению A) в среднем квад-
квадратическом или равномерно при условии достаточной
близости ядер К{х, s) и К^(х, s).
Лит.: [1] Полоний Г. Н., Ч а л е н к о 11. И., «До-
пов1д1 АН УРСР», 1962, М 4, с. 427—31.
А. Б. Бапушииский.
ПОЛОСА — совокупность точек плоскости, лежа-
лежащих между двумя параллельными прямыми этой плос-
плоскости. Координаты точек х, у полосы удовлетворяют
неравенствам C1<iAx-\-By<Ci, где А, В, С1: 6'2 —
нек-рые постоянные, причем А и В одновременно не
равны нулю. Преобразование w=ez конформно ото-
отображает полосу 0<г/<я комплексной плоскости
z=x-\-iy на верхнюю полуплоскость комплексной
ПЛОСКОСТИ IV. ВСЭ-3.
ПОЛОСА, поверхностная полоса (в уз-
узком смысле),— однопараметрическое семейство каса-
касательных плоскостей к поверхности. В общем смысле
поло с о и наз. объединение кривой I и вектора т,
ортогонального в каждой точке кривой ее касательному
вектору. Пусть в евклидовом пространстве И?з кривая I
задана уравнением r=r{s), где s — естественный пара-
параметр кривой, г (s) — радиус-вектор точки кривой.
Вдоль / задается вектор-функция т=т (s), где т (s) —
единичныii вектор, ортогональный касательному век-
гору t~dr,ds в соответствующих точках кривой. В этом
случае говорят, что вдоль кривой I задана поверхност-
поверхностная полоса Ф= {I, т) с нормалью m(s). Вектор т=
= [т, t] наз. вектором геодезической
н о р м а л и полосы Ф; вместе с векторами t и т
вектор т образует трехгранник Френе для П. Относи-
Относительно подвижного трехгранника Френе для П. за-
записываются деривационные формулы Френе:
dm , , .
где kg (геодезия, кривизна П.), kn(s) (нормальная кри-
кривизна П.), xg(s) — (геодезия, кручение П.) — скаляр-
скалярные функции параметра s.
Если в каждой точке кривой I вектор т коллинеарен
вектору главной нормали кривой I, то kg=O и в этом
случае II. наз. геодезической полосой.
Если в каждой точке вектор т. коллинеарон бинормали
кривой, то в этом случае &,,=0, а П. наз. асимпто-
асимптотической полосой.
Лит.: [I] Бляшке В., Введение в дифференциальную
геометрию, пер. с нем., М., 1957. Л. А. Сидоров.
ПОЛУГЕОДЕЗИЧЕСКИЕ КООРДИНАТЫ, гео-
геодезические нормальные координа-
координаты,— координаты х1, . . ., х" в «-мерном римановом
пространстве, характеризующиеся тем, что координат-
координатные линии, соответствующие .г1, являются геодезич.
линиями, на к-рых х1 играет роль нормального пара-
параметра, а координатные поверхности х1-- const — орто-
ортогональны этим геодезическим. В П. к. квадрат линей-
линейного элемента имеет вид
<fc* = №)* + 2" / = 2 8iJ d*1 dxi-
П. к. можно ввести в достаточно малой окрестности
любой точки произвольного риманова пространства.
В двумерных римановых пространствах в ряде случаев
(напр., для регулярных поверхностей строго отрица-
отрицательной кривизны) возможно введение П. к. н целом.
В двумерном случае квадрат линейного элемента в
И. к. принято записывать в виде
dsi = du'2+B2(u, v)dvK
Полная (гауссова) кривизна может быть найдена по
формуле:
к 1_ д*в_
в ди"- •
При изучении двумерных римановых многообразий
знакоопределенной кривизны важную роль играют
специальные П. к.— геодезические поляр-
полярные координаты (г, ср). В этом случае все
координатные геодезич. линии ср— const пересекаются
в одной точке (полюсе), аф является углом между
координатными линиями v~0 и q)=const. Линия г==
= const наз. геодезической окружно-
окружностью. Квадрат линейного элемента в окрестности
полюса в геодезических полярных координатах имеет
вид
—jt- (A"i cos ф + A'j simp)
3) I
где Ко — полная (гауссова) кривизна в точке Р, Kt —
производная от К по 7- в точке Р в направлении геоде-
геодезической ф = 0, К2 — такая же производная в направ-
направлении геодезической qr—л/2.
При определении 11. к. в псевдоримановом прост-
пространстве часто требуется, чтобы геодезические, соответ-
соответствующие хх, не были изотропными. В этом случае
квадрат линейного элемента имеет вид
ds>-^ ± (</*!)* + 2" . = s ВЦ dxf dxi
(знак -f или — выбирается в зависимости от знака
квадрата интервала касательного вектора к линии ж1).
ПОЛУГИПЕРБОЛИЧЕСКОЕ ПРОСТРАНСТВО —
проективное «-пространство, в к-ром метрика опре-
определяется заданным абсолютом, состоящим из совокуп-
совокупности действительного конуса 2-го порядка Qo индекса
10 с (п—т0—1)-плоской вершиной То, {п—т0—2)-
действптельного конуса Qr индекса 1г с (п—ml—1)~
плоской вершиной Тг в (и—т0—1)-плоскости То,
(п—Ш] — 2)-действительного конуса Qi индекса 12 с
(п—тг—1)-плоской вершиной Т2 в (п — ту— 1)-нлос-
кости Тг и т. д. до (п — mr-2—2)-действительного ко-
конуса Qr-i индекса lr-i с (п — шг-\ — 1)-плоской верши-
вершиной Тг_1 и невырожденной действительной (п — mr^1 —
— 2)-квадрикой Qr индекса 1Г в плоскости 7V_],
0<:m0<m1< . . . <тг_!</г. Такое пространство
наз. П. и. индексов 10, 1г, . . ., 1Г и обозначается
KU ¦ ¦ Лг5тот1 • ¦ .тг-!
В случае, когда конус Qo является парой слившихся
плоскостей, совпадающих с плоскостью То (при то=О),
П. п. с несобственной плоскостью То наз. полуевкли-
полуевклидовым пространством'.
/i/2 ¦ • ¦ W пт^г- ¦ ¦ /"/• — 1
Расстояние между точками .Y и Y определяется в за-
зависимости от расположения прямой XY относительно
плоскостей То, 1\, . . ., Тг^г. Если, в частности, пря-
прямая XY не пересекает плоскость 7'0, то расстояние
между точками X и Y определяется с помощью скаляр-
скалярного произведения аналогично соответствующему оп-
определению в квазигиперболическом пространстве.
Если же прямая XY пересекает плоскость То, но не
пересекает плоскость Т^ или пересекает плоскость
Та-.}, но не пересекает плоскость Та, то расстояние
между точками определяется с помощью скалярного
квадрата разности соответствующих векторов точек
X и У.
В зависимости от расположения относительно плос-
плоскостей То, Тх, . . ., Та, , . . абсолюта различаются че-
четыре типа прямых различных порядков: эллиптичес-
эллиптические, гиперболические, изотропные и параболические.
Углы между плоскостями в П. и. определяются по
аналогии с определением углов между плоскостями в
квазигиперболич. пространстве, т. о. с использованием
расстояний в двойственном пространстве.
Проективная метрика П. п. является метрикой наи-
наиболее общего вида. Частным случаем метрики П. п.,
напр., является метрика квазигиперболич. простран-
пространства. В частности,2-плоскость 0152 совпадает с псевдо-
псевдоевклидовой 1В2, плоскость 1052— с копсевдоевклидовой
1я\\ 3-пространства 1XS\ и105з совпадают с квазигипер-
квазигиперболическим 3-пространством, 3-пространство 105з—
с копсевдоевклидовым 1Л3 и т. д.; 3-пространство
100Sl2 двойственно псевдогалилееву пространству 1Г3,
оно наз. копсевдогалилеевым простран-
пространством, его абсолют состоит из пары действительных
плоскостей (конус Qo) и точки Т1 на прямой То пересе-
пересечения этих плоскостей.
Движениями II. н. наз. его коллинеации, переводя-
переводящие абсолют в себя. При пга = ге--тг_а._1 — 1 и при
la—lr~a П. 0. двойственно самому себе. В таком про-
пространстве определяются кодвижения, определе-
определения к-рых аналогичны определению кодвижения в ква-
зигинорболич. пространстве, двойственном самому себе.
Движения, движения и кодвижения образуют группы,
являющиеся группами Ли. Движения (как и кодвиже-
кодвижения) П. п. описываются псевдоортогональными операто-
операторами индексов, определенных индексами пространства.
П. я. является полуримагювым пространством.
Лит.: [1] S о т га е г v i 1 1 с D. M. Y., «Proc. Edinburgh
Math. Soc», 1910, v. 28, p. 25 — 41; [2] P о з е н ф е л ь д Б. А.,
Нееиклидовы пространства, М., 1969. Л. А. Сидоров.
ПОЛУГРУПП МНОГООБРАЗИЕ — класс полу-
полугрупп, задаваемый системой тождеств (см. Алгебраи-
Алгебраических систем многообразие). Всякое П. м. будет либо
периодическим, т.е. состоит из периодич.
полугрупп, либо надкоммутативным, т.е.
содержит многообразие всех коммутативных полугрупп.
Для классификации ряда свойств П. м. выделяются
нек-рые типы тождеств. Тождество u=v наз. норма-
нормальным (а также регулярным, однород-
однородным), если множества переменных, входящих в слова
и и v, совпадают, и аномальным — в противном
случае. Тождество u—v наз. уравновешенным,
если каждая переменная в и и v встречается одно и
то же число раз. Частный случай уравновешенного
тождества — перестановочное тождест-
тождество — если и=х1.. .хт и v получено из и переста-
перестановкой переменных. II. м. надкоммутативно тогда и
только тогда, когда все его тождества уравновешенные.
Базис тождеств П. м. 2Д наз. неприводимым,
если любое его собственное подмножество задает мно-
многообразие, отличное от ЗЛ- Всякое надкоммутативное
П. м. имеет неприводимый базис тождеств. Существу-
Существуют II. м., не имеющие неприводимый базис тождеств.
Примеры конечно базируемых П.м.: любое многообра-
многообразие коммутативных полугрупп, любое периодическое
П.м. с перестановочным тождеством, любое П. м., за-
заданное перестановочными тождествами. Любая полу-
полугруппа с числом элементов <;5 имеет конечный базис
тождеств, но существует б-элементная полугруппа, не
имеющая конечного базиса тождеств.
Следующие условия для П. м. ЗЛ эквивалентны
ЗД1 задано нормальными тождествами; все тождества ЗЛ
нормальны; Ш содержит двухэлементную полурешет-
полурешетку. П. м. ЗЛ имеет среди своих тождеств аномальное
тогда и только тогда, когда ЗЛ периодическое и состоит
из архимедовых полугрупп.
Минимальные П. м. исчерпываются многообразиями
всех: 1) полурешеток, 2) полугрушг левых нулей,
3) полугрупп правых нулей (см. Идемнотентов полу-
полугруппа), 4) полугрупп с нулевым умножением, 5) абе-
левых групп экспоненты р при любом простом р.
В решетке всех П. м. всякий неединичный элемент
имеет покрывающий его элемент; единичный элемент
не может быть равен объединению конечного числа
неединичных элементов. Решетка всех П. м. не удов-
удовлетворяет никакому нетривиальному решеточному тож-
тождеству и имеет мощность континуум. Эту ?ке мощность
имеют подрешетка всех многообразий нильполугрупп
с тождеством х2=0 и подрешетка всех надкоммутатив-
ных многообразий. Для нек-рых П. м. ЗЛ получены
явные описания решетки их подмногообразий L (ЗЛ);
описаны П. м. ЗЛ с нек-рыми ограничениями на ре-
решетку L (Wi-
(Will, м. наз. малы м, если L (ЗЛ) конечна. П. м. ЗЛ
наз. многообразием конечного ин-
индекса, если ступени нильпотентности нильпотент-
ных полугрупп из ЗЛ ограничены в совокупности (это
условие эквивалентно тому, что каждая нилыюлу-
группа изЗЛ нилыготентна, а также тому, что 9Л не со-
содержит многообразия всех коммутативных нилъполу-
групп с тождеством z2=0). Всякое малое П. м. имеет
конечный индекс.
Для периодического П. м. ЗЛ следующие условия
эквивалентны [4]: 9J1 состоит из связок архимедовых
полугрупп; в любой полугруппе из 2Л каждый класс
кручения есть подполугруппа; 2Л не содержит полу-
полугруппы Брандта В2 (см- Периодическая полугруппа).
Этим условиям удовлетворяют П. м. 2Л с модулярной
решеткой L BЛ) и П. м. конечного индекса (в част-
частности, малые II. м.). Малое П. м. л о к а л ь н о ко-
конечно (т. е. состоит из локально конечных полу-
полугрупп) тогда и только тогда, когда локально конечно
многообразие всех групп из 2Л; малое локально конеч-
конечное многообразие групп — это в точности кроссово
многообразие (см. Групп многообразие). О других
локально конечных П. м. см. Локально конечная полу-
полугруппа. Описаны П. м., состоящие из финитно аппрок-
аппроксимируемых полугрупп [3].
Множество всех П. м. относительно мальцевского
умножения образует частичный группоид G. Известны
все идемпотенты в G, их в точности 9. Множество всех
П. м., задаваемых системами тождеств вида и>=0,
образует максимальный группоид в G.
Изучаются также П. м. полугрупп с дополнитель-
дополнительными сигнатурными операциями: многообразия монои-
моноидов (с сигнатурной единицей), многообразия полугрупп
с сигнатурным нулем, многообразия инверсных полу-
полугрупп и др.
Лит.: [1] Evans Т., «Semigroup forum», 1971, v. 2,
,45 1, p. 1—43; [2] Айзенштат А. Я., Б о г у т а Б. К.,
в сб.: Полугрупповые многообразия и полугруппы эндоморфиз-
эндоморфизмов, Л., 1979, с. 3—46; [3] Г о л у б о в Э. А., С а п и р М. В.,
(•Докл. АН СССР», 1979, т. 247, У° 5, с. 1037 — 41; [4] С а п и р
М. В., Суханов Е. В., «Изв. вузов. Математика», 1981,
№ 4, с. 48—55. Л. Н. Шеврин.
ПОЛУГРУППА — множество с одной бинарной опе-
операцией, удовлетворяющей закону ассоциативности.
Понятие П. есть обобщение понятия группы: из аксиом
группы остается лишь одна — ассоциативность; этим
объясняется и термин «П.». П. называют иногда мо-
моноидами, но последний термин употребляется
чаще всего для П. с сигнатурной единицей (т. е. с нуль-
арной операцией, отмечающей единицу).
Теория П. принадлежит к числу сравнительно моло-
молодых областей алгебры. Первые исследования, посвя-
посвященные П., относятся к 20-м гг. 20 в. и связаны с име-
именем А. К. Сушкевича. Он, в частности, определил строе-
строение ядра (наименьшего идеала) конечной П., т. е.
фактически строение конечной П. без собственных идеа-
идеалов. Этот результат позднее был обобщен Д. Рисом
(D. Roes) на произвольные вполне простые полугруппы
и усовершенствован посредством введения понятия
матрицы над группой (см. Рисовская полугруппа мат-
матричного типа). Теорема Риса, к-рую можно считать
нек-рым аналогом теоремы Веддерберна о простых
алгебрах, принадлежит к числу основных фактов
теории П. Другие ранние исследования по теории П.
принадлежат А. Клиффорду (A. Clifford), одним из
первых значительных достижений к-рого было введе-
введение и изучение П., покрываемых группами; эти П.
наз. теперь вполне регулярными, или клиффордовыми
полугруппами. К кон. 50-х гг. 20 в. теория П. сформи-
сформировалась в самостоятельную ветвь современной ал-
алгебры с богатой проблематикой, разнообразными ме-
методами и тесными связями с многими областями мате-
математики как собственно алгебраическими (в первую
очередь, с теорией групп и теорией колец), так и дру-
другими, напр, функциональным анализом (П. операторов
в банаховых пространствах), дифференциальной гео-
геометрией (П. частичных преобразований), алгебраич.
теорией автоматов (П. автоматов).
Примеры П. чрезвычайно многочисленны. Это —
различные множества чисел вместе с операцией сло-
сложения или умножения, замкнутые относительно рас-
рассматриваемой операции, П. матриц относительно ум-
умножения, П. функций относительно «поточечного»
умножения *, задаваемого формулой (/* g) (x)=f(x)
g(x), П. множеств относительно операции пересече-
пересечения или объединения и т. д. В общей теории и нек-рых
приложениях важен следующий пример П. Пусть X —
произвольное множество. На множестве Fx всех ко-
конечных последовательностей элементов из X опреде-
определяется операция, задаваемая формулой
(*1> ¦••> Хп)*(Уи •••> Ут)~(хи ¦•¦> хт Уи ¦¦¦, Ут)-
Тогда Fx относительно операции * является П.;
она наз. свободной П. на множестве X. Вся-
Всякая П. есть гомоморфный образ нек-рой свободной.
Всякая совокупность преобразований произвольного
множества М, замкнутая относительно операции к о м-
позиции (последовательного выполнении, наз.
также суперпозицией), будет П. относительно
этой операции; такова, в частности, совокупность всех
преобразований множества М, наз. с и м метр и-
ческой полугруппой на множестве М.
Многие важные совокупности преобразований оказы-
оказываются П., причем часто они не являются группами.
С другой стороны, всякая П. изоморфна нек-рой П.
преобразований. Таким образом, именно понятие П.
оказывается наиболее подходящим для изучения в са-
самом общем виде преобразований, и в большой степени
через рассмотрение преобразований осуществляются
связи теории П. с другими областями математики.
При этом очень часто П. возникают как П. эндомор-
эндоморфизмов (см. Эндоморфизмов полугруппа) тех или иных
рассматриваемых систем: пространств, алгебр, графов
и т. д. К П. приводит также рассмотрение частичных
преобразований и бинарных отношений относительно
операции умножения.
Как и в других алгебраич. теориях, одной из глав-
главных задач теории П. является классификация всевоз-
всевозможных П., описание их строения. Это осуществляется
прежде всего наложением на рассматриваемые П.
различных ограничений и выделением тем самым раз-
различных типов П. Ограничения могут иметь разную
природу. П. может удовлетворять фиксированной
системе тождеств (типичные примеры — коммутатив-
коммутативные П., П. идемпотентов) или другим условиям, вы-
выражаемым формулой узкого исчисления предикатов
(примеры — П. с законом сокращения, регулярные
П.). Закон сокращения и регулярность представляют
собой примеры ограничений, носящих так или иначе
характер ослабления свойств группы; мведение подоб-
подобных условий было, пожалуй, особенно популярно на
первых порах развития теории П. (среди выделенных
здесь типов, наиболее близких к группам,— правые
группы). Во многих случаях, впрочем, возникающие
на этом пути классы П. включают в себя П., весьма
далекие по своим свойствам от групп (типичный при-
пример — П. идемпотентов).
Понятие регулярной полугруппы возникло шэ анало-
аналогии с понятием регулярного кольца. Класс регулярных
П. принадлежит к числу наиболее интенсивно изучае-
изучаемых в теории П. Он включает в себя следующие важ-
важные классы полугрупп: мультипликативные II. регу-
регулярных колец (и, в частности, П. всех матриц данного
порядка над телом), симметрические П., П. всех час-
частичных преобразований множеств, инверсные П.,
клиффордовы П. и, в частности, П. идемпотентов и
вполне простые П., вполне 0-простые П. и др.
Другой тип распространенных ограничений — ог-
ограничения на систему всех или нек-рых подполугрупп,
в частности идеалов, а также нек-рых отпошений на
П., в частности конгруэнции. Так возникают, напр.,
разнообразные типы простых полугрупп и разнооб-
разнообразные условия конечности (см. Полугруппа с усло-
условием конечности, Периодическая полугруппа, Локально
ьонечная полугруппа, Финитно аппроксимируемая полу-
полугруппа, Минимальный идеал), П. с разными типами иде-
идеальных рядов и идеальных систем (см. Идеальный ряд,
Нилъполугруппа); принципиальную роль в исследо-
исследовании многих вопросов теории П. играют Грина от-
отношения эквивалентности.
Ограничения могут относиться к порождающим
множествам и выделять их типы либо с точки зрения
характера порождающих элементов (напр., идемпо-
тенты; всякая П. вложима в идсмпотентно иорогкден-
ную П.) или их числа (конечно порожденные П. су-
существенно участвуют во многих исследованиях), либо
с точки зрения взаимодействия порождающих элемен-
элементов — изучаются П., заданные определяющими соот-
соотношениями и, в частности, конечно определенные П.
(см. Алгоритмическая проблема, Полугруппа с усло-
условием конечности), либо с объединенной точки зрения
(см., напр., Бициклическая полугруппа).
При изучении строения П. важную роль играют раз-
различные конструкции, сводящие описание рассматри-
рассматриваемых П. к тем или иным «более хорошим» типам.
Довольно часто в качестве последних выступают
группы, и принцип описания «по модулю групп» рас-
распространен в теоретико-полугрунповых исследова-
исследованиях, он проявился еще в упоминавшейся классич.
теореме Риса, согласно к-рой всякая вполне 0-простая
(вполне простая) П. изоморфна регулярной рисовской
П. матричного типа над группой с нулем (группой).
Группы участвуют в конструкциях, описывающих
инверсные П., и в конструкциях, описывающих ком-
коммутативные архимедова полугруппы с законом сокра-
сокращения и без идемпотентов. Описание П. с многими ус-
условиями конечности сводится к группам с соответст-
соответствующими условиями.
Среди конструкций, участвующих в описании П.,
имеются как общеалгебраические, напр, прямые про-
произведения, подпря.мые произведения, так и специфи-
специфически теоретико-иолугрупповые. К последним отно-
относятся уже упоминавшиеся рисовские П., а также ряд
других, из к-рых следует упомянуть конструкцию
связки — такого разбиения на подполугруппы,
что соответствующее отношение эквивалентности есть
конгруэнция. Среди связок особую роль играют ком-
коммутативные связки (или полурешетки) и матричные
(прямоугольные) связки (см. Связка полугрупп). В
терминах связок описываются многие типы П. Так,
теорема Клиффорда о вполне регулярных П. означает,
по существу, что эти П. исчерпываются полурешет-
полурешетками вполне простых П.; вполне простые П.— это
в точности прямоугольные связки групп; теорема
Тамуры — Кимуры утверждает, что любая коммута-
коммутативная П. единственным образом разложима в связку
архимедовых П. (см. [3]).
Как и всюду в алгебре, существенную роль в теории
П. играет понятие гомоморфизма и, соответственно, по-
понятие конгруэнции. П. принадлежат к числу универ-
универсальных алгебр, конгруэнции к-рых не определяются
однозначно нек-рым своим каноническим смежным клас-
классом («ядром») подобно тому, как это, напр., имеет место
в группах и кольцах. Эта более сложная ситуация
привела к развитию довольно обширного направления
теории П., посвященного изучению конгруэнции П.
с различных точек зрения. Решаемые здесь задачи
делятся в основном на два вида: 1) выделяются те или
иные специальные типы конгруэнции на произвольных
П.; 2) описываются все конгруэнции на тех или иных
специальных П., принадлежащих важным в каком-то
отношении классам П. К первому виду относится, в
частности, рассмотрение главных конгруэнции (см.
[3]), а также идеальных, или рисовских,
конгруэнции, сопоставляемых каждому дву-
двустороннему идеалу (если / — идеал полугруппы S,
то соответствующая рисовская конгруэнция имеет
своими классами / и одноэлементные подмножества
{х}, где x?S\I), к-рые часто используются в различ-
различных вопросах н объясняют важность рассмотрения
идеалов; факторполугругшу но рисовскои конгруэнции
наз. фактор полугруппой Риса по соот-
соответствующему идеалу. Из решенных задач второго
вида следует отметить описание конгруэнции на сим-
симметрических П., на вполне 0-простых П.; весьма да-
далеко продвинуто изучение конгруэнции на инверсных
П.; изучение радикалов П. развивается не без влияния
аналогичного раздела теории колец. Рассмотрение
гомоморфизмов ГТ. в П. с заданными «хорошими» свой-
свойствами способствовало формированию направления,
занимающегося аппроксимацией (см. Сепаративная
полугруппа. Финитно аппроксимируемая полугруппа).
В исследованиях, связанных с рассмотрением под-
подполугрупп, выделяется самостоятельное направление,
посвященное изучению решеточных свойств П., т. е.
взаимосвязей между свойствами П. и свойствами ре-
теток их подполугрупп (см. Решетка подалгебр).
Широкое направление теории II. посвящено изуче-
изучению различных вложений П. Истоки этого направле-
направления восходят к классич. проблеме вложения полугрупп
в группы. О нек-рых задачах и результатах этого на-
направления см. в ст. Расширение полугруппы.
Интенсивно развивается теория многообразий П.;
об исследованиях в этом направлении см. в ст. Полу-
Полугрупп многообразие. Начинает развиваться теория
квазимногообразий П. (см. Алгебраических систем
квазимногообразие) и нек-рых других классов П.,
близких в том или ином смысле к многообразиям.
Связи общей теории П. с конкретными П. осуществ-
осуществляются многими путями. Решаются проблемы абстракт-
абстрактной характеризации тех или иных важных конкретных
П. (напр., П. преобразований: известно, в частности,
несколько характеризации симметрических П.), опи-
описываются различные их абстрактные свойства. О нек-
рых основных результатах, касающихся П. преобра-
преобразований, см. Преобразований полугруппа. Изучаются
изоморфизмы и гомоморфизмы абстрактных П. в раз-
различный конкретные П., прежде всего П. преобразо-
преобразований и П. матриц (см. Представление полугруппы).
Исследованием гомоморфизмов П. в нок-рые числовые
П., нрелвде всего в мультипликативную П. комплекс-
комплексных чисел, занимается теория характеров полугрупп.
К специальным разделам теории П. приводит рас-
рассмотрение П. с дополнительными структурами, согла-
согласованными с операцией умножения. Здесь следует, в
первую очередь, отметить структуру топологич. про-
пространства (см. Топологическая полугруппа) и структуру
порядка, частичного или линейного (см. Упорядочен-
Упорядоченная полугруппа).
Развивается и теория нек-рых видов обобщенных
II. В первую очередь это алгебры с одной «-арной
операцией, подчиненной обобщенному ассоциативному
закону (их наз. ;;-а ссоциативами, или п-
полугруппами). Рассматриваются также ал-
алгебры с одной частичной ассоциативной бинарной
операцией (одна из естественных ситуаций подобного
рода возникает в теории категорий).
Лит.: [1] С у ш к спич А. К., Теория обобщенных групп,
Хар,— К., 1937; 12] Линии К. С., Полугруппы, М., 19Н0;
L3] Клиффорд А., Престон Г., Алгебраическая тео-
теория полугрупп, пер, с англ., т. 1—2, М., 1972; [41 Алгебраиче-
Алгебраическая теория автоматов, языков и полугрупп, пер. с англ., М.,
1975; [5] Фукс Л., Частично упорядоченные алгебраические
системы, пер. с англ., М., 1965; [В] Итоги науки. Алгебра. То-
Топология. 1962, М., 1963, с. 33—58; [7] Итоги науки. Алгебра.
1964, М., 1966, с. 161—202; [8] Итоги науки. Алгебра. Тополо-
гия. Геометрия. 1966, М., 1968, с. 9—56; La] Semigroups, N.Y.—
L., 1969; [10] Howie J., An introduction to semigroup theory,
L,—N.Y.—S.P., 1976; [11] Pctrich M., Introduction to semi-
semigroups, Columbus, 1973; [12] его же, Lectures in semigroups,
В., 1977; [13] Redei L., The theory of finitely generated com-
commutative semigroups, Oxf. — [a.o.], 1965; [14] Hofmann К. Н.,
Mostert P. S., Elements of compact semigroups, Columbus,
1966; [15] Lallement G., Semigroups and combinatorial
applications, N.Y. — [a.o.], 1979; [16] Eilenberg S., Auto-
Automata, languages and machines, N.Y.—S.F.—L., v. A, 1U74; v. В.,
1976. .7. II. Шеврин.
ПОЛУГРУППА НЕЛИНЕЙНЫХ ОПЕРАТОРОВ-
однопараметрическос семейство операторов S(t), 0<?<
<оо, определенных и действующих в замкнутом под-
подмножестве С банахова пространства X, обладающее
свойствами:
1) S(t+T)x^S(t)(S(i)x) при х?С, t, т>0;
2) S{0)x=x для любого х?С;
'Л) при каждом х?С функция S (t)x (со значениями
п .V) непрерывна но t на [0, go).
Полугруппа S (t) имеет тип со, если
\\S(t)x-S (t) y$<e«« ix-y I, x, у?С, t >0.
Полугруппа типа 0 наз. с ж и м а ю щ е й.
Так жо, как и для полугрупп линейных операторов,
вводится понятие производящего опера-
оператора Ао полугруппы S (t):
Аох= lim (S (li)x—x)/h
h -* о
на тех элементах х? С, для к-рых этот предел существу-
существует. Если полугруппа сжимающая, то Ао — диссииатив-
ный оператор. При этом оператор А в банаховом про-
пространстве X д и с с и и а т и в е н, если \\х—у—X (Ах—
—Ау)\\^\\х— у\\ при х, у?О (А), Я,>0. Диссипативный
оператор может быть многозначным, тогда в определе-
определении под Ах понимается любое его значение на х. Дисси-
Диссипативный оператор наз. m-д иссинативным,
если Im(/—ХА)=Х при Х>0. Если S (t) — типа со, то
А 0—со/ диссииативен.
Основная теорема о порождении
полугруппы: если оператор А —со/ диссииативен
и при достаточно малых А>0 образ Im (/—\А) операто-
оператора / - -Х.4 содержит D {А), то существует полугруппа
типа со на D (А) такая, что
SA (t)x= lim (l
где x?D (.4), при этом сходимость равномерна на любом
конечном промежутке изменения t. (Существование
полугруппы S^(t) можно показать, если заменить ус-
условно Im (/—XA)^D (А) более слабым:
lim Х~Ч (lm(I — XA), i)-(),
X -* О
где d — расстояние между множествами.)
С оператором А можно связать задачу К о ш и
-^ ?Аи (t), I > 0, и@)=х. (*)
Если существует сильное решение задачи
(*), т. е. непрерывная на [0, оо) функция u(t), абсолютно
непрерывная на любом компакте из @, оо), принимаю-
принимающая при почти всех t>0 значения в D(A), имеющая
при почти всех t>0 сильную производную, удовлетво-
удовлетворяющую включению (*), то u(t)=S^(t)x. Любая функ-
функция SA(t)x является единственным т.н. интеграль-
интегральным решением задачи (*).
Если в условиях основной теоремы пространство X
рефлексивно и А замкнут, то при x?D(A) функция
u(t)—S^(t) дает сильное решение задачи Коши (*), ripn
этом -г- ?A°u(t) почти везде, где A°z — множество эле-
элементов минимальной нормы из Az. В этом случаи про-
изводящий оператор Ао полугруппы SA(t) плотно задан:
D (A0)~D (А). Если, сверх того, X и X' равномерно
выпуклы, то оператор А" однозначен и при всех i^O
существует правая производная -^-=Л°«(?); эта функ-
функция непрерывна справа на [0, оэ) и непрерывна во всех
точках, кроме, быть может, счетного множества, в этом
случае Z> (Ло) — D (А) и А0~А°.
Если X рефлексивно (соответственно Х = У, где
У — еепарабельно), а оператор А однозначен и облада-
обладает тем свойством, что из хп —>¦ х в X и Ахп —> у в слабой
топологии а (X, X') (соответственно а(Х, У)) следует
у=Ах, то и (t)?D (A), i>0, и u(t) слабо (соответственно
слабо *) непрерывно дифференцируемое решение за-
задачи (*). В не рефлексивном случае известны примеры,
когда выполнены условия основной теоремы при D (А)=
— X и функции u(t) = SA(t)x не имеют даже слабой
производной в X ни при каких х?Х, iJsO.
Пусть А — непрерывный оператор, определенный
на всем X и такой, что А—со/ диссипативен. Тогда
lmG — кА)=-Х при А.>0, ^ш<1 и для любогог?Х зада-
задача (*) имеет единственное непрерывно дифференцируе-
дифференцируемое на [0, оэ) решение и (t) = SA(t)x. Если оператор А
непрерывен в замкнутой области определения D(A),
то для того, чтобы он был производящим оператором
полугруппы типа и наК(Л), необходимо и достаточно,
чтобы А—со/ был диссипативным и lim "k~1d(x-\-'kAx,
D(A))--=0 при x?D(A).
В гильбертовом пространстве II сжимающая полу-
полугруппа на множестве С может быть продолжена для
сжимающей полугруппы на замкнутом выпуклом мно-
множестве С из //. При этом производящий оператор Ао
расширенной полугруппы будет определен на плотном
в С множестве. Существует единственный ти-диссипа-
тивный оператор такой, что D{A)~C и А0=А°. Если
А есть m-диссипативнын оператор, то D (А) выпукло
и существует единственная сжимающая на D (А) полу-
полугруппа S(t) = SA(t), для к-рой Ао—А".
Если на действительном гильбертовом пространстве
// задан выпуклый полунепрерывный функционал ф
и д<р — его субдифференциал, то оператор Ах=—Зф (х)
(для тех х, при к-рых ду(х) непусто) является дисси-
диссипативным. Полугруппа SA(t) обладает свойствами,
сходными со свойствами линейных аналитич. полугрупп.
В частности, SA(t)x?D (A) (i>0) при любомx?D (А) и
и (t)~SA(t)x является сильным решением задачи Коши
(•?), причем
для всех i>0, v?D (А). Если ф достигает минимума,
то u(t) слабо сходится при (-> со к нок-рой точке ми-
минимума.
Для приближенного решения задачи Коши сущест-
существенную роль играют теоремы об аппроксимации полу-
полугрупп. Пусть X, Х„, ге=1, 2, ...,— банаховы простран-
пространства, операторы А в X и Ап в Хп однозначны и удов-
удовлетворяют условиям основной теоремы с общим типом
со, операторы рп : X —*¦ Хп — линейны и \<рЛхч-х ^
<:const. Тогда из сходимости резольвент (Х>ОДсо<1)
при x?D(A) следует сходимость полугрупп
равномерная на каждом конечном промежутке.
Мультипликативные формулы Ли, полученные им в
конечномерном линейном случае, обобщены на нели-
нелинейный случай. Если А, В и А-\-В суть да-диссипа-
тивные однозначные операторы в гильбертовом прост-
пространстве и замкнутое выпуклое множество CdD (A)f\
f)D(B) инвариантно относительно (/—ХА)'1 и (/—
—ХВ)-1, то при любом x?C(\D(A)(\D(B)
SA + B(t)x= lim VsA(±)sB(-L)~\nx.
Эта формула справедлива также в произвольном
банаховом пространстве X для любого х?Х, если А —
плотно заданный линейный m-диссипативный оператор,
а В — заданный на всем X непрерывный диссипативный
оператор. В обоих случаях
В приводимых ниже примерах нелинейных дифферен-
дифференциальных операторов, удовлетворяющих условиям ос-
основной теоремы о порождении полугрупп, указывается
лишь пространство X и краевые условия, а точное опи-
описание D (А) опускается. Во всех примерах Я — огра-
ограниченная область в Rn с гладкой границей; р", у — мно-
многозначные максимальные монотонные отображения R -»•
-*- R, Р(О)ЭО, у(О)ЭО;г|) : R->-R — непрерывная стро-
строго возрастающая функция, ф@)=0. Пример 1.
X=Lp(Q), 1 </>«», Аи=Аи—р"(и), — ^€y(«) на Г.
Пример 2. X = L1(Q), 4u=M|>(u), —|?€7(м)на Г.
Пример 3. X=W21(Q), Au=Aty(u), и=0 на Г.
Пример 4. Z=C(Q) или Z=-L«(Q), Ли=гЬ(Д«),
и=0на Г. Пример 5. X = Li(R"), Au=di\f(u),
где /GC1(R) со значениями в R™, /@) = 0. Пример 6.
X=A(>,(R), /4«=/(«x), где / : R —>- R непрерывна.
Лит.: 11] В а г Ь u V., Nonlinear semigroups and differen-
differential equations in Banach spaces, Bueurejti, 1976; [2] В г 6-
z i s H., Operateurs maximaux monotones et semi-groupes de
contractions dans les espaces de Hilbert, Amst.—L.—N.Y.,
1973; [3] Brezis H. Pazy A., «J. Funct. Anal.», 1972,
v. 9, Л» 1, p. 63 — 74; [4] С r a n d a 1 1 M. G., L i g g e t t Т. М.,
«Amer. J. Math.», 1971, v. 93, № 2, p. 265—98; [5] К о b a-
y a s h i Y., «J. Math. Soc. Japan», 1975, v. 27, № 4, p. 640—65;
[6] Konislii Y., «Proc. Japan. Acad.», 1972, v. 48, № 2,
p. 62—66; [7] Martin R. H., «Trans. Amer. Math. Soc»,
1973, v. 179, p. 399—414; [8] Webb G. F., «J. Funct. Anal»,
1972, v. 10, №2, p. 191—203; [9] Хазан М. И., «Докл.
АН СССР», 1973, т. 212, № 6, с. 1309—12; [10] его же, там
же, 1976, т. 228, № 4, с. 805—808.
С. Г. Нрейн, М. И. Хазан.
ПОЛУГРУППА ОПЕРАТОРОВ — семейство опера-
операторов {Т} в банаховом или топологическом векторном
пространстве, обладающее тем свойством, что компо-
композиция любых двух операторов семейства снова принад-
принадлежит семейству. Если операторы Т «занумерованы»
элементами нек-рой абстрактной полугруппы 31 и би-
бинарной операции полугруппы отвечает композиция
операторов, то полугруппа {Т} наз. представле-
представлением полугруппы Щ. Наиболее подробно изу-
изучены одпопарамепгрические полугруппы линейных огра-
ограниченных операторов в банаховом пространстве X,
дающие представление аддитивной полугруппы всех
положительных чисел, т. е. семейства Т (t) со свойством
Т (t + T)x=T (t) T (x)x, t, х > 0, х?Х.
Из сильной измеримости T(t), ?>0, следует, что
Т (t) — сильно непрерывная полугруппа, поэтому в
дальнейшем только такие и рассматриваются.
Существует число
со= lim t-4n\IT (t)\\
/->- да
— тип и о л у г р у п п ы. Все функции Т (t)x растут
не быстрее экспоненты.
Важной характеристикой является и н ф и н и т е-
з и м а л ь н ы й оператор полугруппы
Лог= lim if-1 [Г (t)x — x],
t^ О
определенный на линейном множестве D(A0) тех эле-
элементов х, на к-рых предел существует, и его замыкание
А (если оно существует) — производящий опе-
оператор полугруппы. Множество D (Ао) плотно
на подпространстве Хо, являющемся замыканием объе-
объединения всех значений T(t)x. Если в Ха нет ненулевых
элементов, на к-рых 7'(?).г=0, то существует произво-
производящий оператор А . В дальнейшем всегда предполагает-
предполагается, что Хо—Х и что из Т (t)x=O следует х—0.
Наиболее простой класс полугрупп — класс Со — вы-
выделяется условием: Т(t)x —>- х при t—>-0 и любом х?Х.
Для выполнения этого условия необходимо и достаточ-
достаточно, чтобы функция ||Г(?)|| была ограниченной на каком-
нибудь промежутке @, а\. В этом случае Т(t) имеет про-
производящий оператор А=А0, для резольвенты R (X, А) =
= (Л—К/) к-poro выполнено
|| Л" (Я, ЛI|<М(Я —со)-", п = 1, 2, . ..; Я>со, A)
где и — тип полугруппы. Обратно, если А — замкну-
замкнутый оператор с плотной в X областью определения, для
резольвенты к-рого выполнено A), то он является про-
производящим оператором нек-рой полугруппы Т D) клас-
класса Со, причем \\ТA)\\^:Меа*. Условия A) выполняются,
если
||R (Я, Л)Ц<(Я-ш)-1
(условие Хилле — Иосиды). Если при этом
со=0, то Т (t) —сжатий полугруппа: \\T(t)\\^.\.
Суммируемая полугруппа — та, для
к-рой функции ||r(i)^ll суммируемы на любом конечном
отрезке при всех х?Х. Суммируемая полугруппа имеет
производящий оператор А=А0. Оператор Ао замкнут
тогда и только тогда, когда при любом х?Х
lim 4- [* Т (s)xds = x.
t-* о г Jo
Для суммируемой полугруппы при ВеЯ>ш опреде-
определено преобразование Лапласа
f'rl'I1 {t)xdt = — R (Я) ж, B)
J о
дающее линейный ограниченный оператор R (X), обла-
обладающий многими свойствами резольвенты.
Для того чтобы замкнутый оператор А с плотной в X
областью определения был производящим оператором
суммируемой полугруппы T(t), необходимо и достаточ-
достаточно, чтобы для нек-рого со существовала резольвента
R (X, А) при Re Я>со и выполнялись условия: а) ||Л (Я,
Л )||<:М, Re Я>со; б) существуют такие неотрицательная
и непрерывная по совокупности переменных функция
Ф (t, х), *>0, х?Х, и неотрицательная функция ф(?),
ограниченная на любом промежутке [о, Ь]с@, оо), что
при со1>со
["e-'^'ifit, x)dt < оо,
Dm t~l lncp (/) < оо, ф {t, хХф (/)
t
t-
цк«(я, A)x\\< ,„_;„, \ -0««-ч<-»ф(A j;)rf«.
При этом
Если дополнительно потребовать, чтобы функция
IIГ(t)II была суммируемой на конечных промежутках,
то необходимо и достаточно существование такой непре-
непрерывной функции q>(i), что при со1>ш
ф(Ое"ю'* Л < оо, C)
IIR" (Я, Л) к
мФ(')Л, Яхв, re^l, 2, ... D)
При :>том ||7" (<)||-а?:<р (*). Выбирая различные функции,
удовлетворяющие C). можно выделять различные под-
подклассы суммируемых полугрупп. Если ср (t)~Meal,
то получается класс Са и из D) вытекает A). Если ф (*) —
Mt~aeat, 0<:сс<1, то из D) получается условие
V ' '" (п- 1)! (Я- ш)"-а
Полугруппа со степенными особенностями. Если
в предыдущем примере а>1, то в D) интегралы при ге<:
<а—1 расходятся. В соответствии с этим производящий
оператор соответствующих полугрупп может не иметь
резольвенты ни при каких X, т. е. иметь спектр, совпа-
совпадающий со всей комплексной плоскостью. Однако для
таких операторов, начиная с нек-рого п, существуют
функции Sn(k, А), совпадающие в предыдущих случаях
с Rn + l(k, А). Оператор-функция Sn(k, А) наз. ре-
резольвентой порядка п, если она аналитична
в нек-рой области ОсС и при X
Sn(k, A)Ax = ASn(k, А)х,
и из того, что Sn(K, A) х=0 при всех X ?G, следует, что
х=0. Если D (Ап + 1)=Х, то оператор может иметь един-
единственную резольвенту порядка п, для к-рой имеется
максимальная область аналитичности, наз. резоль-
резольвентным множеством порядка п.
Пусть для сильно непрерывной полугруппы Т (t)
выполняется неравенство
|| Т (t)\\<M
при а>1. Тогда ее производящий оператор В имеет
резольвенту порядка п при п><х — 1, причем
Sn(k, B)x = J_ f°° t"e~uT (t)x dt, ReX>CD,
n! J о
d*Sn (Я, В) „
Обратно, пусть оператор В имеет при Re Я>0 резоль-
резольвенту Sn(k, В) порядка п, для к-рой выполнено E) при
га>а—1. Тогда существует единственная полугруппа
Т (t) с оценкой
|| Г (t){\<Mt-<*e<*>t,
для производящего оператора А к-рой Sn(k, A) =
= Sn(X, В).
Гладкая полугруппа. Если x?D (Ав), то функция
Т (t)x непрерывно дифференцируема и
Существуют полугруппы класса Со, для к-рых при
хфБ (Ao)-—D (А) функции Т (t)x нсдифференцируемы
при всех t. Однако для важных классов полугрупп на-
наблюдается явление повышения их гладкости с увеличе-
увеличением t. Если Т(t)x, i>iOi дифференцируемы при любом
х?Х, то из полугруппового свойства следует, что Т (t)x
дважды дифференцируема при ?>2?0, трижды — при
<>3<0 и т. д. Поэтому если Т(t)x дифференцируемы при
любых г>0 и х?Х, то Т(t)x бесконечно дифференциру-
дифференцируемы.
Для того чтобы для полугруппы класса Со при нек-ром
?05г0 функции Т (t)x были дифференцируемы при всех
х? X и i>?0, необходимо и достаточно существование та-
таких чисел а, Ь, с>0, что резольвента R (К, А) определе-
определена в области
ReA, > а — Ып\ ImJi |
и в этой области
|| Ro (Л., Л)||<с| 1тЯ|.
Для того чтобы Т (t)x были бесконечно дифференцируе-
дифференцируемыми при всех х?Х и ?>0, необходимо и достаточно,
чтобы для каждого Ь>0 нашлись такие аь, еь, что ре-
резольвента R (X, а) определена при
Re Л > аь— Ып\ Im А.|
и
\\R(\, А)\\<сь\\тХ\.
Достаточные условия: если при нек-ром ц.>ш
lim In | т | || i? (ц + it, А) \\ = t0 < со ,
то Т(t).c дифференцируемы при t>@ и х?Х, если ^0=0,
то 7'(*)ж бесконечно дифференцируемы при всех ?>0
и .г?Л'.
Иногда о гладкости полугруппы можно судить по ее,
поведению в нуле; напр., если для каждого е>0 сущест-
существует такое бс, что при 0<t<6c
\\I-T(t)\\<L2-ctlnt-\
то Т (t)x бесконечно дифференцируемы при всех i>0,
х?Х.
Имеются условия гладкости суммируемых полугрупп
и полугрупп степенного роста. Если полугруппа сте-
степенного роста а бесконечно дифференцируема при ?>0,
то функция
dt —" W ~
часто также имеет степенной рост:
Между числами а и Р в общем случае нет жесткой связи,
и число Р может служить для более детальной класси-
классификации бесконечно дифференцируемых полугрупп
степенного роста.
Аналитическая полугруппа. Важный класс полугруп-
полугруппы, связанный с уравнениями с частными производными
цараболич. типа, состоит из полугрупп T(t), допускаю-
допускающих аналитич. продолжение в нек-рый сектор комплекс-
комплексной: плоскости, содержащий положительную полуось.
Для того чтобы полугруппа класса Со обладала этим
свойством, необходимо и достаточно, чтобы в нек-рой
правой полуплоскости Re Я>ш для резольвенты выпол-
выполнялось неравенство
|| Re (Я, А) || < М | X— col.
Также необходимо и достаточно, чтобы полугруппа
была сильно дифференцируемой и чтобы для ее произ-
производной имелась оценка
dT
dt
Наконец, из неравенства
lim" || / — Г (t)[\ < 2
также следует аналитичность T(t).
Если полугруппа Т (t) допускает аналитич. продол-
продолжение Т (z) в сектор |arg z\ <ср<я/2 и имеет степенной
рост в нуле, ||7'(z)||<c[z|a, a>0, то резольвента Sn(X, A)
порядка га>ос—1 ее производящего оператора А допу-
екает аналитич. продолжение в сектор |arg Ц <л/2+ф
и в любом секторе |arg Я| <я/2+ф, ч|з<ф, допускает
оценку
\\Sn(X, 4)||<|A,|«-«-»M (ф).
Обратно, пусть резольвента Sn(X, В) оператора В опре-
определена в секторе |arg Я| <л/2+г|з и справедливо нера-
неравенство
\\Sn(k, В)\1^\"-п-1М.
Тогда существует аналитическая в секторе |ai'gz|<i|)
полугруппа Т (z) роста а, для производящего оператора
А к-рой 5„(Я, A)=Sn(X, В).
Полугруппа-распределение. В соответствии с общей
концепцией теории распределений (обобщенных функ-
функций) можно отказаться от того, чтобы оператор-функция
Т (t) была определена при каждом f>0, а потребовать
с + °°
лишь вычислимость интегралов \ Т (/)ф (t)dt для всех
Ф из пространства D (R) всех финитных бесконечно диф-
дифференцируемых функций. Тогда возникает определение:
полугрупп он-рас предел он и ом в ба-
банаховом пространстве X наз. линейное непрерывное
отображение Т (ц>) пространства D (R) в пространство
L (X) всех линейных ограниченных операторов в X.
обладающее свойствами: а) 7т(ф)=-(), если supp фс:
С{—оо, 0); б) для ф, \|з из пространства /)H(R), состоя-
состоящего из всех функций из D (R) с носителями в @, оо),
Г(ф*1|))=Г(ф)ГA]з), где свертка
ф * ф — \ ф (t — s) \p (s) ds
(полугрушювое свойство); в) если Г(ф).г--0 для всех
(p?D + (R), то ж— 0; г) линейная оболочка объединения
всех значений Г(ф)г, ф?/) + ^). ^^Х, плотна в А";
д) для любого у—Т(ty)x ci|)^D + (R) существует такая
непрерывная на @, оо) функция и (t) со значениями в X,
что и(О) = у и
для всех ф??> (R).
И н ф и н и т е з и м а ль н ы й оператор Ай
нолугрупны-расироделення определяется так: если су-
существует дельта-последовательность {p,,}czD + (R) та-
такая, что Т (рп)х -*¦ х и Т (—Р'п)х-+У при п—>-оо, то
ж??> (Ло) и (/—Лот. Инфинитезилкигьный оператор допу-
допускает замыкание А~А0, к-рое наз. производя-
производящим оператором полугруппы-рас-
полугруппы-распределения. Множество П/Г=1^ Ио) плотно в X
и содержит Т((р)Х при любой ф^Д + fR).
Замкнутый линейный оператор А с плотной в X об-
областью определения является производящим операто-
оператором полугруппы-распределения тогда и только тогда,
когда найдутся числа а, Ь^О, с>0 и натуральное m
такие, что при Re X,^a In A-} |Я|)-| Ь существует ре-
резольвента В (X, А) и выполнено неравенство
ця (Я, л)||<СA + |я|)'я. F)
Если А — замкнутый линейный оператор в X, то
множество D"=i?> (А") можно превратить в пространст-
пространство Фреше X», введя в нем систему норм
Сужение А„ оператора А на Х«, оставляет Х„ инвари-
инвариантным. Если А — производящий оператор полугруп-
полугруппы-распределения, то Л к, —производящий оператор
полугруппы класса Со (непрерывный при /^0, Т@) = 1)
в пространстве Х„. Обратно, если X*, плотно в X, опе-
оператор А имеет непустое резольвентное множество и яв-
является производящим оператором полугруппы класса
С-'о в Хоо, то Л — производящий оператор полугруппы-
распределения в X.
Полугруппа-распределение имеет экспоненциальный
порядок роста не выше д,1«7<со, если при нек-ром
ы>0 отображение ехр(—ы*<?O'(ф) непрерывно в топо-
топологии, индуцированной на D + пространством S (R) бы-
быстро убывающих функций. Для того чтобы замкнутый
линейный оператор был производящим оператором та-
такой полугруппы-распределения, необходимо и доста-
достаточно, чтобы он имел резольвенту R (К, А), для к-рой
выполнено F) в области
где a, p>0. В частности, если <?--1, то полугруппа наз.
экспоненциальной и неравенство F) выпол-
выполняется в нек-рой полуплоскости. Имеется характери-
характеристика полугрупп указанных типов в терминах свойств
оператора Л„. Для полугрунпы-распределений изучены
вопросы гладкости и аналитичности.
Полугруппа операторов в (отделимом) локально вы-
выпуклом пространстве X. Определение сильно непре-
непрерывной полугруппы непрерывных в X операторов Т (t)
остается таким же, как и в банаховом пространстве.
Аналогично класс Со выделяется свойством Т (t)x —*¦ х
при (—>-0 и любом х?Х. Полугруппа наз. локаль-
локально э к в и и о н р е р ы в н о й (принадлежит классу
1С0), если семейство операторов Т (t) равностепенно
непрерывно, когда t пробегает любой конечный проме-
промежуток из @, со). В бочечном пространстве полугруппа
класса 6'0 нсегда локально эквинепрерывна.
Полугруппа наз. эквинопрерывной (при-
(принадлежит классу иС0), если семейство T(t), 0<:?<oo,
равностепенно непрерывно.
Инфините.чимальный и производящий операторы по-
полугруппы определяются так же, как и в банаховом
случае.
В дальнейшем предполагается, что пространство X
секвенциально полно. Для полугрупп класса 1С0 произ-
производящий оператор А совпадает с инфинитезимальным,
его область определения D (А) плотна в X и, более
того, плотно в X множество ПгТ-i-D (Ап). Полугруппа
Г (t) оставляет D (А) инвариантной и
,r = AT (t)x=T (t) Ax, 0<< < оо,
Если А — производящий оператор полугруппы клас-
класса иС0, то при Re Х>0 определена резольвента R (X, А)
и она является преобразованием Лапласа от полу-
полугруппы.
Линейный оператор А является производящим опера-
оператором полугруппы класса иС0 тогда и только тогда,
когда он замкнут, имеет плотную в X область опреде-
определения и существует такая последовательность поло-
положительных чисел Xf, —>¦ оо, что для любого %k определе-
определена резольвента ЯСК/,, А) и семейство операторов
[Xfcfl (Xft, А)]п, к, n=l, 2, ... , равностепенно непрерыв-
непрерывно. При этом полугруппа может быть построена по фор-
формуле
T(t)x= lini (exp [—Xft — XlR (%k, A)]t)x,
к -»¦ оо
В ненормируемом локально выпуклом пространстве
производящий оператор полугруппы класса 1С0 может
d
не иметь резольвенты ни в одной точке. Пример: А = ~^г
в пространство С°° бесконечно дифференцируемых функ-
функций от s на R. В качестве оператора, заменяющего ре-
резольвенту, может быть взят непрерывный оператор, ум-
умножение к-рого на оператор А— XI справа и слева «ма-
«мало» отличается от единичного оператора.
Непрерывный оператор Я (к), определенный для к
из множества ЛсС, паз. асимптотической
резольвентой линейного оператора А, если
оператор А В (к) непрерывен в X, оператор В (к)А допу-
допускает расширение с D (А) до непрерывного оператора
В (Я) в X и существует такая предельная точка к0 мно-
множества Л, что Н + {к)х -> 0, Н~(к)х —>• О при к -¦+- к0 для
любого х из X, где
Я+ (Я) = (Л — к!) Я (л) — /, Я- (Я) = 5 (Я)—Я/? (Я)—/.
Асимптотич. резольвента обладает рядом свойств, близ-
близких к свойствам обычной резольвенты.
Для того чтобы замкнутый линейный оператор А
<¦ плотной в X областью определения был производящим
оператором полугруппы класса 1С0, необходимо и до-
достаточно, чтобы существовали такие числа ы и сс> О,
что при Я>а> определена асимптотич. резольвента Я (к)
оператора А, обладающая свойствами: функции Я (к),
Н+(к), Н~(к) сильно бесконечно дифференцируемы при
Х>м, семейства операторов
>. d"H±W Kn^ dnR (Я)
е <И1» ' »| <й« - Л > w' л—и, 1, ...,
равностепенно непрерывны.
Теоремы порождения получены и для других классон
П. о. в локально выпуклом пространстве.
Сопряженная полугруппа. Если Т (t) — полугруппа
класса Со в банаховом пространстве X, то сопряженные
операторы образуют полугруппы ограниченных опера-
операторов в сопряженном пространстве X'. Однако соотно-
соотношение T'(t)f —*¦ / при t—>- 0 и любом /?А" выполняется
лишь в смысле слабой топологии о (X', X). Если А —
производящий оператор, то сопряженный оператор А'
будет слабым производящим оператором T'(t) в том
смысле, что D (А') состоит из всех тех /, для к-рых суще-
существует в смысле слабой сходимости предел t~l[T'(t)—/|/
при i->- 0, равный A'f. Область определения D(A')
плотна в X' в смысле слабой топологии, и оператор А'
замкнут в этой топологии.
Пусть Х+ — совокупность тех элементом из А",
для к-рых Т'(}) —<- / при t —>¦ 0 в сильном смысле, тогда
Х+ — замкнутое подпространство А", инвариантное
относительно всех Т (t). В Х+ операторы Т (t) образуют
полугруппы класса Со. Пространство А+ может быть
получено как сильное замыкание и X' множества
D(A'). Если исходное пространство рефлексивно, то
Х + = Х'. Для полугрупп класса Со в локально выпук-
выпуклых пространствах справедливы аналогичные факты.
Полугруппы классов 1С0 и иС0 порождают полугруппы
таких же классов в пространстве X +.
Полугруппа-распределение в (отделимом) локально
выпуклом пространстве. Полугруппа-распределение
Г(ф) в секвенциально полном локально выпуклом про-
пространстве определяется так же, как и в банаховом прост-
пространстве. Полугруппа Т (ф) наз. локально экви-
непрерывной (класса Ш'), если для любого ком-
компакта KcD(R) семейство операторов {Г(ф)}, ф?Я,
равностепенно непрерывно. В бочечном пространстве X
всякая полугруппа-распределение принадлежит классу
ID'. Аналогично случаю банахова пространства опреде-
определяется инфинитезимальный оператор Аа полугруппы-
распределения. Для полугрупп класса ID' он замкнут
(А0=А), f\n=iD (Ап) плотно в X, при любых т?Х и
??>(К) выполпено
T((p)x?D(A). Г(фI=4Г(ф)^ф@I
Обобщенную функцию Т с носителем на [0, оо), обла-
обладающую свойствами G), естественно нызпать фунда-
фундаментальной функцией оператора
-JJ- —А. Таким образом, если А — производящий one-
ратор полугруппы Т класса ID', то Т является фунда-
фундаментальной функцией оператора -др—А. Обратное ут-
утверждение верно при дополнительных предположениях
относительно порядка сингулярности фундаментальной
функции Т (точнее, функций f(T((p)x), где /?А").
Для характеризации полугруппы в локально выпук-
выпуклом пространстве полезным является понятие обоб-
обобщенной резольвенты. Через ф обозначается
образ функции ф?Д(К) при преобразовании Лапласа,
в пространстве D (R) всех образов вводится топология,
индуцируемая преобразованием Лапласа из топологии
D (R). Преобразование Лапласа Х-значной обобщенной
функции F определяется равенством F (<p)=F(ф). При
этом F является непрерывным отображением из Ъ (R)
в пространство L (X) линейных непрерывных операто-
операторов на .Y. Пусть Ь'+ -- пространство всех F, получен-
полученных из F с носителем на @, оо), с естественной тополо-
rneii. Если А — линейный оператор в X, то его можно
«поднять» до оператора Л в пространстве D+ с помощью
равенства
Таким образом, он определен на тех F?D + , для к-рых
правая часть определена при любой ф??> (R) и продол-
продолжает обобщенную функцию из D + . На В'+ определяет-
определяется непрерывный оператор X равенством
(XF) (Ф)= XF ($) = *" (Ф) = -/' (ф').
Если оператор А —X имеет непрерывный обратный Я на
D + , то R ааз. обобщенной резольвентой
оператора А .
Оператор А имеет обобщенную резольвенту тогда
и только тогда, когда у оператора -jj- —Л существует
локально эквинепрерывная фундаментальная функция
Т, к-рая строится по формуле:
П<г)*-(ДA®*)) (Ф). 4>e0(R), •*€*.
где
A ® т) (ф) = (б @ х) ф = ф @) х.
При дополнительных условиях Т будет полугруппой-
распределением. В терминах обобщенной резольвенты
получена также теорема порождения П. о. класса 1С0.
См. также Полугруппа нелинейных операторов.
Лит.: [1] Хилле Э.,Филлипс Р., Функциональный
анализ и полугруппы, пер. с англ., 2 изд., М., 1962; [2] В у в у-
нинян Ю.М., в кн.: Теория операторов в функциональных
пространствах, Новосиб., 1977, с. 99—120; [3] Забрейко
П. II., 3 а ф и е в с к и й А. В., «Докл. АН СССР», 1969,
т. 189, Ni 5, с. 934 -37; [4] 3 а ф и е в с к и й А. В., «Тр. Ма-
тем. ф-та Воронеж, ун-та», 1970, в. 1, с. 206—10; [5] И о с и-
да К., Функциональный анализ, пер. с англ., М., 1967; [6]
К р е й н С. Г., Линейные дифференциальные уравнения в ба-
банаховом пространстве, М., 1967; [7] Сильченко Ю. Т.,
«Дифференц. уравнения», 1979, т. 15, Н 2, с. 363—66; [8] С h a-
г а га i n J. «J. Funct. Analys.», 1971, v. 7, № 3, p. 386—446;
[9J G i о г a n e s с u J., «J. Math. Analys. and Appl.», 1971,
v. 34, p. 34—41; [10] её же, «Rev. roum. math, pures et
appl.», 1977, v. 22, №8, p. 1053—68; [ill К a to Т., «Proc.
Amer. Math. Soc», 1970, v. 25, MS 3, p. 495—98; [12] LionsJ.,
«Portugal. Math.», 1960, v. 19, p. 141—64; [13] Pazy A.,
«J. Math. Mech.», 1968, v. 17, № 12, p. 1131—41; [14] его же,
«Proc. Amer. Math. Soc», 1971, v. 30, № 1, p. 147—50; [15j
U s h i j i m а Т., «Sci. Papers College Gen. Edic. Univ. To-
Tokyo», 1971, v. 21, p. 93—122; [16] его же, «J. Рас. Sci. Univ.
Tokyo. Sect. 1A», 1972, v. 19, MS 1, p. 65—127; [17] Wild C,
«C. r. Acad. sci.», 1977, t. A 285, p. 437—40.
Ю. M. Вувуникян, С. Г. Крейн.
ПОЛУГРУППА С УСЛОВИЕМ КОНЕЧНОСТИ —
полугруппа, обладающая нек-рым свойством в таким,
что всякая конечная полугруппа обладает этим свойст-
свойством (такое свойство в наз. условием конечно-
с т и). В определении свойства Н могут фигурировать
элементы полугруппы, ее подполугруппы и т. п.
Примеры условий конечности: периодичность (см.
Периодическая полугруппа), локальная конечность (см.
Локально конечная полугруппа), финитная аппроксими-
аппроксимируемость (см. Финитно аппроксимируемая полугруппа),
конечная порожденность, конечная определенность.
Исследования конечно определенных полугрупп в зна-
значительной степени ведутся с точки зрения алгоритмич.
проблем. Наиболее известное условие, при к-ром конеч-
конечная порожденность полугруппы влечет ее конечную оп-
определенность,— коммутативность (теорема Ре-
Редей). Всякая счетная полугруппа вложима в полу-
полугруппу с двумя порождающими, а также в полугруппу
с тремя идемпотентными порождающими [8].
Целый ряд условий конечности формулируется в тер-
терминах решетки подполугрупп (напр., условие мини-
минимальности для подполугрупп). Полугруппа S тогда и
только тогда удовлетворяет условию минимальности
для подполугрупп, когда S периодическая, имеет лишь
конечное число классов кручения, в каждом классе
кручения Ке наибольшая подгруппа Ge удовлетворяет
условию минимальности для подгрупп, а разность Ke\Ge
конечна [2]. Аналогичное строение имеют полугруппы
конечного ранга (конечность ранга означает, что мини-
минимальное число порождающих каждой конечно порож-
порожденной подполугруппы полугруппы S не превосходит
фиксированного числа), полугруппы конечной ширины
(конечность ширины для S означает, что из любого ко-
конечного множества М ее элементов можно выделить
подмножество, порождающее ту же подполугруппу, что
и М, мощность к-рого не превосходит фиксированного
числа), периодические полугруппы с условием макси-
максимальности для подполугрупп и др. (см. [3], [4]).
Инверсная полугруппа удовлетворяет условию мини-
минимальности для инверсных подполугрупп тогда и только
тогда, когда она обладает главным рядом (см. Идеальный
ряд полугруппы), каждый фактор к-рого есть Брандта
полугруппа с конечным числом идемпотентов, все макси-
максимальные подгруппы к-рой удовлетворяют условию ми-
минимальности для подгруппы. Аналогичные описания
получены для условия максимальности, конечности
ранга и др. (см. [5]).
Из условий конечности, формулируемых в терминах
частично упорядоченного множества идеалов полу-
полугруппы, наиболее известны условия минимальности Mi,
Мr, Mj для главных левых, правых, двусторонних
идеалов (эти условия часто определяются в терминах
Х-, SH- и ^-классов, см. Грина отношения эквивалент-
эквивалентности). Аналогично определяется условие Мц для ffl-
классов. Конъюнкция условий Mi и Mr эквивалентна
конъюнкции условий Mj и Мн, в остальном эти усло-
условия независимы; в частности, полугруппа с условиями
Mi и Mj не обязательно удовлетворяет условиям Mr
и Ми- Вместе с тем полупростая (см. Главный фактор
полугруппы) полугруппа с условием Mi или Mr удов-
удовлетворяет условию Mj. Для регулярных полугрупп все
четыре условия эквивалентны; всякая полугруппа с ус-
условием Mff будет квазипериодической. Конечно порож-
порожденная полугруппа с условием Mi или Mr, все под-
подгруппы к-рой конечны, сама конечна [6].
Полугруппа с условием минимальности для правых
конгруэнции является периодической, удовлетворяет
условию Mi и двойственному условию максимальности
для главных левых идеалов; если при этом все ее под-
подгруппы конечны, то сама полугруппа конечна [6]. В ин-
инверсных полугруппах условие минимальности для пра-
правых конгруэнции эквивалентно условию минимальности
для левых конгруэнции, а также тому, что полугруппа
имеет лишь конечное число идемпотентов и удовлетво-
удовлетворяет условию минимальности для подгрупп [7]. Изучен
ряд свойств полугрупп с условием максимальности для
односторонних конгруэнции. Коммутативная полу-
полугруппа удовлетворяет условию минимальности (макси-
(максимальности) для конгруэнции тогда и только тогда, когда
она имеет главный ряд и удовлетворяет условию мини-
минимальности для подгрупп [7] (конечно порождена).
Лит.: [1] Клиффорд А., Престон Г., Алгебраи-
Алгебраическая теория полугрупп, пер. с англ., т. 2, М., 1972; [2] Ш е в-
рин Л. Н., «Изв. АН СССР. Сер. матем.», 1965, т. 29, №3,
с. 553—66; [3] его же, «Матем. заметки», 1974, т. 15, № 6,
с. 925—35; [4] его же, «Изв. ВУЗов. Матем.», 1974, М 5,
с. 205 —15; [5] Ершова Т. И., там же, 1977, № 11, с. 7 —14;
[6] Hotzel E., «J. Algebra», 1979, v. 60, №2, p. 352 — 70;
[7] Kozhukhov I. В., «Semigroup Forum», 1980, v. 21,
.Mi 4, p. 337—50; [8] Pastijn F., там же, 1977, v. 14, К» 3,
p. 247 — 64. Л. Н. Шеврин.
ПОЛУГРУППОВАЯ АЛГЕБРА — алгебра Ф (S)
над полем Ф, обладающая базисом S, являющимся
одновременно и мультипликативной полугруппой. В ча-
частности, если базис S является группой, получается
групповая алгебра. Если полугруппа S содержит нуль,
то он обычно отождествляется с нулем алгебры ФE).
Задача описания всех линейных представлений полу-
полугруппы S над полем Ф равносильна задаче описания
всех представлений алгебры ФE). Значение П. а. для
теории полугрупп состоит в возможности применения
более богатого аппарата теории алгебр для изучения
линейных представлений полугрупп. Пример такого
рода результата: алгебра Ф (S) конечной полугруппы S
полупроста тогда и только тогда, когда все линейные
представления полугруппы S над полем Ф приводимы.
Лит.: [1] Клиффорд А., Престон Г., Алгебраи-
Алгебраическая теория полугрупп, пер. с англ., т. 1, М., 1972.
Л. М. Глускип.
ПОЛУДЕДЕКИНДОВА РЕШЕТКА, полуде-
декиндова структура, полу моду-
модулярная решетка (структура),— решетка,
в к-рой отношение модулярности симметрично, т. е.
аМЬ влечет ЪМа для любых элементов решетки а и Ъ.
Отношение модулярности при этом
определяется следующим образом: говорят, что элемен-
элементы а и Ь образуют модулярную пару или что
аМЬ, если a (fc+c) = afc-j-c для любого c*s.a. Решетка,
в к-рой всякая пара элементов модулярна, паз. м о-
дулярной решеткой или дедекиндовой ре-
решеткой.
Решетка конечной длины полудедекиндова тогда и
только тогда, когда она удовлетворяет условию
покрытия: если хну покрывают ху, то х-\-у по-
покрывает х и у (см. Покрывающий элемент). В любой
И. р. конечной длины выполняется условие
Иордана — Дедекинда для цепей (все
максимальные цепи между двумя фиксированными эле-
элементами имеют одну и ту же длину), что позволяет
развивать в них теорию размерности. П. р. конечной
длины является решеткой с относительными дополне-
дополнениями тогда и только тогда, когда каждый ее элемент
есть объединение атомов. Такие решетки наз. гео-
геометрическими. Важный класс П. р. образуют
близкие к геометрическим матроидные решетки (см.
[3]). Каждая конечная решетка изоморфна подрешетке
конечной П. р. Класс П. р. не замкнут относительно
гомоморфных образов.
Наряду с П. р., называемыми также полудеде-
киндовыми сверху, рассматриваются п о л у-
дедекиндовы снизу решетки, опреде-
определяемые двойственным образом. Примерами П. р., кроме
дедекиндовых решеток, являются решетки всех разбие-
разбиений конечных множеств и решетки линейных многооб-
многообразий аффинных пространств.
Лит.: [1] Б и р к г о ф Г., Теория структур, пер. с англ.,
[2 изд.], М., 1952; [2] В i r k h о f f G., Lattice theory, [3 ed.].
Providence, 1967; [3j M a e d a F., M a e d a S h., Theory of
symmetric lattices, В. —Hdlb.—N. Y., 1970. Т. С. Фофанова.
ПОЛУЕВКЛИДОВО ПРОСТРАНСТВО — действи-
действительное аффинное re-пространство, в к-ром определено
скалярное произведение векторов так, что при надле-
жащем выборе базиса скалярный квадрат (ж, on) всякого
вектора имеет вид
iaKoo П. и. называется П. п. индекса I и дефекта d,
обозначается l + (-d^Rn. При 1—0 выражение скалярного
квадрата вектора является квадратичной нолуопредс-
ленной формой, и II. п. наз. «-пространством дефекта
d, обозначается {d)Rn-
[I. u. в проективной классификации могут быть опре-
определены как соответственно полуэллиптич. пространст-
пространство или полугиперболич. пространство с несобственной
абсолютной плоскостью, к-рые являются пространства-
пространствами с проективными метриками наиболее общего вида.
В П. п. определяется т.н. полунеевклидово
пространство как метрическое п-пространство,
являющееся гиперсферой с отождествленными диамет-
диаметрально противоположными точками в П. п. индекса I
и дефекта d. Таким образом, нолуэллиптич. и полуги-
иерболич. пространства могут быть интерпретированы
как указанные гиперсферы (т. е. как иолунеевклидовы
пространства) в П. п. с соответствующими индексом и
дефектом.
Геометрич. интерпретация механики Галилея — Нью-
Ньютона приводит к П. п. A) Rn (см. |2j).
П. п. является полуримановым пространством нуле-
нулевой кривизны.
Лит.: [1] Sommerville D. М., «Ргоо. Edinburgh Math.
Soc», 1910, v. 28, p. 25 — 41; [2] Котельников А. П.,
Принцип относительности и геометрия Лобачевского, в кн.:
In memoriam N.I. Lobacevski, т. 2, Казань, 1926; [3] Розен-
фельд Б. А., Неевклидовы пространства, М., 1969.
ПОЛУИНВАРИАНТ — общий собственный век-
вектор семейства эндоморфизмов векторного пространства
или модуля. Если G — множество линейных преобра-
преобразований векторного пространства V над полем А', то П.
множества G — это такой вектор ь'? V, что v^O и
где у, : G —>¦ К — функция, называемая несом и о-
луин варианта v. П. веса 1 наз. также и н в а-
р и а н т о м. Чаще всего рассматривается случай,
когда GcGL (V) — линейная группа, тогда % : G -> К*
есть характер группы G и продолжается до полиноми-
полиномиальной функции на End V. Если ф : G —>- GL (F) —
линейное представление группы G в пространстве V,
то П. группы ф (G) наз. также полуинвариан-
полуинвариантом представления ф. Пусть G — линейная
алгебраич. группа, Н — ее замкнутая подгруппа,
flCQ — алгебры Ли этих групп. Тогда существуют
такое точное рациональное линейное представление
Ф : G —>- GL (E) и такой полуинвариант v?E группы
ф(Я), что Н и f) являются максимальными подмноже-
подмножествами в G и д, для образов к-рых в End E вектор v
есть П. Это означает, что соответствие ail h* K(f(a)v,
a^G, есть изоморфизм алгебраического однородного
пространства на орбиту прямой Kv в проективном про-
пространстве Р(Е).
Часто П. множества GcEnd V наз. полиномиальную
функцию на End V, являющуюся П. множества линей-
линейных преобразований т| (G) пространства К [End V], где
g?G, f?K [End V], XgEndK.
Если GcGL(F) — линейная алгебраич. группа, д —
ее алгебра Ли, то G обладает такими П.
/„ ..., /„€ К [End V)
одинакового веса, что G и CJ суть максимальные под-
подмножества в GL(F) и End V, для к-рых /1; ... , /„ суть
i i. (теорема Ш е в а л л е).
Лит.: [1J Б о р с л ь А., Линейные алгебраические группы,
пер. с англ., М., 1У72; [2] Хамфри Д ж., Линейные алгеб-
алгебраические группы, пер. с англ., М., 1980; [3] Ш е в а л л е К.,
Теория групп Ли, пер. с франц., т. 2, М., 1958.
А. Л. Оиищик.
ПОЛУКОЛЬЦО — непустое множество с двумя
ассоциативными бинарными операциями -|- и •, свя-
связанными дистрибутивными законами:
(а-\- Ь) ¦ с =_ а¦ Ъ -\ а-с
и
а-F 4-с) = а-Ь 4-а-с.
В большинстве случаев дополнительно предполагается,
что сложение коммутативно и что существует нуль 0,
для к-рого a-\-Q~ а при любом а. Важнейшие примеры
II.— кольца и дистрибутивные решетки. При наличии
единицы 1 относительно умножения оба эти класса объ-
объединяются требованием
V.r ЗУ (х 4- !/ = 1).
Неотрицательные целые числа с обычными операциями
образуют П., не удовлетворяющее этому требованию.
Л. А. Скорняков.
ПОЛУКУБИЧЕСКАЯ ПАРАБОЛА — плоская алге-
алгебраическая кривая 3-го порядка, уравнение к-рой в
прямоугольных координатах имеет вид
Начало координат есть точка во.чнрата (см.
рис.). Длина дуги от точки 0:
кривизна:
У
Иногда П. п. наз. параболой II е й л я.
Лит.: [1] Саве лов А. А., Плоские кривые, М., 1960;
[2] Смогоржевский А. С., Столова 3. С, Спра-
Справочник по теории плоских кривых третьего порядка, М., 1961.
Д. Д. Соколов.
ПОЛУЛИНЕЙНОЕ ОТОБРАЖЕНИЕ — отображе-
отображение а (левого) модуля М в (левый) модуль ..V над одним
и тем же кольцом А, удовлетворяющее условиям:
а (х4-у) = а (х) 4-а (у),
a (ex) ---саа (х),
где .г, ц?М, с?А, с—>-са— нек-рый автоморфизм коль-
кольца А . В атом случае говорят, что а полулиней-
полулинейно относительно автоморфизма а.
И.о. векторных пространств над полем С относительно
комплексного сопряжения е°=с наз. также а н т и л и-
нейным отображением. П. о. А-модуля М
в себя наз. полулинейным преобразо-
преобразованием.
Пример. Гомотетия Л-модуля М, т. е.
отображение х —>¦ ах (х?М), где а — фиксированный
обратимый элемент кольца А, есть полулинейное преоб-
преобразование относительно автоморфизма сA=аса~1.
Для П. о. остаются справедливыми многие свойства
линейных отображений и гомоморфизмов модулей.
В частности, ядро и образ П. о. являются подмодулями;
П. о. свободных модулей с конечными базисами пол-
полностью определяются своей матрицей; для П. о. вектор-
векторных пространств определяется ранг, совпадающий с
рангом его матрицы, и т. д.
Лит.: [1] Б у р б а к и Н., Алгебра. Алгебраические струк-
структуры. Линейная и полилинейная алгебра, пер. с франц., М.,
1962. А. Л. Оиищик.
ПОЛУМАРКОВСКИЙ ПРОЦЕСС — случайный про-
процесс X (t) с конечным или счетным множеством состоя-
состояний Л/—{1, 2, ...}, имеющий ступенчатые траектории
со скачками в моменты времени 0<Т|<т?<... . Значе-
ния П. п. X (т„) в моменты скачков образуют Маркова
цепь с переходными вероятностями
P,7 = P{X(TB) = /|X(Tn-i)-i}.
Распределения моментов скачков хп описываются с по-
помощью функций распределения F[j(x) следующим об-
образом:
Р {т„ —Tn_j < х, X (т„) = / | X (т„_!) = i}=PijFij (х)
(и при этом не зависят от состояний процесса в более
ранние моменты времени). Если
F'ij(x) =e~%ilX', zSsO,
для всех i,i?jV, то П. п. X (t) является цепью Маркова
с непрерывным временем. Если все распределения вы-
вырождены в одной точке, то получают цепь Маркова с
дискретным временем.
П. п. служит моделью многих процессов массового
обслуживания и теории надежности. С П. п. связаны
процессы марковского восстановления (см. Восстанов-
Восстановления теория), описывающие количество посещений
процессом X (t) состояний <?Л' за время |0, t\.
Изучение П. п. и марковских процессов восстановле-
восстановления аналитически сводится к системе интегральных
уравнений восстановления. ;
Лит.: Ill К о р о л ю к В. С, Тур 0 и н А. Ф., 11 <>.'i v, — j
марковские процессы и их приложения, If., J!>7(i.
П. А. Севастьянов.
ПОЛУМАРТИНГАЛ — понятие, равносильное по-
понятиям субмартингала или супермартингала. Именно,
стохастич. последовательность X =--(Xt,§~t), t? Гс=[0,оо),
заданная на вероятностном пространстве (Я, §~, Р) с вы-
выделенным на нем убывающим семейством сг-алгебр
(?t)tzTi ?s^?fSf. s<z> наз. и о л у м а р т и н г а-
л о м, если Е|Л"(|<оо, Xf является ^-измеримой и с
вероятностью 1 или
E(Xt\pfs)<Xs. B)
В случае A) П. наз. с у б мартингалом, в слу-
случае B) — с у и е р м а р т и н г а л о м.
В современной литературе термин «П.» или не упо-
употребляют, или отождествляют с понятием субмартин-
субмартингала (супермартингал определяется изменением знака
из субмартингала и наз. иногда нижним П.). См. также
Мартингал. А. В. Прохоров.
ПОЛУНАСЛЕДСТВЕННОЕ КОЛЬЦО слева —
кольцо, все конечно порожденные левые идеалы к-рого
проективны. П. к. являются кольцо целых чисел, коль-
кольцо многочленов от одного неизвестного над полем, регу-
регулярные кольца и смысле Неймана, наследственные коль-
кольца, кольца конечно порожденных свободных идеалов
(полу-ЛТ-кольца). Аналогично определяется правое
П. к. Левое П. к. не обязано быть правым П. к. Однако
локальное левое П. к. оказывается областью целостно-
целостности и правым П. к. Кольцо матриц над П. к. является
II. к. Если Н ость П. к. и e2=-e?R, то еНе есть П. к.
Конечно порожденный подмодуль проективного моду-
модуля над П. к. изоморфен прямой сумме нек-рого множе-
множества конечно порожденных левых идеалов основного
кольца и, следовательно, проективен. Каждый такой
модуль может быть представлен и как прямая сумма
модулей, двойственных конечно порожденным правым
идеалам основного кольца.
Для коммутативного кольца Я эквивалентны следую-
следующие свойства: A) R есть П. к.; B) (A f]B)C^ACf\BC,
где А, В и С — произвольные идеалы кольца Я; C)
полное кольцо частных кольца R регулярно в смысле
Неймана, и для всякого максимального идеала lit коль-
кольца R кольцо частных Rm является кольцом нормирова-
нормирования; D) все 2-порожденные идеалы кольца R проектив-
ны. Кольцо многочленов от одного переменного над ком-
коммутативным кольцом R оказывается П. к. в том и
только в том случае, когда R регулярно в смысле
Неймана.
Лит.: [1] Картан А., ЭйленбергС, Гомологиче-
Гомологическая алгебра, пер. о англ., М., 1960; [2] Итоги науки и техни-
техники. Алгебра. Топология. Геометрия, т. 14 М. 1976, с. 57 —190,
т. 19, М., 1981 с. 31 — 134. Л. А. Скорняков.
ПОЛУНЕПРЕРЫВНАЯ ФУНКЦИЯ — функция из
первого Бэра класса. Подробнее, числовая функция /,
определенная на полном метрич. пространстве X, наз.
полунепрерывной снизу (сверху)
в точке ха?Х, если
Ит, _ х> f (х) = / (*„) (Шх ^ Xt / (х) = / (*„)).
Функция / нач. полунепрерывной снизу (сверху) на X,
если она полунепрерывна снизу (сверху) для всех х?Х.
Предел монотонно возраста7ощей (убывающей) последо-
последовательности полунепрерывных снизу (сверху) в точке
.г0 функций есть П. ф. снизу (сверху) в ,т0. Если и{х) и
v(x) есть П. ф. соответственно снизу и сверху на X и
для всех х?Х имеет место «(.г)<Гс(.г), н(.г)>—оо, i>(.r)<
<+оо, то существует непрерывная на X функция / та-
такая, что v(x)^f(x)^u(x) для всех х?Х. Если (х — неот-
неотрицательная мера на R", то для любой ц-измеримой
функции / : К" —у R существуют две последователь-
последовательности функций {ип(х)} и {vn(.c)}, удовлетворяющие ус-
условиям: \) ип(х) полунепрерывны снизу, и„(х) полуне-
полунепрерывны сверху, 2) каждая функция ип(х) ограничена
снизу, каждая функция vn(x) — сверху, 3) последова-
последовательность {и,,} невозрастающая, последовательность
{г,,} неубывающая, 4) для всех х имеет место неравен-
неравенство
«п (х) 5&/ И ^vn(x),
5) fi-почти всюду
lim un(x)~ lim vn(x) = f(x),
а -у да п -* со
6) если для ?cR" функция / суммируема, f?L(E), то
«я. v,i€L{E) и
lim f undu,= lim \pvn dp = \ f dp
(теорема Витали — Каратоодори).
Лит.: [1] Натансон И. II., Теория функций вещест-
вещественной переменной, 3 изд., М., Г,O4; [2] С а к с Г.., Теория
интеграла, нер. с англ., М., 1949. И. А. Виноградова.
ПОЛУНЕПРЕРЫВНОЕ ОТОБРАЖЕНИЕ с н е р-
х у (с н и з у) — отображение / одного топологии. про-
пространства X в другое Y такое, что из
\\тхп = х
следует
ITS / (хп) < / (х) (\im_f (хп) S3: / (х))
(здесь lim (lim)— верхний (нижний) предел).
М. И. Войцеховский.
ПОЛУНЕПРЕРЫВНОЕ РАЗБИЕНИЕ с н и зу
(сверху) — разбиение ?>, т. е. замкнутое дизъюнкт-
дизъюнктное покрытие пространства X, такое, что проекция
р : X —>- D является открытым (замкнутым) отображе-
отображением, м. И. Ъойцеховский.
ПОЛУНЕПРЕРЫВНЫЙ МЕТОД СУММИРОВА-
СУММИРОВАНИЯ — метод суммирования рядов и последовательно-
последовательностей, определенный с помощью последовательности
функций. Пусть {ak(u))}, к—О, 1, ... ,— последователь-
последовательность функций, заданных на нек-ром множестве Е изме-
изменения параметра со, и ш0 — точка сгущения этого мно-
множества (конечная или бесконечная). Данную последо-
последовательность {sn} с помощью функций а/г(м) преобразу-
преобразуют в функцию а(ш):
Если ряд в A) сходится для всех со, достаточно близких
к ш0, и
lim а (со) = s,
(О -»¦ (О0
то последовательность {sn} наз. суммируемой к пределу
.< полунепрерывным методом с у м м и-
)) о в а н и я, определенным последовательностью функ-
функций {aii(o.))}. Если {sn} — последовательность частич-
частичных сумм ряда
то ряд B) в этом случае наз. суммируемым полунепре-
полунепрерывным методом к сумме s. П. м. с. при шп-= оо является
аналогом матричного метода суммирования, определен-
определенного матрицей ||anfe||, причем целочисленный параметр п
заменен непрерывным параметром ы. Последователь-
Последовательность функций ак(со) в этом случае наз. полуне-
полунепрерывной матрицей.
П. м. с. может задаваться преобразованием непо-
непосредственно ряда в функцию с помощью заданной по-
последовательности функций, напр. {#/г(ш)}:
Y И =-2"=0?ft <«)«*• C)
В этом случае ряд B) паз. суммируемым к сумме s, если
lim у (со) = s,
где ш0— точка сгущения множества Е изменения пара-
параметра со, а ряд в (З)предполагается сходящимся для всех
со, достаточно близких к со0.
II. м. с. в нек-рых случаях являются более удобны-
удобными, чем методы суммирования, определенные обычными
матрицами, т. к. позволяют использовать аппарат
теории функций. Примерами П. м. с. являются Абеля
метод суммирования, Бореля метод суммирования,
Линделёфа метод суммирования, Миттаг-Леффлера
метод суммирования. Класс П. м. с. составляют методы
с полунепрерывными матрицами вида
а* Н = pk Ш*/2Г= оРгШ''
где в знаменателе стоит целая функция, не сводящаяся
н многочлену.
Условия регулярности П. м. с. аналогичны условиям
регулярности матричного метода суммирования. Напр.,
условия
для всех со, достаточно близких к со(|,
lim afe(@)=-0, fc = 0, 1, 2, ...,
lim "V afc (со) — 1
являются необходимыми и достаточными, чтобы П. м. с,
определенный преобразованием A) последовательности
{¦s/e} D функцию, был регулярным (см. Регулярности
признаки).
Лит.: Ш Харди Г., Расходящиеся ряды, пер. с англ.,
М., 1951; [2] Кук Р., Бесконечные матрицы и пространства
последовательностей, пер. с англ., М., i960; L3] Zeller К.,
Bukmann W., Theorie der Limitierungsverfahren, 2 Aufl.,
В. —Hdlb.—N.Y., 1970. И.И.Волков.
ПОЛУНОРМА — конечная неотрицательная функ-
функция р на векторном пространстве Е (над полем дей-
действительных или комплексных чисел),, подчиненная
условиям:
К)\К\(
Р (х + у)<р (х)-\-р (у)
шя всех х, у?Е и скаляров Я. Примером П. служит
норма; отличие заключается в том, что для П. допус-
допустимо р (х) — 0 при хуЬО. Если на векторном пространстве
задана полунорма р, а на его подпространстве — линей-
линейный функционал /, подчиненный условию \f(x)\ <:p (х),
то его можно продолжить на все пространство с сохра-
сохранением этого условия (теорема Хана — Бана-
Банаха). В математич. анализе наиболее употребительны
отделимые топологические векторные пространства, ба-
базис окрестностей нуля в к-рых можно составить из вы-
выпуклых множеств. Такие пространства наз. локаль-
локально выпуклыми. В этих пространствах базис мо-
может быть описан неравенствами р(х)<1, где р — не-
непрерывные П. В то же время в практике математич.
анализа встречаются и такие топологич. векторные про-
пространства (в том числе и с метризуемой топологией), на
к-рых нет нетривиальных непрерывных П. Простейшим
пример такого рода — пространство LJ0, 1), где 0<
<<!
?<
Лит.: [1] Б у р б а к и Н., Топологические векторные
пространства, пер. с франц., М., 1959; [2] Р у д и н У., Функ-
Функциональный анализ, пер. с англ., М., 1975. Е. А. Горин.
ПОЛУОГРАНИЧЕННЫЙ ОПЕРАТОР — симметри-
симметрический оператор S в гильбертовом пространстве Я,
для к-рого существует такое число с, что
(Sx, х) Эг с (х, х)
для всех векторов я, лежащих в области определения S.
П. о. S всегда имеет полуограниченное самосопряжен-
самосопряженное расширение А с той же нижней гранью с (т е о р е-
ма Фридрих с а). В частности, их индексы дефек-
дефекта совпадают.
Лит.: [1] Рисе Ф., Сёкефальви-Надь Б., Лек-
Лекции по функциональному анализу, пер. с франц., 2 изд., М.,
1979. В. И. Ломоносов.
ПОЛУОПРЕДЕЛЕННАЯ ФОРМА — квадратичная
форма над упорядоченным полем, представляющая
либо только неотрицательные, либо только неполо-
неположительные элементы поля. В первом случае квад-
квадратичная форма наз. неотрицательной
(д(х)^О для всех значений .т), во втором — неполо-
неположительной квадратичной формой
(</(.т)<0). Чаще всего II. ф. рассматриваются над полем
R действительных чисел. Над полем С аналогично
определяются полуопределенные (неотрицательные и
неположительные) эрмитовы квадратичные формы (см.
Эрмитова форма).
Если Ь — симметрическая билинейная или эрмитова
форма, причем q(x) = b(x, x) является П. ф., то и форму
Ь также иногда называют полуопределенной (неотрица-
(неотрицательной или неположительной). Если q — квадратичная
или эрмитова П. ф. в векторном пространстве V, то
.V— {х? V\g(x)—0} является подпространством, совпа-
совпадающим с ядром формы Ъ, причем на V/N естественным
образом индуцируется положительно определенная или
отрицательно определенная форма. о. А. Иванова.
ПОЛУПЛОСКОСТЬ — совокупность точек плос-
плоскости, лежащих по одну сторону от нек-рой прямой
этой плоскости. Координаты точек П. удовлетворяют
неравенству Ах-\-Ву-\-С>0, где А, В, С — нек-рые по-
постоянные, причем А и В одновременно не равны нулю.
Если сама прямая Ах-\-Ву-\-С=0 (граница П.)
причисляется к П., то говорят о замкнутой П.
На комплексной плоскости z—x-\-iy рассматриваются
верхняя полуплоскость y=Imz>0,
нижняя полуплоскость y=Imz<(), л е-
вая полуплоскость х— Rez<0, правая
полуплоскость л—:Re2>0 и т. д. Верхняя П.
комплексной плоскости z конформно отображается на
круг |н>|<1 с помощью дробно-линейной функции
где в — произвольное действительное число, a Inx fS>0.
BCD-:;.
463 ПОЛУПРАВИЛЬНЫЕ
ПОЛУПРАВИЛЬНЫЕ МНОГОГРАННИКИ, тела
Архимед а,— выпуклые многогранники, все грани
к-рых суть правильные многоугольники, а многогран-
многогранные углы конгруэнтны или симметричны. Данные о
П. м. приведены в таблице, где В — число вершин,
Р — число ребер, Г — число граней, 1\ — число п^-
Полуправильные многогранники
Усеченный тетраэдр . . . .
Усеченный куб
Ромбокубооктаэдр
Плосконосый куб
Усеченный нубооктаэдр • .
Кубооктаэдр
Усеченный октаэдр
Усеченный додекаэдр ....
Ромбоикосододекаэдр . . .
Усеченный икосододекаэдр
Икосододекаэдр
Усеченный икосаэдр ....
Плосконосый додекаэдр . .
Правильная призма (п = 3,
5, 6,...)
Антипризма (п = 4, 5, 6,...)
J* на
рис.
1
г
3, 4
5
6
7
S
9
10
11
12
13
14
IS
16
12
24
24
24
48
12
24
60
60
120
30
60
60
2тг
18
36
48
60
72
24
36
90
120
180
60
90
150
Зп
in
14
26
38
26
14
14
32
62
62
32
32
92
п + 2
2п+2
10
Г,
угольных граней, s — число граней, сходящихся в каж-
каждой вершине, в том числе sx ^-угольных, s2 гс2-угольных
и т. д. В евклидовом пространстве R3 существует 13 П.
м. [см. рис., 1—14, иногда выделяют два вида ромбоку-
бооктаэдра (рис., 3—4), к-рые различаются тем, что
верхняя часть многоугольника, состоящая из 5 квадра-
квадратов и 4 правильных треугольников, повернута как це-
целое на угол я/4] и две бесконечные серии — призмы
(рис., 15) и антипризмы (рис., 16).
Нсвыпуклых (звездчатых) П. м. больше 51.
Лит.: [1] Энциклопедия элементарной математики, кн. 4—
Геометрия, М.—Л., 1963; [2] Л ю с т е р н и к Л. А., Выпуклые
фигуры и многогранники, М., 1956; [3] Bruckner M.,
Vielecke und Vielflache. Theorie und Geschichte, Lpz., 1900;
[4] В е н и и н д ж е р М., Модели многогранников, пер. с
англ., М., 1974. А. Б. Иванов.
ПОЛУПРОСТАЯ АЛГЕБРА относительно
радикала г — алгебра, являющаяся г-полупростым
кольцом (см. Полупростое кольцо). В нек-рых классах
алгебр при подходящем выборе радикала г удается
описать строение П. а. (см. Классически полупростое
кольцо, Альтернативные кольца и алгебры, Йорданова
алгебра, Ли полупростая алгебра).
МНОГОГРАННИКИ 464
Часто под П. а. понимается конечномерная алгебра
над полем, являющаяся прямой суммой простых ал-
алгебр. Л. А. Скорняков.
ПОЛУПРОСТАЯ АЛГЕБРАИЧЕСКАЯ ГРУППА --
связная линейная алгебраич. группа положительной
размерности, содержащая лишь тривиальные разре-
разрешимые (или, что равносильно,
абелевы) связные замкнутые
нормальные подгруппы. Фак-
Факторгруппа связной неразреши-
неразрешимой линейной алгебраич. груп-
группы по радикалу полупроста.
Связная линейная алгебра-
алгебраич. группа G положительной
размерности наз. простой,
если она не содержит собст-
собственных связных замкнутых
нормальных подгрупп. Центр
Z(G) простой группы G ко-
конечен, и G/Z(G) проста как
абстрактная группа. Алгеб-
Алгебраич. группа G полупроста
тогда и только тогда, когда
G разлагается в произведение
простых связных замкнутых
нормальных подгрупп.
В случае, когда основное
поле есть поле С комплексных
чисел, П. а. г.— это не что
иное как полупростая группа
Ли над С. Оказывается, что
классификация П. а. г. над
произвольным алгебраически
замкнутым полем К аналогич-
аналогична случаю К—С, т. е. что П.
а. г. определяется с точностью
до изоморфизма своей корне-
корневой системой и нек-рой подре-
шеткой в решетке весов, со-
содержащей все корни. Точнее,
пусть Т — максимальный тор
в П. а. г. G, Х(Т) — группа
характеров тора Т, рассматри-
рассматриваемая как решетка в прост-
пространстве E=X(THR. Для
любого рационального ли-
линейного представления р груп-
группы G группа р(Т) является
диагонализируемой. Ее соб-
собственные значения, являющи-
являющиеся элементами группы Х(Т), наз. весами пред-
представления р. Ненулевые веса присоединенного
представления Ad наз. корнями группы G. Ока-
Оказывается, что система %(Z.X(T) всех корней группы G
является приведенной корневой системой в пространстве
Е, причем неприводимые компоненты системы 2 — это
системы корней простых замкнутых нормальных под-
подгрупп группы G. Далее, <?B)^Х (Т)^Р B), где <?B) —
решетка радикальных весов, а Р B)= {К^Е\а*(К) ? %
для всех а?2} — решетка весов корневой сис-
системы 1. В случае К=С пространство Е естественно
отождествляется с вещественным подпространством
tjjet*, где t — алгебра Ли тора Т, натянутом на диф-
дифференциалы всех характеров, а решетки в t, двойствен-
двойственные к Q(E)c=:X (T)^P B), совпадают (с точностью до
множителя 2яг) с ГХ=2Г (б)ЭГ0 (см. Ли полупростая
группа).
Основная теорема классификации утверждает, что
если G' — другая П. а. г., Т' — ее максимальный тор,
2'с?" — система корней группы G' и если существует
линейное отображение Е -*¦ Е', определяющее изомор-
463 ПОЛУПРАВИЛЬНЫЕ
ПОЛУПРАВИЛЬНЫЕ МНОГОГРАННИКИ, тела
Архимед а,— выпуклые многогранники, все грани
к-рых суть правильные многоугольники, а многогран-
многогранные углы конгруэнтны или симметричны. Данные о
П. м. приведены в таблице, где В — число вершин,
Р — число ребер, Г — число граней, 1\ — число п^-
Полуправильные многогранники
Усеченный тетраэдр . . . .
Усеченный куб
Ромбокубооктаэдр
Плосконосый куб
Усеченный нубооктаэдр • .
Кубооктаэдр
Усеченный октаэдр
Усеченный додекаэдр ....
Ромбоикосододекаэдр . . .
Усеченный икосододекаэдр
Икосододекаэдр
Усеченный икосаэдр ....
Плосконосый додекаэдр . .
Правильная призма (п = 3,
5, 6,...)
Антипризма (п = 4, 5, 6,...)
J* на
рис.
1
г
3, 4
5
6
7
S
9
10
11
12
13
14
IS
16
12
24
24
24
48
12
24
60
60
120
30
60
60
2тг
18
36
48
60
72
24
36
90
120
180
60
90
150
Зп
in
14
26
38
26
14
14
32
62
62
32
32
92
п + 2
2п+2
10
Г,
угольных граней, s — число граней, сходящихся в каж-
каждой вершине, в том числе sx ^-угольных, s2 гс2-угольных
и т. д. В евклидовом пространстве R3 существует 13 П.
м. [см. рис., 1—14, иногда выделяют два вида ромбоку-
бооктаэдра (рис., 3—4), к-рые различаются тем, что
верхняя часть многоугольника, состоящая из 5 квадра-
квадратов и 4 правильных треугольников, повернута как це-
целое на угол я/4] и две бесконечные серии — призмы
(рис., 15) и антипризмы (рис., 16).
Нсвыпуклых (звездчатых) П. м. больше 51.
Лит.: [1] Энциклопедия элементарной математики, кн. 4—
Геометрия, М.—Л., 1963; [2] Л ю с т е р н и к Л. А., Выпуклые
фигуры и многогранники, М., 1956; [3] Bruckner M.,
Vielecke und Vielflache. Theorie und Geschichte, Lpz., 1900;
[4] В е н и и н д ж е р М., Модели многогранников, пер. с
англ., М., 1974. А. Б. Иванов.
ПОЛУПРОСТАЯ АЛГЕБРА относительно
радикала г — алгебра, являющаяся г-полупростым
кольцом (см. Полупростое кольцо). В нек-рых классах
алгебр при подходящем выборе радикала г удается
описать строение П. а. (см. Классически полупростое
кольцо, Альтернативные кольца и алгебры, Йорданова
алгебра, Ли полупростая алгебра).
МНОГОГРАННИКИ 464
Часто под П. а. понимается конечномерная алгебра
над полем, являющаяся прямой суммой простых ал-
алгебр. Л. А. Скорняков.
ПОЛУПРОСТАЯ АЛГЕБРАИЧЕСКАЯ ГРУППА --
связная линейная алгебраич. группа положительной
размерности, содержащая лишь тривиальные разре-
разрешимые (или, что равносильно,
абелевы) связные замкнутые
нормальные подгруппы. Фак-
Факторгруппа связной неразреши-
неразрешимой линейной алгебраич. груп-
группы по радикалу полупроста.
Связная линейная алгебра-
алгебраич. группа G положительной
размерности наз. простой,
если она не содержит собст-
собственных связных замкнутых
нормальных подгрупп. Центр
Z(G) простой группы G ко-
конечен, и G/Z(G) проста как
абстрактная группа. Алгеб-
Алгебраич. группа G полупроста
тогда и только тогда, когда
G разлагается в произведение
простых связных замкнутых
нормальных подгрупп.
В случае, когда основное
поле есть поле С комплексных
чисел, П. а. г.— это не что
иное как полупростая группа
Ли над С. Оказывается, что
классификация П. а. г. над
произвольным алгебраически
замкнутым полем К аналогич-
аналогична случаю К—С, т. е. что П.
а. г. определяется с точностью
до изоморфизма своей корне-
корневой системой и нек-рой подре-
шеткой в решетке весов, со-
содержащей все корни. Точнее,
пусть Т — максимальный тор
в П. а. г. G, Х(Т) — группа
характеров тора Т, рассматри-
рассматриваемая как решетка в прост-
пространстве E=X(THR. Для
любого рационального ли-
линейного представления р груп-
группы G группа р(Т) является
диагонализируемой. Ее соб-
собственные значения, являющи-
являющиеся элементами группы Х(Т), наз. весами пред-
представления р. Ненулевые веса присоединенного
представления Ad наз. корнями группы G. Ока-
Оказывается, что система %(Z.X(T) всех корней группы G
является приведенной корневой системой в пространстве
Е, причем неприводимые компоненты системы 2 — это
системы корней простых замкнутых нормальных под-
подгрупп группы G. Далее, <?B)^Х (Т)^Р B), где <?B) —
решетка радикальных весов, а Р B)= {К^Е\а*(К) ? %
для всех а?2} — решетка весов корневой сис-
системы 1. В случае К=С пространство Е естественно
отождествляется с вещественным подпространством
tjjet*, где t — алгебра Ли тора Т, натянутом на диф-
дифференциалы всех характеров, а решетки в t, двойствен-
двойственные к Q(E)c=:X (T)^P B), совпадают (с точностью до
множителя 2яг) с ГХ=2Г (б)ЭГ0 (см. Ли полупростая
группа).
Основная теорема классификации утверждает, что
если G' — другая П. а. г., Т' — ее максимальный тор,
2'с?" — система корней группы G' и если существует
линейное отображение Е -*¦ Е', определяющее изомор-
физм корневых систем 2 и 2' и отображающее X (Т) на
Х(Т'), то G~G'. Кроме того, для любой приведенной
корневой системы 2 и любой решетки Л, удовлетворяю-
удовлетворяющей условшо Q (Zy~\^P B), существует такая П. а. г.
G, что 2 есть система ее корней относительно макси-
максимального тора Т и А=Х(Т).
Классифицированы также все изогении (в частности,
все автоморфизмы) II. а. г.
Лит.: Ш С т е Я н б е р г Р. Г., Лекции о группах Шевал-
ле, пер. с англ., М., 1975; [2] Хамфри Д ж., Линейные ал-
алгебраические группы, пер. с англ., М., 1980. А. Л. Опищик.
ПОЛУПРОСТАЯ ГРУППА (в смысле нек-рого ра-
радикала) — группа, радикал к-рой совпадает с единич-
единичной подгруппой. Таким образом, понятие П. г. целиком
определяется выбором радикального класса групп.
В теории конечных групп и групп Ли под радикалом
обычно понимают наибольшую (связную) разрешимую
нормальную подгруппу. В этих случаях описание П. г.
сводится к описанию простых групп.
Лит.: Ш К у р о ш А. Г., Теория групп, 3 изд., М., 1967;
[2} Понтрягин Л. С, Непрерывные группы, :( изд., М.,
1973. А. Л. Шмелъкип.
ПОЛУПРОСТАЯ МАТРИЦА — квадратная матрица
над полем F, подобная матрице вида diag [d1, ..., d{\,
где dj — матрица над F с неприводимым в F \х]
характеристическим многочленом, j~i, ¦¦¦, к. Для
матрицы А над полем F следующие три утверждения
эквивалентны: A) А полупроста; B) минимальный мно-
многочлен матрицы А не имеет кратных множителей в
F [а-]; C) алгебра F [А] полупроста.
Если F — совершенное поле, то П. м. над F подобна
диагональной матрице над нек-рым расширением F.
Для всякой квадратной матрицы А над совершенным
полем имеется единственное представление в виде А —
—As-\~Ajy, где А^ есть П. м., Ар? нильпотентна,
А$Аjf—AjyA$; матрицы А$ и А^ принадлежат ал-
алгебре F [А].
Лит.: [1] Бурбаки Н., Алгебра, пер. с франц., М.,
1966, гл. 8. Д. А. Супрунепко.
ПОЛУПРОСТОЕ КОЛЬЦО — кольцо Я с нулевым
радикалом. Точнее, если г — нек-рый радикал (см. Ра-
Радикалы колец и алгебр), то кольцо И наз. r-п о л у-
простым в случае, когда r(R) — 0. Часто, говоря
об ассоциативном П. к., имеют в виду классически
полупростое кольцо. л- А- Скорняков.
ПОЛУПРОСТОЕ ПРЕДСТАВЛЕНИЕ — то же, что
вполне приводимое представление (см. Вполне приводи-
приводимое множество).
ПОЛУПРОСТОИ МОДУЛЬ — то же, что вполне
приводимый модуль.
ПОЛУПРОСТОЙ ЭЛЕМЕНТ линейной ал-
алгебраической группы G — элемент g?Gcz
dGL(V), где V — конечномерное векторное простран-
пространство над алгебраически замкнутым полем К, являю-
являющийся полупростым эндоморфизмом пространства V.
Понятие П. э. не зависит от реализации группы G в виде
линейной группы, а определяется лишь структурой ал-
гебраич. группы на G. Элемент g(^G полупрост тогда и
только тогда, когда для оператора правого сдвига
Pg в К [G] существует базис из собственных векторов.
При любом рациональном линейном представлении
ф : G —>- GL(VF) множество П. э. группы G отображает-
отображается на множество П. э. группы cp(G).
Аналогично определяются полупростые эле-
элементы алгебраической алгебры Ли
3, отвечающей группе G; дифференциал dtp : Д —*¦
-+0,{(W) представления <р отображает множество
П. э. алгебры д на множество П. э. своего образа.
Полупростой элемент алгебры Ли
$ — это элемент X?fl такой, что присоединенное ли-
линейное преобразование ad X является полупростым
эндоморфизмом векторного пространства it. Если
qg {V) — алгебра Ли редуктивной линейной ал-
гебраич. группы, то X есть П. э. алгебры й тогда и
только тогда, когда X — полупростой .-эндоморфизм
пространства V.
Лит.: [1] Б о р е л ь А., Линейные алгебраические группы,
пер. о англ., М., 1972; [2] Мерзляков Ю. И., Рацио-
Рациональные группы, М., 1980; [3] Хамфри Дж., Линейные
алгебраические группы, пер. с англ., М., 1980. А. Л. Онищи-к.
ПОЛУПРОСТОЙ ЭНДОМОРФИЗМ, п о л у п р о-
стое линейное преобразование, век-
векторного пространства V над полем К — эндоморфизм а
пространства V такой, что всякое подпространство в Г,
инвариантное относительно а, обладает инвариантным
прямым дополнением. Другими словами, требуется,
чтобы а определял на V структуру полупростого модуля
над кольцом К \Х]. Напр., любое ортогональное, сим-
симметрическое или кососимметрическое линейное преоб-
преобразование конечномерного евклидова пространства, а
также любое диагонализируемое (т. е. за-
записывающееся в нек-ром базисе диагональной матри-
матрицей) линейное преобразование конечномерного вектор-
векторного пространства являются П. э. Полупростота эндо-
эндоморфизма сохраняется при переходе к инвариантному
подпространству WcV и к факторпространству V/W.
Пусть dim F<oo. Эндоморфизм а. : V -> V является
П. э. тогда и только тогда, когда его минимальный мно-
многочлен не имеет кратных множителей. Пусть, кроме
того, L — расширение поля К и ссш= а(Х}1 — продолже-
продолжение эндоморфизма а на пространство Va)= V0/<L. Ес-
Если ос(/_) полупрост, то и а полупрост, а если ZTcenapa-
бельно над К, то верно и обратное. Эндоморфизм а наз.
абсолютно полупростым, если а<д полу-
полупрост для любого расширения LzdK; для этого необ-
необходимо и достаточно, чтобы минимальный многочлен
не имел кратных корней в алгебраич. замыкании А"
поля К, т. о. чтобы эндоморфизм а — был диагонализи-
(К)
руем.
Лит.: [1] Бур баки Н., Алгебра. Модули, кольца,
формы, пер. е франц., М., 1966. А. Л. Опищик.
ПОЛУПРЯМАЯ — одна из частей прямой, на к-рые
разбивается прямая любой ее точкой О. Если точка О
отнесена к П., то П. наз. замкнутой П. (или
Л у Ч ОМ). БС9-3.
ПОЛУПРЯМОЕ ПРОИЗВЕДЕНИЕ группы А
на группу В — группа G~AB, являющаяся про-
произведением своих подгрупп А и В, причем В нормальна
в G, и А П В - - {1 }. Если также и А нормальна в G, то
П. п. превращается в прямое произведение. П. п. по
группам А к В строится неоднозначно. Для построения
П. и. нужно еще знать, какие автоморфизмы на группе
В вызывают сопряжения элементами из А . Точнее, если
G~AB — П. п., то каждому элементу а?А соответст-
соответствует автоморфизм aa?Auti?, являющийся сопряже-
сопряжением элементом а:
При этом соответствие а \-^ аа есть гомоморфизм А —>-
-> Aut В. Обратно, если А и В — произвольные груп-
группы, то для любого гомоморфизма ср : А —у Aut В суще-
существует единственное П. п. группы А на группу В такое,
что ай=ф(а) для любого а^Л. П. п. является частным
случаем расширения группы В с помощью группы
А , такое расширение наз. расщепляющимся.
Лит.: [1] К у р о ш А. Г., Теория групп, 3 изд., М., 19A7.
А. Л. Шлгелъпин.
ПОЛУПСЕВДОЕВКЛИДОВО ПРОСТРАНСТВО —
векторное пространство с вырожденной индефинитной
метрикой. П. п. ''• • JrR%'- • -mr-i определяется как
п-мерное пространство, в к-ром задано /¦ скалярных
произведений
2V
где 0-mn<m.j<. . .<тгаг=п; a—I, 2, .,., г; ia~'nu_1+
+ 1, ..., та, е- = ±1, причем — 1 среди чисел е^
а а
встречается 1а раз. Произведение (х, у)а определено
для тех векторов, для к-рых все координаты х' при с<:
<та_! равны нулю. На этих векторах справедливо
равенство (х, #)o_i—0. Первый скалярный квадрат про-
произвольного вектора х П. п. является вырожденной квад-
квадратичной формой от координат вектора:
(X, *) = - (*!)*-(*„)*- . . . _(ж1,)»+(я'+1)»+ . . . -|-
где / — индекс, d=n—тх — дефект П. п. При
/1™Z2=- • . = ^ = 0 П. п. является полуевклидовым про-
пространством. В П. п. определяются m-мерные плоско-
плоскости (т<Сп), прямые, параллельность, длина вектора так
же, как в псевдоевклидовых пространствах. В П. п.
1 + <"'>/?„ можно выбрать ортогональный базис, состоя-
состоящий из I векторов мнимой длины, п—I—d вещественной
длины и d изотропных векторов. Через каждую точку
П. п. дефекта d можно провести d-мерную изотропную
плоскость, каждый вектор к-рой ортогонален всем век-
векторам П. п. См. также Галилеево пространство.
Лит.: [1] Розенфельд Б. А., Неевклидовы простран-
пространства, М., 1969. Д. Д. Соколов.
ПОЛУПСЕВДОРИМАНОВО ПРОСТРАНСТВО —
многообразие с вырожденной индефинитной метрикой.
П. п. li---hy^i--.mr-, определяется как гс-мерное мно-
многообразие с координатами х1', в к-ром задано г линейных
элементов
где O = mo<m1<. . .<mr=«; a=l, 2, ..., г; ia = ma^YA7
-j-1, ..., та, причем индекс квадратичной формы g(a),y
равен 1а. Линейный элемент ds% определен для тех век-
векd
р а р
торов, для к-рых все координаты dx' при i<ma_i равны
нулю (для этих векторов справедливо равенство ds^-i—
— 0). При i1=/2=... = /r=0 П. п. является полурима-
новым пространством. Пространства V™ и klV™ яв-
являются квазир и меновыми простран-
пространствами. В П. п. определяются основные понятия
дифференциальной геометрии (напр., кривизна) по ана-
аналогии с римановыми пространствами (см. [1]).
Лит.: [1] Розенфельд Б. А., Неевклидовы про-
пространства, М., 1969. Д. Д. Соколов.
ПОЛУ РЕШЕТКА, полуструктура,— ком-
коммутативная идемпотентная полугруппа, т. е. полу-
полугруппа с тождествами х-\-у=у-\-х и х-\-х--х. Всякая
полурешетка р=<р, +> может быть превращена в час-
частично упорядоченное множество (частичный порядок<:
вводится соотношением a<:b<=?a-j-6— 6), в к-ром для
любой пары элементов существует точная верхняя грань
sup {a, Ь}=а-\-Ь. Обратно, всякое частично упорядо-
упорядоченное множество с точными верхними гранями для лю-
любых пар элементов является П. относительно операции
a-{-6=sup {a, ft}. В этом случае говорят, что частично
упорядоченное множество является верхней по-
л у р е ш е т к о й (или полурешеткой по
объединениям, или V-n олурешеткой).
Нижняя полуре тетка, называемая также
полурешеткой но пересечениям, или
Л-п о л у р е ш е т к о й, определяется дуально как
частично упорядоченное множество, в к-ром для любых
двух элементов существует точная нижняя грань.
Т. С. Фофанова.
ПОЛУРИМАНОВО ПРОСТРАНСТВО — пространст-
пространство с полуримановой метрикой (с вырожденным метрич.
тензором). П. н. является обобщением понятия римано-
ва пространства. Определение П. п. может быть выра-
выражено с помощью понятий, применяемых при определе-
определении риманова пространства. В определении риманова
пространства Vn используется в качестве касательного
пространства евклидово пространство R", причем ка-
касательные векторы в каждой точке Х(хх. . .xn)?Vn ин-
инвариантны при параллельных переносах Vп (метрич.
тензор а,-у пространства Vn абсолютно постоянен).
Если в качестве касательного пространства в каждой
точке пространства Vп берется полуевклидово простран-
пространство д™1т㦕¦mr-ii T0 метрика пространства Vn будет яв-
являться вырожденной, метрит, тензор также абсолютно
постоянен, но является теперь вырожденным, его мат-
матрица имеет ранг тх и имеет неособенную подматрицу.
Определяется второй вырожденный метрич. тензор в
(п—т1)-плоскости (a^xi—Q), к-рая наз. нулевой (n—nij)-
плоскостью тензора at/; его матрица также обладает
неособенной подматрицей я т. д. Последний, г-ж мет-
метрич.. тензор, определенный в нулевой (п—тг_1)-плоско-
сти (г—1)-го тензора,— невырожденный тензор с неосо-
неособенной матрицей. Такое пространство и наз. П. п. и в
атом случае обозначается символом у™>тг---тг-1. Ана-
Аналогично определяется П. п. вида lth---irym<ms...mr_1^
т. е. когда в качестве касательного пространства берется
полупсевдоевклидово пространство (Л...'гнто1гI,...тг_1^
Пространства \'% и klV™ наз. к в а з и р и м а н о-
выми пространствами.
Как и в римановом пространстве, в П. п. вводится
понятие кривизны в двумерном направлении. Полуги-
перболич. и полуэллиптич. пространства являются
П. а. постоянной ненулевой кривизны, а полуевклидово
пространство — П. п. постоянной нулевой кривизны.
Таким образом, П. п. может быть определено как
пространство аффинной связности (без кручения), каса-
касательные пространства к-рого в каждой точке являются
полуевклидовыми (или полупсевдоевклидовыми), при-
причем метрич. тензор II. н. является абсолютно постоян-
постоянным.
В П. п. дифференциальная геометрия линий и по-
поверхностей строится по аналогии с дифференциальной
геометрией линий и поверхностей в Vп с учетом указан-
указанной выше специфичности П. п. Поверхности полуги-
перболич. и полуэллиптич. пространств сами являются
П. п. В частности, m-орисфера полугиперболич. прост-
пространства m + lSn изометрична П. п. V^i"*'1, метрика
к-рого сводится к метрике цолуэллиптич. пространства
5j*_m_i; этот факт является обобщением изометричнос-
ти орисферы пространства Лобачевского евклидовому
пространству.
Лит.: [1J Р о з е и ф е л ь д Б. А., Неевклидовы простран-
стна, М., 1969. Л. А. Сидоров.
ПОЛУСИМПЛЕКТИЧЕСКОЕ ПРОСТРАНСТВО —
проективное B??4-1)-пространство, в к-ром задана
B;г—2та— 1)-плоскость Т„, в ней — Bп^2ш1~^-плос-
Bп^2ш1~^-плоскость Тх и т. д. до Bп—1mr-\ — 1)-плоскости Тг-\, при
атом в пространстве задана нуль-система, переводящая
все точки пространства в плоскости, проходящие через
плоскость То; в плоскости То задана абсолютная нуль-
система, переводящая все ее точки в Bn—2m0—2)-
плоскости, лежащие в ней и проходящие через Bи—
—2т1 — 1)-плоскость Тх и т. д. до абсолютной нуль-
системы Bn—2mr-i — 1)-плоскости Тг~г, переводящей
все ее точки в Bп—2mr-x—2)-плоскости, лежащие в
ней, 0<m0<mj<... <mr_!<7i. П. п. обозначается
о_2т„+ 1, ..., 2тг_1 + 1
П. п. получается методом, аналогичным переходу от
эллиптич. и гиперболич. пространств к полуэллиптич.
и полугиперболич. пространствам, и является более
общим по отношению к квазисимплектич. пространству.
Коллинеации П. п., переводящие в себя плоскости
Т',-, перестановочные с пуль-вистемами, наз. пол у-
симплектическими преобразовани-
преобразованиями П. п.
Существуют инварианты полуспмплектич. преобра-
преобразований, аналогичные симплектич. инварианту симплек-
тич. пространств. Полусимплектич. преобразования об-
образуют группу, являющуюся группой Ли.
Лит.: [1] Розенфельд Б. А., Неевклидовы про-
пространства, М., 19В9. Л. А. Сидоров.
ПОЛУСИМПЛИЦИАЛЬНЫЙ КОМПЛЕКС — преж
нее название симплициального множества, данное при
первом рассмотрении объектов такого рода.
М. И. Войц?ховский.
ПОЛУСОВЕРШЕННОЕ КОЛЬЦО — кольцо, каж-
каждый конечно порожденный левый (или каждый конечно
порожденный правый) модуль над к-рым обладает про-
проективным накрытием. Кольцо R с радикалом Джекоб-
сона / оказывается П. к. тогда и только тогда, когда R
полулокально и у каждого идемпотента факторкольца
R/J имеется идемпотентный прообраз в R. Первое усло-
условие можно заменить требованием классич. полупро-
полупростоты факторкольца RIJ, а второе— возможностью
«поднимать» из RIJ в R модульные прямые разложения.
П. к. характеризуются также условием, что каждый
модуль допускает прямое разложение, относительно
к-рого дополняемы максимальные прямые слагаемые.
Кольцо матриц над П. к. является П. к.
См. также Совершенное кольцо и лит. при этой статье.
Л. А. Скорняков.
ПОЛУТОРАЛИНЕЙНАЯ ФОРМА — функция от
двух переменных на модуле (напр., на векторном про-
пространстве), линейная по одному переменному и полули-
полулинейная по другому. Точнее, П. ф. на унитарном модуле
Е над ассоциативно-коммутативным кольцом А с едини-
единицей, снабженным автоморфизмом а -> а", наз. отобра-
отображение ср : ЕХ.Е -*¦ А, линейное при фиксированном
втором аргументе и полулинейное (см. Полулинейное
отображение) при фиксированном первом аргументе.
Аналогично определяется полутора линейное
отображение Ех !•'-*¦ G, где Е, /•', G—А -модули.
В случае, когда а° — а (а?А), получается понятие би-
билинейной формы, (и билинейного отображения). Другой
важный пример П. ф. получается, когда V — вектор-
векторное пространство над полем С и аа = а. Специальным
случаем П. ф. являются эрмитовы формы (а также косо-
эрмитовы формы).
П. ф. можно рассматривать и на модулях над неком-
некоммутативным кольцом А; в этом случае предполагается,
что а — антиавтоморфизм, т. е. что
(ab)a = 6СТ аст, а, Ь?А.
Для П. ф. удается ввести многие понятия теории били-
билинейных форм, напр. понятия ортогонального подмоду-
подмодуля, левого и правого ядра, невырожденной формы,
матрицы формы в данном базисе, ранга формы, сопря-
сопряженных гомоморфизмов.
Лит.: Ш Б у р б а к и Н., Алгебра. Модули, кольца,
формы, пер. с франц., М., 1966; [2] Л е н г С, Алгебра, пер.
с англ., М., 1968. А. Л. Онищип.
ПОЛУУПОРЯДОЧЕННОЕ ПРОСТРАНСТВО — об-
общее название векторных пространств, в к-рых опреде-
определено бинарное отношение частичного порядка, согласо-
согласованное определенным образом с векторной структурой
пространства. Введение порядка в функциональных
пространствах позволяет исследовать в общих рамках
функционального анализа такие задачи, к-рые сущест-
существенно связаны с неравенствами между функциями, с вы-
выделением классов положительных функций. Однако, в
отличие от множества действительных чисел, допускаю-
допускающего полное упорядочение, естественный порядок в
функциональных пространствах оказывается лишь час-
частичным; напр., в пространстве С \а, Ь] естественно счи-
считать, что функция / мажорирует функцию g, если f(t)^
^g(t) при всех t?\a, b]. Но при таком определении по-
порядка многие функции окажутся несравнимыми между
собой.
Упорядоченные векторные пространства (у. в. п.).
Векторное пространство А' над нолем действительных
чисел наа. упорядочении м, если в нем опре-
определено бинарное отношение порядка, причем х^у влечет
х-\--z^y-\-z для любого з^Х и Хх^Ку для любого числа
Я^О. Таково, напр., С \а, 1>\ с естественным порядком.
Если отношение ^ есть порядок, то множество X + =
~-~ {х?Х : ,с>0} — конус, наз. положительным
конусом. Обратно, если в векторном пространстве
X задан конус К с вершиной в нуле, то в X может быть
введен такой порядок, при к-ром Х+ ~К; следует поло-
положить х~^у, если х—у?К. Рассматриваются и более об-
общие у. в. п., в к-рых определена лишь структура квази-
квазипорядка. В этом случае множество Х+ есть клин, а
всякий клин с вершиной в нуле порождает в X квази-
квазипорядок.
Пусть у. в. н. X наделено порядком. Конус Х+ наз.
воспроизводящим, если Х + —Х + = Х. Это
свойство конуса Х+ необходимо и достаточно, для того
чтобы любое конечное подмножество из X было ограни-
ограниченным (сверху и снизу). Те у. в. п., в к-рых всякое
ограниченное сверху множество имеет верхнюю грань,
иначе — точную верхнюю границу, или супремум (а
тогда и всякое ограниченное снизу множество имеет
нижнюю грань, иначе — точную нижнюю границу, или
инфимум), на», н о р я д к о в о полными или
(о)-полными. Более слабый вид полноты в у. в. п.
определяется следующим образом: у. в. п. наз. д е д е-
к и н д о в о полны м, если всякое его ограничен-
ограниченное сверху и направленное вверх подмножество имеет
верхнюю грань (множество EczX направлено вверх,
если для любых xlt x.2?E существует такой х3?Е, что
х3'^х1, х2). Если это требование выполнено для огра-
ограниченных возрастающих последовательностей, то у. в. п.
наз. дедекиндово (о)-нолным. Дедекиндова
полнота слабее (о)-гшлноты. Напр., если X — произ-
произвольное бесконечномерное банахово пространство,
ц?Х, 0<г<1И1, а К — конус, натянутый на замк-
замкнутый шар S (и; г) и элемент 0, и с помощью К в X
введен порядок, то X — дедекиндово полное, но не
(о)-полное. У. п. п. наз. архимедовым, если в
нем выполнена Архимеда аксиома. В частности, архиме-
архимедовым является всякое дедекиндово (о)-нолное у. в. п.
В у. в. и. вводится понятие порядковой схо-
д и м о с т и: последовательность {хп} (о)-с х о Д и т с я
к элементу х(хп—кг), если существуют такие возрас-
возрастающая и убывающая последовательности {уп} и {z,,},
что (/„«.г„<г„ и sup yn = x—inl za. (о)-п редел обла-
обладает многими свойствами предела в множестве действи-
действительных чисел, однако нек-рые из них справедливы
лишь в архимедовых у. в. п.
Линейный оператор А , действующий из у. в. п. X
в у. в. п. Y (в частности, линейный функционал с дей-
действительными значениями), наз. п о л о ж и т е л ь-
н ы м, если А X л czY + . Для положительных функцио-
функционалов справедлива следующая теорема о р а с-
п р о с т ране н и и. Пусть Е — линейное подмноже-
подмножество в X, мажорирующее конус Х+ (это означает, что
для любого .т?Х+ существует такой у?Е, что у^х).
Всякий линейный функционал, заданный на Е и по-
положительный относительно конуса Е f\ X +, допускает
линейное положительное распространение на все X.
Векторная решетка (в. р.) — у. в. п., в к-ром от-
отношение порядка определяет структуру решетки. При
этом для определения в. р. достаточно постулировать
для любых двух элементов из у. в. п. существование од-
одной из граней: верхней х\>у или нижней х/\у. Напр.,
если существует х'у у, то хлу— х-\-у—xvy. Если X —
в. р., то конус X + наз. м и н и э д р а л ь н ы м. В в. р.
для любого ее элемента .г существуют положитель-
положительная и отрицательная части: ,rf -jvO hi_ = (-i)vO,
При этом т—,г+—,г_, и эта формула дает «минималь-
«минимальное» представление х в виде разности положительных
элементов, т. е. если г у—:., где у, г>0, то ,г4_<:;/,
.¦/¦_<:г. Миниэдральный конус является воспроизводя-
воспроизводящим. Элемент |ж| = ж++ж- наз. модулем элемента х.
В пространстве С [а, Ь] с естественным упорядочением
положительный конус миниэдрален, положительная
часть любой функции х (t) из С получается из x{t) заме-
заменой ее отрицательных значений нулем, а модуль есть
функция |x(i)|. В в. р. всякое конечное множество эле-
элементов имеет обе грани. Модуль элемента в. р. обладает
многими свойствами абсолютной величины действитель-
действительного числа.
В. р. наз. дистрибутивно и, если для произ-
произвольного множества ее элементов {ха}, у к-рого сущест-
существует sup xa, при любом у?Х справедлива формула: г/Л
Asup ха~sup {улха}. Тогда верна и двойственная
формула: г/vinf xa=inf {y\Jxa}.
Теорема о двойном разбиении поло-
положительных элементов: если x=y-\-z, где у, zJ^O, и одно-
одновременно х=.Г] + ... + х,„ где все х^О, то каждый .г,-
можно представить в виде xi---yi-\-zi так, что все г/,-, z,-^0
и что
У=У1~\- ¦¦ ¦ +Ут z = Z!+...+zn.
Два элемента х, у в. р. наз. д и з ъ ю н к т н ы м и
(xdy), если \х\ Л |г/| = 0. Два множества А , В наз. д и з ъ-
юнктными, если adb для любых а?А, Ь?В. В про-
пространстве С [а, Ь] дизъгонктность xdy означает, что
х (t)y (t)^sO. Положительный элемент е наз. слабой
единицей (единицей в смысле Фрей-
Фрейде н т а л я), если 0 — единственный элемент, дизъ-
дизъюнктный се. ВС [о, Ь] слабой единицей является любая
функция, к-рая больше 0 на всюду плотном множестве.
Если же элемент е таков, что для любого х существует
X, при к-ром \х\ <Яе, то е наи. сильной едини-
единицей, а X с сильной единицей наз. в. р. ограни-
ограниченных элементов. В С [а, Ь] сильная еди-
единица — любая функция, для к-рой min ж(()>0. Если
в архимедовой в. р. X с сильной единицей е положить
l|.r||=min {к : |.г|<Я«}, то ^Y становится нормиро-
нормированной решеткой.
На плоскости любой конус, кроме одномерного (т. е.
луча), миниэдрален. Но в пространствах с большим чис-
числом измерений среди замкнутых конусов много не ми-
ниэдральных, напр, таковы все «круглые» конусы в R3.
Для того чтобы конус (с вершиной в нуле) в п-мерном
архимедовом у. в. п. был миниэдральным, необходимо
и достаточно, чтобы он был натянут на (п — 1)-мерный
симплекс с линейно независимыми вершинами. Всякая
архимедова n-мерная в. р. изоморфна пространству R"
с покоординатным упорядочением.
К-пространства (К.-п.), пространства Кан-
Канторовича, суть (о)-полные в. р. Это — основной
класс П. п., они всегда архимедовы, (о)-сходимость в
К.-п. описывается с помощью верхнего и нижнего пре-
пределов, именно, для огранич. последовательности {хп}
lim хп = inf sup xm, lim?n=sup inf xm
n /я >- n n m >- n
и тогда хп—yx означает, что x= lim xn= lim xn. ЦуСТ1)
X есть К.-и. Для любого множества ЕаХ его дизъюн-
дизъюнктным дополнением наз. множество Ed — {ж? X :х dE).
Всякое множество, к-рое является дизъюнктным допол-
дополнением (к какому-либо множеству), наз. полосой.
Для любого множества Е существует наименьшая поло-
полоса, содержащая Е, именно Edd\ она наз. и о л о с о й,
порожденной множеством Е. Если само
Е есть полоса, то Edd=E. Полоса, порожденная одно-
олементным множеством, наз. главно й. Понятие
полосы вводится и в любой в. р., однако в К.-и. оно иг-
играет особую роль, поскольку справедлива т е о р е м а
<} проектировании на полосу: если К — полоса
в X, то для любого .г ? X существует единственное разло-
разложение ar—y-j-z, где ?/?Л\ z?Ed. Определенный при этом
линейный оператор .у— VrEx наз. проектором
на полосу Е. Если задана произвольная совокуп-
совокупность попарно дизъюнктных полос Еа, полная в том
смысле, что 0 — единственный элемент из X, дизъюнкт-
дизъюнктный всем Еа, то любой х?Х + представим в виде х--
= sup ха, 1'Де ха—1'гЕах. Всяких! i-идеал YaX также
является К.-п. Однако если xn?Y и хп—>х в X, то это
соотношение верно и в У только в том случае, когда по-
последовательность {хп} ограничена в Y.
Примером К.-п. служит пространство S всех действи-
действительных почти всюду конечных измеримых функций на
[О, 1], в к-ром эквивалентные функции отождествляют-
отождествляются. Функция x?S считается положительной, если x(t)^
JsO почти всюду. Если А~{хп} — счетное ограничен-
ограниченное сверху подмножество из S (ограниченность сверху
означает, что существует такая y?S, что xn{t)<.y(t)
почти всюду для любого п), то функция x(t) = sup xn(t)
и будет верхней гранью множества А , т. е. sup А вычис-
вычисляется поточечно. Однако для несчетных множеств вы-
вычисление граней таким же способом уже невозможно,
и существование у несчетных множеств ограниченных
множеств в S устанавливается сложнее, (о)-сходимость
в S означает сходимость почти всюду. Все пространства
Lp—[0, 1], p>0, являются ^-идеалами в S, и потому они
тоже являются К.-п.
Важную роль играет теорема Рисса — Канторовича
о том, что множество всех порядково ограни-
ограниченных операторов (т.е. линейных операто-
операторов, переводящих ограниченные по упорядочению
множества в такие же) из в. р. в К.-п. при естествен-
естественном порядке (А^В означает, что Ах^Вх при всех
х^О) само является К.-п. Теория К.-п. нашла приложе-
приложения в выпуклом анализе и теории экстремальных
задач. Многие результаты здесь основываются на тео-
теореме Хана — Банаха — Канторовича о продолжении
линейных операторов со значениями в К.-п.
К.-п. наз. расширенным, если всякое множе-
множество его попарно дизъюнктных элементов ограничено.
В расширенном К.-п. всегда существует слабая единица.
Для любого К.-и. X существует единственное (с точ-
точностью до изоморфизма) расширенное К.-п. У, в к-рое
X погружается как Z-идеал, а полоса в У, порожденная
X, совпадает с У. Такое У наз. максимальным
расширением К. - п. Пространство S [О, 1] —
максимальное расширение для всех пространств Ьр\0,
1]. Понятие расширенного К.-п. играет существенную
роль во всей теории П. п., в частности при представле-
представлении К. п. с помощью функций.
С в. р. и К.-п. тесно связано понятие решеточно-
нормированного пространства — векторного простран-
пространства, каждому элементу к-рого сопоставлена его обоб-
обобщенная норма, являющаяся элементом фиксированной
в. р. и удовлетворяющая обычным для нормы акси-
аксиомам, в к-рых знак неравенства понимается в смысле
порядка и указанной в. р. Такие пространства исполь-
используются в теории функциональных уравнений (теоремы
существования; методы приближенного решения; метод
Ньютона — Канторовича; монотонные процессы после-
последовательных приближений и т. д.).
Топологические нолуупорядоченные пространства.
В функциональном анализе используются также у. в. п.,
в к-рых одновременно определена еще нек-рая тополо-
топология, согласованная с порядком. Простейший п важ-
важнейший пример такого пространства — банахова ре-
решетка. Обобщением понятия банаховой решетки слу-
служит локально выпуклая решетка.
Важный класс банаховых К.-п. составляют KB
и р о с т р а н с т в а (КВ-п.), Канторович а -
Баваха пространства. Так называется ба-
банахово К.-п., удовлетворяющее двум дополнительным
условиям: 1) хп\О влечет ||zn||-»-0 (порядковая непре-
непрерывность нормы); 2) если последовательность {хп} воз-
возрастает и не ограничена по порядку, то ||zn|| —»-+оо.
В КВ-п. удается описать с помощью нормы многие фак-
факты, опирающиеся по своему смыслу только на порядок.
Напр., хп _!+ О означает, что |||zn|v. . .v\xn+m\\\-*-0
П—>оо
равномерно относительно т. Для того чтобы множество
в КВ-п. Е было ограничено по порядку, необходимо и
достаточно, чтобы ограниченным было множество всех
чисел вида Нк^ч/. . .v|xn|||, гцех;?Е. КВ-п. есть регу-
регулярное К.-п.
Пример КВ-п.: Lp[0, 1] при 1 «:/> <-|-оо.
Пусть X — произвольное локально выпуклое про-
пространство, наделенное структурой у. в. п. и имеющее
т. н. нормальный конус Х + ; при этом нормальность X +
равносильна тому, что в X существует база окрестно-
окрестностей нуля, состоящая из абсолютно выпуклых и поряд-
ково насыщенных множеств U (последнее означает, что
если х, y?U и г<г/, то и весь интервал [ж, у] ? U). Для
того чтобы каждый непрерывный линейный функцио-
функционал на локально выпуклом у. в. п. был представим
в виде разности положительных непрерывных линейных
функционалов, необходима и достаточна нормальность
конуса Х+ в слабой топологии. Для нормированных
пространств нормальность конуса в слабой и сильной
топологии равносильны.
Лит.: [1] В у л и х Б. 3., Введение в теорию полуупорядо-
полуупорядоченных пространств, М., 1961; [2] Канторович Л. В.,
Вулих Б. 3., Пинскер А. Г., Функциональный анализ
в полуупорядоченных пространствах, М.— Л-, 1950; [3] Ш е-
ф е р X., Топологические векторные пространства, пер. с англ.,
М., 1971; [4] Красносельский М. А., Положитель-
Положительные решения операторных уравнений, М., 1962; [5] Анто-
Антоновский М. Я., Болтянский В. Г., Сарымса-
ков Т. А., Топологические алгебры Буля, Таш., 1963; [в]
Б ир к г о ф Г., Теория структур, пер. с англ., М., 1952; [7]
Канторович Л. В., А к и л о в Г. П., Функциональный
анализ, 2 изд., М., 1977; [8] Функциональный анализ, М., 1972
(Справоч. матем. б-ка); [9] Вулих Б. 3., Введение в теорию
конусов в нормированных пространствах, Калинин, 1977; L10]
Крейн М. Г., Рутман М. А., «Успехи матем. наук»,
1948, т. 3, в. 1, с. 3—95; [11] Бух валов А. В., В е к-
слер А. И., Лозановский Г. Я., «Успехи матем.
наук», 1979, т. 34. в. 2, с. 137—83; 112] А кил ов Г. П.,
Кутателадзе С. С, Упорядоченные векторные простран-
пространства, Новосибирск, 1978. Б. 3. Вулих.
ПОЛУЦЕПНОЕ КОЛЬЦО, полуцепное
слева (справа) кольц о,— кольцо, являющее-
являющееся левым (правым) полуцепным модулем над самим собой.
Л. А. Скорняков.
ПОЛУЦЕПНОЙ МОДУЛЬ — модуль, разлагающий-
разлагающийся в прямую сумму цепных подмодулей (см. Цепной мо-
модуль). Все левые Д-модули оказываются П. м. тогда и
только тогда, когда R — обобщенно однорядное кольцо.
Л. А. Скорняков.
ПОЛУЭЛЛИПТИЧЕСКОЕ ПРОСТРАНСТВО —
проективное «-пространство, в к-ром метрика опреде-
определяется заданным абсолютом, состоящим из совокупно-
совокупности мнимого конуса 2-го порядка Qo с (га—т0 — 1)-
плоской вершиной То, (п—т0—2)-мнимого конуса Q± с
(п—т1 — 1)-плоской вершиной 7\ в (п—та—1)-плоскости
То, (п—т±— 2)-мнимого конуса Q2 с (га—го2—1)-плоской
вершиной Т2 в (га — т1—1)-плоскости 7\ и т. д. до (га—
— mr-i—2)-мнимого конуса Qr-\ с (п—тг-\—2)-пло-
ской вершиной Гг_! и невырожденной мнимой (п—
—mr~i—2)-квадрикой Qr в (п—тТ-\ — 1)-нлоскости
Tr_x, 0<.m0<m1<. . .<mr_i<n. Индексы конусов Qk,
к=0, 1, ..., г—1 равны: Zo—mo-f-l; 1а~m0 — ma-i, 0<
<a<r\ lr—n~mr^1. П. п. обозначается s^"m' — mr-1 .
В случае, когда конус Qu является парой слившихся
плоскостей, совпадающих с плоскостью То (при то~-О),
пространство с несобственной плоскостью То наз. полу-
евклидовым пространством R™imi-mr-i^
Расстояние между точками X и У определяется в за-
зависимости от расположения прямой XY относительно
плоскостей То, Тх, ... , Тг^1. Если, в частвости, прямая
XY не пересекает плоскость То, то расстояние между
точками X и У определяется с помощью скалярного
произведения аналогично определению расстояния в
квазиэллиптическом пространстве. Если же прямая
ЛГУ пересекает плоскость То, но не пересекает плоскость
Тх или пересекает плоскость Га_1, но не пересекает
плоскость Та, расстояние между точками определяется
с помощью скалярного квадрата разности соответствую-
соответствующих векторов точек X л Y.
В зависимости от расположения относительно пло-
плоскостей абсолюта в П. п. различаются четыре типа пря-
прямых.
Углы между плоскостями в П. п. определяются ана-
аналогично определению углов между плоскостями в квази-
эллиптич. пространстве, т. е. с использованием расстоя-
расстояний в двойственном пространстве.
Проективная метрика П. п. является метрикой наи-
наиболее общего вида. Частным случаем метрики П. п.
является, напр., метрика квазиэллиптич. пространства.
В частности, 2-плоскость S% совпадает с евклидовой,
Si — с коевклидовой, 3-пространство S^ — с квази-
квазиэллиптическим, ?° — с евклидовыми 3-пространствами,
3-пространство S является галилеевым, SlJ12 — флаго-
флаговым пространством и т. д. 3-пространство S1^ соответ-
соответствует по принципу двойственности галилееву 3-про-
странству Г3 и наз. когалилеевым пространством. (Абсо-
(Абсолют когалилеева пространства состоит из пары мнимых
плоскостей (конус Qo) и точки Т1 на прямой Го пересече-
пересечения этих плоскостей.)
Движениями П. п. являются его коллинеации, пере-
переводящие абсолют в себя. В случае та=п—тТ-а-\—1,
la=lr-a П. п. является двойственным самому себе, в
нем определяются кодвижения, определение к-рых ана-
аналогично определению кодвижений квазиэллиптич. про-
пространства.
Движения, движения и кодвижения образуют груп-
группы, являющиеся группами Ли. Движения (как и ко-
кодвижения) описываются ортогональными операторами.
П. п. являются полуримановыми пространствами.
Лит.: [1] Розенфельд Б. А., Неевклидовы простран-
пространства, М., 1969. Л. А. Сидоров.
ПОЛЬКЕ — ШВАРЦА ТЕОРЕМА: любой полный
плоский четырехугольник может служить параллель-
параллельной проекцией тетраэдра, подобного любому данному.
Теорема впервые высказана в иной форме К. Польке
(К. Pohlke, 1853), обобщена Г. Шварцем (Н. Schwarz,
1864).
Лит.: [1] Энциклопедия элементарной математики, кн. 4—
Геометрия, М., 1963. А. Б. Иванов.
ПОЛЮС — 1) П. координат — начало координат
в полярных координатах.
2) П.— центр инверсии.
3) П. прямой р относительно линии 2-го порядка —
точка Р, для к-рой прямая р является полярой точки Р
относительно данной линии 2-го порядка, а. Б.Иванов.
ПОЛЮС — изолированная особая точка а однознач-
однозначного характера аналитич. функции f(z) комплексного
переменного z такая, что \f(z)\ неограниченно возрас-
возрастает при приближении к a, lim/(z)=oo. В достаточно
z-*a
малой проколотой окрестности V— {zfC : 0<]z—a\ <
<г} точки афса или F'={z?C : r<|zf<oo} в случае
бесконечно удаленной точки а== оо функция / (z) пред-
ставима в виде ряда Лорана специального вида:
или соответственно
с конечным числом отрицательных степеней в главной
части при а ф оо или соответственно конечным числом
положительных степеней при а= оо. Натуральное число
т в этих разложениях наз. порядком, или крат-
кратностью, полюса а; при т=\ П. наз. прос-
простым. Разложения A) и B) показывают, что функция
р (z) = (z—a)mf(z) при аф оо или р (z) = z~mf (г) при а= оо
аналитически продолжается в полную окрестность по-
полюса а, причем р(а)^0. Иначе полюс а порядка т
можно еще охарактеризовать тем, что функция i/f(z)
имеет в этой точке а нуль кратности т.
Точка а=(а1, ... , ап) комплексного пространства
С", и^2, наз. П. аналитич. функции /(z) многих комп-
комплексных переменных z=(zx, ... , zn), если выполняются
следующие условия : 1) f (z) голоморфна всюду в нек-рой
окрестности U точки а, за исключением множества Pel
dU, а?Р; 2) f(z) не продолжается аналитически ни в
одну точку Р; 3) существует голоморфная в U функция
q (z)^=0 такая, что голоморфная в [т\ Р функция
р (z) = q(z)i(z) голоморфно продолжается во всю окрест-
окрестность U, причем р(а)фО. Здесь также
lim /(z) = lim ?Щ- =-- оо,
однако при гСз*2 П., как и особые точки вообще, не мо-
могут быть изолированными.
Лит.: [1] Ш а б а т Б. В., Введение в комплексный анализ,
2 изд., М., 197Й. Е. Д. Соломенцев.
ПОЛЯ ОПЕРАТОР — линмшое слабо непрерывное
отображение / ->- cp/,/(;?>L(R4), пространства #Л(К4) ос-
основных функций f{x), ,r? R4, принимающих значения из
конечномерного векторного пространства L, в множе-
множество операторов (вообще говоря, неограниченных), опре-
определенных на плотном линейном многообразии D(j ^ Н
нек-рого гильбертова пространства Н. При этом пред-
предполагается, что как в L, так и в Я действуют нек-рые
представления g—>- Tg(B L) и g -+¦ Ug (в Н), #?G, неод-
неоднородной группы Лоренца G, причем так, что выполне-
выполнено равенство
где
В зависимости от представления в L (скалярного, век-
векторного, сшшорного и т. д.) поле {ф^, /^?)i(R4)} наз.
соответственно скалярным, векторным
или спинорным. Семейство П. о. {(fy, .1^О1{^)}
вместе с представлениями {Tg, g?G}n {U g, g?G}, для
к-рых выполнено условие (**, а также еще ряд общих
требований (см. [1]), паз. квантовым (или кван-
квантованным) полем.
Кроме нек-рых моделей, относящихся к двумерному
или трехмерному миру (см. 12], [4]), построены A983)
только простые примеры т. н. свободных квантовых по-
полей [3].
Лит.: [1] Й о ст Р., Общая теория квантованных нолей,
пер. с англ., М., 1967; [2] Саймон Б,, Модель Р (ср)г евкли-
евклидовой квантовой теории поля, пер. с англ., М., 1976; [3] Бого-
Боголюбов Н. Н., Ширков Д. В., Введение в теорию кван-
квантованных полей, М., 1957; [4] Евклидова теория поля. Марков-
Марковский подход, пер. с англ., М., 1978. Р. А. Миняос.
ПОЛЯРА — 1) П. точки Р относительно
невырожденной линии 2-го порядка — мно-
множество точек N, гармонически сопряженных с точкой Р
относительно точек Мг и Мг пересечения линии 2-го
порядка секущими, проходящими через точку Р. Поля-
Поляра является прямой линией. Точку Р наз. полюсом.
Если точка Р лежит вне линии 2-го порядка (через точ-
рис
Рис. 2.
ку Р можно провести две касательные к линии), то П.
проходит через точки касания данной линии с прямыми,
проведенными через точку Р (см. рис. 1). Если точка Р
лежит на линии 2-го порядка, то П. является прямая,
касательная к данной ли-
линии в этой точке. Если П.
точки Р проходит через
точку Q, то П. точки Q
проходит через точку Р
(см. рис. 2).
Всякая невырожденная
линия 2-го порядка опре-
определяет биекцию точек про-
проективной плоскости и мно-
множества ее прямых — по-
поляритет (полярное пре-
образование). Соответст-
Соответствующие при этом преобразовании фигуры ная. в з а-
и м н о полярными. Фигура, совпадающая со
своей взаимно полярной, на.ч, авто полярной
(см., напр., автоиоляр-
ный трехвершинник PQR
на рис. 2).
Аналогично определяет-
определяется П. (полярная
плоскость) нек-рой
точки относительно невы-
невырожденной поверхности
2-го порядка.
Понятие II. относитель-
относительно линии 2-го порядка
обобщается на линии п-то
порядка. При этом задан-
заданной точке плоскости ставится в соответствие п—1 по-
поляр относительно линии л-го порядка. Первая из этих
П. является линией порядка п — 1, вторая, являющаяся
П. заданной точки относительно первой П., имеет по-
порядок п—2 и т. д. и, наконец, (п—1)-я П. является
прямой линией.
Лит.: [1] Ефимов Н. В., Высшая геометрия, 6 изд.,
М., 1978; [2] Постников М. М., Аналитическая геомет-
геометрия, М., 1973. А.Б.Иванов.
2) П. А° подмножества А локально выпуклого топо-
топологического векторного пространства Е — множество
функционалов / из сопряженного пространства Е', для
к-рых |<.т, />|<1 для всех х?А (здесь <х, /> значение
/в х). Би полярой А°° наз. множество векторов х
пространства Е, для к-рых |<г,/>|<;1 для всех/?Л°.
П. выпукла, уравновешена и замкнута в слабой то-
топологии. Биполяра А°° является слабым замыканием
выпуклой уравновешенной оболочки множества А.
Кроме того, (А°°)°—А°. Если А — окрестность нуля и
пространстве Е, то ее поляра А" является компактом в
слабой * топологии (теорема Банаха — А л а-
о г л у).
П. объединения Ua^a любого семейства {Аа} мно-
множеств из Е есть пересечение П. этих множеств. П. пере-
пересечения слабо замкнутых выпуклых уравновешенных
множеств А а есть замкнутая в слабой * топологии вы-
выпуклая оболочка их П. Если А — подпространство в Е,
то его П. совпадает с подпространством в ?", ортого-
ортогональным к А.
За фундаментальную систему окрестностей нуля,
определяющих слабую * топологию пространства Е',
можно принять систему множеств вида М", где М про-
пробегает все конечные подмножества пространства Е.
Подмножество функционалов пространства Е' равно-
равностепенно непрерывно тогда и только тогда, когда оно
содержится в П. нек-рой окрестности нуля.
Лит.: [1] Эдварде Р., Функциональный анализ, пер.
с англ., М., 1969. В. И. Ломоносов.
ПОЛЯРИЗОВАННОЕ АЛГЕБРАИЧЕСКОЕ МНО-
МНОГООБРАЗИЕ —¦ пара (F, I), где V — полное гладкое
многообразие над алгебраически замкнутым полем к, \
из Pic I'.'IMe'T — класс нек-рого обильного обратимого
пучка, Pic°F —связная компонента абелевой схемы
Пикара Pic V. В случае, когда V — абелево многооб-
многообразие, определено также понятие степени по-
поляризации П. а. м.; она совпадает со степенью
изогении фjg : V —>¦ Pic°F, определяемой пучком
а именно:
где Тх — морфизм сдвига на х, ж? V. Поляризация сте-
степени 1 наз. главной поляризацией.
Понятие П. а. м. тесно связано с понятием поляризо-
поляризованного семейства алгебраич. многообразий. Пусть
/: X —>¦ S — семейство многообразий с базой S, то
есть / — гладкий проективный морфизм схемы X в.а
нётерову схему S, слоями к-рого являются алгебраич.
многообразия. Поляризованным семей-
семейством наз. пара (X/S, |/5), где XIS — семейство
/ : X ->- S с базой S, a \l'S — класс относительно обиль-
обильного обратимого пучка J?xis в Нот E, Pic X/S) по мо-
модулю Нот E, Vic°X/S), где Pic X/S — относительная
схема Пикара.
Введение понятий поляризованного семейства и
П. а. м. необходимо для построения пространств моду-
модулей алгебраич. многообразий (см. Модулей теория).
Так, напр., не существует пространства модулей всех
гладких алгебраич. кривых рода gjsl, а для поляризо-
поляризованных кривых такое пространство модулей существует
[4]. Одним из первых вопросов, связанных с понятием
поляризации многообразий, является вопрос об одно-
одновременном погружении в проективное пространство по-
поляризованных многообразий с фиксированными чис-
численными инвариантами. Если (К, ?) содержится в каче-
качестве слоя в поляризованном семействе (X/S, %/S) со
связной базой S и относительно обильным пучком
%x!s(z&S, то существует ли такая константа с, завися-
зависящая только от многочлена Гильберта h (и)=%( V, JS"),
что при п>с пучки JSs с многочленом Гильберта h(n)
и с H'(XS, JPsn)^=O при г>0 очень обильны для всех
П. а. м. (Xs, |j), где s?S? Для гладких П. а. м. над
алгебраически замкнутым полем характеристики 0 от-
ответ на этот вопрос положителен [3], а в случае поверх-
поверхностей основного типа с канонич, поляризацией кон-
константа с не зависит даже от многочлена Гильберта (см.
[1], [2]).
Лит.: [1] Bombieri E., «Publ. malh. IHES», 1972,
X 42, р. 447—95; [2] К о da i га К., «J. Math. Soc. Jap.»,
1968, v. 20, № 1—2, p. 170—92; [3] M a t s и s a k а Т., М « m-
ford D., «Ашег. J. Math.», 1964, y. 86, № 3, p. 608—84; [4]
Mumford D., Geometric invariant theory, В., 1965.
В. С. Нуликов.
ПОЛЯРИТЕТ, полярное прообразов а-
н и е,— корреляция л, для к-рой я2-—id, то есть л(У)-
= Х тогда и только тогда, когда л(Х)- Y. П. разбивает
все подпространства на пары, в частности, если пара об-
образована подпространствами So и 5„_ь где ?„---¦
— n(Sn-i) —точка, a Sn-l~n(S0) —гиперплоскость,
то So наз. полюсом гиперплоскости
5п-1, a Sn-1 наз. полярой точки So. Простран-
Пространство Un(K) над телом К обладает П. тогда и только тог-
тогда, когда тело допускает и н в о л то т и в н ы й ин-
инверсный автоморфизм а (т. е. а2"id).
Пусть л представляется полубилинейной формой ja(.r,
у). Тогда л будет П. в том и только в том случае, когда
из fa{x, у)=0 следует fa(y, x)-—0.
Поляритет я является либо с и м п л е к т и ч е с к о й
корреляцией, характеризующейся тем, что
Pczn(P) для любой точки Р (в этом случае j{x, у)
является кососимметрич. формой на Л„ + ь а А' — по-
полем), либо л представляется а-симметрнч. формой на
А„ + г : a(ia(x, y))~fa{y, *) (симметрически й
П.), в этом случае существование нестрого изотропного
нулевого подпространства равносильно тому, что ха-
характеристика тела саг К— 2 (в частности, если Саг Кф
7=2, то любое нулевое подпространство строго изотроп-
изотропно).
Относительно поляритета я определяется разложение
проективного пространства на подпространства, позво-
позволяющее привести полубилинейную форму, представля-
представляющую л, к каноипч. виду. Важнейшими среди них яв-
являются:
М — максимальное неизотропное нулевое подпрост-
подпространство, его размерность я(л)— 1, где п четно и наз.
дефектом я, / кососимметрична;
U ¦— максимальное строго изотропное нулевое под-
подпространство, его размерность i(n) — 1, i наз. индек-
индексом :, /=0;
J — компонента, свободная от нулевых подпрост-
подпространств, неизотропна, причем / является положительно
или отрицательно определенной, М [\J~- 0;
W-M-\-U — максимальное нулевое подпространст-
подпространство, его размерность г(я) + п(л) — 1.
Проективное преобразование F наз. л-д опусти-
мым (относительно поляритета я), если n,F=Fn.
Полулинейное преобразование (F, ф) тогда и только
тогда индуцирует я-допустимое проективное преобра-
преобразование, когда в К существует с такое, что f(Fx, Fy) =
-cq>{j(x, у)), л-доиустимые преобразования образуют
группу Gn (наз. группой П.). Если группа Gn
транзитивна, то либо каждая точка пространства П„
является нулевой (и бл в этом случае наз. с и м п л е к-
тической), либо нет ни одной нулевой точки (и
Gn наз. в этом случае ортогональной при
а =¦ id и унитарной при oc=cid).
Лит.: [1] Ефимов Н. В., Высшая геометрия, 6 изд.,
М., 1978. М. И. Войцеховский.
ПОЛЯРНОЕ МНОЖЕСТВО — 1) П. м. анали-
аналитической функции /(г) комплексных пере-
переменных z~(z1, ... , zn), n^l,— такое множество Р точек
нек-рой области О комплексного пространства С",
что: a) /(z) голоморфна всюду в D\P\ б) / {?) не про-
продолжается аналитически ни в одну точку Р; в) для лю-
любой точки а^Р существуют такие окрестность Ua и го-
голоморфная в Uа функция ge(s)=?=O, что голоморфная в
D[\{Ua\P} функция pa{z)--qa(z)f(z) продолжается
голоморфно u Uа. Во всякой точке а?Р имеем да(о)=0.
П. м. Р состоит из полюсов а^Р функции f(z), в к-рых
ра(а)ф{), и точек неопределенности а?Р функции
f(z), в к-рых ра(а) 0 (предполагается, что pa(z) и qa(z)
не имеют общих множителей, голоморфных и равных ну-
нулю в а). Всякое II. м. есть аиалитич. множество комп-
комплексной размерности п—1.
2) П. м. в теории потенциала — множе-
множество Е точек евклидова пространства R", п^1, такое,
что существует потенциал и^(х), x?Rn, нек-рой бо-
релевской меры ц, принимающий значение ~f-oo в точ-
точках Е и только в них.
В случае логарифмического потенциала при д=2 и
ньютонова потенциала при п^'А для того, чтобы огра-
ограниченное множество Е было П. м., необходимо и до-
достаточно, чтобы Е было множеством тина Gg и имело
нулевую внешнюю емкость. При этом в определении
П. м. можно заменить «потенциал» на «супергармониче-
«супергармоническую функцию». Основные свойства П. м. для этого слу-
случая : а) множество {а}, состоящее из одной точки а? R",
есть П. м.; б) счетное объединение П. м. есть П. м.;
в) любое П. м. имеет лебегову меру нуль в R"; г) при
конформных отображениях П. м. переходит в П. м.
Локальный критерий П. м. см. в ст. Разреженность
множества.
Лит.: [1] Ш а б а т Б. В., Введение в комплексный анализ,
2 изд., ч. 2, М., 1976; [2] Л а н д к о Ф Н. С, Основы совре-
современной теории потенциала, М., 1986; [3] Б р е л о М., Основы
классической теории потенциала, пер. с франц., М., 1964.
Е. Д. Соломенцев.
ПОЛЯРНОЕ РАЗЛОЖЕНИЕ — 1) П. р. лине й-
ного преобразования — разложение линей-
линейного преобразования конечномерного евклидова (или
унитарного) пространства L в произведение самосопря-
самосопряженного и ортогонального (соответственно унитарного)
преобразования. Каждое линейное преобразование А
пространства L допускает П. р.
A-=S-U,
где S — положительно полуопределенное самосопря-
самосопряженное линейное преобразование, a U — ортогональ-
ортогональное (или унитарное) линейное преобразование, причем
S определяется единственным образом. Если А невы-
невырожденно, то преобразование S является даже положи-
положительно определенным, а V также определяется одно-
однозначно. Для одномерного унитарного пространства
П. р. совпадает с представлением комплексного числа z
в тригонометрии, форме. а. Л. Онищик.
2) П. р. оператора — представление операто-
оператора А , действующего я гильбертовом пространстве, в ил-
Д»1
где U — частично изометрический, а Т — положитель-
положительный операторы. Всякий замкнутый оператор А допу-
допускает П. р., причем Т- (А*А) /г (часто используют обо-
обозначение Г=-|-4|), a U отображает замыкание Ид*
области определения сопряженного оператора А на
замыкание области значений R А оператора А (теоре-
(теорема Неймана, см. [1]). П. р. становится единст-
единственным, если потребовать, чтобы начальное и конечное
подпространства оператора U совпадали соответствен-
соответственно с На* и Яа. С другой стороны, U всегда можно вы-
выбрать унитарным, изометрическим или коизометриче-
ским — в зависимости от соотношения коразмерностей
подпространств На* и Д^. В частности, если
dim II Q TiA, =dim // Q ЯА,
то можно выбрать U унитарным п найти такой эрмитов
оператор Ф, что U~- ехр(М>). Тогда II. р. оператора А
запишется в пидс
А — \ А |ехр(гФ),
полностью аналогичном П. р. комплексного числа.
Перестановочность сомножителей в П. р. имеет место
тогда и только тогда, когда оператор нормален.
Получен (см. [2], [3]) аналог П. р. для операторов в
пространстве с индефинитной метрикой.
3)П.р. функционала на алгебре
Неймана — представление нормального функцио-
функционала / на алгебре Неймана А в виде /= up, где р — поло-
положительный нормальный функционал на Л, и?А — час-
частичная изометрия (то есть и*и и ии* — проекторы),
умножение понимается как действие на функционал р
оператора, сопряженного к левому умножению на и
в A :f(x)=p(ux) для всех х?А. П. р. всегда можно
осуществить таким образом, чтобы выполнялось усло-
условие: u*f—p. При этом условии П. р. определено одно-
однозначно.
Всякий ограниченный линейный функционал / на
произвольной С*-алгебре А можно рассматривать как
нормальный функционал на универсальной обертываю-
обертывающей алгебре Неймана А"\ соответствующее П. p. f~up
наз. обертывающим полярным разло-
разложением функционала /. Сужение функцио-
функционала р на А называется абсолютной вели-
величиной функционала и обозначается )/); сле-
следующие свойства однозначно определяют функционал
1/1:111/111 = 11/11 и I / (*) 12< II/И/К***).
В случае, когда А — С (X) — алгебра всех непрерыв-
непрерывных функций на компакте, абсолютная величина
функционала соответствует полной вариации опреде-
определенной им меры.
П. р. функционала во многом позволяет сводить из-
изучение функционалов на С*-алгебрах к изучению поло-
положительных функционалов. С его помощью, напр., мож-
можно построить для каждого f?A' такое представление л
алгебры А, в к-ром / реализуется векторно (т. е. суще-
существуют векторы |, г] из //л такие, что f(x) = (n(x)%, r\),
x?A)t— таким свойством будет обладать представление
л |/| , построенное по положительному функционалу
Я|/| с помощью конструкции Гельфанда — Наймарка —
Сегала ГНС-конструкции).
4) П. р. элемента С*-а л г е б р ы — представ-
представление элемента С*-алгебры в виде произведения поло-
положительного элемента на частично изометрический.
П. р. возможно не для всех элементов: в обычном П. р.
оператора Т в гильбертовом пространстве положитель-
положительный сомножитель принадлежит С*-алгебре, порожден-
порожденной Т, но о частично изометрическом сомножителе мо-
можно утверждать лить, что он принадлежит порож-
порожденной Т алгебре Неймана. Поэтому определяют и
используют т. н. обертывающее П. р. элемента
а?А : a=ut, где t={a*aI/2?A — частично изомет-
рич. элемент универсальной обертывающей алгебры
Неймана А" (предполагается, что А канонически вло-
вложена в А").
Лит.: И] Н а й м а р к М. А., Нормированные кольца,
2 изд., М., 19В8; [2] В о g n a г J., «Stud. Scient. Math. Hung.»,
19E6, t. 1, № 1/2, p. 97 — 102; [3] Д и к с м ь с Ж., С*-алге0ры
и их представления, пер. с фрарщ., М., 1974. В. С. Шулълнт.
ПОЛЯРНОЕ СООТВЕТСТВИЕ — соответствие двух
поверхностей, при к-ром в соответствующих точках ра-
радиус-вектор одной из них параллелен нормали другой и
наоборот. Для каждой гладкой поверхности F в Е3 с
радиус-вектором х существует (при определенных усло-
условиях) полярная ей поверхность F* с радиус-вектором
.г* = —-—— , где п — нормаль, а (.т, и) — опорная
функция к /*', так что
Иногда эти условия также входят в определение П. с.
Понятие П. с. получает наиболее яркое выражение (в
смысле полной двойственности) в цонтроаффинной гео-
геометрии. М. И. Войцеховский.
ПОЛЯРНЫЕ КООРДИНАТЫ — числа риф (см.
рис.), связанные с декартовыми прямоугольными коор-
координатами х к у формулами:
где 0<р<оо, 0<ф<2л. Коорди-
Координатные линии: концентрической
окружности (р= const) и лучи
(9=const). Система П. к.— ор-
ортогональная система. Каждой
точке плоскости Оху (за исклю-
исключением точки 0, для к-рой р=0,
а ф не определено, т. е. может
быть любым числом 0 <ф <2я)
соответствует пара чисел (р, ф) и обратно. Расстояние
р точки Р от точки @, 0) (и о л го с а) наз. ноля р-
н ы м радиусом, а угол ф — полярным уг-
л о м.
Коэффициенты Ламе:
Lp = 1, ?ф = р.
Элемент площади:
da — p dpdy.
Векторные дифференциальные операции:
1
p
1
1 f
дар
I Э2/ 82f
J Эф2 Эр2
1 day _
P Эф '
+ "р~~Эр~ + "
1 Э2/
p2 9ф2
' p ap I ^ эр
Обобщенными П. к. наз. числа г и t|), свянан-
ные с декартовыми прямоугольными координатами
х к у формулами:
х = аг cos гр, г/ == br sin л|э,
гдеО<:г<оо, 0<1|><2я, а>0, Ь>0, афЪ. Координатные
линии: эллипсы (r=const) и лучи (\|)=const).
Д. Д. Соколов.
ПОМЕХОУСТОЙЧИВОСТЬ — понятие, характери-
характеризующее способность системы передачи информации
противостоять искажающему действию помех. Пре-
Предельно достижимую П. для оптимального метода пере-
передачи часто наз. потенциальной П. В теории
передачи информации П. конкретной системы передачи
информации характеризуют сообщений точностью вос-
воспроизведения и, в частности, ошибочного декодирования
вероятностью переданного сообщения.
Лит.: [1] X а р к е в и ч А. А., Борьба с помехами, 2 изд.,
М., 1965; [2] Возенкрафт Д ж., Джекобе И., Тео-
Теоретические основы техники связи, пер. с англ., М., 1969.
Р. Л. Добрушин, В. В. Прелое.
ПОНТРЯГИНА ДВОЙСТВЕННОСТЬ — 1) П. д.—
двойственность между абелевыми топологич. группами
и их характеров группами. Теорема двойст-
двойственности утверждает, что если G — локально
компактная абелева группа и X (G) — ее группа харак-
характеров, то естественный гомоморфизм G ~+ X (X (G)),
переводящий «^Св характер ша : X (G) —>• Т, заданный
формулой
есть изоморфизм топологич. групп. Из этой теоремы
выводятся следующие утверждения.
I. Если Н — замкнутая подгруппа в G и
— ее аннулятор в X (G), то И совпадает с аннулятором
{a?G\a(a)=0
подгруппы Н*\ при этом группа Х(Н) естественно изо-
изоморфна X(G)/H*, а X(GIH) — группе Н*.
II. Если ф : G—*¦ Й — непрерывный гомоморфизм
локально компактных абелевых групп, то после отож-
отождествления группы G с X (X (G)) и группы Н с X (X (Н))
при помощи изоморфизмов а —*¦ ша гомоморфизм (ф*)*
отождествляется с ф.
III. Вес группы X (G) (как топологич. пространства)
совпадает с весом группы G.
П. д. сопоставляет компактным группам G дискрет-
дискретные группы X (G) и наоборот. При этом компактная
группа G метризуема тогда и только тогда, когда X (G)
счетна, и связна тогда и только тогда, когда группа
X (G) без кручения. Конечномерность компактной груп-
группы G равносильна тому, что X (G) имеет конечный ранг
(см. Ранг абелевой группы). Конечномерная компакт-
компактная группа G локально связна тогда и только тогда,
когда X (G) конечно порождена. Если G конечна, то
П. д. совпадает с двойственностью конечных абелевых
групп, рассматриваемой над полем С комплексных
чисел.
Топологич. группы, для к-рых верна теорема двойст-
двойственности, наз. рефлексивными. Они не исчер-
исчерпываются локально компактными группами, т. к. лю-
любое банахово пространство, рассматриваемое как топо-
логич. группа, рефлексивно [8]. О характеризации реф-
рефлексивных групп см. [9].
Аналог П. д. известен и для некоммутативных групп
(теорема двойственности Танака —
К р е й н а) (см. [4], [6], [7]). Пусть G — компактная
топологич. группа, R — алгебра комплекснозначных
представляющих функций на G, S (R) — множество всех
ненулевых гомоморфизмов алгебр ш : R —>- С, удовле-
удовлетворяющих условию ш(/)=ш(/), /?Д- В S (R) опреде-
определяется умножение (а, |3) —>- а|5, удовлетворяющее сле-
следующему условию: если р : G —>- U (т) — неприводимое
непрерывное унитарное представление группы G и
Pif(g) — его матричные элементы, то
I («Р) (Р,7) 11 = 11 «(Р.7) 11-1 Р(Р«7) И-
Это умножение и естественная топология превращают
S (R) в топологич. группу. Каждому g?G отвечает го-
гомоморфизм a.g?S (R), задаваемый формулой
Тогда соответствие g —>• ag есть изоморфизм топологич.
группы G на S(R). Дано также алгебраич. описание
категории алгебр R, к-рая оказывается, таким образом,
двойственной категории компактных топологич. групп.
Эта теория допускает обобщение на случай однородных
пространств компактных топологич. групп (см. [4|).
Лит.: [1] П о н т р я г и н Л. С, «Ann. Math.», 1934, v. .'iu,
№ 2, p. 361—88 (рус. пер.— «Успехи матем. наук», 1936, в. 2,
с. 177—95); [2] его же, Непрерывные группы, 3 изд., М.,
1973; [3] К a m p e n E. van, «Ann. Math.», 1935, v. 36, p.
448—63; [4] К р е й н М. Г., «Укр. матем. ж.», 1949, т. 1, Jfl 4,
с. 64—98; 1950, т. 2, № 1, с. 10—59; [5] Моррис С, Двой-
Двойственность Понтрягина и строение локально компактных абе-
левых групп, пер. с англ., М., 1980; [6] Наймарк М. А.,
Нормированные кольца, 2 изд., М,, 1968; [7] Хьюитт Э.,
Росс К., Абстрактный гармонический анализ, иер, с англ.,
т. 2, М., 1975; 18] Smith M. F., «Ann. Math.», 1952, v. 56,
№2, p. 248—5.4; [9] Venkataraman К., «Math. Z.»,
1976, Bd 149, H. 2, S. 109 — 19. А. Л. Опищи-к.
2) П. д. в топологии — изоморфизм между
р-мерной группой когомологий Александрова — Чеха
Нр (A; G) с коэффициентами в группе G компактного
множества А, лежащего в re-мерном компактном ориен-
ориентируемом многообразии М", и (п — р — 1)-мерной груп-
группой гомологии H°n-p-i(B; G) дополнения В~Мп ч.4
в предположении, что НР(М"; G) = HP + 1(Mn; G) О
(гомологии и когомологий в размерности нуль — при-
приведенные; символ с означает компактные носители).
Для случая, когда А или В — конечный полиэдр, этот
изоморфизм был установлен Дж. Александером (J.Ale-
(J.Alexander). Н. Стинрод (N. Steenrod) установил наличие
такого изоморфизма для любого открытого подмноже-
подмножества АсМ", а К. А. Ситников — для произвольного
подмножества А.
В приведенном виде закон двойственности Понтря-
Понтрягина был сформулирован П. С. Александровым. В пер-
первоначальной форме утверждалась двойственность в
смысле теории характеров между группами Нр(А; G*)
и Hcn^p-i(B; G), где G* — бикомпактная группа ха-
характеров дискретной группы G. Эквивалентность обеих
формулировок закона двойственности следует из тога,
что группа Нр(А; G*) есть группа характеров группы
НР(А; G). Из предположения об ацикличности многооб-
многообразия в размерностях р и р-\-1 и из точной последова-
последовательности когомологий пары (Мп, А) вытекает, что
Нр(А; G) = Hp + 1(M", A; G), поэтому П. д.—простое
следствие двойственности Пуанкаре — Лефшеца (см.
Пуанкаре двойственность).
Наиболее общая форма соотношений двойственности
рассматриваемого типа состоит в следующем. Пусть
М" — произвольное многообразие (возможно, обоб-
обобщенное, не обязательно компактное и не обязательно
ориентируемое), <§ — локально постоянная система
коэффициентов со слоем G, А — произвольное подмно-
подмножество в М" и Ф — семейство всех замкнутых в М"
множеств, содержащихся в В--М"\А. Тогда если
Пр{М"; $)=Нр + 1(М"; $) = Q, то НР(А; &?„{•§)) =
= 11^ _Х(В; '§). Здесь Н^ — гомологии с замкнутыми
носителями, содержащимися в Ф (т. е. прямой предел
групп Hq{F; g), /"'^Ф), а Жг№) — локально постоян-
постоянная система коэффициентов, образованная группами
Нп(Мп, Мп\х; <§), х?Мп. В приведенном равенстве
коэффициенты ,9Jfn(;§) для когомологий могут быть за-
заменены на g, если рассматривать гомологии с коэффи-
коэффициентами в нек-рой специально определяемой системе.
Лит.: [1] Александров П, С, Топологические тео-
теоремы двойственности, ч. 1 — Замкнутые множества, М., 1955
(Тр. Матем. ин-та АН СССР, т. 48); [2] Масси У., Теория
гомологии и когомологий, пер. с англ., М., 1981.
Е. Г. Скляренко,
ПОНТРЯГИНА ИНВАРИАНТ — инвариант осна-
оснащенных перестроек поверхности с заданным на ней ос-
оснащением. Пусть (М2, U) — замкнутая ориентируемая
поверхность с re-мерным оснащением U в Sn + 2, т. е.
тривиализацией нормального «-мерного расслоения
над поверхностью М2 n Sn + 2. Любой элемент z?Ht(M2,
%) может быть реализован гладко иммерсированнои ок-
окружностью с самопересечениями, к-рыо являются толь-
только двойными и трансверса мьными. Пусть выбрана и за-
зафиксирована нек-рая ориентация окружности S1;
пусть !/,((/), и2(у), ... , ип(у) — ортогональные векторы,
возникающие из оснащения U, ограниченного на точку
f(y)i y?C; un + i(y) — вектор, касательный в точке j(у)
к кривой C=f(y), согласно выбранной ориентации S1;
un + i(y) — вектор, касательный к М2 в точке f(y), орто-
ортогональный un + i(y) и направленный так, что последова-
последовательность векторов их(у), ... , и „(у), ип + 1(у), ип + 2(у)
дает стандартную ориентацию сферы Sn + 2. Возникаю-
Возникающее отображение h: S1 -*¦ SOn+2 задает элемент из
группы m-,(iSOn + 2), к-рая при п^1 изоморфна %г.
Пусть |3^0, если h гомотопно нулю, и Р=1, если h не
гомотопно нулю, и пусть значение функции Фо : Н^М2,
%.)-*¦%z равно сумме по mod 2 числа двойных точек
кривой С, реализующей элемент z, и числа Р, определен-
определенного по кривой С. Так, определенное значение Ф0(г)
зависит только от гомологич. класса z, и функция
Ф0(г) удовлетворяет следующему условию:
Фо (Zl 4- z2) ^ Ф„ (zj) + Фо (z2) + Ф (Ч, z2) mod 2,
где Ф : Я1(Л/2, 1)ХНХ(М2, й) ->- Z — форма пересе-
пересечений одномерных гомологии поверхности М2. arf-кн-
вариант функции Фо и наз. инвариантом П о н-
т р я г и н а пары (ЛЯ, U). Пара (М2, U) оснап;енно пе-
перестраивается до пары (S2, U) тогда и только тогда, ког-
когда П. и. пары (М2, U) равен нулю (теорема Понт-
р я г и н а).
П. и. может быть реализован (га+2)-мерным оснаще-
оснащением на торе, п^2, и является единственным инвариан-
инвариантом двумерных оснащенных кобордизмов. П. и. задает
изоморфизм я„., 2(S")«g2, »^2.
Лит.: 11] П о н т р я г и н Л. С, Гладкие многообразия и
их применения в теории гомотопий, 2 изд., М., 1976.
М. А. Штанъко.
ПОНТРЯГИНА КВАДРАТ — когомологическая опера-
операция 5^2 типа (з ^, 2я; % ft + 1, 4»), т. е. отображение
5\: Н-ЦХ,?; z^ —-Я*» (*, У; 2г* + 1),
определенное для любой пары топологич. пространств
(X, Y) и такое, что для любого непрерывного отобра-
отображения / : (X, Y) —у (X', У) имеет место равенство
/*552=5:>2/* (естественность).
П. к. обладает следующими свойствами:
4>> где г: Z%k—+%ik + l
— вложение;
2)р5>2и = и2 и Р2ри = и\ где p:H*(X,Y;z^ + 1)-+
-->//*(*, У; Z2k)
— гомоморфизм приведения по mod 2;
3) 5^,2-2^, где 2 : Н^~\Х; G) -+IP"BX; G) —
изоморфизм надстройки, а ^р — Постникова квадрат
(иными словами, когомологич. надстройкой над {р2
является $*). Если
5V K{Ztit, 2n)-*K(Ztk^, in)
5>: К B2Й, 2n-l)-+K(Z2fl + 1, An — I)
— представляющие отображения, то Qff>2==9s-
Свойства 1), 2) однозначно характеризуют П. к. и
потому могут быть приняты за определяющие его акси-
аксиомы. Конструктивно П. к. определяется формулой
где и?Сгп(Х; z) — коцикл mod 2ft (о {/(-произведениях
см. ст. Стипрода квадрат).
Существует (см. [5], [6]) обобщение П. к. на случай
произвольного нечетного простого р. Это обобщение яв-
является когомологич. операцией типа B ?, 2п; % д + 1,
2рп) и наз. р-й степенью Понтрягина ^рр.
Для операции ff>р имеют место формулы (к-рые эту опе-
операцию однозначно характеризуют):
где i : % k -*¦ й й + j — вложение;
где р : Н*(Х, У; % k,-,)—>-H*(X, Y\% .,)—гомомор-
V + V
физм приведения по модулю р, обобщающие соответст-
соответствующие формулы для !р2. Аналог формулы 3) для $*р
имеет вид5>р2 = 0, означающий, что когомологич. над-
надстройка над 3>р при р>2 равна нулю. При р>2 имеет
место равенство ?Р p(uv)= ffi pu)(^pv), в к-ром умноже-
умножение можно считать как внешним (X-умножением),
так и внутренним ((J-умноженном). При р~2 соответст-
соответствующее равенство имеет место только с точностью до
слагаемых порядка 2.
Наиболее общим образом П. к. определяется для ко-
гомологий над произвольной конечно порожденной абе-
левой группой я (см. [2], [3]). Окончательный вид этого
обобщения (см. [6]): П. к. представляет собой кольцевой
гомоморфизм
5>*: Г(П2"(Х; л))~^Н*(Х; Г (я)),
где Г — функтор разделенных степеней алгебры. Если
л=1,р, то р-я компонента этого гомоморфизма совпа-
совпадает с р-й степенью Понтрягина ^р (при р = 2 — с II. к.
Лит.: [1] П о н т р я г и н Л. С, «Докл. АН СССР», 1942,
т. 34, с. 39—41; [2] Болтянский В. Г., Гомотопическая
теория непрерывных отображений и векторных полей, М., 1955;
[3] Постников М. М., «Докл. АН СССР», 1949, т. 64.
№ 4, с. 461—62; [4] В го w d e r W., Thomas E., «Quart,
J. Math.», 1962, v. 13, p. 55—60; [5] Thomas E., «Proc
Nat. Acad. Sci. USA», 1956, v. 42, p. 266—69; [6] его ж и.
The generalized Pontrjagin cohomology operations and rings with
divided powers, Providence, 1957.
C. II. Малыгин, M. М. Постников,
ПОНТРЯГИНА КЛАСС — характеристический класс,
определенный для действительных векторных расслое-
расслоений; П. к. введены в 1947 Л. С. Понтрягиным 111. Для
векторного расслоения | с базой В П. к. обозначаются
символом pj(^)?IJ4' (В) и полагаются равными
j°/(S)=(—1)' С2< F(Х)С), где ?(х)С — комплексификация
расслоения |, a ct — Чжэня классы. Полным П. к.
наз. неоднородный характеристик, класс р - 1-!-/>!+
-fp2+... . Иначе говоря, 11. к. определяются как
классы когомолопш pi?llil(BOn), задаваемые равен-
равенством />,-—/*(( — 1)' c2l), где / : ВОп~+ (BUn) — отобра-
отображение, соответствующее комплексификации униРер-
сального расслоения, a cn?H2k(BU ,t) — классы Чжэня.
Пусть (x,,)R — овеществление универсального рассло-
расслоения v.n над BUn. Полный П. к. р((х„)к) расслоения
(xn)R совпадает с Il^l + yp ?H*(BUn), где хи ..., хп —
образующие By (см. Характеристический класс).
Частичное описание кольца когомологий Н*(ВОп)
может быть получено в терминах образующих By сле-
следующим образом. Отображение g : BV^n,,-. —>- ВОп, соот-
соответствующее расслоению (>C|n/.,i)R либо (x[h/2i)r®0i
где 6, — одномерное тривиальное расслоение, индуци-
индуцирует гомоморфизм колец g*:ll*(BOn) —у ll*(BU^nj,,-^),
при к-ром подкольцо кольца П*(ВОп), порождаемое
П. к. ру, р2, ..., pln'2\ отображается мономорфпо на
подкольцо кольца Н*(В1'п), состоящее из всех четных
спмметрич. полиномов от образующих By. Четность по-
понимается в том смысле, что каждая переменная я,- долж-
должна входить в полином в четной степени. Тем самым
получается выражение любого элемента кольца Z (Р\,.--
..., prnf2-,)dH*(BOn) через образующие By, что важно
для ирактич. вычислений с П. к. Характеристич. класс,
определяемый четным симметрич. полиномом от обра-
образующих By, может быть выражен через П. к. следую-
следующим образом. Полином выражается через элементарные
симметрич. функции переменных х\, ... , х%, а затем
вместо элементарных симметрич. функций подставляет-
подставляется П. к.
Если Ъ,, г) — два действительных векторных расслое-
расслоения над общей базой, то класс когомологий р (?©т)) —
—/j(?)p(T|) имеет порядок не больше двух; это связано
с, том, что для первого класса Чжэня сх(Х)=—^(Х).
Пусть нек-рое кольцо Л, содержащее V2, рассматри-
рассматривается в качестве кольца коэффициентов и пусть />,- —
П. к. со значениями в //*(¦; Л). В этом случае имеет
место равенство
р
или
Кольцо Н**(ВОп; Л) мономорфно отображается в
H**(BU,,,-.; Л), и образ этого отображения совпадает
с подкольцом всех четных симметрич. рядов с образую-
образующими By в качестве переменных. При этом полный П. к.
переходит в полином n^pii+xj), а П. к.— в элемен-
элементарные симметрич. функции от переменных х\, ..., хп .
Теорема:
Н**(ВОп; А)=Л[[Р1, .... Р[п/2]]].
Кольцо когомологий H*(BSOn) содержит кроме П. к.
также эйлеров класс e?H"(BSOn). Теорема:
И** (BSO2k + 1; Л) =Л [[/>!, ..., рк, е]],
H**(BSO2k; Л)=Л[[рь ..., Рк-г, е]],
для пространства BSO^ имеет место равенство р^~е2.
Отображение g : ви^^-*-ВО„ пропускается через
5?/ _>. BSOn. Индуцированное отображение
H**{B~SOn) ->#**0Bt/)[rl/2] переводит е в нуль при
нечетном га и в Uf^x; при четном га.
Пусть /(/) ? Q |[(Ц —четный формальный степенной
ряд над полем Q. Тогда ряд nf™/j]/(^,) определяет не-
к-рый неоднородный элемент кольца Н**(ВОп\ Q), т. е.
характеристич. класс. Допуская нек-рую вольность,
можно записать
Характеристич. класс х стабилен (то есть (|)
= ж(§), где G — тривиальное расслоение) тснда ti только
тогда, когда свободный член рнда / (t) parson единице.
Если положить f(t) — t/th t, то построенный описанным
способом характеристич. класс обозначается через L
и наз. L-к л а с с о м Хирцебруха,
Стандартная процедура выражения ряда П/(г/) через
элементарные симметрич. функции переменных х\, ...
..., хп приводит к представлению класса L в виде ряда
от П. к. Другой важный для приложений характери-
характеристич. класс получается, если положить
' sh(</2) e'/2-c-</2
Класс, задаваемый четным симметрич. рядом
Х./2
наз. А -классом. Аналогично, А -классом
наз. характеристич. класс, задаваемый рядом П/(ж,),
где /W—ihTT)- Оба эти класса, как и L, могут быть
выражены через П. к.
Топологическая инвариантность.
В 19С5 С. П. Новиков [2J доказал, что П. к. с рацио-
рациональными коэффициентами двух гомеоморфных многооб-
многообразий совпадают. До этой работы было известно, что
рациональные П. к. кусочно линейно инвариантны, т. е.
совпадают для двух кусочно линейных гомеоморфных
многообразий. Более того, были определены (см. [4])
рациональные П. к. для кусочно линейных многообра-
многообразий (возможно с краем). Был дан пример (см. [5]), пока-
показывающий, что целочисленные П. к. не являются тоио-
логич. инвариантами.
В 1969 было доказано (см. [7]), что слой Top/PL рас-
расслоения BPL —>- В Тор имеет гомотопич. тип про-
пространства Эйленберга —Маклейна Л'(„¦;.,, 3). Отсюда
следует топологич. инвариантность рациональных П.
к., а также вытекает опровержение о с н о в н о ii
гипотезы комбинаторной топологии
(Hauptvermutung).
Обобщенные классы Понтрягина.
Пусть h* — обобщенная теория когомологий, в к-рой
определены классы Чжэня а,-. Если для одномерного
комплексного векторного расслоения к выполнено ра-
равенство 01(Я) = — <Ji(A,), то П. к. со значениями в тео-
теории h* можно определить прежней формулой />,•(!)-¦=
=(—1)'сг2,'(?®С). Определенные таким образом классы
будут обладать свойством Р (|0n) = -P (QP (п), где Р =
=-1 + Р1+^>2+---— полный П. к., рассматриваемый в
теории й*(ХJ [1/2].
Однако во многих практически используемых обоб-
обобщенных теориях (напр., в /f-теории) приведенное ра-
равенство для ai не имеет места. В таких теориях нецеле-
нецелесообразно определять П. к. описанным способом, т. к.
при таком определении не выполняется обычная форму-
формула для полного класса суммы Двух расслоении, даже
после включения V2 в коэффициенты. Можно определять
обобщенные П. к. следующим образом. Пусть h* —
мультипликативная теория когомологий, в к-рой уни-
универсальным образом задана ориентация и A®С) ?
?( ) расслоения ?®C, где ? — произвольное
«-мерное действительное расслоение над В. Пусть
<Ч?®С) — эйлеров класс расслоения |(g)C, e(?(g)C)=
= i*u(\@C), где i : В ->¦ #5®^ _ включение нулевого
сечения. П. к. в теории h* наз. характеристик, классы
Р(, определенные для действительных векторных рас-
расслоений и удовлетворяющие следующим условиям.
1) P,(g)=O, если г > 2dimg;
2) /",-(?©8)= -/",•(!), где в — тривиальное расслоение;
3) pk(l®<\) — ^ipi(l)pk-iW) — элемент порядка сте-
степени двойки;
4) Рп(%) = (—1)"е(|®С), где it = dim|.
Доказано существование и единственность характе-
ристич. классов с перечисленными свойствами. II. к.
в этом смысле приводят к понятию двузначной формаль-
формальной группы над кольцом li*(pt), соответствующей тео-
теории h*.
Характеристич. классы я,- в ЛТ-теории определяются
следующей формулой:
где s— t—t2, здесь у,- — Чжэня класса в ;22-градуиро-
ванной АГ-теории.
Лит.: [1] Понтрягин Л. С, «Матем. сб.», 1947, т.
21, с. 233—84; [2] Новиков СП., «Докл. АН СССР»,
1965, т. 163, с. 298—300- [3] Бухштабер В. М., «Матем.
сб.», 1970, т. 83, с. 575—95; [4] Рохлин В. А., Ш в а р ц
А. С, «Докл. АН СССР», 1957, т. 114, с. 490—93; [5] М и л-
н о р Д ж., «Математика», 1959, т. 3, № 4, с. 3—53; 1965, т. 9,
№ 4, с. 3—40; [6] С т о н г Р., Заметки по теории кобордизмов,
пер. с англ., М., 1973; 17] К i г b у R., Siebenmann L.,
Foundational essays on topological manifolds, smoothings and
Iriangulations, Princeton, 1977. А. Ф. Харшиладзе.
ПОНТРЯГИНА ПОВЕРХНОСТИ — лежащие в че-
четырехмерном евклидовом пространстве R4 двумерные
континуумы Ст, dim Cm~2, такие, что их гомологиче-
гомологическая размерность по данному модулю т=2, 3, ... равна
1 и что они в этом смысле «размерно неполноценны».
Л. С. Понтрягин [1] построил такие поверхности С2,
Cs, что их топологич. произведение С=С2Х С3 есть кон-
континуум размерности 3. Этим была опровергнута гипо-
гипотеза, что при топологич. перемножении двух (метриче-
(метрических) компактов их размерности складываются. Им же
эта гипотеза доказана для гомологич. размерности по
простому модулю и вообще по всякой группе коэффици-
коэффициентов, являющейся полем. Построен также [2] двумер-
двумерный континуум С в R4, топологич. квадрат к-рого С2=
= СХС трехмерен.
Лит.: [1] Понтрягин Л. С, «С.г. Acad. sci.», 1930,
t. 190, p. 1105—07; [2] Болтянский В., «Успехи матем.
наук», 1951, т. 6, в. 3, с. 99—128; [3] Александров П. С,
Введение в гомологическую теорию размерности и общую ком-
комбинаторную топологию, М., 1975. П. С. Александров.
ПОНТРЯГИНА ПРИНЦИП МАКСИМУМА — со
отношения, выражающие необходимые условия силь-
сильного экстремума для неклассической вариационной за-
задачи оптимального управления математической теории.
Сформулирован в 1956 Л. С. Понтрягиным (см. [4]).
Принятая формулировка П. п. м. относится к сле-
следующей задаче оптимального управ-
управления. Дана система обыкновенных дифференциаль-
дифференциальных уравнений
i = /(ar, и), A)
где x?Rn — фазовый вектор, м? ГУ — управляю-
управляющий параметр, / — вектор-функция, непрерыв-
непрерывная по совокупности переменных и непрерывно диффе-
дифференцируемая по х. В пространстве R? задано множест-
множество U допустимых значений управляющего параметра и;
в фазовом пространстве R" даны точки х° и я:1; фикси-
ронаи начальный момент времени t0. Д о п у с т и м ы м
у и р а и л о н и о м является любая кусочно непре-
непрерывная функция и (?), iu <:?<*!, со значениями во множе-
множестве U. Говорят, что допустимое управление w=u(t)
переводит фазовую точку из положения х° в по-
положение х1 (х° -vx1), если соответствующее ему решение
x(t) системы A), удовлетворяющее условию x(to)=xa,
определено при всех t^\t0, 1г] и х (t^^^x1. Среди всех
допустимых управлений, переводящих фазовую точку
из положения х° в положение ж1, требуется найти о п-
тимальное управление — функцию u*(t),
минимизирующую функционал
*), u(l))dt, B)
здесь /°(т, и) — заданная функция того же класса, что
и компоненты f(x, и), x(t) — решение системы A) с
начальным условием x(to)~xn, отвечающее управлению
u(t), t-t — момент прохождения этого решения через
точку х1. Под решением задачи понимают пару, состоя-
состоящую из оптимального управления u*(t) и отвечающей
ему оптимальной траектории x*(t) системы A).
Пусть
Я (if, х, u) = (ip, j(x, и))
— скалярная функция (гамильтониан) переменных ij,,
.г, и, где if=(ifn, ^)?R" + \ ipo?R\ ifi?R«, /=-(/«, /).
Функции //(if, x, и) ставится в соответствие канониче-
каноническая (гамильтонова) система (относительно if, x)
dx _<]!? йф__ дВ_ .о.
dt~ ()il> ' dt~~ ~дх *¦ '
(первое из этих уравнений есть система A)). Пусть
М (г|), x) = sup{H (if, x, и) | u?U}.
Принцип максимума Понтрягнна:
если u*(t), x*(t) (t?\ta, <x]) — решение задачи оптималь-
оптимального управления A), B) (зя—>-х1, u?U), то су1цествует
такая ненулевая абсолютно непрерывная функция
if (i)> что тройка функций if (*), x*(t), u*(t) удовлетворя-
удовлетворяет на \t0, tx] системе C) и для почти всех t?[tl), гх] вы-
выполняется условие максимума
#(if (i), x*(l), u*(t)) = M(y(t),x*(t)), D)
а в конечный момент t1 — условия
o, t,((,)<a (-5)
Если функции if(<), x(t), u(t) удовлетворяют соотно-
соотношениям C), D) (то есть x(t), u(t) образуют экстре-
экстремаль П о н т р я г и н а), то имеют место условия
o?(t) = M(y (t), a:@)ssconst, ifo(*) = const.
Из данного утверждения вытекает принцип максиму-
максимума для задачи о быстродействии (/°=1, J—^—ц). Это
утверждение допускает естественное обобщение на неав-
неавтономные системы, задачи с подвижными концами тра-
траекторий и задачи с ограничениями йа фазовые коорди-
координаты (условием г(г) ?.Х, где X — замкнутое множество
фазового пространства R", удовлетворяющее нек-рым
дополнительным ограничениям (см. [1])).
Допущение к рассмотрению замкнутых множеств U,
X (ати области могут, в частности, задаваться система-
системами нестрогих неравенств) обусловило неклассич. ха-
характер задачи. Основные необходимые условия класси-
классического вариационного исчисления с обыкновенными
производными вытекают из П. п. м. (см. [1], а также
Вейерштрасса условия).
Распространенное доказательство изложенной фор-
формулировки П. п. м., основанное на использовании т. н.
игольчатых вариаций (т. е. на рассмотре-
рассмотрении допустимых управлений, отклоняющихся от опти-
оптимального произвольным образом, но зато лишь на конеч-
ном числе малых интервалов времени), состоит в линеа-
линеаризации задачи в окрестности оптимального решения, в
построении нек-рого выпуклого конуса вариаций опти-
оптимальной траектории и последующем использовании тео-
теоремы об отделимости выпуклых конусов (см. [1]). Соот-
Соответствующее условие далее записывается в аналитич.
форме D), C), в терминах максимума гамильтониана
II (ty, х, и) от фазовых переменных х, управлений и и
сопряженных переменных г|5, играющих
роль, аналогичную Лагранжа множителям в класси-
классическом вариационном исчислении. Эффективное исполь-
использование П. п. м. часто приводит к необходимости решать
двухточечную краевую задачу для системы C).
Наиболее полное решение задачи оптимального уп-
управления получено для линейных систем, где соотноше-
соотношения П. п. м. часто выступают не только как необходи-
необходимое, но и как достаточное условие оптимальности.
П. п. м. получил многочисленные обобщения, напр.,
в направлении охвата более сложных неклассич. огра-
ограничений (в том числе смешанных ограничений на управ-
управления и фазовые координаты функциональных и разно-
разнообразных форм интегральных ограничений), в изучении
достаточности соответствующих условий, в рассмотре-
рассмотрении обобщенных решений, т. н. скользящих режимов,
систем дифференциальных уравнений с негладкой пра-
правой частью, дифференциальных включений, задач опти-
оптимального управления для дискретных систем и систем
с бесконечным числом степеней свободы, описываемых,
в частности, уравнениями с частными производными,
уравнениями с последействием (в том числе с запаздыва-
запаздыванием), эволюционными уравнениями в банаховом про-
пространстве и т. д. Последнее привело к рассмотрению но-
новых классов вариаций соответствующих функционалов,
введению т. н. интегрального принципа максимума,
линеаризованного принципа максимума и т. д. Весьма
общие классы вариационных задач с неклассич. огра-
ограничениями (в том числе в виде нестрогих неравенств)
или негладкими функционалами принято называть
задачами н о н т р я г и н с к о г о типа. От-
Открытие П. п. м. послужило важным стимулом в созда-
создании математич. теории оптимального управления. Оно
стимулировало новые исследования в теории дифферен-
дифференциальных уравнений, функциональном анализе и тео-
теории экстремальных задач, вычислительной математике
и других смежных областях.
Лит.: [1] П о н т р я г и н Л. С, Б о л т я н с к и й В. Г.,
Г а м к р о .г и д л е Р. В., М и щ е н к о К. Ф., Математиче-
Математическая теория оптимальных процессов, 3 изд., М., 1976.
А. Б. Куржапскийщ
ПОНТРЯГИНА ПРОСТРАНСТВО — гильбертово
пространство с индефинитной метрикой Пх, имеющей
конечный ранг индефинитности х. Основные факты гео-
геометрии П. п. установлены Л. С. Понтрягиным [1]. По-
Помимо фактов, общих для пространств с индефинитной
метрикой, имеют место следующие.
Если 5Р — любой неотрицательный линеал в Пк , то
dim ^<:x; если !р — положительный линеал и dim,*/3
= х, то его /-ортогональное дополнение Лг является
отрицательным линеалом и Пи /yV,.Y. При атом N
представляет собой полное пространство но отношению
к норме \х\= У—/(х, х). Если линеал LdTLx невырож-
невырожден, то невырождено его /-ортогональное дополнение М
и UK = MQ>L.
Спектр (в частности, дискретный спектр) /-унитарно-
/-унитарного (/-самосопряженного) оператора симметричен отно-
относительно единой окружности (действительной оси), все
элементарные делители, отвечающие собственным чис-
числам X, |Я|>1, имеют конечный порядок р^, р^<:х, р^—
=р^—X. Сумма размерностей корневых подпространств
/-унитарного (/-самосопряженного) оператора, отве-
отвечающих собственным числам X, |Я|>1 Aш Х>0), не
превосходит числа к.
Основой теории /-самосопряженных операторов,
действующих н П. п. Пи , является следующая теорема
[1]: у каждого /-самосопряженного оператора A (D (А)~-
= Пх) существует х-мерное (максимальное) неотрица-
неотрицательное инвариантное подпространство J7", в к-ром все
собственные значения оператора А имеют неотрицатель-
неотрицательную мнимую часть, и х-мерное неотрицательное инвари-
инвариантное подпространство $", в к-ром все собственные
значения имеют неположительную мнимую часть.
Аналогичное утверждение с заменой верхней (нижней)
полуплоскости на внешность (внутренность) единичного
круга справедливо и для /-унитарных итераторов, а
при нек-рых дополнительных условиях — даже для
операторов в пространстве .П^.
Если U есть /-унитарный оператор, то его макси-
максимальные инвариантные неотрицательные подпростран-
подпространства $~, ?Г' могут быть выбраны таким образом, чтобы
порядки элементарных делителей операторов U ф-=
= U\$~, U (я-/= U\$" были минимальны. Для того чтобы
многочлен Р(А), не имеющий корней внутри единичного
круга, обладал свойством: (P(U)r, Р (f/)z)<:0, а-^Пх,
необходимо л достаточно, чтобы он делился на мини-
минимальный аннулирующий многочлен онератора U а~ .
Если оператор U — циклический, то его неотрицатель-
неотрицательные инвариантные подпространства размерности к
определяются единственным образом. В этом случае
указанное свойство многочлена Р, корни {А,} к-рого
лежат вне единичного круга |л,-|>1, эквивалентно
делимости Р (А) на характеристич. многочлен оператора
U вг-
В П. н. Пи у каждого вполне непрерывного /-само-
/-самосопряженного оператора А такого, что нуль принадле-
принадлежит его непрерывному спектру, остаточный спектр от-
отсутствует. Корневые векторы такого оператора образуют
базис Рисса в Пи по отношению к (дефинитной) норме
(|/|.г, х).
Многие факты об инвариантных подпространствах и
спектре обобщаются на случай /-изометрических и /-не-
растягивающих операторов. Так, если Ах, ... , А„ —
произвольная совокупность собственных значений /-
изометрического оператора, A,-Afe?il, i, k=\, ... , п,
и порядок элементарного делителя в точке А/, то ^^р,-^
<:к. Всякий /-нерастягивающий ограниченно обрати-
обратимый оператор Т обладает х-мерным инвариантным не-
неотрицательным подпространством ^Гтаким, что все соб-
собственные значения сужения Т\$~ лежат в единичном
круге [2]. Аналогичный факт верен для максимальных
/-диссипативных операторов. Вообще /-диссипативный
оператор A, D (A)aD (А*), имеет не более х собствен-
собственных значений в верхней полуплоскости. Между /-изо-
/-изометрическими и /-симметрическими (и, более широко,
/-нерастягивающими и /-диссицативными) операто-
операторами устанавливается связь с помощью Кэли преобра-
преобразования, к-рое в пространстве IIх обладает всеми ес-
естественными свойствами [2]. Это позволяет развивать
теорию расширений одновременно для /-изометриче-
/-изометрических и /-симметрических операторов. В частности, вся-
всякий /-изометрический (/-симметрический) оператор
может быть расширен до максимального. Если его ин-
индексы дефекта не одинаковы, то у него нет /-унитарных
(/-самосопряженных) расширений. Если же они оди-
одинаковы и конечны, то любое максимальное расшире-
расширение является /-унитарным (/-самосопряженным).
Для вполне непрерывных /-диссипативных операто-
операторов в П. н. Пи верен также ряд утверждений о полноте
системы корневых векторов, аналогичных соответствую-
соответствующим фактам из теории диссипативных операторов в про-
пространствах с дефинитной метрикой.
Лит.: [1] Ионтрягин Л. С, «Изв. АН СССР. Сер.
матем.», 1944 т. 8. с. 243—80; [2] И о х в и д о в И. С, К р е й н
М. Г., лТр. Моск. матем. об-ва», 1956, т. 5, с. 367 — 432; [3]
и х ж е, там н.с, 1959, т. 8, с. 413—96; [4] А з и з о в Т. Я.,
И о х в и д о п И. С, «Успехи матем. наук», 1971, т. 26, в. 4,
с. 43—92; [5] К р е й н М. Г., в кн.: Вторая летняя математи-
математическая школа, [т.Л, К., 1965, с. 15—92; [6] Наймарк М.
А., И с м а г и л о в Р. С, в кн.'. Итоги науки. Математический
анализ, 19«8, в. 17, М., 1969, с. 73—105; [7J Надь К.,
Пространства состояний с индефинитной метрикой в квантовой
теории поля, пер. с англ., М., 1969.
Н. К. Никольский, Б. С. Павлов.
ПОНТРЯГИНА ХАРАКТЕР ph — характеристи-
характеристический класс, определяемый равенством ph(g) = ch(|(g)
®С), где |(g)C — комплексификация расслоения f,
ch — Чжэня характер. П. х. как элемент кольца
Н**(ВОп; Q) задается четным симметрич. рядом
2i,i=i (е ~^~е ) и обладает свопствами
Индексный класс /(|) полагается равным Г(|(х)С),
где Т?-H**(BU,,; Q) — Тодда класс. Индексный класс
I(Zff**(BOn; Q) выражается через образующие By по
формуле
= П—i— П-
1-е ' 1-е '
Имеет место следующая теорема о связи П. х. с клас-
классом А. Пусть \ — действительное векторное расслоение
над баяой В, имеющее Spin „-структуру, n=dim |=8fc.
Для таких расслоений имеется изоморфизм Тома в дей-
действительной А'-теории:
Ф: КО* (В)—* КО* (В1).
Пусть
Фя: Я*(б; Q)—^ff*(Bl; Q)
— изоморфизм Тома, однозначно определенный ориен-
ориентацией расслоения %. Тогда
Эта формула является точным аналогом соответствую-
соответствующего утверждения о связи характера Чжэня с классом
Тодда.
Если I — комплексное векторное расслоение, то
T{%)==A{(E,)R)eCl{^)>"i, здесь (?)R — овеществление рас-
расслоения, Т — класс Тодда.
Лит. см. при ст. Поитрягина класс. А. Ф. Харшиладзе.
ПОНТРЯГИНА ЧИСЛО — характеристическое чис-
число, определенное для действительных замкнутых мно-
многообразий и принимающее рациональные значения.
Пусть x?JJ**(BO; Q) — произвольный (необязательно
однородный) стабильный характеристический класс.
Для замкнутого ориентированного многообразия М
рациональное число х[М] — (х(тМ), [М]у наз. чис-
числом Понтрягина многообразия М, соответст-
соответствующим классу х, здесь хМ — касательное расслоение.
П. ч. у \М\ зависит лишь от однородной компоненты
степени dim М класса х. Пусть ш— {i1, ... , ij.} — раз-
разбиение числа п, т. е. набор целых неотрицательных
чисел (j, ..., ikvil-\~...-\-ib=ni&pe>=pi, ...,pt ?Hin(BO).
k
Рациональные числа ри,\М\ определены для замкнутого
многообразия М размерности in и всех разбиений со
числа и.
П. ч. х \М\, х [N] двух бордаитных (в ориентирован-
ориентированном смысле) многообразий М, N равны: х [М\ -х [N]
(теорема Понтрягина).
Согласно этой теореме каждый характеристпч. класс
x(ZH**(BO; Q) индуцирует гомоморфизм х [ J : Q» —>-
—v Q, а каждый элемент [М] ? Q* индуцирует гомомор-
гомоморфизм Н**{ВО; Q) -> Q, х ->- х [М]. Другими словами,
имеется отображение
-> Hom(ff**(fiO;Q); Q).
Если вое П. ч. и Штифеля числа двух ориентированных
замкнутых многообразий совпадают, то эти многообра-
многообразия бордантиы (в ориентированном смысле).
Задача, аналогичная проблеме Милнора — Хирце-
бруха для квазикомплексных многообразий, состоит г
том, чтобы описать образ отображения ср. Решение :>то!;
задачи основано на рассмотрении П. ч. в Я-теории, соот
ветствующих Понтрягина классам я,- в К -теории. Пусть
ф— {slt ... , гп} — набор целых неотрицательных чисел.
S(o(p) и S^e^) — характерпстнч. классы, определяе
мые четными симметрич. рядами
S«> (х\, ..., з-l) и ?м (e*i + e-*. — 2, ..., ех*-\-е~Хп — 2)
соответственно, здесь ¦SM(f1, ..., tn) — минимальный
симметрич. полином, содержащий одночлен ti , ... , lk'\
«>*!+... + ift. Пусть B..,cziiom(II**(BO; Q); <Q) -
множество таких гомоморфизмов b : Н** (ВО; Q) —>- Q,
для к-рых 6 (?(„(/>))€ Z, *Eи(е/,)Х,)б2 [1/2] при всех
наборах со. Тогда образ гомоморфизма
ф: QSO _ нот (Я** (SO; С); Q)
совпадает с 5„. (теорема Стонга — Хаттори).
Характеристич. числа Tj \М\ и А [М], соответствую-
соответствующие классам L, А ?11**(ВО; Q), паз. L-p о д о м ц
4-р о д о м соответственно многообразия М.
Для замкнутого многообразия М, размерность к-рого
делится на 4, имеет место равенство L \M]-- I(M), где
I(M) - сигнатура многообразия, т. е. сигнатура квад-
квадратичной формы пересечения, определенной uaHn^2(M),
n~dim M (теорема Хирцебруха). Для
замкнутого спинорного многообразия М четной раз-
размерности спинорный индекс М, т. с. индекс оператора
Дирака на М, совпадает с А [М\.
Лит. см. при ст. Понтрягина класс. А. Ф. Харшиладзе.
ПОПЕРЕЧНИК множества — величина, ха-
рактерпзуюгцая уклонение множества в метрич. прост-
пространстве от нек-рой системы объектов (как правило, ко-
конечномерных) при определенном методе приближения,
а также величина, характеризующая точность восста-
восстановления элемента из данного множества при опреде-
определенном методе кодирования. Наиболее изучены П., ха-
характеризующие возможность аппроксимации множества
конечномерными компактами и копечномерными линей-
линейными многообразиями (поперечники но Александрову
и поперечник по Колмогорову).
Пусть X — нормированное пространство с единичным
шаром В, СаХ — аппроксимируемое подмножество
в X, 3!-— {А }, А сХ,— нек-рая совокупность аппрок-
аппроксимирующих подмножеств, F (С, А) — нек-рая совокуп-
совокупность отображений / : С —v А, наконец, т5=^ (С 21)=
= UA g ^F (С, А) — заданная совокупность отображе-
отображений из аппроксимируемого в аппроксимирующее мно-
множества. Число
рв(С, Х)= inf sup Л*-/(х) Ц A)
fsSxeC
характеризует величину уклонения аппроксимируемого
множества С от совокупности аппроксимируемых мно-
множеств Щ при методе аппроксимации %.
Большинство П., характеризующих аппроксимаци-
онные свойства того или иного аппарата приближения,
задаются по типу A).
Если ЭД=йЛдг— совокупность {Мр/} всех линейных
многообразий (т. е. сдвигов линейных подпространств)
размерности <:JV, a F (С, М^) — совокупность всех
отображений из С в Mjy, то величина A), называемая
N-n оперечником по Колмогорову
множества С и обозначаемая обычно dj^(C, X), характе-
характеризует минимальное уклонение данного множества С
от ДГ-мерных линейных многообразий, т. е. характери-
характеризует аппроксимативные возможности iV-мерных линей-
линейных многообразий. Другие равносильные и общеприня-
общепринятые определения d^ таковы (см. [1]):
им (С, Х) = inf sup inf \\х— 2/|| =
{м у} хеС yeMN
= inf inf fe > 0| С cr MN + e,m. ^1')
{MN} e
Если 31=Щ1дг (или=€^ — совокупности всех под-
подпространств {Ltf} размерности <JV, a F(C, Mjv)(F(C,
Ltf)) — совокупность всех аффинных (линейных) не-
непрерывных отображений из С в M^(L^), то величина
A), обозначаемая адт(С, Х)(Х^(С, X)) и называемая а ф-
финным (линейным) JV-n о п е р е ч н и к о м,
характеризует аппроксимативные возможности аффин-
аффинных (линейных) JV-мерных отображений.
Если Э1=|Сдг есть совокупность {Kpj} всех jV-мерных
компактов (или, равнозначно, всех N-мерных полиэд-
полиэдров), a F(C. Км) — множество всех непрерывных ото-
отображений из С в Ж^у, то величина A), называемая JV-п о-
перечником по Александрову и обоз-
обозначаемая адг(С, X), характеризует степень аппроксима-
аппроксимации множества С JV-мерными компактами.
Если 91=2дг — совокупность {Едг} всех JV-точечных
множеств gjvfo, ... , xN) в X, a F(C, |^) — совокуп-
совокупность всех отображений из С в |дг, то П. A), обозначае-
обозначаемый 8дг(С, X), характеризует наименьшее уклонение
данного С от JV-точечных мпожеств, т. е. характеризует
аппроксимативные возможности iV-точечных множеств.
Все введенные выше аппроксимативные П. зависят
от объемлющего пространства X и могут изменяться
при погружении С с его метрикой в другое нормирован-
нормированное пространство.
Другой тип П. связан с задачами «кодирования»
элементов множества С элементами другой природы
или, как этот процесс еще иначе называют, с задачей
восстановления. Пусть С — метрич. пространство, Z—
= {?,} — нек-рая совокупность «кодирующих» множеств,
Ф (С, ?) — нек-рая совокупность отображений / : С —*¦
-*¦?,. Наконец, Ф^Ф (С. Z)— U^g/Ф (С, Q — заданная
совокупность методов кодирования. Величина
рф(С) = т{ sup i)(/-4z)), B)
/еФ геЦС)
где через D (Е) обозначен диаметр множества Е, харак-
характеризует восстановимость элементов .множества С по
информации, «закодированной» элементами множеств ?
из Z с помощью отображений из Ф. Большинство П.,
связанных с процессами восстановления, задается по
типу B).
Если Ф — совокупность всевозможных отображений
из С в Z, состоящего из одного множества {1, ... , N],
то П. B), обозначаемый e,N(С), характеризует точность
восстановления элемента с помощью таблицы, состоя-
состоящей из N элементов. Если С лежит в линейном норми-
нормированном пространстве X и Ф — совокупность всех не-
непрерывных аффинных отображений из X в Кл , то ве-
величина, равная рф(С)/2, где рф(С) определено в B).
называемая N - а о и е р е ч н и к о м но Г е л fa-
фа н д у и обозначаемая dN(C), характеризует точность
восстановления элементов но их образам при аффинных
отображениях в КЛ>. Для центрально-симметричных
множеств величины dN имеется другое равносильное
определение:
N
dN(C)= inf sup||х|| = inf sup{e >0|СП?с:еЯ}, B')
{N} X?CnLN {'V> Ё
где LN — замкнутое подпространство коразмерности N.
Пусть Z состоит из всех iV-мерных компактов {Км},
ф (С, Км) — совокупность всех непрерывных отоора-
жений из С в .йГдг, Ф= иф (С, Kjy), тогда B) называется
Ikn]
iV-поперечником и о У р ы с о н у и обозна-
обозначается идг(С). Другое равносильное и общепринятое оп-
определение поперечника Урысона таково: и^(С) есть
нижняя грань диаметров покрытий множества С крат-
кратности <:JV+1. Поперечник по Урысону характеризует
степень iV-мерности (с точки зрения брауэровской раз-
размерности) множества С.
Впервые величину, названную впоследствии П., ввел
в 1923 П. С. Урысон (см. [2]), когда он определил и^т.
В 1933 П. С. Александров [3] вскрыл аппроксиматив-
аппроксимативные аспекты теории размерности, что привело его к
определению адг. В 1936 А. Н. Колмогоров [1] опреде-
определил dp/ — именно этот П. наиболее интенсивно изучал-
изучался далее в теории приближений. В 1931 Л. С. Понтря-
гин и Л. Г. Шнирельман (см. [4]) выразили размерность
(топологич. характеристику), использовав асимптоти-
асимптотическую метрич. характеристику Ne (С) (обратную к по-
поперечнику en(C)), равную для метрич. пространства С
наименьшему числу элементов 2е-покрытия для множе-
множества С. Интерес к подобным величинам возрос в 50-х гг.,
когда А. Н. Колмогоров [5], базируясь на идеях теории
информации, ввел величину Ne (С, X) (обратную к попе-
поперечнику г^(С, X)) и сформулировал программу иссле-
исследований величин типа NE(C), Ne(C, X) и им подобных
как специальный раздел теории приближений, связан-
связанный с вопросами наилучшего табулирования функций.
Двоичный логарифм величины Ne (С, X) получил на-
название е-энтропии множества С, a log2Ng (С) — абсо-
абсолютной е-энтропии множества С.
Получено множество конкретных результатов, где
те или иные П. (названные выше и иные) вычислялись
для различных функциональных классов и геометрич.
объектов. Такие вычисления можно разделить на две
группы — асимптотические и точные.
Вот нек-рые результаты, касающиеся асимптотич.
вычислений П. Соболевских классов. Пусть Wp —
совокупность функций х(-) на конечном отрезке (ска-
(скажем, на [0, 1]), у к-рых (/•—1)-я производная абсолютно
непрерывна и для r-й производной выполнено неравен-
неравенство
\\^гЧ-Пр-~=( V \*{п tt)\P dtI/P<l, рЗП,.<г = 1, 2, ... .
\ i) 0 /
Доказана следующая асимптотич. формула:
Из частных случаев верхней строки формулы C) сле-
следует, что асимптотически наилучшим аппроксимирую-
аппроксимирующим пространством является пространство тригономет-
рич. полиномов или пространство сплайнов с равномер-
равномерно распределенными узлами.
Ожидалось, что всегда имеет место такая асимпто-
асимптотика, т. е. подпространство тригопометрич. полиномов
данной степени всегда будет асимптотически экстре-
экстремальным. Однако оказалось, что это не так (см. [10],
[13]). Тригонометрич. полиномы lin {cos nt, sin nt, 0<
<re<:iV} оказались асимптотически не экстремальными.
Однако в ряде случаев «переставленные» гармоники,
т. е. ~^N гармоник, взятых в «неправильном» порядке,
все-таки оказались экстремальными.
Решение задачи о П. Соболевских классов опирается
на исследование вопроса о поперечнике и-октаэдров
в R":
При p7s?q величина d2\@p, l") определяется точно; при
р<</ точно вычислена величина dj\r(O'l, $), она оказа-
лась равной ( 1—— J ' . Принципиальную роль при
вычислении колмогоровских П. соболевских классов иг-
играют следующие оценки (см. [13]):
A) dN{0i, /^)<2iV~1
Б) dpj \0", i
где А — постоянная;
В) если Я?@, 1), то при п^ <:Лг<:п имеет место нера-
неравенство
dN @i, '»)< CxN''1'.
Рассмотрен вопрос и об асимптотич. поведении алек-
александровских П. соболевских классов. Оказалось, что
N Lq)Xj^ при i<p, g <cc, r?N.
Решить вопрос о точном вычислении П.— это найти
экстремальный для данного класса аппарат приближе-
приближения. Первый результат этого рода принадлежит
А. Н. Колмогорову [1], к-рый решил задачу о вычисле-
вычислении поперечника d^(W2, L2 [0, 1]) и аналогичную зада-
задачу для периодич. класса Wz в метрике L2(\—л, л]).
Для вычисления точного значения поперечника
dtf{WL, Leo[—л, я]) впервые привлечены (см. [7]) топо-
логич. методы (теорема о поперечнике шара, сводящаяся
к теореме Борсука об антиподах). Эта теорема была об-
обобщена (см. [12]) и применена к нахождению других
точных решений. Впоследствии обнаружились интерес-
интересные связи с вариационным исчислением и оптимальным
управлением (см. [9]).
О поперечниках едг, е-^ и обратных к ним величинах
NE (С) и NE(C, X) см. в-энтропия.
Вопросы о П. имеют тесное соприкосновение с разно-
разнообразными задачами геометрии. Напр., задача об асимп-
асимптотике величины JVg (С, R") тесно связана с задачей
о наилучшем замощении пространства R™ сферами.
Зависимость асимптотических П. от объемлющего про-
пространства привела к идее введения абсолютных П.—
величин
PAF{C)=mipF(C, X),
где нижняя грань берется по всем вложениям С с его
метрикой в объемлющее пространство X. При атом
оказывается (см. [9]), напр., что
4 (С)=4-е"(С),
Лит.: [1] Колмогоров А. Н., «Ann. Math.», 1936,
v. 37, p. 107--H); [2] У р ы с о н П. С, Труды по топологии
и другим областям математики, т. 1, М.— Л., 1951, с. 483;
L3] Александров П. С, «Fund, math.», 1933, v. 20,
p. 140—50; [4] II о н т р я г и н Л., Шнирельман Л. Г.,
в кн.: Гуревич В., Волмэн Г., Теория размерности,
пер. с англ., М., 1948, с. 210—18; [5] К о л м о г о р о в А. Н.,
«Докл. АН СССР», 195«, т. 108, № 3, с. 385—88; [BJ Б р у д-
н ы « Ю. А., Тима н А. Ф., там же, 1959, т. 12(i, .M. Г),
с. 927—30; L7) Тихомиров В. М., «Успехи мат™, наук»,
1960, т. 15, в. 3, с. 81—120; 1965, т. 20, в. 1, с. 227-30; [8]
его же, Некоторые вопросы теории приближений, М., 197В;
[9] его ж е, в кн.; Теория приближения функций. Тр. Межд.
конф. по теории приближения функций. Калуга. 1975, М., 1977,
с. 359—65; [10] Исмагилов Р. С, в кн.: Геометрия
линейных пространств и теория операторов, Ярославль, 1977,
с. 75—113; 111] его же, «Успехи матем. наук», J974 т. 29,
в. 3, с. 161—78; [12] М а к о в о з Ю. И., «Матем. сб.», 1972,
т. 87, №1, с. 136 — 42; [13] Кашин Б. С, «Изв. АН СССР.
Сер. матем.», 1977, т. 41, № 2, с. 334—51; L14] Корнейчук
Н. П., Экстремальные задачи теории приближения, М., 1976.
В. М. Тихомиров.
ПОПОЛНЕНИЕ топологического векторного прост-
пространства X — топологическое векторное пространство А'
такое, что X является подпространством X и X плот-
плотно в X. Под П. понимают также и операцию перехода
от X к X; стандартное ее осуществление — с помощью
направлепносшей (в частности, последовательностей
Коши). М- И. Войцеховский.
ПОПОЛНЕНИЕ РАВНОМЕРНОГО ПРОСТРАНСТВА
X — отделимое полное равномерное пространство
X такое, что существует равномерно непрерывное отоб-
отображение i: X—уХ и для любого равномерно непрерывно-
непрерывного отображения / пространства X в отделимое полное
равномерное пространство У существует, и притом
единственное, равномерно непрерывное отображение
#: Х-уУ, причем f=goi. Подпространство i(X) плотно
в X, и образы при отображении гХг окружений для
X являются окружениями для i(X), а замыкания по-
последних в XXX образуют фундаментальную систему
окружений для А'. Когда X отделимо, i инъективно
(что позволяет отождествить X с t(X). Отделимое по-
пополнение подпространства АсгХ изоморфно замыканию
t(^4)ClX. Отделимое пополнение произведения равно-
равномерных пространств изоморфно произведению отдели-
отделимых пополнений пространств-сомножителей.
Доказательство существования X по существу обоб-
обобщает построение Г. Кантора (G. Cantor) множества дей-
действительных чисел из чисел рациональных.
Лит.: [1] Бурбаки Н., Общая топология. Основные
структуры, пер. с франц., М., 1968. М. И. Войцеховский.
ПОПОЛНЕНИЕ СЕЧЕНИЯМИ, пополнение
М а к-Н е й л а, частично упорядоченного множества
М — полная решетка L, получаемая из множества М
следующим образом. Пусть М=М (если М обладало
нулем) или получается внешним присоединением наи-
наименьшего элемента О к М (если М не имело нуля).
И пусть Р(М) — упорядоченное отношением включе-
включения множество всех непустых подмножеств множест-
множества М. Для любого X ?Р(М) пусть
для
для всех
Условие (p(X)~-~(X&)v определяет замыкания отноше-
отношение ф на множестве Р(М). Решетка L всех ср-замкну-
тых подмножеств множества Р(М) является полной.
Для любого х?М множество (х&)^ является глав-
главным идеалом, порожденным элементом х. Полагая i(.i-) -
=(х&)У для всех х?М, получают изоморфное вложе-
вложение i множества М в полную решетку L, сохраняющее
все точные верхние и нижние грани, существующие
в М. В применении к упорядоченному множеству ра-
рациональных чисел описанная конструкция дает попол-
пополнение множества рациональных чисел дедекиндовымн
сечениями.
Лит.: [1J М а с п е i 1 1 е Н. М., «Trans. Amer. Math. Soc»,
1937, v. 42, p. 41K—60. Т. С. Фофанова.
ПОПОЛНЕНИЯ МЕТОД — метод вычисления об-
обратной матрицы, основанный на рекуррентном перехо-
переходе, использующем вычисление матрицы (C-f uv)-1, где
и— вектор-столбец, г; — вектор-строка, по формуле
(C-\ruv)-1=C-1 — — C-1uvC~\ y = 1 + !;C~1«-
Вычислительная схема метода такова. Пусть А =
— 1Ку!1 —данная матрица n-го порядка. Рассматривает-
Рассматривается последовательность А0=Е, Аъ . . ., Ап, где Ак=
=Л^_!+е^а^, ek есть fc-й столбец единичной матрицы
Е, ak={aja, . . ., аА, а-1, ak, k_b ak> k + 1, . . ., akn).
Тогда Ап=А и матрица А-1 получается в результате
и-кратного применения описанного выше процесса.
Расчетные формулы при этом имеют следующий вид:
если ау ' есть /-й столбец Ак, то для к — 1,2,.. ., п;
<1*"'*' ^Х), /=1. 2, .... п. (*)
Для матрицы Л j^ достаточно вычислять элементы
первых к строк, т. к. последующие строки совпадают
со строками единичной матрицы.
Известны другие способы организации вычислений
в П. м., основанные на модификации (*), напр. т. н.
метод Ершова (см. [1]).
Лит.: [1] Фаддеев Д. К., Ф а д д е е в а В. Н., Вы-
Вычислительные методы линейной алгебры, 2 изд., М.— Д., 1963.
Г. Д. Ким.
ПОРИСТОСТИ ТОЧКА для множества Е из гс-мер-
ного евклидова пространства R" —точка x^^R",
п^1, для к-рой существует последовательность
открытых шаров Вк с радиусами rft-v0 и общим
центром в точке х0 таких, что для каждого fc—1, 2, ...
найдется открытый шар G^czB/^E радиуса ^Сгк,
где С положительно и не зависит от к (но, вообще гово-
говоря, зависит от хп и Е). Множество Е ная. пористым,
если каждая его точка является П. т. для него. Мно-
Множество Е наз. о-а о р и с т ы м, если его можно пред-
представить в виде конечного или счетного объединения
пористых множеств (см. [1]). П. т. для Е является
П. т. для его замыкания Е и не является точкой плот-
плотности в смысле Лебега ни для Е, ни для Е. Каждое
пористое или а-пористое множество EczR" имеет
первую категорию по Бэру и нулевую меру Лебега
в R". Обратное, вообще говоря, неверно: существуют
даже совершенные нигде не плотные множества EdR1,
имеющие меру нуль, но не являющиеся а-пористыми
(см. f2J). Для множества Е, лежащего на гладком мно-
многообразии Sc:Rn, П. т. xn?S множества Е относитель-
относительно многообразия S определяется, как выше, при допол-
дополнительном условии, что центры шаров В^ лежат на S.
Лит.: [II Д о л ;ц е н к о К. П., «Изв. АН СССР. Сер.
матем.», 1967, т. HI, Л» 1, с. 3—14; 12] Z а ] i с е k L., «Caso-
pis pest, mat.», 1976, sv. HU, s. 350 — 59. E. II. Долженко.
ПОРЦИЯ множества — пересечение множест-
множества с интервалом в случае множества на прямой и с от-
открытым кругом или шаром, с открытым прямоуголь-
прямоугольником или параллелепипедом в случае множества
в re-мерном (?г5г2) пространстве. Важность этого по-
понятия оправдывается следующими обстоятельствами.
Множество А является всюду плотным в множестве Б,
если каждая П. множества В содержит точку мно-
множества А, иначе говоря, если замыкание AzzB. Мно-
Множество А является нигде не плотным в множестве В,
если А не будет всюду плотным ни в какой П. мно-
множества В, т. с. если не существует П. множества Б,
содержащейся в А. А. А. Конюшков.
ПОРЯДКА СООТНОШЕНИЕ, сравнение
функций, О — о-с оотношения, асимп-
асимптотические со отношен и я,— понятие, воз-
возникающее при изучении поведения одной функции
относительно другой в окрестности нек-рой точки (быть
может, бесконечной).
Пусть х0— предельная точка множества Е. Если
для функций f(x) и g{x) существуют такие постоян-
постоянные с>0 и 5>0, что |/(.r)|<c|g(*.t)| при \х—хо\<6,
х^х0, то говорят, что / является ограниченной по срав-
сравнению с g функцией в нек-рой окрестности точки х0,
и пишут
/ (х) = О (я (х)) при х —* ха
(читается: «/(.г) есть О большое от g(.r)»); x —> ха озна-
означает, что рассматриваемое свойство имеет мест.о лишь
в нек-рой окрестности точки х„. Естественным образом
это определение переносится на случай х —у оо, х —у
->¦ ±00.
Если функции f(x) и g(x) такие, что f=O(g) и g=O(f)
при х —V .г„, то они наз. функциями одного
порядка при х —>- х0. Напр., если функции а,(х),
Р(х) таковы, что а(х)фО, $(х)фО при хфх0 и суще-
существует предел
то они одного порядка при х —v x0.
Две функции / (х) и g (x) наз. эквивалентны-
эквивалентными (асимптотически равными) при
i-noii пишут f~g, если в нек-рой окрестности точки
х0, кроме, быть может, самой точки х0, определена
такая функция ц>(х), что
/ (х) = ф (х) g (х) и lim ф (х) = 1. (*)
Условие эквивалентности двух функций симметрично,
т. е. если j~g, то и #~/ при х —>- х0, и транзитивно,
т. е. если/~? и #~/г, то f~k при г ->¦ х0. Если в нек-poii
окрестности точки х0 при ж^г0 справедливы неравен-
неравенства /(.с)фО, я(х)фО, то условие (*) эквивалентно
любому и а следующих
lim --^ = 1, lim j|2z = l.
Если a(x) = e(x)f (x), где lim e(z) = 0, то говорят, что
х->-.т0
а. является бесконечно малой функцией
по сравнению с функцией /, и пишут
а = о (/) при х —>¦ х0
(читается: «а есть о малое от /»). Если j (х) ФО при хфх0,
то <%=<?(/), когда lim а//=0. В случае, если / является
бесконечно малой при х —»- ,т0, то говорят, что функция
а - о (/) при х -у хд является бесконечно ма-
малой более высокого порядка, чем /.
Если же g(x) и [f{x)]k— величины одного порядка,
то говорят, что g является величиной поряд-
порядка/с относительно /. Все формулы указанного выше
вида наз. асимптотическими оценка-
м и, они наиболее интересны для бесконечно малых и
бесконечно больших функций.
Примеры: ех — 1 = оA) (х -»• 0); cos x2=O(i),
(In x)a=o(xP) (x -*- оо; a, f> — любые положительные
числа); [x/sin A/.т)] — О(х2) (х —>- оо).
Некоторые свойства символов о и О:
O(af)=O(f) (a—const);
O(O(f))=O(f);
если 0 <ж<.г0 и f—O(g), то
Формулы, содержащие о-, О-символы, читаются только
слева направо, это не исключает того, что отдельные
формулы оказываются справедливыми и при чтении
справа налево. Символы о и О для функций комплекс-
комплексного переменного и для функций многих переменных
вводятся аналогично тому, как они были определены
выше для функций одного действительного переменного.
М. И. Шабунин.
ПОРЯДКОВАЯ СТАТИСТИКА— член вариационного
ряда, построенного по результатам наблюдений. Пусть
наблюдается случайный вектор Х~ (X,, Х.2, . . ., Хп),
принимающий значения х=(х1, х2, . . ., хп) в ге-мерно.м
евклидовом пространстве R", гс^2, и пусть в R" задана
функция ф(-) : R" —у R", определенная по следующему
правилу:
ф (X) =.l@, x?R",
гдеж^)=(з;(п1),ж(п2,, . . ., .т(„„)) —вектор из R», получен-
полученный из вектора х в результате перестановки его коор-
координат хъ х2, . . ., хп в возрастающем порядке, т. е.
компоненты х{п1), x{ni), . . ., xinn) вектора z<-> удовлет-
удовлетворяют следующему соотношению
В этом случае статистика Х(')=ф (X)=(X(ni), . . ., Х{п„{)
наз. вариационным рядом (или векто-
вектором) порядковых статистик, а ее к-я
компонента Хп^ (А=1, 2, . . ., п) наз. /с-й порядко-
порядковой статистикой.
В теории П. с. наиболее полно изучен случай, когда
компоненты Хх, Х2, ..., Хп случайного вектора X суть
независимые одинаково распределенные случайные ве-
величины, что в дальнейшем и будет предполагаться.
Если F (и) — функция распределения случайной вели-
величины Х{, г=1, 2, . . ., п, то функция распределения
Fn/l(u) к-й П. с. X(n?) вычисляется по формуле
F nk(u) = P {Х{Ш<и} = /F(u) (к, п — к + 1), \и\ <оо, B)
где
— неполная бета-функция. Из B) следует, что если
функция распределения F (и) имеет плотность вероятно-
вероятности f(u), то плотность вероятности in^(u) к-а П. с.
X(nk)> &=1, 2, . . ., п, тоже существует и выражается
формулой
C)
В предположении существования плотности / (и) была
получена совместная плотность вероятности
1nr..,. -W, и2. • • •. щ) П. с. X(nri), Х(„г,„ . . ., Х( ,,
, k , , *
l<rrj<r2 < . . . < гк<сп; /с<:п, к-рая выражается фор-
формулой
XFI г (их) / (ux) [F (u2)-F Ы}г*-Г1~ l 1 (щ)...
...\i-F(uk)}n~rkf(uk), D)
— oo < щ < м2 < ... < afj < oo.
Формулы B) — D) позволяют, напр., найти распреде-
распределение вероятностей т.н. экстремальных II. с.
Х<ш>= п»п №, А'2, ..., Х„) и
ХШп)= max (Zb X2, ..., Хп),
а также распределение статистики Wn=X(nny—X(nlh
к-рую наз. размахом. Напр., если функция рас-
распределения F (и) непрерывна, то функция распределе-
распределения размаха Wn выражается формулой
P{Wn<w} = n [* [F(u-\-w) — F(«)]«-W(u),itCaO. E)
Формулы B) — E) показывают, что, как и в общей
теории выборочных методов, точные распределения
П. с. невозможно использовать при получении ста-
тистич. выводов, если функция распределения F (и) не-
неизвестна. Именно поэтому в теории II. с. получили ши-
рокое развитие асимптотич. методы исследования рас-
распределений П. с. при неограниченном увеличении раз-
размерности п вектора наблюдений. В асимптотич. теории
П. с. изучаются предельные распределения соответ-
соответствующим образом нормированных последовательно-
последовательностей П. с. {Х^к)}, когда и—voo; при этом, вообще говоря,
порядковый номер к может меняться в зависимости
от п. Если с ростом п порядковый номер к меняется
таким образом, что существует lim kin, отличный от
О и 1, то соответствующие П. с. Х(п>!) рассматриваемой
последовательности {Х(я/е)} наи. центра л ь н ы м и
или средними П. с. Если же lim kin равен 0 или
п->- со
1, то П. с. Х^пЬ) наз. крайними.
В математич. статистике центральные П. с. исполь-
используют при построении состоятельных последовательно-
последовательностей оценок для квантилей неизвестной функции рас-
распределения F (и) по реализации случайного вектора
X или, иначе говоря, при оценивании функции Л1-1 (и).
Напр., пусть хр—квантиль уровня Р @</*<1) функ-
функции распределения F(u), про к-рую известно, что ее
плотность вероятности f(u) непрерывна и строго поло-
положительна в нек-рой окрестности точки хр. В этом
случае последовательность центральных П. с. {Ху,^}
с порядковыми номерами /с=[(ге+1)-Р+0,5], где [а] —
целая часть действительного числа о, является состоя-
состоятельной последовательностью оценок для квантили
хр, п—уоо. Более того, эта последовательность ТТ. с.
{X{,,k)} асимптотически нормально распределена с
параметрами
Р A-Р)
Хр и nv(»+i)'
т. е. для любого действительного числа х
Нт р ( jj»MZ!g_ f (xd) < х \ = ф w, F)
где Ф (х) — функция распределения стандартного нор-
нормального закона.
Пример 1. Пусть Х<->=(ХШ), . . ., Х(пп)) — век-
вектор П. с, построенный по случайному вектору Х=
= (Х1, . . ., Хи), компоненты к-рого суть независимые
случайные величины, подчиняющиеся одному и тому
же вероятностному закону, плотность вероятности
к-рого непрерывна и строго положительна в нек-рой
окрестности медианы х^ . В этом случае при п—>-оо
последовательность выборочных медиан {|х„}, опреде-
определяемых для любого и>2 по правилу
( Х(п, л»+1ъ если п—нечетное число,
\ т'Х<'»я> + -Х-'".'в + 1>)'если 1 —четное число,
асимптотически нормально распределена с параметрами
х1/2 и {4 (л + 1)/" (*!/,)}-1-
В частности, если
{fi^!} 1<ю' а>0-
то есть X,- подчиняется нормальному закону N (а, а2),
то в этом случае последовательность {|х„} асимптоти-
асимптотически нормально распределена с параметрами х,,=а
и ., t, . Если последовательность статистик {цп}
сравнить с последовательностью наилучших несмещен-
несмещенных оценок
{Хп}, Xn = -^2J._1Xi,
математич. ожидания а нормального закона, то следует
отдать предпочтение последовательности {Хп}, т. к.
для любого
Пример 2. Пусть Х"=(ХШ), . . ., ХЫп)) -
вектор П. с, построенный но случайному вектору
Х=(Хг, . . ., Хп), компоненты к-рого независимы и
равномерно распределены на отрезке [a—h; a-\-h],
причем параметры а и k неизвестны. В этом случае
последовательности статистик {Yn} и {Zn}, где
Yn = -2 (Х(„1) + Х(пп)) и ^"~^(п-1
являются состоятельными последовательностями сверх-
сверхаффективных несмещенных оценок для параметров а
и h соответственно, причем
у _ 2ft* _ 2ft' _.
Можно показать, что последовательности статистик
{Yn} и {2„} определяют наилучшие оценки для о
и /j в смысле минимума квадратичного риска в классе
линейных несмещенных оценок, выраженных в тер-
терминах П. с.
Лит.: [1] Крамер Г., Математические методы статис-
статистики, пер. с англ., 2 иуд., М., 1975; 1.2] У и л к с С., Матема-
Математическая статистика, пер. с англ., М., 19E7; [3] Д э й в и д Г.,
Порядковые статистики, пер. с англ., М., 1979; [4] Г у м б е л ь
Э., Статистика экстремальных значений, пер. с англ., М., 1965;
[5] Гаек Я., Ш и д а к 3., Теория ранговых критериев, пер.
с англ., М., 1971; [а] Г н е д е н к о Б. В., «Докл. АН СССР.
Новая серия», 1941, т. 32, jsft 1, с. 7—9; [7] его же, «Ann.
Math.», 1943, v. 44, № 3, p. 423—53; 18] С м и р н о в Н. В.,
«Тр. Матем. ин-та», 1949, т. 25, с. 5—59; [9] его же, «Теория
вероятн. и ее применен.», 1967, т. 12, №2, с. 391—92; [10]
Чибисов Д. М., там же, 1064, т. 9, Л/5 1, с. 159—Но; [11]
Craig А. Т., «Ашег. J. Math.», 193-2, v. 54, p. 353 — E6; [12]
Tippe tt L. H. С, «Biometrika», 1925, v. 17, p. 364—87;
[13] Pearson E. S., там же, 1932, v. 24, p. 404—17.
M. С. Никулин.
ПОРЯДКОВАЯ ТОПОЛОГИЯ — топология ^т< на
линейно упорядоченном множество X, порожденная
линейным упорядочением <, базу к-рой образуют все-
всевозможные интервалы из X. М. И. Войцеховский.
ПОРЯДКОВОЕ ЧИСЛО, трансфинитное
число, ординальное число, орди-
ординал, — порядковый тип вполне упорядоченного мно-
множества. Понятие П. ч. ввел Г. Кантор (G. Cantor,
1883, см. [2]). Напр., П. ч. множества натуральных чи-
чисел, упорядоченного отношением <:, есть со. П. ч. мно-
жества, состоящего из числа 1 и чисел вида 1— — ,
еслии--1, 2, . . ., упорядоченного отношением <:, есть
со+1. Говорят, что П. ч. а равно (меньше) П. ч. р.
и пишут а=Р(а<Р), если множество типа а подобно
множеству (отрезку) типа E. Для произвольных П. ч. а
и р выполняется одна и только одна из возможностей
а<Р, а=р, а>C. Множество {C : Р<а} всех П. ч.,
меньших а, вполне упорядочено по типу а отношением
<. Более того, каждое множество П. ч. вполне упо-
упорядочено отношением <, т. е. в каждом непустом мно-
множестве П. ч. есть наименьшее П. ч. Для каждого мно-
множества Z П. ч. существует П. ч., превосходящее каждое
П. ч. из Z. Таким образом, не существует множества
всех П. ч. Наименьшее среди П. ч., следующих за
П. ч. а, паз. последователем аи обозначается
а-|-1. И. ч. а наз. предшественником II. ч.
а+1- П. ч. наз. предельным числом, если
оно не имеет предшественника. Таким образом, 0 —
предельное число. Каждое П. ч. можно представить
в виде а=к-\-п, где X — предельное число, п — нату-
натуральное, а сумма понимается как сложение порядко-
порядковых типов.
Трансфинитной последователь-
последовательностью типа а, или а-п оследовательно-
с т ь ю, наз. функция <р, определенная на {|5 : E<сс}.
Если значениями этой последовательности служат П. ч.
и из 7<р<а следует фG)<ф(Р)> т0 эта последователь-
последовательность наз. возрастающей. Пусть гр обозначает
^.-последовательность, где X — предельное число. На-
Наименьшее среди П. ч., больших каждого из чисел
<p(Y), где у<Л, наз. пределом последовательности
ф(у) для у<Х и обозначается lim ф (f). Напр., со-—
г<я
= lim re=lim re2. П. ч. X конфинально предельному
п<со п<и>
числу а, если X является пределом возрастающей
а-последовательности: a,= lim<p(§).
?
?<
П. ч. наз. регулярным, если оно не конфи-
нально никакому меньшему П. ч., и сингуляр-
сингулярным в противном случае. П. ч. наз. начальным
П. ч., мощности т, если оно наименьшее среди II. ч.
мощности т (т. е. среди порядковых типов вполне упо-
упорядоченных множеств мощности т). Начальное П. ч.
мощности т обозначается со(т). Множество {со F) : 6<т}
всех начальных П. ч. бесконечных мощностей, мень-
меньших чем т, вполне упорядочено. Если П. ч. а является
его порядковым типом, то полагается со (т) — соа. Таким
образом, каждое начальное П. ч. снабжается индексом,
равным порядковому типу множества всех начальных
П. ч., меньших, чем данное. Различным начальным чис-
числам соответствуют различные индексы. Каждое П. ч. а
является индексом нек-рого начального числа. Каждое
предельное П. ч. Xj=O конфинально начальному числу
Ша — наименьшему из П. ч., конфинальных Я.
Начальное число соа наз. слабо недостижи-
м ы м, если оно регулярно и его индекс а — предельное
число. Напр., со=соо слабо недостижимо, а сош сингу-
сингулярно и потому не будет слабо недостижимо. Если а >0,
то соа слабо недостижимо тогда и только тогда, когда
а=соа = с/(а), где с/(а) — наименьшее число | такое,
что а конфинально сор.
Слабо недостижимые П. ч. допускают классификацию,
аналогичную классификации недостижимых кардиналь-
кардинальных чисел. Сумма и произведение двух II. ч. являются
П. ч. Если множество индексов вполне упорядочено, то
вполне упорядоченная сумма П. ч. является П. ч. Для
П. ч. можно определить возведение в степень по транс-
трансфинитной индукции: yo==1i Y^+1=Y*'Y> Y*" = lim V > гДе
|<я
X — предельное число. Число уа наз. степенью числа
у, у — основанием степени и а — показателем степе-
степени. Напр., взяв у=(й, ао=1, получают a1=Ya°=co,
«2=01®, а3=соа)М, .... Предел этой последователь-
последовательности e=lim an является наименьшим критич. числом
П<0)
функции со^> т. е. наименьшим из П. ч., для к-рых
соЕ=е. Числа е, для к-рых выполняется это равенство,
наз. э п с и л о н-о рдинал а ми.
Возведение в степень можно использовать для пред-
представления П. ч. в виде, напоминающем представление
натуральных чисел в десятичной системе. Если у7>1,
l<:a<YT1i то существуют такое натуральное число п
и такие последовательности E1; р2, . . .,Р„ и %, г]2,
. . ., г)„, что
a = YT"Pi + YTl2P2 + .--4YT!"Pn, A)
¦П >тI>тJ>...>т)„, О«СР,- < у, B)
для i=l, 2, . . ., п. Формула A) для чисел Ру и т)у,
удовлетворяющих условиям B), наз. разложени-
разложением числа а по основанию у. Числа fS; наз. цифрами,
а числа ii,- — показателями степеней этого разложения.
Разложение П. ч. по данному основанию единственно.
Разложение П. ч. по основанию со используется для оп-
определения натурального сложения и натурального
умножения П. ч.
Лит.: [1] Александров П. С, Введение в общую тео-
теорию множеств и функций, М.— Л., 1948; [2] Кантор Г..
и кн.: Новые идеи в математике. Сб. 6, СПБ, 1914, с. 90—184;
[3] Хаусдорф Ф., Теория множеств, пер. с нем., М.— Л.,
1937; [4] К у р а т о в с к и й К., М о с т о в с к и й А., Тео-
Теория множеств, пер. с англ,, М., 1970; [5] S i е г р i A s k i W.,
Cardinal and ordinal numbers, 2 ed., Warsz., 1965.
Б. А. Ефимов.
ПОРЯДКОВЫЙ ТИП линейно упорядоченного мно-
множества А — свойство множества А, к-рое присуще
любому линейно упорядоченному множеству В, по-
подобному А. При этом два множества А я В, линейно
упорядоченные соотношениями R и S, наз. подоб-
подобными, если существует функция /, взаимно одно-
однозначно отображающая А на В и такая, что для любых
точек х, у?А выполнено xRy^z^i(x)Sf (у). Г. Кантор
(G. Cantor) определял П. т. как такое свойство линейно
упорядоченного множества, к-рое остается, если от-
отвлечься лишь от свойств элементов этого множества,
но не от их порядка. Чтобы подчеркнуть, что прове-
проведен один этот акт абстракции, Г. Кантор для обозначе-
обозначения П. т. множества А ввел символ А . Для часто встре-
встречающихся множеств их П. т. обозначается специальны-
специальными буквами. Напр., если ч,+ —множество всех на-
натуральных чисел, упорядоченное отношением <, то
2;+ = <в. Если Q — множество всех рациональных
чисел, также упорядоченное отношением <:, то <Q=ti.
Линейно упорядоченное множество А имеет тип со
тогда и только тогда, когда: A)А имеет первый эле-
элемент а0, B) каждый элемент х множества А имеет
последующий х-\-\, C) если ao?XczA и множество X
содержит последователь каждого своего элемента, то
Х=А. Существует только один П. т. г\ непустых мно-
множеств, плотных, счетных, не имеющих ни первого, ни
последнего элемента (теорема Кантора). Ли-
Линейно упорядоченное множество имеет П. т. к — множе-
множества всех действительных чисел, если оно непрерывно и
содержит плотное в нрм подмножество А, П. т. к-рого
есть т), имеющее с ним общее начало и общий конец.
Доказана независимость в системе аксиом (ZF) Суслина
проблемы, см. Щ.
Для П. т. определяются операции, до нек-рой сте-
степени аналогичные арифметич. операциям.
Пусть а и Р — два П. т., А и В — такие два ли-
линейно упорядоченные множества, что Л = а, B = f> и
А Г\В=0. Суммой а+Р наз. П. т. а+Р=лЦв, где
множество А[)В упорядочено так, что все элементы
множества А предшествуют всем элементам множества
В, а в каждом из множеств А ш В порядок сохраняется.
В частности, если а и Р — натуральные числа, то оп-
определение суммы П. т. совпадает с определением суммы
натуральных чисел. Имеют место равенства (a+P)+Y=
=a+(P+Y) и a+0=a=0+a, где 0 — И. т. пустого
множества. Закон коммутативности в общем случае
не выполняется, напр. со+1=^=1+со.
Пусть а=А и $=В. Произведением сх-|3 наз.
П. т. a-fi=AxB, где множество ^4x5 упорядочено
так, что если {х, у}, {xlt yt} — два его элемента, то
первый элемент предшествует второму, когда yKyi
или (в случае совпадения ординат) х<Сх1 (принцип по-
последних различных членов). Имеют место равенства
(a-p)-Y=a-(P-Y), a-l=l-a, a-0=0-a=0, где 1 —
П. т. одноэлементного множества. Умножение, как и
сложение, некоммутативно. Напр., со-2=с2-со. Закон
дистрибутивности выполняется: a(P+Y)=a-P+a-T-
Произведение К-к представляет непрерывный П. т.
мощности континуума, не содержащий счетного плот-
плотного подмножества.
С суммой и произведением ТТ. т. тесно связаны сумма
произвольного упорядоченного множества П. т. и
лексикографич. произведение вполне упорядоченного
множества П. т. Пусть {Ат : т?М} — семейство линей-
линейно упорядоченных множеств, индексированное вполне
упорядоченным множеством М, и А = П{Ат: т?М}—
декартово произведение этого семейства.
Лексикографическим произведени-
произведением семейства {Ат : т?М} наз. множество А, наделен-
наделенное следующим порядком. Если {ат} и {Ьт} элементы
ая А, то {ат}<{Ьт} тогда и только тогда, когда или
о1<61, или существует то?М такое, что ат—Ът для
всех m<m0 и ama<ibma (принцип первых различных члеt
нов). Если ат = Ат и А — лексикографич. произведе-
произведение семейства {Ат: т?М}, то а=П{ая: mfM}=^
наз. произведением семейства П. т.
{ат:т^М}. С помощью лексикографич. произведения
и обобщенной континуум-гипотезы построено для каж-
каждого кардинального числа т такое линейно упорядочен-
упорядоченное множество г\х мощности т, что каждое линейно упо-
упорядоченное множество мощности <:т подобно нек-рому
подмножеству множества т)т. Если т является сильно
недостижимым кардинальным числом, то обобщенная
континуум-гипотоза для доказательства этой теоремы
не нужна. В частности, для т=#0 таким множеством
является любое линейно упорядоченное множество
П. т. т).
Лит.: Jl"| Иех Т., Теория множеств и метод форсинга,
пер. с англ., М., 1073. Б. А. Ефимов.
ПОРЯДОК — 1) П. алгебраич. кривой F(х, у) = 0,
где F (х, у) — многочлен от х и у, наз. наивысшую сте-
х2
пень членов этого многочлена. Напр., эллипс "^г+
+рг==1 есть кривая второго П., а лемниската (х%-\-
+ (/2J=а2 (г2—у2) — кривая четвертого П. 2) П. бес-
бесконечно малой величины а относительно бесконечно
малой величины Р есть такое число п, что существует
конечный предел lira —z, отличный от нуля. Напр.,
Р
sin2 Зх при z-vO есть бесконечно малая второго П. от-
.. sin2 Ззс
носительно х, так как am :—=9. Вообще говорят,
что а — бесконечно малая высшего П., чем [3, если
lim ~р-=0, и низшего П., чем р, если lim -g-=oo.
Аналогично определяют П. бесконечно больших ве-
величин. 3) П. нуля (соответственно полюса) о функции
f(x) есть такое число п, что существует конечный пре-
предел lim л (соответственно lim (л:—a)"f(x)), отлич-
ж->-а (х—а>
ный от нуля. 4) П. производной — число дифференци-
дифференцирований, к-рые надо произвести над функцией, чтобы
получить эту производную. Напр., у'"— производная
третьего П., ^гхо%у — производная четвертого П. Ана-
Аналогично определяют П. дифференциала. 5) П. диффе-
дифференциального уравнения — наивысший из ТТ. произ-
производных, входящих в уравнение. Напр., у'"у—(у"J=
-=1 — уравнение третьего П., у"—Зу'-{-у=0 — урав-
уравнение второго П. 6) П. квадратной матрицы — число ее
строк или столбцов. 7) П. конечной группы — число
элементов группы. Если группа G бесконечна, то гово-
говорят, что G — группа бесконечного П. Не сле-
следует путать порядок группы с порядком в группе, о
к-ром см. Упорядоченная группа, Частично упорядочен-
упорядоченная группа. 8) П. элемента группы — целое положи-
положительное число, равное числу различных элементов в
циклической подгруппе, порождаемой этим элементом,
либо оо, если эта подгруппа бесконечна. В послед-
последнем случае элемент наз. элементом бесконечного
П. Если П. элемента а конечен и равен п, то п явля-
является наименьшим из чисел, для к-рых о" = 1. 9) Правый
П. в кольце Q — такое подкольцо R кольца Q, что
для всякого x^Q найдутся а, Ь?Д такие, что Ь обра-
обратим в 9 и х=аЪ~1. Другими словами, R — это такое
подкольцо в Q, что Q является классич. правым коль-
кольцом частных кольца R (см. Частных кольцо). 10) Ес-
Если при нек-ром исследовании или вычислении отбра-
отбрасываются все степени нек-рой малой величины, начиная
i (л—|-1)-й, то говорят, что исследование или вычисле-
вычисление ведется с точностью до величин и-го П. Напр., при
исследовании малых колебаний струны пренебрегают
величинами, содержащими вторые и высшие степени
прогиба и его производных, получая благодаря этому
линейное уравнение (линеаризуя задачу). 11) Слово
«П.» употребляется также в исчислении конечных раз-
разностей (разности различных П.), в теории многих спе-
специальных функций (напр., цилиндрич. функции и-го П.)
и т. д. 12) При измерениях говорят о величине порядка
10™, подразумевая под этим, что она заключена между
0,5-10" и 5-10".
По материалам одноименной статьи из БСЭ-3.
ПОРЯДОК, отношение порядк а,—
бинарное отношение на нек-ром множестве А, обычно
обозначаемое символом ¦< и обладающее следующими
свойствами: A) а<^а (рефлексивность); B) если
а<6и Ь<с, то о<с (транзитивность); C) если
а<Ь и Ь<:а, то а=Ь (антисимметричность).
Если <: — П., то отношение <, определяемое условием
а<Ь, если а<;Ь и афЬ, наз. строгим П. Строгий П.
может быть определен и как отношение, обладающее
свойствами B) и C') : а<Ъ и 6<о не могут выпол-
выполняться одновременно. Запись а<:Ь обычно читается как
«а меньше или равно Ь» или «6 больше или равно о»,
а о<& — как «о меньше 6» или «Ь больше о». П. наз.
л и н е й н ы м, если для любых а, Ь?А имеет место
а^Ь или 6<о. Отношение, обладающее свойствами
A) и B), наз. предпорядком< или к в а з и п о-
рядком. Если <] — квазипорядок, то отношение
а~Ь, определяемое условиями а<\Ь и Ь<]о, оказывается
эквивалентностью. На фактормножестве по этой экви-
эквивалентности можно определить П., полагая [а]<. [Ь],
где [о] — смежный класс, содержащий элемент о,
если а<\Ь. Примеры и лит. см. при ст. Частично упоря-
упорядоченное множество. Л. А. Скорняков.
ДОСЛЕДОВАНИЯ ОТОБРАЖЕНИЕ для гладкого
или хотя бы непрерывного потока {Sf} и трансверсаль-
ной к нему гиперповерхности V — отображение Т,
сопоставляющее точке v?V первую по времени точку
пересечения с V исходящей из v положительной полу-
полутраектории потока (и определенное для тех v, для к-рых
такое пересечение имеется). (Гиперповерхность V наз.
при этом сечением, секущей поверх-
поверхностью, трансверсаль ю.) Когда размер-
размерность dim V=l (так что {Sf} — поток на плоскости
или двумерной поверхности", в этом случае V наз.
также дугой без контакта) и V параметри-
параметризована числовым параметром s, то смещение точек V
под действием П. о. описывается нек-рой числовой
функцией / одного переменного (если v отвечает значе-
значению параметра s, то Tv — значению параметра s+
+/ (s)), к-рая наз. функцией последования.
Впервые П. о. использовал А. Пуанкаре (Н. Poincare,
[1]), поэтому иногда П. о. наз. отображением
Пуанкаре.
Если любая полутраектория пересекает V, то П. о.
(определенное в данном случае на всем V) в значитель-
значительной степени определяет поведение всех траекторий по-
потока. Однако такие «глобальные» сечения существуют
далеко не всегда (в частности, у гамильтоновой систе-
системы на многообразии постоянной энергии, не проходя-
проходящем через критнч. точки гамильтониана, т. е. равнове-
сия положения, нет замкнутых — как многообразия —
глобальных сечений; см. [3] гл. VIII, п. 4.7).
Для неавтономной системы с периодической правой
частью
x = f(t,x),
возникает аналог П. о.: точке х сопоставляют точку
Тх=ц> (т, х), где ф (t, x) — решение системы (*) с началь-
начальным значением ф @, х) = х. Это «отображение сдвига на
период» можно даже формально рассматривать как
П. о., если (*) рассматривать как автономную систему
в «цилиндрическом» фазовом пространстве. Отображе-
Отображение Т определено всюду, если решения системы (*)
определены при всех t.
Чаще приходится иметь дело с «локальным» сече-
сечением — его пересекает только часть траекторий и не-
нередко только часть пересекающих ого траекторий вновь
возвращается на V. Примером может служить малень-
маленькая гладкая «площадка» коразмерности один, транс-
версально пересекающая нек-рую замкнутую траекто-
траекторию L. В этом случае П. о. определено вблизи V[)L и
характеризует поведение траекторий вблизи L.
В теории слоений также вводится П. о. (см. [2]), яв-
являющееся обобщением предыдущего примера (и охва-
охватывающее также П. о. для обыкновенных дифференци-
дифференциальных уравнений в комплексной области).
Лит.: [1] Пуанкаре А., О кривых, определяемых диф-
дифференциальными уравнениями, пер. с франц., М., 1947; Ш
Т а м у р а И., Топология слоений, пер. с япон., М., 1979; [3]
Годбийон К., Дифференциальная геометрия и аналитиче-
аналитическая механика, пер. с франц., М., 1973. Д. В. Аносов.
ПОСЛЕДОВАТЕЛЬНОСТЕЙ КАТЕГОРИЯ — част-
частный случай общей конструкции категории функторов
или категории диаграмм. Пусть % — множество целых
чисел, снабженное обычным отношением порядка.
Тогда % можно рассматривать как малую категорию,
объектами к-рой являются целые числа, а морфизма-
ми — всевозможные пары вида (г, /), где ?, /?g иг «г/.
Пара (i, j) — это единственный морфизм объекта г
в объект /. Композиция морфизмов определяется следую-
следующим равенством: (i, ;) (/, k) = (i, к).
Для произвольной категории JT категория кова-
риантных функторов %(Z, .1i) из I, в Я наз. ка-
категорией пос ледова те л ь н о с т е й над
,1?. Чтобы задать функтор F : Ъ —*-Й\ достаточно
указать семейство объектов из .4, заиндексированное
целыми числами, и для каждой пары объектов А;,
A[ + i выбрать произвольный морфизм ее,-_ ,¦ +1 : А,—уА ; + i •
Тогда отображенияF(i) — A,,F (i, i-f-1 ) = «,-_ ; + 1 однознач-
однозначно продолжаются до функтора F : Z —у§(. Естественное
преобразование ф функтора F : Z —*¦ Я в функтор
G : % —у Й\ т. е. морфизм категории последователь-
последовательностей, задается таким семейством морфизмов
ф. : F(i) -yG(i), что <ffi(i, j+l)=F(i, S+1). Ф; + 1 для
любого i ? % .
Если ,ft — категория с нулевыми морфизмами, то
в П. к. % (Z, Ш) выделяется полная подкатегория
комплексов, т. е. таких функторов F : % —у Л, что
F(i, f+1) F(i+\, i+2) = 0 для любого i?Z. Для абе-
левой категории 91 П. к. и подкатегория комплексов
являются абелевыми категориями.
Вместо категории % можно рассматривать ее под-
подкатегории, состоящие только из неотрицательных или
только из неположительных чисел. Соответствующие ка-
категории диаграмм также наз. П. к. м. Ш. Цаленпо.
ПОСЛЕДОВАТЕЛЬНОСТЬ элементов за-
заданного множества — функция, определен-
определенная на множестве натуральных чисел, множество зна-
значений к-рой содержится в рассматриваемом множестве.
Э л е м е н т о м, или членом, последовательно-
последовательности / : N—уХ, где 7V — множество натуральных чисел,
X — заданное множество, наз. упорядоченная пара
(п, х), x=f(n), n?N, x?X, к-рая обозначается через
хп. Натуральное число п наз. номером элемен-
элемента последовательности хп, а элемент
х?_ X — его з н а ч е п и е м. Последовательность
/ : N—*-X обычно обозначается через {хп} или хп, п=
= 1,2
Множество элементов П. всегда счетно, причем два
различных члена П. отличаются по крайней мере номе-
номерами. Множество значений элементов П. может быть и
конечным; так, множество значений всякой стаци-
стационарной П., т. е. последовательности {хп}, все
элементы к-рой имеют одно и то же значение: хп=а,
га=1, 2, . . ., состоит из одного элемента.
Если щ<Спг, то член хП1 последовательности {хп}
наз. предшествующим члену хПг, а член
хП1 —'Следующим за членом хпг Таким образом,
множество элементов П. упорядочено.
Того или иного рода П. встречаются в различных
разделах математики и с их помощью описываются
многие свойства изучаемых объектов. Напр., если
X — топологич. пространство, то среди П. его точек
важную роль играют сходящиеся П., т. е. П.,
к-рые имеют предел в этих пространствах. В терминах
сходящихся П. удобно (во всяком случае, при наличии
счетной базы) описывать свойство компактности, су-
существование предела отображения, его непрерывность
и т. п. Если все элементы П. нек-рых объектов (точек,
множеств, отображений и т. д.) обладают каким-либо
свойством, то часто бывает нужным выяснить, сохра-
сохраняется ли это свойство для предела П.; напр., выяснить,
как ведут себя свойства измеримости, непрерывности,
дифференцируемости, интегрируемости при предельном
переходе для различных видов сходимости функций
(поточечной, почти всюду, равномерной, по мере, в
среднем и т. п.).
Иногда отображение / : 1, п—vX конечного множества
1, п йе— {1, 2, . . ., п\ натуральных чисел в множество
X наз. конечной П. и обозначается через {xlt x2,
. . ., хп}, где xn=f(k), к={, 2, . . ., п. П. может за-
задаваться формулой ее общего члена (напр., П. членов
арифметич. прогрессии), рекуррентной формулой
(напр., П. чисел Бернулли) или просто словесным описа-
описанием с той или иной степенью эффективности (напр.,
П. всех простых натуральных чисел в порядке их воз-
возрастания). См. также Двойная последовательность,
Кратная последовательность. Обобщением понятия
П. является направленность. л. Д. Кудрявцев.
ПОСЛЕДОВАТЕЛЬНЫЙ АНАЛИЗ — раздел ма-
тематич. статистики, характерной чертой к-рого явля-
является то, что число производимых наблюдений (момент
остановки наблюдений) не фиксируется заранее, а
выбирается по ходу наблюдений в зависимости от зна-
значений поступающих данных. Стимулом к интенсивному
развитию и применению в статистич. практике после-
последовательных методов послужили работы А. Вальда
(A. Wald). Им было установлено, что в задаче различе-
различения (по результатам независимых наблюдений) двух
простых гипотез т. н. последовательный критерий от-
отношений вероятностей дает значительный выигрыш в
среднем числе производимых наблюдений по сравнению
с наиболее мощным классич. способом различения (оп-
(определяемой леммой Неймана — Пирсона) с фиксиро-
фиксированным объемом выборки и теми же вероятностями
ошибочных решений.
Основные принципы П. а. состоят в следующем.
Пусть ?i, ?2> • • • — последовательность независимых
одинаково распределенных случайных величин и функ-
функция распределения Fq (x)=Pq {^-о:} зависит от не-
неизвестного параметра В, принадлежащего нек-рому
параметрич. множеству 0. Задача состоит в том, чтобы
по результатам наблюдений вынести то или иное реше-
решение об истинном значении неизвестного параметра 9.
В основе любой статистич. задачи решения лежат
пространство D заключительных (терминальных) ре-
решений d (о значениях параметра Э) и правило т, опре-
определяющее момент прекращения наблюдений, в к-рый
и выносится заключительное решение. В классич.
методах наблюдений момент х является неслучайным
и фиксированным заранее; в последовательных методах
т является случайной величиной, не зависящей от «бу-
«будущего» (марковский момент, момент остановки). Фор-
Формально, пусть rtFM=a{co : Si, ¦ ¦ •, SH} есть a-алгебра,
порожденная случайными величинами \г, . . ., gn. Слу-
Случайная величина т~-т(со), принимающая значения
О, 1, . . ., -}- оо, наз. марковским моментом,
если событие {t«ji}?;Fk для каждого ге>0 ($"„=
= {0, S3})- Пусть qF% — совокупность тех измеримых
множеств А , для к-рых А П {t<ra}€eFn и Для каждого
«JsO. Если gfn интерпретируется как совокупность
событий, наблюдаемых до случайного момента п (вклю-
(включительно), то §~% можно интерпретировать как сово-
совокупность событий, наблюдаемых до случайного момента
т (включительно). Заключительное (терминальное) ре-
решение d=d(a>) есть §~х -измеримая функция со значе-
значениями в пространств D. Пара 6= (х, d) таких функции
наз. (последовательным) решающим
правилом.
Для выделения среди решающих правил «оптималь-
«оптимального» задают функцию риска W(t, в, d) и рассматрива-
рассматривают математич. ожидание ?в W(x, В, d). Существуют
разные подходы к определению понятия оптимального
решающего правила 6* = (х*, d*). Один из них, бейесов-
ский, основан на предположении, что параметр Э явля-
является случайной величиной с априорным распределени-
распределением я=я(^Э). Тогда имеет смысл говорить о я-риске
и называть правило б* = (т*, d*) оптимальным
бейесовским решением (или л-о п т и-
м а л ь н ы м), если До* (я)<Лб (я) для любого другого
(допустимого) правила. Наиболее распространенной
формой риска W(x, 0, d) является риск вида ет+
~\-Wt(Q, d), где константа с^О интерпретируется как
стоимость единичного наблюдения, а ^(9, d) является
функцией потерь от заключительного решения.
В бейесовских задачах отыскание оптимального за-
заключительного решения d*, как правило, не вызывает
трудностей, и основные усилия направлены на оты-
отыскание оптимального момента остановки т*. При этом
большинство задач П. а. укладывается в следующую
схему «оптимальных правил остановки».
Пусть Х=(хп, §~п, Рх), ге^О, х?Е, — цепь Мар-
Маркова в фазовом пространстве (Е, 53), где хп — состоя-
состояние цепи в момент времени п, a-алгебра ,Тп интерпре-
интерпретируется как совокупность событий, наблюдаемых до
момента времени п (включительно), аРя — распределе-
распределение вероятностей, отвечающее начальному состоянию
х?Е. Предполагается, что, прекращая наблюдение в
момент времени п, получают выигрыш g(xn). Тогда
средний выигрыш от остановки в момент т есть Bxg(xx),
где х —¦ начальное состояние. Функцию s(x) =
= sup Exg(x%), где sup берется по всем (конечным)
моментам остановки т, наз. ценой, а момент т?1
для к-рого s(x)*s?.xg(xx )-\-в для всех х?Е, наз. е-
оптимальным моментом остановки.
О-оптимальные моменты наз. оптимальными.
Основные вопросы теории «оптимальных правил оста-
остановки» таковы: какова структура цены s(x), как ее
найти, когда существуют е-оптимальные и оптимальные
моменты, какова их структура. [1иже приведен один
из типичных результатов, касающихся поставленных
вопросов.
Пусть функция g (.r) ограпичена: \g (,т)| <:с<оо.
Тогда цена s (х) является наименьшей эксцессивной
мажорантой функции g (.с), т.е. наименьшей из функций
j(x), удовлетворяющих двум свойствам
?(*)</И, Tf(x)<f(x),
где Tf (x) = Exg (xt). При этом момент
Te=inf{rt5s0: sfijX?^) . е}
является е-оптимальньш для всякого е>0, цена «(г)
удовлетворяет уравнению Вальда — Беллмана
s(x) = max{g(x), Ts(x)}
и может быть найдена по формуле
s(x)= lim <?ng(z),
где
<?g(x)= max {?(*), Г^г(ж)}.
В том случае, когда множество Е конечно, момент
то = Ы {гегэО: s(*n) = g(zn)}
будет оптимальным. В общем случае момент т0 является
оптимальным, если Рх{т0<оо }=1, х^Е.
Пусть
С = {х: s (х) > g (х)}, Г = {х: s (х) = ^ (л:)}.
В соответствии с определением
Иначе говоря, прекращение наблюдений следует произ-
производить при первом попадании в множество Г. В связи
с этим множество С наз. множеством продолжения
наблюдений, а Г — множеством прекращения наблю-
наблюдений.
Иллюстрацией этих результатов может служить зада-
задача различения двух простых гипотез, на к-рой А. Вальд
продемонстрировал преимущество последовательных
методов по сравнению с классическими. Пусть параметр
8 принимает два значения 1 и 0 с априорными вероят-
вероятностями я и 1—я соответственно и множество заключи-
заключительных решений D состоит также из двух точек:
d ~1 (принимается гипотеза Дх : 6=1) и d=0 (прпни-
астся гипотеза II0 : 6=0). Если функцию W1(Q, d)
выбрать в виде
( а, 9 = 1, d = 0,
WiiQ, rf)=- b, 0 = 0, rf=l,
(О, в остальных случаях
и положить
W(x, 0, d) = ct-{ W^e, d),
то для R6 (л) получают выражение
А6 (я) = сЕя х + аа„ (б) + Ь$л (б),
где
аЯ(б) = Ря{й = 0|6 = 1}, ря(б) = Рл{й = 1 | 0 = 0}
— вероятности ошибок первого и второго рода, а Ря оз-
означает распределение вероятностей в пространство
наблюдений, отвечающее априорному распределению
я. Если лп=Р{в=Ц$~п} — апостериорная вероят-
вероятность гипотезы Н1 : 0— 1 относительно а-алгебры
,|Г„=о-{со : Ij, . . ., L). то
где
?(Я)=НПП(ЯЯ, 6A—л)).
Из общей теории оптимальных правил остановки, при-
примененной к хп=(п, я„), следует, что функция р(л) =
= infT/^(.T,) удовлетворяет уравнению
Отсюда, в силу выпуклости вверх функций р(я), g(n),
Тр(п), можно вывести, что найдутся два числа 0<:
<:Л <fi<:l такие, что область продолжения С= {п : А <
<л<С#}, а область прекращения наблюдений Г=
= [0, 1]\(Л, В). При этом момент остановки
является оптимальным (я„=л).
Если ро(х) и jDj (х) — плотности распределений F0(x)
и Ft (ж) (по мере d|x= -у (dF^dFj)), a
V Po(ll)"-Po(ln)
— отношение правдоподобия, то область продолжения
наблюдений (см. рис. 1) может быть записана в виде
С =
т0 выносится реше-
решех : 9=1. Если же
и T0=inf {> ф„^}
При этом если срг Js -jtrg —7
ние d=l, т. е. принимается гипотеза
ЧЧ„ "^ Т^а ^Г ' то ~ гипотеза Но : 9=0.
Структура этого оптимального решающего правила
сохраняется и для задачи различения гипотез в ус-
ловноэкстремаль н о й
постановке, состоя-
состоящей в следующем.
Для каждого решаю-
решающего правила б=(т,
d) вводят вероятности
ошибок a{b)-=Pi(d=
= 0), pF) = P0(d=l)
и задают два числа
а>0 и р>0;ипусть,
далее, Д (а, Р) — сово-
совокупность всех реша-
решающих правил с а(б)«:а, Р(б)<Р и Е0т<оо, !<
Следующий фундаментальный результат был получен
А. Вальдом. Если а+C<1 и среди критериев б=(т,
d), основанных на отношении правдоподобия <р„ и
имеющих вид
-<р„
С-область продолжения
наблюдений
1
3 4 5
Рис. 1.
T=inf
ф„ (jt (а, Ь)},
_ (l, Фт5зЬ
\ 0, <рт<а
найдутся такие а=а* и Ь=Ь*, что вероятности ошибок
первого и второго рода в точности равны а и р, то
решающее правило б* = (т*, d*) ca=a* и Ъ=Ь* является
в классе Д (а, Р) оптимальным в том смысле, что
Еот*<Еот, E^siEiT
для любого б?Д(а, р).
Преимущества последовательного решающего прави-
правила б* = (т*, d*) по сравнению с классическим проще
проиллюстрировать на примере задачи различения двух
гипотез Но : 0=0 и Н1 : 0=1 относительно локального
среднего значения 0 винеровского процесса ^j с еди-
единичной диффузией. Оптимальное последовательное ре-
решающее правило б*= (т*, d*), обеспечивающее за-
заданные вероятности ошибок аир первого и второго
рода соответственно, описывается следующим образом:
T* = iiif {t^sO: Xt$-(a*, b*)},
^_ /1, \
~ \0, Я
где )vj=ln ян и отношение правдоподобия (производная
меры, отвечающей 9=1, по мере, отвечающей 6=0) ф/=
~е 2 , а Ь* = 1п—g-, й* = 1п-[ГГр (см. рис. 2).
Оптимальное классич. правило б=(т, а!) (согласно
лемме Неймана — Пирсона) описывается следующим
образом:
Г=*(«, Р),
I, X-S&feft
"\0, К7 < й(а' Р)>
'С-область продолжений _ j 1, X г ^ & (a, f>),
наблюдений ^ )
где
Рис. 2. h
& Су — корень уравнения
1 г-ое -х2/2 ,
V2n J с.,
Поскольку Е0т*=2со(а, Р), Е1т* = 2ш(р, а), где
то
«> ("'Р>...
(<=а + ^J '
Численный подсчет показывает, что при а, р<:0,03
«(а, Р) ^ 30 ' t (а,3) ~—30 '
Иначе говоря, при рассматриваемых значениях ошибок
первого и второго рода оптимальный последовательный
метод различения требует примерно в два раза меньше
наблюдений, чем оптимальный метод с фиксированным
числом наблюдений. Более того, если а=Р, то
Лит.: [1] Вальд А., Последовательный анализ, пер.
с англ., М., 1960; [2] Ширяев А. Н., Статистический по-
последовательный анализ, М., 1976. А. Н. Ширяев.
ПОСЛЕДОВАТЕЛЬНЫХ ПРИБЛИЖЕНИЙ МЕ-
МЕТОД, метод повторных подстановок,
метод простой итераци и,— один из общих
методов приближенного решения операторных уравне-
уравнений. Во многих случаях хорошая сходимость построен-
построенных этим методом приближений позволяет приме-
применять его в практике вычислений.
Пусть Е — нек-рое множество, на к-ром задан
оператор А, отображающий Е в себя. Требуется найти
неподвижную точку этого отображения, т. е. решение
уравнения
х=А(х), х?Е. A)
Пусть уравнение A) имеет решение г„ и каким-
либо способом указано его начальное приближение
хо?Е. Все остальные приближения в П. п. м. строятся
по формуле
хп+1^Ахп, я = 0, 1, 2, ... B)
Этот процесс наз. простой одношаговой
итерацией.
Для исследования сходимости последовательности
B), а также для доказательства существования реше-
решения уравнения A) широко применяется ниже сформули-
сформулированный принцип сжимающих отобра-
отображений.
Пусть Е — полное метрич. пространство с метрикой
р; оператор А определен в замкнутом шаре S радиуса 6
с центром в х0:
S = {x?E: р(х, хо)<:8};
для всяких элементов х и у из шара S верно соотноше-
соотношение
р(Ах, ijXapfi, у), 0 < a = const < 1;
для начального приближения х() выполнено неравенст-
неравенство р(Аха, х0) <: т, для чисел а, б, т соблюдается ус-
условие ml (\—а) <: б.
Тогда: 1) последовательные приближения хт вы-
вычисляемые по правилу B), могут быть найдены при
всяком значении п, и все они принадлежат шару S;
2) последовательность хп сходится к нек-рой точке
х* ?S; 3) предельный элемент х% есть решение урав-
уравнения A); 4) для приближения хп верна следующая
оценка близости к решению х^:
р(хп,
Далее, во всяком подмножество цространства Е, где
для двух любых точек х, у верно неравенство р(Ах,
Ау) <р{х, у), уравнение A) не может иметь более
одного решения.
Пусть E=Rn — арифметическое re-мерное простран-
пространство и оператор А в A) имеет вид Ax=BxJ\-b, где В—
— lla,'fel! — квадратная матрица n-го порядка, 6= (bt,. . .,
Ьп) — заданный, а х— (хъ . . ., х„) — искомый векто-
векторы в R". Если в этом пространстве метрика определена
формулой
р (х, у)=тах\х1 — у(\
и элементы матрицы В удовлетворяют условию
для всех i, i=\,. . ., re, то из принципа сжимающих
отображений следует, что система алгебраич. уравне-
уравнений х—Ах имеет единственное решение вК.",к-рое
можно получить П. п. м., исходя из произвольного
начального приближения хп ? R".
Если в R" действует евклидова метрика
, v)=
тогда получается другое условие сходимости последо-
последовательных приближений:
Пусть A) — интегральное уравнение, в к-ром
Ах (t) =/(/) + Я [ К (t, s)x(s)ds,
где известные функции /, К интегрируемы с квадратом
соответственно на множествах [а, Ъ\ и \а, Ь] X [а, Ь],
X — числовой параметр. Тогца из принципа сжимаю-
сжимающих отображений следует, что если
то рассматриваемое интегральное уравнение имеет един-
единственное решение в пространстве L2([a, b]), к-рое мож-
можно построить П. п. м.
Лит.: Ш Фаддеев Д. К., Ф а д д е е в а В. Н., Вы-
Вычислительные методы линейной алгебры, 2 изд., М.— Л., 1963,
['-] Крылов В. И., Бобков В. В., М о н а с т ы р~
ный П, И., Вычислительные методы, т. \—2, М., 11G6 77;
['М К о л л а т ц Л., Функциональный анализ и вычислитель-
вычислительная математика, пер. с нем., М., 1969. Б. В. Хведелидзе.
ПОСТА АЛГЕБРА — алгебра вида (Р Q), где Р
является множеством функций, a Q — множеством
операций, равносильных операциям композиции с раз-
различного рода ограничениями. Примерами П. а. явля-
являются конечнозначные и счетнозначные логики, логики
неоднородных функций и т. п. Проблематика П. а. по
существу совпадает с проблематикой для многозначных
логик.
Лит. см. при ст. Многозначная логика. В. Б. Кудрявцев.
ПОСТА КАНОНИЧЕСКАЯ СИСТЕМА, и с ч и с-
ление Пост а,— способ задания перечислимых
множеств слов. Понятие П. к. с, предложенное
'•'. Постом (Е. Post) в 1943, было первым общим поня-
понятием исчисления, пригодным для задания произвольных
перечислимых множеств и не привязанным к логич.
структуре порождаемых объектов, к их семантике и к
логике вывода правил. П. к. с. задается четверкой
А, Р, Л, я;, где А — алфавит исчисления, Р (не имею-
имеющий общих букв с А) — алфавит переменных, Л —
список слов в А (аксиом исчисления), я — список пра-
правил вывода вида
Gi,iPi,i- ¦ -Gi mPi, nfii, ni + i
(*)
Gm, lPm, 1'' Gm, nmpm, nmGm, nm+l
G1p1- ¦ •GnVnGn +1
(G^ j суть обозначения слов в А , р,_ у — обозначения
букв из Р). Слово Q получается из Q\,. . ., Qm приме-
применением правила (*), если для каждой входящей в (*)
буквы из Р можно подобрать слово в А (значение этой
переменной), подставляя к-рое вместо всех вхождений
рассматриваемой переменной в (*), мы получим после
такого замещения всех переменных слова Qx,. . ., Qm —
над чертой и Q — под чертой. На основе этого понима-
понимания правил определяется выводимость в П. к. с. В тео-
теории исчислений применяется следующее определение
перечислимого множества слов в А,
эквивалентное обычному: М наз. перечислимым,
если оно совпадает с множеством слов в А, выводимых
в нек-рой П. к. с, алфавит к-рой содержит А (необхо-
(необходимость расширения А хотя бы одной буквой \ неустра-
неустранима, но можно потребовать, чтобы помимо М были
выводимы лишь слова вида ?<?, где Q из А).
Рассматриваются различные специализации понятия
П. к. с: 1) нормальные системы Поста
(все правила имеют вид z^v), 2) локальные ис-
исчисления (правила вида 'g, *), 3) ограничен-
ограниченные исчисления (алфавит однобуквенный, правила
одноиосылочны) и др. Упомянутые специализации
предполагаются одноаксиомными, к каждой из них
можно свести произвольную П. к. с. (установленная
Постом эквивалентность П. к. с. и нормальных исчис-
исчислений имеет фундаментальное значение для работ этого
направления, для нахождения неразрешимых систем).
Лит. см. при ст. Исчисление. С. Ю. Маслов.
ПОСТА КЛАСС — замкнутый относительно опе-
операции суперпозиции класс функций алгебры логики
(ф. а. л.). Э. Пост (Е, Post) установил, что таких
классов в точности счетное множество, и дал их
явное описание. Им же показано, что все они являют-
являются конечно порожденными, построена решетка по
включению, образованная этими классами. Множество
указанных классов исчерпывается списком С,-, А,-, D j,
Lk, Ot, Sr, Pr, /f, FT, где »=1, 2, 3, 4; / = 1, 2, 3;
fc=l,. . ., 5; 1 = 1,. . ., 9; г = 1, 3, 5, 6; s=l, . . .,
8; ц = 2, 3,. . .
Класс Cj содержит все ф. а. л.; С2 состоит из всех
ф. а. л. /(-г1!, . . ., х„) таких, что /@,. . ., 0)--0; Ся —
извсехф. а. л. таких, что/A, . . ., 1)-"-1; С4 — C.zf]C3.
Класс Лх состоит из всех монотонных ф. а. л.;
-4a=C2rMi; A3=Car\Ai, At = -42П-4з- Класс D3 до-
достоит из всех ф. а. л. /(jj, . . ., х„) = f(xx, . . ., хп);
D1=Cif\Da; D.2=A1{\D3. Класс Lx состоит из всех
ф. а. л. f(xu x2, . . ., zn) = z1+z2+. . .+xn+d(mod 2),
?{0, 1}; Z,2=C2nii; L3=C3n?i; ?4=Л? ^
Класс О9 состоит из всех ф. а. л., существенно зави-
зависящих не более чем от одного переменного; О8=А 1ГКЛъ
О4=?3ПО9; О5=С2ПО,; Ов^С3ПОя; О^О^О^, О7
состоит из всех константных функций; O2=Obf]O7;
оя=оапо7.
Класс Se состоит из всех ф. а. л. f(xt, . . ., хп) =
— х1\/х2\/. . -\/хп и всех константных ф. а. л.; S3—
=с2П'?б; sb=c3f\s6\ s1=s3f\s:i.
Класс Рв состоит из всех ф. а. л. f{xu х2, . . ., хн)=
&& . . . &хп и всех константных ф. а. л.; Ръ=
РС(Р РРГР
2Г[, 33(\Ь; уьГ[й
Ф. а. л. удовлетворяет условию с№, если любые ц
наборов, на к-рых она равна 0, имеют общую координа-
координату, равную нулю. Аналогично с заменой 0 на 1 вво-
вводится условие А^.
Класс Fi состоит из всех ф. а. л. со свойством а^;
F?=CtnFi\ F^A^Ft; F$=flr\F$; F$ состоит из
всех ф. а. л. со свойством А^; /?^=C4f)/?^; F7X=A3[]
Ф. а. л. удовлетворяет условию а°°, если все наборы,
на к-рых она равна нулю, имеют общую координату,
равную нулю. Аналогично с заменой 0 на 1 вводится
свойство А °°. Класс ^4° состоит из всех ф. а. л. со свой-
ством a»; F? = Ctr\FT; F? = A1()FT; /? = ^ГП^? ;
F™ состоит из всех ф. а. л. со свойством А °°; Fs'=Ci(]
OF?; F? = AbC\F?; F? = F?nF?.
Решетка по включению, образованная этими клас-
классами, изображена на рисунке. На нем классы изобра-
изображены точками. Две точки соединены дугой, если ниже-
нижележащая точка обозначает класс, непосредственно
содержащийся в верхнем классе (т. е. между ними нет
промежуточных классов).
Лит.: [11 Полонский СВ., Гаврилов Г. П.,
Кудрявцев В. Б., Функции алгебры логики и классы
Поста, М., 1966. В. Б. Кудрявцев.
ПОСТА МАШИНА — один из вариантов Тьюринга
машины.
ПОСТА НОРМАЛЬНАЯ СИСТЕМА, нормаль-
нормальное исчислена е,— важный частный случай
Поста канонической системы. с. Ю. Маслов.
ПОСТА РЕШЕТКА — решетка по включению Поста
алгебр.
ПОСТА СИСТЕМА ПРОДУКЦИЙ, нормаль-
нормальная система Поста, нормальное
исчисление Пост а,— частный случай Поста
канонической системы, когда все правила вывода имеют
°1>
вид ^-, и имеется только одно исходное слово (одна
аксиома рассматриваемого исчисления). Э. Пост [1]
установил эквивалентность П. с. п. и канонич. систем
Поста в широком смысле. П. с. и. были использованы
Э. Постом ц А. Л. Марковым A947) при построении
первых примером ассоциативных исчислений с неразре-
неразрешимой проблемой распознавания равенства слов (проб-
(проблема Т v о).
Лит.: [1] Post E. L., «Amer. J. Math.», 1943, v. 65,
№ 2, p. 197—215; [2] Марков А. А., Теория алгорифм»»,
M., 1954 (Тр. Матем. ин-та АН СССР, т. 42). С. И. Адлн.
ПОСТНИКОВА КВАДРАТ — когомологическая опе-
операция типа 0A, А, 3, В), где А, В — абелевы груп-
группы с фиксированным гетероморфизмом т):
А —>- В, т. е. таким отображением, что функция
билинейна и г) (—g) = r\(g). Пусть \ : F -+ А — эпи-
эпиморфизм, a F = ф2 •— свободная абелева группа.
Для 1-коциклов П. к. определен формулой
где ей — такая коцепь с коэффициентами в F, что
|ej=«1. Надстройкой над П. к. является Понтрягина
квадрат. Для односвязного X П. к., для к-рого А =
= я2(А'), В = пя(Х), a i| определяется композицией с
отображением Хипфа й'я —>- S'1, используется при клас-
классификации отображений трехмерных полиэдров в X.
П. к. введен М. М. Постниковым [1].
Лит.: [1] Пост и к о ii M. М., «Докл. АН СССР», 1949,
Т. 64, «V» 4, с. 461 — 62. А. Ф. Харшиладзе.
ПОСТНИКОВА СИСТЕМА, натуральная
система, гомотопическая резоль-
резольвента, П-р азложение общего тип а,—
последовательность расслоений
Pre + i v Pn v Pn-i Pi v ,
• • • * Лп f. Л„_! >• • • >. Л0 — pi,
слоями к-рых являются Эйленберга — Маклейна про-
пространства К(пп, п), где я„ — нек-рая группа (абелева
при п > 1). Введена М. М. Постниковым [1]. Про-
Пространство А',г наз. п-м членом (или n-м этажом)
П. с. {рп : Хп-+ Ап_,}. П. с. {рп : Хп-+ Хп^г} наз.
сходящейся к пространству X, если ее обратный
предел lim {pn : Хи —>- Хп_1} слабо гомотопически
эквивалентен пространству X. В этом случае простран-
пространство X наз. пределом П. с. {рп : X п —>- Л'п_1}.
Морфизмом П. с. {/)„ : Л'„ ->- Xп~\} в П. с.
{qn : Yn-+Yn-i} наз. последовательность непрерыв-
непрерывных отображений /„ : Xп —>- Yn, для к-рых диаграмма
гомотопически коммутативна. Морфизм {/„} индуци-
индуцирует отображение lim /„ : limXn —>-limy,,, называемое
его продолом.
Из определения П. с. следует, что для каждого п ^1
отображение р,г является («— 1)-оквпвалентностью
(см. Гомотопический тип), в частности я,(^„_1) =
ал,- (А'„) при i < л, пп(Хп) s п., и я,- (Х„) = 0 при
i > п. Пространства X и Х„ имеют один и тот же
(п+1)-тцц. В частности, если П. с. конечна, т. е. для
нек-рого числа N при всех п > N группа пп тривиаль-
на, то пространства X и Xjy гомотопически эквивалент-
эквивалентны. В общем случае при i ¦*? п имеют место изоморфиз-
изоморфизмы //j(Xn) э= Н,(Х) и п,-(Х„) =s я,-(Х), т. е. с ростом п
группы гомологии и гомотопич. группы стабилизиру-
стабилизируются. Для любого кле-
клеточного разбиения К > Хл ''" » X?-i > *-Х,
размерности < re mho- i . | , i
жества [К, X] н [А', Г" г Г" \h
Х„] совпадают. Харак- *-У"—2_^у,;_,—¦ —Y,
теристич. класс ftn= Рис j
(РиN („,;
{я„}) расслоения р„ : Хп -*¦ Хл_ь т. е. образ при
трансгрессии
т: Я" («(я, и); л)—*#»+ЧЯ; W)
фундаментального класса i,,?Hn(K (я, ге); я), наз.
ге-м &-и нвариантом (или ге-м постников с-
к и м фактором) П. с. пли ее предела X. Для лю-
любого п ^ 1 n-й член И. с, а потому и (п-И)-тип про-
пространства X полностью определяются группами пи . ..,
л„ и ^-инвариантами klt . . ., /en_i- Часто П. с. наз.
двойная последовательность
{ль ки ..., лп, кт ...}.
Пространство X тогда и только тогда является пре-
пределом П. с. {рп : Хп —у- Хп-х), когда существуют
такие (п — 1)-эквивалентности р„ : X —>- Хп, что ря_]~
~Рл°Рп Для любого п ^ 1. Аналогично характеризу-
характеризуются пределы морфизмов П. с.
Существует вариант понятия П. с, иногда оказываю-
оказывающийся более полезным. В этом варианте пространства
Хп предполагаются клеточными разбиениями, обла-
обладающими тем свойством, что Хп_гс:Х% и X^JLi—Х"^ .
а отображения рп : Хп -*- Хп-\ — такими клеточными
отображениями (уже не являющимися расслоениями),
что, во-первых, pn\Xn~^1=id и, во-вторых, гомотопич.
слой отображения рп (т. е. слой этого отображения,
превращенного в расслоение) является пространством
К (л„, п). Такие П. с. наз. клеточными. Преде-
Пределом клеточной П. с. является клеточное разбиение X,
для к-рого Х"—Х% при любом п ^ 1. Произвольная
П. с. гомотопически эквивалентна клеточной П. с.
Основная теорема теории П. с. утверждает (см. [1],
[6]), что каждое пространство X является пределом
нек-рой однозначно (с точностью до изоморфизма) оп-
определенной П. с. {рп : Хп —у Xn_i}. Эта П. с. наз.
системой Постникова пространст-
пространства X. Имеет место также вариант основной теоремы
для отображений: любое отображение / : X —»- Y яв-
является пределом нек-рого морфизма {/„ : Хп -+УВ}
П. с. {рп : Хп—>- Хя_]} пространства X в П. с.
{Яп '¦ Yn-+ yn_i} пространства Y. Этот морфизм наз.
системой Постникова отображения
/ (др. названия: гомотопическая резоль-
резольвента отображения, П-с и с т е м а о б щ е го
типа отображения, система Мура—
Постникова отображения). Для постоян-
постоянного отображения с : X —>- pt линейно связного про-
пространства X его П. с. совпадает с П. с. пространства X.
В приложениях большое распространение получили
т. н. стандартные системы Пост ник о-
в а (к-рые зачастую наз. просто системами Пост-
Постникова), представляющие собой П. с, составленные
из главных расслоений ;;„ : Х„—>-А'„_,, индуцирую-
индуцирующихся из стандартных расслоений Серра К(пп, п) —>-
-+ЕК (л„, п -f- 1) —>- К (я„, п -\- 1) постниковскими фак-
факторами kn? fftl + 1(X,,_1; я„), интерпретируемыми в силу
представимости групп когомологий как отображения
кп : Xn_i —у К(пп, п -f- 1). Стандартными П. с. обла-
обладают все пространства, гомотопически простые во всех
размерностях (в терминологии [21 — абелевы прост-
пространства), и только они (см. [3], [4]).
Стандартные П. с. применяются для решения задач
распространения и задач понятия, к которым сводят-
сводятся многие задачи алгебраической тополо-
|А ""У гни. Объединенная постановка этих задач
|р заключается в следующем. Пусть име-
| ется (гомотопически) коммутативный ква-
X »-В драт пространств и отображений, в кото-
jill(, ¦> ром отображение i является замкнутым
корасслоением с кослоем XIА, а р — рас-
расслоением со слоем F. Спрашивается, существует ли
такое отображение X —»- Y, чтобы оба получающихся
треугольника были (гомотопически) коммутативными.
Далее, если такое отображение существует, то тре-
требуется вычислить мно-
g"~'»Yn »-EKI>fl(F},fl+i] жество [X, Y]b гомото-
I I классов отображе-
ji) вА:.
Рис. 3 . Пусть для расслоения
р : Y —у В существует
стандартная П. с. {р„ : Yn^-Yn_1, Уо=5} (для этого
достаточно, напр., потребовать, чтобы пространства Y
и В были одиогвязными). Задачу относительного под-
поднятия решают шаг за шагом.
Рассмотрим «элементарную» задачу относительного
поднятия отображения fn~\. X —*¦ Yn_Y с (п.—1)-го
члена П. с. на гс-й член П. с. (рис. 3).
Отображения /„_i и g;!_x определяют отображение
XIA -> К(пп, (F), п -(- 1), т. е. класс когомологий
сп + 1^//п+1(Х, A, nn{F)), называемый препятст-
препятствием. Отображение /„_i тогда и только тогда можно
поднять в Yn, когда с" + 1==0. Два поднятия f'n и fn опре-
определяют элемент dn?Hn(X, A; nn(F)), называемый
различающей, к-рый тогда и только тогда равен
нулю, когда поднятия f'n и \"п гомотопны.
Таким образом, задача относительного поднятия
будет решена, если последовательно возникающие пре-
препятствия cn+1 равны нулю (напр., если Нп + 1(Х, А;
nn(F))~0. Поднятие будет единственно, если последо-
последовательно возникающие различающие d" равны нулю
(напр., если Нп(Х, А; лп(Р))—0). В случае, когда ко-
корасслоение i является вложением клеточных разбиений,
препятствие сп + 1 ж различающая d" совпадают с обыч-
обычными «поклеточными» препятствием и различающей.
Для односвязных пространств X, группы гомологии
к-рых конечно порождены, П. с. эффективно вычисли-
вычислима [5] и, следовательно, эффективно вычислим гомото-
пич. тип пространства X. Однако на практике для боль-
большинства пространств из-за резко возрастающей слож-
сложности вычислений удается вычислить только начальные
отрезки П. с. Для вычислений используется метод
когомологических операций.
Двойственной к П. с. является система Кар та-
тана — Серра
¦¦¦ »• Лп i.Xn-i )-••• >.li-i~A
пространства X, состоящая из расслоений, слоями
к-рых являются пространства Эйленберга — Маклейна
К(лп (X), п — 1). Пространство X%s наз. (п + 1)-м
убивающим пространством для X. Чле-
Члены XnS системы Картана — Серра являются гомото-
пич. слоями (п — 1)-эквивалентностей р„ : X ->- Хп
для П. с. пространства X, а члены Хп П. с.— простран-
пространствами петель над слоями расслоений Хп —>- X.
Расщепленной И. с. наз. последовательность
главных расслоений
¦••—у Хп—>.Xn_i.—*¦¦¦—>.X0=pt,
слоями к-рых являются пространства Эйленберга —
Маклейна К(лп, sn), где sn <: sn + 1. Расщепленные П. с.
являются основным технич. средством изучения т. н.
нильпотентных пространств и, в частности, их локали-
локализаций (см. [2], [6], G]). Имеются и другие варианты
П. с. (см. [6]).
Лит.: [1] Постников М. М., Исследования по гомото-
гомотопической теории непрерывных отображений, ч, 1—2, М., 1955:
[2] его же, «Успехи матем. наук», 1077, т. 32, п. 6, с. 117—81;
[3] Мошер Р., Тангора М., Когомологические опера-
операции и их приложения в теории гомотопий, пер. с англ., М.,
1970, гл. 13; [4] Спеньер Э., Алгебраическая топология,
пер. с англ., М., 1971, гл. 8; [5J В р а у н Э. X., «Математика»,
1958, т. 2, № 2, с. 3—24; [6] В a u e s H. J., Obstruction theory
of the homotopy classification of maps, В.—Hdlb.—N.Y., 1977;
[7] Hilton P., Mislin G., Roitberg J., Localiza-
Localization of nilpotent groups and spaces, Amst., 1976.
С. Н. Малыгин.
ПОСТОЯННОЙ КРИВИЗНЫ ПРОСТРАНСТВО —
риманово пространство М, у к-рого секционная кривиз-
кривизна К (а) по всем двумерным направлениям а постоянна:
если К(а) — к, то говорят, что П. к. п. имеет кривиз-
кривизну к. Согласно теореме Шура, риманово пространство
Мп, ге>2, есть П. к. п., если для любой точки р^М
секционная кривизна К(а) по направлению любых
двумерных подпространств а касательного простран-
пространства ТрМ одна и та же. Тензор кривизны1 П. к. п.
выражается через кривизну к и метрич. тензор g;j по
формуле
П. к. п. является локально симметрическим простран-
пространством.
С точностью до изометрии существует единствен-
единственное полное одиосвязное re-мерное риманово пространство
S"(k) постоянной кривизны к. При &=0 это евклидово
пространство, при к > 0 — сфера радиуса \l\Z~k,
при к < 0 — Лобачевского пространство.
Пространства S" (к) являются максимально однород-
однородными пространствами, т. е. обладают группой двшке-
п(п+1) „
нии максимально возможной размерности —g—. Все
отличные от S" {к) максимально однородные римановы
пространства исчерпываются проективными (иначе,
эллиптическими) пространствами, к-рые получаются
из сфер отождествлением диаметрально противополож-
противоположных точек.
Полные, но неодносвязные П. к. п. наз. простран-
пространственными формами. Они получаются из
односвязного пространства Sn(k) факторизацией по
свободно действующей дискретной группе движений
пространства S"{k). Известны все пространственные
формы положительной кривизны. Проблема классифи-
классификации пространственных форм нулевой и отрицатель-
отрицательной кривизны до конца A983) ее решена.
П. к. п. выделяются среди всех римановых прост-
пространств одним из следующих характористич. свойств:
1) П. к. п. удовлетворяют аксиоме плоскости, т. е.
любое геодезическое в точке подмногообразие в П. к. п.
является вполне геодезическим. 2) П. к. п. является
локально проективно плоским пространством, т. е.
допускает локально проективные отображения в евкли-
евклидово пространство.
Понятие П. к. п. не обладает свойством корректно-
корректности, т. е. пространство с мало меняющимися секцион-
секционными кривизнами может сильно отличаться от П. к. п.
Однако нек-рые общие свойства П. к. п., напр, топо-
логич. строение, при этом сохраняются (теорема Ада-
мара—Картана, теорема о сфере и др., см. Кривизна,
[2]). Совершенно иначе обстоит дело для ксевдорн-
мановых П. к.п.— любое псевдориманово пространство
знакооиределенной секционной кривизны, размерность
к-рого больше двух, является П. к. п.
П. к. п. являются также локально конформно евк-
евклидовыми, т. е. допускают локальные конформные ото-
отображения в евклидово пространство.
Лит.: [1] Вольф Дж., Пространства постоянной кри-
кривизны, пер. с англ., М., 1982; [2] Б ур аго Ю. Д., 3 а л-
галлер В. А., «Успехи матем. наук», 11O7, т. 32, в. 3,
с. 3—55. Д. Д. Соколов.
ПОСТОЯННОЙ ШИРИНЫ КРИВАЯ — плоская
выпуклая кривая для к-рой расстояние между любыми
парами параллельных опорных пря-
прямых одинаково. Это расстояние наз.
шириной П. ш. к. Кроме окруж-
окружности, существует бесконечно много
других, вообще говоря, негладких
П. ш. к. Простейшей из них яв-
является треугольник Р ё-
л о, состоящий из трех дуг окружно-
окружности одного радиуса я, к-рые соеди-
соединяют вершины равностороннего треу-
треугольника со стороной а (см. рис. 1).
Ширина треугольника Рёло равна а.
Площадь фигуры, ограниченной треугольником Рёло,
равна iLff я2—-LjL V Из всех П. ш. к. данной ширины а
треугольник Рёло ограничивает фигуру наименьшей
площади. Примеры других П. ш. к., где дуги П. ш. к.,
описанные вокруг различных многоугольников, пред-
представляют собой дуги окружностей, см. на рис. 2. Длина
П. ш. к. ширины а равна па (Барбье теорема).
Рис. 1.
Рис. 2.
Понятие П. ш. к. можно обобщить на случай объектов
с высокой коразмерностью. Пусть V — гладкое под-
подмногообразие n-мерного евклидова пространства. Про-
Пространство V наз. транснормальным прост-
пространством (см. [2]), если для каждой точки р на V
нормальное многообразие v (p) таково, что для каждой
точки q^v(p)f]V выполнено условие v(g) = v(p). Класс
плоских транснормальных кривых совпадает с классом
гладких П. ш. к. (о пространственных транснормаль-
транснормальных кривых см. [3]).
Лит.: [1] Бляшке В., Круг и шар, пер. с нем., М.,
1967; [2] Robertson S. A., «Michigan Math. J.», 1964,
v. 11, p. 97—105; [3] Wegner В., «Math. Nachr.», 1972, Bd
53, S. 337—44; 1975, Bd 67, S. 213 — 23. Д. Д. Соколов.
ПОСТОЯННОЙ ШИРИНЫ ТЕЛО — выпуклое тело,
для к-рого расстояние между любыми парами параллель-
параллельных опорных плоскостей одинаково. Это расстояние наз.
шириной П. ш. т. Кроме шара существует беско-
бесконечно много других, вообще говоря, негладких П. ш. т.
Простейшим из них является тело, ограниченное поверх-
поверхностью, полученной путем вращения треугольника Рёло
вокруг одной из его осей симметрии. Класс П. ш. т.
совпадает с классом выпуклых тел постоянно-
постоянного охвата, для к-рых границы ортогональных про-
проекций на всевозможные плоскости имеют совпадающие
длины.
Кроме П. ш. т., иногда рассматривают тела по-
постоянной яркости, к-рые характеризуются
тем, что площади поперечного сечения всевозможных
ортогональных проекций атих тел совпадают.
Лит.: [1] Бляшке В., Круг и шар, ijoji. с нем., М.,
1967. Д. Д. Соколов.
ПОТЕНЦИАЛ, потенциальная. функ-
функция, — одна из характеристик векторного поля.
Скалярный потенциал — скалярная
функция v(M) такая, что a = gradv(M) во всех точках
области задания поля а(М) (иногда, напр, в физике,
П. наз. величину, противоположную по знаку). Если
такая функция существует, то векторное поле наз.
потенциальным полем.
Векторный потенциал — векторная
функция А (М) такая, что a=rotA (Л/) во всех точках
области задания поля а(М). Если такая функция су-
существует, то векторное поле а (М) наз. соленоидальным
полем.
В зависимости от распределения порождающих П.
масс или зарядов рассматриваются П. точечного заряда,
поверхностный П. (простого или двойного слоя), объем-
объемный П. и др. (см. Потенциала теория). А. Б. Иванов.
ПОТЕНЦИАЛА ТЕОРИИ ОБРАТНЫЕ ЗАДАЧИ -
задачи, в к-рых требуется найти форму и плотности
притягивающего тела по заданным значениям внешнего
(внутреннего) потенциала этого тела (см. Потенциала
теория). В другой постановке одна из таких задач
состоит в отыскании такого тела, чтобы его внешний
объемный потенциал заданной плотности совпадал вне
этого тела с заданной гармонич. функцией. Первона-
Первоначально П. т. о. з. рассматривались в связи с задачами
теории фигуры Земли и небесной механики. П. т. о. з.
связаны с задачами фигур равновесия вращающейся
жидкости и задачами геофизики.
Центральное место в исследовании П. т. о. з. состав-
составляют проблемы существования, единственности, устой-
устойчивости, а также создание эффективных численных ме-
методов их решения. Теоремы существования решений в
малом имеются для случая тела, близкого к данному,
но при этом имеются значительные трудности в иссле-
исследовании уравнений, как правило, нелинейных, к к-рым
сводятся эти задачи. Критериев существования гло-
глобальных решений нет A983). Во многих случаях су-
существование глобальных решений предполагается за-
заранее, что естественно во многих приложениях, и ис-
исследуются проблемы единственности и устойчивости.
Одним из основных моментов в исследовании проблемы
единственности является выявление дополнительных
условий на решения, обеспечивающих их единствен-
единственность. С проблемой единственности связана проблема
устойчивости. Для задач, записанных в виде уравнения
1-го рода, вообще говоря, сколь угодно малым вариаци-
вариациям правой части могут соответствовать конечные вариа-
вариации решений, т. е. эти задачи относятся к некорректно
поставленным задачам. Для того чтобы задача стала
корректной, накладывается ряд дополнительных огра-
ограничений на решения; при этих ограничениях получа-
получаются различные характеристики отклонения решения
в зависимости от отклонения правой части.
Ниже сформулированы обратные задачи ньютонова
(объемного) потенциала и потенциала простого слоя
для уравнения Лапласа в трехмерном евклидовом про-
пространстве R3, хотя указанные задачи исследуются
и в «.-мерном (ге>2) евклидовом пространстве для по-
потенциалов общих эллиптич. уравнений (см. [7]).
Пусть Та, а---1, 2,— односвязные ограниченные
области с кусочно гладкими границами Sa;
— ньютонов потенциал;
— потенциал простого слоя, где \х—у\ — расстояние
между точками х— (х1, ,т2, xs) и у= (z/lt z/2, ;/3) в R3,
»а(.'/) Ф 0 (?аЫ Ф 0) почти всюду в Ta(Sa). И пусть
где C, у — действительные числа, PJ+Ya Ф
Общая в н е ш н я я П. т. о. з. состоит в нахождении
формы и плотности притягивающего тела по заданным
значениям внешнего потенциала Z (х). Для получения
условий единственности решения этой задачи она фор-
формулируется следующим образом: найти такие условия
для областей Та и плотностей u.a, t,a, чтобы из равенст-
равенства внешних потенциалов Zx(x) и Z2(x):
Z1 (x) = Z2 (х) для х ? R>\(f\U f2) (I)
следовало равенство ТХ=Т2, (х1=ц2, ?i=?2- Если мно-
множество R3\G'iU Т2) состоит из одной компоненты, то ус-
условие A) выполняется, когда Z1(x)^Z2(х) для |х|>Д, где
R — достаточно большое, или когда на границе шара
\x\-R задаются данные, обеспечивающие совпадение
7i\{x) и Z2(x) вне этого шара. В качестве таких данных
могут быть выбраны данные Дирихле на всей границе
шара либо данные Коши на куске границы шара и т. д.
В дальнейшем для простоты считается, что множества
T'=Tif\T2 и T"=R3\(F1\jfi) состоят из одной ком-
компоненты.
Решение общей внешней П. т. о. з. единственно, если
Ш=И'2==И' > °> Si= ?2= S > U. а области Та контакт-
контактны, т. е. такие, что для каждого из множестн 7" и Т"
существует общий участок iS#(mes5^^0) границ
So., причем mes[E1(j52) \ S,„]—0.
П. т. о. з. для ньютоновых потенциалов получается,
когда в A) C=1 и 7=0. Пусть Та, а=1, 2,— области,
звездные относительно общей точки, а функции [ха (у)
имеют вид ua(i/)=6av(i/), где 6a=const, v > 0 и не за-
зависит от р= \у\. Если ньютоновы потенциалы удовлетво-
удовлетворяют условию A) и, кроме того, существует точка
ЯоС^ПЛ такая, что U1{x0)= U2(x0), то ТХ=Т2,
Ц1=М-2-
Если в условиях A) положить u.1=u.2=fx, p=l, -у=0,
то получается задача об определении формы притяги-
притягивающего тела по известным значениям внешнего ньюто-
ньютонова потенциала U(х) заданной плотности. Решение
этой задачи единственно в классе областей Та, звездных
относительно общей точки, в случае заданных плотно-
плотностей (г(у), монотонно неубывающих с ростом \у\.
Если в условиях A) положить C = 0, 7—li ?i—?г>
то получается задача об определении формы притяги-
притягивающего тела по известным значениям внешнего потен-
потенциала простого слоя V(х) заданной плотности ?. Для
выпуклых тел постоянной плотности решение этой зада-
задачи единственно.
Если в условиях A) положить 7\" Т2- Т, C = 1, "\>=0,
то получается задача об определении плотности при-
притягивающего тела по известным значениям внешнего
ньютонова потенциала. Решение задачи единственно,
если функции ца{у) имеют вид (ха(г/) = т) (y)va(y), где
g g
Общая в н у т р е н н я я П. т. о. з. состоит в нахож-
нахождении формы и плотностей притягивающего тела по
заданным значениям внутреннего потенциала Z(x).
Для получения теорем единственноети используется сле-
следующая формулировка этой задачи: найти условия для
областей Та и плотностей ц.а, ?а, чтобы из совпадения
внутренних потенциалов Z1(x) и Z2(x):
Z1(x) = Z2(x) для х ? ГхП^а B)
следовали равенства ТЛ=Т2, \ii==\i2, ^x= 5г-
Если в условиях B) р" = 1, 7=0, то в классе выпуклых
тел переменной положительной плотности решение един-
единственно. Если же в условиях B) Р=0, 7=1> Si=S2=C=
=const, то в классе выпуклых тел решение также
единственно.
Пусть ищется тело Т такое, что его внешний нью-
ньютонов потенциал U (х; Т1, ц) данной плотности ц(х)
равен вне тела Т1 заданной гармонич. функции Н(х),
Н (х) —у- 0 при \х\ —>- оо и -ff (ж) близка в смысле нек-рой
функциональной метрики к внешнему ньютонову по-
потенциалу U(х; 7', ц) заданного тела Т плотности ц.
Для односвязных областей Т с гладкой границей S
при условии (.1 (.с) 15 ф 0 решение задачи существует и
единственно.
Внутренняя задача ставится аналогично внешней,
причем Н (х) является решением неоднородного урав-
уравнения Лапласа в конечной области
Л# = —(Л (х) для x?G0.
Ищется тело 7\ такое, что для
grad Н (х) =grad U (х; Ти ц).
В отличие от внешней внутренняя задача имеет, вооб-
вообще говоря, не единственное решение; число решений
определяется уравнением разветвлений.
Плоские П. т. о. з. (ге=2) ставятся аналогично
пространственным с учетом соответствующего поведения
потенциалов на бесконечности. В связи с этим ряд ут-
утверждений, приведенных выше для п = 3, видоизменя-
видоизменяется. Плоские П. т. о. з. иногда удобно исследовать
методами теории функций комплексного переменного и
конформных отображений.
Плоская в н е га н я я П. т. о. з. Пусть ,и=1 —
заданная плотность, причем вместо логарифмич. по-
а 1/9
тенциала масс введена его производная -^ = — ( -^ —
9 \
~*Иу)' на комплекснои плоскости z=x-\-iy вне круга
К (О, R) = {\z\ < R} задана аналитич. фуйкция H(z),
7/(оо) = 0, особые точки к-рой при ее аналитич. продол-
продолжении находятся внутри области D#, 0?.О„. Требуется
найти конечную односвязную область D с жордановой
границей, D^dDdDdK(О, R), такую, чтобы #(z) =
= U(z, D) для \z\ > R, где
U (z, D) = —
Решением этой задачи считается функция z(t), отобра-
отображающая конформно единичный круг |i| < 1 комплекс-
комплексной плоскости t на область D плоскости z=x-\-iy и
удовлетворяющая условиям z@) = 0, z'@)>0.
Пусть D — заданная конечная односвязная область
с жордановой границей, функция f/a(z)=Cf(z, D) для
z ? R2\D. Тогда функция удовлетворяет уравнению
где
Если z(t) является решением уравнения C), в к-ром
Ua (z) заменена указанной выше функцией Н (z), причем
z(t) однолистна при UI < 1, z@) = 0, z @) > 0, тоЯ(г)=
= U(z, D) для UI > R.
Из уравнения C) можно получить ряд связей между
функцией Ua(z) и функцией z(t). Напр., если внешний
потенциал Ua (z) можно аналитически продолжить
внутрь D через всю границу 8D, то z(t) — аналитич.
функция при |t| = l; если
*(s) =z (-4-4) при | s| Sal.
Это позволяет иногда решить плоскую П. т. о. з. в ко-
конечном виде. Пусть Н(z)— ^ь_,~~?, ст5с0. Тогда соот-
к—1 X
ветствующее нелинейное уравнение для z{t) эквивалент-
эквивалентно, вообще говоря, нелинейной системе алгебраич.
уравнений относительно коэффициентов а1, . . ., ат.
Функция z (t), вообще говоря, но однолистная при \t\ <1,
находится как решение этой алгебраич. системы урав-
уравнений. Класс однолистных в круге \t\ < 1 решений
z{t), удовлетворяющих условиям z@)--, z @) > 0,
является решением поставленной П. т. о. з.
Аналогичное исследование можно провести для
внешней обратной задачи логарифмич. потенциала
простого слоя, а также для внутренних обратных задач
логарифмич. потенциалов, причем как для внешних,
так и для внутренних П. т. о. з. можно рассматривать
переменные плотности.
Лит.: [1J Нов и к о и П., «Докл. АН СССР», 1938, т. 18,
Ms 3, с. 165—08; [2J Тихонов А. Н., там же, 1943, т. 39,
№ 5, с. 195—98; [3] С, р с т с н с к и й Л. II., Теория ньюто-
ньютоновского потенциалу, М.— Л., 1946; [41 И и а н о в В. К.,
«Изв. АН СССР. Сер. мятсм.», 195E, т. 20, .N5 6, с. 793—818;
[5] его же, «Докл. АН СССР», НM5, т. 105, № 3, с. 409—11;
1956, т. 106, №4, с. 598 — 9!); Гй] Лаврентьев М. М.,
О некоторых некорректных задачах математической физики,
Новосиб., 1962; [7] Г1 риле п к о А. И., «Дифференциальные
уравнения», 19В6,т. 2, № 1, с. 107—24; 19E7, т. 3, .\5 1, с. 30—
44; 1970, т. 6, № 1, с. 27 —49; 1972, т. 8, № 1, о. 118-25; его
ж е, «Сиб. матем. ж.», 1965, т. 6, .К» 6, с. 1332—56; 1971, т. 12,
Л 3, с. 630—47; Ml 4, с. 828 — 36; Л» 6, с. 1341 — 53; 18] Тих о-
н о в А. Н., А р с е н и н В. Я., Методы решения некорректных
задач, 2 изд., М., 1979. A. if. Прилепко.
ПОТЕНЦИАЛА ТЕОРИЯ — и первоначальном по-
понимании — учение о свойствах сил, действующих по
закону всемирного тяготения. В формулировке этого
закона, данной И. Ньютоном (I. iNewton, 1687), речь
идет только о силах взаимного притяжения, действую-
действующих на две материальные частицы малых размеров, или
материальные точки, прямо пропорциональные произ-
произведению л псе, этих частиц и обратно пропорциопальные
квадрату расстояния между частицами. Поэтому первой
и важнейшей с точки зрения небесной механики и геоде-
геодезии задачей было изучение сил притяжения материаль-
материальной точки ограниченным гладким материальным телом—
сфероидом и, в частности, эллипсоидом (ибо многие
небесные тела имеют именно эту форму). После первых
частных достижений И. Ньютона и др. ученых основ-
основное значение здесь имели работы Ж. Лагранжа (J. Lag-
range, 1773), А. Лежандра (A. Legendre, 1784—94) и
П. Лапласа (P. Laplace, 1782—99). Ж. Лагранж уста-
установил, что ноле сил тяготения, как говорят теперь,—
потенциальное, и ввел функцию, к-рую позже Дж. Грин
(G. Greet), 1828) назвал потенциальной, а К. Гаусс
(С. Gauss, 1840) — просто потенциалом. Ныне достиже-
достижения этого первоначального периода обычно входят в
курсы классич. небесной механики (см. также [2]).
Еще К. Гаусс и его современники обнаружили, что
потенциалов метод применим не только для решения
задач теории тяготения, но и вообще для решения
широкого круга задач математич. физики, в частности
электростатики и магнетизма. В связи с этим стали
рассматриваться потенциалы не только физически
реальных в вопросах взаимного притяжения положи-
положительных масс, но и «масс» произвольного знака, или за-
зарядов. В П. т. определились основные краевые задачи
такие, как Дирихле задача и Неймана задача, электро-
статич. аадача о статич. распределении зарядов на
проводниках, или Рибена аадача, задача о выметании
масс (см. Выметания метод). Для решения указанных
задач в случае областей с достаточно гладкой границей
оказались эффективным средством специальные разно-
разновидности потенциалов, т. е. специальные виды интег-
интегралов, зависящих от параметров, такие, как потенциал
объемно распределенных масс, потенциалы простого и
двойного слоя, лошрнфмич. потенциалы, потенциалы
Грина и др. Основную роль в создании строгих методов
решения основных краевых задач сыграли работы
А. М. Ляпунова и В. А. Стеклова кон. 19 в. Изучение
свойств потенциалов различных видов приобрело в
И. т. и самостоятельное значение.
Мощный стимул в направлении обобщения основных
аадач и законченности формулировок П. т. получила
начиная с 1-й пол. 20 в. на основе использования
общих понятий меры в смысле Радона, емкости и обоб-
обобщенных функций. Современная П. т. тесно связана в
своем развитии с теорией аналитпч. функций, гармонич.
функций, субгармонич. функций и теорией вероятно-
вероятностей.
Наряду с дальпейшим углубленным изучением клас-
классических краевых задач и обратных задач (см. Потен-
Потенциала теории обратные задачи) для современного
периода развития П. т. характерно применение методов
и понятий современной топологии и функционального
анализа, применение абстрактных аксиоматич. методов
(см. Потенциала теория абстрактная).
Основные типы потенциалов и их свойства. Пусть
S — гладкая замкнутая поверхность, то есть (п — 1)-
мерное гладкое многообразие без края, в п-мерном
евклидовом пространстве R", re 5s 2, ограничивающая
конечную область G=G+, 9G=S, и пусть G~ =
= Rn\(G + \JS) — внешняя бесконечная область. Пусть
1 1 п
„ , s v I, u %("-2) |х-»Г! ' "" '
Е (х, у) = Е(\х-у\) =
— главное фундаментальное решение уравнения Лап-
Лапласа Au=y^k=1d2uldxl=Q в R", где
1/2
— расстояние между точками х=(х1: . . ., хп) и ;/=
=(Уи- ¦ ¦, Уп) в R"> со„=2я"'2/Г(ге/2) — площадь единич-
единичной сферы в R", Г — гамма-функция. Три интеграла,
зависящих от х как от параметра:
Р (У) Е (x, у) dy,
V(x) = \ a(y)E(x, y)dS(y), V A)
где пу — направление внешней относительно G+ нор-
нормали к S в точке y?S, наз. соответственно объем-
объемным потенциалом, потенциалом прос-
простого слоя и потенциалом двойного
слоя. Функции р(г/), ц (у) и v (у) наз. плотно-
плотностям и соответствующих потенциалов; ниже они бу-
будут предполагаться абсолютно интегрируемыми соответ-
соответственно на G или S. При ге=3 (а иногда и при п ^ 3)
интегралы A) наз. ньютоновым объемным
потенциалом, ньютоновыми потен-
потенциалами простого и двойного слоя,
при п=2 — логарифмическими потенци-
потенциалами м а с с, и р о с т о г о и двойного слоя.
Пусть р принадлежит классу C1(G[JS). Тогда объем-
объемный потенциал и его производные 1-го порядка непре-
непрерывны всюду в R", причем их можно вычислить по-
посредством дифференцирования под знаком интеграла, то
есть Z?CL(R"). Далее,
lim (Z(x)/E(x, Q))=M, M=[ o(y)dy.
| .V I -> CO •) U
Производные 2-го порядка непрерывны всюду вне S,
но при переходе через поверхность S они претерпевают
разрыв, причем в области G+ удовлетворяется уравне-
уравнение Пуассона — AZ=p(x), x^G'~, а в G~ — уравнение
Лапласа AZ—O, x?G~. Перечисленные свойства харак-
характеризуют объемный потенциал.
Еглп G, — конечная область пространства R" с гра-
границей S1--dG1 класса С1, то справедлива формула
Гаусса для объемного потенциала:
Пусть ц^С1E'). Потенциал простого слоя V (х) есть
гармонич. функция при x(?S, причем
lim (V(x)/E(x, 0)) = Л/, M^[ a(y)dS(y);
| X I ->
в частности, lim l'(i)-0 при re > 3, но lim V(x) = 0
|.Y|->-« |ж|->-00
при п==2 тогда и только тогда, когда \ fi(y)dS (y)—Q.
Потенциал простого слоя непрерывен всюду в R",
V?C(Rn), причем V(х) и его касательные производные
непрерывны при переходе через поверхность S. Нор-
Нормальная производная потенциала простого слоя при
переходе через поверхность S испытывает скачок:
dnj ~ 2 И*Л дПх
/ ov\+ / av \ -
где f g^ I и ( g^ 1 — предельные значения нор-
нормальной производной соответственно ил Gh и б~, то
есть
гДЛ+ = lim
Через д\'(хIдпх здесь обозначено т. н. прямое
значение нормально» н р о и л в од н о и
потенциала простого слоя, вычисленное
на поверхности S, то есть
-ТЙ-гЧ* I'M <?*<*• y)*S(y),x?S,
к-рое является непрерывной функцией точки x?S,
а ядро дЕ (х, уIдпх имеет слабую особенность на S,
а
const
Перечисленные свойства характеризуют потенциал
простого слоя.
Пусть v^C1E). Потенциал двойного слоя W(x)
есть гармонич. функция при x(?S, причем
lim со„| х I"-1 W (х) = М, М—\ v(y)dS(y).
| J5
I к |
5
При переходе через поверхность 5 потенциал двойного
слоя испытывает скачо-к:
W+ (x) = -±.v(x) + W(x), W-(x)=±v(
где W+ (х) и W~ (x) — предельные значения потенциала
двойного слоя соответственно из G+ и G~, то есть
W+ (ж)= lim И' (х'), ТУ- (ж)= lim W{x').
x'-+x,x'?G+ x'^*x,x'ed~
Через W(x) при x?S обозначено т. н. прямое
значение потенциала двойного слоя,
вычисленное на поверхности S, то ость
W(x)=[ v(y)-?-E(x, y)dS(y), x?S,
Jo У
к-рое является непрерывной функцией точки x?S,
а ядро дЕ(х, уIдпу имеет слабую особенность на 5,
4
const
-у ["-'
| х-у [
У
Касательные производные потенциала двойного слоя
также испытывают скачок при переходе через поверх-
поверхность S, но нормальная производная dW(x)ldnx сохра-
сохраняет свое значение при переходе через S:
Перечисленные свойства характеризуют потенциал
двойного слоя.
В случае постоянной плотности V— 1 имеет место
формула Гаусса для потенциала
двойного слоя:
(I, *?G + ,
d?-E(<x' y)dS(y)=q(x) = < 1/2, x?S,
y I 0, x?G~.
Интеграл в левой части этого равенства интерпрети-
интерпретируется как (деленный на соп(д—2)) телесный угол, под
к-рым видна поверхность S из точки х.
Ниже дополнительно приводятся нек-рые свойства
потенциалов при меньших ограничениях на плотности
и поверхность S.
Если p(zLi(G), то Z (х) — гармония, функция при
х ? G~ и Z (х) суммируема в G <". Если p?LJG), 1<р<:
<ге/2, toZ?L(.(R«), l/p + l/g=l, I <g<np/(re—2p); если
p?Lp(G), p>n/2, то Z?C(R"). Если p?Lp(G), 1<р<ге,
то Z? W^(R"), i<q<np/(n—p); если p?Lp(G), p>n, то
Z?G1(Rn). Если pgZ»2(G), то существуют обобщенные
производные 2-го порядка от Z (х), они также принадле-
принадлежат классу А2(С) и выражаются с помощью сингулярных
интегралов:
y)dy,
i, / = 1, 2, ..., п,
где 6,у=1 при ?=/, о',у = 0 при ???;; если p?
<р<оо, то все обобщенные производные jj
также существуют и принадлежат LJR"). Если р^
?Lp(G), 1<р<+оо, то Z(x) есть обоощенное решение
уравнения Пуассона —А2=р(ж), x?G. Если pg
gC(». «)(б) и 5gC'i. a>, 0<а<1, то Z^C<2. а> в G+
или G-. Если pGc</' а> С?) и 5gC<*+i. «>, 0<а<1, I,
к — целые, 0<i<fc, то Z?C<-1+*. a>(G^ ).
¦ Пусть S ?С^ а>, 0<а<1, D — замкнутая конечная
область такая, что G? \JSCDaDaRn. Тогда если
\i€Lp(S), p=l,2, то VgZ,^), V?Lp(S), dV/дх^
?Lp(D), p—l, 2; i=l, 2, ..., re. Если плотность п. огра-
ограниченная и суммируемая, то
V ? С<°. *>VX g @, 1).
Если ц?С(о, «)E), 0<а<1, то F^Cd. <*> в G+ или
G-. Если v^C<°. а»E), то ТУ^СО. <*> в G+ или б~.
Если ц?СС а)E) и ^gC***-1. «>,0<а<1, г, А: — це-
целые, ()<;<&, то К^6'<41. *) в G+ или G-. Если vg
gCC «'(•!>) и 5gC(fe + 1- а), 0<а<1, I, к — целые,
0<г<А;+1, то WgCC. а) в G+ или G-.
Для доопределенных по непрерывности потенциалов
и их производных на поверхности S описанные выше
свойства гладкости также остаются в силе при соответ-
соответствующих условиях гладкости на плотность и поверх-
поверхность S.
Представление функций и решение основных крае-
краевых задач теории потенциала с помощью потенциалов.
Пусть Ф (х) — функция класса C'-(G[JS), S —• гладкая
поверхность класса С2. Тогда справедливо интеграль-
интегральное тождество (формула Грина):
АФ (у) Е (х, у, dy+t (ЩШе(х,у)-
о j s v у
B)
В частности, в области G функция Ф (х) представима в
виде суммы объемного потенциала и потенциалов про-
простого и двойного слоя соответственно с плотностями
, v (у)-=—Ф (у).
Для гармонической в области G функции и (х) класса
C1(G[JS) имеет место тождество
У ' дпУ J
и поэтому такая функция и (х) представима в G в виде
суммы потенциалов простого и двойного слоя соответст-
соответственно с плотностями \у(у)~ди(уIдпу, v(y)=—u(y).
Однако эти плотности в формуле C) не могут задаваться
произвольно на S, они связаны интегральным соотно-
соотношением, получающимся из C) при x?G~.
Центральное место в П. т. занимают краевые задачи
Дирихле и Неймана (наз. также первой и второй крае-
краевыми задачами) для областей G *¦ (внутренние задачи)
и G~ (внешние задачи), к-рые в предположении доста-
достаточной гладкости поверхности удается полностью иссле-
исследовать сведением их к интегральным урав-
уравнениям П. т.
Внутренняя задача Дирихле: найти
гармоническую в G+ функцию и{х) класса С(G+ \JS),
S ?C<i. <*>, 0<а<1, удовлетворяющую краевому усло-
условию и(х) = (р + (х), х?S, где (f + (x) — данная непрерывная
функция на S. Решение этой задачи всегда существует,
единственно и может быть найдено в виде потенциала
двойного слоя
u(x)=tv(y)-?-E(z, y)dS(y)
J ¦J У
с плотностью v, к-рая находится как единственное ре-
решение интегрального уравнения Фредгольма 2-го рода
Внутренняя задача Неймана: найти
гармоническую в области G+ функцию и(х) класса
C1(G+ \JS), 5?СA- a>, 0<а<1, удовлетворяющую крае-
краевому условию du(x)/dnx—i!p + (x), x?S, гдег|) + (х) — дан-
данная непрерывная функция на S. Решение этой задачи
существует тогда и только тогда, когда функция г|) + (-с)
удовлетворяет условию ортогональности
^г|)+ (x)dS(x) = O. D)
Это решение определяется с точностью до произвольной
аддитивной постоянной С в виде и(х)= V(x)-\-C, где
V (х) = ^s ц (у) Е (х, у) dS (у)
— потенциал простого слоя, плотность ц к-рого опре-
определяется из интегрального уравнения Фредгольма 2-го
рода
Соответствующее однородное уравнение имеет нетриви-
нетривиальное решение цо(х)> а неоднородное уравнение E)
разрешимо при выполнении условия D), причем его
общее решение имеет вид \x(x)~\-cixo(x), где с — произ-
произвольная постоянная.
В н е ш н я я з а д а ч а Дирихле: найти гармо-
гармоническую в области G~, 0?G4, функцию и (х) класса
C(G-\JS), S?C<i. «>, 0<а<1, удовлетворяющую крае-
краевому условию м(ж) = ф-(х), x?S, где ф~(ж) —данная
непрерывная функция на S; при этом и(х) предпола-
предполагается регулярной на бесконечности, т. е.
lim | х \"~2 и (х) = const.
Решение этой задачи всегда существует, единственно
и может быть найдено в виде
где А — постоянная,
v(y)-^-E(x, y)dS(y)
— потенциал двойного слоя, плотность v к-рого являет-
является решением интегрального уравнения Фредгольма
2-го рода
f v(y)~E(x, y)dS(y) =
J S У
(b)
Соответствующее однородное уравнение имеет нетриви-
нетривиальное решение vn-= 1. При надлежащем выборе постоян-
постоянной А решение неоднородного уравнения F) имеет вид
где С — произвольная постоянная, a v~(y) — частное
решение ур-ния F). Постоянная А подбирается в виде
А = — \ s ф - (х) v0 (x) dS (x),
где плотность vn должна удовлетворять условию
yo(y)j^rdS(y)=i. G)
Эта плотность vn есть нетривиальное решение уравне-
уравнения E) внутренней задачи Неймана с даннымиг|) + (ж) = О,
x?S, удовлетворяющее эквивалентному G) при п^'\
условию нормировки
Потенциал простого слоя V0(x) плотности vo(x) наз.
равновесным потенциалом, или п о-
тенциалом Робена. Плотность vo(.t) дает ре-
решение задачи Робена или электростатич. задачи о рас-
распределении зарядов на проводнике S, создающем равно-
равновесный потенциал, постоянный в области G+. Нек-рая
сложность решения внешней задачи Дирихле происхо-
происходит из-за того, что регулярная на бесконечности гармо-
нич. функция и(х), вообще говоря, убывает при \х\ —>- оо
медленнее, чем потенциал двойного слоя, и поэтому и (.г)
в общем случае нельзя представить в виде одного только
потенциала двойного слоя.
Внешняя задача Неймана: найти гармо-
гармоническую в области G~, О^С1 , функцию и(х) класса
C1(G~ [JS), 5^CA" a>, 0<а<1, удовлетворяющую крае-
краевому условию du(x)/dnx=ty~(x), x?S, где я|)~(.г) — дан-
данная непрерывная функция на 5; при этом и(х) предпо-
предполагается регулярной на бесконечности. При ге^З ре-
решение этой задачи всегда существует и единственно;
при п=- 2 решение существует тогда и только тогда,
когда выполняется условие
^>- (x)dS(x)=Q, (8.
причем решение определено лишь с точностью до про-
произвольной аддитивной постоянной. Решение внешней
задачи Неймана представимо в виде потенциала прос-
простого (МОЯ
плотность (х к-рого есть решение интегрального уравне-
уравнения Фредгольма 2-го рода
-yl'W+jjMrt-^fi (х, y)dS(y) =
= ij)- (x), x?S. (9)
При н^З решение этого уравнения всегда существует и
единственно. При п=2 соответствующее однородное
уравнение имеет нетривиальное решение \lu(x), поэтому
неоднородное уравнение (9) при выполнении условия
разрешимости (8) имеет единственное решение \i(x)
такое, что
а его общее решение имеет вид ц, (я-)—и. (х)-\-с\хо(х),
где с — произвольная постоянная.
Решение краевых задач П. т. может быть получено
также с помощью Грина функции. Напр., для (внутрен-
(внутренней) задачи Дирихле функция Грина имеет вид
G(x, у) = Е(х, y) + g(x, у), x?G+\JS, y?G+,
где g(x, у) — гармонич. функция в G f ti непрерывная
в G+(J^ по л1, для каждого у ?G+ удовлетворяющая
краевому условию G (х, у)~-0, .г ? S. Решение (внутрен-
(внутренней) задачи Дирихле и (х) класса C2(G 'r) f]C (G+ \)S)
для уравнения Пуассона - Аи (.т) — /(.г), a-g G + , с крае-
краевым условием и(х) Ф +(.'•), x?S, представимо в виде
и(х) =
Зависящие от параметра и iihtci ралы
" , р {у) С (х, у) dy, [ v(y)JL-G (x, у) dS (у)
J С
наз. соответственно объемным потенциа-
потенциалом Грина (задачи Дирихле), п о т е н ц и а-
л о м Грина д в о й и ого с л о я. Их свойства
аналогичны свойствам потенциалов A).
С помощью функции Грина к интегральным уравне-
уравнениям сводятся задачи на собственные значения. Напр.,
задача Дирихле — Аы = Я.и(.г), ,r?G + ,c краевым усло-
условием и (х) = 0, х?5, сводится к интегральному уравне-
уравнению Фредгольма 2-го рода с самосопряженным ядром
Дальнейшее обобщение некоторых основных поня-
понятий теории потенциала. Параллельно с углубленным
изучением свойств потенциалов A), определяемых плот-
плотностями более или менее общего вида, и их применений
само понятие потенциала подверглось начиная пример-
примерно с 20-х гг. 20 в. глубокому обобщению, связанному с
понятием меры и интеграла Радона.
Пусть }.^>Л) - положительная борелевская мера на
пространстве R" с компактным носителем supp X.
Потенциал меры
EK(x)=<\jE(x,y)dK(y) A0)
существует всюду в R" в смысле отображения EX : R" ->
-->¦ [0, ос] при ?2^3 и Е% : R2 -> (—ос, со] при п~2
(т. е. здесь допускается и значение +ос) и является
гупергармонической функцией всюду в R", гармониче-
.кой — вне носителя меры supp X. Для меры X произ-
вольного знака с компактным носителем потенциал Ек
определяется, исходя из канонич. разложения Х=
- к + —к~, Х-< >0Д->0, и виде Ек=Ек+—Ек~.В тех
точках x?-R", где оба потенциала Ек + (х) и ЕХ~(х) при-
принимают значение + оо, этот потенциал не определен.
Если мера Х^О сосредоточена на гладкой поверхности
S, то аналогично A0) определяется и потенциал двой-
двойного слоя меры Л:
Потенциал A0) конечен, Ек<.-\-со, всюду в R", за
исключением точек полярного множества, к-рое харак-
характеризуется как множество внешней емкости нуль. Если
ЕХ(х)=-:0 всюду, кроме множества внешней емкости
нуль, то к=0. Если мера Х~^§, ХфО сосредоточена на
множестве емкости нуль, то sup Ек=-\-оо. Справедлив
следующий принцип максимума:
Ек (x)s^ supp {EX (у): y?suppk},
т. е. верхняя грань ЕХ(х) есть верхняя грань сужения
Ек на supp X. Если это сужение непрерывно (в обоб-
обобщенном смысле, включая значение -j-oo) в точке хо?
?supp X, то потенциал ЕХ(х) непрерывен в точке хд
в R". Потенциалы мер Ек сводятся к потенциалам плот-
плотностей A) тогда и только тогда, когда мера X абсолютно
непрерывна по мере Лебега соответственно на G или на
5 (см. [3]-[6]).
Если Т — обобщенная функция, или распределение,
в R", то потенциал распределения
определяется как свертка Е*Т, являющаяся также об-
обобщенной функцией. Напр., если Т — финитная обоб-
обобщенная функция, то в R" в смысле обобщенных функ-
функций справедливо уравнение Пуассона А(ЕТ) = — Т.
Потенциалы мер можно рассматривать как частный слу-
случаи потенциалов распределений. О потенциалах распре-
распределений см. [3], 14], [9].
Для областей G--G + с достаточно гладкой границей S
метод потенциалов дает эффективное решение задачи
Дирихле. Одно из основных направлений развития П. т.
состоит в открытии методов доказательства существова-
существования и единственности решения задачи Дирихле для все
более широких классов областей (см. Выметания метод,
Дирихле принцип, Перрона метод, Шварца альтерни-
альтернирующий метод). Однако в 1910 С. Заремба (S. Zaremba)
заметил, что для плоской области G при наличии изо-
изолированных точек границы flG= S задача Дирихле в
приведенной выше классич. постановке не всегда раз-
разрешима; более того, в 1912 А. Лебег (Н. Lebesgue) по-
показал, что она не всегда разрешима и для пространст-
пространственных областей, гомеоморфных шару, при наличии до-
достаточно острого входящего в область острия границы
(т. н. острие Лебега, см. Иррегулярная гранич-
граничная точка), т. е. существуют такие непрерывные функ-
функции ф + (.г), x?dG, для к-рых задача Дирихле не разре-
разрешима никаким способом.
Поэтому важное значение имеет полученное в ходе
развития люто да Перрона обобщенное реше-
решение в смысле Перрона — Винера зада-
задачи Д и р и л л с для уравнения Лапласа. Как показал
Н. Винер (N. Wiener, 1924), при этом любая конечная
непрерывная функция ф=ф+, заданная на границе 5 =
-~дЬ произвольной конечной области GcM", p а з-
р е ш и м а, т. е. для нее существует и притом единст-
единственное обобщенное решение Нц, (х) в смысле Перрона —
Винера. Вообще, в 1939 М. Брело (М. Brelot) показал,
что конечная измеримая функция ф на S разрешима
тогда и только тогда, когда ф интегрируема по гармони-
гармонической мере на S.
Обобщенное решение Д"ф (х) не во всех граничных точ-
точках принимает заданные значения ф. Точка. xo?-S наз.
регулярной, если для любой конечной непрерыв-
ной функции ф на S обобщенное решение 11ф (.г) прини-
принимает значение q (г„), то есть
lim Яф (х) = ф (хй), ж?С.
Прочие точки х0 ? 5 наз. иррегулярными, к ним
относятся изолированные точки границы при г?^2 и
острие Лебега лри п^З. Как оказалось (Келлога —
Эеанса теорема, 1933), множество иррегулярных точек
имеет внешнюю емкость нуль, т. е. является в нек-ром
смысле разреженным. Множество регулярных точек
плотно на S.
Для задачи Дирихле строится соответственно и
обобщенная функция Грина G, к-рую
можно определить, напр., для произвольно фиксиро-
фиксированной точки y(^G следующим образом:
G(x, у) = Е(х, y)-HE(xy){x),x?G.
Обобщенная функция Грина сохраняет нек-рые свойст-
свойства классич. функции Грина, папр. свойство симметрии
G{x, y)=G{y, х), но iim G(x, у)-0, .r?G, тогда и только
х-*х0
тогда, когда х0 — регулярная точка границы S (см.
[4], [6]).
Важное значение имеют также исследования задачи
Дирихле для компактов и устойчивости задачи Дирихле
(см. [6], [4]).
Интенсивно разливается изучение потенциалов с
другими ядрами, отличными от ядра Е(х, у), и их при-
применений для решения краевых задач (см. Весселев по-
потенциал, Нелинейный потенциал, Рисса потенциал,
а также [3], [11]).
Лит.: [1] Г ю н т е р Н. М., Теория потенциала и ее при-
применение к основным задачам математической физики, М., 1953;
[2] Сретенски й Л. Н., Теория ньютоновского потен-
потенциала, М.— Л., 1946; [3] Л а н д к о ф Н. С, Основы совре-
современной теории потенциала, М., 1966; [4] Брело М., Основы
классической теории потенциала, пер. с франц., М., 1964; [5]
Kellogg О. D., Foundations of potential theory, В., 1929;
[6] Келдыш М. В., «Успехи матем. наук-», 1941, в. 8, с. 171 —
231; [7] Вица язе А. В., Уравнения математической фи-
физики, М., 197В; [8] его ж е, Краевые задачи дли эллиптиче-
эллиптических уравнений второго порядка, М.. l%(i; [!)] Владими-
Владимиров В. С, Уравнения математической физики, 4 изд., М.,
1981; llu] Курант Р., Уравнения с частными производными,
пер. с англ., М., 1964: I1J] М и р а и д а К., Уравнения с част-
частными производными эллиптического типа, пер. с итал., М..
1957; [12] М и х л и и С Г., Линейные уравнения в частных
производных, М., 1977; [13] Тихонов А. Н., Самар-
Самарский А. А., Уравнения математической физики, Г> изд., М.,
1977. Л. И. Лрилепко, Е. Д. Соломепцев.
ПОТЕНЦИАЛА ТЕОРИЯ АБСТРАКТНАЯ — тео-
теория потенциала на абстрактных тоиологич. пространст-
пространствах. П. т. а. возникла веер. 20 в. из стремления охва-
охватить единым аксиоматпч. методом широкое многообра-
многообразие свойств различных потенциалов, применяемых при
решении разнообразных задач теории дифференциаль-
дифференциальных уравнений с частными производными. Первое до-
достаточно полное изложение аксиоматики «гармониче-
«гармонических» функций (т. е. решений допустимого класса урав-
уравнений с частными производными) и соответствующих
потенциалов было дано М. Брело A957 — 58, см. [1]), но
оно охватывало только уравнения зллиптич. типа. Рас-
Расширение теории, пригодное и для широкого класса
уравнений параболич. типа, получено X. Бауиром
A960—63, см. [3]). Весьма плодотворным оказался ве-
вероятностный подход к П. т. а., начало к-рому было по-
положено еще в работах П. Леви (P. Levy), Дж. Дуба
(J. Doob), Г. Ханта (G. Hunt) и др.
Для изложения П. т. а. удобно понятие гармониче-
гармонического пространства. Пусть X— локально компактное
топологич. пространство. Пучком функций
на X наз. отображение ?•, определенное на семействе
всех открытых множеств X н такое, что
1) % (U) для любого открытого множества UdX ecu.
семейство функций и : Г —>- R = [—оо, оо];
2) если открытые множества U, V таковы, что Ua Vcz
СX, то сужение любой функции пз J-(F) на U принад-
принадлежит $(U);
3) если для любого семейства {U,}, i?/, открытых
множеств UjCzX сужения нек-рой определенной на
U i € ; Ui функции и на U,- для всех i ? 1 принадлежат
$(?/,•), то u€%(\JielUi).
Пучок функций ЗИ на X нал. гармоническим
пучком, если для любого открытого множества
UczX семейство Щ(и) есть действительное векторное
пространство непрерывных функций на U. Функция и,
определенная на нек-ром множестве 5с1, содержащем
открытое множество U, паз. Ж-ф у н к ц и е й, если
сужение u\U принадлежит 2В(С). Гармонич. пучок Ш
н е в ы р о ж д е н в точке .г ? X, если в окрестности
.г существует ЗВ-функция и такая, что и(х)^сО.
Реальные различия в аксиоматиках Бауэра, Брело,
Дуба характеризуются свойствами сходимости Ж-
функций.
а) Свойство сходимости Бауэра со-
состоит в том, что если возрастающая последовательность
ЗБ-функций локально ограничена на нек-ром открытом
множестве UczX, то предельная функция v есть Ш-
функция.
б) Свойство сходимости Дуба состоит
п том, что если предельная функция и конечна на плот-
плотном множестве в X, то v есть Ж-функция.
в) Свойство сходимости Брело состо-
состоит в том, что если предельная функция и возрастающей
последовательности Sffi-функций на нек-рой области
UczX конечна в точке х? U, то v есть 2В-функция.
Если пространство X локально связно, то имеют
место импликации в) => б) =Ф а).
Пучок функций U на X наз. гипергармояи-
ческим пучком, если для любого открытого
множества UczX семейство il(U) есть выпуклый конус
полунепрерывных снизу функций и : U —>-{—оо, оо];
U-ф у н к ц и я определяется аналогично Ж-функции.
Отображение U -+ 1\(U)f\(—VL(U)) есть гармонич.
пучок 2В=Жи, порожденный пучком U; только этот
гармонич. пучок будет использоваться в дальнейшем.
Пусть на границе 0U открытого множества UczX
дана непрерывная функция ф : 0U —>-(—оо, оо) с ком-
компактным носителем. Гипергармонич. пучок Ц позволяет
построить Перрона методом обобщенное решение зада-
задачи Дирихле для нек-рых открытых множеств в классе
соответствующих ЗУ-функций. Пусть U<j> — семейство
полунепрерывных снизу Ц-функций к, ограниченных
снизу на U, положительных пне нек-рого компакта и
таких, что
lim inf и (яKг ф (у),
можно положить Иф =• —11ф • Пусть теперь
и В<р~ос, если Цф — 0- Аналогично,
7/ф (г)= sup {и (х): k
или Hq, = —оо. Функция наз. разрешимо й, если
для нее IJtp и Яф совпадают, Я(г— Яф—Яф, и Яф являет-
является 2Б-функцией; эта функции // и есть обобщенное ре-
решение задачи Дирихле в классе 21!-функний. Открытое
множество UczX р а з р с ш и м о относительно Ц,
если разрешима любая конечная непрерывная функция
с компактным носителем на ol:. Для разрешимого мно-
множества U отображение Яф : Ck(dU) —>- R есть положи-
положительный линейный функционал,.к-рый, следовательно,
определяет положительную меру \хх, x?U, наз. г а р-
ионической мерой на dU в точке х (относи-
(относительно II).
Локально компактное пространство X с гигшргар-
монич. пучком Ц превращается в гармоническое
пространство, если для него выполняются со-
соответствующие четыре аксиомы (см. Гармоническое про-
пространству), причем в аксиоме сходимости имеется в ви-
виду свойство Бауэра.
Часто (в классич. примерах именно так и обстоит
дело) за основу берется гармонич. пучок 2В, а аксиома
мажоранты служит тогда определением гипергармоннч.
пучка. Напр., евклидово пространство R", «23=2, с
пучком классич. решений уравнения Лапласа или
уравнения теплопроводности в качестве 26 является
гармонич. пространством. Гармонич. пространство ло-
локально связно, не содержит изолированных точек it
имеет базис из связных разрешимых множеств (разреши-
(разрешимых областей).
Открытое множество U гармонич. пространства X с
сужением И \U в качестве гипергармонич. пучка есть
гармоническое пространство X. Ги-
Гипергармонич. функция и на UcX наз. супергар-
супергармонической функцией, если для любого
относительно компактного разрешимого множества V,
VcU, наибольшая миноранта \ivu является гармони-
гармонической, \xvu ?2B(F). Многие свойства классических су-
пергармонич. функций (см. Субгармоническая функция)
выполняются п здесь. Потенциалом наз. такая
положительная супергармонич. функция и, для к-рой
наибольшая гармонич. миноранта \ivu на X тождествен-
тождественно равна нулю. Гармонич. пространство X наз. ($-г а р-
ионическим (или 5^-г армоническим)
пространством, если для любой точки х?Х
существует положительная супергармонич. функция и
(соответственно потенциал и) на X такая, что м(ж)>0.
Любое открытое множество ^-гармонического прост-
пространства разрешимо.
Принимая :sa основу гармонич. пучок 36 и определяя
соответствующий пшергармонич. пучок 2В* с помощью
аксиомы мажоранты, получают пространство
Бауэра, совпадающее с гармонич. пространством
для 26*. Если гармонич. пучок 28 для любого открытого
множества UczR"X R состоит из решений h уравнения
теплопроводности Ah—dh/dt=Q, то 26 обладает свойст-
свойством сходимости Дуба и R"XR с этим пучком Ш есть
^-пространство (Бауэра). При этом v — гипергармо-
гипергармонич. функция класса С2 тогда и только тогда, если Аи—
—Ov/dt^.0.
Пространство Брело характеризуется
следующими условиями: X не имеет изолированных
точек и локально связно; регулярные множества отно-
относительно 2Б образуют базу X (регулярность — это раз-
разрешимость классич. задачи Дирихле в классе 2В);
Ш обладает свойством сходимости Брело. Пространства
Брело составляют собственный подкласс т. н. эллип-
эллиптических гармонич. пространств (см. [4|), т. е. эллип-
тич. пространств Бауэра. Если гармонич. пучок 2В
для любого открытого множества UdRn, п^Л, состоит
из решений и уравнения Лапласа Ли=0, то R2 с этим
пучком есть (^-пространство Брело, a R" при rC^-Ъ есть
^-пространство Брело. При этом v — гипергармонич.
функция класса С2 тогда и только тогда, если Лу«:0.
Точка у границы dU разрешимого множества U гар-
гармонич. пространства наз. регулярной гранич-
граничной точкой, если для любой конечной непрерывной
функции ф на dU имеет место предел
lira #<p (x)=(p(y), x?U,
*->¦ у
а в противном случае у наз. иррегулярной
граничной точно й. Пусть F — фильтр на U',
сходящийся к у. Барьером фильтра F наз. строго
положительная гипергармонич. функция v, определен-
определенная на пересечении U с нек-poii окрестностью у и сходя-
щаяся к 0 вдоль F. Если для относительно компактного
разрешимого множества U (\-гармонического простран-
пространства все фильтры, сходящиеся к точкам y?dU, имеют
барьер, то U — регулярное множество,
т. е. все его граничные точки регулярные. Если U —
относительно компактное открытое множество $|?-гар
ионического пространства, на к-ром существует строги
положительная гннергармопич. функция, сходящаяся
к 0 в каждой точке 1/^G 6, то Г — регулярное множе-
множество.
Кроме изучения разрешимости и регулярности в за-
даче Дирихле, к основной проблематике П. т. а. отно-
относятся: теория емкости точечныу множеств на гармонич.
пространствах X; теория выметания (см. Вылетания
метод) функций и мер на X; теория интегральных пред-
представлений положительных супергармонич. функций на
X, обобщающая представления Мартина (см. Мартина
граница).
Уже в нач. 20 в. была замечена тесная связь теории
потенциала с нек-рыми вопросами теории вероятностей,
такими, как броуновского движения процесс, винеровский
процесс, марковский процесс. Напр., вероятность того,
что траектория броуновского движения в плоской об-
области GczR2, исходящая из точки .'0(]G, встретит в пер-
первый раз границу дС на (борелевском) множестве EcOG,
есть не что иное, как гармоническая мера множества Е
в точке ха; полярные множества границы дв суть при
этом те множества, к-рые траектории не встречают поч-
почти наверное. В дальнейшем вероятностные методы спо-
способствовали более глубокому пониманию нек-рых идей
теории потенциала и привели к ряду новых результа-
результатов; с другой стороны, теоретико-потенциальный под-
подход уменьшает отчужденность теории вероятностей и
также приводит в ней к новым результатам.
Пусть X — локально компактное пространство со
счетной базой, Ск и Со — классы конечных непрерыв-
непрерывных функций на X соответственно с компактным носи-
носителем и стремящихся к 0 на бесконечности. Ядро-мера.
N {х, Е)~^0 есть (борелевская) функция от х?Х для
каждого относительно компактного (бореловского) мно-
множества ЕаХ. С помощью 7V каждой функции /^0, / ? С /,,
ставится в соответствие потенциал-функция
Nf(x) = \jf(y)N(x,dy), z?X,
а мере 9^0 соответствует потенциал-мера
&N(E) = С N(x, E)dQ(x).
Единичное ядро I (х, Е) равно 0 при х(?Е и равно 1 при
х?Е, оно не изменяет/(ж) и Q(E). Напр., в евклидовом
пространстве R3 ядро
определяет ньютонов потенциал Nf с плотностью /, а
ЭЛ^ есть мера с плотностью, равной ньютонову потен-
потенциалу меры G (см. Потенциала теория).
Ядро-произведение имеет вид
MN [х, Е) = { N (у, Е) М (х, dy).
Семейство ядер {Лг^}, iJ^O, с законом композиции
Nf + s= NfNs является однопараметрич. полугруппой.
Ядро N удовлетворяет полному принципу максимума,
если для любых /, g^=0 из С^ и а>0 выполнение нера
венства N]<.Ng-\-a на множестве, где />0, влечет за
собой выполнение итого неравенства всюду на X.
Основная в этой теории теорем'а Хан та в про-
простейшей форме состоит в том, что если образ Сь при
отображении N плотен в Сд и N удовлетворяет полному
принципу максимума, то существует полугруппа {Pf},
O такая, что
(феплеровская полугруппа); при этом
Pf отображает Ck в Со, Ро — единичное ядро, lim Pfj~-~
i->-0
=/. f?C0, локально равномерно и Pt(l)<l. Функция
/^0 наз. :) к с ц е с с и в я о й функцией относи-
относительно полугруппы {Pf}, если всегда Pff<-f и lim Ptf
=/; если Ptf=f, то/ наз. инвариантной функ-
функцией. Соответствующие построения имеют место и
для потенциала-меры 07V.
Очерченная теория Г. Ханта A957—58) имеет непо-
непосредственный вероятностный смысл. Пусть на X задана
век-рая о-алгебра борелевских множеств Ш. и вероят-
вероятностная мера Р. Случайная величина S=S(x) — это
91-измеримое отображение X в пространство состояний
Д=[ — оо, оо]. Семейство случайных величин {Sf},
0=0,— это случайный марковский процесс, для к-рого
Sf(x) — траектория точки х?Х, если для каждого у,
— оо <:;/ < оо, существует вероятностная мера ?и на 91
такая, что
1) Р*Ч{50 = г/}) = 1; 2) ру(А)> А€%<
— борелевская функция от у; 3) вид траектории, про-
проходящей через у в момент г, при JJsr не зависит от поло-
положения предыдущих ее точек. Применительно к таким
марковским процессам полугруппы {Pt} интерпрети-
интерпретируются как полугруппы мер
Pt(y, B) =
Важное значение имеет изучение эксцессивных и инва-
инвариантных функций относительно полугрупп {Pt}.
С другой стороны, если X есть §K-гармоническое
пространство со счетной базой, то на нем всегда можно
выбрать ядро потенциалов так, чтобы удовлетворялись
условия теоремы Ханта, и эксцессивные функции соот-
соответствующей полугруппы будут тогда в точности неот-
неотрицательными гипергармонич. функциями. Теорема
Ханта обобщается и для нек-рых типов пространств
Бауэра (см. [4], [7]).
И другие понятия П. т. а., такие, напр., как вымета-
выметание, полярные и тонкие множества, также получают
вероятностную интерпретацию в рамках общей теории
случайных процессов, облегчающую их исследование.
С другой стороны, для теории вероятностей оказалась
важной теоретико-потенциальная трактовка ряда по-
понятий, таких, напр., как мартингалы, выходящих за
рамки марковских процессов.
Лит.: [1] В г е 1 о t M., Lectures on potential theory, 2 ed.,
Bombay, 1967; [2] его же, «L'enseign. math.», 1972, t. 18,
JVTs 1, p. 1—36; [3] Bauer H., Harmonische Ratime und ihre
Potentialtheorie, В., 1966; [4] Constantinescu C,
C A Pttil th hi В 1972
entialtheorie, В., 1966; [4] Constantinescu C,
Cornea A., Potential theory on harmonic spaces, В., 1972;
[5] M e й е р П. - А., Вероятность и потенциалы, пер. с англ.,
М., 1973; [6] X а н т Дж. - А., Марковские процессы и потен-
потенциалы, пер. с англ., М., 1962; [7] В 1 u m e n t h a I R., G е-
toor R., Markov processes and potential theory, N.Y.—L.,
1968. E. Д. Соломенцев.
ПОТЕНЦИАЛОВ МЕТОД — метод исследования
краевых задач для уравнений математич. физики путем
сведения их к интегральным уравнениям, основанный
на представлении решений этих задач в виде (обобщен-
(обобщенных) потенциалов.
Пусть в пространстве R", п^2, задано дифференци-
дифференциальное уравнение с частными производными 2-го по-
порядка эллиптич. типа
7
A)
с достаточно гладкими коэффициентами а,у=ау,=
¦-¦-¦¦ ai/(x), e/ - s,(.r), с(.т)<0 и правой частью f(x), причем
с(ж)<—/e2<U вне нек-рой ограниченной области, со-
содержащей внутри область D класса С1. Тогда любое
решение и (х) уравнения A) класса C2(D[)S) можно
представить в виде суммы трех (обобщенных) потенци-
потенциалов: потенциала объемных масс
x, y)p(y)dy, B)
потенциала простого слоя
\sE(x, y)o(y)dsy C)
и потенциала двойного слоя
[sQy[E(x, y)]p(y)dsa, D)
где S — dD — граница области D, Е(х, у) — главное
фундаментальное решение оператора L, символ Qy обо-
обозначает оператор
действующий в точке y?S, N — единичный вектор ко-
пормали в точке y?S,
2j/= i aU cos <v' У/)
v — единичный вектор внешней нормали к S в точке
y?S. Плотности потенциалов р(у), а (у) и ц(у) — доста-
достаточно гладкие функции на /> или S.
Для потенциалов B)—D) остаются в силе, с соответ-
соответствующими изменениями, все дифференциальные и
граничные свойства гармонич. потенциалов, описанные
в ст. Потенциала теория для случая, когда L — опе-
оператор Лапласа. На основании этих свойств удается све-
свести краевые задачи для эллиптич. уравнений типа A)
к интегральным уравнениям, аналогично тому, как это
было описано для задач Дирихле и Неймана для гар-
гармонич. функций в ст. Потенциала теория.
Лит.: [1] Миранда К., Уравнения с частными произ-
производными эллиптического типа, пер. с итал., М., 1957; [2] Б и-
ц а д з е А. В., Краевые задачи для эллиптических уравнений
второго порядка, М., 1966; [3] Владимиров В, С, Урав-
Уравнения математической физики, 4 изд., М., 1981; [4] К у п р а д-
з е В. Д., Методы потенциала в теории упругости, М., 1903;
[5J М и л н - Т о м с о н Л. М., Теоретическая гидродинамика,
пер. с англ., М., 1964. Е. Д. Соломенцев.
ПОТЕНЦИАЛЬНАЯ СЕТЬ, сеть Егоро-
в а,— ортогональная сеть на двумерной прверхности
евклидова пространства, к-рую переводит в себя по-
потенциальное движение жидкости по этой поверхности.
В параметрах П. с. линейный элемент поверхности име-
имеет вид
ви ' 9»
где Ф "Ф(г/, v) — потенциал поля скорости жидкости.
Каждая ортогональная полугеодезич. сеть потенциаль-
потенциальна. Частным случаем П. с. является Лиувилл я сеть.
П. с. впервые рассматривал Д. Ф. Егоров A901).
Лит.: ll] E г о р о в Д. Ф., Работы по дифференциальной
геометрии, М., 1970; [21 Пуликовский В. И., Класси-
Классическая дифференциальная геометрия ь тензорном изложении,
М., 1963. В. Т. Базылев.
ПОТЕНЦИАЛЬНОЕ ПОЛЕ, градиентное
пол е,— векторное поле, образованное градиентами
гладкой скалярной функции /(?) нескольких перемен-
переменных t—it1, ... , t"), принадлежащих нек-рой области Т
n-мерного пространства. Функция / (?) наи. скаляр-
скалярным потенциалом (потенциальной
функцией) этого поля. П. п. вполне интегрируемо
в Т: Пфаффа уравнение (grad/((), dt)~O имеет в ка-
качестве (п—1)-мерных интегральных многообразий ли-
нии (п=2) или поверхности (п~^3) уровня потенциала
f(t). Любое регулярное вполне интегрируемое в Т кова-
риантное ноле z-— (vlt v2, ... , vn) получается умножени-
умножением П. п. на скаляр:
va (t) = с (t) -2L- , 1<а<и.
вг*'
Скаляр i/c(t) наз. интегрирующим множителем уравне-
уравнения Пфаффа (v{t), dt)--=O. Признаком потенциальности
поля va(t) (c(t)~ 1) служат равенства
означающие, что поле v(t) является безвихревым (см.
Вихрь).
Понятие П. п. широко используется в механике и
физике. Большинство силовых и электрич. полей мож-
можно рассматривать как П. п. Напр., если f(t) выражает
давление в точке t идеальной жидкости, заполняющей
область Т, то вектор F=—grad /-dco равен равнодейст-
равнодействующей сил давления, приложенной к элементу объема
da. Если / (t) — температура нагретого тела Т в точке
t, то вектор F=—к -grad /, где к — коэффициент тепло-
теплопроводности, равен плотности теплового потока, иду-
идущего в сторону менее нагретых участков тела (в на-
направлении, ортогональном изотермич. поверхностям
/= Const). Л. II. Купцов.
ПОТЕНЦИАЛЬНЫЙ ОПЕРАТОР — отображение
А банахова пространства X в сопряженное простран-
пространство X*, являющееся градиентом нек-рого функционала
/?Х* т. е. такое, что
Напр., всякий ограниченный самосопряженный опера-
оператор А, определенный на гильбертовом пространстве
Н, является потенциальным:
Лит.: Ill В а й н б е р г М. М., Вариационный метод и
метод монотонных операторов в теории нелинейных уравнений,
М., 1972; [2J Гаевский X., Г р е г о р К., Захариас,
К., Нелинейные операторные уравнения и операторные диффе-
дифференциальные уравнения, пер. с нем., М., 1978. В. И. Соболев.
ПОТЕРЬ ФУНКЦИЯ — неотрицательная функция,
показывающая потери (ущерб) экспериментатора в за"
даче принятия статистич. решения при каждом возмож-
возможном исходе эксперимента. Пусть X — случайная ве-
величина, принимающая значения в выборочном прост-
пространстве (I, S3, Ре), 6?в, и пусть D={d} — прост-
пространство всех возможных решений, к-рые можно при-
принять относительно параметра 0 по реализации случай-
случайного вектора X. В теории статистических решающих
функций любую неотрицательную функцию L (• , •),
определенную на JxD, наз. функцией потерь.
Значение LF, d) П. ф. L (• , •} в произвольной точке
F, d)?%XD интерпретируют как ущерб, к к-рому при-
приводит принятие решения d, d^D, если истинное значе-
значение параметра есть 6, 0?в.
Лит.: [1] В а л ь д А., Статистические решающие функции,
пер. с англ., в кн.: Позиционные игры, М., 1967; [2] Л е м а н
:)., Проверка статистических гипотез, пер. с англ., 2 изд., М.,
1979. М. С. Никулин.
ПОТОК векторного поля — одно из поня-
понятий теории векторного поля. П. векторного поля а
через поверхность dV выражается с точностью до знака
поверхностным интегралом
dxdy),
i де п — единичный вектор нормали к поверхности 3 V
(предполагается, что изменение вектора п по поверх-
ности 0V непрерывно). Для поля скоростей частиц жид-
жидкости П. векторного поля равен объему жидкости,
протекающей за единицу времени через поверхность dV.
ВС 9-з.
ПОТОК, динамическая система с не-
непрерывным временем,— динамическая сис-
система, определяемая действием аддитивной группы дей-
действительных чисел R (или аддитивной полугруппы
неотрицательных действительных чисел) на нек-ром
фазовом пространстве W. Другими словами, каждому
t?R (каждому г2з=О) сопоставлено нек-рое преобразо-
преобразование S-t : W -> W, причем
St (w) =-- w и Si + S (w) = St (Ss (w)).
При этом t обычно наз. «временем» и о зависимости Stw
от t (при фиксированном w) говорят как о «движении»
точки Sfiv; множество всех SfW для данного w наз.
траекторией w (нередко этот термин употреб-
употребляется применительно к функции t\—> Stw). Как и для
любых динамич. систем, обычно фазовое пространство
наделено нек-рой структурой, и П. в каком-то смысле
согласован с ней: преобразования St сохраняют эту
структуру, накладываются определенные условия на
характер зависимости Stw от t.
В приложениях чаще всего встречаются П., описы-
описываемые автономными системами обыкновенных диффе-
дифференциальных уравнений
или, в векторных обозначениях, w~f(w), w? Rn. Непо-
Непосредственное обобщение — поток на дифферен-
дифференцируемом многообразии Wm, определяе-
определяемый («порождаемый») заданным на W" гладким вектор-
векторным полем f(w) класса Ск, к~^1 (гладкий по-
поток класса С*). В этом случае движение точки
SfW, пока она находится в пределах одной карты (ло-
(локальной системы координат), описывается системой ви-
вида (*), в правой части к-рой стоят компоненты вектора
f(w) в соответствующих координатах. При переходе к
другой карте описание движения меняется, поскольку
при этом меняются как координаты точки S^w, так и вы-
выражения для компонент вектора f(w) как функций ло-
локальных координат. См. также Измеримый поток,
Непрерывный поток, Топологическая динамическая си-
система.
П. образуют наиболее важный класс динамич. сис-
систем, к-рый к тому же первым начал изучаться. Термин
«динамическая система» часто употребляют в узком
смысле, понимая под ним именно П. (или П. и кас-
каскады). Д. В. Аносов.
ПОТОК — понятие интуиционистской математики
(см. Интуиционизм); совокупность, вид, состоящий из
конечных кортежей натуральных чисел, называемых
узлами П. (или допустимыми кортежа-
м и П.). Точнее, вид П кортежей натуральных чисел
наз. потоком, если выполняются следующие ус-
условия: 1) существует эффективное правило а (т. н.
закон потока), согласно к-рому для всякого
кортежа (щ, ¦¦¦ , «т> можно выяснить, является ли он
узлом П; 2) пустой кортеж < > является узлом всякого
П.; 3) если кортеж (-п1, ... , пту есть узел П, то всякий
его начальный кортеж вида <И], ... , п,-> при i<:m также
является узлом П; 4) если кортеж <%, ... , пту есть узел
П, то найдется натуральное к такое, что <и17 ... , пт, ку
есть узел П.
Если кортежи натуральных чисел упорядочить, счи-
считая, что т<я тогда и только тогда, когда т есть собст-
собственное начало я, то с точки зрения этого порядка поток
II представляет собой бесконечное дерево с началом < >,
заданное эффективным образом (заданное законом).
Свободно становящаяся последовательность а (или,
более общо, произвольная эффективная функция, пере-
рабатывающая натуральные числа в натуральные)
наз. л л е м с н т о м и о т о к a JJ, символически а?П,
если для лея кого и кортеж <сс(О), ... , а (га—1)> являет-
является узлом П. В приложениях встречается также понятие
оснащенного П. Оснащенный поток Г состоит
из потока П и эффективного правила Гп (т. н. д о и о л-
нительпого закона ИЛ, приписывающего
каждому узлу л потока И нек-рый объект Гп(я). Каж-
Каждому элементу потока И при этом естественным образом
соответствует последовательность объектов, задаваемых
законом Гп.
В языке формального интуиционистского математич.
анализа П. задается функцией — своим законом П.
С этой целью рассматривается стандартное примитивно
рекурсивное взаимно однозначное соответствие между
кортежами натуральных чисел и натуральными чис-
числами. Пусть при этом кортежу < > соответствует О,
операция соединения двух кортежей в один задается
на их номерах примитивно рекурсивной функцией
х*у, х означает номер кортежа с единственным членом
х. Утверждение, что кортеж с номером х является узлом
П., задаваемого а, записывается в виде а(х)~0. Тогда
формула Spr(a), выражающая понятие «функция а за-
задает П.», записывается в виде
а@)=0& уху (а(х* у)=0 Г)а(х\ = 0)&
Ух (а (х) =0э ЗУ (а (х *'у) = 0)).
Наконец, если через а(п) обозначить номер кортежа
<а@), ... , а(п—1)>, где п — длина кортежа, то фор-
формула а?а («а есть элемент П.,заданного а») записывает-
записывается в виде \)ха(а.(х)) — (.).
В основаниях математики употребляются также обоб-
обобщения понятия П., в к-рых используются кортежи не
натуральных чисел, а более сложных объектов, напр,
кортежи, составленные из свободно становящихся по-
последовательностей.
Лит.: []] Рейтинг А., Интуиционизм. Введение, пер.
с англ., М., 19в,г>. А. Г. Драгалин.
ПОТОК В СЕТИ — функция, сопоставляющая ду-
дугам данной сети (ориентированного графа) нек-рые чис-
числа. Каждое число интерпретируется как интенсивность
потока нек-рого груза по данной дуге. П. в с. являются
удобной моделью при исследовании ряда проблем в
транспорте, связи и др. областях, связанных с движе-
движением грузов, информации и т. д. Многие задачи о пото-
потоках являются задачами линейного программирования
и могут решаться общими методами этой теории. Однако
в большинстве случаев задачи о потоках допускают аф-
аффективное решение методами теории графов.
Пусть каждой дуге (х, у) сети А приписано неотрица-
неотрицательное действительное число с (х, у) — пропускная
способность дуги (х, у). Говорят, что поток f(x, у) яв-
является стационарным потоком величины v из вершины г
в вершину .?, удовлетворяющим ограничениям пропуск-
пропускных способностей дуг, если
/~ И-/+ (r)^v,
f~ {x) — /+ (х) = 0 при х ф г, s,
/- (s)~/+ (-') = -у,
0</(i, !/)==? с (я, у) для любой дуги (х, у),
здесь f~(x)=21 ^¦г' У^ —поток, выходящий из вершины
х, a f + (x)^ V }(у, х) — поток, входящий в вершину х.
В задаче о максимальном потоке
между двумя вершинами требуется построить стацио-
стационарный поток из вершины г в вершину s, имеющий мак-
максимально возможную величину г;. Для решения этой
задачи существуют достаточно эффективные алгоритмы.
Пусть X — подмножество вершин сети N такое, что
rf.X, s(feX. Тогда множество дуг (х, у) таких, что х?Х,
y(j~X, наз. разрезом. Пропускной способностью
разреза наз. величина ^jx6_y «{Xе (х> У)- Справедлива
следующая теорема о максимальном
потоке п минимальном разрезе: мак-
максимальна» ветчина потока равна минимальной про-
пропускной способности разрезов. В приложениях часто
используется теорема о целочисленно-
с т и: если пропускная способность дуг целочисленна,
то существует целочисленный максимальный (стацио-
(стационарный) поток.
К задаче о максимальном потоке между двумя вер-
вершинами сводится ряд задач: задача о максимальном
П. в с. с несколькими источниками и стоками; задача о
максимальном П. в с, имеющей неотрицательные огра-
ограничения на потоки по дугам как сверху, так и снизу;
задача о максимальном потоке в неориентированных и
смешанных сетях; задача о максимальном потоке в сети
с пропускными способностями дуг и вершин и др.
Теорема о максимальном потоке и минимальном раз-
разрезе выявила общую основу ряда результатов, полу-
полученных ранее в теории графов и комбинаторике. Оказа-
Оказалось, что как следствия этой теоремы могут быть полу-
получены: теорема о максимальном паросочетании в графе
двудольном, теорема о различных представителях,
теоремы о fe-связности графов (см. Графа связность),
теорема о покрытии частично упорядоченного множест-
множества наименьшим числом цепей и др. Сведение различных
задач к задаче о максимальном потоке является важным
методом теории графов и комбинаторики.
В ряде задач о П. в с. каждой дуге (х, у) сопоставляет-
сопоставляется число а (х, у) — стоимость перевозки единицы груза
но дуге (х, у) и требуется найти поток, удовлетворяю-
удовлетворяющий определенным ограничениям и минимизирующий
общую стоимость потока. Задача о потоке ми-
минимальной стоимости состоит в нахождении
стационарного потока из вершины г в вершину .?, удов-
удовлетворяющего ограничениям пропускных способностей
дуг, причем такого, что величина его равна заданному
числу и, а стоимость минимальна.
В транспортной задаче сеть является
двудольным графом. Вершины одной доли 5j, ... , Sm
интерпретируются как пункты отправления нек-рого
груза, вершины другой Тг, ... , Тп — как пункты на-
назначения. Каждый пункт отправления 5,- имеет опреде-
определенное предложение Ь,-, и каждый пункт назначения Т j
имеет определенный спрос cj. Известна стоимость «,-у
перевозки единицы груза из S/ в Tj. Задача состоит и
отыскании потока минимальной стоимости, удовлетво-
удовлетворяющего спрос во всех пунктах назначения.
Рассматриваются также многопродуктовые потоки и
потоки, изменяющиеся во времени.
Лит.: [1] Форд Л. - Р., Ф а л к е р с о н Д. - Р-, Пото-
Потоки в сетях, пер. с англ., М., 1866. В. Б. Алексее,
ПОТОЧЕЧНАЯ СХОДИМОСТЬ — один из видо!
сходимости последовательности функций (отображений).
Пусть /„ : X -> У, га=1, 2, ... , где X — нек-рое мно-
множество, a Y — топологич. пространство, тогда П. с. оз-
означает, что для любого элемента х?Х последователь-
последовательность точек yn=jn(x), л=1, 2, ... , сходится в простран-
пространстве Y. Важным подклассом класса поточечно сходя
щи.чея последовательностей являются равномерно
сходящиеся последовательности. л. Д. Кудрявца
ПОТОЧЕЧНОЙ СХОДИМОСТИ ТОПОЛОГИЯ
одна нз топологий пространства F(X, Y) отображение
множества X в топологич. пространство Y. Направле
ние {/cc}ae?(C;/''(X, Y) поточечно сходится к f?F(X, Y).
если {/aWlagsi сходится при любом х?Х к f (х) в топо-
топологии пространства Y. Базу окрестностей точки fo?F(X,
У) образуют множества вида {f\f(z/)CZVf ix.\, i—l, ...
... , и}, где хц ... , хп— конечный набор точек из X и
vf (x.) € Vfo(X.) ~ база окрестностей точки fo(xj) прост-
пространства У.
Если Y отделимо, то F(X, Y) также отделимо и Аа
CzF(X, Y) компактно тогда и только тогда, когда при
каждом xGX компактно множество Ах= {f{z)\f?A }.
Лит.: [Л К е л л и Д ж., Общая топология, пер. с англ.,
2 изд., М., 1981. В. И. Соболев.
ПОХГАММЕРА УРАВНЕНИЕ — линейное обык-
обыкновенное дифференциальное уравнение re-го порядка
вида
Q (z) wW — \xQ' (z)w<n-1'<-\- . . .
. . . + (-1)» Mn + Q.-^'n-l) Qm (z) w _
[R (z) u;(n-l)— (fX + 1) R'(z) !(;<"-2)+
+ (_ 1)B-1 (jHlh^±Hzll Rin-l) (z) „j =0,
где fx — комплексная постоянная, <?(z), Я (z) — много-
многочлены степени <n и <n—1 соответственно. П. у. было
исследовано Л. Похгаммером [1] и К. Жорданом [2].
П. у. проинтегрировано с помощью Эйлера преобра-
преобразования, и его частные решения имеют вид
(t — zf+n~lu(t)dt, (*)
где 7 — нек-рый контур в комплексной плоскости t.
Пусть все корни аг, ... , ат многочлена Q(z) простые и
вычеты функции R (z)lQ (z) в этих точках — нецелые
числа. Пусть а — фиксированная точка такая, что
Q(a)^Q, и пусть 7/ — простая замкнутая кривая с на-
началом и концом в точке а, положительно ориентирован-
ориентированная, к-рая содержит внутри себя только корень aj, ]--
= 1, ... , т. Формула (*) дает решение П. у., если
V =
из этих решений ровно т линейно независимы. Для
построения остальных решений используются другие
контуры, в том числе незамкнутые (см. [3], [4]). Вычис-
Вычислена группа монодромии П. у. (см. [3]).
Частными случаями П. у. являются уравнение
Тис со (см. [4]), то есть II. у., в к-ром
и Папперица уравнение.
Лит.: [1] Pochhammer L., «Math. Ann.», 1889, Bd
35, S. 470—94; l2j Jordan C, Cours d'analyse de l'Ecole
Polytechnique, 3 ed., t. 3, P., 1915; [3] Айне Э. Л., Обык-
Обыкновенные дифференциальные уравнения, пер. с англ., Хар.,
1939; [4] Камке Э., Справочник по обыкновенным дифферен-
дифференциальным уравнениям, пер. с нем., 5 изд., М., 1976.
М. В. Федорюк.
ПОЧТИ ВСЮДУ, для почти всех х (относи-
(относительно меры \х),— выражение, означающее, что речь
идет о всех х из измеримого пространства X, за исклю-
исключением, быть может, нек-рого множества Ад^Х меры
нуль: [х(Л) = О. В. И. Битюцков.
ПОЧТИ КОМПЛЕКСНАЯ СТРУКТУРА — поле
/ линейных преобразований касательных пространств
на многообразии М, удовлетворяющее условию
т. е. поле комплексных структур в касательных прост-
пространствах ТрМ, р?М. П. к.с. / определяет разложение
T^M=V + -{-V_ комплексификации Т М касательного
расслоения в прямую сумму комплексно сопряженных
друг другу подрасслоении V + и 7_, состоящих из соб-
собственных векторов аффинора / (продолженного по ли-
линейности на Т М) с собственными значениями i и —i
соответственно. Обратно, разложение Т М в прямую
сумму двух взаимно сопряженных векторных подрас-
слоений S, S определяет П. к. с. на М, для которой
V + -S.
П. к. с. / наз. интегрируемой, если она ин-
индуцируется комплексной структурой на М, т. е. если
существует атлас допустимых карт многообразия М, в
к-рых поле / имеет постоянные координаты I'k- Необ-
Необходимое и достаточное условие интегрируемости П. к. с.
состоит в инволютивности подраселоения V +, т. е. замк-
замкнутости пространства его сечений относительно комму-
коммутирования (комплексных) векторных полей. Условие ин-
волютивностн подрасслоенпя V + равносильно обраще-
обращению в нуль ассоциированной с / векторнозначной 2-фор-
мы N (I, /), задаваемой формулой
N1,1, I)(X, Y) = [IX, IY]—I [X, TY) — T[I, XY] —
где X, Y — векторные поля. Эта форма наз. тензо-
тензором кручения, или тензором Нейен-
х е й с а, II. к. с. Тензор Нейенхейса NA, I) можно
рассматривать как дифференцирование степени 1 алгеб-
алгебры дифференциальных форм на М, имеющее вид
Л'(Л 1)-[Т, [/, d]] + d,
где d — внешний дифференциал, а / рассматривается
как дифференцирование степени 0.
С точки зрения теории G-структур П. к. с. представ-
представляет из себя GL(m, С)-структуру, где m=42 dim M,
а тензор кручения NA,1)—тензор, определяемый пер-
первой структурной функцией отой структуры. Qh(m, С)-
структура является структурой аллиптич. типа, и
поэтому алгебра Ли инфинителимальных автоморфиз-
автоморфизмов П. к. с. удовлетворяет оллпптич. системе дифферен-
дифференциальных уравнений 2-го порядка [11. В частности, ал-
алгебра Ли инфииитезималмшх автоморфизмов П. к. с.
на компактном многообразии конечномерна, а группа
G всех автоморфизмов компактного многообразия с
П. к. с. является группой Ли. Для некомпактных мно-
многообразий ято, вообще говоря, но так.
Если группа автоморфизмов G транзптивна на много-
многообразии М, то П. к. с. 1 однозначно определяется своим
значением /„ в фиксированной точке /> ? М, к-рое пред-
представляет из себя инвариантную относительно представ-
представления изотропии комплексную структуру в касательном
пространстве ТрМ (см. Инвариантный объект на одно-
однородном пространстве). Методы теории групп Ли позво-
позволяют построить широкий класс однородных прост-
пространств, облагающих инвариантной П. к. с. (как интег-
интегрируемой, так и неинтегрируемой) и при тех или
иных предположениях классифицировать инвариантные
П. к. с. (см. [2]). Напр., любое факторнространство GIH
группы Ли G по подгруппе //, состоящей из неподвиж-
неподвижных точек автоморфизма нечетного порядка группы
Ли G, обладает инвариантной П. к. с. Примером яв-
является 6-мерная сфера 5", рассматриваемая как одно-
однородное пространство G2/SU C); ни одна из инвариантных
П. к. с. на iSe не является интегрируемой.
Наличие на многообразии П. к. с. накладывает не-
к-рые ограничения на его топологию — оно должно
быть четномерным, ориентируемым, а в компактном
случае все его нечетномерные классы Штифоля — Уит-
ни должны быть равны нулю. Среди сфер П. к. с. допу-
допускают только сферы размерностей 2 и 6.
Лит.; Ll] Kobayashi S., Transformation groups in dif-
differential geometry, B. — [u.a.3, 1072; 12] К о м р а к о в Б. II.,
Структуры на многообразиях и однородные пространства,
Минск, 1978; [3] Лихнерович А., Теория евязностей
в целом и группы голономий, пер. с франц., М., 19В0; [4J
Уэллс Р., Дифференциальное исчисление на комплексных
многообразиях, пер. с англ., М., 1976; [5] X е р м а н д е р Л.,
Введение в теорию функций нескольких комплексных перемен-
переменных, пер. с англ., М., 1968. Д. В. Алексеееский.
ПОЧТИ ПЕРИОД — понятие теории почти периоди-
периодических функций, являющееся обобщением понятия пе-
периода. Для равномерной почти иериодич. функции
1(х), —оо <.т<оо, число т=тДе) наз. 8-п о ч т и пери-
периодом функции f(x), если для всех х выполняется не-
неравенство
|/( ()|
Для обобщенных почти периодич. функций понятие
П. п. определяется сложнее. Напр., в пространстве
SP функций Степанова е-почти период т определяется
неравенством
sP х <е,
где Dsplf, ф] — расстояние между функциями {(х) и
<р(х) в метрике пространства Sf.
Множество П. п. функции/(.г) наз. относитель-
относительно плотным, если существует число L = L (с, /)>0
такое, что в каждом интервале (a, a.-\-L) действитель1
ной оси найдется хотя бы одно число этого множества.
Определение равномерных почти периодич. функций и
почти периодич. функций по Степанову может быть ос-
основано на требовании существования относительно
плотных множеств е-почти периодов у этих функций.
Лит.: [1] Левитан Б. М., Почти-периодические функ-
функции, М., 1953. Е. А. Бредихина.
ПОЧТИ ПЕРИОДИЧЕСКАЯ ФУНКЦИЯ — функ-
функция, к-рая может быть представлена обобщенным рядом
Фурье. Существуют различные способы определения
классов П. п. ф., основанные на понятиях замыкания,
почти периода, сдвига. Каждый из классов П. п. ф.
получается в результате замыкания в том или ином
смысле одной и той же совокупности конечных тригоно-
метрич. сумм.
Пусть DG[f(x), (f(x)] — расстояние между функция-
функциями / (х) и ф (х) в метрич. пространстве G. Далее в каче-
качестве G рассматривается одно из пространств U, Sp
Wp, ВР, где U — совокупность непрерывных ограничен-
ограниченных на действительной оси функций с метрикой
Du[f(x),<f(x)]= sup \f(x)-<f(x)\;
— 00 < Х<00
Sf, Wp, Bp — совокупности функций, измеримых н
суммируемых со степенью р, p^i, в каждом конечном
интервале действительной оси с метриками:
S?
= sup
D [f(x), q>(*)]= lira D p\f (x), q (x)],
W I > CD Sf
I —> CD
DBP[f (x), q>(*)]= Г Шп 4г^
Пусть T— множество тригонометрии, полиномов вида
S k
где Xjj — любые действительные числа, а^ — комплекс-
комплексные коэффициенты. Через Нq{T) обозначается замыка-
замыкание в пространстве G множества Т. Классы Ни(Т) =
= U-a. п., HsftT)=Sf-n.n., Hwp(T)=WP-n.n.,
НвР=Вр-п. п. наз. соответственно классами равно-
равномерных П. п. ф., или Бора почти периодических функ-
функций, Степанова почти периодических функций, Вейля
почти периодических функций, Везиковича почти перио-
периодических функций. Все определенные выше классы
П. п. ф. инварианты относительно сложения. Вместе с
f{x) в каждый класс входит /(г), \f (х)\ и произведение
/ (x)ei)uc, где Я — действительное число. Расстояния
Dsp[f(x), q>(x)] при различных лначениях I тошшогиче-
ски эквивалентны, и потому можно считать 2=1. Пусть
S\-u. u. = Sp-u. п., Sl-n. n.=S-n. п., Вг-п. u.=B-a. п.,
тогда имеют место включения
U-n.nc:Sp-n.nc:Wp-n.HCBp-n.n., рЗг 1;
и. если рх<р2, ру>\,
S -u.ncS"' -п.и., WP2 -п.п.С WPl -п.п,
ВР2-п.п. cS''-п.п.
Для каждой f(x)?B-n. п. существует среднее
значение
{/(*)}= lim — Г f (ж)
функция а(Я, f) = M {f(x)e-i^x}, где X, — действитель-
действительное число, может отличаться от нуля не более чем на
счетном множестве значений X; в результате нумерации
в произвольном порядке получается последовательность
{ЯА}, А=1, 2, ... , показателей Фурье функ-
функции /(.г).
Числа Л ^ =а(А,?, /) паз. коэффициентами
Фурье функции /(х). П. п. ф. / (х) любого определен-
определенного выше класса соответствует ряд Фурье вида
Для / (х)?В2-п. II. имеет место равенство Пар-
Парсе в а л я
В классе В^-п. п. обобщается теорема 1' и с с а —
Фишера: пусть {Я,^}, fc—1, 2, ... ,— произвольные
действительные числа, {^4^.}, к=1, 2, ... ,— комплекс-
ные числа, для к-рых ^fe_=1l-4fel2<oo, тогда существует
f(x)?B2-n. п., для к-рой тригонометрич. ряд ^ Л ,е^кх
является ее рядом Фурье.
Теорема единственности понимается
в следующем смысле: если две функции /(•2')^//(jG1) и
<р(ж)^//0(Г) имеют один и тот же ряд Фурье, то выпол-
выполняется равенство
Da[i(x), ф (*)]=0.
В-частности, для равномерных П. п. ф. теорема единст-
единственности означает, что /(х) =ср {.г) (для II. и. ф. Степано-
Степанова — почти всюду). Теорема едннотнениости, понима-
понимаемая в том же смысле, что и для рядов Фурье — Ле-
Лебега 2я-периодических функций, не имеет места для
П. п. ф. Вейля — Безиковича.
Классы равномерных П. п. ф. и II. п. ф. Степанова
являются соответственно нетривиальными расширени-
расширениями класса непрерывных на всей числовой оси и сумми-
суммируемых на [0,2я] 2я-периодичес,К1[х функций. Для
этих классов П. п. ф. сохраняется теорема единствен-
единственности.
Другие, менее формальные определения П. п. ф. рас-
рассматриваемых классов опираются на понятие почти пе-
периода и на обобщения этого понятия.
Следствием определения классов П. п. ф. через iro-
нятие замыкания является теорема аппрок-
аппроксимации: для каждой П. п. ф. / (.г) из U (или
Sp, Wp) и каждого е>0 можно указать конечный три-
тригонометрич. полином Р (х) из множества Т, удовлетво-
удовлетворяющий неравенству
Dulf(x), Р(х)} <е
WsP\iW), PW1 <s, Dwp[f(x), P(x)] < е).
Теирема . аппроксимации может служить отправным
пунктом определения различных классов П. п. ф. При
этом аппроксимирующие полиномы Р (х) могут содер-
содержать «посторонние», т. е. отличные от показателей
Фурье функции f(x), показатели. Однако для нек-рых
приложений теоремы аппроксимации важен тот факт,
что можно совершенно избежать введения в Р (х) пока-
показателей, отличных от показателей Фурье функции f(x).
В связи с представимостью П. п. ф. обобщенными ря-
рядами Фурье возникает вопрос о признаках сходимости
для этих рядов и приобретают значение разнообразные
методы суммирования обобщенных рядов Фурье (метод
Бохнера — Фейера и др.)- Так, получены признак аб-
абсолютной сходимости обобщенных рядов Фурье с ли-
линейно независимыми показателями Фурье, признак рав-
равномерной сходимости рядов Фурье, когда 1^1 -> оо
при А-> оо, и аналогичный признак в случае, когда
%?. ->- 0 при к —у оо.
Значение признаков равномерной сходимости в тео-
теории П. п. ф. подчеркивается следующей теоремой:
если тригонометрич. ряд ^ft"**""*™ сх°Дится равномер-
равномерно на всей действительной оси, то он является рядом
Фурье своей суммы S {x)cz.U-n. п. Следствие: сущест-
существуют равномерные П. п. ф. с произвольным счетным
множеством показателей Фурье. В частности, показа-
показатели Фурье равномерной П. п. ф. могут иметь предель-
предельные точки на конечном расстоянии или даже распола-
располагаться всюду плотно.
Кроме понятия замыкания или почти периода, для
определения П. п. ф. можно использовать понятие сдви-
сдвига. Так, функция /(.г) будет равномерной П. п. ф. тогда
и только тогда, когда из каждой бесконечной последова-
последовательности функций fix-^h^, f(x-\-h2), ... , где сдвиги
Aj, h.2, ...— произвольные действительные числа, мож-
можно выбрать равномерно сходящуюся подпоследователь-
подпоследовательность. Это определение служит отправной точкой при
рассмотрении П. п. ф. на группах.
Основные факты теории П. п. ф. остаются справед-
справедливыми и в том случае, если рассматривать понятие
обобщенного сдвига. Возможны и полезны другие обоб-
обобщения: П. п. ф. со значениями в евклидовом п-мерном
пространстве, в банаховом или метрич. пространстве,
аналитические и гармонические П. п. ф.
Лит.: [1] Бор Г., Почти периодические функции, пер.
с нем., М.— Л., 1934; [2] В е s i с о v i t с h A. S., Almost
periodic functions, Camb., 1932; [3] Левитан Б. М., Почти-
периодические функции, М., 1953; [4] Купцов Н. П., «Ус-
«Успехи матем. наук», 1968, т. 23, в. 4, с. 117 — 78; [5] R u d i n W.,
Fourier analysis on groups, N.Y.—L., 19B2; [6] Левитин
Б. М., Операторы обобщенного сдвига и некоторые их примене-
применения, М., 1962; [7] Красносельский М. А., Бурд
В. Ш., К о л е с о в Ю. С, Нелинейные почти периодические
колебания, М., 1970. Е, А. Бредихина.
ПОЧТИ ПЕРИОДИЧЕСКАЯ ФУНКЦИЯ АНАЛИ-
АНАЛИТИЧЕСКАЯ — аналитическая функция /(«), s=a+n,
регулярная в полосе —оо <:а<а<Р<+оо и разло-
разложимая в ряд вида
Sik s
апе " ,
где ап — комплексные, %п — действительные числа.
Действительное число т наз. е-п очти периодом
функции /(«), если во всех точках полосы (ее, Р) выпол-
выполняется неравенство
П. п. ф. а.— аналитическая функция, регулярная в
полосе (а, Р) и обладающая для каждого е>0 относи-
относительно плотным множеством е-почти периодов. Анало-
Аналогично определяется П. п. ф. а. в замкнутой полосе
а<а<р. П. п. ф. а. в полосе fa, pi на каждой прямой
полосы является равномерной почти периоднч. функци-
функцией от действительного переменного т, она ограничена в
[а, р], т. е. в любой внутренней полосе. Если функция
/(s), регулярная в полосе (а, Р), является равномерной
почти периодич. функцией хотя бы на одной единствен-
единственной прямой а^ого этой полосы, то ограниченность /(х)
в [а, р] влечет за собой ее почти периодичность во всей
полосе [ос, Р]. В результате теория П. п. ф. а. оказы-
оказывается в основе своей аналогичной теории почти пери-
периодических функций от действительного переменного.
Поэтому на П. п. ф. а. легко переносятся многие важ-
важные факты последней теории: теорема единственности,
равенство Парсеваля, правила действий над рядами
Дирихле, аппроксимационная теорема и ряд др. тео-
теорем.
Лит.: [1] Бор Г.. Почти периодические функции, пор.
с нем., М.— Л., 1934; [2] Левитан Б. М., Почти-периодп-
чесние функции, М., 195,'!. Е. А. Вредихина.
ПОЧТИ ПЕРИОДИЧЕСКАЯ ФУНКЦИЯ НА ГРУП-
ГРУППЕ — обобщение почти периодич. функции, заданных
на R1.
Пусть G — (абстрактная) группа. Комплекснознач-
ная функция j {л), x?G, наз. правой почти пе-
период и ческой функцией (п. л. ф.), если
семейство /(та), где я пробегает всю группу 6', компакт-
компактно в смысле равномерной сходимости на G, т. е. из
каждой последовательности j (хах), f(xa2), ... можно вы-
выделить равномерно на G сходящуюся подноследователь-
ность. Аналогично определяются левая почти
периодическая функция на группе G.
Оказывается, что всякая правая (левая) п. и. ф. яв-
является одновременно левой (правой) п. п. ф., и имеет
место компактность семейства f(axb), где a, b независи-
независимо пробегают группу G. Последнее свойство часто при-
принимается в качестве определения п. п. ф. на G. Сово-
Совокупность всех п. п. ф. на G есть банахово пространство
с нормой ||/1|= sup |/ (х) \.
G
Теория п. п. ф. на группе существенно опирается на
теорему о среднем значении (см. [5],
[8]). Линейный функционал Mx{f(x)}, заданный на
пространстве всех п. п. ф., наз. средним значе-
значение м, если
1) Mx{i}-\, Mx{f(x)}^0 для/(*)>0 и Mx{J{x)}>0
для 1Ф0;
2) Мх{! (га) У- Мх {/ (ах)}= Мх {/ (х-*) }.
Унитарная матрица g(x) = {gij(x)Yi, j=i, заданная на
G, наз. унитарным представлением
группы G, если g(e) = Ir (e — единица группы С,
Ir — единичная матрица порядка г) и для любых але-
ментов .т, у ?б имеет место равенство g(xy) = g(x)g(y).
Число г наз. размерностью представле-
представления g. Матричные элементы g,j(x) суть п. п. ф. на
G. В теории п. п. ф. на группе они играют ту же роль,
что и функции exp(iXx) в теории п. п. ф. на прямой R1.
Два представления g(.x) и g'(x) наз. эквивалент-
эквивалентными, если существует такая постоянная матрица А ,
что g'(x) = A~1g(x)A. Представление g наз. непри-
неприводимым, если семейство матриц g{x), x?G, не
имеет общего нетривиального инвариантного подпрост-
подпространства в Rr. Множество всех неприводимых унитар-
унитарных представлений разбивается на классы эквивалент-
эквивалентных между собой представлений. Пусть из каждого клас-
класса эквивалентных представлений выбрано по одному
представлению и полученное множество обозначено S.
Тогда множество п. п. ф. на G
Я = {Фя(х)}^{ф, ф-^,7, g?S]
оказывается ортогональной (хотя, вообще говоря, не-
несчетной) системой.
Теорема 1 (равенство Парсеваля).
Если для п. п. ф. f (х) положить
\M x
L
Говорят, что представление #?jS входит в ряд
Фурье п. п. ф. f{x), если Mx{f(x)g;j(x)}?:Q для
нек-рых г, /, l<i<r, 1</<г.
Теорема 2 (теорема а п п р о к с и м а-
ц и п). Множество Н плотно в пространстве п. п. ф.,
наделенном нормой
||/Ц= sup |/(х)|,
xeG
причем каждую п. п. ф. можно сколь угодно близко ап-
аппроксимировать конечной линейной комбинацией мат-
матричных элементов представлений, входящих в ее ряд
Фурье.
Если G — топологич. группа, то к определению
п. п. ф. нужно добавить требование ее непрерывности.
В этом случае и представления, входящие в ее ряд Фу-
Фурье, также будут непрерывными.
В случае, когда группа G абелева, непрерывные уни-
унитарные представления одномерны — они наз. харак-
характера м и группы G. Характеры группы G обознача-
обозначаются через у, и равенство Парсеваля таково:
Мх {\ } (х) Г-}=2„ | ап I2. аа = Мх {/ (х) гп (')}¦
В случае G~=Rn непрерывными характерами являют-
являются функции х(г) = схр(гЯ -х), где X?R", к •ж=Я.1ж1+...+
-\-Хпхп. Из теорем 1, 2 следуют основные результаты тео-
теории п. п. ф. одного и многих переменных.
Доказательство основных положений теории п. п. ф.
опирается на рассмотрение интегральных уравнений на
группе (см. [2]). Доказапо [3] существование достаточ-
достаточной системы линейных представлений компактных
групп Ли. В этом случае инвариантное интегрирование
(а значит, и среднее) устанавливается непосредственно.
Построено [4J инвариантное интегрирование на абст-
абстрактной компактной группе, обусловливающее распро-
распространение на этот случай теории Петера — Вейля.
Теорию п. п. ф. на группе можно вывести (см. [3])
из теории Петера — Вейля следующим образом. Пусть
/(.г) — п. п. ф. на группе G и пусть
р(а\ у)= sup I f (axb) — f (ayb) |,
a, us G
тогда множество E— {t?G, p(t, e) = 0} есть нормальный
делитель группы G, a p — инвариантная метрика на
факторгруппе GIE и / равномерно непрерывна на GIE.
Из почти периодичности функции / (т) следует, что
пополнение факторгруппы GIE по метрике р есть ком-
компактная группа, и теоремы 1, 2 следуют из теории Пе-
Петера — Вейля.
Лит.: [1] Левитан Б. М., Почти-периодические функ-
функции, М., 1953; [2] W е у I H., «Matli. Ann.». 1926, Bd 97, 8.
338—56; [3 | P e t er F., We у 1 H., там же, 1927, Bd 97, S.
737—.')j; ['i] Neumann J. von, «Сотр. math.», 1934, v. 1,
.\»l,p. 106—14; [5] e г о же, «Trans. Amer. Math. Soc», 1934.
v. 3fi. p. 4'iri—92; [6J\Vei 1 A., «C. r. Acad. sci.», 1935, v. 200,
p. :;x— 40: |7| И оси да К., Функциональный анализ, пер. с
англ.. М., 10 0 7; [8j M a a k W-, Fast perjodische Funktionen,
В., 195 0. В. В. Жиков, Б. М. Левитан.
ПОЧТИ ПРИВОДИМАЯ ЛИНЕЙНАЯ СИСТЕМА
обыкновенных дифференциальных
уравнений — система
х = А (t)x, x?R",
A (-):R —¦, Horn (Rn, Rn), ^
обладающая свойством: найдется система с постоянными
коэффициентами у---By, n?R", и для каждого к>0
найдется Ляпунова преобразование Le(t) такие, что в ре-
зультате замены x — L{i)y система (*) переходит в сис-
систему
где
sup || С (t) || < е.
Всякая приводимая линейная система почти приводима.
Лит.: [1] Итоги науки и техники. Математический анализ,
т. 12, М., 1974, с. 71 —146. В. М. Миллионщиков.
ПОЧТИ ПРОСТОЕ ЧИСЛО — натуральное число
п, имеющее вид
n = pip2 ¦ ¦ ¦ Pk,
где pi — простые числа, a ftjsd — константа. Простые
числа являются частным случаем П. п. ч. при fe=l.
Для П. п. ч. имеют место теоремы, обобщающие теоре-
теорему о распределении простых чисел в натуральном ряду.
Ряд аддитивных проблем, к-рые еще не решены в про-
простых числах, решаются В П. П. Ч. П. М. Бредихин.
ПОЧТИ СИМПЛЕКТИЧЕСКАН СТРУКТУРА -
невырожденная дифференциальная 2-форма на мно-
многообразии. П. с. с. Q может существовать только
на чотномерном многообразии М (dim M=2m) и опре-
определяет Sp(m, R)-CTpyKTypy BSp(^m R), а именно глав-
главное расслоение реперов на М со структурной группой
Sp(m, R), состоящее из всех реперов г= {е,-, /,-, ?=1,
... , т}, для к-рых
Q (*>,-, «7) = »(/<, //)=0, Q(e; fj) = bu.
Необходимое и достаточное условие существования
на многообразии МП. с. с. (так же, как н почти комп-
комплексной структуры) состоит в возможности редукции
структурной группы касательного расслоения к уни-
унитарной группе U(m). Для этого, в частности, необходи-
необходимо обращение в нуль всех нечетномерных классов Шти-
феля — Уптни многообразия М (см. [1]).
Почти комплексная структура / и риманова метрика
g на многообразии М определяют П. с. с. Q по формуле
Q(X, Y) = g(JX, Y)-g(X, JY),
где X, Y — векторы, и любая П. с. с. может быть по-
получена таким образом. П. с. с. Q наз. интегрируе-
м о й или, иначе, симплектической струк-
структур о И, если в окрестности любой точки в нек-рых
локальных координатах ,г', у1', ?=1, ... , т, она приво-
приводится к виду fi=Sir'Arf,!;'. Согласно теореме Дарбу
для этого необходимо и достаточно, чтобы форма Q
была замкнута. Пример интегрируемой П. с. с. — ка-
каноническая симплектич. структура Q=2dp[Adql на
кокасательном расслоении Т*М произвольного мно-
многообразия М (здесь qi — локальные координаты мно-
многообразия М, pi — соответствующие координаты в
слое). Примером неинтегрируемой П. с. с. является ле-
воинвариантная 2-форма на полупростой группе Ли G,
получающаяся разнесением левыми сдвигами произ-
произвольной невырожденной внешней 2-формы на соответст-
соответствующей группе G алгебре Ли. Так же, как и риманова
метрика, П. с. с. определяет изоморфизм касательных
и кокасательных пространств (а тем самым и про-
пространств контравариантных и ковариантных тензоров),
а также каноническую 2то-форму объема r]~A/m\Qm
и ряд операторов в пространстве Л (М) дифференци-
дифференциальных форм: оператор е,, внешнего умножения па И;
оператор гй внутреннего умножения на Q; оператор
звездочки Ходжа * : \Р(М) ->¦ А2т~р{М), ш -у ifflil, где
оператор Iq внутреннего умножения определяется как
свертка данной формы с р-вектором, соответствующим
р-форме со; оператор кодифференцирования 8=*d*.
В отличие от риманова случая оператор A—d6+6d
оказывается кососимметрич. относительно глобально-
го скалярного произведения <сс, |5> = \ ал*Р и
пространстве р-форм на компактном многообразии М.
Для произвольной р-формы имеет место разложе-
разложение Ходжа — Лепажа со= Q)o-(-eQcut-(-ef,oJ+..., где
ч>1^АР~-1(М) — однозначно определенные эффектив-
эффективные (т. е. аннулируемые оператором ifi) формы [3].
П. с. с. на;;, конформно плоской, если
существует такая функция А,>0, что d(XQ)=O. Это эк-
эквивалентно представимости формы Q в виде:
При т.— 2 необходимым и достаточным условием того,
чтобы П. с. с. Q была конформно плоской, является
замкнутость 1-формы 6fl=iadQ, а при т>2 — выпол-
выполнение равенства dQ=(i/m~ 1) бйдй (см. [1]).
Тензор Т типа A, 2), соответствующий 3-форме tffi
п определяемый равенством Q(TXY, Z)~dQ(X, Y, Z),
где X, Y, Z — векторы, наз. тензором круче-
кручения П. с. с. Q. С ним ассоциируется, вообще говоря,
вырожденная метрика g(X, Y)~tr T^Ty- С произволь-
произвольной П. с. с. связывается класс линейных связностей S/,
аннулирующих форму О и имеющих тензор Т своим
тензором кручения. Две такие связности отличаются на
тензорное поле вида Q'J'Sу^г, где Sj^i — произвольное
симметрическое тензорное поле. Рассматриваемые связ-
связности взаимно однозначно соответствуют сечениям пер-
первого продолжения В1 —у-В для Sp(m, К)-структуры В=--
=BS (m R), являющегося главным расслоением репе-
реперов на -В со структурной группой S3(R2m) (векторной
группой однородных полиномов третьей степени от 2т
переменных). Sp(m, К)-структура является G-структу-
рой бесконечного типа. Поэтому группа автоморфиз-
автоморфизмов П. с. с. может быть бесконечномерной. В частности,
группа автоморфизмов симплектич. структуры всегда
бесконечномерна и является fc-транзитивной группой
для любого А>().
Лит.: [1] bibermann P., ((Bull. Soc. Math. France»,
1955, t. 83, p. 195 — 224; [21 Итоги науки и техники. Алгебра.
Топология. Геометрия, т. 11, М., 1974, с. 153—207; [3] Л ы-
ч а г и н В. В., «Успехи матем. паук», 1979, т. 34, К° 1, с. 137—
165; [4] К о b а у a s h i S h., Transformation groups in differen-
differential geometry, B. — La.o.], 1972. Д. В. Алексеевский.
ПОЧТИКОЛЬЦО — одно из обобщений понятия ас-
ассоциативного кольца. П.— это кольцоид над группой,
т. е. универсальная алгебра, в к-рой имеется ассоциа-
ассоциативная операция умножения и операция сложения;
относительно сложения П. должно быть группой (не
обязательно коммутативной), причем должен также вы-
выполняться правый закон дистрибутивности:
Л. являются также частным случаем мультиоператор-
11 ых групп.
Примерами П. являются множества МS(T) всех отоб-
отображений группы Г в себя, перестановочных с действи-
действием фиксированной полугруппы эндоморфизмов 5 груп-
группы Г. Групповые операции в М${Т) вводятся поточечно,
умножением в MS(T) является композиция отображе-
отображений. Почтикольцо Л?5(Г) является аналогом кольца
матриц. Обычным образом вводятся понятия подпочти-
кольца, идеала, правого модуля над П.
Пусть No (соответственно Nc) — многообразие П.,
задаваемое тождеством 0.г~0 (соответственно Ох=х).
Любое почтикольцо А разлагается в сумму подпочтико-
яецА=А0-\-Ас, где A0?N0, A C?Nс, причем АО[)АС=
- 0. Циклический правый А -модуль М наз. прими-
примитивным типа 0, если М прост, примитив-
примитивным типа 1, если либо хА—(), либо хА = М для
любого х?М, и примитивным типа 2, если М
является простым Л0-модулем. Почтикольцо А наз.
примитивным типа v (v—0, 1, 2), если существует точ-
точный простой А-модуль Г типа v. При атом возникает
плотное вложение почтикольца А в М$(Т) для нек-рой
полугруппы эндо.морфизмов S группы Г. Для 2-прпми-
тивных почтиколец Л с единицей и условием минималь-
минимальности для правых идеалов в Ао имеет место равенство
A=MS(T) (аналог теоремы Веддерберна — Артина).
Для каждого v=0, 1, 2 вводится понятие радикала
Джекобсона типа v, обозначаемого JV(A), он
определяется как пересечение аннуляторов v-нрими-
ттеных А -модулей. Радикал /,, (А) определяется как
пересечение максимальных правых модулярных идеа-
идеалов. Все четыре радикала различны, причем
Л {A) S /1/g (A) <= /х (А) <= Jt (A).
Оказывается, что эти радикалы обладают многими
свойствами радикала Джекобсона ассоциативных колец
(см. [4]).
Для II. справедлив аналог теоремы Оре о почтиколь-
цах частных [4].
Дистрибутивно порожденным поч-
почти к о л ь ц о м наз. П., аддитивная группа к-рого
порождается такими элементами х, что
(у -¦- г) х = ух-{- zx
для всех у, z из П. Все дистрибутивно порожденные П.
порождают многообразие No. Для конечных дистрибу-
дистрибутивно порожденных П. понятия 1- и 2-примитивности
совпадают; 1-примитивные дистрибутивно порожденные
П. имеют вид МВ(Т) для нек-рой группы Г. В дистрибу-
дистрибутивно порожденном П., с тождеством
{ху—ух)п 1х,У1=ху — ух, п(х, у) > 1,
умножение коммутативно (см. [3], [4]).
Каждое П. из Л'о, не содержащее нильпотентных
элементов, является подпрямым произведением П. без
делителей нуля [4]. Почтиалгебра А разлагается в пря-
прямую сумму простых П. тогда и только тогда, когда а) она
удовлетворяет условию минимальности для главных
идеалов, б) в А нет идеалов с нулевым умножением,
в) аннулягор любого минимального идеала максима-
максимален [1].
Для П. получены результаты, аналогичные резуль-
результатам о строении регулярных колец [2], о почтикольцах
частных [5]. П. имеют приложения к изучению групп
подстановок, блок-схем, проективной геометрии [4].
Лит.: [1] Be] I H. E., «Ganad. Math. Bull.», 1977, v. 20
.MSI, p. 25—28; 121 H e a t h e r 1 у H. E., «J. Indian Math.
Soc», 1974, v. 38, p. :i45—54; Ш Ligh S., «J. London Math.
Soc», 1975 v. 12, pt. 1, p. 27—31; [4] P i 1 z G., Near-rings,
Amst., 1977; [5] Oswald A., «Proc. Edinburgh Math. Soc»,
1979, v. 22, № 2, p. 77—86; [6] Полин С. В., в кн.: Кольца,
Новосиб., 1973, с. 41 — 45. В. А. Артамонов.
ПОЯС, л и н к, симплекса а триангуляции Т — со
вокугшость In (a, T) тех симплексов из замкнутой
звезды St(a, T) (объединения симплексов Г, содержа
щих а), к-рые не пересекают а. м. и. Войцехоескип.
ПРАВАЯ ГРУППА — полугруппа, простая справа
(см. Простая полугруппа) и удовлетворяющая левосто-
левостороннему закону сокращения. Всякая П. г. является
вполне простой полугруппой. Свойство полугруппы 5
быть П. г. эквивалентно любому из следующих условий:
а) S проста справа и содержит идемпотент, б) S регу-
регулярна и удовлетворяет левостороннему закону сокра-
сокращения, в) S обладает разбиением на левые идеалы, яв-
являющиеся (необходимо изоморфными) группами, г) S
есть прямое произведение группы и полугруппы пра-
правых нулей (см. Идемпотентов полугруппа). Симметрич-
Симметричным к понятию П. г. является понятие левой г р у н-
п ы. Группы и только они суть одновременно П. г. л
левые группы. Всякая вполне простая полугруппа об-
обладает разбиением на правые (левые) идеалы, являю-
ПРАВИЛЬНАЯ
552
щиеся (необходимо изоморфными) правыми (левыми)
группами.
Лит.: U] Клиффорд А., Простои Г., Алгебраи-
Алгебраическая теория полугрупп, пер. с англ., т. 1, М., 1972.
Л. Н. Шеврин.
ПРАВДОПОДОБИЯ УРАВНЕНИЕ — уравнение,
к-рое составляют при нахождении статистич. оценок не-
неизвестных параметров по максимального правдоподобия
методу. Пусть X — случайный вектор, плотность ве-
вероятности к-рого p{x\Q) содержит неизвестный пара-
параметр 0?в. Тогда уравнение
наз. уравнением правдоподобия, а его
решение 6 — оценкой максимального
(наибольшего) правдоподобия для
параметра 6. В нек-рых случаях П. у. решается эле-
элементарно, но в основном П. у. представляет собой алгеб-
алгебраическое или трансцендентное уравнение, для решения
к-рого пользуются методом последовательных прибли-
приближений.
Лит.: [1] Ван дер Варден Б. л., Математическая
статистика, пер. с нем., М., 19Н0. М. С. Никулин.
ПРАВИЛЬНАЯ ИНТЕРПРЕТАЦИЯ — интерпрета-
интерпретация формальной системы, при к-рой все аксиомы истин-
истинны или принимают значение «истина» при всех значени-
значениях ее параметров, а правила вывода сохраняют свойство
принимать значение «истина». Данное определение от-
относится к двузначным логич. исчисле-
исчислениям. Если истинностных значений
больше и нек-рые из них отмечены, то
в определении П. и. вместо слов «при-
«принимать значение „истина"» надо ис-
использовать слова «принимать отмечен-
отмеченные значения». Если приведенное
свойство интерпретации не выполня-
выполняется, то она наз. неправильной.
П. и. для формальных систем, получающихся добавле-
добавлением к узкому исчислению предикатов какого-то множе-
множества аксиом Т, наз. также моделями системы
аксиом Т или моделями для Т. Произвольные ин-
интерпретации для таких формальных систем наз. алгеб-
раич. системами или просто моделями.
Лит.: И] Ч ё Р ч А., Введение в математическую логику,
пер. с англ., М., 1960. В. Н. Гришин.
ПРАВИЛЬНАЯ ЛИНЕЙНАЯ СИСТЕМА о б ы к-
новенных дифференциальных урав-
уравнений — система вида
= А (t) х,
A)
(где А (¦) — суммируемое на каждом отрезке отображе-
отображение R.+->-Horn (R", R")), обладающая свойством:
lim ~ {' tiA (т) d-v
t^- + oo l JO
существует и равен ^j.=1k[(A), где
!япунова характеристические показатели системы A).
Для того чтобы треугольная система
была правильной, необходимо и достаточно, чтобы су-
существовали пределы
lim
V pu(x)dx, i = l, ..., n
J о
(критерий Ляпунова). Всякая приводимая
линейная система и всякая почти приводимая линейная
система являются правильными.
Роль понятия П. л. с. проясняется на следующей
теореме Ляпунова. Пусть система A) пра-
правильная и к ее характеристич. показателей Ляпунова
отрицательны:
0> К-к^(А)^ ...^1п{А).
Тогда для всякой системы
х^А (t)x-yg(t, x), B)
где g(t, х) удовлетворяет следующим условиям: g, gx
непрерывны, g@, <)=0, \\g'x(x, t)\\=O(\x\z), где
>0 й fe б
рр , \\gx(, )(
—- const >0, найдется fe-мерное многообразие
содержащее точку ж=0, такое, что всякое решение
,r.(t) системы B), начинающееся на Vk (то есть ж@) ? V'*),
экспоненциально убывает при * -*¦ +оо, точнее — удов-
удовлетворяет неравенству
(для всякого 6>0 при нек-ром С&).
Лит.: [1] Ляпунов A.M., Общая задача об устойчи-
устойчивости движения, Хар., 1892 (то же, в кн.: СоОр. соч., т. 2, М.—
Л., 195В); [2J Б ы л о в Б. Ф., Виноград Р. Э., Г р о б-
м а в Д. М., Н е м ы ц к и й В. В., Теория показателей Ля-
Ляпунова и ее приложения к вопросам устойчивости, М., 1966;
[3] Итоги науки и техники. Математический анализ, т. 12, М.,
1974 с 71 —146. В. М. Миллионщиков.
ПРАВИЛЬНЫЕ МНОГОГРАННИКИ, телаПла-
тона,— выпуклые многогранники, все грани к-рых
Рис. 1.
суть одинаковые правильные многоугольники и все
многогранные углы при вершинах правильные и рав-
равные (рис. la—id).
В евклидовом пространстве Е3 существуют пять П. м.,
данные о к-рых приведены в табл. 1, где символ Шлефли
{р, q) (см. Многогранника группа) обозначает П. м. с
р-угольными гранями и g-гранными углами.
Табл. 1. — П р а в и л ь н ы е (выпуклые)
многогранники в ?¦'
Тетраэдр ....
Куб (гексаэдр)
Октаэдр
Додекаэдр ....
Икосаэдр ....
Рис.
1а
16
1«
и
19
Символ
Шлефли
C,3)
D,3)
C,4)
E,3)
C,5)
Число
вершин
4
8
С
20
12
Число
ребер
6
12
12
30
30
Число
граней
4
0
8
12
20
Двойственными многогранниками
{р, q) и {<?, р} наз. такие, к-рые переходят друг в друга
при полярном преобразовании относительно вписанной
Т абл. 2,-
Симплекс . .
Гиперкуб . .
lfi-гранник
24-гранник
120-гранник
ЦОО-грашшк
ГТ р
ч в
и л 1
Символ
Шлефли
C,
D,
{3,
{3,
{5,
{.ч.
3,
3,
3,
4,
3,
3,
3}
3)
4)
3}
3}
5}
> н ы е
Ч исло
иш \\
5
l(i
8
24
600
120
много
Число
ребер
10
.42
24
96
1200
720
г р а н н и
Число
двумер-
двумерных
граней
10
24
32
98
720
1200
t и в Е*
Число
трехмер-
трехмерных
граней
5
8
16
24
120
600
ПРАВИЛЬНАЯ
552
щиеся (необходимо изоморфными) правыми (левыми)
группами.
Лит.: U] Клиффорд А., Простои Г., Алгебраи-
Алгебраическая теория полугрупп, пер. с англ., т. 1, М., 1972.
Л. Н. Шеврин.
ПРАВДОПОДОБИЯ УРАВНЕНИЕ — уравнение,
к-рое составляют при нахождении статистич. оценок не-
неизвестных параметров по максимального правдоподобия
методу. Пусть X — случайный вектор, плотность ве-
вероятности к-рого p(x\Q) содержит неизвестный пара-
параметр 0?в. Тогда уравнение
наз. уравнением правдоподобия, а его
решение 6 — оценкой максимального
(наибольшего) правдоподобия для
параметра 6. В нек-рых случаях П. у. решается эле-
элементарно, но в основном П. у. представляет собой алгеб-
алгебраическое или трансцендентное уравнение, для решения
к-рого пользуются методом последовательных прибли-
приближений.
Лит.: [1] Ван дер Варден Б. л., Математическая
статистика, пер. с нем., М., 19Н0. М. С. Никулин.
ПРАВИЛЬНАЯ ИНТЕРПРЕТАЦИЯ — интерпрета-
интерпретация формальной системы, при к-рой все аксиомы истин-
истинны или принимают значение «истина» при всех значени-
значениях ее параметров, а правила вывода сохраняют свойство
принимать значение «истина». Данное определение от-
относится к двузначным логич. исчисле-
исчислениям. Если истинностных значений
больше и нек-рые из них отмечены, то
в определении П. и. вместо слов «при-
«принимать значение „истина"» надо ис-
использовать слова «принимать отмечен-
отмеченные значения». Если приведенное
свойство интерпретации не выполня-
выполняется, то она наз. неправильной.
П. и. для формальных систем, получающихся добавле-
добавлением к узкому исчислению предикатов какого-то множе-
множества аксиом Т, наз. также моделями системы
аксиом Т или моделями для Т. Произвольные ин-
интерпретации для таких формальных систем наз. алгеб-
раич. системами или просто моделями.
Лит.: И] Ч ё Р ч А., Введение в математическую логику,
пер. с англ., М., 1960. В. Н. Гришин.
ПРАВИЛЬНАЯ ЛИНЕЙНАЯ СИСТЕМА о б ы к-
новенных дифференциальных урав-
уравнений — система вида
= А (t) х,
A)
(где А (¦) — суммируемое на каждом отрезке отображе-
отображение R.+->-Horn (R", R")), обладающая свойством:
lim
4" Г tl
l JO
существует и равен ^j.=1kj(A), где
!япунова характеристические показатели системы A).
Для того чтобы треугольная система
была правильной, необходимо и достаточно, чтобы су-
существовали пределы
lim
V pu(x)dx, i = l, ..., n
J о
(критерий Ляпунова). Всякая приводимая
линейная система и всякая почти приводимая линейная
система являются правильными.
Роль понятия П. л. с. проясняется на следующей
теореме Ляпунова. Пусть система A) пра-
правильная и к ее характеристич. показателей Ляпунова
отрицательны:
0> К-к^(А)^ ...^1п{А).
Тогда для всякой системы
х^А (t)x-yg(t, x), B)
где g(t, х) удовлетворяет следующим условиям: g, gx
непрерывны, g@, <)=0, \\g'x(x, t)\\=O(\x\z), где
>0 й fe б
рр , \\gx(, )(
—- const >0, найдется fe-мерное многообразие
содержащее точку ж=0, такое, что всякое решение
,r.(t) системы B), начинающееся на Vk (то есть ж@) ? V'*),
экспоненциально убывает при * -*¦ +оо, точнее — удов-
удовлетворяет неравенству
(для всякого 6>0 при нек-ром С&).
Лит.: [1] Ляпунов A.M., Общая задача об устойчи-
устойчивости движения, Хар., 1892 (то же, в кн.: СоОр. соч., т. 2, М.—
Л., 195В); [2J Б ы л о в Б. Ф., Виноград Р. Э., Г р о б-
м а в Д. М., Н е м ы ц к и й В. В., Теория показателей Ля-
Ляпунова и ее приложения к вопросам устойчивости, М., 1966;
[3] Итоги науки и техники. Математический анализ, т. 12, М.,
1974 с 71 —146. В. М. Миллионщиков.
ПРАВИЛЬНЫЕ МНОГОГРАННИКИ, телаПла-
тона,— выпуклые многогранники, все грани к-рых
Рис. 1.
суть одинаковые правильные многоугольники и все
многогранные углы при вершинах правильные и рав-
равные (рис. la—id).
В евклидовом пространстве Е3 существуют пять П. м.,
данные о к-рых приведены в табл. 1, где символ Шлефли
{р, q) (см. Многогранника группа) обозначает П. м. с
р-угольными гранями и g-гранными углами.
Табл. 1. — П р а в и л ь н ы е (выпуклые)
многогранники в ?¦'
Тетраэдр ....
Куб (гексаэдр)
Октаэдр
Додекаэдр ....
Икосаэдр ....
Рис.
1а
16
1«
и
19
Символ
Шлефли
C,3)
D,3)
C,4)
E,3)
C,5)
Число
вершин
4
8
С
20
12
Число
ребер
6
12
12
30
30
Число
граней
4
0
8
12
20
Двойственными многогранниками
{р, q) и {<?, р} наз. такие, к-рые переходят друг в друга
при полярном преобразовании относительно вписанной
Т абл. 2,-
Симплекс . .
Гиперкуб . .
lfi-гранник
24-гранник
120-гранник
ЦОО-грашшк
ГТ р
ч в
и л 1
Символ
Шлефли
C,
D,
{3,
{3,
{5,
{.ч.
3,
3,
3,
4,
3,
3,
3}
3)
4)
3}
3}
5}
> н ы е
Ч исло
иш \\
5
l(i
8
24
600
120
много
Число
ребер
10
.42
24
96
1200
720
г р а н н и
Число
двумер-
двумерных
граней
10
24
32
98
720
1200
t и в Е*
Число
трехмер-
трехмерных
граней
5
8
16
24
120
600
553
ПРЕВОСХОДНОЕ КОЛЬЦО
554
или описанной сферы. Тетраэдр двойствен сам себе, гек-
гексаэдр — октаэдру и додекаэдр — икосаэдру.
В пространстве Ех существуют шесть П. м., данные
о к-рых приведены в табл. 2.
В пространстве Еп, к>4, существует три П. м.—
аналоги тетраэдра, октаэдра и куба; их символы Шлеф-
ли- {3 3}, {4,3, ... ,3},'{3, ... ,3,4}.
Если под многоугольником понимать плоские замк-
замкнутые ломаные (хотя бы и самопересекающиеся), то
можно указать еще 4 н е в ы п у к л ы х (з в е з д ч а-
2а
26
Рис.
т ы х) П. м. (т е л а П у а н с о). В этих многогранни-
многогранниках либо грани пересекают друг друга, либо грани —
самопересекающиеся многоугольники (рис. 2» 2,').
Данные о них приведены в табл. 3.
Табл. 3.—Правильные (невыпуклые)
многогранники в Е3
Малый звездчатый додекаэдр
Большой звездчатый додекаэдр
Большой додекаэдр
Икосаэдр
Рис.
2а
26
2 в
2г
Число
вер-
шин
12
20
12
12
Число
ребер
3 0
.40
3 0
30
Число
граней
12
12
12
20
Лит.: [1] Энциклопедия элементарной математики, кн. 4—
Геометрия, М., 1963; [2] Л ю с т е р н и к Л. А., Выпуклые
фигуры и многогранники, М., 1956; [3] Ш к л я р с к и й
Д. О., Ч е н ц о в Н. Н., Я г л о м И. М., Избранные задачи
и теоремы элементарной математики, ч. 3, М., 1954; [4J С о-
xeter H. S. М., Hegular polytopes, 3 ed., N.Y., 1973.
А. Б. Иванов.
ПРАВИЛЬНЫЕ МНОГОУГОЛЬНИКИ — много-
многоугольники, у к-рых равны все его углы и равны все его
стороны. Подробнее см. Многоугольник.
ПРАВОУПОРЯДОЧЕННАЯ ГРУППА — группа G,
на множестве элементов которой задано отношение
линейного порядка <: такое, что для всех х, у, z из
G неравенство .г<# влечет за собой xz<.yz. Множест-
Множество .Р= {ж?С|.г>е} положительных элементов группы
G является чистой (то есть Pf\P~l=0) ли-
линейной (то есть i3(J-P~1U (e}=G) полугруп-
полугруппой. Всякая чистая линейная подполугруппа Р произ-
произвольной группы определяет в ней правый порядок, а
именно порядок ж<г/ S- у ух~1^Р.
Группа А (X) автоморфизмов линейно упорядоченного
множества X естественным образом может быть пра-
воупорядочена. Всякая II. г. порядково изоморфна
нек-рой подгруппе А (X) для подходящего линейно упо-
упорядоченного множества (см. [1]). Архимедова П. г., то
есть П. г., для к-рой верна аксиома Архимеда (см. Ар-
Архимедова группа), порядково изоморфна подгруппе ад-
аддитивной группы действительных чисел. В отличие от
(двусторонне) линейно упорядоченных групп существу-
существуют некоммутативные П. г. бея собственных выпуклых
подгрупп. Класс П. г. замкнут относительно лексико-
графич. расширений. Система всех выпуклых подгрупп
П. г. G линейно упорядочена по включению и полна.
Ота система разрешима тогда и только тогда, когда для
всяких положительных элементов a, b?G существует на-
натуральное число п. такое, что anb~j>a. Если группа об-
обладает разрешимой системой подгрупп $(G), факторы
к-рой не имеют кручения, то G можно так правоупоря-
дочить, что все подгруппы из S (G) окажутся выпуклы-
ми. В локально нильпотентнои П. г. система выпуклых
подгрупп разрешима.
Группа G тогда и только тогда может быть право-
унорядочена, когда для любого конечного набора
{х,- ф е, 1 sg i< n}
элементов из G найдутся числа в,-=±1, l<:t<:n,
такие, что полугруппа, порожденная множеством
{.г^1, ... , г^"}, не содержит единицы группы G.
Всякий структурный (решеточ-
(решеточный) порядок группы есть пересе-
пересечение нек-рых ее правых поряд-
порядков (см. Структурно упорядочен-
упорядоченная группа).
Лит.: [1] К о к о р и н А, И., Ко-
Копы т о в В. М., Линейно упорядочен-
упорядоченные группы, М., 1972; [2] Мига
R. В., R h e m t и 1 1 a A., Orderable
groups, N.Y.—Basel, 1977.
В. M. Копытов.
ПРАНДТЛЯ УРАВНЕНИЕ — основное интегро-диф-
ференциальноо уравнение крыла самолета конечного
размаха. При выводе П. у. делаются предположения,
которые позволяют считать каждый элемент крыла на-
находящимся в условиях обтекания его плоскопарал-
плоскопараллельным потоком. Это дает возможность связать гео-
метрич. характеристики крыла с его аэродинамич.
свойствами. Так, полученное П. у. имеет вид
2г
где F — искомая функция, F'(t) = dF(t)/dt, В и / —
заданные функции B(t) = cb(t), f{t)=va>(t), а несобст-
несобственный интеграл понимается в смысле главного значе-
значения но Коши. Значения входящих в эти равенства ве-
величин следующие: 2а — размах крыла, к-рое предпо-
предполагается симметричным относительно плоскости Oyz,
причем направление оси Oz совпадает с направлением
потока воздуха на бесконечности; Ъ (х) обозначает хорду
профиля, к-рый соответствует абсциссе х; F(x) — цир-
циркуляцию воздушного потока вокруг этого профиля;
с — нек-рую постоянную; v — скорость воздушного
потока на бесконечности; аи — функцию, зависящую
от изогнутости профиля и перекручивания крыла
(см. [1J). Исходя из экспериментальных данных, пола-
полагают, что F(—a) = F(a).
П. у. решается в замкнутом виде лишь при весьма
жестких предположениях. В общем случае удается
П. у. свести к интегральному уравнению Фредгольма
(см. [3]).
П. у. наз. по имени Л. Прандтля (L. Prandtl).
Лит.: [1] Голубев В. В., Лекции по теории крыла,
М.— Л., 1949; [2] Карман Т., Бюргере И., Теорети-
Теоретическая аэродинамика идеальных жидкостей, пер. с англ., М.—
Л., 1939; [3] М у с х е л и ш в и л и Н. И., Сингулярные инте-
интегральные уравнения, 3 изд., М., 1968. В. В. Хведелидзе.
ПРАНДТЛЯ ЧИСЛО — один из критериев подо-
подобия тепловых процессов в жидкостях и газах. П. ч.
зависит только от термодинамич. состояния среды. П. ч.
Pv~v/a = \xcp/X,
где V—иУр — кинематич. коэффициент вязкости, ц —
динамич. коэффициент теплопроводности, р —- плот-
плотность, к — коэффициент теплопроводности, а-~гк1рс„ —
коэффициент температуропроводности, ср — удельная
теплоемкость среды при постоянном давлении.
П. ч. связано с др. критериями подобия — Пепле
числом и Рейнолъдса числом соотношением Pr=Pe/Re.
П. ч. наз. по имени Л. Прандтля (L. Prandtl).
Ho материалам одноименной статьи из БСЭ-3.
ПРЕВОСХОДНОЕ КОЛЬЦО — коммутативное нё-
терово кольцо, удовлетворяющее трем приводимым
ниже аксиомам. Известно, что геометрические кольца
обладают рядом качественных свойств, не присущих
553
ПРЕВОСХОДНОЕ КОЛЬЦО
554
или описанной сферы. Тетраэдр двойствен сам себе, гек-
гексаэдр — октаэдру и додекаэдр — икосаэдру.
В пространстве Ех существуют шесть П. м., данные
о к-рых приведены в табл. 2.
В пространстве Еп, к>4, существует три П. м.—
аналоги тетраэдра, октаэдра и куба; их символы Шлеф-
ли- {3 3}, {4,3, ... ,3},'{3, ... ,3,4}.
Если под многоугольником понимать плоские замк-
замкнутые ломаные (хотя бы и самопересекающиеся), то
можно указать еще 4 н е в ы п у к л ы х (з в е з д ч а-
2а
26
Рис.
т ы х) П. м. (т е л а П у а н с о). В этих многогранни-
многогранниках либо грани пересекают друг друга, либо грани —
самопересекающиеся многоугольники (рис. 2» 2,').
Данные о них приведены в табл. 3.
Табл. 3.—Правильные (невыпуклые)
многогранники в Е3
Малый звездчатый додекаэдр
Большой звездчатый додекаэдр
Большой додекаэдр
Икосаэдр
Рис.
2а
26
2 в
2г
Число
вер-
шин
12
20
12
12
Число
ребер
3 0
.40
3 0
30
Число
граней
12
12
12
20
Лит.: [1] Энциклопедия элементарной математики, кн. 4—
Геометрия, М., 1963; [2] Л ю с т е р н и к Л. А., Выпуклые
фигуры и многогранники, М., 1956; [3] Ш к л я р с к и й
Д. О., Ч е н ц о в Н. Н., Я г л о м И. М., Избранные задачи
и теоремы элементарной математики, ч. 3, М., 1954; [4J С о-
xeter H. S. М., Hegular polytopes, 3 ed., N.Y., 1973.
А. Б. Иванов.
ПРАВИЛЬНЫЕ МНОГОУГОЛЬНИКИ — много-
многоугольники, у к-рых равны все его углы и равны все его
стороны. Подробнее см. Многоугольник.
ПРАВОУПОРЯДОЧЕННАЯ ГРУППА — группа G,
на множестве элементов которой задано отношение
линейного порядка <: такое, что для всех х, у, z из
G неравенство .г<# влечет за собой xz<.yz. Множест-
Множество .Р= {ж?С|.г>е} положительных элементов группы
G является чистой (то есть Pf\P~l=0) ли-
линейной (то есть i3(J-P~1U (e}=G) полугруп-
полугруппой. Всякая чистая линейная подполугруппа Р произ-
произвольной группы определяет в ней правый порядок, а
именно порядок ж<г/ S- у ух~1^Р.
Группа А (X) автоморфизмов линейно упорядоченного
множества X естественным образом может быть пра-
воупорядочена. Всякая II. г. порядково изоморфна
нек-рой подгруппе А (X) для подходящего линейно упо-
упорядоченного множества (см. [1]). Архимедова П. г., то
есть П. г., для к-рой верна аксиома Архимеда (см. Ар-
Архимедова группа), порядково изоморфна подгруппе ад-
аддитивной группы действительных чисел. В отличие от
(двусторонне) линейно упорядоченных групп существу-
существуют некоммутативные П. г. бея собственных выпуклых
подгрупп. Класс П. г. замкнут относительно лексико-
графич. расширений. Система всех выпуклых подгрупп
П. г. G линейно упорядочена по включению и полна.
Ота система разрешима тогда и только тогда, когда для
всяких положительных элементов a, b?G существует на-
натуральное число п. такое, что anb~j>a. Если группа об-
обладает разрешимой системой подгрупп $(G), факторы
к-рой не имеют кручения, то G можно так правоупоря-
дочить, что все подгруппы из S (G) окажутся выпуклы-
ми. В локально нильпотентнои П. г. система выпуклых
подгрупп разрешима.
Группа G тогда и только тогда может быть право-
унорядочена, когда для любого конечного набора
{х,- ф е, 1 sg i< n}
элементов из G найдутся числа в,-=±1, l<:t<:n,
такие, что полугруппа, порожденная множеством
{.г^1, ... , г^"}, не содержит единицы группы G.
Всякий структурный (решеточ-
(решеточный) порядок группы есть пересе-
пересечение нек-рых ее правых поряд-
порядков (см. Структурно упорядочен-
упорядоченная группа).
Лит.: [1] К о к о р и н А, И., Ко-
Копы т о в В. М., Линейно упорядочен-
упорядоченные группы, М., 1972; [2] Мига
R. В., R h e m t и 1 1 a A., Orderable
groups, N.Y.—Basel, 1977.
В. M. Копытов.
ПРАНДТЛЯ УРАВНЕНИЕ — основное интегро-диф-
ференциальноо уравнение крыла самолета конечного
размаха. При выводе П. у. делаются предположения,
которые позволяют считать каждый элемент крыла на-
находящимся в условиях обтекания его плоскопарал-
плоскопараллельным потоком. Это дает возможность связать гео-
метрич. характеристики крыла с его аэродинамич.
свойствами. Так, полученное П. у. имеет вид
2г
где F — искомая функция, F'(t) = dF(t)/dt, В и / —
заданные функции B(t) = cb(t), f{t)=va>(t), а несобст-
несобственный интеграл понимается в смысле главного значе-
значения но Коши. Значения входящих в эти равенства ве-
величин следующие: 2а — размах крыла, к-рое предпо-
предполагается симметричным относительно плоскости Oyz,
причем направление оси Oz совпадает с направлением
потока воздуха на бесконечности; Ъ (х) обозначает хорду
профиля, к-рый соответствует абсциссе х; F(x) — цир-
циркуляцию воздушного потока вокруг этого профиля;
с — нек-рую постоянную; v — скорость воздушного
потока на бесконечности; аи — функцию, зависящую
от изогнутости профиля и перекручивания крыла
(см. [1J). Исходя из экспериментальных данных, пола-
полагают, что F(—a) = F(a).
П. у. решается в замкнутом виде лишь при весьма
жестких предположениях. В общем случае удается
П. у. свести к интегральному уравнению Фредгольма
(см. [3]).
П. у. наз. по имени Л. Прандтля (L. Prandtl).
Лит.: [1] Голубев В. В., Лекции по теории крыла,
М.— Л., 1949; [2] Карман Т., Бюргере И., Теорети-
Теоретическая аэродинамика идеальных жидкостей, пер. с англ., М.—
Л., 1939; [3] М у с х е л и ш в и л и Н. И., Сингулярные инте-
интегральные уравнения, 3 изд., М., 1968. В. В. Хведелидзе.
ПРАНДТЛЯ ЧИСЛО — один из критериев подо-
подобия тепловых процессов в жидкостях и газах. П. ч.
зависит только от термодинамич. состояния среды. П. ч.
Pv~v/a = \xcp/X,
где V—иУр — кинематич. коэффициент вязкости, ц —
динамич. коэффициент теплопроводности, р —- плот-
плотность, К — коэффициент теплопроводности, а—Х/рс^ —
коэффициент температуропроводности, ср — удельная
теплоемкость среды при постоянном давлении.
П. ч. связано с др. критериями подобия — Пепле
числом и Рейнолъдса числом соотношением Pr=Pe/Re.
П. ч. наз. по имени Л. Прандтля (L. Prandtl).
Ho материалам одноименной статьи из БСЭ-3.
ПРЕВОСХОДНОЕ КОЛЬЦО — коммутативное нё-
терово кольцо, удовлетворяющее трем приводимым
ниже аксиомам. Известно, что геометрические кольца
обладают рядом качественных свойств, не присущих
произвольным нётеровым кольцам. Понятие П. к. поз-
позволяет в аксиоматич. форме учесть важнейшие из этих
>войств.
Аксиомы П. к. А.
А1. Кольцо А универсально ценное. (Кольцо А наз.
цепным, если для любых двух его простых идеалов
?>?-р' длины любых неуплотняемых цепочек простых
идеалов p=poczp1cz...(Zpn=p' совпадают. Кольцо
А наз. универсально цепным, если цепным
является любое кольцо многочленов А [Тг, ..., Г/J.)
А2. Формальные слои кольца А являются геометри-
геометрически регулярными, т. е. для любого простого идеала
pczA и гомоморфизма из А в поле К кольцо А, (?)дК
регулярно. Здесь А^ — пополнение локального коль-
кольца А9.
Аи. Для любой целостной конечной Л-алгебры В
найдется ненулевой элемент Ъ?В такой, что кольцо
частных В \Ь~г] регулярно.
ГГ. к. обладают следующими свойствами.
1) Для П. к. А множество регулярных (соответствен-
(соответственно нормальных) точек схемы Spec А открыто.
2) Если превосходное локальное кольцо А приведен-
приведенное (соответственно нормальное, равноразмерное), то
таким же будет пополнение А.
3) Целое замыкание П. к. А в конечном расширении
поля частных кольца А является конечной А -алгеброй.
4) Если кольцо А превосходное, то любая А -алгебра
конечного типа — также П. к.
Два важнейших примера П. к.— полные локальные
кольца (или аналитич. кольца) и дедекиндовы кольца
с полем частных нулевой характеристики. Таким об-
образом, класс П. к. достаточно широк и, в частности, со-
содержит все алгебры конечного типа над полем или над
кольцом целых чисел %.
Превосходность кольца А тесно связана с возмож-
возможностью разрешения особенностей схемы Spec А (см.
[1], [2]).
Лит.: [1] Grothendieck A. [Dieudonne" J.],
Elements de geometrie algebrique, pt. 2, P., 1965; [2] X и р o-
п а к a X., «Математика», 1965, т. 9, № 6, с. 3—70.
В. И. Данилов.
ПРЕДБАЗА — семейство у открытых подмножеств
топологич. пространства X такое, что совокупность
всех множеств, являющихся пересечением конечного
числа элементов у, образует базу X.
М. И. Войцеховспий.
ПРЕДВАРЕННАЯ ФОРМУЛА — формула узкого
исчисления предикатов (УИП), имеющая вид
где Q; обозначает квантор всеобщности v или квантор
существования д, переменные х,-, xj различны при ХФ]
ii f — формула, не содержащая кванторов. П. ф. наз.
также предваренными нормальными
формами или пренекснымн формами.
Для всякой формулы ср языка УИП можно найти
П. ф., логически эквивалентную в классич. исчислении
предикатов формуле ф. Процесс нахождения П. ф. ос-
основан на следующих эквивалентностях, выводимых в
класепч. УИП:
О^Эх' (ф(х')оЧ'),
= Vz' (ф (^') Г) V),
) = V*' (V =3 ф (х1)),
== у^ф, Qy V ф =s д.мр,
где я' — любая переменная, не входящая свободно в
формулы (р(х), Т, и (f(x') получается из ф(.г) заменой
всех свободных вхождений х на х''; переменная у не
входит свободно в VffP, З^ф. Чтобы применять приве-
приведенные эквивалентности, надо предварительно выра-
выразить логич. связки через ZD и ~]; затем, применяя эти
эквивалентности, постепенно передвигать все кванторы
влево. Получающаяся в результате П. ф. наз. пред-
предваренной формой даппой формулы.
Лит.: [1] Мендельсон Э., Введение в математическую
логику, пер. с англ. М., 1971. В. Н. Гришин.
ПРЕДГИЛЬБЕРТОВО ПРОСТРАНСТВО — вектор-
векторное пространство Е над полем комплексных или дей-
действительных чисел, снабженное скалярным произведе-
произведением ЕхЕ —>- С, хХу -*¦ (.г, у), удовлетворяющим сле-
следующим условиям:
1) (х-\-у, z)—(x, z) + (y, z), (he, y) = l(x, у), (у, х)~
= (*, у), х, у, z?E, e
2) (х, х)>0 для х?Е.
На П. п. Е определена полунорма \\x\\~ (х, х) 2 .
Пополнение Е по этой полунорме является гильберто-
гильбертовым пространством. В. И. Ломоносов.
ПРЕДЕЛ — одно из основных понятий математики,
означающее, что какая-то переменная, зависящая от
другой переменной, при определенном изменении по-
последней, неограниченно приближается к нек-рому по-
постоянному значению. Основным при определении П.
является понятие близости рассматриваемых объектов:
только после его введения П. приобретает точный смысл.
С П. связаны основные понятия математич. анализа:
непрерывность, производная, дифференциал, интеграл.
Одним из простейших случаев П. является П. последо-
последовательности.
Предел последовательности. Пусть
X — топологич. пространство. Последовательность его
точек хП} п= 1, 2, ... , наз. сходящейся к точке хо?Х
или, что то же самое, точка х0 наз. пределом дан-
данной последовательности, если для любой
окрестности U точки х0 существует такое натуральное
N, что для всех n>JV выполняется включение zn?U;
при этом пишут
lim xn = x0.
п -> оо
В случае, когда X — хаусдорфово пространство, П.
последовательности а-„? X, и=1,2, ... , если он сущест-
существует, единствен. Для метрич. пространства X точка ,г0
является II. последовательности {хп} тогда и только
тогда, когда для любого е>0 существует такое нату-
натуральное N, что для всех номеров n>N выполняется не-
неравенство р (.г„, х0) <в, где р.(хп, х0) — расстояние меж-
между точками хп и ,г0. Если последовательность точек
метрич. пространства сходится, то она ограничена. По-
Последовательность точек полного метрич. пространства
является сходящейся в том и только в том случае, когда
она фундаментальная. В частности, это верно для чис-
числовых последовательностей, для к-рых исторически
впервые возникло понятие П. последовательности. Для
числовых последовательностей справедливы формулы
lim c = c, lim cxn = c lim xn,
с — произвольное фиксированное число,
lim (х„-\-уп)— lim xn-\ lim у
п —> w п ~-*¦ оо 11 —>- х
lim xnyn—- lim ,г„ lim yn,
а если lim у„ ?tO, то
lim ^ = ^.
Эти свойства числовых последовательностей переносят-
переносятся на П. последовательностей более общих структур.
напр, свойство П. суммы — на последовательности то-
точек линейных топологич. пространств, свойства П. про-
произведения — на последовательности точек топологич.
групп и т. д.
Если действительные числовые последовательности
Яя€к и yn?R сходятся и хп<у„, n—i, 2, ... , то
lira ?„< lira у„,
п ->¦ оо п ~> оо
т. е. при предельных переходах нестрогие неравенства
сохраняются. Если
lira хп = lira У„ = а
п ->- оо п -> оо
я 1„<го<(/„, то последовательность zn, n=i, 2, ... ,
сходится к тому же П.: lim zn=a. Эти свойства обоб-
щаются на П. последовательностей точек упорядочен-
упорядоченных множеств. -
Всякая возрастающая (убывающая) последователь-
последовательность действительных чисел хп, т. е. такая, что ж„<
<хп+1 (соответственно хп^хп+1), л—\, 2, ... , ограни-
ограниченная сверху (снизу), сходится, и ее П. является верх-
верхняя (нижняя) грань множества ее значений. Напр.,
если а>0, к — натуральное число, ап — приближен-
приближенное значение корня ?/а с п десятичными знаками после
запятой, вычисленное с недостатком, то ап, л=1, 2, ... ,
образуют возрастающую последовательность и lim an—
П-* 00
= |/а. Другим примером возрастающей ограниченной
сверху последовательности является последователь-
последовательность периметров правильных многоугольников с п
сторонами, гс=3, 4, ... , вписанных в нек-рую окруж-
окружность, к длине к-рой и сходится эта последователь-
последовательность.
Особую роль в теории числовых последовательностей
играют бесконечно малые последова-
последовательности, т. е. последовательности, сходящиеся
к нулю. Общее понятие П. числовой последовательности
сводится к понятию бесконечно малой в том смысле, что
числовая последовательность сходится к нек-рому чис-
числу в том и только в том случае, когда разность между
членами последовательности и этим числом является
бесконечно малой последовательностью.
Полезным является и понятие, бесконечно
больших числовых последователь-
последовательностей, т. е. последовательностей, имеющих своим
П. либо одну из бесконечностей со знаком +оо или —со,
либо бесконечность без знака оо. Для определения бес-
бесконечных П. вводятся понятия е-окрестностей, е>0,
бесконечностей -f-oo, —оо и оо в множестве действи-
действительных чисел R по формулам
*7 (+00, e)=/xeR:x>-l\ ,
и понятно р-окрестности оо в множестве комплексных
чисел С:
U (со, e)=/2gC:|2| > ±J.
Пишут lim хп—оо (соответственно 1тт.ги—+ оо или
п -> х п * ос
— со), хп? R, л—1, 2, ... , если для любого е>0 сущест-
существует такой номер А7, что для всех номеров n>iV выпол-
выполняется включение хп? U{оо, е) (соответственно включе-
включение х„? ?7(+оо, е) или х„? U(— оо, е)). Аналогично
определяется бесконечный П. для последовательностей
комплексных чисел.
Из всякой ограниченной числовой последовательно-
последовательности можно выделить сходящуюся подпоследователь-
подпоследовательность (см. Волъцано — Вейерштрасса теорема), а из
всякой неограниченной — бесконечно большую.
П. (конечный или бесконечный) какой-либо подпосле-
подпоследовательности данной последовательности наз. час-
частичным пред ел о м последней. В множестве
всех частичных П. всякой последовательности действи-
действительных чисел всегда имеются как наибольший, так и
наименьший (конечные или бесконечные). Наибольший
(соответственно наименьший) частичный П. последова-
последовательности наз. ее верхним (соответственно ниж-
нижним) пределом. Последовательность имеет конечный
или бесконечный П. тогда и только тогда, когда ее верх-
верхний П. совпадает с нижним, причем их общее значение
и является П.
С помощью П. последовательности могут быть опре-
определены другие понятия П., напр. П. функции и П. ин-
интегральных сумм. Определение П. последовательностей
обобщается на случай направленных (частично упоря-
упорядоченных) множеств.
Предел функции (отображения).
Пусть X и Y — топологич. пространства, ВсХ, х0 —
точка прикосновения множества Е, f : Е -у Y — отоб-
отображение Е в Y. Точку a?Y наз. пределом отоб-
отображения /в точке х0 (или, как говорят, при х,
стремящемся к х0) и пишут
lira / (х)=а или / (х) —> а при х —> х0,
Х-+ Х„
если, какова бы ни была окрестность V=V(a) точки а
в Y, существует такая окрестность U= U (х0) точки х0
в X, что для любой точки x?Ef\ U(x0) ее образ f{x) при-
принадлежит V : f(x) ? V. Иначе говоря, если f(Ef\ U)dV.
Если Y — хаусдорфово пространство, то отображение
/ : Е ->- Y может иметь только один П. в точке хо?Х.
В случае, когда E*czE и х0 — точка прикосновения
множества Е*, то П. сужения /?* отображения / на
множестве Е* наз. П. отображения (функции) / по мно~
жеству Е*, при этом пишут
lira /(.r)=-- lim fE.(x).
х-+х0, xsE* х ->¦ х0
Если / : Е —у У, E*aEczX, х„ — точла прикоснове-
прикосновения множества Е* и существует lim f(x), то в точке х0
существует и предел / по множеству Е*, причем
lim /(.*)= lira f (x).
x-*xot х е Е* х -> х0
Если ЕгаХ, Е.2аХ, /: Е^Е2 -»- Y и существуют
lira / (х) -— lim / (x) =а,
х-уха, xeEi x-*xa, ie?j
то существует и
lim / (х) = а.
Х-* Х0
При рассмотрении П. отображения (функции) / : Е -*-
—у Y, ЕаХ, при х —у хо?Х может случиться, что хо?Е
или, наоборот, хо(?Е. Случаи х0 ?Е представляет специ-
специальный интерес, т. к. он приводит к понятию непрерыв-
непрерывной функции: если / : Е —»- Y и х0 ?Е, то для того, чтобы
отображение / имело П. в точке х0, необходимо и до-
достаточно, чтобы
lim / (х) —/ (,г0).
X -> X „
R случае выполнения этого условия отображение /
и наз. непрерывным в точке х0. Если точка
х0 является изолированной точкой множества Е, то в
ней всегда существует предел
lim f{x)=f(x0)
X -f Х„
для любого отображения /:/?—>- У, т. о. любое отобра-
отображение / непрерывно во всех изолированных точках
множества своего определения. Поэтому понятие П.
отображения, в частности его непрерывности, содержа-
содержательно лишь для предельных точек отображаемого мно-
множества. В классич. случае П. функций / : Е —>- У обыч-
обычно предполагается, что хофЕ, т. е. что точка тоне при-
принадлежит тому множеству, по к-рому берется II.
Если в точке хо?Х для пространства X выполняется
первая аксиома счетности, а пространство У — хаус-
дорфоно, то для того, чтобы существовал предел lim /' (?)
отображения f : Е -*¦ Y, ЕаХ, необходимо и достаточ-
достаточно, чтобы для любой последовательности хп?Е, к-1,
2, ... , lim хп~а-0, существовал предел lim/(i,,). При
11-»- ее п-юо
выполнении этого условия предел lim / (xn) не зависит
от выбора указанной последовательности {хп} я их об-
общее значение является П. отображения / в точке х0.
Предел последовательности точек
{у,,} топологич. пространства У является частным слу-
случаем П. отображения (функции): в этом случае ?=N —
множество натуральных чисел, рассматриваемых с дис- ,
кретной топологией, ж0= + со, X=NU {+°° }, окре- 1
стностью + со в X является любое подмножество
UczH вида 17= {п : n^no}{J {-\- оо }, где п0 — нек-рое
натуральное число.
Понятие предела кратной последова-
последовательности, т. е. последовательности, члены к-рой
снабжены целочисленными мультииндексами, также яв-
является частным случаем П. отображения.
Внутренний критерий существования П. отображения
/ : Е —>- У в данной точке хц (он наз. критерием
К о ш и) в случае, когда в точке х0 топологич. прост-
пространства Xz^E выполняется первая аксиома счетности,
а множество У является полным метрич. пространством,
состоит в том, что предел lim/(.г) существует тогда и
х-*х0
только тогда, когда для любого е>0 найдется такая ок-
окрестность U— U (х0) точки х0 в X, что для всех точек г'
и ж", удовлетворяющих условию x'^Ef\U, x"?E[)U,
выполняется неравенство р (/(х"), /(ж'))<е. В частности,
этот критерий справедлив, когда У является множест-
множеством действительных или комплексных чисел.
Некоторые свойства пределов.
Если У — метрич. пространство, /:/?-> У, ЕаХ,
и существует предел lim f(x)~a?Y, то найдется такая
х—ха
окрестность f/=t/(.r0) точки .г0, что при отображении /
образ пересечения Е f) U отображаемого множества Е
с этой окрестностью будет ограниченным подмножест-
подмножеством пространства У.
Если функция / : Е —v R, EczX, R — множество
действительных чисел, имеет в точке хо?Х не равный
нулю конечный П., то существуют такие окрестность
U=U(x0) точки ,г0 и число с>0, что для всех точек
х ? Е П U выполняются неравенства
/ (х) > с, если lim / (х) > О,
х ~* х„
f (х) < —с, если lim / (.г) < 0.
X-f Х„
Если У — топологич. группа (в частности, коммута-
коммутативная с аддитивной записью групповой операции),
/ : Е -у У, ЕаХ, хо?Х, то предел lim /(.r) существует
х^ха
тогда и только тогда, когда функция a(x)^=f(x)a~1
имеет в точке х0 предел, равный единице группы У
(соответственно функция а(а-)=/(з-)— а имеет П. в х0,
равный нулю,— такие функции наз. бесконечно
малыми функциями).
Если У — линейное топология, пространство над по-
полем Р, /,:#->. У, /2 ; К ¦-*- Y, EczX, то П. в точке х„
линейной комбинации отображений /j и /2 равен такой
же линейной комбинации их П. в той же точке:
lira [A,,/] (x)-\-h2f2(x)]=\, lira /i(a:) + A,2 1™ /2 (*).
Если У — множество действительных или комплекс
ных чисел, /j : ? ->- У, /2 : ? ->- У (такие функции на.;
числовыми), EczX, то
lim fi(x)f2{x)= lim j,(x) lim /., (x),
X -> Д'о Л' —>- ЛЦ Л' -*• Ха
а если lim/2(x)yi0, то
S^i0 lim /, (.г)
lim ^' ^'т* = J ""* ж°
, Л /*(•*) I'm Ы*) '
* ° Х-* Л-„
причем в этом случае под lim ^' ^ понимается П.
сужения функции ¦— на пересечение отображаемого
множества Е с нек-рой окрестностью точки х0 такой, что
на указанном пересечении имеет смысл частное -Л- .
Если /i(x)</2(j), x?E, и существуют пределы lim /-,(rr),
lim /2(^), то ж-*-ж0
lim /1 (г) «S lim /2 (ж).
Если X и У получены из множества действитель-
действительных чисел R пополнением его либо бесконечностью без
знака: оо, либо двумя бесконечностями со знаком:
+ оо, —оо, ?cR, /(?)cR и .го^?, то сформулирован-
сформулированное определение П. функции является класснч. опре-
определением конечного и бесконечного П. действительной
функции одного переменного. Аналогично, если прост-
пространства X и У получаются пополнением бесконечностью
оо множества комплексных чисел С, то получают оп-
определение П. (конечного и бесконечного) для функций
комплексного переменного. Если же пространство А'
получается пополнением бесконечностью со простран-
пространства R" (соответственно С"), п>1, то получают опре-
определение конечного и бесконечного П. функции многих
переменных при стремлении аргумента к конечной или
бесконечно удаленной точке.
Для функций, определенных на подмножествах чис-
числовой прямой (или, более общо, на упорядоченных мно-
множествах), существует понятие одностороннего
предела. Примером функций, имеющих по крайней
мере один односторонний П. во всех предельных точ-
точках области определения, являются действительные
монотонные функции: если функция / монотонна на
множестве Е числовой оси и точка ,г0 является предель-
предельной точкой множества ?, то она является и предельной
точкой хотя бы одного из множеств ?1=?f| {x?R : x<C
<я}, Е2=Еf| {.r?R : ж>а}. Если точка х0 предельная
для множества Ех, то у функции / в точке х0 существует
П. слева, а если она предельная для Е2, то справа.
При этом если, напр., функция / возрастает и ограниче-
ограничена сверху, ?1^0, х0 — предельная точка для множе-
множества Ei, то предел lim j (x) конечен.
Основным общим методом отыскания П. функций яв-
является метод выделения главных частей функций в ок-
окрестности данной точки, что обычно делается с помощью
Тейлора формулы. Для вычисления П. часто бывает
полезно Лопиталя правило.
Несмотря на большую общность понятия П. отобра-
отображения, оно не охватывает все существующие понятия
П., имеющиеся в современной математике. Напр., по-
понятие П. интегральных сумм не содержится в понятии
П. отображения (функции). Достаточно общим поняти-
понятием П., в определенном смысле охватывающим все ос-
основные случаи, является П. отображения по фильтру.
Предел фильтра. Пусть X — тонологич.
пространство, Х^0, U= {U} — его база топологии,
55 — фи л ь т р на X (т. е. такое непустое семейство Д-
непустых подмножеств пространства X, что для любых
Л'€$?> ^"€?? существует такое Л ?§, что ЛаА' f\A").
Точка а-,, наз. пределом фильтра ^ или его
предельной точкой, если фильтр $• сильнее фильтра
*8(а-0), являющегося локальной базой топологии в точ-
точке х0, т. е. для любого U ? 58 (хд) существует такое А ?g,
что AaU.
Пусть N — множество натуральных чисел с дискрет-
дискретной топологией. Фильтр на множестве М, состоящий
пз всевозможных дополнений к конечным подмножест-
подмножествам множества N, наз. натуральным фильт-
фильтром и обозначается ^ку- Он не имеет П. в (М- Тот же
фильтр на множестве Jl = M(J {-|-oo }, в к-ром локаль-
локальная база 58(+оо) состоит из всевозможных множеств
Ап~ {т : m? N, m>nQN}, a iP(n) при n?N — из одной
точки п, имеет своим П. бесконечность +оо. Единствен-
Единственность П. фильтра топологич. пространства связана с от-
отделимостью точек пространства: для того чтобы любой
фильтр тонологич. пространства имел не более одного
П., необходимо и достаточно, чтобы пространство было
хаусдорфово.
Пусть X — нек-рое множество, У — топологич. про-
пространство, ф — отображение X в У, f? — фильтр на X.
Точку Ь ? У наз. пределом отображения
Ф по фильтру % и пишут
если фильтр ф(^), состоящий из всевозможных мно-
множеств ф(^4), А ?%, имеет своим П. в пространстве У
точку Ъ.
Если Х=М — множество натуральных чисел, ф —
отображение N в топологич. пространство У, ф(я)—
= г/я?У, n?N, З'ву— натуральный фильтр, то П. отоб-
отображения ф по фильтру %^, в пространстве У совпадает
с обычным П. последовательности {#„} в У. .
Если в X— NX(M, % — фильтр на X, являющийся
произведением двух натуральных фильтров 5J^, т. е.
состоящий из всевозможных множеств вида Ах В, где
А 65[у> ^GSiui Ф — отображение NXN в топологич.
пространство У : ф(я, m)— ynm?Y, re?N, m?IM, то П.
отображения ф по фильтру g в пространстве У совпада-
совпадает с обычным П. двойной последовательности {упт} в У.
Пусть элементами множества X являются, в свою оче-
очередь, множества х, состоящие из какого-либо разбие-
разбиения т—{t,-}^='o нек-рого отрезка [а, Ь]; а—го<{1<...<
«,г_ i<tH=6 и каких-то точек ?,-? [t,-_i, //], i—1, 2, ... ,
то есть
Пусть А г, (для любого Т)>0) — подмножество множе-
множества X, состоящее ии всех элементов х? X, у к-рых мел-
мелкости входящих в них разбиений т= {/,-}[=о меньше ц,
то есть
max (ti — ij'_i) < Ц-
1 = 1, 2, ..., П
Система Я'— {А г\ } является фильтром. Всякая действи-
действительная функция /, определенная на отрезке [а, 6],
порождает отображение ф^ множества А' в числовую ось
R но формуле
1 = П
Таким образом, Ц>](х) является значением интегральной
суммы Римана функции /, соответствующим элементу
х?Х.
П. отображения ф/ в R по фильтру $ совпадает с
обычным П. интегральных сумм Римана функции /
при условии, что мелкости рассматриваемых разбиг
ний стремятся к нулю. Это совпадение имеет место в
том смысле, что оба П. одновременно существуют или
нет, а если существуют, то равны и являются зна-
значениями интеграла Римана от функции / по отрезку
[а, 6].
Предел отображения топологиче-
топологических пространств по фильтру. Пусть
X и Y — топологич. пространства, ЕаХ, g — фильтр
на Е, ф — отображение Е ъ Y. Точку b?Y наз. пре-
пределом отображения срвточке а?Х по
фильтру %, если а является П. фильтра %, а 6
является П. фильтра срE). В этом случае пишут
b~\ims ср (х).
Если 5Р(а) — база окрестностей в точке а, Е=-
— Х\{о}, а фильтр % состоит из всевозможных «про-
«проколотых окрестностей» f(a)\{a} точки a, U(а) ?58 («),
то предел limgcp(x) совпадает с обычным пределом
lim ср(ж) отображения <р в точке а, то есть обобщает
классическое определение П. отображения, сформули-
сформулированное в терминах окрестностей. Непосредственным
обобщением понятия П. последовательности являет-
является П. направленного множества в топологическом про-
пространстве, т. е. такого частично упорядоченного мно-
множества, у к-рого за каждыми двумя элементами име-
имеется следующий. В терминах П. по направленным
множествам можно также сформулировать понятие П.
отображения одного топологич. пространства в дру-
другое (см. Направленность, Сходимость).
Предел последовательности мно-
множеств. Топологический предел. Пусть
А „, л—1, 2, ... ,— множества топологич. пространства
X. Верхним топологическим преде-
пределом \tAn последовательности {Ап} наз. множество
точек х?Х, каждая окрестность к-рых пересекается с
бесконечным числом множеств Ап, а нижним то-
топологическим пределом it An — множе-
множество точек, каждая окрестность к-рых содержит точки
почти всех Ап. Очевидно, It A ncll А п. Если А =
— It АП~It Ап, то последовательность {Ап} наз. схо-
сходящейся, а множество А ее топологическим П. и пишут
A — It А „. Верхний и нижний топологические П. после-
последовательности являются замкнутыми множествами.
Теоретик о-м ножественный предел.
Имеется понятие П. последовательности множеств, не
связанное с топологией. Последовательность множеств
Ап, п=1, 2, ... , наз. сходящейся, если сущест-
существует такое множество А, называемое ее пределом
и обозначаемое
A —lim A n,
что каждая его точка принадлежит всем множествам
Ап, начиная с нск-рого номера, и каждая точка из объе-
объединения всех множеств Ат не принадлежащая А, со-
содержится лишь в конечном числе множеств Ап. Множе-
Множество А является П. последовательности {Ап} тогда и
только тогда, когда оно является одновременно ее верх-
верхним и нижним пределом.
Лит.: [1] Ильин В. А., Позн я к Э. Г., Основы мате-
математического анализа, 3 изд., ч. 1, М., 1971; [2J Ильин В. А.,
Садовничий В. А., Сеидов Б. X., Математический
анализ, М., 1079; [3] Кудрявцев Л. Д., Курс математи-
математического анализа, т. 1—2, М., 1981; [4] Никольский С.
М., Курс математического анализа, 'Л изд., т. 1, М., 1975; 15]
Б у р б а к и Н., Общая топология. Основные структуры, пер.
с франц., 2 изд., М., 1958; [6] 3 а м а н с к и й М., Введение
в современную алгебру и анализ, пер. с франц., М., 1974; 17]
Келли Д ж. Д., Общая топология, пер. с англ., 2 изд.,
М., 1981- [8] X а у с д о р ф Ф,, Теория множеств, пер. с нем.,
М.— Л., 1937. ' Л. Д. Кудрявцев.
ПРЕДЕЛЬНАЯ ТОЧКА множества — точка,
в любой окрестности к-рой содержится по крайней
мере одна точка данного множества, отличная от нее
¦чшон. Рассматриваемые множества и точка предпола-
предполагаются принадлежащими нек-рому топология, про-
пространству. Множество, содержащее все свои П. т., наз.
.1 айкнут ы м. Совокупность всех П. т. множества
М наз. производным множеством и обо-
шачается М'. Если рассматриваемое топология, про-
пространство X удовлетворяет первой аксиоме отделимости
(для любых двух его точек х и у существует окрестность
U (х), не содержащая точку у), то каждая окрестность
П. т. нек-рого множества MdX содержит бесконеч-
бесконечно много точек этого множества и производное мно-
множество М' — замкнуто. Всякая прикосновения точка
множества М является либо его П. т., либо изолиро-
изолированной.
Лит.: [1] Александров II. С., Введение в теорию
множеств и общую топологию, М., 1977; 12] X а у с д о р ф Ф.,
Теория множеств, пер. с нем., М.— Л., 1937.
Л. Д. Кудрявцев.
ПРЕДЕЛЬНАЯ ТОЧКА траектории {f'x}
динамической системы /' — точка
х = lim ftkx A)
а ft-* оо
(а-п редельная точка) пли
х = lim f'kx B)
(ш-п редел-ьная точка), где {^}, fc?N,-- по-
последовательность такая, что tk—>—оо при к—> ос
в A) или tk—»--)- оо при к ¦—<¦ оо в B) и пределы A)
или B) существуют.
Для траектории {/'ж} динамич. системы f1 (или, иначе,
/(*, х), см. [1]) а-П. т. (ш-П. т.) — то же, что а)-П. т.
(а-П. т.) траектории {f~fx} динамич. системы /~* (сис-
(системы с обращением времени). Множество Qx (Ax) всех
ш-П.. т. (а-П. т.) траектории {ffx} наа. ш-и р е д е д ь-
н ы м (а-п ре дельным) множеством этой
траектории.
Лит.: [1] Немыцкий В. В., Степанов В. В.,
Качественная теория дифференциальных уравнений, 2 изд.,
М., 1949. В. М. Миллионщиков.
ПРЕДЕЛЬНОГО ПОГЛОЩЕНИЯ ПРИНЦИП —
способ однозначного выделения решений уравнений,
аналогичных Гелъмголъца уравнению, с помощью введе-
введения бесконечно малого поглощения. Математич. смысл
П. п. п. состоит в следующем. Пусть Q — неограничен-
неограниченная область в R", Р — самосопряженный оператор в
Ьг(й), задаваемый дифференциальным выражением
Р[ х, д-т ), x?Q, и однородными граничными условия-
условиями на 9Q, К — точка непрерывного спектра оператора
Р. Тогда при е=?0 уравнение
однозначно разрешимо в L2(Q) и в нек-рых случаях мож-
можно выделить решения к=к± уравнения
Pu = %u-\-f
с помощью предельного перехода
и [ = lira и .
Е^ ± О
При этом предполагается, что / имеет компактный но-
носитель, а сходимость ие -уи+_ при в -> +0 понимается
в смысле L2(fi'), где п' — иропзнольпая ограниченная
область в Q. Так как К — точка спектра оператора Р,
то указанный предел в I2(fi), вообще говоря, не сущест-
существует.
Впервые П. п. п. был сформулирован для уравнения
Гельмгольца в R2 (см. [1]):
Р = _Д, к = -к*-<0.
Выделяемые с помощью этого принципа решения и__
соответствуют расходящимся или сходящимся волнам
и удовлетворяют излучения условию на бесконечности.
Эти результаты были перенесены (см. B], [3]) на эллип-
эллиптические краевые задачи во внешности ограниченной
области в R" для оператора
д \ «~т п. д / 0 \ i ^
. \ . ^к 1 in,. \ (] ( Т) (]
х) ~k, j=i xk ч xj J
где коэффициенты а/г/(х) достаточно быстро стремятся к
константам при |з,| —v оо. Для справедливости П. п. и.
в этом случае необходимо требовать, чтобы К не было
собственным значением оператора Р или / была ортого-
ортогональна собственным функциям. Теорема Като (см. [3]j
дает достаточные условия отсутствия собственных зна-
значений на непрерывном спектре оператора Р~ — Д+9 (j)
Такая теорема получена для оператора (¦*) (см. [3]).
П. п. и. обоснован для нок-рых областей с некомпакт-
некомпактной границей (см. [3], [4]).
П. п. п. и соответствующие условия излучения най-
найдены для уравнений любого порядка и систем уравнений
(см. [5], [6]); они состоят в следующем.Пусть Р(' gj ) —
эллиптический (или гипоэллинтический) оператор, удо-
удовлетворяющий условиям: 1) многочлен Р (а) имеет дей-
действительные коэффициенты, 2) поверхность Р (а)=0,
a?Rn, распадается на х-связных гладких поверхно-
поверхностей Sj с отличной от нуля кривизной, 3) grad P (а)ф§
на Sj. Пусть на Sj заданы ориентации, т. е. независимо
для каждой поверхности выбраны направления норма-
нормали V. Пусть ffl=rjri , О7=о"у(ш) — точка на Sj, в к-рой v
и со имеют одинаковые направления, и иу(ш)—(о"у(со),
и). Тогда функция и (х) удовлетворяет условиям излу-
излучения, если она представима в виде
" = 2/= 1 <*)> и/ = О('-<1-п)/2),
~ — i\.ij (со) uj = o (rA~n)/2), г —>¦ оо.
Эти условия выделяют единственное решение уравне-
уравнения
для любой функции / с компактным носителем. П. п. п.
для этого уравнения заключается в том, что это же
решение получается в пределе при t —у -\-0 из одно-
однозначного определяемого решения кЕ (x)^L2 (R.") эп-
липтич. уравнения
дх) е
u=f
u
где Q(a) имеет действительные коэффициенты и Q (а)Ф
фО на Sj. В зависимости от набора sign Q(o), 1</<и,
о е s .
в пределе получаются решения с условиями излуче-
излучения, соответствующими той или иной ориентации по-
поверхностей Sj. Этот принцип обоснован для уравнений
и систем любого порядка с переменными коэффициен-
коэффициентами во внешности ограниченной области (гм. [5J,
1В]), а также в случае нсвыпуклых Sj-; для утих урав-
уравнений имеется и теорема единственности типа Като.
Лит.: [1] Игнатове к и й В. С, «Ann. Phys.», 1905,
Bd 18, Mi 13, S. 495—522; [2] Повзнер А. Я., «Матем. сб.»,
1953, т. 32, № 1, с. 109—56; L3] Э й д у с Д. М., «Успехи ма-
матем. наук», 1969, т. 24, в. 3, с. 91 —156; [4] Свешников
А. Г., «Докл. АН СССР», 1951, т. 80, X 3, с. 345—47; [5] В а й н-
fi г р г Б. Р., «Успехи матем. наук», 1966, т. 21, в. 3, с. 115—94;
его же, «Матсы. сб.», 1968, т. 75, Ма 3, с. 454—80.
Б. Р. Вайнберг.
ПРЕДЕЛЬНОЕ МНОЖЕСТВО С (f, z0; S) функции
/(г): G->-Q, определенной в области GaC со значе-
значениями на сфере Римана Q, в точке zo?G по множест-
множеству Sc:G, zo?S, — множество значений a?Q, для к-рых
существуют такие последовательности точек {г„},г„^,
п—1, 2, . . .; lim г„—z0, что
lira f(zn)=a.
п ->- оо
Каждое значение а?С (/, z0; S) наз. предельным
значением функции / в точке z0 по множеству S.
Теория П. м.— это раздел теории функций, в кото-
котором граничные свойства функций изучаются в терми-
терминах топологических и метрических свойств различ-
различных II. м.
Если в качестве множества 5 взята вся область G,
то получается полное предельное мно-
множество С(/, z0; G)=C(f, z0); в случаях строгого
включения SdG соответствующие П. м. С(/, z0; S)
иногда наз. частными. Полное П. м. С(/, z0)
всегда замкнуто; если функция / непрерывна на мно-
множестве S, локально связном в точке zo?S, то П. м.
C(f, z0; 5) либо вырожденное, т. е. состоит из одной
точки, либо является невырожденным континуумом.
Если II. м. C(f, z0; 5) совпадает с Q, то оно наз. т о-
т а л ь н ы м П. м. Значение a?Q принадлежит м н о-
жеству повторяющихся значений
R (/, z0; 5) функции / в точке z0 по множеству 5, если
существует такая последовательность точек {zn}, zn?S,
в=1, 2, . . ., lim zn~z0, что a=f(zn), n~—l, 2, ....
?!-> ее
Всегда R (/, z0; S)aC(f, z0; S). Если для нек-рого
a?Q в области G существует путь L : z=z(t), 0«:i<l,
оканчивающийся в точке z0, zof G, lim z(t)=z0, и
такой, что' lim /(z(t)) = a, то а наз. асимптотическим
t-*l
значением функции / в точке z0 (вдоль пути L). А с и м-
п т о т и ч е с к о о множество А (/, z0; G) —
это совокупность всех асимптотич. значений / в точ-
точке z0.
Понятие П. м. было впервые явно сформулировано
][. Пенлсве в 1895 (под названием «область неопреде-
неопределенности», см. [1]) в связи с изучением поведения ана-
литич. функции вблизи ее особой точки и классифи-
классификацией особенностей таких функций. С тех пор в тео-
теории П. м. изучаются в основном три геометрически про-
простейших случая: a) z0 — изолированная точка грани-
границы VvG или внутренняя точка G; б) G".D={|z|<l} —
единичный круг или, вообще, нек-рая жорданова об-
область, a z0 — точка границы T=FrD; в) граница Е=
= FrG есть всюду разрывный компакт на плоскости
(т. е. вполне несвязный компакт, не содержащий ни-
никакого невырожденного контипуума) и го?Е. Ряд
классич. результатов теории аналитич. функций до-
допускает формулировку в терминах П. м. Напр., Со-
хоцкого теорема в несколько усиленной форме: если
z0 — изолированная точка всюду разрывного ком-
компакта EdG и /(z) — мероморфная функция па G\E,
то П. м. С(/, z0; G\E) либо вырожденное, либо то-
тотальное. Дополнительно к этому Пипара теорема
утверждает, что в случае, когда С'(/, z0; G\E) тоталь-
тотально, т. е. когда z0 — существенно особая точка, мно-
множество CR (/, z0; G\?)—Ь2'\Д(/, z0; G\E) содержит
не более двух различных значений. В этом же случае
СП (/, z0; G\E) a A (/, z0; G\E)
(И верее на теорема).
Основной из результатов, касающийся теории
поведения мероморфных функций вблизи «тощей»
границы (теории Пенлеве), состоит в следую-
следующем (см. [1], [2]): если множество EcG имеет линей-
линейную хаусдорфову меру нуль, ц(?) = (Х] (Е) = 0, и функ-
функция / мероморфна в G\E, то в каждой точке zogiJ
П. м. С(/, z0; G\E) либо вырожденное, либо тоталь-
тотальное; более того, в первом случае / мероморфна и в точ-
точке z0. Таким образом, точка zo?E, в к-рой П. м. C(f,
z0; G\E) вырожденное, является устранимой особой
точкой функции /; изучение устранимых множеств
различных классов функций можно рассматривать
как раздел теории П. м.
Важным усилением теоремы Пикара является т е о-
рема Голубев а: если EaG, (i (?)=0 и / меро-
мероморфна в G\E, то в любой существенно особой точке
zo^? множество CR(f, z0; G\E) имеет аналитичес-
аналитическую емкость нуль (и, следовательно, плоскую Меру
(СДH)
ца(
Началом теории П. м. в случае непрерывной гра-
границы можно считать работу П. Фату (P. Fatou, 1906)
о граничных значениях функций f(z), голоморфных
в единичном круге D= {М<1}. Если такая функция /
ограничена в D, то почти всюду (в смысле меры Лебе-
Лебега) на окружности Г={|г| = 1} она имеет радиальные
и угловые граничные значения (теорема Фату).
Для произвольной точки ?=е<е?Г пусть h(t,, ср.)
обозначает хорду круга D, оканчивающуюся в ? и
образующую с радиусом, проведенным в эту точку,
угол раствора ср, —л/2<ср<я./2. И пусть Д (?, ср1;
Фз) — угловая область с вершиной ??Г, состоящая
из всех точек круга D, заключенных между двумя хор-
хордами
h (?, cpi) и h (?, ср2), — л/2 <q>L < ср2 < л/2-
Точку ?? Г наз. точкой Фату и относят к мно-
множеству F(f), если объединение
(]C(f, i; Д(?, срь <р2))
но всем угловым областям Д (?, срх, ср2) состоит из
единственного значения /(е'е), наз. у г л о в ы м гра-
граничным значением функции / в точке ?.
Иная формулировка теоремы Фату состоит в том, что
для ограниченной голоморфной в круге D функции /
справедливо разложение Г=.Р (/) \J Е, mes ?=0. Резуль-
Результат дополняется теоремой единственности
Ф. и М. Р и с с о в A916): если / голоморфна и ог-
ограничена в круге D и на нек-ром множестве MdF(f),
mes M>0, имеет угловое граничное значение /(?)—«,
??М, то f(z)=a. Это утверждение было независимо
доказано Н. Н. Лузиным и И. И. Приваловым A919),
к-рые существенно распространили его также на слу-
случай произвольных мероморфных функций. В том же
году Н. Н. Лузин и И. И. Привалов опубликовали
граничную теорему единственно с-
т и для случая радиальных граничных значений:
если голоморфная в D функция /на множестве М второй
категории и метрически плотном на нек-рой дуге yczP
имеет одно и то же радиальное граничное значение
agfi, то есть lim /(ге'е) = я, e'e?Af, то /(z)=a.
1
г»1
В 1936 II. И. Привалов отметил, что утверждение
/(z)=const остается в силе и в том случае, когда зна-
значения ag=lim /(re'e) не обязательно одинаковы в точ-
г->1
ках ?=-ei'8?Af, но принадлежат нек-рому множеству
(логарифмической) емкости нуль. Основная идея и
элементы доказательства теорем Лузина — Прива-
лова применимы и в общем случае непрерывных отоб-
отображений / круга D, что и было позднее использовано
во многих работах.
Точку ?? Г— {|z| = l} наз. точкой Плеснера
и относят к множеству /(/), если пересечение
П6'(/, ?; Д(?, фь ср2))
по всем угловым областям А (?, ф1; ф2) с вершиной ?
совпадает с Q. В 1927 А. И. Плоснер доказал, что для
любой мероморфной в круге D функции / почти вес
точки окружности Г принадлежат либо /''(/), либо
/(/), то есть T=F(i){JI(f){]E, mes Е=0. Точку ?€г
наз. точкой М е й е р а и относят к множеству
M(f), если С(i, ?; О)фп и пересечение хордальных
П. м. Г\С(/. ?; А(?, ф)) по всем хордам, проведенным
в точку I, совпадает с C(f, ?; D). К. Мейер (К. Meier.
1961) установил следующий аналог теоремы Плеснера
в терминах категории по Бэру: если / мероморфна
вВ, то все точки окружности Г, за возможным исклю-
исключением множества Е первой категории, принадлежат
объединению М (/)(J I (/)• Получено уточнение теоремы
Мейера, согласно к-рому Е есть множество первой
категории и типа Fa (см. |12] — [14], где получены
усиления теорем Плеснера и Мейера, а также даны
обращение теоремы Мейера и характеризация мно-
множества МA)).
Работа П. Фату послужила первоначальным толч-
толчком к развитию фундаментальных исследований гра-
граничных свойств аналитич. функций. Исследования Ф.
и М. Риссов, Н. Н. Лузина, И. И. Привалова, Р. Не-
ванлинны (R. Nevanlinna), А. И. Плеснера, В. И. Смир-
Смирнова и др. проводились независимо от идей П. Пенлеве,
и для них характерно использование методов, связан-
связанных с теорией меры и теорией интегрирования, с по-
понятием категории по Бэру (см. [4] — [9]).
Основным объектом исследований Ф. Иверсена
(F. Iversen) и В. Гросса (W. Gross) были также меро-
морфные функции / в области D с жордановой грани-
границей F=Fr D. В произвольной точке ?0? Г гранич-
граничное предельное множество С (/, ?0; Г)
определяется следующим образом: если Мг обозна-
обозначает замыкание объединения (jC(f, ?; D) но всем точ-
точкам
se(r\{Eo»u{i г—g01 < г},
то С(/, ?0; Т)=[\Т>ОМг. Одна из основных теорем,
полученных независимо Ф. Иверсеном и В. Гроссом,
утверждает, что при указанных условиях в каждой
точке to 6 Г множество
С,- (/, Со; D)=C(f, So; D)\C (/, ?„; Г)
открыто и все значения a^C^f, ?0; D), за возможными
двумя исключениями, принадлежат множеству по-
повторяющихся значений R (/, ?0; D); кроме того, каж-
каждое исключительное значение (если таковые сущест-
существуют) является асимптотич. значением функции /
в точке ?0.
Исследования Ф. Иверсена и В. Гросса получили
свое дальнейшее развитие в работах А. Бёрлинга
(A. Beurlir,g), В. Зайделя (W. Seidol, он и ввел тер-
термин «П. м.» в 1932) и др. (см. [5] — [9]). Рассмат-
Рассматривались в основном случаи, когда Со принадлежит
нек-рому «малому» множеству Е точек границы Г
нулевой линейной меры или нулевой емкости, и изу-
изучалось П. м. С(/, ?о'> Т\Е), определяемое аналогич-
аналогично множеству С(/, ?; Г). В этих исследованиях ис-
использовались и методы теории потенциала.
Новейшие результаты в этом направлении сформу-
сформулированы ниже для случая круга Д-={|г|<1}. Пусть
фиксировано множество Е на дуге у границы Г— {|z| =
= 1}, mes?=0, S0€^- Каждой точке i,?y\E от-
отнесем жорданову дугу AjC-D, оканчивающуюся в ?.
Пусть м* —замыкание объединения (J С (/, ?; Aj)
по всем точкам
и пусть С* (/, So; Г\?) = П , > ол/л*-
Тогда множество
открыто, множество S (?0)\./? (/, to'* D) имеет емкость
пуль, а каждое значение а? S (?0)\Я (/, Jo; ?>) яв-
является асимптотическим значением функции / либо в
точке ?0, либо в каждой точке нек-рой последователь-
последовательности {?„}, ?«6Г. л=1, 2, . . ., lim ?„=?0- Если ем-
П-VCD
кость ? равна нулю, то для каждой связной компонен-
компоненты Sд. (?0), /е=1, 2, . . ., множества 5 (?0) множество
Sfe(?o)\-R (/, So! -D) состоит самое большее из двух раз-
различных значений.
С помощью нормальных семейств была доказана
т е о р е м а Линделёфа: если голоморфная функ-
функция / ограничена в круге D и имеет асимптотич. зна-
значение а в точке ?о€Г, т0 она имеет в этой же точке
значение айв качестве углового граничного значе-
значения. Нормальность семейства F={f(z)} мероморфных
функций /(z) в области G можно характеризовать
is терминах т. н. сферической производ-
производной
Именно, семейство F нормально тогда и только тогда,
когда сферич. производные p(/(z)), f?F, равномерно
ограничены внутри G, т. е. для любого компакта KG
можно указать такую постоянную С—С {К), что
9(f(z))<C(K), z?K
Однако наиболее важный вклад нормальных се-
семейств в теорию П. м. формулируется при помощи
понятия нормальной функции. Мероморфная в одно-
связной области G функция /(z) наз. н о р м а л ь-
ной функцией в G, если нормально семейство
{f(S (z))}, где S пробегает семейство всех конформных
автоморфизмов области G; f(z) нормальна в много-
многосвязной области G, если она нормальна на универсаль-
универсальной накрывающей поверхности G. Мероморфная функ-
функция /(г) в круге D— {|z|<l} нормальна тогда и только
тогда, когда существует константа C—C(f), 0<C'<oo,
такая, что
р (/ («)) | dz | < с -J-^L..
Здесь левая часть есть элемент длины в т. н. хордаль-
ной метрике на сфере Римана Q для отображения
w=f(z), а стоящее в правой части выражение do(z) —
— \dz\//(l — |z|2) есть элемент длины в гиперболич.
метрике круга D. Ограниченные голоморфные функции
и мероморфные функции, не принимающие трех раз-
различных значений, являются нормальными функциями,
и нек-рые свойства функций названных классов пере-
переносятся ца произвольные нормальные функции. Напр.,
для произвольной нормальной функции справедливо
утверждение теоремы Линделёфа. Класс всех нор-
нормальных мероморфных функций в круге D имеет
нек-рое сходство с классом ограниченного вида функций.
Однако имеются и существенные различия. Напр.,
существуют нормальные мероморфные функции без
асимптотич. значений, а следовательно и без радиаль-
радиальных граничных значений, чего не может быть для
функций ограниченного вида. Важные исследования
асимнтотич. значений были проведены Дж. Мак-
Лейном (G. R. MacLane, см. |7], [9]). Теория Мак-
Лейна позволила получить новые доказательства из-
вестных ранее свойств нормальных функций; так, I
напр., множество точек ?? Г, в к-рых нормальная голо-
голоморфная функция /(z) имеет асимитотич. значение, а
следовательно и угловое граничное значение, плотно
на Г.
С понятием нормальности тесно связано распреде-
распределение значений мероморфных функций. Последова-
Последовательность {zn}точекznединичного круга/), lim |zn| —1,
и—>™
наз. Р-и оследовательностью для меро-
морфной функции /(z) в D, если для любой ее беско-
бесконечной подпоследовательности {zn } и для любого
е>0 множество
Я\Л(/, z; Ul.tizeD:<,(», z^) < г))
состоит самое большее из двух значений. Показано,
что / обладает хотя бы одной /'-последовательностью
в том и только в том случае, если
lirri^ suP9/(z)= + oo, ?/(z) = (l- |z|2)p(/(z)).
Таким образом, распределение значений мероморфной
функции f (z) связано со строением И. м. непрерывной
функции q/(z).
Существенные продвижения имеются в теории П. м.
общих отображений / : D —>- Q, Z)={|z|<l}. Так, еще
а 1955 была доказана теорема о точках
неопределенности: для произвольного отоб-
отображения / : D —>- Q точки ?? Г, в к-рые можно про-
провести две непрерывные кривые L\ и L\ такие, что
С (/, С; L\) ф С (/, С; L\),
образуют самое большее счетное множество. Тео-
Теорема максимальности К о л л и н г в у-
д а: пусть Lo — произвольный континуум в круге D
такой, что 1„Л Г= {z=l}, и пусть континуум Lq полу-
получается из Lo поворотом на угол 6 вокруг начала коор-
координат; тогда для произвольного отображения /:/)->
-> Q точки ?=е'е?Г, в к-рых
С (/, С; Le) ф С (/, S; D),
образуют множество первой категории на Г. Точку
??Г относят к множеству C(f), если П. м. С(/, ?; D)
совпадает с пересечением
П С (/, С; Д (?, ф1, ф2))
по всем угловым областям с вершиной t,. Доказано [10]»
для произвольного отображения / : D —*¦ У, где /? —
множество типа Fo и первой категории. Обратно, для
произвольного множества ?сГ типа Fo и первой
категории существует голоморфная и ограниченная
в D функция /(г), для к-рой ?=Г\С(/). Множество
С (I) является подмножеством множества K(f), состоя-
состоящего из таких точек ??Г, в к-рых
С (/, ?; Д (?, (р1г ф2)) = С (/, ?; Д (?, (pi, (p2))
для любых двух угловых областей Д (?, (plt (p2) и Д (?,
ф(, фа). Пусть ?сгГ и fegr. Для данного е>0 пусть
г ($, е, ?) обозначает длину наибольшой открытой дуги
на Г, лежащей в дуговой е-окрестности {eie:|9—arg ?| <
<s} точки j и не имеющей общих точек с Е; если та-
такой дуги нет, то полагают г(?, е, Е)=0. Множество Е
наз. пористым на Г, если для любой точки ?,?Е
lim sup r (?, е, Е) > 0;
е-»- о
гг-п о р и с т о с множество есть объединение
не более чем счетного числа пористых множеств. Вся-
кое а-пористое множество есть множество первой кате-
категории и линейной меры нуль. Для произвольного
отображения / : D —у Q справедливо равенство Г=
~К (f)[jE, где Е есть а-пористое множество типа G&j.
Обратно, для произвольного а-пористого множества
Е существует голоморфная и ограниченная в D функ-
функция /(г), для к-рой Y\K{f)^)E.
О теории П. м. для функций многих комплексных
переменных см., напр., [15] — [17].
Лит.: [1] Р a i и 1 е v ё P., Lemons sur la theorie analytique
des Equations differentielles..., P., 1897; [2] Zoretti L.,
Lc;ons sur le prolongement analytique..., P., 1911; [3] Голу-
Голубев В. В., Однозначные аналитические функции. Автоморф-
ные функции, М., 1961; Н] Привалов И. И., Граничные
свойства аналитических функций, 2 изд., М.— Л., 1950; [5]
Носиро Киоси, Предельные множества, пер. с англ.,
М., 1963; [6] Колли нгвуд Э., Ловатер А., Теория
предельных множеств, пер. с англ., М., 1971; [7] Мак-Лейн
Г., Асимптотические значения голоморфных функций, пор.
с англ., М., 1966; [8] Маркушевич А. И., Т у м а р к и н
Г. П., Хавиисон С. Я., в кн.: Исследования по совре-
современным проблемам теории функций комплексного переменного,
М., 1961, с. 100—10; [9] Ловатер А., в кн.: Итоги науки
и техники. Математический анализ, т. 10, М., 1973, с. 99—259;
[10] Д о л ж е н к о Е. П., «Изв. АН СССР. Сер. матем.», 1967,
т. 31, № 1, с. 3—14; [11] его же, «Ann. Math.», 1976, v. 2,
p. 191 — 201; [12] Г а в в и л о в В. И., «Докл. АН СССР», 1974,
т. 216, № 1, с. 21—23; [13] Г а в р и л о в В. И. Канатни-
Канатников А, Н., та»! же, 1977, т. 233, №1, с. 15—17; [14] Ка-
Канатников А. Н., там же, 1978, т. 238, № 5, с. 1043—1046;
[15] Р у дин У., Теория функций в поликруге, пер. с англ.,
М., 1974; [16] X е н к и н Г. М., Ч и р к а Е."М., в кн.: Итоги
науки и техники. Современные проблемы математики, т. 4, М.,
1975, с. 13—142; [17] Hudin W., Function theory in the unit
Lall of C, N.Y. — fe.a.], 1980.
B. 11. Гсшрилов, Е. Д. Соломе}1цев.
ПРЕДЕЛЬНОЕ МНОЖЕСТВО траектории
{рх} динамической системы р— мно-
множество Ах всех а-предельных точек (а-п р е д е л ь-
ное множество) или множество ?1Х всех со-
сопредельных точек (со-п редельное множест-
в о) этой траектории (см. Предельная точка траекто-
траектории). Для траектории {/1х} системы (или, иначе, f(t, x),
см. [1]) а-П. м. (соответственно w-П. м.) — то же, что
ш-П. м. (соответственно а-П. м.) траектории {f~h}
динамич. системы f~t (системы с обращением времени).
Поэтому свойства а-П. м. аналогичны свойствам со-
П. м.
Множество пх — замкнутое инвариантное множе-
множество. Если Qx=0, то траектория {/'ж} наз. уходя-
уходящей в положительном направлении;
если Ах=0, то траектория {рх} наз. уходящей
в отрицательном направлении; если
Qx=Ax~0, то траектория наз. у х о д я щ е й. Если
x?Qx, то точка х наз. положительно устой-
устойчивой по Пуассону; если х?А х, то точка х
наз. отрицательно устойчивой по
Пуассону; если х?О,х[\Ах, то точка х наз. у с-
тойчивой по Пуассону. Если х(?О,х и
&ХФ0, то точка х наз. положительно
асимптотической; если x(feA v и Ахф0,
то точка х наз. отрицательно асимпто-
т и ч е с к о й.
Если точка х положительно устойчива по Лаграшку
(см. Устойчивость по Лагранжу), то Q^— непустое
связное множество,
lim d (px, QJ=0
t -> + 00
(где d(z, Y) — расстояние от точки z до множества У)
и в Qx найдется рекуррентная точка (траектория).
Если х — неподвижная точка, то Qx= {х}. Если х —
периодич. точка, то
где Т — период. Если точка х положительно устой-
устойчива по П уасхону, но не неподвижная и не периодиче-
периодическая, а метрич. пространство, на к-ром задана рас-
сматриваемая динамич. система, полно, то в пх всюду
плотны точки, не принадлежащие траектории {fix}.
Если динамич. система задана на плоскости авто-
автономной системой дифференциальных уравнений
(гладким векторным полем f(x)), точка х положительно
устойчива по Лагранжу, но не периодическая и f (х)
не обращается в нуль на множество Qx (т. е. мно-
множество Qx не содержит неподвижных точек), то Qx—
цикл, т. е. замкнутая кривая (траектория периодич.
точки), а траектория {рх} при I—>-4-оэ спиралевидно
наматывается на этот цикл. У динамич. систем, за-
заданных на R", п>2, или на нек-рых двумерных по-
поверхностях, напр, на торе, w-П. м. могут быть устроены
иначе. Напр., у иррациональной обмотки тора (система
Ф=1, "ф=ц, где (ф, -ф) (mod 1) — циклич. координаты
на торе У2, р. — иррациональное число) множество
Qx для всякой точки х =(ф, ty) совпадает со всем то-
тором.
Лит.: [1] Немыцкий В. В., Степанов В. В.,
Качественная теория дифференциальных уравнений, 2 изд.,
М,— Л., 1949; [2] П онтрягин Л. С, Обыкновенные диф-
дифференциальные уравнении, 4 изд., М., 1974.
В. М. Миллионщиков.
ПРЕДЕЛЬНОЙ АМПЛИТУДЫ ПРИШЩП — спо-
способ однозначного выделения решений стационарных
уравнений, описывающих установившиеся колебания,
через предел при t —>¦ оо амплитуды решений соответ-
соответствующих нестационарных уравнений с нулевыми на-
начальными данными и периодической по t правой частью
вида f(x)e±iu>i. Справедливость П. а. п. означает, что
решение v (x, t) указанной нестационарной задачи при
t —к оо имеет вид
v (х, () = и±A)е±1'вЧ»A), (*)
где и . — решения стационарного уравнения.
Впервые этот принцип был предложен (см. [1]) для
уравнения Гельмгольца в R"
он выделяет те же решения этого уравнения, что и
излучения условия и предельного поглощения принцип.
Справедливость П. а. п. исследована: для уравнений
2-го порядка с переменными коэффициентами во внеш-
внешности ограниченной области (см. |2], [3]), уравнения
Гельмгольца в нек-рых областях с некомпактной гра-
границей (см. [3], 14]), задачи Кошн — Пуассона в полосе
(см. [5)), нек-рых уравнений высокого порядка (см.
131, [6]), смешанных задач во внешности ограниченной
области для уравнений и систем любого порядка с
переменными коэффициентами (см. [7]). В последнем
случае условия излучения и принцип предельного
поглощения выделяют 2*, 1<х <оо, решений стацио-
стационарного уравнения, а П. а. п. дает два из них. Указаны
(см. [8]) такие постановки П. а. ц., к-рые позволяют
получить все эти 2К решений.
Для справедливости П. а. п. необходимо, чтобы
f (х) была ортогональна всем собственным функциям
стационарной задачи. Поэтому П. а. п. не справедлив
в ограниченной области. Пусть Р% — оператор, к-рый
соответствует зависящей полиномиально от спектраль-
спектрального параметра X стационарной задаче, полученной из
смешанной задачи для нестационарного уравнения
заменой в уравнении и граничных условиях опера-
оператора дифференцирования ialdt на параметр к. Справед-
Справедливость для оператора Р}. , Я= const, П. а. п. связана
с возможностью аналитич. продолжения ядра резоль-
резольвенты Rx^ssPj} на непрерывный спектр и гладкостью
по Я этого продолжения (см. [3], [7]). Если ядро В},
допускает аналитич. продолжение через непрерывным
спектр и имеет подходящие оценки при X —>¦ оо, то
можно написать асимптотику при t —>¦ со остатка 0 A)
в («), а также получить асимптотику при t —>¦ оо ре-
решений других нестационарных задач (см. [2], [7]).
Указанные свойства R\ получены в [7] для смешанных
задач во внешности ограниченной области для урав-
уравнений и систем любого порядка.
Лит.: [1] Тихонов А. Н., Самарский А. А.,
«Ж. эксперимент, и теоретич. физики», 1948, т. 18, Ла 2, с. 243—
248; Ш Ладыженская О. А., «Успехи матем. наук»,
1957, т. 12, в. 3, с. 161—64; ?3] Э й д у с Д. М., там же, 1ЭВ9,
т. 24, в. 3, с. 91—156; [4] Свешников А. Г., «Докл. АН
СССР», 1950, т. 73, № 5, с. 917—20; [5! Исакова Е. К.,
«Дифференциальные уравнения», 1970, т. 6, № 1, с. 56—71;
[6] Михайлов В. П., «Тр. Матем. ин-та АН СССР», 1067,
т. 91, с. 100—12; [7] Вайнберг Б. Р., «Успехи матем.
наук», 1975, т. 30, в. 2, с. 3—55; [8] его же, «Изв. ВУЗои.
Математика», 1974, № 2, с. 12—23. Б. Р. Вайнберг.
ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ теории вероят-
вероятностей — общее название ряда теорем теории ве-
вероятностей, указывающих условия возникновения тех
или иных закономерностей в результате действия
большого числа случайных факторов. Первые П. т.,
установленные Я. Бернулли (J. Bernoulli, 1713) и
П. Лапласом (P. Laplace, 1812), относятся к распре-
распределению отклонений частоты \inln появления нек-рого
события Е при п независимых испытаниях от его ве-
вероятности р, 0<р<1 (точные формулировки см. в
статьях Бернулли теорема, Лапласа теорема). С. Пу-
Пуассон (S. Poisson, 1837) распространил эти теоремы на
случай, когда вероятность р^ наступления события
Е в ft-м испытании может зависеть от к, описав предель-
предельное поведение при п —у оо распределения отклонений
частоты (х„/ге от среднего арифметического р =—2ь_ ^ft
вероятностей pk, l<:fc<re (см. Пуассона теорема).
Если обозначить через Хк случайную величину, при-
принимающую значение, равное единице при появлении
события Е в к-и испытании, и значение, равное нулю
при ПОЯВЛеНИИ ПРОТИВОПОЛОЖНОГО СОбыТИЯ, }1„ МОЖНО
представить в виде суммы
что позволяет рассматривать перечисленные теоремы
как частные случаи двух более общих утверждений,
относящихся к суммам независимых случайных ве-
величин — больших чисел закона и центральной пре-
предельной теоремы (к-рые приводятся ниже в их клас-
сич. формулировке).
Закон больших чисел. Пусть
-Yb Xa, ..., Хп, ... A,
— последовательность независимых случайных вели
чин, sn — сумма первых п из них:
А,г и Вп — соответственно математич. ожидание
и дисперсия
В\ = Dsn = DXj + DX2 +...+ DXn
суммы sn. Говорят, что последовательность A) под-
подчиняется закону больших ч и с е л, если при
любом е>0 вероятность неравенства
стремится к нулю при п -*¦ оо.
Широкие условия приложимости закона больших
чисел найдены впервые П. Л. Чебышевым A867) и затем
обобщены А. А. Марковым A906). Вопрос о необходи-
необходимых и достаточных условиях приложимости закона
больших чисел был окончательно решен А. Н. Кол ми-
горовым A928). В случае, когда случайные величины
Х„ имеют одну и ту же функцию распределения, эти
условия, как показал А. Я. Хинчин A929), сводятся к од-
одному: величины Хп должны иметь конечные матема-
тич. ожидания.
Центральная предельная теорема. Говорят, что
к последовательности A) применима централь-
центральная предельная теорема, если при лю-
любых z1 и :2 вероятность неравенства
z±Bn < sn—An < z2Bn
имеет пределом при га —*¦ оо величину
Ф (г2) — Ф (zjj,
где
ф(г)=-^.Гг е-"'" dx
- 00
(см. Нормальное распределение). Довольно общие до-
достаточные условия применимости центральной П. т.
были указаны П. Л. Чебышевым A887), но в его до-
доказательстве обнаружились пробелы, восполненные
лишь позже А. А. Марковым A898). Решение вопроса,
близкое к окончательному, было получено А. М. Ля-
Ляпуновым A901). Точная формулировка теоремы
Ляпунова такова: пусть
сА = Е \Xk-~BXk\2 + 6, б>0,
Если отношение Ьп=Сп/В?г+ стремится к нулю при
п->оо, то к последовательности A) применима цент-
центральная П. т. Окончательное решение вопроса об ус-
условиях применимости центральной П. т. получено
в основных чертах С. Н. Бернштсйном A926) и до-
дополнено В. Феллером (W. Feller, 1935). В условиях
центральной П. т. относительная точность аппрокси-
аппроксимации вероятности неравенства типа sn—An>znBn,
где zn неограниченно растет вместе с га, величиной
1—Ф(г„) может быть весьма невысокой. Необходимые
для повышения точности поправочные множители ука-
указываются в П. т. для вероятностей больших отклоне-
отклонений (см. Больших отклонений вероятности, Крамера
теорема). Вслед за Г. Крамером (Н. Cramer) и В. Фел-
Феллером вопрос исследовался Ю. В. Линником и др.
Типичные результаты, относящиеся к этой области,
легче всего пояснить на примере сумм B) независи-
независимых одинаково распределенных случайных величин
\'i, . . ., Хп, ... с EXj — 0 и DXj— 1; в этом случае
.1„-0, Bn=Vn.
Пусть, напр., рассматривается верояипость нера-
неравенства
Эта вероятность равна 1—Fn(zn), где Fn (z) — функция
распределения величины sn: У п и при фиксированных
zn=z и га —»- оо
1-Fn(z)—*1-Ф(г). C)
Если з„ зависит от п, причем так, что zn —*¦ оо при
п -+¦ оо , ТО
i-Fn{za)-*O и 1-Ф(г„)-,0
и формула C) становится бесполезной. Необходимы
оценки для относительной точности аппроксимации,
т.е. для отношения i—Fn(zn) к 1— Ф(х„). В част-
частности, естественно возникает вопрос об условиях, при
к-рых
дли
Соотношение D) может выполняться при любом ро-
росте zn только при условии, что сами слагаемые имеют
нормальный закон (этот вывод верен уже при zn по
порядку, больших У~п). Если же слагаемые не являются
нормальными, то это соотношение может выполняться
лишь в определенных зонах, к-рые по порядку не
превосходят У п. Наиболее «узкие» (логарифмиче-
(логарифмического порядка) зоны получаются при условии конеч-
конечности определенного числа моментов. При этом в оп-
определенных условиях «регулярности» плотности сла-
слагаемых можно проследить переход «нормальной» асим-
асимптотики в степенную. Напр., если плотность слагае-
П A +22I'
то равномерно по z при п —>¦ оо
учитывая, что при z -> оо
1ф(,)~ е\
V 2л г
легко понять, при каких z имеет место D). Расширение
зоны до степенной (вида па, а<1/2), требует условия
Ее Лаа+1<оо E)
и совпадения определенного (зависящего от а) числа
моментов Xj с соответственными моментами нормаль-
нормального распределения. Если же условие совпадения мо-
моментов не выполнено, то отношение в левой части D)
описывается в терминах ряда Крамера (при так наз.
условии Крамера, см. Крамера теорема) или его на-
начальных отрезков (при выполнении условий типа E)).
Оценки вероятностей больших отклонений исполь-
используются в математич. статистике, статистич. физике
и т. д.
Из других направлений работ в области П. т. можно
отметить следующие.
1) Начатые А. А. Марковым и продолженные
С. Н. Бернштейном и др. исследования условий при-
приложимости закона больших чисел и центральной
П. т. к суммам зависимых случайных величин.
2) Даже в случае последовательности одинаково
распределенных случайных величин можно указать
простые примеры, когда «нормированные» (т. е. под-
подвергнутые какому-либо линейному преобразованию)
суммы (sn—ап)/Ьп, где ап, Ь„>0 — постоянные, имеют
в пределе распределение, отличное от нормального
(речь идет о невырожденных распределениях, т. е.
распределениях, не сосредоточенных целиком в одной
точке) (см. Устойчивое распределение). В работах
A. Я. Хинчина, Б. В. Гнеденко, П. Леви (P. Levy),
B. Дёблина (W. Doeblin) и др. полностью изучены
как класс возможных распределений для сумм неза-
независимых случайных величин, так и условия сходи-
сходимости распределений сумм к тому или иному предель-
предельному распределению (в схеме серий случайных вели-
величин при условии асимптотической пренебрегаемости
слагаемых) (см. Безгранично делимое распределение,
Случайный процесс с независимыми приращениями).
3) Значительное внимание уделяется т. п. локальным
предельным теоремам. Пусть, напр., случайные ве-
величины Хп принимают лишь целые значения. Тогда
суммы sn принимают также только целые значения
и естественно поставить вопрос о предельном пове-
поведении вероятностей Рп(т) того, что sn=m, где т —
целое. Простейшим примером локальной П. т. может
служить локальная теорема Лапласа. Другой тип ло-
кальных П. т. описывает предельное распределение
плотностей распределения сумм.
4) П. т. в их классич. постановке описывают пове-
поведение отдельной суммы sn с возрастанием номера п.
Достаточно общие П. т. для вероятностей событий,
зависящих сразу от нескольких сумм, получены впер-
впервые А. Н. Колмогоровым A931). Так, напр., из его
результатов следует, что при весьма широких усло-
условиях вероятность неравенства
max | sk | < zBn
<ft < n
имеет пределом величину
2 { ' e
Наиболее общий способ доказательства подобных
П. т.— предельный переход от дискретных процессов к
непрерывным.
5) Перечисленные выше П. т. относятся к суммам
случайных величин. Примером П. т. иного рода могут
служить П. т. для членов вариационного ряда. Эти
П. т. подробно изучены Б. В. Гнеденко, Н. В. Смир-
Смирновым и др.
6) Наконец, к П. т. относят также и теоремы, уста-
устанавливающие свойства последовательностей случай-
случайных величин, имеющие место с вероятностью, равной
единице (см., напр., Больших чисел усиленный закон,
Повторного логарифма закон).
О методах доказательства П. т. см. в статьях Ха-
Характеристическая функция, Распределений сходи-
сходимость.
Лит.: [1] Гнеденко Б. В., Колмогоров А. Н.,
Предельные распределения для сумм независимых случайных
величин, М.— Л., 1949; [2] Ибрагимов И. А., Пин-
пик Ю. В., Независимые и стационарно связанные величины,
М., 1965; [3] Петров В- В., Суммы независимых случайных
величин, М., 1972; [4] Про х"о ров Ю. В., Розанов
Ю. А., Теория вероятностей, 2 изд., М., 1973.
Ю. В. Прохоров.
ПРЕДЕЛЬНЫЙ КОНУС выпуклой поверх-
поверхности S — поверхность Р (S) конуса, образован-
образованного полупрямыми, исходящими из нек-рой точки
O?S и принадлежащими выпуклому телу, ограничен-
ограниченному S. Л. к. определен однозначно с точностью до
параллельного переноса, зависящего от выбора точ-
точки О. Понятие П. к. определяется и для нек-рых клас-
классов невыпуклых поверхностей, напр, для т. н. сфери-
сферически однолистных седловых поверхностей.
Лит.: [1] П о г о р е л о в А. В., Внешняя геометрия вы-
выпуклых поверхностей, М., 1969. М. И. Войцеховскип.
ПРЕДЕЛЬНЫЙ ЦИКЛ _ замкнутая траектория
в фазовом пространстве автономной системы обыкно-
обыкновенных дифференциальных уравнений, к-рая является
а- или со-предельным множеством (см. Предельное мно-
множество траектории) хотя бы для одной другой траек-
траектории этой системы. П. ц. наз. орбитально
устойчивым, или устойчивы м, если для
всякого е>0 найдется 8>0 такое, что все траектории,
начинающиеся в б-окрестности II. ц. при t— 0, не вы-
выходят из его е-окрестности при г>0. П. ц. соответст-
соответствует периодич. решение системы, отличное от постоян-
постоянного. Если оно устойчиво по Ляпунову, то П. ц. ус-
устойчив. Для того чтобы периодич. решению соответст-
соответствовал устойчивый П. ц., достаточно, чтобы модули
всех его мультипликаторов, кроме одного, были
меньше единицы (см. Орбитальная устойчивость, Анд-
Андронова — Витта теорема). С физич. точки зрения
П. ц. соответствует периодич. режиму, или автоколе-
автоколебанию, системы (см. [2]).
Пусть автономная система
x = f (х), (*)
определенная в области UcVn, где V—дпфференци-
руемое многообразие, напр. F"=R", имеет замкну-
замкнутую траекторию Г. Проведем гиперповерхность я,
пересекающую Г трансверсальио в точке р. Тогда
любая траектория системы, начинающаяся при *=0
в точке eg Vcл, где V — достаточно малая окрест-
окрестность точки р, при увеличении t снова пересечет л
в точке Т (с). Диффеоморфизм Т : V -*. Т (V) имеет
неподвижную точку р и наз. наследования отображе-
отображением. Его свойства определяют поведение траекторий
системы в окрестности Г. П. ц. в отличие от произ-
произвольной замкнутой траектории всегда определяет
отличное от тождественного отображение доследова-
доследования. Если р — седловая точка диффеоморфизма Т,
то П. ц. наз. П. ц. седлового типа. Система,
имеющая П. ц. седлового типа, может иметь гомокли-
нич. кривую, т. е. траекторию, для к-рой П. ц. яв-
является одновременно как а-, так и со-предельным мно-
множеством.
В случае двумерной системы (*) (Х"г= R2) в ка-
качестве я берут прямую и рассматривают функцию
р : р(с)— Г (с)—с, к-рая наз. функцией после-
последов а н и я. Кратность нуля с=р функции р наз.
кратностью П. ц. Предельный цикл четной
кратности наз. пол у устойчив ы м. П. ц. вместо
с точками покоя и сепаратрисами определяют качест-
качественную картину поведения остальных траекторий
(см. Пуанкаре — Вендиксона теория, а также [3J,
\i\). П. ц. в случае аналитич. функций /(х) принадле-
принадлежит к одному из типов: 1) устойчивый, 2) неустойчи-
неустойчивый, т. е. устойчивый П. ц., если изменить направле-
направление t на противоположное, 3) пол у устойчивый. Напр.,
система
f? 1)*,
Яа—1)*,
где w^O, |j,= const, k(zN, имеет при ц<0 ((х>0) и к
нечетном устойчивый (неустойчивый), а при к чет-
четном — полуустойчивый П. ц. кратности к; во всех
этих случаях П. ц. является окружность xt-\-xi=l,
т. е. траектория решения
Если система (*) задана на односвязнои области ,
то П. ц. окружает по крайней мере одну точку покоя
утой системы.
Для разыскания П. ц. в системе 2-го порядка при-
применяется метод, основанный на следующем утвержде-
утверждении: если векторное поле f (х) направлено вовнутрь
(вовне) кольцеобразной области G и в G нет точек по-
покоя, то в G имеется хотя бы один устойчивый (неустой-
(неустойчивый) П. ц. Выбор области G производится из фи-
зич. соображений или результатов аналитических или
численных расчетов.
Лит.: Г1] П о н т р я г и н Л. С, Обыкновенные дифферен-
дифференциальные уравнения, 4 изд., М., 1974; [2] Андронов А. А.,
В и т т А. А., X а й к и н С. Э., Теория колебаний, 2 изд.,
М., 1959; [3] Андронов А. А., Леонтович Е. А.,
Гордон И. И., М а й е р А. Г., Качественная теория дина-
динамических систем второго порядка, М., 1966; [4] их ж е, Тео-
Теория бифуркаций динамических систем на плоскости, М., 1967;
[5] Плисе В. А., Нелокальные проблемы теории колебаний,
М.— Л., 1964; [6] Моисеев Н. Н., Асимптотические методы
нелинейной механики, 2 изд., М., 1981. Л. А. Черкас.
ПРЕДИКАТ — функция, значениями к-рой являют-
являются высказывания об ге-ках объектов, представляющих
значения аргументов; при «=1 П. наз. «свойством»,
при я>1 — «отношением», единичные высказывания
могут рассматриваться как нульместные П.
Чтобы задать га-местный предикат Р (хг, . . ., хп),
следует указать множества Dt, . . ., Dn — области
изменения предметных переменных
.Ti, . . ., хп, причем чаще всего рассматривают случай
D1—D.i~. . .~Вп. С теоретико-множественной точки
зрения П. определяется заданием подмножества М
в декартовом произведении DtX. . ,XDn. При этом
Р (ait . . ., ап) понимают как высказывание «упорядо-
«упорядоченный набор (а1? . . ., ап) принадлежит М». Синтак-
сич. задание га-местного П. осуществляется указанием
формулы логико-математич. языка, содержащей га
свободных переменных. Понятие П. восходит к Арис-
Аристотелю; аппарат оперирования с высказываниями, со-
содержащими в своем составе П., разработан в митема-
тич. логике (см. Логические исчисления, Предикатов
исчисление). С. Ю. Маслов.
ПРЕДИКАТИВНОСТЬ — особый способ образования
понятий, характеризующийся отсутствием «порочного
круга» в определениях: определяемый объект не дол-
должен участвовать в своем собственном определении.
Если язык, на к-ром даются определения, формализо-
формализован, то П. означает, как правило, что определяющая
формула не должна содержать связанной переменной,
в область изменения к-рой входит определяемый объект.
Непредикативные определения, наоборот, отлича-
отличаются наличием в них такого «порочного круга». Яв-
Явление непредикативности встречается также в нек-рых
рассуждениях, когда в процессе обоснования нек-рая
часть проводимого рассуждения сама рассматривается
как объект рассуждения. Именно использование та-
такого типа рассуждений является причиной появления
семантич. антиномий. Типичный пример — установле-
установление противоречия в т. н. парадоксе лжеца: если некто
утверждает — «я лгу», то это утверждение не может
быть истинным и не может быть ложным.
В. Н. Гришин, А. Г. Драгалин.
ПРЕДИКАТНАЯ ПЕРЕМЕННАЯ — переменная,
значениями к-рой могут быть предикаты. При формаль-
формальном построении аксиоматич. систем П. п. отличаются
от индивидных переменных тем, что вместо них можно
подставлять формулы. Так, в исчислении предикатов
2-й ступени, если в аксиоме
Vxy (х) — Ф (t)
х — предикатная переменная для га-местных предика-
предикатов, то в качество t можно взять любую формулу с га
отмеченными переменными. При этом результатом
подстановки формулы t с отмеченными переменными
zx, . . ., zn вместо П. п. х в атомарную формулу х(у1,
. . ., уп), где т, . . ., уп — индивидные переменные,
является формула t (yr'z1, . . ., y,Jzn), получающаяся
из t одновременной заменой свободных вхождений
Zj, . . ., zn на г/1; . ¦ ., уп соответственно.
Лит.: [1] Чёрч А., Введение в математическую логику,
пер. с англ., М., I960; [2] Такеути Г., Теория доказа-
доказательств, пер. с англ., М., 1978. В. Н. Гришин.
ПРЕДИКАТНЫЙ СИМВОЛ, предикатная
буква,— обозначение какого-либо конкретного пре-
предиката. Напр., символом ¦< часто обозначают отноше-
отношение порядка на действительных числах, являющееся
двуместным предикатом. При формальном построении
языка символы, отнесенные к категории предикатных,
должны определенным образом использоваться для
построения выражений языка. Именно, если Р есть
га-местный П. с, то среди синтаксич. правил образо-
образования выражений формализованного языка должно
быть правило: «если t^, . . ., tn — термы, то
P(t1,. . ., tn) — формула». Таким образом, П. с. син-
синтаксически используются для образования формул, а
семантически обозначают предикаты.
Лит.: [1] К л ин и С. К., Введение в метаматематику,
пер. с англ., М., 1957; [2] Ершов Ю. Л., П а л га-
тин Е. А., Математическая логика, М., 1979. В. Н. Гришин.
ПРЕДИКАТОВ ИСЧИСЛЕНИЕ — формальная
аксиоматич. теория; исчисление, предназначенное для
описания логических законов, справедливых для любой
непустой области объектов с произвольными заданны-
заданными на этих объектах предикатами (т. в. свой-
свойствами и отношениями).
Для формулировки П. и. следует вначале формулиро-
формулировать точный логико-математический
язык Q. В наиболее распространенном случае одно-
сортных языков 1-го порядка такой язык содержит
предметные переменные х, у, z, . . ., функциональные
символы /, g, h, . . . с различным количеством аргу-
аргументных мест и предикатные символы (предикатные
буквы) Р, Q, R, ... также с различным количеством
аргументных мест. Из переменных и функциональных
символов конструируются термы языка, содержа-
содержательно интерпретируемые как имена объектов исследо-
исследования теории. Далее, если Р есть n-местный предикат-
предикатный символ языка Q, re^O, a tx, . . ., tn — термы, то
/>(*!, . . ., tn) есть, по определению, атомарная
(элементарная) формула языка Q. Содер-
Содержательно Р (t1} . . ., tn) означает, что истинно выска-
высказывание, гласящее, что объекты tIt ...,(„ связаны
отношением Р.
Из атомарных формул с помощью пропозициональных
связок и кванторов конструируются формулы языка.
Обычный набор связок и кванторов в классическом и
интуиционистском П. и. таков: & или л (конъюнкция,
«и»), V (дизъюнкция, неразделительное «или»), ->- или
Z) (импликация, «влечет», «если..., то»), ~| (отрицание,
«не»), V (квантор «для всех»), 3 (квантор «существует»).
Соответственно неэлементарные формулы этих исчис-
исчислений имеют вид (фЛф), (cpV\]}), (доф), ~~|<Р> V^<P,
Згф. Вхождение переменной х в формулу <р наз.
связанным, если х входит в часть ф вида З^Ф
или V.n|). Остальные вхождения х в ф наз. свобод-
свободными. Переменная х наз. параметром ф,
если найдется хотя бы одно свободное вхождение х в
ф. Интуитивно говоря, формула с параметрами выра-
выражает нек-рое условие, к-рое превращается в конкрет-
конкретное высказывание, если задать модель исчисле-
исчисления, т. е. выбрать нек-рую непустую область объек-
объектов исследования и приписать предикатным символам
предикаты (т. е. отношения на области объектов),
а параметрам приписать в качестве значений определен-
определенные объекты.
П. и. задается с помощью аксиом и правил вывода.
Напр., одна из обычных формулировок классиче-
классического исчисления предикатов содер-
содержит следующие аксиомы:
1. (ф=5A|> =5ф)),
2. ((фЗA|)=5Т))K((ф=I|))=5(ф=5Т1))),
3. ((фЛ1|>)=5ф),
4. ((фЛ1|))=5 1|)),
5. (фЗ(г|)Г) (ф Л г|)))),
И. ((Ф =} г\) =5 (A|з 3 Л) => ((Ф V г|)) Г) Л))),
7. (фГ>(Ф Vi|))),
8. (г|K(ф Vi|))),
9. AфЗ(ф=5 1|))),
10. ((ф=5 1|))=5
11. (ф V ~|ф),
12.
13.
14. (Vz (фГ31|5) Г) (ф =5
15. (Vi (г|) Г) ф) Z5 (Зг<|> 3 ф)).
Здесь ф, i[>, т| обозначают произвольные формулы языка
Q, так что каждая из строчек 1—15 представляет со-
собой аксиомную схему, порождающую конкретную ак-
аксиому исчисления при конкретном выборе формул ф,
г|), т). Далее, в схемах 14 и 15 предполагается, что х —
не параметр формулы ф; в схемах 12 и 13 через q>(x\t)
обозначен результат одновременного замещения всех
свободных вхождений переменной х в ф на терм t
(причем если t оказался на месте х в части формулы ф,
имеющей вид 3jrt|> или Чух, где у входит в t, то следует
дополнительно заменить все связанные вхождения у в
эту часть на переменную, но входящую в ф; это дела-
делается для того, чтобы не допустить искажения смысла ф
при замене х на t; такое искаженно смысла наз. к о л-
лизией переменных).
Далее, П. и. содержит два правила вывода: 1) если
выведены формулы вида ф и (ф:эф), то разрешается
вывести формулу г|) (правило модус поненс) и 2) если
выведена формула ф и х — переменная, то разрешается
вывести формулу Угф (правило обобщения).
Истолкование логич. связок в П. и. такое же, как
и в высказываний исчислении. Что касается истолко-
истолкования кванторов, то они в классическом П. и. тракту-
трактуются с использованием актуальной бесконечности. Если
задать интерпретацию языка, то каждая формула без
параметров получает значение «истина» пли «ложь».
Формула наз. классически общезначи-
общезначимой, если она в любой интерпретации и при любом
приписывании значений параметрам принимает значе-
значение «истина». В силу Гёделя теоремы о полноте в
классическом П. и. выводимы все классически обще-
общезначимые формулы и только они. Эта теорема пред-
представляет собой точное выражение идеи формализации
классич. логики: в классическом П. и. выводятся все
логич. законы, общие для всех моделей.
Интуиционистское исчисление
предикатов отличается от классического том,
что из числа экономных схем исключается схема 11.
Различие двух исчислений отражает различное пони-
понимание логич. связок и кванторов. В последнем исчис-
исчислении это понимание трактуется в рамках интуицио-
интуиционизма. Вопрос о полноте интуиционистского П. и.
оказывается значительно сложнее и допускает различ-
различные решения в зависимости от деталей интуиционист-
интуиционистской семантики, но и здесь может быть развита весьма
содержательная теория моделей, аналогичная классич.
моделей теории (см. Крипке модели, Реализуемость).
Употребляются и другие формулировки П. и., среди
к-рых с точки зрения доказательств теории наиболее
важны исчисления натурального вывода (см. Естест-
Естественный логический вывод) и секвенций исчисление.
П. и. является обычным базисом для построения ло-
логич. исчислений, предназначенных для описания фраг-
фрагментов тех или иных конкретных математич. теорий.
Напр., если мы стремимся описать нек-рый класс ис-
истинных суждений теории множеств, то можно построить
логич. исчисление в языке теории множеств, в к-ром,
кроме аксиом и правил вывода классического П. и. (ло-
(логич. постулатов), будут фигурировать дополпитолышр
н е л о г и ч е с к и е аксиомы, описывающие своп
ства множеств. Примером типичной нслогич. аксиомы
в теории множеств является выбора аксиома.
П. и. иногда наз. узки м и с ч и с л е н п е м
предикатов, исчислением предика-
предикатов 1-го порядка, функциональным
исчислением 1-го порядка, в отличие
от исчислений, содержащих кванторы но предикатам и
соответствующие аксиомы свертывания, утверждающие
существование соответствующих предикатов. Такого
рода исчисления, уже не носящие чисто логич. харак-
характера, часто наз. П. и. высшего порядка. При-
Примером такого исчисления может служить типов теория.
Помимо классического и интуиционистского П. и.,
имеются и другие логич. системы, описывающие логич.
законы, к-рые могут быть выражены иными логич.
средствами или с иных методологич. позиций. Сюда
ОТНОСЯТСЯ П. И. МОДаЛЬНОЙ, ИНДУКТИВНОЙ ЛОГИКИ И Д]1.
Лит.: [1] Гильберт Д., Б с р н а й с П., Ошюнашъч
математики. Логические исчисления и формализации арифме-
арифметики, пер. с нем., 2 изд., М., 1982; [2] К лини С. К., Введение
в метаматематику, пер. с англ., М., 1!>Г>7; [3J II о в и и о в II. и.,
Элементы математической логики, 2 изд., М., 1073; [4] Т а к с-
у т и Г., Теория доказательств, пер. с англ., М., 1978.
А. Г. Драгалин.
ПРЕДКОМПАКТНОЕ ПРОСТРАНСТВО, впол-
вполне ограниченное пространство, —
равномерное пространство X, для всякого окружения
U к-рого существует конечное покрытие X множествами
порядка U. Другими словами, для каждого окружения
UczX должно найтись такое конечное множество
F<z.X, что XcU(F). Равномерное пространство ком-
компактно тогда и только тогда, когда каждая сеть в X
обладает подсетью Коши. Поэтому для того чтобы А'
было П. и., достаточно, чтобы нек-рое пополнение про-
пространства X было компактным, и необходимо, чтобы
каждое пополнение его было компактным.
М. И.. Войцеховский.
ПРЕДЛОЖЕНИЕ — простейшее выражение языка,
представляющее собой такое соединение слов, к-рое
имеет самостоятельный смысл, т. е. выражает закон-
законченную мысль. В формализованных языках П. наз.
формулы, не содержащие свободных переменных, т. е.
параметров. П. в формализованных языках наз. также
замкнутыми формулами. Напр., в языко
1-го порядка (языке узкого исчисления предикатов)
формулы
являются замкнутыми (первая ложная, а вторая и
третья — истинные в области натуральных чисел).
Формулы
3z (i< 2&z< у), z<l
но являются замкнутыми, т. к. содержат параметры
(,с и у — в первой иг — во второй).
Лит.: [1] Чёрч А., Введение в математическую логику,
пер. с англ., М., 1960. В. Н. Гришин.
ПРЕДМЕРА — конечно аддитивная мера с действи-
действительными или комплексными значениями на нек-ром
пространстве Q, обладающая свойством: она определена
на алгебре Ж подмножеств Q, к-рая имеет вид 91—
= U 35а, где ©а — семейство а-алгебр пространства
не А
Я, помеченных элементами нек-рого частичного упоря-
упорядоченного множества А так, что JBc^cSa., при at<a2,
и сужение этой меры на любую a-алгебру iBa счетно
аддитивно. Напр., если Q — хаусдорфово топологич.
пространство, А — совокупность всех компактов, упо-
упорядоченных по вложению, iBa, а?Л, есть а-алгобра
борелевских подмножеств компакта а и C0(Q) — про-
пространство всех непрерывных функции на Q с ком-
компактными носителями, то всякий линейный функционал
на C0(Q), непрерывный относительно топологии равно-
равномерной сходимости в C0(Q), порождает П. на алгебре
31 - U 23«.
ае А
Пусть Q — линейное локально выпуклое простран-
пространство, А — совокупность конечномерных подпространств
сопряженного пространства Q', упорядоченных по
вложению, 58а,ос(;Л,— наименьшая a-алгебра, относи-
относительно которой измерим любой линейный функционал
ф? а. Множества из алгебры 91 = (J $Sa наз. цилин-
ае А
др и чески ми множествами, а любая II. на
31 — цилиндрической мерой (или к в а-
з и м е р о й). Любой положительно определенный
функционал на пространстве Q', непрерывный на любом
конечномерном подпространстве ааЯ, является харак-
тористич. функционалом (преобразованием Фурье)
нек-рой конечной неотрицательной П. на Q.
Лит.: [1] Б у р б а к и Н., Интегрирование. Меры на ло-
локально компактных пространствах. Продолжение меры. Интег-
Интегрирование мер. Меры на отделимых пространствах, пер. с франк.,
М., 1977. Р. А. Мюыос.
ПРЕДМЕТНАЯ ОБЛАСТЬ, универсу м,— тер
мин теории моделей, обозначающий область изменения
(оробегания) предметных переменных данного формаль-
формального языка. В качестве формальных языков берутся
языки узкого исчисления предикатов. Каждый такой
язык полностью описывается множеством
L = {P0, ..., Рп, ..., Fo, ..., Fm, ...},
где Ро, . . ., Р„, ... — предикатные символы, a Fo, . . .,
Fm, . . . — функциональные символы, для каждого из
к-рых указано число его аргументных мест. Модель ЗЛ
(или алгебраич. система) для L задается непустым мно-
множеством М и интерпретирующей функцией /, опреде-
определенной на L и сопоставляющей n-местному предикат-
предикатному символу гс-мостный предикат, т. е. подмножество
декартовой степени Мп множества М, а га-местному
функциональному символу — и-местную функцию
Мп-*-М. Множество М наз. П. о. (или универсумом)
модели !Ш.
Лит.: [1] К л и н и С. К., Математическая логика, пер.
с англ., М., 1973; [2] Кейс л ер Г., Чэн Ч. Ч., Теория
моделей, пер. с англ., М., 1977; [3] Ершов Ю. Л., Па-
лютин Е. А., Математическая логика, М., 1979.
В. Н. Гришин.
ПРЕДМЕТНАЯ ПЕРЕМЕННАЯ — то же, что инди-
индивидная переменная. См. также Предикатов исчисление.
ПРЕДМЕТНЫЙ ЯЗЫК — язык, являющийся пред-
предметом изучения. При формализации какой-либо содер-
содержательной теории различают два языка. Один — это
язык формализуемой теории, или П. я., задаваемый
правилами построения выражений П. я. и семантиче-
семантическими правилами, определяющими, что обозначают его
выражения или какие они выражают суждения. Дру-
Другой — это язык, на к-ром формулируются упомянутые
выше синтаксические и семантич. правила. Этот язык
наз. метаязыком. Обычно метаязык не формализуется.
Однако и его можно формализовать, и тогда он станет
П. я., для изучения к-рого требуется новый метаязык.
Лит.: [1] К лини С. К., Введение в метаматематику,
пер. с англ., М., 1957. В. Н. Гришин.
ПРЕДНОРМА — то же, что полунорма.
ПРЕДПОРЯДОК, квазипорядок, пред-
упорядоченность, квазиупорядо-
квазиупорядоченность, — рефлексивное и транзитивное бинар-
бинарное отношение на множестве. Если ^ есть П. на мно-
множестве М, то отношение а~Ъ*~>а-<Ъ и Ь-^а, a, b?M,
является отношением эквивалентности на М. При
этом П. ^ индуцирует порядок на фактормножестве
Ml~. Т. С. Фофанова.
ПРЕДПУЧОК на топологическом пространстве X
со значениями в нек-рой категории Ж (напр., категории
множеств, групп, модулей, колец, . . .) — контрава-
риантный функтор F из категории открытых множеств
пространства X и их естественных отображений вклю-
включения в категорию SK. В зависимости от Ж предпучок F
наз. пред пучком множеств, групп, мо-
модулей, колец,... . Отвечающие включениям VczU
морфизмы F (U)^-F (V) наз. гомоморфизмами огра-
ограничения.
Всякий П. определяет на X пучок (см. Пучков теория).
Е. Г. Скляренко.
ПРЕДСКАЗУЕМАЯ а-АЛГЕБРА — наименьшая
о-алгебра ^=^>{^) множеств из
порожденная всеми отображениями (ю, /)—>-/(со, t) мно-
жества Я XR + вй, к-рые (для каждого фиксированного
cogQ) являются (но t) непрерывными слева и F-согла-
сованными с неубывающим семейством F=(<Ff)(j,
под-а-алгебр ?Ft{~§~, <>0, где (Q, §~) — измеримое
пространство. П. а-а. порождается также любой из
совокупностей множеств:
1) Л X {0}, где A ?(f 0, и [О, т|, где т — марковские
.мо.менгы, a fo, т]] -- стохастич. интервалы;
2) А X {0}, где A G5, и А X (s, t], где s<« и А 65~
Между опциональными алгебрами и П. а-а. имеет
место соотношение 55("г)=б С7)-
Пит.: [1] Д е л л а ш е р и К., Емкости и случайные про-
процессы, пер. с франц., М., 1975. А. Н. Ширяев.
ПРЕДСКАЗУЕМЫЙ СЛУЧАЙНЫЙ ПРОЦЕСС —
стохастический процесс X=(Xt{a>), (ft), являющийся
измеримым (как отображение (со, t)—*Х (со, t)=Xf (со))
относительно предсказуемой а-алгебры д*=Э*(^)-
А. Н. Ширяев.
ПРЕДСТАВИМОСТИ МАТРИЦ ПРОБЛЕМА —
проблема, заключающаяся в том, чтобы выяснить, мож-
можно ли указать такой единый общий метод (алгоритм),
к-рый по произвольной системе U, Ult . . ., U4 цело-
целочисленных матриц позволял бы за конечное число шагов
ответить на вопрос, представима ли матрица U через
остальные матрицы иг, . . ., Uq с помощью операции
умножения. Наибольший интерес представляет слу-
случай, когда матрицы (У, ?/х, . . ., Uq являются квад-
квадратными и имеют один и тот же порядок. Так сформу-
сформулированная П. м. п. наз. общей. Фиксируя матрицы
Ult . . ., Uq и оставляя матрицу U переменной, полу-
получают т. н. частные П. м. п. Алгоритм, решающий
общую П. м. п., решал бы и все частные проблемы, так
что для установления неразрешимости общей П. м. и.
достаточно указать хотя бы одну неразрешимую част-
частную П. м. и.
П. м. и.— одна из первых алгоритмических проблем
алгебраич. характера, неразрешимость к-рых была ус-
установлена. Первоначально А. А. Марковым было по-
показано (см. [1], [2]), что для любого «5*6 может быть
построена система, состоящая из 91 матрицы порядка
п, такая, что соответствующая ей частная П. м. п.
будет неразрешимой, т. е. будет невозможен алгоритм
(понимаемый в точном смысле этого слова), распознаю-
распознающий по произвольной матрице порядка п, представима
ли она через матрицы данной системы. В дальнейшем
(см. [3]) число матриц в системе было уменьшено до 23
и было показано, что за счет надлежащего усложнения
конструкции системы (включая увеличение числа чле-
членов) условие га^б может быть ослаблено до га^4. Для
любого п^б строится конкретная система, состоящая
из 12 матриц порядка п, с неразрешимой частной
П.м.п. (см. [4]). Путем подходящей фиксации U и
варьирования G3, . . ., Uч доказана неразрешимость
общей II. м. п. для п=3 (см. [5]).
Лит.: [1] М а ]) к о в А. А., «Докл. АН СССР», 1951, т. 78,
Л"> 6, с. 1089—92; [2J его ж е, Теория алгорифмов, М.— Л.,
1954 (Тр. Матем. ин-та АН СССР, т. 42); [3] его же, «Z. math.
Logik und Grundl. Math.», 1958, Bd 4, S. 157—68; [4] На-
Нагорный H. M., «VI Веесоюзн. конференция по матем. логи-
логике», Тб., 1982, с. 124; [51 Paterson M.S., «Studies in
appl. math.», 1970, v. 49, N5 1, P- 105 — 07. II. M. Нагорный.
ПРЕДСТАВИМЫЙ ФУНКТОР — коварнантный
(или контравариантиый) функтор F из нек-рой кате-
категории Я в категорию множеств @, изоморфный одному
из основных теоретико-множественных функторов:
НА(Х) = Н (А, X): .ft-¦-*©.
Функтор F : Й1—>-3 представим тогда и только тог-
тогда, когда найдутся такие объект Л?ОЬЯ и элемент
a?F(A), что для каждого элемента х ? F (X), X?ObJt,
существует единственный морфизм а : А—>-Х, для к-рого
x~aF (а). Объект А называется представляю-
представляющим функтор F; он определен однозначно с точ-
точностью до изоморфизма.
В категории множеств тождественный функтор пред-
представим: представляющим объектом служит одноточеч-
одноточечное множество. Функтор взятия нек-рой декартовой
степени также представим: представляющим объектом
служит множество, мощность к-рого равна этой степени.
В произвольной категории произведение П. ф. F; с
представляющими объектами Aj, i?/, представимо
тогда и только тогда, когда в этой категории существует
копроизведение объектов А;. Всякий ковариантньш
П. ф. перестановочен с пределами, т. е. непрерывен.
П. ф.— аналог понятия «свободная универсальная
алгебра с одним образующим». Для любого функтора
G : Й1—>-<2 и П. ф. F множество естественных преобра-
преобразований Nat (F, G) изоморфно множеству G(A), где
А — представляющий объект. Это показывает, что
П. ф. являются свободными объектами категории функ-
функторов.
Для аддитивных категорий вместо функторов со
значениями в @ рассматриваются аддитивные функторы
со значениями в категории абелевых групп; поэтому
под П. ф. понимается аддитивный функтор, изоморф-
изоморфный основному аддитивному функтору.
Понятие П. ф. первоначально возникло в нлгебраич.
геометрии (см. [2]). Наиболее важными примерами
П. ф. здесь являются функторы Пикара Pic XlS и
Гильберта Hilb XlS, представимые в категории алге-
алгебраических пространств (см. [11). Пусть К — ноле
частных регулярного дискретного нормированного коль-
кольца О с совершенным полем вычетов. Если Хо— глад-
гладкая геометрически неприводимая собственная кривая
рода g>0 над К, то ее минимальная модель представляет
функтор У н> Isom^-(y (g)o К, Хо) из категории регу-
регулярных О-схем. Если А — абелево многообразие над
К, то его минимальная Нерона модель является глад-
гладкой групповой схемой X^t-SpecO, представляющей
функтор У ь» Ношд- (У (Я)о К, А) из категории гладких
О-схем.
Лит.: [1] Артин М., «Математика», 1D70, т. 14, Mi,
с. 3—39; [2] Г р о т е н Д и к А., Дьёдоннс Ж., «Успехи
матем. наук», 1972, т. 27, в. 2, с. 135—48.
С. Г. Танкеев, М. Ш. Цалеико.
ПРЕДСТАВЛЕНИЕ АЛГЕБРЫ ЛИ в вектор-
векторном пространстве V — гомоморфизм р ал-
алгебры Ли L над полем к в алгебру Ли (\l(V) всех
линейных преобразований пространства V над к.
Два представления pt : L—*-&\A\) и р2 : L—*-gl(T'2)
паз. эквивалентными (или изоморфны-
м и), если существует изоморфизм a: Fj_>K2, для к-рого
при любых l^L, v1^V1. Представление р в V наз.
конечномерным, если dim F<oo, и непри-
неприводимым, если в V не существует отличных от нуля
и всего пространства подпространств, инвариантных
относительно всех операторов p(l), l?L.
При заданных представлениях pt : L -*-д1 (К,) и
р2 : Z/->gl( V2) можно построить представления рх(ф р2
(прямая сумма) и Pi®p2 (тензорное произведение)
алгебры L в пространствах Fi(J)F2 и Fi®V2, полагая
(Pi ф Рг) @ ("ь v2) = (рх (I) иг, р2 (/) v2),
(Pi® Рг) (I) *>i®i>a = Pi (О »i®v2 + vi®P2 (О V2
для vt?Vi, y2g F2, l?L. Если р — представление ал-
алгебры Ли L в пространстве V, то формула
< р* (I) и, v> = — <и, p(l)v>
определяет представление р* алгебры L на сопряженном
к V пространстве, наз. контраградиентным
по отношению к р.
Каждое П. а. Ли L однозначно продолжается до
представления универсальной обертывающей алгебры
U (L); тем самым устанавливается изоморфизм катего-
категории П. а. Ли L и категории модулей над U(L). В част-
частности, представлению р алгебры L соответствует идеал
кег р в U (L) — ядро его продолжения р. Если пред-
представление р неприводимо, то идеал кег р примитивен.
Обратно, всякий примитивный идеал в U (L) строится
таким способом по нек-рому (вообще говоря, не един-
единственному) неприводимому представлению р алгебры L.
Изучение пространства примитивных идеалов PrimU(L),
снабженного топологией Джекобсона, является сущест-
существенной частью теории П. а. Ли. Оно проведено пол-
ноетью в случае, когда L — конечномерная разре-
разрешимая алгебра Ли, а к —алгебраически замкнутое
ноле характеристики нуль (см. [21).
Наиболее полно изучены конечномерные представ-
представления конечномерных алгебр Ли над алгебраически
замкнутым полем характеристики нуль. В случае полей
С и R эти представления находятся во взаимно одно-
однозначном соответствии с аналитическими конечномерными
представлениями соответствующих односвязных (ком-
(комплексных или вещественных) групп Ли. В этой ситуа-
ситуации любое представление разрешимой алгебры Ли
содержит одномерное инвариантное подпространство
(см. Ли теорема). Любое представление полупростой
алгебры Ли вполне приводимо, т. е. изоморфно пря-
прямой сумме неприводимых представлений. Неприводимые
представления нолупростой алгебры Ли L полностью
классифицированы: классы изоморфных представле-
представлений взаимно однозначно соответствуют доминант-
доминантным весам, т. е. весам с неотрицательными число-
числовыми отметками, из сопряженного пространства И*
к подалгебре Картана Л алгебры L (см. Картина теоре-
теорема о старшем векторе). Об описании строения неприво-
неприводимого представления по соответствующему ему доми-
доминантному весу (его старшему весу) см. в статьях Крат
иостъ веса, Характеров формула.
Произвольный (не являющийся, вообще говоря, до-
доминантным Бесом) элемент %?Н* также определяет
нек-рое неприводимое линейное представление полу
простой алгебры Ли L со старшим весом X. являющееся,
однако, бесконечномерным (см. Представление со стар-
старшим вектором). Соответствующие {/(?)-модули наз.
модулями Верма (см. [2]). Полной классифи-
классификации неприводимых бесконечномерных представле-
представлений полунростых алгебр Ли пока A983) не получено.
Если к — алгебраически замкнутое иоле характе-
характеристики р>0, то неприводимые представления конеч-
конечномерной алгебры Ли L всегда конечномерны и их раз-
размерность ограничена константой, зависящей от п=
= dim L. Если алгебра L имеет р-структуру, то эта
константа ость р<п~г)/2, где г — минимальная воз-
возможная размерность аннулятора линейной формы на L
в коприсоединенном представлении \А]. Для описания
множества неприводимых представлений в этом случае
применяется следующая конструкция. Пусть Z (L)—
центр алгебры U (L) и Ml— аффинное алгебраич.
многообразие (размерность dim Afi— я), алгебра ре-
регулярных функций на к-ром совпадает с Z (L) (м н о-
гообразие Цассенхауза). Отображение
()\-*kev(()/Z(L)) позволяет сопоставить каждому непри-
неприводимому представлению точку многообразия Цассен-
Цассенхауза. Получаемое отображение сюръективно, прооб-
прообраз любой точки из Ml конечен, а для точрк открытого
всюду плотного подмножества этот прообраз состоит
из одного элемента [7]. Полное описание всех непри-
неприводимых представлений имеется для нилыютентных
алгебр Ли (см. [8]) и нек-рых отдельных примеров
[см. [9], [10]). Получены также разнообразные резуль-
результаты относительно специальных типов представлений.
Лит.: [1] Бур баки Н., Группы и алгебры Ли, пер.
г франц., М., 1976—78; 12] Диксмье Ж., Упинереальные
обертывающие алгебры, пер. с франц., М., 1978; [3] Д ж е к о 6-
с о н Н., Алгебры Ли, пер. с англ., М., 1964; [4] М и л ь н е р
А. А., «Функциональный анализ и его прило>иения», 1980, т. 14,
М 2, с. 67—68; [5] С е р р Ж. - П., Алгебры Ли и группы Ли,
пер. с англ. и франц., М., 1969; [6] Теория алгебр Ли. Тополо-
Топология групп Ли, пер. с франц., М., 1962; [7] Zassenliaus H.,
«Ргос. Glasgow Math. Assoc», 1954, v. 2, p. 1—36; [8] Вей с-
ф ей л ер Б. Ю., Кац В. Г., «Функциональный анализ и
его приложения», 1971, т. 5, № 2 с. 28—36; [9] J a n t г е и
J. С, «Math. Z.», 1974, Bd 140, Н. 1, S. 127—4!); [10] Руда-
Рудаков А. Н., «Изв. АН СССР. Сер. матем.», 1970, т. 34, №4,
с. 735 — 43. А. Н. Рудаков.
ПРЕДСТАВЛЕНИЕ АССОЦИАТИВНОЙ АЛГЕБ-
АЛГЕБРЫ р а з м е р н о с т и п — гомоморфизм алгебры А
над полем F в алгебру матриц Mn(F), т. е. сопостав-
ление каждому а ? А квадратной матрицы Т (а) поряд-
порядка п, при к-ром
T(U + \ib) = XT (a) + \iT (Ь) и Т (аЬ) = Т (а) Т (Ь),
где а, Ь?А, к, \i<zF. Обычно требуется также, чтобы
единице алгебры А соответствовала единичная матри-
матрица; иногда требуется, чтобы и сама алгебра А была ко-
конечномерной.
Всякое неразложимое представление иолуиростой
алгебры эквивалентно прямому слагаемому регулярного
представления. Таким образом, всякая иолупростая
алгебра является алгеброй конечного (п р е д-
с т а в л е н ч е с к о г о) типа, т. е. имеет копсчное
число неизоморфных неразложимых представлений.
Неполупростые алгебры люгут быть как конечного, так
и бесконечного представленческо-
г о тина (такова, напр., А = {1, г, s|r2=s2=rs=4T=0}).
Алгебры бесконечного тина принято делить еще на а л-
гебры дикого типа, задача классификации
к-рых содержит в себе классич. нерешенную з а д а ч у
о паре матриц (т.е. задачу об одновременном
приведении к канонич. форме двух линейных операто-
операторов в конечномерном пространстве), и алгебры
ручного типа.
Основными вопросами, изучаемыми в теории П. а. а.,
являются получение необходимых и достаточных усло-
условий, при к-рых алгебра принадлежит одному из пере-
перечисленных типов, и классификация неразложимых пред-
представлений в конечном и ручном случаях. В общем слу-
случае эти задачи не решены. Описание алгебр конечного
и ручного типа и их представлений получено для ал-
алгебр, у к-рых квадрат радикала равен нулю (см. [2],
14], [8]—[10]). Решены проблемы Брауэра —
Т р э л л а, т.е. доказано, что над любым нолем ал-
алгебра бесконечного типа имеет неразложимые пред-
представления сколь угодно большой размерности, а над
совершенным полем имеется бесконечно много размер-
размерностей, в каждой из к-рых имеется бесконечно много
неразложимых представлений (см. [5], [7]). Любая
алгебра конечного типа над алгебраически замкнутым
нолем имеет мультипликативный базис, т. е. базис, у
к-рого произведение любых двух его элементов либо
равно нулю, либо принадлежит этому базису [6]. Пол-
Полностью решен вопрос о разделении групповых алгебр
на ручные и дикие [1].
С П. а. а. тесно связаны представления нек-рых дру-
других объектов: колчанов, частично упорядоченных мно-
множеств, решеток, боксов.
Лит.: [1] Бондаренко В. М., Д р о а д Ю. А., «За-
«Записки научных семинаров ЛОМИ», 1977, т. 71, с. 24—41; [2]
Кругляк С. А., там же, 1972, т. 28, с. 60—69; [3] К эр т и с
Ч., Райнер И., Теория представлений конечных групп и
ассоциативных алгебр, пер. с англ., М., 1969; [4] Назаро-
Назарова Л. А., «Изв. АН СССР. Сер. матем.», 1973, т. 37, № 4, с.
752—91; [5] Назарова Л. А., Р о й т е р А. В., Категор-
ные матричные задачи и проблема Брауэра — Трэлла, К., 1973",
[(i) P о й т е р А. В., Обобщение теоремы Бонгартца, К., 1981;
[7] его же, «Изв. АН СССР. Сер. матем.», 1968, т. 32, с. 1275 -
1282; [8] D 1 a b V., Ringel С, Indecomposable representa-
representations of graphs and algebras, Prowidence, 1976; [9] Don o-
v a n P., Freislich M. R., The representation theory of
finite graphs and associated algebras, [s. 1., 1974]; [10J Gab-
Gabriel P., «Manus. Math.», 1972, v. 6, № 1, p. 71—103.
A. В. Ройтер.
ПРЕДСТАВЛЕНИЕ БЕСКОНЕЧНОЙ ГРУППЫ —
гомоморфизм бесконечной группы в группу взаимно
однозначных отображений на себя (вообще говоря,
бесконечных) множеств. Чаще всего рассматриваются
П. б. г. автоморфизмами алгебраич. структур; в атом
случае теория П. б. г. связана с теорией представле-
представлений связанных с этими группами групповых алгебр.
Лит.: [1] Кириллов А. А., Элементы теории пред-
представлений, 2 изд., М., 1978; [2] Плоткин Б. И., Группы
автоморфизмов алгебраических систем, М., 1!Ш6. А. И. Штерн.
ПРЕДСТАВЛЕНИЕ БИКОМПАКТНОЙ ГРУППЫ-
непрерывное представление бикомпактной топологич.
группы в топологическое векторное пространство. См.
Компактная группа. А. И. Штерн.
ПРЕДСТАВЛЕНИЕ ГРУППЫ — гомоморфизм груп-
группы в группу всех, обратимых преобразований нек-рого
множества V. Представление р группы G наз. л и-
н е ii н ы м, если V является векторным простран-
пространством над нек-рым нолем к, а преобразования p(g),
g?G,— линейными преобразованиями. Часто линейные
представления называют для краткости просто пред-
представлениями (см. Представлений теория). В тео-
теории представлений абстрактных групп наиболее раз-
разработанным разделом является теория конечномерных
представлений конечных групп (см. Конечной группы
представление, Представление симметрической группы).
Если G — топологи1!, группа, то рассматриваются
непрерывные линейные представления группы G в то-
топологическом векторном пространстве V (см. Непре-
Непрерывное представление, Представление топологической
группы). Если G — группа Ли, а V — конечномерное
пространство над R или С, то непрерывное линейное
представление автоматически является вещественно
аналитическим. Аналитические и дифференцируемые
представления группы Ли можно определить и в бес-
бесконечномерном случае (см. Аналитическое представле-
представление, Бесконечномерное представление). Всякому диф-
дифференцируемому представлению р группы Ли G соот-
соответствует нек-рое линейное представление ее алгебры
Ли — дифференциал представления р. Если G — связ-
связная группа Ли, то ее конечномерные представления
полностью определяются своими дифференциалами.
Наиболее разработанные разделы теории представлений
топологич. групп — это теория конечномерных ли-
линейных представлений полупростых групп Ли, к-рая
часто формулируется на языке алгебр Ли (см. Конечно-
Конечномерное представление, Представления классических
групп, Карта па теорема о старшем векторе), теория
представлений компактных групп, теория унитарных
представлений.
Для алгебраич. групп имеется теория рациональных
представлений, во многом аналогичная теории ко-
конечномерных представлений групп Ли.
Лит.: 11] Ж с л о б е н к о Д. II., Компактные группы
Ли и их представления, М., 1JI70; [2] Кириллом А. А.,
Элементы теории представлений, 2 изд., М., 1978; [3] Най-
марк М. А., Теория представлении групп, М., 1976; [4]
Желобенко Д. П., Штерн А. И., Представления групп
Ли, М., 1981. А. Л. Онищип.
ПРЕДСТАВЛЕНИЕ КОМПАКТНОЙ ГРУППЫ —
гомо.морфизм компактной группы в группу непрерывных
линейных автоморфизмов (комплексного) банахова про-
пространства, непрерывный в сильной операторной топо-
топологии.
Пусть G — компактная группа, V — банахово про-
пространство и ф : G-+GL (V) — представление. Если V—
= Н — гильбертово пространство, а ср (g) — унитар-
унитарный оператор для любого g?G, то (р наз. унитарным
представлением. В Н всегда существует эквивалент-
эквивалентная норма, относительно к-рой данное представление ср
унитарно.
Всякое неприводимое унитарное представление груп-
группы G конечномерно. Пусть {ра,а,?1} — семейство все-
всевозможных попарно неэквивалентных унитарных непри-
неприводимых представлений группы G. Всякое унитарное
представление ф группы G является ортогональной
прямой суммой таких однозначно определенных пред-
представлений фа, а?/, что каждое фа является ортого-
ортогональной прямой суммой нек-рого семейства представ-
представлений, эквивалентных ра.
Если G конечна, то семейство {ра } тоже конечно и
содержит столько элементов, сколько имеется в G
различных классов сопряженных элементов (при этом
2а6 z(dim ра)'-~ |G|). Задача исследования этих пред-
представлений (вычисления их характеров, нахождения
явной реализации и т. п.) составляет предмет обширной
теории (см. Конечной группы представление).
Если G — связная односвязная компактная группа
Ли, a Gj.— ее комплексификация (см. К омплексифика-
ция группа. Ли), то описание семейства {ра, а?/} для G
сводится (посредством сужения представлений на G)
к описанию семейства всех неприводимых попарно
неэквивалентных конечномерных рациональных пред-
представлений редуктивной алгебраич. группы С^. Послед-
Последнее же семейство, в свою очередь, допускает полное
описание с помощью рассмотрения старших весов (см.
Представление со старшим вектором).
В современной теории чисел и алгобраич. геометрии
рассматриваются ?-адические представления компакт-
компактных вполне несвязных групп (см. [5], [6]).
Лит.: [1] Понтрягин Л. С, Непрерывные группы,
3 изд., М., 1973; L2J Н а й м а р к М. А., Теория представле-
представлений групп, М., 1976; [3] Желобенко Д. П., Компакт-
Компактные группы Ли и их представления, М., 1У70' [4] Л е н г С,
Я?2(Д), пер. с англ., М., 1977; [5] Г е л ь ф а н д И. М., Гра-
Граев М. И., Пятецкий-Шапиро И. И., Теория пред-
представлений и автоморфные функции, М., 1966; [6] Серр
Ж. - П., Абелевы i-адические представления и иллиптические
кривые, пер. с англ., М., 1973; [7] Шевалле К., Теория
групп Ли, пер. с англ., т. 1, м., 1948. В. Л. Попов.
ПРЕДСТАВЛЕНИЕ ПОЛУГРУППЫ S в к лассо
полугрупп 8 — гомоморфизм полугруппы S в
нек-рую полугруппу из класса S (в случае изоморфиз-
изоморфизма говорят о точном представлении). Обычно имеются
в виду классы каких-либо конкретных полугрупп.
Наиболее изучены представления в классе полугрупп
преобразований (короче — представления преобразо-
преобразованиями), в классах полугрупп частичных преобразо-
преобразований и бинарных отношений, в классе полугрупп
матриц (т. н. матричные, или линейные, П. п.). В теории
автоматов с каждым автоматом связано представление
свободной полугруппы преобразованиями множества
его внутренних состояний. Специальный характер но-
носят П. п. преобразованиями, связанными тем или иным
образом со свойствами элементов преобразуемого мно-
множества, наделенного какой-либо структурой (эндомор-
(эндоморфизмами, непрерывными преобразованиями и т. п.).
Всякая полугруппа с единицей изоморфно представима
как полугруппа всех эндоморфизмов ориентированного
или неориентированного графа, как полугруппа всех
эндоморфизмов нек-рой алгебры с унарными операция-
операциями и т. п. Известно A983) несколько конструкций, по-
позволяющих получить все П. п. частичными преобразо-
преобразованиями. Они строятся из нек-рых простейших П. п.
при помощи их объединения, кратного повторения,
ограничения на подмножестве и операции погружения
полугрупп.
Присоединив к полугруппе S единицу: Sl ?(J{I}
и продолжив регулярное П. п. S лонымп сдвигом и па
декартову степень Sx полугруппы S1, получают пред-
представление ф/ — /-кратное повторение регулярного П. и.
S. Всякое представление ty полугруппы S преобразо-
преобразованиями множества Q может быть получено (см. |2])
из ф/ с помощью нек-рого отображения 0 : S!—*-Q
так, что
Особую роль играют транзитивные П. п., т. е. такие
ее представления ф преобразованиями множества И,
что для любых a, P?fl найдется а, для которого
(фя)а=р\
П. п. взаимно однозначными частичными преобразо-
преобразованиями связаны с понятием и свойствами инверсных
полугрупп.
При исследовании матричных П. п. привлекаются к
рассмотрению полугрупповые алгебры. Изучается вопрос
о приводимости матричных П. п. Найдены неприводи-
неприводимые представления для ряда полугрупп (в том числе
и для конечных). Матричные представления вполне
простых и вполне 0-простых полугрупп могут быть по-
построены как продолжение представлений их подгрупп.
Матричные представления произвольных полугрупп
могут быть описаны при помощи представлений их фак-
факторов, являющихся простыми и 0-простыми полугруп-
полугруппами.
Лит.: [1] Клиффорд А., Престон Г., Алгебраи-
Алгебраическая теория полугрупп, пер. с англ., т. 1—2, М., 1972; [2]
Вагнер В. В., «Матем. сб.», 1956, т. 38, Л» 2, с. 203—40:
[3] Л я п и н Е. С, там же, 1960, т. 52, № 1, с. 589—96; 14]
Шайн Б. М., там же, 1963, т. 60, N5 3, с. 293—1H3; [5] М с-
А I i s t с г D. В., «Semigroup Forum», 1971, v. 2, Kt 3, p. 189—
263; № 4, p. 288—320; [6] J б n s s о п В., Topics in universal
algebra. В.—N. Y., 1972. Л. M. Глускин, Е. С. Ляпип.
ПРЕДСТАВЛЕНИЕ СИММЕТРИЧЕСКОЙ ГРУП-
ГРУППЫ — линейное представление группы Sm над каким-
либо полем К. Если char K=0, то все конечномерные
П. с. г. вполне приводимы и определены над Q (иначе
говоря, все неприводимые конечномерные представле-
представления над Q абсолютно неприводимы).
Неприводимые конечномерные представления группы
Sm над Q классифицируются следующим образом.
Пусть d — какая-либо Юнга диаграмма, отвечающая
разбиению Х=(ХХ, . . .,ХГ) числа т, Rj (соответственно
Сд) — подгруппа группы Sm, состоящая из всех под-
подстановок, переводящих каждое из чисел 1,2,..., т
в число, находящееся в той же строке (соответственно
столбце) диаграммы й. Тогда
где X' — (Xi , . . ., Xs) — разбиение числа т, сопряженное
к разбиению X. Существует единственное неприводимое
представление Т% : Sm—>GL (U% ) группы Sm (завися-
(зависящее только от X) со следующими свойствами: 1) в про-
пространстве Ui имеется такой ненулевой вектор ud, что
Т\ (g)'id—ud Для любого g?Ra', 2) в пространстве U\
имеется такой ненулевой вектор щ, что Т% (g)u<i -
= e(g)ua для любого g^C^, где e,(g)= 11 — четность
подстановки g. Представления, отвечающие различным
разбиениям, не эквивалентны, и ими исчерпываются
все неприводимые представления группы Sm над Q.
Векторы и^ и и'д определены однозначно с точностью
до умножения на число. Для всех диаграмм, отвечаю-
отвечающих разбиению X, эти векторы нормируются таким обра-
образом, что gud=uga и gu'i =u'gd для любого g?Sm,
где gd обозначает диаграмму, получаемую из d приме-
применением ко всем числам подстановки g. Векторы ud
(соответственно ud), соответствующие стандартным
диаграммам d, образуют базис пространства U\; в этом
базисе операторы представления Тх записываются цело-
целочисленными матрицами. Размерность представления Т%
равна
П
dim У, = ¦
И',' ~IL.y>V
где Z,-—X,-+r—i (i=l, . . ., г), а произведение в знаме-
знаменателе второго выражения берется по всем клеткам
Cjj таблицы Юнга tx 1 причем Х,у обозначает длину соот-
соответствующего крюка.
Разбиению (т) отвечает тривиальное одномерное
представление группы Sm, а разбиению (!,...,!) —
нетривиальное одномерное представление е (четность).
Разбиению X', сопряженному к X, отвечает представле-
представление гТх- Пространство U^ канонич. образом (с точ-
точностью до гомотетии) отождествляется с пространством
Vh так, что Tx,(g)=e(g)Tx (g) для любого g?Sm;
при этом можно считать, что ud ~-ud,, где d! — диаг-
диаграмма, получаемая из d транспонированием.
Построение полной системы неприводимых П. с. Г.
производится с помощью Юней симметризаторов, поз-
позволяющих получить разложение регулярного представ-
представления. Если d — диаграмма Юнга, отвечающая раз-
разбиению к, то представление Тх эквивалентно П. с. г.
Sm в левом идеале групповой алгебры QSm, порожден-
порожденном симметризатором Юнга ед. Апостериорное описа-
описание элемента ed состоит в следующем: Гц («d)=0 при
ифк, а Тх (ed) — оператор ранга 1, действующий по
формуле Тх (e^u—iurf, u)u'd для любого u?Ux, где
( , ) — подходящим образом нормированное инва-
инвариантное скалярное умножение в пространстве Ux- При
Производящая функция для характеров представле-
представлений Тх дается Фробениуса формулой. Однако для вы-
вычисления отдельных значений характеров удобнее
пользоваться рекуррентными соотношениями. Наибо-
Наиболее эффективным из них является правило М у р-
нагана — Накаямы: пусть axVb=ain^ — зна-
значение характера представления Тх на классе []х] со-
сопряженных элементов группы Sm, определенном раз-
разбиением и числа т, ъ пусть разбиение ц содержит число
р. Через и, обозначается разбиение числа т—р, полу-
получаемое из ц выбрасыванием числа р. Тогда
где сумма берется по всем разбиениям к числа т—р,
получаемым удалением косого крюка длины р из таб-
таблицы Юнга t\ , a i (к) обозначает высоту удаленного ко-
косого крюка.
Имеется также метод (см. [5]), позволяющий найти
целиком таблицу характеров группы S,„, т. е. матрицу
4=||ая|х11- Пусть Мх есть П. с. г. Sт, индуцированное
тривиальным одномерным представлением подгруппы
R\=Rd, где d —диаграмма Юнга, отвечающая раз-
разбиению "к. И пусть Mi = 'S.v,millTlx, a M=\\m-Ali\\. Если
считать, что строки и столбцы матрицы М расположе-
расположены в порядке лексикографич. убывания индексов (раз-
(разбиений), то это будет нижняя треугольная матрица с
единицами на диагонали. Значение характера пред-
представления Мх на классе [ц] равно
**~ \Rx\ '
где с^ — порядок централизатора подстановки из клас-
класса [ц|. Матрица .В=|1&Я|Л является верхней треуголь-
треугольной, и имеет место соотношение ММТ=ВС~1ВТ, где
?'=diag(C|x), из к-рого однозначно определяется матри-
матрица М. После этого матрица А находится по формуле
А = М~1В.
Ограничение представления Тх группы Sm на под-
подгруппу S m_1 находится по правилу ветвления:
где суммирование распространяется на те г, для к-рых
kj>k;+1 (включая г). Ограничение представления Тх на
подгруппу Am при kj=k' абсолютно неприводимо, а
при к=Х' распадается над квадратичным расширением
поля Q в сумму двух неэквивалентных абсолютно не-
неприводимых представлений одинаковой размерности.
Получаемые таким образом представления группы A m
исчерпывают все ее неприводимые представления над С.
О II. с. г. в тензорах см. в ст. Представления класси-
классических групп.
Разработана также теория модулярных П. с. г. (см.,
напр., [5]).
Лит.: [1] В е й л ь Г., Классические группы, их инвари-
инварианты и представления, пер. с англ., М.', 1947; [2] М у р н а-
ган Ф. Д., Теория представлений групп, пер. с англ., М.,
1950; [3] Хамермеш М., Теория групп и ее применение
к физическим проблемам, пер. с англ., М., 1966; [4] К э р т и с
Ч., Р айн ер И., Теория представлений конечных групп и
ассоциативных алгебр, пер. с англ., М., 1969; [5] Д ж е им с Г.,
Теория представлений симметрических групп, пер. с англ.,
М., 1982. Э. Б. Винберг.
ПРЕДСТАВЛЕНИЕ СО СТАРШИМ ВЕКТОРОМ —
линейное представление р конечномерной полупростой
расщепляемой алгебры Ли g над полем к характери-
характеристики нуль с расщепляющей К ар тана подалгеброй t,
удовлетворяющее следующим условиям.
1) В пространстве V представления р существует
циклический вектор v (т. е. V — наимень-
наименьшее g-инвариантное подпространство, содержащее v).
2) ' p(h)(v)=k(h)v для всех fe?t, где X — некото-
некоторая фиксированная линейная форма на t со значения-
значениями в к.
3) Если «и . . ., <яг— система простых корней, оп-
определенная нек-рым лексикографич. упорядочением
множества Д всех корней алгебры g относительно t
(см. Корневая система), а еа , ta,, ha — соответ-
соответствующие корню а,- векторы из базиса Шевалле алгебры
9, i=l, . . ., г, то p(ea)(v) = 0 для всех i=l, . . ., г.
Таким образом, к является весом относительно суже-
сужения р на t (см. Вес представления); он наз. стар-
старшим весом. Пространство V наз. цикличе-
циклическим g-м одулем со старшим весом Я
и образующей v, a v наз. старшим векто-
вектором.
Для всякой линейной формы к на t существует
единственное с точностью до эквивалентности неприво-
неприводимое представление р\ алгебры g со старшим весом
к. g-модуль V(k), определяемый ря,, является прямой
суммой весовых подпространств относительно сужения
р^ на t- Их веса имеют вид
где п[— целые неотрицательные числа. Весовое под-
подпространство Г'ц (к) веса р, конечномерно, натягива-
натягивается над к на векторы вида
и для любого h?t ограничение p^(h) на V (к) явля-
является скалярным оператором умножения на fi(ft). Про-
Пространство \\ (к) одномерно; вес к является единствен-
единственным старшим весом представления р^ и может быть оха-
охарактеризован как единственный вес t-модуля V (к)
такой, что любой другой вес имеет вид
где ге,-— целые неотрицательные числа.
Представление р^ конечномерно тогда и только тогда,
когда к — доминантная линейная фор-
форма на t, то есть k(ha ) — целое неотрицательное
число для всех г =1, . . ., /-. Всякое неприводимое ко-
конечномерное линейное представление алгебры g имеет
вид р\ для нек-рой доминантной линейной формы А,
на t (так что все такие представления классифициру-
классифицируются с точностью до эквивалентности доминантными
линейными формами на t). Множество всех весов ко-
конечномерного представления р\ относительно t инва-
инвариантно относительно Вейля группы алгебры g (рас-
(рассматриваемой как группа линейных преобразований
пространства t), и если веса |л и у лежат в одной орбите
группы Вейля, то размерности пространств V^ (к) и
Vy (к) совпадают. Для всякого веса \i и всякого корня
сс? Д число \i(ha) — целое; если при этом |х+а — тоже
вес, то
Р («а) (Уц (X)) ф О
(здесь ha — элемент из t, соответствующий а, а еа—
корневой вектор корня а).
Лит.: [1] Д ж е к о б с о н Н., Алгебры Ли, пер. с англ.,
М., 1964; [2] Теория алгебр Ли. Топология групп Ли. Семи-
Семинар «Софус Ли», пер. с франц., М., 1962; [3] Желобенко
Д. П., Компактные группы Ли и их представления, М., 1970;
[4] Cartan E., «Bull. sci. math.», 1925, t. 49, p. 130—52;
[5] Harish-Chandra, «Trans. Amcr. Math. Soc», 1951,
V. 70, p. 28—96. В. Л. Попов.
ПРЕДСТАВЛЕНИЕ ТОПОЛОГИЧЕСКОЙ ГРУППЫ—
непрерывное отображение группы G в топологич. груп-
группу гомеоморфизмов нек-рого топологич. пространства.
Чаще всего под П. т. г. G понимается линейное представ-
представление, более того — такое линейное представление я
топологич. группы G в топологич. векторном простран-
пространстве (т. в. п.) Е, что вектор-функция g->-n(g)x, g?G,
определяет при любом х?Е непрерывное отображение
группы G в пространство Е. В частности, всякое не-
непрерывное представление группы G является П. т.г. С.
Теория П. т. г. тесно связана с теорией представ-
представлений различных топологических групповых алгебр.
Среди них важнейшей является банахова симметрич-
симметричная алгебра мер М (G) группы G (алгебра всех регуляр-
регулярных борелевских мер на G с конечной полной вариацией,
в к-рой умножение определяется как свертка). Часто
используется также топологическая алгебра С" (G)
всех регулярных борелевских мер на G с конечной
полной вариацией и с компактным носителем. Умно-
Умножение в С (G) определяется как свертка, а инволю-
инволюция ]х-+ц*, [x^C'(G), определяется формулой
Топология алгебры С (G) согласуется с двойственно-
двойственностью между этой алгеброй и алгеброй С (G) (всех не-
непрерывных функций на G), рассматриваемой в компакт-
компактно открытой топологии. Важную роль играют также
различные подалгебры алгебр М (С) и С (G). В част-
частности, если Е — квазиполное бочечное или полное
локально выпуклое пространство (л. в. п.), ал — не-
непрерывное П. т. г. G в Е, то формула
определяет слабо непрерывный линейный оператор я (jt)
в Е и соответствие |х->-я (|х) есть представление алгебры
С (G) в пространстве Е, однозначно определяющее
представление я топологич. группы. При этом П. т. г.—
(топологически) неприводимое представление, оператор-
но неприводимое представление, вполне неприводимое
представление, эквивалентно другому П. т. г. (и т. д.)
тогда и только тогда, когда соответствующее представ-
представление алгебры С (G) обладает соответствующим свой-
свойством.
Пусть я есть П. т. г. G в л. в. п. Е; пусть Е'— со-
сопряженное к Е пространство. Функции на G вида g->
—мр(я(#M), \?Е, наз. матричными элемен-
элементами представления я. Если Е — гиль-
гильбертово пространство и %?Е, |||||=1, то функции вида
g-*-<.n(g)\, |>, g?G, наз. сферическими функ-
функциями, связанными с представлением я.
Пусть Е, Е* суть л. в. п. в двойственности, я есть
П. т. г. G в л. в. п. Е. Формула я* (g)~n(g-v)* опреде-
определяет П. т. г. л* в Е*, наз. с о п р я ж е н н ы м, или
контрградиентным, к я. Пусть ях, я2 суть
П. т. г. G в т. в. п. Ег, Е.2 соответственно, E=Et-{-E2—
прямая сумма и n(g), g?G,— непрерывный линейный
оператор в Е, определенный формулой
Отображение g-+n(g) есть П. т. г. G в т. в. п. Е, наз.
прямой суммой П. т. г. я, и я2. В нек-ры\
случаях (в частности, для унитарных представлении)
может быть определено тензорное произведение П. т. г.
и прямая сумма бесконечного семейства П. т. г. С по-
помощью ограничения или расширения поля скаляров
вводятся операции овеществления и комплексифнкации
для П. т. г.
Представление топологич. группы наз. вполне
приводимы м, если любое замкнутое инвариант-
инвариантное подпространство имеет дополнительное замкнутое
инвариантное подпространство. Представление я то-
топологич. группы G в т. в. и. Е наз. разложимым,
если существуют такие замкнутые инвариантные под-
подпространства Е1, Е2 в Е, что л эквивалентно прямой
сумме подпредставлоний я,, я., представления л, от-
отвечающих подпространствам Et, Ег соответственно; в
противном случае л наз. неразложимым. Не-
Неразложимое приводимое представление я определяется
не только подпродставлением и факторпредставлением,
соответствующими данному инвариантному подпро-
подпространству, но и нек-рым классом одномерных когомо-
логий грушш G с коэффициентами в G-модуло ограни-
ограниченных линейных операторов из пространства фактор-
представлении в пространство представления.
Важнейшими общими задачами теории П. т. г. явля-
являются описание всех неразложимых представлений дан-
данной топологич. группы и изучение возможности опи-
описания (разложения) произвольных П. т. г. с помощью
неразложимых. В общем случае обе задачи далеки
A983) от полного решения, но полученные в этих на-
направлениях результаты делают теорию П. т. г. осно-
основой гармонического анализа абстрактного, обобщаю-
обобщающего теорию рядов и интегралов Фурье, спектральную
теорию унитарных операторов, теорию жордановых
нормальных форм и систем обыкновенных дифференци-
дифференциальных уравнений с постоянными коэффициентами, а
также основой нек-рых разделов эргодической теории,
квантовой механики, статистической физики и теории
поля.
Наиболее важным разделом общей теории П. т. г.
является теория унитарных представлений, имеющих
многочисленные приложении и обладающих рядом
свойств, упрощающих их изучение. В частности, орто-
ортогональное дополнение к инвариантному подпростран-
подпространству унитарного представления инвариантно, поэтому
всякое унитарное П. т. г. вполне приводимо; для уни-
унитарных представлений условия полной неприводимо-
неприводимости, (топологической) неприводимости и операторной
неприводимости равносильны (но, вообще говоря, сла-
слабее условия алгебраич. неприводимости).
Другой класс П. т. г., имеющий многочисленные при
ложения, образуют конечномерные представления. Изу
ченио представлений этого класса во многом облегча-
облегчается относительным упрощением аналитич. сложности
задачи по сравнению с общим случаем; в частности,
неприводимое конечномерное П. т. г. вполне неприво-
димо. Однако теория конечномерных П. т. г. построена
A983) достаточно полно лишь для нек-рых классов
топологич. групп (в частности, для полупростых групп
Ли и для групп R и %). Для несколько более широкого
класса групп, содержащего класс групп Ли, существу-
существует полное описание неприводимых конечномерных
П. т. г.
Теория П. т. г. более разработана для локально
компактных групп. Важнейшим свойством класса
локально компактных групп является его совпадение с
классом полных топологич. групп, на к-рых существует
ненулевая правоинварпантная регулярная борелев-
ская мера т (см. Хаара мера). Этот факт позволяет
включить в число групповых алгебр локально компакт-
компактной группы G банахову симметричную алгебру //, (G) —
~Li{G, m) (относительно свертки), к-рая играет ре-
тающую роль в теории ограниченных (т. е. имеющих
ограниченный образ) П. т. г. G в банаховых простран-
пространствах. Формула
nU)=\af{g)n(g) dm(g), f^L^G),
устанавливает взаимно однозначное соответствие между
ограниченными представлениями л, локально компакт-
компактной группы С и (непрерывными) представлениями я
алгебры L1(G), обладающими тем свойством, что
л(/,] (G))ff л плотно в пространстве Н~ представлении
л; при этом унитарные П. т. г. соответствуют симмет-
симметричным представлениям алгебры L, (G). Другое свой-
свойство локально компактных групп состоит н том, что
их представления в бочечных л. в. п. суть непрерывные
представления.
Наиболее развитая часть теории П. т. г.— теория
унитарных представлений локально компактных групп.
В связи с существованием меры Хаара на локально
компактных группах оказывается возможным изучение
регулярного представления группы G в пространстве
/J2(G), приводящее, в частности, к аналогу Иланшереля
формулы для таких групп, а также к выделению основ-
основной, дополнительной и дискретной серий унитарных
П. т. г. рассматриваемого класса (см. Дополнительная
серия, Дискретная серия). Важнейшими общими зада-
задачами теории унитарных П. т. г. являются задачи по-
построения неприводимых представлений и факторпред-
ставлений, разложения представлений в прямой инте-
интеграл, изучения дуальных объектов'и связанные с ними
вопросы теории сферич. функций, теории характеров и
гармонич. анализа, в том числе — изучения различных
групповых алгебр.
Исключительно богатым приложениями подклассом
класса локально компактных групп является класс
групп Ли. Теория бесконечномерных представлений
групп Ли, включающая теорию представлений классич.
групп, является одним из наиболее быстро развиваю-
развивающихся разделов общей теории П. т. г. Мощным методом
изучения П. т. г. Ли является орбит метод.
Другой важный подкласс класса локально компакт-
компактных групп образуют компактные группы. Представле-
Представления компактных групп — один из наиболее завершен-
завершенных разделов общей теории П. т. г., являющийся ин-
инструментом изучения П. т. г., содержащих компактные
подгруппы. Актуальным разделом теории представле-
представлений компактных групп является группа задач, свя-
связанных с вопросами разложения ограничения на под-
подгруппу н тензорного произведения конкретных пред-
представлений компактных групп Ли. Разделом теории
представлений компактных групп, имеющим много-
многочисленные приложения в алгебре и анализе, является
теория конечных групп представлений.
Не только упомянутая выше задача изучения нераз-
неразложимых П. т. г., но и более простая задача описания
зацеплений вполне неприводимых представлений, свя-
связанная с соответствующей теорией когомологий, реше-
решена A983) лишь для нек-рых групп, несмотря на ее
важность в построении гармонич. анализа на группах.
Действительно, в терминах неразложимых П. т. г. (а
именно, входящих в аналитич. продолжение соответ-
соответствующей основной серии) для нек-рых групп Ли (соот-
(соответственно групп Шевалле) получен аналог теоремы
1Тэли — Винера, дающий описание образа групповой
,1лгебры финитных бесконечно дифференцируемых (соот-
(соответственно финитных локально постоянных) функций
на группе при преобразовании Фурье (т. е. при отоб-
отображении f-+{af(g)n(g)d\i(g), I?K(G), сопоставляю-
сопоставляющем функции на группе операторнозначную функцию
на множестве представителей пространства классов эк-
эквивалентности представлении этой группы). Менее об-
щая задача описания всех вполне неприводимых пред-
представлений данной группы решена A983) лишь для ло-
локально компактных групп, факторгруппа к-рых по
центру компактна (вполне неприводимые представле-
представления таких групп конечномерны, и набора этих пред-
представлений достаточно для получения аналога теоремы
Пэли — Винера) и для нек-рых линейных групп Ли (в
том числе для комплексных полупростых). Как в те-
теории унитарных, так и в теории неунитарных П. т. г.
накоплен богатый фактич. материал, относящийся к
конкретным представлениям конкретных групп и к при-
приложениям этих результатов к отдельным задачам гар-
монич. анализа на таких группах.
Ряд вопросов теории П. т. г. связан с изучением
П. т. г. в пространствах с индефинитной метрикой.
Для нек-рых полупростых групп Ли нолучено полное
описание вполне неприводимых представлений в таких
пространствах (к их числу относятся, в частности, не-
неприводимые конечномерные представления таких групп)
и найдено разложение тензорных произведений нек-рых
неприводимых представлений этого типа на неприводи-
неприводимые унитарные представления. Теория операторно не-
неприводимых представлений полуиростых групп Ли в
пространствах с индефинитной метрикой и определение
структуры их инвариантных подпространств тесно свя-
связаны с аналитич. продолжением основной серии пред-
представлений этих групп.
Успехи теории П. т. г. связаны с развитием теории
проективных представлений, с распространением ряда
методов теории представлений групп Ли (в частности,
метода орбит) на локально компактные группы общего
вида, а также с развитием теории П. т. г., не являю-
являющихся локально компактными (групп гладких функ-
функций на многообразии со значениями в группе Ли, групп
диффеоморфизмов гладких многообразий, бесконеч-
бесконечномерных аналогов классич. групп и нек-рых других).
Изучение представлений таких групп оказалось связан-
связанным с теорией вероятностей (в частности, теорией мар-
марковских процессов) и задачами статистич. физики.
С другой стороны, установлены глубокие связи теории
представлений групп матриц 2-го порядка над локально
компактными полями (и нек-рых связанных с ними
групп) с задачами теории чисел.
Лит.: [1] Б а р у т А., Р о н ч к а Р., Теория представле-
представлений групп и ее приложения, пер. с англ., т. 1—2, М., 1980; [2]
В и л с и и и и Н. Я., Специальные функции и теория пред-
представлений групп, М., 1965; [3] ГельфанД И. М., Гра-
Граев М. II., Л я т е ц к л й - Ш а п и р о И. И., Теория пред-
представлений и антоморфныс функции, М., 1966; [4] Жаке Э.,
Л е н г л ендс Р., Автоморфные формы на GL2, пер. с англ.,
М., 1973; 15] Ж е л о б е н к о Д. П., Компактные группы Ли
и их представления, М., 1970; [6] его же, Гармонический
анализ на полупростых комплексных группах Ли, М., 1974;
[7] Ж е л о б е н к о Д. П., Ш т е р н А. И., Представления
групп Ли, М., 1983; [8] Кириллов А. А., Элементы тео-
теории представлений, 2 изд., М., 1978; [9] К л и м ы к А. У.,
Матричные элементы и коэффициенты Клебша — Гордана пред-
представлений групп, К., 1979; [10] Л е н г С, SL2 (R), пер. с англ.,
М., 1977; [11] Наймарк М. А., Нормированные кольца,
2 изд., М., 1968; [12] его же, Теория представлений групп,
М., 1976; [13] G а а 1 S. A., Linear analysis and representation
theory, В. — [а.о.], 1973; [14] Lie groups and their representa-
lions, Bdpst, 1975; [15] Mackey G. W., Unitary group rep-
representations In physics, probability and number theory, Reading,
1978; fl6] Non-commutative harmonic analysis, B.— [a.o.],
1979. А. И. Штерн.
ПРЕДСТАВЛЕНИЙ КОЛЬЦО — коммутативное
кольцо, определяемое, следующим образом. Аддитив-
Аддитивная группа П. к. порождена классами эквивалентности
представлений группы С в векторных пространствах,
а определяющие соотношения имеют вид л=я1+я2,
где я — класс эквивалентности нек-рого представле-
представления, п1— класс эквивалентности его подпредставления,
а я2— класс эквивалентности соответствующего фактор-
представления я; операция умножения в П. к. сопо-
сопоставляет классам эквивалентности представлений ях и
я2 класс эквивалентности их тензорного произведения.
П. к. иногда наз. кольцом Гротендпка
группы G. Для локально компактных групп П. к.
группы G принято называть коммутативное кольцо,
определенное операциями прямой суммы и тензорного
произведения в множестве классов эквивалентности
непрерывных унитарных представлений группы G.
Изучение структуры П. к. плодотворно для компакт-
компактных групп, где оно приводит к теории двойственности
в терминах блок-алгебр, а также в более общем слу-
случае для групп типа I, где изучение структуры П. к.
может быть сведено к изучению структуры тензорных
произведений неприводимых унитарных представле-
представлений. А. И. Штерн.
ПРЕДСТАВЛЕНИЙ ТЕОРИЯ — теория, изучающая
гомоморфизмы полугрупп (в частности, групп), алгебр
или других алгебраич. систем в соответствующие сис-
системы эндоморфизмов нек-рой подходящей структуры.
Особенно часто рассматриваются линейные
представления, т. е. гомоморфизмы полу-
полугрупп, групп, ассоциативных алгебр или алгебр Ли
в полугруппу, группу, алгебру линейных преобразо-
преобразований нек-рого векторного пространства V. Такое
представление наз. также линейным пред-
представлением в пространстве V, а V
наз. пространством представления.
Часто под П. т. понимают именно теорию линейных
представлений. Если пространство V конечномерно,
то его размерность наз. размерностью пред-
представления, а само представление — к о н е. ч-
номерным. Таким образом, различаются конечно-
конечномерные и бесконечномерные представления. Представ-
Представление наз. точным, если оно инъективно.
Изучение линейных представлений полугрупп, групп
и алгебр Ли сводится к изучению линейных представ-
представлений ассоциативных алгебр. А именно, линейные пред-
представления полугрупп (линейные представления групп)
в пространстве V над полем к находятся в естественном
взаимно однозначном соответствии с представлениями
соответствующей полугрушювоп (групповой) алгебры
над к в пространстве V. Представления алгебры Ли L
над к взаимно однозначно соответствуют линейным
представлениям ее универсальной обертывающей алге-
алгебры.
Задание линейного представления ср ассоциативной
алгебры А в пространстве Г равносильно заданию на V
структуры А -модуля, называемого модулем пред-
представления ф. При рассмотрении представлений
группы G или алгебры Ли L говорят также о С-модулях
пли i^-модулях (см. Модуль). Гомоморфизмы модулей
представлений наз. сплетающими операторами. Изо-
Изоморфным модулям соответствуют эквивалент-
эквивалентные представления. Подмодуль модуля V
представления ф — это подпространство WczV, инва-
инвариантное относительно ф; индуцируемое в W пред-
представление наз. подпредставлением, а пред-
представление, индуцируемое в фактормодуле V/W,—
факторпредставлением представления ф.
Прямые суммы модулей соответствуют прямым суммам
представлений, неразложимые модули — неразложи-
неразложимым представлениям, простые модули — неприводи-
неприводимым представлениям, а полупростые модули — вполне
приводимым представлениям. Определяются также тен-
тензорное произведение линейных представлений, внешняя
и симметрия, степени представления (см. Тензорное
произведение представлений).
Наряду с абстрактной (или алгебраической) П. т.
существует теория представлений топологич. объек-
объектов, напр, топологич. групп или банаховых алгебр
(см. Непрерывное представление, Представление топо-
топологической группы). О. А. Иванова.
ПРЕДСТАВЛЕНИЯ КЛАССИЧЕСКИХ ГРУПП
в тензорах — линейные представления групп
GL(V), SL(V), O(V,f), SO(V,f), Sp(V,J) (где V\
есть n-мерное векторное пространство над полем к,
/ — невырожденная симметрическая или знакопере-
ценная билинейная форма на V) в инвариантных под-
подпространствах тензорных степеней Тт ( V) пространст-
пространства V. Если к — поле нулевой характеристики, то все
неприводимые полиномиальные линейные представле-
представления указанных групп реализуются в тензорах.
В случае к=С перечисленные выше группы яв-
являются комплексными группами Ли. Для всех них, кро-
кроме GL(V), все (дифференцируемые) линейные пред-
представления полиномиальны; всякое линейное представ-
представление группы GL(V) имеет вид g н> (det g)kR (g), где
&6 Z, a R —полиномиальное линейное представле-
представление. Классические компактные группы Ли U„, SUn,
Оп, SOn, Spn имеют те же комплексные линейные
представления и те же инвариантные подпространства
в пространствах тензоров, что и их комплексные обо-
оболочки GLn(C), SLn{C), On(C), SOn(C), Sp2n(C).
Поэтому результаты теории линейных представлений,
полученные для классических комплексных групп Ли,
переносятся на соответствующие компактные группы и
наоборот («унитарный трюк» Вейля). В частности, с,
помощью интегрирования по компактной группе дока-
доказывается полная приводимость линейных представле-
представлений классических комплексных групп Ли.
Естественное линейное представление группы GL(V)
в пространстве Tm(V) определяется по формуле
g(vi®-..®vm) = gvi®...@gvm, g?GL(V), v;?V.
В том же пространстве определено линейное представ-
представление симметрич. группы Sт:
Операторы этих двух представлений перестановочны;
тем самым в Tm(V) определено линейное представле-
представление группы GL(V)XS ,„. Если char к--- 0, то прост-
пространство Tm(V) может быть разложено в прямую сум-
сумму минимальных (GL (Т')Х 5,„)-инвариантных подпро-
подпространств:
Здесь суммирование происходит по всем разбиениям
X числа т, содержащим не более п слагаемых, U\ —
пространство абсолютно неприводимого представления
Т\ группы S,п, отвечающего разбиению X (см. Пред-
Представление симметрической группы), a V%—простран-
V%—пространство нек-рого абсолютно неприводимого представления
Rl группы GL (V). Разбиения X удобно представлять
в виде наборов (Я15 Х2, ¦ . ., Хп) целых неотрицательных
чисел, удовлетворяющих условиям Х{^Х^. . .^Хп,
Подпространство V% ®UidTm (V) разлагается в сум-
сумму минимальных GL (Г)-инвариантных подпространств,
в каждом из к-рых реализуется представление Ri.
Эти подпространства могут быть явно получены приме-
применением к Tm(V) Юнга симметризаторов, связанных с
разбиением X. Напр., для разбиения Х=(т, 0, . . ., 0)
(соответственно Х=A, ...,1,0,..., 0) при т<:и)
dim С/д, = 1 и Vi®U\ есть минимальное GL (['^-инва-
(['^-инвариантное подпространство, состоящее из всех симмет-
симметрия, (соответственно кососимметрич.) тензоров.
Представление R\ характеризуется следующими
свойствами. Пусть BdGL(V) — подгруппа, состоящая
из линейных операторов, к-рые в нек-ром базисе (ех, ...,
еп) пространства V записываются верхними треуголь-
треугольными матрицами. Тогда операторы Кх(Ь), Ь?В, имеют
единственный (с точностью до числового множителя)
общий собственный вектор и^, называемый старшим
вектором представления R%. Соответствующее
собственное значение (старший вес представле-
представления i?x) равно b^L . . . Ъ^п, где Ъц есть i-й диагональ-
диагональный элемент матрицы оператора Ъ в базисе (ех, . . ., е„).
Представления Rx, отвечающие различным разбие-
разбиениям X, не эквивалентны. Характер представления Я \
находится по ф о р м у л е В е й л я:
где zt, . . ., zn— корни характеристич. многочлена опе-
оператора g, Wi — обобщенный определитель Вандер-
монда, отвечающий разбиению X (см. Фробениуса форму-
формула), Wo— обычный определитель Вандермонда. Раз-
Размерность представления Да, равна
где /;-=Яг-+ге—I.
Ограничение представления R\ на унимодулярную
группу SL(V) неприводимо. Ограничения на SL(V)
представлений R\ n Яц эквивалентны тогда и только
тогда, когда fi,-=X,-+s (s не зависит от i). Ограничение
представления Rx группы GLn(k) на подгруппу
GLn_i(k) находится по правилу:
где (х пробегает все наборы (цг, . . ., fin_i), удовлетво-
удовлетворяющие условию
Я* > (хх 32 А,2 Ss (i2 Ss.. .35 (Xn-! ^ Я„.
Для всякой диаграммы Юнга d, отвечающей разбие-
разбиению Я, тензор vil^u'ci^Tm(V) (обозначения см. в ст.
Представление симметрической группы) является ре-
результатом альтернирования по столбцам диаграммы d
тензора^ (X) ¦ . . ®егту гДе h ~~ номер строки диаграм-
диаграммы d, в к-рой находится число к. Тензоры, построен-
построенные таким образом по всем стандартным диаграммам
d, образуют базис минимального Sт-инвариантного
подпространства vi($)U\, в к-ром реализуется пред-
представление Уд, группы Sm.
Линейное представление ортогональной группы
О (V, /) в пространстве Тт (V) устроено следующим
образом. Имеется разложение в прямую сумму двух
(О (V, /) X 5от)-инвариантных подпространств:
где Т™ (V) состоит из бесследных тензоров,
т. е. тензоров, свертка к-рых с формой / но любым двум
индексам равна нулю, а
Пространство T™(V) в свою очередь разлагается в пря-
прямую сумму минимальных (O(V, /)X ?т)-инвариантных
подпространств:
где V\aVx. При этом УхФ® тогда и только тогда,
когда сумма X'i-\-X'2 высот первых двух столбцов таб-
таблицы Юнга, отвечающей разбиению Я,, не превосходит
л,ив этом случае \'\ есть пространство абсолютно не-
неприводимого представления R\ группы O(V, /). Пред-
Представления R\, отвечающие различным разбиениям X,
не эквивалентны. Если разбиение X удовлетворяет
условию ^[-{-Х^^п, то после замены первого столбца
его таблицы Юнга столбцом высоты п—Х\ получается
таблица Юнга нек-рого разбиения X, также удовлетво-
удовлетворяющего этому условию. Соответствующие представле-
представления группы O(V,f) связаны соотношением R-(g)=
А
~(det g) R°x(g) (в частности, они имеют одинаковую
размерность).
Ограничение представления R\ на подгруппу SO(V,f)
абсолютно неприводимо, за исключением случая, когда
п четно и Л=Я (т. е. число слагаемых разбиения X равно
ге/2). В этом последнем случае оно распадается надполей
к или его квадратичным расширением в сумму двух
неэквивалентных абсолютно неприводимых представ-
представлений одинаковой размерности.
При вычислении размерности представления R\
можно считать, 4to_Xi<w/2 (в противном случав сле-
следует заменить X на X). Пусть ij=X,+ re/2—i. Тогда при
нечетном п
=IUl 7ф1 11,./=
а при четном n ж
1=\,г<]
При Х~Х последняя формула дает половину размер-
размерности представления li\, т. е. размерность каждого
из соответствующих ему абсолютно неприводимых пред-
представлений группы SO(V, /).
Разложение пространства Tm(V) относительно сим-
плектич. группы Sp{V, j) аналогично разложению от-
относительно ортогональной группы, с той разницей, что
\ тогда и только тогда, когда Xi<n/2. Размер-
Размерность представления R\ находится в этом случае по
формуле
"/2 '' ТТ"/2
,-, /=l
aim ni -Ц,_, и/2_г+1 11,-
где l^i++
Лит.; [1] В ей ль Г., Классические группы, их инвари-
инварианты и представления, пер. с англ., М., 1947; [2] Ж е л о б е н-
к о Д. П., Компактные группы Ли и их представления, М.,
1970; [3] X а м е р м е ш М., Теория групп и ее применение
к физическим проблемам, пер. с англ., М., 1966.
д. Б. Винберг.
ПРЕДСТАВЛЯЮЩАЯ ФУНКЦИЯ — непрерывная
функция / на топологич. пространстве X, снабжен-
снабженном непрерывным действием нек-рой группы G, орбита
к-рой \g*f\g?G} в пространстве всех непрерывных
функций на X порождает конечномерное подпростран-
подпространство. П. ф. иногда называют также сферически-
м и, или почти инвариантными, функ-
функция м и. П. ф. со значениями в поле k=R или О
образуют С-инвариантную /с-подалгебру F(X, k)o в
алгебре всех /с-значных непрерывных функций F(X, к)
на X. В случае, когда X~G — топологич. группа, дейст-
действующая на себе при помощи левых сдвигов, F(X, fc)c=
-~F(G, k)a совпадает с подпространством в F(G, к),
иорожденным матричными элементами конечномерных
непрерывных линейных представлений группы G. Если
при этом G компактна, то можно ограничиться матрич-
матричными элементами неприводимых представлений. Напр.,
если G=T — группа вращений плоскости, то П. ф. на
С — это тригонометрич. полиномы. Другим примером
являются классические сферич. функции на сфере,
к-рые суть П. ф. для стандартного действия группы вра-
вращений сферы.
Если G — компактная топологич. группа, непрерыв-
непрерывно действующая на пространстве X, являющемся объ-
объединением счетного числа компактов, то F(X, &)g
плотно в F(X, к) относительно компактно открытой
топологии (см. Петера — Вейля теорема). Аналогич-
Аналогичные утверждения справедливы для П. ф. различных
степеней гладкости на дифференцируемом многообра-
многообразии с гладким действием компактной группы Ли. С дру-
другой стороны, если G не допускает нетривиальных непре-
непрерывных гомоморфизмов в компактную группу (на-
(например, G — связная полупростая группа Ли без
компактных простых факторов), то всякая П. ф. на
компактном пространстве X с непрерывным действием
группы G является G-инвариантнон [4].
Если гладкое действие компактной группы Ли G
на дифференцируемом многообразии X имеет лишь
конечное число типов орбит, то алгебра F°°(X, k)Q всех
П. ф. класса С00 конечно порождена над подалгеброй
всех G-инвариантных функций класса 6'°° (см. [5]).
В частности, для однородного пространства X алгебра
F(X, C)q=/'°°(X, С)о конечно порождена и отож-
отождествляется с алгеброй регулярных функций на аффин-
аффинном однородном алгебраич. многообразии над С, мно-
множество вещественных точек к-рого совпадает с X.
Важной для приложений является задача о разложении
С-модуля F(X, C)q в прямую сумму простых G-моду-
лей. В случае, когда X — симметрическое однородное
пространство компактной группы G, она была решена
Э. Картаном [1].
Обобщением П. ф. являются представляю-
представляющие сечения нек-рого векторного С-расслоения
Е над G-пространством Х, т. е. непрерывные сечения,
G-орбиты к-рых порождают конечномерные подпро-
подпространства в пространстве Г(А') всех непрерывных се-
сечений, напр, представляющие тензорные поля на глад-
гладких многообразиях с гладким действием группы Ли
G; они образуют G-иодмодуль Г(?H<гГ(?) (см. [5]).
Если группа G компактна, то подмодуль Г (Е)q плотен
в Т(Е). В случае, когда X — симметрическое однород-
однородное пространство группы G, изучено (см. [3]) разложе-
разложение G-модуля Г(Е)а на простые компоненты. Если же
X — компактное однородное пространство полупро-
полупростой группы Ли G без компактных факторов со связной
стационарной подгруппой, то
dim Г (Е)о < оо
(см. [2]).
Лит.: [1] С. а г t a n E., «Rend. Circ. Mat. Palermo», 192!),
v. 53, p. 217—52; [2] Дао Ван Ч а, «Успехи матем. наук»,
1975, т. 30, в. 5, с. 203—04; [3] Дзядык Ю. В., «Докл.
АН СССР», 1975, т. 220, № 5, с. 1019 — 22; [4] Л у к а ц к и ii
А. М., «Успехи матем. наук», 1971, т.
2«, в. 5, с. 212 — 13; [5] Он и щи к
А. Л., «Тр. Моск. матем. об-ва», 1970,
т. 35 с. 235 — 64. А. Л. Онищип.
ПРЕКРАЩЕНИЯ ТОЧКА —
особая точка плоской кривой, в
к-рой кривая обрывается. Окруж-
Окружность достаточно малого радиуса
с центром в П. т. пересекает -
кривую только в одной точке.
Например, у кривой у~х \пх
П. т.— начало координат (см. рис.). бсэ-з.
ПРЕОБРАЗОВАНИЕ — отображение и нек-рого
множества М (вообще говоря, наделенного нек-рой
структурой) в себя. Образ элемента а?М при преоб-
преобразовании и обозначается и (а), или иа, или аи, или а".
Совокупность всех П. множества М в себя образует
относительно операции умножения (суперпозиции) пре-
преобразований полугруппу, называемую симметри-
симметрической полугруппой на множестве М. Об-
Обратимые элементы этой полугруппы наз. подстановками.
Все подстановки на множестве М образуют подгруппу
симметрич. полугруппы — симметрическую группу.
См. также Подстановок группа, Преобразовании
группа. О. А. Иванова.
ПРЕОБРАЗОВАНИЙ ГРУППА — подстановок груп-
группа (G, М), действующая на множестве М. При этом если
на множестве М определена какая-либо структура и
алементы из G эту структуру сохраняют, то принято
говорить, что С есть группа преобразований этой
структуры. Наименование П. г. обычно отражает в
нек-рой мере наименование структуры, определенной
на М. Так, напр., если М.— векторное пространство
над телом, то группы, сохраняющие эту структуру,
наз. линейными группами. Более общо, линейными
группами наз. часто группы автоморфизмов модулей
над различными кольцами. В частности, если М — сво-
свободный конечномерный модуль над кольцом % целых
чисел, то говорят о кристаллографических группах. Если
М — топологич. пространство, a G состоит из автогомео-
автогомеоморфизмов пространства М, то говорят о группах не-
непрерывных преобразований. Если М=К есть поле, а
G — конечная группа автоморфизмов поля К, то G
является группой Галуа расширения K/L, где L — под-
подполе, состоящее из элементов, неподвижных при дей-
действии элементов из G. Рассматривается также ситуация,
когда группа G и множество М снабжены структурами
одного и того же типа, причем действие группы G на
М является морфизмом в соответствующей категории.
Напр., если G — топологич. группа, непрерывно дейст-
действующая на топологич. пространстве М, то говорят о
топологической группе преобразований; аналогично
определяются Ли группа преобразований, алгебраическая
группа преобразований.
Лит.: Ll] Математика, ее содержание, методы и значение,
т. 3, М., 1950, гл. 20. Л. А. Калужнип.
ПРЕОБРАЗОВАНИЙ ПОЛУГРУППА - всякая
подполугруппа симметрич. полугруппы Гц, где TQ—
совокупность всех преобразований множества Q. Част-
Частным случаем П. п. являются преобразований группы.
П. п. Рг^ Та , P^czTq^ наз. подобными, если
существуют биекции <р : Q1—>-Q2 и ^ : Pi—*-Pa такие,
что при ыа=р(а, P^Qj; u?Pt) имеет место (\ри) (сра)=
= <рР. Подобные П. п. изоморфны, но обратное, вообще
говоря, неверно. Однако в пределах нек-рых классов
П. п. из изоморфизма вытекает подобие. Таков, напр.,
класс II. п., включающих все такие преобразования и,
что uQ состоит из одного элемента. Задание полугруп-
полугруппы как П. п. несет большую информацию, чем ее зада-
задание с точностью до изоморфизма.
Принципиально важно выделение свойств П. п., ин-
инвариантных относительно изоморфизмов. Для нек-рого
класса П. п. Г условие, при к-ром полугруппа S
изоморфна нек-рой полугруппе из Г, наз. абстракт-
абстрактной характеристикой класса Г. Най-
Найдены абстрактные характеристики для нек-рых важных
II. п. Всякая полугруппа изоморфна нек-рой П. п.
Полугруппа S тогда п только тогда изоморфна нек-рой
симметрич. полугруппе Гн, когда она является макси-
максимальным плотным идеальным расширением (см. Рас-
Расширение полугруппы) какой-либо полугруппы А с
тождеством ху~х.
Из общей теории П. п. выделяется направление, при
к-ром преобразуемое множество Q наделено нек-рой
структурой (топологией, действием, отношением в Q и
т. п.), и рассматриваются П. п., связанные с этой
структурой (эндоморфизмы, непрерывные или линей-
линейные преобразования, сдвиги полугрупп и т. д.). Изу-
Изучение соотношений между свойствами структуры в Q
и свойствами полугруппы соответствующих преобразо-
преобразований является обобщением теории Галуа. В частности,
известны случаи, когда указанная П. п. вполне опреде-
определяет структуру (см., напр., Эндоморфизмов полугруппа).
Свойства левых и правых сдвигов полугрупп использу-
используются в общей теории полугрупп.
Обобщением понятия преобразования является ч а с-
тичное преобразование, отображающее
какое-либо подмножество й'сг?2 в Q. Бинарное отно-
отношение на множестве Й иногда трактуют как многознач-
многозначное (вообще говоря, частичное) преобразование этого
множества. Рассматриваемые относительно операции
суперпозиции (определяемой как умножение бинар-
бинарных отношений) однозначные и многозначные частичные
преобразования также образуют полугруппы. Целе-
Целесообразно рассматривать их как полугруппы, наделен-
ные дополнительными структурами (напр., отношением
включения бинарных отношений, включения или ра-
равенства областей определения, включения или равен-
равенства образов и т. д.).
Лит.: И] Л я пин Е. С, Полугруппы, М., 1960; [2]
Клиффорд А. X., Престон Г. Б., Алгебраическая
теория полугрупп, пер. с англ., т. 1—2, М., 1972; [3] Г л у с-
кин Л. М., «Матем. сб.», 1961, т. 55, №4, с. 421—48; [41
S с h e i п В. М., «Semigroup Forum», 1970, v. 1, № 1, p. 1—62.
Л. М. Глускин, Е. С. Ляпин.
ПРЕПЯТСТВИЕ—понятие гомотопич. топологии;
инвариант, равный нулю, если соответствующая задача
разрешима, и отличный от нуля — в противном случае.
Пусть (X, А) — пара клеточных пространств и У —
односвязное (более общо — гомотопически простое)
топологич. пространство. Можно ли данное непрерывное
отображение g : A—>Y продолжить до непрерывного
отображения / : X—>-У? Продолжение можно осуще-
осуществлять по остовам Хп пространства X. Пусть построено
такое отображение / : X" (J A-+Y, что /1 ^ = #• Для любой
ориентированной (ге+1)-мерной клетки Sn—*Y отоб-
отображение /|де„4-1 задает отображение S"~-yY (где S"
есть re-мерная сфера) и элемент ае?я„(У) (именно
здесь и используется гомотопич. простота пространства
Y, позволяющая игнорировать выбор отмеченной точ-
точки). Таким образом, возникает коцепь
с? + х?С» + 1{Х; я„(У)), ^ь1(е« + ')=а,.
Так как для еп + 1аА , очевидно, tf + 1(e"^ *)=0, то на
самом деле
cf + 1?Cn + i(X, A;nn(Y)).
Очевидно, е"+1=0 тогда и только тогда, когда / про-
про"+1
должается на Xn + l, т. е. коцепь с"+1 является пре-
препятствием к продолжению / на Xtt + 1.
Коцепь с" + 1? С"+ 1(Х, А; я„(У)) является коциклом.
Из того, что с—0, вообще говоря, не следует, что g
не продолжается на X : / может не продолжаться на
X" + i в силу неудачного выбора продолжения g на X".
Может оказаться, напр., что отображение /|уп-]М л
\л и л
продолжается на Хп + \ т. е. что продолжение возможно
после отступления на один шаг. Оказывается, что П.
к этому является класс когомологий
4X, А; Яп(У)),
то есть [с"+1] —0 тогда и только тогда, когда существует
такое отображение J: Xn + 1\jA-+-Y, что ~f\xn-i\\A =
=/|^„_1ц^ (в частности, /I =§).Для доказательства
этого утверждения используется конструкция разли-
различающей.
Так как задачу гомотопич. классификации отобра-
отображений X—*-Y можно интерпретировать как задачу про-
продолжения, то теория П. применима и к описанию мно-
множества [X, Y] гомотопич. классов отображений из X в
Y. Пусть /=[0, 1] и пусть А~ХХ {0, 1} — подпрост-
подпространство в XXI. Тогда пара отображений /0, f1 : X-+Y
интерпретируется как отображение G : A—>Y, G(x, i) =
—f[(x), г=0, 1, и наличие гомотопии между /„ и Jx озна-
означает наличие отображения F : X Xl-yY, продолжаю-
продолжающего отображение G. При этом если гомотопия F по-
построена на и-мерном остове пространства X, то П. к ее
продолжению на X есть различающая
В качестве приложения можно укалать описание мно-
множества [X, Y]=-[X, А'(я, п)\, п>1, где А'(я, п) — Эй-
ленберга — Маклейна пространство: я,- (А (я, п))=0
при i^n, я„(А'(я, п))~л. Пусть /0 : X—>-А'(я, п) —
постоянное отображение, а / : X—>-А'(я, п) — произ-
вольное непрерывное отображение. Так как Н!(Х;
я,-(У))=Опри i<n, то/0 и/j гомотопны на Хп~ 1 и можно,
выбрав какую-нибудь такую гомотопию, определить
различающую
*•(/, fo)€C"(X; n.n(Y))=C"(X; л).
Класс когомологий [dn(f, fu)]?H"(X; л) определен
корректно, т. е. не зависит от выбора гомотопии между
/0 и / (в силу того, что я,-(У)=0 при i<n). Далее, если
отображения /, g : X—>-Y таковы, что [dn(f, /0)] =
= [dn(g, /„)], то [d"(f, g)]=0 и, значит, / и g гомотопны
на X". П. к продолжению этой гомотопии на все X лежат
в группах Н'(Х; я,-(У))=0 (так как i>n), и, значит,
отображения / и g гомотопны. Таким образом, гомото-
пич. класс отображения / полностью определяется эле-
элементом [d"(f, fo)]?Hn(X, я). Наконец, для любого
элемента х?Лп(Х,п) найдется отображение / с
[d"(f, /„)]=* и потому [X, К(п, п)]=Я"(Х; я). Ана-
Аналогично: если я,-(У)— г при г<ге и dim Х<:ге,то[Х, У]-~
Я(Х (У))
(; „())
При исследовании задачи продолжения рассматрива-
рассматривалась возможность продолжения после «отступления на
один шаг». Полное решение задачи требует анализа
возможности продолжения после отступления на произ-
произвольное число шагов. Для этой цели используются ко-
когомологические операции или Постникова системы.
Так, для описания множества [X, Y], где яг-(У)=0
при 1<п, л„(У)^0, dim X=n-\-r, требуется, вообще
говоря, исследовать возможность отступления на г+1
шаг, для чего надо исследовать первые п-\-г этажей
системы Постникова пространства Y, т. е. использо-
использовать когомологич. операции порядков <г (в ст. Кого-
Когомологические операции эта задача разобрана для г=1).
Теория П. используется также в более общей ситуа-
ситуации продолжения сечений. Пусть р : Е-+В — нек-рое
расслоение со слоем F (причем я1(^)=0 и пх(В) дей-
действует на щ(Р) тривиально), пусть АаВ и s : A-+E —
нек-рое сечение (т. е. такое непрерывное отображение,
что ps(a)~a). Можно ли продолжить s на все В? Соот-
Соответствующие П. лежат в группах Hn + l(B; nn(F)). За-
Задача продолжения получается из этой задачи, если по-
положить В~Х, E=XXY, p(x, y)=x, s(a) = (a, g(a)).
Аналогичным образом с помощью теории П. исследу-
исследуется и задача классификации сечений.
Наконец, в задаче продолжения можно снять огра-
ограничение гомотопич. простоты пространства Y (и ана-
аналогично в задаче о сечениях); для этого надо использо-
использовать когомологий с локальными коэффициентами.
ЯЗ. Б. Рудяк.
ПРЕСЛЕДОВАНИЯ ИГРА — антагонистическая
дифференциальная игра преследователя (догоняющего)
Р и преследуемого (убегающего) Е, движения к-рых
описываются системами дифференциальных уравнений:
P:'x = f(x, и), E:y = g(y, v),
где х, у — фазовые векторы, определяющие состояния
игроков Р и Е соответственно,; и, v — управляющие
параметры, выбираемые игроками в каждый момент
времени из заданных компактных множеств U, V
евклидовых пространств. Целью Р может быть, напр.,
сближение с Е на заданное расстояние, что формально
означает попадание х в Z-окрестность у A^0). При
этом различаются случаи сближения за минимальное
время (П. и. на быстродействие), к заданно-
заданному моменту времени (П. и. с предписанной
продолжительностью) и до момента дости-
достижения игроком Е нек-рого множества (игра с «линией
жизни»). Сравнительно хорошо изучены игры с полной
информацией, когда оба игрока знают фазовые состоя-
состояния друг друга в каждый текущий момент времени.
Под решением П. и. понимается нахождение ситуации
равновесия.
Лит.: [1] Понтрягин Л. С, «Успехи матем. наук»,
1966, т. 21, в. 4, с. 219—74; [2] К р а с о в с к и й Н. Н., С у б-
ботин А. И., Позиционные дифференциальные игры, М.,
1074; [3] Айзеке Р., Дифференциальные игры, пер. с англ.,
М., 1967; [4] Пе трос ян Л. А., Дифференциальные игры
преследования, Л., 1977. Л. А. Петросян.
ПРИБЛИЖЕНИЕ — то же, что аппроксимация. Тер-
Термин «П.» иногда употребляется и смысле приближаю-
приближающего объекта (напр., начальное П.).
ПРИБЛИЖЕНИЕ В СРЕДНЕМ — приближенно
заданной и интегрируемой на промежутке [а, Ь] функ-
функции f(t) функцией (р(?), когда за мору погрешности
принята величина
li(f,<t)=\ba\f(t)-<p(t)\dt.
В более общем случае, когда
(О (q >0),
где a(t) — неубывающая на [а, Ь\ отличная от постоян-
постоянной функция, говорят о средне степенном (с
показателем д) приближении относительно рас-
распределения da(t). Если a(t) абсолютно непрерывна
и p(t)~o' (t), получают среднестепенное
приближение с весом p(t), если же a(t) —
ступенчатая функция со скачками ck в точках tf. из
[а, Ъ], то приходят к взвешенному средне-
степенному приближению в системе
точек {ifc} с мерой погрешности
М/. ф) = 2***1/ (**)—фС**)!'7-
Естественным образом эти понятия обобщаются на
случай функций многих переменных.
Лит.: Ц] Гончаров В. Л., Теория интерполирования
и приближения функций, 2 изд., М., 1954; [2] Н и к о л ь-
с к и й С. М., Приближение функций многих переменных и тео-
теоремы вложения, 2 изд., М., 1977.
Н. П. Корнейчук, В. П. Моторный.
ПРИБЛИЖЕНИЕ ФУНКЦИЙ — замена по опре-
определенному правилу функции /(/) близкой к ней в том
или ином смысле функцией <p(f) из заранее фиксиро-
фиксированного множества эд (приближающего мно-
множества). Предполагается, что функция / определена
на том множестве Q m-мерного евклидова пространства
(в частности, действительной оси), на к-ром осуществля-
осуществляется приближение, она может быть задана явно через
элементарные функции или быть решением нек-рого
уравнения. Если о функции f(t) располагают неполной
информацией, то тогда речь идет, по существу, о при-
приближении задаваемого этой информацией целого класса
функций.
Практич. необходимость в П. ф. возникает в самых
различных ситуациях, когда нужно функцию /(?) заме-
заменить более гладкой или более простой и удобной для
вычислений, восстановить функциональную зависи-
зависимость по экспериментальным данным и т. п.
В общей задаче П. ф. обычно можно выделить следу-
следующие более частные задачи: выбор приближающего
множества 9J; выбор меры погрешности приближения;
выбор метода приближения, т. е. правила, по к-рому
функции f(t) сопоставляется функция cp(i) из 9(';
исследование и оценка погрешности приближения.
При выборе приближающего множе-
множества 5R, помимо безусловного требования обеспе-
обеспечить нужную точность приближения, руководствуются
стремлением иметь дело С простыми по структуре и
удобными для вычисления функциями ф(/), на к-рые
могут накладываться априорные условия, связанные,
напр., с гладкостью.
Классич. аппаратами приближения являются алге-
алгебраические (если Q — ограниченное замкнутое множе-
множество) и тригонометрические (в периодич. случае)
полиномы одного и многих переменных. Широкое пси-
менение их в качестве приближающего множества обу-
обусловлено, в частности, принципиальной возможность!*
приблизить непрерывную функцию алгебраическими
или тригонометрич. полиномами с любой наперед за-
заданной погрешностью. Точность приближения может
быть повышена за счет увеличения степени полинома,
что, однако, усложняет приближающий аппарат и
увеличивает вычислительные трудности при его не
пользовании. На практике в качестве приближающего
множества берут подпространства алгебраических или
тригонометрич. полиномов фиксированного порядки
и стремятся получить нужную точность с помощью
полиномов возможно меньшей степени. Более общий v.
в то же время более гибкий аппарат приближения полу
чают, рассматривая обобщенные полиномы
гДе {фь • ¦ м 4>n} — нек-рая система линейно незави-
независимых функций, к-рую можно выбирать в зависимости
от условий конкретной задачи и априорных требований
на ф(?)-
Во многих задачах более естественным и удобным с
вычислительной точки зрения, чем классич. полиномы
аппаратом приближения оказались сплайны. Если
Длг={й = т0 < Tj <.. .< Тлг=6}, N Ss2, A
фиксированное разбиение отрезка [а, Ь], то (п о л п н о-
м и а л ь н ы м) сплайном порядка г дефекта
к (k—i, 2, . . ., г) по разбиению Ад- наз. функцию s(t),
«склеенную» в точках хг, т2, . . ., Тдг_х из алгебрап':
многочленов степени г так, что на всем отрезке \а,Ь]
она непрерывна вместе со своими производными дс
(г—к)-ю порядка включительно. Таким образом, s(t)?
^С~к[а, Ь] и s{t) есть алгебраич. многочлен степени г
на каждом промежутке (т,-!, т,), i—i, 2, . . ., Л'.
Напр., ломаная с узлами в точках т,- есть сила п и
первого порядка дефекта 1; непрерывно
дифференцируемая на [й, Ь] функция s(t), совпадающая
на [t;_i, т,'], г=1, . . ., Л', с кубич. многочленом, ест),
кубический сплайн дефекта 2 и т. д.
Аналогично определяются сплайны двух и большего
числа переменных. Имея конечную гладкость, сплайны
обладают большей, чем полиномы, локальной гибко-
гибкостью: изменение значений сплайна на нек-ром проме-
промежутке (а, Р) мало сказывается (или совсем не сказыва-
сказывается) на поведении его вне (ос, E). Преимущества сплай-
сплайнов, помимо простоты машинной реализации, сказы-
сказываются, в частности, там, где информация о приближае-
приближаемой функции имеет дискретный характер, напр, зна-
значения в нек-рых точках самой функции / и, быть может,
нек-рых ее производных.
Если / (t) имеет особенности или приближение осу-
осуществляется в неограниченной области, то удобным
аппаратом приближения являются рациональные дроби
p(t)lq{t), где p(t) и q(t) — алгебраич. многочлены. За-
Заданные на всей действительной оси непериодич. функ-
функции приближают также целыми функциями экспонен-
экспоненциального типа.
Мера погрешности и. (/, ср) выбирается
обычно с учетом условий конкретной задачи и имею-
имеющейся информации о приближаемой функции f(t).
Чаще всего дело сводится к выбору содержащего /
функционального пространства, в метрике к-рого це-
целесообразно оценивать погрешность приближении.
Если
то речь идет оравно мерном, или ч е б ы ш е в-
с к о м, приближении, если же
то говорят о сроднестепенном прибли-
ж е и и и, к-рое при р—Л наз. приближением
в средне л. Особое значение имеет случай р=2 —
среднеквадратическое приближе-
приближение, когда погрешность наилучшего приближения
функции / конечномерным подпространством может
быть точно выражена через нек-рые определители.
В нек-рых задачах требования близости функций /
и q> в различных точках различны; для учета этой не-
неоднородности вводят весовую функцию р(<MгО и рас-
рассматривают взвешенное приближение
с мерой погрешности
u.(/, <p)=sup|/(«) —Ф(<IР(О
tQ
P(.f,<?)=lQ\f(t)-q,(t)\Pp(t)dt, p
0.
Носовая функция позволяет также обеспечить конеч-
конечность погрешности, если, напр., /(t) неограничена.
Если погрешность должна учитывать близость / и
Ф только в отдельных точках ?& (k=i, . . ., iV) из
Q, то в качестве ,и (/, ср) .можно выбрать одну из величин
max \f(tk)—(?(tk)\
в к-рые также могут вводиться весовые коэффициенты.
При решении вопроса о том, по какому правилу вы-
выбирать из множества 5R приближающую функцию
ср (?)=ф (/, t) (n p и выборе метода прибли-
приближения), естественно стремление обеспечить по воз-
возможности более высокую точность приближения и од-
одновременно простоту построения ф (/, t) по имеющейся
информации о приближаемой функции f(t). Первое
требование ориентирует па «ближайшую» к / (t) функ-
функцию ф/(<) из Ш, т.е. такую, что
Ц (/. Ф/)= inf Iх (/> Ф)-
!десь сразу же возникают вопросы о существовании
и единственности такой функции (функции н а и-
[учшего приближения), а также о ее
чарактеристич. свойствах (см. [5]). Существование
гарантируется, если ЭД — замкнутое локально ком-
компактное множество, в частности конечномерное под-
подпространство. Единственность зависит как от свойств
приближающего множества SR (см. Хаара условие,
Чебышева система функций), так и от метрики, опре-
определяющей меру погрешности р, (/, <р). Известен ряд
необходимых и достаточных условий, к-рым должна
удовлетворять функция наилучшего приближения tfy (t)
в той или иной ситуации (см. Наилучшего приближе-
приближения многочлен, Чебышева теорема, Маркова крите-
критерий). Однако эти критерии, как правило, не дают спо-
способов эффективного построения функции q>/(t). Поэтому
большое значение имеют методы, к-рые позволяют по
информации о приближаемой функции / (t) эффектив-
эффективно построить нек-руго функцию ср (/, t) из $i, обеспечи-
обеспечивающую приемлемое приближение. Здесь, в первую
очередь, надо говорить о линейных мето-
методах (когда (f(a.1fr\-a2f2, t)—a^(/,, г)+а2ф(/з> t)),
к к-рым, в частности, относится метод интерполяции.
Зафиксировав точки гх, . . ., tN из Q, можно выби-
выбирать ф(/, () среди тех функций ф (I) из Ш, к-рые удов-
удовлетворяют условию интерполяции
4(tk)^}{tk), k^-l, 2 Лг. B)
Если 9t — линейное многообразие и в нем существует
система функций ф,, . . ., фдг такая, что <р; (*,•)=1»
()° {к), то функция
принадлежит 91 и удовлетворяет условиям B); она
задает интерполяционный метод при-
приближения, являющийся, очевидно, линейным.
Функцию ср (/, t) можно выбирать, требуя совпадения
в точках tk ire только /(/) и ф (/, t), но и нек-рых их
производных; в этом случае говорят об интерпо-
интерполировании с кратными узлами. Если
Q=[a, b], o<i1<<2<. . .<%<&, то существует един-
единственный алгебраич. многочлен степени JV—1, а в не-
иериодич. случае (Ь—о=2я, tpj=t2n~\<ib) — единст-
единственный тригонометрич. полином порядка п—1, совпа-
совпадающий с / (г) в точках tfc. Кратное интерполирование
осуществляют интерполяционные полиномы Эрмита,
частным случаем к-рых является многочлен Тейлора,
когда в одной точке алгебраич. многочленом степени п
интерполируются значения функции и ее первых п
производных.
Интерполирование сплайнами имеет свои особен-
особенности, связанные с выбором точек интерполяции и
краевых условий, обеспечивающих существование и
единственность интерполяционного сплайна. Напр.,
сплайн s(t) порядка г^2 дефекта 1 по разбиению A),
принимающий заданные значения в JV различных
точках t[ интервала (а, Ъ) таких, что т^^г^т,-, i=
= 1, 2, . . ., N, существует и единствен, если задать
определенным образом краевые условия в виде та чи-
чисел s(v)(a) @<v<r—1) и ть чисел я<М-> (Ь) @<u<r—1),
причем та-\-ть—г. Функции f?Ck~J [а, о] можно
однозначно сопоставить сплайн s(f, t) порядка 2г—1
дефекта к A </?</¦) по разбиению A), потребовав вы-
выполнения равенств s(v> (/, x,-)=/(v) (т,-), v=0, I, . . .,
к—1; i=0, 1, . . ., N, а при к<г также нек-рых краевых
условий. При к—-г этот сплайн наз. эрмитовым,
а также локальным, т.к. его поведение на ин-
интервале (т,_1, т,) определяется только значениями
функции f (I) и ее производных /(v)@ (v=l, • . ., к—1)
в точках т,-_1 и т,-.
В П. ф. важную роль играют также линейные ме-
методы, построенные на базе разложения приближае-
приближаемой функции в ряд Фурье по яек-рой ортогональной
системе. В частности, в периодич. случае широко рас-
распространенным аппаратом приближения являются сум-
суммы Фурье по тригонометрич. системе и их различные
усреднения (см. Приближение функций; линейные
методы приближения).
Исследование и оценка погреш-
погрешности приближения — важный с практич.
точки зрения и в то же время наиболее содержатель-
содержательный в идейном отношении этап П. ф. Именно разра-
разработка методов оценки погрешности, изучение зависи-
зависимости ее от гладкостных характеристик приближаемой
функции, исследование и сравнение аппроксиматив-
аппроксимативных свойств различных аппаратов приближения при-
привели к формированию теории приближения функций —
одного из наиболее интенсивно развивающихся разде-
разделов математич. анализа.
Фундамент теории П. ф. был заложен работами
11. Л. Чебышева в 1854—59 (см. [1]) о наилучшем
равномерном приближении непрерывных функций
многочленами и рациональными дробями, а также ра-
работами К. Вейерштрасса [2], доказавшего в 1885, что
для любой непрерывной на отрезке [й, Ь] или непрерыв-
непрерывной на всей оси с периодом 2л функции /(?) сущест-
существует последовательность алгебраических (соответст-
(соответственно тригонометрических) полиномов Р„ (/, t) по-
рядка n=l, 2, ... такая, что при п
М/, Р„(/))
где <J есть [й, Ь] или, соответственно, вся числовая ось.
Аналогичные факты имеют место и в случае, когда
мера погрешности определяется интегральной метри-
метрикой, а также для функций многих переменных. Осо-
Особую важность приобретает исследование скорости убы-
убывания числовой последовательности ц (/, Рп (/)) в за-
зависимости от свойств приближаемой функции и от
выбора приближающих полиномов Р„(/, t). Наиболь-
Наибольший интерес представляет изучение наилучшего при-
приближения, а также приближения, доставляемого ли-
линейными методами, позволяющими по функции } (t)
эффективно построить полином /*„(/, t). Важный этап
в развитии теории П. ф., связанный с именами
Ш. Ж. Балле Пуссена (Ch. J. La Vallee Poussin),
Д. Джексона (D. Jackson), С. Н. Бернштейна, соста-
составили исследования связи между скоростью убывания
погрешности приближения функции /(<) выбранными
тем или иным способом многочленами Pn(f, t) степени
п (при п -*¦ оо) и дифференциально-разностными свой-
свойствами f{t). Оказалось, что эти свойства, т.е. нали-
наличие у f(t) производных, их гладкость и т. д., можно
в ряде случаев охарактеризовать через последователь-
последовательность приближающих полиномов и поведение достав-
доставляемой ими погрешности (см. Приближение функций;
прямые и обратные теоремы). Этим давалась новая,
конструктивная характеристика непрерывных и диф-
дифференцируемых функций. В первой трети 20 в. такая
проблематика была доминирующей в теории прибли-
приближения, что дало повод говорить о ней как о конструк-
конструктивной теории функций.
В 30—40-х гг. появились работы А. Н. Колмого-
Колмогорова, Ж. Фавара (J. Favard) и С. М. Никольского,
к-рые положили начало новому направлению исследо-
исследований, связанному с приближением классов функций
конечномерными подпространствами и получением точ-
точных оценок погрешности через задающие класс диф-
дифференциально-разностные характеристики. Речь идет
об отыскании величин
sup
i 6 «!
/, PN(f)),
где ц (g_, ф) — выбранная мера погрешности прибли-
приближения, Ш — нек-рый класс функций, а PtiJ.fi 1) ~~
приближающий (вообще говоря, обобщенный) поли-
полином, коэффициенты к-рого определяются выбором
метода приближения. Результаты такого рода позво-
позволяют сравнивать методы приближения с точки зре-
зрения их аппроксимативных возможностей и ставить
важную для приложений задачу отыскания для дан-
данного класса функций оптимального (наилучшего) при-
приближающего аппарата (фиксированной размерности
N). Исследования в этом направлении, базирующиеся
как на изучении свойств конкретных методов прибли-
приближения, так и на самых общих положениях функцио-
функционального анализа, оказались весьма плодотворными
и в идейном отношении, т. к. привели к установлению
принципиально новых фактов о связи между различ-
различными по характеру экстремальными задачами, позво-
позволили выявить глубокие и тонкие зависимости в тео-
теории функций. Благодаря этому оказалось возможным
до конца решить ряд экстремальных задач по наилуч-
наилучшему приближению важнейших классов функций
(см. [5], [7], а также Приближение функций; экстре-
экстремальные задачи на классах функций).
О некоторых других аспектах П.ф.
На приближающую функцию <p(t)=q>(/, t) из 9J мо-
могут накладываться дополнительные ограничения. Если
они не связаны с функцией / (напр., ограничения или
связи на коэффициенты приближающего полинома),
то дело фактически сводится к уточнению приближаю-
приближающего множества 41. Новая ситуация возникает, если
ограничения на ср (/, t) связаны с приближаемой фун-
функцией /; один из интересных случаев — одно-
одностороннее приближение, когда ср (/, t)
из 9J должна удовлетворять неравенству ср (/, ()</(*)
(или ^) и погрешность оценивается в интегральной
метрике (см. [19]).
В прикладных задачах наряду с явно задаваемыми
функциями возникает необходимость приближать кри-
кривые и поверхности, допускающие только параметрич.
задание; в качестве аппарата приближения могут слу-
служить, напр., параметрич. сплайны. Меру погрешности
здесь естественнее всего определить через хаусдорфово
расстояние, к-рое хорошо учитывает геометрич. бли-
близость таких объектов, и, напр., для кривых ^ и /2
определяется равенством
r (h, W = max f maxminp (P, Q), max min p(P, Q)\,
[piQi PHQel /
где p (P, Q) — евклидово (или какое-нибудь другое)
расстояние между точками Р и Q. Хаусдорфово рас-
расстояние является более предпочтительным при вы-
выборе меры погрешности и в нек-рых ситуациях П. ф.,
напр, когда разрывную функцию нужно аппроксими-
аппроксимировать функцией гладкой (см. [16]).
Решение ряда задач теории П. ф. тесно связано с
исследованием экстремальных свойств полиномов по
тем или иным конкретным системам функций (нера-
(неравенства для производных многочленов, полиномы,
наименее уклоняющиеся от нуля, и др.). В частности,
доказательство обратных теорем П. ф. существенно
базируется на неравенствах, дающих оценку нормы
(или значения в фиксированной точке) нек-рой про-
производной алгебраического или тригонометрич. поли-
полинома через те или иные характеристики самого поли-
полинома. В этом направлении известен ряд точных ре-
результатов, имеются обобщения на целые функции
(см. [6] - [10]).
Задача об нлгебраич. многочлене (с фиксированным
старшим коэффициентом), наименее уклоняющемся от
нуля в метрике С или Lp на отрезке [а, Ь], эквивалент-
эквивалентная задаче о наилучшем приближении функции V1
многочленами степени п—1, исследовалась П. Л. Че-
бышевым (метрика С) и его учениками (метрика L{).
Решение дают многочлены Чебышева первого (б1) и вто-
второго (Z-х) рода и многочлены Лежандра (L2), имеющие
широкое применение как в теоретических, так и в при-
прикладных исследованиях. Известен ряд результатов
для более общего случая, когда на коэффициенты
многочлена накладывается несколько связей (см. [6]).
Задача о моносплайне минимальной нормы, эквива-
эквивалентная отысканию наилучшего приближения функ-
функции t" сплайнами порядка п—1 со свободными узлами.
приобрела особое значение в связи с тем, что к ней
в ряде случаев сводится задача о наилучшей квадра-
квадратурной формуле (см. [17]).
О П. ф. в комплексной плоскости см. Приближение
функций комплексного переменного.
Лит.: tl] Ч е б ы ш е в П. Л., Вопросы о наименьших ве-
величинах, связанные с приближенным представлением функций
A859), Поли. собр. соч., т. 2, М.— Л., 1947, с. 151—235; [2]
We i erstra ss К., «Sitzungsber. Akad. Berlin», 1885, S. 633—
639, 789—805; [3] Гончаров В. Л., Теория интерполиро-
интерполирования и приближения функций, 2 изд., М., 1954; [4] Натан-
Натансон И. П., Конструктивная теория функций, М.— Л., 1949;
[5] Корнейчук Н. П., Экстремальные задачи теории при-
приближения, М., 1976; [6] Д з я д ы к В. К., Введение в теорию
б фй п М 1977
раномер рближия фуц ма, , ;
[7] Тихомиров В. М., Некоторые вопросы теории прибли-
приближений, М., 1976; [8] Никольский С. М., Приближение
функций многих переменных и теоремы вложения, 2 изд., М.,
1977; [9]- А х и е з е р II. И., Лекции по теории аппроксима-
аппроксимации, 2 изд., М., 1965; НО) Т и ы а н А. Ф,, Теория приОлиже-
ния функций действительного переменного, М., 1960; [11J К о-
р о в к и н П. П., Линейные операторы и теория приближе-
приближений, М., 1959; [12] А л б е р г Д ж., Н и л ь с о н Э., У о л ш
Д ж., Теория сплайнов и ее приложения, пер. с англ., М., 1972;
[13] Стечкин С. Б., Субботин Ю. Н., Сплайны в вы-
вычислительной математике, М., 1976; [14] Лоран П.-Ж.,
Аппроксимация и оптимизация, пер. с франц., М., 1975; [15]
К о л л а т ц Л., Крабе В., Теория приближений. Чебышев-
ские приближения и их приложения, пер. с нем., М., 1978; [16]
Сендов Б., Хаусдорфовые приближения, София, 1979; [17]
Никольский С. М., Квадратурные формулы, 3 изд., М.,
1979; [18] Завьялов Ю. С, К в а с о в Б. И., М и р о ш-
ниченко В. Л., Методы сплайн-функций, М., 1980; [19]
Корнейчук Н. П., Л и г у и А. А., Доронин В. Г.,
Аппроксимация с ограничениями, К., 1982. Н. П. Корнейчук.
ПРИБЛИЖЕНИЕ ФУНКЦИЙ; линейные
методы приближения — методы приближе-
приближения, определяемые линейными операторами. Если
в линейном нормированном пространстве функций X
в качестве приближающего множества выбрано ли-
линейное многообразие Ш, то любой линейный опе-
оператор U, сопоставляющий функции /?Х функцию
?/(/, t)={Uf)(t) из 9с так, что
U (о^/Н-«2/2, t)=-.a.JJ (/i, t) + a,U (f2, t)
(аг и а2 — любые числа), определяет линейный
метод приближения (л. м. п.) функций про-
пространства X функциями множества 91- Л. м- п- наз-
проекционным, если U (/, t)=f (t) для всех /
из Ш, он наз. положительным, если U (/, t)^0
для неотрицательных функций f(t).
Наибольший интерес представляет конечномерный
случай, когда $l = SHp/ есть TV-мерное подпространство,
и тогда
U(f,t) = UN(f, 0 = 2fc-ic*</)«P*@. A)
где {4>k(t)}i — базис" 41 дг, а ск — нек-рые определен-
определенные на X линейные функционалы. Выбор линейно не-
независимой системы {фБ (t) }i и набора функционалов
{c/j}i может определяться той информацией о при-
приближаемой функции /(*), к-рую предполагается ис-
использовать при построении линейного метода. Если
ck(f)=1l{tk)^ где {fft}f—фиксированная система точек
в области определения функции /(t) и q>k(t,-) = O при
{фк, фА(«й)==1, то UN(f, tk)=f(tk), fc=l, . . ., N,
и имеют интерполяционный метод
(напр., интерполяционный многочлен Лагранжа, ин-
интерполяционный сплайн). Если Х = Н — гильбертово
пространство функций и с^ (/) — коэффициенты Фурье
функции / по ортонормированной системе {cpj, (?)}, то
суммы A) дают линейный метод ортого-
ортогонального проектирования X на 5JiVi
причем в этом случае
II /-UN(f) Ця = inf |
т.е. этот метод реализует наилучшее приближе-
приближение функции / линейными комбинациями функции
()
*()
В теории л. м. п. функций особое внимание уделя-
уделяется проблеме сходимости. Пусть X — банахово прост-
пространство, {qpi(i), ф2('),* ...} —линейно независимая
система функций из X, 3i^(N=i, 2, . . .) — подпро-
подпространства, порожденные первыми N функциями этой
системы, Ujy(N=l, 2, . . .) — линейные ограничен-
ограниченные операторы из X в %In- Сходимость U^(f, t) -v
-»- f (t) (в смысле \\Ujyf—fllx-*¦ О ПРИ N -*¦ оо) для лю-
любой функции j (t) из X имеет место тогда и только
тогда, когда 1) последовательность норм ||fjvll опера-
операторов f/дг ограничена (см. Банаха — Ш тейнхауза
теорема) и 2) fjv(/> t)-*¦ f (t) для всех функций f (t)
из множества А, всюду плотного в X. Эти условия вы-
выполняются, в частности, в пространстве 2я-иериоди-
чегких функций Lp—Lp\O, 2я] при 1<р<оо для опе-
операторов Slr оиределяемых суммами Фурье
Sn(f, t) =-Y"f 2^D cos kt + bk sin Ш), B)
n=l, 2, ...,
функции / по тригонометрич. системе, причем в ка-
качестве множества А, на к-ром проверяется условие 2),
можно взять множество всех тригонометрич. полино-
полиномов. Если же X есть пространство С=С\0, 2я] (не-
(непрерывных на всей оси с периодом 2л функций) или
Lx, то ||5„||~1п п при п -> оо (см. Лебега константы)
и, следовательно, существуют в С и в Lx функции /(<),
к к-рым последовательность {5„ (/, t)} не сходится
в соответствующей метрике. Так как в банаховом про-
пространстве функций X с нормой, инвариантной относи-
относительно сдвига, для оператора U^ линейного проекти-
проектирования X на подпространство Т„ тригонометрич.
полиномов порядка п справедливо неравенство Ht^llS*
>||5„|| (см. [3]), то расходимость на С и Lx имеет место
и для последовательности {U^}. В частности, это
имеет место на С для последовательности интерполяци-
интерполяционных операторов Лагранжа по любой треугольной
матрице узлов интерполирования. Аналогичные факты
отрицательного характера наблюдаются и в неперио-
дич. случае для операторов линейного проектирования
пространств С [а, Ь] и Ьг[а, Ь] на подпространства Ап
(ге=1, 2, . . .) алгебраич. многочленов степени п.
Факт расходимости последовательности B) для нек-
рых функций из С побудил ввести в рассмотрение раз-
различные усреднения сумм Фурье, не обладающие таким
недостатком. Таковы, напр., Фейера сумма, Вернштей-
на — Рогозинского метод суммирования, к-рые яв-
являются частным случаем (при определенном выборе
числовых множителей Х^) полиномов вида
Un(l, t)=^ + ^k=^{akcoskt + bksmkt), C)
«=1, 2
Так как
то средние C) входят в весьма широкий класс л. м. п.,
представимых в виде свертки функции / с нек-рым
(сингулярным) ядром, свойствами к-рого (в данном
случае свойствами треугольной матрицы чисел {kk })
и определяется решение вопроса о сходимости. Если
lim ^"' = 1, fc = l, 2, ...,
rt-> да
то суммы C) равномерно сходятся, когда /(*) —три-
—тригонометрич. полином, и значит, выполнено условие 2).
Для ограниченности норм ?7„, как операторов из С
в С, необходимо, чтобы
Ц
hЦт-...Ч г- = 0A)
и Х^—0A) равномерно по п и fc=l, 2, . . ., re. Эти
условия становятся и достаточными для ограничен-
ограниченности последовательности {[|?/л||}7 если наложить на
матрицу {h^iP } нек-рые дополнительные требования
(напр., выпуклость или вогнутость по строкам). По
аналогии с C) с помощью матрицы множителей {к/, }
строятся также средние на базе сумм Фурье — Чебы-
шева (для /?С [—1, 1]), а также на базе интерполя-
ционных полиномов Лагранжа по узлам 2kn/Bn-Jrl)
(в периодич. случае) или по узлам cos [Bfc—1)л,'Bга-|-2)|
на отрезке [—1, 1] (см., напр., [6]).
Вопрос о сходимости линейных положительных опе-
операторов Un , действующих из С [а, Ь] в Ап или из С
в Тп (в частности, операторов вида D) с положитель-
положительным ядром), решается на трех пробных функциях
(см. [1]): для равномерной сходимости последователь-
последовательности Un (/, *) к f(t)?C [я, Ь] ала к f(t)?C необходимо
и достаточно, чтобы это имело место для функций 1, t,
t2 ила соответственно для функций 1, sin t, cos i.
Исследование погрешности приближения, доставляе-
доставляемой л. м. п., сводится, чаще всего, к изучению скорости
сходимости Ujy(f, t) к /(?), оценке погрешности че-
через дифференциально-разностные характеристики при-
приближаемой функции, выяснению вопроса о тбм, как ре-
реагирует л. м. п. на улучшение ее гладкостных свойств.
При оценке аппроксимативных свойств л. м. п. A)
естественным ориентиром служит наилучшее прибли-
приближение Е (/, ?f дОх функции / подпространством 9?л'-
Лебега неравенство
|1/-5в(/)Лг<Я(/1 7\,)-Aпв + 3) E)
показывает в сопоставлении с Джексона неравенством
К (/, 71П)?< Mn-r<*(f<-r\ 1/л)
iui(g, б) — модуль непрерывности функции g?C),
что, хотя порядок приближения суммами Фурье не-
несколько хуже наилучшего (In п в E) нельзя заменить
константой), эти суммы реагируют на любое повыше-
повышение порядка дифференцируемое™ приближаемой функ-
функции. Для иек-рых же л. м. п. порядок приближения
не может быть выше определенной величины, сколько
бы производных ни имела функция f (t) (эффект
насыщения). Так, порядок приближения линей-
линейными положительными полиномиальными операторами
Г'п не может быть выше О (п~2); для сумм Фейера по-
порядок насыщения О(п~г), для сумм Бернштейна —
Рогозинского О(п~2). Интерполяционные сплайны при
определенном выборе узлов склейки обеспечивают наи-
наилучший порядок погрешности приближения не только
самой функции, но и нек-рых ее первых производных ¦—
в зависимости от степени многочленов, из к-рых склеен
сплайн (см. [7], [8]).
В отдельных случаях для конкретных л. м. п. най-
найдены точные или асимптотически точные оценки по-
погрешности на классах функций. Видимо, первый не-
нетривиальный результат такого рода был получен
А. Н. Колмогоровым, к-рый в 1935 установил, что
sup ||/_5n(/)|L=^
где WK (г=1, 2, . . .) — класс функций /?С, у к-рых
/(Г~3) (t) абсолютно непрерывна на [0, 2л] и почти всюду
|/<Г) (t)\ ^.K. В дальнейшем аналогичного характера
результаты были получены для сумм Фурье (и для
нек-рых их средних) на других важных классах функ-
функций, задаваемых, напр., мажорантой модуля непре-
непрерывности г-й производной (см. [2], [6], [9]). Особый
интерес представляют л. м. п. A), в точности реали-
реализующие на том или ином классе функций верхнюю
грань наилучших приближений подпространством ЭДдг.
Таким свойством для классов WK (г—1, 2, . . .) об-
обладают при определенном выборе к? суммы вида C),
напр., при ?—1 надо положить
я in) ?л + hji
а также интерполяционные сплайны порядка г—1 де-
дефекта 1 с узлами склейки Лл/ге (к=0, 1,2,...) (см. [4],
а также Приближение функций; экстремальные задачи
на классах функций, Наилучший линейный метод).
Mum.: UJ К о р о в к и н П. II., Линейные операторы и тео-
теория приближений, М., 1959; [2] Дзядык В. К., Введение
в теорию равномерного приближения функций полиномами, М.,
1977; [3] Тихомиров В. М., Некоторые вопросы теории
приближений, М., 1976; [4] Корнейчук Н. П., Экстре-
Экстремальные задачи теории приближения, М., 1976; [5] Гонча-
Гончаров В. Л., Теория интерполирования и приближения функ-
функций, 2 изд., М., 1954; [6] Тиман А. Ф., Теория приближе-
приближения функций действительного переменного, М., I960; [7] А л-
б е р г Д ж., Н и л ь с о н Э., У о л ш Д ж.. Теория сплай-
сплайнов и ее приложения, пер. с англ., М., 1972; [8] С т е ч к и н
С. Б., Субботин Ю. Н., Сплайны в вычислительной мате-
математике, М., 1976; [9] Степане ц А. И., Равномерные при-
приближения тригонометрическими полиномами. Линейные методы,
К., 1981. Н. П. Корнейчук.
ПРИБЛИЖЕНИЕ ФУНКЦИЙ; прямые и об-
обратные теоремы — теоремы и неравенства,
устанавливающие связь .между дифференциально-раз-
дифференциально-разностными свойствами приближаемой функции и вели-
величиной (а также поведением) погрешности приближения
ее тем или иным методом. Прямые теоремы (п. т.) дают
оценку погрешности приближения функции / (?) через
ее гладкостные характеристики (наличие производных
определенного порядка, модуль непрерывности или
модуль гладкости самой функции / или нек-рой ее
производной и т. п.). В случае наилучшего прибли-
приближения полиномами п. т. известны еще как теоремы
Джексона [1] и их различные обобщения и уточнения
(см. Джексона неравенство, Джексона теорема). Об-
Обратные теоремы (о. т.) характеризуют дифференциаль-
дифференциально-разностные свойства функций в зависимости от ско-
скорости убывания к нулю ее наилучших (или каких-либо
других) приближений. Задача получения о. т. прибли-
приближения функций впервые была поставлена, а в нек-рых
случаях и решена С. Н. Бернштейном [2]. Сопоставле-
Сопоставление п. т. и о. т. позволяет иногда полностью охаракте-
охарактеризовать класс функций, имеющих те или иные глад-
костные свойства, с помощью последовательности, напр.,
наилучших приближений.
Наиболее проста связь между п. т. и о. т. в перио-
дич. случае. Пусть С — пространство непрерывных
на всей оси 2л-иериодических функций с нормой
11/Ц-=тах|/(Щ, E(f,Tn)= inf ||/-cp|U
С t фбГ„ с
— наилучшее приближение функции / из С подпрост-
подпространством Т„ тригонометрич. полиномов порядка и,
со(/, 6) — модуль непрерывности функции /?6'; С
(/•—1, 2. . . .) — множество г раз непрерывно дифферен-
дифференцируемых на всей оси функций из С, С0—С. Пр я м а я
теорема: если f(zCr, то
( i) A)
где константа М не зависит от п. Более сильное ут-
утверждение состоит в том, что можно указать последова-
последовательность линейных методов Un (n — 0, 1, . . .), сопо-
сопоставляющих функции f(t) из С, полином [/„(/, t)?Tn
и таких, что для /?СГ погрешность ||/— ?/л(/)Нс
оценивается правой частью A). Обратная тео-
теорема утверждает, что для
co(f, 6)<M6j^^E(f, Г,,-,), 6>0, B)
где М — абсолютная константа, [16] — целая часть
числа 1/6, а из сходимости при нек-ром натуральном ?¦
ряда
следует, что /?С, причем аналогично B) можно оце-
оценить' со(/<Г). i/n) через E(f, 7',,_i) (n 1, 2, . . .) (см.
[4], [8], [121). Из этих оценок, в частности, следует, что
если
?(/, Г„_1) = О(л-'-а), г = 0, 1, ..., О < а<1,
то/?С и f">(t) удовлетворяет при 0<а<1 усло-
условию Гёльдера
а при а=-1 — условию Зигмунда
:K\t' — t"\. D)
Обозначив :)тот класс функций через КНг^а, полу-
получают его конструктивную характеристику: f(*KHr + a
тогда и только тогда, когда
Я (/. 7'„_1)^О(я-'-«).
2л-перподичеекая функция бесконечно дифференци-
дифференцируема на всей оси в том и только в том случае, если
]im»'/?(/, 7\,_i)=0
Л-»-со
для любого г=\, 2, ....
Аналогичные факты имеют место для приближения
периодич. функций в метрике Ьр\Ь, 2л]A <р <эо),
а также для заданных на всей оси (не обязательно
периодич.) функций в случае приближения их целыми
функциями конечной степени (см. [7], [8]). Пзне-
стны и. т. и о. т. для f?Cr, использующие в качестве
дифференциально-разностной характеристики модуль
гладкости (Ofc(/, б) порядка k=i, 2, ... приближаемой
функции (или нек-рой ее производной) (см. [4], [8]).
Иначе обстоит дело в случае приближения на конеч-
конечном отрезке. Пусть С=С[а, Ь] — пространство непре-
непрерывных на [я, Ь] функций с нормой
С—-С[а, Ь] — множество г раз непрерывно диффе-
дифференцируемых на [а, Ь] функций, С°=С, КНг + а\а, Ь] —
класс функций, определяемый неравенствами C) и D)
при t', t"?[a, b]. Для наилучшего приближения
?(/, Л„_1; а, Ъ)= Inf ||/-p|lc, n = l,2, ...,
функции f?C подпространством Ап-^ алгебраич.
многочленов степени и—1 справедлива оценка вида A)
через модуль непрерывности функции fr) на [а, Ь],
однако обращение, аналогичное периодич. случаю
(с неравенством вида B)), здесь возможно лишь на
отрезке, лежащем внутри интервала (а, Ь). Напр., если
Е (/, А^и а, Ъ) < Ми-г-а, E)
г=0, 1, .. ., 0 < а< Г,
то можно лишь утверждать, что / принадлежит классу
КЯг+а [а1, i>i], определяемому неравенствами C) (при
0<сс<1) и D) (при а=^1) лишь на отрезке [аг, ftjc
cz(a, b), причем константа К зависит от a, ol7 b1 и b
и может неограниченно увеличиваться, если ох -у а,
Ьх —»- Ь. Существуют функции, не принадлежащие
классу KHr+a[a, b], для к-рых, однако,
?(/, Ап_1; а, Ъ) = О (п~'-<*¦).
Напр.,
Е(У~[-~Г*, An-x; —1, l) < 2/ли, ге = 1, 2, ...,
хотя У i—t^^KH0- на [ —1, 11 ни при каком а>1/2..
Оказалось, что алгебраич. многочлены могут, обеспе-
обеспечивая на всем отрезке [а, Ь] наилучший порядок при-
ближенпя функции / ? С, у концов отрезка осуществ
лять приближение существенно лучшее (впервые этот
феномен был обнаружен С. М. Никольским, см. [3]).
Если, в частности, f?KHr+a\a, Ь], то при каждом
п>г существует многочлен />н (Об-^п-! такой, что
\f (t)-PnH)\<M\^V(t -a) (b~t)-\-^\+a, F)
а< t < 6,
где константа М не яависит ни от п, ни от t.- Это утверж-
утверждение, в отличие от E), уже можно обратить: если для
/?б' существует последовательность многочленов
pn(t)?A ,t_t таких, что при нек-рых г=0, 1, ... и
0<а<] выполнено F), то f?KHr+a[a, b\. Известны
и. т. и о. т. для f?C[a, ft], использующие модуль не-
непрерывности и модуль гладкости (см. [4], [8]).
П. т., в к-рых даются порядковые оценки погреш-
погрешности через дифференциально-разностные характе-
характеристики приближаемой функции, доказаны для мно-
многих конкретных методов приближения (см. [6], |8],
|9|), в частности для сплайнов (наилучших и интерпо-
интерполяционных 110]).
Известны п. т. и о. т. для приближения в хаусдор-
фовой метрике (см. [13]). Здесь возникают свои осо-
особенности; в частности, характеризация классов функ-
функций через их наилучшие хаусдорфовы приближения
связана не только с порядком этого приближения, но
и с величиной константы в соответствующем нера-
неравенстве. О п. т. и о. т. в многомерном случае см. При-
Приближение функций; случай многих действительных
переменных.
Лит.: El] Jackson D., tlber die Genauigkeit der Annu-
herung stetiger Funktionen durch ganze rationale Funktionen
gegebenen Grades und trigonometrische Summen gegebener Ord-
nung, Gott., 1911; [2] Берн штейн С. Н., О наилучшем
приближении непрерывных функций посредством многочленов
данной степени A912), Собр. соч., т. 1, М., 1952, с. 11 — 104;
[3] Никольский СМ., «Изв. АН СССР. Сер. матем.»,
1946, т. 10, М« 4, с. 295 — 317; [4] Дзядык В. К., Введение
в теорию равномерного приближения функций полиномами, М.,
1977; [ft] Корнейчук Н. II., Экстремальные аадачи тео-
теории приближения, М., 1976; [6] Тихомиров В. М., Не-
Некоторые вопросы теории приближений, М., 1976; [7J А х и е-
з е р Н. И., Лекции по теории аппроксимации, 2 изд., М., 196о;
[8] Тиман А. Ф., Теория приближения функции действи-
действительного переменного, М., 1960; [9] Коровник П. П.,
Линейные операторы и теория приближений, М., 195U; [101
С т е ч к и н СБ., Субботин Ю. Н., Сплайны в вычис-
вычислительной математике, М., 1976; [11] Даугавет II. К.,
Введение в теорию приближения функций, Л., 1977; [12] С т о ч-
кин С. В., «Изв. АН СССР. Сер. матем.», 1951, т. 15, .N1 3,
с. 219—42; 113] С е н д о в Б л., Хауодорфовые приближения,
София, 1979. Н. П. Корнейчук.
ПРИБЛИЖЕНИЕ ФУНКЦИЙ; случай м п о
гих действительных переменных --
случай, когда приближаемая функция / зависит от двух
и большего числа переменных:
f(t)=f(h, h, ..., tm), mS&2
(см. Приближение функций). По сравнению с одномер-
одномерным случаем исследование вопросов приближения
функции in (m^2) переменных значительно услож-
усложняется ввиду появления принципиально новых об-
обстоятельств, связанных с многомерностью. Прежде
всего это касается области, на к-рой осуществляется
приближение. Просто связный компакт (в одномер-
одномерном случае — отрезок) в Rra (даже на плоскости)
может и.меть самую разнообразную конфигурацию, и
возникает необходимость классифицировать области
в зависимости, напр., от гладкостных свойств их гра-
границ. Сложности появляются и при описании диффе-
дифференциально-разностных свойств функций т перемен-
переменных. Эти свойства могут быть, вообще говоря, различ-
различными по разным направлениям, их характоризация
должна учитывать как геометрию области определе-
определения, так и поведение функции при подходе к границе,
так что большое значение приобретает изучение гра-
ничных свойств функций. Если пытаться упростить
решение аппроксимационной задачи переходом к об-
области более простой структуры, то возникает проблема
возможности продолжения функции /из области QaRm
в нек-рую содержащую Q канонич. область Qx (напр.,
и параллелепипед или на все пространство R) с сох-
сохранением тех или иных гладкостных свойств (см. Про-
Продолжения теоремы). Этот круг вопросов тесно связан
с вложения теоремами, а также с проблемами, возни-
возникающими при решении краевых задач математич.
физики.
Увеличение числа независимых переменных, естест-
естественно, усложняет и аппарат приближения, ибо уве-
увеличивается его размерность при том же, напр., по-
порядке 1ЮЛИН0М0В. Алгебраич. многочлен степени ге1?
. . ., пт соответственно по переменным tlt . . ., tm
имеет вид
рп „я('1. ••¦> '«) = 2«*1 *„/•••¦'*" A)
(ak,, ..., hm ~~ действительные коэффициенты, сумми-
суммирование ведется по kv , v= 1,. . ., т, от 0 до nv), так что,
напр., подпространство многочленов степени 3 по
каждому из т переменных имеет размерность 4га.
Иногда фиксируется суммарная степень многочлена п,
тогда суммирование в A) распространено на индексы,
удовлетворяющие неравенству O-gfcj-l-. . .+&v <»•
Тригонометрический действительный полином порядка
«!, . . ., пт по переменным tlt . . ., tm может быть за-
записан в виде
пи ¦¦¦> п.т (<1> • • • . 1т) =
где комплексные коэффициенты ah j k с индексами
противоположного знака комплексно сопряжены, а
суммирование ведется по kv, v=l, . . ., т, от —nv
до nv . Этот полином можно также представить в виде
линейной комбинации всевозможных произведений
вида фЙ1(() <pft2(y . . . q>hm(tm), где ф^ (tv) есть либо
sin fcvM0<uv <»v). либо coskvtv @<fcv<»v)- Ши-
Широкое применение находят многомерные сплайны,
«склеенные» до определенной гладкости из «кусков»
алгебраич. многочленов т переменных. В случае т=2
наиболее простой вид имеют сплайны, склеенные из
многочленов по прямым, параллельным осям коорди-
координат. В качестве аппарата приближения применяются
также функции g(tlt . . ., ?„,), являющиеся полино-
полиномами или сплайнами лишь по нек-рым из переменных.
Для приближения непериодич. функций, заданных на
всем пространстве R (или на неограниченном мно-
множестве из Rm), могут применяться целые функции
экспоненциального типа, представимые в" виде суммы
абсолютно сходящегося степенного ряда
Gnl nm(ti, ..., tm) =
=24>o,v=i m-*,.....*-¦••¦'«- <2>
при условии, что для любого е>0 при всех комплекс-
комплексных tlt U, . . ., tm
где константа Ме зависит только от е (см. [1]). Следует
заметить, что в отличие от полиномов функция B)
определяется бесконечным числом параметров.
В многомерном случае справедлива теорема
Вейерштрасса о возможности приблизить не-
непрерывную на ограниченном замкнутом множестве
QczRm функцию f(f?C(Q)) или непрерывную на всем
пространстве Rra с периодом 2л по каждому перемен-
переменному функцию f(I^C(Rm)) алгебраическими (со-
(соответственно тригонометрическими) полиномами с лю-
любой наперед заданной степенью точности. Аналогич-
Аналогичный факт имеет место и в пространствах Lp (Q) и (в
периодич. случае) Lp(Rm) A<р<оо). На линейные
нормированные пространства функций т неременных
распространяются общие факты и теоремы о свойствах
наилучшего приближения, о существовании, единст-
единственности и характеристич. свойствах функции наилуч-
наилучшего приближения, а также общие соотношения двой-
двойственности для приближения выпуклым множеством
и, в частности, подпространством (см. [3], [4]). Однако
получение конкретных реализаций этих теорем с уче-
учетом конкретной метрики и специфики приближающего
подпространства в многомерном случае сопряжено
с большими трудностями.
Более полно исследованы вопросы связи порядка
убывания наилучших приближений функции многих
переменных алгебраическими и тригонометрич. поли-
полиномами, а также целыми функциями с гладкостными
свойствами приближаемой функции.
Пусть Q — произвольное открытое множество в Rm
(в частности, Q~Rm), e — единичный вектор из Rm,
А>0 и Qhe — множество точек t(zQ таких, что отрезок
[t, t+he]cQ. Если f?Lp(Q), 1<р<оо, то величина
)= supeII/ (*+*«)-/ (
наз. модулем непрерывности функ-
функции f(ti, . . ., tm) в метрике Lp(Q) по на-
направлению е. Величину
наз. модулем непрерывности функции /
в Lp(Q).
В периодич. случае для наилучших приближений
ЕПи ¦¦.,nm(f>Zp(R'n') тригонометрич. полиномами
Гп> Пт функции i?Lp(Rm), имеющей частные
(вообще говоря, обобщенные по Соболеву) производные
V
'V
84
— целые, Z>y/=/, v=1, . . ., m), справедливы
оценки
Е
п„ ...,
где ev —единичный вектор, направленный вдоль tv,
а константа М не зависит от / и nv . Для функции /
из Lp(R'n), имеющей обобщенные смешанные и не-
несмешанные производные
Drf= — ffLD(R'")
1 m
(r=(rlt . . ., rm)) порядка г=г!+. . .+rm, имеют место
неравенства
Если
т. е. если функции Dr f удовлетворяют Гёльдера ус-
условию, то
~Еп, ..., п ^l^Rm^-—, г-0, 1, ..., О < а<1. E)
В последнем случае обратная теорема утверждает, что
если для функции f?l<p(Rm) при всех п=1, 2, ...
справедлива оценка E), то существуют производные
Drj^Lp(Rm), удовлетворяющие при любом h?Rm
неравенствам
|| Z)'7 (t + h)-Drf (t) \ip{Rn)<.K | Л |a, F)
если 0<а<1, или
| Drf (t + h)-2Drf (t)-DrfA -A) kp{Rm)<K | Л j, G)
если a—I, где К не зависит от длины \/i\ — (kf-\-. . .-[-
+hmY'°- вектора Л=(А1, . . ., hm).
Теоремы, аналогичные приведенным, верны также
для непериодич. функций f?Lp{Rm), если в качестве
аппарата приближения применяются целые функции
экспоненциального типа. Приведенные результаты рас-
распространяются также на классы функций, гладкость
к-рых описывается в терминах модулей непрерывности
(модулей гладкости) более высокого порядка (см. [1]).
В случае приближения функций f^Lp{Q) алгеб-
раич. многочленами Рп< Пт на ограниченном па-
параллелепипеде (и нек-рых других ограниченных мно-
множествах) доказаны прямые теоремы, аналогичные C),
D) и E). Обращение этих теорем, как и для функций,
заданных на конечном отрезке, возможно лишь на
множестве Qx, лежащем строго внутри Q. Известны
обратные теоремы, предполагающие повышение по-
порядка приближения вблизи границы множества Q
(см. [13]), а также прямые теоремы, утверждающие
возможность такого улучшения вблизи угловых то-
точек (см. [14]). Необходимые и достаточные условия,
обеспечивающие принадлежность функции / классу
Не"а (Q) (определяемому в метрике С (Q) условиями,
аналогичными условиям (б), G)) за счет повышения по-
порядка приближения вблизи границы (как в одномерном
случае), неизвестны A983). Однако имеет место сле-
следующий результат отрицательного характера (см.[13]).
Пусть Q~ {t : t?R2, |f|<l}. He существует ни одной
определенной на Q последовательности функций
hn (l*l)> и=1, 2, . . ., 0<а<1, обладающей сле-
следующими двумя свойствами:
1) для всякой функции / из Не (Q) найдется постоян-
постоянная М и последовательность многочленов
р т —V
таких, что
\f(t)-Pn(t)\<MK<naU\t\), t?Q; (8)
2) из того, что для определенной на Q функции /
существуют постоянная М >0 и последовательность
многочленов P,,(t), удовлетворяющих неравенству (8),
следует, что f(zflc(Q)-
В качестве других примеров, отражающих специ-
специфику приближения функций многих переменных,
можно привести следующие результаты.
Пусть Ёщ 1и (/) ? — наилучшее приближение 2л-
периодической функции / двух переменных тригоно-
тригонометрия, полиномами Тп п в метрике X (X=C(R2)
или Х~— iTp(R2)), а Еп^х (/)j— наилучшее прибли-
приближение / в X функциями Тп ж, являющимися триго-
тригонометрия, полиномами порядка щ по переменному 1и
коэффициенты к-рых суть функции от t2. Аналогично
определяются величины Еа п (/)^.
Если 1<р<оо, то выполняются неравенства
где Ар зависит лишь от р.
Если же Х = Г, (R-) или X~C{R2), то
EnunJf)~ < А1п B-^тт {пи п2}) (?„„
Л
(9)
где А — абсолютная постоянная, и множитель In B+
-(-min^!, n.2}) в неравенстве (9) нельзя заменить ни на
какой другой, растущий при mm{nlt n2}-+¦ оо по по-
порядку медленнее (см. [15]).
Принципиальные особенности возникают в задачах
интерполирования функций многих переменных.
Напр., существование алгебраического интерполяцион-
интерполяционного многочлена в отличие от одномерного случая су-
существенно зависит от расположения узлов интерпо-
интерполяции. Разработаны, тем не менее, эффективные спо-
способы построения полиномов и сплайнов, интерполи-
интерполирующих функцию /(<1, . . ., tm) на определенным об-
образом выбранной сетке узлов (см. Интерполирование),
Для многомерных интерполяционных сплайнов в ряде
случаев найдены порядковые оценки погрешности
приближения как самой функции /, так и ее частных
производных, более детально исследованы в этом на-
направлении двумерные сплайны малого порядка, а
также локальные (эрмитовы) сплайны любого порядка
(см. [7], [10] — [12]). Среди других линейных методов
приближения функций многих переменных сравни-
сравнительно лучше исследованы кратные суммы Фурье и
их различные средние. Здесь известны порядковые
оценки приближения на классах функций, в нек-рых
случаях найдена точная асимптотика (см. [5], [6], [8]).
Лит.: [1] Никольский С. М., Приближение функций
многих переменных и теоремы вложения, 2 изд., М., 1977; [2]
Гутер Р. С, Кудрявцев Л. Д., Левитан Б. М.,
Элементы теории функций, М., 1963, с. 106—98; [3] Корне й-
чук Н. П., Экстремальные задачи теории приближения, М.,
1976; [4] Тихомиров В. М., Некоторые вопросы теории
приближений, М., 1976; [5] Д з я д ы к В. К., Введение в тео-
теорию равномерного приближения функций полиномами, М.,
1977; [6] Т и м а н А. Ф., Теория приближения функций дей-
действительного переменного, М., 1960; [7] Стечкин С. Б.,
Субботин Ю. Н., Сплайны в вычислительной математике,
М., 1976; [8] С т е п а н е ц А. И,, Равномерное приближение
тригонометрическими полиномами. Линейные методы, К., 1981;
[9] Лоран П. - Ж., Аппроксимация и оптимизация, пер.
с франц., М., 1975; [10] Алберг Д ж., Ни ль сон Э.,
У о л ш Д ж., Теория сплайнов и ее приложения, пер. с англ.,
М., 1972; [11] Завьялов Ю. С, К в а с о в Б. И., Ми-
Миошниченко В. Л., Методы сплайн-функций, М., 1980;
[12] Варга Р., Функциональный анализ и теория аппрокси-
аппроксимации в численном анализе, пер. с англ., М., 1974; [13] Ни-
Никольский С. М.,«Сиб. матем. ж.», 1969, т. 10, N° 5, с. 1075—
1083; [14] Б р у д н ы й Ю. А., «Докл. АН СССР», 1970, т. 195,
№ 5, с. 1007—09; [15] Темляков В. Н., «Докл. АН СССР»,
1975, т. 223, с. 1079—82. В. Н. Коновалов, Н. П. Корнейчук.
ПРИБЛИЖЕНИЕ ФУНКЦИИ; экстремаль-
экстремальные задачи на классах функций —
задачи, связанные с отысканием верхней грани по-
погрешности приближения на фиксированном классе
функций и с выбором для него наилучшего в том или
ином смысле аппарата приближения. Начало иссле-
исследованиям по экстремальным задачам П. ф. положили
работы А. Н. Колмогорова (см. [1] — [2]), Ж. Фавара
(см. [3] — [4]) и С. М. Никольского (см. [5]—[6]).
Широкое развитие эти исследования получили начи-
начиная с 50-х гг. 20 в.; они стимулировались потребнос-
потребностями вычислительной математики, все больше сталки-
сталкивавшейся с задачами оптимизационного содержания.
Если в нормированном функциональном простран-
пространстве X рассматривается П. ф. из класса *Ш функциями
р
[
фиксированного множества ЭДСГЛ", то интерес пред-
представляют задачи отыскания величин
?C31, 9c)x=sup E(j, )!l)x, A)
few
где E(f, Ш)х= inf Ц/-Ф11*
Ф61)!
— наилучшее приближение функции f(t) множеством
Щ, а также
?№, Ы, U)x^mp U-Ufhc, B)
/ е да
где U — нек-рып конкретный метод приближения,
задаваемый тем или иным оператором, действующим
из Л' в 9?. С геометрич. точки зрения верхняя грань A)
характеризует величину уклонения множества Ш от
Щ в метрике X. Практич. смысл величины Е (Щ}, У1)х
можно видеть в том, что она, во-первых, дает мини-
минимально возможную оценку сверху для наилучшего
приближения множеством "jl функции, о к-рой из-
известно только, что она принадлежит классу 931, а во-
вторых, является определенным ориентиром при оцен-
оценке и сравнении аппроксимативных возможностей кон-
конкретных методов приближения на классе ffli. Что ка-
касается величины B), то наиболее важным является
случай, когда 9i=9tjveCTi> TV-мерное подпространство,
U — линейный метод приближения. Известен целый
ряд точных и асимптотически точных результатов но
приближению классов функций конкретными линей-
линейными методами (в частности, полиномами и сплай-
сплайнами) (см. [1]—[12], [19]), но особый интерес вызы-
вызывают .методы, реализующие точную нижнюю грань
C)
распространенную на все линейные ограниченные опе-
операторы и из X в ЭДдг, т. е. линейные методы, наилуч-
наилучшие для класса ЭД}. Ясно, что всегда
и, естественно, возникает вопрос о возможности здесь
знака равенства. Помимо тривиального случая, когда
X — гильбертово пространство функций и наилучшее
приближение каждой функции доставляют суммы
Фурье по ортонормированному базису ЭДдг, известны
ситуации в нсгильбертовом пространстве, когда ли-
линейный метод реализует наилучшее приближение на
всем классе 331.
Так, если X — пространство 2я-периодических функ-
функций lp—lp\O, 2л] A </><»), SRl",,-!—подпространст-
SRl",,-!—подпространство тригонометрия, полиномов порядка п — 1 (diraJJai-i^
¦=--2и—1), MWp{r-A, 2, . . .) — класс функций f?Lp,
у к-рых f""~1){t) абсолютно непрерывна на [0,2я| и
и/11- <л/; то
Lp
E{MWrp, Mn-i)l =#(MWrp, Шп-Ol =MKrn-r,
P V
p — \, со; п, r = l, 2, ...,
где Kr — константы Фавара, причем наилучшее при-
приближение на классах MW[ u MWrx реализует линей-
линейны ii метод Un-i, построенный на базе сумм Фурье
(См. 1]риближение функций; линейные методы приб-
приближения, формула C)) при определенном выборе мно-
множителей aJ?"~1'=Xj"~1' (r). Построены линейные операто-
операторы со значениями в Шгп-г, реализующие верхнюю грань
наилучших приближений на классах сверток, вклю-
включающих, в частности, классы MWrx и MW[ с дроб-
дробными г>0, а также классы сопряженных функций
'см. [10], [И]).
Для приближения подпространством S'^n 2л-периодп~
ческнх сплайнов порядка т дефекта 1 с узлами склей-
склейки кп/п (dim S^—In) справедливы равенства
E(MWrp, S&)l =g(MWrp, S^1)]: =
p P
наилучшим линейным методом здесь являются сплайны
ar-i(l, t) из S^n1, интерполирующие функцию /({)
в точках Лл/п, если г четно, и в точках кл/п-\-п/2п,
если г нечетно. Относительно класса МWL эти сплай-
сплайны обладают исключительными аппроксимативными
свойствами, т. к. наилучшим образом приближают
функции f (t)^MWL в любой метрике Lp (см. [7]).
Перечисленные случаи, когда величины A) и C)
совпадают и удается построить конкретный линейный
метод, решающий сразу обе задачи, являются, в из-
известном смысле, идеальными. В других ситуациях эф-
эффективным при решении задачи A) оказывается подход,
основанный на использовании общих теорем двойст-
двойственности, отражающих фундаментальные соотноше-
соотношения геометрии выпуклого анализа (см. f7], [8]). Если,
напр., X — произвольное линейное нормированное
пространство, X*— ему сопряженное, 9? — выпуклое
множество в X, то для любого элемента ;r?X
irif \\x-u\\= sup \F(x)— sup F (и)]; D)
«6 9! F6 X*, И Ffl< 1 «6 91
в частности, если 9( — подпространство, то
inf Ij ж — u\\ = sup{F (x\: F?X*, H^IKl,
и е чя
F (и)=0 Чи?Щ. E)
Соотношения D) или E) позволяют в ряде случаев
свести вычисление или оценку верхней грани A) к
более обозримой задаче на экстремум явно задавае-
задаваемого функционала на нек-ром множестве функций,
связанных, если 9? -- подпространство, условиями
ортогональности. Например, используя E), оценку
F.(Wrai %Т \~ A<п, о<оо) можно свести с помощью
ч 2П— 1/ Lp
известных неравенств к вычислению верхней грани
норм \\g\\qi (q'-=ql(q—1)) на множестве функций
l( \)) таких, что
Более тонкая ситуация возникает, если задача A)
решается на классах, задаваемых ограничениями не на
норму r-ii производной f-r)(t), а на ее модуль непрерыв-
непрерывности ш(/(Г|, б)х, в частности когда Щ}= WrJIa (r—
= 0, 1, . . .; WOHa"-H<-o)—класс 2я-периодических
функций f?Cr (C°=C), у к-рых
где со F) — заданный модуль непрерывности, напр.
соF)~Л#6а @<а<:1, 0<:б<я). Здесь применение E)
требует использования тонких свойств дифференци-
дифференцируемых периодич. функций типа теорем сравнения и
Колмогорова неравенств (для норм производных),
но описываемых с помощью аппарата перестановок
(равноизмеримых функций). При условии выпуклости
вверх со (б) справедливы равенства (см. [7], [13])
n = i, 2, ...; ;- = 0, 1, ...,
где Х—-С или Лл, /пг(ш, t) — функция из \УГНШ пе-
периода 2я/п с нулевым средним значением на периоде,
у к-рой /(Г1(ш, t) четна, равна | ы(л/я —2t)\/2 на |(),
я/2и] и равна — [ oiBf--л;n)\i2 на |л,'2н, л-'п\. Нор.мьг
||/чг(ш)|1х допускают ннное выражение, напр.:
II/по И||- =— со (л/л),
1 Гл ? о
где функции <t>j)(t) задаются на [0, я] рекуррентно:
фк @ = 4" Jo ф;г-г (г') <?"•
Решение задач о наилучшем для класса WrH№ линей-
линейном методе из С в ь)с г/г -1 нлн в $2п известно в слу,чае
ш(б) = МЬ @<:6<:л), т. е. когда WrHa=zMWr|].
Интерполяционные сплайны ar{J, l) ия S^n реализуют
верхнюю грань E(WrHa, S^uJq (при любом выпуклом
со (б)) лишь в случае г—1.
При решении экстремальных задач на классах функ-
функций, заданных на конечном отрезке и не связанных
жесткими краевыми условиями, нельзя ждать резуль-
результатов в столь совершенном, как в периодич. случае,
виде: на экстремальных функциях сказывается воз-
возмущающее действие концов промежутка, к-рое усугуб-
усугубляется с увеличением порядка дифференцируемости.
Здесь известны нек-рые результаты с точной асимпто-
асимптотикой. Если MWH*(r=Q,\, . . .; 0<а<1, Mjy°tf<*^
МНа) — класс функций l{t)^Cr[~\, 1J, у к-рых
то для наилучшего равномерного на |—1, 1] прибли-
приближения подпространством }?н алгебраич. многочленов
степени /; — 1 имеют место соотношения
lim n<*E(MIIa, У1п)с = Мла/2, F)
lim
п -+сю
М
-Jo
к-])ые полезно сравнить с соответствующими результа-
результатами в периодпч. случае; при а 1 правые части F)
и G) равны соответственно Л/А'а и MKr hl. Отказавшись
от многочленов наилучшего приближения, можно уси-
усилить эти результаты, существенно улучшив приближе-
приближение у концов отрезка f—1, 1| без потери наилучшей
асимптотики на всем промежутке. Напр., для любой
}?МНа существует последовательность алгебрапч.
многочленов р„(/, 0€9tn таких, что равномерно но
'€1 — 1, Я иРи п -*• оо
\f(t)-Pn(f, «)l<f [ (^
= ? (МЯ«, дгй)с[A-Оа/2Н-о AI-
Аналогичный факт имеет место для функций классов
MW1I1 (/•=!, 2, . . .) (см. [11]). В задачах прибли-
приближения сплайнами (наилучшими и интерполяционными)
классов функций, заданных на отрезке, известны нек-
рые точные (гл. обр., для сплайнов малого порядка)
и асимптотически точные результаты (см. [15]).
В случае одностороннего приближения (в интег-
интегральной метрике) известен ряд точных результатов
но оценке погрешности наилучшего приближения поли-
полиномами и сплайнами на введенных выше классах функ-
функций (см. [19]). При их получении существенно исполь-
использовались соотношения двойственности для наилучшего
приближения при наличии ограничений, задаваемы х
с помощью конуса.
Отыскание наилучшего аппарата приближения (фик-
(фиксированной размерности) для данного класса функций
*Ш приводит к задачам о поперечника х: найти
величины (см. A) и C))
d'N№, X) = inf^(aJl
где нижние грани берутся по всем подпространствам
ЭДдг и:? X (и их сдвигам) размерности N, а также ука-
укапать экстремальные (наилучшие) подпространства, реа-
реализующие эти нижние грани. Оценки сверху для dx
и rfyy дают найденные для конкретных подпространств
4iN величины ?BЛ, Шм)х и ©0-Ш. Шя)х> основная
трудность в задаче о поперечнике обычно состоит
в получении точных оценок снизу. В ряде ситуаций
получить такие оценки удается, привлекая топологич.
соображения, в частности теорему Борсука об анти-
антиподах (см. [8]). Практически во всех случаях точного
решении задачи о наилучшем приближении классов
MW'p и W'H01 периодич. функций подпространствами
^2;i-i (тригонометрич. полиномов порядка ге—1) и
Sfn (сплайнов нек-рого порядка т. дефекта 1 по раз-
разбиению knln) найденные точные верхние грани ?EШ,
Шм)х Да1°т и значения поперечников а(дг этих классов,
причем оказалось, что для периодич. классов din_-^din.
В частности (см. [7], [8]) ,
n, r=l, 2, ...,
а при выпуклом вверх ш(б) и Х=С или Ll
G2п_г (If'#<», X)=d2a(WrlI«>, X) = \\fnrF>)\\x,
n:-=l, 2, .. .; /- = 0, 1, ...
Следует отметить, что подпространство %lln-i является
наилучшим для рассматриваемых классов при всех г
и никакое подпространство размерности 2/г не дает на
этих классах лучшее приближение, чем v3iL-i (имею-
(имеющее размерность In—1). Подпространство сплайнов
S'"n является наилучшим для классов WrJ 1 и WrIIa в С
при т=г и для класса Wp+1 в L1 при т^г. Линейные
поперечники d'^ классов Wx, в С и W[ в Ьг совпадают
с </д-, они реализуются на подпространствах Ш1п-1 и
Son1 наилучшими линейными методами, о к-рых упо-
упоминалось выше. Поперечники dN и йдг класса W^ в Z2
при iV=2re—1 и N~2n равны и реализуются суммами
Фурье по тригонометрич. системе. Для поперечников
классов функций, заданных на отрезке, в ряде случаев
известна точная асимптотика; поперечники d^ и d^
классов WL в С [ —1, 1] совпадают и реализуются ин-
интерполяционными сплайнами порядка г —1 по нерав-
неравномерному разбиению (см. [8]).
Задачу оценки погрешности приближения на множе-
множестве Хг г-х интегралов от функций из X (не являющем-
являющемся локально компактным) можно сделать корректной,
если оценивать для/?Хг при фиксированном у>0 ве-
величину
ЕA, 5Ых/и(/(г), у)х
(а)(^, б)х — модуль непрерывности функции g в прост-
пространстве X) или (в случае приближения конкретным ме-
методом) величину
II/-^v/|Ly>(/('->, y)x.
Отыскание точных верхних граней этих величин на мно-
множестве Хг равносильно нахождению наименьшей кон-
константы в соответствующем Джексона неравенстве;
можно затем говорить о минимизации по всем подпрост-
подпространствам размерности JV. В ряде случаев эти задачи
решены. Напр., в неравенстве
E{f,S2n)e<Mrnw(f7 njn)
наименьшая константа Mr^--Krl2, причем она не может
быть уменьшена, если S^n заменить любым другим под-
подпространством той же размерности (см. [14]). Известны
точные константы в неравенстве Джексона для прибли-
приближении тригонометрич. полиномами в равномерной и ин-
интегральной метрике (см. [7]). В непериодич. случае есть
результаты с точной асимптотикой.
Среди экстремальных задач, в к-рых приближающее
множество, не будучи линейным многообразием, яв-
является выпуклым множеством, интерес представляют
задачи наилучшего приближения одного класса функ-
функций Ш другим классом HTd с лучшими, в том или ином
смысле, гладкостными свойствами. Сначала такая зада-
задача возникла как промежуточная при получении точной
оценки для
(см. [7]); в дальнейшем ее стали рассматривать как
самостоятельную, причем в ряде случаев использование
соотношения D) позволило получить точный результат.
При
mi=M2w% (о< г < к).
здесь обнаруживается связь с задачами о неравенствах
между нормами производных и о наилучшем приближе-
приближении оператора дифференцирования линейными ограни-
ограниченными операторами (см. [16]).
Многие экстремальные задачи приближения функций
можно интерпретировать как задачи оптимального вос-
восстановления (см. [15], [17], [18]). Пусть информация о
функции f?X задается вектором T(f, Л)= {Я^/), ... ,
¦^n(/)}j гДе ^к — заданные на X функционалы (напр.,
значения функции / (t) пли (и) нек-рых ее производных
в фиксированных точках). Зная, что / принадлежит
классу 3J1, требуется по информации T(f, А) восстано-
восстановить с наименьшей погрешностью функцию / или значе-
значение L (/) на ней нек-рого линейного функционала (напр.,
L(f)=f(t), L(f)~\ f(t)dt и т. и.). Минимизация может
Jo
предполагаться не только по методам S, сопоставляю-
сопоставляющим вектору T(f, А) функцию <p(t)^f(t) (или функцио-
функционал I {f)~L(f)), но также и по наборам функционалов
Pi? (к~ 1, ... , N). В зависимости от выбора меры погреш-
погрешности и класса методов S задача оптимального восста-
восстановления функции может быть иногда сведена к отыска-
отысканию поперечников йдг или d'ni, чебышевского центра
или других характеристик класса 3JL Оптимальное вос-
с ь
становление интеграла \ / (t)dt по информации вида
{f(tk)} или {/1V)('ft)} приводит к задаче о наилучшей
квадратурной формуле для класса *Ш. Наилучший аппа-
аппарат восстановления в ряде случаев доставляют сплай-
сплайны; так, напр., сплайны o>_i(/, t) из S^n1, интерполи-
интерполирующие в равностоящих точках t^, восстанавливают
функции / из WL по информации X^f)'- j (tk) в каждой
точке tj=tk с минимально возможной на всем классе
\Vr^ погрешностью.
В пространствах функций двух и большего числа пе-
переменных, если не считать тривиального случая при-
приближения в гильбертовом пространстве, точных реше-
решений экстремальных задач почти нет A983). В немногих
случаях известны асимптотически точные соотношения
для погрешности равномерного приближения классов
функций суммами Фурье и нек-рыми их средними
(см. [12]).
Лит.: [1] Колмогоров А. Н., «Ann. Math.», 1935,
v. 36, jvf« 2, с. 521—26; [2] е г о ж е, там же, 1936, v. 37, Л 1,
р. 107—10; [3] Favard J., «С. г. Acad. sci.», 1936, t. 203,
p. 1122—24: [4] e г о ж е, «Bull. sci. math.», 1937, t. 61,
p. 209—24, 243—56; [5] Никольский С. М., «Тр, МИАН
GCGP», 194.'>, т. 15, с 1—76; [6] его же, «Изв. АН СССР.
Сер. матем.», 1946, т. 10, с. 207—56; [7] Корнейчук Н. П.,
Экстремальные задачи теории приближения, М., 1976; [8] Ти-
Тихомиров В. М., Некоторые вопросы теории приближений,
М., 1976; Е9] Д з я д ы к В. К., Введение в теорию равномер-
равномерного приближения функций полиномами, М., 1977; [10] Ахв-
о з е р Н. И., Лекции по теории аппроксимации, 2 изд., М., 1965;
[11] Т и м а н А. Ф., Теория приближения функций действи-
действительного переменного, М., 1960; [12] С т е п а н*е ц А. И.,
Равномерные приближения тригонометрическими полиномами.
Линейные методы, К., 1981; [13] Корнейчук П. П., «Ма-
«Матем. заметки», 1976, т. 20, №5, с. 655—64; [14] его же,
«Укр, матем. журн.», 1979, т. 31, № 4, с. 380—88; [15] е г о же,
«Изв. АН СССР. Сер. матем.», 1981, т. 45, №2, с. 266 — 90;
116] Арестов В. В., «Тр. Матем. ин-та АН СССР», 1975,
т. 138, с. 3—28; [17] Великий В. Л., «Матем. заметки»,
1977, т. 22, № 5, с. 663—70; [18] Л и г у н A. A., «Anal. Math.»,
1979, v. 5, № 4, p. 269—86; [19] Корнейчук Н. П., Л и-
г у н А. А., Доронин В. Г., Аппроксимация с ограниче-
ограничениями, К., 1982. Я. П. Корнейчук.
ПРИБЛИЖЕНИЕ ФУНКЦИЙ КОМПЛЕКСНОГО
ПЕРЕМЕННОГО — раздел комплексного анализа, изу-
изучающий вопросы приближенного представления (аппро-
(аппроксимации) функций комплексного переменного посред-
посредством аналитич. функций специальных классов. Ос-
Основными в теории П. ф. к. п. являются задачи о воз-
возможности приближения, скорости приближения и об
аппроксимационных свойствах различных способов
представления функций (интерполяционных последова-
последовательностей и рядов, рядов по ортогональным многочле-
многочленам и многочленам Фабера, разложений в непрерывные
дроби и аппроксимаций Паде, последовательностей
полиномов из экспонент и рядов Дирихле и т. п.).
Теория П. ф. к. п. тесно связана с другими разделами
комплексного анализа и математики в целом; в теории
приближений важную роль играют методы и результа-
результаты конформных отображений, интегральные представ-
представления, теория потенциала, теория функциональных
алгебр и др.
Центральная проблематика теории П. ф. к. п. отно-
относится к приближению функций многочленами и рацио-
рациональными функциями, в частности многочленами и ра-
рациональными функциями наилучшего приближения
(существование, характеристич. свойства, единствен-
единственность), а также экстремальные задачи и различные
оценки для многочленов и рациональных функций
(оценки роста, неравенства для производных, много-
многочлены и рациональные функции, наименее уклоняю-
уклоняющиеся ОТ НуЛЯ, И Т. нЛ. А. А. Гончар.
Приближение функций комплексного переменного
многочленами и рациональными функциями. В этом
разделе теории П. ф. к. п. можно выделить несколько
направлений.
1) Изучение возможности приближе-
приближения функции / (z) комплексно! о переменного z с любой
наперед заданной точностью посредством многочленов
и рациональных функций от г в зависимости от свойств
того множества Е, на к-ром задана / и на к-ром проис-
происходит приближение, от свойств метрики уклонения р
и, наконец, от свойств самой функции /.
2) Изучение свойств многочленов и раци-
рациональных функций наилучшего при-
приближения, т. е. таких многочленов Рп (z; f,E, р)
и рациональных функций R,,(z\ /, Е, р) степени не выше
ге, п~0, 1, ... , для к-рых
def
p(f,Pn(z;f, ?,(>)) = ?„(/, E,p)=ini{p(f1P):degP<n},
p(f,Rn(z;!,E,p))^Rn(f,E,p)=inf{p(f,R):degR<n},
где нижние грани берутся соответственно по всем много-
многочленам Р (z) степени deg Р *?п и рациональным функци-
функциям R (z) степени deg R <и (либо по части множества та-
таких многочленов или рациональных функций, выделяе-
выделяемой какими-либо дополнительными условиями). По
существу здесь идет речь о свойствах решений нек-рого
класса экстремальных задач. Сюда можно отнести так-
также изучение и других экстремальных задач на множест-
множествах многочленов, рациональных функций и на нек-рых
классах аналитич. функций, а также исследования
аналитич. свойств многочленов и рациональных функ-
функций (в частности, получение неравенств между различ-
различными нормами этих функций и их производных).
3) Изучение зависимости скорости убывания к нулю
величин En(f, Е, р) и Rn(f, Е, р) при п —> оо от свойств
/, Е и р (так наз. прямые теоремы теории при-
приближения) и зависимости свойств функции / от скоро-
скорости убывания .?„(/, Е, р) или Л„(/, Е, р) к нулю при
«->¦ и и свойств ? и р (обратные теорем ы^.
С этим направлением неразрывно связано изучение
возможностей известных методов П. ф. к. п. (таких,
как ряды по Фабера многочленам, различные интерпо-
интерполяционные процессы и т. п.) и отыскание новых эффек-
эффективных методов приближения.
4) Приближение функций нескольких комплексных
переменных. Здесь решаются в основном те же задачи,
что и в случае одного переменного, однако результаты
и методы их получения, как правило, резко отличаются
от случая одного переменного.
Ниже отмечены нек-рые основные результаты.
1) Задачу о возможности сколь угодно хорошего рав-
равномерного приближения многочленами решают Рунге
теорема (в случае аналитичности / на Е), Лаврентьева
теорема (непрерывность / на Е), Келдыша теорема
(Е — замкнутая область, / непрерывна на Е и анали-
тична внутри Е), Мергеляна теорема (в общем случае:
Е — компакт, / непрерывна на ? и аналитична во вну-
внутренних точках Е).
2) Задачу о возможности приближения голоморфной
функции на замкнутом подмножестве Е расширенной
комплексной плоскости С решает теорема Рунге. При
изучении возможности приближения функций / из
различных пространств в метрике этих пространств по-
посредством рациональных функций важную роль играют
количественные характеристики множеств ее:С, ана-
аналогичные аналитической емкости у(е). В терминах у(е)
задача об описании компактов Е, на к-рых любая не-
непрерывная функция с любой точностью приближается
рациональными функциями, решается следующим об-
образом: необходимо и достаточно выполнение либо ус-
условия
(а) у (а (г, а)\Е) = у(а(г, а)) = г
для любого круга a{r, a)= {z : \z—<г|О}, я?С, г>0;
либо условия
(б) Tim г-2у (а (г, а) \ Е) = оо
для любого а?Е (эквивалентность условий (а) и (б)
выражает т. н. «неустойчивость» аналитической
емкости).
3) Если Е ограничено и измеримо по Лебегу и 1 <р <
<2, то множество всех рациональных функций плотно
в пространстве LP(E).
4) Если р>0, G — односвязная область с жордановоп
спрямляемой границей, то семейство всех многочленов
от г плотно в Смирнова классе Еp(G) тогда и только тогда,
когда G — Смирнова область.
5) Пусть комплекснозначные функции cpjz), ... ,
ф„(г), /(г) непрерывны на компакте ЕаС, /г>1. Среди
всех обобщенных полиномов вида
Р B)=
(ct, ... , cn — произвольные комплексные числа) обоб-
обобщенный полином P0(z) является наименее уклоняющим-
уклоняющимся от / по метрике
рс(/, i>)=max{|/(z) —i>(z)|
тогда и только тогда, когда
min {Re [P (z) (PQ (z)—f (z))]:z?E,
\f(z)-P0(z)\ = t
для каждого P(z).
6) Если Е — компакт со связным дополнением G
и в G существует Грина функция (первой краевой задачи
для уравнения Лапласа) g(z, oo) с полюсом в оо, то
при z ?G для любого многочлена Р (г) степени ге справед-
справедливо неравенство
\Р (z) \<a^Mexp{ng (z, oo)},
M = max{| P (z) \:z?E].
7) Если E -— ограниченный невырожденный конти-
континуум со связным дополнением G, / (z) непрерывна на Е
с модулем непрерывности ш (б) и аналитична во внутрен-
внутренних точках Е, то
Г" it r> \ — /-> / /> / , /Hill
*л (/. Л . РсХ t- / ш d -r-
V V "
где
Если замкнутая область G ограничена аналитической
кривой Г, то условие
En(f, E, рс) = 0(ге-"-а)
эквивалентно выполнению для fiPi (z) в G условия Гёль-
дера порядка а, 0<а<1. Изучед также случай, когда
Г — кусочно гладкая кривая с углами.
8) В ряде случаев эффективным аппаратом прибли-
приближения аналитич. функций являются различные интер-
интерполяционные процессы, в том числе Ладе аппроксима-
аппроксимации и их обобщения.
9) При ге^2 в С" существуют как незамкнутые жор-
дановы кривые, на к-рых не каждая непрерывная функ-
функция равномерно с любой точностью приближается мно-
многочленами от (zx, ... , zn), так н замкнутые жордановы
кривые, на к-рых многочленами равномерно приближа-
приближается любая непрерывная функция. В С1 это невозможно.
10) К настоящему времени A983) имеется сравни-
сравнительно мало прямых теорем теории приближения рацио-
рациональными функциями со свободными полюсами (т. е.
без всяких условий на расположение полюсов прибли-
приближающей функции) и значительное количество обратных
теорем. е. П. Долженпо.
Лит.: [1] Гончаров В. Л., Теория интерполирования
и приближения функций, М., 1954; [2] У о л ш Д ж. Л., Ин-
Интерполяция и аппроксимация рациональными функциями в ком-
комплексной области, пер. с англ., М., 1961 (там же, Приложение:
Мергелян С. Я., О некоторых результатах в теории равно-
равномерных и наилучших приближений полиномами и рациональ-
рациональными функциями, с. 461—99); S3] Смирнов В. И., Ле-
Лебедев Н. А., Конструктивная теория функций комплексного
переменного, М.— Л., 1964; [4] Дзядык В. К., Введение
п теорию равномерного приближения функций полиномами, М.,
1977; [5] Русак В. Н., Рациональные функции как аппарат
приближения, Минск, 1979; [6] Гаме ли н Т., Равномерные
алгебры, пер. с англ., М., 1973; [7] Л е о н т ь е в А. Ф., Ряды
экспонент, М., 1976; [8] Некоторые вопросы теории приближе-
приближений, пер. с англ., М., 1963; [9] К е л д ы ш М. В., «Докл. АН
СССР», 1936, т. 4, с. 163—66; [10] Лаврентьев М. А.,
«Тр. Физ.-матем. ин-та АН СССР», 1934, т. 5, с. 159—245; [11]
Колмогоров А. Н., «Успехи матем. наук», 1948, т. 3,
и. 1, с. 216—21; [12] Мергелян С. Н., там же, 1952, т. 7,
в. 2, с. 31—122; [13] Витушкин А. Г., там же, 1967, т. 22,
в. 6, с. 141—99; [14] Джрбашян М. М., «Матем. сб.»,
1955, т. 36, с. 353—440; [15] Гончар А. А., в кн.: Тр. Меж-
Международного конгресса математиков. Москва, 1966, М., 1968,
с' 329—56; [16] Долженко Е. П., Ульянов II. Л,,
«Вестн. Моск. ун-та. Сер. матем. Мех.», 1980, № 1, с. 3—13;
[17] Мергелян С. Н., в кн.: Математика в СССР за сорок
лет, т. 1, М., 1959, с. 383—98: [18] Гончар А. А., М е р г о-
л я н С. Н., в кн.: История отечественной математики, т. i,
кн. 1, К., 1970, с. 112—93; [19] Там разов П. М.,
Гладкости и полиномиальные приближения, К., 1975; [~0]
Мельников М. С, С и н а н я н Г.. О., в кн.: Современ-
Современные проблемы математики, т. 4, М., 197f>, с. 143—250.
ПРИБЛИЖЕНИЯ ПОРЯДОК, а п п р о к с и м а-
ц и и порядок,— порядок погрешности прибли-
приближения как переменной величины, зависящей от непре-
непрерывного пли дискретного аргумента т, относительно
другой переменной <р(т), поведение к-рой, как правило,
считается известным. Обычно т — нек-рый параметр,
являющийся числовой характеристикой приближаю-
приближающего множества, (напр., размерность этого множества)
или метода приближения (напр., шаг интерполяции);
при этом множество значений т имеет конечную или бес-
бесконечную предельную точку. Функция ф (т) — чаще
всего степенная, показательная или логарифмическая.
В качестве ф(т) может фигурировать непрерывности мо-
модуль приближаемой функции (или нек-рой ее производ-
производной) или его мажоранта.
П. п. характеризует как аппроксимативные возмож-
возможности метода приближения, так и определенные свой-
свойства приближаемого объекта, напр., дифференциально-
разностные свойства приближаемой функции (см. При-
Приближение функций; прямые н обратные теоремы).
В численном анализе П. п. численного метода, имею-
имеющего погрешность O(hm) (h — шаг метода), наз. пока-
показатель т.
Лит.: Ш Гончаров В. Л., Теория интерполирования
и приближения функций, 2 изд., М., 1954; [2] Т и м а н А. Ф.,
Теория приближения функций действительного переменного,
М., 1960; [3] Бахвалов Н. С, Численные методы, т. J,
М., 1975. Н. П. Корнейчук, В. П. Моторный.
ПРИБЛИЖЕНИЯ ТЕОРИЯ, аппроксимации
т е о р и я,— раздел математич. анализа, изучающий
методы приближения одних математич. объектов дру-
другими и вопросы, связанные с исследованием и оценкой
возникающей при этом погрешности.
Основное содержание П. т. относится к приближению
функций. Фундамент П. т. был заложен работами
П. Л. Чебышева A854—59) о наилучшем равномерном
приближении функций многочленами и К. Вейерштрас-
са (К. WeierstraB), установившего в 1885 принципиаль-
принципиальную возможность приблизить непрерывную на конеч-
конечном отрезке функцию алгебраич. многочленами со сколь
угодно малой наперед заданной погрешностью. Раз-
Развитие П. т. в значительной степени определялось осно-
основополагающими работами А. Лебега (Н. Lebesgue),
Ш. Ж. Балле Пуссена (Cl>. J. La Vallee Poussin),
С. Н. Бернштейна, Д. Джексона (D. Jackson), Ж. Фа-
вара (J. Favard), А. Н. Колмогорова, С. М. Никольско-
Никольского о приближении функций и классов функций.
С развитием функционального анализа многие вопро-
вопросы П. т. стали рассматривать в самой общей ситуации,
напр. как приближение элементов произвольного ли-
линейною нормированного пространства X. При этом
выделяют три круга задач, к-рые в определенной сте-
степени соответствуют и основным хронологич. этапам раз-
развития исследований в П. т.
1. Приближение фиксированного элемента а?Х эле-
элементами фиксированного множества ?jc^. Если в ка-
качество меры приближения взять величину
Е (х, 5)()= inf||i —и |,
1
т. е. наилучшее приближение х множеством $1, то, по-
помимо исследования и оценки Е(х, й), возникают во-
вопросы о существовании элемента наилучшего прибли-
приближения и0 из 9{ (для к-рого \\х—и0 ||=Е (х, 5R)), его един-
единственности и характеристич. свойствах. Любой опера-
оператор А , отображающий X в ЭД, задает нек-рый метод
приближения с погрешностью ||.г—Ах]\. Если 91 — ли-
линейное многообразие, то особое значение имеют линей-
ные операторы. Для последовательности {А „} таких
операторов возникает задача об условиях сходимости
А пт —>. х для любого х ? X.
2. Приближение фиксированного множества ЯпсХ
элементами другого фиксированного множества *Я из
Л'. Наилучшее приближение в атом случае выражается
поличиной
Е («Ш, $)= sup ?(,<¦, 90,
л- б ЗД
к-рая дает минимально возможную оценку погрешности
приближения любого элемента л?Х элементами из 9J-
В конкретных случаях задача состоит в том, чтобы оце-
оценить или точно выразить Е (*Ш, 90 через характерис-
характеристики, задающие множества Ш1 и 9J- Если приближение
осуществляется с помощью оператора А , то исследуется
верхняя грань
sup || .г — Ах ||,
л- 6 Ш
а также (если Ш — линейное многообразие) величина
& (Ш, ?()= inf sup || .г —Л* ||,
.4.YC')i хеш
где нижняя грань распространена на все линейные
операторы, отображающие X в 91. Линейный оператор,
реализующий эту нижнюю грань (если он существует),
определяет наилучший линейный метод приближения.
Особый интерес представляет выяснение случаев, когда
§( 90?ffl 9
( )
3. Наилучшее приближение фиксированного множе-
множеЧПХ Щ) а
ства ЧПсХ заданным классом Щ) аппроксимирующих
множеств из X. Предполагается, что в класс {9?}
входят в каком-то смысле «равноценные» множества,
напр, содержащие одно и то же количество элементов
или имеющие одну и ту же размерность. Первый слу-
случай приводит к задаче об е-энтропии множества ЯЛ (от-
(относительно X), второй — к задачам вычисления попе-
поперечников множества fflf} (в пространстве X), в частности
величин
dA B3!, X) == inf Е («Ш, 9Ы, (Ь
где нижние грани берутся но всем подпространствам
9Ztv из X фиксированной размерности N (или по все-
всевозможным их сдвигам 9?лг~г'й)- Таким образом, в за-
задачах A)—B) речь идет об отыскании наилучшего (со-
(соответственно наилучшего линейного) аппарата при-
приближения размерности Л" для множества Ш-
Лит.: 11] А х и е з е р Н. И,, Лекции по теории аппрокси-
аппроксимации, 2 изд., М., 1965; [2] Гончаров В. Л., Теория ин-
интерполирования и приближения функций, 2 изд., М., 1954; [31
Д з я д ы к В. К., Введение в теорию равномерного приближе-
приближения функций полиномами, М., 1977; [4] Никольский
С. М., Приближение функций многих переменных и теоремы
вложения, 2 изд., М., 1977; [5] Корней ч v к Н. П., Экстре-
Экстремальные задачи теории приближения, М., 197ti; [6] Т и х о от и-
ров В. М., Некоторые вопросы теории приближений, М.,
1976; [7] Т и м а н А, Ф., Теория приближения функций дейст-
действительного переменного, М., I960.
Н. 11, Нор}/ейчук, В. TJ. Моторный.
ПРИБЛИЖЕНИЯ ФУНКЦИЙ МЕРА — количе-
количественное выражение погрешности приближения. Когда
речь идет о приближении функции f(t) функцией q>(t),
мера приближения ц (/, ф) обычно определяется метри-
метрикой нек-рого функционального пространства, содержа-
содержащего как /(/), так и q>(t). Напр., если функции lit)
и ф(/) непрерывны на отрезке |я, 6], часто пользуются
равномерной метрикой пространства С \а, Ь], т. е.
полагают
Если же непрерывность приближаемой функции не га-
гарантирована или но условию задачи важна близость
между I(t) и ср(?) лишь и среднем на [я, 6], можно ис-
использовать интегральные метрики пространств L;\a,
6], полагая
И/, ф) = *
где <?B) — нек-рая весовая функция. Здесь наиболее
употребительным и удобным с практич. точки прения
является случай р---2 (см. С реднеквадратическое при-
приближение функций).
П. ф. м. может учитывать значения функций / (t) и
i( (t) лишь в отдельных точках t^, ft—1, ... , п, проме-
промежутка [я, Ь\, напр.:
ц(/, ц>) •-=¦- max |/(tfe)— (p(tfc)l,
i Д
где (jfj. — нек-рые положительные коэффициенты.
Аналогично определяется мера приближения функ-
функций двух и большего числа неременных.
Мера приближения функции f(t)
семейством функций /' обычно определяет-
определяется как наилучшее приближение:
E(f, F)=y.(U F) = inf ц(/, ф).
cpeF
Под мерой приближения класса Щ} функций / (t) функ-
функциями ф(() из фиксированного множества F понимают
величину
? (Ш, F)=n(W, F) = sny inln(/, ф),
I е Ш ф е F
к-рая характеризует максимальное отклонение функций
множества ЗЛ от ближайших к ним функций из F.
В общем случае, когда рассматривается приближе-
приближение в произвольном метрич. пространстве X, мера при-
приближения ц (т, и) элемента х элементом и (множеством
V) есть расстояние р (х, и) (р (х, F)) между х и и (.г и F)
в смысле метрики пространства X.
Лит.: [1] Гончаров В. Л., Теория интерполирования
и приближения функций, 2 изд., М., 1954; [2] Николь-
Никольский СМ., Приближение функций многих переменнйх и
теоремы вложения, 2 изд., М., 1977.
Н. П. Корнейчук, В. 77. Моторный,
ПРИВАЛОВА ОПЕРАТОРЫ, параметр ы
Привалова,— операторы, позволяющие выразить
условие гармоничности функции без использования
частных производных. Пусть и(х) — локально интег-
интегрируемая функция в конечной области D евклидова
пространства R", я^2; ш('*) —объем шара В{х; h)
радиуса h с центром x?D, расположенного в D;
(.v; ft) u ^ dy~u И-
Верхний и ни ж ний операторы П р и-
валова А*и(х) и &*и(х) соответственно опреде-
определяется формулами
~А*и (.<) ТТпТ ( Ahu (х): ттт
А--0 -(«+
Если верхний и нижний П. о. совпадают, то опер а-
тор Привалова А*и(х) определяется формулой
И()() (Н 27^
Если функция и (.т) имеет непрерывные частные irpo-
ианодные до 2-го порядка включительно в точке x?_D,
то в этой точке существует П. о. Д*м(т), и он равен
аначению оператора Лапласа: A*it(,r) = ku(x). Спра-
Справедлива 'I1 сирена Привалов а: если непре-
непрерывная в области U функция и (х) удовлетворяет всюду
в D условию
Д*м
то и(х) — гармонич. функция в D. Отсюда вытекает,
что непрерывная функция \i{x) в D является гармони-
гармонической тогда и только тогда, когда во всякой точке х ? D,
начиная с достаточно малого h, Д^и(.г) —О или, иначе,
1 f
II (.{¦) 1= — \ U ill) A11.
Среднее значение по объему шара здесь можно заменить
средним значением но площади сферы.
Лит.: Ш Привалов It. И., «Матем. сб.», 192о, т. 32,
с. 4t>4—71; [2j его же, С> ^гармонические функции, М.—
Л., 1937; [3] Брело М., Основы классической теории потен-
потенциала, пер. с франц., М., 1964. Е. Д. Соломеицеь.
ПРИВАЛОВА ТЕОРЕМА — 1) П. т. о сопря-
сопряженных функциях: пусть
/ W =af+ 2J= , (ak cos kt + bk sin kt)
— периодическая непрерывная функция с периодом 2л и
— тригонометрически сопряженная функция с f(t);
тогда если f(t) удовлетворяет условию Липшица в по-
показателем а, /? Lip а, 0<а<1, то /?Lip а при 0<а<1
и /имеет модуль непрерывности, не больший Мб In A/6)
при а=1. Эта теорема, доказанная И. И. Приваловым
[1], имеет важные применения в теории тригонометрии,
рядов. Она переносится и на условия Липшица в не-
к-рых других метриках (см., напр., [5]).
2) П. т. единственности аналитиче-
аналитических функций: если однозначная аналитич.
функция / (г) в области D плоскости комплексного пере-
переменного г, ограниченной спрямляемой жордановой
кривой Г, на нек-ром множестве ЯсТ положительной
меры Лебега на Г имеет нулевые угловые граничные
значения, то /(z)s=0 в D. Эта теорема доказана
И. И. Приваловым [2]; ее обобщением является Лузи-
Лузина — Привалова теорема; см. также Единственности
свойство аналитических функций.
3)П.т. о сингулярном интеграле
К о ш и, основная лемма Привалов а,—¦
один из основных результатов теории интеграла типа
Кошн — Стилтьеса (см. Коши интеграл). Пусть Г : ?=
— ?М. 0<s<Z,— спрямляемая (замкнутая) жорданова
кривая на плоскости комплексного переменнЬго z, I --
длина кривой Г, s — длина дуги на Г, отсчитываемая
от нек-рой фиксированной точки; ф=ф($) — угол меж-
между положительным направлением оси абсцисс п каса-
касательной к Г, 1|з (s) — комплексная функция ограничен-
ограниченной вариации на Г. Пусть точка So € Г определяется зна
чением s0 длины дуги, ?о "?(*<>)> O<:so<:Z, и Гб — часть
линии Г, оставшаяся после удаления из Г меньшей ду-
дуги, концами к-рой являются точки t,(s0—6) и ?(so-|-6).
Конечный предел при б -*¦ О
если он существует, пая. сингулярным инте-
интегралом К о ш и —- Стилтьеса. Пусть D ь
и D ~ — соответственно конечная и бесконечная обла-
области, ограничиваемые кривой Г. Формуляров к а
И. т.: если для почти всех но мере Лебега на Г точек Г
существует сингулярный интеграл A), то почти всюду
на Г существуют угловые граничные значения
интеграла типа Коши — Стилтьеса
B)
соответственно из областей D-, причем почти всюду
справедливы Сохоцкого формулы:
Обратно, если почти всюду на Г существуют угловые
граничные значения F+(?o) (или -F~(?o)) интеграла B),
то почти всюду на Г существуют сингулярный интеграл
A) и граничные значения с другой стороны F-(i^0)
(соответственно /г + (?0)), причем выполняются равенства
C). Эта теорема была установлена И. И. Приваловым
для интегралов типа Коши — Лебега (т. е. для случая
абсолютно непрерывной функции -Цз (s), см. [2]), а затем
и для общего случая [3]. Она играет основную роль в
теории сингулярных интегральных уравнений и раз-
разрывных граничных задач аналитич. функций (см. [6]).
4) П. т. о граничных значениях инте-
интеграла типа Коши — Лебега: если жорда-
нова кривая Г кусочно гладкая и без точек заострения,
а комплексная функция /(?), ??Г, удовлетворяет усло-
условию Липшица
l/(Si)-/(C2)l < c\Zi-wi\a, о
то интеграл типа Коши — Лебега
есть непрерывная функция в замкнутой области D+,
причем для граничных значений F±(?) выполняются
условия:
\F±&1)-F±{li)\<C1\L,1-U\a>
если 0<а<1, п
если а=1, IS1-ga|<6<l (см. [2]).
Лит.: [1] Привалов И. И., «Bull. Soc. math. France»,
191H, t. 44, p. 100—03; t2j его ж е, Интеграл Cauchy, Саратов,
1918; [3] его же, Граничные свойства однозначных аналити-
аналитических функций, М., 1941; [4] его же, Граничные свойства
аналитических функций, 2 изд., М.— Л., 1950; [5] Зигмунд
А., Тригонометрические ряды, пер. с англ., М., 1965; [6] X в е-
д с л и д з е Б. В., в кн.; Итоги науки и техники. Современные
проблемы математики, т. 7, М., 1975, с. 5—102.
Е. Д. Соломеацев.
ПРИВЕДЕНИЕ К АБСУРДУ — правило логич. вы-
вывода, позволяющее заключить, что если из списка ут-
утверждений Г, А следует как утверждение В, так и ут-
утверждение "\В, то из списка Г следует ~\А. Правило
П. к а. записывают, напр., в виде
Г,А -уВ; Г, А->-]В
и наз. также правилом введения отрица-
отрицания. П. к а. является допустимым правилом для
подавляющего большинства логико-математич. исчис-
исчислений. С. Ю. Маслое.
ПРИВЕДЕННАЯ СИСТЕМА ВЫЧЕТОВ по моду-
модулю т — набор, составленный из всех чисел полной
системы вычетов по модулю т, взаимно простых с т.
П. с. в. по модулю т состоит из ф (т) чисел, где ц> (т) —
функция Эйлера. В качестве П. с. в. по модулю т обыч-
обычно берутся взаимно простые с т числа полной системы
вычетов 0, 1, ... , го—1. С. А. Степанов.
ПРИВЕДЕННАЯ СХЕМА — схема, локальное коль-
кольцо любой точки к-рой не содержит ненулевых ннльпо-
тентных элементов. Для любой схемы (X, §х) сущест-
вует наибольшая замкнутая приведенная подсхема
(•^redi 6\ ed). характеризуемая соотношениями
где гх — идеал, состоящий из всех нильпотентных эле-
элементов кольца (Зх, х. Групповая схема над полем ха-
характеристики 0 всегда приведена [3]. П. с.— классич.
объект изучения в алгебраич. геометрии.
Лит.: [1] Ар тин М., «Математика», 1970, т. 14, №4,
с. 3—47; [2] Г р о т е н д и к А., Дьёдоине Ж., «Успехи
матем. наук», 1972, т. 27, №2, с. 135—48; [3] Мамфорд
Д., Лекции о кривых на алгебраической поверхности, пер. с
англ., М., 1968. С. Г. Танкеев.
ПРИВИЛЕГИРОВАННЫЙ КОМПАКТ — понятие,
часто используемое в теории комплексных пространств,
в особенности в теории модулей комплексных структур.
Пусть К — компакт в С", Qx — ограничение на К
пучка ростков голоморфных функций в Сп. Компакт К
наз. привилегированным относительно
когерентного аналитического пучка
§~, заданного на К, если существует точная последова-
последовательность отображений 0д'-пучков
О —>¦ Хп —> Хп-\ —> ¦ ¦. —>¦ Х\ —>• Хо —> gf —> 0, A)
в к-рой X(=Qjl с нек-рыми /-,^0, j—0, 1, ... , и,
такая, что порожденная ею последовательность непре-
непрерывных операторов
С— В (К, Хп) Л В (К, ifn_0 —*-...
... —+В(К, Хг)-^В(К, Хо) B)
точна и расщепляема. Здесь
в (к, jei)=B(K,Q)r',
а В (К, 0) есть банахово пространство непрерывных на
К функций, голоморфных внутри К, наделенное равно-
равномерной нормой. Расщепляем ость последова-
последовательности B) означает, что ядро и образ дифференци-
дифференциала d в каждом члене имеет прямое замкнутое допол-
дополнение. Это условие расщепляемости эквивалентно сле-
следующему: существует линейный непрерывный оператор
h в B), переводящий В (К, j?() в В (К, =SP,-+1), такой, что
dhd=d (оператор г о м о т о п и и). Свойство точ-
точности и расщепляемости последовательности B) но за-
зависит от выбора последовательности A).
Пусть точка z принадлежит внутренности компакта
К. Тогда существует морфизм я комплекса B) в слой
комплекса A) над точкой z, переводящий элемент
В (К, ?(), т. е. функцию на К со значениями в С '
в ее росток в точке z. Отсюда вытекает, что последова-
последовательность
в (к, i?о -^в(к, зе0) ^1$-г C)
полуточна. Компакт К наз. gf-n р и в и л е г и р о-
панной окрестностью точки г, если он
^"-привилегирован и последовательность C) точна. Это
свойство также не зависит от выбора последователь-
последовательности A).
Для всякого когерентного аналитич. пучка $~ вся-
всякая точка его области определения обладает фундамен-
фундаментальной системой ^"-привилегированных окрестностей.
В качестве таких окрестностей выбираются поликруги
с определенными соотношениями типа неравенств для
радиусов. Известно достаточное условие ^-привилеги-
^-привилегированности полицилиндра, связывающее пучок §~ с уст-
устройством границы (см. [1]).
Рассматриваются также привилегированные ком-
компакты по отношению к пучку, заданному на произволь-
произвольном комплексном пространстве X, при этом имеют в
виду компакты, привилегированные относительно пуч-
пучков /* (gf), где / карта на X.
Лит.: [1] D о u a d у A., «Ann. Inst. Fourier», 1966, t, IB.
[). 1—Я5. ' В. П. Паламодов.
ПРИВОДИМАЯ ЛИНЕЙНАЯ СИСТЕМА о б ы к н о-
венных дифференциальных уравне-
уравнений — система
x = A(t)x, x?Rn (или С"), (*)
А(-): R —->• Нот (R«, R") (или Нот (С, С")),
переходящая п систему с постоянными коэффициентами
у—By в результате замены x=L{t)y, где /, (/) — нек-рое
Ляпунова преобразование. Если отображение A (t) не-
непрерывно и периодически зависит от t, то система (*)
приводима (теорема Ляпунова). Для приво-
приводимости системы (*) необходимо и достаточно, чтобы
нашлись преобразование Ляпунова L(t) и оператор В
такие, что всякое решение системы (*) имеет вид
x(t)=L(t)etBx@)
(критерий Е р у г и н а).
Лит.: [1] Ляпунов A.M., Общая задача об устойчи-
устойчивости движения, в его кн.: Собр. соч., т. 2, М.— Л., 1956, с. 7—
263; [2] Еругин Н. П., Приводимые системы, Л.— М.,
1946 (Тр. Матем. ин-та АН СССР, т. 13). В. М. Миллионщиков.
ПРИВОДИМОЕ ПРЕДСТАВЛЕНИЕ — линейное
представление, в пространстве к-рого есть собственное
инвариантное подпространство. а. п. Штерн.
ПРИВОДИМОЕ РИМАНОВО ПРОСТРАНСТВО —
риманово пространство М, у к-рого линейная (или,
иначе, однородная) голономии группа приводима, т. е.
имеет нетривиальные инвариантные подпространства.
Риманово пространство с неприводимой группой голо-
голономии наз. неприводимым. Полное односвяз-
ное П. р. п. разложимо (теорема д е Р а м а), т. е.
разлагается в прямое произведение римановых прост-
пространств положительной размерности. Более точно, лю-
любое полное односвязное риманово пространство изомет-
рично прямому произведению МпХ МгХ ...X М^ евкли-
евклидова пространства Мо и полных односвязных неприво-
неприводимых римановых пространств Л/,-, г>0, причем такое
разложение М единственно с точностью до порядка со-
сомножителей.
Ослабленный вариант этой теоремы справедлив для
псевдоримановых пространств: псевдориманово прост-
пространство наз. слабо неприводимым, если все
нетривиальные инвариантные относительно группы го-
голономии Г подпространства касательного пространства
изотропны, т. е. индуцированное на них скалярное про-
произведение вырождено. Любое полное односвязное псев-
псевдориманово пространство разлагается в прямое произ-
произведение слабо неприводимых псевдоримановых прост-
пространств. Если подпространство неподвижных относи-
относительно группы голономии векторов неизотропно, то
такое разложение единственно с точностью до порядка
сомножителей. Слабо неприводимое псевдориманово
пространство не разлагается в прямое произведение
псевдоримановых пространств [3].
Лит.: [1] Лихие рович А., Теория связностсй в це-
целом и групп голономии, пер. с франц., М., I960; [21 К о б а я-
си Ш., Номидзу К., Основы дифференциальной геомет-
геометрии, пер. с англ., т. 1, М., 1981; [3] Wu H., «Illinois J. Math.»,
1964, v. 8, Лэ 2, р. 201—311; [4] Шапиро Я. Л., «Докл.
АН СССР», 1972, т. 206, № 4, с. 831—33. Д. В. Алежеевспий.
ПРИЗМА — многогранник, у к-рого две грани суть
л-угольникп (основания П.), а остальные п гра-
_ ней (боковых) — параллело-
~" граммы. Основания П. конгруэнт-
конгруэнтны и расположены в параллель-
параллельных плоскостях. П. наз. прямо й,
если плоскости боковых граней
перпендикулярны к плоскости ос-
нования. Прямую П. наз. пра-
правильно й, если основанием ее
служит правильный многоугольник. П. бывают тре-
треугольные, четырехугольные и т. д., смотря по тому,
лежит ли в основании треугольник, четырехугольник и
т. д. На рисунке дана шестиугольная П. (слева — пря-
прямая). Объем П. равен произведению площади основа-
основания на высоту (расстояние между основаниями П.).
БСЭ-З.
ПРИЗМАТОИД — многогранник, две грани к-рого
(основания П.) лежат в параллельных плоскостях,
а остальные являются треуголь-
треугольниками или трапециями, причем
у треугольников одна сторона, а
у трапеций оба основания явля-
являются сторонами оснований П.
(см. рис.). Объем П. равен
где h — расстояние между осно-
основаниями П., S и S' —их площа-
площади, S" — площадь сечения, одинаково удаленного от
обоих оснований. бсэ-з.
ПРИКОСНОВЕНИЯ ПРЕОБРАЗОВАНИЕ, каса-
касательное преобразование, контакт-
контактное преобразован и е,— преобразование кри-
кривых на плоскости, при к-ром две касающиеся друг
друга кривые преобразуются в две кривые, также ка-
касающиеся друг друга. См. Контактное преобразование.
ПРИКОСНОВЕНИЯ ТОЧКА — точка г множества
А в топологич. пространстве X такая, что всякая ее ок-
окрестность имеет непустое пересечение с А. Множество
всех П. т. образует замыкание [А] множества А .
М. XI. Войцеховский.
ПРИМАРНОЕ КОЛЬЦО — кольцо с единицей, фак-
торкольцо к-рого по радикалу Джекобсона изоморфно
кольцу матриц над телом или, что то же самое, является
артиновым простым кольцом. Если идемнотенты П. к.
R с радикалом Джекобсона / можно поднимать по мо-
модулю / (т. е. у каждого идемпотента из RIJ существует
пдемпотентный прообраз в R), то R изоморфно кольцу
всех матриц над нек-рым локальным кольцом. Это, в
частности, имеет место, если / есть нильидеал.
Лит.: [1J Джекобсон Н., Строение колец, пер. с англ.,
М., 19Н1; [2] Ф е й с К., Алгебра: кольца, модули и категории,
пер. с англ., т. 1—2, М., 1977—79. Л. А. Скорняков.
ПРИМАРНОЕ ПРЕДСТАВЛЕНИЕ — то же, что
фактор представление.
ПРИМАРНОЕ РАЗЛОЖЕНИЕ — представление
идеала / кольца R (или подмодуля А модуля М) в виде
пересечения примарных идеалов (примарных подмоду-
подмодулей). П. р.-обобщает разложение целого числа в произ-
произведение степеней различных простых чисел. Существо-
Существование П. р. в кольце многочленов доказал Э. Ласкер
|1], в произвольном коммутативном нётеровом кольце —
О. Нётер [2]. Пусть R — коммутативное не'терово коль-
п
цо. П. р. /= П Qi наз. неприводимым, если
П Qi^I для любого /=1, ... , п и радикалы Plt ... , Рп
гф]
идеалов Qu ... , Qn попарно различны (радикалом
примерного идеала Q наз. такой единственный простой
идеал P^2Q, что Pnt=:Q для нек-рого натурального
числа п). Совокупность простых идеалов {Рг, ... , Рп}
определена однозначно идеалом /(первая тео-
теорема единственности П. р.), минимальные
по включению элементы этой совокупности наз. и з о-
л про ванными простыми идеалами
идеала /, остальные — вложенными просты-
простыми идеалами, причем примерные идеалы, соот-
соответствующие изолированным простым идеалам, также
однозначно определены идеалом f (вторая тео-
теорема единственности П. р., см. [3]). Изо-
Изолированным простым идеалам идеала / кольца много-
многочленов над полем соответствуют неприводимые компо-
компоненты аффинного многообразия корней идеала /. Имеют-
Имеются различные некоммутативные обобщения понятия
П. р. Аксиоматизация П. р. привела к развитию ад-
аддитивной теории идеалов.
Лит.: \\\ L a s k о г Е., «Math. Ann.», 1905, Bd 60, S. 20-
116; [2] N о г 1 ]] е I- ]•:., «Math. Aim.», 1921, Bd 8.1, S. 24—60;
[M] А т ь я JL. I a i; д о и а л ь д И., Введение в коммутатив-
коммутативную алгебру, пер. с англ., М., 1972; [4] 3 а р и с с к и й О.,
Самюэль П., Коммутативная алгебра, пер. с англ., т. 1 — 2,
М., 1963; [5] Б у р 6 а к и Н., Коммутативная алгебра, пер.
с франц., М., 1971. В. Т. Марков.
ПРИМАРНЫЙ ИДЕАЛ коммутативного
кольца R — такой идеал IczR, что если a, b?R и
ab?I, то либо Ь?1, либо ан?1 для нек-рого натураль-
натурального числа п. В кольце целых чисел % II. и.— идеал
вида рп1, где р — простое, ;г — натуральное число.
Важную роль в коммутативной алгебре играет представ-
представление любого идеала коммутативного нётерова кольца
в виде пересечения конечного числа П. и.— примарное
разложение. Более общо, пусть Ass (M) обозначает мно-
множество первичных идеалов кольца Я, являющихся ан-
нуляторами ненулевых подмодулей модуля М. Под-
Подмодуль N модуля М над нётеровым кольцом R наз.
примарным, если kss(MlN) — одноэлементное
множество. Если кольцо R коммутативно, то любой
собственный подмодуль нётерова Я-модуля, не пред-
етавнмый в виде пересечения двух строго содержащих
его подмодулей, примерен. В некоммутативном случае
это не так, поэтому предпринимались попытки постро-
построить различные некоммутативные обобщения понятия
примарности. Напр., собственный подмодуль N модуля
М наз. п р и м а р и ы м, если для любого ненулевого
пнъективного подмодуля Е' инъективной оболочки Е
модуля MlN пересечение ядер гомоморфизмов из Е в Е'
тривиально. Другое удачное обобщение — понятие
терциарного идеала [4]: левый идеал / нётерова слева
кольца R наз. терциарным, если для любых
элементов a?R, b?R\I из aRb^I следует, что для лю-
любого c?R\f найдется элемент d?Rc\I такой, что
aRdc^l. Оба эти обобщения приводят к некоммутатив-
некоммутативным аналогам примерного разложения. Каждый тер-
терциарный идеал нётерова кольца Я примарен в том и
только в том случае, когда кольцо R удовлетворяет
условию А р т и н а — Риса: для любых
левых идеалов /, / кольца R найдется натуральное
число п такое, что In[}J<^IJ (см. [3]).
Лит.: 11] Б у р б а к и Н., Коммутативная алгебра, пер.
с франц., М., 1971; [2] 3 а р и с с к и й О., С а м ю я л ь П.,
Коммутативная алгебра, пер. с англ., т. 1, М., 1963; [3] Go] d-
гаап О., «J. Algebra», 1969, v. 13, K> 1, p. Ю-,47; [4] L e-
sieur L, Croisot R., Algebre noetherienne non commuta-
commutative, P., 1963. В. Т. Марков.
ПРИМИТИВНАЯ ГРУППА ПОДСТАНОВОК —
группа подстановок (G; М), сохраняющая лишь триви-
тривиальные отношения эквивалентности на множестве М
(т. е. равенство и аморфную эквивалентность). Изуча-
Изучаются главным образом конечные П. г. п.
П. г. п. транзитивна и всякая 2-транзитивная группа
примитивна (см. Транзитивная группа). В точности
1-транзптивные (т. е. не являющиеся уже 2-транзитив-
ными) группы подстановок наз. у н и п р и м и т и в-
н ы м и. Коммутативными П. г. п. являются циклит,
группы простого порядка и только они. Транзитивная
группа подстановок примитивна тогда и только тогда,
когда стабилизатор Ga каждой точки а ? М есть макси-
максимальная подгруппа в группе G. Другой признак прими-
примитивности основан на сопоставлении каждой транзитив-
транзитивной группе (G; М) ее графов, соответствующих бинар-
бинарным орбитам этой группы. Группа (G; М) примитивна
тогда и только тогда, когда графы, соответствующие
нерефлекспвны.м 2-орбнтам. связны. Число 2-орбит наз.
рангом группы (G; М). Ранг равен 2 для дважды транзи-
транзитивных групп, а ранг унипримитивной группы не мень-
меньше 3.
Всякий иеедшшчный нормальный делитель 1J. г. п.
транзитивеи. Всякая транзитивная группа подстановок
погружается в кратное сплетение П. г. п. (правда, та-
такое представление не однозначно).
Многие вопросы теории групп подстановок сводятся
к обозрению П. г. п. Известен список всех П. г. п.
степени < 50 (см. f4]). Изучаются связи между П. г. п.
и простыми конечными группами.
Обобщение понятия П. г. п.— кратно прим н-
тивные группы. Группа подстановок (G; М)
наз. к раз примитивной, если она к раз транзитивна
и фиксатор (к—1)-й точки действует примитивно на ос-
остальных точках.
Лит.: [1] Cameron P., «Bull. London Math. Soc», 1981,
v. 13, p. 1—22; [2] Krasner M., Kaloujnino L.,
«Acta Scient. math. (Szeged)», 1951, v. 14, p. 39—66; [3] W i e-
landt H., Finite permutation groups, N.Y.—L., 1964; [41
Погорелой Б. А., в кн.: VI Всесоюзный симпозиум по
теории групп. Сборник, К., 1980,с. 14В—57: [5] Шмидт О. Ю.,
Абстрактная теория групп, 2 изд., М. ,ч., 1933.
.7. Л. Калужпин.
ПРИМИТИВНАЯ РЕКУРСИЯ — способ определе-
определения функций от натуральных аргументов с натуральны-
натуральными значениями. Говорят, что (п + 1)-местная функция
/ (хх, ... , хп, у) получена примитивной рекур-
рекурсией из re-местной функции g(x{, ... , хп) и (и+2)-
местной функции h(xt, ... , яр„, у, z), если для всех нату-
натуральных значений хх, ... , хп, у имеет место
/ (Ч, ¦¦¦, zn, 0) = g (x1, ..., хп)
и
I \хх, ..., .г„, y-\-i)^h(x1, ..., хп, у,
/ (А, • • •, ¦'•«, У))-
Для данных g и h такая функция / всегда существует и
единственна. При п—0 определяющие равенства для /
записываются в виде
Фундаментальным свойством П. р. является то, что
при любом разумном уточнении понятия вычислимости
функция /, полученная из вычислимых функций g и h
с помощью П. р., сама вычислимая. П. р.— одно из ос-
основных правил порождения из исходного набора про-
простейших функций всех примитивно рекурсивных и всех
частично рекурсивных функций.
Лит.: [1] Успенский В. А., Лекции о вычислимых
функциях, М., 1960; [2] Мальцев А. И., Алгоритмы и ре-
рекурсивные функции, М., 1965; [3J Роджерс X., Теория ре-
рекурсивных функций и эффективная вычислимость, пер. с англ.
М., 1972. С. Я. Артемов.
ПРИМИТИВНО РЕКУРСИВНАЯ ФУНКЦИЯ —
функция от натуральных аргументов с натуральными
значениями, к-рую можно получить из простейших
функции
s (.<¦)= х + 1, о{х).=--0, I'm(xi, .. ., хп)-=хт
конечным числом операций суперпозиции и примитив-
примитивной рекурсии.
Поскольку исходные функции являются вычислимы-
вычислимыми, а операторы суперпозиции и примитивной рекурсии
вычислимость сохраняют, множество всех П. р. ф. есть
подкласс класса всех вычислимых функций. Каждая
П. р. ф. задается описанием ее построения из исходных
функций (примитивно рекурсивное о п и-
с а н и е) и, следовательно, класс всех П. р. ф. счетен.
Практически все арифметик, функции, употребляемые
в математике по конкретным поводам, являются П. р.
ф., напр.: .r+г/, х-у, хУ, sg(ap), j-i-~j, остаток от деления
х на у, я (.г) — простое число с номером х и т. д.
Отношение P(xt, ... , хп) на натуральных числах наз.
примитивно рекурсивным отношен и-
ем (п. р. о.), если функция g(xu ... , хи), равная 1,
когда Р (хх, ... , хп) истинно, и 0, когда Р (х1: ... , ,;;„)
ложно, является П. р. ф. Говорят, что отношение
Р (xlt ... , .с,,, г) получено из отношения Q(xlf ... , хп,
;/, ;) с помощью ограниченного квантора,
если
P(.vu ..., хп, z)&Vy(y<z=> Q (*i, •¦¦,¦'„, У, z))
или
Р(хъ ...,хп, z)&3y(y<z&Q (хъ ...,хп, у, z)).
Класс п. р. о, замкнут относительно применения всех
логнч. связок (включая отрицание) и ограниченных
кванторов.
Пусть f1, ... , /S1 i суть «-местные П. р. ф., a Pi, ...
... , Ps — такие п. р. о., что на любом наборе значений
аргументов истинно не более одного из них. Тогда
функция
I fl&l, ¦¦ ., Х„), ОС ЛИ Pl(X1, ...,?„),
/ (Xi, . . . , X „) = ¦!
ts(xu •¦•>л:п)> если Ps(xu ...,xn),
'- fs + i(xi, ¦¦¦ixn), в ДРУГнх случаях,
является П. р. ф.
Говорят, что функция f(xu ... , х„, г) получена из
всюду определенной функции g(x}, ... , хп, у, z) приме-
применением ограниченного оператора м и-
н и м и з а ц и и, если f (хг, ... , хп, г) равно минималь-
минимальному у такому, что г/<г и g(xlt ... , хт у, z) = 0, и равно
г+1, если такого у нет. Класс П. р. ф. замкнут относи-
относительно применения ограниченных операторов миними-
минимизации.
Функция Ф (у, ,<i, ... , хп) наз. универсальной
для класса всех re-местных П. р. ф., если для каждой
П. р. ф. f (*1, ... , хп) найдется натуральное число к
такое, что
Для каждого п~^\ такая универсальная функция су-
существует, но она не может быть П. р. ф.
Всякое рекурсивно перечислимое множество есть
область значений П. р. ф.; всякое рекурсивно перечис-
перечислимое отношение R (хг, ... , хп) представимо в виде
ЗуА (у, x-i, ... , хп), где А — п. р. о. Всякая П. р. ф.
представима в арифметике формальной, т. е. для каж-
каждой П. р. ф. /(хг, ... , хп) найдется арифметич. формула
F(y, хи ... , хп) такая, что для натуральных klt ... , kn,
т при /(fej, ... , kn) = m в формальной арифметике выво-
выводима формула ?(т, klt .- , kn), а при f(kr, ... , kH)^m
выводима "\F(m, klt ..., kn) (здесь ku ... , kn, m — ариф-
арифметич. термы, изображающие в формальной арифме-
арифметике натуральные числа kly ... , кп, т). Этот факт зани-
занимает центральное место в доказательстве неполноты
формальной арифметики (см. [4]).
Лит.: [1] Успенский В. А., Лекции о вычислимых
функциях, М., 1960; [2] Мальцев А. И., Алгоритмы и ре-
рекурсивные функции, М., 1965; [3] Роджерс X., Теория ре-
рекурсивных функций и эффективная вычислимость, пер. с англ.,
М., 1972; L4] Мендельсон Э., Введение в математичес-
математическую логику, пер. с англ., М.. 1976. С. Я. Артемов.
ПРИМИТИВНОЕ КОЛЬЦО правое — ассоциа-
ассоциативное кольцо, обладающее правым точным неприводи-
неприводимым модулем. Аналогично (с помощью левого неприво-
неприводимого модуля) определяется левое примитив-
примитивное кольцо. Классы правых и левых П. к. не сов-
совпадают. Всякое коммутативное П. к. является нолем.
Всякое полупростое (в смысле Дженобсона радикала)
кольцо является подпрямым произведением П. к. Про-
Простое кольцо либо является П. к., либо радикально.
П. к. с ненулевыми минимальными правыми идеалами
описываются теоремой плотности. П. к. с условием
минимальности для правых идеалов (т. е. артпновы
П. к.) являются простыми.
Кольцо Я примитивно тогда и только тогда, когда оно
обладает максимальным модулярным правым идеалом
1, к-рый не содержит двусторонних идеалов кольца R,
отличных от нулевого идеала. Это свойство может быть
принято за определение П. к. в классе неассоциативных
колец.
Лит.: [1] Д ж е к о б с о н Н., Строение колец, пер. с англ.,
М., 1961; [2] Херстейн И-, Некоммутативные кольца, пер.
с англ., М., 1972. И. А. Жевлаков.
ПРИМИТИВНЫЙ ИДЕАЛ, и р а в о п р и м л т и в-
ный идеал,— такой двусторонний идеал Р ассоци-
ассоциативного кольца R, что факторкольцо R/P является
(правым) примитивным кольцом. Аналогично, с по-
помощью левых примитивных колец может быть опреде-
определен л е в о п р и м и т и в н ы й идеал. Множество
П всех П. и. кольца, снабженное нек-рой топологией,
оказывается полезным при изучении отдельных классов
колец. Обычно множество II топологизируется при по-
помощи следующего замыкания отношения:
А = {Р'\Р'€П, Р'=> (f]P, Р?А)},
где А подмножество в П. Множество всех П. и. кольца,
снабженное такой топологией, наз. структурным
пространством этого кольца.
Лит.: [1] Д ж е к о б с о н Н., Строение колец, пер. с
англ., М., 1961. К. А. Жевлапов
ПРИМИТИВНЫЙ КЛАСС алгебраических
систем — то же, что многообразие (см. Алгебраи
ческих систем многообразие).
ПРИМИТИВНЫЙ МНОГОЧЛЕН — многочлен
f(X)?R[X], где R — ассоциативно-коммутативное
кольцо с однозначным разложением на множители,
коэффициенты к-рого не имеют нетривиальных общих
делителей. Любой многочлен g{X)?R[X] можно запи-
записать в виде g(X) — c(g)f{X), где /(X) ~ П. м., a c(g) —
наибольший общий делитель коэффициентов многочле
на g(X). Элемент c(g)?R, определенный с точностью
до умножения на обратимые элементы из R, наз. с о-
держанием многочлена g(X). Справедли-
Справедлива лемма Гаусса: если gi(X), g2(X)?R[X],
то с (gigi)=c(g1)c(g2). В частности, произведение П. м.
снова примитивно.
Лит.: [1] Зарисский О., Самюэль П., Коммута-
Коммутативная алгебра, пер. с англ., т. 1, М., 1363. Л. В. Кузьмин.
ПРИОРИТЕТА МЕТОД — метод, применяемый в
рекурсивной теории множеств для построения просто
устроенных с рекурсивной точки зрения (в простей-
простейших случаях — рекурсивно перечислимых) множеств
(функций, нумераций и т. п.), удовлетворяющих бес-
бесконечной системе условий определенного типа. Спе-
Специфика допустимых условий такова, что для того
чтобы удовлетворить отдельному условию из данной
системы, обычно бывает достаточно, чтобы в строяще-
строящееся множество был включен определенный (зависящий
от рассматриваемого условия) элемент. Однако на каж-
каждом этапе построения (представляющего собой нек-рый
вычислительный процесс, чем и обеспечивается рекур-
рекурсивная простота строения искомого объекта) каждое
из условий системы (к-рое определяется, вообще гово-
говоря, бесконечным множеством конструктивных объектов)
представлено нек-рой своей конечной аппроксимацией.
Включение в строящееся множество элемента, обеспе-
обеспечивающего выполнение аппроксимации у-го условия,
еще не дает гарантии, что тем самым будет удовлетво-
удовлетворено само у-е условие. П. м. позволяет в известных
случаях обходить это препятствие. С этой целью у-му
условию данной системы, /=1, 2, 3, . . ., в процессе
построения ставится в соответствие натуральное число,
являющееся кандидатом на роль элемента, включение
к-рого в строящееся множество удовлетворяет ;-му
условию; про такой элемент принято говорить, что
он помечен маркером у
(снабженным, возможно, до-
дополнительными индексами). Каждый такой кандидат
может в процессе построения заменяться (пли, что то
же самое, маркер может сдвигаться), но при этом в
простейших приоритетных конструкциях сама после-
довательность, в к-рои выполняются попытки удовлет-
удовлетворить данным условиям, организуется так, что каж-
каждый маркер может изменить свое положение лишь
конечное число раз, причем в своем заключительном
положении он с необходимостью отмечает элемент,
гарантирующий выполнение соответствующего условия.
П. м. был создан при решении проблемы Поста о
существовании нетривиальных рекурсивно перечисли-
перечислимых степеней. Впоследствии он был использован в
многочисленных задачах, возникших при изучении
тьюринговых и других степеней, структуры рекурсивно
перечислимых множеств (упорядоченной отношением
включения), теории вычислимых нумераций и др. При
этом возникли различные модификации первоначаль-
первоначального П. м. (в частности, иногда допускается, чтобы
нек-рые маркеры меняли свое положение бесконечно
много раз), поэтому нередко предпочитают говорить
о методах приоритета.
Лит.: [1] Роджерс X., Теория рекурсивных футщий
и эффективная вычислимость, пер. с англ., М., 1972;
[2) Sacks G- E., Degrees of unsolvability, Princeton (N.J.),
1963. В. А. Душский.
ПРИСОЕДИНЕННАЯ ГРУППА группы G —
линейная группа Ad G, являющаяся образом группы
Ли или алгобраич. группы G при присоединенном пред-
представлении. П. г. Ad G содержится в группе Aut д
всех автоморфизмов алгебры Ли д группы G, а ее
алгебра Ли совпадает с присоединенной алгеброй ad д
алгебры Ли д. Связная полупростая группа есть
группа присоединенного типа (т. е.
она изоморфна своей П. г.) тогда и только тогда, когда
ее корни порождают группу рациональных характеров
максимального тора; центр такой группы тривиален.
Если основное поле имеет характеристику 0 и G связ-
связна, то Ad G однозначно определяется алгеброй Ли д
и наз. иногда П. г., или группой внутрен-
внутренних автоморфизмов, алгебры Ли д. В част-
частности, если G полупроста, то Ad G совпадает со связной
компонентой единицы в Aut д.
Лит.: [1] П о н т р я г и н Л. С, Непрерывные группы,
3 изд., М., 1973; [2] С е р р Ж. - П., Алгебры Ли и группы Ли,
пер. с англ. и франц., М., 1969; [3] Хамфри Д ж., Линей-
Линейные алгебраические группы, пер. с англ., М., 1980.
ПРИСОЕДИНЕННАЯ ПОВЕРХНОСТЬ — поверх-
поверхность Y, находящаяся с данной поверхностью X
в Петерсона соответствии, причем асимптотич. сети
на Y соответствует на X сопряженная сеть а с рав-
равными инвариантами, и наоборот. П. п. Y является
вращения индикатрисой для X, п наоборот. Если сеть
а — главное основание изгибания X, то Y — Бианки
поверхность. Я. X. Сабитов.
ПРИСОЕДИНЕННОЕ ПРЕДСТАВЛЕНИЕ груп-
группы Л и или алгебраической группы
G — линейное представление Ad группы G в каса-
касательном пространстве Те (G) (или в алгебре Ли д
группы G), сопоставляющее каждому a?G дифферен-
дифференциал Ad a=d(Int а)е внутреннего автоморфизма Int a :
х—^-аха,-1. Если Gg^GL(V) —линейная группа в про-
пространство V, то
(Ad a) X^aXa-1, X?Te(G).
Ядро Ker Ad содержит центр группы G, а в случае,
когда G связна и основное поле имеет характеристику О,
совпадает с центром. Дифференциалом П. п. группы
G в точке е служит присоединенное представление ad
алгебры д.
Присоединенным представлением
алгебры Ли д наз. линейное представление ad
алгебры д в модуле д, действующее по формуле
(ad.г) у = [х, у], х, г/?д,
где [ , ] — операция в алгебре д. Ядро Ker ad есть
центр алгебры Ли д. Присоединенные операторы
ad x являются дифференцированиями алгебры g и наз.
внутренними дифференцирования-
м и. Образ ad g называется присоединенной
алгеброй и является идеалом в алгебре Ли
Der g всех дифференцирований алгебры д, причем
Der g/Ad g есть пространство Я1(д, д) 1-мерных кого-
мологий алгебры Ли д, определяемых П. п. В част-
частности, ad g=Der g, если g — полупростая алгебра Ли
над полем характеристики 0.
Лит.: L1] Джекобсон Н., Алгебры Ли, пер. с англ.,
М., 1964; [2] Понтрягин Л. С, Непрерывные группы,
3 изд., М., 1973; [3] С е р р Ж. - П., Алгебры Ли и группы Ли,
пер. с англ. и франц., М., 11N9; [41 Хамфри Д ж., Линей-
Линейные алгебраические группы, пер. с англ., М., 1980.
А. Л. Онищик.
ПРИСТРЕЛКИ МЕТОД, стрельбы метод,—
метод решения краевой задачи для обыкновенного диф-
дифференциального уравнения, к-рый заключается во вве-
введении управляющих переменных (параметров) и после-
последующем нахождении их на системы уравнений, при
этом выбор параметров имеет решающее значение для
успешного решения задачи.
Пусть имеется при a<$.x^.b дифференциальное урав-
уравнение
y' = F(x,y) A)
с граничным условием
g(y(a), y(b)) = h, B)
где вектор-функция у={у1, . . ., г/n)" от х подлежит
определению, вектор-функции F=(F1, . . ., Fn)^ и g=
= (gi, ¦ ¦ ., gn)~^ известны, числовой вектор h=(h1, . , .,
/г„)Т задан.
Пусть задача Коши
dZjdx-F (x, Z), C)
Z (а, г)-—г, D)
где Z=(Zj, . . ., Zn)T, r—fa, . . ., г„)т, имеет единствен-
единственное решение Z(x, г), определенное при а<:а-'<:Ь, г?Еп.
При подстановке в B) вместо у (а) заданного значения
Z(a, r) = r, а вместо </(Ь) найденного значения Z{b, r)
получают уравнение
g(r, Z(b, r)) = h E)
относительно параметра г.
Алгоритм П. м. состоит в следующем: сначала на-
находят решение г--ч- * уравнения E), а затем — иско-
искомое решение граничной задачи A) — B) как решение
задачи Коши
y' = F(x,y), y(a) = r*.
Для решения упоминавшихся здесь задач Коши могут
быть использованы численные методы. Для решения
уравнения E) целесообразно избрать какой-либо ите-
итерационный метод.
В случае, когда нек-рые из компонент вектора g
зависят только от у (а), а остальные компоненты —
только от у(Ь), выгоден другой выбор параметров (см.
[1], а также Нелинейная краевая задача; численные
методы решения). Имеются другие варианты П. м.
(см. [4]). П. м. применяют и при решении сеточной
краевой задачи.
Лит.: [1] Бахвалов Н. С, Численные методы, '2 изд.,
М., 1975; [2] Годунов С. К., Рябенький В. С,
Разностные схемы, 2 изд., М., 1977; 13] Крылов В. И.,
Бобков В. В., Монастырный П. И., Вычислитель-
Вычислительные методы, т. 2, М., 1977; [4] Современные численные методы
решения обыкновенных дифференциальных уравнений, пер.
с англ., М., 1979. А. Ф. Шаппин.
ПРИТЯЖЕНИЯ ОБЛАСТЬ устойчивого
распределения — совокупность всех функций
распределения F (х) таких, что для последовательности
независимых одинаково распределенных случайных
величин Xj, X2, ... с функцией распределения F (х)
при подходящем подборе постоянных Ап и 5„>0,
га=1, 2, . . ., распределения случайных величин
H, n = l, 2, ..., (»)
слабо сходятся при п -> оо к невырожденной функции
распределения Г (.г), к-рая с необходимостью оказыва-
оказывается устойчивой.
Одной из основных задач теории устойчивых зако-
законов является описание П. о. устойчивых законов. Так,
для нормального распределения в 1935 А. Я. Хинчи-
ным, В. Феллером (W. Feller) и П. Леви (P. Levy)
было установлено, что F'(.г) принадлежит П. о. нор-
нормального закона тогда и только тогда, когда при ж->-оо
Позже Б. В. Гнеденко A939) и В. Дёблин (W. Doeblin,
1940) дали описание П. о. устойчивого закона с пока-
показателем а, 0<а<2: для принадлежности F(x) П. о.
невырожденного устойчивого закона V (х) с показате-
показателем а необходимо и достаточно, чтобы
F{r-x)l[l — F(x) + F(-x)]—+c1l(c1 + c2) при x-^v>
для нек-рых Cj^O, c2=^0, ci~rc2>0, определяемых по
V(x), и
[l—F (x) + F (-я)]/[1 —F (tx)-r-F(-tx)] ¦—> t*
при х —>¦ оо
при каждом постоянном t>0. Ограничение на характер
поведения нормирующих коэффициентов Вп, га=1,
2, . . ., приводит к уменьшению совокупности функций
распределения, для к-рых имеет место сходимость по
распределению для последовательности (•*). Совокуп-
Совокупность функций распределения F(x), для к-рых функ-
функции распределения последовательности случайных ве-
величин (*) при подходящем выборе последовательности
Ап, ге=1, 2, . . ., постоянной с>0 и Вп=сп~1^а, п=\,
2, . . ., слабо сходятся к устойчивой функции распреде-
распределения V (х) с показателем а, наз. областью нор-
нормального притяжения V(x). Нормальная
П. о. нормального распределения совпадает с сово-
совокупностью невырожденных распределений с конечной
дисперсией.
Нормальная П. о. невырожденной устойчивой функ-
функции распределения V(х) с показателем а @<а<2)
образована функциями F(x) такими, что существуют
и конечны
lira F(x)/\x\a = c,^0,
lim A — F (х))/ха = с2 5= 0,
где Cj и с2 определяются устойчивым законом V(x).
Лит.: [1] Гнеденко Б. В., Колмогоров А. Н.,
Предельные распределения для сумм независимых случайных
величин, М.— Л., 1949; [2] Ибрагимов И. А., Л и н-
ни к Ю. В., Независимые и стационарно связанные величины,
М., 1965; [3] Петров В. В., Суммы независимых случайных
величин, М., 1972. Б. А. Рогозин.
ПРОБЛЕМНО-ОРИЕНТИРОВАННЫЙ ЯЗЫК — спе-
специализированный язык программирования задач,
принадлежащих нек-рому четко выделяемому классу.
Выделение лласса производится либо фиксацией ма-
тематич. объектов, лежащих в основе решаемых задач
(напр., класс задач линейной алгебры), либо фиксаци-
фиксацией области применения ЭВМ (напр., класс задач опе-
оперативного планирования и учета на предприятии).
Проблемная ориентация обычно производится п кон-
контексте нек-рого универсального языка программиро-
программирования, по отношению к к-рому П.-о. я. является либо
над-, либо пред-, либо подъязыком. Надъязык
получается обогащением универсального языка до-
дополнительными конструкциями, особенно удобными
для формулирования задачи из класса. Обычные кон-
конструкции универсального языка используются либо
для «скрепления» дополнительных конструкций в це-
целостную программу, либо для программирования «не-
«нестандартных» компонент задачи. В пред ъ языке
дополнительные конструкции полностью «загоражива-
«загораживают» универсальный язык и переводятся на него спе-
специальным препроцессором. Подъязык получает-
получается из универсального языка отказом от конструкций,
неупотребительных в данном классе задач, либо пред-
предварительным составлением библиотеки «стандартных
программ», в совокупности достаточных для выраже-
выражения любой задачи из класса. Во всех случаях выгода
от употребления П.-о. я. состоит в том, что вместо
программирования заново каждой задачи из класса
достаточно лить указать средствами П.-о. я. пара-
параметры, отличающие одну задачу от другой.
А. П. Ершов.
ПРОГОНКИ МЕТОД — метод переноса одноточеч-
одноточечного граничного условия с помощью дифференциаль-
дифференциального или разностного уравнения, соответствующего
данному уравнению. Применяется для решения гра-
граничной задачи в том случае, когда пристрелки метод
не эффективен.
Щ'сть на отрезке a<?x*?b задано линейное обыкно-
обыкновенное дифференциальное уравнение
у' (х) + А (x)y(x)=i(x), A)
где квадратная матрица А (х) порядка п и вектор f (х)=
=[fi(x), . . ., fn(x)]J — известные непрерывные функ-
функции, дифференцируемая вектор-функция у(х) = [у1(х),
. . ., yn(x)]J подлежит определению. К уравнению A)
присоединены граничные условия в форме
<рТу(а)=а, г|)тг/(Ь) = Р, B)
где известные матрицы ф и г|з имеют размеры reX к и
nXl и ранги к и I соответственно,
а=[сц, ...,о*]Т, Р = [РЬ ...,р?]Т.
Используя дифференциальные уравнения
у' (х) = иТ (x)f(x)
с начальными условиями м(я) = ф, у (а) —а, где иско-
искомая дифференцируемая матрица-функция и{х) имеет
размеры пХк, у(х) — [у1(х), . . ., Vfe(x)]"I"? можно опре-
определить и(х) и у(х) на всем отрезке а<х<:/7 (прямой
ход прогонки). С помощью уравнения
ит (Ь)у(Ъ) = у(Ъ)
и второго из граничных условий B) можно определить
значение у(Ь), если квадратная матрица [и(Ь), г|з] име-
имеет ранг п. Искомое решение граничной задачи A)—B)
вычисляется теперь как решение задачи Коти для
уравнения A) в направлении от точки х=Ь к точке
х=а (обратный ход прогонки). Указан-
Указанный метод применим и к многоточечной задаче, когда
условия вида B) задаются не только на концах, но
и в нескольких внутренних точках отрезка а^сх^Ь.
Разработаны варианты метода прогонки для переноса
линейных граничных условий, отличных от B) (см.
HI).
Достоинства II. м. видны на примере следующей
граничной задачи:
i/n-\-Q(x)y(x) = f(x), C)
у' (a)-\-qiy (a)--a, D)
2ЛЬ) + ф2/F) = Р, E)
где квадратная матрица Q(x) порядка п и вектор f(x)
размера п — известные непрерывные функции, дваж-
дважды дифференцируемая вектор-функция у(х) подлежит
определению, известные квадратные матрицы ф и г|з
имеют порядок п, а=(а15 . . ., а„)т, Р=(РЬ . . ., Р„)т-
Используя дифференциальные уравнения
у' (x) = v(x)y(x) + f(x)
с начальными условиями v(a) = cf, у(а) — <х, где искомая
дифференцируемая квадратная матрица-функция v(x)
имеет порядок п, у(х) = [у1{х), . . ., уп{х)Р , ищутся
v(x) и у{х) на всем отрезке а<л;<6 (прямой х о д
прогонки).
С помощью уравнения
y'(b) + v(b) у{Ь)=у{Ь)
и граничного условия E) можно определить значение
j/F) = [y(b)-t|5]-1[v(&)-PJ. F)
если матрица v(b) — г|; имеет ранг п. Искомое решение
граничной задачи C) — E) находится как решение
задачи Коши для уравнения
У' (z)--'rv (x) у (х) = у(х)
с начальным условием F) (обратный ход п р о-
г о н к и). Таким образом, П. м. для задачи C) — E)
является методом понижения порядка дифференци-
дифференциального уравнения C).
В случае конечной последовательности линейных
алгебраич. уравнений
Я(ф<--1 — bj-qPi + W + i— h, « = 1,2, ...,п, G)
где коэффициенты «,-, с,-, Ь,- — известные квадратные
матрицы порядка v, а /,¦ п Ф,- — известный и. искомый
вектор-столбцы размера v, ax=0, сп~0, алгоритм про-
прогонки определяется следующим образом:
Р,- + 1 = (&«—в/Р,-)-1^-, (8)
Ч + 1 = {Ьг — а^-Ца/г!— /,•), i = l, 2, ..., п, (9)
при условиях Pi=0, з1=0 (прямой х о д) и
«Pi=Pi+i?i+i+z,- + i, A0)
iz=n, n — 1, ..., 1,
при условии ф« + 1=0 (обратный ход). Здесь
|3,- — квадратная матрица порядка v, г,- и ф,- — вектор-
столбцы размера v. Изложенный метод наз. методом
правой прогонки. Аналогично формулам (8)—
A0) получаются формулы левой прогонки.
Комбинируя левую и правую прогонки, получают метод
встречных прогонок. При решении урав-
уравнений G) с сильно меняющимися коэффициентами при-
применяется потоковый метод прогонки.
Для нахождения периодич. решения бесконочной по-
последовательности уравнений вида G) с периодич. ко-
коэффициентами используется циклическая про-
прогонка (см. [4]).
См. также Ортогональной прогонки метод.
Лит.: [1] Бахвалов Н. С, Численные методы, 2 иуд.,
М., 1975; [2] Крылов В. И., Бобков В. В., Монас-
Монастыри в й П. И., Вычислительные методы, т. 2, М., ]977;
[3] Марчук Г. И., Методы вычислительной математики,
2 изд., М., 1980; [4] Самарский А. А., Николаев
Е. С, Методы решения сеточных уравнений, М., 1978.
А. Ф. Шапкин.
ПРОГРАММ ОПТИМИЗИРУЮЩИЕ ПРЕОБРАЗО-
ПРЕОБРАЗОВАНИЯ — применяемые при трансляции направлен-
направленные преобразования программы, представленной в
нек-рой ее промежуточной форме, с целью улучшения
рабочих характеристик программы, связанных с ис-
использованием ею ресурсов ЭВМ, главными из к-рых
являются время выполнения ц объем занимаемой
памяти.
Обычно каждое применение П. о. п. изменяет ло-
локальную семантику фрагментов программы, но сохра-
сохраняет семантику программы в целом — результирующая
программа либо эквивалентна исходной, либо является
ее доопределением на более широкое множество
входов.
Различают машинно-зависимые П. о. п.,
к-рыс определяются особенностями машинного языка
или другими характеристиками конкретной ЭВМ, и
универсальные П. о. п. (такие, напр., как
удаление из программы операторов, недостижимых от
начала), к-рые определяются только семантикой, вкла-
вкладываемой в исходную запись алгоритма, и применимы
для широкого класса ЭВМ.
Основные способы улучшения машинной программы
при П. о. п. заключаются в удалении вычислений или
объектов из процессов выполнения программы или в
замене в них сложных вычислений на более простыв
(на основе априорных оценок сложности вычислений).
Это требует учета управляющих, информационных и
частотных отношений, возникающих в этих процессах
между операторами и объектами программы. П. о. п.
по существу включает в себя: нахождение необходимых
ему отношений указанного типа по локальной семан-
семантике операторов программы — т. н. потоковый
анализ программа; проверку нек-рых свойств
собранной информации — т. н. контекстных
условий; преобразование фрагмента программы
в случае удовлетворения этих свойств — собственно
трансформация данного П. о. п.
По величине той части программы (т. н. участка
э к о н о м и и), к-рая обрабатывается П. о. п. неза-
независимо от окружения, П. о. п. разделяются на л о-
к а л ь н ы е, участок экономии к-рых не более опе-
оператора; глобальные, участком экономии к-рых
является вся программа; кваз и локальные,
где участок экономии — нек-рый фрагмент програм-
программы, имеющий фиксированную внутреннюю структу-
структуру,— напр., луч (линейная последовательность опе-
операторов), зона (нетривиальный сильно связный
подграф управляющего графа программы), не содер-
содержащая других зон, или гамак (подграф, связан-
связанный с остальной частью управляющего графа в точ-
точности двумя вершинами — входной и выходной; вход-
входная вершина принадлежит гамаку, а выходная нет),
не содержащий других гамаков и зон.
Для уменьшения временной и емкостной сложности
глобального П. о. п. часто используется фактори-
факторизация — замена глобального П. о. п. серией квази-
квазилокальных, применяемых к фрагментам программы
в соответствии с их вложенностью.
Только для узких классов программ таких, как,
напр., класс линейных программ, можно построить
конечный полный набор П. о. п. Поэтому в конкрет-
конкретных трансляторах набор П. о. п. в значительной сте-
степени строится на эвристич. основе и существенно за-
зависит от класса задач, для к-рых предназначен транс-
транслятор. Важным является выбор последовательности
применений П. о. п., поскольку, как правило, исполь-
используемые наборы П. о. п. не являются системами Чёр-
ча — Россера, в к-рых результат не зависит от порядка
применения преобразований.
Набор П. о. п. для трансляторов с наиболее распро-
распространенных проблемно-ориентированных языков (та-
(таких, напр., как алгол, фортран, ПЛИ) является хо-
хорошо исследованным и позволяет получать машинные
программы, сравнимые по качеству с программами,
написанными вручную. Он содержит преобразования
по удалению повторных вычислений с одинаковым ре-
результатом, частичному выполнению программы при
трансляции, по чистке программы от оесполезных
объектов и действий, замене сложных вычислений на
более простые, уменьшению суммарного размера одно-
одновременно существующих объектов, сокращению раз-
размера программы.
Лит.: llj А х о А., У л ь м а н Д ж., Теория синтаксиче-
синтаксического анализа, перевода и компиляции, цер. с англ., т. 2, М.,
1978; 12] Б а б с ц к и й Г. И. и др., Альфа-система автома-
автоматизации программирования, Новосиб., 1967; [3] Касья-
iioii В. Н., Поттосйн И. В., Технология трансляции,
Новосиб., i 979. В. Н. Касьянов.
ПРОГРАММА — план действий, подлежащих вы-
выполнению нек-рым исполнителем, обычно автомати-
автоматическим устройством, чаще всего ЭВМ; предписание,
алгоритм. П. представляется в виде конечной совокуп-
совокупности команд (инструкций), каждая из
к-рых побуждает исполнителя выполнить нек-рую
элементарную операцию над данными, хранящимися
в памяти исполнителя и имена к-рых являются пара-
параметрами команды. Автоматизм исполнения достигает-
достигается тем, что любая текущая команда, кроме завершаю-
завершающей, указывает однозначно на команду П., к-рая долж-
должна выполниться после текущей. Особенностью испол-
исполнения является наличие команд ветвления (ус-
(условных переходов), в к-рых выбор одного из несколь-
нескольких указанных продолжений делается на основании
проверки свойств данных, упоминаемых в команде.
Другой особенностью является возможность многократ-
многократного выполнения отдельных команд. Эти особенности
приводят к тому, что последовательность выполняемых
команд и ее длина при исполнении П. могут варьиро-
варьировать, однозначно определяясь входными данными. Та-
Таким образом, П., являясь конечным объектом, побуж-
побуждает исполнителя закономерно реагировать на потен-
потенциально бесконечное разнообразие входных данных.
Тем самым П. так же, как и теоремы с их доказатель-
доказательствами, реализуют свойство всеобщности математич.
закономерностей.
Математнч. абстракции П. изучаются программиро-
программированием теоретическим. П. важна не только как пред-
предписание для ЭВМ, но и как источник операционного
знания для человека. Том самым алгоритмические язы-
языки, созданные для записи П., несут также коммуни-
коммуникативную функцию, свойственную естественным язы-
языкам .
Составление П. для ЭВМ, или программирование,
стало в связи с широким применением ЭВМ новой мас-
массовой формой математич. практики.
Лит.: [1] Ершов А. П., «Кибернетика», 1972, ЛЬ 5, с.
i'o—99; [2] Туре к и й В., Методология программирования
>Т., 1981. ' А. П. Ершов.
ПРОГРАММИРОВАНИЕ — 1) процесс составления
программы, плана действий; 2) дисциплина, изучающая
методы и приемы составления программ. С определен-
определенной долей условности П. как дисциплина делится на
программирование теоретическое, изучающее матема-
шч. абстракции программ и способов их построения,
системное п р о г р а м м и р о в а н и е, имею-
имеющее дело с разработкой математического обеспечения
ЭВМ, т. е. программных- комплексов массового и дли-
длительного применения, и прикладное про-
программирование, обслуживающее конкретные
применения ЭВМ во всем их разнообразии.
Составление программы является творч. задачей,
т. к. поиски способа достижения даже четко сформу-
сформулированной цели в общем случае требуют выработки
или привлечения нового знания. В нек-рых частных
случаях возможно нахождение более систематической
п формальной процедуры П. Так, если задание на П.
уже сформулировано в виде алгоритма, то П. сводится
к переводу с языка записи алгоритма, или алгоритми-
алгоритмического языка, к языку, непосредственно воспринимае-
воспринимаемому исполнителем. В нек-рых математич. моделях
задача перевода решается исчерпывающе. Напр., если
задача сформулирована в виде теоремы существования
ЧхЗ\уР (х, у),
где Р (.с, у) — нек-рая формула узкого исчисления
предикатов, то из доказательства теоремы в конструк-
конструктивной логике эффективно извлекается рекурсивное
описание функции <f(x), для к-рой yxP(,r, <f(x))
(теорема Клини — Нельсона). Поиски
систематич. процедур перевода записей алгоритма в
программы и извлечения программы из условия задачи
и дополнительной информации составляют предмет ав-
автоматизации программирования и ее частного слу-
случая — трансляции программ.
Методика П. уделяет особое внимание способам опи-
описания исходной спецификации задачи, подлежащей П.,
поскольку умелое использование заложенной в специ-
спецификации информации позволяет придать П. более до-
достоверный характер. Важным аспектом П. является
забота о четкой структуре программы, облегчающей
проверку ее правильности, а главное — выделение и
изоляцию тех фрагментов программы, дальнейшая де-
детализация к-рых требует привлечения нового знания.
Нек-рое представление о способе перехода от спе-
спецификации задачи к программе дает следующий пример
П. задачи возведения х в натуральную степень п.
Исходное знание: х^~х, .rnirm — xn-xm, xnm=(xn)m.
Обнаруживая, что эти соотношения позволяют свести
решение задачи х" к более простой (т. е. с меньшим п),
пытаются придать исходному знанию простейшую фор-
форму (творч. шаг):
Содержательный анализ показывает, что третье соот-
соотношение эффективнее, нежели второе, но зато приме-
применимо не всегда. Второе соотношение переписывается
в виде случая, дополнительного к третьему (творч.
шаг):
Используя обратимость функций 2л и re-f-t и логич.
несовместимость соотношений, получают рекурсивное
соотношение методом разбора случаев (формальный
шаг):
( если п = 0, то 1;
*"-=•{ если п четное, то (хп12)г\
[ если п нечетное, то х-хп~^.
Остается переписать это правило на каком-либо алго-
ритмич. языке, напр, алгол-60 (формальный шаг):
real power (x, n); real х1 integer n;
power. = \i ге = 0 then I else
if even(n) then power(x,nil)t2 else xXpower(x, re—1).
Определение процедуры проверки четности even (n)
становится отдельной, более частной задачей П.
Важной составной частью П. является проверка
правильности программы. Одним из способов обеспе-
обеспечения правильности является придание процессу П.
формы, сходной с доказательством теоремы, т. е. ког-
когда каждый шаг построения программы сопровождается
рассуждением, подтверждающим непротиворечивость
этого шага исходному знанию о программе и дополни-
дополнительному знанию, использованному в данном таге.
Возникающие при этом формальные дедуктивные си-
системы также изучаются в программировании теорети-
теоретическом. Дополнительным средством проверки правила
ности уже составленной программы является ее о т-
л а д к а, т. е. систематич. испытания программы на
машине и сравнение эффекта, производимого програм-
программой, с ожидаемым. Хотя на практике отладка является
преимущественным способом проверки программ, тео-
теоретически она не может быть исчерпывающей, т. к.
установление правильности программы путем коне>1-
ной системы испытаний может быть достигнуто только
для очень узких классов задач (см. Автоматов теория).
Лит.: [1] Л ю б и м с к и й Э. 3., Мартынюк В. В.,
Трифонов Н. П., Программирование, М., 1980; 12] Д е fl-
flic стр а Э. В., Дисциплина программирования, пер. о англ.,
М., 1978; [3] Мейер В., В о д у э н К., Методы программи-
программирования, пер. с франц., т. 1 — 2, М., 1982. А. П. Ершов.
ПРОГРАММИРОВАНИЕ МАТЕМАТИЧЕСКОЕ —
см. Математическое программирование.
ПРОГРАММИРОВАНИЕ ПАРАЛЛЕЛЬНОЕ —
раздел программирования, связанный с изучением и
разработкой методов и средств для: а) адекватного
описания в программах естественного параллелизма
моделируемых в ЭВМ и управляемых ЭВМ систем и
процессов, б) распараллеливания обработки информа-
информации в многопроцессорных и мультипрограммных ЭВМ
с целью ускорения вычислений и аффективного ис-
использования ресурсов ЭВМ.
В отличие от программирования последовательных
вычислений, концептуальную основу к-рого составля-
составляет понятие алгоритма, реализуемого по шагам строго
последовательно во времени, в П. п. программа порож-
порождает совокупность параллельно протекающих процес-
процессов обработки информации, полностью независимых
или связанных между собой статическими или динами-
динамическими пространственно-временными или причинно-
следственными отношениями.
Вычислительный параллелизм выступает в разных
конкретных формах в зависимости от этапа програм-
программирования, от сложности параллельных фрагментов и
характера связей между ними.
В текстах, описывающих задачи и программы, мож-
можно выделить уровни сложности фрагментов, для к-рых
задача распараллеливания, т. е. со-
составления параллельной программы, решается по-раз-
по-разному: выражения со скалярными данными; выражения
над структурными данными (векторы, матрицы, де-
деревья и т. п.), записываемые в алгоритмнч. языках с
помощью операторов цикла; подзадачи и подпрограм-
подпрограммы; независимые задачи и программы в мультипроцес-
мультипроцессорных системах.
Предпосылкой для распараллеливания выражений
служит тот факт, что входящие в них операции и функ-
функции удовлетворяют нек-рым соотношениям, индуцирую-
индуцирующим на всем множестве выражений отношение эквива-
эквивалентности по результатам (например, для арифметич.
операций — ассоциативность, коммутативность, дист-
дистрибутивность). Задача распараллелива-
распараллеливания состоит в построении но заданному выражению
Е эквивалентного выражения Е', к-рое может быть
исполнено за наименьшее число параллельных шагов,
где параллельный шаг — это совокупность действий,
выполняемых одновременно на разных вычислителях
(процессорах). Напр., выражение
f)^ 8
преобразуется в эквивалентное выражение
исполнение к-рого осуществляется за 3 параллельных
шага. Отношение числа параллельных шагов испол-
исполнения к числу последовательных шагов наз. уско-
ускорением распараллеливания. Любое
арифметич. выражение с п операндами может быть
вычислено параллельно за О (log n) шагов с использо-
использованием п процессоров. Относительная простота алго-
алгоритмов распараллеливания выражений позволяет реа-
реализовать их автоматически в ЭВМ с помощью специ-
специальных программ или аппаратными средствами.
Большее ускорение может быть получено за счет
распараллеливания обработки структурных данных.
В алгоритмич. языках типа алгол или фортран выраже-
выражения над структурными данными программируются с
помощью операторов цикла дида FOR/=<4, В, С,
DO S, где / — целочисленный параметр цикла, А —
ого начальное значение, В — конечное значение, С -
шаг изменения параметра, S — тело цикла, задающем
действия, выполнимые на одном шаге итерации. Для
распараллеливания системы вложенных циклов рас
сматрипается «-мерное целочисленное пространство
итераций с координатными осями /ъ /2, . . ., /„. Вы
полнение Aj-й итерации по параметру 1г, K2-& итерации
по параметру /2, . . ., Кп-ж итерации по параметру 1п
изображается точкой (Ки . . ., Кп) этого пространства.
В пространстве итераций ищется семейство поверх
ностей, удовлетворяющих условию: все итерации (Ki7
. . ., К„), лежащие на любой из этих поверхностей,
могут выполняться параллельно. Для программного
представления параллельной обработки структурных
данных необходимы специальные языковые средства.
С этой целью разработаны модификации существующих
языков программирования (в основном — фортрана),
в к-рые вводятся параллельные операторы циклов,
напр., вида
FORALL(/, /, K)/[l:N\ 1:L; 1:M],
при исполнении к-рых тело цикла копируется но опре-
определенным правилам на параллельно исполняемые ите-
итерации. Эти языки снабжаются также более развитыми
средствами описания структурных данных и средства-
средствами управления размещением их в памяти для обеспе-
обеспечения быстрого параллельного доступа к структурным
данным. Дальнейшее повышение уровня языкоа прог-
программирования состоит в использовании групповых
операций над структурными данными таких, как по-
покомпонентное умножение и сложение векторов и мат-
матриц, скалярное и векторное произведение, обращение
матриц и т. п. Применение таких языков позволяет
заменить автоматич. распараллеливание последова-
последовательных циклов, к-рое на практике осуществимо, но
относительно сложно, на непосредственное задание
параллельных групповых операций.
Параллельные выражения могут исполняться асин-
асинхронно или синхронно. В первом случае
не фиксируется связь между временами выполнения
параллельных операций, во втором случае времена их
выполнения должны вкладываться в жесткие рамки
тактированного расписания. Если операции имеют
фиксированные длительности и известно число про-
процессоров, доступных в любой момент исполнения, то
целесообразно применять синхронный метод вычисле-
вычислений, в противном случае — более гибкий асинхронный.
Управление асинхронным исполнением выражений ос-
основано на потоковом принципе: операция может выпол-
выполняться в любой момент времени после того, как для
нее подготовлены операнды.
Распараллеливание на уровне подзадач и подпро-
подпрограмм существенно сложнее. В этом случае параллель-
параллельные процессы могут иметь сложную внутреннюю струк-
структуру, длительность их выполнения не фиксирована;
процессы взаимодействуют, обмениваясь данными и об-
обращаясь к общим ресурсам (общие данные и программы
в памяти, внешние устройства и т. п.). Автоматич.
распараллеливание на этом уровне требует сложных
алгоритмов анализа задач и учета динамич. ситуаций
в системе. В связи с этим особое значение имеет созда-
создание языков П. п., позволяющих программисту непо-
непосредственно описывать сложные взаимодействия па-
параллельных процессов.
В большинстве языков и систем П. п. принята час-
частично асинхронная организация вычислений. В язы-
языках П. п. имеются средства выделения (порождения)
параллельных процессов и сродства их синхронизации,
к-рые в аппаратуре поддерживаются механизмами
прерываний — принудительных остановок процессов
с запоминанием их. текущих состоянии и с последую-
последующей активацией или возобновлением др. процессов.
Наиболее известными и простыми программными ме-
механизмами синхронизации являются семафоры и собы-
события. Семафор — это специальная управляющая
переменная, принимающая целочисленные значения.
Семафор обычно связан с нек-рым конфликтным ресур-
ресурсом. К семафору применимы только две операции Р и
V. Если в ходе исполнения процесса встретится опера-
операция P(s), где s — семафор, то процесс может продол-
продолжаться с уменьшением значения s на 1 только в том
случае, когда значение s положительно; в противном
случае он приостанавливается и занимает место в оче-
очереди q(s) процессов, ждущих соответствующего ресур-
ресурса. Операция V увеличивает значение s на 1 и возобнов-
возобновляет первый в очереди q(s) процесс. Механизм семафо-
семафоров широко используется в языках управления про-
процессами в операционных системах ЭВМ и в ряде уни-
универсальных языков программирования (напр., алгол-
68). Механизм событий включает управляющие
переменные, текущие значения к-рых отмечают на-
наступление каких-либо программных или системных
событий (завершение процессов, прерывания и т. п.),
и специальные операторы ожидания событий.
Семафоры и события являются универсальными сред-
средствами синхронизации, но они слишком примитивны, и
неправильное их использование может привести к ава-
аварийным ситуациям таким, как взаимная блокировка
процессов (напр., два процесса требуют для своего
продолжения но два ресурса и каждый «захватил» по
одному). Стремление повысить надежность программи-
программирования приводит к появлению более сложных меха-
механизмов синхронизации: «почтовые ящики» —
особые структуры для обмена сообщениями, для к-рых
фиксированы правила работы с ними параллельных
процессов; мониторы — наборы процедур и дан-
данных, к к-рым процессы могут обращаться только по-
поочередно и к-рые содержат заданные программистом
правила организации взаимодействий.
Чисто асинхронное П. п. используется для органи-
организации вычислений в распределенных вычислительных
системах, в к-рых полностью исключены конфликты
по ресурсам. Стремление упростить организацию взаи-
взаимодействий между процессами с общими ресурсами
привлекает внимание к асинхронным методам вычисле-
вычислений, в к-рых разрешен нерегламентированный доступ
параллельных процессов к общим ресурсам. Напр.,
разрабатываются асинхронные алгоритмы, в к-рых
параллельные процессы обмениваются данными с об-
общей памятью, причем неупорядоченный доступ к па-
памяти не мешает достижению однозначного результата.
В теории П. п. разрабатываются формальные модели
параллельных программ, процессов и систем и с их
помощью исследуются различные аспекты П. п.: авто-
матич. распараллеливание последовательных алгорит-
алгоритмов и программ; разработка параллельных методов
вычислений для разных классов задач и разных клас-
классов параллельных вычислительных систем; оптималь-
оптимальное планирование параллельных вычислений и распре-
распределение ресурсов между параллельными процессами;
формальное описание семантики программ и языков
П. п. Среди таких моделей — схемы параллельных
программ, отражающие с разной степенью детализа-
детализации структурные свойства программ; графовые модели
и асинхронные сети (Петри сети), являющиеся мате-
матнч. абстракциями дискретных процессов и систем.
Лит.: [1] Котов В. Е., «Кибернетика», 1974, № 1, о.
1—16; №2, с. 1 — 18; [2] Н а р и н ь я н и А. С, там же, Л» 3,
с. 1—15; № 5, с. 1 — 14; [3] Ф а д д е е в а В. Н., Ф а д д е-
е в Д. К., там же, 1977, №6, с. 28—40; [4] К и с k D. J.,
«Сотр. Surveys», 1977, v. 9, № 1, p. 29—59. В. Е. Нотой.
ПРОГРАММИРОВАНИЕ ТЕОРЕТИЧЕСКОЕ —
математическая дисциплина, изучающая математич.
абстракции программ, трактуемых как объекты, вы-
выраженные на формальном языке, обладающие опреде-
определенной информационной и логич. структурой и подле-
подлежащие исполнению на автоматич. устройствах. П. т.
сформировалось преимущественно на основе двух мо-
моделей вычислений: последовательных программ с па-
памятью, или операторных программ, и рекурсивных про-
программ. Обе модели строятся над нек-рой абстрактной
алгебраич. системой <?>, Ф, П>, образованной пред-
предметной областью D, конечным набором (сигнатурой)
функциональных Ф—{q>i, • • ч 4>т) и предикатных
П= {я1г . . ., лп} символов с заданным для каждого
символа числом его аргументов (арностью).
Определение класса программ слагается из трех
частей: схемы программы (синтаксиса), интерпретации
и семантики. Схема программы — это кон-
конструктивный объект, показывающий, как строится
программа с использованием сигнатуры и других фор-
формальных символов. Интерпретация — это за-
задание конкретной предметной области и сопоставление
символам сигнатуры конкретных функций и предика-
предикатов (базовых операций), согласованных с предметной
областью и арностью символов. Семантика —
это способ сопоставления каждой программе резуль-
результата ее выполнения. Как правило, с программами
связывают вычисляемые ими функции. Интерпретация
обычно входит в семантику как параметр, поэтому
схема программы задает множество программ и вы-
вычисляемых ими функций, к-рое получается при варьи-
варьировании интерпретаций над нек-рым запасом базовых
операций.
Схема программы с памятью, назы-
называемая также алголоподобной, или опе-
операторной, схемой, задается в виде конечного
ориентированного графа переходов, име-
имеющего обычно одну входную и одну выходную верши-
вершины, вершины с одной (преобразователи) и двумя (рас-
(распознаватели) исходящими дугами. С помощью символов
сигнатуры и счетного множества символов переменных
и констант обычным образом строится множество функ-
функциональных и предикатных термов. Каждому распо-
распознавателю сопоставляется нек-рый предикатный терм,
а преобразователю — оператор присваивания, имею-
имеющий вид !/:=т, где у — символ переменной, а т — функ-
функциональный терм. Конечная совокупность всех пере-
переменных в схеме образует ее память. Интерпрета-
Интерпретация в дополнение к конкретизации базовых операций
предписывает каждой переменной область ее измене-
изменения, а каждой константе — ее значение. Для программ
с памятью наиболее обычна т.н. операционная
семантика, состоящая из алгоритма выполне-
выполнения программы на заданном состоянии памяти. Про-
Программа выполняется при движении по графу перехо-
переходов. При попадании на распознаватель вычисляется
предикатный терм и происходит переход по дуге, со-
соответствующей значению предиката. При попадании на
преобразователь с оператором г/:=т вычисляется зна-
значение т и присваивается переменной у. Результат вы-
выполнения программы — состояние памяти при попа-
попадании на выходную вершину.
Схема рекурсивной программы, или
рекурсивная схема, использует кроме функ-
функциональных т. н. условные термы, образу-
образующие вместе с первыми множество вычислительных
термов. Условный терм задает вычисление методом
разбора случаев и имеет вид (я|Т]|т2), где я — преди-
предикатный, a tj и т2 — вычислительные термы, и соответ-
соответствует конструкции условного выражения в алголе:
if л then ti else т2.
Термы строятся над счетным множеством входных и
формальных неременных, констант и символов опреде-
ляемых функций. Рекурсивная схема состоит из глав-
главного вычислительного терма с входными переменными
и конечного набора рекурсивных уравнении вида
/(^i, . . ., хп)=х, где / — символ определяемой функ-
функции, х1г . . ., хп — формальные переменные, а т —
терм с переменными из множества \хх, . , ., хп) и с
определяемыми функциями из набора уравнении. При
естественных предположениях на интерпретацию ба-
базовых операций система уравнений относительно опре-
определяемых функций всегда имеет т. и. и а и м е н ь-
тн у к) неподвижную то ч к у (п. н. т.) —
совокупность функций, удовлетворяющих уравнениям,
с графиками, принадлежащими графикам любых дру-
других решений уравнений. Подставляя в главный терм
вместо символов определяемых функций соответствую-
соответствующие компоненты н. н. т., получают функциональный
терм, задающий нек-рую функцию входных перемен-
переменных, к-рая и объявляется функцией, вычисляемой ре-
рекурсивной программой. Поскольку такой способ со-
сопоставления программе вычисляемой ею функции по
дает конкретного алгоритма вычисления, определенная
так семантика наз. денотационной.
Указанные формализмы как бы отмечают диапазон
уровней изобразительных средств языков программи-
программирования: если операторные схемы близки к структуре
машинной программы, то рекурсивные схемы ближе
к исходной формулировке задач, подлежащих програм-
программированию.
Исследования но П. т. несут на себе отпечаток об-
щематематич. средств, используемых при изучении мо-
моделей программ. Формально-комбинаторные методы
формируют теорию схем программ, к-рая
изучает свойства программ, инвариантные относитель-
относительно выбора интерпретации базовых операций. Логич.
методы изучают способы определения семантики про-
программы, а также ищут закономерности в процессе по-
построения программы. Алгебраич. методы, отвлекаясь
от конкретной структуры программы, концентрируют
свое внимание на изучении множеств, возникающих
при рассмотрении программы или класса программ.
Сложившиеся разделы IT. т. охватывают в основном
модели последовательных вычислений, выполняемых
одним активным устройством. Изучение проблем, воз-
возникающих при необходимости организовать совмест-
совместную работу ансамбля машин, объединяемых для ре-
решения одной задачи или взаимодействующих посредст-
посредством передачи сигналов и информации, составляет пред-
предмет новой дисциплины — т. н. программирования па-
параллельного.
Теория схем программ. Отправным понятием теории
схем программ является понятие функциональной эк-
эквивалентности. Две схемы функционально
эквивалентны, если для любой интерпретации
соответствующие программы вычисляют одинаковые
функции. Каждому выполнению программы можно
сопоставить его протокол-- особого рода терм
в сигнатуре базовых операций, отражающий порядок
их выполнения. Если известны значения истинности
предикатов, входящих в программу, то протокол по
этим значениям строится однозначно, при этом для
построения не нужно знать интерпретации базовых
операций. Если выбирать значения истинности пре-
предикатов произвольно, то в результате для схемы про-
программы создается нек-рое множество формальных
протоколов, называемое ее детерминантом.
Две схемы формально эквивалентны, если их детерми-
детерминанты совпадают. Формальная эквивалентность кор-
корректна, если из нее следует функциональная эквива-
эквивалентность. Поскольку детерминант строится чисто
комбинаторно на основе произвольного выбора из ко-
конечного множества, он образует формальный язык, вос-
воспринимаемый нек-рым автоматом. Представляют особый
интерес такие определения протокола схем программ,
к-рые приводят к разрешимым детерминантам. Для
таких детерминантов можно ставить вопрос о поис-
поиске системы преобразований схем программ, полной
в том смысле, что любые две формально эквивалентные
схемы переводимы одна в другую этими преобразо-
преобразованиями.
Структура теории схем программ сложилась на базе
основополагающих работ А. А. Ляпунова и 10. И. Яно-
ва (см. [5], [10]). Последний полностью изучил
простейшую модель операторных схем о сигнатурой
одноместных операций и допускающих в программе
только одну церемонную (схемы Я н о в а). Про-
Протоколом схемы Янова является последовательность
выполняемых операций, перемежаемых значениями
предикатов. Автомат, воспринимающий детерминант,
оказывается конечным автоматом, а формальная экви-
эквивалентность разрешима, при этом она совпадает с
функциональной. Для схем Янова найдена полная
система преобразований.
Для общей модели операторных схем функциональ-
функциональная эквивалентность оказалась неразрешимой, однако
удалось найти форму протокола — т. н. л о г и к о -
термальную и с т о р и ю, к-рая приводит
к разрешимому детерминанту. Этот протокол фикси-
фиксирует последовательность выполнения и значения пре-
предикатов схемы, а для каждого аргумента предиката
указывает функциональный терм, к-рый вычислял
значение данного аргумента при выполнении програм-
программы. Автоматом, воспринимающим детерминант, ока-
оказывается двухлонточный конечный автомат. Для логи-
логико-термальной формальной эквивалентности также най-
найдена полная система преобразований.
Существенное место в теории схем программ зани-
занимают вопросы перевода схем программ из одной вычис-
вычислительной модели в другую. Операторные схемы эффек-
эффективно переводятся в рекурсивные схемы в той же сиг-
сигнатуре, однако обратная трансляция невозможна, т. к.
выполнение рекурсивной программы требует, вообще
говоря, сколь угодно большого числа ячеек памяти.
Детерминант рекурсивной схемы может быть задан
в виде контекстно-свободного языка (см. Грамматика
бесконтекстная), однако вопрос о разрешимости соот-
соответствующей формальной эквивалентности остается
пока A983) открытым.
Теория схем программ занимается также изучением
отдельных классов схем программ с целью выделить
случаи разрешимых эквивалентностей, она также обо-
обогащает базовую вычислительную модель дополнитель-
дополнительными конструкциями языков программирования, изу-
изучая при этом выразительную силу обогащений и во-
вопросы сводимости.
Логическая теория программ. Говорят, что програм-
программа А частично правильна относительно
входного условия Р и выходного условия Q (обозначе-
(обозначение Р {А } Q), если в случае, когда Р истинно для вход-
входных значений переменных и А завершает работу, Q
истинно для выходных значений переменных. При этом
Р наз. предусловием, а (>—-постусло-
(>—-постусловие м программы А . Программа А тоталь-
тотально правильна (обозначение Р<.А >(•>), если А
частично правильна относительно Р и Q, а также А
завершает работу для входных значений переменных,
удовлетворяющих условию Р. Для доказательства час-
частичной правильности последовательных программ часто
используется метод Ф л о й д а, к-рый состоит в
следующем. На схеме программы выбираются контроль-
контрольные точки так, чтобы любой циклич. путь проходил
но крайней мере через одну точку. Контрольные точки
также связываются с входом и выходом схемы. С каж-
каждой контрольной точкой ассоциируется специальное
условие (т. н. индуктивное у т в е р ж д е н и е,
или инвариант цикла), к-рое истинно при
каждом переходе через ату точку. С входной и выходной
точками ассоциируются входное и выходное условия.
Затем каждому пути программы между двумя соседни-
соседними контрольными точками сопоставляется т. н. условие
правильности. Выполнимость всех условий правиль-
правильности гарантирует частичную правильность программы.
Один из способов доказательства завершения работы
программы состоит во введении в программу дополни-
дополнительных счетчиков и установлении ограниченности
этих счетчиков на выходе программы в процессе дока-
доказательства частичной правильности.
Было предложено задавать аксиоматич. семантику
языков программирования посредством конечной ак-
аксиоматич. системы (т. н. логики X о а р а), со-
состоящей из аксиом и правил вывода, в к-рой в качество
теорем выводимы утверждения о частичной правиль-
правильности программ. Напр., для оператора присваивания
схема аксиом имеет вид
Р (х + -е) {х := е) Р,
где Р (-г-*—е) означает результат подстановки в Р выра-
выражения е вместо всех вхождений переменной х, а для
оператора цикла типа while правило вывода имеет вид
(Р АВ){А}Р\-Р {while П do A} (Pa ~\R)
(то есть Р является инвариантом цикла).
Пусть рассматривается логика Хоара, у к-рой в
качестве языка для записи условий взят язык ариф-
арифметики 1-го порядка. Утверждение о частичной пра-
правильности программы наз. выводимым, если оно выво-
выводимо в расширении этой логики посредством добавле-
добавления истинных формул арифметики, и наз. истинным,
если оно истинно по отношению к операционной (или
денотационной) семантике программы. Логика Хоара
наз. состоятельной, если каждое выводимое
в ней утверждение истинно, и наз. полной (отно-
(относительно арифметики), если каждое истинное утверж-
утверждение выводимо в ней. Состоятельная и полная логика
Хоара построена, в частности, для языка программи-
программирования, содержащего простые переменные и опера-
операторы присваивания, составной, условный, цикла и
процедуры (возможно, рекурсивные, но с рядом огра-
ограничений).
Важным обобщением логики Хоара является т. н.
алгоритмическая (или динами ч е с к а я)
логика. Пусть P{A}Q представлено в виде PZD
ZD\A]Q, где \A]Q есть самое слабое предусловие, для
к-рого справедливо утверждение о частичной правиль-
правильности программы А с постусловием Q. Аналогично для
случая тотальной правильности пусть P<A>Q пред-
представлено в виде PZD<iA^>Q. Формулы алгоритмич.
.чирики строятся из формул базового логич. языка (для
записи условий) и программ с помощью булевых опе-
операций, кванторов, а также операций вида [A]Q, <A >Q.
В алгоритмич. логике выразимы различные утвержде-
утверждения о программах, напр, их эквивалентность. Анало-
Аналогично логике Хоара для алгоритмич. логики построена
состоятельная и полная конечная аксиоматич. систе-
система в случае языка программирования, допускающего
и недетерминированные программы.
Для доказательства утверждений о рекурсивных
программах часто используется специальная индук-
индукция, связанная с определением н. н. т. Пусть для про-
простоты рекурсивная программа задается одним уравне-
уравнением /=т(Л. а се денотационная семантика — н. н. т.
/н. При естественных предположениях об условии Р
справедлив следующий принцип индукции: если фор-
формула Р (Q) истинна и из Р (т'(Q)) следует Р (т' fl (Q)),
то выполняется Р (fH) (здесь й —нигде не определен-
определенная функция). Для описания денотационной семантики
языков программирования высокого уровня исполь-
G(x в
91 сч
зуется задание области данных в виде т.н. полных
решеток Скотта.
Задачу синтеза программы можно формализовать
как задачу построения доказательства теоремы
V-1'ЭуП (.г, у) и последующего извлечения программы
из этого доказательства. Построен алгоритм, к-рый по
доказательству в интуиционистской логике дает про-
программу на языке алгол-68. Если доказательство ис-
использует правило индукции, то ему соответствует в
программе цикл вида for to ... do ... od. Извлекаемая
программа будет приемлемой сложности, если исполь-
использовать предположение, что она строится из стандарт-
стандартных (т. е. заданных) функций и предикатов, свойства
к-рых описаны аксиомами специального вида.
Алгебраическая теория программ. Примером приме-
применения алгебраич. методов в П. т. может служить про-
проблема эквивалентности дискретных преобразователей
Глушкова, в к-рые естественно вкладываются опера-
операторные схемы программ. Пусть Ш — конечный автомат
Мили с входным алфавитом X и выходным алфавитом
У и с заданными начальным и заключительным состоя-
состояниями. Пусть G — полугруппа с множеством образу-
образующих У и единицей е. Пусть рассматривается автомат
Мура G^ (возможно, бесконечный) с множествами со-
состояний G, входов У, выходов X, начальным состоя-
состоянием е, функцией выходов \х (g) и функцией переходов
q(g, У) = 8У- Автомат %, работающий совместно с вц,
наз. дискретным преобразователем,
если 31 воспринимает в качестве входа выход Gp,, a
G воспринимает в качестве входа выход 31. Выходом
читается при этом состояние G^ в момент останов-
остановки 51. Дискретные преобразователи эквивалентны
относительно полугруппы G, если для каждого отобра-
отображения |.i из G в X они оба не останавливаются при
работе с G^ либо оба останавливаются с одинаковым
выходом. Установлена разрешимость проблемы экви-
эквивалентности дискретных преобразователей относи-
относительно полугруппы с левым сокращением, неразло-
неразложимой единицей, в к-рой разрешима проблема тож-
тождества слов. Описаны также все разрешимые и нераз-
неразрешимые случаи эквивалентности дискретных преобра-
преобразователей относительно коммутативной полугруппы.
П. т. оказывает свое влияние на практику прежде
всего как концептуальный багаж при изучении про
граммирования и — более тохнич. путем — через тео-
теорию формальных языков программирования. Здесь
свойства абстрактных моделей вычислений использу-
используются для уточнения семантики языков программиро
вания и для обоснования различных манипуляций с
программами (см. Трансляция программ, Программ
оптимизирующие преобразования).
Лит.: [1] Г л у ш к о в В. М., Летпчсвский А. Л.,
н кн.: Избранные вопросы алгебры и логики, Новосиб., 197:-:.
с. 5—39; [2] Ершов А. П., Введение в теоретическое про-
программирование, М., 1977; [3] Котов В. Е., Введение в тео-
теорию схем программ, Новосиб., 1978; [4] Лавров С. С,
«Программирование», 1978, № 6, с. 3—10; [о] Л я п у н о в
А. А., «Проблемы кибернетики», 1958, в. ), с. 46—74; [Bj Н е-
н е й в о д а Н. Н., «Программирование», 1979, JV» 1, с. 15—25;
[7] П л к) ш к я в и ч ю с Р. А.-; [и др.], «Кибернетика», 1979,
Л» 2, с. 12 — 19; [8] Семантика языков программирования. Сб.
статей, пер. с англ., М., 1980; [9] С к о т т Д., «Кибернетический
сборник», 1977, в. 14, с. 107—21; [10] Янов Ю. П., «Проб-
«Проблемы кибернетики», 1958, в. 1, с. 75—127; 111] Manna Z.,
Mathematical theory of computation, N.Y., —la.o.], 1974.
A. П. Ершов, В. А. Непомнящий.
ПРОГРАММИРОВАНИЯ ЯЗЫК — формальная зна-
знаковая система, служащая общению человека с ЭВМ.
Решая вычислительные задачи или управляя испол-
исполнительными механизмами, ЭВМ с ее программным обес-
обеспечением демонстрирует сложные формы поведения,
обычно относимые к умственной деятельности челове-
человека. Именно dto сходство функций, отражающее общ-
общность кибернетич. законов обработки информации в
живых организмах и автоматич. устройствах, нозволя-
ет говорить о языке ЭВМ, о понимании машиной пере-
передаваемой ей информации, об общелии человека и
ЭВМ.
Основное назначение П. я.— быть средством про-
программирования, т. е. формулирования программ, под-
подлежащих выполнению на ЭВМ. Осмысленная програм-
программа для ЭВМ представляет собой своеобразную опера-
операционную и информационную модель нек-рой законо-
закономерности внешнего мира, причем программа фиксирует
эту закономерность в точной и воспроизводимой форме.
Эта документальная сторона программирования дела-
делает П. я. также важным средством профессионального
общения людей.
Наиболее распространенным видом П. я. являются
алгоритмические языки, формулирующие алгоритм ре-
решения задачи на ЭВМ. Обычно П. я. носит универсаль-
универсальный характер, допуская формулирование алгоритмов
решения разнообразных задач, подлежащих решению
на разных ЭВМ. В то же время для более удобного
представления задач из нек-рого четко выделяемого
класса создают проблемно-ориентированные языки, а
для более полного использования возможностей кон-
конкретной ЭВМ создают машинно-ориентированные язы-
языки. Наиболее распространенные П. я. в 1970-е гг.—
алгол, фортран, кобол, FIJI I I, алгол-68. К более спе-
специальным языкам относятся лиса, симула, снобол.
В СССР получили распространение также языки альфа
и рефал.
Лит.: [1] Криницки й Н, А., Миронов Г. А.,
Фролов Т. Д., Программирование и алгоритмические язы-
языки, 2 изд., М., 1979; [2] П р а т т Т., Языки программирова-
программирования: разработка и реализация, пер. с англ., М., 1979.
А. П. Ершов.
ПРОГРАММЫ СХЕМА — формальный конструк-
конструктивный объект, получающийся из программы абстра-
абстрагированием от лексич. особенностей использованного
при ее записи формального языка программирования и
от смысла элементарных действий и объектов, употреб-
употребляемых в программе. П. с. изучаются в программиро-
программировании теоретическом. А. П. Ершов.
ПРОГРЕССИЯ — см. Арифметическая прогрессия,
Геометрическая прогрессия.
ПРО-р-ГРУППА — проконечная группа, являюща-
являющаяся проективным пределом конечных р-групп. Напр.,
аддитивная группа кольца %р целых р-адических чисел
является П.-р-г. В теории Галуа П.-р-г. появляются
как группы Галуа р-расширений полей.
Пусть G есть П.-р-г. Ее системой образую-
образующих наз. подмножество EcG, обладающее свойства-
свойствами: 1) G совпадает с минимальной замкнутой подгруп-
подгруппой группы G, содержащей Е, 2) в любой окрестности
единицы группы G содержатся почти все (т. е. все,
кроме конечного числа) элементы из Е.
Пусть / — множество индексов и Fr — абстрактная
свободная группа с системой образующих {a,|i?/}.
Проективный предел F (/) системы групп F[lN, где
N — такие нормальные делители группы F/, что ин-
индекс подгруппы N в F[ является степенью числа р,
а почти все элементы a,-, i?I, лежат в N, является
П.-р-г., к-рая наз. свободной П.-р-г. с системой
образующих {а,-|??/}. Всякая замкнутая подгруппа
свободной П.-р-г. сама является свободной П.-р-г. Вся-
Всякая П.-р-г. G есть факторгруппа свободной П.-р-г., то
есть существует точная последовательность гомомор-
гомоморфизмов П.-р-г.
где F — подходящая свободная П.-р-г. (эта последо-
последовательность яаз. представлением группы
G с помощью F). Подмножество EdR наз.
системой соотношений группы G, если R
является наименьшим замкнутым нормальным дели-
делителем в R, содержащим Е, и любой открытый нормаль-
нып делитель в R содержит почти все элементы из Е.
Мощности минимального (относительно включения)
множества образующих и минимальной системы соот-
соотношений соответствующего представления П.-р-г. G до-
допускают когомологич. интерпретацию: первая мощ-
мощность совпадает с размерностью над %1р% пространства
H1(G) = H1 (G, ж/pZ), а вторая — с размерностью над
iJpZ пространства Н'2 (G)= H'1 (G, %'-р%). Здесь g/pS
рассматривается как дискретный G-модуль с триви-
тривиальным действием. Если G — конечная р-группа, то
4 dim Н2 (G) Ss (dim IP (G) — IJ;
из итого результата выводится отрицательное решение
классич. проблемы башни, полей классов [4].
Лит.: [1] С е р р Ж. - П., Когомологии Галуа, пер. с
франц., М., 1968; [2] Кох X., Теория Галуа р-расширений,
пер. с нем., М., 1973; [3] Алгебраическая теория чисел, пер.
с англ., М., 1969; [4] Голод Е. С, Ш а ф а р е в и ч И. Р.,
«Изв. АН СССР. Сер. матем.», 1964, т. 28, J41 2, с. 261—72.
ПРОДОЛЖАЕМОСТЬ РЕШЕНИЙ ДИФФЕРЕН-
ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ — свойство решений
обыкновенных дифференциальных уравнений быть про-
продолженными на больший интервал независимого пере-
переменного. Пусть
x=<p(t), t?I, A)
— решение системы
x = f(t,x),x?R». B)
Решение x=ty(t), t?J, системы B) наз. продол-
продолжением решения A), если JzdI и -ф(t)=(p(t),
t?I.
Пусть функция
f (t, x) — (fx (t,xu ..., г„), ..., fn(t,xu ...,!„))
определена в области Gt=R?,4.i и to?I. Решение A)
наз. неограниченно продолжаемым
(неограниченно продолжаемым впе-
вперед (вправо), неограниченно продол-
продолжаемым назад (в лев о)), если существует ого
продолжение, определенное на оси — оо<г<оо (соот-
(соответственно на полуоси {0<:г<оэ, на полуоси— с» <?<
<:<0). Решение A) наз. продолжаемым впе-
вперед (вира по) до границы Г области G,
если существует его продолжение ж=г|)(?), io<:i<:i4 <
<со, обладающее свойством: для любого компакта
FdG найдется значение t=tp, io<<p<i+, такое, что
точка (tf, ф (*у=-)) не содержится в F. Аналогично опре-
определяется продолжаемость назад (вле-
(влево) до границы Г. Решение, к-рое нельзя
продолжить, наз. не продолжаемым.
Если функция / (t, x) непрерывна в области G, то
всякое решение A) системы B) может быть продолжено
вперед (назад) либо неограниченно, либо до границы
Г. Другими словами, всякое решение системы B)
может быть продолжено до непродолжаемого решения.
Если частные производные
dfildxj, i, / = 1, ..., re, C)
непрерывны в области G, то такое продолжение единст-
единственно .
Интервал / наз. максимальным интер-
интервалом существования решения системы
B), если его нельзя продолжить на больший интервал.
Для любого решения линейной системы
к =¦ 2"= 1 aU @
@.
с непрерывными на интервале / коэффициентами ац (t)
и правыми частями }[{t), l<;i,/<<!, максимальный
интервал существования решения совпадает с /. Для
решений нелинейных систем максимальный интервал
существования может быть разным для ранных ptxuie-
ний, и его отыскание — трудная задача. Напр., для
решения задачи Коши
х=х~, x{to)=xo
имеет место
/ = (го-[^о~\ со)
при хо<О,
/ = (—оо, to + xo1)
при хо>О,
/ = (—оо, оо)
при хо~О.
Достаточные условия, при к-рых можно указать
максимальный интервал существования решения, дает,
напр., теорема Уинтнера: пусть функция
f(t, x) непрерывна при t?J=\t0, to-\-a], x?Rn и в этой
области выполняется оценка
где L (г) —непрерывная при К>0 функция, ?(г)>0 и
тогда максимальный интервал существования любого
решения системы B) совпадает с /.
Эта теорема справедлива и в том случае, когда /=
— \t0, оо). Большой интерес представляют достаточные
условия неограниченной продолжаемости решений.
Напр., если функция f(t, x) и ее частные производные
C) непрерывны при ?0<?<oo, x?Rn и при этих зна-
значениях t, х выполняются оценки
\dfildxj\^c(t) < оо, г, / = 1, ..., и,
то решение системы B) такое, что x(to)=xB, существует
при i0<?<oo для любого xo^R".
Пусть рассматривается задача Коши
x = f{x), x(to)=xo D)
для автономной системы, причем функция f(x) непре-
непрерывно дифференцируема в области Gt=R". Если при
возрастании t фазовая траектория решения ,r=cp(i)
задачи D) остается в компактном подмножестве FdG,
то это решение можно продолжить на полуось ?0<:?<оо.
Лит.: [1] Понтрягин Л. С, Обыкновенные дифферен-
дифференциальные уравнения, 3 изд., М., 1970; [2] Арнольд В. И.,
Обыкновенные дифференциальные уравнения, М., 1971; [3]
Немы цкий В. В., Степанов В. В., Качественная тео-
теория дифференциальных уравнений, 2 изд., М.— Л., 1949; [4]
К о д д и н г т о и Э. А., Л е в и н с о н Н., Теория обыкно-
обыкновенных дифференциальных уравнений, пер. с англ., М., 1958;
[51 X а р т м а н Ф., Обыкновенные дифференциальные урав-
уравнения, пер. с англ., М., 1970; Об] Ч е з а р и Л., Асимптотиче-
Асимптотическое поведение и устойчивость решений обыкновенных диффе-
дифференциальных уравнений, пер. с англ., М., 1964; [7] Wintner
A., «Amer. J. Math.», 1945, v. 67, p. 277—84.
JVf. В. Федорюк.
ПРОДОЛЖЕНИЙ И ОХВАТОВ МЕТОД — метод ис-
исследования различных дифференциально-геометрич.
структур на гладких многообразиях и их подмногооб-
подмногообразиях. В основе П. и о. м. лежат дифференциально-
алгебраич. критерии операций, позволяющих в инва-
инвариантной (безкоординатной) форме присоединять к
данной структуре внутренне связанные с ней струк-
структуры, в том числе и их дифференциальные инварианты.
Исторически П. и о. м. возник вслед за методом по-
подвижного репера как инвариантный метод исследова-
исследования подмногообразий однородных пространств или про-
пространств со связностью. Впоследствии П. и о. м. был
распространен на геометрию произвольных расслоен-
расслоенных пространств. В отличие от главной цели метода
подвижного репера — построения канонич. поля репе-
реперов и дифференциальных инвариантов изучаемой струк-
структуры путем последовательного сужения соответствую-
соответствующих главных расслоенных пространств, П. и о. м.
ставит целью построение инвариантов и инвариантно
присоединяемых структур без сужения главных рас-
расслоений реперов. В необходимых случаях П. и о. м.
включает и процесс канонизации репера.
Пусть G — группа Ли и К (G) — класс всех G-npo-
странств с левосторонним действием группы Ли G на них
как группы преобразований. G-o хватом наз. такое
гладкое сюръективное отображение
f-X—>Y; X, Y?K (G),
что для любого g?G коммутативна диаграмма
где lg и lg — преобразования G-пространств X и У со-
соответственно, определяемые элементом g. В этом слу-
случае говорят, что пространство У с помощью / охва-
охвачено пространством X или простран-
пространство X является продолжением про-
пространства У. Класс К (G) становится категорией
с морфизмами — G-охватами.
Примеры G-охватов.
1) Пусть Т(р, q)?K (GL (n, Я)) — пространство тен-
тензоров типа (р, q), pj>l, q^i. Охватом является отобра-
отображение свертки
Т(р, 9)_н.7-(р_1, g_l).
Полная свертка тензоров пространства Т(р,р)
Т(Р, P):T(p,p)-*R
является примером охвата инварианта.
2) Если X, Y?K(G), то XXY с помощью pry и pry
охватывает X и У соответственно. Иными словами,
XXY является продолжением как X, так и У.
Понятие охвата естественным образом распростра-
распространяется на классы расслоенных пространств, присоеди-
присоединенных к главным расслоениям. Пусть я : Р(М, Н) —>-
—>-М — главное расслоенное пространство со структур-
структурной группой II, действующей на Р правым образом, и
F ? К (Н) — любое левое Я-пространство. Объектами
класса К (Р) присоединенных к Р расслоенных про-
пространств являются пространства типа
где факторизация подразумевается по следующему
правому действию группы // на PXF:
(I, Y)h^&h, h-W); A,Y)?PXF,
Пространство F(P)?K(P) является расслоенным над
базой М пространством с типовым слоем F. Элемент
у?Р(Р), определяемый парой (|, Y)?PxF, записы-
записывают в виде y=%Y. Если F, Ф?К(Н) и / : F -> Ф —
отображение Я-охвата, то в силу конструкций F (Р) и
Ф(Р) f индуцирует послойное сюръективное отображение
/ : F (Р) _». ф (Р), называемое Р-о хватом. Р-ох-
ват / определяется по закону:
I№')-¦= If (Y), l?P,
Таким образом, класс К (Р) присоединенных к Р рас-
расслоенных пространств является категорией с морфиз-
морфизмами тина Р-охватов /¦ Соответствие Fh-F(P), fy-*f
является биективным функтором категории К (Н) на
категорию К(Р). Следовательно, достаточно изучать
операции охвата в категориях Я-пространства.
Если s : М —*¦ F (Р) — сечение расслоенного прост-
пространства F (Р) (поле геометрического
объекта типа F), то Р-охват / : /' (Р) -> Ф (Р)
присоединяет к сечению s сечение s=/Qs охваченного
расслоения ф (Р); иными словами, поле геомртрич.
объекта s(x), ,r?M, охватывает ноле геометрлч. объек-
объекта j js(x). Если s(x) —структурный объект яек-рой
G-структуры, то изучение G-структуры и ее инвариан-
инвариантов сводится во многом к отысканию охватываемых гео-
геометрия, объектов. В процессу отыскания охватываемых
геометрич. объектов важную роль играют дифференци-
дифференциальные критерии охватов, формулируемые в терминах
структурных дифференциальных форм расслоенных
пространств и составляющие основу П. и о. м.
Лит.: И] Лаптев Г. Ф., «Тр. Моск. матем. об-ва», 1953,
т. 2, с. 275—382; [2] его ж е, в кн.: Тр. Третьего Всесоюзного
матем. съезда. Москва, 195И, т. 3, М., 1958, с. 409—18.
Л. Е. Евтушик.
ПРОДОЛЖЕНИЯ ПО ПАРАМЕТРУ МЕТОД —
включение данной задачи в однопараметрическое @«:
•<а<:1) семейство задач, связывающее данную задачу
(а=1) с известной разрешимой задачей (а—О), и изу-
изучение зависимости решений от параметра а. Метод
широко используется в теории дифференциальных урав-
уравнений.
Пусть, напр., требуется доказать разрешимость в
классе Гёльдера задачи Дирихле
в ограниченной Л^-мерной области D?A<-n' Iх) для ли-
линейного эллиптич. оператора 2-го порядка
Lu=2,, /=1 аи (х) ^7^7+2, =,ь' и ш^л-с и и,
с(.г)<0, а,7, Ъ;, с?С(п~2- ^]ф), D^--D+dD,
re 5s 2, ц > 0.
Вводится семейство эллиптич. операторов
Lau = a.Lu-\- A — а) Дн, 0<а<1,
и рассматривается для него задача Дирихле
Пусть 91 — множество тех а?[0, 1], для к-рых задача
B) однозначно разрешима в классе С'"- Д) (D) при любых
/ и ф, /gC<"-2. й)(Р), ф^С". W EД). Множество 21
не пусто, поскольку при а--0 (т. е. для оператора Ла-
Лапласа) задача B) однозначно разрешима в классе
С(и. м) (Д), как это следует из теории потенциала. Мно-
Множество Э? одновременно открыто и замкнуто на [0, 1]
и, следовательно, совпадает с [0, 1]. Таким образом,
а=1 принадлежит % и задача A) разрешима.
П. по п. м. (в варианте аналитич. продолжения по
параметру) был предложен и развит в ряде работ
С. Н. Бернштейна (см. [1], [2]). В дальнейшем этот метод
нашел широкое применение в различных вопросах
теории линейных и нелинейных дифференциальных
уравнений, причем идея аналитич. продолжения по
параметру была дополнена более общими функциональ-
функциональными и топологич. принципами (см. [3]).
Лит.: [1] Берн штейн С. Н., «Math. Ann.», 1904,
Bd 59, S. 20—7B; [2] его же, Собр. соч., т. 3, М., I960; [3]
Лерэ Ж., Шаудер К)., «Успехи матем. наук», 1946, в.
3/4, с. 71 — 95. 11. А. Шишмарев.
ПРОДОЛЖЕНИЯ ПО ПАРАМЕТРУ МЕТОД —
метод приближенного решения нелинейных функцио-
функциональных уравнений. П. по п. м. состоит в том, что ре-
решаемое уравнение Р (.г) = 0 обобщается к виду F (х, ?) —О
путем введения параметра t, принимающего задан-
заданные значения на конечном интервале to<s.t*g.t*, так,
что первоначальное уравнение получается при
t—t*:F(x,t*)—-P(x), а уравнение F(x, to)-Q легко
решается или известно его решение х0 (см. [1] — [3]).
Ofiouiценное уравнение F(.r,t) — () последовательно
решается при отдельных значениях I : tu, t}, . . ., lk--t*.
Уравнение при t=ti + 1 решается каким-либо итераци-
итерационным методом (методом Ньютона, простой итерации,
итерационным методом вариации параметра f4] и др.),
начиная с полученного решения Х{ уравнения F (т, t)—0
при t--~ t,-. Применение на каждом шаге но i, напр, п
итераций метода Ньютона, приводит к следующей фор-
формуле:
i=0, 1,2, ...,k-~\; v- 0,1,2, ...,n — l; x^U^xp.
Ксли разность t{ + x—it достаточно мала, то значение
.г/ может оказаться достаточно хорошим начальным
приближением, обеспечивающим сходи.моеть, для полу-
получения решения :гц , при t=t;+1 (см. [1], [3], [5]).
На практике часто исходная задача естественным об-
образом зависит от нек-рого параметра, к-рый может
быть выбран в качестве параметра t. ¦
П. по и. м. применяется как для решения систем
нелинейных алгебраич. и трансцендентных уравнении
(см. |1], [21), так и для более общих нелинейных функ-
функциональных уравнений в банаховых пространствах
(см. [5] - [7])'.
П. по п. м. иногда наз. также прямой метод вариа-
вариации параметра (см. [2], [6]), а также комбинированный
метод прямого и итерационного методов вариации пара-
параметра. В этих методах построение решений обобщенно-
обобщенного уравнения сводится путем дифференцирования по
параметру к решению дифференциальной задачи с на-
начальными условиями (задачи Коши) методами числен-
численного интегрирования обыкновенных дифференциаль-
дифференциальных уравнений. Применяя простейший метод Эйлера
в прямом .методе вариации параметра к задаче Коши
приближенные значения .г(?,)=?,-, г=1, 2, . . ., А, ре-
решения х (t) уравнения F (j, t)=0 можно определить
следующими равенствами:
*i ,1=*; — (ч + 1 — ч) [К (*/, ti)]~1F't (.г,-, /,•),
Олемеит ,г^ будет искомым приближенным решением
исходного уравнения Р(.г)==6. Уточнение всех или
нек-рых значени14 х[ + 1 можно проводить итерационным
.методом вариации параметра D] (или методом^ Ньюто-
Ньютона). Обобщенное уравнение при атом рассматривается
обычно в виде
F(x, /,- + i):----(!-Я)/'(^@)- </ + i). x^=xin
на конечном промежутке 0<;Я<1 или, наменян здесь
1—к на е~%, на бесконечном промежутке 0<?т<оо.
Метод вариации параметра применен к широкому
классу задач как для построения решений, так и для
доказательства их существования (см., напр., [3], [4J,
[6], [7]).
Jlu.ni.: [J] La ha у е Е., «Acad. Hoy. Belg. Bull., Cl. Sci.
Ser. 5». 1048, t. 34, p. 809—27: til Давид енко Д. Ф.,
«Укр. матем. ж.», 195Я, т. S, Л« 2, с. JOB—20B; [3] О рте г а
Д ж., Р е й н б о л д т В., Итерационные методы решении не-
нелинейных систем уравнений со многими неизвестными, пер.
г, англ., М., 1975; [4] Д а в и д е н к о Д. Ф., «Ж. иычисл.
матем. и матем. физ.», 1975, т. 15, JSS 1, с. 30—47; [51 Д е м е tt-
т ь е в а А. М., «Докл. АН СССР», 1971, т. 201, Л! 4, с. 774 —
777; [6] Д а в и д с и к о Д. Ф., «Укр. матем. ж.», 1955, т. 7,
Л» 1, с. 18—28- [7] Шидловска п И, А., «Уч. зап. ЛГУ»,
1958, К» 271, в. 33, с. 3 — 17. Д. Ф. Давидент.
ПРОДОЛЖЕНИЯ ТЕОРЕМЫ — теоремы о продол
жении функции с нек-рого множества на более широкое
таким образом, что продолженная функция обладает
определенными свойствами. К II. т. относятся прежде
всего задачи об аналитическом продолжении функции.
Примером теорелгы существования непрерывного про-
продолжения непрерывной функции является т е о р е м а
Б р а у о р а — Урысона: если Е —замкнутое под-
подмножество нормального пространства Ja/:?->R-
непрерывная действительная ограниченная функ-
функция, то существует такая непрерывная ограниченная
функция F : X -> R, что F—f на Е. К числу П. т.
относится Хана — Банаха теорема о продолжении ли-
линейных функционалов в векторных пространствах.
В евклидовом пространстве П. т. в основном связаны
с решением следующих двух задач: 1) продолжение
функций с областей, лежащих в пространстве, на все
пространство; 2) продолжение функций с границы
области на саму область. В обоих случаях требуется,
чтобы продолженная функция обладала определен-
определенными свойствами гладкости, т. е. принадлежала опре-
определенному функциональному классу, зависящему от
свойств продолжаемой функции.
Задача о продолжении функции с сохранением непре-
непрерывности частных производных с области с достаточно
гладкой границей на все пространство была решена
М. Хестенсом [3] и X. Уитни [4]. Если на (п — 1)-мер-
ной границе dG области G, лежащей в н-мерном прост-
пространстве R", заданы функции <pk : dG -+¦ R, A-=0, 1,
. . ., /п, то задача построения такой функции и : G—>- R,
что для нее
где п — нормаль к dG, в случае, когда гладкость функ-
функций ср? и границы dG описывается в терминах непрерыв-
непрерывности и принадлежности Гёльдерову пространству
(при наличии, быть может, нек-рых особенностей), рас-
рассматривалась :). Леви [5], Ж. Жиро [6] — [7J и М. Жевре
[8]. Изучался также порядок роста частных производ-
производных порядка &>ш при стремлении аргумента к границе
0G области G.
Систематически обе указанные задачи о продолжении
функций в разных метриках Lp, 1 ¦</> o-f- с», для разных
измерений и в различных функциональных пространст-
пространствах изучались С. М. Никольским и его учениками (см.
[9], [10]). В терминах ряда функциональных пространств
установлены наилучшие характеристики дифферен-
дифференциальных свойств функций, к-рые можно получить при
продолжении функции, обладающей заданными диффе-
дифференциально-разностными свойствами (см. Вложения
теоремы). Для задачи (*) было найдено продолжение,
наилучшее с точки зрения роста производных порядка
&>т при подходе к граничному многообразию (см.
[11], [12]).
Часто методы продолжения функций и систем функ-
функций (».) с границы области на всю область основаны на
интегральных представлениях функций. Подобные ме-
методы продолжения функций обычно являются линей-
линейными. Существуют и другие методы продолжения функ-
функций, напр., основанные на разложении функций в ряды
с последующим продолжением каждого члена ряда.
!)тот метод, вообще говоря, не линейный. Имеются
случаи, когда заведомо не существует линейного метода
продолжения [13].
Лит.: [1] X а у с д о р ф Ф., Теория множеств, пер. с нем.,
М.~ д., 1937; [2]' Ко л м о v о р о в А. Н., Ф о ы и н С. В.,
Элементы теории функций и функционального анализа, 5 изд.,
М., 1981; [3] Hestenes M. R., Extension of the range of
differentiable function, «Duke Math. J.», 1941, v. 8, p. 183—92;
Ц] Whitney H., «Trans. Amer. Math. Soc», 1934, v. 3ti,
p. 63—89: 1936, v. 40, p. ;1O9—17; [5] Lfvi E. E., «Mem. Soc.
It. dei XL», 1909, v. 16, p. 3—112; [fi] G i г a u d G., «Ann. EC.
norm, sup.», 1929, t. 4(i, p. 131 — 245; [7] его ж с, там же,
1932, t. 49, p. 1 — 104, 245—308; t8] Gevrey M., «Ann. Ёс.
norm, sup.», 1935, t. 52, p. 39—108; [9] Никольский
С. М., Приближение функций многих переменных и теоремы
вложения, 2 изд., М., 1977; [10] Бесов О. В., Ильин
В. П., Н и к о л ь с к и й С. М., Интегральные представле-
представления функций и теоремы вложения, М., 1975; [11] Кудряв-
ц е в Л. Д., «Тр. Матем. ин-та АН СССР», 1959, т. 55; [12]
У г II с л с к и й С. В., (.С.нС. матем. ж.», 1966, т. 7, .V I,
с. 192-4)9; JY. 2, с. 409—18; [13] Б у р е н к о в В. Ы.
Гольдман М. Л., «Тр. Матем. ин-та АН СССР», 1979,
т. 150, с. 31 — 51. Л. Д. Кудрявцев.
ПРОДОЛЖЕНИЯ ТЕОРЕМЫ в аналитиче-
аналитической геометрии — утверждения о продолже-
продолжении функций, сечений аналитич. пучков, аиалитич.
пучков, аналитич. подмножеств, голоморфных и меро-
морфных отображений с дополнения Аг\4 и аиалитич.
пространстве X к подмножеству А (как правило, тоже
аналитическому) на все пространство X. Класспч. ре-
результатами о продолжении функции являются две тео-
ромы Римана.
Первая теорема Г и м а н а утверждает,
что всякая аналитич. функция на Х\А, где X — нор-
нормальное комплексное пространство, а А его аналитич.
подмножество коразмерности 5э2, продолжается до
аналитич. функции на всем X. В т о р а я т о о р о м а
Римана утверждает, что всякая аналитич. функция
/ на Х\А , где А нигде не плотное аналитич. подмноже-
подмножество нормального комплексного пространства X, локаль-
локально ограниченная на X, продолжается до аналитич. функ-
функции на всем X. Существуют обобщения этих теорем на
произвольные комплексные пространства X, а также
на сечения когерентных аналитич. пучков (см. Локаль-
Локальные когомологии).
Важнейшими результатами о продолжениях анали-
аналитических подмножеств являются теорема Реммерта —
Штейна — Шифмана и теорема Бишопа. Теорема
Реммерта — Штейна — III нфмана утвер-
утверждает, что всякое чисто р-мерное комплексное аналитич.
подмножество в Х\А, где X — комплексное аналитич.
многообразие, а А его замкнутое подмножество, имею-
имеющее нулевую Bр—1)-мерную меру Хаусдорфа, про-
продолжается до чисто р-мерного комплексного аналитич.
подмножества во всем X. Теорема Бишопа
утверждает, что всякое чисто р-мерное комплексное ана-
аналитич. подмножество V в Х\А, где X — комплексное
аналитич. многообразие, а А — его комплексное анали-
аналитич. подмножество, продолжается до чисто р-мерного
комплексно аналитич. подмножества V во всем X,
если 1* имеет локально конечный объем в нек-poii окрест-
окрестности U множества А в X.
Имеются критерии продолжаемости аналитич. отоб-
отображений, обобщающие классич. Пикара теорему. Напр.,
всякое аналитич. отображение Х\А—>-У, где X—комп-
X—комплексное многообразие, А — его аналитическое нигде не
плотное подмножество, a Y — гиперболическое ком-
компактное комплексное многообразие, можно продол-
продолжить до аналитич. отображения X—>-У. Всякое не всюду
вырожденное аналитич. отображение X\A-*Y, где
X—комплексное многообразие, А — его аналитич. под-
подмножество, Y — компактное комплексное многообразие
с отрицательным первым классом Чжэня, можно про-
продолжить до мероморфного отображения X-+-Y.
Лит.: 11] Гриффите Ф., Кинг Д ж., Теория Неван-
линньт и голоморфные отображения алгебраических многооб-
многообразий, пер. с англ., М., 197U; [2] К о С а я с и Ш., «Матема-
«Математика», 1973, т. 17, в. 1, с. 47—96; [3] Харви Р., Голоморф-
Голоморфные цепи и их границы, пер. с англ., М., 1979.
Д. А. Пономарев.
ПРОДУКТИВНОЕ МНОЖЕСТВО — множество на-
натуральных чисел А , для к-рого существует такая час-
частично рекурсивная функция <р, что (р(х)?А— Wx для
всякого рекурсивно иеречислимого множества Wx с
геделевым номером х, содержащегося в А. Известно,
что для всякого П. м. А существует такая общерекур-
общерекурсивная функция \р, что уже для каждого х в зависимости
от взаимного расположения множеств А и Wx имеет
место либо ty(j)?A—Wx, либо ty(x)?Wx—А. Таким
обрааом, П.м. «эффективно» отличается от любого ре-
рекурсивно перечислимого множества. С другой стороны,
всякое П. м. содержит бесконечное рекурсивно пере-
числимое подмножество, в силу чего П. м. противопо-
ставляются иммунным множествам, хотя иммунны-
иммунными и продуктивными множествами не исчерпывается со-
совокупность множеств, не являющихся рекурсивно по-
речислимыми. Продуктивными оказываются многие
множества, играющие важную роль в рекурсивной тео-
теории множеств (напр., множество всех гёделевых номеров
общерекурсивных функций в нек-рой гёделевой нуме-
нумерации всех частично рекурсивных функций) и в ее при-
приложениях (в частности, множества всех номеров истин-
истинных и ложных формул элементарной арифметики при
естественной нумерации всех ее формул). Рекурсивно
перечислимые множества, дополнение к-рых (до нату-
натурального ряда) является продуктивным, наз. кре-
креативными; они образуют важный класс рекурсив-
рекурсивно перечислимых множеств.
Лит.: [1] Роджерс X., Теория рекурсивных функций
и эффективная вычислимость, пер. с англ., М., 1972.
В. А. Душский.
ПРОЕКТИВНАЯ АЛГЕБРА в узком смысле —
алгебра точек на проективной прямой; проективно-
инвариантные конструкции для определения сложения
и умножения точек проективной прямой I, расположен-
расположенной в нек-рой проективной плоскости я, для к-рой вы-
выполняется Дезарга предложение. Эти конструкции за-
зависят от выбора на
I трех различных
точек О, Е, U.
Конструк-
Конструкция I определяет
для любых двух
точек А и В, отлич-
отличных от U, третью
точку А+В, также
отличную от U и
называемую с у м-
м о й т о ч е к А
ВТ
Рис. 1.
и В. Для этого в плоскости я проводятся три прямые а,
Ъ и и, отличные от I, не проходящие через одну точку и
проходящие соответственно через точки А, В и U.
Пусть Р — точка пересечения прямых ип a, Q — точка
пересечения прямых и и Ъ, R — точка пересечения пря-
прямых OQ и a, S — точка пересечения прямых Ь и UR.
Тогда прямая PS пересекает прямую I в определенной
точке Т=А-\-В (общий случай — на рис. 1). Оказывает-
Оказывается, так построенная точка зависит лишь от А, В, О, U
и не зависит от выбора прямых и точки Е.
Конструкция II определяет для любых двух
точек А и В, отличных от U, третью точку А -В, также
отличную от U, называемую произведением
точекЛ ж В. Для этого в плоскости проводятся три
прямые а, Ь, и, проходящие соответственно через точки
А, В ж U, отличные от I и не проходящие через одну точ-
точку. Пусть Р — точка пересечения прямых и и о, Q —
точка пересечения прямых и и Ъ, R — точка пересечения
прямых EQ и a, S — точка пересечения прямых OR
и Ь. Тогда прямая
PS пересекает пря-
прямую I в определен-
определенной точке Т=А-В
(общий случай —
на рис. 2). Оказы-
Оказывается, так постро-
построенная точка зави-
зависит лишь от А , В,
О, Е, U, но не за-
зависит от выбора
прямых о, Ъ и и.
Относит е л ь н о
этих операций сло-
сложения и умноже-
умножения точки прямой I (отличные от U) образуют тело К (О,
Е, U). Поменяв ролями А и В в конструкции II, полу-
получают инверсно изоморфное тело К*{0, Е, U). Если О',
Рис. 2.
E', U' — любая другая упорядоченная тройка точек на
прямой I из той же плоскости я, то соответствующее тело
К'(О', Е', U') изоморфно А" (О, Е, V) вследствие того,
что между прямыми I и V существует проективное соот-
соответствие; поэтому любое тело К, изоморфное им, наз.
просто телом данной проективной плоскости (или даже
данной проективной геометрии); говорят также, что
имеет место проективная геометрия над
т е л о м К. В общих случаях конструкций I и II фигу-
фигурируют четыре лежащие в одной плоскости точки Р, Q,
Я, S, никакие три из к-рых не коллинеарны; они обра-
образуют т. н. (полный) четырехвер шинник с
тремя нарами противоположных сторон PQ, RS; PS,
QR ; PR, QS, Точки пересечения Z, X, Y этих пар проти-
противоположных сторон называется диагональ-
диагональными точкам и, а прямые, соединяющие диаго-
диагональные точки,— диагоналями. Специальный
случай, не покапанный на рисунке, соответствует той
ситуации, когда X, Y, Z коллинеарны (см. Фано по-
постулат).
Аналогичные построения проводятся и в пучке пря-
прямых, проходящих через одну точку с использованием
(полного) четырехсторонника — фигуры,
двойственной четырехвершиннику, и приводят к телу
К*, инверсно изоморфному К.
Свойства проективной прямой I как алгебраич. сис-
системы определяются геометрическими (проективно-ин-
вариантными) свойствами проективной плоскости, в
к-рой она расположена. Так, напр., коммутативность К
эквивалентна выполнению Паппа аксиомы; то, что ха-
характеристика К не равна 2, эквивалентно постулату Фа-
Фано; при отсутствии автоморфизмов у тела К, отличных
от внутренних, любое проективное преобразование есть
коллинеация, и т. д.
С помощью тела К на прямой, а затем и в проективном
пространстве, ее содержащем, вводятся проективные
координаты, описывающие алгебраич. модель проектив-
проективного пространства, так что содержание проективной гео-
геометрии по существу определяется свойствами того тела
К, над к-рым она построена.
В широком смысле П. а. исследует совокупность под-
подпространств проективного пространства, являющуюся
дедекиндовой решеткой с дополнениями; при этом конеч-
конечномерности пространства не требуется, но накладывают-
накладываются условия полноты, существования однородного базиса
и т. д., благодаря чему устанавливаются разнообразные
связи с теорией простых и регулярных колец, теорий
операторных абелевых групп и др. разделами алгебры.
Лит.: [1] Ход» В., Пи до Д., Методы алгебраической
геометрии, пер. с англ., т. 1, М., 1954; [2] Ар тин Э., Гео-
Геометрическая алгебра, пер. с англ., М., 1969.
М. И. Войцеховспий.
ПРОЕКТИВНАЯ ГЕОМЕТРИЯ — раздел геометрии,
изучающий свойства фигур, не меняющиеся при проек-
проективных преобразованиях, напр, при проектировании.
Такие свойства наз. проективным и; к ним отно-
относятся, напр., прямолинейное расположение точек
(коллинеарность), порядок алгебраич. кри-
кривой и т. д.
При проектировании точек одной плоскости П на
другую плоскость П' не каждая точка П' имеет прооб-
прообраз в II и не каждая точка из П имеет образ в ГГ. Это
обстоятельство привело к необходимости дополнения
евклидова пространства т. н. бесконечно удаленными
элементами (несобственными точками,
прямыми и плоскость ю)ик образованию
нового геометрия, объекта — трехмерного проективно-
проективного пространства. При этом каждая прямая дополняется
одной несобственной точкой, каждая плоскость — од-
одной несобственной прямой, все пространство — одной
несобственной плоскостью. Параллельные прямые до-
дополняются одной и той же несобственной точкой, не-
непараллельные — разными, параллельные плоскости
дополняются одной п той же несобственной прямой, не-
непараллельные — разными. Несобственные точки, кото-
которыми дополняется плоскость, принадлежат несобствен-
несобственной прямой, дополняющей ту же плоскость. Все несоб-
несобственные точки и несобственные прямые принадлежат
несобственной плоскости. Дополнение евклидова прост-
пространства до проективного пространства приводит к тому,
что проектирование становится взаимно однозначным.
Аналогичная процедура применима и для n-мерного про-
пространства .
Существуют различные способы аксиоматич. построе-
построения проективного пространства. Наиболее распростра-
распространенным является видоизменение системы аксиом, пред-
предложенной в 1899 Д. Гильбертом (D. Hilbort) для обо-
обоснования элементарной геометрии (см. Гильберта систе-
система аксиом). Проективное пространство рассматривается
как совокупность элементов трех родов: точек, прямых
н плоскостей, между к-рыми установлено основное для
П. г. отношение инцидентности, характеризующееся
надлежащими аксиомами. Они отличаются от соответст-
соответствующей группы аксиом элементарной геометрии тем, что
требуют, чтобы каждые две прямые, лежащие в одной
плоскости, имели общую точку, и на каждой прямой
имелось, по крайней мере, три различные точки. В кон-
конкретных случаях для получения более «богатой» П. г.
эта совокупность аксиом дополняется аксиомами по-
порядка и непрерывности (для действительного проектив-
проективного пространства), Паппа аксиомой (для П. г. над ком-
коммутативным телом), Фано постулатом (для П. г. над те-
телом, характеристика к-рого Ф2) и т. д.
Замечательным положением П. г. является двойствен-
двойственности принцип. Говорят, что точка и прямая (точка и
плоскость, прямая и плоскость) инцидентны, ес-
если точка лежит на прямой (или прямая проходит через
точку) и т. д. Тогда если верно нек-рое предложение Л
о точках, прямых и плоскостях проективного прост-
пространства, сформулированное только в терминах инци-
инцидентности между ними, то будет верно и двойственное
предложение аЗ, к-рое получается из Jl заменой слова
«точка» на слово «плоскость», слова «плоскость» на слово
«точка» и с сохранением слова «прямая».
Важную роль в П. г. играет Дезарга предложение,
выполнение к-рого необходимо и достаточно для введе-
введения проективными средствами системы проективных
координат, составленных из элементов нек-рого тела К,
естественным образом связанного с точками проектив-
проективной прямой (см. Проективная алгебра).
Основы П. г. были заложены в 17 в. Ж. Дезаргом
(G. Desargues) (в связи с развитием им учения о перс-
перспективе) и Б. Паскалем (В. Pascal) (в связи с изучением
им нек-рых свойств конич. сечений). Большое значение
для последующего развития П. г. имели работы Г. Мон-
жа (G. Monge, 2-я пол. 18 — нач. 19 вв.). Как самостоя-
самостоятельная дисциплина П. г. была изложена Ж. Понселе
(J. Poncelet, нач. 19 в.). Заслуга Ж. Понселе заключа-
заключалась в выделении проективных свойств фигур в отдель-
отдельный класс и установлении соответствий между метри-
метрическими и проективными свойствами этих фигур. К это-
этому же периоду относятся работы Ж. Брианшона (J. Bri-
anchon). Дальнейшее развитие П. г. получила в трудах
Я. Штейнера (J. Steiner) и М. Шаля (М. Cliasles). Боль-
Большую роль в развитии П. г. сыграли работы К. Штаудта
(Ch. Staudt), в к-рых были намечены также контуры ак-
аксиоматич. построения П. г. Все эти геометры стреми-
стремились доказывать теоремы П. г. синтетич. методом, поло-
положив в основу изложения проективные свойства фигур.
Аналитич. направление в П. г. было намечено работами
А. Мёбиуса (A. Mobius). Влияние на развитие П. г.
оказали работы Н. И. Лобачевского по созданию неев-
неевклидовой геометрии, позволившие в дальнейшем А. Кэ-
ли (A. Cayley) и Ф. Клейну (F. Klein) рассмотреть раз-
различные геометрич. системы с точки зрения П. г. Разви-
тие аналитич. методов обычной П. г. и построение на
атой базе комплексной П. г. (Г). Штуди, Е. Study, Э. Кар-
тан, Е. Cartan) поставили задачу о зависимости тех или
иных проективных свойств от того тела, над которым
построена геометрия. В решении этого вопроса боль-
больших успехов добились А. Н. Колмогоров и Л. С. Пон-
трягин.
Лит.: [1] Глаголев Н. А., Проективная геометрия,
2 изд., М.—Л., 1963; [2] Гильберт Д., К о н - Ф о с-
сен С., Наглядная геометрия, пер. с нем., 3 изд., М., 1981;
[3] К о к с т е р X. С. М., Действительная проективная плос-
плоскость, пер. с англ., М., 1959; [4] Гильберт Д., Основания
геометрии, пер. с нем., М.— Л., 1948; [5] Хартсхорн Р.,
Основы проективной геометрии, пер. с англ., М., 1970; 16]
Ефимов Н. В., Высшая геометрия, 6 изд., М., 1978; [7]
Александров П. С, Лекции по аналитической геомет-
геометрии . . ., М., 1968; [8] Ефимов Н. В., Р о з ен д о р н
Э. Р., Линейная алгебра и многомерная геометрия, М., 1970;
[9] Ар тин Э., Геометрическая алгебра, пер. с англ., М.
1969; [10] V е b I e n О., Y о u n к J. W., Protective geometry,
v. 1—2, Boston—N.Y., 1910—18; fill В 1 a s с h k e W., Pro-
jektive Geometrie, 3 Aufl., Basel, 1954. M. И. Войцеховспий.
ПРОЕКТИВНАЯ ГРУППА от п переменных
над тел ом AT — группа PGLn (AT) "преобразований
(п—1)-мерного проективного пространства Рп_\(К),
индуцированных невырожденными линейными преоб-
преобразованиями пространства К". Имеется естественный
эпиморфизм
P:GLn(K)-+PGLn(K),
ядром к-рого служит группа гомотетий пространства
К", изоморфная мультипликативной группе Z* центра
Z тела К. Элементы группы PGLn{K), наз. проек-
проективными преобразованиями, являются
коллинеациями пространства Рп-\ (К). Наряду с груп-
группой PGLn (К), яаз. также полной проектив-
проективной группой, рассматривают уни модуляр-
модулярную проективную группу PSLn (К) и
вообще группы вида P(G), где G — нек-рая линейная
группа.
При я^2 группа PSLn (К) проста, за исключением
двух случаев, когда и=2 и |/П = 2 или 3. Если К — ко-
конечное поле из q элементов, то
) (g)
Лит.: Ll] Дьедонне Ж., Геометрия классических
групп, пер. с франц., М., 1974, д. Б. Винберг.
ПРОЕКТИВНАЯ ДИФФЕРЕНЦИАЛЬНАЯ ГЕО-
ГЕОМЕТРИЯ — раздел геометрии, изучающий дифферен-
дифференциально-геометрические свойства кривых и поверх-
поверхностей, сохраняющихся при проективных преобразова-
преобразованиях. Таковы, напр., понятия асимптотич. направле-
направления или, более общо, сопряженных направлений, сопри-
соприкасающейся квадрики (в частности, квадрики Ли, пучка
квадрик Дарбу и т. п.), проективной нормали и т. д.
Важную роль в П. д. г. играет двойственности прин-
принцип, так, напр., поверхность в проективном простран-
пространстве может рассматриваться и как двухпараметрич.
семейство точек, и как огибающая двухпараметрич.
семейства плоскостей. Разработанными разделами
П. д. г. являются (проективная) теория прямолинейных
конгруэнции, вопросы проективного изгибания, асим-
асимптотич. преобразования (в частности, преобразования
Бэклунда, Бианки, Эйзенхарта, Лапласа и др.).
Первые исследования по П. д. г. начались в коя. 19
в.; здесь особенно важны работы Г. Дарбу (G. Darboux)
по теории поверхностей и конгруэнции. Первой книгой,
где систематически изложена классич. П. д. г., явилась
работа [1]. В дальнейшем появились монографии [2],
[3], L], в к-рых П. д. г. предстает уже широко развитой
геометрич. теорией, связанной с другими разделами
геометрии и имеющей широкие приложения, напр, в
теории дифференциальных уравнений (в особенности
нелинейных, что выяснилось в последнее время нри «бес-
«бесквадратурном» получении их решений путем аналогов
асимптотич. преобразований, см., напр., Синус Гордо-
Гордона уравнение).
Г. Фубияп (G. Ftibini) и И. Чех (Е. Cecil) дали изло-
изложение П. д. г. в тензорной форме, используя ковариант-
ное дифференцирование и положив в основу фунда-
фундаментальные формы (см., напр., Фубини фирма). Так
была решена задача нроективно инвариантного оснаще-
оснащения поверхности 3-мерного пространства. Большой
вклад в П. д. г. внесен С. П. Финиковым и его школой,
в особенности это касается теории конгруэнции и тео-
теории пар конгруэнции и jiv преобразований. Проблема
проективно инвариантного оснащения многообразия в
многомерном проективном пространстве исследовалась
Г. Ф. Лаптевым и др.
Эффективным средством изучения II. д. г. многомер-
многомерных пространств является метод нормализа-
ц и и А. П. Нордена [6]. В этом методе с каждой точкой х
/«-мерной поверхности Хт проективного пространства
Рп ассоциируется инцидентная х(п— та)-мерная плос-
плоскость (н о р м а л ь 1 - г о рода), пересекающая ка-
касательную плоскость в единственной точке х, а в каса-
касательной m-мерной плоскости выбирается (т—1)-мерная
плоскость (нормаль 2-го рода), не инци-
инцидентная точке х. При этом на поверхности Xт индуци-
индуцируется аффинная связность без кручения, свойства к-рой
зависят как от строения X т, так и от выбора норма-
нормализации. В случае нормализованной гиперповерхности
возникает двойственная конструкция, приводящая к
внутренним связностям Г;! кручения 1-го и 2-го рода,
сопряженным относительно асимптотич. тензора гипер-
гиперповерхности. При специальном выборе нормализации в
общую схему включается дифференциальная геометрия
пространств, отвечающих подгруппам проективной
группы: аффинных, биаксиальных, неевклидовых и ев-
евклидовых пространств.
Наконец, в работах Э. Картана (Е. Caitan) построена
общая теория пространств проективной связности.
Г. Ф. Лаптев, используя метод внешних форм, иссле-
исследовал их как расслоенные пространства, структурная
группа к-рых является группой проективных преобра-
преобразований проективного пространства.
Лит.: [I] Wilczynski F., «Mem. publ. Acad. Bel-
gique», 1911, t. 3, pt. 2; [2] P u Ъ 1 n i G., С е с h E., Gpometria
proiectiva differenziale, t. 1—2, Bol., 1926—27; [3] В о 1 G.,
Projective DiHerentialgeometrie, t. 1—3, Gott, 1950—07; [4]
Фиников СП., Проективно дифференциальная геометрия,
М.— Л., 1937; [5] его же, Теория конгруэнции, М.— Л..
1950; [б] Норден А. П., Пространства аффинной связ-
связности, 2 изд., М., 1976; [7] Каган В. Ф., Основы теории по-
поверхностей в тензорном изложении, ч. 2, М.— Л., 1948.
А. П. Норден, А. П. Широков.
ПРОЕКТИВНАЯ МЕТРИКА — метрика р (г, у) в
подмножество R проективного пространства Р" такая,
что кратчайшая относительно этой метрики является
частью или всей проективной прямой. При этом полага-
полагают, что R не принадлежит ни одной гиперплоскости и
что 1) для любых трех неколлинеарных точек .г, у, z не-
неравенство треугольника выполняется в строгом смысле
р(х, у) + р(у, z) > р(х, 2);
2) если х, у — различные точки из R, то пересечение
1(х, у) прямой /, проходящей через х и //, с R естг. либо
вся I (бол ь ш о й круг), либо получается из I
удалением нек-рого отрезка (могущего сводиться и к
одной точке) (метрическая прямая).
Множества R, наделенные П. м., наз. проектив-
проективно метрическими пространствами
(п. м. п.).
В одном и том же п. м. п. не могут одновременно су-
существовать оба типа линий: либо все они — метрич.
прямые (т. е. изометричны отрезку из R1), либо же
все они — большие круги одинаковой длины (т е о р е-
м а Г а м е л я). Пространства первого типа наз. о т-
крытыми (они совпадают с подмножествами аффин-
ного пространства, то есть с Р", из к-рого удалена нек-
некрая гиперплоскость); геометрия открытых и. м. п. па::,
также Гильберта геометрией. Пространства второго
типа наз. замкнутыми (они совпадают со всем Р").
Проблема определения всех П. м.— это так на.ч.
4-я проблема Гильберта (см. |2]), полное ее решение
дано А. В. Погореловым A974).
С П. и. связано, как частный ее случай, т. н. проек-
проективное мероопределение — введение в подмножества
проективного пространства методами проективной гео-
геометрии такой метрики, при к-рой эти подмножества
оказываются изоморфными евклидову, гиперболиче-
гиперболическому и эллиптическому пространствам. Так, геометрия
открытых п. м. ц., подлежащее множество к-рых сон
падает со всем аффинным пространством, наз. г е о-
м е т р и е и М и н к о в с к о г о. Евклидова
геометрия — это одновременно геометрия Гиль-
Гильберта и геометрия Минковского.
Гиперболическая геометрия — гео-
геометрия Гильберта, в к-рой существуют отражения от
всех прямых. Для этого необходимо и достаточно, чтобы
И было внутренностью эллипсоида.
•Эллиптическая геометрия (или Ри-
мана геометрия) — геометрия п. м. п. второго типа.
Лит.: [1] Б у з е м а н Г., К е ,ч л и II. Д т., Проективная
геометрия и проективные метрики, пер. с англ., М., 1957; [2J
Проблемы Гильберта, пер. с нем., М., 19В9.
М. И. Войцеховспий.
ПРОЕКТИВНАЯ НОРМАЛЬ — обобщение понятия
нормали в метрич. геометрии. В отличие от последней,
где нормаль вполне определяется касательной плос-
плоскостью к поверхности (т. е. окрестностью первого по-
порядка), в проективной геометрии ато не так. Даже и
члены третьего порядка малости не определяют вершину
координатного тетраэдра, не лежащую в касательной
плоскости (т. е. к выбранной Дарбу квадрике можно
построить но один автополярный тетраэдр). Это естест-
естественно: проективная группа значительно шире группы
движений, а потому ее инварианты должны быть более
высокого порядка; но и окрестность 4-го порядка не
определяет единственной прямой, к-рую можно принять
за третью ось тетраэдра. На атом пути, напр., получа-
получаются:
директриса Вильчи иск ого
ребро Грина
С =Л' + -1 {^РяЦ.-±.Аи Т'/р)гр.
ось Ч е х а
C = N + ± (gis^L-± AJkTUk) r.t
нормаль Ф у б и н и
(здесь N — аффинная нормаль).
Все они лежат в одной плоскости.
Лит.: II] Ши р о и о н II. А., Широков А. П., Аф-
Аффинная дифференциальная геометрии, М,, 19Г>9; 12] Н о р д е и
А. П., Пространства аффинной связности, 2 изд., М., I97C; [3]
Фиников СП., Проективно-дифференциальная геометрия,
М.— Л., 1937. М. И. Войцеховский.
ПРОЕКТИВНАЯ ПЛОСКОСТЬ, двумерное
проективное пространство,— инци-
дентностная структура п--- {^р, X, /}, где элементы мно-
множества у наз. точками, элементы множества X —
и р я м ы м и, а / — отношение инцидентности. Ин-
цидентностная структура удовлетворяет следующим
аксиомам:
1) для любых двух различных точек р и q существует
единственная прямая L такая, что pIL и qlL;
2) для любых двух различных прямых L и М сущест-
существует единственная точка р такая, что pIL u piM;
3) существуют четыре точки, никакие три из к-рых
не инцидентны одной прямой.
Напр., пучок П прямых и плоскостей трехмерного аф-
аффинного пространства, проходящих через точку О,
является П. и., если в качестве проективной точки счи-
считать прямую пучка П, а в качестве проективной
прямой — плоскость из П. В этой интерпретации полу-
получают прозрачный геометрич. смысл однородные коорди-
координаты точки П. п. над полем как координаты какого-
либо вектора прямой, изображающей эту точку (см.
Проективная геометрия, Проективные координаты).
Другим примером является П. п., состоящая из семи
точек А{, г=1, . . ., 7, и семи прямых {А1, А2, А4},
{А2, А3, Аь}, {А3, Ait Ап}, {А4,
А6, А,}, {А:„ А6, А,}, {Л6, А7,
А2), {А7, Аи А3) (рис. 1),—
представитель класса конечных
проективных плоскостей. П. п.
Р B, п) наз. конечной
проективной плос-
плоскостью порядка гс, если от-
отношение инцидентности удов-
удовлетворяет еще одной аксиоме:
4) существует прямая, инци-
инцидентная ровно п-4-1 точке.
^ В Р B, п) каждая точка (пря-
*s мая) инцидентна п+1 прямой
(точке), а число точек плоскости
Рис' ]' равно числу прямых и равно
п'г-\- re-f-1 .Остается невыясненным
A983) вопрос, для каких значений п существует П. п.
/'B, п). Доказано существование конечной П. п., поря-
порядок к-рой есть степень простого числа (см. |4]). Доказа-
Доказано также (см. [5]) отсутствие П. п. Р B, п) для широкого
класса чисел: если п сравнимо с 1 или 2 но модулю 4 и
1'слп в разложении этого числа на простые множители
встречается в нечетной степени хотя бы одно простое
число, сравнимое с 3 по модулю 4, то Р B, п) не сущест-
существует; таковы, напр., п—Ь, 14, 21, 22, .... Вопрос отно-
относительно ге= 10, 12, 15, 18, . . . остается открытым.
Важной задачей теории конечных П. и. является изу-
изучение подплоскостей заданной плоскости РB, п). Так,
если Р B, т) является собственной подплоскостью ко-
конечной П. п. Р B, п), то т2-\-т^п или т"—п (см. [5]).
Специфическим для П. п. является понятие двойст-
двойственности. Две П. п. наз. двойственным и, или
дуальными, если между точками (прямыми) од-
одной плоскости и прямыми (точками) другой можно уста-
установить взаимно однозначное соответствие, сохраняю-
сохраняющее инцидентность. Нек-рые П. п. (напр., П. п. над
полем к) допускают двойственное отображение на себя,
к-рое наз. корреляцией, а П. п., допускаю-
допускающие корреляцию, наз. автодуальными. Для
П. п. имеет место т. н. малый принцип двойственности:
если верно нек-рое предложение Л о точках и прямых
П. п., сформулированное только в терминах инцидент-
инцидентности между ними, то будет верно предложение ей?, двой-
двойственное Л, т. е. предложение, к-рое получается из Л
заменой слова «точка» на слово «прямая» и наоборот.
Изоморфное отображение П. п. на себя наз. к о л-
.1 и н е а ц и е п. Коллинеация конечной П. п. Р B, п)
является подстановкой множества точек и подстановкой
множества прямых, причем эти подстановки подобны.
Конечная П. п. наз. д е з а р г о в о й, если она имеет
группу коллинеаций, дважды транзитивную на ее точ-
точках. Группа коллинэаций дезарговой П. п. PGB, ph)
имеет порядок
Группа коллинеаций недезарговой П. п. РB, п) имеет
порядок, но превосходящий
IIs (п2-\ К + 1) (rt2-f п)п2(п — IJ,
где s<ln2». Порядки групп коллинеаций известных
недезарговых П. п. не превосходят порядков групп кол-
коллинеаций дезарговых плоскостей того же порядка.
На рассмотрении 53 типов множеств
T(G) = {(z, X)\G является (х, ,Х)-транзитивной},
определенных для полной группы коллинеаций G,
основана классификация Ленца — Б а р-
т о л о ц ц и П. п. Одним из основных путей изучения
П. и. является введение в ней координат и тернарной
операции. Каждому возможному типу П. п. классифика-
классификации Ленца — Бартолоцци соответствует система алгебра-
ич. законов, к-рой должно удовлетворять натуральное
тело П. и., определенное через тернарную операцию.
Напр., П. п. является дезарговой (иапповой) тогда и
только тогда, когда во всех ее натуральных телах вы-
выполняется ассоциативный (коммутативный) закон. Де-
ларгова конечная П. и. РB, п) является папновои.
Особенность дезарговой П. п. J'GB, n) в том, что она
обладает коллинеацией порядка n2-f-n-f-1, циклической
на точках и прямых. Этот результат дает возможность
представить П. и. PGB, n) в виде циклич. таблицы. Та-
Такое представление PGB, n) заключается в том, что точ-
точки плоскости, занумерованные натуральными числами
от 1 до пг-\-п-{-\, располагаются в прямоугольной табли-
таблице ия п+1 строки и ге2+и+1 столбца таким образом,
что каждый столбец, означающий прямую со всеми
на ней точками, получается прибавлением к каждому
элементу предыдущего столбца единицы по модулю
п2+л+1. Напр., представление плоскости Р B, 2) име-
имеет вид 12 3 4 5 6 7
2 3 4 5 6 7 1
4 5 6 7 12 3.
Плоскости Р B, п), где ге<:8, единственны с точностью до
изоморфизма — это дезарговы плоскости или плоскости
Галуа (см. [G]), а уже для п.—9 известны четыре неи.чо-
морфные плоскости (см. [7]).
Если к аксиомам П. п. и предложению Дезарга при-
присоединить аксиомы порядка (к-рыми описывается раздо-
ленность двух пар точек, лежащих на одной прямой:
напр., на рис. 2 пара С, D разделяет пару А, В, а, пара
А , С не разделяет пару В, D) и аксиому непрерывности,
то полученная П. п. оказывается изоморфной действи-
действительной аффинной плоско-
плоскости, пополненной несобст- С р
венными алементами: к д ^
каждой прямой присо-
присоединяется несобственная Рис. 2.
(бесконечно удаленная)
точка, к параллельным прямым — одна и та же, а к
непараллельным — разные, причем все несобственные
точки лежат на одной несобственной прямой.
II. и. наз. топологической, если множества
ее точек и прямых являются топологич. пространства-
пространствами, причем отношение инцидентности является непре-
непрерывным. В топология, плоскости тернарная операция
непрерывна но всем своим аргументам. С топологич.
точки зрения множество точек действительной П. п.
(равно как и множество прямых) представляет собой
замкнутое неориентируемое многообразие, эйлерова
характеристика к-рого равна 1.
Лит.: [1] Ко к стер X., Действительная проективная
плоскость, пер. с англ., М., 1959; [2] Бэр Р., Линейная ал-
алгебра и проективная геометрия, пер. с англ., М., 1955; 1;Л
Скорняков Л. А., «Успехи матем. наук», 1951, т. В, в. С,
с. 112—54; f'i] К а р т е с и Ф-, Введение в конечные геомет-
геометрии, пер. с англ., М., 1980; [5] Холл М., Теория групп, пер.
с англ., М., 1962, гл. 20; [fl] Demiowski P., Finite geo-
geometries, В.—N.Y.. 19158; [7] Room Т. G., К i r k p a t-
rick P. В., Miniquaternion geometry, Camb., 1971.
В. В. Афанасьев.
ПРОЕКТИВНАЯ ПРЯМАЯ — проективное простран-
пространство размерности 1; П. п., рассматриваемая как само-
самостоятельный объект, является замкнутым одномерным
многообразием. П. п. является своеобразным проектив-
проективным пространством — на ней нет интересных отноше-
отношений инцидентности, как у проективных пространств
большей размерности. Единственным инвариантом П. п.
служит число ее точек. П. п. наз. непрерывной,
дискретной или конечной, если она инци-
инцидентна со множеством точек мощности континуума,
счетным или конечным соответственно.
П. п. наз. упорядоченной, если на ней зада-
задано отношение разделения двух пар различных точек.
Предполагается, что разделение не зависит от порядка
пар и порядка точек в парах и любая четверка различ-
различных точек разбивается на две взаимно разделяющиеся
пары единственным образом, а также принимается ак-
аксиома расположения, связывающая пять различных
точек (см., напр., [1]). Упорядочение П. п. над полем R
связано с упорядоченностью этого поля, а именно: пара
точек {А, В} разделяет пару {С, D}, если двойное от-
отношение (А , В; С, D) отрицательно, и не разделяет, если
(А, В; С, D) положительно. Конечную П. п. PGA, q)
над Галуа полем нечетного порядка q можно упорядо-
упорядочить аналогично вещественной П. п. Полагают (см.
[4]), что пара точек {А, В} разделяет пару {С, D}
тогда и только тогда, когда (А, В; С, D) — квадратич-
квадратичный вычет поля Галуа GF(q).
П. п. приобретает определенное геометрич. строение,
если она вложена в проективное пространство большей
размерности; так, напр., П. п. однозначно определяет-
определяется двумя различными точками, а аналитич. определе-
определение П. п. как множества классов эквивалентности пар
элементов тела к, не равных одновременно нулю, по
существу эквивалентно вложению П. п. в проективное
пространство Р п (к), к^2. Если Рх(к) является П. п.
над полем к, то группа автоморфизмов П. п. Aut Pi{k)
может быть представлена на точках Ps(k) в параметрич.
форме как множество отображений
к —->¦ ft(Xa+b , а, Ъ, с, п?к, ad —be ф 0, agAutfc.
hac + d
Группа алгебраич. автоморфизмов действительной П. п.
изоморфна группе перемещений действительной плос-
плоскости Лобачевского, а порядок группы Aut PG(\, ph)
равен h{psfl—ph).
На П. п. можно построить другие геометрии. Так,
напр., плоскость Мёбиуса порядка р допускает интер-
интерпретацию на П. п. J°G(l,p2) (см. [5]). Другой традицион-
традиционной геометрич. конструкцией является изображение
проективного пространства Рп{к) на П. п. Р^к) (см.
[2]), при к-ром точки из Рп (к) изображаются набором
п точек П. п. Pi(k) (здесь к — алгебраически замкну-
замкнутое поле).
Лит.: Ell Глаголев Н. А., Проективная геометрия,
М., 1963; [2] III а ф а р е в и ч И. Р., Основы алгебраической
геометрии, М., 1972; [3] Hughes D. R., Piper F. С,
Projective planes, N. Y., 1973; [4] Kustaanheimo P.,
«Comment, phys.-math.», 1957, v. 20, Ms 8; [5] V e Ь 1 e n O.,
Young J. W., Projective geometre, v. 1, Boston, 1910.
В. В. Афанасьев.
ПРОЕКТИВНАЯ СВЯЗНОСТЬ — дифференциаль-
дифференциально-геометрическая структура на гладком многообра-
многообразии М; специальный вид связности на многообразии,
когда приклеенное к М гладкое расслоенное простран-
пространство Е имеет своим типовым слоем проективное прост-
пространство Рп размерности «=dim M. Структурой такого
Е к каждой точке х? М присоединяется экземпляр про-
проективного пространства {Pn)xi к-рый отождествляется
(с точностью до гомологии с инвариантной связкой
прямых в точке х) с касательным центроаффинным про-
пространством Тх (М), дополненным бесконечно удаленной
гиперплоскостью. П. с, как связность в таком Е, пре-
предусматривает сопоставление каждой гладкой кривой
? с началом ,г0 и каждой ее точке xt проективного
отображения (Р„)х^(Рп)Хп так' что удовлетворяется
следующее условие. Пусть М покрыто координатными
областями, в к-рых фиксировано гладкое поле репера
(Pn)xi У к-рого вершина, определяемая вектором е0,
совпадает с х. (Репер в Рп определяется классом экви-
эквивалентности базисов в векторном пространстве Vn + 1,
если эквивалентными считаются те {еа} и {е'а}, 06=0,1,
. . ., га, у к-рых е'а=~-Хеа, Ят=О.) Тогда при t—>-0 отобра-
отображение семейства должно стремиться к тождественному
отображению, причем главная часть его отклонения от
последнего должна определяться относительно поля
реперов в нек-рой окрестности точки х0 матрицей ли-
линейных дифференциальных форм
j O, A)
а, 0 = 0, i, ..., n; i, / = 1, ..., га,
общей для всех L. Другими словами, образ репера в точ-
точке х^ при отображении (Рп)х+ ->(Pn)x0 должен быть оп-
определен векторами
где X — касательный вектор к L в точке х0 м
lim —г—— =0. Возможность перехода к эквивалентным
t->-o ?
базисам приводит к тому, что среди форм A) существен-
существенны только
о4, e{- = G)j —6[чв8, со?. B)
При преобразовании репера поля в произвольной точке
х?М согласно формулам еа/=Ла»ер , ер=Л р'еа,, где
Aif=Ao'=O, т. е. при переходе к произвольному эле-
элементу главного расслоенного пространства П реперов в
пространствах {Р„)х, формы A) заменяются следующи-
следующими а-формами на П:
^¦ = A%'dAl, + Al,A\'b$. C)
2-формы
Q^ = dw^ + w^ лооГ' D)
являются полубазовыми, т. е. линейными комбинация-
комбинациями шоЛсоо, и тензорными, т. е. при преобразовании ре-
репера матрицами А\ имеют место формулы
где Й^', составлены из C) аналогично D). Для сущест-
существенных форм B) имеют место структурные уравнения
П. с. (где для простоты опущены штрихи):
Лоо-1 8} лсо? = й5, |
? + с4 л (fi{w? -- ftiw?) - ei:, | E)
)
где ef=Q{—б/й5- Здесь правые части полубазовы;
они составляют систему форм кручения-кривизны П. с.
Равенство Qo=O имеет инвариантный смысл. В этом
случае говорят о П. с. нулевого кручения; для нее
0{-!=-0|. Инвариантные тождества
й< ^ о, в\ ^ 0,
выделяют специальный класс П. с, называемых (по
Картану) нормальными П. с.
Формы A) определяют П. с. на М однозначно: об-
образ при отображении (Рп)Х1—>-{Р„)х0 репера в точке xt
определяется решением {ea(t)} системы
при начальных условиях иа @) — еа, где х' = х' (t) —урав-
—уравнения кривой L в нек-рой координатной окрестности ее
точки х0 с координатами х' @).
Любые 1-формы wo, Q{, w°, заданные на П и удовлет-
удовлетворяющие уравнениям E) с правыми частями, выражаю-
выражающимися через сооЛШо, где mi), i=l, ..., п, линейно неза-
независимы, определяют в этом смысле нек-рую П. с. на М.
Кривая, к-рую описывает в (Рп)Ха точка, определяе-
определяемая первым вектором eB(t) решения \ea(t)} системы F),
наз. разверткой кривой L. Кривая наз. геоде-
геодезической линией П. с. на Л/, если ее разверт-
развертка в нек-рой окрестности произвольной ее точки х яв-
является прямой пространства (Р„)х. Уравнения .г' —
=x'(t) геодезич. линии определяются с помощью функ-
функций
из системы
df+ p (Q})xit) (i (*)) = <**«> (* @) ?'\
где d — нек-рая 1-форма. В репере, где <oi=dxi,
S'=j', эта система имеет вид
d^x" „
(dxny v \ dxn ' ' ' '' da
.1 ,jx" -1
dx" ' •••' dx"
где Qa и Qn — многочлены 2-го порядка, коэффициенты
к-рых есть функции он1, . . ., х".
Теорема Картава: если на гладком много-
многообразии М задана система кривых, локально определяе-
определяемая системой дифференциальных уравнений вида G),
то существует одна и только одна нормальная П. с,
для к-рой эта система кривых является системой геоде-
геодезич. линий.
Теория П. с. дает, таким образом, средство для инва-
инвариантного исследования систем дифференциальных
уравнений специального вида. П. с. полезны также при
исследовании геодезических (или проективных) отобра-
отображений пространств аффинной связности. П. с. сводится
к аффинной связности, если на М существуют локаль-
локальные поля реперов, относительно к-рых co?=-J°?y(ui.
Для каждой аффинной связности на М существует
единственная нормальная П. с, имеющая общие геоде-
геодезич. линии, из к-рой она может быть получена. Две аф-
аффинные связности геодезически (или проективно) экви-
эквивалентны, если их нормальные П. с. совпадают. В част-
частности, аффинная связность на М при dim M>2 проек-
проективно евклидова тогда и только тогда, когда ее тензор
проективной кривизны К1Ы обращается в нуль.
Лит.: [1] Саг tan К., «Bull. Soc. math. France», 1924,
t. 52, p. 205—41; [2] его ж е, Leyons sur la theorie des espaces
a connexion projective, P., 1937; [3] его же, Пространства
аффинной, проективной и конформной связности, пер. с франц.,
Казань, i 9E2; [4] К о Ь а у а в h i S., N a g a n о Т., «J. Math,
and Mecih.», 1964, v. 13, № 2, p. 215—35. Ю. Г. Лумисте.
ПРОЕКТИВНАЯ СХЕМА — замкнутая подсхема
проективного пространства Р%; в однородных координа-
координатах х0, . . ., хп на Р% проективная схема задается систе-
системой однородных алгебраич. уравнений:
/i (ж0. • • •. хп) = 0, . .., fr (xg, ..., хп) — 0.
Каждая П. с. является полной (компактной в случае
к=С); обратно, полная схема проективна, если на ней
есть обильный обратимый пучок. Имеются и другие
критерии проективности.
Обобщением понятия П. с. служит проективный мор-
физм. Морфизм схем /: X —>¦ Y наз. проективным
(a X — схемой, проективной над У), если X является
замкнутой подсхемой проективного расслоения Ру((§),
1Де $ — локально свободный (З^-модуль. Композиция
проективных морфизмов цроективна. Проективность
морфизма сохраняется и при замене базы; в частности,
слои проективного морфизма являются проективными
схемами (но не обратно). Если схема X проективна, а
X ->- Z — конечный сюръективный морфизм, то и Z
проективна.
Любая П. с. (над У) может быть получена при помо-
помощи конструкции проективного спектра.
Ограничиваясь случаем аффинной базы, У*--Spec Л;
пусть А— ф А{ — градуированная Л-алгебра, цри-
i> о
чем Д-модуль Аг имеет конечный тип и порождает ал-
алгебру А, и пусть Рго](Л) —множество однородных
простых идеалов раА, не содержащих Ах. Снабженное
естественной топологией и структурным пучком мно-
множество I'roj (А) является проективной У-схемой; более
того, любая проективная У-схема имеет такой вид.
Лит.: [1J Мам форд Д., Алгебраическая геометрия,
т. 1 — Комплексные проективные многообразия, пер. с англ.,
М., 1979; [2] Итоги науки и техники. Алгебра. Топология. Гео-
Геометрии, т. 10 М., 1972, с. 47 — 112. В. И. Данилов.
ПРОЕКТИВНОЕ АЛГЕБРАИЧЕСКОЕ МНОЖЕСТ-
МНОЖЕСТВО — подмножество точек проективного пространст-
пространства Рп, определенного над полем к, имеющее (в однород-
однородных координатах) вид
У(/) = {(а0, ..., ап)?Р»\ 1(аа, ..., ои)=0
для любого
Здесь / — однородный идеал в кольце многочленов
к[Х0, . . ., Хп]. (Идеал / однороден, если из /?/ и /=
= 2/i> гДе все /i—однородные многочлены степени (,
следует, что все /,-?¦/.)
Свойства П. а. м.:
2) V (
3) если /j С /2, то V {Iг) d V (/x);
4) V(I) = V(VrT),
где УI — радикал идеала /. Из свойств 1)—3) следует,
что на V (I) можно ввести топологию Зариского. Если
/= УI, то / однозначно представляется в виде пересе-
пересечения однородных простых идеалов:
В случае, когда / — однородный простой идеал,
П. а. м. VA) на.ч. проективным многое б-
р а з и е м.
Лит.: [1] Ш а ф а р е в и ч И. Р., Основы алгебраической
геометрии, М., 1972; [2] 3 а р и с с к и й о., Самюэль П.,
Коммутативная алгебра, пер. с англ., т. 1—2, М., 1963.
Bun. С. Иулипов.
ПРОЕКТИВНОЕ ИЗГИБАНИЕ — распространение
на проективную геометрию понятия изгибания (нало-
(наложения) в метрич. теории поверхностей, дано Г. Фубини
(G. Fubini, 1916) (обобщение этого понятия на геометрию
любой группы преобразований получил Э. Картан,
Е. Cartan, 1920) с использованием понятия т. н. качения
одной поверхности по другой.
Пусть G — группа преобразований пространства Е.
Поверхность S' налагается на поверхность S (или ка-
катится no S) в геометрии группы G, если между их точ-
точками устанавливается взаимно однозначное соответст-
соответствие так, что каждой паре соответствующих точек M?S,
М' ?6" можно присоединить преобразование y?G, к-рое
переводит S' в положение S. При этом требуется, чтобы
1) М' совмещалась с М;
2) каждая кривая V ?S', проходящая через М, имела
в атой точке касание n-го порядка с соответствующей
кривел l?S (т. е. расстояние между точками М'* и
М*, близкими к общей точке М' — М, будет бесконечно
малым порядка и-f-l по сравнению с расстоянием их от
общей точки). Соответствие S и S', характеризующееся
числом п, наз. наложением и-г о порядка.
Содержащееся здесь понятие расстояния не вносит
ограничения на геометрию группы. Однако здесь речь
идет о порядке касания кривых в несколько более тес-
тесном, чем обычно, смысле слова (отличие состоит в том,
что соответствие между точками обеих кривых уже уста-
установлено наложением, тогда как обычно оно устанавли-
устанавливается при определении порядка касания).
Пусть, далее, G — группа проективных преобразова-
преобразований и пусть S и 5' проективно налагаются. Тогда П. и.
есть преобразование поверхности Л1 с сохранением про-
проективного линейного элемента
где F2 и F3 — Фубипи формы (при этом здесь — нало-
наложимость 2-го порядка). И оказывается, что, кроме ли-
линейчатых поверхностей, только т. н. поверхности Я
(см. [1]) допускают нетривиальное П. и.
Проективная геометрия занимает некое среднее по-
положение между метрической, где, вообще говоря, вся-
всякая поверхность может изгибаться, и аффинной, где
понятие изгибания не имеет места: любые две. поверх-
поверхности допускают наложение 1-го порядка и никакие
две различные не могут иметь наложение 2-го порядка.
Лит.: [1] Фиников СП., Проективно-дифференциаль-
ная геометрия, М.— Л., 1937; [2] Н о р д е н А. П., Простран-
Пространства аффинной связности, 2 изд., М., 1976.
М. И. Войцеховский.
ПРОЕКТИВНОЕ МЕРООПРЕДЕЛЕНИЕ — вве-
введение в подмножествах проективного пространства
методами проективной геометрии такой метрики, при
к-рой эти подмножества оказываются изоморфными ев-
евклидову, гиперболическому или эллиптическому прост-
пространствам. Это достигается выделением из класса всех
проективных преобразований таких преобразований,
к-рые порождают в этих подмножествах группу преоб-
преобразований, изоморфную соответствующей группе дви-
движений. Наличие движений позволяет «откладывать»
отрезки от данной точки в данном направлении и тем са-
самым ввести понятие длины отрезка.
Чтобы получить евклидово мероопределение в га-
мерном проективном пространстве Р, выделяют в нем
одну (п—1)-мерную гиперплоскость я, называемую н е-
собственной гиперплоскостью, и ус-
устанавливают в этой гиперплоскости эллиптическое по-
полярное соответствие П точек и (п—2)-мерных гиперплос-
гиперплоскостей (т. е. полярное соответствие, при к-ром никакая
точка не принадлежит соответствующей ей (га—2)-мер-
ной плоскости).
Пусть Еп — подмножество проективного пространст-
пространства Р, получающееся удалением из него несобственной
гиперплоскости; X, Y, X', У — точки, принадлежащие
Еп. Два отрезка XY и X'Y' наз. конгруэнтны-
м и, если существует проективное преобразование ф,
переводящее точки X и Y соответственно в точки X' и
У, при к-ром сохраняется поляритет П.
Определенное таким образом понятие конгруэнтнос-
конгруэнтности отрезков позволяет в Еп ввести метрику евклидова
пространства. Для этого в проективном пространстве Р
вводится система проективных координат с базисным
симплексом ОА1А2- ¦ -А п, причем точка О не принад-
принадлежит несобственной гиперплоскости я, а точки А1г
А2, ¦ ¦¦, А„ принадлежат этой плоскости. Пусть точка О
в этой системе имеет координаты 0,0, . . ., О, 1, а точки
Л,-, (=1, 2, . . ., га, имеют координаты
Тогда эллиптическое полярное соответствие П, задан-
ное в гиперплоскости я, может быть записано в виде
«i- = 2.= 1 a;jXj, г = 1, 2, ..., п.
Матрица ||я,-7-|| этого соответствия будет симметричес-
симметрической, а соответствующая ей квадратичная форма
Q (хи хг, ..., xn) = '^Laijxixj
— положительно определенной. Пусть
A' = (o1:a2:...:on:on + i) и Y= Fi:62:.. . :bn:bn+1)
— две точки, принадлежащие Еп (то есть ап + 1^0,
Ьп + 1фО). Можно положить:
-^xn,
Тогда расстояние р между точками X и У определяется
соотношением
р(Х, У) =!/"«? (хг — уи х2—у2, ..., х„—у„).
Для установления П. м. в га-мерном гиперболич.
пространстве в n-мерном проективном пространстве Р
рассматривается множество U внутренних точек дей-
действительной овальной гиперповерхности S 2-го порядка.
Пусть X, Y, X', Y' принадлежат множеству U, тогда
отрезки XY и X'Y' считаются конгруэнтными, если
существует проективное преобразование пространст-
пространства Р, при к-ром гиперповерхность S отображается на
себя, переводящее точки X и Y соответственно в точки
X' и У. Введенное таким образом понятие конгруэнт-
конгруэнтности отрезков приводит к установлению во множестве
U метрики гиперболич. пространства. Длина отрезка в
этой метрике определяется соотношением
р(Х, Y)=c\\a(XYPQ)\,
где Р и Q — точки пересечения прямой XY с гиперпо-
гиперповерхностью S, а с — положительное число, связанное
с кривизной пространства Лобачевского.
Для введения в проективном пространстве Р эллип-
тич. метрики в этом пространстве рассматривается эл-
эллиптическое полярное соответствие Л. Два отрезка XY
и X'Y' нал. конгруэнтными, если существует проек-
проективное преобразование <р, переводящее точки X и Y еда-
ответственно в точки X' и Y', при к-ром сохраняется
поляритет II (т. е. для любой точки М и ее поляры т
полярой точки <p(Af) будет (f(m)). Если эллиптическое
полярное соответствие П задано соотношениями
то матрица (а,у) будет симметрической, а соответствую-
соответствующая ей квадратичпая форма — положительно опреде-
определенной. Тогда если
Х = (х1:х2:... :хп:хп + 1), К = {Ul: уг:... :уп:уп+1),
то
р(Х, У) =
B(X, X)VB(Y, Y)
где В — билинейная форма с матрицей ||а,-у||.
Во всех рассмотренных случаях (если дополнить дей-
действительное проективное пространство до комплекс-
комплексного проективного пространства) при проективных пре-
преобразованиях, определяющих конгруэнтность отрезков,
т. е. движениях, остаются инвариантными нек-рые ги-
гиперповерхности 2-го порядка, наз. абсолютами.
В случае евклидова мероопределения абсолютом будет
мнимая (п—2)-мерная овальная поверхность 2-го по-
порядка, в случае гиперболич. мероопределения — оваль-
овальная (га—1)-мерная действительная гиперповерхность
2-го порядка, в случае эллиптич. мероопределения —
мнимая (га—1)-мерная овальная гиперповерхность 2-го
порядка.
Лит.: [1] Ефимов Н. В., Высшая геометрия, В изд.,
М., 1978; [2] Глаголев Я. А., Проективная геометрия,
2 изд., М., 1963; [;i] Б у з е м а н Г., К е л л и II. Д ж., Про-
Проективная геометрия и проективные метрики, пер. с англ., М.,
1957. П. С. Моденов, А. С. Пархоменко.
ПРОЕКТИВНОЕ МНОЖЕСТВО — множество, крое
может быть получено из борелевских множеств повтор-
повторным применением операций проектирования и перехода
к дополнению. П. м. классифицируются по классам,
образующим проективную иерархию. Пусть /= шш—
бэровское пространство (гомеоморфное пространству
иррациональных чисел). Множество Pczlm принадле-
принадлежит: 1) классу Лх, если Р есть проекция борелевского
множества пространства /от+1; 2) классу САп (Р есть
САп-ш н о ж о с т в о), если его дополнение 1т\Р есть
/(„-множество (»^1); 3) классу Ап (Р есть А п-м н о-
ж е с т в о), если Р есть проекция С А „^-множест-
„^-множества пространства I'n+l, п^2; 4) классу Вп, если Р при-
принадлежит одновременно классам Ап шСАп, п^\. Те
же классы получаются заменой проекции непрерыв-
непрерывным образом (множества того же пространства 1т).
В силу Суслика теоремы класс А1 совпадает с клас-
классом А -множеств (следовательно, класс САГ — с классом
СА-множеств), а класс В1 — с классом борелевских
множеств. Для каждого класса Ап построено универ-
универсальное множество, и при его помощи доказана следую-
следующая теорема о проективной иерар-
х и и (теорема «существования», теорема «о непустоте
классов»): В „С А паВ „ + 1 (следовательно, ВпаАпа
C-Bn + i), где каждое из включений — строгое. Мощ-
Мощность множества всех П. м. пространства / равна 2"'.
Каждое А 2-множество — объединение $х борелевских
множеств и, значит, счетно или имеет мощность tft или
2^° (см. [2], [7]). Для класса А2 выполнены принципы
униформизации и редукции, а для класса С А 2 — (пер-
(первый) принцип отделимости. Каждый из проективных
классов с номером п^2 инвариантен относительно А-
операции. Для каждого из классов А п, С А п существует
bs-операция, дающая в точности все множества итого
класса, исходя из замкнутых множеств. Изучение П. м.
(даже второго класса) — трудная задача. Многие во-
вопросы теории П. м. оказались неразрешимыми в клас-
сич. смысле, что полностью подтвердило предвидение
(см. [6]): «область П. м. есть область, где принцип ис-
исключенного третьего уже не применим». Теория П. м.
получила свое дальнейшее продвижение с привлече-
привлечением сильных теоретико-множественных предположе-
предположений, таких, как МС (существует измеримый кардинал),
PD (аксиома проективной определимости), V=L.
В предположении МС: каждое А 2-множество измеримо
(по Лебегу), обладает Бэра свойством и, если несчетно,
содержит (непустое) совершенное подмножество; каж-
каждое Л3-множество может быть униформизировано А4-
множеством.
В предположении PD: 1) каждое П. м. измеримо, об-
обладает свойством Бэра и, если несчетно, содержит совер-
совершенное подмножество, может быть униформизировано
П. м., точнее: принцип униформизации выполнен для
классов Л 2„ и СА2п+л; 2) для классов А 2п и С А 2п + 1 вы-
выполнен принцип редукции, следовательно, для классов
А-2.ПЛ 1 и CAin — принцип отделимости.
В предположении V=L: 1) существует несчетное СА-
множество, не содержащее совершенного подмножества,
и неизмеримое В2-множество без свойства Бэра; 2) при
п^2 для класса Ап выполнен принцип униформизации.
Если для класса Ап выполнен принцип униформиза-
униформизации, то выполнен и принцип редукции. При га>3 об-
обратная импликация не доказуема в ZFC. Если сущест-
существует неизмеримое (или без свойства Бэра) А 2-множество,
то существует несчетное С А -множество, не содержащее
совершенного подмножества. Если каждое несчетное
СЛ-множество содержит совершенное подмножество,
то это ;ко верно для каждого несчетного А 2-множества
(см. [7]).
Отмеченные результаты справедливы не только для
пространства /, но и для числовой прямой и, вообще,
для любого полного сеиарабельного метрмч. прост-
пространства. Имеет место следующая теорема о топологич.
инвариантности П. м.: гомеоморфный образ П. м. дан-
данного класса, расположенный в том же или любом другом
полном сепарабельном метрич. пространстве, есть П. м.
того же класса.
Лит.: [1] Лузин Н. Н., «С. г. Acad. sci.», 1925, v. 180,
p. 1572 (пер.: [6], с. 304—306); [2J S i е г р i rt s k i W., «Fund,
math.», 1925, t. 7, p. 237—43; 13] Куратовский К., То-
Топология, пер. [с англ.], т. 1, М., 1966; [4] Куратовский
К., Мостовский А., Теория множеств, пер. с англ., М.,
1970; [5] Sierp iriski W., Les ensembles projectifs et ana-
lytiques, P., 1950; [6] Лузин H. H., Собр. соч., т. 2, M.,
1958, с. 242, 268; [7] Jech Т., Set theory, N.Y., 1978; [81
Hlnman P. Recursion theoretic hierarchies, В., 1978;
[9] Новиков II. С, Избр. труды, М., 1979; [10] Коз-
Козлова 3. И., «Или. АН СССР. Сер. матем.», 1962, т. 26, № 2,
с. 223—60; [11] Канторович л. В., Л и в е н с о н Е. М.,
«Fund, math.», 1932, t. 18, p. 214 — 79; [12] Martin D., в
кн.: Handbook of mathematical logic, Amst., 1977, p. 783—815:
[13] Moschovakis Y., в кн.: Proc. of the Inter. Congr.
of Mathern. (Vancouver, 1974), v. 1, Montreal, 1975, p. 251—57:
[14] К а Н о в е й В. Г., «Докл. АН СССР», 1980, т. 253, № 4.
с. 800—03; [15] Л ю б е ц к и й В. А., в сб.: Исследования по
теории множеств и неклассич. логикам, М., 1976, с. 96—122:
[16] Kechris А., в кн.: Logic colloquim'77, Amst., 1978,
p. 155—60; [17] M a u I d I n R., «Mathematika», 1970, v. 23,
,M'. 2 p. 151—55; [181 Marcus S., «Main. Nachr.», 1959, Bd
17, .Nj 3—6, S. 143—50; 1.191 Козлова 3. И., Филип-
Филиппов В. П., «Изв. ВУЗов. Матем.», 1978, №7, с. 33—39.
ПРОЕКТИВНОЕ ПРЕДСТАВЛЕНИЕ г р у п* п"ы
G — гомоморфизм этой группы в группу PGL(V) про-
проективных преобразований проективного пространства
Р (V), связанного с векторным пространством V над по-
полем к.
С каждым П. п. ф группы G связано центральное рас-
расширение этой группы
где р — естеств. проекция группы GL(V) на PGL(V).
i — вложение мультипликативной группы поля к в
GL(V) в виде скалярных матриц, а E<9=p-1(y(G)).
Каждое сечение s проекции р над ф (G) задает отображе
ние
xP = s°y:G —+GL (V),
обладающее свойством
где с: GxG^-k* —двумерный коцикл на группе G.
Класс когомологии h этого коцикла не зависит от выбор;;
сечения s. Он определяется П. п. ф и определяет клаег
эквивалентности расширения (*). Условие h=0 необ
ходимо и достаточно для того, чтобы П. п. ф получалось
факторизацией линейного представления группы G.
П. п. естественным образом возникают при изучение
линейных представлений расширении групп. Важней-
Важнейшие примеры П. п.: спинорное представление ортого-
ортогональной группы и представление Вейля симплектич.
группы. На П. п. непосредственно переносятся опреде-
определения эквивалентности и неприводимости линейных
представлений. Классификация неприводимых П. п.
конечных групп получена И. Шуром (I. Scliur, 1904).
П. п. наз. унитарным, если пространство V
гильбертово, а отображение 4яможно выбрать так, чтобы
оно принимало значение в группе U(V) унитарных
операторов в V. Изучались унитарные неприводимые
П. п. топологич. групп [4]; для связной группы Ли С
их изучение сводится к изучению унитарных неприводи-
неприводимых представлений односвязной группы Ли G, алгебра
Ли к-рой является центральным расширением алгебры
Ли д группы С с помощью tf-мерной коммутативной ал-
алгебры Ли, где d=dim H2 (д, R).
Лит.: Ш Кириллов А. А., Элементы теории представ-
представлений, 2 изд., М., 1978; [2] К ер тис Ч., Р айн ер И.
Теория лредставлений конечных групп и ассоциативных алгебр'
пер. с англ., М., 1969; [3] Маске у G. W., «Acta math.»'
1958, v. 99, p. 265—311; [4] В а г g m a n n V., «Ann. Math.»'
1947, v. 48, p. 568—640. А. А. Кириллов'
ПРОЕКТИВНОЕ ПРЕОБРАЗОВАНИЕ — взаимно
однозначное отображение F проективного пространства
П„ на себя, сохраняющее отношение порядка частично
упорядоченного (по включению) множества всех под-
подпространств П„, т. е. отображение П„ в себя такое, что
1) если Sp<=Sq, то F(Sp)<=F(Sq);
2) для каждою Sp существует Sp такое, что F(Sp) —
=sp;
3) Sp~Sq тогда и только тогда, когда F(Sp) = F(Sq).
При П. п. сохраняются сумма и пересечение подпро-
подпространств, точки отображаются в точки, независимость
точек сохраняется. П. п. образуют группу, наз. н р о-
ективной группой. Примеры П. п.: коллине-
ация, перспектива, гомология.
Пусть пространство П„ интерпретируется как сово-
совокупность подпространств Рп(К) левого векторного про-
пространства А „ +1 (К) над телом К; полулинейным
преобразованием An + i в себя наз. пара
(F, ф), состоящая из автоморфизма F аддитивной группы
А „+1 и автоморфизма ф тела К такого, что для любых
а?Ап + х и к?К имеет место: F(ka) = y(k) F(a); в част-
частности, полулинейное преобразование (/•', ф) является л и-
н е и и ы м, если ф (k)s=k. Полулинейное преобразова-
преобразование (/', ф) индуцирует П. п. F. Обратное утверждение —
первая основная теорема проек-
проективной геометрии: если га^2, то каждое П. п.
F индуцируется нек-рым полулинейным преобразова-
преобразованием (F, ф) пространства Апх\ (К).
Лит.: [11 Бэр Р., Линейная алгебра а проективная гео-
геометрия, пер. с шил., М., 1955; [2] Ходи В., Пи до Д.,
Методы алгебраической геометрии, пер. с англ., т. 1, М., 1954.
М. II. Войцеховский.
ПРОЕКТИВНОЕ ПРОСТРАНСТВО — совокупность
всех подпространств инцидентноетнои структуры я~
^{!р, X, /}, где элементы множества 53 на;^- точка-
м и, а элементы множества jf-прямыии, I —
отношение инцидентности. Подпрост-
Подпространством инцидентноетнои структуры я наз. под-
подмножество S множества 53, для к-рого справедливо ус-
условие: если р, q?S и p?=q, то множество точек прямой,
проходящей через точки р и q, также принадлежат S.
Инцидентностная структура я удовлетворяет следую-
следующим требованиям:
1) для любых двух различных точек р и q существует
единственная прямая L такая, что plL, qlL;
2) каждая прямая инцидентна по крайней мере с
тремя точками;
3) если две различные прямые L, М пересекаются в
точке р и выполнено qlL и rlL, a sTM, tIM, то прямые,
проходящие через пары точек г, I и .?, q, пересекаются.
Подпространство S пор о ж д е н о множеством s
точек из 53 (пишут S— <*•>), если S является пересе-
пересечением всех подпространств, содержащих s. Множество
точек s наз. независимым, если для любого x?s имеет
место :r?<s\{:r}>. Упорядоченное максимальное и
независимое множество точек подпространства S наз.
базисом S, а число его элементов d(S) — раз-
размерностью подпространства S. Подпространство
размерности 0 является точкой, размерности 1 --- про-
проективной прямой. Подпространство размерности 2 наз.
проективной плоскостью.
В П. п. определены операции сложения и пересече-
пересечения подпространств. Суммой Pm-\-Pk подпространств
Рт и Pf/ наз. наименьшее из подпространств, содержа-
содержащее и Рт, и Pk. Пересечением Pm[\Pk подпространств
P',„ и Pk наз. наибольшее из подпространств, содержа-
содержащееся и в Р,„, и в /V Размерности подпространств Рт,
Рк, их суммы и пересечения связаны соотношением
m + k = d(Pm OPk) + d(Pm + Pk).
Для любого Рт существует PH_m_i такое, что Pmf\
дополнение Рт в />„), и если РтаРг, то
для любого Р^(дедекиедово п р а в и л о), т. е.
относительно введенных операций П. п. является деде-
киндовой решеткой с дополнениями.
ГГ. п. размерности больше двух дезаргово (см. Де-
зарга предложение), а следовательно, изоморфно П. п.
(левому или правому) над подходящим телом к (см. [1]).
Р'п (к) (напр., левое) размерности п над телом к — сово-
совокупность линейных подпространств нек-рого (га-{-1)-
мерного левого линейного пространства Ап+1(к) над
телом к; точками Р!п (к) являются прямые А!1 + 1 (к), т. е.
множества классов эквивалентности слева строк (х0,
х1, . . ., х„), составленных из элементов тела к и не рав-
равных одновременно нулю (строки (х0, хх, . . ., ,т„) и
{Уо, i/n ¦ • •> Уп) эквивалентны слева, если существу-
существует такое А,?А;, что .г, — Ал/,-, i~0,i, . . ., га); подпространст-
подпространствами Рт(к), т.~Л, . . ., п, являются (т+1)-мерные под-
подпространства Ат+г(к). Можно установить нек-рое со-
соответствие между левым Рп (к) и правым Ргп (к) П. п., при
к-ром подпространству р[ (к) соответствует Pn-s-i (к)
(подпространства Р[(к) и Prn-s-\ (к) наз. дуаль-
дуальными друг другу), пересечению подпространств со-
соответствует сумма, а сумме — пересечение. Если нек-рое
утверждение, основанное только на свойствах ли-
линейных подпространств, их пересечений и сумм, спра-
справедливо для Рп(к), то справедливо и соответствующее
утверждение для Ргп(к). Это соответствие между свойст-
свойствами пространств Рп(к) и Ргп(к) наз. п р и н ц и пом
двойственности для П. п. (см. [2]).
Конечное тело необходимо коммутативно, следова-
следовательно, конечное П. п. размерности больше двух и по-
порядка q изоморфно П. и. над Галуа полем PG(n, q).
Конечное П. п. Р (га, q) содержит (qn + 1 — !)/(<?—1) то-
точек и ТТЛ (gn + J-' — 1)/ ТТГ (grj w--1) подпро-
-L-l(=o •*"•-»=¦ о
странств размерности г (см. [4]).
К о л л и н е а ц и е и П. и. является перестанов-
перестановка ее, точек, к-рая отображает прямые в прямые, при
этом подпространства отображаются на подпространст-
подпространства. Нетривиальная коллинеация П. п. имеет не более
одного центра и не более одной оси. Группа коллинеа-
ции конечного П. п. PG(n, ph) имеет порядок, равный
Каждое П. п. PG(n, q) допускает циклическую транзи-
транзитивную группу коллинеаций (см. [3|).
КорреляциейбП. п. является перестановка
подпространств, к-рая меняет включения, т. е. если
SczT, то S6^T6. П. п. допускает корреляцию, только
если оно конечномерно. Важное значение в проектив-
проективной геометрии играет корреляция порядка два, наз.
поляритетом.
Лит.: [1] Ар тин Э., Геометрическая алгебра, пер. с
англ., М., 1909; [2] Ходи р., П и д о Д., Методы алгебраи-
алгебраической геометрии, пер. с англ., т. 1, М., 1954; [3] I) e m b о w-
ski P., Finite geometries, В. —[а. о.], 1968; [4] Segre В.,
Lectures on modern geometry, Roma, 19B1. В. В. Афанасьев.
ПРОЕКТИВНЫЕ КООРДИНАТЫ — взаимно од-
однозначное соответствие между элементами проективного
пространства П„ (К) (проективными подпространства-
подпространствами Sц) и классами эквивалентных упорядоченных ко-
нечных подмножеств элементов тела К. П. к. подпрост-
подпространств S(l при </>() (паз. также г р а с с м а н о в ы ы и
координатам и) определяются через координаты
точек @-мерных подпространств), лежащих в Sq, и
потому достаточно определить П. к. точек проектив-
проективного пространства.
Пусть в совокупности строк (хО, х1, . . ., хп)~х не
равных одновременно нулю элементов тела Л' (к-рые
наз. также однородными координата-
координатами т о ч е к) введено отношение эквивалентности
слева (справа): х~у, если существует к?К такое, что
.r'-'h/1' (,т''=у'Я), i~0, . . ., га. Тогда совокупность
классов эквивалентности находится во взаимно одно-
однозначном соответствии с совокупностью точек 53 проек-
проективного пространства Р1п (К) (Ргп(К)). Если 53 интерпре-
интерпретируется как множество прямых левого (правого) век-
векторного пространства Ап+1 (К) (Ап+х{К)), то однород-
однородные координаты точки М имеют смысл координат век-
векторов, принадлежащих прямой I, представляющей ату
точку, а П. к.— совокупности всех таких координат.
В общем случае П. к. точек проективного простран-
пространства П„ относительно нек-рого базиса вводятся чисто
проективными средствами (при обязательном выпол-
выполнении в П„ Дезарга предложения) следующим образом.
Множество on(n-\-i) независимых точек Ао, . . ., Ап
пространства П„ наз. симплексом, при этом
точки Ао, . . ., 4,-_1, Ai + 1, . . ., Ап также независимы
и определяют нек-роо подпространство SH_i-~2', наз.
гранью этого симплекса. Существует нек-рая точ-
точка Е, не лежащая ни на одной из граней 2'. Пусть i0,
![, . . ., ln— любая перестановка чисел 0, 1, . . ., п.
Точки А:., , . . ., А; , /с>0, и Е оказываются незави-
симыми и определяют нек-рое ?„_?. Далее, точки
Aja, . . ., А; определяют тоже нек-рое S?, а так как
суммой Sk и Sn_k является все пространство П„, то S^
и Sn-k имеют в точности одну общую точку Ein _ _ ,¦ , не
лежащую ни в одном из (/с—1)-мерных подпространств,
определяемых точками Л,о, . . ., А,-._ ,А,-., . . ., А/',
при этом Ej ___ ,-., Л,- , . . ., Л,- также незави-
независимы. Таким образом получается 2п + 1—1 точек
^;0 ... it' включая точки ?,-=Л,- и Ео «"¦?", к-рые
и образуют репер пространства 5„=ПП
симплекс ап является его остовом.
На каждой прямой А ;А у имеются три точки А/, А у
Ец, пусть они играют роль точек О, U, Е в определении
тела К рассматриваемой проективной геометрии (см.
Проективная алгебра). Тела К (А,-, Ец, А у) и К(А^,
F'kii A i) изоморфны друг другу, причем изоморфизм
устанавливается проективным соответ-
соответствием Т ц между точками двух прямых AjAy и
AfrAi таким, что точки А ь, Е^, At отвечают точкам А,,
Ejy, Ay. Элемент тела AT, соответствующий точке Р пря-
прямой А /А у, наз. проективной координатой р
точки Р в шкале (А/, Ец-, А у). В частности, П. к. Ец
всегда равна 1, а П. к. Р в шкале (Лу, Ец-, At) есть
Пусть Р — точка пространства, не лежащая ни на од-
одной из граней симплекса а„: Ао, . . ., Ап, образующего
вместе с нек-рой точкой Е репер Я. Если использовать
точку Р вместо Е в вышеприведенной конструкции ре-
репера, то получится последовательность точек />,-, Рц,
Piyki ¦ ¦ •, где Р/о ... и лежит в подпространстве, опре-
определяемом A iB, . . ., А и (но не лежит ни в одной из гра-
граней симплекса а^, образованного этими точками). Пусть
Рц — координата точки Рц (лежащей на А ;А у) в шкале
(А/, Ец-, Ау). Тогда если i, j, к попарно различны, то
Пусть ,r0 — произвольный элемент К, отличны)! от
нуля, а •'/ = /о/);'п> ¦г?=0, <~ 1, . . ., и (при :ito\i оказыкает-
оказыкается, что /-),¦/=¦'/ .',¦). Тогда совокупность эквивалентных
между собой строк, определяемых различными элемен-
элементами хй, и дает П. к. точки Р относительно репера R.
Пусть Р лежит в подпространстве Sд., определяемом
точками A i . . ., А ,• , по не лежит ни в одной из граней
симплекса, определяемого этими точками. Пусть сово-
совокупность эквивалентных строк (д,-,(|, . . ., х;^) является
П. к. точки Р относительно репера R подпространства
S/t, определяемого симплексом а& и точкой Е / ,-fe.
Тогда П. к. точки Р относительно репера И задаются
следующим образом: у,-=ж,-, i== j0, . . ., <&; !/,=0, 1Ф
фц, . . ., tfc.
Любая совокупность эквивалентных между собой
слева (справа) (и+1) строк, построенная вышеизложен-
вышеизложенным способом, соответствует одной и только одной точ-
точке Р пространства П„ и определяет поэтому в нем П. к.
Лит.: [1] Ходж В., Пи до Д., Методы алгебраической
геометрии, пер. с англ., т. 1, М., 1954. М. И. Войцеховский.
ПРОЕКТИВНЫЙ МОДУЛЬ — модуль Р, удовлетво-
удовлетворяющий любому из следующих эквивалентных условий:
1) для любого эпиморфизма модулей а: В-+С и любого
гомоморфизма р": P—*-С найдется такой гомоморфизм у:
Р —>- С, что Р=ау; 2) модуль Р является прямым слага-
слагаемым свободного модуля; 3) функтор Нот (Р,—) точен;
4) любо» эпиморфизм модулей А —>¦ Р расщепляется.
Т о о р с м а К а п л а н с к о г о |2], утверждаю-
утверждающая, что всякий П. м. является прямой суммой П. м.
со счетным числом образующих, сводит изучение струк-
структуры П. м. к счетному случаю. П. м. с конечным числом
образующих изучаются в алгебраической А"-теории.
Простейшим примером П. м. является свободный мо-
модуль. Над кольцами, разложимыми в прямую сумму,
всегда существуют П. м., отличные от свободных. Сов-
Совпадение классов проективных и свободных модулей
доказано для локальных колец [2], колец многочленов
над полем от нескольких переменных (см. [3], [4]).
Лит.: [1] К а р т а н А., Эйленберг С, Гомологи-
Гомологическая алгебра, пер. с англ., М., 1960; L2] Kaplansky J.,
«Ann. Math.», 1958, v. 68, № 2, p. 372—77; [3] С У с л и н А. А.,
«Докл. АН СССР», 1976, т. 229, № 5, с. 1003—68; [4] Q u 1 1-
1 е n D., «Invent. Math.», 1976, v. 36, p. 167 — 71. В. Е. Говоров.
ПРОЕКТИВНЫЙ ОБЪЕКТ категори и —поня-
—понятие, формализующее свойства ретрактов (или прямых
слагаемых) свободных групп, свободных модулей и т.п.
Объект Р категории Я наз. проективным, если
для всякого эпиморфизма v: A -*¦ В и произвольного
морфизма у. Р-+В найдется такой морфизм у': Р—*-А,
что y—y'v. Другими словами, объект Р проективен,
если основной функтор Нр(Х)—Н(Р, X) из .ft1 в ка-
категорию множеств <S переводит эпиморфизмы из Я1
в эпиморфизмы категории 2>, т. е. в сюръективные
отображения.
Примеры. 1) В категории множеств всякий объ-
объект проективен. 2) В категории групп проективны сво-
свободные группы и только они. 3) В категории ЛЭД1 левых
модулей над ассоциативным кольцом Л с единицей
модуль проективен тогда и только тогда, когда он яв-
является прямым слагаемым свободного модуля. Опи-
Описание колец, над к-рыми всякий проективный модуль
свободен, составляет содержание проблемы Се р-
р а. 4) В категории Л2I все модули проективны тогда
и только тогда, когда кольцо Л классически полу-
полупросто. 5) В категории функторов JF C), ®) из малой
категории 3) в категорию множеств @ каждый объ-
объект проективен тогда и только тогда, когда 3) — диск-
дискретная категория.
В определении П. о. иногда предполагают, что функ-
функтор Яр переводит в сюръективные отображения не
все эпиморфизмы, а морфизмы выделенного класса (?.
В частности, если Ц — класс допустимых эпиморфиз-
мов бикатегории j?= (й, (?, 5Ш), то Р наз. допус-
допустимым проективным объектом. Напр.,
в нек-рых многообразиях групп свободные группы этого
многообразия являются допустимыми П. о. относи-
относительно класса всех сюръективных гомоморфизмов, но
не являются П. о., поскольку существуют несюръек-
тивные эпиморфизмы.
Дуальным к понятию П. о. является понятие и н ъ-
ективного объекта. Фундаментальная роль
проективных и инъективных объектов была выявлена
при построении гомологич. алгебры. В категориях
модулей всякий модуль представим в виде фактор-
модуля проективного модуля. Это свойство позволяет
строить т. н. проективные резольвенты и исследовать
различные типы гомологич. размерности.
Лит.: [1] Карта н А., Э й л е н б е р г С, Гомологи-
Гомологическая алгебра, пер. с англ., М., 1960; [2] Мак лейн С,
Гомология, пер. с англ., М., 1966. М. Ш. Цаяенко.
ПРОЕКТИВНЫЙ ПРЕДЕЛ, обратный пре-
предел,— конструкция, возникшая первоначально в тео-
теории множеств и топологии, а затем нашедшая широкое
применение во многих разделах математики. Наиболее
часто используется П. п. семейства однотипных мате-
матич. структур, индексированных элементами нек-рого
предупорядоченного множества. Пусть / — множество,
снабженное отношением предпорядка •<, и каждому
элементу i?I сопоставлено множество X,-, а каждой
паре (i, j), i, /?/, в к-рой i</, сопоставлено отобра-
отображение (fij-Xf -+ Xj, причем ф,-,-, i?I,— тождественные
отображения и ф(уф//г= ф;k ПРИ i-Kj-^k. Множество X
паз. проективным пределом семей-
семейства множеств X; и отображений ф,у, если выполнены
следующие условия: а) существует такое семейство
отображений я,-: X -+- X;, что л,?ф,-у=лу для любой
пары г<0'; б) для любого семейства отображений а,-: Y—y-
-у X/, i?I, произвольного множества У, для к-рого
выполнены равенства а;ф,у=а/ при г<(/, существует
такое однозначно определенное отображение a: Y -у- X,
что а, = ая,- для всех i?/. Конструктивно П. п. можно
описать следующим образом: рассматривается прямое
произведение ТТ. Х,-ив нем выделяется подмножество
всех функций/: / —у Uis/X,-, для к-рых выполняются
равенства Ф,у (/@)~/0) ПРИ '¦Ki- Это подмножество
является П. п. семейства А',-. Если все Xt снабжены
дополнительной однотипной структурой, к-рая пере-
переносится на JJ. Х{, то лта же структура индуцируется
и в П. п. Поэтому можно говорить о П. н. групп, мо-
модулей, топологич. пространств и т. д.
Естественным обобщением понятия П. п. является
понятие П. п. функтора. Пусть F : 3) —>¦ it — одномест-
одноместный ковариантный функтор из малой категории 35 в
произвольную категорию if. Объект Х^ОЫХ, вместе
с морфизмами nD: X —>- F (D), D ?ОЬ 3), наз. проек-
проективным пределом (обратным пре-
пределом, или просто пределом) функтора
/•', если выполнены следующие условия: а) яд/'1(ф)==
= Я?)' для любого морфизма ф: D -*-?)'; б) для всякого
семейства морфизмов ар ¦ Y -*- t~ (D), Для к-рого
cldF (ф) = об?>' при ф : D -у- D', существует такой един-
единственный морфизм а : Y -у- X, что <xd~olud• для любого
1>?ОЬ2). Обозначение: lira F— (X, nD). Аналогично
определяется проективный предел контравариантного
функтора.
Примеры П. п. 1) Пусть / — дискретная кате-
категория. Тогда для произвольного функтора F: I —>- М'
проективный предел функтора F совпадает с прямым,
произведением семейства объектов F (i), i?I.
2) Пусть 35—категория с двумя объектами А, В
и двумя неединичными морфизмами а, р": А —у В. Тогда
предел любого функтора F : 35 —>- Й является ядром
нары морфизмов F(a), /'(p").
Если в категории Я1 существуют произведения лю-
любых семейств объектов и ядра пар морфизмов, то в Я
существует предел любого функтора F : -D—vtf' из про-
произвольной малой категории Ж. м. ш. Цаленко.
ПРОЕКТИВНЫЙ СПЕКТР кольца— схема Х =
= Proj(i?), сопоставляемая градуированному кольцу
Л=2 _п-Кп- Как множество точек X представляет
собою множество однородных простых идеалов pdR,
таких, что Р^>2 -^и" Топология на X определяется
следующим базисом открытых множеств: Х/= {p\f$.p}
для f?Rn, re>0. Структурный пучок Qx локально
окольцованного пространства X задается на базисных
открытых множествах так: Г(Ху, Qx)=\R(f)\o, т- е-
подкольцо элементов степени 0 кольца частных Яф
по мультипликативной системе {/"}„^.о-
Наиболее важным примером П. с. является Рп=
= Proj Z[T0, Тъ . . ., Тп]. Множество его fc-значных
точек Pi для любого поля к находится в естественном
соответствии с множеством точек проективного га-мер-
га-мерного пространства над полем к.
Если все кольца Rm как Л „-модули натянуты на
® ®R то на Proj (/?) определена еще дополни-
тельная структура. А именно, покрытие {Xf | /^ Лх} и
единицы fig определяют 1-коцикл Чеха на Proj(i?),
к-рому отвечает обратимый пучок, обозначаемый через
CA). Через Q(n) принято обозначать ге-ю тензорную
степень Q(iy^n пучка 0A). Существует канонич.
гомоморфизм Rn-">F(X, б (re)), указывающий гео-
метрич. смысл градуировки кольца R (см. [1]). Если,
напр., R^k[T0, . . ., Тп], то 0A) соответствует пучку
гиперплоских сечений в Р%.
Лит.: [1] М а м ф о р д Д., Лекции о кривых на алгебраи-
алгебраической поверхности, пер. с англ., М., 1ЯН8; 12] G г о t h e n-
d i е с k A., Elements de gftmielrie alcffbrique t. 1 — 4, P., 19G0—
1967 (Publ. IHES). - В. В. Шакуров.
ПРОЕКТОР, п р о о к ц и о н и ы и о п е р а т о р,—
линейный оператор Р и векторном пространстве X
такой, ЧТО Р2=Р. м. И. Войцеховский.
ПРОЕКЦИОННЫЕ МЕТОДЫ — методы отыскания
приближенного решения операторного уравнения в
заданном подпространстве, основанные на проектиро-
пании уравнения па пек-рос (вообще говоря, другое)
подпространство. И. л. являются основой построения
различных вычислительных схем решения краевых
задач, в том числе метода конечных элементов и ме-
метода коллокации.
Пусть L — оператор, область определения D (L)
к-рого лежит в банаховом пространстве X, а область
значений R (L) — в банаховом пространстве Y. Для
решения уравнения
Lx^y A)
проекционным методом выбирают две последователь-
последовательности подпространств {Хп} и {Г„},
XnczD(L)(=X, У„с=У, м = 1, 2, ...,
а также проекторы Рп, проектирующие Y на Yп. Урав-
Уравнение A) заменяется приближенным
PnLxn = Pny, xn^Xn. B)
В случае X—Y, Xn=Yn, ra=l; 2, ... П. м. B) при-
принято называть методом Галеркина (иногда
последний метод трактуется более широко, см. Галер-
Галеркина метод).
Имеет место теорема сходи мости П. м. для
линейных уравнений (для случая конечномерных
подпространств Хп и Yn). Пусть L линеен и переводит
D (L) на R (L) взаимно однозначно, причем D (L) и
R (L) плотны в Х и Y соответственно; подпространства
Х„ и Y п конечномерны, dim A'n=~dim Yn, n "I, 2. . . .,
а проекторы Рп ограничены равномерно по п, то есть
\\Рп||<с= const, n=l, 2, . . . Тогда следующее усло-
условие а) равносильно набору условий б) и в):
а) начиная с нек-рого п=п0 существует единственное
решение х„ уравнения B) и \\Lxn—y\\ -*¦ 0 при любом
б) последовательность подпространств LXn предель-
предельно плотна в Y, т. е. расстояние d(y, LXn)—>0 при
п —>¦ со для 4y?F;
в) T=limTn>0, где ти= inf \\Р„уп\\-
Vnn, ||Уп11
Быстрота сходимости при соблюдении условий б)
и в) характеризуется неравенством
d(y, LXn)^\\Lxn~y\\< (l+c/xn)d(y,LXn). C)
В случае, когда пространства X и Y гильбертовы,
а Рп и Qn — ортопроекторы, проектирующие У со-
соответственно на >*„ и LX,,, условие в) равносильно
условию
в') 6i= lim 6„<1, где 0„= \\Pn—Qn\\ — раствор под-
пространств Yn и LXn\ вместо C) получается оценка
|| у - Q „у II < I Lxn - у || < -~=- \\ У - Q пУ \\ ¦
В случае Yn~LXn (метод наименьших квадратов)
0„=О, n—i, 2, . . ., и критерием сходимости является
условие б).
Теорема дает условие сходимости певязки \\Lxn—у\\.
Если L~x ограничен и у ? Л (L), то из сходимости не-
невязки следует сходимость самих приближений хп к
решению x=L~xy уравнения A). Из теоремы можно
извлечь удобный критерии сходимости метода Галер-
кина; для метода Галеркина — Петрова следует до-
дополнительно наложить условие типа в').
Пусть / — линейная ограниченная форма, а о — би-
билинейная ограниченная форма на действительном гиль-
гильбертовом пространстве Н (или полуторалинейная в слу-
случае комплексного Я). Допускается, что а предсташша
в Ш1де а—а-\-Ь, так что
а (и, и)-:;у||и||2 Чи?Н, Y = eonst;-t),
а билинейная форма Ъ вполне непрерывна, т. е. слабые
сходимости и„ —>- u, vn —>- v в Н влекут за собой схо-
сходимость Ъ(ип, г„)—>-Ь(и, v) (симметричность форм а,
а, Ь не обязательна). Пусть поставлена задача: найти
и?Н такое, что
а (и, 1») = г (v) \jv?H. D)
Метод Галеркина решения задачи D) заключается в
следующем. Выбирают какие-нибудь (замкнутые) под-
подпространства Н„СН, и=1, 2, . . ., и находят ип?Нп
такое, что
а(ип, vn)=--l(vn) \/vn^Hn. E)
Имеет место следующая теорема: пусть {Нп} пре-
предельно плотпа в Н, выполнены наложенные выше на а
условия, и задача D) имеет единственное решение
и?Н (равносильное условие: однородная задача оты-
отыскания и из условия а(и, v) = 0 Vv?If имеет лишь три-
тривиальное решение и=0); тогда задача E) при всех
достаточно больших п имеет единственное решение
ип?Нп и \\ип—ti|| —>-0 с оценкой
|| и — Опи || < |! ип-и'\ < с I и-Опи ||,
где О„ — ортопроектор, проектирующий Я на Я„,
с = const.
В применении к краевым задачам для уравнений эл-
липтич. типа в качестве И, как правило, выбирается
знергетич. пространство главной части соответству-
соответствующего дифференциального оператора.
Лит.: [1] Красносельский М. А. [ид р.], Прибли-
Приближенное решение операторных уравнений, М., 1969.
Г. М. Вайникко.
ПРОЕКЦИОННЫЙ СПЕКТР — индексированное
направленным множеством (А, » семейство симплици-
альных комплексов {Na : а,?А } такое, что для каждой
пары индексов а, а'?Л, для к-рых а'>а, определено
симплициалыюс отображение (проекция) л«' ком-
комплексов Na> на комплекс Na- При этом требуется,
чтобы Ла"=па'па", когда а">а'>а (условие транзи-
транзитивности). Тогда и говорят, что задан проекцион-
проекционный спектр S= {Na, я?', А }, или просто S= {Na,
л*'}. Это понятие принадлежит П. С- Александрову
(см. [2]); оно, по сути, эквивалентно общему понятию
обратной системы, или обратного
спектра (см. Спектр в категории). Действитель-
Действительно, каждый комплекс Na естественным образом пре-
превращается в частично упорядоченпое множество сим-
симплексов зтого комплекса, а следовательно в тополо-
топологическое Го-пространство Na- При этом проекции л,"'
становятся непрерывными отображениями. Обратно,
если {Na, Па } — обратная система из топологических
Г0-иространств и непрерывных проекций я% , то каж-
каждое Го-пространство Na естественно превращается в
частично упорядоченное множество, а это частично
упорядоченное множество реализуется в виде симпли-
циального комплекса Na- При этом непрерывные про-
проекции я« становятся симшгациальными отображения-
отображениями. Таким образом, 11. с— это в точности обратная
система из топологических Г0-пространств (см. [3]).
Понятия «П. с.» (а следовательно, и обратной си-
системы пространств) и и е р и а системы множеств (см.
ниже) оказали огромное влияние не только на разви-
развитие топологии, но и на развитие всей теоретико-мно-
теоретико-множественной математики. После этого стало возможным
говорить о теории аппроксимации сложных топологи-
топологических и алгебро-топологич. объектов более простыми.
Если для каждого а?А комплекс Na конечен, то
спектр S— {Na, Ла } паз. конечным п р о е к-
ц и о н н и м с п е к т р о м. С каждым П. с. 5= {Na,
л"'} связываются следующие понятия. Всякий набор
симплексов |= {ta : а?А } по одному из каждого ком-
комплекса Л'а спектра S на.-s. нитью этого спектра, если
при а' >а всегда Jta'ia.--?a, где ta, ta,?'?,. Множество
S всех нитей с топологией, базу к-рой образуют мно-
множества вида Ota.,= {|'65 -t'a,<ta0}, гдеао?Л, tan?Na0
произвольны, a ta,,<-ta0 означает, что симплекс ta0
нити s' и комплексе Naa является гранью симплекса
tao, наз. полным пределом спектра S,
Та же топология получается, если индуцировать на S
топологию тихоновского произведения П (оДРа •' а € А },
где ,ДГ'а — соответствующее комплексу Na топологи-
топологическое Подпространство. Нить |'={*а} объемлет нить
|т= {ta}, если для каждого <х?А выполнено ta^ta.
Нить | наз. м а к с и м а л ь н о й (соответственно м и-
нимальной). гели не существует никакой отлич-
отличной от нее нити, для к-poii она была бы объемломой (со-
(соответственно объемлющей). Подпространство полного
предельного пространства S спектра S, состоящее из
всех максимальных (соответственно из всех минималь-
минимальных) нитей, наз. верхним (соответственно н и ж-
ним) пределом спектра S. Полный предел
S является полурегулярным (в другой терминологии —
семирегулярным) Го-пространством, а верхний S
и нижний S пределы суть Г]-пространства. Если S - -
конечный П. с, то S, S и S -- бикомпактные прост-
пространства.
В основе всей теории аппроксимации топологич.
пространств полиэдрами, вернее симплициальными
комплексами, лежит введенное П. С. Александровым
(см. [1]) понятие нерва системы множеств. Нервом
данной системы а множеств наз. симплициальнып комп-
комплекс Na, вершины к-рого взаимно однозначно соот-
соответствуют элементам системы а таким образом, что
каждое множество вершин определяет симплекс ком-
комплекса Na тогда и только тогда, когда соответствующие
этим вершинам множества системы а имеют непустое
пересечение.
Удобнее рассматривать т. н. канонич. покрытия
пространства X. Локально конечное (конечное) по-
покрытие а пространства X наз. каноническим,
если его элементы — канонические множества (замк-
(замкнутые) (в другой терминологии — регулярные замкну-
замкнутые) с дизъюнктными открытыми ядрами. Если из
двух канонич. покрытий пространства X покрытие а'
следует за покрытием а, т. е. а' вписано в а (в этом слу-
случае а'>а), то определено естественное симилициаль-
ное отображение Яа' (проекция) нерва No,- на нерв No.*
к-рое возникает, если каждому элементу Аа'?а' по-
покрытия а' поставить в соответствие тот единственный
элемент Аа покрытия а, для к-рого AaZ)Aa'. Пусть
Ш(Х) (соответственно %0(Х)) обозначает совокупность
всех локально конечных (конечных) канонич. покрытий
пространства X. Для каждого а?%(Х) (соответственно
а?*йо(Х)) обозначена вся совокупность всех локально
конечных (конечных) канонич. покрытий пространства
X. Для каждого а ?21 (А') (соответственно а?210(А))
рассматривается комплекс Na, являющийся нервом по-
покрытия а. Если а' >а, то определено симплициальное
отображение л?' : JVa< -*¦ Na- Полученный таким
образом П. с. S—{Na, л"'} наз. полным (соот-
(соответственно конечным) П. с. топологич. простран-
пространства X. П. С. Александров [2] еще в 1928 доказал, что
каждый метрический (л-мерный) компакт является
верхним пределом (re-мерного) конечного П. с. над счет-
счетным множеством индексов. А. Г. Курош в 1934 до-
доказал, что каждый бикомпакт есть верхний предел
своего конечного П. с. В 1961 В. И. Пономарев доказал,
что каждый паракомпакт есть верхний предел своего
полного П. с, то есть спектра, построенного над мно-
множеством 'й(Х) всех локально конечных канонич.
покрытий пространства X. В. И. Пономарев ввел по-
понятие расслабления симплициального ком-
комплекса К, понимая под этим всякий замкнутый под-
подкомплекс К'сК, содержащий все вершины комплекса
А'. Нульмерный комплекс, состоящий из всех вершин
комплекса К, наз. его полным расслабле-
расслаблением (или остовом). Заменяя все комплексы
данного П. с. их (полным) расслаблением и сохраняя
при этом проекции, получают (полное) расслабление
спектра. Исследование неприводимых совершенных
отображений паракомпактов сводится к исследованию
расслаблений их полных Л. с. При этом предел пол-
поллого расслабления полного Л. с. паракомпакта X
есть т. н. абсолют X паракомпакта А", а предел пол-
полного расслабления конечного И. с. любого регуляр-
регулярного пространства — бикомпактное расширение Сто-
Стоуна — Чеха $Х абсолюта X этого регулярного про-
пространства. Всякий конечный абстрактный П. с. эк-
эквивалентен спектру над нек-рым направленным из-
измельчающимся множеством конечных канонических
покрытий нек-рого полурегулярного бикомпактного
7\гпространетва, т. е. получается из этого спектра
посредством конечного числа следующих операции:
1) замена спектра изоморфным ему спектром, 2) замена
снектра его конфинальной частью, 3) замена спектру
спектром, содержащим данный в качестве конфиналь-
ной части (теорема Зайцева).
Понятия нерва и П. с. доставили средства для ре-
редукции свойств общих пространств, и прежде всего
паракомпактов, бикомпактов и метрич. компактов, к
свойствам комплексов и их симплициальных отобра-
отображений. Это позволило определить и изучать гомоло-
гомологические и когомологические инварианты общих про-
пространств, а не только полиэдров (см. Александрова —
Чеха гомологии и когомологии, С центральные гомологии).
Все это привело к синтезу геометрических и теоретико-
множественных идей в топологии.
Лит.: [1] Александров П. С, «С.г. Acad. sci.», 1927,
t. 184, p. 317—20; L2] его же, «Ann. Math.», 1929, v. 30, p.
101—87; IS] его же, «Успехи матем. наук», 1947, т. 2, в. 1,
с. 5—57; [4] его же, Введение в теорию множеств и общую
топологию, М., 1977; 15] Александров П. С, Поно-
Пономарёв В. И., в кн.: General topology and its relations to mo-
modern analysis and algebra, v. 2, Prague, 1967, p. 25—30; [6]
Александров П. С, Федорчук В. В., «Успехи ма-
матем. наук», 1978, т. 33, в. 3, с. 3—i8; [7] Пономарев В. И.,
«Матем. сборник», 1963, т. ВО, .\5 1, с. 89—119; [8] Зайцев
В. И., «Труды Моск. матем. об-на», 1972, т. 27, с. 129—93.
В. И. Пономарев,
НРОЕКЦИЯ — термин, связанный с операцией про-
проектирования (проецирования), к-рую
можно определить следующим образом (см. рис.);
выбирают произволь-
произвольную точку S простран-
пространства в качестве ц ен-
т р а проекти-
проектирования и пло-
плоскость П', не прохо-
проходящую через точку S,
в качестве плоско-
плоскости проекций.
Чтобы спроектиро-
спроектировать точку А (прообраз) пространства на пло-
плоскость П' через центр проекций S, проводят прямую
SA до ее пересечения в точке А' с плоскостью ГГ.
Точку А' (образ) наз. проекцией точки А;
проекцией фигуры F наз. совокупность П. всех ее
точек. Описанная ГГ. наз. центральной (или
конической). П. с бесконечно удаленным цент-
центром проектирования наз. параллельной (или
цилиндрической). Если плоскость П. распо-
расположена перпендикулярно к направлению проекти-
проектирования, то 11. наз. ортогонально й (или пря-
прямоугольной).
Параллельные П. широко используются в начерта-
начертательной геометрии для получения различных видов
изображений (см., напр., Аксонометрия, Перспектива).
Имеются специальные виды П. на плоскость, сферу и
др. поверхности (см., напр., Картографическая про-
проекция, Стереографическая проекция). А. В. Шиное.
ПРОИЗВЕДЕНИЕ семейства объектов
категории — понятие, описывающее на языке
морфизмов конструкцию декартова произведения. Пусть
Ai, i?I,— индексированное семейство объектов ка-
категории ,ft. Объект PgObfi1 (вместе с морфизмами
я,-: Р -*¦ Ah i?l) наз. произведением семейства объек-
объектов A/, i?/, если для всякого семейства морфизмов
а,-: X ->¦ A;, t? Г, существует такой единственный мор-
физм а : X ->- Р, что ая,-=а,-, i?/. Морфизмы я,- наз.
проекциями произведения; П. обозна-
обозначается JJ* 7Л,-(Д(-), или JJ. А[, или АгХ. . .ХА„
в случае /={1, . . ., п). Морфизм а, входящий в
определение П., иногда обозначается Ц^е;а'' или
(X){6ja,-. П. семейства Л;, г?/, определено однозначно
с точностью до изоморфизма; оно ассоциативно и ком-
мутативно. Понятие П. семейства объектов двойствен-
двойственно понятию копроизведения семейства объектов.
Произведением пустого семейства объектов является
правый нуль (терминальный объект) ка-
категории. В большинстве категорий структуризованных
множеств (категории множеств, групп, топологич.
пространств и т. д.) понятие 11. семейства объектов
совпадает с понятием декартова (прямого) П. этих
объектов. Тем не менее такое совпадение не является
обязательным: в категории периодических абелевых
групп П. семейства групп G,-, г?/, есть периодич.
часть декартова П. этих групп, к-рая в общем случае
отличается от самого декартова П.
В категориях с нулевыми морфизмами для любого
произведения Р= JJ. А,- (л,-) существуют такие од-
однозначно определенные морфизмы а,-: Л,-—v P, i?I,
что а[л,= 1^., а,-Яу=0 при 1ф]. Если / конечно, то в
абелевой категории л^-!-. • .-\-лпап=1 и П. семейства
объектов Аг, . . ., Ап совпадает с их копроизведением.
Лит.: [1] Ц а л е н к о М. Ш., Ш у л ь г е и ф е р Е. Г.,
Основы теории категорий, М., 1974. М. Ш. Цаленпо.
ПРОИЗВОДНАЯ — одно из основных понятий ма-
тематич. анализа. Пусть действительная функция
f(x) действительного переменного х определена в
нек-рой окрестности точки х0 и существует конечный
или бесконечный предел
lim
Этот предел и наз. производной от функ-
ц и и I (х) в точке х0. Если положить y — f(x),
то предел (*) запишется так:
Ах
— f (xo) = f (хо + Дх) —/ (xg) =Д(/,
я та
lim
Ах -*¦ О
Используют также обозначения /' (х0), — , у',
7' 7 ^х^ и нек-Рые ДРУгие-
Операцию вычисления П. наз. дифференци-
дифференцированием. Если производная /' (х0) конечна, то
функцию /(х) наз. дифференцируемой в
точке х0. Функцию, дифференцируемую в каждой
точке нек-рого множества, наз. дифференцируемой на
этом множестве. Дифференцируемая функция всегда
непрерывна. Однако существуют непрерывные функ-
функции, не имеющие П. во всех точках заданного проме-
промежутка (см. Недифференцируемая функция).
Пусть функция дифференцируема в нек-ром проме-
промежутке. Ее производная /' (х) может оказаться при этом
разрывной функцией. Однако по классификации Бэра
(см. Бэра классы) она всегда является функцией 1-го
класса и обладает свойством Дарбу: приняв два зна-
значения, принимает и все промежуточные.
Обобщением понятия П. является понятие П. по
множеству. Пусть действительная функция / (х) оп-
определена на нек-ром множестве Е действительных
чисел, х0 — предельная точка этого множества, хо?Е,
и существует конечный или бесконечный предел
lim —z— ,
X — Ха
х -> х0, х е Е
к-рый и наз. производной от функции
f(х) по множеству Е в точке х0 и обозначают
символом ]'е(х0). П. функции по множеству есть обоб-
обобщение понятия П. Разновидностями этого обобщения
являются понятия односторонней производной, произ-
производного числа, аппроксимативной производной.
Данное определение П. (и его обобщение), а также
простейшие ее свойства почти без изменений распро-
распространяются на комплексные функции и вектор-функции
действительного или комплексного переменного. Кроап
того, существуют понятия П. скалярной функции
точки евклидова пространства R" (см. Градиент).
И. функции множества по мере (в частности, по пло
щади, по объему и т. п.), понятие П. распространяют
на вектор-функции точки абстрактного пространства
(см. Дифференцирование отображения).
О геометрич. и механич. истолковании П., о про-
простейших правилах дифференцирования, о П. высших
порядков, о частных П., а также лит. см. в ст. Диффе-
Дифференциальное исчисление. Г П. Толстое
ПРОИЗВОДНОЕ МНОЖЕСТВО — совокупности
М' всех предельных точек множества М в топологич.
пространстве. Множество М, совпадающее со своим
П. м., наз. сове рш е н н ы м. м. и. Войцеховский.
ПРОИЗВОДНОЕ ПРАВИЛО вывода для дан-
данного исчисления — вывода правило, заключе-
заключение к-рого выводимо из его посылок в рассматриваемом
исчислении. Напр., в высказываний исчислении правило
вывода
лзв.взс
является П. п., поскольку в этом исчислении имеет
место выводимость из посылок:
Az> В, BziC \—Az>C.
Всякое П. п. является допустимым правилом, но не
всякое допустимое правило является П. п. Напр.,
подстановки правило в исчислении высказываний яв-
является допустимым правилом, но не производным.
Лит.: [1] К л и н и С. К., Введение в метаматематику,
пер. с англ., М., 1957. С. Н. Артемов.
ПРОИЗВОДНОЕ ЧИСЛО, производное чис-
число Дин и,— понятие теории функций действитель-
действительного переменного. Верхним правым П. ч.
Аа наз. верхний предел отношения —— —- при
Xi—X
ij-> j, где ху^>х. Аналогично определяют ниж-
нижнее правое %а, верхнее Ag и нижнее
Xg л е в ы е П. ч. Если Аа—\а (Ag—Xg), то f (х) имеет
в точке х одностороннюю правую (левую) производную.
Обыкновенная производная существует, если все че-
четыре П. ч. конечны и совпадают. П. ч. были введены
У. Дини [1]. Как показал Н. Н. Лузин, если все че-
четыре П. ч. конечны на нек-ром множестве, то функция
имеет обычную производную всюду на этом множе-
множестве, кроме точек множества меры нуль.
Лит.: [1] D i n i U., Fondamenti per la icorica delle funzio-
nl di variabili reali, Pisa, 1878; [2] Сакс С, Теория интеграла,
пер. с англ,, М., 1949. Т. П. Лукашенко.
ПРОИЗВОДНЫЙ АВТОМОРФИЗМ в э р г о д и ч с>-
ской теории — преобразование Тх, определя-
определяющееся но автоморфизму Т пространства с мерой
(М, ц.) и измеримому подмножеству положительной
меры ХсМ, почти все точки к-рого под действием
итераций Т снова попадают в X. Для каждой такой
точки х определяют Тх {х) как ту точку траектории
Тпх, в к-рой эта траектория впервые после х возвра-
возвращается в X (согласно Пуанкаре теореме о возвращении,
условие, чтобы почти все точки из X со временем
снова возвращались в А', автоматически выполняется,
если |х(М)<оо). Преобразование 1'х оказывается
автоморфизмом (точнее, автоморфизмом по mod 0)
пространства X с индуцированной на нем мерой (по-
(последняя есть мера (х, рассматриваемая только на под-
подмножествах X; если |i(X)<oo, то обыкновенно эту
меру еще нормируют).
Обратно, если U п>ц ТпХ=~М (это условие автома-
автоматически выполняется, если автоморфизм Т эргодичен),
то исходный автоморфизм Т восстанавливается (с точ-
точностью до сопряжения посредством нек-рого изо-
изоморфизма пространств с мерой) по Тх и времени
возвращения
nx(x)=mm{n > 0:Тпх ? X}.
А именно, Т ость специальный автоморфизм, постро-
построенный по Тх и пх- Д. В. Аносов.
ПРОИЗВОДНЫЙ ФУНКТОР — функтор, «измеряю-
«измеряющий» отклонение основного функтора от точного.
Пусть Т (А, С) —аддитивный функтор из категории
.Rj-модулей и Д2-модулей в категорию Д-модулей,
ковариантный по первому аргументу и контравариант-
вын по второму. Для инъективной резольвенты X
модуля А л проективной резольвенты Y модуля С
получают дважды градуированный комплекс Т (X, Y).
Группы гомологии ассоциированного одинарного ком-
комплекса Т (А, С) не зависят от выбора резольвент, об-
обладают функторными свойствами и иаз. правыми
производными функторами Rn Т (А , С) функтора Т (А, С).
Основное свойство П. ф.— существование бесконеч-
бесконечных точных последовательностей
^ R»T (A',C)—rR"T (A, C)-^R"T (Л"С)—+
—> RnT (А, С")—* RnT (А, С) —* R"T (А, С) —*
—¦+R"±l(A, С")—>...,
индуцированных короткими точными последователь-
последовательностями
О -—»- А' —* А —* А" —>• О,
О—+С ^С—*С"—+0.
Левые П. ф. определяются двойственным образом.
И. ф. функтора Нот обозначаются Ext^. Функтор
Extj^(.4, С) классифицирует все расширения модуля
А с ядром С с точностью до эквивалентности (см.
Бэра умножение, Когомологии алгебр}.
Лит.; [1] К а р т а н А., Э й л е н б е р г С, Гомологическая
a ire6pa, пор. с англ., М., 1960; [2] М а к л с и н С, Гомология,
нер. с англ., М., 1966. В. Е. Говоров,
ПРОИЗВОДЯЩАЯ ФУНКЦИЯ, i е н е р а т р и с а,
числовой или функциональной последовательности
{ап (х)} — сумма степенного ряда
F (х, w) = y2jDn=Qan(x)w"
с положительным радиусом сходимости. Если известна
П. ф., то для изучения последовательности {ап(х)}
используются свойства коэффициентов Тейлора ана-
литич. функций. Для многочленов {Рп (х)}, ортого-
ортогональных на интервале (а, Ь) с весовой функцией h(x),
при нек-рых общих условиях существует П. ф.
Для классических ортогональных многочленов П. ф.
представляется в явном виде через весовую функцию
h (x) и используется для вычисления значений этих
многочленов в отдельных точках, а также для вывода
различных тождественных соотношений между этими
многочленами и их производными.
В теории вероятностей II. ф. случайной величины ?,
принимающей целочисленные значения {п}^ с вероят-
вероятностями {Р| (га)}, определяется формулой
F(t, z) = 2"^oPs(re)z«, |z|«;l.
С помощью П. ф. вычисляются распределения вероят-
ностей случайной величины §, ее математич. ожидание
и дисперсия:
D6 = 7-2. (g, l) + ^i(E, i)-I>«(s, Dp.
П. ф. случайной величины g можно определить как
математич. ожидание случайной величины zl, то есть
Лит.: [1] Cere Г., Ортогональные многочлены, пер. с
англ.,М., 1962; [2] Суетин П. К., Классические ортогональные
многочлены, 2 изд., М., 1979; [3] Ф е л л е р В., Введение в тео-
теорию вероятностей и её приложения, пер. с англ., 2 изд., т. 1 — 2,
М., 19G7. П. К. Суетин.
ПРОИЗВОДЯЩИЙ ОПЕРАТОР полугруппы —
производная в нуле от полугруппы линейных ограничен-
ограниченных операторов Т (i), ()<?<оо, действующих в ком-
комплексном банаховом пространстве X. Если Т (t) не-
непрерывна по норме операторов, то она имеет вид Т (t)=
= eW», где Ао — ограниченный оператор,
lim t~l[T (t)x~x]=Aox A)
t -+ о
при любом х?Х и А0 есть П. о. T(t). Обратно, если
предел слева существует при всех х?Х, то Т {t)=etA«.
Более сложная картина возникает, когда Т(t) только
сильно непрерывная полугруппа. В атом случае предел
A) существует не при всех х. Оператор Ао, определен-
определенный на линейном множестве D (Ао) всех тех х, для
к-рых предел существует, является линейным неогра-
неограниченным оператором и наз. и н ф и н и т е з и м а л ь-
ным оператором. В частности, Ап определен
на всех элементах вида \ T(t)ydt, a, Р>0, у?Х.
Если обозначить через Хо аамыкание объединения
областей значений всех операторов Т (t), i>0, то D (Ао)
плотно в Хо и, более того, f\nD(Ao) плотно в Хо.
Все значения оператора Ао также лежат в Хо. Если
оператор Ао неограничен, то D(A0) является множе-
множеством первой категории в Хо-
Если в Хо нет элементов х, на к-рых Т (t)x=O, то
оператор Ао допускает аамыкание А—Ао, к-рое и наз.
производящим оператором полугруппы
T(t). В этом случае при x?D(A)
Т (()i-r(s)i=f'r (т) Ах dx,
B)
dTff Х=4,Г (t)x = T(t)Ax.
Равенство B) определяет замкнутый оператор А,
к-рый, вообще говоря, шире, чем замыкание Ао. Его
иногда наз. обобщенным производящим
оператором полугруппы Т (t).
На множестве D% тех же х?Х, для к-рых сходится
несобственный интеграл
Т (s)x ds, C)
J
определен оператор
Я (X) х= lim [ °° е-^Т (s) xds
t -* о •>'
при Re Х>и, где со — тип полугруппы T{t). Этот опе-
оператор обладает свойствами:
1) R(k)DRcDR;
2) R(X)x — Л (n)z = (|x —Х)Яа) R (ц)ж;
3) R (к) (Х1-А0)х=х, х g D (Ао);
4) (M-A)R(X)x=x, x?DRnX0.
Если интеграл C) абсолютно сходится при любом
х^Х, то 11. о. А существует тогда и только тогда, когда
из Т(?)ж=0, х?Х0, следует х=0; оператор R (к) огра-
iinioH, и, если Хо —.Y, он совпадает с резольвентой
оператора А ; для того чтобы Ло был замкнутым (А = Ад),
необходимо и достаточно, чтобы
lim -г \ 1 (s) j: ,
t ~> 0 J°
при любом ?0
Основной задачей теории полугрупп операторов яв-
является установление связи между свойствами полу-
полугрупп и свойствами их П. о., причем последние обычно
формулируются в терминах операторов Я(Х).
Лит.: [1] X. и л л е Э., Ф и л л и п с Р., функциональный
анализ и полугруппы, пер. с англ., М., 1962; [2] Забрей-
ко И. II., Зафиевский А. В., «Докл. АН СССР», 1969.
т. 189, ,Ni> 5, с. 934 —37;[3l его ж е, там же, 1970, т. 195, К» 1,
с. 24—27. С. Г. h'jieUH.
ПРОИЗВОЛЬНЫХ ПОСТОЯННЫХ ВАРИАЦИЯ —
метод решения линейных неоднородных обыкновенных
дифференциальных систем (или уравнений). Этот метод
позволяет записать в замкнутой форме общее решение
неоднородной системы, если известно общее решение
соответствующей однородной системы. Идея метода
П. п. в. состоит в том, что произвольные постоянные,
входящие в общее решение однородной системы, за-
заменяются функциями независимой переменной, к-рые
подбираются так, чтобы удовлетворить неоднородной
системе. В конкретных задачах этот метод применялся
еще Л. Эйлером (L. Euler) и Д. Бернулли (D. Bernoul-
Bernoulli), но его полная разработка принадлежит Ж. Лаг-
ранжу [1].
Пусть рассматривается задача Коши для линейной
неоднородной системы
i = A(t)x + f(t), х(Ц)=х0, A)
где
А:(а, Р) —>Hom(R", R«),
— суммируемые на каждом конечном отрезке отобра-
отображения, to€(a> Р)- Если Ф (t) — фундаментальная мат-
матрица решений однородной системы
y = A(t)y, B)
то ;/=Ф (t)r, c?R",— общее решение этой системы.
П. н. в. представляет собой замену переменных в си-
системе A):
и приводит кформуле Коши для решения за-
задачи A):
) V Ф!()/()г
к-рую наз. иногда формулой вариации
(произвольных) постоянных (см. также
Линейное дифференциальное уравнение обыкновенное).
Идею П. п. в. иногда удается использовать в более
общей нелинейной ситуации для описания связи реше-
решений возмущенной полной системы и решений невоз-
невозмущенной укороченной системы (см. [3], [4]). Напр.,
для решения x(t) задачи
x = A(t)x + f(t, х), x(to)=xo
(где А, / — непрерывные отображения и где обеспечи-
обеспечивается условие единственности решения) справедлива
формула Л. п. в., являющаяся интегральным уравне-
уравнением:
х (t) =Ф (t) ф-i (*„) хо + Ф @ V Ф-1 (т) / (т, х (т)) dx;
*j • о
здесь Ф (t) — фундаментальная матрица решепий си-
системы B).
Лит.: [1] Las г л п к с J., lEuvres, t. IV, P., 18B9, p. 151-
251; [2] П о н т р я г и ii „I. С, Обыкновенные дифференциаль-
дифференциальные уравнения, 5 изд., М., 19X3; [3] А л е к с е е в В. М., «Вестн.
Моск. ун-та», 1961, № 2, с. 28—36; Ы Р е й з и н ь Л. Э., Ло-
Локальная эквивалентность дифференциальных уравнений, Рига,
1971. Я. X. Розов.
ПРОКОНЕЧНАЯ ГРУППА — топологическая груп-
группа, являющаяся проективным пределом системы ко-
конечных групп G(, i?/, снабженных дискретной топо-
топологией (/ — предупорядоченное множество). П. г.
G обозначается lim G,-. Как подпространство прямого
произведения JJ. G,-, снабженного компактной топо-
топологией (базой окрестностей единицы является система
ядер проекций JJ. Gt-*-G[), она замкнута и потому
компактна.
Примеры. 1) Пусть / — множество целых
чисел, больших нуля, с естественным отношением
порядка и Gi='Ei'p'r?- Пусть т,-+1 : Gi + 1-+- G,- — естест-
естественный эпиморфизм и
для любых i</. Тогда lim G; — (аддитивная) группа
кольца Zp целых р-адических чисел.
2) Всякая компактная аналитич. группа над полом
р-адических чисел (напр., SL,,(ZP)) является (как
топологич. группа) П. г.
3) Пусть G — абстрактная группа и {//,-, *€^} "-
семейство всех ее нормальных делителем"! конечного
индекса. На / можно ввести отношение <, положив
?<:/, если Н;~Я/. Это отношение превращает I в
предупорядоченное множество. Сопоставляя каждому
i(zi группу GI'//,¦ и каждой паре i</ из I— естественный
гомоморфизм х\ : GH у —>- G/Н',-, получают П. г. G=
= lim GlH;, паз. а с с о ц и и р о в а н и о ii с G \\. г.;
она является отделимым пополнением группы G от-
относительно топологии, определенной подгруппами ко-
конечного индекса. Ядро естественного гомоморфизма
G -+ G является пересечением всех подгрупп конеч-
конечного индекса. В этой конструкции можно было бы вме-
вместо семейства всех нормальных делителей конечного
индекса рассматривать лишь те, индекс к-рых есть
степень фиксированного простого числа р. Соответст-
Соответствующая группа обозначается Gp и является про-р-
группой.
4) П. г. следующим образом естественно возникают
в теории Галуа (вообще говоря, бесконечных) алгеб-
раич. расширений полей. Пусть Klk — Галуа расши-
расширение и {Кilk, i?/} — семейство всех конечных рас-
расширений Галуа поля к, лежащих в К. Тогда К= \J {g jKj.
На I можно ввести отношение <, положив i</, если
K^Kj. Тогда / становится предупорядоченным мно-
множеством. Пусть Ga]F{j/k — группа Галуа расширения
Kjlk. Каждой паре ;<:; из I сопоставляется естествен-
естественный гомоморфизм
^G*\ К ilk.
Тогда соответствующая П. г. lim Gal Kjlk (абстрактно)
изоморфна группе Gal Klk, что позволяет считать
Gal Klk П. г. Система подгрупп Gal K/K{ образует в
Gal Klk систему окрестностей единицы (см. Галуа
топологическая группа). Эта конструкция получает
обобщение в алгебраич. геометрии при определении
фундаментальной группы схемы. П. г. могут быть
охарактеризованы как компактные вполне несвязные
группы (см. Компактная группа), а также как ком-
компактные группы, у к-рых имеется множество открытых
нормальных делителей, образующее систему окрест-
окрестностей единицы. Теория когомологии П. г. (см. Кого-
мологии групп, Галуа когомологии) играет важную
роль в современной теории Галуа.
Лит.: [1] С е р р Ж.-П., Когомологии Галуа, пер. (; франц.,
М., 19В8; [2] К о х X., Теория Галуа р-расширений, пер. с нем.,
М., 1973; [3] Алгебраическая теория чисел, пер. с англ., М.,
1969. В. Л. Попов.
ПРОМЕЖУТОК, открытый промежуток,
интервал,— множество точек, заключенных меж-
между двумя данными, т. е. удовлетворяющих условию
вида a<ix<_b. П. не включает концов и обозначается
(а, Ь), в отличие от отрезка \а, Ь] (замкнутого П.),
включающего концы, т. е. состоящего из точек а^.х-^:Ь.
БСЭ-З.
ПРОМЕЖУТОЧНАЯ ЛОГИКА высказыва-
высказываний — произвольное непротиворечивое множество
пропозициональных формул, замкнутое относительно
правила вывода модус поненс и правила подстановки
и содержащее все аксиомы интуиционистского исчис-
исчисления высказываний I.
Наиболее естественным способом задания П. л.
являются промежуточные пропозицио-
пропозициональные исчисления. Каждое такое исчис-
исчисление задается указанием нек-рого числа классически
общезначимых пропозициональных формул, добавля-
добавляемых к аксиомам исчисления /.
Совокупность всех П. л. образует дистрибутивную
решетку относительно включения с:, причем конечно
аксиоматизируемые П. л. образуют в ней подреглетку,
в к-рую изоморфно вложима любая конечная дистри-
дистрибутивная решетка.
П. л. L наз. разрешимой, если существует
алгоритм, к-рый по каждой пропозициональной фор-
формуле А распознает, принадлежит А П. л. L или нет.
Так, разрешимыми являются интуиционистская и
классическая П. л. Вообще, всякая финитно аппрок-
аппроксимируемая (см. ниже) конечно аксиоматизируемая
П. л. разрешима. Построен пример конечно аксиома-
аксиоматизируемой неразрешимой П. л. (см. [7]).
П. л. L наз. дизъюнктивной, если из (А V B)?L
следует, что А ? L или B?L. Этим свойством обладает,
напр., интуиционистская П. л., но не обладает клас-
классическая П. л. Существует бесконечно много дизъюнк-
дизъюнктивных П. л.
Интерполяционное свойство П. л.
(теорема К р е й г а) состоит в том, что если
формула А3M принадлежит П. л. L, то существует
формула С, содержащая только общие для А и В пере-
переменные и такая, что (ЛЗ)СN^ и (CZ)B)? L; если А и В
не имеют общих переменных, то ~]Л ?L или B?L. По-
Показано, что интерполяционным свойством, кроме ин-
интуиционистской и классической П. л., обладают еще
ровно пять П. л. (см. [6]).
Формула А наз. выразимой через формулы Вг,
В2, ... в П. л. L, если А можно получить из Вг,
В 2, . . . с помощью конечного числа замен на эквива-
эквивалентные (в L) формулы и конечного числа подстановок
ранее полученных формул вместо переменных. Список
формул 2= {jSj, В 2, ...} функционально
полон в П. л. L, если всякая формула выразима в
L через 2. Алгоритмическая проблема распознавания
функциональной полноты любого стека формул раз-
разрешима для интуиционистской и нек-рых других
П. л. (см. [3]). Другая алгоритмич. проблема — про-
проблема распознавания выразимости А через 2 по дан-
данным формуле А и списку 2 — положительно решена
лишь для нек-рых П. л.; она остается пока A983)
открытой для интуиционистской П. л.
Другой способ задания П. л. дает т. н. семантич.
подход. Под семантикой здесь понимается нек-рое
множество S структур (моделей) ЯЛ, на к-рых опреде-
определено отношение истинности ЭД}[=е/1 данной пропози-
пропозициональной формулы А при данной оценке 6 (о ц е н-
к а — отображение, сопоставляющее переменным фор-
формулы А нек-рые значения в ЭД1). Формула А, истинная
в ЯЛ при любой оценке, наз. общезначимой
на Щ] (обозначение *Bl\=A). Если S^S, то П. л. iE,)
есть совокупность всех формул, общезначимых на
любой структуре 2Jl?Sj. Для данной семантики S
естественно определяется отношение семантиче-
семантического следования Г f^ $Л, где Г состоит из
формул; это отношение означает, что для любой струк-
структуры m?S из Ш\=В для всех В?Г следует ?Ш(=Л.
Семантики St и S2 наз. эквивалентными,
если отношения \^s, и |=g, совпадают. Основное
требование, предъявляем-ое к семантике,— это ее
корректность: из Г|—ГА должно следовать
Г(=5^- Все упоминаемые ниже семантики корректны.
Другое важное свойство семантики — полнота. П. л.
L наз. полной относительно семан-
семантики S, если А ? L<&L )p $А .
Алгебраическая семантика S А со-
состоит из псевдобулевых алгебр, т. е.
алгебр вида
Ш1=(Л/, &, v, =5, П; 1, 0),
где ~] — унарная, а &, V, =3 — бинарные операции
на М, соответствующие связкам ], &, v, ID, причем
(М, &, V) — дистрибутивная решетка, а 1 и 0 — наи-
наибольший и наименьший элементы в М. Операции f5
и ~] удовлетворяют свойствам: для любых а, Ъ,
Отношение ЗЛ^е^ здесь означает, что А принимает
в Щ} значение 1 при данной оценке 6.
Каждая П. л. полна относительно конечно порож-
порожденных псевдобулевых алгебр. Если П. л. L полна
относительно множества конечных псевдобулевых ал-
алгебр (одной конечной псевдобулевой алгебры), то она
наз. финитно аппроксимируемой (со-
(соответственно табличной). Простейшей табличной
П. л. является классическая П. л. Дизъюнктивные
П. л., в частности интуиционистская, табличными не
являются. Имеется пример не финитно аппроксими-
аппроксимируемой конечно аксиоматизируемой П. л. (см. [3]).
Семантика Кринке Sк состоит из Крапке
моделей, имеющих в данном случае вид EШ, G), где
*Ш= (Л/, «О — частично упорядоченное множество,
наз. также остовом, или ш к а л о й, а значениями
оценки 0 являются подмножества М, причем для
любых а, E?Л/ из <%?б(р,-) и а<^E следует Р?6 (/),¦).
Между семантиками S^ и Sg имеется тесная связь
(см. [5]), однако они не эквивалентны; в частности,
существуют П. л., не полные относительно 5^-
(см. [3]).
Конструктивные семантики — это се-
семантика реализуемости Sg (см. [1]) и семантика фи-
финитных задач Sр. Эти семантики не полны даже для
интуиционистской П. л., более того, существуют фор-
формулы, общезначимые в S^ и не общезначимые в S р,
и наоборот.
Предикатные П. л. определяются по анало-
аналогии с II. л. высказываний, т. е. это — расширения
интуиционистской логики предикатов LI, содержащие-
содержащиеся в классич. логике предикатов. В отличие от пропо-
пропозициональных П. л. все предикатные П. л. неразреши-
неразрешимы. Семантика предикатных П. л. аналогична соот-
соответствующей семантике П. л. высказываний (см. [2]).
Лит.: [1] Новиков П. С, Конструктивная математи-
математическая логика с точки зрения классической, М., 1977; [2] Д р а-
галин А. Г., Математический интуиционизм. Введение в тео-
теорию доказательств, М., 1979; [3] Кузнецов А. В., в кн.:
Логический вывод, М., 1979, с. 5—33; [4] его ж е, «Математи-
«Математические исследования», 1975, т. 10, в. 2, с. 150—58; [5] Эсакиа
Л. Л., в кн.: Логический вывод, М., 1979, с. 147 — 72; [6] М а к-
симока Л. Л.,«Алгебра и логика», 1977 т. 1В с. 643—81'
[7] Шехтман В. В., «Докл. АН СССР», 1978, т. 240, № 3,
с. 549—52; [8] Hosoi Т., О no H., «J. Tsuda College»,
1973, v. 5, р, 67 — 82. С. К. Соболев.
ПРОМЕЖУТОЧНЫЙ ЯКОБИАН — набор комплекс-
комплексных торов, определяемых нечетномерными когомоло-
гиямн комплексного кэлерова многообразия, геомет-
геометрия к-рых тесно связана с геометрией самого много-
многообразия.
Пусть Нп(Х, R) (соответственно Нп(Х, %)) — про-
пространство и-мерных когомологий с действительными
(соответственно с целыми) коэффициентами комплексно-
аналитич. кэлерова многообразия X. На веществ, торе
при нечетном п можно двумя различными способами
ввести комплексную структуру, используя представ-
представление «-мерных когомологий с комплексными коэф-
коэффициентами в виде прямой суммы Нп(Х, С) =
~(r!P + q = n^F'Ч пространств Нр''' гармонич. форм
типа (р, д). Пусть Ppq :'Нп(Х, С) ->- Нр' q — проек-
проекция, а
— операторы, переводящие когомологий с действи-
действительными коэффициентами в себя. Полагая
(а-\- ib) со = аш-|-&С1р (со) и (а-\~ 1Ъ) ш = асо-[-йС0 (со),
для любого со из Нп(Х, R), a, b?R, получают ком-
комплексные структуры на Т"(Х), первая из к-рых Т% (X)
наз. промежуточным якобианом В е й-
л я, а вторая Tq (X) — промежуточным то-
тором Гриффитса. Если X — многообразие Ход-
Ходжа, то ходжева метрика на X канонически определяет
на П. я. Т\/ (X) структуру поляризованного абелева
многообразия, что не всегда имеет место для Т'а (X).
С другой стороны, при голоморфной вариации много-
многообразия X промежуточные торы Tq (X) варьируются
голоморфно [2], а П. я. Вейля этим свойством могут
не обладать. Cup-произведеиие, задающее спаривание
пространств Нп(Х, R) и Hd~n(X, R), где d=dimRZ,
определяет комплексное спаривание торов Та (X) и
Та~п(Х) и двойственность между абелевыми много-
многообразиями Т'у/{Х)м Тууп(Х). В случае, когда di
= 2fc+l, П. я. Туу+г(Х) является самодвойственным
абелевым многообразием с главной поляризацией, а
Т'ск+1(Х) — главным тором.
П. я. служит важным инвариантом кэлеровых мно-
многообразий. Если для двух многообразий X и Y из
совпадения Т^(Х)=- T'w(Y) (соответственно Та (X)—
— T'g(Y)) следует, что X^Y, то говорят, что для X
выполнена теорема Т о р е л л и. Теорема То-
реллп выполняется, напр., для алгебраич. кривых.
С помощью П. я. была доказана нерациональность
общей кубики в проективном пространстве РА (см.
[1]) и нек-рых других многообразий Фано.
Лит.: [1] Clemens С, Griffiths V h., «Ann. Math.».
1972, v. 95, № 2, p, 281 —35e; [2] С г i f f i t h s P li., «Araer. J.
math.» 1988, v. 90, p. 568—626, 805—B5; [3] W e i 1 A., «Amer. J.
math.», 1952, v. 74 p. 865—04. Bun. С. Куликов.
ПРОНОРМАЛЬНАЯ ПОДГРУППА — подгруппа Н
группы G, удовлетворяющая следующему условию:
если К — подгруппа из G, сопряженная с Н, то К
сопряжена с // в подгруппе, порожденной Н и К.
Силова подгруппы в конечных группах, Холла под-
подгруппы и Картера подгруппы в конечных разрешимых
группах пронормальны. Понятие П. п. тесно связано
с понятием абнирмалъной подгруппы. Любая абнор-
мальная подгруппа пронормальна, а нормализатор
П. и. абнормален.
Лит.: [1] Ш е м е т к о в Л. А., Формации конечных групп
М., 1978. В. Д. Мазуров
ПРОПОЗИЦИОНАЛЬНАЯ ПЕРЕМЕННАЯ — сим
вол формального языка, служащий для обозначения
произвольного высказывания. с К Соболев
ПРОПОЗИЦИОНАЛЬНАЯ СВЯЗКА — символ
формального я<1ыка, служащий для обозначения логи-
логической операции, с помощью к-рой из данных выска-
высказываний можно получать новые высказывания. Важ-
Важнейшими П. с. являются конъюнкция & (иначе Л).
дизъюнкция v, импликация :э (иначе —>- или =»,
отрицание ~| (иначе ~), эквивалентность = (иначе <-»
или ^). Эти П. с. соответствуют в русском языке
выражениям «и», «или», «влечет», «не верно, что» и
«равносильно». Иногда рассматриваются и другие
П. с, напр. т. н. Шеффера штрих.
Символ = обычно вводится не как независимая П. с,
а как сокращение:
A^B?z;(Az>B)&(B=)A). A)
Если же в языке имеется пропозициональная кон-
константа _|_, обозначающая «ложь», то отрицание можно
рассматривать как сокращение: ~]Аt^(AZ)JJ.
П. с. &, V, ID и не являются независимыми в
классич. логике, поскольку в ней верны эквивалент-
эквивалентности:
B)
В), C)
D)
т. е. каждая из П. с. &, V, :э выражается через "|
и одну из остальных. Поэтому при формулировках
классического пропозиционального исчисления выска-
высказываний в качестве исходной можно брать две П. с:
~) и одну из П. с. &, v, Z3, а остальные рассматривать
как сокращения, согласно A) — D). В интуицио-
интуиционистской логике П. с. &, v, Z3 и ~] являются неза-
независимыми. С. К. Соболев.
ПРОПОЗИЦИОНАЛЬНАЯ ФОРМА, в ы с к а з ы-
вательная форм а,— языковое выражение, со-
содержащее переменные, вместо к-рых можно подстав
лять высказывания, получая при этом новые выска-
высказывания. В формализованных языках П. ф. наз. фор-
формулы, содержащие свободные вхождения пропозицио-
пропозициональных переменных, принимающих значения в множе-
множестве истинностных значений.
П. ф. наз. также выражения, построенные по типу
пропозициональной формулы, в к-рых вместо пропози-
пропозициональных переменных используются символы мета-
метаязыка, обозначающие произвольные формулы выска-
высказываний исчисления.
Лит.: [1] М е и д е л ь с, о н Э., Введение в математическую
логику, пер. с англ., М., 1971. В.Н.Гришин.
ПРОПОЗИЦИОНАЛЬНАЯ ФОРМУЛА — выраже
ние, построенное из пропозициональных переменных
с помощью пропозициональных связок &, V, ^>, ~~), =
(и, возможно, нек-рых других) по следующим прави-
правилам: 1) каждая пропозициональная переменная есть
П. ф.; 2) если А, В суть П. ф., то (А&В), (А у В),
(Az^B) и ("И) суть также П. ф.
Если а — нек-рый набор пропозициональных связок
(сигнатура), то под П. ф. сигнатуры а понима-
понимается такая П. ф., в построении к-рой в 2) использо-
использовались ЛИШЬ СВЯЗКИ ИЗ а. С. К, Соболев.
ПРОПОЗИЦИОНАЛЬНАЯ ФУНКЦИЯ — функция,
аргументами и значениями к-рой являются истинност-
истинностные значения. Этот термин употребляют, когда речь
идет об интерпретации формализованного логич. языка.
Если Q — множество истинностных значений формул
данного языка, то П. ф.— это любое отображение вида
Q™ -*- Q (п^О). Этими функциями интерпретируются
пропозициональные связки, позволяющие образовывать
из предложений или формул новые предложения пли
формулы. При классической двузначной интерпретации
множества истинностных значений, т. е. когда Q= {0,1},
такие функции наз. также функциями алгеб-
алгебры ЛОГИК И. В. Н. Гришин.
ПРОПОЗИЦИОНАЛЬНОЕ ИСЧИСЛЕНИЕ, ц с ч п с
ление высказываний,— логическое исчисле-
исчисление, в к-ром выводимыми объектами являются пропо-
пропозициональные формулы. Каждое П. и. задается набором
аксиом (произвольных пропозициональных формул)
и вывода правил. Формула, выводимая в данном П. п.,
наз. теоремой этого П. и. В качестве правил
вывода обычно берут модус поненс и подстановку (про-
(произвольных пропозициональных формул вместо пере-
переменных). Иногда П. и. задают не аксиомами, а аксиом
схемами; тогда правило подстановки оказывается
излишним.
Классическое П. и. задается следующими
аксиомами:
1) pz^(q=>p),
2) (р ГЗ (q ГЭ г)) ZD ((p =,q)=>(p^) r)),
3) (р &q)=>p,
4) (p&q)=)q,
5) pr>(q=)(p&q)),
6) p
7) q
9) (p =} q) => ((p =>~\q) =>~\p),
10) llp=>p.
В этом П. и. пропозициональные связки &, v, Z3, ~1
не являются независимыми. Его можно задать с по-
помощью только аксиом 1), 2), 9) и 10), основываясь на
связках Z3, ~] в качестве исходных. Тогда связки &
и v рассматриваются как сокращения:
A&Bt^~\(Az3~]B), A\/В^ ~\А^В,
а аксиомы 3) — 8) становятся теоремами. Классиче-
Классическое П. и. наз. также полным П. и., поскольку
добавление к нему любой невыводимой в нем формулы
в качестве аксиомы приводит к н р о т и в о р с ч и-
в о м у П. и., т. е. к такому, в к-ром выводимы все
пропозициональные формулы. Часто классическое П. и.
паз. просто П. и.
Интуиционистское (конструктив-
(конструктивное) П. и. получается из классического П. и. заменой
аксиомы 10) более слабой аксиомой
И) -]p=)(p=>q).
П. и., получаемое из конструктивного П. и. добавле-
добавлением конечного (или рекурсивного) числа аксиом, наз.
промежуточным, суперинтуициони-
с т с к и м (или суперконструктивным).
См. также Промежуточная логика.
Другими примерами П. и. являются импликативное
пропозициональное исчисление, минимальное пропози-
пропозициональное исчисление, позитивное пропозициональное
исчисление.
Интерпретация П. и. осуществляется с
помощью алгебр (матриц) вида
Ш = <М, D; &*, v*, Z3*, Т>,
где М — множество истинностных значений, D —
множество выделенных истинностных значений,
DcM, а &*, V*, Z3*, 1*
— операции на М, соответствующие связкам &, V, 3 и
~"|. Множество D должно удовлетворять следующему
условию: для любых a, b?D, если agflu (azD*b)?D, то
b?D (согласованность с правилом модус поненс). Фор-
мула наз. общезначимой на матрице Щ, если
она принимает выделенное значение при любой интер-
интерпретации ее переменных элементами М. Простейшей
матрицей является матрица Щ}2> состоящая из двух
элементов 1, 0 («истина», «ложь») ц одного выделенного
значения 1, а операции &*, v*, и*, "*]* определяются
обычным образом (см. Алгебра логики). Пропозицио-
Пропозициональная формула, общезначимая на 5Л2, наз. тавто-
тавтологией. Формула является тавтологией тогда и
только тогда, когда она является теоремой классиче-
классического П. и.
Лит.: [1] Ч ё р ч А., Внедснис в математическую логику,
пер. с англ., М., 1960. С. К. Соболев.
ПРОСТАЯ АЛГЕБРА — неодноэлементная алгебра
без двусторонних идеалов, отличных от 0 и всей алгебры.
П. а. без единицы может и не быть простым кольцом,
т. к. в этом случае не всякий идеал кольца является
идеалом алгебры. Для нек-рых классов алгебр из-
известна классификация конечномерных П. а. (см. Аль-
Альтернативные кольца и алгебры, Йорданова алгебра., Ли
алгебра). Любая ассоциативная алгебра над полем,
обладающая единицей, вложима в II. а. с той же еди-
единицей.
Лит. см. при ст. Простое кольцо. Л. А. Скорняков.
ПРОСТАЯ ГИПОТЕЗА в математической
статистике — утверждение, согласно к-рому на-
наблюдаемая случайная величина подчиняется конкретно
заданному распределению вероятностей. Распределе-
Распределение вероятностей, определяемое П. г., наз. гипоте-
гипотетическим распределением. Наир., если
наблюдается случайная величина X, то утверждение
«X подчиняется закону Пуассона с параметром 1»
является П. г. См. также Сложная гипотеза.
М. С. Никулин.
ПРОСТАЯ ГРУППА — группа, не имеющая нор-
нормальных подгрупп, отличных от всей группы и еди-
единичной подгруппы. Описание всох простых конечных
групп является центральной проблемой в теории
конечных групп. В теории бесконечных групп значе-
значение П. г. значительно меньше ввиду их необозримости.
Простой является группа всех четных подстановок,
каждая из к-рых перемещает конечное подмножество
элементов множества М, если мощность М не меньше 5.
;)та группа бесконечна, если М бесконечно. Сущест-
Существуют конечно порожденные и даже конечно опреде-
определенные бесконечные II. г. Всякая группа вложима в
П. г. В теории групп Ли и алгебраич. групп опреде-
определении П. г. несколько отличается от приведенного
выше (см. Ли полупростая группа). а. Л. Шмелькин.
ПРОСТАЯ ДУГА — гомеоморфный образ отрезка.
Внутренняя характеристика: П. д.— это линия, имею-
имеющая в двух точках индекс ветвления 1 (конце п ы е
точки), а во всех остальных точках — индекс ветв-
ветвления 2 (внутренние точки).
М. И. Войцеховский.
ПРОСТАЯ КОНЕЧНАЯ ГРУППА — конечная груп-
группа, в к-poii нет нормальных подгрупп, отличных от
всей группы и от единичной подгруппы. П. к. г.—
наименьшие «строительные блоки», из к-рых с помощью
расширении может быть «собрана» любая конечная
группа. Каждый фактор композиционного ряда конеч-
конечной группы является П. к. г., а минимальная нормаль-
нормальная подгруппа — прямое произведение П. к. г. Про-
Простейшими примерами П. к. г. служат циклич. группы
простых порядков. Только таким П. к. г. изоморфны
факторы композиционных рядов разрешимых групп.
Все остальные П. к. г. неразрешимы и их порядки
четны [см. Бёрнсайда проблема — 1)]. Бесконечные
серии примеров неразрешимых П. к. г. дают знако-
знакопеременные группы ?(„, проективные специальные
линейные группы PSL{n, q) над конечным полем по-
порядка q, проективные симплектич. группы PSPBn, q),
проективные ортогональные группы PQ (n, q) и про-
701
ПРОСТАЯ
702
ективные унитарные группы PSU(n, q2). Все перечис-
перечисленные II. к. г. были известны еще в прошлом веке.
Кроме них, в кон. 19 в. были открыты еще 5 групп (см.
Матъё группа). В нач. 20 в. построены конечные
аналоги простых групп Лп тина G2 (см. Диксона группа).
Открытия новых бесконечных серий II. к. г., сделан-
ные в 50-х гг., позволили получить большинство
типов известных простых групп из групп автоморфиз-
автоморфизмов простых алгебр Ли (см. Шевалле группа). Извест-
Известные бесконечные серии П. к. г. представлены в таблице.
идеалов и не являющаяся двухэлементной полугруппой
с нулевым умножением, бипростая — состоящая
из одного б/)-класса (см. Грина отношения эквивалент-
эквивалентности), 0-6 ипростая — состоящая из двух б?-
классов, один из к-рых нулевой, простая отно-
относительно конгруэнции — не имеющая кон-
конгруэнции, кроме универсального отношения и отноше-
отношения равенства.
Всякая простая слева или справа полугруппа бп-
проста; всякая бппростая полугруппа идеально про-
Обозначение,
связанное с
типом соот-
соответствующей
алгебры Ли
А1 №
В, (д)
С1 A)
nt(q)
Е, (д)
¦Е» (9)
F4 (q)
Gz(q)
>AL (q')
¦Dl (g*)
'-E, (g2)
3Л4 ((!•')
lB2(q)
2G2 (9)
Другое
обозначение
\"
PSL(l+\, q)
PQ- BJ+1, <()
PSp BJ, 9)
PQ+ B1, q)
PSU (l + i, q°)
PQ- B1, 9)
Sz(q)
H (9)
Условия
существования
II. к. г.
р — простое число
/>2; 1=1, д>4
;>з; г=2, а>з;
г = 1, д>4
г>3; / = 2, 9>3;
«5 3; ( = 2, д>3
1 = 1, 9>4
д = 22' + »
д = За' + 1
д = 2"^ — »
Порядок группы
р
g? (i + l)/2 (g2_l) (9a_l)...(g' + ]_ l)/t(
g'2(92-l) <q«-l)---(qj/-l)/d
9'2(92-1)(9'-1)--(9!г-1)/<^
9'B-1'(g2_1)(,4_i)...(,^-2_])(9;_1)/d
936 (92-1) (9s-1) (9е-1) (gs-l) (g"- О (912- D/rf
9" (g2- 1) (9e-l) (g*- 1) (gI0-l) ((/i;- 1) (q14- 1) E"-l)/d
giao (9!~1) (g»-l) (g12-l) (g14-l) (918-1) (9гэ-1)-
(g24-l)(q=»-l)
g2* (9г- 1) (ge- 1) (9*- 1) (912- 1)
96 (g2-l) (9ъ-1)
g/a+l)/2№_i)(g,+ 1)(9«_1)...(^ + . + (_i)/)/d
ql (I-l)/2 (g«_l) (g*-i). ..(g**-«-l) (g' + l)/d
q3> (g2- 1) (gs+ 1) (g6- 1) (g8- 1) (g» + 1) (912- \)ld
q\i (g2_ i) (q«- 1) (q«+g4+ 1)
4- (9-l)(92+l)
(/-'(g-i) (g3+D
912 (g— i) (gJ+1) (94—i) (gG+ i)/d
d
(l+i, g-l)
B, g-l)
B, g-l)
D, g'-l)
C. 9-D
B, 9-1)
(l+i, 9+1)
D, g' + i)
C, 9+1)
2 при 9 = 2
1 при q>2
Здесь q — ненулевая степень простого числа, I — на-
натуральное число, (s, t) — наибольший общий делитель
чисел s и I. Кроме перечисленных в таблице, известны
еще 26 П. к. г., не входящих ни в одну бесконечную
серию П. к. г. (т. н. спорадические простые группы).
Главной задачей теории П. к. г. является проблема
классификации П. к. г., содержанием к-рой служит
доказательство того, что каждая П. к. г. изоморфна
одной из известных простых групп. Другая задача
состоит в изучении свойств известных простых групп:
изучении их матричных представлений (см. Конечной
группы представление), описании примитивных под-
подстановочных представлений (см. Подстановок группа)
или, более общо, представлений в виде групп автомор-
автоморфизмов различных математич. объектов (графов, ко-
конечных геометрий), описании подгрупп, в частности
максимальных подгрупп, и т. д.
Лит.: [1] Картер Р., «Математика», 1986, т. 10, № 5,
с. 3 47; L2] А ш б а х е р М., «Успехи матем. наук», 1981, т. 36,
.4? 2 с. 141-72; [3] Н и р р е г t В., Endliehe Gruppcn, iBd]
1 В. 1967; Ы Blackburn N., H upper I B., Finite
groups II, III, В., 1981. В. Д. Мазуров.
ПРОСТАЯ ПОЛУГРУППА — полугруппа, не содер-
содержащая собственных идеалов или конгруэнции того
пли иного фиксированного типа. В зависимости от
рассматриваемого типа возникают различные типы
II. п.: идеально п р о с т а я — не содержащая
собственных двусторонних идеалов (термин «II. п.»
часто относят только к таким полугруппам), про-
простая слева (справа) — не содержащая соб-
гтвенных левых (нравы1.) идеалов, 0-и р о с т а я
(слова, справа) — нолу1 руина с нулем, не содержащая
собственных ненулевых двусторонних (левых, правых)
ста, но существуют идеально И. п., не являющиеся
бипростыми (и даже такие, что все их ^-классы одно-
одноэлементны). Важнейшим типом идеально 11. и. @-про-
стых полугрупп) является вполне простая полугруппа
(вполне 0-цростая полугруппа). Важнейшие примеры
бипростых, но не вполне П. п.: бициклическая полу-
полугруппа, четырехспиралъная полугруп-
п a Spi (см. [11]) — это полугруппа, заданная порож-
порождающими а, Ь, с, d и определяющими соотношениями
dc—c, cd—d, da=d; полугруппа Spt изоморфна рисов-
ской полугруппе матричного типа над бициклич. по-
полугруппой с порождающими и, г, где uu—i, с сэндвич-
матрицей
1 У II
Четырехспиральная полугруппа является в нек-ром
смысле минимальной среди бипростых и не вполне
П. п., порожденных конечным числом пдемпотентов,
и нередко возникает как подполугруппа таких полу-
полугрупп. -
Простые справа полугруппы (п. с. п.) наз. также
полугруппами с правым делением
или полугруппами с правой обрати-
обратимостью. Основанием для этих терминов является
следующее свойство таких полугрупп, эквивалентное
определению: для любых элементов а и Ъ существует
элемент х такой, что ах—-Ь. П. с. п., содержащие идем-
нотенты,— это в точности правые группы. Важный
пример п. с. п. без пдемпотентов доставляет полугруппа
Т(М, б, р, q) всех таких преобразований ср множества
701
ПРОСТАЯ
702
ективные унитарные группы PSU(n, q2). Все перечис-
перечисленные II. к. г. были известны еще в прошлом веке.
Кроме них, в кон. 19 в. были открыты еще 5 групп (см.
Матъё группа). В нач. 20 в. построены конечные
аналоги простых групп Лп тина G2 (см. Диксона группа).
Открытия новых бесконечных серий II. к. г., сделан-
ные в 50-х гг., позволили получить большинство
типов известных простых групп из групп автоморфиз-
автоморфизмов простых алгебр Ли (см. Шевалле группа). Извест-
Известные бесконечные серии П. к. г. представлены в таблице.
идеалов и не являющаяся двухэлементной полугруппой
с нулевым умножением, бипростая — состоящая
из одного б/)-класса (см. Грина отношения эквивалент-
эквивалентности), 0-6 ипростая — состоящая из двух б?-
классов, один из к-рых нулевой, простая отно-
относительно конгруэнции — не имеющая кон-
конгруэнции, кроме универсального отношения и отноше-
отношения равенства.
Всякая простая слева или справа полугруппа бп-
проста; всякая бппростая полугруппа идеально про-
Обозначение,
связанное с
типом соот-
соответствующей
алгебры Ли
А1 №
В, (д)
С1 A)
nt(q)
Е, (д)
¦Е» (9)
F4 (q)
Gz (9)
^ («*)
2D, (g«)
s?. (92)
3Л4 (q>)
lB2(q)
*Сг (9)
2j?4 (qy
Другое
обозначение
\"
PSL(l+\, q)
PQ- B.1+i, q)
PSp B1, 9)
PQ+ B1, q)
PSU (l + i, g")
PQ- B1, 9)
Sz(q)
4 (9)
Условия
существования
II. к. г.
р — простое число
/>2; 1=1, д>4
;>з; г=2, а>з;
г = 1, д>4
г>3; г = 2, д>3;
;= 1, д>4
«5 3; ( = 2, д>3
1 = 1, 9>4
д = 22' + »
^ = За' + 1
q_2aZ — »
дг(г + 1)/2(8
д'2(92-1) (д<
g'2(92-i)(9'
938(92-D(9s
9" (92-D (9е
д'го(д!-1)(д
(дг4-1)(а=»
92«(9г-1)(9в
96 (9г-1) (дъ
ql A+1I2 (q
ql (I-l)/2 (?2
дз« ((/2-l) (Ч*
912 (92-D (ge
q- (9-l)(92 +
(/¦' (9- И (g3 +
912 (g-l) (gJ
-l)
-l)
-i)
1) (9
-1)
-1)
-1)
-1)
-1)
-1)
+ 1)
-1)
1)
1)
t-1) (
Порядок группы
p
(,»_!)...(i' + l-D/d
...(<j2/_l)/d
• •¦(g''-D/d
'-l)-(qU-2-l)(q'.-l)/d
(g«- 1) (g8- 1) ((/•- I) (q12- l)/rf
(gb~l) (g10 — 1) (c/12— 1) (914- i) (g18 — l)/d
i (g12— 1) (g14—1) (g]8-l) (930 — l)-
(9'-l) (912-1)
W-l)...(q2l-'-i)(qi + l)/d
(g6- 1) (g8- 1) (g» + 1) (912- l)/d
(9B + 94+ 1)
(j4_]) (G=+ i)/d
(г
B
B
D
C
B
d
4 1, g-l)
, g-D
. 9-1)
, g'-D
. 9-D
¦ 9-1)
(l+i, 9+1)
D
C
2
1
. 9г + 1)
, 9+1)
при 9 = 2
при q>2
Здесь q — ненулевая степень простого числа, I — на-
натуральное число, (s, t) — наибольший общий делитель
чисел s и I. Кроме перечисленных в таблице, известны
еще 26 П. к. г., не входящих ни в одну бесконечную
серию П. к. г. (т. н. спорадические простые группы).
Главной задачей теории П. к. г. является проблема
классификации II. к. г., содержанием к-рой служит
доказательство того, что каждая П. к. г. изоморфна
одной из известных простых групп. Другая задача
состоит в изучении свойств известных простых групп:
изучении их матричных представлений (см. Конечной
группы представление), описании примитивных под-
подстановочных представлений (см. Подстановок группа)
или, более общо, представлений в виде групп автомор-
автоморфизмов различных математич. объектов (графов, ко-
конечных геометрий), описании подгрупп, в частности
максимальных подгрупп, и т. д.
Лит.: [1] Картер Р., «Математика», 1986, т. 10, № 5,
с. 3 47; L2] А ш б а х е р М., «Успехи матем. наук», 1981, т. 36,
•Ns 2 с. 141-72; [3] Н и р р е г t В., Endliehe Gruppcn, iBd]
1 В. 1967; Ы Blackburn N., H upper I B., Finite
groups II, III, В., 1981. В. Д. Мазуров.
ПРОСТАЯ ПОЛУГРУППА — полугруппа, не содер-
содержащая собственных идеалов или конгруэнции того
пли иного фиксированного типа. В зависимости от
рассматриваемого типа возникают различные типы
II. п.: идеально п р о с т а я — не содержащая
собственных двусторонних идеалов (термин «II. п.»
часто относят только к таким полугруппам), про-
простая слева (справа) — не содержащая соб-
гтвенных левых (нравы1.) идеалов, 0-и р о с т а я
(слова, справа) — нолу1 руина с нулем, не содержащая
собственных ненулевых двусторонних (левых, правых)
ста, но существуют идеально И. п., не являющиеся
бипростыми (и даже такие, что все их ^-классы одно-
одноэлементны). Важнейшим типом идеально 11. и. @-про-
стых полугрупп) является вполне простая полугруппа
(вполне 0-цростая полугруппа). Важнейшие примеры
бипростых, но не вполне П. п.: бициклическая полу-
полугруппа, четырехспиралъная полугруп-
п a Spi (см. [11]) — это полугруппа, заданная порож-
порождающими а, Ь, с, d и определяющими соотношениями
dc—c, cd—d, da=d; полугруппа Spt изоморфна рисов-
ской полугруппе матричного типа над бициклич. по-
полугруппой с порождающими и, г, где uu—i, с сэндвич-
матрицей
1 У II
Четырехспиральная полугруппа является в нек-ром
смысле минимальной среди бипростых и не вполне
П. п., порожденных конечным числом пдемпотентов,
и нередко возникает как подполугруппа таких полу-
полугрупп. -
Простые справа полугруппы (п. с. п.) наз. также
полугруппами с правым делением
или полугруппами с правой обрати-
обратимостью. Основанием для этих терминов является
следующее свойство таких полугрупп, эквивалентное
определению: для любых элементов а и Ъ существует
элемент х такой, что ах—-Ь. П. с. п., содержащие идем-
нотенты,— это в точности правые группы. Важный
пример п. с. п. без пдемпотентов доставляет полугруппа
Т(М, б, р, q) всех таких преобразований ср множества
г р у
171).
является частным случаем процесса восстановления
(см. Восстановления теория). С П. п. связан пуассо-
новскии процесс ?(?), равный числу событий потока в
отрезке времени @, /). П. п. и соответствующий
ему пуассоновский процесс удовлетворяют следующим
условиям.
Стационарность. Для любых 0<?0, 0<?х<
<?2<. . . <3ь распределение случайных величин
I (trrh)-t(ti-i+h), 2 = 2, •-., к,
не зависит от 1„.
Ординарность. Вероятность появления в
интервале (t, t~\~ \t) двух или более событий потока
равна о (tit) при At —у 0.
М, что 1) ядро ф равно отношению эквивалентности б
на М, 2) мощность фактормножества М1Ь равна р,
3) множество Л/<р пересекается с каждым б-классом не
более чем по одному элементу, 4) множество б-классов,
не пересекающихся с М<р, имеет бесконечную мощ-
мощность q, причем д*^р. Полугруппа Т(М, б, р, q) наз.
полугруппой Тесье типа (р, q), а в случае,
когда б — отношение равенства, она наз. пол j-
i у и и о й Бэра — Леви типа (р, q) (см. [6],
Полугруппа Тесье — пример п. с. п. без идем-
нотентов, не обязательно удовлетворяющей правосто-
правостороннему закону сокращения. Всякая п. с. п. без идем-
потентов вкладывается в подходящую полугруппу
Тесье, а всякая п. с. п. без идемиотентов и с право-
правосторонним законом сокращения вкладывается в под-
подходящую полугруппу Бэра — Леви (причем в обоих
случаях можно выбрать p=q).
Различные типы П. п. часто возникают в качестве
«блоков», из к-рых строятся рассматриваемые полу-
полугруппы. По поводу классич. примеров П. п. см. Вполне
простая полугруппа, Врандта полугруппа, Правая
группа; о бипростых инверсных полугруппах (в том
числе структурные теоремы при нек-рых ограничениях
на полурешетку идемпотентов) см. [1], [8], [9]. Суще-
Существуют идеально простые инверсные полугруппы с
произвольным числом б/)-классов. При изучении вло-
вложений полугрупп в П. п. обычно либо указываются
условия для возможности соответствующего вложения,
либо устанавливается, что всякая полугруппа вклады-
вкладывается в подходящую П. п. рассматриваемого типа;
напр., любая полугруппа вкладывается в бипростую
полугруппу с единицей (см. [1]), в бипростую полугруп-
полугруппу, порожденную идемпотентами (см. [10]), в простую
относительно конгруэнции полугруппу (к-рая может
обладать теми или иными наперед заданными свой-
свойствами: наличие или отсутствие нуля, полнота, пу-
пустота подполугруппы Фраттини и т. д., см. [3] — [5]).
Лит.: [1] Клиффорд А., Престон Г., Алгебраичес-
Алгебраическая теория полугрупп, пер. с англ., т. 1—2, М., 1972; [2] Л н-
н и н Е. С, Полугруппы, М., 1960; [3] Б о к у т ь Л. А., «Сиб.
мятем. ж.», 1963, т. 4, № 3, с. 500—18; [4]Ш у то в Э. Г., «Ма-
«Матом, сб.», 1963, т. 62, № 4, с. 496—511; [5] К л и м о в В. Н.,
«Сиб. матем. ж.», 1 973, т. 14, № 5, с. 1025—36; [6] В а е г R., L е-
v i F., «Sitzungsber. Heidelberg. Akad. Wiss. Math.-naturwiss.
Kl.», 1932, Abh. 2, S. 3—12; [7] T e i s s i e r M., «Compt. rend.
Acad. sci.», 1953, v. 236, JMs 11, p. 1120—22; [8] M u n n W. D.,
в кн.: Semigroups, N. Y. L., 1969, p. 107--23; [9] H о w i e J.,
An introduction to semigroup theory, L.— [a. o.], 1976; [10]
Pastijn F., «Semigroup Forum», 1977, v. 14, N» 3, p. 247 —
263; [11] В у le en К., М с a kin J., Pastijn F., «J. Algeb-
Algebra», 1978, v. 54, p. 6 — 26. Л. Н. Шеврин.
ПРОСТЕЙШИЙ ПОТОК — случайная последова-
последовательность моментов времени 0<т!<т2<. . ., в к-рые
происходят события нек-рого потока событий (напр.,
потока вызовов, приходящих на телефонную станцию),
удовлетворяющая условию независимости и одинако-
одинаковой показательной распределенности разностей т,- + 1—
т.,-. П. п. с распределением
Отсутствие последействия. При 0<
<<j<<2<- • -<tn случайные величины %(tt) — i(ti^{j,
2=1, . . ., к, независимы.
Доказывается, что при выполнении этих условий
и при условии
Р {|
поток будет простейшим с показательным распределе-
распределением (*).
Лит.: [1] X и н ч и н А. Я., Работы по математической теории
массового обслуживания, М., 1963. Б. А. Севастьянов.
ПРОСТОГО СЛОЯ ПОТЕНЦИАЛ — выражение вида
h(\x-y\)f(y)do(y), A)
где S — замкнутая поверхность Ляпунова (класса
641. я.)) в евклидовом пространстве R™, ri^-1, разде-
разделяющая R™ на внутреннюю область Z) + и внешнюю
D~; h(\x—у\) — фундаментальное решение оператора
Лапласа:
и)„=2яп/12/Г(и/2) — площадь единичной сферы в R",
\х — у\ — расстояние между точками х и у, da (у) —
элемент площади S.
Если /(x)gC@>(S), то П. с. п. и(х) определен всюду
в R". П. с. и. представляет собой частный случай
ньютонова потенциала, порождаемого массами, рас-
распределенными на поверхности S с поверхностной плот-
плотностью /(#), и обладает следующими свойствами.
В D + и D~ П. с. п. и(х) имеет производные всех
порядков, к-рые можно вычислять под знаком интег-
интеграла, и удовлетворяет уравнению Лапласа Аи(х)=0,
т. е. является гармонической функцией. При и^З
эта функция регулярна на бесконечности, гг(со) = 0.
П. с. п. и(х) непрерывен во всем пространстве R",
причем ц(ж)^С(°. V)(R") при любом v, 0<v<X. При
переходе через поверхность S производная по направ-
направлению внешней нормали п„ к S в точке уп ? S терпит
разрыв. Предельные значения нормальной производ-
производной из области D + и из области D ~ существуют и
непрерывны всюду на S и выражаются соответственно
формулами
lim
du
<iu (г/о) / (у»)
x^y,- '¦ dn° 2
d"ft/o) i /(]/o)
B)
11111 dna\l~~ dn0 ~ 2 '
X -*¦ Уа i
где
— т. н. прямое значение нормальной
производной П. с. п. в точке yo?S, причем
du (yn)/dnn?C(°' V~>(S) при всех v, 0<v<X. Если f(y)(z
?С(о. *.)(S), то частные производные функции и (х)
непрерывно продолжаются r D + и в D ~ до функций
классов С(°. M(JD + ) и 6"<°. *-)(D -) соответственно. В
этом случае также
du(yo)/dno ? Cto. ^)(,S).
Эти свойства обобщаются в различных направлениях.
Напр., если f (у)?L1 (S), то и(х)(^1Л внутри и вне 51,
формулы B) имеют место почти всюду на S, причем
интеграл C) суммируем на S. Изучены также свойства
П. с. п., понимаемых как интегралы по произвольной
радоновской мере |х, сосредоточенной на S:
здесь также и(х) — гармонич. функции вне S, формулы
B) имеют место почти всюду на S по мере Лебега с
заменой / (у) на производную меры \х' (у0) но мере
Лебега. В определении A) фундаментальное решение
оператора Лапласа можно заменить на произвольную
функцию Леви для общего эллиптич. оператора 2-го
порядка с переменными коэффициентами класса С(°. *•)
с заменой нормальной производной d/dn0 на произ-
производную по конормали. При этом перечисленные свой-
свойства остаются в силе (см. [2] — [4]).
П. с. п. используется при решении краевых задач
для эллиптич. уравнений. Представление искомого
решения 2-й краевой задачи в виде П. с. п. с неизвест-
неизвестной плотностью / (у) и использование свойства C)
приводит к интегральному уравнению Фредгольма
2-го рода на S для определения f(y) (см. [2] — [5]).
При решении краевых задач для параболич. урав-
уравнений используется тепловой потенциал
простого слоя вида
v(x, г)=
где
G(x, t; у, т) =
— фундаментальное решение уравнения теплопровод-
теплопроводности в n-мерном пространстве, f(y, т) — плотность.
Функция v (x, t) и ее обобщение на случай произволь-
произвольного параболич. уравнения 2-го порядка обладают
свойствами, аналогичными указанным для и(х) (см.
[3], 14], [6]).
Лит.: [1] Г юнтер Н. М., Теория потенциала и ее при-
применение к основным задачам математической физики, М., 1953;
12] М и р а н д а К., Уравнения с частными производными эллип-
эллиптического типа, пер. с итал., М., 1957; 13] Тихонов А. Н.,
Самарский А. А., Уравнения математической физики,
."> изд., М., 1977; [4] С м и р н о в В. И., Курс высшей матема-
математики, т. 4. 5 изд., М., 1958; [5] Фридман А., Уравнения с
частными производными параболического типа, пер. с англ., М.,
1968; [6] Б и ц а д з е А. В., Краевые задачи для эллиптических
уравнений второго порядка, М., 1966. Е. Д. Соломенцев.
ПРОСТОЕ КОЛЬЦО — неодноэлементное кольцо бе.ч
двусторонних идеалов, отличных от 0 и всего кольца.
Ассоциативное П. к. с единицей, содержащее мини-
минимальный односторонний идеал, изоморфно кольцу
матриц над нек-рым телом. Без предположения су-
существования единицы такое кольцо оказывается ло-
локально матричным над нек-рым телом D, т. е. каждое
его конечное подмножество содержится в подкольце,
изоморфном кольцу матриц над D (см. [2]). Сущест-
Существуют П. к. без делителей нуля (даже нётеровы), от-
отличные от тел, а также нётеровы П. к. с делителями
нуля, но без идемпотентов [3]. Известны П. к., ради-
радикальные в смысле Джекобсона (см. [1]). Однако от-
открыт вопрос о существовании простых нильколец.
Описание строения альтернативных П. к. сводится
к ассоциативному случаю (см. Альтернативные кольца
и алгебры). См. также Простая алгебра.
Лит.: [1] Б о к у т ь Л. А., Ассоциативные кольца, ч. 1 — 2,
Новосиб., 1977—81; [2] Джекобсон Н., Строение колец,
пер. с англ., М., 1961; [3] 3 а л е с с к и й А, Е., Н е р о с л а в-
г к и й О., «Communs. Alg.», 1977, v. 5, № 3, p. 231—44; [4]
Ф е й с К., Алгебра: кольца, модули и категории, пер. с англ.,
т. 1—2, М., 1977—79; [5] Cozzens J., Faith С, Simple
Noetherian rings, Camb.— [a. o.], 1975. Л. А. Скорняков.
ПРОСТОЕ МНОЖЕСТВО — рекурсивно перечисли-
перечислимое множество натуральных чисел, дополнение к-рого
ость иммунное множество. П. м. являются промежу-
промежуточными в смысле так наз. m-сводимости (см. Рекур-
сивнак теория множеств) между разрешимыми множе-
множествами и творческими (креативными) множествами —
последние'являются наибольшими среди неречиелимых
множеств в смысле m-сводимости. Пусть Р — произ-
произвольное П. м., а К — произвольное креативное множе-
множество натуральных чисел (напр., множество гёделевых
номеров теорем формальной арифметики). Тогда не
существует общерекурсивной функции f(x), сводящей
К к Р, т. е. такой, что
Сводимость Р к К имеет место всегда, а к Р не сводится
ни одно разрешимое множество.
Лит.: [1] Успенский В. А., Лекции о вычислимых
функциях, М., 1960; [2] М а л ь ц е в А. И., Алгоритмы и рекур-
рекурсивные функции, М., 1965; [3] Роджерс X., Теория рекур-
рекурсивных функций и эффективная вычислимость, пер. с англ., М.,
1972. С. Я. Артемов.
ПРОСТОЕ ОТНОШЕНИЕ трех точек Мх, М, Мг на
прямой — число X такое, что
При этом говорят, что точка М делит отрезок М^М2
в отношении А. Если (хи у^) и (х2, у2) ~ координаты
точек Мх и М2, то координаты точки М определяются
по формулам
i+л ' у— l + x '
П. о. является инвариантом аффинных преобразований.
'Л. S. Иванов.
ПРОСТОЕ ПОЛЕ — поле, не содержащее собствен-
собственных подполей. Каждое поле содержит единственное
простое подполе. П. п. характеристики 0 изоморфно
нолю рациональных чисел. П. п. характеристики р
ИЗОМОрфнО ПОЛЮ ВЫчетОВ ПО МОДУЛЮ р. О. А. Иванова.
ПРОСТОЕ ПРЕДСТАВЛЕНИЕ — то же, что непри-
неприводимое представление.
ПРОСТОЕ ЧИСЛО — натуральное (целое положи-
положительное) число р>1, имеющее только два делителя
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, ...
Числа, имеющие не менее трех различных делителей,
наз. составными. Понятие П. ч. является ос-
основным при изучении делимости натуральных чисел.
Так, основная теорема элементарной
теории чисел утверждает, что всякое натуральное
число, отличное от единицы, либо простое, либо, если
оно составное, может быть представлено в виде произ-
произведения простых чисел. При этом такое представление
единственно (с точностью до расположения сомножи-
сомножителей). Запись этого произведения в виде степеней
одинаковых П. ч., а самих П. ч. в порядке возрастания,
дает канонич. разложение натурального числа:
fe
С помощью канонич. разложений натуральных чисел
1, а2, . . ., ак находят наибольший общий делитель
d— (о1? а2, . . ., ak) и наименьшее общее кратное т=
= [а,, а2, . . ., afe] этих чисел. С помощью канонич.
разложения натурального числа п вычисляются зна-
значения теоретико-числовых функций т(ге), S(п) и Ц>(п),
к-рые обозначают соответственно число делителей,
сумму делителей числа п и количество натуральных
чисел т^.п, взаимно простых с п (т. е. таких, что
(т, ге)—1):
p,-l p.-l
.. d
V pk
Существенной особенностью этих формул является их
зависимость от арифметич. структуры натурального
аргумента п.
П. ч. играют роль своеобразных «кирпичиков», из
к-рых строятся все остальные натуральные числа.
Еще в 3 в. до н. э. Евклид доказал бесконечность мно-
жества П. ч., а Эратосфен нашел способ отсеивания
П. ч. из множества натуральных чисел (см. Эратос-
фена решето). Л. Эйлер (L. Euler) нашел доказатель-
доказательство бесконечности множества П. ч., основанное на
использовании средств математич. анализа. Даль-
Дальнейшее развитие аналитич. метода Эйлера оказалось
очень плодотворным (см. Аналитическая теория чи-
чисел). П. Л. Чебышев открыл ряд новых законов, к-рым
подчиняются П. ч. В частности, с помощью элемен-
элементарных рассуждений, использующих канонич. раз-
разложение для числа га!, П. Л. Чебышев нашел нера-
неравенства, к-рым должно удовлетворять количество
я (ж) простых чисел
где я<1, Ь>1 —нек-рые положительные константы.
Наиболее глубокие закономерности, к-рым подчиня-
подчиняется поведение последовательности П. ч., были полу-
получены путем углубления исходных идей П. Л. Чебы-
шева с помощью аналитических и, в ряде случаев,
элементарных методов (см. Распределение простых
чисел).
П. ч. связаны не только с мультипликативной, но
и с аддитивной структурой натуральных чисел. До-
Достаточно характерной в этом отношении является
Гольдбаха проблема о разбиении натуральных чисел
на сумму трех П. ч., решенная в 1937 И. М. Виногра-
Виноградовым (см. Аддитивная теория чисел). Изучение
законов разложения П. ч. в алгебраич. полях проли-
проливает свет на свойства обычных П. ч. Напр., рассмат-
рассматривая закон разложения П. ч. рФ2 в поле гауссовых
чисел, получают теорему Гаусса: p=a2+fc2
тогда и только тогда, когда pesl (mod 4).
Существует много пока A983) еще не решенных
проблем, относящихся к П. ч. Напр.:
будет ли бесконечным множество П. ч. Мерсепна:
р = 21 — 1, где q — простое;
будет ли бесконечным множество П. ч. Ферма:
/> = 22" + 1, где п 5а 0 — целое;
существует ли бесконечное множество П. ч. рх и р2
«близнецов», т. е. таких, что р1—р2—2.
Экспериментальные и эвристич. соображения сви-
свидетельствуют в пользу положительного решения сфор-
сформулированных выше проблем и др. аналогичных задач.
Лит.: Щ X а с С е Г., Лекции по теории чисел, пер. с нем.,
М., 1953. Б. М. Бредихин.
ПРОСТОИ ГОМОТОПИЧЕСКИЙ ТИП - класс
клеточных комплексов, принадлежащих одному гомо-
гомотопическому типу, такой, что Уайтхеда кручение
соответствующей гомотопич. эквивалентности равно
нулю. м. И. Войцеховский.
ПРОСТОЙ ИДЕАЛ — двусторонний идеал Р кольца
R такой, что из АВ^Р, где А и В — идеалы в И,
следует, что либо Ас^Р, либо В^Р. Для ассоциатив-
ассоциативного кольца эквивалентным определением на языке
элементов будет следующее:
aRb ^ Р —+ а ? Р или Ь?Р,
где а, Ъ — элементы кольца R. Всякий примитивный
идеал прост.
Пусть R — ассоциативно-коммутативное кольцо с
единицей. Тогда простота идеала PczR эквивалентна
тому, что ab?P-*-a?P или Ь?Р,т. е. тому, что фактор-
кольцо RIP есть область целостности. В этом случае
всякий максимальный идеал прост, а пересечение всех
простых идеалов кольца R является радикалом нуле-
нулевого идеала (т. е. множеством нильпотентных элемен-
элементов).
Обобщением понятия П. и. служит понятие прим ар-
арного идеала. В теории примарных разложений П. и.
играют ту же роль, что простые числа в разложении
целых чисел по степеням простых, а примарные идеа-
идеалы — роль степеней простых чисел.
Идеал Р решетки L наз. простым, если
аЬ ? Р -—, а ? Р или Ь?Р.
Идеал Р прост тогда и только тогда, когда F=
простой фильтр, т. е. если a-{-b?F —*¦ a?F или
Лит.: [1] Бурбаки Н., Коммутативная алгебра, пер.
с франц., М., 1971; [2] Д ж е к о 6 с о н Н., Строение колец,
пер. с англ., М., 1961; [3] 3 а р и с с к и й О., С а м ю ч л ь П.,
Коммутативная алгебра, пер. с англ., т. 1, М., 19i>3; U I С к о р-
н я ко в Л. А., Элементы теории структур, М,, 1970.
О. Д. Иванова.
ПРОСТОЙ ИНТЕРВАЛ частично упорядо-
упорядоченного множества — подмножество, состоя-
состоящее из двух элементов а<^.Ь таких, что между ними в
данном частично упорядоченном множестве нет других
элементов, т. е.
а <ж < b =ф а = х/\Ъ — х.
О. А. Иванова.
ПРОСТОЙ ИТЕРАЦИИ МЕТОД — метод прибли-
приближенного решения системы линейных алгебраич. ypars-
нений Ах—Ъ, к-рая преобразуется к виду .т— ВхЛ,-с
и решение к-рой находится как предел последователь-
последовательности xk+i=^Bxk-\-c, к~0, \, . . ., где х'и — начальное
приближение. Для сходимости П. и. м. при любом
начальном приближении х° необходимо и достаточно,
чтобы все собственные значения матрицы В были по
модулю меньше единицы; и достаточно, чтобы какая-
либо норма матрицы В была меньше единицы. Если
для нормы матрицы В, согласованной с нормой вектора
х, имеет место оценка ||#||<р<1, то П. и. м. сходится
со скоростью геометрич. прогрессии и для погрешности
метода верна оценка
\[хт X t| ^Pm || 2° X ||.
Для случая кубической, октаэдрической и сфериче-
сферической векторных норм условие ||5||<:р будет выпол-
выполнено, если имеют место оценки:
-Л' 2' •••» п'
Простейший вариапт метода соответствует случаю,
когда в качестве матрицы В выбирают матрицу Е — А ,
где Е — единичная матрица. Если все диагональные
элементы матрицы А отличны от нуля, то, выбирая
b=D~l(l)--A) и c~D~xb, где D — диагональная
матрица, диагональные элементы к-рой совпадают с
диагональными элементами матрицы А , получают Якоби
метод или метод одновременных смещений.
Частным случаем П. и. м. является метод В = Е—хА
и с=т6, где т — итерационный параметр, к-рый выби-
выбирается из условия минимума но х нормы матрицы
Е—%А . Если Yi и 7г — минимальное и максимальное
собственный значения симметричной положительно
определенной матрицы А, то при т= —-— для
сферич. нормы матрицы В имеет место оценка ||В||«:р,
Для нелинейной системы алгебранч. уравнении
(р/(ж)=0, 1<г<ге, х = (хи хг, ..., х„),
II. и. м. имеет вид
Вопрос о выборе итерационного параметра т решается
в зависимости от дифференциальных свойств функций
Ф;(ж). Часто он подчинен требованию локальной схо-
сходимости метода в окрестности решения.
Лит.: Ш Ф а д д е е в Д. К., Ф а д д е е в а В. Н., Вычис-
Вычислительные методы линейной алгебры, 2 изд., М., 1УВЗ; [2] Б е-
р е з и н И. С, Жидков Н. ГГ., Методы вычислений, 3 изд.,
т. 1, М., 1966; [3] О р т е г а Д ж., РейнболдтВ., Ите-
Итерационные методы решении нелинейных систем уравнений со
многими неизвестными, пер. с англ., М., 1975; [4] С а м а р-
с к и й А. А., Н и к о л а е в Е. С, Методы решения сеточных
уравнений, М., 1978. Е. С. Николаев.
ПРОСТОЙ ЭЛЕМЕНТ — обобщение понятия просто-
простого числа. Пусть G — область целостности или коммута-
коммутативная полугруппа с единицей, удовлетворяющая
закону сокращения. Ненулевой элемент p?G, не яв-
являющийся делителем единицы, наз. просты м, если
произведение аЬ может делиться на р лишь в том слу-
случае, когда хотя бы один из элементов а или b делится
на р. Всякий П. э. является неприводимым,
т. е. делится только на делители единицы и ассоцииро-
ассоциированные с ним элементы. Неприводимый элемент не
обязан быть простым, однако в гауссовой полугруппе
эти два понятия совпадают. Более того, если всякий
неприводимый элемент из G является простым, то
полугруппа G гауссова. Аналогичные утверждения
имеют место для факториальнызг колец. Элемент кольца
является простым тогда и только тогда, когда главный
идеал, порожденный этим элементом,— простой идеал.
Существуют обобщения этих понятий на некомму-
некоммутативный случай (см. [2]).
Лит.: Ш Кон П., Свободные иольца и их связи, пер. с
англ.,М., 1975; [2] К у р о ш А. Г., Лекции по общей алгебре,
2 изд., М., 1973; [3] Л е н г С, Алгебра, пер. с англ., М., 1968.
О. А. Иванова.
ПРОСТРАНСТВЕННЫЕ ФОРМЫ — связные полные
римановы пространства постоянной кривизны. Про-
илема классификации «-мерных римановых пространств
произвольной постоянной кривизны была сформули-
сформулирована В. Киллпнгом (W. Killing, 1891), к-рый на-
шал ее проблемой пространственных
форм Клиффорда — Клейна; современ-
современная формулировка этой проблемы дана X. Хонфом
(И. Hopf, 1925).
Примеры П. ф.: евклидово пространство Е"
размерности п есть П. ф. нулевой кривизны (так на-
называемое плоское пространство); сфера S" в Еп + 1 ра-
радиуса г>0 есть П. ф. положительной кривизны \1г°;
пространство Лобачевского (гиперболич. пространство)
Л" есть П. ф. отрицательной кривизны; плоский тор
Тп=Е"/Г, где Г— n-мерная решетка в А1","есть П. ф.
мулевой кривизны (плоское пространство).
Любая П. ф. М" кривизны а может быть получена
из односвязной П. ф. Мп той же кривизны фактори-
факторизацией по дискретной группе Г движений пространства
М", действующих свободно (т. е. без неподвижных
точек); при этом два пространства Мп— Мп1Т и М'п =
= MnlY' изометричны в том и только в том случае,
когда Г и Г' сопряжены в группе всех движении Мп.
Тем самым проблема классификации П. ф. сводится
к задаче описания всех несопряженных групп движе-
движений пространств S", Еп в А", действующих свободно.
Пространство М" наз. сферической прост-
пространственной ф о р м о й (с. п. ф.), если М"~
= S"/T, евклидовой пространственной
формой (е. п. ф.), если М"—Еп/Г, и гипербо-
гиперболической пространственной фор-
формой (г. п. ф.), если Мп—\"/Т; фундаментальная
группа Мп изоморфна Г. При изучении проблемы
классификации П. ф. ненулевой кривизны а значение
\о\ не играет существенной роли, поэтому обычно
считают |а| = 1.
Если п четно, то единственным движением сферы
Sn без неподвижных точек является центральная сим-
симметрия, переводящая каждую точку сферы в диамет-
диаметрально противоположную; факторпространство Sn/V
по группе Г, порожденное этим движением, есть
пространство Римана (эллиптич. пространство). Любая
с. п. ф. четной размерности п изометрична либо 5™,
либо Р". Были классифицированы трехмерные с. и. ф.
(см. [2]). Следующим шагом в направлении класси-
классификации с. п. ф. явилась общая программа решения
этой проблемы и её применение для классификации
с. п. ф. размерности 4&+1 (см. [4]). Поскольку сфера
Sn компактна, дискретная группа Г движений S"
конечна, то для классификации n-мерных с. п. ф.
достаточно описать все несопряженные конечные под-
подгруппы ортогональной группы 0(п+1), действующие
свободно на S". Говорят, что ортогональное представ-
представление л конечной группы G в ?в + 1 свободно от
неподвижных точек, если для всех g ? G\ {I }
преобразование n{g) сферы Sn не имеет неподвижных
точек; в частности, л — точное представление. Согласно
программе, изложенной в |4|, решение проблемы
с. п. ф. Клиффорда — Клейна можно разбить на ряд
этапов. Во-первых, найти необходимые и достаточные
условия для того, чтобы абстрактная группа G могла
служить фундаментальной группой с. п. ф. и класси-
классифицировать такие группы; получается нек-рое семей-
семейство {G\} групп. Во-вторых, описать нее неэквивалент-
неэквивалентные неприводимые ортогональные представления каж-
каждой из групп {Gx } и выделить среди них представления,
свободные от неподвижных точек. Наконец, определить
все автоморфизмы групп {Gx} и выяснить, какие из
найденных представлений эквивалентны по модулю
автоморфизма соответствующей группы. Эта программа
в полном объеме была реализована в [5], что привело
к исчерпывающей классификации с. п. ф. Любая
конечная циклич. группа принадлежит семейству
{G% }; чтобы нециклич. группа порядка N могла слу-
служить фундаментальной группой n-мерной с. п. ф., не-
необходимо (но не достаточно), чтобы .V было взаимно
просто с ге+1 и делилось на квадрат какою-либо
целого числа.
Глобальная теория е. п. ф. возникла как приложение
нек-рых результатов геометрич. кристаллографии. В ра-
работе [3] был использован известный с кон. 19 в. список
кристаллографич. групп в Е3 и получена топологиче-
топологическая, а в компактном случае аффинная, классификация
трехмерных е. п. ф. Теоремы Бибербаха о кристалло-
кристаллографич. группах в Е" приводят к структурной теории
компактных е. и. ф. произвольной размерности, В част-
частности, для любого л^2 существует только конечное
число разных классов эквивалентных компактных
е. п. ф. размерности п, при этом две компактные е. п. ф.
Mn=En/V и М'п = Еа1Т' аффинно эквивалентны, если
и только если их фундаментальные группы Г и Г'
изоморфны. Напр., любая двумерная компактная
е. п. ф. гомеоморфна (а следовательно, аффинно экви-
эквивалентна) либо плоскому тору, либо поверхности
Клейна. Абстрактная группа Г тогда и только тогда
может служить фундаментальной группой компактной
е. п. ф. М", когда а) Г имеет нормальную абелеву
подгруппу Г* конечного индекса, изоморфную %п\
б) Г* совпадает со своим централизатором в Г; в) Г
не имеет элементов конечного порядка. Если такая
группа Г реализована в виде дискретной подгруппы
в группе всех движений пространства Е", ю Г* сов-
совпадает с множеством параллельных сдвигом, принад-
принадлежащих Г, и имеется нормальное накрытие /¦ про-
пространства Л-]" — Е"/Г шшскн.м тором Tn=EniV*, оп-
определенное формулой р(Т* (я)) —Г (л:) для всех х?Е".
Конечная группа Г/Г* изоморфна группе накрываю-
накрывающих преобразований для р, к-рая в свою очередь
изоморфна голономии группе пространства М". Ком-
Компактная е. п. ф. всегда имеет конечную группу голоно-
голономии. Справедливо и обратное утверждение: компакт-
компактное риманово пространство, группа голономии к-рого
конечна, является плоским. Доказано, что любая
конечная группа изоморфна группе голономии нек-рой
компактной е. п. ф. Аффинная классификация ком-
компактных е. п. ф. заданной размерности п в настоящее
время A983) известна только для »<:4. При «-=3
имеется 6 классов ориентируемых и 4 класса неориен-
тируемых аффинно эквивалентных компактных е. н. ф.
Классифицированы компактные е. п. ф. с циклич.
группами голономии простого порядка. Семейство всех
неизометричных плоских торов Тп можно параметри-
параметризовать элементами из
SL(n, %,)\GL+ (re, R)/SO(n),
где GL+(n, R) — связная компонента единицы в
GL(n, R), а изометрич. классификация компактных
е. п. ф. размерности ге непосредственно следует из их
аффинной классификации и изометрич. классификации
торов Тп. Некомпактные е. п. ф. классифицированы
(с точностью до изометрии) только в размерностях
2 и 3; в частности, двумерная некомпактная е. и. ф.,
отличная от Е2, гомеоморфна цилиндру, либо листу
Мёбиуса. Любая некомпактная е. п. ф. допускает дей-
действительную аналитич. ретракцию на компактное впол-
вполне геодезич. плоское подмногообразие; класс фунда-
фундаментальных групп некомпактных е. п. ф. совпадает с
классом фундаментальных групп компактных е. п. ф.
Исследование двумерных г. п. ф. по существу нача-
началось в 1888, когда А. Пуанкаре (Н. Poincare, [1]),
изучая дискретные группы дробно-линейных преоб-
преобразований верхней полуплоскости Im(z)>0 комплекс-
комплексной плоскости — фуксовы группы, заметил, что их
можно трактовать как группы движений плоскости
Лобачевского А2. Пусть X — группа движений А2,
сохраняющих ориентацию; Ах, . . ., Aim, m^2,— вы-
выпуклый 4т-угольник в А2 с попарно конгруэнтными
геодезич. сторонами
где г=1, . . ., m, A4m + 1=At, сумма углов к-рого 2л.
Элементы а,- и 6,- из X переводят АА[_3А^_., в
соответственно (на рис. показан случай т~ 2). Тогда
подгруппа TczX, порожденная элементами а,-, &,-,
действует на Л2 без неподвижных точек, а заданный 4т-
угольник служит фундамен-
фундаментальной областью этой груп-
группы; при этом Г имеет единствен-
единственное определяющее соотношение
Пт
Факторпространство А2/Г явля-
является ориентируемой компактной
г. п. ф. рода т, и каждая двумер-
>г*"" ная ориентируемая компактная
1 г. п. ф. может быть получена та-
таким способом. Пусть теперь Г— абстрактная группа, изо-
изоморфная фундаментальной группе ориентируемой замк-
замкнутой поверхности рода т. Тогда существует непре-
непрерывное отображение <р:ГХ Л6™-6-->Х, удовлетво-
удовлетворяющее условиям: а) для всех x^R6m~li отображение
<рх : g —>ф(#, <¦) является мономорфизмом Г в X;
б) подгруппы r.v = <|\v (Г) и Гх,--=--ц>х>(Г) сопряжены в
X тогда и только тогда, когда ж— х'; в) если дискрет-
ная подгруппа Г"сX изоморфна Г, то она сопряжена
с Гх для нек-рого x^Rbm~li. Таким образом, семейство
неизоморфных компактных г. п. ф. размерности 2
рода т зависит от 6т—6 действительных параметров.
Двумерная компактная г. п. ф. естественным образом
наделяется структурой римановой поверхности, и
только что сформулированное утверждение первона-
первоначально было доказано средствами теории униформи-
зации; геометрич. доказательство было дано в [7].
Указанные результаты обобщаются на некомпактные
г. п. ф., гомеоморфные сфере с конечным числом ручек
и дырок, а также на неориентируемые г. п. ф. раз-
размерности 2. В противоположность двумерному случаю
не существует непрерывных семейств неизометричных
компактных г. п. ф. размерности больше 2. А именно,
компактные г. п. ф. размерности п^'А, имеющие изо-
изоморфные фундаментальные группы, изометричны. Дру-
Других общих результатов, непосредственно относящихся
к классификации и-мерных г. п. ф., в настоящее время
A983) нет; примеры г. п. ф. размерности ге^З приве-
приведены в [6], [8J.
Кроме римановых П. ф. изучались их обобщения:
исевдоримановы, аффинные и комплексные П. ф. и
П. ф. симметрич. пространств (см., напр., [9]).
Лит.: [1J Пуанкаре А., Избр. труды, т. 3, М., 1974;
[2] т h г с 1 f а 1 1 W., S e i f e r t H., «Math. Ann.», 1930, Bd
104, S. 1—70; 13] Nowacli W., «Comment, math, helv.»,
1934, v. 7, p. «1—93; [4] V i n с е n t G., там же; 1947, v. 20,
p. 117—7t; Г5] Вольф Д ж., Пространства постоянной кри-
кривизны, пер. с англ., М., 1982; [6] В и н б е р г Э. Б., «Матем.
сб.», 1969, т. 78, № 4, с. 633—39; [7] На тан зон С. М.,
«Успехи матем. наук», 1972, т. 27 в. 4, с. 145—60; [8] Mil 1-
son J. J., «Ann. Math.», 1976, v. 104, p. 235—47; [9] В о-
r e 1 A., «Topology», 1963, JSft 2, p. 111—22. H. P. Камышанспий.
ПРОСТРАНСТВО — логически мыслимая форма (или
структура), служащая средой, в к-рой осуществляются
другие формы и те или иные конструкции. Напр., в
элементарной геометрии плоскость или пространство
служат средой, где строятся разнообразные фигуры.
В большинстве случаев в П. фиксируются отношения,
сходные по формальным свойствам с обычными прост-
пространственными отношениями (расстояние между точ-
точками, равенство фигур и др.)) так что о таких П. можно
сказать, что они представляют логически мыслимые
пространственно-подобные формы. Первым и важней-
важнейшим математич. П. является трехмерное евклидово
пространство, представляющее приближенный абст-
абстрактный образ реального П. Общее понятие «П.» в
математике сложилось в результате обобщения и видо-
видоизменения понятий геометрии евклидова П. Первые
П., отличные от трехмерного евклидова, были введены
в 1-й иол. 19 в. Это были Лобачевского пространство
и евклидово П. любого числа измерений (см. Многомер-
Многомерная геометрия)'. Общее понятие о математич. П. как
«многократной протяженности» было выдвинуто в 1854
Б. Риманом (В. Riemann); оно обобщалось, уточня-
уточнялось и конкретизировалось в разных направлениях: та-
таковы, напр., риманоео пространство, финслериво про-
пространство, векторное пространство, гильбертово про-
пространство, метрическое пространство, топологическое
пространство. В современной математике П. опреде-
определяют как множество каких-либо объектов, к-рые наз.
его точками; ими могут быть геометрич. фигуры, функ-
функции, состояния физич. системы и т. д. Рассматривая
их множество как П., отвлекаются от всяких их
свойств и учитывают только те свойства их совокупно-
совокупности, к-рые определяются принятыми во внимание или
введенными но определению отношениями. Эти отно-
отношения между точками и теми или иными фигурами, т. е.
множествами точек, определяют «геометрию» П. При
аксиоматич. ее построении основные свойства этих от-
отношений выражаются в соответствующих аксиомах.
Примерами П. могут служить: 1) метрич. П., в к-рых
определено расстояние между точками; напр., П. не-
прерывных функции на к.-л. отрезке \а, Ь], где точка-
точками служат функции f(x), непрерывные на [a, b], a рас-
расстояние между fj(х) и fz(x) определяется как максимум
модуля их разности:
r = max| /x (x)—fa(x) |.
2) «П. событий», играющее важную роль в геометрия,
интерпретации теории относительности. Каждое собы-
событие характеризуется положением — координатами х,
у, z и временем t, поэтому множество всевозможных
событий оказывается четырехмерным П., где «точка» —
событие определяется 4 координатами х, у, z, t. 3) Фа-
Фазовые П., рассматриваемые в теоретич. физике и меха-
механике. Фазовое П. физич. системы — это совокупность
всех ее возможных состояний, к-рые рассматриваются
при ЭТОМ как ТОЧКИ ЭТОГО П. А. Д. Александров.
Д-ПРОСТРАНСТВО — топологическое пространство
с умножением, обладающим двусторонней гомотопич.
единицей. Подробнее, пунктированное топологич. про-
пространство (X, е), для к-рого задано непрерывное ото-
отображение т : XX X -*- X, наз. //-пространст-
//-пространством, если т(е, е) = е и отображение X —> X, х —>-
-*-т(х, е) и х-^-т(е, х) гомотопны rel(e, e Тождествен-
Тождественному отображению. Отмеченная точка е наз. гомо-
гомотопической единицей //-П. X. Иногда
термин «//-П.» употребляется в более узком смысле,
при к-ром требуется, чтобы отображение т : ХХХ^-
-+Х было гомотопически ассоциатив-
ассоциативным, т. е. чтобы отображения
т°(тХ id), т о (id X т):Х X X X X —>¦ X
были гомотопны rel (е, е, е) между собой. Иногда тре-
требуется также существование гомотопически
обратных элементов. Это значит, что долж-
должно быть задано отображение ц : (X, е) —*¦ (X, е), для
к-рого отображения
X —> X, х —>- т (х, [I (х)), х —»¦ т (ц (х), х)
гомотопны постоянному отображению X -*¦ е. Напр.,
для любого пунктированного топологич. пространства
Y петель пространство QY является гомотопически
ассоциативным //-П. с гомотопически обратными эле-
элементами, a Q2Y=Q(QY) является также и комму-
коммутативным Д-П., то есть таким, что отображения
X X Х—+Х, (х, у) —>- т (х, у), (х, у) —> т (у, х)
гомотопны. Группы когомологий //-П. образуют Хопфа
алгебру.
Лит.: [U БорцманДж., Фогт Р., Гомотопически ин-
инвариантные алгебраические структуры на топологических про-
пространствах, пер. с англ., М., 1977. А. Ф. Харшиладзи.
БГ-ПРОСТРАНСТВО, Канторовича про-
пространство,— порядково полное векторное про-
пространство, т. е. векторное полуупорядоченное про-
пространство, в к-ром всякое ограниченное сверху мно-
множество имеет верхнюю грань. Открыто Л. В. Канто-
Канторовичем [1].
Лит.: [1] К а н т о р о в и ч Л. В., «Матем. сб.», 1937, т. 2,
с. 121 — 68. М. И. Войцеховский.
ПРОСТРАНСТВО НАД АЛГЕБРОЙ — пространство,
обладающее дифференциально-геометрической струк-
структурой, точки к-рого могут быть снабжены координата-
координатами из нек-рой алгебры. В большинстве случаев алгебра
предполагается ассоциативной с единицей, иногда —
альтернативной с единицей (см. Ассоциативные кольца
и алгебры, Альтернативные кольца и алгебры).
Для построения широкого класса П. н. а. можно
исходить из понятия унитарного модуля над алгеброй,
определение к-рого получается из определения век-
векторного пространства над телом путем замены тела
на ассоциативную алгебру с единицей (см. [1], [31).
В результате присоединения к элементам модуля, на-
зываемым векторами, новых элементов, называемых
точками, связанных с векторами теми же аксиомами,
что и точки аффинного пространства с его векторами,
получается аффинное пространство над ассоциативной
алгеброй с единицей. Аффинные преобразования в
аффинном пространстве над алгеброй имеют в коор-
координатах вид
где f(x) — непрерывный автоморфизм алгебры, ге-мер-
ное аффинное пространство над алгеброй, имеющей
ранг г над нек-рым полем, допускает естественную мо-
модель (представление) в иг-мерном аффинном простран-
пространстве над тем же полем. В этой модели каждая точка
аффинного пространства над алгеброй изображается
точкой rer-мерного аффинного пространства над рас-
рассматриваемым полем, координатами к-рой являются
коэффициенты разложений координат точек простран-
пространства над алгеброй по базисным элементам алгебры.
В случае, когда базисные элементы гА, A = i, . . ., г,
алгебры связаны между собой структурными уравне-
уравнениями
где улв — структурные константы алгебры, каждому
базисному элементу ед соответствует в модели линейное
преобразование с матрицей
У А
(*)
О ... уА
где по диагонали стоят п одинаковых r-мерных блоков
ул=||у$в11- В аффинных пространствах над алгебрами
можно задать эрмитову метрику (евклидову и псевдо-
псевдоевклидову), а в случае коммутативных алгебр и квад-
квадратичную (евклидову и псевдоевклидову) метрику. Для
этого в унитарном модуле определяется скалярное
произведение векторов (а, Ь), в первом случае обла-
обладающее свойством
(а, Ь) = (Ь, а)',
где / — инволютивный антиавтоморфизм (инволюция)
в алгебре, а во втором случае — свойством
(а, Ь) = (Ь, а).
Скалярный квадрат вектора А В определяет метрич.
инварианты пары точек А ж В; движения евклидовых
и псевдоевклидовых пространств — аффинные преоб-
преобразования, сохраняющие скалярное произведение век-
векторов. При замене в определении эллиптических и ги-
гиперболических П. н. а. скалярного произведения век-
векторов скалярным произведением векторов (аз, у), для
к-рого (ж, у)——(у, жI или (аз, у)=—(у, аз), полу-
получается эрмитово, или квадратичное
с и м п л е к т и ч е с к о е, П. н. а.
Многообразие одномерных подмодулей (п-\-^-мерно-
(п-\-^-мерного унитарного модуля над алгеброй К наз. ге-мерным
проективным пространством над
алгеброй К; точками этого пространства наз.
одномерные подмодули, а координаты векторов этих
подмодулей наз. проективными координатами точек.
В проективном П. н. а. определяются так же, как в
проективных пространствах над полями, коллинеации
и корреляции. В проективных координатах коллинеа-
коллинеации имеют вид
где / (i) — непрерывный автоморфизм алгебры, а кор-
корреляции имеют вид
где f(x) — непрерывный антиавтоморфизм алгебры, а
Uj — проективные координаты гиперплоскости. Вье-
дение скалярного произведения векторов в унитарном
модуле позволяет определить в проективном простран-
пространстве, построенном с помощью этого модуля, эрмитовы
пли, в случае коммутативной алгебры, квадратичные
эллиптические и гиперболич. метрики. Метрич. инва-
инварианты точек этих пространств определяются скаляр-
скалярными произведениями векторов м и ц соответствующих
подмодулей с помощью двойного отношения
W=(x, ж)-1 (ж, .'/)(.'/, ,'/)~Ч.'/> »")•
В том случае, когда W — действительное число, инва-
инвариант со, для к-poro W=cos2 со, на:), расстояни-
е м между соответствующими точками (см. [2]).
Проективные, эллиптические, гиперболические и
силшлектич. пространства над действительными про-
простыми алгебрами (напр., алгебрами действительных,
.омплексных и кватернионных матриц) обладают тем
свойством, что их фундаментальные группы являются
простыми группами Ли бесконечных серий. Евклидо-
Евклидовы, псевдоевклидовы и квазиэллиптические, квазиги-
квазигиперболические и квазисимплектич. пространства над
теми же алгебрами обладают тем свойством, что их
фундаментальные группы являются квазипростыми
группами Ли тех же серий (см. [2]); тем же свойством
обладают проективные, эллиптические, гиперболиче-
гиперболические и симплектич. пространства над полупростыми
алгебрами, к к-рым относится алгебра дуальных чисел.
Несколько сложнее определяются проективные и
эрмитовы (эллиптические и гиперболические) плоско-
плоскости над альтернативными алгебрами. Фундаментальные
группы этих плоскостей являются простыми или ква-
квазипростыми группами Ли нек-рых особых классов.
Лит.: [1] Б у р б а к и Н., Алгебра. Алгебраические струк-
структуры. Линейная и полилинейная алгебра, пер. с франц., М.,
1962; 12] Р о з е н ф е л ь д Б. А., Неевклидовы пространства,
М., 1969; [3] Bern W., Vorlesungen iiber Geometric dcr Algeb-
ren, В., 1973. Б. А. Розепфельд, А. П. Широков.
ПРОСТРАНСТВО ОТОБРАЖЕНИЙ т о и о л о г и-
4 е с к о е — множество F отображении множества X
в топологич. пространство Y с какой-нибудь естествен-
естественной топологией Т на F. При фиксированных множестве
X и пространстве Y получаются различные П. о. в
зависимости от того, какие отображения X —*¦ Y вклю-
включаются в F и какая естественная топология берется
на /'. Выбор F связан с наличием на А' и Y дополни-
дополнительных структур и спецификой рассматриваемой ситуа-
ситуации. Так, в качестве F могут фигурировать: множество
всех непрерывных отображений множества X в прост-
пространство Y, множество всех отображений множества X
в пространство Y, множество всех непрерывных ли-
линейных отображений топологического векторного про-
пространства X в топологическое векторное пространство
Y, множество всех непрерывных гомоморфизмов топо-
топологич. группы X в топологич. группу Y, множество
всех гладких отображений отрезка в прямую и т. д.
Важность рассмотрения П. о. в определенной мере
вызвана тем, что отображения представляют собой
наиболее общий способ сравнения математич. объек-
объектов.
Естественные топологии (па множестве F) обычно
определяются по следующей схеме. В F фиксируется
семейство S подмножеств, и предбаза топологии Т на F
составляется из множеств вида
V(A, V) = [f б F; t(A)c V},
где А ? S и V — любое открытое множество в F. Если
5 — семейство всех конечных (или одноточечных) под-
множеств множества X, то Т наз. топологи е и
поточечной сходимости на X. Если S
состоит из всех компактных подмножеств тонологич.
пространства X, то Т наз. компактно откры-
открытой топологией. Если X ? S, то Т наз. топо-
топологией равномерной сходимости (на
X). Впрочем, всякую топологию Т на F, получаемую
по этой схеме, наз. топологией равномерной сходимо-
сходимости на элементах семейства S.
В зависимости от области математики те пли пные
П. о. оказываются особенно важными. К числу цент-
центральных объектов функционального анализа относятся
банаховы пространства непрерывных функций на ком-
компактах в топологии нормы, т.е. топологии
равномерной сходимости, ив слабой т о п о л о-
г и и, к-рая описывается в терминах поточечной схо-
сходимости. В теории гомотопий важную роль играет
пространство путей в топологич. пространстве, т. е.
пространство непрерывных отображений действитель-
действительного отрезка в это пространство. Гомотонии одного
отображения в другое представляются путем в прост-
пространстве отображений. П. о. сфер в сферы возникает
при определении гомотопических и когомотопических
групп.
Особенно естественной на множестве всех отображе-
отображений одного /^-пространства в другое оказывается ком-
компактно открытая топология. Преимуществом топологии
равномерной сходимости (на всем пространстве) явля-
является ее метризуемость. Эта топология — сильнейшая
в большом классе естественных топологий на П. о.
Но обладает важными преимуществами и топология
поточечной сходимости — слабейшая в том же круге
топологий. Во-первых, эта топология обладает наи-
наибольшим запасом компактов, как слабейшая, а ком-
компактность является одним из наиболее полезных свойств
множества функций. Во-вторых, имеет место фундамен-
фундаментальный результат Дз. Нагаты (J. Nagata), к-рым изу-
изучение любых тихоновских пространств ставится в
прямую связь с исследованием топологич. колец.
А именно, тихоновские пространства X и У гомеоморф-
ны в том и только в том случае, если топологически
изоморфны топологич. кольца С^(Х) и Сp(Y) непре-
непрерывных функций на X и Y, взятые в топологии пото-
поточечной сходимости.
Рассмотрение топологич. свойств П. о. полезно при
доказательстве теорем о существовании отображений
с тем или иным свойством. Полнота мотрич. пространст-
пространства непрерывных действительных функций на компакте
через принцип сжатых отображений применяется для
доказательства фундаментальной теоремы о существо-
существовании решения дифференциального уравнения в из-
известных предположениях. Следствием полноты метрич.
пространства функций является Бэра свойство. На этой
основе доказывается, напр., существование непрерыв-
непрерывной нигде не дифференцируемой функции иа отрезке.
Свойство Бэра П. о. играет центральную роль при
доказательстве теорем общего положения, при доказа-
доказательстве известной теоремы о вложимости каждого
re-мерного компакта со счетной базой в Bга-|-1)-мерное
евклидово пространство, ц т. п.
Влияние пространств действительных функций на
общую топологию проявилось в следующей задаче
общего характера: как связаны свойства пространств X
и Y, если пространства непрерывных действительных
функций над ними (в топологии поточечной сходимости,
в компактно открытой топологии) гомеоморфны (ли-
(линейно гомеоморфны). Известно, напр., что линейные
гомеоморфизмы сохраняют компактность и размерность.
Существенное значение имеет наследование двойст-
двойственности между свойствами топологич. пространства и
топологич. свойствами пространства функций над ним
в топологии поточечной сходимости. Примером полез-
ного результата и атон ооласти может служить теорема:
любая конечная степень пространства линделёфова в
том и только в том случаи, если пространство функций
над ним имеет счетную тесноту. Этот результат при-
применяется, в частности, при исследовании строения
компактов Эберлейна — компактов, лежа-
лежащих в банаховых пространствах, наделенных слабой
топологией.
Лит.: [1] К е л .1 и Д ж. Л., Общая топология, пер. с англ.,
М., 1981. А. В. Архангельский.
ПРОСТРАНСТВО С ИНДЕФИНИТНОЙ МЕТРИКОЙ,
G-n ространств о,— пара объектов (?', G), из
к-рых первый есть векторное пространство Е над нолем
комплексных чисел, а второй есть билинейная (точнее,
полутора линейная) форма G над Е; эта форма наз.
также S-метрикой. Если G — положительно оп-
определенная (т. н. дефинитная) форма, то G есть скаляр-
скалярное произведение в Е, и с помощью G можно канонич.
способом (см., напр., Гильбертово пространство с ин-
индефинитной метрикой) ввести норму и расстояние
(т. е. обычную метрику) для элементов из Е. В случае
общей полуторалпнейной формы нет норм или метрик,
канонически связанных с G, и термин «G-метрика» лишь
напоминает о тесной связи дефинитных полуторалиней-
пых форм с нек-рыми метриками в векторных прост-
пространствах.
Теория конечномерных пространств
с и н д с ф и н и т и о й м е т р и к о й, наз. чаще
билинейно метрич. пространствами или прост-
пространствами с билинейной м е т р и к о и,
разработана еще Г. Фробениусом и излагается в курсах
линейной алгебры (см. [1]).
Основной целью общей теории П. с и. м.
является выделение и исследование сравнительно про-
простых, но важных для приложений классов несамосопря-
несамосопряженных операторов и гильбертовом пространстве. П. с
11. м. впервые введены Л. С. Понтрягиным [2] (подроб-
(подробное см. Нонтрягина пространство).
Теория П. с н. м. развивается но двум направлени-
направлениям — геометрия этих пространств и линейные операто-
операторы в них.
Геометрия общих П. с и. м. в основном исследует:
а) связь С-метрики с различными топологиями на /'.';
б) классификацию векторных подпространств (линеа-
(линеалов) в Е относительно С-метрики (особенно т. н. дефи-
питных подпространств; см. ниже); в) свойства G-npo-
сктирования; г) базисы G-пространств.
В случае эрмитовой (/-метрики (Сэ-
метрик и), т. е. такой, что G(.r, у) - G(y, х) для
нсех х, у?Е, важнейшими понятиями и результатами
геометрии П. с н. м. являются следующие. Пусть каж-
каждому вектору у?? поставлен в соответствие линейный
Функционал G,, : х —>- G(.r, у), х?Е. Топология
т на Е наз. подчиняющей G-метрик у,
если функционал Gy непрерывен в т для всех у?Е;
топология т наз. согласующейся с
f/'-м е т р и к о й, если она подчиняет С и каждый
т-непрерывный функционал имеет вид Су, у?Е. В про-
пространстве Е с индефинитной метрикой можно задать
не более одной топологии Фреше, подчиняющей G, и,
однако, не каждая G-метрика допускает такую тополо-
i пю (см. [4]). Если подчиняющая G-метрику топология
пвляется предгильбертовой топологией на Е и задается
в Е скалярным произведением Н(-, •), то форма Я
наз. эрмитово неотрицательной м а-
,к о р а н т о п формы G; в этом случае
\G(x, у)\"<СН (х, х)Н(у, ;/), С-const, х, у с Е.
После пополнения по //-норме получается г и л ь б е р-
т о в о пространство с индефинитной
м е т р и к о й (Ё, G), где G — продолжение G по не-
прерывности на все пространство Е. При этом метрика
G может оказаться вырожденной, даже если G — невы-
невырожденная метрика. Этого вырождения не происходит,
если метрика С невырождена и наибольшая из размер-
размерностей х положительных подпространств в Е конечна.
В последнем случае получается пространство Понтря-
гина Пх.
Подпространство L в пространстве (Е, G) с индефи-
индефинитной метрикой наз. положительным под-
подпространством, отрицательным под-
подпространством (общее название — дефинит-
дефинитным иод пространством) пли н о и т-
ралъным подпространством, в зависи-
зависимости от того, будет ли G(x, -r)>0, G(,r, .r)<<) или
G(x, х) = 0 для любого x?L; подпространство м a к с и-
м а л ь н о положительно, если оно положи-
положительно и не может быть расширено с сохранением этого
свойства. Всякое подпространство одного из названных
типов содержится в максимальном подпространстве
того же типа.
Важную роль в классификации подпространств и
пространствах с индефинитной метрикой играют поня-
понятия к а н о н и ч е с к о i о р а з л о ж с н и я и G-
ортогонального проектирования.
Вектор х?Е наз. G-o р т о г о н а л ь н ы м к под-
подпространству LC.E (;& изотропным
подпространством относительно L), если
G(x, г/) = 0 для любого у?Е. Подпространство L наз.
вырожденным, если оно содержит хотя бы
один ненулевой вектор, изотропный относительно L.
Если L — подпространство в пространстве Е с ин-
индефинитной метрикой, то L'= {у : G(x, y) = 0, yx?L}—
его G-o рто тональное дополнение. Всег-
Всегда L"=LT, где т — любая топология, согласующаяся
с G. G-ортогоналыюе дополнение L' вырожденного пек-
торного подпространства L является вырожденным
векторным подпространством, замкнутым относительно
любой топологии т, согласующейся с G, a L(~\L^ есть
векторное подпространство изотропных элементов.
Подпространство L наз. u р о с к ц и о н в о по л-
н ы м, если каждый вектор у ?Е имеет С-п р о е к ц и ю
на L, т. е. существует такое //0?Ь, что G (х, у—j/0)=0
для каждого x?L. Единственность G-нроекции па L
равносильна невырожденности подпространства L, а
ее существование зависит от непрерывности функцио-
функционала Gy в топологиях на L, соыасующпхея с G. Если
М и iV'являются G-ортогональными подпространствами
и M-\-N=E, то М и N проекционно полны; если L —
проекционно полное подпространство, то L-\-L' = E,
причем сумма есть прямая сумма, если Е — невырож-
невырожденное пространство с индефинитной метрикой.
Пусть L — дефинитное подпространство в прострап-
стве с индефинитной метрикой Е; оно наз. р е г у-
л я р н ы м, если каждый функционал Gy, y^E, не-
непрерывен на L в норме \\x\\q—\G(x, x)\ '2. В противном
случае оно наз. сингулярным. Всякое невы-
невырожденное бесконечномерное пространство с индефи-
индефинитной метрикой содержит сингулярные; подпростран-
подпространства. Дефинитное подпространство L проекционно
полно в том и только в том случае, если оно регулярно
и если для любого у?Е найдется такой вектор x?L,
что
!!.т,!?гН|Су!!о- = С(з:, у)-
Линейные операторы в пространствах с индефинитной
метрикой изучались в основном в гильбертовых прост-
пространствах с индефинитной метрикой; имеется обзор
банаховых аналогов (см. [8]).
Как и в случае гильбертовых пространств с индефи-
индефинитной метрикой, важным инструментом изучения
геометрии П. с и. м. и линейных операторов в прост-
ранствах (Е, G), наделенных нек-рой топологией,
согласованной с G, являются так наз. G-o р т о н о р-
мированные базисы в Е, т. е. такие базисы
{еп} топологического векторного пространства Е, что
(Gek, «n)=±Sfen; A. «=1, 2, ... (см. [4]).
Лит.: L1] Мальцев А. И., Основы линейной алгебры,
3 изд., М., 1970; [2] П о н т р я г и н Л. С, «Изв. АН СССР.
Сер. матем.», 1944, т. 8, с. 243—80; [3] Иох видов И. С,
К р е н н Ш. Г., «Тр. Моск. матем. об-ва», 1956, т. Г>, с. 367 —
432; [4] Гинзбург 10. И., Иохвидов И. С.. «Успехи
матем. наук», 1962, т. 17, JVJ 4, с. 3—56; [5] Крсйи М. Г.,
в кн.: Вторая летняя матем. школа, ч. 1, К., 1965, с. 15—92; [6]
А з и з о в Т. Я., И о х в и д о в И. С, «Успехи матем. наук»,
1971, т. 26, в. 4, с. 43—92; [71 Надь К., Пространства состоя-
состояний с индефинитной метрикой в квантовой теории поля, пер. с
англ., М., 1969; [8] И о х в и д о в И. С, «Изв. АН Молд. ССР»,
1968, № 1, с. 60—80. Н. Я. Никольский, Б. С. Павлов.
ПРОСТРАНСТВО С МЕРОЙ (X, А, ц) — измеримое
пространство (X, А) с заданной на А мерой а (т. е.
счетно аддитивной функцией со значениями в [0, оо],
для к-рой (х@) = О; последнее свойство следует из
аддитивности, если мера конечна, т. е. не принимает
значения оо, и даже если имеется хоть одно Y ? А с
(,1У<оо). Запись (X, А, ц) часто сокращают до (X, ц.)
и говорят, что fi есть мера на X; иногда эту запись со-
сокращают даже до X. Основной случай — когда А
является а-алгеброй и X можно представить в виде
Un=iXn с Хп?А и цХп<^оо; меру в атом случае на;|.
(вполне) ст-к о н е ч н о й (а если [iX<со, то
(вполне) конечной). Такова, напр., мера Ле-
Лебега на R (см. Лебега пространство). Однако иногда
встречаются и не а-конечные меры, как, напр., /с-мер-
ная Хаусдорфа мера на R" при k<in. Встречаются так-
также модификации, когда |л принимает значения в (—оо,
оо], комплексные или векторные значения, а также
когда (.1 всего лишь конечно аддитивна.
Лит.: [1] Халмош П., Теория меры, пер. с англ., М.,
1953; [2]ДанфордН., ШвардДж., Линейные операторы,
ч. 1 — Общая теория, пер. с англ., М., 1962. Д. В. Аносов.
ПРОСТРАНСТВО-ВРЕМЯ — термин, обозначающий
геометрич. конструкцию, к-рая описывает пространст-
пространственные и временные отношения в тех физич. теориях,
в к-рых эти отношения рассматриваются как взаимо-
зависящие (эти теории принято наз. релятивистскими).
Впервые понятие П.-в. возникло при формулировке
и систематизации основных положений теории относи-
относительности. П.-в. этой теории является четырехмерным
псевдоевклидовым пространством EfLi 3j с линейным
элементом
ds* = c2dt2 — dx2 — dy2 — dz2,
где х, у, z — пространственные координаты, at —
временная координата, с — скорость света. Эта систе-
система координат называется в физике галилеевой системой
координат и соответствует инерциалъной системе от-
отсчета. Переход между различными галилеевыми систе-
системами координат, соответствующий рассмотрению инер-
циальных систем отсчета, движущихся друг относитель-
относительно друга, осуществляется с помощью Лоренца преобра-
преобразований. То, что значение временной координаты в но-
новой системе координат оказывается при этом выражен-
выраженным как через временную, так и через пространствен-
пространственные координаты старой системы координат, отражает
взаимозависимость пространственных и временных от-
отношений в специальной теории относительности. П.-в.
специальной теории относительности принято называть
также П.-в. Минковского, лоренцевым
П.-в.
В общей теории относительности в качестве П.-в.
используются различные четырехмерные нсевдорима-
новы пространства сигнатуры A, 3). Отличие метрики
этого П.-в. от плоской метрики П.-в. специальной
теории относительности описывает в общей теории от-
относительности гравитационное поле (см. Гравитация).
В свою очередь метрика П.-в. связана с распределени-
ем и свойствами негравитационных полей и различных
видов с помощью Эйнштейна уравнений.
Выработка концепции П.-в. сыграла важную роль в
преодолении метафизич. подхода к пространству как
абсолютному вместилищу тел и к времени как абсо-
абсолютной длительности, не связанной с реальными фи-
зич. процессами.
В дальнейшем концепция П.-в. в той или иной форме
входит в структуру других физич. теорий, рассматри-
рассматривающих релятивистские эффекты (релятивистской кван-
квантовой механики, квантовой теории ноля и др.)- В общей
теории относительности были изучены многие типы
П.-в., являющиеся решениями уравнений Эйнштейна.
Качественное различие между пространственными и
временными отношениями с точки зрения релятивист-
релятивистской физики находит свое отражение в наличии в
П.-в. векторов различной природы — пространственно-
и времениподобных векторов, образующих в касатель-
касательных пространствах конусы. Соответственно, метрика
П.-в. оказывается индефинитной, пространственно- и
времениподобные векторы имеют разные знаки ска-
скалярного квадрата. Границу между конусами прост-
пространственно- и времениподобных векторов образует
изотропный конус, изотропные векторы к-рого имеют
нулевой скалярный квадрат и соответствуют движению
спета и других частиц с нулевой массой покоя.
Многие споцифич. эффекты теории относительности
связаны именно с индефинитностью метрики П.-в. и
с наличием структуры изотропных конусов на П.-в.
Напр., лоренцево замедление времени есть следствие
обратного неравенства треугольника в пространстве с
индефинитной метрикой, согласно к-рому в двумерном
псевдоевклидовом пространстве наклонная всегда ко-
короче своей проекции.
Во многих случаях оказывается полезным в различ-
различной степени отвлекаться от конкретного строения мет-
метрики П.-в. и рассматривать лишь свойства структуры
изотропных конусов на П.-в., то есть рассматривать
различные т. н. общие пространства кинематич. типа,
или времениподобные пространства.
При ретроспективном анализе предшествующих фи-
физич. теорий с точки зрения теории относительности
были построены различные типы П.-в., к-рые можно
условно поставить в соответствие ньютоновской меха-
механике (галилеево пространство) и даже физич. пред-
представлениям Аристотеля (см. [51). Эти П.-в. являются
различными пространствами с вырожденным изотроп-
изотропным (световым) конусом (напр., полуримановым прост-
пространством). Именно вырождение изотропного конуса
позволяет рассматривать эти пространства как пре-
предельные случаи П.-в. теории относительности и сопо-
сопоставлять их тем теориям, исходной внутренней струк-
структуре к-рых концепция П.-в. была чужда.
Лит.: [11 Эйнштейн А., Собр. науч. трудов, т. 1 — 4,
М., 196а — A7; I.2J А л е к с а н д 1) о в А. Д., «Вопросы филосо-
философии», 19Г>9, ,К» J, с. A7—84; [3] Ландау Л. Д., Лиф'
ш и ц Е. М., Теория поля, в изд., М., 1973 (Теоретич. физика,
т. 2); [4] Р а ш с в с к и й 11. К., Риманова геометрия и тензор-
тензорный анализ, 3 изд., М., 1967; [5] П е н р о у з Р., Структура про-
пространства-времени, пер. с англ., М., 1972. Д. Д. Соколов.
ПРОТИВОПОЛОЖНАЯ ТЕОРЕМА — теорема, по-
получающаяся путем замены условия и заключения дан-
данной исходной теоремы их отрицаниями.
ПРОТИВОРЕЧИВЫЙ КЛАСС — класс К формул
языка узкого исчисления предикатов (УИП) такой,
что существует такая формула ср, что средствами УИП
из К выводимо как ф, так и ~)ср (отрицание <р). Другими
словами, если к аксиомам УИП добавить все формулы
из УС в качестве новых аксиом, то в полученном исчис-
исчислении будет выводима как формула ср, так и формула
~|ф. В. Н. Гришин.
ПРОТИВОРЕЧИЕ — формула <р языка узкого ис-
исчисления предикатов (УИП) такая, что во всех моделях
этого языка она ложна. Формула <р является П. тогда
и только тогда, когда ~|<р выводимо в УИП.
ПРОТИВОРЕЧИЯ ЗАКОН — логический закон!
утверждающий, что никакое высказывание не может
быть истинным одновременно со своим отрицанием.
В языке исчисления высказываний П. з. выражается
формулой
1 (А&-] А).
Эта формула выводима как в классическом, так и в
интуиционистском исчислении высказываний.
В. Н. Гришин.
ПРОЦЕДУРА — 1) Последовательность действий, вы-
выполняемая закономерно, согласно точному предписа-
предписанию; алгоритм.
2) П.— особым образом оформленная программа, ре-
решающая задачу, частную по отношению к другой,
более широкой задаче; фундаментальная конструкция
алгоритмических языков.
П. является главным средством преодоления слож-
сложности программирования путем систематич. разделения
задачи на части. Различают два способа выделения П.
при программировании: нисходящий и восходящий.
При нисходящем способе П. возникает при
однократном разбиении задачи на малое число стан-
стандартно сопрягаемых подзадач; тем самым П. иденти-
идентифицируется до того, как будет построена ее программа.
При восходящем способе П. заготавлива-
заготавливается впрок, с тем чтобы в дальнейшем быть использо-
использованной при решении более широкой задачи как эле-
элементарное действие.
Программа, образующая П., обычно содержит сво-
свободные переменные, называемые формальными пара-
параметрами П. При обращении к выполнению П. формаль-
формальным параметрам придаются их значения, называемые
фактич. параметрами. Описание П. обычно состоит из
четырех частей: тела П., т. е. собственно программы,
образующей П., имени П., списка формальных пара-
параметров и атрибутов — перечня свойств П. Обычно
атрибуты характеризуют множества, к-рым принадле-
принадлежат значения формальных параметров и результатов
П. Простейшим видом П. являются процедуры-
функции. Для них формальные параметры явля-
являются аргументами функции, а обращение к П.-функции,
имеющее вид имени П., за к-рым стоит в скобках список
фактич. параметров, означает «команду» вычисления
значения функции, соответствующего этим парамет-
параметрам. А. П. Ершов.
ПРЮФЕРА ПОВЕРХНОСТЬ — пример двумерного
действительного аналитич. многообразия, не имеющего
счетного базиса открытых множеств; приведен в работе
Т. Радо [1]. Имеется обобщение П. п. на случай любой
четной размерности (см. [2]). Однако всякая риманова
поверхность имеет счетный базис открытых множеств
(теорема Радо).
Лит.: [1] R a d 6 Т. «Acta Szeged», 1925, v. 2, p. 101—21;
[2] С a 1 a b i E., R о s e n 1 i с h t M., «Pruc. Amer. Math. Soc»,
1953, v. 4, p. 335—40; [3] Спрингер Д ж., Введение
u теорию римановых поверхностей, пер. с англ., М., 1960; [4]
Неванлинна Р., Униформизацил, нер. с нем., М., 1955.
Е. Д. Соломенцев.
ПРЯМАЯ — одно из основных геометрич. понятий.
П. обычно косвенным образом определяется аксиома-
аксиомами геометрии; напр., евклидова П.— аксиомами инци-
инцидентности, порядка, конгруэнтности, непрерывности.
П. наз. проективной, аффинной, гиперболической и
т. д. в зависимости от плоскости, в к-рую она вложена.
П. можно изучать по ее преобразованиям, индуцируе-
индуцируемыми коллинеациями плоскости. Так, напр., группа
алгебраич. автоморфизмов действительной проектив-
проективной П. изоморфна группе перемещений действительной
плоскости Лобачевского. Топологически все П. одной
плоскости эквивалентны. Так, эллиптическая и дейст-
вительная проективная П. топологически эквивалент-
эквивалентны окружности евклидовой плоскости, а комплексная
проективная П.— двумерной сфере евклидова простран-
пространства. П. na:s. непрерывной, дискретной или конеч-
конечной, если она инцидентна со множеством точек мощно-
мощности континуума, счетным или конечным множеством
с оответетвенно.
В плоскости над произвольным полем под П. пони-
понимают алгебраич. линию 1-го порядка. В прямоуголь-
прямоугольной системе координат (х, у) евклидовой плоскости
R2 ГГ. задается линейным уравнением
Ах+Ву-\-С~ О,
коэффициенты А, В определяют координаты нормаль-
нормального вектора этой прямой.
Прямой (А , В) аффинного пространства над полем к
(но Вейлю) наз. множество таких точек М, что АМ=
— tAB, ГДе if к. В. -В- Афанасьев, Л. А. Сидоров.
ПРЯМАЯ СУММА — конструкция, широко исполь-
используемая в теориях таких математич. структур, категории
к-рых близки к абелевым категориям; в неабелевом
случае конструкция прямой суммы обычно наз. дис-
дискретным прямым произведением.
Пусть U — нек-рый класс однотипных алгебраич.
систем, содержащих одноэлементную (нулевую) под-
подсистему. Прямой суммой пли (дискретным) прямым
произведением систем Xh if/, из класса Ц наз. под-
подсистема прямого произведения -X^JJ. 7^'' С0СТ0ЯП1ая
из таких функций / : /->Х, все значения к-рых, кро-
кроме конечного числа, принадлежат соответствующим
нулевым подсистемам. П. с. обозначается одним из
следующих способов:
п
Для конечного числа слагаемых используются также
обозначения
Непосредственно из определений следует совпадение
П. с. и прямого произведения в случае конечности
числа слагаемых.
Для каждого слагаемого П. с. Х= JJ. X,- существу-
существует канонич. вложение ?,- : X,¦ —>- X, к-рое элементу
zfX,- сопоставляет функцию </,(.г) : / -». X, прини-
принимающую значение х при значении аргумента i и равную
нулю в остальных случаях. Следовательно, можно
считать, что П. с. содержит свои слагаемые. В случае
?2-групп (в частности, в случае групп, абелевых групп,
векторных пространств, колец) можно дать «внутрен-
«внутреннее» определение П. с. fi-группа G является П. с. своих
Q-подгрупп G(, if/, если выполнены следующие усло-
условия: a) G порождается G,-, if/; б) каждая Q-подгруппа
G,- является идеалом в G; в) пересечение G,- с U-под-
группой, порожденной остальными идеалами, является
нулевой подгруппой для каждого I.
Всякое векторное пространство есть П. с. одномер-
одномерных подпространств. Всякая свободная абелева группа
является П. с. бесконечных циклич. групп. Всякая
конечная абелева группа есть П. с. примерных циклич.
групп. Всякое ассоциативное кольцо с единицей, удов-
удовлетворяющее условию минимальности для идеалов,
есть П. с. конечного числа полных колец линейных
преобразований подходящих конечномерных вектор-
векторных пространств.
В теории групп, решеток и категорий глубокое раз-
развитие получила проблема изоморфизма прямых разло-
разложений, начало к-рой было положено теоремой Рема-
ка — Шмидта о центральном изоморфизме прямых
разложений групп, обладающих главным рядом (см.
Крулля — Ремака — Шмидта теорема).
В теории категории иногда II. с. наз. понятие,
двойственное понятию произведения, т. е. копроизве-
дение объектов категории. м. Ш. Цаленко.
0-ПРЯМОЕ ОБЪЕДИНЕНИЕ полугрупп с н у-
л е м — полугруппа, полученная из данного семейства
{Sa} полугрупп с нулем, попарно пересекающихся
лишь по этому нулю, заданием на объединении (jSa
операции умножения, совпадающей с исходной опера-
операцией на каждой полугруппе Sa и такой, что SaSp=O
для любых различных а, р\ 0-П. о. наз. также орто-
ортогональной суммой. Описание ряда типов
полугрупп устанавливает возможность их разложения
в 0-П. о. тех или иных известных полугрупп (см.,
напр., Максимальный идеал, Минимальный идеал,
Регулярная полугруппа).
Лит.: 1U Клиффорд А., II р е с т о н Г., Алгебраиче-
Алгебраическая теория полугрупп, пер. с англ., т. 2 М., 1972.
Л. Н. Шеврин.
ПРЯМОЕ ПРОИЗВЕДЕНИЕ — одна из основных
общематоматич. конструкций, идея к-рой принадлежит
Декарту; поэтому П. п. наз. также декартовым
произведением. П. п., или просто произведе-
произведением, двух непустых множеств X и Y наз. множество
XXY, состоящее из всех упорядоченных пар вида
(х, у), где.т?Х, y?Y:
Если одно из множеств X или Y пусто, то произведение
пусто. Множество XX Y можно отождествить с мно-
множеством функций, определенных на двухэлементном
множестве {1, 2} и принимающих значения в множест-
множестве X при значении аргумента, равном 1, и в множестве
Y при значении аргумента, равном 2. Это отождествле-
отождествление позволяет распространить определение П. п. на
случай любого количества множителей. Пусть / —
нек-рое множество индексов и пусть Х{ — произволь-
произвольное семейство множеств, заиндексированных элемента-
элементами множества /. П. п. семейства множеств X;, i?I,
наз. множество таких функций / : 1 ->¦ X, где Х=- U X;,
ге I
что f(i)?X,- для каждого i?/. Обычно П. п. обозна-
обозначается JT. X,-; для конечного множества индексов
/= {1, .. ., и} используются также обозначения JJ..-Х^1
или Х1ХХ2Х . . .ХХп. Если / состоит из одного эле-
MeHTal, то ТТ; = j Хх— Хх. Иногда П. п. конечного числа
множителей определяется индуктивно:
П,-=1 Х1 = Хг, П,2=1 Х,- = {(.ть xt)\ri е Л',, г, g Л'.,},
Значение конструкции П. п. определяется прежде
всего тем, что в нем естественно вводится дополни-
дополнительная структура, если все множители являются одно-
тинными математич. структурами. Напр., пусть X,-,
i^J,— однотипные алгебраич. системы, т.е. мно-
множества с общей сигнатурой конечноместных предика-
ioh и операций. Тогда произведение ^=JJ. ,Х( пре-
превращается в алгебраич. систему с той же сигнатурой:
для функций Д, . . .,/„:/ —>- X и re-арной операции со
действие функции /х. . ./„со на элемент i определяется
равенством
значение предиката Р (f1} . . ., /„) истинно, если для
любого i^l истинно значение P(f1(i), . . ., fn(i)). При
этом выполнение во всех X,- определенных тождеств
влечет за собой их выполнение в произведении. По-
этому П. п. полугрупп, групп, колец, векторных про-
пространств и т. п. снова являются полугруппами, груп-
группами, кольцами, векторными пространствами соответ-
соответственно.
Для любого множителя П. п. X—"j^ X,- существует
естественная проекция pj : X —у Xj, оп-
определяемая равенством fp;~f{i)- Множество X и се-
семейство проекций р^ i? /, обладают следующим у н и-
версальным свойством: для любого се-
семейства отображений #,- : У —>¦ -V, существует такое
однозначно определенное отображение h : Y —v X, что
Si — hPi Для каждого i?/. Это свойство сохраняется
в случае, когда все X,¦ — однотипные алгебраич. си-
системы, и позволяет определить подходящую топологич.
структуру П. п. топологич. пространств. Сформулиро-
Сформулированное свойство лежит в основе определения произве-
произведения объектов категории.
Многие задачи математики связаны с описанием ма-
тематич. объектов, неразложимых в П. п., и с выясне-
выяснением условий, при к-рых множители произведения оп-
определены однозначно с точностью до изоморфизма.
Классич. результатами здесь являются теорема о
строении конечно порожденных модулей над кольцом
главных идеалов и теорема Ремака — Шмидта о цент-
центральном изоморфизме прямых разложений групп с
главным рядом.
П. п. иногда наз. полным прямым произ-
произведением в отличие от дискретного прямого про-
произведения (или прямой суммы), к-рое определяется в
тех случаях, когда дополнительная структура в мно-
множителях позволяет выделить одноэлементные под-
подструктуры (напр., единичные подгруппы, нулевые
подпространства и т. п.). Как правило, П. п. конечного
числа множителей совпадает с дискретным произведе-
произведением. М. Ш. Цнленко.
ПРЯМОЙ ПЕРЕСЧЕТ — пересчет элементов нек-рого
множества натуральных чисел в порядке их возраста-
возрастания. Точнее, П. и. множества А натуральных чисел
есть строго возрастающая функция натурального ар-
аргумента, область значений к-рой совпадает с Л. В тео-
теории алгоритмов рекурсивность и скорость возраста-
возрастания 11. п. множества являются его важными характе-
характеристиками. Напр., общерекурсивность (примитивная ре-
рекурсивность) П. п. бесконечного множества эквивалент-
эквивалентна разрешимости (примитивно рокурсишюп разреши-
разрешимости) этого множества. Множества натуральные чи-
чисел, П. п. к-рых но мажорируются никакой общерекур-
общерекурсивной функцией, наз. гипериммуыны м п, они
играют существенную роль в теории табличной сво-
сводимости.
Лит.: Ill Успенский В. А., Лекции о вычислимых
функциях, М., 1960; [2] Р о д ж е р с X., Теория рекурсивных
функций ir эффективная вычислимость, пер, с англ.. М., 1972.
С. Я. Артемов.
ПРЯМОУГОЛЬНИК — четырехугольник, у к-рого
все углы прямые. П. является параллелограммом.
ПРЯМОУГОЛЬНИКОВ ФОРМУЛА — формула вы-
вычисления интеграла по конечному промежутку [а, Ь\:
где h=(b—a)lN и а?[а, а+й]. Алгебраич. степень
точности равна 1 при a.--~a-\-hl2 и равна 0 в остальных
случаях.
Квадратурная формула (*) точна для тригонометрич.
функций
cos-f^-A-z, ain—L-Aa; д—0, 1, 2, ..., Л' —1.
п — а ' Ь — а ''
В случае Ь — а-=2л квадратурная формула (*) точна
для всех тригонометрич. полиномов порядка не выше
Лг — 1, более того, ее тригонометрич. степень точности
равна N — 1. Никакая другая квадратурная формула с
N действительными узлами не может иметь тригоно-
тригонометрич. степень точности, большую чем N — 1. так что
П. ф. при Ь— а — 2л обладает наивысшей тригонометрич.
степенью точности.
Пусть И (/, а) — погрешность П. ф., то есть разность
между легюй и правой частями приближенного равен-
равенства (*). Если подинтегральная функция /(х) дважды
непрерывно дифференцируема на [а, Ь], то при а~
= a-\-h/2 справедливо представление
Л/ г h \ Ь~ а , 9?„ ,*..
(/, a + Y) = ^л~Н ' (^'
где | — нек-рая точка промежутка [а, Ь]. Если функ-
функция / (х) — периодическая с периодом Ъ—а и имеет не-
непрерывную производную порядка 2к (к — натуральное
число) на всей действительной оси, то при любом
a€U, a+h]
R(f, а) = -F-в)Я,*-^г/(«)(т1),
где т) — точка промежутка [а, Ъ] и В^ — число Бер-
нулли. И. П. Мысовских.
ПРЯМЫХ МЕТОД — метод численного решения диф-
дифференциальных уравнений с частными производными
(см. [1] — [3]). Применим для нелинейных уравнений
эллиптического [4], гиперболического [5] и параболи-
параболического [6] типов любых порядков и систем уравнений.
П. м. позволяет проводить числепные расчеты в облас-
областях с криволинейными границами [7]. П. м. использу-
используется для решепия разнообразных задач механики [8].
В П. м. производится аппроксимация операции диф-
дифференцирования по нек-рым направлениям, что позво-
позволяет понизить размерность задачи и заменить решение
исходной системы дифференциальных уравнений с част-
частными производными расчетом аппроксимирующей ее
системы меньшего порядка.
С помощью П. м. решен ряд задач газовой динамики
[9]. При этом задача интегрирования исходной системы
дифференциальных уравнений с частными производ-
производными сводится к расчету аппроксимирующей ее систе-
системы обыкновенных дифференциальных уравнений.
В П. м. область интегрирования разбивается поперек
ударного слоя рядом прямых лучей па полосы. Замы-
каюший луч расположен в сверхзвуковой области.
Лучи располагаются соответственно узлам многочлена
Чебышева или равномерно. Газодинамич. функции
аппроксимируются кусочно линейно вдоль каждой
полосы либо полиномиально с узлами интерполяции
на всех л-учах. Получаемая аппроксимирующая система
обыкновенных дифференциальных уравнении интегри-
интегрируется вдоль каждого луча от ударной волны к телу.
В отличие от интегральных соотношений метода не
составляются интегральные соотношения и не выделя-
выделяется минимальная область влияния затупления, что
приводит к снижению точности, но упрощает вид ап-
аппроксимирующей системы (см. flO]).
П. м. проведены расчеты двумерного обтекания ряда
тел вращения совершенным [11], равновесным [12] и
неравновесным [13] газом. П. м. решена задача сверх-
сверхзвукового обтекания сферы горючей смесью с исполь-
использованием модели детонационной волны [14], ударной
волны и фронта пламени [15] и др. С применением три-
тригонометрич. аппроксимаций по меридиональному углу
П. м. распространен на пространственно-трехмерный
случай (см. [16], [17]), в том числе для неравновесного
обтекания затупления [18].
Лит.- [1] Rothe E. H., «Math. Ann.», 1930, Bd 102, S.
650—70; [2] К о л м о г о р о в А. Н., Петровский И. Г.,
И и с к у н о в Н. С, «Бюлл. МГУ. Секц. А», 1937, т. 1, в. 6,
с. 1—20; [3J Дородницын А. А., в кн.: Конференция
«Пути развития советского математического машиностроения
и приборостроения», М., 1956; [4J Костюкович Б. X.,
«Докл. АН СССР», 1958, т. 118, № 3, с. 433—35; [5J Лебе-
Лебедев В. И., «Вест. МГУ», 1955, №10, с. 47—57; Ш О л е й-
н и к О. А., Калашников А. С, Чжоу Юй-линь,
«Изв. АН СССР. Сер. матем.», 1958, т. 22, J* 5, с. 667—704:
17] Б у д а к Б. М., Горбунов А. Д., «Докл. АН СССР»,
1958, т. 118, ,М. 5, с. 858 — Gl; [8J А л и х а ш к и н Я. II., «Вы-
«Вычислит, матем.», 1957, ,N» 1, с. 13E- —52; 19] Г и л и н г г, и » С. М.,
ТеленинГ. Ф., Т и н я к о в Г. П., «Изв. АН СССР. Мсхан.
и машиностр.», 1904, JN» 4, с. 9—28; [10] Б е л о ц"е р i; о в-
с к и й О. М., Ч у ш к и н П. И., «Ж. вычисл. матем. и матем.
физ.», 1902, т. 2, .№ 5,о. 731—59; [11] Росляков Г. С, Т е-
л е н и н Г. Ф., в кн.: СО. работ ВЦ Моск. ун-та, 19f>8, .N't 11,
с. 9.4—112; [12] Т о л е н и и Г. Ф., Т и н я к о п Г. П., «Докл.
АН СССР», 1964, т. 159, № 1, с. 39—42; [13] С т у л о в В. П.,
в кн.: Некоторые применения метода сеток в газовой динамике.
в. 5, М., 1974, с. 140—227; [14] Гилинекий СМ., 3 а п-
р я и о и 3. Д., Черный Г. Г., «Изв. АН СССР. Мсхан. жид-
жидкости и газа», 1966, № 5, с. 8 — 13; [15] Г и л и и с к и ii С. М..
Ч е р н ы й Г. Г., там же, 19R8, .№ 1, с. 20 — 32; [10] Миног-
цеп В. Б., Те ленип Г. Ф., Тиняков Г. П., «Докл.
АН СССР», 1908, т. 179, № 2, с. 304 — 07; 117] Б а з ж и н А. П.,
Ч е л ы m e и а И. ф., «Изв. АН СССР. Механ. жидкости и
газа», 1967, .N5 3, с. Н9—23; [18] Семен и хина О. Н.,
Ш к а д о п а В. П., там же, 1973, № 2, с. 99—103.
Ю. М. Давыдов.
ПСЕВДОБАЗА топологического про-
пространства X — семейство открытых в Л" множеств
такое, что каждая точка пространства X является пе-
пересечением всех содержащих ее элементов этого семей-
семейства. II. существует только в пространствах, все одно-
одноточечные подмножества к-рых замкнуты (т. е. в 7V
пространствах). Если ^-пространство с баяой й наде-
наделить другой более сильной топологией, то ей уже не
будет базой нового топологич. пространства, но оста-
останется его П. В частности, счетную П. имеет дискретное
пространство мощности континуум, в к-ром счетном
базы нет. Однако для бикомпактов (т. е. бикомпактных
хаусдорфовых пространств) из наличия счетной П.
следует существование счетной базы.
Лит.: [1] Архангельский А. В., Понома-
Пономаре в В. И.,'Основы общей топологии в задачах и упражнениях,
М., 1974. А. В. Архангельский
ПСЕВДОБУЛЕВА АЛГЕБРА — решетка L--={L, <).
содержащая наименьший элемент 0 и такая, что
для любых ее элементов а и Ъ во множестве {х ? L :
аЛз:<Ь} существует наибольший элемент <Ob, где
а Ах — наибольшая нижняя грань для а и х. Элемент
аэб наз. псевдодополнением а отно-
относительно Ъ, или импликацией от а к
Ь. Всякая П. а. является дистрибутивной решеткой
с наибольшим элементом 1 (таковым будет любой эле-
элемент вида «Da).
П. а. служат алгебраич. моделями интуиционист-
интуиционистского исчисления высказываний Рейтинга и характеризу-
характеризуют его аналогично тому, как булевы алгебры характе-
характеризуют классич. исчисление высказываний. П. а. наз.
также алгебрами Рейтинга.
Решетки с относительным псевдодополнением рас-
рассматривал еще в 1919 Т. Сколем [1], правда без связи
с логикой. Впервые такая связь появилась при рас-
рассмотрении решеток, двойственных П. а. (т. е.
решеток, получающихся из П. а. обращением отноше-
отношения <:; см. [2]). Такие решетки были названы алгеб-
алгебрами Б р а у я р а. Позднее алгебрами Брауэра
стали называть и П. а.
Класс П. а., рассматриваемых как универсальные
алгебры (L; 0, л, V, Э) с константой 0 и двуместными
операциями л, V, HJ, может быть задан с помощью
нек-рой системы тождеств.
Конгруэнция Rg^LX L универсальной алгебры (Z-;
0, Л, V, из), являющейся П. а., полностью определя-
определяется классом эквивалентности, содержащим 1, т. е.
множеством
по формуле
<х, у} ? R<=>(x=)y ? V и у ох ? у)- B)
Множество A) является решеточным фильт-
фильтром, т. е. удовлетворяет условиям
V и (х ? у п y?v)=»* Л и g V
Наоборот, всякий непустой решеточный фильтр v
произвольной П. а. Л определяет по формуле B) кон-
конгруэнцию на алгебре (L; О, Л , V , из), класс эквивалент-
эквивалентности единицы к-рой совпадает с исходным фильт-
фильтром у-
В П. a. (L, <:) выполняется также бесконечный дис-
дистрибутивный закон
«Asup X — sup {алх:х ? X) C)
для любого a?L и любого множества ХЯкЬ, имеющего
в L наименьшую верхнюю грань sup X. Если решетка
(L, <:) полна, т. е. sup X существует для любого Х-Я=Ь,
то, наоборот, из того, что в ней справедливо тождество
C), вытекает, что она является И. а. Операция из
определяется равенством
а ИЗ Ь —- sup {х ? Ь:алх^Ь}.
Полные П. а. (т. е. полные решетки, удовлетво-
удовлетворяющие тождеству C)) рассматривают как алгебры
(L; 0, л, sup) с константой 0, двуместной операцией
Л : LXL —»- L и «бесконечноместной» операцией sup :
{X : X<^L} —> L. Этот подход определяет для полных
П. а. смысл таких понятий, как гомоморфизм, конгру-
конгруэнция, подалгебра. Так, для конгруэнции RczLXL
должно выполняться условие: если Х={х,:1^1} и
Y= {у; : i?I} — два подмножества в L таких, что для
всякого ??/ имеет место <?,•, г/,>?Л, то <sup X,
supF>?i?. Класс полных П. а., рассматриваемых
как алгебры (L; О, л, sup), может быть задан нек-рой
системой тождеств, содержащих операции О, Л, sup.
Поэтому он замкнут относительно подалгебр, фактор-
алгебр и прямых произведений семейств алгебр. В клас-
классе полных П. а. существуют свободные алгебры с
любым множеством образующих.
Если J : L —*¦ L — мультипликативный
оператор замыкания на полной П. а. ?—
=(L, ¦<), т. е. такая функция, что в L тождественно
выполняются условия
)=.J(J(x)) и J(x/\y)=J {x)/\J(y),
то отношение
Rj={<x, yy'€LxL:J(x)-J(y)} D)
является конгруэнцией на алгебре A (L; О, Л, sup),
а множество JL={x?L : J(x) = x} с индуцированным
из Л порядком <1л. — полной П. a. (JL; <:!//.),
изоморфной факторалгебре A/Rj. Наоборот, произ-
произвольная конгруэнция R на А определяет по формуле
JR(x) = suV{y ?L:<y, x> ?R} E)
мультипликативный оператор замыкания /^ : L —»- L.
Отображения Jv^Rj и R\-^Jд, определяемые формула-
формулами D) и E), взаимнообратны.
Примеры П. а. 1) Множество {X : X<=t/}, упо-
упорядоченное по включению <=, является полной П. а.
Его подалгебрами будут топологии на Р и только они.
2) Если функция / : L —>- L на полной П. а. (/,, <)
тождественно удовлетворяет условиям
), F)
то множество /L= {x?L : Ix—x) с индуцированным
отношением порядка образует подалгебру алгебры
(L; 0, л, sup). Всякую подалгебру Jlgi этой алгебры
можно получить указанным способом из единственной
функции /, удовлетворяющей условиям (б). Она опре-
определяется равенством
I (x) — s\i-p'{a ? А:а^х}.
Функция /, удовлетворяющая условиям F), наз.
ояератором взятия внутренности.
3) Если определить на множестве Ф всех формул
языка интуиционистского исчисления высказываний
отношение х^.у так, что А <:? тогда и только тогда,
когда формула Az^B выводима в этом исчислении и
факторизовать это множество но отношению эквива-
эквивалентности ?<:</& .у<:.-?, то получится свободная П. а.
Лит.: [1] S k о Ге m Т., Selected works in logic, Oslo, 1970,
p. 67—101; [2] McKinsey J. С. С, Tarski A., «Ann.
Math.», 1946, v. 47, p. 122—62; [3] P а с ё в а Е., Coop-
с к и й Р., Математика метаматематики, пер. с англ., М., 1972;
[4] Д р а г а л и н А. Г., Математический интуиционизм. Введе-
Введение в теорию доказательств, М., 1979; [5] Applications of shea-
sheaves. Proc. ...of sheaf theory to logic, algebra and analysis, B.—
N. Y., 1979. В. Н. Гришин.
ПСЕВДОВЕКТОР — то же, что осевой вектор.
ПСЕВДОВЫПУКЛОСТЬ И ПСЕВДОВОГНУТОСТЬ -
свойства областей в комплексных пространствах, а
также комплексных пространств и функций на них,
аналогичные свойствам выпуклости и вогнутости об-
областей и функций в пространстве R". Вещественная
функция ф класса С2 на открытом множестве UczC"
наз. р-п севдовыпуклой (или р-в ы п у к-
л о й), если эрмитова форма
имеет в каждой точке области U ни менее чем п—р + 1
неотрицательных собственных значений. В случае,
когда #(<р) имеет не менее чем ге—р+1 положительных
собственных значений, говорят, что ф сильно (или
строго) р-п севдовыпукла. В частности,
(сильно) 1-псевдовыпуклые функции — это (строго)
плюрисубгармонические функции класса С2. Функция
на аналитич. множестве XcU наз. (сильно) р-выпук-
лой, если она является ограничением сильно р-псевдо-
выпуклой функции на U. Наконец, (сильно) р-выпуклая
функция на произвольном комплексном пространстве
X — это непрерывная функция на X, к-рая в окрест-
окрестности любой точки представляется (сильно) р-выпуклон
функцией в соответствующей локальной модели (см.
Аналитическое пространство).
Комплексное пространство X наз. (р, q)-B ы п у к-
ло-вогнутым, если существуют непрерывная
функция ф : X -»- R и такие d0, с0, где —оо <d0<c0<oo,
что для любых с^с0 и d«:d0 множество
относительно компактно в X, а ф сильно р-выпукла
на Х^, Г|) и сильно д-выпукла на Х^„, -»• Если do=—оо
или р0-=оо, то пространство X наз. сильно р-
и с е в д о в ы п у к л ы м или сильно q-ъ о г н у-
т ы м соответственно. Если же do=co=—оо, то X наз.
р-п о л н ы м.
Примеры. 1) Открытое множество X с гладкой
границей дХ в комплексном многообразии М на.ч.
строго р-п с е в д о в ы п у к л ы м (строго /)-
псевдовогнутым), если всякая точка хо?дХ
обладает окрестностью U, в к-рой существует такая
сильно р-выпуклая функция ф, что X f\U—{x?
?Uiq>(j:)<0} (соответственно Xf\ U= {xg U\<f> (x) >0})-
Всякое строго р-исевдовыпуклое (строго р-псевдово-
гнутое) относительно компактное открытое множество
является сильно р-вынуклым (сильно р-вогнутым) мно-
многообразием. Если нек-рые компоненты границы дХ
удовлетворяют условию р-псевдовыпуклости, а дру-
другие — условию (/-псевдовогнутости, То получаются
примеры (р, д)-выпукло-вогнутых многообразий.
2) Компактные комплексные пространства естествен-
естественно считать О-выпуклыми.
3) Класс 1-полных пространств совпадает с классом
Штейна пространств.
4) Класс сильно 1-выпуклых пространств совпадает
с классом пространств, получающихся из пространсти
Штейна путем собственной модификации в конечном
множестве точек.
5) Пусть X — компактное комплексное многообра-
многообразие размерности п, S— его замкнутое подмногообразие,
тс компоненты к-рого имеют размерность q. Тогда
А'\5 является сильно (</+1)-вогнутым, а если нор-
нормальное расслоение над S положительно — сильно
(в—</)-выпуклым пространством.
6) Если S — замкнутое подмногообразие коразмер-
коразмерности р в многообразии Штейна А", то X\S />-полно.
7) Голоморфное векторное расслоение Е ранга г
над многообразием X наз. р-и оложительным
(}-о трицательным), если на Е существует та-
такая послойная эрмитова метрика h, что функция
X(v)——h(v, v) на Е является сильно (р + г)-выиуклой
(соответственно —у_ является сильно g-выпуклой) вне
нулевого сечения (в случаях р=1 и д=1 получают по-
понятия положительного расслоения и отрицательного
расслоения). Если X компактно, то пространство ^-поло-
^-положительного расслоения Е является сильно (р +^-вог-
+^-вогнутым, а пространство (/-отрицательного расслоения —
сильно g-выпуклым. Пространство голоморфного век-
векторного расслоения над р-полным пространством всегда
/J-ПОЛНО.
Для (р, </)-выпукло-вогнутых пространств доказаны
теоремы о конечномерности и отделимости нек-рых
пространств когомологий со значениями в когерентных
,1Налитич. пучках (см. Конечности теоремы в теории
аналитических пространств). Аналогичные теоремы ко-
конечности доказаны также и для сильно (р, д)-выпукло-
вогнутых отображений (см. [1], [2]). Пространство X
является сильно 1-выпуклым тогда и только тогда,
когда dim W(X, /')<оо для всех г и любого когерент-
когерентного аналитич. пучка f на X. Если X р-п|олно, то
НГ(Х, /') —0 для всех г~^р и любого когерентного ана-
аналитич. пучка F на X.
Группы гомологии /з-выпуклых и р-полных про-
пространств обладают следующими свойствами. Если X
есть n-мерное приведенное сильно р-выпуклор (р-пол-
ное) комплексное пространство, то dim Hr(X, С)<оо
(соответственно НГ(Х, С) = 0) для г~^п-\-р. Для сильно
1-выпуклых пространств известно также, что группы
Hr(X, Z) конечно порождены при г^п-\-1, а для р-
полных многообразий,- - что //Г(Х, /,) 0 для г^ге+р
и что группа ИПгр-\ (X, Г?) свободна.
Комплексное пространство X на.ч. исевдовог-
i у т ы м, если в X существует относительно компакт-
компактное открытое множество U, пересекающее каждую не-
неприводимую компоненту пространства X и удовлетво-
удовлетворяющее следующему условию: любая точка xo?i)U
обладает такой окрестностью V в X, что для любых
точек х? V, достаточно близких к х0,
I / (*) К S»P \Пу)\
vu '
1ля всех голоморфных функций / в V. Если X есть
«мерное многообразие, и^2, то достаточно, чтобы
множество V было сильно (п—1 )-псевдовогнутым в X.
,1юбое компактное пространство псевдовогнуто. Для
нсевдовогнутых пространств X доказаны следующие
георемы конечности: пространство голоморфных сече-
сечений любого голоморфного векторного расслоения над
X конечномерно; если X связно, то все голоморфные
функции на X постоянны; ноле мероморфных функций
на X есть поле алгебраич. функций, степень транс-
трансцендентности к-рого не превосходит dim X. Послед-
Последняя теорема имеет важные приложения к автоморфным
функциям, основанные на том, что пространство D/Г,
где Г — собственно разрывная группа автоморфизмов
ограниченной области D в С", во многих случаях ока-
оказывается псевдовогнутым (в этом случае говорят, что
Г — псевдовогнутая группа). Напр.,
нсевдовогнутыми являются арифметич. подгруппы
групп автоморфизмов ограниченных симметрич. об-
областей.
Лит.: [1] Е rm i n e J. L., «Ann. Sc. norm. sup. Pisa. CA.
sci», 1Я79, v. (i, Л;> 1, p. 1 -IS; [2] Итоги пауки и техники. Алгеб-
Алгебра. Топология. Геометрия, т. 15, М., 1977, с. 93—171.
А. Л. Онищик.
ПСЕВДОГАЛИЛЕЕВО ПРОСТРАНСТВО — проек-
проективное ^-пространство с выделенной бесконечно уда-
удаленной (п — 1)-плоскостью То аффинного ге-пространст-
ва, в к-рой, в свою очередь, выделена бесконечно уда-
удаленная (и—2)-плоскость Тг псевдоевклидова простран-
пространства '/?„_], а в (ге— 2)-плоскости Тг выделена (ге—3)-
квадрик.) Q2, являющаяся абсолютом гиперболического
(п—1)-пространства индекса I. Совокупность плоскос-
плоскостей То, Т1 и квадрики Q2 образует абсолют (базис) П. п.,
обозначаемого гГ„. Напр., 3-пространство 1Т:} имеет
своим абсолютом 2-плоскость То, прямую Тг в То и пару
действительных точек Q% на прямой Tj. П. п. можно
определить как аффинное ^-пространство, в бесконечно
удаленной плоскости к-рого при дополнении до про-
проективного n-пространства определена геометрия псев-
псевдоевклидова (п — 1)-пространства индекса I.
Расстоянии между точками определяется аналогич-
аналогично определению расстояния в галилеевом пространстве.
Движениями 11. п. 1Гп являются его коллинеации,
переводящие абсолют в себя. Движения образуют
группу, являющуюся группой Ли.
Пространство, абсолют к-рого двойствен абсолюту
П. п. 'Гл, наз. копсевдозалилеевим пространством. Фла-
Флаговое пространство — предельный случай П. п. 1Тп.
Лит.: L1] Р о з е н ф с л ь д В. А., Неевклидовы про-
пространства, М., 1969. Л. А. Сидоров.
ПСЕВДОГРУППА преобразований диф-
дифференцируемого многообразия М —
семейство диффеоморфизмов открытых подмножеств
многообразия М в М, замкнутое относительно компо-
композиции отображений, перехода к обратному отображе-
отображению, а также сужения и склейки отображений. Точнее,
псевдогруппа преобразований (п. п.) Г многообразия
М состоит из локальных преобразова-
преобразований, т. е. пар вида p—(Dr>, р), где Dр — открытое
подмножество в М, а р — диффеоморфизм D р -у М,
причем предполагается, что 1) р, q?_ r=^>poq~(q-1 (Dp[\
(]q{Dq)), poq)?r, 2) p?r=>p-i=(p(Dp), р-*)?Г,
3) (M, id)?r, 4) если р —диффеоморфизм открытого
подмножества DcM в М и D— |J aDa, где Da —^откры-
—^открытые подмножества в М, то (D, p)?V ФФ (Da, р1оа)?Г
для любого а. Видоизменяя должным образом усло-
условия 1)— 4), можно определить п. п. произвольного то-
пологич. пространства (см. [7]) или даже произволь-
произвольного множества. Так же, как группа преобразований,
п. п. определяет на М отношение эквивалентности;
классы эквивалентности наз. ее орбитами. П. п. Г
многообразия М низ. транзитивной, если М—
ее единственная орбита, и наз. примитивной,
если в М нет нетривиальных гладких Г-инвариантных
слоений (в противном случае п. п. наз. и м п р и м и-
т и в н о й).
П. п. Г дифференцируемого многообразия М наз.
п. п. Л и, определяемой системой S дифференциаль-
дифференциальных уравнений в частных производных, если Г состоит
из тех и только тех локальных преобразований много-
многообразия М, к-рые удовлетворяют системе S. Напр.,
П. конформных преобразований плоскости — это п. п.
Ли, определяемая уравнениями Коши — Римана. По-
Порядком п. п. Ли наз. минимальный порядок определяю-
определяющей ее системы дифференциальных уравнений.
Примеры п. п. Л и. 1) П. всех голоморфных ло-
локальных преобразований «-мерного комплексного
пространства С". 2) П. всех голоморфных локальных
преобразований пространства С" с постоянным яко-
бианом. 3) П. всех голоморфных локальных преобра-
преобразований пространства С" с якобианом, равным I.
4) Г а м и л ь т о н о в а псевдогруппа, со-
состоящая из всех голоморфных локальных преобразова-
преобразований пространства С" (п четно), сохраняющих дифферен-
дифференциальную 2-форму
</24+ . . . -\-dz"-1Adzn.
5) П. всех голоморфных локальных преобразований
пространства С", сохраняющих форму со с точностью
до постоянного множителя. 6) Контактная
псевдогруппа, состоящая из всех голоморфных
локальных преобразований пространства С" (при
га=2то+1, т.^Х), сохраняющих с точностью до (функ-
(функционального) множителя дифференциальную 1-форму
dz" + 2-" (z! dzm + i — zm + i dz').
7) Вещественные аналоги комплексных п. п. из приме-
примеров 1) — 6). Порядки п. п. Ли из примеров 1), 3) — 6)
раины 1, а в примере 2) порядок равен 2.
Любая группа Ли G преобразований многообразия
М определяет п. и. Г (G), состоящую из ограничений
преобразований из G на открытые подмножества мно-
многообразия М. П. п. вида Г (G) наз. глобализ у е-
м ы м и. Так, П. локальных конформных преобра-
преобразований сферы S" глобализуема при ге>2 и не глобали-
глобализуема при п=2.
П. п. Ли Г наз. п. и. конечного типа, если
найдется такое натуральное число d, что любое локаль-
локальное преобразование р? Г однозначно определяется
своей d-струей в нек-рой точке x?Dp; наименьшее
такое число d наз. степенью, или типом, п. п.
Г; если же такого d не существует, то Г наз. п. п.
бесконечного типа. TI. п. в примерах 1) —
6) — примитивные п. и. Ли бесконечного типа.
Пусть Г — транзитивная п. и. Ли re-мерного диффе-
дифференцируемого многообразия М и С (Г) —совокуп-
—совокупность всех r-струй локальных преобразований из Г,
сохраняющих точку О ?М, т. е. таких р?Г, что U^_Dp
и р(О) = О. Множество С (Г), снабженное естественной
структурой группы Ли, наз. группой изотро-
изотропии г-го порядка п. п. Г (группа Gl (T) наз.
также линейной группой изотропии
п. п. Г). Алгебра Ли йг(Г) группы С (Г) естественным
образом вкладывается в алгебру Ли r-струй векторных
полей на М в точке О. Если Г — п. п. Ли первого
порядка, то ядро Gtr) (Г) естественного гомоморфизма
С + 1 (Г) —>¦ С (Г) при любом г^1 зависит только от
линеппой группы изотропии G1 (Г) и наз. ее r-м н р о-
д о л ж е н и е м. П. п. Ли Г первого порядка тогда
и только тогда является п. п. конечного типа d, когда
dimGC-1>(D ± 0 и dim G<rf> (Г) =0.
Если при этом линейная группа изотропии G1 (Г) не-
приводима, то d<2 (см. [5]). Для того чтобы п. п. Ли I'
первого порядка была п. п. конечного типа, необходи-
необходимо, а в комплексном случае и достаточно, чтобы алгебра
Ли Я1 (Г) не содержала эндоморфизмов ранга 1 (-см.
110]). Такие линейные алгебры Ли наз. эллипти-
эллиптическими.
Для п. п. Ли Г первого порядка в терминах ее ли-
линейной алгебры изотропии вычислены алгебры Ли всех
продолжений Gir)(r), т^1. А именно, алгебра Ли
ct<r) (Г) группы G<r)(r) состоит из (г+1)-струй вектор-
векторных полей на М в точке О, имеющих в нек-рой локаль-
локальной системе координат (х1, х2, . . ., хп) вид
?4 Hii ... lr Эх'
где v\^ ir — произвольный тензор, симметричный по
нижним индексам и удовлетворяющий условию: при
любых фиксированных /lt l2, . . ., ir матрица
ir/, и, i- ir\i, /=1. 2, ••-. п
содержится в алгебре Ли 91(Г), отнесенной к системе
координат (х!).
Пусть М — re-мерное дифференцируемое многообра-
многообразие над полем К=& или С. Всякая транзитивная п. п.
Ли Г порядка к многообразия М совпадает с П. всех
локальных автоморфизмов нек-рой Gk (Г)-структуры
(см. G-структура) порядка к на М (первая ос-
основная теорема Карта на). Классифика-
Классификация всех примитивных п. п. Ли бесконечного типа
впервые была получена Э. Картаном [2]. Согласно его
теореме всякая примитивная п. п. Ли бесконечного
типа, состоящая из голоморфных локальных преобра-
преобразований, локально изоморфна одной из п. п. примеров
1)—6). Эта теорема неоднократно передоказывалась; ее
современные доказательства получаются чисто алге-
браич. средствами. При этом локальное изучение тран-
транзитивной п. п. Ли Г сводится к изучению нек-рой фильт-
фильтрованной алгебры Ли (см. [9]). Классификация таких
фильтрованных алгебр Ли может быть проведена на
основе классификации простых градуированных ал-
алгебр Ли (см. [3]). Классификация примитивных п. п.
Ли получена также и в вещественном случае, причем
условие аналитичности действия п. п. заменено более
слабым условием бесконечной дифференцируемое™
(см. [81, [9]).
1 Гостроены нек-рые абстрактные модели транзитивных
п. п. Ли, к-рые призваны играть в теории п. п. беско-
бесконечного типа такую же роль, какую в конечномерном
случае играют абстрактные группы Ли (см. [6], [9]).
Лит.: [ЦСтернберг С, Лекции по дифференциальной
геометрии, пер. с англ., М., 1970: 12] Car ta n Ё., Oeuvres
completes, v. 2, P., 1953, p. 571 -714 857—925; 1335 — 84; Ы
G u i 1 1 e m i n V., «J. Diff. Gcora.», 1970, v. 4, .Ni 3, p. 257—82:
[4] Kobayashi S., Transformation groups in differential
geometry. В.— [u. a.], 1972; [5] Kobayashi S., N a g a-
n о Т., «J. Math, and Mech.», 1964, v. 13 .No'5, p. 875 — 907; 1965,
v. 14 p. 679—706; [6] К u r a n i s h 1 M.. «Nagoya Math. J.»,
1959, v. 15, p. 225—60; 1961, v. 19, p. 55 —91; [7] Liber-
m a n n P., «Bull. Soc. math. France», 1959, t. 87, ,\» 4, p. 409—25:
18] S h n i d e r S., «J. Diff. Geom.», 1970, v. 4, Л« 1, p. 81—89;
[9] Singer I. M., Sternberg S., «J. d'Analyse math.»,
1965, t. 15, p. 1 114; [10] W i 1 so n R. L., «Prnc. Amer. Math.
Soc», 1971, v. 29 ,N« 2, p. 243—49. 9. Б. Винберг.
ПСЕВДОГРУППОВАЯ СТРУКТУРА на мно-
многообразии М — максимальный атлас А глад-
гладких локальных диффеоморфизмов многообразия М на
фиксированное многообразие V, все функции перехода
между к-рыми принадлежат данной псевдогруппе 1'
локальных преобразований многообразия V. Псевдо-
Псевдогруппа Г на:). определяющей псевдо-
псевдогруппой, а многообразие V — модельным про-
пространством. П. с. с определяющей псевдогруппой Г наи.
также Г-с труктурой. Более подробно, множество
А F-значных карт многообразия М (т. е. диффеомор-
диффеоморфизмов ф : U —>- V открытых подмножеств UczM на
открытые подмножества q>(U)c:V) называется П. с.
если а) любая точка х?М принадлежит области
определения нек-рой карты ф из А; б) для любыл
карт ф : U -v V, т|з : W -*¦ V на А функция перехода
фоф-1 : ф (t/fl W) —>- \р (U[) W) является локальным
преобразованием данной псевдогруппы Г; в) множество
А является максимальным множеством карт, удовле-
удовлетворяющих условию 2).
Примеры П. с. 1) Псевдогруппа Г преобразова-
преобразований многообразия V задает П. с. (V, Г) на V, картами
к-рой служат локальные преобразования из Г. Она
наз. стандартной плоской Г-струк-
турод. 2) Пусть V=Kn есть n-векторное пространст-
пространство над K=R, С или левый модуль над телом кватернио-
кватернионов К—Н, а Г — псевдогруппа локальных преобра-
преобразований V, главные линейные части к-рых принадлежат
группе GL(n, К). Соответствующая Г-структура на
многообразии М есть структура гладкого многообразия
при K=R, комплексного аналитич. многообразия при
К—С и специального кватерпиоиного многообразия
при К=Н. 3) Пусть Г — псевдогруппа локальных
преобразований векторного пространства V, сохра-
сохраняющих данный тензор 5. Задание Г-структурьт равно-
равносильно заданию интегрируемого поля тензоров типа
S на многообразии М. Напр., рели S — невырожден-
невырожденная кососимметричная 2-форма, то Г-структура есть
симплектич. структура. 4) Пусть Г — псевдогруппа
локальных преобразований пространства R2n + 1, со-
сохраняющих с точностью до функционального множи-
множителя дифференциальную 1-форму
Тогда Г-структура есть контактная структура. 5) Пусть
V—G/H — однородное пространство группы Ли G, а
Г — псевдогрупп» локальных преобразований V, про-
продолжающихся до преобразований из группы G. Тогда
Г-структура наз. П. с, определяемой однородным
пространством V. Примерами таких структур являются
структура пространства иостояшюй кривизны (в част-
частности, локально евклидова пространства), плоские
конформные и проективные структуры.
Пусть Г — транзитивная псевдогруппа Ли преобра-
преобразований пространства V~Rn порядка I; Г-структура
А на многообразии М определяет главное подрасслое-
ние я/j : В1г —>- М расслоения кореперов любого поряд-
порядка к на М, состоящее из Zc-струн карт из Л:
Структурной группой расслоения яд. является группа
изотропии А-го порядка Gk (Г) псевдогруппы Г, к-рая
действует на Вк по формуле
& (a) jx4 = /* (а о <р).
Расслоение я^ наз. к-м структурным рас-
расслоением или Gk (Г)-с т р у к т у р о й, опреде-
определяемой П. с. А. Расслоение л(, где I — порядок псев-
псевдогруппы Г, в свою очередь, однозначно определяет
П. с. А как множество карт ф : U -у V, для к-рых
]х(а °ф)?#'> если а?Г, аоф(ж) = 0.
Геометрия расслоения л^ характеризуется наличием
канонической Gfc (Г)-эквивариаптной горизонтальной
относительно проекции Вк -^- Бк~х 1-формы 9* : ТВк —*.
—»-У+д*(Г) со значением в пространстве Т"-гЙ*(П,
где д*(Г) — алгебра Ли группы изотропии С*(Г).
Она задается формулой
где
<pt(xt)=0, t?[0, e],
и удовлетворяет нек-рому структурному уравнению
Маурера — Картана. Алгебра Ли инфинитезимальных
автоморфизмов Г-структуры может быть охарактери-
охарактеризована как алгебра Ли векторных полей на В1, сохра-
сохраняющих каноническую 1-форму в'.
Основной проблемой теории 11. с. является проблема
описания П. с. на многообразии с определяющей псев-
псевдогруппой Г с точностью до аквивалентности. Две П. с.
на многообразии наз. эквивалентными, если
одна из них может быть переведена в другую диффео-
диффеоморфизмом многообразия.
Пусть Г — глобализуемая транзитивная псевдогруп-
псевдогруппа преобразований односвязного многообразия V. Лю-
бое односвязное многообразие М с Г-структурой А
допускает отображение р : М —у V, называемое раз-
разверткой Картана, к-рое локально является изомор-
изоморфизмом Г-структур. Если Г-структура А обладает
нек-рым условием полноты, в частности, если многооб-
многообразие М компактно, то отображение р является изо-
изоморфизмом Г-структур и все Г-структуры рассматривае-
рассматриваемого типа являются формами стандартной Г-структуры
V, т. е. получаются из V факторизацией по свободно
действующей дискретной группе автоморфизмов (Г, Г).
Так обстоит дело, напр., с (псевдо)римановыми струк-
структурами постоянной кривизны и с конформно плоскими
структурами на компактных многообразиях Мп, и>2.
Важное место в теории П. с. занимает теория деформа-
деформаций, пергюначалыто развитая для комплексной струк-
структуры. В ней изучается вопрос об описании нетривиаль-
нетривиальных деформаций Г-структуры А, т.е. семейств Af
Г-структур, содержащих данную Г-структуру и гладко
зависящих от параметров t по модулю тривиальных
деформаций. Пространство формальных инфинитези-
мальных нетривиальных деформаций данной Г-струк-
Г-структуры описывается как пространство Н1 (М, Q) одно-
одномерных когомологий многообразия М с коэффициента-
коэффициентами в пучке ростков в инфинитезимальных автомор-
автоморфизмов Г-структуры А . Тривиальность этого простран-
пространства влечет жесткость Г-структуры. Тривиальность
двумерных когомологий: II2 (М, в) —0 позволяет при
нек-рых условиях доказать существование нетривиаль-
нетривиальных деформаций Г-структуры, соответствующих данной
инфшштезимальнок деформации из IIх (Л/, в).
Лит.: [)] К а р т и гт О., Геометрия римановмх пространств,
пер. с франц., М.— Д., 1930; 12] (iuillcmin V., Stern-
h о г g S , Deformation theory of pseudogroup structures, Provi-
Providence, 19B0 («Mem. Amer. Math. Soc», .№ «/«); l:s] P о 11 а с k A. S.,
«J. Diff. Geom.», 1974, v. 9, №3, p. :ift!i_9ft; [4] Grif-
Griffith s P. A., «Math. Ann.», 1904, Bd 155, H. 4, S. 292 — 315;
1905, Bd 158, H. 5, S. 326 — 351; [5] P о m m a r e t J. F., «Ann.
Inst. H. Poincare, n. Ser.», 1973, v. 18, p. 285—352; [С] В е г а г d
BergpryL., Boursuignon J. P., Lafontaine J.,
«Proc. Syrfip. Pure Math.», 1975, v. 27, p. 3—32; [7] S p e ri-
rice r D. C, «Ann. Math.», 1902, v. 76, Kt 2, p. 306—398; .Ns 3,
p. 399—A45. Д. Б. Алексеевский.
ПСЕВДОДИФФЕРЕНЦИАЛЫ1ЫЙ ОПЕРАТОР —
оператор, действующий в функциональных пространст-
пространствах на дифференцируемом многообразии и локально
по определенным правилам записываемый с помощью
нек-рон функции, обмчно наз. символом П. о., и удов-
удовлетворяющей оценкам производных определенного ти-
типа, аналогичных оценкам производных полиномов,
являющихся символами дифференциальных операторов.
Пусть Q — открытое подмножество в R", С'(Г (Й) —
пространство бесконечно дифференцируемых функций
с компактным носителем, принадлежащим Q. Простей-
Простейший П. о. в О — это оператор Р : СГ (Q) -»- С" (О),
задаваемый формулой
Ри (х) = Bл)-" ^ eis^p (x, 1) u(l)dl, A)
где m?C"(Q), ??R , d\ — мера Лебега на R", x-\ —
обычное скалярное произведение векторов х и ?, и (|) —
преобразование Фурье функции и, то есть
u(l)='\)e~ix^u(x)dx
(интеграл здесь и выше берется по R"), р (х.Ъ,) — глад-
гладкая функция на QX R™, удовлетворяющая нек-рым
условиям и называемая символом П. о. Р. Опе-
Оператор Р вида A) обозначается также р (х, D) или
р(х, Dx). Если
— многочлен от | с коэффициентами ра 6 С°
(здесь а — мультииндекс, т.е. а=(ах, . . ., а„), ау
о^ —целые, |a|=a, + . . .+а„, ga^|"' ...?""), то
p(x, D) совпадает с дифференциальным оператором,
получаемым, если в выражение для р (.г, |) вместо с;
подставить вектор D= —-^ ¦
Часто используется класс символов р (х, |)?C°°(QX
XR"), удовлетворяющих условиям
I 0* $р (х, |) | < С в - A + | | \)т-р (а) + б «Ч B)
где а, 6 — мультииндексы, 9,— -г— , д% — -гг-,
5?"— компакт в Q. Этот класс обозначается ¦?'? б (или
¦<?? s(QXR»)).
Обычно предполагается, что 0<р<1, 0<8<1. Через
Lp' а (или Lp, б (й)) обозначается класс операторов
(также называемых П. о. в Q) вида р(х, D)-\-K, где
p^S'p, б, а К — интегральный оператор с бесконечно
дифференцируемым ядром, т. е. оператор вида
Ки(х)=^К(х, у) и (у) dy,
где К(х, у)?С°° (QXfi). Функцию р(х, |) по-прежнему
наз. символом П. о. р (х, D)-t-K, хотя теперь она опре-
определена уже не однозначно, а с точностью до символов,
принадлежащих 5-°°= f) maRS"', о- Оператор A ?L™t g
наз. П. о. порядка не вышет итипар, S.
Описанный выше дифференциальный оператор принад-
принадлежит классу Lilo. Наименьшее возможное значение т
часто наз. порядком П. о. Классы S™, &, L™ (,
часто наз. классами Хёрмандера.
Можно задавать П. о. в Q с помощью двойных сим-
символов, т. е. в виде
Ри= Bп)-" [^ е{<х-У)*а(х, у, I) и (у) dyd\. C)
При а(х, у, ?)=?> (х, |) эта формула переходит в A). •
Обычно предполагается, что а(х, у, D^^p! б (QXQX
X R"), то есть
| д\ dl'dfa (х, у, |
a,P,p,* D)
где Ж — компакт в О. Если 0<:б<р<1, то построен-
построенный класс операторов вида C) (со всевозможными
функциями ag5™ б) совпадает с классом L™ б (О). При
этом символ р (х, ?) (определенный с точностью до
символов из S~°°) имеет следующее асимптотич. раз-
разложение:
где a!=aj! . . . а„! и суммирование ведется по всем
мультииндексам. Эта запись означает, что разность
между р (х, g) и частью суммы, взятой но тем а, для
к-рых |а| <:iV, является символом, принадлежащим
S'p,^' , т. е. символом, порядок к-рого не выше наи-
наибольшего из порядков оставшихся членов.
П. о. Р продолжается по непрерывности или с помо-
помощью двойственности до оператора Р : $' (ii)-^t-D' (Q),
где D' (Q) и $' (Q) — пространства обобщенных
функций и обобщенных функций с компактным носи-
носителем в Q соответственно. Если б<1, то при этом П. о.
обладает следующим свойством псевдолокаль-
псевдолокальности: если u?t§' (Q) ПС°° (?}'), где Q'cfi, то
Ри?С°° (О')- Другая формулировка свойства псевдо-
псевдолокальности: ядро К (х, у) (в смысле Шварца) операто-
оператора Р бесконечно дифференцируемо по х, у при хфу.
Классический П. о. порядка т в Q — П. о.
"о, символ к-рого р(х, |) допускает асимптотич.
разложение
p(:r, l)~^=oyJl)Pm-j(.r, I),
где xF)GC»(R»), XF)=l при |?|>1, xF) = 0 прь
|||<1/2, рт-/(х, I) ? С" (Q X (К"\0)) и положительно
однородна по | порядка т—;
Примером классического П. о. является дифференци-
дифференциальный оператор (с гладкими коэффициентами). Функ-
Функция рт (х, |) наз. главным символом клас-
классического И.о.
И. о. в И наз. собственным (или П. о. с
собственным носителем, или П. о. с
компактным носителем), если проекции
носителя его ядра при проектировании ЙХЙ на каж-
каждый сомножитель являются собственными отображе-
отображениями. Собственный П. о. Р отображает С" (Q) в
6'о° (Q) и продолжается по непрерывности до отображе-
отображений C°°(Q)^ C~(Q), <g'(Q) -+<g'(Q) и D' (Q)-rD' (Q),
он может быть записан в виде A) с символом р(х, %)=
=e~ix'^P (е'ж'^), где экспонента в скобках рассматри-
рассматривается как функция от х, а ? является параметром.
Пусть А, В — два П. о. в Q, из к-рых один является
собственным. Тогда имеет смысл их произведение (ком-
(композиция) С=АВ. Важную роль в теории П. о. играет
теорема о композиции: если А ? L™' 6 ,
B?L™>6, О«б«р<1, то C=AB€L™'+6m>. Если при
этом 6<р, с(х, |), а (х, |), Ъ(х, |) — символы операто-
операторов С, А, В, то
с (х, g) - Stt ^T [3f a (x, I)] [Oaxb (х, 6)].
В частности, если А, В — классические П. о. поряд-
порядков тл, т2, то С — классический П. о. порядка тх-\-т^
с главным символом с„,1 + т^(х, l)—-am, (x, i)bmi{x, |),
где ami (х, 5), 6Й1 (г, I) — главные символы операторов
А и И.
Если P?L™t а, 0<:8<:р<:1, то существует и единствен
сопряженный И.о. P*G^p! 6> Для к-рого
(Ри, v)={u, P*v), и, у?С0°°(Й), где (и, v)—^u(xO{x)dx —
скалярное произведение и к v в L2(Q). Если при этом
8<р и р* (х, Ъ,) — символ П. о. Р*, яр(х, |) — символ
Р, то
Таким образом, собственные П. о. при 8<р образуют
алгебру с инволюцией, задаваемой переходом к сопря-
сопряженному оператору. Произвольные П. о. образуют
модуль над этой алгеброй.
Теорема об ограниченности П. о.
классов Хёрмандера в Z2~H°PMax B наиболее точной
форме состоит в следующем (см. [8]): пусть il=R",
оператор Р имеет вид C) с двойным символом а (х, у, %),
удовлетворяющим оценкам D), где числа т, р, 6 удов-
удовлетворяют условиям
0<р<1, 0<6< 1, т<0, р — S— ^-5гО; E)
тогда оператор Р продолжается до ограниченного опе-
оператора Р : L2(Rn) -> L2(R"). В частности, при усло-
условии E) ограничены в L2 (Rn) П. о. вида A) с символами,
удовлетворяющими оценкам B) равномерно по х (т. е.
с постоянными С а, $,Х=Са, 0, не зависящими от SK).
Отсюда следует, напр., ограниченность в L2(Rn) опе-
операторов Р?1-р,б, если 0<6<:р<1 и ядро оператора Р
имеет компактный носитель (или оценки символа опять-
тмки равномерны по х). При р<б или при 6—1 опера-
операторы такого вида уже но обязательно ограничены. Ана-
Аналогично, в общей ситуации невыполнение одного из
двух последних условий E) уже дает класс II. о., со-
содержащий неограниченные операторы.
В терминах оценок символа можно дать условия ог-
ограниченности П. о. в L^-нормах, а также в гёльдеровых
и в жевреевских нормах (см. [8]).
Если в Rn дан оператор Р=р(х, D), где P?S™r а,
0<6<р<:1, причем оценки B) равномерны по х? R", то
этот оператор продолжается до ограниченного оператора
Р : IIs{К") ->- Hs-m(RnI s?R, где #f(R") означает
обычное пространство Соболева на R" (иногда обозна-
обозначаемое также wi(R")).
Класс П. о. i™ 6 при 1—р<6<р<1 в естественном
смысле инвариантен относительно диффеоморфизмов
так же, как и его подкласс классических П. о. Это
позволяет определить класс П. о. L™y g (X) и классиче-
классические П. о. на произвольном гладком многообразии
Л". Формула замены переменной в символе при диффео-
диффеоморфизме и : Q —>- Qx, где Q, Qj — области в X, имеет
вил
ai(у, 4)\y=*ix)~Yiaha{^a){xi> и'
где а (г, %) — символ оператора А ? Lp1, a (Q), at (у, ц) —
символ оператора A1^L!pt e (Qi), заданного формулой
.1,и = [Л (мои^ои, т. е. полученного из А заменой
переменных х; и' (х) обозначает якобиан отображения
х, V(x) — транспонированная матрица,
а(а) (х,1)=.д?а(х, 1),х"х{г)=у.{г) — х(х) — -л' (х) (z—x).
В частности, отсюда следует, что главный символ клас-
классического П. о. на многообразии X является коррект-
корректно определенной функцией на кокасательном расслое-
расслоении Т*Х.
Если X — компактное многообразие (без края), то
П. о. на X образуют алгебру с инволюцией, если вво-
вводить инволюцию с помощью скалярного произведения,
задаваемого гладкой положительной плотностью. Опе-
Оператор A?Ll? б(Х) ограничен в L2(X), а если А?
?L™ б{Х), где т<0, то такой П. о. компактен в L2(X).
Для классических П. о. А порядка 0 на X
sup |о„(.г, Е)|,
( |Г*Х
где а0 (х, |) — главный символ оператора А, а. К про-
пробегает множество всех компактных операторов в L2 (X).
Оператор A?L™s(X) непрерывно отображает НХ(Х)
в Hs-"> (X) при'любом s?R.
Параметриксом П. о. А наз. такой П. о. В,
что /—АВ и /—ВА — П. о. порядка —оо, т. е. интег-
интегральные операторы с гладким ядром. Пусть А ? I™, б№),
0<:6<р<:1, a (x, |) — символ оператора А. Доста-
Достаточным условием существования параметрикса oirepa-
тора А является выполнение оценок:
\а(х. I) | S& Е | % |»о, ЩЗйЯ, Е>0, ')
В этом случае существует параметрикс В ? Av~™° (Q).
Простейшим следствием существования параметрикса
является гипоэллиптичность оператора А: если iitg
^C°°(Q'), где Q'dH, то и?С°° (Q'). Иными словами,
sing supp Au~sing supp и. Верен также следующий
более точный факт (теорема регулярно-
регулярности): если Ли?Я)ОС@'),тои?#|+сто@')- Имеет место
и микролокальная теорема регулярности: WF(Аи)—
= WF (и), где WF (и) означает волновой фронт обобщен-
обобщенной функции и.
Условия F) при 1—р<6<р<1 инвариантны отно-
относительно диффеоморфизмов. Поэтому имеет смысл со-
соответствующий класс операторов на многообразии X.
Если X — компактное многообразие, то такой опера-
оператор А фредгольмов в С°° (X), т. е. имеет в С°° (X) конеч-
конечномерные ядро и коядро, а также замкнутый образ.
Классический П. о. А порядка т с главным символом
ат (х, |) наз. эллиптическим, если ат (х, |)^0
при 1^0. Такой оператор удовлетворяет условиям
F) с то=т и имеет параметрикс, также являющийся
классическим П. о. порядка — т. На компактном мно-
многообразии X такой П. о. задает фредгольмов оператор
A:Hs (X) —+ Hs~m (X), s?R.
Все эти определения и факты переносятся на П. о.,
действующие в вектор-функциях или, более общо, в
сечениях векторных расслоений. Для эллиптич. опера-
оператора на компактном многообразии X индекс задавае-
задаваемого им отображения А : Hs (X) —»- Hs~m(X) на собо-
левских классах сечений не зависит от s?R и может
быть явно вычислен (см. Индекса формулы).
Роль П. о. состоит в том, что имеется ряд операций,
выводящих за класс дифференциальных операторов, но
сохраняющих класс П. о. Напр., резольвента и комп-
комплексные степени эллиптического дифференциального
оператора на компактном многообразии являются клас-
классическими П. о., они возникают при сведении на гра-
границу эллиптической граничной задачи (см., напр., 17],
[8] и предпоследнюю статью в [1]).
Существуют разные варианты теории П. о., приспо-
приспособленные к решению различных задач анализа и ма-
тематич. физики. Часто возникают П. о. с параметром,
необходимые, напр., для изучения резольвенты и асимп-
асимптотики собственных значений. Важную роль играют
различные варианты теории П. о. на R", учитывающие
эффекты, связанные с описанием поведения функции на
бесконечности, и частично инспирированные матема-
тич. вопросами квантовой механики, возникающими
при изучении квантования классич. систем (см. [5], [1]).
В теории локальной разрешимости уравнений с част-
частными производными и в спектральной теории полезны
П. о., поведение к-рых описывается с помощью весовых
функций, заменяющих \\\ в оценках типа B) (см. [8],
[14]). Построена алгебра П. о. на многообразии с краем,
содержащая, в частности, параметрикс эллиптической
граничной задачи (см. [3], [13]).
Частным случаем П. о. являются многомерные син-
сингулярные интегральные и интегро-дифференциальные
операторы, изучение которых подготовило появление
теории П. о. (см. [10]).
Теория П. о. служит основой для изучения интеграль-
интегральных операторов Фурье (см. [7], [10]), играющих ту же
роль в теории гиперболич. уравнений, что и П. о. в те-
теории эллиптич. уравнений.
Лит.: [Ц Псевдодифференциальные операторы, пер. с
англ., М., 1967; [2] Агранович М. С, В и ш и к М. И.,
Лсендодифференциальные операторы, М., 1968; 13]ЭскинГ. И.,
Краевые задачи для эллиптических псевдодифференциальных
уравнений, М., 1973; [4] Грушин В. В., Псевдодифференци-
Псевдодифференциальные операторы, М.. 1975; [5] III у б и н М. А., Псевдодиффе-
Псевдодифференциальные операторы и спектральная теория, М., 1978; [6]
Friedrichs К. О., Pseudo-differential operators, N. Y.,
1970; |7] Treves F., Introduction to pseudo-differential
and Fourier integral operators, v. 1—2, N. Y., 1980; 18] T a y-
1 о г M., Pseudo-differential operators, В.— lu. a.j, 1974;
[9] Kumano-go H., Pseudo-differential operators, Camb.,
1981; [10] Duistermaat J., Fourier integral operators,
N. Y., 1973; [И] М а с л о в В. П., Ф е д о р ю к М. В., Квази-
Квазиклассическое приближение для уравнении квантовой механики,
М., 1976; [12] Агранович М. С, «Успехи матем. наук»,
1965, т. 20, в. ft, с. 3—120; 113] Boutet de MonvelL.,
«Acta math.», 1971, v. 126, p. 11—51; 114] HGrmanderL.,
«Gomm. Pure Appl. Math.», 1979, v. 32, JV« 3, p. 359—443.
M. А. Шубин.
ПСЕВДОДУГА — наследственно неразложимый со-
держаицш более одной точки змеевидный континуум.
Таков, напр., Кнастера континуум, м. И. войцеховспий.
ПСЕВДОЕВКЛИДОВО ПРОСТРАНСТВО — действи-
действительное аффинное пространство, в к-ром каждым двум
векторам а и Ь поставлено в соответствие определенное
число, называемое скалярным произведе-
произведением (а, Ь).
1) Скалярное произведение коммутативно:
(а, Ь) = (Ь, «)•;
2) скалярное произведение дистрибутивно относи-
относительно сложения векторов:
(а(Ь + с)) = (а, Ь) + (а, с);
3) числовой множитель можно вынести за знак ска-
скалярного произведения:
(fea, &)=fc (a, b);
4) существуют такие п векторов а,-, что
(ас, ас) > 0, с < I; (ad, а4) < 0, d > I;
(я,-, ау)=О, 1Ф1-
Число п наз. размерностью П. п., 2 — индексом,
пара чисел (I, р), р=п—/, — сигнатурой. П. п.
обозначается Еа р) (или 1Еп). Пространство Еа<3) нау.
Минковского пространством. В пространстве Ец, р) во
всякой системе п векторов bh для к-рых F,-, 6,)т=0 п
F,-, 6у)=0 при i-ф), число векторов Ьь для к-рых F,-,
6,-)>0, равно I, а число векторов 6,-, для к-рых (б,-,
l>i)<0, равно д—I (закон инерции квадра-
квадратичной формы).
М о д у л ь \а\ вектора а П. п. может быть определен
как неотрицательный корень ]^|(й, а)\. Векторы, ска-
скалярные квадраты к-рых равны 1 и —1, наз. соответст-
соответственно единичными и мнимоединич-
н ы м и векторами. Векторы ж, для к-рых
(а-, ж) = 0, обладают нулевым модулем и наз. изо-
изотропными векторами; направления изо-
изотропных векторов — изотропными направ-
направлениям и.
В П. п. имеются три вида прямых: евклидовы, на-
направляющий вектор к-рых имеет положительный ска-
скалярный квадрат ((», «)>0), псевдоевклидовы (а, »)<0)
и изотропные ((а, а)=0). Совокупность всех изотроп-
изотропных прямых, проходящих через нек-рую точку, наз.
изотропным конусом.
В П. п. имеется несколько видов плоскостей: евкли-
евклидовы плоскости Е2, псевдоевклидовы плоскости Е^. ^
и плоскости, содержащие изотропные векторы,— т. н.
полуевклидовы плоскости сигнатуры @,1) и A,0) и
дефекта 1 (см. Полуевклидово пространство) и изотроп-
изотропные плоскости, все векторы к-рых изотропны.
За расстояние между точками А (ж) и В (ж) принима-
принимается модуль вектора А В, и оно может быть вычислено
следующим образом:
1в* = \у-х\* = \(у-х), (у-ж)\.
П. п. не является метрич. пространством, т. к. в нем
не выполняется неравенство треугольника. Если век-
векторы а и Ь принадлежат евклидовой плоскости (или
псевдоевклидовой плоскости индекса 0), то для них вы-
выполняется неравенство треугольника, а если они при-
принадлежат псевдоевклидовой плоскости индекса 1, то
для них выполняется т. н. обратное неравенство тре-
треугольника:
В П. п. имеются три вида сфер: сферы с положитель-
положительным квадратом радиуса: (х, ж)=р3, сферы с отрицатель-
отрицательным квадратом радиуса: (ас, ас)=— о2 и сферы нулевого
радиуса: (ж, х)=0, совпадающие с изотропным конусом.
Д в и ж е н и я П. п. являются аффинными преобра-
преобразованиями и могут быть записаны в виде
х' = Ujp-\-u.
Оператор С" удовлетворяет условию |17а;1=|х|, т.е.
сохраняет расстояние между точками. Движения П. и.
образуют группу по умножению; она зависит от
п (ге+1)/2 независимых параметров. Движения П. п.
наз. движениями 1-го или 2-го рода, если они являются
аффинными преобразованиями соответствующего рода.
Антидвижением П. п. называют геометрич.
преобразование, при к-ром всякий вектор а переходит
в вектор а' такой, что (а, а)——(«.', а').
В П. п. можно ввести основные операции векторной
и тензорной алгебры. Основные дифференциально-гео-
метрич. понятия строятся в соответствии с правилами
геометрии псевдоримановы'с пространств. Метрич. тен-
тензор П. п. имеет вид (в галнлеевой системе координат)
1
О
О
—1
П. п. является плоским, т. е. его Римана тензор равен
нулю. Если тензор Римана псевдориманова пространст-
пространства равен нулю тождественно, то оно является л о-
каль но псевдоевклидовым прост-
пространством.
Подмногообразия П. п. могут нести различные мет-
метрики: положительно или отрицательно определенную
риманову метрику, псевдориманову метрику и вы-
вырожденную метрику (см. Индефинитная метрика).
Так, напр., сферы П. п. несут (вообще говоря, индефи-
индефинитную) метрику постоянной кривизны. В Еа< „_d
сфера с положительным квадратом радиуса является
(п—1)-мерным пространством, изометричным простран-
пространству Лобачевского.
П. п. EUp) (l-\-p=n) и евклидово пространство Е"
можно рассматривать как подпространства комплекс-
комплексного пространства с формой ds2=^i=ldz}. Если х1 —
координаты П. п., у/—действительного евклидова
пространства, zJ — комплексного евклидова простран-
пространства, то уравнения подпространств имеют вид
^' = Re z', 0 < / < I; х1—\ш z>, I < 7 < п, у} = Re zL
Метрику П. п. можно формально получить из метрики
евклидова пространства заменой xf-~iyJ, ^</<д.
Лит.: [1] Е ф и м о в Н. В., Р о з е н д о р н Э. Р., Линей-
Линейная алгебра и многомерная геометрия, М., 1970; [2] Розен-
фельд Б. А., Многомерные пространства, М., 1966; [3] Л а ве-
веда у Л, Д., Л и ф ш и ц Е. М., Теория поля, 6 изд. М., 1973.
ПСЕВДОКОМПАКТНОЕ ПРОСТРАНСТВО ^впол-
^вполне регулярное пространство X такое, что всякая дей-
действительная функция, определенная и непрерывная
на X, ограничена. В классе нормальных пространств
объемы понятий счетной компактности и псевдоком-
псевдокомпактности СОВПадаЮТ. М. Я. Войце.ховский.
ПСЕВДОКОНФОРМНОЕ ОТОБРАЖЕНИЕ — биголп-
морфное отображение области D пространства С" на
область D'czC" при ге>1. Название связано с тем,
что при ге>1 это отображение не является, вообще гово-
говоря, конформным отображением. Е. д. Соломенцев.
ПСЕВДОМЕТРИКА на множестве А' —
неотрицательная действительная функция р, определен-
определенная на множестве всех пар элементов множества X
(т. р. на А'Х X) и подчиненная следующим трем ограни-
ограничениям, наз. а к с и о м а м и п с е и д о м е т р н-
ки: а) если х=у, то р(х, у) — 0; и) р(.т, у)=р(у, х);
в) рх, z)<p(z, г/Lр(г/, г), где х, у, z — любые элемен-
элементы множества X.
Не требуется, чтобы из р(х, г/) = 0 следовало, что х=
=у. По псевдометрике р на множестве X определяется
топология на X: точка х принадлежит замыканию мно-
множества АаХ, если р(,г, Л)—0, где
р(х, /4) = inf {р(х, у):у?А).
Эта топология вполне регулярна, но не обязательно
хаусдорфова: одноточечные множества могут быть не-
незамкнуты. Каждая вполне регулярная топология мо-
может быть задана семейством П. как структурное объе-
объединение отвечающих этим П. топологий. Аналогично,
семейства П. могут служить для определения, описания
и исследования равномерных структур.
Лит.: [1] Келли Дж., Общая топология, пер. с англ.,
2 изд., М., 1981. А. В. Архангельский.
ПСЕВДОМЕТРИЧЕСКОЕ ПРОСТРАНСТВО — мно-
множество X, наделенное псевдометрикой. Каждое П. м.
нормально и удовлетворяет первой аксиоме счетности.
Вторая аксиома счетности выполняется в том и только
в том случае, когда X — сепарабельное пространство.
М. И. Войцеховский.
ПСЕВДОМНОГООБРАЗИЕ «-мерное замк-
замкнутое (соответственно, с краем) — конечное сим-
шшциальное разбиение со следующими свойствами.
а) Неразветвленность: каждый (п—1)-мер-
ный симплекс является гранью ровно двух (соответст-
(соответственно, одного или двух) и-мерных симплексов; б) с и л ь-
ная связность: любые два re-мерных симплекса
можно соединить «цепочкой» «-мерных симплексов, в
к-рой каждые два соседние симплекса имеют общую
(п—1)-мерную грань; в) размерностная од-
однородность: каждый симплекс является гранью
нек-рого n-мерного симплекса. Если нек-рая триангу-
триангуляция тогюлогич. пространства является П., то и лю-
любая его триангуляция является П., поэтому можно
говорить о свойстве топологич. пространства быть (или
не быть) П.
Примеры П.: триангулируемые связные компактные
гомологич. многообразия над ж; комплексные алгебра-
ич. многообразия (даже с особенностями); Тома прост-
пространства векторных расслоений над триангулируемыми
компактными многообразиями. Наглядно П. можно
считать комбинаторной реализацией общей идеи мно-
многообразия с особенностями, образующими множество
коразмерности два. Для П. имеют смысл понятия ориен-
ориентируемости, ориентации и степени отображения, при-
причем при комбинаторном подходе П. образуют естествен-
естественную область определения этих понятий (тем более что
формально определение П. проще, чем определение ком-
комбинаторного многообразия). Циклы в многообразиях
можно в нек-ром смысле реализовать посредством П.
(см. Стинрода задача).
Лит.: [1]ЗейфертГ.,ТрельфалльВ., Топология,
пер. с нем., М,— Л., 1938; |2] Спеньер 9., Алгебраическая
топология пер. с англ., М., 1971. Д. В. Аносов.
ПСЕВДОНОРМИРОВАНИЕ — обобщение понятия
мультипликативного нормирования, заключающееся в
ослаблении одной из аксиом: вместо условия w (а, Ъ)~
—w(а) ю(Ъ) требуется только w(a, b)<w(a) w(b). При-
Пример П.: в кольце всех непрерывных действительных
функций/(.т), определенных на отрезке [0,1], П., не
являющееся нормированием, определяется формулой
G) = шах ! / (х) |.
дге [0, 1]
Всякая действительная конечномерная алгебра может
быть псевдонормирована.
Лит.: [1] К у р о ш А. Г., Лекции по общей алгсоре, 2 изд.,
М., 1973. О. А. Иванова.
ПСЕВДООТКРЫТОЕ ОТОБРАЖЕНИЕ — непрерыв-
непрерывное отображение / : Л' —*- Y такое, что для всякой
точки у ? Y и любой окрестности U множества \~лу в
X непременно y?lntfU (здесь intfU— множество всех
внутренних точек fU относительно У).
М. И. Войце.ховс.кип.
ПСЕВДОПЕРИОДИЧЕСКАЯ ФУНКЦИЯ с п е р и о-
,4 а л и со0, сох, . . ., аг — функция /(?, ии . . ., иг)
от r-j~l переменных, удовлетворяющая условиям:
f(t, ии . .., и,- + ш,-, ..., иг) =
^f(t, их, ..., щ, ..., ur), i = l, ..., г;
f{t-\-a>0, щ, ..., ur) = f(t, "i + co0, ..., иг-\-щ).
Пример: если fo(t) и Д(г) —непрерывные периодич. функ-
функции с периодами со0 и (?>! соответственно, причем отно-
отношение ао/ац иррационально, то f(t, u1)—f0(t)-\-f1{t-\-u1)
является П. ф.
П. ф. связана с квазипериодической, функцией п опре-
определяется по ней единственным образом: функция F (t)
квазинериодична с периодами со0, соъ . . ., ч>г тогда п
только тогда, когда существует такая непрерывная
П. ф. f(t, их, . . ., иг) с периодами со0) ^ъ ¦ ¦ •> шг> чт0
F(t) = f(t, 0, . . ., 0). Ю. В. Номленко.
ПСЕВДОРИМАНОВА ГЕОМЕТРИЯ — совокуп-
совокупность геометрич. свойств поверхностей и кривых в
псееОоримаповом пространстве lVп. Эти свойства ьыте-
кают из свойств псевдоримановой метрики этого прост-
пространства, к-рая является знаконеопределенноы квадра-
квадратичной формой индекса I:
Длина дуги кривой I выражается формулой
она может быть действительной, чисто мнимой или нулем
(изотропная кривая). Геодезич. линии в lVn даже в
малых своих частях теряют экстремальные свойства,
оставаясь линиями стационарной длины. Длина дуги
I может быть больше или меньше длины геодезич. от-
отрезка, соединяющего концы дуги /. Если рассматри-
рассматривается пространство n~1Vn, то отрезок геодезической
А В действительной длины дает длиннейшее расстояние
между точками А, В (в предположении, что ату дугу
геодезической можно вложить в полугеодезическую ко-
координатную систему в виде координатной линии и что
для сравнения берутся гладкие кривые действительной
длины из области, где определена эта координатная
система). В случае, когда рассматривается псевдорима-
ново пространство n~xRn, можно всякую прямую дей-
действительной длины принять за ось хп ортонормиро-
ванной координатной системы, в к-рой скалярный квад-
квадрат вектора х имеет вид
Здесь любой прямолинейный отрезок действительной
длины (вдоль оси х") будет служить длиннейшим рас-
расстоянием между точками, являющимися его концами.
В случае пространства 1Vn (или 1Л„) отрезок геодезич.
линии мнимой длины будет служить длиннейшим рас
стояниед! по сравнению со всевозможными гладкими
кривыми мнимой длины, концы к-рых совпадают с кон-
концами геодезич. отрезка.
На основе псевдоримановой метрики развертывается
дифференциальная геометрия поверхностей и кривых
в псевдоримановом пространстве, определяются кри-
кривизны кривых и поверхностей и т. д.
П. г. возникает также на поверхностях в гиперболич.
пространствах. Простейшим случаем П. г. является
геометрия псевдоевклидова пространства lRn и, в част-
частности, геометрия Минковского пространства.
Лит. см. при ст. ПсевОориманово пространство.
Л. А. Сидоров.
ПСЕВДОРИМАНОВО ПРОСТРАНСТВО — простран-
пространство аффинной связности (без кручения), касательное
пространство в каждой точке к-рого является псевдоев-
псевдоевклидовым пространством.
Пусть Ап есть га-пространство аффинной связности
(без кручения) и lRn — касательное псевдоевклидово
пространство в каждой точке пространства А ю в этом
случае П. п. обозначается lVn. Как и в собственном
римановом пространстве, метрич. тензор пространства
lVn является невырожденным и абсолютно постоянным,
а метрич. форма пространства lVn является квадратич-
квадратичной формой индекса I:
ds2 = gjj dx1 dxJ, i, / = 1, ..., n,
gij (X) — метрич. тензор lVn, det\\gij\\^:O. Пространст-
Пространство lVn можно определить как «-мерное многообразие,
в к-ром задана инвариантная дифференциальная квад-
квадратичная форма индекса I.
Простейшим примером П. п. является пространство
'Я». ,
П. п. lVn наз. приводимым, если в окрестности каж-
каждой его точки существует такая система координат
(а-1, . . ., х"), что все координаты х' можно разделить
на группы х а такие, что giaja?z^ лишь для тех индексов
ia, /а, к-рые принадлежат одной группе, a giaja явля-
являются функциями только координат этой группы.
В П. п. определяется кривизна пространства в дву-
двумерном направлении, она может быть истолкована как
кривизна геодезической (неизотропной) 2-поверхности,
проведенной в данной точке в данном двумерном на-
направлении. Если значение кривизны в каждой точке
одно и то же по всем двумерным направлениям, то оно
является постоянным во всех точках (теорема
Ш у р а) и П. п. наз. в этом случае П. п. постоянной
кривизны. Примером П. п. постоянной отрицательной
кривизны ягвляется гиперболич. пространство lSn от-
отрицательной кривизны — оно является П. п. n~lVn;
пространство lRn есть П. п. нулевой кривизны.
Лит.: [1] Р а ш е в с к и й П. К., Риманова геометрия и
тензорный анализ, 3 изд., М., 1967; [2]РозенфельдБ. А.,
Неевклидовы пространства, М., 1969; [3] Эйнштейн А.,
Собр. науч. трудов, т. 1, М., 1965. Л. А. Сидоров.
ПСЕВДОСКАЛЯР — величина, не изменяющаяся
при переносе и повороте координатных осей, но изменя-
изменяющая свой знак при замене направления каждой оси на
противоположное. Примером П. может служить сме-
смешанное произведение трех векторов и скалярное про-
произведение (ш, Ь), где а — осевой вектор, Ь — обычный
(полярный) вектор. всэ-з-
ПСЕВДОСКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ, косое
произведение, avb ненулевых векторов а и
Ь — произведение их модулей на синус угла ф положи-
положительного (против часовой стрелки) вращения от а к 0:
а\/Ь — \ а 11 6 | sin ф.
Если я = 0 и (или) 6=0, то П. п. полагают равным нулю.
См. Векторная алгебра. А. Б. Иванов.
ПСЕВДОСЛУЧАЙНЫЕ ЧИСЛА — см. Случайные
и псевдослучайные числа.
ПСЕВДОСФЕРА — поверхность постоянной отрица-
отрицательной кривизны, образованная вращением трак-
трактрисы вокруг ее асимптоты (см. рис.). Линейный эле-
элемент в полугеодезич. координатах имеет вид (линия
и=0— геодезическая):
— dv2, a = const;
в изотермич. коордтшатах:
, о n dx2 + di/2 .
ds~--~az j-^- , a = const.
Всякая поверхность посто-
постоянной отрицательной кри-
кривизны наложима на П.
Внутренняя геометрия П. ло-
локально совпадает с геометрией Лобачевского (см. Белъ-
трами интерпретация).
Лит.: И] В ы г о д с к и й М. Я., Дифференциальная гео-
геометрия, М.— Л., 1949; [2] К а г а н В. Ф., Основы теории по*
верхностей в тензорном изложении, ч. 2, М.— Л., 1948.
А. Б. Иванов.
ПСЕВДОТЕНЗОР — тензор, рассматриваемый с точ-
точностью до произвольного функционального множителя.
ПСЕВДОХАРАКТЕР множества А в то-
топологическом пространстве X — на-
наименьший из всех бесконечных кардиналов т таких,
что существует семейство мощности т открытых в X
множеств, пересечение к-рых есть А. Обозначается
обычно ty(A, X). Псевдохарактер -ф (Л., X) определен
для всех подмножеств А пространства А* в том и только
в том случае, если в X все одноточечные подмножества
замкнуты. Под псевдохарактером \%>(х, X) точки х?Х
в топологич. пространстве X понимается псевдохарак-
псевдохарактер 1|)({х}, X) множества {х} в X.
Псевдохарактер ty(X) топологич. пространства X —
наименьший бесконечный кардинал т такой, что каждая
точка является пересечением семейства мощности <:т
открытых в X множеств. Пространства счетного П.—
те, в к-рых каждая точка имеет тип Gq . Каждое тополо-
топологич. пространство можно представить как образ при
непрерывном открытом отображении нек-рого пара-
компактного хаусдорфова пространства счетного П.
Для бикомпактных хаусдорфовых пространств счет-
ность П. равносильна первой аксиоме счетности. Вооб-
Вообще, П. замкнутого множества А в бикомпактном хаус-
дорфовом пространстве X равен мощности некото-
некоторой определяющей системы окрестностей множества
А в X.
Лит.: [1] Архангельский А. В., П о н о м а-
р е в В. И., Основы общей топологии в задачах и упражнениях,
М., 1974; [2] Архангельский А. В., «Успехи матем.
наук», 1981, т. 36, в. 3, с. 127—46. А. В. Архангельский.
ПСЕВДОЭЛЛИПТИЧЕСКИЙ ИНТЕГРАЛ — интег-
интеграл вида
J R(z,
J R(z
где R — рациональная функция двух аргументов,
/ (z) — многочлен 3-й или 4-й степени без кратных кор-
корней, к-рый может быть выражен элементарно, т. е.
через алгебраич. функции от z и логарифмы от таких
функций. Напр.,
г z' dz
есть П. И. См. Эллиптический интеграл. Е. Д Соломенцев
ПСИ-ФУНКЦИЯ, ^-функция Гаусса,
дигамма-функция,— первая производная от
логарифма гамма-функции.
ПТОЛЕМЕЯ ТЕОРЕМА: во всяком выпуклом четы-
четырехугольнике, вписанном в окружность, произведение
длин диагоналей равно сумме произведений длин его
противоположных сторон. Названа по имени Клавдия
Птолемея B в.), к-рый использовал ее для вывода
нек-рых соотношений в тригонометрии, л. С. Моденов.
ПУАНКАРЕ ГИПОТЕЗА — утверждение, приписы-
приписываемое А. Пуанкаре (Н. Poincare) и гласящее: любое
замкнутое односвязное трехмерное многообразие го-
меоморфно трехмерной сфере. Естественным обобщением
является следующее утверждение (обобщенная
гипотеза Пуанкаре): любое замкнутое
н-иррнор многообразие, гомотопически эквивалентное
«-мерной сфере S", гомеоморфно ей; в настоящее время
A983) доказана для всех и, кроме я=3 (при и =4 —
лишь для гладких многообразий). ю. Б. Рудяк.
ПУАНКАРЕ ГРУППА — группа движений прост-
пространства Минковского. П. г. является полупрямым про-
произведением группы преобразований Лоренца и группы
четырехмерных сдвигов (трансляций). П. г. названо но
имени А. Пуанкаре (Н. Poincare), который впервые
A905) установил, что преобразования Лоренца образу-
образуют группу. Л. Б. Иванов.
ПУАНКАРЕ ДВОЙСТВЕННОСТЬ — изоморфизм
р-мерных групп (модулей) гомологии n-мерного много-
многообразия М (в том числе обобщенного) с коэффициентами
в локально постоянной системе % групп (модулей),
изоморфных G, (п—р)-мерным когомологиям М с коэф-
коэффициентами в ориентирующем пучке Жп (<§) над М
(слой этого пучка в точке х?М совпадает с локальной
группой гомологии Н%—Нп(М, М\х; <§)). При этом
обычные гомологии Н°р {М\ <§) изоморфны когомологиям
Н? (М; ЖпКЪ)), 9=п~Р, с компактными носителями
(когомологиям «второго рода»), в то время как гомоло-
гомологии «второго рода» Нр(М; <§) (определяемые «беско-
«бесконечными» цепями) изоморфны обычным когомологиям
ЦЧ (М; ЖЛ%))- В более общем виде имеют место изо-
изоморфизмы Н%(М; ^) = Н^(М; &?„(<§)), где Ф-любое
семейство носителей.
Аналогичные отождествления имеются также для
гомологии и когомологии подмножеств АаМ и пар
(М, А) (двойственность Пуанкаре —
Л е ф ш е ц а). Именно, пусть А — открытое или зам-
замкнутое подпространство в М и В=М\А . Пусть Ф/В —
семейство всех тех множеств из Ф, к-рые содержатся в
В, и пусть Ф ГМ —семейство множеств вида Ff\A,
РаФ. Тогда точная последовательность гомологии пары
(М, В)
¦ ¦ ¦ HfB (В; <§) -^Hf(M;$)-^ Н® (М; В; <§) —
fL* (В- S) —... (*)
совпадает с когомологич. последовательностью пары
(М, А)
...-+Н«,(М, А; Жп (%)) — И% (М- Мп (»)) —
с
Группы Н®/в (В; $) = Я*/В (М; <?) совпадают
ИСр(В; <§) в случае, когда Ф=- с, и с Нр (В; g) в случае,
когда Ф — семейство f всех замкнутых в М множеств,
а множество В замкнуто (в этом случае символ Ф в
первой последовательности может быть опущен, при-
причем имеет место изоморфизм Нр (М, В\ <§)~ Н р (Л; <?)).
В случае, когда ф—^, а В открыто, символ Ф можно
опустить лишь во втором и третьем членах гомологич.
последовательности, т. к. гомологии Н®1В (В; g) за-
зависят не только от топологич. пространства В, но и от
вложения ВсМ.
В случае, когда Ф=?, этот символ (вместе с Ф[~|Л)
может быть опущен в когомологич. последовательности
пары (М, А). Если А замкнуто, то
= #S/B(S; SVnCS)),
при Ф— W возникающие когомологии В зависят не толь-
только от В, но и от вложения ВаМ. ЕслиФ = с и А замкну-
замкнуто, то Ф[)А можно заменить на с, и в этом случае
также Hi (М; А ; Жп^^^с (В; Жп (?)) — когомоло-
гни «второго рода» пространства В. Если Ф=е, но А
открыто, то когомологип И^пл (^' 3%nAi)) отличаются
от Н?(А; $%„($)) (и зависят от вложения АаМ).
Двойственность Пуанкаре — Лефшеца легко может
быть применена для описания двойственности между
гомологиями и когомологиями многообразия с краем.
Полезно иметь в виду, что если все отличные от нуля
слои пучка ЗКп (К) изоморфны основному кольцу R,
то Жп{%)=Жп{Щ®нЪ-
В случае, когда пучок эъп \Щ локально постоянен,
существует единственный с точностью до изоморфизма
локально постоянный пучок X(R), для к-рого
¦?{R)®RS%n(R)—R- Поэтому если в гомологич. по-
последовательности (*) вместо g использовать пучок ко-
коэффициентов =5?(Д)®д^, то в когомологич. последова-
последовательности станет (вместо ffln ('§)) фигурировать пучок <§.
Таким образом, наперед заданные коэффициенты в изо-
изоморфизмах двойственности могут фигурировать как в
гомологиях, так и в когомологиях.
Наиболее естественное доказательство П. д. получает-
получается средствами теории пучков. П. д. в топологии —
частный случай соотношений двойственности
типа Пуанкаре, справедливых для производ-
производных функторов в гомологич. алгебре (другой частный
случай — двойственность типа Пуанкаре для гомоло-
гомологии и когомологий групп).
Лит.: El] Скляренко Е. Г., «Успехи матем. науки»,
1979, т. 34, в. 6, с. 90—118; [2] е Г о же, «Матем. заметки»,
1980, т. 28, № 5, с. 769—76; [3] М а с с и У., Теория гомологии
и когомологий, пер. с англ., М., 1981. Е, Г. Скляренко.
ПУАНКАРЕ ДИВИЗОР — дивизор, заданный есте-
естественной поляризацией на якобиане алгебраич. кри-
кривой. Форма пересечений одномерных циклов гомологии
алгебраич. кривой X индуцирует унимодулярную косо-
симметрич. форму на решетке периодов. В соответствии
с определением поляризованного абелева многообразия
эта форма определяет главную поляризацию на якобиа-
якобиане кривой 1(Х). Поэтому эффективный дивизор всг
dl (X), заданный этой поляризацией, определен одно-
однозначно с точностью до сдвига на элемент «?./(X). Гео-
Геометрия П. д. в отражает геометрию алгебраич. кри-
кривой X. В частности, размерность множества особых
точек П. д. dim q sing Q^g—4, где g — род кривой X
(см. [1]).
Лит.: [1] Andreotti A., Mayer A., «Ann. Sc. norm,
sup. Pisa», 1967, V. 21, № 2, p. 189—238. Вик. С. Куликов.
ПУАНКАРЕ ЗАДАЧА: найти гармоническую в ко-
конечной односвязной области S + функцию по условию на
границе L области:
где A (s), B(s), c(s), f(s) — заданные на L действитель-
действительные функции, s — дуговая абсцисса, п — нормаль к
L. К этой задаче пришел А. Пуанкаре (Н. Poincare,
1910), разрабатывая математич. теорию приливов, и дал
(неполное) решение задачи в случае, когда A(s)=l,
r(s) = 0, контур L и функции B(s), f(s) — аналитичес-
аналитические.
См. также Граничные задачи теории аналитических
функций. А. Б. Иванов.
ПУАНКАРЕ ИНТЕРПРЕТАЦИЯ — модель, реали-
реализующая геометрию плоскости Лобачевского (гипербо-
лич. геометрию) на плоскости комплексного переменно-
переменного. В П. и. с круговым абсолютом каждая точка единич-
единичного круга Е~ {z : \z\ <1} в плоскости z наз. гипер-
гиперболической точкой, а сам круг — гипер-
гиперболической плоскостью. Дуги окруж-
окружностей (и диаметр) в Е, ортогональные к граничной ок-
ру?кности Q= {z : |z| = l}, наз. гиперболичес-
гиперболическими прямыми. Каждая точка Q наз. иде-
идеальной точкой. Гиперболич. прямые с общей
гиперболич. точкой наз. пересекающимися
прямыми; с общей идеальной точкой —парал-
—параллельными прямым и; прямые, к-рые не пере-
сокаготся и не параллельны,— г и и е р и а р а л л е л ь-
н ы м и (расходящимися) пряными. Так,
напр., на рис. 1 изображены две прямые, проходящие
через точку z1; параллельно прямой z2z3.
В П. и. в полуплоскости //= {z=x-\-iy\y>0} каждая
точка верхней полуплоскости наз. гиперболи-
гиперболической точкой, а сама полуплоскость — ги-
гиперболической плоскостью. Полуок-
Полуокружности и полупрямые, ортогональные действитель-
действительной оси, наз. гиперболиче-
гиперболическими прямыми. Множе-
Множеством идеальных точек (абсолю-
(абсолютом) является действительная
ось и бесконечно удаленная точка
Рис. 1.
Рис. 2.
плоскости z. Аналогично П. и. с круговым абсолютом
определяются параллельные, пересекающиеся и рас-
расходящиеся прямые. Так, напр., на рис. 2 изображены
две прямые, проходящие через точку zx параллельно
прямой z2 zs.
Движения описываются конформными преобразова-
преобразованиями, переводящими абсолют в себя. Расстояния опре-
определяются с помощью двойного отношения четырех то-
точек
p(zx, z2) = fcln (zb z2, г*, zl),
где zi — идеальная точка полупрямой, исходящей из
z1 и проходящей через z2; гг — идеальная точка полу-
полупрямой, исходящей из z2 и проходящей через zt; к —
произвольное положительное постоянное;
(«I
Z2>
Величины углов в П. и. совпадают с величинами углов
в геометрии Лобачевского.
П. и. предложена А. Пуанкаре (Н. Poincare, 1882).
Лит.: [1] Клейн Ф., Элементарная математика с точки
прении высшей, пер. с нем., т. 2, М.— Л., 1934; [2] Каган
В. Ф., Лобачевский и его геометрия, М., 1955; [3] Гиль-
Гильберт Д., Кон-Фоссен С, Наглядная геометрия, пер. с
нем., 3 изд., М.— Л., 1981; [4] Пуанкаре А., Избранные
труды, [пер. с франц.], М., 1974; [5] Неванлинна Р.,
Униформизация, пер. с нем., М., 1955; [6] Sansone G.,
Gerre tsenJ., Lectures on the theory of functions of a comp-
complex variable, [v.] 2, Geometric theory, Groningen, 1909.
А. Б. Иванов.
ПУАНКАРЕ КОМПЛЕКС — обобщение понятия
многообразия; пространство, группы гомологии к-рого
устроены в нек-ром смысле так же, как группы гомоло-
гомологии замкнутого ориентируемого многообразия. А. Пу-
Пуанкаре (Ы. Рошсаге) обнаружил, что группы гомоло-
гомологии многообразия удовлетворяют нек-рому соотноше-
соотношению (изоморфному Пуанкаре двойственности). П. к.
представляет собой пространство, где аксиоматизи-
аксиоматизирован этот изоморфизм (см. также Пуанкаре простран-
пространство).
Алгебраический комплекс Пуан-
Пуанкаре — цепной комплекс с формальной двойствен-
двойственностью Пуанкаре — аналог прежнего.
Пусть С= {С,} — пополненный цепной комплекс с
С,=0 при г>0 такой, что его группы гомологии конеч-
конечно порождены. Пусть, кроме того, комплекс С снабжен
такой (цепной) диагональю A: С —>-С(?)С, что (е@?I)Д =
(®), где р. : С ->. % — пополнение (и С отож-
отождествляется с 6'gJi и Z®C). Наличие диагонали поз-
позволяет определить спаривание
Я* (С) ® Я„ (С) —>- Я„_ й (С), г (g) у -^ х П г/.
Комплекс С наз. геометрически м, если ладана
цепная гомотопия между Л и ГА, где Т : С0С -> С®
®С — перестановка сомножителей Г(а(ХN) =6@а.
Геометрич. цепной комплекс наз. алгебраическим
П. к. формальной размерности п, если существует такой
элемент бесконечного порядка и.?Я„(С), что для лю-
любого к гомоморфизм 0\л : Hk (С) ->- Hn_k(C) есть изо-
изоморфизм.
Примерами алгебраич. П. к. являются комплекс син-
сингулярных цепей ориентируемого замкнутого многооб-
многообразия или, более общо, П. к., определенный выше,
с подходящими условиями конечности. Можно опреде-
определить также цепные пары Пуанкаре —
алгебраич. аналоги пар Пуанкаре (X, А). Рассматрива-
Рассматриваются также П. к. (и цепные пары Пуанкаре) модулей
над подходящими кольцами. Ю. Б. Рудяк.
ПУАНКАРЕ ПРОСТРАНСТВО — 1) П. п. фор-
формальной размерности п — топологическое простран-
пространство X, где задан элемент \if Hn(X)=<?, что гомо-
гомоморфизм Пц : Я* (X) -> Hn-k (X) виДа x->-xf\[i яв-
является изоморфизмом для любого к (здесь Г) —опера-
—операция Уитни умножения, высечение). При этом [)ц наз.
изоморфизмом двойственности Пу-
Пуанкаре и элемент ц порождает группу Нп (Х)= Z •
Любое замкнутое ориентируемое re-мерное связное
топологич. многообразие является П. п. формальной
размерности п; в качестве (х берется ориентация (фунда-
(фундаментальный класс) многообразия.
Пусть X — конечное клеточное пространство, вло-
вложенное в евклидово пространство R" большой размер-
размерности N, и U — замкнутая регулярная окрестность это-
этого вложения, a 0U — ее край. Стандартное отображе-
отображение р : dU —*¦ X превращается (по Серру) в расслоение.
Теорема: пространство X является П. п. формаль-
формальной размерности п тогда и только тогда, когда слой этого
расслоения гомотопически эквивалентен сфере SN ~п~х.
Возникающее над П. п. X описанное расслоение (слой
к-рого — сфера) единственно с точностью до стацио-
стационарной эквивалентности и наз. сферическим
нормальным расслоением, или рас-
расслоением С п и в а к а, П. п. X. При этом конус
проекции р : 0U -> X есть Тома пространство нормаль-
нормального сферич. расслоения над X.
Если ограничиться лишь гомологиями с коэффици-
коэффициентами is нек-ром поле F, то получится т. н. прост-
ранствоПуанкаре над F.
Рассматриваются также пары Пуанкаре
(X, .4) (обобщение понятия многообразия с краем), где
для нек-рой образующей (х?Я„(Х, А)=%, и любого
к имеется изоморфизм двойственности Пуанкаре:
П(х:Я*(Х) — Я„_ПХ, А).
П. и. естественным образом возникают в задачах
существования и классификации структур на много-
многообразиях. Содержательна также задача сглаживания
(триангуляции) П. п., то есть отыскания гладкого (ку-
(кусочно линейного) замкнутого многообразия, гомото-
гомотопически эквивалентного данному П. п.
2) П. п. ге-м е р н о е — замкнутое re-мерное много-
многообразие М, гомологии группы Н; (М) к-рого изоморфны
группам гомологии Я,- (Sn) гс-мерной сферы S"; другое
название — гомологическая сфера.
Односвязное П. и. гомотопически эквивалентно сфере
(см. Гомотопический тип). Для группы я, реализуемой
как фундаментальная группа нек-рого П. п., имеют мес-
место равенства Н1(п)---Н2(п)~0, где Я,-(я) — группы го-
гомологии группы я. Обратно, для любого ?г^5 и любой
конечно представимой группы л с //,(я) — Н$(я)--0 су-
существует «-мерное П. п. М с л,(Л#)л.
Для « = 3,4 этих условий недостаточно для реализа-
реализации группы л в виде я=я1(.М'). Так, напр., фундамен-
фундаментальная группа любого трехмерного П. п. допускает
непредставление с одинаковым числом образующих
и соотношений. Единственная конечная группа, реа-
реализуемая как фундаментальная группа трехмерного
П. п., есть бинарная группа икосаэдра <ж, у(: г2=г/5=1>,
являющаяся фундаментальной группой додекаэдра про-
пространства — исторически первого примера П. п.
Лит.: [1] Браудер В., Перестройки односвязных мно-
многообразий, пер. с англ., М., 1983. Ю. Б. Рудяк.
ПУАНКАРЕ СФЕРА — сфера в пространстве К:!
с отождествленными диаметрально противоположными
точками. П. с. диффеоморфна проективной плоскости
RP2\ она была введена А. Пуанкаре (Н. I'oincare, см.
[1]) для исследования поведения на бесконечности фазо-
фазовых траекторий двумерной автономной системы
х = Р(х, у), y=Q(x, у) A)
в случае, когда Р nQ — многочлены. П. с. обычно изоб-
изображают так, чтобы она касалась плоскости (х, у); при
проектировании из центра П. с. взаимно однозначно
отображается на RP'2, причем паре диаметрально про-
противоположных точек экватора отвечает бесконечно уда-
удаленная точка. Соответственно, фазовые траектории сис-
системы A) отображаются на кривые на сфере.
Эквивалентный метод исследования системы A) —
применение преобразований Пуанкаре:
а) ж= -1 , у= ~ н б) х=г 2. : у— _L .
Первое (соответственно второе) из них пригодно вне
сектора, содержащего ось у (ось .г). Напр., преобразо-
преобразование а) приводит систему A) к виду
¦? = *•(«, *), |т=Р*К «), (!')
где dt—-zndx и п — наибольшая из степеней Р, Q;
особые точки системы A') наз. бесконечно уда-
удаленными особыми точками системы A).
Если многочлены iJ, Q взаимно просты, то многочлены
Р*, Q* также взаимно просты и система A) имеет ко-
конечное число бесконечно удаленных особых точек.
Лит.: [1] Пуанкаре А., О кривых, определяемых диф-
дифференциальными уравнениями, пер. с франц., Ы., 1947; [21
Андронов А. А., Л е о и т о в и ч К. А., Г о р д о Н И. И.,
М а й е р А. Г., Качественная теория динамических систем вто-
второго порядка, М., 19В8; [3] Л е ф ш е ц С, Геометрическая тео-
теория дифференциальных уравнений, пер. с англ., М., 1961.
М. В. Федорюп.
ПУАНКАРЕ ТЕОРЕМА: пусть на гладком замкну-
замкнутом двумерном римановом многообразии V определено
векторное поле X, имеющее конечное число изолиро-
изолированных особых точек Ах, . . ., Аь-
Тогда
здесь } (X, А ,-) — индекс точки А,- относительно А' (см.
Особой точки индекс), % — Эйлерова характеристика
V. Установлена А. Пуанкаре (Н. Poincare, 1881).
М. И. Войцеховский.
ПУАНКАРЕ ТЕОРЕМА в теории устойчи-
устойчивости — см. Устойчивость по Пуассону.
ПУАНКАРЕ ТЕОРЕМА ВОЗВРАЩЕНИЯ — одна из
основных теорем общей теории динамич. систем с инва-
инвариантной мерой.
Пусть движение системы описывается дифференци-
дифференциальными уравнениями
dx,
jl^Xiixi, ..., хп), г = 1 п, A)
где однозначные функции X; (хъ . . ., хп) удовлетворя-
удовлетворяют условию
V" 9 (Mxi)
дх.
¦ =о,
так что уравнения A) допускают положительный ин-
интегральный инвариант
dXl ... dxn. B)
Предполагается такжо, что если изображающая точка
Р с координатами х1} . . ., хп в начальный момент вре-
времени t0 находится внутри нек-рой области V конечного
объема, то она будет оставаться неопределенно долго
внутри этой области, и что
dxL ... dxn< со.
П. т. в.: если рассматривается область Uo, содержа-
содержащаяся в V, то можно выбрать бесконечным числом спо-
способов начальное положение точки Р таким образом,
чтобы эта точка пересекла область Uo бесконечно много
раз. Если этот выбор начального положения делается
наудачу внутри Uo, то вероятность того, что точка Р
не пересечет обла U б б
бесконечно мала.
Другими словами, если начальные условия не явля-
являются исключительными в указанном смысле, то точка
Р пройдет бесконечно много раз сколь угодно близко
от своего начального положения.
Движение, при к-ром система бесконечное число раз
возвращается в окрестность начального состояния,
А. Пуанкаре (Н. Poincare) назвал устойчивым
в смысле Пуассона. П. т. в. была впервые
установлена А. Пуанкаре (см. [1], [2]), а его доказатель-
доказательство было улучшено К. Каратеодори [3].
Введя в метрич. пространстве R с помощью четырех
аксиом абстрактное понятие меры цА любого множест-
множества AczR и рассматривая динамич. систему f(p, t) (p-=
=Р для 2=0), заданную в R, К. Каратеодори назвал
меру (.1 инвариантной относительно системы f(p, t), ес-
если для любого ц-измеримого множества А имеет место
равенство
\if (A, t)=-\iA, — оо < t <-foo.
Инвариантная мера представляет собой естественное
обобщение интегрального инварианта B) для дифферен-
дифференциальных уравнений A). Предположив меру всего про-
пространства R конечной, К. Каратеодори доказал, что:
1) если (А.4 = т>0, то найдутся значения t, UIS>1,
такие, что \i[A -f(A, 2)]>0, где A-f(A, t) — множество
точек, принадлежащих одновременно множествам А и
l(A,t);
2) если в пространстве R со счетной базой цЯ=1 для
инвариантной меры (х, то почти все точки р ? R (в смыс-
смысле меры ц) устойчивы по Пуассону.
А. Я. Хинчин [5] уточнил часть 1) этой теоремы, до-
доказав, что для всякого измеримого множества Е, \хЕ=
s=m>0, и любого t, —со<2<+оо, неравенство
VL(t)=li(,E.f(E, 0) > W2
выполняется для, относительно плотного множества
значений t на оси —оо<г<+оо (при любом А,<1).
Н. Г. Четаев (см. [6], ]7]) обобщил П. т. в. на случай,
когда функции X, в A) зависят также от времени t
периодически. Именно, пусть а) действительным сос-
состояниям системы отвечают лишь действительные зна-
значения переменных; б) функции X; в дифференциаль-
дифференциальных уравнениях движения A) суть периодические отно-
относительно t с одним общим им всем периодом т; в) в сво-
своем движении точка Р не выйдет из нек-рой замкнутой
области R, если ее начальное положение Ро находятся
P
[
где-либо внутри определенной области г0; г) mes W^^
^а mes Wo, где mes W^= \ d.r, ... dxn обозначает меру
множества W^ (объем в смысле Лебега), к-рое запол-
заполняют в момент t=to-\-kx движущиеся точки, вышедшие
в 10 из Wo; к — нек-рое целое число, постоянная а пред-
предполагается не бесконечно малой. Тогда почти всюду
(кроме, быть может, множества точек меры нуль) в
области г0 траектории имеют устойчивость в смысле
Пуассона.
Н. М. Крылов и Н. Н. Боголюбов [8] для весьма ши-
широкого класса динамич. систем дали построение меры,
инвариантной относительно данной динамич. системы
(см. также [4]).
Лит.: [1] Р о i n с а г ё Н., «Acta math.», 1890, v. 13,
. 1—270; [2] е г о же, Избр. тр., пер. с франц., М., 1972;
.3] Caratheodory С, «Sitz. Pres. Acad. Wiss. Berlin»
1919, S. 580; [4] Немыцкий В. В., Степанов В. В.
Качественная теория дифференциальных уравнений, 2 изд.
М.— Л., 1949; [5] X и н ч и н А. Я., «Сотр. math.», 1934, v. I
p. 177—79; [6] Ч е т а е в Н. Г., «С. г. Acad. sci.», 1928, t. 187,
p. 637—38; 17] e г о же, «Уч. зап. Казанск. ун-та», 1929, т. 89
кн. 2, с. 199—201; [8] К р ы л о в Н. Н., Б о г о л ю б о в Н. Н.
«Ann. Math.», 1937, v. 38, Nt 1, p. 65—113. В. В. Румянцев,
ПУАНКАРЕ ТЕОРЕМА ПОСЛЕДНЯЯ: пусть К —
кольцо на плоскости, ограниченное окружностями с
радиусами г=а и г=Ь, и дано отображение его в себя
(9 — полярный угол)
г = ф (г, 9), 9 = 1K (г, 9),
удовлетворяющее условиям: 1) отображение сохраняет
площадь, 2) каждая граничная окружность переходит
в себя ф(а, 9)=а, ф(Ь, 9)=&, 3) точки с г^а передвига-
передвигаются против часовой стрелки, а точки с г=Ь — по ча-
часовой стрелке, то есть ть(а, 9)>9, tf>(&, 9)<9. Тогда
это отображение имеет две неподвижные точки. Вместо
сохранения площади, более общо, можно потребовать,
чтобы никакая подобласть не преобразовывалась в свою
(собственную) часть.
Эта теорема высказана А. Пуанкаре [1] в 1912 в свя-
связи с нек-рыми задачами небесной механики; доказана
им в ряде частных случаев, однако общего доказатель-
доказательства этой теоремы он не получил. Работа была послана
А. Пуанкаре в итальянский журнал (см. [1]) за две не-
недели до смерти, причем автор в сопроводительном пись-
письме редактору выразил уверенность в справедливости
теоремы в общем случае.
Полное доказательство дал через полгода Дж. Бирк-
гоф [2].
Лит.: [1] Р о i n с а г ё Н., «Rend. circ. mat. Palermo»,
1912, v. 33, p. 375—407; [2] Birkhoff G., «Trans. Amer.
Math. Soc», 1913, v. 14, p. 14—22; [3] II a p с Л. А., Аналити-
Аналитическая динамика, пер. с англ., М., 1971. М. И. Войцеховский.
ПУАНКАРЕ УРАВНЕНИЯ — общие уравнения
механики голономных систем, представимые с помощью
нек-рой группы Ли бесконечно малых преобразований.
Пусть xj, i~l, . . ., п,— переменные, определяю-
определяющие положение голономной механич. системы, стеснен-
стесненной идеальными связями, зависящими явно от времени.
Если система имеет к степеней свободы, то существует
пнтранзптивная группа бесконечно малых преобразова-
у — a_i V" р! д у — V" р! д
а = 1, ..., к,
позволяющая перевести систему в момент времени t из
положения xj в бесконечно близкие действительное
положение xj-^-dx; и возможное положение ж,-+6ж,- бес-
бесконечно малыми преобразованиями группы (X0-j-
-j-~S\ riaXa)dt и подгруппы V w/X,- соответ-
ственно. Здесь ша и Т)а — независимые переменные,
определяющие соответственно возможные и депствл
тельные перемещения системы,— связаны уравнениями
da- v^k
6т1/ = -ЗГ-А*. p=i саЭ.-Ша1р. ' = 1, ...,*,
если группа возможных перемещений Ха определена
своими структурными постоянными еар,-:
(хахр) = хахр — Хр ха = 2=1 сар,-х,-,
а, Р = 1, ..., fc,
а оператор Хо перестановочен с группой возможных
перемещений
(Х0Ха) = 0, а = 1, ..., к.
Эти условия далее предполагаются выполненными.
П. у. имеют вид обыкновенных дифференциальных
уравнений 2-го порядка
d dL <«n&
21
где / — 1, .. ., к,
L(t, xt хп, тц, ..., цк)
— функция Лагранжа, T{t, х, ц) — кинетич. энергия,
U(t, x) — силовая функция.
Уравнения A) были получены впервые А. Пуанкаре
(см. [1]) для случая транзитивной группы возможных
перемещений, когда связи не зависят явно от времени,
и применены (см. [2]) для исследования движения
твердого тела с эллипсоидальной полостью, целиком
заполненной идеальной жидкостью, совершающей од-
однородное вихревое движение. Н. Г. Четаев (см. [3])
обобщил П. у. на случай интразитивной группы переме-
перемещений, когда связи зависят явно от времени, и разра-
разработал их теорию (см. [3]—[5]), а также преобразовал к
более простому канонич. виду (см. Четаееа уравнения).
В частности, им был дан (см. [5]) метод построения груп-
группы возможных и действительных перемещений, когда
голономные связи заданы в дифференциальной форме,
и введено важное понятие циклич. перемещения.
Перемещения Xr, r—s-f-1, . . ., к, наз. цикли-
циклическими, если они удовлетворяют условиям:
1) ХД, = О,
2) (ХГХР)^О, г = я + 1, .... к, р = 1, ..., к.
Согласно 2) циклич. перемещения Xг образуют абелеву
подгруппу группы возможных перемещений, переста-
перестановочную со всеми операторами Хр. Для циклич. пе-
перемещений существуют первые интегпалы П. у.
-— = ar = const, r = s-)-l, . .., к.
Из этих соотношений переменные х\г можно выразить
через постоянные аг и переменные t, 27, г\1г . . ., i)s и
ввести функцию Рауса
R (t, хи ..., хп\ г\и . .., 1Ы as + 1, ..., ak)^=
Тогда для нециклич. перемещений П. у. принимают
вид уравнений
¦^г Sj=2еа№^ Щ;+2 c«/vioov+xjr. B)
а, у, Р--1, ..., s; v = s-fl, .... к.
После интегрирования уравнений B) значения х\г оп-
определяются равенствами
Если дополнительно винолняются равенства caijy—O,
а, /=1, . . ., s; y=s+l, . . ., к, т. е. если нециклич. пе-
перемещения Х$, р=1, . . ., к, представляют собой под-
подгруппу группы возможных перемещений, то по отноше-
отношению к этой подгруппе рассматриваемая механич. сис-
система образует как бы самостоятельную голономную сис-
систему с s степенями свободы, описываемую уравнениями
A) при а, /, E=1, . . ., s, где роль функции L играет
функция R.
П. у. содержит как частные случаи: Лагранжа урав-
уравнения, когда группа преобразований, увеличивающая
одну из переменных на бесконечно малую постоянную,
приводится к группе перестановочных между собой
преобразований; Эйлера уравнения вращения твердого
тела, когда роль т](- играют проекции р, д, г мгновенной
угловой скорости.
Лит.: И] Р о i n с а г k Н., «С. г. Acad. sci.», 1901, t. 132, p.
369—71; [2] e г о же, «Bull. Astron.», 1910, t. 27, p. 321—56;
[3] Ч е т а е в Н. Г., «Докл. АН СССР», 1928, jN» 7, с. 103—04;
[4] е г о же, «С. г. Acad. sci.», 1927, t. 185, p. 1577—78; Г5]
его же, «Прикл. матем. и механ.», 1941, т. 5, № 2, с. 253—62.
В. В. Румянцев.
ПУАНКАРЕ — ББНДИКСОНА ТЕОРИЯ — раздел
качественной теории дифференциальных уравнений и
теории динамич. систем, относящийся к предельному
(при <-у ± оо) поведению траекторий автономных систем
двух дифференциальных уравнений 1-го порядка:
ii = fi(x1, хг), j = l, 2 (*)
(условия, обеспечивающие существование и единствен-
единственность решений, подразумеваются выполненными). В на-
наиболее важном случае, когда в ограниченной части плос-
плоскости система имеет только конечное число равновесия
положений, основной результат А. Пуанкаре (Н. Poin-
сагё, см. [1]) и И. Бендиксона (I. Bendixson, см. [2])
состоит в том, что любая ограниченная полутраекто-
полутраектория (положительная или отрицательная) либо стремит-
стремится к положению равновесия, либо навивается (наподо-
(наподобие спирали) на предельный цикл, либо аналогичным
образом навивается на замкнутую сепаратрису или «се-
паратрисный контур», состоящий из нескольких се-
сепаратрис, «соединяющих» нек-рые положения равнове-
равновесия, либо сама является положением равновесия или
замкнутой траекторией. Наиболее часто используемое
следствие: если полутраектория не выходит из нек-рой
компактной области, не содержащей положения рав-
равновесия, то в этой области имеется замкнутая траекто-
траектория. Для тех случаев, когда положений равновесия
бесконечное число или когда полутраектория не явля-
является ограниченной, тоже имеется достаточно полное,
хотя и более сложное описание (см. [4]). Наконец, мож-
можно рассматривать непрерывный поток на плоскости, не
предполагая, что он задается дифференциальными урав-
уравнениями (*), ибо при этом все еще возможно использо-
использовать основные «технические» предпосылки П.- Б. т.:
Жордана теорему и наследования отображение для
локальных сечений, гомеоморфных отрезку (существо-
(существование их доказано в [7], см. также [8]).
К П.— Б. т. примыкают: открытая А. Пуанкаре связь
между вращением векторного поля на границе области
н индексами положений равновесия внутри нее (см.
Особой точки индекс); результаты И. Бендиксона и
Л. Брауэра (L. Brouwer) о возможных типах поведения
траекторий возле положений равновесия (см. [2] —
[5]); результаты, уточняющие роль «особых траекто-
траекторий» — положений равновесия, предельных циклов и
сепаратрис — в «качественной картине», возникающей
на фазовой плоскости (см. [61).
Хотя общая теория дает исчерпывающую информацию
о вариантах поведения фазовых траекторий, возмож-
возможных для систем (*), это не отвечает на вопрос, какой
вариант реализуется для той или иной конкретной
системы. Решению подобных вопросов (обычно не для
отдельной системы, а для нек-рого класса систем) по-
посвящено большое количество работ, в к-рых, как пра-
правило, существенно используется общая теория, но
к-рые никоим образом не сводятся к ее автоматич. при-
применению.
Лит.: [1] Пуанкаре А., О кривых, определяемых диф-
дифференциальными уравнениями, пер. с франц., М., 1947; [2]
Бе ч дик сон И., «Успехи матем. наук», 1941, в. 9, с. 191—.
211; [3J В г о u w е г L. E., «Verhandel. Konikl. nederl. akad.
wet. Afd. natuurkunde. I. reeks», 1909, v. 11, p. 850—58; 1910,
v. 12, p. 716—34; 1910, v. 13, № 1, p. 171—86; [4] H e м ы ц-
к и й В. В., Степанов В. В., Качественная теория диффе-
дифференциальных уравнений, 2 изд., М., 1949; [5] X а р т м а н Ф.,
Обыкновенные дифференциальные уравнения, пер. с англ., М.,
1970; [6] Андронов А. А., Леонтович Е. А., Г о р-
д о и И. И., М а й е р А. Г., Качественная теория динамических
систем второго порядка, М., 1966; [71 Whitney H., «Ann.
Math.», 1933, v. 34, № 2, p. 244—70; [8] Н е м ы ц к и й В. В.,
«Вестн. Моск. ун-та», 1948, JM» 10, с. 49—61. Д. В. Аносов.
ПУАНКАРЕ — БЕРТРАНА ФОРМУЛА — формула
перестановки порядка интегрирования в повторных не-
несобственных интегралах в смысле главного значения
по Коши.
Пусть Г — простая замкнутая или разомкнутая глад-
гладкая линия на комплексной плоскости; ср(?, tj)—опреде-
tj)—определенная на Г (вообще говоря, комплекснозначная) функ-
функция, удовлетворяющая равномерно условию Гёльдера
по t, ti, ta — фиксированная точка на Г, отличная от
. концов, если Г разомкнута. Тогда имеет место П.—
Б. ф.
г at
Jr 7=Га
Формула справедлива и при более общих предполо~
жениях относительно линии Г и функции ср (см. [4]),
Если ф (t, h)=a(t) Р(г,), где a?Lp, Р€ V , р>1, р'=*
—р/(р—1), то равенство A) справедливо для почти всех
го?г (см. [5], [6]). Если линия Г замкнута и функция (р
зависит от одного аргумента, то равенство A) прини-
принимает вид
и имеет место для всех или почти всех („^ Гв зависимос-
зависимости от того, удовлетворяет ф условию Гёльдера или
ф€^,р> Р>1- Равенство B) также наз. П.— Б. ф.
Построены аналоги формулы A) в случае кратных
интегралов (см. [8]—[И]).
Формула A) при определенных условиях была полу-
получена Г. Харди (см. [7]) ранее А. Пуанкаре (см. [1]) и
Ж. Бертрана (см. [2], 13]).
Лит.: El] Poincare H., Legons de mecanique celeste
t. 3, P., 1910; [2] Bert rand G., «С. г. Acad. sci.», 1921, t. 172,
p. 1458—61; [3] e г о те, «Ann. sci. Ecole norm, super.», 1923,
t. 40, p. 151—258; 14] M у с х е л и ш в и л и Н. И., Сингуляр-
Сингулярные интегральные уравнения, 3 изд., М., 1968; [5] X в е д е-
п и д з е Б. В., «Сообщ. АН Грув. CGP», 1947, т. 8, № 5, с. 283—
90; [6] е г о ж е, в кн.: Итоги науки и техники. Современные
проблемы математики, т. 7, М., 1975, с. 5—162; Е7] Н а г-
d у G. H., «Proc. London Math. Soc», 1909, v. 7, № 2, p. 181—208;
[8] T r i с о m i F., «Math. Z.», 1928, Bd 27, S. 87—133; [9] G i-
raud G., «C. r. Acad. sci.», 1936, t. 202, № 26, p. 2124—26;
[10] его же, «Ann. sci. Ecole norm, super.», 1934, t. 51, f. 3—
4, p. 251—372; [11] Михлин С. Г., «Успехи матем. наук»,
1948, т. 3, в. 3, с. 29—112; [12] его же, Многомерные сингу-
сингулярные интегралы и интегральные уравнения, М., 1962.
Б. В. Хведелидзе.
ПУАССОНА ИНТЕГРАЛ — интегральное представ-
представление решения Дирихле задачи для Лапласа уравнения
в простейших областях. Так, П. и. для шара Вп (О, R)
евклидова пространства R", п^ 2, радиуса R с центром
в начале координат имеет вид
: ,„ RJ(y)PBn(x, V)dSa(y), A)
п (О, Н)
где f(y) — данная непрерывная функция на сфере
Sn@, R) радиуса R,
РВ (х и) 1 я"-<Д'-1*1')
fUn(X, У)—ап \Х-у\П
— ядро Пуассона для шара, а„~
=ил"'/2Л»-1/Г(п/2+1) площадь сферы 5„ (О, Я), (IS,., —
элемент площади Sn@, R).
С. Пуассон [1] пришел к формуле A) в случае и 2
как к интегральной форме записи суммы тригонометрии,
ряда
где ak, bk — коэффициенты Фурье функции f(y)=/(e'f),
(г, 6) и A, <р)— полярные координаты соответственно
точек ж=ге'е и y=ei{f , когда ядро Пуассона имеет вид
ЯЛ., (х, у) = РВ2(геМ, е^) = ±- — Ц?—-—- B)
(о применениях П. и. в теории тригонометрич. рядов
см. [3], а также Абеля — Пуассона метод суммирова-
суммирования).
П. и. для полупространства
имеет вид
и[х)—\ nf{y)PRn+(.t, y)dR'^(y), C}
где
dR'i — элемент площади Ri, f (у) — ограниченная не-
непрерывная функция на Ro,
2Г(т+1
РД"<*'*> = —ЪТГ- |х-Н»
— ядро Пуассона для полупросч-
р а н с т в а. Формулы A) и C) суть частные случаи
формулы Грина
дающей решение задачи Дирихле для областей
с гладкой границей Г при помощи производной
dG(x, y)ldny функции Грина G(x, у) по направлению
внутренней нормали к Г в точке 2/?Г. Иногда форму-
формулу D) также наз. П. и.
Основные свойства П. и.: 1) и(х) есть гармонич. функ-
функция координат точки х; 2) П. и. дает решение задачи
Дирихле с граничными данными / (у) в классе (ограни-
(ограниченных) гармонич. функций, т. е. функция и(х), про-
продолженная на границу области значениями f(y), не-
непрерывна в замкнутой области. На этих свойствах ос-
основаны применения П. и. в классической математич.
физике (см. [4]).
П. и., понимаемый в смысле Лебега, от суммируемой
Функции /(у), напр, на Sn (О, R), наз. интегра-
интегралом Пуассона — Лебега; интеграл вида
по произвольной конечной борелевской мере ц, сосредо-
сосредоточенной на Sn (О, Л), наз. интегралом Пуас-
Пуассона — Стилтьеса. Класс А гармонич. функций
и (я), представимых интегралом E), характеризуется
тем, что любая функция и (х) ? А есть разность двух
неотрицательных гармонич. функций в В „(О, R). Класс
функций, представимых интегралом Пуассона — Ле-
Лебега, есть правильный подкласс класса А , содержащий,
в свою очередь, все ограниченные гармонич. функции в
Вп (О, R). Для почти всех точек у ?SU (О, R) но мере Ле-
Лебега на Sn@, R) интеграл Пуассона — Стилтьеса E)
имеет угловые граничные значения, совпадающие со
значением производной ц' (у) меры и. по мере Лебега.
Теория интегралов Пуассона — Стилтьеса и Пуассо-
Пуассона — Лебега строится и для случая полупространства
(см. [5]).
Большую роль в теории аналитич. функций многих
комплексных переменных и в ее применениях к кванто-
квантовой теории поля играют различные модификации П. и.
Напр. ,ядро Пуассона для поли к руг а
комплексного пространства С" получается при пере-
перемножении ядер B):
Соответствующий П. и.
uo остову поликруга Тп— {?= (?,, ¦ ¦ ., ?п)?Сп: |?/| = 1,
/ = 1, . . ., п} даеткратногармонич. функцию и (г), z?Un,
принимающую на остове Тп непрерывные значения
/ (?). Рассматриваются также обобщения в виде интег-
интегралов Пуассона — Лебега и Пуассона — Стилтьеса
(см. [6]).
В квантовой теории поля применяются П. и. для
трубчатых областей Тс комплексного пространства С"
над выпуклым открытым острым конусом С в прост-
пространстве R" (с вершиной в начале координат) вида
П. и. для полуплоскости вида C) при п=2 есть частный
случай таких П, и. для трубчатых областей. П. и. для
ограниченных симметрии, областей пространства С"
представляется так же, как П. и. для трубчатой области
в пространство матриц. Понимая плотность П. и. / как
обобщенную функцию, а сам П. и.— как свертку / с
ядром Пуассона, приходят к важному понятию П. и.
от обобщенных функций определенных классов (см.
[7]-[9]).
Лит.: U] Poisson S. D., «J . Ecole polytechn.o, 1820, t. 11,
p. 295—341; 1823, t. 12, p. 404 — 509; [2] Schwarz H. A.,
«Vierteljahrsschr. Naturforsch. Ges. ZUrich», 1870, Bd 15, S. 113 —
28; [3] Б а р и Н. К., Тригонометрические ряды, М., 1961; [4]
Тихонов А. Н., Самарский А. А., Уравнения мате-
математической физики, 5 изд., М., 1977; ЫСоломенцевЕ. Д.,
Итоги науки. Математический анализ. Теория вероятностей.
Регулирование. 1962, М., 19134, с. 83—100; 1E] Рудин У.,
Теория функций в поликруге, пер. с англ., М., 1974; [7] В л а-
д и м и р о в В. С, Обобщенные функции в математической фи-
физике, Wf., 1976; [8] Хуа Л о - к е н, Гармонический анализ
функций многих комплексных переменных в классических об-
областях, пер. с кит., М., 1959; [9] С т е й н И., В е й с Г., Введе-
Введение в гармонический анализ на евклидовых пространствах,
пер. с англ., М., 1974. Е. Д. Соломенцев,
ПУАССОНА МЕТОД СУММИРОВАНИЯ — то же,
что Абеля — Пуассона метод суммирования.
ПУАССОНА ПРЕОБРАЗОВАНИЕ — интегральное
преобразование вида
где a(t) — функция ограниченного изменения в каждом
конечном интервале, а также преобразование
^W'lJ-x 1 + (ж-*J dt'
вытекающее из (*), если a(t) — абсолютно непрерыв~
пая функция. Пусть
и~г [g (х -[ и) ^2g (х) + g (x-u)\ da
Имеют место следующие формулы обращения для П. п.:
а. (ж+0) + а (х-0) с. ( + 0L а (-0)
2 3
= lim Г* Г*/ (и) <*и
/ -»- 1-0 Jo
при всех х и
<p(z) = lim 7y(s)
* -». i-о
для почти всех х.
Пусть С — выпуклый открытый острый конус в R"
с вершиной в нуле и С* — сопряженный конус, т. с.
Функция
наз. ядром Коши трубчатой области 7"с= {г=
=x-\-iy; x?Rn, у?С} П. п. (обобщенной) функции/
наз. свертка
где
|Кс(х + 1!/) |2
Рс(х, У)= Bя)П кс (гу)
— ядро Пуассона трубчатой области Тс (см. [2]).
Пит.: [1] Pollard H., «Trans. Amer. Math. Soc», 1955,
v. 78, № 2, p. 541—50; [2] Владимиров В. С, Обобщенные
функции в математической физике, М., 1976.
Ю. А. Брычков, А. П. Прудников.
ПУАССОНА РАСПРЕДЕЛЕНИЕ — распределение
вероятностей случайной величины X, принимающей
целые неотрицательные значения к— 0,1,2, . . ., с веро-
вероятностями
где Я,>0 — параметр. Производящая функция и харак-
теристич. функция П. р. определяются соответственно
равенствами
<p(z) = e?b(z-1) и /(O=exp[Ji(e'f —1)].
¦ Математич. ожидание, дисперсия и все семиинварианты
более высокого порядка равны к. Функция распределе-
распределения П. р.
в точках Л=0,1,2, . . . выражается формулой
F (k)=~±
где 5k + 1 (к) — значение в точке к функции гамма-рас-
гамма-распределения с параметром А+1 (или формулой F (к)=
=1—H2kl2BX), где H2k+2 BA.) — значение в точке 2к
функции «хи-квадрат» распределения с 2к-\-2 степенями
свободы), откуда, в частности, следует соотношение
Сумма незаписимых случайных величин Хг, . . ., Хп,
имеющих П. р. с параметрами Хг, . . ., Хп, подчиняется
П. р. с параметром кх -)-...+ кп.
Обратно, если сумма Х1-\-Х2 двух независимых слу-
случайных величин Xt и Х2 имеет П. р., то каждая случай-
случайная величина X, и 12 подчинена П. р. Имеются общие
необходимые и достаточные условия сходимости рас-
распределения сумм независимых случайных величин к
II. р. При А—>-оо случайная пеличина /,_ имеет в про-
дело стандартное нормальное распределение.
П. р. было впервые получено С. Пуассоном (S. Ро-
issou, 1837) при выводе приближенной формулы для
биномиального распределения в условиях, когда п (чи-
(число испытаний) велико, а р (вероятность успеха) мало.
См. Пуассона теорема 2). П. р. с хорошим прибли-
приближением описывает многие физич. явления (см. [2], т. I,
гл. 6). П. р. является предельным для многих дискрет-
дискретных распределений, таких как, напр., гипергеометриче-
гипергеометрическое распределение, отрицательное биномиальное рас-
распределение, Пойа распределение, для распределений,
возникающих в задачах о размещении частиц по ячей-
ячейкам при определенном изменении их параметров. В ве-
вероятностных моделях П. р. играет большую роль как
точное распределение вероятностей. Природа П. р.
как точного распределения вероятностей наиболее пол-
полно раскрывается в теории случайных процессов (см.
Луассоновский процесс), где П. р. появляется как рас-
распределение числа X (t) нек-рых случайных событий,
происходящих в течение фиксированного интервала вре-
времени t:
Р{Х {t)=^k} = e-u(^, k = 0, i, 2, ...
(параметр Я — среднее число событий в единицу вре-
времени), или, более общо, как распределение случайного
числа точек в нек-рой фиксированной области евкли-
евклидова дространства (параметр распределения пропор-
пропорционален объему области).
Наряду с П. р., как оно одределено выше, рассматри-
рассматривают и так наз. обобщенное или сложное
П. р. Так называют распределение вероятностей суммы
X14-X2-j-...-j-Xv случайного числа v одинаково рас-
распределенных случайных величин Х1? Хг, . . . (при этом
v, Хх, Х2, . . .. считают взаимно независимыми, и v —
распределенным по П. р. с параметром Я). Характерис-
тич. функция ф(г) обобщенного П. р. равна
где 'ф(<) —¦ характеристич. функция Xv . Напр., отрица-
отрицательное биномиальное распределение с параметрами п
и р является обобщенным П. р., так как для него
можно положить
l|3(f)=^-log-^-77, k = log±,q = l-p.
Обобщенные П. р. безгранично делимы и каждое
безгранично делимое распределение является пределом
обобщенных П. р. (может быть «сдвинутых», т. е. с ха-
характеристич. функциями вида ехр(?\,„A)з„(г)—1 — itan)).
Вместе с тем все безгранично делимые распределения
(и только они) могут быть получены как пределы рас-
распределений сумм вида Ап1Х„1+ . . . +hnkiXnkn—An,
где (Хп1, . . ., Xnit ) образуют схему серий независи-
независимых случайных величин с П. р., А„йп>0 и Ап—действи-
Ап—действительные числа.
Лит.: [1] Poisson S. D., Recherches sur la probabilite
des jugements on matiere criminelle et en matiere civile, prficedges
des regies generates du calcul des probabilites, p., 1837; [2] Ф е л-
л е р В., Введение в теорию вероятностей и ее приложения, пер.
с англ., 2 изд., т. 1—2, КГ., 1967; [3] Б о л ь ш е в Л. Н., Смир-
Смирнов Н. В., Таблицы математической статистики, 2 изд., М.,
1968; [4] Л и н н и к Ю. В., Островский И. В., Разло-
Разложения случайных величин и векторов, М., 1972.
А. В. Прохоров.
ПУАССОНА СКОБКИ — дифференциальное выра-
выражение
зависящее от двух функций u(q, p) и v(q, f>) In перемен-
переменных q= {qt, . . ., qn), p= (plt . . ., pn). Введены С. Пуас-
Пуассоном [1]. П. с— частный: случай Якоби скобок. П. с.
есть билинейная форма от функций и, v, причем
(и, у) = —(у, и),
и имеет место тождество Якоби (см. [2])
(и, (и, w)) + (v, (w, и)) + (ш, {и, v))=0.
П. с. применяются в теории дифференциальных уран-
нений с частными производными 1-го порядка и являют-
являются удобным математич. аппаратом в аналитич. механике
(см. [3]—[5]). Напр., если q, р — канонич. переменные
и дано преобразование
<?=-<? (?, р), Р = Р(<1, Р), B)
где <?=(<?!, . . ., (?„), P=(Plt . . ., Рп) и (иХн)-мат-
рицы
(Р, Р), «?, Q), (V, Р) C)
составлены из элементов (Pit Pj), (Qh Qj), (Qit Pj) со-
соответственно, то B) является канонич. преобразованием
тогда и только тогда, когда первые две матрицы в C)
нулевые, а третья —¦ единичная.
П. с, вычисленные для случая, когда в A) и и v
замещены какой-либо парой координатных функций от
q, p, наз. фундаментальными скобками.
Лит.: fl] Poisson S., «J. Ecole polytechn.», 1809, t. 8,
p. 266—344; E2] J а с о b i C.,' «J. reine und angew. Math.», 1862,
Bd 60, S. 1—181; [3] УиттекерЕ. Т., Аналитическая дина-
динамика, пер. с англ., М.— Л., 1937; [4] Л у р ь е А. И., Аналити-
Аналитическая механика, М., 1961; [5] Г о л д с т е й н Г., Классичес-
Классическая механика, пер. с англ., 2 изд., М., 1975. А. П. Солдатов.
ПУАССОНА ТЕОРЕМА — 1) П. т.— предельная тео-
теорема теории вероятностей, являющаяся частным слу-
случаем больших чисел закона. П. т. обобщает Бернулли
теорему на случай независимых испытаний, вероятность
появления в к-рых нек-рого события зависит от номера
испытаний (т. н. схема Пуассона). Формули-
Формулировка П. т. такова: если в последовательности независи-
независимых испытаний событие А наступает с вероятностями
Pk, зависящими от номера испытания к, А-—-1, 2, . . .,
ц„/ге — частота А в первых п испытаниях, то при любом
8>0 вероятность неравенства
будет стремиться к 1 при n->oo. Теорема Бернулли сле-
следует из П. т. при Pi~. . ¦=рп- П. т. была установлена
С. Пуассоном [1]. Доказательство П. т. было получено
С. Пуассоном из варианта Лапласа теоремы. Простое
доказательство П. т. было дано П. Л. Чебышевым A846),
к-рому также принадлежит первая общая форма закона
больших чисел, включающая П. т. в качестве частного
случая.
2) П. т.— предельная теорема теории вероятностей
о сходимости биномиального распределения к Пуассона
распределению: если Рп(т) — вероятность того, что в
п испытаниях Бернулли нек-рое событие А наступает
ровно т раз, причем и вероятность А в каждом испыта-
испытании равна р, то при больших значениях п и 1/р вероят-
вероятность Рп (т) близка к
пр(пр)т
Величина Х=пр равна среднему значению числа нас-
наступлений А в п испытаниях, а последовательность зна-
чевий е-*- —^ , та=0,1, 2, . . ., Я,>0, образует распреде-
распределение Пуассона. П. т. была установлена С. Пуассоном
[1] для схемы испытаний, более общей, чем схема Бер-
Бернулли, когда вероятности наступления события А
могут меняться от испытания к испытанию так, что рп—»-0
при п —>- оо. Строгое доказательство П. т. в этом случае
основано на рассмотрении схемы серий случайных ве-
величин такой, что в я-й серии случайные величины неза-
независимы и принимают значения 1 и 0 с вероятностями
и рп 1—р„ соответственно. Более удобна форма П. т.
в виде неравенства: если A,=pt+. . .+р„, 6=jt?f+. . .
. . .-\-pti, то при ге^2
Это неравенство указывает ошибку при замене Рп (т)
величиной е~^ —- . Если рх— . . . =рп=к/п, то б =
—Х2/п. П. т. и теорема Лапласа дают исчерпывающее
представление об асимптотич. поведении биномиального
распределения.
Последующие обобщения П. т. создавались в двух
основных направлениях. С одной стороны, появились
уточнения П. т., основанные на асимптотич. разложе-
разложениях, с другой — были установлены общие условия схо-
сходимости сумм независимых случайных величин к рас-
распределению Пуассона.
Лит.: [1] Poisson S. - D., Recherches sur la probability
des jueements en matiere criminelle et en matiere civile..., P.,
1837; [2] Лоэв М., Теория вероятностей, пер. с англ., М.,
1962; |3] Боровков А. А., Теория вероятностей, М., 197В.
А. В. Прохоров.
ПУАССОНА УРАВНЕНИЕ — дифференциальное
уравнение с частными производными, к-рому удовлет-
удовлетворяет объемный потенциал внутри областей, занятых
создающими этот потенциал массами. Для ньютонова
потенциала в пространстве R", nj>3, и логарифмичес-
логарифмического потенциала в R2 П. у. имеет вид
где p=p(z1, . . ., хп) — плотность распределения масс,
о"(?")=геяп/2/Г(л/2+1) — площадь единичной сферы
S" в R", Г(га/2+1) — значение гамма-функции.
П. у. является основным примером неоднородного
уравнения эллиптич. типа. П. у. впервые рассмотрено
С. Пуассоном (S. Poisson, 1812).
Лит.: [1] Б и ц а д з е А. В., Уравнения математической
физики, М., 1976; [2] К у р а н т Р., Уравнения с частными про-
производными, пер. с англ., М., 1964. Е. Д. Соломенцев.
ПУАССОНА УРАВНЕНИЕ; численные мето-
методы решения — методы, заменяющие исходную
краевую задачу для уравнения Пуассона
Au(X) = Z,r = 1 ~^ = f ^' * — (*!' Х2. •¦¦> xd) С1)
системой из jV линейных алгебраич. уравнений
LN(uN)=fN, B)
решение к-рой u^s^^i, u2, . . ., и^т) позволяет постро-
построить нек-рую аппроксимацию pnun Для решения исход-
исходной задачи, TV-^oo.
В зависимости от способа сравнения решений исход-
исходной задачи A) и дискретной задачи B) определяются
такие важнейшие понятия, как погрешность численного
метода и оценка погрешности (точности). Другими ха-
характеристиками численных методов служат алгебраич.
свойства систем B) (дискретных аналогов краевых за-
задач), связанные с устойчивостью их решений (коррект-
(корректностью дискретных задач) и возможностью отыскания
точных или приближенных решений B) теми или ины-
иными прямыми или итерационными методами при выпол-
выполнении соответствующей вычислительной работы и соот-
соответствующих требованиях на объем используемой па-
памяти ЭВМ (см. Минимизация вычислительной работы).
Важность численного решения краевых задач для
П. у. определяется не только тем, что эти задачи часто
возникают в разнообразных областях науки и техники,
но и тем, что они нередко служат и средством решения
более общих краевых задач как для уравнений и систем
уравнений эллиптич. типа, так и различных нестацио-
нестационарных систем. Основными численными методами для
решения рассматриваемых краевых задач являются
проекционные методы и разностные методы.
Проекционные методы включают в себя
ряд методов: вариационные, наименьших квадратов,
Галеркнна, проекционно-разностные, проекционно-се-
точные, конечных алементов. Для всех них характерно
сведение исходной краевой задачи к операторному урав-
уравнению
L(u)=f C)
(оператор L действует, напр., из гильбертова прост-
пространства Н в Я) с последующим выбором конечномерных
подпространств Ядг и F ^ {N—>са)\ сама задача C) в
этих методах заменяется задачей нахождения
т?!;ой, что для любого
(LuN—f, v)H=-0.
Тогда при заданных базисах в Ядг и FN система B)
является системой относительно коэффициентов раз-
разложения идг по базису Ядг и за pjvupj можно принять
саму функцию идг; погрешность метода естественно
определить как \\и—идг||//. В наиболее важных случаях
Н является нек-рым подпространством пространства
Соболева И^Й), Ядг—/дг, и если tyx(x), ^2(x), . . .,
^{) — базис Яд', то система B) принимает вид
2 \ &d Vj 8rad ¦*« (*) dx =r-
, i = l, 2, ..., N. D)
Погрешность метода при этом определяется расстоя-
расстоянием в Я от решения исходной задачи до иодпрост-
ранства Ядг (см. [1], [5]—[9]). В современных вариантах
проекционных методов подпространства Ядг стремятся
шбирать так, чтобы функции tyi(x) имели локальные
носители и в каждом уравнении D) лишь конечное чис-
число коэффициентов было отлично от нуля. Методы такого
чипа и наз. нроекционно-сеточными ме-
методами (проекционно-разностными, вариационно-
разностными, конечных элементов) (см. [1], [4], [7] —
[9], [11]). Наибольшим достоинством этих методов яв-
является их применимость при достаточно сложной гео-
геометрии области Q, в к-рой рассматривается краевая
задача. К проекционным методам примыкает и относи-
относительно редко применяемый коллокаций метод.
Разностные (конечноразностные)
методы используют аппроксимацию исходной об-
области Q нек-рой сеточной областью Одг, содержащей N
узлов сетки, и обычно приводят к системе B) на основе
аппроксимации П. у. и соответствующих граничных
условий их разностными (сеточными) аналогами, ис-
использующими лишь значения функции в выбранных
узлах (см. [1]). Погрешность метода обычно получается
сравнением вектора г*дг и вектора, получаемого суже-
сужением искомого решения на множество рассматриваемых
узлов. Корректность и аппроксимация могут изучаться
при различных выборах норм, в частности возможно
использование принципа максимума; сходимость полу-
получается как следствие корректности и аппроксимации
(см. [1]-[4]).
Системы B) могут выводиться и на основе нек-рых
дискретных аналогов соответствующих вариационных
задач и на основе аппроксимации нек-рых интеграль-
интегральных соотношений (см. [1], [2], |4], |10]); такие подходы
несколько сближают эти варианты разностных методов
с проекционно-разностными.
Методы решения систем сеточ-
сеточных уравнений B) наиболее интенсивно изу-
изучались для простейших разностных аналогов на парал-
лелепипедной сетке (см. [1], [9], [11]—[19]). В случае
двух переменных и области Q на плоскости, являющейся
прямоугольником, часто применяются для ряда гра-
граничных условий прямые методы, позволяющие найти
решение B) при затрате O(iVln N) арифметич. дейст-
действий. Это — метод разделения переменных, использую-
использующий дискретное преобразование Фурье, и метод редук-
редукции (см. [12], [13]); известны и методы с оценкой O(N)
действий (см. |14]). При d"^2 и наличии разделения пе-
переменных (Й в этом случае — параллелепипед) решение
B) с точностью е>0 можно найти при затрате O(N In
N\ln е|) действий с помощью итерационного метода
переменных направлений (см. [1], [12]); итерационные
методы с факторизуемыми операторами (метод последо-
последовательной сверхрелаксации с симметризацией, непол-
неполной матричной факторизации, попеременно-треуголь-
попеременно-треугольный) позволяют найти решение B) с точностью е при
затрате O(JV1 + 1/2d |ln г)) действий (см. 112], [15]) для
довольно общих ситуаций.
В случае односвязных и многосвязных областей Q
на плоскости, составленных из конечного числа прямо-
прямоугольников, решение системы B) с точностью е может
быть найдено при затрате O(Nln iV-)-iV3/'<t|ln e| In N)
действий на основе разрезов Q на прямоугольники
(см. [15], [16]). Похожая асимптотика для дискретных
аналогов задачи Дирихле в случае некоторых обла-
областей получена с помощью метода емкостей (см. [17])
и фиктивных неизвестных (см. [18]). Для ряда систем
B), являющихся цроекционно-разностными аналога-
аналогами исходных задач, затраты типа O(N In N\\n е|), a
иногда и O(N\nN) (при eX^V1, а>0) достигаются
с помощью итерационных методов, использующих эк-
эквивалентность операторов по спектру (см. [11], [17],
[19]). Использование последовательностей сеток в ряде
случаев позволяет получить итерационные методы,
дающие решение B) с точностью eXiV-a, a>0, при
асимптотически минимальных затратах вычислительной
работы (число действий есть 0{N)) (см., напр., [1], [9],
[И], [19]).
Лит.: [1] Годунов С. К., Рябенький В. С,
Разностные схемы, 2 изд., М., 1977; [2] Л а д ы ж е н-
с к а я О. А., Краевые задачи математической физики, М., 1973;
[3] М а р ч у к Г. И., ШайдуровВ. В., Повышение точнос-
точности решений разностных схем, М., 1979; 14] С а м а р-
с к и й А. А., А н д р с е в В. Б., Разностные методы для эллип-
эллиптических уравнении, М., 1976; [5] М и х л и н С. Г., Численная
реализация вариационных методов, М., 1966; [6] К р'а с н о-
с е л ь с к и й М. А. [и др.], Приближенное решение оператор-
операторных уравнений, М., 1969; [7] О б э н Ж. П., Приближенное реше-
решение эллиптических краевых задач, пер. с англ., М,, 1977; [8]
Стренг Г., Фикс Д ж., Теория метода конечных элемен-
элементов, пер. с англ., М., 1977; [9] Оганесян Л. А., Р и в-
к и н д В. Я., Р у х о в е ц Л. А., Вариационно-разностные
методы решения эллиптических уравнений, ч. 1—2, Вильнюс,
1973—74 (Дифференциальные уравнения и их применение, в.
5, 8); [10] Самарский А. А., ФрязиновИ. В., «Успехи
матем. наук», 1976, т. 31, в. 6, с. 167—97; [11] Д ьяконов Е. Г.,
в кн.: Вариационно-разностные методы в математической физи-
физике, Новосиб., 1978, с. 149—84; [12] С а м а р с к и й А. А., Н и-
к о л а е в Е. С, Методы решения сеточных уравнений, М., 1978;
[13] Barker R. I., в кн.: Mathematical models and numeri-
numerical methods, Warsz., 1978, p. 255—68 (Banach center publicati-
publications, v. 3); 114] Bank R. E., Rose D. J., «SIAM J. Numer.
Anal.», 1975, v. 12, № 4, p. 529—40; [15] К у з н е ц о в Ю. А.,
в кн.: Вариационно-разностные методы в математической физи-
физике, Новосиб., 1978, с. 178—212; [16] Дьяконов Е. Г., в
кн.: Численные методы в математической физике, Новосиб.,
1979, с. 45—68; [17] А с т р а х а н ц е в Г. П., в кн.: Разност-
Разностные и вариационно-разностные методы, Новосиб., 1977, с. 63—
72; [18] Капорин И. Е., Николаев Е. С, «Дифферен-
«Дифференциальные уравнения», 1980, т. 16, JNI5 7, с. 1211—25; [19] К о р-
н е е в В. Г., Схемы метода конечных элементов высоких поряд-
порядков точности, Л., 1977. Е. Г. Дьяконов.
ПУАССОНА ФОРМУЛА — 1) То же, что Пуассона
интеграл.
2) Формула, дающая интегральное представление
решения задачи Коши для волнового уравнения в про-
пространстве R3:
~ — а2Аи-,0, t > 0, М = (х, y,z),
00 < Ж, IJ, Z < -j- 00,
В(Л/.О)=Ф(Л/),
и имеющая вид
где
ф
- среднее значение функции ср на сфере Sat в нромран-
. тве (х, г/, z) радиуса at с центром в точке М, dQ —
элемент площади единичной сферы. В случае неоднород-
неоднородного волнового уравнения в формуле A) добавляется
третье слагаемое (см. [2]).
Из формулы A) спуска методом получаются формулы
решения задачи Коши для случая двух (Пуассона
формула) и одного (Д' Аламбера форму-
л а) пространственного переменного (см. [2]). См. также
Кирхгофа формула.
3) Иногда П. ф. наз. интегральное представление
решения задачи Коши для уравнения теплопроводности
в пространстве R3:
-^- —а2 Дм=0, t > 0, М --^(х, у, г),
— оо < х. у, z < -!- оо ,
и(М, 0)-<р(Л/),
имеющее вид
I МР\*
Формула B) непосредственно обобщается на любое
число пространственных переменных п ^ 1.
Лит.: [1] Poisson S. D., «Mem. Acad. sci.», 1818, t. 3,
p. 121—76; [2] Тихонов А. Н., Самарский А. А.,
Уравнения математической физики, 5 изд., М., 1977; [3] В л а-
д и м и р о в В. С, Уравнения математической физики, 4 изд.,
М., 1981. Е. Д. Соломенцее.
ПУАССОНА ФОРМУЛА СУММИРОВАНИЯ — фор-
формула
П. ф. с. имеет место, если, напр., функция g(x) абсо-
абсолютно интегрируема на интервале (—оо, +оо), имеет
ограниченное изменение и 2g(x)—g(xJr6)Jrg(x—0).
П. ф. с. записывается также в виде
где а п Ъ — любые два положительных числа, удовлет-
удовлетворяющие условию aft—2л, а %(и) есть преобразова-
преобразование Фурье функции g:
.Itim.: [1] Зигмунд А., Тригонометрические ряды, пер.
с англ., т. 1, М., 1965; [2] Т и т ч м а р ш Е., Введение в теорию
интегралов Фурье, пер. с англ., М.— Л., 1948. И. И. Волков.
ПУАССОНОВСКИЙ ПОТОК — то же, что пуассонов-
ский процесс. Этот термин используют, как правило, в
теории массового обслуживания.
ПУАССОНОВСКИЙ ПРОЦЕСС — случайный процесс
X(t) с независимыми приращениями X (t2)—X (t,),
*2 ^* *и имеющими Пуассона распределение. В однород-
однородном П. п. для любых t2 > t1
*=0, 1, 2, ... A)
Коэффициент X > 0 наз. интенсивностью пу-
ассоновского процесса X (t). Траектории
П. и. X (Q представляют собой ступенчатые функции со
скачками размера 1. Моменты скачков 0 < тх < т2<. . .
образуют простейший поток, описывающий поток тре-
бований во многих системах массового обслуживания.
Распределения случайных величин хп—гп_1 независи-
независимы при га=1,2,. . . и имеют показательную плотность
Хе-М, t > 0.
Одним из свойств П. п. является следующее: услов-
условное распределение моментов скачков 0 < т, < т2 < . . .
<т„ < t при X (t) — X @) = п совпадает с распределе-
распределением вариационного ряда независимой выборки объема
п с равномерным распределением на [0, t]. С другой
стороны, если 0 < т± < т2 < . . . <т„ — описанный
выше вариационный ряд, то при п -> оо, t -> со, с nlt-+
—*¦ X получают в пределе распределение скачков П. п.
В неоднородном П. п. интенсивность X(t) зависит от
времени t и распределение X(t2)—X(tl) определяется
формулой
ГС * Я (u)du I - V *
P{X(t)X(^) = A}-LJ<1 ieJ''
du
При определенных условиях П. п. может быть пока-
показан как предел суммы неограниченно возрастающего
числа независимых «редких» потоков довольно общего
вида. О нек-рых поучительных парадоксах, связанных с
П. п., см. [3], т. 2, гл. 1.
Лит.: [1] Боровков А. А., Теория вероятностей, М.,
1976; [2] ГихманИ. И., С к о р о х о д А. В., Ядрен-
к о М. И., Теория вероятностей и математическая статистика,
К., 1979; [3] Ф е л л е р В., Введение в теорию вероятностей и её
приложения, 2 изд., дер. с англ., т. 1 — 2, М., 1967.
Б. А. Севастьянов.
ПУЛЬВЕРИЗАЦИЯ на дифференцируе-
дифференцируемом многообразии М — векторное поле W на
касательном пространстве ТМ, имеющее в терминах ло-
локальных координат (г1,. . ., х", v1,. . ., vn) на ТМ, ес-
естественным образом связанных с локальными координа-
координатами (.г1,. . ., хп) на М, компоненты (и1,. . ., и", f1,. . ., /"),
где /'==/' (х1,. . ., .г", у1,. . . , и") — функции класса
С1, причем при фиксированных х1,. . ., хп они являют-
являются положительно однородными функциями от v1,. . ., v"
степени 2 (эти свойства W не зависят от конкретного
выбора локальных координат). Определяемая этим по-
полем система дифференциальных уравнений
dxl : dvl ,: , , „i „\ ¦ 1
Г=У ' ~йТ~ {х ' •¦¦' х ' " ' ••••")• t=~ !' ••¦' "'
лкпппалентна системе дифференциальных уравнении
2-го порядка
d'x -- // (r1 rn ,,1 ,,n\
at* — ' ^ ' '''' > ' • ¦ ¦ > />
поэтому П. описывает (причем инвариантным образом,
т. е. не зависящим от системы координат) систему таких
уравнении на М.
Важнейший случай П.— когда /' суть многочлены
2-й степени от v':
f=2 rU (s1, ¦ • ¦. ^
В этом случае Tfk задают на М аффинную связность с
нулевым тензором кручения. Обратно, для всякой
аффинной связности уравнения геодезич. линий зада-
задаются нек-рой П. с /' вида (*) (причем при переходе от
связности к пульверизации T)k симметризуются по ниж-
нижним индексам). Если поле W — класса С2, то /' обя-
обязаны иметь вид (*). В общем случае W, каким бы глад-
гладким оно ни было вне нулевого сечения расслоения ТМ,
не обязано быть полем класса С2 возле этого сечения.
В такой ситуации иногда говорят об обобщенной П.,
оставляя термин «П.»' только для специального случая
(*). Дифференциальные уравнения для геодезических в
финслеровой геометрии приводят к обобщенной П.
Можно дать определение П. в инвариантных тер-
терминах, пригодное и для банаховых многообразий
(см. [1]).
Лит.: [l] Л е н г С, Введение в теориго дифферендир>емы\
многообразий, пер. с англ., М., 1967. Д. В. Аносов.
ПУНКТИРОВАННОЕ ПРОСТРАНСТВО — тополо-
топологическое пространство X с отмеченной точкой х0 в нем;
пунктированный объект категории топологич. прост-
пространств, и. И. Войцеховский.
ПУНКТИРОВАННЫЙ ОБЪЕКТ категории
С, обладающей финальным объек-
объекте м,— пара (X, х0), где Х?0ЬС, х0 — морфизм фи-
финального объекта в X. Важнейший пример: пунктиро-
пунктированное топологич. пространство, т. е. пара (X, х0),
где X — топологич. пространство, хо?Х — точка,
называемая отмеченной. Пунктированные топологнч.
пространства образуют категорию, морфизмами в к-рой
являются отображения, переводящие отмеченную точку
В отмеченную. А. Ф. Харшиладзе.
ПУНКТИФОРМНЫЙ НАРОСТ — нарост топологич.
пространства X в его бикомпактном расширении Y
такой, что всякий связный бикомпакт в Y\X состоит
ИЗ ОДНОЙ ТОЧКИ. М. И. Войцеховский.
ПУСТОЕ МНОЖЕСТВО — множество, не содержа-
содержащее элементов. Обозначения: 0, А. Ипаче, 0= {^ :
х Ф х}, при этом' вместо х j~ x в этом определении
можно было бы использовать любое всегда ложное
утверждение. П. м. является подмножеством любого
множества. М. И. Войцеховский.
ПУСТЫХ ЯЩИКОВ КРИТЕРИЙ — статистический
критерий проверки гипотезы Но о принадлежности не-
независимой выборки фиксированному распределению.
Подробнее, пусть Хг,. . ., Хп — независимая выборка,
взятая из непрерывного распределения F(x). Точки
zo= —oo<z! < z2 < ... <гЛг_1<г„=оо выбираются
так, чтобы F(zk) — F(zft_x) = 1/JV, fc=l,2,. . ., N. Кри-
Критерий строится на основе статистики ц0, равной числу
полуинтервалов (z^_i, z^,], в к-рые но попало ни одного
наблюдения ж,-. Этот критерий имеет следующий вид:
если ц0 <: С, то гипотеза По принимается; если |л0 > С,
то гипотеза Но отвергается. Константа С выбирается из
условия, что ошибка 1-го рода, т. е. вероятность отверг-
отвергнуть гипотезу ff0 если она верна, равна заданному
значению. Вычисление константы С и расчет мощности
П. я. к. при больших п к N произиодится с помощью
предельных теорем в случайных размещениях.
Лит.: [I] КоячинВ. Ф., СевастьяновБ. А., Чи-
Чист я к о в В. П., Случайные размещения, М., 1976.
Б. А. Севастьянов.
ПУТЕЙ ПРОСТРАНСТВО — пространство Е рас-
расслоения (Е, р, X), называемое расслоением
путей, где X — линейно связное пространство с отме-
отмеченной точкой *, Е — множество путей в X, начинаю-
начинающихся в *, р — отображение, сопоставляющее каждому
Пути его концевую точку; при этом Е рассматривается в
компактно открытой топологии. Слоем этого расслоения
(являющегося Серра расслоением) является петель
пространство QX — множество всех петель простран-
пространства X в точке *. П. п. стягивается но себе в точку,
так что гомотопич. группы лп(Е)-—0, и гомотопич. пос-
последовательность расслоения путей вырождается в
т. н. изоморфизмы Гуревича:
na(QX) «яя + 1(АГ).
М. И. Войцеховский.
ПУТЬ — непрерывное отображение / отрезка [0, 1]
в тоиологич. пространство X. Точки /@) и /A) наз.
начальной и концевой точками пути /.
П., определенный по / формулой t —>f(i—t), t?@, 1],
паз. путем, обратным /, и обозначается /-'.
П., определяемый по путям Д и/2 с/1A)=/2@) формулой
t _^ ( fBt), *< 1/2,
~ * \ 1Bt-i),
наз. п р о и з в е д о н и е м п у т е и fx и /2 и обозна-
обозначается fj2- Совокупность всех П. линейно связного
пространства X с отмеченной точкой *, начинающихся
в ней, образует путей пространство. м.'И. Войцеховский.
ПУЧКОВ ТЕОРИЯ — специальный математич. ап-
аппарат, обеспечивающий единый подход для установле-
установления связи между локальными и глобальными свойствами
топологич. пространств (в частности, геометрич. объек-
объектов) и являющийся мощным средством исследования
многих задач в современной алгебре, геометрии, топо-
топологии и анализе.
На тоиологич. пространстве X задан предпучок
F, если каждому открытому подмножеству UcX сопо-
сопоставлена абелева группа (кольцо, модуль над кольцом
и т. п.) F(U) и всякой паре открытых множеств VczU—
гомоморфизм Fy : F(U) ->¦ F(V) такой, что Fy—тож-
Fy—тождественный изоморфизм и Fw^FwFv Для каждой
тройки W с: V a U. Другими словами, предпучок —
контравариантный функтор из категории открытых
подмножеств X и их вложений в категорию групп (ко-
(колец и т. п.) и их гомоморфизмов. Отображения Fy ?
наз. гомоморфизмами ограничения (напр.,
если F(U) — функции какого-либо типа, Fy — огра-
ограничения их на меньшее подмножество). На множестве
?= U dfx. гДе fл — прямой предел lim F(U),
х е х xeU
следующим образом определена топология: для всякого
U а X и любого a?F(U) в |р объявляется открытым
множество S, состоящее из тех точек ,f~x, r,?U, к-рые
служат образами а при определении $ х. В этой топо-
топологии слои ^f x дискретны и замкнуты в дГ, определяе-
определяемые прямыми пределами послойные алгебраич. операции
на f непрерывны, а естественная проекция р : f —>¦
-> X, при к-рой ^гх=Р~1(ж)' является локальным
гомеоморфизмом. Пространство f вместе с послойными
алгебраич. операциями и проекцией р наз. пучком
абелевых групп (колец и т. п.) над X, определяемым
предпучком F.
Всякое непрерывное отображение s : U -> $~, для
к-рого х~ ps(x), наз. сечением $ над U. Сечение g~
над X, определяемое всеми нулями в §~х, наз. н у л е-
в ы м. Если нек-рое сечение s равЬо нулю в точке х,
то s совпадает с нулевым сечением в нек-рой окрест-
окрестности х, поэтому множество тех точек, в к-рых s отлично
от нуля (носитель сечения s), замкнуто в U.
Пусть ГF^, JF) (соответственно -Рф(Х, §"), где Ф —
нек-рое семейство замкнутых множеств в X, в частно-
частности ГС(Х; §~)) — группа (кольцо, модуль и т. п.) всех
сечений над U (соответственно сечений над X с носите-
носителями из Ф, в частности сечений с компактными носите-
носителями). Соответствие U —>. Г({/, Jp) является предпуч-
предпучком над X, к-рып наз. предпучком сечений
пучка Цр'. Используемое при определении топологии на
if соответствие а -> s определяет также гомоморфизмы
F(U) -> Г (С/, §~), коммутирующие с ограничениями на
V a U, т. е. гомоморфизм предпучков. Этот гомомор-
гомоморфизм является изоморфизмом при условии, что исход-
исходный предпучок F удовлетворяет требованиям: а) если
U= U Uk и a, o'?F{U), то о"=0', если равны ограни-
я
чения а, а' па все U},; б) если U= (J U\, а ста, ?F(U\)-~
Л
такой набор элементов, что ограничения а\, Оц на Ut, П
П С/р, совпадают, то существует a?F(U), ограничения
к-рого на каждое U\ совпадают с а\. Понятие предпуч-
ка, удовлетворяющего этим требованиям, эквивалентно
понятию порожденного им пучка, поэтому такие пред-
пучки также нередко наз. пучками.
Пучок вида X X G, где G — нек-рая группа, наз.
постоянными обозначается через G. J1 о к а л ь-
н о и о с т о я н и ы м наз. пучок, постоянный в доста-
достаточно малых окрестностях х?Х. Топология таких
пучков отделима, если X — отделимое пространство.
В более типичных ситуациях топология ff" может
быть неотделимой, даже если отделимо X (таков, напр.,
пучок ростков непрерывных (или дифференцируемых)
функций, порожденный предпучком F, где F(U) —
непрерывные (дифференцируемые) функции на U; од-
однако пучок ростков аналитич. функций на многообра-
многообразии отделим).
Всякий гомоморфизм предпучков F -> F' приводит
к отображению соответствующих пучков JF—>-,f"',
к-рое является локальным гомеоморфизмом и гомомор-
гомоморфно отображает слои в слои; такое отображение пучков
наз. гомоморфизмом пучков. Стандарт-
Стандартным образом определяются моно- и эпиморфизмы. При
любом гомоморфизме / : |р' —> ff~ образ /(JF') есть
открытая часть Jp, замкнутая по отношению к послой-
послойным алгебраич. операциям. Всякая часть <р", удовлет-
удовлетворяющая этим требованиям, наз. подпучком
в Jp. Факторпучок пучка ff~ по подпучку §г'
определяется как пучок Jf", порожденный предпучком
U -> ГA7, <р")/Г(?/, gr'); при этом имеется эпиморфизм
W-*¦ ?" 1 причем ff"x=Wxl?x- Для всякого открытого
UczX через $ц обозначается подпучок в $, являющий-
являющийся объединением p~1(U) с нулевым сечением Jp над X,
а через ff'xw — соответствующий факторпучок (огра-
(ограничение к-рого на X\U совпадает с ограничением §г).
Возможность употреблять по отношению к пучкам
над X такие привычные термины, как гомоморфизм,
ядро, образ, подпучок, факторпучок и т. д., вкладывая
в эти понятия такой же смысл, как в алгебре, позволяет
рассматривать их с категорной точки зрения и приме-
применять в П. т. конструкции гомологической алгебры. Воз-
Возникающие над X категории пучков родственны таким
классическим, как категория абелевых групп или ка-
категория модулей; в частности, для пучков определя-
определяются прямые суммы, бесконечные прямые произведе-
произведения, индуктивные пределы и др. понятия.
Аппарат П. т. проник в разнообразные области мате-
математики благодаря тому, что определены естественные
когомологии Н* (X, ,f) пространства X с коэффициен-
коэффициентами в пучке ff'', причем без каких-либо ограничений
на X (что существенно, напр., в алгебраич. геометрии,
где возникающие пространства, как правило, неотде-
неотделимы), и что другие когомологии (в тех или иных кон-
конкретных условиях) сводятся к пучковым по крайней
мере в тех ситуациях, где их применение оправдано.
Для определения Н* (X, |р) сначала строится кано-
каноническая резольвента
где C°(g~) — пучок, определяемый предпучком F,
для к-рого F(U)—группа всех (включая разрывные)
сечений <р" над U, при этом Г (С/, С°(^))—
=F{U), СЧГ)--=С»(С")(^-)'|-), ... , C + 1(f)=
=C°(C(g')/lm C~x(<f)), .... По определению,
HP(X, §r) = HP(T(X, С*($-)){НРф(Х, f) получа-
получаются заменой символа Г на Гф)). При этом сам пучок If
удаляется из С* (f), так что Н°Ф(Х, Зг)=Тф(Х, f)
(для классич. когомологии /7° (X, G)—группа локально
постоянных функций на X со значениями в G). Резоль-
Резольвента С* (§~)—точный ковариантный функтор от Jp:
точной тройке «коэффициентов» 0 —>- !jj~'—у Uf -> ff'"—*- О
отвечает точная тройка резольвент. Функтор Гф ока-
оказывается точным на членах Ср, р ^ 0, резольвент, по-
поэтому указанным коэффициентам отвечает точная по-
последовательность когомологии
(X, Г') -^н%(х, «г") ¦-
нф
начинающаяся с 0 -v Гф(Х, $") -> Гф(Х, f )->... .
Когомологич. последовательность пары (X, А) отве-
отвечает тройке 0 ->- ?х\Л -*¦ ? -* ? д ->¦ ° й —замк-
—замкнутое множество).
Когомологии Нф(Х, If) обладают следующим свой-
свойством «универсальности», раскрывающим их значение:
для любой другой резольвенты X* (т.е. начинающейся
с $~ точной последовательности пучков ХЧ) имеется
естественный гомоморфизм «сравнения» Нр (Гф(Х,
X*)) -> #ф(Х, <р"), для описания к-poro в терминах
Яф(Х, Xя) применяются спектральные последователь-
последовательности. Важен случай, когда пучки резольвенты Ф-
а ц и к л и ч н ы, т. е. когда Л?(Х, J?4)=0 при р ^1:
в этом случае указанный гомоморфизм есть изоморфизм.
Основными примерами ацикличных пучков являются
вялые пучки (для всех f/cX отображения Г(Х, X) ->
-> Г {U, X) эпиморфны) и мягкие пучки (любое сечение
над замкнутым множеством продолжается до сечения
над всем X). Канонич. резольвента состоит из вялых
пучков. Если X — паракомпактное пространство, то
всякий вялый пучок является также и мягким.
Свойство универсальности позволяет сравнивать с
пучковыми (а следовательно, и между собой) когомоло-
когомологии, возникающие в более конкретных ситуациях,
определять для них те естественные границы, в к-рых
их применение эффективно, а также применять методы
П. т. для решения конкретных задач. Напр., когомоло-
когомологии Александрова — Чеха можно определить с помощью
коцепей, получающихся из коцепей специально подоб-
подобранной системы открытых покрытий переходом к прямо-
прямому пределу. Эти коцепи оказываются сечениями пучков
ростков коцепей (определяемых аналогично пучкам
ростков функций), составляющих резольвенту группы
(или даже пучка) коэффициентов, к-рая оказывается
мягкой, если пространство паракомпактно. Таким об-
образом, для паракомпактных пространств когомологии
Александрова — Чеха совпадают с пучковыми. Ана-
Аналогичный вывод имеет место для пространств Зариского
(в частности, для алгебраич. многообразий). Сечения-
Сечениями пучков резольвенты оказываются и коцепи Алек-
сандера •— Спеньера, причем резольвента состоит из
мягких пучков, если X паракомпактно, в частности, в
этом случае когомологии Алоксандера -— Спеньера и
Александрова — Чеха естественно изоморфны. В случае
сингулярных когомологии отождествление коцепей,
совпадающих друг с другом на сингулярных симплек-
симплексах мелкости (произвольных) открытых покрытий, при-
приводит к т. н. локализованным коцепям (дающим те же
когомологии), к-рые являются сечениями пучков, оп-
определяемых предпучками обычных сингулярных коце-
коцепей. Пучки оказываются мягкими, если X паракомпакт-
паракомпактно (а если X наследственно паракомпактно, то даже вя-
вялыми), но образуют резольвенту при дополнительном
требовании, чтобы X было слабо локально стягиваемым
(в каждой окрестности U каждой точки х ? X найдется
меньшая окрестность, стягиваемая в точку внутри U).
Классич. примером является теорема де Рама:
когомологии комплекса дифференциальных форм диф-
дифференцируемого многообразия совпадают с обычными
когомологиями с коэффициентами в поле R действи-
действительных чисел (пучки ростков дифференциальных форм
являются мягкими и образуют резольвенту R: вблизи
каждой точки каждая замкнутая дифференциальная
форма является точной).
Имеются также резольвенты, отвечающие любым от-
открытым или локально конечным замкнутым покрытиям
и позволяющий сравнивать когомологии X с когомоло-
когомологиями покрытий (спектральные последовательности
покрытий). В частности, изоморфизм обеспечивается
условием Н9=0 при д ^ 1 для всех элементов покрытия
и их конечных пересечений (теорема Лере).
Переход к прямому пределу по открытым покрытиям
дает изоморфизм когомологий Александрова — Чеха
Н* с пучковыми и для непаракомпактных X при усло-
условии, что в X имеется достаточно много мелких откры-
открытых множеств U, для к-рых Hq(U, Hf)~O при q > 1
(теорема Картана). Это означает, что приме-
применяемые в алгебраич. геометрии когомологий Н* с коэф-
коэффициентами в когерентных пучках также изоморфны
стандартным пучковым когвмологиям Н*.
Общие конструкции, обеспечивающие гомоморфизм
сравнения, позволяют также сравнивать когомологий
Нр(Х, &?9) с Н* (Г(Х, X*)) [аналогично Н% (X, SKq)
с Н* (Тф(Х, ЛБ*))\ в случае, когда X* — любой диф-
дифференциальный пучок (т. е. пучок, в к-ром
для любого q композиция Xq -> c5f*+2 равна нулю) с
ацикличными Xя', где $%1 — производные пучки от X*
(являющиеся факторпучками ядер по образам в каждой
размерности q). Соответствующие этому спектральные
последовательности имеют много различных примене-
применений. При этом, если ^f?=0 при q > 1, то Н*(Т(Х,
Х*))=Н*(Х, $jf°). Напр., если в качестве X* взять
пучок цепей Jf^ (оператор границы понижает размер-
размерность на единицу, T(U, %>*) — цепи пары (X, X\U),
слои Ж;=1шЯ,A, X\U)=Hq(X, X\x)), то
получается зависимость гомологии Hf(X, G) от все-
всевозможных Н^(Х, Жц)- На многообразии fflq=0 при
q < /i=dimX и Hf(X, G)=H?-p(X, $?„), т. е. имеет
место Пуанкаре двойственность. Если А — открытое
или замкнутое подмножество локально компактного
X, то гомологии А определяются теми сечениями Й"*,
носители к-рых содержатся в Л, а гомологии пары (X,
А) — сечениями ограничения и", на Х\А. Наоборот
(и это — тоже одно из проявлений двойственности
Пуанкаре), если ё"* — любая вялая резольвента для
когомологий, то ограничение 1§* на Х\А определяет
когомологий Х\А, а сечения #* с носителями в А —
когомологий пары (X, Х\А). Пучки #* вялые, и в
случае многообразия гомологич. последовательность
пары (X, А) совпадает с точностью до обратной нуме-
нумерации с когомологич. последовательностью пары
(X, Х\А). Это означает, что двойственности в много-
многообразиях, подобные Лефшеца двойственности Нр(Х,
U, G)=Hn~p(X\U, ffln), являются частными случая-
случаями двойственности Пуанкаре. Оказывается, что соот-
соотношения двойственности, не укладывающиеся в эту
схему, являются следствиями двойственности Пуанкаре
и ацикличности многообразия в нек-рых размерностях.
Такая же ситуация возникает в случае непрерывного
отображения / : X —у Y. Резольвента для когомологий
X определяет на Y нек-рый дифференциальный пучок
X*, для к-рого слои SKу СУТЬ прямые пределы когомо-
когомологий Я?(/-1(С/), JF) по окрестностям U точек у (а
для замкнутых отображений Ну=Н1 (f~1{y), JF)),
причем Н* (X, §r)=H*(T(Y, X*)). Возникающая за-
зависимость Н* (X, $f) от HP(Y, Ж4) описывается спект-
спектральной последовательностью Лере отображения /
(частным случаем к-рой является спектральная после-
последовательность Серра расслоения). Обращение в нуль
J^f* отвечает ацикличным отображениям, обеспечивая
изоморфизмы когомологий X и Y с соответствующими
коэффициентами (теорема Вьеториса и ее
обобщения). Упоминавшиеся выше общие конструкции
дают также спектральную последовательность отобра-
отображения, учитывающую (наряду с их когомологич. струк-
турой) степень несвязности прообразов точек, к-рая
особенно эффективна для нульмерных или конечно-
кратных отображений (в случае накрытий она прев-
превращается в спектральную последовательность Картана).
Имеются также специальные спектральные последова-
последовательности в категориях G-пространств (пространств,
на к-рых определено действие группы G).
В пучковых когомологиях естественным образом оп-
определяется мультипликативная структура. Существо-
Существование специальных вялых резольвент, отображения
внутри к-рых определяются нек-рой полусимплициаль-
ной структурой, позволяет дать явные формулы для
умножения коцепей, аналогичные обычным. Одновре-
Одновременно это дает возможность определить в П. т. и др. ко-
гомологич. операции.
Аппарат П. т. находит много применений всюду, где
существенно использование абстрактных гомологич.
методов: в топологии (гомологич. и когомологич. раз-
размерность, локальные гомологии и двойственность,
структура различных классов непрерывных отображе-
отображений, в том числе вложений на плотные подмножества,
в частности бикомпактификаций, и т. п.), в теории
аналитич. многообразий [гомологии и когомологии с
коэффициентами в когерентных аналитич. пучках и их
приложения, когомологии и аналитические дифферен-
дифференциальные формы, гомологии и аналитич. потоки (ана-
(аналог теоремы де Рама и т. п.)], а также в абстрактной ал-
гебраич. геометрии (когомологии аффинных, проектив-
проективных и полных алгебраич. многообразий с коэффициен-
коэффициентами в когерентных алгебраич. пучках, алгебраич.
двойственность Серра, алгебраическая (комбинатор-
(комбинаторная) размерность и др.).
Нек-рые основные идеи П. т. и спектральных после-
последовательностей появились в работе Ж. Лере (J. Leray,
1945 и позже) в связи с изучением гомологич. свойств
непрерывных отображений локально компактных про-
пространств, к-рым было дано также определение когомо-
когомологии (с компактными носителями) с коэффициентами в
пучке. Довольно полное изложение теории пучков с
применением резольвент было дано позже А. Картаном
(Н. Cartan). Большое влияние на развитие П. т. ока-
оказали данное А. Вейлем (A. Weil, 1947) доказательство
теоремы де Рама и работы Ж. П. Серра (J.-P. Serre,
нач. 50-х гг.) по алгебраич. многообразиям. Когомоло-
Когомологии с коэффициентами в пучке определялись первона-
первоначально способом Александрова — Чеха. Завершенный
вид П. т. приобрела в конце 50-х гг. в работах А. Гро-
тендика (A. Grothendieck) и Р. Годмана (R. Godement),
в к-рых была достигнута максимальная общность, а
методы значительно упрощены. В частности, было пока-
показано, что в категории пучков над X имеется образующая
(т. е. пучок /, допускающий ненулевые гомоморфизмы
в любой ненулевой пучок; для пучков абелевых групп
J=^jjUc:x 2u)i так чт0 каждый пучок вкладывается в
инъективный (теорема Гротендика). В
этом состоит причина формальной аналогии между
теорией когомологии с коэффициентами в пучках и тео-
теорией производных от функторов в категории модулей:
в категории пучков над X «достаточно» инъективных
объектов (хотя, как правило, мало проективных), и
поэтому можно свободно применять все соответствую-
соответствующие средства гомологич. алгебры, в частности опреде-
определять когомологии Нф(Х, |р) (без каких-либо огра-
ограничений на X) как производные точного слева функтора
Гф(^1 Ю (и даже как Ext* (Zx, W))- Это же пролива-
проливает свет и на общую природу, напр., таких понятий,
как когомологич. размерность (над %) пространства,
алгебраич. размерность многообразия и глобальная
размерность кольца. А. Гротендиком дано описание
спектральной последовательности для функтора Ext,
необходимой в алгебраич. геометрии. Более простои
способ конструирования инъективных пучков был най-
найден Р. Годеманом. Он показал также, что для построе-
построения теории когомологий вполне достаточно пользовать-
пользоваться предложенной им канонической вялой резольвентой,
к-рая с точки зрения гомология, алгебры оказывается
просто одной из ацикличных резольвент пучка. Р. Годо-
ман первым стал применять вялые и мягкие пучки, ока-
оказывающиеся ацикличными в том же смысле (мягкие
ацикличны лишь при условии паракомпактности X,
чем объясняется их использование преимущественно в
топологии).
Лит.: [1] Bred on G. E., Sheaf theory, N. Y., 1967; [2]
Годеман Р., Алгебраическая топология и теория пучков,
пер. с франц., М., 1961; [3] Гротондик А., О некоторых
вопросах гомологической алгебры, пер. с франц., М., 1961;
[4] S w a n R., The theory of sheaves, Chi.— L., 1964.
E. Г. Скляренко.
ПУЧОК — 1) П.— предпучок F такой, что для всяко-
всякого объединения U — ^kUk открытых подмножеств U%
топологич. пространства X выполнены следующие
условия: 1) если ограничения на каждое Ux элементов
sbs' из F (U) совпадают, то «'=*"; 2) если sx?F(U\)
таковы, что для любой пары индексов Я, fi ограничения
si и sji на 17% П U^ совпадают, то существует элемент
s?F(U), ограничения к-рого на все Ux совпадают с
sx. Всякий П. на X изоморфен П. ростков непрерыв-
непрерывных сечений некоторого накрывающего пространства
Р : Е —>- X над X, к-рое определяется однозначно с точ-
точностью до изоморфизма (под накрывающим пространст-
пространством понимается непрерывное отображение ? на А',
являющееся локальным гомеоморфизмом), поэтому под
II. обычно понимается также и само накрывающее ото-
отображение р : Е —>- X (см. Пучков теория).
К. Г. Скляренко.
2) П.— однопараметрическое семейство линий на
плоскости или поверхностей в пространстве, линейно
зависящее от параметра. Пусть Ру и Fг — функции двух
переменных, непропорциональные друг другу. Семей-
Семейство линий на плоскости, определяемых уравнением
x1f1+x2f2 = o
при всевозможных значениях параметров 'ку и к2 (кро-
(кроме Яг=0, Я2=0), представляет собой П. (фактически П.
зависит от одного параметра кг : к2). Аналогично запи-
записывается уравнение П. поверхностей в пространстве.
Два уравнения ^1=0, /'2-=0 дают два элемента П.
(две линии или две поверхности), к-рые определяют
весь П. Каждые два элемента П. пересекаются по од-
одному и тому же множеству точек — носителю.
Носитель П. может содержать как действительные,
так и мнимые точки. Если исходные кривые П. являют-
являются алгебрапч. кривыми порядков т и и, то носитель
состоит из тп точек (действительных или мнимых,
собственных или несобственных).
Пучок прямых — множество всех прямых,
лежащих в одной плоскости и проходящих через фик-
фиксированную точку (собственный П.) пли парал-
параллельных фиксированной прямой (несобствен-
(несобственный П.). Уравнение П. прямых имеет вид
Пучок плоскостей — множество всех плос-
плоскостей, проходящих через фиксированную прямую
(собственный П.) или параллельных нек-рон
фиксированной плоскости (несобственный П.).
Уравнение П. плоскостей имеет вид
Пучок окружностей — однонараметриче-
ское семейство окружностей, линейно зависящее от
параметра. П. окружностей содержит окружности и
одну прямую. Носителем (собственного) П.
окружностей являются две круговые точки и две соб-
собственные точки а и Ь. Если a jb Ь, то П. окружностей
можно определить как множество окружностей (считая
прямые окружностями бесконечного радиуса), проходя-
проходящих через точки а и Ь; если а-~Ь, нужно дополнительно
требовать, чтобы окружности касались друг друга в
точке а. Если а и Ъ действительные и различные, П.
Рис. 1.
Рис. 2.
окружностей наз. эллиптическим (рис. 1), если
совпавшие (действительные) — параболиче-
параболическим (рис. 2), если мнимые (различные) — гипер-
гиперболическим (рис. 3). Несобственным
И. окружностей наз. совокупность концентрических
окружностей (рис. 4).
У каждого собственного П. окружностей существует
так наз. радикальная ось — прямая, каждая точка к-рой
Рис. з.
Рис. 4.
имеет одинаковую степень точки (различную для раз-
различных точек) относительно всех окружностей П. Ра-
Радикальная ось эллиптического П. проходит через общие
точки окружностей; параболического — является их
общей касательной; гиперболического — линией цент-
центров двух окружностей, ортогональных ко всем окруж-
окружностям П. Центры окружностей П. лежат на прямой,
перпендикулярной радикальной оси. Точка пересече-
пересечения линии центров П. и его радикальной оси нал.
центром П. Степень центра П. относительно любой
окружности П. одинакова и наз. степенью П. Если
ось абсцисс является линией центров окружностей
П., а ось ординат — радикальной осью П., то уравне-
уравнение произвольной окружности П. имеет вид
где t — параметр, определяющий данную окружность,
р — степень П. Для эллиптического П. р < 0, для
параболического П. р=0, для гиперболического р > О
(степень несобственного П. можно считать бесконечной).
Окружности, ортогональные всем окружностям дан-
данного П., сами образуют П.; про этот II. говорят, что он
сопряжен с данным. Эллиптический П. сопряжен с
гиперболическим, параболический — с параболиче-
параболическим.
Любой П. окружностей является пересечением двух
связок окружностей.
Пучок сфер — однопараметрическое семейство
сфер, линейно зависящее от параметра. Любые две
сферы II. пересекаются по нек-рой окружности дейст-
действительного, нулевого или мнимого радиуса. В первом
случае П. сфер наз. эллиптически м, он состоит
на всех сфер, проходящих через данную окружность;
во втором — параболическим, П. состоит из
всех сфер, касающихся друг друга в общей точке; в
третьем — гиперболическим, П. состоит из
всех сфер, ортогональных к нек-рым трем данным сфе-
сферам, пересекающимся в двух точках. У П. сфер имеется
так наз. радикальная плоскость, каждая
точка к-рой имеет одинаковую степень (различную для
разных точек) относительно сфер П.; центры всех сфер
П. лежат на одной прямой, перпендикулярной ради-
радикальной плоскости.
П. офер является пересечением трех сетей сфер,
центры к-рых не лежат на одной прямой.
В проективной геометрии алгебраическим
пучком прямых наз. множество всех прямых
проективной плоскости, координаты иь и2, и3 к-рых
удовлетворяют уравнению
F (их, м2, и3) --0,
где Р(иъ и2, и3) — не равный тождественно нулю
многочлен, однородный относительно переменных иг,
и2, и3; степень многочлена F наз. степенью (или
п о р я д к о м) П. прямых. Алгебраический П. прямых
первого порядка задается уравнением
а1щ + а2иг -{- а3и3 = О
и представляет собой множество всех прямых, проходя-
проходящих через точку с координатами (alt я2, а3).
Алгебраический П. прямых второго поряд-
к а задается уравнением
-!-2/23и2и3 = 0, /,7 = /,¦,-, i, / = 1,2, 3,
pfifij — действительные числа, среди к-рых по крайней
мере одно отлично от нуля. Если дискриминант 6=
'--\fij\i i=l! 2, 3, отличен от нуля, П. прямых второго
порядка наз. невырожденным, если 6=0 —
вырожденным. Каждый невырожденный П.
второго порядка является множеством касательных к
невырожденной линии второго порядка; каждая невы-
невырожденная линия второго порядка является огибающей
нек-рого невырожденного П. второго порядка.
Лит.: [1] П о с т н и к о в М. М., Аналитическая геометрия,
М., 1S73. А. Б. Ивапое.
ПФАФФА ПРОБЛЕМА — проблема описания ин-
интегральных многообразий максимальной размерности
для системы Пфаффа уравнений
6«=-0, « = 1, ..., q, (*)
задаваемой набором ия q дифференциальных 1-форм в
нек-роп области Л/crR" (или на нек-ром многообразии),
линейно независимых в каждой точке. Подмногообразие
MczM наз. интегральным м н о г о о б р а з и-
о м системы (*), если ограничение форм 9а на N тож-
тождественно равно нулю. П. п. была поставлена И. Пфаф-
Пфаффом (J. Pfaff, 1814).
С геометрич. точки зрения система (*) определяет
(п—д)-мерное распределение (Пфаффа структуру)
в М, т. е. поле
(п—д)-мерных подпространств, а П. п. состоит в опи-
описании подмногообразий максимальной возможной раз-
размерности, касающихся этого поля. Важность П. и.
определяется тем, что интегрирование произвольного
уравнения с частными производными может быть све-
сведено к (соответствующим образом уточненной) П. и.
Напр., интегрирование уравнения 1-го порядка
F (х>, и, ди/дх') — 0
сводится к П. п. для уравнения Пфаффа O^sdu— p(dv' - О
на многообразии (вообще говоря, с особенностями),
задаваемом в пространстве R2n + i уравнением
F(xi, и, р,) = 0.
Вполне интегрируемая система Пфаффа (а также
одно уравнение Пфаффа постоянного класса) локально
может быть приведена к простому канонич. виду.
В этих случаях решение П. п. сводится к решению обык-
обыкновенных дифференциальных уравнений. В общем слу-
случае (в классе гладких функций) П. п. не решена A983).
В аналитич. случае П. п. была решена Э. Картаном
(Е. Cartan) в его теории систем в инволюции. Формули-
Формулировка основной теоремы Картана основана на понятии
регулярного интегрального элемента, ft-мерное подпро-
подпространство Еь касательного пространства ТХМ наз. к~
мерным интегральным элементом
системы («), если
0, dQa (Ek а Ек) _0, а^1, ...,</.
Подпространство S (?&) кокасательного пространства
ТхМ, порожденное 1-формами Qa\x, E^ jdQa\x, где
J — операция внутреннего умножения, наз. поляр-
полярной системой интегрального элемента Е^. Ин-
Интегральный элемент Е^ наз. per у л я р н ы м, если су-
существует такой флаг EkiDEk + 1ZD . . . ZdExZdO, для
к-рого
dim Я, — i, dim S (Е;) = max dim S (El),
где максимум берется по всем г-мерным интегральным
элементам Е\, содержащим ?7_i. Теорема Кар-
Картана утверждает следующее: пусть N есть fe-мерное
интегральное многообразие системы Пфаффа с ана-
аналитич. коэффициентами и для нек-рого x?N касатель-
касательное пространство TXN является регулярным интеграль-
интегральным элементом. Тогда для любого интегрального эле-
элемента Ek + i^)TxN размерности fc+1 существует в нек-
некрой окрестности точки х интегральное многообразие
N, локально содержащее TV, для к-рого #? + i= TXN.
Теорема Картана была обобщена на произвольные диф-
дифференциальные системы, задаваемые идеалами в алгебре
дифференциальных форм на многообразии (теорема
Картана — Кэлера).
Лит.: [1] Карта я О., Внешние дифференциальные сис-
системы и их геометрические приложения, пер. с франц., М., 1962;
[2] его ж е, Интегральные инварианты, пер. с франц., М.—
Л., 1940; [3] Раневский U.K., Геометрическая теория
уравнений с частными производными, М.— Л., 1947; [4] Стерн-
бергС, Лекции по дифференциальной геометрии, пер. с англ.,
М., 1970. Д. В. Алексеевспий.
ПФАФФА СИСТЕМА — система Пфаффа уравнений
(см. также Пфаффа структура).
ПФАФФА СТРУКТУРА, рас преде лени е,—
векторное подрасслоение я : Р ->- М касательного рас-
расслоения ТМ ->- М многообразия М. Размерность р
слоев Рх=п~1 (х) наз. размерностью П. с. я,
а число q—n—р (где re=dim М) — рангом, или к о-
раз мерностью. П. с. размерности р можно рас-
рассматривать как поле />-мерных подпространств х н> Рх
на многообразии М.
Обычно П. с. задают системой Пфаффа уравнений
91=. . .= 9?=0 или, двойственным образом, указанием
векторных полей, значения к-рых в произвольной
точке х?М образуют базис подпространства Рх.
Подмногообразие NczM наз. интегральным
многообразием П. с, если TxNaPx для всех
x?N. П. с. наз. вполне интегрируемой,
если через каждую точку х ? М проходит р-мерное ин-
интегральное многообразие или, что эквивалентно, если
локально она может быть задана системой уравнений
Пфаффа dy1=. . .= б2,7/?=О, где у1, . . ., уп — нек-рыо
локальные координаты в М. Это понятие соответствует
понятию вполне интегрируемой системы уравнений
Пфаффа. Пусть Г (л) — пространство сечений рас-
слоения п : Р —*¦ М, a L (я) — пространство дифферен-
дифференциальных 1-форм, обращающихся в нуль на Р. Соглас-
Согласно т е о р е м о Ф р о б с н и у с а, П. с. я вполне инте-
интегрируема тогда и только тогда, когда пространство
Г (л) является подалгеброй алгебры Ли D (М) вектор-
векторных полей на М или, что эквивалентно, если идеал,
порожденный пространством L (л) в алгебре Q (М)
дифференциальных форм, замкнут относительно опе-
оператора внешнего дифференцирования.
Пусть А (л) — алгебра Ли инфинитезимальных
автоморфизмов П. с. л, т. е. множество векторных
полей Х?Г(п), для к-рых [X, Г(я)]сГ(я). Алгебра
А (л) есть подалгебра алгебры Ли D (М) и одновре-
одновременно модуль над кольцом F (М) гладких функций на А/.
Фактормодуль Г (л)/А (л) характеризует степень неин-
неинтегрируемости П. с.
П. си наз. регулярной, если размерность про-
пространства Ар(п)= {Хр, Х?А (л)} не зависит от р?М.
В этом случае А (л) есть пространство сечений вполне
интегрируемой П. с. л' : Р'= \Jpi и-^-р (я) ~"*" м> к"Рая
наз. характеристической системой
П. с. л. Ранг структуры я' наз. классом П. с. я,
он равен наименьшему возможному числу координат
локальной системы координат, через к-рые выражаются
все 1-формы из Ь(л). Класс регулярной П. с. ранга 1
(т. е. поля гиперплоскостей) нечетен и образует пол-
полную систему локальных инвариантов: локально в нек-
некрой системе координат П 2\1
уравнением Пфаффа
Другим важным локальным инвариантом П. с. яв-
является ее р о д, указывающий размерность максималь-
максимальных интегральных неособых многообразий (см. Пфаффа
проблема). Полная система локальных инвариантов
П. с. размерности р при 1 < р < п — 1 неизвестна.
П. с. можно рассматривать как G-структуру беско-
бесконечного типа, где G — группа линейных преобразова-
преобразований пространства R", оставляющих инвариантной
р-мерную координатную плоскость. Ее структурная
функция 1-го порядка соответствует F (А/)-билиней-
ному отображению с : Г (л)ХГ (л) —>¦ D {M)/Y (я), к-рое
определяется коммутированием векторных полей. Про-
Пространство А (л) совпадает с ядром векторнозначной
билинейной формы с.
Лит. см. при ст. Пфаффа проблема. Д. В. Алексеевский.
ПФАФФА УРАВНЕНИЕ — уравнение вида
. . . -\-ап (ос) dxn=0, «ЗгЗ, A)
где xQDczR", о) — дифференциальная 1-форма, функ-
функции aj(x), /=1,. . ., п, действительнозначны. Пусть
aj(x)?C1(D) и векторное поле а (х)=(а1(х),. . ., а„(х))
не имеет критич. точек в области D.
Многообразие #*cR" размерности й>1 и класса С1
наз. интегральным многообразием
П. у. A), если @=0 на Mk. П. у. наз. вполне ин-
интегрируемым, если через каждую точку области
D проходит интегральное многообразие максимально
возможной размерности п—1 и притом только одно.
Теорема Фробениуса: для того чтобы П. у.
A) было вполне интегрируемым, необходимо и доста-
достаточно выполнение условия
йюл<в = 0. B)
В этом случае интегрирование П. у. сводится к интегри-
интегрированию семейства систем обыкновенных дифферен-
дифференциальных уравнений.
В трехмерном евклидовом пространстве П. у. имеет
вид
Pax+Qdy + Rdz^Q, C)
гдр Р, Q, R — функции от х, у, z, а условие B) полной
интегрируемости принимает вид
или
(rot F, F)=0, где F = (P, Q, Я).
В этом случае существуют гладкие функции ц, U
(jj, ^fc 0) такие, что
Pdx+Qdy-\-Rdz*=\idU,
и интегральные поверхности П. у. C) задаются урав-
уравнениями V' (х, у, z)=const. Если F есть нек-рое сило-
силовое поле, то поле [ь~гР имеет потенциальную функ-
функцию, равную U. Если П. у. C) не вполне интегрируе-
интегрируемо, то оно не имеет интегральных поверхностей, но
может иметь интегральные кривые. Если заданы про-
произвольные функции x=x(t), y=y(t), то C) будет обык-
обыкновенным дифференциальным уравнением для z и кри-
кривая x=x(t), y=y{t), z=z(t) будет интегральной.
Постановка задачи об исследовании уравнения A)
для произвольного п>3 и о приведении дифферен-
дифференциальной 1-формы со к канонич. виду принадлежит
И. Пфаффу [1]. Условие D) впервые было получено
Л. Эйлером в 1755 (см. [2] гл. IX).
Локально любое П. у. с помощью гладкой замены
переменных приводится к виду
где у0,. . ., Ур, Zj,- . ., Zp — новые независимые пере-
переменные Bр + 1 < п, р > 0). Число 2р + 1 наз. клас-
классом П. у.; здесь р — наибольшее число такое, что
дифференциальная форма coAdcoA ... Adco степени
2p-j-l не равна тождественно нулю. При р=0 П. у.
вполне интегрируемо. Функции уа(х),. . ., ур(х) наз.
первыми интегралами П. у. E), а его
интегральные многообразия максимально возможной
размерности п—р—1 задаются уравнениями
Уа И=с0, ..., ур (х)=ср.
Системой Пфаффа наз. система уравнений
гшда
o)!=.0, ..., <% = (), к < п, F)
где x?DczRn, а у — дифференциальные 1-формы:
@у =2 k = i@/ft (,z)dzft, / = 1, ..., к.
Ранг г матрицы ||ш_/^ (х)\\ наз. рангом системы
П ф а ф ф а в точке х. Система Пфаффа наз. вполне
интегрируемой, если через каждую точку ж? U
проходит интегральное многообразие максимально воз-
возможной размерности п—г и притом только одно.
Теорема Фробениуса: для того чтобы
система П ф а ф ф а F) была вполне интегрируемой,
необходимо и достаточно выполнение условий
d(Oj А а>1 А •.. A Wfe=-0, / = 1, ..., к.
Задача об интегрировании любой конечной нелиней-
нелинейной системы дифференциальных уравнений с частными
производными эквивалентна задаче об интегрировании
нек-роп системы Пфаффа (см. [6]).
Получен ряд результатов по аналитич. теории сис-
систем Пфаффа. Рассматривалась вполне интегрируемая
система Пфаффа
dy----x~Pfdx-\- z-4gdz
из т уравнений, где р, q — положительные целые
числа, а вектор-функции/(.г, у, z),g(x, у, z) голоморф-
голоморфны в точке л:=0, у—0, z=(); указаны достаточные
условия существования голоморфного в начале коорди-
координат решения (см. [7]), приведены обобщения на большее
число независимых переменных.
Лит.: [1] Р f a ( f J. F., «Berl. Abh.», 1814—1815, S. 76—135;
[2] Эйлер Л., Дифференциальное исчисление, пер. с лат.,
М.— Л., 1949; [3] П е т р о в с к и й И. Г., Лекции по теории
обыкновенных дифференциальных уравнений, 6 изд., М., 1970;
[4] Богданов Ю. С, Лекции по дифференциальным уравне-
уравнениям, Минск, 1977; [5] К а р т а н Э., Внешние дифференциаль-
дифференциальные системы и их геометрические приложения, пер. с франц.,
М., 1962; [6] Р а ш е в с к и й П. К., Геометрическая теория
уравнений с частными производными, М.— Л., 1947; [7] Equa-
Equations differentielles et systemes de Pfaff dans le champ complexe,
В., 1979. M. В. Феворюк.
ПФАФФА ФОРМА — дифференциальная форма
степени 1.
ПФАФФИАН знакопеременной матри-
матрицы X — многочлен PiX от элементов матрицы X, квад-
квадрат к-рого равен detZ. Точнее, если Х=||а:1у|| — знако-
знакопеременная (т. е. удовлетворяющая условиям х,-;- --
= —xji, хц=0) матрица порядка 2п над коммутативно-
ассоциативным кольцом А с единицей, то PfX есть эле-
элемент кольца А, вычисляемый по формуле
где суммирование ведется по всевозможным разбиениям
s множества {1, . . ., 2п) на непересекающиеся пары
{ia, 7a}> причем считается, что ia </a, а=1, ...,«,
a e(s) — знак подстановки
12 ... 2п — 1 Ъп
»i/i ¦¦¦ in In
П. обладает следующими свойствами:
1) Pf (СТХС) = (det С) (Pf X)
для любой матрицы С порядка 2п;
2) (PfXJ = drtZ;
3) если Е — свободный Л-модуль . с базисом
еь . . ., ein и
u=~S^ x/iei A e,- ^ AM,
*-1 i < 1 J
ТО
\и = п\ (Pf X) ег А ... Л е»„.
Лит.: {1] Б у р б а к и Н., Алгебра. Модули, кольца, формы,
пер. с франц., М., 1966. А. Л. Онищик.
ПЬЕРПОНТА ВАРИАЦИЯ — одна из числовых ха-
характеристик функции нескольких переменных, к-рую
можно рассматривать как многомерный аналог вариации
функции одного переменного. Пусть функция f (х)=
=f(xlt. . ., хп), ге=2,3,. . ., задана на re-мерном парал-
параллелепипеде
Dn=[ai, 6J X ... X К, Ъ„]
и И*1, к— 1, . . ., га,— разбиение отрезка [ak, bk] на т,
т.= 1, 2, . . ., равных между собой отрезков точками
n) .
Эти разбиения порождают разбиение
параллелепипеда Dn на т" параллелепипедов dt,
d2, . . ., dmn с ребрами, параллельными координатным
осям.
Пусть
где и>(/, dj) —колебание функции f(х) на dj. Тогда
def ,
Р((, Dn) = sup sup
sup sup Л
т Пт т"
Если P(f, Dn) < oo, то говорят, что функция f(x)
имеет ограниченную (конечную) П. в. на Dn, а класс
всех таких функций обозначается через P(Dn). Это
определение предложил Дж. Пьергюнт [1]. Класс
Р (Dn) содержит в себе класс A (Dn) функций, имеющих
ограниченную Арцела вариацию на Dп.
Лит.: ll] Picrpont J., Lectures on the Iheory of fun-
functions of real variables, v. 1, N. Y., 1959; [2] Hahn H., Theorie
der reellen Funktionen, Bd 1, В., 1921. Б. И. Голубое.
ПЭЛИ — ВИНЕРА ТЕОРЕМА: функция /?L2(— oo,
+ °о) тогда и только тогда обращается в нуль почти
всюду вне отрезка [~А, А], когда ее преобразование
Фурье
удовлетворяет условию
F(y) \*dy < oo
J — 00
и является ограничением на действительную прямую
нек-рой целой аналитич. функции F (г) комплексного
переменного г, причем |.F(z)| <ел'2' для всех z?C
(см. [1]). Аналогом П.— В. т. наз. описание образа
нек-рого пространства функций или обобщенных функ-
функций на локально компактной группе при Фуръе преобра-
преобразовании или другом инъективном интегральном преобра-
преобразовании; чаще всего аналогом П.— В. т. наз. описание
образа пространства Со° (G) финитных бесконечно
дифференцируемых функций или пространства S (G)
быстро убывающих бесконечно дифференцируемых
функций на локально компактной группе G при преоб-
преобразовании Фурье на группе G. Такие аналоги известны,
в частности, для абелевых локально компактных
групп, для нек-рых связных групп Ли, для нек-рых
подалгебр алгебры Со° (G) на вещественных полупростых
группах Ли, а также для нек-рых других интегральных
преобразований.
Лит.: [1] Винер Н., П э л и Р., Преобразование Фурье
в комплексной области, пер. с англ., М., 1964; [2] В л а д и м и-
ров В. С, Обобщенные функции в математической физике,
М., 1976; [3] Гельфанд И. М., Г р а е в М. И., В и л е н-
к и н Н. Я., Интегральная геометрия и некоторые связанные с
ней вопросы теории представлений, М., 1962; [4] Желобе н-
к о Д. П., Гармонический анализ на полупростых комплексных
группах Ли, М., 1974; [5] Рудин У., Функциональный ана-
анализ, пер. с англ., М., 1975. А. И. Штерн.
ПЮИЗЁ РЯД — см. Ветвления точка.
ПЯТЫЙ ПОСТУЛАТ, аксиома параллель-
параллельности Евклида,— через точку Р вне прямой
А А' в плоскости, проходящей через Р и АА', можно
провести лишь одну прямую, не пересекающую АА'.
В «Началах» Евклида П. п. был приведен в следую-
следующей эквиналентной формулировке: «И если прямая,
падающая на две прямые,- образует внутренние и по
одну сторону углы, меньшие двух прямых, то продол-
продолженные неограниченно эти две прямые встретятся с той
стороны, где углы меньше двух прямых» (см. [1]). У ком-
комментаторов Евклида возник взгляд, что это предложе-
предложение можно доказать, опираясь на остальные аксиомы.
Попытки доказательств возникли еще в Древней* Гре-
Греции. Эти попытки продолжались на Средневековом
Востоке, а затем в Западной Европе. Если не говорить
о прямых логич. ошибках, то обычно неявно (а иногда
и с отчетливым пониманием) вводилось предположение,
не выводимое из остальных аксиом, к-рое оказывалось
таким образом эквивалентным П. п. Напр., расстояние
между параллелями ограничено, пространство допус-
допускает «простое» (поступательное) движение (все траек-
траектории — прямые линии), две сближающиеся прямые
всегда пересекаются, существуют подобные не равные
фигуры, сумма углов треугольника равна двум прямым
и др. Дж. Саккери (G. Saccheri, 1733) рассматривал
четырехугольник с прямыми углами при основании и
равными боковыми сторонами. Ранее такой четырех-
четырехугольник рассмотрел Омар Хайям A1—12 вв.). Из трех
возможных гипотез об остальных двух равных углах
(они тупые, они острые, они прямые) он стремился от-
отвергнуть две первые, т. к. из третьей вытекал П. и.
Дж. Саккери удалось привести к противоречию следст-
следствия из первой гипотезы, но он совершил логич. ошибку
в опровержении гипотезы острого угла. И. Ламберт
(J. Lambert, 1766, опубл. 1786) при аналогичном
подходе опровергнул гипотезу острого угла, тоже со-
совершив при этом серьезную ошибку. О и высказал пред-
предположение, что такая геометрия осуществляется на мни-
мнимой сфере. А. Лежандр (A. Legendre, 1800) в первых
изданиях учебника «Элементы геометрии» исходил из
суммы S углов треугольника. Опровергнув гипотезу
S > 2d, он допустил ошибку при выводе следствий из
гипотезы S < 2d, а именно, он неявно ввел аксиому,
что для любой точки внутри острого угла существует
прямая, проходящая через эту точку и пересекающая
обе стороны угла. Решение проблемы П. п. (точнее
ее снятие) было получено путем создания Н. И. Лоба-
Лобачевским A826) геометрии, отрицающей П. п. Из непро-
непротиворечивости Лобачевского геометрии следует незави-
независимость П. п. от др. аксиом евклидовой геометрии.
Лит.: [1] Начала Евклида, пер. с греч., т. 1—3, М.— Д.,
1948—50; [2] К а г а н В. Ф., Основания геометрии, ч. 1, М.—
Л., 194Я; [3] Ефимов Н. В., Высшая геометрия, 5 изд., М.,
1971; [4] Об основаниях геометрии. Сб. классических работ
но геометрии Лобачевского..., М., 195fi; 1й| Р о з е и ф с л ь д
Б. А., История неевклидовой геометрии, М., 197fi.
Б. Л. Лаптев.
РААБЕ ПРИЗНАК сходимости число-
в ы х рядов: ряд > ап сходится, если при доста-
точно больших п выполняется неравенство
r, где г>1;
если Rn <: 1, начиная с нек-рого номера п, то ряд рас-
расходится .
Установлен Й. Раабс (J. Raabe). Е. Г. Соболевская.
РАВЕНСТВА АКСИОМЫ — аксиомы, регулиру-
регулирующие употребление отношения равенства в математич.
доказательствах. Аксиомы эти утверждают рефлексив-
рефлексивность отношения равенства и возможность замены рав-
равного равным. Символически Р. а. записываются так:
X = X,
х = у Л <?(y/v) =ф<р(ж/1)),
x = y=>t (y/v) = t (x/v),
где ф — произвольная формула, a t — произвольный
терм рассматриваемого языка; х, у, v — переменные,
имеющие одну и ту же непустую область изменения;
выражения вида ф (x/v) и t (x/v) обозначают результат
намены всех свободных вхождений переменной v в фор-
формуле ф или терме t на х.
С помощью Р. а. можно доказать симметричность и
транзитивность отношения равенства. Для этого и
качестве ф надо взять формулу y=v в первом случае и
формулу v=z во втором.
Если формулы и термы рассматриваемого языка стро-
строятся из атомарных формул и термов с помощью логич.
связок и суперпозиций, то приведенные Р. а. можно
вывести из их частных случаев, когда в качестве ф
и t берутся атомарные формулы и термы. Символи-
Символически:
•'7 = 2// Л Р (хи .. .,х{, ...,xn)=$P(xu...,yh .. .,хп).
<7 = !/i => / (*i> ¦••,*/, • • • , ¦cn)=f On, • • •, Hi, ••-.*„),
где Р и / суть «-местные предикатный и функциональ-
функциональный СИМВОЛЫ. В. Н. Гришин.
РАВНОВЕЛИКИЕ И РАВНОСОСТАВЛЕННЫЕ ФИ-
ФИГУРЫ — две фигуры в R2, имеющие равные площади и
соответственно два многоугольника М± и М2 такие, что
их можно разрезать на многоугольники так, что части,
составляющие Ми соответственно конгруэнтны частям,
составляющим Мг.
Для R", п ^ 3, равновеликость означает равенство
объемов; равносоставленность многогранников опреде-
определяется аналогично с R2. Эти понятия обобщаются также
на неевклидовы геометрии.
Площадь (многоугольника) есть функция s(M), удов-
удовлетворяющая следующим аксиомам:
(a) s(M) ^ 0 для любого многоугольника М;
(р) если М ость объединение многоугольников
Mi,- ¦ •, Л1k, попарно не имеющих общих точек, то
s(M)=s(Mi)-\-...-\-s(Mk);
(у) если Mi а Мг конгруэнтны, то s(M1) — s(M2);
F) площадь квадрата, стороной которого является
единица длины, равна 1.
С помощью этих аксиом определяется площадь пря-
прямоугольника.
Теорема. Если два многоугольника равносостав-
лены, то они равновелики.
На этой теореме основан метод разбиения,
известный еще Евклиду: для вычисления площади мно-
многоугольника пытаются разбить его на конечное число
частей, из к-рых можно составить фигуру известной
площади. Напр., параллелограмм равносоставлен с
прямоугольником, имеющим то же основание и ту же
Рис. 1. Рис. 2.
высоту (см. рис. 1); треугольник равносоставлен с па-
параллелограммом, имеющим то же основание и вдвое
меньшую высоту (см. рис. 2). Таким образом, вся теория
площадей многоугольников может быть построена на
основе теоремы о площади прямоугольника.
Существует и другой способ вычисления площадей,
основанный на аксиомах (Р) и (у),- метод допол-
дополнения. Два многоугольника наз. равнодоиол-
н я е м ы м и, ес-
если их можно до- / Tl
полнить соответ- / /J /
ственно конгру- / / | /
энтными частями ^ ?-_J l—
так, чтобы полу- рио 3.
чились конгру-
конгруэнтные многоугольники. Напр., параллелограмм и пря-
прямоугольник с одинаковыми основаниями и одина-
одинаковыми высотами равнодогюлняемы (см. рис. 3) и потому
равновелики.
В евклидовой плоскости два многоугольника в том
и только в том случае равновелики, если они равносо-
ставлены (а также если они равнодополняемы). Анало-
Аналогичная теорема справедлива в плоскости Лобачевского
и в эллиптической плоскости. Напротив, в неархи-
медовои геометрии эквивалентны лишь равновеликость
и равнодополняемость; равповеликость же им не экви-
эквивалентна.
Теория объемов в R3 базируется на аксиомах (а),
(Р), (т)> (б), аналогичных аксиомам площади. Однако
для вычисления объема тетраэдра со времен Евклида
используется предельный переход («чертова лестница»),
а в современных учебниках — интеграл, определение
к-рого также связано с предельным переходом. Обосно-
нание использования «лишнего» (по сравнению с пла-
планиметрией) предельного перехода, доказательство
того, что методами разбиения и дополнения невозможно
вычислить объем произвольного тетраэдра, составили
третью проблему Гильберта. В 1900 М. Ден (М. Delm)
решил третью проблему, доказав, что правильный
тетраэдр и равновеликий ему куб не равносоставлены.
Для равносоставленности двух равновеликих много-
многогранников М-у и М2 в R3 необходимо и достаточ-
достаточно, чтобы для каждого инварианта Дена / (М) (нек-рой
функции от длин ребер и величин соответствующих
двугранных углов, си. |2]) выполнялось равенство
/(Л/) /(М)
Х) /B)
Имеются многомерные обобщения инвариантов Дена,
с помощью к-рых сформулировано необходимое условие
равносоставленности и доказано, что при п ^ 3 пра-
правильных! и-мерный симплекс не равносоставлен с рав-
равновеликим ему кубом. В R4 необходимое условие
равносоставленности является также и достаточным.
Пусть G — нек-рая группа движений плоскости.
Два многоугольника Мг и М2 наз. G-к онгруэнт-
н ы м и, если существует такое движение g?G, что
g(M1)=M2. Два многоугольника М1 и М2 наз. G-
равносоставленными, если их можно раз-
разрезать на части таким образом, что части, составляю-
составляющие М1, соответственно конгруэнтны частям, состав-
составляющим Мг. Аналогично определяется G-равносостав-
ленность многогранников.
Пусть S — группа движений, состоящая из всех
параллельных переносов и центральных симметрии.
Понятия равносоставленности и ^-равносоставленности
в R2 эквивалентны. В частности, равновеликие много-
многоугольники можно разбить на части таким образом, что
соответствующие их части не только конгруэнтны, но и
имеют соответственно параллельные стороны.
Равносоставленность в том и только в том случае эк-
эквивалентна G-равносоставленности, если GidS в случае
R2 и GaD0 в случае R3, где Do — группа всех движе-
движений, сохраняющих ориентацию.
Ниже приводится определение флаговых инвариантов,
позволяющих дать необходимое и достаточное условие
Г-равносоставленности, где Т — группа всех параллель-
параллельных переносов. Пусть R™-1, . . ., R', 1 < i <: п—1,—
такая последовательность подпространств простран-
пространства R", что R"-1^) . . . пэК-!' (верхний индекс означает
размерность). Пусть, далее, для каждого/=?+1,. . ., п
фиксировано одно из двух полупространств, на к-рое
RJ разбивается подпространством R/-1; это полупро-
полупространство наз. «положительным» и обозначено через
PJ. Последовательность Ф= (Рп, . . ., Р' + 1) наз. фла-
флагом порядка i в R". Пусть, наконец, Q— (М"'1, . . .,
М') — такая последовательность граней многогранни-
многогранника MnczRn, что М"-1^} . . . =)ЛЯ\ Если MJW.J для
всех ; = i,. . ., п—1, то полагают
где lAf'l есть i-мерный объем грани М', а е,/—±1
в зависимости от того, примыкает ли MJ + 1 к М/ с поло-
положительной стороны или нет. Если же MJ' % RJ хотя бы
для одного /, то Нф (<?)=0; Нф (Мп) — сумма ^Нф (Q)
по всем последовательностям Q, составленным из граней
многогранника Мп.
Два равновеликих многогранника в том и только в
том случае 77-равносоставлены, если для каждого
флангового инварианта Нф его значения на этих мно-
многогранниках одинаковы.
Многогранник MndR" наз. к-к ратной суммой
М и н к о в с к о г о, если существуют такие много-
¦-рапникн Л'],. . ., Nk (положительных размерностей),
несущие плоскости к-рых порождают разложение прост-
пространства Rn в такую прямую сумму, что Mn=N1-\- . . . +
+iV/j (в смысле векторной суммы множеств). Многогран-
Многогранник называется принадлежащим классу 3fe> если Мп
мондао разбить на конечное число многогранников,
каждый из к-рых Г-равносоставлен с многогранником,
представляющимся в виде Ажратной суммы Мин-
ковского.
Многогранник Л#™?;!& в том и только в том случае,
если Нф{М")=0 для всех флаговых инвариантов Нф
порядков, меньших к.
Пусть Г — группа, состоящая из всех гомотетий с
положительными коэффициентами и параллельных пе-
переносов. В R" любые два многогранника Г-равносостав-
лены. Рис. 4 иллюстри-
иллюстрирует Г-равносоставлен-
ность треугольника и пря-
прямоугольника (одинаковы-
(одинаковыми цифрами обозначены
Г-конгруэнтные много-
многоугольники).
Пусть при гомотетии с
коэффициентом X > О
объем n-мерного много-
многогранника увеличивается
в V раз. Если принять Рис. 4.
это утверждение как ак-
аксиому, то объем любого многогранника может быть
найден методом разбиения.
Пусть группа движений G в «-мерном евклидовом,
гиперболическом или эллиптич. пространстве почти
транаитивна (т. с. орбита точки всюду плотна); два
многогранника в этом пространстве тогда и только тог-
тогда G-равнодополняемы, когда они G-равносоставлены.
Лит.: [1] Проблемы Гильберта, М., 1969; [2] Болтян-
Болтянский В. Г., Равновеликие и равносоставленные фигуры, М.,
1956; [3) его же, Третья проблема Гильберта, М., 1977;
[4] X а д в и г е р Г., Лекции об объеме, площади поверхности
и изопериметрии, пер. с нем., 1966; [5] lessen В., Т h о-
rup A., «Math. Scand.», 1978, v. 43, fasc. 2, p. 211—40.
В. Г. Болтянский.
РАВНОВЕСИЯ ПОЛОЖЕНИЕ системы обыкновен-
обыкновенных дифференциальных уравнений
x = f{t, х), х? Rn, (*)
— точка |? R" такая, что я=| является (постоянным по
времени) решением системы (*); Р. п. наз. также и само
это решение. Точка |? R" есть Р. п. системы (*) тогда и
только тогда, когда
/ (/, ?) —0 при всех t.
Пусть x~<p(t) — произвольное решение системы (*).
Замена переменных x=cp(J)+2/ переводит это решение в
Р. п. у=0 системы
y = F(t,y), F(t, y)^f(t,<p(t) + y)-f(t, <p(i)).
Поэтому, напр., в теории устойчивости без ограничения
общности можно считать, что речь всегда идет об иссле-
исследовании устойчивости Р. ц. в начале координат К".
Р. п. д;=0 неавтономной системы (*) часто наз.
тривиальным, или нулевым, р е ш е н и-
е м, а термин Р. п. предпочитают использовать в теории
автономных систем обыкновенных дифференциальных
уравнений и в теории динамич. систем. Здесь употреб-
употребляется много синонимов этого термина: особая
точка, неподвижная точка, стацио-
стационарная точка, точка покоя, состоя-
ниеравновесия. н. х Розов.
РАВНОВЕСИЯ СООТНОШЕНИЕ — соотношение,
выражающее связь между ростом функции f(z), меро-
морфной при |z| < R < оо, и ее распределением
значений (см. Распределения значений теория). Каждая
мероморфная функция /(z) обладает следующим с во й-
ствол равновесия: сумма ее считающей функ-
функции N (г, а, /), характеризующей плотность распреде-
распределения а-точек f(z), и функции приближения т(г, а, /),
характеризующей скорость среднего приближения
/(z) к данному числу а, остается инвариантной для
различных значений а. Наиболее эффективным Р. с.
становится при использовании сфернч. метрики.
Пусть
[в, !>]¦= |Ц-Ь|
1 1 + | а | г • >' 1
означает сферич. расстояние между двумя числами
а и ?i и пусть для каждого комплексного числа в
где
a (a, /) — lim In ¦
z -> о
ав=я@, а, /) означает кратность а-точки / (z) при z¦¦¦- 0.
При г-> Л функция пг (г, а, /) отличается от неванлин-
новской функции приближения то (г, а, /) на ограни-
ограниченное слагаемое. Поэтому на окружности |z| — г < Л
функция т (г, а, /) по-прежнему характеризует среднюю
скорость приближения f(z) к числу а. Имеет место сле-
следующее утверждение. Для каждого значения г, О ^
¦ёг < Я, любого комплексного числа а из расширенной
комплексной плоскости и для произвольной мероморф-
ной при \z\ < Я <оо функции /(z) выполняется ра-
равенство (соотношение равновесия):
m(r,a, f) + N(r,a, f)=m(r, oo, f)+N(r, со, /),
где
N(r, a, /) = J |j[n(*, а, /)-в@, а, /)]^ +
+ ге @, а, /) In г,
а и (?, а, /) означает число а-точек /(z), попавших в
круг {z : \z\ <: «}¦
После основополагающих работ Р. Неванлинны [1]
Р. с. были перенесены на р-мерные целые кривые (см.
[3]) и на голоморфные отображения (см. [4], [5]).
Лит.: [1] Nevanlinna R., Analytic functions, N. Y.—
В., 1970; [2] В и т т и х Г., Новейшие исследования по однознач-
однозначным аналитическим функциям, пер. с нем., М., 1960; [3] We-
у 1 Н., Meromorphic functions and analytic curves, Princeton,
1943; [4J Ш а б а т Б. В., Введение в комплексный анализ, 2
изд., ч. 2, М., 1976; [5] Г р и ф ф и т с Ф., К и н г Д ж., Теория
Неванлинны и голоморфные отображения алгебраических мно-
многообразий, [пер. с англ.], М., 1976. В. П. Петренко.
РАВНОМЕРНАЯ АЛГЕБРА — замкнутая относи-
относительно равномерной сходимости подалгебра А алгебры
С (X) всех непрерывных комплексных функций на ком-
компакте X, содержащая все функции-константы и разде-
разделяющая точки компакта X. Последнее условие озна-
означает, что для каждой нары х, у различных точек из X
в алгебре А имеется функция /, для к-рой / (х) Ф f (у).
Р. а. обычно снабжают sup-нормой:
||/|| = sup|/(x) |.
При этом ||/2|| —- il/S]2. Каждая банахова алгебра с еди-
единицей (даже без предположения коммутативности;,
норма в к-рой подчинена последнему условию, изоморф-
изоморфна нек-рой Р. а.
Р. а. составляют важный подкласс класса комму-
тативпых банаховых алгебр над полем С комплексных
чисел.
Каждой точке х?Х отвечает гомоморфизм ц>х : А ->
-у С, действующий по правилу <px(f)~f(x). Поэтому X
естественно топологически вкладывается в пространство
максимальных идеалов алгебры А и при соответствую-
соответствующем отождествлении поглощает границу Шилова. При
изучении Р. а. важную роль играют точки пика
(т. е. такие точки из X, в к-рых достигается строгий
максимум модуля хотя бы для одного элемента из А),
мультипликативные вероятностные меры на X (т. о.
представляющие меры гомоморфизмов из Л в С) и
ортогональные к А меры на X. Многие конкретные
результаты, относящиеся к Р. а., касаются связей
между этими объектами.
Р. а. наз. симметрично и, если вместе с каж-
каждой функцией к алгебре принадлежит и комплексно
сопряженная ей функция. Согласно теореме Стоуна —
Вейерштрасса, каждая симметричная Р. а. на компакте
X совпадает с С(Х). Полярный класс составляют т. н.
антисимметричные Р. а., вовсе не содержа-
содержащие действительных функций, кроме констант. Типич-
Типичный пример — алгебра всех функций, аналитических к
открытом единичном диске комплексной плоскости и не-
непрерывных в его замыкании (диск-алгебра). Теоре-
Теорема Шилова — Бишопа: каждая Р. а. опреде-
определенным способом может быть «склеена» из антисиммет-
антисимметричных. Известны и более тонкие классификационные
теоремы. Вместе с тем произвольные Р. а. но сводятся
к алгебрам аналитич. функций типа диск-алгебра.
Напр., можно сконструировать такую Р. а. на одно-
одномерном компакте, который совпадает с ее пространст-
пространством максимальных идеалов, что все точки компакта
являются точками пика и одновременно среди эле-
элементов алгебры только тождественны и нуль может
принимать нулевое значение на непустом открытом под-
подмножестве .
Лит.: Ш Гаме лин Т., Равномерные алгебры, пер. с
англ., М., 1973. Е. А. Горин.
РАВНОМЕРНАЯ НЕПРЕРЫВНОСТЬ — свойство
функции (отображения) /: X ->- Y, где X и Y—метрич.
пространства, означающее, что для любого е > 0 су-
существует такое б > 0, что для всех хх?Х, х2?Х, удов-
удовлетворяющих условию р(х1, х2) < б, выполняется
неравенство р (/(%), /(а-2)) < в.
Если отображение / : X ->- Y непрерывно на X и
X — компакт, то / равномерно непрерывно на X.
Композиция равномерно непрерывных отображений
равномерно непрерывна.
Р. н. отображений встречается и в теории топологич.
групп. Напр., отображение / : Хо —>- Y, где Х„сХ, X
и Y — топологич. группы, наз. равномерно
непрерывным, если для любой окрестности
Uу единицы группы Y существует такая окрестность
Uх единицы группы X, что для любых элементов хх^Хй,
х2?Х0, удовлетворяющих условию хххг^ ? Ux (со-
(соответственно Xi1x.i?Uy), выполняется включение
/(zjH/Cra)]-^^ (соответственно \j{х^-'Ч(x2)^Uv).
Понятие Р. н. обобщается на отображения равномер-
равномерных пространств.
Лит.: Щ К олмогоровА. Н., Ф о м и н С. В., Элемен-
Элементы теории функций и функционального анализа, 5 изд., М.,
1981; [2] II о н т р я г и н Л. С, Непрерывные группы, 3 изд.,
М., 1973; [3] К е л л и Д ж. Л., Общая топология, 2 изд., пер.
с англ., М., 1981; [4] Б у р б а к и Н., Общая топология, пер. с
франц., М., 19С8. Л. Д. Кудрявцев.
РАВНОМЕРНАЯ ОГРАНИЧЕННОСТЬ сверху
(снизу) — свойство семейства действительных функ-
функций /« : X -*- R, где а ?21, Ш — нек-рое множество ин-
индексов, X — произвольное множество, означающее,
что существует такая постоянная с > О, что для всех
а?91 и всех х?Х выполняется неравенство fa(x)<-c
(соответственно fa (х) ^ — с).
Семейство функций /а : X -> R, а?ЭД, наз. рав-
равномерно ограниченным, если оно равно-
равномерно ограничено как сверху, так и снизу.
Понятие Р.о. семейства функций обобщается на слу-
случай отображений в нормированные и полунормировап-
ные пространства: семейство отображений /а : X —>- ^*,
где <х?5Д, X — произвольное множество, а У — полу-
полунормированное пространство с полунормой (нормол)
II-||у, наз. равномерно ограниченным,
если существует такая постоянная с > 0, что для всех
а?91и всех х?Х выполняется неравенство \\fa(x)\\Y^-
<с. Если в пространстве {X —>¦ Y} ограниченных отоб-
ражений / : X -> У ввести полунорму (норму) по фор-
формуле
И / II {* _> у) = SUp ||/ (*) II У,
1 ' хех
то Р. о. множества функций /а : X —>- У, a?3t, озна-
означает ограниченность этого множества в пространстве
{X-*-Y} с полунормой Ц-Н^^у}.
Понятие Р. о. снизу и сверху обобщается на случай
отображений / : X —к У в упорядоченные в том или
ином смысле множества У. л. д. Кудрявцев.
РАВНОМЕРНАЯ ПОДГРУППА локально
компактной топологической груп-
группы G — такая замкнутая подгруппа HczG, что фактор-
пространство GlH компактно. С понятием Р. п. близко
связано понятие квазиравномерной подгруп-
подгруппы в G, т. е. такой замкнутой подгруппы // в G, для к-рой
на GlH существует G-инвариантная мера и, с (х (G/7/)<со.
Напр., подгруппа SL2(f,) группы SL2(JH) квазиравно-
квазиравномерна, но не равномерна в ней. С другой стороны,
подгруппа Т всех верхнетреугольных матриц из
Л7>2 (R) — Р. п. в SL2(R), не являющаяся квазирав-
квазиравномерной (на факторпространстве SL2(R)/T нет
SL2 (К)-инвариантных мер). Однако всякая связная
квазиравномерная подгруппа в группе Ли G является
Р. п. (см. [1]), а всякая дискретная Р. п. в G квазирав-
квазиравномерна [2]. (О дискретных Р. п. в группах Ли см. Диск-
i/етная подгруппа.) Если G — связная группа Ли и//—
1'. п. в G, то нормализатор Nq(IP) в G связной компо-
компоненты единицы Н° группы II содержит максимальную
связную треугольную подгруппу группы G (см. [3]).
Алгебраич. подгруппа // связной алгебраической
комплексной линейной группы Ли G тогда и только тог-
тогда является Р. п., когда U — параболич. подгруппа в
G. Описаны все связные Р. п. в полупростых группах
Ли (см. [4]). Недискретная Р. п. Н связной полупростой
группы Ли G обладает свойством сильной жест-
жесткости (см. [5]), к-рое состоит в том, что в G имеется
конечное число таких подгрупп Н;, i—1,. . ., т, что
любая подгруппа H'czG, изоморфная Н, сопряжена
одной из подгрупп //,-. Важные примеры равномерных
и квазиравномерных подгрупп строятся следующим
образом. Пусть G — линейная алгебраич. группа,
определенная над полом рациональных чисел Q, GA —
ее группа аделей и G^dGA — подгруппа главных аде-
лей. Тогда Gq — дискретная подгруппа в Gj[, причем
Cq является Р. и. в G^ тогда и только тогда, когда
'I) У группы G нет нетривиальных рациональных ха-
характеров, определенных над полем Q, и 2) все унипо-
тентные элементы группы Gq принадлежат ее радикалу
(см. [6], [7]). В частности, если G — уншютентная
алгебраич. группа, определенная над Q, то Gq есть Р. п.
в G^j. Условие 1) является необходимым и достаточным
для квазиравномерности Gq в Ga.
Лит.: [1] М о s t о w G. D., «Ann. Math.», 1962, v. 75, № 1,
p. 17—37; [2] P агун ат ан М., Дискретные подгруппы групп
Ли пер. с англ., М., 1977; [з] О н и щ и к А. Л., «Матем. си.»,
I960, т. 71, № 4, с. 483—94; [4] е г о же, там же, 1967, т. 74,
.№ 3, с. 398—416; [5] Goto M., Wang H,- С, «Math. Ann.»,
1972 Bd 198 Н. 4 S. 259—86; [8] Б о р е л ь А.,«Математика»
1964, т. 8, М 2, с. 73 — 75; [7] М о s t о w G. D., T a m a g a-
w а Т., «Ann. Math.», 1962, v. 76, № 3, p. 446 — 63.
В. Л. Попов.
РАВНОМЕРНАЯ СХОДИМОСТЬ последова-
последовательности функций (отображений) —
свойство последовательности /„ : X —>- У, где X —
произвольное множество, У — метрич. пространство,
п = 1, 2,. . ., к функции (отображению) / : X —>Y,
означающее, что для любого е > 0 существует такой
номер пг, что для всех номеров п > гее и всех точек
х ? X выполняется неравенство
Р(/(*)| /Я (*))<*•
Это условие равносильно тому, что
lim sup pAn(x), /(ж))=0.
п -> се .v 6 Е
Чтобы последовательность {/„} равномерно сходилась
на множестве X к функции /, необходимо и достаточно,
чтобы нашлась такая числовая последовательность
{а,,}, что lim an — 0, и существовал такой номер п0, что
П-*-00
для всех п > пй и всех х?Х выполнялось неравенство
Р (/„(*), /(*))<«„.
Пример. Последовательность/,, (j) =.г", ге—1,2, . . .,
равномерно сходится на любом отрезке [0, а], 0 <
< а < 1 и не сходится равномерно на отрезке [0, 1].
Необходимое и достаточное условие Р. с. последова-
последовательности функций без использования понятия предель-
предельной функции дает Коши критерий равномерной сходи-
сходимости.
Свойства равномерно сходящих-
сходящихся последовательностей.
1. Если У — линейное нормированное пространство
и последовательности отображений /„ : X —>- У и
gn : X -»- У, п — 1, 2,. . ., равномерно сходятся на
множестве X, то при любых \?С и и,?С последова-
последовательность {Я/„--| ц#п} также равномерно сходится на X.
2. Если У — линейное нормированное кольцо,
последовательность отображений /„ : X —>- У, ге— 1,
2,. . ., равномерно сходится на множестве X я g : X —*¦
->У — ограниченное отображение, то последователь-
последовательность {gfn} также равномерно сходится на X.
3. Если X — топологич. пространство. У — метрич.
пространство и последовательность непрерывных в
точке хо?Х отображений fn : X —>- У равномерно на
множестве X сходится к отображению / : X —>- У, то
это отображение также непрерывно в точке х0, то есть
lim lim /„ (х) = lim fn(x0)= lim lim fn{x).
Условие равномерной сходимости последовательности
{/я} на X является в этом утверждении существенным в
том смысле, что существуют даже последовательности
числовых непрерывных на отрезке функций, сходящие-
сходящиеся во всех его точках к функции, не являющейся не-
непрерывной на рассматриваемом отрезке. Примером
такой последовательности является fn(x)=xn, n—\,
2,. . ., на отрезке [О, 1]. Р. с. последовательности не-
непрерывных функции не есть необходимое условие
непрерывности предельной функции. Однако если мно-
множество X — компакт, У — множество действитель-
действительных чисел R, последовательность непрерывных функ-
функций /„ : X -> R во всех точках х?Х одновременно
возрастает или убывает и имеет конечный предел,
lim jn(x)=j(x),
п —>- оо
то для того, чтобы функция / была непрерывной на
множестве X, необходимо и достаточно, чтобы последо-
последовательность {/„} сходилась равномерно на этом мно-
множестве. Необходимые и одновременно достаточные
условия для непрерывности предела последователь-
последовательности непрерывных функций в общем случае даются в
терминах квазиравномерной сходимости последователь-
последовательности.
4. Если последовательность интегрируемых по Ри-
ману (по Лебегу) функций /„ : \а, Ь] ->. R, п=1,2,. . .,
равномерно на отрезке [а, Ь], сходится к функции
/ : [а, Ь] —>- R, то эта функция также интегрируема по
Риману (соответственно по Лебегу), и для любого
х?[а, Ь] имеет место равенство
lim f */„
n-*-ceJa
(t)dt= lim fn(t)dt,
н сходимость последовательности М Л /„ (t)dt > па отрез-
отрезке [а, Ъ\ к функции \ / (t)dt равномерна. Формула (*)
обобщается на случай Стилтьеса интеграла. Если же
последовательность интегрируемых на отрезке [а, Ь]
функций /„, ге=1, 2, . . ., просто сходятся в каждой
точке этого отрезка к интегрируемой же на нем функции
/, то формула (*) может не иметь места.
5. Если последовательность непрерывно дифферен-
дифференцируемых на отрезке [а, Ъ] функций fn 'Ли, b\~*-R,
п = 1, 2,. . ., сходится в нек-рой точке хо?[а, b], a
последовательность их производных I —О- > равномерно
сходится на [а, Ъ], то последовательность {]„} также
равномерно сходится на отрезке [а, Ь], ее предел яв-
является непрерывно дифференцируемой ни этом отрезке
функцией и
4- lim fn(x)^- lim ЩМ., a^x^b.
Пусть X — произвольное множество, tx Y — метрич.
пространстве). Семейство функций (отображений) ja :
: X —>¦ Y, a?3l, где 21 — топологич. пространство, наз.
равномерно сходящимся при а —>-а0^2t
к функции (отображению) / : X -> Y, если для любого
8 >0 существует такая окрестность ?/(а0) точки а0,
что для всех а? U (а0) и всех х?Х выполняется нера-
неравенство
р (/(*), fa (х)) <г.
Для равномерно сходящихся ceMeiicTB функций имеют
место свойства, аналогичные указанным выше свой-
свойствам Р. с. последовательностей функций.
Понятие Р. с. отображений обобщается на случай,
когда Y — равномерное пространство, в частности,
когда Y — топологич. группа.
Лит.: [1] Александров П. С, Введение в теорию
множеств и общую топологию, М., 1977; [2] К о л м о г о-
р о в А. Н., Ф о м и н С. В., Элементы теории функций и функ-
функционального анализа, 5 изд., М., 1981; [3] К е л л и Д ж. Л.,
Общая топология, пер. с англ., 2 изд., М., 19SL
Л- Д. Кудрявцев.
РАВНОМЕРНАЯ ТОПОЛОГИЯ — топология, по-
порожденная равномерной структурой. Подробнее, пусть
X — множество, наделенное равномерной
структурой (т.е. равномерное пространство) О',
и пусть для каждого х ? X через В (х) обозначено мно-
множество подмножеств V (х) множеств X, где V пробегает
все окружения U. Тогда в X существует и притом
только одна топология, для к-рой В (х) является фильт-
фильтром окрестностей точки х при любой х?Х. Топология
наз. р а в и о м е р и з у е м о й, если существует рав-
равномерная структура, ее порождающая. Не всякое то-
топологич. пространство равномеризуемо: таковы, напр.,
не регулярные пространства. м. Я- Войцеховский.
РАВНОМЕРНАЯ УСТОЙЧИВОСТЬ — устойчи-
устойчивость по Ляпунову, равномерная относительно началь-
начального момента. Решение rB(t), i?IR ", системы дифферен-
дифференциальных уравнений
i = /(«, х), х g R»,
наз. равномерно устойчивым, если для
всякого е>0 найдется б > 0 такое, что для всякого
/0?R+ и всякого решения х (t) той же системы, удов-
удовлетворяющих неравенству
выполнено неравенство
\x(t)-xo(i)\ < s
для всех t ^ t0.
Устойчивая по Ляпунову неподвижная точка авто-
автономной системы дифференциальных уравнений x—f(x),
x?Rn, равномерно устойчива, но устойчивое по Ляпу-
Ляпунову решение, вообще говоря, может не быть равномер-
равномерно устойчивым. Напр., решение x(t)~0, t?K+, урав-
уравнения
л-= [sin In A + 0— ol]x A)
при каждом а? A/к 2, 1) устойчиво, но не равномерно
устойчиво.
Пусть дана линейная система дифференциальных
уравнений
x = A(t)x, х ? R", B)
где А (•) — суммируемое на каждом отрезке отобра-
отображение R+-к Hom(R«, R«).
Для того чтобы решение х=0 системы B) было рав-
равномерно устойчивым, необходимо, чтобы верхний осо-
особый показатель Q0 (А) системы B) был меньше или равен
нулю. Напр., в случае уравнения A) верхний особый
показатель Q0 (А)— 1—а, а Ляпунова характеристичес-
характеристический показатель Х1 (А )¦= тт= —а. Для существования б>0
такого, чтобы решение а—0 всякой системы
x^-A(l)x-\-g(t, х), х ? R»,
удовлетворяющей условиям теоремы существования и
единственности решения задачи Коши и условию
\g(t,x)\< 6-И ,
было равномерно устойчиво, необходимо и достаточно,
чтобы верхний особый показатель О°(Л) системы B)
был меньше нуля.
Лит.: [1] Персидский К., «Матем. сб.», 1933, т. 40,
№ 3, с. 284—93; [2J Д е м и д о в и ч Б. П., Лекции по мате-
математической теории устойчивости, М., 1967; [3] Д а л е ц-
к и й Ю. Л., К р е и н М. Г., Устойчивость решений дифферен-
дифференциальных уравнений в банаховом пространстве, М., 1970.
В. М. Миллионщиков.
РАВНОМЕРНО НАИБОЛЕЕ МОЩНЫЙ КРИТЕ-
КРИТЕРИЙ — статистический критерий с заданпым уровнем
значимости для проверки сложной гипотезы Но против
сложной альтернативы Нг, мощность к,-рого не меньше
мощности любого другого статистич. критерия, пред-
предназначенного для проверки Но против Нх и имеющего
тот же уровень значимости.
Пусть проверяется сложная гипотеза 7/0 : 8?в0с;в
против сложной альтернативы Н1 : 8^в1=в\в0 и
пусть задана верхняя грань а, 0 < а < 1, вероятпо-
стей ошибок 1-го рода, к-рые можно совершить, от-
отклоняя проверяемую гипотезу Но с помощью статистич.
критерия, когда она в действительности верна (число а
паз. уровнем значимости критерия,
а про сам критерий говорят, что он имеет уровень а).
Таким образом, ограничение на вероятности ошибок 1-го
рода сужает множество всех статистич. критериев,
предназначенных для проверки Но против Нг, до клас-
класса критериев уровня а. В терминах функции мощности
|}(9), О?в=-вои01> статпетич. критерия фиксирова-
фиксирование уровня значимости а означает, что
sup P(9)-^a.
060»
Если в классе всех статистич. критериев уровня а,
предназначенных для проверки Яо против Нъ сущест-
существует такой, что его функция мощности р* (9) удовлетво-
удовлетворяет условию
sup р»(в)=о, р»(вK=Р(в), 0€ Ох.
e0
где Р @) — функция мощности любого другого критерия
из этого же класса, то такой , критерий наз. р а в-
но мерно наиболее мощным крите-
критерием уровня а для проверки Но против Н1. Р. н. м.к.
является наилучшим критерием, если сравнение кри-
критериев производят в терминах мощности критериев.
Лит.: [1] Л е м а н Э., Проверка статистических гипотез,
пер. с англ., 2 изд., М., 1979. М. С. Никулин.
РАВНОМЕРНО СХОДЯЩИЙСЯ РЯД — функцио-
функциональный ряд
с (вообще говоря) комплексными членами, сходящийся
на множестве X, и такой, что для любого е > 0 суще-
существует номер пе , что для всех п > пе и всех .г?Х вы-
выполняется неравенство
\sn(x) — s (x)\ < е,
где
Иными словами, последовательность частичных сумм
sn(x) является равномерно сходящейся последователь-
последовательностью. Определение Р. с. р. равносильно выполнению
условия
Km sup | rn (x) | = 0,
л-noiei"
что означает равномерную сходимость к нулю на мно-
множестве X последовательности остатков
ряда A).
Пример. Ряд
равномерно сходится на каждом конечном круге комп-
комплексной плоскости и не сходится равномерно на всем
множестве С комплексных чисел.
Условие равномерной сходимости ряда A) на мно-
множестве X без использования понятия суммы ряда дает
Коши критерий равномерной сходимости ряда. Доста-
Достаточное условие равномерной сходимости ряда дается
Вейерштрасса признаком.
Ряд2 _< ап{х) наз- правильно сходящим-
сходящимся на множестве X, если существует такой числовой
ряд ^ап, а„^0, что для всех п=1, 2,. . . и всех х?Х
выполняется неравенство
\ап(х)\<ап,
т. е. если ряд A) удовлетворяет условиям признака
Вейерштрасса равномерной сходимости рядов. В силу
этого признака правильно сходящийся на множестве X
ряд равномерно сходится на этом множестве. Обратное,
вообще говоря, неверно; однако во всяком равномерно
сходящемся на множестве X ряде можно так объеди-
объединить следующие друг за другом его члены в конечные
группы, что получившийся при этом ряд будет уже пра-
правильно сходиться на множестве X.
Имеются признаки равномерной сходимости ряда,
аналогичные признакам Дирихле и Абеля для- сходимо-
сходимости числового ряда. Эти признаки равномерной сходи-
сходимости ряда впервые встречаются в работах Г. Харди
(G. Hardy). Если в ряде
2 я» (ж) Ьп (х) B)
функции а„ (х) и Ъп(х), га—1, 2, . . ., определенные на
множестве X, таковы, что последовательность {ап(х)}
монотонна при каждом х^Х и равномерно стремит-
стремится к нулю на А', а последовательность частичных сумм
{/У„(.г) } ряда 2 Ьп{х) равномерно ограничена на множе-
множестве X, то ряд B) равномерно сходится на этом множе-
множестве .
Если последовательность {ап(х)} равномерно ограни-
ограничена на множестве X и монотонна при каждом фиксиро-
фиксированном х?Х, а ряд ]?bn(x) равномерно сходится
на множестве X, то ряд B) также равномерно сходится
на X.
Свойства равномерно сходящих-
сходящихся рядов. Если ряды 2 ап (<г) т 2 ''" (J) РавН0МеРН0
сходятся на множестве X, А?С и [xfJjC, то ряд
также равномерно сходится на множестве X.
Если ряд 2 ап (х) равномерно сходится на множестве
X, &Ъ(х) — ограниченная на этом множестве функция,
то ряд 2 Ъ (х) ап (х) также равномерно сходится на X.
Непрерывность суммы ряда. Для
изучения свойств суммы функционального ряда явля-
является полезным понятие «точки равномерной сходимости
ряда». Пусть X— топологич. пространство и ряд A)
сходится на X. Точка хо?Х наз. точкой равно-
равномерной сходимости ряда A), если для любого
е>0 существует такая окрестность U~U(x0) точки
х0 и такой номер х„г, что для всех x?U и всех га>п?
выполняется неравенство |г„(ж)| <е.
Если множество А — компакт, то, для того чтобы
ряд A) равномерно сходился на А, необходимо и доста-
достаточно, чтобы каждая точка х?Х являлась точкой его
равномерной сходимости.
Если X — топологич. пространство, ряд A) сходит-
сходится на X, х0 — точка равномерной сходимости ряда A)
и существуют конечные пределы
lim ап(х)—са, п—Л, 2, ...,
х-+ха
то числовой ряд 2^ сходится, сумма s(x) ряда A)
имеет предел при х —>- х0, причем
lim s(x) = lim 2anW = 2 lim a«W=2c«' C)
X-+Xo X-+ Xo X-*- Xa
т. е. при сделанных предположениях в ряде A) возмо-
возможен почленный переход к пределу в смысле формулы
C). Отсюда следует, что если ряд A) сходится на X, его
члены непрерывны в точке равномерной сходимости
.г„?А, то его сумма также непрерывна в этой точке:
lim s(z) = V lim an (x) = V ч-п Ы — s (x0).
х-*-д:0 х-± ха
Поэтому если ряд непрерывных функций сходится
равномерно на топологич. пространстве, то его сумма
непрерывна на этом пространстве. В случае, когда про-
пространство X является компактом и члены ряда A) не-
неотрицательны на X, то равномерная сходимость ряда
A) является и необходимым условием для непрерыв-
непрерывности на X суммы ряда A) (см. Дипи теорема).
В общем случае необходимым и достаточным услови-
условием для непрерывности суммы сходящегося на тополо-
топологич. пространстве X ряда A), члены к-рого непрерывны
на X, является квазиравномерная сходимость последо-
последовательности его частичных сумм sn{x) к его сумме s(x)
(теорема Ар цела — Александрова).
Ответ на вопрос о существовании точек равномерной
сходимости у сходящихся рядов, непрерывных на отрез-
отрезке функций, дает теорема Осгуда — Гобсо-
н а: если ряд A) сходится в каждой точке отрезка [а, Ъ]
и члены ап(х) этого ряда непрерывны на [a, b], то
на отрезке [а, Ь] существует всюду плотное множество
точек равномерной сходимости ряда A). Отсюда следу-
следует, что сумма всякого ряда непрерывных функций,
сходящегося па нек-ром отрезке, непрерывна на всюду
плотном множестве этого отрезка. Вместе с тем сущест-
существует и сходящийся во всех точках отрезка ряд непре-
непрерывных функций такой, что точки, в к-рых он сходится
не равномерно, образуют всюду плотное множество
рассматриваемого отрезка.
Почленное интегрирование рав-
равномерно сходящихся рядов. Пусть
Х = [а, 6]. Если члены ряда
2 ««И, *€[<*. Ь]. D)
интегрируемы по Риману (по Лебегу) на отрезке [а, Ъ],
л ряд D) равномерно сходится на этом отрезке, то
его сумма s(x) также интегрируема по Риману (но Ле-
Лебегу) на [а, Ь] и для любого а-?[а, Ь] имеет место
равенство
причем ряд, стоящий в правой части равенства, схо-
сходится равномерно на отрезке [а, Ъ].
В этой теореме нельзя заменить условие равномерной
сходимости ряда D) просто условием его сходимости на
отрезке [а, 6], так как существуют сходящиеся на от-
отрезке ряды даже непрерывных функций с непрерыв-
непрерывной суммой, для к-рых неверна формула E). Вместе
с тем существуют различные ее обобщения. Ниже при-
приведен результат для интеграла Стилтьеса.
Если g(x) — возрастающая на отрезке [а, Ь] функция,
а„ (х) — интегрируемы по Стилтьесу относительно функ-
функции g(x), ряд D) сходится равномерно на отрезке [а, Ъ],
то сумма s(x) ряда D) также интегрируема по Стилтье-
Стилтьесу относительно функции g (х),
и ряд, стоящий в правой части равенства, сходится рав-
равномерно на отрезке [а, Ь].
Обобщается формула E) и на функции многих пере-
переменных.
Условия почленного дифферен-
дифференцирования рядов в терминах рав-
равномерной сходимости. Если члены ряда
D) непрерывно дифференцируемы на отрезке [а, 6],
ряд D) сходится в нек-рой точке этого отрезка, а ряд,
составленный из производных членов ряда D), рав-
равномерно сходится на [а, 6], то сам ряд D) также равно-
равномерно сходится на отрезке [а, Ь], а его сумма s (x) не-
непрерывно дифференцируема на нем и
w2(J () F)
В этой теореме условие равномерной сходимости ря-
ряда, получающегося из данного почленным дифференци-
дифференцированием, нельзя заменить просто условием его сходи-
сходимости на отрезке [а, Ь], так как существуют равномерно
сходящиеся на отрезке ряды непрерывно дифференци-
дифференцируемых функций, для к-рых ряды, получающиеся из
них почленным дифференцированием, сходятся на от-
отрезке, однако сумма исходного ряда либо недифферен-
цируема на всем рассматриваемом отрезке, либо диф-
дифференцируема, но ее производная не равна сумме ряда
из производных.
Таким образом, наличие свойства равномерной сходи-
сходимости у рядов, так же как и свойства абсолютной сходи-
сходимости (см. Абсолютно сходящийся ряд), позволяет пере-
перенести на эти ряды нек-рые правила действия с конеч-
конечными суммами: равномерная сходимость — возможность
почленно переходить к пределу, почленно интегриро-
вать и дифференцировать ряды (см. формулы C) —
F)), а абсолютная сходимость — возможность пере-
переставлять члены ряда в любом порядке бея изменения его
суммы и перемножать ряды почленно.
Свойства абсолютной и равномерной сходимости
функциональных рядов независимы друг от друга.
Так, ряд
поскольку все его члены не отрицательны, абсолютно
сходится на всей числовой оси, но заведомо точка х=0
но является его точкой равномерной сходимости, т. к.
его сумма
( 1 +?2, если х э= О,
s (х) — <
| 0, если x = U
разрывна в этой точке.
Ряд
равномерно сходится на всей действительности оси, но
не сходится абсолютно ни в какой ее точке.
Лит. см. при ст. Ряд. Л. Д. Кудрявцев.
РАВНОМЕРНОЕ ПРИБЛИЖЕНИЕ — то же, что
чебышевское приближение.
РАВНОМЕРНОЕ ПРОСТРАНСТВО — множество с
определенной на нем равномерной структурой. Рав-
Равномерная структура (равномер-
(равномерность) на множестве X определяется заданием
нек-рой системы 3t подмножеств произведения XXX.
При этом система Щ должна быть фильтром (т. е. для
любых V1, F2?3C пересечение Fjf|F2 также содержится
вК, и если WzdV, F?2t, то JF?2{) и должна удовлетво-
удовлетворять следующим аксиомам.
U1) Всякое множество F?2l содержит диагональ Д=
= {(z, х): х?Х}.
U2) Если F?2t, то V~1={(y, х) : (х, i/)GF}?2l.
U3) Для любого F?8l существует PF^3t такое, что
W° WczV, где Wo PF= {{x, у): существует такое z?X,
что {х, z) ? W и (z, у)? W}. Элементы Щ наз. окр уж е-
н и я м и равномерности, определяемой системой Щ.
Равномерность на множестве X может быть определе-
определена также путем задания на X системы покрытий ©,
удовлетворяющей следующим аксиомам.
С1) Если a?S и а вписано в покрытие Р, то Р?©.
С2) Для любых alt a2g(S существует покрытие Р?®,
к-рое звездно вписано ва1ива2(т. е. для лю-
любой точки х?Х все элементы р4, содержащие х, лежат
в нек-рых '.элементах ai и а2). Покрытия, принадлежа-
принадлежащие ©, наз. равномерными покрытия-
покрытиями X (относительно равномерности, определяемой сис-
системой ©).
Указанные два способа задания равномерной струк-
структуры эквивалентны. Напр., если равномерная структура
на X задана системой окружений Щ, то система ©
равномерных покрытий X может быть построена так.
Для всякого F?© семейство a (F)= {Y(x) : х?Х} (где
V(x)~{y: (x, y)?V}) является покрытием X. Покрытие
а принадлежит (S тогда и только тогда, когда существу-
существует вписанное в а покрытие вида a(F), F?3l. Обратно,
если ($, — система равномерных покрытий Р. п., сис-
систему окружений образуют множества вида (J {НУ.II :
:Н?а}, а?©, и всевозможные множества, их содержа-
содержащие.
Равномерная структура на X может быть задана так-
также с помощью системы псевдометрик. Всякая равномер-
равномерность на множестве X порождает топологию: Т= {GczX:
для любой точки x?G существует такое V?2l, что
)?}
Свойства Р. п. являются обобщением равномерных
свойств метрических пространств. Если (X, р) — ме-
трич. пространство, на X возникает равномерность,
порожденная метрикой р. Систему окружений зтой
равномерности образуют всевозможные множества, со-
содержащие множества вида {(х. у) : р(х, i/)<e}, e>0.
При этом топологии на X, индуцированные метрикой и
равномерностью, совпадают. Равномерные структуры,
порожденные метриками, наз. м е т р и з у е м ы м и.
Р. п. были введены в 1937 А. Вейлем [1] (посредством
окружений; определение Р. и. посредством равномер-
равномерных покрытий было дано в 1940, см. [4]). Однако идея
использования многократной звездной вписанности для
построения функций появилась ранее у Л. С. Понтря-
гина (см. [5]) (впоследствии эта идея была использова-
использована при доказательстве полной регулярности топологии
отделимого Р. п.). Первоначально равномерные струк-
структуры использовались как инструмент для изучения (по-
(порожденных ими) топологий (подобно тому, как метрика
на метризуемом пространстве часто используется для
и.чучения топология, свойств этого пространства). Од-
Однако теория Р. п. имеет и самостоятельное значение,
хотя и тесно связана с теорией топологич. пространств.
Отображение /:1-*У Р.п, X в Р. и. У наз. рав-
равномерно непрерывным, если для любого
равномерного покрытия а пространства У система /~1а=
={f~1U : U?a} является равномерным покрытием X.
Всякое ралномерно непрерывное отображение является
непрерывным относительно топологий, порожденных
равномерными структурами на X и У. Если равномер-
равномерные структуры на X и У индуцированы метриками, то
равномерно непрерывное отображение / : X -*¦ У ока-
оказывается равномерно непрерывным в классич. смысле
как отображение метрич. пространств.
Более содержательной является теория Р. п., к-рая
удовлетворяет дополнительной аксиоме отделимости:
(в терминах окружений) или (в терминах равномерных
покрытий):
СЗ) для любых двух точек х, у^Х, хфу, существует
такое a ?(S, что никакой алемент а не содержит точки х
и у одновременно.
Далее речь будет идти только о Р. п., наделенных
отделимой равномерной структурой. Топология, поро-
ждепная на А" отделимой равномерностью, является
вполне регулярной и обратно, всякая вполне регуляр-
регулярная топология на X порождается нек-рой отделимой
равномерной структурой. Как правило, существует
много различных равномерностей, порождающих оди-
одинаковую топологию на X. В "частности, метризуемая
топология может порождаться неметризуемои отделимой
равномерностью.
Р. "п. (X, Ж) является метризуемьш тогда и только
тогда, когда Щ. имеют счетную базу. При этом базой
равномерности наз. (в терминах окружений) всякая
подсистема 93сЩ, удовлетворяющая условию: для лю-
любого V?3i существует такое W?2B, что WczV, или
(в терминах равномерных покрытий) подсистема ЭГс©
такая, что для любого а ?6 существует P?2t, к-рое
вписано в а. Весом Р. п. (X, Щ.) наз. наименьшая
мощность базы равномерности 3t.
Пусть М — подмножество Р. п. (X, Щ. Система окру-
окружений Жм= {(MXM)(]V : F?2f} определяет равномер-
равномерность на М. Пара (М, 2ГЛ1) наз. подпространст-
подпространством Р. п. (X, Щ. Отображение / : X ->- У Р. п. (X, 3t)
в Р. п. (У, W) наз. равномерным вложе-
вложением, если / взаимно однозначно, равномерно непре-
непрерывно и отображение /-1 : (/X, Щх)->¦ (X, 31) также
равномерно непрерывно.
Р. п. А' наз. полны м, если всякий фильтр Коши
в X (т. е. фильтр, содержащий нек-рый элемент всякого
равномерпого покрытия) имеет точку прикосновения
(т. е. точку, лежащую в пересечении замыканий эле-
элементов фильтра). Метризуемое Р. п. является полным
тогда п только тогда, когда полна метрика, порождаю-
порождающая его равномерность. Любое Р. п. (X, Ж) может
быть равномерно вложено в качестве всюду плотного
подмножества в единственное (с точностью до равномер-
равномерного изоморфизма) полное Р. п. (X, ЗТ), к-рое наз. п о-
полнением (А', 31). Топология пополнения (X,
Щ) Р. и. (X, Щ бикомпактна тогда и только тогда,
когда Щ является прекомпактной равно-
равномерностью (т.е. такой, что в любое равномерное
покрытие можно вписать конечное равномерное покры-
покрытие). В этом случае пространство X является биком-
бикомпактным расширением X и наз. расширением
Самюэля пространства X относительно равномер-
равномерности Ш. Для всякого бикомпактного расширения ЬХ
пространства X существует единственная прекомпакт-
ная равномерность на X, расширение Самюэля относи-
относительно к-рой совпадает с ЪХ. Таким образом, на языке
прекомпактных равномерностей описываются все би-
бикомпактные расширения ЬХ. На бикомпактном прост-
пространстве существует единственная равномерность (пол-
(полная и прекомпактная).
Всякая равномерность Щ на множестве X индуци-
индуцирует близость 6 по следующей формуле:
A6B&(AxB)(}V ф в
для любого F?2t. При этом топологии, порожденные на
X равномерностью 31 и близостью S, совпадают. Лю-
Любое равномерно непрерывное отображение является
близостно непрерывным относительно близостей, поро-
порожденных равномерностями. Как правило, существует
много различных равномерностей, порождающих на X
одну и туже близость. Тем самым множество равномер-
равномерностей на X распадается на классы эквивалентности
(две равномерности эквивалептны, если индуцирован-
индуцированные ими близости совпадают). Каждый класо эквива-
эквивалентных равномерностей содержит ровно одну преком-
пактную равномерность, причем расширения Самюэля
относительно этой равномерности совпадают с расшире-
расширениями Смирнова (см. Близости пространство) относи-
относительно близости, индуцированной равномерностями это-
этого класса. В множестве равномерностей на X задается
естественный частичный порядок: Щ>ЗГ, если 21о2Т.
Среди всех равномерностей, порождающих на X фик-
фиксированную топологию, есть наибольшая — т. н. у н и-
версальная равномерность, к-рая ин-
индуцирует на X близость Стоуна — Чеха. Всякая пре-
прекомпактная равномерность является наименьшим эле-
элементом в классе эквивалентных ей равномерностей.
Если & — система равномерных покрытий нек-рой рав-
равномерности на X, то система равномерных покрытий
эквивалентной прекомпактной равномерности состоит
из таких покрытий X, в к-рые можно вписать конечные
покрытия из ®.
Произведением Р. п. (X;, Щ), t?T, наз. Р. п.
(UX-t, иЩ), где n§tf — равномерность на UXt, базу
окружений к-рой образуют множества вида
, i = i, ..., и},
Топология, индуцированная на HXf равномерностью
n3(f, совпадает с топологией тихоновского произведе-
произведения пространств Xt- Проекции произведения Р. п.
на сомножители равномерно непрерывны. Всякое Р. п.
веса % может быть вложено в произведение % экземпля-
экземпляров метризуемых Р. п.
Семейство F непрерывных отображений топология,
пространства X в Р. п. (У, 3() наз. равностепен-
но непрерывным (относительно равномернос-
равномерности 31), если для любой точки х?Х и любого F?2t су-
существует окрестность Ох^х такая, что (f(x), f(x'))^V
при х'?Ох af?F. Имеет место следующее обобщение
классич. теоремы Асколи: пусть X есть ^-пространство,
(Y, Щ) — равномерное пространство и Yx — прост-
пространство непрерывных отображений X в Y с компактно
открытой топологией. Для того чтобы замкнутое под-
подмножество FdYX было бикомпактным, необходимо и
достаточно, чтобы F было равностепенно непрерывно
относительно равномерности % и все множества {/ (х) '¦
/?/'}, x?X, имели бикомпактные замыкания в Y
(fc-пространства — это хаусдорфовы пространства, яв-
являющиеся факторным образом локально компактных
пространств; класс fc-пространств содержит все хаус-
хаусдорфовы пространства с первой аксиомой счетности и
i:ce хаусдорфовы локально бикомпактные пространства).
Топология метризуемого Р. п. паракомпактна в си-
силу теоремы Стоуна. Однако решается отрицательно
проблема Исбелла о равномерной паракомпактности
метризуемых Р. п. Построен пример метризуемого Р. п.,
имеющего равномерное покрытие.
В теории размерности Р. п. основными являются рав-
равномерные размерностные инварианты 6d и Ad, опреде-
определяемые аналогично топологич. размерности dim (Sd —
при помощи конечных равномерных покрытий, a Ad —
при помощи всех равномерных покрытий), и равномер-
равномерная индуктивная размерность 6Ind. Размерность SInd
определяется по аналогии с большой индуктивной раз-
размерностью Ind индукцией по размерности близостных
перегородок между далекими (в смысле близости, поро-
порожденной равномерностью) множествами. При этом
множество Л наз. близостной перегород-
перегородкой между А и В (где А б В), если для любой б-окрест-
ности U множества Л такой, что Uf\{A [}В)Ф0, имеет
место X\U=A'\JB', где А'Ъв', АсА', ВсВ' (U наз.
6-окрестностью Л, если Л &(X\U). Таким образом,
размерность SInd (равно как и 6d) является не только
равномерным, но и близостным инвариантом. Размер-
Размерность Sd P. п. (X, U) совпадает с обычной размер-
размерностью dim расширения Самюэля, построенного по эк-
эквивалентной 3t прекомпактной равномерности. Если
размерность AdX конечна, то AdX = 6dX. Однако
может быть 6dX=0, a AdX^oo. Для метризуемого
Р. п. всегда SdX<5lnd X= AdX (и если AdX<oo,
то 6dZ=SIndX=AdA:). Равенства SdX^O и 5IndX=0
эквивалентны для любого Р. п. Если Р. п. метризуемо,
то эквивалентны также равенства SdX~О и AdX~0.
Если Р. п. X' является всюду плотным подмножеством
Р. п. X, то SInd X'>SInd X. Всегда SInd X<Ind X.
Для размерности Sd имеет место аналог теоремы о пе-
перегородках.
Различные обобщения Р. п. получаются путем ослаб-
ослабления аксиом равномерности. Так, в аксиоматике ква-
квазиравномерности (см. [8]) исключена аксиома симмет-
симметрии. При определении обобщенной равномерности (см.
IЮ]) (/-равномерности) вместо равномерных покрытий
рассматриваются равномерные семейства подмножеств
X, к-рые, вообще говоря, по являются покрытиями
(тела этих семейств оказываются всюду плотными в
X в топологии, порожденной /-равномерностью). Одно
из обобщений равномерности — так наз. 6-р а в н о-
мерность — связано с наличием топологии на
Р. п. Она определяется семействами 0-покрытий хаус-
дорфова пространства; 0-покрытиями наз. система х\
канонических открытых множеств X, удовлетворяющих
следующему условию: для любой точки х ? X существуют
Vj, . . ., Vn?r\ такие, что г? int U ._, L Vj]-
Лит.: []] Wei I A., Sur les cspaccs a structure uniforme et
sur le topologie generate, P., 1937; [2l Б у р б а к и Н., Общая
топология. Основные структуры, пер. с франц., 2 изд., М,,
1968; [3] е г о ж е, Общая топология. Использование вещест-
вещественных чисел в общей топологии. Функциональные пространст-
пространства. Сводка результатов. Словарь, пер. с франц., М., 1975; [4]
Т и к е у J., Ann. of Math. Studies 2, Princeton, 1940; [5] П о н-
трягин Л. С, Непрерывные группы, 3 изд., М., 1973; [б]
I shell J., Uniform spaces, Providence, 1964; [7] Samu-
Samuel P., «Trans. Amer. Math. Soc», 1948, v. 64, p. 100—32; [8]
С s a s z a r A., Foundations of general topology, Oxford —[etc.1,
1963; [9] Ф е д о р ч у к В. В., «Докл. АН СССР», 1970, т. 192,
Ni 6, с. 1228—30; [10] К u I p a W., «Colloq. Math.», 1972, v. 25,
p. 227—40; [11] Щ е п и н Е. В., «Докл. АН СССР», 1975, т. 222,
№ 3, с. 541—43. А. В. Иванов, Н. С. Стреколовская.
РАВНОМЕРНОЕ РАСПРЕДЕЛЕНИЕ — общее на-
название класса распределений вероятностей, возникаю-
возникающего при распространении идеи «равновозможности
исходов» на непрерывный случай. Подобно нормально-
нормальному распределению Р. р. появляется в теории вероят-
вероятностей как точное распределение в одних задачах и как
предельное — в других.
P.p. на отрезке числовой прямой
(прямоугольное распределение).
Р. р. на каком-либо отрезке [а, 6], я<й, — это распре-
распределений вероятностей, имеющее плотность
\ 0, *$[о, Ь].
Понятие Р. р. на [а, Ъ] соответствует представлению о
случайном выборе точки на этом отрезке «наудачу».
Математич. ожидание и дисперсия Р. р. равны, соот-
соответственно, (Ь+а)/2 и F—аJ/12. Функция распределе-
распределения задается формулой
а характеристич. функция — формулой
Случайную величину с Р. р. на [0,1] можно постро-
построить, исходя из последовательности независимых слу-
случайных величин X-l, Х2, . . ., принимающих значения 0
и 1 с вероятностями 1li, полагая
X =Zjn_1 Xn2~n
(Хп являются цифрами в двоичном разложении X).
Случайное число X имеет Р. р. на отрезке [0,1]. Этот
факт имеет важные статистич. приложения, см., напр.,
Случайные и псевдослучайные числа.
Если независимые случайные величины Zt и Х2 име-
имеют Р. р. на [0,1], то их сумма Хг-\-Хг имеет так наз.
треугольное распределение на [0,2]
с плотностью и2(х)=1 —11—х|для ж?[0,2]и и2(ж)=0 для
хф [0,2]. Сумма трех независимых случайных величин
с Р. р. на [0,1] имеет распределение на [0,3] с плот-
плотностью
[х2_3 (х^1у2+3 (х-2J}/2, 2 <z < 3,
I 0, sg[O, 3].
В общем случае сумма Х1-\-Х2+. . . -\-Хп независимых
величин с Р, р. на [0,1] распределена с плотностью
для 0«ж» и ип(т)—-0 для xf. [0, п]; здесь
_; г, z>o,
Z+~ \ 0, z<Q.
Распределение суммы Xj+. . ,-\-Хп, нормированной
математич. ожиданием nl'l и среднеквадратич. отклоне-
отклонением Уп/i'i, с ростом п быстро сближается с нормаль-
нормальным распределением с параметрами 0 и 1 (уже при ге=3
приближение удовлетворительно для многих практич.
целей).
В статистич. приложениях процедура построения
случайной величины с заданной функцией распределе-
распределения F (ж) основана на следующем факте. Пусть случай-
случайная величина У распределена равномерно на [0,1] и
функция распределения F (х) непрерывна и строго воз-
возрастает. Тогда случайная величина X = F~1(Y) имеет
функцию распределения F (х) (в общем случае надо за-
заменить в определении X функцию F~1(y) на нек-рый ее
аналог, а именно / (г/)-- inf {х : F (x)^ys^F (я-f-O)}).
X
P.p. на отрезке как предельное
распределение. Ниже приводятся типичные
примеры возникновения Р. р. на [0,1] is качестве пре-
предельного.
1) Пусть A'j, Х2, . . ., Хп, ... — независимые слу-
случайные величины, имеющие одну и ту же непрерывную
функцию распределения. Тогда распределение их сум-
суммы Sn, приведенной по mod 1, т. с, иными словами,
распределение дробной части {?„}суммы Sn, сходится
к равномерному на [0, 1] распределению.
2) Пусть параметры аир имеют абсолютно непрерыв-
непрерывное совместное распределение; тогда при t—>.оо распре-
распределение {осН~Р} сходится к равномерному на [0,1].
3) Р. р. встречается как предельное распределение
дробных долей нек-рых функций g (га) натурального
аргумента п. Напр., при иррациональном а доля тех
т, 1<т<:п, из п для к-рых
0 s? a s? {па} < Ь < 1,
имеет пределом при п—>-оо величину Ъ—а.
P.p. на подмножествах R*. Пример Р. р. в
прямоугольнике встречается уже в В юффона задаче (см.
также Геометрические вероятности, Стохастическая
геометрия). Р. р. на нек-ром ограниченном множестве
D в евклидовом пространстве R* определяется как рас-
распределение, имеющее плотность
С фО, x?D,
|;
где С обратив /с-мерному объему (или лебеговой мере)
области D.
Рассматривают также и Р. р. на поверхностях. Так,
«случайное направление» (напр., в R3) определяют век-
вектором, идущим из начала координат в случайную точку
поверхности единичной сферы, равномерно распреде-
распределенную в том смысле, что вероятность ее попадания в
какую-либо часть поверхности пропорциональна пло-
площади этой части.
Роль Р. р. на алгебраич. группах играет нормиро-
нормированная Хаара мера.
Лит.: [1] Ф е л л е р В., Введение п теорию вероятностей и
ее приложения, пер. с англ., 2 изд., т. 2, М., 19В7.
А. В. Прохоров.
РАВНОМЕРНОЙ СХОДИМОСТИ ТОПОЛОГИЯ —
топология пространства ff~ (X, Y) отображений множест-
множества X в равномерное пространство У, порожденная
равномерной структурой множества ?F(X, Y), базой
окружений к-рой являются совокупности всех пар
(/, ?)€<F(*, Y)xg-(X, Y) таких, что (/(.г), g{x))?v
для любого х ? X и v пробегает базу окружений прост-
пространства У. Сходимость направления {fa }ae3lc:JF(X, У)
к /o?JF (^i Y) в такой топологии наз. сходимостью /«
к /0. равномерной на множестве X. Если У полно, то
!jf(X, У) — полное пространство в топологии равно-
равномерной сходимости. Если X — топологич. пространст-
пространство и % (X, У) — множество всех непрерывных в топо-
топологии пространства X отображений X в У, то % (X, У)
замкнуто в !jf (X, У) в Р. с. т.; в частности, предел fo(x)
равномерно сходящейся последовательности fn(x) не-
непрерывных на X отображений ость отображение, так-
также непрерывное на X.
Лит.: L1] Б у р 0 а к и Н., Общая топология. Использова-
Использование вещественных чисел в общей топологии. Функциональные
пространства. Сводка результатов. Словарь, пер. с франц., М.,
1975; [2] К е л л и Д ж., Общая топология, пер. с англ., 2
изд., М., 1981. -В. И. Соболев.
РАВНОСИЛЬНОСТЬ, или эквивалентность,
утверждений (формул) А и В — понятие, означающее,
что при каждом допустимом наборе значений парамет-
параметров утверждения А и В оба истинны или оба ложны.
Напр., Р. уравнений, неравенств и их систем означает
совпадение множеств их решений. Р. формул выска-
высказываний исчисления есть совпадение задаваемых ими
булевых функций.
Лит.: [1] Новиков П. С, Элементы математической ло-
логики, 2 изд., М., 1973. С. Я. Артемов.
РАВНОСИЛЬНЫЕ МЕТОДЫ СУММИРОВАНИЯ —
методы, суммирующие одни и те же последовательно-
последовательности (быть может, к разным пределам); иначе, Р. м. с—
методы суммирования, имеющие одно и то же сумми-
суммируемости поле. Иногда Р. м. с. наз. методы, к-рые име-
имеют одинаковые поля суммируемости и являются сов-
совместными методами суммирования. Примерами равно-
равносильных и совместных методов суммирования являются
Чезатро метод суммирования (С, к) и Рисса метод
суммирования (R, п, к) (при одном и том же &Э=0), Че-
заро метод суммирования {С, к) и Гёльдера метод
суммирования (Н, к) (при одном и том же целом
А->0). Существуют Р. м. с, не являющиеся совмест-
совместными .
Иногда рассматривают не полные поля суммируемос-
суммируемости, а их подмножества, принадлежащие нек-рому мно-
множеству U. Если для двух методов суммирования эти
подмножества совпадают, то говорят, что методы сум-
суммирования равносильны на множестве U. Методы сум-
суммирования действительных последовательностей наз.
вполне равносильными, если равенство
их полей суммируемости остается справедливым при
включении в них последовательностей, суммируемых
к +°° и —оо. Аналогично определяется равносильность
методов суммирования для специальных видов сумми-
суммируемости (абсолютной, сильной и др.).
Матричные методы суммирования, определенные пре-
преобразованиями последовательности в последователь-
последовательность посредством матриц [|а„&|| и l|bnfc||, наз. абсо-
абсолютно равносильными (абсолютно
эквивалентными) на множестве U последо-
последовательностей {sfc}, если т„ — %п —*¦ 0, п —>-оо, для лю-
любой {.4k}c:U, где •
а ряды в выражениях для т;г и тп сходятся для всех п.
Лит.: L1] Кук Р., Бесконечные матрицы и пространства
последовательностей, пер. с англ., М., I960' [2] Харди Г.,
Расходящиеся ряды, пер. с англ., М., 1951; [3] К а н г р о Г. Ф.,
и сб.: Итоги науки и техники. Математический анализ, т. 12,
М., 1974, с. 5—70. И. И. Волков.
РАВНОСТЕПЕННАЯ НЕПРЕРЫВНОСТЬ м н о-
жества функций — понятие, тесно связанное
с понятием компактности множества непрерывных функ-
функций. Пусть X, Y — компактные метрич. пространства и
С(Х, У) — множество непрерывных отображений X в
У. Множество DaC (X, У) наз. равностепенно
непрерывным, если для любого 8>0 существует
такое 6>0, что из pxi^j, х2) <6 вытекает pr(/(^i), /(ж2))<;
<е для всех xlt .z2?X, f?D. P. н. D эквивалентна от-
относительной компактности D в С(Х, У), наделенном
метрикой
(/(ж), g{x)),
хе.х
что составляет содержание теоремы Арцела —
А с к о л и. Понятие Р. н. переносится на топологич.
пространства.
Лит.: [1] К о л м о г о р о в А. Н., Ф о м и н С. В., Элемен-
Элементы теории функций и функционального анализа, 5 изд., М.,
1081; [2] Э д в а р д с Р., Функциональный анализ, пер. с англ,,
IT., 1969. Е. М. Семенов.
РАВНОСХОДЯЩИЕСЯ РЯДЫ — такие сходящиеся
или расходящиеся числовые ряды V а,, и V Ьп,
разность к-рых является сходящимся рядом с суммой,
равной нулю: ^ _Лап—Ьп)~0- Если же их разность
.шляется лишь сходящимся рядом, то исходные ряды
наз. равносходящимися в широком
смысле.
Если ап—ап(х) и Ьп=Ъп(х) — функции, напр. ап :
X ->- R, Ь„: X —>- R, где X — произвольное множество,
a R — множество действительных чисел, то ряды
2°°_ ап(х) и 2-1 Ъц(х) наз- равномерно
равносходящимися (равномерно рав-
равносходящимися в широком с м ы с л е) на
множестве X, если их разность есть ряд, к-рый равно-
равномерно сходится на X и его сумма равна нулю (соответст-
(соответственно просто равномерно сходится на X).
Пример. Если две интегрируемые на отрезке
| —л, я] функции равны на интервале /с[—я, я], то
их ряды Фурье — равномерно равносходящиеся на
каждом интервале /*, внутреннем к интервалу /, а
сопряженные ряды Фурье — равномерно равносходя-
равносходящиеся на /* В широком смысле. Л. Д. Кудрявцев.
РАДЕМАХЕРА СИСТЕМА — ортонормированная на
отрезке [0,1] система {гь(х)}. Введена X. Радемахером
[1J. Функции гк(х) можно определить равенствами
rk(x)=signsin2knx, x?[0, 1], А- = 1, 2, ...
Другое определение функций Радемахера гь(х) по-
получается путем рассмотрения двоичных разложений
чисел отрезка [0,11: если в двоичном разложении числа
х на к-м месте стоит цифра 0, то полагают гъ(х)==1, если
же на к-ж месте стоит 1, то г&(.г) = —1; в случае же, ког-
когда х=0 или число х допускает два разложения, по-
полагают г^(а;) = О. Согласно этому определению отре-
.)ок [0,1] распадается на 2* равных подинтервала, в
каждом из которых функция г^(х) принимает' попе-
попеременно значения 4-1 и —1, а на концах подинтерва-
лов г^(.г) = 0.
Система {^(ж)} представляет типичный пример сто-
стохастически независимых функций и имеет применения
как в теории вероятностей, таки в теории ортогональ-
ортогональных рядов.
Одно из важных свойств Р. с. устанавливается тео-
теоремой Радемахера: если ^j с\ <-|- а>, то ряд
2^ cfe г^(х) сходится почти всюду на [0,1], и т о о р е м о й
X и и ч и п а — К о л м о г о р о в а: если ^j c%~ f oo,
то ряд 2^ck rk(-r) расходится почти всюду на [0,1].
Так как функции Радемахера в двоично иррацио-
иррациональных точках интервала [0,1] принимают лишь зна-
значения ±1, то рассмотрение ряда 2 сп г„(х) означает,
что у членов ряда ^ с„ выбирается распределение зна-
знаков ±1, зависящее от точки х. Если х~0, aL a2. . .
a,, . . .— представление числа z?[0,l] в виде бесконеч-
бесконечной двоичной дроби, то при а„=0 перед сп ставится
знак -|- и при <х„~1 ставится знак — .
Вышеприведенные теоремы в терминах теории веро-
вероятностей означают, что если ^Cj?<--|-oo, то ряд 2j±cn
сходится для почти всех распределений знаков (сходит-
(сходится с вероятностью 1), и если ^ <;„== +со, то ряд ^±с„
расходится для почти всех распределений знаков (рас-
(расходится с вероятностью 1).
Наоборот, ряд теорем теории вероятностей можно
сформулировать в терминах функции Радемахера.
Напр., теорема Кантелли о том, что при игре «в герб и
решетку» со ставкой 1 средний выигрыш с вероятностью
1 стремится к нулю, означает, что почти всюду на [0,1]
выполняется равенство
lim 7Г 2" Гк (х) ~°-
Лит.: [ll Rademacher H., «Math.. Ann.», 1922, Bd 87,
S. 112—38;[2] К а ч м а ж С, Ш т е й н г а у з Г., Теория орто-
ортогональных рядов, пер. с нем., М., 1958; [3] А л е к с и ч Г.,
Проблемы сходимости ортогональных рядов, пер. с англ., М.,
1963; [4] К а ц М., Статистическая независимость в теории веро-
вероятностей, анализе и теории чисел, пер. с англ., М., 1963.
А. А. Талаляи.
РАДИАЛЬНОЕ ГРАНИЧНОЕ ЗНАЧЕНИЕ — значе
ние функции /(z), определенной в единичном круге
D~ {z?C : |z|<l} в граничной точке ?=f''e, равное
пределу
lim /('•«¦) = /*(«•)
г-* 1-0
функции /(z) по множеству точек радиуса^/Г= {z=reie :
0<г<1}, проведенного в точку l,. Термин «Р. г. з.»
иногда употребляется в обобщенном смысле для функ
ций /(z), заданных в произвольных областях (включая
многомерные) D, причем в качестве // берется множест
во точек нормали (или ее аналога) к границе D, прове
денной в граничной точке. Напр., в случае бикруга
под Р. г. з. в точке ?— (е ', е ') понимается предел
lim f(re'\ гею>) = /*(?).
г-+ 1-0
Лит.: [1] Маркушевич А. И., Теория аналитических
функций, 2 изд., т. 1 —2, М., 1967—68; [2] II р и в а л о в И. И.,
Граничные свойства аналитических функций, 2 изд., М.— Л.,
1950. Е. Д. Соломенцев.
РАДИАН —• угол, соответствующий дуге, длина
к-рой равна ее радиусу; содержит приблизительно
57°17'44", 80625. Р. принимается за единицу измере-
измерения углов при т. н. круговом, или радианном, измере-
измерении углов. Если круговая мера угла равна а Р., то угол
содержит 180° аЫ градусов; обратно, угол в п° имеет
круговую меру яга°/180° Р. БСЭ-з.
РАДИКАЛ —• 1) Р.— математический знак V~ (из
мененное латинское г), к-рым обозначают извлечение
корня, т. е. решение двучленного алгебраич. урав-
уравнения вида хп—а-=0. Под символом\/ а подразумева-
подразумевается один из корней этого уравнения.
Проблема решения алгебраич. уравнений над полем
С комплексных чисел в Р.: выразить корни алгебраич.
уравнения (с комплексными коэффициентами) черен
его коэффициенты с помощью конечного числа дейст-
действий сложения, вычитания, умножения, деления, возвы-
возвышения в степень и извлечения корня. Уравнения выше
4-й степени, вообще говоря, нельзя решить в Р. (см.
Галуа теория).
Знак Р. используется также для обозначения ради-
радикала идеала.
2) Р. в нек-ром классе алгебраических систем — поня-
понятие, связанное с понятием радикального свойства.
Первые примеры Р. возникли в теории ассоциативных
колец (см. подробнее Радикалы колец и алгебр), пост-
построение общей теории Р. было начато С. Амицуром
(S. Amitsur) и А. Г. Курошем.Теория Р. может быть раз-
развита в любой категории алгебраич. систем, обладаю-
обладающей нек-ры.ми необходимыми свойствами (напр., в ка-
категории мультиоператорных групп). Многие вопросы
теории Р. изучаются в рамках теории категорий. См.
также Радикал группы, Радикал в классе полугрупп.
О. А. Иванова.
РАДИКАЛ в классе полугрупп — функция
р, ставящая в соответствие каждой полугруппе S ее
конгруэнцию p(i9) и обладающая следующими свойст-
свойствами: 1) если S изоморфна Т и рE)—0 (через 0 обозна-
обозначено отношение равенства), то р(У)=О; 2) если
0 — конгруэнция на S и рE/0)==О, то р(?)<0; 3)
р(?/р(?))=О. При выполнении 1) и 3) свойство 2) рав-
равносильно неравенству
sup{p(>S), 0}/0 <: р (S/0)
для всякой конгруэнции 0 на S. Полугруппа S наз. р-
полупростой, если р(?)=0. Класс р-полупрос-
тых полугрупп содержит одноэлементную полугруппу
и замкнут относительно изоморфизма и подпрямых
произведений. Наоборот, каждый класс полугрупп, об-
обладающий этими свойствами, служит классом р-полу-
простых полугрупп для нек-рого радикала р. Если
p(S)=SxS, то полугруппа S наз. р-р а д и к а л ь-
н о й. В отличие от колец Р. в полугруппах не опреде-
определяется соответствующим радикальным классом. Если
в определении Р. ограничиться рассмотрением конгру-
конгруэнции, определяемых идеалами, то возникает другое
понятие Р., где соответствующая функция выделяет
в каждой полугруппе идеал.
Если Я — класс полугрупп, замкнутый относительно
изоморфизма и содержащий одноэлементную полугруп-
полугруппу, то функция, ставящая в соответствии каждой полу-
полугруппе S пересечение всех ее конгруэнции 8 таких, что
?/0?.ft\ оказывается Р., напр. рх. Класс .ft1 совпадает с
классом рч-полупростых полугрупп тогда и только
тогда, когда он замкнут относительно подпрямых про-
произведений. В этом случае на S/px(S) можно смотреть
как на наибольшую факториолугруппу полугруппы S
среди лежащих в .ft (ср. Реплика).
Пример. Пусть St — класс полугрупп, допускаю-
допускающих точное неприводимое представление. Тогда
ps(S) = {(a, 6)| a, b?S, (а,
для всех s?S\J0}, где
ц(а) = {(ж, у)\х, y?S
для некоторых т, }
Рассматривались Р., определенные на данном клас-
классе полугрупп, замкнутом относительно гомоморфных
образов.
С каждым радикалом р связан класс левых полигонов
2(р). Именно, если А — левый S-полигон, то конгру-
конгруэнция 0 на полугруппе S наз. А -аннулирующей, если
(К, |л)?8 влечет за собой Xa=\ia для всех а ? А. Точная
верхняя грань всех Л-аннулирующих конгруэнции
оказывается .4-аннулирующей конгруэнцией и обозна-
обозначается Ann А. Класс 2(р), по определению, состоит
из всех таких левых ^-полигонов А, что рE/Апп А)—
=0, причем S пробегает класс всех полугрупп. Если 0—
конгруэнция на S, то левый E/0)-полигон лежит в
2 (р) тогда и только тогда, когда он лежит в 2 (р), бу-
будучи рассматриваемым как левый S-полигон. Наоборот,
если дан класс 2 левых полигонов, обладающий этим
свойством, и 2E) —класс всех левых ^-полигонов,
лежащих в 2, то функция
( SxS, если 2E) пусто,
Р ( ) ~ i П Ann А в противном случае
оказывается Р.
Лит.: [1] Клиффорд А., Престон Г., Алгебраиче-
Алгебраическая теория полугрупп, пер. с англ., т. 2, М., 1972; [2] С к о р-
н я к о в Л. А., в кн.: Избр. вопросы алгебры и логики, Ново-
сиб., 1973, с. 283—99;[3] Clifford A. H., «Semigroup Forum»,
1970, v. 1..М2, p. 103—27; [4] R о i z К. N., S с li e i n В. М.,
там же, 1978, v. IB, № 3, p. 299-344. Л. А. Скорняков.
РАДИКАЛ группы G — наибольшая нормал,ь-
ная подгруппа группы G, принадлежащая данному ради-
радикальному классу групп. Класс групп наз. ради-
радикальным, если он замкнут относительно гомоморф-
гомоморфных образов, а также относительно «бесконечных рас-
расширений», т. е. если классу обязана принадлежать вся-
всякая группа, обладающая возрастающим нормальным
рядом с факторами из данного класса (см. Нормальный
ряд). Во всякой группе имеется наибольшая радикаль-
радикальная нормальная подгруппа — радикал. Фактор-
Факторгруппа по Р. является полупростой груп-
группой,!, е. имеет единичный радикал.
Примером радикального класса является класс групп,
обладающих возрастающим субнормальным рядом с
локально нильпотентными факторами. Иногда термин
«Р.» используется именно применительно к наибольшей
локально нильпотентной нормальной подгруппе
(в случае конечных групп — это пилыютептпый Р., или
подгруппа Фиттинга). Важнейшим Р. в конечных груп-
группах является разрешимый Р. (см. Разрешимая группа).
Конечные группы, имеющие тривиальный разрешимый
Р., допускают нек-рое описание и терминах простых
групп и их групп автоморфизмов (см. [1]).
Лит.: [1] К у р о ш А. Г., Теория групп, 3 изд., М., 1967.
А. Л. Шмелъкин.
В классе групп Ли радикалом наз. наибольшую
связную разрешимую нормальную подгруппу. В лю-
любой группе Ли G существует радикал R, причем R —
замкнутая подгруппа Ли в G. Если Н — нормальная
подгруппа Ли в G, то группа GUI полупроста (см. Ли
полупростая группа) тогда и только тогда, когда ЯЭЛ.
Подалгебра алгебры Ли д группы Ли G, соответствую-
соответствующая Р., совпадает с Р. алгебры Ли д.
Радикал алгебраической груп-
группы — наибольшая связная разрешимая нормальная
подгруппа алгебраич. группы G, всегда замкнутая в G.
Радикал R (G) линейной алгебраич. группы G совпадает
со связной компонентой единицы в пересечении всех
Бореля подгрупп группы G; он является наименьшей
из таких замкнутых нормальных подгрупп //, что груп-
группа GlH полуироста (см. Полупростая алгебраическая
группа). Множество R{G)U всех унипотентных элемен-
элементов в R (G) есть связная унипотентная замкнутая нор-
нормальная подгруппа в G, являющаяся наибольшей среди
всех связных унипотентных нормальных подгрупп.
Эта подгруппа наз. унипотентным радика-
радикалом г р у п п ы G и может быть охарактеризована
как наименьшая из таких замкнутых нормальных
подгрупп Н в G. что GlH редуктивна. а. л. онищик.
РАДИКАЛ ИДЕАЛА А ассоцпатпвно-ком-
мутативного кольца R — множество всех
элементов Ь?Д, нек-рая степень к-pwx содержится в
А. Это множество обозначается У А. Оно является
идеалом в R, причем Y AzdA и К У~А = УА.
Обобщением этого понятия является понятие ради-
радикала подмодуля. Пусть М — модуль над R а
N — его подмодуль. Радикалом подмодуля N наз. мно-
множество всех элементов a?R таких, что anMciN для
нек-рого целого п (вообще говоря, зависящего от п).
Радикал подмодуля будет идеалом в R. о. а. Иванова.
РАДИКАЛЫ колец и алгебр— понятие,
впервые возникшее в классической структурной теории
конечномерных алгебр в нач. 20 в. Под Р. первоначаль-
первоначально понимался наибольший иильпотентный идеал конеч-
конечномерной ассоциативной алгебры. Алгебры с нулевым
Р. (называемые полупростыми) получили в
классич. теории достаточно полное описание: любая
полупростая копечномерная ассоциативная алгебра
является прямой суммой простых матричных алгебр
над подходящими телами. Впоследствии было обнару-
обнаружено, что наибольшие нилытотентные идеалы сущест-
существуют в любых ассоциативных кольцах и алгебрах с
условием минимальности для левых (или правых) идеа-
идеалов, т. е. в любых артиновых кольцах и алгебрах, и
описание артиновых полупростых колец и алгебр сов-
совпадает с описанием конечномерных цолупростых ал-
алгебр. В тоже время оказалось, что Р., как наибольший
нильпотентный либо разрешимый идеал, может быть
определен и во многих классах конечномерных неас-
неассоциативных алгебр (альтернативных, йордановых,
лиевых и др.). При этом, как и в ассоциативном слу-
случае, полупростые алгебры оказываются прямыми сум-
суммами простых алгебр нек-рого специального вида.
В связи с тем, что в бесконечномерном случае наиболь-
наибольшего нильпотентного идеала может и не существовать,
появилось много различных обобщений классического
Р.: радикал Бэра, радикал Джекобсона, радикал Ле-
Левицкого, радикал Кёте и др. Наиболее часто используе-
используемый из них — Джекобсона радикал. Выли введены так-
также Р., в нек-ром смысле противоположные классиче-
классическому. Так, напр., все классически п о л у-
цростые кольца (т. е. прямые суммы полных
матричных колец) радикальны в смысле регулярного
радикала Неймана и наследственно идемпотентного ра-
радикала Блэра. Построение общей теории Р. было начато
в работах С. Амицура [1] и А. Г. Куроша [2].
Общая теория радикалов. Всюду в дальнейшем го-
говорится только об алгебрах (имеются в виду алгебры
над произвольным фиксированным ассоциативно-ком-
ассоциативно-коммутативным кольцом с единицей); кольца являются
частным случаем таких алгебр. Под идеалом алгебры,
если это не оговорено специально, понимается двусто-
двусторонний идеал.
Пусть Щ — нек-рый класс алгебр, замкнутый отно-
относительно взятия идеалов и гомоморфных образов, т. е.
содержащий вместе со всякой алгеброй любой ее идеал
и любой ее гомоморфный образ. И пусть г — нек-рое
абстрактное свойство, к-рым может обладать или не
обладать алгебра из 3t. Алгебра, обладающая свойст-
свойством г, наз. r-а л г е б р о й. Идеал / алгебры А наз. ее
г-ж д е а л о м, если / является r-алгеброй. Алгебра
наз. r-а олу простой, если она не имеет ненуле-
ненулевых r-идеалов. Говорят, что г является радикаль-
радикальным с в о и с т в о м в классе Щ или что в Щ. задан
радикал (в смысле Куроша), если выполняются
следующие условия:
(A) гомоморфный образ r-алгебры есть г-алгебра;
(Б) каждая алгебра ,А класса 3t обладает наиболь-
наибольшим r-идеалом, т. е. идеалом, содержащим любой г-
идеал этой алгебры, и этот максимальный г-идеал
наз. тогда r-р адикалом этой алгебры и обозна-
обозначается г (А);
(B) факторалгебра Air (А) г-полупроста.
Алгебра, совпадающая со своим Р., наз. ради-
радикально й. В любом классе алгебр и для любого ра-
радикала {0} является единственной одновременно ради-
радикальной и полупростой алгеброй. Подпрямое произве-
произведение любого множества полупростых алгебр само полу-
полупросто.
С каждым радикалом г связаны два подкласса алгебр
в ЭД: класс Si (r) всех r-радикальных алгебр и класс
!Р(г) всех r-полупростых алгебр. По любому из этих
классов однозначно находится радикал г (А) для каж-
каждой алгебры А из Щ, а именно:
г (Л) = 2 {Л'-идеал в А, Г ? & (г)};
г(Л)=Г){/|/-идеал в А, А/1?Р(г)}.
Алгебра r-радикальна тогда и только тогда, когда она
не может быть отображена гомоморфно ни на одну не-
ненулевую r-полупростую алгебру.
Известны условия на подклассы алгебр, необходимые
и достаточные для того, чтобы эти подклассы служили
классами всех радикальных или классами всех полу-
полупростых алгебр для каких-либо Р. в ?[. Такие подклас-
подклассы алгебр принято называть соответственно ради-
радикальными и полупростыми под-
подклассами.
Частичная упорядоченность радикальных классов
по включению индуцирует частичный порядок на клас-
классе всех Р. в Ж- А именно, считается, что rj^^r^, если
ZA (гх) содержит У1 (г2) (и в этом случае также 5* (rj)
содержит Т (г2)).
Для каждого подкласса М класса % нижним
радикальным классом I (M), порожден-
порожденным классом М, наз. наименьший радикальный класс,
содержащий М, а соответствующий ему Р. наз. ниж-
нижним радикалом, определяемым классом М.
Верхним радикальным классом
и(М), определенным классом М, наз. наибольший ради-
радикальный класс, относительно Р. к-рого все алгебры из М
полупросты (этот Р. наз. верхним радика-
радикалом, определяемым классом М). Для любого класса М
нижний радикальный класс I (Л/) существует. Если 91 —
класс ассоциативных алгебр, то верхний Р. для любого
подкласса М также всегда существует. В неассоциатив-
неассоциативном случае верхний Р. может не существовать. Извест-
Известны достаточные условия на класс М, при к-рых верх-
верхний радикал для М существует. Этим условиям, в част-
частности, удовлетворяет всякий класс, содержащий только
простые алгебры.
Для любого Р. всякая простая алгебра либо ради-
радикальна, либо полупроста. Таким образом, каждому ра-
радикалу г соответствует разбиение простых алгебр на
два непересекающихся класса: St — класс г-полупрос-
тых простых алгебр, или верхний класс, и 52
класс всех r-радикальных простых алгебр, или ниж-
нижний класс. Принято говорить, что радикал г
соответствует этому разбиению. Обратно, для произ-
произвольного разбиения простых алгебр на два непересе-
непересекающихся класса, один из к-рых 5Х назван верхним,
а другой S2 — нижним, существует радикал, соот-
соответствующий данному разбиению. Такими будут верх-
верхний радикал rlt определяемый классом 51, а также ниж-
нижний радикал г2, определяемый классом S2; радикалы
rt и г2 наз. соответственно верхним и нижним
радикалами данного разбиения
простых алгебр. Для любого радикала г, соответствую-
соответствующего тому же разбиению простых алгебр, r^r^r2.
В классе всех ассоциативных алгебр для любого раз-
разбиения простых алгебр гх>г2. Классический Р. в классе
конечномерпых ассоциативных алгебр над полем со-
соответствует тому разбиению простых алгебр, нижний
класс которого пуст, причем является единственным
нетривиальным Р., соответствующим этому раз-
разбиению.
Наследственные радикалы. Радикал г наз. и д е-
ально наследственным рад и к а-
л о м, или кручением, в классе Щ, если для вся-
всякого идеала / алгебры А этого класса: r(I) = r(A)f\I.
Идеально наследственные Р. есть в точности те Р., для
к-рых классы У1(г) и 53 (г) замкнуты относительно идеа-
идеалов. Радикал г наз. наследственным, если
класс tii (r) замкнут относительно идеалов. В классах
ассоциативных, а также альтернативных алгебр каж-
каждый наследственный Р. является кручением. Радикал
г наз. строго наследственным, если
класс У (г) замкнут относительно подалгебр.
Класс всех кручений является полной дистрибутив-
дистрибутивной «решеткой» (см. Дистрибутивная решетка). Упот-
Употребление кавычек здесь связано с тем, что совокупность
элементов этой «решетки» является не множеством, а
классом.
В классе всех кручений выделены два противополож-
противоположных подкласса: класс наднильпотентных
кручений, т. е. таких кручений г, что все алгебры
с нулевым умножением r-радикальны, и класс п о д-
идемпотентных кручений — таких кру-
кручений г, что все алгебры с нулевым умножением г-полу-
просты (а все r-радикальные алгебры идемиотентны).
Важным частным случаем наднильпотентных Р. явля-
являются специальные радикалы — такие
кручения г, что все г-полунроетые алгебры разлагают-
разлагаются в подпрямое произведение первичных г-полупростых
алгебр. Существуют наднилыютентные неспециальные
Р. (см. [5], [7]).
Радикалы в классе ассоциативных колец. Пусть
31 — класс всех ассоциативных колец. И пусть:
Ф — нижний Р., определяемый классом всех простых
колец с нулевым умножением;
Р (нижний радикал Бэра)— нижний
Р., определяемый классом всех нильпотентных колец;
верхний Р., определяемый классом всех первичных
колец; наименьший специальный Р.; равен пересече-
пересечению простых идеалов кольца;
X (радикал Левицкого) — нижний Р.,
определяемый классом всех локально нильпотентных
колец; равен сумме всех локально нильпотентных иде-
идеалов кольца и содержит любой односторонний локально
нильпотентный идеал кольца;
Ж (верхний нильрадикал, или р а-
д и к а л К ё т е) — нижний Р., определяемый клас-
классом всех нильколец;
^ (радикал Джекобсона) — верхний Р.,
определяемый классом всех примитивных колец; ра-
равен пересечению всех примитивных идеалов кольца,
а также пересечению всех модулярных максимальных
правых (левых) идеалов, является квазирегулярным
идеалом, содержащим все квазирегулярные правые
(левые) идеалы;
<§~ (радикал Брауна — Маккоя) — верх-
верхний Р., определяемый классом всех простых колец
с единицей, совпадает с верхним Р. своего разбиения;
равен пересечению всех максимальных модулярных
идеалов кольца;
т — верхний Р., определяемый классом всех матрич-
матричных колец над телами;
Л (обобщенный нильрадикал) —
верхний Р., определяемый классом всех колец бе.ч дели-
делителей нуля;
F — верхний Р., определяемый классом всех полей.
В классе всех ассоциативных колец имеют место
строгие неравенства:
SfC < Л <F.
В классе колец с условием минимальности первые
семь Р. совпадают и соответствуют классическому Р.
Если радикал г индуцирует в классе колец с условием
минимальности классический Р., то ф<г<т. Для колец
с условием максимальности $=-Х=-Ж. Для коммута-
коммутативных колец у-^-?Г=-т— /'. р = Х= Л'= Л- Радикалы
Р, X, Ж, ^-, Jr, т, Л, F являются специальными. Ра-
Радикалы ф, Р, X соответствуют одному и тому н;е раз-
разбиению простых колец, а ^, ?Г, х, Л, /"--другим по-
попарно различным разбиениям.
Лит.: [1] A m i t s u r S. A., «Amer. ,). Math.», 1952, v. 74,
p. 774—86: 1954, v. 76 p. 100—36; МНурош А. Г.,«Матем.
сб.» 1953, т. 33, в. 1, с. 13 -26; [3] D i v i n s k у N., Rings and
radicals, Toronto, 19l>5;[4] Artin E., Nesbitt C, Til»-
rail R., Rings with minimum condition, Ann Arbor, 1944; 15]
Итоги науки. Алгебра. Топология. Геометрия. 1967 М., 1969,
с. 28 — 32; [6] Кольца, т. 2, Новосиб., 1973, с. 3—6; [7] А н Д р у-
н а к и е в и ч В. А., р я б у х и и К). М., Радикалы алгебр и
структурная теория, М., 1979; [8] Ж е в л а к о в К. А.,
С л и н ь к о А. М., Шестаков И. П., Ширшов А. II.,
Кольца, близкие к ассоциативным, М., 1978.
В. А. Андрунакиевич.
В классе алгебр Ли обычно радикалом наз. наиболь-
наибольший разрешимый идеал, т. е. разрешимый идеал г, со-
содержащий все разрешимые идеалы данной алгебры
Ли. В конечномерной алгебре Ли g существует также
наибольший нильпотентный идеал п (называемый иног-
иногда нильрадикалом), к-рый совпадает с наи-
наибольшим идеалом, состоящим из нилыготентных эле-
элементов, а также с множеством таких г?й, что присо-
присоединенный оператор adx содержится в Р. ассоциативной
алгебры линейных преобразований пространства д,
порожденной присоединенной алгеброй Ли adg. Рас-
Рассматривается также нильпотентный ради-
радикал g алгебры Ли g — это множество таких z?g.
что а (.г)—0 для любого неприводимого конечномерного
линейного представления а алгебры д. Нильпотентный
Р. совпадает также с наибольшим из идеалов, пред-
представляемых нильпотентными операторами при любом
конечномерном линейном представлении алгебры д.
При этом v^2n^2§. Если характеристика основного
поля равна 0, то § — это наименьший из идеалов jc
eg, для к-рых д/f — редуктивная алгебра Ли. В этом
случае нильпотентный Р. связан с радикалом г, соот-
соотношениями
§-=[9, r] = fg, g]flr;
любое дифференцирование алгебры Ли g переводит
X в п и 8 в §. Нильрадикал и нильпотентный Р.,
однако, не являются Р. в смысле общей теории Р. ко-
колец и алгебр.
Лит.: [1] Джекобсон Н., Алгебры Ли, пер. с англ.,
М., 1964; [2] Теория алгебр Ли. Топология групп Ли. Семинар
«Софус Ли», пер. с франц., М., 1982; [3] Ш е в а л л е К.,
Теория групп Ли, пер. с франц., т. 3, М., 1958. А. Л. Онищик.
РАДИКАЛЬНАЯ ОСЬ — совокупность точек плос-
плоскости, имеющих относительно двух неконцентрич. ок-
окружностей
z2 + У2 — 2а2х — 2Ь2у — 2с2 = О
одинаковую степень точки. Уравнение Р. О.:
(a.1 — a1)x^(b2 — bl) у -г(га —ci)=0.
Р. о. двух непересекающихся окружностей проходит
вне окружностей и перпендикулярна прямой, проходя-
проходящей через их центры (иногда принимают, что Р. о.
концонтрич. окружностей является несобственная пря-
прямая). Р. о. двух пересекающихся окружностей являет-
является прямая, проходящая через точки их пересечения;
а Р. о. двух касающихся окружностей — их общая ка-
касательная. Для любых трех окружностей с неколлинеар-
ными центрами Р. о. каждой пары окружностей прохо-
проходят через одну точку (радикальный центр).
А. Б. Иванов.
РАДИУС окружности — отрезок, соединяю-
соединяющий точку окружности (или сферы) с центром. Р. наз.
также длину этого отрезка. бсэ-з.
РАДИУС-ВЕКТОР точки пространства—
вектор, идущий в эту точку из нек-poii заранее фикси-
фиксированной точки, называемой полюсом. Если в ка-
качестве полюса берется начало декартовых координат,
то проекции Р.-в. точки М на оси координат (декар-
(декартовых прямоугольных) совпадают с координатами точ-
точки М. БСЭ-З.
РАДО КВАДРАТУРНАЯ ФОРМУЛА — квадратур
ная формула наивысшей алгебраич. степени точности
для промежутка [a, fc]^[—1, 1] и веса р(х)-—1 с одним
фиксированным узлом — концом промежутка, напр.—1.
Р. к. ф. имеет вид
J'_ 5
/ (х) dx з= Af (-1) +
Узлы xj — корни ортогонального на [ —1,1] с весом
1+ж многочлена Якоби Р{„л) {х), А=2/(п+1)'\ Коэф-
Коэффициенты Cj положительны. Алгебраич. степень точ-
точности равна 2 п. Существуют таблицы узлов и коэффи-
коэффициентов для Р. к. ф., напр, для га—1A) 6 см. [2].
Формула найдена Р. Радо [1].
Лит.: li] R a d а 11 R., «J. math, pures et. appl.», 1880. v. В,
p. 283—336; [2] Крылов В- И., Приближенное вычисление
интегралом, 2 изд., М., 1967. И. П. Мысавских.
РАДОНА ИНТЕГРАЛ — интеграл по Радона мере.
Подробнее, пусть даны а-алгебра 2 подмножеств мно-
множества Т и конечная счетно аддитивная функция <р
на 2 (мера Радона). Тогда в совокупности всех измери-
измеримых функций выделяется класс функций, называемых
с у м м и р у е м ы м и по ф у н к ц и и ф, к-рым
сопоставляется нек-рое конечное число, к-рое и нал.
и и т е г р а л о м Р а д о я а. М. и. Войцеховскии.
РАДОНА МЕРА, внутренне регулярная
м е р а,— конечная мера ц, определенная нп борелев-
ской а-алгебре S3(А') топологич. пространства А', об-
обладающая следующим свойством. Для любого е;>()
найдется компакт К=Кг ?Х такой, что и. A\Де )<е.
Введена И. Радоном (J. Radon, 1913), исходные по-
построения к-рого относились к мерам на а-алгебре
,5g(R") - - борелевской а-алгебре пространства R", и
=1,2, . . . .Топологич. пространство X наз. р а д о и о-
в ы м пространством, если любая конечная
мера, определенная на а-алгебре 33(Х), является Р. м.
Лит.: II] Бурбаки Л., Интегрирование. Меры, интег-
интегрирование мер, пер. с франц., М., 1967; [2] Дан форд Н.,
Шварц Дч!., Линейные операторы. ОГяцая теории, пер. с
англ., т. 1, М\, 1962. Р. А. Минлос.
РАДОНА ПРЕОБРАЗОВАНИЕ — интегральное пре-
преобразование функций от нескольких переменных, род-
родственное Фурье преобразованию. Введено И. Радоном
(см. [1]).
Пусть f (хи . . ., хп) — непрерывная и достаточно
быстро убывающая на бесконечности функция от дей-
действительных переменных xi^R1, г-~1, 2, . . ., п, и=1,
Для любой гиперплоскости в R"
R\
определяется интеграл
^'E!, ¦¦-, In, С) -
где Fr — евклидовым (га — 1)-мерный объем на гипер-
гиперплоскости Г. Функция
f(iu .-., I», С), (gx, .... %„, С) g R» + l,
наз. преобразованием Радона функ-
ции /. Она является однородной функцией своих пе-
переменных степени —1:
F(a|lt ..., а|„; аС)^-^ F Aи ..., ?„; С)
и связана с преобразованием Фурье /(Si, . . ., !„),
5i ^ R-1, функции / формулой
С Р. п. непосредственным образом связана задача,
восходящая к И. Радону, о восстановлении функции /
по значениям ее интегралов, вычисленных по всем ги-
гиперплоскостям пространства R" (т. е. задача об обраще-
обращении Р. п.).
Лит.: [1] Radon J., «Вег. Verh. Sachs. Acad.», 1917, Bd
69, S. 262—77; [2J Г е л ь ф а н д И. М., Граев М. И., В и-
л е н к и н Н. Я., Интегральная геометрия ..., М., 1962.
Р. А. Минлое.
РАДОНА — НИКОДИМА ТЕОРЕМА: у заряда V,
абсолютно непрерывного относительно нек-рой меры ц,
существует плотность Р= — относительно \i, суммируе-
суммируемая по этой мере. Установлена И. Радоном [1] и О. Ни-
кодимом [2]. Точнее, пусть на измеримом пространстве
(X, 23), SJ3 — нек-рая а-алгебра подмножеств X, оп-
определены заряд v, т. е. счетно аддитивная действитель-
действительная или комплексная функция, заданная на 23, и мера
(г, причем заряд v абсолютно непрерывен относительно
fi. Тогда существует такая суммируемая по мере (г
функция р(х), х?Х, что для любого множества 4^33
имеет место
г*
v(A)—\p (х) d\i (x).
Функция р единственна (с точностью до изменения на
множестве нулевой ц-меры) и наз. плотностью
заряда v относительно меры ц. Имеются (см. [3])
обобщения этой теоремы на случай, когда заряд при-
принимает значения из нек-рого векторного пространства.
Лит.: [1] R a d о n J. «Acad. Wiss.», Wien, 1919, t. 128,
S. 1083 — 1121; [2] N i с о d у m О., «Fund, math.», 1930, t. 15,
p. 1.41—79; [3] Данфор д'П., Ш в а р ц Д., Линейные опера-
операторы, ч. 1 — Общая теория, пер. с англ., М., 1902; [4] D 1 е s-
t e 1 J., U h I J., Vector measures, Providence, 1977.
P. А. Минлое.
РАЗБАВЛЕНИЕ РЯДА — включение в ряд между
его соседними членами любого конечного числа нулей.
Для ряда
разбавленный ряд имеет вид
.. .+0 + ц, 4 0 + ••• +0-f u,-!-
Р. р. не отражается на его сходимости, однако может
нарушить суммируемость ряда (суммируемый к числу
s каким-либо методом суммирования ряд (*) после раз-
разбавления может оказаться вообще не суммируемым этим
методом или суммируемым к числу афя).
И. И. Волков.
РАЗБИЕНИЕ — 1) Р.— представление заданного
множества в виде объединения системы множеств, не
имеющих попарно общих точек.
В дискретной геометрии часто рассматривают Р.
пек-рого пространства на замкнутые области, к-рые
покрывают все пространство и попарно не имеют общих
внутренних точек (граничные точки могут быть общими).
Напр., если зафиксировать любую точечную решетку
евклидова пространства R" и сопоставить каждой точ-
точке решетки те точки пространства, к-рые удалены от
этой точки не более, чем от любой другой точки решет-
решетки, то получается т.н. разбиение Дирихл е—
Вороного. Р. пространства наз. правильным,
если для любых его областей Dl и D.2 существует такое
движение М, что D2~M (Dx) и />¦¦-¦ Л/(Р). См. также
Вороного типы решеток.
В комбинаторной геометрии имеется ряд задач и
результатов, относящихся к специальным Р. нек-рых
множеств. Примером такой задачи является Борсука
проблема: можно ли разбить любое множество диаметра
d, лежащее в R", на и+1 таких частей, что каждая из
них имеет диаметр <d? В R" существуют такие ограни-
ограниченные множества, разбиение к-рых на меньшее число
таких частей невозможно. Любое Р. определяет нек-
некрое покрытие и из любого покрытия можно получить
нек-рое Р. Разбиения имеют тесную связь с освещения
задачами и с Хадвигера гипотезой.
Лит.: [1] Болтянский В. Г., С о л т а н П. С, Комби-
Комбинаторная геометрия различных классов выпуклых множеств,
Киш., 1978; [2] Г р ю н б а у м Б., Этюды по комбинаторной
геометрии и теории выпуклых тел, пер. с англ., М., 1971.
П. С. Солтан.
2) Р. пространства X — система Щ} его
дизъюнктных подмножеств, объединение к-рых есть X.
Множество ЭД1 превращается в топологич. пространство,
если объявить открытыми в нем множествами всякие
множества 9?с2Л, прообразы к-рых при естественном
отображении ц: X —>- Щ} (каждой точке х?Х ставится
в соответствие единственное содержащее его множест-
множество Ма'Ш) являются открытыми множествами в X.
3) Р.— локально конечное покрытие простран-
пространства, элементами к-рого являются замкнутые кано-
нич. множества с дизъюнктными открытыми ядрами.
М. И. Войцеховский.
РАЗВЕРТКА — 1) Р.— область на плоскости, изо-
метричная заданной области на развертывающейся по-
поверхности. Пример: Р. боковой поверхности конуса,
разрезанного но образующей, есть плоский сектор. При-
Приближенное построение Р. может осуществляться графи-
графически, средствами начертательной геометрии.
2) Р. многогранной поверхности —
набор многоугольников (граней Р.) с указанием правила
склеивания их сторон, порождающий многогранную
метрику, изометричную внутренней геометрии задан-
заданной многогранной поверхности. Грани Р. не обязаны
совпадать с истинными гранями поверхности: при на-
наложении на поверхность они могут переламываться.
В. А. Залгаллер.
РАЗВЕРТЫВАЮЩАЯСЯ ПОВЕРХНОСТЬ, торс-
линейчатая поверхность нулевой гауссовой кривизны.
Во всех точках одной и той же образующей Р. п. имеет
одну и ту же касательную плоскость. Параметр распре-
распределения Р. п. равен нулю. Если образующие Р. п.
параллельны одной и той же прямой, то она — ц и-
л и н д р. Если образующие Р. п. проходят через одну
точку, то она — конус. В остальных случаях Р. п.
образована касательными к нек-рой кривой — реб-
ребру возврата Р. п. Для того чтобы кривая на по-
поверхности была ее линией кривизны, необходимо и до-
достаточно, чтобы нормали вдоль этой линии образовыва-
образовывали Р. п.
Р. п.— огибающая однопараметрич. семейства плос-
плоскостей (напр., спрямляющая поверхность) и потому
локально является изгибанием куска плоскости.
РАЗВЕТВЛЕНИЯ ТОЧКА — то же, что еетвлеТия
точка аналитич. функции.
РАЗДЕЛЕНИЯ ПЕРЕМЕННЫХ МЕТОД — то же,
что Фурье метод.
РАЗДЕЛИТЕЛЬНАЯ ДИЗЪЮНКЦИЯ — одна из
логич. связок. Предложение А уВ, получающееся
из двух предложений А и В с помощью Р. д. V , считает-
считается истинным в случае, если истинно А и ложно В, или
в случае, если ложно Л и истинно В. В остальных слу-
случаях оно считается ложным. Таким образом, Р. д. мо-
жет быть выражена через обычную (не разделительную)
дизъюнкцию по формуле
> {А\уВ)&~\ (АаВ).
В. Н. Гришин,
РАЗЛИЧАЮЩАЯ, различающая ко-
коцепь,— препятствие к продолжению гомотопии меж-
между отображениями. Пусть X — нек-рое клеточное про-
пространство, У — односвязное топологии. пространство;
пусть, далее, даны два отображения /, g: X —>¦ У и
гомотопия
(где /=fO, 1] и X" есть n-мерный остов пространства X)
между ними на (п—1)-мерпо.ч остове. Для каждой ори-
ориентированной n-мерной клетки еп пространства X ог-
ограничение отображения F на д (е X /) задает отображе-
отображение S" —>¦ У (Sn есть «-мерная сфера) и, значит, элемент
группы л„(У). Таким образом возникает коцепь
d"(f, g)€c"{X; я„(У)) (более точным было бы обозначе-
обозначение dnp(], g)), к-рая и паз. различающей ко-
коцепью; коцепь dn(f, g) япляется препятствием к
продолжению отображения /•' на ХХО \JX"XI\JXX
XI=(XXI)"-1\JXX{O, 1}.
Справедливы следующие утверждения: 1) d"(f, g)=0
тогда и только тогда, когда гомотопия между fug
продолжается на X"; 2) коцепь
d"U, g) GC(XX/, Xx{0, 1}; л„(У))
является коциклом; 3) класс когомологий
[<*"(/, g)]?H"(XXl, XX{O, 1}; яп(У))
тогда и только тогда раиен нулю, когда между fag
имеется гомотопия на X", совпадающая с F па Хп~2.
Без ограничения общности можно считать, что fug
совпадают на Хп~х и что F (x, t) = f(x)=g (х) для х?
?Хп~2. При этих предположениях справедливы сле-
следующие утверждения:
1) d"(f, g)=—d"(g, /), в частности d"(f, /) = 0;
2) d"(f, g) + d"(g, h)=rd"(f, h)\
3) для любого отображения /: 1-+Уи любой коце-
коцепи d^C"(X\ .in(Y)) существует такое отображение g,
что }\xn-r-g\xn--, и d"(f, g)=d.
Пусть теперь заданы два отображения /, g: X" —>- У
/I vn-i = ^l vn-i и пУсть с?-1-1 и с"+1 — препятствия к
продолжениям соответствующих отображении. Роль Р.
в теории препятствий определяется следующим предло-
предложением:
c^ + 1-4+1 = 6d«(/, g).
Таким образом, если g продолжается на Хп + 1, то
[1]0, а если [с^ + 1]=0, то /| „_j продолжается на
Ю. Б. Рудяк.
РАЗЛИЧАЮЩИЙ ЭЛЕМЕНТ в К-т е о р и и — эле-
элемент группы К (X, А) (где (X, А) — пара пространств,
при этом обычно X считается конечным клеточным про-
пространством и А — его клеточным подпространством),
строящийся по тройке (|, т), ?), где | и т) — вектор-
векторные расслоения одной и той же размерности над X и
? : Ь\а —>¦ flU— изоморфизм векторных расслоений (здесь
а|д — часть векторного расслоения а над X, располо-
расположенная над подпространством А). Построение Р. э.
осуществляется следующим образом. Пусть сначала
расслоение т) триииально и фиксирована какая-нибудь
тривиализация расслоения т) над X. Тогда ? задает
тривиализацию расслоения Ц^ и, значит, задает эле-
элемент группы К (XIА )=К (X, А). Этот элемент не зависит
от выбора тривиализации расслоения ц над всем А'.
В общем случае подбирается такое расслоение а над X,
что расслоение r\Qja тривиально и тройке (|, т), ?) со-
Хп
поставляется тот же элемент, что и тройке {?©ст, ^фо",
?©id а). ю. б. рудяк.
РАЗЛИЧНЫХ ПРЕДСТАВИТЕЛЕЙ СИСТЕМА для
заданного семейства подмножествF= {F;, i ? / }множест-
}множества S — множество R={n(i), i?I] при любом взаимно
однозначном отображении я : I —>¦ S, обладающем свой-
свойством: n(l)?Fi для любого t?/ (здесь / — произволь-
произвольное множество индексов). Другое название Р. п. с.
R — трансверсаль семейства F. Рас-
Рассматриваются также частичные трансвер-
сали семейства F — множества вида {я (г),
i?/0}, где /0 — подмножество /, ц: 10 —у S — взаим-
взаимно однозначное отображение.
Р. п. с. применяются как в чисто комбинаторных
математич. исследованиях, так и в их приложениях
к линейному программированию, математич. экономике
и кибернетике. В пределах комбинаторной математики
Р. п. с. играют существенную роль в той ее части,
к-рая связана с задачами выбора и экстремальными за-
задачами. Они используются, в частности, при изучении
латинских прямоугольников, в задаче о назначениях,
при исследовании матриц с неотрицательными элемен-
элементами и с суммами элементов по строкам и столбцам, ле-
лежащими в заданных границах.
Критерий существования Р. п. с. для конечного /
дается теоремой Холла: пусть на множестве
S задано семейство F—{Ft, i?/} из \1\ = п элементов,
п конечно; для существования Р. п. с. необходимо и
достаточно, чтобы \F(l[jFi2\J. . .\JFlk\^k для каждого
/с-подмножества {it, i2, . . ., ik)—I и каждого к, к—
=1, 2, . . ., п. Теорема Холла представляет собой утвер-
утверждение, эквивалентное теореме Кёнига (см. Выбора
теоремы) о матрицах из нулей и единиц. Этот фунда-
фундаментальный критерий применим также к бесконечному
/, когда все Fh ig/, конечны. Упомянутыми случая-
случаями, вообще говоря, исчерпывается, как показывают
примеры, область применения критерия Холла, но он
послужил отправной точкой для различных критериев
в ряде других случаев (см. [3]), напр.: а) когда сущест-
существует такое подмножество Ioczl, что /—/0 конечно, а
Fj конечны при всех i?/0; б) когда / — счетное мно-
множество.
Ввиду широкого использования Р. п. с. представля-
представляют интерес алгоритмы, разработанные для их практич.
нахождения (см. [11).
Одной из основных задач о Р. п. с. является задача
о числе Р. п. с. для конечных семейств, состоящих из
конечных множеств; она связана с вычислением перма-
перманента матрицы, состоящей из нулей и единиц. Для
числа Р. и. с. существуют оценки снизу. Пусть семей-
семейство F состоит из п подмножеств Fb . . ., Fn и пусть
они упорядочены по мощности: m=l^1|<|F2| <. . .<
s?:|FH|. Тогда если F удовлетворяет критерию Холла,
то число Р. п. с. не меньше, чем
Вопросы, связанные с системами представителей,
разрабатываются также в рамках теории матроидое
(иначе — пространств независимости, комбинаторных
геометрий). Связь теории представителей с матроида-
ми дается теоремой Эдмондса — Фал-
к е р с о н а: для заданного семейства подмножеств
конечного множества совокупность всех частичных
трансверсалей есть совокупность независимых подмно-
подмножеств нек-рого матроида. Матроид, полученный таким
образом из семейства F, наз. трансверсаль-
ным матроидом для F. Многие матроиды могут
быть представлены как трансверсальные для нек-рого
семейства подмножеств.
Понятие Р. п. с. обобщается в различных направле-
направлениях, напр.: а) р-т рансверсали для заданного
семейства F= [Fj, . . ., Fn) и целочисленного вектора
р— (pj, . . ., р„) суть множества {яA), . . ., я(гс)},
где я(г)?//,-, i=l, . . ., п,— такие попарно различные
подмножества S, что 1<|я (i)\ <p,-; б) k-t p а н с в е р-
с а л и для F= {Fj, i?I} и целого числа к~^\ суть под-
подмножества R= {я (i), i?^} Для отображений л : I -> S
со свойствами n(i)?Fi и 1<:| {я~1(яA))}|<:А;, i?/.
Лит.: И] X о л л М., Комбинаторика, пер. с англ., М., 1970;
[2] М i г s k у L-, Transversal theory, N. Y.— L., 1971; [3] T a-
p а к а н о в В. Е., в кн.: Вопросы кибернетики, в. 16, М., 1975,
с. 110—24. В.В.Тараканов.
РАЗЛОЖЕНИЕ ЕДИНИЦЫ — однопараметрическое
семейство{ ??t }, — °° <^-<оо, проекционных операторов,
действующих в гильбертовом пространстве ffl, такое,
что
1) Е\<^.Ец, если А<и.;
2) Е%. сильно непрерывно слева, т. е. Е\-0=Е\ для
любого Х?( — оо, оо);
3) Е^-^-0 при А,-» оо и Е\-*гЕ при А,-*- оо, здесь О
и Е — нулевой и единичный операторы в пространстве
$ft ¦ Условие 2) можно заменить на условие непрерыв-
непрерывности справа в каждой точке А,? (— оо , оо).
Всякий самосопряженный оператор А, действующий
в $%, порождает соответствующее ему вполне опреде-
определенное Р. е. При этом кроме условий 1)—3) выполняют-
выполняются еще условия:
4) если В — ограниченный оператор такой, что В А =
=АН, то BEi ~Ех В для любого К;
5) если А — ограниченный оператор, т, М — его
нижняя и верхняя грани соответственно, то
Е,=0, — оо<Я,</га, и Е, — Е при М < К < оо.
Р. е., порожденное оператором А, полностью опреде-
определяет спектральные свойства этого оператора, а именно:
(а) точка X есть регулярная точка оператора А тогда
и только тогда, когда она является точкой постоянст-
постоянства, т. е. когда существует б>0 такое, что ?|х = ?^для
(Р) точка Хо речь собственное значение оператора А
тогда и только тогда, когда в этой точке Е% имеет ска-
скачок, т. е. Е^ +0—Е^ >0;
(у) если ?'(Д)=?(х—Ei, то LE,^~E (A)ffl есть инва-
инвариантное подпространство оператора А .
Поэтому Р. е., порожденное оператором А, наз. так-
также спектральной функцией этого опера-
оператора.
Обратно, каждое Р. е. {Ех } однозначно определяет
самосопряженный оператор А, для к-рого это Р. е.
является спектральной функцией. Область определе-
определения D (А) оператора А состоит из тех и только тех х(~
для к-рых
и имеет место представление оператора А в виде опера-
операторного интеграла Стилтьеса
Лит.: [1] Рисе Ф., С ё к е ф а л ь в и - Н а д ь Б., Лекции
по функциональному анализу, пер. с франц., 2 изд., М., 1979;
[2] А х и е з е р Н. И., г л а зм а н И. М., Теория линейных опе-
операторов в гильбертовом пространстве, 2 изд., М., 19BU; [3] К а н-
т о р о в и ч Л. В., А к и л о в Г. П., Функциональный анализ,
2 изд., М., 1977. В. И. Соболев.
РАЗЛОЖИМАЯ ГРУППА над полем к, рас-
расщеп и м а я группа над к, к-р а -л л о ж и-
мая групп а,— линейная алгебраич. группа, оп-
определенная над к и содержащая разложимую над к
Бореля подгруппу; при этом связная разрешимая линей-
линейная алгебраич. группа В наз. разложимой над к, если
она определена над к и обладает таким композицион-
композиционным рядом B^BozdB1ZDB2ZD. . .Z^Bf= {I }, что все
fl,- — связные, определенные над к алгебраич. подгруп-
пы, а каждая из факторгрупп BtlB; + 1 изоморфна над к
либо одномерному тору Gm—GL1, либо аддитивной од-
одномерной группе Ga. В частности, алгебраический тор
тогда и только тогда разложим над it, когда он опреде-
определен над к и изоморфен над к прямому произведению
нескольких экземпляров группы Gm. Для связных
разрешимых Аг-разложимых групп справедлива Бореля
теорема о неподвижной точке. Определенная над it
редуктивная линейная алгебраич. группа тогда и
только тогда разложима над к, когда она обладает
разложимым над к максимальным тором, т. е. когда
ее fe-ранг совпадает с ее рангом (см. Ранг алгебраиче-
алгебраической группы). Образ it-разложимой группы при любом
определенном над к рациональном гомоморфизме яв-
является fc-разложимой группой. Всякая определенная
над к линейная алгебраич. группа G разложима над
алгебраич. замыканием ноля к; если, кроме того,
группа G редуктивна или разрешима и связна, то она
разложима над нек-рым конечным расширением поля к.
Если поле к совершенно, то связная разрешимая оп-
определенная над к линейная алгебраич. группа тогда
и только тогда разложима над fc, когда она приво-
приводится над к к треугольному виду. Если char /с=0,
то определенная над к линейная алгебраич. группа
тогда и только тогда разложима над к, когда ее ал-
алгебра Ли L является разложимой (или рас-
расщепляемой) над к алгеброй Ли; послед-
последнее, по определению, означает, что алгебра Ли L об-
обладает расщепляющей подалгеброй
К а р т а н а, т. е. такой Картана подалгеброй IIL
что все собственные значения каждого оператора
А?//, принадлежат полю к.
Если GR— вещественная группа Ли, совпадающая
с группой вещественных точек полупростой R-разло-
жимой алгебраич. группы G, a Gp— комплексификация
группы Ли GR, то GR наз. нормальной вещест-
вещественной формой комплексной группы Ли Gq.
Существуют квазиразложимые группы над полем к,
не являющиеся Р. г. над к; примером при /, К может
служить группа 50C, 1).
Лит.: U1 Б о р е л l А., Линейные алгебраические группы,
пер. с англ., М., 1972; [2] Б о р е л ь А., Т и т с Ж., «Математи-
«Математика», 1967, т. 11, № 1, с. 43—111; [3] М е р з л я к о в Ю. И.,
Рациональные группы, М., 1980: 14] Хамфри Д ж., Линей-
Линейные алгебраические группы, пер. с англ., М., 1980. В. Л. Пипов.
РАЗМАХ выборки — разность
wn^= #niax "**-min
между наибольшим хтах = хп и наименьшим хт\и~хг
значениями в выборке
получающейся с помощью п независимых измерений
одной и той же случайной величины А". Пусть F (х) —
=Р{ЛГ<ж} — функция распределения случайной вели-
величины X. Тогда распределение вероятностей для зна-
значений Р. равно
^^ (F (x + t)-F (x))»-ldF (x),
Лит.: ll] В а н д о р В а р д е н Б. Л., Математическая
статистика, пер. с англ., М., 19E0; [2] Большее Л. Н.,
Смирнов Н. В., Таблицы математической статистики 2
изд., М., 1968. Т. Ю. Понови.
РАЗМЕРНОСТЕЙ АНАЛИЗ — метод установления
связи между фпзпч. величинами, существенными для
изучаемого явления, основанный на рассмотрении
размерностей этих величин. В Р. а. рассматриваются
проблемы установления различных систем единиц
измерения, вопросы о выборе первичных величин и
соответствующих им опытных единиц измерения и
связанное с выбором первичных единиц измерения
образование вторичных единиц измерения для величин,
определяемых через первичные.
В качестве величин, для к-рых выбираются пер-
первичные единицы измерения, можно брать различные.
В разных областях приложений выгодно и удобно
выбирать в качестве первичных единиц измерения
свои местные единицы. В связи с этим и с установив-
установившимися обычаями на практике были созданы различ-
различные системы единиц измерения и возникла задача
о переходе (задача пересчета) от одной системы единиц
измерения к другой. Распространены многочисленные
системы единиц измерения: в числе главных — система
СГС, в к-рой первичные сантиметр, грамм-масса и
секунда; система МКГСС, в к-рой первичные метр,
килограмм-сила и секунда; система СИ, в к-рой пер-
первичные метр, килограмм-масса, секунда, ампер, кель-
вин, кандела. Число первичных единиц измерений в
употребляемых или потенциально допустимых системах
единиц измерения может быть разным: меньшим трех,
равным трем, как в системах СГС и МКГСС, и др.
Выражение производной единицы измерения через
основные единицы наз. формулой размер-
размерности, к-рая записывается через символы первичных
единиц измерения и имеет вид степенных одночленов.
Напр., в системе СГС формулы размерности содержат
три аргумента: единицу длины L, единицу времени Т
и единицу массы М\ на основании определения силы
через массу и ускорение формула размерности силы К
имеет вид
MLT-K A)
В системе СГС формулы для любой величины N ме-
механической, тепловой или электромагнитной природы
имеют вид
N^L'TW1*, B)
где показатели степеней I, t, m — нек-рые целые или
дробные действительные числа, к-рые наз. показа-
показателями размерности, или размерно-
размерностью, величины N. Принимают, что размерность
первичной величины в отношении себя равна единице,
а в отношении любой другой первичной величины —
нулю.
Формулы размерности позволяют определить чис-
численные масштабные множители для пересчета соот-
соответствующих характеристик при изменении величин
первичных единиц измерения. Если вместо заданных
единиц измерения длины /., времени Т и массы М
перейти к новым единицам измерения, меньшим для
длины в а раз, для времени в Р раз и для массы в у рая,
то новая единица измерения для величины N с размер-
размерностью по формуле B) будет меньше первоначальной
в а.1$*ут раз.
Если l--t~m~0, то численное значение величины
не зависит от выбора масштабов для первичных еди-
единиц и, следовательно, такая величина будет безраз-
безразмерно й, или отвлеченной. Примерами без-
безразмерных величин являются: число Рейиольдса Re=
~ру//|х;. число Фруда Fr = r^ . число Маха M=v/a,
число кавитации х— 2ДР/р(Л2, где для характерных
в нек-рых явлениях размерных величин приняты
следующие обозначения: р — плотность, v — скорость,
I — линейный размер, ji — динамич. коэффициент вяз-
вязкости, АР — характерная разность давлений, g — ус-
ускорение силы тяжести.
Число первичных единиц намерения можно увели-
увеличивать, если кроме уже выбранных первичных единиц
измерения выбирать по соглашению независимо еди-
единицы измерения для любых др. величин, напр, можно
взять независимо единицы измерения: для тепловой
энергии — калорию и для механич. энергии — кило-
граммометр. прибавив соотношение: / — тепловая энер-
энергия в калориях или механич. энергия в килограммо-
килограммометрах, где / — размерная «физическая» постоянная,
называемая механич. эквивалентом тепла.
Физич. законы, содержащие размерные постоянные,
можно использовать для сокращения числа первичных
единиц измерения. Так, напр., постоянную скорости
света можно считать абсолютной постоянной, т. е.
безразмерной величиной, и таким путем выразить
единицу измерения и размерность длины через единицу
измерения и размерность времени; при рассмотрении
гравитационной постоянной как абсолютного безраз-
безразмерного числа можно выразить размерность и единицу
измерения для массы через размерность и единицы
измерения для длины L и времени Т.
В нек-рых вопросах явно проявляется тенденция
к стандартизации путем введения единой универсальной
системы единиц измерения. Однако привязывание
универсальной системы единиц измерения к опреде-
определенным физически фиксированным масштабам или к
соответствующим физич. постоянным является искус-
искусственным. Наоборот, возможность использования про-
произвольных единиц измерения и независимость рас-
рассматриваемых закономерностей от выбора систем еди-
единиц измерения могут служить источником ценных
выводов.
Физич. закономерности, вообще говоря, не зависят
от выбора системы единиц измерения. Это обстоя-
обстоятельство обусловливает особую структуру функций
и функционалов, выражающих собой через посредство
размерных величин физич. закономерности, независи-
независимые от систем единиц измерения. Эта специальная
структура функциональных соотношений устанавли-
устанавливается я-т d о р е м о й: всякое соотношение между
размерными характеристиками, имеющее физич. смысл,
представляет собой, по существу, соотношение между
отвлеченными безразмерными комбинациями, к-рые
можно составить из размерных определяемых м опре-
определяющих величин, среди к-рых должны учитываться
и размерные физич. постоянные, имеющие существен-
существенное значение в рассматриваемых явлениях.
Дополнительные данные об отсутствии нек-рых физич.
постоянных в рассматриваемом соотношении приводят
к сокращению в этих соотношениях существенных
аргументов. Напр., если в рассматриваемых тепловых
и механич. явлениях нет преобразования — перехода
тепловой энергии, измеряемой в калориях, в механи-
механическую, измеряемую в эргах, то постоянная механич.
эквивалента тепла будет отсутствовать среди аргу-
аргументов функции, описывающей соответствующую за-
закономерность.
Для получения полезных выводов с помощью Р. а.
необходимо схематизировать проблему и, прежде
всего, фиксировать общее моделирование явлений и
свойств рассматриваемых объектов. Во многих случаях
такая схематизация может быть связана с рядом рабо-
рабочих гипотез. В рамках нек-рых моделей устанавли-
устанавливается система характеристик, к-рые связаны между
собой физич. соотношением и к-рые согласно л-тоореме
должны представляться как соотношения между без-
безразмерными параметрами. Таким образом, нужно
ввести систему определяющих параметров постоянных
или переменных, вытекающую из постановки выделя-
выделяемого класса задач и характеризующую, вообще го-
говоря, полностью для данной среды каждую отдельно
взятую задачу.
При выделении минимального числа определяющих
параметров требуется учитывать условия симметрии
и выбор выгодных систем координат. Независимые
переменные (координаты точек пространства и времени')
и физич. параметры типа коэффициентов теплопровод-
теплопроводности, вязкости, модулей упругости и т. п. необхо-
димо включать в таблицу определяющих параметров.
Такие постоянные, как ускорение силы тяжести или
механич. эквивалент тепла, тоже должны фигурировать
в перечне определяющих параметров, когда грави-
гравитация или переход тепловой энергии, измеряемой в
калориях, в механическую, измеряемую в килограм-
килограммометрах (или в эргах), существенны.
Для выделенного класса задач необходимо включать
в число определяющих параметров размерные или без-
безразмерные характеристики заданных границ рассмат-
рассматриваемых тел и задаваемых функций, участвующие
в формулировке начальных, краевых или каких-либо
других условий.
Если рассматриваемая задача сформулирована как
математическая, то можно выписать полную таблицу
аргументов для соотношений вида
я — / («1, я2, . . ., ап), C)
где а — искомая величина, а %, . . ., а,г — определя-
определяющие параметры. В зависимости от постановки задачи
число п может быть конечным или бесконечным. Обычно
при соответствующем фиксировании класса рассмат-
рассматриваемых задач можно ограничиваться случаями, когда
п конечно и, вообще говоря, невелико. Параметры
alt . . ., ап составляются из задаваемых величин, вхо-
входящих в основные уравнения, граничные условия и
начальные данные. Определяющие, параметры — это
все исходные данные, к-рые надо знать предварительно
по смыслу постановки матеммтпч. задачи для вычис-
вычисления искомой функции различными путями, в том
числе и при расчетах на специальных машинах или
с помощью аналоговых систем.
Определяющие параметры при получении нужных
ответов с помощью экспериментов — это величины,
характеризующие каждый отдельный опыт, величины,
к-рые необходимы и достаточны для повторения и
сравнения различных экспериментов.
Можно выписать систему определяющих параметров
и в тех случаях, когда детальные свойства модели и
системы уравнений, описывающих рассматриваемые яв-
явления, вообще говоря, неизвестны: достаточно опе-
опереться на предварительные данные или гипотезы о
виде задаваемых функций и о постоянных, к-рые
входят или могут входить в определение модели, и на
др. условия, выделяющие конкретные решения задачи.
Выводы Р. а. получаются на основании л-теоремы о
существовании соотношения вида C), к-рое выпол-
выполняется для определяемой величины и определяющих
величин аг, . . ., ап в любой системе единиц измерения.
Система аргументов в соотношении C) должна в
смысле теории размерностей обладать полнотой. Это
значит, что если величина а отлична от нуля или бес-
бесконечности, то существуют числа ах, . . ., а„ такие, что
размерности величины а и комбинаций а™1 а™2. . .а*"
одинаковы. На основании этого и л-теоремы соотно-
соотношение C) можно переписать в виде
я = = g(n1, л2, ..., л„_ь), D)
Г/. re „ г/., п v L' ^' ' " к' ' х '
где я1? . . .. я„_?— степенные безразмерные одно-
одночлены (аналогичные л=3,14. . .), образованные из
alf . . ., ап, причем /Ь<и. Число к равно числу пара-
параметров среди а1? . . ., ап с независимыми размерно-
размерностями .
После явной записи физич. закономерностей в виде
D) по существу заканчиваются возможности приме-
применений Р. а. Соответствующие результаты, полученные
таким путем, носят ограниченный характер. Если
видоизменить любым способом уравнения движения
без внесения в них каких-либо новых параметров, то
физич. закономерности D) могут сильно измениться,
но основной вывод, содержащийся в формуле D),
сохраняет свою силу.
Существует целый ряд примеров получения плодо-
плодотворных выводов и установления целесообразных
удобных методов обработки экспериментальных ре-
результатов с использованием Р. а. и л-теоремы. Особая
польза достигается за счет сокращения числа аргумен-
аргументов у искомых функций; это сокращение обеспечи-
обеспечивается л-тооремой и во многих случаях достигается на
основании постановки задачи с использованием опыт-
опытных данных или нек-рых гипотез о механизмах сущест-
существенных эффектов в изучаемых вопросах.
Основная практич. польза состоит в установлении
возможности перенесения результатов опыта в одних
условиях на др. условия, в к-рых опыт не проводился.
Напр., но опытам с водой, движущейся в трубе с фик-
фиксированным диаметром, можно давать автоматически
нужные ответы о движении воды в трубах той же
формы, но других размеров, о движении в трубах
нефти, воздуха и т. п. Однако для возможности перене-
перенесения результатов данного опыта на др. опыты необ-
необходимо обеспечивать в соответствующих случаях оди-
одинаковые значения безразмерных параметров. Значения
нек-рых из этих величии легко обеспечиваются гео-
метрич. условиями постановки опытов. Значения дру-
других параметров связаны с физико-механич. условиями
проведения опытов.
Примерами применения Р. а. являются примеры уста-
установления из постановки задач автомодельности иско-
искомых решений. Свойство автомодельности
состоит в следующем. При нервом подходе к математич.
разрешению ставящейся задачи можно отметить неза-
независимые переменные аргументы функций; обычно это
три координаты точек в нок-ром объеме пространства
и время. Кроме этих неременных величин среди аргу-
аргументов искомых функции могут фигурировать нек-рые
задаваемые постоянные параметры, возникающие при
описании свойств изучаемой модели и при выделении
конкретной схематизированной задачи. Всякую задачу
можно сформулировать в безразмерных переменных
как для Искомых функций, так и для их независимо
изменяющихся аргументов. А итоМодельность прояв-
проявляется в том, что сокращается число независимых без-
безразмерных пережчишх аргументов по сравнению с
числом размерных.
Эффективные результаты, связанйыо с автОмодель-
ностью, получаются в теории нек-рых одномерных Не-
Неустановившихся задач со сферическими, цилиндриче-
цилиндрическими и плоскими волнами, когда имеются только две
независимые переменные: координата г с размерностью
длины и время t. Если из определяющих размерных
постоянных, присутствующих в постановке задачи,
нельзя образовать две комбинации — <3дну с размер-
размерностью длины, а другую с размерностью времени,
то единственным переменным безразмерным аргумен-
аргументом в искомых безразмерных функциях будет параметр
вида К=Grit13-, где а — нек-рый показатель, а С —
размерная постоянная, выражающаяся через заданные
постоянные, фигурирующие в постановке задачи.
В частности, если математич. задача сводилась к реше-
решению нек-рой системы дифференциальных уравнений с
частными производными по г и t, то при паличйи только
одного переменного параметра X уравнения с частными
производными по г и г преобразуются к обыкновенным
дифференциальным уравнениям с одной независимой
переменной Я, вследствие чего математич. задача
сильно упрощается. Таким путем было получено ре-
решение многих практически важных задач, напр. задачи
о возмущенном движении воздуха, вызванном кон-
концентрированным атомным взрывом в атмосфере.
Соображения Р. а. для автомодельных процессов
Могут служить не только для сведения уравнений с
частными производными к обыкновенным, но и для
получения конечных соотношений между искомыми
функциями (интегралов этих уравнений), что позво-
позволяет находить решения нек-рых автомодельных задач
в замкнутом формульном виде. Эти методы были про-
продемонстрированы при решении задач о сильном взрыве
в атмосфере и в задачах о распространении взрывных
волн в газовых средах, в к-рых в исходном состоянии
плотность переменна и изменяется вдоль радиуса по
степенному закону. Эти задачи ставятся как сильно
схематизированные модели взрыва звезд.
Р. а. непосредственно связан с понятием о физич.
подобии, к-рое изучается в подобии теории.
Лит.: [1] Б р и д ж м е н П. В., Анализ размерностей, пер.
с англ., Л.— М., 1934; [2] Седов Л. И., Методы подобия и
размерности в механике, 9 изд., М., 1981. Л. И. Седое.
РАЗМЕРНОСТИ АДДИТИВНЫЕ СВОЙСТВА —
свойства, выражающие связь размерности топологич.
пространства X, представленною в виде суммы своих
подпространств Ха, с размерностями пространств Ха.
Имеется несколько видов Р. а. с.
Теорема суммы. Если хаусдорфово и нор-
нормальное пространство X представимо в виде конечной
или счетной суммы своих замкнутых подмножеств X,-,
то
dim X,= sup dim X;.
i
Если, дополнительно, пространство X совершенно
нормально или наследственно паракомпактно, то
Ind X = sup Ind Xj.
i
Локально конечная теорема с у м-
м ы. Если хаусдорфово и нормальное пространство X
представлено в виде суммы локально конечной системы
своих замкнутых подмножеств Ха, то
dim X = sup dim Xa.
а
Если, дополнительно, пространство X совершенно
нормально или наследственно паракомпактно, то
Ind X = sup Ind Xа.
а
Теорема сложения. Если пространство X
хаусдорфово, наследственно нормально и Х=А [JB, то
dim X < dim A + dim В +1
(формула Менгера — Урысона). Если,
кроме того, пространство X совершенно нормально, то
IndXsjInd/1+IndS + l-
Метрич. пространство Я имеет размерность dim R^.n
тогда и только тогда, когда
л+1
Д= (J Д,-, dimfl,-<0, i = l, ...,ге + 1;и = 0, 1. 2, ....
i=i
В хаусдорфовом наследственно нормальном про-
пространстве X для любого замкнутого подмножества F
выполняются равенства
dim X =max (dim F, dim X\F),
, lndX\F).
В. А. Пасынков.
РАЗМЕРНОСТИ ТЕОРИЯ — часть топологии, в
к-рой для каждого компакта, а впоследствии и для
более общих классов топологич. пространств тем или
иным естественным образом определяется числовой то-
топологич. инвариант — размерность, совпадающий, если
-Y есть полиэдр (в частности, многообразие), с его чис-
числом измерений в смысле элементарной или дифферен-
дифференциальной геометрии. Первое общее определение раз-
мерности было дано Л. Брауэром (L. Brouwer, 1913)
для компактов и даже более широкого класса полных
метрич. пространств. Определение строится по индук-
индукции следующим образом. Пустому множеству припи-
приписывается размерность — 1. В предположении, что
определены пространства, а значит и лежащие в них
множества, размерности <:п, говорят, что пространст-
пространство X имеет размерность <:ге+1, если между любыми
двумя дизъюнктными замкнутыми множествами А и В
пространства X имеется перегородка Ф размерности
<п (при этом перегородкой между множест-
множествами А и В в пространстве X наз. такое замкнутое
множество Ф этого пространства, что дополнение Х\Ф
есть сумма двух дизъюнктных открытых множеств С
и D, из к-рых одно содержит множество А, а другое —
множество В). В 1921 П. С. Урысон и К. Менгер
(К. Menger) независимо от Л. Брауэра и друг от друга
пришли к эквивалентному в случае компактов и даже
любых сепарабельных метрич. пространств определе-
определению, отличающемуся от брауэровского тем, что одно из
двух замкнутых множеств А, В предполагается со-
состоящим из одной точки. Определения размерности п
смысле Браузра и в смысле Урысона и Монгера мо-
могут быть сформулированы для любых хаусдорфовых
пространств, и определяемые ими топологич. инвариан-
инварианты наз. соответственно большой и малой ин-
индуктивно)! размерностями и обозначают-
обозначаются Ind X и ind X, причем всегда ind Xs?lnd X.
Совершенно иной подход к понятию размерности бе-
берет начало от А. Лебега (Н. Lebesgue), высказавшего
следующую теорему: n-мерный в смысле элементарной
геометрии куб Q" при любом положительном числе е
может быть покрыт конечным числом замкнутых мно-
множеств (даже кубов) диаметра <е таким образом, что
кратность этого покрытия равна ге-f-l, тогда как при
достаточно малом е>0не существует покрытия куба Qn,
крое имеет кратность <n-f-l и состоит из замкнутых
множеств диаметра <е (при этом кратностью какой-либо
'.коночной) совокупности множеств наз. наибольшее це-
целое число т такое, что в данной совокупности имеется
т множеств с непустым пересечением). Теперь можно
теорему Лебега сформулировать так. Число измерений
куба Q" есть наименьшее такое целое число и, для
к-рого имеется сколь угодно мелкое (т. с. состоящее из
элементов сколь угодно малого диаметра) покрытие
кратности ге+1 замкнутыми множествами. Эта теоре-
sia, впервые доказанная лишь Л. Брауэром, приводит
к следующему определению. Размерностью dim X
компакта X (определенной посредством покры-
покрытии) наз. наименьшее число п такое, что при любом
е>0 компакт X имеет покрытие кратности га+1, со-
состоящее из замкнутых множеств диаметра <:е. Не ме-
меняя содержания этого определения, можно заменить
в его формулировке замкнутые множества открытыми.
При определении размерности компакта X применя-
применяется понятие диаметра множества, относящееся к мет-
метрике, а не к топологии компакта X. Однако доказы-
доказывается, что определенное так число dim X тем не менее
является тоиологич. инвариантом компакта X, т. е.
что два гомеоморфные между собою компакта имеют
одну и ту же размерность dim Х- Этот факт устанавли-
устанавливается непосредственно, но его легко вывести и из то-
того, что числу dim X можно дать и непосредственно то-
топологич. определение, опирающееся лишь на тополо-
топологию компакта X.
Покрытием данного топологич. пространства
нал. любая конечная совокупность его открытых мно-
множеств, дающих в своей сумме все это пространство.
Покрытие а' мельче покрытия а, если а' вписано в а,
т. е. если каждый элемент покрытия а' является под-
подмножеством хотя бы одного элемента покрытии а.
Оказывается, размерность dim X можно определить
так: число dim X есть наименьшее целое число п та-
такое, что для всякого покрытия пространства X су-
существует вписанное в него покрытие кратности re-f 1.
Но это определение, очевидно, может быть сформули-
сформулировано не только для компактов, а для любых тополо-
гич. пространств, и позволяет определить для них раз-
размерность. Размерность dim X, определенная таким об-
образом для топологич. пространств, позволяет построить
содержательную и богатую математич. фактами тео-
теорию, оставаясь, по крайней мере, в классе нормальных
пространств (а значит, в частности, и метризуемых
пространств).
Одной из главных проблем Р. т. является выясне-
выяснение наиболее широких условий, в к-рых имеет место
т. н. основное тождество Урысона, а
именно:
Оказывается, оно имеет место для всех соиарабельных
метризуемых пространств, т. е. для всех нормальных
пространств со счетной базой, а также для пространств
локально бикомпактных групп (теорема Пасын-
Пасынков а). Без предположения сепарабельности для мет-
метризуемых пространств можно утверждать лишь спра-
справедливость формулы Катетова
а для бикомпактов — формулы Алекса ндро-
в а
dim X sg: ind X < Ind X,
причем имеются бикомпакты X, для к-рых
dim X ф ind X
(пример Лунц а—Л окуциевского), и би-
бикомпакты X, для к-рых
ind X ф Ind X
(пример Филиппова).
Большое общепознавательное значение имеет следую-
следующая теорема Нёбелинга — Понтряги-
н а: необходимое и достаточное условие для того, что-
чтобы топологич. пространство X было гомеоморфно под-
подпространству какого-либо евклидова пространства ко-
конечного числа измерений, заключается в том, чтобы
X было нормальным пространством конечной размер-
размерности, имеющим счетную базу. Это позволяет при изу-
изучении конечномерных компактов и вообще конечно-
конечномерных нормальных пространств со счетной базой рас-
рассматривать их как подпространства евклидовых про-
пространств.
В связи с этим приобретает особый интерес т.н. те о-
р о м а об е-с д в и г а х: для того чтобы компакт X,
лежащий в каком-либо евклидовом пространстве Rm,
имел размерность dim X<.n, необходимо и достаточно,
чтобы при любом е>0 этот компакт мог быть превра-
превращен в полиэдр размерности <:ге посредством е-сдвига
в пространстве &т (при этом е-сдвигом подпростран-
подпространства X в евклидовом пространстве Rm наз. такое
непрерывное отображение / этого подпространства X
в содержащее его евклидово пространство Rm, при
к-ром расстояние ()(ж, jx) любой точки х?Х от ее
образа fx меньше числа е). Интуитивное содержание
этой теоремы состоит в том, что всякий компакт дан-
данной конечной размерности п, рассматриваемый как мно-
множество, лежащее в каком-либо евклидовом простран-
пространстве Rm, может быть сколь угодно малым непрерыв-
непрерывным видоизменением (к чему и сводится его е-сдвиг)
превращен в полиэдр той же, но не меньшей, размер-
размерности. Эта теорема так же, как и определение размер-
размерности dim X для компактов, может быть переформули-
переформулирована в чисто топологич. терминах, причем снова
«сколь угодно малые» числа е>0 заменяются «сколь
угодно мелкими» покрытиями ю. Это позволяет ана-
аналогичную теорему сформулировать для любых нормаль-
нормальных пространств и придти к заключению, что в нек-
ром (все же наглядном) геометрическом смысле вся-
всякое re-мерное нормальное пространство «похоже» и
даже «сколь угодно мало отличается» от n-мерного по-
полиэдра.
Одной из важнейших теорем Р. т. является т. н.
теорема о существенных отображе-
отображениях, лежащая в основе значительной части всей
этой теории. Пусть / — непрерывное отображение (нор-
(нормального) пространства X на и-мернын шар Q" с гра-
границей S"-1. Пусть ФсХ — прообраз сферы S"-1
при этом отображении, <!)=f~1Sn~1. Отображение
/ : X-*Qn наз. существенным, если р.сякое не-
непрерывное отображение g : X->Qn, совпадающее с / во
всех точках х?Ф, есть отображение на весь шар Q".
Упомянутая теорема Александрова утвер-
утверждает, что нормальное пространство X тогда и только
тогда имеет размерность dim X^n, когда пространство
X можно существенно отобразить на re-мерный шар.
Из этой теоремы выводится теорема суммы (доказан-
(доказанная для компактов П. С. Урысоном и К. Менгером еще
в самом начале развития Р. т.): если (нормальное)
пространство X размерности dim X=n является объ-
объединением конечного или счетного числа своих замк-
замкнутых множеств Ф^, то по крайней мере для одного
из этих Ф(; имеет место dim©fe=«.
Теорема о существенных отображениях лежит в ос-
основе т. н. гомологической теории раз-
размерности, позволяющей применить к изучению
размерности в весьма общих предположениях методы
алгебраич. топологии. Понятие гомологической размер-
размерности связано с понятиями цикла и гомологии и по-
поэтому предполагает, что наряду с топологич. прост-
пространством X дана и нек-рая коммутативная группа ©,
к-рая наз. группой коэффициентов. Тогда можно го-
говорить о циклах компакта X но этой группе коэффи-
коэффициентов, об их носителях ФсХ и, в частности, о
циклах, гомологичных нулю в X по области коэф-
коэффициентов (#, причем ути понятия можно эквива-
эквивалентным образом понимать как в смысле теории го-
гомологии Александрова — Чеха, так и в смысле гомо-
логич. теории Вьеториса.
После этого можно определить гомологич. размер-
размерность компакта X по группе коэффициентов E5 как
наибольшее целое число п такое, что в компакте X
имеется (п—1)-мерный цикл Zn~1, гомологичный ну-
нулю в X, но не гомологичный нулю на нек-ром своем
носителе Ф. Оказывается, что dim X есть гомологич.
размерность по группе х, являющейся факторгруппой
группы всех действительных чисел по подгруппе целых
чисел, и она является наибольшей среди всех вообще
гомологич. размерностей.
Если от циклов и гомологии перейти к коциклам и
когомологиям, то получится когомологическая размер-
размерность, причем когомологич. размерность компакта но
данной дискретной группе 31 равна гомологич. раз-
размерности по бикомпактной группе 58, двойственной
группе 31 в смысле теории характеров Понтрягина.
Отсюда следует, что размерность dim X совпадает с
когомологической размерностью по группе целых
чисел.
Лит. см. при ст. Размерность. 11. С. Александров.
РАЗМЕРНОСТИ ФУНКЦИЯ — целочисленная функ-
функция d на решетке L (т. е. отображение d : L—*-%),
удовлетворяющая условиям: 1) d(z+y)Jrd(xy)—d(x)^\-
+<2 (у) для любых х, у ? L; 2) если \х, у]—простой интер-
интервал в L, то d(y) = d(x)-\-l. Для решетки, все ограничен-
ограниченные цепи к-рой конечны, существование Р. ф. экви-
эквивалентно дедекиндовости этой решетки.
Существует и более общее определение Р. ф. на ор-
томодулярной решетке или ортомодулярном частично
упорядоченном множестве, где значениями Р. ф. мо-
могут быть произвольные действительные числа или даже
функции (см. [3]).
Лит.: [1] С к о р н я к о в Л. А., Элементы теории структур,
М., 1970; [2] В i r k h о f f G., Lattice theory, 3 ed., Providence,
1967; [3] К a 1 m b а с h G., Omolattices, L., 1981.
Т. С. Фофанова.
РАЗМЕРНОСТНЫЙ ИНВАРИАНТ — целое число
d(X), определяемое для каждого топологич. простран-
пространства X данного класса Ж и обладающее достаточным
количеством свойств, сближающих его с обычным чис-
числом измерений евклидовых многомерных пространств.
При этом от класса Ж требуется, чтобы он содержал
все кубы любого числа измерений и вместе с любым
данным пространством X, являющимся его элементом,
содержал в качестве элемента и всякое пространство,
гомеоморфное пространству X. От Р. и. d(X) пред-
предполагается, во всяком случае, что для гомеоморфных
пространств X и X' всегда d(X)=d(X') и что для
n-мерного куба /" выполняется rf(/") = n. Среди Р. п.
важнейшими являются т. н. к л а с с и ч е с к и о
размерности — Лебега размерность dim X и
(большая и малая) индуктивная размерность Ind X,
ind X.
Имеют место следующие предложения, выделяющие
размерность dim X среди всех Р. и., определенных со-
соответственно в классе всех (метрических) компактов,
всех метризуемых и всех сепарабельных метризуемых
пространств и тем решающие для этих пространств
проблему аксиоматич. определения размерности. Един-
Единственный, удовлетворяющий нижепоречисленным усло-
условиям 1), 2), 3), определенный в классе Ж всех (метри-
(метрических) компактов X размерностный инвариант d(X)
есть размерность dim X=Ind X=ind X (теорема
Александрова).
Условие 1) (аксиома Пуанкаре). Ес-
Если пространство принадлежит к классу Ж \\d(X) рав-
равно неотрицательному целому числу га, то в X содер-
содержится замкнутое подпространство Хо, Для к-рого
d(xo)<ft и такое, что множество Х\Х0 несвязно.
Условие 2) (а к с и о м а коночной сум-
суммы). Если принадлежащее к классу Ж пространство
X есть объединение двух замкнутых подпространств
Xj и Х->, для к-рых d(Xi)^n, d(X2)«?n., то и d(X)<re.
Условие 3) (аксиома Б р а у э р а в
метрической форме). Если X — принадле-
принадлежащее к классу Ж пространство и d(X) есть неотрица-
неотрицательное целое число п, то существует такое положи-
положительное число е, что для всякого пространства Y, яв-
являющегося образом пространства X при каком-либо
е-отображении, имеет место неравенство d(Y)^n. При
этом отображение / компакта X на компакт У наз.
е-о т о б р а ж е н и е м, если оно непрерывно, и пол-
полный прообраз f-1 (у) каждой точки y?Y имеет в X
диаметр <|.
Теорема Щ е п и н а [2]. Размерность dim X
есть единственный, определенный соответственно в
классе Ж всех метрических, всех сепарабельных мет-
рич. пространств X размерностный инвариант d(X),
удовлетворяющий следующим условиям (т е о р е м а
Щеиина).
У с л о вне 1) (аксиома Пуанкаре, см.
выше).
Условие 2) (аксиома счетной с у м-
м ы). Если принадлежащее к классу Ж пространство
X есть объединение счетного числа своих замкнутых
подпространств Xs, it=l,2,. . ., для каждого из к-рых
d(Xft)<:rc, то и d{X)<n.
Условие 3) (аксиома Б р а у э р а в об-
общей фор м е). Если для принадлежащего к классу
Ж пространства X имеется d(X)«:ra, то существует та-
кое конечное открытое покрытие ш пространства X,
что для всякого, принадлежащего к классу Ж про-
пространства У, являющегося образом пространства X при
каком-либо ю-отображении, будет d(Y)^n. При этом
отображение / пространства X, на к-ром зафиксировано
нек-рое открытое покрытие ю, на пространство У наз.
м-о тображением, если каждая точка у про-
пространства У имеет окрестность Оу, полный прообраз
к-рой /-1 (Оу) содержится в нек-ром элементе покры-
покрытия ю.
Лит.: [1] А л е к с а н д р о в П. С, в кн.: Тр. Международ-
Международного симпозия по топологии и ее применениях. Херцег-Нови-
19В8, Beograd, 1969, с. 38—42;[2] Ще п и н В., «Докл. АН СССР»,
1972, т. 206, № 1, с. 31 — 32; [3] Александров II.С ., П а-
сынков Б. А., Введение в теорию размерности, М., 1973.
А. А. Мальцев.
РАЗМЕРНОСТНЫЙ МНОГОЧЛЕН расшире-
расширения дифференциальных полей — мно-
многочлен, описывающий количество производных констант
в решении системы уравнений с частными производ-
производными и являющийся аналогом Гильберта многочлена.
Пусть G — дифференциальное расширение дифферен-
дифференциального поля F. Максимальное подмножество ноля
G, дифференциально сепарабельно независимое над F,
наз. базисом дифференциальной се-
сепарабельности. Базис дифференциальной сепа-
сепарабельности расширения G над F, дифференциально ал-
алгебраически независимый над F, наз. дифферен-
дифференциальным базисом трансцендент-
трансцендентности.
Пусть G — конечно порожденное дифференциальное
расширение: G=F (щ,. . .,т]„> и (гц,. . . ,п„) — общий
нуль простого дифференциального идеала pdF{Yx,. . .,
Yn}. Дифференциальная степень трансцендентности по-
поля G над F наз. дифференциальной раз-
размерностью идеала р (она обозначается d(p)).
Если q — другой простой дифференциальный идеал
и pdq, то d(p)~^d(q), причем равенство может иметь
место даже для строгого включения. По этой причине
желательно иметь более тонкую меру для измерения
идеалов.
Фильтрация кольца дифференциальных многочленов
F{Yl,. . . ,У„} по степеням дифференцирований Э?0
индуцирует фильтрацию нолей расширения G=F<t\1,
. . .,цп> поля F:
F = @0 С ®i С • d®s С...
Существует (см. [2]) многочлен, значение к-рого в
точках 4'?25 Для всех s^N0 равно степени трансцен-
трансцендентности расширения ©5 поля F. Он наз. р а з-
мерностным многочленом расшире-
расширения ®/F и имеет вид
r|/F V / ^Jo < i< ш l
где т — мощность множества дифференцирований А,
а а,- — целые. Р. м. является бнрациональным инва-
инвариантом поля, то есть F (¦n)=^(g)=>co11^J?=a)wf, но
не является дифференциальным бирациональным инва-
инвариантом, то есть из F<r] >-"/''<?>, вообще говоря,
не следует, что в1)/у=и?,}.. Тем не менее этот много-
многочлен содержит в себе дифференциальные бирациональ-
ные инварианты, каковыми являются степень много-
многочлена T=deg (оц,р (она наз. дифференциаль-
дифференциальным типом расширения F <т| > над F) и
старший коэффициент ах (называемый типовой
дифференциальной размерностью).
Среди дифференциальных Р. м., соответствующих раз-
различным системам дифференциальных образующих диф-
дифференциального расширения, существует минимальный
относительно нек-рого отношения порядка на множе-
множестве всех целозначны.х многочленов, являющийся, та-
ки.м образом, дифференциальным бирациональным ин-
инвариантом расширения.
Многочлен дифференциальной размерности опреде-
определяется также и для дифференциальных модулей.
Р. м. вычислен для расширений, задаваемых сле-
следующими системами (см. |1], где Р. м. наз. мерой жест-
жесткости системы уравнений поля): 1) волновое уравне-
уравнение; 2) уравнение Максвелла для пустого пространст-
пространства; 3) уравнения электромагнитного поля, задаваемого
потенциалами; 4) уравнения Эйнштейна для пустого
пространства. Другие примеры вычисления Р. м. см.
в [3].
Лит.: ШЭйнштейн А., Собрание научных трудов, т. 2,
М., 1966; [2] К о 1 с h i n В. R., Differential algebra and algeb-
algebraic groups, N. Y.~ L., 1973; [3J Михалев А. В., П а н-
к ратьевЕ. В., в кн.: Алгебра, М., 1980, с. 57—67.
Е. Б. Панкратьев.
РАЗМЕРНОСТЬ топологического про-
пространства X — целочисленный инвариант dim X,
определяемый следующим образом. Тогда и только
тогда dim Х=—1, когда Х=ф. О непустом тополо-
гич. пространстве X говорят, что оно не более чем п-
мерно, и пишут dim Х<л, если в любое конечное от-
открытое покрытие пространства X можно вписать ко-
конечное открытое покрытие пространетна X кратности
<:«+!, «—О, 1, 2, . . .. Если dim X<:« для нек-рого
п—- —1,0,1,. . ., то пространство X наз. конечно-
конечномерным, пишется dim X <oo и считается
dim X = min {п.: dim X < п}.
При этом если dim X = n, то пространство наз. гс-мер-
ным. Понятие Р. топологич. пространства обобщает
элементарно-геомотрич. понятие числа измерений евк-
евклидова пространства (и полиэдра), т. к. размерность
и-мерного евклидова пространства (и любого «-мерного
полиэдра) равна п (теорема Брауэра — Ле-
Лебега).
Важность понятия Р. топологич. пространства вы-
выявляется теоремой Нёбелинга — Понт-
рягина — Г уревича - - Куратовского:
«-мерное метризуемое со счетной базой пространство
вкладывается в Bп-\-1 )-мерное евклидово пространст-
пространство. Таким образом, класс пространств, топологически
эквивалентных подпространствам всевозможных /г-мер-
ных евклидовых пространств, п=1, 2,. . ., совпадает
с классом конечномерных метризуемых пространств со
счетной базой.
Размерность dim X иногда наз. лебеговой,
т.к. ее определение отталкивается от т е о р е м ы Ле-
Лебега «о м о с т о в ы х»: «-мерный куб для любого
е>0 обладает конечным замкнутым кратности <ге+1
покрытием с диаметром элементов <г; существует та-
такое ео>О, что кратность любого конечного замкнутого
покрытия «-мерного куба ^ге+1, если диаметр эле-
элементов этого покрытия <е0.
К определению Р. тонологич. пространства возмо-
возможен другой — индуктивный — подход (см. Индуктив-
Индуктивная размерность), основанный на разбиении простран-
пространства подпространствами меньшего числа измерений.
Этот подход к понятию Р. восходит к А. Пуанкаре
(Н. Poincare), Л. Брауэру (L. Brouwer), П. С. Урысону
и К. Менгеру (К. Mengor). В случае метризуемых про-
пространств он эквивалентен лебеговскому.
Основы теории Р. были заложены в 1-й пол. 20-х
гг. 20 в. в работах П. С. Урысона и К. Менгера. К кон.
30-х гг. была построена теория Р. метризуемых про-
пространств со счетной базой, а к нач. 60-х гг.— теория
Р. любых метризуемых пространств.
Ниже все рассматриваемые топологич. пространства
считаются нормальными и хаусдорфовыми. В этом слу-
случае в определении Р. без ущерба вписываемые открытые
покрытия можно заменить на замкнутые.
Лебегов подход к определению Р. (в отличие от ин-
индуктивного подхода) позволяет в случае любых рас-
рассматриваемых пространств геометризовать понятие Р.
посредством сравнения исходного топологич. простран-
пространства с простейшими геометрич. образованиями — поли-
полиэдрами. Грубо говоря, пространство «-мерно тогда и
только тогда, когда оно сколь угодно мало отличается
от re-мерного полиэдра. Точнее, имеет место теорема
Александрова об со-о тображениях:
тогда и только тогда dim Х«:ге, когда для любого ко-
конечного открытого покрытия со пространства X суще-
существует ю-отображение пространства X на не более чем
«-мерный, (г=0,1,2,. . ., (компактный) полиэдр. Осо-
Особую наглядность сформулированная теорема приобре-
приобретает в случае компактов: для компакта X тогда и толь-
только тогда dim X <7i, когда для любого е>0 существует
е-отображоние компакта на не более чем п-мериый
полиэдр. Если еще X лежит в евклидовом или гиль-
гильбертовом пространстве, то е-отображение можно за-
заменить е-сдвигом (теорема Александрова
об Ё-о тображениях и е-сдвигах).
Следующее утверждение позволяет выяснить, какова
Р. пространства, посредством его сравнения со все-
всевозможными п-мерными кубами: тогда и только тогда
dim Х^п, когда пространство обладает существенным
отображением на «-мерный куб, «=0,1,2,. . . (тео-
(теорема Александрова о существенных
отображениях).
Этой теореме можно придать следующую форму. Тог-
Тогда и только тогда dim Х<:«, когда для любого замкну-
замкнутого в X множества А и любого непрерывного отобра-
отображения / : A—>Sn в га-мерную сферу существует непре-
непрерывное продолжение F : X-+Sn, re=0,l,. . ., отобра-
отображения /.
Следующая характеристика Р. указывает на роль
этого понятия в вопросах существования решений си-
систем уравнений: тогда и только тогда dim X^n, п=
=1,2,..., когда в X существует такая система дизъюнкт-
дизъюнктных нар замкнутых множеств Ait Bj, i=l,. . ., «, что
для любых непрерывных на X функций /,-, удовлетво-
удовлетворяющих условию //.л^О,/;|в(.<0, ?=1,. . ., «, най-
найдется точка i^X, в к-рой /,-(.т) = 0, ?=1,. . ., « (тео-
(теорема Отто — Эйленборга — Хеммингсе-
н а о перегородках).
Одно из важнейших свойств Р. выражает теорема
суммы М и н г о р а — У р ы с о н а — Чоха:
если пространство X есть конечная или счотная сумма
своих замкнутых подмножеств размерности <:ге, то и
dim Х<«. н = 0,1,. . .В этой теореме можно условие
конечности или счетности суммы заменить условием
ее локальной конечности. Аналогичное теореме суммы
утверждение для большой и Малой индуктивных Р.
не выполняется уже в классе бикомпактов. Следующие
утверждения принадлежат к числу основных общих
фактов теории Р. и позволяют сводить рассмотрение
любых пространств к рассмотрению бикомпактов. Для
любого нормального пространства
а) dimpX = dimX, Ind px = IndX, где РХ — мак-
максимальное бикомпактное расширение Стоуна — Чеха
пространства Х\ в то же время неравенство ind EХ>
>ind X = Ind X возможно;
б) существует бикомпактное расширение ЬХ про-
пространства X, вес к-рого ш(ЪХ) равен весу ivX, и раз-
размерность dim ЬХ равна размерности dim X; аналогич-
аналогичное утверждение верно и для большой индуктивной Р.
Особенно интересен случай счетного веса пространства,
т.. к. в этом случае расширение ЬХ мотризуемо.
Утверждение б) может быть усилено следующим пред-
предложением: для любого «=0,1,. . . и любой бесконеч-
бесконечной мощности существует бикомпакт ТТ веса т и
размерности dim ТТ =п, содержащий гомеоморфный
образ любого нормального пространства X веса <т
и размерности dim X<n (теорема об универсальном
бикомпакте данного веса и размерности). Аналогичное
утверждение верно и для большой индуктивной Р. При
этом в качестве II можно взять канторово совершен-
совершенно j
ное множество, а в качестве ТТ — менгеровскую
На
универсальную кривую.
Казалось бы, что Р. должна обладать свойством мо-
монотонности: dim A <:dim X, если AdX. Это так, если
а) множество А замкнуто в X или сильно паракомпакт-
но, или б) пространство X метризуемо (и даже совер-
совершенно нормально). Однако уже для подмножества А
наследственно нормального пространства X может быть
dim A >dim X и Ind A >Ind X. Но всегда ind A <:
s?:ind X при АаХ.
Одним из важнейших вопросов теории Р. является
поведение Р. при непрерывных отображениях. В слу-
случае замкнутых отображений (к ним принадлежат и все
непрерывные отображения бикомпактов) ответ дается
формулами В. Гуревича (W. Hurewicz), полученными
им первоначально в классе пространств со счетной ба
ЗОЙ.
Формула Гуревича для повышаю-
повышающих размерность отображений: если
отображение / : X—>Y непрерывно и замкнуто, то
кратность f + dim X — 1 За dim У,
где кратность f—s\iip{\f~1y\:y?Y}.
Формула Гуревича для понижаю-
понижающих размерность отображений: для
непрерывного замкнутого отображения /:Х-*-У на па-
ракомпакт Y выполняется неравенство
dim X — dim /< dim У, A)
где
dim/ = sup {dim/-1!/:;/ ? К}.
Для произвольного нормального пространства У эта
формула, вообще говоря, неперна.
В случае непрерывных отображений конечномерных
компактов установлено, что непрерывное отображение
/ размерности dim /=fc является суперпозицией к не-
непрерывных отображений размерности 1 (это — уточ-
уточнение формулы A) и аналог того факта, что /с-мерный
куб есть произведение к отрезков).
В случае открытых отображений можно показать,
что образ нульмерного бикомпакта нульмерен и в то
же время гильбертов кирпич есть образ одномерного
компакта, даже если соответствующее отображение /
имеет размерность dim /, равную нулю. Однако в слу-
случае открытого отображения / : X—>-У бикомпактов X
и У кратности <So выполняется равенство dim X —
—dim У.
Поведение Р. при взятии топологич. произведения
описывают следующие утверждения:
а) существуют такие конечномерные компакты X и
У, что dim XXY<dimX+dimY;
б) если один из сомножителей произведения X X У
бикомпактен или метризуем, то dim Xxys?dimX+
+dim У;
в) существуют такие нормальные пространства X и
У, что dim Xxy>dimX+dimy.
В случае бикомпактных X и У всегда Ind ХХУ<оо,
если Ind X<t» и Indy<oo, но может быть IndXxy>
IndX+Indy. Если же бикомпакты X и У совершенно
нормальны или одномерны, то Ind Xxy«:IndX+
-find У.
Наиболее содержательна теория Р. прежде всего в
классе метрич. пространств со счетной базой и затем
В классе любых метрич. пространств выполняется р а-
венство Катетова
в классе любых метрич. пространств. В классе мет-
рич. пространств со счетной базой выполняются р а-
венства Урысона
B)
р а-
C)
и может быть ind X = 0<IndX=l.
В случае метрич. пространств понятие re-мерного про-
пространства следующими двумя способами может быть
сведено к понятию нульмерного пространства. Для мет-
метрич. пространства X тогда и только тогда dim Х<:гс,
и=0,1,. . ., когда
а) пространство X может быть представлено в виде
не более чем я-|-1 нульмерных слагаемых;
б) существует непрерывное замкнутое отображение
кратности <:гс+1 нульмерного метрич. пространства
на пространство X.
Для любого подмножества А метрич. пространства
X найдется такое подмножество BzdA типа G& в X,
что dim B = dim A.
В классе метрич. пространств веса <:т и размерности
<гс существует универсальное (в смысле вложений)
пространство. Важную роль в построении теории Р.
любых метрических (и более общих) пространств сыг-
сыграла теорема Даукера: тогда и только тогда
dim X<:n, когда в любое локально конечное открытое
покрытие пространства X можно вписать открытое по-
покрытие кратности <:я+1.
Одним из наиболее важных вопросов теории Р. яв-
является вопрос о соотношениях между лебеговой и ин-
индуктивными Р. Хотя для произвольного пространства
X вначения размерностей dim X, ind X, Ind X, вооб-
вообще говоря, попарно различны, однако для нек-рых
классов пространств, в том или ином смысле близких
к метрическим, выполнено, напр., следующее:
а) если пространство X обладает непрерывным замк-
замкнутым отображением / размерности dim /=0 на мет-
метрич. пространство, то выполняется равенство C), от-
отсюда следуют равенства B) для локально бикомпакт-
пых групп и их факторпространств;
б) если существует непрерывное замкнутое отобра-
отображение метрич. пространства на пространство X, то
выполняются равенства B).
Еще одно общее условие для выполнения равенства
C) для паракомпакта X выглядит так: dim X~n и
пространство X является образом нульмерного про-
пространства при замкнутом отображении кратности <:«+
4-1, и=0,1,. . .
В случае произвольного пространства X всегда вы-
выполняются неравенства dim X<:IndX и indX<:Ind.Y,
а равенства dim X — 0 и IndX = 0 равносильны. Для
сильно наракомпактного (в частности, бикомпактного
или финально компактного) пространства X выпол-
выполняется неравенство dim X«sindX. Для бикомпактов
равенства ind Х=1 и IndX=l равносильны. Суще-
Существуют бикомпакты, удовлетворяющие первой аксиоме
счетности (и даже совершенно нормальные в предполо-
предположении континуум-гипотезы), для которых dim X=i,
ind X=n, n—2,3,. . . Построен пример топологич. од-
однородного бикомпакта с dim X<ind X. Для совершен-
совершенно нормальных бикомпактов всегда ind X=Ind X. Су-
Существуют бикомпакты даже с первой аксиомой счет-
счетности, для к-рых ind X<IndX. Существует ли такое
т, что для каждого ге>т найдется бикомпакт (метрич.
пространство) X с ind X = m, Ind Х = ге,— неизвестно
A983).
В случае неметризуемых пространств Р. может не
только не быть монотонной, но и обладает другими
патологич. свойствами. Для любого ге=2,3,. . . построен
пример такого бикомпакта 9,„ что любое замкнутое
подмножество его имеет Р. или 0 или n=dim 6„. Ана-
Аналогичный пример в случае индуктивных Р. невозмо-
невозможен. Построен также для любого /г=1,2,. . .пример
такого бикомпакта Ф„, что любое разбивающее этот
бикомпакт замкнутое множество имеет размерность ге=
=dim Ф„. Таким образом, подход к определению Р. в
случае неметризуемого пространства в принципе отли-
отличен от индуктивного подхода А. Пуанкаре, основанного
на разбиении пространства подпространствами мень-
меньшего числа измерений. Бикомпакты Ф„ имеют непо-
непосредственное отношение к следующему утверждению:
в любом re-мерном бикомпакте содержится «-мерное
канторово многообразие.
Подмножество n-мерного евклидова пространства Еп
тогда и только тогда гс-мерно, когда оно содержит
внутренние относительно Е" точки. Компакт имеет раз-
размерность <:ге тогда и только тогда, когда он обладает
отображением Р. нуль в Еп, и, таким образом, с точ-
точностью до нульмерных отображений re-мерные ком-
компакты не отличимы от ограниченных замкнутых, содер-
содержащих внутренние (относительно Е") точки подмно-
подмножеств Еп.
См. также Размерности теория.
Лит.: [1] Александров II. С, Пасынков Б. А.,
Введение в теорию размерности, М., 1973; [2] Г у р е в и ч В.,
В о л м э н Г., Теория размерности, пер. с англ., М., 1948; [3]
У р ы с о н П. С., Труды по топологии и другим областям мате-
математики, т. 1—2, М.— Л., 1951. Б. А. Пасынков.
РАЗМЕЩЕНИЕ с повторениями из т
элементов по ге — конечная последовательность а =
= (а,-1, а,- ,. . .,а,- ) элементов нек-рого множества А =
={аг, а2,. . -,ат}. Бели все члены а различны, то а наз.
Р. без повторений. Число всех возможных Р.
с повторениями из т по ге равно тп, а без повторений —
(т)п--т(т — 1). . . (т—п — 1).
Р. можно рассматривать как функцию ср, заданную
на Zn={\, 2, . . ., п) и принимающую значения из А:
ср (fc=)o,v,ft=l,2,. . ., ге. Элементы А принято называть
ячейками (или урнами), а элементы Zn — ча-
частицами (или шарами); ср определяет запол-
заполнение различных ячеек различными частицами. Бели
речь идет о неразличимых частицах или ячейках, то
подразумевается, что рассматриваются классы Р.
Так, если все частицы одинаковы, то два Р., определя-
определяемые соответственно функциями ср и -ф, относятся к
одному классу, если найдется подстановка а множе-
множества Zn такая, что ср (a (A;)) — ip (k) для всех k?Zn.
В этом случае число таких классов, или, как говорят,
число размещений ге одинаковых частиц но т различ-
различным ячейкам, есть число сочетаний с повторениями
из л по т.
Если говорят, что все ячейки одинаковы, то имеют
в виду, что Р. разбиваются на классы так, что два Р.,
определяемые функциями ср и ф соответственно, отно-
относятся к одному классу, если существует подстановка
х множества Л, при к-рой т (ср (/с)) = 1[> (к) для всех
k?Zn. В этом случае число размещений п различных
частиц по т одинаковым ячейкам, т. е. число классов,
равно 2™- S (re> ^)' где -S (и, fe) — ч и с л а С т и р-
линга Ирода:
S(n, k) = S(n — l, k — l) + kS(n — l, к), S@,0)=l,
S (re, k)=0 при к > re и к = 0, п>0.
Если не различать как частицы, так и ячейки, то
получают размещение п одипаковых частиц по т оди-
одинаковым ячейкам; число таких Р. равно У Рп(к)>
гдер„(/с) — число разбиений п на к натуральных сла-
слагаемых.
Рассматриваются и другие разбиения Р. на классы,
напр, когда вышеупомянутые подстановки а и т. бе-
берутся из подгрупп симметрии, групп соответственно
степеней пит (см. об этом и других обобщениях в |1],
|2]). Синонимами «Р.» являются термины ««-переста-
««-перестановка», «упорядоченная re-выборка из генеральной со-
совокупности».
Лит.: [1] С а ч к о в В. Н., Комбинаторные методы дискрет-
дискретной математики, М., 1977; [2] Риордан Дж., Введение и
комбинаторный анализ, пер. с англ., М., 1963. В. М. Михеев.
РАЗНОСТНАЯ ВАРИАЦИОННАЯ СХЕМА — раз-
разностная схема, построенная на основе вариационной
задачи, соответствующей краевой задаче для дифферен-
дифференциального уравнения. Основная идея построения Р.
в. с. состоит в том, чтобы при специальном выборе ко-
координатных функций в Ритиа методе получить систе-
систему линейных алгебраич. уравнений, совпадающую по
структуре с системой разностных уравнений; обычно
неизвестными параметрами являются приближенные
значения в узлах сетки точного решения и, возможно,
нек-рых его производных. В качестве таких коорди-
координатных функций можно использовать кусочно линей-
линейные, полилинейные и др. функции.
Разностные схемы можно получать также, выбирая
специальным образом координатные функции в Галер-
Галеркина методе. Метод получения разностных схем с по-
помощью метода Галеркина наз. вариационно-
разностным методом (или проекцион-
но-разностным методом). Вариационно-
разностный метод иногда наз. методом конеч-
конечных элементов, хотя последнее названии упо-
употребляется в более общем смысле.
Пусть поставлена краевая задача:
— (p(x)u'(x))' = f(x), 0 < jc < 1, A)
u@)=u(l)=0, B)
где /(х) — непрерывная функция, р (.г) — непрерывно
дифференцируема и р (лMгро>О.
Умножение A) на произвольную функцию ф (.г), удов-
удовлетворяющую условиям B), и интегрирование по х:
приводит к тождеству
L {и, ф) = \ ри ф' дх~\ )ц>а"х, C)
к-рому удовлетворяет решение задачи A), B). Справед-
Справедливо и обратное утверждение: функция и(х), удов-
удовлетворяющая граничным условиям B) и тождеству C)
при произвольных функциях ф(т), ф@) = фA) = 0, яв-
является решением задачи A), B). Тождество C) исполь-
используется для построения приближенного решения методом
Галеркина. Промежуток [0,1] разбивается на N ча-
частей точками x{=ih, г=1,. . ., JV— I, h=N~1. Множе-
Множество {ж,} наз. сеткой, точки х/ — узла м и сетки,
h — шагом сетки. В качестве координатных функ-
функций в методе Галеркина берутся функции
где
\ 0 при |(|>1.
Функции ф((?)=0 вне промежутка [x;-i, x,-+1]. Это
свойство координатных функций принято называть
свойством локальности. Пусть прибли-
приближенное решение задачи ищется в виде
v^Jjtfj^vWiW' D)
1'де i'i — искомые параметры, к-рые являются значе-
значениями приближенного решения в узлах сетки:
vt = и (Х[), ? = 1, ..., N — 1.
Пусть К — множество функций вида D). Функции
из К линейны на промежутках [х(, 27+1]. непрерывны
на |0,1] и равны нулю при х=0 и х=1. Система метода
Галеркина получается при подстановке в C) функции
v(х) вместо и(х) и функций ц((х) вместо ф(.г):
V,A'- I (Ч ¦ , - ,
Т *-'/=1 У J О
=-; ^ / И<р!(г) dx. ' = 1. ••-, iV —1. E)
При этом
1/А при а:,-_! < а: < а:,-,
— 1/А при г,- < х < х, + 1
лишь для /— I — 1, г, г+1, т. е. в каждом уравнении
имеется не более трех неизвестных.
Система E) может быть записана в виде
? = 1, ..-, Л- —1,
1'ДС
а. 1, =й-Л ' р {х) dx,
•)A'l-l
+1 / (х) ф,- (ж) da:, yo = ^jv =
Эта система по структуре сходна с обычной разност-
разностной. Системы уравнений, полученные таким способом,
и наз. разностными вариационными
схемами. В отличие от обычных разностных схем
коэффициенты o-i_i, и /,- являются не значениями функ-
функций р и / в фиксированных точках, а их усреднениями.
Это обстоятельство позволяет использовать Р. в. с.
для уравнений с «плохими» (напр., разрывными) коэф-
коэффициентами.
Пусть Lit={L(tpj, q>j)} — матрица системы E). Так
как L (фу, ф,-)--А (ф,-, фу), то матрица L^ симметрична.
Имеет место равенство
(Lhwh, wh)--
где 4'fi~~{u'i)c=i - произвольный вектор из евклидова
пространства En-\ размерности N—1, (.,.) — скаляр-
скалярное произведение в ?n-i,
w = yNLl w -<х)
Из неравенства
и' (I) dl ) < \ (u'J dx,
и /Jo
справедливого для произвольной непрерывно!! и диф-
дифференцируемой функции, удовлетворяющей условию
и @) = @), следует оценка
\ 1 р (х) (w' (ж)J dx^spomax (w (а:)J За
Jo х
-м\-1 ±
из к-рой выводится неравенство
(Lhwh, wh)l^pah(wh, irh). (в)
Матрица Lh положительно определена; система E) од-
однозначно разрешима.
При малых значениях h спстема E) состоит из боль-
большого числа уравнений. Точность решения системы ал-
гсбраич. уравнений и объем необходимой для этого
работы в большой степени зависят от величины т. н.
числа обусловленности Р = ^maxAmin
матрицы системы, где Хтах и Xmjn — наибольшее и
наименьшее собственные значения матрицы /./,. Из не-
неравенства F) следует, что ^minsSPo^- Справедлива так-
также оценка
^тах <4й тахр (х).
х
Число обусловленности Р=О (h~"), что совпадает но
порядку h с известными оценками для матриц обычных
разностных схем.
Сходимость приближенного решения к точному до-
доказывается по обычной для метода Галеркина схеме.
Из C) и E) для произвольной функции ф из К следует,
что
L(u — v, ф) = 0, G)
откуда
L (и—v, и—i>)=L(u — v, и—ш), (8)
где w - произвольная функция из К. Правая часть
(8) оценивается с помощью неравенства
Таким образом,
L (и—v, и — и) = \ р (х) (и' — у'J Ах-.
< inf \Х р (х) {u'—w'fdx.
Обозначение
.1/2
(число | и | наз. энергетической нормой
функции и) позволяет переписать последнее неравен-
неравенство в виде
\и — y|<ii)f|« — w\.
K
weK
Оценка погрешности Р. в. с. сводится к оценке наилуч-
наилучшего приближения точного решения функциями класса
А.'. Если в качестве w(x) взять кусочно линейную функ-
функцию
совпадающую с функцией и (х) в узлах сетки, то спра-
справедлива оценка:
(х) С1 (u"Jdx,
где С — постоянная.
На рассмотренном примере видны нек-рые характер-
характерные черты вариационно-разностного метода: локаль-
локальность координатных функций, обеспечивающих бли-
близость Р. в. с. по структуре к разностным схемам, и при-
применимость техники проекционных методов к исследо-
исследованию сходимости Р. в. с.
Основным при построении Р. в. с. является выбор
локальных координатных функций, обладающих тре-
требуемыми аппроксимационными свойствами. Задача ап-
аппроксимации ставится в различных функциональных
пространствах. Для задач математич. физики важны
пространства Соболева WP(Q), т.е. линейные множе-
множества функций с конечной нормой
где Q — область в Еп, p^l, I — неотрицательное целое
число, а— (<Х],. . . ,а„)— вектор с целочисленными коор-
координатами, |a|=aj+a2+. . .+an,
Многие классы локальных координатных функций
строятся по следующей схеме. Пусть заданы функции
ФЧЕ). Фа (?->,- • ->фг(?), принадлежащие И7* (Я„) и рав-
равные нулю вне re-мерного куба |?у|<й, /=1,2,. . .,ге.
Пусть h={h1,. . .,hn) — заданный вектор с положи-
положительными координатами, l= (iX). . ., /„) — произволь-
произвольный целочисленный вектор,
Через / обозначено множество векторов i таких, что
«-мерный параллелепипед \h[1xJ-— ij\ <Д, / = !,. . .,
п, пересекается с Q. Для данной области Q в качестве
координатных функций выбираются функции вида
<$ (х)=у* (h~lx — i), i?I, [i = l, ..., г,
т. е. функции, полученные из исходных функций мас-
масштабированием аргументов и сдвигом на вектор i. Та-
Такие координатные функции принято называть регу-
регулярными. Пусть классом К наз. множество функ-
функций вида
Если любой полином P(_i степени I от % можно пред-
представить как линейную комбинацию фа(^),. . ., фг(?),
то для произвольной фупкции и (х)? Wp (Q) можно ука-
указать функцию w?K такую, что справедливо аппрок-
симационное неравенство
я*||и||,1/, 0<к<1, (9)
где fe=max hj, С не зависит от А и и.
Р. в. с. для краевых задач для эллиптич. уравнений
строятся на основе эквивалентных задач нахождения
функций, удовлетворяющих интегральным тождествам.
Многие из этих задач состоят в нахождении функции
u^Wtl(Q), удовлетворяющей при произвольной функ-
функции ф? W^(Q) интегральному тождеству
где S — граница Q, аар(х), Ьрт(х) и /(х) — заданные
функции. Предполагается, что
и L (и, и) ;зг у IIй Ik т, Y = const > 0.
Применение к A0) метода Галеркина с координатными
функциями iff приводит к Р. в. с. для задачи A0).
Пусть решение и(х) задачи A0) принадлежит W^(Q),
1>т, и функции ф^ удовлетворяют условиям, при
к-рых справедливо неравенство (9). Для оценки по-
погрешности Р. в. с. используют стандартную технику
метода Галеркина:
< inf L(u—w, и — u>XC7i2 <'-"»> II ulg,,
weK '
где v — приближенное решение.
Задачи вида A0), для к-рых в качестве функции <р
может быть взята произвольная функция из И/21(У),
наз. задачами с естественными крае-
выми условиями. Существует другой класс
краевых задач, в к-рых на границе 6 ставятся краевые
условия вида
(Ц\а\<тЪкОаи)\8=0, 0</<v, v<m-l. A1)
В этом случае краевым условиям A1) в тождестве A0)
должны удовлетворять и функции ф? Wf(Q). Для при-
приближенного решения таких задач методом Галеркинн
необходимо, чтобы координатные функции удовлетво-
удовлетворяли условиям A1). Введенные выше координатные
функции <$ (х), в силу самого способа их построе-
построения, вообще говоря, не пригодны для представления
приближенного решения, удовлетворяющего условиям
(И).
Один из приемов построения Р. в. с. для задач с
краевыми условиями вида A1) связан с использованием
метода штрафа. Пусть, напр., требуется ре-
решить задачу Дирихле для уравнения Пуассона. Эта
задача эквивалентна определению функции и(х), и\$—
=0, удовлетворяющей при произвольной функции ф (х),
cpls=O, интегральному тождеству
+ рЛ) dQ^\ fy dQ.
дх ' ду ду ) J Я т
В методе штрафа вводится в рассмотрение функция v,
удовлетворяющая при произвольных функциях ф ин-
интегральному тождеству
f<fdQ,. e>0.
Функция v является решением задачи с естественным
краевым условием. Доказывается, что при малых зна-
значениях е решения и и и близки. Для приближенного
решения последней задачи можно применить Р. в. с.
с использованием регулярных координатных функций.
Общий способ построения координатных функций та-
таков.
Пусть для произвольного положительного числа h
в Q задано множество точек z,-, t —1, 2,. . ., N, наз.
узлами сетки, такое, что каждая точка области отстоит
от какого-либо узла не более чем на h. Пусть для каж-
каждого узла z,- определен набор функции ф[, фа,. . .,
<f-v(i) из W'T{Q), удовлетворяющих заданным гранич-
граничным условиям A1), причем v(i)<?.M, где М не за-
зависит от i и h. Пусть при каждом i и всех / интеграл
отличен от нуля лить для числа индексов к, ограничен-
ограниченного числом, не зависящим от i и h (условие локально-
локальности координатных функций). Пусть К — класс функ-
функций вида
l=l
где X) — числовые параметры.
Если решение и (х) краевой задачи может быть при-
приближено функциями класса К с точностью, характери-
характеризуемой неравенством
inf \\u-w\\it га<СА'-га||м|2,г, т<1,
то для решения, полученного при помощи Р. в. с,
справедлива оценка погрешности
\\u — v\\.2. т<СМ-"\\и\\2, I.
Нерегулярные сетки применяются иногда для более
полного учета свойств задачи. Напр., для более точ-
ного воспроизведения функции в окрестности угловой
точки границы можно расположить узлы на радиально-
кольцевой сотке.
Для численной реализации матрица Р. в. с. должна
обладать не слишком плохой обусловленностью. Для
задач вида A0) оптимальной считается обусловленность,
выражаемая соотношением Р=О (N2m^n), где Р — число
обусловленности матрицы Р. в. с, N — число узлов
сетки, п — размерность пространства, содержащего об-
область Q. Для многих конкретных задач такая обуслов-
обусловленность действительно имеет место.
Использование Р. в. с. сочетает достоинства метода
сеток и проекционных методов. Структура Р. в. с.
позволяет использовать экономичные методы решения
разностных схем. Легко устанавливается разрешимость
Р. в.с: матрица Р. в. с. положительно определена, если
положительно определен дифференциальный оператор.
Вопрос о сходимости сводится к вопросу об аппрокси-
аппроксимации точного решения координатными функциями Р.
в. с, и, следовательно, скорость сходимости опреде-
определяется дифференциальными свойствами точного реше-
решения. Р. в. с. можно применять при весьма слабых
ограничениях на данные задачи.
Исследования но Р. в. с. проводятся в следующих
основных направлениях:
1) создание координатных функций, удовлетворяю-
удовлетворяющих краевым условиям, исследование их аппроксима-
ционных свойств;
2) получение оценок точности в различных нормах;
3) построение Р. в. с. для задач, имеющих те или
иные особенности (линии разрыва коэффициентов, уг-
угловые точки границы и т. д.);
4) разработка методов решения Р. в. с. и способы
оптимизации методов решения;
5) решение нелинейных уравнений;
6) применение Р. в. с. для нестационарных уравне-
уравнений.
Лит,: [1] О г а н с с я и Л. А., Р и в к и н д В. Я., Р у х о-
d e ц Л. А., Вариационно-разностные методы решения эллипти-
эллиптических уравнений, ч. 1—2, Вильнюс, 197 3—74; [2) S t г a n g G.,
Fix G., An analysis of the finite element method, En^lewood
Cliffs, 1973; [3] A u b i n J.-P., Approximation of elliptic bo-
boundary — value problems, N. Y., 1972; [4] Варга P., Функ-
Функциональный анализ и теория аппроксимации В Численном ана-
анализе, пер. с англ., М., 1974; [Г>| М и х л и н С. Г., «Зап. научн.
семинаров ЛОМИ», 1974, т. 48, с. 32 — 188; [(>] М а р ч у к Г.II.,
Методы вычислительной математики, 2 изд., М., 1980; [7] Д ь я-
конов Е. Г., Разностные методы решения краевых аадач,
М., 1971. Л. А. Оганесян.
РАЗНОСТНАЯ СХЕМА — система разностных урав-
уравнений, аппроксимирующих дифференциальное урав-
уравнение и дополнительные (начальные, граничные и др.)
условия. Аппроксимация исходной дифференциальной
задачи Р. с.— это один из способов приближенной дис-
дискретизации Исходной задачи. Он заключается в том,
что заданную область изменения независимых перемен-
переменных G заменяют дискретным множеством точек GA —
с е т к о и, а производные, входящие в дифференциаль-
дифференциальное уравнение, заменяют на сетке GA разностными от-
отношениями. В результате такой замены возникает зам-
замкнутая система большого числа алгебраич. уравнений
(линейных или нелинейных в зависимости от исходной
дифференциальной задачи), к-рая и представляет собой
Р. с. По существу Р. с.— это семейство разностных
уравнений, зависящих от шагов сетки. Решение Р. с.
также зависит параметрически от шагов сетки. Р. с.—
многопараметрический и сложный объект. Помимо ко-
коэффициентов исходного дифференциального уравнения
она содержит свои собственные параметры такие, как
шаги по времени и пространству, весовые множители
и др. Влияние этих параметров может существенно ис-
исказить представление о поведении исходной дифферен-
дифференциальной задачи.
В связи с разностной аппроксимацией дифференци-
дифференциальных задач изучаются следующие вопросы: о спо-
собал построения Р. с, о сходимости при измельчении
сетки решения разностной задачи к решению исходной
дифференциальной задачи, о методах решения систем
разностных уравнений. Все перечисленные вопросы рас-
рассматривает разностных схем теория. Разработаны эф-
эффективные численные методы решения типичных Р. с.
для обыкновенных дифференциальных уравнений
и уравнений с частными производными, предполагаю-
предполагающие использование быстродействующих ЭВМ.
Ниже приводится простой пример Р. с. Пусть име-
имеется дифференциальная задача
и" (х) — q (x) u(x) = — f (х), (/ (х) 5з 0, 0 < х < ]
и' @)-=<та @) — (Да, иA)=ц2, а > 0.
Область G{O<?<1} заменяется сеткой
G/l = {x( = ih, г = 0, 1, ..., Л', ЛЛ' = 1}.
Р. с. для задачи A) имеет вид
' + * f 'г ~~1 п -и • / • j — 1 9 Лг i
. 2 11 УI / / ) А)? • . « , i T 1,
где ijj=y(xi), qi=q(xj), Xj^Gh. Можно показать, что
при А->-0 решение разностной задачи B) сходится к
решению исходной задачи A) и при достаточной глад-
гладкости функции g (x), f(x).
Р. с. B) имеет второй порядок точности, т. е.
max | yi — и (х{) | < Мft2,
О < с < N
где М— постоянная, не зависящая от h. Решение Р. с.
B) находится методом прогонки.
Лит.: [1] Самаре к и й А. А., Теория разностных схем,
31., 1977; [2] С а м а р с к и й А. А., Николаев Е. С, Ме-
Методы решения сеточных уравнений, М., 1978.
А. В. Тулин, А. А. Самарский.
РАЗНОСТНОЕ МНОЖЕСТВО, совершенное
разностное множество,— множество D, со-
состоящее из к вычетов dx, d2,. . ., dfe по модулю нек-
рого натурального числа г, причем для каждого a?D,
а^ЁО (mod с), существует точно к упорядоченных пар
(dj, dj) элементов из D таких, что
a s dj — dj (mod v)\
числа v, к, к наз. параметрами Р. м. Напр.,
множество ?> = {1, 3, 4, 5, 9} вычетов по модулю 11 есть
Р. м. с Х=2.
Р. м. тесно связаны с блок-схемами, а именно: суще-
существование Р. м. равносильно существованию симмет-
симметричной блок-схемы с параметрами (v, k, к), обладаю-
обладающей циклич. группой автоморфизмов порядка и (блоки
такой схемы суть множества {dj-f-i,. . .,d/i-\-i}, ? = 0,1,. . .,
i>—1). Идея Р. м. обобщается следующим образом: мно-
множество D, состоящее из к различных элементов dx,. . .,
dji группы G порядка г, наз. (v, к, к)-р а з н о с т-
н ы м множеством в G, если для любого
a?G, аф\, существует в точности к упорядоченных
пар (dj, dj), dj, dj?G, таких, что d\djl~a (или, что то
же, к nap (dj, dj) с djldj=a). Тогда определенное выше
Р. м. наз. циклическим Р. м. (т. к. группа
классов вычетов по mod v есть циклич. группа). Су-
Существование (v, к, Л)-разностны.\ множеств в группе G
порядка v равносильно существованию симметричной
блок-схемы с параметрами v, к, к, допускающей G в
качестве регулярной (т. е. без неподвижных элементов)
группы автоморфизмов (эта схема получается отожде-
отождествлением элементов блок-схемы с элементами группы
и блоков — с множествами {^i^,. . -А?}, где g пробе-
пробегает G).
Основным в теории Р. м. является вопрос о сущест-
существовании и построении Р. м. с заданными параметрами.
77*
При его изучении оказывается полезным понятие мно-
множителя Р. м,: автоморфизм группы G наз. множи-
множителем (v, к, Я)-разностного множества I) в G, если
он является также автоморфизмом блок-схемы, опре-
определяемой Р. м. D. Для циклического Р. м. множитель —
это число t, взаимно простое с сие том свойством, что
{tdlt ..., tdk} = {dt + i, ..., dk + i}
для нек-рого i, 0<U<:i> —1. Множители цикличес-
циклического Р. м. образуют группу. Справедливо утверждение:
если D — циклическое (v, к, Л)-разносТное множество
и если р — простое число, делящее к—X и такое, что
(р, v)=\ и р~>к, то р — множитель D (теорема о
множителе Р. м.). При построении Р. м. поле-
полезен следующий результат: для любого множителя (у,
к, Я)-разностного множества D в абелевой группе G
порядка v в блок-схеме, определяемой D, существует
блок, фиксируемый этим множителем; при (i>, fc)=l
существует блок, фиксируемый любым множителем.
Р. м. обычно строятся прямыми Методами с исполь-
использованием свойств конечных нолей, полей Деления круга
(см. Круговое поле), а также конечных геометрий.
Известно несколько бесконечных семейств Р. м., напр.
следующие типы S и Q.
Тип S (р а з н о с т н ы е множества Зин-
Зингера): это — гиперплоскости в п-мерной проективной
геометрии над полем из q элементов; параметры".
у = (дЛ+1 —1)/(9 —1),
fe = (g« — l)/(g — 1), X = (g"-1—l)/(g — 1);
тип Q: квадратичные вычеты в поле GF (рг) при
//=3(mod 4) (р — простое число); параметры:
Другие бесконечные семейства Р, м. см. в [1]—[3].
Наряду с Р. м. часто рассматриваются обобщен-
обобщенные Р. м., или разностные семейств а,—
это множества ?)ь. . ., Dr, состоящие из вычетов по
mod v и такие, что для любого афО (mod v) сущест-
существует точно X упорядоченных пар (dh dj), d[, dj?Dk,
с a s d(—dj (mod v)
для нек-рого к, 1</с<г.
Имеются также другие обобщения Р. м.
Лит.: [1] X о л л М., Комбинаторика, пер. с англ., М., 1970;
[2] В а и m e r t L. D., Cyclic difference sets, В.— Hdlb.—N.Y.,
1971; [3] Hall M., «Math. Centre Tracts», 1974, v. 57, p. 1—26.
В. Е. Тараканов.
РАЗНОСТНОЕ УРАВНЕНИЕ — уравнение, содержа-
содержащее конечные разности искомой функции. Пусть у (п)—
—Уп — функция целочисленного аргумента гс=0,±1,
±2,. . .;
А1уп = Ауп, т<=1, 2, ...,
— конечные разности. Выражение Атуп содержит зна-
значения функции у в (т-(-1)-й точке п, ге+1,. . ., п-\-т.
Справедлива формула
Amyn = ^=l)(-i)m-kCkmyn + k. A)
Разностным уравнением наз. уравнение
вида
F(n; Уп, Ауп, ..., Д"»у„)=О, B)
где у — искомая и F — заданная функции. Замена
в B) конечных разностей их выражениями через зна-
значения искомой функции согласно A) приводит к урав-
уравнению вида
F (п\ Уп, Уп+i, •••> Уп + т) = 0. C)
Если i—=^0, jr- фО, т. е. уравнение C) деист-
"Уп "Уп 4- tn
вительно содержит как ;/„, так и у„+т, то уравне-
вие C) наз. разностным уравнением
m-го порядка, или дифференциально-
разностным уравнением.
Наиболее развита теория линейных Р. у., к-рая
имеет много общего с теорией обыкновенных линейных
дифференциальных уравнений (см. [1] — [3]). Линей-
Линейным Р. у. m-го порядка наз. уравнение
ат (п) Уп + т + ат-1 (") Уп + т~1+ ¦ ¦ ¦ +«0 (") Уп — fm D)
где in—i(n) — заданная функция, ak(n), к=0, 1, . . .,
т, — заданные коэффициенты, причем ат(п)?=0,
аа(п)ф0. Решением Р. у. D) наз. всякая функция у„-=
=У (n)i Удовлетворяющая уравнению D). Как и в случае
дифференциальных уравнений, различают частное и
общее решения Р. у. D). Общим решением Р. у.
D) наз. его решение, зависящее от т произвольных
параметров и такое, что каждое частное решение
может быть получено из этого общего решения при
нек-ром значении параметров. Обычно конкретные
значения параметров находятся из дополнительных
условий. Типичной является задача Коши: по задан-
заданным у0, у1, . . ., ym-i, jn найти решение уп уравнения
D) при п= т, т-\-1, . . . Существование и способ
построения решения Р. у. D) устанавливаются по
следующей схеме. Наряду с D) рассматривается одно-
однородное Р. у.
ат (п) Уп+т + ат-1 М Уп + т -1 + • ¦ • + «о («) У„ = 0. E)
Справедливы следующие утверждения.
1) Пусть у\}\ у^, . . ., 2/п' — решения уравнения
E) и си с2, . . ., eft — произвольный набор постоянных.
Тогда функция с1уп1)+с2уп2)+. . ¦ + ckynk) также яв-
является решением уравнения E).
2) Если уп, ¦ ¦ ., уп суть т решений уравнения
E) и определитель
у?
отличен от нуля, то общее решение однородного Р. у.
E) имеет вид
где с? — произвольные постоянные.
3) Общее решение неоднородного Р. у. D) представ-
представляется в виде суммы какого-либо частного его решения
и общего решения однородного Р. у. E).
Частное решение неоднородного уравнения E) можно
построить, исходя из общего решения F) однородного
уравнения, путем применения метода вариации про-
произвольных постоянных (см., напр., [2]). В случае
Р. у. с постоянными коэффициентами
атУт + п + ат-1Ут + п-1+--- -'гОоУп^О G)
можно непосредственно найти т линейно независимых
частных решений. Для этого рассматривается харак-
теристич. уравнение
+ a,B_ig'B-1+---+a1)-0 (8)
и ищутся его корни gt, q2, ¦ ¦ ., qm. Если все корни
простые, то функции
,,B) —„<"' „(ш) — „"
Уп — 92 , • • •, Уп — Чт
образуют линейно независимую систему решений урав-
нения G). В случае, когда q^ — корень кратности г,
линейно независимыми являются решения
п п ¦¦> п г 1 и
Як, Щк, п'Як, ¦••> «< 9ft-
Если коэффициенты а0, аг, . . ., ат действительные
и уравнение (8) имеет комплексный корень, напр,
простой корень </?= р (coscp-f j'sin ф), то вместо ком-
комплексных решении q%, f/ft" иьтделяют два линейно не-
независимых действительных решения
р™ cos щ, р" sin иф.
Пусть имеется Р. у. 2-го порядка с постоянными
действительными коэффициентами
а-гУп + 2 + а,.уп + 1 + а0уп=:0. (9)
Характеристич. уравнение
имеет корни
9i,2 = {—а1 ±у а'х—4а0а2)/Bа2).
Общее решение уравнения (9) в случае q2?=9i Удобно
записывать в виде
+ с2 — , A0)
где cj и с2 — произвольные постоянные. Если дх и д2 —
комплексно сопряженные корни:
9i, а=-Р (совф ± i sin <p),
то другое представление общего решения имеет вид
у„ = ClP + С2Р ^ ¦ A1)
ап " SlIKf ' iV 81Пф V '
В случае кратного корня общее решение может быть
получено предельным переходом' из A0) или A1).
Оно имеет вид
Уп = — ci (« —1) 9i + c-iii'li^1-
Как и в случае уравнений произвольного порядка,
для Р. у. 2-го порядка можно рассматривать задачу
Коши или различные краевые задачи. Напр., для
задачи Коши
Tlt + 3(j:) — 2u;Tnli(r)+Tn(x)=.O, /i = 0, I,...,)
7'eW-l, Ti{x)=x, ]
где х — любое действительное число, решением A2)
является многочлен Т„ (х) степени п (многочлен
Чебышева 1-го рода), к-рый определяется
формулой
Т п {х) = cos (n arccos .r) ---
= 0,5 [(х+ У~х* — \ )" + (*+ V^^T)~n].
Краевая задача Р. у. 2-го порядка состоит в нахож-
нахождении функции !/„, удовлетворяющей при га=1, 2, . . .,
N—1 уравнению
^Уп = апУп-1—<:пУп + 1>пУп+1=—(п A3)
и двум линейно независимым краевым условиям. Та-
Такими краевыми условиями могут быть, напр., условия
ao = *i</i+|-ii, yN=XyN-i + \*-2 A4)
или условия
г/о = Н-1. г/д^Я-2- A5)
Для Р. у. 2-го порядка справедлив следующий
принцип максимума. Пусть дана задача A3), A5)
и пусть выполнены условия
<*п > 0, Ьп > 0, с„-^ап-\-Ьп, п = 1, 2, ..., N — i.
Тогда если ?(/„>0 (Li/n<0), ге=1, 2, . . ., iV—1, то
^ не может принимать наибольшего положи-
гельного (наименьшего отрицательного) значения при
/г=1, 2, . . ., JV—1. Из принципа максимума следует
однозначная разрешимость краевой задачи A3), A5)
л устойчивость ее решения относительно изменения
граничных условий filt ц.2 и правых частей /,г. Для
решения разностных краевых задач A3), A4) приме-
применяется прогонки метод (см. [2]).
Построить в явном виде решения нелинейных Р. у.
*/„ + ! = /« (!/„), ге = 0, 1, ... A6)
удается лишь в отдельных очень частных случаях.
Для уравнений вида A6) изучаются в основном каче-
качественные вопросы поведения решений при п —»-оо и
развита теория устойчивости, аналогичная теории
устойчивости обыкновенных дифференциальных урав-
уравнений (см. [4], [5]).
При разностной аппроксимации уравнений с част-
частными производными возникают многомерные Р. у.
(см. [2], [6]). Напр., уравнение Пуассона
чожно аппроксимировать Р. у.
». + i.y-2".-. ;+».•-!. j , »1.у + 1-2«
,.2
где
... ._„ /T(i) T</>\ r@_/b r(/)_;l,
i, 1=0, +1, ±2, ...,
'?!, fe2 — шаги сетки.
Система многомерных Р. у. в совокупности с до-
дополнительными начальными и граничными условиями
образует разностную схему. В связи с многомерными
Р. у. изучаются такие вопросы, как корректность раз-
разностных задач, методы их решения, сходимость при
измельчении сетки к решениям исходных дифференци-
дифференциальных уравнений (см. Разностных схем теория).
Хотя существуют различные математические и тех-
нич. модели, приводящие к Р. у. (см., напр., [4], [5]),
основной областью их применения являются прибли-
приближенные методы решения дифференциальных уравнений
(см. [6], [9]).
Лит.: [1] Г е л ь ф о н д А. О., Исчисление конечных раз-
разностей, 3 над., М., 1967; [2] Самарски й А. А., Нико-
Николаев Е. С, Методы решения сеточных уравнений, М., 1978;
13J Самарский А. А., Карамзин 10. Н., Разностные
уравнения, М., 1978; [4] МартынюкД. И., Лекции по ка-
качественной теории разностных уравнений, К., 1972; [5] X а л а-
н а й А., В е к с л е р Д., Качественная теория импульсных сис-
систем, пер. с рум., М., 1971; [tij Самарский А. А., Теория
разностных схем, М., 1977; [7] Березин И.О., Жид-
Жидко в Н. П., Методы вычислений, 2 изд., т. 2, М., 19E2; [8 ]Б а х-
налов Н. С, Численные методы, 2 изд., М., 1975; [9] Гор-
Горбунов А. Д., Разностные уравнения, М., 1972,
А. В. Тулин, А. А. Самарский.
РАЗНОСТНЫЕ МЕТОДЫ — методы приближенного
решения дифференциальных уравнений, основанные
на замене этих уравнений уравнениями относительно
функций дискретного аргумента. См. Гиперболическо-
Гиперболического типа уравнение, численные методы решения; Пара-
Параболического типа уравнение, численные методы реше-
решения; Эллиптического типа уравнение, численные методы
решения; Дифференциальное уравнение обыкновенное,
приближенные методы решения. н. с. Бахвалов.
РАЗНОСТНЫЙ ОПЕРАТОР — оператор, действую-
действующий в пространстве сеточных функций. Р. о. возникают
при аппроксимации дифференциальной задачи разност-
разностной и являются предметом изучения разностных схем
теории. Разностную схему можно рассматривать как
операторное уравнение с операторами, действующими
в нек-ром функциональном пространстве, а именно
в пространство сеточных функций. Под пространством
сеточных функций понимается множество функций,
определенных в точках заданной сетки и образующих
конечномерное векторное пространство. Пространства
сеточных функций обычно возникают при аппрокси-
аппроксимации того или иного пространства функций непре-
непрерывного аргумента.
Пример 1. Пусть С [О, 1] — пространство непре-
непрерывных функций, заданных на отрезке 0<?х<:1 с
нормой
|| и ||с = max \u(x)\.
xeio, l]
Вводится сетка
u>h = {xi = ih, * = 0, 1, ..., N, hN = i)
и рассматривается множество Сд [0, 1] функций у=
= {j/(}o. yi=y(xi), заданных на сетке w^. Множество
Сй[0, Я образует (#+1)-мерноо векторное пространство
относительно покоординатного сложения и умножения
на число. Норма в Сн [0, 1]
|| у ||с = max | yi |
* 0 < t < Л?
согласована с нормой в С [О, 1] в том смысле, что для
любой функции и?С [О, 1] определен вектор
"ft = K}^€Cft[0, 1], Щ = и{х{),
и существует
lim|uft||c = \\и\\с.
h -* 0 ft
Любой линейный Р. о. А[г как оператор, действую-
действующий в конечномерном пространстве, может быть пред-
представлен матрицей. Характерными свойствами матриц,
порождаемых разностными операторами, являются их
большой размер и относительно большое число нулевых
элементов.
В общем случае конструкция пространств сеточных
функций и Р. о. может быть весьма сложной. Наи-
Наиболее изучены свойства Р. о., действующих в про-
пространствах с гильбертовой метрикой. В этом случае
наибольший интерес представляют такие свойства
Р. о., как самосопряженность и положительность.
В основе математич. аппарата, позволяющего иссле-
исследовать свойства Р. о., лежат разностные аналоги
формул дифференцирования произведения и интегри-
интегрирования но частям.
Пример 2. Пусть задано множество действитель-
действительных функций на сетке c%. Вводятся обозначения:
_ Vj-Vj-1 _ Vj+l-Vj , Vj + j-Vj-i
Jx, i~ h > Ух,1— h - yx,i~' 2ft '
(У, "]^^t=iyiVih, [y, ")-'Zi
Справедливы следующие формулы:
ivx, /•
Имеет место также формула суммирования по частям
(У' vx] = — {Ух, v) + VNuN—yovo-
Из последней формулы следует, в частности, самосо-
самосопряженность и положительность оператора второй
разностной производной
на множестве функций, заданных на сетке wft и обра-
обращающихся в нуль на границе l—Q, i- N.
Многочисленные исследования посвящены изучению
свойств разностных аппроксимаций дифференциальных
операторов эллиптич. типа (см. [1] — [4]). Для по-
построения соответствующих Р. о. используются такие
эффективные методы, как метод баланса, конечных
элементов, вариационные и проекционные методы.
[1айденные разностные аппроксимации хорошо моде-
шруют основные свойства исходных операторов, такие,
напр., как эллиптичность, выполнение принципа мак-
максимума и др. Построены также Р. о., аппроксими-
аппроксимирующие эллиптические дифференциальные операторы
в областях сложной формы при различных типах
краевых условий и в случае нерегулярных сеток
(см. [5]).
Свойства стационарных Р. о. используются для
изучения устойчивости нестационарных разностных
задач и для построения итерационных методов. При
этом теория итерационных методов может быть изло-
изложена как один из разделов общей теории устойчивости
разностных схем (см. [6], [7]).
В связи с построением экономичных разностных
схем для многомерных задач математич. физики ис-
исследованы факторизованные Р. о., то есть
многомерные Р. о., продставимые в виде произведения
одномерных Р. о. (см. [1]). Изучались и нелинейные
Р. о. (см. [8]).
Лит.: [1] С а м а р с к и й А. А., Теория разностных схем.
М., 1977; [2] С и м а р с к и й А. А., А н д р с е ь В. В., Разност-
Разностные методы для эллиптических уравнений, М., 1976; 13] К о р-
н е е в В. Г., Схемы метода конечных элементов высоких поряд-
порядков точности, Л., 1977; 14] О б о н Ж.-П., Приближенное реше-
решение эллиптических красных задач, пер. с англ., М., 1977; [5J
Самарский А. А., Ф р я з и л о и И. В., «Успехи матем.
наук», 1976, т. 31, и. (i, с. 167—97; [6] С а м а р с к и й А. А.,
Г у л и н А. В., Устойчивость разностных схем, М., 1973; [7]
Самарский А. А., Николаев Е. С, Методы решения
сеточных уравнений, М., 1978; [8] КарчевекиЙМ. М.,
Л я ш к о A.j Д., «Изв. вузов. Математика», 1972, № 11, с.
23—31; 1973, М 3, с. 44—52. А. В. Тулин, А. А. Самарспий.
РАЗНОСТНЫХ СХЕМ ТЕОРИЯ — раздел вычисли-
вычислительной математики, изучающий методы приближен-
приближенного решения дифференциальных уравнений путем их
замены конечноразностными уравнениями (разност-
(разностными схемами).
Р. с. т. изучает способы построения разностных
схем, исследует корректность разностных задач и схо-
сходимость решения разностной задачи к решению ис-
исходной дифференциальной задачи, занимается обосно-
обоснованием алгоритмов решения разностных задач. Метод
конечных разностей (называемый также методом
сеток) является универсальным вычислительным
методом, позволяющим эффективно решать сложнейшие
задачи математич. физики, включая нелинейные за-
задачи. Отличительной чертой современной Р. с. т.
является ориентация на построение и исследование
методов, пригодных для ЭВМ.
Основные понятия. Метод конечных разностей при-
применяется в теории дифференциальных уравнений как
эффективное средство доказательства теорем сущест-
существования. Для целой вычислительной математики за-
задачи Р. с. т. существенно меняются. Решая приближенно
ту или иную задачу математич. физики, заранее пред-
предполагают, что эта задача поставлена корректно; при
этом основной целью Р. с. т. становится нахождение
и обоснование наилучшего метода решения исходной
дифференциальной задачи, формулировка общих прин-
принципов построения разностных схем с заданными свой-
свойствами для широких классов задач математич. физики.
Ниже излагаются на достаточно общем примере ос-
основные понятия, к-рьгми оперирует Р. с. т.— понятия
аппроксимации, устойчивости, сходимости; демонстри-
демонстрируется один из возможных подходов к построению
Р. с. т.
Пусть в ;?-мерной области G с границей Г ищется
решение дифференциального уравнения
A)
с дополнительными (граничными, начальными) ус-
условиями
1и(х)=ц(х), х?Г, B)
где L и I — линейные дифференциальные операторы,
f (х) и ц (х) — заданные функции. Пусть в нек-ром
классе функций задача A), B) поставлена корректно
(т. е. ее решение и(х) существует, единственно и не-
непрерывно зависит от входных данных /(х), \i(x)).
В методе конечных разностей область G—G+Г при-
приближенно заменяют дискретным множеством точек —
сеткой Gft=G/j+Fft. Параметр h—(h^ . . ., hn),
шаг сетки, характеризует плотность сетки, и обычно
при \h\ ->¦ 0 последовательность сеток Gh стремится
заполнить всю область G. Производные, входящие в
A), B), аппроксимируются на сетке бЛ соответствую-
соответствующими разностными отношениями. В результате полу-
получается система линейных алгебраич. уравнений
C)
где ijh{x) — искомая сеточная фупкция, <р/,(х), %ь(х) —
заданные сеточные функции L^, lh — разностные опе-
операторы. Семейство уравнений C), зависящее от пара-
параметра h, паз. разностной схемой. Хотя урав-
уравнение C) получено путем аппроксимации исходной
задачи A), B), его можно рассматривать как незави-
независимый математич. объект. Из корректности задачи
A), B) не следует, вообще говоря, корректность раз-
разностной задачи C). Поэтому одной из основных задач
Р. с. т. является исследование корректности задачи
C). Кроме того, Р. с. т. изучает сходимость при h ->¦ О
решения yh (x) разностной задачи к решению и (х)
исходной дифференциальной задачи. Корректность и
сходимость тесно связаны между собой.
Пусть множество сеточных функций, заданных на
Gh, образует векторное пространство II h, а операторы
?fti 'ft действуют в этом пространстве; в пространствах
решений у/г(х) и правых частей фд(ж), %/i(h) вводятся
нормы Il-Il(lft), IHI(ift), IHI(,ft).
Говорят, что разностная задача C) поставлена кор-
корректно, если для всех достаточно малых \h\ и при
любых фй, Х/2^11/1 ее рмпенмг существует, единственно
и для него выполняется оценка
с константой М, не зависящей от h. Последнее свой-
свойство, означающее равномерную по h непрерывную
зависимость решения от входных данных, наз. устой-
устойчивостью разностной схемы. Оценки
вида D) решения разностной задачи через известные
правые части наз. априорными оценкам и.
Получение априорных оценок составляет основу Р. с. т.
Для оценки погрешности решение задачи C) пред-
представляется в виде суммы
где ufl(x) — проекция решения и (х) задачи A), B)
в пространство Н^, zh(x) —погрешность приближен-
приближенного решения. В силу линейности задачи C) для по-
погрешности zft (x) получаются уравнения
Lhzh (x)=yh (x), x?Gh- lhzh (x)=yh (x), x?Th, E)
где
4>/i (x) = Фл (x) — Lhuh (x); vft (x) = Xh (x) ~ lhuh (x),
функции "ф/j (x) и V/, (.г) наз. погрешностями
а п и р о к с и м а ц п и разностной схемой C) урав-
уравнения A) и дополнительного условия B) соответствен-
но. Говорят, что схема C) аппроксимирует задачу
A), B) с т-м порядком аппроксимации, если
) = O(|fe|<»), l|v||Cft) = O(|fe|'»), m>0.
Схема C) имеет m-й порядок точности или сходится
со скоростью O(\h\m), если
Для сходимости разностной схемы одной только ап-
аппроксимации, вообще говоря, недостаточно: надо по-
потребовать еще, чтобы разностная задача C) была кор-
корректна. Именно, справедливо следующее утверждение:
если разностная схема C) корректна и имеет т-й
порядок аппроксимации, то она сходится со скоростью
0(|А|»>) (см. [28]).
Возможны и другие подходы к построению Р. с. т.
Так, в теории Лакса (см. [8]) сходимость разностных
схем изучается не в пространствах сеточных функций,
а в пространстве решений исходной дифференциальной
задачи; здесь доказана т. н. теорема аквивалентности:
если исходная задача A), B) корректна и схема C)
аппроксимирует задачу A), B), то устойчивость не-
необходима и достаточна для сходимости. Возможны
и другие постановки вопроса о связи устойчивости и
сходимости (см., напр.. [9]). Исследование сходимости
разностных схем проводилось и в пространствах обоб-
обобщенных решении (см. 1.10]).
Требования к разностным схемам; При расчетах на
'¦овременных ЭВМ не всегда достаточно требовать от
разностной схемы только сходимости при \h\ —»-().
Использование реальных сеток при конечном шаге
сетки предъявляет к схемам ряд дополнительных тре-
требований. Они сводятся к тому, что разностная схема
помимо обычной аппроксимации и устойчивости должна
\орошо моделировать характерные свойства исходного
дифференциального уравнения. Кроме того, разност-
разностная схема должна удовлетворять определенным усло-
условиям простоты реализации вычислительного алго-
алгоритма. Ниже рассматриваются нек-рые из этих допол-
дополнительных требований.
Под однородной разностной схемой
(ем. [1], 111]) понимается разностная схема, вид к-рой
не зависит ни от выбора конкретной задачи из данного
класса, ни от выбора разностной сетки. Во всех узлах
сетки для любой задачи из данного класса разностные
уравнения имеют один и тот же вид. К однородным
разностным схемам относятся, в частности, схемы
сквозного счета для решения уравнений с сильно
меняющимися или разрывными коэффициентами. Схемы
сквозного счета не предусматривают явного выделения
точек разрыва коэффициентов и позволяют вести вы-
вычисления по одним и тем же формулам. Широко ис-
используются схемы сквозного счета при расчетах раз-
разрывных решений уравнений газовой динамики (см.
[1], [51, [12]).
Требование консервативности раз-
разностной схемы означает, что данная разност-
разностная схема имеет на сетке такой же закон сохранения,
что и исходное дифференциальное уравнение. В част-
частности, если L - самосопряженный оператор и схема C)
консервативна, то Лд — самосопряженный в Н^ опе-
оператор, т. е. консервативная схема сохраняет свойство
самосопряженности.
Регулярным методом получения консервативных
однородных схем является т. и. м с т о д баланса,
пли интегро-интер по ляп, ионный ме-
метод. Сущность метода баланса состоит в аппрокси-
аппроксимации на разностной сетке интегрального закона
сохранения (уравнения баланса), соответствующего
данному дифференциальному уравнению. Метод ба-
баланса нашел широкое применение при аппроксимации
уравнений с переменными, в том числе и разрывными,
коэффициентами. Другой группой методов построения
разностных схем, сохраняющих свойства самосопря-
самосопряженности и положительности исходного оператора,
являются методы, основанные на вариационных прин-
принципах (метод Ритца, метод конечных элементов) (см.
Разностная вариационная схема).
При конструировании разностных схем для уравне-
уравнений газовой динамики нашел применение принцип
полной консервативности (см. [5]). Для уравнений
гинсрболич. типа оказалось полезным исследование
дисперсионных свойств соответствующих разностных
уравнений (см. [13]).
Если известно, что лри t -> со решение исходной
дифференциальной задачи стремится к нулю, то естест-
естественно требовать того же и от решения аппроксимиру-
аппроксимирующей разностной задачи. Схемы, обладающие этим
свойством, низ. асимптотически устой-
устойчивы м и (см. [4]).
Другой подход к построению разностных схем луч-
лучшего качества состоит в получении схем, удовлетво-
удовлетворяющих тем же априорным оценкам, к-рые характерны
(неулучшаемы) для исходных дифференциальных урав-
уравнений (см. [14]).
Экономичные разностные схемы для многомерных
задач математической физики. При решении систем
разностных уравнений, аппроксимирующих нестацио-
нестационарные многомерные задачи математйч. физики (с
числом пространственных переменных два или более),
возникают специфич. затруднения, связаннее с тем,
что число арифметич. операций, необходимы* для
отыскания решения на новом временной слое, резко
возрастает при измельчении сетки. В то же время
решение одномерных нестационарных задач осуществ-
осуществляется методом прогонки, к-рып .-экономичен в том
смысле, что он требует конечного (не зависящего от
шага сетки h) числа действий на одну точку сетки.
В общем случае разностную схему наз. экономич-
н о й, если отношение числа действий, необходимых
для отыскания решения на новом временном слое к
числу узлов пространственной Сетки, не зависит от
числа узлов сетки. Обычные неявные разностные
схемы не являются экономичными. Наиболее эффек-
эффективным приемом построения экономичных разностных
схем является метод сведения многомерных задач к
нескольким одномерным задачам (метод переменных
направлений, метод расщепления) (см. [1], [15], [16]).
Новые алгоритмы стимулировали и новый подход
к основным понятиям теории разностных схем: ап-
аппроксимации, устойчивости, сходимости. Напр., ока-
оказалось плодотворным понятие суммарной аппрокси-
аппроксимации или аппроксимации в слабом смысле (см. [1],
[16]). Сформулирован принцип аддитивности, позво-
позволяющий в общем случае строить экономичные разност-
разностные схемы, обладающие свойством суммарной ап-
аппроксимации (см. [17]). Дальнейшим обобщением раз-
разностных схем переменных направлений явились схемы
с уравнениями на графах и векторные схемы (см. [18]).
Методы исследования корректности и сходимости
разностных схем. Для линейных задач из устойчивости
и аппроксимации следует сходимость. Поэтому основ-
основное внимание в Р. с. т. уделяется получению априор-
априорных оценок, из к-рых следует корректность задач в
той или иной норме. Методы получения априорных
оценок для разностных схем во многом аналогичны
тем же методам в теории дифференциальных урав-
уравнений, напр, можно указать следующие методы: раз-
разделение переменных, преобразование Фурье, принцип
максимума, энрргетич. неравенства.
Методы решения сеточных уравнений. Любой сеточ-
сеточный метод для дифференциальных уравнений приводит
к большим системам линейных алгебраич. уравнений.
Напр., в случае многомерных задач число уравнений
достигает порядка 104 —106. Одномерные разностные
задачи обычно решают методом прогонки (см. [2]),
представляющим собой вариант метода последователь-
последовательного исключения неизвестных. Наиболее распростра-
распространенными методами решения многомерных сеточных
уравнений являются итерационные методы. В вычис-
вычислительной практике широко используются такие ите-
итерационные методы, как метод Ричардсона с чебышев-
ским набором параметров, итерационные методы пере-
переменных направлений, двухступенчатые итерационные
методы, представляющие собой комбинацию методов
переменных направлений (внутренняя итерация) с
каким-либо классич. методом (внешняя итерация).
Часто используются также метод верхней релаксации
и попеременно-треугольный итерационный метод (см.
[2], [6]). Теория итерационных методов может быть
изложена как один из разделов общей теории устой-
устойчивости разностных схем (см. [2]).
Наметилась тенденция к использованию прямых (не-
(неитерационных) методов решения многомерных разност-
разностных задач. К таким методам относятся матричная
прогонка, быстрое дискретное преобразование Фурье
и его обобщения, метод суммарных представлений.
Нелинейные задачи. Развита теория однородных
разностных схем для нелинейных уравнений парабо-
лич. типа (см. [19]). Обобщена на нелинейный случай
теорема Лакса о связи между устойчивостью и сходи-
сходимостью (см. 120], [21]). Рассматривались разностные
схемы для нелинейных эллиптич. уравнений (см. [23],
[24]) и для нелинейных параболич. уравнений (см.
[21], [22]). Имеется ряд общих теорем о корректности
разностных схем для нелинейной абстрактной задачи
Коши (см. [25]). Изучалась сходимость разностных
схем для нелинейных эволюционных уравнений (см.
[26], [27])
Лит.: [U Самарский А. А., Теория разностных схем,
М., 1977; [2] С а м а р с к и й А. А., Н и к о л а е в Е. С, Ме-
Методы решения сеточных уравнений, М., 1978; [3] Самар-
Самарский А. А., Андреев В. Б., Разностные методы для а.п-
липтических ураннений, М., 197(i; UJ С а м а р с к и и Л. Л.,
Гулин А. В., Устойчивость ра.ишетпых схем, М., 1973; 15]
Самарский А. А., Подов Ю. П., Разностные методы
решения задач газовой динамики, М., 1980; [6] М а р ч у к Г. И.,
Методы вычислительной математики, 2 изд., М., 1980; [7] Г о-
д у н о в с. К., Рябенький В. С, Разностные схемы. Вис-
дение в теорию, М., 1973; [8] Рихтмайср Р. Д., М о р-
тон К., Разностные методы решения краевых задач, пер. с
англ., М., 1972; [9] Гудович II. Н., «Ж. вычисл. матем. и
матем. физ.», 1966, т. 6, № 5, с. 916—21; [10] Кузне-
ц о в Н. Н., там же, 1972, т. 12, Л» 2, с. 334—51; [11] Тихо-
Тихонова. Н., С а м а р с к и й А. А., там же, 1961, т. 1, № 1, с.
5 — «3: [12] Рождественский Б. Л., Я н е н к о Н. Н.,
Системы квазилинейных уравнений и их приложения к газовой
динамике, М., 1978; [l.'i] П о т т ер Д., Вычислительные методы
в физике, пер. с англ., М., 1975; [14] М о к и н Ю. И., «Ж. вы-
вычисл. матем. и матем. физ.», 1075, т. 15, J\» 3, с. 661—71; [15]
Фрязинов И. В., там же, 1076, т. 16, ."№ 4, с. 008—021;
[16] Яненко Н. Н., Метод дробных шагов решения много-
многомерных задач математической физики, НоносиО., 1067; [17]
Самарский А. А., «Докл. АН СССР», 1965, т. 165, J4» 6,
с. 1253—5й; [18] Самарский А. А., Фрязинов И. В.,
«Beitr. Numer. Math.», 1975, № 4, S. 191—203; [10] Самар-
Самарский А. А. «Ж. вычисл. матем. и матем. физ.», 1062, т. 2
Mi 1, с. 25 — 56; [21]] Якут Л. И., «Докл. АН СССР», 1064
т. 156, № 6, с. 1304—07; [21] А п s о г р с R., Hass R., Коп-
vergenz von Differenzenverfahrcn fur Hncare und nichtlineare
Anfangswertaufgaben, В., 1070; [22] Дьяконов Е. Г., Раз-
Разностные методы решения краевых задач, в. 2 — Нестационарные
задачи, М., 1972; [23] КарчевскийМ. М., Л я ш к о А. Д.,
«Изв. высш. учебн. заведений. Математика», 1972, JM& 11, с. 23—
31; 1073, № 3, с. 44—52; [24] СапаговасМ. II., «Ж. вычисл.
матем. и матем. физ.», 1965, т. 5, № 4, с. 638 — 47; [25] К а р-
ч е в с к и й М. М., Л а п и н А. В., Л я ш к о А. Д., «Изв. высш.
учебн. заведений. Математика», 1972, J\s 3, с. 23—31; [26] Да-
ii и н А. В., Л )! ш к о А. Д., там же, 1973, № 1, с. 71 — 77; [27]
R a v i a r t P. A., «J. math, pures et appl.», 1067, t. 46, J\Ts 1
p. 11 —107; № 2, p. 109—83; [28] P я б е н ь к и й В. С, Ф и-
л и пп о в А. Ф., Об устойчивости разностных уравнений, М.,
1Я56. А. В. Гулин, А. А. Самарский.
РАЗНОСТЬ множеств — одна из операций
над множествами. Пусть имеется два множества А и В
(из к-рых второе может и не содержаться в первом).
Тогда множество тех элементов множества А, к-рые
не являются элементами множества В, наз. разно-
разностью этих множеств.
Р. множеств А и В обозначается А\В.
М. И. Войцгховский.
РАЗРЕЖЕННАЯ МАТРИЦА — матрица с малым
числом ненулевых элементов. Системы линейных урав-
уравнений с такими матрицами возникают, в частности, при
аппроксимации дифференциальных уравнений конеч-
норазностными или вариационно-разностными.
РАЗРЕЖЕННОСТЬ МНОЖЕСТВА EczR" ' в Точке
г/0?К« — локальный признак того, что Е является по-
полярным множеством. Непустое множество EaR." наз.
разреженным в точке /Уо€^"в ДВУХ слу-
случаях: 1) если у0 не является предельной точкой Е,
то есть iinfeE', где Е'— производное множество для Е;
2) если уо(^Е' и в окрестности у0 существует сунергар-
монич. функция и(х) (см. Субгармоническая функция)
такая, что
lim \i\lv (х) > v (у0).
х-* у о
хеЕ\{у0}
Множество Е является полярным тогда и только
тогда, когда оно — разреженное множество (р. м.)
в каждой из своих точек. Для произвольного множества
Е подмножество тех точек, в к-рых Е есть р. м., яв-
является полярным. Любое непустое подмножество р. м.
в точке г/о€^" является р. м. в у0. Объединение коноч-
коночного числа р. м. в точке уо? R" является р. м. в точке ;/0.
Отрезок на плоскости R2 но является р. м. ни в
одной из своих точек. Если A'cR2 — р. м. в точке у0,
то существуют сколь угодно малые окружности с
центром у0, не пересекающиеся с Е. Полярное множе-
множество Ec'R- вполне разрывно. Однако канторово мно-
множество меры нуль на оси абсцисс не является р. м.
ни в одной из своих точек. Вместе с тем в пространстве
R3, напр., множество точек
Е = {(х, у, z) : V(x, у, z)^k > 1},
имеющее острие в точке @, 0, 0), где
17 \ С1 ttlt
V(x,y, z)=\
Jo V(x-t)'+y'+zt
— ньютонов потенциал плотности t на отрезке @<.z<:
<1, 0, 0), есть р. м. в острие @, 0, 0) ??' (пример
Лебег а).
Лит.: Ш Б р с л о М., Основы классической теории потен-
потенциала, пер. с франц., М., i'JH'i; [2] Л а н д к о ф Н. С, Основы
современной теории потенциала, М., 1966. Е. Д. Соломепцев.
РАЗРЕЗ области DaC по разомкнутой простой
дуге 7~ {z(<):0<«<:1} — удаление из области D точек
дуги у, т. е. переход от области D к области (или об-,
ластям) D\y, а также само множество у. При этом'
предполагается, что области D принадлежит либо
вся дуга у, либо вся дуга за исключением начальной
или конечной точек z@), z(l), a z@) или z(l) принад-
принадлежат границе 3D. Каждой точке z(t) разреза у при
0<?<1 соответствуют два граничных элемента приле-
прилегающей к у части области D: левый и правый. В сово-
совокупности эти элементы образуют соответственно л е-
вый и правый берега разреза у.
Е Д. Соломенцев.
РАЗРЕЗА МНОЖЕСТВО, множество раз-
раздела, от точки О — множество тех точек х риманова
многообразия W. к-рые либо соединимы с О более
чем одной кратчайшей Ох, либо Ох не продолжима как
кратчайшая за точку х. В двумерном случае Р. м.
является одномерным графом без циклов (см. [2]);
в аналитическом W любой размерности — полиэдром
из аналитич. подмногообразий (см. [3]). Р. м. непре-
непрерывно зависит от О. Р. м. определяется не только от
точки, но и от других подмножеств, напр, от края 6W,
а также в пространствах, отличных от римановых,
напр, на выпуклых поверхностях (см. [4]) и в двумер-
двумерных многообразиях ограниченной кривизны.
Лит.: [1] Громе л Д., Клингенберг В., Мей-
ер В., Риманова геометрия в целом, пер. с нем., М., 1971; [2J
MyersS. В., «Duke Math. J.», 1935 v. 1, p. 376—91; [3]
В u с li n e г M. A. «Proc. Amer. Math. Soc», 1977, v. 64,
.Ns 1, p. 118—21; [4] К u n г e J., Der Schnittort auf konvexert
Verheftungsflachen, B. 1969. В. А. Залгаллер.
РАЗРЕШАЮЩАЯ ФУНКЦИЯ — то же, что Сколема
функция.
РАЗРЕШЕНИЕ ОСОБЕННОСТЕЙ, десингуля-
ризация,— замена особого алгебраич. многооб-
многообразия на бирационально изоморфное неособое много'
образие. Более точно, Р. о. алгебраич. многообразия
X над основным полем к наз. собственный бирацио-
нальный морфизм/ : Х'-*-Х такой, что многообразие X'
неособое (гладкое). Аналогично определяется Р. о.
схемы, комплексно-аналитического пространства и
т. д. Существование Р. о. позволяет сводить многие
вопросы к неособым многообразиям, при изучении
к-рых можно использовать теорию пересечений и
аппарат дифференциальных форм.
Обычно Р. о. происходит путем последовательного
применения операции моиоидальиого преобразования.
Известно, что если центр D моноидального преобра-
преобразования Х'-+Х допустим (то есть D неособо, а X —
нормальное плоское многообразие вдоль D), то чис-
численные характеристики особенностей многообразия
(кратность, функция Гильберта и т. д.) не хуже, чем
у X. Проблема состоит в пыборе центра раздутия так,
чтобы особенности у X' действительно улучшились.
В случае кривых проблема Р. о. сводится по существу
к нормализации. В двумерном случае ситуация слож-
сложнее. Доказано существование Р. о. у любого много-
многообразия над полем к нулевой характеристики. Точнее,
для приведенного многообразия Хо существует конеч-
конечная последовательность допустимых моноидальных
преобразований /,•: X[+\-*-Xj, i~0, I, . . ., г, с цент-
центрами D/CX,- такая, что ?>,¦ содержатся в множествах
особых точек X,-, а Хг -~ неособое многообразие.
Аналогичный результат верен для комплексно-ана-
комплексно-аналитических пространств. В положительной характе-
характеристике существование Р. о. установлено A983) для
размерностей <:3.
С задачей Р. о. тесно связана задача разрешения
вложенных особенностей, формулируемая следующим
образом. Пусть X вложено в неоеобое алгебраич. мно-
многообразие Z; существует ли собственное отображение
f:Z'-+Z с неособым Z' такое, что а) / индуцирует изомор-
изоморфизм Z'X/-1 (X) на Z\X, б) /-1 (X) является дивизором
с нормальными пересечениями? (Дивизор на неособом
многообразии имеет нормальные пересечения, если
локально он задается уравнением tx . . . ife=0, где
t[, . . ., tk — часть регулярной системы параметров
на Z.)
Задача разрешения вложенных особенностей яв-
является частным случаем задачи тривиализации пучка
идеалои. Пусть Z — неособое многообразие, / — коге-
когерентный пучок идеалов на Z, a Dc:Z — неособое замк-
замкнутое подмногообразие. Слабым прообразом идеала /
при раздутии j:Z'-+Z с центром в О ная. пучок идеалов
на Z', где D' — f-l(D), a m —кратность идеала / в
общей точке D. Тривиалишщин кучка идеалов состоит
в нахождении последовательности раздутий с неосо-
неособыми центрами, при к-рых слабый прообраз / стано-
становится структурным пучком. Пусть Zo — неособое мно-
многообразие над нолем нулевой характеристики, /0 —
когерентный пучок идеалов на Zo и, кроме того, задан
нек-рый дивизор Ео на Zn с нормальными пересече-
пересечениями. Тогда существует последовательность раздутий
ff.Zi+l-+Zj, 1=0, 1, . . ., г—1, с неособыми центрами
L>iCzZ;, обладающая следующими свойствами: если
определить /,-+1 как слабый прообраз /,• при разду-
раздутии /;> а ?, + 1-как fj1 (Е^^ЦИ), то Ir=6Zr >
a ?,. имеет лишь нормальные пересечения (теорема
X и р о н а к а). Более того, можно считать, что Dj
лежит в множестве точек максимальной кратности /,-
и имеет нормальные пересечения с Е{. В положитель-
положительной характеристике аналогичный результат известен
лишь при dim Z<:3.
Другой задачей этого типа является задача исклю-
исключения точек неопределенности рационального отобра-
отображения. Пусть f:X-+Y — рациональное отображение
неособых алгебрзич. многообразий. Существует ли
последовательность раздутий с неособыми центрами
X г —> X г __ 1 —>... —> Xq = X
такая, что индуцированное отображение Хг—>-У яв-
является морфизмом? Эта задача сводится к задаче су-
существования тривиализации пучка идеалов, и ответ
утвердителен, если char k=0 или если dim X<:3.
Лит.: [1] Abhyankar S., Resolution of singularities
of embedded algebraic surfaces, N. Y.— L., 1966; в кн.: Тр. Меж-
Международного конгресса математиков. 1966, М., 1968, с. 469—
481; [2] L i p m a n J., в кн.: Algebraic geometry, Providence,
1975, p. 531—46; [3] Хиронака X., «Математика» 1965,
т. 9, № 6, с. 2—70. В. И. Данилов.
РАЗРЕШЕНИЯ ПРОБЛЕМА — алгоритмическая
проблема, в к-рой для заданного множества А требуется
построить алгоритм, разрешающий А относительно
другого множества В, включающего А {АЯ^В), т. е.
такой алгоритм 91, к-рый применим ко всякому эле-
элементу из В, причем Щ(.г)=1, если х^А, и Ш.(х) = 0,
если х?В\А. Важным классом алгоритмич. проблем
являются Р. п. для формальных теорий, то есть Р. п.
множества всех доказуемых в теории формул (множе-
(множество А) относительно множества всех формул теория
(множество В).
Термин «Р. п.» следует отличать от термина «проб-
«проблема разрешимости», означающего вопрос о разреши-
разрешимости той или иной математической (напр., алгорит-
алгоритмической) проблемы. В. в. Плиско.
РАЗРЕШИМАЯ ГРУППА — группа, обладающая ко-
конечным субнормальным рядом с абелевыми факторами
(см. Подгрупп ряд). Она также обладает нормальным
рядом с абелевыми факторами (такие ряды наз. раз-
разреши м ы м и). Длина кратчайшего разрешимого
ряда группы наз. ее длиной, или ступенью
разрешимости. Важнейшим из таких рядов
является ряд коммутантов, или производный ряд (см.
Коммутант группы). Термин «Р. г.» возник в теории
Галуа и связан с разрешимостью алгебраич. уравнений
в радикалах.
Конечные Р. г. обладают субнормальным рядом с
факторами простых порядков. Эти группы характе-
характеризуются справедливостью следующего обращения
теоремы Лагранжа: для любого разложения п=п1п3
порядка п группы на два взаимно простых сомножи-
сомножителя существует подгруппа порядка пг, и все под-
подгруппы порядка «j сопряжены между собой. Если
порядок конечной группы делится только на два
простых числа, то такая группа разрешима. В классе
Р. г. конечные группы выделяются как конечно по-
порожденные периодич. группы.
Частными случаями Р. г. являются нильпотентные
группы, полициклические группа, метабелевы группы.
Важный подкласс образуют конечно порожденные
группы, являющиеся расширениями своей абелевой
нормальной подгруппы с помощью полициклич. фак-
факторгруппы. Они удовлетворяют условию максималь-
максимальности для нормальных подгрупп (см. Обрыва цепей
условие) и финитно аппроксимируемы (см. Финитно
аппроксимируемая группа). Всякая связная разрешимая
группа Ли, «а также Р. г. матриц, связная в Зариского
топологии, имеют нилыютентпый коммутант. Всякая
матричная Р. г. над алгебраически замкнутым полем
имеет подгруппу конечного индекса, сопряженную с
подгруппой треугольной группы (см. Ли — Полчина
теорема).
Все Р. г. длины, не препосходящей числа /, образуют
многообразие (см. Групп многообразие). Свободные
группы таких многообразий наз. свободными
разрешимыми группами.
Лит.: [1] К у р о ш А. Г., Теория групп, 3 изд., М., 1967;
[2] Каргаполов М. И., Мерзляков Ю. И., Основы
теории групп, 2 изд., М., 1977. А. Л. Шмелъкин.
я-РАЗРЕШИМАЯ ГРУППА — обобщение понятия
разрешимой группы. Пусть я — нек-рое множество
простых чисел. Конечная группа, каждый индекс
композиционного ряда к-рой либо не делится ни на
одно число из я, либо совпадает с нек-рым числом из я,
наз. я-р азрешимой группой. Основные свой-
свойства я-Р. г. подобны свойствам разрешимых групп.
я-Р. г. является я^Р. г. для любого яхс:я; подгруппы,
факторгруппы и расширения л-Р. г. с помощью л-Р. г.
также являются л-Р. г. В л-Р. г. G каждая я-п о д-
группа (т. е. подгруппа, все простые делители
порядка к-рой принадлежат я) содержится в нек-рой
холловской я-п одгрупне (я-подгруппа наз.
холловской, если ее индекс в группе не делится ни
на одно число из л), а каждая я'-подгруппа (где л' —
множество, дополняющее я в множество всех простых
чисел) — в нек-рсш холловской я'-подгругше; все
холловские я-цодгрушш, а также холловские я'-
подгрущщ сопряжены в G; индекс максимальной под-
подгруппы группы G либо не делится ни на одно число из
я, либо равен степени одного из чисел множества
я (см. [1]). Число холловских я-подгруш! в G равно
aia2 ... at, где a,=l (mod p/) для каждого р,-?я,
делящего порядок группы G, причем а,- делит порядок
одного из главных факторов группы G (см. B]).
Лит.: [1] Ч у н и хин С. А., Подгруппы конечных групп,
Минск, 1964; [2] В г а и е г W.,«Arch. Math.», 1968, Bd 19,
Xt 3, S. 245 — 55. С. П. Струнков.
РАЗРЕШИМАЯ ФОРМУЛА (в данной системе) —
такая формула А данной формальной системы, что
либо она доказуема в этой системе (т. е. является тео-
теоремой), либо опровержима (т. с. доказуемо ее отрица-
отрицание ~\а). Если всякая замкнутая формула данной
формальной системы разрешима в ней, то такая си-
система наз. полной. (Следует заметить, что нельзя
требовать, чтобы в системе были разрешимы все фор-
формулы, а не только замкнутые. Так, формула х=0,
где х — переменная для натуральных чисел, не вы-
выражает ни истинное, ни ложное суждение, и поэтому
ни она, ни ее отрицание не являются теоремами фор-
формальной арифметики.)
Название «Р. ф.» связано с тем, что вопрос об ис-
истинности или ложности су?кдения, выражаемого такой
формулой, может быть решен на основе данной си-
системы аксиом. В силу Гёделя теоремы о неполноте в
любой формальной системе арифметики найдется не-
неразрешимое предложение, т. е. замкнутая формула,
к-рая не является разрешимой в этой системе. В част-
частности, неразрешимой оказывается формула, выражаю-
выражающая утверждение о непротиворечивости такой системы.
Термин «Р. ф.» следует отличать от термина «разре-
«разрешимый предикат». в. е. Плиско.
РАЗРЕШИМОЕ МНОГООБРАЗИЕ, солвмного-
о б р а з и е,— компактное факторпространство связ-
связной разрешимой группы Ли (иногда, впрочем, ком-
компактности не требуют). Частпый случай — нильмного-
образие. По сравнению с последним общий случай
значительно сложнее, но для него тоже имеется полная
структурная теория.
Лит.: [1] Auslander L. «Bull. Amer. Math. Sue».
1973, v. 79, № 2, p. 227 —Bl. Д. В. Аносив.
РАЗРЕШИМОЕ МНОЖЕСТВО — множество кон-
конструктивных объектов какого-либо фиксированного
типа, допускающее проверку принадлежности к нему
его элементов при помощи алгоритма. Фактически
мы можем ограничиться понятием Р. м. натуральных
чисел, т. к. более общий случай может быть сведен к
данному при помощи соответствующей нумерации
рассматриваемых объектов. Множество М натураль-
натуральных чисел наз. разрешимым, если существует
такая общерекурсивная функция /, что М= {n\f(n) = 0}.
В этом случае / и представляет собой алгоритм, прове-
проверяющий принадлежность к М натуральных чисел.
В самом деле, п?М равносильно тому, что /(п)—-0.
Р. м. натуральных чисел часто наз. также о б щ о р е-
курсивным, или рекурсивным, множе-
множеством.
Многие известные математич. проблемы (такие, как
проблема тождества, проблема гомеоморфии, 10-и
проблема Гильберта, проблема разрешимости в мате-
математич. логике) состоят в требовании доказать или
опровергнуть утверждение о том, что нек-рые кон-
конкретные множества суть Р. м. Известные (отрицатель-
(отрицательные) решения перечисленных выше проблем состоят в
установлении неразрешимости соответствующих им
множеств (см. также Алгоритмическая проблема).
Лит.: [1] Успенский В. А., Лекции о вычислимых
функциях, М., 1960. Н. М. Нагорный.
РАЗРЕШИМЫЙ ПОТОК — поток на разрешимом
многообразии M=GlH, определяемый действием на М
какой-нибудь однопараметрич. подгруппы gf разреши-
разрешимой группы Ли G: если М состоит из смежных клас-
классов g#, то под действием Р. п. такой класс за время t
переходит в класс gfgH. Частный случай Р. п.— ниль-
поток; в общем случае свойства Р. п. могут быть зна-
значительно более разнообразными.
Лит.: [1]Ауслендер Л., Грин Л., Хан Ф., Потоки на
однородных пространствах, пер. с англ., М., 1966; 12] Сте-
Степи н А. М., «Успехи матем. наук», 1969 т. 24 в. 5, с. 241—42;
[3] Auslander L., «Bull. Amer. Ma1h. Sue», 1973, v. 79,
Mi 2, p. 262—85; [4] Сафонов А. В., «Функциональный
анализ и его приложения», 19S0, т. 14, JM» 4, с. 81—82.
Д. В. Аносов.
РАЗРЕШИМЫЙ ПРЕДИКАТ — такой гс-местный
предикат Р, заданный на нек-ром множестве кон-
конструктивных объектов (напр., натуральных чисел) М,
для к-рого существует алгоритм, позволяющий для
любого набора аь . . ., ап элементов множества М
найти значение (И или Л) предиката Р на этом наборе.
Иными словами, предикат является разрешимым,
если он, рассматриваемый как га-местная функция
на М со значениями .во множестве {И, Л}, является
вычислимой функцией.
Когда в качестве математич. уточнения понятия
вычислимости используется понятие рекурсивной функ-
функции или какое-либо эквивалентное понятие, то вместо
«Р. п.» обычно употребляется термин «рекурсивный
предикат». в. е. Плиско.
РАЗРЫВА ТОЧКА — точка, принадлежащая мно-
множеству X определения функции /: X ->- У, где X и
У — топологич. пространства, в к-рой эта функция
не является непрерывной. Иногда к Р. т. относят и
точки, к-рые хотя и не принадлежат множеству опре-
определения функции, но в этом множестве содержатся
нек-рые их проколотые окрестности.
Среди Р. т. функций, определенных в проколотых
окрестностях точек числовой оси, различают точки
разрыва 1-го и 2-го рода. Если точка хй является
Р. т. функции /, определенной в нек-рой окрестности
этой точки, кроме, быть может, ее самой, и в ней су-
существуют конечные пределы слева /(.г0—0) и справа
f (хо+О) функции / (по проколотой окрестности точки
zq), to эта точка наз. точкой разрыва 1-г о
рода, а число / (хо-\- 0)—/ (х0—0) скачком функции
/ в точке ./¦„, п])ичем если он равен нулю, то х0 наз.
точкой устранимого разрыва. Если
Р. т. не является точкой разрыва 1-го рода, то она наз.
ТОЧКОЙ разрыва 2-Г О р О Д а. Л. Д. Кудрявцев.
РАЗРЫВНАЯ ВАРИАЦИОННАЯ ЗАДАЧА — зада-
задача вариационного исчисления, в к-рой экстремум функ-
функционала достигается на ломаной экстремали. Лома-
Ломаная экстремаль — кусочно гладкое решение
Эйлера уравнения, удовлетворяющее в угловых точках
нек-рым дополнительным необходимым условиям. Эти
условия принимают конкретный вид в зависимости от
типа Р. в. з. Так, в Р. в. з. 1-го рода ломаная экстре-
экстремаль разыскивается при обычных предположениях
относительно непрерывности и непрерывной диффе-
ренцируемости подинтегральной функции. Для про-
простейшего функционала
F (х, у, y')dx, y(xi)~yi, у(х2) = у2, A)
в угловой точке х0 ломаной экстремали необходимо
шполнение условий Вейерштрас. са —
Ч р д м а н а
Fv,(x0, y(x0), y'(xo — O)) = Fy,(xo, y(x0), у'(хо + О)), B)
F (х„, у (х0), у' (.г0 —0)) —
-у' (хо-О) Fy, (*„, у (*„), у' (ха-0)) =
= F(x0, y(x0), у' (
(x0, у(хо), у'(хо + О)). C)
В случае, когда F зависит от п неизвестных функций,
т. е. у в A) есть «-.мерный вектор у= (</х, . . ., уп), ус-
условия Веперштрасса — Эрдмана в угловой точке имеют
вид, аналогичный B), C):
Г 9F "| г of . , ...
—г = —- , i = l, ..., п, (А)
I дШ Jxo-o I дУ( Jx0 + o
^,л ' OF
y
E)
Для задач на условный экстремум, в к-рых подинте-
гральная функция зависит от п неизвестных функций
и имеется т дифференциальных ограничений типа
равенства (см. Больца задача), условия Вейерштрас-
а—Эрдмана формулируются с помощью функции
1агранжа L и имеют вид D), E) с заменой F на L.
В термипах теории оптимального управления необ-
необходимые условия в угловой точке ломаной экстремали
требуют непрерывности сопряженных переменных и
функции Гамильтона в точках разрыва оптимального
управления. Как следует из Понтрягина принципа
максимума, эти условия автоматически выполняются,
если управление вдоль ломаной экстремали опреде-
определяется пл условия максимума функции Гамильтона.
В Р. в. я. 2-го рода подинтегральчая функция раз-
разрывна. Пусть, напр., F (х, у, у) претерпевает разрыв
вдоль линии у—ф(,г) так, что F(x, у, у') соответственно
равна Fx(x, у, у') и F2(.r, у, у') по одну и другую
сторону от линии у~(р(х). Тогда если оптимальное
решение существует, то оно достигается на ломаной
экстремали, имеющей; угловую точку (,г0, <р(ж0)) и
вместо функционала A) получают функционал
J = \X°t\(x,y,
Вариация функционала (fi) сводится к вариации функ-
функционалов Jl и /2 на кривых сравнения, имеющих соот-
соответственно правый п левый подвижные концы, смеща-
смещающиеся вдоль линии у=<р(х). Для того чтобы ломаная
экстремаль доставляла минимум функционалу F),
необходимо, чтобы в угловой точке (х0, <р(х0)) выпол-
выполнялось условие
G)
Для случая, когда F зависит от п неизвестных функций
У= (j/ii • • •> Уп)-> а поверхность разрыва F задана в виде
Ф(х, у)=0, (8)
необходимые условия в угловой точке ломаной экстре-
экстремали, находящейся на поверхности (8), принимают вид
I-
1
¦1 -Hrfl
дУп \х„-о I d«n 1
аф
Необходимые условия G), @) дают недостающие
условия для вычисления произвольных постоянных,
определяющих ломаную экстремаль — частное реше-
решении уравнения Эйлера, удовлетворяющее граничным
условиям. Действительно, равенства (9) дают п необ-
необходимых условий, к-рые в совокупности с 2ге гранич-
граничными условиями, п условиями непрерывной стыковки
ломаной экстремали в угловой точке и уравнением
(8) дают 4п+1 условий, с помощью к-рых можно
определить абсциссу угловой точки х0 и in произ-
произвольных постоянных — по 2п для каждой из экстре-
экстремалей, лежащих по разные стороны от поверхности (8).
Лит.: [1] Г ю н т е р Н. М., Курс вариационного исчисле-
исчисления, Л.— М., 1941; [2] С м и р н о в В. И., Курс высшей мате-
математики, 5 изд., т. 4, М., 1958; [3] П о н т р я г и н Л. С. [и др.],
Математическая теория оптимальных процессов, 3 изд., М., 1976.
И. Б. Вапнярский.
РАЗРЫВНАЯ ФУНКЦИЯ — функция /: X -» Y,
где X и Y — топологии. пространства, не являющаяся
непрерывной функцией на пространстве X. Среди
разрывных действительных функций /: X -*¦ R важные
классы составляют Бэра классы, кусочно непрерывные
функции, ступенчатые функции.
Р. ф. возникают, напр., при интегрировании по
параметру элементарных функций (см. Дирихле раз-
разрывный множитель), при вычислении суммы функцио-
функциональных рядов, членами к-рых являются элементарные
функции, в частности при вычислении суммы тригоно-
метрич. рядов, в задачах оптимального управления.
Примеры.
., у=° х" _1 0, если х = 0,
+-*п = а A+.т2)« |1_)_л;2] если хфО.
„ V" sum* \ 0, если х = 0,
г> А,=1 —Т- - \ JLI2L , если 0 < х < 2п.
Л. Д. Кудрявцев.
РАЗРЫВНЫЙ МНОЖИТЕЛЬ — величина, завися-
зависящая от одного или более параметров и принимающая
два (или больше) значения. Напр.,
2ni
1
Bfe) !
J2
¦(i
— i'OD
s (s
0,
+ 1)...(
если i
если (
s + 2ft)
)=^ У
Р. ы. применяются для формального расширения
области суммирования или интегрирования, для све-
сведения данного выражения к другому, к к-рому можно
применить заданные формулы или преобразования.
Другие примеры — Дирихле разрывный множитель,
дельта-функция Дирака и т. п. К. Ю. Булота.
РАМА КОГОМОЛОГИИ, де Рама когомо-
л о г и и, алгебраического многообразия — теория ко-
гомологий алгебраич. многообразий, основанная на
дифференциальных формах. С каждым алгебраич.
многообразием X над полем к связывается комплекс
регулярных дифференциальных форм (см. Дифферен-
Дифференциальная форма на алгебраическом многообразии);
его группы когомологий HPr>R (Х/к) наз. группами Р. к.
многообразия X. Если X гладко и полно, a char fc=0,
то Р. к. являются Вейля когомологиями (см. [2], [3]).
Если X гладко и аффинно, а к—С, то справедлив сле-
следующий аналог Рама теоремы:
HPDR(X/k)~HP(Xan, С), р^О,
где Хап — комплексное аналитич. многообразие, со-
соответствующее алгебраич. многообразию X (см. [1]).
Напр., если X — дополнение к алгебраич. гиперпо-
гиперповерхности в Р"(С), то когомологий НР(Х, С) могут
быть вычислены при помощи рациональных диффе-
дифференциальных форм на Р" (С) с полюсами на атой
гиперповерхности.
Для любого морфизма / : X —> S можно определить
относительный комплекс де Рама 2р>0 ^ (®x/s) (см-
Дифференциалов модуль), приводящий к относи-
относительным когомологиям де Рама
#dr(X/S). В случае, когда A'=Spec А и 5=Spec В
аффинны, относительный комплекс де Рама совпадает
с KQrA,s. Когомологий ЙС^ъ (X/S) комплекса пучков
2p;?o/*^x/s на $ наз- пучками относитель-
относительных когомологий де Рама. Эти пучки
когерентны на S, если / — собственный морфизм.
Лит.: [1] G г о t h e n d i е с k A., «Publs math. IHES»,
196В, t. 29, p. 351—59; [2] Hartshorne R., Ample sub-
varieties of algebraic varieties, В., 1970; [3] e г о же, «Ma-
nuscr. math.», 1972, v. 7, p. 125—40. А. Л. Онищип.
РАМА КРУЧЕНИЕ, де Рама кручен и е,—
инвариант, позволяющий различать многие струк-
структуры в дифференциальной топологии; то же, что Рей-
демейстера кручение.
РАМА ТЕОРЕМА, де Рама теорем а,—
теорема, выражающая вещественные когомологий диф-
дифференцируемого многообразия М при помощи ком-
комплекса дифференциальных форм на М. Если Е* (М)^
= 2 _п,Ер (Щ — комплекс де Рама многообразия М,
где ЕР (М) — пространство всех бесконечно диффе-
дифференцируемых р-форм на М', снабженный внешним диф-
дифференциалом, то Р. т. устанавливает изоморфизм меж-
между градуированными алгебрами когомологий Н* (Е*(М))
комплекса Е* (М) и когомологий Н* (М, Щ
многообразия М со значениями в R. Явная интерпре-
интерпретация этого изоморфизма состоит в том, что каждой
замкнутой р-форме со сопоставляется линейная форма
у —». |^ со на пространстве р-мерных сингулярных
циклов у в М.
Р. т. впервые была установлена Ж. де Рамом [1], хо-
хотя идея связи между когомологиями и дифференциаль-
дифференциальными формами восходит к А. Пуанкаре (Н. Рошсагё).
Существует ряд вариантов Р. т. Напр., когомологпи
Н* (Ее (М)) комплекса ?с* (М) с компактными носи-
носителями изоморфны алгебре вещественных когомологий
Нс (М, R) многообразия М с компактными носите-
носителями. Когомологий многообразия М со значениями в
локально постоянном пучке векторных пространств
изоморфны когомологиям комплекса дифференциаль-
дифференциальных форм со значениями в соответствующем плоском
векторном расслоении [3]. Когомологии симплициаль-
ного множества S со значениями в любом ноле к ха-
характеристики 0 изоморфны когомологиям соответст-
соответствующего полиномиального комплекса де Рама над к.
В случае, когда S — сингулярный комплекс произ-
произвольного тоиологич. пространства К, получают таким
образом градуированно-коммутативную дифференци-
дифференциальную градуированную fc-алгебру Awr(X), алгебра
когомологии Н* (Adr(X)) к-рой изоморфна алгебре
сингулярных когомологий II* (X, к) (см. [4]). Если
X — гладкое аффинное алгебраич. многообразие над
С, то когомологии Н*(Х, С) изоморфны когомоло-
когомологиям комплекса регулярных дифференциальных форм
на М (см. Рама когомологии).
Лит.: [1] Rham J. de, «J. math, pures et appl. 9 se"r.», 1931,
t. 10, p. 115—200; [2] Рам Ж. д е, Дифференцируемые много-
многообразия, пер. с франц., М., 195E; [3] Рагунатан М., Дис-
Дискретные подгруппы групп Ли, пер. с англ., М., 1977; [4] Гомо-
Гомотопическая теория дифференциальных форм, пер. с англ. и
франц., М., 1981. А. Л. Онищик.
РАМАНУДЖАНА ГИПОТЕЗА — высказанное С. Ра-
мануджаном [1] предположение, что коэффициенты
Фурье т(п) функции Д (параболич. формы веса 12)
удовлетворяют неравенству
| т (р)К2/I1/2,р — простое,
т(п) наз. также Рамануджаиа функцией. Функция
Д есть собственная функция операторов Гекке, т(п) —
соответствующие собственные значения. Петерсон (Н.
Petersson) обобщил Р. г. на случай собственных зна-
значений операторов Гекке модулярных форм веса к,
к — целое 5=2 (гипотеза Петерсон а). П. Де-
линь (P. Deligne, см. [2]) свел гипотезу Петерсона к
гипотезе Вейля, затем доказал последнюю A974).
Этим была доказана и Р. г.
Лит.: [1] Raman u Jan S., «Trans. Camb. Phil. Socj>,
1916, v. 22;[2] Д е л и н ь П., «Успехи матем. наук», 1975, т. 30,
в. 5, с. 159—90; 13] Фом е н к о О. М., в ни.: Итоги науки и
техники. Алгебра. Топология. Геометрия, т. 15, М., 1977, с.
5—91. И. К). Пцлопт.
РАМАНУДЖАНА СУММЫ — зависящие от двух
целочисленных параметров /си п тригонометрич. суммы
2ren/ii \ 'V 2япЛ
где h пробегает все целые неотрицательные числа,
меньшие, чем к, и взаимно простые с к. Основные
свойства Р. с.— мультипликативность относительно
индекса к:
ckk' (n) = ck(n)ck> (n), если (к, к')=1,
а также представление через функцию Мёбиуса ц:
Р. с. являются ограниченными, если ограничено к
либо п. В частности, с^A)=1.
Многие мультипликативные функции от натураль-
натурального аргумента разлагаются в ряды по Р. с. и наобо-
наоборот, основные свойства Р. с. позволяют проеуммиронать
суммы вида
где /(я) — мультипликативная функция, <; — целое
число. В частности,
E(s)
где ? (s) — дзета-функция Римана, аа (п) — сумма а-х
степеней делителей числа п. Такие суммы тесно свя-
заны с особыми рядами нек-рых аддитивных проблем
теории чисел, напр, представление натуральных чисел
в виде четного числа квадратов. С. Рамануджаном [1]
были получены многие формулы, содержащие Р. с.
Jlum.:[l]'R а т a n u ) a nS., «Trans. Camb. Phil. Soc», 1918,
v. 22, p. 259—7fi; L2] H a r d у G. H., «Proc. Camb. Phil. Soc»,
1920/21, v. 20, p. 263—71; [3] Ramanujan S., Collected
papers, ed. G. H., Hardy, [a. o.l, Camb., 1927, p. 137—41; [4]
V о 1 k m a n и В., «J. reine und angew. Math.», 1974, Bd 271,
S. 203—13; 15] T и т ч м а р ш Е. К., Теория дзета-функции
Римана, пер. с англ., М., 1953; 16] Л е в и н В. И., в кн.: Исто-
рико-математические исследования, т. 13, М., 1960.
К. Ю. Вулота.
РАМАНУДЖАНА ФУНКЦИЯ — функция п -> т(п),
где х(п) — коэффициент при х" (л>1) разложения
произведения
в степенной ряд:
Если положить
Д (z) — D (e2"iz), Imz>0,
то Р. ф. является n-м коэффициентом Фурье параболич.
формы Д (z), впервые исследованной С. Рамануджаном
fl]. Нек-рые значения Р. ф.: тA)=1, тB)=—24,
тC) = 252, т D)=--1472, тE)=483,0, т F)=—6048,
тG)=-—16744, тC0)= 9458784518400.' С. Рамануджан
предположил (а Л. Дж. Морделл, L. J. Mordell, до-
доказал) справедливость следующих свойств Р. ф.:
х {тп) — х {т) х {п); если (т, п)~Л,
т(рп + г) = х(р")х(р)—р1х(рп~1), если р -простое,
Следовательно, вычисление х (п) сводится к вычислению
т(р), р — простое. Известно, что |т(/»)| <:2p"/i (см.
Рамануджана гипотеза). Известны многие сравнения,
к-рьш удовлетворяет Р. ф. Напр., С. Рамануджану
оыло известно сравнение
Примеры позже найденных сравнений:
х (п) = ап (н) (mod 21), если re = 1(mod8);
т (р) =р + Р10 (mod 25);
LI Т. П.
Лит.: [1] Ramanujan S., «Trans. Camb. Phil. Soc»,
1916, v. 22, p. 159—84; [2] Cepp Ж.-IL, «Математика», 1969,
r. 13, ,N» 4, с 3—15; [3] Фоменко О. М., в кн.: Итоги науки и
техники. Алгебра. Топология. Геометрия, т. 15, М., 1977, с 5—
41. К. Ю. Вулота.
РАМСЕЯ ТЕОРЕМА — название нескольких теорем
в дискретной математике, сформулированных и до-
доказанных Ф. Рамсеем [1].
Первую из этих теорем Ф. Рамсей сформулировал
следующим образом. Пусть Г— бесконечный класс
ii \х иг — положительные целые числа; и пусть все
ге подклассы Г, к-рые имеют г элементов или, иначе,
лее r-сочетания элементов Г, разделены любым спо-
собом на \1 взаимно исключающих классов С,-, / = 1, 2,
. . .,ii, так, что каждое r-сочетание является элементом
одного и только одного класса С,-; тогда, предполагая
справедливой аксиому выбора, класс Г должен содер-
содержать бесконечный подкласс Д такой, что все г-соче-
гания членов Д принадлежат одному и тому же классу
С;. К о н е ч н ы й аналог этой Р. т., также уста-
установленный Ф. Рамсеем, можно сформулировать сле-
следующим образом.
Пусть S — множество, содержащее N элементов,
и Т — семейство всех подмножеств множества S,
содержащих в точности г элементов из S. Пусть се-
семейство Т разбито на t (непересекающихся) подсе-
подсемейств Т1, Т2, . . ., Tf и пусть <h, q2, . . ., qf, r — целые
числа, q^r^l, i=l, 2, . . ., t. Тогда существует такое
минимальное число п (qx, q%, . . ., qt, г), зависящее
только от qx, q2, . . ., qt, r и не зависящее от множества
S, что если N^n(qj, q2, . . ., qt, г), то для нек-рого г,
г=1, 2, ...,/, в 5 существует подмножество Л,- из </<¦
элементов, все г-подмножества к-poro находятся в
семействе Г,- (доказательства этой теоремы содержатся
также в [2], [3]).
Последнюю теорему можно пояснить примером, в
к-ром вычисляется число п C, 3, 2). Рассматриваются
шесть точек на плоскости, связанных попарно дугами,
каждая из к-рых окрашена либо в красный, либо в
голубой цвета. Существуют три точки такие, что дуги,
соединяющие их, окрашены в один и тот же цвет. Из
пяти дуг, соединяющих нек-рую точку Ро с пятью дру-
другими точками, три дуги одного цвета (напр., красного).
Пусть это дуги P0Pi, Po^2i РцРз- Если какая-нибудь
из дуг РгР2, Р\Рз, РцРз красная, то она и две другие,
соединяющие ее концы с точкой Ро, образуют красный
треугольник, если же они все голубые, то сами обра-
образуют голубой треугольник. Это означает, что /?. C, 3, 2)<:
<:E. Однако пять точек на плоскости можно так по-
попарно соединить красными и голубыми дугами, что
при этом не найдется треугольника одного цвета. Для
этого пусть дуги РгР2, РХР3, Р2Р4, РаР^, Р4РЬ будут
красными, а остальные — голубыми. Это показывает,
что гаC, 3, 2)>5. Таким образом, иC, 3, 2) = 6.
Из Р. т. вытекает следующий результат: для данного
натурального гс^З существует целое число N—N(n)
такое, что любые N точек в плоскости, никакие три из
к-рых не лежат на одной прямой, содержат п точек,
образующих выпуклый «-угольник (см. [4]).
Лит.: [1] R а га s е у Р. Р., «Ргос. London Math. Soc. Ser. 2»,
1930, v. 30, p. 264—86; [2] P а й з е р Г.- Д ж., Комбинаторная
математика, пер. с англ., М., 1966; [3] X о л л М., Комбинато-
Комбинаторика, пер. с англ., М., 1970; [4] Е г d б s P., SzekeresG.,
«Compositio math.», 1985, v. 2, p. 463—70; [5] E r d б s P.,
I! a d о R., «Bull. Amer. Math. Soc», 1956, v. 62, p. 427—89.
M. П. Минеев.
РАНГ — понятие, тесно связанное с понятием
базиса. Обычно Р. определяется либо как минимальная
из мощностей порождающего множества (так, напр.,
вводится базисный ранг а л г е б р а и ч е-
с к о и с и с т е м ы), либо как максимальная мощность
независимой в нек-ром смысле подсистемы элементов.
Ранг системы векторов в векторном
пространстве над телом — это максимальное число
линейно независимых векторов в этой системе (см.
Линейная независимость). Ранг, или р а з м е р-
ность, векторного пространства, в
частности, равен числу элементов базиса этого про-
пространства (Р. не зависит от выбора базиса: все базисы
имеют одну и ту же мощность). Для модулей ситуация
сложнее. Существуют такие ассоциативные кольца R,
что даже свободный модуль над R может обладать
двумя базисами с различным числом элементов (см.
Ранг модуля, Свободный модуль). Если каждый свобод-
свободный Д-модуль имеет единственный Р., то говорят, что
R обладает свойством инвариантности базисного числа.
Таким кольцом является всякое ассоциативно-комму-
ассоциативно-коммутативное кольцо с единицей, что позволяет определить,
напр., ранг (Прюфера) абелевой группы (к-рую можно
рассматривать как модуль над кольцом %). В неабе-
левом случае вводятся два понятия Р. группы —
общий и специальный Р. (см. Ранг группы). Особым
образом определяются ранг алгебраической группы
и ранг группы Ли.
Ранг алгебры (над телом) понимается как Р.
ее аддитивного векторного пространства. Однако особо
существует еще понятие Р. в теории алгебр Ли (см.
Ранг алгебры Ли).
Ранг матрицы определяется как Р. системы
векторов ее строк (строчный ранг) или си-
системы ее столбцов (столбцовый ранг). Для
матриц над телом или коммутативным кольцом с еди-
единицей оба эти понятия Р. совпадают. Для матрицы
над полем Р. равен также максимальному порядку
отличного от нуля минора. Р. произведения матриц
не больше Р. каждого из сомножителей. Р. матрицы
не меняется при умножении ее на невырожденную
матрицу.
Ранг линейного отображения —
это размерность образа этого отображения. В конеч-
конечномерном случае он совпадает с Р. матрицы этого
отображения.
Вводятся также понятия ранга билинейной
формы (см. Билинейная форма) и ранга квад-
квадратичной формы (см. Квадратичная форма).
Они также (в конечномерном случае) совпадают с Р.
Матрицы соответствующей формы. О. А. Иванова.
РАНГ линейного обыкновенного дифференциального
уравнения в комплексной области
2]"= о Pi (z) wU> ~J) = °' P° (z) =1' A)
— число r=A+l, где
k--= max ray//,
l < / <; n
Коэффициенты уравнения A) — сходящиеся при
больших \г\ ряды
Понятие Р. употребляется только тогда, когда z—
= оо — особая точка дифференциального уравнения A).
Р. дифференциального уравнения наз. также рангом
особой точки z= оо. Если эта точка — регуляр-
регулярная особая точка, то г=0; если иррегулярная особая
точка, то г>0. Число к наз. п о д р а н г о м. Р. урав-
уравнения — целое или дробпое число. Если подранг
дробный, со знаменателем q~^2, то подранг уравнения,
полученного из A) заменой переменной z=?1/'9, будет
целым. Р. уравнения инвариантен относительно за-
замены переменной вида z— ?ф(?)> гДе функция ф(?)
голоморфна и отлична от нуля в точке ?~оо.
Понятие Р. уравнения и особой точки используется
при исследовании структуры решении уравнения A)
на бесконечности. Пусть Q (z) — многочлен степени р,
— формальный ряд, s^l — целое число. Ряд
наз. нормальным (соответственно поднор-
поднормальным) порядка pis, если «= 1 (соответственно
s5=2). Решение уравнения A), представимое сходящим-
сходящимся в окрестности точки z= оо нормальным (поднор-
(поднормальным) рядом, наз. нормальным (поднор-
(поднормальным) решением того же порядка (см. [2], [3]).
Порядок нормального (поднормального) решения
не превосходит Р. уравнения; это верно и для фор-
формальных решений вида B). Если ранг г уравнения A)
целый, то оно имеет по крайней .мере одно формальное
решение вида B) порядка г. Подстановка ir (z) = eQ(z)«(z)
не меняет Р. уравнении. Если подранг k=plq, где р,
q — взаимно простые целые числа u cf^'l. то уравнение
имеет не менее q формальных решений вида B) по-
порядка г.
Уравнением Гамбургера паз. урав-
уравнение A) с рациональными коэффициентами, если оно
имеет ровно две особые точки: регулярную z О и
иррегулярную z=oo. Для уравнения Гамбургера
получены достаточные условия, при к-рых оно имеет
нормальные решения, а при ге=2 — необходимые
и достаточные условия существования нормальных
и поднормальных решений (см. [2J).
Понятие Р. вводится и в том случае, когда урав-
уравнение A) имеет конечную особую точку (см. [2], |3|).
В случае линейной системы из п обыкновенных
дифференциальных уравнений в комплексной области
w'^z'A (z) w, C)
где г^ — 1 — целое число, матрица-функция Л (г) голо-
голоморфна в точке z= оо и А (оо)^=0, число г+1 наз. ран-
рангом системы C), или рангом особой
точки z— сю, число г — ее подрангом (см.
[4] — [6]). Если г=—1, то точка z= оо — регулярная
особая точка; в отличие от скалярного уравнения A),
точка z=oo может быть регулярной особой, если г>—1
(см. [4]).
Лит.: El] Poincare H., «Acta math.», 1886, v. 8; [2]
Айне Э. Л., Обыкновенные дифференциальные уравнения,
пер. с англ., Харьков, 1939; [3] Латышева К. Я., Т е-
Р е щ е н к о Н. И., О р е л Г. С, Нормально-регулярные реше-
решения и их приложения, К., 1974; U] К о д д и н г т о н Э., Л е-
винсон Н., Теория обыкновенных дифференциальных урав-
уравнений, пер. с англ., М., 1958; [5] Камке Э., Справочник по
обыкновенным дифференциальным уравнениям, пер. с нем.,
5 изд., М., 1976; [6] В а з о в В., Асимптотические разложения
решений обыкновенных дифференциальных уравнений, пер. с
англ., М., 1968. М. В. ФеЭорюк.
РАНГ особой точки — см. Ранг линейного
обыкновенного дифференциального уравнения.
РАНГ АЛГЕБРАИЧЕСКОЙ ГРУППЫ G — размер-
размерность любой из ее Картана подгрупп (эта размерность
не зависит от выбора подгруппы Картана). Наряду с
Р. а. г. G рассматриваются ее полупростой
ранги редуктивный ранг, к-рые, по оп-
определению, равны соответственно Р. а. г. GIR и Р. а. г.
GlRu, где R — радикал алгебраич. группы G, a Ru —
ее унипотентный радикал. Редуктивный Р. а. г. G
равен размерности любого из ее максимальных торов.
Редуктивным k-тр а н г о м линейной алгебраич.
группы G, определенной над полем к (а в случае, когда
группа G редуктивна,— просто ее к-р а н г о м), наз.
размерность любого ее максимального /с-разложимого
•гора (эта размерность не зависит от выбора тора; см.
Разложимая группа). Если /с-ранг определенной над к
редуктивной линейной алгебраич. группы G равен
нулю (соответственно рангу G), то группа G наз. ани-
анизотропной (соответственно разложимой)
над к (см. также Анизотропная группа).
Примеры. 1) Р. а. г. Т'„ всех невырожденных
верхнетреугольных квадратных матриц порядка п
равен ее редуктивному рангу и равен п; полупростой
ранг группы Тп равен нулю. 2) Р. а. г. V'„ всех верхне-
верхнетреугольных квадратных матриц порядка п с едини-
единицами на главной диагонали равен ее размерности
п(п—1)/2, а редуктивный и полупростой ранги группы
Un равны нулю. 3) Р. а. г. Ои(к. /) всех автоморфизмов
определенной над полем к квадратичной формы / в п-
мерном векторном пространстве над к равен [п/2], а
/с-ранг группы Оп(к, /) равен индексу Витта формы /.
Если характеристика основного поля равна 0, то
Р. а. г. G совпадает с рангом ее алгебры Ли L (см.
Ранг алгебры Ли) и равен минимальной из кратностей
собственного значения Х---1 всевозможных присоеди-
присоединенных операторов Ad/я (минимум берется по всем
g?G). Элемент g?G, для к-рого эта кратность равна
Р. а. г. G, наз. регулярным. Множество регу-
регулярных элементов группы G открыто в G в топологии
Зариского.
Лит.: [1] Ш е в а л л е К., Теория групп Ли, пер. с франц.,
т. 3, М., 1958; [2] Борель А., Тите Ж., «Математика»,
I !№7, т. 11, JM1 1, с. 43—И 1; Ы Борель А,, Линейные алге-
Гцкшчеекие группы, пер. с англ., М., 1972; [4] X а м ф р и Д ж.,
Линейные алгебраические группы, пер. с англ., М., 1980.
В. Л. Попов.
РАНГ АЛГЕБРЫ ЛИ—минимальная из кратностей
собственного значения А=0 для линейных операторов
adz.,r по всем х из алгебры Ли L. Предполагается,
что алгебра L конечномерна. Элемент х, для к-рого
эта кратность минимальна, наз. регулярным.
Множество регулярных элементов алгебры Ли открыто
в ней (в топологии Зариского). Р. а. Ли равен размер-
размерности любой из ее Картана подалгебр. Ранг rkL нену-
ненулевой алгебры Ли L удовлетворяет неравенствам
причем равенство rkL=dimL имеет место тогда и
только тогда, когда L нилыютентна. Для полупростых
алгебр Ли над нолем к ранг совпадает со степенью
трансцендентности над к иодполя поля рациональных
функций па L, порожденного всеми коэффициентами
характеристич. многочлена эндоморфизма ad/я.
Р. а. Ли 1.1 R, где R — радикал в L, наз. полу-
полупростым рангом алгебры L.
Пример ы. Пусть L — одна из следующих
алгебр Ли: 1) алгебра ©1„ всех квадратных матриц
порядка п с элементами из ноля к\ 2) алгебра EЧ„ всех
.матриц с нулевым следом; 3) алгебра всех верхнетре-
верхнетреугольных матриц; 4) алгебра всех диагональных мат-
матриц; 5) алгебра всех верхнетреугольных матриц с ну-
нулями на главной диагонали. Для этих алгебр ранг и
полупростой ранг равны соответственно п, п—1, п, п,
п(п—1)/2 и га—1, га—1, 0, 0, 0.
Лит.: 11] Д ж е к о П с о н П., Алгебры Лц, пер. с англ., ЭД.,
1964; 121 С е р ц Ж.-П., АлгеГфы Ли и группы Ли, пер. с
англ. и франц., м., 19И9; [3] Ш е в а л л е К., Теория групп
Ли, пер. с франц., т. 3, М., 1958. jB- Л. Попов.
РАНГ ГРУППЫ (общий и специальный) — понятие
еории групп. Группа G имеет конечный общий
I) а н г г, если г — наименьшее число с тем свойством,
•I го всякая конечно порожденная подгруппа группы G
содержится в подгруппе, обладающей г' образующими
(г'¦<;•). Группа G имеет конечный специальный
ранг г, если г является наименьшим числом с тем
свойством, что всякая конечно порожденная под-
подгруппа группы G обладает системой образующих,
содержащей не более чем г элементов. В случае, если
соответствующего конечного числа не существует,
общий (специальный) Р. г. считается бесконечным.
Общий Р. г. меньше или равен ее специальному
рангу. Существуют группы, общий ранг к-рых конечен
(п даже равен двум), в то время как специальный
ранг бесконечен. Такова, напр., счетная симметрия,
группа. Для абелевых групп общий и специальный
ранги совпадают с рангом Прюфера (см. Абелева группа).
Лит.: [1] К у р о ш А. Г., Теория групп, Зизд., М., 1967.
О. А. Иванова.
РАНГ ГРУППЫ ЛИ (вещественной или комплекс-
чой) — размерность (соответственно вещественная или
комплексная) любой из ее Картана подгрупп. Р. г.
Ли равен рангу ее алгебры Ли (см. Ранг алгебра Ли).
Если группа Ли G совпадает с множеством вещест-
вещественных или комплексных точек линейной алгебраич.
группы 6, то Р. г. Ли G равен рангу алгебраической
группы G. в. Л. Попов.
РАНГ МОДУЛЯ — 1) ранг левого модуля
М над кольцом R, вложимым в тело к — размерность
тензорного произведения кд(?)М, рассматриваемого
как векторное пространство над к. Если R— 2 —
кольцо целых чисел, то это определение совпадает с
обычным определением ранга абелевой группы. Если
тело к является плоским R-модулем (напр., к — тело
частных кольца R), то для точной последовательности
О—>-М' —*¦ М —>¦ М" —> О
выполняется следующее равенство между рангами:
гкЛ# = гкМ'+гкЛ#".
2) Ранг свободного модуля М над
произвольным кольцом R определяется как число его
свободных образующих. Для колец, вложимых в
тело, это определение совпадает с определением из
пункта 1). В общем случае ранг свободного модуля
определяется неоднозначно. Существуют кольца (на-
(называемые «-^/-кольцами), над к-рыми любой свобод-
свободный модуль с не более, чем п свободными образующими,
имеет однозначно определенный ранг, а для свободных
модулей с числом образующих, большим л, это свой-
свойство не верно. Достаточным условием однозначности
ранга свободного модуля над кольцом R является
существование гомоморфизма <р: R —*¦ к в тело к. В этом
случае понятие Р. м. распространяется на проективные
модули следующим образом. Гомоморфизм <р инду-
индуцирует гомоморфизм групп проективных классов
(г*: K0R -»- Кок~ g и рангом проективно-
проективного модуля Р наз. образ представителя модуля Р в
2. Гомоморфизм ф существует для произвольного ком-
коммутативного кольца R.
Лит.: [1] Кон П., Свободные кольца и их связи, пер. с
англ., М., 1975; 12] М и л н о р Дж., Введение в алгебраиче-
алгебраическую К-теорию, пер. с англ., М., 1974. В. Е. Говоров.
РАНГОВ ВЕКТОР — векторная статистика R—
— (R1, . . ., Rn), построенная по случайному вектору
наблюдений Х= (Xlf . . ., Хп), i-я компонента к-рой
Rj-Rj(X), г~1, 2, . . ., п, определяется по правилу
где б (х) — характеристическая функция множества
[О, + оо), т. е.
J *> если ж3г0'
0, если х < 0.
Статистика Д,- наз. рангом г-й компоненты X?., г=1,
2, . . ., п, случайного вектора X. Определение Р. в.
будет корректным при выполнении следующего ус-
условия:
к-рое заведомо выполняется, если распределение веро-
вероятностей случайного вектора X задается плотностью
р(х)-=р(х1, . . ., хп). В этих условиях из определения
Р. в. следует, что статистика R принимает значения в
пространстве 9t= {г} всех перестановок г= {гг, г2,
. . ., г„) чисел 1, 2, . . ., п, при этом реализация г,-
(г,= 1, 2, . . ., п) ранга Л,- численно равна количеству
компонент вектора X, наблюденные значения к-рых
не превосходят реализации i-й компоненты A',-, i=l, 2,
. . ., п.
Пусть Х<->= {ХШ) , . . ., Х(ил)) — вектор порядко-
порядковых статистик, построенный по вектору наблюдений
X. Тогда пара (R, Х1)) является достаточной стати-
статистикой для распределения вектора X, причем сам
вектор X однозначно восстанавливается по достаточной
статистике {R, Х()). Кроме того, при дополнительном
предположении о симметричности плотности вероят-
вероятности р (х) случайного вектора X относительно пере-
перестановок аргументов компоненты Я и Х1' достаточной
статистики (R, Х^*) независимы и
В частности, если
Р (X) =Р (*1, *2, • • • , Хп) = J["=i f (Xj) , A)
т. е. компоненты Хх, Х2, . . ., Х„ случайного вектора
X суть независимые одинаково распределяемые слу-
чайные величины (/(ж/) — плотность вероятности слу-
случайной величины X;), то
> у I п(П—1) ' ^ •" ^ > ^ B)
г, j, к, т = 1, 2, . . ., п,
Ы, 2,..., n,j
для любого k=l, 2, . . ., ?}.
При выполнении условия A) существует совместная
плотность вероятности q{x;, к), к~Л, 2, . . ., п, слу-
случайных величин Xi и Hi, к-рая выражается формулой
q(xh к) —
- (fe-Tn'LU), [ffr)]*-1!!-*1 (*<)]"-*/(*/), C)
где F (х;) — функция распределения случайной ве-
величины Х[. Из B) и C) следует, что условная плотность
вероятности q(xi\Ri=k) случайной величины Х{ при
условии, что R(=k (k=l, 2, . . ., п), выражается
формулой
Последняя формула позволяет проследить внутреннюю
связь, существующую между вектором наблюдений X,
Р. в. R и вектором порядковых статистик X(j), так
как D) есть не что иное, как плотность вероятности к-п
порядковой статистики Xfnk), к=1, 2, ... , п. Кроме
того, из C) следует, что условное распределение ранга
Hi выражается формулой
tp /Y.\l*-l fl F (X ¦)
_
(h-l)i(n-h)!
И, наконец, при допущении о существовании моментов
B{Xj} и D{A'i} и выполнении A) из B) и C) следует,
что коэффициент корреляции р(Х,-, Д,-) между X,- и Л,-
равен
В частности, если X,- подчиняется равномерному рас-
распределению на отрезке [0,1], то
В случае, если X,- подчиняется нормальному распреде-
распределению N (а, а2), то
причем р (X,-, i?,) не зависит от параметров нормального
закона.
Лит.: Ll] Hoeffding W., в кн.: Ргос. 2 Berkeley sympo-
symposium on mathematical statistics and probability, Berkeley — Los
Ang., 1951, p. 83—92;[2] Га ек Я., Шидак 3., Теория ранго-
ранговых критериев, пер. с англ., М., 1971;[3] Т а р а с е н к о Ф. П.,
Непараметрическая статистика, Томск, 1976. М. С. Никулин.
РАНГОВАЯ СТАТИСТИКА — статистика, постро-
построенная по вектору рангов. Если R—{R1} ... , Л„) —
рангов вектор, построенный но случайному вектору
наблюдений Х=(Х1? ... , Хп), то любая статистика
T=T(R), являющаяся функцией от R, наз. ранго-
ранговой статистикой. Классич. пример Р. с. дает
коэффициент т ранговой корреля-
корреляции Кендалла между векторами R и 1 = A,
1, ... , 1), к-рый определяется по формуле
В классе всех Р. с. особое положение занимают т. н.
линейные Р. с, к-рые определяются следующим обра-
образом. Пусть А~\\аA, /)|| — произвольная квадратная
матрица порядка п. Тогда статистика
наз. линей но ii ранговой статистикой.
Напр., коэффициент р ранговой корре-
корреляции Спирмена между векторами R и 1,
определяемый по формуле
K~~ n(n-i) ^J; =
является линейной Р. с.
Линейные Р. с, как правило, просто устроены в вы-
вычислительном отношении и их распределения вероятно-
вероятностей нетрудно находить. Именно поэтому в теории Р. с.
играет большую роль понятие проекции Р. с. в семей-
семейство линейных Р. с. Если Т — нек-рая Р. с, построен-
построенная по случайному вектору X, относительно распреде-
распределения вероятностей к-рого высказана гипотеза Но, то
проекцией f = T (R) Р. с. Г в семейство линейных
Р. с. наз. такую линейную Р. с, что Е{(Г — ГJ} мини-
минимально при справедливости По. Как правило, проекция
Т достаточно хорошо аппроксимирует Р. с. Т, и раз-
разность Т—Т пренебрежимо мала, когда п-*-оо. При
справедливости гипотезы Но, согласно к-рой компо-
компоненты Хи ... , Хп случайного вектора X суть незави-
независимые случайные величины, проекция Г Р. с. Т опре-
определяется по фор.муле
где a(i,j ) = Е {Т\/?,— /}, l<i, j<n (см. [1]).
Существует внутренняя связь между Р. с. т и р.
Как показано в [1], при справедливости гипотезы Но
проекция т коэффициента корреляции Кендалла т
в семейство линейных Р. с. с точностью до постоянного
множителя совпадает с коэффициентом ранговой кор-
корреляции Спирмена р, а именно:
Из этого равенства следует, что коэффициент корреля-
корреляции corr(jj, т) между р и т равен
ГО1Т (р, Т) =
т. е. при больших п Р. с. р и т асимптотически эквива-
эквивалентны (см. [2]).
Лит.: [1] Г а е к Я., Ш и д а к 3., Теория ранговых крите-
критериев, пер. с англ., М., 1971; [2] Kendall M. G., Rank corre-
correlation methods, 4cd.,L., 1970. M. С. Никулин.
РАНГОВЫЙ КРИТЕРИЙ — статистический крите-
критерий, оспованный на ранговой статистике. Напр.,
критерии Вилкоксона и Манна — Уитни являются
ранговыми. Р. к. инвариантны относительно группы G
всех преобразований, задаваемых непрерывными строго
возрастающими функциями и, следовательно, являются
инвариантными относительно изменений параметров
сдвига и масштаба. Кроме того, во многих задачах ста-
тистич. проверки гипотез наиболее мощные инвариант-
инвариантные критерии хорошо аппроксимируются Р. к.
См. также Непараметрический критерий.
Лит.: [1] Гаек Я., III и д а к 3., Теория ранговых крите-
критериев, пер. с англ., М., 1971; 12] Л е м а н Э., Проверка статисти-
статистических гипотез, пер. с англ., 2 изд., М., 1979. М. С. Никулин.
РАНДОМИЗАЦИИ КРИТЕРИЙ, перестано-
перестановок критерий,— статистический критерий, пред-
предназначенный для проверки гипотезы о симметричности
плотности вероятности наблюдаемого случайного век-
вектора относительно перестановки ее аргументов.
Пусть по реализации х={х1, ... , хп) случайного век-
вектора Х=(Х1, ... , Хп) надлежит проверить гипотезу Но,
согласно к-рой неизвестная плотность вероятности
р(х)=р(х1, ... , хп) случайного вектора X симметрична
относительно перестановок своих аргументов, т. е.
Р (-4, ¦¦-, х„)=р (хп, ..., хГп),
где (Г], ... , г„) — вектор, получающийся в результате
произвольной перестановки координат вектора A,
2, ... , п). Далее, пусть ,Х(-> и Л — вектор порядковых
статистик и вектор рангов соответственно, построенные
по вектору наблюдений X, и пусть W~W (A''-', R) такая
статистика, что
почти всюду для нек-рого а ? @; 1). В таком случае ста-
статистич. критерий с критич. функцией <р, связанной со
статистикой W соотношением q>(X) = W (Х1ж), R), наз.
критерием рандомизации. В силу того
что Х<р) является полной достаточной статистикой,
то при справедливости гипотезы На семейство подобных
критериев совпадает с семейством критериев переста-
перестановок.
Лит.: [1] Гаек Я., Ш и д а к 3., Теория ранговых крите-
критериев, пер. с англ., М., 1971; [2] Л е м а н Э., Проверка статисти-
статистических гипотез, пер. с англ., 2 изд., М., 1979. М. С. Никулин.
РАНДОМИЗАЦИЯ — статистическая процедура, в
к-рой решение принимается случайным образом. Пусть
но реализации х случайной величины X, принимающей
значения в выборочном пространстве (ЭЁ, 93, Ре ), 8?в
надлежит принять решение \ из измеримого пространст-
пространства решений C, Л) и пусть на этом пространстве (Н, Л)
задано семейство {Qx}, а-^ЭЁ, т. н. переходных вероят-
вероятностных распределений Qx(-) таких, что для любого
фиксированного события А, А?Л, функция Q.(A) яв-
является ^-измеримой от х. В таком случае статистич.
процедура принятия решения, в к-рой но наблюденной
реализации х случайной величины X решение прини-
принимается с помощью розыгрыша по вероятностному за-
закону Qx( •), наз. рандомизацией.
Лит.: [1] Ч е н ц о в Н. Н., Статистические решающие пра-
правила и оптимальные выводы, М., 1SJ72. М. С. Никулин.
РАО — БЛЭКУЭЛЛА — КОЛМОГОРОВА ТЕОРЕ-
ТЕОРЕМА — утверждение из теории статистпч. оценивания,
на основе к-рого построен метод улучшения несмещен-
несмещенных статистич. оценок.
Пусть X — случайная величина, принимающая зна-
значения в выборочном пространстве (i, 93, Ро ), Э?в,
причем семейство вероятностных распределений {Ре,
Э?в} обладает достаточной статистикой Т-~Т(Х), и
пусть ф=ф(Х) —нек-рая векторная статистика с ко-
конечной матрицей вторых моментов. В этом случае ма-
тематич. ожидание Ее {ф} статистики ф существует и,
кроме того, условное математич. ожидание ф* =
= Ее {ф1 Т} является несмещенной оценкой для Ее {ф},
то есть
В этих условиях Р.— Б.— К. т. утверждает, что квад-
квадратичный риск статистики ф* не превосходит квадра-
квадратичного риска статистики ф равномерно по всем Э?в,
т. е. для любого вектора г, имеющего ту же размер-
размерность, что и статистика ф, выполняется неравенство
гЕ0 {(Ф-Е0 МO" (<Р-Е0
для всех Э?в. В частности, когда ф является одномер-
одномерной статистикой, то при любом 9^6 дисперсия О^ф*
статистики ф* не превосходит дисперсии Dg<p статис-
статистики ф.
В самом общем случае Р.— Б.— К. т. утверждает,
что операция осреднения по достаточной статистике не
приводит к увеличению риска относительно произволь-
произвольной выпуклой функции потерь, откуда следует, что хо-
хорошие статистич. оценки нужно искать только в терми-
терминах достаточных статистик, т. е. в классе необходимых
статистик.
В случае, когда семейство {Ре } является полным,
т. е. когда единственной несмещенной оценкой нуля
является функция, почти всюду равная нулю, несме-
несмещенная оценка с равномерно минимальным риском,
получаемая с помощью Р.— Б.— К. т., является един-
единственной. Таким образом, Р.— Б.— К. т. дает рецепт
построения наилучших несмещенных оценок: нужно
взять любую несмещенную оценку, а затем осреднить
ее по достаточной статистике. Именно таким образом
в следующем примере, принадлежащем А. ТТ. Колмо-
Колмогорову, строится наилучшая несмещенная оценка функ-
функции распределения нормального закона.
Пример. Пусть по реализации случайного векто-
вектора X=(Xt, ... , Хп), компоненты к-рого X/, i~\,
2, ... , п, л^З, суть независимые случайные величины,
подчиняющиеся одному и тому же нормальному закону
iVjE, о2), следует оценить функцию распределения
о / 1 2л a J - oo
Предполагается, что параметры fe и а2 неизвестны. Так
как семейство
нормальных законов является полным и существует
достаточная статистика Т=(Х, S2), где
Х=±(Х1+...+Хп)
то для построения наилучшей несмещенной оценки
функции распределения ф(^-^~) следует воспользо-
воспользоваться Р.— Б.— К. т. В качестве исходной статистики
Ф можно взять, напр., функцию эмпирич. распределе-
распределения, построенную по какой-то одной компоненте век-
вектора X, напр. Хи то есть
_ (О, если х < Xi
И, если х^Ху,
к-рая является тривиальной несмещенной оценкой для
Ф( —— ), так как
Осреднение оценки <р по достаточной статистике Т
приводит к оценке
' s Г
В силу того что статистика
V-
являющаяся дополнительной к достаточной статистике
Г, имеет равномерное распределение на (»—2)-мерной
сфере радиуса п и, следовательно, не зависит ни от не-
неизвестных параметров % и о2, ни от достаточной стати-
стики Т, то (Х1—X)'S тоже не зависит от |. о2 и Т,
причем
Р | -b-zl < ,Л = Г„_2 (и), | и | < ]/";Т^Т, B)
где
Ш
— функция распределения Томпсона с / степенями
свободы. Таким образом, и.ч A)—C) следует, что наи-
[ X—' \
лучшей несмещенной оценкой для Ф1—-), построен-
Hoii по п независимым наблюдениям Хх, ... , Хп, яв-
является
где Sf(-) —функция распределения Стыодента с /
степенями свободы.
Лит.: [1] Колмогоров А, И., «Пан. АН СССР. Се]),
ыатеы.», 1950, т. 14, „\« 4, с. 303—26; [2] Р а и с. Р., Линейные
статистические методы и их применения, пер. с англ., М., 1968;
[3] В а п дер В а р д е н Б. Л., Математическая статистика,
пер. с нем. М., I960; [4] В 1 а с k w е 1 1 D., «Ann. Math. Sta-
Statistics»), 1047, v. 18, p. 105 — 10. M. С. Никулин.
РАО — КРАМЕРА НЕРАВЕНСТВО, неравен-
неравенство Фроше, неравенство информа-
ц п и,— неравенство в математич. статистике, устанав-
устанавливающее нижнюю границу риска в задаче статистич.
оценивания неизвестного параметра относительно квад-
квадратичной функции потерь.
Пусть распределение вероятностей случайного векто-
вектора A'—(.Y,, ... , Хп), принимающего значения в «-мер-
«-мерном евклидовом пространстве R", задается плотностью
вероятности р(х\в), х—{х1, ... , .г„)г, Э^всгК1, и пусть
в качестве оценки неизвестного скалярного параметра 6
используется статистика Т—Т(Х) такая, что
Ев Г = 8 + 6F),
где Ь(9) — нек-рая дифференцируемая функция, назы-
называемая с м е щ с н и е м статистики Т. В таком случае
при определенных условиях регулярности семейства
(р(ж|Э)}, одно из к-рых заключается в отличии от нуля
информационного количества Фи-
Фишера
имеет место неравенство Рао — Крамера
устанавливающее нижнюю границу для среднеквадра-
среднеквадратичной ошибки Eel?" — Э|2 всех оценок Т неизвестного
параметра В, имеющих одну и ту же функцию смещения
Ь(й)
(й).
В частности, если статистика Т является несмещенной
оценкой параметра G, то есть Ее Т=6, то из A) следует,
что
ОГ = Ее|Г-в|^г155. B)
Таким образом, в этом случае Р.— К. н. показывает
нижнюю границу для дисперсий несмещенных оценок Т
параметра 6, к-рая равна 1//(9), и, кроме того, Р.—
К. н. демонстрирует, что существование состоятельных
оценок связано с неограниченным ростом информацион-
информационного количества Фишера 7F) при п —>- ос. В случае
если в Р.— К. н. B) достигается равенство для какой-то
несмещенной оценки Т, то она является наилучшей в
смысле минимума квадратичного риска в классе всех
несмещенных оценок и наз. эффективной
о ц е н к о й. Напр., если Jf,, Х%, ... , Хп — незави-
независимые случайные величины, подчиняющиеся одному и
тому же нормальному закону Л'F, 1), то статистика
Т= — (Xj+...-j-Х,;) является эффективной оценкой не-
неизвестного математич. ожидания G.
В общем случае равенство в B) достигается тогда и
только тогда, когда семейство {р(х\В)} является экс-
ноненциальным, т. е. плотность вероятности случай-
случайного вектора X представима в виде
р (х j 9) =с (х) ехр {и F) ф (x) — v F)},
причем эффективной оценкой для параметра 0 в этом
случае является достаточная статистика Т—<р(Х).
В тех случаях, когда эффективные оценки не существу-
существуют, нижнюю границу дисперсий несмещенных оценок
следует уточнять в силу того, что Р.— К. н. дает лишь
нижнюю границу, к-р'ая не обязательно является точ-
точной нижней границей. Напр., если Xlt ... , Хп — не-
независимые случайные величины, подчиняющиеся одно-
одному и тому же нормальному закону N (а ", 1), то нижней
границей для дисперсий несмещенных оценок парамет-
параметра а является
п ~ «2 ~ п" '
в то время как
1 _ 9п«
Вообще, если в Р.— К. н. B) равенство не достигается,
то это пи означает, что найденная оценка не является
наилучшей, т. к. она может оказаться единственной не-
несмещенной оценкой.
Существуют различные обобщения Р.— К. н. на слу-
случай векторного параметра, а также на случай, когда
оценивается неизвестная функция от итого параметра.
Именно в этих случаях большую роль играют уточне-
уточнения нижней границы в Р.— К. н.
Неравенство A) было получено независимо друг от
друга М. Фреше (М. Frechet), Рао (С. R. Rao), Г. Кра-
Крамером (Н. Cramer).
Лит.: 11] Крамер Г., Математические методы статистики,
пер. с англ., 2 изд., М., 1975; [2] В а н дер Варден Б. Л.,
Математическая статистика, пер. с нем., М., 196A; [3] Б о л ь-
ш е в Л. Н., «Теория вероятностей и се применения», 19(il, т. В
Л» 3, с. 319—2В; 14] В h a I t а с h а г у у a A., «Sankhya», 1946,
v. 8, Л5 1, р. 1 — 141 1947 v 8 № 3, р. 201 — 18; 1948, V. 8, Л!» 4
р. 315 — 28. М. С. Никулин.
РАСКРОЯ ЗАДАЧА, задача рациональ-
рационального раскроя,— выбор такого размещения за-
заготовок в кусках материала, к-рое дает заготовки, как
правило, и требуемой комплектности при минимальном
расходе материала. В соответствии с особенностями в
технологии и организации раскроя различаются мате-
математич. модели рационального раскроя (р. р.) для мас-
массового и индивидуального производства: для прямых
(отрезки, прямоугольники, параллелепипеды) и фи-
фигурных заготовок, для случая кусков материала по-
постоянных размеров и формы и с разбросом формы или
размещения пороков (см. [1J). В зависимости от отрасли
производства и используемого оборудования учитыва-
учитываются ограничения на допустимые виды раскроев. С Р. з.
совпадает постановка нек-рых задач размещения грузов
в сушильных печах, в вагонах, на палубах судов.
В массовом производстве при поступлении одинако-
одинаковых кусков материала, если можно перечислить все
(--1. 2, ... , N доступные способы раскроя одного куска
материала на нек-рые из /-=1, ... , m нужных видов за-
заготовок, Р. з. сводится к решению задачи линейного
программирования: найти интенсивность применения
j-,-^0 каждого из раскроев, при к-рых z^.av—min и для
каждого / соблюдено условие ^,л;уу,-^6у, где а,-у— ко-
количество /-х заготовок в i-м раскрое, a bj — необходи-
мое на одно изделие количество этих заготовок. На
практике обычно нельзя перечислить все допустимые
раскрои. Упомянутую задачу линейного программиро-
программирования решают исходя из нек-рого набора допустимых
раскроев методом последовательного улучшения пла-
плана. Одновременно нередко изменяют список допущен-
допущенных к рассмотрению раскроев. На каждом шаге состав-
составляют (генерируют на ЭВМ) один из тех раскроев, к-рые,
согласно оценкам двойственной задачи линейного про-
программирования, способны улучшить план раскроя в
целом. В случае «линейного» материала (к-рый надо
кроить только по длине) упомянутое генерирование
осуществимо в приемлемое время средствами динамиче-
динамического программирования (см. [1], |2]). При раскрое ли-
листов на прямоугольники этот путь принципиально тоже
осуществим, но в реальных задачах может становиться
громоздким. Генерирование улучшающих раскроев
тогда ведут эвристич. алгоритмами: ограничиваются
целенаправленным составлением раскроев с участием
не более трех разнотипных заготовок (см. [2], |3|).
Сходно ставятся и решаются Р. з. при возможности
выбора одного или нескольких стандартных размеров
материала или при необходимости использовать имею-
имеющийся в наличии материал нескольких размеров (см.
|1]). В программах решения Р. з. для прямых и прямо-
прямоугольных заготовок учитываются ограничения, связан-
связанные со спецификой используемого оборудования (см.
|2], [3]). В программы включают составление подеталь-
подетальных норм и печать карт раскроя.
В массовом производстве часто используют линей-
линейный материал смешанных длин. Здесь Р. з. состоит в
выборе, раскроя очередного куска конкретной длины.
IS машиностроении целесообразно применять специаль-
специально рассчитываемую линейку, предписывающую раскрои
остатка, к-рый возникает после отрезания нескольких
заготовок |1]. В ш не ином производстве при составлении
настилов ткани из рулонов разной длины используют
также малые специализированные ЭВМ (см. [4]), решаю-
решающие только эту Р. з. В металлургии на прокатных
станах замеряют на ходу длину прокатного металла и,
па основе решения Р. з. на ЭВМ, осуществляют в авто-
матнч. режиме управление раскройным устройством
(см. |5]). В зарубежной стекольной промышленности
автоматизируют обнаружение пороков стекла и решают
на ЭВМ Р. з., подчиняя ее обходу пороков. В лесопи-
лесопилении бревна также имеют разброс размеров и формы,
но массовость задачи придает коэффициентам а,-у& (ха-
(характеризующим для Л--Й группы бревен выход досок /.-го
иида при установке пил Км способом) устойчивый ста-
шстнч. характер. Р. з. в лесопилении математически
поставлена давно (см. [ ]]) и эффективно решена в произ-
яодственных условиях (см. [6]).
Для фигурных заготовок в массовом производстве
есть вполне применимые программы выбора оптималь-
оптимального положения заготовок при однорядной и двухряд-
двухрядной штамповке из бесконечной ленты (см. [7], [8]), а
также при штамповке из лент, нарезаемых из заданного
листа. Остается эффективным также глазомерное состав-
[снпе наборов, включающих разные фигурные заго-
говкн раскроев с последующим решением задачи ли-
неппого программирования только на этом множестве
раскроев.
При индивидуальном производстве Р. а. требует вме-
вместо линейного программирования решения более слож-
сложной задачи целочисленного программирования, снова
с неявно заданной матрицей коэффициентов, поскольку
все допустимые раскрои не перечислены. Для линейных
и прямоугольных заготовок запрограммированы прак-
практичные эвристич. алгоритмы приближенного решения
этой задачи (см. |2j).
Для фигурных заготовок при индивидуальном произ-
овдстве имеются различные разработки, но цока нет
A983) достаточно удовлетворительных приемов решения
Р. з. на ЭВМ. Надобность в таком решении ощущает
и первую очередь судостроительная промышленность.
Довольно эффективны диалоговые алгоритмы, при к-рых
глазомерные возможности человека сочетаются с пере-
переносом на ЭВМ труда по воспроизведению поправок,
обсчету и оформлению возникающих вариантов.
Лит.: [1] Канторович Л. В., 3 а л г а л л е р В. А.,
Рациональный раскрой промышленных материалов, 2 изд.,
Новосиб., 1971; [2] Мухачева Э. А., «Кузн.- штамп, про-
из-во», 1979, № 6, с. 14—17; [3] Математическое обеспечение рас-
расчетов линейного и прямоугольного раскроя, Уфа, 1980 (Тр. Все-
Всесоюзного науч. семинара); [4] Г а л ы н к е р И. И., С а ф р о-
н о в а П. В., Механическая технология производства одежды,
М., 1977: [5] Э п ш т е й н В., Л а г у т и и А., «Материально-
техн. снаож.», 1976, К* 11, с. 77—81; [6] С о б о л е в И. В., Уп-
Управление производством пиломатериалов, Петрозаводск, 197ti;
[7] Белякова Л. Б., Рябинина Н. О., «Кузн.- штамп,
произ-во», 1977, Л'в 11, с. 25 — 28; [8] С т о >г н Ю. Г., Пана-
сен к о А. А., Периодическое размещение геометрических
объектов, К., 1978. В. А. Залгаллер, Л. В. Канторович.
РАСПАДА РАЗРЫВА МЕТОД — один иа методов
численного решения задач математич. физики. Термин
«распад разрыва» привнесен из газовой динамики. Он
означает процесс, возникающий при соприкосновении
двух масс газа с различными состояниями газодннамич.
величин (плотности, скорости, давления, внутренней
энергии). Применительно к численному решению задач
газовой динамики метод заключается в следующем.
В области, где численно решается задача, строится раз-
разностная сетка (см. Подвижных сеток метод). Прини-
Принимается, что в пределах каждой ячейки разностной сетки
газодинамич. величины постоянны и равны нек-рым
средним значениям, полученным из имеющегося их
распределения. Затем на каждой из границ ячеек сетки
решается задача о распаде разрыва применительно к со-
состоянию газов в двух соседних ячейках. Ее решение
достаточно просто алгоритмизируется для двух полу-
полубезграничных, соприкасающихся по плоской поверх-
поверхности |-азов, в каждом из к-рых распределение газоди-
газодинамич. величин постоянно. Значения газодинамич. ве-
величин из решения этой задачи, отвечающие пространст-
пространственно-временному положению границы, разделяющей
ячейки сетки, принимаются за значения на соответст-
вующей границе ячейки. Это приближение справедливо
но крайней мере на промежутке времени At, пока ни
одно из попарных взаимодействий на границах сосед-
соседних ячеек не будет влиять друг на друга. Рассчитав
потоки по значениям газодинамич. величин на границах
ячеек и зная исходное ступенчатое распределение на
момент t0, из балансов массы, импульса, полной энергии
по каждой ячейке разностной сетки рассчитывается сту-
ступенчатое распределение на момент to\ At. Сама разност-
разностная сетка может перестраиваться в ходе расчета. Ее
движение может задаваться независимо или опреде-
определяться в соответствии с особенностями решаемой зада-
задачи. Уполшнутое выше ограничение на временной шаг
At является по своей сути условием устойчивости
описанной схемы расчета.
Изложенный подход к построению вычислительных
алгоритмов обобщается применительно к решению задач
гидродинамики с теплопроводностью, теории упругости
и др. Благодаря наглядной физич. интерпретации,
адекватности граничных условий исходной дифферен-
дифференциальной постановке и универсальности, Р. р. м. полу-
получил широкое распространение в практике численного
решения задач математич. физики.
Лит.: Ш Л а и Д а у Л. Д., Л и ф ш и ц Е. М., Механика
сплошных сред, 2 изд., М., 1У.">4; [2] Численное решение много-
многомерных задач газовой динамики, М., 197U. А. В. Забродин.
РАСПИСАНИЙ ТЕОРИЯ — ветвь прикладной мате-
математики (раздел исследования операций), изучающая ма-
математич. постановки и методы решения задач оптималь-
оптимального упорядочения и согласования выполнения нек-рых
действий во времени. К Р. т. относятся вопросы, свя-
занные с построением оптимальных расписаний (кален-
(календарных планов, графиков) выполнения конечных (пли
повторяющихся) комплексов операции. Область при-
приложения результатов Р. т. включает в себя управление
производством, транспортам, строительством, вычисли-
вычислительными системами и др.
Исследуемые в Р. т. задачи часто формулируются
как задачи оптимизации процесса обслуживания ко-
конечного множества требований в системе, содержащей
ограниченные ресурсы. Конечное множество требова-
требований отличает модели Р. т. от сходных с ними моделей
массового обслуживания теории, где в основном рас-
рассматриваются бесконечные потоки требовании. В ос-
остальном эти теории имеют близкие отправные точки.
В Р. т. для каждого требования задается момент его
поступления в систему. Находясь в системе, требование
должно пройти одну или несколько, в зависимости от
условий задачи, стадий обслуживания. Для каждой
стадии указываются допустимые наборы ресурсов и
длительности обслуживания требования при использо-
использовании этих наборов. Оговаривается возможность пре-
прерываний процесса обслуживания отдельных требова-
требований. Ограничения на очередность обслуживания
задаются, как правило, транзитивным, антирефлексив-
антирефлексивным бинарным отношением. Алгоритмы расчета ха-
характеристик больших частично упорядоченных мно-
множеств требований составляют основное содержание
раздела Р. т., к-рый носит название теории сетевого
планирования. Иногда в моделях Р. т. указываются
длительности переналадок при переходе от обслужива-
обслуживания одного требования к обслуживанию следующего
требования и др. условия.
Следует отметить, что исходя из практич. направ-
направленности Р. т. не стремится к унификации терминоло-
терминологии: наряду с термином «требование» употребляются,
напр., термины «работа», «операция» и т. д. По той же
причине по-разному формально определяется расписа-
расписание обслуживания требований. В общем случае под
расписанием можно понимать однозначное отображе-
отображение, ставящее в соответствие каждому требованию в
каждый момент времени определенный набор ресурсов.
В качестве критериев обычно выбираются критерии
суммарного и максимального штрафов, имеющие сле-
следующий вид:
= 2
neN
здесь ta(s) — момент завершения обслуживания требо-
требования а в расписании .?, Л' — множество требований»
а Фа(-) — неубывающие функции, именуемые функция-
функциями штрафа. В практич. постановках функции штрафа
имеют обычно конкретный экономим, смысл (напр.,
омертвление оборотных средств, ущерб от потери по-
потребителей и т. д.). Рассматриваются многокритери-
многокритериальные задачи.
Помимо детерминированных изучаются и стохастич.
модели. В этом случае обычно рассматривается либо
задача минимизации математич. ожидания значения од-
одного из используемых в детерминированных постанов-
постановках критериев, либо задача минимизации вероятности
нек-рого события. Таким событием может быть, напр.,
запаздывание в обслуживании требований относительно
заданных сроков.
Основным подходом к решению детерминированных
задач Р. т. является общая алгоритмич. схема последо-
последовательного анализа вариантов. Именно на этом пути
удалось решить наиболее адекватные практике задачи,
отработать оптимизационные процедуры планирования
работ во времени (календарное планирова-
планирование), реализуемые в автоматизированных системах
управления. Вместе с тем для ряда детерминирован-
детерминированных задаа получены быстродействующие решающие
правила, доказаны необходимые и достаточные условия
их применимости, предложены эффективные приемы,
имеющие значение для дискретной оптимизации в це-
целом (см., напр., [1] — [4]). При разработке таких опти-
оптимизационных алгоритмов находят применение, в част-
частности, результаты графов теории и математич. програм-
программирования. Опубликованные в нач. 70-х гг. 20 в. рабо-
работы по теории Л'Р-полноты привели к появлению много-
многочисленных исследовании сложности задач Р. т. (см.,
напр., [5]). Результаты этих исследований повысили
интерес к алгоритмам приближенного решения и оцен-
оценке точности таких алгоритмов (см., напр., [6]). Для
многих подходов и приемов решения задач дискрет-
дискретной оптимизации Р. т. представляет легко формули-
формулируемые практически значимые «пробные камни» —
примеры.
Лит.: [1] Т а н а е в В. С, Ш к у р б а В. В., Введение в
теорию расписаний, М., 1975; [2] К о н в е й Р. В., Макс-
Максвелл В. Л., Миллер Л. В., Теория расписаний, пер. с
англ., М., 1975; [3] Computer and job-shop scheduling theory,
N. Y.—[a. o.], 1976; [4] G о n z a 1 e z M. J., «А С Т Computing
Surveys», 1977, v. 9, .№ 3, p. 173—204; L5] Lenstra J. K.,
R i n n о о у К а п А. Н. G., «Operations Research», 1978 v. 26,
№ 1, p. 22—35; [til G а г е у M. R., Graham R.L., John-
eon D. S., там же, р. 3 — 21. Я. Б. Зиндетр, В. В. Шкурба.
РАСПОЗНАВАНИЕ ОБРАЗОВ — раздел математнч.
кибернетики, разрабатывающий принципы и методы
классификации, а также идентификации предметов,
явлений, процессов, сигналов, ситуаций — всех тех
объектов, к-рые могут быть описаны конечным набором
нек-рых признаков или свойств, характеризующих
объект.
Описание объекта представляет собой n-мерный век-
вектор, где п — число признаков, используемых для ха-
характеристики объекта, причем j-я координата этого
вектора равна значению i-ro признака, i=l, ...,«.
В описании объекта допустимо отсутствие информации
о значении того или иного признака. Если необходимо
расклассифицировать предъявленные объекты по не-
нескольким группам (образам) только на основе их
описаний, причем число групп не обязательно известно,
то такая задача Р. о. наз. задачей таксоно-
таксономии (кластера, обучения без учите-
учителя, самообучения). Собственно для задач
Р. о. (о б у ч е н и я с учителе м), кроме описания
объектов, необходимы дополнительные сведения о при-
принадлежности этих объектов к тому или иному классу
(образу). Количество классов конечно и задано. Классы
могут пересекаться.
Совокупность описаний объектов, для к-рых известны
образы, к к-рым они принадлежат, образует т. н.
обучающую последовательность (на-
(набор эталонов). Основная задача Р. о. заклю-
заключается в том, чтобы исходя из обучающей последова-
последовательности определить класс, к к-рому принадлежит
описание нек-рого объекта, подвергаемого классифика-
классификации или идентификации. К такой схеме приводится лю-
любая задача принятия решений, если только процесс
принятия решения базируется в основном на изучении
ранее накопленного опыта.
Прикладные задачи, решаемые методами Р. о., воз-
возникают при идентификации машинописных и рукопис-
рукописных текстов, идентификации фотоизображений, при
автоматич. распознавании речи, в медицинской диагно-
диагностике, при геологич. прогнозировании, прогнозирова-
прогнозировании свойств химич. соединений, оценке экономических,
политических, производственных ситуаций, при клас-
классификации социологич. материала и т. и. Для решения
¦.(тих задач накоплено большое число т.н. эвристи-
эвристических алгоритмов распознавания,
ориентируемых на специфику каждой конкретной за-
задачи. Кроме того, на основе нек-рых интуитивных
принципов строятся модели алгоритмов
р а с,п о з.н а в а н и я, т. е. семейства:алгоритмов для
решения классификационных задач. Наиболее употре-
употребительны следующие модели: модели, построенные с ис-
использованием принципа разделения, задающие класс
поверхностей, разделяющих образы; модели, построен-
построенные на принципе потенциалов; модели вычисления
оценок (голосования); структурные модели; статистич.
модели.
На уровне модели ставится задача отыскания экстре-
экстремального но качеству алгоритма распознавания (модель
вычисления оценок). О качестве работы распознающего
алгоритма обычно судят по результатам работы алго-
алгоритма на нек-ром тестовом наборе объектов (контроль-
(контрольная последовательность), для к-рого исследователю
априори известна достоверная классификация. При
построении общей теории распознающих алгоритмов
наиболее полные результаты получены в рамках алгеб-
раич. подхода. Распознающий алгоритм представляется
в виде произведения распознающего оператора и решаю-
решающего правила. Введение над распознающими операто-
операторами операций сложения, умножения, умножения на
скаляр позволяет доказать существование в рамках
нек-рого алгебраич. расширения исходного набора рас-
распознающих операторов такого распознающего алгорит-
алгоритма, к-рый обладает экстремальным качеством на любой
контрольной последовательности.
К задачам Р. о. относятся также задачи минимиза-
минимизации описания исходных объектов, выделения информа-
информативных признаков.
Лит.: [1] Журавлев Ю. И., «Проблемы кибернетики»,
1978, в. 33, с. 5—68; [2] Айзерман М. А., Б р а в е р-
ман Э. М., Розоноэр Л. И., Метод потенциальных функ-
функций в теории обучения машин, М., 1970; [3] В а п и и к В. Н.,
Червоненкис А. Я., Теория распознавания образов, М.,
1974; [4] Ф у К. С, Структурные методы в распознавании об-
образов, пер. с англ., М., 1977. П. П. Кольцо».
РАСПРЕДЕЛЕНИЕ — то же, что обобщенная функ-
функция.
/''-РАСПРЕДЕЛЕНИЕ — см. Фишера f'-распределе-
f'-распределение.
t-РАСПРЕДЕЛЕНИЕ — см. Стъюдента распределе-
распределение.
Т'2-РАСПРЕДЕЛЕНИЕ — см. Хотеллипга Т^-распре-
деление.
W'-РАСПРЕДЕЛЕНИЕ — см. Уишарта распределе-
распределение.
^-РАСПРЕДЕЛЕНИЕ — см. Фишера z-распределение.
В-РАСПРЕДЕЛЕИИЕ — см. Бета-распределение.
Г-РАСПРЕДЕЛЕНИЕ — см. Гамма-распределение.
^-РАСПРЕДЕЛЕНИЕ — см. «Хи-квадрат» распре-
распределение.
(¦^-РАСПРЕДЕЛЕНИЕ — см. «Омега-квадрат» рас-
распределение.
РАСПРЕДЕЛЕНИЕ ВЕРОЯТНОСТЕЙ — одно из
основных понятий вероятностей теории и математиче-
гкой статистики. При современном подходе в качестне
математич. модели изучаемого случайного явления бе-
берется соответствующее вероятностное пространство
{Q, S, Р}, где Q — множество алементарных событий,
S — выделенная в Q а-алгебра подмножеств, Р — опре-
определенная на S мера со свойством Р(Я)=1 (вероятност-
(вероятностная мера).
Любую такую меру на {Я, S} и называют распре-
распределением вероятностей (см. [1]). Однако
)то определение, являющееся основой аксиоматики
Л. Н. Колмогорова A933), при последующем развитии
теории оказалось чрезмерно общим и было, с целью
исключения нек-рых «патологических» случаев, заме-
заменено более ограничительным, напр, требованием «со-
«совершенности» вероятностной меры Р (см. [2], особенно
добавление к англ. переводу [3] этой книги). От Р. в.
в функциональных пространствах требуют обычно вы-
выполнения нек-рого свойства регулярности, формули-
формулируемого как сепарабельность, но допускающее форму-
лировку и в других терминах (см. Сепарабельний про-
процесс, а также D]).
Р. в., встречающиеся в большинстве конкретных за-
задач теории вероятностей и математич. статистики, весь-
весьма немногочисленны. Все они давно известны и связаны
с основными вероятностными схемами [5]. Они описы-
описываются или вероятностями отдельных значений (см.
Дискретное распределение) или плотностями вероятно-
вероятности (см. Непрерывное распределение). В необходимых
случаях для них составлены таблицы [6].
Из этих основных Р. в. одни связаны с повторениями
независимых испытаний (см. Биномиальное распределе-
распределение, Геометрическое распределение, Полиномиальное
распределение), а другие — с соответствующими этой
вероятностной схеме предельными закономерностями,
возникающими при неограниченном возрастании числа
испытаний (см. Нормальное распределение, Пуассона
распределение, Арксинуса распределение). Однако эти
предельные распределения могут возникать и как точ-
точные: в теории случайных процессов (см. Винеровский
процесс, Пуассоновский процесс) или как решения урав-
уравнений, возникающих в т. н. характеризационных тео-
теоремах (см. также Нормальное распределение, Показа-
Показательное распределение). Равномерное распределение ве-
вероятностей, принимаемое обычно как математич. выра-
выражение равновозможности соответствующих исходов
опыта, также может быть получено как предельное
(напр., при приведении по какому-то модулю суммы
большого числа случайных величин или каких-либо
других случайных величин с достаточно гладкими «рас-
«расплывающимися» распределениями). Из упомянутых
выше основных Р. в. получают другие Р. в. с помощью
функциональных преобразований рассматриваемых слу-
случайных величин. Так, напр., в математич. статистике из
нормально распределенных случайных величин полу-
получают величины, имеющие «хи-квадрат» распределение,
нецентральное «хи-квадрат» распределение, Стъюдента
распределение, Фишера F-распределение и др.
Важные классы распределений были открыты в связи
с развитием асимптотич. методов теории вероятностей
и математич. статистики (см. Предельные теоремы, Ус-
Устойчивое распределение, Безгранично делимое распреде-
распределение, «Омега-квадрат» распределение).
С теоретической и прикладной точек зрения важно
умение определить понятие близости распределений.
Совокупность всех Р. в. на {Q, S] может быть различ-
различными способами превращена в топологич. пространство.
При этом основную роль играет слабая сходимость Р. в.
(см. Распределений сходимость). В одномерном и конеч-
конечномерном случаях основным средством изучения сходи-
сходимости Р. в. является аппарат характеристических
функций.
Часто полное описание Р. в. (напр., при помощи
плотности вероятности или распределения функции)
заменяют заданием небольшого числа характеристик.
Из этих характеристик наиболее употребительны мате-
математическое ожидание (среднее значение), дисперсия,
медиана и моменты в одномерном случае. О числовых
характеристиках многомерных Р. в. см. Корреляция,
Регрессия.
Статистическим аналогом Р. в. является эмпирическое
распределение. Эмпирич. распределение и его характе-
характеристики могут быть использованы для приближенного
представления теоретического Р. «. и его характеристик
(см. Оценка статистическая). О способах измерения
степени согласия эмпирич. распределения с гипотети-
гипотетическим Р. в. см. Статистических, гипотез проверка,
Непараметрические методы статистики.
Лит.: [1] Колмогоров А. Н., Основные понятия тео-
теории вероятностей, 2 изд., М., 1974; [3] Гн еден к о Б. В.,
Колмогоров А. Н., Предельные распределения для сумм
независимых случайных величин, М.— Л., 1949; [3] и х ж е,
Limit distributions for sums of independent random variables,
Camb. Mass. 1954; [4] Прохоров Ю. В., в кн.: Pi-ос, fourth
Berkeley symposium on mathematical statistics and probability,
V. 2, Berkeley — Los Ang., 1961, p. 4A,4— 19; |5] Ф с л л е р В.,
Введение в теорию вероятностей и ее приложения, пер. с англ.,
2 изд., т. 1—2, М., 1967; 16] Большее Л. Н., С м и р-
но в Н. В., Таблицы математической статистики, 2 изд., М.,
1968; [7] Гнсденко В. В., Курс теории вероятностей, Г>
изд., М., 1969; [8] Крамер Г., Математические методы ста-
статистики, пер. с англ., 2 изд., М., 1975: [Я] Н е в ё Ж., Математи-
Математические основы теории вероятностей, пер. с франц., М., 196!).
Ю. В. Прохоров.
РАСПРЕДЕЛЕНИЕ ДРОБНЫХ ДОЛЕЙ — распреде-
распределение в единичном интервале [0.1) дробных долей {а,-}
последовательности действительных чисел а,-, / =
=1,2, . . . Последовательность дробных долей {«/},
/=1,2, . . . , на.1), равномерно распределен-
распределенной в и н т.е р в а л е @,1), если для каждого интер-
интервала [а,6)с[0,1) имеет место равенство
lim Фя (ц, bK_i a
п -* во п '
где ф„(о, ft) — число первых п членов {ау}, 1</<гс,
последовательности {ау}, /=1,2, . . . , попавших в
|й, ft). При атом последовательность чисел а,-, /=
=1,2, ¦ ¦ . , Ha:i. равномерно распределен-
распределенной по мод у л ю 1.
Критерий В е й л я (см. [11) для равномерно
Р. д. д.: бесконечная последовательность дробных долен
{oLj}. }—i, 2. ... , равномерно распределена в единичном
интервале [0, 1) тогда и только тогда, когда
f (х) clx
для любой интегрируемой по Риману на отрезке 0<:.?<:
<:1 функции 1{х). Это утверждение эквивалентно сле-
следующему. Для того чтобы последовательность а;-, /—
~1, 2, была равномерно распределена по модулю 1,
необходимо и достаточно, чтобы
lim L у" e-nimai =0
для каждого целого тфЧ. Из критерия Вейля и его
оценок тригонометрии, сумм
следует, что если хотя бы один ил коэффициентов aSl
l<s</i-, многочлена
/(x) = afex*-)~.. ,+агх
иррационален, то последовательность дробных долей
{/(п)}, » — 1, 2, ... , равномерно распределена в интер-
интервале [0, 1).
Понятию равномерного Р. д. д. {ay}, /=1, 2, ... ,
можно придать количественный характер, если ввести
в рассмотрение величину
Dn= sup
0 < а < i<
называемую отклонением первых п членов последова-
последовательности {а,}, /—1, 2, ... (см. [2], [3)).
Лит./ ll] W с у 1 II., «Math. Ann.», 1916, Bd 77, S. .413—52;
12] В и н о г р я д о в II. М., Метод тригонометрических сумм л
|е'ории чисел. М., 1971; [3] X у а Ло - к е н, Метод тригономет-
тригонометрических сумм и его применения в теории чисел иер. с нем.,
\1., 1064. С. А. Степанов.
РАСПРЕДЕЛЕНИЕ ДРОБНЫХ ДОЛЕЙ МНОГО-
МНОГОМЕРНОЕ — распределение в re-мерном единичном кубе
Е, 0<г,-<1, г-=1, 2, ... , и, дробных долен {Pj}-~
=({^i')}, •¦• , {г(/'}) последовательности точек /г-люр-
иого евклидова пространства Pj—{x['\ ... , х'/'), ;'=1,
2, ... . Здесь { } — знак дробной доли.
Последовательность дробных долей {Р;}, }— 1, 2, ... ,
иаа. равномерно распределенной в
единичном «-мерном кубе Е, если для каждого прямо-
прямоугольника V, содержащегося в ?\ имеет место равенство
lim Ф»«(V) __ | у i
т - > ее т ' ''
гдефга(Г)—число точек среди первых т членов после-
последовательности {Pj}, попавших в V, и |Г| — мера пря-
прямоугольника V.
Последовательность Р;-, /=1, 2, ... , точек и-мерного
пространства наз. равномерно распреде-
распределенной по модулю 1, если соответствующая ей
последовательность дробных долей {Р/} равномерно
распределена в единичном кубе Е.
Критерий Вейля для Р. д. д. м. Последовательность
{Pj}, j Л, 2, ... , равномерно распределена в единичном
кубе Е тогда и только тогда, когда
lim — \\ е" ' '':
для каждого набора целых чисел (аъ а2, ... , ап)
0. . .0). Частным случаем этой теоремы является Вейля
критерий для равномерного распределения по модулю
1 последовательности действительных чисел. Из кри-
критерия Вейля следует теорема Кронекера:
пусть 8j, 82, ... , 6„, 1 — действительные числа, линей-
линейно независимые над полем рациональных чисел, а1(
а2, ... , а„ — произвольные действительные числа и
N, е — положительные числа; тогда существуют целые
т и рх, р2, ... , рп такие, что
т > Лг, | тв; — Pi — а; [ < 8
для всех i=l, 2, ... , п. Иначе говоря, последователь-
последовательность т%—(т*дг. шбо, ... , твп), гя-=1, 2, ... , равномер-
равномерно распределена по модулю 1.
Лит.: [1] К а с с е л с Д ж. В. С, Введение в теорию дио-
фантовых приближений, пер. с англ., М., 1901.
С. А. Степанов,
РАСПРЕДЕЛЕНИЕ ПРОСТЫХ ЧИСЕЛ — раздел
теории чисел, в к-ром изучаются закономерности рас-
распределения простых чисел (п. ч.) среди натуральных
чисел. Центральной является проблема наилучшего
асимптотич. выражения при х —>- оо функции л (х),
обозначающей число п. ч., не превосходящих х, а также
функции л (х; d, I), обозначающей число п. ч., не пре-
превосходящих ,т в арифметич. прогрессии dn-\-l при 1<;
•*il^.d, и--Q, I, 2, ... , для растущих вместе с х значе-
значений d.
Основная теорема арифметики:
каждое натуральное число д>1 является или п. ч. или
единственным (с точностью до перестановки сомножи-
сомножителей) произведением п. ч.
(т. н. каноническое представление
числа ?;), где />,, ... , рь — различные и. ч., пг, ...
... , я/, — натуральные числа. Таким образом, п. ч,
сеть базис му.'и.тпи.чнь'ативного построения ряда нату-
натуральных чмсе.1. )то, однако, непосредственно ничего
не говорит о величине я (х).
Для нахождения п. ч. от 1 до г служит известный с
Я в. до тт. а. метод Эратосфена решета. Решето Эрато-
сфена является простейшей процедурой получения по-
последовательности п. ч. Однако аналитпч. формула ре-
решета
где d пробегает делители произведения всех п. ч. <^У~х,
v (d) — число простых делителей d, [и] — целая часть
и, непригодна для изучения л (а-) при ж—>-оо.
Рассмотрение последовательности п. ч. от 1 до х:
2, 3, 5, 7, 11, 14, ..., р A)
показывает, что с увеличением х она становится в сред-
среднем все более редкой. Существуют сколь угодно длин-
длинные отрезки ряда натуральных чисел, среди к-рых нет
ни одного п. ч. Напр., п—1 натуральных чисел вида
п\-\-2, ... , н\~\-п для любого iC^2 являются составными
числами. В то же время в A) встречаются и. ч. такие,
как 8004119 и 8004121. разность между к-рыми равна 2
(п. ч.— близнецы). Проблема поведения л (х) при
х—>- зо является одной из наиболее трудных и интерес-
интересных проблем теории чисел.
Первый результат о величине л (х) — т е о р е м а
Е в к л и д а: л (х) -*¦ оо при х —*¦ оо. Л. Эйлер (L. Eu-
ler, 1737. 1749, см. [1]) ввел функцию
и показал, что при s>l
где ряд распространяется на все натуральные числа,
а произведение на все п. ч. Тождество C) и его обобще-
обобщения играют фундаментальную роль в теории Р. п. ч.
Исходя из него, Л. Эйлер доказал, что ряд ^^/р и про-
произведение ТТ A -) по простым/) расходятся. Это—
новое доказательство бесконечности числа и. ч. Более
того. . I. Эйлер установил, что п. ч. «много», ибо
и, в то же время, почти все натуральные числа являют-
являются составными, т. к.
л (х) х'1 —>• 0 при х - -у оо.
Далее значительного успеха достиг If. Л. Чебышев
A851—52, см. [2)). Он доказал, что:
1) для любых »(>0, М >0 есть последовательности
х~*¦ оо, у—*- оо, для к-рых
л (х)—Их < Мх log~w х,
л (.(/) —li у >—Му log- у;
2) если существует предел частного л (х) log x!x при
х —>- оо, то он равен 1.
Тем самым впервые был решен вопрос о существова-
существовании простой функции
J 2 1°S u
Юк.т ' log* .г '•¦•IV -' • lQgr
к-рая служит наилучшим приближением для я (.г).
Затем II. Л. Чебышев установил истинный порядок
роста л (л), т. е. существование постоянных а>0, А >0
таких, что
ат^Ь<л{х) < Аш~^- D)
приче.\г, а=-(),92... , Л —1,05... для j-^.r0. Он же до-
доказал, что при любом ii^'i в интервале (п, 2п) содер-
содержится по крайней .мере одно и. ч. (п о с т у л а т
Бертрана). В основе вывода неравенств D) лежит
тождество Ч е бы ш е в а
в к-ром введенная П. Л. Чебышевым функция^ опреде-
определяется суммой по степеням р'", m—i, 2, ... , п. ч. р:
Именно, комбинация log \u]\ для л^30 в форме
вследствие E), дает тождество
F* Н = ф (.г) -!)¦ (^-) + i|> (-
из к-рого следует, что
Отсюда, вследствие асимптотич. формулы Стирлинга
для п\, вытекает аналог неравенств D) для ij;(.r), из
к-рых частичным суммированием получаются неравен-
неравенства D). Функция Чебышева \^(.г) оказалась более удоб-
удобной, чем п(х), при изучении Р. п. ч., поскольку наи-
наилучшим приближением ее является сам аргумент х. По-
Поэтому обычно сначала рассматривают ip(x), а затем час-
частичным суммированием получают соответствующий ре-
результат для я (х).
Принцип Римана. В 1859—60 Б. Риман (В. Riemann,
см. [3]) рассмотрел введенную Л. Эйлером для s>l
функцию Z, (s) как функцию комплексного переменного
s~a-\-it, где a, t — действительные переменные, опре-
определяемую рядом B) при О">1 (см. Дзета-функция),
и обнаружил исключительную важность этой функции
для теории Р. ц. ч. В частности, он указал выражение
разности я (.г)—li x через ,т и нули функции ?(«), лежа-
лежащие в полосе 0<:ст<1. к-рыс наз. нетривиаль-
н ы ми нуля м и функции ? (s).
Вместо формулы Римана обычно используется более
простой конечный ее аналог для ty(x), доказанный
(наряду с формулой Римана) X. Мангольдтом (Н. Man-
Mangold t, 1895). Именно, для .с>1
l
lv \<T
где |>=|i+i'V пробегает нетривиальные нули ?(s), T —
любое -:У1.
Носко. и>ку
формула F) показывает, что величина разности г)з(г)—х
в главном определяется величиной р" (действительной
частью самых правых нулей р). В частности, если t,(s)^=
ФО правее вертикали а=0, 1/.2<0<1, для функций
•ф(а-), -!(¦'¦) справедливы следующие асилштотич. выра-
выражения:
¦ф (х)=х-\-0 (хв ]og2x),
Наоборот, из этих соотношений следует, что ?()
для а:>6. Если справедлива гипотеза Римана, т. е.
все нетривиальные нули ? (s) лежат на одной прямой
o"~V2, тогда асимитотнч. закон распределения п. ч.
должен илють вид
1)з (x)=r-\-O(V'^log2x),
n(x)=\i.c-L-O (Y~x\ogx).
Причем эти соотношения существенно усилить нельзя,
т. е. существую! последовательности х—>-х, у -^ оо
такие, что
Я .Г -.
^У)-^У> + У)Ч^^1
Таким образом, согласно принципу Римана проблема
асимптотич. выражения функции Р. п. ч. if (я), я (j;)
сводится к прцбледге границы действительной части не-
нетривиальных нулей функции ?(.<). До сих нор A983),
однако, не удалось найти какое-либо постоянное 8,
161 с yc.nu:iie\i р_>0. Искодтя граница для р
оказывается связанной с мнимой частью у нулей р,
причем так, что прямая а=1 является для нее асимп-
асимптотой.
Методы Адамара и Балле Пуссена. Асимптотич. закон
Р. п. ч. в простейшем виде
был получен в 1896 независимо Ж. Адамаром (J. Hada-
mard) и III. Балле Пуссеном (Ch. La Vallee Poussin),
к-рые доказали, что ?(l+it)=^0, т. е. что на прямой а=Л
нет нулей функции ?(s). В 1899 Ш. Балле Пуссен
показал, что 1,(<з+и)фЬ в области а>1— c/log(|/| + 2).
Тем самым было доказано, что
п(х) — \\х-\-0 (хехр ( — 6
при постоянных а>0, Ь>0.
Были получены также дальнейшие расширения об-
области свободной от нулей функции ?(s) (см. [4] — [12]).
Метод Вейля — Литлвуда. Существует определенная
связь между ростом модуля функции ? (s) и ее нулями
вблизи прямой а=1. Именно, если ?(s)<exp (ф (t)) при
1—0(г)<:сг<:2, где q>(t), 1/0@ — положительные неубы-
неубывающие функции t^O такие, что 6(?)<1, ф (t) —*¦ оо при
t —*¦ оо и <р (г)/0 (<)<^ехр ф(<), то существует постоянная
Л такая, что ?(s)=^0 в области
При этом для оценки ?(«) используется частная сумма
ее ряда B), к-рая сводит вопрос к оценке тригономет-
рич. сумм вида
Sexp (it log n).
V < Л < U
За счет оценок таких сумм по Вейля методу Дж. Литл-
вуд (J. Littlewood, 1921) показал, что для t>A ?(«)<
<log5< при a^l—log2log //log t и, следовательно, ?(.?) /=
=^=0 в области
а Эг 1 — Л log log г/log t.
Отсюда
я (x) = lix + O (x exp (— а у log ^ log log.r)).
Метод Виноградова. Дальнейший прогресс в оцен-
оценках п(х), i|) (х) связан с созданием И. М. Виноградовым
(см. Виноградова метод) нового, значительно более
мощного метода оценок тригонометрич. сумм. При по-
помощи этого метода им в 1938 было доказано, что t(s)?=O
при
— c/log3/4(| t | + 2) log3/4log (| t | + 2)
и соответственно что
л (i) = lix + O (.г ехр ( — a \ogi!'x log~3/?log.r)).
В 1858 И. М. Виноградов и другие (см. [6]— fll])
показали, что t,(s)^O при
Это пока A983) лучший результат о границе нетриви-
нетривиальных нулей функции ?(s), к-рому отвечает лучший
результат в Р. п. ч.:
л(х) = Пх + О(хехр( — a Iog3/5.r log" 1/5 log x)),
¦ф (а-) =т+О (т ехр ( — h Iog3/5.rlog~1/6log.r)).
Из асимптотики л (х) следует асимптотика 7г-го простого
числа рп~п log п. Показано (см. [21]) также, что />„>
>п log п для всех п^1 и что для 17100 wo
—^ <п(х) < logx_
для
Юк х + 2 < Л ^ < 1ол.т-4 '
Элементарные методы. Так называют методы изуче-
изучения асимптотик, закона Р. п. ч., не опирающиеся на
принцип Римана (нули дзета-функции) и, вообще, на
какие бы то ни было положения теории функций комп-
комплексного переменного. Впервые такой метод открыли в
1948 А. Сельберг [16] и П. Эрдёш [17]. В основе лежит
элементарная формула Сельберга
(-?-) А (п)=2х logx + O (x). G)
Дальнейшая задача состоит в том, чтобы из асимптотики
в среднем для г|)(и) в виде G) вывести асимптотику ij) (,r).
Это можно сделать по-разному, но общим во всех слу-
случаях является использованием факта медленного коле-
колебания функциит)) (см. [18]). В 1962 Э. Бомбьери (Е. Вот-
bieri) и Э. Вирзинг (Е. Wirsing) доказали, что при лю-
любом фиксированном А >0
¦ф (х)=х-\-0 (xlog-^x).
В 1970 X. Дайамонд и Дж. Стейниг (см. [19]) существен-
существенно усовершенствовали идею и технику оценок элемен-
элементарного метода и доказали, что для .т^ехр ехр 100
| г|) (х) —х | <х ехр ( — log1//7x log log x).
Наконец, в 1973 А. Ф. Лаврик и А. Ш. Собиров [20]
показали, что при элементарном методе доказательства
справедлива теорема: для ж^ехр ехр 10:i
| ij; (x)—х\ < х ехр (— Iog1//f'x log log x).
Этот результат представляет пока лучшее достижение
элементарного метода в изучении Р. п. ч., хотя он не-
несколько слабее того, к-рый получен аналитич. методом,
в принципе эти результаты близки между собой.
Разность между простыми числами. Существует мно-
много вопросов Р. п. ч., касающихся разности между п. ч.
Среди них выделяются вопросы поведения dn=pn + 1—
—ри — разности между соседними п. ч.; проблема ко-
количества п. ч. близнецов, или, более общо, пар п. ч.
разности 2к и, вообще, числа систем р, р-\-и^, ... , р+ит
из т-\-1 п. ч., лежащих на отрезке [1, х].
С помощью гипотезы Римана доказано, что dn<<
<^]^p,,log p,t; а нек-рые эвристич. рассуждения показы-
показывают, что, вероятно, справедлива оценка dn^log-pn.
Лучшей к 1983 является оценка dn<g,pn, где б=-^+е,
е>0, полученная М. Н. Хаксли (М. N. Huxley, 1973)
по методу большого решета. Что касается пар п. ч.
разности, равной 2 (близнецов), или разности, равной
1к, к~\, 2, ... , то до сих пор A983) неизвестно, являет-
является количество их бесконечным или нет. Пусть лк(х)
есть число пар и. ч., не превосходящих .г, разности 2к.
В 1919 В. Брун (V. Вгип) нашел метод решета (см.
Вруна решето), к-рый позволил получить ожидаемую
оценку сверху для л*(.т):
Кроме этого, за счет оценок И. М. Виноградова триго-
нометрич. сумм с п. ч. (см. Виноградова метод) доказано
круговым методом (см. [13]), что если положить
f(x)-2Tl
2 V (P-l)V J2 lOH» и
то при любых фиксированных Л>1, М>0
Отсюда, в частности, следует, что при Х = х log-^x для
всех l<ck<z.X, исключая не более X log~Mx из них,
Ль(х) имеет асимптотич. выражение в виде
х-^-ТТ ^
log2 х Х±р\к, р > 2 р-г •
Аналогичные результаты получены для систем п. ч.
/), p + Wj, ... , р + И/я при любом m^Sl.
Простые числа арифметической прогрессии. Первый
способ (Евклида) доказательства бесконечности чис.ча
п. ч. можно перенести и на нок-рые арифметич. прогрес-
прогрессии. Но доказать таким путем, что в каждой арифметич.
прогрессии dn-\-l, первый член к-рой I и разность d
взаимно просты, содержится бесконечно много п. ч.,
до сих пор A983) не удалось. Задачу другим методом
решил П. Дирихле (P. Dirichlet, 1837—40), распро-
распространив идею Л.Эйлера о том, что ^1/р" —>- оо при
s -*¦ 1 + 0 на п. ч. p=l (mod d). Для этого он ввел ариф-
арифметич. функции — характеры %=х(п, d) (см. Дирихле
характер) и функции L(s, %) (см. Дирихле L-фунщия),
которые подобно функции ? (s) для л (х), \р (х) служат
в качестве основного аппарата изучения функции
п(х; d, l) и ее аналога
г|> (х; d, г) = 2„<*, ПзцтоАс1)\(п).
В случае фиксированного значения d, 1<J«2, (I, d)—\,
большинство результатов, указанных выше для я(,<)
иг|з(ж), перенесены и на функции я (.*¦; d, I) и ф (х; d, I).
Однако особый интерес здесь представляют результаты
для растущих вместе с х значений d, к-рые важны в ад-
аддитивной теории чисел и ряде других задач. В таком
случае возникают значительные дополнительные труд-
трудности, связанные прежде всего с оценкой величины
d — наибольшего действительного нуля функции L (s,%)
по mod d. При помощи Пейджа теорем доказано, что
для l<d<(log x)'2-z, 0<e<V2,
а вследствие оценки К. Зигеля (К. Siegel, 1935) для
любого фиксированного А >1 при 1 i^
где ф (d) — функция Эйлера, а — положительная по-
постоянная, Cj^-c^A) — неэффективная постоянная >0,
то есть cj не может быть вычислена по заданному А.
Если справедлива расширенная Римана гипотеза, то
для d^.x
+ С A^^ log2 x).
Гакпм образом, к 1983 доказано, что п. ч. равномерно
распределены по всем <р (d) прогрессиям 1</<:й, (/, d) —
=--1, разности d лишь при d<c\ogAx. Что же касается
отрезков прогрессий dn-\-l-^x разности, напр. d=xs с
каким бы то ни было постоянным е>0, то из предыду-
предыдущего не следует даже, что такая прогрессия содержит
\отя бы одно п. ч.
Метод решета Бруна, как и его модификация, пред-
предложенная А. Сольбергом в 1947, показывает, что для
нсех l<?.d<Cx, l<Z<:d, (I, d)=l, имеет место неравенство
сверху
п(х; d, Z)< ^ -,
Ф (d) log ~
с абсолютной константой <, но никаких оценок снизу
для л (х; d, l) эти методы дать не могут.
Выражение для \р(х; d, I) no принципу Римана через
нули ()¦— PH-t7i лежащие в полосе 0«:а«:1 функции
L (s, X), имеет вид
где штрих у суммы — знак суммирования по комплекс-
комплексным 5С me<l ^> a — действительны!! нуль функции
L (*'> Х)> если он существует и больше 1—C(,/log d,
«<x7--4og2dj+^1/4 log ж,
Г — любое ~5 2.
Из (8) видно, если не считать слагаемого, отвечаю-
отвечающего а, что остаточный член асимптотики ty(x; d, I)
определяется величиной двойной суммы, зависящей и от
действительной части нулей р и от количества чсех,
L (s, у) с % mod d, имеющих нули р с Re р=р. Если для
0,5<:а<1 через Л'(а, Т, %) обозначить число нулей
функции L(s, %) в прямоугольнике: a<Re s«l, U|«7\
то вопросы оценки остаточного члена для т|> (х\ d, I)
и его среднего значения сводятся к вопросам оценки
плотности распределения нулей L-функции в виде
Таким образом, понижение разного рода оценок для
п. ч. связывается не только с отсутствием нулей L (s, %)
в критич. полосе, но и с сравнительно редким их рас-
распределением здесь.
Реализация этой идеи была одним из центральных
направлений исследований Р. п. ч. последних 40 лет.
Начало положил 10. В. Линник открытием в 1941 мето-
метода большого решета (см. [22], а также [14], [15], {24]).
Особо важными являются теоремы о наименьшем п. ч.
в арифметической прогрессии, о поведении я (х; d, l) и
ф(,г; d, l) в среднем по d^.D и о двойном усреднении
этих функций по l<Z<d, (I, d)—l, и d-^D.
Именно, в 1944 Ю. В. Линник [23] показал, что при
d -+ оо сумма N-i в (9) имеет оценку <rfa(i - °), где а —
постоянная; отсюда он вывел существование постоян-
постоянной с такой, что любая арифметич. прогрессия dn^-l, где
l<Z<rf, (/, d)=1, содержит п. ч., меньшее dc. Послед-
Последняя к 1983 оценка постоянной Линника имеет вид
с=17; а если верна плотностная гипотеза: Л^чС
<(d7'J(i-c + e)i то С=2+Е.
В 1965 А. И. Виноградов и Э. Бомбьери независимо
получили сильные оценки сумм JV2 из (9). Более совер-
совершенствованный метод оценки этих сумм разработал
Г. Монтгомери (Н. Montgomery, 1969). Одним из след-
следствий оценок N .у является следующий результат о
Р. п. ч. в арифметич. прогрессиях в среднем:
_ _B max max \\p(y;d, I) —
max max я (у; d, 1) -|-
d<,Vx\ou хУ<хA,<1) = 1
<^ г-log-^ я,
при любом постоянном А и 5 = 4 + 7/2. Эти оцедки су-
существенно усилить уже нельзя, т. к. из расширенной
гипотезы Римана следует, что В = Л + 2.
Другие вопросы распределения простых чисел. Пусть
nv(x; d, l) есть количество чисел вида dn-^-l^g-x, к-рые
являются произведением простых v чисел. X. Рихерт
(Н. Richrrt, 1953) доказал, что
лг(.с; d, /) =
+0
<p(d) ^m=0 *- h=0 'lvv*' "'
где r(i) = cVAlog.r, r>20, ft=fc(e), e>0, Л (h, m, d)
определяется рядами, зависящими от h, m. d и v.
Э. Ландау (Е. Landau, 1903—1918) перенес нек-рые
результаты Р. п. ч. на алгебраические числовые поля.
Пусть К — алгебраическое .числовое поле «-Й степени.
л \х\ К) — есть число простых идеалов с нормой <.с
в К. Тогда
л(х; К)--=И
где с — абсолютная положительная постоянная, и
n(x) — liz=±Q -—^ log log lug x,
где Q — отрицание символа о (малое).
Много изучалась функция F (х, у), обозначающая
число натуральных чисел <х, не содержащих простых
делителей, меньших у. Для ;у=х1'*, |=;(i)->- oo при
т—v оо, такие числа наз. квази просты м и
ч и с л а м и. Методом решета для этих чисел получена
Достаточно полная теория их распределения, аналогич-
аналогичная ожидаемой теории Р. п. ч. Рассматривалось также
распределение чисел с малыми простыми делителями
(см. [25]).
Лит.: [1] Эйлер Л., Введение в анализ бесконечных,
пер. с латин., 2 изд., т. 1, М., 1961; [2] Ч е б ы ш е в П. Л.,
Избр. матгм. труды, М.— Л., 1946; [3] Р и м а н Б., Соч., пер.
с нем., М.— Л., 1948;,[4] И н г а м А. Е., Распределение прос-
простых чисел, пер. с англ., М.— Л., 1936; [5] Виногра-
Виноградов II. М., Избр. труды, М., 1952; [6] е г о ж с, «Изв. АН
СССР. Сер. матем.», 1958, т. 22, № 2, с. 161—64; [71 е г о же,
Метод тригонометрических сумм в теории чисел, М., 1971; [8]
Титчмарш Е., Теория дзета-функции Римана, пер. с англ.,
М., 1953; [9] П р а х а р К., Распределение простых чисел, пер.
с нем., М., 1967; [10] Карацуба А. А., Основы аналити-
аналитической теории чисел, М., 1975; [11] X у а Л о-к е н, Метод три-
тригонометрических сумм и его применения в теории чисел, пер. с
нем., М., 1964; [12] Ч у д а к о в Н. Г., Введение ь теорию L-
функций Дирихле, М.— Л., 1947; [13] Л а в р и к А. Ф. «Тр.
Матем. ин-та АН СССР», 1961, т. 64, с. 90—125; [14] Д о вен-
порт Г., Мультипликативная теория чисел, пер. с англ., М..
1971; [15] Монтгомери Г., Мультипликативная теория
чисел, пер. с англ., М., 1974; [16] S е 1 b е г е; A., «Ann. Math.»,
1949, v. 5A, p. 305—13; [17] Е г d о s P. «Prop. Nat. Acad. Sci.
USA», 1949, v. 35, p. 371—84; Ll8] Л а в р и к А. Ф. (Обзорный
доклад международной конференции по теории чисел, М., 1981);
[19] Diamond H.G., SteinigJ. «Inveni. Math.», 1970,
V. 11, p. 199—258; [20] Л а в р и к А. Ф., С о б и р о в А. Ш.,
«Докл. АН СССР», 1973, т. 211, Ks 3, с. 534—36; [21] Ro s s e г В.,
«Ргос. London math. Soc», 1939, v. 45 B), p. 21—44; L22] Л и н-
н и к Ю. В., «Докл. АН СССР», 1941, т. 30, №4, с. 290—92;
[23] его же, «Матем. сб.», 1944, т. 15, с. 139—78; [24] Л а в-
р и к А. Ф., «Успехи матем. наук», 1980, т. 35, в. 2, с. 55—65;
[25] Halherstam H., Richert Н. Е., Sieve Methods,
L.— [etc], 1Я74. А. Ф. Лпврик.
РАСПРЕДЕЛЕНИЕ СТЕПЕННЫХ ВЫЧЕТОВ И НЕ-
НЕВЫЧЕТОВ — распределение среди чисел 1, 2,. . .,
т — 1 тех значении х, для к-рых сравнение
у" = х (mod m),
»>1 — целое, разрешимо (неразрешимо). В вопросах,
связанных с Р. с. в. и н.. наиболее полно изучен случай
простого модуля р. Пусть ч=(п, р — 1). Тогда сравнение
yn=x(mod р) разрешимо при р ~ ' значениях х из мно-
множества 1, 2, ... , р — 1 и неразрешимо при остальных
(q—1) значениях х (см. Двучленное сравнение).
Однако сравнительно немного известно о том, как рас-
расположены эти значения среди чисел 1, 2,. . ., р — 1.
Первые результаты о распределении степенных вы-
вычетов были получены еще К. Гауссом (С. Gauss, см. [11)
в 1790. С того времени и до работ И. М. Виноградова
в вопросах о Р. с. в. и н. были получены лишь отдель-
отдельные частные результаты. В 1915 И. М. Виноградов
(см. [2]) доказал ряд общих результатов о распределе-
распределении степенных вычетов и невычетов, а также первооб-
первообразных корней но модулю р среди чисел 1, 2,. . ., р.
В частности, им была получена оценка
для наименьшего квадратичного невычета Л'т,п и
оценка
Л-тт<22* f~p\np,
где к — число различных простых делителей р — 1, для
наименьшего первообразного корня Л,*пп1 по простому
модулю р. Кроме того, И. М. Виноградовым был вы-
высказан ряд гипотез о распределении квадратичных вы-
вычетов и невычетом (см. Виноградова гипотезы), стимули-
стимулировавших ряд исследований в :>тон области. Так,
К). В. Линник |3] доказал, что при достаточно большом
N на отрезке [JVE , Л'] количество простых чисел /;, для
к-рых iVmjn >pR , не превосходит нек-рой константы
C(t), зависящей лишь от е>0. Таким образом, простые
числа р, для к-рых Nm\n>p? , если только они сущест-
существуют, встречаются очень редко. Другим существенным
шагом в исследовании гипотез Виноградова явилась
теорема Д. Бёрджесса [4]: для любого фиксированного
сколь угодно малого 6>0 максимальное расстояние
d(p) между соседними квадратичными невычетами удов-
удовлетворяет неравенству
— + 6
d (р) < A (S) р 4
Отсюда, в частности, следует оценка
В этих неравенствах константы А (Л). В (Л) зависят
только от S и не зависят от р. Доказательство теоремы
Вёрджесса, сложное само по себе, основывалось на тео-
теореме Хассе — Вейля о числе решений гнпераллиптич.
сравнения
доказательство к-рой требовало привлечения аппарата
абстрактной алгебраич. геометрии. Простой вывод тео-
теоремы Бёрджесса см. в [5], [6].
Лит.: 1П Г а у с с К. Ф., Труды по теории чисел, пер. с
нем., М., 1959; 12] Виноградов И. М., Шоранные труды,
М., 1952; [3] Л и и н и к Ю. В., «Докл. АН СССР», 1942, г. 36,
с. 13); [4] Bcrdgcss D., «Matliematika», 1957, v. 4. ,Ni 8,
p. 106 — 12; [5] С т еп а н о в С. А. «Тр. Матем. ин-та АН СССР»,
1973, т. 132, с. 237-46; [б] Кара ц у о а А. А., «Докл. АН
СССР», 1968, т. 180, Л5 6, с. 1287—8 9 С. А. Степанов.
РАСПРЕДЕЛЕНИЙ ПОЛНОЕ СЕМЕЙСТВО — се-
семейство вероятностных .мер {Ро , 0?6c:R*}, заданное
на измеримом пространстве (J. 5J3), для к-рого единст-
единственной несмещенной оценкой нуля в классе ф-измери-
мых функций на ? является функция, тождественно
равная нулю. т. е. для любой ^-измеримой функции
/(•), определенной на ЭВ и удовлетворяющей соотно-
соотношению
[ / (х) tZPe (г)=0 для любого 9 ? в, (*)
следует, что/(.г)^^0. Напр., экспоненциальное семейство
распределений является полным. Если соотношение
(¦¦::) выполняется при дополнительном предположении
об ограниченности функции /(х), то семейство {Ре,
6?6} наз. ограниченно полным. Ограни-
Ограниченно полные семейства распределений достаточных
статистик играют важную роль в математич. статисти-
статистике, в частности в задаче построения подобных критериев,
обладающих Неймана структурой.
Лит.: El] Лини и к ГО. В., Статистические задачи с меша-
мешающими параметрами, М., 1ЯИВ; [2] Леиан Э., Проверка ста-
статистических гипотез, пер. с англ., 2 изд., М., 1979.
М. С. Никулин.
РАСПРЕДЕЛЕНИЙ СХОДИМОСТЬ — в основном
слабая сходимость и сходимость по вариации, опреде-
определяемые следующим образом. Последовательность рас-
распределений (вероятностных мер) {Рп} на боре .невских
множествах метрич. пространства S ная. с л а б о
сходящейся к распределению Р, если
lim Г /<*/>„= f fdP (*)
п JS JS
для любой действительной ограниченной непрорывной
функции /на S. Слабая сходимость является основным
типом сходимости, рассматриваемым в теории вероят-
вероятностей. Обозначают ее обычно знаком =Ф. Следующие
условия равносильны слабой сходимости:
1) соотношение (*) выполняется для любой ограни-
ограниченной равномерно непрерывной действительной функ-
функции /;
2) соотношение (*) выполняется для любой ограничен-
ограниченной непрерывной Р-почти всюду действительной функ-
функции /;
3) m^Pn(FXP(F)
п
для любого замкнутого множества FCS;
4) \\m_Pn(G)^P(G)
п
для любого открытого множества GczS;
5) lim Pn(A)=P (A)
п
для любого борелевского множества ACS такого, что
Р (дА)=0, где дА —граница А;
6) Птр(Р„, Р) = 0,
п
где р есть Леей — Прохорова метрика.
Пусть U — замкнутый относительно пересечений
класс подмножеств S такой, что всякое открытое мно-
множество и.ч S есть конечное или счетное объединение
множеств из U. Тогда если lim PH(A)—P (А) при всех
п
А ? U, то Р„=>Р. Если S----R* и /•'„, F — функции рас-
распределения, отвечающие Рп и Р соответственно, то
Pn=z>P тогда и только тогда, когда Fn(x)-*-F(x)
в каждой точке х непрерывности функции /'.
Пусть пространство S сенарабельно и $~ — класс
ограниченных борелевских действительных функций на
6\ Для того чтобы \ fdPn~>\ fdP равномерно по /?С5Г
J 5 J S
для всякой последовательности \Рп} такой, что
Р необходимо и достаточно, чтобы:
„ д
а) sup со/- (S) < оо ,
fnF
б) lim sun Р ({х:ш, (Sx, Е) > 6})= О, V& > О,
где
a>f(A)^sup{\f(J:) — f(y)\, х, у?А],
и где Sx, е — открытый шар радиуса е с центром в .г.
Если класс §~ образован индикаторами множеств из
нек-рого класса Е, то условия а) и б) сводятся к условию
lim sup Р (А*\А-?)^О.
вф о А е?
где
АЕ = UxeAS*. s,A-e=S-*JS \Л)?
(когда всякий открыты!! шар в 6' связен, Ле\.4~Е —
()). Если S=Rk и распределение Р абсолютно
непрерывно по мере Лебеги, то Р„=$Р тогда и только
тогда, когда Рп(А) -»• Р (А) равномерно по всем боре-
левским выпуклым множествам А.
Пусть Рп, Р — распределения на метрич. простран-
пространстве S, Р„=5>Р и h — непрерывное /"-почти всюду из-
измеримое отображение S в метрич. пространство S';
тогда Pnh~l=±> Ph~1, где для любого распределения Q
на S распределение Qh,-1 есть его Л-образ на 6":
для любого борелевского A ?S'.
Семейство распределений у* на S наз. слабо
относительно компактны м, если всякая
последовательность его элементов содержит слабо схо-
сходящуюся подпоследовательность. Условие слабой отно-
относительной компактности дает теорема Прохорова. Се-
Семейство !р наз. плотным, если Ve>0 существует
компакт Kc:S такой, что Р{к)>1— е ЧР??р. Тео-
Теорема Прохорова: если fp плотно, то оно отно-
относительно компактно, а если S сепарабельно и полно,
то слабая относительная компактность Цр влечет его
плотность. В случае, когда S=R*, семейство распре-
распределений уъ слабо относительно компактно тогда и толь-
только тогда, когда соответствующее jp семейство характс-
рнстич. функций равностепенно непрерывно в нуле.
Пусть теперь Рп, Р — распределения на измеримом
пространстве (X, А), где А есть а-алгебра. Под с х о-
д и м о с т ь ю по нар и а ц и и Р„ к Р понимают
равномерную сходимость по всем множествам из А или,
что равносильно, стремление вариации
к нулю; здесь (Рп—Р)+ и (Рп—Р)~—компоненты
разложения Жордана — Хана обобщенной меры Рп—Р.
Лит.: [13 Биллингс л и П., Сходимость вероятностных
мер, пер. с англ., М., 1977; [2] Л оэв М., Теория вероятностей,
пер. с англ., М.. 1962; [3] Б х а т т а ч а р и я Р. Н., Р. Ран-
Ранга Ра о, Аппроксимация нормальным распределением и асим-
асимптотические разложения, пер. англ., 1982. В. В. Сазонов.
РАСПРЕДЕЛЕНИЙ ТИП — совокупность распреде-
распределений вероятностей случайных величин, получаемых
одна из другой каким-либо линейным преобразованием.
Точное определение в одномерном случае таково: рас-
распределения вероятностей случайных величин Х1 и A'j,
называют однотипными, если существуют посто-
постоянные А и i?>0 такие, что распределения величин Х2 и
ВХг-\ А совпадают. Соответствующие функции распре-
распределения связаны при атом соотношением
где Ь=МВ и а=—А,!В.
Таким образом, множество функций распределения
разбивается на попарно непересекающиеся типы. При
итом, напр., все нормальные распределения образуют
один тип, все равномерные распределения также обра-
образуют один тин.
Понятие типа широко используется в предельных тео-
теоремах теории вероятностей. Распределение сумм Sn
независимых случайных величин часто «неограничен-
«неограниченно расплываются» при п —*¦ оо и сходимость к пре-
предельному распределению (например, к нормальному)
окапывается возможной только после линейной «норми-
«нормировки», т. е. для сумм " ~—-> где ап и />„>0 — нек-рые
константы, Ьп ->- оо при п —у- оо. При этом если для ка-
каких-либо случайных величин Х„ распределения вели-
велики-ап хп-а'п
чин -—5 и ;— сходятся к невырожденным нре-
дельным распределениям, то эти последние обязательно
однотипны. Поэтому можно дать следующее определе-
ние сходимости типов (А. Я. Хинчив, 1938). Пусть
Т (F) — тип, к-рому принадлежит функция распреде-
распределения F (из дальнейшего изложения исключается вы-
вырожденный тип — тип, к-рому принадлежат вырожден-
вырожденные распределения). Говорят, что последовательность
типов Тп сходится к типу Г, если существует последо-
последовательность функций распределения Fn?Tn, сходящая-
сходящаяся (слабо) к функции распределения F? Т.Топологизи-
рованное таким образом множество типов есть хаус-
дорфово нерегулярное пространство и, следовательно,
неметризуемо (В. Дёблин, W. Doeblin, 1939).
Пусть, теперь, Stl — суммы независимых одинаково
распределенных случайных величин и Fп — соответст-
соответствующие функции распределения. Тогда класс типов,
предельных для T(Fn), совпадает с классом всех ус-
устойчивых типов, т. е. таких типов, что из FX^T и F.Z?T
вытекает, что свертка F1 и /<\2 принадлежит Т (т. е.,
иными словами, сумма двух независимых случайных
величин с распределениями типа Т снова имеет тип Г,
см. Устойчивое распределение).
Понятие Р. т. может быть распространено на много-
многомерный случай. Однако это распространение неодно-
неоднозначно. Выбирая какую-либо подгруппу G полной груп-
группы матриц, можно получить соответствующее понятие
Р. т. Случайные векторы Х1 и Х.2 со значениями из R"
называют G-однотипными, если существует такое пре-
преобразование #?G, что Х2 и gXt имеют одно и то же рас-
распределение. Соответственно можно ввести понятие
G-устойчивости Р. т. По отношению к полной группе
матриц устойчивы только нормальные распределения
(Г. Сакович, 1960).
Лит.: [1] Г н е д е н к о Б. В., Колмогоров А. Н.,
Предельные распределения для сумм независимых случайных
величин, М.—Л., 1МЯ. Ю. В. Прохоров.
РАСПРЕДЕЛЕНИЯ ЗАКОН в теории веро-
вероятностей — удобный описательный термин, мо-
могущий означать, в зависимости от контекста, распреде-
распределение вероятностей (напр., какой-либо случайной ве-
величины) или соответствующую распределения функцию
или плотность вероятности. Ю. В. Прохоров.
РАСПРЕДЕЛЕНИЯ ЗНАЧЕНИЙ ТЕОРИЯ — теория
распределения значений мероморфных функций, по-
построенная в 20-х гг. 20 в. Р. Неванлинной (R. Nevan-
linna, см. [1]), основной задачей к-рой является изуче-
изучение систем {zn} точек области G, в к-рых функция w(z)
принимает заданное значоние w—а (так наз. а-т о ч е к);
при этом рассматриваются всевозможные значения
Основные понятия. Основные положения неванлин-
новской теории можно проиллюстрировать на случае,
когда w=f(z) является трансцендентной мероморфной
функцией во всей открытой комплексной плоскости С.
Пусть n(t, a, /) обозначает число я-точек /(z) с учетом
их кратностей, попавших в круг {|г|<<}. И пусть для
произвольного комплексного числа а
N(r, a, f) — \ \n(t, a, /) — re @, a, f)]d\nt-
-f-re @, я, /) In r,
то (r, a, f) = m ( r, oo, -^-^ ) , a # ao,
m (r, oo , /) ——
Г (r, i)^m(r, oo, /) + yV(r, ao, /).
Функция T (r, /) наз. неванлинновской
характеристикой (или характери-
характеристической функцией) мероморфной функции
f(z). Функция т(г, а, /) характеризует скорость сред-
среднего приближения f(z) к числу а при \z\ —>- оо, а функ-
функция N (г, а, /) характеризует среднюю плотность рас-
распределения a-точек /(z). Справедлива следующая тео-
рвма, допускающая геометрич. интерпретацию харак-
характеристики Т (г, /). Пусть if7, обозначает часть римановои
поверхности /(г), соответствующей кругу {|z|<:r}, а
лА (г, /) — сферич. площадь поверхности Fr, тогда
Т (г, f) = YQ A (s,f) dins+0A) (г—оо).
С помощью характеристики Т (г, /) определяются поря-
порядок роста р функции / (z) и се нижний порядок роста X:
•р— 1п7(г, /) . ,.„. In Т (г, f)
P=lim ' Шг ' *-=L?l In г •
r~* со /•-»¦»
Первая основная теорема Неван-
л и н н ы: при г —»- со
т. е. сумма m (r, a, f)~\-N(r, а, /), с точностью до огра-
ограниченного при г -+ оо слагаемого, сохраняет постоян-
постоянное для различных а значение Т (г, /). В этом смысле
все значения w для мероморфной функции /(z) являются
равноправными. Особый интерес представляет поведе-
поведение при г —>- оо функции N (г, а, /). В Р. з. т. исполь-
используются следующие количественные характеристики
роста функций Л' (г, а, /) и пг {г, а, /) по сравнению с рос-
ростом характеристики Г (г, /):
Величина 6 (а, /) наз. дефектом f(z) в точке а
в смысле Неванлинны, а величина А (а, /) —
дефектом /(z) в точке а в смысле Ва-
Вали р о н а. Пусть
D (/) = {а:Ь (a, /) > 0}, V (/) = {а: А (а, /) > 0}.
Множество D (/) наз. множеством дефектных значений
f(z) в смысле Неванлинны, а множество VЦ) — множе-
множеством дефектных значений /(z) в смысле Валирона.
Теорема Неванлинны о величинах дефектов
и о множестве дефектных значений /(z): для произ-
произвольной мероморфной функции /(z) справедливы ут-
утверждения: а) множество D (/) не более чем счетно;
б) дефекты / (z) удовлетворяют соотношению
(соотношение дефектов). Постоянная 2,
фигурирующая в A),— это эйлерова характеристика
всей замкнутой плоскости C[j{oo}, к-рую накрывает
риманова поверхность функции /(z).
Структура множества D(f). Утверждение Р. Неванлин-
Неванлинны о том, что множество D (/) но болоо чем счетно, уси-
усилить нельзя. Справедлива теорема: каково бы ни было
конечное или счетное множество Е точек из расширен-
расширенной комплексной плоскости и каково бы ни было число
р, 0<р<:ао, существует мероморфная функция /p (z)
порядка р, для к-рой Е совпадает с множеством ее де-
дефектных значений О(/р). Для мероморфных функций
нулевого нижнего порядка D (/) может содержать самое
большее одну точку. Таким образом, вопрос о струк-
структуре множества D (/) полностью решен.
Кроме того, показано, что для каждого р>0,5 су-
существует целая функция #р (z) порядка р, для к-рой мно-
множество D (#р ) является счетным. Целые функции ниж-
нижнего порядка Я<0,5 не могут иметь конечных дефект-
дефектных значений.
Структура множества V(j). Множество валиронов-
ских дефектных значений VЦ) исследовано A983) не в
полной мере. Ж. Валирон (G. Valiron) показал, что су-
существует целая функция g(z) 1-го порядка, для к-рой
множество V(g) имеет мощность контиуума. С другой
стороны, справедлива теорема: для произвольной меро-
морфной функции /(z) множество V (j) всегда имеет
нулевую логарифмич. емкость.
Для каждого множества Е класса Fo нулевой лога-
логарифмич. емкости существует целая функция g (z) бес-
бесконечного порядка, для к-рой Ecz.V(g).
Свойства дефектов мероморфных функций конечного
нижнего порядка. Для мероморфных функций беско-
бесконечного нижнего порядка величины дефектов, вообще
говоря, не удовлетворяют никаким дополнительным
соотношениям, кроме основного соотношения A). Одна-
Однако если ограничиться рассмотрением мероморфных
функций конечного нижнего порядка, то картина резко
меняется. Справедлива теорема: если /(z) имеет конеч-
конечный нижний порядок X, то при любом а, 11'3^а-^1,
2(д)ба(а, f)<K(X, а), B)
где постоянная К (X, а) зависит лишь от А, и а. С другой
стороны, существуют мероморфные функции конечного
нижнего норядка, для к-рых при <х<1/3 ряд, стоящий
слева в B), уже может расходиться. Наличие у меро-
мероморфной функции /(z) нижнего порядка Х<0,5 одного
дефектного значения а такого, что б (а, /)>1— cos пХ,
влияет на се асимптотич. свойства: такая функция но
может иметь других дефектных значений.
Обратная задача Р. з. т. В несколько упрощенном
виде обратную задачу Р. з. т. в каком-либо классе Ж
-мероморфных функций можно сформулировать в сле-
следующем виде. Каждой точке нек-рой последовательно-
последовательности {а;,} из расширенной комплексной плоскости по-
поставлено в соответствие число б(а^), 0<6(ajj)<l, так,
что 2fc6(afc)<:2. Требуется указать мероморфную функ-
функцию /(z)?a5T такую, что 6(a^, /) = 6(й?), k—l, 2, ... , и
Ь(а, /)==0 для каждого афа^, к=\, 2, ... , либо дока-
доказать отсутствие таких функций в Ж. Обратная задача
полностью решена положительно в классе целых функ-
функций бесконечного нижнего порядка и в классе мероморф-
мероморфных функций бесконечного нижнего порядка. При ре-
решении обратной задачи в классе мероморфных функций
конечного нижнего порядка возникают определенные
трудности, к-рые объясняются тем, что в этом случае
величины дефектов, кроме основного соотношения A),
подчинены еще другим соотношениям (см. B)).
Рост мероморфных функций. Пусть для мероморфной
функции /(z)
L (г, оо, /)= max In+ I / (z) I,
L (r, a, f)=L (r, oo, ~^J , а ф оо
Величина ft (a, f) наз. величиной отклонения
мероморфной функции /(z) от числа а, а множество
Q(f)—{a : Р(а, /)>0} наз. множеством положительных
отклонении мероморфной функции /(z); D(f)czQ-(f).
Доказано, что если g(z) — целая функция конечного
порядка р, то
\ -Д2—, если 0< р<0,5,
Р@0, g)< 81ПЯР ' V
\ яр, если р?эО,5.
(Справедлива также теорема: если мероморфная функция
/(z) имеет конечный нижний порядок X, то а) множество
Q(/) не более чем счетно; б) для каждого а
I пХ если 0 < X < 0,5,
Р (а, /) «?.' втяХ, '
( лХ, есл
в) при любом а, 0,5<а<:1.
2(а)Ра(«, /
где постоянная К (к, а) зависит лишь от Я, и а;
г) Q(/)?= V(j).
Кроме этого, существуют мероморфные функции бес-
бесконечного нижнего порядка, для к-рых множество Q, (/)
имеет мощность континуума. Множество Q (/) (подобно
V (f)) для каждой мероморфной функции /(z) имеет
нулевую логарифмич. емкость. Следующая теорема
характеризует отличия в свойствах величин б (а, /)
и E (а, f): для любого X, 0<Х<оо, существует мероморф-
ная функция /^ (z) нижнего порядка X, для к-рой при
нек-ром а выполняются соотношения
б (а, /)=0 И Р(а, /)=з1.
Исключительные значения мероморфных функций
в смысле Пикара и Бореля. Значение а наз. исключи-
исключительным значением мероморфной функции /(z) в смысле
Пикара, если число а-точек /(z) при {|z|<oo} конечно.
Значение а наз. исключительным значением /(z) в смыс-
смысле Бореля, если п(г, а, /) при г —»- оо растет в опреде-
определенном смысле медленнее Т(г, /). Каждая мероморфная
функция, отличная от постоянной, не может иметь
более двух борелевских (а значит, и пикаровских)
исключительных значений.
Успешно развивается теория распределения значе-
значений голоморфных отображений комплексных многооб-
многообразий — многомерный аналог теории Неванлинны (см.
[6], [7]), а также теория распределения значений мини-
минимальных поверхностей (см. [9], [10]).
Распределение значений функций, мероморфных в
круге. Выше описана теория распределения значений
мероморфных во всей открытой плоскости функций; это
параболич. случай. Теория роста и распределения зна-
значений построена также и для случая гиперболического,
т. е. когда f(z) является функцией, мероморфной в еди-
единичном круге {|z|<l} (см. [1], [8]). При атом функции
N (г, а, /), m(r, а, /), L (г, а, /) и Т (г, /) определяются
для каждого г, 0<г<1, точно так же, как и в параболи-
параболическом случае. Дефект /(z) в точке а в смысле Неван-
Неванлинны и в смысле Валирона определяется соответствен-
соответственно так:
m (г, а, О
б (а, /)=
А величина
наз. величиной отклонения /(z) относительно значе-
значения а.
Пусть ?>(/)= {а : б (а, /)>0},
П/) = {а:Д(а, /) > 0} и Q (/) - {а:Р (а, /) > 0}.
Основные положения параболич. случая о величинах
б (а, /), Д (а, /) и [5 (а, /), а также о структуре множеств
^(/), V(f) и Q (/) сохраняются и в гиперболич. случае,
но не для всех функций, а лишь для функций с быстро
растущей (в определенном смысле) при г —у 1 характе-
характеристикой Т (г, /).
Лит.: [1] Неванлинна Р., Однозначные аналитические
функции, пер. с нем., М.— Л., 1941; [2] X с й и а и У.-К.,
Мероморфные функции, пер. с anr.ii., М., 1У66; [3] Араке-
л я н Н. У., «Докл. АН СССР», 1966, т. 170, № о, с. 999—10«2;
[4] Г о л ь д б е р г А. А., О с т р о в с к и й и. В., Распределе-
Распределение значений мероморфных функций, М,, 1970; [5] П с т р е н-
к о В. И. «Изв. АН СССР. Сер. матем.», НШ9, т. :).'!, № G, с. 1U30—
1348; 1970, т. 34, № 1,с. 31—5В;[й] Гр иффитс Ф., КингД ж.,
Теория Неванлинны и голоморфные отображения алгебраичес-
алгебраических многообразий, пер. с англ., М., 1076; [7] Ш а б а т Б. В.,
Введение в комплексный анализ, 2 изд., ч, 2, М., 197В; [8] 11 с т-
ренко В. II., Рост мероморфных функций, Хар., 1978; [9J
е г о ж е, «Докл. АН СССР», 1981, т. 256, № 1, с. 40- '.2; [10]
Bcckenbach E. P., Hutchison G. A., «Pacific J.
Math.», 1969, v. 28, .№ 1, p. 17 — 47, В. П. Петренко.
РАСПРЕДЕЛЕНИЯ ФУНКЦИЯ какой- л ибо
случайном величины X — функция действи-
действительного переменного х, принимающая при каждом х
значение, равное вероятности неравенства Л'<>.
Каждая Р. ф. F(х) обладает следующими свойствами:
1) F(x')<F(x") при х'<х";
2) F (х) непрерывна слева при каждом х;
3) lim F(x)--^0, limf(j)-l
(иногда Р. ф. определяют как вероятность неравенства
Х*Сх, и тогда она оказывается непрерывной справа).
В математич. анализе Р. ф. называют любую функ-
функцию, для к-рой имеют место свойства 1)—3). Существует
взаимно однозначное соответствие между распределе-
распределениями вероятностей Рр на 0-алгебре <В борелевских
подмножеств числовой прямой R1 и Р. ф. Это соответст-
соответствие определяется формулой: для любого интервала
Га, Ь)
PF([a, b))=-F(b)-F(a).
Каждая функция F, обладающая свойствами 1)—3),
может рассматриваться как Р. ф. нгк-poit случайной ве-
величины „Y (напр., случайной величины X (х) = х, задан-
заданной на вероятностном пространстве (R1, <й), Рр}).
Всякая Р. ф. может быть однозначно представлена
в виде суммы
F (х) = aiF! (x) -f а^\ (х) -\- a3F3 (.r),
где а1, а2, а3 — неотрицательные числа, сумма к-рых
равна 1, a Ft, F2, F3 — Р. ф. такие, что Fx(x) абсолютно
непрерывна:
Fi(x) = [X P(z)dz,
^ - »
F2(x) — «ступенчатая функция»:
—лк *- л
где xjj — точкп скачков F(x), а ;^>0 пропорциональны
размеру этих скачков; F3(x) — «сингулярная» компо-
компонента — непрерывная функция, производная к-рой
почти всюду равна нулю.
Пример. Пусть Xk, к— 1, 2, 3, ... ,— бесконечная
последовательность независимых случайных величин,
принимающих значения 1 и 0 с вероятностями
•<1/2 и <7fe=l—рь, соответственно. Пусть
Y ¦
k=i 2"
тогда
1) если pfc=gf;^l;2 при всех к, то Л" имеет абсолютно
непрерывную Р. ф. (с р(х)=1 для 0<.г<:1, т. е. X рав-
равномерно распределена на [0, 1]);
2) если 2ft- ,/'*<ос' т0 Л' имеет «ступенчатую»
Р. ф. (она имеет скачки во всех двоично-рациональных
точках отрезка [0, 1]);
3) если ^ _ pj.= oo, pt->-() при к—*- со, то Л'
кмеет «сингулярную» Р. ф.
Этот пример является иллюстрацией одной теоремы
П. Леви (P. Levy), в соответствии с к-рой предел бес-
бесконечной свертки дискретных Р. ф. может содержать
только одну из указанных выше компонент.
«Расстояние» между распределениями Р и Q на число-
числовой прямой часто определяют в терминах соответствую-
щих Р. ф. F и S, полагая, напр.,
Pl(P, (?)=sup|f И-5(.г)|
X
или
(см. Распределений сходимость. Леей метрика. Харак-
Характеристическая функция).
Р. ф. наиболее употребительных распределений ве-
вероятностей (напр.. нормального, биномиального, пуас-
соновского распределений) табулированы.
Для проверки гипотез о Р. ф. /' по результатам неза-
независимых наблюдений используют так или иначе изме-
измеренное отклонение F от эмпирической Р. ф. (см. Колмо-
Колмогорова критерии. Колмогорова — Смирнова критерий,,
Крамера — Мизеса критерий).
Понятие Р. ф. естественным образом распространяет-
распространяется на многомерный случай, но многомерные Р. ф. зна-
значительно менее употребительны, чем одномерные.
О приближенном представлении Р. ф. см. Г рама —
Шарлъе ряд, Эджворта ряд, Предельные теоремы.
Лит.: [1] К р а м е р Г., Случайные величины и распределе-
распределения вероятностей, пер. с англ., М., 1947; [2] е г о ж с, Матема-
Математические методы статистини, пер. с англ., 2 изд., М., 1975; ы)
Ф е л л е р В., Введение в теорию вероятностей и ее приложения,
пер. с англ., 2 изд., т. 1—2, М., 1967; [4] Большее Л. Н.,
Смирнов Н. В. Таблицы математической статистики,
2 изд., М., 19G8. Ю. В. Прохоров.
РАССЕИВАНИЕ ВЫБОРКИ — одна из скалярных
характеристик разброса выборки на прямой относи-
относительно какой-либо конкретной точки, называемой
центром рассеивания, численно равная
сумме квадратов отклонений значений случайных ве-
величин, образующих выборку, от центра рассеивания.
Пусть Х„ ... , А'„ — независимые случайные величины,
подчиняющиеся одному и тому же закону, и пусть точ-
точка х, x^R1, выбрана в качестве центра рассеивания.
Тогда величина
наз. рассеиванием выборки Xt, ... , Хп
относительно центра рассеивания х. Так как для лю-
любого х
S,t (х) = Sn (X) + n (X-xf :--a Sn (X),
где Х = —(Х-,-\-...-\-Х,,), то Р. в. будет минимальным,
п
если в качестве центра рассеивания выбрать X. Малые
значения Р. в. говорят о сосредоточенности элементов
выборки около центра рассеивания, и наоборот: боль-
большие значения Р. в. говорят о большой разбросанности
элементов выборки. Понятие Р. в. естественным обра-
образом распространяется на многомерные выборки.
Лит.: [1] У и л к с С, Математическая статистики, пер.
с англ., М., 1967. м. С. Никулин.
РАССЕИВАНИЯ ЭЛЛИПСОИД — эллипсоид в про-
пространстве реализаций случайного вектора, характери-
характеризующий сосредоточенность его распределения вероят-
вероятностей возле нек-рого заданного вектора в терминах
моментов 2-го порядка. Пусть случайный вектор X,
принимающий значения x=(xt, ... , хп)Т и га-мерном
евклидовом пространстве R", имеет невырожденную ко-
ковариационную матрицу В. В таком случае для любого
фиксированного вектора a, a?R", в пространстве реа-
реализаций R" можно определить эллипсоид
(х — а)' В~х (х — а) = п-\ 2., x?R",
к-рын наз. э л л н н с о и д о м рассеивания
распределения вероятностей случайного вектора X от-
относительно вектора а, или эллипсоидом рассеивания
случайного вектора X. В частности, если а = ЕХ, то
Р. э. является геометрич. характеристикой концентра-
ции распределения вероятностей случайного вектора X
около его математич. ожидания ЕЛ'.
Ь задаче статистич. оценивания неизвестного к-мер-
к-мерного параметра 0 с помощью понятия Р. ;>. можно
ввести отношение частичного упорядочивания на мно-
множестве т= {Т} всех несмещенных оценок Т параметра 8,
имеющих невырожденные ковариационные матрицы,
считая, что из двух оценок 7\, Т2^г предпочтительней
является оценка Тг, если Р. э. оценки Т1 лежит цели-
целиком внутри Р. э. оценки Г2. Именно в этом смысле не-
несмещенные эффективные оценки неизвестного вектор-
векторного параметра являются наилучшими, то есть Р. :>.
несмещенной эффективной оценки лежит внутри Р. о.
любой другой несмещенной оценки. См. Рао — Краме-
Крамера неравенство, Эффективная статистика, Информа-
Информации количество.
Лит.: [1] К р а м с р Г., Математические методы статистики,
иер. с англ., 2 изд., М., 1975; [2] А н д е р с о н Т., Введение в
многомерный статистический анализ, иер. с англ., М., 1963;
[3] Ибрагимов И. С, Хае ъ мине кий Р. 3., Асимп-
Асимптотическая теории оценивания, М-, 1979. М. С. Никулин.
РАССЕЛА ПАРАДОКС —см. Антиномия.
РАССЕЯНИЯ МАТРИЦА, tf-м а т р и ц а,— совокуп-
совокупность величин (матрица), описывающая процесс пере-
перехода квантовомоханич. систем из одних состояний в
другие при их взаимодействии (рассеянии).
При рассеянии система переходит из одного кванто-
квантового состояния, начального (его можно отнести к момен-
моменту времени <-= — оо), в другое, конечное (<--= + оо).
Если обозначить набор квантовых чисел, характери-
характеризующих начальное состояние, через i, а конечное —
через у, то амплитуда рассеяния (квадрат модуля к-poi'r
определяет вероятность данного рассеяния) может быть
записана как S/j. Совокупность амплитуд рассеяния об-
образует таблицу с двумя входами, к-рая и наз. м а т-
рицей рассеяния S.
Нахождение Р. м.— основная задача квантовой ме-
механики и квантовой теории поля. Р. м. содержит всю
информацию о поведении системы, если известны
не только численные значения, но и аналитич. свойства
ее элементов; в частности, ее полюсы определяют свя-
связанные состояния системы (а следовательно, дискрет-
дискретные уровни энергии). Из основных принципов кванто-
квантовой теории следует важнейшее свойство Р. м.— ее
унитарность.
По материалам ст. Матрица рассеяния в БСЭ-1,
РАССЛОЕНИЕ — непрерывное сюръектпвноо отобра-
отображение п : X ->- В пространства X на пространство В
(следует различать Р. как процесс и Р. как объект (X,
л, В)). При этом X наз. пространством Р.,
?—базой Р., л — проекцией Р., л ~] F) —
слое м над Ь. Р. представляет собой объединение сло-
слоев я~1F), параметризованных базой В и склеенных
топологией пространства X. Напр., расслоение -
произведение л : BXF —у В, где л — проек-
проекция на первый сомножитель; расслоение-баз а
я : В —*¦ В, где n~=id, X отождествляется с В; р а с-
слоение над точкой* . где X отождествляет-
отождествляется с (единственным) пространством /¦*.
Сечением Р. наз. непрерывное отображение
s : В —»- X такое, что ns= id.
Ограничением расслоения я : X —>- В
на подмножестве AczB наз. расслоение п' : X' -*¦ Л,
где Х1—л~1(А) и л' = я| Обобщением операции огра-
ограничения является построение индуцированного расслое-
расслоения.
Отображение F : X -*¦ X' наз. м орфизмом
расслоения я : X —*¦ В в расслоение я' : X' —>-
->- В', если оно переводит слои в слои, т. е. если для
каждой точки ЬаВ существует такая точка Ь'?В',
что А'(л-1F))сл~1 (Ь'). Отображение F определяет
согласно формуле /(Ь) — л'F (я (Ь)) нек-рое отобра-
отображение f.B—yB'; F является накрытием / и имеет
мосто равенство л'о/?=/ол; ограничения Fb '¦ л~х (Ь) —>-
—»- (л') (Ь') суть отображения слоев. Если В —В'
и /—id, то морфпзм F наз. й - м о р ф и з м о м. Р.
и их морфизмы образуют категорию, содержащую в ка-
качестве подкатегории Р. над В и их /7-морфизмы.
Всякое сечение расслоения л : X —»- В представляет
собой Д-морфизм s : В —»- X расслоения (В, id, В)
в расслоение (X. л, В). Если АаВ, то канонич. вло-
вложение i : п~1(А)-*¦ В является морфизмом расслое-
расслоения л|_} в расслоение л.
Гомсоморфяое отображение F наз. изоморфи з-
м о м. Р., изоморфное расслоению-произведению, на.:
тривиальным Р., а изоморфизм 9 : X -*-В X /¦'
т р и в и а л и а а ци ей л.
Если каждый слой л~'(Ь) расслоения гомеоморфен
пространству F, то расслоение л наз. расслое-
расслоением со слоем F. Напр., в любом локально
тривиальном Р. над связной базой В всо слои zi~1(h)
гомеоморфны, и в качестве F можно взять любое
л~'(Ь0); таким образом, определены гомеоморфизмы
Ц>Ь '¦ F —V Л~' (Ь). М. И. Войцеховский.
Г/РАССЛОЕНИЕ, расслоение со струк-
структурной г р у иной,— обобщение понятия прямо-
прямого произведения двух тоиологич. пространств.
Пусть G — топологич. группа, а X — эффективное
правое (J-пространство, т. е. топологич. пространство
с заданным правым действием группы G таким, что
xg=x влечет g=l, .r?X, g?G. Пусть Х*сХХХ —
подмножество таких пар (х, х'), что r' = xg для нек-
рого g?G, B=X/q — пространство орбит и р : X —>
—»- В — отображение, сопоставляющее с каждой точкой
оо орбиту. Если отображение X*-+¦ G : (х, .rg) —»- g
непрерывно, то набор §=(.?, р, В) наз. главным
расслоением со структурной груп-
п о й G.
Пусть /' — левое (J-иространство. Топологич. прост-
пространство X X /•' снабжается правым действием группы G
но формуле (xf)g-(xg, g~4),f?F. Композиция X XF_?
''•* X it В индуцирует отображение Хр-(Х XF) G LZ.
^F В (здесь Xр — пространство орбит действия С на
XX F). Набор (X р, рр, В, F) наз. расслое ни.ем
со структурной группой, ассоци-
ассоциированным с главным расслоением s,
а набор (Хр, Рр, F, с,) — расслоением со
слоем F, базой В и структурно и груп-
н о й G. Таким образом, главное расслоение со
структурной группой является частью структуры лю-
любого расслоения со структурной группой, и оно одно-
однозначно определяет расслоение для любого левого G-
пространства F.
Если |==(А", р, В), ?'— (Х\ р', В') — два главных
расслоения со структурной группой С, то морфизмом
!•—»-!' наз. отображение 6т-иространств h : X -+ А".
Отображение h индуцирует отображение / : В —у В'.
Главное расслоение со структурной группой наз.
тривиальны м, если оно изоморфно расслоению
следующего вида:
(BxG, ргд, В), F, g)g' = (b, gg'), b?B, g,x'?G.
Пусть (X, p, В) — главное расслоение и / : В' —*¦
—»- В — непрерывное отображение произвольного то
пологич. пространства В' в В. Пусть X'CZB'XX -
подмножество таких нар (Ь, х), что f(b) = p(x). Про
екция ргй, : В' X X —>- В' индуцирует отображение
р' : X' —*¦ В'. Пространство Х'обладает естественной
структурой правого С-пространства, и тропка (X',
р'. В') представляет собой главное расслоение, оно ин-
индуцировано расслоением (X, р, В) с помощью отобра-
отображения / и наз. индуцированным расслое-
расслоением. Если / : В' —»- В — включение нодпростран-
ства, то (X', р', В') наз. ограничением (X, р,
В) над подпространством В'.
Главное расслоение со структурной группой наз.
локально тривиальным, если его ограничение
на нек-рую окрестность любой точки базы В триви-
тривиально. Для широкого класса случаев требование ло-
локальной тривиальности излишне (напр., если G —
компактная группа Ли, X — гладкое С-многообра-
зие). Поэтому часто термин «расслоение» со структур-
структурной группой используется в смысле локально триви-
тривиального расслоения (или косого произведения).
Пусть (Хр, pf, F, I), (Xf, p'f, F, %') пара расслое-
расслоений с одной структурной группой и одним (J-прост-
ранством в качестве слоя. Для морфизма h : | —*¦ |'
главных расслоений отображение fcXid : XXF -*-X'XF
индуцирует непрерывное отображение ср : Xf—*- X'f,
и пара (h, ср) наз. морфизмом расслоений со структур-
структурной группой (XF, pF, F, I) ->- (X'f, PF, F, i'). •
Локально тривиальное расслоение ц=(Хр, pp,
F, ?) допускает следующее описание, лежащее в основе
другого, также общепринятого определения расслое-
расслоения со структурной группой. Пусть U= {иа} — откры-
открытое покрытие базы В для к-рого ограничение т| на иа
при всех а тривиально. Выбор тривиализации и их
сравнение на пересечениях иа П "Р приводит к непре-
непрерывным функциям (наз. функциями пере-
перехода) {gap}, ЯаР '• "aD"v ->¦ G- в пересечениях трех
окрестностей "а(]и$ [}иу имеет место равенство
ga{j°gfSy°gya=i€G' а выбор других тривиализации над
каждой окрестностью приводит к новым функциям
g'ajS^hag^hp1- Таким образом, функции {#ар} обра-
образуют одномерный коцикл в смысле Александрова —
Чеха с коэффициентами в пучке ростков (J-значных
функций (коэффициенты неабелевы), и локально три-
тривиальное расслоение определяет этот коцикл с точ-
точностью до кограницы.
Лит.: ШХьюзмоллер Д., Расслоенные пространства,
пер. с англ., М., 1970; [2] Стинрод Н,, Топология косых
произведений, пер, с англ., М., 1953. А. Ф. Харшиладзе.
РАССЛОЕННАЯ ВЫБОРКА — выборка, разбитая
на несколько выборок меньших объемов по нек-рым
отличительным признакам. Пусть каждый элемент
какой-то выборки объема N^2 обладает одним и
только одним из /е>2 возможных признаков. В таком
случае исходную выборку можно разбить на к выборок
объемов н1; . . ., «fe соответственно («i+. . •+«?=
= N):
Хи, .... Х1п„
Л 21, • • • , Х2„2,
исходя из принципа: в i-ю выборку Хц, . . ., Х/,,1
отнесены только те элементы исходной выборки, к-рые
обладают г-м признаком. В результате такого разбие-
разбиения первоначальная выборка оказывается как бы
расслоенной на к слоев Хц, . . ., Х(п., i=l, . . ., к,
причем именно i-i'i слой содержит информацию об j-м
признаке. К понятию Р. в. приходят, наблюдая, напр.,
реализации компоненты X двумерной случайной вели-
величины (X, Y), вторая компонента к-рой Y подчиняется
дискретному распределению.
Лит.: [1] У и л к с С., Математическая статистика, пер. с
англ., М., 1967. М. С. Никулин.
РАССЛОЕННОЕ ПРОИЗВЕДЕНИЕ объектов
категории — частный случай понятия (обрат-
(обратного или проективного) предела. Пусть Ж— произ-
произвольная категория и пусть заданы морфиамы а: А —>-
—»- С, Р: В -*¦ С из Я. Объект D, вместе с морфизмами
ф: D —>- А ф; D —»- В, наз. расслоенным про-
изведен и ем объектов А а В (над а и р"),
если tpa=i|;P и для любой пары морфизмов у: X —> А,
6: х -*¦ В, для которой va=6p\ существует такой
единственный морфизм | : X -*¦ D, что ?<p = Y> ?1|> = 0-
Коммутативный квадрат
D—* В
ч>\ | Р
Л — >С
а
часто наз. универсальным, или декарто-
декартовым, квадратом. Объект D вместе с морфиз-
мами фиф есть предел диаграммы
В
I'
А—*С .
а
Р. п. объектов А и В над « и f обозначают одним из
следующих способов:
АхВ, АХВ, Aj[fJ.
С а, р ар
Р. п., если оно существует, определено однозначно
с точностью до изоморфизма.
В категории с конечными произведениями и ядрами
пар морфизмов Р. п. объектов А и В над а и f> строится
следующим образом. Пусть Р = АХВ — произведе-
произведение А и В с проекциями ях и я2 и пусть (D, и.) — ядро
пары морфизмов л^, я2Р : Р —»¦ С. Тогда D, вместе
с морфизмами ^лх=ф и ил2=г(), есть Р. и. А и В над
а и р. Во лшогих категориях структуризованных мно-
множеств D является подмножеством произведения (А X
ХВ), состоящим из всех таких пар (а, Ь), где а?А,
Ь?В, ДЛЯ К-рыХ аа=Ь$. М. Ш. Цаленко.
РАССЛОЕННОЕ ПРОСТРАНСТВО — тотальное про-
пространство расслоения. М. И. Войцехоеский.
РАСТЯГИВАЮЩЕЕ ОТОБРАЖЕНИЕ — дифферен-
дифференцируемое отображение / замкнутого многообразия М
на себя, под действием к-рого длины всех касательных
векторов (в смысле какой-нибудь, а тогда и любой,
римановой метрики) растут с экспоненциальной ско-
скоростью, т. е. существуют такие константы С>0 и
А,>1, что для всех Х?ТМ и всех ге>0
| Г/<"> (X) || 5= Ск» || X ||.
Имеется также вариант понятия Р. о. без условия диф-
ференцируемости, охватывающий, в частности, многие
ранее изучавшиеся одномерные примеры. Свойства
Р. о. аналогичны свойствам У-систем и отчасти даже
проще (так, Р. о. класса С3 всегда имеет конечную ин-
инвариантную меру, задаваемую в терминах локальных
КООрДИНат ПОЛОЖИТеЛЬНОЙ ПЛОТНОСТЬЮ). Д. В. Аносов
РАСХОДЯЩАЯСЯ ПОСЛЕДОВАТЕЛЬНОСТЬ — по-
последовательность точек топологич. пространства, не
имеющая предела. Из всякой расходящейся последо-
последовательности метрич. компакта можно выделить схо-
сходящуюся подпоследовательность. В классе Р. п. нор-
нормированных пространств выделяют бесконечно боль-
большие последовательности, т. е. такие последователь-
последовательности {х,г} точек этих пространств, что lim||xn||=oo.
Понятие Р. п. обобщается на кратные последователь-
последовательности и на направленные (частично упорядоченные)
множества. Л. Д. Кудрявцев.
РАСХОДЯЩИЙСЯ ИНТЕГРАЛ — понятие, противо-
противоположное понятию сходящегося интеграла (см. Не-
Несобственный интеграл). Напр., если функция опреде-
определена на конечном или бесконечном промежутке [а, Ь),
— оо<а<:Ь<оо, если для любого ng[a, b] она интег-
интегрируема на отрезке [a, 1]J и не существует конечного
предела
lim I / (x) dx,
r\ -> b J a
то говорят, что интеграл \ f(x)dx расходится. В слу-
J B
чае, когда
/ (х) dx = + оо или — оо,
ч - - v a
говорят, что Р. и. \ f (x)dx равен соответственно
+ оо ИЛИ —оо. Л. Д. Кудрявцев.
РАСХОДЯЩИЙСЯ РЯД — ряд, у к-рого последова-
последовательность частичных сумм не имеет конечного предела.
Напр., ряды
1 + 1 + 1 + 1 + 1+...,
1-1 + 1-1 + 1-...,
1_2 + 3—4 + 5-...,
расходятся.
Р. р. стали появляться в работах математиков
17—18 вв. Л. Эйлер (L. Euler) первым пришел к вы-
выводу, что нужно ставить вопрос, не чему равна сумма,
а как определить сумму Р. р., и нашел подход к реше-
нию этого вопроса, близкий к современному. Р. р.
до кон. 19 в. не находили применения и были почти
забыты. Накопление к кон. 19 в. различных фактов
математич. анализа вновь пробудило интерес к Р. р.
Стал выдвигаться вопрос о возможности суммирова-
суммирования рядов в нек-ром смысле, отличном от обычного.
Примеры. 1) Если перемножить два ряда
-,С0 ^-,00
а„ и V Ь„,
сходящихся соответственно к А и В, то полученный
в результате перемножения ряд
2Г=0С" =2Г=0 (aohn±ilba-l + ¦¦¦+апЬо) A)
может оказаться расходящимся. Однако если сумму
ряда A) определить не как предел частичных сумм х„,
а как
lim
то в этом смысле ряд A) всегда будет сходиться (т. е.
предел в B) будет существовать) и его сумма в этом
смысле равна С=АВ.
2) Ряд Фурье функции f(x), непрерывной в точке х0
(или имеющей разрыв 1-го рода), может расходиться
в этой точке. Если же сумму ряда определить по фор-
формуле B), то в этом смысле ряд Фурье такой функции
всегда будет сходиться и его сумма в этом смысле равна
f(x0) (или соответственно \f(x0 + O)-\-f(xB—0)]/2, если
х0 — точка разрыва 1-го рода).
3) Степенной ряд
сходится для |z|<l к сумме 1/A—z) и расходится для
|5sl. Если сумму ряда определить как
где *¦„ — частичные суммы ряда C), то в этом смысле
ряд C) будет сходиться для всех z, удовлетворяющих
условию Re z<l, причем его суммой будет функция
1/A—z).
Для обобщения понятия суммы ряда в теории Р. р.
рассматривают нек-рую операцию или правило, в ре-
результате к-рого Р. р. ставится в соответствие опреде-
определенное число, наз. его суммой (в этом определении).
Такое правило наз. суммирования методом. Так, пра-
правило, описанное в примере 1), наз. методом суммиро-
суммирования средних арифметических (см. Чезаро методы
суммирования). Правило, определяемое в примере 2),
наз. Бореля методом суммирования.
См. также Суммирование расходящихся рядов.
Лит.: [1] В о г е 1 Е., Lecons sur les series divergentes, P.,
1Я28; [2] Харди Г., Расходящиеся ряды, пер. с англ., М.,
1П51; [3] Кук Р., Бесконечные матрицы и пространства после-
последовательностей, пер. с англ., М., 196A; [4] Р е у е г i m h о f f
A., Lectures on summability, В., 1969; [5] К n о р р К., Theory
and application on infinite series. N. Y., 1971; [6] Z e 1 1 e r K.,
Beekmann V., Theory der Limitierungsverfahren, B.—
Hdlb. — N. Y., 1970. И. И. Волков.
РАСШИРЕНИЕ алгебры Л и S с ядром А —
алгебра Ли G с эпиморфизмом <р : (J —»- S, ядром к-рого
служит идеал A C.G, это равносильно заданию точной
последовательности
Д
Р. наз. р а с щ е п и м ы м, если существует подал-
подалгебра S^S такая, что G—S^A (прямая сумма моду-
модулей). Тогда ф индуцирует изоморфизм S!~S, и потому
определено действие алгебры S на А дифференцирова-
дифференцированиями. Обратно, по любому гомоморфизму а : S —¦-
-*¦ Der A , где Der A — алгебра дифференцирований
алгебры А, однозначно строится расщепимое расшире-
расширение Sfp'A c законом умножения
[(s, a), (s', a')] = ([s, s'], a (s) a' ~ a(s') a + [a, a']).
Для конечномерных алгебр Ли над полем характери-
характеристики 0 справедлива теорема Л е в и: если S полу-
полупроста, то всякое расширение алгебры S расщепимо.
Из нерасщепимых Р. наиболее изучены абелсвы Р.,
то есть Р. с абелевым ядром А. В этом случае действие
алгебры G на А индуцирует действие алгебры G/A^S
на А, то есть А есть 5-модуль. Для алгебр Ли над
полем всякое абелево Р. алгебры S, ядром к-рого
служит 5-модуль А, имеет вид SQ)A со следующим
законом умножения:
[(*, a), (s1, a')\ = ([s, s'\, a (s) a' — a (s') а + ф (s, s')),
где ф — нек-рое линейное отображение SaS—>-A.
Тождество Якоби равносильно тому, что ф — двумер
ный коцикл (см. Когомологии алгебр Ли). Р., к-ры.м
эквивалентны когомологичные коциклы, эквивалент-
эквивалентны в естественном смысле; в частности, Р. расщепимо
тогда и только тогда, когда ф когомологичен нулю.
Таким образом, абелевы Р. алгебры S с ядром А опи-
описываются группой когомологии У/2 (S, А). К случаю
абелсвых Р. сводится изучение Р. с разрешимым ядром.
Лит.: [1] Д ж е к о б с о н Н., Алгебры Ли, пер. с англ.,
М., 1964. А. К. Толпыго.
РАСШИРЕНИЕ ассоциативной алгебры
Я над коммутативным кольцом К — гомоморфизм
Ф : S —»- R К -алгебры S на алгебру R. Если Кегф---
— / — алгебра с нулевым умножением, то Р. наз.
сингулярным. В этом случае на / естествен-
естественным образом вводится структура й-модуля. На мно-
множестве всех Р. ассоциативной алгебры R с яд-
ядром / вводится отношение эквивалентности (так же,
как для групп, модулей и т. д.), и множество классов
эквивалентных Р. обозначается F(R, I). Если алгеб-
алгебра R является К -проективной, то алгебра S разложима
в прямую сумму /f-модулей S=I-\-R, и элементы ал-
алгебры S можно записать в виде нар (и, г), u?I, r?R,
к-рыс перемножаются по правилу
(ult г,) (м2, ri)---(u1r2 + r1ui-{-a(r1, г.,),
где а : R@R —»- /. Ассоциативность умножения на-
кладывает ограничения на функцию а, превращая се
в коцикл. Сопоставление Р. его коцикла устанавли-
устанавливает изоморфизм К -модуля F(tt, J) со второй группой
когомологип Я2 (Я, I) алгебры Я с коэффициентами в /.
Р. алгебры Я наз. также алгебру, содержащую Я.
Такие Р. часто связаны с конкретной конструкцией
(многочлены над Я, локализация Я, кольцо частных
алгебры Я и т. д.)- См. также Расширение поля.
Лит.: [1] М a is л с й н С',., Гомология, пер. с англ., М., 1966;
[2] Hochschild G., «Ann. Math.», 1Я45, v. 4B, p. 58—67.
В. Е. Говоров.
РАСШИРЕНИЕ группы — группа, содержащая
данную группу в качестве нормального делителя.
Обычно фиксируется и факторгруппа, т. е. расши-
расширением группы А и р и п о м о щ и г р у п-
п ы В наз. группа G, содержащая А в качестве нор-
нормального делителя и такая, что GiAsB, или точная
последовательность
e-^a—>g\b^e. A)
Иногда группу G наз. расширен и о м г р у п и ы
В при помощи групп ы А (см., напр., [2]) или
эпиморфизм у : G —»- В — Р. группы В (см., [1]). На-
Наконец, точная последовательность A) может назы-
называться пак Р. группы А при помощи группы В, так
и Р. группы В при помощи группы А. Р. группы А
при помощи группы В всегда существует, однако груп-
группы А \\ В определяют его неоднозначно. Необходимость
описания всех Р. группы А при помощи группы В
вызвана как потребностями самой теории групп, так
и ее приложениями. Такое описание естественно про-
проводить с точностью до эквивалентности. Два Р. груп-
группы А при помощи группы В наз. э к в и в а л с н т-
н ы м и, если коммутативна диаграмма
Е -ч-А ¦ С - Я ^Е
Произвольное Р. A) определяет путем трансформи-
трансформирования элементами группы С гомоморфизм
a-.G-^kniA, a(g)a — gag-1,
для к-рого а, (А) содержится в группе hi А внутрен-
внутренних автоморфизмов группы А, и, следовательно,
Определяет гомоморфизм
$:В —-* Aut Л/1и А.
Тройку (А , В, Р) наз. абстрактным ядром Р.
Фиксируя Р. A). выбирают для каждого Ь?Я пред-
представителя u(b)?G так, чтобы удовлетворялись усло-
условия уи(Ь) = Ь и иA)=1. Тогда сопряжение элементом
и (Ь) порождает автоморфизм ф (Ь) группы А:
ф (Ь) а —и (Ъ) а и(Ь)~х- аь .
Произведение и Fj) и (Ь2) равно u {I'll',) с точностью до
множителя /(Ьх, Ь2)?А:
u(b1)u(b2)=f(bl, b2)u(bl Ь2).
Легко проверяется, что введенные функции должны
удовлетворять условиям
[ф(Ы/(&2. b3)]f(l>u Мз) =-/(''!, Ъ„I(Ъф2, Ь3), B)
(/¦^(«^"¦•^У'Ч C)
где в равенстве C) неявно присутствует функция
Ф : В ->- Aut A .
Задание групп /1 и В и функций f:BXB-*-A,
Ф : Я —у Aut А , удовлетворяющих условиям B) и C)
и условиям нормализованное™:
ф(])= 1, /(«, 1)^1^/A, Ь),
определяет Р. A) в следующем смысле. Множество
Па(А, В, ф, /) пар (я, Ь), а?А, Ь?В,
является группой относительно операции
(а, Ъ)(аи bi)=-(a4f(b, /м), bb,).
Гомоморфизмы а Ь» (а, 1), (а, Ь) (-» 6 задают Р.
Если задано абстрактное ядро (А, В, р"), то всегда
можно найти нормализованную функцию (|>, удовлет-
удовлетворяющую условию C). Естественно возникает функ-
функция /, однако условие B) не всегда выполняется; в об-
общем случае
j(b,. Ья) f (Ьи Ь2 Ьа) = -- к FЬ Ь2, Ь3) f (bu b2) f (h b.2, b3),
где k(bi, b2, bs)?A. Функция f:BXB-+A наз.
системой факторов, а функции к : В А Их
ХВ -*¦ А наз. препятствиями к Р. Ксли
группа А абелева, то системы факторов составляют
группу Z2(B, А) относительно их естественного сло-
сложения. Факторы, соответствующие полупрямым про-
произведениям, составляют подгруппу В.2(В, А) группы
Z2(B, А). Факторгруппа Z2(B, А)/В2(В, А) изоморфна
второй группе когомологий группы В с коэффициен-
коэффициентами в группе А. Аналогичную интерпретацию имеют
препятствия в третьей группе когомологий.
Идея изучения Р. с помощью систем факторов по-
появилась давно (О. Гёльдер, О. Holder, 1893). Однако
упоминание систем факторов обычно связано с именем
О. Шрайера (О. Schreier), предпринявшего с их по-
помощью первое систсматич. изучение расширений.
Р. Бэр (R. Ваег) впервые начал инвариантные исследо-
исследования Р. групп без участия систем факторов. Теория
Р. групп явилась одним из истоков гомологич. алгебры.
Лит.: [11 К а р т а н А., Э й л е н б е р г С, Гомологическая
алгебра, пер. с англ., М., 1960; [2] Кириллов А. А., Эле-
Элементы теории представлений, М., 1978; [3J К урош А. Г.,
Теория групп, 3 изд., М., 1967; 14] М а к л е й н С., Гомологии,
пер. с англ., М., 1968. В. Е. Говоров.
РАСШИРЕНИЕ дифференциального
поля Fo — дифференциальное поле F'ZdFq с таким
множеством дифференцирований Д, что ограничение
Д на Fo совпадает с множеством дифференцирований,
заданных на /•'„. В свою очередь Fo будет диффе-
дифференциальным п о д п о л е м поля F.
Пересечение любого множества дифференциальных
подполен в F является дифференциальным подполом
поля /'. Для любого множества элементов Ее/' су-
существует наименьшее дифференциальное подполе в /•',
содержащее все элементы из 2 и Fo; оно обозначается
F0CL) и наз. расширением поля Fo, п о-
рожденным множество м 2 (при ;>том
говорят, что 2 является множеством, или семейством,
образующих расширения F0(Z) над Fa). P. наз. к о-
н е ч н о порожденным, если оно имеет конеч-
конечное множество образующих, и наз. просто п о-
р о ж д с н н ы м, если множество образующих состоит
из одного элемента. Если Ь\ и F2 — два дифферен-
дифференциальных нодполя в F, то подполе
F1F2=FL <F2> = /•! (F2) =/\j (Ft) -. F, </¦',>,
являющееся дифференциальным подполом поля F,
наз. к о м и о з и т о м полей Fx и F2.
Пусть в — свободная коммутативная полугруппа
с множеством свободных образующих Д (ее элементы
паз. дифференциальными операто-
операторами). Семейство (a,)i€7 элементов дифференциаль-
дифференциального поля F наз. дифференциально алгеб-
алгебраически завися м ы м над дифферен-
дифференциальным нолем FocF, если семейство @а,); е , 0 g e
алгебраически зависимо над /•'„, в противном случае
семейство (<х,-);6 j наз. дифференциально а л-
г с б р а и ч е с к и независимым над /<т0, или
семеме твом дифференциальных неизве-
с т н ы х над Fo. Говорят, что элементы (a,)i6 (Диф-
(Дифференциально с е " а р а б е л ь н о з а в и-
о и м ы над Fo, если семейство @a,)i6 / ge g сенарабель-
но зависимо над /<-0; в противном случае семейство
(a,)i€ j наи. дифференциально с с и а р а-
б е л ь н о независимы м над Fa.
Распшрение F наз. д и ф ф е р е н ц и а л ь н о а л-
г с б р а и ч о с к и м над /'V если таковым является
каждый элемент ноля F. Аналогично, /' наз. диффе-
дифференциально сепарабелъным над /-'0,
если таковым является каждый элемент из F. Для
дифференциальных Р. справедлива теорема о прими-
примитивном элементе: пусть множество 0 независимо на
/'о, тогда всякое конечно порожденное дифференци-
дифференциально сепарабельное расширение F ноля Fo порож-
порождается одним элементом.
Пусть / —¦ нек-рое множество и F0\(y,e )(c j е€ в]_
алгебра многочленов над Fu от семейства неизвест-
неизвестных (i/g) j? j g6 e с множеством индексов /Х0. Лю-
Любое дифференцирование 6?Д поля Ftt единственным
образом продолжается до дифференцирования кольца
/•oi(j//e);ej,fi6H], отображающего г//е в i//6r Это диф-
дифференциальное кольцо наз. кольцо м д и ф ф е-
р е н ц и а л ь н ы х много ч л е н о в от диффе-
дифференциальных неизвестных ///, /?/, и обозначается
Fq {(У j)j e j }• Его дифферсн ц и а л ь н о е по л е
частных (т. е. ноле частных с продолжением диф-
дифференцирований) обозначается F0((y)j? j), л элементы
итого поля наз. д и ф ф с р о н ц и а л ь н ы м и фун-
функциями над /-'о от дифференциальных неизвест-
неизвестных (i/.);-6j- Для обыкновенных дифференциальных
нолей имеет место аналог теоремы Л ю р о т а:
пусть /' — произвольное дифференциальное Р. диф-
дифференциального поля Fo, содержащееся в F0(ti), тогда
/'' содержит элемент г; такой, что /<'--F0(i>).
Для любого дифференциального поля /•' существует
с е п а р а б е л ь н о е п о л у у н и в е р с а л ь н о е
р а с ш и р е н и с, т. е. такое Р.. в к-рое вкладывается
«сякое конечно порожденное сепарабельное Р. ноля F.
Нолее того, существует сепарабельное у н и-
нереальное расширение U, т. е. такое
Р., к-рое является полууниверсальным над каждым
конечно порожденным Р. дифференциального ноля F,
содержащимся в U.
В теории дифференциальных полей нет объекта,
соответствующего алгебраически замкнутому полю
в теории полей. До нек-рой степени их роль играют
стесненно замкнутые ноля. Основным свойством та-
такого ноля /*' является то, что любая конечная система
алгебраических дифференциальных уравнении и по-
пора венств с коэффициентами в F, имеющая решение,
рациональное над нек-рым Р. поля /•', имеет решение,
рациональное над/'. Семейство 1l=Oly)j6,/ элементов
из нек-рого Р. дифференциального ноля F наз. с т е с-
ц е н и ы м над /•', если существует дифференциальный
многочлен c?F {(yj))a j} такой, что с(ц)Ф() и с(т]')—-О
для любой необгцей дифференциальной специализации
ц' точки 1] над /'. Расширение '§ поля F наз. с т о с-
п с н н ы м над /•', если любая конечная система
.моментов %, .. . , i|«6^ является стесненной над
/•'; это равносильно тому, что произвольный элемент
из <§ является стесненным над /•'. Дифференциальное
иоле, не имеющее нетривиальных стесненных Р., наз.
стесненно замкнуты м. Пример такого но-
ноля — универсальное дифференциальное поле нулевой
характеристики (универсальное Р. поля рациональ-
рациональных чисел Q). Для любого дифференциального поля
нулевой характеристики существует стесненное
замыкание, т. е. стесненно замкнутое Р. поля F,
к-рое вкладывается в любое другое стесненно замкну-
замкнутое I3. ноля F.
Определение нормального Р. из теории полей может
быть перенесено в дифференциальную алгебру раз-
различными способами. В дифференциальной теории Га-
луа основную роль играют сильно нормальные Р.
Пусть U — фиксированное универсальное дифферен-
дифференциальное поле характеристики 0 с полем констант К.
Все дифференциальные ноля, встречающиеся ниже,
предполагаются лежащими в U, а все упоминаемые
далее изоморфизмы предполагаются дифференциаль-
дифференциальными изоморфизмами, т, с. коммутируют с операто-
операторами из множества Д. Пусть /• и g — дифференциаль-
дифференциальные поля, над к-рыми U универсально. Пусть С —
иоле констант ноля '§. Изоморфизм о поля f, наз.
сильным, если гг оставляет инвариантным
каждый элемент из С, agcrgAT и gcagA (то есть
gA—gaA"). Сильно нормальным Р. диффе-
дифференциального ноля F наз. конечно порожденное рас-
расширение g поля /•' такое, что всякий изоморфизм
поля g над F является сильным. Сильно нормальные
Р. являются стесненными. Множество сильных изо-
изоморфизмов сильно нормального расширения g над
71' имеет естественную структуру алгебраич. группы,
определенной над полем К (обозначаемой через
GC§/F)). Это — Г илу а дифференциальная группа
расширения %! F. Частным случаем сильно нормаль-
нормальных Р. являются расширения Пик ара
В е с с и о, т. о. расширения, сохраняющие поле коп
стант и получающиеся присоединением к полю F базис
решений какой-либо системы линейных однородны •-
дифференциальных уравнений с коэффициентами из /
Для таких Р. группа Галуа G($/F) является алгеп
раической матричной группой, т. о. алгебраич. под-
подгруппой группы ОЬд-(ге) для нек-рого целого ге>0.
Дифференциальные группы Галуа типичных диф-
дифференциально-алгебраических Р. имеют следующий
вид.
1) Пусть <§=-F(a), где а удовлетворяет системе
уравнений 6,-a=aI-a, 6,-?Д, а,?Р, г=1, . . ., т, и
пусть поля констант нолей g и F совпадают. Тогда
g является расширением Пикара — Всссио ноля F
и дифференциальная группа Галуа G (?//<') является
подгруппой мультипликативной группы поля К (то
есть ОЬд-A)= А'*). Если элемент а трансцендентен
над F, то G($//'')»А'*, а если а алгебраичен, то a
удовлетворяет уравнению вида уа—ft—0, где b?F и
G{% F) — %d (группа корней из 1 степени d). Расширение
g ноля F наз. Р. ц р и п о м о щ и экспонент ы.
2) Пусть (§=Р{а), где а удовлетворяет системе
уравнений fi,a — a,-, 6\?Д, a,-g/(', /—1, . . ., т (такой
элемент а наз. прим и т и в н ы м над F). II пусть
ноле констант поля F(a) совпадает с С. Если <*?/•',
то а трансцендентен над F. Полученное Р. является
расширением Пикара — Вессио, и группа Галуа
G(F{a)lF) изоморфна аддитивной группе поля К.
Такие Р. наз. расширениями н р и п о м о щ и
интеграла.
3) Пусть g2, g3 — элементы поля С такие, что
#¦¦>—27^1=^0. Элемент a?U наз. в е и е р ш т р а с-
с о в ы м над /<', если а удовлетворяет системе уравнений
F,-a)-—«¦•Da3~-j?2a—g3); 6,-?Д, a;?F, l<t</n. Рас-
Расширение 4}--F(a) является сильно нормальным пад
F, однако, если а трансцендентен над F, оно но яв-
является расширением Пикара — Вессио. Имеется моно-
мономорфизм
c:G (F<a> /л ¦—¦> WK,
где W/(— группа точек кубмч.
Если а трансцендентен над F, то с является изомор-
изоморфизмом.
4) Пусть F —дифференциальное поле, ах, . . ., an?F
и (щ, . . ., цп) — фундаментальная система нулей
уравнения ^1п>-(-а1#<п-1)-|-. • • +ал2/=0, к-рая порождает
расширение Пикара — Вессио поля F. Группа Галуа
G(/'<T|1 ,. . ., r\n>/F) содержится в SL/((n) тогда и
только тогда, когда уравнение у'-\-а1у=0 имеет не-
нетривиальный нуль в /•'. В частности, если F=C{x) —
дифференциальное поле рациональных функций од-
одного комплексного переменного с дифференцирова-
дифференцированием dldx и Bv=j"+i"V+(l—v2x~2)y— дифферен-
дифференциальный многочлен Бссселя, то группа Галуа соот-
соответствующего Р. совпадает с SLA-B) при v—1/2фЖ-
Если v—I ?,?_%, то группа Галуа совпадает с К*.
Для любого натурального п можно построить Р. диф-
дифференциальных полей ?з.Р такое, что G ($//")« GLA* (n).
Существует соответствие Галуа между множеством
дифференциальных подполен сильно нормального Р.
и множеством алгебраич. подгрупп его группы Галуа.
Как и в обычной теории Галуа, в дифференциальном
случае рассматриваются две общие задачи.
а) Прямая задача: задано сильно нормальное рас-
расширение % дифференциального поля F. Определить
его группу Галуа.
б) Обратная задача: заданы дифференциальное поле
/' и алгебраич. группа G. Описать множество сильно
нормальных Р. поля F, группа Галуа к-рых изоморфна
группе G (в частности, определить, не пусто ли оно).
Существует другой способ обобщения нормальности
на случай Р. дифференциальных нолей и построения
дифференциальной теории Галуа, использующий ме-
методы дифференциальной геометрии [4].
Лит.: [1] Ritt J. F., Differential algebra, N. Y., 1950;
[2] К о 1 с h i n E. R., Differential algebra and algebraic groups,
N. Y., 1973; [3] К а п л а н с к и й И., Введение в дифферен-
дифференциальную алгебру, пер. с англ., М., 1959; [4] Pommarct
J. F., Differential Galois theory, N. Y.-L.-P., 1983.
А. В. Михалев, E. В. Панкратьев.
РАСШИРЕНИЕ модуля — любой модуль X, со-
содержащий данный модуль А в качестве подмодуля.
Обычно, говоря о Р, модуля А, фиксируют фактормо-
дуль XIА, т. е. расширением модуля А
с помощью модуля В наз. точную последива-
тельность
0—+ А~^Х —+ В—>0.
Такой модуль X всегда существует (напр., прямая сум-
сумма А и В), но не определяется модулями А ж В одно-
однозначно. Как в теории модулей, так и в ее приложениях
возникает потребность в обозрении всех различных
Р. модуля А с помощью В. С этой целью в классе всех
Р. модуля А с помощью В вводится отношение эквива-
эквивалентности, а на классах эквивалентных Р.— операция
умножения (см. Бэра умножение), относительно к-рой
множество классов эквивалентности Р. модуля А над
кольцом В образует абелсву группу Ext#(/1, В). Эта
конструкция обобщается и на п-к ратные Р. мо-
модуля А с помощью В, т. е. на точные последо-
последовательности вида
0 —* А —>¦ Х„-! -*...—*-.?„ ¦—* В---+ 0,
к-рым соответствует группа Ext %{A , В). Группы
Ext % (Л, В), « = 1, 2, ...,
являются производными функторами функтора
Нотд(Л, В) и вычисляются с помощью проективной
резольвенты модуля А или инъективнои резольвенты
модуля В. Расширение X модуля А наз. сущест-
существенны м, если для любого подмодуля S модуля X
из Sf]A = O следует S—0. Всякий модуль обладает мак-
максимальным существенным Р., являющимся минималь-
минимальным инъективным модулем, содержащим данный.
Лит. см.' при ст. Расширение группы. В. Е. Говоров,
РАСШИРЕНИЕ оператора — линейный опе-
оператор, график к-рого содержит график данного линей-
линейного оператора. Тот факт, что оператор В есть Р. опе-
оператора А, записывается в виде АаВ. Обычные задачи
теории Р.: максимально расширить оператор, сохраняя
определенное свойство, или изучить Р. оператора,
обладающие нек-рым дополнительным свойством.
Пусть, напр., дан изометрич. оператор А в гильбер-
гильбертовом пространстве II с областью определения D (A)CZH
и областью значений R (A)CZlI; тогда изометрические Р.
оператора А находятся во взаимно однозначном соот-
соответствии с изометрич. отображениями из H+--D (ЛI
в Н^ — Я(А)Х-. В частности, А имеет унитарные Р.,
когда размерности Н + и //_ совпадают.
Расширения симметрических опе-
операторов. Наиболее развитой (и важной для прило-
приложений) является теория самосопряженных Р. симмет-
рич. операторов в гильбертовом пространстве. Опера-
Оператор Т является симметрическим тогда и только тогда,
когда TczT*, где Т* — сопряженный к Т оператор.
Поэтому область определения любого симметрического
Р. оператора Т содержится в D (Т*), и это Р. есть с у-
ж е н и е оператора Т*. Тем самым описание симметри-
симметрических Р. сводится к нахождению их областей опреде-
определения. Подпространство LczD (T*) является областью
определения нек-рого симметрического Р. оператора Т
тогда и только тогда, когда (Т*х, у)=(хТ*у) для любых
х, y?L. Оказывается, что
где 7V±=KerGT* ^ г) — дефектные подпрост-
подпространства (их размерности re_i_ = dim N± наз. д е-
ф е к т н ы м и числами), и симметрические Р.
оператора Т находятся во взаимно однозначном соответ-
соответствии с изометрич. отображениями из N + в 7V_: каждо-
каждому такому отображению V соответствует Р. оператора Т
с областью определения D (T)\-Yv, где Гу — график
оператора V. Самосопряженные Р. соответствуют уни-
унитарным операторам V и, следовательно, существуют
тогда и только тогда, когда дефектные числа равны.
Области определения Р.симметрич. операторов удоб-
удобно описывать с помощью т.н. (абстрактных) граничных
условий. Граничным значением для сим-
метрич. оператора Т наз. всякий линейный функционал
на D(T*), непрерывный относительно нормы (х) =
— AИ1а+ЦГ*ж||2)'/'! и равный нулю на D (Т); гранич-
граничным условием наз. уравнение f(x) = O, где / —
граничное значение. Граничные значения определяются
своими значениями на N + +N-. Если дефектные числа
симметрич. оператора Т конечны, то всякое его симмет-
рич. расширение Т определяется семейством гранич-
граничных условий, то есть D (Т)= Г) j=iKer /,-, где /; — гра-
граничные значения. Семейства граничных значений, оп-
определяющие самосопряженные Р. оператора Т с дефект-
дефектными числами п + = п_~п, описываются следующим
образом. Пусть фъ ... , ф„ — ортонормированный базис
в N + , а г[I, ... , фл — в N - и пусть для 1<(<ге
fi(x)=,(T*x, щ)-(х, Г*Ф/),
Тогда всякое самосопряженное расширение Т операто-
оператора Т определяется граничными условиями
ГДС Il9iyll — унитарная (гсХгс)-матрица.
В нск-рых случаях удается установить существова-
существование самосопряженных Р. (и найти нск-рые из них), не
решая трудной задачи нахождения дефектных подпрост-
ранств и дефектных чисел. Напр., если Т коммутирует
с (антиунитарной) инволюцией пространства Н, то он
допускает самосопряженное Р. Это часто используется
в теории дифференциальных операторов, где в качестве
инволюции берется комплексное сопряжение простран-
пространства Хг. Равенство дефектных чисел имеет место и в том
случае, когда на действительной оси есть точки регу-
регулярного типа оператора Т (точка к наз. точкой
регулярного типа, если \\Тх— Лх||>с|Ы| при
нек-ром с >0 и для всех х ? D (Т)).
Расширения полуограниченных
операторов. Оператор Т наз. полуограни-
полуограниченным снизу числом a?R, если его число-
числовая область {(Тх, х) : ||х||=1, x?D (T)} лежит в
интервале (а, оо); оператор, полуограниченный снизу
нулем, наз. положительным. Если Т полу-
полуограничен снизу числом а, то все числа Х<а — его точ-
точки регулярного типа, дефектные числа равны и сущест-
существуют самосопряженные Р. Одно из них можно постро-
построить следующим образом. Полуторалинейная форма
яАх> у)=(Тх, у), определенная на D (T)xD (Г), допу-
допускает замыкание q-p. Но, как всякой замкнутой симмет-
симметричной билинейной форме, форме дт соответствует един-
единственный самосопряженный оператор Т такой, что qq-CZ
dqj. Оператор Т наз. расширением Фрид-
Фридрих с а оператора Т, он полуограничен, и нижняя
грань его спектра равна нижней грани числовой обла-
области оператора Т. Это — единственное самосопряженное
Р., область определения к-рого содержится в области
определения формы qT. С помощью расширения Фрид-
рихса можно описать другие полуограниченные Р. опе-
оператора Т (если дефектные числа оператора Т конечны,
то все его самосопряженные Р. полуограничены). Для
этого достаточно найти все положительные Р. положи-
положительных операторов (общий случай сводится к данному
добавлением оператора, кратного единичному). Пусть
Г — положительный оператор, L=Ker T*, тогда по-
положительные самосопряженный Р. оператора Т одно-
однозначно соответствуют положительным ограниченным
операторам В в L: для каждого такого оператора В под-
подпространство D (T)-ir(T~1-^B)L — область определе-
определения соответствующего Р. (см. [4]).
Построение расширения Фридрихса обобщается на
с е к т о р и а л ь н ы е операторы, т. е. опера-
операторы, числовая область к-рых содержится в нек-ром
угле {zgC : | arg(z—zo)\ <0<л/2}; существует Р., яв-
являющееся максимальным секториальным оператором,
числовая область к-рого находится в том же угле и к-рое
обладает свойством минимальности, аналогичным свой-
свойству расширения Фридрихса. Рассмотрен случай опе-
операторов, действующих из банахова пространства в со-
сопряженное к нему (см. [5]).
Диссипативньге расширения. В нек-рых
задачах возникает необходимость строить симметриче-
симметрические Р. симметрич. операторов. Типичный результат
состоит в следующем. Оператор А наз. д и с с и н а-
т и в н ы м, если его числовая область лежит в левой
полуплоскости, и максимальным д и с с и п а-
т и в н ы м, если он диссипативен и не имеет диссипа-
тивных Р. Всякий симметрич. оператор имеет Р. вида
iA, где А — максимальный диссипативный оператор;
все такие Р. описываются с помощью сжимающих отоб-
отображений N+ в N- (см. [8]).
Расширения дифференциальных опе-
операторов. Важные применения теория Р. операто-
операторов имеет при исследовании дифференциальных опера-
операторов. Пусть
i (у) =^2L0 с-1)"-' (Pi (*) j/'»-'))"»-'»
— формально самосопряженное дифференциальное вы-
выражение на интервале (а, 6); пусть D ? Jf2(a, Ь) — под-
подпространство, состоящее из всех функций с абсолютно
непрерывными квазипроизводными порядков 0, 1, ... ,
2(г — 1 и 2гс-й квазипроизводной, принадлежащей Jf2(a,
t>), где Do — подпространство в D, состоящее из функ-
функции, носители к-рых не содержат концов интервалов.
Формула Ту=1(у) при y?D определяет оператор Т;
пусть То — его сужение на Do. Оператор То — симмет-
симметрический, Т'0*=Т и пусть ТО=Т'О — его замыкание.
Область определения оператора То в регулярном слу-
случае (т. е. когда интервал (a, b) конечен и функция
1-Vo суммируема) образована всеми функциями из D,
первые 2ге—1 квазипроизводных к-рых обращаются
в Она концах интервала. В сингулярном случае D (То)
описывается более сложно (см. [2]). Дефектные числа
оператора То равны, причем в регулярном случае они
равны 2п, а в сингулярном — не превосходят 2ге.
Таким образо.м, 3 всегда обладает самосопряженными
Р.; их спектры, спектральные разложения и резольвен-
резольвенты являются основными объектами теории дифференци-
дифференциальных операторов, поскольку выбор того или иного
самосопряженного Р. является фактически точной
постановкой нек-рой спектральной задачи. Это особен-
особенно наглядно проявляется в регулярном случае: (аб-
(абстрактные) граничные условия, задающие область оп-
определения самосопряженного Р. оператора То, запи-
записывается тогда в виде обычных граничных условий:
7 = 1, ..., 2ге,
где a,fc, P,-fe — набор чисел (такое описание следует из
вышеприведенного описания (абстрактных) граничных
условий, поскольку в регулярном случае определены
граничные значения yj{y) = yl'\a), ty/(y) = y^4b)).
При ро(х)>О оператор То является полуограничен-
полуограниченным снизу, и его расширение фридрихса соответствует
граничным условиям у^Ца) = у^{Ь) — О, ().</<2гс—-1.
В общем случае самосопряженные Р. оператора То
.можно описать следующим образом. Пусть
для любых функций у и z из D; тогда существуют пре-
пределы
lim [у, ;]х~[у, z]u, lim [у, z](x) = [y, z]b,
X -* а х ->- b
причем
\У, г]ь — [у, z]a = (Ty, z) — (y, Tz)
(формула Л а г р а н ж а). Поэтому для описания
самосопряженных Р. оператора То достаточно выбрать
базисы <рх, ... , ф^ и \|)t, ... , ф,, в дефектных подпрост-
подпространствах N+ и N_ (удобно считать, что г|з,-=ф;) и каж-
каждой унитарной матрице ||В,у|| поставить в соответствие
самосопряженное расширение Те , область определения
к-poro состоит из всех функций y^D, удовлетворяющих
граничным условиям
где
Расширения, отвечающие краевым
задача м. Р. оолуограниченных операторов играют
центральную роль в теории эллиптических краевых
задач. Пусть, напр., Цу) — эллиптическое дифферен-
дифференциальное выражение 2-го порядка в области G ге-мер-
ного пространства и пусть Ао и А — ,40 — минимальный
и максимальный операторы, определенные этим выра-
выражением. Тогда оператор Ао положительно определен,
его дефектные числа бесконечны и дефектное подпрост-
подпространство L0=Ker А (оно наз. пространством
/-гармонических функций в G) допу-
допускает естественную реализацию в виде пространства
функций на границе dG области G. Таким образом,
различные Р. оператора Ап соответствуют тем или иным
граничным условиям и определяют различные краевые
задачи. В частности, расширение Фридрихса Ао опре-
определено на всех функциях из пространства Соболева
W\{G), обращающихся в нуль на dG, и уравнение
Лои—/ соответствует задаче Дирихле:
Теории уравнений с частными производными диктует
постановку многих общих задач о Р. симметрии, опера-
операторов. Среди них задачи об условиях единственности
самосопряженного Р. (т.н. существенная
самосопряженность), о существовании ком-
коммутирующих Р. у коммутирующих (в том или ином смы-
смысле) симметрнч. операторов, о существовании проме-
промежуточных Р. с заданными свойствами (напр., с условия-
условиями на спектр) и т. д. (см. [7]— [9]).
Расширения с выходом из гильбер-
гильбертова пространства. Всякий симметрия,
оператор, действующий и гильбертовом пространстве
II, может быть расширен до самосопряженного опера-
оператора, действующего в нек-ром пространстве Н^Н (см.
[10]), откуда следует существование у всякого симмет-
симметрия, оператора обобщенной спектральной функции.
С этим также связаны различные результаты о Р. с вы-
выходом из пространства и дилатациях (см. [11]). Так,
всякое сжатие, т. е. оператор с нормой <:1. гиль-
гильбертова пространства может быть расширено до коизо-
метрического (т. е. сопряженного к изометрическому)
оператора; всякое сжатие, степени к-рого сильно схо-
сходятся к нулю, может быть расширено до обратного од-
одностороннего сдвига (т. с. сопряженного к односторон-
одностороннему сдвигу). Результаты о Р. с выходом из простран-
пространства обобщаются на коммутативные семейства, полу-
полугруппы и т. Д.
Лит.: [1] Д а н ф о р д Н., Шварц Д ж.- Т., Линейные
операторы, пер. с англ., т. 2, М., 1966; [2] Н а й парк М. А.,
Линейные дифференциальные операторы, 2 изд., М., 1969; 13]
К а т о Т., Теория возмущения линейных оператором пер. с
англ., М., 1972; 14] Крсйн М. г.,«Матем. cfi.», J 047, т. 20,
с. 431—98, т. 21, с. 365—404; [5] Бирман М. Ш., там же,
1956, т. 38, с. 431—50; [6] Филипс Р. С, «Математика»,
1ПВ2, т. 6, № 4, с. 11—70; [7] М о р е н К., Методы гильбертова
пространства, пер, с польск., М,, 1965; [8] Б с у е з а н-
с к и й Ю. М., Разложение но собственным функциям самосо-
самосопряженных операторов, К., 1965; (Я] Михлин С. Г., пробле-
проблема минимума квадратичного функционала, М.— Л., 1952; [10]
Наймарк М. А., «Изв. АН СССР. Сер. матем.» 1940 т. 4 с.
277—318; 111] С с к с ф а л ь в и - Н а д ь Б., Ф о я ш Ч., Гар-
Гармонический анализ операторов в гильбертовом пространстве
пер. с франц., М., 1970; [12] Brow и L., DoiiglasH., F i 1-
lmore Р., в кн.: lJroc. Conference operator theory, В.—
fa.o.], 1973; [13] A r v с s о n W., «Duke math. J.», 1977, v. 44,
As 2, p. 329—55; [14] Рид М., Саймон Б., Методы сов-
современной математической физики, пер. с англ., т. 2 — Гармо-
Гармонический анализ. Самосопряженность, М., 1978.
А. И. Логинов, В. С. Шульман.
РАСШИРЕНИЕ и о л у г р у п п ы А — полугруп-
полугруппа S, содержащая А в качестве подполугруппы. Обычно
речь идет о расширениях полугруппы Л, связанных с А
теми или иными условиями. Наиболее развита теория
идеальных Р. полугрупп (полугрупп, содержащих А
в качестве идеала). Каждому элементу s идеального
расширения S полугруппы А сопоставляют ее левый и
правый сдвиги ks, ps : ksx=sx, xps= xs(x?A); пусть ts—
— (Л.«! Ps)- Отображение т является гомоморфизмом по-
полугруппы 5 в сдвиговую оболочку Т(А) полугруппы А
л.щ нзоморчтгтгом, если А слабо редуктивна (см. Свей-
ги полугрупп). Полугруппа xS наз. т и п о м и д е-
а л ь н о г о расширения S. Среди идеальных
расширений S полугруппы А выделяют строгие
Р., для к-рых rS=%A , и чистые Р.. в к-рых т~хтЛ--
= А. Каждое идеальное Р. полугруппы А является чи-
чистым Р. нек-рого ее строгого Р.
Идеальное расширение S полугруппы А наз. п л о т-
н ы м (иногда существе н н ы м), если всякий
гомоморфизм полугруппы S, инъоктивный на А, яв-
является изоморфизмом. Полугруппа А тогда и только
тогда обладает максимальным плотным идеальным рас-
расширением D, когда А слабо редуктивпа; в этом случае D
единственна с точностью до изоморфизма и изоморфна
Т(А), а полугруппа А наз. плотно вложен-
вложенным идеалом в D. Подполугруппы Т (А), содер-
содержащие хА, и только они изоморфны плотным идеаль-
идеальным Р. слабо редуктивной полугруппы А.
Если S — идеальное Р. полугруппы А и факторполу-
группа S/A изоморфна Q, то S называется Р. полугруп-
полугруппы А при помощи полугруппы Q. Хорошо изучены иде-
идеальные Р. вполне простых полугрупп, идеальные Р.
группы при помощи вполне 0-нростой полугруппы,
коммутативной полугруппы с сокращением при помощи
группы с присоединенным нулем и т. д. В общем случае
задача описания всех идеальных Р. полугруппы А
при помощи полугруппы Q далека от решения.
Среди Р. полугруппы А других типов выделяются
полугруппы S, обладающие конгруэнцией, одним из
классов к-рой является А, в частности т. н. ш р е и е-
р о в ы Р. полугруппы с единицей [1] —- аналог шрейе-
шрейеровых расширений групп. При изучении различных
видов таких Р. полугрупп (в частности, для инверсных
полугрупп) используются когомологии полугрупп.
Другим широким направлением теории Р. полугрупп
являются различные задачи о существовании Р. полу-
полугруппы А, принадлежащих фиксированному классу по-
полугрупп. Так, всякую полугруппу А можно вложить
в полную полугруппу, в простую относительно кон-
конгруэнции полугруппу, в бипростую полугруппу с ну-
нулем и единицей (см. Простая полугруппа); всякую ко-
конечную или счетную полугруппу — в полугруппу с дву-
двумя образующими. Известны условия, при к-рых полу-
полугруппу А можно вложить в полугруппу без собствен-
собственных левых идеалов, в инверсную полугруппу, в группу
(см. Вложение полугруппы) и т. д.
Лит.: [1] Клиффорд А,, Престон Г., Алгебраичес-
Алгебраическая теория полугрупп, пер, с англ., М., 1972, т. 1; [2] Р е t-
richM., Introduction to semigroups, Columbus, 11O3.
>'J. M. Глуспин.
РАСШИРЕНИЕ и о л я — поле, содержащее данное
поле в качестве подполя. Запись К/к означает: А' —
расширение поля к. Поле К в этом случае наз. также
надполем поля к.
Пусть К/к и Llk — два Р. ноля к. Изоморфизм полей
ф : К —*¦ L наз. и з о м о р ф и з м ом рас ш и р е-
н и и (или к- и з о м о р ф и з м о м н о л е й), если ф
тождествен на к. Если изоморфизм Р. существует, то
Р. наз. изоморфными. В случае K-=L(f наз. авто-
м о р ф и з м ом рас ш и р с и и я К/к. Множество
всех автоморфизмов Р. образует группу G(Klk) —
= Aut (/f/fc), наз. группой Г а л у а ноля К
относительно к, или группой Г а л у а
расширения К/к. Расширение наз. а б е л е-
в ы м, если эта группа абелева.
Элемент поля а наз. алгебраическим над к,
если он удовлетворяет нек-рому алгебраич. уравнению
с коэффициентами из поля к, и трансцендонт-
н ы м — в противном случае. Для каждого алгебраич.
элемента а существует единственный многочлен fa(x)
со старшим коэффициентом, равным 1, неприводимый
в кольце многочленов к \х] и такой, что /а(а) = 0, и
всякий многочлен над к, корнем к-рого является эле-
элемент а, делится на /«(я). Этот многочлен наз. мини-
малынл многочленом элемента а.
Расширение К1к наз. алгебраически м, если
всякий элемент из К алгебраичен над к. Р., не являю-
являющееся алгебраическим, над. трансцендентным.
Р. наз. н о р м а л ь н ы м. если оно алгебраическое
и всякий неприводимый в к \.г] многочлен, обладающий
корнем в Л", разлагается в К \.т] на линейные множите-
множители. Подполе к наз. алгебраически замкну-
т ы м п А', если каждый алгебраический над к элемент
из А' на самом деле лежит в к, т. е. всякий элемент из
Klk трансцендентен над к. Поле, алгебраически замкну-
замкнутое в любом своем Р.. является алгебраически замкну-
замкнутым полем.
Расширение К Ik наз. конечно порожден-
н ы м (или расширением конечного
тина), если в К существует такое конечное подмно-
подмножество элементов S. что К совпадает с наименьшим нод-
полем, содержащим S и к. В этом случае говорят, что
К порождается множеством б1 над к. Если К может быть
порождено над к множеством из одного элемента а, то
Р. наз. просты м и обозначается К =/с(а). Простое
алгебраич. расширение к (а) полностью определяется
минимальным многочленом /а порождающего элемен-
элемента ос. Точнее, если к (fi) —другое простое алгебраиче-
алгебраическое Р. и /а:=г/р , то существует изоморфизм расширении
к (а) -*¦ к (Р), переводящий а в E. Далее, для любого
неприводимого многочлена /?/г [.г] существует простое
алгебраич. расширение к (а) с минимальным многочле-
многочленом /«-=/. Оно можот быть построено как факторколь-
цо к \x]!fk [х]. С другой стороны, для всякого простого
трансцендентного расширения к (а) существует изомор-
изоморфизм расширений к (а) —*-к(х), где к (х) — поле рацио-
рациональных функции от х над к. Любое Р. конечного типа
может быть получено с помощью конечной цепочки
простых Р.
Расширение К/к наз. конечным, если А* как
алгебра конечномерна над полем к, и б е с к о н е ч-
п ы м, если эта алгебра бесконечномерна. Размерность
зтой алгебры наз. степенью расширения
К'к и обозначается [А' : к]. Каждое конечное Р. являет -
1'я алгебраическим и каждое алгебраическое Р. конеч-
конечного типа — конечным. Степень простого алгебраиче-
алгебраического Р. совпадает со степенью соответствующего ми-
минимального многочлена. Напротив, простое трансцен-
трансцендентное Р. бесконечно.
Пусть дана последовательность расширений KcLc
~М. Расширение Ml К является алгебраическим тогда
и только тогда, когда и L!К и М L — алгебраические
Р. Далее, М К конечно тогда и только тогда, когда ко-
конечны L.'K н MIL, причем
Если Р,к и Q,k — два алгебраических Р. и PQ ¦-
композит нолей Р и Q в нек-ром их общем надполе, то
PQlk также алгебраическое Р.
См. также Сепарабелъное расширение. Трансцендент-
юе расширение.
Лит.: ГЦ Б у р б а к и Н., Алгебра. Многочлены и поля.
Упорядоченные группы, пер. с франц., М., 1965; [2] В а н д е р
В а р д е и Б. Л., Алгебра, 2 изд., пер. с нем., М., 1979; [3]
! а р и с с и и и О., С, а м га э л ь П., Коммутативная алгебра,
1, пер. с англ., М., 1ЯВЗ; [41 Л с н г С, Алгебра, пер. с англ.,
AT., 10K8. О. А. Иипновч.
РАСШИРЕНИЕ т о и о :\ о г и ч е с к о г о п р о-
I' т р а н с т в а X — топологическое пространство У,
в к-ром X является всюду плотным подпространством.
Если У бикомпактно, то оно наз. бикомпакт-
бикомпактным расширением, если У хаусдорфово —
х а у с д о р ф о в ьт м расширен и е м.
Д/. //. Войцсховский.
РАСШИРЕНИЯ ОБЛАСТИ ПРИНЦИП, п р п н-
ц и п К а р л е м а н а: гармоническая мера о> (г, a, D)
дуг а границы Г области D может только возрастать
при расширении области D через дополнительные дуги
рсГ, a UP" Г- Точнее, пусть граница Г области U на
плоскости комплексною переменного z состоит из ко-
конечного числа жордановых кривых, а — часть Г, со-
состоящая из конечного числа дуг Г, и пусть область D'
есть расширение области D через допол-
дополнительные дуги р-=- ГЧ а, то есть Dczf)' и а ость часть
границы Г' области D'. Тогда для гкрмонич. мер спра-
справедливо неравенство ш (г, а ,Л)<со (г, а, I)'), zgO,
причем знак равенства здесь имеет место только в случае
D'=D. P. о. п. справедлив и для гармонич. меры отно-
относительно областей евклидова пространства R", ге^2,
ИЛИ С", 74>1.
Р. о. п. находит важные применения в различных си-
ситуациях, связанных с оценками гармонич. меры. Напр.,
еще Т. Карлеман [11 дал при помощи Р. о. п. решение
следующей проблемы К а р л е м а н а — М и п ю.
Пусть граница Г односвязной области D состоит из ко-
конечного числа жордановых дуг, точка ? расположена
на Г или l?CD, A={z: |z—l,\<.R) — круг радиуса R
с центром ?, а а — часть Г, цопавшая в &r=A[]D.
Требуется найти оценку снизу для гармоннч* меры
о) (г, a, A/j), зависящую только от/? и |г-~?|, ?Д
Решение выражается неравенством
«o(z, a, A*)^.larctg(TOIn -ттгёг). A)
где RQ(R) - сумма длин дуг пересечения
{z: \z-Z\~
Поскольку 9(Я)<:2л, то
to(z, a, Aw)si2.arctg
Имеются обобщения проблемы Карлемана — Мийю и
уточнения формул A), B) (см. [3]). Р. о. п. позволяет
доказать также Линделёфа теоремы. Многочисленные
применения Р. о. п. и формул типа A), B) дал А. Мийю
(см. [2], а также [3], [4]).
Лит.: 11] Carle ш а п Т., «Ark. Mat. Astron. Fys.», 1Я21,
v. 15, J\is 10; [2] M i 1 1 о и x H., «.I. math, pures et appl.», 9 ser.,
11J4, t. 3; [3] H e в а и л п и и а Р., Однозначные аналитические
функции, пер. с нем., М. Л., 1941; [4] Е в г р а ф о в М. А.,
Аналитические функции, 2 изд., М., 1Я68. Е. Д. Соломенцгв.
РАСШИРЕННАЯ КОМПЛЕКСНАЯ ПЛОСКОСТЬ —
плоскость комплексного переменного С, компактифи-
компактифицированная посредством добавления бесконечно удален-
удаленной точки оо и обозначаемая С. Окрестностью оо яв-
является внешность любого круга в С, т. е. множество
вида {oe}U{zgC:| z — z0 | > У?'}, R~?Q. P. к. п. есть
Александрова бикомпактное расширение плоскости С,
гомеоморфное и конформно' эквивалентное Рим а на
сфере. С ф е р и ч с с к а я, или хордальная,
м е т р и к а на С дается формулами
V 1 + | z I* V 1 + 1
P(Z, QO)^
VTTUT2
Лит.: [1] M a p к у ш e n и ч \. П.. Теория аналитических
функций, 2 инд., т. 1 — 2, М., 1<Ц>7 l>8; L2] Шабат Б. В.,
Введение в комплексный анализ, 2 изд., ч. 1—2, М., 1976.
Е. Д. Соломенцев.
РАСЩЕПЛЕНИЯ МЕТОД — сеточный метод реше-
решения нестационарных задач со многими пространствен-
пространственными переменными, в к-ром переход от заданного вре-
временного слоя tn к новому слою *., + 1=(„-|-т осуществля-
осуществляется за счет последовательного решения сеточных ана-
аналогов родственных нестационарных задач с меньшим
числом пространственных переменных (см. [1] — [4]).
Часто в этом классе методов могут быть найдены такие,
что 1) весь переход от сеточного слоя в момент времени
tn к новому сеточному слою t~tn+\ является достаточно
простым и может быть осуществлен при затрате О (N)
арифметич. действий, где jV — число узлов простран-
пространственной сетки; 2) гарантируется абсолютная устой-
устойчивость метода; 3) гарантируется наличие приемлемой
точности метода (наличие аппроксимации в том или
ином смысле). Р. м. довольно широко применяются
при практич. решении многомерных задач математич.
физики, связанных, напр., с линейными и нелинейны-
нелинейными системами параболического, гиперболического или
смешанного типа (см. [1] — [8]).
Обычно для задачи с р пространственными перемен-
переменными переход от tn к tn+i в Р. м. производится с ис-
использованием р вспомогательных (дробных) шагов:
4"' u" + sJP~B(sn) (и", un+i/P, ..., и»-1^), A)
где
u"^u(ln), un + k/»^u(tn + 1), A{n)
— матрица, соответствующая разностной аппрокси-
аппроксимации нек-рого дифференциального оператора, со-
содержащего производные только по xs (одномерного диф-
дифференциального оператора), а правые части A) легко
вычислимы. При соответствующей нумерации неизвест-
неизвестных, связанной с выбором направления xs, матрицы
А$п) становятся обычно диагональными и решение
систем A) при каждом s сводится к многократному
решению одномерных разностных систем по направле-
направлению xs. Поэтому часто Р. м. наз. также или переменных
направлений методом или дробных шагов методом.
Одним из типичных примеров в случае уравнения
с начальным условием u\f=g=<((x1, х2) и краевым ус-
условием ы|1-.=-ф(ж1, х2, t), где Q=@, 1)Х@, 1), Г— гра-
граница Q, может служить следующий метод, построенный
на квадратной сетке с шагом h:
+ [Л1(ои« + 1'а+A-оI^)], = /?+1/3.
t/2
u,i =я|з" + 1/2 при -г,?Г, u"+1 = 1|)"+1 при ,
— ^ h[A2@^ + 1 + (l-0)"" + ]'2)Ji =
= ф ((га+1/2) т, jc,-), — Лх и Л2—простейшие разно-
разностные аппроксимации для —- и --'-_ , 52П— совокуи-
дх'{ дх\
ность внутренних узлов j;,-, 0^=1/2.
Имеются два альтернативных подхода к теории Р. м.
В одном из них промежуточные шаги ни в чем сущест-
существенном не отличаются от целых шагов, и сами разно-
разностные уравнения на дробных шагах и граничные усло-
условия для них, подобно методу B), устроены одинаково,
и можно ожидать, что м" и ип+1'2 будут служить ап-
аппроксимациями для решения исходной задачи в момен-
моменты времени tn и tn+]/.,= tn-\-т/2. Этот подход основан
на использовании понятия составной схемы и суммар-
суммарной аппроксимации (см. [2]). Схемы такого типа часто
на:!, локальноодно мерными схемами
или аддитивными схема м и; их можно также
трактовать как обычные разностные схемы для нек-
рого уравнения с сильно осциллирующими по времени
коэффициентами, решение к-рого должно быть близко
к решению исходной задачи (см. [1]—[4]). Достоинства
этого подхода в его простоте и общности, напр, обоб-
обобщения метода B) возможны и для случая криволиней-
криволинейных областей Q и более общих задач. Точность же полу-
получаемых на этом пути методов обычно не очень высока.
Известны и иногда успешно применяются варианты
Р. м., в к-рых расщепление производится не по про-
пространственным неременным, а но физич. процессам
(см. [5]).
Второй подход в плане анализа устойчивости и схо-
сходимости исключает какие-либо дробные шаги из рас-
рассмотрения. Сама разностная схема и аппроксимация
трактуются традиционным образом. Необычность раз-
разностной схемы проявляется лишь в том, что на верх-
верхнем слое схемы появляется необычный разностный опе-
оператор. Напр., вместо метода B) рассматривается метод
u'l=^'l при х;?Г,
где А^Е+атА-,) (?+атЛ2), Е — тождественный опе-
оператор. Такие операторы А обычно наз. расщепля-
расщепляющимися или факторизованны ми
операторами. Дробные шаги связываются лишь
с методом решения возникающих систем и для одной
и тон же схемы C) могут быть введены различными спо-
способами, граничные условия для них должны выбираться
в зависимости от этого. Сами схемы типа C) можно трак-
трактовать как обычные схемы с весом для е-уравнения,
напр., вида
ди дги д-и | Ььи , > ,.
решения к-рого отличаются от решения исходной зада-
задачи на О (г) (см. [4]). В случае области Q, составленной
из прямоугольников, матрицы возникающих систем в
методах типа C) уже не представимы в виде произве-
произведения «одномерных» матриц. Все же решения подобных
систем могут быть найдены при затрате O(N) арифме-
тич. действий (см. [4]), операторы подобного типа наз.
расширенно расщепляющимися опе-
операторами. При исследовании устойчивости и схо-
сходимости схем с расщепляющимися и расширенно рас-
расщепляющимися операторами большую роль играет
метод энергетич. неравенств (см. [2], [4], [6] — [8]).
Лит.: ШМарчукГ. И., Методы вычислительной мате-
математики, 2 изд., М., 1!)80; [2] С а м а р с к и й А. А., Теория раз-
разностных схем, М., 1977; [3] Яне и к о Н. Н., Метод дробцых
шагов решения многомерных задач математической физики, Но-
восиб., 1067; [4] Д ь я к о н о в Е. Г., Разностные методы реше-
решения краевых задач, в. 1—2, М., 1071—72; [5] К о в е н я В. М.,
Я н с н к о Н. Н., Метод расщепления в задачах газовой дина-
динамики, Новосиб., 1981; [6] Д р ы я М., в кн.: Banach center pub-
publications, v. ,'i, Warszawa, 1978, p. 59—67; [7] 3 л о т н и it A. A.,
«Ж. вычислит, матем. и матем. физ.», 1980, т. 20, J4» 2, с. 422—32;
[8] Н a yes L. J., «S1AM J. Numer. Analysis», 1981, v. 18, № 4,
p. 627—43. E. Г. Дьяконов.
РАСЩЕПЛЯЕМАЯ ГРУППА — группа G, порож-
порожденная своими подгруппами Н и К такими, что Н
инвариантна в G и пересечение tlf\K = E (так что фак-
факторгруппа Gill изоморфна К). В этом случае G наз.
также расщепляемым расширением
группы // при помощи группы К, или п о л у и р я-
м ы м произведением //на К. Если подгруп-
подгруппы 11 и К поэлементно перестановочны, то их полупря-
полупрямое произведение совпадает с прямым произведением
НХ К. Полуирямое произведение G группы // на группу
К существует тогда и только тогда, когда существует
гомоморфизм т|) группы К в группу Aut II автоморфиз-
автоморфизмов группы В. В зтом случае для любых /е?А', ?II
справедлива формула
определяющая умножение в G. В случае, когда
K=Aut II и т|) — тождественное отображение, группа
G наз. голоморфом группы Н.
Лит.: Ll] Gorenstein D., Finite groups, N. Y.— L.,
1968. H. H. Вильяме.
РАСЩЕПЛЯЮЩАЯСЯ ПОСЛЕДОВАТЕЛЬНОСТЬ—
точная последовательность
f g
О—>Л—+#—>С—^0 (*)
в абелевой категории, изоморфная последовательности
прямой суммы:
причем этот изоморфизм таков, что А и С отображаются
в А и С соответственно тождественным образом. Для
расщепляемое™ последовательности (*) достаточно су-
существования правого обратного /' для отображения /
или левого обратного g' для отображения g. Класс
расщепляющихся точных последовательностей явля-
является нулем группы Ext%(A,C) (см. Бэра умноже-
умножение). В категории векторных пространств (т.е. моду-
модулей над фиксированным полем) все точные последо-
последовательности являются расщепляемыми.
Для относительной гомологической алгебры типич-
типична ситуация, когда рассматриваются точные последо-
последовательности одной категории, являющиеся Р. п. в дру-
другой Категории. В. Е. Говоров.
РАУСА ТЕОРЕМА — теорема, позволяющая для
многочлена / (х) с действительными коэффициентами
(в регулярном случае) определить с помощью схемы
Рауса число комплексных корней этого многочлена с
положительной действительной частью.
Пусть многочлен / (х) для удобства записан в виде
/ (х) =ао^ + 6ох™-1 + а1х«-2 + 61^-з+ ...{айф 0).
Схемой Pa уса этого многочлена наз. система чи-
чисел
сос1с2 . . .
В этой схеме первые две строки составлены из коэф-
коэффициентов многочлена f(x), а каждая строка, начиная
с третьей, получается из двух предыдущих следующим
образом: из первой строки вычитается вторая, умно-
умноженная на такое число, чтобы первый элемент обра-
обратился в нуль. Выбрасывая этот первый нуль, полу-
получают искомую строку. Напр., в третьей строке
c, = aI- + 1-b/ + 1-^-, /=0, 1, 2, ... .
В первой строке схемы Рауса число элементов равно
п + 1
целой части числа —^— , во второй — целой части числа
'-- , в к-й строке при /с>2 число элементов на 1 меньше,
чем в (к — 2)-й строке. Вся схема содержит п+1 строку.
Регулярным наз. тот случай, когда в схеме Ра-
Рауса многочлена все числа первого столбца отличны от
нуля.
Теорема Рауса. Для многочлена с действи-
действительными коэффициентами в регулярном случае число
корней, лежащих в правой полуплоскости (т. е. име-
ющих положительные действительные части), равно
числу перемен знака в ряду чисел первого столбца
схемы Рауса. В регулярном случае многочлен не может
иметь корней, лежащих на мнимой оси. Критерий
Рауса: для того чтобы все корни многочлена f(x) с
действительными коэффициентами имели отрицатель-
отрицательные действительные части, необходимо и достаточно,
чтобы все числа первого столбца схемы Рауса были
отличны от нуля и имели одинаковые знаки. Эти тео-
теоремы были установлены Э. Раусом [1]. Метод Рауса
применяется для определения числа корней многочле-
многочлена в правой полуплоскости и в нек-рых нерегулярных
случаях.
Построение схемы Рауса возможно лишь для много-
многочленов с, заданными числовыми коэффициентами. Более
широко применим метод, в к-ром роль схемы Рауса
играет матрица Гурвица, а роль первого столбца схе-
схемы Рауса — последовательность главных миноров Д,-,
(=1, 2, . . ., п (см. Рауса — Гурвица критерий). При
этом аналогом Р. т. будет теорема Рауса —
Гурвица: если все миноры Л,- отличны от нуля,
то число корней многочлена j(x), лежащих в правой
полуплоскости, равно числу перемен знака в ряду чисел
„ Л дг А3
°0> &1, Х" ' "л~~
и /(.г) не имеет корней, лежащих на мнимой оси. Этот
метод применим при нек-рых дополнительных условиях
к случаю, когда отдельные из миноров Д,- равны нулю.
Лит.: [1] R о u t h E. J., Treatise on the stability of a given
state of motion..., L., 1877; [2] его ж е, The advanced, part of
a treatise on the dynamics of a system of rigid bodies, 6 ed., L.,
1905; 13] Ляпунов А. М., Общая задача оО устойчивости
движения, М.— Л., 1950; [4] Г а н т м а х е р Ф. Р., Теория мат-
матриц, 3 изд., М., 1967. И. В. Проскуряков.
РАУСА — ГУРВИЦА КРИТЕРИЙ, Гурвица
критерий, — необходимое и достаточное условие
того, чтобы псе корни многочлена
/ (х) = аах"
с действительными коэффициентами и ао>О имели от-
отрицательные действительные части. Р.—Г. к. состоит
в том, чтобы были положительными все главные ми-
миноры Д/, i=l, 2, . . ., п, матрицы Гурвица
//, где Н — матрица порядка п, i-н строка к-рой имеет
вид
а2-11 а4-A •••! а2п-('
и, по определению, ак— 0, если &<0 или &>« (усло-
(условия Гурвица, условия Рауса — Гур-
Гурвица). Этот критерий получен Л. Гурвицем [1] и
является обобщением работы Э. Рауса (см. Рауса
теорема).
Многочлен /(х), удовлетворяющий условиям Гур-
Гурвица, наз. многочленом Гурвица, или
устойчивым многочленом, что связано
с применениями Р.— Г. к. в теории устойчивости ко-
колебательных систем. Известны и другие критерии ус-
устойчивости многочленов: критерий Рауса, Лъенара —
Шипара критерий, а также способы определения числа
корней многочлена.
Лит.: [llHnrwitz A., «Math. Ann.», 1895, Bd 46, S. 273—
84; [21 Г а и т м к х е р Ф. Р., Теория матриц, 3 изд., М., 1967.
К. Я. Кузьмин.
РАЦИОНАЛЬНАЯ КРИВАЯ — одномерное алгеб-
раич. многообразие, определенное над полем к, иоле
рациональных функций к-рого является чисто транс-
трансцендентным расширением поля к степени 1. Все неосо-
неособые полные Р. к. изоморфны проективной прямой Р1.
Полная неособая кривая X рациональна тогда и
только тогда, когда ее геометрич. род g=0, то есть
когда на X нет регулярных дифференциальных форм.
В случае, когда к=С — ноле комплексных чисел,
неособая полная Р. к. X — это сфера Римана С (J {оо }.
Вик. С. Куликов.
РАЦИОНАЛЬНАЯ ОСОБЕННОСТЬ — нормальная
особая точка Р алгебраич. многообразия или комплек-
комплексно аналитич. пространства А', допускающая разре-
разрешение особенности л : Г->-А', при к-ром прямые об-
образы W'n^Oy структурного пучка Оу тривиальны при
г>1. Тогда этим свойством будет обладать и любое
разрешение данной особенности. Если основное поле
имеет характеристику 0, то особенность является Р. о.
тогда и только тогда, когда X — многообразие Коэна —
Маколея и вложение л» : шу-+шу дуализирующих
пучков является изоморфизмом [5].
Р. о. являются, например, особые точки фактор-
пространства С"/С, где G — коночная группа линейных
преобразований; особая точка 0 гиперповерхности
4»-!-. . .-!- 4" =0 при 2 "=1 йт'>1 (см. [8]); торичес-
кие особенности.
Если Р?Х — горенштеннона изолирован-
изолированная особенность (т. е. пучок и>х локально свободен)
над полем С и со — образующая пучка и>х, то Р явля-
является Р.о. тогда и только тогда, когда
\ у
в достаточно малой окрестности U точки Р (cur. [7J).
В случае, когда dim Х—-2, особенность Р рациональ-
рациональна тогда и только тогда, когда Л1(Од) = 0 для каждого
цикла D на исключительной кривой Е=л~1(Р) рая-
решения я. В атом случае для Р. о. все компоненты А",-
кривой Е изоморфны проективной прямой Р1, А" —
дивизор с нормальными пересечениями и граф Г раз-
разрешения является деревом.
Фундаментальным циклом особенности наз. мини-
минимальный цикл Z>0 на Е, для к-рого Z -Е^О для всех i.
В терминах цикла Z можно дать критерий рациональ-
рациональности: hl(Og) = 0, а также вычислить кратность осо-
особенности и размерность касательного пространства [1].
Обозначение
О„ , л » 4
Уравнение
Т3 + ^* + 22
X1 + X/3 + 72
i3 + у5 + г2
Граф
о^ <^
G
Вп~г
Т
0
1
Р. о. гиперповерхностей X в трехмерном аффинном
пространстве А* или, что эквивалентно, двумерные
Р. о. кратности 2 наз. двойными Р. о. Двойные
Р. о. имеют ряд эквивалентных характеризаций и
несколько различных названий: о с о б е и и о с т и
К л е й н а, особенно с т и Д ю 13 а л я. и р о-
стне о с о б е н н о с т и. Уравнения двойных Р. о.
возникают как уравнения, связывающие инварианты
групп симметрии правильных многогранников (см.
[6]). Это соответствует характеризацин двойных Р. о.
как особенностей факторпространст» A' --C2/GcCs,
где G — конечная подгруппа в SL B, С); с точностью
до сопряженности такие подгруппы . исчерпываются
списком: Сп— циклич. группа порядка п, бинарные
группы диэдра Dn, группа тетраэдра 7\ группа октаэд-
октаэдра О, группа икосаэдра I. Если л — минимальное
разрешение двойной. 1'. о., то все Е\~ —2 и взвешенный
граф Г совпадает со схемой простых корней одной из
полупростых алгебр Ли Ап, D,,, Ев, Е-, Ея, обозначе-
обозначения к-рых переносятся и на особенности. С точностью
до изоморфизма такая особенность определяется своим
взвешенным графом Г (|3|, 1111), см. таблицу, кол. 915.
Двойные Р. о. могут быть охарактеризованы как дву-
двумерные горенштейновы Р. о. Они наз. также кано-
каноническими особенностями, т. к. это
в точности те особенности, к-рые появляются на ка-
нонич. моделях алгебраич. поверхностен основного
типа.
Если Р?Х горенштейнова Р. о. произвольной раз-
размерности, то ее общее гиперповерхностное сечение есть
либо рациональная, либо эллиптическая горенштейнова
особенность, что позволяет, в частности, описать трех-
трехмерные Р. о. (см. |81).
В произвольной размерности справедливы следующие
факты (см. [4]). 1) Деформация Р. о. есть снова Р. о.
2) Если / : А->5 — плоский морфизм, х?Х, причем
точка s=f(x) является Р. о. в S, ах — Р. о. слоя
Xs: = f-](s), то х является Р. о. в X. 3) Если деформация
/ : X-+S имеет гладкую базу S и допускает одновре-
одновременное разрешение особенностей, то точка х?Х явля-
является Р. о. тогда и только тогда, когда х является Р. о. в
своем слое /~1(/(х)).
В случае dim А"=2 любая деформация многообразия
У, разрешающего Р. о. Р?Х, определяет деформацию
особенности Р, к-рая получается, если стянуть исклю-
исключительные кривые слоев данной деформации. В ре-
результате получается морфизм q. : Def У—>-Def А* баз
нереальных деформации многообразия У и особенности
Р. Образ A -=(p(Def У) есть неособая неприводимая
компонента » Del' X, называемая компонентой
А р т и н а, а ср : Del' У-+А — накрытие Галуа, груп-
группа W к-рого может быть найдена при помощи графа
Г особенности Р (см. |2], [Ю]). В частности, для двойной
Р. о. ф сюръектинно и W совпадает с группой Вейля
соответствующей алгебры Ли, т. с. версальная дефор-
деформация Р. о. одновременно разрешается после накрытия
Галуа базы деформации с группой Вейля W (см. [9]).
Лит.: [1] А г t i n M., «Amer. ,1. Math.», 1966, v. 88, p. 129 —
36; [2] его же, «J. Algebra», 1974, v. 29, №2, p. 330—48;
Ш Brieskorn B. «Invent, main.», 19И8 v. 4, p. 336—58;
[4] Elkik R., там же, 1978, v. 47, p. 139 — 47; [5] К е m p f
G., в кн.; Toroidal embedding, v. 1, B.— [u. a.], 1B73, p. 41—52;
ifi/ Klein F., Yorlesungen flber das Ikosaeder und die Auf-
losung der Gleichung von funften Grade, Lpz., 1884; 17] I, a u-
f e г Н. В., «Amer. .1. Math.», 1972, v. 94, p. 597—608; [8] К е i d
Н,,вш.: Geometric н1кёЬг1цие, rfockviil, 1980, p. 273—.411; [9]
Slodowy P. J., Simple singularities and simple algebraic
groups, В.,4980; [10] Wahl J., «Compos, math.», 1979, v. 38,
p. 43—54: [11] Тюри и а Г Н., «Изв. АН СССР. Сер. матем.»,
19()8, т. ,42, с. 943—70. Вал. С. Куликов.
РАЦИОНАЛЬНАЯ ПОВЕРХНОСТЬ — двумерное ал-
гебраич. многообразие, определенное над полем к,
иоле рациональных функции к-рого является чисто
трансцендентным расширением поля к степени 2. Лю-
Любая Р. и. X бирацпонально изоморфна проективному
пространству Ра.
Геометрии, род pg и иррегулярность q полной глад-
гладкой Р. н. X равны 0, то есть на X нет регулярных диф-
дифференциальных 2-фор.м и 1-форм. Все кратные роды
Рп—й\тМа(Х,Ох(пКх)) гладкой полной Р. п. X
также равны 0, где Кх— канонпч. дивизор поверхно-
поверхности X. Эти бирациональные инварианты выделяют
Р. и. среди всех алгебраич. поверхностей, а именно,
всякая гладкая полная алгебраич. поверхность с ин-
инвариантами pg—q—-P2-—l) является Р. ц. (крит е-
р и й рациональности К а с т е л ь н у о-
в о). Согласно другому критерию р а ц и о н а л ь-
н о с т и гладкая полная алгебраич. поверхность
А" является Р. п. тогда и только тогда, когда на X
летит неособая рациональная кривая С, индекс са-
самопересечения к-рой (С2)д->0.
Каждая алгебраич. поверхность, кроме Р. п. н ли-
линейчатых поверхностей, бирационально изоморфна
единственной минимальной модели. В классе Р. и. име-
имеется счетное множество относительно минимальных
моделей. Это — проективное пространство Р2 и поверх-
поверхности ?'„^Р (%п) (проективизации двумерных линей-
линейных расслоений над проективной прямой Р1), =5?,,=^
^ОргРОр^—п), где п^О и п=^=1. Другими словами,
поверхность Fn— ото расслоение на рациональные
кривые над рациональной кривой, у к-рого есть се-
сечение Sn— гладкая рациональная кривая с индексом
самопересечения (<?л)^——п. Поверхность Fo изо-
изоморфна прямому произведению Р'хР1, а поверхности
/¦'„ получаются из Fo с помощью последовательности
элементарных преобразований (см. [1]).
Р. п. имеют большую группу бирациональных преоб-
преобразований (т. н. г р у п п у кремоновых пре-
преобразований).
Если на гладкой полной Р. п. антнканонич. пучок
(>х(—А'я) обилен, то X наз. поверхностью
Д е л ь Пецц о. Наибольшее целое число г>0 та-
такое, что —Kx~rD для нек-рого дивизора D на X, наз.
индексом поверхности Д ел ь II е ц ц о. Ин-
юкс г может принимать значения 1, 2, 3 (см. f'2]). По-
Поверхность Дель Пеццо индекса 3 изоморфна Р-. Для
поверхности Дель Пеццо X индекса 2 рациональное
отображение ф0 (V) : Х->-Р3, определяемое пучком
<>x{D), дает бирациональный изоморфизм на квадрику
в Р3. Поверхности Дель Пеццо индекса 1 могут быть
получены п моноидальными преобразованиями пло-
плоскости Р2 с центрами в точках общего положения, где
1<га«8 (см. [2]).
Лит.: ll] Алгебраические поверхности, М., 19ti5 [Тр. Ма-
Маем, ин-та АН СССР, т. 75] ; [2] И с к о в с и и х В. А., в сб.:
"временные проблемы математики, т. 12, М., 1979, с. 59—157;
|.ч] Хартсхорн Р-, Алгебраическая геометрия, пер. с
шгл., М. 1981. But;. С. Куликов.
РАЦИОНАЛЬНАЯ ФУНКЦИЯ — 1) Р. ф.—'функ-
ф.—'функция w—R(z), где Я (z) — рациональное выражение
от z, т. е. выражение, полученное из независимого
переменного z и нек-рого конечного набора чисел (дей-
(действительных или комплексных) посредством конечного
числа арифметич. действий. Р. ф. можно записать (не
единственным образом) в виде
где Р, Q — многочлены, ()(г)фО. Коэффициенты этих
многочленов наз. коэффициента м и Р. ф.
Дробь PiQ наз. несократимой, если Р, Q ые имеют об-
общих нулей (то есть Р, Q — взаимно простые многочле-
многочлены). Всякую Р. ф. можно записать в виде несократимой
дроби R (z) — P (z)/Q (z); если при итом Р имеет степень
га, a Q — степень п, то степенью Р. ф. Л (г) наз. пару
( II, п) ИЛИ ЧИСЛО
iV = max {m, n].
Р. ф. степени (т, п) при я—0, т. е. многочлен, наз.
целой рациональной функции й, в
противном случае — дроби о-рациональной
функцией. Р. ф. R (г)--Л) не имеет степени. При
т<.п дробь R ыаз. правильной, при т>к — неправиль-
неправильней. Неправильную дробь можно единственным обра-
образом записать в виде
где Р,— многочлен, наз. целой частью дроби PiQ,
a l'.tiQ — правильная дробь. Правильная дробь с не-
несократимой записью R(z)—P(z).'Q(z), где
может быть единственным образом разложена в сумму
простейших дробей:
Если P(x)lQ(x) — правильная Р. ф. с действительными
коэффициентами и
Q (х)=Ъ„(х-1>1I. . .(x~br)h (x"--\-p,xAr4l)U.. .
где b0, bu . . ., br, рг, qx, . . ., ps, qs — действитель-
действительные числа, p2j—4qy<(), /=!,..., s, то P(x)'Q(x) также
единственным образом представляется в виде
(*-»1)'1.
г и ¦ x + t. . П , х + Е ¦
D;f'^A.
¦••+
где все коэффициенты действительны. Эти коэффициен-
коэффициенты, как и с,-.- в A), могут быть найдены неопределенных
коэффициентов методом.
Р. ф. степени (га, п) в несократимой записи опреде-
определена и аналитична в расширенной комплексной пло-
плоскости (т. е. плоскости, дополненной точкой z=oo)
за исключением конечного числа особых точек— по-
полюсов в нулях ее знаменателя, а при ш>>! еще и в точ-
точке оо; при атом сумма кратностей полюсов функции Я
равна ее степени N. Обратно, всякая аналитич. функ-
функция, имеющая в расширенной комплексной плоскости в
качестве особых точек только полюсы, является Р. ф.
В результате арифметич. действий над Р. ф. полу-
получают также Р. ф. (деление на Я (z)^=0 исключается),
так что все Р. ф. образуют ноле; вообще, Р. ф. с ко-
коэффициентами ш) нек-рого поля образуют иоле. Если
Я1{г), B2{z) суть Р. ф., той Я1(Н2(г)) является Р. ф.
Производная порядка р от Р. ф. степени iV есть Р. ф.
степени <:(p-!-l)iV. Неопределенный интеграл (пер-
(первообразная) от Р. ф. представляет собой сумму нек-рой
Р. ф. и выражений вида crh\(z — Ьг). Если Р. ф. R (х)
действительна при действительном х, то неопределен-
неопределенный интеграл \ R (x)d.c может быть записан в виде сум-
суммы нек-рой Р. ф. Я0(х) с действительными коэффици-
коэффициентами, выражений вида
c;l In | x — bi |, Mj In (x- -\-pjx-\- qj),
2x i Vj
Nj arctg .¦ - , i = 1, ..., r; / = 1, ..., s,
V i^j-p)
и произвольной постоянной С (здесь числа с,- , Ь,-,
Pj, i/j— те же, что н в B), Mj, Nj— нек-рые действи-
действительные числа). Функцию Яо (,т) но Остроградского
метооу можно найти, минуя разложение Я (х) на про-
простейшие дроби B).
Удобные длн вычислений, Р. ф. используются для
приближенного представления функций. Рассматрива-
Рассматриваются также Р. ф. от нескольких действительных или
комплексных переменных Я— P/Q, где Р, Q — много-
многочлены от соответствующих переменных (Ощ&О), а также
абстрактные Р. ф.
ft А1Ф1+ . . . +А,„Фт
Б,Ф,+ . . . +В„Фп '
где Фг, Фо, . . . — линейно независимая система не-
непрерывных функций на нек-ром бикомпакте X, а
Аг, . . ., А,а, Ви . . ., Вп — числа.
См. также Дробно-линейная функция, Жуковского
функция.
Лит.: [1] Привалов И. И., Введение в теорию функций
комплексного переменного, 12 изд., М., 1977; [2] К у р о ш А. Г.,
Курс высшей алгебры, И изд., М., 1!OГ). Е. П. Долженко.
2) Р. ф. на алгебраическом многооб-
многообразии — обобщение классич. понятия рациональной
функции (см. п. 1). Р. ф. на неприводимом алгебраич.
многообразии X — это класс эквивалентности пар
(U, /), где X— непустое открытое подмножество в А',
а / — регулярная функция на U. Две пары (U, /) и
(F, g) наз. эквивалентными, если f=g на U[)V. P. ф.
на X образуют поле, обозначаемое к(Х).
В случае, когда X=Spec R — аффинное неприводи-
неприводимое многообразие, ноле Р. ф. на X совпадает с полем
частных кольца R. Степень трансцендентности над
к поля к (X) наз. размерностью многооб-
многообразия X.
Лит..- [1] Ш а ф а р е в и ч И. Р., Основы алгебраической
геометрии, М., 1972. Вин. С. Куликов.
РАЦИОНАЛЬНОЕ МНОГООБРАЗИЕ — алгебраиче-
алгебраическое многообразие X над алгебраически замкнутым но-
нолем к, поле рациональных функции к(Х) к-рого изо-
изоморфно чисто трансцендентному расширению конеч-
конечной степени поля к. Другими словами, Р. м.— это
алгебраич. многообразие X, бирационально изоморф-
изоморфное проективному пространству Р".
Полное гладкое Р. м. X обладает следующими бира-
циональными инвариантами. Размерности всех про-
пространств Ни(Х, Их) регулярных дифференциальных
к -форм на X равны 0. Кроме того, кратный род
Н° (X, Ох (пКх)) = 0 при п > 0,
где Кх— канонич. дивизор алгебраич. многообразия
X, т. е. кодаировская размерность Р. м. X равна 0.
В малых размерностях перечисленные выше инвари-
инварианты однозначно выделяют класс Р. м. среди всех ал-
алгебраич. многообразий. Так, если dinijX = l и род ал-
алгебраич. кривой X равен 0, то X — рациональная
кривая. Если dinifcX=2, а арифметич. род
Pa = dimkH°(X, Qx)-AimkH»(X,Qx)=0
и кратный род Р2=0, то X — рациональная поверх-
поверхность. Однако в случае dim^ Х^З нет хорошего крите-
критерия рациональности из-за отрицательного решения
Люрота проблемы.
Лит.: [1] Ш а ф а р е в и ч И. Р., Основы алгебраической
геометрии, М., 1972. Вик. С. Куликов.
РАЦИОНАЛЬНОЕ ОТОБРАЖЕНИЕ — обобщение
понятия рациональной функции на алгебраич. мно-
многообразии. А именно, рациональным отоб-
отображением неприводимого алгебраич. многообра-
многообразия X в алгебраич. многообразие Y (оба определены
над полем к) наз. класс эквивалентности пар (U, еру),
где Г — непустое открытое подмножество в X, а ц>ц—
морфил.м из U в У. При этом пары (U, фу) и (V, ц>у)
считаются эквивалентными, если (рц и фу совпадают на
U(]V. В частности, Р. о. многообразия X в аффинную
прямую есть рациональная функция на многообразии
X. Для каждого Р. о. ср : X >-У существует такая
пара (U, Ц>ц), что U'g^U для любой эквивалентной ей
пары (U, ц>ц) и фу является ограничением ф^ на U,
Открытое подмножество U наз. областью регу-
регулярности Р. о. ф, а ф (U) — образом мно-
многообразия X (обозначается ф(Х)) при Р. о. ф.
Если ф : X >- У — Р. о. алгебраич. многооб-
многообразий и образ ф (X) плотен в Y, то <р определяет вло-
вложение полей ф*: &(У)—>-fc(X). Обратно, вложение полей
рациональных функций ф* : к (Y)-+-k (X) определяет
Р. о. многообразия X в Y. Если Р. о. ф индуцирует изо-
изоморфизм полей рациональных функций к (X) и /г (У),
то ф наз. бирациональным отображе-
отображением.
Множество точек из X, в к-рых Р. о. <р: X vY
не регулярно, имеет в общем случае коразмерность 1.
Но если У — полное многообразие, а X — гладкое не-
неприводимое многообразие, то множество точек из X,
в к-рых ф не регулярно, имеет коразмерность не мень-
меньше двух. Если X и У — полные неприводимые мно-
многообразия над алгебраически замкнутым полем харак-
характеристики 0, то Р. о. ф: X —>-У может быть вклю-
включено в коммутативную диаграмму (см. [2]):
(*)
где т], / — морфиямы алгебраич. многообразия Z,
и т] является композицией моноидальных преобразова-
преобразований. Если ф : X— >-У — бирациональное отобра-
отображение полных неособых поверхностей, то существует
диаграмма (*), в к-рой оба морфизма / и Г| являются
композициями моноидальных преобразований с неосо-
неособыми центрами (теорема 3 а р и с к о г о), т. е.
любое бирациональное отображение полных неособых
поверхностей раскладывается в композицию моно-
моноидальных преобразований с неособыми центрами и об-
обратных к ним отображений. В случае dim Х~^Ъ ана-
аналогичный вопрос о разложении бирационального отоб-
отображения открыт A983).
Лит.: [1] Шафаревич И. Р., Основы алгебраической
геометрии, М., 1972; [2] Hironaka H., «Ann. Math.», 1964
V. 79, Л» 1 — 2, р. 109 — 326. Виг,. С. Куликов.
РАЦИОНАЛЬНОЕ ПРЕДСТАВЛЕНИЕ алгеб-
алгебраической группы G — линейное представле-
представление алгебраич. группы G над алгебраически замкнутым
полем к в конечномерном векторном пространстве V
над к, являющееся рациональным (и тем самым регу-
регулярным) гомоморфизмом группы G в GL(F). Говорят
также, что V — рациональный G-м о д у л ь.
Прямая сумма и тензорное произведение конечного чис-
числа Р. п. группы G являются Р. п.; подпредставление и
факторпредставление нек-рого Р. п. являются Р. п.;
симметрическая или внешняя степень любого Р. п. яв-
является Р. п.; представление, контрагредиентное к Р. п.,
является Р. п.
Если G конечна, то всякое ее линейное представле-
представление будет Р. п. и теория Р. п. сливается с теорией пред-
представлений конечных групп. В наибольшей степени
сиецифич. методы теории линейных алгебраич. групп
используются при исследовании Р. п. в том случае,
когда рассматриваемая группа связна, причем наибо-
наиболее глубоко развита теория Р. п. связных полупростых
алгебраич. групп. Далее G — такая группа. Пусть
Т — ее максимальный тор, Х(Т) — его группа рацио-
рациональных характеров (записываемая аддитивно), 2 —
система корней группы G относительно Т, W — ее груп-
группа Вейля. И пусть ф : G—>-GL(F) есть Р. п. Ограни-
Ограничение представления ф на Т разлагается в прямую
сумму одномерных представлений, точнее
где РсрСХ(Т) — нек-рое множество характеров то-
тора Т, называемых весами представления, а
Множество весов Ру инвариантно относительно W.
Если char к=-0, то всякое Р. п. группы G вполне при-
приводимо, но если char /r>0, то это уже не так (см. Мам-
форда гипотеза). Однако при любой характеристике
поля к имеется полное описание неприводимых Р. и.
Пусть В — борелевская подгруппа в G, содержащая
Т, и Д — определяемая ею система простых корней в
2. Группа Х(й) рациональных характеров группы В
отождествляется с ХG'). В пространстве V любого не-
неприводимого Р. п. ф :G—>-GL(F) существует единст-
единственное одномерное весовое подпространство V'F<p),
бф ?Pq>, инвариантное относительно группы В. Харак-
Характер fiif ная. старшим весом неприводимо-
неприводимого Р. п. ф; он доминантен, т. е. скалярное произве-
произведение (fi(p, а)^0 для любого а?А, а всякий другой
вес Х?Рф имеет вид
Отображение ф(-»6(р определяет биекцию между клас-
классами эквивалентных неприводимых Р. п. и доминант-
доминантными элементами из Х(Т). Явная конструкция всех
неприводимых Р. п. может быть получена следующим
образом. Пусть k[G] — алгебра регулярных функций
на G. Для любого х?Х(Т) — Х(В) рассматривается
подпространство
Оно конечномерно и является рациональным G-mo-
дулем относительно действия группы G левыми сдви-
сдвигами. Геометрич. смысл этого пространства таков:
оно канонически отождествляется с пространством ре-
регулярных сечений одномерного однородного векторного
расслоения над G/B, определенного характером —%.
Пусть wo?W — элемент, переводящий положительные
корни в отрицательные. Тогда если k[G]_m ,^^=0, то
•( — доминантный характер и минимальный ненулевой
G-подмодуль в /c[G]_u,[(x) является неприводимым ра-
рациональным G-модулем со старшим весом у. Всякий
неприводимый рациональный G-модуль получается при
помощи такой конструкции. Если char k~0, то уже сам
ff-модуль к [G]_Wi)(x> неприводим.
Для получения неприводимых Р. п. часто использу-
используются упомянутые выше операции над Р. п. Напр., если
Ф/— неприводимое Р. п. со старшим весом Хп г=1,
..., rf, то нек-рое факторнредставление (fi® . . -®4>d
является неприводимым Р. п. со старшим весом ул-\-
¦+• • -+Xd (оно наз. к а р т а н о в с к о й к о м и о-
:( и ц и е й Р. п. фг, . . ., ф^). Если ср — неприводи-
неприводимое Р. п. со старшим весом %, то нек-рое факторпредстав-
.|рние Sv является неприводимым Р. п. со старшим
весом dX, а ф* — неприводимо и его старшим весом
является — '"о(х)'
Пусть з — алгебра Ли группы G. Если ф : G—>-GL( V)
есть Р. п., то его дифференциал &р является представле-
представлением алгебры Ли fl. P. п. ф наз. инфинитези-
инфинитезимально неприводимым, если Лр — непри-
неприводимое представление алгебры д. Инфинитезимально
неприводимое Р. п. неприводимо, а в случае char &=0
верно и обратное (что в значительной степени сводит
теорию Р. п. группы к теории представлений ее алгеб-
алгебры Ли), однако в случае char &>0 это уже не так.
Инфинитезимально неприводимые Р. п. в этом случае —
это в точности неприводимые Р. п. со старшими весами
X, для к-рых
О < 2,(*'а) < Р ПРИ любом <*?Л-
Более того, все неприводимые Р. п. могут быть построе-
построены при помощи инфинитезимально неприводимых.
Точнее, если С односвязна, т. е. если X (Т) совпадает с
решеткой весов корневой системы 2, то всякое непри-
неприводимое Р. п. одаодначно разлагается в. тензорное, про-
наведение вида
где ф_о> <Pi, • • -, ф<* инфинитезимально неприводимы,
а <pfr — представление, полученное применением к
матричным элементам представления ф,- автоморфиз-
автоморфизма Фробениуса a\-*ap'(a?k), Р =с.Ьаг к.
Лит.: [1] Б о р е л ь А., Линейные алгебраические группы,
пер. с англ., М., 1972; [2] е г о ж е, в кн.: Algebraic geometry,
Providence, 1975, p. 421—40 (Proc. Symposia in pure math.,
v. 29, Arkata, 197'»); L3] X а м ф р и Д ж.. Линейные алгебраи-
алгебраические группы, пер. с a?irji., M., 1980; [4] Семинар по алгебра-
алгебраическим группам, пер. с англ., М., 1973; [5] С т е й н б е р г Р.,
Лекции о группах Шевалле, пер. с англ., М., 1975; [li] его же,
«Nagoya math. J.», 1963, v. 22, p. 33—56; [7] Hochschild
G., The structure of Lie groups, S. F., 1965; 18] Humph-
Humphreys ,1. E., Introduction to Lie algebras and representation
theory, N. Y. — [a. o.], 1972. В. Л. Попов,
РАЦИОНАЛЬНОЕ ЧИСЛО — число, выражаемое ра-
рациональной дробью. Формальная теория Р. ч. строится
с помощью пар целых чисел. Рациональной
дробью -jj- наз. упорядоченная пара (а, Ь) целых
чисел а и Ь, у к-рой ЪфО. Две рациональные дроби -^
и -j- наз. эквивалентными (равными)
тогда и только тогда, когда ad-—be. Это соотношение
эквивалентности, будучи рефлексивно, симметрично
и транзитивно, разбивает множество всех рациональ-
рациональных дробей на классы эквивалентности. Рацио-
Рациональным числом наз. каждый класс эквива-
эквивалентности рациональных дробей. Разные классы опре-
определяют разные Р. ч. Множество Р. ч. счетно. Р. ч.,
содержащее рациональную дробь вида -^-, наз. н у-
л е м. Если г есть Р. ч. и у-?г, то Р. ч., содержащее
рациональную дробь — , наз. рациональным числом,
противоположным Р. ч. г, и обозначается через —г.
Р. ч. г на.ч. положительным (отрицатель-
н ы м), если оно содержит рациональную дробь ~ ,
у к-рой а и b одного знака (разных знаков). Если Р. ч.
положительно (отрицательно), то противоположное ему
число отрицательно (положительно). В множестве Р. ч.
вводится упорядоченность: всякое отрицательное Р. ч.
считается меньшим всякого положительного, положи-
положительное Р. ч. г' считается меньшим положительного
Р. ч. г" : г'<г", если существуют такие рациональные
дроби ¦?-?г' и -^ ? г", а>0, Ь>0, с>0, d>0, что ad<
<bc; всякое отрицательное (положительное) Р. ч. г счи-
считается меньше (больше) нуля: г<0 (г>0); отрицательное
Р. ч. г' считается меньшим отрицательного Р. ч. г",
если положительное Р. ч.— г' больше положительного
Р. ч.— ;•": —г' > — г". Абсолютная величина |г| Р. ч.
определяется как обычно: \г\ = г, если г^О, и |Н = —г,
если г<0.
Суммой рациональных дробей-г- и -у нал. рацио-
рациональная дробь "' * , а произведением ~ . Сум-
Суммой и произведением Р. ч. г' и г" наз.
классы эквивалентных рациональных дробен, содер-
содержащие соответственно сумму или произведение раци-
рациональных дробей -г- и ¦—, принадлежащих г' и г":
— ?г',— ?г". Упорядоченность, сумма и произведение
Р. ч. г 'и г" не зависят от выбора представителей в соот-
соответствующих классах эквивалентности — ?г' и -j-?r",
т. е. однозначно определяются самими Р. ч. г' и г".
Р. ч. образуют упорядоченное поле, обозначаемое Q.
Для обозначения Р. ч. г применяются рациональные
дроби -г из класса эквивалентности, задающего это число:
-~-?г. Таким образом, одно и то же Р. ч. может быть
лаписано разными, но эквивалентными рациональными
1,])ОбяМИ.
Если каждому Р. ч., содержащему рациональную
чробь вида — , поставить в соответствие целое число а,
к» получится изоморфное отображение множества
укапанных Р. ч. на кольцо '? целых чисел. Поэтому
Р. ч., содержащие рациональные дроби вида ~ , обо-
.шачают через а.
Всякая функция вида
а A)
является метрикой в поле Р. ч. Q, то есть удовлетво-
удовлетворяет условиям:
1) ф(г)>0 при любом r i= О, ф @) 0;
2) ф(г'-!-7-"Хф(г') + ф(О;
3) ф(г', r")^(f(r')(f(r")
при любых г' ?Q и г"?<0. Поле Р. ч. не является пол-
полным в метрике A). Пополнением поля Р. ч. по метрике
A) является поле действительных чисел.
Функция
^(r)-pv<r>, B)
где р — простое число, r—V. ч., представнмое в виде
,. _pv CO _^
(х (г) — целое, — несократимая рациональная
дробь, причем числа а и Ь не делятся на р), ар - фик-
фиксированное число, ()<р<1, также является метрикой
в поле Р. ч. Q. Она наз. р-'л д и ч е с к о ii м е т р и-
к о ii. Поле Р. ч. Q с метрикой B) не является нолньш.
Пополнением поля Р. ч. по метрике B) является ноле
р-адических чисел. Метрики A) и B) (для всех простых
чисел) исчерпывают все нетривиальные метрики в поло
Р. ч.
В десятичной записи Р. ч. и только они цредстави-
мы периодическими десятичными дробями.
Лит.: HJ Б о р е и и ч 3. И., Ш а ф а ]) е в и ч И. Р., Тео-
Теория чисел, 2 изд., М., 1972; [2] II и :) о Ш., Л а м а н с к и й М.,
Курс математики. Алгебра и анализ, jtcjt. с франц., М.., 1971.
.7. Д. Кудрявцев.
РАЦИОНАЛЬНОСТИ ТЕОРЕМЫ д ля алге б-
р а и ч е с к и х групп — утверждения о рацио-
рациональности (унирациональности) или нерациональности
тех или иных групповых алгебраич. многообразий.
Так как абелевы многообразия всегда нерациональны,
то основной интерес представляют Р. т. для линейных
алгебраич, групп, Здесь проблема рациональности
имеет два существенно различных аспекта: геометри-
геометрический и арифметический, отвечающие соответственно
алгебраически замкнутому и незамкнутому основному
полш А'. Первые Р. т. над полем С комплексных чи-
чисел были фактически доказаны еще Э. Никаром (Е. Pi-
card) и в современной терминологии устанавливают
унирациональность многообразий связных комплекс-
комплексных групп. В явной форме проблема рациональности
групповых многообразий была поставлена К. Шевалле
[1] лишь в 1954. Прогресс в этом направлении тесно
связан с достижениями структурной теории алгебра-
алгебраич. груди. Так, разложение Лови позволяет свести
проблему рациональности к редуктивным группам, а
разложение Бшоа — доказать рациональность много-
многообразий редуктивных групп над любым алгебраиче-
алгебраически замкнутым нолем. Таким образом, в геометрич.
случае имеется окончательный результат.
Гораздо более сложной оказывается ситуация для
незамкнутых полей А*. Примеры нерациональных К-
многообразин доставляют уже алгебрапч. торы; напр.,
трехмерный норменный тор Т - - Я у^ (С,„), соответ-
соответствующий биквадрат чном у расширению/^— А"( У a, V~b)
ноля А' (см. |1]). Этот пример минимален, ибо то-
торы размерности <:2 рациональны. В общем случае
алгебраич. торы всегда унирациональны. Произволь-
Произвольные связные А'-группы не обязательно унирацио-
унирациональны [3], однако, если ноле К совершенно или группа
0 редуктивна, унирациональность имеет место (см.
11] — [4]). Тем самым проблема рациональности груп-
групповых многообразий имеет характер Люроша проблемы
над незамкнутым полем.
Так как произвольная редуктивная группа является
почти прямым произведением тора и полуиростой
группы, то естественно различать два основных слу-
случая: 1) G — тор; 2) G — полупростая группа. В пер-
первом случае исследование проводится при помощи раз-
различных когомологич. инвариантов (для иолунростых
групп :>тп инварианты оказываются неэффективными).
Достаточно законченные результаты имеются для то-
торов, разложимых над абелевым расширением ноля оп-
определения (см. [5]). Первый пример нерационального
многообразия в классе полупростых групп был неодно-
связной группой, конструкция к-рой фактически со-
содержится в [10]. Возникшая при этим гипотеза о
том, что многообразия односвязных групп всегда ра-
рациональны, была решена отрицательно В. П. Плато-
Платоновым при помощи развитой им приведение и
АГ-теории (см. [(ij, |7]). Оказалось, что приведенная
группа Уайтхеда SKi(D) конечномерной центральной
простой А'-алгебры П тривиальна, если многообразие,
определяемое SL(l, D), рационально над А'. Эти ре-
результаты были перенесены на унитарные группы [12].
Ряд результатов связан с исследованием рационально-
рациональности спинорных многообразий Spin (и, /), где / — невы-
невырожденная квадратичная форма над К от п переменных
(char Кф2). Спинорные многообразия рациональны,
если либо /г<:5, либо поле К является недискретным ло-
локально компактным или полем рациональных чисел
(см. [8], [9], [11]); для я!>6 существуют нерациональные
спинорные многообразия |8]. Последний результат
удивителен тем, что Spin (/(, /) является двулистным
накрытием рационального многообразия SO(«, /).
Термин «Р. т.» иногда употребляется в теории ал-
алгебраич. групп в несколько ином смысле, примени-
применительно к утверждениям о свойствах групп над не обя-
обязательно алгебраически замкнутым полем. К утвержде-
утверждениям такого типа относится, напр., теорема Р о-
з е н л и х т a — Г р о т е н д и к а о том, что любая
связная А"-группа обладает максимальным тором, опре-
определенным над К (см. [4]).
Лит.: Ш С h с v а 1 I е у С, «J. Math. Soc. Japan», 1954,
v. ti, .M 3/4, p. 303—24; [21 b e m a •/. n r e M., G г о t U e n d i-
cck A., Schemes en troupes, B.— I», aj, 1970; l.'ij К о s e n-
1 i с U t M., «Ann. mat. pura aypl.», 1957, v. 43, p. 25—50; [4]
Б о р е л ь А., Линейные алгебраические группы, пер. с англ.,
М., 1972; 151 Воскресенский В. Е., Алгебраические
•горы, М., 1977; [й] Платонов В. П., «Тр. Матем. ин-та АН
СССР», 1H7U, т. 142, с. 198 — 207; [71 е г о ж е, «Докл. АН БССР»,
1977 т. 21, Л1 3, с. 197 — 98; [8] его ж е, «Докл. АН СССР»,
1979, т, 248, Л! 3, с. 524 — 27; [9] е г о ж е, «Тр. Матем. ин-та
АН СССР», 1981, т. 157, с. 1Н1—69; [1 0] С е р р Ж,-Н., Когомо-
логии Галуа, пер. с франц., М., 1968; [11] Ч е р н о у с о в В. И.,
«Докл АН БССР», 1981, т. 25, Л5 4, с. 293—96; [12] Я н ч е в-
с к и й В. И., «Матем. сб.», 1979, т. 110, № 4, с. 579 — 96.
А. С. Рапинчуп.
РЕАЛИЗУЕМОСТЬ — один из видов неклассич.
интерпретаиий логических и логико математических
языков. Различные интерпретации типа Р. определя-
определяются по следующей схеме. Для формул логико-матема-
тич. языка определяется отношение «объект е реализует
замкнутую формулу F», к-рое сокращенно записыва-
записывается 4erF». Определение носит индуктивный характер:
сначала отношение erF определяется для элементарных
формул /<', а затем для сложных формул в предполо-
предположении, что для составляющих их более простых фор-
формул это отношение уже определено. Замкнутая формула
F наз. реализуемой, или истинной при данной
интерпретации, если существует такой объект е, что
erF. Формула F, содержащая свободные неременные
хь . . ., хп, считается реализуемой, если реализуема
замкнутая формула Чхх . . . yx,,F.
Впервые интерпретация такого вида, известная как
рекурсивная реализуемость, была предложена С. Кли-
ни (см. [1], [2]) с целью уточнения интуиционистской
(конструктивной) семантики языка формальной ариф-
арифметики в терминах рекурсивных функций. Другие по-
понятия Р. являются модификациями рекурсивной Р.
Интуитивный смысл отношения erF такой: объект е
кодирует информацию об истинности формулы V.
Напр., в рекурсивной Р. натуральное число 0 реализует
элементарную формулу вида s—t тогда и только тогда,
когда эта формула верна (т. е. значения термов s и t
совпадают); если число е реализует дизъюнкцию AVB,
то по нему можно выяснить, какой ее член реализуем,
и найти число, его реализующее; по числу, реализую-
реализующему формулу УхА (х). можно построить алгоритм,
к-рый по любому натуральному числу п строит реали-
реализацию формулы А (и). В качестве реализаций, т. е.
объектов, реализующих формулы, чаще всего высту-
выступают натуральные числа. Однако при интуиционистской
интерпретации языка математич. анализа в качестве ре-
реализаций могут использоваться и другие объекты, напр,
одноместные теоретико-числовые функции (см., напр.,
13]).
Для формул логич. языков, напр. для пропозицио-
пропозициональных или предикатных формул, Р. определяется
обычно через понятие Р. для того или иного логико-ма-
тематич. языка Q. Логич. формула ЗС считается реа-
реализуемой, если реализуема всякая формула языка
1>, получающаяся подстановкой в 31 формул языка
12 вместо предикатных переменных.
Интерпретации типа Р. нашли широкое применение
и исследовании неклассических, прежде всего интуи-
интуиционистских и конструктивных, логических и логико-
чатоматич. теорий. Имеется описание различных поня-
isrii P. и их применений в теории доказательств для
исследования интуиционистских теорий (см. [3], [4]).
Лит.: [1] К 1 е с п с S. С, «.Г. Symbolic Logic», 1945, v. 10,
p. 109—24; [2] К ;i и н и С. К., Введение в метаматематику,
нер. с англ., М., 1957; L.1] К л и н и С, В е с л и Р., Основании
интуиционистской математики..., пер. с англ., М., 1978; 14]
Д р а г а л и н А. Г., Математический интуиционизм. Введение
в теорию доказательств, М., 1979. В. Е. Плиско.
РЕБРО многогранника — сторона грани
многогранника.
РЕГРЕССИИ КОЭФФИЦИЕНТ — коэффициент при
независимой переменной в уравнении регрессии. Так,
напр., в уравнении линейной регрессии Е (Y\X — x)~
= p4-pt;r, связывающей случайные величины К и X,
Р. к. E0 и Р, равны:
где р — корреляции коэффициент X и У, »ij—EX,
m2=EV. Oi-=DA', 02=-Dy. Вычисление оценок Р. к.
(выборочных Р. к.) — основная задача регрес-
регрессионного анализа. д, в. Прохоров
РЕГРЕССИИ МАТРИЦА — матрица В коэффици-
коэффициентов регрессии Ру/, /- 1, . . . т, i— 1, . . ., г, в мно-
многомерной линейной модели регрессии
лесь X — матрица с элементами Xjk, /=1, . . ., т.
к=\, . . ., n, Xjk, к=1, . . ., п. — наблюдения над
/-й компонентой исходной m-мерной случайной ве-
величины; Z — матрица известных регрессионных пере-
менных Zik, i—Л, . . ., г, А—1, . . ., п; р — матрица
ошибок с/*, /—1, . . ., т, п=\, . . .. п, с E8/fc=0.
Элементы ру,- Р. м. В неизвестны и подлежат оценке.
Модель (*) является обобщением на m-мерный случай
общей линейной модели регрессионного анализа.
Лит.: [1] К ен д а л л М. Д ж., Ст ьюарт А., Многомерный
статистический анализ и временные ряды, пер. с англ., М.,
1976. А. В. Прохоров.
РЕГРЕССИИ ПОВЕРХНОСТЬ (гиперповерхность) —
общее геометрич. представление уравнения регрессии.
Если заданы случайные величины Хг, Х2, . . ., Х„ и
f (х2, . ..,*„) ~Ь(Х1\Хг = х2, ...,Хп^=хп)
— регрессия Х1 по Х.2, . ¦ ., Х„, то уравнение у —
~-/(j-2, • . -. .'Си) задает в п-мерном пространстве соот-
соответствующую Р. п. При и-- 2 Р. и. обычно наз. к р и-
в о и регрессии. Иногда эти термины используют-
используются для того, чтобы подчеркнуть, что соответствующие
уравнения регрессии не являются линейными. В ли-
линейном случае Р. и. наз. соответственно плоек о-
стью регрессии и пряной р е г р е с с и и.
См. Регрессия. А. В. Прохоров.
РЕГРЕССИИ СПЕКТР — спектр случайного процес-
процесса, входящего в регрессионную схему для стационарных
временных рядов. Именно, пусть случайный процесс
j//, наблюдаемый при t=l, . . ., и, представляется в
виде
yt^mt + xt, A)
где .i-j— стационарный процесс с tx^ssQ, а среднее зна-
значение Еу1~пц выражено в форме линейной регрессии
где ф(*' ---(ф^*) , . . ., ф**'), k—i, . . ., s,— известные ре-
регрессионные векторы, 0j, . . ., ps— неизвестные ре-
регрессии коэффициенты. Пусть М (X) — спектральная
функция распределения регрессионных векторов фA),
. . ., Ф(Л|. Спектром регрессии для М (к)
наз. множество всех К таких, что М (Х2) — Af (Хх)>0
для любого интервала (Яь А,2), содержащего К, Я,1<Я<Я,2.
Р. с. играет важную роль в задачах оценки коэффи-
коэффициентов регрессии в схеме A) — B). В терминах эле-
элементов Р. с. выражается, напр., необходимое и доста-
достаточное условие асимцтотич. эффективности оценок р1
по методу наименьших квадратов.
Лит.: [II Grcnandf r U., Rosenblatt M., Statisti-
Statistical analysis of stationary time series, Stockh., 195E.
А. В. Прохоров.
РЕГРЕССИОННЫЙ АНАЛИЗ — раздел математич.
статистики, объединяющий практич. методы исследова-
исследования регрессионной зависимости между величинами по
статистич. данным (см. Регрессия). Проблема регрессии
в математич. статистике характерна тем, что о распреде-
распределениях изучаемых величин нет достаточной информации.
Пусть, напр., имеются основания предполагать, что
случайная величина У имеет нек-рое распределение
вероятностей при фиксированном значении х другой
величины, так что
Е (У |*) = «(*, Р),
где Р — совокупность неизвестных параметров, опре-
определяющих функцию g(x), и нужно но результатам
наблюдении определить значения параметров. В зави-
зависимости от природы задачи и целей анализа результаты
эксперимента (хг, уг), . . ., (х„, у„) по-разному интер-
интерпретируются в отношении неременной х. Для установ-
установления связи между величинами в эксперименте исполь-
используется модель, основанная на упрощенных допущени-
допущениях: величина х является контролируемой величиной,
значения к-рой заранее задаются при планировании
эксперимента, а наблюдаемые значения у представили в
виде
Vi=g(^i, Р) + в/, г = 1, ..., и,
где величины в,- характеризуют ошибки, независимые
при различных измерениях и одинаково распределен-
распределенные с нулевым средним и постоянной дисперсией. В слу-
чае неконтролируемой переменной результаты наблю-
наблюдений (x-i, у1,); . . ., (хп, ц„) представляют собой выбор-
выборку из нек-рой двумерной совокупности. Методы Р. а.
одинаковы и в том, и в другом случае, однако интер-
интерпретация результатов различается (в последнем слу-
случае анализ существенно дополняется методами теории
корреляции).
Исследование регрессии по экспериментальным дан-
данным производится методами, основанными на принципах
средней квадратич. регрессии. Р. а. решает следую-
следующие основные задачи: 1) выбор модели регрессии, что
заключает в себе предположения о зависимости функ-
функций регрессии от i я р, 2) оценка параметров E в выб-
выбранной модели методом наименьших квадратов, 3) про-
проверка статистич. гипотез о регрессии.
Наиболее естественной с точки зрения единого
метода оценки неизвестных параметров является модель
регрессии, линейная относительно этих параметров:
g(x, P)
Выбор функций gi(x) иногда определяется по располо-
расположению экспериментальных значений (х,у) на диаграм-
диаграмме рассеяния, чаще — теоретич. соображениями. Пред-
Предполагается также, что дисперсия в* результатов на-
наблюдений постоянна (или пропорциональна извест-
известной функции от х). Стандартный метод оценки регрес-
регрессии основан на использовании многочлена нек-рой
степени т, 1 <;»</;:
или в простейшем случае — линейной функции (линей-
(линейная регрессия)
g(x, P) = Po+Pi^.
Существуют критерии линейности и рекомендации но
выбору степени аппроксимирующего многочлена.
В соответствии с принципами средней квадратич.
регрессии оценка неизвестных регрессии коэффициентов
Ро, . . ., ри и дисперсии о2 осуществляется методом наи-
наименьших квадратов. Согласно этому методу в качестве
статистич. оценок параметров ро, . . ., (Зж выбираются
такие значения ро, . . ., {5т, к-рые обращают в мини-
минимум выражение
2"=1 (у,—* (**))••
Многочлен g(x)=$u+. . .-\-^>mxm, построенный мето-
методом наименьших квадратов, наз. эмпирической
линией, регрессии и является статистич.
оценкой неизвестной истинной линии регрессии. При
гипотезе линейности регрессии уравнение эмпирич.
прямой регрессии имеет вид
g(« = pVbPV,
где
Z г-/—-у) (Vi — У)
= У — Pi*, Pi=
Случайные величины р0, . . ., рот наз. выбороч-
выборочными коэффициентами регрессии.
Несмещенная оценка параметра о2 дается формулой
Если дисперсия зависит от х, то метод наименьших
квадратов применим с нек-рыми видоизменениями.
Если изучается зависимость случайной величины Y
от нескольких переменных х1, . . ., xk, то общую линей-
линейную модель регрессии удобнее записывать в матричной
форме: вектор наблюдений у с независимыми компонен-
компонентами i/x, . . ., уп имеет среднее значение и ковариаци-
ковариационную матрицу
Е(У |zi, ...,2» = А'р\ D(V I*-!, ...,xk) = o4, (*)
где p=(Px, . . ., fik) — вектор коэффициентов регрес-
регрессии, Х = ||г/у||, i— 1, . . ., п, у —1 ,. . ., к, — матрица
известных величин, связанных друг с другом, вообще
говоря, произвольным образом, / — единичная мат-
матрица и-го порядка; при этом п>к и \ХГ Х\у^(). В более
общем случае допускается корреляция между наблюде-
наблюдениями г/,-:
Е(У |*„ ...,*fc) = Xp, D(Y\xu ...,хк)=о*А,
где .матрица А известна, но эта схема сводится к мо-
модели (*). Несмещенной оценкой р4 по методу наимень-
наименьших квадратов является величина
а смещенной оценкой для а2 служит
s =-^z%(y У— Р х У)-
Модель (*) является наиболее общей линейной мо-
моделью, поскольку она применили к различным регрес-
регрессионным ситуациям и включает в себя все виды пара-
параболической регрессии Y но х1, . . ., х% (в частности, рас-
рассмотренная выше параболич. регрессия У по х поряд-
порядка m может быть сведена к модели (*), в к-рой m ре-
регрессионных переменных функционально связаны).
При таком линейном понимании Р. а. задача оценки р и
вычисления ковариационной матрицы оценок Dp -
= а2(Х X) сводится к задаче обращения матрицы
ХТХ.
Укапанный метод построения эмпирич. регрессии
в предположении нормального распределения результа-
результатов наблюдений приводит к оценкам для р1 и о2, со-
совпадающим с оценками наибольшего правдоподобия.
Однако оценки, полученные этим методом, являются
в нек-ром смысле наилучшими и в случае отклонения
от нормальности, если только объем выборки достаточ-
достаточно велик.
В данной матричной форме общая линейная модель
регрессии (*) допускает простое обобщение на тот слу-
случай, когда наблюдаемые величины у; являются век-
векторными случайными величинами. При этом никакой
новой статистич. задачи не возникает (см. Регрессии
матрица).
Задачи Р. а. не ограничиваются построением то-
точечных оценок параметров р4 и а2 общей линейной мо-
модели (*). Проблема точности построенной эмпирич.
зависимости наиболее аффективно разрешается при до-
допущении, что вектор наблюдений у распределен нор-
нормально. Если вектор у распределен нормально и лю-
любая оценка |3 является линейной функцией от у, можно
заключить, что величина E,- распределена нормально
со средним Р,- и дисперсией DC,- = a2b,7, где Ъц— диа-
диагональный элемент матрицы (ХТА')~1. Кроме того,
оценка s2 для о2 распределена независимо от любой ком-
компоненты вектора р\ а величина (п—k)s2/a2 имеет ахи-
квадрат» распределение с (п—к) степенями свободы.
Отсюда следует, что статистика
* = (?,— ?,¦)/№/]1/2
подчиняется Стъюдента распределению с п—к степеня-
степенями свободы. Этот факт используется для построения до-
верительных интервалов для параметров C,- и для про-
проверки гипотез о значениях, к-рые принимает величина
Р,-. Кроме того, появляется возможность найти довери-
доверительные интервалы для Е(У\хх, . . ., xk) при фиксиро-
фиксированных значениях всех регрессионных переменных и
доверительные интервалы, содержащие следующее
(н + 1)-е значение величины у (т. н. интервалы пред-
предсказания). Наконец, можно на основе вектора выбороч-
выборочных коэффициентов регрессии f) построить доверитель-
доверительный эллипсоид для вектора р1 или для любой совокуп-
совокупности неизвестных коэффициентов регрессии, а также
доверительную область для всей линии или прямой ре-
регрессии.
Р. а. является одним из наиболее распространенных
методов обработки экспериментальных данных при
изучении зависимостей в физике, биологии, экономике,
технике и др. областях. На моделях Р. а. основаны
такие разделы математич. статистики, как дисперсион-
дисперсионный анализ и планирование эксперимента, ати модели
широко используются в многомерном статистическом
анализе.
Лит.: [1] К е н д а л л М. Д ж., Стьюарт А., Статисти-
Статистические выводы и связи, пер. с англ., М., 1973; [2] Смир-
Смирнов Е В., Дунин-Барковский Н. В., Курс теории
вероятностей и математической статистики для технических
приложений, 3 изд., М., 1969; [3] А й в а з я н С. А., Статисти-
Статистическое исследование зависимостей, М., 1968; [4] Рао С. Р.,
Линейные статистические методы и их применения, пер. с англ.,
М., 19R8; [5] Д р е й п е р Н., С м и т Г., Прикладной регрес-
регрессионный анализ, пер. с англ., М., 1973. А. В. Прохоров.
РЕГРЕССИЯ — зависимость среднего значения ка-
какой-либо случайной величины от нек-рой другой вели-
величины или от нескольких величин. Если, например,
при каждом значении х~~х,- наблюдается и/ значений
уц, . . ., у[„. случайной величины Y, то зависимость
средних арифметических
этих значений от ж,- и является Р. в статистич. понима-
понимании этого термина. При обнаруженной закономерности
изменения у с изменением х предполагается, что в ос-
основе наблюдаемого явления лежит вероятностная за-
нисимость: при каждом фиксированном значении х
случайная величина Y имеет определенное распределе-
распределение вероятностей с математич. ожиданием, к-рое явля-
является функцией х:
Зависимость у=т(х), где х играет роль «независимой»
переменной, наз. регрессией (или функци-
функцией регрессии) в вероятностном понимании этого
термина. График функции т (х) наз. линией ре-
регрессии, или кривой регрессии, вели-
величины Y по х. Переменная х наз. регрессионной
переменной, или регрессором. Точность,
с к-рой линия регрессии Y по х передает изменение Y
и среднем при изменении х, измеряется дисперсией ве-
величины Y, вычисляемой для каждого значения х:
D(Y\x)=e*(x).
Графически зависимость дисперсии аг(х) от х выража-
выражается т. н. скедастической линией. Если
аг(х)—0 при всех значениях х, то с вероятностью 1 ве-
ветчины связаны строгой функциональной зависимо-
сгью. Если а2 (х)ф() ни при каком значении х и т (х) не
:ависит от х, то регрессия Y по х отсутствует.
В теории вероятностей задача Р. решается примени-
н'льно к такой ситуации, когда значения регрессион-
регрессионной переменной х соответствуют значениям нек-рой
случайной величины X и предполагается известным сов-
честное распределение вероятностей величин X и Y
(при этом математич. ожидание Е (Y\x) и дисперсия
D(F|,r) будут соответственно условным математич.
ижиданием и условной дисперсией случайной величины
Y при фиксированном значении Х~х). В этом случае
определены две Р.: У пот X по у, и понятие Р. может
быть использовано также для того, чтобы ввести нок-
рые меры взаимосвязанности случайных величин X
и Y, определяемые как характеристики степени кон-
концентрации распределения около линий Р. (см. Корре-
Корреляция).
Функции Р. обладают тем свойством, что среди всех
действительных функций j(x) минимум математич.
ожидания Е (Y—/(ж)J достигается для функции f(x)=
= т(х), то есть регрессия Y uo x дает наилучшее (в ука-
указанном смысле) представление величины Y. Наиболее
важным является тот случай, когда регрессия Y по х
линейна, т. е.
Коэффициенты Ро и |5j, наз. коэффициентами
Р., легко вычисляются:
Ро-гоу-р-^тх, Pi = P-~
А Л
(здесь р — корреляции коэффициент X и Y, тх=?Х,
my—?Y, Ox = DX, o=DF), и прямая регрес-
регрессии Y по х имеет вид
y = mK + p-J^-(z — mx)
(аналогичным образом находится прямая регрессии
X по у). Точная линейная Р. имеет место в случае,
когда двумерное распределение величин X и Y является
нормальным.
В условиях статистич. приложений, когда для точ-
точного определения Р. нет достаточных сведений о форме
совместного распределения вероятностей, возникает
задача приближенного нахождения Р. Решению этой
задачи может служить выбор из всех функций g{x),
принадлежащих заданному классу, такой функции,
к-рая дает наилучшее представление величины Y в
том смысле, что минимизирует математич. ожидание
Е (Y—g(X)J. Найденная функция наз. средней
квадратической Р.
Простейшим будет случай линейной средней
квадратической Р., когда отыскивают наи-
наилучшую линейную аппроксимацию величины Y по-
посредством величины X, т. е. такую линейную функцию
^(а:)=ро+р1ж, для к-рой выражение Е (У—g(X)J
нринимает наименьшее возможное значение. Данная
экстремальная задача имеет единственное решение
PiP'
А
т. е. вычисление приближенной линии Р. приводит к
тому же результату, к-рый получен в случае точной
линейной Р.:
y^my + p-^ix — mx).
Л
Минимальное значение ?(Y—g(X)J при вычисленных
значениях параметров равно ОуA—р2). Если регрессия
т (х) существует, то при любых ро и р\ имеет место соот-
соотношение
откуда следует, что прямая средней квадратич. ре-
регрессии г/=C0+Р1.т дает наилучшее приближение к ли-
линии регрессии т (х), если измерять расстояние вдоль
оси у. Поэтому если линия т(х) есть прямая, то она
совпадает с прямой средней квадратической Р.
В общем случае, когда Р. сильно отличается от ли-
линейной, можно поставить задачу нахождения многочле-
многочлена g(x)=po+Pi^+-- ¦^г^тх"> нек-рой степени т, для
к-pore среднее значение Е (У—?(т))? имеет возможно
меньшее значение.
Такое решении задачи соответствует параболи-
параболической (или полиномиальной) средней
квадратической Р. (см. Параболическая регрессия) по-
порядка т. Кривая y=g(x) есть парабола т-то порядка,
дающая наилучшую аппроксимацию истинной линии
Р. Обобщением параболической Р. служит функция Р.,
выраженная линейной комбинацией тех или иных
заданных функций:
g (х) = Р„ф0 (х) + р1ф1 (х) + . . . -f Р,лФ,л (х).
Наиболее важное значение имеет случай, когда ф0 (х).-
¦ . ., ф,л (х) — ортогональные многочлены соответст-
соответствующих порядков, построенные по распределению Х>
Дру! ими примерами нелинейной (криволи-
(криволинейной) Р. являются случаи тригонометрической Р.,
показательной Р., и т. п.
Понятие Р. естественным образом обобщается на
тот случай, когда вместо одной регрессионной пере-
переменной рассматривается нек-рое множество переменных.
Если случайные величины ХЛ, Х2, . . ., Хп имеют
совместное распределение вероятностей, то м н о ж е-
ственная Р. определяется, напр., как регрессия
Хг по х2, . . . , хп:
Е № | Х2 = х2, ..., Xn—xll) = m1 (х2, ...,х„).
Соответствующее уравнение определяет поверх-
поверхность регрессии Х^ no х2, . . ., х„. Линейная
регрессия Xj no г2, . . ., хп имеет вид
Е (Х1 | х2, .. ., хп) т= $.гх2~>Г . .. -f- р„хп,
где f52, . . ., р„— коэффициенты Р. (при ЕХ^—0).
Линейная средняя квадратическая Р. величины A"j uo
х2, . ¦ ., хп определяется как наилучшая линейная
оценка величины Хх величинами Х2, ¦ ¦ ., Хп в смыс-
смысле обращения в минимум выражения
Соответствующая плоскость Р. дает наилучшую
аппроксимацию поверхности регрессии ;r1=m(x2,
. . ., хи), если последпяя существует. Если поверх-
поверхность Р. есть плоскость, то она необходимо совпадает
с плоскостью средней квадратической Р. (так будет
в случае, когда совместное распределение всех и ве-
величин нормально).
Простым примером регрессии Y по X является за-
зависимость между Y и X, к-рая выражается соотно-
соотношением У— и (х)п б, где u(x) = E(Y\X = x), а случай-
случайные величины X и 6 независимы. Это представление
полезно, когда планируется эксперимент для изучения
функциональной связи у=и(х) между неслучайными
величинами у и х. Эта же модель Р. используется во
многих приложениях при изучении характера зависи-
зависимости случайной величины У от неслучайной величи-
величины х. На практике выбор функции у--и(х) и оцепку
неизвестных коэффициентов Р. по экспериментальным
дапным производят методами регрессионного анализа.
Лит.: [1] К р а м е р Г., Математические методы статисти-
статистики, пер. с англ., 2 изд., М., 1975; [2] К е н д а л л М. Д ж.,
С т ь ю а р т А., Статистические выводы и связи, пер. с англ.,
М., 1973. А. В. Прохоров.
РЕГУЛЯРИЗАЦИИ МЕТОД — метод построения
приближенных решений некорректных задач, состоя-
состоящий в том, что в качестве приближенных ре-
решений некорректных задач [точнее — некорректно
поставленных задал (н. п. з.)] берутся значения
регуляризирующего оператора с учетом приближен-
приближенного характера исходной информации (см. Некоррект-
Некорректные задачи).
Для определенности ниже рассматривается задача
нахождения решений функциональных уравнений вида
Az—u, в к-рых z и и — элементы метрич. пространств
F и 11 с расстоянием р^(,) и рц(,)- Если, напр., А —
вполне непрерывный оператор, то решения такого урав-
уравнения не обладают свойством устойчивости к малым
изменениям правой части и. Пусть вместо точных зна-
значений исходной информации (А, и) дапы их приближе-
приближения (А, и). В этих условиях речь может идти лишь о
нахождении приближений к решению z уравнения
Az=u. Нельзя в качестве приближенного решения
н. п. з. такого вида с приближенной исходной инфор-
информацией (А, и) брать точное решение уравнения Az~-и,
т. к. такого решения может не существовать, а если
оно и существует, то не будет устойчивым к малым из-
изменениям исходной информации и, следовательно, та-
такое «решение» может не допускать физич. интерпрета-
интерпретации. В дальнейшем полагается для простоты, что при-
приближенной может быть лишь правая часть и, а оператор
А задан точно.
Пусть 6 — оценка уклонения и от и, т. е. расстоя-
расстояния (>?,'("> ")> и FocF—заданный класс возможных
решении (моделей сравнения). Естественно искать
приближенные решения уравнения Az=u среди эле-
элементов z?F0, сопоставимых с исходной информацией,
т.е. таких, что pu(Az, и)<6. Пусть Л'б —• множество
всех таких элементов из Fo . Если в выбранном классе
/•'„ возможных решений нет элементов (напр., функции
z(s)), сопоставимых с исходными данными, то ото зна-
значит, что элементы z из Fo имеют слишком упрощенную
(грубую) структуру. В этом случае надо расширять
класс Fo, беря, возможно, последовательность расши-
расширяющихся классов Fo a F^. . .cFnci. . ., пока не
найдется класс Fn, содержащий элементы (наир., функ-
функции), сопоставимые с исходными данными.
Если Fn не пусто, то оно может содержать сущест-
существенно отличающиеся друг от друга элементы(функции).
В таких случаях одно лишь требование'сопоставимости
возможных решений с исходными данными не может
служить критерием нахождения однозначно опреде-
определенных приближенных решений уравнений Az=u, т. к.
нет достаточных оснований для выбора в качестве при-
приближенного решения того или иного сопоставимого
элемента из Fn.
Для однозначного определения устойчивых решений
необходим нек-рый принцип отбора сопоставимых с и
решений. Обычно его формулируют, пользуясь смыслом
задачи. Такой отбор может быть произведен, напр.,
но принципу выбора элемента (функции) из Fn, име-
имеющего минимальную сложность. Понятие сложности
элемента z может быть формализовано, напр., с по-
помощью функционалов сложности Й[г] — непрерыв-
непрерывных, неотрицательных и удовлетворяющих нек-рым
специальным условиям (см. [1]). За меру сложности
элемента z принимается значение функционала U[z|.
Так, если элементами z являются непрорывные на от-
отрезке [а, Ь] функции z(s) класса W\, то функционал
сложности fifz] можно взять, напр., в виде
Желание искать приближенные решения уравнений
Az=u среди простейших элементов (функций), сопо-
сопоставимых с исходными данными, приводит к задаче
нахождения элемента из F(,, минимизирующего il\z]
на Fe . Если оператор А линейный и функционал ?2[z] не
имеет локальных минимумов на области своего опре-
определения F?), то эта задача может быть сведена (см. под-
подробнее в [1]) к задаче нахождения элемента za из мно-
множества Ftj (}Ра, шпш.ми.чируклцего функционал
Л/a [г, A, Z\ =- р2у (Az, й) + аЙ [г].
Значение параметра а (параметра регуляризации) долж-
по быть согласовано с уровнем погрешности исходных
данных. Его можно определить, напр.. по невязке, т. е.
из условия pu(Aza, г*) —6, если известно число б. Но
возможны и др. способы определения а (см. [1]). Та-
Таким образом, параметр а должен зависеть от 6 и и,
а=аF\ и). Элемент za^:u) и принимается за прибли-
приближенное решение уравнения Az~u. Это и есть одна
из форм разработанного в [2], [3] Р. м. Аналогично
строятся приближенные решения уравнений Лz = и с
приближенно заданным оператором А и правой частью
и. При этом минимизируется функционал тина Ma[z, A,
и] (см., напр., [1]). Возможны и другие формы Р. м.
и применение его к иным классам задач(см. [11). Р. м.
развит и для решения нелинейных задач (см. [1], [4]).
Лит.: [1] Тихонов А. Н., Арсении В. Я., Методы
решения некорректных задач, 2 изд., М. 1979; [2] Тихо-
Тихонова. Н., «Доил. АН СССР», 1963, т. 151, л» 3, с. 501— O'i :
[3] с г о ж с, там же, т. 153, № 1, с. 'iS—52; [4] Л а в р е н т ь-
е в М. М., О некоторых некорректных задачах математической
фи.тки, Повосиб., 1962. В. Я. Арсении, А. II. Тихонов.
РЕГУЛЯРИЗАЦИЯ — использование той или иной
формы отбора допустимых решений при построении
устойчивых к исходной информации приближенных
решений некорректно поставленных задач (ом. также
Некорректные задачи и Регуляризации метод).
В. Я. Арсенин, А. II. Тихонов.
РЕГУЛЯРНАЯ ГРАНИЧНАЯ ТОЧКА — точка
у0 границы Г области D евклидова пространства R",
л>2. в крой для любой непрерывной на Г функции
/((/) обобщенное решение и (х) Дирихле задачи в смысле
Винера — Перрона (см. Перрона метод) принимает
граничное значение /((/0), то есть
lim и (x) = f (y0).
х -+ у а. -теп
Р. г. т. для области D образуют множество R, в
точках к-рого дополнение CD = R"\D не является
разреженным множеством; множество Г\Д иррегуляр-
иррегулярных граничных точек есть полярное множество типа Fa-
Если все точки Г суть Р. г. т., то область D шля. р е-
г у л я р н о й относительно задачи Дирихле.
Для того чтобы точка уо? Г была Р. г. т., необходимо
и достаточно, чтобы в пересечении U0=Uf]D области
D с нек-рой окрестностью U точки у0 существовал
барьер, т. о. супергармонич. функция w(z)>0 в UO та-
такая, что Нпш (х)=0 (критерий барьера Ле-
¦v-h/,,
бег а). А. Лебиг (Н. Lebesgue, 1912) впервые показал,
что при /(Js3 вершина достаточно острого входящего в
D острия может не быть Р. г. т.
Пусть
ck~C(Ek) -- емкость Л'&. Для того чтобы точка i/0? Г
была Р. г. т.. необходимо и достаточно, чтобы расхо-
расходился ряд
2i0° 2*'n-2)ffc, «3*3,
при п— 2 ряд
причем здесь
(к р и т е р и и В и н о р а).
При и--2 точка г/о?1' является Р. г. т., если суще-
существует непрерывный пуп. x(t), 0<i<l, такой, что
гA)=г/0, x(t)?CD при Ос:/<1. При п>3 точка ;/0€г
является Р.' г. т., если w можно коснуться вершиной
прямого кругового конуса, принадлежащего CD в
достаточно малой окрестности у0. В случае области
D компактифицированного пространства R", и^З,
бесконечно удаленная точка оо?Г всегда является
Р. г. т.; при л=2 бесконечно удаленная точка оо ? Г
является Р. г. т., если существует непрерывный
путь x(t), 0<<<1, такой, ч-to x(t)? CD при 0«t<l
n lim x(t)=oo.
t-+i-o
См. также Иррегулярная граничная точка.
Лит.: [1] К е л д ы ш М. В., «Успехи матем. наук», 1941,
в. 8, с. 171—232; [2] Л а н д к о ф Н. С, Основы современной
теории потенциала, М., 1906; [3] X е й м а н У. Кенне-
Кеннеди П., Субгармонические функции, пер. с англ., М., 1980.
Е. Д. Соломенцев.
РЕГУЛЯРНАЯ />-ГРУППА — р-группа G такая,
что для любых ое элементов а, Ъ и любого целого п=ра
справедливо равенство
где s,, . . ., s/— нек-рые элементы из коммутанта под-
подгруппы, порожденной -элементами а и Ь. Подгруппы и
факторгруппы I', p-r. регулярны. К'онечная р-группа
регулярна тогда и только тогда, когда для любых ее
элементов а и Ь справедливо равенство
apbp=(abfsP,
где s — нек-рый элемент коммутанта подгруппы, по-
порожденной элементами а и Ь.
Элементы Р. р-т. G, имеющие вид аРа, a?G, обра-
образуют характеристич. подгруппу Ca(G), а элементы по-
порядка, не большего числа ра,— вполне характеристич.
подгруппу Ca(G).
Примерами Р. р-г. являются любая р-грунпа, класс
нильпотентности к-рой меньше р, а также любая р-
грунпа порядка, не большего числа рР. Для любого
р существует нерегулярная р-группа порядка p^ + 1, a
именно, силовская подгруппа Sр симметрия, группы
S (р2) степени р2 (она изоморфна сплетению цпклич.
группы порядка р с самой собой).
Лит.: [1] X о л л М., Теория групп, пер. с англ., М., 19IS2.
РЕГУЛЯРНАЯ МЕРА — мера, определенная на ио-
ролевской сг-алгебре И(Т) топологич. пространства Т
такая, что для любого борелевского множества X ? $$(Г)
и любого е>0 найдется открытое множество GaT, по-
покрывающее X : XdG и jx(G\A')<k. Равносильное
определение: для любого X?S8G') и е>0 найдется
замкнутое множество FczX такое, что (л (Х\/')<е.
Р. А. Минлос.
РЕГУЛЯРНАЯ ОСОБАЯ ТОЧКА — понятие теории
обыкновенных линейных дифференциальных уравнений
с комплексным независимым переменным. Точка а?С
наз. Р. о. т. уравнения
, + а„ (t) у = 0 A)
или системы
'z = A(t)z, 2gC«, B)
с аналитич. коэффициентами, если а — изолированная
особенность коэффициентов и все решения уравнения
A) или системы B) растут не быстрее, чем |i—a\d
для нек-рого d?R, когда t стремится к а, оставаясь
внутри произвольного острого угла с вершиной а.
Последнее ограничение вызвано тем, что в окрестно-
окрестности Р. о. т. решения являются неоднозначными ана-
аналитич. функциями и при ?-«г но произвольной кривой
могут расти существенно быстрое, чем при стремлении
t-*-a по лучу с вершиной а.
Для того чтобы особая точка коэффициентов урав-
уравнения A) или системы B) была Р. о. т., необходимо,
чтобы она была полюсом, а не существенно особой точ-
точкой коэффициентов. Для уравнений A) имеет место
условие Фукса: особая точка t— 0 коэффициен-
тов a,j(t) регулярна для уравнений A) тогда и только
тогда, когда все функции (t—a)! aj(t), j = \, . . ., п, го-
голоморфны в нуле. Для систем B) справедливо следую-
следующее достаточное условие: если элементы матрицы A (t)
имеют простой полюс в точке я, то эта точка — Р. о. т.
системы B). Явное условие на матрицу A (t), необходи-
необходимое и достаточное для того, чтобы точка а была Р. о. т.
системы B), пока A983) не получено.
Лит.: [1] ГолубевВ. В., Лекции по аналитической теорий
дифференциальных уравнений, 2 изд., М.— Л., 1950; [2] К о д-
дингтон Э. Л., Левинсон Н., Теория обыкновенных
дифференциальных уравнений, пер. с англ., М., 1958; [3] L е-
v e I t A. H. M., «Proc. Koninkl. Nederl. akad. wet. Ser. A», 1961,
v. 04, № 4, p. 362—403; [4] D e 1 1 g n e P., Equations differen-
tiellesa points singuliers reguiliers, В., 1970 (Lect. Notes in Math.,
№ 16.3); La] Plemel] J., Problems in the sense of Riemann
and Klein, Univ. of Adelaide, 1964. Ю. С. Илъяшенко.
РЕГУЛЯРНАЯ ПОЛУГРУППА — полугруппа, каж-
каждый элемент к-рой регулярен.
Произвольная Р. п. S содержит идемпотенты (см.
Регулярный элемент), и строение S в значительной
степени определяется «строением» и «расположением»
в S множества всех ее идемпотентов Е (S). Р. п. с един-
единственным идемпотентом — это в точности группы. На
Е (S) прежде всего можно смотреть как на частично
упорядоченное множество относительно естественного
частичного порядка (см. Идемпотент); известны
структурные теоремы, описывающие Р. п. S с нек-рыми
естественными ограничениями на множество E(S).
Одно из таких ограничений (для полугрупп с нулем)
состоит в том, что все ненулевые идемпотенты прими-
примитивны (см. Вполне простая полугруппа); полугруппа
с этим свойством наз. примитивной. Следую-
Следующие условия для полугруппы S эквивалентны: a) S
есть примитивная Р. п., б) S есть Р. п., равная объе-
объединению своих О-минимальных (см. Минимальный
идеал) правых идеалов, в) S есть 0-прямое объединение
вполне 0-простых полугрупп. Описано строение Р. п.,
у к-рых Е (S) есть цепь, упорядоченная по типу отри-
отрицательных целых чисел [2].
Более информативный взгляд на Е (S) состоит в рас-
рассмотрении на этом множестве частичной операции °,
заданной следующим образом. Если для <?, f?E(S)
хотя бы одно из произведений ef, fe равно одному из
элементов е, /, то ef?E(S); полагают тогда' еэ/=е/.
Возникающая частичная алгебра может быть охарак-
охарактеризована аксиомами, использующими два отноше-
отношения квазипорядка о/ и ц/, тесно связанные с заданной
частичной операцией (реализация этих отношений в
Е (S) такова: еш;/ означает /е=е, ешг/ означает ef—e;
тогда и/ П мг есть отношение естественного частичного
порядка на Е (S)); такая частичная алгебра наз. б и-
упорядоченным множеством (см. [5]).
Произвольная Р. п. может быть определенным обра-
образом сконструирована из би упорядоченного множества
и групп. Таким образом, в терминах биупорядочен-
ных множеств можно проводить классификацию Р. п.
Среди исследованных в этом направлении типов полу-
полугрупп— комбинаторные Р. п. (см. [7]), т. е.
имеющие лишь одноэлементные подгруппы.
Гомоморфный образ Р. п. будет Р. п. Всякий нор-
нормальный комплекс Р. п., являющийся подполугруппой,
содержит идемпотент. Произвольная конгруэнция на
Р. п. однозначно определяется своими классами, содер-
содержащими идемпотенты. Конгруэнция на Р. п. S разде-
разделяет идемпотенты тогда и только тогда, когда она со-
содержится в отношении $f? (см. Грина отношения эк-
эквивалентности); множество таких конгруэнции состав-
составляет модулярную подрешетку с нулем и единицей в ре-
решетке всех конгруэнции на S. Р. п. наз. ф у и д а м е н-
т а л ь н о и, если ата подрешетка состоит лишь из
отношения равенства. Всякая комбинаторная Р. п. бу-
будет фундаментальной. Фундаментальные Р. п. важны
не только как один из более обозримых типов Р. п.,
но и в силу определенной «универсальности» их класса
для Р. и. Л именно, для любого биупорядоченного мно-
множества Е можно канонич. образом сконструировать фун-
фундаментальную Р. п. Tg, для к-рой Е будет биупорядо-
ченным множеством всех идемпотентов, причем для
любой Р. п. S такой, что Е (S)~E, существует разделя-
разделяющий идемпотенты гомоморфизм ф : S-.>-Тр, для к-рого
Ф E) будет подполугруппой в Т?-, содержащей Е (о
различных конструкциях для ТЕ см. [3], |5], |8], A0|).
Р. п. S фундаментальна тогда и только тогда, когда
гомоморфизм ф инъективен.
Если S — Р. п., то подполугруппа <E(S)>, порож-
порожденная всеми ее идемпотентами, также будет Р. п,
Подполугруппа <Е (S)> оказывает существенное влия-
влияние на строение S. Р. п. идемпотентно порождена тогда
и только тогда, когда таков каждый ее главный фактор
[10]. В идемпотентно порожденной Р. п. S для произ-
произвольного элемента х существует представление ж=
= е1е2 . . . е„, где et?E(S) и e,(i?U54)<?, + i при 1=
— 1, . . ., п—1 (здесь X и 54 — отношения эквивалент-
эквивалентности Грина) (см. [5]). Последовательность идемпотен-
идемпотентов ег, е2, . . ., еп с указанным свойством наз. Е - це-
цепью. В би простой идемпотентно порожденной полу-
полугруппе любые два идемпотента связаны нек-рой Е~
цепью, и если они сравнимы в смысле естественного
частичного порядка, то длина такой цепи ^4.
Если (Е (S)>=E (S), т.е. произведение любых двух
идемпотентов снова есть идемпотент, то Р. п. S наз.
ортодоксальной. Класс ортодоксальных по-
лугрупп содержит, в частности, все инверсные полу-
полугруппы. Полугруппа ортодоксальна тогда и только
тогда, когда каждый ее главный фактор ортодоксален.
Имеются структурные теоремы об ортодоксальных
полугруппах (см. [4], [9]).
Отношение естественного частичного порядка на
Е (S) может быть продолжено на Р. п. S следующим
образом: х<.у, если существуют идемпотенты ей/
такие, что х — ey—yj. В случав, когда S инверсна, от-
отношение <: превращается в отношение естественного
частичного порядка, для произвольной Р. п. оно также
наз. отношением естественного частич-
частичного порядка. Отношение <: на Р. п. S сог-
согласовано с умножением тогда и только тогда, когда
для любого идемпотента е подполугруппа eSe инверсна
[6]. Р. п., обладающие таким свойством, наз. псев-
псевдоинверсными. Более широкий класс состав-
составляют псевдоортодоксальные полугруппы
(для любого идемпотента е подполугруппа eSe ортодок-
ортодоксальна). Для указанных классов полугрупп использо-
использовались также термины «локально инверсная» и «ло-
«локально ортодоксальная». Р. п. наз. естествен-
естественной, если множество всех ее групповых элементов
(см. Регулярный элемент) есть подполугруппа. Имеются
структурные теоремы о псевдоинверсных, псевдоор-
псевдоортодоксальных [И] и естественных [12] Р. п.
Многие структурные теоремы о различных типах Р. п.
представляют собой (подчас весьма далекие) обобще-
обобщения и модификации конструкции рисовской полугруппы
матричного типа или суммы прямого спектра групп
(см. Клиффордова полугруппа), либо опираются па те
или иные представления полугрупп и разложения их
в нодпрямые произведения (см. [1], [13]). См. также ст.
Полугруппа.
Лит.: [1] К л и ф ф о р д А., П р е с i- о н Г., Алгебраичес-
Алгебраическая теория полугрупп, пер. с англ., т. 1 — 2, М., 1972; 12] М u n n
W. D., «Glasgow Math. .Г.», 1988, v. 9, pt. 1, p. 4E--(Hi; [3] Clif-
Clifford A., «Semigroup Forum», 1975, v. 10, p. 84-112; 141 его
ж e, «J. pure and appl. algebra», 197У, v. 8 p. 23—50; t.r>] N a m-
b о о r i p a d K. S. S., «Mem. Amer. Math. Soc», 1979, v. 22,
.№ 224; [6] e г о же, «Proc. Edinburgh Math. Soc», 1980,
v. 23, pt 3, p. 249—60; [7] N a m b о о r i p a d K. S. S. S., ii я j a n
A. R., «Quart. J. Math.», 1978, v. 29, № ll(i, p. 489 — 504; [8l
Grillet P. A., «Semigroup Forum», 1974, v. 8, p. 177—83;
p. 254—«5; p. 3B8 —73; [9] H a 1 1 Т. Е., «Pacif. J. Math.», 1971,
v. 39, p. 677—86; [10] его же, «J. Algebra», 1973, v. 24,
p. 1—24; [11] M e а к i n J., N a m b о о г i p a d К. S. S.,
«.). Austral. Malli. Soc», 1980/1981, v. 30, p. 73 86; [12] W a I'-
I'll e К. Л., n km.: Algebraic theory of semigroups, Amst., 1970
p. «85 — 720; Ll.'iJ L a 1 1 e m с n t G., «Semigroup Forum», 1972,
v. 4, p. 95 — 123. Л. Н. Шеврин.
РЕГУЛЯРНАЯ РЕШЕТКА, структура ре-
регулярна я,— условно полная решетка (структура),
в к-рой выполняется следующее условие (наз. также
аксиомой регулярности): для любой по-
последовательности {?„} ограниченных множеств, для
к-рой
(о) (о)
sup Еп —* a, inf Е„ —>¦ 6,
найдутся конечные подмножества E'naEn с тем же
свойством (S°X_ означает сходимость по упорядочению).
Такие структуры (в первую очередь регулярные К-
пространства и булевы алгебры) чаще всего встреча-
встречаются в функциональном анализе и теории меры. Они
естественно возникают в задаче продолжения гомомор-
гомоморфизмов и линейных положительных операций. В Р. р.
выполняются следующие два принципа: а) принцип диа-
диагонали (если хпт^Ххп, хп^%х, то х,Шп^\х для нек-poii
последовательности индексов тп) и б) принцип счет-
ности типа (всякое бесконечное ограниченное множество
содержит счетную часть с теми же гранями). В свою
очередь, а) и б)вместе эквивалентны аксиоме регуляр-
регулярности. Примеры Р. р.: всякое /ТВ-пространство и, в
частности, всякое Lp, l<gp<+oo; булева алгебра
mod 0 измеримых множеств произвольного пространст-
пространства с конечной счетно аддитивной мерой. Другие из-
известные примеры регулярных булевых алгебр основы-
основываются на отрицании Суслика гипотезы.
Лит.: [1] Канторович Л. В., В у л и х Б. 3., П и н-
с к е р А. Г., Функциональный анализ в пол у упорядоченных
пространствах, М.— Л., 1950. Д. А. Владимиров.
РЕГУЛЯРНАЯ СХЕМА — схема (X, Qx), локаль-
локальное кольцо Qx.x любой точки х к-рой регулярно.
Для схем конечного типа над алгебраически замкну-
замкнутым нолем к регулярность эквивалентна тому, что пучок
дифференциалов &x/k локально свободен. Регулярные
локальные кольца факториальны, поэтому любая зам-
замкнутая приведенная неприводимая подсхема кораз-
коразмерности 1 на Р. с. (X, 0х) локально задается одним
уравнением (см. [2]). Важной задачей является постро-
построение Р. с. (X, Qx) с заданным полем К рациональных
функций, снабженной собственным морфизмом X-+-S на
нек-рую базисную схему S. Эта задача решена в слу-
случае, когда S — спектр ноля характеристики 0 (см.
[3J), а для малых размерностей схемы и в случае простой
характеристики, а также в случае, когда S — спектр
дедекиндовой области и dim X/5<1 (см. [1]).
Лит.: Ill A lih у a n k а г S h. S h., в кн.: Тр. Международ-
Международного конгресса математиков (Москва — I960), М., 1968, с. 469 —
481; L2J М а м ф о р д Д., Лекции о кривых на алгебраической
поверхности, пер. с англ. М., 1968; [3| I и р о н а к а X., «Ма-
«Математика», 19С5, т. 9, № 6 с. 2 — 70; 1966, т. 10, J45 1, с. 3—89;
N- 2 с. 3—58. С. Г. Танкеев.
РЕГУЛЯРНАЯ ФУНКЦИЯ, правильная
функция, в области — функция /(z) комплексно-
комплексного переменного z, однозначная в этой области и имею-
имеющая в каждой ее точке конечную производную (см.
Аналитическая функция). Р. ф. в точке а — это
Р. ф. в нек-рой окрестности а. ю- Д- Максимов.
РЕГУЛЯРНАЯ ФУНКЦИЯ МНОЖЕСТВА — адди
тивная функция ц, определенная на системе множеств
топологич. пространства, полная вариация к-рой \ц\
удовлетворяет условию
| ц | (Е) ^inf | р. | (G) =sup | ц 1 (F), G гз Е =3 F,
G — внутренность множества G, F — замыкание
множества F(E, G, F — из области определения |х).
Ограниченная аддитивная Р. ф. м., определенная на
полукольце множеств бикомпактного топологич. про-
странства, является счетно аддитивной функцией (т е-
о р е м а Александрова).
Свойство регулярности можно относить и к мере
как частному случаю функции множества и говорить
о регулярной мере, заданной на топологич.
пространстве. Примером регулярной меры является
Лебега мера.
Лит.: [1] Д а н ф о р я Н., Ш в а р ц Д ж., Линейные опе-
операторы, пер. с англ., ч. 1, М., 1962; [2] А л е к с а н д р о в А. Д.,
«Матем. сб.», 1941, т. 9, с. 5ВЗ—628. А. П. Терехин
РЕГУЛЯРНАЯ ЭКСТРЕМАЛЬ, неособенная
экстремаль,— экстремаль у (х), во всех точках
к-рой выполняется условие
Fy.y{x, y(x), у'(х)) фО, A)
где F (х, у, у') — подинтегральная функция, входящая
в минимизируемый функционал
F(x, у, y')dx.
Как всякая экстремаль, Р. э. есть, но определению,
гладкое решение Эйлера уравнения
Точки экстремали, в к-рых выполнено условие A),
наз. регулярными точками. Доказано, что
в каждой регулярной точке экстремаль имеет непре-
непрерывную 2-ю производную у"(х). На Р. э. 2-я производ-
производная у"(х) непрерывна. Для Р. э. уравнение Эйлера
Fy-Fy,x-Fy,yy'-Fy,y,y" = O
можно записать в виде, разрешенном относительно
старшей производной
</" = /(*, У, У')-
Свойство регулярности A) непосредственно связано
с необходимым Лежандра условием (в усиленной форме),
согласно к-рому во всех точках экстремали должно вы-
выполняться неравенство
Fy,y,(x, у(х), у' (х)) <0.
Регулярность существенно используется при доказа-
доказательстве возможности включения экстремали у (х) в
окружающее ее поле экстремалей. Если хотя бы в од-
одной точке условие A) нарушается, то экстремаль не
всегда может быть включена в поле. Условие включения
экстремали в поле является одним из достаточных ус-
условий экстремума.
Приведенное определение Р. э. дано для простейшей
задачи вариационного исчисления, в к-рой рассматри-
рассматривается функционал, зависящий от одной неизвестной
функции. Для функционалов, зависящих от п неизвест-
неизвестных функций:
= U
Уп>
Р. э. наз. такая экстремаль, во всех точках к-рой опре-
определитель л-го порядка
Fh
B)
Для более общих задач вариационного исчисления
па условный экстремум (см. Болъца задача) Р. э, оп-
определяется аналогично: только вместо /' в B) следует
подставить Лагранжа функцию L.
Экстремаль, у к-рой на нек-ром участке условие ре-
регулярности (A) или B)) нарушается во всех точках,
наз. особой экстремалью, а указанный уча-
участок наз. участком особого режима.
Для особых режимов выведены необходимые условия,
дополняющие известные классические необходимые
условия экстремума (см. Оптимальный режим особый).
Лит.: If] Б л и с с Г. А., Лекции по вариационному исчис-
исчислению, пер. с англ., М., 1950; [2] Лаврентьев М. А.,
Л ю с т е р н п к Л. А., Курс вариационного исчисления, 2
изд., М.—Л., 1950. И. Гу. Папнярский.
РЕГУЛЯРНОЕ КОЛЬЦО в коммутативной
алгебре — нётерово кольцо А, все локализации
Ау к-рого регулярны; здесь р — иростой идеал в А.
При этом локальное нётерово кольцо А с максимальным
идеалом т наз. регулярным, если m порожда-
порождается п элементами, где n=dim А, т. е. если касательное
пространство m/m2 (как векторное пространство над
полем вычетов) имеет размерность, равную dim A ¦ Это
равносильно отсутствию особенностей у схемы Spec A.
Локальное Р. к. А всегда целостно и нормально, а так-
также факториально (теорема Ауслендора —
ij у к с б а у м а), глубина его равна dim А. Ассо-
Ассоциированное градуированное кольцо
изоморфно кольцу многочленов k[Xi, . . ., Хп\. Ло-
Локальное нётерово кольцо А регулярно тогда и только
тогда, когда регулярно его пополнение А; вообще, если
ACZB — плоское расширение локальных колец и В
регулярно, то и А регулярно. Для полных локальных
Р. к. имеет место структурная теорема
К о э п а: они имеют вид Д[[ХХ, . • ., X,,]], гдо В --
поле или кольцо дискретного нормирования. Любой
модуль конечного типа над локальным Р. к. обладает
конечной свободной резольвентой (см. Гильберта те-
теорема о сизигиях); верно и обратное (см. [2]).
Р. к. являются любое поле и любое дедекиндово коль-
кольцо. Если А регулярно, то регулярно кольцо многочле-
многочленов AlXi, . . ., Хп] и кольцо формальных степенных
рядов Л[[Х];, . . ., X„]] над А. Если а?А — необрати-
необратимый элемент локального Р. к., то Ala А регулярно тогда
и только тогда, когда афт2.
Лит.:[1] Зарисский О., Самюэль П., Коммутатив-
Коммутативная алгебра, пер. с англ., т. 2, М., 1963; [2] С с р р Ж,- П.,
«Математика», 1963, т. 7, № о, с. 3—93; [3] G г о t h e n d i-
е с k A., Dieudonne J. (red.), Elements de geometrie al-
gebrique, chap. 4, P., 196/t. В. И. Данилов.
РЕГУЛЯРНОЕ КОЛЬЦО (в смысле Неймана) —
ассоциативное кольцо (обычно с единицей), в к-ром
уравнонпо аха~а разрешимо для любого а. Следующие
свойства ассоциативного кольца В с единицей равно-
равносильны: а) В есть Р. к.; б) каждый главный левый иде-
идеал кольца В порождается пдемпотентом; в) главные
левые идеалы кольца В образуют нодрешетку в решетке
всех его левых идеалов, являющуюся дедекиндовой ре-
решеткой с дополнениями; г) каждый главный левый
идеал кольца В имеет дополнение в структуре всех его
левых идеалов; д) все левые Я-модули плоские; е) име-
имеют место правые аналоги свойств б) — д) (см. [3], [4],
[5], [8], [10]).[Ввиду д) Р. к. иногда наз. абсолютно
плоским и. Коммутативное кольцо регулярно
тогда и только тогда, когда инъективны все простые
модули над ним (см. [5]). Любой конечно порожденный
левый (нравый) идеал Р. к. оказывается главным и,
следовательно, выделяется прямым слагаемым. Вся-
Всякий неделитель пуля в Р. к. обратим. Радикал Дже-
кобсона Р. к. равен нулю. Кольцо матриц над Р. к. ока-
оказывается Р. к. Класс Р. к. замкнут относительно пере-
перехода к прямым произведениям и факторкольцам. Идеал
Р. к. является Р. к. (возможно, без единицы). Если
Р. к. нётерово или совершенно (слева или справа),
то оно оказывается классически пол упростим кольцом.
Всякое классически иолупростое кольцо регулярно.
Колее того, регулярным оказывается кольцо эндомор-
эндоморфизмов векторного пространства над телом (даже бес-
бесконечномерного), а также факторкольцо кольца эндо-
эндоморфизмов инъективного левого (правого) модуля над
любым кольцом по его радикалу Джекобсона (см. [3]).
В частности, всякое самоинъективное слева (справа)
колыю с нулевым рплнкплом Джекобсопа регулярно.
Групповое кольцо группы С над Р. к. регулярно тогда и
только тогда, когда любая конечно порожденная под-
подгруппа в G конечна и порядок каждой из таких
подгрупп обратим в исходном Р. к. (см. [3]). Кольца
эндоморфизмов всех свободпых левых Я-модулей ре-
регулярны в том и только в том случае, когда R класси-
классически полуиросто Г 6]. Счетно порожденные односторон-
односторонние идеалы Р. к. ироективны [8].
Если R есть Р. к., то конечно порожденные подмоду-
подмодули левого Л-ыодуля R" «-мерных строк над В образу-
образуют дедекиндову решетку L с дополнениями, являющу-
являющуюся подрешеткой решетки всех подмодулей модуля R".
Решетка L содержит однородный базис
а^, . . ., ап, то есть эти элементы независимы (см. Де-
декиндова решетка), их сумма равна наибольшему эле-
элементу из L (а именно, R") и любые а; и а,- перспек-
перспективны, что означает существование для них общего
дополнения. Наоборот, всякая дедекиндова решетка с
дополнениями, обладающая однородным базисом, со-
содержащим не менее четырех элементов, изоморфна ре-
решетке L для подходящего Р. к. R. Решетка L изоморф-
изоморфна решетке главных левых идеалов кольца всех (пХп)-
матриц над R (см. [4], [10]).
Важный частный случай Р. к.— строго регу-
регулярное кольцо, в к-ром, по определению, раз-
.решимо уравнение а?х=а. Равносильны следующие
свойства Р. к. R: a) R строго регулярно; б) R не содер-
содержит ненулевых пилыютентных элементов; в) все идем-
потенты кольца R центральны; г) каждый левый (или
каждый правый) идеал кольца R является двусторон-
двусторонним; д) решетка главных левых (правых) идеалов коль-
кольца R дистрибутивна; е) мультипликативная полугруппа
кольца R является инверсной полугруппой (см. [7],
[8]).
Другой подкласс класса Р. к. образуют м-р е г у л я р-
ные кольца, где, по определению, уравнение
аха = а имеет в качестве решения обратимый элемент.
В классе Р. к. u-регулярные кольца характеризуются
транзитивностью перспективности в решетке конечно
порожденных подмодулей суммы двух экземпляров ос-
основного кольца, а также возможностью сокращать
прямую сумму на конечпо порожденный проективный
модуль (см. [4], [8]).
Р. к. наз. непрерывным слева, если не-
непрерывна решетка его главных левых идеалов. Не-
Непрерывное Р. к. и-регулярно и разлагается в прямую
сумму строго Р. к. и самоипъективного кольца. На
Р. к. может быть определена псевдоранг-функция, яв-
являющаяся апалогом меры на булевой алгебре. Она
определяет псевдометрику. Пополнение Р. к. по зтой
метрике оказывается самоинъективным Р. к. (см. [8]).
Р. к. являются частным случаем п-р е гул ирных
колец, в к-рых, по определению, для каждого эле-
элемента а найдутся элемент х и натуральное число п
такие, что а"ха"=а".
Как двусторонний аналог Р. к. можно рассматривать
бирегулярные кольца, и к-рых, но опре-
определению, каждый главный двусторонний идеал порож-
порождается центральным идемпотентом. Каждый двусто-
двусторонний идеал бирегулярного кольца является пересе-
пересечением его максимальных двусторонних идеалов. Вся-
Всякое бирегулярное кольцо с единицей изоморфно кольцу
глобальных сечений с бикомпактными носителями пуч-
пучка простых колец с единицей над бикомпактным впол-
вполне несвязным хаусдорфовым топологич. пространством,
и всякое такое кольцо глобальных сечении бирегулярпо
(см. [2]). В коммутативном случае классы бирегуляр-
ных, строго Р. к. и Р. к. совпадают, и простые кольца
в последней теореме заменяются полями.
Близки к Р. к. б л р о в с к и е коль ц а, опре-
определяемые тем условием, что каждый левый (или, что
при пплпчнн едитнп.г р.тппспльпо, каждый правый)
аннулятор порождается идемпотентом. Примерами ба-
ровскпх колец служат кольцо эндоморфизмов вектор-
векторного пространства над телом и кольцо ограниченных
операторов гильбертова пространства. Бэровское кольцо
наз. а б е л е в ы м, если все его идемпотенты централь-
центральны, и конечным (и о Д е д е к и н д у), если ху= )
влечет за собой ух=1. Идедшотент е воровского кольца
R наз. абелевым (конечным), если кольцо
eRe абелево (конечно по Дедекинду). Различаются сле-
следующие типы бэровских колец: Ifjn — конечные коль-
кольца, содержащие абелев идемнотент, не принадлежащий
никакому собственному прямому слагаемому; 1}П{ —¦
бесконечные по Дедекинду (т. о. не содержащие нену-
ненулевых конечных центральных идемпотентов) кольца,
содержащие абелев идедшотент, не принадлежащий ни-
никакому собственному прямому слагаемому; Ппп (или
11:) — конечные по Дедекинду кольца без ненулевых
абелевых идемпотентов, содержащие конечный идем-
потент, но принадлежащий никакому собственному
прямому слагаемому; IIinf — бесконечные по Дедекин-
Дедекинду кольца с условием, указанным в Ilf in; П1 — кольца
без ненулевых конечных идемпотентов. Каждое бэров-
бэровское кольцо единственным способом разлагается в
прямую сумму колец перечисленных типов (см. [9]).
Р. к. были введены для координатизации непрерыв-
непрерывных геометрий, бирегулярные — в связи с исследова-
исследованием функциональных представлений колец, бэровские
(и риккатовы) — при исследовании колец операторов.
Рассматривались неассоциативные Р. к. См. также
•*-регулярное кольцо, риккартово кольцо.
Лит.: [1] Б у р б а и и Н., Коммутативная алгебра, пер. с
франц., М., 1971; [2] Дауне Д ж., Гофман К., «Математи-
«Математика», 1968, т. 12, JMb 4, с. 3—24; [3] Л а мб ек И., Кольца и модули,
пер. с англ., М., 1971; [4] С к о р н я к о в Л. А., Дедениндовы
структуры с дополнениями и регулярные кольца, М., 19В1;
15] Ф е й с К., Алгебра: кольца модули и категории, пер. с
англ., т. 1—2, М., 1977—79; [В] Цукерман Г. М., «Снб.
матем. ж.», 1966, т. 7, № 5, с. 1161—67; [7] Шайн Б. М.,
«Изв. ВУЗов. Математика», 1966, № 2, с. 111—22; [8J G о о d е-
arl К. К., Л'оп Neumann regular rings, L.— [а. о.], 1979; [9]
KaplanskyJ I., Rings of operators, N. Y.— Amst., 1968;
[10] Neumann J., Continuous geometry, Princeton, 1960.
Л. А. Скорняков.
*-РЕГУЛЯРНОЕ КОЛЬЦО — регулярное кольцо,
допускающее инволюционный антиавтоморфизм аН>а*
такой, что асс* = 0 влечет за собой а=0. Идемпотент е
из *-Р. к. наз. проекцией, если е* = е. Каждый ле-
левый (правый) идеал *-Р. к. порождается однозначно
определенной проекцией. Поэтому можно говорить о
решетке проекций *-Р. к. Если эта решетка полна,
то она является непрерывной геометрией. Дедекиндова
решетка с дополнениями, обладающая однородным ба-
базисом Oj, . . ., ап, где п^4 (см. Регулярное кольцо), яв-
является решеткой с ортодополнениями тогда и только
тогда, когда она изоморфна решетке проекций нек-рого
*-Р. к.
Лит.: [1] С к о р н я к о в Л. А., Дедекиндовы структуры с
дополнениями и регулярные кольца, М., 1961; [2] Berber!-
nan S. К., Bacr "-rings, В.— [а. о.], 1972; 13] Kaplans-
k у I., Kings of operators, N. Y.— Amst., 1968.
Л. А. Скорняков.
РЕГУЛЯРНОЕ ПРЕДСТАВЛЕНИЕ — 1) P. п. (л е-
п о о) алгебры А — линейное представление L
алгебры А в векторном пространстве Е~А, определяе-
определяемое формулой L(a)b~ab для всех а, Ь?А; аналогично,
формула R(a)b = ba, а,Ь?А, определяет (анти)-пред-
етавление алгебры А в пространстве Е = А, наз. (пра-
(правым) Р. п. А. Если А — топологич. алгебра (с умно-
умножением, непрерывным по совокупности переменных),
то L ц 11 — непрерывные представления. Если А —
алгебра с единицей или полупростая алгебра, то все
ее Р. п.— точные.
2) Р.п. (правое) группы G — линейное пред-
представление 11 группы G в пространстве Е комплексно-
значных функций па G, определенное формулой
причем пространство Е разделяет точки группы G и
обладает тем свойством, что функция Ki-*-f(gig), gi?G,
принадлежит пространству Е для всех f?E, g?G. Ана-
Аналогично, формула
определяет (левое) Р. п. группы G в пространстве Е,
если функция gi-*-f(g~'gj), gi?G, принадлежит Е
для всех'g^G, /?Л'. Если G — топология, группа, то в
качестве пространства Е часто рассматриваются про-
пространства непрерывных функций на G. Если G — ло-
локально компактная группа, то (правым) Р. п. группы
С наз. (правое) Р. п. группы G в пространстве L~(G),
построенном по иравоинвариантной мере Хаара на G;
Р. п. локально компактной группы является ее непре-
непрерывным унитарным представлением, причем левое и
правое Р. п. унитарно эквивалентны. а. И. Штерн.
РЕГУЛЯРНОЕ ПРОСТОЕ ЧИСЛО — простое нечет-
нечетное число р, для к-рого число классов идеалов кругового
поля R (егзх1/р) не делится на р. Все остальные про-
простые нечетные числа наз. иррегулярными
(см. Иррегулярное простое число). О. А. Иванова.
РЕГУЛЯРНОЕ ПРОСТРАНСТВО — топологическое
пространство, в к-ром для каждой точки х и каждого
не содержащего ее замкнутого множества А найдутся
непересекающиеся множества U и V такие, что x?U
и А ? V. Регулярными являются все вполне регулярные
пространства и, в частности, все метрические про-
пространства.
Если в Р. п. все одноточечные подмножества зам-
замкнуты (а это выполняется не всегда!), то оно наз.
Т3-и р о с т р а н с т в о м. Не всякое Р. п. вполне
регулярно: существует бесконечное Т3-пространство,
на к-ром каждая непрерывная действительная функция
постоянна. Тем более, не каждое Р. п. является нор-
нормальным пространством. Однако если пространство
регулярно и из каждого его открытого покрытия можно
выделить счетное подпокрытие, то оно нормально. Про-
Пространство со счетной базой метризуомо в том и только
в том случае, если оно является Т3-пространством.
Регулярность наследуется любыми пространствами и
мультипликативна.
Лит.: [1] К о л л и Д ж., Общая топология, пер. с англ,»
2 изд., М., 1981; [2] Архангельский Л. В., П оном а-
р е в В. И., Основы общей топологии в задачах и упражнениях,
М., 1974. А. В. Архангельский.
РЕГУЛЯРНОЕ СОБЫТИЕ — множество слов конеч-
конечного алфавита, к-рое на алгебраич. языке может быть
задано с использованием выражений специального ви-
вида — регулярных выражений. Пусть А —
конечный алфавит и U > °> * — символы операций,
наз. объединением, конкатенацией и
итерацией соответственно. Регулярные
выражения в алфавите А задаются индуктивно:
1) каждая буква из алфавита А есть регулярное вы-
выражение, 2) если Вл, R2 и R — регулярные выражения,
то (fljU^), (R1oR2) и R* суть также регулярные вы-
выражения. Язык регулярных выражений интерпретиру-
интерпретируется следующим образом.
Пусть А*—множество всех слов в алфавите Л,
3fi^/l *, 312—А * • Символ любой буквы из А пони-
понимается как множество, состоящее из одной буквы, а
2ti U ЭГ2 — как обычное теоретико-множественное объе-
объединение. Множество 3tio3t2 состоит из всех слов,
к-рые представимы в виде a^j, где а^ЗГц а2?312>
причем если 4i\ n 3f2 содержат пустое слово Л, то
Ла2=а2, а1Л=а1, ЛЛ=Л. Пусть Щ.Я^А* и для лю-
любого ?г^2 имеет место обозначение 5С"~5Ь . . . °Э1
(п раз). Тогда 31* совпадает с 3tU?BU?PU • • •, т. е.
если a?31*, то существует m.^l такое, что с/, предста-
вимо в виде ах а2 . . . а,л, где а,-??( для любого г =
= 1, . . ., т. Таким образом, множество слов конечного
алфавита является регулярным событием
тогда и только тогда, когда оно может быть получено
из однобуквенных множеств с помощью применения
конечного числа операций объединения, конкатенации
и итерации. Р. с. могут быть заданы и с помощью дру-
других операций, сохраняющих регулярность (напр., пе-
пересечение, дополнение и т. п.), а также путем задания
множества слов, выводимых в формальных системах
типа систем полу-Ту:) (см. Туя система), грамматик и
т. д.
Понятие «Р. с.» возникло при исследовании поведе-
поведения автомата конечного, рассматриваемого в качестве
акцептора. Одной из основных для конечных автоматов
является теорема: событие представимо в конечном
автомате тогда и только тогда, когда оно регулярно.
В связи с этим в теории автоматов рассматривают две
задачи: задачу анализа — по данному авто-
автомату, представляющему нек-рое событие, построить ре-
регулярное выражение, задающее это событие; и зада-
задачу синтеза — имея нек-рое регулярное выраже-
выражение, построить автомат, представляющий соответствую-
соответствующее событие.
Множество всех подмножеств слов в конечном алфа-
алфавите А (событий) вместе с введенными на этом множе-
множестве операциями образуют нек-рую алгебру со-
событий; важнейшими среди таких алгебр являются
алгебры Р. с. с операциями, позволяющими все Р. с.
получить из однобуквенных множеств. Наибольший
интерес представляет вопрос о конечно-аксиоматизируе-
мости алгебр Р. с, то есть вопрос о существовании в та-
таких алгебрах конечных полных систем тождеств. В са-
самой общей постановке ответ на этот вопрос отрицателен,
хотя существуют важные подалгебры алгебр Р. С, в
к-рых конечная полная система тождеств существует.
См. также Автомат, Автоматов способы задания,
Синтеза задачи.
Лит.: [1] Кудрявцев В. Б., Алешин СВ., П од-
кол з к н А. С, Элементы теории автоматов, М., 1978; [2]
С а л о м а а А., «Проблемы кибернетики», 1966, в. 17, с. 237—
24«; [3] Янов Ю. И., там же, 1964, в. 12, с. 253—58; 1966, в. 17,
с. 25D — 58; [4] Ушчумлич Ш., «докл. АН СССР», 1979,
т. 247, № 3, с. 561—65. В. А. Буевич.
РЕГУЛЯРНОСТИ ПРИЗНАКИ для методов
суммирования — условия регулярности сумми-
суммирования метода.
Для матричного метода суммирования, определен-
определенного преобразованием последовательности в последова-
последовательность посредством матрицы ||ал^|!, п, Л=1, 2, . . .,
условия:
2) lim а„ь = 0,
являются необходимыми и достаточными для регуляр-
регулярности метода суммирования. Для матричного метода
суммирования, определенного преобразованием ряда в
последовательность посредством матрицы ||gnfe||, n,
к=1, 2, . . ., необходимыми и достаточными усло-
условиями регулярности являются:
B)
2) lim gnk^i. I
n ->¦ о» J
Условия A) первоначально были установлены О. Тёп-
лицем [1] для треугольных методов суммирования, а
затем X. Штейнхаузом [2] распространены на про-
произвольные матричные методы суммирования. В свя-
связи с этим матрицу, удовлетворяющую условиям A),
наз. матрицей Теплица, или Т-м а т р и-
ц е й.
Для полунепрерывных методов суммирования, опре-
определенных преобразованием последовательности и функ-
функцию посредством полунепрерывной матрицы ||"fc(w)!l
или преобразованием ряда в функцию посредством полу-
полунепрерывной матрицы ||gfc@))||, P. и- подобны соответ-
соответственно условиям A) и B).
Регулярный матричный метод суммирования явля-
является вполне регулярным, если все элементы
матрицы преобразования неотрицательны. Это условие
в общем случае не является необходимым для полной
регулярности.
Лит.: [l] T oepl i t z О., «Prace mat.-fizyczne», 1911, v. 22,
p. 113—19; [2] S t e i n h a u s H., там же, р. 121—34; [3] X a p-
ди Г., Расходящиеся ряды, пер. с англ., М., 1951; М Кук Р.,
Бесконечные матрицы и пространства последовательностей,
пер. с англ., М., 1960. i И. И. Волков.
РЕГУЛЯРНЫЕ МЕТОДЫ СУММИРОВАНИЯ, и е р
манентные методы суммировани я,—
методы суммирования рядов (последовательностей),
суммирующие каждый сходящийся ряд (последователь-
(последовательность) к той же сумме, к к-рой этот ряд (последова-
(последовательность) сходится. Р. м. с. являются частным слу-
случаем консервативных методов сумми-
суммирования — методов, к-рые каждый сходящийся ряд
(последовательность) суммируют к конечной сумме,
хотя быть может и отличной от той, к к-рой он сходится.
Если Р. м. с. определен преобразованием последова-
последовательности {sn} в последовательность {ап} посредством
бесконечной матрицы ||а„&||:
°"п = 2Г=1 ""***' ге=' 2' ••• W
(см. Матричные методы суммирования), то преобразо-
преобразование (*) и матрицу этого преобразования ||а„^|| наз.
регулярными.
Наиболее распространенные методы суммирования,
как правило, регулярны. Напр., регулярными явля-
являются Чезаро метод суммирования (С, к) при к^О,
Гёлъдера методы суммирования, Абеля метод сумми-
суммирования и др. Существуют нерегулярные методы сум-
суммирования. Напр., метод суммирования Чезаро (С, к)
при fe<0, Римана метод суммирования не являются ре-
регулярными.
Метод суммирования наз. вполне регуляр-
регулярным методом суммирования, если он
регулярен и каждый ряд (последовательность) с дей-
действительными членами, сходящийся к -(-оо (или —оо),
суммируется этим методом также к -|- оо (соответственно
— оо). Р. м. с, определенный положительной матри-
матрицей, является вполне регулярным (см. также Регуляр-
Регулярности признаки).
Лит.: [1] Харди Г., Расходящиеся ряды, пер. с англ.,.
М., 1951; [2] К у к Р., Бесконечные мат.рицы и пространства пос-
последовательностей, пер. с англ., М., 1960; [3] К а и г р о Г. Ф.,
в сб.: Итоги науки и техники. Математический анализ, т. 12,
М., 1974, с. 5—70; [4] Барон С, Введение в теорию сумми-
суммируемости рядов, Таллин, 1977. И. И. Воль-ив.
РЕГУЛЯРНЫЙ АВТОМОРФИЗМ — автоморфизм
(р группы G такой, что gq>^=g ни для какого неединич-
неединичного элемента g группы G (т. е. образы всех неединич-
неединичных элементов группы при Р. а. должны быть отличны
от своих прообразов). Если <р — Р. а. конечной группы
G, то для каждого простого р, делящего порядок груп-
группы, он оставляет инвариантной (т. е. отображает в
себя) единственную силовскую р-нодгруппу Sp и
любая инвариантная относительно <р р-иодгрунна груп-
группы G содержится в Sp. Конечная группа, допускающая
Р. а. простого порядка, нильпотентна [2], однако су-
существуют разрешимые ненильпотентные группы, допу-
допускающие Р. а. составного порядка.
Лит.: [1] Gorcnstein D., Finite groups, N. Y., 1968;
[2] T h о m p s о n J. О., «Proc. Nac. Res. Acad. Sci.», 1959,
v. 45, p. 578 — 81. H. H. Вильяме.
РЕГУЛЯРНЫЙ ИДЕАЛ — то же, что и модулярный
идеал.
РЕГУЛЯРНЫЙ TOP — алгебраический тор в связ-
связной алгебраич. группе G, содержащийся лишь в конеч-
конечном числе борелевских подгрупп. Максимальные торы
в G всегда регулярны. В общем случае тор SczG явля-
является регулярным тогда и только тогда, когда его цен-
централизатор Cq(S) — разрешимая группа. В теории
алгобраич. групп важную роль играют одномерные
Р. т. S и соответствующие им однопараметрич. под-
подгруппы k : Gm—*-S (т.н. регулярные пара-
параметры). Тор, не являющийся регулярным, наз. с и н-
г у л я р н ы м. Для редуктивной группы G можно
дать критерий сингулярности тора SczG в терминах
системы корней. А именно, если Т — максимальный
тор в G, содержащий S, и Ф(Т, G) — соответствующая
система корней, то S сингулярен в том и только в том
случае, если ScrKer а для нек-рого а?ФG\ G).
Иногда под Р. т. в б понимают тор S, содержащий"
регулярный элемент (элемент s?S регу-
регулярен, если размерность централизатора Ca(s) в G ми-
минимальна), и называют нолурегулярным тор,
являющийся регулярным в смысле первоначального
определения (см., напр., [1]). Для редуктивных групп
оба ити определения эквивалентны.
Jlvm.: [11 Б о р е л ь А., Линейные алгебраические группы,
пер. с англ., М., 1972; [2] X а м ф р и Д ж., Линейные алгебраи-
алгебраические группы, пер. с англ., М., 1980. В. П. Платонов,
РЕГУЛЯРНЫЙ ЭЛЕМЕНТ полугруппы —
элемент а такой, что а=аха для нек-рого элемента х
данной полугруппы; если при этом ах=ха, то а наз.
вполне регулярным. Если а — Р. э. полу-
полугруппы S, то главный правый (левый) идеал в S, по-
порожденный а, порождается нек-рым идемпотентом;
обратно, каждое из этих двух симметричных свойств
влечет регулярность а. Если aba—а и ЬаЬ=Ь, то эле-
элементы а и Ь наз. инверсными друг к другу
(а также обобщенно обратными, регу-
регулярно сопряженными). Всякий Р. э. имеет
инверсный к ному элемент, вообще говоря, не обяза-
обязательно единственный (ср. Инверсная полугруппа.) Полу-
•г>\'ппы, в к-рых всякие два элемента инверсны друг
к другу, — это в точности прямоугольные полугруппы
(l.'.i. ИОемпотентов полугруппа). Всякий вполне Р. э.
а имеет инверсный к нему элемент, перестановочный
с а. Элемент вполне регулярен тогда и только тогда,
когда он групповой, т. е. принадлежит нек-рой под-
подгруппе полугруппы (ср. Клиффордова полугруппа).
О регулярных ^-классах см. Грина отношения экви-
г,а,1ентности.
hnn.: [1] К л и ф ф о р д А., Преет он Г., Алгебраическая
теория полугрупп, пер. с англ., т. 1, М., 1972; [2] Л я пи и Е. С,
-- |\тр>1шы, М., I960. Л. Я. Шеврин.
РЕГУЛЯТОР поля К алгебраических
ч и с е л — число Дд-, к-рое, по определению, равно 1,
если Л есть поле Q или мнимое квадратичное расшире-
„ v
нис поля Ц, а в остальных случаях равно у , где
г —ранг группы Е единиц поля К (см. Алгебраическое
число, Алгебраическая теория чисел), a v—г-мерный
объем основного параллелепипеда r-мерной решетки в
Kr + 1, являющейся образом группы Е при ее лога-
логарифмическом изображении I в Rr + 1.
При этом гомоморфизм I определяется следующим обра-
лом. Пусть а1, . . ., as — все вещественные, а <т^ + 1, . . .,
os + f — комплексные попарно несопряженные изомор-
изоморфизмы К в С; s+2i=diniQ К (см. Дирихле теорема о
единицах). Тогда r+l=s+t, а гомоморфизм I : E-*-Rr + 1
определяется формулой
( In | о,- (a) | при 1
' \ In | a,- (a) |2 при s
Образом гомоморфизма I является r-мерная решетка в
КЛ + 1, лежащая в плоскости "Vr+ xL—0 (ж,—канонич.
координаты). 1~
Единицы ej, . . ., гг, для к-рых l(ej), . . ., l(er)
является базисом решетки 1(Е), наз. основными
единицами ноля К и
Имеются и другие формулы, связывающие Р. с други-
другими инвариантами поля К (см.,напр., Дискриминант, 3)).
Если вместо Е рассматривать пересечение этой груп-
группы с каким-либо порядком Q поля К, то аналогично
можно определить регулятор R,- порядка Q.
Лит.: [1] Б о р е в и ч 3. И., ШафаревичИ. Р., Тео-
Теория чисел, 2 изд., М., 1972; [2] Л е н г С, Алгебраические числа,
пер. с англ., М., 1UBB. В. Л. Попов.
РЕДУКТИВНАЯ ГРУППА — линейная алгебраич.
группа G, удовлетворяющая одному из следующих
эквивалентных условий: 1) радикал связной компонен-
компоненты единицы G0 группы G есть алгебраический тор,
2) унипотентный радикал группы G0 тривиален, 3) груп-
группа G0 разлагается в произведение замкнутых нормаль-
нормальных подгрупп S и Т, являющихся соответственно по-
полупростой алгебраической группой и алгебраич. тором.
При этом S — коммутант группы G°, a T совпадает с
радикалом группы G0, а также со связной компонентой
единицы ее центра; S[\T конечно, любая полуиростая,
а также любая унипотентная подгруппа группы G"
содержится в S.
Линейная алгебраич. группа G наз. линейно
редуктивной, если выполнено любое из следую-
следующих двух эквивалентных условий: а) каждое рацио-
рациональное линейное иредставление группы G вполне при-
приводимо, б) для каждого рационального линейною пред-
представления р : G—>GL(W) и любого р^-инвариант-
р^-инвариантного вектора w?W\{0} существует такая p(G)-
инвариантная линейная функция / на W, что /(ш)=^=0.
Всякая линейно Р. г. является Р. г. Если характери-
характеристика основного поля К равна 0, то верно и обратное.
В случае char Л">0 это не так — всякая связная ли-
линейно Р. г. является алгебраич. тором. Однако и в
общем случае Р. г. могут быть охарактеризованы в тер-
терминах теории представлений. Линейная алгебраич. груп-
группа G наз. геометрически редуктивной
(или полуредуктивной), если для каждого ра-
рационального линейного представления р : G—>-GL(W)
и любого р(С)-инвариантного вектора if ? VF%{0} су-
существует такая р (С)-инвариантная полиномиальная
функция / на W, что /(if)=?tO. Линейная алгебраич.
группа тогда и только тогда является Р. г., когда она
геометрически редуктивна (см. Мамфорда гипотеза).
Для Р. г. справедлива обобщенная Гильберта теоре-
теорема об инвариантах. Верно и обратное: если G — линей-
линейная алгебраич. группа над алгебраически замкнутым
полем К и при любом ее локально конечномерном ра-
рациональном представлении автоморфизмами произ-
произвольной конечно порожденной ассоциативно-коммута-
тивной /f-алгебры А с единицей алгебра инвариантов
Аа конечно порождена, то G есть Р. г. (см. [4]).
Каждая конечная линейная группа является Р. г.,
а если ее порядок не делится на char if, то и линейно
Р. г. Связные Р. г. допускают структурную теорию,
во многом аналогичную структурной теории редуктив-
ных алгебр Ли (система корней, группа Вейля и т. п.,
см. [2]). Эта теория распространяется и на группы вида
Gfe, где G — связная Р. г., определенная над нек-рым
подполем kCZK, a G&— группа ее fe-рациональных то-
точек (см. [3]). При этом роль борелевских подгрупп,
максимальных торов, групп Вейля играют соответ-
соответственно минимальные определенные над к параболич.
подгруппы, максимальные разложимые над к торы,
относительные группы Вейля (см. Вейля группа). Лю-
бые две минимальные определенные над к параболич.
подгруппы группы G сопряжены над к, т. е. при по-
помощи элемента группы G/,; то же верно и для любых двух
максимальных ft-разложнмых торов группы G.
Если G — связная Р. г., определенная над нолем
к, то G — разложимая группа над нек-рым сепарабель-
ным расширением конечной степени поля к; если,
кроме того, ноле А- бесконечно, то 0^ плотна в G в
смысле топологии Зариского. Если G — Р. г. и Н —
ее замкнутая подгруппа, то факторпространство GlH
аффинно тогда и только тогда, когда Н — Р. г. Линей-
Линейная алгебраич. группа над полем характеристики 0 ре-
дуктивна тогда и только тогда, когда ее алгебра Ли
является Ли редуктивной алгеброй или когда она яв-
является комилексификацией нек-рой компактной груп-
группы Ли (см. Комплексификация группы Ли).
Лит.: [1] Спрингер Т., Теория инвариантов, пер. с
англ., М., 1981; [2] Хамфри Дн:., Линейные алгебраические
группы, пер. с англ.. М., 1980; [3] Б о р е л ь А. Тите Ж.
«Математика», 1967, т. 11. № 1, с. 43—111; ЛГ« 2, с. 3—31; [4]
П о п о в В. Л., «Докл. АН СССР», 1979, т. 249, JV« 3, с. 551 — 55.
В. Л. Попов.
РЕДУКТИВНОЕ ПРОСТРАНСТВО — такое одно
родное пространство G'H связной группы Лн G, что
в алгебре Ли g группы G существует Ad (//)-инва-
риантное подпространство, дополнительное к подалгеб-
подалгебре \)СС[, являющейся алгеброй Лн группы Н. Вы-
Выполнение любого из следующих условии достаточно
для того, чтобы однородное пространство GlH было
Р. п.: 1) линейная группа Ad (Я) вполне приводима,
2) на cj существует Ad. (//)-инвариантная билинейная
форма, сужение к-рой на !) невырождено. В частности,
всякое однородное риманово пространство является
Р. п. Если M--G/H — Р. п. и группа G действует эф-
эффективно на М, то линейное представление изотропии
группы Н в касательном пространстве М0 к многообра-
многообразию М в точке о = еН?М точно. С каждым Ad^ (Н)-
инвариантным подпространством ШСД, дополнитель-
дополнительным к I), связаны две важные G-инвариантные аффин-
аффинные связности на М: каноническая связ-
связность и естественная с в я з н о с т ь б е з
к р у ч е н п я. Канонич. связность на Р. п. M=GlH
с фиксированным Adfl (Я)-инвариантным разложением
3^ Г) Ии — единственная G-инвариантная аффинная
связность на М, обладающая том свойством, что для
любого вектора X?ttl и любого репера и в точке о
кривая (exp tX)u в главном расслоении реперов над
М горизонтальна. Канонич. связность полна и множе-
множество ее геодезических, проходящих через точку о, сов-
совпадает с множеством кривых вида (exp tX) о, где Х?т.
После естественного отождествления пространств m
и Мо тензор кривизны Я и тензор кручения Т канонич.
связности определяются формулами (В (X, Y) Z)o=
--|[Х, У]„ , Z] и T(X,YH=-[X,Y]m, где X, Y,
а через We и Wm обозначены проекции вектора
на Г) и m соответственно. Тензорные ноля R и
Т параллельны относительно канонич. связности так
же, как и любое другое G-инвариантное тензорное поле
на М. Алгебра Ли линейной группы голономии (см.
Голономии группа) канонич. связности на М с опор-
опорной точкой о порождается множеством {).(\X,Y]c)
\Х, Y?m}, где К — линейное представление изотро-
изотропии алгебры Ли Г) в пространстве М0. Всякое связное
односвязное многообразие, снабженное полной аффин-
аффинной связностью с параллельными нолями кривизны и
кручения, может быть представлено в виде Р. п., кано-
канонич. связность к-рого совпадает с заданной аффинной
связностью. На Р.н. М GlH с фиксированным
Ad (У/)-пнвариантным разложением t]=v-f)_j-m су-
существует единственная б'-пнвариантная аффинная связ-
связность с нулевым кручением, имеющая те же геодезиче-
скис, что и канонич. связность. Эта связность наз. е с-
т ест венной связностью без круче-
кручения на М (относительно разложения t]=---f)-fm).
Однородное риманово или псевдоримапово пространст-
пространство M--G/II наз. естественно р е д у к т п в-
н ы м, если оно допускает такое Adfl (/^-инвариант-
(/^-инвариантное разложение 9=^+tn, что
для всех X, Y, Z?m, где В — невырожденная сим-
симметрическая билинейная форма на ш, индуцированная
римановой (исевдоримановой) структурой на М при ес-
естественном отождествлении пространств m и Мо. Если
M—G/H — естественно редуктивное риманово или псев-
дориманово пространство с фиксированным Adfl (#)-
инвариантным разложением д=f)-f-nt, удовлетво-
удовлетворяющим условию (*), то естественная связность без
кручения совпадает с соответствующей римановой или
псевдоримановой связностью па М. Если М — одно-
связное естественно редуктивное однородное риманово
пространство и М = Мо X М1X . . .X Мг — его разложе-
разложение др Рама, то М может быть представлено в видо
М С II. причем G=-G0XG1y< .. .xGr, H=1IOXJI1X.
X. . . ,.llr и Mi=Gi//I; (i---d. 1, 2. .'. ., r).
Нижним обобщением Р. п. являются v-редуктивные
однородные пространства [4]. Однородное пространство
G/H наз. v-p едуктнвн ы м. если его стационар-
стационарная подалгебра I) допускает разложение в пря-
прямую сумму подпространств 1р Г)г]-1J+ - . .-i'ljv, где
FjvT^fO}, причем в (j существует такое дополнитель-
дополнительное к Г) подпространство т, что ff),-, m]cf),-_i, »=
= 1, 2, . . ., v, где fH=m. При этом 1-редуктивные
однородные пространства — это в точности Р. п.;
примерами 2-редуктивных однородных пространств яв-
являются проективное и конформное пространства, на
к-рых действуют группа проективных преобразований
и группа конформных преобразований соответственно.
Если M=G/1I есть v-редуктивное однородное про-
пространство и v>4, то линейное представление изотропии
алгебры Ли I) не является точным (так как [(),-, ill let)
при i>l) и, следовательно, на М не существует С-
инвариантной аффинной связности. Однако на v-pe-
дуктивном однородном пространстве существует кано-
каноническая G-инвариантная связность, слоем к-poii явля-
является однородное пространство век-рой транзитшшо-
диффоренциальной группы порядка v (см. [4]).
Наряду с Р. п. рассматриваются также ч а с т и ч н о
редуктивные пространства, т. е.
такие однородные пространства G/U, чю существует
разложение алгебры Ли С] в прямую сумму двух нену-
ненулевых Adfl (//)-инвариантвых подпространств, одно из
к-рых содержит подалгебру Г) (см. [5]).
Лит.: [1] К о б а я с и Ш., Н о м и д з у К., Псионы диффе-
дифференциальной геометрии, пер. с англ., т. 2, М., JUKI; Ы Ра ш с:
raizn К., «Ашег. J. Mutli.», IH.Vj, v. 7B,
ок и й П. К., «Тр. Се
в. 9, с. 49—74; [3] N о .... , -. -. -. , .. .-,
JN1. 1, р. 33—65; [4] Кантор И. Л., «Тр. Семинара по игкт. и
тонн, анализу», 1966, в. 13, с. 310—98; [5] Винбсрг Э. Б.,
«Тр. Моск. матем. об-ва», 1960, т. 9, с. 191—210.
Д. В. Алексееаский.
РЕЗИДУАЛЬНОЕ ОТОБРАЖЕНИЕ — пзогонное
отображение ф частично упорядоченного множества Р
в частично упорядоченное множество Р', для к-рого
существует изотовнос отображение ср' из Р' в Р такое,
ото ср' (ф(х))>ж для всех л?Р и <р (ф'(^'))<х' для всех
х' ?Р'. Если Р и Р' — полные решотки и ф сюръектив-
но, то это равносильно равенству
ф (sup A) --sup ф (Л)
для всякого подмножества А из Р. Совокупность Р. о.
частично упорядоченного множества Р в себя образует
полугруппу, к-рую можно сделать частично упорядо-
ченной (см. Упорядоченная полугруппа), полагая
Ф«?ф, если ф (х).<ф(я) для всех х?Р. Свойства этой
частично упорядоченной полугруппы тесно связаны со
свойствами частичпо упорядоченного множества Р
(см. Решетка). Л. А. Скорняков.
РЕЗНАЯ ПОВЕРХНОСТЬ — поверхность, образо-
образованная лз ортогональных траекторий однонараметрич.
семейства плоскостей. Р. п. имеет одно семейство пло-
плоских линий кривизны, к-рые одновременно являются
для Р. п. геодезическими. Если семейство плоскостей
вырождается в пучок, то Р. п. будет поверхностью вра-
вращения. Сечения Р. п. плоскостями семейства наз. м е-
ридианами, а ортогональные траектории — па-
пара л л с л я м и Р. н. Все меридианы конгруэнтны,
так что Р. п. можно образовать движением плоской
линии L (меридиана), плоскость к-рой катится без
скольжения по нек-рой развертывающейся поверхно-
поверхности, называемой направляющей поверхностью
Р. ц. и являющейся одной из полостей ее эволюты.
Если р (s) — радиус-вектор одной параллели, то ра-
радиус-вектор Р. п. есть
где р — v cos 6+Р sin 6, g= —v sin G+P cos G, v — глав-
главная нормаль, ^-бинормаль, х — кручение кривой Г,
a G= — \xds. Ее линейный элемент:
ds2 = [1 + k (Isin 6 — т] cos б)]2 ds2+ (t)'! + ?'2) dv",
где г] (v), ?(и) — уравнения Г, а к — кривизна.
И. X. Сабитов.
РЕЗОЛЬВЕНТА — 1) Р. алгебраического
уравнения f(x) = 0 степени п — алгебраическое
уравнение g(y)=O с коэффициентами, рационально
зависящими от коэффициентов f(x), такое, что знание
корней этого уравнения позволяет найти корни данного
уравнения f(x) = 0 в результате решения более простых
уравнений, степеней не больших п. Иногда Р. называют
само рациональное выражение y—y(xlt . . ., хп).
Пусть f(x) — сепарабельный многочлен пад полем к
с группой Галуа G и Н — нормальный делитель группы
G. Пусть у=у(х1, . . ., хп) — рациональное выражение
от xj, . . ., хп, остающееся инвариантным при всех
подстановках корней хх, . . ., хп из группы II, и уфк.
Тогда у является корнем нек-рого уравнения g(y)=O
с коэффициентами из к, группа Галуа к-рого является
собственной факторгруппой группы G. Таким образом,
решение уравнения f(x) = 0 сводится к решению урав-
уравнения g{y)==O и решению уравнения /(х) —0 над полем
к (и,, . . ., ys).
'апр., для решения уравнения 4-й степени
дх.]- г = 0
(любое уравнение 4-й степени приводится к такому ви-
виду) используют кубич. Р.
корни к-рой уг, у2. у3 связаны с корнями xs, x2. x,s, ,r,
соотношениями у^Хх^х^) (ха-\-хА), г/2==(ж1Н"-г'з)C'2+
+z.i). .Уз —(г2+*4) (хг+хз). Корни у1, у2, у3 определя-
определяются с помощью формулы Кардано, что позволяет
определить и корни xlt x2, хъ, xt.
Последовательное применение метода Р. позволяет
свести решение любого уравнения с разрешимой груп-
группой Галуа к решению цепочки уравнений с циклич.
группой Галуа. Для решения последних использу-
используются резольвенты Лагранжа.
Пусть /(.т) = 0 — уравнение над полом к с циклич.
группой Галуа G порядка п и пусть к содержит пер-
первообразный корень пз единицы ?„ степени п. Для эле-
элемента а, принадлежащего полю разложения многочле-
многочлена f(x), и характера % группы G в группу корней из
единицы степени и резольвента Лагранжа
р(Х,а) определяется формулой
Пусть а=хг— один из корней многочлена /(.г) и '/
пробегает все характеры группы G. Тогда система
линейных уравнений (*) позволяет определить корни
х1г х2, . . ., хп, если известны резольвенты Лагранжа
для всех характеров % группы G.
Для t?G выполняется соотношение
к-рое показывает, что элементы «=p(y_,a)" и 6,-=
= р(%, a)~'p(x', a) при любом целом г инвариантны от-
относительно G и, следовательно, являются однозначно
определенными рациональными выражениями от коэф-
коэффициентов многочлена / (х) и корня ?„. Если % порождает
группу характеров группы G, то имеют место равен-
равенства р(х, а)=уа и р(х', a)=bip(x, a)' для х'=Х'-
Резольвентой Галуа уравнения / (х)*=0
наз. такое неприводимое над данным полем алгебраич.
уравнение у(х) — 0 (см. Галуа теория), что в резуль-
результате присоединения одного из его корней к атому полю
получается поле, содержащее все корни уравнения
/(;о
;
Лит.: [1] В а и д е р К а ji д е и Ь. Л., Алгсира. пёр. с
нем., 2 изд., М., 1971). Л. В. Кузьмин.
2) В теории интегральных уравнений под Р. (раз-
(разрешающим ядром) уравнения
tf(s, t)<p(t)dt = f(s) (**)
иопимают функцию Г (s, t; X) переменных s, t и пара-
параметра X, при помощи к-рой решение уравнения (**)
представляют в виде
/М+а, \bT(s,t, x)f(t)dt,
если Я но есть собственное значение уравнения (**),
напр, для ядра К (s, t)=s-\-t резольвентой является
функция
ВС9-3.
3) Р.о и оратора — оператор /??., обратный к Гх =
—А —КТ, где А — замкнутый линейный оператор, опре-
определенный на плотном множестве Dj банахова прост-
пространства X со значениями в том же пространстве, при
условии, что X таково, что J'^1 ость линейный непрерыв-
непрерывный оператор, определенный на всем X. Точки К, для
к-рых Р. существует, наз. регулярными точ-
точками оператора А, а совокупность исех регулярных
точек — резольвентным множеством р(/1)
этого оператора. Множество р(А) — открытое и на
каждой его связной компоненте оператора Rx являет-
является аналитич. функцией параметра к.
Свойства Р.:
1) В} —/?n = fX—|x)i??,2?(j, для любых двух точек К,
Л
Р();
2) из В\х=0 следует л-—0; t
3) если X — гильбертово пространство, то liy—R%-
Лит.: [1] И о с и д а К., Функциональный анализ, пер. с
англ., М., 1967; 12] А х и с з е р Н. И., Г л а з м а н И. М.,
Теория линейных операторов в гильбертовом пространстве,
2 изд., М., 19В6; [3] Канторович Л. В., Ак и л о в Г. П.,
Функциональный анализ, 2 изд., М., 1977. В. И. Соболев.
4) Б гомологической алгебре Р. моду л я — комп-
комплекс С, определенный для положительных степеней и
снабженный пополняющим гомоморфизмом А-уС (мо-
дуль А рассматривается как комплекс, равный нулю
в ненулевых степенях) таким образом, что последова-
последовательность 0—»v4—>-6'°—vC1—»-. . . точна. Р. наз. и н ъ е к-
т и в н о й, если все С' инъективны. Двойственным об-
образом определяется проективная резольвен-
т а. Р. является основным средством вычисления произ-
производных функторов. В частных случаях удобно исполь-
использовать специальные виды Р. Напр., для кольца много-
многочленов Л—k[xi,. . .,хп] внешняя алгебра Ед(и1у. . ., ип)
превращается в Р. тривиального Л-модуля к, если за-
задать дифференциал д(и{) = Х{ и пополняющий гомомор-
гомоморфизм е(и,)=0. Эта' конструкция применима к кольцам
степенных рядов (как сходящихся, так и формальных)
и носит название комплекса Козюля.
В. Я. Говоров.
РЕЗОЛЬВЕНТНОЕ МНОЖЕСТВО — множество
р(Г), где Т — линейный оператор в банаховом прост-
пространстве, такое, для к-рого существует оператор R2=
--(Г— z/)-1, ограниченный и имеющий область опре-
определения, плотную в X. Дополнительное к Р. м. мно-
множество есть спектр оператора Т.
Лит.: [I] Рисе Ф., Сёкефальви-НадьБ., Лекции
по функциональному анализу, пер. с франц., 2 изд., М., 1979.
М. И. Войцеховский.
РЕЗОНАНС — явление увеличения амплитуды
вынужденных колебаний при приближении частоты внеш-
внешнего воздействия к одной из частот собственных коле-
колебаний динамич. системы. Явление Р. имеет наиболее
простой характер в линейной динамич. системе. Диф-
Дифференциальное уравнение движения линейной системы
с одной степенью свободы в среде с вязким трением при
гармонич. воздействии имеет вид
aq-^-bq-\-cq = H sin (pt -f- б),
где 7 — обобщенная координата; а, Ъ, с — постоянные
параметры, характеризующие систему; Я, р, б — соот-
соответственно амплитуда, частота, начальная фаза внеш-
внешнего воздействия. Установившиеся вынужденные коле-
колебания происходят по гармонич. закону с частотой р и
амплитудой
я
?> = -
где к= Ус/а—частота собственных колебаний при отсут-
отсутствии рассеивания энергии (Ь=0). Амплитуда D имеет
максимальное значение при — ^ -\/ 1 —— и при малом
ft У 2ас
рассеивании энергии близка к ее значению при р--к.
Принято называть резонансом тот случай, когда
р=к. Если Ь=0, то при р=к амплитуда вынужденных
колебаний возрастает пропорционально времени.
Если линейная система имеет п степеней свободы,
то Р. наступает при совпадении частоты внешней силы
с одной из собственных частот системы. При негармо-
нич. воздействии Р. может иметь место лишь при сов-
совпадении частот его гармонич. спектра с частотами соб-
собственных колебаний.
Лит.: [1] Стрелков С. П., Введение в теорию колеба-
колебаний, М.— Л., 1951. Н. В. Бутеиин.
РЕЗОНАНСНЫЕ ЧЛЕНЫ —те члены fPQXpx
Хехр {i<Q,Y>} ряда Тейлора — Фурье
f(X, Y) = ^fPQXPexp{i<Q, У>}, A)
у к-рых показатели Р и Q удовлетворяют линейному
соотношению вида
<Р, Л>-Н<<?, Q> = c. B)
Здесь fpQ — постоянные коэффициенты, <<?, Y} —
скалярное произведение Q и У; постоянные (кх,. . .,
^•т) = Л и (colt. • ., й)„) = й — обычно собственные зна-
значения и базис частот нек-рой системы обыкновенных
дифференциальных уравнений; константа с не зависит
от Р и Q, она определяется ролью ряда A) в рассмат-
рассматриваемой задаче.
Если в линейной системе
xj = XjXj, ] — l,...,m, yk = <ak, к = \, . .., п, C)
все Лу чисто мнимые и в B) с—0, то сумма Р. ч. ряда A)
совпадает с осреднением этого ряда вдоль решений си-
системы C). Систему обыкновенных дифференциал иных
уравнений в окрестности нек-рых инвариантных много-
многообразий можно привести к нормальной форме, в к-рой
ряды содержат только Р. ч. (см. [1]). Так, для гамилъ-
тоновой системы в окрестности неподвижной точки га-
гамильтониан может быть приведен к виду A), где п=0,
и выполнено B) с с—0, причем А=(Х1,. . ., Xi,—Xl,...,
—Xt) — вектор из собственных значений линеаризован-
линеаризованной системы (см. [2]). В этом случае иногда члены с
pj-—pj-+h / = 1, . . ., I, наз. вековыми (для них
B) выполняется тривиально), а резонансными наз. ос-
остальные члены ряда A), для к-рых выполнено B).
Выделение Р. ч., производимое в задачах с малым па-
параметром, зачастую также может быть обосновано с по-
помощью нормальной формы (см. [1]). Для точечного пре-
преобразования с мультипликаторами (|Xf,. . ., \im)=M по-
показатели Р. ч. ряда A) с ге= 0 удовлетворяют соотноше-
соотношению Мр=1; если положить А=1пМ и йI=1, то по-
получится соотношение B) с е=0.
Лит.: [1] Брюно А. Д., Локальный метод нелинейного
анализа дифференциальных уравнений, М., 1979; [2] е г о же,
«Тр. Моск. матем. об-ва», 1971, т. 25, с. 119—262; 1972, т. 26,
с. 199—239. А. Д. Брюно.
РЕЗУЛЬТАНТ многочленов f(x) и g (x) —
элемент ноля Q, определяемый формулой
Я (/, g) -albS IIL П1=1 <a<—М- (*>
где Q — поле разложения многочлена fg, «,-, Р;- — кор-
корни многочленов
* (z) = «.„*'+ М*+ •••+*,
соответственно. Если aobo=?O, то многочлены тогда и
только тогда имеют хотя бы один общий корень, когда
их Р. равен нулю. Имеет место равенство
R(g, 1) = (-\)nsR(i,g).
Р. можно записать в любом из следующих видов:
я(/, г) = (-1гь'о' П'=1/(М- C)
Выражения A), B) и C) неудобны для вычисления Р.,
так как они содержат корни многочленов. Через ко-
коэффициенты многочленов Р. можно выразить в виде
следующего определителя порядка re-J-s:
a0
bob1
bo
... an
«n
... bs
bn
¦ an-
«! .
-lbs
¦ bs_
h .
i an
¦¦a.n-1
i bs
In
b,
Этот определитель в первых s строках содержит коэф-
коэффициенты многочлена f(r), в последних п строках —
коэффициенты многочлена g(x), а на свободных мо-
мостах — нули.
Р. многочленов f(x) и g(x) с числовыми коэффициен-
коэффициентами .можно предсталить в виде определителя порядка
п (или s). Для этого находят остаток от деления
xk g(x) na j(x), к^О, 1, 2,. . ., п — 1. Пусть это будет
Тогда
eoo eoi ••¦ аов-1
«10 аП ¦ ¦ ¦ а1 п-1
n-lo °»-ii ••• °п-Гя-1
Дискриминант D (f) многочлена
выражается через Р. многочлена /(.rj и его производ-
производной /' (х) следующим образом:
п (п-1)
Д (/) = (—1) 2 a»1 R(f, 1').
Применение к решению систем
уравнений. Пусть дана система двух алгебраич.
уравнений с коэффициентами из поля Р:
Многочлены fag записывают по степеням х:
f (х, у) = а0 (у) х" + в1 (у)х*-*+. • • +ak (у),
E)
и по формуле D) вычисляют Р. этих многочленов как
многочленов от х. Получается многочлен, зависящий
только от у.
R(f,g) = F(v)-
Говорят, что многочлен F (у) получен путем исключе-
исключения х из многочленов /(х,у) и g(x, у). Еслих=а, у=$—
решение системы E), то ^(р")=0, и обратно, если
F (Р)=:0, то или многочлены f(x, P), g(x, P) имеют об-
общий корень (к-рый надо искать как корень их наиболь-
наибольшего общего делителя), или а0 (Р)=Ь0 (Р)=0. Тем са-
самым решение системы E) сводится к вычислению кор-
корней многочлена F(y) и общих корней многочленов
/ (х, Р), g(x, P) с одним неизвестным.
Аналогично можно решать и системы уравнений с
любым числом неизвестных, но эта задача приводит
к весьма громоздким вычисл ниям (см. также Исклю-
Исключения теория).
Лит.: 11] К у Р о ш А. Г., Курс высшей алгебры, 11 изд.,
М., 1975; [2] О к у н е в Л. Я., Высшая алгебра, 4 изд., М.—
Л., 1041); [3] В а н дер Варден Б. Л., Алгебра, пер. с
нем., 2 изд., М., 1979; Щ X о д ж В., II и д о Д., Методы ал-
алгебраической геометрии, пер. с англ., т. 1—3, М., 1954—55.
И. В. Проскуряков.
РЕЙДЕМЕЙСТЕРА КРУЧЕНИЕ, кручение
де Рама, кручение Франц а,— инвариант,
позволяющий различать многие структуры в дифферен-
дифференциальной топологии, напр, узлы, гладкие структуры
на многообразиях, в частности на линзовых простран-
пространствах. Впервые Р. к. введено К. Рейдемейстером (см.
[1]) при изучении трехмерных линз, обобщения для
и-морных линз были независимо получены в [2] и [3].
Пусть С — свободный комплекс левых А -модулей,
г;|,о А — ассоциативное кольцо с единицей. Пусть, да-
далее, h — матричное представление кольца А, т. е. го-
гомоморфизм кольца А в кольцо Я"хя всех действитель-
действительных (геХп)-матриц. И пусть в модулях С^ комплекса С
отмечены базисы ck, а комплекс С ~ R"Xn ®дС Л"Х«-
модулей ацикличен; тогда определено Уайтхеда кру-
кручение х {C')?K1Rnxn = ~KXR = R + , где Л+—мульти-
л.шкаптная группа ноля действительных чисел. Чи-
Число т(С') наз. кручением Рейде мейстера
комплекса С, а также действительным Р. к.
Эффективность замены кручения Уайтхеда на Р. к.
основывается на т е о р е м е Б а с с а [4]: если л —
конечная группа, то элемент u>?Wh(n) имеет конеч-
конечный порядок, если Л*(ш)=1 для любого представле-
представления h, где й*(со) — Р. к., индуцированное элементом со.
Лит.: [1] ReUemeister К., «Abhandl. math. Semin.
Univ. Hamburg», 1935, Bd 11, S. 102—09; [2] Franz W.,
«J. fur r. und ang. Math.», 1935, Bd 173, S. 176—84; [3] R h a m G.
d e, «Матем. сб.», 1936, т. 1, № 5, с. 737—43; [4] Bass H.,
«Publ. math.», 1964, JMb 22, p. 5 — 60 [1HES). А.С.Мищенко.
РЕЙНОЛЬДСА ЧИСЛО — один из критериев по-
подобия для течений вязких жидкостей и газов, характе-
характеризующий соотношение между инерционными силами
и силами вязкости:
где р — плотность, ц — динамич. коэффициент вязко-
вязкости жидкости или газа, v — характерная скорость по-
потока, I — характерный линейный размер.
От Р. ч. зависит также режим течения жидкости,
характеризуемый критическим Р. ч. ReKp.
При Re<ReKp возможно лишь ламинарное течение
жидкости, а при Re>ReKp течение может стать тур-
турбулентным.
Р. ч. названо по имени О. Рейнольдса (О. Reynolds).
По материалам одноименной статьи из БСЭ-3.
РЕКУРРЕНТНАЯ ТОЧКА динамической
системы— точка х динамич. системы /' (или, в
иных обозначениях, /((,¦), си. [2]), заданной на мет-
рич. пространстве S, удовлетворяющая условию: для
всякого е>0 найдется 7'>0 такое, что все точки тра-
траектории рх содержатся в е-окрестности всякой дуги
временной длины Т этой траектории (иными, словами,
при любом t?R е-окрестность множества
содержит всю траекторию f'x). В этом случае /'ж наз.
рекуррентной траекторией.
Теорема Биркгофа: если пространство S
полное (напр., 5=Rn), то 1) для того чтобы точка бы-
была рекуррентной, необходимо и достаточно, чтобы за-
замыкание ос траектории было минимальным множеством;
2) для того чтобы существовала Р. т., достаточно, что-
чтобы существовала точка, устойчивая по Лагранжу (см.
Устойчивость по Лагранжу).
Р. т. устойчива по Лагранжу и по Пуассону (см.
Устойчивость по Пуассону). Почти периодическая (в
частности, неподвижная или периодическая) точка ди-
динамич. системы рекуррентна. Вообще, всякая точка
строго эргодической динамич. системы рекуррентна, но
сужение динамич. системы на замыкание рекуррентной
траектории (минимальное множество) может но быть
строго эргодической динамич. системой (пример
Маркова, см. [2]).
Лит.: [1] Б и р к г о ф Д. Д., Динамические системы пер. с
англ., М., 1941; [2] Н е м ы ц к и й В. В., С т е п а н о в В. В.,
Качественная теория дифференциальных уравнений, 2 изд.,
М.— Л., 1949. В. М. Миллгюшцикан.
РЕКУРРЕНТНАЯ ФОРМУЛА — то же, что рекур-
рекуррентное соотношение.
РЕКУРРЕНТНАЯ ФУНКЦИЯ — функция, являю-
являющаяся рекуррентной точкой сдвигов динамич. системы.
Эквивалентное определение: функция ф : R-+S, где S —
метрич. пространство, наз. рекуррентной, если она
имеет предкомпактное множество значений, равномер-
равномерно непрерывна и для всякой последовательности чисел
tk ?R такой, что существует предел
Ф(О= Hm
h-> сю
(предел в компактно открытой топо-
топологии, т. е. равномерный на каждом отрезке), най-
дется последовательность чисел tj?R такая, что
q>{t)=. lini (( [Tk + t)
к -> со
в компактно открытой топологии.
Если (p:R—>-R" — ограниченная равномерно непре-
непрерывная функция, то найдутся ?k?fv такие, что предел
Ч' (/)-- lim ч {'к г г)
ft ->¦ ж
(в компактно открытой топологии) существует и явля-
является Р. ф. Веяная почти периодич. функция и, в част-
частности, всякая периодич. функция являются Г. ф.
Лит.: [11 Итоги науни и техники. Математический анализ,
т. 12, М., 1974, с. 71 — 146. В. М. Миллионщиков.
РЕКУРРЕНТНОЕ СООТНОШЕНИЕ, рекуррент-
рекуррентная формула,— соотношение вида
к-рое позволяет вычислять все члены последовательно-
последовательности а±, а2, а3.. . ., если заданы ее первые р членов. При-
Примеры Р. с: 1) an + 1—q-an(q?=Q) —геометрия, прогрес-
прогрессия, 2) a,J + 1=an+d — арифметич. прогрессия, 3) а„ + 2=
="re+i+an — последовательность чисел Фибоначчи.
В случае, когда Р. с. линейно (см. Возвратная после-
последовательность), задача описания множества всех по-
последовательностей, удовлетворяющих данному Р. с,
имеет аналогии с решением обыкновенного одпород-
ного линейного дифференциального уравнения с по-
постоянными коэффициентами.
Лит.: [1] М а р к у m e в и ч А. И., Возвратные последова-
последовательности, 2 изд. М., 1975. С. Л. Артемов.
РЕКУРРЕНТНЫЕ СОБЫТИЯ в последова-
последовательности повторных испытаний со
случайными исходами — ряд событий
Аъ А 2,. . ., Ап,. . . таких, что наступление события
Ап определяется исходами первых п испытаний,
ге=1,2,. . ., а при условии, что наступило событие Ап,
наступление события Ат, туп, определяется исхода-
исходами (ге+1)-го, (п-\-2)-то и т.д. до m-го испытаний, при-
причем при условии одновременного наступления событий
Ап и А,„ (m>n) исходы первых п и последующих m—п
испытаний условно независимы.
Более точно, пусть X — совокупность (коночная или
счетная) всех исходов отдельного испытания, х'-1'"-' —
пространство последовательностей (.с^,. . ., -г,,), j/^.Y,
?=1,. . ., п, исходов при п испытаниях, м—1, 2, 3,. . .,
и А'' ' °°'— пространство бесконечных последовательно-
последовательностей (xj,. . ., хп...), ?;?Х, ?=1,2,. . ., ге,. . ., исходов,
в к-ром задано пек-рое распределение вероятностей р.
Пусть в каждом пространство X1'' "', п --1,2,. . ., выде-
выделено нек-рое подмножество еп^Х^'п' так, что для
любых и и m, \<^l.n<im <l&, последовательность .г —-
M.i Лл)€-^[''т1 такая, что
пршгадле;кит tm в том и только в том случае, когда
последовательность
Если послодпее условие выполнено и
'i-fvl'' ¦¦").Ilffl.-"[ ! ¦ (Z V[1 > 'х 1 ¦ г "
где для последовательности х~(хи. . .,хп,. .
через х \ обозначена последовательность
Событие
на:к рекуррентным событием, наступив-
наступившим поело и испытаний.
Примеры. 1) В последовательности независимых
бросаний монеты события, состоящие, соответствен-
соответственно, I! том, что при и не питаниях герб и решка выпадут
одинаковое Число раз (такое событие возможно только
при четных п).
2) При случайном блуждании точки по одномерной
решетке Z1, начинающемся в нуле (с независимыми
при разных шагах переходами в соседние точки с ве-
вероятностями р и q, p^\-q=l), события, состоящие, соот-
соответственно, в том, что блуждающая точка окажется в
нуле после п-то шага, п=2,4,. . ., являются рекуррент-
рекуррентными.
Лит.: [1] Ф е л л е р В., Введение в теорию вероятностей и
ее приложения, пер. с англ., 2 ИЗД., Т. 1, М., 1067.
Г. ГО. Попова.
РЕКУРСИВНАЯ ИГРА — стохастическая игра
с терминальным выигрышем (см. также Динамическая
игра). Ввиду того, что Р. И. может никогда не закон-
закончиться, необходимо определять выигрыши игроков в
случае бесконечных партий. Анализ любой игры Шти-
Штили может быть сведен к анализу нек-рой Р. п., но из-за
возможности бесконочных партии исследование Р. и.
к общем случае сложнее, чем исследование стохастич.
игр. Любая антагонистическая конечная Р. и. обладает
значением, и оба игрока имеют стационарные е-опти-
мальные стратегии. X. Эворетт [1] указал метод на-
нахождения как значений игры, так и оптимальных стра-
стратегий.
Лит.: [1] Everett H.( в кн.: Contributions to the theory
of games, v. 3, Princeton, 1957, p. 47 — 78. В. К. Домапс-кий.
РЕКУРСИВНАЯ РЕАЛИЗУЕМОСТЬ уточнение
интуиционистской семантики арифметич. суждений на
основе понятия частично рекурсивной функции, пред-
предложенное С. Клини (см. [1], [2]). Для всякой замкнутой
арифметич. формулы F определяется отношение «нату-
«натуральное число е реализует формулу /•'», обозначаемое
erf1. Отношение erF определяется индуктивно в соот-
соответствии с построением формулы /•'.
1) Если F — элементарная формула бе:\ свободных
переменных, т. е. формула вида s- I. где s и t — по-
постоянные термы, то erF тогда и только тогда, когда е=
—О и значения термов sat совпадают.
Пусть А и В — формулы без свободных переменных.
2) ег(А&В) тогда и только тогда, когдг! с~-2а-Зь,
где агА , ЬгВ.
3) er(AvB) тогда и только тогда, когда е=2°-За и
агА или е^=21-3!) и ЬгВ.
4) ег(А^зВ) тогда и только тогда, когда е — гёделев
номер такой одноместной частично рекурсивной функ-
функции ф, что для любого натурального числя а. если агА,
то ф применима к а и ф (а)гВ.
5) ег(~]А) тогда и только тогда, когда сг(.4г:1--0).
Пусть А [х) — формула без свободных перемепных,
отличных от х\ если и натуральное1 число, то // --
терм, изображающий и формальном арифметике чис-
число п.
6) ег(ЗхА (х)) тогда и только тогда, когда с -2" -За
и пгА (п).
7) ег (у.сА(х)) тогда и только тогда, когда с — гёде-
лен номер такой общерекурсинной функции /, что для
любого натурального п число 1(п) реализует А (п.).
Замкнутая формула /•' называется р с а л и з у е-
м о и, если существует число е, реализующее F. Фор-
Формула А (г/!,. . .,!/„,), содержащая свободные перемен-
переменные ух,. . ., у,„, может рассматриваться как предикат
от у1:. . ., ;/,„ («формула A (yit. . .,ym) реализуема»).
Если формула F выводима и Я реализуемых формул в
интуиционистском арифметическом исчислении, то F
реализуема (см. [3]). В частности, всякая формула, до-
доказуемая в интуиционистской арифметике, реализуема.
Можно указать такую формулу Л(х), что формула
Уз1 (А (х) v ~\А (х)) не реализуема. Соотвотстненно, в
этом случае формула ~] ух (А (х) v А (х)) реализуема,
хотя является классически ложной.
Всякая предикатная формула Э1, доказуемая в ин-
интуиционистском, исчислении предикатов, обладает тем
свойством, что каждая арифметич. формула, получаю-
получающаяся пи 21 подстановкой, реализуема. Предикатные
формулы, обладающие этим свойством, паз. реал и-
з у с м ы м и. Было показано [4], что пропозициональ-
пропозициональная формула
(niD3D)D(Tl #V1 D))r>(Tl 0V D),
где 1) обозначает формулу ~}p\Z~\q, реализуема, no
не выводима в интуиционистском исчислении высказы-
высказываний.
Лит.: [1] KleencS. С, «J. Symbolic Logic», 1945, v. 10,
p. 109—24; [2] К ли ни С. К., Введение в метаматематику,
пер. с англ., М., 1957; [3] Nelson D., «Trans. Amer. Math.
Soc», 1947, v. 01, p. 307—68; [4] RoseG. F., там же, 1953, v. 75,
p. 1 —19; [5] H о в и к о в II. С, Конструктивная математичес-
математическая логика с точки зрения классической, М., 1977.
РЕКУРСИВНАЯ ТЕОРИЯ МНОЖЕСТВ — раздел тео-
теории рекурсивных функций, в к-ром рассматриваются
и классифицируются подмножества натуральных чисел
с алгоритмич. точки зрения, а также исследуются струк-
структуры, возникающие в результате такой классификации.
Для каждого множества А, к-рое является подмноже-
подмножеством множества всех натуральных чисел N, можно
сформулировать следующую проблему разре-
разрешимости: существует ли алгоритм, позволяющий
для любого х ? N ответить на вопрос о принадлежности
х к А?
Математическая постановка проблем такого рода,
как и развитие Р. т. м., стала возможна лишь в 40-х гг.
20 в. после успешной формализации интуитивного по-
понятия (алгоритмически) вычислимой функции. Области
значений таких функций образуют семейство реку р-
с и в н о перечислимых множеств (р. п.
м.). Множества, для к-рых сформулированная выше
проблема разрешима, наз. рекурсивными. Точ-
Точнее, А рекурсивно тогда и только тогда, когда А и N\A
оба являются р. п. м. Первы.ми примерами нерекур-
нерекурсивных р. п. м. оказались т. н. креативные (творческие)
множества. Именно, р. п. м. К наз. к р е а т и в п ы м,
если существует вычислимая функция, к-рая по номе-
номеру любого р. п. м. А, не пересекающегося с А', выдает
число, принадлежащее N\{K\JA). Одновременно с
креативными множествами были обнаружены и другие
нерекурсивные р. п. м., в частности простые. Р. п. м.
наз. просты м, если оно имеет бесконечное дополне-
дополнение, к-рое не содержит бесконечных р. п. м. Таким об-
образом, уже для р. п. м. возникает тонкая проблема
классификации их проблем разрешимости. Одним из
инструментов для такой классификации служит поня-
понятие сводимости. На интуитивном уровне мно-
множество А сводимой множеству В, если существует
алгоритм, к-рый решал бы проблему вхождения эле-
элементов для множества Л при условии, что есть возмож-
возможность по мере надобности пользоваться информацией
о принадлежности тех или иных натуральных чисел
множеству В. В этом случае А оказывается в опреде-
определенном смысле «рекурсивным» относительно Н, а обыч-
обычные рекурсивные множества — «рекурсивными» отно-
относительно любого множества. Такая сводимость в са-
самом общем виде (точная формулировка к-рой достаточ-
достаточно сложна) наз. тьюрингово й, или Г-с вод и-
м о с т ь ю. Накладывая те или иные ограничения на
алгоритм, участвующий, в понятии сводимости, прихо-
приходят к определению других сводпмостей, напр. 1-, т-,
btt- или U-сводимости. В частности, А т-с водимо
к Л, если существует всюду определенная вычислимая
функция / такая, что для всех х из N
Если / можно выбрать разнозначной, то говорят, что
А 1 -с в о д и м о к В.
Обобщением ш-сводимости является табличная
(U-) сводимость. Множество А «-сводимо к множеству
В, если существует алгоритм, к-рый для каждого х
дает набор чисел <2*, t%,. . ., йш> и булеву фун1;цшо
Рх(г/1- • ¦. Умх)), причем
где yu(()=l, если t?B,n %(t)—0 в противном случае. Если
А можно таблично свести к В так, что п (х) будет ограни-
ограничено нек-рой константой, то говорят, что А ограни-
ограниченно таблично (Ьи-) сводится к В.
Пусть г — нек-рая сводимость. Пишут А <ГВ, если
множество А r-сводимо к В. Отношение <г должно
быть иредпорядком. Если положить
Л =г Д 4Э (A <rS & В<ГА),
то ssr будет отношением эквивалентности, отдельный
класс к-poii наз. r-с т е н е п ь ю (и рекурсивно пере-
перечислимой r-стененью, если этот класс содержит р. н. м.).
Тьюринговы степени известны п литературе и как
степени неразрешимости. Отношение <Л
порождает частичное упорядочение всех г-етепенеп.
Сводимость г' слабее, чем г, если А <ГВ влечет Л <.Г-В.
Частично упорядоченные множества г-стопеней для
т- и более слабых сводимостей образуют верхние полу-
полурешетки (что неверно для 1-степеней), имеющие наи-
наименьший элемент 0 —/--степень рекурсивных множеств.
Если ограничиться изучением только рекурсивно пере-
перечислимых r-степеней, то они имеют также и наиболь-
наибольший элемент 1, к-рый наз. полной г - с т. е п с-
ц ь ю. Р. п. м., содержащиеся в полной r-степени, на:).
r-п о л н ы м и. Минимальными r-с т е п е н я-
м и наз. такие, к-рьте имеют лишь единственную стро-
го меньшую r-степень, а именпо 0.
После определения той или иной сводимости ее изу-
изучение развивается в основном в двух направлениях.
Первое связано с вопросами описания верхней полу-
полурешетки степеней относительно введенной сводимости.
Известным примером проблемы такого типа явилась
проблема Поста [1]: верно ли, что все рекур-
рекурсивно перечислимые нерекурсивные множества имеют
одну и ту же степень неразрешимости? Или, другими
словами, верно ли, что полурешетка рекурсивно пере
числимых степеней неразрешимости состоит лишь из
двух элементов? Получено отрицательное решение этой
проблемы [2]. Решения этих вопросов о строении верх-
верхних нолурешеток рекурсивно перечислимых т-, it- и
Г-степеней являются определенными вехами в изуче-
изучении сводимостей. В нач. 1960-х гг. было доказано, что
иолурешетка 7'-степеней (везде ниже подразумеваются
нолурошетки рекурсивно перечислимых степеней) не
является решеткой и не имеет минимальных элементов;
тогда же было отмечено существование минимальных
m-стоиеней и показано, что полная m-стеиень не яв-
является точной верхней гранью двух несравнимых т-
степеней. Позднее выяснилось, что этот факт не имеет
места для Ьи- и более слабых сводимостей. 10. Л. Ер-
Ершов [4] доказал, что верхняя полурешетка т-стопеной
не является решеткой и что под нок-рыми ее элемента-
элементами нет минимальных. Аналогичные результаты, а так-
также существование минимальных элементов, были по-
получены для полурешеток Ьи- и «-степеней [5]. Установ-
Установлено, что элементарные теории полурешеток т-, Ьи-,
tt-, T- и нек-рых других степеней попарно различны.
Второе направление связано с вопросами о том, ка-
какие r-стеиени, сколько их и как они расположены в сте-
пенях относительно более слабой сводимости, чем г.
В частности, полная T(tt-, Ьи-)-степень содержит счет-
счетное число рекурсивно перечислимых и (соответственно
btt-, т-)-степеней. С другой стороны, существуют не-
нерекурсивные Т (бМ-)-степени, состоящие из одной
М(т-)-ст(Ч1ени, но каждая нерекурсивная it-степень
содержит, по крайней мере, две fttt-стспени.
К изучению р. п. м. имеются и другие подходы, не
связанные с понятием сводимости. Один из них заклю-
заключается в следующем. Все р. ц. м. вместе с операция-
операциями объединения и пересечения образуют решетку <$¦?.
Нек-рое свойство р. и. м. наз. теоретик о-р е ш е-
точным, если оно сохраняется при всех автомор-
автоморфизмах $. Такими, напр., являются свойства «быть
рекурсивным», «быть простым» или «быть максималь-
максимальным» множеством. Р. п. м. А наз. максим ал ь-
н ы м (r-м аксимальным), если его дополнение
бесконечно и не может быть разбито р. п. м. (соответ-
(соответственно рекурсивным множеством) на две бесконечные
части. Классич. результатами, связанными с изуче-
изучением $, могут служить теоремы о существовании мак-
максимальных множеств и о возможности разбиения любого
нерекурсивного р. п. м. на два нерекурсивных р. п. м.
(см. [2]) и теорема о существовании г-максимального
множества без максимальных надмножеств (см. [3]).
Понятие максимального множества возникло в связи
с надеждой, что они окажутся не Г-полными. Это было
бы естественным решением проблемы Поста. Сам
Э. Пост, накладывая все более жесткие ограничения на
дополнения р. п. м., определил классы гиперпростых и
1 мпергиперпростых множеств, показав, что гинерпростые
множества не могут быть it-полными. При этом р. п. м.
.1 с бесконечным дополнением наз. гиперпрос-
т ы м (г и п е р г и п е р н р о с т ы м), если не су-
существует вычислимой последовательности попарно не-
непересекающихся конечных (соответственно рекурсивно
перечислимых) множеств, каждое из к-рых имеет не-
непустое пересечение с дополнением А . Определение этих
классов множеств дается не в теоретико-решеточных
терминах, и в действительности удалось показать, что
«быть гиперпростым» не является теоретико-решеточ-
теоретико-решеточным свойством. Однако доказано, что р. п. м. А с бес-
бесконечным дополнением является гипергиперпростым
тогда и только тогда, когда для любого р. п. м. В су-
существует рекурсивное множество R такое, что Дс=8
п (В"^A)^R, т.е. свойство «быть гипергиперпростым»
оказалось теоретико-решеточным. Было построено ги-
нергипериростое множество без максимальных над-
надмножеств, а также доказано, что для любого нерекур-
нерекурсивного р. п. м. Л существует автоморфизм Ф решетки
$ такой, что Ф(А) является Г-полным множеством
[6]. Таким образом, надежда найти теоретико-решеточ-
теоретико-решеточное свойство, к-рым не обладали бы рекурсивные и
Г-полные множества, не оправдалась.
Имеется также концепция (в духе [7]), согласно
к-рой Р. т. м. должна изучать свойства подмножеств N,
сохраняющиеся при рекурсивных перестановках. В со-
соответствии с этим говорят, что множества А и В имеют
один и тот же тип рекурсивной эквива-
эквивалентности, если существует разнозначная вычис-
вычислимая функция / такая, что f(A)=B и f~1(B)=A.
Типы рекурсивной эквивалентности, не содержащие
множеств, имеющих бесконечные рекурсивно перечис-
перечислимые подмножества, наз. и з о л я м и. После опре-
определения для изолей подходящим образом операции сло-
сложения и умножения стала развиваться «арифметика»
изолей.
Изучение свойств р. п. м. и сводимостей не только
взаимосвязано с другими направлениями теории ре-
рекурсивных функций, но и находит применение в логи-
логике, теории моделей и алгебре. Р. т. м. имеет в своем
арсенале собственные, присущие пока только ей мето-
ды исследований. Наиболее известным является т. н.
приоритета метод, с помощью к-рого получаются осо-
особенно глубокие результаты.
Лит.: [1] Р о s t E. L. «Bull. Amer. Math. Soc.» 1944, v. 50,
p. 284 — 316; [2] Friedberg R. M., «J. Symbolic Logic»,
1958, v. 23, p. 309 —IB; [3] Lachlan A. H., «Trans. Amor.
Math. Soc», 1968, v. 130, № 1, p. 1—37; [4] Ершов Ю. Л.,
«Алгебра и логика», 1969, т. 8, № 5, с. 523—52; [5] Д е г т е в
А. Н., «Успехи матем. наук», 1979, т. 34, в. 3, с. 137—68; [6]
S о а г е R. I., «Bull. Amer. Math. Soc», 1978, v. 84, № 6, p.
1149—81; [7] D e k k e г J. С. Е., М у h i 1 1 J., «Univ. Calif,
publ. math.», 1960, v. 3, № 3, p. 67—213; [8] M а л ь ц е в А. И.,
Алгоритмы и рекурсивные функции, М., 1965; [9] Род ж с р г X..
Теория рекурсивных функций и эффективная вычислимость,
пер. с англ., М., 1972. А. Н. Дегтее.
РЕКУРСИВНАЯ ФУНКЦИЯ, частично ре-
рекурсивная функци я,— одно из матсматич.
уточнений интуитивного понятия вычислимой функции,
определяемое следующим образом. Рассматриваются
функции, заданные на натуральных числах и с нату-
натуральными значениями. Функции предполагаются ч а-
с т и ч н ы м и, т. е. определенными, вообще говоря,
не для всех значений аргументов. Следующие функ-
функции наз. простейшими: S (x)=x-\-i, о (х)=0,
lm(xi,- ¦ .Ai)=xm(l<m<rc). Будем говорить, что ге-ме-
стная функция г|з получена из m-местной функции ф и
re-местных функций /ь. . .,fm с помощью операто-
оператора суперпозиции, если для всех х1,. . .,хп име-
имеет место равенство
..,*„) =ф(/1(*1, ...,*„), ...,fm(xu ...,xn)).
Скажем, что (ге-|-1)-местная функция / получается из
n-местной функции ф и (га+2)-местной функции г|з с
помощью оператора примитивной ре-
рекурсии, если при любых значениях жь. . ., хп, у
выполняются равенства
f (xu ...,xn, у-$-1)=У(хи ...,хп, у, f (хи ...,хп, у)).
Будем говорить, что n-местная функция / получается
из (п+1)-местной функции ф с помощью операто-
оператора минимизации, или наименьшего числа опе-
оператора, если для любых хи. ..,хп, у выполнено усло-
условие / (хг,. . ., хп)=у тогда и только тогда, когда значе-
значения Ц>(х1,. . .,хп,0),. . ., ф(х1). . ., хп, у — 1) определе-
определены и не равны 0, а ф (х1,. . .,хп, у)=0. Частичная функ-
функция / наз. рекурсивной, если она может быть
получена из простейших функций с помощью конеч-
конечного числа применений операторов суперпозиции, при-
примитивной рекурсии и минимизации.
Иными словами, / является Р. ф., если существует
такая конечная последовательность частичных функ-
функций glt. . .,gft, что gk—J'R каждая функция этой после-
последовательности либо является простейшей, либо полу-
получается из предыдущих с помощью операторов супер-
суперпозиции, примитивной рекурсии или минимизации.
С помощью метода арифметизации можно получить
пересчет всех таких описаний Р. ф., а именно, можно
указать алгоритм, к-рый каждому натуральному числу
х сопоставляет нек-рое описание Р. ф. Задаваемую этим
описанием Р. ф. обшчно обозначают q>x, a x наз. ее г ё-
деловым номером.
Всюду определенные Р. ф. наз. общерекур-
общерекурсивными. Существуют Р. ф., к-рые не могут быть
продолжены до обще рекурсивных.
Для любой Р.ф. можно указать алгоритм вычисления
ее значений, т. е. все Р. ф. суть вычислимые функции.
Распространенная гипотеза, известная под названием
тезиса Ч ё р ч а, состоит в том, что всякая вычис-
вычислимая функция является Р. ф. Эта гипотеза подтверж-
подтверждается рядом фактов. Так, все рассматривавшиеся в
математике конкретные функции, признаваемые вычис-
вычислимыми в интуитивном смысле этого слова, оказыва-
оказывались рекурсивными. Понятие Р. ф. оказывается совпа-
совпадающим по объему с другими математич. уточнениями
понятия вычислимой функции (напр., с понятиями функ-
функции, вычислимой на машине Тьюринга, вычислимой
с помощью нормального алгорифма Маркова и др.).
Возможны различные определения класса всех Р. ф.
через исходные функции и порождающие операции.
В частности, всякая Р.ф. может быть получена из функ-
функций
а(х, у)=х-гу, т{х, у)=х-у, 1т
/О, если х < у,
{ 1, если х ^ у,
с помощью конечного числа применений операторов
суперпозиции и минимизации.
Лит.; [1] Мальцев А. И., Алгоритмы и рекурсинные
функции, М., 1965; [2] Роджерс X., Теория рекурсивных
функций и эффективная вычислимость, пер. с англ., М., 1972.
В. Е. Плиско.
РЕКУРСИВНОЕ ОПРЕДЕЛЕНИЕ — часто приме-
применяемый в математике способ задания функций, при
к-ром значение искомой функции в данной точке опре-
определяется через ее значения в предшествующих точках
(при подходящем отношении предшествования). Р. о.
теоретико-числовых функций являются объектами изу-
изучения в теории алгоритмов (см. Рекурсия). В теории
множеств постоянно используется для определения
функций на ординалах траисфинитная рекурсия. В
более общем плане Р. о. рассматриваются в теории до-
допустимых множеств, в основе к-рой лежит некий син-
синтез идей теории множеств и теории алгоритмов (см.
[2]).
Лит.: AJ Р о д ж е р с X., Теория рекурсивных функций и
эффективная вычислимость, пер. с англ., М., 1972; 12] Bar-
wise J., Admisible sets and structures, В., 1975.
H. В. Белякин.
РЕКУРСИВНОЕ ОТНОШЕНИЕ — такое отношение
i?SN", где N — множество натуральных чисел, что
функция /, определенная на № условием
1, если (х^, ..., xny?R,
О, если <жь ..., xn>(j:R,
является рекурсивной функцией. В частности, при лю-
любом п универсальное отношение N" и нуль-отношение
0 являются Р. о. Если R и S суть re-местные Р. о.,
то отношения R\JS, R[)S, R'=Nn\R,R\S также бу-
будут Р. о. Относительно операций U, П,' система всех
re-местных Р. о. образует булеву алгебру, в. е. плиско.
РЕКУРСИВНОЙ ЭКВИВАЛЕНТНОСТИ ТИП -класс
эквивалентности для отношения рекурсивной эквива-
эквивалентности, т. е. совокупность всех подмножеств нату-
натурального ряда, каждые два из к-рых могут быть приве-
приведены во взаимно однозначное соответствие с помощью
частично рекурсивной функции. Таким образом, поня-
понятие Р. э. т. служит в рекурсивной теории множеств
аналогом понятия мощности в классич. теории мно-
множеств. Так как любые два конечных множества рекур-
рекурсивно эквивалентны тогда и только тогда, когда они
содержат одинаковое число элементов, то Р. э. т. ко-
конечного множества полностью характеризуется мощ-
мощностью этого множества. Для бесконечных множеств
натуральных чисел, несмотря на их равномощность,
это не так: совокупность всех таких множеств распа-
распадается на множество континуальной мощности различ-
различных Р. э. т. При этом всякий Р. э. т. (кроме Р. э. т.
пустого множества) сам является счетным множеством.
Множества, принадлежащие одному Р. э. т., сходпы в
отношопии нек-рых алгоритмич. свойств. Так, беско-
бесконечные рекурсивно перечислимые множества (как ре-
рекурсивные, так и нерекурсивные) образуют один Р. э. т.
Так как множество, рекурсивно эквивалентное про-
продуктивному, само является продуктивным, всякий
Р. э. т., содержащий продуктивное множество, состоит
=l
{
только пз продуктивных множеств; так же обстоит дело
с иммунными множествами. Теория Р. э. т. иммунных
множеств, называемых вместе с Р. э. т. конечных мно-
множеств изолями, разрабатывалась особенно интенсивно.
Над Р. э. т. определяются алгебраич. операции,
важнейшими из к-рых являются сложение и умножение:
если А -я В суть Р. э. т., а?А, $?В, причем а состоит
из четных чисел, а р" —из нечетных, то А-\-В есть
Р. э. т. множества a(JP; А -В есть Р. э. т. множества
/ (а X Р), где / — общерекурсивная функция, взаимно од-
однозначно отображающая декартов квадрат натураль-
натурального ряда на натуральный ряд. Алгебра Р. э. т. тесно
связана с алгеброй кардинальных чисел, развиваемой
без аксиомы выбора. Совокупность изолей замкнута
относительно указанных операций.
Предпринимались попытки перенесения понятия
Р. э. т. на классы множеств.
Лит.: [1] Р о д ж е р с X., Теория рекурсивных функций и
эффективная вычислимость, пер. с англ., М., 1972; [2] D e k-
к е г J. С. Е., М у h i I 1 J., Recursive equivalence types, Berk.—
Los Ang., 1960. В. А. Душский.
РЕКУРСИВНЫЙ ОПЕРАТОР - всюду определен-
определенный частично рекурсивный оператор. в Е Пгиспо
РЕКУРСИВНЫЙ ПРЕДИКАТ - предикат Р (хи
. . .,х„), определенный на натуральных числах и та-
такой, что функция /, заданная на натуральных числах
условием
( 1, если Р (xi, ..., хп) истинно,
\ 0, если Р (хг, . .., хп) ложно,
является рекурсивной функцией. В. Е. Плиско.
РЕКУРСИИ ВЫСШИХ СТУПЕНЕЙ — рекурсивные
определения, в к-рых в качестве вспомогательных объ-
объектов наряду с числовыми функциями используются
нек-рые функционалы более высоких типов. Напр., для
случая рекурсии второй ступени такопыми являются
«подстановочные» функционалы вида
7х,...жп(°1' ¦••>а'»' /(*!> ••¦ixn))=fD, •••, ап),
а также функционалы, получаемые из них посредством
этой рекурсии. Интересное свойство Р. в. с. заклю-
заключается в том, что многократную рекурсию можно свести
к однократной за счет перехода к более высокой сту-
ступени. На этом основан метод приведения многократных
рекурсий к нормальной форме. Следует иметь в виду,
что терминологию в этой области нельзя считать окон-
окончательно установившейся. В частности, под термином
«Р. в. с.» иногда понимают нормальные формы много-
многократных рекурсий.
Лит.: fl] Петер Р., Рекурсивные функции, пер. с нем.,
М., 1954. Н. В. Велякин.
РЕКУРСИЯ — способ определения функций, яв-
являющийся объектом изучения в теории алгоритмов и
других разделах математич. логики. Этот способ давно
применяется в арифметике для определения числовых
последовательностей (прогрессии, чисел Фибоначчи и
пр.). Существенную роль играет Р. в вычислительной
математике (рекуррентные методы). Наконец, в теории
множеств часто используется трансфинитная Р.
Долгое время термин «Р.» употреблялся математика-
математиками, не будучи точно определенным. Его приблизитель-
приблизительный интуитивный смысл можно описать следуюпщм об-
образом. Значение искомой функции / в произвольной
точке х (под точкой подразумевается набор значений
аргументов) определяется, вообще говоря, через зна-
значения этой же функции в других точках у, к-рые в
каком-то смысле «предшествуют» х. (Само слово «ре-
«рекурсия» означает «возвращение».) Конечно, в нок-рых
«исходных» точках значения / должны задаваться не-
непосредственно. Иногда при помощи Р. определяются
одновременно несколько функций; тогда вышеприве-
вышеприведенные разъяснения нуждаются в соответствующей мо-
днфикацви. Примеры разнообразных Р. будут даны
ниже. Отношение «х1 предшествует х2» (где xlt х2
принадлежат области определения искомой функции)
и разных видах Р. («рекурсивных схемах») может
иметь разный смысл, однако оно должно быть «фунди-
«фундированным» (т. с. пе должно существовать бесконечной
последовательности точек хп, п—0, 1,2,. . ., такой, что
хп + 1 предшествует .г,,). Кроме того, неявно подразу-
подразумевается, что оно является «достаточно естественным»
(напр., желательно, чтобы ато отношение усматривалось
из самого описайия рекурсивной схемы, а но из про-
процесса ее применения). Последнее условие имеет чисто
:>вристич. значение (напр., для определения каких-
нибудь специальных, сравнительно простых видов Р.).
Уточнение этого условия но существу неотделимо от
уточнения самого понятия Р., а для этого необходимо
установить, какого рода формальные выражения могут
быть нризпаны в качестве рекурсивных определений.
В тех случаях, когда речь идет о рекурсивных опи-
описаниях числовых функций (т. е. функций от натураль-
натуральных аргументов и с натуральными значениями), обыч-
обычно подразумевается, что такие описании задают способ
вычисления определяемых функций. Ниже всюду (кро-
(кроме заключительных замечаний) термин «Р.» будет пони-
пониматься именно в таком смысле. Простейшей и наиболее
употребительной рекурсивной схемой является и р и-
м и т и в н а я Р.:
/(О, хи ...,хп) = <?{хи ...,ха),
1 (!/ + 1, *i, ¦¦¦,xn) = h{y, / (у, хи ..., хп), xlt ...,xn),
где функции g, h предполагаются известными, / —
определяемая функция, у — неременная, по к-рой ве-
ведется Р., хх,. . ., хп — параметры, не участвующие в
Р. Ближайшим обобщением этой схемы является т. н.
возвратная Р., охватывающая такие виды ре-
рекурсивных определений, у к-рых, подобно примитивной
Р., только одна переменная участвует в Р., а соответ-
соответствующее отношение предшествования совпадает с
обычным упорядочением натуральных чисел (иногда,
впрочем, этот термин употребляется и в более широком
смысле). Наиболее типичная разновидность возврат-
возвратном Р. такова:
/ @, хи • • ¦, xtl)^-g (xx, ..., хп),
/ (У-1-1, хг, ..., хп) —
= Л(У, / («1 (у), хи • ¦-, *„), .••, /(<х*Ы> хи •••- хп),
XI, . . ., Хп),
гдр а,-(;/)-.»//, ( 1,. . ., /г. Представляет интерес тот
фаьч, что нпзвратпую I'. можно заменить конечным чис-
числом примитивных I1. и подстановок. Другой пример
рекурсивной схемы, сводящейся к примитивной Р.,
дас* одни и [> и »l e u н ц и Р. вида
/;@, хи ..., л„)—A',-(a:i, ..-, хп),
lii'J + i, *и •••, хп)-~
¦—hi(y, f1(y, xu ...,?„), ..., (к(у, хи ...,хп),
хи ¦••, х„),
где i=l,. . ., к. Математич. логика часто имеет дело с
примитивно рекурсивными ф у и и ц и-
я ы и, т. е. с такими, к-рые можно получить за конечное
число шагов при помощи подстановок и примитивных
Р., исходя из нек-рого фиксированного запаса совсем
простых функций (напр., /(х)=ж-1-1, /(х, у)=у п т. п.).
Последовательность функциональных равенств, опи-
описывающая такое построение, наз. примитивно
рекурсивным описанном соответствую-
соответствующей функции. Эти описания суть синтаксич. объекты
(т. с. цепочки символов), обладающие определенной
эффективно распознаваемой структурой. Практически
все числовые функции, употребляемые в математике по
какому-либо конкретному поводу, оказываются при-
примитивно рекурсивными. Этим в значительной мере объ-
объясняется интерес к данному классу функций.
Более сложные виды рекурсивных определений полу-
получаются, когда Р. идет сразу по нескольким переменным.
Такие определения, вообще говоря, выводят вд класса
примитивно рекурсивных функций, хотя соответствую-
соответствующее отношение предшествования может выглядеть как
вполне естественное. Напр., в определении /(.г, у) мо-
могут участвовать значения /(и, и), где и<.х или и—ж,
1><г/, как это имеет место в следующей схеме дву-
двукратной Р.:
/(я. У)=ё(х, У), если х^О или у —О,
= h(x, у, 1(х, а(х, у, /(.г-fl, у))), f (х-\Л, у)).
Эта схема уже не сводится к примитивной Р. С другой
стороны, к ней сводимы многие более сложные рекур-
рекурсивные определения (см. |1]).
Перечисленные частные виды Р. имеют точные мате-
матич. определения — в отличие от расплывчатых «око-
«около математических» представлений о «рекурсии вооб-
вообще». Уточнение этих представлений естественно мыс-
мыслить как отыскание подходящего алгоритмич. языка
(т. е. формального языка для описания вычислитель-
вычислительных процедур), включающего все вообразимые виды
Р., но и не слишком широкого. Правомерно ожидать,
что выработка такого уточнения может потребовать
дополнительных соглашений, вносящих нечто новое в
интуитивное понимание Р. В этой связи небезинтереспо
отметить, что все рассмотренные выше рекурсивные
схемы ориентированы на порождепие тотальных (всю-
(всюду определенных) функций. Так, если в схеме прими-
примитивной рекурсии g, h тотальны, то такова же и /.И во-
вообще, рекурсивные определения, задающие частичные
функции, с интуитивной точки зрения выглядят не-
несколько искусственно. Однако есть причины привлечь
такие Р. к рассмотрению. Это связано ст. н. диаго-
диагональ н ы м методом. Именно, пусть дан алгорит-
алгоритмич. язык L, в к-ром определимы лишь тотальные
функции, и Пусть синтаксич. конструкции L не выво-
выводят за пределы интуитивно понимаемой рекурсивно-
сти. Конечно подразумевается, что выражения языка
L (являющиеся описаниями функций) алгоритмически
распознаваемы и что имеется единообразный способ
вычисления функций, представимых в L, по их опи-
описаниям. Если рассматривать выражения в L просто
как цепочки символов, то каждую такую цепочку мож-
можно считать изображением натурального числа в под-
подходящей системе счисления, являющегося «кодом» дан-
данного выражения. Пусть теперь функция G(m, х) опре-
определена так. Если т есть код ¦ описания (в языке L)
нек-рой одноместной функции fm, то G(m, T)---jm(x).
В противном случае G(m, х)—ц>{х), где ф — какая-
нибудь фиксированная функция, представимая в L.
Ясно, что G (т, х) вычислима и тотальна и такова же
функция F(x)=G(x, x)-\-l. Но F невыразима в L, ибо
ни при каком т невозможно равенство F (m)~jm (m).
(В этом рассуждении существенно использована то-
тотальность F.) Возникает вопрос: является ли данное.
описание F рекурсивным? Если в качестве L взять язык
примитивно рекурсивных описаний, то оно оказывает-
оказывается сводимым к двукратной Р. В общем случае ситуа-
ситуация неясна из-за расплывчатости интуитивных пред-
представлений о Р., так что положительный ответ на по-
поставленный вопрос представляет собой дополнительное
соглашение. Если принять его (как это неявно делает
современная логика), то язык /., описывающий в точ-
точности все яиды «тотальной» Р., оказывается невозмож-
невозможным.
Между тем, если в L выразимы также частичные
функции (и их описания признаются рекурсивными),
то диагопализация не обязательно выводит за пределы
L, так что такой язык в принципе может быть пригод-
пригодным для адекватного уточнения рокурсивности. Прав-
Правда, это связано с нок-рым переосмыслением самого по-
понятия Р., и современное строгое определение этого по-
понятия не вполне согласовано с имевшимися ранее
шттунпшпыми представлениями. В новом уточненном
смысле Р. есть нек-рая синтаксич. операция (с фикси-
фиксированной интерпретацией), употребляемая для построе-
построения выражений в различных алгоритмич. языках. Если
L—один из таких языков, то естественно Предполагать,
что в нем ость и другие синтаксич. операции, от к-рых
зависит конкретный вид рекурсивных описаний в /..
Вообще говоря, выражения языка L не обязательно
описывают только числовые функции. Нек-рые из них
.могут задавать функциональные операторы и другие
объекты. Это нужно, в частности, для определения Р.
Рекурсивные описания в L — это системы функцио-
функциональных уравнений вида /,-=Г,-(/], ... , /„), i=l, ... , п.
где /,¦ -- определяемые функции, а 7',- — выражения в
L, задающие в совокупности нек-рый оператор. Но все
выразимые в L операторы должны быть эффективными
(поскольку L — алгоритмич. язык) и потому монотон-
монотонными (т. е. они сохраняют отношение ф —i -ф, означаю-
означающее, чго-ф доопределяет ф). В силу этого всякая система
указанного вида обладает минимальным (в смысле от-
отношения -=?) решением и, по определению, является
рекурсивным описанием функций, составляющих это
решение. Исходя из данного описания, искомое мини-
минимальное решение можно получить посредством следую-
следующего процесса. Для i=i, ... , п пусть /"—нигде не
определенная функция и /*+1 — Г/(/*, ... , /*), так чю
/*-3/г+1. Нетрудно убедиться, что искомые функции
/,• получаются «объединением» /^ (к=0, 1, 2, ...). Тем
самым задан способ совместного вычисления /,-. Этот же
процесс задает более или менее естественное отношение
предшествования на аргументах, к-рое и оправдывает
(в удовлетворительной мере) употребление термина
•<Р.>> в данной связи.
Для того чтобы приведенные ранее рекурсивные
схемы подходили под такое определение, необходимо,
чтобы язык Л был не слишком беден. Так. уже в случае
примитивной р. нужны подстановка и «кусочное» опре-
определение (т. е. задание функции несколькими равенст-
равенствами). Вместе с тем этих двух синтаксич. операций,
в сочетании с только что определенной Р., уже доста-
достаточно для получения всех вычислимых функций (исходя
из простейших). При соответствующих предположениях
об L можно также достаточно уверенно утверждать, что
данное определение Р. охватывает все интуитивно мые-
.ишые рекурсивные описания. В то же время введенное
общее определение обладает характерными чертами не-
неформально понимаемой рекурсивности, к-рые призна-
признаются существенными в современной математике.
Плодотворность данного определения Р. заключается
не только и ого значении для теории алгоритмов, но и в
том, что оно позволяет взглянуть с «алгоритмической»
(в обобщенном смысле) точки зрения также и на нек-рые
конструкции абстрактной математики, имеющие опре-
определенное сходство с «числовыми» Р. (трансфинитная
Р., индуктивные определения, рекурсивные иерархии
11 Т. П.).
Лит.; [1] II е т е р Р., Рекурсивные функции, пер. с нем.,
М., 1954; [2] М адь ц е в А. И., Алгоритмы и рекурсивные
' г~т.. е н с к и й В. А., Лекции о вычисли-
Введенне в мета-
¦ITXtA X Ч/iTXt* л СЖ 41 J , А*ир« \s (ЛК.1.1 см . f J.u..r Л. V V i , LVJ J.T* \J tj \j lI OVtlKlb 1» It » ,
Elementary induction on abstract structures, Amst.,— [a. o.],
1974. H. В. Белякин.
п., 1904; lisj мальцев А. и., Алгоритмы и р(
функции, М., 1965; [3] V с п е н с к и й В. А., Лекции
мых функциях, М., 1ЙвО; U] К л и аи С. К., Введен
математику, пер. С ан?л., М., 1957; [5] М 0 s с п. о v a
РЕЛАКСАЦИИ МЕТОД, ослабления ме-
метод,— метод итерационного решения системы линей-
линейных алгсбраич. уравнении Ах~Ь, элементарный шаг
к-рого состоит и изменении только одной компоненты
вектора неизвестных, причем! номера изменяемых ком-
компонент выбираются в нек-ром циклпч. порядке. Наибо-
Наиболее часто Р. м. используется для решении систем с по-
положительно определенной матрицей А .
Если изменение одной компоненты вектора неизвест-
неизвестных хк осуществляется так, что для НОВОГО приближе-
приближения xk^1 квадратичная форма (А (х* + 1—х), xk + 1—х)
минимизируется, то Р. м. наз. методом полной
релаксации. Если же за один элементарный таг
значение квадратичной формы лишь уменьшается, но
не минимизируется, то Р. м. наз. Методом непол-
неполной релаксации.
Наиболее полно исследован метод последо-
последовательной верхней релаксации, ког-
когда матрица А обладает т. и. пшйством (Л) и согласо-
согласованно упорядочена. Матрица А наз. матрицей, обла-
обладающей свойством (А), если сущепнует матрица
перестановок Р такая, что матрица РАР1 имеет форму
Цк'лЛ > гДе fli и flj - квадратные диагональные мат-
матрицы.
Итерационная схема I'. м. п.меог следующий вид:
(D-\-aL)x* + 1=-((i—(u)D~(>>U)x'i-j-(ob, А —0, 1, ...,
где (о — параметр релаксации, I) — диагональная. L —
нижняя треугольная и U — верхняя треугольная мат-
матрицы из разложений A—D-\-L-p U. Если ш>1, то метод
наз. методом верхней релаксации
(сверхрелаксации), если со<1 — методом
нижней релаксации. Параметр со выбирается
из условия минимизации спектрального радиуса матри-
матрицы S перехода от итерации it итерации:
-)-1((l— «) D — aV).
Если А — симметричная матрица с положительными
диагональными элементами и А,- -- корпи детерминант-
ного уравнения dot (L-\-\D-\- ?/)=0, то оптимальное
значение параметра со дается формулой
Ы = ц)„ = -
где Xo=mnx Л;. Для со=соо спектральный радиус мат-
матрицы S равен
Рассмотрены случаи, когда пек рие ).,- комплексны.
Разработаны Методы блочной релаксации.
Лит.: [1] Y о и 11 g D. M., «Trans. Лшсг. Matli. Soc», 1054,
v. 7В, Л;-> 1, р. 92 ill; [2] его н; е, Iterative solution of larpc
linear systems, N. Y. — L., 1671; lifj В а а о n В., Ф о ii-
c а й т Д щ., РазИОШШе мстОЙы решения диффир'чщиапьиых
уравнений в частных производных, пер. с англ., М., l'JU.'i; 1'iJ
Фаддеев Д. К.,Фадде6ваВ. Н., Вычислительные ысто-
ды линейной алгебры, М., 19G0. К. С. Hv-колаев.
РЕЛАКСАЦИОННОЕ КОЛЕБАНИЕ — периодичес-
периодический' процесс, при к-ром медленное, плавное изменение
состояния объекта в течение конечпого промежутка
времени чередуется с быстрым, скачкообразным изме-
изменением его состояний за бесконечно малое время. Токио
колебательные процессы наблюдаются во мношх реаль-
реальных механических, радиотехнических, биологических
и др. объектах (см., напр., [1]—[3]).
Математич. моделью, описывающей Р. к., являются
автономные системн обыкновенных дифференциальных
уравнений с МальШ параметром при части производных:
tx = j (х, у), y' = g(x,y), ' = d/dt, A)
Периодическое по времени t решение такой системы и
наз. релаксационным колебанием.
Классич. примером системы с одной степенью свободы,
имеющей Р. к., служит Ван дер Поля уравнение
d2x - ,. п. dx /л ,,-,.
_._я. A-я»)-^4^=0 B)
при больших положительных значениях параметра X
(с этой точки зрения уже значение Х=10 можно считать
большим). Если положить
то уравнение B) приводится к системе типа A):
ах = у — у+1, у = — х.
Вопрос о существовании и числе Р. к. системы A)
решается в терминах вырожденной системы
/(*, У)^0, ij = g(x, у), C)
являющейся гибридной системой уравнений. Траекто-
Траектории системы C) в фазовом пространстве R'xRm ес-
естественно трактовать как пределы фазовых траекторий
невырожденной системы A) при е ->¦ 0.
В частности, траектория Р. к. системы A) при е —>- 0
стремится к замкнутой траектории системы C), состоя-
состоящей из чередующихся участков двух типов: участков,
проходимых фазовой точкой системы C) за конечное
время (каждый из них лежит на поверхности f(x, г/)—
= 0), и участков, проходимых фазовой точкой сис-
системы C) мгновенно (каждый из них начинается в точ-
точке срыва, т. е. в точке, где
лежит в плоскости, параллельной R*, и кончается на
поверхности/(х, у)=0). Решение системы C), соответст-
соответствующее такой замкнутой траектории, наз. разрыв-
разрывным периодическим решением, а по-
потому Р. к. системы A) часто наз. периодическим
решением, близким к разрывному,
или даже просто разрывным колебанием.
(Система C) может иметь замкнутую траекторию, цели-
целиком лежащую на поверхности |(ж, г/)=0 и не проходя-
проходящую через точки срыва. В таком случае система A)
имеет близкую к ней замкнутую траекторию, однако со-
соответствующее ей периодич. решение системы A) не
будет Р. к.; см. [6].)
Важной задачей является асимптотич. (при е ->¦ 0)
вычисление фазовой траектории Р. к. системы A), а так-
также получение асимптотич. формул для характери-
характеристик этого колебания — его периода, амплитуды и т. д.
Вычисление траектории Р. к. уравнения Ван дер Поля
B) проводил А. А. Дородницын [7], построивший асим-
асимптотич. приближения при X —>- оо для амплитуды
и для периода (см. также [8])
Г ^ 1,613706X4-7,01432Я" */з — |-'-^ —1,3233Л-Ч-
В случае системы A) 2-го порядка (т. е. при k—m=i)
с точками срыва общего положения проблема асимп-
асимптотич. вычисления Р. к. решена полностью [9]. В част-
частности, выяснена структура асимптотич. разложения
при е ->¦ 0 периода Р. к.:
/ \ п , 2 Уз
где х(п) =т + ~9~~
a Kn, v — коэффициенты, эффективно вычисляемые не-
непосредственно по функциям f(x, у) и g(x, у) (см. [10]).
Для общей системы A) произвольного порядка остается
A983) не перекрытым результат Л. С. Понтрягина и
Е. Ф. Мищенко, вычисливших асимптотику Р. к. с
точностью до О (г) (см. [И], [12], [9]).
Изучался также вопрос о периодич. решениях типа
Р. к. неавтономных систем обыкновенных дифференци-
дифференциальных уравнений (см., напр., [13]).
Лит.: [1] Андронов А. А., Витт А. А., X а й-
кин С. Э., Теория колебаний, 2 изд., М., 1959; [2] Л а н-
д а П. С, Автоколебания в системах с коночным числом степеней
свободы, М., 1980; [3] Романовский Ю. М., Степа-
новаН. В., Чернявский Д. С, Математическое модели-
моделирование в биофизике, М., 1975; [4] V a n ierPol В., «1'hil.
Mag. Ser. 7», 1926, v. 2 №11, p. 978—92; [5] Желез-
ц о в Н. А., Р о ды г и н Л. В., «Докл. АН СССР», 1951, т. 81,
№ 3, с. 391—94; L6] А н о с о в Д. В., «Матем. сб.», I960, т. 50,
.№ 3, с. 299—334; [7] Дородницын А. А., «Прикл. матом,
и механ.», 1947, т. 11, № 3, с. 313—28; [8] Ж а р о в М. И., М и-
щ е н к о Е. Ф., Р о з о в Н. X., «Докл. АН СССР», 1981, т. 261,
JMS 6, с. 1292—96; [9] М и щ е н к о Б. Ф., Р о з о в Н. X., Диф-
Дифференциальные уравнения с малым параметром и релаксационные
колебания, М., 1975; [10] Розов Н. X., «Докл. АН СССР»,
1962, т. 145 № 1, с. 38—40; [11 ] II о н т р я г и н Л. С, «Изв.
АН СССР. Сер. матем.», 1957, т. 21, Ni 5, с. 605 — 26; [12J М и-
ценно Е. Ф., там же, с. 627—54; [13] Levi M., «Mem.
Amer. Math. Soc», 1981, v. 32, jM 244. H. X. Розов.
РЕЛЕЙНО-КОНТАКТНАЯ СХЕМА — математиче-
математическая модель электротехнич. устройств, состоящих из
контактов и промежуточных реле, функционирующих
в дискретные моменты времени. Р.-к. с.— один из пер-
первых классов управляющих систем, рассмотренных с ма-
тематич. точки зрения, а также один из первых вариан-
вариантов понятия автомата конечного. Первые описания
Р.-к. с. появились в 1938—44 (см. [1]—[3]).
Математически Р.-к. с. представляет собой конечный
граф, всем ребрам и нек-рым выделенным вершинам
к-рого приписаны символы из алфавитов
х={хи ~хи ..., хп, хп), Y = {Ylt ..., Ym},
y^i'Ji, Ух, ¦¦¦, Ут> Ут}> а = {а+, а_, аи ..., as}
следующим образом. Каждой выделенной вершине гра-
графа (эти вершины наз. полюсами) приписан символ
из алфавита а так, что различным полюсам приписаны
различные символы. Множество ребер графа разбито
на три непересекающиеся подмножества: R, Кх, К2.
Ребрам каждого из этих подмножеств приписаны сим-
символы из Y, х, у следующим образом. Каждому ребру из
R приписан символ из Y, всем ребрам из R приписаны
различные символы, и все символы из Y приписаны реб-
ребрам из R. Каждому ребру множества Кг (соответствен-
(соответственно К2) приписаны символы из х (соответственно у) так,
что каждый символ может быть приписан нескольким
ребрам, нек-рые символы могут быть не приписаны ни-
никаким ребрам. Если множество Y пусто, то пусто и мно-
множество К2. В таком случае (если непусто только Кг)
Р.-к. с. является контактной схемой. Две Р.-к. с. наз.
изоморфными, если изоморфны их графы и соответст-
соответствующим ребрам и полюсам приписаны одинаковые сим-
символы.
Полюс а+ наз. входным, полюсы а1; ... , as паз.
выходными, полюс а_ может иногда также быть
выходным. Ребра, к-рым приписаны символы из х,
наз. контактами основных реле (или
основными контактами); множество всех
ребер, помеченных символами Yi, yi, г/,-, наз. i-м про-
промежуточным реле, i=l, ... , то; ребра, поме-
помеченные символами из у, наз. контактами про-
промежуточных реле; робра, помеченные симво-
символами из Y, наз. обмотками. Последовательность
контактов и обмоток между нек-рыми вершинами Р.-
к. с, соответствующая простой цепи графа, наз.
цепью.
Функционирование Р.-к. с. происходит в дискретные
моменты времени 1, 2, ... , t, ... и рассматривается в тер-
терминах проводимостей, к-рые в каждый момент представ-
представляют собой (в рассматриваемой модели) функции ал-
алгебры логики. Проводимость контактов xj, xj, j-'l,
... , «, в любой момент t равна значению соответствую-
соответствующей переменной (ху или х/). Проводимость
контакта г/,-, t = l, ... , то, промежуточного реле в
момент 1 равна нулю, проводимость контакта у/ в мо-
момент 1 равна единице; проводимость обмот-
к и всегда равна единице. Всякая обмотка в момент t
может находиться в различных состояниях. Состояние
обмотки в момент t (в рассматриваемой двузначной мо-
модели — 1 и 0 — «возбуждена» и «не возбуждена») может
определяться по-разному. Напр., обмотка У; находится
в состоянии 1 в момент времени t тогда и только тогда,
когда либо а) существует цепь о между полюсами а+ и
я_, проходящая через У, и имеющая в момент t прово-
проводимость 1; либо б) выполнено условие а) и не сущест-
существует цени, состоящей только из контактов, имеющей
в момент t проводимость 1 и соединяющей некоторые
вершины цепи о, расположенные по разные стороны
от У,-.
Проводимость промежуточного контакта у; (у;) в мо-
момент t зависит от состояния обмотки У; в момент t—1,
а именно: проводимость (/,- с ним совпадает, проводи-
проводимость iji — противоположна. Проводимость цепи Р.-
к. с. между двумя вершинами в момент t равна конъ-
конъюнкции нроводимостей в момент t образующих ее кон-
контактов и обмоток. Состояния обмоток, таким образом,
в момент г, вообще говоря, зависят от последовательно-
последовательности наборов значений переменных ц, ... , хп в предыду-
предыдущие моменты времени. При подаче в последовательные
моменты времени на переменные хг, ..., хп последова-
последовательности наборов значений между парой полюсов а +
и afr, fc==l, ... , s, а в частном случае и между а+ и а_,
реализуется ограниченно-детерминированная функция.
Изоморфные Р.-к. с. реализуют одну и ту же ограничен-
ограниченно-детерминированную функцию. Если Р.-к. с. такова,
что при подаче на переменные xlt ... , хп одного и того
же набора значений (oj, ... , а„), начиная с нек-рого
момента ?, обмотки промежуточных реле не меняют
своих состояний (и так для каждого набора значений
переменных xlt ... , х„), то говорят об «установившихся»
состояниях обмоток, и посредством Р.-к. с. реализуются
функции алгебры логики. Если стабилизация обмоток
с момента t наступает сразу для всех наборов значений
переменных i\, ... , х„, то Р.-к. с. наз. о д н о т а к т-
н о и; если стабилизация наступает в момент ?+т, то
Р.-к. с. наз. т-т а к т н о й.
Сложность Р.-к. с. определяется как сумма
весов (или индексов сложности) всех основных контак-
контактов, промежуточных контактов и обмоток Р.-к. с.
Аснмитотич. выражение для сложности самой простой
Р.-к. с., реализующей самую сложно реализуемую функ-
функцию алгебры логики, имеет вид р2п/п, где р — констан-
константа, зависящая от выбранного способа функциониро-
функционирования, топологии схем и сложности контактов и обмоток
реле.
Лит.: [1] Шеннон К., Работы по теории информации и
кибернетике, пер. с англ., М., 1963, с. 9—45; L2] Гавр и-
¦ ¦ и М. А., Теория релейно-контактных схем, 2 изд., Минск,
i: [3] Ш е с т а к о в В. И., «Уч. зап. МГУ. Математика»,
1, в. 73, кн. 5, с. 45—48; [4] Л у п а н о в О. В., «Проблемы
кнчернетики», 1964, в. 11, с. 25 — 47. Н. А. Карпова.
РЕЛЬЕФ АНАЛИТИЧЕСКОЙ ФУНКЦИИ — то же,
что аналитический ландшафт.
РЕЛЯТИВИСТСКАЯ ДИНАМИКА — раздел част-
частной теории относительности, посвященный изучению
движения материальных тел под действием приложен-
приложенных к ним сил.
В теории относительности свободные, т. е. не подвер-
подверженные действию сил, материальные точки имеют в ка-
качестве своих мировых линий времениподобные или изо-
изотропные геодезические. Этот факт является выражением
закона инерции в теории относительности.
Если на частицу действуют силы, то ее мировая ли-
линия не совпадает с геодезической. Для описания дви-
движения частицы вводятся понятия четырехмерного век-
вектора энергии-импульса р' и вектора четырехмерной
силы gi. Именно,
р' = (Е/с; р), A)
где Е — энергия частицы, т — масса покоя, р — трех-
трехмерный импульс частицы. Вектор gl определяется соот-
соотношением
FV F
:2Vl— V'/C ' cVl—V'/c'
где V—трехмерная сила, V — скорость. С использова-
использованием этих векторов основные уравнения Р. д. могут
быть записаны в виде, аналогичном виду уравнений
второго закона Ньютона:
8' =ЧГ~тС1п" (>
Конкретный вид силы g' устанавливается в тех разделах
теории относительности, к-рые изучают конкретные
свойства различных взаимодействий. Напр., сила, дей-
действующая на частицу в электромагнитном поле —
сила Лоренца, имеет вид
где е — заряд частицы, F'k — тензор электромагнит-
электромагнитного поля, u/i — четырехмерная скорость.
Лит.: [1] Л а н д а у Л. Д. >>Л и ф ш и ц Е. М., Теория поля,
6 изд., М., 1973. Д. Д. Соколов.
РЕЛЯТИВИСТСКАЯ ИНВАРИАНТНОСТЬ — свой-
свойство физич. законов сохранять свой вид при преобразо-
преобразованиях Лоренца, описывающих переход от одной инср-
циальной системы отсчета к другой. Это свойство фи-
физич. законов наз. л оренц-инвариантностью.
В тех случаях, когда необходимо подчеркнуть, что Р. и.
включает и инвариантность при параллельных перено-
переносах во времени и пространстве, говорят о п у а к к а-
ре-инвариантности. Лоренц-инвариантность
означает равноправие всех инерциальных систем и од-
однородность пространства-времени.
В общей теории относительности инвариантность фи-
физич. законов при переходе от одной локальной
инерциальной системы отсчета к другой наз. локаль-
локальной лоренц-инвариантностью. В нек-рых
случаях в общей теории относительности рассматри-
рассматривают также величины, к-рые определены при задании
конгруэнции линий времени (т. е. задании системы от-
отсчета) и инвариантны относительно выбора пространст-
пространственных сечений. Эти величины наз. хронометри-
хронометрическими инвариантами.
Лит.: 11] Фок В. А., Теория Эйнштейна и физическая от-
относительность, М., 1067. Д. Д. Соколов.
РЕЛЯТИВИСТСКОЙ АСТРОФИЗИКИ МАТЕМАТИ-
МАТЕМАТИЧЕСКИЕ ЗАДАЧИ — задачи, возникающие при изу-
изучении астрофизич. явлений, в к-рых существенны реля-
релятивистские эффекты, т. е. эффекты специальной пли
общей теории относительности.
Принято разделять Р. а. м. з. на задачи, относящие-
относящиеся к космологии — науке о строении и эволюции Все-
Вселенной, и задачи релятивистской астрофизики отдель-
отдельных небесных тел. Примером космологич. решения,
описывающего расширение (или сжатие) однородной и
изотропной Вселенной, является решение А. Л. Фрид-
Фридмана. Однородные анизотропные космологич. решения
классифицированы (выделено 9 типов по Ьианки) и
хорошо изучены. Детально изучены анизотропные а не-
однородные решения, представляющие собой малые от-
отклонения от решения Фридмана (линейное приближе-
приближение), и построены некоторые простые нелинейные
решения.
Особое место занимает проблема, связанная с наличи-
наличием особой точки в общем космологии, решении, в к-рой
достигается бесконечная плотность вещества и беско-
бесконечная кривизна прострапства-времени. Показано, что
сингулярность неизбежна в прошлом в условиях, имею-
имеющих место в реальной Вселенной, и построено общее
решение уравнений общей теории относительности с
сингулярностью. Активно исследуется возможность по-
построения космологич. решений без сингулярности,
связанная с выходом за рамки классической общей тео-
теории относительности.
Гюлыпой класс Р. а. м. з. связан с изучением взаимо-
взаимодействия реликтового излучения, заполняющего прост-
пространство, с веществом в ходе расширения Вселенной и
физич. процессов, способных породить такое излучение.
Р. а. м. з. для отдельных небесных тел касаются рав-
равновесия и устойчивости звезд и звездных скоплений.
Найдены равновесные массы белых карликов и ней-
нейтронных звезд и изучен релятивистский коллапс более
массивных звезд, превращающихся в т. н. «черные
дыры» — объекты, к-рые можно обнаружить лишь по
проявлению их гравитационного ноли. Л связи с зада-
задачей поиска и изучения релятивистских объектов (ней-
(нейтронных звезд, «черных дыр» и др.) рассматривается
задача об аккреции на них вещества с магнитным
полем.
К Р. а. м. з. относится также исследование гравита-
гравитационного излучения. В слабом гравитационном поле в
пустоте возмущения, напр, инварианта кривизны, под-
подчиняются волновому уравнению, и ноле тяготения рас-
распространяется в пространстве подобно электромагнит-
электромагнитным волнам.
Лит.: [1] 3 е л ь я о в и ч Я. Б-, Н о в и к о в И. Д., Реля-
Релятивистская астрофизика, М., 1967; [2J и х ж е, Теория тяготе-
тяготения и ано.шошш лр.езд, М., 1 Г»71; [:tl и х ж е, Строение II :шолю-
ция Вселенной, М., 1!>75; [\\ 11 и 0 л с, II., Физическая космоло-
космология, пор. с англ., М., 197.V, 15] М и а и с р Ч., Т о р и К., У и-
л с р Д и;., Гравитация, т. 2-У, пер. о анг.1., М., 1У77; LHI
Лнф'шиц К. М., «Ж. иксперименталынш и тсоретич. физи-
физики», 1946, т. 16, с. 587—602; [7] Б е л и и о к и й В. А., Л и ф-
ш и ц Е. М., Халатников И. М., «Успехи физ. наук»,
1970, т. 102, с. 463—500; L8] Б р а г и иски и В. Б., там н.е,
1965, т. 86, с. 433 — 46. А. А. Рувмайкин.
РЕЛЯТИВИСТСКОЙ ГИДРОДИНАМИКИ МАТЕ-
МАТЕМАТИЧЕСКИЕ ЗАДАЧИ — задачи для системы урав-
уравнений, описывающей точения жидкости со скоростями,
близкими к скорости света с, и ее взаимодействие с силь-
сильными гравитационными полями. В предельном случае
малых скоростей v<^.c и слабых гравитационных нолей
ср<^с2, где ср — гравитационный потенциал, Р. г. м. з.
сводятся к гидродинамики математическим задачам.
Система уравнений релятивистской гидродинамики об-
образуется путем приравнивания к нулю ковариантных
дивергенций тензора энергип-имнульса и вектора плот-
плотности потока вещества:
Tik—te+P) UiUk- Pgik+iik, A)
nr-=nUi+vh i, k = \, 2, 3, 4, B)
где е, p и n — плотность анергии, давлепис it плотность
числа частиц в системе отсчета, покоящейся относитель-
относительно рассматриваемого элемента жидкости, gjk — метрич.
тензор, и,- — четырехмерная скорость, т,-? и V; — части
тензора энергии-импульса и вектора потока вещества,
описывающие эффекты, связанные с вязкостью (см. [1]).
Пример решений Р. г. м. з.: распространение звука
в веществе с ультрарелятивистским уравнением состоя-
состояния р — е/'д, для возмущения давления пли плотности
энергии получается волновое уравнении со скоростью
звука ii—cV^'d.
Р. г. м. з. возникают, напр., при рассмотрении фи-
:!нч. процессов, протекающих и окрестности звезд, об-
обладающих сильными гравитационными полями (ней-
(нейтронные звезды и т. н. «черные дыры») и расширяющей-
расширяющейся Вселенной, заполненной излучением и веществом.
Лит.: [1] Л и и Д а у Л. Д., Л и ф ш и ц Е. М., Механика
сплошных сред, - изд., М., 1954; [2] Зельдович Я. Б.
Н о в и к о в И. Д., Теория тяготения и эволюция звезд, М.
1971; 13J и х ж е, Строение и эволюция Вселенной, М., 1975
I U Ы и влср Ч., Т о р н К., У и л с р Д ж., Гравитация, пер
с англ., т. 2, М., 1977. А. А. Рузмайкин
РЕЛЯТИВИСТСКОЙ ТЕРМОДИНАМИКИ МАТЕ-
МАТЕМАТИЧЕСКИЕ ЗАДАЧИ — установление соотноше-
соотношений между величинами, характеризующими макроско-
пич. состояния тел (термодинампч. величинами), при
наличии сильных гравитационных нолей и скоростей,
сравнимых со скоростью света.
Обычно рассматривается равновесная термодинамика
идеальной жидкости с заданным химич. составом. Уста-
Установленные в нерелятивистской термодинамике соотно-
соотношения между термодина.мич. величинами сохраняются
как при релятивистском макроскопич. движении час-
частиц, составляющих тело, так и релятивистском движе-
движении самого тела, а также в сильных гравитационных
полях, если значения термодинамич. величин взяты в
системе отсчета, покоящейся относительно рассматри-
рассматриваемого элемента объема жидкости или тела, и в энер-
энергию и химич. потенциал включены все формы энергии
(в частности, энергия покоя).
Основные уравнения релятивистской термодинамики
формулируются в следующем виде:
(ли'),/—0 — закон сохранения барионов,
de—^dn-trnTda — первый закон термодинамики,
(аи'),1~0 — условие адиабатичности,
где и' — четырехмерная скорость (величины п — плот-
плотность барионов, е — плотность энергии, Т — темпера-
е+р
тура, ц= —— — химич. потенциал, р — давление, а —
плотность энтропии относятся к системе отсчета, покоя-
покоящейся относительно рассматриваемого элемента объе-
объема). При этом давление и плотность энергии связаны
соотношением р<к/3. При переходе к дпижущейся от-
относительно элемента объема системе отсчета или к ло-
локализованному наблюдателю (при наличии гравитаци-
гравитационных полей) нек-рыс величины (папр., плотность ба-
барионов п или энтропия S) не изменяются, т. е. являют-
являются скалярами, другие преобразуются, напр.
Т = Ти<>, |1 = |ш°,
где компонента четырехмерной скорости и" берется
вдоль мировой линии, описываемой данной точкой тела.
Следствием этого является, напр., тот факт, что в по-
постоянном гравитационном поле условие теплового рам-
новесия требует постоянства вдоль тела пе температуры,
а величины r|/^^00=const, где gu0 — компонента
мстрич. тензора, goo~-l — 2cp/c2 в слабом гравитационном
поле (ф — гравитационный потенциал, с — скорость све-
света). А температура, измеренная наблюдателем, относи-
относительно к-рого тело движется со скоростью v, равна
Релятивистская инвариантность энтропии S позво-
позволяет записать второй закон термодинамики в форме,
принятой в норолятивистской термодинамике:
где изменение тепла 6Q и Т преобразуются по одинако-
одинаковому закону. Равенство достигается для обратимых
процессов.
Лит.: [1] Ландау Л. Д., Л и ф ш и ц К. М., Статисти-
Статистическая физика, 2 изд., М., 19В4; 12] Мианср Ч., Т о р и К.,
Уилер Д н<-, Гравитация, нер. с англ., т. 2—3, М., 1977;
[3] М ё л л е р К., Теория относительности, пер. с англ., 2 изд.,
М., 1975, А. А. Рузмайник.
РЕЛЯТИВНАЯ ГЕОМЕТРИЯ — геометрия конфи-
конфигурации, состоящей ии двух п о по рх посте и So : п=п(и1,
и2) и S : г—Г (и1, к2), находящихся в Петерсопа соот-
соответствии. Аналогия между этим соответствием и сфери-
сферическим отображением позволила ввести понятия реля-
TiiBiKiii площади, полной и сродней кривизны и т. д.,
в частности релятивно минимальной поверхности
(см. [1]).
Рассмотрение деривационных уравнений для репера
ой1' Ш*' ** привело к понятию внутреннен Р. г. по-
поверхности S (см. [2]). Это есть геометрия аффинной связ-
связности (точнее эквиаффинной) без кручения. Было вве-
введено понятие геометрии 2-го рода, аналогичной геомет-
геометрии сферич. отображения (см. [3]).
Р. г. позволяет включить в общую схему, кроме
геометрии поверхностей евклидова и нсевдоевклидова
пространств, также и геометрию аффинной дифферен-
дифференциальной геометрии. Вектор п аффинной нормали ха-
характеризуется том, что асимптотич. сеть поверхности
S — чебышевская (см. [3]).
Дальнейшим обобщением Р. г. является теория
нормализованных поверхностей (см.
[4]). С каждой точкой поверхности S проективного про-
пространства связываются две прямые: нормаль 1-го рода,
проходящая через точку поверхности А, но не имеющая
с касательной плоскостью а других общих точек и нор-
нормаль 2-го рода, принадлежащая а, но не проходящая че-
через А . На поверхности S определяются при этом две
внутренние геометрии, сопряженные относительно
асимптотич. сети. Построения Р. г. допускают много-
многомерное обобщение (см. [4]).
Лит.: [1] М ii 1 1 е г Е., «Monatsh. Math und Physik», 1921,
Bd 31, S. 3—19; [2] N о r d e n A. P. (H о р д е н A. II.), «C. r.
\cad. sci.», 1931, t. 192, p. 1ЗГ) — 37; [3] e г о же,«Изв. ВУЗои.
Математика», 1958, .\« 4, с. 172—83; [4] его же, Простран-
.тна аффинной связности, 2 изд., М., 1978. А. П. Норвеи.
РЕНЬИ КРИТЕРИЙ — статистический критерий,
применяемый для проверки простой непараметрич.
гипотезы Но, согласно к-рой независимые одинаково
распределенные случайные величины Xj, ... , Хп имеют
заданную непрерывную функцию распределения Ь'(х),
цршни альтернатив следующего вида:
Я Г : кир г|) [F (x)\ (?Fn (х) -1< (х)) > 0.
I л-1 < *>
ЯГ : inf г|) [/-' (х)] (?F,— (x)F (x)) < 0.
#i : sup \\, [/•' (х)] | Ef „ (x) — F (x) | > О,
где Fn (х)-- функция амиирич. распре деления, nocipii-
еннан но выборке Xt, ... , X,„ if (/•'), >|'^0, - весовая
4|ункция. В случае, если
1/1 /(
Tr v"»- I 0 при F(x) < а,
ill' a - любое фиксированное "нсло и:! отрезка [О. ]|.
-го Р.к., предназначенный для проверки У/о против
указанных альтернатив НХ. Н\ , ^i , основан на соот-
соответствующих им статистиках Р е н ь и:
V I V
Нп (а. 1)= sup =— = тах
F[Xm))>a F (X
F(x)>a b {x)
FIX \ ^—-
(" (m))
Л„(«,1)= «up |y»(?-f'*"
л+(в, 1), Rn(a, 1)},
где ХA), ХB), ... , Х(,г) — члены вариационпого ряда
цостроенного по наблюдениям Хх, ..., Х(„>.
Статистики Rn(a, 1) и Я а (а, 1) подчиняются одному
и тому же вероятностному закону, и если 0<а<1, то
1A11 р \Vr=ZRn (а- ^ <г)=2Ф(*)-1, х>и, A)
=/, (х), ж> 0, B)
где <1> (г) — функция распределения стандартного нор-
нормального закона, L (х) — функция распреде-
распределения Реньи, определяемая формулой:
М-П -1Г^А = О 2ftf 1LXP I 87'
В случае, если а=0, то
р{я;Г(о, 1)=э^}-1-~, х>о.
Из A) и B) следует, что при больших значениях п для
вычислении (^-процентных критич. значений @%«?<
<50%) для статистик Rn{a, 1) и Rn(a, 1) можно вос-
воспользоваться следующими приближенными значениями:
-1 A-0,01 У)
соответственно, где Ф~)-(а;) и L~J(a;) функции, обратные
Ф (х) и Л (х) соответственно, при этом имеют в виду, что
если 00/о«?<10%', то ф-1A— 0,005<?)«?-Н1— 0,02<?).
Кроме того, если .с>2,99, то при вычислении значе-
значений функции распределения Реньи L(x) рекомендуется
пользоваться приближенным равенством
L (х) я 4Ф (х)~3,
погрешность к-рого пе превосходит 5-Ю.
Кроме рассмотренных Р. к., существуют аналогичные
критерии, отвечающие весовой функции
1 0, если F (х) > а,
где а — любое фиксированное число из отрезка [0, 1].
.'hurt.: tl] R б n у i A., «Ada math. Acad. sciont. hung.»,
1953, v. 4, p. 191—231; [2] Г а е к Я., Ш и Д а и 3., Теории 1>нн-
говых критериев, пер. с англ., М., 1971; U] Большие .11. 11.,
Смирнов Н. В., Таблицы математической статистики, 2
изд., М., 1068. М. С. Никулин.
РЕПЕР — совокупность линейно независимых век-
векторов, взятых в определенном порядке и отложенных от
общего начала. Для векторов в пространстве Р. может
служить любая тройка непараллельных одно» плоско-
плоскости векторов. Если векторы, составляющие Р., попарно
ортогональны, то Р. наз. ортогональны м;
если при этом векторы имеют длину, равную единице,
то Р. наз. ортонормировании м. HC3-:s.
РЕПЛИКА алгебр а и ч е с к о й с и с т с м ы
Л в заданном классе ,ft алгебраических систем чип ;ке
сигнатуры — алгебраическая система Ко из ,(f, обла-
обладающая следующими свойствами: 1) существует сюръек-
тивный гомоморфизм ср0 системы А на Ко; 2) если /<?,№
и ф — гомоморфизм системы А в К, то ф = фог|- для пе-
к-рого сюръективного гомоморфизма if) системы А'о на
К. Р. системы А в классе Я1 (если она существует) опре-
определяется однозначно с точностью до изоморфизма.
Класс Л1 наз. реплично полным, если он со-
содержит Р. любой алгебраич. системы той же сигнатуры.
Класс алгебраич. систем фиксированной сигнатуры
реплично полон тогда и только тогда, когда он содержит
одноэлементную систему и замкнут относительно под-
систем и прямых произведений. Аксиоматизируемыми
реплично полными классами являются квазимногооб-
квазимногообразия и только они.
Лит.: [1] Мальцев А. И., Алгебраические системы,
М., 1970. Л. А. Скорняков.
РЕПЛИКА эндоморфизма X конечномерного
векторного пространства F над полем к характеристики
О — элемент наименьшей, содержащей X, алгебраич.
подалгебры Ли gl(F) (см. Ли алгебраическая алгебра).
Эндоморфизм X'?ftl(F) является Р. эндоморфизмах
тогда и только тогда, когда всякий тензор на V, аннули-
аннулируемый эндоморфизмом X, аннулируется также и эндо-
эндоморфизмом X'.
Каждая Р. эндоморфизма X может быть представлена
в виде многочлена от X с коэффициентами из ноля к
с нулевым свободным членом. Полупростая и нильпо-
тентная компоненты эндоморфизма X (см. Жордана раз-
разложение, 2) являются его Р. Подалгебра алгебры Ли
$I(F) тогда и только тогда алгебраична, когда она со-
доржит все Р. любого своего элемента. Эндоморфизм
.Y пространства V тогда и только тогда нипьпотентен,
когда Тг ХХ'=0 для любой реплики X' эндоморфиз-
эндоморфизма X.
Пусть к алгебраически замкнуто, ф — автоморфизм
поля к, X — нолупростоп эндоморфизм пространства V,
а гр (X) — такой эндоморфизм пространства V, что вся-
всякий собственный вектор эндоморфизма X, отвечающий
собственному значению к, является собственным вежто-
ром и для ф(Х), но отвечающим собственному значению
ц>(Х). Эндоморфизм X'?ft((F) тогда и только тогда
является Р. эндоморфизма X, когда Х'=ф(Х) для
нек-рого автоморфизма ф поля /с.
Лит.: [1] С е р р Ж.-П., Алгебры Ли и группы Ли, пер.
с англ. и франц., М., 1969; [2] Теория алгебр Ли. Топология
групп Ли, пер. с франц., М., 1982; [3] Ш е в а л л е К., Теория
групп Ли, пер. с франц., т. 2, М., 1958. В. Л. Попов.
РЕПРЕЗЕНТАТИВНОЕ ПОДПРОСТРАНСТВО —
подпространство X топологич. пространства У такое,
что включение XCZ.Y является слабой гомотопич. экви-
эквивалентностью. А. Ф. Харшиладзе.
РЕТРАКТ объекта категории — понятие,
обобщающее соответствующие понятия алгебры и топо-
топологии. Объект R категории .ft наз. ретрактом
объекта А, если существуют такие морфизмы
|i: R —> А и v : А —у R,
что |j,v=l/j. Морфизм |j, при этом оказывается мономор-
мономорфизмом и, более того, ядром пары морфизмов 1^, vfi.
Двойственно, морфизм v — эпиморфизм и, более того,
коядро пары морфизмов 1^, v|i. Иногда |j, наз. сече-
сечением, av — расслоением.
Если R есть Р. объекта А и объект R' изоморфен R,
то R' есть ретракт А. Поэтому изоморфные Р. образуют
один подобъект объекта А . Каждому рстракту R, опре-
определяемому морфизмами и. : Л —у A hv : А —»- R, соответ-
соответствует идемпотентный морфизм ф=уц : Д-wl. Два рет-
ракта R и R' объекта А принадлежат одному и тому же
иодобъекту тогда и только тогда, когда им соответствует
общий идемпотент. Р. любого объекта произвольной ка-
категории образуют множество. м. ш. Цалеико.
РЕТРАКТ топологического простран-
пространства X — подпространство А этого пространства,
для к-рого существует ретракция X на А . Если прост-
пространство X хаусдорфово, то всякий Р. пространства X
замкнут в X. Всякое непустое замкнутое множество кан-
торова совершенного множества является его Р. При
переходе от пространства к его Р. сохраняются многие
важные свойства. В частности, всякое свойство, сохра-
сохраняющееся при переходе к непрерывному образу, равно
как и любое свойство, наследуемое замкнутыми под-
подпространствами, устойчиво относительно перехода к Р.
Поэтому компактность, связность, линейная связность,
сепарабельность, ограничение сверху на размерность,
паракомпактность, нормальность, локальная компакт-
компактность, локальная связность сохраняются при переходе
к Р. В то же время Р. пространства может быть устроен
гораздо проще его самого, более обозрим, более удобен
для конкретного исследования. Так, одноточечное мно-
множество является Р. отрезка, прямой, плоскости и т. д.
Если пространство X имеет свойство непо-
неподвижной точки, т.е. для каждого непрерывного
отображения / : X -+¦ X существует точка х?Х такая,
что }(х) — х, то и каждый Р. пространства X обладает
свойством неподвижной точки. В частности, п-мерная
сфера не является Р. (и+1)-мерного шара евклидова
пространства, где п=0, 1, ... , так как замкнутый шар
обладает свойством неподвижной точки (т е о р и м а
Б р а у э р а), а сфера этого свойства не имеет. Под-
Подпространство А пространства X наз. окрестное т-
н ы м Р. этого пространства, если существует в X от-
открытое подпространство, содержащее А, ретрактом
к-рого А является. Понятие Р. имеет прямое отношение
к вопросу о продолжаемости непрерывных отображений.
Так, подпространство А пространства X является его
Р. в том и только в том случае, если всякое непрерывное
отображение пространства А в произвольное тополо-
гич. пространство Y можно продолжить до непрерыв-
непрерывного отображения всего пространства X в Y.
Метризуемое пространство X наз. абсолютным
Р. (абсолютным окрестностным Р.),
если оно является Р. (соответственно окрестностным
Р.) всякого метризуемого пространства, содержащего X
в качестве; замкнутого подпространства. Для того чтобы
метризуемое прост-ранство X было абсолютным Р.,
необходимо, чтобы оно было Р. нек-рого выпуклого
подпространства линейного нормированного простран-
пространства, и достаточно, чтобы X было Р. выпуклого подпро-
подпространства локально выпуклого линейного пространства.
Таким образом, все выпуклые подпространства ло-
локально выпуклых линейных пространств являются аб-
абсолютными Р.; в частности, таковы точка, отрезок, шар,
прямая и т. д. Из приведенной характеристики вы-
вытекают следующие свойства абсолютных Р. Всякий Р.
абсолютного Р. снова есть абсолютный Р. Каждый аб-
абсолютный Р. стягиваем по себе и локально стягиваем.
Все гомологические, когомологические, гомотопические
и когомотопич. группы абсолютного Р. тривиальны.
Метризуомое пространство Y является абсолютным Р.
в том и только в том случае, если, каковы бы ни были
метризуемое пространство X, его замкнутое подпрост-
подпространство А и непрерывное отображение пространства А
в Y, его можно продолжить до непрерывного отображе-
отображения всего пространства X в Y. Абсолютные окрестност-
ные Р. характеризуются как Р. открытых подмножеств
выпуклых подпространств линейных нормированных
пространств. К их числу относятся все компактные по-
полиэдры. Существенным их свойством является ло-
локальная стягиваемость.
Если ретракция пространства X на его подпростран-
подпространство А гомотопна тождественному отображению прост-
пространства X на себя, то А наз. деформационным
Р. пространства. X. Деформационный Р. пространства
гомотопически эквивалентен этому пространству, т. е.
имеет с ним один и тот же гомотопич. тип. Обратно, два
гомотопически эквивалентных пространства всегда мож-
можно вложить в нек-рое третье пространство таким обра-
образом, что оба они будут его деформационными Р.
JIvm.: [1] Борсук К., Теория ретрактов, пер. с англ.,
М., 1971. А. В. Архангельский.
РЕТРАКЦИЯ — непрерывное отображение f топо-
логич. пространства X на его подпространство А, тож-
тождественное на А, то есть такое, что f(.r)--x при всех
х?А. IW. И. Бопцехоиский.
РЕФАЛ, алгоритмический язык ре-
рекурсивных функци и,— алгоритмический язык,
ориентированный на задачи преобразования символьной
информации; в первоначальном варианте назывался
«метаалгоритмическим языком» (см. 11J). Р. был создан
как универсальный метаязык для описания преобразо-
преобразований языковых объектов. Он используется для транс-
трансляции с одного алгоритмич. языка на другой, для ма-
машинного выполнения аналитич. выкладок, доказатель-
доказательства теорем, перевода с естественных языков и т. п.
Запись алгоритма на Р. представляет описание не-
к-рого числа рекурсивных функций на множестве в ы-
ражений (т.е. последовательностей символов и
скобок), правильно построенных (в обычном смысле)
относительно скобок. Значение функции ф при аргу-
аргументе ? изображается на Р. в виде Ку?—, где К —
знак конкретизации, служащий для явного
указания на необходимость вычисления значения функ-
функции, а символ — означает закрывающую скобку для К.
Описание функции распадается на несколько предло-
предложений (правил конкретизации), относя-
относящихся к случаям, когда аргумент имеет тот или иной
частный вид. Напр., функция сложения в рекурсивной
арифметике описывается на Р. двумя предложениями:
1)
2)
Предложение состоит из левой и правой частей, раз-
разделяемых знаком =2, и может включать свободные пере-
переменные (в примере это — -ЕЛ и MB). Оно считается при-
применимым для конкретизации выражепия вида Кср^1—,
если это последнее может быть отождествлено с левой
частью предложения при нек-рых значениях входящих
в нее свободных переменных. Применение предложения
состоит в замене конкретизируемого выражения на
правую часть предложения, в к-рой свободные перемен-
переменные замещены их значениями. Для вычисления значе-
значения фупкции предложения рассматриваются последова-
последовательно, и применяется первое из них, оказавшееся под-
подходящим. Этот процесс повторяется, пока в объект ра-
работы входят знаки К.
Для реализации программ на Р. разработаны эффек-
эффективные трансляторы (см. [3], [4]; пример использования
Р. для машинного выполнения выкладок в теоретич.
физике см. в [5]).
Лит.: [1] Т у р ч и н В. Ф., «Кибернетика», 1988, М 4, с.
'.5—54; [2] Т у р ч и н В. Ф., С е р д о б о л ь с к и й В. И.,
¦ Кибернетика», 1969, № 3, с. 58—62; [3] Ф л о р е н ц е в С. Н.,
О л ю н и н В. Ю., Т у р ч и н В. Ф., «Тр. 1 Всесоюзн. конфе-
конференции по программированию», К., 1968, с. 114—33; 14] Р о-
м а н е н к о О. А., Т у р ч и и В. Ф., «Тр. 2-й Всесоюзн. кон-
конференции по программированию», Новосиб., 1970, с. 31—42;
[5] Б у дн и к А. П. [и др.], «Ядернан физика», 1971, т. 14,
с. 304—13. В. Ф. Турчин.
РЕФЛЕКСИВНОЕ ПРОСТРАНСТВО — банахово про-
гтранство X, совпадающее при каноническом вложении
о споим вторым сопряженным X**. Подробнее, пусть
X* — пространство, сопряженное с X, то есть совокуп-
совокупность всех непрерывных линейных функционалов, оп-
определенных на X. Если <х, /> — значение функционала
f?X* на элементе х?Х, то при фиксированном х и /,
пробегающем X*, выражение <я, />—§"x(f) будет ли-
линейным функционалом на X*, то есть элементом прост-
пространства X**. Пусть XdX** — множество таких функ-
функционалов. Соответствие х-*-§~х есть изоморфизм, не
.юняющий нормы ||x|| = ||JFх\\. Если А'—Л'**, то прост-
пространство X наз. рефлексивным. Пространства
1р и Lp(a, b), р>1, рефлексивны, пространство С [а, Ь]
не рефлексивно.
Пространство X рефлексивно тогда и только тогда,
когда X* рефлексивно. Другим критерием рефлексив-
рефлексивности банахова пространства X является слабая ком-
компактность единичного шара этого пространства.
Р. п. слабо полно, и замкнутое подпространство Р. п.
рефлексивно.
Понятие рефлексивности естественным образом рас-
распространяется на локально выпуклые пространства.
Лит.: [1] Д а н ф о р д Н., Ш в я р ц Д ж., Линейные опе-
операторы, ч. 1 — Общая теория, пер. с англ., М., 19В2; [2] И о-
оида К., Функциональный анализ, пер. с англ., М., 1967;
13) Канторович Л. В., А к и л о в Г. П., Функциональ-
Функциональный анализ, 2 изд., М., 1977. В. И. Соболев.
РЕФЛЕКСИВНОСТЬ — одно из свойств бинарных
отношений. Отношение R на множестве А наз. реф-
рефлексивным, если aRa для любого а?А. Примера-
Примерами рефлексивных отношений являются равенство, эк-
эквивалентность, ПОРЯДОК. Г. С. Фофанова.
РЕФЛЕКТИВНАЯ ПОДКАТЕГОРИЯ — подкатего-
подкатегория, содержащая «наибольшую» модель любого объекта
категории. Точнее, полная подкатегория (S категории
St наз. рефлективной, если (S, содержит ©-реф-
©-рефлектор (см. Рефлектор) для любого объекта категории.
Полная подкатегория (S категории ,Й рефлективна тог-
тогда и только тогда, когда функтор вложения Ida, « : Й—>-й'
обладает сопряженным слева функтором S : Jf —*¦ Й.
Функтор S сопоставляет каждому объекту А из
St его (J-рефлектор S(А); морфизмы па • А ->- S (А).
входящие в определение (S-рефлектора, определяют
естественное преобразование тождественного функтора
Ids в композицию функторов 5Id®,«. Двойственным
к понятию Р. п. является понятие к о р е ф л е к т и в-
н о и подкатегории.
Р. п. (S наследует многие свойства объемлющей ка-
категории St. Напр., морфизм fx?Mor(? тогда и только
тогда является мономорфизмом в S, когда он мономор-
мономорфизм в Si. Поэтому всякая Р. п. локально малой слева
категории локально мала слева. Р. п. обладает произ-
произведениями тех семейств объектов, для к-рых произве-
произведение существует в самой категории, при этом оба
произведения оказываются изоморфными. То же самое
справедливо и для любых пределов. С другой стороны,
функтор S переводит копределы из SX в копределы в (S,.
Поэтому Р. п. полной (слевп) категории является пол-
полной (слева) категорией.
Пусть Щ — полная локально малая категория. Вся-
Всякая полная подкатегория (S, категории ,й, замкнутая от-
относительно произведений и подобъектов своих объектов
и содержащая правый нуль, является Р. п. В частности,
всякое многообразие категории .ft' есть Р. п.
E-рефлектор произвольного объекта А строится сле-
следующим образом. Выбираются представители (v,-, Л,),
i?/, таких факторобъектов объекта А, что А^ОЪ Ё
Произведение
принадлежит E, и S-рефлектор S (А) является обра-
образом однозначно определенного морфизма у : А —у Р,
для к-рого YJt,-=v,-, i?I.
Примеры. 1) Пусть R — область целостности.
Полная подкатегория инъективных модулей без круче-
кручения является Р. п. категории Я-модулей без кручения:
рефлекторами являются инъектмвные оболочки моду-
модулой. В частности, подкатегория полных абелевых групп
без кручения есть Р. п. категории абелевых групп бе.ч
кручения.
2) Полная подкатегория нормальных топологич.
пространств есть Р. п. категории вполне регулярных
топологич. пространств: рефлекторы строятся с по-
помощью компактификации Чеха.
3) Полная подкатегория пучков есть Р. п. категории
предпучков: рефлекторы определяются функтором ас-
ассоциированного пучка. М. Ш. Цаленко.
РЕФЛЕКТОР объекта категории — поня-
понятие, описывающее «наибольшую» модель данного объек-
объекта в нек-ром классе объектов. А именно, пусть (S --
подкатегория категории SX; объект #?(.Я наз. реф-
рефлектором объекта Л?М' в ($, или (S - р е ф-
л е к т о р о м, если существует такой морфизм л : А ->
—у Л, что для любого объекта X из ($, отображение
Нх{п): На(В, Х)->НЯ(А, X)
биективно. Другими словами, для любого морфизма
а : А —>- ,Y существует такой единственный морфизм
а' : й—>- Х?(^, чтосс=яа'. ©-рефлектор объекта А опре-
определен неоднозначно, но любые два Ц-рефлектора объек-
объекта Л изоморфны. (S-рефлектор левого нуля (инициаль-
(инициального объекта) категории й является левым нулем в ($.
Пример ы. В категории групп факторгруппа G'G'
произвольной группы G по коммутанту является Р.
группы G в подкатегории абелевых групп. Для абеле-
вой группы А ее факторгруппа А/Т (А) по периодич.
подгруппе Т(А) является Р. группы А в полной подка-
подкатегории абелевых групп без кручения. Пополнение
(инъективная оболочка) Л группы А/1л(А) является Р.
групп А и А/Т (А) в подкатегории полных абелевых
групп без кручегшя.
Обычпо Р. рассматриваются в полных подкатегориях.
Полная подкатегория 1\ категории ,н\ в к-рой сущест-
существуют Р. для любых объектов из ,ft\ наз. р е ф л е к т и в-
II О п. м. Ш. Цпленко.
РЕШАЮЩАЯ ФУНКЦИЯ, решающая про-
процедура, статистическое решающее
н р а в и л о,- - правило, согласно к-рому на основании
полученных наблюдений делают статистич. выводы (при-
(принимают решения).
Пусть Y — случайная величина, принимающая зна-
значения в выборочном пространстве (J, ®, Ре), 6?6, и
пусть 1)—- {<!} — множество всех возможных решений d,
к-рые можно ш.шести относительно параметра S по реа-
реализации случайной величины X. Согласно терминоло-
терминологии, принятой в матсматич. статистике и теории игр,
любое ^-измеримое отображение б : Ж -»- D простран-
пространства реализаций X случайной величины X в множество
возможных решений О наз. Р. ф. Напр., в задаче стати-
статистич. оценивания параметра 0 любая точечная оценка
0~0(.Y) является Р. ф. Основной задачей статистики
при получении статистич. выводов является выбор та-
такой Г. (!). о'(-)) к-рая минимизирует риск
П (9, &) = Ee[L (в, б (X))]
относительно используемой функции потерь L(-, •).
Попяше I'. ф. является основным в теории статисти-
статистических Р.ф., созданной Л. Вальдом (A. Wald).
Лит.: 1.11 г1 о н и " и Н.Ш., Статистические решающие пра-
правила и оптимальные выводы, М., 1972; [2] В а л ь д А., Статис-
Статистические решающие функции, в сб.: Позиционные игры, М., 1967,
о. :@0 -522. М. С. Никулин.
РЕШЕНИЕ в теории игр — исход (или мно-
множество исходов), удовлетворяющий принятому в данной
модели принципу оптимальности. Выделяют следующие
основные типы Р.: 1) решение по Н э ш у (см.
/бескоалиционная игра), в частности седловая точка
функции выигрыша в антагоплстич. играх; 2) р е га е-
н и о по II о й м а н у — Морген Штерн у
(Н — М -решение) — множество дележей, никакие
два из к-рых не доминируют друг друга, причем для
каждого дележа, не принадлежащего этому множеству,
найдется доминирующий его дележ из этого множества
(см. Доминирование); 3) решение Н э ш а в арбит-
арбитражных схемах.
Лит.: [1] II <! й м я н Д ж., Моргенштерн О., Теория
игр и гн.ипомичРское поведение, пер. с англ., М., 1970; [21 О у-
о н Г., Теория игр, пер. е англ., М., 1971. А. Я. Ляпунов.
РЕШЕТА МЕТОД — один на общих методов теории
чисел, обобщающий принцип высеивания составных чи-
чисел из натурального ряда (см. Эратосфена решето).
Проблема Р. м. состоит в оценке для конечного мно-
множества А целых чисел количества тех элементов, к-рые
не делятся ни на какоо простое число р из пек-рого мпо-
жества Р простых чисел. Оценивается «просеивающая»
функция S(A; P, z), обозначающая количество указан-
указанных элементов и:» А при дополнительном условии: p<.z.
Для получения оценок просеивающей функции часто
используется информация о числе N (А ч) элементов
множества Aq, состоящего из элементов А , к-рые делят-
делятся на свободное от квадратов число q. При <7=1 множе-
множество Aq = A . Поэтому обычно оценивается более общая
просеивающая функция S(Aq; Р, z).
При выборе ожидаемого значения для N (Aq) в форме
(a(q)/q)X, где X — ожидаемое значение для N (А) и
о) (q) — мультипликативная функция, руководствуются
тем, чтобы погрешность
R(X, q) = N(Aq)-((B(q)/q)X
была относительно мала. Если при этом а>(р)=гк (по
крайней мере, «в среднем»), то к наз. размерностью
решета.
Общая теория Р. м. с ее приложениями продвинулась
наиболее далеко в случае линейного решета (при /г=1).
Существуют различные специализации Р. м., наиболее
важные из к-рых принадлежат В. Бруну (V. Bruu; см.
Вруна решето) и Л. Сельбергу (A. Selberg; см. Селъ-
берга решето).
В приложениях Р. м. к аддитивным задачам (см.
Аддитивная теория чисел), кроме оценок просеивающей
функции сверху, необходимы оценки этой функции
снизу. Получение оценок снизу может fii.ni, основано
на логическом комбинаторном тождестве
S (Л,; P, *) = ЛГ(Лв)-2Р<г. p6PS(Aqp; P, P).
Наиболее точные оценки снизу получаются с добавле-
добавлением комбинаторных соображений, связанных с ис-
использованием весовых функций. Сильный результат
в приложениях Р. м. с весовыми функциями состоит в
том, что каждое достаточно большое четное число Л'
представимо в виде JV=/) + P2i ГДе Р — простое число,
содержит не более двух простых оже
Лит.: [1] Праха р К., Распределение простых чисел
пер. с нем., М., 1967; [2] Г е л ь ф о н д А. О., Лини и к Ю. В.
Элементарные методы к аналитической теории чисел, М., 1902
[3] Halberstam II., Riclieit Ы., Sieve methods
L.— La. о.], 197'i. Б. М. Бредихин.
РЕШЕТКА в группе Ли — дискретная под-
подгруппа Г группы Ли G такая, что G/V имеет конечный
объем относительно G-инварнантпой меры.
Р. размерности (или ранга) ив вектор-
векторном пространстве V над R или С — свободная абелева
подгруппа в V, порожденная п векторами, линейно не-
независимыми над полем R. Подгруппа аддитивной груп-
группы конечномерного векторного пространства V над R
дискретна тогда и только тогда, когда она является ре-
решеткой [1].
Лит.: [1] Моррис С, Двойственность Понтрягина и отро-
отроение локально-компактных абелевых групп, не]), о аш-л., М.,
1980. А. Л. Онищик.
РЕШЕТКА, структ ур а,— частично упорядочен-
упорядоченное множество, в к-ром каждое двухэлементное под-
подмножество имеет как точную верхнюю, так и точную
нижнюю грани. Отсюда вытекает существование :>тих
граней для всякого непустого конечного подмножества.
Пример ы. 1) Линейно упорядоченное множество
М (или цепь), где для а, Ъ ? М, если а<6, то
sup-{а, Ь} — Ъ, inf {а, Ъ} = а.
2) Подпространства векторного пространства, упоря-
упорядоченные по включению, где
sup {А, В} = {х | х = a-f-.
inf {А, В} — ,
3) Подмножества данного множества, упорлдочеппыо
по включению, где
sup {Л, В}—-А\}П,
inf {Л, Ц)—.А(\Н.
4) Неотрицательные целые числа, упорядоченные но
делимости: а^,Ь, если Ъ~ас для нек-рого с, где sup {я,
Ь} — наименьшее общее кратное а и b, a inf {a, !>} —
наибольший общий делитель а и Ъ.
5) Действительные функции, определенные на от-
отрезке [0, 1] и упорядоченные условием: /-<g, если
(t) <g(t) для всех г?[0, 1], где
sup {/, g} = u,
причем
и (I) -max {/(t), g(t)},
а
inf {/, g} = v,
причем
i>(i)=min{/@, g@b
Пусть Л/ — решетка. Д/ становится универсальной
алгеброй с двумя бинарными операциями, если опреде-
определить
o-b = inf {a, 6}
(вместо + и ¦ часто употребляются символы U и П или
V и Л). Эта универсальная алгебра удовлетворяет сле-
следующим тождественпым соотношениям:
A) a-fa = a; (Г) я-а = я;
B) а + Ь = Ь-|-а; B') а-Ъ^Ь-а;
Наоборот, если М — множество с двумя бинарными
операциями, обладающими перечисленными выше свой-
свойствами A) — D), A')—D'), то на М можно задать поря-
порядок <:, полагая а<6, если а+Ь=6 (при этом окажется,
что а<6 тогда и только тогда, когда а -Ь—а). Возникаю-
Возникающее частично упорядоченное множество будет Р., при-
причем
sup {а, 6} = а-{-Ь, a inf {a, b} = а-Ь.
Таким образом, Р. можно определить как универсаль-
универсальную алгебру, описываемую тождествами A)—D), A')—
D'), то есть Р. образует универсальных алгебр много-
многообразие.
Если частично упорядоченное множество рассматри-
пать как малую категорию, то оно оказывается Р. в том
II только в том случае, когда для любых двух объектов
:>той категории существует их произведение и копроиз-
нрдение.
Если Р и Р' — решетки и / — изоморфизм этих час-
частично упорядоченных множеств, то / является также
изоморфизмом соответствующих универсальных ал-
. ебр, т. е.
f(x + y)=f(x)+f(y) И f{xy)=f(x)-f(y)
^ля любых х, у?Р- Однако произвольное изотопное ото-
отображение решетки Р в решетку Р' не обязано быть го-,
юморфизмом этих Р., рассматриваемых как универ-
универсальные алгебры. Так, для любого а?Р отображения
f(x) — x-\-a и g(x) = x-a — изотонные отображения ре-
решетки Р в себя, являющиеся гомоморфизмами лишь в
том и только в том случае, когда Р — дистрибутивная
решетка. Впрочем, первое из этих отображений являет-
является гомоморфизмол! полурешетки Р с операцией -f-, а вто-
второе— гомоморфизмом полурешетки Р с операцией-. Со-
Совокупность всех Р. образует категорию, если .«орфиз-
.«орфизмами считать гомоморфизмы.
Антигомоморфизм решетки Р i ре-
решетку Р' есть такое отображение /: Р -+¦ Р', что
/(•*-[¦*/) = /(*)•/(*/) и / (х-y) — f (x) +f (У)
для любых х, у?Р. Последовательное выполнение двух
антигомоморфизмов является гомоморфизмом. Частично
упорядоченное множество, алтиизоморфное Р., есть Р.
Под координатизацией Р. понимают на-
нахождение алгебраической системы (чаще, универсальной
алгебры) такой, что данная Р. изоморфна Р. подсистем,
Р. конгруэнции или какой-либо другой Р., связанной с
этой алгебраич. системой или универсальной алгеброй.
Произвольная Р. с 0 и 1 координатизируется частично
упорядоченной полугруппой ее резидуальных отобра-
отображений в себя, оказываясь изоморфной Р. правых анну-
ляторов этой полугруппы. Сама полугруппа является
бэровской, т. е. как правый, так и левый ан-
нулятор каждого из ее элементов порождается идем-
потентом.
Наиболее важные результаты получены для Р., под-
подчиненных тем или иным дополнительным ограничениям
(см. Алгебраическая решетка, Атомная решетка, Брау-
эра решетка, Векторная решетка, Дедекипдова решет-
решетка, Дистрибутивная решетка, Мультипликативная
решетка, Ортомодулярпая решетка. Полная решетка,
Свободная решетка, Решетка с дополнениями, Булева
алгебра). Но отдельным вопросам теории Р. см. Идеал,
Фильтр, Пополнение сечениями. Особую роль играют
алгебраич. образовании, являющиеся в то же время Р.
(см. Структурно упорядоченная группа). Наибольшее
число приложений теории Р. связано с булевыми алгеб-
алгебрами. Другие классы Р. использовались в квантовой
механике и физике.
Появление понятия «Р.» относится к сер. 19 в. и свя-
связано с тем, что многие факты, касающиеся множества
идеалов кольца и множества нормальных подгрупп
группы, выглядят аналогично и могут быть доказаны в
рамках теории дедекиндовых Р. Как самостоятельное
направление алгебры теория Р. сформировалась в
30-х гг. 20 в.
Лит.: [)J Биркгоф Г., Теория решеток, пер. с англ.,
М., 1983; [2] Гретцер Г., Общая теория решеток, пор. с
англ., М., 1982; [3]СалийВ. Н., Лекции по теории решеток,
Саратов, 1970; [4] Скорняков Л. А., Дедекиндовы струк-
структуры с дополнениями и регулярные кольца, М., 19В1; 15] е г о
ш е, Элементы теории структур, 2 изд , М., 1982; [G] Итоги нау-
науки. Алгебра. 1964, М., I960, с. 237—74; [7] Итоги пауки. АлгоО-
ра, топология, геометрия. 1968, М., 1970, с. 101—54; [81 Уии-
рндоченные множества и решетки, в. 3, Саратов, 1975; 1V*J
В 1 у t h Т., J а п о w i t ъ М., Residuation theory, N. Y., 1972.
Л. А. Скорняков.
РЕШЕТКА ПОДАЛГЕБР универсальной
алгебры А — частично упорядоченное (отношени-
(отношением теоретико-множественного включения) множество
Sub А всех подалгебр алгебры А. Для произвольных
A', Y? Sub Л их супремумом будет подалгебра, порож-
порожденная X и Y, а их пнфинумом — пересечение Х[]У'.
Пересечение подалгебр может быть пустым, поэтому
для нек-рых типов алгебр (напр., для полугрупп и ре-
решеток) к числу подалгебр относят и пустое множество.
Для любой алгебры А Р. п. Sub А является алгебраиче-
алгебраической и обратно, для любой алгебраической решетки L
существует алгебра А такая, что LssSub А (теорема
Биркгофа — Фринка). Любая решетка вло-
жиыа в решетку Sub А для нек-рой группы А.
Р. п. Sub A — одна из основных производных струк-
структур, сопоставляемых алгебре А (наряду с такими струк-
структурами, как группа автоморфизмов, полугруппа эндо-
эндоморфизмов, решетка конгруэнции и т. п.). Проблемати-
Проблематика, посвященная изучению связей между алгебрами
и их Р. п. делится на такие аспекты: решеточные изо-
изоморфизмы, решеточные характеристики тех или иных
классов алгебр, исследование алгебр с различными огра-
ограничениями на Р. п. Алгебры А ж В наз. решет очно
изоморфными, если Sub /l~Sub В; всякий изо-
изоморфизм Snb А на Sub В наз. решеточным и з о-
морф измом (или проектированием)
А на Д. Изоморфные алгебры решеточно изоморфны,
обратное же далеко не обязательно. Говорят, что ал-
алгебра А решеточно определяется (в дан-
данном классе Ж), если для любой однотипной с ней алгеб-
алгебры В (из Ж) из Sub fiasSub А следует Вг^А. В некото-
рых случаях (напр., для полугрупп) понятие рогаеточ-
iioii определяемое™ расширяют добавлением в заклю-
заключение импликации условия «или В антиизоморфна Л»,
так как антиизоморфные полугруппы также решеточно
изоморфны. Классический пример решеточной опреде-
ляемости доставляет первая основная теорема проек-
проективной геометрии (см. [1]), где в качестве А рассматри-
рассматриваются векторные пространства над телами. Решеточно
определяющимися являются также всякая абелева груп-
группа, содержащая два независимых элемента бесконечно-
бесконечного порядка, всякая свободная группа (свободная полу-
полугруппа) и группа (полугруппа), нетривиально разло-
разложимая в свободное произведение, всякая нильпотентная
группа без кручения, всякая коммутативная полугруп-
полугруппа с законом сокращения и без идемпотентов, всякая
свободная полугруппа идемпотентов, свободная полу-
полурешетка более чем с двумя свободными образующими.
При этом нередко оказывается, что каждое проектиро-
проектирование алгебры индуцируется ее изоморфизмом (или ан-
антиизоморфизмом). Класс однотипных алгебр Ж может
содержать решеточно не определяющиеся алгебры, но
обладать тем свойством, что из А?Ж и Sub fi=Sub A
вытекает, что В?Ж; в этом случае говорят, что Ж р е-
шеточно определяется (или решеточ-
решеточно замкнут); если при этом алгебры В берутся
только из класса q$, to к соответствующему термину
добавляют «в классе о#>>. Среди решеточно замкнутых
классов — класс всех разрешимых групп.
Многие ограничения, накладываемые на изучаемые
алгебры, формулируются в терминах Р. п.; классиче-
классический пример — условия минимальности и максималь-
максимальности для подалгебр. Sub Л удовлетворяет условию мак-
максимальности тогда и только тогда, когда все подалгебры
в А конечно порожденные (см. также Группа с условием
конечности, Полугруппа с условием конечности). В ка-
качестве других накладываемых на Р. п. ограничений рас-
рассматриваются такие теоретико-решеточные свойства
как дистрибутивность, модулярность, различные виды
полумодулярности, условие Жордана — Дедекинда, до-
дополняемость, относительная дополняемость и т. д.
Напр., для группы А Р. п. дистрибутивна тогда и только
тогда, когда А локально циклическая (теорема
О р е); условия дистрибутивности изучены и в случае
полугрупп, ассоциативных колец, модулей, алгебр Ли
и др.
Наряду с изоморфизмами Р. п. рассматриваются д у а-
л и з м ы (т. е. антиизоморфизмы), гомоморфизмы. В
случае, когда А — топологическая алгебра, наиболее
естественно сопоставлять ей решетку всех замкнутых
подалгебр; соответствующая проблематика также ак-
активно разрабатывается.
Лит.: [1] Б э р Р., Линейная алгебра и проективная геомет-
геометрия, пер. с англ., М., 1955; [2] С у д з у к и М., Строение груп-
группы и строение структуры ее подгрупп, пер. с англ., М., 1980;
[3] С к о р н я к о в Л. А., Дедекиндовы структуры с дополне-
дополнениями и регулярные кольца, М., 1961; [4] К о н II., Универсаль-
Универсальная алгебра, пер. с англ., М., 1908; [5] С а д о в с к и й Л. Е.,
«Успехи матем. наук», 1908, т. 23, в. 3, с. 123—57; L6J А р ш и-
н о в М. II., С а д о в с к и й Л. Е., там же, 1972, т. 27, в. 6,
с. 139—80; [7] Ш е в р и н Л. Н., «Сибирск. матем. ж.», 11H2,
т. 3, №3, с. 440—4 70; [8] Итоги науки. Алгебра. 1904, М.,
1906, с. 237—74; [9] Итоги науки. Алгебра. Топология. Геомет-
Геометрия. 1968, М., 1970,с. 101—54; [10] Упорядоченные множества
и решетки, в. 3, Саратов, 1975, с. 50—74. Л.Н.Шеврин.
РЕШЕТКА С ДОПОЛНЕНИЯМИ — решетка L
с нулем 0 и единицей 1, в к-рой для любого элемента а
существует такой элемент Ъ (наз. дополнением
элемента а), что a\Jb—\ и ал 6=0. Произвольную
решетку можно вложить в решетку, каждый элемент
к-рой обладает единственным дополнением. Если для
любых a, 6?L интервал [а, Ь] является Р. с д\, то L наз.
решеткой с относительными допол-
дополнениями. Каждая модулярная Р. с д. является
решеткой с относительными дополнениями. Решетка L
с нулем 0 называется: а) решеткой с частич-
частичными дополнениями, если каждый ее интер-
интервал вида [0, а\, a?L, является Р. с д.; б) р е ш е т к о и
со слабыми дополнениями, если для лю-
любых а, b?L существует такой элемент с^L, что аЛс=0
и бЛс^О; в) решеткой с полудополнени-
полудополнениями, если для любого a?L, аф\, существует такой
элемент b?L, ЬфО, что алЬ=0; г) р с m e т к о и с
псевдодополнениями, если для любого
a?L существует такой элемент а*, что аЛх=0 тогда и
только тогда, когда х<а*; д) решеткой с квази-
квазидополнениями, если для любого x?L сущест-
существует такой элемент y?L, уфх, что xW у является
плотным элементом. Большую роль играют также решет-
решетки с ортодополнениями (см. Ортомодулярная решет-
решетка). О связи между различными типами дополнений в
решетках см. [4].
Лит.: [1] Б и р к г о ф Г., Теория структур, пер. с англ.,
М., 1952; [2] С к и р н я к о в JI. А., Элементы теории структур,
2 изд., М., 1982; [3] е г о ж е, Дедекиндовы структуры с допол-
дополнениями и регулярные кольца, М., 1961; [4] G r i 1 1 е t P. А.,
Varlet J. С, «Bull. Soe. roy. Sci. Liege», 1967, t. 3G,
№ 11 — 12, p. 628—42. Т. С. Фофанова.
РЕШЕТОЧНО УПОРЯДОЧЕННАЯ ГРУППА — то
же, что структурно упорядоченная группа.
РЕШЕТЧАТОЕ РАСПРЕДЕЛЕНИЕ — дискретное ве-
вероятностное распределение, сосредоточенное на мно-
множестве точек вида a-\-nh, где А>0, а — действительное
число, га=0, ±1, ±2, ... . Число h наз. шагом P.p.,
и если ни при каких аг и ht1>h распределение не сосредо-
сосредоточено на множестве вида a^nh^ и—О, ±1, ±2, ... ,
то шаг h наз. максимальным. Частным случаем
Р. р. является арифметич. распределение.
Для того чтобы вероятностное распределение с харак-
теристич. функцией /(*) было решетчатым, не-
необходимо и достаточно, чтобы существовало действи-
действительное число to^O такое, что |/(@)| = 1; причем h яв-
является максимальным шагом тогда и только тогда, ког-
когда |/(/)|<1 при 0<г<2л/А и |/Bл/й)| = 1. Характери-
стич. функция Р. р. является периодич. функцией.
Формула обращения для Р. р. имеет вид
*" —2я ]\t
\t\<nlhe
гДе Рп — вероятность, к-рую Р. р. приписывают точке
а-\-пЛ, f(t) — соответствующая характеристич. функ-
функция. Справедливо также равенство
Свертка двух Р. р. с тагами h1 и h2 является Р. р.
тогда и только тогда, когда hjh2 — рациональное число.
При исследовании предельного поведения сумм неза-
независимых случайных величин, имеющих Р. р., основной
результат центральной предельной теоремы о сходимо-
сходимости к нормальному распределению существенно допол-
дополняется локальными теоремами для Р. р. Простейшим
примером локальной теоремы для P.p. является Лапла-
Лапласа теорема. Ее обобщением служит следующее утверж-
утверждение: пусть Xlt X%, ...— последовательность незави-
независимых одинаково распределенных случайных величин
с BXj — m, DXj = ct2 и Sk=X1-\-...JrX/l и Х1 принимает
значения вида a-\-nh, /г>0; тогда если
для выполнения при к —>- оо предельного соотношения
' ka+nh-km ', .
-О
равномерно относительно п, необходимо и достаточно,
чтобы шаг h был максимальным.
Лит.: [1] Г н е д е н к о Б. В., Курс теории вероятностей,
5 изд., М., 1969; [2] П е т р о в В. В., Суммы независимых слу-
случайных величин, М., 1972; [3] Прохоров Ю. В., Роза-
Розанов Ю. А., Теория вероятностей, 2 изд., М., 1973.
Н. Г. Ушаков.
РИБОКУРА КОНГРУЭНЦИЯ — конгруэнция пря-
прямых, развертывающиеся поверхности к-рой секут ее
среднюю поверхность по сопряженной сети линий.
Пусть 5 — средняя поверхность Р. к. Тогда сущест-
существует семейство поверхностей, к-рые соответствуют по-
поверхности S ортогональностью линейных элементов и в
каждой паре соответствующих точек имеют нормаль,
параллельную лучу конгруэнции. Наоборот, если зада-
задана пара поверхностей S и S, соответствующих ортого-
ортогональностью линейных элементов, то конгруэнция, об-
образованная лучами, проходящими через точки поверх-
поверхности S и коллинеарными нормалям поверхности S в
соответствующих точках, является Р.к. со средней по-
поверхностью S. Поверхность S наз. образующей
поверхностью Р.к. Линии кривизны образую-
образующей поверхности S соответствуют тем линейчатым по-
поверхностям конгруэнции, линии сжатия к-рых пересе-
пересекают луч в центре. Развертывающиеся поверхности
Р. к. соответствуют асимптотич. линиям образующей
поверхности S. У нормальной Р. к. образующая по-
поверхность минимальная. Такая конгруэнция образована
нормалями поверхности с изотермическим сферич. из-
изображением линий кривизны.
Конгруэнция впервые рассмотрена А. Рибокуром
(A. Ribaucour, 1881).
Лит.: [1] Фиников С. П., Проективно-дифференциаль-
ная геометрия, М.— Л., 1!>37; [2] е г о же, Теория конгруэн-
конгруэнции, М.— Л., 1950. ~ " ¦'
РИБОКУРА КРИВАЯ — пло-
плоская кривая, радиус кривизны
И к-рой в произвольной точке
М пропорционален длине отрез-
отрезка нормали МР (см. рис.). Урав-
Уравнение Р. к. в декартовых пря-
прямоугольных координатах:
, р ру
В. С. Малаховский.
JL _1
\
где ге~ мр . Если n=l/A (h — любое целое число), то
И
параметрич. уравнения Р. к.:
V sin"» + 1tdt, y^C sinm + 1 t,
где т——(n-\-i)n. При т = 0 Р. к. есть окружность, при
т=1 — циклоида, при ти = —2 — цепная линия, при
т=—3 — парабола.
Длина дуги Р. к.:
l = (m + i)C V sin« t dt;
радиус кривизны:
/? = — (m+ljCsin"» t.
Эту кривую исследовал А. Рибокур (A. Ribaucour,
1880).
Лит.: [1] С а'в е л о в А. А., Плоские кривые, М., I960;
[2] F а ш е в с к и й П. К., Курс дифференциальной геометрии,
4 изд., М., 1956. Д. Д. Соколов.
РИККАРТОВО КОЛЬЦО левое, левое РР-к о л ь-
ц о,— кольцо, в к-ром левый аннулятор любого эле-
элемента порождается идемпотептом (симметричным обра-
образом определяются правые Р. к.). Р. к. характери-
характеризуются проективностью всех главных левых (правых)
идеалов. Риккартовыми являются регулярные, бэров-
ские и полунаследственные кольца. Левое Р. к. не
обязано быть правым Р. к. Может не быть риккартовым
и кольцо матриц над Р. к. Кольца эндоморфизмов всех
свободных левых Я-модулей суть Р. к. тогда и только
тогда, когда Я наследственно слева. Все эти кольца
будут правыми Р. к. в том и только в том случае, когда
R наследственно слева, совершенно слева и когерентно
справа. Сами же кольца эндоморфизмов при этих усло-
условиях оказываются бэровскими (см. Регулярное кольцо).
Коммутативное кольцо R является Р. к. тогда и только
тогда, когда его полное кольцо частных регулярно в
смысле Неймана и для всякого максимального идеала
lit кольца R кольцо частных Нт не имеет делителей ну-
нуля. Кольцо многочленов над коммутативным Р. к. яв-
является Р. к.
Кольцо с инволюцией * наз. риккартовым
¦ -кольцом, если левый аннулятор любого элемен-
элемента порождается проекцией, т. е. таким элементом е,
что е=-е-—е*. Аналогичное свойство для правых анну-
ляторов при этом выполняется автоматически. Проек-
Проекции риккартова *-кольца образуют решетку. Эта ре-
решетка полна в том и только в том случае, когда проек-
проекцией порождается аннулятор любого множества. Такие
кольца наз. бэровскими «-кольцами.
Термин «Р. к.» введен в честь Ч. Риккарта, рас-
рассмотревшего соответствующее свойство в кольцах опе-
операторов (см. [1]).
~ 1.: [1] R
Лит.: [1] R i с k a r t С. Е., «Ann. math.», 1946, v. 47, Г'
1972
528—50; [2] В е г Ь е г i a n S. К., В а е г «-rings, В— [а. и.,
1972; [3J К а р 1 a n s к у I., Rings of operators, N. Y.— Amst.
1968; [4] Итоги науки и техники. Алгебра. Топология. Геомет
рия, т. 15, М., 1981, с. 31 —134. Л. А. Скорнякои
РИККАТИ УРАВНЕНИЕ — обыкновенное диффе-
дифференциальное уравнение 1-го порядка вида
z'+az2 = bta, A)
где а, Ъ, а. — постоянные. Впервые это уравнение ис-
исследовал Я. Риккати A723, см. [1]); отдельные частные
случаи рассматривались раньше. Д. Бернулли (D. Ber-
Bernoulli, 1724—25) установил, что уравнение A) интегри-
интегрируется в элементарных функциях, если <х=—2 или а=
= —ikBk— 1), где к— целое число. Ж. Лиувилль
(J. Liouville, 1841) доказал, что при других значениях а,
решение уравнения A) нельзя выразить в квадратурах
от элементарных функций. Общее решение уравнения
A) может быть записано с помощью цилиндрически*
функций (см. [1]).
Дифференциальное уравнение
z'=-2a(t)z + h(t)-c(t)z\ B)
где a(t), b(t), c(t) — непрерывные функции, наз. о б-
щим уравнением Риккати (в отличие от
него уравнение A) наз. специальным уравне-
уравнением Риккати). При с(г)=О общее Р. у. является
линейным дифференциальным уравнением, при Ъ (?)&
^sO — Бернулли уравнением; решения этих двух урав-
уравнений находятся в квадратурах. Изучены также другие
случаи интегрируемости общего Р. у. (см. [2]).
Уравнение B) тесно связано с системой дифференци-
дифференциальных уравнений:
x' = a(t)x+b(t)y, \ ,3
y' = c(t)x-a(t)y. f К '
Если (j?(t), у (I)) — решение системы C) при t?I=(t0, tt)
и y(t) не обращается в нуль на /, то z=x(t)y~1{t) есть
решение уравнения B); если z(t) — решение уравнения
B), a y(t) — решение уравнения
y'=~-[c(t)z(t)-a(t)}y,
то пара (x(t)=--z(t)y(t), y(t)) является решением систе-
системы C). В частности, решения уравненияB) при с(/)---!
связаны с решениями уравнения
равенством z(i) = j/'(i)'/~1(t)i если У(*) не обращается
в нуль на /. В силу отмеченной связи, уравнение B)
часто привлекается для исследования колеблемости,
неосцилляции, приводимости и многих других вопро-
вопросов качественного поведения линейных уравнений и
систем 2-го порядка (см. [3], [4]).
Уравнение
Z'-A(i)Z+B(t)-ZC(t)Z-ZD(t), D)
где ZsssZ (t) — неизвестная (/( X т)-матрица-функция, а
матрицы-функции А, В, С, D имеют размеры пХп,
пХт, тХп, тХт соответственно, наз. матрич-
матричным уравнением. Р и к к а т и. Решения Z (t)
матричного Р. у. D) связаны с решениями (X (t), Y (())
матричной линейной системы:
(t)Y, \
D(t)Y I K>
равенством X (t)~ Z (t)Y (t).
Матричное Р. у. играет важную роль в теории линей-
линейных гамильтоповых систем, вариационном исчислении,
задачах оптимального управления, фильтрации, ста-
стабилизации управляемых линейных систем и др. (см. [6],
[7]). Напр., оптимальное управление ы0 в задаче мини-
минимизации функционала
zT('i) Фх (<!))+ [','[xJ(t) М (t) х @+ит@ N @ и (Л] dt
на решениях системы
x' = A(t)x + n (t) и, x(to)=xa,
((яХи)-матрицы Ф, М(t) симметричны и неотрицатель-
неотрицательно определены, а (тХт)-матрица N(t), положительно
определенная при t?[t0, tt]), дается ранеигпюи
ut)(t)^~N-^(t)BT(t)Z(t)x,
где Z(t) — решение матричного Р. у.
Z'=— ZA(t)— AT(t)Z-\-ZB(t)N-1(t) BJ(t)Z — M(t) F)
с граничным условием Z (tj)—Ф (см. [5], [8]).
В задачах управления на бесконечном интервале вре-
времени важными являются вопросы о существовании у
матричного Р. у. неотрицательно определенного огра-
ограниченного на [t0, оо) решения, о существовании периоди-
периодического или почти периодического решения (в случае
периодических или почти периодических коэффициен-
коэффициентов уравпения) и о способах приближенного построения
таких, решений.
IS вариационных задачах с дискретным временем и
задачах дискретной оптимизации аналогом уравнения
D) служит матричное р е к у р р е ц т и о е
уравнение Р и к к а т и
Уравнению D) можно естественным образом поста-
поставить в соответствие динамич. систему на многообразии
Грассмаиа Gm< „ (см. [9]), что позволяет привлечь
к исследованию уравнения D) теорию динамич. систем.
Напр., если матрицы А, И, С, D в уравнении D) пери-
периодичны с периодом ш>0 и 1^1 <|Л,а| <-. .<|Л,„ + т1. где
)>i - мультипликаторы (см. флоке — Ляпунова теоре-
теорема) системы E), то соответствующая динамич. система
порождается диффеоморфизмом Морса — Смейла (см.
Морса — Смейла система), ц потому она структурно
устойчива.
Лит.: [I] E iccati J., Opere, Treviso, 1758 B Aufl., Luc-
Lucca, 17lil—6Г)); [2] Камке Э., Справочник по обыкновенным
дифференцальным уравнениям, иер с нем., 5 изд., М., 1976;
|:t] !•; ii у г и н II. П., Книга для чтения по общему курсу диффе-
]1спцм.1.:1Ы1ыч уравнений, 3 изд., Минск, 1979; 14] его же,
. liini'iinue системы обыкновенных дифференциальных уравне-
уравнений, Минск, 1UU3; [5] R e i d W. Т., Kiecati differential equati-
equations, N. Y.-~ L., 1972; [6] К а л м а н Р., Ф а л б П., А р б и б М.,
Очерни но математической теории систем, пер. с англ., М., 1971;
L7) Л и о н с Ж.-Л., Оптимальное управление Системами, опи-
описываемыми уравнениями с частными производными, пер. с
франц., М., 1972; [8] 3 а х а р - II т к и н М. X., «Успехи мэтем.
наук», 1973, т. 28, в. 3, с. 83 — 120; [9] S с h n e i d e r С. R.,
«Math. Syst. Theory», 1973, v. 7, Я. 3, p. 281 —8B. E. Л. Гонков.
РИМАНА ГЕОМЕТРИЯ, эллиптическая
геоиетри я,— одна из неевклидовых геометрий,
т. е. геометрич. теория, основанная на аксиомах, тре-
бовапия к-рых отличны от требований аксиом евклидо-
евклидовой геометрии. 13 отлично от евклидовой геометрии в
Р. г. осуществляется одно из двух возможных отрица-
отрицаний аксиомы параллельности евклидовой геометрии:
в плоскости через точку, но инцидентную данной пря-
прямой, пе проходит ни одной прямой, пе пересекающей
данную; другое отрицание евклидовой аксиомы парал-
параллельности осуществляется в Лобачевского геометрии:
в плоскости через данную точку, не инцидентную данной
прямой, проходит по крайней мере две прямые, не пере-
пересекающие данную.
Система аксиом трехмерной Р. г. может быть постро-
построена по основе тех же понятий, что и Гильберта система
аксиом евклидовой геометрии, где в качестве основных
понятий полагаются «точка», «прямая», «плоскость».
«Прямая» и «плоскость» понимаются как нек-рые классы
«точек», а под «пространством» подразумевается сово-
совокупность всех объектов: «точек», «прямых» и «плоско-
«плоскостей».
Система аксиом состоит из четырех групп.
I rpyuua — аксиомы п р и и а д л о ж п о с-
т и — содержит все аксиомы, составляющие I группу
гильбертовой системы аксиом, и, кроме того, допол-
дополняется еще одной аксиомой: каждым двум различным
прямым в плоскости принадлежит одна и только одна
общая им точка.
II группа — аксиомы порядка, или р а-
с и вложения точек на прямой. Аксиомы
этой группы описывают понятно «ралдсленноеть двух
пар точек прямой», с помощью к-рого определяется по-
порядок точек на прямой. П^ Каковы бы ни были три раз-
различные точки А, В, С произвольной прямой, сущест-
существует на отой примой такая точка D, что пара А, В раз-
разделяет пару С, D (обозначается AB^CD). Если АВ-г-
^CD, то все четыре точки А, В, С, D различны. И2.
Если AB-CD, то BA—CD и CD+AB. Н3. Каковы
бы ни были четыре различные точки А , В, С. 1) прямой,
из них могут быть всегда и единственным образом
составлены две разделенные пары. П4. Пусть точки А,
В, С, D, Е лежат на одной прямой, если CD—AB и
СЕ-т-АВ, то пара DE не разделяет пару АВ. НГ). Если
пары CD и СЕ не разделяют пару АВ, то и пара !)!•', пе
разделяет пару АВ (см. П4). Не- Пусть четыре различ-
различные прямые нек-рого пучка пересекаются двумя раз-
различными прямыми соответственно в точках А, В, С, D
и Ах, Вх, Сг, Dlt тогда если AB-t-CD, то и А^В^С^х.
III группа — аксиомы конгруэнтнос-
конгруэнтности — описывает отношение «конгруэнтность» отрезков,
углов и т. д. Под отрезком подразумевается множество
точек прямой, определенное нарой различных точек А,
В этой прямой следующим образом. Вследствие аксиом
II группы на прямой существует такая пара точек М, N,
что AB^-MN; множество точек X, к-рые удовлетворяют
соотношению АВ^-МХ, образуют класс внутренних
точек отрезка, определяемого точками А и В; обозна-
обозначается [АВ]м. Точки прямой, внешние относительно
[АВ]м, образуют взаимно дополнитель-
дополнительный отрезок \АВ]\г, точки А и В паз. концами
отрезков [АВ]ц1 и [Лй]дг. В аксиомах, относящихся к
понятию отрезка, под отрезком подразумевается псегда
класс внутренних точек или всегда класс внешних то-
точек. Ш^ Каждый отрезок конгруэнтен самому себе.
Ш2. Если первый отрезок конгруэнтен второму, то вто-
второй отрезок конгруэнтен первому. Ш3. Если первый
отрезок конгруэнтен второму, а второй конгруэнтен
третьему, то и первый конгруэнтен третьему. III,,.
Из конгруэнтности двух отрезков следует конгруэнт-
конгруэнтность их взаимно дополнительных отрезков. Ш5. Каж-
Каждый отрезок не конгруэнтен своей части. П о л у п р Я'
м ы м и наз. конгруэнтные взаимно дополнительные
отрезки одной прямой. Концы таких отрезков низ. про-
тивоположными точками прямой. П1(!. Для каждой точ-
точки прямой существует ей противоположмая. 11I-. Нее
полупрямые конгруэнтны между собой. 1118. Если от-
отрезок [АВ] конгруэнтен отрезку [/^fij] и точка С есть
внутренняя точка первого отрезка, то внутри второго
отрезка существует такая точка С±, что отрезок [ЛХСХ]
конгруэнтен отрезку [.-1С] и отрезок [CjBj] конгруэн-
конгруэнтен отрезку [67?]. Пусть на сторонах угла, образован-
образованного двумя прямыми, отмечены противоположные точ-
точки относительно вершины угла, тогда отрезком, соот-
соотнесенным углу, наз. отрезок прямой, проходящий через
эти две точки, к-рьш расположен внутри данного угла.
Два угла наз. конгруэнтными, если конгру-
конгруэнтны соотнесенные им отрезки. Ш9. Если в двух тре-
треугольниках ABC и А1В1С1 сторона АВ конгруэнтна
стороне А1В1, а сторона АС — стороне АХСХ., то угод А
конгруэнтен углу Аг тогда и только тогда, если конгру-
штны стороны ВС и В1С\.
IV группа — аксиома непрерывности.
Пусть внутренние точки отрезка [АВ\К разделены на
два класса таких, что 1) каждая точка отрезка попадает
н один из этих классов, 2) каждый класс но пуст, 3) если
ючка X принадлежит первому классу, а точка Y —
нторому, то X — всегда внутренняя точка отрезка
1ЛУ]д[. Тогда на отрезке [АВ]м существует такая точка
С, что всякая внутренняя точка отрезка [ЛС]м принад-
принадлежит первому классу, а всякая внутренняя точка
отрезка [СВ]м —второму.
Имеются и другие системы аксиом Р. г., в основе
к-рых лежат иные основные понятия и отношения (см.,
напр., [3], [5]).
Метрич. свойства Р. г. «в малом» совпадают с метрич.
свойствами нек-рой гиперсферы в соответствующем
евклидовом пространстве. Напр., для любой точки
плоскости Римана существует содержащая эту точку
часть плоскости, изометричная нек-рой части сферы и
¦-мерном евклидовом пространстве, радиус г этой сфе-
сферы — один и тот же для всех плоскостей данного прост-
пространства Римана — наз. радиусом кривизны этого про-
пространства; метрич. свойства 3-мерного пространства
Римана «в малом» совпадают с метрич. свойствами ги-
«ерсферы 4-мерпого евклидова пространства и т. д.
Число /с=1/г? наз. кривизной пространст-
I! а Римана.
Ниже приведены основные факты Р. г. прямой, пло-
¦ кости и 3-мерного пространства.
Прямая Римана (эллиптическая
прямая) — замкнутая конечная линия Э1. Моделью
прямой в евклидовой плоскости Ег может служить ок-
окружность радиуса г с отождествленными диаметрально
противоположными точками. Две различные точки пря-
прямой делят ее на две части. Взаимное расположение то-
точек на прямой определяется с помощью понятия «раз-
деленности двух пар точек». Расстояние между двумя
точками прямой определяется двузначно: меньшее из
пих не превышает яг/2, большее — превосходит яг/2.
Длина всей прямой равна яг. Две точки, расстояние
.между к-рыми равно яг/2, наз. взаимно поляр-
н ы м и; каждой точке прямой соответствует единст-
единственная, полярная ей.
Плоскость Римана (эллиптическая
плоскость) — замкнутая конечная односторонняя
поверхность З2, гомеоморфная листу Мебиуса, граница
к-рого заклеена кругом. Моделью плоскости Р. г. с кри-
кривизной 1/г2 в 3-мерном евклидовом пространстве может
служить сфера радиуса г с отождествленными диамет-
диаметрально противоположными точками. Прямая не разде-
разделяет плоскость на две области.
Всякие две прямые на плоскости обладают общим пер-
перпендикуляром; его длина равна аг, где а — угол между
прямыми, г — радиус кривизны плоскости Римана.
Две различные прямые делят плоскость на две области,
к-рые ii;i:i. у г л ;i м и. Трехсторонник разделяет всю
плоское I'll па 'i оГ>.ч;1сти, i; рыг» ii;i:!. т |> е у г о л ь н п-
К Л М IF.
Метрич. соотношения в треугольнике на плоскости Э".
кривизны 1/г2 выражаются соответствующими соотно-
соотношениями сферич. тригонометрии на сфере радиуса г
в евклидовом пространстве Е3. Вообще, формулы три-
тригонометрии в Э'2 Р. г. тождественны формулам сфериче-
сферической тригонометрии на сфере соответствующего ради-
радиуса в евклидовом пространстве, однако существуют оп-
определенные условия справедливости сферич. формул
на плоскости Э2.
Множество точек плоскости, отстоящих от данной
точки (полюса) на расстоянии л г/2, есть прямая —
поляра полюса. Любая прямая однозначно опре-
определяется своим полюсом и, обратно, определяет свой
полюс. Полюсы прямых, проходящих через данную точ-
точку, располагаются на поляре этой точки, а поляры то-
точек, лежащих на нек-рой прямой, пересекаются в по-
полюсе этой прямой. Взаимно полярные тре-
треугольники имеют вершинами полюсы соответст-
соответствующих сторон. Для двух взаимно полярных треуголь-
треугольников имеет место теорема Шаля о пересечении
в одной точке трех прямых, соединяющих соответствую-
соответствующие вершины этих треугольников. Если вершины тре-
треугольника янляются полюсами его сторон, то его наз.
авто полярным треугольником.
Сумма углов треугольника больше л; ого площадь
?=г2-Д пропорциональна угловому илбытку Д = Л +
-\-B-\-C—я, где г — радиус кривизны плоскости Ри-
мана.
Окружность в З3 — множество точек, распо-
расположенных на одинаковом расстоянии от нек-рой точки
(ее центра). Под радиусом окружности R можно
понимать любой из взаимно дополнительных отрезков
длины Н и лг —Я, обычно выбирается радиус, не боль-
больший л г/2. Окружность является эквидистантой нек-рой
прямой (базы окружности). При R = nr/2 ок-
окружность является прямой — полярой центра.
Длина окружности радиуса R равна 2пг sin (Rlr), a
площадь круга равна 4nr2sin2(if/2r).
Существуют четыре и только четыре окружности,
проходящие через три данные точки, не лежащие на
одной прямой. Две различные окружности могут пере-
пересекаться не более, чем в четырех различных точках.
Площадь всей плоскости Э'1 радиуса кривизны г равна
2яг2.
В Р. г. плоскости имеет место принцип двой-
двойственности: во всяком верном утверждении мож-
можно взаимно заменить термины «точка» и «прямая», в ре-
результате получается верное утверждение.
Пространство Римана трехмерное (э л-
ли н т и чес кое пространство) — замкну-
замкнутое конечное двустороннее (ориентируемое) простран-
пространство 0s. Моделью пространства Э3 в евклидовом прост-
пространстве А'4 может служить гиперсфера радиуса г с отож-
отождествленными диаметрально противоположными точ-
точками. Пространство Римана с радиусом кривизны г
имеет объем я2;-3.
Плоскость не разделяет пространство на две области.
Дво различные плоскости в Э3 пересекаются но прямой.
Прямая, не лежащая в плоскости, пересекает ее в одной
точке.
Множество точек пространства, отстоящих от данной
точки (п о л ю с а) на расстоянии лг/2, есть плоское п. -
поляра полюса. Любая плоскость определяется
однозначно споим полюсам и обратно, определяет свой
полюс. Если три плоскости проходят через одну пря-
прямую, то их полюсы лежат на одной прямой и обратно,
если полюсы трех плоскостей лежат на одной прямой,
то ати плоскости пересекаются по одной прямой. Для
каждон прямой существует такая скрещивающаяся с
ней прямая, что полюсы плоскостей, проходящих через
одну прямую, лежат на другой, а полярные плоскости
точек, лежащих на одной прямой, проходят через дру-
другую. Такие скрещивающиеся прямые наз. взаимно
полярными (взаимные поляры). Две скрещиваю-
скрещивающиеся прямые паз. косыми, если они не являются
взаимными 1голяра.ми или если каждая из них не пере-
пересекает поляру другой. Две косые прямые имеют два
общих перпендикуляра, являющихся взаимными по-
полярами. Если дпа общих перпендикуляра косых пря-
прямых неравнопелики (имеют разные длины), то эти косые
прямые наз. расходящимися, а длины общих
перпендикуляров дают наименьшее и наибольшее рас-
расстояния одной прямой от другой. Две косые прямые,
имеющие бесконечное множество общих перпендикуля-
перпендикуляров одинаковой длины, наз. параллелями
Клиффорда (равноотстоящими, п а-
ратактичными прямыми). Через каждую
точку пространства, лежащую вне данной прямой и вне
полярной ей прямой, проходят две параллели Клиффор-
Клиффорда к даппой прямой. Множество точек, отстоящих от
данной прямой на одном и том же расстоянии, меньшем
яг/2, наз. поверхностью Клиффорда.
Данная прямая наз. осью, а расстояние р точек от оси —
радиусом поверхности Клиффорда. Эта поверхность
имеет две взаимно полярные оси и соответственно два
радиуса, дополняющих друг друга до полупрямой.
Плоскости, проходящие через ось поверхности Клиф-
Клиффорда, пересекают ее по окружности. Через каждую
точку поверхности Клиффорда проходят две прямые,
равноотстоящие от ее осей и целиком принадлежащие
поверхности; эти прямые наз. прямолинейны-
прямолинейными образующими поверхности Клиф-
Клиффорда. Всякие три прямые, равноотстоящие друг от
друга, определяют поверхность Клиффорда, для к-рой
они являются образующими. Каждая пара прямоли-
прямолинейных образующих различных семейств пересекается
под постоянным углом. Поверхность Клиффорда изо-
метрична евклидову ромбу с острым углом, равным углу
между образующими различных семейств, и стороной
длины яг, у к-рого отождествлены точки противополож-
противоположных сторон, соединяемых прямыми, параллельными
другим сторонам. Иными словами, поверхность Клиф-
Клиффорда несет на себе евклидову геометрию. Площадь
поверхности Клиффорда радиуса р равна n2r2sinBp/r).
Сфера в Э3 — множество точек, расположенных
на одинаковом расстоянии от нек-рой точки (ее ц е н т-
р а). Сфера является эквидистантой нек-рой плоскости
(базы сферы). Площадь сферы радиуса R равна
4nr2sin2(/J/r).
В Р. г. пространства имеет место принцип двой-
двойственности: во всяком верном утверждении мож-
можно взаимно заменить термины «точка» и «плоскость»,
в результате получается также верное утверждение.
По-видимому, первое сообщение о Р. г. сделано
Б. Риманом (В. Riemann) в его лекции «О гипотезах,
лежащих в основании геометрии» A854, опубл. 1867,
см. [1]), где Р. г. рассматривалась как риманова
геометрия постоянной положительной гауссовой
кривизны.
Лит.: Ш Р и м а н Б., в кн.: Об основаниях геометрии, М.,
1950, с. 30U—25; L2] Ефимов Н. В., Высшая геометрия, 6
изд., М., 1978; [3] Р о з е н фе л ь д Б. А., Неевклидовы прост-
пространства, М., 1969; [4] Каган В. Ф., Основания геометрии,
ч. 2, М., 1956; [5] Б о г о м о л о в С. А., Введение в неевклидо-
неевклидову геометрию Римана, Л.— М., 1934. Л. А. Сидоров.
РИМАНА ГИПОТЕЗЫ в аналитической
теории чисел — пять гипотез, высказанных
В. Риманом (В. Riemann, 1876) относительно распреде-
распределения нетривиальных нулей дзета-функции ?(s) и от-
относительно выражения через эти нули числа простых
чисел, не превосходящих х (см. Дзета-функция). Не
доказана и не опровергнута одна Р. г.: все нетриви-
нетривиальные нули диета-функции ? (s) лежат на прямой
Re S~V2. Л. Ф. Лаврип.
РИМАНА ДЗЕТА-ФУНКЦИЯ — см. Дзета-функция.
РИМАНА ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ —
линейное однородное обыкновенное дифференциальное
уравнение 2-го порядка в комплексной плоскости, име-
имеющее три заданные регулярные особые точки а, Ь, с
с соответствующими характеристич. показателями а,
а'> Р> Р> У' ?' в этих точках. Общий вид такого уравне-
уравнения впервые выписал Э. Паппериц (Е. Papperitz), из-за
чего оно также наз. Напперица уравнением. Решения
Р. д. у. записываются в виде так наз. Р-ф у н к ц и и
Р и м а н а
fa b с \
\а Р v 4-
U' Р' V' )
Р. д. у. принадлежит Фукса классу уравнений с тремя
особыми точками. Частным случаем Р. д. у. является
гипергеометрическое уравнение (особые точки: 0, 1, оо);
поэтому само Р. д. у. иногда наз. обобщенным
гипергеометрическим уравнением.
Р. Д. у. приводится к Похгаммера уравнению, а потому
решение Р. д. у. можно записать в виде интеграла по
специальному контуру в комплексной плоскости.
Лит. см. при ст. Папперица уравнение. Н. X. Розов.
РИМАНА ИНТЕГРАЛ — обобщение понятия Ноши
интеграла на нек-рый класс разрывных функций,
введенное Б. Риманом (В. Riemann, 1853). Пусть функ-
функция f(x) задана на отрезке [а, Ь] и а— жо<х1<...<г,_1<
<x,-<...<xn=b, i=l, 2, ... , п, хг-х;_1=Лх,-. Сумму
вида
•¦¦+f(tn)(*n-*n-i), A)
где х._1 <|,-<:х,-, наз. интегральной суммой,
отвечающей данному разбиению отрезка [а, Ь] точками
.г,- и выбору точек ?,-. Число / наз. пределом интеграль-
интегральных сумм A) при max Дж,-<8, если для любого е>0 най-
г
дется 8>0 такое, что при max Дж,- —>- 0 справедливо не-
г
равенство \а—/| <е. Если существует конечный предел
/ интегральных сумм при max Ax, -> 0, то функцию
г
/ (х) наз. интегрируемой в смысле Рима-
н а на отрезке [а, Ь] при а<?>, а указанный предел —
определенным интегралом Римана
от функции f(x) но отрезку [а, Ь] и обозначают
$*/(*)<**¦ B)
При а=Ь, по определению, полагают
5>>*.=о,
а при а>Ь определяют интеграл B) с помощью равен-
равенства
Необходимым и достаточным условием интегрируе-
интегрируемости / (х) на [а, Ь\ в смысле Римана являются ограни-
ограниченность f (х) на этом отрезке и равенство нулю Лебега
меры множества всех точек разрыва/(х), содержащихся
на [а, Ь].
Свойства Р. и. 1) Всякая интегрируемая по Ри-
ману на отрезке [а, Ь] функция f(x) ограничена на атом
отрезке (обратное неверно: примером ограниченной и
пеинтегрнруемой на [а, Ь] функции служит Дирихле
функция).
2) Лине иное свойство: для любых постоян-
постоянных а и Р из интегрируемости на [а, Ъ] каждой из функ-
функций / (х) и g (.r) следуют интегрируемость на этом отрез-
отрезке функции [а/(.т)+Pg (я) 1 и равенство
С* [а/ И + Pg (ж)] <fa = a \b f (x) rf^+f3 f b g (x) dx.
3) Из интегрируемости на отрезке [а, Ь] каждой из
функций /(ж) и g(.r) следует интегрируемость на этом
отрезке произведения f(x)g(x).
4) Аддитивность: из интегрируемости функ-
функции f(x) на каждом из отрезков [а, с] и [с, Ь] следуют ин-
интегрируемость /(ж) на отрезке [а, Ь] в равенство
/ И *х = ^ / (х) dx+ J* / (*) dx.
5) Если функции /(х) и g(.r) интегрируемы на [а, Ь]
и если f(x)^g(x) всюду на этом отрезке, то
6) Из интегрируемости на [а, Ь] функции f(x) следуют
интегрируемость аа этом отрезке функции \f{x)\ и спра-
справедливость оценки
Ц*
/(*)<**(< j* \f(x)\dx.
7) Формула среднего значения: если
функции /(.г) и g(x) интегрируемы на [а, Ь], функция
g (x) неотрицательна или неположительна всюду на этом
отрезке, а М и т. — точные верхняя и нижняя грани
/(х) на [а, Ь], то найдется число (г из отрезка m<.\i<.M
такое, что справедлива формула
g(x)dx. C)
Если, кроме того, функция f(x) непрерывна на [а, Ь],
то на этом отрезке найдется точка | такая, что в форму-
формуле C)
8) Вторая формула среднего значе-
значения (формула Бонне): если функция f(x) ин-
интегрируема на [а, Ь], а функция g(х) монотонна на этом
отрезке, то найдется точка g на [а, Ъ) такая, что справед-
справедлива формула
Лит.: [1] R i е щ a n n B. «Gottinger Akad. Abhandl.»,
1868, Bd 13; [2] И л ь и н В. А., П о з н я к Э. Г., Основы мате-
математического анализа, з изд., ч. 1, М., 1971, 2 изд., ч. 2, М., 1980;
[3] Кудрявцев л. Д., Курс математического анализа,
т. 1—2, М., 1981; [4] Никольский С. М., Курс математи-
математического анализа, 2 изд., т. 1—2, М., 1975. В. А. Ильин.
РИМАНА МЕТОД, Римана — Вольтерра
метод,— метод решения Гурса задачи и Коши задачи
для линейных гиш>рболич. тина уравнений 2-го порядка
с двумя независимыми переменными
Lus=uxy-\-a (x, у) их-\-Ь (х, у) иу-\-с (х, у)и^
= 1(х,у)- A)
В Р.м. фундаментальную роль играет функция
Римана Д = Л(.г, у; ?, ц), к-рая при определенных
предположениях Относительно заданных функций а, Ь,
с и / однозначно определяется как решение специаль-
специальной задачи Гурса:
У, I, т))=ехр \у a(l,t)dt;
Г. I, Ti) = exp [Xb{t, i\)dt
для сопряженного уравнения
Функция Л по переменным |, т) является решением
однородного уравнения
a F, r\)Ri + b F, 17) Я„ +<• F, 11) в = 0.
При а— 6=0, e=const функция Д = 0С(
где /0(z) — функция Бесселя порядка нуль.
Функцию Римана можно определить как решение
нагруженного интегрального уравнения Вольтерра:
Я (*, у; I, Т))— [У а (х, т) R (х, т; g, ц) dx—
(t, y)R(t, у; I, i\)dt +
c(f, т)Л(*, т; Б, ti)dT = l. B)
Р. м. решения задачи Гурса реализуется следующим
образом: для любой дифференцируемой до соответству-
соответствующего порядка функции и = и(х, у) имеет место тож-
тождество
^L.[uR(x,y; g, 4I —Я (х, у; l,i\)Lu =
из к-рого интегрированием по частям получается, что
любое решение и уравнения A) представляет собой ре-
решение нагруженного интегрального уравнения:
и (х, y) = R (x, у0; х, у) и (х, уо)-\-
, У, I, У) и (*о, У) — И (*о> У о,
1 Ь V> уо) R С у* *,
x
iL ' ' . . - - . - . „( _¦
СиГ
y Га(х0, т) Л (ж0, т; х, у) —
У a L
dR (x0, t; x, y) ~|
ЙТ J " (*o. T)
Л (/, t; x, y) f{x, x) dx, x > x0, у > y0. C)
Из (З) непосредственно вытекает корректность задачи
Гурса
u (г1 Уо) =ф (х)> u (^0) i/o) =4| (У)| Ф (жо) =ty (^о)
для уравнения A).
Р. м. приводит решение задачи Коши для уравнения
A) с начальными данными на любой гладкой нехаракте-
ристич. кривой к нахождению функции Римана и дает
возможность в квадратурах выписать решение этой
задачи.
Р. м. обобщен на широкий класс линейных гипербо-
лич. уравнений и систем.
Для случая гиперболич. типа системы линейных
уравнений с частными производными 2-го порядка
"л* — иу,,+а{х> У)"х+Ь{х, у)иу + с(х, y)u=-.j(x, у),
где а, Ъ, с — заданные действительные квадратные сим-
метрич. матрицы порядка т, /=(/i, ... , fm) — заданный,
а и = (и1, ... , ит) — искомый векторы, матрица
Римана однозначно определяется как решение
системы нагруженных интегральных уравнений Воль-
Вольтерра вида B), в правой части к-рой стоит единичная
матрица / порядка т.
В. Вольтерра (V. Volterra) впервые обобщил Р, м. на
волновое уравнение
ихх -i-"ui/ —"« = / (*> У, t). D)
Роль функции Римана, позволяющей выписать в квад-
квадратурах решение задачи Коши с начальными данными
на плоскости t= const и задачи Гурса с данными на ха-
рактеристич. конусе для уравнения D), играет функция
где )+1)
Метод предложен Б. Риманом (В. Riemann, 1860).
Лит.: [1] Б и ц а д з е А. В., Уравнения смешанного типа,
М., 1959; [2] Курант Р., Уравнения с частными производ-
производными, пер. с англ., М., 1964; [3] С м и р н о в В. И., Курс выс-
высшей математики, 5 изд., т. 4, М., 1958. А. М. Нахушев.
РИМАНА МЕТОД СУММИРОВАНИЯ — один из
методов суммирования числовых рядов. Ряд У ап
суммируется методом Римана к числу S, если
\S.
inniA2!
7nrJ \
Впервые этот метод ввел и доказал его регулярность
Б. Риман (В. Riemann, см. |1]) в 1854. Р. м. с. приме-
применяется в теории тригонометрич. рядов, где его обычно
формулируют следующим образом; тригонометрич. ряд
-гг + ^, j o.n cos nx-\-bn sin пх
с ограниченными коэффициентами аа, Ъп суммируется
методом Римана в точке j0 к числу S, если функция
г, . . аох* Vе0 ancosnx + bn sinnx
имеет в точке х0 Римана производную, равную S.
Лит.: [1] Риман Б., Соч., пер. с нем., М.—Л., 1948;
[2] Б а р и Н. К., Тригонометрические ряды, М., 1961; [3] 3 и г-
мунд А., Тригонометрические ряды, пер. с англ., т. 1, М.,
1965; [4] Харди Г., Расходящиеся ряды, пер. с англ., М.,
1951. Т. П. Лукашенко.
РИМАНА ОБОБЩЕННАЯ ГИПОТЕЗА — высказы-
высказывание О нетривиальных нулях Дирихле L-функций,
дзета-функций Дедекинда и нек-рых других подобных
функций, вполне аналогичное Римана гипотезе относи-
относительно нетривиальных пулей дзета-функции Римана
?(s). P. о. г. в случае Дирихле L-функций наз. также
расширенной гипотезой Римана.
А. Ф. Лаврик.
РИМАНА ПРОИЗВОДНАЯ, производная
Шварца, вторая симметрическая
производная, функции f(x) в точке ,г0 — предел
D*f (х0) = lim/C + *>-3/('.> + /С-*) .
h0
Введена Б. Риманом (В. Riemann, 1854); он доказал,
что если в точке х0 существует 2-я производная f"(x0),
то существует Р. п. и D2f(x0) — f"(x0). Верхний и нижний
пределы
/ ( йJ/ () f( h)
при h -v 0 наз. соответственно верхней D"f(x0) и ниж-
нижней D_2f(x0) P. п.
Р. п. получила широкое применение в теории пред-
представления функций тригонометрич. рядами; в частно-
частности, в связи с Римана методом суммирования.
Т. П. Лукашенко.
РИМАНА СООТНОШЕНИЕ, билинейные со-
соотношения Риман а,— см. Абелев дифферен-
дифференциал.
РИМАНА СФЕРА — сфера в евклидовом простран-
пространстве R3 (§, т|, t), на к-рую расширенная комплексная
плоскость С отображается взаимно однозначно и кон-
конформно при помощи стереографической проекции.
Напр., в качестве Р. с. можно взять единичную сферу
а плоскость С совместить с плоскостью t=0 так, чтобы
действительная ось совпала с осью г|=— 0, t— 0, а мнимая
ось — с осью |=0, t=0 (см. рис.). Каждой точке z=
=х-\-1уфоэ при стерео-
графич. проекции соот-
соответствует точка сферы
МA, ц, *)=*=Р@, 0, 1),
получающаяся как точ-
точка пересечения луча со
сферой S2, проведенно-
проведенного из северного полюса
сферы Р@, 0, 1) в точку
z; бесконечно удаленной
точке z= оо соответствует северный полюс Р@, О, 1).
Аналитически это соответствие выражается форму-
формулами
2г , Iz|'-1 g + in ,»
Иначе говоря, соответствие (*) определяет дифференци-
дифференцируемое вложение одномерного комплексного проектив-
проективного пространства СР1 в пространство Ra в виде сферы
S2. Во многих вопросах теории функций расширенную
комплексную плоскость отождествляют с Р. с. От ис-
ключительпой роли бесконечно удаленной точки плос-
плоскости С можно избавиться, если за расстояние между
двумя точками z, н;?С принять хордальное,
или сферическое. |) ас стояние %(z, w)
между их образами М, ?
(,, „•) = 2|2-ц'1 , х [z, оо) = 2
Вложение многомерного комплексного проективного
пространства СР", /i>l, в пространство R"<«- -) мож-
можно осуществить при помощи формул комплексно ге-мер-
ной стереографич. проекцлп. обобщающих формулы (*)
(см. [2]).
Лит.: [1] Ш а б а т Б. В., Введение в комплексный анализ,
2 изд., ч. 1—2, М., 1976; [2] Фукс D. А., Введение в теорию
аналитических функций многих комплексных переменных,
[2 изд.), М., 1962. Е. Д. Соломенцев.
РИМАНА ТЕНЗОР — четырехвалентный тензор,
рассматриваемый в теории кривизны пространств.
Пусть Ln — пространство аффинной связности, Г;/ —
объект связности пространства /_,„, компоненты (коор-
(координаты) Р. т., один раз контраиарпантпого и трижды
ковариаптного. имеют вид
Rik, i =-^k~-^i Г'р] ftf + ГйрГ,,-,
l, к, i, 9 = 1, 2, . .., и,
где —g — символ дифференцирования по пространст-
пространственной координате xk, к=\, ... , п. В римановом прост-
пространстве Vn с основным метрич. тензором g,y, кроме
тензора R%y ,-, рассматривается четырежды ковари-
антный Р. т.', получаемый опусканием верхнего индек-
индекса q с помощью метрич. тензора
Здесь Г*/=Г/,-, так как У„ снабжено римановой связ-
связностью (без кручения). В произвольном пространстве
с аффинной связностью без кручения координаты Р. т.
удовлетворяют тождеству Рпччп
т.е. циклирование по трем первым (нижним) индексам
дает пуль.
Р. т. обладает следующими свойствами:
1) Rlki ,7 = Л,7, lk; 2) Я? « = - Я?, ы;
если оба индекса одной пары одинаковы, то соответст-
соответствующая координата равна нулю: Raa, ;==0;.
5) для абсолютных производных Р. т. имеет место
тождество Бианки
где v« — символ ковариантного дифференцирования
по координате хт. Аналогичное тождество имеет место
и для тензора R^, «/¦
Р. т. имеет всего ге4 координат, где и —- размерность
пространства, из них п2(п2—1)/12 существенных, между
к-рымц нет тождественных зависимостей, вытекающих
из указанных свойств.
В случае п=2 Р. т. имеет одну существенную коорди-
координату -й12,12, к-рая входит в определение внутренней,
или римановой, кривизны поверхности A'— d^' lz (см.
Гауссова кривизна).
Р. т. был определен Б. Риманом (В. Riemann) в 1861
(опубл. в 1876).
Лит.: [1] Р а ш е в с к и й П. К., Риманова геометрия и тен-
тензорный анализ, 3 изд., М., 1967; [2] Эйзенхарт Л. П.,
Риманова геометрия, пер. с англ., М., 1948; L3] Г р о м о л Д.,
Клингенберг В., М е й е р В., Риманова геометрия в це-
л.:м, пер. с нем., М., 1971. Л. А. Сидоров.
РИМАНА ТЕОРЕМА — 1) Р. т. о конформном
отображении: каковы бы ни были две односвяз-
ные области Gt и <?2 расширенной комплексной плоско-
плоскости С, отличные от С, а также от С с какой-либо ис-
исключенной из нее точкой, найдется бесконечное число
аналитических и однолистных в области Gt функций,
каждая из к-рых осуществляет взаимно однозначное и
конформное отображение G1 на G2. При этом для любой
лиры точек а?ОиаФ<х>, и b?G2 и любого действительно-
действительного числа а, 0 <:а<:2л, найдется, ивритом единственна я,
функция / этого класса, для к-рой f(a)=b, arg/'(a) — a.
Условие arg f'(a)~a геометрически означает, что каж-
каждый бесконечно .малый доктор, выходящий из точки а,
при отображении w—j{z) переходит в бесконечно малый
нектор. направление к-рого образует с направлением
исходного вектора угол а.
Р. т. является основной в теории конформных ото-
отображений и вообще в геометрич. теории функций
комплексного переменного. Вместе со своими обоб-
обобщениями на многосвязные области она имеет обшир-
обширные применения в теории функций комплексного
переменного, математич. физике, теории упругости,
аэро- и гидромеханике, электро- и магнитостатике
и т. д. Эта теорема для более общего случая односвяз-
ных и, вообще говоря, неоднолистных областей над ком-
комплексной плоскостью была сформулирована Б. Рима-
Риманом (В. Riemann, 1851). При этом вместо условий
нормировки <</(а)=6, arg/'(a) = a» конформного отобра-
отображения w=f(z), обеспечивающих его единственность, в
формулировке Б. Римана для той же цели использова-
использовались условия <</(a)=fe, /(?) = <»», rflea^Gj, b?G2, а ^и
со — наперед заданные точки гранид областей Gx и G2
соответственно. Последние условия при современном
определении понятия односвязной области не всегда
корректны. Б. Риман доказывал свою теорему в значи-
значительной степени исходя из физич. представлений, к-рые
его также убедили в важности этой теоремы для прило-
приложений. В современном понимании математич. строгость
доказательству Б. Римана придал Д. Гильберт (D. Ш1-
bert), обосновавший использованный Б. Риманом в его
доказательстве т. н. Дирихле принцип.
См. также Конформное отображение.
Лит.: 11] Рима и В., Соч., пер. с нем., М.—Л., 1948,
с. 49—87; [2] II р и в а л о в И. И., Введение в теорию функций
комплексного переменного, 12 изд., М., 1977; [3] Г о л у-
з и н Г. М., Геометрическая теория функций комплексного пере-
переменного, 2 изд., М., 196Й. Е. П. Должен то.
2) Р. т. о перестановке членов ряда:
если ряд, члены к-рого являются действительными чис-
числами, сходится, но не абсолютно, то каково бы ни было
число А, можно так переставить члены этого ряда, что
сумма получившегося ряда будет равна А . Кроме того,
члены ряда можно так переставить, что его сумма будет
равна одной из наперед заданных бесконечностей со
знаком -j-oo или —оо, а также так, что его сумма не
будет равна ни -j-oo, ни —оо, но последовательность его
частичных сумм будет бесконечно большой, и, наконец,
так, что последовательность его частичных сумм не
будет иметь ни конечного, ни бесконечного предела
(СМ. Ряд). Л. Д. Кудрявцев.
РИМАНА ТЕТА-ФУНКЦИЯ — суперпозиция
тета-функций 1-го порядка Q/j(u), u~- (mj, ... , Up),
с полуцелыми характеристиками И и абелевых интегра-
интегралов 1-го рода, примененная Б. Риманом (В. Riemann,
1857) для решения Якоби проблемы обращения.
Пусть F (и, w)=0 — алгебраич. уравнение, опреде-
определяющее компактную риманову поверхность F рода р',
фх, ... , ф^ — базис абелевых дифференциалов 1-го рода
на F с матрицей периодов размера рХ2р:
О ... О аи а12 ... а1р
О
А || =
О 0 ... J4 Upi Up2 ¦ . . Upp
Пусть
u(w)=(u1(u>i) = Р'фь ¦•¦' UP (wp) = \ ~РФ/
— вектор базисных абелевых интегралов 1-го рода, где
(clt ... , Ср) — фиксированная система точек на F, а ш=
= (ш1, ... , wp) — текущая система точек на F. Для
любой тета-характеристики
hi ... h
p
h'p
где целые числа hh he принимают только значения О
или 1, можно построить тета-функцию 0//(") с матрицей
периодов W, причем Qfj(u) удовлетворяет основным со-
соотношениям:
\ A'
где ер, есть |х-я вектор-строка единичной матрицы Е,
1-1=1, ... , р-
Если z=(z1, ... , zp) — нек-рый фиксированный век-
вектор в комплексном пространстве Ср, то тета-функ-
ция Римана Ф//(ш) представляет из себя супер-
суперпозицию
ФнМ-ей(«м-2). B)
В области F*, получающейся из F после удаления раз-
разрезов вдоль циклов a]b1 ... apbp базиса гомологии F,
Р. т.-ф. B) всюду определены и аналитичны. При пере-
переходе через разрезы Р. т.-ф., вообще говоря, умножаются
на мультипликаторы, значения к-рых определяются из
основных соотношений A). Особую роль при этом игра-
играет тета-функция 1-го порядка Q(u)=Q0(u) с нулевой
характеристикой Н~0. Именно нули тI? ... , цв соот-
ветствующей Р. т.-ф. Ф(ю)=Ф0(и;) определяют реше-
решение проблемы обращения Якоби.
Для фактич. построения аналитич. выражений, ре-
решающих проблему обращения, используются отноше-
отношения Р. т.-ф. вида Чг//(ю)=в//(гг (w)) с общим знаменате-
знаменателем ? (w)=&(u(w))=Q0(u(w)). Из A) видно, что такие
отношения 4r//(w)/4f (w) могут иметь в качестве нетри-
нетривиальных мультипликаторов только —1, а квадраты
этих отношений являются однозначными мероморфны-
ми на F функциями, т. е. рациональными функциями
точки поверхности F. Используемые при этом квадраты
и другие рациональные функции от отношений тета-
функций представляют собой специальные абелевы
функции с 2р периодами. Специализация выражается
в том, что р(р-\-1I2 различных элементов a^v симмет-
рич. матрицы А при р >3 связаны определенными соот-
соотношениями, налагаемыми конформной структурой по-
поверхности F, так что независимых среди них остается
Р. т.-ф., построенные для случая гиперэллиптич.
поверхности F, когда F(u, w) = w2—P(u), где Р (и) —
многочлен степени и>5 без кратных корней, иногда вы-
выделяются под названием гиперэллиптиче-
гиперэллиптических тета-функций.
Лит.: [1] Чеботарев Н. Г., Теория алгебраических
функций, М.— Л., 1948, гл. 9; [2] М а р к у ш е в и ч А. И.,
Введение в классическую теорию абелевых функций, М., 1979;
13] Krazer A., Lehrtmcli der Thetafunktionen, Lpz., 1903;
L4] С о n f о r t о F., Abelsche Punktionen und algebraische Geo-
metrie, В., 1956. E. Д. Соломенцев.
РИМАНА ФУНКЦИЯ — 1) P. ф. в теории три-
тригонометрических рядов — функция, вве-
введенная Б. Риманом (В. Riemarm, 1851) (см. [1]} для изу-
изучения вопроса о представимости функции тригономет-
рич. рядом. Пусть дан ряд
с ограниченными последовательностями {«„}, {Ьп}.
Функцией Римана для этого ряда наз. функ-
функция F (х), полученная почленным двукратным интегри-
интегрированием данного ряда:
С, D = const.
Теоремы Римана. 1) Пусть ряд (*) сходится
в точке х0 к числу S. Тогда производная Шварца
ZJF(x0)=5. 2) Пусть ат 6,,-vO при п->¦ оо. Тогда в
любой точке х
lira F(x+ft> + F(x-ft>-2* W _q
П
причем сходимость на любом промежутке равномерная,
то есть F(х) — равномерно гладкая функция.
Если ряд (*) сходится на [0, 2я] к /(ж) и
f(x)?L [0, 2я], то D2F(x)^f(x) на [0, 2л] и
F (х) = fat ^[f [и) du+Cx+D.
Пусть ап, Ьп ->- 0 при п —>- оо и пусть
S_(x) — lim Sn (x) и 5 (х) = Шп Sn (x)
и —*• ос п -*¦ ав
конечны в точке х, а
s<*) = тE (*)+5"(*)), в (*) = 4(* (*)-?(*)).
Тогда нижняя и верхняя производные Шварца D2F(.r)
и D2F (х) принадлежат [5—цб, 5+цб], где |д — нек-рая
абсолютная постоянная (лемма Дюбуа-Рей-
м о н а).
Лит.: И] Риман Б., Соч., пер. с нем., М.— Л., 1948'.
Г2] Бари Н. К., Тригонометрические ряды, М., 1961.
А. А. Нонюшнов.
2) Р. ф. в теории дифференциальных
уравнении — см. Римана метод.
РИМАНА — ГИЛЬБЕРТА ЗАДАЧА— см. Гранич-
Граничные задачи теории аналитических функций.
РИМАНА — ГУРВИЦА ФОРМУЛА, формула
Гурвица, соотношение Гурвица, —
формула, связывающая род замкнутой римановой по-
поверхности с числом ее листов и кратностью точек
ветвления. Пусть R — замкнутая риманова поверхность
рода g, R —- накрывающая R риманова поверхность,
имеющая т листов над R, конечное число точек ветвле-
ветвления с кратностями к1, ... , ks и род g. Тогда имеет место
Р.— Г. ф.:
В частности, если риманова поверхность R рассматри-
рассматривается как накрывающая поверхность над Римана
сферой, то g=-0 и Р.— Г. ф. дает соотношение
Р.— Г. ф. позволяет подсчитать род алгебраич. функ-
функции (т. е. род соответствующей рюнановол поверхно-
поверхности), определяемой алгебраич. уравнением F (z, u>)=0.
В более общем понимании Р.— Г. ф. связыиает род g
поля алгебраич. функций с родом g его конечного (се-
парабельного) расширения степени т к индексами ветв-
ветвления ftv (см., напр., |4], |5]).
Р.— Г. ф. была высказана В. Риммном [1] и доказана
А. Гурвицем [2].
Лит.: [1] R i e m a n n В. Gesammelte malliematische
Werke, Lpz., 1876, S. 129; [2] Hurwih A., Mathematische
Werke, Bd 1, Basel, 1932, S. 321—83; [3] Г у р в и ц А., К у-
р а н т Р., Теория функций, пер. с нем., М., 19Н8: I'll II с » а н-
линии Р., Униформизация, пер. снем., М., 1 !iri."i; | г>I .1 i- n r г,.,
Введение в алгебраические и абелевы функции, мер. >• aiir.i.,
М., 1970. К. ( Ciijiu.urmiee.
РИМАНА — КРИСТОФФЕЛЯ ТЕНЗОР — четырех-
валентный тензор, координаты (компоненты) к-povo оп-
определяются объектами Г,-}-* связности пространства,
называемыми Кристоффеля символами 2-го рода. Р.—
К. т. наз. также Римана тензором. .7. л. Сидоров.
РИМАНА — РОХА ТЕОРЕМА — теорема, позволя-
позволяющая выразить эйлерову характеристику % (Е) локаль-
локально свободного пучка Е на алгебраическом или аналитич.
многообразии X в терминах характеристич. классов
Чжэня пучка Е и многообразия X. Она может быть
применена для вычисления размерности пространства
сечений пучка Е (проблема Римана — Роха).
Классическая Р.— Р. т. относится к случаю неособых
алгебраич. кривых X и утверждает, что для любого
дивизора D на А^
где l(D)— dim H°{X, Ox(D)) — размерность простран-
пространства функции J?k(X), для к-рых (/)-)-/.>>(). /\ х кано-
нич. дивизор, a g — род кривой А . I! сер. lil и. li. Ри-
Риман (В. Riemann) аналитич. дагол.мш иолучил нераиен-
ство
Равенство (*) было доказано Э. Рохом (Е. Roch).
Р.— 1'. т. для кривых представляет собой одномер-
одномерный случай более общей теоремы Римана — Роха —
Хирцебруха — Гротендика. Пусть X — неособое про-
проективное многообразие размерности п, а Н'Х — подхо-
подходящая теория когомологий: либо Н'Х — Н'(Х, Q) —
сингулярные когомологий в случае, когда основное
поле /t=C, либо НХ^А (X)®Q, где А (X) — Чжоу
кольцо, либо ИХ — кольцо, присоединенное к кольцу
Гротендика К°(Х) (см. К-фунптор в алгебраической
геометрии) относительно нек-рой специальной у-филь-
трации (см. [2], [7]). Пусть Е —локально свободный
пучок ранга г на X. Для пучка Е следующим образом
определяются универсальные многочлены с рациональ-
рациональными коэффициентами ch (—) и td (—) от классов Чжэня
Cj(E)?H'X пучка Е. Для многочлена Чжэня рассмат-
рассматривается разложение на множители
где а,- — формальные символы. Экспоненциальный ха-
характер Чжэня определяется формулой
и, соответственно, класс Тодда
ch (E) и td (E) — симметрия, функции от о,-, и их можно
записать в виде многочленов от с ,•(?).
Теорема Римана — Роха — Хирцебру-
х а: если X — неособое проективное многообразие или
компактное комплексное многообразие размерности п,
Е — векторное расслоение ранга г на X, то
где Тх — касательный пучок на X, a deg( )„ обозна-
обозначает компоненту степени п в Н'Х. Эта теорема была до-
доказана Ф. Хирцебрухом (F. Hirzebruch) в случае ос-
основного поля С. В случае п=2 и обратимого пучка Е—
~6x(D) она приводит к равенству
=\D (D-Kx) + j^(Kx +et),
где с2—сг(Х) —2-й класс Чжэня поверхности А', а
Кх — ее канонич. класс. В частности, при D — 0 полу-
получается формула Нётера
Для трехмерных многообразий (п=3) теорема приводит
к равенству
В частности, при D = 0
В 1957 А. Гротендик (A. Grothendieck) обобщил
теорему Римана — Роха — Хирцебруха на случай мор-
физмов неособых многообразий над произвольным
алгебраически замкнутым полем (см. [1]). Пусть К0Х
и К°Х — группы Гротендика соответственно когерент-
когерентных и локальных свободных пучков на X. Функтор
КаХ является ковариантным функтором ии категории
схем и собственных морфизмов в категорию абелевых
групп, при этом для собственного морфизма / : X -*- Y
гомоморфизм / : КпХ -v К„У определяется формулой
/.(<F) = 2 (-1)''Я'ЫГЬ
где If — произвольный когерентный пучок на X;
К°Х — контравариантный функтор в категорию колец.
Для регулярных схем с обильным пучком группы
К0Х и К"Х совпадают и обозначаются К(X). Характер
Чжэня ch : К(Х)-+ Н'Х является гомоморфизмом ко-
колец; Н'Х также является ковариантным функтором:
определен гомоморфизм Гизина /* : НX ->- HY.
В случае, когда 1ГХ = Н'(Х, Q), гомоморфизм /* по-
получается из /* для гомологии с помощью двойственно-
двойственности Пуанкаре. Обобщенная А. Гротендиком теорема
выражает меру отклонения от коммутативности гомо-
гомоморфизмов ff и ch.
Теорема Римана—-Роха — Хирцебру-
х а — Г р о т е н д и к а: пусть / : X —>- Y — гладкий
проективный морфизм неособых проективных много-
многообразий; тогда для любого х?К(X) в //'.Y справедливо
равенство
ch(/,(.r))=/#(ch(a;)tdG'/)),
где jT/= Тх—f*(Ty) ? Кх (о т носите л ь н ы и к а-
с а т е л ь н ы й пупок м о р ф и з м а /).
В случае, когда Y — точка, эта теорема сводится к
теореме Римана — Роха — Хирцебруха. Имеются об-
обобщения (см. [5]—[7]) на случаи, когда Y — нётерова
схема, обладающая обильным обратимым пучком, когда
/ — проективный морфизм, слои к-рого — локально
полные пересечения, а также на особые квазипроек-
квазипроективные многообразия.
Нек-рые варианты Р.— Р. т. тесно связаны с пробле-
проблемой индекса аллиптич. операторов (см. Индекса форму-
лы). Напр., теорема Римана — Роха — Хирцебруха
для компактных комплексных многообразий является
частным случаем теоремы Атьи — Зингера об индексе.
Лит.: [1] Боре ль А., С с р р Ж.-П., «Математика»,
1961, т. 5, № 5, с. 17—54; [2] М а н и н Ю. И., «Успехи матем.
наук», 1969, т. 24, в. 5, с. 3—86; [3] X а р т с х о р н Р., Ал-
Алгебраическая геометрия, пер. с англ., М., 1981; [4] X и р ц е о-
р У х Ф., Топологические методы в алгебраической геометрии,
пер. с англ., М., 1973; [5] В a u m P., Fulton W., Mac,
Pherson R. «Publ. Math. IHES», 1975 M, 45, p. 101 — 45;
[61 их же, «Acta math.», 1979, v. 143, № 3—4, p. 155—92;
[7] Theorie des intersections et theor&me de Riemami — Roch
(SGA, A6), В.— [е. a,], 1971, Вал. С. Куликов.
РИМАНА — СТИЛТЬЕСА ИНТЕГРАЛ — см. Стил-
тьеса интеграл.
РИМАНА — ШВАРЦА ПОВЕРХНОСТЬ — мини-
малъная поверхность, натянутая на полигональный
контур, многоугольник. Она представляет собой одно
из первых достаточно общих решений Плато задачи.
Аналитически выражается с помощью Кристоффеля —•
Шварца формулы. Рассмотрена впервые Б. Риманом
(В. Riemann, 1872) и Г. Шварцем (Н. Schwarz, 1874).
М И. Войцеховский.
РИМАНА — ШВАРЦА ПРИНЦИП, принцип
симметрии Римана — Шварц а,— метод про-
продолжения конформных отображений и аналитич. функ-
функций комплексного переменного, сформулированный
Б. Риманом (В. Riemann) и обоснованный Г. Шварцем
(Н. Schwarz) в 19 в.
Р.— Ш. п. для конформных отображе-
отображений состоит в следующем. Пусть области Du ?>2 на
комплексной плоскости С симметричны относительно
действительной оси R и не пересекаются, а их границы
содержат общий интервал ycR, причем D=D1(jy\J
(J?>2 — тоже область. Пусть аналогично определены
Dl, dI, у* и D*. Если функция /х, непрерывная на
-DjUT' конформно отображает D± на Dt и если /i(y)=
=у*, то функция /(z), равная/i(z) при z^DxU7 и /i(z)
при z?D2, осуществляет конформное отображение об-
области D на область D*.
Более общая формулировка Р.— III. п. получается,
когда Dlt D2 и Dv., D2 — области на Римана сфере С,
симметричные относительно окружностей С, С*сС
соответственно, и y(Z.C, усС* — открытые дуги (см.
Симметрии принцип).
Р.— III. п. для голоморфных функций.
Пусть граница области flcC содержит открытый уча-
участок у, к-рый является гладкой вещественно аналити-
аналитической дугой. Если функция / голоморфна в D, непре-
непрерывна в D U у и ее значения на у принадлежат нек-рой
другой гладкой вещественно аналитической дуге у*, то
/ аналитически продолжается 'в нск-рую окрестность
дуги у.
Р.— Ш. п. используется для построения конформных
отображений плоских областей, а также в теории ана-
литич. продолжения функций одного и многих комп-
комплексных переменных.
Лит.: [1] Л а в р е н т ь е в М. А., Ш а б а т Б. В., Ме-
Методы теории функций комплексного переменного, 4 изд., М.,
1973. Е. АГ. Чирка.
РИМАНОВА ГЕОМЕТРИЯ — теория риманова про-
пространства. Римановым пространством
наз. «-мерное связное дифференцируемое многообразие
Мт на к-ром задано дифференцируемое поле ковари-
антного, симметрического и положительно определен-
определенного тензора g ранга 2. Тензор g наз. метриче-
метрическим тензором. Р. г. есть многомерное обобще-
обобщение внутренней геометрии двухмерных поверхностей
в эвклидовом пространстве Е3. Метрика риманова про-
пространства с точностью до первого порядка малости,
по сравнению с размерами рассматриваемой области,
совпадает с евклидовой метрикой. Отличие этих метрик
оценивается (локально) римановой кривизной — мно-
многомерным обобщением понятия гауссово?! кривизны
поверхности в Е'3.
В основании Р. г. лежат три идеи. Первая идея —
осознание факта существования неевклидовой геомет-
геометрии — геометрии Н. И. Лобачевского. Вторая идея —
понятие внутренней геометрии поверхностей, создан-
созданной К. Гауссом (С. Gauss). Третья идея — понятие га-
мерного пространства, разработанное в 1-й пол. 19 в.
Б. Риман (В. Hiemann) соединил и обобщил эти идеи в
лекции «О гипотезах, лежащих в основании геометрии».
Понятия Р. г. сыграли важную роль в создании А. Эйн-
Эйнштейном (A. Einstein) общей теории относительности,
дальнейшее ее развитие связано с созданием аппарата
тензорного исчисления. Р. г. и ее многочисленные об-
обобщения успешно развиваются, особенно в той ее части,
к-рая наз. римановой геометрией в целом, и находят
обширные и глубокие механические и физич. примене-
применения.
Основные понятия Р. г. следующие.
Скалярное произведение. В каждом
касательном пространстве (ТМп) р?М", тензору оп-
определяет скалярное (внутреннее) произведение < •, ¦ >
по формуле
<Х, У> = *(Х, У), X, У?(ТМ")р.
Верно и обратное: если для любого р ? Мп в (ТМп)р оп-
определено скалярное произведение, дифференцируемо за-
зависящее от р, то оно определяет тензорное поле g с ука-
указанными выше свойствами. Степени гладкости Мп и g
варьируются в зависимости от поставленной задачи.
В большинстве случаев достаточно потребовать, чтобы
Мп было трижды непрерывно дифференцируемо, а поле
тензора g — дважды непрерывно дифференцируемо (да-
(далее необходимая степень гладкости указываться не
будет). В локальных координатах {./¦'} с локальным ба-
базисом {б,-}, г=1, ... , га, компоненты тензора g имеют
вид
так что
где
Y/d,.
Риманово пространство как метри-
метрическое пространство. Длина I гладкой
кривой c{t) : [О, 1] —> Мп определяется формулой
где с — касательный вектор к c{t). Длина кусочно
гладкой кривой равна сумме длин ее гладких звеньев.
Если x'--.r'(t) — уравнения c(t) в локальных коорди-
вттах, то
~«i=i at " Jo у -?ji,j=ig4 at at
Имея в виду эту формулу, метрику на М" записывают
в традиционной форме
и ds наз. элементом длины, а функции gn{x) — коэф-
коэффициентами метрической (основной, первой квадратич-
квадратичной) формы. Угол можду двумя кривыми в точке их
пересечения определяется как угол между касательны-
касательными к ним. Объём V(U) области U, принадлежащей ко-
координатной окрестности, определяется формулой
V (U) = [ \g |1/2 dx1... dx",
где g=det \\gjj\\. Обт,ем произвольной области равен
сумме объемов ее частей, причем каждая из частей ле-
лежит в нек-рой координатной окрестности.
Расстояние р(р, q) между точками р, q?Mn
определяется как точная нижняя грань длин всех ку-
кусочно гладких кривых, соединяющих ред. Аналогично
определяется метрика рц в произвольной связной обла-
области U. Два римановых пространства М\ и М" наз.
изометричными, если существует отображение
ф : М" -*¦ М%, при к-ром
рмп(р, A)--=рмП(ц>(р), ф(?)),
или, что то же, Цс)=Ц(р(с)), где с — произвольная кри-
кривая в М\. Если ф — изометрия, то для любой точки
р?М1 с5'Ществует координатная окрестность U^p и
координатная окрестность 6'2Эф(/:>) такие, что g)j(x) =
==Sij(<P(x))> ж€ Ux, i, j — I, ... , п. Иаометрич. отображе-
отображение Мп на себя наз. д в и ж е н и е м.
Кривая с концами в точках р и q наз. кратчай-
кратчайшей, если ее длина равна р(р, q). Стационарная кри-
кривая функционала длины / наз. геодезической
линией. Каждая кратчайшая в Мп есть геодезическая,
и каждая достаточно малая дуга геодезической есть
кратчайшая. Область UcMn на.з. геодезически
выпуклой, если кратчайшие, определенные по
метрике рц, есть геодезические Мп. Если x' — jcl'(t),
z'=l, ... , п,— уравнения геодезической в локальной
системе тсоордннат {•'¦'}, ю функции .r'(t) удовлетворяют
системе уравнений, к-рпя в cjry4ae, |;огда t — параметр,
пропорциональный длине дуги, имеет вид
к
dx n .
где
г
ih'a
— символи Кристоффеля, gab — элементы матрицы,
обратной к WuijW, i, /, к, а, 6=1, ... , п.
Риманово пространство наз. полным (геоде-
(геодезически полным), если оно полно как метрич.
пространство (если любую дугу геодезической можно
неограниченно продолжить в обе стороны). Риманово
пространство полно тогда и только тогда, когда оно
геодезически полно. В полном римановом пространстве
любые две точки можно соединить кратчайшей (не обя-
обязательно единственной). На любом дифференцируемом
многообразии можно ввести структуру полного римано-
ва пространства.
Р и м а н о в о пространство как много-
многообразие со связностью. Ковариантная
производная у наз. симметрической и сов-
совместной с метрикой g пространства М", если
выполняются условия симметричности
VxY-vyX = [X, У]
и совместности
Z<X, Y> = <vzX, Y> + <X, у7Г>,
где X, Y, Z — дифференцируемые векторные поля, а
[X, Y] — их коммутатор. Этими условиями производ-
производная v определяется однозначно через поле метрич.
тензора g. В локальных координатах {.г1} компоненты
связности v имеют вид Tkjii <Vfc^/, #,-> и совпадают
с символом Кристоффеля 1-го рода, а
Аналогичной формулой определяется ковариантная
производная любого тензора.
Векторное поле Y (t) вдоль кривой с (() наз. парал-
параллельным, если V.y=0. Аналитически параллель-
с
ное поле Y (t) определяется решением системы
где x'~x'(t) — уравнения кривой c(t). Решения этой
системы при различных начальных условиях дают отоб-
отображение (TM")cUl) в (ТМп)с{1); оно оказывается изо-
метричным и наз. параллельным перене-
перенесением Л е в и - Ч и в и т а. Результат перенесе-
перенесения зависит, вообще говоря, не только от конечных то-
точек с@) и сA), но и от самого пути сA). Кривая, для
к-рой у г—О, является геодезической, и ото свойство
г
геодезической можно взять за ее определение.
Подмногообразия р п м а н о в а прост-
пространства. Если Мк, &<:«,— дифференцируемое под-
подмногообразие риманова пространства Мп, то в каждом
кисан1 п.ном пространстве к Мк((ТМк)рС(Т'М")р) инду-
lUipyi'ic.M скалярное произведение и тем самым на Мк
возникает структура риманона мространст.' с хммрнч.
тензором а, компоненты к-poro вычисляются но форму-
формулам
где х' = х'(их, ... , м*) — уравнения Мк в локальных
координатах. Внешняя геометрия Л'/*, к^2, описывает-
описывается вторыми квадратичными формами Б(\р), к-рые опре-
определяются для каждой единичной нормали vp к Мк фор-
формулой
B(vp)(X, Y)=-(vxv, Y),
где X и Y — векторные поля на Мк, a v — произволь-
произвольное поле единичных нормалей, содержащее vp. Для
любой формы В (Vp) определяются нормальные кривиз-
кривизны, главные направления и кривизны, средняя и полная
кривизны и т. д. и выводятся уравнения Гаусса — Ко-
дацци — Риччи, связывающие коэффициенты первой
и вторых квадратичных форм. Свойствами вторых форм
характеризуются важные классы подмногообразий,
напр, минимальные, вполне геодезические, выпуклые
и т. п. Для Af'--^e(t) (гладкая криная) строится теория.
аналогичная теории кривых в Еп, определяются пер-
первая, вторая и т. д. кривизны п выводятся уравнения,
аналогичные формулам Френе. Первая кривизна кри-
кривой кг обычно наз. геодезической кривиз-
н о н и вычисляется по формуле
если t — длина дуги; в локальных координатах
где
11! — I >
~dT dt
a x'=xl(t) — уравнения сA).
Большой круг задач Р. г. связан с изометрическими
погружениями одного риманова пространства в другое
и изучением свойств этих погружении. Эти задачи труд-
трудны и исследованы мало (более подробно — в двумерном
случае).
Экспоненциальное отображение
expg : (ТМп)ц —>- Мп определяется условием: exp<jX=
= г, где г — конец дуги геодезической с началом в q, с
направлением X(^(TMn)q и длины |Х|. Если в окрест-
окрестности точки р ввести систему координат, сопоставляя
точке р декартовы координаты точки ехр
то окажется
Гм \x=a = Tjk: i \x=q =0, то есть
= 0, г, /, fr = l, га;
ах1 х=я
это — т. н. (римановы) нормальные коорди-
н а ты.
Кривизна. Если в окрестности точки q ввести
нормальные координаты, то компоненты метрич. тен-
тензора записываются в виде
1 -, и и
ГДе 8ift, /l -> 0 при х' -*¦ 0, i, j, к, 1=\, ... , га. Отсюда
выводится важное свойство римановой метрики: для
любой точки g?Mn экспоненциальное отображение срз
=exp<7 : (TMn)q —> Мп обладает свойством
ХA+г(Х, У)),
где е(Х, Y) -> 0 при |Х|, |У| -> 0. Добиться более вы-
высокого по порядку малости совпадения метрик М" и
(ТМп)ч за счет удачного выбора отображения ср в общем
случае невозможно. Поэтому коэффициенты eikjl ха-
характеризуют отличие метрики М" от евклидовой метри-
метрики (TMn)q. Эти коэффициенты являются компонентами
т. н. тензора кривизны, или тензора
Римана — Кристоффеля (в точке q). В ло-
локальных координатах {ж'} они выражаются через коэф-
коэффициенты метрич. тензора и их первые и вторые произ-
производные по формуле
R.k .,- ' ( 91gn | 92gkJ a?g'7 dZgkl ) |
2 \дхк Ox' dxl dxl dxk dxl dxl dx' )
+ 2a, ft=1 S"" (Г*/\ a Г,'!, Ь-Г«. а, Г,7, „),
i, /, fc, Z, a, b = l, .. ., re.
С тензором кривизны связан целый ряд других понятий,
также (с разных сторон) характеризующих меру отли-
чия метрики Мп от евклидовой. Так, через тензор кри-
кривизны онределяюн я си.юрн Р и ч ч и
и Эйнштейна
где
— т. н. скалярная кривизна Мп.
Трилинейное отображение, сопоставляющее трем
векторным полям X, У, Z поле
R(X, yJ=vK(VjrZ)-VJf(VK2)-V[A'n2,
наз. преобразованием кривизны. Его
свойства:
1) R(X, Y)Z + R(Y, X)Z = 0;
2) R (X, Y)Z + R(Y,Z)X+R(Z, X)Y = 0 (тожде-
(тождество Риччи);
3) <R (X, У) Z, W> = <R (X, Y) W, Z>;
4).<Я(ЛГ, Y)Z, W>^<R(Z, W)X, У>.
Кроме того, имеет место тождество Бианки
Преобразование кривизны можно связать нек-рой кон-
конструкцией с параллельным перенесением. Ллгебраич.
свойства тензора кривизны выводятся из свойств преоб-
преобразования кривизны, т. к. через него, а именно через
«биквадратичную форму» к(Х, У) = <Я(Х, Y)Y, Х>,
тензор кривизны (точнее, его значения на векторах X,
Y, Z, W) однозначно (алгебраически) выражается
(см. Кривизна).
Секционная кривизна. Пусть F2 — дву-
двумерная поверхность в Мп, проходящая через р, а=
= (TF2)p, Г — простая замкнутая кривая на Г2, про-
проходящая через р, S — площадь области на F-, ограни-
ограниченной кривой Г, z? (TF2)p, z — вектор, полученный из
г параллельным перенесением вдоль Г, ф — угол меж-
между вектором z и касательной составляющей вектора г.
Тогда при стягивании Г к точке р существует предел
К (р, a)=lim -^-, к-рый наз. римановой секцион-
секционной кривизной пространства Мп в данной точ-
точке р и в данном двумерном направлении а (Л(р, о) не
зависит от поверхности F2, а зависит только от а). Сек-
Секционная кривизна показывает меру «искривления» М"
в данной точке и в данном двумерном направлении.
Вообще говоря, в разных двумерных направлениях это
искривление различно; но если в каждой точке кривиз-
кривизна К (р, а) не зависит от выбора а, то она не меняется
и от точки к точке (теорема Шура). Тождествен-
Тождественное обращение секционной кривизны в нуль — необхо-
необходимое и достаточное условие того, чтобы М" выло ло-
локально изометрично Еп (в целом оно может отличаться
от Еп). Секционную кривизну М" можно связать и с
другими объектами Р. г., напр, с дефектом (избытком)
геодезич. треугольника (см. Гаусса — Бонне теорема).
Сам Б. Риман определял секционную кривизну как
гауссову кривизну двумерной поверхности ехр^о, вы-
вычисленную по формуле Гаусса в точке р. В свою оче-
очередь, по секционной кривизне метрика Мп определяет-
определяется однозначно в следующем смысле: если у двух много-
многообразий М" и Ml секционные кривизны постоянны и
равны одному и тому же числу а, то М\ и М% локально
изометричны, если они к тому же оба односвязны, то —
просто изометрнчны. Односвязное риманово простран-
пространство постоянной секционной кривизны а изометрично:
«-мерному пространству Лобачевского Л„ при а <0; п-
мерному евклидову пространству Е„ при я—0; «-мер-
«-мерной сфере S" в Еп + 1 радиуса \/У~а при я>0. В общем
случае известен следующий результат. Если М\ —
аналитическое риманово пространство непостоянной
секционной кривизны п существует диффеоморфизм
Ф : Ml -v M", при к-ром К(р, o)~K(q>(p), dip (а)), то
при 7?Js=4 отображение ц> — изометрия; в случае л~3
это утверждение доказано при нек-рых дополнительных
предположениях, а в случае п~2 теорема не верна.
Однако неизвестно A983), кроме двумерного случая, ка-
какова должна быть функция К (р, а), чтобы для нее суще-
существовала метрика g, для к-рой А' (р, а) была бы секцион-
секционной кривизной. В этом направлении известны только
нек-рые отрицательные результаты.
Секционная кривизна связана с преобразованием
кривизны формулой
<Д (^ Y Х Y
к, л -
А{р'а) -
а через компоненты тензора кривизны выражается так:
К (р, о) =
-X'Y1) (XkYl-Xl Yk)
у"
где а определено векторами
Значение тензора Риччи Л,у на векторе X связано с сек-
секционной кривизной следующим образом: пусть векторы
X, Yj, ... , Yn_f образуют ортонормированный базис
в (ТМп)р, тогда
где ak — двумерное направление векторов X и Yk.
Классы римановых пространств.
Помимо общих (произвольных) римановых пространств
существуют римановы пространства, на к-рых могут
быть введены дополнительные структуры. Эти структу-
структуры возникают тогда, когда непосредственно на метрику
или на кривизну накладываются те или иные условия
геометрического или алгебраич. характера. Таким
способом определяются важные классы римановых
пространств: многообразия постоянной секционной кри-
кривизны (см. Пространственные формы), однородное про-
пространство, симметрическое пространство, эрмитовы и
кмеровы многообразия, пространства Эйнштейна и т. д.
Обобщения. Развитие идей Р. г. и геометрии
в целом привело к ряду обобщений понятия Р. г.
Псевдориманова геометрия — теория
псевдориманова пространства. Псевдоримановым про-
пространством наз. дифференцируемое многообразие, на
к-ром задано поле знакопеременного симметричного
невырожденного тензора.
Финслерова геометрия — теория диффе-
дифференцируемого многообразия, на касательном расслое-
расслоении к-рого задана функция F{x, А), однородная первой
степени по К. Длина I кривой c(t) вычисляется:
1= [ 1 F (с, с) dt.
Пространства ограниченной кри-
кривизны — теория двумерных метрич. многообразий с
внутренней метрикой (без всяких предположений глад-
гладкости), в к-рых определена интегральная кривизна лю-
любого ограниченного борелевского множества. Сюда, в
частности, относится внутренняя геометрия выпуклых
поверхностей. Этот класс метрич. пространства можно
получить, присоединяя к двумерным римановым прост-
пространствам двумерные метризованные многообразия, мет-
метрика к-рых в окрестности каждой точки допускает рав-
равномерное приближенно римановыми метриками с огра-
ограниченными в совокупности интегралами от абсолютной
гауссовой кривизны.
Пространства кривизны не больше
К — теория полных метрич. многообразий с внутрен-
внутренней метрикой, в к-рых сумма верхних углов треуголь-
треугольников, составленных из кратчайших, не превосходит
суммы углов треугольника на плоскости постоянной
кривизны К с такими же длинами сторон (кроме того,
предполагается, что любые две точки можно соединить
единственной кратчайшей).
См. также Геодезических геометрия, Конформная гео-
геометрия, Риманово пространство обобщенное.
Лит.: [1] Рима и Б., Соч., пер. с нем., М.-—Л., 1948; [2]
Рашевский П. К., Риманова геометрия и тензорный ана-
анализ, 3 изд., М., 1967; [3] Э й з е н х а р т Л. П., Риманова гео-
геометрия, пер. с англ., М., 1948; [4] Г р о м о л Д., К л и н г е н-
б е р г В., М е й е р В., Риманона геометрия в целом, пер. с
нем., М., 11171; [5] Александров А. Д., Внутренняя
геометрии выпуклых поверхностей, М.—Л., 1948; [6] Б у р а-
го Ю. Д., Залгаллер В. А., «Успехи матем. наук»,
1977, т. 32, в. 3, с. 3—55; [7] М и л н о р Д ж., Теория Морса,
пер. с англ., М., 1965; [8] К а р т а н Э., Геометрия римановых
пространств, пер. с франц., М.—Л., 1936; Г9] Kulkarni R. S.,
(.Ann. Math.», 1971), v. 91, .\j 2, p. 311 — 31; [10] W о 1 f J. A.,
Spaces of constant curvature, N. Y., 1967. В. А. Тояоногое.
РИМАНОВА ГЕОМЕТРИЯ В ЦЕЛОМ — раздел рима-
новой геометрии, изучающий связи между локальными
и глобальными характеристиками римановых многооб-
многообразий (р. м.). Термин Р. г. в ц. обычно относят к опре-
определенному кругу проблем и методов, характерных для
геометрии в целом. Основное место в Р. г. в ц. занимает
изучении связи между кривизной и топологией р. м.
При этом исследуются вопрос о топологическом и мет-
метрич. строении р. м. с данными условиями на кривизну
и вопрос о существовании на заданном гладком много-
многообразии римановой метрики с предписанными свойст-
свойствами кривизны (секционной кривизны Ка , Риччи кри-
кривизны Ric, скалярной кривизны KtK). Большая часть по-
полученных результатов относится к пространствам с
кривизнами постоянного знака. Р. г. в ц. тесно сопри-
соприкасается с теорией однородных пространств и вариа-
вариационной теорией геодезических линий. О подмногооб-
подмногообразиях Р. м. см. в статьях Изометрическое погружение
и Погруженных многообразий геометрия.
Методы Р. г. в ц. носят синтетич. характер. Наряду
с локальной дифференциальной геометрией широко ис-
используются теория дифференциальных уравнений и
Морса теория. Но основные достижения связаны с на-
нахождением удачных конструкций, напр, построением
замкнутых геодезических, минимальных пленок или
пленок из геодезических, орисфер, выпуклых множеств.
Исследованию топологии р. м. обычно предшествует
изучение их метрич. свойств. Последнее часто осуществ-
осуществляется путем сравнения р. м. с подходящим эталонным
пространством (см. ниже теоремы сравнения).
Топологическое строение. Для замк-
замкнутых поверхностей связь между кривизной и тополо-
топологией но существу исчерпывается формулой Гаусса —
Бонне. Среди замкнутых поверхностей метрику положи-
положительной кривизны могут нести только сфера S% и про-
проективная плоскость Р2, а нулевой кривизны — тор и
бутылка Клейна. Строение р. м. размерности п>2 из-
известно хуже A983). Вот примеры известных теорем.
Полное односвязное р. м. Мп с Ка <:0 диффеоморфно
R" (теорема Адамара — К ар тан а), при-
причем для любой точки х ? Мп экспоненциальное отобра-
отображение expv есть диффеоморфизм касательного простран-
пространства ТХМ" на М".
Для иамкнутых р. м. с Ко >0 имеет место следующая
теорема о сфер е: полное р. м. Мп с 0<6'<:
<:/fa <:! наз. б-з ащем ленным; если оно одно-
связно и б>1/4, то Мп гомеоморфно Sn. Для четных п
граница здесь точная: при б=1/4 существуют Мп, не-
гомеоморфные S", это — симметрические пространства
ранга 1 и только они. Для нечетных п теорема о гомео-
гомеоморфности Мп и S" верна и при б — 1/,. При ге<7, ге?=4,
гомеоморфность сфере S" влечет диффеоморфность. При
п^7 дцффеоморфность сфере установлена при более
жестком, чем в теореме о сфере, защемлении (доста-
(достаточно взять б>(),87, а при п —>- оо взять б>0,66). Из-
Известно также, что при еще более жестком защемлении
(достаточно б>0,98 и 6>0,66 при п —>- оо) неодносвязное
М" диффеоморфно пространству постоянной кривизны
(факторпространству S" но дискретной подгруппе изо-
метрий). Есть ряд результатов об условиях на Ка, обе-
обеспечивающих гомеоморфизм симметрич. пространству
ранга 1 (см. [14J, [15]).
Открытое, т. е. полное некомпактное, р. м. с Л"ст >0
всегда диффеоморфно R". Множество X(z.Mn наз.
абсолютно выпуклым, если каждая геодези-
геодезическая с концами в X вся лежит в X. Пусть М" — от-
открытое р. м. с Ко^(), тогда в Мп существует вполне
геодезическое абсолютно выпуклое замкнутое подмно-
подмногообразие N такое, что Мп диффеоморфно пространству
v (N) нормального расслоения N в Мп (если Ко >0, то
dim N=0). В случаях dim N—l или re—1, а для одно-
однородных пространств — всегда, М" даже изометрично
v(N) со стандартной метрикой нормального расслоения.
При ;г<:3 это дает полную классификацию открытых
р. м. с Ка ^0.
Прямой на.), полная геодезическая, кратчайшая
на любом своем участке. Теорема о цилиндре:
открытое М" с Ко ^0 изометрично прямому метрич.
произведению Д/"-*Х R*, 0<ft<re, где Af™-* не содер-
содержит прямых. Условие Ко^0 здесь можно заменить на
Шс>0.
Фундаментальная группа. При Ка >0
и четном п замкнутое Мп либо ориентируемо и односвяз-
но, либо неориентируемо и фундаментальная группа
пх{Мп)=%г\ при нечетном п оно всегда ориентируемо,
но о лх(Мп) за пределами теоремы о сфере мало что из-
известно. Даже для Мп постоянной кривизны Ка =1 пол-
полное описание возможных строений яг(Л/") для нечет-
нечетных п оказалось трудной задачей (см. [9J).
Если Ка — 0, то универсальное накрывающее Мп
пространства М" изометрично R" и фундаментальная
группа пх(Мп) изоморфна дискретной группе изометрий
Rra без неподвижных точек; она содержит подгруппу
сдвигов конечного индекса. (Тем самым Мп допускает
конечное изометрич. накрытие плоским тором.)
Если в Мп все Ка «0, то М" диффеоморфно R". По-
Поэтому все гомотопич. группы Л/ (Мп) для i>l тривиаль-
тривиальны, и гомотопич. тип определяется я1(Л/"). Если Ко <0,
то п^Мп) полностью некоммутативна в том смысле, что
любая аоелева (и даже любая разрешимая) ее подгруп-
подгруппа является бесконечной циклической. В случае А"о <:0
известно следующее. Пусть Г — разрешимая подгруппа
я1G1/"). Тогда Г изоморфна дискретной группе изомет-
изометрий R" (без неподвижных точек) и Мп содержит ком-
компактное вполне геодезич. подмногообразие, изометрпч-
ное R"/F. Вместо Ка <:0 достаточно при этом потребо-
потребовать отсутствия на геодезических сопряженных точек.
Для двух многообразий одинаковой постоянной отри-
отрицательной кривизны и одинаковой размерности ге^З
изоморфизм ях влечет изометрию (теорема Мос-
Мостов а).
Рпмановы многообразия, для к-рых max \Ka\X
Xdiam 71/"<е, наз. е-п л о с к и м и. Такие многообра-
многообразия могут при произвольном е>0 топологически отли-
отличаться от локально плоских. Для них при любом п^2
существует такое е„, что для е„-плостеого Мп в л,(М")
есть нильпотентная подгруппа конечного индекса. При
этом М" допускает конечное (с кратностью, зависящей
лишь от п) накрытие, диффеоморфное факторпростран-
ству нильпотентной группы Ли по ее дискретной под-
подгруппе (см. [8]).
Полное р. м. с кривизной Шс5гя>0 имеет конечный
diam Мп<.п1У а и потому конечную группу пк(Мп).
Если для замкнутого Мп Ric^O, то существует такая
конечная нормальная подгруппа Гся1(Л/'1), что л^'Г —
дискретная группа изометрий R*, 0<&<:;г, причем М"
разлагается в прямое метрич. произведение M*xRfl,
где М* замкнуто, разложение инвариантно относи-
относительно nt(M"), а Г — тривиальна на R*.
Наряду с изучением щ(Мп) получены с помощью
теории гармонических дифференциальных форм нек-рые
оценки для чисел Бетти Ьк для б-защемленных М". Так,
&2=0 при 6>(и—3)Dгс—9) и нечетном гС^Ъ.
Теоремы сравнения. Многие глобальные
свойства р. м. доказываются путем сравнения конст-
конструкции в изучаемом р. м. с аналогичными конструкция-
конструкциями в эталонном пространстве. В качестве последнего
берут многообразие постоянной кривизны, реже —
другое симметрия, пространство. Ниже с - п л о с-
костью называем R2 при с—0, сферу Sc радиуса
с~Чг при с>0, плоскость Лобачевского кривизны с при
с<0.
Многочисленные применения имеет следующая тео-
теорема Топоногова сравнения углов.
Пусть в р. м. Мп все Ка^с и аг, а2, а3 — углы тре-
треугольника из кратчайших, а а%, <х'ъ, а3 — соответствую-
соответствующие углы треугольника с теми же длинами сторон на
с-плоскости; тогда а.{^а.\. Если Ко <с и любые две точ-
точки сторон рассматриваемого в Мп треугольника соеди-
соединимы единственной кратчайшей, то a,-<aj-. Эта теорема
эквивалентна следующему условию выпукло-
с т и: если в Мп кратчайшие ab, ас образуют тот же
угол, что кратчайшие а'Ь', а! с тех же длин на с-плоско-
с-плоскости, то рмп(Ь, с)<:рсF', с'). Здесь по существу сравни-
сравнивается быстрота расходимости кратчайших.
В теореме сравнения Рауха сравни-
сравниваются скорости движения концов bub' кратчайших
ab, а'Ь' в двух р. м. Мп и М'п при условии, что ab и а'Ь'
поворачиваются вокруг своих начал а, а' с одинаковой
скоростью в условиях, когда (при нек-ром естественном
сопоставлении) секционные кривизны в Мп не меньше,
чем в М'п. Тогда скорость движения Ь не больше, чем
скорость I/. В основном случае (при сравнении с с-пло-
скостью) теорема Рауха равносильна инфинитезималь-
ному варианту теоремы сравнения углов.
Имеются аналоги теоремы Рауха, в к-рых точки а, а'
смещаются по гиперповерхностям, к к-рым ab, a'b'
остаются ортогональными. Есть также теоремы сравне-
сравнения для объемов трубчатых окрестностей подмногооб-
подмногообразий (см. [13], [16]).
Экстремальные теоремы. Теоремы срав-
сравнения приводят к оценкам таких характеристик М",
как диаметр, радиус инъективности, длина замкнутой
геодезической, объем шара данного радиуса и т. п. От-
Ответы на вопросы о случаях достижения равенства в та-
таких оценках дают экстремальные теоремы.
Для Мп с Ka^i всегда diam Л/"<:л. Равенство до-
достигается только для единичной сферы. Если М" замк-
замкнуто и 0<А'а <1 при четном п или 1/4<А'а <1 при не-
нечетном п, то радиус инъективности Г(п(Мп)^л. и длина
замкнутой геодезической ^2я. Если при этом в Мп есть
замкнутая геодезическая у длины 2я, то при четном п в
М" существует вполне геодеяич. поверхность, содержа-
содержащая 7 и изометричная S", а при 1/4<А'о <1, независимо
от четности п, М" изометрично Л? (см. [6]). Объем шара
D радиуса г<г,-„(Л/") в М" с Ка <сс(Ка^с) не меньше
(не больше), чем объем шара Ос того же радиуса в про-
пространстве постоянной кривизны с, с равенством, лишь
если D изометрично Dc.
Экстремальные теоремы не всегда связаны с оценками
кривизны. Пусть, напр., на замкнутой поверхности F
для любой точки множество точек, ей сопряженных,
состоит из единственной точки. Тогда F изометрично
сфере.
Конечность топологических типов.
Среди замкнутых р. м. с равномерно ограниченными
кривизнами и ограниченными снизу радиусами инъек-
тивности Vol МпК.С1, г,„>6'2>0, Ко <С3, есть лишь
конечное число попарно гомотоиически неэквивалент-
неэквивалентных, а при замене Ко <С'а на \КО |<С3 — лишь конеч-
конечное число попарно негомеоморфных. В этом утвержде-
утверждении условие rjn>C2>0 можно заменить обеспечиваю-
обеспечивающими его, но легче проверяемыми условиями Vol М"^
>С4>0, diam М"<С& (см. [14]).
Для р. м. со знакопостоянными Ко условия, обеспе-
обеспечивающие конечность их топология, типов, упрощают-
упрощаются. Напр., для четных п и Ко >0 достаточно условия
max Ko <C min Ко.
При и>3 для Мп с — 1 <:/fa <0 справедлива оценка
Vol Мп~>СA + diam Л/"). Потому при п-^3 конечно
число топология, типов замкнутых р. м., удовлгтноряю-
щих условиям Vol М"<ССи 6'2<А'О <(). Но при и 3 су-
существует бесконечная серия попарно негомеоморфных
М3, удовлетворяющих условиям (см. |12]).
Метрики с заданной к р и в и з н о й.
Пусть х — эйлерова характеристика замкнутой по-
поверхности М2. Чтобы гладкая функция / на М" была
кривизной нек-рой римановой метрики на Л/, необхо-
необходимо: max />0 при х>0, min /<0 при х<0 и f меняет
знак или /ssO при %=0. Эти условия и достаточны. Ус-
Уснеобходимо и достаточно, чтобы 2-
\
форма о) была формой кривизны ш= \ К dS римановой
метрики на М2. Если М2 — открытое подмногообразие
замкнутого многообразия 7V2, то любая гладкая / на М2
есть кривизна нек-рой (быть может, неполной) римано-
римановой метрики на М2. Необходимые и достаточные усло-
условия, при к-рых / есть кривизна полной римановой мет-
метрики на некомпактной поверхности, выяснены A983)
лишь для конечносвязных поверхностей.
С ростом размерности число независимых компонент
тензора кривизны растет быстрее числа компонент
мстрич. тензора. Условия, при к-рых данное поле тен-
тензора служит, хотя бы локально, полем тензора кривиз-
кривизны нек-рой метрики, неизвестны A983). Но для скаляр-
скалярной кривизны при ге>2 каждая гладкая функция / на
замкнутом М", для к-рой min /<0, является скалярной
кривизной нек-рой римановой метрики па Мп (см. |4]).
Существуют многообразия, не допускающие метрики с
положительной скалярной кривизной, напр, трехмер-
трехмерный тор (см. [5]).
Выпуклые функции. Существование на р. м.
М" скалярной функции /, выпуклой вдоль любой гео-
геодезической, налагает жесткие ограничения на строение
такого Ма. Напр., если на Мп есть выпуклая функция
/, то Vol M"=oo. Если / строго выпукла и при любом
с компактны множества /~'(с), то М" диффеоморфно R".
В ряде случаев выпуклые функции удается постро-
построить. Напр., при А'ст <0 выпуклы функции /i(.r)=ft(x, p),
f2(x) = p(x, рJ, р?Мп. Если Ка <0 и у: М" -> М" —
изометрия, то выпукла функция 6у (*)=--(>(*, ух). При
Ко 5=0 существуют выпуклые / с компактными /-1(с);
это связано с абсолютной выпуклостью (при Ка ^0)
дополнений к орншарам и с тем обстоятельством, что
при Ка^:0 выпуклость множества UcM" влечет выпук-
выпуклость множества {x?U : p(x, U)}
Изучались и проблемы Р. г. в ц. для р. м. с дополни-
дополнительными структурами, напр, для калеровых многооб-
многообразий (см. [10]).
Лит.: [1] Г р о м о л Д., КлингенбергВ., Мейер
В., Риманова геометрия в целом, пер. с нем., М., 1971; [2] Б у -
р а г о Ю. Д., 3 а л г а л л е р В. А., «Успехи матем. наук»,
1977, т. 32, в. 3, с. 3—55; [3] Cheeger J., EbinD., Com-
Comparison theorems in riemannian geometry, Amst.—Oxf.—N. Y.,
1975; [4] Исследования по метрической теории поверхностей,
пер. с англ. и франц., М., 1980; [5] Schoen R., Van S.,
«Ann. Math.», 1979, v. 110, p. 127—42; [6] T о п о н о г о к В. А.,
«Сиб. матем. ж.», 1974, т. 15, № 6, с. 1348—71; [7] G г о m о v M.,
Lawson В., «Ann. Math.», 1980, v. Ill, Ms 2, p. 209—30;
[8] Buser P., KarcherH Gromov's almost flat mani-
manifolds, «Asterisque», 1981, v. 81; [9] Вольф Дж., Пространст-
Пространства постоянной кривизны, пер. с англ., М., 1982; [10] Gold-
Goldberg S., Curvature and homology, N. Y., 1963; [11] Б е с с е А.,
Многообразия с замкнутыми геодезическими, пер. с англ., М.,
1981; [12J Т li u г s t о n W., The geometry and topology of 3
manifolds, Preprint, Princeton, 1978; [13] HeintzeE.,
Karcher H., «Ann. scient. Ecole norm, super.»., 1Я78, v. 11,
№4, p. 451—70; [14] Cheeger J., «Amcr. ,T. Math.», 19(i!>,
v. 91, M*? 3, p. 807 — 34; [15] M i n-0 o, R u h I:., «Ann. scient.
Ecole, norm, super.», 1979, v. 12, p. 335—53; [l(i] Gray A.,
«Topology», 1982, v. 21, M5 2, p. 201—28.
Ю. Д. Bi/раго В. А. Топоногов.
РИМАНОВА КРИВИЗНА — мера отличия метрик
риманова и евклидова пространств. Пусть М — точка
риманова пространства, F — двумерная регулярная
поверхность х' = х'(и, v), проходящая через М, L —
простой замкнутый контур на F, проходящий через М,
а — площадь участка поверхности, ограниченного кон-
контуром L. Пусть произвольный вектор а', касательный к
поверхности F (т. е. линейно выражающийся через
векторы |i- , ~ J, перенесен параллельно по L. Тогда
составляющая перенесенного вектора, касательная к F,
окажется повернутой по отношению к а* на угол ф
(положительное направление отсчета углов должно сов-
совпадать с направлением обхода L). Если при стягивании
L в точку М существует предел
ЛГ = Шп-2.,
то он наз. римановой кривизной (кривизной
риманова пространства) в данной точке в направлении
двумерной поверхности; Р. к. зависит не от поверхно-
поверхности, а лишь от ее направления н точке М, т. е. от на-
направления двумерной плоскости касательного евклидо-
ва пространства, содержащего векторы ^- , ~ .
Р. к. К связана с тензором кривизны формулой
где
дхтдх1
ди dv
дх1вхт\
ди dv j
причем параметры и, v выбраны так, что площадь
параллелограмма, построенного на векторах ~ , ?f— ,
равна 1.
По материалам ст. Риманова геометрия в БСд-3.
РИМАНОВА МЕТРИКА — метрика пространства,
задаваемая положительно определенной квадратичной
формой. Если в пространстве Vn введена локальная си-
система координат (хх, ... , хп) и в каждой точке X (х1, ... ,
... , хп)? Vn определены функции gij(X), i, /=1, 2, ... ,
га, det (gij) >0, gij(X) = gji(X), являющиеся компонента-
компонентами ковариантного симметричного тензора второй ва-
валентности, то этот тензор наз. основным мет-
метрическим тензором пространства Vn. С помо-
помощью основного тензора выражается длина ds контрава-
риантного вектора (dz1, ... , dxn):
ds2 = gij (X) dx> dxJ;
форма gjjdx'dxJ является положительно определенной
квадратичной формой. Метрика пространства Vn, опре-
определенная с помощью формы ds2, наз. римановой, а про-
странство с введенной в нем Р. м. наз. римановым про-
пространством. Задание Р. м. на нек-ром дифференцируе-
дифференцируемом многообразии означает задание на этом многообра-
многообразии евклидовой структуры, дифференцируемым образом
зависящей от точки.
Р. м. является обобщением первой квадратичной фор-
формы поверхности в трехмерном евклидовом пространст-
пространстве — внутренней метрики поверхности. Геометрия про-
пространства Vn, основанная на определенной Р. м., наз.
римановой геометрией.
Существуют обобщения понятия Р. м. Так, псевдо-
риманова метрика определяется с помощью неопреде-
неопределенной квадратичной формы (см. 11севдориманово прост-
пространство и Относительности теория). Вырожденная
Р. м., то есть метрич. форма, определенная с помощью
функций gij(X), для к-рых det (?/_,-) —0, определяет не-
к-роо полуриманово пространств!).
Лит.: [1] ЭЯ зенхарт Л. 11., Риманова геометрия, пер.
с англ., М., 1948; [2] Р а ш е в с к и й II. К., Риманова гео-
геометрия и тензорный анализ, 3 изд., М., 1967; [3J Р и м а н Б.,
О гипотезах, лежащих в основании геометрии, пер. о нем., вкн.:
Об основаниях геометрии, М., 195В. Л. А. Сидоров.
РИМАНОВА ОБЛАСТЬ, комплексное (а н а-
литичоское) многообразие над С",—
аналог римановой поверхности аналитич. функции w=
~f(z) одного комплексного переменного z для случая
аналитич. функции w=j(z), z^{zx, ..., ztl), многих ком-
комплексных переменных zlt ..., zH, /t^=2.
Точнее, линейно связное хаусдорфово топологич.
пространство Л наз. (абстрактной) римано-
римановой областью, если существует локальный гоме-
гомеоморфизм (проекция) я : Л —> С" такой, что для
каждой точки pB<r_R существует окрестность U(р0; е),
гомеоморфно отображающаяся на нек-рый поликруг
D(z«; e) = {z = (Zl, ...,
\zj-z°,\ <e, / = 1, ..., n}
в комплексном пространстве С". Р. о. сепарабельна.
Комплексная функция g наз. голоморфной
на Л, если для любой точки ро?К функция g [n~1(z)]
от п комплексных переменных z1; ..., zn голоморфна в
соответствующем поликруге D (z°; в). Проекция я зада-
задается набором п голоморфных функций л=(л1, ..., я„),
соответствующих координатам zt, ..., zn в С". Исходя
из данного регулярного элемента аналитич. функции
w=/(z). ее Р. о. строится аналогично тому, как строится
рп.маиова поверхность данной аналитич. функции од-
одного комплексного переменного, т. с. сначала посред-
посредством аналитич. продолжения строится полная аналити-
аналитическая функция w=f(z), а затем с помощью окрестно-
окрестностей вводится топология на множестве элементов пол-
полной аналитич. функции. Так же, как и римановы по-
поверхности, Р. о. неизбежно возникают при аналитич.
продолжении данного элемента аналитич. функции, ког-
когда полную аналитич. функцию w=/(z) стремятся пред-
представить, следуя идеям Б. Римана (В. Riemann), как од-
однозначную функцию точки соответствующей Р. о.
В частности, Р. о. возникают как многолистные голо-
голоморфности области аналитич. функций многих комп-
комплексных переменных. Теорема Ока утверждает,
что Р. о. является областью голоморфности тогда и
только тогда, когда она голоморфно выпукла (см. Голо-
Голоморфно выпуклое комплексное пространство).
Современное изучение Р. о. проводится в рамках об-
общей теории аналитич. пространств. Обобщение поня-
понятия области голоморфности приводит к Штейна про-
пространствам.
Лит.: [1] Щ а П а т Б. В., Введение в комплексный анализ,
2 изд., ч. 2, М., 197й; [2] Г а н н и в г Р., Р о с си X., Анали-
Аналитические функции многих комплексных переменных, пер. с англ.,
М., 1969; [3J Хермавдср Л., Введение в теорию функций
нескольких комплексных переменных, пер. с англ., М., 1968.
Е. Д. Соломекцев.
РИМАНОВА ПОВЕРХНОСТЬ аналитической
функции w=f(z) комплексного пере-
переменного 2 — поверхность Л такая, что данная
полная аналитическая функция w=f(z), вообще говоря
многозначная, может рассматриваться как однозначная
аналитич. функция w=F(p) точки р поверхности Л.
Понятие Р. п. возникло в связи с изучением алгебра-
ич. функций w=f(z), определяемых алгебраич. уравне-
уравнением
а0 (г) W»+ai (z) u;"»-i+ . .. +am (z) = 0, A)
где aj(z), /=0, ..., m,— многочлены с постоянными
коэффициентами, ao(z)^O, am(z)^0. В работах В. Пюи-
зё (V. Puiseaux, 1850—51) было достигнуто ясное по-
понимание многозначности, присущей этим функциям
w=f(z), когда каждому значению переменного z ста-
ставится в соответствие т значений переменного w. Б. Ри-
ман (В. Riemann, 1851—57, см. [1]) впервые показал, как
для любой алгебраич. функции построить поверхность,
на к-рой ее можно рассматривать как однозначную ра-
рациональную функцию точки. Полученную Р. п. можно
отождествить с алгебраич. кривой, определяемой урав-
уравнением A). Вообще, для всего дальнейшего развития
теории Р. п., связанного с именами Ф. Клейна (F. Klein),
А. Пуанкаре (Н. Poincare), П. Кебе (P. Koebe)
и др., характерно (то усиливающееся, то несколько ос-
ослабевающее) взаимопроникновение, с одной стороны,
идей и методов теории функций комплексного перемен-
переменного, с другой — алгебры и алгебраич. геометрии.
Важной вехой в этом развитии явилось первое издание
книги Г. Вейля [18], в к-рой было сформулировано об-
общее понятие абстрактной Р. п.
Определение А: связное хаусдорфово топо-
логич. пространство R наз. абстрактной ри-
мановой поверхностью, или просто р и-
мановой поверхностью, если оно допуска-
допускает покрытие открытыми множествами U с соответствую-
соответствующим каждому множеству U гомеоморфным отображени-
отображением а : U —>--Ь, где D= {z?C : |z|<l} есть единичный
круг на плоскости С комплексного переменного z,
причем если точка p?R принадлежит Uu U', то взаимно
однозначное соответствие z'=a'a~1(z) есть конформное
отображение I рода в окрестности точки a(p)?D, то
есть z' = a'a~1(z) есть однолистная аналитич. функция в
окрестности точки a(p)?D. Иначе говоря, абстрактная
Р. п. есть двумерное комплексное аналитич. многооб-
многообразие.
Определение римановой поверхности с
краем R отличается от определения А тем, что наря-
наряду с гомеоморфизмами а : U —>- D допускаются гомеомор-
гомеоморфизмы а : U-^Do, где Do={z?C : |г|<1, imz>0}
— единичный полукруг на плоскости С, причем
обычно предполагается, что R не является Р. п. в смыс-
смысле определения А. Точки Р. и. с краем R, имеющие
окрестности, гомеоморфные D, наз. внутренними, а
остальные точки, отображающиеся в точки отрезка
{z=x-i-iy?C: — l <х < 1, г/ = 0},
образуют край dR. Совокупность внутренних точек R
(внутренность Л) есть Р. п. в смысле опреде-
определения А. Таким образом, в случае Р. п. с краем обычно
край предполагается непустым множеством.
Р. п. (или Р. п. с краем) есть триангулируемое и ори-
ориентируемое многообразие со счетной базой, к-рое, сле-
следовательно, сепарабельно и метризуемо. Компактная
Р. п. (без края) наз. замкнутой Р. п.; более ши-
широкий класс конечных Р. п. включает замкнутые
Р. п. и компактные Р. п. с краем, состоящим из конеч-
конечного числа связных компонент. Некомпактные Р. п. с
краем или без него наз. открытыми Р. п. В не-
к-рых случаях в определении А более удобно допускать
конформное отображение не только I рода, но н II рода.
Получающаяся при таком подходе Р. п. с краем R (или
без него) не является уже, вообще говоря, ориентируе-
ориентируемой, но в предположении ее конечности она может
быть вложена конформно в ориентируемую замкнутую
Р. л.— дубль римановой поверхности R (см. [8]).
• Пусть аналитич. функция u>=f(z) задана одним из
своих регулярных элементов (а, Р)=(а, P(z—a)), т. е.
парой, состоящей из точки a?C и степенного ряда
с центром а и радиусом сходимости r(a), 0<r(a)<:oo.
Аналитическое продолжение элемента (а, Р) вдоль все-
всевозможных путей в расширенной плоскости С позво-
позволяет получить все регулярные элементы такого же типа
(b, Q), составляющие в совокупности полную аналитич.
функцию, к-рую мы будем продолжать обозначать ш=
—/(z). Кроме того, при аналитич. продолжении появ-
появляются элементы более общей природы
(Ь, S) = (b,
т.е. пары, состоящие из точки 6?С и обобщенного
степенного ряда (ряда П ю и з ё):
или (в случае, когда Ь= оо — бесконечно удаленная
точка):
где т — целое, are — натуральное числа, причем эти
ряды сходятся соответственно при \z—6|О(&) или при
|z|>r(oo)>0. Обобщенные элементы (b, S), а точнее
их классы эквивалентности, составляют в совокупности
аналитический образ Af, соответствующий данной
аналитич. функции w=f(z). Среди составляющих ана-
аналитич. образ классов эквивалентности элементов (b, S)
различаются регулярные с ге=1 и разветвленные с л>1.
Введение подходящей топологии на аналитич. образе
Af превращает его в Р. и. Rf аналитич. функции го=
= /(z). Это получается, напр., если задавать окрест-
окрестность элемента F, S), Ьф<х>, как множество, состоящее
из самого элемента (Ь, S) и всех тех регулярных элемен-
элементов (а, Р) из Af, для к-рых \Ь—а|<р", p<r(t>) и ряд
Р (z—а) сходится к одному из п определений ряда
S('\/z—Ъ) в их общей области определения, т. е.
где е — один из корней из единицы степени п, е"=-1.
Окрестность элемента (оо, S) состоит из самого элемен-
элемента (ас, S) и всех тех регулярных элементов (а, Р) из Af,
для к-рых \а\ >р~", р<г(й) и ряд Р (z—a) сходится к од-
одному из п определений ряда 5(z-i/n). Пространство Rf
удовлетворяет всем условиям определения А.
Таким образом, каждой аналитич. функции w=f(z)
соответствует Р. п. Rf, на к-рой эта функция представ-
представляется как однозначная аналитич. функция точки w—
= F(p), р=(Ь, S)?Rj. Это означает, что в окрестности
любой точки po — (b, S) существует локальный униформи-
зирующий параметр t=r^/'z—Ъ, через к-рый w выра-
выражается как однозначная аналитич. функция iv=P(t) =
— F(p). Иначе говоря, Р. п. Rf аналитич. функции есть
геометрич. конструкция для глобальной униформиза-
ции многозначного, вообще говоря, соотношения м>=
— /(г). В окрестности каждой точки po=(b, S)?Rf оно
уннформизируется посредством двух однозначных ана-
аналитич. функций z=b~i~t'! и w=S(t). С другой стороны,
отображение проектирования П : (Ъ, S) —>- Ь, ставящее
в соответствие каждому элементу pa=(b, S)?Rf его
центр Ь, показывает, что Р. п. Rj аналитич. функции
есть (разветвленная) накрывающая поверхность над
расширенной комплексной плоскостью С или, что то
же, над Римана сферой. Проекции разветвленных
элементов (b, S) с п>1 суть точки ветвления этого на-
накрытия.
В то же время каждой априори заданной Р. п. R
соотнртствует бесконечно много аналитич. функций и>=
=-/(z), для к-рых именно R является их Р. п., Rf=R.
Это утверждение для случая замкнутых Р. п. было вы-
высказано и обосновано еще Б. Риманом в 1851. Централь-
Центральным пунктом соответствующего доказательства являет-
является конструкция гармонич. функций на R с заданными
особенностями. Данное Б. Риманом обоснование опи-
опиралось на некритич. применение т. н. Дирихле прин-
принципа; строгое доказательство впервые было дано П. Кё-
бе A909); позднее были даны более простые доказатель-
доказательства этого фундаментального положения, в том числе
и опирающиеся на надлежащим образом применяемый
принцип Дирихле (см., напр., [3], [4], [17], [18]).
Какова бы ни была ориентируемая топологич. по-
поверхность S, можно построить Р. п. Я, гомеоморфную
S, т. е. построить Р. п. R того же топологич. тина, что
и S. Замкнутые Р. п. топологически вполне характе-
характеризуются одним числом — родом g, 0<g<+oo. Топо-
Топологич. тип такой Р. п. R при g—0 есть сфера, при g=
= 1 — тор, при g>l — обобщенный тор, или сфера с g
ручками. Разрезав Р. п. R рода g--0 вдоль нек-рой ду-
дуги, получают в качестве ее топологич. .модели, или нор-
нормальной формы, двуугольник с символомs=aa~1,
указывающим, что точки сторон а и а~г отождествляют-
отождествляются; при g^l необходимо сделать 2g канонических разре-
разрезов alt Ь1? ..., a.g, Ь„, после чего получается нормальная
форма замкнутой Т3. п. R — многоугольник с 4g сторо-
сторонами, попарно отождествляемыми, символ s=a1 ... дол-
должен указывать порядок следования сторон. Напр., на
рис. 1 изображены нормальные формы сферы при g=0 и
тора при g—i с их символами. С аналитич. точки зрения
замкнутая Р. п. R характеризуется тем, что она есть
Р. п. нек-рой алгебраич. функции w=f(z), определяе-
определяемой алгебраич. уравнением A) степени т. Эту Р. п. R
можно представлять себе также в виде т листов, про-
9=0,
>
s=aa~'
V
«
Рис. 1.
стирающихся над сферой Римана и определенным об-
образом соединяющихся между собой в точках ветвления
и вдоль нек-рых линий, соединяющих эти точки (способ
соединения определяется конкретным видом уравне-
уравнения A)). При этом род g P. и. R выражается через число
k k Р
р
листов т и порядки kl,
на — Гурвица формулой
р р
ks точек ветвления Рима-
РимаКонечные Р. и. R топологически вполне характери-
характеризуются родом g, 0<#<оо, и числом I связных компо-
компонент края, 0<?<оо; их топологич. типом является сфе-
сфера с g ручками и I отверстиями. В нормальной форме
конечной Р. п. число сторон не обязательно четное,
нек-рые стороны, соответствующие компонентам края,
остаются свободными, не отождествляются. Понятие
рода обобщается и для открытых Р. п. R, напр. при
помощи исчерпания R последовательностью {Rv}v=i
принадлежащих R компактных Р. п. с краем Rv та-
таких, что Rv содержится внутри Rv+i, (Jv=i.ffv=-ff-
Род g Р. п. R полагают равным g==lim #v, где g — род
Rv. Этот предел существует и не зависит от выбора ис-
исчерпания {i?v}i 0<:g<-|-оо. Однако род не полностью
определяет топология, тип открытой Р. п.; топологич.
типы открытых Р. п. могут быть весьма разнообразны-
разнообразными. Так, на рис. 2 изображены две модели с g=0 и
g=--2.
Важной топологич. характеристикой Р. п. R являет-
является порядок связности: R наз. односвязной,
если любую простую замкнутую кривую на R можно
непрерывно деформировать в точку, не выходя за пре-
пределы R, т. е., иначе говоря, если фундаментальная
группа поверхности R тривиальна. В противном слу-
случае Р. п. R наз. много связно и. Важный класс
составляют Р. п., подобные однолистным:
так наз. Р. п. (с краем или без края), к-рые разделяются
любой простой замкнутой кривой на две непересекаю-
непересекающиеся части. Напр., на рис. 2, а представлена тополо-
топологич. модель многосвязной Р. п., подобной однолистной.
Р. п., подобная однолистной, необходимо имеет род
нуль. Р. п. R, подобная однолистной, наз. ге-с в я з-
Рис 2.
ной, если минимальнее число разрезов, превращаю-
превращающих R в односвязную Р. п., равно п — 1, пЭ=1 (см.
рис. 2, б).
Топологич. свойства Р. п. R отнюдь не определяют
полностью аналитич. свойства R, т. е. топологич. свой-
свойства R не определяют полностью поведение функций
различных классов на Л. В частности, пусть / : R1 —>-
-> R2 — функция на Р. п. R1 со значениями на другой
Р. п. R2. Функция / наз. аналитической на Rlt если для
любой точки PoG-^i' /(Po) —9oi можно найти локальные
униформизирующие параметры соответственно ?=<р(р)
в окрестности р0 на Дх и т =ф (q) в окрестности q0 на R2
такие, что сложная функция
является аналитич. функцией комплексного перемен-
переменного t в окрестности значения *о=ф(Ро)- Две Р- п- ^i и
R2 наз. конформно эквивалентными,
или принадлежащими одному и тому же конформному
классу, если существует аналитич. функция f : R1—>-
—>¦ R2, взаимно однозначно отображающая Rt на R2.
С точки зрения поведения аналитич. функций на Р. п.,
конформно эквивалентные Р. п. следует рассматривать
как одну и ту же Р. п., но топологически эквивалентные
Р. п. не всегда являются конформно эквивалентными.
Применительно к Р. п. можно следующим образом
сформулировать теорему Римана о кон-
конформном отображении: всякая односвяз-
ная P. rr. H конформно эквивалентна одной из трех об-
областей: 1) расширенной комплексной плоскости С=
= С U {оо }, или сфере Римана (эллиптический
с л уча »); 2) конечной комплексной плоскости С,
или сфере Римана с одной выколотой точкой (парабо-
(параболический случай); 3) единичному кругу D =
= {z?C : |z|<l} на плоскости С, или сфере Римана с
разрезом положительной длины (гиперболиче-
(гиперболический случай). Важный результат состоит в том,
что любая Р. п., подобная однолистной, конформно эк-
эквивалентна нек-рой канонич. области расширенной ком-
комплексной плоскости. В качестве такой канонич. области
можно взять всю расширенную плоскость с конечным
или бесконечным числом разрезов, параллельных дейст-
действительной оси, причем нек-рые из этих разрезов могут
вырождаться в точки. Как указано выше, в случае од-
носвязноп Р. п. канонич. область либо не имеет ни од-
одного разреза (эллиптический тип), либо раз-
разрез вырождается в точку (параболический
тип), либо разрез имеет положительную длину (г и-
п е р б о л и ч е с к и й тип). Все три типа односвяз-
ных Р. н. конформно различны, хотя последние два из
них топологически эквивалентны. Проблема ти-
п а, пока A983) не получившая полного решения,
состоит в разыскании дополнительных условий на одно-
связную Р. п., при к-рых она принадлежит гиперболи-
гиперболическому или параболич. типу (см. [6], [7], [10], [11|).
В общем случае произвольной Р. п. R односвязной
Р. п. будет всегда ее универсальная накрывающая по-
поверхность R, к-рая, следовательно, принадлежит одно-
одному из трех указанных типов. Сама Р. п. Л считается
Р. п. эллиптического, п а р а б о л и ч е с к о-
г о пли гиперболического типа в соответствии
с тем. какого типа будет ее универсальная накрываю-
накрывающая R. Эта классификация Р. и. оправдывается следую-
следующими соображениями. Пусть D — одна из трех обла-
областей: расширенная комплексная плоскость, конечная
комплексная плоскость или единичный круг, а Л —
нек-рая группа дробно-линейных отображений области
D на себя (автоморфизмов), не имеющая неподвижных
точек в D. Конформное отображение w=W(q) универ-
универсальной накрывающей R на D переводит группу Л пре-
преобразований накрытия Д, изоморфную фундаменталь-
фундаментальной группе n^R), в нек-рую группу Л автоморфизмов
области D. При этом w= W (q) можно рассматривать как
конформное отображение факторпространства Я/Л на
факторпространство М/А, а В./А можно отождествить
с R. Таким образом, w= W(q) можно рассматривать как
конформное отображение Р. п. R на факторпространст-
факторпространство DIA с нек-рой группой автоморфизмов Л, изоморф-
изоморфной фундаментальной группе ях(Д).
Так как Р. п. R эллиптич. типа обязательно односвяз-
на, то группа Л тривиальна, а значит, такая Р. п. есть
обязательно Р. п. функции, обратной рациональной.
Односвязная Р. п. параболич. типа обязательно яв-
является Р. п. функции, обратной мероморфной в конеч-
конечной плоскости. Компактная Р. п. рода g—-0, g=i и g>l
является соответственно Р. п. эллиптического, парабо-
параболического и гиперболич. типа.
В связи с конформной эквивалентностью Р. н. воз-
возникает также вопрос о строении группы 2 конформных
автоморфизмов Р. п. R. За нек-рыми простыми исклю-
исключениями эта группа 2 дискретна, а для компактных
Р. и. рода g>l она конечна (теорема Шварца).
Исключительных случаев, когда группа 2 непрерывна,
всего семь, а именно (указаны представители соответст-
соответствующих конформных классов): сфера в эллиптич. слу-
случае; сфера с одной или двумя выколотыми точками и тор
в параболич. случае; круг, круг с выколотой точкой и
кольцо в гинерболич. случае.
Важное значение имеет также проблема м о д у-
л е й Р. п. в различных постановках. Это вопрос о воз-
возможном описании разнообразия конформно неэквива-
лентных Р. п. того или иного вида. Напр., легко уста-
устанавливаются следующие положения. Множество видов
конформно неэквивалентных двусвязных Р. п., подоб-
подобных однолистным (колец), зависит от одного действи-
действительного параметра (модуля) А:, 0<&<1; т.е. два
кольца U<rv <|z| <RV , v= 1, 2, конформно эквивалент-
эквивалентны тогда и только тогда, когда совпадают отношения их
радиусов: k=(rl/R,)=(r2/R2). Множество видов конфор-
конформно неэквивалентных «-связных Р. п., подобных одно-
однолистным, при п >2 зависит от Зге — 6 действительных
параметров. Множество видов конформно неэквивалент-
неэквивалентных замкнутых Р. п. рода gjsl при g=l зависит от
двух действительных параметров, а при g>l — от
6g — б действительных параметров (см. Римановых
поверхностей конформные классы, а также [3], [12], |13],
[15], [16]; относительно поведения функций других
классов на Р. п. см. Римановых поверхностей класси-
классификация).
Важным аспектом теории Р. п. является связь с по-
понятием униформизации. Для многозначной, вообще го-
говоря, аналитич. функции
W = f (Z) {?)
ее Р. п. Rf дает геометрич. средство униформизации:
многозначное соотношение B) заменяется двумя одно-
однозначными представлениями:
w = F(p), z=g(p), p?Rf, C)
выражающими переменные z и и> однозначно во всей
области существования функции B) как полной анали-
аналитич. функции. С другой стороны, подход К. Вейерштрас-
са (К. Weierstrass) к построению понятия полной ана-
аналитич. функции B) состоит в использовании локального
униформизирующего параметра t, позволяющего выра-
выразить переменные z и w аналитически в виде однозначных
аналитич. функций z=z(t) и w--w(L) локально и окрест-
окрестности нек-рой точки (z0, w0), wo—f(z0). Задача унифор-
униформизации в ее простейшей классич. постановке есть зада-
задача синтеза этих двух идей. Требуется заменить соот-
соотношение B) во всей области его определения двумя
аналитич. представлениями z=z(t), w=w(t), где t —
униформизирующее комплексное переметки-. изменяю-
изменяющееся в нек-рой области на плоскости.
Возможность униформпзации в указанной постановке
установлена П. Кёбе и независимо А. Пуанкаре почти
одновременно в 1907. Если Р. п. Rf функции B) одно-
связна или подобна однолистной, то задача униформи-
униформизации сводится к построению конформного отображе-
отображения (р : Rf—>¦ D Р. п. Rf на плоскую область D. Пред-
Представления C) тогда дают искомую униформизацию:
Конформное отображение / на плоскую область суще-
существует для Р. п. Rf, подобных однолистным, и толь-
только для них (общая теорема униформы-
з а ц и и).
В общем случае произвольного аналитич. соотно-
соотношения B) P. a. Rf не является подобной однолистной,
но ее универсальная накрывающая Rf односвязна, и
следовательно, существует конформное отображение
1|з: Д/—> D,
где D — одна из упоминавшихся областей: С, С или
единичный круг. Функция w--f(z) мероморфна на Р. п.
Rf, а следовательно и на Rf, причем она зависит только
от проекции p--p(q), pfRf, точки г/{^Лу. Таким обра-
образом, получается геометрич. унпформизация в виде
а отсюда и аналптич. униформизация:
где z и w выражаются как мероморфные функции Ф (<)
и 'F (t) переменного t?D. Эти функции Ф («)' и ? (<) суть
автоморфные функции в области Z) относительно группы
автоморфизмов Л, изоморфной фундаментальной груп-
группе я, (НА Р. п. Я, униформизируемойфункции (см. [3],
[7], [15], 116]).
Лит.: [1] Р и м а н Б., Соч., пер. с нем., М.—Л., 1948;
[2] М а р к у ш е в и ч А. П., Теория аналитических функций,
2 изд., т. 1—2, М., 1967—В8; [3] Г у р в и ц А., К у р а н т Р.,
Теория функций, пер. с нем., М., 19R8; [4] Стой лов С,
Теория функций комплексного переменного, пер. с рум., т. 1—2,
М., 1962; [5] е г о же, Лекции о топологических принципах
теории аналитических функций, пер. с франц., М., 1964: Lt>]
Спрингер Д ж., Введение в теорию римановых поверх-
поверхностей, пер. с англ., М., 1960; [7] Неванлинна Р., Уни-
Униформизация, пер. с нем., М., 1955; [8] Ш и ф ф е р М., С л е н-
сер Д. К., Функционалы на конечных римановых поверхнос-
поверхностях, пер. с англ., М., 1957; [9J Чеботарев Н. Г., Теория
алгебраических функций, М.—Л., 1948; [10] Волновые-
к и й Л. И., «Тр. Матем. ин-та АН СССР», 1950, т. 34, с. 3—171;
[ 11J его же, «Успехи матем. наук», 1956, т. 11, в. 5, с. 77—84;
[12] К р у ш к а л ь С. Л., Квазиконформные отображения и
римановы* поверхности, Новосиб., 1975; L13] Крушкаль
С. Л., Апанасов Б. Н., Гусеве кий Н. А., Клейно-
вы группы в примерах и задачах, Новосиб., 1978; [141 Итоги
науки и техники. Алгебра. Топология. Геометрии, т. 1й, М.,
1978, с. 191—245; [15] А л ь ф о р с Л., Б е р с Л., Простран-
Пространства римановых поверхностей и квазиконформные отображения,
пер. с англ., М., 1961; [16] Б ер с Л., «Успехи матем. наук»
1973, т. 28, в. 4, с. 153—98; 1974, т. 29, в. 2, с. 86—102; [17]
Klein F., Riemannsche Flachen... Vorlesung von F. Klein,
Gott. 1894; [18] Weyl H., Die Idee der Riemannschen
Flache, 3 Aufl., Stuttg., 1955; [19| A h 1 f о r s L., S a r i о L.,
Riemann surfaces, Princeton, I960; [20] P f 1 u к e r A., Theorie
der Riemannschen Flachen, B.— [u. a.], 1957; 121] S a r i о L.,
Nakai M., Classification theory of Riemann surfaces, B.—
[u. a.], 1970; [22] H e i n s M., Hardy classes on Riemann sur-
surfaces, В.— [u. a.], 1969; [23] G u n n i n g R. C, Lectures on
Riemann surfaces, Princeton, 1966; [24] его же, Lectures on
Riemann surfaces, Jacobi varieties, Princeton, 1972; [25] Форс-
Форстер О., Римановы поверхности, пер. с нем., М., 1980.
Е. Д. Сояоменцев.
РИМАНОВА СВЯЗНОСТЬ — аффинная связность на
римановом пространстве Л/, относительно к-рой мет-
рич. тензор пространства g;,- является ковариантно по-
постоянным. Если аффинная связность на М задана с по-
помощью матрицы локальных форм связности
\
J
и метрич. формой на М является dss—g,-y-co'<o/, то по-
последнее условие выражается в виде
M'j B)
Оно может быть выражено еще следующим образом:
при параллельном перенесении вдоль любой кривой мно-
многообразия М скалярное произведение <Х, У> =
= ,?,yu)'(Z)(o^(F) произвольных двух векторов сохра-
сохраняет свое значение, т. е. для любых векторных полей
X, Y, Z на М справедливо равенство
Z<A\ Y> = <vzX, У>+<Х
где V?Х — векторное поле, называемое ковариантной
производной поля X относительно поля Z и определяе-
определяемое формулой
со' (vzX)=Zco< (Х)+со^B)со*(Х).
Если на М перейти к локальному полю ортонормиро-
ванных реперов, то #,у —6,-у (если ограничиться случаем
положительно определенной ds2) и условие B) прини-
принимает вид
со(- fco/==0,
т. е. матрица со, составленная из форм A), принимает
значения в алгебре Ли группы движений евклидова
пространства Еп размерности n=dim М. Поэтому Р. с.
может быть интерпретирована как связность в рас-
расслоенном пространстве ортонормированных реперов в
касательных к М евклидовых пространствах. Голоно-
мии группа Р. с. есть нек-рая подгруппа группы дви-
движений пространства Еп; римановой связностью для
нок-рой римановой метрики на М является каждая
аффинная связность, группа голономии к-рой — груп-
группа движений или нек-рая ее подгруппа.
Если в A) o)' — dxl (то есть М отнесено к полю нату-
натуральных реперов локальной координатной системы),
то
I 1 ст k hj
Щ г Sii~~ ё g
где
— т. н. символ Кристоффеля и Sij=Tij—Yjk — тензор
кручения Р. с. Существует одна и только одна Р. с.
без кручения (т. о. такая, что Stj— 0), к-рая определяет-
определяется формами °>'j—{jk\'Jdxk и паз. Леви-Чивита связ-
связностью.
Лит.: [1] Г р о м о л Д., К л и н г е н б е р г В., М е й е р
В., Риманова геометрия в целом, пер. с нем., М., 1971; [2] Л и-
хнерович Л., Теория связностей в целом и группы голо-
номий, пер. с франц., М., I960. Ю. Г. Лумисте.
РИМАНОВО МНОГООБРАЗИЕ — дифференцируемое
многообразие, наделенное римановой метрикой. По
существу Р. м.— то же, что и риманово пространство.
М. И. Войцеховский.
РИМАНОВО ПРОСТРАНСТВО — пространство, в ма-
малых областях к-poro имеет место приближенно (с точ-
точностью до малых высшего порядка сравнительно с раз-
размерами областей) евклидова геометрия, хотя в целом
такое пространство может не быть евклидовым. Р. п.
названо по имени Б. Римана (В. Riumami), наметившего
в 1854 основы теории таких пространств (см. Риманова
геометрия). Простейшими Р. П. являются евклидово
пространство и примыкающие к нему два других про-
пространства постоянной кривизны, в к-рых имеет место
Лобачевского геометрия и Римана геометрия (не смеши-
смешивать последнюю с общей римановой геометрией, к-рая
изучает Р. п. вообще).
Г/о MuviejmonuM одноименной статьи в БСЭ-3.
РИМАНОВО ПРОСТРАНСТВО ОБОБЩЕННОЕ —
пространство с внутренней метрикой, подчиненное не-
к-рым ограничениям на кривизну. К ним относятся
пространства с «кривизной, ограниченной сверху»,
и др. (см. [3]). Р. и. о. отличаются от римановых прост-
пространств не только большей общностью, но и тем, что они
определяются и исследуются, исходя из метрики, без
координат. При нек-ром соединении условий на кри-
кривизну и поведении кратчайших (т. е. кривых, длины
к-рых равны расстояниям между концами) Р. п. о.
оказывается римаповым, что дает чисто метрич. опреде-
определение риманова пространства.
Определения Р. п. о. исходят из классич. связи кри-
кривизны с избытком геодезического треугольника (избы-
(избыток- сумма углов минус я). Эти понятия переносятся
на пространство с внутренней метрикой такое, что у
каждой точки его есть окрестность, любые две точки
к-рой соединены кратчайшей. Это условие далее подра-
подразумевается без оговорок. Треугольником /=
= АВС наз. тройка кратчайших АВ,ВС, СА — сторон
треугольника, соединяющих попарно три различных
точки А, В, С — вершины треугольника. Угол опреде-
определяется между кривыми в любом метрич. пространстве.
Пусть L, M — исходящие из одной точки О кривые в
пространстве с метрикой р. Выбираются точки X?L,
Y?M (X, УфО), строится евклидов треугольник со
сторонами z=p(O, X), у=р(О, Y), z=p(X, Y) и углом
у(х, у), противолежащим стороне z. Определяется
верхний угол между L и М:
а= Пт у(х, У)- (D
ху-+о
Верхние углы треугольника —это верхние углы а, р\
у между его сторонами при вершинах А, В, С, а избы-
избыток треугольника 6 (Т)=а-\-$-\-у—я.
Р. п. о. с ограниченной кривизной (¦</? и ^К') опре-
определяется условием:
(А) для каждой последовательности треугольников
Тп, стягивающихся к точке,
где а (Тп) — площадь евклидова треугольника с такими
же сторонами, что Тп (если ст(Уи) —0, то &(Тп)=0).
Такое пространство оказывается римановым при двух
естественных дополнительных условиях:
A) локальная компактность прост-
пространства (в пространстве с внутренней метрикой
это уже обеспечивает условие локального существо-
существования кратчайших);
B) локальная продолжаемость крат-
кратчайших — у каждой точки существует окрестность
U такая, что любую кратчайшую XY, где X, Y?U,
можно продолжить за ее концы. При всех этих услови-
условиях пространство является римановым (см. [4]), причем
в окрестности каждой точки можно ввести координаты
х' так, что метрика будет задаваться линейным элемен-
элементом ds^gijdx'dxi с коэффициентами g/j? Wqf] С1- а,
0<а<1. Тем самым имеется параллельный перенос (с
непрерывными T/k) и почти везде — тензор кривизны.
Кроме того, доказано [7], что координаты х' можно
взять гармоническими, т. е. удовлетворяющими равен-
равенствам ?l..gi-frlj=Q. Гармонич. системы координат со-
составляют атлас класса С3- а при любом а, 0<а<1.
Р. п. о. с ограниченной кривизной при К-=К',
удовлетворяющее условиям A) и B), является рима-
римановым пространством постоянной римановой кривизны
К (см. [3]).
Всякое риманово пространство с римановой кривиз-
кривизной, заключенной между К и К'(К'^.К), является
Р. п. о. кривизны <Я и >#' и удовлетворяет услови-
условиям A) и B).
«Пространство с кривизной <сК» определяется левым
неравенством B), т. е. условием:
(А~) для любой последовательности треугольников
Тп, стягивающихся в точку,
Другое равносильное определение и начало исследо-
исследования Р. п. о. исходят из сравнения произвольного
треугольника Т=ABC с треугольником Tk со сторонами
той же длины в пространстве постоянной кривизны К.
Пусть afe, Рй, Yk — углы такого треугольника; от-
относительный верхний избыток треугольника Т опреде-
определяется как бАG')=(а-|-^+у)—(afe+Pfe+Vfe). Условие
(А ~) в определении пространства с кривизной </f мож-
можно заменить на условие:
(ЛГ) у каждой точки есть окрестность А'д., в к-рой
б(!Gт)<:0 для всякого треугольника Т. Выполняется и
более сильное свойство вогнутости метрики. Именно,
пусть L, M — кратчайшие, исходящие из одной точки
О, и Ук(х, у) — угол в треугольнике Tk со сторонами
х=р(О, X), у=р(О, X), z=p(X, Y), X?L, Y?M, в
пространство постоянной кривизны К, противолежащий
стороне z. В Ft/, (локально) угол Yk(x, у) оказывается
неубывающей функцией (y*0*i, i/i)<Yfc(z2, уг) при ^<
<:.г2, г/!<1/2)- Отсюда следуют локальные свойства:
(I) между любыми двумя кратчайшими, исходящими
из одной точки, существует угол и даже «угол в сильном
смысле» ac=lim y^(x, у) (так что, в частности, если
ху->-о
!/=const, то lim-r— =cos a^);
х-»-о
(II) для углов а, р, у треугольника вД^в соответст-
соответствующего треугольника Г*
(III) в Rk, если An->-A, Bn^-B, кратчайшие
А„Вп —>. АВ (тем самым кратчайшая в R^ с данными
концами единственна).
Двойственными пространствами с кривизной ^.К бу-
будут пространства с кривизной ^К, определяемые ана-
аналогично через нижние избытки, к-рые вычисляются по
нижним углам в сильном смысле. Для кратчайших L,
М этот угол есть
a= lim у (х, у).
Нижний избыток треугольника есть б=а+Р-(-Т—л-
Пространство с кривизной ^К ~ это такое простран-
пространство, в к-ром вместо (А~) выполняется условие:
(А+) для любой последовательности Тп треугольни-
треугольников, стягивающихся к точке,
Неравенство с верхним избытком б, противоположное
неравенству C), не дает содержательных результатов,
их не дает и неравенство с избытком, вычисляемым про-
просто с нижними углами
lim y(x,y).
ху-*о
Условие (А+) можно заменить на условие:
A у каждой точки есть окрестность Rk , в к-рой
О для всякого треугольника Т. В R^ (локально)
угол Yfc(.r, у) для двух кратчайших L, М оказывается
невозрастающей функцией (выпуклая метрика).
Аналогично пространствам с кривизной <:/? для
пространств с кривизной ^К выполняются (локальные)
свойства, подобные (I) и (II): между кратчайшими
существует угол в сильном смысле; a^a^, P^P^i Y=S=
:>Yfe Для всякого треугольника в Rt. Вместо (III) вы-
выполняется условие неналегания кратчайших или, что
то же, единственность их продолжения: если AC~z>AB
и АСг~эАВ в R& , то либо АС2ЭАС1г либо AC-^dAC.
Таким образом, пространство с ограниченной кри-
кривизной получается соединением условий, определяю-
определяющих оба класса пространств — с кривизной, ограни-
ограниченной сверху или снизу (причем в левой части нера-
неравенства C) нет нужды брать б). Условие (А) можно за-
заменить, подобно (At) и (Ai), на условие:
(Аг) у каждой точки есть окрестность Rkk', гд"
б«г(Г)<0, бй.(У)^О для всякого треугольника Т. Это
оказывается также равносильным следующему:
(А2) для всякой четверки точек в Rkk' существует
четверка точек с теми же попарными расстояниями в
пространстве постоянной кривизны к, где А"<А-<:А" и
к зависит, вообще говоря, от выбранной четверки точек
в R
Примером Р. п. о. с кривизной ^.К(~^К') является
область риманова пространства, в к-рой риманоны кри-
кривизны всех двумерных площадок во всех точках огра-
ограничены сверху (снизу) числом К (К1).
Множество V в пространстве с внутренней метрикой
наз. выпуклым, если любые две точки X, Y? V
можно соединить кратчайшей X, У и всякая такая
кратчайшая содержится в У.
Установлен [8] следующий результат: если простран-
пространство R с внутренней метрикой получено склеиванием
двух пространств R', R" кривизны *?К по выпуклым
множествам V'CR" и V"cR", то R само есть простран-
пространство кривизны <К. Условие склеивания заключается
в том, что Я = Д'и#", V'=V"=-R'f\R" и в R', R"
индуцируется метрика пространства R.
Две выходящие из точки О кривые А, М (по опреде-
определению) имеют в О одинаковое направле-
направление, если верхний угол между ними равен нулю
(если L=M, то говорят, что А имеет в О определенное
направление). Направление в точке О опреде-
определяется как класс кривых, имеющих в О одинаковое
направление. Направления в точке О образуют метрич.
пространство, в к-ром расстояние между направления-
направлениями определяется верхним углом между любыми их пред-
представителями. Это пространство наз. простран-
пространством направлений в точке О.
Доказано [5]: если точка О содержится в окрестности
пространства кривизны <К, гомеоморфной Е", то
пространство направлений в точке О является прост-
пространством кривизны <1. Неизвестно A983), гомеоморф-
но ли оно (ге — 1)-мерной сфере.
В двумерном случае теория многообразий ограничен-
ограниченной кривизны (см. Двумерное многообразие ограничен-
ограниченной кривизны) включает в себя как частный случай тео-
теорию многообразий с кривизной <#. Примером двумер-
двумерного многообразия с кривизной <.К является линейча-
линейчатая поверхность в Jfj, снабженная внутренней метри-
метрикой, т. е. поверхность, образованная внутренними
частями кратчайших, концы к-рых зачеркивают две
спрямляемые кривые А1; А2. Если кривая А2 вырож-
вырождается в точку О, поверхность наз. конусом крат-
кратчайших, натянутым из точки О на кривую At. Если
Aj есть треугольник ОАВ, то такой конус наз. п о-
верхностным треугольником (см. [3]).
Отображение ф : Мг —v M2 метрич. пространства наз.
нерастягивающим, если рл1,(^, У)^РЛь(ф {X),
if (К)) для любых X, Y^MX. Отображение <р : 1\ -*• Г2
.(нмкнутой кривой Tj в Mt на замкнутую кривую Г2 в
.1/2 наз. эквилонгальным, если длины соот-
соответствующих при отображении ф дуг кривых 1\ и Г2
говпадают. Пусть V — выпуклая область в простран-
пространстве постоянной кривизны К и А — краевой контур V.
Область V мажорирует замкнутую кривую Г в
метрич. пространстве М, если существует нарастающее
отображение области V в М, эквилонгально отображаю-
отображающее А на Г. Само отображение наз. мажорирую-
щ и м.
Пусть Rk — выпуклое пространство с внутренней
метрикой; С — конус кратчайших, натянутый на замк-
замкнутую спрямляемую кривую Г в Rk из точки О ? Г,
причем в случае К >0 длина I кривой Г меньше 2л/ У К ¦
Тогда в пространстве постоянной кривизны К сущест-
существует выпуклая область V, мажорирующая Г, такая, что
<p(F)=C для соответствующего мажорирующего ото-
отображения ф. Это свойство характеризует пространства
кривизны <:ЛГ. Достаточным является уже существо-
существование эквилонгального нерастягивающего отображе-
отображения контура А области V на Г.
Повсрхнос т J, то в метрич. пространстве М
наз. непрерывное отображение / круга R в М. Пусть
Р — триангулируемый многоугольник, т. е. комплекс
из треугольников 71,-, вписанный в В. Треугольнику Г,
с вершинами X, У, Z сопоставляется евклидов треуголь-
треугольник Тс со сторонами, равными расстоянию между
точками f{X), /(У), f(Z). Пусть S0(P) обозначает сумму
площадей S(Г°) всех треугольников Т°; тогда пло-
площадь S(/) поверхности / определяется (см.
[3]) как нижний предел величин S0{P) при условии,
что вершины комплекса Р неограниченно сгущаются в
В : S(f)=lim S0(P). Это определение модифицировано
так (см. [6]). Вместо точек f(X), f(Y), f(Z) вершинам
X, Y, Z треугольника Т/ комплекса Р сопоставляются
нек-рые точки Хр, Yp, Zp в М, причем вершинам ком-
комплекса Р сопоставляются одинаковые точки в том и
только в том случае, когда образы вершин при отобра-
отображении / совпадают. За площадь L(f) поверхности /
принимается нижний предел сумм площадей евклидо-
евклидовых треугольников Г° со сторонами, равными расстоя-
расстояниям между точками Хр, У , Zp при дополнительном
предположении, что p(f(X^), Xk) по всем вершинам Х^
комплекса Р стремится к нулю. Всегда L (/)<:?(/).
1) Если последовательность поверхностей /„ в i?&
равномерно сходится к поверхности /, то
L (/) s? litnL (/„) (иолунепрерывность).
2) Если р — нерастягивающее отображение из Я&
в Rk и / — поверхность в R^, то
L (р о /) < L (/) (принцип Колмогорова).
3) Площадь S (/) поверхностного треугольника Т в
Rk не больше площади соответствующего треугольника
Г* и равна ему тогда и только тогда, когда треугольник
Т изометричен Тк (локальное свойство).
4) В условиях теоремы о существовании мажорирую-
мажорирующего отображения (см. выше) площадь S (G) не больше
площади круга в пространстве постоянной кривизны К
с периметром I (изопериметрическое неравенство) (см.
[3], [6]).
Решается [6] задача Плато в R/, о существовании по-
поверхности минимальной площади, натянутой на замкну-
замкнутую кривую Г. Доказано следующее. Пусть R^ — мет-
метрически полное пространство кривизны *sK (при /f >0
диаметр d(R/l)<ni2V~K), Г — замкнутая жорданова
кривая в Я&. Тогда существует поверхность / мини-
минимальной площади L(/), натянутая на кривую Г. Пусть
Г, Г„, ге=1, 2, ... ,— замкнутые жордановы кривые
в таком пространстве и а (Г), а (Г„) — минимальные пло-
площади поверхностей, натянутых соответственно на Г и
Г„. Если Т„ равномерно сходятся в нек-рых парамет-
параметризациях к Г, то а (Г)<:lim я (Г„),
Рассматривались двумерные многообразия с инде-
индефинитной метрикой ограниченной кривизны. Не ре-
решена A983) задача бескоординатного определения мно-
многомерных пространств с индефинитной метрикой огра-
ограниченной кривизны, в частности пространств общей тео-
теории относительности.
Лит.: [1] Александров Д. Д., Внутренняя геомет-
геометрия выпуклых поверхностей, М.—Д., 1948; [2] е г о ж е, «Тру-
«Труды Матем. ин-та АН СССР», 1951, т. 38, с. 5—23; И е г о ж е,
«Schrift. Inst. Math. Deutsch. Acad. Wiss.», 1957, H. 1, S. 33—
84; [4] Б е р е с т о в с к и й В. Н., «Сиб. матем. ж.», 1975,
т. 16, № 4, с. 651—62; [5] Николаев И. Г., там же, 1978,
т. 19, М« 6, с. 1341—48; [6] е г о же, там же, 1979, т. 20, № 2,.
с. 345—53; [7] Р е ш е т н я к Ю. Г., «Матем. сб.», 1960, т. 52,
№ 3, с. 789—98; [8] е г о же, «Сиб. матем. ж.», 1968, т. 9, № 4,
с. 918—27. А. Д. Александров, В. И. Берестовский.
РИМАНОВО ПРОСТРАНСТВО ОДНОРОДНОЕ —
риманово пространство (М, у) вместе с транзитивной
эффективной группой G его движений. Пусть К — ста-
стационарная подгруппа фиксированной точки о?М.
Тогда многообразие; М отождествляется с факторпрост-
ранством GiK с помощью биекции G/K^gK<^z^go^M,
а риманова метрика у рассматривается как G-инвариант-
ная метрика на GIК. Обычно предполагается дополни-
тельно, что группа G замкнута в полной группе дви-
движений. В этом случае стационарная подгруппа К ком-
компактна.
Пусть К — компактная подгруппа группы Ли G, не
содержащая нормальных делителей группы G. Тогда
однородное пространство M—G/'К допускает инвариант-
инвариантную риманову метрику у, к-рая определяется следую-
следующим образом. Пусть (M=,ff-j-2ft — редуктивная струк-
структура в М, т. е. разложение алгебры Ли ® группы Ли G
в прямую сумму алгебры Ли Ж группы К и подпро-
подпространства [ДО, инвариантного относительно присоеди-
присоединенного представления Ad К группы К в пространстве
№. Пространство ЯЛ естественным образом отождеств-
отождествляется с касательным пространством T0M^&/St точки
о = еК, а представление изотропии группы К в Т0М —
с представлением Ad А'|ЗЛ. Любая G-инвариантная ри-
манова метрика у на М получается из нек-рого Ad K-
инвариантиого скалярного произведения у0 в ЯЛ раз-
разнесением с помощью преобразований из G:
yg0(X, Y)^yo(g~1X, g~xY), X, Y?Tg0M, g?G.
Существование такого скалярного произведения следу-
следует из компактности группы изотропии Ad A |Щ1.
Любое Р. и. о., локально изометрнчное односвязному
Р. п. о. М, получается из М факторизацией по произ-
произвольной дискретной группе изометрий Клиффорда —
Вольфа (т. е. движений многообразия М, перемещаю-
перемещающих все точки на одинаковые расстояния [2]).
Наиболее изученными классами Р. п. о. являются
римановы симметрич. пространства, однородные кэле-
ровы пространства и однородные кватернйонные про-
пространства, изотропно неприводимые Р. п. о. (классифи-
(классифицированы в [9], [10]), нормальные Р. п. о., в к-рых
скалярное произведение уи в ЯЛ продолжается до невы-
рожденпой симметрической Ad G-инвариантной били-
билинейной формы на ($, естественно редуктивные Р. п. о.,
характеризуемые тем, что в них любая геодезическая
является траекторией однопараметрич. группы движе-
движений.
Изучена структура Р. п. о. с различными условиями
на тензор кривизны. Напр., известна классификация
Р. п. о. положительной секционной кривизны [5]. Опи-
Описана структура просто транзитивных групп движений
Р. п. о. неположительной кривизны [8], неотрицатель-
неотрицательной кривизны и неотрицательной кривизны Риччи [4].
Р. и. о. с разрешимой группой движений G всегда имеет
неположительную скалярную кривизну sk, и случай
sk=O возможен только для локально евклидова про-
пространства. Любая инвариантная риманова метрика на
односвязно.м Р. п. о. GIК имеет неположительную
скалярную кривизну тогда и только тогда, когда К
есть максимальная компактная подгруппа группы G
(см. [4]).
Р. п. о. (М, у) наз. эйнштейновым, если его
тензор Риччи р пропорционален метрике: р=А/у, Х=
= const. Проблема описания эйнштейновых Р. п. о. не
решена A983). Известен ряд частных результатов. Пусть
(M=GlK, у) — эйнштейново Р. п. о. со скалярной
кривизной sk. 1) Если sk>0, то многообразие М ком-
компактно. Описаны все такие пространства: а) если (М,
у) — кватернионное пространство, б) если М диффео-
морфно симметрии, пространству ранга один, в) для
нек-рого класса естественно редуктивных Р. п. о. (см.
[7]) и для u.'ioipoiiHO неприводимых Р. п. о. (см. [10]).
2) Если sk=O, то М есть локально евклидово простран-
пространство. 3) Если sk<0 и группа G унимодулярна (т. е. оп-
определитель операторов ее присоединенного представле-
представления равен 1), то группа G полупроста.
Лига.: [1] К о б а я с и Ш., Н о м и д з у К., Основы диф-
дифференциальной геометрии, пер. с англ., т. 2, М., 1981; [2]
В о .'л ь ф Дж., J 1]Л1С1ранстка постоянной кривизны, пер. с
англ., ML, 1982; [31 X е л г а с о н С, Дифференциальная гео-
геометрия и симметрические пространства, пер. с англ., М.,
1964; [4] Berard Bergery L., «Ann. sci Ёс. norm, sup.»,
1978, t. 11, Л5 4 p. 543—76; [5] e г о же «J. Math, pures et
appl.», 1976, t. 55, p. 47—67; [6] J e n s e n G. R., «J. Dif.
Geom.», 1973, v. 8, p. 599—614; [7]D'Atri J. E., Z i I 1 e r W.,
«Mem. Amer. Math. Soc», 1979, v. 18 p. 1—72; [8]Azencott
R., Wilson E. N.. там же, 1976, v. 8, p. 1 — 102; [9J
Мант у ров О. В., «Тр. сем. по вект. и тенз. анализу»,
1966, т. 3, 68—145; [10] Wolf J., «Acta math.», 1968, v. 120,
p. 59—148. Д. В. Ллексеевский.
РИМАНОВЫ КООРДИНАТЫ — см. Геодезические
координаты.
РИМАНОВЫХ ПОВЕРХНОСТЕЙ КЛАССИФИКА-
КЛАССИФИКАЦИЯ — изучение римановых поверхностей (р. п.), свя-
связанное с рассмотрением поведения функций различных
классов на этих поверхностях.
Комплексная функция / : R —>- С на р. п. R наз.
аналитической на Я, если для любой точки
Роб Я существуют окрестность U и локальный уиифор-
мизирующий параметр z=(p(p), <р(Ро)=О, отображаю-
отображающий гомеоморфно U на единичный круг D-
= {z?C : |г|<1} и такой, что сложная функция F(z) = -
=f [ф~1(г)] является однозначной аналитич. функцией
в D. Аналогично определяются на р. п. действительные
и комплексные гармонич. функции, субгармонич. функ-
функции и др. Пусть W — нек-рый конформно инвариант-
инвариантный класс функций на р. п. R, содержащий константы.
Задача Р. п. к. в простейшей постановке состоит в оп-
определении условий, при к-рых данная р. п. R принад-
принадлежит или не принадлежит классу Ow таких р. п., что
класс W на них состоит только из констант. Теория
Р. п. к. выросла в 20 в. из классич. теоремы Римана
о конформном отображении односиязпых р. п., пробле-
проблемы типа, проблемы существования Грина функции
р. п. и понятия идеальной границы р. п.
Теорема Римана утверждает, что любая одно-
связная р. п. R отображается конформно (и, следова-
следовательно, гомеоморфно) на плоскую область D одного ия
трех видов: D=C=С (J {оо} — расширенная комп-
комплексная плоскость (случай р. п. R эллиптиче-
эллиптического типа); D — C — конечная комплексная пло-
плоскость (R — параболического типа); D—
--={z?C : \z\ <1} — единичный круг (R — гипер-
гиперболического типа). Поскольку эллиптич.
случай отличается от остальных уже топологически,
остается трудная задача распознавания, когда данная
р. п. R принадлежит гиперболическому или параболич.
типу. Это и есть классич. проблема типа, пол-
полностью пока не решенная A983). Известно, что замкну-
замкнутая р. п. рода g при g=0 эллиптич. типа, при g= 1 пара-
параболич. типа, при #>1 гиперболич. типа, поэтому про-
проблема типа важна в основном для открытых р. п. В слу-
случае произвольной р. п. R, не обязательно односвязной,
ее типом является тип ее универсальной накрывающей
поверхности (см. Универсальное накрытие) R, к-рая
всегда односвязна.
Для односвязных конечных р. п. R задача отыскания
конформного отображения R на единичный круг D
эквивалентна задаче отыскания функции Грина G (р, р0)
для R, т. е. положительной гармонич. функции с лога-
рифмич. особенностью вида In A/ |з—zo|) в полюсе р0 (; Я
(z—(f(p) — параметр в окрестности pOi z0=<p(p0),
обращающийся в нуль во всех точках края dR). Функ-
Функция Грина строится и для многосвязных конечных р. п.
гиперболич. типа. В случае произвольной открытой
р. п. R можно построить исчерпание {i?vKT=i поверх-
поверхности R с помощью конечных р. п. Rv с краем, имею-
имеющих функции Грина
Gv (Р, Ро) —1" | г_г0| +Yv +0 (|г — го|), z —<- z0
(или Gy{p, р0)=+оо, начиная с нек-poro номера v),
и таких, что Rv(zRv+i, \Jv=iRv—R- Постоянная
Vv> — со <Yv¦< ~Ь а> • наз. Робена постоянной р. п. Д\п
cv=e v есть емкость края dRy (относительно фикси-
фиксированного полюса ра?Я). При стремлении v к оо зна-
значения Gv(p, p0) и yv могут только возрастать. Функ-
Функция Грина открытой р. п. R определяется как предел
G(p, Po) возрастающей последовательности {Gv(p, p0)},
если он существует; в противном случае, когда
lim Gv (p, р„) ==+<»,
говорят, что р. п. R не имеет функции Грина, причем
существование или несуществование функции Грина не
зависит от выбора полюса ро?Я. Класс р. п., для
к-рых функция Грина не существует, обозначается f)(i.
Иными словами, класс Qa характеризуется тем, что
lim yv = + oo или lim cv = 0,
нричем эти соотношения также не зависят от выбора
полюса.
Пусть R — открытая р. ц. и {Av}v°=i — т.н. о и р е-
деляющая последовательность замк-
замкнутых на R областей Av. т. е. такая последовательность,
что 1) граница Av есть простая замкнутая кривая на Я\
2) Av+iCZAv, v=l, 2, ... ; 3) riv°=iAv=0> ™ есть Av
не компактны на Я. Две определяющие последователь-
последовательности {Av} и {Av} эквивалентны, если каждому v соот-
соответствуют такие п и т, что AnCZAv и AmcAv. Классы
эквивалентности определяющих последовательностей
наз. граничны м и :> л е м е н т а м и р. п. R,
а совокупность всех граничных элементов образует
идеальную границу Г р. п. Я, рассматри-
рассматриваемой как топологнч. поверхность. Напр., идеальная
граница единичного круга D состоит из одного гранич-
граничного элемента. Отметим, что функция Грина открытой
р. и. /?, в отличие от случая гиперболич. конечной р. п.,
не обязательно обращается в нуль на всех элементах
идеальной границы Г. Класс Qq характеризуется так-
также как класс р. п. с идеальной границей нулевой
емкости, или, короче, как класс р. п. с нулевой грани-
границей; если R(?()q, то lim cv-=c>0 наз. емкостью иде-
v~>oo
альиой границы. Существование или несуществование
функции Грина р. п. R, а также объем других функцио-
функциональных классов на Я определяются прежде всего этой
и другими более тонкими характеристиками идеальной
границы, связанными с самими функциональными клас-
классами.
Основными функциональными клас-
классами W на р. п. Я являются следующие:
А В — класс ограниченных однозначных аналитич.
функций на R;
AD — класс однозначных аналитич. функций /(z)
на Я с конечным Дирихле интегралом
IIP, HB и HD —классы однозначных гармонич. функ-
функций на R соответственно положительных, ограниченных
и с конечным интегралом Дирихле. Эти классы могут
комбинироваться, напр. ABD — класс ограниченных
однозначных аналитич. функций на if с конечным
интегралом Дирихле. Для соответствующих классов
Ciw Р- п- ^ установлены следующие строгие включения
и равенства:
Qhb с Qhd с: 6ad, Qhbd—Qhd-
Для плоских областей R эти соотношения упрощаются:
6а = 6 нр -= бнв =
Важное значение имеют также классы Харди
АН„, 0<р<+оо, однозначных аналитич. функций ш=
=/(z) на р. п. R. При ()<р<+°° функция f?AHp,
если субгармонич. функция |/|^ имеет на всей р. п. R
гармонич. мажоранту, а АН^ — АВ (см. Граничные
свойства аналитических функций).
Р. п. иараболич. тина принадлежит классу (Зо.
поэтому иногда вопрос о характеризации р. п. класса
Оа наз. обобщенной проблемой типа.
Имеется много результатов, в к-рых в различных терми-
терминах устанавливаются условия принадлежности р. п.
указанным выше классам. Глубокие исследования были
посвящены выяснению внутренних свойств р. п. опре-
определенных классов. В частности, оказалось, что р. п. с
нулевой границей во многих отношениях аналогичны
замкнутым р. и. На них строятся аналоги абелевых
дифференциалов и соответствующие интегралы.
Более тонкие свойства идеальной границы р. п. Я
удается исследовать также с помощью различных ком-
пактификаций R. Напр.. пусть N (R) — винеровская
алгебра функций и на р. и. R, ограниченных, непре-
непрерывных и гармонизуемых на R; последнее означает,
что для любой регулярной области GczR существует
обобщенное решение задачи Дирихле в смысле Вине-
Винера — Перрона (см. Перрона метод) с граничными дан-
данными и на границе dG. Компактификациен.
Винера р. п. R наз. компактное хаусдорфово про-
пространство R* такое, что R есть открытое плотное под-
подпространство Я*, каждая функция u?N(R) непрерыв-
непрерывно продолжается на R* и N (R) разделяет точки R*.
Компактификация Винера существует для любой р. п.
R. Множество Г(Д)=Д*\Д над. винеровской
идеальной границей р. п. R, а подмножест-
подмножество Л (Л)сГ(/?), состоящее из тех точек if?*, в к-рых все
потенциалы из N(R) обращаются в нуль,— вине-
винеровской гармонической границей.
В этих терминах, напр., включение ff^6o равносиль-
равносильно равенству Д(Я)-=0; отсюда получается также стро-
строгое включение QhP^-Qhr-
С Р. и. к. связан также вопрос об устранимых множе-
множествах на р. п. Так, компакт К на р. п. R нац. AR-
устранимым, если для нек-рои окрестности f/'Э
ЗЭЛ" на Я все /45-функции на U\K имеют аналитич.
продолжение на всю окрестность U.
Внимание многих исследователей привлечено также
к вопросам классификации римановых многообразий
произвольных размерностей N^2, связанной с рассмот-
рассмотрением описанных выше классов функций.
Лит. см. при ст. Романова поверхность.
РИМАНОВЫХ ПОВЕРХНОСТЕЙ КОНФОРМНЫЕ
КЛАССЫ — классы, состоящие из конформно экви-
эквивалентных римановых поверхностей. Замкнутые рима-
новы поверхности (р. п.) имеют простой топологич.
инвариант — род g; при этом любые две поверхности
одного рода гомеоморфны. В простейших случаях то-
нологич. эквивалентность двух р. п. обеспечивает и их
принадлежность к одному и тому же Р. п. к. к., то
есть конформную эквивалентность, или, говоря иначе,
совпадение их конформных структур. Это выполняет-
выполняется, напр., для поверхностей рода 0, то ость гомеоморф-
ных сфере. В общем случае дело обстоит по так. Еще
Б. Риман (В. Riemann) заметил, что классы конформной
эквивалентности р. п. рода #>1 зависят от 3g—3 комп-
комплексных параметров, называемых модулями римановых
поверхностей; для конформно эквивалентных поверх-
поверхностей эти модули совпадают. Случай g= 1 описан ниже.
Если же рассматривать компактные р. п. рода gen
аналитич. компонентами края, то для их конформной
эквивалентности требуется совпадение tig—6-j-3rc дейст-
действительных параметров-модулей (g^Q, ге^О, 6g—6+
-|-Зге>0). В частности, для га-связных плоских облаете!!
(ге^З) таких модулей Зге—6; всякая двусвязная плоская
область конформно эквивалентна кольцу с определен-
определенным отношением радиусов.
Указанное выше замечание 1j . Римана послужило ис-
истоком классич. проблемы модулей р. п.,
к-рая заключается в том, чтобы изучить природу этих
параметров и, если возможно, ввести их так, чтобы они
определяли на множестве р. п. данного рода g комплекс-
но-аналитич. структуру. Имеются два подхода к проб-
проблеме модулей: алгебраический и аналитический. Алгеб-
раич. подход связан с изучением полей К (S) мероморф-
ных функций на р. н. S. В случае замкнутой поверх-
поверхности К (S) есть поле алгебраич. функций (для g=0 —
это поле рациональных, а для g= 1 — поле эллиптич.
функций). Каждая замкнутая р. п. S конформно экви-
эквивалентна р. п. нек-рой алгебраич. функции, определяе-
определяемой уравнением Р (z, ш)=0, где Р — неприводимый
многочлен над С. Это уравнение задает плоскую алгеб-
алгебраич. кривую X, и поле рациональных функций на X
отождествляется с полем мероморфных функций на S.
Конформной эквивалентности р. п. соответствует бира-
циональная эквивалентность (совпадение) полей их ал-
алгебраич. функций или, что равносильно, бирациональ-
ная эквивалентность определяемых этими поверхно-
поверхностями алгебраич. кривых.
Аналитич. подход опирается на геометрические и ана-
аналитич. свойства р. п. Оказывается удобным ослабить
конформную эквивалентность р. п., наложив топологич.
ограничения. Вместо р. п. S данного рода g^i берутся
пары (S, /), где / — гомеоморфизм фиксированной по-
поверхности So рода g на S; две пары (S, /), (S', /') счита-
считаются эквивалентными, если существует такой кон-
конформный гомеоморфизм h : S —>¦ S', что отображение
гомотопно тождественному. Множество классов эквива-
эквивалентности {(S, /)} наз. пространством Т а й х-
м ю л л е р а Т (So) поверхности So. В Т(Sa) вводится
метрика с помощью квазиконформных гомеоморфизмов
S—^-S'. Аналогичным образом определяется простран-
пространство Тайхмюллера и для некомпактной р. п., но тогда
берутся только квазиконформные гомеоморфизмы /.
Для замкнутых поверхностей So данного рода g прост-
пространства Т E0) изометрически изоморфны, и можно
говорить о пространстве Тайхмюллера Tg поверхно-
поверхностей рода g. Пространство Rg P. п. к. к. рода g полу-
получается факторизацией Тg no нек-рой счетной группе Г^
его автоморфизмов, называемой модулярной группой.
Наиболее простым является случай поверхностей
рода 1 — торов. Каждый тор S после конформного ото-
отображения его универсальной накрывающей на ком-
комплексную плоскость С представляется в виде C/G,
где G — группа сдвигов с двумя образующими щ, со2
такими, что 1т(оJ/ш1)>0; при этом два тора S и S'
конформно эквивалентны тогда и только тогда, когда
отношения т— <ajo^1 и t' = uJ/u>i соответствующих об-
образующих связаны модулярным преобразованием
а, Ь, с, d?Z-
В качестве (комплексного) модуля данного Р. п. к. к.
{S } можно взять значение эллиптической модулярной
функции /(т). Пространство Тайхмюллера Тх совпадает
с полуплоскостью //={т^С : Im т>0}, Pj есть эллип-
эллиптическая модулярная группа SLB,'?)l{±i}, а Л,=
= Т1/Г1 - риманова поверхность, конформно эквива-
эквивалентная С\{0, 1}. Все эллиптич. кривые (и поверх-
ности рода 1) допускают одновременную униформиза-
цию с помощью функции Вейерштрасса $>(z; 1, т) и ее
производной $>' (г; 1, т).
При ?>1 ситуация значительно сложнее. Установ-
Установлены, и частности, следующие основные свойства про
странства Tg: I) Tg гомеоморфно Д"?~е; 2) Tg биголо
морфно вкладывается в виде ограниченной области i:
С3?~3, к-рая голоморфно выпукла; 3) модулярная
группа Tg дискретна (даже собственно разрывна) и при
g >2 является полной группой биголоыорфных автомор-
автоморфизмов Tg; 4) накрытие Tg -> TgIYg является развет-
разветвленным, a TglTg=Rg есть нормальное комплексное
пространство с неуниформизируемыми особенностями.
Такие же свойства, за отдельными исключениями в 3),
имеют место и для более общего случая замкнутых р. ц.
с конечным числом проколов, к-рым соответствуют ко-
конечномерные пространства Тайхмюллера. Указанное
биголоморфное вложение Тg в С3?~3 получается с по-
помощью униформизации и свойств квазиконформных ото-
отображений. Поверхность So представляется в виде
Sa — H/ro, где Гр — фуксоеа группа, действующая раз-
разрывно в верхней полуплоскости Н (определяемая с
точностью до сопряжения в группе всех конформных
автоморфизмов Н), и рассматриваются квазиконформ-
квазиконформные автоморфизмы w^f^z) плоскости С=С(_|{°°}'
т. е. решения уравнения Бельтрами w-—[i(z)u?z, где
\i (z)dz/dz — инвариантные относительно Го формы с но-
носителями в Н, ||u||j <1. Пусть еще /^ оставляют не-
неподвижными точки 0, 1, оо. Тогда Tg можно отождест-
отождествить с пространством сужений fv\R или, что равносиль-
равносильно, сужений fV-\L, L={z?C : Im z<0}, и Tg биголо-
морфно эквивалентно области, заполняемой производ-
производными Шварца
в комплексном пространстве В (L, Го) голоморфных в L
решений уравнения
с нормой
при этом A\mB(L, rB)=3g~3. Используя это вложе-
вложение, можно построить расслоенное пространство Tg
с базой Tg, также допускающее введение комплексной
структуры, и голоморфные функции ф^ ... , i^-s на
fg, позволяющие дать параметрич. представление всех
алгебраич. кривых рода g в комплексном проективном
пространстве Рп, п^2. Указанная конструкция, свя-
связанная с вложением Tg в B(L, Го), обобщается на про-
произвольные р. п. и фуксовы группы. В частности, для
компактных р. п. с аналитич. границами получающееся
пространство Тайхмюллера допускает введение в нем
глобальной вещественно аналитич. структуры соответ-
соответствующей размерности.
Другое описание Р. и. к. к. рода #>1 получается с
помощью т. н. матриц периодов этих поверх-
поверхностей. Это — симметрические (g X #)-матрицы с по-
положительно определенной мнимой частью. Пространст-
Пространство Tg голоморфно вкладывается во множество всех та-
таких матриц (верхнюю полуплоскость Зигеля) Не (см.
[4], [5]).
Имеются замкнутые р. п. с определенной симметрией,
конформные классы к-рых зависят от меньшего числа
параметров. Это — г и и е р ;> л л и п т и ч е с к и е по-
поверхности, эквивалентные двулистным р. п.
функций w= Yp(z), где р (z) — многочлены вида
(z—zx) ... (z—z2g + 2). Они допускают конформную инво-
люцию и зависят от 2g—1 комплексных параметров. Все
поверхности рода 2 гиперэллиптичны; при #>2 такие
поверхности образуют в Tg аналитич. подмногообразия
размерности 2g—1.
С Р. п. к. к. связан вопрос о конформных автомор-
автоморфизмах данной римановой поверхности S. За исключе-
исключением нескольких частных случаев группа Aut S таких
автоморфизмов дискретна. В случае замкнутых поверх-
поверхностей рода g>l она конечна, причем тогда порядок
Aut S не превосходит 84(g— 1).
Имеющаяся классификация некомпактных р. п. бес-
бесконечного рода основана на выделении отдельных кон-
конформных инвариантов и не определяет Р. и. к. к. пол-
полностью; обычно это делаетсн в терминах существовании
аналитических или гармонич. функций с определенными
свойствами.
Лит.: [1] Н е в а н л и н н а Р., Униформизация, пер. с
нем., М., 1955; [2] Спрингер Дж., Введение в теорию ри-
мановых поверхностей, пер. с англ., М-, 1960: [3] Крушкаль
С. Л., Квазиконформные отображения и риыановы поверхно-
поверхности, Новосиб., 1975; [4] Б е р с Л., «Успехи матем. наук», 1973,
т. 28, в. 4, о. 153—98; [5] Ш и ф ф е р М., Спенсер Д. К.,
Функционалы на конечных римановых поверхностях, пер. с
англ., М., 1957; [6] Abikoff W., The real analytic theory of
Teichmuller space, В.— [u. a.], 1980. С. Л. Нрушкалъ.
РИМСКИЕ ЦИФРЫ — цифры древних римлян.
Система Р. ц. основана на употреблении особых знаков
для десятичных разрядов 1 = 1, Х=10, С=100, М=1000
и их половин V=5, L=50, D=500. Натуральные числа
записываются при помощи повторения этих цифр.
При этом если большая цифра стоит перед меньшей, то
они складываются (принцип сложения), если же мень-
меньшая — перед большей, то меньшая вычитается из боль-
большей (принцип вычитания). Последнее правило приме-
применяется только во избежание четырехкратного повторе-
повторения одной и той же цифры. Выполнение арифметич.
действий над многозначными числами в этой записи
весьма неудобно. Система Р. ц. в настоящее время не
применяется, за исключением, в отдельных случаях,
обозначения веков, годов н. э. и месяцев при указании
дат, порядковых числительных, а также иногда тфоиз-
водных небольших порядков, больших трех: у , у
И Т. Д. БСЭ-3.
РИСК статистической процедуры —
характеристика, выражающая средние потери экспери-
экспериментатора в задаче принятия статистич. решения и этим
самым определяющая качество используемой статистич.
процедуры.
Пусть по реализации случайной величины X, прини-
принимающей значения в выборочном пространстве (j, 23,
Ре), в ?8, надлежит принять решение d из измеримого
пространства решений (D, ..</) относительно параметра
0. Далее, пусть потери статистика от принятия решения
d, если случайная величина X подчиняется закону Р0)
равны L(Q, d), где L — нек-рая функция потерь, задан-
заданная на 8X.D. В таком случае, если статистик в задаче
принятия решения d пользуется нерандомизированной
решающей функцией б : j?-*-?*, то в качестве харак-
характеристики этой решающей функции б используют функ-
функцию
R F, 6) = EeL F, б (*))=$/ О, б (А')) ЙРе (*),
называемую функцией риска, или просто р и-
с к о м, статистич. процедуры, основанной на решаю-
решающей функции б относительно функции потерь L.
Понятие Р. позволяет ввести отношение частичного
упорядочивания на множестве Д= {6} всех нерандоми-
нерандомизированных решающих функций, при этом считают, что
из двух различных решающих функций 8г и б2 предпоч-
предпочтительнее является 6j, если Я F, 61)<ЯF, о2) равно-
равномерно по всем 6.
В случае, если решающая функция 6 является ран-
рандомизированной, Р. статистич. процедуры определяется
по формуле
я F, в)= Г Г i (e, d) #<?Л (d) rfPe и,
J 3t J D
где {Qx(d)} — семейство марковских переходных рас-
распределений вероятностей, определяющих процедуру
рандомизации.
[3] В а льдА., Статистические решающие функции, в сб.:
Позиционные игры, М., 1967. М. С. Никулин.
РИСОВСКАЯ ПОЛУГРУППА МАТРИЧНОГО ТИ-
ТИПА— теоретико-полугрупповая конструкция, опреде-
определяемая следующим образом. Пусть S — произвольная
полугруппа, / и Л — (индексные) множества, P=(p%i)—
(ЛХ/)-матрица над S, т. е. отображение декартова про-
произведения Лх/ в S. На множестве M=IXSxA опре-
определяется операция посредством формулы
(i, s, Я) (/, t, (i) =(;, spx.t, |х).
Тогда М превращается в полугруппу, к-рая наз. Р. п.
м. т. над полугруппой S и обозначается cS(S; I, Л; Р);
матрица Р наз. сэндвич-матрицей полу-
полугруппы aS(S; /, Л; Р). Если S есть полугруппа с нулем
0, то Z={(i, 0, X)\i?I, Х?Л} есть идеал в M=eS(S;
1, Л; Р) и факторполугруппа Риса M/Z (см. Полугруппа)
обозначается ^'(S; /, Л; Р); в случае, когда S=G° есть
группа G" с присоединенным нулем, вместо eS°(G°; /, Л;
Р) пишут a?°(G; I, Л; Р) и называют эту полугруппу
Р. п. м. т. над группой с присоединенным нулем G0.
Для полугрупп cJl(G; /, Л; Р) и qS°{G; I, Л; Р) группа G
наз. структурной группой.
Другое представление Р. п. м. т. над полугруппой S
с нулем и (Л X/)-сэнДвич-матрицей Р осуществляется
следующим образом. (/XЛ)-матрица над S наз. мат-
матрицей Риса, если она содержит не более одного
ненулевого элемента. Через \\a\\t% обозначается матрица
Риса над S, у к-рой в ?-и строке и Х-ш столбце стоит а,
а на остальных местах — нули. На множестве всех
(/ХЛ)-матриц Риса над S задается операция:
где в правой части — «обычное» матричное умножение.
Относительно этой операции указанное множество об-
образует полугруппу. Отображение ||a||a h* (i, я, Я) яв-
является изоморфизмом этой полугруппы на полугруппу
aS°(S; I, Л; Р); обозначение aS°(S; /, Л; Р) применяется
для обеих этих полугрупп. Формула (*) объясняет тер-
термин «сэндвич-матрица» для Р. Если G — группа, то
полугруппа eM°(G; I, Л; Р) будет регулярной тогда и
только тогда, когда каждая строка и каждый столбец
матрицы Р содержит ненулевой элемент; всякая полу-
полугруппа cS(G; /, Л; Р) вполне проста, всякая регулярная
полугруппа o#°(G; /, Л; Р) вполне 0-проста. Обращение
последних двух утверждений составляет основное со-
содержание теоремы Риса [1]: всякая вполне про-
простая (вполне 0-простая) полугруппа изоморфно пред-
ставима Р. п. м. т. над группой (регулярной Р. п. м. т.
над группой с присоединенным нулем). Если qM°(G; I,
Л; Р) и qM°(G'\ !', Л'; Р') изоморфны, то группы G и С
изоморфны, / и /' равномощны, Л и Л' равномощны;
необходимые и достаточные условия изоморфизма полу-
полугрупп e?°(G; I, Л; Р) и Ж{С\ Г, Л'; Р') хорошо извест-
известны и наряду с только что приведенными условиями
включают вполне определенную связь между сэндвич-
матрицами Р и Р' (см. [1] — [3]). В частности, любая
вполне 0-простая полугруппа изоморфно представима
I'. п. м. т., у сэндвич-матрицы Р к-рой каждый элемент
в данной строке и данном столбце равен либо 0, либо
единице структурной группы; такая сэндвич-матрица
наз. нормализованной. Аналогичные свой-
свойства выполняются для вполне простых полугрупп.
Лит.: [1] R e e s D., «Proc. Camb. Phil. Soc»., 1940, v. 36,
p. 387 — 400; [2] Клиффорд А., Престон Г., Алгебра-
Алгебраическая теория полугрупп, пер. с англ., т. 1. М., 1972; [3]
Дяиня Е. С, Полугруппы, М., 1960. Л. Н. Шеврин.
РИССА БАЗИС — см. Рисса система.
РИССА ИНТЕРПОЛЯЦИОННАЯ ФОРМУЛА — фор-
формула, дающая выражение для производной тригономет-
тригонометрия, полинома в нек-рой точке через значения самого
полинома в конечном числе точек: если Тп(х) —
тригонометрич. полином с действительными коэффи-
коэффициентами степени п, то для любого действительного ,т
имеет место равенство
где x'f=Bk — l)n/2n, k=l, 2, ... , In.
Р. и. ф. обобщается на целые функции экспоненци-
экспоненциального типа: если / — целая функция, ограниченная
на действительной оси R и имеющая степень а, то
причем ряд, стоящий в правой части равенства, сходит-
сходится равномерно на всей действительной осп.
Установлена М. Риссом [1].
Лит.: [1]R i с s z М.,«С. г. Acad. sci.», 1914, t. 158, p. 1152—
54; [21 Б е р н ш т е й н С. Н., Экстремальные свойства поли-
полиномов и наилучшее приближение непрерывных функций одной
вещественной переменное, ч. 1, Л.—М., 1937; [3] Н и к о л ь-
с к и и С IU., ПриПлиячение функций многих переменных и
теоремы вложения, 2 над., М., 1977. Л. Д. Кудрявцев.
РПССА МЕТОД СУММИРОВАНИЯ — метод сум-
суммирования числовых и функциональных рядов; обозна-
обозначается (R, X, к). Ряд У ап суммируем методом
суммирования Р и с с а (Я, к, к) к сумме s,
если
lim у
где &>0, О«гЛо<А,1<...<Л,г—»- оо, ш — непрерывный
параметр. Метод был введон М. Риссом [1] для суммиро-
суммирования рядов Дирихле. Метод (Я, X, к) регулярен; при
Хп=п равносилен Чезаро методу суммирования (С, к)
и совместен с ним.
М. Рисе рассматривал также метод, в к-ром сумми-
суммируемость ряда У ап определяется через предел по-
последовательности {от}, где
Этот метод обозначается (R, рп). Метод (Я, Я, к) яв-
является модификацией метода (/?, рп) (при А:=1) и обоб-
обобщением его на произвольные &>0.
Лит.: [1]R i с s z М. «С. г. Acad. sci.», I 911, t. 152, p. 1651 —
54; [2] e г о же, там же, 1!H9, t. 119, р. 18—21; [3l Hardy
G. П., Riesz M., The truneral theory of Dirichlet's series,
Camb., 1915; [4] Хард и Г., Расходящиеся ряды, пер. с англ.
М., 1951. И. И. Волков.
РИССА НЕРАВЕНСТВО — 1) Пусть {ф„} — орто-
нормированная система функций на отрезке [а, Ь],
|cpn|<:iW почти всюду на \а, Ь] для любого п.
а) Если f?Lp[a, b], 1<;j<2, то ее коэффициенты
Фурье
удовлетворяют неравенству Рисса
II {«?„} ||, < М-'Р-^ || }\\р, l/p + l/g = l.
б) Для любой последовательности {с,,} с ||{с„}|(^<оо,
1<р<:2, существует функция f?Li\a, Ь], имеющая сп
своими коэффициентами Фурье и удовлетворяющая
неравенству Р и с с а
2) Если /?Z/|0, 2л], 1<р<оо. то сопряженная функ-
функция f?Lp[Q, 2л] и справедливо неравенство
Р и с с а
где Ар — постоянная, зависящая только от р.
Утверждение 1) впервые доказано Ф. Риссом [1],
частные случаи этого утверждения ранее рассматрива-
рассматривали У. Юнг (W. Young) и Ф. Хаусдорф (F. Hausdorf).
Утверждение 2) впервые доказано М. Риссом [2].
Лит.: [1] Riesz F. «Math. Z.», П 923, Bd 18, S. 117—24;
[2] Riesz M., там же, 1927, Bd 27, S. 218 — 44; [3] Бари
H. К., Тригонометрические ряды, М., 1981, с. 211, 566; [4]
Зигмунд А., Тригонометрические ряды, пер. с англ., 2 изд.,
т. 1—2, М., 1965, с. 404 (т. 1), с. 154 (т. 2). т п Лупашенко.
РИССА ПОТЕНЦИАЛ, а-п о т е н ц и а л,— потен-
потенциал вида
где (х — положительная борелевская мера с компакт-
компактным носителем на евклидовом пространстве R", ге^2,
\х—у\ — расстояние между точками х, j/?R". При ге^З
иа=в—2 Р. п. совпадает с классическим ньютоновым
потенциалом; при ге=2 и a -*¦ 0 предельным случаем
Р. п. в нек-ром смысле является логарифмический по-
потенциал. При n^'i и 0<а<«—2 Р. п. есть супергар-
монич. функция во всем пространстве R"; при этом в
классич. случае о.= п—2 вне носителя S'(\v) меры (х
потенциал V(x)=Vn^^{x) есть гармонич. функция. При
а>ге—2 Р. п. Va(x) есть субгармонич. функция вне
S(\i). При всех а>0 Р. п. Va(x) — полунепрерывная
снизу функция в R", непрерывная вне 5([х).
Из общих свойств Р. п. важнейшими являются сле-
следующие. Принцип непрерывности: если
xo?S([i) и сужение Va{x)\S(\x) непрерывно в точке х0,
то Va(x) непрерывен в х„ как функция на всем R".
Ограниченный принцип максимума:
если Va.(x)\S(n)<szM, то Va(x)<2aM всюду в R". При
п—2<:а<;г справедлив более точный принцип
максимума: если Va(x)\S ([х)«:М, то Va(x) <: М
всюду в R" (это утверждение остается верным и при
ге=2 и a -*- 0, то есть для логарифмич. потенциала).
Теория емкости для Р. п. строится, напр., исходя
из понятия a-энергии меры (х:
, a>0.
Для компакта К можно положить
где нижняя грань берется по всем мерам (х, сосредото-
сосредоточенным на К и таким, что [х (А")= 1; тогда a-е м к о с т ь
равна
Если Vа(К) <^-\-<х>, то нижняя грань достигается на со-
сосредоточенной на К емкостной мере 'к,
Я(А')==1, порождающей соответствующий е м к о с т-
н ы п a-п отенциал V (х; а, К). Дальнейшее по-
построение a-емкостей произвольных множеств произво-
производится так же, как и для классич. емкостей.
Р. п. назван по имени М. Рисса (см. [2]), получившего
ряд важных свойств Р. п.; впервые такие потенциалы
были исследованы О. Фростманом (см. [1]).
Лит.: [1] Frostmann О., «Medd. Lunds Univ. Mat.
Sem.», 1935, v. 3; [2] Riesz M., «Acta sci. math. Szeged»,
1938, v. 9, p. 1—42; [3] Л а н д к о ф Н. С, Основы современ-
Г=1 d+«fetos nkx), ~1^'l > 1. |afcl<l, A)
ной теории потенциала, М., 1966; [4] Хейман У., Кен-
Кеннеди Л., Субгармонические функции, пер. с англ. т. 1, М.,
1980. Е. Д. Соломенцев.
РИССА ПРОИЗВЕДЕНИЕ — бесконечное произве-
произведение вида
П
для всех ftgN- x? [0, n].
С помощью таких произведений (ak=\, и&=3* при
всех к?Щ) Ф. Рисе (F. Riesz) указал первый пример
непрерывной функции с ограниченным изменением,
коэффициенты Фурье к-рой не равны of— \ Если д>3,
то тождество
П
h=1 (I +akcos nkx) =
определяет ряд
о к-ром говорят, что он представляет Р. п. A). В случае,
когда д>3, — 1<яА<1 для всех k?N, ряд B) есть ряд
Фурье — Стилтьеса неубывающей непрерывной функ-
функции /'. Если </>3,
при всех fc?N, то Р' (х) — 0 почти всюду. Если дополни-
дополнительно afe -*¦ 0, то ряд B) сходится к нулю почти всюду-
Ряд проблем, относящихся в основном к теории триго-
нометрич. рядов, удалось решить, используя естествен-
естественное обобщение Р. п., когда в A) вместо a^cos nkx запи-
записаны специально выбранные тригонометрич. полиномы
Тк(х).
Лит.: [1] Б а р и Н. К., Тригонометрические ряды, М.,
1961; [2] Зигмунд А., Тригонометрические ряды, пор. с
англ., т. 1—2, М., 1965. В. Ф. Емельянов.
РИССА ПРОСТРАНСТВО, векторная решет-
решетка,— вещественное частично упорядоченное векторное
пространство X, в к-ром
1) структуры векторного пространства и упорядочен-
упорядоченного множества согласованы, т.е. из х, у, z?X и
х < у следует x-rz < у -j- г и иа х?Х, х > О, Я?К,
Я > 0 следует Хх > 0;
2) для любых двух элементов ,г, // су;цествует sup (x,
у)?Х. В частности, существуют sup и iuf любого конеч-
конечного .множества.
В отечественной литературе Р. п. обычно наз. Я-л и-
н е а л а м и. Впервые такие пространства были вве-
введены Ф. Риссом (F. Riesz, 1928).
Примером Р. и. может служить пространство С [а, Ь]
действительных непрерывных на С [а, Ь] функций с
поточечным упорядочением. Для любого элемента
х Р. п. определяются ^4=sup(^, 0), :r_ = sup(—х, 0)
и |; \=х+ + х-. При этом оказывается, что х=х+ — х~.
В Р. п. вводятся два вида сходимости последователь-
последовательности {хп}. Порядковая сходимость,
о
о-с х о д и м о с т ь: х„->,г0, если существуют моно-
монотонно возрастающая последовательность {уп} и моно-
монотонно убывающая последовательность {z,,} такие, что
уп <: хп <: zn и sup yn — ml zn—-z0. Относи т о л ь-
по равномерная сходимость, /-с х о-
г
д и м о с т ь: хп -v х0, если существует элемент и > 0
гакой, что для любого к > 0 существует ге0 такое, что
I сп — хо1 < ги "Р*1 п s3= i0 (г-сходимость наз. также
сходимостью с регуляторе м). Понятия
о- и г-сходимости обладают многими обычными свой-
свойствами сходимости числовых последовательностей и
естественным образом распространяются на направле-
направления {ха}а^%аХ.
Р. и. паз. архимедовым, если из х, у?Х и
их <: у для «=1,2,. . . следует х <; 0. В архимедовом
Р. п. из Кп ->- Хо и хп-^х0 следует Хпхп -»- Яого Aп,
^€^, хп, ^об^О и из г-сходимости следует о-схо-
димость.
Лит.: [llRlesi F., в кн.: Atti del Gongr. Int. dei Math.,
v. 3, Bologna, 1930, p. 143—48; [2] Luxemburg W., Z a a-
nen A., Rieszspaces, v. 1, Amst.—L., 1971; [3] В у лих
Б. 3., Введение в теорию полуупорядоченных пространств, М.,
1961. В. И. Соболев.
РИССА СИСТЕМА — понятие теории ортогональных
систем. Пусть фиксирована в пространстве L2~TJ (а,Ь)
полная система функций {г|з„}. Ее считают нормирован-
нормированной или, более общо, почти нормированной, т. е. до-
допускают наличие чисел т > 0 и М > 0, при к-рых
т <: ||ij),,|| ¦< М для всех га? N- Ослабляя требования
ортогональности системы {tyn), предполагают, что су-
существует полная в L2 система функций {gn} и такая,
что (i|)n, #„)—1. (i|)n, gm) —0 для всех п Ф т. В частном
случае, когда система {чр,,} ортонормирована, gn=tyn
для всех re?N- Если ряд
сходится в />2 к функции /, то а„= (/, д„) при всех re?N-
Поэтому имеет смысл называть число а„= (/, gn) re-
коэффициевтом Фурье функции / по системе {tyn}- В до-
доказательстве ряда теорем теории ортогональных рядов
играют важную роль неравенство Бесселя и теорема
Рисса—Фишера. В общем случае эти теоремы не верны,
и поэтому приходится выделять специальный класс
Р. с. с помощью следующих требований к системе {1|з„}.
1) Для любой функции / сходится ряд из квадратов
коэффициентов Фурье, т. е. .
2) Для любой последовательности чисел {Q
существует функция /, имеющая числа ап своими re-
коэффициентами Фурье по системе {§„}, то есть а„=
(/ ) €N
(/ n €
Первое требование к системе {tyn} заменяет неравен-
неравенство Бесселя, второе — теорему Рисса — Фишера.
II. К. Бари доказала (см. [2]), что система {ty,,} есть
Р. с. тогда и только тогда, когда существует линейный
непрерывный обратимый в L2 оператор А такой, что
система функций {Л1|)„} является полной и ортонорми-
рованной. Поэтому Р. с. наз. также базисом Рис-
с а, эквивалентным ортонормированному. Н. К. Бари
указала удобный критерий для Р. с. Полная в L2 си-
система функций {ф,,} является Р. с. тогда и только тогда,
когда матрица Грама ||(i|)rl, "фт)|| определяет линейный
непрерывный обратимый оператор в Р. Если в Р. с.
переставить произвольно члены, то получится Р. с.
Обратно, если базис в L2 остается базисом после любой
перестановки его членов, то, нормируя его, получают
Р. с. Естественное обобщение Р. с. получают, если за-
заменить L'1 на замыкание линейной оболочки системы
{i|)n} по норме того гильбертова пространства, из к-рого
взяты элементы тЬ„ (см. [4]).
Лит.: [1] Б а р и Н. К., «Докл. АН СССР», 194G, т. 54,
с. 383—86; [21 ее же, «Уч. зап. МГУ», 1951, в. 148, Ml 4,
с. 69—107; [3] Г о х б е р г И. Ц., К р е ft н М. Г., Введение
в теорию линейных несамосопряшенных операторов в гильбер-
гильбертовом пространстве, М., 1985; [4] Гапошкин В. Ф., «Ус-
«Успехи матем. наук», 1966, т. 21, в. 6, с. 3 — 82. В. Ф. Емельянов.
РИССА ТЕОРЕМА — 1) Р. т. о представле-
представлении субгармонической функции: если
и(х) —субгармонич. функция в области D евклидова
пространства R", п ^ 2, то существует единственная
положительная борелевская мера ji на D такая, что для
любого относительно компактного множества KD
справедливо представление Рисе а функ-
функции и (х) в виде суммы потенциала и гармонич. функции
1{)
где
j l
п > 3, \х—у\ — расстояние между точками х, y?
(см. [1]). Мера (х наз. ассоциированной ме-
мерой для функции и(х) или мерой Рисса.
Если К=Н есть замыкание области //, причем су-
существует обобщенная функция Грина g(x, у; Н), то
формулу A) можно записать в виде
g(x, У. H)dli(y) + h* (х), B)
где h* (х) —наименьшая гармонич. мажоранта и (х) в
области Н.
Формулы A), B) можно распространить при нек-рых
дополнительных условиях на всю область D (см. Суб-
Субгармоническая функция, а также [3], [5]).
2) Р.т. о среднем значении субгармо-
субгармонической функции: если и (х) —субгармонич.
функция в кольцевой области {x?Rn : 0 <: г <; \х—
—хо\ <: R }, то ее среднее значение по площади сферы
Sn(xoi Р) с центром х0 и радиусом р, г <: р ¦< R, рав-
равно
где о„(р) — площадь Sn(x0, p), и является выпуклой
функцией относительно 1/р"-3 при ге>3 и относитель-
относительно 1пр при ге=2. Если же и (х) — субгармонич. функ-
функция во всем шаре {x?Rn: \х—хо\ <<Л }, то /(р), кроме
того,— неубывающая непрерывная функция относи-
относительно р при условии, что J(Q)=u(x0) (см. [1]).
3) Р. т. об аналитических функциях
классов Харди Д"б, S > 0: если / (z) — регу-
регулярная аналитич. функция в единичном круге D =
= {z=re»'6?C : |z| < 1} класса Харди #б, б >0 (см.
Граничные свойства аналитических функций), то для
нее имеют место соотношения
lim
С | / (ге'в) |б de= f
1 J? J
lim
r-»l
где Е — любое множество положительной меры на ок-
окружности Г= {z=eie : |z| = l}, f(ece) — граничные
значения /(z) на Г. Кроме того, /(z)?#j тогда и только
тогда, когда ее первообразная непрерывна в замкнутом
круге D LJ Г и абсолютно непрерывна на Г (см. [2]).
Теоремы 1) — 3) доказаны Ф. Риссом (см. [1], [2j).
Лит.: [ll Riesz F., «Acta math.», 1926, v. 48, p. 329 — 43;
1930, v. 54, p. 321—60; [2] e г о we, «Math. Z.», 1923, Bd 18,
S. 87—95; [3] Привалов И. И., Субгармонические функ-
функции, М.—Л., 1937; [4] его же, Граничные свойства аналити-
аналитических функций, 2 н;зд., М.—Л., 1950; [5] Хсйман У. К.,
Кеннеди П. Б., Субгармонические функции, пер. с англ.,
т. 1, М., 1980. Е. Д. Соломенцев.
РИССА ТЕОРЕМА ВЫПУКЛОСТИ: логарифм
In М (а, Р) точной верхней грани модуля М (а, C) би-
билинейной формы
на множестве
X^m i _. 11 /rx л VIш ... ,1/В^.л
(если а—0 или C— 0, то соответственно |х,|<:1, /=-1,
. . ., т или \yj\ <: 1, / = 1,. . . , п) является выпуклой
функцией от параметров а и р1 в области а ^ 0, р1 ^ О,
если форма действительна К/,^, j/,-^RT), и в области
0<а, Р<1, а + Р > 1, если форма комплексна
(a;j, xj, y/?C). Эта теорема была доказана М. Рис-
сом [ 1 ].
Обобщение Р. т. в. на линейные операторы (см. [3]):
пусть Lp, 1 ¦< р <: оо,— совокупность всех комплек-
созначных суммируемых в р-й степени при 1 < р < оо
и существенно ограниченных при р= оо функции на
нек-ром пространстве с мерой; пусть, далее, Т : ?р,—»-
->- Lq , 1 < pj, qt < оо, s = 0, 1,— линейный непре-
рывный оператор; тогда Т является непрерывным опе-
оператором из Lp в Lq , где
и норма и; оператора Г (как оператора из Lp в Lq\
удовлетворяет неравенству kf<ko~ кг (т. е. является
логарифмически выпуклой функцией). Эту теорему
наз. теоремой Р и с с а Горина об ин-
интерн о л я ц и и, но иногда г е о р е м ой вы-
выпуклости Р и с с а 14].
Р. т. в. явилась отправным пунктом для целого на-
направления в анализе, где изучаются интерполяционные
свойства линейных операторов. Среди первых из обоб-
обобщении Р. т. в.— теорема М а р ц и н к е в и ч а
об интерполяции [5], к-рая гарантирует при 1 ¦< /?,-¦<
«:</,-<: оо, г—0, 1, непрерывность оператора Т : L(l
б б
''г/ > г€@> 1)> "Ри более слабых предположениях,
чем в теореме Рисса — Торина. См. также Интерполи-
Интерполирование операторов.
Луш.: [1] R 1 е s z M., «Ada math.». 1926, v. 49, p. 465—97;
[2] X a p д и Г., Л и т т л ь в у д Д., И о л и а Г., Неравен-
Неравенства, пер. с англ., М., 1948; [3] Thorin G., «Comm. Sem,
Math. Univ. Lund.», 1939, v. 4, p. 1—5; [4] С т е й н И., В е й с
Г., Введение в гармонический анализ на евклидовых простран-
пространствах, пер. с англ., М., 1974; [51 Marcinkicwicz J.,
«С. г. Acad. Sci.», 1939, t. 208, p. 1272—7H; 1б1 К р е ft н С. Г.,
П е т у н и а Ю. И., Семенов Е. 11., Интерполяция ли-
линейных операторов, М., 1978; [7] Т г i с Ь е 1 Н., Interpola-
Interpolation theory, В., 1978. В. Ы. Тихомиров,
РИССА — ФИШЕРА ТЕОРЕМА — теорема, устанав-
устанавливающая связь между пространствами I'2 и I? |я, ft]:
если система функций {q)re(i)|^=i ортонормироваца на
отрезке [a, b], a последовательность чисел {сп\п=\
такова, что
(то есть Сп?Р), то существует функция /(i)^L2 [а, Ь],
для к-рой
При этом функция f(t) единственна как элемент про-
пространства L- [а, Ь], т. е. с точностью до ее значений
на множестве нулевой меры Лебега. В частности, если
ортонормированная система {<fn(t)} замкнута (полна) в
//- [a, ft], то с помощью Р.— Ф. т. устанавливается, что
пространства V1 и L2 [a, ft] изоморфны и изометричны.
Р.— Ф. т. доказана независимо Ф. Риссом [1] и Э. Фи-
Фишером |2|.
Лит.: [1] R i е 8 z F., «С. г. Acad. sci.», 1907, t. 144, p. 615_
19; 12] Fischer E., там же, 1907, t. 144, p. 1022—24, 1148—
50; L3] H а т а н с о н И. П., Теория функций вещественной
переменной, 3 изд., М., 1974, с. 168. Б. И. Голубое.
РИССОВ ТЕОРЕМА — 1) Р. т. единственно-
единственности для ограниченных аналитичес-
аналитических функций: если /(z) — ограниченная регуляр-
регулярная аналцтич. функция в единичном круге D=={z?C :
\z\ < 1}, имеющая радиальные граничные значения
нуль на множестве Е точек окружности Г= {z : |z|—-1}
положительной меры, mes Е > 0, то / (z) г=з 0. Теорема
сформулирована п доказана братьями Ф. Риссом и М.
Риссом (F. Riesz, M. Riesz, 1916, см. 11]).
Это — одна из первых граничных теорем единствен-
единственности для аналитич. функций. Независимо от братьев
Риссов наиболее общие граничные теоремы единствен-
единственности были получены Н. Н. Лузиным и И. И. При-
Приваловым (см. [2], [3]).
2) Р. т. об и н т е г р а л е К о ш и: если f(z) есть
интеграл Коши
' У > 2Я!
в единичном круге D и его граничные значения /(?)=
=/(<?'е) образуют функцию ограниченной вариации
на Г, то /(?) есть абсолютно непрерывная функция на Г
(см. [1]).
Эта теорема допускает обобщение для интегралов
Коши по любому спрямляемому контуру Г (см. [3]).
Лит.: [1] Riesz F. CEuvres completes, t. 1, P.— Bdpst,
1960, p. 537—54; [2] Привалов Н. И., Интеграл Cauchy,
Саратов, 1918; [3] e г о же, Граничные свойства аналитиче-
аналитических функций, 2 изд., М. — Л., 1950. Е. Д. Соломенцев.
РИТЦА МЕТОД — метод решения задач вариацион-
вариационного исчисления и вообще бесконечномерных задач на
экстремум, основанный на минимизации функцио-
функционала на конечномерных подпространствах или много-
многообразиях.
Пусть поставлена задача нахождения точки миниму-
минимума ограниченного снизу функционала J :{/->¦ R на
сепарабельном банаховом пространстве U. Задается
нек-рая (т. н. координатная) система элементов {ф„}Гс
CZU, полная в U. По Р. м. минимизирующий элемент в
га-м приближении разыскивается в линейной оболочке
первых п координатных элементов фх, . . ., ф„, т. е.
коэффициенты с[п\ . . ., с^ приближения
определяются из условия минимальности J{un) среди
элементов указанного вида. Вместо координатной систе-
системы можно задать последовательность подпространств
IJndU, не обязательно вложенных друг в друга.
Пусть // — гильбертово пространство со скалярным
произведением (и, v), A — самосопряженный, положи-
положительно определенный, вообще говоря, неограниченный
оператор в Н, а Нд—гильбертово пространство,
получаемое пополнением области определения D (А)^Н
оператора А по норме ЦмЦ^, порожденной скалярным
произведением (и, и)д~(Аи, v), и, v?D(A). Пусть
нужно решить задачу
Au = f. A)
i >на равносильна задаче отыскания точки минимума
квадратичного функционала
Ф{и)=?(Аи, и) —(и, /)-(/, и),
ii-рый можно записать в виде
где ий—А -1/ — решение уравнения A). Пусть НпсНА,
н~ 1, 2, . . .,— замкнутые (обычно конечномерные)
подпространства такие, что \\и—Рпи|[д —*¦ 0 при /г->-оо
для каждого и?Нд, где Рп — ортопроектор в Яд,
проектирующий на Нп. Минимизируя Ф в Нп, полу-
получают ритцовское приближение ип=Рпий к решению
уравнения A); при этом ||м„—ио\\А = \\щ — Рпи0\\А-+ 0
приге->оо. Если dim Нп=п и ф<1">, • .-., ф(^* — базис
//„, то коэффициенты элемента
определяются из линейной системы уравнений
К ритцовскому приближению можно прийти и минуя
вариационную формулировку задачи A). А именно,
определив приближение B) из условий
(Aun~f, <р<»>) = о, 4 = 1, .... и
(метод Галеркина), приходят к той же системе
уравнений C). Поэтому Р. м. для уравнения A) иногда
наз. методом Ритца — Галеркина.
Р. м. широко применяется и при решении задач на
собственные значения, краевых задач и вообще опера-
операторных уравнений. Пусть А и В — самосопряженные
операторы в Н, причем А положительно определен, В
положителен, D (A)<^D (В) и оператор А~ХВ вполне
непрерывен в пространстве IIА. В силу наложенных
условий А~1В самосопряжен и положителен в II &
и спектр задачи
A hB D)
состоит из положительных собственных значений:
^4«fc = X/,i?«fc, 0 < А,1<Я2<-• •; %k—*" °° ПРИ ^—*в0-
Р. м. основан на вариационной характеризации соб-
собственных значений. Напр.,
и, проведя минимизацию лишь по подпространству
Нп(^.Нд, получают ритцовские приближения Х1п, щп к
Кх, их. Если <р! , . . ., фп"\ как и выше, базис Нп, то
ритцовские приближения Я&„ к Я&, к=1,. . ., п, опре-
определяются из уравнения
а вектор коэффициентов oktn—(c("k, ¦ ¦ ., ад) прибли-
приблик Mft определится как нетривиальное решение линейной
однородной системы (Ап—Я^„2?„)с^„=0. Р. м. прибли-
приближает собственные значения сверху, то есть Я^„ ^ Я^.,
/с=1, . . ., ;г. Если к-е собственное значение задачи
D) простое (ЯА_! < Xk < Яд + 1), то быстрота сходимости
Р. м. характеризуется соотношениями
*п—«fe IU = A+еы) II uk—pnuk IU.
где e#n, е^п ->- 0 при re—>- оо. Подобные соотношения
распространяются и на случай кратного Я&, но требуют
нек-рых уточнений (см. [2]). В. Ритц [4] предложил
свой метод в 1908, но ранее Рэлей (Rayleigh) применял
этот метод при решении нек-рых задач на собственные
значения. В связи с этим Р. м. часто наз. методом
Рэлея — Ритца, особенно, если речь идет о реше-
решении проблемы собственных значений.
Лит.: [1] В а и н б е р г М. М., Вариационный метод и
метод монотонных операторов в теории нелинейных уравнений,
М., 1972; [2] Красносельский М. А. 1и др.], Приб-
Приближенное решение операторных уравнений, М., 1969; [3] М и х-
л и н С. Г., Вариационные методы в математической физике,
2 изд., М., 1970; [4] R i t z W., «J. reine und angew. Math.»,
1908, Bd 135 S. 1 —B1. Г. М. Вайникко.
РИЧАРДСОНА ЭКСТРАПОЛЯЦИЯ — метод уско-
ускорения сходимости решений разностных задач (см.
Аппроксимация дифференциальной краевой задачи
разностной). Основная идея метода состоит в исследо-
исследовании решения и/г (,г) сходящейся разностной задачи
при фиксированных .г как функции параметра h разно-
разностной сетки, стремящегося к нулю, в подборе подходя-
подходящей интерполяционной функции %(h), построенной по
нескольким значениям решения и^ (х) при различных
Л, и вычислении величины %@), являющейся прибли-
приближенным значением искомого решения и (.г) — предела
последовательности uh(x) при h —>¦ 0. Чаще всего функ-
функция %(h) ищется в виде интерполяционного многочлена
от h.
Метод носит имя Л. Ричардсона [1]. к-рый впервые
использовал его как средство для улучшения точности
решений разностных задач и называл постепен-
постепенным переходом к пределу.
Теоретич. основой применимости метода служит су-
существование разложения вида
u,h (x) = u (
где В > f>m-\ >. . .>Pi > 0 и функции <;,- не зависят
от h, a r|ft(.r) — значения сеточной функции, ограни-
ограниченные при h —>¦ 0. Имеется несколько теоретич. прие-
приемов для выяснения существования таких разложе-
разложений [4].
Чаще всего используется линейная экстраполяция:
с помощью т значений uh (х) в одной точке х для раз-
различных параметров h=hlt . . ., li,a вычисляется экстра-
экстраполированное значение и^(х) по правилу
где веса Yj. определяются из системы уравнений:
Если среди hk нет слишком близких значений, то
\uH{x) — u(j)\=O(fiB),
где ft-~max h^, то есть величина ы//(.г) сходится к и (.г)
Kft<
K<
при i-j-О с порядком В, что больше f>1 — порядка
сходимости и/г(х) к и(х). В двух частных случаях су-
существуют алгоритмы вычисления величины иц(.г), ми-
минуя определение коэффициентов у*-'
а) в случае р1,- = 1р, р > 0, i — 1, . . ., т — 1, метод
приводит к интерполяции многочлена от kp и из cBoiicTu
Лагранжа интерполяционной формулы следует, что
где
af = uhj(x), / = 1, 2 т;
/ = 1, ••., т—г, г = 1, ..., т
б) в случае h;—ho?, 0 < Ь < 1, /— 1, .... т — 1,
формула (*) заменяется следующей:
(i) (i)
Этот алгоритм, называемый правилом Р о м-
б е р г a (W. Roraberg, 1955), нашел распространение
при конструировании квадратурных формул (см. [5]).
Для того чтобы при различных /г,- сетки DhV (см. Ап-
Аппроксимация дифференциального оператора разност-
разностным) имели возможно больше общих узлов для осуще-
осуществления Р. э., параметры h,- выбирают как часть одной
из последовательностей: А,-=йо/г, i=l, 2, ...; й(-=/г021-'',
i=l, 2, ... ; h0, ho/2, ko'3, ho/i, ho/&, ho/8, ho'i2, ....
Линейная экстраполяция не является единственно
возможной. Напр., в случае f>,~ip. p > 0. в качестве
интерполяционной функции х С') используют рацпо-
нальные функции вида y(hp)/\p(hp), где (p(i), i|i(i) — много-
многочлены от t степени Цт—1)/2] и [т/2] соответственно.
Тогда результат рациональной экстраполяции u//(z)=
= X @) может быть вычислен с помощью рекуррентной
процедуры:
d^1) = 0, /==2, ..., т;
SV = uh.(x), / = 1, 2, .... т;
7 = 1, ..., т—i, i—A, ..., т—1;
) Н»
Р. э. удобна для реализации на ЭВМ, поскольку
для достижения высокой точности использует много-
многократное решение простых разностных задач (иногда
с небольшими модификациями) невысокого порядка ап-
аппроксимации, для к-рых обычно хорошо разработаны
стандартные приемы решения и программы для ЭВМ.
Лит.: [1] Richardson L. F., «PMlos. Trans. Rosr- Soc.
Ser. A», 1910, v. 210, p. 307 — 57; [2] В u 1 i r s с h R., S t о е г ,T.,
«Numer. Math.», 19B4, Bd B, H. 5, S. 413—27; 13] J о i с e D. C,
«SIAM Review,), 1971, v. 13, № 4, p. 435—90; [4] M a p ч у к
Г. И., Ш а й д у р о в В. В., Повышение точности решений
разностных схем, М., 1979; [5] Бахвалов Н. С, Числен-
Численные методы, 'I изд., М., 1975. JS. Б. Шайдуров.
РИЧЧИ КРИВИЗНА риманова многооб-
многообразия М в точке р^дИ — число, сопоставляе-
сопоставляемое каждому одномерному подпространству из каса-
касательного пространства Мр по формуле
_ (сД) (V, у)
Г()" g(v,v) '
где cR — Риччи тензор, v — вектор, порождающий
одномерное подпространство, g — метрич. тензор рима-
риманова многообразия М. Р. к. выражается через секцион-
секционные кривизны многообразия М. Пусть Кр(а, Р) —
секционная кривизна в точке р?М в направлении
площадки, определяемой векторами а и |3, 1л, . . .,
/„_, —норлщрованные векторы, ортогональные друг
другу и вектору v, п — размерность М, тогда
Для лшогообраяшг М размерности больше двух идтеет
место следующее предложение: если Р. к. в точке р?М
имеет одно и то же значение г по всем направлениям
л1, то Р. к. имеет одно и то же значение г во всех точках
многообразия. Многообразия с постоянной Р. к. наз.
пространствами Эйнштейна. Тензор
Риччи пространства Эйнштейна имеет вид cti—rg, где
г — Р. к. Для пространства Эйнштейна выполняется
равенство
nRijRii — S- — 0,
где Rjj, R'i ~ ковариантные и контравариантные коор-
координаты тензора Риччи. п — размерность пространства,
s — скалярная кривизна пространства.
Р. к. может быть определена и на псевдоримановых
.многообразиях с помощью аналогичных формул, в этом
случае вектор предполагается неизотропным.
По Р. к. однозначно восстанавливается тензор Риччи:
(cR)(u, v) = -~ [г (u \-v) g (u-\-v, и \-v) — r (и) g (и, и) —
— г (v) g (v, v)].
Лит.: [1] Г р о м о л Д., КлингенбергВ., Мей-
ер В., Риманова геометрия в целом, пер. с нем., М., 1971;
[2] Петров А. 3., Пространства Эйнштейна, М., 1961.
Л. А. Сидоров.
РИЧЧИ ТЕНЗОР — дважды ковариантный тензор,
получаемый из Римана тензора Rjki путем свертыва-
свертывания верхнего индекса с нижним:
В римановом пространстве VnP. т. является симметри-
симметрическим: 11 Ri~ lijk- В результате свертывания Р. т. с
контраваршштным метрич. тензором gU пространства
Vn получается скалярная величина R = g'JRjj, назы-
называемая инвариантом кривизны, или ска-
скалярной кривизной' V,,. Компоненты Р. т.
выражаются через основной метрич. тензор %ц про-
пространства Vn: _ _
„ _ ачп У и 2_r*_i_rmr* ^т 9 in Т я
'7~~~&?а1Г axklii + liklmj-l4 Ох,„ '
где g=det gfj, Vlj — символы Кристоффеля 2-го рода,
вычисленные относительно тензора g/y.
Тензор введен Г. Риччи [1].
Лит.: [1] R i с с i G., «Atti Reale Inst. Veneto», 1903—04,
t. 53, J* 2, p. 1233—39; [2] Э й з е н х а p т Л. П., Риманова
геометрия, пер. с англ., М., 1948. Л. А. Сидоров.
РИЧЧИ ТЕОРЕМА: для того чтобы поверхность
S с метрикой ds2 и гауссовой кривизной К <: О была
локально изометрична нек-рой минимальной поверх-
поверхности F, необходимо и достаточно, чтобы метрика ds2 —
= У—/ids2 имела (во всех точках, где К < 0) гауссову
кривизну А' —0. И. X. Сабитов.
РИЧЧИ ТОЖДЕСТВО — 1) Тождество, выражающее
одно из свойств Римана тензора R(j,k, (или R^ ^ fc;);
Для ковариантного тензора R[j ^i тождество имеет вид
т. е. циклирование по трем первым иядексам дает
нуль.
2) Тождество, к-рому должны удовлетворять кова-
риантные производные 2-го порядка относительно мет-
метрич. тензора gi/ риманова пространства Vn, отличаю-
отличающиеся лишь порядком дифференцирования. Если X; —
тензор 1-й валентности, Л,-,/? — ковариаятная произ-
производная 2-го порядка по х) и'по xk относительно тензора
gji, то Р. т. имеет вид
где RiJt ь — тензор Римана, определяемый метрич.
тензором gjj, то есть в метрике пространства V"„ (иными
словами, альтернированная 2-я абсолютная производ-
производная тензорного поля Я, в метрике g;j выражается через
тензор Римана и компоненты к;).
Для ковариантного тензора 2-й валентности а,у Р. т.
имеет вид
Вообще, для ковариантного тензора т-й валентности
аГи..гт тождество имеет вид
ar1...rm,kl — ar1...rm, 1к =
ar,...rr,_,hrr,J_,...rJirr,H-
Аналогичные тождества образуются и для ковариант-
ных и смешанных тензоров в Vn. P. т. применяется,
напр., при построении геометрии подпространств в Vn
в качестве условия интегрируемости основных дерива-
риационных уравнений, из к-рого выводятся уравне-
уравнения Гаусса и Петерсона — Кодацци для подпространств
в Vn.
Тождество установлено Г. Риччи (см. [1]).
Лит.: [1] R i с с i G., L e v i-C i v i t а Т., «Math. Ann.»,
19A1, Bd 54, S. lliTi—201; [2] P а ш е в с к и й 11. Ь., Риманова
геометрия и тензорный анализ, 3 изд., М., 1907; 13] Э й з е н-
харт Л. II., Риманова геометрия, пер. с англ., М., 1948.
Л. А. Сидоров.
РИШАРА ПАРАДОКС — см. Антиномия.
РОБЕНА ЗАДАЧА, задача равновесия,
электростатическая задач а,— задача о
таком распределении положительной борелевской
меры Я на границе S компакта К в га-мерном евклидовом
пространстве R", n 5s 2, к-рое создает постоянный
ньютонов потенциал при л > 2 или логарифмический
потенциал при п~ 2 на каждой из связных компонент
внутренности Л', т. о. задача о равновесном распределе-
распределении алрктрпч. заряда Я (А) на поверхности S провод-
проводника К.
В простейшем классич. случае, когда К есть гомео-
морфная шару замкнутая область в R", ограниченная
гладкой простой замкнутой поверхностью или (при
ге=2) кривой S класса С1. а, 0 < а < 1, 0?К, решение
Р. з. сводится к отысканито нетривиального решения
v(x), x?S, однородного интегрального уравнения Фред-
гольма 2-го рода
-i-v(.r)-i—i- {V(y)?-En(x, y)dS (jO=0, x?S, A)
с условием нормировки
Здесь
Я2 (*. У) = 1п т^1ГТ • Еп (г, у) =.__ *,
при п ^ 3, \х—у\ — расстояние между точками
х, J/^R", пх — направление внешней нормали к S в то-
точке z?S, v(z) — производная, или плотность, абсо-
абсолютно непрерывной меры Я по мере Лебега на S,
к -2я к - 2<"-2>""/2
А2-2я, А„_- г(п/2)
при « ^ 3, dS (у) — элемент площади поверхности S.
Уравнение A) получается при рассмотрении внутрен-
внутренней задачи Неймана для области с границей S при нуле-
нулевых граничных данных, т. к. потенциал простого слоя
и (х)^.и (х; А') = Jsv (у) Еп (х, у) dS (у),
называемый потенциалом Робена, или рав-
равновесным потенциалом, должен, по усло-
условию Р. з., иметь постоянное значение на К (см. Потен-
Потенциала теория, а также [2]). Решение v(^) задачи A),
B) при указанных условиях всегда существует в клас-
классе непрерывных функций C(S). Мера
Я(Я)=Г v (y)dS(y), EaS,
дающая решение Р. з., наз. равновесной ме-
р о й. Аналогично решается Р. з. и в более сложном
случае, когда граница компакта К состоит из конечного
числа непересекающихся простых замкнутых поверх-
поверхностей или (при п=2) кривых класса С1< а, 0 < а < 1
(см. [2]). При зтом на ограниченных связных компо-
компонентах открытого множества G= CK= Rn\K потен-
потенциал Робена и (х) также сохраняет постоянное зна-
значение, т. е. на границах этих компонент плотность
у(х)=0.
Пусть компакт К есть связное множество. Постоянное
значение потенциала Робена и (х) на К
У='\:У(У)Еп(х, у) dS (у), х
наз. постоянной Робена компакта К. При
п ^ 3 она связана с гармонической, или ньютоновой,
емкостью компакта К простым соотношением С (К) —
= 1/7, причем 0 < у < -| ¦ оо, 0 <С(А)<+оо. При п — 2
постоянная Робена может принимать все значения
— оо < y < + оо, гармонич. емкость выражается фор-
формулой С (К)—е-"*.
Иначе, равновесная мера X определяется как мера,
дающая минимум интегралу энергии
кхкЕп(х, У) d\i (x) dp (у)
в классе всех мер р, сосредоточенных на А" и таких,
что (х ^ 0, (х (К) = 1. Такая мера X в случае компакта
К с гладкой границей совпадает с найденной выше, но
она существует и в общем случае произвольного ком-
компакта KcRn, п ^ 2, если только С (А) > 0. Соответ-
Соответствующий равновесный потенциал
'п(х, y)dX(ij),
являющийся обобщением потенциала Робена, сохраняет
постоянное значение 7= 1/С(К) при гс>3 или 7= —1пС(А')
при п=2 всюду на А, за возможным исключением точек
нек-рого множества емкости нуль.
Название Р. з. связано с исследованиями Г. Робена
(см. [1]).
Лит.: L1J Robin G., «Ann. sci. Ёс. norm, super.»,
188S, v. 3; [2] Г ю н т е р Н. М., Теория потенциала и ее при-
применение к основным задачам математической физики, М., 1953;
[3] Л а н д к о ф Н. С, Основы современной теории потенциа-
потенциала, М., 1966; [4] X е й м а н У., Кеннеди П., Субгармони-
Субгармонические функции, пер. с англ., т. 1,М., 1980. Е. Д. Соломенцев.
РОБЕНА ПОСТОЯННАЯ — численная характерис-
характеристика множества точек евклидова пространства R",
п Js 2, тесно связанная с емкостью множества.
Пусть К — компакт в R", (х — положительная боре-
левская мера, сосредоточенная на А и нормированная
условием р(К)=1. Интеграл
КхКЕп(х, у) dp {х) dp {у),
где
Е2(х, j/)=--ln, * , , Еп(х,у) = - ^~г_
\х—у\ — расстояние между точками х, y?Rn, есть
энергия меры (х. Постоянной Робена ком-
компакта К наз. нижняя грань 7 (&') = inf v (Ю по
всем мерам (х указанного вида. Если у(К) <-|-оо,
то эта грань конечна и достигается на нек-рой (един-
(единственной) равновесной (или емкостной)
мере X > 0, y(K)=V(X), X(K)=i, сосредоточенной
на К; если у(К)—-\-<х, то F(jx)= + oo для всех мер (i
указанного вида. Р. п. компакта А* связана с его ем-
емкостью соотношениями
y(K) = i/C (К) при ге^аЗ,
7 (А) = — In С (К) при и = 2.
Если граница S компакта К достаточно гладкая, напр,
состоит из конечного числа попарно непересекающихся
простых замкнутых поверхностей (при п ^ 3) или кри-
кривых (при п=2) класса С1- а, 0< а< 1, то равновесная
мера X сосредоточена на части ScS, к-рая составляет
границу той связной компоненты дополнения СК=
= Rn\K, к-рая содержит бесконечно удаленную точку.
Равновесный потенциал, т. е. потенциал
равновесной меры
u(z)=\En{x, y)dX(y),
в этом случае принимает на S постоянное значение, рав-
равное у (К), что и позволяет вычислить Р. п. компакта в
простейших случаях (см. Робена задача). Напр., Р. п.
круга радиуса г > 0 в RS равна — In г, а Р. п. шара
радиуса г > 0 в R", п > 3, равна i/rn~2. В случае
произвольного компакта А положительной емкости
всюду и(х) ¦< у (К) и и(х)=у(К) всюду на носителе
¦S (Я) равновесной меры Я, кроме, быть может, точек
нек-рого полярного множества, причем всегда S (X)dK.
Пусть D — область расширенной комплексной плос-
плоскости С, содержащая внутри бесконечно удаленную
точку и допускающая функцию Грина g(z, оо) с полю-
полюсом в бесконечности. Тогда имеет место представление
g(z, oo) = ln|z| + V(?>) + e(z, oo), A)
где z— x-\-iy — комплексное переменное, y(D) — по-
постоянная Робена области D, e(z, со) —
гармонич. функция в D, причем
lim e (z, оо) = 0.
1*1-+°°
Определяемая формулой A) Р. п. области D совпадает
с Р. п. компакта dD, 'у (D) = y(dD). Если функция Грина
для области D не существует, то полагают у (D) — + оо.
Обобщая представление A), для римановой поверх-
поверхности R, допускающей функцию Грина, может быть
получено локальное представление функции Грина
Н(Р, Ро) с полюсом po^zR'-
g(p, Po) = lnlz_1Zi||+V(fl; Po) + e(p,Po), B)
где z=z(p) — локальный униформизирующий пара-
параметр в окрестности нолюса р0, z(po)—za, y(R', Po) —
постоянная Робена римановой поверхности R относи-
относительно полюса р0, е(р, р0) — гармонич. функция в
окрестности рп, причем lime(p, ро)-~О. Для римановых
поверхностей R, не допускающих функцию Грина, по-
полагают y(R; p0)= + oo. В выражении B) значение Р. п.
y(R; Po) зависит уже от выбора полюса Ро^Р, но соот-
соотношения y(R; Ро)< +оо и y(R; Po)= + °° не зависят
от выбора полюса, что и позволяет использовать по-
понятие Р. п. для классификации римановых поверхно-
поверхностей.
Лит.: [1] Неванлинна Р., Однозначные аналитиче-
аналитические функции, пер. с нем., М.—Л., 1941; [2] С т о и л о в С,
Теория функций комплексного переменного, пер. с рум., т. 2,
М., 1962; [3] Sario-L., N a k a i M., Classification theory of
Riemann surfaces, В.—N. Y., 1970. E. Д. Соломенцев.
-6-Р0Д — характеристическое число, соответствую-
соответствующее L-классу Хирцебруха (см. Понтрягина класс).
А. Ф. Харшиладзе.
РОД АЛГЕБРАИЧЕСКОЙ ФУНКЦИИ — см. Алгеб-
Алгебраическая функция.
РОД КРИВОЙ — численный инвариант одномерного
алгебраич. многообразия, определенного над полем
к. Род g гладкой полной алгебраич. кривой X равен
размерности пространства регулярных дифференци-
дифференциальных 1-форм на X. Род алгебраич. кривой X, но опре-
определению, равен роду полной гладкой алгебраич. кри-
кривой, бирационально изоморфной кривой X. Для любого
целого g ^ 0 существует алгебраич. кривая рода g.
Алгебраич. кривая над алгебраически замкнутым по-
полем рода g=0 является рациональной кривой, т. е.
бирационально изоморфна проективной прямой Р1.
Кривые рода g=i (эллиитич. кривые) бирационально
изоморфны гладким кубич. кривым в Р2. Алгебраич.
кривые рода g > 1 распадаются на два класса: гипер-
аллиптич. кривые и негиперэллиптич. кривые. Для
негиперэллиптич. кривых X рациональное отображе-
отображение <jw . : X -*¦ PS-1, определяемое канонич. классом
К% полной гладкой кривой, является изоморфным вло-
вложением. Для гиперэллиитич. кривой X отображение
Ф|К | • X -*- P2~L является двулистным накрытием
рациональной кривой ср,к <(Х), разветвленным в
2g+2 точках.
Если X — проективная плоская кривая степени т,то
де d — неотрицательное целое число, измеряющее
отклонение от гладкости кривой X. Если X имеет толь-
только обыкновенные двойные особые точки, то Нравно чис-
числу особых точек алгебраич. кривой А. Для простран-
пространственной кривой X имеет место оценка
{ (Ш~и ^ > е('ли т — четн0>
если т-нечетно,
где т — степень кривой X в Р3.
Если &—С — поле комплексных чисел, то алгебраич.
кривая X может быть рассмотрена как риманова по-
поверхность. В этом случае гладкая полная кривая X ро-
рода g гомеоморфна сфере с g ручками.
Лит.: [1] III а ф а р е в и ч И. Р., Основы алгебраической
геометрии, М., 1972; [2] Хартсхорн Р., Алгебраическая
геометрия, пер. с англ., М., 1981. Вин. С. Куликов.
РОД ПОВЕРХНОСТИ — численный бирациональный
инвариант двумерного алгебраич. многообразия, опре-
определенного над алгебраически замкнутым полем к.
Различают два рода — арифметический и геометриче-
геометрический. Геометрическийродр^ полной гладкой
алгебраич. поверхности X равен
размерности пространства регулярных дифференци-
дифференциальных 2-форм на А'. А р и ф м е т и ч е с кии род
ра полной гладкой алгебраич. поверхности А' равен
т (X, Ох)-длхпкЦ1 (X, Ох).
Геометрический и арифметич. роды полной гладкой
алгебраич. поверхности X связаны соотношением pg—
~Pa~4i гДе Ч — иррегулярность поверхности X, рав-
равная размерности пространства регулярных дифферен-
дифференциальных 1-форм на X.
Лит.: [1) Алгебраические поверхности, М., 1965 (Труды
МИАН СССР, т. 75). Вик. С. Куликов.
РОД ЦЕЛОЙ ФУНКЦИИ — целое число, равное наи-
наибольшему из чисел р и q в предмавлении целой функции
f(z) в форме
-L+JL+ +~
"k 2al' К- (*)
где q — степень многочлена Q(z), a p — наименьшее
целое, удовлетворяющее условию
Vю
Число р наз. родом произведения, участ-
участвующего в формуле (*).
Лит.: [1] Л е в и н Б. Я., Распределение корней целых
функций, М., 1956. А. Ф. Леонтьев.
"РОД ЭЛЕМЕНТА арифметической группы—
совокупность элементов группы единиц G связной ал-
гебраической Q-группы G, сопряженных с данным эле-
элементом а в группах Go и G,7 для всех простых р, где
Q, Ър — соответственно поле рациональных чисел и
кольцо целых р-адических чисел; класс злемента а
определяется как его класс сопряженности в G . Число
непересекающихся классов, на к-рые распадается род
элемента а, конечно 11], обозначается /о(а) и наз. ч и с-
лом классов в роде .элемента а. Возни-
Возникающая здесь функция /0 на G является важной
арифметич. характеристикой, выражающей отклоне-
отклонение от локально-глобального принципа в вопросах со-
сопряженности. Вообще говоря, /о(а) > 1. Более того,
если группа G полупроста, а группа G бесконечна, то
sup /q (я)— оо для любой арифметич. подгруппы /ГС
CG (см. [1], [3]). Рассмотренные понятия Представля-
Представляла
ют естественную модификацию соответствующих клас-
сич. понятий из теории квадратичных форм и приме-
применяются при исследовании финитной аппроксимируе-
аппроксимируемости арифметич. групп относительно сопряженности
(см. [2]).
Лит.: [1] Платонов В. П., «Докл. АН СССР», 1971,
т. 200, № 4, с. 793—96; [2] II л а т о н о в В. П., Матвеев
Г. В., «Докл. АН БССР», 1970, т. 14, П 9, с. 777—79; [3]
Ра пи н чу к А. С, «Докл. АН БССР», 1981, т. 25, №2,
с. 101—04. А. С. Рапинчук.
РОД РИГ А ФОРМУЛА — 1) Р. ф. — формула, свя-
связывающая дифференциал нормали п к поверхности с
дифференциалом радиус-вектора г поверхности в глав-
главном направлении:
dn~—h\dr или dn ——k2dr,
где kL n k2 — главные кривизны.
Формула получена О. Родригом (О. Rodrigues, 1815).
А. Б. Иванов.
2) Р. ф.— представление ортогональных многочле-
многочленов через весовую функцию с помощью дифферент
рования. Если весовая функция h (x) удовлетворяет
дифференциальному уравнению Пирсона
h'(x) Ро + Р.х __ А(х) ,, ,.
h(x) ga + qlX + q^ — В (ж)
причем на концах интервала ортогональности выполня-
выполняются условия
lim h(x)B(x) = lim h(x) В (х)—0,
х-щ+0 x-rb-Q
то ортогональный многочлен Рп(х) представляется в
виде формулы Родрига
где с„ — постоянная. Р. ф. имеет место только для
классических ортогональных многочленов и для мно-
многочленов, полученных из последних линейными преоб-
преобразованиями аргумента. Первоначально эта формула
была установлена О. Родригом[1] для Лежандра много-
многочленов.
Лит.: [1] Rodrigues О., «Correspondence sur l'Ecole
polytechnique», 1816, t. 3, p. 361—85. П. И. Cyemun.
РОЖДЕНИЯ И ГИБЕЛИ ПРОЦЕСС — марковский
процесс с состояниями 0, 1, 2, . . ., в к-ром за время
(t, t-\rh) возможны переходы из состояния п в состоя-
состояния ге-Н и п — 1 с вероятностями Xn(t)h-\-o(h) и \x.n(t)h-\-
-\-о (К) соответственно, а вероятность остальных пере-
переходов равна о (Л). При специальном выборе коэффици-
коэффициентов размножения \,,{t) и гибели \xu(t) получаются
частные случаи, к-рые дают удовлетворительное опи-
описание различных реальных процессов: радиоактивных
превращений, работы телефонных станций, эволюции
биологич. популяций и т. д. Использованию Р. и г. п.
в приложениях способствует простота уравнений для
переходных вероятностей, к-рые часто удается найти в
явном виде. Напр., в случае пуассоновского процесса
%n(t)—\, |г„(*)=0, вероятности P,,(t) (Pn(t) — веро-
вероятность нахождения в момент времени t в состоянии
п, если процесс начался из состояния 0) удовлетворяют
системе уравнений:
P'0{t)=r-~%,P0{t)
P'n{t)=-bPn
Решение этой системы:
Более общим является процесс, для к-рого Хп(t)-=nk,
н„(?) = 0. Этот тип процесса был впервые изучен
Дж. Юлом (G. Jule, 1924) в связи с математич. теорией
1В0ЛЮЩШ. Процесс Юла является частным слу-
случаем процесса чистого размножения,
к-рый получается из общего Р. и г. п., если положить
'•л(')=^н! ^л(*)=0- Если Хп растут очень быстро, то за
конечное время можно с положительной вероятностью
пройти по всем состояниям и тогда
Условие
для процесса чистого размножения выполняется тогда
и только тогда, когда расходится ряд 2 1/^п- Если
Xn(t)=iik-\r\, (х„(г) = пи, то Р. и г. п. представляет
собой ветвящийся процесс с иммиграцией, в к-ром со-
состояние п означает число частиц, причем каждая ча-
частица за время ((, t-\-h) с вероятностью (x/i+o(/i) поги-
погибает, с вероятностью Kh-{-o(h) делится на две и, кроме
того, извне иммигрирует одна частица с вероятностью
v/i-fo(h). Если v=0, то получится простейший вет-
ветвящийся процесс без иммиграции.
Если Я=0, a v > 0, то этот вид процесса с иммиграцией
можно применить к описанию работы телефонной си-
системы с бесконечным числом линий. Состоянием тогда
является число занятых линий. Коэффициент размно-
размножения Я„(()=л> характеризует поступающий поток
вызовов, ар. — длительность разговора.
Лит.: 11] Ф е л л с р В., Введение в теорию вероятностей
и ее приложения, пер. с англ., т. 1—2, М., 1964—67; [2] С е в а-
пьяно» Б. А.,'Теория ветвящихся процессов, в кн.: Итоги
науки. Серии Математика, т. 14— Теория вероятностей. Мате-
Математическая статистика. Теоретическая кибернетика. 1967, М.,
1968, с. 5—46; [3] Саати Т. Л., Элементы теории массового
обслуживания и ее приложения, пер. с англ., М., 1965.
В. П. Чистяков.
РОЖДЕНИЯ ОПЕРАТОРЫ — семейство замкнутых
линейных операторов {а* (/), /?#}, где Я — нек-рое
гильбертово пространство, действующих в Фока про-
пространстве, построенном над Н, и являющихся сопря-
сопряженными к уничтожения операторам {«(/), f?H).
Р. А. Минлос.
РОЗЫ — плоские кривые, уравнения к-рых в поляр-
полярных координатах имеют вид
р = а sin fcq>,
где а и А" — постоянные. Если к=т!п — число рацио-
рациональное, то Р.— алгебраич. кривая четного порядка.
Порядок Р. равен
го+я, если тип —
нечетные числа, и ра-
равен 2(т + »), если
одно из чисел т или
п — нечетное. Вся
кривая расположена
внутри круга радиу-
радиуса а, состоит из кон-
конгруэнтных лепестков
(см. рис.). Если А: —
целое, то Р. состоит
из к лепестков при
к нечетном и из 2к
лепестков при к чет-
четном. Если к--т/п и
m, n —взаимно про-
простые, то Р. состоит
из т лепестков, ког-
когда т и п нечетные,
и из 2т лепестков, если одно из чисел т или п явля-
является четным.
При иррациональном к лепестков бесконечное мно-
множество. Р. относятся к семейству циклоидальных
кривы.!-. Р. являются гипоциклоидами, если /,>1, и
эпициклоидой, если Л-<1.
С семейством циклоидальных кривых Р. связаны и
тем, что они являются подэрами эпи- и гипоциклоид
относительно центра их неподвижного круга.
Длина дуги Р. выражается эллинтич. интегралом
2-го рода. Площадь одного лепестка: S — na-/ik.
Р. наз. также кривыми Гуидо Гранди
(G. Grandi), впервые описавшего их в 1728.
Лит.: [1] С а в е л о в А. А., Плоские кривые, М., 1960.
Д. Д. Соколов.
РОЛЛЯ ТЕОРЕМА: если действительная функция
/ непрерывна на нек-ром отрезке [а, Ь], имеет в каждой
его внутренней точке конечную или определенного знака
бесконечную производную, а на его концах принимает
равные значения, то на интервале (а, Ь) существует по
крайней мере одна точка, в к-рой производная функции
/ равна нулю.
Геометрич. смысл Р. т. состоит в том, что на графике
функции /, удовлетворяющей условиям Р. т., сущест-
существует такая точка (|, /(?)), а < ? < Ь, что в ней каса-
касательная к графику параллельна оси х.
Механич. интерпретация Р. т. означает, что для ма-
материальной точки, непрерывно двигающейся по пря-
прямой и вернувшейся через нек-рый промежуток времени
в исходную точку, существует момент времени, в к-рый
ее мгновенная скорость равнялась нулю.
Впервые теорема была получена для алгебраич. мно-
многочленов М. Роллем [1].
Лит.: fll R и 1 1 е М., Traitt d'algebre, P., 1690; [2] Ни-
к о л ь с [. и II О. М., Курс математического анализа, 2 изд.,
т. 1, М., J!>7"j. ' Л. Д. Кудрявцев.
РОМБ — плоский четырехугольник с равными сто-
сторонами. Р. можно рассматривать как частный случай
параллелограмма, у к-рого или две смежные стороны
равны, или диагонали взаимно перпендикулярны, или
диагональ делит угол пополам. Р. с прямыми угля mi*
наз. квадратом. Б(
РОМБЕРГА МЕТОД, правило Р о м б е р г а. -¦
метод вычисления определенного интеграла, основан-
основанный на Ричардсона экстраполяции. Пусть вычисляется
значение / нек-рого функционала, при этом вычисляе-
вычисляемое приближенное значение Т (h) зависит от параметра
h, так что в результате вычисления получается прибли-
приближенное равенство 1 =к T(h). Пусть известна информа-
информация о поведении разности 1 — Т (Л) как функции от h,
а именно:
I — Т (h) - a.hm, A)
где m — натуральное число и а зависит от приближае-
приближаемого функционала и той функции, на к-рой он вычисля-
вычисляется, от способа приближения и (слабо) от h. Если на-
наряду с Т (h) вычислено TBh), то способ Ричардсона
дает для / приближение
2'"Т (ft)-TB/t) .„
= ^пГГу • ^>
Это приближение тем лучше, чем слабее а из равенства
A) зависит от h. В частности, если а от h не зависит, то
в B) имеет место точное равенство.
Р. м. применяется к вычислению интеграла
Промежуток [0, 1] взят для простоты записи, он может
быть любым конечным. Пусть
del г __п'г_ 1 -1
[2 2/:=1 /(/2-*)-b/(l)J, C)
, 1, 2, ... .
Вычисления в P.m. сводятся к составлению следующей
таблицы:
т
т
п
п
т
т
_;
-1,
00
10
0
0
Т
Т
Т
Т
п-2,
п-1,
01
11
1
1
Т
' 02
Ti2
-2, 2
0. п-1
1,11-1
где первый столбец состоит из квадратурных сумм C)
формулы трапеций. Элементы (/+2)-го столбца получа-
получаются из элементов (i+l)-ro столбца по формуле
+>1'f" *', * = 0,l,2, ...,„-1-1.D)
При составлении таблицы главная часть вычислитель-
вычислительного труда затрачивается на вычисление элементов
первого столбца. Элементы следующих столбцов вычис-
вычисляются чуть сложнее конечных разностей.
Каждый элемент Tki таблицы есть квадратурная
сумма, приближающая интеграл
Is±Tkl. E)
Узлами квадратурной суммы Тк1 являются точки
J~к~1, /=0, 1, 2, ..., 2* + ', а ее коэффициенты —
положительные числа. Квадратурная формула E) точ-
точна для всех многочленов степени не выше 2/+1.
В предположении, что подинтегральная функция
/(х) имеет непрерывную производную порядка 2Z-J-2
на [0, 1], разность / — Ты имеет представление вида
A), в к-ром т—-11-\-1. Отсюда следует, что элементы
(Z+2)-ro столбца, вычисляемые по формуле D), явля-
являются улучшениями по Ричардсону элементов (Z+l)-ro
столбца. R частности, для погрешности квадратурной
формулы трапеций справедливо представление
и способ Ричардсона дает более точное приближение
к /:
Тк1 оказывается квадратурной суммой формулы Сгош-
сона, и т. к. для погрешности этой формулы справед-
справедливо представление
^^, A = 2-*-i, TiCfO, Ц,
то снова можно воспользоваться способом Ричардсона
и т. д.
В Р. м. в качестве приближения к / берется ТОп, при
этом предполагается, что существует непрерывная
производная /(-'" (х) на [0, 1]. Ориентировочное пред-
представление о точности приближения Топ можно полу-
получить, сравнивая То„ и 7*1, n-i-
Впервые метод изложен В. Ромбергом [1].
Лит.: [И Romberg W., «Kgl. norske vid. selskabs for-
handl.», 1955, Bd 28, № 7,' s. 30—36; [2] В a u e г F. L., R u-
t i s h a u s e г H., Stiefel E., «Proc. Symp. Appl. Math.»,
1963, v. 15, p. 199—218. И. П. Мысовских.
РОМБИЧЕСКАЯ СЕТЬ, к о н ф о р м н о-ч е б ы-
шевская сеть,— сеть, в каждом четырехуголь-
четырехугольнике к-рой, образованном двумя парами линии различ-
различных семейств, стороны равны с точностью до бесконечно
малых 1-го порядка. На поверхности вращения ее асим-
асимптотическая сеть есть Р. с. Напр., на гиперболоиде
вращения его прямолинейные образующие составляют
|J_ с А. В. Пеанов.
РОСТА ИНДИКАТРИСА, индикатор целой
у н к ц и и,— величина
ш
характеризующая рост целой функции /(z) конечного
порядка р > 0 и конечного типа о вдоль луча arg г=ф
при больших г(г=ге1ч>). Напр., для функции
порядок равен р и Р. и. равна h (ф) = о со8рф-)~Ь sin рф;
для функции sin z порядок р=1 и й(ф)=|атф|. Функ-
Функция h (ф) всюду конечна, непрерывна, имеет в каждой
точке производную слева и справа, имеет производную
всюду, кроме, быть может, счетного множества точек;
всегда h (ф) <s а и имеется, по крайней мере, одно ф,
когда Л(ф)=а; обладает характерным свойством
тригонометрич. выпуклости, т.е. еслл
А (ф!Х# (фх), й(ф2х#(ф2),
II (ф) = a cos рф-f-b sin рф,
ф! < ф2, ф2 — ф1 < min ( л/р, 2л
то А(ф)<Я(ф),
Выполняется неравенство
|/(re'<P)|<el'!<41>+e]''P, r>ro(e), Ve>0,
где го(е) не зависит от ф.
Р. и. вводится также для функции, аналитической в
угле и имеющей в этом угле конечный порядок или уточ-
уточненный порядок и конечный тип.
Лит.: [1] Левин Б. Я., Распределение корней целых
функций, М., 1956; [2] Маркушевич А. П., Теория ана-
аналитических функций, 2 изд., т. 2, М., 196S. А. Ф. Леонтьев.
РОСТОК — термин, означающий точечную локализа-
локализацию различных математич. объектов (Р. функций, Р.
отображений, Р. аналитических множеств и т. п.).
Пусть, напр., х есть точка топологич. пространства и
F — нек-рое семейство функции, определенных в ок-
окрестности х (каждая в свое»). Функции /, g считаются
эквивалентными (в точке х), если они совпадают в нек-
некрой окрестности х. Класс эквивалентности по этому
отношению наз. ростком функций класса F
в точке х. Так определяются Р. непрерывных функций,
дифференцируемых функций в точках дифференцируе-
дифференцируемого многообразия, голоморфных функций в точках
комплексного многообразия и т. п. Если семейство F
обладает нек-рой алгебраич. структурой, то множество
Р. функций семейства F наследует эту структуру (опе-
(операции при помощи представителей классов). В частно-
частности, Р. голоморфных функций в точке z образуют коль-
кольцо. Элементы поля частных этого кольца наз. рост-
ростками мероморфных функций в точке z.
Аналогично определяется Р. семейства подмножеств
топологич. пространства. Напр., в точках аналитич.
многообразия есть Р. аналитических множеств (класс
эквивалентности определяется по совпадению в окрест-
окрестности данной точки). На Р. семейств подмножеств есте-
естественно определяются теоретико-множественные опе-
операции и отношения. Понятие Р. имеет смысл и для
других объектов, определенных на открытых подмно-
подмножествах топологич. пространства.
См. также Аналитическая функция, Мероморфная
функция, Пучок.
Лит.: [1] Ганнинг Р., Росси X., Аналитические
функции многих комплексных переменных, пер. с ан!'.н., М.,
1969. К. М. Чирка.
РОТОР — то же, что вихрь.
РУЛЕТТА — название плоской кривой, рассматри-
рассматриваемой как траектория точки, жестко связанной с нек-
некрой кривой, катящейся по другой неподвижной кри-
кривой. В случае, когда окружность катится по прямой,
Р. есть циклоида; если окружность катится по окруж-
окружности — циклоидальная кривая; если по прямой катится
гипербола, эллипс или парабола — Штурма кривая.
Траектория точки эллипса, катящегося но др. эллипсу,
наз. э п и э л л и п с о м. Каждая плоская кривая
многими способами может быть рассмотрена как Р.;
напр., всякая кривая может быть образована качением
прямой по эволюте.
Лит.: [1] С а в е л о в А. А., Плоские кривые, М., I960.
Д. Д. Соколов.
РУНГЕ ОБЛАСТЬ, область Рунге перво-
первого рода,— область G в пространстве С" комплексных
переменных (zl5. . ., zn), обладающая тем свойством,
ЧТО ДЛЯ любой ГОЛОМОрфнОЙ В G фуНКЦИИ /(Zj, . . ., Zn)
существует последовательность многочленов
сходящаяся в G к f(z1, . . ., zn) равномерно на каждом
замкнутом ограниченном множестве EcG. Определение
Р.о. второго рода получается отсюда заменой
последовательности (*) последовательностью рацио-
рациональных функций {-Rfc(zb. . ., zn)}k=i. Приге=1 всякая
односвязная область является Р. о. первого рода, вся-
всякая область — Р. о. второго рода (см. Рунге теорема).
При п 5s 2 не всякая односвязная область есть Р. о.
и не всякая Р. о. односвязна.
Лит.: [1] Ф у к с Б. А., Специальные главы теории анали-
аналитических функций многих комплексных переменных, М., 1!№3:
[2]' Владимиров В. С, Методы теории функций многих
комплексных переменных, М., 1964. Е. П. Должепко.
РУНГЕ ПРАВИЛО — один из методов оценки по-
погрешности формул численного интегрирования. Пусть
R = hkM — остаточный член формулы численного ин-
интегрирования, где h — длина отрезка интегрирования
или какой-то его части, к — фиксированное число и М —
произведение постоянной на производную иодинтег-
ральной функции порядка к—1 в какой-то точке про-
промежутка интегрирования. Если J — точное даачение
интеграла, а / — его приближенное значение, то /=
I+hkM
Согласно Р. п. вычисляется тот же самый интеграл
по той же формуле численного интегрирования, но
вместо h берется величина hi2. При этом, чтобы получить
значение интеграла по всему отрезку, формула интег-
интегрирования применяется дважды. Если производная,
входящая в М, меняется не сильно на рассматриваемом
промежутке, то
где /х — значение интеграла, вычисленное по Л/2.
Р. п. используется и при численном решении диффе-
дифференциальных уравнений.
Правило предложено К. Рунге (С. Runge, нач. 20 в.).
Лит.: [1] Б е р е з и н И. С, Ж и д к о в Н. П., Методы
вычислений, 3 изд., т. 1, М., 1966; 2 изд., т. 2, М., 1962; [2]
Современные численные методы решения обыкновенных диффе-
дифференциальных уравнений, пер. с англ., М., 1979.
А. Б. Иванов.
РУНГЕ ТЕОРЕМА — теорема о возможности поли-
полиномиальных приближений голоморфных функций, впер-
впервые доказанная К. Рунге (С. Runge, 1885).
Пусть D — односвязная область на плоскости комп-
комплексного переменного z. Тогда всякая функция /,
голоморфная в D, приближается равномерно внутри D
многочленами от z. Точнее, для любого комиакта KcD
и любого е > 0 найдется многочлен р (z) с комплексны-
комплексными коэффициентами такой, что |/(z) —p(z)l <e для
всех z(^K.
В иной формулировке: любая функция /, голоморф-
голоморфная в односвязной области DaC, представляется в
виде ряда из многочленов от z, абсолютно и равномерно
сходящегося к / внутри D.
Эквивалентная формулировка Р. т.: пусть К —
компакт на комплексной плоскости С со связным до-
дополнением С\К; тогда всякая функция, голоморфная
в окрестности Л", равномерно на А' приближается много-
многочленами от z. В такой форме Р. т. есть частный случай
Мергеляна теоремы.
Р. т. наз. также следующая теорема о рацио-
рациональных приближениях: всякая функция
/, голоморфная в области DcC, равномерно внутри D
приближается рациональными функциями с полюсами
вне D.
Р. т. имеет многочисленные применения в теории
функций комплексного переменного и в функциональ-
функциональном анализе. Аналог Р. т. справедлив на некомпактных
римановых поверхностях. Обобщением Р. т. для функ-
функций многих комплексных переменных является теорема
Ока — Вейля (см. Ока теоремы).
Лит.: [1]МаркушевичА. И. Краткий курс теории
аналитических функций, 4 изд., М., 1978; [2] Ш а б а т Б. В.,
Введение в комплексный анализ, 2 изд., ч. 1, М., 1976.
Е. М. Чирка.
РУНГЕ — КУТТА МЕТОД — одношаговый метод чи-
численного решения задачи Коши для системы обыкно-
обыкновенных дифференциальных уравнений вида
«*'=/(', и). A)
Основная идея Р.— К. м. была предложена К. Рунге
[1] и развита затем В. Кутта [2] и др. Первоначально
эта идея использовалась лишь для построении явных
схем Р.— К. м., к-рые разыскивались в виде
^+i = »/+ii2j=1?;. B)
где
, n = 2, 3, ..., q,
при этом значения постоянных А[,ап, $пт, s=l, 2,..., д;
ге=2, 3, . . ., q; m=l, 2, . . ., п—1, определялись из
требования, чтобы погрешность равенства B) на точ-
точном решении уравнения A) имела возможно высокий
порядок малости в сравнении с шагом т для любых урав-
уравнений вида A).
В отличие от Адамса метода и др. многошаговых ме-
методов, Р.— К. м., как и всякий одношаговый метод, не
требует предварительного построения начала таблицы
значений приближенного решения и дает возможность
вести вычислительный процесс при естественных для
уравнения A) начальных условиях, что позволяет ис-
использовать его непосредственно и в случае неравно-
неравномерных сеток. Однако поскольку в этом методе не ис-
используется информация о решении в предыдущих узлах
сетки, то он, вообще говоря, оказывается локально
менее экономичным, чем, напр., метод Адамса.
Наиболее широко известным (см., напр., [3]) среди
Р.— К. м. является метод
*! = /(«/, У/), k2 = f
принадлежащий зависящему от двух свободных пара-
параметров семейству методов четвертого порядка точности
вида B) с д=4. Популярен и простейший явный Р.—
К. м. первого порядка точности, получающийся из
B) при <7=1. Этот метод известен под названием мето-
метода Эйлера. При значениях q, равных 2 и 3, из B)
могут быть найдены семейства Р.— К. м. второго и
третьего порядка точности, зависящие от одного и двух
свободных параметров соответственно. В случае q > 4
имевшее место ранее соответствие между значением q
и порядком точности метода уже нарушается. Р.— К. м.
вида B) пятого порядка точности удается построить
лишь при q=6, шестого — при q=7, седьмого — при
<7=9 и т. д. В этом случае с увеличением значения q
на единицу расширение множества подлежащих вы-
выбору в B) постоянных At, an, $пт часто оказывается
уже недостаточным, чтобы удовлетворить условиям,
возникающим из требования повышения на единицу
порядка точности явного Р.— К. м. С целью увеличе-
увеличения числа выбираемых в B) параметров можно рассмот-
рассмотреть, напр., следующее обобщение конструкции одно-
шаговых методов, основанных на идее К. Рунге:
п = 1, 2, ..., q. (')
Методы вида B), C) в общем случае являются уже
неявными, что значительно осложняет их численную
реализацию: величины кп, ге=1, 2, . . ., q, на каждом
шаге приходится находить из системы, вообще говоря,
нелинейных уравнений C). Однако за счет достигнутого
здесь значительного увеличения числа подлежащих вы-
выбору констант такие методы приобретают следующее
свойство (см. [4]): для каждого значения q существует
неявный Р.— К. м. порядка точности 'lq. Кроме того,
при таком расширении класса Р.— К. м. появляются
методы, хорошо ориентированные на случай жестких
дифференциальных систем.
Имеется еще одно видоизменение (см., напр., [5])
идеи К. Рунге конструирования одношаговых методой
численного решения уравнений вида A). Именно, ис-
исходя из A) записывается равенство
и (t/+x)-u (tj) = x ^Qf (tj + ax, u (tj+ax)) da.
Приближенное представление последнего интеграла
квадратурной формулой с q узлами дает
и (tj + x) ~ и (tj)+x'2f.= i Atf («у-Ьа/Т, и (/,-+а,-г)). D)
Если выбор узлов а,- и кояффициентов A;, i=l, 2, . . . ,
q, рассматриваемой квадратурной формулы подчинить
условиям
п = 1,2,...,р-1, E)
то погрешность приближенного равенства D) будет
величиной порядка xP + i. При р < 2q система уравне-
уравнений E) разрешима и приближенное равенство D) может
быть построено. Аналогично можно записать прибли-
приближенные равенства для неизвестных величин и(?/+а,т),
входящих в правую часть D), при этом требования к их
точности могут быть понижены на порядок, и т. д.
В качестве примера так построенного одногаагового
метода ниже приводится (см. [6]) метод третьего порядка
точности предсказывающе-исправляющего характера:
Если положить в D) одно из значений а,- равным
единице, на этом пути можно строить также и неявные
методы, напр, метод
ff{t/, yj+i — т/(*/+т,
второго порядка точности.
Рассмотренные выше на примере уравнений вида A)
подходы к построению численных методов могут быть
распространены на обыкновенные дифференциальные
уравнения высших порядков (см. [6], [7]), а также
использованы при конструировании разностных схем в
случае дифференциальных уравнений с частными про-
производными.
Лит.: [HRiinge С, «Math. Ann.», 1895, Bd 46, S. 167 —
178; [2] К u t t a W.,«Z. Math, und Phys.», 1901, Bd 46, S.
435—53; [3] Бахвалов Н. С, Численные методы, 2 изд.,
M., 1975; li] В u t о h е г J. С, «Math. Сотр.», 1964, v. 18, p.
50—64; [5] Бобков В. В., «Becitf АН БССР. Сер. ф13.-мат.
навук», 1967, №4, с. 27—35; [6] Крылов В. И., Боб-
Бобков В. В., МонастырныйП. И., Вычислительные ме-
методы, т. 2, М., 1977; [7J Коллатц Л., Численные методы
решения дифференциальных уравнений, пер. с нем., М., 1953.
В. В. Бобков.
РУЧЕК ТЕОРИЯ — один из методов изучения тополо-
гич. многообразий, основанный на представлении мно-
многообразия в виде объединения топологич. шаров с не-
непересекающимися внутренностями и специальным обра-
образом пересекающимися краями.
Пусть Мп есть n-мерное многообразие, к — такое
целое число, что 0 <: к •< п, и пусть топологич. шар Н
является образом гомеоморфного отображения
h : Вк X В"~к —>¦ Мп, где Вт обозначает стандартный
/«-мерный шар с центром в точке О. Тогда пара (Н, h)
(или просто Н) наз. ручкой индекса к в многооб-
многообразии Мп. Гомеоморфизм h наз. характерис-
характеристическим отображением ручки 11,
диск h(Bk X О) — срединным, а диск Л (ОХ
Xfi«-«) — секущим. Сфера к(дВкХО) наз. при-
приклеивающей (или подошвенной) сферой,
а сфера к(ОхдВп~к) —секущей. Пространство
к(дВкУ..Вп~к) наз. подошвой ручки Я.
Если многообразие М" кусочно линейно, то имеет
смысл говорить о кусочно линейных ручках, имея в
ниду кусочную линейность характеристич. отображе-
отображения. Точно также в случае гладкого многообразия
Мп можно говорить о гладких ручках.
Пусть (//, h) — ручка индекса к в многообразии
Мп, Р — ее подошва и Ml — такое подмногообразие
Мп, что НС\М\ =/". Операция перехода от многообра-
многообразия Ml к многообразию М"=м1[]Н наз. опера-
операцией приклеивания ручки индекса к.
Вложение / --h » „в-* наз. приклеивающим
I О-В Х.В
отображением. С точностью до неподвижного
на Л/" гомеоморфизма многообразие Ml полностью
определяется приклеивающим отображением / и не за-
зависит от объемлющего многообразия М. Если / —
произвольное вложение дВк X В"~к в дМ", то резуль-
результат приклеивания ручки но вложению / можно описать
так: М1~(М1{](ВкХВп~к)I^п, где отношение экви-
эквивалентности с/э порождено отождествлением точек
дВкХВ"~к и 0М1 но вложению /. Операция перехода
от дМ'[ к дМ" наз. сферической пере-
перестройкой. По аналогии с этим приклеивание ру-
ручек наз. иногда пристройками. Многообразия,
получающиеся приклеиванием ручки по изотопным вло-
вложениям, гомеоморфны. На рис. 1 изображено приклеи-
приклеивание трехмерных ручек индексов 1 и 2. Приклеивание
к Ml ручки индекса 0 состоит в добавлении к Ml
отдельно взятого шара размерности п. Добавление
ручки индекса п заключается в заклеивании ге-мерным
шаром одной из компонент дМ1.
Рис.
Если многообразие Mi и приклеивающее вложение
/ : дЛ^ХВп~к —у дМ1 кусочно линейны, то многообра-
многообразие Ml, получающееся приклеиванием ручки по вло-
вложению /, также кусочно линейно. В случае гладких
М" и / многообразие М" обладает естественной гладкой
структурой во всех точ-
точках, кроме «угловых»
точек, объединение к-рых
совпадает с краем подош-
подошвы ручки. Эту структуру
можно единственным об-
образом продолжить до
гладкой структуры на
всем м1. Такое продол-
продолжение наз. сглажива-
сглаживанием углов. В глад-
гладком случае операцию
сглаживания углов вклю-
включают в операцию прикле-
приклеивания ручки. Прикле-
Приклеивание гладкой ручки полностью определяется при-
приклеивающей сферой вместе с тривиализацией ее нор-
нормального расслоения.
Представление компактного многообразия Мп в
виде объединения конечного упорядоченного семейства
ручек в М" наз. разложением Мп на ручки,
если каждая следующая ручка пересекается с объедине-
объединением предыдущих в точности по своей подошве. Дру-
Другими словами, М" допускает разложение на ручки,
если его можно получить из шара (или из пустого
множества) последовательным приклеиванием ручек.
Аналогично, под разложением пары (Мп, Ml), где Мо —
подмногообразие многообразия М", понимается пред-
представление М" в виде результата последовательных
приклеиваний ручек к м". В частности, разложе-
разложением бордизма (W, Мо, Мг) на ручки наз.
разложение пары (W, МаХ1), где МйХ1 — воротник
Мо. Разложение на ручки некомпактного многообразия
Мп состоит из бесконечного числа ручек. При этом
обычно требуется, чтобы разложение было локально
конечным, т. е. чтобы каждый компакт в М" пересе-
пересекался только с конечным числом ручек.
Применяя приведение в общее положение секущих
сфер уже приклеенных ручек и подошвенной сферы при-
приклеиваемой ручки и заме-
заменяя приклеивающие ото-
отображения на изотопные,
можно добиться, чтобы
ручки одного индекса не
пересекались и чтобы ин-
индексы последовательно
приклеиваемых ручек не
убывали. Такое разложе-
разложение на ручки наз. пра-
правильным.
Каждое кусочно линей-
линейное многообразие раскла-
раскладывается на кусочно ли-
пейные ручки. Если Т —
триангуляция М" и Т" —
ее второе барицентриче-
барицентрическое подразделение, то в
качестве ручек индекса к можно взять замкнутые
звезды в Т" барицентров А-мерных симплексов Т (см.
рис. 2; определение звезды дано в ст. Комплекс).
Существует тесная снизь между разложениями глад-
гладкого многообразия М" на гладкие ручки и гладкими
функциями на М" с невырожденными критич. точка-
точками — Морса функциями. Эта связь заключается в сле-
следующем. Пусть хй — такая критич. точка индекса к
Рис.
функции Морса / : М" -»¦ R, что для нек-рого е > 0 в
прообразе отрезка lf(x0)— е, f(xo)+e] нет других кри-
тич. точек, и пусть Мс= {х?Мп : f(x)<c}. Тогда
многообразие Af/(Xo) + e получается из многообразия
Мпх ) е приклеиванием гладкой ручки индекса к.
Таким образом, каждая функция Морса на компактном
многообразии М" порождает разложение Мп на глад-
гладкие ручки, причем число ручек индекса к в этом разло-
разложении совпадает с числом критич. точек индекса к.
Этим доказывается существование разложения любого
гладкого многообразия на гладкие ручки. Обратно,
каждое разложение М" на гладкие ручки порождено
нек-рой функцией Морса на Мп.
Сложнее обстоит дело с разложением на ручки топо-
логич. многообразий. Известно, что любое замкнутое
топологич. многообразие размерности re ^ 5 расклады-
раскладывается на топологич. ручки. Многообразия размернос-
размерности га <: 3 комбинаторно триангулируемы и поэтому
раскладываются на ручки. Доказано, что существует
многообразие размерности 4, не допускающее разло-
разложения на ручки.
Если в правильном разложении на ручки многообра-
многообразия Мп последовательно стянуть все ручки на их сре-
срединные диски, то получится клеточное пространство
К. Каждой ручке индекса к в разложении М" отвечает
Ar-мерная клетка в клеточном разбиении пространства
К. Пространство К имеет тот же гомотопический тип,
что и Мп. В случае замкнутого М" цространство К
совпадает с М".
Из определения ручки следует, что каждая ге-мерная
ручка Н индекса к является одновременно ручкой ин-
индекса п—А:. Если Р^ — подошва // как ручки индекса
к, а Р„-ц — подошва Н как ручки индекса п—к, то
Pk\JP,,-k=0H и Pkr\Pn_k=dPk=dPn_k. Каждое
разложение замкнутого многообразия М" на ручки
порождает т. н. двойственное разложе-
разложение Мп на ручки. Двойственное разложение состоит
из взятых в обратном порядке ручек исходного разло-
разложения, причем каждая ручка индекса к считается уже
ручкой индекса га—к. Этот факт служит геометрич. ос-
основой Пуанкаре двойственности. Если многообразие
М" имеет край, то двойственное разложение можно
рассматривать как разложение пары (M"\J (дМпх1),
дМпх1).
Пусть Hi, H2 — непересекающиеся ручки индекса к,
приклеенные к многообразию М" с односвязным краем
по вложениям jt /2 : dBkXBn~k -> дМ". Пусть к > 2
и п—к ^ 2, а [/] обозначает элемент группы л^-л (дМ"),
определяемый отображением /. Тогда вложение /2
изотопно в д(Мп\]Н1) такому вложению /а : дВкХ
X?""*-+()if", что [/a] = [/i] + [/2l. Это означает, что
многообразия 7kf"U#iU#2 и M"\J^il)^i где Нг —
ручка, приклеенная по вложению /а, гомеоморфны.
Операция перехода от многообразия Мп\}И\\$Н-ъ к
многообразию Mn\JH1[}IIi наз. сложением
ручек.
Пусть многообразие Ml получено из многообразия
М\ последовательным приклеиванием ручки Нх ин-
индекса к и ручки //2 индекса к-\-1 так, что подошвенная
сфера ручки 7/2 трансверсально пересекает секущую
сферу ручки Н1 ровно в одной точке. Тогда эту пару
ручек можно устранить. Это означает, что существует
гомеоморфизм М" на м", неподвижный вне окрестно-
окрестности /fi\JJI2. Операция устранения иногда наз. сок-
сокращением дополнительных ручек.
Сложение ручек и сокращение ручек можно произво-
производить, оставаясь в рамках кусочно линейной или гладкой
категории. С помощью сокращения ручек индексов О
и 1 можно, напр., любое разложение на ручки связного
компактного многообразия М" заменить на разложение
с ровно одной ручкой индекса 0. Если М" односвяано и
п > 5, то, складывая и сокращая ручки, можно любое
разложение на ручки свести к разложению с минималь-
минимальным числом ручек, совместимым с гомологич. структу-
структурой Мп.
Пусть (Я, h) — топологич. ручка индекса к в кусоч-
кусочно линейном многообразии М", причем характериетич.
отображение h кусочно линейно в окрестности дВкХ
xBn-k. Существует ли неподвижная на окрестности
дВкХВп~11 изотопия отображения h, выпрямляющая
ручку Н, т. е. переводящая ее в кусочно линейную руч-
ручку? Если бы ответ на этот воцрос был всегда положи-
положительным, то на каждом топологич. .многообразии можно
было бы ввести кусочно линейную структуру, согласовы-
согласовывая структуры на координатных окрестностях с помо-
помощью выпрямления кусочно линейных ручек одной ок-
окрестности внутри другой. На самом деле ответ зависит
от индекса к и размерности п ручки //. Если п < 3
или п 5г 5 и к ф 3, то любая ручка выпрямляема. Из-
Известно, что при п 5а 5 существуют невыпрямляемые
ручки индекса 3, причем препятствие к выпрямлению
лежит в группе ч_2. В размерности 4 ручки индексов 0
и 1 выпрямляемы, а индексов 2 и 3, вообще говоря,
нет. Препятствием к сглаживанию кусочно линейных
ручек служат т. н. группы Милнора Г&.
Лит.: [1] Смей л С, «Математика», 1062, т. 6, № 3,
с. 138 — 55; [2] е г о же, там же, 196 4, т. 8, №4, с. 95 — 108;
[3] е г о же, «Успехи матем. наук», 1964, т. 19, в. 1, с. 125—38;
[4] К i r b у R. С, Siebenmann L. С, «Ann. Math.
Stud.», 1977, А1! 88; [5] Рурк К., Сандерсон Б., Введение
в кусочно линейную топологию, пер. с англ., М., 1974; [6] Рох-
Рохлин В. А., Ф у к с Д. В., Начальный курс топологии. Гео-
Геометрические главы, М. 1977. С. В. Матвеев.
РУЧНОЕ ВЛОЖЕНИЕ — вложение топологич.
полиэдра Р в пространство R" такое, что существует
гомеоморфизм R" на себя, при к-ром Р переходит в
прямолинейный полиэдр. Тогда Р ная. ручным.
В противном случае Р наз. диким, а вложение —
диким вложением. м. И. Войцеховский.
РУШЕ ТЕОРЕМА: пусть f(z) и g(z) — регулярные
аналитич. функции комплексного переменного z в об-
области D, простая замкнутая кусочно гладкая кривая Г
вместе с ограничиваемой ею областью G принадлежит
D и всюду на Г выполняется неравенство |/(z)| > |g(z)|;
тогда в области G сумма f(z)-\-g(z) имеет столько же
нулей, сколько и /(z).
Эта теорема была получена Э. Руше [1]. Она является
следствием аргумента принципа, и из нее в свою оче-
очередь получается основная теорема алгебры многочле-
многочленов.
Справедливо также обобщение Р. т. для много-
многомерных голоморфных отображений, напр, в следующем
виде. Пусть /(z)= (/i(z),. . ., /„(z)) и g(z)= (g, (z),. . .,
gn (z)) — голоморфные отображения области D комп-
комплексного пространства С" в С", п^ 1, с изолирован-
изолированными нулями, пусть гомеоморфная сфере гладкая
поверхность Г вместе с ограничиваемой ею областью С
принадлежит D и всюду на Г выполняется неравенство
Тогда отображение /(z) -f- g(z) имеет в G столько же
нулей, сколько и f(z).
'Лит.: [1] RoucheE., «J. Ecole polyt.», 1858, t. 21;
I'A M a p к у ш е в и ч А. И., Теория аналитических функций,
2 изд., т. 1,М., 1967; [31 Ш а б а т Б. В., Введение в комплек-
комплексный анализ, 2 изд. ч. 1—2, М., 197U. Е. Д. Соломенцев.
РЭЛЕЯ РАСПРЕДЕЛЕНИЕ — непрерывное распре-
распределение вероятностей с плотностью
Р(Х)М^
'О , ,
зависящей от масштабного параметра а > 0. Р. р.
имеет положительную асимметрию, его единственная
мода находится в точке х= а. Все моменты Р. р. конеч-
конечны, математич. ожидание и дисперсия равны соответ-
соответственно у ~ а и 2а2 М—2.J. Функция распреде-
распределения Р. р. имеет вид
Р. р. является частным случаем распределения с плот-
плотностью
2 х„-лГхЧ*«>
при ге=2 и, следовательно, при о=1 Р. р. совпадает с
распределением арифметического квадратного корня и;;
случайной величины, имеющей чхи-квадрат» распреде-
распределение с двумя степенями свободы. Иначе, Р. р. может
быть интерпретировано как распределение длины век-
вектора в прямоугольной системе координат на плоскости,
координаты к-рого независимы и имеют нормальное
распределение с параметрами 0 и а2. Аналогом Р. р. в
3-мерном пространстве служит Максвелла распределе-
распределение.
Р. р. находит основное применение в теории стрельбы
и статистич. теории связи. Р. р. впервые рассмотрено
Рэлеем (Rayleigh, 1880), как распределение результи-
результирующей амплитуды при сложении гармонич. колебаний.
Лит.: [1] СтреттД». В. (лорд Р э л е й), Волновая
теория света, пер. с англ., М.— Л., 1940. А. В. Прохоров.
РЭЛЕЯ УРАВНЕНИЕ — нелинейное обыкновенное
дифференциальное уравнение 2-го порядка
x-\-F (x)+x = 0, x = dx/dt, (*)
где функция F (и) удовлетворяет предположению:
uF (и) < 0 при малых | и |,
uF (и) > 0 при больших | и |.
Р. у. описывает типичную нелинейную систему с од-
одной степенью свободы, в к-рой возможны автоколеба-
автоколебания. Названо по имени Рэлея (Rayleigh), изучавшего
уравнение такого типа в связи с задачами акустики [1].
Если уравнение (*) продифференцировать, а затем
положить у~х, то получится Лъенара уравнение
O; f(u) = F' (и).
Частным случаем Р. у. при
F (u) = —A, [b-jI , X — coast,
является Ван дер Поля уравнение. Иногда Р. у. наз.
частный случай уравнения (*):
х— (а — Ьх2)х'+х = 0, а>0, Ъ > 0.
Имеется большое число работ, в к-рых выясняются
условия существования и единственности устойчивого
предельного цикла у Р. у., то есть условия возникнове-
возникновения автоколебаний. Вопрос о периодич. решениях
изучался и для различных обобщений Р. у., напр.
для
где e(t) — периодич. функция.
Системой типа Рэлея часто наз. урав-
уравнение
x + F (x)-\-G (x) = H (t, х, х),
x?R", F:Rn—с R«, G:R"—>¦ R",
причем обычно предполагается, что
G=geadg, g:R"-^R
a II — ограниченная и периодическая по t вектор-
функция. Представляет интерес получение достаточ-
достаточных условий существования периодич. решений таких
систем.
Лит.: [1] С т р е т т Дж. В. (л о р д Р э л е й), Теория
звука, пер. с англ., 2 изд., т. 1, М.— Л., 1955; [2] Ч е з а р и Л.,
Асимптотическое поведение и устойчивость решений обыкновен-
обыкновенных дифференциальных уравнений, пер. с англ., М-, 1964. См.
также лит. при ст. Лъенара уравнение. Н. X. Розов.
РЯД, бесконечная сумма,— последова-
последовательность элементов (наз. членами данного
ряда) нек-рого линейного топологич. пространства и
определенное бесконечное множество их конечных сумм
(наз. частичными суммами ряда), для
к-рых определено понятие предела. Простейшими при-
примерами Р. являются следующие.
Однократные числовые ряды. Пара последователь-
последовательностей комплексных чисел {ап} и {sn} таких, что
sn = ai + a2+- ••+"„, л = 1, 2, ..., A)
наз. числовым (однократным) рядом и
обозначается так:
или
Элементы последовательности {я„} наз. членами
ряда, а элементы последовательности {sn} — его
частичными суммами, причем ап наз. п-м
членом Р. B), a sn — его частичной суммой порядка п.
Р. B) однозначно определяется каждой из двух после-
последовательностей {ап} и {sn}: члены последовательности
{sn} получаются из членов последовательности {ап} по
формуле A), а последовательность {ап} восстанавли-
восстанавливается по последовательности {s,,} согласно формулам
ei = «i, an + ]—.'„.pi —sB, n — l, 2, ...
В этом смысле изучение Р. равносильно изучению пос-
последовательностей: для каждого утверждения о Р. мож-
можно сформулировать равносильное ему утверждение о
последовательностях.
Р. B) наз. сходящимся, если последовательность
его частичных сумм {«„} имеет конечный предел
s— lim sn,
п-> х
к-рып наз. суммой Р. B), и пишут
Таким образом, обозначение B) применяется как для
самого Р., так и для его суммы. Если последователь-
последовательность частичных сумм Р. B) не имеет конечного предела,
то он наз. расходящимся.
Примером сходящегося Р. является сумма членов
бесконечной геометрич. прогрессии
при условии, что |г/| < 1. В этом случае ее сумма равна
1 ¦чл" 1
-j^, то есть 2jn=l1n=zJ—^ ¦ Если же \д\ > 1, то Р.
C) дает пример расходящегося Р.
Если Р. B) сходится, то последовательность его чле-
членов стремится к нулю:
lim e,, = 0.
Обратное утверждение неверно: последовательность
/ 1 \
членов i — / гармонического ряаа
стремится к нулю, однако этот Р. расходится. Ряд
2Г j^n + fe наа- остатком порядка п Р. B). Если
Р. сходится, то каждый его остаток сходится. Если
нек-рый остаток Р. сходится, то и сам Р. сходится. Если
остаток порядка п Р. B) сходится и его сумма равна
гп, то есть гп=У^=1ап + к, то
Если Р. B) и ряд
%Ьп D)
сходятся, то сходится и ряд
наа. суммой рядов B) и C), причем его сумма равна
сумме этих Р.
Если Р. B) сходится и X — комплексное число, то ряд
2]Xan, наз. произведением Р. B) на число К,
также сходится и ^Ал„—%2jan.
Условие сходимости Р., не использующее понятие
его суммы, дает Коши критерий сходимости Р.
Если все члены Р. B) являются действительными
числами: a,,?R, то Р. B) наз. действительным. Важ-
Важную роль в теории Р. играют действительные Р. с не-
неотрицательными членами:
2>„, в,„5а 0, ге = 1, 2, .... E)
Для того чтобы Р. E) сходился, необходимо и дос-
достаточно, чтобы последовательность его частичных сумм
была ограничена сверху. Если же он расходится, то его
частичные суммы стремятся к бесконечности:
поэтому в этом случае пишут
Для Р. с неотрицательными членами существует много
различных признаков сходимости. Основными являются
следующие.
Признак сравнения. Если для Р. E) и
2*и- ьп^0, л = 1, 2, ... , F)
с неотрицательными членами существует такая посто-
постоянная с > 0, что 0 < ап < cba, то из сходимости Р.
F) следует сходимость Р. E), а из расходимости Р.
E) — расходимость Р. F).
При применении признака сравнения для исследова-
исследования сходимости заданного Р. с неотрицательными чле-
членами часто оказывается целесообразным выделить глав-
главную часть его п-то члена относительно — при п —у со в
виде — (а — нек-рая постоянная), а в качестве Р.,
„а
с к-рым сравнивается данный Р., взять ряд
сходящийся при a > 1 и расходящийся при a <: 1.
Как следствие признака сравнения в случае, когда в
качестве Р. сравнения взят Р. G), получается следую-
следующее правило: если
lim naan — b,
/!->ОО
то при а > 1 и 0<b<+coP. E) сходится, а при
а <: 1 и 0 < Ь ¦< + а> Р- E) расходится.
Следствиями признака сравнения являются также
Д'Аламбера признак и Коши признак сходимости чис-
числовых рядов с положительными членами. Для таких
Р. имеются еще Бертрана признак, Гаусса признак,
Ермакова признак, Куммера признак, Раабе при-
признак.
Интегральный признак с ходим о с-
т и дает достаточные условия сходимости Р. E) с не-
неотрицательными членами, образующими убывающую
последовательность: ап is an + 1 Js- 0, п =- 1, 2,. . .
Пусть Р. E) таков, что для него существует функция /
определенная и убывающая при х 5s 1, У к-рой ее зна-
значения в целочисленных точках совпадают с членами
данного ряда: f(n)~an, я=1, 2,. . . . Тогда если sn—
частичные суммы, а г„ — остатки ряда E), то для них
имеют место следующие оценки:
f(x)dx+c + en, n = i, 2, ...,
где с — нек-рая постоянная, а
lim sn = 0.
Поэтому Р. E) сходится тогда и только тогда, когда
сходится интеграл
Если же Р. E) расходится, то его частичные суммы «„
растут так же, как интегралы
т. е. sn асимптотически равны указанным интегралам:
f(x)dx, п—>+«>.
Для Р. E), члены к-рого образуют убывающую пос-
последовательность, имеет место теорема Коши:
если члены Р. E) убывают, то он сходится или расходит-
расходится одновременно с рядом
Необходимым условием сходимости Р. E) с убываю-
убывающей последовательностью членов является условие
Пример расходящегося ряда
Vе 1
показывает, что условие (8) не является достаточным
для сходимости Р. E) с убывающей последовательностью
членов.
Важный класс числовых Р. составляют абсолютно
сходящиеся ряды, т. е. такие Р. B), для к-рых сходятся
ряды ^У|я„|. Если Р. абсолютно сходится, то он просто
сходится и его сумма не зависит от порядка следования
слагаемых. Сходящиеся, но не абсолютно сходящиеся
Р. наз. условно сходящимися. Примером
условно сходящегося Р. является ряд
„» (-1)»-'
2
Сумма условно сходящегося Р. зависит от порядка его
членов (см. Римана теорема о перестановке членов
ряда): каковы бы ни были а и р\ принадлежащие
множеству действительных чисел, дополненному бес-
бесконечностями -|-оо и —оо, а <Р, можно так переста-
переставить члены любого условно сходящегося Р., членами
к-рого являются действительные числа, что для час-
частичных сумм sn полученного Р. будут иметь место ра-
равенства
lim sn — a, lims,, = p.
Таким образом, для условно сходящихся Р. не имеет
места коммутативный закон сложения. Не для всех
Р. оказывается справедлив и ассоциативный закон сло-
сложения: если Р. расходится, то Р., полученный из дан-
данного последовательной группировкой его членов, может
сходиться, причем его сумма зависит от способа груп-
группировки членов исходного Р. Напр., ряд
расходится, а ряды A—1)+A—1)+. . . и 1—A—1)—
A—1) —. . ., полученные из него попарной группиров-
группировкой его членов, сходятся и имеют различные суммы.
Однако если Р. сходится, то, конечно, всякий Р.,
получающийся последовательной группировкой его
членов, сходится, и его суммой является сумма дан-
данного Р., ибо последовательность частичных сумм но-
нового Р. есть подпоследовательность частичных сумм
исходного Р.
Среди Р. с членами разных знаков выделяют знако-
знакочередующиеся Р., для к-рых имеется Лейбница признак
сходимости. Различные признаки сходимости для про-
произвольных числовых Р. могут быть получены с помощью
Абеля преобразования сумм попарных произведений,
напр. Абеля признак, Дедекинда признак, Дирихле
признак, Дюбуа-Реймона признак сходимости Р.
Умножение рядов. Для умножения Р. су-
существуют различные правила. Наиболее известно пра-
правило Коши, согласно к-рому при перемножении рядов
B) и D) сначала суммируются по конечным «диагона-
«диагоналям» попарные произведения атЪп, т. е. такие, у к-рых
сумма индексов т-\-п имеет одно и то же значение:
и ряд^Ср, членами к-рого являются полученные суммы,
наз. произведением данных Р. Это правили
умножения Р. подсказывается формулой умножения
степенных рядов:
Пусть Р. B), D), (9) сходятся и
2 «¦»=*• 26«=&- Ъср=с-
Если Р. B) и D) абсолютно сходятся, то Р. (9) также
абсолютно сходится и аЪ—с. Если Р. B) абсолютно
сходится, а Р. D) сходится, то сходится Р. (9) и ab=c
(теорема М е р т е н с а). Если же ряды B) и D)
условно сходятся, то Р. (9) может не сходиться; напр.,
РЯД
^п=1 Vn
условно сходится, а ряд
/у» (- 1)"-'\2
:1 1 /i 1 П-Н1
расходится. Если все три Р.—B), D), (9)—сходятся,
то ab=c.
Примером другого правила умножения Р. является
Суммирование сначала попарных произведений ambn,
у к-рых произведение индексов тп имеет фиксирован-
фиксированное значение
и определение произведения рядов B) и D) как ряда
2.,Ср. Это правило умножения Р. подсказывается фор-
формулой умножения Дирихле рядов:
Sam V Ь_п__ у J>
Встречаются также Р., члены к-рых ап занумерованы
всеми целыми числами и=0, ±1, ±2,... . Они обозна-
обозначаются:
Р. A0) наз. сходящимся, если сходятся ряды
2n=1«»-i и 2„=,в-»'
и сумма этих Р. наз. суммой Р. A0).
Числовыми Р. более сложной структуры являются
кратные ряды, члены а „ к-рых снабжены
1 ¦¦¦ т
мультииндексами, где п^ — натуральные числа, к=
= 1, 2, . . ., т, т=2, 3, .... В теории кратных Р.
рассматриваются различные типы частичных сумм: тре-
треугольные
s« = 2*l + ...+ftm<r!aft1...*m'
прямоугольные
сферические
и др. В зависимости от выбора типа частичных сумм
определяется понятие суммы кратного Р. как соответ-
соответствующего их предела. В случае т=2 кратный Р. наз.
двойным рядом. Для кратных Р., в отличие от однократ-
однократных, члены Р. уже могут не определяться заданием
множества частичных сумм, т. е., вообще говоря, для
того чтобы кратный Р. был определен, необходимо за-
задать как кратную последовательность членов Р., так и
множество его частичных сумм.
В математич. анализе находят применение не только
сходящиеся Р., но и расходящиеся. Для последних
разработаны разнообразные методы суммирования.
В виде сумм числовых Р. записываются многие важ-
важные иррациональные постоянные, напр.:
а также значения определенных интегралов, первооб-
первообразные подинтегральных функций к-рых не выражаются
через элементарные функции:
с 1 arctg х , -^,00 (-I)"-'
Jo I~i|,=in°1
Функциональные ряды, функциональным
(однократным) рядом
наз. пара функциональных последовательностей {а„ {х) }
и \sn(x)}, состоящих из числовых функций, определен-
определенных на нек-ром множестве X и таких, что
)-'r.+a(x) и = 1, 2, ...
Как и в случае числовых Р., элементы последователь-
последовательности \пп(х)} наз. членами Р. A1), а последова-
последовательности {sn (x) } — его частичными сумма-
м и. Р. A1) наз. сходящимся на множе-
множестве X, если при любом фиксированном хо?Х схо-
сходится числовой ряд
2 а« (¦*«)•
Пример. Ряд
у,» ?2 = ег
сходится на всей комплексной плоскости, а ряд
только при z=0.
Сумма сходящегося Р. непрерывных, напр, на нек-
ром отрезке, функций не обязательно является непре-
непрерывной функцией, напр, ряд
сходится на отрезке [0, 1], его члены непрерывны на
этом отрезке, а сумма
если 0<ж < 1,
Ч?:
s и
' ^ л если
разрывна в точке х=\. Ряд условий, при к-рых на
функциональные Р. переносятся свойства непрерывнос-
непрерывности, дифференцируемости и интегрируемости конечных
сумм соответственно непрерывных, дифференцируемых
или интегрируемых функций, формулируется в терми-
терминах равномерной сходимости рядов (см. Равномерно
сходящийся ряд).
Ряды измеримых функций. Пусть X —
измеримое по Лебегу подмножество re-мерного евклидова
пространства R", (J. — мера Лебега и члены ак(х) ряда
2 «ft И, z?X<=R», A2)
являются измеримыми почти всюду конечными на X
функциями, принимающими значения из расширен-
расширенной числовой прямой (т. е. наряду с действительными
числами они могут принимать значения +оо и —оо).
Если Р. A2) сходится почти всюду на множестве X,
то его сумма s(x) также является измеримой функцией
и, в силу Егорова теоремы, для любого е > 0 сущест-
существует такой компакт ЕсХ, что \i(X\E) < e, а Р.,
членами к-рого являются сужения я&(жIя функций
a.k{x) на компакте Е, сходится на нем равномерно и
его суммой является s(x)\e — сужение суммы Р. A2)
на рассматриваемом компакте.
Пусть Ьр(Х), 1 < р «+оо,—пространство функ-
функций / : X -> R соответственно с нормой
при 1<р<+оо и с нормой
vrai|/(*)|
р
хеХ
прир=оо. Р. A2) наз. сходящимся в простран-
пространстве Lp(X), если последовательность его частичных
сумм {su(x)} сходится в Lp(X) и ее предел s(x) наз.
суммой Р. A2) в этом пространстве:
.1(х) = ^ак(х) в Lp(X).
Если Р. A2) сходится в Lp(X) и s(x) — его сумма,
то существует подпоследовательность последователь-
последовательности его частичных сумм, к-рая сходится к s(x) почти
всюду на X.
Почленное интегрирование рядов.
Обобщением теоремы о почленном интегрировании рав-
равномерно сходящихся Р. являются следующие теоремы.
Теорема 1. Если существует такая суммируемая
на множестве X функция /, что для всех то=1, 2,. . .
и всех х?Х частичные суммы sn(x) P. A2) удовлетво-
удовлетворяют неравенству
P. A2) сходится почти всюду на X и его сумма равна
s(х), то
~~ ~~ " ак (х) dx. A3)
Теорема 2. Если ak(x)?Lp(X), s(x)?Lp(X),
1 <р < +00, цА' < +оо, и последовательность ча-
частичных сумм {sm(x)} P. A2) слабо сходится на мно-
множестве X к функции s(x) (т.е. для любой функции
b = b(x)?Lg(x), 1/p+ l/g = l, выполняется условие
lim (s—sm, 6)=lim Г [s (ж)—sm (х)] Ь(х) dx--=O),
т-*-Ф m-*-QDJx
то имеет место формула A3).
Можно почленно интегрировать и Р. A2), все члены
к-рых неотрицательны на множестве X. У таких Р.
последовательность их частичных сумм в каждой точке
х?А' возрастает и потому имеет конечный или беско-
бесконечный предел, к-рый наз. значением суммы s(x) рас-
рассматриваемого Р. в этой точке.
Теорема 3. Если члены Р. A2) неотрицательны,
то имеет место формула A3).
В предположениях теоремы 3 обе части формулы A3)
могут обратиться в + оо. Достаточные условия их ко-
конечности даются следующей теоремой.
Теорема 4. Если члены Р. A2) неотрицательны
и интегралы от его частичных сумм sm (x) ограничены в
совокупности:
5sm (x) dx <c, где с — постоянная,
X
т = 1, 2,
то сумма «(ж) Р. A2) является суммируемой функцией.
Почленное дифференцирование
рядов. Пусть R" есть n-мерное арифметическое
евклидово пространство точек х— (xt, х2,- ¦ •> ж«). ау? R,
G — открытое в R" множество, / : G —>¦ R. И пусть
Dx.f — обобщенная производная функции / по пере-
переменной х{, i—i, 2,. . ., п. Если ak(x)?Lp(G),
— фиксировано), 1 <: р <: +оо,
и ряды ^ а & (ж), ~S\DX. ак(х), x?G, сходятся в
Lp (G): s (х) = 2 ak (.г), а (х) =2 Dx. ak И, то функ-
ция s (х) имеет в G обобщенную производную по пере-
переменной х и Dx s(x)—g(z), to есть
Dx, S ak (*) = 2 Dx. ak (x) в L (G).
Среди функциональных Р. особо важную роль играют
степенные ряды, Фурье ряды, Дирихле ряды и вообще
Р., получающиеся при разложении функций по собст-
собственным функциям того или иного оператора. Многие из
перечисленных свойств функциональных Р. обобщаются
на более общие Р., когда их членами являются функ-
функции со значениями в линейных нормированных прост-
пространствах или, более общо, в линейных топологич.
пространствах, а также на кратные функциональные
Р., то есть Р., члены к-рых снабжены мультииндексами:
2аш • ¦ • "/я П-
Теория функциональных рядов дает удобные и весьма
общие методы для изучения функций, поскольку функ-
функции весьма широкого класса могут быть представлены в
определенном смысле в виде суммы нек-рого ряда эле-
элементарных функций. Напр., однозначная аналитич.
функция является в окрестности каждой внутренней
точки из множества своего определения суммой своего
Тейлора ряда; всякая непрерывная на отрезке функ-
функция янляется суммой равномерно сходящегося на этом
отрезке ряда, членами к-рого являются алгебраич.
многочлены; наконец, для всякой измеримой и конечной
почти всюду на отрезке [—-п, л] функции существует
тригономотрич. ряд
сумма к-рого почти всюду совпадает с заданной функ-
функцией.
Разложение функций в Р. применяется в различных
разделах математики: в анализе для исследования функ-
функций, при отыскании решений в виде Р. тех или иных
уравнений, содержащих неизвестные функции, напр.
неопределенных коэффициентов методом, р численных
методах для приближенного вычисления значений
функций и т. п.
Историческая справка. К понятию бесконечных сумм
подошли еще ученые Др. Греции, у них уже встречалась
сумма членов бесконечной геометрич. прогрессии с
положительным знаменателем, меньшим единицы. Как
самостоятельное понятие Р. вошел в математику в
17 в. И. Ньютон (J. Newton) и Г. Лейбниц (G. Leibniz)
систематически использовали Р. для решения как ал-
алгебраических, так и дифференциальных уравнений.
Формальная теория Р. усиленно развивалась в 18 —
19 вв. в работах Я. и И. Бернулли (Jakob iind .Tohann
Bernoulli), Б. Тейлора (В. Taylor), К. Маклорена
(С. Maclaurin), Л. Эйлера (L. Euler), Ж. Д'Аламбера
(J. D'Alembert), Ж. Лагранжа (J. Lagrange) и др.
В этот период использовались как сходящиеся, так и
расходящиеся Р., хотя не было полной ясности в вопро-
вопросе о законности действий над ними. Точная теория Р.
была создана в 19 в. на основе понятия предела в
трудах К. Гаусса (С. Gauss), Б. Больцаио (В. Bolzano),
О. Коши (A. Cauchy), П. Дирихле (P. Dirichlet),
Н. Абеля (N. Abel), К. Веперштрасса (К. Weierstrass),
Б. Римана (В. Riemann) и др.
Лит.: [1] Колмогорова. Н., Фомин С. В., Эле-
Элементы теории функций и функционального анализа, 5 изд.,М.,
1981; [2] Л у з и н Н. Н., Теория функций действительного
переменного, 2 изд., М., 1948; [3] Н и к о л ь с к и И С. М.,
Приближение функций многих переменных и теоремы вложения,
2 изд., М., 1977; 1.4] Харди Г., Расходящиеся ряды, пер. с
англ., М., 1951; [5] Бахвалов Н. С, Численные методы,
2 изд., М., 1975; 161 И л ь и н В. А., И о з н я к Э. Г., Осно-
Основы математического анализа, 3 изд., ч. 1, М., 1971, 2 изд., ч. 2,
М., 1980; [7] К у д р я в ц е в Л. Д., Курс математического ана-
анализа, т. 1—2, М., 1981; [8] Никольский С. М., Курс ма-
математического анализа, 2 изд., т. 1—2, М., 1975; [9] Н е м ы ц-
кийВ., Слудская М., Черкасов А., Курс матема-
математического анализа, 2 изд., т. 1—2, М.— Л., 1944.
Л. Д. Кудрявцев,
САККЕРИ ЧЕТЫРЕХУГОЛЬНИК — четырех-
четырехугольник А В CD, имеющий при вершинах А и В
прямые углы и равные стороны AD и ВС. Рассматри-
Рассматривался Дж. Саккери (G. Saccheri, 1733) при попытках
доказать постулат Евклида о параллельных. Из трех
предположений о величинах углов при вершинах С и
D: либо углы прямые, либо углы тупые, либо острые,
первая гипотеза является утверждением, эквивалент-
эквивалентным постулату Евклида о параллельных; вторая при-
приводит к противоречию с др. аксиомами и постулатами
Евклида. Относительно третьей гипотезы Дж. Саккери
пришел к ошибочному выводу, что она противоречит
др. аксиомам и постулатам Евклида.
Лит.: [1] Каган В, Ф., Основания геометрии, ч. 1,
М.— Л., 1949; [2] П о г о р е л о в А. В., Основания геомет-
геометрии, 3 изд., М., 1968. А. Б. Иванов.
САЛОННАЯ ИГРА — игра с несколькими участни-
участниками, в к-рон исход определяется не только искусством
играющих, но и случайными факторами (раскладами
карт, выпадениями игральных костей и т. п.). Иссле-
Исследование Си. (преимущественно карточных) занимает
значительное место в игр теории. С. и., с одной сторо-
стороны, являются неисчерпаемым источником интересных
с математич. точки зрения игровых моделей; а с дру-
другой — сами являются моделями более серьезных конф-
конфликтов — военных, экономических и т. п. Покер, пер-
первая модель к-рого исследовалась Дж. Нейманом в
1928 (см. [1]), сыграл при возникновении теории игр
роль, аналогичную роли игры в кости в возникновении
теории вероятностей. Позднее были построены и ре'
шены многие частные модели игр типа покера, а в сер.
50-х гг. С. Карлином (S. Karliii) и Р. Рестрепо (R. Rest-
геро) были заложены основы общей теории антагонисти-
антагонистических игр типа «покер». В их модели игрок I (II) знает
свою карту % (соответственно ц) — реализацию случай-
случайной величины, имеющей распределение F (|) [соответ-
[соответственно б(т])]. Стратегии игроков I и II представляют
собой соответственно векторы <р (!) и 1|)(п), а функция
выигрыша имеет вид
К (Ф, \р) = J J Р [g, n, Ф (g), ф (п)] dF (I) dG (n).
С. Карлин и Р. Рестрепо нашли достаточно эффектив-
эффективные методы решения подобных игр (см. [2]).
Довольно много исследований было посвящено бри-
бриджу. Ввиду того что в бридже два партнера представ-
представляют собой фактически одного игрока, он является
примером игры без полной памяти.
Лит.: [1] Нейман Д ж., в сб.: Матричные игры, М.,
1961, с. 173—204; [2] Карлин С, Математические методы
в теории игр, программировании и экономике, пер. с англ., М.,
1964; [3] Т h о m p s о n G. L., в кн.: Contributions to the the-
theory of games, v. 2, Princeton, 1953, p. 267—77.
В. Н. Доманский.
САМОИНЪЕКТИВНОЕ КОЛЬЦО левое — коль-
кольцо, инъективное как левый модуль над собой. Симмет-
Симметричным образом определяется правое С. к. Клас-
Классически полупростые кольца и все кольца вычетов
суть С. к. Если R — С. к. с радикалом Джекобсона
/, то факторкольцо RlJ регулярно в смысле Неймана
(см. Регулярное кольцо). Регулярное С. к. непрерывно.
Всякое счетное С. к. квазифробениусово. Левое С. к.
может не быть правым С. к. Кольцо матриц над С. к.
и полное кольцо линейных преобразований векторного
пространства над телом самоинъективны. Кольца
эндоморфизмов всех свободных левых i?-модулей явля-
являются С. к. тогда и только тогда, когда R квазифробе-
ниусово. Если М — кообразующий категории левых
Я-модулей, то End^M есть С. к. Если сингулярный
идеал кольца R равен нулю, то его инъективная обо-
оболочка естественным образом превращается в С. к.
Групповое кольцо RG самоинъективно слева тогда и
только тогда, когда R есть С. к., а группа G конечна.
Прямое произведение самоинъективных колец самоинъ-
самоинъективно. Кольцо R изоморфно прямому произведению
полных колец линейных преобразований над телами в
том и только в том случае, когда R — левое С. к. без
нилъпотентных идеалов, каждый ненулевой левый идеал
к-рого содержит минимальный левый идеал.
Лит.; [1] Итоги науки и техники. Алгебра. Топология. Гео-
Геометрия, т. 14, М., 1976, с. 57—190; [2] Фей с К., Алгебра:
кольца, модули и категории, пер. с англ., т. 1—2, М., 1977—79;
C] Lawrence J., «Prop,. Amer. Math. Soc», 1977, v. 05,
,14» 2, p. 217 — 20. Л. А. Скорняков.
САМОПЕРЕСЕЧЕНИЯ ТОЧКА — одна из особых
точек кривой или поверхности. См., напр., Двойная
точка.
САМОПЕРИМЕТР — длина 2ns центрально-сим-
центрально-симметричной замкнутой выпуклой кривой S на плоскости,
измеренная в той метрике Минковского, для к-рой са-
сама S играет роль единичной окружности. Всегда 3<
<:яз <:4 (см. [1]). При обобщении на несимметричный
случай С. приписывается направленной кривой S и за-
зависит от выбора начала внутри S (см. [2], [3]). Рассмот-
Рассмотрен случай звездной S (см. [4]). Существуют различные
обобщения С. для единичной сферы S в нормированном
пространстве размерности, большей двух (см. [51, [6]).
Лит.: [1] Решетник Ю. Г., «Успехи матем. наук»,
1933, т. 8, в. 6, с. 125—26; [2] Сорокин В. А., «Уч. зап.
Моск. гос. нед. ин-та», 19155, № 243, с. 160—85; [3] С h a k е-
г i a n G. D., Т а 1 1 е у W. К., «Arch, math.», 1909, v. 20,
№ 4, p. 431—43; [4] G о \ ?| b S., «Colloq. math.», 1966, v. 15,
M 1, p. 141—44; [5] SchafferJ. J.,«Math. Ann.», 1971,
Bd 190, № 3, S. 242—47; 16] P e t t у С. М. «Geom. dedic»,
1974, v. 3, № 1, p. 77—97. В. А. Залгаллер.
САМОПРИКОСНОВЕНИЯ ТОЧКА — одна из осо-
особых точек кривой или поверхности. См., напр., Двойная
точка.
САМОСОПРЯЖЕННОЕ ДИФФЕРЕНЦИАЛЬНОЕ
УРАВНЕНИЕ — линейное обыкновенное дифферен-
дифференциальное уравнение 1(у) — 0, совпадающее с сопряже>1-
иым дифференциальным уравнением I* (у)~0. Здесь
I* (у) = (-1)" (ад)<«> + . . . + (-1)»-*
ГДР
yW^-dvy/dtv, у {¦)?€" (I), afc (•)€?>"*(/),
«о @ #0, *?/;
СтA)—пространство т раз непрерывно дифференцируе-
дифференцируемых комплекснозначных функций на /-— (а, р1); черта
означает операцию комплексного сопряжения.
Левая часть всякого С. д. у. 1{у)~0 есть сумма вы-
выражений вида
где pm(t), qm{t) — действительнозначные достаточно
гладкие функции, г'2=—1. С. д. у. с действительными
коэффициентами — обязательно четного порядка и
имеет вид
(рвуШ)) Ш+ .. . +(ркуШ-к)) «я-*>_|_.. . +рту = 0
(см. [1] - [3]).
Линейная система дифференциальных уравнений
Цх)=0, L(x)^x+A (t)x, t?I,
с непрерывной комплекснозначной (пХге)-матрицей
A (t) наз. самосопряженной, если A (t)=
= —A* (t), где A* (t)—эрмитово сопряженная матри-
матрица к матрице A {t) (см. [1], [4]). Это определение не
согласовано с определением С. д. у. Напр., система
эквивалентная С. д. у.
— самосопряженная только в том случае, если
Краевая задача
Цу)^0. t?\ = [to, *,], A)
Uk(y)=0, к=1, ..., n, B)
где Uъ : Сш) (А) —»- R1 — линейные и линейно неза-
независимые функционалы, описывающие краевые условия,
наз. самосопряженной, если она совпадает со
своей сопряженной краевой задачей, то есть A) —
С. д. у., a Uk(y)=Uk{y) для всех г/(-)€с"(д) и всех
к=\,. . ., п (см. [1] — [3], [5]). Если A), B) — самосо-
самосопряженная краевая задача, то справедливо равенство
(см. Грина формулы)
для любой пары функций у(-), %(')?С"(А), удовлет-
удовлетворяющей краевым условиям B).
Все собственные значения самосопряженной задачи
l(y) = X,j, Uk(y)=O, к = 1, ..., п,
действительны, а собственные функции ф,, ф.,, отвечаю-
отвечающие различным собственным значениям Л17 Х2, ортого-
ортогоЛинейная краевая задача
L(x) = 'x-\-A(t)x = 0, U (x) = 0, t^A, C)
где A (t) — непрерывная комплекснозначная пХп мат-
матрица, U есть «-вектор-функционал на пространстве
Сп (А) непрерывных комплекснозначных функций х :
Д —v R", наз. самосопряженной, если она
совпадает со своей сопряженной краевой задачей,
L*(x)=0, U*(x) = Q, t^A,
т. е.
L (х) = — L* (х), U (х) = U* (х)
для всех >с( •)€ Сп(А). Самосопряженная краевая задача
обладает свойствами, аналогичными свойствам задачи
A), B) (см. 14]).
Понятия С. д. у. и самосопряженной краевой задачи
тесно связаны с понятием самосопряженного оператора
[6]. С. д. у. и самосопряженная краевая задача опре-
определяются также для линейного уравнения с частными
производными (см. [5], [7]).
Лит.: [1] Камке Э., Справочник по обыкновенным диф-
дифференциальный уравнениям, пер. о нем., 5 изд., М., 1У76; [21
Н а й м а р к М. А., Линейные дифференциальные операторы,
2 изд., М., 1969; [31 К о д д и н г г о н Э. А., Л е в и н с о н Н.,
Теория обыкновенных дифференциальных уравнений, пер. с
англ., М., 1958;[4] Владимиров В. С, Уравнения мате-
математической физики, 4 изд., М., 1981; [5] X а р т м а н Ф., Обы-
Обыкновенные дифференциальные уравнения, пер. с англ., М., 1970;
[6] Д а н ф о р д Н., Ш в а р ц Д ж. Т., Линейные операторы.
Спектральная теория. Самосопряженные операторы в гильбер-
гильбертовом пространстве, пер. с англ., ч. 2, М., 1966; [7] М и х а й-
л о в В. П., Дифференциальные уравнения в частных производ-
производных, М., 1976. Е. Л. Тонкое.
САМОСОПРЯЖЕННОЕ ЛИНЕЙНОЕ ПРЕОБРАЗО-
ПРЕОБРАЗОВАНИЕ — линейное преобразование евклидова или
унитарного пространства, совпадающее со своим
сопряженным линейным преобразованием. В евклидовом
пространстве С. л. п. наз. также симметричес-
симметрически м, а в унитарном пространстве — эрмитовым.
Необходимое и достаточное условие самосопряжен
ности линейного преобразования конечномерного про
странства состоит в том, что его матрица А в произволъ
ном ортонормированием базисе совпадает с сопряжен
ной матрицей А*, т. е. является симметрич. матрицей
(в евклидовом случае) или эрмитовой матрицей (в уни-
унитарном случае). Собственные значения С. л. п. действи-
действительны (даже в унитарном случае), а собственные
векторы, отвечающие различным собственным значе-
значениям, ортогональны. Линейное преобразование конеч-
конечномерного пространства L является самосопряженным
тогда и только тогда, когда в L существует ортонорми-
рованный базис, состоящий из собственных векторов,
и в :>том базисе записывается действительной диа-
диагональной матрицей.
С. л. п. А наз. неотрицательным (или по
ложительно полуоцределенным),
если (Ах, х) ^ 0 для любого вектора ж,иположи-
тельно определенным, если (Ах, х) > 0
для любого вектора х ф 0. Для неотрицательности
(положительной определенности) нек-рого С. л. п. в
конечномерном пространство необходимо и достаточно,
чтобы все его собственные значения были неотрицатель-
неотрицательны (соответственно положительны) или чтобы соответ-
соответствующая ему матрица была положительно полуопре-
полуопределенной (соответственно положительно определен-
определенной). В этом случае существует единственное неотрица-
неотрицательное С. л. и. В, удовлетворяющее условию В2=
= А — квадратный корень из С. л. п. А.
САМОСОПРЯЖЕННЫЙ ОПЕРАТОР, эр м иТо"в
о п е р а т о р,— линейный оператор А, определенный
на линейном всюду плотнодг множестве D (А) гильберто-
гильбертова пространства И и совпадающий со своим сопряжен-
сопряженным оператором А, т.е. такой, что D (A)=D (А*) и
<Ах, уУ-^ix, Ау> (*)
для любых j-, y?D(A). Всякий С. о. замкнут и не до-
допускает расширения с сохранением равенства (*) на
более широкое, чем D(A), линейное многообразие, в
силу чего С. о. наз. также гипер максима л ъ -
н ы м. Поэтому если А ограниченный С. о., то он опре-
определен на всем пространстве Н.
Каждый С. о. однозначно определяет разложение еди-
единицы Fi, —оо < А,< оо; имеет место интегральное пред-
представление
Ах=.\т Id Fix,
О -»
где интеграл понимается как сильный предел интегра-
интегральных сумм, для каждого x?D(A) и
D(A)=lx\['B ХЧ <Eix, .с) < оо ) .
Спектр Со. А не пуст и лежит на действительной
оси. Квадратичная форма К (А)=<Аа-, аг>, порожден-
порожденная С. о. А, действительна, что позволяет ввести поня-
понятие положительного оператора.
С помощью Со. описываются многие краевые задачи
математич. физики.
Лит.: [1] Л ю с т е р н и к Л. А., Соболев В. И.,
Элементы функционального анализа, 2 изд., М., 1965; [2] А х и-
езерН. И., ГлазманИ. М., Теория линейных операто-
операторов в гильбертовом пространстве, М., 1966; [3] Рисе Ф.,
Сёкефальв и-Н а д ь Б., Лекции по функциональному
анализу, пер. с франц., 2 изд., М., 1979. JB. И. Соболев.
САРДА ТЕОРЕМА: пусть / : М-*- N — отображение
класса С многообразий М и N размерности т и п
соответственно; если г > max @, т—п), то критические
значения f образуют множество меры нуль. Множество
же регулярных значений оказывается массивным и
всюду плотным. Установлена А. Сардом [1].
Лит.: [1] Sard A., «Bull. Amer. Math, Soc», 1942, v. 48,
p. 883—90. M. И. Войцеховский.
СБАЛАНСИРОВАННОЕ КОЛЬЦО левое (пра-
(правое) — кольцо, над к-рым все левые (правые) модули
сбалансированы. Кольцо сбалансировано слева тогда
и только тогда, когда все его факторкольца суть QF-1-
кольца, т. е. все точные левые модули над ними
сбалансированы. В частности, кольцо сбалансировано,
если все эти факторкольца квазифробениусовы. Всякое
С. к. разлагается в прямую сумму однорядного кольца
и колец матриц над локальными кольцами специального
типа. Любое С. к. полусовершенно. Нётерово С. к.
оказывается артиновым.
Лит.: [1] Итоги науки и техники. Алгебра. Топология.
Геометрия, т. 19, М., 1981, с. 31—134; [2] Ф е й с К., Алгебра:
кольца, модули и категории, пер. с англ., т. 1—2, М., 1977—79.
Л. А. Скорняков.
СБАЛАНСИРОВАННЫЙ МОДУЛЬ — модуль
М такой, что естественный кольцевой гомоморфизм
ц> : R -*¦ EndKnd MM, в случае правого модуля оп-
определяемый равенством ц>(г)(т) = тг для любых r?R
и т?М, сюръективен. Модуль Р над кольцом R ока-
оказывается образующим категории Я-модулей тогда и
только тогда, когда Р есть С. м. как Я-модуль, проек-
тивен и конечно порожден как End#.P-модуль.
Лит.: [1] Ф с й с К., Алгебра: кольца, модули и категории,
пер. с англ. т. 1 — 2, М., 1977 — 79. Л. А. Скорняков.
СВЕРТКА ф у н к ц и л / (х) и g (х), принадле-
принадлежащих L (— оо, оо),— функция h(x), определяемая
равенство»!
h(x)=\a> f(x~y)g(y)dy=\w f(y)g(x-y)dy
и обозначаемая символом (f*g)(x). Функция f*g опре-
определена почти всюду и также принадлежит L(—ос, оо).
Свертка обладает основными свойствами операции ум-
умножения, а именно: f*g=g*f,
для любых трех функций из L (—оо, оо). Поэтому
L (— оо, оо) с обычным сложением и умножением на
число, с операцией С. в качестве умножения элементов
из L(—оо, оо) и с нормой
превращается в банахову алгебру (при такой норме
№*g\\ <: 11/11 ¦ Ы)- Если >[/] — преобразование Фурье
функции /, то
F [hg] = V2n F [f] F (g)
и это используется при решении ряда прикладных задач.
Так, если задача сведена к интегральному уравнению
вида
—оо.оо),
sup | F [К] (х)\^~,
г Л
то в предположении, что f(x)dL(— оо, оо), применяя к
уравнению (*) преобразование Фурье, получают
откуда
1/1 1-1 2 л F [К] '
и обратное преобразование Фурье приводит к решению
уравнения (*).
Свойства С. функций находят важные приложения в
теории вероятностей. Если f(x) и g(x) являются плот-
плотностями вероятности Независимых случайных величин
X и Y, то С. (f*g)z есть плотность вероятности слу-
случайной величины X-\-Y.
Операция С. распространяется на обобщенные функ-
функции. Если / и g — обобщенные функции, из к-рых по
крайней мере одна имеет компактный носитель, и ф (х)
принадлежит пространству основных функций, то f*g
определяется равенством
<f*g, 4>> = </
где f(x)Xg(y) — прямое произведение обобщенных
функций / и g, т. е. функционал в пространстве основ-
основных функций двух независимых переменных такой, что
def
</WXfW, u(x, ?/)> = </ (х), <g{y), u(x, ;/)»
для любой финитной бесконечно дифференцируемой
функции и(х, у).
С. обобщенных функций также обладает свойством
коммутативности, линейности по каждому аргументу,
а если по крайней мере две из трех обобщенных функций
имеют компактные носители, то и свойством ассоциатив-
ассоциативности. Справедливы равенства:
где D оператор дифференцирования и а — любой
мультииндекс, (Da6)*f=Daf, в частности б*/=/, где
6 — дельта-функция, и если/,,, п=\, 2,. . .,— обобщён-
обобщённые функции такие, что /„ ->¦ /0 и существует компакт
то
fn*g -> fo*8-
Наконец, если g — финитная обобщенная функция и
/ — обобщенная функция медленного роста, то к /*g
применимо преобразование Фурье и снова
Flf*g]=V~2~nF[f]F\g\.
С. обобщенных функций широко используется при ре-
решении краевых задач для уравнений с частными произ-
производными. Так, интеграл Пуассона, написанный в виде
U(x, *)=(i(*).ri7=e-*Vlt,
дает решение уравнения теплопроводности для беско-
бесконочного стержня, когда начальная температура и. (х)
может быть но только обычной, но и обобщенной функ-
функцией.
Понятие С. как обычных, так и обобщенных функций
естественным образом переносится на случай функций
многих независимых переменных: надо в предыдущем
считать х, у не действительными числами, а векторами
из R".
Лит.: [1] В л а д и м и р о в В. С, Уравнения математичес-
математической физики, 4 изд., М., 1Я81; [2] Г с л ъ ф а н д И. М., III и от о в
Г. Е., Обобщенные функции и действия над ними, М., 1958;
[3] Титчмарш Е., Введение в теорию интегралов Фурье,
пер. с англ.. М.— Л. 1948. В. И. Соболев.
СВЕРТКА ТЕНЗОРА — операция тензорной алгебры,
ставящая в соответствие тензору а] " р, р ^ 1,
q > 1, тензор н ¦¦ lq
bt....i к.-*, +а"'-1р ++<»;'• ¦•;''
(здесь свертка производится по паре индексов ilt jq).
Аналогично определяется С. т. по любой паре верхнего
и нижнего индексов, р-кратная С. т., р раз ковариант-
ного и р раз.контравариантного, является инвариантом.
Так, С. т. а) есть инвариант а\, называемый следом
тензора Sp(aj), или tr а). Сверткой произведения
двух тензоров наз. свертка их произведения по верх-
верхнему индексу одного сомножителя и нижнему индексу
ДРУГОГО. А. Б. Иванов.
СВЕРТКИ ПРЕОБРАЗОВАНИЕ — интегральное пре-
преобразование вида
F(x)=[<* GLx-t)f(t)dt.
J - сю
- сю
Функция G(x) наз. ядром С. п. Для определенных
типов ядер G после соответствующих замен перемен-
переменных С. п. переходит в одностороннее Лапласа преобра-
преобразование, Стилтьеса преобразование, Мейера преобра-
преобразование. Обращение С. п. осуществляется линейными
дифференциальными операторами бесконечного поряд-
порядка, инвариантными относительно сдвига.
С. п. введено также для нек-рых классов обобщенных
функций (см. [2]).
Лит.: [1] X и р ш м а н И. И., У и д д е р Д. В., Преоб-
Преобразования типа свертки, пер. с англ., М., 1958; B] Б р ы ч-
к о в Ю. А., II р у д н и к о в А. П., Интегральные преобра-
преобразования обобщенных функций, М., 1Я77.
Ю. А. Брычков, А. П. Прудников.
СВЕРХРАЗРЕШИМАЯ ГРУППА — группа G, об-
обладающая конечным инвариантным рядом подгрупп
в к-ром каждая факторгруппа Л,_[/Л,- циклична.
Всякая С. г. является полициклической группой. Под-
Подгруппы и факторгруппы С. г. также сверхразрешимы,
коммутант С. г. нильпотентен. Конечная группа явля-
является С. г. тогда и только тогда, когда все ее максималь-
максимальные подгруппы имеют простые ийдексы (теорема
X у п п е р т а). н. н. Вильяме.
СВЕРХРЕЛАКСАЦИИ МЕТОД, последова-
последовательной верхней релаксации м е-
т о д,— метод решения систем алгебраич. уравнений.
См. Релаксации метод.
СВЕРХСХОДИМОСТЬ — сходимость нек-рой подпос-
подпоследовательности частных сумм ряда в области, боль-
большей, чем область сходимости ряда. Имеют место сле-
следующие теоремы о сверхсходимости:
1) если в степенном ряде
с радиусом сходимости R, 0 < R < оо, показатели
Хп таковы, что для бесконечного множества значений
пу индекса п
где 9 — фиксированное положительное число, то по-
последовательность частных сумм порядков rev
сходится равномерно в достаточно малой окрестности
каждой точки z0 окружности \z\ = R, в к-poii сумма
ряда /(г) регулярна;
2) если
то последовательность {Snv(z)} сходится равномерно в
любой замкнутой ограниченной части области суще-
существования функции /(г).
Имеет место и следующая теорема (обратная первой
теореме): если у степенного ряда
с радиусом сходимости Л, 0 < Л < оо, имеется под-
подпоследовательность частных сумм, к-рая равномерно
сходится в нек-рой окрестности точки г0, |zo| ^ Л,
то данный степенной ряд может быть представлен
суммой ряда с радиусом сходимости, большим R , и
лакунарного степенного ряда
2Г=1 <*»**¦"• %nk+1-Kk > exBft, *=i, 2, ...; e > о.
Первые теоремы верны и для многих других рядов,
в частности для рядов Дирихле.
Лит.: [1] Б и Сербах Л., Аналитическое продолжение,
пер. с нем., М., 19В7; [2] Г о л у з и н Г. М., Геометрическая
теория функции комплексного неременного, 2 изд., М., 1966;
[3] Леонтьев А. Ф., Ряды экспонент, М., 197й.
А. Ф. Леонтьев.
СВЕРХЭФФЕКТИВНАЯ ОЦЕНКА, с у п е р э ф-
фективная оценка, — общепринятое сокра-
сокращение термина «сверхэффективная (суперэффективная)
последовательность оценок», употребляемого по отно-
отношению к состоятельной последовательности асимпто-
асимптотически нормальных оценок неизвестного параметра, к-
рая является более эффективной, чем состоятельная по-
последовательность оценок максимального правдоподобия.
Пусть Хх, Х2,. . ., Хп — независимые одинаково
распределенные случайные величины, принимающие
значения в выборочном пространстве (ЗЕ, ,53, Ре),
9? в, и пусть семейство распределений {Pq} таково,
что существует состоятельная последовательность
{§„} оценок 9„=6,г (Xi,. . ., Хп) максимального прав-
правдоподобия параметра 9. Далее, пусть {Тп} — последо-
последовательность асимптотически нормальных оценок Тп=
= Т,1(Х1. . ., Хп) параметра 6. Если при всех 6^0
где / @) — информационное количество Фишера,
и, кроме того, хотя бы в одной точке 6*, 6*?в, вы-
выполняется строгое неравенство
то такая последовательность оценок {Т} наз. сверх-
эффективной (суперэффективной)
относительно квадратичной функции потерь, а точки
6*, в к-рых выполняется (*), наз. точками суперэф-
суперэффективности.
Лит.: [1] Ибрагимов И. А., Хасьминскйй
Р. 3., Асимптотическая теория оценивания, М., 1979; [2]
Шметтерер Л. Введение в математическую статистику, пер.
с нем., М., 197В; [3] L e Cam L., «Univ. California .Publ.
Stat», 1953, v. 1, p. 277 — 330. M. С. Никулин,.
СВОБОДНАЯ АБЕЛЕВА ГРУППА — группа, сво-
свободная в многообразии всех абелевых групп (см. Сво-
Свободная алгебра). Прямые суммы (в конечном или бос-
конечном числе) бесконечных циклич. групп и только
они являются свободными группами в классе аиелевых
групп. При этом совокупность образующих элементов
всех циклич. прямых слагаемых служит системой
свободных образующих (называемой также базой)
С. а. г. Не всякая максимальная линейно независимая
система элементов С. а. г. служит для нее базой. С. а. г.
изоморфны тогда и только тогда, когда их базы равно-
мощны. Мощность базы С. а. г. совпадает с рангом
Прюфера этой группы. Всякая подгруппа С. а. г., от-
отличная от нулевой, сама свободна. Абелева группа
свободна тогда и только тогда, когда она обладает
возрастающим рядом подгрупп (см. Подгрупп ряд),
каждый фактор к-рого изоморфен бесконечной циклич.
группе.
Лит.: [1] К у р о ш А. Г., Теория групп, 3 изд., М., 1967;
[2] Каргаполов М. И., Мерзляков Ю. И., Осно-
Основы теории групп, 3 изд., М. 1982. О. А. Иванова.
СВОБОДНАЯ АЛГЕБРА класса Й универсаль-
универсальных алгебр — алгебра F из класса Й, обладающая
свободной порождающей системой
(или базой) X, т. е. таким множеством порождаю-
порождающих X, что всякое отображение множества X в любую
алгебру А из й продолжается до гомоморфизма алгеб-
алгебры F в А (ср. Свободная алгебраическая система). С. а.
обладает любой непустой класс алгебр, замкнутый
относительно подалгебр и прямых произведений и
содержащий неодноэлементные алгебры. В частности,
С. а. всегда существует в нетривиальных многообразиях
и квазимногообразиях универсальных алгебр (см.
Универсальных алгебр многообразие, Алгебраических
систем квазимногообразие). С. а. класса, состоящего из
всех алгебр данной сигнатуры Q, наз. абсолютно
свободной. Алгебра А сигнатуры Q является С. а.
нек-рого класса универсальных алгебр сигнатуры Q
тогда и только тогда, когда Л внутренне сво-
свободна, т. е. обладает таким порождающим множест-
множеством X, что всякое отображение X в А продолжается
до эндоморфизма алгебры А. Если С. а. обладает
бесконечной: базой, то все ее базы имеют одну и ту же
мощность (см. Свободная абелева группа, Свободная
алгебра над ассоциативно-коммутативным кольцом,
Свободная ассоциативная алгебра, Свободная булева
алгебра, Свободная группа, Свободная полугруппа, Сво-
Свободная решетка, Свободный группоид, Свободный модуль,
а также Свободное произведение). Ясно, что каждый эле-
элемент С. а. с базой X записывается как слово в алфавите
X в сигнатуре рассматриваемого класса. Естествен воп-
вопрос: когда различные слова равны как элементы С. а.?
В нек-рых случаях ответ почти тривиален (полугруппы,
кольца, группы, ассоциативные алгебры), в других —
достаточно сложен (алгебры Ли, решетки, булевы ал-
алгебры), а иногда и не поддается решению (альтернатив-
(альтернативные Кольца). Л. А. Скорняков.
СВОБОДНАЯ АЛГЕБРА над ассоциативно-комму-
ассоциативно-коммутативным кольцом Ф — свободная алгебра многообра-
многообразия алгебр над Ф (см. Кольца и алгебры). Элементами
такой С. а. со свободной порождающей системой Л'
служат линейные комбинации элементов свободного
группоида со свободной порождающей системой X с
коэффициентами из Ф. Другими словами, эта С. а. яв-
является свободным модулем над Ф с вышеупомянутым
группоидом в качестве базы. Если Ф — кольцо целых
чисел, то С. а. над Ф наз. свободным кольцом
(ср. Свободная ассоциативная алгебра). Ненулевая
подалгебра С. а. над полем Ф сама является С. а.
Л. А. Скорняков.
СВОБОДНАЯ АЛГЕБРАИЧЕСКАЯ СИСТЕМА —
свободный объект в нек-ром классе алгебраич. систем.
Пусть й — непустой класс алгебраич. систем (см.
Алгебраических систем класс). Система F наз. свобод-
свободной в к л а с с е М, или М-с вободной, если она
принадлежит классу Й и обладает таким множеством
X порождающих, что всякое отображение ф„:Х-^Л
множества X в любую систему А из Й продолжаемо до
гомоморфизма ц> : F —у А . В этом случае говорят также,
что ^свободна над X в классе Й'. Множество
порождающих X с таким свойством наз. Й'-е в о б о д -
н ы м базисом с и с т е м ы F, а его мощность —
рангом системы/'. й'-свободные системы одного
и того же ранга изоморфны. Если класс ,ff обладает
свободной системой ранга г, то всякая система из Я,
допускающая порождающее множество мощности <:г,
является ее гомоморфным образом. Я-свободный базис
X й-свободной системы является и ее минимальным
порождающим множеством, поэтому если класс Я обла-
обладает изоморфными свободными системами F и F' раз-
различных рангов г и г', то оба кардинала гиг' конечны.
Класс алгебраич. систем наз. тривиальным,
или вырожденным, если в каждой его системе
истинно тождество х~у, т.е. все его системы одноэле-
одноэлементны. В противном случае класс наз. нетриви-
нетривиальны м, или невырожденным. Во всяком
невырожденном квазимногообразии (многообразии) ал-
алгебраич. систем (см. Алгебраических систем квазимно-
квазимногообразие, Алгебраических систем многообразие) су-
существует С. а. с. любого ранга. Всякий вырожденный
класс алгебраич. систем обладает только свободной
системой ранга 1.
Пусть класс Я обладает свободными системами
Fi и Fk конечных рангов I и к соответственно и к < I.
Изоморфизм Ff^Ft имеет место тогда и только тогда,
когда существуют такие термы
si (xii •-•> xk)-> i = l, •••, I,
t; ix\, ..., X/), } = 1, ..., к,
в сигнатуре класса Я, что в классе Я истинны тожде-
тождества
Si" (^1 (*^ 1 '••) *^/)т ***) ^ k (*^1 t * * * J ^l)) ~~= ^ I J
где i=l,. . ., I, /=1,. . ., к. Если же класс Ж содержит
конечную систему А мощности ^2, то Й-свободные
системы различных рангов не изоморфны. В частности,
во всех многообразиях групп, полугрупп, решеток,
ассоциативных колец свободные системы различных
рангов не изоморфны. С другой стороны, в нек-рых
многообразиях модулей (см. Свободный модуль) все сво-
свободные модули конечного ранга изоморфны.
Существуют также многообразия алгебраич. систем
конечного тина (см. Алгебраическая система), в к-рых
все С. а. с. конечных рангов изоморфны между собой;
напр., многообразие 1U, 2 алгебр <Л, q>lt ф2, ю> типа
<1, 1, 2>, определяемое тождествами
«Pi (ш (xi, x2)) = xt, i = l, 2,
w(<Pi("t), Фг (х))=х.
Доказано (см. [3]), что в многообразиях %т,„ A<
<т < п) алгебр <Л, (plt. . ., ф„, coj,. . ., com> с
m-арными операциями ц>х,. . ., ср„ и n-арными опера-
операциями сох,. . ., соот, определяемых тождествами
ф,- (<»i (-ci, ¦••,*„), ...,ыт(х1, ...,xn)) = xh
ю/(ф1(а;1, ...,хт), ...,<р„(хи ..., xm)) = xj,
i=i, .. ., re, /—1, .. ., т,
при фиксированных т и п свободные алгебры конечных
рангов к ф I изоморфны тогда и только тогда, когда
к ss I (mod (п — то)), к^т, l^rn.
Существуют универсальные классы, не имеющие сво-
свободных систем. Примером такого класса может служить
класс групп, определяемый универсальными формулами
(х2 = 1) v (a^ = l), xy = yx
(кванторы опущены). Универсальный класс 11, обла-
обладающий свободной системой любого конечного ранга,
имеет свободные системы любых рангов.
Пусть 2 — совместное множество универсальных
формул G(xl,. . ., х„) вида
V ... V "\Gp V Gp+1 V ... V G
q,
где (?!,. . ., Gq — атомные формулы сигнатуры Q. Пусть
ngG = Gi& ... &Gp.
Говорят, что 2 обладает r-п одстановочным
свойством (г ^ 1), если для любой формулы G(x1,. . .,
.г„) из 2 и любых термов
tt (хи .... я,), ..., tn(xu . .., .г,)
от г переменных ,rlf. . ., ?,- верно утверждение:
В невырожденном универсальном классе [2], опреде-
определяемом множеством универсальных формул 2, свобод-
свободная система г;онечного ранга г ^ 1 существует тогда и
только тогда, когда S обладает r-подстановочным свой-
свойством [4]. В частности, если все формулы из 2 несокра-
несократимы и 2 содержит позитивную формулу
(V*!) ... (V*r) Gi V ... V Cq
с числом дизъюнктных членов q ^ 2, то универсальный
класс [2] не имеет свободных систем ранга п^-г.
Напр., класс линейно упорядоченных групп в сигнатуре
«;, •, -1> не имеет С. а. с. ранга г > 2.
Лит.: [1] М а л ь ц е в А. И., Алгебраические системы,
М., 1970; [2] J б п в в о п В. Tarski A., «Math. Scand.»,
19fil, v. Я, p. 95-101; [3] SwierczkowskiS., «Fund.
Math.», 1961, v. 50, Ml, p. 35—44; 14] GiStur G., «Math.
Nachr.», 196K, lid Уй Н. 3/4, S. 135—40. Д. М. Смирнов.
СВОБОДНАЯ АССОЦИАТИВНАЯ АЛГЕБРА — ал-
алгебра к < X > многочленов (со свободными членами)
над полем к от некоммутирующих переменных X. С в о й-
ство универсальности определяет алгебру
к < X > единственным с точностью до изоморфизма
образом: существует отображение i : X ->- к < X >
такое, что любое отображение X в нек-рую ассоциатив-
ассоциативную алгебру А с единицей над к можно единственным
образом пропустить через отображение i. Основные
свойства алгебры к < X > :
1) алгебра к < X > вложима в тело (теорема
М а л ь ц е в а — II е й м а н а);
2) алгебра к < X > обладает слабым алгоритмом
деления, т. е. из соотношения
max,- {rf („,-) + «* F,)},
где а,-, ft,-^ft<X>, все я,-, 1<1«?п, не равны нулю,
й(в]) <:. . .<^d(an), всегда следует, что существуют
целое число г, 1 < г < ге, и элементы clt. . ,,cr_x такие,
и d (a,-) + d (с,-) < d (ar), 1 < i < r — 1
(здесь d(a) — обычная степень многочлена a
d@)=-oo);
3) алгебра /с < X > является левым (правым) кольцом
свободных идеалов (т. е. любой левый (правый) идеал
алгебры к < X > является свободным модулем одноз-
однозначно определенного ранга);
4) централизатор любого нескалярного элемента ал-
алгебры к < X > (т. е. множество элементов, перестановоч-
перестановочных с данным) изоморфен алгебре многочленов над к
от одного переменного (теорема Бергмана).
Лит.: [1] Кон П., Универсальная алгебра, пер. с англ.,
М., 1968; [2] его же, Свободные кольца и их связи, пер. с
англ., М., 1975. Л. А. Бопутъ.
СВОБОДНАЯ БУЛЕВА АЛГЕБРА — булева алгеб-
алгебра, обладающая такой системой образующих, что вся-
всякое отображение этой системы в какую-либо булеву
алгебру допускает продолжение до гомоморфизма.
Любая булева алгебра изоморфна факторалгебре нек-
некрой С. б. а.
Для любого кардинального числа а существует един-
единственная с точностью до изоморфизма С. б. а. с а обра-
образующими. Бе стоуновский бикомпакт есть топологич.
произведение а простых двоеточий — двоичный дискон-
дисконтинуум.
Конечная булева алгебра свободна тогда и только
тогда, когда число ее элементов имеет вид 22"; здесь
п — число образующих. Такая С. б. а. реализуется в
виде алгебры булевых функций от п переменных. Счет-
Счетная С. б. а. изоморфна алгебре открыто-замкнутых под-
подмножеств канторова множества. Всякое множество
попарно дизъюнктных элементов Сб. а. конечно или
счетно.
Бесконечная С. б. а. не может быть полной. В то же
время мощность любой бесконечной полной булевой ал-
алгебры есть верхняя грань мощностей ее свободных под-
подалгебр (см. [5]).
Лит.: [1] С и к о р с к и й Р., Булевы алгебры, пер. с англ.,
М., 1969; [2] В л а д и м и р о в Д. А., Булевы алгебры, М.,
1969; [3] Н а 1 m о s Р. В., Lectures on Boolean algebras, Pri-
Princeton — [а.о.], 1963; [4] Биркгофф Г., Теория структур,
пер. с англ., М., 1952- [5] К и с л я к о в С. В., «Сиб. матем.
ж.», 1973 т. 14, Л"! 3, с. 569—81. Д. А. Владимиров.
СВОБОДНАЯ ГРУППА — группа F с системой X
порождающих элементов такая, что любое отображение
множества X в любую группу G продолжается до гомо-
гомоморфизма F в С Такая система X наз. системой
свободных порождающих; ее мощность
наз. рангом свободной группы F. Мно-
Множество X наз. также алфавитом. Элементы из F
представляют собой слова в алфавите X, т. е. выраже-
выражения вида
где хп?Х, еу= ±1 при всех ;, а также пустое слово.
Слово v наз. несократимым, если х\1. ф х~е1 + '
при любом /—1, 2,. . ., п—1. Несократимые слова яв
ляются разными элементами С. г. F, и каждое слово
равно единственному несократимому слову. Число п
наз. длиной слова и, если оно несократимо.
Преобразованиями Нильсена конечно-
конечного упорядоченного множества элементов %,..., а^
группы называются: 1) перестановка двух элементов в
этом множестве, 2) замена одного из а,- на сц1, 3) за-
замена одного из а,- на а,-ву, где ;' Ф i. Если С. г. F имеет
конечный ранг, то преобразования Нильсена над систе-
системой свободных порождающих приводят к новым систе-
системам свободных порождающих, причем любая система
свободных порождающих может быть получена из любой
другой последовательности применением этих преобра-
преобразований (теорема Нильсена, см. [2]). Зна-
Значение С. г. определяется тем, что всякая группа изо-
изоморфна нек-рой факторгруппе подходящей С. г. Всякая
подгруппа С. г. также свободна (теорема Ниль-
с е н а —Ш р а й е р а, см. [1], [2]).
С. г. групп многообразия S8 определяется аналогично
С. г., но в пределах 2$. Ее наз. также 23-с вободной
г р у п я о и, или относительно свободной
(а также приве денно свободной). Если 35
определяется системой тождеств и=1, где у? V, то
С. г. многообразия SS с системой X свободных порож-
порождающих изоморфна факторгруппе F/V(F) С. г. F с
системой X свободных порождающих по вербальной
подгруппе V (F) — подгруппе, порожденной всеми
значениями слов v? V в F. С. г. нек-рых многообразий
имеют специальные названия, напр.: свободная абелева,
свободная нильпотентная, свободная разрешимая,
свободная бернсайдова — С. г. многообразий Ш, 9tc>
W, 5В„ соответственно.
Лит.: [1] К у р о ш А. Г., Теория групп, 3 изд., М., 1967;
[2] М а г н у с В., К а р р а с А., С о л и т э р Д., Комбина-
Комбинаторная теория групп, пер. с англ., М., 1974: [3] Н е й м а н X.,
Многообрааия групп, пер. с англ., М., 1969.
А. Л. Шмелъкин.
СВОБОДНАЯ ПЕРЕМЕННАЯ, свободное вхо-
вхождение переменной,— вхождение неремен-
неременной в языковое выражение, являющееся параметром
этого выражения. Строгое определение этого понятия
может быть дано только для формализованного языка.
Для каждого яаыка дается свое определение С. п., зави-
зависящее от правил образования выраженип данного яаыка.
Семантич. критерием здесь служит следующее требо-
требование: лодстановка какого-либо объекта из подразуме-
подразумеваемой интерпретации на место данного вхождения пе-
переменной не должна приводить к бессмысленному
выражению. Напр., в выражении {(х, y)\x2Jry'— z2},
обозначающем множество точек окружности радиуса z,
переменная z входит свободно, а переменные х и у
нет (см. Связанная переменная). Если / обозначает
отображение вида X X Y —>¦ Z и переменные я, у про-
пробегают множества X, У соответственно, то в выраже-
выражении f(x, у) переменные х и у свободны (так же, как и /,
если / рассматривать как переменную по функциям).
При фиксировании х и варьировании у получается
функция вида F-+2. Она обозначается через Xyf(x, у).
В этом выражении х свободно, а у нет. В выражении
(Xyf (x, у)) (у), обозначающем значение функции Ху}(х, у)
в произвольной точке ;/, последнее вхождение пере-
переменной у будет свободным. Два других вхождения не
являются свободными. Первое наз. операторным
(находящимся под знаком оператора), второе — свя-
связанным.
Для неформализованных языков, т. е. в реальных
математич. текстах, у отдельно взятого выражения но
всегда можно определенно выяснить какие перемен-
переменные у него свободны, а какие связанны. Напр., в вы-
выражении 2. aik B зависимости от контекста перемен-
переменная i может быть свободной, а к связанной или наобо-
наоборот, но обе свободными быть но могут. Указание на то,
какая переменная считается свободной, дается с по-
помощью дополнительных средств. Напр., если это
выражение встречается в контексте вида «пусть / (к)=
2*i<}laik't>-, то к свободна. Иногда принимают согла-
соглашение, что по к суммирование производиться не будет;
тогда к — это параметр. Выражение {а,}, часто исполь-
используемое в математике, обозначает иногда одноэлемент-
одноэлементное множество, и тогда переменная i входит свободно;
а иногда оно обозначает множество всех я,-, когда
i пробегает отведенную ему область предметов, и тогда
переменная I входит связанно. в. Н. Гришин.
СВОБОДНАЯ ПОЛУГРУППА над алфавитом
А — полугруппа, элементами к-рой являются всевоз-
всевозможные конечные последовательности элементов из А
(букв), а операция состоит в приписывании одной после-
последовательности к другой. Элементы С. и. принято назы-
называть словами, а операцию часто называют конкате-
конкатенацией. Ради удобства нередко рассматривают
также и пустое слово 1 (длина к-рого но определению
равна нулю), полагая wl — lw~w для любого слова w;
возникающая таким образом полугруппа с единицей наз.
свободным моноидом над А. С. п. (свобод-
(свободный моноид) над А часто обозначают A + (соответствен-
(соответственно А*). Для С. п. А+ алфавит А является единствен-
единственным неприводимым порождающим множеством; он
состоит в точности из элементов, неразложимых в
произведение. Буквы из А наз. свободными об-
образующими. С. п. определяется однозначно с
точностью до изоморфизма мощностью своего алфавита;
эта мощность наз. рангом свободной полу-
полугруппы. С. п. ранга 2 имеет подполугруппы, яв-
являющиеся С. п. счетного ранга.
С. п. являются свободными алгебрами в классе всех
полугрупп. Следующие условия для полугруппы F
эквивалентны: 1) F есть С. п.; 2) F имеет порождаю-
щее множество А такое, что любой элемент из Р един-
единственным образом представим в виде произведения эле-
элементов из А; 3) F удовлетворяет закону сокращения,
не содержит идемпотентов, каждый элемент из F имеет
конечное число делителей, и для любых ц, v, и', v ?F
равенство uv=u'v' влечет, что и=и' или один из эле-
элементов и, и' есть левый делитель другого.
Всякая подполугруппа Я в С. п. имеет единственное
неприводимое порождающее множество, состоящее из
элементов, неразложимых в Я в произведение; однако
не всякая подполугруппа С. п. сама свободна. Сле-
Следующие условия для подполугруппы Н в С. п. F экви-
эквивалентны: 1) // есть С. п.; 2) для любого w?F из того,
что wH[\H ф ф и Hwf]II Ф ф, следует, что w?H\
3) для любого «.>?/•' из того, что юН[)НшГ\Нфф, сле-
следует, что «>?//. Для произвольных различных слов и.
v в С. п. F либо и и v являются свободными образую-
образующими порожденной ими подполугруппы, либо сущест-
существует w?F такое, что u=wk, v=wl для нек-рых нату-
натуральных к, I; вторая альтернатива выполняется тогда
и только тогда, когда uv=vu. Всякая подполугруппа с
тремя образующими в С. п. будет конечно определен-
определенной полугруппой, но существуют подполугруппы с
четырьмя образующими, не являющиеся конечно опре-
определенными.
С. п. естественно возникают в автоматов алгебраи-
алгебраической теории (см. также [5], [6]), теории кодирова-
кодирования (см. Кодирование алфавитное, [4] — [6]), теории
формальных языков и формальных грамматик (см. [3].
[5], [6]). С указанными областями связана проблематика
решения уравнений в С. гг. (см. [7] — \Щ)- Существует
алгоритм, распознающий разрешимость произвольных
уравнений в С. п.
Лит.: [1] К л и ф ф о р д А., Престон Г., Алгебраиче-
Алгебраическая теория полугрупп, пер. с англ., т. 1—2, М., 1972; [2] Л я-
пин Е. С, Полугруппы, М., 1960; [3] Гросс М., Л а н-
тен А., Теория формальных грамматик, пер. с франц., М.,
1971; [4] Марков А. А., Введение в теорию кодирования,
М., 1982; [5] EilenbcrgS. Automata, languages and ma-
machines, v. А—В, N. Y,—L., 1974—76; [6] L a 1 1 e m e n t G.,
Semigroups and combinatorial applications, N. Y.— ta. o.],
1979; [7] Lentin A., Equations dans les monoides libres,
P., 1972; [8] Хмелев с (i ий Ю. И., Уравнения в свободной
полугруппе, М., 1971 (Тр. Матем. ин-та АН СССР, т. 107);
[9] М а к а н и н Г. С, «Матем. сб.», 1977, т. 103, N? 2, с. 147—
236. Л. Н. Шеврин.
СВОБОДНАЯ РЕЗОЛЬВЕНТА — частный случай про-
проективной резольвенты. Всякий модуль М над ассоциа-
ассоциативным кольцом R является фактормодулем Po/No
свободного Я-модуля Fo по нек-рому его подмодулю
No. Для подмодуля No существует аналогичное пред-
представление P1/N1 и т. д. В результате получается точная
последовательность свободных модулей
Fo*- F1*~F2*- ... <- Fn*-,
называемая С. р. модуля М. Канонич. гомоморфизм
^о ->• М наз. пополняющим гомоморфиз-
М О М. В. Е. Говоров.
СВОБОДНАЯ РЕШЕТКА — свободная алгебра мно-
многообразия всех решеток. Решены [1] проблемы тожде-
тождества слов и канонич. представления слова в С. р.
Лит.: [1] Whitman P. M., «Annals Math.», 1941, v. 42,
p. 325 — 30; 1942, v. 43, p. 104 — 15. Т. С. Фофанова.
СВОБОДНО СТАНОВЯЩАЯСЯ ПОСЛЕДОВАТЕЛЬ-
ПОСЛЕДОВАТЕЛЬНОСТЬ — см. Интуиционизм.
СВОБОДНОЕ ГАРМОНИЧЕСКОЕ КОЛЕБАНИЕ —
синусоидальное колебание. Если механическая или фи-
зич. величина x(t), где t — время, меняется по закону
x(t)=. Л соь (сог + ср), A)
то говорят, что x(t) совершает С. г. к. Здесь А , со, ф ¦—
действительные постоянные, А > 0, ш > 0. Величины
А, ш, ф наз. соответственно амплитудой, час-
частотой, фазой С. г. к. П е р и о д С. г. к. равен
Г=2л/со. В физике и технике часто употребляется
такая терминология: С. г. к. наз. гармониче-
гармоническим колебанием, или простым гармо-
гармоническим колебанием, функция вида A)
наз. гармоникой, переменная величина cot-ftp наз.
мгновенной фазой, а постоянная ср — на-
начальной фазой. Величина со наз. также кру-
круговой, или циклической, частотой, а /=<о/2я—
частотой. С. г. к. A) можно записать в виде
х (t) = a cosШ-\-ЬsinШ,
где а, 6 и А, ф связаны соотношениями
Л= Va"-+b"-, coscp = 1— . sincp = —_Ё ,
Va' + Ъ2 Vra' + b*
или в виде
Часто фазой наз. не ср, а —ср.
Малые колебания механических или физич. систем
с одной степенью свободы вблизи устойчивого невы-
невырожденного положения равновесия представляют собой
С. г. к. с большой степенью точности. Таковы, напр.,
малые колебания маятника; колебания груза, подвешен-
подвешенного на пружинке; колебания камертона; изменение
напряжения и силы тока в электрическом колебатель-
колебательном контуре; качка кораблям т. д. Система, совершаю-
совершающая С. г. к., наз. линейным гармоническим
осциллятором, и ее колебания описываются
уравнением
Для математич. маятника длины I и массы т : со2=
= gll, для груза массы т на пружинке с коэффициентом
упругости k : us'i—-klm; для электрического колебатель-
колебательного контура, состоящего из емкости С и индуктивности
L : co2=l/CL. На фазовой плоскости (х, х) положение
равновесия х—0, х=0 для С. г. к. есть центр, а фазовые
траектории — окружности.
Сумма двух С. г. к. x1{t) + x2(t),
где xj{t) = Aj cos (vjt+qj), jf = l, 2,
с соизмеримыми частотами со1? со2 есть С. г. к. Если же
частоты coj, co2 несоизмеримы, то x1(t)-\-x2(t) есть почти
периодическая функция и
sup (х, Ц)-\-хг (t)) = A1+A2= — inf (^ (t) + xt (t)).
(е R ieR
Сумма п С. г. к. с частотами &1,. . ., со„, к-рые рацио-
рационально независимы, также есть почти нериодич. функ-
функция. Для суммы двух С. г. к. величина 0=103! —со2)
наз. расстройкой. Если расстройка мала:
O/ ^j 1, а ю1, со2 — одного порядка, то
¦Ч (t)+x-2 (t) = A (t) cos ((М+ф (t)),
A* (t) = Al + A* + 2AtA2 cos (ip (*)-<fi),
«Амплитуда» A (t) — медленно меняющаяся функция,
имеющая период 2я/Й, и A2 (i) меняется в пределах от
(^! — Л2J до (Аг+А2J. Колебание x1{t)+x2(t) наз.
биением: «амплитуда» A (t) поочередно увеличи-
увеличивается и уменьшается. Этот случай важен для анализа
приемных устройств.
Пусть имеется система из п уравнений:
где М, К — действительные симметрические положи-
положительно определенные матрицы с постоянными элемен-
элементами. С помощью ортогонального преобразования
х= Ту эта система приводится к расиадающейся си-
системе:
Координаты ylt . . ., уп наз. нормальными.
В нормальных координатах x(t) есть векторная сумма
С. г. к. вдоль координатных осей.
Лит.: [1] Андронов А. А.,ВиттА. А., X а й к и н
С. Э., Теория колебаний, 2 изд., М., 1981; [2] Го р е л и к Г. С,
Колебания и волны, М., 1959; [3] Ландау Л. Д., Л и ф-
ш и ц Е. М,, Механика, 3 изд., т. 1, М., 1973.
М. В. Федорюк.
СВОБОДНОЕ МНОЖЕСТВО в векторном
пространстве I над полем К — то же,
что линейно независимая система векторов из X, т. е.
множество элементов A — {at}aX, {? Т, такое, что соот-
соотношение 2?/a<=0, где §t=0 для всех кроме конечного
числа индексов t, влечет ?(=0 для всех (. Несвободное
множество наз. также зависимым.
Свободное множество в топологическое
векторном пространстве X над полем К (топологи-
(топологически свободное множество) — множе-
множество 4 = {в/}сХ такое, что для любого s? T замкнутое
подпространство, порожденное точками a/, tj=s, не со-
содержит as. Топологически С. м. является С. м. вектор-
векторного пространства; обратное неверно. Напр., в норми-
нормированном пространстве С непрерывных функций на [О,
1] функции e'ifcnfx, k?Z, образуют топологически
С. м. в отличие от функций ,г* (поскольку х содержится в
замкнутом подпространстве, порожденном {ж2*}).
Совокупность всех (топологически) С. М. в X, вообще
говоря, но индуктивна относительно включения; кроме
того, она не обязательно содержит максимальное то-
топологически С. м. Напр., пусть X — пространство
над R, образованное непрерывными функциями и на-
наделенное отделимой топологией: соответствующая фун-
фундаментальная система окрестностей нуля в X состоит
из уравновешенных поглощающих множеств Vs, e=
= {х : \f(x) | ¦< 6 всюду вне (зависящего от /) открытого
множества меры <е, 0<?<1, б >0}. Тогда каждый
непрерывный линейный функционал равен нулю и в X
не существует максимального С. м.
Для того чтобы А было (топологически) С. м. в ослаб-
ослабленной топологии о(Х, X*) в X, необходимо и доста-
достаточно, чтобы для каждого t существовал элемент bf? X*
такой, что <af, Ь(>^Ои <я$, Щ>=0 для всех s=jtt.
Для локально выпуклого пространства С. м. в ослаб-
ослабленной топологии является С. м. и в исходной топологии.
М. Я. Войцеховский.
СВОБОДНОЕ ОБЪЕДИНЕНИЕ — операция в нек-ром
классе универсальных алгебр, сопоставляющая задан-
заданной совокупности алгебр из этого класса в нек-ром смыс-
смысле «самую свободную» алгебру этого же класса, содер-
содержащую подалгебры, изоморфные заданным, и порож-
порождаемую ими. Термин в настоящее время вытеснен тер-
термином свободное произведение. О. А. Иванова.
СВОБОДНОЕ ПРОИЗВЕДЕНИЕ в классе ft уни-
универсальных алгебр A a, a?fi, из класса ,Я — алгебра А
из класса Й, содержащая все А а в качестве подалгебр и
такая, что любой набор гомоморфизмов алгебр Аа в
любую алгебру В из $ продолжается до гомоморфизма
алгебры А в В. С. п. заведомо существует, если Я —
многообразие универсальных алгебр. Каждая свобод-
свободная алгебра является С. п. однопорожденных свободных
алгебр. В классе всех абелевых групп С. п. совпадает
с прямой суммой. В нек-рых случаях поддаются описа-
описанию подалгебры С. п.; напр., в группах (см. Свободное
произведение групп), неассоциативных алгебрах, ал-
алгебрах Ли.
С. п. в категориях универсальных алгебр совпадает
с копроизведением в этих категориях, л. .4. Скорняков.
СВОБОДНОЕ ПРОИЗВЕДЕНИЕ групп G,,
i ?1,— группа G, порожденная группами (?,-, причем
любые гомоморфизмы ср,- : G,¦ ->¦ Н групп G, в любую
группу // продолжаются до гомоморфизма ц> : G -> Н.
Для обозначения С. и. используется знак *, напр.:
в случае конечного множества /. Каждый не равный
единице элемент С. и. G единственным образом выра-
выражается в виде несократимого слова "—g/jg'iv ¦ -gin,
где gij€.Gjj, gi-ф 1, и при любом /=--1,2, . . ., я —1,
ijz?ij + l. Конструкция С. п. является важной и изу-
изучении групп, заданных множеством порождающих
элементов и определяющих соотношений. В этих тер-
терминах оно может быть определено следующим образом.
Пусть каждая группа G,- задана множествами X,- порож-
порождающих и Ф, определяющих соотношений, причем
•Х/П-Ху—0, если i Ф ). Тогда группа G, заданная мно-
множеством Х,-= Uigj-^i порождающих и множеством Ф=
= Uie^< определяющих соотношений, будет С. п.
групп Gi, i?/.
Всякая подгруппа С. п. G сама разлагается в С. п.
своих подгрупп, из к-рых нек-рые являются бесконеч-
бесконечными циклическими, а каждая из других сопряжена с
нек-рой подгруппой какой-либо группы G/, входящей в
свободное разложение группы С (теорема К у-
р о ш а).
Лит.: [1] К у р о ш А. Г., Теория групп, 3 изд., М., 19Н7;
И Магнус В., К а р р а с А., С о л и т э р Д., Комби-
Комбинаторная теория групп, пер. с англ., М., 1974.
А. Л. Шмелъкин.
СВОБОДНЫЙ ВЕКТОР — см. Вектор.
СВОБОДНЫЙ ГРУППОИД — свободная алгебра
многообразия всех группоидов. С. г. с множеством X
свободных образующих совпадает с группоидом слов,
если под словом понимать любую упорядоченную систе-
систему элементов из X с любыми повторениями, причем в
этой системе задано распределение скобок (каждый
символ считается взятым в скобки, а затем скобки
расставлены так, что каждый раз перемножаются лишь
две скобки). Произведением слов (а) и (Ь) считается сло-
слово ((а) (Ь)). О. А. Иванова.
СВОБОДНЫЙ МОДУЛЬ — свободный объект (сво-
(свободная алгебра) в многообразии модулей над фиксиро-
фиксированным кольцом R. Если R — ассоциативное кольцо с
единицей, то С. м.— это модуль, обладающий базисом,
т. е. линейно независимой системой порождающих.
Мощность базиса С. м. наз. его рангом. Ранг не всегда
определен однозначно, т. и. существуют кольца, над
к-рыми С. м. может обладать двумя базисами, состоя-
состоящими из различного числа элементов. Это равносильно
существованию над кольцом R двух прямоугольных
матриц А и В, для к-рых
АВ = 1т, ВА = 1п, т ф п,
где Iт и /„ — единичные матрицы порядков тип
соответственно. Неоднозначность, однако, имеет место
лишь для конечных базисов, если же ранг С. м. беско-
бесконечен, то все базисы С. м. равномощны. Кроме того,
над кольцами, допускающими гомоморфизм в тело (в
частности, над коммутативными кольцами), ранг С. м.
определен всегда однозначно.
Кольцо Л, рассматриваемое как левый модуль над
самим собой, является С. м. ранга один. Всякий левый
С. м. является прямой суммой С. м. ранга один. Лю-
Любой модуль М представим как фактормодуль Fjlla
нек-рого С. м. Fo. Подмодуль Нв в свою очередь пред-
представим как фактормодуль F1jH1 С. м. Ft. Продолжая
этот процесс, получают точную последовательность:
... ->F2->Fi ->F0-+M -*0,
к-рая наз. свободной р е з о л ь в е н т о ii моду-
модуля М. Тела могут быть охарактеризованы как кольца,
над к-рыми все модули свободны. Над областью глав-
главных идеалов подмодуль С. м. свободен. Близкими к
С. .ч. являются проективные модули и плоские модули.
Лит.: [1] Кон П., Свободные кольца и их свяаи, пер. с
англ., М., 1975; [2] М а к л е й н С, Гомология, пер. с англ.,
М., 196В. В. Е. Говоров.
СВОДИМОСТИ АКСИОМА — аксиома, добавленная
Б. Расселом (В. Russell) к его разветвленной теории ти-
типов с целью избежать расслоения понятий (см. Непре-
Непредикативное определение). В разветвленной теории типов
множества данного типа разделяются на порядки.
Так, вместо понятия множества натуральных чисел по-
появляется понятие множества натуральных чисел дан-
данного порядка. При этом множество натуральных чисел,
определяемое формулами без использования каких-либо
множеств, принадлежит первому порядку. Если в опре-
определении используется совокупность множеств первого
порядка, а совокупности множеств высшего порядка
не используются, то определяемое множество принад-
принадлежит второму порядку, и т. д. Напр., если S — се-
семейство множеств, состоящее из множеств одного и
того же порядка, то множество
должно принадлежать следующему порядку, т. к. в его
определении содержится квантор по множествам дан-
данного порядка. С. а. утверждает, что для каждого мно-
множества существует равнообъемное ему (т. е. состоящее
из тех жо самых элементов) множество первого порядка.
Таким образом, С. а. фактически сводит разветвленную
теорию типов к простой теории типов.
Лит.: [1] Гильберт Д., Аккерман В., Основы
теоретической логики, пер. с нем., М., 1947.
В. Н. Гришин.
СВЯЗАННАЯ ПЕРЕМЕННАЯ, связанное
вхождение переменной,— тип вхождения
переменной в языковое выражение. Точное определе-
определение для каждого формализованного языка — свое и
зависит от правил образования этого языка. Вместо
С. п. нельзя подставлять объекты. Такая подстановка
приводит к бессмысленным выражениям. Но замена
С. и. всюду, где она встречается, на новую для данного
выражения переменную приводит к выражению с тем
же самым смыслом. Напр., в выражениях
[f(x, y)dx, {x\f(x, у)=-.О}
переменная х является связанной. Подстановка вместо
х какого-нибудь числа приводит к бессмысленным вы-
выражениям. В то же время, написав всюду вместо х,
например z, получают выражения, обозначающие те
же самые сущности.
С. п. всегда возникают при применении к нек-рому
выражению е со свободными вхождениями переменной
х какого-нибудь оператора с операторной переменной
х (см. Свободная переменная). В получившемся выра-
выражении все вхождения переменной х в е, бывшие свобод-
свободными, становятся связанными. Ниже указаны нек-рые
наиболее употребительные операторы (помимо уже ис-
использованных операторов \. . .dx и {.г\. . .}), в к-рых
х является операторной переменной:
Vx(. . .), Зх(. . .) — кванторы общности и существо-
существования;
\ . . . dx — определенный интеграл по х\
2*. . . — сумма по х;
Кх(. . .) — функция от х, значение к-рои в точке х
равно . . .
Вместо многоточий можно подставлять определенные
языковые выражения.
В реальных (не формализованных) математич. текстах
возможно неоднозначное употребление одних и тех же
выражений, в свяаи с чем выделение С. п. в данном
выражении зависит от контекста и смысла выражения.
В формализованных языках имеется формальная про-
процедура выделения свободных и связанных вхождений
переменных. В. Н. Гришин.
СВЯЗАННЫЙ ВЕКТОР — см. Вектор.
СВЯЗКА — двупараметрическое семейство линий на
плоскости или поверхностей в пространстве, линейно
зависящее от параметров. Пусть l<\, f\, F3 — функции
двух переменных, из к-рых ни одна не является линей-
линейной комбинацией двух других. Семейство .'ишпй на
плоскости, определяемых уравнением
при всевозможных значениях параметров }п, к2, Л3
(кроме >ч=0, Я2=0, Я3=0), представляет собой С. (фак-
(фактически зависит от двух отношений кг : Я,2 : Л;|). Ана-
Аналогично записывается уравнение С. поверхностей в
Рис. 1.
пространстве. Три уравнения /^=0, F.,— 0, /•',-,-¦ 0
дают три элемента С. (три линии или три поверхности),
к-рые определяют всю С.
Связка прямых — множество всех прямых,
каждая пара из к-рых лежит в одной плоскости. В
евклидовой геометрии С. прямых — множество всех пря-
прямых, проходящих через одну точку. Если эта точка ко-
конечная, то С. прямых наз. эллиптической, ес-
если бесконечно удаленная, — параболической.
Связка плоскостей — множество всех
плоскостей, проходящих через одну точку (собст-
(собственная С.) или параллельных нек-роп прямой
(несобственная С).
Связка окружностей — двупараметрич.
семейство окружностей, линейно зависящее от парамет-
параметров. Собственной С. окружностей является
множество тех окружностей, относительно к-рых данная
Рис.
Рис. 3.
точка (центр С.) имеет данную степень точки. И с-
собст венной С. окружностей наз. множество
всех окружностей, центры к-рых принадлежат нек-рой
фиксированной прямой (т. н. фундаменталь-
фундаментальной прямой) (см. рис. 1). Если @,0) — центр
собственной связки, то ее уравнение
х*-\~у* — 2ах — 2Ьу-\-р = 0, а'*-\-Ь- > р,
где а и Ь — параметры, определяющие окружность,
p — степень центра С. относительно окружностей С.
(степень несобственной С. считается бесконечной).
Имеются три типа собственных С. окружностей:
1) г и п е р б о л и ч е с к а я С. (р > 0), состоящая
из всех окружностей, ортогональных нек-рой данной
окружности (фундамен-
(фундаментальной окружно-
окружности) (см. рис. 2);
2) параболическая
С. (p = Q), состоящая из всех
окружностей, проходящих
через нек-рую данную точку
(центр С.) (см. рис. 3);
3) э л л и и т и ч е с к а я
С. (р < 0), состоящая из
окружностей, пересекающих
нек-рую данную окружность Рис 4
в двух диаметрально проти-
противоположных точках последней (см. рис. 4).
Пересечение двух С. окружностей является пучком
окружностей. Эллиптическая С. содержит только эллип-
тич. пучки, параболическая С.— только эллиптич. и
нараболич. пучки, гиперболическая С.— три типа соб-
собственных пучков. Несобственная С. содержит как не-
несобственные пучки, так и собственные пучки всех трех
типов.
Пересечение двух С, из к-рых одна эллиптическая,
может быть только эллиптич. пучком. Пересечения
двух С, из к-рых одна параболич., может быть только
эллиптическим или параболич. пучком. Пересечение
двух С, из к-рых одна собственная, может быть только
собственным пучком.
Связка сфер — двупараметрич. семейство сфер,
линейно зависящее от параметров. С. сфер состоит из
множества сфер, относительно к-рых точки нек-рой пря-
прямой (радикальной оси) имеют одинаковую
степень (различную для разных точек). Радикальная
ось пересекает все сферы С. в двух точках. В зависимо-
зависимости от того, являются ли эти точки действительными
(различными), комплексно сопряженными или совпадаю-
совпадающими, С. сфер наз. эллиптической С, к-рая
состоит из всех сфер, проходящих через две общие
точки; гиперболической С, к-рая состоит из
всех сфер, ортогональных двум нек-рым пересекаю-
пересекающимся сферам; параболической С, к-рая
состоит из всех сфер, касающихся нек-рой данной пря-
прямой в данной точке. Центры всех сфер С. лежат в одной
плоскости, перпендикулярной к радикальной оси.
С. является пересечением всех общих сфер двух сетей
сфер.
В проективной геометрии С.— множество всех пря-
прямых и плоскостей, проходящих через данную точку.
Лит.: [1] Постников М. М., Аналитическая геомет-
геометрия, М., 1973; [2] Моденов П. С, Аналитическая геомет-
геометрия, М., 1969. А. Б. Иванов.
СВЯЗКА ПОЛУГРУПП данного семейства
{Sa } — полугруппа S, обладающая разбиением на под-
подполугруппы, классы к-рого суть в точности полугруппы
Sa, и для любых Sa, S(з существует 6'v такая, что 5а5р^
g^Sy . В этом случае говорят также, что S разложи-
разложима в связку полугрупп Sa- Другими словами, S
есть С. п. Sa, если все Sa— подполугруппы в S и су-
существует конгруэнция р на S такая, что р-классы суть в
точности Sa- Полугруппы Sec наз. компонентами
данной связки. Термин «С. п.» согласуется с использо-
использованием нередко слова «связка» как синонима термина
«полугруппа идемпонентов», так как конгруэнция р
на полугруппе S определяет разложение S в связку
тогда и только тогда, когда факторполугруппа S/p —
полугруппа идемпотентов.
Многие полугруппы разложимы в связку полугрупп
с теми или иными «более хорошими» свойствами; таким
образом, изучение их строения в известной мере сво-
сводится к рассмотрению типов, к к-рым принадлежат ком-
компоненты связки, и к рассмотрению полугрупп идемпотен-
тов (см., напр., Архимедова полугруппа, Вполне простая
полугруппа, Клиффордова полугруппа, Периодическая
полугруппа, Сепаративная полугруппа).
С. п. 5аназ. коммутативной, если для соот-
соответствующей конгруэнции р факторгголугруппа Sip
коммутативна; тогда Sip — полурешетка (в этом случае
часто говорят, что S есть полурешетка полугрупп
Sa, в частности, если S/p — цепь, то говорят, что S
есть цепь полугрупп Sa)- С. п. наз. прямоуголь-
прямоугольной (иногда — матричной), если S/p — прямо-
прямоугольная полугруппа (см. Идемпотентов полугруппа).
Это эквивалентно тому, что компоненты связки могут
быть индексированы парами индексов Six., где i и X
пробегают нек-рые множества / и Л соответственно,
причем для любых Sn, 5/д выполняется включение
Si\Sjii^Si\i. Любая С. п. есть полурешетка прямо-
прямоугольных связок, т. е. ее компоненты могут быть рас-
распределены на подсемейства так, что объединение ком-
компонент каждого подсемейства есть прямоугольная
связка этих компонент, а исходная полугруппа разло-
разложима в полурешетку указанных объединений (теоре-
(теорема Клиффорда [1]). Поскольку свойства быть
полугруппой идемпотентов, полурешеткой, прямоуголь-
прямоугольной полугруппой характеризуются тождествами, на лю-
любой полугруппе S для каждого из перечисленных свойств
О существует наименьшая конгруэнция, для к-рой
соответствующая факторполугруппа обладает свойст-
свойством 0, т.е. существуют наибольшие (или наи-
наиболее дробные) разложения S в С. п.,
в коммутативную С. п., в прямоугольную С. п.
К специальным тинам Си. относится сильная
связка [4]: для любых элементов а и Ь из разных
компонент произведение ab равно степени одного из
этих элементов. Важным частным случаем сильной
связки и одновременно частным случаем цепи полу-
полугрупп является о р д и н а л ь н а я сумма (или п о-
с лед о ват оль но аннулирующая связка):
множество ее компонент {Sa} линейно упорядочено
и для любых Sa, 5р таких, что Sa< Sp , и любых a?Sa,
6^5р имеет место равенство ab=ba= а. Заданием
компонент и способа их упорядочения ординальная
сумма определяется однозначно с точностью до изо-
изоморфизма.
Лит.: 11] С 1 i f f о г d A., «Proc. Amcr. Math. Soc.|>, 1954,
v. a, p. 499—504; [2] Клиффорд А., Престон Г.,
Алгебраическая теория полугрупп, пер. с англ., т. 1, М., 1972;
[3J Л :f п и н Е. С, Полугруппы, М., 1960; [4] Ш е в р и н Л. Н.,
«Изв. вузов. Матем.», 1965, № 6, с. 156—65. Л. Н. Шеврин
СВЯЗНАЯ КОМПОНЕНТА ЕДИНИЦЫ группы
G — наибольшее связное подмножество G° топологи-
топологической (или алгебраической) группы G, содержащее
единицу этой группы. С. к. е. С° является замкнутой
нормальной подгруппой в G; смежные классы по этой
подгруппе совпадают со связными компонентами груп-
группы G. Факторгруппа GIG' вполне несвязна и хаусдорфо-
ва, причем G" — наименьшая из таких нормальных
подгрупп HaG, что GIH вполне несвязна. Если G
локально связна (напр., G — группа Ли), то G" открыта
в G и G/G° дискретна.
В произвольной алгебраич. группе G С. к. е. G"
также открыта и имеет конечный индекс, причем G°
является минимальной замкнутой подгруппой конеч-
конечного индекса в G. Связные компоненты алгебраич. груп-
группы С совпадают с неприводимыми компонентами. Для
любого регулярного гомоморфизма ф : G —>- G' алгеб-
алгебраич. групп справедливо равенство tp (G°)=<$ (G)°. Если
G определена над нек-рым полем к, то и G° определена
над /г.
Если G — алгебраич. группа над полем С, то ее С. к.е.
G" совпадает со С. к. е. группы G, рассматриваемой как
комплексная группа Ли. Если G определена над К,
то группа G° (R) вещественных точек в GD не обязательно
связна в топологии группы Ли G(R), но число ее связ-
связных компонент конечно и имеет вид 2', где I ^ 0. Напр.,
группа GLn(C) распадается на две компоненты, хотя
GLn(R) связна. Псевдоортогональная унимодулярная
группа SO(p, д), к-рая может рассматриваться как
группа вещественных точек связной комплексной ал-
гебраич. группы SOp+q (С), связна при р=0 или <7=0
и распадается на две компоненты при р, д > 0.
Лит.: [1] Борель А., Линейные алгебраические груп-
группы, пер. с англ., М., 1972; [2] Понтрягин Л. С, Непре-
Непрерывные группы, 3 изд., М., 1973; [3] Хелгасон С., Диф-
Дифференциальная геометрия и симметрические пространства, пер.
г англ., М., 1964; [4] Ш а ф а р е в и ч И. Р., Основы алгебра-
алгебраической геометрии, М., 1972. А. Л. Онищик.
СВЯЗНАЯ СУММА семейства множеств —
объединение этих множеств в единое связное множество.
Само понятие С. с. возникло из необходимости отличить
такого рода объединение от понятия несвязной или
открыто-замкнутой суммы, т. е. такого объединения
множеств, когда они не пересекаются и связными под-
подмножествами в этом объединении могут быть только под-
подмножества-слагаемые. В. И. Малыхин.
СВЯЗНОЕ МНОЖЕСТВО — подмножество объемлю-
объемлющего множества, в к-ром определено понятие связности
и в смысле к-рого само подмножество связно. Напр..
См. пространства действительных чисел являются
выпуклые множества и только они; С. м. графа явля-
является такое множество, в к-ром любые две точки соеди-
соединены путем, целиком лежащим в этом множестве.
В. И. Малыхин.
СВЯЗНОЕ ПРОСТРАНСТВО — топологическое про-
пространство, к-рое нельзя представить в виде суммы двух
отделенных друг от друга частей или, более строго,
непустых непересекающихся открыто-замкнутых под-
подмножеств. Пространство связно тогда и только тогда,
когда каждая непрерывная числовая функция прини-
принимает на нем все промежуточные значения. Непрерывный
образ С. п., произведение С. п., пространство замкну-
замкнутых подмножеств в топологии Вьеториса С. п. суть С. п.
Каждое связное вполне регулярное пространство имеет
мощность не менее континуума, хотя существуют и
счетные связные хаусдорфовы пространства.
В. И. Малыхип.
СВЯЗНОСТИ НА МНОГООБРАЗИИ — дифферен-
дифференциально-геометрические структуры на гладком много-
многообразии М, являющиеся связностями в приклеенных к
М гладких расслоенных пространствах Е с однород-
однородными типовыми слоями GlH размерности dim M. В за-
зависимости от выбора однородного пространства Gill
получаются, напр., аффинные связности, проективные
связности, конформные связности и др. на многообразии
М. Общее понятие С. на м. ввел Э. Картан 11]; он назвал
многообразие М с заданной на нем связностью «пеголо-
номным пространством с фундаментальной группой».
Современное определение С. на м. опирается на по-
понятие гладкого расслоенного пространства, приклеен-
приклеенного к многообразию М. Пусть F—G/H является
однородным пространством размерности dim M (напр.,
аффинным пространством, проективным пространством
и т. н.). Пусть р : Е —>- М является гладким локально
тривиальным расслоением с типовым слоем F и пусть в
этом расслоении существует и фиксировано гладкое
сечение s, т. е. такое гладкое отображение s : М —*¦ Е,
что р (s(x)) = x для любого х(^М. Последнее условие
гарантирует, что s является диффеоморфизмом М на
s(M), и поэтому М и s(M) можно при желании отож-
отождествлять. Другими словами, к каждой точке х?М
присоединен экземпляр Fх однородного пространства F
размерности dimM — слой расслоения р : Е —>- М над
х—с фиксированной в ней точкой s(x), отождествляе-
отождествляемой С X.
С. на м. является частным случаем общего понятия
связности; самостоятельно она может быть определена
следующим образом. Пусть для каждой кусочно глад-
гладкой кривой L(x0, xt) многообразия М определен изо-
изоморфизм VL : FXt —>¦ FXo касательных однородных про-
пространств в концах кривой (напр., если F является аф-
аффинным, проективным и т. д. пространством, то ГЬ —
соответственно аффинное, проективное и т. д. отобра-
отображение). Пусть, кроме того:
1) при Ь(г0, г-,), L' {хХ1 х2), L-i (.гх, х„) и LL' (х0, х2)
справедливы ГЬ~^ (ГЬ)-1, Г (ЬЬ')= (ГЬ) (ГЬ');
2) для каждой точки х?М и касательного вектора
Xx$z ТХ(М) изоморфизм FLt:Fxt ->¦ Fx, где Lf — образ
отрезка [0, t] при параметризации % ; [О, i]—>L(x, xi)
кривой L с касательным вектором X, стремится при
I-+0 к тождественному изоморфизму, и его отклоне-
отклонение от последнего зависит в своей главной части только
от х и X, причем гладко.
В этом случае говорят, что на многообразии М дана
связность Г типа F; изоморфизм VL наз. параллельным
перенесением вдоль Ь. Для каждой кривой Ь(.т, x,i)?M
определяется ее развертка: кривая в Fx, состоящая
из образов точек х\ кривой Ь при параллельном перене-
перенесении вдоль Lt. Из 2) следует, что кривые с общим
касательным X в точке х дают развертки с общим ка-
касательным вектором Y, гладко зависящим от х и X,
вследствие чего для каждой точки х возникает отобра-
отображение
fx:Tx(M)-*Ttlx) (Fx).
Наиболее изучены линейные С. на м., к-рые облада-
обладают следующим дополнительным свойством:
3) элемент со (X) в алгебре Ли g структурной группы
G, к-рый определяет главную часть отклонения изо-
изоморфизма TLf от тождественного изоморфизма при t —>-0
относительно нек-рого поля реперов, зависит от X ли-
линейно.
В этом случае отображение fx является линейным.
Если fx оказывается изоморфизмом для любой точки
х, то говорят о невырожденной С. на м. или о связ-
связности Картана;в этом случае изоморфизм /~'
трактуется также как приклеивание расслоения р:
Е -*¦ М к базе М (вдоль заданного сечения S). Связ-
Связность Картана на М наз. полно й, если для каж-
каждой точки х всякая гладкая кривая в Fх с началом в х
является разверткой нек-рой кривой в М.
С точки зрения общей теории связностей, где линейная
связность в расслоении р : Е—>-М задается с помощью
горизонтального распределения Л на Ё, отображение
fx является композицией изоморфизма s*, отображаю-
отображающего X в соответствующий касательный к s (M) вектор,
и последующей проекции пространства Ts{x)(E)--
= ^six)®^six) (Fx) на второе прямое слагаемое. Отсю-
Отсюда следует, что связность невырождена тогда и только
тогда, когда As{x)f\ Ts(x) (s(M))~ {0} для любой точки
х?М. На М применимы все понятия и результаты
общей теории связностей, напр, такие, как голономии
группа, кривизны, форма, теорема о голономии и др.
Дополнительная структура расслоения, приклеенного
к многообразию М, позволяет, однако, ввести нек-рые
более специальные понятия. Кроме развертки наиболее
важным из них является понятие кручения формы связ-
связности на М в точке х.
Особое место в теории С. на м. занимают связности
Картана в случае, когда F=GlH является однородным
редуктивным пространством, т. е. когда существует
прямое разложение g=h-[-m со свойством [hm]cim.
В этом случае происходит расщепление формы кривизны
Q на два самостоятельных объекта: ее компонента в т
порождает форму кручения, а компонента в h порождает
форму кривизны. Здесь наиболее известным примером
является аффинная связность на М, у к-рой F является
аффинным пространством размерности dim M.
Редуктивное пространство F обладает инвариантной
аффинной связностью. Вообще, если на F существует
инвариантная аффинная или проективная связность, то
определяются геодезические линии связности типа F
на М как такие линии в М, развертки к-рых являются
геодезич. линиями указанной инвариантной связности.
Лит.: Ш С а г t a n E., «Acta math.», 1926, I. 48, p. 1—42
(в рус. пер. — Картин Э., Группы голоиомии обобщенных
пространств, иер, с франц., Казань, 1933)', 12] Лап-
Лаптев Г. Ф., «Тр. Моск. матем. об-ва», 1953, т. 2, с. 275 — 382;
13] Ehresmann С, Coll. de Topologie (Bruxelle, 1950),
P., 1951, p. 29—55; [4] Kobayashi S., «Canad. J. Math.»,
1956, V. 8, N 2. p. 145 — 156; [5] С 1 i ( t о n Y. H., «J. Math.
and Mech.», 196*6, v. 16, Л» в, p. 5В9—76. 10 Г. Лумисте.
СВЯЗНОСТИ ОБЪЕКТ — дифференциально-геоме-
дифференциально-геометрический объект на гладком главном расслоенном
пространстве Р, с помощью к-рого задается горизонталь-
горизонтальное распределение Д связности в Р. Пусть R0(P) явля-
является расслоением всех таких реперов в касательных к
Р пространствах, что первые г векторов е1, . . ., ег ка-
сательны к слою и порождаются определенными г
базисными элементами в алгебре Ли структурной
группы G пространства Р, г- dim G. Со. составляют
тогда функции Гр на R0(P) такие, что подпространство
распределения А натянуто на векторы е, + ГРер (р,
а=1,. . ., г; i, /,. . .=г+1,. .., г-\-п). Условия, к-рым
должны удовлетворить функции Гр на Ло (Р), чтобы они
составили Co., следующие".
*Г?-Г?Ш{+Г%8+а)? = Г>Л A)
Ojjh выражены с помощью 1-форм на Ro (P), входящие
в структурные уравнения для форм со', сор , составляю-
составляющих дуальный кобазис к {е,-, ер }:
Gш' = а>/ л ту, ^1
dcoP = —i- СРтш<? л сох +ш' Л (of, \ B)
С. о. определяет также связности форму 0 согласно фор-
формуле 0p=ioP— rfffl' и кривизны форму Q согласно
формулам
qp = _ * Др-ш' л со/,
Напр., пусть Р является пространством аффинных
реперов в касательных пространствах re-мерного глад-
гладкого многообразия М. Тогда вторые из уравнений B)
имеют вид
daj= —со* Л со/ + сой л co/ft
и A) сводятся к
При параллельном перенесении должно быть (о) —
— Г/й(о*=0. Если на М выбрана локальная карта и в ее
области сделан переход к натуральному реперу карты,
то (tik=dzk и параллельное перенесение определяется с
помощью со}=Гу/гйа:*. Классич. определение С. о. аф-
аффинной связности иа М как совокупности функций Г/ь
заданных на области каждой карты и преобразующих-
преобразующихся при переходе к координатам другой карты по форму-
формулам
¦pi' _(!.*'' дх/ дхк _ С . дгх' дх1'
1 /' R' : ; Т~~ 1 jk Н г~ ' ~7 ,
дх' дх1 д.\л' flxJ дхк' dx'
следует из условия инвариантности перенесения.
Ю. Г. Лумисте.
СВЯЗНОСТИ ФОРМА — линейная дифференциаль-
дифференциальная форма G на главном расслоенном пространстве Р,
к-рая принимает значения в алгебре g структурной
группы G пространства Р, определяется нек-роп ли-
линейной связностью Г в Р и сама определяет эту связ-
связность однозначно. По связности Г значение С. ф. Qy(Y),
где у?Р, Y?Ty(P), определяется как тот элемент в g,
к-рый в действии G на Р порождает вторую компо-
компоненту вектора У относительно прямого расслоения
Ty(P)=kyQ)Ty(Gy), где Gy — слой, содержащий у,
а Д — горизонтальное распределение связности Г.
По С. ф. 6 горизонтальное распределение Л, а тем са-
самым и связность Г, восстанавливается следующим об-
образом.
Теорема Картава — Лаптева. Чтобы
нек-рая форма 6 на Р со значениями в g была С. ф.,
необходимо и достаточно следующее: 1) при Y? Ту (Gy)
значением Qy (Y) является тот элемент в g, к-рый в
действии G на Р порождает Y, 2) g-значная 2-форма
= de + -i. [9, в],
составленная из 0, является полубазовой, или горизон-
горизонтальной, т.е. Qy(Y, У) = 0, если хотя бы один из
векторов Y и Y' принадлежит Ty(Gy). 2-форма Q
наз. кривизны формой связности. Если в g задан базис
{е1,. . ., ег}, то условие 2) выражается локально в
виде равенств:
(р, о, т = 1, ..., г; i, j = r + l, ..., r+n
где со1,. . ., со" —• нек-рые линейно независимые полу-
базовые 1-формы. В такой форме необходимость условия
2) установил Э. Картан [1]; его достаточность при вы-
выполнении условия 1) доказал Г. Ф. Лаптев [2]. Урав-
Уравнения (*) на компоненты С. ф. наз. структурны-
структурными уравнениями связности в Р, в них Rfy
составляют объект кривизны.
Пусть Р, в качестве примера, является пространст-
пространством аффинных реперов в касательных пространствах
re-мерного гладкого многообразия М. Тогда G и g яв-
являются соответственно группой и алгеброй Ли матриц
вида
1* * A, cietMJl ^0,
/ II
В силу теоремы Картана — Лаптева g-значная 1-форма
О со''
О cof
на Р является С. ф. нек-рой аффинной связности на М
тогда и только тогда, когда
rfco' + co/ л со/= 4" rj-feco/ л со*,
dcot-j-cofe л со/ = — Rjki w* л со'.
Здесь Tjk и Rjki составляют соответственно тензор
кручения и тензор кривизны аффинной связности на М.
Последние два уравнения на компоненты С. ф. наз.
структурными уравнениями полученной на М аффинной
связности.
Лит.: [1] С а г t а п Е., «Acta math.», 1926, v. 48, p.1—42;
[21 Лаптев Г. Ф., «Тр. Моск. матем. об-ва», 1953, т. 2, о.
275 — 382; [3J К о 6 а я с и HI., H о м и д з у К., Основы диф-
дифференциальной геометрии, т. 2, пер. с англ., М., 1981.
Ю. Г, Лумисте.
СВЯЗНОСТИ ЧИСЛО — мощность семейства ком-
компонент связности топологич. пространства. Напр.,
если из числовой прямой выбросить п точек alt . . .,
а„, то компонентами остатка являются множества
] —оо, at [, }а1, а2[, ..., ]ап, оо [
и, !аким образол!, С. ч. остатка равно га+1.
Термин «С. ч.» используется и в следующем смысле:
область евклидова пространства наз. «-с в я з н о и,
если ее граница состоит из п непересекающихся связ-
связных подмножеств. Напр., внутренность круга — одно-
связная область, внутренность кольца — двусвязная.
В. 11. Малыхип.
СВЯЗНОСТЬ — свойство топологич. пространства,
состоящее в том, что пространство нельзя представить
в виде суммы двух отделенных друг от друга частей,
или, более строго, непустых непересекающихся откры-
открыто-замкнутых подмножеств. Пространство, не являю-
являющееся связным, наз. несвязным. Напр., обычная
евклидова плоскость — связное пространство; если
удалить из нее точку, то остаток связен; если удалить
какую-нибудь окружность, не сводящуюся к точке, то
остаток уже несвязен.
Абстрактное свойство С. выражает интуитивное
представление о С. пространства в единое целое, об
отсутствии в нем каких-либо изолированных «остров-
«островков». С. топологич. пространства сохраняется при го-
гомеоморфизмах и является одним из важнейших свойств
топологич. пространства.
Подмножество топологич. пространства наз. свя-
связным, если оно — связное подпространство. После
введения этого понятия можно утверждать, что прост-
пространство связно, если любые его две точки лежат в нек-
ром связном подмножестве, т. е. их можно соединить
нек-рым связным множеством. С этой точки зрения аб-
абстрактное свойство С. можно рассматривать как обоб-
обобщение линейной связности, т.е. свойства
пространства, заключающегося в возможности свя-
связать любые его две точки нек-рым путем — непрерыв-
непрерывным образом отрезка. Открытое связное подмножество
наз. областью. Области и выпуклые подмножества
в евклидовых пространствах являются линейно связ-
связными и, тем более, связными.
Если семейство связных подмножеств имеет непустое
пересечение, то объединение этого семейства — связ-
связное множество. Для всякой точки топологич. прост-
пространства объединение всех связных подмножеств, ее
содержащих, есть наибольшее связное подмножество,
ее содержащее, оно наз. компонентой этой
точки. Компоненты — замкнутые множества, различ-
различные компоненты не пересекаются.
К ваз и компонентой точки наз. пересече-
пересечение всех содержащих ее открыто-замкнутых подмно-
подмножеств. Компонента точки содержится в ее квазиком-
квазикомпоненте. В бикомпактных пространствах компоненты
и квазикомпоненты совпадают.
Пространство наз. наследственно н е с в я з-
н ы м (дисперсным), если все его компоненты одното-
одноточечны, т. е. все его связные подмножества только одно-
одноточечны. Пространство наз. вполне несвяз-
несвязным (нигде не связным), если все его квазикомпоненты
одноточечны. Пространство наз. экстремально
несвязным, если замыкание любого открытого
множества открыто. Хаусдорфово экстремально не-
несвязное пространство вполне несвязно, а всякое вполне
несвязное пространство наследственно несвязно. Су-
Существует связное пространство, содержащее точку
дисперсии, по удалении к-рой остаток есть вполне не-
несвязное пространство. Пример — Курагповского —
Кнастера веер.
Связное бикомпактное пространство наз. кон т и-
н у у м о м. Пересечение убывающего семейства не-
пустых континуумов есть непустой континуум. Однако
никакой континуум нельзя разложить в объединение
счетного семейства непустых непересекающихся замк-
замкнутых подмножеств (теорема Серпиньс-
к о г о).
Пространство наз. неприводимым между
нек-рыми своими двумя точками, если оно связно и
эти две точки нельзя соединить никаким связным мно-
множеством, отличным от всего пространства. Всякий
континуум для любых своих двух точек содержит
неприводимый между ними подконтинуум (т е о р и м а
Мазуркевича — Янишевского).
Пространство наз. локально связным в
точке, если всякая окрестность этой точки содержит
нек-рую связную ее окрестность.
Пространство наз. связным в размерности п,
если каждое непрерывное отображение re-мерной сферы
в него продолжается до непрерывного отображения
n-мерного шара. С. в размерности 1 эквивалентна
тривиальности фундаментальной группы пространства.
Непрерывное отображение одного топологич. прост-
пространства в другое наз. монотонным, если прооб-
прообраз каждой точки — связное подмножество. Для замк-
замкнутых отображений монотонность эквивалентна связ-
связности прообраза каждого связного подмножества.
Лит.: [1J А л с к с а в д р о в П. С, Введение в теорию
множеств и общую топологию, М., 1977; [2] К у р а т о в-
с к и й К., Топология, пер. с англ., т. 2, М., 1969.
В. И. Малыхип.
СВЯЗНОСТЬ на расслоенном простра-
пространстве — дифференциально-геометрическая струк-
структура на гладком расслоенном пространстве со струк-
структурной группой Ли, обобщающая связности на много-
многообразии, в частности, напр., Леви-Чивита связность
в римановой геометрии. Пусть р : Е —>- В является
гладким локально тривиальным расслоением, на типо-
типовом слое F к-рого эффективно и гладко действует
группа Ли G. С. в этом расслоении — это отображение
категории кусочно гладких кривых базы В в катего-
категорию диффеоморфизмов слоя на слой, к-рое кривой
L=L{x0, хх) с началом х0 и концом х1 сопоставляет
диффеоморфизм TL : р~1 (хх) -^-р~1 (х0) и удовлетво-
удовлетворяет следующим аксиомам:
1) при L(xu, хх), L'(xL, хг), L-i{xy, x0) и LL' (хв, хл)
справедливы
2) при произвольном тривиализующем диффеомор-
диффеоморфизме ф : UXF —>¦ р (U) и при L (xu, X\)^U диффео-
диффеоморфизм ф (Г?)фЛ1 : (хх, F) -> (х0, F), где фх -=ф|(х, F),
определяется действием нек-рого элемента gcj>?fi;
3) для нек-рой кусочно гладкой параметризации
X : [0,1] —>- L (x0, Xi)cU отображение t h» g^, где
Lf — образ отрезка [0, t] при X, определяет кусочно
гладкую кривую в G, начинающуюся в единице е—
= ?ф°! причем X и X' : [0, 1] -v V (х0, xj)^ U с общим
ненулевым касательным вектором X ?ТХ В опреде-
определяют пути в G с общим касательным вектором в<р(х0,
X)?Te(G) = g, гладко зависящим от х0 и X.
Диффеоморфизм TL наз. параллельным перенесением
вдоль L. Параллельные перенесения вдоль всевоз-
всевозможных замкнутых кривых L (х0, ,г0) составляют
голономии группу связности Г в точке х0, изоморфную
нек-рой подгруппе Ли в G, не зависящей от х0. Кривая
А(у0, j/i) в Е наз. горизонтальной для связности Г,
если Т(pAf)yf=y0 для любого ??[0, 1] при нек-рой ее
кусочно гладкой параметризации. Если заданы L(x0,
xi) и .'/обР (хо)> то всегда существует единственная
горизонтальная А(у0, г/х), наз. горизонта л ь-
ным поднятием кривой L, такая, что
pA=L; она состоит из TLJ1y0. Множество горизонталь-
горизонтальных поднятий всех L в В определяет связность Г од-
однозначно: TL отображает концы всех поднятий кри-
кривой L в их начала.
С. наз. линейной, если 0ф (х, X) при произвольных
фиг зависит от X линейно или, что равносильно, если
для любой у?Е касательные векторы горизонтальных
кривых с началом у образуют в Ту (Е) векторное под-
подпространство Л у, наз. горизонтальным подпростран-
подпространством. При этом Ту(Е)=АуфТу(Ру), где Fy — слой,
проходяпнм через у, то есть Fy—p~l{p(y)). Гладког
распределение Л: у (-* А„ наз. горизонтальным рас-
пределением линейной связности Г. Оно определяет Г
однозначно: горизонтальными поднятиями являются
его интегральные кривые.
Расслоенное пространство Е наз. главным (соответ-
(соответственно пространством однородного типа) и обозначает-
обозначается Р (соответственно Q), если G действует на F просто
транзитивно (соответственно транзитивно), т. е. если
для произвольных z, z' ? F существует точно один
(соответственно существует) элемент g?G, к-рый пере-
переводит z в z'. Пусть G действует на F слева; тогда на Р
определяется ее естественное правостороннее дейст-
действие, в к-ром g определяет Rg : z н> zag. При этом Q
отождествимо с фактормногообразием Р/Н, состав-
составленном из орбит уоН, где // — стационарная под-
подгруппа нек-рой точки из F=GlH. Общее Е отождест-
отождествимо с фактормногообразием (PXF)lG орбит (у, z)oG
относительно действия, определяемого формулой
(У, z)°g=(y°g, g~loz).
Гладкое распределение А на Р является горизон-
горизонтальным распределением нек-рой линейной С. (к-рую
оно определяет однозначно) тогда и только тогда, когда
для произвольных у^Р и g?G. Все горизонтальны!
распределения на Q (соответственно Е) являются об-
образами таких А при канонич. проекции Р —>- Q=P/B
(соответственно естественных поднятий таких А на
PXF при канонич. проекции PXF -+¦ E=(PXF)/G).
Часто линейная С." определяется прямо как распреде-
распределение с указанными выше свойствами. Известно, что
в каждом Р, а вместе с тем и в каждом Q и Е, сущест-
существует нек-рая линейная С.
Исследование линейной С. в Р проводится обычно
с помощью связности формы, к-рая определяет С.
однозначно и может быть положена в основу еще од-
одного ее определения. Важной ее характеристикой яв-
является кривизны форма, с помощью к-рой можно вы-
вычислить алгебру Ли группы голономии.
Впервые понятие С. возникло в 1917 в работе Т. Ле-
ви-Чивита [1] о параллельном перенесении вектора
в римановой геометрии. Уже в 1918 Г. Вейль [2] дал
понятие аффинной связности. В 20-е гг. Э. Картан
(см. [3] — [5]) перешел к исследованию проективной
связности и конформной связности, в 1926 дал общую
концепцию «неголономного пространства с фундамен-
фундаментальной группой» (см. Связности на многообразии), где
эти пространства освещены с точки зрения общей тео-
теории С. В 40-е гг. В. В. Вагнер развивал еще более об-
общую концепцию, близкую по духу (но не но методу)
к современному понятию С. Решающим был 1950,
когда появились сводное изложение В. В. Вагнера [6],
первые заметки Г. Ф. Лаитева, открывающие новые
подходы, особенно в части аналитич. аппарата, и ра-
работа Ш. Эресмана [7], положившая начало современ-
современной глобальной теории С. См. также Вейля связность,
Линейная связность, Риманова связность, Симплекти-
ческая связность, Эрмитова связность.
Лит.: [1] Lev i-C i v i t а Т., «Rend. circ. mat. Palermo»,
1P17, t. 2, p. 173—205; [2] Wcyl H., Raum, Zeit, Materie,
5 Аи!]., В., 1923; [3] Cartan В., «Ann. Soo. poi. math.»,
1923, t. 2. p. 171—221; [4] его же, «Bull. Soc. math, de Fran-
France», 1924 t. 52, p. 205—41; b] его я; е, «Acta math.», 1926,
t. 48, p. 1—42; [6] Вагнер В. В., «Тр. Семин, по вент, и
тенз. анализу», 1950, в. 8, с. 11—72; [7] Ehresmann С,
в кн.: Coll. de Topologie. Bruxelles, 1950, P., 1951, p. 29—55;
[8] Лаптев Г. Ф., «Тр. Моск. матем. ofi-ва», 1953, т. 2, с.
275 —382; [9] Н о М и д з у К., Группы Ли и дифференциальная
геометрия, пер. с англ., М., 1960; [10] Л и х н е р о в и ч А.,
Теория спязностей в целом и группы голономий, пер. с франц.,
ЭТ., I960; [111 Лумисте 10. Г., в кн.: Итоги науки. Сер.
Математика, в. 21 — Алгебра. Топология. Геометрия. 1969,
М., 1971, с. 123—68. Ю. Г. Лумисте.
СГУЩЕНИЯ ТОЧКА, накопления точка,—
то же, что предельная точка. м. И. Войцеховский.
СДВИГ — аффинное преобразование плоскости, при
к-ром каждая точка смещается по направлению оси Ох
па расстояние, пропорциональное ее ординате. В де-
декартовой системе координат С. задается соотношениями
х' ~х-\-ку, у' = у, к Ф 0.
При С. сохраняются площади и ориентация.
С. пространства по направлению оси Ох задается
соотношения ми
х' =x-\-kz, y' = y, z' = z, кфО.
При С. пространства сохраняются объемы и ориента-
ориентация. А. Б. Иванов.
СДВИГА ОПЕРАТОР — оператор Tt, зависящий от
параметра / и действующий на нек-ром множестве Ф
отображений <р : А —>- Е (где А — абелева полугруппа,
Е — множество) по формуле
(говорят также, что Tf — оператор сдвига
на t). В качестве А часто фигурируют R, R+ (тогда
Tf — сдвиг в том или ином пространстве функций
действительного переменного), Z или N (тогда Tf —
сдвиг в том или ином пространстве последовательнос-
последовательностей). Множество Е, а соответственно этому и мно-
множество Ф, обычно наделено нек-рой структурой (век-
(векторного, векторного топологического, нормированного,
метрического, вероятностного пространства).
С. о. используется, в частности, в теории динамич.
систем (см. Сдвигов динамическая система, Бернулли
автоморфизм). Употребляется также термин «С. о. по
траекториям дифференциальных уравнений» (см. Ноши
оператор). П. Л/. Миллионщиков.
СДВИГА ПАРАМЕТР — параметр 0, О^всг/?*,
семейства функций {<pe(-)}i заданных на Я* по сле-
следующему правилу:
фе (•)=ф(- —0) для любого
где <р@ — нек-рая заданная функция на Rk.
Лит.: [1] И б р а г и м о в И. А., Хасьминский
Р. 3., Асимптотическая теория оценивания, М., 1979.
М. С. Никулин.
СДВИГИ ПОЛУГРУПП —преобразования полугрупп,
удовлетворяющие специальным условиям: правым
с д в и г о м полугруппы S наз. преобразование р
такое, что для любых х, y?S имеет место (ху)р=х (ур)\
левый сдвиг определяется симметричным образом, при
этом ради удобства левые сдвиги чаще записывают как
левые операторы. Таким образом, левый сдвиг
полугруппы S — такое ее преобразование X, что для
любых х, y?S имеет место Х(ху) = {Хх)у. Соответственно
последовательность выполнения двух левых сдвигов
в произведении (см. Преобразований полугруппа) осу-
осуществляется справа налево. Произведение двух ле-
левых (правых) С. п. само будет левым (правым) С. п.,
так что множество Л (S) (соответственно Р (S)) всех ле-
левых (правых) С. п. S будет подполугруппой симметрич.
полугруппы of~s- Для произвольного элемента a?S пре-
преобразование Ха(ра), заданное формулой hax— ax (хра=
= .'«) является левым (правым) сдвигом, соответствую-
соответствующим элементу я. Он наз. внутренним левым
(правым) сдвигом. Множество Ло (S) (соот-
(соответственно P0(S)) всех внутренних левых (правых)
С. п. 5 есть левый идеал в Л (S) (правый идеал в P(S)).
Левый сдвиг X и правый сдвиг р полугруппы S наз.
связанны м и, если х(куУ=(хр)у для любых х,
y^S; в этом случае пару (к, р) наз. бисдвигом S.
Для любого a?S пара (ка, ра) есть бисдвиг; он наз.
внутренним бисдвигом, соответствующим
элементу а. В полугруппах с единицей и только в них
всякий бисдвиг внутренний. Множество ТE) всех
бисдвигов полугруппы S есть подполугруппа декар-
декартова произведения ЛE)ХРE); она наз. сдвиго-
сдвиговой оболочкой полугруппы S. Множество
ТоE) всех внутренних бисдвигов есть идеал в ТE);
он наз. внутренней частью Т (S). Отобра-
Отображение т: S—*-Tq(S), заданное формулой х(а) = (Ха,
ра), есть гомоморфизм S на ТоE), называемый, ка-
каноническим. Полугруппа S наз. слабо р е-
д у к т и в н о й, если для любых a, b?S из того, что
ах=--Ьх и ха=хЪ для всех x?S, следует а=Ъ\ т. е. ка-
нонич. гомоморфизм полугруппы S есть изоморфизм.
Если S слабо редуктишта, то Т (S) совпадает с идеади-
затором T0(S) в ЛE)ХРE), т. е. с наибольшей под-
подполугруппой из ЛE)ХРE), содержащей ТоE) в ка-
качестве идеала.
С. п. и, в частности, сдвиговые оболочки играют
существенную роль при изучении идеальных расшире-
расширений полугрупп. Роль сдвиговой оболочки при этом
в известной етепени аналогична роли голоморфа груп-
группы в теории групп.
Лит.: [1] Клиффорд А., Престон Г., Алгебраи-
Алгебраическая теория полугрупп, пер. с англ., т. 1, М., 1972; [2] Pet-
rich М., Introduction to semigroups. Columbus, Ohio, 1973;
[3] его же, «Semigroup Forum», 1970 v. 1, p. 283—360.
Л. Я. Шеврин.
СДВИГОВ ДИНАМИЧЕСКАЯ СИСТЕМА — дина
мическая система ft (или, в иных обозначениях, f(t, ¦))
на пространстве непрерывных функций ф : R —>- S (S —
метрич. пространство), наделенном компактно
открытой топологией (т. е. топологией
равномерной сходимости на отрезках), заданная фор-
формулой
где Tf — сдвига оператор на t, то есть
Таким образом, траектория точки ф в С. д. с. есть
множество всех сдвигов функции ф, т. е. всех функций
вида ф (( 1--т) переменного t?R, а замыкание этой
траектории — множество всех функций вида
где Предел равномерен на каждом отрезке. С. д. с.
наделяется нормированными инвариантными мерйми,
существующими в силу теоремы Боголюбова — Кры-
Крылова (инвариантные меры Боголюбова — Крылова со-
сосредоточены на компактах).
С. д. с. используется в теории динамич. систем, глав-
главным образом — для построения примеров (при этом
в качестве S обычно берут R; пример Маркова
не строго эргодич. системы на компакте, каждая тра-
траектория к-рой всюду плотна, и др.), а также в теории
неавтономных систем обыкновенных дифференциальных
уравнений, где в качестве S берется обычно R" или
нек-рое пространство отображений R" —>. R™ (в теории
линейных однородных неавтономных систем обычно
берется 5=Hom(R", R")).
См. также Особые показатели, Центральные пока-
показатели, в, jif. Миллионщипов.
СЕГМЕНТ — 1) С. на плоскости — плоская
фигура, заключенная между кривой и ее хордой. Пло-
щадь С. круга (кругового сегмента) S=-
= 2y2hr—/*"-, где г — радиус круга, h — высота С.
2) С. в пространстве — часть тела, ограни-
ограниченная плоскостью и отсекаемой ею частью поверх-
поверхности. Объем С. шара (шарового сегмента):
V=1/3nh'i('SR—h), где Л — радиус шара, h — высота
С. шара. Площадь кривой поверхности С. шара: S~
= 2nRk, ^ Л. Б. Иванов.
СЕГМЕНТ — см. Интервал и сегмент.
СЕГРЕ ВЛОЖЕНИЕ — вложение ф : Р» ></>«->-
-+PN произведения проективных пространств РпХРт
в проективное пространство PN, где N~ пт-\-п-\-т.
Если х'^(и0 . . . ип)€Р", !/=(!;„ . . . vm)?Pm, a wtj,
i—О, . . ., п, /==0, . . ., т, — однородные координаты
в PN, то отображение определяется формулами
где wij=u;Vj. Отображение ф корректно определено и
является замкнутым вложением. Образ С. в.(р (РпХ Рт)
наз. многообразием Сегре. Случай и= т= 1
имеет простой геометрич. смысл: (f(P1xP^)— это невы-
невырожденная квадрика в Р3 с уравнением wnw00=w01w10.
Образы (р(хХР1) и <р(Р^Ху) дают два семейства
прямолинейных образующих на квадрике.
Названо в честь Б. Сегре (В. Segre).
Лит.: [)] Ш а ф а ]) с в и ч И. Р., Оснсшы алгебраической
геометрии, М., 1972. Вал. С. Куликов.
СЕДЛО — тип расположения траекторий автономной
системы обыкновенных дифференциальных уравнений
2-го порядка:
x — f(x), x?R'\ f:GczR'l'-+R-, (*)
f^C(G), G — область единственности, в окрестности
особой точки (равновесия положения) х0. Этот тип ха-
характеризуется следующим образом. Существует ок-
окрестность U точки х0 такая, что для всех траекторий
системы, начинающихся в f/\{^0}, как положительные,
так и отрицательные иолутраектории являются уходя-
уходящими (с течением времени покидают любой компакт
VCU). Исключение составляют лишь четыре траекто-
траектории (сепаратрисы седла). Для двух из них
отрицательные полутраектории являются уходящими,
а положительные полутраектории примыкают к точке
х0, для двух других — наоборот. Первые две сепарат-
сепаратрисы наз. устойчивым и, две вторые — неус-
неустойчивыми. Устойчивые сепаратрисы, будучи
дополнены точкой х0, образуют проходящую через .г0
гладкую кривую — устойчивое м н о г о о б-
разие седла. Неустойчивые сепаратрисы вместе
с точкой х0 образуют гладкое неустойчивое
многообразие седла.
С. при этом наз. и сама точ-
точка х0.
Седло z0 неустойчиво по
Ляпунову. Его индекс Пуан-
Пуанкаре равен —1. Для системы
{¦*) класса С1 (/ ? С1 (G)) с нену-
ненулевой матрицей А-=[' (х0) точка
покоя х0 является С. в случае,
когда собственные значения Хх,
Рис. 1. ^2 матрицы 4 удовлетворяют ус-
условию XLX2 <0 (простое С., рис. 1,
где жо--О). но может быть Сив тех случаях, ко-
когда ~K1=()^X2 или %1=X.i=0. В любом из этих случаев
сепаратрисы С. касаются в точке х0 направлений,
определяемых собственными векторами матрицы А.
Если система (*) линейна (f(x) = A (х—х0), А —
постоянная матрица с собственными значениями Х1,к2),
то для нее точка х0 является С. лише> при условии
Х1Х2<_0. Сепаратрисы седла ха в этом случае прямоли-
прямолинейны, а все остальные траектории (отличные от точки
.r0) суть аффинные образы гипербол вида х2=с\х1\ 2/"',
c€R\{0} (рис. 2).
Термин «С.» применяют и для наименования любого
расположения траекторий системы (%) в окрестности
U изолированной
точки покоя х0, при
к-ром из i/\ {.iB} к
точке х0 примыкает .
лишь конечное чис-'
ло т (^2) траекто-
траекторий, и каждая из ЩГШГ Рис. 2.
них, будучи дополне-
дополнена точкой х0, касается в ней определенного направле-
направления (т-с епаратрисное С). С. наз. и пек-рые
типы точек покоя автономных систем обыкновенных
дифференциальных уравнений порядка /гГ^З.
Лит. см. при ст. Особая точка дифференциального уравне-
уравнения А. Ф. Андреев.
СЕДЛО В БЕСКОНЕЧНОСТИ, несобственная
седловая точк а,— тип расположения траекто-
траекторий динамич. системы. Говорят, что динамич. система
/' (или, иначе, /(,р), см. [1]), заданная на R», имеет
С. в б., если найдутся точки хь и числа т^<0, 9&Х),
такие, что последовательности
6
feeN feN
— сходящиеся, a \xk | —>- со при k ->¦ со. Это определе-
определение В. В. Немыцкого было обобщено М. В. Бебутовым
на динамич. системы, заданные на произвольном мет-
рич. пространстве; при этом требование ч\хк\ —*¦ со при
к -*¦ со» заменяется требованием: «последовательность
{¦ik} не содержит ни одной сходящейся подпосле-
подпоследовательности» .
Отсутствие С. в б.— необходимое условие глобаль-
глобальной выпрямляемости динамич. системы (см. Полная не-
неустойчивость). Для того чтобы вполне неустойчивая
динамич. система, заданная на метрич. пространстве,
не имела С. в б., необходимо и достаточно, чтобы фак-
торпространство динамич. системы было хаусдорфовым.
Лит.: 11} Н е м ы ц к и й В. В., С т с п а и о в В. В.,
Качественная теория дифференциальных уравнений, 2 изд.,
М. 1949. В. М. Миллионщиков.
СЕДЛОВАЯ ПОВЕРХНОСТЬ — обобщение поверх-
поверхности отрицательной кривизны. Пусть М — поверх-
поверхность в трехмерном евклидовом пространстве, опреде-
определяемая погружением / : W ->- Е3 двумерного многооб-
многообразия W в Е'-К Плоскость а отсекает от М горбушку,
если среди компонент прообраза множества М\а в W
имеется компонента с компактным замыканием. Часть
поверхности М, соответствующая этой компоненте,
наз. горбушкой (см. рис.). Поверхность М наз.
С. п., если от нее нельзя отсечь горбушки никакой
плоскостью. Примерами С. п. являются однополост-
ный гиперболоид, гиперболич. параболоид, линейча-
линейчатые поверхности. Для того чтобы дважды непрерывно
дифференцируемая поверхность была С. п., необхо-
необходимо и достаточно, чтобы в каждой точке поверхности
ее гауссова кривизна была неположительна. Поверх-
Поверхность, все точки к-рой седловие точки, является С. п.
С. п., ограниченная спрямляемым контуром, по своей
внутренней метрике, индуцированной метрикой прост-
пространства, является двумерным многообразием неполо-
неположительной кривизны. На класс С. п. можно обобщить
ряд свойств поверхностен отрицательной кривизны,
однако эти поверхности не образуют, по-видимому,
столь же естественного класса поверхностей, как вы-
выпуклые поверхности.
Лит.: [1] Б а к е л ь м а н И. Я., Вернср А. Л.,
Кантор Б. Б., Введение в дифференциальную геометрию
«в целом», М., 1973; [2] Ш е ф е л ь С. 3., Исследования по гео-
геометрии седловых поверхностей, Новосиб., 1963.
Д. Д. Соколов.
СЕДЛОВАЯ ТОЧКА — точка гладкой поверхности,
вблизи к-рой поверхность лежит по разные стороны от
своей касательной плоскости. Если С. т. является
точкой двукратно непрерывно дифференцируемой по-
поверхности, то ее гауссова кривизна в этой точке не-
неположительна. С. т. является обобщением гипербо-
лич. точки. д. д. Соколов.
СЕДЛОВАЯ ТОЧКА (в теории игр) функции
F, заданной на декартовом произведении двух множеств
XXY,— точка (х*, y*)?XXY, для к-рой
F(x*, y*) = maxF(x,
хеХ
i/eY
у).
Наличие С. т. у функции F равносильно существованию
оптимальных стратегий у игроков в антагонистической
игре Г=(Х, У, F). В. Л. Крепе.
СЕДЛО-УЗЕЛ — тип расположения траекторий ав-
автономной системы обыкновенных дифференциальных
уравнений 2-го порядка:
i = f(x), x?R\ /:G-^R2, (*)
/?C(G), G — область единственности, в окрестности
особой точки х0. Этот тип характеризуется следующим
образом: нек-рая окрестность U точки х0 разбивается
примыкающими к х0 полутраекториями (сепарат-
(сепаратрисами С.-у.) на т криволинейных секторов
C<:т<-|-о°), из к-рых h, 2<:fe<m, являются седловы-
ми, а остальные — открытыми узловыми; каждая
примыкающая к х0 полутраектория, будучи дополне-
дополнена точкой х0, касается в ней определенного луча.
С.-у. наз. при этом и сама точка х0.
С.-у. неустойчив по Ляпунову. Его индекс Пуанкаре
равен 1—(А/2). Если f^C1(G), а матрица A=f (хо)^О,
то особая точка х0 может быть для системы (*) С.-у.
лишь в случаях, когда собственные значения Хг, Х2
матрицы А удовлетворяют одному из следующих усло-
условий:
а) К1 = 0 Ф Х2; б) А,1 = А,а = 0.
В любом из этих случаев точка х0 может быть для сис-
системы (*) также седлом или узлом, а в случае б) и точ-
точкой иного типа. Если же она является С.-у., то для
Рис. 1.
Рис. 2.
нее m=3, k=2, а все примыкающие к х0 полутраекто-
рии системы касаются в этой точке направлений, оп-
определяемых собственными векторами матрицы А (см.
рис. 1 и 2, где жирными линиями изображены сепарат-
сепаратрисы С.-у. хо = (), а стрелки указывают налравление
движения по траекториям системы с возрастанием t;
оно может быть и противоположным).
Лит.: [1] Б а у т и н Н. Н., ЛеонтовичЕ. А., Ме-
Методы и приемы качептпен-ного исследования динамических сис-
систем на плоскости, М., 197Н. А. Ф. Андреев,
СЕКАНС — одна иа тригонометрических функций:
и = sec х = ,
•' cos х '
другое обозначение sc т. Область определения — вся
числовая прямая за исключением точек, абсциссы
к-рых
* = -5.Bв+1), и = 0, ±1, ±2, ...
С.— неограниченная четная периодическая (с периодом
2л.) функция. Производная С:
(sec х)' = s'"'x =tg x sec x.
к ' cos2 ж в
Интеграл от С:
\sec??te = ln tg (—+т) +С-
С. разлагается в ряд
|
5 |
т; — (т) - (т) -ж2
Ю. А. Горькое.
СЕКВЕНЦИАЛЬНО КОМПАКТНОЕ ПРОСТРАНСТ-
ПРОСТРАНСТВО — топологическое пространство (условие
Больцано — Вейерштрасса), любая бес-
бесконечная последовательность точек к-poro содержит
сходящуюся подпоследовательность. В классе TV
пространств С. к. п. является счетно компактным
пространством. Если к тому же пространство удов-
удовлетворяет первой аксиоме счетности, то из его счет-
счетной компактности следует секвенциальная компакт-
компактность. С. к. п. не обязательно является бикомпактным
пространством: таково, напр., множество всех поряд-
порядковых чисел, меньших первого несчетного числа, на-
наделенное топологией, база к-рой — всевозможные ин-
интервалы, м. II. Войцеховекий.
СЕКВЕНЦИАЛЬНОЕ ПРОСТРАНСТВО — топологи-
топологическое пространство X такое, что из АсХ и Л?=(Л]
(т. е. множество А незамкнуто) следует существование
последовательности х/,, k~ i. 2, . . ., точек из А, схо-
сходящихся к нек-рой точке [Л]\4. Если из х?[А]сХ
всегда следует, что существует последовательность х^
точек из А, сходящаяся к х, то X наз. простран-
пространством Ф р е Ш е — У р Ы С О Н а. М. И. Войцеховекий.
СЕКВЕНЦИЙ ИСЧИСЛЕНИЕ — одна из формули-
формулировок предикатов исчисления. Благодаря удобной фор-
форме вывода Си. находит широкое применение в до-
доказательств теории, основаниях математики, при ав-
томатпч. поиске вывода. С. и. было предложено Г.
Генценом в 1934 (см. fl|). Ниже приводится один из
вариантов классич. исчисления предикатов в форме
Си.
Набором формул чаз. конечное множество
формул нек-рого логико-математического языка О,
причем в этом множестве допускаются повторения фор-
формул. Порядок формул в наборе Г несуществен, но для
каждой формулы указано, в скольких экземплярах
она присутствует в Г. Набор формул может быть и
пустым. Набор фГ получается из Г присоединением
одного экземпляра формулы ф. Секвенцией наз.
фигура вида Г-vA, где Г и Д —наборы формул,
Г наз. антецедентом секвенции, а Д—ее
с у к ц е д е н т о м.
Аксиомы Си. имеют вид фГ —v Дф, где Г, Д — про-
произвольные наборы формул, а ф — произвольная ато-
атомарная (элементарная) формула. Правила вывода ис-
исчисления устроены очень симметрично и вводят ло-
гич. связки в антецедент или сукцедент секвенции:
<И>Г->-Д , > Г-> Лф; Г^ Дф .
(л ->)¦
v ' (Ф V ip) Г-> Д ' v v ' Г-
, _ ,, Г -> АФ; i|J -> А , (^-j)^
Д(фЛ*
(фЭ1|))Г->Д ' v ~^ Г — Д (ф Э
,1 г - Д(Р • /* ~п Фг -*¦ д .
-]фГ-»д ' > '' г
И*! <)Г->- А . , . Г->-Аф
Г1
, ч фГ-> Д , , Г -»¦ Дф (ж I 1) эжф
' ""*"' э^ф (г/1 х) г -* д ' '"*" ' г -»¦ дзжф ¦
Здесь в правилах (->- V) и C ->-) предполагается, что
переменная у не есть параметр Г и А, а ж не есть па-
параметр ф.
Си. эквивалентно обычной форме исчисления преди-
предикатов в том смысле, что формула ф выводима в исчис-
исчислении предикатов тогда и только тогда, когда секвен-
секвенция —>- ф выводима в С. и. Для доказательства этого
утверждения существенна основная теоре-
теорема Генцена (или теорема о нор мал и-
з а ц и и), к-рая для С. и. может быть сформулирована
следующим образом: если в С. и. выводимы секвенции
Г -> Аф и фГ —v А, то выводима и секвенция Г —»- Д.
„ Г->- Дф; фГ->- А
Правило вывода г^ д наз. правилом
сечения, и теорема о нормализации утверждает,
таким образом, что правило сечения допустимо в
Си. или что добавление правила сечения не изме-
изменяет объема выводимых секвенций. Ввиду этого теоре-
теорему Генцена наз. также теоремой об устра-
устранении сечения.
Симметричное устройство С. и. в значительной мере
облегчает изучение его свойств, поэтому в теории до-
доказательств важное .место занимает поиск секвенциаль-
секвенциальных вариантов прикладных исчислений: арифметики,
анализа, теории типов и доказательство для таких ис-
исчислений теоремы об устранении сечения в той или
иной форме (см. [2], [3]). Найдены секвенциальные
варианты и для многих исчислений, основанных на
неклассич. логиках — интуиционистской, модальных
и релевантных логиках и др. (см. [3], [4]).
Лит.: [1] Математическая теория логического вывода. Сб.
переводов, М., 1967; [2] Т а к е у т и Г., Теория доказательств,
пер. с англ., М., 1978; [3] Д р а г а л и н А. Г., Математический
интуиционизм. Введение в теорию доказательств, М., 1979;
HJ Ф е й с Р., Модальная логика, пер. [с англ.], М., 1974.
А. Г. Драгалин.
СЕКВЕНЦИЯ — выражение вида
Аи ..., А„-> Ви ..., Вт,
где Ai, . . ., А„, #ь . . ., Вт— формулы. Читается:
«при допущениях Аг, . . ., Ап имеет место Вг или В2,
или . . ., или Вт». Часть С, стоящая слева от стрелки,
наз. антецедентом; часть С, стоящая справа
от стрелки, наз. сукцедентом (консеквен-
том). Формула (Ах&. . . . &A,J)z^(B1 V ... VBm)
(пустая конъюнкция обозначает ложь, пустая дизъюн-
дизъюнкция — истину) наз. формульным обра-
образом С. Г. Е. Минц.
СЕКТОР — 1) С. на плоскости — плоская
фигура, ограниченная двумя полупрямыми, исходя-
исходящими из внутренней точки фигуры, и дугой контура.
С. круга (круговой сект о р) —¦ фигура, ог-
ограниченная двумя радиусами и дугой, на к-рую они
опираются. Площадь С. круга: S=ir/2, где г — ра-
радиус круга, I — длина дуги.
2) С. в пространстве — часть тела, ограни-
ограниченная конич. поверхностью, вершина к-рой нахо-
дится внутри тела, и вырезаемой частью поверхности
тела. Шаровой сектор — тело, возникающее
при вращении сектора большого круга вокруг одного
из радиусов (шаровой С. 1-го рода) или вокруг диа-
диаметра, не пересекающего его дуги (шаровой С. 2-го
рода). Объем шарового сектора: F—- 1/3яЛ2/г, где i? —
радиус сферы, h — проекция хорды, стягивающей дугу
С. на ось вращения. бсэ-з.
СЕКТОР в теории обыкновенных диф-
дифференциальных уравнений. 1) С— от-
открытый криволинейный сектор S с вершиной в изо-
изолированной особой точке О автономной системы обык-
обыкновенных дифференциальных уравнений 2-го порядка:
{¦*)
^ G — область единственности, удовлетворяю-
удовлетворяющая следующим четырем условиям. 1) Каждая из бо-
боковых стенок S является ТО-к р и в о и системы (*)
(полутраекторией, примыкающей при | t\—>--\- оок точке
О, касаясь в ней определенного направления). 2) Зад-
Задней стенкой S является простая параметрич. дуга
(гомеоморфный образ отрезка). 3) В 5\{0} нет особых
точек системы (*). Четвертым условием является
одно из трех следующих. 4а) Все траектории системы
(*), начинающиеся в S, покидают этот сектор как
с возрастанием, так и с убыванием t; такой С. наз.
гиперболическим, или седловым (рис. 1).
46) Все траектории системы (*), начинающиеся в S
в достаточной близости от О, с возрастанием t, не вы-
выходя из S, примыкают к точке О, а с убыванием t
покидают S (или наоборот); такой С. наз. парабо-
параболическим, или открытым узловым
(рис. 2). 4в) Все траектории системы (*), начинаю-
начинающиеся в S в достаточной близости от О, как с возрас-
возрастанием, так и с убыванием t, не выходя из S, примы-
примыкают к точке О, образуя вместе с О замкнутые кривые
(петли), причем из любых двух петель одна охва-
охватывает другую; такой С. наз. эллиптическим,
или замкнутым узловым (рис. 3).
Для аналитич. системы (*), имеющей ГО-кривые,
круг Q достаточно малого радиуса с центром в точ-
точке О всегда может быть разбит на конечное число С.
описанного вида: h гиперболических, р параболиче-
параболических и е эллиптических (см. [1], [2]). Выявить все
эти С, определить тип каждого из них и установить
для них закон следования друг за другом при обходе
точки О по границе круга Q (и тем самым выяснить
топологич. структуру расположения траекторий сис-
системы (*) в окрестности точки О) можно, напр., с по-
помощью Фроммера метода. Для чисел k, p и е имеются
априорные оценки сверху через порядок малости нор-
нормы ||/(г)|| при х-+0 (см. [1], [4], [5]).
Иногда (см., напр., [3]) понятие «С.» определяется
свободнее: в гиперболич. и иараболич. С. допускается
наличие петель, покрывающих множество, не имеющее
предельных точек на задней стенке С, а в эллиптпч.
С.—наличие петель, не охватывающих друг друга.
При этом первая фраяа предыдущего абзаца сохраня-
сохраняет силу и для систем (*) общего вида, а индекс
Пуанкаре особой точки О системы (*) выражается
формулой Бен диксон а:
i= l+{e — h)/2.
Лит.: [1] Bcndixson I., «Acta math.», 1901, v. 24,
p. 1—88; [2] Андронов А. А., Л е о н т о в и ч Е. А.,
Гордон И. И., М а й е р А. Г., Качественная теория дина-
динамических систем второго порядка, M.,sl966; [3] Хартман Ф.,
Обыкновенные дифференциальные уравнения, пер. с англ.,
М., 1970; [4] Б е р л и н с к и й А. Н., «Докл. АН СССР»
1969, т. 187, Л» 3, с. 502 —05; [5] С а г а л о в и ч М. Е., «Диф-
ференц. уравнения», 1979, т. 15, №2, с. 360—62.
2) Сектор Фроммера, нормальная
область Фроммера,— круговой С.
Л' = {(г, ср)|О < г^б, |<р —<pol<e}
с вершиной в изолированной особой точке О(х=х0)
системы (*) (см. п. 1), боковыми стенками ОА и ОВ,
Фл=фо—8, фв=фо+е, и задней стенкой ЛВ (здесь
г, <р — полярные координаты на ж-плоскости с по-
полюсом в точке О, б, е, фо?К), удовлетворяющий сле-
следующим условиям:
A) ф~({'(| -исключительное направ-
направление гнете .м ы (*) в точке О, т.е. сущест-
существует последовательность хк~хй~\-{гь cos Фь '> si" Ч'к),
/с=-1, 2, . . ., г^-»-0, ф^ —v ф0 при к —v+oo, такая,
что если а (*) = (/(.г) О1 х— ха), то tg а (хь) -*¦ 0 п])и
к—у--оо, и такое направление единственно и А,
B) tga(i)^=0 для любого х?ОА()ОВ,
C) а(х)фк/2 для любого x?N.
в
ff
Рис. 4.
Пусть угол а (х) отсчитывается от вектора .г—х0 и
имеет знак направления отсчета. Сектор N называется:
нормальной областью Фроммера
1-го типа (обозначение N{), если tg a (.t)<0 при
х?ОА, tga(a;)>0 при х?ОВ;
нормальной областью 2-го типа
(JV2), если tga(i)>0 на ОА, tg a (i)<0 на OB;
нормальной областью 3-го типа
(Лгз), если tg а(х) на О А и на ОВ имеет один и тот же
знак. Эти области были вве-
введены М. Фроммером [1].
Траектории системы (*)
в нормальных областях
Фроммера ведут себя
следующим образом. Об-
Область N1 покрыта О-кри-
выми системы (рис. 4).
Они образуют открытый
пучок — семейство одно-
1 именных О-кривых, не-
Рис 0 прерывно зависящее от
параметра, пробегающего
открытый промежуток. В области N2 существует
либо (а) единственная О-кривая (рис. ), либо (б)
бесконечно много О-кривых (замкнутый пучок, рис. 6).
В области Л'з либо (а) существует бесконечно много
О-кривых (полуоткрытый пучок, рис. 7), либо (б) не
существует О-кривых (рис. 8). В нормальной области
N любого типа О-кривые при t —>- -|- оо (или t -*¦ —оо)
примыкают к точке О по направлению Ф=фо, а с убы-
убыванием (возрастанием) t покидают область N; все ос-
остальные траектории покидают область Л' как с воз-
возрастанием, так и с убыванием t. Задачи различения
случаев (а) и (б) для областей N2 и JV3 наз. соответст-
соответственно 1-й и 2-й проблемами различе-
различения Фромм ер а.
Если система (*) имеет в точке О конечное число
(>0) исключительных направлений, каждое из них
В
Рис. 7. Рис. R.
можно заключить в нормальную область N, и для всех
областей N, и JV3 будут решены проблемы различения
Фромме ра, то топологич. структура расположения
траекторий системы в окрестности точки О будет вы-
выяснена полностью, ибо секторы с вершиной в О, рас-
расположенные между нормальными областями, в доста-
достаточной близости от точки О полностью пересекаются
траекториями системы (как на рис. 8). Такая ситуация
имеет место, напр., в случае, когда
), Р = (Ри Р.г),
Pi, Р> — формы степени п^1 от компонент хг, х%
вектора х,
р (х)=о (flarf) при ;:./¦ ' ->0,
причем выполняются следующие условия: форма
xiPi(x)—X2^"i (-r) имеет действительные линейные мно-
множители; формы Pj, P2 не имеют общих действительных
линейных множителей; p?t'n + 1. При этом в каж-
каждой из областей Л'г, Л будет иметь место располо-
расположение (а).
Аналоги нормальных областей Фроммера введены и
для систем вида (*) порядка ^3.
Лит.: Ш F rummer M., «Math. Ann.», 1928, Bd 99, S.
222—72; [2] H e м ы ц и и й В. В., Степанов В. В.,
Качественная теория дифференциальных уравнений, 2 изд.,
М.—Л., 1949; [3] .Андреев А. Ф., в сб.: Тр. Четвертого
Всесоюзного матем. съезда, т. 2, JT., 1964, с. 3^4—402.
А. Ф. Андреев.
СЕКУНДА — единица измерения плоских углов,
равная ]/збоо части градуса или 1/т части минуты;
обозначается знаком ". Метрическая С. —1/106
часть прямого угла; обозначается знаком сс.
СЕКУЩИХ МЕТОД — метод вычисления нулей не-
непрерывных функции. Пусть в [а, Ь] содержится нуль а
непрерывной функции /(х); х0, хх — различные точки
этого отрезка. Итерационная формула С. м.:
^ = Хft = 1 2 A)
Если последовательность {хк} сходится, то обязатель-
обязательно к нулю функции /(.г). При наличии у / непрорывной
производной на [а, Ь] локальная сходимость С. м.
к простом}' корню будет сверхлинейной. Если усилить
требования к гладкости /, можно указать точный по-
порядок (локальной) сходимости [1]. Именно, для /?
?С-[а, Ь\ и а такого, что /(а)=0, /' (а)=^0, /"(а)^=0,
lim L^±iZ^J = fc
ft^x \xk-a\P
Здесь р = (\гЪ+1)/2~1,Ы8, fr--|/"(a)/2/'(а)|.
Сверхлинейпая сходимость См. для гладких функ-
функций — очень важное обстоятельство, поскольку вы-
числения производных не требуется и на каждом шаге
вычисляется лишь одно новое значение функции. Так,
для сравнения, в методе Ньютона, порядок (локаль-
(локальной) сходимости к-рого равен 2, на каждом шаге тре-
требуется вычисление значения функции и ее производ-
производной, что, как правило, но менее трудоемко, чем вычис-
вычисление двух значений функции.
Поскольку сходимость С. м. зависит от гладкости
функции и выбора начальных приближений, в стан-
стандартных машинных подпрограммам вычисления нулей
непрерывных функций этот метод комбинируется с
каким-либо методом, обладающим гарантированной
сходимостью, напр, методом деления отрезка пополам.
На каждом шаге такого комбинированного метода ко-
корень а локализован в отрезке [а^, Ьк], на концах
к-рого функция меняет знак (предполагается, что ято
условие выполнено для исходного отрезка [а, Ь]).
В соответствии с нек-рым тестом очередное приближе-
приближение выбирается либо по формуле A), либо по формуле
деления пополам. При этом если / (.т) — гладкая функ-
функция, то итерации, начиная с нек-рого номера к0,
автоматически идут по С. м. Возможна еще более
сложная комбинация методов, напр, алгоритм ZEROIN
(см. [2]), в к-ром, кроме упомянутых выше, исполь-
используется еще метод обратной квадратичной интерполя-
интерполяции. Иногда С. м. называют метод с итерационной
формулой
**-(/(ЖА) _/(Л** / (я.Й_Х) , k = U 2, ... B)
Другое название метода B) — метод ложного
положения, или regula falsi. Такой метод схо-
сходится лишь линейно.
При обобщении См. на случай системы уравнений
возможен двоякий взгляд на итерационную формулу
A). Можно считать, что она получена из формулы ме-
метода Ньютона дискретной аппроксимацией производ-
производной. Другая возможность — считать, что для f(x)
произведена линейная интерполяция по точкам
(жА_], ](xk-i))Ti (хь, ](хк)) и заж* + 1 взят нуль линейной
интерполянты. Обе интерпретации позволяют получить
большое количество многомерных аналогов С. м.;
нек-рые из них (но далеко не все) имеют тот же поря-
порядок (локальной) сходимости р=A-(- У5 )/2 (см. [3]).
Лит.: [1] Brent R. P., Algorithms for minimization wit-
without derivatives, Englewood cliffs (N. J .), 1973; Г2] Ф о p-
c а й т Д ш., Малькольм М., М о у л е p К., Машинные
методы математических вычислений, пер. с англ., М., 1980;
[3] Ортета Дж., Рейнболд-tB., Итерационные методы
решения нелинейных систем уравнений со многими неизвест-
неизвестными, пер. с англ., М., 197Г). X, Д. Нкримов.
СЕКЦИОННАЯ КРИВИЗНА — риманова кри-
кривизна дифференцируемого риманова многообразия М
в точке р в направлении двумерной плоскости а (в на-
направлении бивектора, определяющего плоскость а
В ТОЧКе р Многообразия М). Л. А. Сидоров
СЕЛЬБЕРГА РЕШЕТО, Сельберга метод,—
специальный и в то же время достаточно универсаль-
универсальный решета метод, созданный А. Сельбергом [1].
С. р. позволяет хорошо оценивать сверху просеиваю-
просеивающую функцию S (A; P, z), обозначающую количество
элементов конечного множества А целых чисел, к-рые
не делятся на простые числа р <г и принадлежат нек-
рому множеству Р простых чисел.
Пусть P(z)=JJ pp. Метод Сельберга основан
на очевидном неравенстве
S(A;P, *)<2asABd|a;dlP(z)^J' <*)
к-рое верно при Ях=1 для произвольных действитель-
действительных чисел \д (d^2). Идея Сельберга состоит в том,
чтобы, положив A.rf=0 для djsz, минимизировать пра-
правую часть неравенства (*) путем надлежащего вы-
выбора оставшихся чисел Xd2rf
В комбинации с другими методами решета С. р.
позволяет получать оценки снизу, особенно сильные
при использовании весовых функций.
Лит.: [1] S е 1 h е г к A., «Norske Vid. Sclsk. Forh.», 1947,
Bd 19, ,M 18, p. 64—67; [2] П р а х а р К., Распределение про-
простых чисел, пер. с нем., М., 1967; [3] Halberstam H.,
К i chert H., Sieve methods, L.— [а. о.], 1974.
Л. М. Бредихин.
СЕМАНТИКА в математической логи-
логике — исследование интерпретаций логического исчисле-
исчисления, формальной аксиоматич. теории; изучение смысла
и значения конструкции формализованного языка
теории, способа понимания его логич. связок и фор-
формул. С. уделяет внимание возможности точного опи-
описания и определения таких понятий, как «истина», «оп-
«определимость», «обозначение», по крайней мере приме-
применительно к точно описанным языкам. В несколько
более узком смысле под С. формализованного языка
понимают систему соглашений, определяющих пони-
понимание формул языка, задающих условия истинности
атих формул.
С. логич. связок в классической и интуиционистской
логике носит экстенсиональны и харак-
характер, т. е. истинность сложного высказывания опре-
определяется только характером истинности составляющих
его высказываний. В иных классич. логиках, напр,
релевантных, может учитываться и смысловое содер-
содержание понятий (такие логики наз. интенсио-
интенсиональными). В такого рода логиках, напр., не
обязательно, чтобы все истинные высказывания были
эквивалентны.
Построение четкой С. достаточно сложных форма-
формализованных языков типа языков аксиоматической тео-
теории множеств является трудной проблемой. Это
связано ио существу с тем, что процесс абстрагирова-
абстрагирования в математике является весьма сложным и много-
многоступенчатым с привлечением таких глубоких и неоче-
неочевидных абстракций, как абстракция актуальной бес-
бесконечности ИЛИ абстракция потенциальной осущест-
осуществимости. В результате объем объектов исследования
в математике, способы обращения с этими объектами
и способы доказательства утверждений относительно
таких объектов, как множества произвольной при-
природы, становятся весьма неопределенными. При не-
неосторожном обращении с принципами доказательства
в рамках теории возникают антиномии, напр, пара-
парадокс Рассела в теории множеств, В такой ситуации
приходится отказываться от построения исчерпываю-
исчерпывающей и интуитивно убедительной С. языка и ограничи-
ограничиваться формулировкой нек-рых семантич. соглашений.
При формализации теории при этом стремятся, чтобы
правила вывода полученного исчисления были кор-
корректны по отношению к этим соглашениям, т. е. при
применении к верным формулам вновь давали верные
формулы. Полученная формальная система может
уже изучаться в рамках нек-рой метатеории с более
ясной С.
Часто семантич. понятия для нек-рого языка могут
быть точно сформулированы в рамках более богатого
языка, играющего для первого роль метаязыка. Напр.,
средствами теории мпожеств можно дать строгое мате-
матич. определение (классической) истинности фор-
формулы данного языка 1-го порядка на алгебраич. си-
системе. Это понятие является основным в моделей теории.
С другой стороны, как показал А. Тарский (A. Tarski,
193A), для достаточно богатых теорий их истинность
не может быть выражена на языке самой теории.
Широко изучаются С. неклассич. теорий, напр, ма-
тематич. теорий, развиваемых в рамках интуициониз-
интуиционизма. Роль моделей в таких исследованиях играют ал-
алгебраич. структуры, учитывающие неклассич. характер
понимания логич. связок. Таковы, напр., Крипке мо-
дели, реализуемость по Клини, ступенчатая семанти-
семантическая система А. А. Маркова.
Лит.: Ш Карнап Р., Значение и необходимость пер.
с англ., М., 1959; [2] Ч ё р ч А., Введение в математическую
логику, пер. с англ., М., 1960; [3] К л и п и С. К., Введение в
метаматематику, пер. с англ., М., 1957; [4] Д р а г а л и н А. Г.,
Математический интуиционизм. Введение в теорию дока-
доказательств, М., 1979; [5] Ф е й с Р., Модальная логика, пер. с
англ., М., 1974. А. Г. Драгалин.
СЕМИИНВАРИАНТ — 1) С— то же, что полуин-
полуинвариант. 2) С.— одна из числовых характеристик
случайных величин, родственная понятию момента
старшего порядка. Если ?=(§j, . . ., |&) — случайный
вектор, фг {t)=Eel<>- s> _ его характеристич. функ-
функция, *=(*!, . . ., tk), t?R
и для нек-рого n^l моменты Ell/I"<°°, г~1, . . ., к,
то существуют (смешанные) моменты
для всех неотрицательных целочисленных v,,
таких, что Vj-f-- . .+Vft<:n. Тогда
Ф6 (*) =
где 1*1=^1 + . • -+l*fel и для достаточно малых \t\
главное значение In ф* (t) представимо по формуле
Тейлора в виде
VA)
*
где коэффициенты «g " •••¦ v*> наз. (смешанными)
семиинвариантами, или кумулянта-
кумулянтами, порядка v=(vb . . ., vk) вектора |=(|j, . . .,|fc).
Для независимых случайных векторов i^dx,...
• • -, Ik) и ¦П=('Пь • • •> f\k)
то есть С. суммы независимых случайных векторов
есть сумма С. Именно это и послужило причиной тер-
термина «семиинвариант», отражающего свойство адди-
аддитивности для случая независимых величин (но это
свойство уже, вообще говоря, не верно для зависимых
величин).
Между моментами и С. справедливы следующие фор-
формулы связи:
m(v)_'V*- - ТТ9
1 ~ Zu q J,O)!...l«l! XXp = l "l| >
где 2* означает суммирование по всем упорядочен-
упорядоченным наборам целых неотрицательных векторов X{f>),
1 | >0, дающих в сумме вектор v. В частности, если
— случайная величина (fc=l), mn=m%i>=?'Eln, srl=
sin\ то
тз = S3 -(- 3sjs2 -)- «
Cm*.
Лит.: [1] Леонов В. II., Ширяев А. Н., «Теория
вероятн. и ее примен.», 1959, т. 4, в. 3, с. 342—53.
А. Н. Ширяев.
СЕМИМАРТИНГАЛ — стохастический процесс, пред-
ставимый в виде суммы локального мартингала и
процесса локально ограниченной вариации. При фор-
формальном определении С. исходят из допущения, что
всв рассмотрения ведутся на стохастич. базисе (Q,
JF, F, Р), где F=(JFt)t>o- Стохастич. процесс Х=
= (Х/, <f"})(^о наз- семимартингалом, если
его траектории непрерывны справа и имеют пределы
слева и он представим в виде X-t=Mf\-Vf, где М=
= (Mf, ft) — локальный мартингал, a V=(Vf, Jfj) —
процесс локально ограниченной вариации, т. е.
|d^(w) |< оо, t >0, ш?Й.
Такое представление, вообще говоря, неоднозначно.
Однако в классе разложений с предсказуемыми про-
процессами V рассматриваемое представление единственно
(с точностью до стохастич. эквивалентности). К классу
С. относятся (помимо локальных мартингалов и про-
процессов с локально ограниченными вариациями) ло-
локальные супермартингалы и субмартингалы, процессы
X с независимыми приращениями, для к-рых функ-
функция f(t)=^ei^Xi является функцией локально огра-
ограниченной вариации для любого A?R (и значит — все
процессы со стационарными независимыми прираще-
приращениями), процессы Ито, процессы диффузионного ти-
типа и др. Класс С. инвариантен относительно эквива-
эквивалентной замены меры. Если X есть С, а /=/ (х) — дваж-
дважды непрерывно дифференцируемая функция, то /(Х)=
~(f(Xf), JF() также С. При этом (формула Ито)
=/ (X,) |-^/'(X,_)<LY,+yJ/' (X,_) d [X, Х]\+
или, что эквивалентно,
'(Xs-) dXs+±[j" (Xs-)d[X,X]s
t [f(xs)-f(Xs-)-f{Xs-)AXs-
< , <
где [X, X]—([X, X]f, <fFf) — квадратич. вариация
семимартингала X, то есть
[X, X]t=Xl+2\jtQXs-dXs,
ix, xrt = [X,xh-^o<s<t{AXs),
— непрерывная часть квадратич. вариации [X, X],
ДХ5.= Х5—Xs_, а рассматриваемые интегралы по-
понимаются как стохастич. интегралы по С.
Если X есть С, то процесс Х(<1)={Х\<1), JFt) с
имеет ограниченные скачки, | AX(t<:l>| <1, и в силу
этого он допускает единственное представление вида
где B = {Bt, JFf) — предсказуемый процесс локально
ограниченной вариации, a M-~(Mf, gft) — локаль-
локальный мартингал. Этот мартингал однозначным образом
представим как M=-MCjrMd, где МС={МС^() —
непрерывный локальный мартингал (непрерывная мар-
гннгальная составляющая семимартингала X), а
Md=(Mt, JF?) — чисто разрывный локальный мар-
мартингал, к-рый может быть записан в виде
где d(x=jx (со, dt, dx) — случайная мера скачков семи-
мартингала X, то есть
ц(ш, @, f], Г)=2о<«<«/(А-
a dv=v(co, d«, <?r) — ее компенсатор. Поскольку
У ДХ./МДЛГЛ > 1)=Г f 4*^Щ
то всякий семимартингал X допускает представление
|i |> xd»,
к-рое наз. каноническим представле-
представлением (разложением).
Набор (предсказуемых) характеристик (?, <Мс>, v),
где <iW"c> — квадратич. характеристика Мс, т. е.
такой предсказуемый возрастающий процесс, что
(МсJ— <Л/<> является локальным мартингалом, наз.
¦г р и п л е т о м локальных (предсказуемых) характе-
характеристик X.
Лит.: LU J а с о d J., Calcul slocliastique et problemes de
mar-tingales, В., 1979 (Lecture notes in mathematics, № 714).
A. H. Ширяев.
СЕПАРАБЕЛЬНАЯ АЛГЕБРА — конечномерная по-
полупростая ассоциативная алгебра А над полем к,
остающаяся полупростой при любом расширении К
поля к (т.е. алгебра А^^К полупроста для любого
поля К^к). Алгебра А сепарабельна тогда и только
тогда, когда центры простых компонент этой алгебры
(см. Ассоциативные кольца и алгебры) являются сепа-
рабельными расширениями поля к.
Лит.: Ll] Ван дер ВарденБ. Л., Алгебра, пер. с
нем., 2 изд.,М., 1979; [2] К э р т и с Ч., Р а й н е р И., Теория
представлений конечных групп и ассоциативных алгебр, пер.
с англ., М., 19U9. Л. А. Бокутъ.
СЕПАРАВЕЛЬНОЕ ОТОБРАЖЕНИЕ — доминантный
морфизм / неприводимых алгебраич. многообразий X
и Y, / : X —>- У, для к-рого поле К (X) является сепа-
рабельным расширением подполя f*K(Y) (изоморф-
(изоморфного К (Y) ввиду доминантности). Несепарабельные
отображения существуют только тогда, когда характе-
характеристика р основного поля больше нуля. Если / — ко-
конечный морфизм и его степень не делится на р, то он
сепарабелен. При С. о. для точек в нек-ром открытом
подмножестве UcX дифференциал (df)x отображения /
сюръективно отображает касательное пространство
Тх. х в ^"к,/(л) и наоборот: если точки х и f(x) неосо-
неособые и Xdj)x — сюръективен, то / есть С. о.
Термин «сепарабельность» употребляется для мор-
физмов и в ином смысле. Морфизм / : X —у Y схем X
и Y наз. сепарабельным, или (чаще) о т д е-
л и м ы м, если диагональ в XX уХ замкнута. Компо-
Композиция отделимых морфизмов отделима; f : X —>¦ Y
отделим тогда и только тогда, когда для любой точки
y?Y существует такая окрестность V^y, что морфизм
/:/~1A7)-> V отделим. Морфизм аффинных схем
всегда отделим. Существует критерий отделимости
ДЛЯ Нётеровых схем. А. Н. Рудаков.
СЕПАРАБЕЛЬНОЕ ПРОСТРАНСТВО — топологиче-
топологическое пространство, обладающее счетной базой. Про
такие пространства иногда говорят, что они удовлет-
удовлетворяют второй аксиоме счетности. м. И. Войцеховский.
СЕПАРАВЕЛЬНОЕ РАСШИРЕНИЕ поля — рас-
расширение К/k такое, что для нек-рого натурального п
поля К ж У линейно разделены над к (см. Линейно
разделенные расширения). Расширение, не являющееся
сепарабельным, наз. не сепарабельным.
В дальнейшем рассматриваются только алгебраич.
расширения (о трансцендентных сенарабельных рас-
расширениях см. Трансцендентное расширение). Конеч-
Конечное расширение сеиарабельно тогда и только тогда,
когда отображение следа Sp : К —у к является ненуле-
ненулевой функцией. Алгебраич. расширение сепарабельно,
если любое конечное его подрасширение сепарабельно.
В характеристике 0 все расширения сепарабельны.
С. р. образуют отмеченный класс рас-
расширений, т. е. в башне полей Lz)XZ3fe расшире-
расширение Ык сепарабельно тогда и только тогда, когда
сепарабельны и ЫК и К/к. Если Кх!к и К2/к суть
С. р., то и K-^Kjk сепарабельно; для С. р. К/к и про-
произвольного расширения Ык расширение KL/L снова
сепарабельно. Расширение К/к сепарабельно тогда и
только тогда, когда оно допускает погружение в нек-
некрое расширение Галуа L/k. При этом для конечного
расширения К/к число различных /с-изоморфизмок
поля К в L совпадает со степенью [К : к]. Любое ко-
конечное Ср. является простым.
Многочлен f(x)?k\X] наз. сепарабельным
над к, если его неприводимые множители не имеют
кратных корней. Алгебраич. элемент а наз. сепа-
сепарабельным (над к), если он является корнем
сепарабельного над к многочлена. В противном слу-
случае а наз. несепарабельным. Элемент а
наз. чисто несепарабельным над к, если
аРп?к для нек-рого п. Неприводимый многочлен /(х)
несепарабелен тогда и только тогда, когда производ-
производная /' (х) тождественно равна 0 (это возможно только
в случае, когда к имеет характеристику р и f(x)=
—/1 (хР) • Произвольный многочлен / (х) однозначно
представим в виде f(x)~g(xPe), где g(x) — сепарабель-
ный многочлен. Степень многочлена g (x) и число е
наз. соответственно редуцированной сте-
степенью и индексом многочлена /(х).
Пусть Ык — произвольное алгебраич. расширение.
Все элементы поля L, сепарабельные над к, образуют
поле К, к-рое является максимальным С. р. поля к,
содержащимся в L. Поле К наз. сепарабель-
сепарабельным замыканием поля к в L. Степень [К : к]
наз. сепарабельной степенью расшире-
расширения L/k, а степень [L : К] — несепарабель-
ной степенью, или степенью несепа-
несепарабельности. Несепарабельная степень равна
нек-рой степени числа p=char к. Если К=к, то поле к
наз. сепарабельно замкнутым в L.
В этом случае расширение Ык наз. чисто несе-
несепарабельным. Расширение К/к чисто несепара-
бельно тогда и только тогда, когда
т. е. когда любой элемент поля К чисто несепарабелен
над к. Чисто несепарабельные расширения поля к
образуют отмеченный класс расширений. Если рас-
расширение К/к одновременно сепарабельно и чисто не-
сецарабельно, то К—к.
Лит. см. при ст. Расширение поля. Л. В. Кузьмин.
СЕПАРАБЕЛЬНЫЙ ПРОЦЕСС — случайный про-
процесс, поведение траекторий к-рого по существу опре-
определяется их поведением на нек-ром счетном прост-
пространстве. Именно, определенный на полном вероятност-
вероятностном пространстве {Q, JF, Р} действительный случай-
случайный процесс {Х(, t?T}, где Т — подмножество дейст-
действительной прямой R, сепарабелен относи-
относительно класса Л подмножеств R, если су-
существует счетное множество TxczT (сепаранта)
и множество Nc$F, P(JV)=O, такое, что для любого
АЛ и любого открытого интервала /cR
П, е it, № € Л}\ Г) 16 IT {Xt 6 A}cN.
Наиболее важны понятия сепарабельности относи-
относительно класса замкнутых множеств и относительно
класса замкнутых интервалов (в последнем случае
процесс называется просто сепарабельным).
Если процесс {Xt, t?T} сепарабелен, то для любого
? и любого открытого интервала JR
inf Xt (со) = inf Xt (со), sup -У4(со) = sup Zf(co), A)
«err, telT teir1 te.1T
inf -JTt (со) s? Л', (со) s? sup A't(co), ??/7\ B)
isiT, (е/Г,
lim inf Xu (со) == lim inf Хи(со), "]
u-*(, нет, u^i.nel !
lim sup ZH(co) = lim sup .Ув (со), t ? 7\ |
linvinf 1д(и)<Х((ч))< lim sup ЛГв(со), г ?7. D)
M->i, ite T, >t->i, utT
Каждое из свойств A) — D) равносильно сепарабель-
сепарабельности. Если t — левая предельная точка множества 7',
то существует последовательность tn\t точек из Т
такая, что
lim inl'Xf =liminf Хи, limsup^( —limsupA",,
n n u-*t + Q n n u-*-t+0
с вероятностью 1 (аналогично для пределов справа).
Если Х-t — сепарабельный случайный процесс, непре-
непрерывный но вероятности, то любое всюду плотное в Т
счетное множество Тха'Г является сепарантой; кроме
того, для любого открытого интервала /, 1[)Тфф
и любой последовательности sn= \snk, k<.kn} конеч-
конечных подмножеств IT, удовлетворяющей условию
sup inf \t—snk\ ->0,
te IT h
inf X, ->¦ inf Xt, sup X -*¦ sup Xt E)
ft nk telT h nh telT
по вероятности. Сходимость в E) можно заменить схо-
сходимостью с вероятностью 1, если Xt непрерывен с ве-
вероятностью 1.
Для всякого случайного процесса Xt, t?T, суще-
существует на том же вероятностном пространстве сепара-
сепарабельный относительно класса замкнутых множеств
процесс Xfi *€^i принимающий значения из расши-
расширенной числовой прямой, и такой, что Р {Xt—Xt}^-
= 1, t?T. Понятие сепарабельности и его свойства
обобщаются на процессы, у к-рых Т и область значений
суть различные общие топология, пространства. Пере-
Переход к С. п. позволяет утверждать применимость ряда
важных функционалов и множеств, связанных с про-
процессом. Альтернативный подход состоит не в измене-
изменении случайных величин, образующих процесс, а в рас-
расширении а-алгебры, на к-рой он определен (напр.,
в случае функционального пространства — произве-
произведения хаусдорфовых компактов меру с обычной а-ал-
а-алгебры, порожденной цилиндрич. множествами, мож-
можно однозначно продолжить на весьма богатую а-ал-
гебру борелевских множеств).
Лит.: [1] Д у б Д ж. Л., Вероятностные процессы, пер.
с англ., М., 195В; [2] Л о эв М., Теория вероятностей, пер. с
англ., М., 1962; [3] Г и х м а н И. И., Скороход А. В.,
Теория случайных процессов, т. 1, М., 1971; [4] D о о b T. L.,
«Bull. Amer. Math. Soc», 11L7, v. 53, Hi 1, p. 15—30; [5] Nel-
Nelson E., «Ann. Math.», 1959, v. 09, Ml 3, p. 630 — 43.
СЕПАРАТИВНАЯ ПОЛУГРУППА — полугруппа',0в
к-рой для любых элементов х, у из х-—ху—у'* следует
х=у. Если полугруппа S обладает разбиением на
подполугруппы, удовлетворяющие закону сокраще-
сокращения, то S будет С. п. Для коммутативных полугрупп
верно и обратное; более того, всякая коммутативная
С. п. разложима в связку полугрупп (автоматически
в полурешетку) с законом сокращения. Коммутатив-
ная полугруппа будет С. п. тогда и только тогда,
когда она вложима в клиффордову полугруппу. Пе-
риодич. полугруппа будет С. п. тогда и только тогда,
когда она клиффордова. Коммутативная полугруппа S
будет С. п. тогда и только тогда, когда ее характеры
отделяют элементы S.
Лит.: [1] Клиффорд А., Престон Г., Алгебраичес-
Алгебраическая теория полугрупп, пер. с англ., т.1,М.,1972. Л. Н. Шеврин.
СЕПАРАТРИСА — термин качественной теории диф-
дифференциальных уравнений.
1) С. в первоначальном смысле слова — траектория
{Sfp} потока {S^} на плоскости, стремящаяся (при
?—>-+°° или при t ->¦ —оо) к нек-рому равновесия по-
положению р0, причем сколь угодно близко к ней имеются
траектории, к-рые вначале приближаются к р0, как бы
«идя вдоль траектории {S^p}», а затем отходят от него
на нек-рое конечное расстояние. Формально послед-
последнее означает существование таких окрестности U
точки р0, последовательности точек р„ -> р и последо-
последовательностей чисел sn, tn, что sn —>• оо (соответственно
SsnPn->P0, StnPn? и, tn > sn (hi < sn)-
Основной пример — С. невырожденного (или прос-
простого) седла. Для последнего под С. может пониматься
также его устойчивое (соответственно неустойчивое)
многообразие, т. е. (в даннод1 случае) линия, включаю-
включающая седло и обе траектории, стремящиеся к нему при
t—>+°° (соответственно при t —>-—оо).
Название «С.» связано с наблюдением, что С. наряду
с замкнутыми траекториями делят фазовую плоскость
на области с одинаковым поведением траекторий. Это
наблюдение может быть строго формализовано (см. [1],
[3]). С. могут входить в состав предельных множеств
траекторий. Так, траектория может навиваться на
«петлю С.» — замкнутую кривую, образованную тра-
траекторией, стремящейся к одному и тому же седлу как
при t -у —оо, так и при t —»- оо, или на «сецаратрисный
контур (цикл)» — замкнутую кривую, состоящую из
нескольких С, соединяющих седла. При малом воз-
возмущении из петли С. может возникнуть предельный
цикл (это один из основных типов бифуркаций для по-
потоков на плоскости; см. [2], [3]).
2) В многомерном случае под С. (или с е п а р а т-
р и с н ы м и многообразиями) чаще всего
понимают устойчивое и неустойчивое многообразия
гиперболич. положения равновесия или периодич.
траектории.
Имеются попытки выделить под названием «С.» класс
траекторий, входящих в множества, которые в неко-
некотором смысле «разделяют» траектории с различным по-
поведением. Непосредственное обобщение случая плос-
плоскости имело бы ограниченную применимость, по-
поскольку в многомерном случае фазовое пространство,
вообще говоря, не разбивается на области, запол-
заполненные траекториями с одинаковыми предельными мно-
множествами (тогда как на плоскости такая ситуация «ти-
«типична»). Предложенные формулировки являются до-
довольно сложными (см. [4]), и не приходится ожидать
полного описания различных типов С. и составленных
из них множеств.
Лит.: [11 А н д р о н о в А. А., ЛеонтовичЕ. А.,
Гордой И. И., М а й е р А. Г., Качественная теория дина-
динамических систем второго порядка, М., 1966;[2] и х ж е, Теория
бифуркаций динамических систем на плоскости, М., 1987; 13]
Г> а у т и и II. Н., Л е о н т о в и ч Е. А., Методы и приемы
качественного исследования динамических систем на плоскости,
М., 1976; [4] Hartzman С. S. «Aequationes math.», 1980,
v. 20, № 1, p. 59 — 72. Д. В. Амосов.
СЕРВАНТН АЯ ПОДГРУППА, чистая п о д г р у п-
п а,— такая подгруппа С абелевой группы E, что
для любого элемента с^ С из разрешимости в G урав-
уравнения пх=с следует его разрешимость в подгруппе С.
Примерами С. п. служат нулевая подгруппа, сама
1117
группа G, периодич. часть данной группы и прямые
слагаемые. Даже для примерной группы не всякая
С. п. должна быть ее прямым слагаемым. Однако если
С — периодическая С. п. абелевой группы G, причем
порядки ее элементов ограничены в совокупности, то
С — прямое слагаемое в G. Имеется (см. [1]) полное
описание абелевых групп, в к-рых каждая С. п. слу-
служит прямым слагаемым. Полностью исследован также
вопрос о мощности множества С. п. абелевой группы.
Лит.: [1] К у р о ш А. Г., теория групп, 3 изд., М., 1967.
О. А. Иванова.
СЕРИАЛЬНЫЙ КОЭФФИЦИЕНТ КОРРЕЛЯЦИИ —
статистика, к-рая служит оценкой автокорреляции
(автокорреляционной функции) временного ряда.
Именно, пусть х1, т2, . . ., х^— временной ряд. С. к. к.
порядка к наз. статистика г^, задаваемая формулой
1 Ж-Т Л7 h ) I 1 Т-1ДГ Ь \( ^
В
СЕРПИНЬСКОГО КРИВАЯ
СЕРИЙ СХЕМА, последовательность
сери и,— двойная последовательность случайных ве-
величин 1„к, 1<й</с„, к„^ оо, и->1, в к-рой случайные
величины gHl, %ni, . . ., tnktt< образующие п-ю серию,
взаимно независимы при любом п. Простейшая С. с.
соответствует случаю кп~п. Класс случайных вели-
величин, образующих С. с, играет в предельных теоремах
теории вероятностей особую роль, к-рая определяется
предельным поведением при п ->. оо распределений
сумм случайных величин:
-k2ji=i \ ' IV-h
г-
При определенных условиях класс предельных рас-
распределений для таких последовательностей совпадает
с классом безгранично делимых распределений. Имен-
Именно, пусть С. с. lnk удов-
удовлетворяет условию беско-
бесконечной малости (условию
асимптотической пренебре-
гаемости), то есть нри
п —у оо
biJV—ft
¦т/ + к
¦}"Г
к
С.
качестве С. к. к. используются статистики, близкие
(*) несколько упрощенного вида. Совокупность
к. к. наз. коррелограммой; этот термин употреб-
употребляется также для обозначения графика г& как функ-
функции к.
При различных предположениях относительно рас-
распределений х,- имеются точные и приближенные выра-
выражения для распределения С. к. к. и их моментов. С. к. к.
используются в статистич. задачах для обнаружения
зависимости членов временного ряда.
Наряду с термином «С. к. к.» используется термин
«выборочная автокорреляци я».
Лит.: [1]Андерсон Т., Статистический анализ времен-
временных рядов, пер. с англ., М., 1976; [2] К е н д а л л М., С т ь н>-
а р т А., Многомерный статистический анализ и временные ряды,
пер. с англ., М., 1976; [3] X е н н а и Э., Анализ временных ря-
рядов, пер. с англ., М. 1964. В. Г. Ушаков.
СЕРИИ ПРЕДСТАВЛЕНИЙ — семейства (непре-
(непрерывных неприводимых унитарных) представлений ло-
локально компактной группы (точнее, неприводимые
множества классов унитарной эквивалентности таких
представлений), обладающие общими свойствами по
отношению к регулярному представлению этой группы.
Так, семейство неприводимых унитарных представле-
представлений группы, матричные элементы к-рых являются рав-
равномерными на компактах пределами матричных эле-
элементов регулярного представления, образуют о с-
новную серию представлений; ос-
остальные неприводимые унитарные представления (если
они существуют) образуют дополнительную
серию представлений; семейство (классов
эквивалентности) неприводимых прямых слагаемых
регулярного представления образует дискрет-
дискретную серию представлений данном
группы. Для редуктивных групп Ли или групп Ше-
валле понятие С. п. имеет смысл также для подмно-
подмножеств множества классов эквивалентности представ-
представлений этой группы, элементы к-рых обладают теми
или иными свойствами по отношению к регулярному
представлению редуктивных факторгрупп параболич.
подгрупп этой группы. Так, семейство представлений
редуктивной группы, индуцированных конечномер-
конечномерными представлениями ее параболич. подгруппы, обра-
образует связанную с этой параболич. подгруппой часть
пространства представлений, называемую соответст-
соответствующей основной (основной вырожденной, если пара-
параболич. подгруппа не является борелевской) С. п.
Лит.: [1] К и р и л л о в А. А., Элементы теории представ-
представлений, 2 изд., М., 1978; L21 N g u e n Н и и A n h., «Ann. Inst.
Fourier», 1980, v. M, fasc. 1, p. 152—92; [3] С a 1 1 e z J., Les
sous-groups paraboliques de SV (p, q) et Sp (n, Я) et applications,
P., 1979. А. И. Штерн.
0.
B)
Говорят,
с е р и н.
max P {|§Я|
К ft <; kn
что |nj образуют нулевую схему
Тогда множество распределений, предель-
предельных в смысле слабой сходимости для распределений
A), где \„ъ — нулевая С. с, удовлетворяющая усло-
условию бесконечной малости, совпадает с множеством
безгранично делимых распределений.
Известны условия сходимости распределений т)„
к заданному безгранично делимому распределению
(см. [1]). В частности, условие сходимости к нормаль-
нормальному распределению имеет следующий вид.
Пусть |„? есть С. с, Рпк — функция распределения
|nfc. Для того чтобы !,,k удовлетворяла условию B)
и распределение сумм A) слабо сходилось к нормаль-
нормальному распределению с параметрами а и Ь, необходимо
и достаточно, чтобы для любого фиксированного е>0
выполнялись условия:
f|<e
x^xdFnk(x)~+a.
Изучение предельных распределений для нормиро-
нормированных частичных сумм последовательности незави-
независимых случайных величин сводится к С. с.
По поводу С. с. см. также Безгранично делимое рас-
распределение, Больших чисел закон, Предельные тео-
теоремы. Так, напр., в классич. вариантах центральной
предельной теоремы и закона больших чисел рассмат-
рассматриваются частные случаи С. с, образованные случай-
случайными величинами
где ?k — независимые случайные величины.
Лит..' [1] Г н е д е и к о Б. В., Колмогорова. Н.,
Предельные распределения для сумм независимых случайных
величин, М.—Л., 1949; [2} Прохоров Ю. В., Роза-
Розанов К). А., Теория вероятностей, 2 изд., М., 1973; [31 П е т-
р о в В. В., Суммы независимых случайных величин, М., 1972;
I'll Ф е л л е р В., Введение в теорию вероятностей и ее прило-
приложения, пер. с англ., 2 изд. т. 2, М., 1967. Н. Г. Ушаков.
СЕРПИНЬСКОГО КРИВАЯ, ковер Серпинь-
с к о г о,— пример канторовой кривой, содержащей
подмножество, гомеоморфное любой наперед заданной
СЕРИЙ СХЕМА, последовательность
сери и,— двойная последовательность случайных ве-
величин с,пк, 1<:/с<:А:„, к„^ оо, njsl, в к-рой случайные
величины ?н1, %„%, . ¦ ., %Hk > образующие п-ю серию,
взаимно независимы при любом п. Простейшая С. с.
соответствует случаю кп~п. Класс случайных вели-
величин, образующих С. с, играет в предельных теоремах
теории вероятностей особую роль, к-рая определяется
предельным поведением при п —v оо распределений
сумм случайных величин:
При определенных условиях класс предельных рас-
распределений для таких последовательностей совпадает
с классом безгранично делимых распределений. Имен-
Именно, пусть С. с. lnk удов-
удовлетворяет условию беско-
бесконечной малости (условию
асимптотической пренебре-
гаемости), то есть нри
п —у оо
v—ftT. Л
max P {|?я*|5ае}->.0. B)
К ft <; кп v '
Говорят, что !„* образуют нулевую схему
сери й. Тогда множество распределений, предель-
предельных в смысле слабой сходимости для распределений
A), где E,nk — нулевая С. с, удовлетворяющая усло-
условию бесконечной малости, совпадает с множеством
безгранично делимых распределений.
Известны условии сходимости распределений т)„
к заданному безгранично делимому распределению
(см. [1]). В частности, условие сходимости к нормаль-
нормальному распределению имеет следующий гшд.
Пусть \nk есть С. с, Fnk — функция распределения
|nfc. Для того чтобы |„ь удовлетворяла условию B)
и распределение сумм A) слабо сходилось к нормаль-
нормальному распределению с параметрами а и Ъ, необходимо
и достаточно, чтобы для любого фиксированного е>0
выполнялись условия:
Изучение предельных распределений для нормиро-
нормированных частичных сумм последовательности незави-
независимых случайных величин сводится к С. с.
По поводу С. с. см. также Безгранично делимое рас-
распределение, Больших чисел закон, Предельные тео-
теоремы. Так, напр., в классич. вариантах центральной
предельной теоремы и закона больших чисел рассмат-
рассматриваются частные случаи С. с, образованные случай-
случайными величинами
%
Snfe
где Ik ~ независимые случайные величины.
Лит..- tl] Гнеденко Б. В., Колмогорова. Н.,
Предельные распределения для сумм независимых случайных
величин, М.— Л., 1949; [2] Прохоров Ю. В., Роза-
Розанов К). А., Теория вероятностей, 2 изд., М., 1973; [3J П е т-
р о в В. В., Суммы независимых случайных величин, М., 1972;
L'i] Ф е л л е р В., Введение в теорию вероятностей и се прило-
приложения, пер. с англ., 2 изд., т. 2, М., 19157. Н. Г. Ушаков.
СЕРПИНЬСКОГО КРИВАЯ, ковер Серпинь-
с к о г о,— пример канторовой кривой, содержащей
подмножество, гомеоморфное любой наперед заданной
канторовой кривой. Построена В. Серпиньским [1],
конструкцию см. в ст. Линия. Эта кривая в каждой
точке имеет континуальный индекс ветвления.
Лит.: [1] S i е г р i rt s k i W., «Compt. Rend. Acad. sci.»,
1915, v. 160, p. 302; 1916, v. 162, p. 623; [2] Александр о в
П. С, Введение в теорию множеств и общую топологию, М.,
1977; [3] Куратовекий К., Топология, пер. с англ.,
т. 2, М., 1969. М. И. Войцеховский.
СЕРРА ПОДКАТЕГОРИЯ — ненулевая полная ло-
локально малая подкатегория @ абелевой категории 9t
такая, что для каждой точной последовательности
О -> А-* В -*С -+0
в 91 верно, что #?2 эквивалентно А ?© и С?5-
Локальная малость категории есть условие:
совокупность представителей классов эквивалентных
подобъектов любого объекта составляет множество.
С. п. можно охарактеризовать как ядро точного функ-
функтора в категории 31.
С. п. позволяет определить факторкатегорию ЭГ/S,
объектами к-рой являются объекты категории 91, a
морфизмы определяются равенство»
Факторкатегория 91/© является абелевой.
С. п. наз. локализующей, если канонич.
функтор Т : Щ —у Ш/:? имеет правый сопряженный
функтор S : 91/© ->- Ш, наз. функтором се-
сечений. Если 91 — Гротендика категория, обладаю-
обладающая копроизведениями, то локализующий функтор
существует. Таким образом получается обобщение
классич. теории локализации модулей над коммута-
коммутативным кольцом. Этот метод охватывает многочислен-
многочисленные конструкции колец частных и теории кручений
(радикалов) модулей над ассоциативными кольцами.
Понятие «С. п.» было введено Ж. П. Серром [1] и
названо им классом. Используя это понятие, он полу-
получил далеко идущее обобщение теоремы Гуревича (см.
Гомотопическая группа).
Лит.: [1] Serre J.-P., «Ann. Math.», 1953, v. 58, №2,
p. 258—94 (pytvnep., в сб.: Расслоенные пространства и их при-
приложения, М., 1958, с. 124—59); [2] Ф е й с К., Алгебры; коль-
кольца, модули и категории, пер. с англ., т. 1, М., 1977; [3] Р о-
р е s с о N.. Gabriel Р., «С. г. Acad. sci.», 1964, t. 258,
№ 17, p. 4188—90. В. Е. Говоров.
СЕРРА РАССЛОЕНИЕ — тройка (X, р, Y), где
X, Y — топологич. пространства, р : X —у Y — непре-
непрерывное отображение, обладающее следующим свойст-
свойством (наз. свойством существования накрывающей
гомотопии для полиэдров). Для любых конечного поли-
полиэдра К и отображений
f:Kx[Q, i]-*Y, F0:K
существует отображение
F:(Kx[0, l])-*X
такое, что F\(KX {0})=F0, poF—f. С. р. было опре-
определено Ж. П. Серро.м (J.-P. Serre) в 1951 (см. [1]).
Лит.: L1] Расслоенные пространства и их приложения. Сб.
пер., М., 1958, с. 9—114. А. Ф. Харшиладэе.
СЕТЕВАЯ МОДЕЛЬ — интерпретация программы
(плана) реализации нек-рого комплекса взаимосвя-
взаимосвязанных работ в виде графа ориентированного без кон-
контуров, отражающего естественный порядок выпол-
выполнения работ во времени с нек-рыми дополнительными
данными комплекса (стоимость, ресурсы, продолжи-
продолжительность и т. д.). Обычно С. м. изображают графи-
графически на плоскости и в этом случае ее наз. сетевым
графиком. См. лежит в основе метода сетевого
планирования и управления и календарного планиро-
планирования. В зависимости от условий при обработке ин-
информации С. м. может иметь и другие формы представ-
лония — табличную, цифровую и т. п. Все формы
представления С. м. равносильны.
Основой С. м. является ее структура, т. е. граф
комплекса работ, к-рый, как правило, определяется
следующим образом. Пусть v1, у2, . . ., vn — комплекс
работ (напр., возведение многоэтажного здания), для
к-рого определены стадии ху, х2, . . ., хт: начало .тц
конец.г m и, в зависимости от логики частичного порядка,
обусловленной взаимосвязью работ, каждая проме-
промежуточная стадия г,- (напр., нельзя закончить монтаж
каркаса десятого этажа, не выполнив соответствую-
соответствующие работы но девятому этажу). Промежуточные ста-
стадии, равно как и их число, являются в достаточной
мере условными и во многом определяются ответст-
ответственными за реализацию комплекса. Пусть V— {г,-} —
комплекс работ, а X={xi) — множество стадий.
Если теперь определить граф б, для к-рого X является
множеством вершин, а работа vj, /—1, 2, . . ., п, имею-
имеющая началом стадию хг и концом стадию xs, является
его дугой, то полученный ориентированный граф G=
— {X, V) без контуров и есть искомая структура С. м.
рассматриваемого комплекса работ. На языке С. м.
работы г1; v2, . . ., vn наз. операциями, а стадии
я\, х2, . . ., хт — с о б ы т и я м и.
С. м. строится на основе своей структуры в зависи-
зависимости от целей, к-рые ставятся при этом относительно
комплекса работ. Напр., в случае, когда относительно
комплекса ставится задача выполнить его в минималь-
минимальный срок при заданных ресурсах, то С. м. включает
в себя и данные о времени, необходимом для выпол-
выполнения каждой работы vj, и в этом случае говорят,
что С. м. построена по критерию времени.
С. м. может быть построена и по другому критерию
или одновременно но нескольким критериям. В зави-
зависимости от этого См. наз. одномерной или
многомерной. Различают См. канониче-
канонические и альтернативные (см. [1], [3]).
Первые определяются при помощи фиксированной
структуры и условия, что любая операция v;~(xr, xs)
не может быть начата, пока не выполнены все операции
с концом в хг. Вторые имеют переменную структуру и
допускают начало нек-рой операции vj=(.rr, rs) после
выполнения какой-либо одной операции с концом в
хг. С. м. бывают также детерминированны-
детерминированными и вероятностными в зависимости от
того, точны критерии или прогнозированы с какой-
либо вероятностью.
Лит.: [1] Основные положения по разработке и применению
систем сетевого планирования и управления, 3 изд., М., 1974;
[2] Энциклопедия кибернетики, К., 1974; [3] Л о п а т н и к о в
Л. И., Краткий экономико-математический словарь, М., 1979.
Я. С. Солтан.
СЕТЕВОЕ ПЛАНИРОВАНИЕ, сетевой м е т о'д
планирования и управления, — метод
управления при реализации нек-рого комплекса работ
(проекта, программы, темы и т. п.) на основе сетевой
модели комплекса, известной также иод названием
ПЕРТ (см. [2]). С. и. позволяет существенно поднять
качество планирования и управления при реализации
комплекса работ, в частности оно дает возможность
четко координировать деятельность всех сторон (орга-
(организаций), участвующих в реализации комплекса, вы-
выделить наиболее важные задачи, судить о наиболее
целесообразных сроках реализации проекта, своевре-
своевременно корректировать планы реализации и т. д.
С. п. может быть условно разбито на два этапа: 1) по-
построение сетевой модели (с. м.) комплекса работ,
2) использование с. м. для планирования и управления
при реализации комплекса работ (см. [1]—[3]). Пост-
Построение см. комплекса сводится к отображению в виде
специально ориентированного графа множества ста-
стадии (событий) и естественного порядка (вообще гово-
говоря, частичного) самих работ (операций) комплекса, а
также и нек-рой числовой информации, необходимой
при этом (время выполнения каждой операции, ресур-
ресурсы и др.). В зависимости от сформулированных целей,
после составления см. приступают к ее анализу для
лучшей подготовки плана их достижения. Напр., если
с. м. построена по критерию времени, т. е. когда не-
необходимо добиться минимальной продолжительности
всего комплекса работ при заданных ресурсах, то этот
анализ сводится к нахождению критич. пути и выяс-
выяснению того времени, меньше к-рого делает задачу
реализации комплекса неразрешимой. Это означает
следующее. Пусть G~(X, V)—структура см. ком-
комплекса, где
Х~{х1, х2, ..., хт} и V = {i>i, v2, ..., vn]
— соответственно множества событий и операций, а
t(vj) — время выполнения операции vj?V. Рассмат-
Рассматривается множество Р всех путей графа G, максималь-
максимальных по включению. Таких путей в G, вообще говоря,
.много, и для более простой ситуации, когда имеется
одно начальное событие х±я одно конечное событие хт,
все эти пути начинаются в^и кончаются в хт. Среди
всех и утей множества Р ищется тот, к-рый обладает
наибольшей длиной (под длиной пути р=
~~ {у/ь vj2, •••, vjk) понимается число t(p)—t{vj1)-\-
~И (yji)+- ¦ --{-t(vfk))- Путь р?Р, обладающий этим
свойством, наз. критическим путем см.,
и его длина выражает, что реализация комплекса ра-
работ за меньшее время, чем t(p), невозможна. Поэтому
метод С. п. наз. также методом критиче-
критического пути (см. [1] — [4]).
С. ц. на период самой реализации комплекса работ
играет роль механизма в управлении, помогающего об-
обрабатывать информацию о фактам, состоянии работ
для данного момента времени и о прогнозируемых из-
изменениях и необходимой корректировке планов для
выполнения оставшихся работ.
Лит.: [1] Основные положения по разработке и применению
систем сетевого планирования и управления, 3 изд.,М., 1974;
[2] К о ф м а н А., ДебазейГ., Сетевые методы планиро-
планирования. Применение системы ПЕРТ и ее разновидностей при уп-
управлении производственными и научно-исследовательскими про-
проектами, пер. с франц., М., 1908; 13] Сетевое планирование и
управление, М., 1967; [4] А б р а м о в С. А., Мариничев
М. И., Поляков П. Д., Сетевые методы планирования
и управления, М., 1965; [5] Энциклопедия кибернетики, К.,
1974; [6] Лопатин ков Л. И., Краткий экономико-мате-
экономико-математический словарь, М., 1979. П. С. Солтан.
СЕТЕВОЙ ГРАФИК — сетевая модель, изображен-
изображенная графически на плоскости. п. с. Солтап.
СЕТОК МЕТОД — собирательное название группы
приближенных методов решения дифференциальных,
интегральных и интегро-дифференциальных уравне-
уравнений. Применительно к дифференциальным уравнениям
с частными производными термин «С. м.» используется
в качестве синонима терминов «метод конечных раз-
разностей» и «разностный метод». С. м.— один из наиболее
распространенных приближенных методов решения
задач, связанных с дифференциальными уравнениями.
Широкое применение С. м. объясняется его большой
универсальностью и сравнительной простотой реали-
реализации на ЭВМ.
См. Разностных схем теория.
По материалам одноименной статьи в БСЭ-3.
СЕТЬ — обобщение понятия графа. С. задается
парой вида (V, &), в к-рой V — нек-рое множество,
g—(E0; Ег, Е2, . . .) — семейство наборов элементов
из V. В наборах ?,?<? элементы могут, вообще гово-
говоря, повторяться. Элементы множества V наз. вер-
вершинами С, элементы набора Ео — полюса-
м и С, наборы Eh i=l, 2, . . .,— ребрами С.
В случае, когда множество полюсов пусто и каждый
из наборов Ei является множеством, С. представляет
собой гиперграф. Если каждый из наборов Е;, i =
= i, 2, . . ., содержит ровно диа улемента, С. есть
граф с выделенными полюсами. Час-
Часто под С. понимается граф (с полюсами или без них),
элементам к-рого приписаны символы из нек-рого
множества. Напр., граф с полюсами, ребрам к-рого
приписаны неотрицательные числа, называемые про-
пропускными способностями, представляет собой транс-
транспортную сеть.
Понятие С. используется в определении и описании
управляющей системы и специальных классов управ-
управляющих систем (контактные схемы, схемы из функцио-
функциональных элементов), диаграмм переходов автоматов,
коммуникационных сетей и др.
Лит.: [1] Яблонский С. В., «Проблемы кибернетики»,
1959, в. 2, с. 7 — 38; [2] Форд Л., Фалкерсон Д., По-
Потони в сетях, пер. с англ., М., 1966; Гз] К u n t г т a n n J.,
Theorie des rcseaux Graphes, P., 1972. А. А. Сапоженко.
СЕТЬ — система 2„={а1, а2, . . ., а"} п семейств
(и>2) достаточно гладких линий, определенных в об-
области G и-мерного дифференцируемого многообразия М
так, что 1) через каждую точку x?G проходит точно
по одной линии каждого семейства а'; 2) векторы, ка-
касательные к этим кривым в точке х, образуют базис
пространства Тх — касательного пространства к мно-
многообразию М в точке х. Векторы, касательные к ли-
линиям одного семейства а', принадлежат одномерному
распределению Д[, определенному в области G. Ус-
Условия того, что семейства линий составляют С. в нек-
некрой окрестности точки, могут не выполняться при
продолжении линии. Линии семейства а< являются
интегральными кривыми распределения Д{. Сеть
~ZndG определяется заданием п одномерных распреде-
распределений Д| таких, что в каждой точке x?G касательное
пространство Тх является прямой суммой подпрост-
подпространств Al, ?=1, 2, . . ., га. Сеть 2nCZG определяет
в области G (п—1)-мерные распределения ДА-i такие,
что в каждой точке x?G подпространство Дп-i (х)аТх
является прямой суммой и — 1 одномерных подпрост-
подпространств Д'х (х), }'Ф1. Различают следующие типы С:
голономные С, для к-рых каждое из распреде-
распределений Дя_1 интегрируемо (при га=2 всякая С. голо-
номна); частично голономные С., для
к-рых нек-рые из распределений ДА-i интегрируемы,
а остальные неинтегрируемы (такие С. подразделяются
по числу неинтегрируемых распределений); не го-
голономные С., для к-рых все распределения Дп-1
неинтегрируемы.
Если распределение Дп-ь «>2, интегрируемо и
у' — интегральная кривая распределения Д{, то через
каждую точку х?у' проходит интегральное многооб-
многообразие распределения Дп-i, несущее сеть ^„.^i) из
кривых, принадлежащих семействам oJ, /фг.
Сеть 2ncG можно задать также одним из следующих
способов: а) системой векторных полей XjCZ&i, б) си-
системой дифференциальных 1-форм со' таких, чтош1 (Xj)
=¦=6/, в) полем аффинора Ф такого, что Ф"=? {Е —
единичный аффинор).
При изучении С. рассматриваются три основные
проблемы: внутренние свойства С, внешние свойства
С. и исследование диффеоморфизмов С.
Внутренние свойства С. индуцируются структурой
многообразия, несущего С. Напр., сеть 2„ в прост-
пространстве М аффинной связности V наз- геодези-
геодезической сетью, если все ее линии геодезические.
Если риманово многообразие М со связностью без
кручения, в к-рой метрич. тензор ковариантно постоя-
постоянен, несет ортогональную чебышевскую сеть 1-го рода,
то М — локально евклидово. Связь таких С. с парал-
параллельным перенесением векторов на поверхности была
установлена Л. Бьянки (L. Biauchi, 1922). Эта связь
была положена А. П. Норденом в основу определения
чебышевской С. 1-го рода в прострагк'тнс аффинной
связности.
Внешние свойства С. индуцируются структурой
объемлющего пространства Е. Так, напр., пусть сеть
2„, заданная в нек-рой области G на гладкой поверх-
поверхности Vn проективного (ге+А:)-мерного пространства
(fc;==l), — сопряженная С, то ость в каждой
точке x?G сопряжены направления Al(x), А{(х) ка-
касательных к любым двум линиям С, проходящим
через точку х (два направления сопряжены, если каж-
каждое из них принадлежит характеристике касательной
плоскости Тх при ее смещении в другом направлении).
Если Vn не вмещается в проективное пространство
размерности, меньшей п-\-к, то при к=1 поверхность
Vn несет бесконечное множество сопряженных С;
при к=2 поверхность несет в общем случае единст-
единственную сопряженную С, но существуют и такие га-
мерные поверхности, на к-рых нет ни одной сопряжен-
сопряженной С; при &>2 только га-мерные поверхности специ-
специального строения несут сопряженную С. При ге>2 со-
сопряженная С. может и не быть голономной (см. [3]).
Частным случаем голономной сопряженной С. явля-
является ге-с опряженная система: сеть 2 „,
обладающая тем свойством, что касательные к линиям
каждого семейства, взятые вдоль любой линии любого
тругого семейства, образуют развертывающуюся по-
поверхность. Сопряженные системы существуют в про-
¦ктивном пространстве любой размерности га+/с при
га>2, А^гО. Поверхности Vn, несущие п-сопряженную
гпстему в проективном (п+&)-мерном пространстве,
когда к^п, и в каждой точке x?Vn соприкасающееся
к Vn пространство (пространство вторых дифференциа-
дифференциалов точки х) размерности 2га, впервые рассматривал
'¦). Картан [4] под названием «многообразия особого
фоективного типа» (поверхности Картан а).
:1а такие С. было распространено понятие Лапласа
преобразования (см. [5], [6]).
При изучении диффеоморфизмов С. по известным
свойствам сети ~2,паМ описываются свойства сети
ФBп)оЛГ при заданном диффеоморфизме ф : М —*¦ N
inanp., при изгибании или при конформном отображе-
отображении поверхности, несущей С.) или ищется диффеомор-
диффеоморфизм <р, сохраняющий нек-рые из свойств сети 2„.
Так, напр., сеть 22 на поверхности евклидова прост-
пространства наз. ромбической сетью (конформно-чебышев-
( кой), если она допускает конформное отображение
на чебышевскую С. На всякой поверхности вращения
асимптотическая сеть является ромбической.
• Чип.: [1] Норден А. П., Пространства аффинной связ-
связности, 2 изд., М., 1976; [2] Д у б н о в Я. С, Ф У к с С. А.,
..Докл. АН СССР», 1940, т. 28, JV5 2, с. 102 — 04; [3] Б а з ы л е в
В. Т., в кн.: Итоги науки. Геометрия, 1963, М., 1965;Ч4] С а г-
I а п Е., «Bull. Soc. math, de France», 1919, t. 47, p. 125—60; [5]
ChertS. S., «Proc. Nat. Acad. Sci. USA», 1944, v. 30, p. 95—
!I7; [6] Смирнов Р. В., «Докл. АН СССР», 1950, т. 71, № 3,
i>. 437—439. В. Т. Вазылев.
СЕТЬ — отображение направленного множества в
(топологическое) пространство. м. и. Войцехоеский.
СЕТЬ сфер — совокупность всех сфер, относительно
к-рых данная точка (центр С, или радикал ь-
н ы и цент р) имеет данную степень р — с т е-
ir e н ь С. Существуют три типа С. сфер:
1) гиперболическая С. (р>0), состоящая
из всех сфер, ортогональных нок-рой данной сфере;
2) эллиптическая С. (р<0), состоящая из
ксех сфер, переселающих нек-рую данную сферу по
какому-либо большому кругу последней;
3) параболическая С. (р = 0). состоящая
из всех сфер, проходящих через нек-рую данную
гичку. Совокупность всех общих сфер двух С. наз.
• низкой сфер. Совокупность всех общих сфер, центры
к-рых не лежат на одной прямой, наз. пучком сфер.
А. В. Иванов.
СЕТЬ топологического пространст-
в а Л' - семейство ^р подмножеств этого пространства
такое, что для каждой точки ,г?Л' и каждой ее окрест-
окрестности Ох найдется элемент М семейства $* такой, что
Семейство всех одноточечных подмножеств прост-
пространства и каждая его база всегда является его С. От-
Отличие С. от базы в том, что элементы С. не обязаны
быть открытыми множествами. С. появляются при не-
непрерывных отображениях: если / — непрерывное от-
отображение топологич. пространства X на топологич.
пространство Y и 33 — база пространства X, то об-
образы элементов базы 33 при / составляют сеть 5*=
= {fU: U?33} пространства Y. Далее, если прост-
пространство X покрыто каким-либо семейством {Ха'¦<*¦?
?А} своих подпространств, то, фиксируя при каждом
<х?А какую-либо 33а пространства Ха и соединяя все
эти базы вместе, получают сеть 5s == U{33a :a?/4}
пространства X. Пространства со счетной С. характе-
характеризуются как образы сепарабельных метрич. прост-
пространств при непрерывных отображениях.
Минимум мощностей всевозможных С. пространства
X наз. сетевым весом этого пространства и
обозначается nw(X). Сетевой вес пространства всегда
не превосходит его веса, но, как показывают примеры
счетных пространств без счетной базы, сетевой вес
может отличаться от веса. Для всех бикомпактных
хаусдорфовых пространств сетевой вес совпадает с ве-
весом. Это утверждение распространяется на локально
бикомпактные пространства, пространства, полные по
Чеху, и на перистые пространства. Отсюда, в част-
частности, следует, что вес не увеличивается при отобра-
отображениях на такие пространства. Другое следствие:
если перистое пространство X (в частности, биком-
бикомпакт) представлено в виде объединения семейства мощ-
мощности <:т своих подпространств, вес каждого из к-рых
не превосходит кардинала т, предполагаемого беско-
бесконечным, то и вес всего пространства X не больше,
чем т.
Лит.: [1] Архангельский А. В., II оном а-
р е в В. И., Основы общей топологии в задачах и упражнениях,
М., 1974; [2] Архангельский А., «Докл. АН СССР»,
1959, т. 126, № 2, с. 239—41. А. В. Архангельский.
СЕЧЕНИЕ, секущая поверхность, рас-
расслоения р : X —>- Y — непрерывное отображение
s : Y —>¦ X такое, что pos=idy- Если (X, р, Y) — рас-
расслоение Серра, обладающее С, то
Для главного расслоения из существования С. сле-
следует его тривиальность. Векторное расслоение всегда
обладает т. н. нулевым сечением.
А. Ф. Харшиладзе.
СЕЧЕНИЕ ОТОБРАЖЕНИЯ р : X -> У — отоб-
отображение s:Y-*-X, для к-рого pos=idy. В более
широком смысле С. о. любого морфизма в произволь-
произвольной категории — обратный справа морфизм.
А. Ф. Харушладзе.
СЖАТИЕ — аффинное преобразование плоскости,
при к-ром каждая точка смещается к осп Ох по на-
направлению оси Оу на расстояние, пропорциональное
ее ординате. В декартовой системе координат С. за-
задается соотношениями
х' —х, у' — ky, k > 0.
С. пространства к плоскости Оху по папраилсншо
оси ()z задается соотношениями
Х'=х,у'=у, S'=kz, k>0. н.в.реведа„,
СЖАТИЕ, сжимающий о п е р а т о р,— ог-
ограниченное линейное отображение Т гильбертова
пространства Н в гильбертово пространство Н' с
||Л|<1. При#=#' сжатие Т наз. вполне н е у н и-
тарпы м, если оно не является унитарным операто-
оператором ни при каком отличном от {0} приводящем Т
подпространстве. Таковы, напр., односторонние сдвиги
(и отличие от двусторонних сдвигов, являющихся
унитарными С.)- Всякому С. в Н отвечает единствен-
единственное ортогональное разложение Л~В0(?)Н1 на приво-
приводящие Т подпространства такое, что 71о=У|яо уни-
тарен, а 7\ = -Ля, вполне неунитарен. Т=ТофТ1 наз.
каноническим разложением сжатия Т.
Дилатацией, или растяжением, дан-
данного сжатия Т, действующего в II, наз. ограниченный
оператор В, действующий в нек-ром объемлющем
гильбертовом пространстве KZDH и такой, что Т"=
= РВп, га—1, 2, . . ., где Р — ортопроектор из К на
//. Всякое С. в гильбертовом пространстве Н обладает
унитарной дилатацией U в пространстве KZ3H и при-
притом минимальной в том смысле, что А = з. л. о.
{U"JI)nZ-cc (теорема Сёкефальви-Надя).
Минимальные унитарные дилатации и определенные на
основе спектральной теории функции от них позво-
позволяют построить функциональное исчисление для С,
развитое в основном для ограниченных аналитич.
функции в открытом единичном круге D (класс Харди
//""). Вполне неунитарное сжатие Т принадлежит, по
определению, классу Со, если существует функция
и^В", и(\)=?0, такая, что и(Т) — 0. Класс С0 содер-
содержится в классе 6'00 сжатий Т, для к-рых Т" -»- 0, Т*п -*¦
—*¦ О при п —>- оо. Для всякого сжатия Т класса Со
существует т.н. минимальная функция
mj{k) (т.е. внутренняя функция и?Н°°, |ц(А,)|<1 в
a), \u(e't\\ = l почти всюду на границе D) такая, что
и(Т)=0 и и (к) является делителем всех прочих внут-
внутренних функций, обладающих тем же свойством. Мно-
Множество нулей минимальной функции mj- (А) сжатия Т
в D вместе с дополнением до единичной окружности
к объединению тех дуг, через к-рые mj-(X) допускает
аналитич. продолжение, совпадает со спектром о(Т).
Понятие минимальной функции сжатия Т класса Со
юзноляет распространить для этого класса С. функцио-
функциональное исчисление на нек-рые мероморфные в D
функции.
Теоремы об унитарных дилатациях получены не
только для индивидуальных С, но и для дискретных
[Т"}, га=0, 1, . . ., и непрерывных {T (s)}, 0<s<cc,
полугрупп С.
Как и для диссипативных операторов., для С. пост-
построена теория их характеристич. оператор-функций
и на ее основе — функциональная модель, позволяю-
позволяющая изучать структуру С. и соотношения между спект-
спектром, минимальной функцией и характеристич. функ-
функцией (см. [1]). Преобразованием Кэли
А = A + Т)A-Т)~1, 1<?арG'),
сжатие Т связано с максимальным аккретивным опе-
оператором А, т. е. таким, что iA — максимальный дис-
сипативный оператор. На этой основе строится тео-
теория диссипативных расширений Во симметрич. опе-
операторов Ао (соответственно диссипативных по Филлип-
су расширений iB0 консервативных операторов 1А0).
Для С. разработана теория подобия, квазиподобия
и одноклеточности. Теория С. тесно связана с теорией
прогнозирования стационарных случайных процессов
и теорией рассеяния. В частности, схему Лакса — Фил-
липса [2] можно рассматривать как континуальный
аналог теории Сёкефальви-Надя—Фоягаа С. класса С00.
Лит.: [1] Секефальв и-Н а д ь В., Ф о я ш Ч., Гар-
¦юнический анализ операторов в гильбертовом пространстве,
.ер. с франц., М., 1970; [2] Л а к с П. Д., Ф и л л и п с Р. С,
|'рория рассеяния, пер. с англ., М., 1971. И. С. Иохеидое.
СЖАТИЕ алгебры Ли, стягивание
алгебры Ли,— операция, противоположная де-
деформации алгебры Ли. Пусть g — конечномерная
вещественная алгебра Ли, {с/,} — набор ее структур-
них констант в фиксированном базисе е\, .... е„ и
A (t), 0<<<:1,— кривая в группе невырожденных
линейных преобразований пространства g такая, что
АA) = Е. Пусть ei(t)=A (t)e,- и cf/(J) — структурные
константы алгебры g в базисе {«,-(()}. Если с,/(?) при
t —у 0 стремятся к нек-роыу пределу е//@), то алгебра
д, определяемая этими константами в исходном ба-
базисе, наз. сжатием исходной алгебры д. Сжатие
д также является алгеброй Ли, причем д можно
получить путем деформации алгебры д. Если д —
алгебра Ли группы Ли G, то группу Ли С, соответст-
соответствующую д, также наз. сжатием группы G.
Хотя dim g=dim g, эти алгебры, вообще говоря,
не изоморфны: напр., если A (t) = tE, то c*/(t)=tc?/->0,
так что при таком С. предельная алгебра всегда
коммутативна. Естественное обобщение этого примера
состоит в следующем: пусть а — подалгебра в д, Ь —
дополнительное к а подпространство, причем [a, b]cS
i=b, и A(t)v=v цля v?a, A{t)v—tv для i>?C. Тогда
в пределе Ь становился коммутативным идеалом ал-
алгебры д, в то время как умножение в а и тзрисоеди-
ненное действие алгебры а на Ь остаются неизмен-
неизменными.
В частности, иусть G — группа Лоренца, g — ее
алгебра Ли, а — подалгебра, соответствующая под-
грунпо вращений 3-мерного пространства. Тогда опи-
описанное С. алгебры g дает алгебру Ли группы Гали-
Галилея G (см. Галилея преобразование, Лоренца преобра-
преобразование). Соответственно алгебра Лоренца является
деформацией алгебры Галилея и можно показать, что
комнлексификация алгебры Галилея других дефор-
деформаций не имеет; в вещественном случае алгебру Га-
Галилея можно получить также С. ортогональной ал-
алгебры Ли so D). Эквивалентный способ получения ал-
алгебры Галилея из алгебры Лоренца состоит в том,
чтобы определить алгебру Лоренца как алгебру, со-
сохраняющую форму Минковского x2-\-y2J\-z2—c2t2, и
затем устремить скорость света с к оо. Пока с<оо, воз-
возникающие алгебры изоморфны д. Аналогично, дефор-
деформируя алгебру Пуанкаре (неоднородную алгебру Ло-
Лоренца), можно получить алгебры де Ситтера so D,1) и
so C,2) движений пространства постоянной кривизны.
Соответственно, устремляя кривизну к 0, получают
группу Пуанкаре как С. групп де Ситтера.
Связь между этими алгебрами продолжается на
представления. Если, как в описанных примерах,
существует матрица А (()) —Hm A (t), то каждое нред-
(-*0 _
ставление S алгебры g порождает представление S
сжатой алгебры по формуле
S(x) = S(A@)x)
для любого ж^д. Обратная операция (деформация
представлений), вообще говоря, невозможна.
Лит.: [1] Б а р у т А., Р о н ч к а Р., Теория представле-
представлений групп и ее приложения, пер. с англ., т. 1, М., 1980; [2]
InOniiE., W i 6 п е г Е. P. «Proe. Nat. Aead. Sci. USA»,
1953, v. 39, p. 510 — 24; [3] S a 1 e t a n E. J., «J. Math. Phys.»,
1961, v. 2, p. 1--22. А. К. Толпыго.
СЖАТИЙ ПОЛУГРУППА — однопараметрпческгт
сильпо непрерывная полугруппа T(t), 0«:?<oo,
7@)=/, линейных операторов в банаховом прост-
пространстве Е, для к-рых ]]Г(г)|]<1. Плотно определенный
в Е оператор А будет производящим опера-
оператором (генератором) С. п. тогда и только
тогда, когда выполнено условие Хилле — Иосиды
||DWLl<
при всех Я>0. В других терминах: плотно определен-
определенный оператор А — генератор С. п. тогда и только
тогда, когда он является максимальным диссипатив-
пым оператором.
Детально изучены С. п. в гильбертовом пространстве
Н, Частными видами С. п. являются полугруппы
изометрий (||Гх||=]|а:||), унитарные по-
полугруппы (Т* (t)=T~1(t)), самосопряжен-
самосопряженные полугруппы (Т* (t)=-~ T (t)), нормаль-
нормальные полугруппы (Г* (t)T{t)= T(t)T*(t)).
Вместо генератора А иногда удобно рассматривать его
преобразование К э л и: В=(А-\-1) (А — I)-1
(к о г е н е р а т о р). Оказывается, что полугруппа бу-
будет полугруппой изометрий, унитарной, самосопря-
самосопряженной, нормальной полугруппой тогда и только
тогда, когда когеператор соответственно будет изо-
изометрическим, унитарным, самосопряженным, нормаль-
нормальным оператором.
С. п. наз. вполне неунитарной, если ее
сужение на любое инвариантное подпространство не
является унитарным. Для вполне ноунитарной полу-
полугруппы (Т(t)x, у)-+0 при (->- оз и любых х, у?П-
Для того чтобы С. п. была вполне не унитарной, до-
достаточно, чтобы она была устойчивой, т. е. чтобы
||Г(*)ж||->.0 при г-*-оо и х?Н.
Для всякой ?. н. Т (t) существует такое ортогональ-
ортогональное разложение Н--Н1фВ2 на инвариантные относи-
относительно Т(t) подпространства, что на Н1 полугруппа
унитарна, а на Н2 вполне неунитарна.
Если Т (t) есть С. п. в гильбертовом пространстве Н,
то су[цествует более широкое гильбертово простран-
пространство П, содержащее Н как подпространство, и в нем
такая унитарная группа U(t), — оо<г<а>, что Т (i)=
~=PU(t) при t^sO, где Р — ортогональный проектор
из Н на Н. Группа V (t) наз. унитарной дила-
тацией полугруппы T(t). Дилатация определя-
определяется однозначно с точностью до изоморфизма, если
потребовать, чтобы II совпадало с замкнутой линейной
оболочкой .множества [)U(i)H ( — оо<г<оо) (мини-
(минимальная дилатация).
Пусть N — гильбертово пространство и L2 (^> N) —
гильбертово пространство всех измеримых TV-значных
функций f(s), s?R, с интегрируемым квадратом нор-
нормы. В атом пространстве определена унитарная группа
двустороннего сдвига (U(t)f)(s)~f(s~t). Аналогично,
в пространстве Z8(R + , N), R + = @, oo) определена
полугруппа одностороннего сдвига
(U (t) f) (s) = / (s—t) при A<(<!иО при t > s.
Всякая вполне неунитарная полугруппа изометрий
изоморфна одностороннему сдвигу в L2(R. + , N), при
нек-ром вспомогательном пространстве N.
Если Т (t) — вполне неунитарная С. п. и V (t) —
ее минимальная унитарная дилатация, то на нек-ром
инвариантном подпространстве Я (а если Т (t) устой-
устойчива, то и на всем Н) группа изоморфна двусторон-
двустороннему сдвигу. О полугруппах сжатия с нелинейными
операторами см. Полугруппа нелинейных операторов.
Лит.: [1] Davies E., One-parameter semigroups, L.—
[а.о.], 1980; 12]Секефальв и-Н а д ь Б., Ф о я ш Ч., Гар-
Гармонический анализ операторов в гильбертовом пространстве,
иор. с франц., М., 1970. С. Г. К-рей-н.
СЖАТЫХ ОТОБРАЖЕНИЙ ПРИНЦИП — одно из
основных положений теории метрич. пространств о
гуществовании и единственности неподвижной точки
множества при нек-ром специальном («сжимающем»)
отображении его в себя. См. Сжимающих отображений
принцип.
СЖИМАЮЩИХ ОТОБРАЖЕНИЙ ПРИНЦИП, сжа-
сжатых отображений принцип,— теорема, утверждающая
сущесхвовавио и единственпость неподвижной точки
у отображения / полного метрич. пространства (А', р)
(или замкнутого подмножества такого пространства)
в себя, если для любых х', х" выполняется неравенство
Р (/(*'), t{x"))<q9(x', х"), A)
где 0<<?<1. Этот принцип широко используется для
доказательства существования и единственности ре-
решения не только уравнения вида j(x)=x, но и урав-
уравнений ](х)=у путем замены такого уравнения на эк-
эквивалентное: ](х) — х, где j(x) — x±(f{x)—y).
Схема применения С. о. п. обычно такова: исходя
из свойств отображением / находят сначала замкнутое
множество МсХ, обычно замкнутый шар, такое, чти
f{M)dM, а затем доказывают, что на этом множестве у
является отображением сжатия. После этого, отправ
ляясь от произвольного элемента хо?М, строят по-
последовательность {*„}, xn—f(xn^-i), ге=1, 2, . . .,
принадлежащую М, к-рая сходится к нек-рому эле-
элементу х?М. Это и будет единственное решение урав-
уравнения j(x)—-x, а х„ будут последовательными прибли-
приближениями решения.
В общем случае условие A) нельзя заменить условием
р (/(*'), /(*•))< р(*', *"), B)
однако если это условие выполняется на компактном
множестве К, к-рое / отображает в себя, то условие B)
обеспечивает у / существование единственной непод-
неподвижной точки х?К.
Имеет место следующее обобщение С. о. п. Пусть
снова / отображает полное метрич. пространство А'
в себя и
р (/(*'), /(*"))<<? (а, Р)р(*', х")
при а<р(з:\ ж")<р\ где 0<д(а, |3)<1 для 0<а<р"<оо.
Тогда отображение / имеет на X единственную непод-
неподвижную точку.
Лит.: [1] Колмогоров А. Н., Ф о м и н С. В., Эле-
Элементы теории функций и функционального анализа, 5 изд., М.,
1981; [2] Красносельский М. А. 1и др.], Приближен-
Приближенное решение операторных уравнений, М., 1969; [3] Л ю с т е р-
н и к Л. А., Соболев В. И., Элементы функционального
анализа, 2 изд., М., 1965; Е4] треногий В. А., Функцио-
Функциональный анализ, М., 1980. В. И. Соболев.
СИГНАТУРА — 1) С. алгебраической си-
системы — совокупность отношений и операций, дей-
действующих на основном множестве данной алгебраич.
системы, вместе с указанием их арностей. Алгебраич.
система Eгниверсальная алгебра) с сигнатурой Q нал.
также Q-c и с т е м о й (соответственно fi-a л г е б-
р о й).
2) С. квадратичной или симметриче-
симметрической билинейной формы над упорядо-
упорядоченным полем — пара целых неотрицательных чисел
(р, д), где р — положительный, a q — отрицательный
индекс инерции данной формы (см. Инерции закон,
Квадратичная форма). Иногда С. формы наз. число
р—q. О. А. Иванова.
3) С. многообразия ikf"— сигнатура квад-
квадратичной формы
Qm{x) = (x\Jx, О),
гДе U — внутреннее когомологическое умножение,
О?Нп (М\ %) — фундаментальный класс. Многообра-
Многообразие предполагается компактным и ориентируемым.
С. обозначается а(М).
Если гаЗЮ mod 4, то полагают а(М)=0. С. обладает
свойствами:
1) о (М-{-М')=о {М)+о (М1);
2)
3)
С. многообразия может быть представлена как линей-
линейная функция от его Понтрягина классов (см. [2]).
О представлении С т\к ui.,i.'Kca нек-рого дифферен-
дифференциального оператора см. Иноекса формулы.
Лит.: [1] Дольд А., Лекции по алгебраической тополо-
топологии, пер. о англ., М., 1976; 12J М и л н о р Д ж., С т а ш е ф
Д ж., Характеристические классы, пер. с англ., М., 1979.
М. И. Войцеховский.
СИГНУМ — функция действительного переменного
х, равная 1, если х положительно, равная 0, если х
равно нулю, и равная —1, если х отрицательно. Обо-
Обозначение: sgn х или sign х. Таким образом,
/ 1, если х > О,
sgn х — < 0, если х = О,
I —1, если х < 0.
Ю. А. Горькое.
СИЗИГИЯ — астрономический термин, означающий
расположение трех небесных тел на одной прямой.
В алгебре употребляется в значении соотношения.
Пусть М —¦ левый Л-модуль, (m,)J6j — семейство эле-
элементов из М; соотношением, или сизигией, между
(т,) паз. набор (at)iei элементов кольца А такой,
что 2iaimi~0. Так возникает модуль сизигий, цепь
сизигчй и т. д. См. Гильберта теорема о сизигиях.
В. И. Данилов.
СИ ЛОВА ПОДГРУППА, с и лове к ая подгруп-
п а,— максимальная я-подгруппа группы, где л —
нек-рое множество простых чисел, т. е. периодич.
подгруппа, порядки элементов к-рой делятся только
на простые числа из я, и не содержащаяся ни в какой
большей подгруппе с таким свойством (силовская
л-подгрупп а). Основное значение для теории
групп имеют силовские р-подгруппы, то есть
С. п., множество л у к-рых состоит из единственного
простого числа р. Название дано в честь Л. Силова
(L. Sylow), доказавшего ряд теорем о таких подгруп-
подгруппах в конечной группе (см. Силова теорема).
С. п. играют важную роль в теории конечных групп.
Так, вопрос о дополняемости нормальной абелевой
подгруппы сводится к такому же вопросу для силов-
ских подгрупп; существование нетривиальной р-фак-
торгрушш связано с существованием нетривиальной
/(-факторгруппы у нормализатора силовской р-подгруп-
пы; строение конечной простой группы во многом оп-
определяется строением ее силовской 2-подгрушш. В тео-
теории бесконечных групп, исключая теорию локально
конечных групп, роль С. п. меньше, поскольку уже
основной вопрос о сопряженности силовских р-под-
групп решается положительно только в отдельных
классах бесконечных групп.
Лит.: [1] КаргаполовМ. И., Мерзляков Ю. И.,
Основы теории групп, 3 изд., М., 1982; [2] Ш е м е т к о в Л. А.,
«Успехи матем. наук», 1975, т. 30, У« 2, с. 179—98; [3] Итоги
науки. Алгебра. Топология. Геометрия. 1965, М., 1967, с. 45—
61; [4] Huppert В., Bndliche Gruppen, [Bd] 1, В., 1974.
В. Д. Мазуров.
СИЛОВА ТЕОРЕМЫ — три теоремы о максимальных
р-подгруппах конечной группы, доказанные Л. Си-
Силовым fl] и играющие большую роль в теории конеч-
конечных групп. Иногда объединение всех трех теорем наз.
теоремой Силова.
Пусть G — конечная группа порядка p'ns, где р —
простое число, не делящее число s. Тогда имеют место
следующие теоремы.
Первая теорем а Силова: группа С
содержит подгруппы порядков р' для всех г=1, 2,
. . ., т, причем каждая подгруппа порядка р1'1 яв-
является нормальной подгруппой по крайней мере в од-
одной подгруппе порядка р'. Из этой теоремы, в част-
частности, следуют такие важные утверждения: в группе G
существует Силова подгруппа порядка р'п; любая
р-подгруппа группы G содержится в нек-рой силов-
силовской р-подгруппе порядка рт, индекс силовской р-
подгрушш не делится на р; если U--P есть группа
порядка р'п, то любая ее собственная подгруппа со-
содержится в нек-рой максимальной подгруппе порядка
р'п~х и все максимальные подгруппы группы Р нор-
нормальны.
Вторая теорема Силова: все силов-
ские р-подгруппы конечной группы сопряжены между
собой. Для бесконечных групп аналогичное утвержде-
утверждение, вообще говоря, неверно.
Третья теорема Силова: число силов-
ских р-подгрупп конечной группы делит порядок
группы и сравнимо с единицей по модулю р.
Для произвольных множеств я простых чисел ана-
аналогичные теоремы о силовских я-подгруппах получены
лишь в классе конечных разрешимых групп (см. Холла
подгруппа). В неразрешимых группах ситуация иная.
Напр., в знакопеременной группе Аъ степени 5 для
п= {2, 3} есть силовская я-подгруппа S порядка 6,
индекс к-рой делится на число из я. Кроме того, в Аъ
есть силовская я-подгруппа, изоморфная Л4 и несоп-
несопряженная с S. Число силовских я-подгрупп в Л Г) не
делит порядок группы Аъ.
Лит.: Ш S у 1 о w L., «Math. Ann.», 1872, Bd 5, S. 584—94;
[2] Холл М., Теория групп, пер. с англ., М., 1962.
В. Д. Мазуров.
СИЛЬНАЯ ГОМОЛОГИЯ — см. Слабая гомология.
СИЛЬНАЯ ПРОИЗВОДНАЯ — то же, что Фреше
производная.
СИЛЬНО НЕПРЕРЫВНАЯ ПОЛУГРУППА — се-
семейство линейных ограниченных операторов T(t),
?>0, в банаховом пространстве X, обладающее свой-
свойствами:
1) Т (t+x)x=T (t) T (х)х, t, х > 0, х?Х;
2) функции Т (t)x непрерывны на @, оо) при любом
х?Х.
При выполнении 1) из измеримости всех функций
T(t)x, х?Х, и, в частности, из односторонней (справа
или слева) слабой непрерывности следует сильная не-
непрерывность T(t). Для С. н. п. конечное число
ш= inf t-1ln\\T(t)\\= lim г-ЧпЦГ(г)[|
t > 0 t ->¦ 00
наз. типом полугруппы. Таким образом,
нормы всех функций Т (t)x растут на со не быстрее
экспоненты eU)t. Классификация С. н. п. основана на
их поведении при t-> 0. Если существует такой огра-
ограниченный оператор /, что \\T(t)~-J\\ ->- 0 при 1->-О,
то / — проекционный оператор и T(t)—JetA, где
А — ограниченный линейный оператор, коммути-
коммутирующий с /. В этом случае Т (t) непрерывна по норме
операторов. Если /=/, то T(t)=etA, —оо<г<оо,—
равномерно непрерывная группа операторов.
Если T(t)x -*¦ Jx при каждом х?Х, то J—также
проекционный оператор, проектирующий X на под-
подпространство Хо — замыкание объединения всех зна-
значений T(t)x, 4>0, х?Х.
Для того чтобы / существовал и равнялся /, необ-
необходимо и достаточно, чтобы ||Г(г)Н была ограничена
на @,1) и чтобы Х0~~Х. В этом случае полугруппа
T(t), доопределенная равенством Т@)=1, сильно
непрерывна при i^O (удовлетворяет С0-у с л о в и ю).
Для более широких классов полугрупп предельное со-
соотношение Т (t) -*¦ 1 выполняется в обобщенном смыс-
смысле:
lim— Г Т (x)xdx=--x, xCX
(суммируемость по Чезаро, Сх-у с л о в и е), пли
e-^T (x)xdx^x, x?X
(суммируемость по Абелю, А -условие). При этом
предполагается, что функции ||Г(()г||, х?Х, интегри-
руемы на [0,1] (а значит, и на любом конечном от-
отрезке).
Поведение С. н. п. при 1-vO может быть совсем
нерегулярным. Напр., функции ||7'(Z)z|| могут иметь
при г=0 степенную особенность.
Для плотного в Хо множества элементов х функции
Т (t)x дифференцируемы на [0, оо). Важную роль иг-
играют С. п. п., для к-рых функции Т(t)x дифференци-
дифференцируемы при всех х для t>0. В этом случае оператор
Т' (t) ограничен при каждом t и его поведение при
t ->- 0 дает новые возможности для классификации
полугрупп. Выделены классы С. н. п., для к-рых Т(t)
допускает голоморфное продолжение в сектор комп-
комплексной плоскости, содержащий полуось @, оо).
См. Полугруппа операторов, Производящий оператор
полугруппы.
Лит.: [1] X и л л е Э., Ф и л л и п с Р., Функциональный
анализ и полугруппы, пер. с англ. М. 1062 С. Г. Нрейн.
СИЛЬНОЕ ДИФФЕРЕНЦИРОВАНИЕ неопределен-
неопределенного интеграла — нахождение сильной производной
неопределенного интеграла
действительнозначной функции /, суммируемой на
открытом подмножество G «-мерного евклидова прост-
пространства, рассматриваемого как функция сегмента.Если
|/| (In A + |/I))"-1
суммируема на G (в частности, если f?Lp(G), р
то интеграл F от / сильно дифференцирует почти всюду
на G. Для любой <р(и), м^О, положительной, неубы-
неубывающей и такой, что
ф (й)=О (U In"!*)
при м->-оо, существует такая суммируемая на G
функция/^0, что ф (/(*)) также суммируема и отношение
F (I)I\I\ неограниченно в каждой точке x?G при /,
стремящемся к х, то есть F не является С. д.
Лит.: [1] Jcssen В., MarcinkiewiczJ., Zyg-
m u n d A., «Fund. Math.», 1935, v. 25, p. 217—34; [2] S a k s S.,
«Fund. Math.», 1935, v. 25, p. 235—52; [3] Сакс С, Теория ин-
интеграла, пер. с англ., М., 1949; [4] 3 и г м у н д А., Тригономе-
Тригонометрические ряды, пер. с англ., [2 изд.], т. 2, М., 1965.
Т. П. Лукашенко.
СИЛЬНОЕ РЕШЕНИЕ дифференциального уравне-
уравнения
в области D — это локально интегрируемая функция и,
к-рая имеет локально интегрируемые обобщенные про-
производные всех порядков <т и удовлетворяет урав-
уравнению (*) почти всюду в области D.
Понятие «С. р.» может быть введено и таким об-
образом. Функция и наз. С. р. уравнения (*), если су-
существуют такие последовательности гладких (напр.,
класса С°°) функций {ип}, {/„}, что ип-+и, /„_>./ и
];iin=fn при каждом п, где сходимость понимается
в L±(K) для любого компакта K<=D. В этих опреде-
определениях Lx можно заменить классом Lp локально ин-
интегрируемых со степенью pj&l функций. Наиболее
употребительным является класс L2.
В случае эллиптич. уравнения (*) оба понятия
С. р. совпадают. А. П. Солдатов.
СИЛЬНЫЙ ИНТЕГРАЛ — интеграл лебеговского
типа от функций со значениями в линейном топологич.
пространстве по скалярной мере или от скалярной
функции по мере со значениями в векторном прост-
пространстве. При этом предельные процессы, с помощью
к-рых определяется интеграл, понимаются в смысле
сильной топологии. Примерами С. и. являются:
1) Бохнера интеграл от векторнозначной функции;
2) Даниеля интеграл, если значения подинтеграль-
пой функции принадлежат а-полной векторной ре-
шртко;
3) интеграл \ XdFx, дающий спектральное разло-
жение самосопряженного оператора, действующего
в гильбертовом пространстве.
В Си. от скалярных функций по векторной мере
значения меры во многих случаях предполагаются
принадлежащими векторному полуупорядоченному про-
пространству.
Лит.: [1] Данфорд Н., Шварц Д ж.-Т., Линейные
операторы, пер. с англ., т. 1—2, М., 1962—66; [2] Н i I d e b-
г a n d t Т. Н., «Bull. Amor. Malli. Soc.» 1953, v. fi9, p. Ill —
139. B. II. Соболев.
СИЛЬНЫЙ ОТНОСИТЕЛЬНЫЙ МИНИМУМ — ми-
минимальное значение J (у), достигаемое функционалом
J (у) на кривой у(х), х1^.х ^.х2, такое, что
J(y)<J(y) A)
для всех кривых сравнения у (х), удовлетворяющих
условию е-близости нулевого порядка:
\у(х)-у(х)\<г B)
на всем промежутке [tj, .т2]. Предполагается, что кри-
кривые у (.г), у (х) удовлетворяют заданным граничным
условиям.
Если, помимо условия B), требующего 8-близости
по ординате, добавить условие е-блиаости по произ-
производной:
на всем промежутке [хх,х2], то говорят об условии е-
близости первого порядка.
Значение, достигаемое функционалом J (у) на кри-
кривой у(х), для к-рого неравенство A) выполняется для
всех кривых сравнения у (х), удовлетворяющих усло-
условию е-близости первого порядка, наз. слабым
относительным минимумом.
Поскольку условие е-близостн нулевого порядка
B) выделяет более широкий класс кривых по срав-
сравнению с условием е-близости первого порядка B),
C), то всякий сильный минимум является одновре-
одновременно слабым минимумом, но не всякий слабый мини-
минимум является сильным. В связи с указанным разли-
различием необходимые, а также достаточные условия опти-
оптимальности для сильного и слабого относительного ми-
минимума имеют неодинаковый вид.
Наряду с понятием С. о. м. можно ввести понятие
абсолютного минимума. Абсолютный ми-
минимум — это минимальное значение J {у), достигаемое
функционалом J (у) на всем множестве кривых, на
к-рых функционал J (у) имеет смысл. Абсолютный
минимум является глобальным, а сильный и слабый
относительные минимумы— локальными минимумами.
Абсолютный минимум является одновременно и
С. о. м., но не всякий С. о. м. является абсолютным
минимумом.
Вариационную задачу, имеющую более одного С. о.
м., наз. многоэкстремальной задачей. При решении
практических вариационных задач С. о. м. находят
приближенно, используя численные методы вариацион-
вариационного исчисления (см. Вариационное исчисление; чис-
численные методы).
Для задач, в к-рых С. о. м. единственный, необхо-
необходимые условия оптимальности С. о. м. являются одно-
одновременно достаточными условиями абсолютного ми-
минимума. Такая ситуация имеет место, напр., в теории
оптимального управления для линейных задач опти-
оптимального быстродействия (см. Оптимального быстро-
быстродействия задача), а также для нек-рых других классов
задач вариационного исчисления.
Лит.- HI Л а в р е н т ь е в М. А., ЛюстерникЛ. А.,
Курс вариационного исчисления, 2 изд., М.—Л., 1950; [2]
С м я р но в В. И., Курс высшей математики, 3 изд., т. 4, М.,
И. В. Вапнярский.
1Л1ЛЫ1ЫИ ЭКСТРЕМУМ — минимальное или мак-
максимальное значение J(y), достигаемое функционалом
J (у) на кривой у (.с), ^<.с<:.т2, для к-рого выполня-
выполняется одно из неравенств
/ (j/X / (у) или J (у) з- J (у)
для всех кривых сравнения у(х), находящихся в е-
окрестности кривой у(х). Кривые у (х), у (х) должны
удовлетворять заданным граничным условиям.
Поскольку максимизация функционала J (у) эк-
эквивалентна минимизации функционала — J(y)t T0
часто вместо сильного экстремума говорят о сильном
минимуме. Термин «сильный» подчеркивает, что на
кривые сравнения у (х) наложено условие е-близости
только по у(х):
на всем промежутке [х1, х2], тогда как по производной
кривые у (a) vi у (.г) могут отличаться как угодно «силь-
«сильно».
По самому своему определению С. :>. является силь-
сильным относительным экстремумом, поскольку дает
экстремум не абсолютный, т. е. не на всем классе
допустимых кривых сравнения у(х), на к-рых функцио-
функционал J (у) имеет смысл, а локальный, относительный,
соответствующий подмножеству всех допустимых кри-
кривых сравнения, находящихся в е-окрестности кривой
у (х). Однако для краткости термин «относительный»
часто опускают и говорят о С. э., имея в виду сильный
относительный экстремум (см. Сильный относитель-
относительный минимум).
Лит.: [1] Лаврентьев М. А., Лгостерник Л. А.,
Курс вариационного исчисления, 2 изд., М.—Л., 1950; [2]
Смирнов Б. И., Курс высшей математики, 3 изд., т. 4,
М., 1957. Я. Б. Вапнярский.
СИМВОЛ ОПЕРАТОРА — скалярная или матричная
функция, ассоциированная с оператором и обладающая
свойствами, в той или иной форме отражающими свой-
свойства этого оператора. Обычно считается, что Со. за-
заданы для операторов, принадлежащих нек-рой ал-
алгебре. Тогда, как правило, при сложении операторов
их символы складываются, а при умножении — пере-
перемножаются с точностью до членов, в нек-ром смысле
являющихся младшими, но иногда и точно. Бывает,
что С. о. — это функция со значениями в нек-рой ал-
алгебре (в частности, операторной алгебре), более про-
простой, чем исходная.
Обычно символы ассоциируются с операторами, дей-
действующими в функциональных пространствах. Тогда
одна из типичных ситуаций состоит в том, что если
оператор действует на функции от п переменных (или,
более общо, на функции на и-мерном многообразии),
то его символ — функция от 2га переменных (или на
2ге-мерном многообразии). На основе использования
таких С. о. строится теория псевдодифференциальных
операторов. Соответствие между символами и операто-
операторами является основой квантования, при к-ром символ
является классич. величиной, а сам оператор — соот-
соответствующей квантовой величиной.
Символы операторов в R". Пусть дан
полином.
а(Р, ч) = 2|а + р1<т
где 9, p6R"> <? = -(«!, • . ., qn), p-=(?i, . . ., р„) — муль-
тииндексы (т. е., напр., a^aj, . . ., а„), ау>0, а,- —
целые, \tx\~tXi-\-. . .-faH, ^арбС). Тогда по нему
несколькими различными способами .можно пост- i
роить оператор А, действующий на функциях на R"'
подставляя вместо ijy оператор qj умножения на одну
из координат xj в R", а вместо pj — оператор р/=
== Т эх7 ' гЯе 1= ' —1' 'г — произвольная постоянная
(играющая роль постоянной Планка). Если при этом
менять порядок букв q и р, то получатся разные опе-
операторы. Если положить
I i
то в (<j, /?) нал. qp- с и м в о л о м, или левым о и м-
полом оператора А. Получаемое таким образом со-
соответствие между левыми символами и операторами яв-
является взаимно однозначным соответствием между
полиномами и дифференциальными операторами с по-
полиномиальными коэффициентами и может быть рас-
распространено на значительно более широкие классы
операторов и символов, если воспользоваться форму-
формулой
(Au)(x) = Bnh)-Aeh а (т. |) и (у) dy rf?.
где z?—Zj^j-}-. . . + zn|,j для и-мерных векторов z~
;"(zi. • • •, 2„) и i== (ix, . . ., \n), dy — dyv . . ., dyn,
d%=dlx ... d\n.
Оператор А с pq-c и м в о л о м, или правым
символом a(q, p) определяется формулой
A = a\q, p;=
или для более общих символов
(у) i
а (г/, |) и (i/) dy d?.
Более симметричный способ построения оператора
по полиному a(q, p) получается, если ввести для не-
коммутирующих операторов В, С симметризованное
произведение (ВкС1) формулой
а затем полошить
Тогда a (q, p) наз. символом Вейля опера-
оператора А. Оператор А может быть записан через символ
Вейля по формуле
(Au)(x)==Bnh)'"^eh Х Ю а ^±1, Щи (у) dydc,.
Вторичное квантование приводит к появлению еще
двух видов символов операторов на R" — виковского
и антивиковского. А именно, если ввести операторы
рождения a-=qj — ipj и операторы уничтожения aj —
= qj-\-ipj и записать дифференциальный оператор с по-
полиномиальными коэффициентами в виде
или в виде
то его виковский символ с(д, р) и анти-
виковский символ а (<?, р) задаются соот-
соответственно формулами
С(Ч, Р) = 2,а^<хЦ ($—*р
О формулах, связывающих разные виды символов од-
одного и того же оператора, см. в \\] -|4(.
Символы операторов на м н о г о о б-
р а з и и. Если символы описанных выше типов на R™
взаимно однозначно соответствуют операторам нек-
рых достаточно широких классов, то на многообразии,
как правило, нет естественных символов, для к-рых
существовало бы такое взаимно однозначное соответ-
соответствие. На многообразии важную роль играет т. п.
главный символ, к-рый определяется для
нек-рых псевдодифференциальных операторов и яв-
является однородной функцией на Т*Х\О — кокасатель-
ном расслоении многообразия X без нулевого сече-
сечения. Его обратимость означает, что рассматриваемый
оператор А является эллиптическим и гарантирует
выполнение теоремы регулярности, т. е. гладкости
решений уравнения Ли=/ с гладкой правой частью /,
а также фредгольмовость оператора А (в случае ком-
компактного X) в подходящих пространствах Соболева.
При сложении и умножении операторов их главные
символы соответственно складываются и перемно-
перемножаются. Главный символ не меняется при добавле-
добавлении к оператору членов меньшего порядка.
Символы операторов на многооб-
многообразии с краем. На многообразии с краем X
псевдодифференциальный оператор имеет вид мат-
матрицы (см. f5]):
he -© \
rp /") T1 1С* \ T1 / C1 \
1 vi i (l*l) 1 (")
где Elt E2 — векторные расслоения на X, Gx, G2 —
векторные расслоения на Y, A — псевдодифференци-
псевдодифференциальный оператор на X, удовлетворяющий трансмиссии
условию, Т — граничный оператор, т. е. оператор
взятия каких-то граничных условий (вообще говоря,
псевдодифференциальных), К — кограничный опе-
оператор, или оператор типа потенциала, В — сингуляр-
сингулярный оператор Грина (так называются композиции гра-
граничных и кограничных операторов и нек-рые более
общие операторы аналогичной структуры), Q— псевдо-
псевдодифференциальный оператор на У. Оператор 91 имеет
символы двух типов: внутренний и граничный. Вну-
Внутренний символ о0C1) — это обычный символ
оператора А, являющийся функцией на Т*Х\О,
точнее, сечением расслоения Нот(я*?1, п*Е2), где
я : Т*Х\О —>- X — канонич. проекция. Гранич-
Граничный символ ау(Ш) — это функция на T*Y\O,
значения к-рой — операторы на полуоси [0, оо),
получающиеся из 91 замораживанием коэффициентов
главной части в точке границы (в координатах, в к-рых
граница является гиперплоскостью) и последующим
преобразованием Фурье по касательным переменным.
Обратимость о°(Щ — это обычная эллиптичность опе-
оператора А. Если предположить эту эллиптичность, то
обратимость оу (W) в классах убывающих функций на
полуоси —• это фактически условие эллиптичности гра-
граничной задачи, определяемой оператором 91, или i
т. н. условие Шапир о — Л опатинского. I
Таким образом, символом Ж естественно называть
пару {о°(91), оу(Ш)}. Если обратимы оба символа
о0 (91) и ау (91), то Щ наз. эллиптическим, и
в этом случае для него верны обычные теоремы о ре-
регулярности и фредгольмовости (последняя — когда X
компактно).
Лит.: [1] Б е р е з и и Ф. А., Метод вторичного квантова-
квантования, М., 1965; [2] М а с л о в В. П., Операторные методы, М.,
1973; E3J Ш у 0 и н М. А., Псевдодифференциальные операторы
и спектральная теория, М., 1978; [4] Б е р е з и н Ф. А., «Ма-
тем. сб.», 1971, т. 86, ЛЬ 4, с. 578—610; [5] В о u t e t d е М о п-
v е 1 L., «Acta math.» 1971 v. 126 p. 11—51. M. А. Шубин.
СИМВОЛИЧЕСКАЯ ДИНАМИКА — 1) С. д. в уз-
узком смысле слива — исследование определяемого ниже
топологич. автоморфизма Бернулли о — его инва-
инвариантных замкнутых подмножеств, инвариантных мер
и т. д. Т о пологи чески й а в т о .« о р ф и з м
В е р н у л л и а действует в пространстве Q беско-
бесконечных двусторонних последовательностей символов
из нек-рого алфавита А (обычно конечного), снабженном
топологией прямого произведения бесконечного числа
экземпляров А (в каждом из к-рых обычно берется
дискретная топология). А именно, а переводит после-
последовательность со={ш,} в со'-={ш;}, где coi=co, + i
(«сдвиг последовательности на один шаг налево»).
Очевидное обобщение — действие группы (или полу-
полугруппы) G в пространстве А°.
Пусть нек-рые пары (а, Ъ) символов из А объявлены
«допустимыми». Всевозможные последовательности
{ш,}, для к-рых при всех i пары (<в/, co,- + i) допустимы,
образуют нек-рое замкнутое инвариантное (относи
тельно о) подмножество ихсй. Это — важнейший
пример инвариантного подмножества топологич. ав
томорфизма Бернулли. Динамич. система в Qj, порож-
порожденная сдвигом а\пг, наз. топологической
цепью Маркова.
2) С. д. п широком смысле слова — применение С. д.
в узком смысле слова к исследованию динамич. систем,
к-рые сами по себе определяются совершенно незави-
независимо от Q и а.
Лит.: [1] Алексеев В. М., Символическая динамика.
К., 197В (Одиннадцатая [летняя] математическая школа, ч. 1);
|2] Б о у э н Р., Методы символической динамики, пер. с англ.,
М., 1979 (Новое в зарубежной науке. Математика, в. 13).
Д. В. Аносов.
СИММЕТРИЗАЦИИ МЕТОД (в теории функций) —
один из методов решения экстремальных задач геомет-
рич. теории функций. В основе метода лежит понятие
симметризации замкнутых и открытых множеств п-
мерного евклидова пространства. Впервые С. м. в
теории функций был применен к изучению свойств
трансфинитного диаметра (см. [1]), несколько позд
нее — к решению проблемы Карлемана — Миллу (см.
12]), а затем использовался достаточно широко (см.
[3] - [6], [9]).
Использование С. м. в теории функций основано на
монотонном характере изменения емкости конденса-
конденсатора и внутреннего радиуса области при различных
видах симметризации. Возможность применения С. м.
при решении экстремальных задач геометрич. теории
функций обусловливается определенной симметрией
экстремальных отображений. Опираясь на свойство
неубывания внутреннего радиуса области при ее сим-
симметризации относительно прямой или луча, с помощью
теоремы об изменении внутреннего радиуса области
при отображении ее посредством регулярной функции
был получен следующий принцип с и м м е т-
р и з а ц и и (см. [4]): если функция w--f(z), f@)=w0,
/' @) = аь регулярна в круге Е: \z\ <1, Ef — множество
значений функции w=f(z) в Е, Ef— результат сим-
симметризации Еj относительно луча или прямой, прохо-
проходящих через w=w0, a r(Ef, w0) — внутренний радиус
области Ef относительно точки w~w0, то
r
(E},
Равенство в («) имеет место тогда и только тогда, когда
функция г/;—/(г) однолистна в Е, а область Ef совпа-
совпадает с Ef (при симметризации Штейнера) или полу-
получается из Ef в результате поворота вокруг w~u:0
(при симметризации Uoiia). Аналогичный результат
имеет место и для других видов симметризации, для
к-рых справедливо свойство неубывания внутреннего
радиуса. Дополнительное исследование обычно не-
необходимо для выяснения условий достижимости в (*)
равенства.
Имеются обобщения принципа симметризации на
случай кольца и областей произвольной связности
(см. [6]). Плодотворным оказывается сочетание С. м.
с другими методами решения экстремальных задач
геометрич. теории функций (экстремальной метрики
методом, теорией квадратичных дифференциалов и
др.). Таким путем был получен ряд теорем покрытия
и искажения для различных классов регулярных в
данной области функций (однолистных, однолистных
в среднем, слабо р-листных в круге или в кольце и
др., см. [4J — [6]).
С. м. применяется также при изучении свойств про-
пространственных квазиконформных отображений. Это
обстоятельство особенно существенно в связи с огра-
ограниченными возможностями исследования таких ото-
отображений. С. м. позволяет находить среди двусвязных
пространственных областей, обладающих определен-
определенными геометрич. свойствами, область с наибольшим
конформным модулем. Определение такой области в
свою очередь позволяет установить нек-рое экстремаль-
экстремальное свойство квазиконформного отображения. В част-
частности, с помощью С. м. установлены нек-рые теоремы
искажения для квазиконформнглх отображений в трех-
трехмерном евклидовом пространстве (см. [7], [8]).
Лит.: [1] FaberG., «Sitzungsber. Bayer. Akad. Wiss.
Math.-naturwiss. Kl.», 1920, Bd 20, S. 49—64; [2] В о u r 1 i n ff
A., Etudes sur un probleme de majoration, Uppsala, 1933;l3] П o-
ji я а Г., Сегё Г., Изопериметрические неравенства в мате-
математической физике, пер. [с англ.], М., 1962; [4] Хеймап
B. К., Многолистные функции, пер. с англ., М., 1960; [5]
Дженкинс Дж.( Однолистные функции и конформные
отображения, пер. с англ., М., 1962; [6] Г о л у з и я Г. М.,
Геометрическая теория функций комплексного переменного,
2 изд., М., 1966; [7] Шабат Б. В., «Докл. АН СССР»,
1960, т. 132, № 5, с. 1045—48; [8] Gehring F. W., «Trans.
Amer. Math. Soc», 1961, v. 101, ,№ 3, p. 499—519; [9]
Baernstein A., «Acta math.», 1974, v. 133, p. 139—69.
И. II. Митюк.
СИММЕТРИЗАЦИЯ — сопоставление каждому объ-
объекту F объекта F* (того же класса), обладающего
нек-рой симметрией. Обычно С. подвергают замкнутые
множества F в евклидовом пространстве Е" (или в
пространстве постоянной кривизны), а также отобра-
отображения, причем С. строится так, что F* непрерывно
зависит от F. С. сохраняют одни и монотонно изме-
изменяют другие характеристики объекта. С. использу-
используются в геометрии, математич. физике, теории функций
при решении экстремальных задач. Впервые С. вве-
введена Я. Штейнером (J. Steiner) в 1836 для доказатель-
доказательства изопериметрического неравенства.
С. относительно плоскости Еп~к в
Е": для каждого непустого сечения множества F пло-
плоскостью Ek\ Fjn~k в Ек строят шар с центром ?* Л Е"~к
и тем же /с-мерным объемом, что Ff]Ek; заполняемое
шарами множество F* есть результат симметризации.
C. относительно плоскости сохраняет объем, выпук-
выпуклость, не увеличивает площадь границы и интегралы
поперечных мер (см. [2]). При /с=1 эта С. есть сим-
симметризация Штейнера, при к—п—1 —
симметризация Шварца.
С. относительно полуплоскости
1{п-к в ?п- дЛЯ каждого непустого сечения F сферой
Sk, имеющей центр на границе dlln~k и лежащей в
Ек + 1±дН'1~к, строят сферич. планочку S^f]D" (?>"—
шар с центром H"~k{\Sk) того же /с-мерного объема,
что F[]Sk\ заполняемое шапочками множество /'*
есть результат С. При к— п—1 это — сферическая
С, если ге=2 — круговая С.
С. смешением: для выпуклого множества
FcEn строят симметричное ему относительно пло-
плоскости .Б* множество F'; результатом С. является
множество F*-— (F-\-F')i2, где сложение множеств
понимается как векторная сумма.
С. окатыванием: для выпуклого тела FcKn
его опорная функция усредняется на параллельных
сечениях единичной сферы; результатом С. считается
тело F*, восстановленное по получившейся опорной
функции.
В Es симметризация Штейнера не увеличивает ем-
емкость; симметризация Шварца сохраняет непрерывность
гауссовой кривизны границы и не уменьшает ее ми-
минимум; С. относительно полуплоскости не увеличивает
основную частоту области и площадь границы; сфери-
сферическая С. не увеличивает емкость; С. смешением со-
сохраняет интеграл средней кривизны границы и не
уменьшает площадь последней; С. окатыванием со-
сохраняет ширину (см. [1], [3]).
В Ёг симметризация Штейнера не увеличивает по-
полярный момент инерции, внешний радиус, емкость,
основную частоту; не уменьшает жесткость кручения,
максимальный внутренний конформный радиус (см.
[3]).
В связи с многократным применением С. рассматри-
рассматриваются вопросы сходимости С. Определения аналогов
С. для незамкнутых множеств допускают ветвления.
О применении С. в теории функций см. Симметри-
Симметризации метод.
Лит.: [1] Б л я ш к о В., Круг и шар, пер. с нем., М., 1967;
[2] Хадвигер Г., Лекции об объеме, площади поверхности
и изопериметрии, пер. с нем., М., 1966; [3] Полна Г., С е-
г ё Г., Изопериметрические неравенства в математической физи-
физике, пер. с англ., М., 1962; [4] L e i с h t w e i s s К., Konvexe
Mengen, В., 1980. С. Л. Печерский.
СИММЕТРИИ КРИТЕРИЙ — статистический кри-
критерий для проверки гипотезы //„, согласно к-рой
одномерная плотность вероятности симметрична от-
относительно нуля.
Пусть проверяется гипотеза симметрии Но, согласно
к-рой плотность вероятности р (х) вероятностного
закона, к-рому подчиняются независимые случайные
величины Xi, . . ., Х„, симметрична относительно
нуля, то есть р {х)—р (—х) для любого х из области
определения плотности р(х). Любой статистич. крите-
критерий, предназначенный для проверки На, наз. крите-
критерием симметрии.
Наиболее часто в качестве альтернативы к Но рас-
рассматривается гипотеза Hi, согласно к-рой все рас-
рассматриваемые случайные величины Х±, . . ., Х„ имеют
плотность вероятности р (х—Д), Д=^=0. Иначе говоря,
согласно гипотезе Н± плотность вероятности случайной
величины X,- получается в результате сдвига плотности
р (х) вдоль оси Ох на расстояние |Д| вправо или влево,
в зависимости от знака Д. Если знак смещения Д из-
известен, то конкурирующая гипотеза /If наз. одно-
односторонней^ противном случае — двусторон-
двусторонней. Простой пример С. к. дает знаков критерий.
С. к. является частным случаем рандомизации
критерия.
Лит.: Ш Гаек Я., Ш и Д а к 3., Теория рангоиых кри-
критериев, пер. с англ., М., 1971; [2] К е н д а л л М., С т ь ю а р i
Л., Статистические выводы и связи, пер. с англ., М., 1!O;t.
М. С. Никулин.
СИММЕТРИИ ПРИНЦИП, п р и н ц и п с и м м е т-
р и и Шварца,принцип симметрии Р и-
м а н а — Ш в а р ц а для аналитических функции:
пусть область G расширенной комплексной плоскости С
ограничена замкнутой жордановой кривой Г, в со-
состав к-рой входит дуга I окружности L расширенной
комплексной плоскости С. Пусть, далее, функция
f(z) определена и непрерывна на G{}1, аналитична в G,
а на 1 принимает значения, принадлежащие пек-рой
окружности С расширенной комплексной плоскости С.
Тогда / (z) продолжается через дугу I в область С*,
симметричную с, G относительно L, до функции, анали-
аналитической в области G\Jl[jG*- Такое продолжение
(через I) единственно и определяется следующим свой-
свойством продолженной функции f(z): если точки z?G
и z*?G* симметричны (инверсны) относительно L, то
точки ш=/(г) п iu*=/(z*) симметричны относительно С.
В частности, если L и С совпадают с действительной
осью плоскости С, то f{z)=f(z) при z?G\Jl[JG*. Под
окружностями расширенной комплексной плоскости
понимаются как собственно окружности, так и пря-
прямые. Непрерывность также может пониматься как в
обычном, так и в обобщенном смысле, т. е. когда /(z)
наз. непрерывной в точке z0, если f(z) -у f (z0) при z ->-z0,
независимо от конечности или бесконечности величины
/(z0). Кривая Г, равно как и I, может проходить через
точку оо. По условию, f(l)czC, но не обязательно
/ A)= С. Кроме того, если G и G* имеют общие внутрен-
внутренние точки, то продолженная функция в этих точках
может быть неоднозначной.
С. п. для гармонических ф у н к ц и й при
тех же G, L, I и G* формулируется так: если функция
и (х, у) гармонична в G, непрерывна на G\Jl и равна
нулю на I, то и продолжается через I в G* до функции,
гармонической в GU^U^*. При этом если точки (х, y)?G
и (х*, y*)?G* симметричны относительно L, то
!( (х*, у*)= — и{х, у).
Обобщением С. п. на случай аналитич. дуг I (и С)
является принцип Шварца аналитич. продолжения
аналитических и гармонич. функций (см. [1], [2]).
Обобщение С. п. для гармонич. функций на случай
функции любого числа переменных наз. отражения
принципом. С. п. широко используется в приложениях
теории аналитических и гармопич. функций (при кон-
конформных отображениях областей с одной или несколь-
несколькими осями симметрии, в теории упругости, гидролр-
ханике, электростатике и т. д.).
Лит.: [1] Schwarz H., Gesammelte mathematische АЬ-
handlungen, Bd 2, В., 1890; [2] П р и в а л о в И. И., Введение
в теорию функций комплексного переменного, 12 изд.. М., 1977,
с. 350—60; [3] Л а в р е н !Г ь е в М. А., Ш а б а т Б. В., Ме-
Методы теории функций комплексного переменного, 4 изд., М.,
1973, с. 158 — 97, 214—15. Е. П. Долженхо.
СИММЕТРИКА на множестве X — неотри-
неотрицательная действительная функция d, определенная
на множество пар всех элементов множества X и удов-
удовлетворяющая следующим аксиомам:
1) d(x, </)=0 в том и только в том случае, если х=у;
2) d{x, y)=d(y, x) при любых х, у?Х.
В отличие от метрики и псевдометрики С. может
не удовлетворять аксиоме треугольника. По симмет-
рике d на множестве X определяется топология на X:
множество АсХ замкнуто (относительно симметрики
й) в том и только в том случае, если d(x, Л)>0 для
каждого х ? Х\А . При этом
d(x, A) = inf{d(x, y):y?A}.
Замыкание множества А в так определенном топологич.
пространстве содержит множество всех тех точек х?Х,
для к-рых d(x, A)=0, но может этим множеством не
исчерпываться. Соответственно, е-шары вокруг точек
множества X могут иметь пустую внутренность. То-
Топологич. пространство наз. симметризуемым,
если топология его порождается по указанному пра-
правилу нек-рой С. Класс спмметризуемых пространств
гораздо шире класса метризуе.чых пространств: сим-
метризуемое пространство может не быть ни параком-
пактным, ни нормальным, ни хаусдорфовым. Кроме
того, симметризуемое пространство может не удовле-
удовлетворять первой аксиоме счетности.
Но каждое симметрнзуемое пространство X сек-
секвенциально, т. е. его топология определяется
сходящимися последовательностями по правилу: мно-
множество А замкнуто в том и только в том случае, если
предел каждой сходящейся п X последовательности
точрк .множества А принадлежит А . Для бикомпактных
хаусдорфовых пространств сим.метризуемость равно-
равносильна метризуемости.
Лит.; [1] Архангельский А. В., Понома-
Пономарев В. 1-1., Основы общей топологии в задачах и упражнени-
упражнениях, М., 1974; [2] Не дев С. Й., «Тр. Моск. матем. об-ва»,
1971, т. 24, с. 201—36. А. В. Архангельский.
СИММЕТРИРОВАНИЕ, симметризаци я,—
одна из операций тензорной алгебры, при помощи к-рой
по данному тензору строится симметричный (по группе
индексов) тензор. С. всегда производится над несколь-
несколькими верхними или нижними индексами. Тензор S
о координатами {«*'••'V, i<'v, /ц<п} является ре-
результатом С. тензора Т с координатами {tl.'"'\P ,
3,--3q
l<:jv, /ц<ге}по m верхним индексам, напр, по группе
индексов /= (ij, г2, . . ., im), если
3, ¦ ¦ ¦ 3q~"mT^I~>a )\---iq
Здесь суммирование производится по всем пг\ переста
новкам а= (аг, а2, . . ., ат) группы индексов /. G.
по группе нижних индексов определяется аналогично.
С. по группе индексов обозначается взятием этих
индексов в круглые скобки ( ). Посторонние индексы
(не участвующие в С.) отделяются вертикальными
черточками. Напр.,
,D|5|17)_ 1
Последовательное С. по группам индексов /х и J2,
Jidz, совпадает с С. по группе индексов /2. Другими
словами, если*; t- ^=\h _(jft h) ...^.то.^ ...h=t{ji _hl)
(внутренние скобки снимаются).
Тензор, не изменяющийся при С. по нек-poii групп-
индексов, наз. симметрическим тензором.
С. по нек-рой группе индексов тензора, альтерниро-
альтернированного (см. Альтернирование) по этой группе, даем
нулевой тензор.
Умножение двух и более тензоров с последующим С.
их произведения по всем индексам наз. с и м м е т р и
ческим умножением. С. тензоров, наряду <
операцией альтернирования, применяется для разли
жепия тензора па тензоры более простого строения
С. применяется также для образования сумм вида (*;
с многоиндексными слагаемыми. Напр., если эле-
элементы матрицы
а] а\. .. а\
п п п
ах а>... ап
коммутируют при умножении, то выражение
наз. перманентом матри ц ы.
Лит.: El] Ш и р о к о в И. А., Тензорное исчисление, 2 млн.,
Казань, 1961; [2] Беклемишев Д. В., Курс аналитичес-
аналитической геометрии и линейной алгебры, М., 1971; [3] С х о у т е и
Я. А., Тензорный анализ для физиков, пер. с англ., М., 196.">.
Л. Л. Купцов.
СИММЕТРИЧЕСКАЯ АЛГЕБРА — обобщение ал-
алгебры многочленов. Если М — унитарный модуль над
коммутативно-ассоциативным кольцом А с единицей,
то С. а. модуля М наз. алгебра S(M)~- T (M)ll, где
Т(М) — тензорная алгебра модуля М, I — ее идеал,
порожденный элементами вида х@у — у@х (.г, у?М).
С. а.— коммутативно-ассоциативная Л-алгебра с еди-
единицей; она градуирована:
где Sp(M) - Гр{МI1{\ Тр{\1), примем S° (,)!)-= А ,
SL (M) = M. Модуль Sf(M) наз. p-ii с л м м р т р и ч е-
ской степенью модуля М. Если М —
свободный модуль с конечным базисвм х+, . . ., хп,
то соответствие x-t -*- X,- (i=l, . . ., п) продолжается
до изоморфизма алгебры S (М) на алгебру многочленов
1 [Xi, . . ., Хп] (см. Многочленов кольцо).
Для любого гомоморфизма А -модулей /: М -*¦ N
р-я тензорная степень TP(f): ТР{М)->- ТР (N) индуци-
индуцирует гомоморфизм SP(f): SP (М) ->. Sp(N) (р-я сим-
симметрическая степень гомоморфиз-
м а /). Получается гомоморфизм Л-алгебр S (/): S (М) ->
->-S(N). Соответствия f—>-SP(f) и / —>- S (/) являются
соответственно ковариантными функторами из кате-
категории А -модулей в себя и в категорию Л-алгебр. Для
любых двух Л-модулей М и N имеет место естествен-
естественный изоморфизм S (M(BN)=±S (M)®S (N).
Если М — векторное пространство над полем харак-
характеристики 0, то симметрирование а: Т (М) ->- Т (М)
определяет изоморфизм С. a. S (М) на алгебру S (М)С
СТ(М) симметрических контравариантных тензоров
на М относительно симметрич. умножения:
и vp = a(u®i)), u?Sp (M),
Лит.: [1] Б у р б а к и Н., Алгебра. Многочлены и поля.
Упорядоченные группы, пер. с франц., М., 1965; 12] К о с т-
р и к и н А. И., Манин Ю. И., Линейная алгебра и гео-
геометрия, М., 1980. А. Л. Онищик.
СИММЕТРИЧЕСКАЯ ГРУППА — группа всех под-
подстановок (биекций) нек-рого множества X с операцией
суперпозиции (см. Подстановок группа). С. г. подста-
подстановок множества X обозначается S (X). Для равномощ-
ных X и X' группы S (X) и S (X') подобны. В случае
конечного множества Х={1, 2, . . ., п) С. г. обозна-
обозначается Sn. Всякая абстрактная группа изоморфна под-
подходящей подгруппе симметрич. группы S (X) нек-рого
множества X (теорема К эли).
Пусть множество X конечно. Всякая подстановка л
на X однозначно записывается в виде произведения
независимых или взаимно простых циклов (цикло-
(цикловая запись подстановки); числовой век-
вектор
z (л) = (в!, а2, ..., ап),
где а,- — число циклов длины i в цикловой записи
подстановки л, наз. цикловым типом подста-
подстановки я. Две подстановки я и я' сопряжены в группе
Sn тогда и только тогда, когда они имеют один и тот
же цикловой тип. Подстановки с цикловым типом
{п-2, 2, 0, ...,0}
наз. транспозициями; их совокупность яв-
является системой образующих группы Sn. Множество
транспозиций 2—{(i, i-f-l)|?=l, . . ., п—1} является
минимальной системой образующих (базой) для Sn.
Вообще, множество Д={(??, jk)\ik?=ik} образует базу
для Sn, если граф с X в качество множества вершин и с
нарами (ifc, /&) в качестве ребер является деревом [2].
Число таких баз равно ге"~2.
Знакопеременная группа Ап — нормальный дели-
делитель в группе Sn, причем если пф1*., то Ап — един-
единственный нетривиальный собственный нормальный
делитель, а 54 содержит еще один нетривиальный
нормальный делитель — четверную группу
Клейна :#4={1, A 2), C 4), A3), B 4), A4), B 3)}.
При и<:4 группа Sn разрешима, а при м>5 неразре-
неразрешима и Ап — простая неабелева группа. Теорема
Гёльдера: при «=^2,6 группа Sn совершенна
(см. Совершенная группа). Х^руппа S2 коммутативна, а
группа Se обладает внешним автоморфизмом порядка 2.
Известны все максимальные интранзитивные и им-
примитивные подгруппы в Sn. Для всякого разбиения
п—т1-\-т2, m1=jtm2, максимальными интранзитивньши
в S,, будут все подгруппы Smi-\-Smi и только они.
Транзитивными имяри.митивнымн максимальными iгод-
группами в 6'„ будут сплетения Siai с Smi (для всякого
разложения n=mim2) и только они. Примитивные мак-
максимальные подгруппы в Sn не описаны A983), но из-
известны нек-рые их бесконечные серии. Напр., группа
Sn естественным образом действует на множестве В
всех подмножеств мощности т множества конечной
мощности п; при пф1т тем самым определяется при-
примитивная группа подстановок множества В™. Она
максимальна в S(B%), если (т, п)фB,6), B,8), C,10),
D,12), (т, 2т), (т, bn+i) (см. ?1]). Другая серия (см.
[6]) получается при рассмотрении группы YLn(GF(q))
полулинейных преобразований пространств G(F(q))
над конечным полем из q элементов. Эта группа опре-
определяет примитивную группу подстановок Грассмана
многообразия Gtum(GF(q)), l<:m<:n—1, к-рая мак-
максимальна в S (G,u m (GF (q)) при п^З.
Пусть X — бесконочное множество. Группа всех
подстановок множества X, перемещающих лишь ко-
конечное число элементов из X, наз. финитной, или
ограниченной симметрической, груп-
группой множества X и обозначается SF(X), а ее под-
подгруппа, состоящая из всех четных подстановок, наз.
финитной, или ограниченной знако-
знакопеременной, группой множества X и обо-
обозначается AF(X). Подгруппы SF(X) и AF(X) — нор-
нормальные делители в S (X). Более общо, пусть а — мощ-
мощность множества X и р<а — нек-рое бесконечное кар-
кардинальное число; совокупность всех подстановок мно-
множества X, перемещающих не более чем р элементов
множества X, является подгруппой в S(X), обознача-
обозначаемой 5р (X). Наряду с SF(X) и AF(X) группы Sp (X) —
нормальные делители в S (X) для всех р"«х, и других
нетривиальных нормальных делителей у S (X) нет (т с о-
рема Шрейера — Улама — Бэра, см. [3]).
Лит.: 11] К а л у ж н и н Л. А., К л и HjM. X., «Матем.
сб.», 1972, т. 87, № 1, с. 91—121: [2] О р е О., Теория графов,
пер. с англ., 2 изд., М., 1980; 13] П л о т к и н Б. И., Группы
автоморфизмов алгебраических систем, М., 1966; [4] У с т и-
м е н к о-Б акумовский В. А., «Докл. АН СССР», 1978,
т. 240, № 6, с. 1305—08. См. также лит. при ст. Подстановок
группа. Л. А. Налужнин.
СИММЕТРИЧЕСКАЯ МАТРИЦА — квадратная ма-
матрица, в к-poii любые два элемента, расположенные
симметрично относительно главной диагонали, равны
между собой, т. е. матрица A = ||a,-|j||i, совпадающая
со своей транспонированной матрицей
aik = aki, i, fc = l, ..., п.
Действительная С. м. порядка п имеет ровно п дей-
действительных собственных значений (с учетом кратно-
кратности). Если А есть С. м., то А~1 и АР суть С. м., если
А и В суть С. м. одного порядка, то А-\-В есть С. м.,
а произведение АВ есть С. м. тогда и только тогда,
когда АВ = ВА. Т.С. Пиголкина.
СИММЕТРИЧЕСКАЯ ОБЛАСТЬ — комплексное мно-
многообразие D, изоморфное ограниченной области в
С", для каждой точки р к-рого существует инволютив-
ное голоморфное преобразование ар: D —»-/), имеющее р
единственной неподвижной точкой. С. о. является
эрмитовым симметрич. пространством отрицательной
кривизны относительно метрики Бергмана. Группа ее
автоморфизмов как комплексного многообразия со-
содержится в группе движений и имеет ту же связную
компоненту G(D), к-рая является некомпактной ве-
вещественной полупростой группой Ли без центра. Ста-
Стационарная подгруппа Н(D) точки p?D в группе G(D)
есть связная компактная группа Ли с одномерным
центром. Как вещественное многообразие С. о. диффео-
морфна R2".
Всякая С. о. единственным образом разлагается в
прямое произведение неприводимых С. о., перечислен-
перечисленных в следующей таблице (где Л/р, q обозначает про-
пространство комплексных матриц размера pXq).
Тип по
Э. Кар-
тану
I
II
III
IV
V
VI
Тпп
G(D)
"р
°Р
-°р/2 + 1
В(р + 1)/2
Е.
Е,
Тип
Н (D)'
AP-1 +
A>>Ч)
ЛР-г
AP-i
Dp/2-l
В(р-1)/2
Ds
Е,
dim V
РЧ
Р(Р-1)
2
Р(Р+1)
2
16
27
Модель D
{ZeM^ (/:Z*Z<B}
<ZeJVWzt=~Zi
Z*Z<E)
{zeMpp-.zt=z,
Z*Z<E)
{ 26C'
<т('+
С. о. типа III может быть представлена как верхняя
полуплоскость Зигеля:
{Z?Mp p:Z* = Z, Im Z > 0}.
Ее точки параметризуют главно поляризованные абе-
левы многообразия. Остальные Со. также могут быть
представлены как Зигеля области первого или второго
рода (см [2]).
Лит.: И] 3 и г е л ь К., Автоморфные функции нескольких
комплексных переменных, пер. с англ., М., 1954; [2] П я т е ц-
к и й-Ш а п и р о И. И., Геометрия классических областей
и теория автоморфных функций, М., 1961; [3] Cartan E.,
«Abh. Math. Sem. Univ. Hamburg», 1935, Bd 1, S. 116—62;
f4] Drncker D., Exceptional Lie algebras and the structure
of hermitian symmetric spaces, Providence, 1978 (Mem. Amer.
Math. Soc, v. 16, № 208). Э. Б. Винберг.
СИММЕТРИЧЕСКАЯ ПРОИЗВОДНАЯ — обобще-
обобщение понятия производной на случай функций множе-
множества Ф в re-мерном евклидовом пространстве. С. п. в
точке х есть предел
lim Ф(8(х;г>) - —
+ 0
I S(х; г) |
где S (х\ г) — замкнутый шар с центром в точке х и
радиусом /-. С. п. II о р я д к агав точке х функции
действительного переменного f (х) наз. предел
Ansf(x, ft)
hm -Ц^ =
h -> о
Функция действительного иоременного /(.г) пмеет
С. и. в точке х порядна 2г.
если
порядка 2г+1:
_ (/ (x + h) — f (x—h))— 2,k= ofWi Bh7T)! =
Если в точке х существует «-я производная /(л) (х),
то в этой точке существует (в обоих смыслах) С. п. и
она равна /1п) (х). Если f (х) имеет в точке х производ-
пую D'z'j(x) или D2r+lf(x), то она имеет производную
D"f(x). Обратное утверждение справедливо при ус-
условии существования всех производных Dnf(x) мень-
меньшего порядка той же четности.
JIvm.: [1] Сакс С, Теория интеграла, пер. с англ., М.,
1949; [2J James R. D., «Trans. Amer. Math. Sue.», 1934,
V. 76, Mi 1, p. lA'J -7B. T. II. Лукашенко.
СИММЕТРИЧЕСКАЯ РАЗНОСТЬ множеств —
одна из операций над множествами. Пусть имеются два
множества А и В. Тогда их с и м м е т р и ч о с к а я
разность обозначается А АД и определяется ра-
равенствами
где символы (J , ПЛ\> ' означают соответственно опе-
операции объединения, пересечения, разности и допол-
дополнения надлежащих множеств. м. и. Войцеховский.
СИММЕТРИЧЕСКАЯ РАЗНОСТЬ порядка п в
точке х функции действительного переменного f(x) —
выражение
(х, к)
Часто также симметрия, разностью называют выраже-
выражение
2*-о С« (—1^ (^+(«—2fe) ft),
получающееся из вышеприведенного заменой It на 2А.
Если функция / (ж) имеет в точке х производную /" (х)
порядка га, то
Ansf(x, h)=fM(x)h»+o(h").
Т. П. Лукашенко.
СИММЕТРИЧЕСКАЯ ФУНКЦИЯ — функция, не из-
изменяющаяся при любой перестановке своих аргумен-
аргументов. С. ф. являются, напр., х1+х2+. . .-\-х„, хххг. . .хп,
1, Х2, . . . , Хп),
цифры в десятичной записи суммы произвольного
количества одноразрядных чисел, «функция голосо-
голосования», к-рая характеризуется тем, что ее аргументы
принимают лишь два значения: 1 («за») и 0 («против»),
а сама функция равна 1, если больше половины ее
аргументов равны 1, и 0 в противном случае. Триви-
Тривиальными примерами С. ф. являются константы и функ-
функция одной переменной.
Любая С. ф., отличная от константы, существенно
зависит от всех своих переменных. Поэтому при до-
добавлении несущественных переменных отличная от
константы функция становится несимметрической, а
при их изъятии может стать С. ф. Таким образом,
понятие С. ф. связано с точным указанием всех ее
переменных. Простой критерии симметричности функ-
функции f(xi, . . ., х„) состоит в одновременном выполнении
двух равенств:
f {хи х2, хя, ..., xj = f(x2, xi, х3, ..., хп),
f(xi, х2, х3, ..., xn) = f (х„, xlt х,2, ..., xn_i)
или п равенств вида
/ (хъ ..., xt, xi + 1, ...,xn)=f (х-у, . . .,xi + 1,xit ...,xn).
К С. ф. относятся симметрические многочлены. Вся-
Всякая рациональная С. ф. (над полем характеристики 0)
является отношением двух симметрия, многочленов.
Любая булева С. ф. на наборах значений аргументов,
содержащих одинаковое число единиц, принимает оди-
одинаковые значения. Эти функции играют важную роль
в математич. кибернетике и се приложениях, в част-
частности они встречаются при схемной реализации ариф-
арифметических н нек-рых других операций.
Лит.: [1] Ban дер Варден Б. Л., Алгебра, пер. с
нем., 2 изд., М., 1979; [2] Яблонский С. В., Введение и
дискретную математику, М., 197Я. В. М. Храпченко.
СИММЕТРИЧЕСКИЙ МНОГОЧЛЕН — многочлен /
с коэффициентами из нек-рого поля или ассоциативно-
коммутативного кольца К с единицей, являющийся
симметрической функцией от своих переменных, т. е.
инвариантный при любых подстановках переменных:
f(xu ..., xn) = f(n(x1), ..., л(х„)). (*)
С. м. образуют алгебру 5(жх, . . ., хп) над К.
Важнейшие примеры С. м.— элементарные
симметрический многочлены
Sfr (xi, . . . , Х„) = V X: X; . . .X,
и степенные с у м м ы, т. е. многочлены
pk(Xi, ..., х„)=хк + хЬ+...-\-ХЬ.
Для выражения степенных сумм pk&i, ¦ ¦ ., хп) в
виде многочленов от элементарных симметрия, много-
многочленов имеются рекуррентные формулы, называемые
формулами Ньютона:
Pk~ Pk-lSi + Pk-2s2+ ¦ ¦ •
... + (-l)ft-1;>1ss_i + (-l)*foft = O при l<fc<n;
Pk — Рк-1Ч+Рк-2*>2+- • ¦
...+(—^"-^fc-n + iSn-i + Hl)nPft-i»*n = 0 при к>п.
Элементарные С. м. от корней произвольного много-
многочлена одной переменной со старшим коэффициентом
1 с точностью до знака совпадают с остальными коэф-
коэффициентами этого многочлена (см. Виета теорема).
Основная теорема о симметриче-
симметрических многочленах: каждый С. м. является
многочленом от элементарных С. м., причем представим
в этом виде единственным образом. Другими словами,
элементарные С. м. являются свободной системой
образующих алгебры S (хх, . . ., хп). Если поле имеет
характеристику 0, то многочлены рх, . . ., рп также
являются системой свободных образующих алгебры
S(xi, . . ., хп).
К о с о с и м м с т р и ч е с к и м, или знакопе-
знакопеременным, многочленом наз. многочлен
f(xi, . . ., хп), удовлетворяющий соотношению (*),
если подстановка л четная, и соотношению
/(Xi, ..., Хп) = — f (lt(Zi), ..., П(хп)),
если я нечетная. Любой кососимметрич. многочлен
представим в виде А„г, где g есть С. м,, а
Это представление не однозначно, поскольку имеется
соотношение An=Dis(s1, . . ., sn).
Лит.: [1] К у р о ш А. Г., Курс высшей алгебры, 11 изд.,
М., 1975; [2] К о с т р и к и н А. И., Введение в алгебру, М.,
1977; [3] М и ш и н а А. II., Проскуряков И. В.,
Высшая алгебра, 2 изд., М., 1965. О. А. Иванова.
СИММЕТРИЧЕСКИЙ ОПЕРАТОР — отображение
А множества D^ гильбертова пространства Н (в общем
случае комплексного) в себя такое, что <Ах, г/>=О, А у)
для любых х, у?Од. Если Dд— линейное многооб-
многообразие, всюду плотное в Н (что предполагается в даль-
дальнейшем), то А — линейный оператор. Если Вд~Н,
то А ограничен и, следовательно, непрерывен на Н.
С. о. А порождает на DA билинейную эрмитову форму
И (х, у)-=<.Ах, г/>, т. е. такую, что В (х, у) = В (у, х).
Соответствующая квадратичная форма (.Ах, х)> дей-
действительна. Обратно, действительная на Da форма
(Ах, ,г> влечет симметричность А. Сумма А-\-В С. о.
А н В с общей областью определения Вд-Пв есть
снова С. о., и если Л действительно, то КА также сим-
метричен. Для всякого С. о. А существует однозначно
определенное замыкание А и сопряженный оператор
А*^)А. В общем случае А* не является С. о. и А*ФА-
Если А* = А, то С. о. наз. самосопряжен-
самосопряженным оператором. Таким будет, в частности,
С. о., определенный на всем Н. С. о., ограниченный на
Од, допускает продолжение на все Н с сохранением
симметричности и ограниченности.
Примеры. 1) Пусть бесконечная матрица \\ay\\,
i, /—1, 2, . . ., такова, что а^=а.., и
Тогда система равенств
Tji=S/°li a'jh' i=i' 2> •••>
ставящая в соответствие элементу х= {?,¦} ? 12 элемент
y=={r\i)i определяет ограниченный С. о., причем он
оказывается самосопряженным в комплексном про-
пространстве 1
2) В
А = i -тг , определенный на множестве Од абсолютно
непрерывных на [0, 1] функций, имеющих суммируемую
с квадратом производную и удовлетворяющих условию
х@)=х A)=0, есть С. о., не являющийся самосопря-
самосопряженным.
Лит.: [1] Л ю с т е р н и к Л. А., Соболев В. И.,
Элементы функционального анализа, 2 изд., М., 1965; [2] Рисе
Ф.,Секефальви-Надь Б., Лекции по функциональному
анализу, пер. с франц., М., 1954. В. И. Соболев.
СИММЕТРИЧЕСКИЙ ТЕНЗОР, симметрич-
симметричный тензор, по паре индексов — тензор, к-рый
но меняется при перестановке данной пары индексов.
Результат альтернирования С. т. по этой паре индек-
индексов равен нулю. Тензор симметричен по груп-
группе индексов, если он симметричен по любым
двум индексам из этой группы. А. В. Иванов.
СИММЕТРИЧЕСКОЕ ПРОИЗВОДНОЕ ЧИСЛО в т о ч-
к е х — обобщение понятия производного числа на
случай функций множества Ф в re-мерном евкллдовом
пространстве. С. п. ч. в точке х есть предел
Ф (S (ж; г О)
где S {х, г/;) — век-рая последовательность замкнутых
шаров с центрами в точке х и радиусами r^, rj, —г* 0.
С. п. ч. п о р я д к а п в точке х функции действитель-
действительного переменного f(x) наз. предел
\У (ж, hk)
lim -5 =- =
%
k
= lim
где h^—yO при к —>- oo, Asf(x, hfc) — симметрическая
разность f.
Лит.: [1] Сакс С, Теория интеграла, пер. с англ., М.,
1949. Т. 11. Лукашенко.
СИММЕТРИЧЕСКОЕ ПРОСТРАНСТВО — общее на-
название нескольких видов пространств, встречающихся
в дифференциальной геометрии.
1) Многообразие с аффинной связностью наз. а ф-
финным локально симметрическим
пространством, если тождественно равны нулю
тензор кручения и ковариантная производная тензора
кривизны.
2) (Псевдо) риманово многообразие нал. (п с е в д о)
римановым локально симметрия е-
ским пространством, если ковариантная
производная тенаора его кривизны тождественно рапна
нулю.
3) Псевдориманово многообразие (соответственно
многообразие с аффинной связностью) М наз. п с е в-
доримановым (аффинным) глобально
симметрическим пространством, ес-
если с каждой точкой х?М связана изометрия (аффинное
преобразование) Sx многообразия М такая, что 5^=id
и х есть изолированная неподвижная точка преобра-
преобразования Sx.
4) Пусть G — связная группа Ли, Ф — ее инволю-
тивный автоморфизм (CP2=id), бф— замкнутая под"
группа всех Ф-неподвижных точек, Gjf — компонента
единицы группы (of и Н — замкнутая подгруппа в G,
удовлетворяющая условию
Тогда однородное пространство Gill наз. симмет-
симметрическим однородным пространст-
в о м.
5) Симметрическим пространством
в смысле Лоса наз. многообразие М, на к-ром
задано умножение
МхМ—>¦ М, (х, уI—*-х-у,
удовлетворяющее следующим четырем условиям:
а) х-х=х\
6) х-(х-у) = у;
в) x-(yz) = (x-y)-(x-z);
г) для каждой точки х ? М существует такая окрест-
окрестность U, что х-у~у=$>у—х для Vj/? U.
Каждое аффинное (псевдориманово) глобально сим-
метрич. пространство является аффинным (псевдори-
мановым) локально симметрич. пространством и одно-
однородным С. п. Любое однородное С. п. есть аффинное
глобально симметрич. пространство и симметрич.
пространство в смысле Лоса. Всякое связное С. п.
Лоса есть однородное С. п.
Пусть М — связное С. п. Лоса, а значит и однород-
однородное пространство: M=G/H. Пространство G/H можно
снабдить инвариантной аффинной связностью без кру-
кручения, обладающей следующими свойствами: 1) ко-
ковариантная производная тензора кривизны равна
нулю, 2) каждая геодезическая у есть траектория
нек-рой одноиараметрич. подгруппы ty группы G, и
параллельный реренос векторов вдоль у совпадает с
их трансляцией с помощью гр; 3) геодезические замк-
замкнуты относительно умножения и наз. одномерными
подпространствами. Аналогично вводится понятие про-
произвольного подпространства М как такого подмного-
подмногообразия N в М, к-рое замкнуто относительно умно-
умножения и с индуцированным умножением является
С. п. Замкнутое подмножество N в М, устойчивое
относительно умножения, является подпространством.
Аналог алгебры Ли для С. п. G/H вводится следующим
образом. Пусть g и h — алгебры Ли групп G и Н, а
<р — йФг (дифференциал в единице), где Ф — инволю-
гивный автоморфизм, определяющий симметрическое
однородное пространство GlH. Собственные векторы
тдоморфизма пространства ф, соответствующие соб-
собственному значению —1, образуют подпространство го
такое, что g есть прямая сумма подпространств го и h,
a m можно отождествить с касательным пространством
к пространству GlH в точке о=Н. Если ввести в век-
векторном пространстве го трилинейную композицию
mXmXro—>т. (X, У, Z) i—> R (X, Y)Z,
где R ¦— тензор кривизны, то m станет Ли- тройной
системой. Если N — подпространство пространства М,
проходящее через точку о, то касательное пространство
к N в точке о есть подсистема в т и обратно.
Если М есть С. и. Лоса, то произведение МХЛ1
также является С. п. Лоса. Пусть Л есть подпростран-
подпространство в МХМ и отношение эквивалентности в М.
Тогда R наз. конгруэнцией. Это понятие ис-
используется для построения теории накрывающих для
С. п. Две точки х, у^М наз. коммутирующими, если
Центром Z (М) пространства М относительно
точки о(~М наз. лгножество всех точек из М, к-рые
коммутируют с точкой о. Центр Z (М) есть замкнутое
подпространство в М, к-рое можно снабдить струк-
структурой абелевой группы. Пусть М — односпязное С. п.
Тогда разыскание С. п., для к-рых М является накры-
накрывающим пространством, сводится к классификации
дискретных подгрупп группы Z (М).
Большое внимание при построении теории С. п.
уделяется вопросам классификации (см. [2]). Пусть
М — локально симметрическое риманово пространство;
оно наз. приводимым, если в нек-рой системе
координат его основная квадратичная форма может
быть представлена в виде
, ..., xk) (fa''dx/ + gap(.t* + 1, ...,xn) dxadx^,
i, / = 1, ..., к; a, C = /с-р1, ..., п.
В противном случае пространство наз. неприво-
неприводимым. Э. Картан (Е. Cartan) показал, что разы-
разыскание всех неприводимых локально симметрических
римановых пространств сводится к классификации
инволютивных автоморфизмов вещественных компакт-
компактных алгебр Ли, и проделал эту классификацию. Вместе
с тем была решена задача локальной классификации
симметрических однородных пространств с простыми
компактными основными группами. Получена клас-
классификация симметрических однородных пространств с
простыми некомпактными основными группами (см.
[2], [3], [5]).
Лит.: [1] Широков II. А., Избранные работы по гео-
геометрии, Казань, 1966; [2] Картан Э., Геометрия групп Ли
и симметрические пространства, пер. с франц., М., 1949; [3]
В е г s е г М., «Ann. Sci. Ecole norm, super,», 1957, v. 74, p. 85—
177; [4] Loos O., Symmetric spaces, t. 1—2, N. Y.— Amst.,
1969; E5] Хелгасон С, Дифференциальная геометрия и
симметрические пространства, пер. с англ., М.,1964.
СИММЕТРИЧНАЯ АЛГЕБРА - алгебр!' VTa^
полем комплексных чисел, снабженная инволюцией
х -^- х*, х?Е. Примерами С. а. являются: алгебра
непрерывных функций на компакте, в к-рой инволюция
определяется как переход к комплексно-сопряженной
функции; алгебра ограниченных линейных операторов
в гильбертовом пространстве, в к-рой инволюция
определяется как переход к сопряженному оператору;
групповая алгебра локально компактной группы;
алгебра мер на локально компактной группе. Элемент
х* алгебры Е наз. сопряжении м к элементу х;
элемент х?Е наз. самосопряженным, или
эрмитовым, если х* = х, и нормальным,
если х*х=хх*; если алгебра Е содержит единичный
элемент 1, то элемент х?Е, удовлетворяющий условию
х*х=хх* = 1, наз. унитарным. Множество Е^
эрмитовых элементов алгебры есть действительное
векторное подпространство в Е, и любой элемент х?Е
однозначно представляется в виде x—x1J\-ixz, где хг,
xz?.Eh'> элемент х?Е нормален тогда и только тогда,
когда элементы хъ х% перестановочны. Всякий элемент
вида х*х эрмитов; единичный элемент эрмитов. Если х
обратим, то х* также обратим и (х*)~1= (.г--1)*. Спектр
каждого эрмитова элемента симметричен относительно
действительной оси. С. а. Е нан, вполне си м м е т-
р и ч н о й а л г е б j) о ii, если спектр любого эле-
элемента вида х*х, х?Е, содержится в множестве неотри-
дательных действительных чисел. Примерами вполне
симметричных алгебр являются: С. а. непрерывных
функций на компакте; С. а. ограниченных линейных
операторов в гильбертовой пространстве; групповые
алгебры компактных и коммутативных локально ком-
компактных групп. Групповые алгебры некомпактных по-
полупростых групп Ли не являются вполне симметрич-
симметричными. Коммутативная С. а. Е тогда и только тогда
вполне симметрична, когда все максимальные идеалы
в Е симметричны, или тогда и только тогда, когда
всякий характер коммутативной алгебры Е эрмитов.
Любая С*-алгебра вполне симметрична.
Подмножество М С. а. Е паз. симметричным,
если х*?М для всех х?М. Отображение ф С. а. Е в
С. a. F наз. симметричным, если <р (ж)* = ф (х*)
для всехж? Е. Ядро симметричного гомоморфизма С. а.
Е в С. a. F есть симметричный двусторонний идеал;
всякий симметричный односторонний идеал является
двусторонним, и факторалгебра С. а. по симметричному
идеалу естественно снабжается структурой С. а. Ра-
Радикал С. а. симметричен. Симметричная подалгебра F
в С. а. Е является С. а. Пусть Е — прямая сумма
С. а. Е и ноля С, в к-рой линейные операции и инво-
инволюция определяются покомпонентно, а умножение
определяется формулой
{х, Ц{у, P} = {xy + by + \ix, кр]
для всех X, ц?С, х, у?Е; тогда Е есть С. а. с единич-
единичным элементом.
Линейный функционал / на С. а. наз. эрмито-
эрмитовым, если f(x*)=f(x) для всех х?Е, и положи-
положительным, если f(x*, ж)>0 для всех х?Е. Множество
Eh эрмитовых линейных функционалов на Е есть дей-
действительное векторное подпространство пространства
Е', сопряженного Е, и Е' есть прямая сумма подпро-
подпространств E'h и iE'h. Если Е содержит единицу 1, то
всякий положительный функционал / на Е эрмитов
и \f(x)\2^.f(i)f(x*x) для всех х?Е. Если / — положи-
положительный функционал на С. а. Е, то f(y*x) = f(x*y) и
\f(y*x)l**?f(y*y)f(x*x) для всех х, у?Е.
Пусть С. а. Е снабжена нормой, превращающей Е
в нормированную алгебру и удовлетворяющей условию
||г*||= ||z|| для всех х?Е; тогда Е наз. нормирован-
нормированной С. а. Если Е полна относительно рассматриваемой
нормы, то Е наз. банаховой С. а. Всякая нор-
нормированная С. а. Е может быть вложена в нек-рую
банахову С. а. Е, содержащую Е как плотную .сим-
.симметричную подалгебру; Е определена однозначно с
точностью до изометрического симметричного изомор-
изоморфизма: Е наз. пополнением Е. Если Е — бана-
банахова С. а., причем Е имеет аппроксимативную единицу,
то всякий положительный функционал / на Е непреры-
непрерывен и допускает продолжение до положительного ли-
линейного функционала на Ё. Если Е содержит единич-
единичный элемент 1 и ||1||=1, то для любого положительного
линейного функционала / на Е выполняются соотно-
соотношения II/H = /A) и f(x*x)<*.f(i)r(x*x), где г(х*х) —
спектральный радиус элемента х*г (см. Банахова ал-
алгебра).
Эрмитов элемент вполне С. а. имеет действительный
спектр, для любого максимального замкнутого левого
идеала / во вполне С. а. ? с единичным элементом су-
существует такой положительный линейный функционал
/ на Е, что /= {х?Е: f(x*x)=0}, и элемент х?Е обратим
слева в Е тогда и только тогда, когда f(x*x)>0 для
всех ненулевых положительных функционалов / на "Е.
Радикал вполне С. а. Е совпадает с множеством таких
элементов .г ?/¦.'. что ](х*х) — 0 для всех положительных
линейных функционалов / на Е. Банахова С. а. Е
с единичным элементом 1 тогда и только тогда вполне
симметрична, когда r(x*x)=svtp f(x*x), где верхняя
грань берется по множеству таких положительных
линейных функционалов / на Е, что /A)=1.
Лит.: [1] Н а й м а р к М. А., Нормированные кольца,
2 изд., М.,1968;[2]Диксмье Ж.,С *-алгебры и их представ-
представления, пер. с франц., М., 1974; [3] Р t a k V., «Manuscripts
Math.», 1972, v. 6, ATs 3, p. 245—90; [4] Хьюитт Э..
Росс К., Абстрактный гармонический анализ, пер. с англ.,
т. 2, М., 1975. А. И. Штерн.
СИММЕТРИЧНОЕ ПРЕДСТАВЛЕНИЕ — представ-
представление я симметричной алгебры. А непрерывными ли-
линейными операторами в гильбертовом пространстве
такое, что я {х)*=п (х*) для всех х?А (здесь х* ¦— об-
образ X при ИНВОЛЮЦИИ А). А.И. Штерн.
СИММЕТРИЧНОСТЬ — одно из свойств бинарных
отношений. Отношение R на множестве А наз. с и м-
метричным, если для любой пары элементов а,
Ъ?А из aRb следует, что bRa, т. е. если R~xczR, При-
Примером симметричного отношения является эквивалент-
эквивалентность. Т. С. Фофанова.
СИММЕТРИЧНЫЙ ОПЕРАТОР — см. Симметри-
Симметрический оператор.
СИММЕТРИЯ — 1) С.— инволютивное ортогональ-
ортогональное преобразование, изменяющее ориентацию; инво-
лютивность преобразования означает, что двукратное
применение его дает тождественное преобразование.
Напр., отражение относитель-
относительно плоскости а в пространстве (от-
(относительно прямой а на плоскости)
есть С, при к-рой каждая точка М
переходит в точку М' такую, что от-
отрезок ММ' перпендикулярен пло-
плоскости а (прямой а) и делится ею по-
пополам. Плоскость а (прямая а) наз.
плоскостью (осью) С. (рис. 1).
Любое ортогональное преобразование
можно осуществить последовательным
конечного числа отражений.
2) С.— свойство геометрич. фигуры Ф совмещаться
с собой при действии нек-рой группы С ортогональных
преобразований, наз. группой симметрииф;
таким образом, С. отражает нек-рую
правильность формы фигуры, инвари-
инвариантность ее при действии преобразова-
преобразований из G. Напр., если на плоскости фи-
фигура Ф такова, что повороты относитель-
относительно какой-либо точки О на угол 360°/п,
п — целое, переводят ее в себя, то Ф
обладает С. н-го порядка, а О наз.
центром С. /7-го порядка (рис. 2);
здесь С — циклическая группа n-го по-
порядка. Окружность обладает С. бесконечного поряд-
порядка (поскольку совмещается с собой поворотом на лю-
любой угол).
Простейшими видами пространственной С, помимо
С порожденной отражениями, являются:
а) С. относительно прямой re-го порядка:
в этом случае фигура накладывается на себя вращением
вокруг нек-рой прямой (оси С.) на угол 360°/п. Напр..
плоская фигура, симметричная относительно прямой
АВ, имеет в пространстве эту прямую осью С. 2-го
выполнением
1
к
/
>
Рис. 2.
I
Рис. 3.
Рис. 4.
порядка (рис. 3). Куб имеет прямую АВ осью С. 3-го
порядка, а прямую CD — осью С. 4-го порядка (рис. 4);
вообще, правильные и полупраиильные многогранники
симметричны относительно ряда прямых. Располо-
Расположение, количество и порядок осей С. играют основную
роль в кристаллографии.
б) С. переноса; в этом случае фигура наклады-
накладывается на себя переносом вдоль нек-рой прямой (о с и
переноса) на ка-
какой-либо отрезок.
Напр., фигура с един-
единственной осью пере-
переноса обладает беско-
бесконечным множеством
плоскостей С. (по-
(поскольку любой пере-
перенос можно осущест-
осуществить двумя последо-
последовательными отраже-
Рис. 5. Рис. 6. ниями), перпендику-
перпендикулярных оси перено-
переноса (рис. 5). Фигуры, имеющие несколько осей пе-
переноса, играют важную роль при исследовании кри-
сталлнч. решеток.
Комбинации С, порожденные отражениями и враще-
вращениями (исчерпывающие простейшие виды С. конечных
фигур), а также переносами,
представляют интерес и
являются предметом иссле- ..
дования в различных об- и
Рис. 7.
Рис. 8.
ластях естествознания, искусства и т. д. Напр., вин-
винтовая С, осуществляемая поворотом на нек-рый угол
вокруг оси, дополненным переносом вдоль той же оси,
наблюдается в расположении листьев у растений
(рис. 6). С. широко распространена как один из при-
приемов построения бордюров и орнаментов (плоских
фигур, обладающих одной или несколькими С. пере-
переноса в сочетании с отражениями) (рис. 7, 8).
Лит.: [1] Шубников А. В., Симметрия. (Законы сим-
симметрии и их применение в науке, технике и прикладном искусст-
искусстве), М,— Л., 1940;[2] К о к с т е р Г. С. М., Введение в геомет-
геометрию, пер. с англ., М., 1966; [3] В е й л ь Г., Симметрия, пер.
сангл., М., 1968. М. И. Войцеховский.
СИМПЛЕКС — re-мерный многогранник, являющий-
•¦¦<ч выпуклой оболочкой п+1 точек (вершин С),
к-рые не лежат в (п—1)-мерной плоскости. При ге=О,
1, 2, 3 С.— точка, отрезок, треугольник, тетраэдр.
Грани С. суть С. меньшей размерности. Два С. оди-
одинаковой размерности аффинно эквивалентны. Каждой
точке С. соответствует единственный способ распре-
распределения единичной массы между вершинами С. так,
чтобы центр тяжести был в данной точке С. Это ис-
используется при введении в С. барицентрич. координат,
а также служит источником обобщения понятия С.
для бесконечномерного случая (см. Шоке симплекс).
С. может приписываться одна из двух ориентации,
что индуцирует определенную ориентацию его (п—1)-
мерных граней. В. А. Залгаллер.
СИМПЛЕКС — топологическое пространство \А\,
точками к-рого служат неотрицательные функции
у:А -»- R, определенные на конечном множестве А и
удовлетворяющие условию VJ ф (а) = 1. Топология
в |Л| полагается индуцированной из R-4 - простран-
пространства всех функций из А в R. Действительное число
Ф (а) наз. а-й барицентрической коорди-
координатой точки ф, размерностью симплекса
М| наз. число саг йА—1. В случае, когда А является
линейно независимым подмножеством евклидова про-
пространства, симплекс \А | гомеоморфен выпуклой обо-
оболочке множества А (гомеоморфизм задается соот-
соответствием ф —v 'V ,ф (а) -а). В связи с этим выпуклая
оболочка линейно независимого подмножества евкли-
евклидова пространства наз. евклидовым С.
Для любого отображения /: А -> В конечных мно-
множеств формула (|/|ф) (b)=V ,ф(а), Ь?В, определяет
непрерывное отображение |/|:М|->|В|, являющееся
для евклидовых С. аффинным (неоднородным линейным)
отображением, продолжающим отображение /. Этим
задается функтор из категории конечных множеств в
категорию топологич. пространств. Если ВаА и
i:B —>¦ А — соответствующее вложение, то |?| — гомео-
гомеоморфизм на замкнутое подмножество, наз. гранью
симплекса \А\ и обычно отождествляемое с \В\. Нуль-
Нульмерные грани наз. вершинами (как правило,
вершины отождествляются с элементами множества А).
Топологическим упорядоченным С.
наз. топологич. пространство X, для к-рого задан
гомеоморфизм h: А" —*¦ X, где Д" — стандартный сим-
симплекс. Образ граней Д" при гомеоморфизме h наз.
гранью топологического упорядоченного симплек-
симплекса X. Отображение X —у Y топологических упорядо-
упорядоченных симплексов X и Y наз. линейным, если
оно имеет вид koFoh*1, где к и h — заданные гомео-
гомеоморфизмы, F — произвольное отображение Д" -*¦ А"
вида |/|.
Топологическим С. (размерности п) наз.
топологич. пространство X, наделенное (и+1)! гомео-
гомеоморфизмами Д" ->. X (то есть (л+1)! структурами
топологического упорядоченного С), отличающимися
на гомеоморфизмы Д" —v А" вида |/|, где / — произ-
произвольная перестановка вершин. Аналогично, отобра-
отображение топологического С. наз. линейным, если
оно является линейным отображением соответствующих
топологических упорядоченных С.
С. наз. также элементы симплициалъных множеств
и отмеченные подмножества симплициалъных схем.
А. В. Хохлов.
СИМПЛЕКСНЫЙ МЕТОД, с и м п л и к с - м е т о д,
метод последовательного улучше-
улучшения плана,— метод решения общей задачи ли-
линейного программирования:
" ' = !,...,«,
где Af---- (av; . . ., amj)T, / = 0, . . ., п.
С. м.— наиболее распространенный метод линей-
линейного программирования (л. п.). Он состоит в движении
по соседним вершинам многогранного множества за-
задачи л. п., определяемого ее ограничениями, и реализу-
реализуется в виде конечной последовательности итераций.
Базисом вершины х= (х±, . . ., хп) много-
многогранного множества задачи наз. такая система т ли-
линейно независимых векторов As, . . ., As (sa>l, a=l,
. . ., т), что Х]-=0, если /^Efo, . . ., sm}. Исходная
информация для каждой итерации С. м. складывается
из базиса Ах= (ASi, . . ., А$т) вершипы х, параметров
xjj, определяемых из соотношений
Aj ^ 2'/11 X'J A*i> / -= 0, 1, ..., n
(в частности, х;0= xs.— базисные компоненты вер-
вершины х), и параметров
Если Д/>0, V/ A), то х — искомое решение задачи
л. п. В противном случае выбирается отрицательный
параметр Д&. Отсутствие среди хц^, t=l, . . ., т,
положительных величин B) указывает на неразреши-
неразрешимость задачи л. п., обусловленную неограниченно-
неограниченностью целевой функции задачи на ее многогранном
множестве. В случае положительности нек-рых x,f. C)
вершина х заменяется вершиной х'=х-\-вхк, где
х* = (х![, ..., X*), х\ =—xik, l = \, ..., т, z| = l,
остальные компоненты хк — нули,
6= min ^^-
i:xik>0 Xik Xrk
Вершина х' имеет базис АХ', отличающийся от Ах
тем, что ASr заменен на А^. Параметры х'.- и &'¦, свя-
связанные с АХ', определяются по простым рекуррент-
рекуррентным формулам, исходя из x,j и Ду.
Случай A) означает, что вдоль каждого ребра мно-
многогранного множества задачи, выходящего из вершины
л, целевая функция задачи не возрастает. Случаи B)
и C) соответствуют наличию ребра, вдоль к-рого целе-
целевая функция возрастает, причем в случаи B) это реб-
ребро — луч, а в случае C) — отрезок, другой конец
к-рого — вершина х'. Итерации проводятся до полу-
получения оптимальной вершины либо до выяснения не-
неразрешимости задачи л. п.
Программная реализация См., рассчитанная на зада-
задачи достаточно большого размера, обычно основывается
на иной его алгоритмич. реализации, в к-рой основой
исходной информации для каждой итерации служит
обратная матрица А^1 базиса Ах (м е т о д обрат-
обратной матрицы). Она предназначена для задач
л. п., матрица условий А— (А-^А^.- ¦ -Ап) к-рых обла-
обладает свойством слабой заполненно-
заполненности (число ненулевых ац мало по сравнению с тп).
Слабо заполненные матрицы хранятся в запоминающих
устройствах ЭВМ в компактном виде, когда фиксиро-
фиксированы лишь ненулевые элементы и их позиции. Разра-
Разработаны специальные приемы хранения обратного ба-
базиса, направленные на сокращение информации, не-
необходимой для восстановления А^1. Они основаны на
представлении А'1 в виде произведения матричных
множителей (мультипликаторов), отличающихся от
единичной матрицы лишь одним столбцом. Заполнен-
Заполненность нетривиальных столбцов мультипликаторов за-
зависит от порядка введения векторов в базис. Поэтому
после накопления нек-рого числа мультипликаторов
организуется т. н. повторение, в результате к-рого
образуется более экономное мультипликативное пред-
представление А'1.
Важная часть алгоритма С. м.— стратегия выбора
вектора Ак для включения в базис. С одной стороны,
она должна способствовать сокращению информации,
необходимой для хранения А; с другой стороны —
препятствовать попаданию в плохо обусловленный
базис.
Существуют программные реализации С. м., позво-
позволяющие решать на ЭВМ задачи л. п. с мало заполненной
матрицей условий при т порядка тысяч и п порядка
десятков тысяч. Разработаны многочисленные вари-
варианты С. м., учитывающие особенности различных
специальных классов задач л. ц. (блочные задачи, за-
задачи транспортного типа и др.).
Несмотря на то, что С. м. теоретически не достаточно
эффективен (он имеет экспоненциальную оценку тру-
трудоемкости на всем классе задач л. п., хотя алгоритмич.
сложность этого класса всего лишь полиномиальна),
опыт его применения и сравнения с другими методами
позволяет сделать вывод, что для него пока A983)
нет серьезного конкурента.
Лит.: [1] Ю д и н Д. Б., Гольштейн К. Г., Линей-
Линейное программирование, М., 1963; [2] Данциг Д ж., Линей-
Линейное программирование, его применения и обобщения, пер. с
англ., М., 1966; [3] Ашманов С. А., Линейное програм-
программирование, М., 1981. Е. Г. Голыитейн.
СИМПЛЕКСНЫЙ ПОИСК — один из методов мак-
максимизации и минимизации функций многих перемен-
переменных, при к-ром выбор направления спуска (подъема)
производится упорядоченным перебором вершин до-
допустимого многогранного множества (см. Симплекс-
Симплексный метод). Л. Б. Иванов.
СИМПЛЕКТИЧЕСКАЯ ГРУППА — одна из клас-
классических групп, определяемая как группа автоморфиз-
автоморфизмов знакопеременной билинейной формы Ф на левом
^-модуле Е, где К — коммутативное кольцо. В слу-
случае, когда Е=К2т и матрица формы Ф в канонич.
базисе {«,-} модуля Е имеет вид
О 1а
т -Л» о
где 1т— единичная матрица порядка т, соответст-
соответствующая С. г. называется С. г. от 2т переменных над
кольцом К и обозначается Sp(ro, А) или Sp2m(A).
Матрица любого автоморфизма из Sp2m(K) в базисе
{е,-} наз. симплектической матрицей.
Пусть К — поло и Ф — невырожденная знакопере-
знакопеременная билинейная форма в «-мерном векторном про-
пространстве Е над К. Тогда п четно, ассоциированная с
формой Ф С. г., изоморфная группе Spn(K), порож-
порождается всевозможными линейными преобразованиями
пространства Е вида ае, а,
х i—*ае, а (х) — х-\-аФ (е, х)е,
где е?Е, а?А'. Линейные преобразования вида о>, а
наз. симплектическими трансвекция-
м и, или сдвигами, в направлении прямой Ке.
Центр Z группы Spn(Ar) состоит из матриц 1п и —/„,
если спагА=й=2; если же char K= 2, то Z-- {/„}. Фактор-
Факторгруппа Spn(A')/Z наз. проективной симп-
симплектической группой и обозначается
PSpn(A'). Вес проективные С. г. просты за исключением
PSp2(F3) = Sp2(/'1a), PSp4(F2) = Sp4(/-'2) и PSp2U''3),
к-рые изоморфны соответственно симметрич. группам
S3 и S& и знакопеременной группе Ai (через Fq обо-
обозначено поле из q элементов). Порядок С. г. Sp2m (Fq)
равен
(q2m — 1) g2«-l (92я>-2_1) g2m-3. . .(?2 —1) q.
С. г. Sp2(Ar) совпадает со специальной линейной груп-
группой SL2 (К); если char Кф2, то группа PSp4 (А) изоморф-
изоморфна факторгруппе группы Qb(K, /) пи ее центру (где
&ь(К, /) — коммутант ортогональной группы симмет-
симметрической билинейной формы / от пяти переменных
индекса 2).
За исключением случая m=2, char К— 2, всякий
автоморфизм ф группы Sp2m (К) может быть представ-
представлен в виде
где х — автоморфизм поля К, hi^Sp2m(K) и h2 — ли-
нейное преобразование пространства Е, представля-
представляющееся в базисе {е;} матрицей вида
Но р/я
(Р — ненулевой элемент поля К).
С. г. Sp2m (К) совпадает с группой К-точвк линейной
алгебраич. группы Sp2m, задаваемой уравнением
ALJmA=Jm. Эта алгебраич. группа, тоже называ-
называемая С. г., является простой односвязной линейной
алгебраич. группой типа Ст, ее размерность равна
2та+то.
В случае, когда К=С или R, С. г. Sp2m (К) есть
связная односвязная простая комплексная (соответ-
(соответственно вещественная) группа Ли. Группа Sp2m (R)
является одной из вещественных форм комплексной
С. г. Sp2m(C). Остальные вещественные формы этой
группы тоже иногда называют С. г. Это — подгруппы
Sp(p, ?), Р, 9^0, P-\-Q=m, выделяемые из группы
Sp2m (С) условием сохранения эрмитовой формы вида
где в,-=1 при l<i<p и m-\-i<.i<.m-\-p и в,= —1
при остальных i. Группа Sp(O, m) — компактная
вещественная форма комплексной С. г. Sp2m(C). С. г.
Sp(p, ?) изоморфна группе всех линейных преоб-
преобразований правого векторного пространства Н'л
над телом кватернионов Н размерности т=р-\-д,
к-рые сохраняют кваторнионную эрмитову форму
индекса min(p, q), то есть форму вида
где
x=(xi, хг, . . ., хт), у= (уи у2, . . ., ут) ?Н'Л,
а черта означает переход к сопряженному кватер-
кватерниону.
Лит.: [1] А р т и н Э., Геометрическая алгебра, пер. с англ.,
М., 1969; [2] Б у р б а к и Н., Алгебра. Модули, кольца, фор-
формы, пер. с франц., М., 1966; [3]Дьёдонне Ж., Геометрия клас-
классических групп, пер. с франц., М., 1974; [4] X е л г а с о н С,
Дифференциальная геометрия и симметрические пространства,
пер. с англ., М., 1964; [5] Ш е в а л л е К., Теории групп Ли,
пер. с англ., т. 1, М., 1948. В. Л. Попов.
СИМПЛЕКТИЧЕСКАЯ СВЯЗНОСТЬ — аффинная
связность на гладком многообразии М размерности 2п,
обладающая ковариантно постоянной относительно нее
невырожденной 2-формой Ф. Если аффинная связность
на М задана с помощью локальных форм связности
Ф— й/уш' Л ш^, пц— —ay/,
то условие ковариантного постоянства Ф выражается
в виде
2-форма Ф определяет на М симплектич. структуру
(или почти гамильтонову структуру), превращая каж-
каждое касательное пространство ТХ(М) в симплектич.
пространство с кососимметрич. скалярным произве-
произведением Ф (X, Y). С. с. можно определить так же,
как аффинную связность на М, сохраняющую при
параллельном перенесении векторов это прои&ведение.
Репер в каждом ТХ(М) может быть выбран так, что
Все такие реперы образуют главное расслоенное про-
пространство над М, структурной группой к-рого является
симплектич. группа. С. с.—это связность в этом глав-
главном расслоенном пространстве. Существуют многообра-
многообразия М четной размерности, на к-рых нет невырожден-
невырожденной глобально определенной 2-формы Ф и, следователь-
следовательно, нет С. с. Однако если Ф существует, то С. с.
относительно к-рой Ф ковари антно постоянно, опре-
определяется неоднозначно.
Лит.: Шстернберг С, Лекции по дифференциальной
геометрии, пер. с англ., М., 1970. Ю. Г. Лумисте.
СИМПЛЕКТИЧЕСКАЯ СТРУКТУРА — инфини-
теаималъиая структура 1-го порядка на четномерном
гладком ориентируемом многообразии М2п, к-рая оп-
определяется заданием на М?" невырожденной 2-фор-
2-формы Ф. В каждом касательном пространстве Тх(М2п)
возникает структура симплектич. пространства с ко-
сосимметрическим скалярным произведением Ф (А', >').
Все касательные к М2п реперы, адаптированные к
С. с. (т. е. реперы, относительно к-рых Ф имеет кано-
нич. вид
Ф=2 2™=1 щ<х А со"+«),
образуют главное расслоенное пространство над М2п,
структурной группой к-рого является симплектич.
группа Sp(?()- Вообще, задание С. с. на М2п равно-
равносильно заданию Sp (я)-структуры на Af?n, как нек-рой
G-струкшуры.
На Мгп со С. с. существует изоморфизм между мо-
модулями векторных полей и 1-форм на М?л, к-рый
векторному полю X ставит в соответствие 1-форму
сох: У->Ф(Х, Y). Образ скобки Ли [X, Y] наз. при
этом скобкой Пуассона [ах, со^]; в частности, когда
соя и сок полные дифференциалы, получается понятие
скобки Пуассона двух функций на М2п, к-рое обобщает
соответствующее классич. понятие.
С. с. наз. почти гамильтоновой струк-
структурой^ если Ф замкнута, т. е. йФ=0, то г а м и л ь-
топовой структурой; впрочем, иногда ус-
условие <2Ф=0 включают в определение С. с. Эти струк-
структуры, находящие применения в глобальной аналитич.
механике, основаны на том факте, что на касательном
расслоенном пространстве Т* (М) любого гладкого
многообразия М существует каноническая гамильто-
нова структура. Она определяется формой Ф=й0,
где 1-форма 0 на Т* (М), наз. формой Л и у-
в и л л я, задается следующим образом: &и(^и)~
— и(л%Хп) для любого касательного вектора Х„ в
точке и?Т* (М), где л—проекция Т* (М)—>¦ М. Если
па М выбраны локальные координаты .г1, . . ., х" и
u=i/;(i()d-cjj(I(), то в=т/,-Аг', вследствие чего O = dyiAdx'.
В классич. механике М интерпретируется как конфи-
конфигурационное пространство, а Т* (М) как фазовое про-
пространство.
Векторное поле X на Мгп с гамильтоновой структурой
наз. г а м и л ь т о н о в ы м (или гамильтоно-
гамильтоновой с и с т е м о й), если 1-форма со^ замкнута.
Бели она, кроме того, точна, т. е. сох=—dH', то функ-
функция // на М2п наз. гамильтонианом и явля-
является обобщением соответствующего классического
понятия.
Лит.: Шстернберг С, Лекции по дифференциальной
геометрии, пер. с англ., М., 1970; [2] Годбийон К., Диф-
Дифференциальная геометрия и аналитическая механика, пер. с
франц., М., 1973. Ю. Г. Лумисте.
СИМПЛЕКТИЧЕСКОЕ МНОГООБРАЗИЕ — мно-
многообразии, снабженное симплектической структурой.
СИМПЛЕКТИЧЕСКОЕ ПРОСТРАНСТВО — нечет-
номерное проективное пространство Pzn+i над полем /.:
с заданной в нем инволюционной корреляцией — нуль-
системой; обозначается Sp2n+i.
Пусть характеристика поля к не равна 2. Абсолют-
Абсолютная нуль-система в Span+i всегда может быть записана
в виде Ui—aijxl', где ||а,-у|| — косоеимметрич. матрица
(а,у= —в/,-). В векторной форме абсолютная нуль-си-
нуль-система может быть записана в виде и—Ах, где А —ко-
сосимметрич. оператор, матрица к-рого надлежащим
выбором базиса приводится к виду
О +1
—1 О
О 4-1
- 1 0 41
-1 О
В этом случае абсолютная нуль-система принимает
канонич. вид:
Абсолютная нуль-система порождает билинейную фор-
форму, к-рая записывается в канонич. виде:
Коллинеации пространства Sp2«+i, перестановочные
с его нуль-системой, наз. симплектическими
преобразованиями; операторы, определя-
определяющие эти коллинеации,— с и м п л е к т и ч е с к и-
м и. Для указанной выше канонич. формы матрицы
\]А\\ определяется Bя4-2)-матрица симплектич. опе-
оператора U, элементы к-рой удовлетворяют условиям
= 6y, ft_i —6y-, ft + 1,
где ба_ ь — символ Кронекера, а матрица такого опе-
оператора U наз. симплектической; ее опре-
определитель равен единице. Симплектич. преобразования
образуют группу, являющуюся группой Ли.
Всякая точка пространства Sp2n+i лежит в Bп—1)
плоскости, соответствующей ей в абсолютной нуль-
системе. Можно определить также и пулевые то-пло-
скости в Sp2n+i- Многообразие нулевых прямых про-
пространства Sp2n+i наз. его абсолютным линей-
линейным комплексом. В связи с этим симплектич.
группа наз. также группой линейного
комплекса, или комплекс-группой.
Всякая пара прямых и соответствующих в нуль-
системе двух Bп—1)-плоскостей определяют единст-
единственный в пространстве Sp2n+i симплектич. инвариант
относительно группы симплектич. преобразований этого
пространства. Через каждую точку обеих прямых
проходит трансверсаль этих прямых и Bге—^-плоско-
Bге—^-плоскостей так, что определяет проективные четверки точек.
Это составляет геометрический смысл симплекти-
ческого инварианта, который утверждает
равенство двойных отношений получаемых четверок
точек.
Симплектич. 3-пространство допускает интерпрета-
интерпретацию в гиперболич. пространстве, что указывает, в
частности, на связь симплектич. пространств с гипер-
гиперболическими. Так, группа симплектич. преобразований
пространства Sp3 изоморфна группе движений гипер-
гиперболич. пространства 2?4. В этой интерпретации сим-
симплектич. инвариант связан с расстоянием между точ-
точками гиперболич. пространства.
Лит.: [1] Розенфельд Б. Д., Неевклидовы простран-
пространства, М., 1969. Л. А. Сидоров.
СИМПЛЕКТИЧЕСКОЕ ПРОСТРАНСТВО ОДНОРОД-
ОДНОРОДНОЕ — симплектическое многообразие (М, со) вме-
вместе с транзитивной группой Ли G его автоморфиз-
автоморфизмов. Элементы алгебры Ли д группы G можно рас-
рассматривать как сшгплектические векторные поля на М,
т е.нолн А", сохраняющие симплоктическую 2-форму со:
где точкой обозначена производная Ли, ix— оператор
внутреннего умножения на X, d — внешний диффе-
дифференциал. С. п. о. наз. строго симплектиче-
с к и м, если все поля Х?д гамильтоновы, то есть
г^ш—d//x, где Нх функция на М (гамильтониан поля
X), причем гамильтониан Нх можно выбрать так,
чтобы отображение X i—* Нх было гомоморфизмом ал-
алгебры Ли з в алгебру Ли функций на М относительно
скобки Пуассона. Примером строго С. п. о. является
орбита Ма= (Ad*G)a группы Ли G относительно ко-
присоединенного представления Ad*G группы G в
пространстве д* линейных форм на д, проходящая
через произвольную точку a?g*. Инвариантная сим-
плектическая 2-форма со на Ма задается формулой
со(Хр, Ур) = <*р(Х, У)эрр, У]),
где Хр, Ур —значения векторных полей X, У?
точке $?Ма- Поле Х?$ имеет гамильтониан ЯТ
Для произвольного строго С. п. о. (.?, со, G) опре-
определено G-эквивариантное отображение момента
к-рое отображает М на орбиту ц (М) группы G в д*
и является локальным изоморфизмом симплектич.
многообразий. Таким образом, любое строго С. п. о.
группы G является накрытием над орбитой группы G
в коприсоединенном представлении.
Односвязные С. п. о. с односвязной, но не обязатель-
обязательно эффективно действующей группой автоморфизмов G
находятся во взаимно однозначном соответствии с
орбитами естественного действия группы G в про-
пространстве Z2 (g) замкнутых 2-форм на ее алгебре Ли д.
Соответствие определяется следующим образом: ядро
Я° любой 2-формы a?Z?(g) является подалгеброй
алгебры Ли д. Соответствующая $° связная под-
подгруппа Ка группы Ли G замкнута и определяет одно-
связное однородное пространство М0 = G/Ka . Форма а
задает невырожденную 2-форму в касательном про-
пространстве Т0Ма =^g/At0 точки о=еК° многообразия
М°, к-рая продолжается до G-инвариантной симплек-
симплектич. формы ш° на Ма. Таким образом, форме а отве-
отвечает односвязное С. п. о. (Л/°, соа). Если St° не со-
содержит идеалов алгебры Ли д, то действие G на Ма
локально эффективно. С. п. о. М° и Ма' изоморфны
тогда и только тогда, когда формы а, а' принадлежат
одной орбите группы G в Z2(g). Для точной 2-формы
а—da С. п. о. М° отождествляется с универсальной
накрывающей С. п. о. Ма, являющегося орбитой
точки а в коприсоединенном представлении. Если
[д, д] = д, то орбита Go любой точки a?Z2(g) ка-
канонически снабжается структурой С. п. о. и любое
С. п. о. односвязной группы G изоморфно накрытию
над одной из таких орбит. В частности, Ма есть уни-
универсальная накрывающая орбиты Go.
Пусть (М, со) — компактное С. п. о. односвяа
ной связной группы G, действующей локально эффек-
эффективно. Тогда G есть прямое произведение полупр<>
стой компактной группы S и разрешимой группы 11,
разлагающейся в полупрямое произведение абеле-
вой подгруппы и абелева нормального делителя, а
С. п. о. (М, со) разлагается в прямое произведение
С. п. о. с группами автоморфизмов S и Я соответст-
соответственно.
Частным случаем С. п. о. является сичплектическог
групповое пространство — группа Ли вместе с лево-
инвариантной симплектич. формой со. Известно, что
из редуктипности группы Ли, допускающей левоин-
вариантную симметрич. форму, следует ос коммутатив-
коммутативность, а из унимодулярности — разрешимость. Все
такие группы размерности <:4 разрешимы, но начиная
с размерности 6 существуют неразрешимые симплек-
тические групповые пространства [3].
Лит.: [1] К и ри л л о в А. А., Элементы теории представ-
представлений, 2 изд., М., 1978; [2] Г и й е м и н В., Стернберг С,
Геометрические асимптотики, пер. с англ., М., 1981; Из] Ghu
B.-Y., «Trans. Amer. Math. Soc», 1974, v. 197, p. 145—59;
14] Z w а г t P h. В., В о о t h b у W. M., ((Ann. Inst. Fouri-
Fourier», 1980, t. 30, JSfi 1, p. 129—57. Д. В. Алексеевский.
СИМПЛИЦИАЛЬНАЯ СХЕМА (прежние названия —
симплициальный комплекс, абстракт-
абстрактный симплициальный комплекс) —
множество, элементы к-рого наз. вершинами и в к-ром
выделены такие конечные непустые подмножества, наз.
симплексами, что каждое непустое подмноже-
подмножество симплекса s является симплексом, наз. гранью
симплекса s, и каждое одноэлементное подмножество
является симплексом.
Симплекс наз. q-м е р н ы м, если он состоит из q-\-i
вершин. Размерностью &imK симплициальной
схемы К наз. максимальная размерность ее симплексов
(она может быть и бесконечной). С. с. наз. локаль-
локально конечной, если каждая ее вершина принад-
принадлежит лишь конечному числу симплексов. С. с. наз.
упорядоченной, если на ней задано частичное
упорядочение, линейное на каждом симплексе.
Пример С. с. Пусть X — множество и U—
= {Ua\o-?A} — нек-рое семейство его непустых под-
подмножеств. Непустое конечное подмножество а?А наз.
симплексом, если множество Па6/1^а непусто. Полу-
Получающаяся С. с. Л наз. нервом семейства U.
Симплициальным отображением
С. с. Kf в симшшциальную схему А'2 наз. такое ото-
отображение f : К1—>- К2, что для каждого симплекса s
в С. с. Кг его образ f(s) является симплексом в С. с.
Кг. С. с. и их симшшциальные отображения состав-
составляют категорию.
Если симплициальное отображение / : L -> К яв-
является вложением, то С. с. L наз. с и м плиц и а л ь-
н о й подсхемой С. с. Л. Все симплексы С. с.
К размерности, меньшей или равной п, составляют
симплициальную подсхему С. с. К, к-рая обозначается
К" и наз. я-м е р н ы м (или ге-м) остовом С. с.
К. Симплициальная подсхема L С. с. К наз. полной,
если каждый симплекс в К, нее вершины к-рого при-
принадлежат L, сам лежит в L.
Каждой С. с. К канонически сопоставляется сим-
плициалъное множество О (К), симплексами размерно-
размерности п к-рого являются (я-|-1)-члонные последователь-
последовательности (х0, . . ., хп) вершин С. с. К, обладающие тем
свойством, что в К существует такой симплекс s, что
X[?s для любого 2—0, 1, . . ., п. Операторы граней d,-
и вырождения s; этого симнлициального множества
определяются формулами
**1 (xai • • • 1 хп) — (^Oi • • • > ^ii ¦ ¦ • > xnli
Sj(*O, •••, Xn) = (x0, ..., Xh X;, Xl + 1, ..., Xn),
где знак л означает, что символ, стоящий под ним,
опускается. Для упорядоченной С. с. К определено
симплициальное подмножество 0+ (К)сО(К), состоя-
состоящее из тех симплексов (х0, . . ., хп), для к-рых Xg^xj^^.
<:. . .<:.?„. Группы (ко)гомологий симплициального
множества О (К) изоморфны группам (ко)гомологий
симплициального множества О + (К) и наз. группами
(ко)гомологий С. с.
Каждому симплициальному разбиению (симплици-
альному пространству) X отвечает С. с. симплициаль-
пого разбиения, вершинами к-рой являются вершины
разбиения X, а симплексами — те непустые конечный
множества вершин, на к-рые в X натянут симплекс.
Для каждой С. с. К существует однозначно опреде-
определенное с точностью до изоморфизма симплициальное
разбиение, С. с. к-рого является К. Оно наз. г е о-
метрической реализацией (или телом)
С. с. К и обозначается \К\. Им является геометрич.
реализация в смысле Дживера — Ху (см. Симплици-
алъное множество) ||0(.ЙГ)|| симплициального множе-
множества О (К), а если С. с. К упорядочена —геометрич.
реализация в смысле Милнора \О+ (К)\ симплициаль-
симплициального множества 0+ (К). Соответствие К -> \\О (К)\\
является ковариантным функтором из категории С. с.
в категорию клеточных разбиений (клеточных про-
пространств). Тонологич. пространство X, гомеоморфнос
толу \К\ нек-рой С. с. К, наз. полиэдром (;\
также триангулируемым пространст-
в о м), а пара (К, /), где / : IК\ —*¦ X — гомеоморфизм,
наз. триангуляцией пространства X.
Точки топологич. пространства \К\ можно отожде-
отождествить с функциями а : К —>- [0, 1], для к-рых множе-
множество {х?К\а (х)ФО} является симплексом в К и
Число а (.г) наз.' х-й барицентрической
координатой точки а. Формула
d (a, P) =
определяет на множестве 1 К\ метрику, но соответст-
соответствующая метрич. топология, вообще говоря, сильнее
топологии пространства \К\. Множество \К\, снаб-
снабженное метрич.'топологией, обозначается \K\d.
С. с. К изоморфна нерву семейства звезд вершин
пространства \К\, т. е. открытых подмножеств St.z=
^{а€\К\\а(х)фО}, где х?К.
Следующие утверждения равносильны: 1) С. с. К
локально конечна; 2) пространство \К\ локально ком-
компактно; 3) 1^1 = 1^1^; 4) пространство \К\ метризуемо;
5) пространство \К\ удовлетворяет первой аксиоме
счетности. Пространство \К\ сепарабельно (компактно)
тогда и только тогда, когда С. с. л не более чем счетна
(конечна).
Клетки клеточного разбиения \К\ находятся в би-
биективном соответствии с симплексами С. с. \К\, и за-
замыкание |*| клетки, соответствующей симплексу s,
определяется формулой
Оно гомооморфно g-мерному (q—dims) замкнутому
шару (так что клеточное разбиение ]К\ регулярно).
Более того, на каждом множестве Ы имеется канонич.
линейная (аффинная) структура, но отношению к
к-рой оно изоморфно стандартному симплексу А*.
Отсюда и из того, что IsRs'l — Ы Rls'l Для любых
симплексов s, s'czK, вытекает, что пространство \К\
может быть гомеоморфно отображено (вложено) в
пространство R" (возможно, с трансфинитным п) так,
чтобы все замкнутые клетки |s| оказались (прямоли-
(прямолинейными) симплексами. Это означает, что образ \К\
в R" является симплициалъным пространством (по-
(полиэдром), т. е. объединением замкнутых симплексов,
пересекающихся только по целым граням. Это сим-
плициальное пространство наз. реализацией
С. с. К в R».
С. с. К тогда и только тогда реализуется в прост-
пространстве R" с конечным п, когда С. с. К локально
конечна, ие более чем счетна и ее размерность конеч-
конечна. При этом, если dim А'<:и, то К реализуется в R2«+1.
С. с, состоящая из 2м+3 вершин, каждое (л+1)-
элементное подмножество к-рой является симплексом,
в R2" не реализуется.
По любой С. с. К можно построить новую С. с. BdA',
вершинами к-рой являются симплексы С. с. К, а сим-
симплексами — такие семейства (sa, . . ., ху) симплексов
из К, что SoCZSjC:. . .CIs,,. С. с. BdK наз. барицент-
барицентрическим измельчением (или и о д р а з-
д е л е н и е м) С. с. К. Клеточные пространства I В&К\
и \К\ естественно гомеоморфны (но не изоморфны).
При этом гомеоморфизме каждая вершина \s\ из |BdA|
(т. е. нульмерная клетка, отвечающая вершинеs^Bd/i")
переходит в центр тяжести (барицентр) замкнутого
симплекса |s| СПI АГ|.
С. с. BdA естественным образом упорядочена. Если
С. с. К упорядочена, то соответствие s —*- (первая
вершина s) определяет симплициальное отображение
BdK-^-K, сохраняющее упорядоченность. Оно наз.
каноническим сдвигом. Его геометрич.
реализация (являющаяся непрерывным отображением
|Bd/f| ->-\K\) гомотопна естественному гомеоморфизму
|Bd#||tf|
Симплициальное отображение ф : К —*¦ L (или его
геометрич. реализация |<р|: \К\ -> \L\) наз. с и м п л и-
циальной аппроксимацией непрерывно-
непрерывного отображения f :\K\ —*-\L\, если для каждо11 точки
а?\К\ точка |ф| (а) принадлежит минимальному замк-
замкнутому симплексу, содержащему точку /(а), т. о.,
что равносильно, если для каждой вершины ж? К имеет
место вложение /(SteJcSttp (х). При этом отображения
/ и |ф| гомотопны. 1
Теорема о с и м п л и ц и а л ь н о и аппрок-
аппроксимации утверждает, что если С. с. К конечна,
то для каждого непрерывного отображения j:\K\ -*¦ \L\
найдется такое число N, что для всех n^N существует
симплициальная аппроксимация Bd"^ —>• L отобра-
отображения / (рассматриваемого как отображение IBd"^ —v
—*¦ \L\).
Лит.: [1] С пень ер Э., Алгебраическая топология, пер.
с англ., М., 1971; [2] X и л т о н П.7Д ж., У а й л и С, Теория
гомологии. Введение в алгебраическую топологию, пер. с англ.,
М., 1966; [3] Whitehead 1. Н. С, «Ргос. London Math.
Soc», 1939, v. 45, p. 243—327.
С. Н. Малыгин, М. М. Постников.
СИМПЛИЦИАЛЬНОЕ МНОЖЕСТВО (прежние наз
вания — полусимплициальный комп-
комплекс, полный полусимплициальный
комплекс) — симплициальный объект категории
множеств Ens, т. е. система множеств (м-х слоев)
Кп, ?г^0, связанных отображениями d, : A'n->A'n_1,
0<:i<:re (операторами граней), и s,-: Кп —v
->- Кп+1, 0<г<п (операторами вырожде-
вырождения), удовлетворяющих соотношениям
d{dj = dy_iti;, если i < ;',
sisj == sj + i*/> если i < /;
( Sj_idi, если i < j,
d(Sj= id, если i = j или i = /
' sjdj_i, если i > /-f-
Точки слоя Кп наз. n-м е р н ы м и симплексами
С. м. К. Если заданы только операторы й,-, удовле-
удовлетворяющие соотношениям d/rfy=dy_irf,-, i</, то система
{Кп, dn} наз. полусимплициальным мно-
множеством.
Симнлициальным отображением
/: К —>- К' С. м. К в С. м. К' наз. морфизм функторов,
т. е. последовательность отображений fn:Kn-+Kn>
удовлетворяющих соотношениям
С. м. и их симплициальные отображения образуют ка-
категорию A°Ens. Если все отображения /„ являются
вложениями, то С. м. К наз. с и м п л и ц и а л ь н ы м
подмножеством С. м. К'. При этом опера-
операторы граней и вырождения в С. м. К представля-
представляют собой ограничения соответствующих операторов в
С. м. А".
Для любого топологич. пространства X опррделено
С. м. S (X), наз. с и н г у л я р н ы м С. м. пространства
X, симплексами к-рого являются сингулярные сим-
симплексы пространства X (см. Сингулярные гомологии),
т. о. непрерывные отображения а : А" -> X, где Д" —
га-мерный геометрический стандартный симплекс
Операторы граней d; и вырождения S; этого С. м.
определяются формулами
Соответствие X >—>¦ S (X) является функтором (наз.
сингулярным функтором) ин категории
Т01ЮЛ0ГИЧ. пространств Тор в категорию С. м. A°Ens.
Произвольная симплициальная схема К определяет
С. м. О (К), симплексами размерности п к-рого явля-
являются (ге+1)-членные последовательности (х0, . . ., хп)
вершин схемы К, обладающие тем свойством, что в К
существует такой симплекс s, что'х,?s для любого i--0,
1, . . ., re. Операторы граней dj и вырождения s,- этого
С. м. определяются формулами
..., х„)^(х0, ..., х;, ..., х„),
п)=^(х0, ..., х,-, xi, xi + i, ..., хп),
где знак л означает, что символ, стоящий под ним,
опускается. Если симплициальная схема К упорядо-
упорядочена, то симплексы (х0, . . ., хп), для к-рых жо<. . .<.хп,
образуют симплициальное подмножество О+ (К) С. м.
О (К). Соответствие К t-> О (К) (и К н-*- 0+ (К)) являет-
является функтором из категории симплициальных схем (упо-
(упорядоченных симплициальных схем) в категорию A°Ens.
Для произвольной группы я определено С. м. К (л),
симплексами размерности п. к-рого являются классы
пропорциональных (ге-)-1)-членных последовательно-
последовательностей (х0, . . ., хп), ,г,-?я(по определению (х0, . . ., хп)
~ (хо, ¦ ¦ ., хп), если существует такой элемент у^я,
что x'l—yxi для всех г—0, . . ., л).. Операторы гра-
граней dj и вырождения s,- С. м. К (л) определяются фор-
формулами
di(x0:... :хп) = (х„:... :xi_1:xl + 1:.. .:хп),
si (хо: ¦ • • :хп) = (хо'- • • ¦ •Zi-i'-xi'-Zi'xi + i' ¦ ¦ ¦ '¦хп)ш
С. м. К (л) является на самом деле симплициальной
группой.
Для произвольной абелевой группы я и любого
целого п>1 определено С. м. (на самом деле, симпли-
симплициальная абелева группа) Е(п, п), симплексами раз-
размерности q к-рого являются n-мерные коцепи (/-мер-
(/-мерного геометрического стандартного симплекса &1 с
коэффициентами в группе л (таким образом, Е (я, п)ч—
= С"(Д?; л)). Обозначая вершины симплекса А?
символами е\, /-^0, . . ., (/, определяют симнлициаль-
ные отображения б,-: A9~i~^A'/ и о,-: A?->A?-J фор-
формулами
[ еЧ, если j < i,
\ е/+1' если ^'5з';
f еЧ~г, если /< г,
' \ ^-1' если / > L
Индуцированные гомоморфизмы групп коцепей
d/ = 6t: С" (Д?; я) —г С (Д9-1; я),
47 = с*: С" (Д''-1; л) -->¦ Сп (Д1?; я)
являются, по определению, онераторами граней и
вырождения С. м. Е(я, п). Симплексы, являющиеся
коциклами, образуют симплициальное подмножество
С. м. Е (я, п.), к-рое наз. С. м. Эйленберга —
Маклейна и обозначается К(п, п). Кограничный
оператор на группах С* (Д?; я) определяет канониче-
каноническое симплициальное отображение Е (я, п) ->
->¦ К (я, п-\-1), к-рое обозначается б. Поскольку поня-
понятие одномерного коцикла имеет смысл и для неабеле-
вой группы я (см. Неабелевы когомологии), С. м. К (л, 1)
определено и без предположения, что группа я абелева.
Это С. м.изоморфно С. м. К (я) (следует каждому сим-
симплексу z?K(n, 1)?=Z1(A?, я) сопоставить значения
нульмерной коцепи, кограницей к-рой является
коцикл z, на вершинах е^).
Сопоставив каждому слою Кп С. м. К свободную
абелеву группу, им порожденную, получают симпли-
циальную абелеву группу и, следовательно, цеппо и
комплекс. Этот комплекс обозначается С (К) и наз.
комплексом цепей С. м. X. Группы (ко)го-
мологий комплекса С (К) (с коэффициентами в группе
G) наз. группами (ко)гомологий Я*(К; G)
и Н* (К; G) С. м. К. Группы (ко)гомологий сингуляр-
сингулярного С. м. S (X) являются сингулярными группами
(ко)гомологий топологич. пространства X. Группы
(ко)гомологий С. м. О (К) и 0+ (К) изоморфны и наз.
группами (к о)г о ы о л о г и й с и м п л и ц и-
альной схемы if. Группы (ко)гомологий С. м.
К (я) суть группы (к о)г о м о л о г и й г р у п-
II Ы Я.
Симплекс х?К„ С. м. К наз. вырожденным,
если существует такой симплекс у?Кп-\ и такой опе-
оператор вырождения s,-, что x=siy. Лемма Эйлен-
Эйленберга — Зильбера утверждает, что любой сим-
симплекс х?Кп С. м. К единственным образом представ-
представляется в виде x=K(s)y, где s — нек-рый эпиморфизм
s,-: [я] —у [то], т^.п, а у ?Кт— невырожденный симп-
симплекс. Наименьшее симплициальное подмножество С. м.
К, содержащее все его невырожденные симплексы
размерности, меньшей или равной я, обозначается К"
или SknK и наз. я-м е р н ы м о с т о в о м С. м. К.
Геометрические стандартные симплексы
составляют косимплициальное топологич. пространство
относительно операторов кограней б,- и ковырождения
а,-, определенных формулами
б,- (t0, ..., tn_1) = (t0, ..., li,-i, 0, /,-, ..., tn_1),
В дизъюнктном объединении Un~oKnXA", где все
Кп рассматриваются как дискретные множества, фор-
формулы
(diX, и) ~ (х, 6,-а), х ? К„, и ? Д»-1;
(stx, и) ~ (х, aiu), х ?Кп, и? Д« + 1,
определяют отношение эквивалентности, факторпро-
странство по к-рому является клеточным разбиением
(клеточным пространством), клетки к-рого находятся
в биективном соответствии с невырожденными симплек-
симплексами С. м. К. Это клеточное разбиение обозначается
\К\ или RK и наз. геометрической реали-
реализацией в смысле М и л н о р а С. м. К. Каж-
Каждое симплициальное отображение / : К -> L индуци-
индуцирует по формуле
Rf[x, и] = [/(*), и]
непрерывное отображение Rf : RK -*¦ RL, н соответст-
соответствия К 1—> RK, f i—> Rf представляют собой функтор R:
A°Ens -> Тор. Этот функтор сопряжен слева к сипгу-
лярному функтору S : Тор -> A°Ens. Соответствующие
изоморфизмы функторов
q>:A°Ena(K,S(X))—*Tojs(RK, X),
г|> : Top (RK, X) —¦* Д» Ens (Я, 5 (X))
определяются формулами
ф (/)[*, "]=/(*)(«),
№(?)(*))(") = ?[*. и],
где
х ? А'„, и ? А», / ? A» Ens (К, S (X)), g ? Top (RK, X).
Морфизм сопряжения Ф(Х) : BS (X) -у X является
для любого топологич. пространства X слабой гомото-
пич. эквивалентностью (это, в частности, доказывает,
что произвольное топологич. пространство слабо го-
мотопически эквивалентно клеточному разбиению).
Конструкция геометрич. реализации \К\ обобщается
на симплициальные топологич. пространства К. Можно
также определить геометрическую реали-
реализацию в смысле Дживера — Ху \\K\\,
учитывающую только операторы граней dj (в этой
реализации имеются клетки для всех симплексов из К,
а не только невырожденных). Если каждый оператор
вырождения $i является замкнутым корасслоением
(условие, автоматически выполненное для С. м.),
то естественное отображение р : \\К\\-*-\К\ является
гомотопич. эквивалентностью.
Категория Д°Ем допускает произведения, при этом
для любых С. м. К={Кп, df, sf} и L={Ln, d'i, sf)
их произведением будет С. м. KXL, для к-рого
s/CXL-_ SK xjt,
В частности, для каждого С. м. К определено его
произведение на снмилициальный отрезок Д1. Про-
Проекции Лх: К X L —>¦ К и я 2: К X L -> L определяют би-
биективное отображение
Лл1ХЛл2 : R(KxL)—+RKxRL,
к-рое является гомеоморфизмом, когда произведение
RK X RL представляет собой клеточное разбиение
(напр., если оба С. м. К и L счетны или же если одно
из клеточных разбиений RK или RL локально ко-
конечно). Отсюда, в частности, следует, что геометрич.
реализация любого счетного симплициального моноида
(группы, абелевой группы) является топологич. мо-
моноидом (группой, абелевой группой).
Симплициальные отображения /, % : К -> L наз.
гомотопными, если существует такое симп-
лпциальное отображение (г о м о т о п и я) /': А'ХД1-*-
-> L, что
F(x,
F(x,
для любого симплекса х ^ Кп и для любой композиции s
(длины п) операторов вырождения. Ото определение
(моделирующее обычное определение гомотопии не-
непрерывных отображений) равносильно (для случая
С. м.) общему определению гомотопности симшшци-
альных отображений любых симплициальных объек-
объектов.
Имея понятие гомотопии, можно развивать теорию
гомотопии С. м. аналогично теории гомотопии полиэд-
полиэдров. Оказывается, что эти две теории полностью па-
параллельны; это находит свое выражение в том, что
соответствующие категории эквивалентны (эквивалент-
(эквивалентность осуществляется функтором геометрич. реали-
реализации). В частности, геометрич. реализации гомотоп-
пых спмшшциальных отображений гомотопны, и,
напр., геометрич. реализация С. м. К(зх, п) будет Эй-
ленберга —Маклейна пространством К(п, п). Од-
пако фактич. построение теории гомотопий для С. м.
в деталях несколько отличается от построения теории
гомотопий для топологич. пространств. Основное от-
отличие состоит в том, что отношение гомотопности сим-
плициальных отображений не является, вообще говоря,
отношением эквивалентности. Эта трудность преодо-
преодолевается следующим образом.
Симплициальное отображение A'l—*- К стандартного
фунтика (см. Стандартный симплекс) в С. ж. К наз.
фунтиком в К. Каждый фунтик однозначно за-
задается (а+1)-членной последовательностью гс-мерных
симплексов х0, хх, . . ., хь-i, Xk+л, ¦ ¦ ¦> xn+i, Для
к-рых d{Xj=dj-X х{ при любых г'</, 1фк. Говорят, что
фунтик заполняется, если он распространяется
на все С. м. Дп + 1, т. е. найдется такой (п+1)-мерный
симплекс ,г, что d/x~xi для каждого 1фк. С. м. К наз.
полным (или удовлетворяющим усло-
условию Капа), если каждый его фуитйк заполняется.
Сингулярное С. м. S (X) произвольного топологич.
пространства X всегда полно. Любая симилициальная
группа полпа, в частности полны С. м. Эйленберга —
Маклейна К(п) и К (я, п). Значение полных С. м. со-
состоит в том, что отношение гомотопности симплициаль-
ных отображений произвольного С. м. в полное С. м.
является отношением оквивалентности. Поэтому на
подкатегории полных С. м. построение теории гомо-
гомотопий принципиальных трудностей не вызывает. Вме-
Вместе с тем существует [4] функтор Ex~:A°Eris-> A°Ens,
сопоставляющий каждому См. К полное С. м. Ех°°К,
геометрич. реализация к-рого гомотопически эквива-
эквивалентна геометрич. реализации С. м. К и к-рое поэтому
вполне заменяет С. м. К во всех гомотопических во-
вопросах.
Два n-мерных симплекса х и х' С. м. К наз. срав-
сравнимыми, если d[x=djx', 0<:i<;m. Сравнимые сим-
симплексы наз. гомотопными, если существует
такой (и-]-1)-мерный симплекс у, что dny~x, dn + 1y= x'
и dii/~sn_1djX=sn_id;x', 0<:г<:«. Для полных С. м.
это отношение является отношением эквивалентности,
причем симплексы тогда и только тогда гомотопны,
когда их характеристические симплициальные ото-
отображения гомотопны relSk"~1A".
С. м. К наз. пунктированным, если в нем
отмечен нек-рый нульмерный симплекс 0 (тем же сим-
символом 0 обозначаются все вырождения этого симплек-
симплекса, а также порожденное им симплициальное подмно-
подмножество, к-рое обычно наз. отмеченной точкой
в К). Для полного пунктированного С. м. К множество
лп(А") классов гомотопных гс-мерных симплексов, срав-
сравнимых с симплексом 6. является при я^1 группой.
Эта группа наз. п-и ерной гомотопической
г р у и п о й пунктированного полного С. м. К; эта
терминология оправдывается тем, что пп(К)=пп(\К\I
и в частности пп (К (л, п)) = ли я,(ЛГ(я, п)) =0 при 1фп.
См. К, для к-рого щ(К) = 0 при всех (<ге, наз. ге-связ-
н ы м; при этом 0-связное С. м. наз. связным, а
1-связное С. м.— о д н о с в я з н ы м. Сложение в
группе и „(К), п^1, индуцируется операцией, сопо-
сопоставляющей симплексам х и у (сравнимым с 0) симп-
симплекс dnz, где z — симплекс размерности ге-j-l, запол-
заполняющий фунтик .г,--- 0, г<п—2, хп-\_ — х, хп+1 = у.
Если С м. К является опмилициальным моноидом с
единицей 0, то сложение индуцируется также умноже-
умножением в этом моноиде (произведение двух симплексов,
сравнимых с G, сравнимо с 0).
Поскольку любой симплекс х, сравнимый с 0, яп-
ляется циклом (цепного комплекса С (К), определя-
определяемого С. м. К), то возникает естественный г о м о м о р-
физм Гуревича h : пп (К) —v Hn{K), при п— 1
индуцирующий изоморфизм
л^ЩЦп^К), щ(К)]-+Н±(К)
(теорема Пуанкаре), а при ге>1 являющийся
изоморфизмом, когда С. м. К (п—1)-связно (теорема
Гуревича). Для полных С. м. справедлива также
и теорема Уайтхеда в обоих ее вариантах, т. е. симп-
лициалыше отображение / : К -> L полных С. м. тогда
и только тогда является гомотопич. эквивалентностью,
когда оно индуцирует изоморфизм гомотопич. групп,
причем для односвязных С. м. это условие равносильно
тому, что индуцированные гомоморфизмы групп го-
гомологии являются изоморфизмами.
В случае, когда К является симплициальной груп-
группой, гомотопич. группа пп(К) изоморфна группе
гомологии Нп{К) цепного (не обязательно абелева)
комплекса К, для к-рого
_
а граничный оператор является ограничением на Кп
оператора (— l)ndn. Если симплициальная группа К
абелева, то комплекс К является подкомплексом этой
группы, рассматриваемой как цепной комплекс, и,
более того, ее цепным деформационным ретрактом, и,
в частности, ее прямым слагаемым. Оказывается, что
дополнительным прямым слагаемым служит подком-
подкомплекс, порожденный вырожденными симплексами. По-
Поэтому соответствующий факторкомплекс комплекса К
ему цепно эквивалентен. Напр., для групп когомоло-
гий произвольного С. м. К отсюда следует (теорема
о нормализации), что они изоморфны нормали-
нормализованным группам когомологий, т. е. группам, полу-
получающимся, если ограничиться коцепями, равными
нулю на всех вырожденных симплексах. Кроме того,
КЕ(К)
Функтор К i—*• К осуществляет эквивалентность
теории гомотопны симплициальных абелевых групп
с теорией гомологии цепных комплексов. Отсюда,
в частности, следует, что любая связная симпли-
симплициальная абелева группа К гомотопически экви-
эквивалентна произведению С. м. Эйленберга — Маклейна
К(кп(К), п).
Полное С. м. К наз. минимальны м, если срав-
сравнимые симплексы тогда и только тогда гомотопны,
когда они совпадают. С. м. К (л, п) минимально. Вся-
Всякая гомотопич. эквивалентность минимальных С. м.
является изоморфизмом. Каждое полное С. м. К об-
обладает минимальным симплициальным подмножеством.
Оно является его деформационным ретрактом, и по-
поэтому с точностью до изоморфизма определено одно-
однозначно.
Симплициальное отображение р : Е -> В наз. рас-
расслоением в с м ы с л е К а н а, если в Е запол-
заполняется любой фунтик / : Afe-> E, для к-рого фунтик
pof:Ak-*- В заполнен, причем для любого заполнения
g ; д»+! _>. В фунтика p°f существует такое заполне-
заполнение /:Д" + '-> Е фунтика /, что p°f=g. Расслоение в
смысле Кана является симплицнальным аналогом
расслоения в смысле Серра и для него имеет место
теорема о накрывающей гомотопии
в следующей формр: если для симплициальных отоб-
отображений J-.K —> Е и Ф:Л'ХД] —>- В имеет место равен-
равенство Фо (id x6j)-=p о/, то существует такое симплици-
симплициальное отображение Ф:#Х Д1 —>-?, что Ф^ (idX6;[)=7
и роф=ф. Если расслоение р является сюръективным
отображением, то С. м. Е полно тогда и только тогда,
когда полно С. м. В. Слоем расслоения р:Е -> В
наз. (автоматически полное) С. м. F—р~1@), где G —
отмеченная точка в В. Для любого расслоения в смысле
Ceppa p : E —>. В симплициальное отображение S (p):
S (E) —*• S (В) является расслоением п смысле Кана,
и для любого расслоения в смысле Кана р : Е —v В
отображение Rp : RE -> RB является расхлоением в
смысле Серра (см. [5]).
Пусть К — полное пунктированное С. м. и ге^О.
Положим хп у, где.г, y?Kq, если dix—diy для всех
i<.n, т. е. если
(см. Стандартный симплекс). Это отношение является
эквивалентностью, и фактормножества (CosknK)q=
= Kgln составляют (по отношению к индуцированным
операторам граней и пырождения) С. м. CosknK, к-рое
наз. n-м к о о с т о в о м С. м. К. По определению,
полагается Cosk"/f=A'. Для любого ге^О С. м. Cosk" A
полно и nq(CosknK)=0 при </>«. Кроме того, для
любого 7гс<:ге естественное сюрьективноо еимплици-
альное отображение
р? : Cosk" К —^ Cosk"» К
является расслоением, индуцирующим в размерностях,
меньших или равных т, изомо*рфизм гомотопич. групп.
В частности, слой расслоения p'n-i гомотопически
эквивалентен См. Эйленберга — Маклейна К (пп(К), п).
Последовательность расслоени!1
К —>¦. ..¦—±Cosk« + 1K -^ Cosk" А' —> Cosk''-1 К —>. . .
наз. Постникова системой полного С. м. К. Если
С. м. К минимально, то эта последовательность яв-
является его резольвентой (см. Гомотопический тип).
Конструкция системы Постникова непосредственно
обобщается на произвольное расслоение р:Е —>- В
полного С. м. Е над полным С. м. В. Пусть Cosk"p
есть С. м., слоями (Cosknp)q к-рого являются фактор-
п
множества слоев Ец по отношению х~у, к-рое имеет
место тогда и только тогда, когда р (х)—р (;/) и d(X=dn/
при всех ?<:«. По определению, полагается Cosk°°p~E.
При этом Gosk0p=B. При ?«<«<:оз естественное сюръ-
ективное симплициальное отображение
pjjj : Cosk" p —>¦ (;oskm p
является расслоением, индуцирующим в размерно-
размерностях, меньших или равных т и больших ге+1, изо-
изоморфизм гомотопич. групп. В частности, слой рас-
расслоения pn-i гомотопически эквивалентен С. м. Эйлен-
Эйленберга— Маклейна K(nn(F), n). Слоем расслоения
p":Cosknp -у В является С. м. Cosk"/'1, где F — слой
расслоения р'.Е —»- В. Последовательность расслоений
Е —>...—>Cosk"*1 p—i-Cosk" р —^Cosk"-1 p—>-. ..—*В
наз. системой Мура — Постникова рас-
расслоения р:Е -> В.
На языке С. м. удобно определять спектры. С и м-
п л и ц и а л ь н ы м спектром наз. последова-
последовательность {Х(д)} пунктированных множеств (его эле-
элементы наз. симплексами, отмеченный симплекс обо-
обозначается 0), определенных для произвольного целого
числа q, снабженная отображениями d;:X(g) —>- Х(?_и,
?>0 (операторами гране й), и s,-:Z(?)->
-^- Xfq-i), г>0(о ператорами вырождения),
к-рые удовлетворяют соотношениям (*) и следующему
условию: для каждого симплекса х?Х существует
такое целое п, что d,vr=9 при ?>ге. Каждому спектру X
и произвольному целому п можно сопоставить С. м.
Хп, определив его формулой
при I > q, d0, ..., dqX~
Для так определенных С. м. Хп имеют место вложения
SXnCZXn+i, где 5 — надстройка. По последователь-
последовательности С. м. Хп и вложений SXnCZX„+i симплициаль-
ный спектр X, в свою очередь, восстанавливается
однозначно. Если все С. м. X полны, то X,,~=QXu+i,
где Q — функтор петель. Функтор геометрич. реали-
реализации осуществляет эквивалентность категории си.м-
ллициальных спектров с категорией тоиологич. спект-
спектров. Симплициальные спектры могут быть определены
для произвольной категории. Категория абелевых
групповых спектров изоморфна категории (абелевых)
цепных комплексов.
Лит.: [1] Г а б р и е л ь П., Д и с м а н М., Категории
частных и теория гомотопий, пер. с англ., М., 1971; Е«] May
•Г. P., Simplicial objects in algebraic topology, Princeton, 1967;
[3] I, amotkeK., Semisimpliziale algebraische Topologie,
В.— [u. a.], 1968; [4] К a n D., «Amer. J. Math.», 1957, v. 79,
p. 449_76; 15] Q u i 1 1 e n D., «Proc. Amer. Math. Soc», 1968,
v. 19, p. 1499—500; [6] Браун Э. X., «Математика», 1958,
т. 2, № 2, с. 3—24; [7] Каи Д., таги же, 1962, т. 6, № 1,
с. 3 — 32; [8] е г о же, там же, 19В6, т. 10, № 3, с. 12—28.
С. Ц. Малыгин, М. М. Постников.
СИМПЛИЦИАЛЬНОЕ ОТОБРАЖЕНИЕ — морфйзм
либо категории симплициалъных пространств, либо
категории симплициалъных схем. А- в- Хохлов.
СИМПЛИЦИАЛЬНОЕ ПРОСТРАНСТВО — тополо-
топологическое пространство X, снабженное таким покры-
покрытием топологическими симплексами (наз. т р и а н г у-
л я ц и е и), что грани любого симплекса триангу-
триангуляции принадлежат триангуляции, пересечение любых
двух симплексов триангуляции является гранью каж-
каждого из них (возможно, пустой); множество FczX тогда
п только тогда замкнуто, когда замкнуто его пересе-
пересечение с любым симплексом триангуляции. Каждое
С. п. является клеточным пространством. Задание
триангуляции равносильно заданию гомеоморфизма
\S\-t-X, где |?| — геометрич. реализация нек-рой
симплициалъной схемы. С. п. наз. также с и м п л и ц и-
альными к о м и л е к с а м и, с и м п л и ц и а ль-
н ы м и разбиениями. С. п. являются объек-
объектами категории, морфизмами к-рой X -> У служат ото-
отображения такие, что каждый симплекс триангуляции
пространства X линейно отображается на нек-рый сим-
симплекс триангуляции пространства У. Морфизмы наз.
также симплициальными отображени-
отображениями. А. В. Хохлов.
СИМПЛИЦИАЛЬНЫИ КОМПЛЕКС — то же, что
симплициалъное пространство.
СИМПЛИЦИАЛЬНЫИ ОБЪЕКТ к а г о г о р и и
Й" — произвольный контравариантный функтор X:
Д _>. g" (или, что то же самое, ковариантный функтор
X : Д°Р —>- й") из категории Д, объектами к-рой явля-
являются упорядоченные множества [ге]={0, 1, . . ., п),
rc>0, а морфизмами — неубывающие отображения ц:
[ге]->[от]. Ковариантный функтор Х.А —*¦ $" (или,
что то же самое, контравариантный функтор X: A°J' ->¦
—>. $) наз. к о с и м п л и ц и а л ь н ы м о б ъ е к-
т о м категории Ч@.
Морфизмы
категории А, определенные формулами
осли / За ',
I /, если ;'< i,
\ I — 1, если у ;э i,
порождают любой морфизм категории Д, так что С. о.
X полностью определен, если для любого ге^О задан
объект Х([п])=Хп (наз. гс-м слое м, или ге-й к о м-
п о н е н т о и, С. о. X) и морфизмы
dt - X (б,-): Хи -* А'„_ ! и в,- ^ X (о,-): Хп -, Х„ _ г
(наз. соотвртетвенно операторами граней п
операторами вырождения). В случае,
когда to является категорией структуризованных
множеств, точки множества Хп наз. обычно и-м е р-
ными симплексами С. о. X. Отображения
6,- и а,- удовлетворяют соотношениям
б,-б(- = 6,-6у_1, если i < /,
GjO; =а,-а/ + 1, если i<j;
( б,-а;-_!, если i < /', V (*)
0yS,- = <j id, если i — j или г' = / + 1, I
' S/.xoy, если i > /+1; J
причем любое соотношение между этими отображе-
отображениями является следствием соотношений (*). Это оз-
означает, что С. о. X можно отождествить с системой
{Хп, dj, s,}, состоящей из объектов Хп, гс^О, кате-
категории <Ё и морфизмов dj\ Xn ->- Xn~i, 0<i<re, и
«,-: Х„—»-А'п+1, 0<:i«:?!, удовлетворяющих соотно-
соотношениям
didj=dJ--1dh если г < /;
S(Sf=:S/ + 1s;, если «</';
/ sJ_1di, если г < /,
id, если / —/ или г — / + 1,
Sjdi-.1, если i > /+1.
Аналогично, косимплициальный объект X можно
рассматривать как систему {Л'„, d!, s'}, состоящую жл
объектов X", гс>0 (п -.г к о с л о о в), и морфизмов d':
X" —>. X", 0<:г<:?г (операторов кограней),
и s': Z" + 1-»-X", Ocgj<re (операторов к о-
вырождения), удовлетворяющих соотношениям
(*) (в к-рых положено 6,-=d', Oi=s!).
С и м п л и ц и а л ъ н ы м отображением /:
X -> Y С. о. X в С. о. Y (одной и той же категории %)
наз. произвольное преобразование (морфизм) функ-
функтора X: Д —>- $ в функтор Y: Д —>- if, т. е. такая
система морфизмов /„: Хп ->- К„, ге>0, критерии g1,
что
Симплициальные объекты категории to и их симнли-
циальные отображения образуют категорию Д0^.
С и м п л и ц и а л ь н о и г о м о т о п и е й h: f^=g,
связывающей симплициальные отображения /, g: X —>У
еимшшциальных объектов категории С, наз. такое
семейство морфизов А;: Хп —>- Y,, + i, 0«i-<re, катего-
категории %, что
dh f
idi, если i < /,
j_x, если i = / > О,
j-i, если i >
если is
_
^ | /г/''1 еСЛП
На основе этого определения в категории Д°^ над
произвольной категорией if можно воспроизвести по
существу всю обычную теорию гомотопий. В случае
категории множеств или топологии, пространств функ-
функтор геометрич. реализации (см. Симплициальное мно-
множество) переводит эту «симплициальную» теорию в
обычную.
Примеры С. о.: симпдициалъное множество,
симплициальное топологич. пространство, симплици-
симплициальное алгебраич. многообразие, симшшциальная груп-
группа, симшшциальная абелева группа, симпдициальная
алгебра Ли, симплициальное гладкое многообразие
и т. д.
Каждая симплпциальная абелева группа является цеп-
цепным комплексом с граничным оператором d~2 (—l)'d;.
Лит.: [1] Габриель П., Ц и с м а н М., Категории час-
частных и теории гомотопий, пер. е англ., М., 1971; [2] М а у J. Р.,
Simplicial objects in algebraic topology, Princeton, 1967; [3] L a-
motkeK., Semisimpliziale algebraische Topologie, B.—
Ш. a.j, 1968. С. Я. Малыгин, М. М. Постников.
СИМПСОНА ФОРМУЛА — частный случай Ньюто-
Ньютона — Котеса квадратурной формулы, в к-рой берутся
три узла:
/ {х) dx
« Ц? [/ (а) +4/ (а-±-ь) +/F)] . A)
Пусть промежуток [а, Ъ] разбит на н частичных про-
промежутков [ж/, xi + i\, /—0, 1, 2, . . ., п—1, длины h=-
—- (b—а)/п, при этом п считается четным числом, и
для вычисления интеграла по промежутку \x2/i, rl
использована квадратурная формула A):
Суммирование по к от 0 до ге/2—1 левой и правой
частей этого равенства приводит к составной С. ф.:
J* / (х) *г s у {/ («)+/ (Ь)+2 [/ (х2)-|-/ (*4) + ...
•"• ¦ +/ ('В-«I +4 [/ (*!)+/ (*»)+ • • ¦ +/ (*»-!)]}, B)
где xj—a-\-]h, J -0, 1, 2, . . ., re. Квадратурную формулу
B) также иалыииют С. ф. (без добавления слова со-
составная). Алгебраич. степень точности квадратурной
формулы B), как и формулы A), равна 3.
Если подинтегральная функция f(x) имеет непре-
непрерывную производную 4-го порядка на [а, Ь], то по-
погрешность Я (/) квадратурной формулы B) — разность
между левой и правой частями приближенного ра-
равенства B) — имеет представление
где ? — нек-рая точка из промежутка [а, Ъ].
С. ф. названа по имени Т. Симпсона (Th. Simpson),
получившего ее в 1743, хотя эта формула была и.ч-
вестна ранее, напр. Дж. Грегори (J. Gregory, 1668).
И. II. Мысовских.
СИМСОНА ПРЯМАЯ — прямая, на к-рой лежат ос-
основания перпендикуляров, опущенных из произволь-
произвольной точки Р окружности, описанной вокруг треуголь-
треугольника, на его стороны. С. п. делит на две равные части
отрезок, соединяющий точку Р с точкой пересечения
высот треугольника. С. н. названа по имени Р. Симео-
Симеона (R. Simson), хотя она впервые была указана ранее.
А. В. Иванов.
СИМУЛА (от англ. «SIMLJlation LAnguage», т. е.
«язык моделирования») — название двух алгоритмич.
языков, разработанных на основе алгола в Норвежском
вычислительном центре и неофициально различаемых
как симула 1 и симула-67.
С и м у л а 1 — проблемно-ориентированный язык для
моделирования систем с дискретными событиями
(напр., систем массового обслуживания), разработан
и 1964. Спецификация модели сопоставляет компо-
компонентам системы (клиентам, станкам, материалам и т. п.)
процессы. Процесс имеет атрибуты (структуру
данных) и программу действий (алгоритм). Модель
работает по принципу квази параллелизма:
в каждый момент активен только один процесс; ис-
исполняя свою программу, он может использовать свои
и чужие атрибуты, порождать новые процессы, пла-
планировать себе и другим процессам события — но-
новые фазы активности (применяя встроенное в язык
понятие дискретного времени), приостановить себя.
Реализация С.1 привела к разработке алюритмич.
средств большой общности, позволяющих выразить
также иные подходы к моделированию (и не только
дискретному). Включение их в язык привело к со-
созданию С.-67.
Симула-67 определена как база для построе-
построения проблемно-ориентированных языков. Ее элемен-
элементарные средства включают весь алгол-60 (с небольшими
изменениями), а механизм расширения основан на
концепции класса объектов.
Понятие объекта возникло из понятия процесса С.1
путем абстрагирования от сравнительно частной орга-
организации квазипараллельного исполнения в терминах
дискретного времени. Оригинальные средства задания
программы и атрибутов объектов через описания клас-
классов составляют главное достижение С.-67. Особенно
пажен принцип префиксации классом, по-
позволяющий включить в описание нового класса объ-
объектов (напр., класса «студент») атрибуты и действия
оолее общего класса (напр., «человек»). Префиксация
применима и к блокам в смысле алгола; такой блок
с префиксом получает «пролог» и «эпилог» из
программы своего префикса, а также все его атрибуты
(переменные и процедуры)-. Это позволяет оформить
разработку проблемно-ориентированного языка как
описание класса. В частности, поставив префиксом
стандартный класс SIMULATION, пользователь полу-
полумает доступ к средствам, эквивалентным средствам С. 1
(и описанным через базу).
Идеи С.-67 оказали большое влияние на позднейшие
языки программирования. Понятие объекта как соче-
сочетания действий и данных привело к концепции а к-
т о р а во многих языках программировании задач
искусственного интеллекта и повлияло на развитие
концепции абстрактных типов данных. Непосредст-
Непосредственно средствами С.-67, помимо языков моделирования,
описаны языки работы с базами данных, машинной
графики и т. д.
С.-67 реализована на БЭСМ-6 и ЕС ЭВМ.
Лит.: [1] Д а л О. И., Н и г а р д К., СИМУЛА — язык
для программирования и описания систем с дискретными собы-
событиями, пер. с англ., «Алгоритмы и алгоритмические языки»,
1967, в. 2, с. 3 — 72; [2] Д а л У. И., М ю р х а у г Б., Н ю г о р д
К., СИМУЛА-67 универсальный язык программирования,-пер.
с англ., М., 1969. В. В. Околънишпиков, С. Б. Покровский.
СИНГУЛЯРНАЯ ФУНКЦИЯ — отличная от пос-
постоянной непрерывная ограниченной вариации функция,
производная к-рой почти всюду на рассматриваемом
отрезке равна нулю. С. ф. входят в качестве слагаемых
в Лебега разложение функций ограниченной вариации.
Напр., всякая непрерывная функция ограниченной
нариации }{х) на отрезке [а, Ь] единственным образом
представима в виде суммы /(а;) — <р (х)-{-г (х), где <р (х) —
абсолютно непрерывная функция, удовлетворяющая
условию ф (a)—f (a), a r (х) есть С. ф. или тождественный
нуль.
П р и м е р. Пусть Х = [0, 1]. Любое х?Х может быть
представлено в виде
где а,-=0, 1 или 2, г=1, 2, ... При этом если х?С,
где С — катпорово множество, то а,-—0 или 2, ?— 1, 2,
.... Пусть п=-~п(х)—первый индекс, при к-ром а„=1;
если таких индексов нет, то полагают п(х)=ао. Функ-
Функция
является монотонной С. ф.
Лит.: [1] Л е и е г А., Интегрирование и отыскание прими-
примитивных функций, пер. с франц., М.—Л., 1934; 12] Н а т а н с о н
И. П., Теория функций вещественной переменной, 3 изд., М.,
1974; [3] X а л м о ш П., Теория меры, пер. с англ., М., 1953.
Б. И. Голубое.
СИНГУЛЯРНОЕ ИНТЕГРАЛЬНОЕ УРАВНЕНИЕ —
уравнение, содержащее искомую функцию под знаком
несобственного интеграла в смысле главного значения
по Коши. В зависимости от размерности многооб-
многообразия, но к-рому распространены интегралы, разли-
различают одномерные и многомерные С. и. у. По сравнению
с теорией уравнений Фредгольма теория С. и. у. яв-
является более сложной. Так, напр., теории одномерных
и многомерных С. и. у. как в смысле формулировок
окончательных результатов, так и применяемых для
их установления методов значительно отличаются
друг от друга. Теория одномерных С. и. у. разработана
более полно, причем ее результаты формулируются
проще, чем аналогичные результаты в многомерном
случае. Ниже в основном будет рассмотрен одномерный
случай.
Важным классом одномерных С. и. у. являются
уравнения с ядром Коши:
t ? г, A)
где а, Ъ, к, f — известные функции, из к-рцх к — ядро
Фредгольма (см. Интегральный оператор), <р — иско-
искомая функция, Г — плоская линия, а несобственный
интеграл понимается в смысле главного
значения по Коши, т. е.
где Ге — I'NJe , le обозначает дугу t'tt" линии Г такую,
что длины дуг и' и tt" равны е.
Оператор К, определяемый левой частью равенства
A), наз. сингулярным оператором (иног-
(иногда его наз. общим сингулярным опера-
то р о м):
B)
где / — тождественный оператор, S — сингуляр-
сингулярный интегральный оператор (иногда
его наз. сингулярным интегральным
оператором с ядром Коши), т. е.
V — интегральный оператор с ядром к (t, т).
Оператор Ku=aI-\-bS наз. характеристи-
характеристической частью сингулярного опе-
оператора К, или характеристическим
сингулярным оператором, а уравне-
уравнение
^S^T.==/W, t€r, C)
— характеристическим С. и. у., функции а, Ъ — коэф-
коэффициентами соответствующего оператора или урав-
уравнения.
Уравнение
наз. союзнымс уравнением A), а оператор
K' = aI-\-SbI-\-V' (V — интегральный оператор с яд-
ядром к (т, ?)) — союзным с оператором К.
В частности, K'o—al-\-SbI является союзным с А"о.
Операторы К, Ко, К', Ко или соответствующие им
уравнения наз. нормального типа, если
функции
A=a+b, B = a — b
пс обращаются в нуль нигде на Г. В этом случае го-
норят т;и;,ке, что коэффициенты оператора пли урав-
уравнения удовлетворяют условию нормально-
с т и.
Пусть На(Г), 0<а<1,—класс функций {/}, оп-
определенных на Г и удовлетворяющих условию
Когда предполагается, что функция / принадлежит
классу На (Г) при нек-ром допустимом значении а
и не требуется знания численного значения а, то будет
употребляться обозначение /?// (Г) или /?//, если из
контекста ясно, о какой линии Г идет речь.
Множество Н наз. функциональным клас-
классом Г ё л ь д е р а; если /?//, то говорят, что /
удовлетворяет условию Гёльдера или что / является
Н-ф у н к ц и е й.
Пусть G — комплекснозначная непрерывная функ-
функция, не обращающаяся в нуль на ориентированной
замкнутой простой гладкой линии Г, и
где [ ]г обозначает приращение функции, заключен-
заключенной в скобках, при однократном обходе линии Г в
положительном направлении. Целое число и наз.
индексом функции G: x=md<3.
Решение характеристического и союзного с ним
С. и. у. Пусть Г — простая замкнутая, ориентирован-
ориентированная гладкая линия, на к-рой положительное направ-
направление выбрано так, что оно оставляет конечную область
с границей Г слева, начало координат лежит в этой
области и а, Ъ, /?#(Г), причем а, Ъ удовлетворяют
условию нор.мальности. Пусть, далее ~л определено
равенством D), в к-ром
G=±± . E)
а+Ь ч '
Тогда справедливы следующие утверждения.
1) Если xJsO, то уравнение C) разрешимо в классе
И(V) при любой правой части /?#(Г) и все его П-
решения представляются (см. [1], [2]) формулой
где
а , Ь
ри-!— произвольный многочлен степени к —1 (р_г~
= 0). Если х<0, то уравнение C) разрешимо в классе
Я (Г) тогда и только тогда, когда правая часть / удов-
удовлетворяет условиям
^¦/W* = 0, k = 0, 1, ..., -х-1.
При соблюдении этих условий уравнение C) имеет
единственное /Y-решение, определяемое формулой @),
U К-рОЙ ри-1~0.
2) Союзное с C) С. и. у.
разрешимо в классе // при любой правой части
если и«0, и все его //-решения представляются
формулой
co(()
Если же х>0, то уравнение G) разрешимо тогда и
только тогда, когда правая часть g удовлетворяет у.
условиям:
(t) g(t)dt=O, k^O, 1, ..., и —1,
при соблюдении к-рых решение дается формулой (8),
где нужно положить р_и_1=0.
Теоремы Нётера. Пусть v и v' — числа линейно
независимых решений однородных уравнений Коц>=О
и Koty=O соответственно. Тогда разность v—v' наз.
индексом оператора Ко или уравнения
А"оф=0:
idK = v— v'.
Теорема!. Однородные С. и. у. /Гоф=О и /С0\|)=0
имеют конечное число линейно независимых решений.
Теорема 2. Необходимые и достаточные условия
разрешимости неоднородного уравнения C) заклю-
заключаются в том, что
1(t)^>j(t)dt-,Q, /-1, 2, ..., v',
где г|зи . . ., фу— полная система линейно независи-
независимых решении союзного однородного уравнения К'$§=-А).
Теорема 3. Индекс оператора Ко равен индексу
функции G, определяемой равенством E), т. е.
Эти теоремы остаются в силе и в случае общего
С. и. у. A), то есть в сформулированных теоремах
операторы Ко, К'о можно заменить операторами К, К'.
Надо только иметь в виду, что в случае общих С. и. у.
числа v и v', вообще говоря, оба отличны от нуля, в
отличие от характеристических С. и. у., когда одно
из этих чисел обязательно равно нулю.
Теоремы 1—3 наз. теоремами Нётера, в
честь Ф. Нётера (F. Noether), впервые доказавшего их
(9] в случае одномерного С. и. у. с Гильберта ядром:
a (s) Ф (s) + Щ?- J * я ф (г) ctg t? dt +
k(s, t) ф (t) dt = / (s), — jt<s<n. A0)
-я
Эти теоремы аналогичны теоремам Фредгольма (см.
Фредгольма уравнение) и отличаются от них только тем,
что числа линейно независимых решений однородного
уравнения и союзного с ним уравнения, вообще го-
говоря, различны, т. е. тогда как индекс уравнения
Фредгольма всегда равен нулю, С. и. у. может иметь
отличный от нуля индекс.
Формулы F), (8) так же, как теоремы Нётера, ос-
остаются в силе и в случае, когда Г= (J Гд состоит из
конечного числа гладких взаимонепересекающихся
замкнутых линий. В этом случае в равенстве D) символ
[ ]г обозначает сумму приращений выражения, за-
заключенного в скобках при обходе отдельных линий Г&.
Случай же, когда Г— конечная совокупность гладких
разомкнутых взаимонепересекающихся линий (Г=
= (_|Г/г), требует специального рассмотрения.
Если функция ф является //-функцией внутри каж-
каждой из закрытой части линий Г/j, не содержащей концов
этой линии, вблизи же любого конца с представима в
виде ф(г)=ф* @1*—с\~а, 0<a=const<l, где ф* яв-
является Я-функцией в окрестности с, включая с, то
говорят, что ф принадлежит классу II*.
Если a, b?H, /, g?H* и решения уравнений C), G)
разыскиваются в классе #*, то можно так определить
число ¦к и функцию со, что и в этом случае остаются
в силе формулы F), (8). Далее, если соответствующим
образом определить подклассы класса //*, в к-рых
разыскиваются решения данного и союзного с ним
С. и. у., то остаются в силе и теоремы Нётера (см. [1]).
Указанные выше результаты обобщены в различных
направлениях. Показано (см. [1]), что при нек-рых
условиях они остаются справедливыми и в случае
кусочно гладкой линии Г (т. е. когда Г-объединение
конечного числа гладких разомкнутых дуг, к-рые
могут попарно пересекаться только по своим концам).
С. и. у. исследованы также в функциональных про-
пространствах Лебега Ьр(Т) и Lp(T, p), где р>1, ар —
пек-рый вес (см. [4] — [7]). В работах [4] — |6] при-
недецы результаты, к-рые непосредственно обобщают
выше сформулированные утверждения.
Пусть уравнение простой спрямляемой линии Г
есть t~t(s), 0Ks<.\, где s — дуга этой линии, отсчи-
отсчитываемая от нек-рой фиксированной точки на ней,
у — длина Г. Говорят, что функция /, определенная
на Г, почти воюду конечна, измерима, интегрируема
и т. д., если функция f(t(s)) на сегменте [0, у] обладает
соответствующим свойством. Интеграл Лебега от /
на Г определяют равенством
f (t (s)) V ($) ds.
Через Lp(T) обозначается множество измеримых
на Г функций таких, что \j\p интегрируема на Г. Функ-
Функциональный класс Lp(Y), p^i, превращается в бана-
банахово пространство, если норму элемента / определить
равенством
Если в уравнениях C), G), в к-рых равенства со-
соблюдаются почти всюду, коэффициенты а, Ь непрерывны
и удовлетворяют условию нормальности, /, g?Lp(Y),
р>1, то остаются в силе утверждения 1) и 2), если в
них класс Н заменить классом Lp(T), р>1. Далее,
если решения уравнения K<p=f, где оператор К имеет
вид B), разыскиваются в банаховом пространстве
Ьр{Г), р>1, а решения союзного однородного с ним
уравнения ЛС'-ф=О — в пространстве LP'(T), где р' =
=р/(р—1), то остаются в силе и теоремы Нётера, при-
причем V может быть любым вполне непрерывным опе-
оператором в Lp(T).
Когда Г является конечной совокупностью разомк-
разомкнутых линий или Г замкнута, но коэффициенты С. и. у.
терпят разрывы, то решения уравнений часто разыски-
разыскиваются в весовых функциональных пространствах
Lp(T, р), р>1 (/?/,, (Г, p)<*=>p/eVr)>- Приопре-
деленных условиях относительно весовой функции р
остаются справедливыми результаты, аналогичные вы-
вышеприведенным.
Задача регуляризации. Одной из основных задач,
возникающих при построении теории С. и. у., явля-
является задача регуляризации, т. е. задача приведения
С. и. у. к уравнению Фредгольма.
Пусть Е и Е1 — банаховы пространства, к-рые могут
и совпадать, А — линейный ограниченный оператор
А: Е -> Ef. Ограниченный оператор В наз. левым
регуляризатором оператора А, если
BA=I-\-V, где I, V — тождественный и вполне непре-
непрерывный операторы в Е. Если уравнения Лф=/ и ВА
=5/ эквивалентны, каков бы ни был элемент f?lf
то В наз. левым эквивалентным регу-
регуляризатором оператора А. Ограничен-
Ограниченный оператор В наз. правым регуляриза-
регуляризатором оператора А, если AB=I1-\-V1, где
/л, Vi — тождественный и вполне непрерывный опе-
операторы в Ег соответственно. Если при любом J^E1
уравнения Ац>—] и ABty=f одновременно разрешимы
или неразрешимы, причем в случае разрешимости
между их решениями существует связь <р—#ф, то В
наз. правым эквивалентным ре гуля-
риза тором оператора Л. Если В является
одновременно левым и правым регуляризатором опе-
оператора А, то его наз. двусторонним регу-
регуляризатором, или просто регуляриза-
регуляризатором, оператора А. Говорят, что оператор А
допускает регуляризацию левую,
правую, двустороннюю, эквивалент-
н у ю, если существует его регуляризатор (соот-
(соответственно левый, правый, двусторонний, эквивалент-
эквивалентный).
Пусть К — оператор, определяемый равенством B),
где Г— замкнутая простая гладкая линия, а, Ь сутг,
Я-функции (или непрерывные функции), удовлетво-
удовлетворяющие условию нормальности, V — вполне непрерыв-
непрерывный оператор в пространстве Lp(T), />>1. Тогда в
атом последнем пространстве оператор К имеет бес-
бесчисленное множество регуляризаторов, среди к-рых
находится, напр., оператор
М — а Г Ь Я
Для того чтобы оператор К допускал левую эквива-
эквивалентную регуляризацию, необходимо и достаточно,
чтобы индекс х оператора К был неотрицательным [7].
В качестве эквивалентного левого регуляризатора
можно взять оператор М. Если х<0, то оператор К до-
допускает правую эквивалентную регуляризацию, к-рую
можно осуществить с помощью оператора М (см. [1]).
Системы С. и. у. Если в A) а, Ь, к — квадратные
матрицы п-то порядка, рассматриваемые как матрицы
линейных преобразований искомого вектора <р— (фх,
. . ., ф„), а /— (/j, . . ., /„) — известный вектор, то A)
наз. системой С. и. у. Система A) наз. нормального
типа, если матрицы А = а-\-Ъ и В = а — Ъ неособенные
на Г, то есть У(г?Г) detA^O, detB^O.
Теоремы Нётера остаются в силе для системы С. и. у.
ь классе Н (см. [1], [3]) и обобщаются на случай функ-
функциональных пространств Лебега (см. [4], [5]). В отли-
отличие от одного уравнения характеристич. системы С.
и. у. в общем случае не решаются в квадратурах, но
для вычисления индекса и в этом случаен айдена (см.
[1]) формула, аналогичная формуле (9):
ind К = -— [arg det А'1 В]т .
В случае системы С. и. у. задачи регуляризации (см.
[3]) аналогичны задачам регуляризации для одного
С. и. у.
В различных постановках исследованы как одно
С. и. у., так и их системы, когда нарушаются условия
нормальности (см. [11] и указанную там библиогра-
библиографию).
Многомерные С. и. у. Так называются уравнения вида
A1)
где Г — область евклидова пространства Ет, т>1;
Г может быть конечной или бесконечной, в частности
может совпасть с Ет; t, т — точки пространства Ет.
?•=](—т|, ¦&= (т—t)/r, dx -- элемент объема в про-
пространстве Ет, V — вполне непрерывный оператор в
банаховом функциональном пространстве, в к-ром
ищется решение ф; a, g — заданные функции; несоб-
несобственный сингулярный интеграл понимается в смысле
главного значения, т. е.
точка t наз. полюсом, функция g (t, ¦&) —харак-
—характеристикой, функция ф — плотностью спн-
гулярного интеграла A2). Предел в равенстве A1),
как правило, не существует, если не выполняется
условир
\t(t, O)tto = 0, A3)
где а — единичная сфера с центром в начале коор-
координат. Поэтому условие A3) всегда предполагается
выполненным.
В теории многомерных С. и. у. важную роль играет
понятие символа сингулярного оператора А, к-рый
строится с помощью функций a, g, причем но данно-
данному символу сингулярный оператор восстанавливает-
восстанавливается с точностью до вполне непрерывного слагаемо-
слагаемого. Композиции сингулярных операторов соответству-
соответствует произведение их символов. Доказано [7], что при
иек-рых ограничениях уравнение A1) допускает ре-
регуляризацию в пространстве Lp, р>1, тогда и толь-
только тогда, когда модуль его символа имеет положи-
положительную нижнюю грань и в этом случае справед-
справедливы теоремы Фредгольма.
Историческая справка. Исследование одномерных
С. и. у. было начато, почти одновременно с построением
теории Фредгольма уравнения в работах Д. Гильберта
(D. Hilbert) и А. Пуанкаре (A. Poincare). В одном
частном случае С. и. у. с ядром Коши было рассмо-
рассмотрено гораздо раньше в докторской диссертации
К). В. Сохоцкого, опубликованной в Петербурге в
1873; однако это исследование осталось незамеченным.
Основополагающие результаты по построению об-
общей теории уравнения A), A0) были получены в нач.
20-х гг. 20 в. Ф. Нётером [9] и Т. Карлеманом [10].
Ф. Нётер впервые ввел понятие индекса и доказал
сформулированные выше теоремы 1—3 с помощью
применения способа левой регуляризации. Этот спо-
способ впервые был указан (в различных частных случаях)
А. Пуанкаре и Д. Гильбертом, но в общем виде он
появляется именно у Ф. Нётерп. Основным моментом в
реализации упомянутого способа является применение
формулы перестановки (композиции) в повторных
сингулярных интервалах в смысле главного значения
по Коши (Пуанкаре — Бертрана формула). Т. Кар-
леман для нек-рых частных классов уравнения C)
дал основную идею метода редукции этого уравне-
уравнения к следующей граничной задаче теории аналити-
аналитических функций (задача линейного сопря-
сопряжения, см. [1]):
ф+ (()=5(()Ф
и указал путь построения явного решения. Т. Кар-
леману и И. Н. Векуа принадлежит способ регуляри-
регуляризации уравнения A) с привлечением решения характе-
ристич. уравнения C).
Большое теоретическое и прикладное значение С. и. у.
особенно проявилось с кон. 30-х гг. в связи с решением
нек-рых весьма важных задач механики сплошной
среды (теории упругости, гидро- и аэромеханики и
др.) и теоретич. физики. Теория одномерных С. и. у.
была значительно продвинута в 40-х гг. и получила в
определенном смысле законченный вид в трудах со-
советских математиков. Изложение такой теории одно-
одномерных С. и. у. в гёльдеровых классах функций дано
в монографин одного из создателей этой теории
IT. И. Мусхелишвили (см. [1]). Эта монография стиму-
стимулировала научные исследования и в нек-рых других
направлениях, напр, в теории С. и. у., не удовлетворя-
удовлетворяющих условию нормальности по Хаусдорфу, С. и. у. с
недиагональными особенностялш (со смещениями), урав-
уравнений Винера — Хопфа, многомерных С. и. у. и т. д.
Первые исследования по многомерным С. и. у. при-
принадлежат Ф. Трикоми (F. Tricomi, 1928), к-рый уста-
установил формулу перестановки двумерных сингулярных
интегралов и применил ее к решению одного класса
С. и. у. В этом направлении фундаментальное исследо-
исследование принадлежит Ж. Жиро (G. Giraud, 1934), дока-
доказавшему справедливость теорем Фредгольма для нек-
рых классов многомерных С. и. у. на ляпуновских
многообразиях.
Лит.: [1] МусхелишвилиН. И., Сингулярные ин-
интегральные уравнения, 3 изд., М., 1968; [2] Г а х о в Ф. Д.,
Краевые задачи, 3 изд., М., 1977; [3] В е к у а Н. П., Системы
сингулярных интегральных уравнений и некоторые граничные
задачи, 2 изд., М., 1970; [4] X в е д е л и д з е Б. В., «Тр.
Тбилисск. матем. ин-та АН Груз. ССР», 1956, т. 23, с. 3—158;
[5] Д а н и л ю к И. И., Нерегулярные граничные задачи на
плоскости, М., 1975; [6] Г о х б е р г И. Ц., К р У п н и к Н.,
Введение в теорию одномерных сингулярных интегральных опе-
операторов, Киш., 1973; [7] М и х л и н С. Г., Многомерные син-
сингулярные интегралы и интегральные уравнения, М., 1962; [8]
БицадзеА. В., Краевые задачи для эллиптических уравне-
уравнений второго порядка, М., 1966; [9] N о е t h e г P., «Math. Ann.»,
1921, Bd 82, S. 42—63; [10] С u r 1 e m а п Т., «Arkiv mat.,
astron. ocli fys.», 1922, Bd 16, JA 26, S. 1 — 19; 111] П р е с д о р ф
3., Некоторые классы сингулярных уравнений, пер. с нем.,
М., 1979. А. В. Бицадзе, Б. В. Хведелидве.
СИНГУЛЯРНОЕ РАСПРЕДЕЛЕНИЕ — распределе-
распределение вероятностей в R", сосредоточенное на множестве
нулевой меры Лебега и приписывающее каждому
одноточечному множеству нулевую вероятность.
На прямой R1 определение С. р. эквивалентно сле-
следующему: распределение сингулярно, если со-
соответствующая функция распределения непрерывна,
а ее множество точек роста имеет нулевую меру Ле-
Лебега .
Примером С. р. па прямой может служить распреде-
распределение, сосредоточенное на канторовом множестве,
т. н. канторово распределение, к-рое
можно описать следующим образом. Пусть Xj, X2, ¦¦¦
. . .— последовательность независимых случайных ве-
величин, каждая из к-рых принимает значения 0 и 1 с
вероятностями 1/2. Тогда случайная величина
¦чгл00 1
имеет канторово распределение, и его характеристич.
функция равна
/(o=**//sn" ,cos —•
Пример С. р. в R" (reJS=2) — равномерное распреде-
распределение на сфере положительного радиуса.
Свертка двух С. р. может быть либо сингулярной,
либо абсолютно непрерывной, либо представлять со-
собой смесь сингулярного и абсолютно непрерывного
распределений.
Любое вероятностное распределение Р может быть
единственным образом представлено в виде
где Рд — дискретное, Ра — абсолютно непрерывное,
a Ps — С. р., а^О, ах-\-аа-\-а3=1 (разложение
Лебега).
Иногда сингулярность понимается в более широком
смысле: вероятностное распределение F является С. р.
по отношению к мере Р, если оно сосредоточено на
множестве N таком, что P{N}—0. При таком опреде-
определении каждое дискретное распределение является С. р.
по отношению к мере Лебега.
По поводу сингулярных функций множеств см.
также Абсолютная непрерывность функции множества.
Лит.: Ш П р о х о р о в Ю. В., Р о з а и о в Ю. А., Тео-
Теория вероятностей, 2 изд., М., 1973; [2] Ф е л л е р В., Введение
в теорию вероятностей и ее приложения, пер. с англ., 2 изд.,
т. 2, М., 1967. -В- Г. Ушаков.
СИНГУЛЯРНЫЕ ГОМОЛОГИИ — гомологии, опре-
определяемые исходя из сингулярных симплексов тополо-
топология, пространства X таким же образом, как обычные
(симшшциальные) гомологии (и когомологии) полиэд-
полиэдра — исходя из линейных симплексов. Под с и н г у-
лярным симплексом ст" понимается непре-
непрерывное отображение n-мерного стандартного симп-
симплекса А" в .V. причем образ о" обычно наз. носите-
носителем а" и обозначается \ап\. Сингулярные
цепи — это формальные линейные комбинации син-
сингулярных симплексов коэффициентами в абелевой
группе С. Они образуют группу Sn(X; G), изоморфную
прямой сумме групп Gon—G (по всем а"). Группы
цепей объединяются в сингулярный ценной комплекс
S^iX; G) с граничным гомоморфизмом д: Sn{X; G) —>-
—>- Sn-i (X; G), определяемым соотношением
да" = 2- (-- 1)'о"",
где а;~ — композиция с а" стандартного наложения
А" на i-ю грань А". Как обычно, циклами считаются
цепи, принадлежащие ядру, а границами — цепи,
содержащиеся в образе д". Группа n-мерных сингу-
сингулярных гомологии //„ (X; G) определяется как фак-
факторгруппа группы «-мерных циклов по подгруппе
границ.
Если АсХ, то группы 11%(A; G) определяются
подкомплексом в 5» (Х'\ G), состоящим из всех цепей
с носителями в А, а группы пары Нп (X, A; G) — со-
соответствующим факторкомнлексом. Имеет место точная
гомологич. последовательность
...—>Пп(А; G)-+H%{X; G)-+H%{X, A; G) Л
являющаяся ковариантным функтором на категории
пар (X, А) топологич. пространств и их непрерывных
отображений.
Гомоморфизм б определяется границей в X цикла
пары (X, А), представляющего соответствующий эле-
элемент из Hn(X, A; G). С. г.— гомологии с компакт-
компактными носителями в том смысле, что группы X равны
прямому пределу гомологии компактных СаХ.
Сингулярные ко гомологии определя-
определяются дуальным образом. Комплекс коцепей S* (X; G)
определяется как комплекс гомоморфизмов в G комп-
комплекса целочисленных сингулярных цепей St(X; %).
Менее формально, коцепи — это функции ?, опре-
определенные на сингулярных симплексах и принимающие
значения в G, а кограничный гомоморфизм d определя-
определяется формулой
Сингулярные когомологии Н^(Х; G) — это фактор-
факторгруппы групп re-мерных коциклов (ядер d) по
подгруппам кограниц (образов в). Когомологии
подпространства А совпадают с когомологиями огра-
ограничения S* (X; G) на А, в то время как когомологии
пары Hs(X, A; G) — с подкомплексом в S* {X; G),
состоящим из всех коцепей, обращающихся в нуль на
сингулярных симплексах из Л-. Имеет место точная
последовательность
...—Я§(Х, A; G)-^Hns(X; G) —>
—v Hns(A; G)\ffns+1(X, A; C)-^...,
япляющаяся контравариантны-м функтором (X, А).
Отображение б определяется кограницей в X коцикла
из А, представляющего нужный элемент Hs(A; G).
Гомологии и когомологии с коэффициентами в про-
произвольной группе G могут быть выражены через цело-
целочисленные гомологии с помощью формул универсаль-
универсальных коэффициентов. Когомологии с коэффициентами ь
группе G связаны с целочисленными когомологиями
формулами универсальных коэффициенте и только для
конечно порожденных групп G.
В категории полиэдров сингулярная теория экви-
эквивалентна симплициальной (а также клеточной). Этим
обычно устанавливается топологич. инвариантность
последних. Однако значение групп С. г. этим не ис-
исчерпывается. Имея простое описание, они применимы
в достаточно широких категориях топология, прост-
пространств, гомотопически инвариантны. Естественные
связи с теорией гомотопий делают сигнулярпую теорию
незаменимой в гомотопич. топологии.
Однако, хотя грушш С. г. определены для любых
топологич. пространств без каких-либо ограничений,
их применение оправдано лишь при существенных
ограничениях типа локальной стягиваемости или
гомологической локальной связности. Сингулярные
цепи, будучи по своей природе «слишком» линейно
связными, не несут в себе информацию о «непрерывных»
циклах, если они не являются «достаточно» линейно
связными. Возможны и другие «аномалии» (напр.,
гомологии компактных подпространств евклидова про-
пространства могут отличаться от нуля в сколь угодно
высоких размерностях, гомологии и когомологии пары
(X, А) могут неизоморфно отображаться при отобра-
отображении X на факторцространство XIА , отвечающее замк-
замкнутому подмножеству АсХ, и т. п.). Поэтому в общих
категориях топологич. пространств вместо сингуляр-
сингулярных обычно используются когомологии Александро-
Александрова — Чеха и ассоциированные с ними гомологии. Эти
теории свободны от указанных недостатков и совпа-
совпадают с сингулярной всякий раз, когда ее применение
не вызывает сомнений.
Лит.: [1] Д о л ь д А., Лекции по алгебраической тополо-
топологии, пер. с англ., М., 1976; [2] Массе У., Теории гомологии
и когомологии, пер. с англ., М., 1981, гл. 8—9; [3] С к л я р ен-
к о Е. Г., «Успехи матем. наук», 1979, т. 34, в. 6, с. 90—118;
[4] Masse у W., Singular homology theory, N. У., 1980.
Е. Г. Скляренко.
СИНГУЛЯРНЫЙ ИНТЕГРАЛ — интеграл
/„(/, х)= $*/(*)Ф„С. x)dt
с особенностью в точке х, определенный для интегри-
интегрируемой на [а, Ь] функции f{x), ядро к-рого ФпA, х)
удовлетворяет условиям: для любого б>0 и произ-
произвольного интервала [a, P]cz[a, Ъ]
,П г . ,ПФП(*. х) dt = i, A)
„.* х Ля, Ь]п[*-6. х + 6] пк
lim ( ФпС. x)dt — 0 B)
vrai max |Ф„(/, x) | ==? Фх (fi). C)
t?[a, x-6J U t.v т 6, b]
причем Фх F) зависит только от б и х и пе зависит от п.
Если условия A), B) и C) выполняются равномерно
на ж-множестве Eczla, b], то интеграл /„ (/, .г) наз.
равномерно сингулярным на Е. Наи-
Наиболее изучены свойства т. н. положительных ядер
{Фп{1, л)>0), Дирихле ядер
2п+ 1 .
sin —=— (*-л-)
2 sin—те-
sin—теФейера
Fn(t, *) = ¦
ядер Пуассона — Абеля
ядер, порожденных различными методами суммиро-
суммирования ортогональных разложений по ортонормирован-
ным полиномам.
Понятие «С. и.» введено А. Лебегом [1], указавшим
на его важность при исследовании вопросов сходи-
сходимости. Так, к исследованию сходимости С. и. приводят
вопросы сходимости и суммируемости тригонометрич.
рядов Фурье, рядов по ортогональным многочленам,
а также разложений по общим ортогональным систе-
системам.
А. Лебегом был установлен критерий сходимости
С. и. для непрерыиных функций /(х) с ограниченной
вариацией. Д. К. Фаддеев [2] установил необходимые
и" достаточные условия для сходимости С. и. в точках
Лебега суммируемой функции f(x). Так как данные
А. Лебегом и Д. К. Фаддеевым условия сходимости
С. и. трудно проверяемы для конкретных С. и., то
целый ряд работ был посвящен отысканию эффектив-
эффективных достаточных условий сходимости С. и. как в от-
отдельных точках, так и для равномерной сходимости.
Для сходимости С. и. в точках непрерывности до-
достаточна ограниченность нормы оператора /„ (/, .г),
т. е. ограниченность интеграла
а для сходимости в точках Лебега необходимо сущест-
существование т. н. «горбатой мажоранты» для ядра Ф„B, х),
т. е. такой интегрируемой функции 4n{t, x)~^Q, к-рая
монотонно возрастает на [я, х), монотонно убывает
на (х, Ь] и для почти всех t?[a, Ъ]
t, х),
причем
Лит.: [l]Lebesque H., «Ann. Fac. sci. Univ. Toulou-
-(>», 1909, v. 1, p. 25 — 117; [2] ф а д д е е в Д. К., «Матем. сб.»,
'.'.Ч(>, т. 1, с. 351 — 68; [3] К о р о и к и н II. П., Линейные опе-
i агоры и теория приближений, М., 1959; [4] Натансон
П. И. Теория функций вещественной переменной, 3 изд., М.,
1974; [5] А л е к с и ч Г., Проблемы сходимости ортогональных
рядов, пер. с англ., М., 1963; [6] Ефимов А. В., «Изв. АН
СССР. Сер. матем.», 1960, т. 24, в. 5, с. 743—56;[7] Т е л я к о-
v с к и й С. А., там же, 19G4, т. 28, в. 6, с. 1209—36.
А. В. Ефимов.
СИНТАКСИС в математической логи-
логике — описание и изучение формальной аксиоматич.
теории как чисто знаковой системы (в отличие от
семантики, исследующей смысл и содержание объек-
объектов формальной теории). Различие между С. и семан-
семантикой особенно существенно в основаниях математики,
когда изучаются формальные теории, семантика к-рых
интуитивно недостаточно ясна. В этом случае описание
и исследование С. формальной теории часто может
быть осуществлено гораздо более надежными и инту-
интуитивно убедительными средствами в рамках нек-рой
метатеории и, таким образом, может служить обо-
обоснованием и косвенным разъяснением существенных
черт сложной семантики изучаемой теории. Напр., в
аксиоматической теории множеств известный резуль-
результат К. Гёделя (К. Godel) о совместности аксиомы вы-
выбора можно трактовать как синтаксическое и финитно
доказываемое утверждение о том, что если формальная
(ория Цермело — Френкеля непротиворечива, то она
тается таковой и после присоединения аксиомы
мбора.
Вне рамок оснований математики в доказательств
"И'ории различие между С. и семантикой не столь
существенно. Употребляются т. п. п о л у ф о р м.а л ь-
н ы е систем ы, понятие вывода в к-рых зависит
or тех или иных семаытич. соглашений. Формальные
языки могут определяться существенно теоретико-
множественно, с привлечением бесконечно длинных
формул и т. п. С другой стороны, для формальных
языков с ограниченными выразительными возможно-
возможностями типа языков комбинаторной логики или алгорит-
алгоритмических языков семантика может быть точно сформу-
сформулирована в чисто синтаксических терминах самого
языка.
Лит.: [1] С а г n a p R., Logische Syntax der Sprache, Wien,
1934; [2] Ч ё р ч А., Введение в математическую логику, пер.
с англ., М., 1960; [3] К л и н и С. К., Введение в метаматема-
метаматематику, пер. с англ., М., 1957. А. Г. Драгалин.
СИНТАКСИЧЕСКАЯ СТРУКТУРА — математичес-
математическая конструкция, используемая в математической
лингвистике для описания строения предложений
естественного языка. Наиболее широко употребляются
два типа С. с— системы составляющих
и отношения синтаксического под-
подчинения. Понятие системы составляющих можно
определить следующим образом. Пусть х — непустая
цепочка {слово) в алфавите V', вхождения символов
(букв) в цепочку в дальнейшем наз. ее точками;
множество точек цепочки, имеющее вид {г|я<л;<:6},
где а, Ъ — фиксированные точки, наз. отрезком
цепочки. Множество С отрезков цепочки х наз. си-
системой составляющих :>той цепочки, если 1) С содержит
отрезок, состоящий из всех точек х, и все одноточечные
отрезки х; 2) любые два отрезка из С либо не пересе-
пересекаются, либо один из них содержится в другом. Эле-
Элементы С наз. составляющими. Если алфавит
V интерпретируется как множество слов естественного
языка пх — как предложение, то при подходящем
выборе системы составляющих для х нетривиальные
составляющие (т. е. отличные от входящих в С по п. 1)
представляют собой словосочетания, т. е.
группы слов, к-рые интуитивно ощущаются носителем
языка как «синтаксически связные» куски предложе-
предложения. Напр., предложение
„Объединение двух замкнутых множеств есть замкнутое множество"
допускает следующую «естественную» систему состав-
составляющих (границы нетривиальных составляющих отме-
отмечены скобками):
(Объединение (двух (замкнутых множеств))) (есть (замкнутое множество)).
Если па системе составляющих С введено отношение
непосредственного включения, то С представляет
собой по этому отношению дерево с корнем (корнем
служит составляющая, состоящая из всех точек х) —•
дерево составляющих, к-рое для приве-
приведенного примера имеет следующий вид
Объединение двух замкнутых множеств есть замкнутое множества
объединение двух замкнутых множеств, есть замкнутое множество
I /
\
I / \
объединение» двух замкнутых множеств есть замкнутое множество
/ \ /' \
двух замкнутых множеств замкнутое- множества
/ \
замкнутых множеств
Обычно составляющие снабжаются метками,
к-рые представляют собой «синтаксические характе-
характеристики» словосочетаний (составляющая может иметь
более одной метки). В приведенном примере состав-
составляющую, совпадающую со всем предложением, ес-
естественно пометить символом ПРЕДЛ, означающим
«предложение», составляющую «объединение двух замк-
замкнутых множеств» — символом 5Ср.ед,им) означающим
«группа существительного среднего рода в единствен-
единственном числе и именительном падеже», я т. д. Получаемый
при этом объект — дерево с помеченными вершина-
вершинами — наз. размеченным деревом со-
составляющих.
Другой способ описания строения предложения
получается, если определить на множестве X точек
цепочки х бинарное отношение -> таким образом, чтобы
граф (X; ->) был (ориентированным) деревом с корнем.
Всякое такое отношение наз. отношением (син-
(синтаксического) подчинения, а соответ-
соответствующее дерево — деревом (синтаксиче-
(синтаксического) подчинения. Понятие отношения под-
подчинения является формализацией обычного в «школь-
«школьной» грамматике, в частности русского языка, пред-
представления о подчинении одних слов в предложении
другим. При графич. изображении дерева подчинения
обычно располагают точки цепочки на горизонтальной
прямой и проводят стрелки сверху от нее. Приведенное
выше предложение допускает следующее «естественное»
дерево подчинения:
Объединение двух замкнутых множеств есть гамкнуиш множество
(корнем дерева подчинения принято считать сказу-
сказуемое, т. к. оно представляет собой организующий эле-
элемент предложения).
Дуги дерева подчинения часто снабжаются метками,
указывающими типы представляемых этими дугами
синтаксич. связей. В рассмотренном примере связь
между «есть» и «объединение» естественным образом
получает «предикативный» тип, связь между «множеств»
и «замкнутых» — «определительный» тип и т. д.
Деревья подчинения предложений, встречающихся
в деловых и научных текстах, удовлетворяют, как
правило, т. н. условию проективности,
к-рое при указанном выше способе графич. изобра-
изображения формулируется так: во всякую точку, лежащую
под нек-рой стрелкой, идет путь из начала этой стрел-
стрелки; отсюда следует, в частности, что никакие две
стрелки не пересекаются (последнее условие иногда
называют условием слабой проектив-
проективности). В художественной литературе это условие
часто нарушается, но такие нарушения обычно зна-
значимы, т. е. служат цели создания определенного худо-
художественного эффекта.
Одно предложение может допускать несколько раз-
различных «естественных» систем составляющих (деревь-
(деревьев подчинения). Чаще всего это бывает в тех случаях,
когда смысл предложения можно понимать по-раз-
по-разному, и разные системы составляющих (деревья под-
подчинения) отвечают разным толкованиям смысла (с и н-
таксическая омонимия). Напр., предло-
предложение «Гости из Москвы уехали» может означать, что
либо «московские гости уехали (откуда-то)», либо
«(какие-то) гости уехали из Москвы»; первому смыслу
отвечают система составляющих «(Гости (из Москвы))
уехали» и дерево подчинения
.Гости из"
Москвы уехали"
второму — соответственно «Гости ((из Москвы) уе-
уехали)» и
«Госта из Москвы уехали".
Если на цепочке задано дерево подчинения и а —
точка цепочки, то множество точек цепочки, в к-рые
идут пути из а (включая саму точку а), наз. г р у и-
пой зависимости точки а. Всякое множество,
получающееся из группы зависимости точки а выбра-
выбрасыванием групп зависимости нек-рых (или всех) точек,
подчиненных а (т. е. таких, в к-рые из а идут дуги),
наз. усеченной группой зависимости
точки а.
Система составляющих С цепочки х и заданное на х
дерево подчинения наз. согласованными, если
группы зависимости всех точек х являются состав-
составляющими и каждая составляющая есть группа зави-
зависимости или усеченная группа зависимости нек-рой
точки цепочки х. «Естественные» система составляющих
и дерево подчинения, построенные для одного и того
же предложения и отвечающие одному и тому же его
смыслу, обычно согласованы (см. приведенные выше
примеры). Дерево подчинения, согласованное с си-
системой составляющих, ироективно. Для данной си-
системы составляющих может существовать больше од-
одного согласованного с ним дерева подчинения; однако,
если дополнительно задать нек-рое отношение «гла-
«главенствования» между составляющими, можно добиться,
чтобы «естественное» дерево подчинения определялось
однозначно. Именно, если в системе составляющих С
цепочки х для каждой неточечной составляющей
выделить в множестве всех непосредственно вложен-
вложенных в нее составляющих одну, называемую глав-
главной,™ упорядоченная пара (С, С'), где С" — множе-
множество всех главных составляющих, наз. иерархи-
зованной системой составляющих;
нерархизованная система составляющих связана
с деревом подчинения, если система С согласована с
этим деревом и для каждой неточечной составляющей
А корень отвечающего ей поддерева дерева подчинения
совпадает с корнем поддерева, отвечающего главной
из непосредственно вложенных в А составляющих.
«Естественная» система составляющих предложения
при «естественной» иерархизации, как правило, свя-
связана с «естественным» деревом подчинения. Так, если
в рассмотренном выше примере иерархизовать систему
составляющих следующим образом: ([Объединение]
(двух [замкнутых [множеств]])) [[есть] (замкнутое
[множество])] (главные составляющие выделены квад-
квадратными скобками), то полученная иерархизованная
система составляющих будет связана с указанным
выше для данного предложения деревом подчинения.
Не все типы предложений допускают достаточно
адекватное описание с помощью систем составляющих
и деревьев подчинения. В частности, затруднения воз-
возникают при описании предложений, содержащих сло-
словосочетания с «особо тесными» внутренними связями
(напр., сложные формы глагола), а также сочиненные
конструкции. Кроме того, при описании строения
предложений и иных отрезков речи на более «глубо-
«глубоких» уровнях возникает необходимость использовать
графы более сложного вида, чем деревья. Для боль-
большей адекватности описания языка нужно учитывать
наряду с синтаксическими еще т. н. анафориче-
анафорические связи — связи между вхождениями слов,
«называющими одно и то же»; напр.:
«Если f есть отображение ? на F
и существует обратное отображение
/"'Г'ю последнее есть отображение F на .?*.
Поэтому разрабатываются и другие, более сложные
концепции С. с.
Лит.: [ljTesniereL., Elements de syntaxe structuralc, 2
изд., Р., 1965; [2] П а д у ч е в а Е. В., «Вопросы языкознания»,
1964, Л 2, с. 99—113; [3] Гладкий А. В., «Научно-техни-
ческая информация. Сер. 2», 1971, .4» 9, с. 35—.48; |4] его
же, Формальные грамматики и языки, М., 1Н73; [5] его
же, «Slavica», 1981, v. XVI1, XVIII. А. В. Гладкий.
СИНТАКСИЧЕСКАЯ ТЕОРЕМА — теорема синтак-
синтаксического языка, т. е. теорема о формализованной тео-
теории. Примеры С. т.: теорема дедукции для исчисления
предикатов, теорема Гёделя о неполноте арифметики.
Эти теоремы относятся к элементарному синтаксису.
Примером неэлементарной С. т., то есть теоремы, дока-
доказательство к-рой существенно использует бесконечные
совокупности, может служить теорема о непротиворе-
непротиворечивости элементарной арифметики. в. н. Гришин.
СИНТАКСИЧЕСКИЙ ЯЗЫК — язык, предназна-
предназначенный для изучения формализованного языка в от-
отвлечении от его главной интерпретации. Понятие о
С. я. возникло в математич. логике в связи с вопросами
формализации и исследования содержательных мате-
чатич. теорий. Результатом формализации какон-
шбо содержательной теории является формальная
система, к-рую можно рассматривать как самостоя-
самостоятельный объект исследования, забыв о ее происхож-
происхождении. Для исследования формальных систем в тако.м
плане служит С. я.
В С. я. дается описание языка формальной системы,
т. е. его исходных символов, термов, формул и пр.,
определяется понятие вывода в формальной системе,
формулируются и доказываются теоремы о формальной
системе. Таким образом, с формальной системой свя-
связываются два языка: один — исследуемый язык самой
формальной системы (объектный, или пред-
четны п, я з ы к), другой — язык, на к-ром ведется
исследование формальной системы (С. я.).
С. я. должен содержать имена для символов и формул
языка-объекта, а также переменные, значениями к-рых
являются сами символы и формулы. При этом символы
и формулы языка-объекта выступают в С. я. в каче-
качестве своих собственных имен (т. е. в качестве имен,
обозначающих сами эти символы и формулы). С. я.,
как правило, не должен содержать языковых средств
д. ж рассуждения о бесконечных совокупностях как
самостоятельных объектах. Чтобы подчеркнуть это
обстоятельство, говорят об э л е м е н т а р н о м син-
синтаксисе для данной формальной системы, в про-
противоположность синтаксису теоретиче-
теоретическом у, в к-ро-м допускается рассмотрение произволь-
произвольных образований. Язык теоретич. синтаксиса наз. также
метаязыком. Достаточно четко очерченный С. я. может
быть формализован и стать объектным языком. Многие
достаточно сильные формальные системы могут служить
формализациями своего собственного элементарного
С. я. На этом факте основано доказательство Гёделя
теоремы о неполноте формальных систем.
В языках теоретич. синтаксиса можно рассматривать
модели данной формальной системы и говорить об
истинности формул формальной системы в моделях.
В качестве примера формализованного языка теоретич.
¦интаксиса элементарной арифметики можно указать
на язык арифметики 2-го порядка.
Лит.: [1] Чёрч А., Введение в математическую лотику
пер. с англ., М., 1060. В. Н. Гришин'.
СИНТЕЗА ЗАДАЧИ — совокупность задач, концент-
концентрирующихся вокруг проблемы построения управля-
управляющей системы, (у. с), имеющей предписанное функцио-
функционирование. У. с. строится из элементов, к-рые обычно
сами являются простыми у. с. (Три синтезе заранее
заданы состав элементов, правила их соединения между
собой и способ определения но структуре у. с. функ-
функции, к-рую она реализует.
С каждым классом у. с. естественным образом свя-
связан определенный класс функции. Задача син-
синтеза в ее исходной постановке состоит в том, чтобы
по заданной функции из этого класса построить реа-
реализующую ее у. с. Напр.: 1) задана булева функция —
требуется построить формулу, к-рая ее реализует;
2) задана система булевых функций — требуется по-
построить многонолюсную контактную схему, реали-
реализующую эту систему; 3) имеется точное описание
поведения автомата — требуется построить такой ав-
автомат; 4) задана вычислимая функция — требуется
найти алгоритм, к-рый ее вычисляет, либо составить
соответствующую программу.
Приведенные примеры относятся к дискретной ветви
математики. Однако аналогичные примеры харак-
характерны и для непрерывной ветви математики: 1) задана
логарифмическая амплитудно-частотная характеристи-
характеристика системы автоматич. регулирования (или, в более
общем случае, условия ее работы, т. е. возмущающие
н управляющие воздействия, помехи, ограничения по
времени работы и т. д.) — требуется синтезировать
систему автоматич. регулирования, обладающую за-
заданной характеристикой; 2) задана система линейных
уравнений и неравенств, а также нек-рая линейная
функция — требуется построить схему вычисления,
к-рая максимизирует заданную линейную функцию
на множестве решений заданной системы; 3) задана
система дифференциальных уравнений и указана не-
необходимая точность ее решения — требуется найти
алгоритм численного решения этой системы с указан-
указанной точностью.
Имеется определенная условность в том, что послед-
последние три примера отнесены к непрерывной математике,
ибо поиск приближенного численного решения уже
предполагает аппроксимацию непрерывных функций
дискретными, а значит, в этих задачах непрерывная
ветвь математики тесно переплетается с дискретной.
Математическая постановка С. з. предполагает точ-
точное указание языка, на к-ром задается функция. От
этого языка зависит, какие трудности могут возник-
возникнуть при решении С. з. В большинстве случаев сущест-
существует сравнительно простой метод построения у. с.
канонич. вида.
Однако (если только класс у. с. не слишком беден)
задача имеет и много других решений; естественно
возникает задача выбора среди них в каком-то смысле
наилучшего. При таком подходе вводится параметр,
характеризующий качество у. с. Это может быть число
элементов у. с, ее стоимость, занимаемый ею объем,
максимальное число ее элементов, находящихся в
активном состоянии (т. е. мощность), время ее работы,
вероятность выхода ее из строя и т. д. Важно, чтобы
этот параметр, обычно наз. сложностью, пра-
правильно отражал требующееся свойство у. с. и по воз-
возможности просто но ней вычислялся. В уточненной
постановке С. з. состоит в том, чтобы по заданной
функции построить такую реализующую ее у. с, на
к-poii достигается минимум сложности.
На самом деле столь определенная постановка за-
задачи возможна лишь для конечных моделей у. с. Как
следствие, для них и вся синтезная проблематика
оказывается очерченной лучше. Поэтому ниже основ-
основное внимание уделено конечным моделям.
Для конечных моделей у. с. типична ситуация, когда
существует тривиальное решение поставленной за-
задачи. Напр., если минимизируется число элементов в
схеме, то тривиальный метод решения состоит в пере-
переборе сначала всех схем, содержащих один элемент, с
проверкой того, есть ли среди них схема, реализующая
заданную функцию, затем в переборе всех схем, содер-
содержащих два элемента, и т. д. до тех пор, пока не встре-
встретится схема, реализующая заданную функцию. На
этой схеме и достигается минимум числа элементов.
Однако из-за большого числа требующихся шагов
тривиальный метод малоэффективен. Более того, если
сложность реализуемой функции превышает нек-рый
сравнительно невысокий порог, то тривиальный метод
становится практически неосуществимым, причем ис-
использование самых быстрых вычислительных машин
лишь несущественно расширяет границы его приме-
применимости. Это означает, что требуется дальнейшее уточ-
уточнение постановки С. з.
Сложившиеся здесь тенденции продемонстрированы
ниже на примере одного из классов у. с.— схем из
функциональных эле.чеитов для одного частного слу-
случая, когда сложность понимается как число элементов
в схеме. Функции, реализуемые этим классом у. с,—
это функции алгебры логики (булевы функции).
Прежде всего следует отметить, что неприемлемость
решения, к-роо дает тривиальный метод,— это лишь
одна из причин, ведущих к пересмотру постановки С. я.
Существует гшготеаа, что любой алгоритм, к-рый для
каждой булевой функции строит схему с минимальным
числом элементов, неизбежно содержит в себе в ка-
каком-то смысле перебор всех булевых функций. В пользу
этой гипотезы говорит теорема- о том, что если рас-
рассмотреть бесконечное множество булевых функций,
содержащее при каждом числе переменных по одной
самой сложной функции, и замкнуть это множество
относительно операций переименования переменных
(без отождествления) и подстановки констант, то полу-
получится множество, состоящее из всех вообще булевых
функций (с точностью до несущественных переменных
функции). Эта гипотеза получила много других кос-
косвенных подтверждений, причем нек-рые из них свиде-
свидетельствуют о том, что если даже ослабить требование
по числу элементов, допуская построение схем, близ-
близких к оптимальным, но сохранить требование приме-
применимости алгоритма к каждой булевой функции, то
перебор не должен существенно уменьшиться. Идея
о принципиальной неизбежности перебора и является
основной причиной видоизменения постановки С. з.
Здесь имеется несколько возможностей.
Шенноновский подход (по имени К. Э. Шеннона,
к-рый впервые предложил его для контактных схем)
связан с рассмотрением функции
L (л) = тах1, (/),
где L (/) — минимально возможное число элементов
в схеме, реализующей функцию /, а максимум берется
по всем булевым функциям / от га переменных. При
этом L(f) и Цп) зависят от базиса, т. е. от множества
функциональных элементов, к-рые можно использо-
использовать при построении схем. С. з. состоит в том, чтобы
найти эффективный метод построения для каждой
булевой функции от п переменных схем с числом эле-
элементов, существенно не превосходящим Цп).
При более общей постановке задачи каждому функ-
функциональному элементу Е сопоставляется положитель-
положительное число L (Е) —сложность этого элемента, к-рая
зависит только от функции, реализуемой элементом Е,
а каждой схеме S приписывается сложность
где суммирование производится по всем элементам схе-
схемы S. Для каждой булевой функции / определяется
сложность ее реализации (в заданном базисе):
L (/) =
где минимум берется по всем схемам S, реализующим
функцию /. Затем, как и раньше, вводится L (п)=
= maxL(/) и требуется для произвольной булевой
функции от п переменных построить схему, имеющую
сложность не выше (или не на много выше), чем L(n).
При таком подходе нужно уметь вычислять или
хорошо оценивать хотя бы снизу величину Ь(п). Ока-
Оказывается, что неплохую нижнюю оценку для L (л)
дает уже м о щ н о с т н о й м е т о д, основанный на
следующем соображении: число всевозможных схем,
реализующих булевы функции от п переметших и
имеющих сложность не более Л(п), должно быть не
меньше числа всех булевых функций от п. переменных.
В мощностном методе требуется только получить удов-
удовлетворительную верхнюю оценку для числа рассмат-
рассматриваемых схем.
После этого о качестве любого универсального
метода синтеза (т. е. метода, пригодного для произ-
произвольной булевой функции) можно в значительной мере
судить по тому, во сколько раз сложность построенных
им схем при соответствующем п отличается от нижней
оценки для Ь(п). Одновременно сложность этих схем
служит конструктивной верхней оценкой для L(n).
Основным достижением в этом направлении является
создание эффективного универсального метода синтеза,
к-рый дает схемы со сложностью, мало отличающейся
от нижней оценки для L(n), а при п —>- оо асимптоти-
асимптотически совпадающей с ней. Таким образом, это асимп-
асимптотически наилучший метод синтеза, позволяющий к
тому же установить асимнтотич. поведение функции
L{n). Пусть
p = minZ (E)l(i-i),
где i — число входов элемента Е, а минимум берется
по всем элементам, имеющим не .менее двух входов.
Тогда
L (п) ~ р — .
Для других классов у. с. сложность L(S), а с ней
и сложности L (/) и L (и) вводятся аналогичным обра-
образом. Обычно L (S) для контактной схемы S есть число
контактов в ней, а для формулы S — это число сим-
символов переменных в ней. Для автоматов и машин Тью-
Тьюринга L (S) иногда вводится как число состояний ав-
автомата S или машины Тьюринга S. Соответствующее
асимптотическое поведение величины L (и) для этих
классов показано в таблице 1.
Таблица 1
Классы управляющих
спетом
Схемы из функциональ-
функциональных элементов
Контактные схемы
Формулы
Автоматы
Машины Тьюринга
L (п)
•>п
'I'1
log, п
~а (п) ——
а
2"
n(fc-l)
Примечание
, L (Е)
p=min .
1<а (п) < 2
k — число букв во
внешнем алфавите
машины Тьюринга
Если понятие сложности вводится иначе, напр, как
вероятность ошибки, или если рассматривается другой
класс у. с, напр, автоматы, то соответствующее асимн-
асимнтотич. соотношение .может содержать не один, а два
и более параметров, причем в общем случае задача
о получении асимптотики, напр. для автоматов, алго-
алгоритмически неразрешима.
Анализ нижней оценки для L (п) показывает, что
на самом деле для почти всех булевых функций от п
переменных сложность реализации асимптотически
не меньше L(n). Это означает, что данный метод син-
синтеза для почти всех булевых функций дает почти самые
простые схемы.
Однако, во-первых, при достаточно большом п ни
одну из функций этого класса, несмотря на то, что
он содержит почти все булевы функции, не удается
явно указать, а во-вторых, этот класс состоит из наи-
наиболее сложно реализуемых функции, к-рые, по-види-
по-видимому, не встречаются в задачах прикладного харак-
характера. Поэтому такие функции не представляют боль-
большого интереса. И снова появляется необходимость в
видоизменении постановки С. з.
При этом следует иметь в виду, что функции, для
к-рых С. з. актуальна, составляют ничтожную долю
всех булевых функции, и что любой эффективный
универсальный метод синтеза (если гипотеза о необхо-
необходимости перебора верна в полном объеме) для нек-рых
из них заведомо даст далеко не самые простые схемы.
Описать множество таких функций невозможно, но
проблема классификации булевых функций для целей
синтеза возникает. Такой подход к постановке С. з.
связан с выделением важных классов функций, со-
созданием для них специальных методов синтеза, каждый
из к-рых ориентирован на функции определенного
класса, а также с оценкой качества получающихся при
этом схем.
Эффективно решать такие задачи позволяет прин-
принцип локального кодирования. Этот
принцип предполагает такое кодирование функций из
рассматриваемого класса, при к-ром значение функции
можно вычислять по сравнительно небольшой части
кода. Если при этом удается достаточно просто реа-
реализовать нек-рые вспомогательные операторы, то
принцип локального кодирования дает асимптоти-
асимптотически наилучший метод синтеза для рассматриваемого
класса, причем в доволь-
Таблица 2 но широких пределах
справедливо соотноше-
соотношение
Т (Л: N __ г, log» I N» I ,
L (Л "> P log2 log* I A'H |
где Nn — подмножество
тех функций из рассмат-
рассматриваемого класса, к-рые
зависят от заданных п
переменных, а
Число точек,
и к-рых
функция
равна 1
AоВ,п>'.е>1
пс, О 0
2п°, 0<с< 1
2™.и<е<1
L (Атп)
-n(loK,n) —
(c+l)log2n
с
с 2« 1ок2п
где максимум берется по
всем булевым функциям
/ из Nn. (здесь р=1).
Конкретный вид, ко-
который может иметь это
асимптотическое соотно-
соотношение, удобнее всего
проиллюстрировать на классах булевых функций, при-
принимающих значение 1 в заданном числе точек, Наибо-
Наиболее характерные примеры приведены в таблице 2.
На основе принципа локального кодирования были
получены хорошие методы синтеза и для весьма узких
классов функций (напр., для симметрнч. функций),
т. е. для тех функций, к-рые с практической точки
зрения наиболее интересны. Однако в данном случае
нижняя оценка, получающаяся мощностным методом,
оказывается слишком слабой, для того чтобы по ней
судить о качестве схем. По мере сужения класса рас-
рассматриваемых функций в какой-то момент это неиз-
неизбежно должно было произойти, поскольку предельным
i-лучаем узкого класса является класс, содержащий
не более чем по одной функции от каждого числа пере-
переменных. Фактически это означает, что рассматрива-
рассматриваются отдельные конкретные функции.
Здесь возникают две проблемы: 1) построить для
заданной конкретной функции / схему с возможно
меньшим числом элементов и тем самым получить
верхнюю оценку для /<(/); 2) получить возможно луч-
лучшую нижнюю оценку для L (/). Среди :>тих задач первая
обычно бывает легче, так как для ее решения доста-
достаточно, в конечном счете, построить одну схему, а вторая
требует в каком-то смысле просмотра всех схем, реа-
реализующих функцию /. По этой причине возникло целое
направление, связанное с поиском методов получения
нижних оценок для конкретных функции.
Получение нижних оценок, линейных относительно
п — числа аргументов функции (или в общем случае
относительно объема входной информации), обычно
все-таки не вызывает больших трудностей. Получение
более сильных нижних оценок — значительно более
сложная задача. Первыми примерами в этом направ-
направлении были нижняя оценка порядка п1-ъ для формул
в базисе {&, V, ~}, реализующих линейную функ-
функцию (сумму по модулю 2) п аргументов, и нижняя
оценка порядка nll\o%2n для нормальных алгорифмов
Маркова, к-рые обращают слова длины п. Наиболее
высокие нижние оценки, к-рые к настоящему времени
A984) удалось получить, имеют порядок iil, если не счи-
считать оценок, получающихся при очень сильных ограни-
ограничениях на класс у. с. (напр., неполнота системы эле-
элементов) либо при использовании столь мощных средств
для задания функции, что они фактически содержат в
себе перебор всех функций.
О нетривиальности исследования сложности реали-
реализации конкретных функций говорит и то, что многие
задачи, такие, как умножение целых чисел, умноже-
умножение матриц, распознавание симметрии слова на мно-
многоленточных машинах Тьюринга, для к-рых ожидались
сравнительно высокие нижние оценки, оказались на
самом деле проще, чем предполагалось раньше.
При минимизации других параметров схем — за-
задержек, вероятности сбоя и т. д.— возникают при-
примерно такие же задачи. При этом удается установить
определенную связь между различными параметрами,
причем благодаря моделированию одних объектов на
других такую связь часто удается установить между
различными параметрами у. с. из разных классов.
Таким образом, полученные в С. з. результаты не яв-
являются изолированными, а тесно переплетаются друг
с другом и часто переносятся из одной области в другую.
Многое из сказанного выше относится и к бесконеч-
бесконечным моделям у. с. Однако с постановкой задачи син-
синтеза, а тем более с ее решением дело обстоит значи-
значительно сложнее.
Лит.: [1] Л у панов О. Б., «Проблемы кибернетики»,
1965, в. 14 с. 31 — 110; [2] Я б л о н с к и й С. В., там же,
1959, в. 2, с. 75 — 121. В. М. Храпченко.
СИНУС — одна из тригонометрич. функций:
Область определения — вся числовая прямая, область
значений — отрезок [ — 1; 1]; С.— функция нечетная,
периодическая с периодом 2л. С. и косинус связаны
формулой
i2
С. и косеканс связаны формулой
1
sin х = .
cusec к
Производная С:
(sin x)' = cos х.
Интеграл от С:
\ sin х dx — — cosi
С. разлагается в степенной ряд:
. ~3 vb
~{-~ — ..., —оо<г<оо.
Функция, обратная С, наз. арксинусом.
С. и косинус комплексного аргумента z связаны с
показательной функцией формулами Э й л е р а
i sm z,
eiz-e~iz
Sm Z = 21 " '
если z—ix (чисто мнимое число), то
sin ix = — sh x,
где shi — гиперболич. синус.
Ю. Л. Горькое.
СИНУС АМПЛИТУДЫ, эллиптический с и-
н у Q,— одна из трех основных Якоби эллиптических
функций, обозначаемая
snu — s>n(u, /c) = sinamu.
Синус амплитуды определяется через тета-
функции или при цомощи рядов следующим образом:
. , > О, @) 1», (г)
sn 1/ = sn (и, к) ---- I ' =
где к — модуль С. а. (чаще всего 0<:/с<1), г=и/2ш,
2со=я'дз@). При к=0, 1 соответственно sn(u, 0) —
= sin и, sn(u, l) = th и.
Лит.: [1] Г у р в и ц А., Курант Р., Теория функций,
пер. с нем., М., 1968, ч. 2, гл. 3. Е. Д. Соломеицев
СИНУС ГИПЕРБОЛИЧЕСКИЙ — см. Гиперболи-
Гиперболические функции.
СИНУС ГОРДОНА УРАВНЕНИЕ, Sine-Gordon
уравнение,— релятивистски инвариантное урав-
уравнение, в пространственно-временных переменных име-
имеющее вид
— оо < х, t < оо, ugR1, m > 0. (А)
Название предложено \1. Крускалом по аналогии с
линейным Клейна — ГорОина уравнением (где вместо
sin и стоит и). В характеристических (светонодобных)
переменных С. Г. у. выглядит так:
-^^ + m2sin» = 0, а, т, NgR1, m > 0. (В)
Как в случае (А), так и в случае (В) С. Г. у. допускает
представление Лакса
с линейными операторами L и М, что позволяет при-
применить к нему метод обратной задачи рассеяния ([L,
M]—LM—ML).
Задача Коши для С. Г. у. формулируется следующим
образом.
С (
i (.г) ss о (mod 2я).
Случай (А):
dx ' 2
Случай (В):
и
i о ~
€S(R1);
flu
"!' ~dt
lim
lim и0 (о)зе0 (тоА2п).
I сг | -* х
Здесь ^(К1) — пространство Шварца быстроуЙыва-
ющих функций. Задачи Коши (А) и (В) при нек-рых
дополнительных ограничениях на начальные данные
однозначно разрешимы в указанных классах, и мно-
множества их решений совпадают. Эволюция данных
/рассеяния соответствующих /--операторов дается яв-
явными формулами, а решения и (.т, t) и и (а, т) находятся
с помощью интегральных уравнений типа Гельфанда —
Левитана — Марченко.
Периодич. задача для С. Г. у. может быть исследо-
исследована с помощью алгебро-геометрич. метода (подобно
тому, как это делается для Кортевега — де Фриса урав-
уравнения); в частности, получены явные выражения для
конечнозонных решений С. Г. у. через б-функции на
соответствующих абелевых многообразиях.
Гамильтонова формулировка С. Г. у. заключается в
том, что, напр., в случае (А) оно представляет собой
гамильтонову систему с гамильтонианом
Ра = Т S-- (т я2 <*> + Т (Ir)' + т* <* -cos "О dx'
Y > О,
и симплектич. формой
Q = T S-I d:l <*) Л du (х) dx, я = |f .
Эта система является вполне интегрируемой, и пере-
переход от переменных и и л к данным рассеяния соот-
соответствующего оператора L является канонич. преоб-
преобразованием к переменным типа действие-угол. Фазовое
пространство параметризуется канонически сопряжен-
сопряженными переменными трех типов:
1) 0<р(р) < оо, 0<ф(р) < 2я, pgR1;
2) Pa, <?a€Rl, «=-1, •••, -Vi, Л'^0, TVigZ;
3) Чъ, !fc€R1, 0<ab<-^L,0<pb<2n. 6 = 1, ...-.Лз,
7V2Sa0, Лг2?2.
Полная энергия Ро и полный импульс
^i — — \ л (х) -^— dx
поля u в новых переменных выглядят следующим
образом:
Po== j-«
-4-
P + Zia=iPa + 2-Ь=1ЦЬ'
&m „ v
В случае (В) также получается вполне интегриру-
интегрируемая гамильтонова система.
Одно из приложений к квантовой
теории поля. П}'сть и (,r, t) — скалярное поле
с лагранжианом
(здесь у — константа связи). С. Г. у. является урав-
уравнением Эклера — Лагранжа для этого лагранжиана.
При квазиклассич. квантовании поля и основную
роль играют приведенные выше выражения для Ра
п Р1. Первые члены в правых частях указанных формул
отвечают частицам с массой m — частицам основного
поля. Переменным второго и третьего типов соот-
соответствуют локализованные решения С. Г. у.— солитоны
и двойные солитоны с массами М и 'IM sin 6. Система
обладает законом сохранения (топологич. заряд):
Частицы первого и третьего типов имеют заряд, рав-
равный 0, а у частиц второго типа заряд равен +1. Ча-
Частицы с одинаковыми зарядами отталкиваются, а с
разными зарядами — притягиваются. Наличие бес-
конечного числа законов сохранения означает, что при
рассеянии сохраняются количества частиц каждого
типа; я-частичная 5-матрица сводится к парным
S-ыатрицам. С помощью интеграла по траекториям
можно вычислить квантовые поправки к массам и к
квазиклассической ^-матрице солитонов. Одним из
нетривиальных свойств указанной модели является
появление целого спектра частиц (солитонов), в то
время как лагранжиан теории содержит только одно
поле. Кроме того, в приближении слабого взаимодей-
взаимодействия (т. о. когда у мало) солитоны — тяжелые ча-
частицы и сильно взаимодействуют.
Лит.: [1] A b 1 о w i t z M. [и др.], «Phys. Rev. Lett.»,
4973, v. 30, р, 1262—64*, [2] Т а х т а д ж я н Л. А., Ф а д д е-
е в Л. Д., «Теоретич. и матем. физика», 1974, т. 21, № 2, с. 160—
174; [3] и х ж е, «Тр. Матем. ин-та АН СССР», 1978, т. 142,
с. 254—66; [4] К о з е л В. А., К о т л я р о в В. П., «Докл.
АН УССР, сер. А.», 1976, № 10, с. 878—81; [5] К о р с-
п и н В. Е., Фаддеев Л. Д., «Теоретич. и матем. физика»
1975, т. 25, № 2, с. 147—63; [6] В i a n с h i L., Leziuni di geo-
metria differenziale, v. 2, pt 1—2, Pisa, 1923—24; [7] Ф и н и-
к о в С. П., Изгибание на главном основании..., М.— Л., 1937;
19] Пел и нов с кий Е. Н., «Изв. вузов. Радиофизика», 1976
т. 19, ,№ 5—6, с. 883—901. Л. Л. Тахтаджян.
СИНУСОВ ТЕОРЕМА: для произвольного треуголь-
треугольника со сторонами а, Ь, с и противолежащими им уг-
углами А, В, С имеют место соотношения
sin A sin В sin С
=2Д,
где R — радиус описанного круга. ю. А. Горькое.
СИНУСОИДА — график функции y=sia x (см. рис.).
С.— непрерывная кривая с периодом 7'=2я. Пересе-
X /ОСУ*/XV /OCX
NJ
чения с осью Ох — точки (к л, 0); они же — точки пере-
перегиба с углом ±п/А наклона к оси Ох; экстремумы
Ц™ I /2/1 V 1) ) •
График функции г/^cos х--Ап(х+я1.2) — косину-
косинусоида — представляет собой С, сдвинутую влево
на л/2. Пересечения косинусоиды с осью Ох — точки
((А:+1/2)я, 0); экстремумы (кп, (—1)*).
Многие колебательные процессы описываются иерио-
дич. функцией вида у=а sin (bx-\-c), где а, Ь и с —
постоянные. График этой функции (т. н. общая
синусоида, по сравнению с графиком функ-
функции j/=sin х (обыкновенная синусоида)
вытянут вдоль оси Оу в \а\ раз, сжат вдоль оси Ох
в Ъ раз, сдвинут влево на отрезок с/Ь и при а<0 зер-
зеркально отражен относительно оси Ох; период Т = 2п/Ь,
пересечения с осью Ох — точки ( ~— , 0); экст-
экстремумы ( " , ( — 1 ) а ). ю. А. Горькое.
СИНУСОИДАЛЬНАЯ СПИРАЛЬ — плоская кривая,
уравнение к-рой в полярных координатах имеет вид
рот _ am cog тф_
При рациональном т С. с. является алгебраич. кривой.
В частности, при т — \ —окружность, при т=—1 —
равносторонняя гипербола, при т:=1/2 — кардиоида,
при т~—1/2 —парабола.
В общем случае для т> 0 С. с. проходит через полюс
и полностью помещается внутри круга радиуса а.
При отрицательном т радиус-вектор кривой может
принимать сколь угодно большие значения и не про-
проходит через полюс. С. с. симметрична относительно
полярной оси, при рациональном m=plq (где р и q
взаимно простые числа) име-
имеет р осей симметрии, про-
проходящих через полюс. При
целом положительном т
радиус-вектор С. с. являет-
является периодич. функцией с
периодом 2л./т. При измене-
изменении ф от 0 до 2я кривая'
состоит из т лепестков, каж-
каждый из которых распола-
располагается внутри угла, равного
л/т. Полюс в этом случае—¦
кратная точка (см. рис.).
При дробном положительном
/ге=р'<7 кривая состоит из р пересекающихся лепест-
лепестков. При целом отрицательном т С. с. состоит из \т\
бесконечных ветвей, к-рые могут быть получены ин-
инверсией спирали с т'=—т.
Лит.: [1] Сап ело в А. А., Плоские кривые, М., 1960.
Д. Д. Соколов.
СИНУС-ПРЕОБРАЗОВАНИЕ ФУРЬЕ — см. Фурье
преобразование.
А -СИСТЕМА — счетно ветвящаяся система множеств,
т. е. семейство {Ап п.) подмножеств множества X,
занумерованных всеми конечными последовательно-
последовательностями натуральных чисел. Л-С. {Ап } наз. ре-
регулярной, если Ащ nknk + 1CZAni nk. После-
Последовательность Ап , ..., Ап , ... элементов А-С,
занумерованных всеми отрезками одной и той же бес-
бесконечной последовательности натуральных чисел, наз.
цепью этой А-С. Пересечение всех элементов цепи
наз. ее я д р о м, а объединение ядер всех цепей А-С.—
ядром этой А-С, или результатом Л-о пера-
ц и и, примененной к этой А-С, или Л-м н о ж е с т-
в о м, порожденным этой А-С. Всякая А-С. может
быть регуляризована без изменения ядра (достаточно
положить A'ni ,,. „fe— Anif\ ...Г)ЛП| .. „k). Если а/И —
нек-рая система множеств, то ядра Л-С, составленных
из элементов системы оМ, наз. /[-множествами,
порожденными системой оМ,- Л-множества, порожден-
порожденные замкнутыми множествами топологич. пространства,
наз. Л-множествами этого пространства.
Лит.: [1] Александров II. С-, Введение в теорию
множеств и общую топологию, М., 1977; [2] К у р а т о в с к и й
К., Топология, пер. с франц., т. 1, М., 1966. А. Г. Ельцин.
/Т-СИСТЕМА {Г'} — такой измеримый поток (К-
поток) или каскад (К-к а с к а д) в Лебега прост-
пространстве, что существует измеримое разбиение Ъ, фазового
пространства со следующими свойствами: а) оно воз-
возрастающее (в более старой терминологии — и н-
вариантное) относительно {Т }, то есть '1 §
мельче | mod 0 при г>0; б) оно является двусто-
двусторонним образующим для {Т1}, т. е. един-
единственным mod 0 измеримым разбиением, к-рое мельче
mod 0 всех Г'|, является разбиение на точки; в) един-
единственным mod 0 измеримым разбиением, к-рое крупнее
mod 0 всех Г'|, является тривиальное разбиение,
единственный элемент к-рого — все фазовое прост-
пространство.
Автоморфизм пространства с мерой, итерации к-рого
образуют АГ-каскад, наз. К-& в т о м о р ф и з м о м.
Если {Р} — К-С, то все Т1 с t=^=0 являются ii-авто-
морфизмами; обратно, если для измеримого потока
или каскада {Т1} хоть одно Т* является ^-автоморфиз-
^-автоморфизмом, то {Т*} — К-С. АГ-система обладает сильными
эргодич. свойствами: положительная энтропия, эрго-
эргодичность, перемешивание всех степеней, счетнократ-
ный лебеговский спектр (см. Спектр динамической
системы, а также [2]).
Эндоморфизм пространства Лебега имеет вполне
положительную энтропию, если любой
его нетривиальный факторэндоморфизм имеет положи-
положительную энтропию. Среди таких эндоморфизмов со-
содержатся как А*-автоморфизмы (именно последние
суть в точности автоморфизмы с вполне положитель-
положительной энтропией), так и другие интересные объекты {точ-
{точные эндоморфизмы). Имеются обобщения А-С. в других
направлениях: на случай бесконечной инвариантной
меры (см. [6], [7], [11]) и для действия группы, отличной
ox R и z (см. [8] — [10], [12]).
К-С. наз. также системами (потоками
и т. д.) Колмогорова, к-рый впервые ввел их
(см. [1]) под названием «квазирегулярных». Последнее
подчеркивает аналогию с регулярными случайными
процессами (см. [4]). Если случайный процесс {Xf},
стационарны)'] в узком смысле слова, интерпретиро-
интерпретировать как динамич. систему, то значения процесса «в
прошлом» определяют нек-рое измеримое возрастающее
разбиение ? — наименьшее, относительно к-рого из-
измеримы все Х{ с <<0. Если | обладает свойствами б)
и в) (закон «все или ничего»), то процесс наз. регу-
регулярным. В частности, вероятностное происхож-
происхождение имеет простейший пример Л'-автоморфизма —
Бернулли автоморфизм.
Если у измеримого потока или каскада в простран-
пространстве Лебега одно из преобразований Г* изоморфно
автоморфизму Бернулли, то и все они (при i=^=0) изо-
изоморфны автоморфизмам Бернулли; в этом случае ди-
динамич. система наз. бернуллиевской (см. [5]).
Существуют К-С, не являющиеся бернуллиевскими.
А'-С. (даже бернуллиевские) естественно возникают не
только в теории вероятностей, но и в других вопросах
(алгебраической, геометрической и даже физич. при-
природы; см. [2], [3], [5]).
Лит.: [1] К о л м о г о р о в А. Н., «Докл. АН СССР», 1Я58,
т. ИР, Л1 5, с. 801—04; 1959, т. 124, Л» 4, с. 754 — 55; [2]
Корнфельд И. П., С и н а й Я. Г., Фомине. В.,
Эргодическая теория, М., 1980; [3] Итоги науки и техники.
Математический анализ, т. 13, М., 1975, с. 129—262; [4]
Розанов Ю. А., Стационарные случайные процессы, М.,
1983; 15] О р н с т с и н Д., Эргодическая теория, случай-
случайность и динамические системы, пер. с англ., М., 1978; [6]
Parry W., «Proc. Amer. Math. Soc.» 1965, v. 16, №5,
p. 960—66; [7] D u g d a 1 e .1. K., «Publ. math.», (Debrecen),
1967, 1. 14, M 1/4, p. 79—81; [8] Conze J. P., «Z. Wahrs-
chemlichkeitstheorie und verw. Gebiete», 1972, Bd 25, H. 1,
S. 11 — .40; 191 BirtoiiR. M., там же, 1979, Bd 47, H. 2,
S. 207 — 12: [10] D a n i S., «Amer. J. Math.», 1976, v. 98, К 1,
p. 119- B.'-i; [11] Kremcl П. Sucleiton L, «Ann.
Math. Statistics», 1969, v. 40, >j 2, p. 694—96; [121 К a m i rt s k i
В., «Bull. Acad. polon. sci. Ser. sci. math., astron. et phys.»,
1978, v. 26, № 2, p. 95—97. Д. В. Аносов.
У-СИСТЕМА — гладкая динамич. система (поток
или каскад) с компактным фазовым многообразием,
к-рое все является гиперболическим множеством. Диф-
Диффеоморфизм, порождающий У-каскад, наз. У-д и ф-
феом орфизмом. У-С. были введены Д. В. Ано-
Аносовым (см. [1], [2]), поэтому иногда их наз. систе-
системами Аносова.
У-С. являются грубыми системами, причем при
малом (в смысле С1) возмущении У-С. снова получа-
получается У-С; число периодич. траекторий У-С. периода
но больше Т :>кспотенциально растет с ростом Т. У-С.
обладают сильными эргодич. свойствами но отношению
к широкому классу т. н. «гиббеовских» инвариантных
мер (см. [4]—[6]). [В частности, если У-С. имеет ко-
конечную инвариантную меру, «совместимую с гладко-
гладкостью», т. е. задаваемую в терминах локальных коорди-
координат положительной плотностью (в первых работах
только такие меры и рассматривались, см. [1] — [3]),
то эта мера — гиббеовская.] Так, если у У-диффео-
У-диффеоморфизма нет блуждающих точек, то он метрически
изоморфен Бернулли автоморфизму; сходимость вре-
временных средних к пространственному среднему в
широких предположениях подчиняется центральной
предельной теореме, а скорость леррмешивания —
экспоненциальная («экспоненциальное убывание кор-
корреляций») .
При исследовании У-С. нередко используется сим-
символическая динамика, что стало возможным благодаря
введенным в 17], [8] (окончательный вариант в [5])
марковским разбиениям. Ряд результатов об У-С.
оказался справедливым и для нек-рых других типов
гииерболич. множеств; имеются и менее непосредствен-
непосредственные обобщения, при к-рых несколько ослабляются ус-
условия гиперболичности (см. [6], [14]).
У-С. являются гиперболич. автоморфизмы торов и
геодезические потоки на замкнутых многообразиях
отрицательной кривизны; имеются и другие примеры
родственной алгебро-геометрич. природы. В этих при-
примерах У-С. имеет инвариантную меру, совместимую
с гладкостью. При малом возмущении такая мера мо-
может исчезнуть, но ввиду грубости все точки остаются
неблуждающими. Принципиально иной характер имеют
примеры У-С. с блуждающими точками (см. [9]).
Существование У-С. на многообразии налагает ог-
ограничения на его тонологич. свойства. В общем случае
об этом известно немногое (см. [10], [11]); хорошо изу-
изучен тот случай, когда устойчивое или неустойчивое
подпространство (см. Гиперболическое множество) од-
одномерно (см. [9], [12], [13]).
Лит.: [1] А н О с о в Д. В., «Докл. АН СССР», 1962, т. 145,
ЛЬ 4, с. 707—09; 1963, т. 151, Л1» В,с. 1250—52; [2] е г о же,
Геодезические потоки на замкнутых римановых много-
многообразиях отрицательной кривизны, М., 1967; [3] Аносов
Д. В., С и н а й Я. Г., «Успехи матем. наук», 1967, т. 22, п. 5,
с. 107 — 72; [4] С и н а й Я. Г., там же, 1972, т. 27, в. 4, с. 21 —
В4; [о] Б о у э н Р., Методы символической динамики, пер. с
англ., М., 1979; [В] Итоги науки и техники. Математический
анализ т. 13 М., 1975, с. 129- -262; [7l A d I e r R. L, Weiss
В., «Ргос. Nat, Acad. Sci. USA», 1067, V. 57. Mi 6, p. 1573 — 76;
[8] Синай Я. Г., «Функциональный анализ и его приложе-
приложения», 1968, т. 2, № 1, с. 64—89; L9] Franks J. M., W i 1-
1 i am s В., в кн.: Global theory of dynamical systems, B.—
[u. a.], 1980, p. 158—74 (Lecture notes in math., № 819); [10]
Hirschl. W., «Topology», 1971, v. 10, № 3, p. 177—83; [11]
S h i г a i w a K., «Nagoya Main. J.», 1973, V. 49, p. Ill —15;
[12] Гладкие динамические системы, пер. с англ., М., 1977;
[13] Vcrjovsky A., «Bolet. Soc. Matem. Mexicana», 1974,
v. 19, Л 2, p. 49—77; [14] F a t h i A., L a u d e n b а с h F.,
Foe naru V., «Asterisque», 1979, t. 86—67, p. 71—78, 139—
58, 225 — 42. Д. В. Аносов.
СИСТЕМНОЕ ПРОГРАММИРОВАНИЕ — ]) Инже-
Инженерная дисциплина, разрабатывающая методы пост-
построения системных программ, т. е. программ,
входящих в состав больших программных комплексов
(программных систем), придающих вычислительным
средствам постоянные функции нек-рой специальной
системы обработки информации.
2) Процесс составления системных программ — в
этом качестве все больше становится синонимом иро-
фессионального программирования, т. е. составления
программ (иначе называемых программным продук-
продуктом) , отчуждаемых от их автора и ирименяемых
впоследствии многократно.
В начальный период применения ЭВМ, главным
образом для математич. расчетов, основной сферой
приложения С. п. была разработка базового матема-
тич. обеспечения: операционных систем, систем про-
программирования, библиотек стандартных подпрограмм.
В связи с расширением и усложнением применения
ЭВМ в методах С. п. все больше начинает нуждаться
разработка прикладного математич. обеспечения —
пакетов прикладных программ, автоматизированных
систем управления и банков данных.
С. п. в своем развитии встречается с рядом трудно-
трудностей. Главными источниками их являются большой
объем программных систем (до 1 млн. машинных ко-
команд), сугубо нелинейная зависимость сложности от
объема, слабая устойчивость системных программ к
ошибкам программиста и отказам оборудования.
!¦> методах С. п. различается программирование «в
малом», т. с. методы разработки системной программы
одним человеком, и «в большом», т. е. методы объеди-
объединения индивидуального программного продукта в
большую систему.
В С. п. «в малом» на первый план выступают мате-
матич. методы программирования: описание и свой-
свойства математич. модели программируемой задачи, ме-
методы сиете.чатич. преобразования исходной формули-
формулировки задачи л программный текст, методы доказа-
доказательства правильности (верификации) программы. С. п.
«в большом» сближается с теорией больших систем,
общей системотехникой, методами организации кол-
коллективной работы и даже с вопросами эволюции ди-
намич. систем.
Лит.: [1] Б р у ь с Ф., Как проектируются и создаются
программные комплексы. Мифический человеко-месяц, пер. с
И1ГЛ., М., 1979; 121 Создание качественного программного
обеспечения. Тр. Рабочей конференции Междунар. федерации по
обработке информации, пер. с англ., т. 1 — 2, Новосиб., 1978.
А. П. Ершов.
СКАЛЯР — величина, каждое значение к-рой может
быть выражено одним (действительным) числом (см.
Величина). В общем случае С.— элемент иек-рого поля.
СКАЛЯРНАЯ КРИВИЗНА риманова мно-
многообразия в точке р — след Риччи тензора
по отношению к метрич. тензору g. Скалярная кривизна
s(p) связана с Риччи кривизной г и секционной кривизной
к формулами
где «1, . . . , еп — ортонормированный базис касатель-
касательного пространства. В эквивалентной индексной форме
эти равенства имеют вид
где Н{] и ftkijl — координаты тензора Риччи и тензора
кривизны соответственно, gH — контравариантные ко-
координаты метрич. тензора.
Лит.: [1] Г р о м о л Д., К л и н г с н б е р г В., М е й е р В..
Риманова геометрия в целом, пер. о нем., М., 1971; [2] Р а ш е в-
с к и и П. К., Риманова геометрия и тензорный анализ, 3 изд.,
М., 1967. Л. А. Сидоров.
СКАЛЯРНОЕ ПОЛЕ — скалярная функция точки об-
области нек-рого пространства. Примеры С. п.: поле тем-
температуры внутри тела, поле плотности.
СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ, внутреннее
и ]i низведение («,, Ь) ненулевые векторов а, и
Ь, — произведение их модулей на косинус угла ц> между
ними:
(<*, &) = [«, | [ б(созф.
За ц принимается угол между векторами, не превосхо-
превосходящий я. Если A-0 и 6=0, то С. п. полагают равным
нулю. С. п. (я- ,а) ¦—-- а2~\а\2 наз. скалярным
квадратом вектора а. См. Векторная алгебра.
С. и. двух и-мерных векторов а = (Я], я3, ... ап) п
6=iFi, b.,, ... Ьп) в случае действительных координат
наз. число
(а, Ь) = а1Ь1-[ а.-,Ь2-\-... -\-апЪп,
в случае комплексных координат — число
(о, t>) =r- ф
Бесконечномерное векторное пространство, в к-ром
определено С. п. и выполнена аксиома полноты, наз.
гильбертовым пространством. а В Иванов.
СКАНИРОВАНИЯ МЕТОД — метод максимизации и
минимизации функции путем последовательного пере-
перебора и сравнения значений функции во всех точках
нек-рого подмножества допустимого множества. В отли-
отличие от перебора методом Монте-Карло указанные точки
в С. м. лежат на заранее детерминированной траектории.
Название «С. м.» иршило из техники, где часть задач
обзора и обнаружения целей эквивалентна максимиза-
ции или минимизации функции яркости и решается с
помощью аналоговых или цифровых разновидностей
С. м. В дальнейшем С. м. привлек внимание в качестве
удобного средства оптимизации на ЭВМ в диалоговом
режиме.
Траектория сканирования, в частности, может обра-
образовывать всюду плотное множество в допустимом мно-
множестве аргумента.
Достоинствами С. м. являются отсутствие ограниче-
ограничений на способ задания функции и функциональные клас-
классы, к к-рым она может принадлежать. Последнее (наря-
(наряду с большой трудоемкостью перебора) является в то
же время и главным недостатком С. м.: не используется
для сокращения вычислений дополнительная информа-
информация, имеющаяся у вычислителя. Поэтому в вычислитель-
вычислительной практике С. м. редко применяется без комбинации
с другими методами оптимизации. Например, для
функций, удовлетворяющих условию Липшица, поиск
глобального экстремума эффективнее производить вме-
вместо С. м. методом «перебора на неравномерной сетке»
(см. [2], [3]).
Лит.: [1] Р а с т р и г и н Л, А., Системы экстремального
управления, М., 1974: 12] Евтушенко Ю. Г., Методы
решения экстремальных задач и их применение в системах
оптимизации, М., 1982; [3j Towards Global Optimisation
v. 1—2, Amst,— N. Y., 1975—78.
Ю.П. Иванилов, В. В. Охрименпо.
СКАЧКОВ ФУНКЦИЯ — одна из трех компонент
в Лебега разложении функции ограниченной вариации.
Пусть /(.т) — ограниченной вариации функция на от-
отрезке fa, Ь]. Пусть dx(x)=f(x)—f(x—0) при «<.<«&
и dn (¦?)=/(л-ЬО)—/(.г) при a<:i<6. Число dn(x) наз.
скачком функции / в точке х слева,
а число dn(х) — скачком функции / в точ-
точке х справа. Если а<х<Ъ, то число
d (x) = f(x + ») — f (x — 0) = d, (x) + dn {x)
наз. скачком функции / в точке г. Пусть
{.г;} — последовательность всех точек разрыва функ-
функции / на отрезке [а, Ь\ и
Функция s(x) наз. функцией скачков для
функции j(x). При этом разность /(х)—s(x)-~(p(x)
является непрерывной функцией ограниченной вариа-
вариации па отрезке [я, Ь], причем V'*(/)= F*((p)+ V?(s),
гДе Vg{F) — вариация функции F на отрезке [а, Ь].
При этом
Лит.: [1] Л еб ег А., Интегрирование и отыскание примитив-
примитивных функций, пер. с франц., М.—Л., 1У34; [2] На та н с о н й- П.,
Теория функции вещественной переменной, 3 изд., М., 1874.
В. И. Голубое.
СКАЧКООБРАЗНЫЙ ПРОЦЕСС — случайный про-
процесс, к-рый изменяет свое состояние только в случайные
моменты времени, образующие возрастающую последо-
последовательность. Иногда термин «С. п.» относят к любому
процессу с кусочно постоянным» траекториями.
Важный класс С. п. образуют марковские С. п. Мар-
Марковский процесс является С. п., если его переходная
функция P(s, х, t, В) такова, что
lim[P(s, х, t, B)—IB(x)]/(t — s)^q(s, x, В), A)
as
где /f,(x) — индикатор множества В в фазовом прост-
пространстве (Е,$), и выполнены условия регулярности,
заключающиеся в том, что сходимость в A) равномерна
и ядро q(s, х, В) удовлетворяет нек-рым требованиям
ограниченности и непрерывности.
Пусть
a(t, s) = —q(t, x, {x}), a(t, x, B) = q(t, x, ?\{x}),
П (/, x, B) = a(t, x, B)/a(t, x), если a(t, x) > 0,
и U(t, x, B)^0.
— в противном случае. Введенные величины допускают
следующую интерпретацию: с точностью до о (At) (при
At—>.0) a(t, x)At есть вероятность того, что в промежуток
времени (t, t+At) процесс покинет состояние х; U(t,
х, В), когда a(t, x)>0, есть условная вероятность попа-
попадания процесса во множество В при условии, что в мо-
момент, t .он покидает состояние х.
При выполнении условий регулярности переходная
функция С. п. дифференцируема по t при t>s, no s
при s<* и удовлетворяет прямому и обратному урав-
уравнениям Колмогорова с соответствующими
граничными условиями:
[е a(t, у, B)P(s, х, t, dy),
WmP(s, x, ts B) = JB(x);
— ^ P(s, у, t, B)U(s, x, dy)
lim P (s, x, t, B) = lB(x).
Пусть X=(Xt) - — непрерывный справа строго мар-
марковский С. п., Т„ — момент re-го скачка процесса,
Т0=0, Yn=XT , Sn — время пребывания в я-м состоя-
состоянии, Tx> = limTn — момент обрыва, Хт = 6, где б —
точка вне Е. Тогда последовательность (Т„, У„) обра-
образует однородную цепь Маркова. При этом если X —
однородный марковский процесс, то распределение Sn
при заданном Yn=x—показательное с параметром к (х).
Естественным обобщением марковских С. п. являют-
являются полумарковские С. п., для к-рых последовательность
(У„) является цепью Маркова, однако время пребыва-
пребывания в и-м состоянии зависит от У„ и Ул + 1 и имеет про-
произвольное распределение.
При исследовании общих С. и. оказался плодотвор-
плодотворным т. н. мартингальный подход. В рамках этого под-
подхода удастся получить содержательные результаты без
дополнительных предположений о вероятностной струк-
структуре С. п. При мартингальном подходе предполагается,
что на вероятностном пространстве (Q, §~, Р), где за-
задан С. п. X, фиксировано неубывающее непрерывное
справа семейство о-алгебр F=(<fPf)f >0, §~^^, причем
для каждого t случайная величина Xf является Jp^-
измеримой и, значит, моменты Тп— марковскими.
Пусть у — предсказуемая а-алгебра на Qx R + , $=
= 5>Х (§. Случайная мера г\ на (R+ X?,59(R + )(g)(^) наз.
предсказуемой, если для любой неотрицатель-
неотрицательной ^-измеримой функции / процесс (/*Л<Ь> , где
f(t, x)r)(dt, dx),
J@, f]\E
является предсказуемым.
Пусть [х=[х(Л, dx) —мера скачков ироце?Са_Х,^г. е.
целочисленная случайная мера на (R+XE, ~
определенная равенством
При весьма широких предположениях на (Е, $)
(выполненных, в частности, когда Е — полное сепара-
бельное метрпч. пространство с борелевской а-алгеброй
~) существует предсказуемая случайная мера v— v(dt,
х) такая, что имеет место любое из следующих двух
эквивалентных условий:
1) ?/*|лте = ?/*гос для любой неотрицательной 3>-v№
меримой функции /;
2) при любых п^{ и В?(§ процесс
(ц([0, t л Тп]хВ)-\{[0, tATny-B))r>0
является мартингалом, выходящим из нуля.
Предсказуемая случайная мера v определена одно-
однозначно с точностью до множества Р-меры нуль п наз.
к о м п с и с а т о р о м (или дуальной пред-
предсказуемой проекцией) ц. Можно выбрать
такой вариант v, что
v((roo, oo)x?)=0, v({i})x?)<l, v*- B)
Пусть Q — пространство траекторий С. п. X, при-
принимающих значения в (Е,?), g~t=a(Xs,s<gt),§r — uiF<i
t > о
Ро — вероятностная мера, для к-рой выполнено B).
Тогда на (Q, §~) найдется и притом единственная веро-
вероятностная мера Р такая, что v является компенсатором
[х относительно Р и сужение Р на $~0 совпадает с Ро.
Доказательство этого утверждения опирается на явную
формулу, связывающую условные распределения вели-
величин (Тп, Yn) и компенсатор, к-рьгй в ряде случаев ока-
оказывается более удобным средством для описания С. п.
С. п. является процессом с независимыми прираще-
приращениями тогда и только тогда, когда ему отвечает детерми-
детерминированный компенсатор.
Лит.: [1] Колмогоров А. П., «Успехи матем. наук»,
19.48, т. 5, с. 5—41; [2] Г и х м а н И. И., С к о р о х о д А. В.,
Теория случайных процессов, т. 2, М., 1973; [3] Jacod J.,
Calcul stochastique ct problemes de martingales, B.— [a.o. I
1979. Ю. М. КаОатк;.
СКЕЛЕТ КАТЕГОРИИ — минимальная полная под-
подкатегория категории, эквивалентная самой категории.
В произвольной категории St существует, вообще гово-
говоря, много скелетов. Любой скелет можно построить
следующим образом. В каждом классе изоморфных объ-
объектов категории Я' выбирается по одному представите-
представителю. Тогда полная подкатегория категории ,\\, порож-
порожденная выбранным подклассом объектов, является
С. к. Si-
Две категории эквивалентны тогда и только тогда,
когда их скелеты изоморфны. С. к. наследует многие
свойства самой категории: локальную малость, наличие
бикатегорных структур, различные ниды полноты и
Т. Д. М. Ш. Цаленко.
СКЛЕИВАНИЯ МЕТОД в теории поверх-
поверхностей — метод построения поверхностей, изомет-
ричных данной. С. м. имеет приложения к доказательст-
доказательствам реализуемости абстрактно заданных выпуклых
метрик, к вопросам изгибания выпуклых поверхностей
и к количественным оценкам изгибаемости; сила его
в том, что он работает там, где дифференциальные урав-
уравнения бессильны.
Теорема Александрова: пусть Gu . . . ,
Gn — замкнутые области в многообразиях с внутренней
метрикой и положительной кривизной, ограниченные
конечным числом кривых с ограниченной вариацией
поворота. Пусть G — многообразие, составленное из
областей G; путем отождествления точек их границ та-
таким образом, что 1) отождествленные отрезки границ
областей С,- и Gj имеют равные длины; 2) сумма поворо-
поворотов отождествленных отрезков границ областей G, и
Gf со стороны этих областей неотрицательна; 3) сумма
углов секторов в отождествленных точках областей Gk
со стороны этих областей не превосходит 2л. Тогда
многообразие G имеет внутреннюю метрику положи-
тельной кривизны, совпадающую с метриками ооластеи
в окрестностях соответствующих точек.
Лит.: [1J А л е к с а н д р о в А. Д., 3 а л г и л л о р В. А.,
Двумерные многообразия ограниченной кршш uu.i, м.—Л.,
1962; [2] По гор ело в А. В., Изгибание выпуклых поверх-
поверхностей, М.—Л., 1951. М. 11. Вопцеховский.
СКЛЕИВАНИЯ ТЕОРЕМЫ теоремы, к-рые уста-
устанавливают существование аналитич. функций, подчи-
подчиненных определенным соотношениям на границе об-
области.
Теорема склеивания Лаврентьева
[1]: какова бы ни была аналитич. функция .Г] = ф(х),
определенная на сегменте [ — i,i], ц<{ ±i)= ±i, у' (ж)>0,
можно построить две аналитич. функции Д (z, h) и
f.,{z, h), z~x\iy, /i=const, отображающие однолистно
и конформно прямоугольник |.г|<1, ~h<y<Q и прямо-
прямоугольник | х |<1, 0< у <h соответственно на области Dx
и D2 без общих точек так, что /i (.г, й) = /2(ф(г), h).
Эта С. т. была использована (см. [6]) для доказательст-
доказательства теоремы о существовании функции w- /(z), /@) = 0,
/A)=1, осуществляющей квазиконформное отображе-
отображение круга |zj«:l на круг |«?|<:1 и обладающей почти
всюду заданной характеристикой h(z), где
h (z) = w-/wz, \h(z)l*zh6<i,
h (z) — измеримая функция, определенная почти для
всех zz=x-\-iy, |z|«:l. С. т., являющаяся видоизменени-
видоизменением С. т. Лаврентьева, была также использована при
решении вопроса о конформном отображении односвяз-
нои римановой поверхности на однолистный круг [5].
Были получены и другие С. т. (см. [2]), сыгравшие
важную роль в теории римановых поверхностей (при
этом брались более слабые ограничения на функцию
типа а.] = ф(х)). Имеет место следующая С. т. (см. [3],
[5]): пусть на окружности |z|=l дана дуга Yi с конца-
концами а и Ь, афЬ, и на Yi задана функция g(z), обладаю-
обладающая свойствами: 1) она регулярна во всех внутренних
точках дуги Yi и в них />'' (z)=^0; 2) функция z1=g(z)
устанавливает взаимно однозначное отображение дуги
7i на дополнительную дугу "Уз на lz|—l c сохранением
концов а и Ь; тогда существует функция
регулярная в |z|<:l, на исключением точек 0, а и 1>,
и во внутренних точках дугиу! удовлетворяющая соот-
соотношению F(z)-=F(g(z)).
Доказано также существование функции F(z), одно-
однолистной в |г|<1 (см. [4], гл. 2).
Лит.: IU ЛавревтьевМ. А., «Матем. сб.», 1Я35, т. 42
ЛЬ 4, с. 407—24; [2] В о л к о в ы с к и й jr. Ы., там же 1940
т. 18, Л» 2, с. 1йэ—212; [3] S с h a e f { е г А. С. S р е п с с г D. С.
«Duke Math. J.», 1947, v. 14 №4,p. 949—ее- [4]их же «Amer
Math. Soc. Colloq. Puhl.», 1950.V. 35: [5] Г о л у з и н Г. М.
Геометрическая теория функций комплексного переменного,
2 изд., М., 1966, гл. 11, § 1—2; [6] Б е л и н с к и й II. П., Об-
Общие свойства квазиконформных отображений, Новосиб., 1974,
гл. 2, § 1. Е. Г, Голузина.
СКОЛЕМА ПАРАДОКС — следствие теоремы Лёвен-
хейма—Сколема (см. Гёделя теорема о полноте), со-
состоящее в том, что всякая непротиворечивая формаль-
формальная аксноматич. теория, заданная счетным семейством
аксиом, выполнима в счетной области. В частности,
если предположить непротиворечивость аксиоматич.
системы теории множеств Цермело — Френкеля или
простой теории типов (см. Аксиоматическая теория
множеств), то существует интерпретация этих теорий
на счетной области. И это несмотря на то, что сами эти
теории предназначены для описания весьма обширных
фрагментов наивной теории множеств н в рамках этих
теорий можно доказать существование множеств весьма
большой несчетной мощности, так что в любой интерп-
интерпретации этой теории должны существовать несчетные
множества.
Следует подчеркнуть, что С. п. не является парадок-
парадоксом в строгом смысле этого слова, т. е. отнюдь не сви-
свидетельствует о противоречивости теории, в рамках к-рой
он установлен (см. также Антиномия). Кажущаяся
парадоксальность С. и. может быть прояснена тем, что
счетно-бесконечная интерпретация теории множеств
является в нек-ром роде нестандартной. Элемент интер-
интерпретации может оказаться счетным в широком интуитив-
интуитивном смысле и несчетным внутри сапой теории. Послед-
Последнее означает, что среди элементов интерпретации отсут-
отсутствует функция, задающая взаимно однозначное соот-
соответствие между элементами данного множества и эле-
элементами множества натуральных чисел, в то время как
с теоретико-множественной точки зрения существова-
существование такой функции можно доказать.
Лит.: [11 К лини С. К., Введение в метаматематику, пер.
с анг.ч., М , 1957. А. Г. Драгплич.
СКОЛЕМА ФУНКЦИЯ, функция Скуле-
-м а, с к о л е м о в с к а я функция, — понятие
логики предикатов. Если А (ль .... ,г„. у)—преди-
у)—предикатная формула от индивидных переменных х-[, ... ,
лп, у, области изменения к-рых суть множества Xi,
¦ . . , Хп, Y соответственно, то функция / : X-iX . . . X
X Хп—yY наз. функцией С к о л е м а, или раз-
разрешающей функцией, для формулы дг/
А (хи . . . , хп, у), если для всех с^^Х^, . . . , хп?Хп
имеет место импликация
ЗуА (.гь . .., ,г„, у) => А (,си ..., х„, f (хи ..., ./¦„)).
С. ф. были введены Т. Сколемом (Т. Skolem) в 20-х гг.
20 в. Понятие С. ф. широко применяется в работах по
математич. логике. Объясняется это тем, что с помощью
С. ф. можно исключить чередование кванторов у и д.
Так, напр., для всякой формулы А языка узкого ис-
исчисления предикатов можно построить формулу вида
g X), . . . , хп у Ул • ¦ ¦ ¦, у т С * называемую с к о л е м о в-
с к о и нормальной формой формулы
А , где С не содержит кванторов, но содержит новые
(т. е. не встречающиеся в А) предикатные символы, и
такую, что в исчислении предикатов формула А выводи-
выводима тогда и только тогда, когда выводима ее сколемов-
ская нормальная форма.
Идея С. ф. используется в таких фундаментальных
теоремах математич. логики, как теорема Эрбрана, сво-
сводящая вопрос о выводимости в исчислении предикатов
предикатной формулы к исследованию вопроса о вы-
выводимости в исчислении высказываний бесконечной
последовательности пропозициональных формул, теоре-
теорема Лёвенхейма — Сколема и др.
В тех случаях, когда предметная область, на к-рой
рассматриваются формулы, обладает дополнительной
структурой, можно потребовать от С. ф. определенной
связи с этой структурой. Напр., если рассматриваемая
предметная область принадлежит иерархии конструк-
конструктивных по Г'ёделю множеств, то можно потребовать,
чтобы С. ф. также принадлежали определенному уров-
уровню в конструктивной иерархии. Существование С. ф.,
удовлетворяющих дополнительным свойствам, не всегда
гарантировано, но эффект от их использования в слу-
случае, когда они существуют, оказывается более значи-
значительным.
В качестве примера можно указать на результат
Йенсена о выводимости гипотезы Чэна о
двух кардиналах (см. [6]) и отрицания Сус-
лина гипотезы (см. [51) из аксиомы конструктивности
Гёделя. Теорема Новикова — Кондо об униформиза-
ции ^-отношений из дескриптивной теории множеств
утверждает существование определенного рода С. ф.
(см. [2], с. 280).
Лит.: [I] Но и и к о в II. С, Элементы математической
логики, 2 изд., М., 107.4; [2] Ш е н ф и л д Дж. Р., Математиче-
Математическая логика, пер. с англ., М., 1975; [3]Кейс.перГ., ЧпнЧ.Ч.,
Теория моделей, пер. с англ., М., 1977; |4] К р ш п н ю Л .
II a .'i к) т и н Е. А., Математическая логика М.. 1Н7Я; [.i]
Handbook of malliematical logic, Amst., 1977; [Bl D e v 1 i n K. J.,
Aspects of construrtibility, B.— [а. о.] 1973. В. Н. Гришин
СКОЛЬЖЕНИЙ ГРУППА регулярного на-
накрытия р: X—t-Y -- группа Г (р) таких гомеомор-
гомеоморфизмов у пространства X на себя, что ур-- р (X и Y —
свячные локально линейно связные хаусдорфовы тоно-
логич. пространства). Так, С. г. накрытия окружности
действительной прямой R, определяемого формулой
t h>(cos t, sin t), будет группа сдвигов t\-* t-\-2лп, » ? Z •
Группа Т(р) является дискретной группой преобра-
преобразований пространства X, действующей свободно (т. е.
у (х)-~ х =$> у= i), и пространство Y естественно изоморф-
изоморфно факторнростраиству Х/Т(р). С. г. Г(р) изоморфна
факторгруппе фундаментальной группы щ (Y, у0). где
</о€у> п0 образу группы щ (X, х0), где р (аго) = г/о, при
гомоморфизме, индуцированном отображением р.
В частности, для универсального накрытия р С. г.
изоморфна фундаментальной группе пространства )'.
Лит.: X v С ы-ц з я н, Теория гомотопий, пер. с англ,, М.,
19E4. ' Э. Б. ВинПерг.
СКОЛЬЗЯЩЕГО СРЕДНЕГО ПРОЦЕСС — стационар-
стационарный в широком смысле случайный процесс, к-рый может
быть получен с помощью применения нек-рого линей-
линейного преобразования к процессу с некоррелированными
значениями (т. е. к процессу белого шума). Часто С.
с. н. наз. также более частный процесс X (t) с дискрет-
дискретным временем t -¦ 0, ±1, . . . , представимый в виде
X(/)--=V(O-r-foiV(*-l)-r- • • . + b(,Y(t-q), A)
где BY (t) ~ 0, BY (t) Y (s) —a'2bts, b1s — символ Кронеке-
pa (так что Y (t)—процесс белого шума со спектраль-
спектральной плотностью а-/2я), q—нек-рое целое положитель-
положительное число, a 6lt . . . , bq — постоянные коэффициенты.
Спектральная плотность / (X) такого С. с. п. определя-
определяется формулой
а его корреляционная функция r(k)~EX(t)X (t—к)
имеет вид
г (?) = О22*=0 b]bj + \k\ при \k\<q,
г (к) —0 при | к | > q.
Обратно, если корреляционная функция г (к) стацио-
стационарного процесса X (t) с дискретным временем t облада-
обладает тем свойством, что г (к)— 0 при |/с|>? для какого-то
целого положительного q, то X (t) — это С. с. п. поряд-
порядка q, т. е. он допускает представление вида A), где
Y(t) —белый шум (см., напр., |1|, §5.7).
Наряду со С. с. и. конечного порядка q, представимы-
ми и виде A), существуют также два типа С. с. п. с
дискретным временем бесконечного порядка, а именно:
односторонние С. с. и., допускающие представление
вида
где Y(t) — белый шум, а ряд в правой части B) схо-
сходится в среднем квадратичном (и, значит, V. |^/р<
<оо), и более общие двусторонние С. с. п., иредстави-
мые в виде
где Y(I) — белый шум, a ~S\. |Ь<|2 <оо. Класс дву-
сторонних С. с. и. совпадает с классом стационарных
процессов X(t), имеющих спектральную плотность
/(^), а класс односторонних С. с. п.— с классом про-
цессов, имеющих спектральную плотность ;(/.) такую,
что
log/(A)dA > — оо
(см. [2], jt), [3]).
Односторонним или соответственно двусторонним
С. с. п. с непрерывным временем наз. стационарный
процесс X(t),— оо <<<оо, нредставимый в виде
X(t)=[* b(!,)dY(t—s). [* I b (s) I* ds < oo,
или соответственно в виде
b(s)dY{t — s), f°° (/i (s) \-ds < oo,
I — ОС
где B[dY (t)\'~ -O2dt, т. e. Y' (t)—обобщенный процесс
белого шума. Класс двусторонних С. с. п. с непрерыв-
непрерывным временем совпадает с классом стационарных про-
процессов X (/), имеющих спектральную плотность /(А),
а класс односторонних С. с. п. с непрерывным време-
временем— с классом процессов, имеющих такую спектраль-
спектральную плотность / (к), что
log / (к) (l-l-A2) dk > — оо
(см. [4], [31, [5]).
Лгст.: [1] Андерсон Т., Статистический анализ времен-
временных рядов, пер. с англ., М., 197Н; 12] К о л м о г о р о в А. Н.,
«Бюлл. Моск. гос. ун-та», 1941, т. 2, в. В, с. 1 —40; [,')] Л, у б Дж.,
Вероятностные процессы, пер. с англ., М.. 1956: I \ 1 К а г h u-
п en К., «Ann. Acad. Sci. Fennicae. Ser. A. Math.-Phys.», 1947,
.V' Я7, p. .4 — 79; L5J Роза н о в Ю. А., Стационарные случай-
случайные процессы, М., 1!Ж,Ч. А. М. Яглом.
СКОЛЬЗЯЩИЙ ВЕКТОР — см. Вектор.
СКРЕЩЕННОЕ ПРОИЗВЕДЕНИЕ г р у и п ы 6' и
кольца К — ассоциативное кольцо, определяемое
следующей конструкцией. Пусть заданы однозначное
отображение а группы G в группу автоморфизмов ассо-
ассоциативного кольца К с единицей и семейство
P=iPg,n \g, h?G)
обратимых элементов кольца К, удовлетворяющее
условиям
a«i<J-gitf_()-i a(gigj) о р
для всех а? К и #,, g.,, ,г3 g G. Семейство р наз. спет е-
мой факторов. Элементами С. п. группы G и
кольца Л' при системе факторов р и отображении сг будут
всевозможные формальные конечные суммы вида
(lg — ciniBOjr, однозначно сопоставляемый каждому
элементу g g G), а операции определяются формулами
V aJg+Y, P_^=V (сб„-ЬC); •
¦г)то кольцо обозначается Jt (G, р, о); элементы tg обра-
образуют А'-базис С. и. К (G, р, о).
Если о отображает G в единичный автоморфизм коль-
кольца К, то С. ц. К (G, р) наз. скрещенным груп-
групповым кольцо м, а если, кроме того, р^ Л— 1
для всех g, h ? G, то К (G, р, а) — групповое к о л ь-
ц о группы G над кольцом К (см. Групповая, алгебра).
Пусть К — ноле и о — мономорфизм. Тогда С. п.
K(G, р, о) — простое кольцо, являющееся С. п. поля
с его группой Галуа.
Jlvm.: [I] Sehgal S. К., Topics in group rinss, N. Y.,
1978; [2] Б о в д и А. А., «Сиб. матом, ж.». l!hi;j, т. 4, с. 481 —
500; [3] Итоги науки и техники. Современные проблемы матема-
математики, т. 2, М., 197, с. 5 — 118. А. А. Вовди.
СКРЕЩЕННЫЕ МОДУЛИ — понятие, родственное
понятию G-модулей (см. Модуль). Группа М (не обя-
обязательно коммутативная) с группой операторов G, снаб-
снабженная гомоморфизмом / : M-^G таким, что для любо-
любого g?G и любых х, у?М имеют место соотношения
наз. скрещенным (G, /)-м о д у л е м. Тогда и
только тогда М является G-модулем (то есть М — абеле-
ва группа), когда /=COHSt (s=e?G). M. И. Вопцеховсутп.
СКРЕЩЕННЫЙ ГОМОМОРФИЗМ группы G в опе-
операторную группу Г над G — отображение ф : G-э-Г,
удовлетворяющее условию ф (аЬ) --- ф (а) {ац> (Ь)). Если
G действует на Г тождественно, то С. г. — это обычный
гомоморфизм. С. г. наз. также 1-к о л. и к л а м и
группы G со значениями в Г (см. Неабелевы когомологии).
Каждый элемент у?Т определяет С. г. ф (а) — у-1 (ау)
(я?6), наз. главным С. г., или коциклом, кого-
мологггчным е. Отображение ф .' G—>-Г является С. г. тог-
тогда и только тогда, когда отображение р группы G в голо-
голоморф группы Г, заданное формулой р(а)=;(ф(а), а(а)),
где о : Г-э-Aut Г — гомоморфизм, определяющий
на Г структуру операторной группы, является гомомор-
гомоморфизмом. Напр., если о — линейное представление груп-
группы G в векторном пространстве Г, то С. г. ф> : G—Л"
определяет представление р группы G аффинными пре-
преобразованиями пространства V. Ядром С. г. f наз.
множество ц~' (e)czG; оно всегда является подгруппой
В G. А. Л. Онищик.
СКРЕЩИВАЮЩИЕСЯ ПРЯМЫЕ — прямые в про-
пространстве, не лежащие в одной плоскости.
Углом между С. п. нал. любой из углов между
двумя параллельными им прямыми, проходящими через
произвольную точку пространства. Если о и b — на-
направляющие векторы С. п., то косинус угла между
С. п. выражается формулой
(«, 6)
Общим перпендикуляром двух С. п.
ная. прямая, пересекающая каждую и» прямых и им
перпендикулярная. Для любых двух С. п. существует
единственный общий перпендикуляр. Уравнения (как
линии пересечения двух нек-рых плоскостей) общего
перпендикуляра к двум С. п. r~r\-\-atx и г—гг+Ы2
имеют вид
{(г-п), а, [а. Ь})=0,
((r-r2), U, [о, й]) = 0.
Расстоянием между Си. ная. длина отрезка
общего перпендикуляра к этим двум прямым, концы
к-рого лежат на отих прямых (или расстояние между
параллельными плоскостями, в к-рых лежат С. п.).
Расстояние d между С. п. выражается формулой
j I (С-1-'1»). "¦ *I
1[й,6][
А. Б. Иванов.
СЛАБАЯ ГОМОЛОГИЯ — отношение эквивалентно-
эквивалентности между циклами, приводящее к определению групп
спектральных гомологии IIр(С\ G). Известно, что го-
гомологии Стинрода — Ситникова компактного прост-
пространства IIр(С\ G) отображаются на Нр (С; G) эииморф-
но, причем ядро К этого отображения изоморфно пер-
первому производному функтору lim1 от обратного предела
гомологии II„(a; G) нервов открытых покрытий а про-
пространства С. Первоначально группы Вр определялись
is терминах циклов Вьеторнса, причем циклы, задающие
элементы подгруппы Кс.Нр(С\ G), наз. слабо г о-
м о л о г и ч н ы м и и у л ю- Наоборот, циклы Вьото-
риса, гомологичные нулю в укапанном выше определе-
определении групп II р, иногда наа. сильно го м о л о г и ч-
н ы м it н у л ю (а соответствующее отношение гжви-
валентности между ними — сильной г о м о л о-
г и ей). В случае, когда G — компактная группа или
поле, ядро К равно нулю, и понятия сильной и слабой
гомологии оказываются эквивалентными.
Лит.: [1] Александров П. С, «Тр. Матем. ин-та АН
СССР», 1959, т. 5/,, с. 3—136; [2] М а с с и У., Теория гомологии
и когомологий, пер. с англ., М., 1981. Е. Г. Скляренко.
СЛАБАЯ ОСОБЕННОСТЬ, полярная о с о-
б е н н о с т ь,— неограниченность ядра интегрально-
интегрального оператора К (.х, s) при ограниченном произведении
\х—s\aK (.г, s), (x, s)?QXB, где Q — множество прост-
пространства R", \х—s\ — расстояние между точками х, s и
0<a=const</i. Интегральный оператор, к-рый порож-
порождается таким ядром
JM (ж, s)
Q ]x—s |
пая. интегральным оператором со
слабой особенностью (или слолярноп
особенностью). Пусть Q — компактное под-
подмножество пространства Rn. Тогда если М (х, s) непре-
непрерывна на QxQ, то оператор A) вполне непрерывен и
пространстве непрерывных функций С (О), а если М —
ограниченная функция, то — в пространстве L2(Q).
Ядро
(Кх * ЙГ2) (х, s) = f K1 (x, t) Kz (t, s) dt B)
наз. сверткой ядер Кх ж Кг. Пусть эти ядра
имеют Co., причем
I К{ (х, s) | < —^—^5—, а,- = const < п, i = l,2,
lx-siai
тогда их свертка B) ограничена или будет ядром со
С. о., а именно:
/ с если сс\-\-(Х2 < ft,
|(A'i * А'г) (i, s) |< < с | In | x — s ||, если aj4-as = n,
| с \x — .s |"~ai~a*, если ai + a2 > n,
где с — нек-рая постоянная.
Если ядро имеет С. о., то псе его итерированные ядра,
начиная с нек-рого, ограничены.
Лит.: [1] Смирнов В. И., Курс высшей математики, т. Г), М.,
1959; [2] Владимиров В. С, Уравнения математической
физики, 3 изд., М., 1976; [3] К р а с н о с е л ь с к и й М. А.
[и др.], Интегральные операторы в пространствах суммируе-
суммируемых функций, М., 19R6. Б. В. Хведелидае.
СЛАБАЯ ПРОИЗВОДНАЯ — то же, что Гато про-
производная.
СЛАБАЯ ТОПОЛОГИЯ — локально выпуклая топо-
топология на векторном пространстве X, порожденная се-
семейством полунорм р (,г)=|/(.г)|, где / пробегает нек-рое
подмножество F сопряженного пространства X'.
Лит.: [1] Л ю с т е р и и к Л. А., С о б о л е в В. И., Крат-
Краткий курс функционального анализа, м., 1982; [2] Ш с ф с р X.,
Топологические ьекторные пространства, пер. с англ., М., 1971.
Ы. И. Войцеховский.
СЛАБО БЕСКОНЕЧНОМЕРНОЕ ПРОСТРАНСТВО —
топологическое пространство X, для любой бесконечной
системы пар множеств к-рого
(А;, В;), А(ПВ;=0, i = l, 2, ... ,
найдутся перегородки С\ (между А; и В,¦) такие, что
ПС,= 0- Пространство, не являющееся слабо беско-
бесконечномерным, наз. сильно бесконечно мер-
н ы м. С. б. п, наз. также А-с лабо бесконеч-
бесконечно м е р н ы м. Если в определении С. б. п. еще по-
потребовать, чтобы пары множеств были дизъюнктны, то
получится понятие iS-c лабо бесконечномер-
бесконечномерного пространства.
Л-ит.: ГЦ Александров П. С, Пасынков Б, А.,
Введении в теорию размерности, М., 1973. М. И. Войцеховский.
СЛАБО БЛУЖДАЮЩЕЕ МНОЖЕСТВО для обрати-
обратимого измеримого преобразования Т измеримого прост-
пространства (X, SB) — измеримое подмножество AczX, для
к-рого существует такая бесконечная иоследователь-
п.
ность целых чисел щ, что множества Т 'Л попарно не
пересекаются (здесь обратимость Т подразумевает изме-
измеримость Т~х). Если Т имеет а-конечнуго квазиинвари-
квазиинвариантную меру ц (определенную на %$), то необходимое и
достаточное условие существования у Т конечной инва-
инвариантной .меры, эквивалентной и., состоит в том, чтобы
для любого С. б. м. А было цА=0.
Лит.: [ 1 ] HaiianA. В., Kakutanl Sh., «Trans. Araei-
Math. Soc.», 19B4, v. HO, ft» 1, p. 136— 51; 121 H a j i a n A..
I to Y., «J. math, and mech.», 1969, v. 18, До 12, p. 1203— IB-
Д. В. Аносов-
СЛАБОЕ РЕШЕНИЕ дифференциального
уравнения
в области D — локально интегрируемая функция
м, удовлетворяющая равенству
\ и L*ffdx =
к/ D
для любой гладкой (напр., класса С°°) функция ф с
компактным носителем в D. Здесь коэффициенты аа(.г)
уравнения (*) предполагаются достаточно гладкими и
L* означает формально сопряженный но Лагранжу
с L дифференциальный оператор
Напр., обобщенную произродную f=^Dau можно опре-
определить как такую локально интегрируемую функцию /,
что и есть С. р. уравнения Dau = f.
При рассмотрении Ср. уравнения (*) возникает за-
задача: при каких условиях они являются сильными, ре-
решениями. Напр., для эллиптич. уравнений всякое С. р.
является сильным.
Лит.: [1] Бицадзе А. В., Некоторые классы уравнений
в частных производных, М., 1981. А. П. Солдатов.
СЛАБЫЙ ОТНОСИТЕЛЬНЫЙ МИНИМУМ — мини
мальное значение /(г/), достигаемое функционалом
J (у) на кривой у (.г), zj^as^a-j, такое, что / ((/X/ (у)
для всех кривых сравнения у(х), удовлетворяющих
условию е-близости 1-го порядка
| у (х) — у(х)\<е, I у' (х) — ~у' (х)\<г A)
на всем промежутке \х1, х2]. Предполагается, что кри-
кривые у(х), у(х) удовлетворяют заданным граничным ус-
условиям.
Если в A) отбросить условие е-близости по производ-
производной, то это приведет к условию е-близости нулевого
порядка. Минимальное значение функционала J (у) в
g-окрестности нулевого порядка наз. сильным относи-
относительным минимумом.
Поскольку условие е-близости нулевого порядка вы-
выделяет более широкий класс кривых по сравнению с
условием е-близости 1-го порядка, всякий сильный от-
относительный минимум является одновременно С. о. м.,
но не всякий С. о. м. является сильным относительным
минимумом.
Для того чтобы экстремаль у{х) доставляла С. о. м.,
необходимо, чтобы на ней выполнялось Лежандра ус-
условие. Для сильного относительного минимума вместо
условия Лежандра необходимо выполнение более об-
общего Вейерштрасса условия. В терминах теории опти-
оптимального управления это различие в формулировках
необходимых условий означает следующее: для С. о. м.
необходимо, чтобы Гамильтона функция в точках экст-
экстремали достигала локального максимума, а для силь-
сильного минимума — абсолютного максимума по управле-
управлению (в соответствии с принципом максимума Понтря-
гина).
Достаточные условия С. о. м. налагают нек-рые тре-
требования только на экстремаль у(х), тогда как в слу-
случае сильного минимума требуется выполнение сходных
но смыслу условий не только на экстремали у (г), но и
в нек-рой ее е-окрестности нулевого порядка. Экстре-
Экстремаль доставляет С. о. м., если вдоль нее выполняется
усиленное условие Лежандра и усиленное условие Яко-
би. Экстремаль доставляет сильный относительный ми-
минимум, если она может быть окружена полем экстрема-
лгй и для всех точек этого поля функция Вейершт-
расса неотрицательна.
Лит.: [1] Лаврентьев М. А., ЛюстерникЛ. А.,
Курс вариационного исчисления, 2 изд., М.—Л., 1950; [2]
Смирнов В. И., Курс высшей математики, 3 изд., т. 4,
М., 1957. И. Б. Вапнярский.
СЛАБЫЙ ЭКСТРЕМУМ —минимальное или макси-
максимальное значение J (у), достигаемое функционалом J(у)
на кривой у{х), г, <,г<:х2, для к-рого выполняется одно
пз неравенств
J(y)<J (у) или / (у) 5а / (у)
для всех кривых сравнения у(т), находящихся в е-
близости от кривой у(х) как по ординате, так и по про-
производной:
[ у (.г) — у (х)\ < е, \у' (х) —'у' (х)\ < е.
Кривые у(х), у(х) должны удовлетворять заданным
граничным условиям.
Поскольку максимизация функционала J (у) эквива-
эквивалентна минимизации функционала — J (у), то часто вме-
вместо С. э. говорят о слабом минимуме. Термин «слабый»
подчеркивает, что на кривые сравнения у (х) наложе-
наложено условие е-близости не только по ординате, но и по
производной (в отличие от сильного экстремума, где от
у(х) требуется е-близость к у(х) только по ординате).
По определению, С. э. является слабым относитель-
относительным экстремумом, поскольку дает экстремум не абсо-
абсолютный, т. е. не на всем классе допустимых кривых
сравнения у (г), на к-рых функционал J (у) имеет смысл,
а локальный, относительный, соответствующий нек-
рому подмножеству всех допустимых кривых сравне-
сравнения. Однако для краткости употребляют термин «С.э.».
Лит.: Ц] Лаврентьев М. А., Л ю с т е р н и к Л. А.,
Курс вариационного исчисления, 2 изд., М.—Л., 1950; [2]Смир-
н о и В. И., Курс высшей математики, 3 изд., т. 4, М., 1957.
Л. Б. Вапнярский.
СЛАВЯНСКИЕ ЦИФРЫ — цифры древнерусского
счета, в к-ром каждое из целых чисел от 1 до 9, а также
десятки и сотни обозначались буквами славянского ал-
алфавита с надписанным над ними знаком (титло). Целые
числа до 999 составлялись с помощью рядом стоящих
С. ц. Тысячи обозначались с помощью приставки нек-
рого знака к цифре, выражающей число тысяч.
СЛЕД — отображение Sp^/ ^ поля К в поле к (где
К — расширение к), являющееся гомоморфизмом адди-
аддитивных групп и ставящее в соответствие элементу <х?К
след матрицы к-линейного отображения K^r-К, пере-
переводящего В из if в ар.
Если К/к — сепарабельное расширение, то
SP/c/ft(a) = >jcr,-(a).
где о,- пробегают все й-изоморфизмы поля К в алгебраич.
замыкание к поля к. Отображение следа обладает свой-
свойством транзитивности: если LlК и К/к — конечные
расширения, то для любого a?L
sPi/fc (a) = sPK/ft (SPl/K (a))-
Л. В. Кузьмин.
СЛЕД квадратной матрицы — сумма эле-
элементов этой матрицы, стоящих на главной диагонали.
С. матрицы А — \\ау\\ обозначается tr А или Sp A:
Пусть А — квадратная матрица порядка п над полем
Л'. С. матрицы А совпадает с суммой корней характе-
ристич. многочлена матрицы А. Если К — поле харак-
характеристики 0, то п следов: tr А, . . . , tr А" однозначно
определяют характеристич. многочлен матрицы А; в
частности, матрица А нилыютентна тогда и только
тогда, когда tr Ак = 0 для всех к = \, . . . , п.
Если А и В—квадратные матрицы одного порядка
над полем К, а а, Р?А', то
= а tr Л + р tr В,
tr АВ ~tr В А
п при det ВфО
triBAB'^^tr А.
С. тензорного произведения квадратных матриц над по-
полем равен произведению следов сомножителей.
Д. А. Супруненко.
СЛЕД на С*-а л г е б р е А — функция / на мно-
множестве А + положительных элементов алгебры А, при-
принимающая значения и [0, -f- oo], аддитивная, однородная
относительно умножения на положительные числа и
удовлетворяющая условию j (xx*)~=f(x*x) для всех
х?А. След / наз. конечным, если /(.г)<+оо
для всех х?-А +; полуконечным, если f(x)~-
= mp{f{y) : у?А, у<.х, /((/)<+оо }для всех х?А + . Ко-
Конечные следы на А суть ограничения на А + таких
положительных линейных функционалов ф на А, что
ц>{ху) = у(ух) для всех .г, у?А. Пусть / — след на А,
31/—множество таких элементов jc?A, что /(а-.т*)<
<-(-оо, Ш1/— мноя1ество линейных комбинаций попар-
попарных произведений элементов из gj^; тогда 5t/ и Ш1у— са-
самосопряженные двусторонние идеалы в А и на ijJf/ су-
существует однозначно определенный линейный функцио-
функционал ф, совпадающий с / на ЯЯуП^ + • Пусть / — полуне-
полунепрерывный снизу полуконечный след на С*-алгебре
А; формула s(x, y)= ф(г/*.г) определяет на ¦>)}/ эрмитову
форму, и для любого 2 ?А отобрагкение 'kj(x) : у—>ху
пространства 9?/ в себя непрерывно относительно этой
формы. Пусть Nj~ {>"??{/, s(x, x)=*0), Hj — пополнение
факторпространства 4\fiNf относительно скалярного
произведения, определенного формой s. Операторы
%/(х) определяют при переходе к факторпространству
и пополнению нек-рые операторы л^(х) п гильбертовом
пространстве Н f, и отображение х—>-л^(х) есть пред-
представление С*-алгебры А в Нf. Соответствие /—>-л^ есть
взаимнооднозначное соответствие между множеством
полунепрерывных снизу полуконечных следов на С*-
алгебре А и множеством представлений С*-алгебры
А со следом, определенных с точностью до квазиэкви-
квазиэквивалентности.
Лит.: [1]ДиксмьеЖ., С*-алгебры и их представления,
пер. с франц., М., 1974. А, И. Штерн-
СЛОВО — горизонтальный ряд буке нек-рого алфа-
алфавита. Напр., ряд знаков «слововалфавите» является
С. в алфавите, состоящем из букв е, т, и, в, а, ф, л, о, с.
Для удобства к рассмотрению допускается и пустое
слово, т. е. С, не содержащее ни одной буквы. Оно
является С. в любом алфавите.
Возможно, несколько более точной является и н-
д у к т и в н а я х а р а к т с р и з а ц л я С, соглас-
согласно к-рой С. в алфавите А определяются как объекты,
получающиеся в результате развертывания порождаю-
порождающего процесса, определяемого следующими правилами:
а) пустое С. считается С. в алфавите А; б) если объект Р
оказался С. в алфавите А , а | является буквой этого
алфавита, то объект Pi, также считается С. в алфавите
А. Индуктивная характеризацпя С. делает оправдан-
оправданным применение правила индукции для доказательства
утверждений типа всеобщности о С. в данном алфавите.
С. представляет собой достаточно общий тип кон-
структиеного объекта, и в силу этого обстоятельства
понятие С. играет важную роль в конструктивной ма-
математике. Понятие С. широко используется также в
алгебраич. исследованиях, работах по математич. линг-
лингвистике и т. п.
Лит.: [1]Марков А. А., Теория алгорифмов, М,—Л., 1954
(«Тр. матем. ин-та АН СССР», т. 42, с. 12—25). If. M. Нагорный.
СЛОЕНИЕ на п - мерном многообра-
многообразии Мп — такое разбиение Мп на линейно связные
подмножества, именуемые слоями, что М" можно
покрыть координатными окрестностями Ua с локаль-
локальными координатами х^, ... , ж?, в терминах к-рых
локальные слои — компоненты связности пере-
пересечения слоев с [7а, задаются уравнениями жР + 1=
— const, . . . , .r? = consV. С. в атом смысле наз. топо-
топологическим С.; требуя же, чтобы Мп имело
кусочно линейную, дифференцируемую или аналитич.
структуру и чтобы локальные координаты были кусочно
линейными, дифференцируемыми (класса С) или ана-
аналитическими, получают определение кусочно л ;•;-
нейного, дифференцируемого (клас-
(класса С) или аналитического С. Определение
дифференцируемого С. класса С формально годится
и при г— 0, совпадая в этом случае с определением топо-
логич. С. Обычно, говоря о дифференцируемом С, под-
подразумевают, что г^\. Слои естественно снабжаются
структурой п-мерных многообразий (топологических,
кусочно линейных, дифференцируемых или аналитиче-
аналитических) и тем самым оказываются подмногообразиями
(i! широком смысле слова) многообразия М". Число
р (размерность слоев) наз. размерностью G.,
a q «=и—р — его коразмерностью. Рассмат-
Рассматривая С. на многообразии с краем, обычно требуют
либо трансверсальности слоев к краю, либо же того,
чтобы слой, пересекающийся с краем, целиком в нем
содержался. Очевидным образом определяются к о м п-
лексн о -аналитические С. Основным в тео-
теории С. является дифференцируемый случай (ниже С. и
отображения, как правило, подразумеваются диффе-
дифференцируемыми) .
Отображение
Фа • Ua — R?. » — {<' («*) .•¦¦.< <"))
является еубмерсиеп. Локальные слон суть ф~1(с),
c?R*. Система локальных субмерсий {(Ua, Ф«)} явля-
является согласованной в том смысле, что если u?Ua{)Ufi,
то возле и можно перейти от Ц>а(") к фр('') с помощью
нек-рого локального диффеоморфизма Фр«, и (клас-
(класса С) пространства R?, т. е. для всех v, достаточно
близких к и, имеет место срр A')"гФр<х, и фа М- Обратно,
если М" покрыто областями Ua и заданы субмерсий
фа: {/а_^?, согласованные в том же смысле, что и
выше, то путем подходящего «склеивания» ф~а (с) между
собой получается такое С., что каждое ф-1 (с) содержится
в нек-ром слое.
Сопоставление каждой точке и?М" касательного
пространства к проходящему через эту точку слою,
приводит к нек-рому полю р-мерных касательных под-
подпространств (по другой терминологии, р-мерному р а с-
с л о р н и ю), к-рое наз. касательным по-
полем С. При р~ 1 любое поле р-мерншх касательных
подпространств, при самых минимальных требованиях
дифференцируемости, является касательным полем нек-
рого однозначно определенного С. При р>1 это не
так. Данный вопрос имеет локальный характер (см.
Фробениуса теорема). Непосредственное применение
теоремы Фробениуса к инволютивному распределению
показывает, что при выполнении соответствующих ус-
условий имеется система согласованных локальных суб-
мерсии, для к-рых заданное поле касается, переход к
С. осуществляется путем надлежащих «склеиваний»
(и других терминах :>то описано в [3]).
Формирование понятия С. произошло в 40-х гг. 20 и.
в цикле работ Ж. Риба (G. Reeb) и Ш. Эресмана (Ch.
Eltresmann), завершившемся книгой |1] (в связи с исто-
историей см. B]), и было связано с переходом к глобальной
точке зрения. Этому отчасти способствовала теория
гладких динамических систем, где разбиение фазового
многообразия (с выкинутыми равновесия положениями)
на траектории потока является одномерным С. Особое
положение, к-рое в этой теории занимают потоки на
поверхностях (Пуанкаре — Вендиксона теория, Диффе-
ренциальние уравнения на торе, Кнезера теорема).
Особое положение, где траектории локально разбивают
пространство, способствовало привлечению внимания
к С. коразмерности 1. Другой пример С, проанализи-
проанализированный в 40-х гг.,— разбиение группы Ли на смеж-
смежные классы но аналитич. подгруппе (не обязательно
замкнутой) (см. [3J). Наконец, в комплексной области
решения дифференциального уравнения dwldz—j (z, w)
с аналитической правой частью образуют (с веществен-
вещественной точки зрения) двумерное С.
После первых работ наступил перерыв в развитии
теории С, к-рая тогда была еще бедна значительными
результатами. Интенсивное развитие началось с работ
А. Хефлигера [41 и С. П. Новикова [7J, наиболее извест-
известные результаты к-рых таковы (см. [17]): С. коразмер-
коразмерности 1 на трехмерной сфере имеет компактный слой
[7] п не может быть аналитическим [4], хотя еще Ж. 1'иб
построил С. класса С°°. Тогда же при изучении нек-рых
динамич. систем (У~системы и родственные им) возник-
возникли нек-рые вспомогательные С. (уже не одномерные,
что тоже стимулировало исследование С. (см. [7], [8]).
Все эти работы и ряд последующих можно отнести к
«геометрическому» или «качественному» направлению
[16]. В нем большое внимание уделяется С. коразмер-
коразмерности 1, существованию компактных слоев, теоремам
устойчивости (устанавливающим, что при определенных
условиях С. с компактным слоем устроено в его окрест-
окрестности и глобально как расслоение; первые такие теоре-
теоремы доказал еще Ж. Риб, см. [17]), характеристике «рос-
«роста» слоев (т. е. зависимости р-мерного объема геодезич.
тара радиуса г на слое от г) или их фундаментальных
групп. Отметим также недавнее решение вопроса: если
на замкнутом Мп имеется р-мерное С, все слои к-рого
компактны, то обязательно ли ограничен р-мерный объ-
объем слоев? Д. Эпстейн (D. Epstein), Д. Сулливан (D. Sul-
Sullivan) и др. выяснили, что ответ положительный толь-
только при ?<2 Сем. [9]).
Позднее возникло «гомотопическое» направление,
прообразом к-рого послужила гомотопич. теория рас-
расслоений. Отличия, возникающие для С, отчасти свя-
связаны с тем, что для С, вообще говоря, нет аналога
индуцированному расслоению. Это вынуждает перейти
от С. к более общим объектам — Хефлигера структурам
(нечто вроде С. с особенностями), для к-рых такой ана-
аналог имеется.
Слоения /'о и 1'\ па М наз. конкордангны-
м и, если на «цилиндре» А/Х[0, 1] существует такое С
(той же коразмерности), слои к-рого трансверсальны
ко «дну» и «крышке» цилиндра и «высекают» на них слое-
слоения Fo и F1. Сходным образом определяется конкор-
дантность структур Хефлигера. Всякая структура Хеф-
Хефлигера конкордантна такой, к-рая вне множества «осо-
«особых точек» на М соответствует нек-рому С, причем
выполняются определенные условия о поведении слоев
последнего возле этих точек. В этом смысле структуру
Хефлигера можно представить себе как С. с особеннос-
особенностями. Имеется естественное биективное соответствие
«генчду классами конкордатных структур Хефлигера
и гомотопич. классами непрерывных отображений М
n т. н. к .ч а с с и ф н ц н р у ю щ р с п р о с т р а н-
с т в о IIVг (// укалывает коразмерность, г — класс
гладкости структуры Хефлигера).
Голютонич. теория устанавливает, какие гомотопич.
объекты определяют конкордантность С: дна С. конкор-
дантны тогда л только тогда, когда они конкордантны
как структуры Хефлигера, а их касательные поля гомо-
гомотопны (см. [6], [10], A1J). Родственный результат —
доказательство существования/i-мерных С. на любых
открытых М (см. [6]) и на таких замкнутых М, на к-рых
существует непрерывное поле /(-мерных касательных
подпространств (что является очевидным необходимым
условием существования С, см. [10], [11]), ранее раз
личными учеными было доказано существование С.
на ряде многообразий путем непосредственных по-
построений [12J. Идея (см. [101, [11]) состоит в том, чтобы,
начав со С. с особенностями, ликвидировать их путем
нек-рых модификаций С. Случай </>1 оказывается бо-
более простым (см. [10], [131) и ликвидация особенностей
может быть проведена в духе «геометрической» теории
[14]; случай </==1 сложнее [11].
Отображение / : ЛР!—<-ВГг порождает отображение
когомологий, что приводит к характеристическим клас-
классам, С. В возникающую здесь «гомологическую» или «ко-
«количественную» теорию С. (см. [13], [15], 110]) включают-
включаются и нек-рые результаты, полученные ранее без обра-
обращения к №г„, напр, инвариант Годбийона—Вея; для
«=3 (см. [17]) или указанные P. Bottom (R. Bott(
условия, необходимые дли того, чтобы непрерывное
поле касательных подпространств было гомотопно каса-
касательному полю С.
Лит.: [1] н с е b G., в кн.: Actualites Sci. Ind.,№ 1183, P.,
1952; [2] R e e b G., Schweitzer P. А., в кн.: Differential
topology..., В., 1978; t.i] III e в а л л е К., Теория групп Ли, пер.
сангл.,т. 1,М., 19iS; [4] Н a et I i g e r A., «Ann. Scuola norm.
Sup. Pisa», ser. 3, 1962, t. 16, p. 367—97; Ы его ж е, в кн.: Ma-
Manifolds, Amst., 1970, В., 1971; [6] его ж е, «Topology», 197U,
v. 9, .М 2, р. 183—94; [7J Н о в и к о в С. 11., «Тр. Моск. матем.
об-ва», 1965, т. 14, с. 248—78; [8] Гладкие динамические систе-
системы, Inep.], M., 1977; [9] Б е с с е А., Многообразия с замкнуты-
замкнутыми геодезическими, пер. с англ., М., 1981; [lOjThursto n W.,
«Comm. math. Helv.», 1974, У. 49, p. 214—31; [11] его же,
«Ann. Math.», 197ti, v. 104, ,\Ь 2, p. 249—68; [12] L a w s о n H.,
«Bull. Amer. Math. Soc», 1974, v. 80, p. 36Й—418; [13] e г о ж е,
The quantitative theory Cf foliations, Providence, 1977; [14] M и-
ш а ч е в Н. М., Элиашберг Я. М., «Функц. анализ л его
прил.», 1977, т. 11, № 3, с. 43—53; [1о] Ф у к с Д. В., в кн.:
Итоги науки и техн. Сер. Совр. пробл. матем., М., 1978, т. 10, с.
179—285; fl6] его же, вкн.: Итоги науки и техн. Сер. Алгебра.
Топология. Геометрия, М., 1981, т. 18, с. 151—213; [17] Т а м у-
р а И., Топология слоений, пер. сяпон., М., 1979. Д. В. Аносов.
СЛОЖЕНИЕ — одна из основных арифметич. опе-
операций. Результат С наз. сум м о и. Сумма чисел
а и Ъ обозначается о+Ь, при этом а и Ь наз. слагае-
слагаемыми. С. чисел коммутативно: а+й==й+а, и ассо-
ассоциативно: (а-\-Ь)-\-с--=а-\- (Ь+с). Операция, обратная С,
наз. вычитанием.
Обычно С. называют также операцию в абелееой
группе (аддитивная запись) и ту бинарную операцию
в кольце, относительно к-рой элементы кольца образу-
образуют абелеву группу. Здесь также С. ассоциативно и
коммутативно. Иногда сложением наз. и некоммутатив-
некоммутативная операция в группе, напр, операция в мулътиопера-
торной группе. О. А. Иванова.
СЛОЖЕНИЕ множеств — векторное сложение
и нек-рые другие (ассоциативные и коммутативные)
действия над множествами А{. С. рассматривается чаще
всего для выпуклых множеств А; в евклидовом прост-
пространстве R".
Векторная сумма (с коэффициентами А,,-)
определяется в линейном пространстве правилом
где ?м- — действительные числа (см. [1]). В пространстве
R" векторная сумма наз, также с у м м о п М и н-
к о у, с к о ]' о. С зависимостью объема 5 от А,,- связана
смешанны.г обтл'мов теория. Для выпуклых А{ С. со-
сохраняет выпуклость и сводится к С. опорных функции,
а для t--гладких строго выпуклых Л;С:К" характери-
характеризуется С. средних значений радиусов кривизны в точ-
точках с общей нормалью.
Рассматриваются также: С. множеств с точностью
до сдвига; С. замкнутых множеств, сопровождаемое
замыкаинс-м результата (см. Выпуклых множеств про-
пространство); интегрирование континуального семейства
множеств; С. в коммутативных полугруппам (см. D1).
р-с у м м ы Ф а й р и определены в классе выпук-
выпуклых тел AfCR", содержащих нуль. При р~^\ опорная
функция р-суммы определяется как B,#f)ll;), где
Я; — опорные функции слагаемых. При р<:— 1 выпол-
выполняют (—р)-сложение полярных для Л,- тел и берут
поляру результата (см. [2]). р-сумма Файри непрерывна
по A i и р. Проекция р-суммы на подпространство есть
р-сумма проекций. При р-=1 сумма совпадает с вектор-
векторной, при р- —1 нал. инверсной су м м о й
(см. [1], с. 38), при р - ее дает выпуклую оболочку
слагаемых, при р~- — со --• их пересечение. При этих
четырех значениях р-сумма многогранников есть мно-
многогранник; при р== ±2 сумма эллипсоидов есть эллип-
эллипсоид (см. [2]).
Сумма Бляшке определена для выпуклых
тел Л iC;R", рассматриваемых с точностью до сдвига.
Определяется сложением поверхностных функций |3].
Сумма вдоль подпространства оп-
определена в векторном пространстве X, разложенном и
прямую сумму подпространств У и Z. Сумма А,- вдоль
У определяется как
где Yz — так сдвинутое У, что Yzf\Z~ {z} (см. [1]).
Лит.: [1] Рокафсллар Р., Выпуклый анализ, пер. с
англ., М., 1973; [2] Р i г е у W. J., «Pacif. J. Math.», 1964, v. 14,
p. 53—60; [3] e г о ж e, «Proc. O.olloq. on Com'.», Copenhagen,
1965, Kbh., 1967, p. 94— 101; [4J D i n g h а я A., Minkowskische
Summen und Integrate. Superadditive mengen-funktionale. I sope-
rimetrische UnRleichungen, P., 1961. В. П. Федотов.
СЛОЖНАЯ ГИПОТЕЗА — утверждение (предполо-
(предположение) о принадлежности функции распределения (плот-
(плотности вероятности) случайной величины нек-рому мно-
множеству функций распределения, содержащему более
одного элемента. См. Статистических гипотез проверка,
Простая гипотеза.
Лит.: [1] К р а м е р Г., Математические методы статистики,
пер. с англ. 2 изд., М., 1975. М. С. Никулин.
СЛОЖНАЯ СИСТЕМА — собирательное название си-
систем, состоящих из большого числа взаимосвязанных
элементов. Следует подчеркнуть неформальность этого
понятия, поскольку на современном этане развития
науки нет строгого математич. определении С. с, охва-
охватывающего все интуитивные представления о реальных
С. с. Типичными примерами С. с. являются: нервная
система, мозг, ОВМ, система управления в человеческом
обществе и т. д.
В 20 в. в связи с необходимостью изучения все более
сложных объектов к понятию С. с. подошли многие
науки: биология, техника, экономика, социология и
др. Особо следует отметить рождение кибернетики как
самостоятельной науки, основным предметом к-рой
являются сложные управляющие системы. В результате
этого процесса появился также ряд специальных дис-
дисциплин, имеющих в своем названии слово «система»:
системный анализ, системотехника, общая теория си-
систем и др.
Существуют различные подходы к математич. описа-
описанию и изучению С. с. в зависимости от используемого
математич. аппарата. Можно выделить два тина мате-
математич. моделей С. с: дискретные п непрерывные. Пер-
Первые изучаются преимущественно в математич. киберне-
тике (теория управляющих систем) и опираются на ап-
аппарат дискретной математики, а вторые - в теории
динамических систем и теории автоматич. управления,
математич. основой к-рых является теория дифферен-
дифференциальных уравнений. Широко применяются также при
изучении С. с. вероятностно-статистические методы —
теория массового обслуживания, методы стохастяч.
программирования it стохастнч. моделирования. Не-
Несмотря на различие форм и математич. аппарата, все
эти подходы к описанию С. с. объединяет общая мето-
методология и общий предмет изучения.
Одним пи наиболее трудных моментов при всех по-
попытках математич. описания С. с. является формализа-
формализация понятии с л о ж н о с т п. Реальным С. с. прису-
присущи многие характерные черты «сложности»: большое
число элементов, из к-рых состоит система; многообра-
многообразие возможных форм связи элементов системы между
собой; сложное функционирование; иерархичность
структуры и т. д. Необходимо отметить, что понятия
С. с. и «большая система» но являются синонимами, т. к.
последний термин охватывает системы, обладающие
лишь одной чертой сложности — большим числом эле-
элементов.
К настоящему времени A983) основные продвижения
в формализации понятия сложности в математич. изуче-
изучении С. с. получены для достаточно простых (модельных)
классов управляющих систем — Тьюринга машин, схем
из функциональных элементов, автоматов конечных
и т. и. Дальнейшее изучение С. с. идет по пути рассмот-
рассмотрения все более сложных математич. моделей, позволяю-
позволяющих полнее отразить структуру и функционирование
реальных С. с. При этом многие закономерности, уста-
установленные для более простых моделей, часто перено-
переносятся на более сложные.
Лит.: 11J Л я п у н о в А. А., Я Г> л о н с к и й С. В., «Проб-
«Проблемы кибернетики», 1963, в. 9, с. .">- 22; 121 Б у с л е н к о Н. П.,
Калашников В. В., Ковал1 и i, о II. Н., Лекции по
теории сложных систем, М., 197.4; LoJ Энциклопедия кибернети-
кибернетики, т. 2, К., 1975, с. 373—75. Н. Н. Кузюрип.
СЛОЖНАЯ ФУНКЦИЯ — функция, представленная
как композиция нескольких функций. Бели множество
значений У,- функции /,¦ содержится во множестве опре-
определения Xj + 1 функции /,+), т. е.
/«:*,•-+y.-C:.V; + l, t = l, 2, ..., и-1,
то функция
/и°/п-1° • • ¦ °/i, я^2,
определяемая равенством
(/„"/„-,»¦¦. -к) (X) = /„(/»-! (••• (/lW) •••)), X$Xi,
наз. сложной функцией или (п—1)-крат-
ной к о м позицией (супе р п о з и ц и е й)
функций /,, /2, . . ., /„. Напр., всякая рациональная
функция любого числа неременных является компози-
композицией четырех арифметич. действий, т. е. композицией
функций х-\-у, х—у, ху, х/у.
С. ф. сохраняет многие свойства функций, компози-
композицией к-рых она является. Так, композиция непрерывных
функций непрерывна. Это означает, что если функция
fl : X —>-У непрерывна в точке ,г0 <?Х, а функция /2 : У—>¦
->Z непрерывна в точке 11 (,г0) ?Y, то С. ф. /2°/i также
непрерывна в точке х0 (здесь X, Y и Z являются, напр.,
ТОПОЛО1-ИЧ. пространствами). Подобным образом, ком-
композиция п раз (непрерывно) дифференцируемых функ-
функций представляет собой также п раз (непрерывно) диф-
дифференцируемую функцию, П---1, 2, ... Композиция
возрастающих (убывающих) функций есть возрастаю-
возрастающая (соответственно убывающая) функция. При ком-
композиции функций иногда меняется количественные
характеристики свойств функций: композиция функ-
функций /х и /2. удовлетворяющих условию Гёльдера нек-
рых степеней, есть функция, удовлетворяющая усло-
условию Гёльдера степени, равной произведению степеней
условий Гёльдера, к-рым удовлетворяют функции
fi и /2. Нек-рые характеристики функций не сохра-
сохраняются при композиции. Так. ко.мпозиция функций,
интегрируемых по Риману или но Лебегу, не является,
вообще говоря, функцией, интегрируемой по Риману
или, соответственно, но Лебегу; композиция абсолютно
непрерывных функций может оказаться не абсолютно
непрерывной функцией. Вместе с тем, согласно резуль-
результатам Н. К. Бари и Д. Е. Меньшова [1], композиция
трех абсолютно непрерывных на отрезке функций не
приводит к новому классу функций но сравнению с
композицией двух абсолютно непрерывных функций.
Н. К. Бари [2] доказала, что любая непрерывная на
отрезке функция может быть представлена в виде сум-
суммы трех композиций абсолютно непрерывных функций,
и есть такие непрерывные функции, к-рые не могут
быть представлены в виде суммы двух таких компо-
композиций. Вместе с тем, всякая непрерывная на отрезке
функция является суммой двух композиций функций
с ограниченным изменением; однако «-кратные компо-
композиции функций с ограниченным изменением для каж-
каждого л—1, 2, ... приводят к существенно новым клас-
классам функций и существуют однократные композиции
функций с ограниченным изменением, не являющиеся
непрерывными функциями [3].
Понятие композиции функций представляет собой
наиболее широкое понимание термина «представление
функции формулой». Задача о представлении функций
в виде композиций возникла в связи с отысканием фор-
формул для решений алгебраич. уравнений. Всякий ко-
корень уравнения степени не выше четвертой может быть
представлен формулой, выражающей его через коэф-
коэффициенты уравнения и представляющей собой компо-
композицию четырех арифметич. действий и радикалов.
Всякое уравнение степени и^5 может быть с помощью
подстановки (наз. преобразованием Чирнгаузона) при-
приведено к виду
х" + аул"-4-f . . . f а„_,т +1 =-0.
Таким образом, каждый корень уравнения степени
гС^Ъ представляет собой функцию п—4 параметров.
Задача состоит в выяснении: можно ли эти функции
представить в виде композиции алгебраич. функций
меньшего числа переменных. Одна из 23 проблем
Д. Гильберта (D. Hilbert), поставленных им на Меж-
Международном конгрессе математиков в Париже в 1900,
относилась к этой задаче. Именно, 13-я проблема со-
состояла в следующем (см. DJ): представляется ли ко-
корень / уравнения
yP + zf+ 1 = 0 (*)
через коэффициенты ,r, pi этого уравнения посредст-
посредством композиций каких-либо непрерывных функций
двух неременных (следует отметить, что всякая функ-
функция конечного числа переменных является компози-
композицией разрывных функций двух неременных). Д. Гиль-
Гильбертом была показана невозможность получения всех
аналитич. функций трех переменных в виде компози-
композиций аналитич. функций двух переменных. Он же для
уравнения 9-й степени доказал [5|, что решение
уравнения 9-й степени можно представить в виде ком-
композиции алгебраич. функций четырех неременных (вме-
(вместо пяти, как это сразу следует из применения преоб-
преобразования Чирнгаузена). Эти исследования были про-
продолжены многими математиками (см. [6] — |19]).
А. Г. Витушкин в 1954 доказал A01, что если нату-
натуральные числа т, л, т1 и пг удовлетворяют неравен-
неравенству '^ >^?, то можно указать п раз дифференцируе-
дифференцируемую функцию т переменных, непредставимую в виде
композиции п\ раз дифференцируемых функций от
nil переменных. В частности, при всяком п можно
указать функцию п переменных наперед заданной
гладкости, непредставимую композицией функций
jiem.iiici (i числа переменных той же гладкости. В этом
с.мыс.и- среди гладких функций любого числа пере-
переменных существуют функции, существенно зависящие
от всех своих аргументов.
В 1956 А. Н. Колмогоров показал [11], что всякая
определенная на «-мерном (»^4) кубе непрерывная
функция является композицией непрерывных функций
трех переменных. Затем В. И. Арнольд уменьшил
число неременных с трех до двух. Именно, он доказал
[12], что любую непрерывную на кубе функцию трех
переменных можно представить в виде композиции
непрерывных функций двух переменных (и даже, более
точно, в виде суммы 9 функций, каждая из к-рых яв-
является однократной композицией непрерывных функ-
функций двух неременных). Тем самым было показано, что
каждая непрерывная на n-мерном (гс^З) кубе функция
нредставнма в виде композлции непрерывных функций
двух переменных. Это явилось последним словом по
опровержению гипотезы Гильберта о невозможности
представления корней уравнения (*) в виде компози-
композиций непрерывных функций двух переменных. Работы
Л. Н. Колмогорова и В. И. Арнольда дали, в частности,
положительный ответ на вопрос о представимости кор-
корней алгебраич. уравнений любой степени в виде ком-
композиции непрерывных функций не более чем двух
неременных. Для композиций аналитич. и и.'п ебраич.
функций аналогичный вопрос не решен. До сп\ пор
A983) неизвестно, являются ли корни уравнения (;.)
композицией аналитич. функций или нет.
Этот цикл работ завершает следующая теорема
Колмогорова [13]: любая непрерывная функ-
функция п переменных может быть получена с помощью
композиции непрерывных функций одного перемен-
переменного и единственной функции двух переменных
.!,'(./•, .у) .''-'-.у; именно, он доказал, что любая функция
/, непрерывная на «-мерном кубе, может быть пред-
представлена в виде
где функции h[ и ф,у— непрерывны, а функцшг ф,у,
кроме того, стандартны, т. е. не зависят от выбора
функции /.
А. Г. Витушкин показал [14], что для любых ко-
конечных наборов непрерывных функций pk и непрерыв-
непрерывно дифференцируемых функций qk, зависящих от п
переменных, k—i, 2, ..., т, n~*i, 2, ..., существуют
даже аналитич. функции п переменных, не представи-
мые композицией вида
Sft = i Рк° Уь°Як),
где !к — произвольные непрерывные функции од-
одного переменного.
Лит.: [1] Б а р и Н. К., Меньшов Д. Е., «Ann. di Mat.»,
1927, v. Г>, p. 19—54; [2] Бар и Н. К., «Math. Ann.», 193», Bd 103,
S. 185— 248, pt 2, S. 598—053; [3] e e ж е, «Матем. сб.», 1933, т. 40,
с. 326—72; [4] Проблемы Гильберта, М., 1969; [5J II i I b с г t D.,
«Math. Ann.», 1927, Bd 97, S. 243 — 51; [6] В i e b e r b а с h L.,
«J reinc u. angew. Math.», 1931, Bd 165, S. 89—92; [7J Чебо-
Чеботарев H. Г., Собр. соч., т. 1, М.— JJ , 1949,с. 255—.440; [8]Че-
ботаревГ. Н. «Уч. зап. Казанск. ун-та»,1954, т. 114, кн. 2.
с. 189—93; [9] М о р о з о в В. В., там же, 1954, т. 114, кн. 2,
с. 173—87; [10J Витушкин А. Г., О многомерных вариаци-
вариациях М., 1955; A1] Колмогоров А. Н., «Докл. АН СССР»,
1956, т. 108, № 2, с. 179—82; [12] А р н о л ь д В. II., там же,
1957, т. 114, JMs 4 с. 679—81; [13] Колмогорова. Н., там
же 1957 т. 114, .V 5, с. 953—56; [14] Витушкин А. Г., там
же, 1964, т. 156, Ли 6, с. 1258—61; [15] L о г е n t г G. G., Appro-
Approximation of functions N. Y.,—[а.о.], 1966; [16] Spree her D. A.,
«J. Approvim. Theory», 1972, v. 6, № 2, p. 123—34; [17] К a h a-
n e J. P., там же, 1975, v. 13, p. 229—34; [18] Л ин В. Я., «Функц.
анализ и его прилож.», 1976, т. 10, Л» 1, с. 37—45; [19] В и т у ш-
к ин А. Г., «Enseign. math.», 1977, t. 23, p. 255—320.
Л. Д. Кудрявцев.