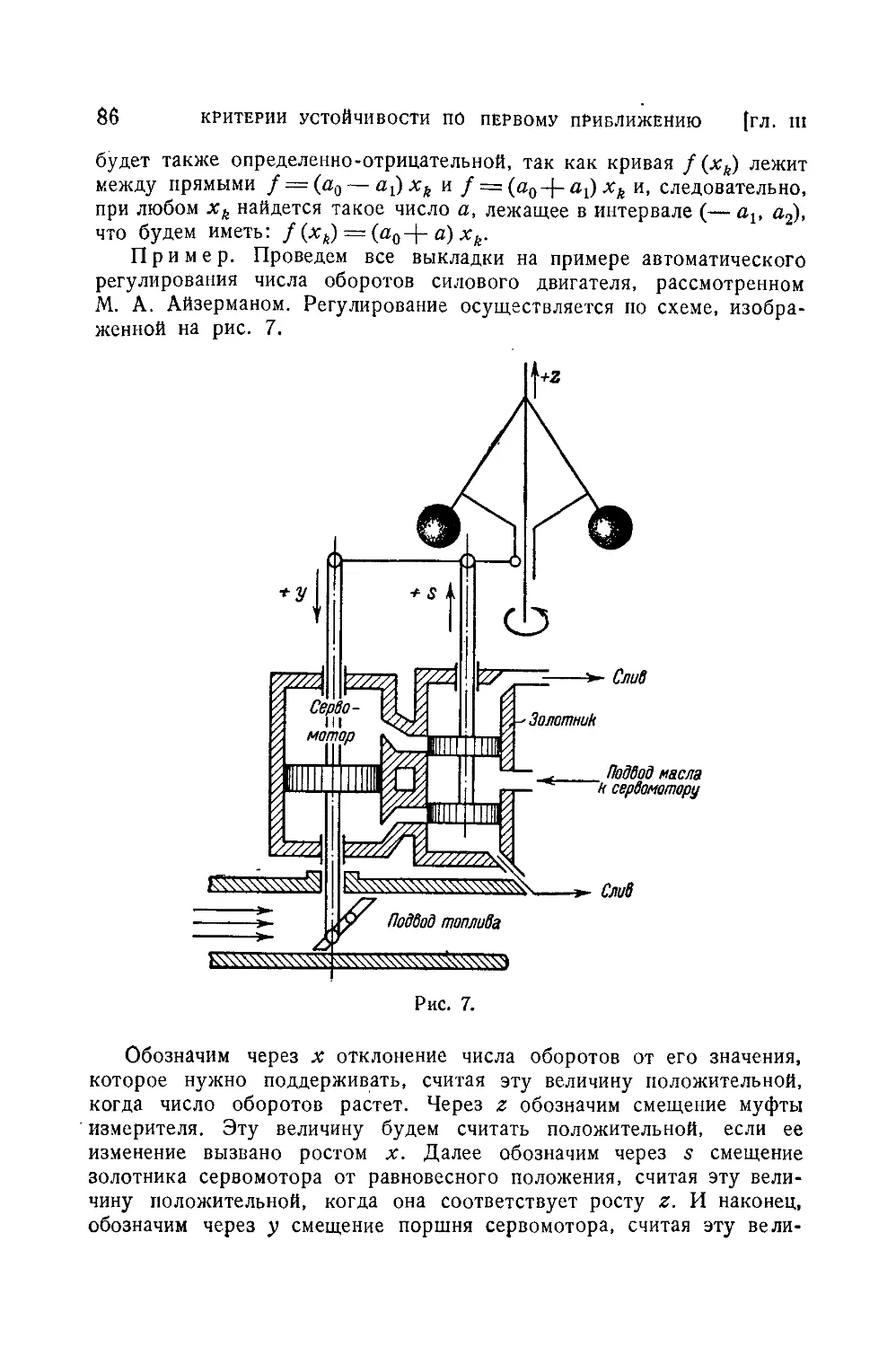
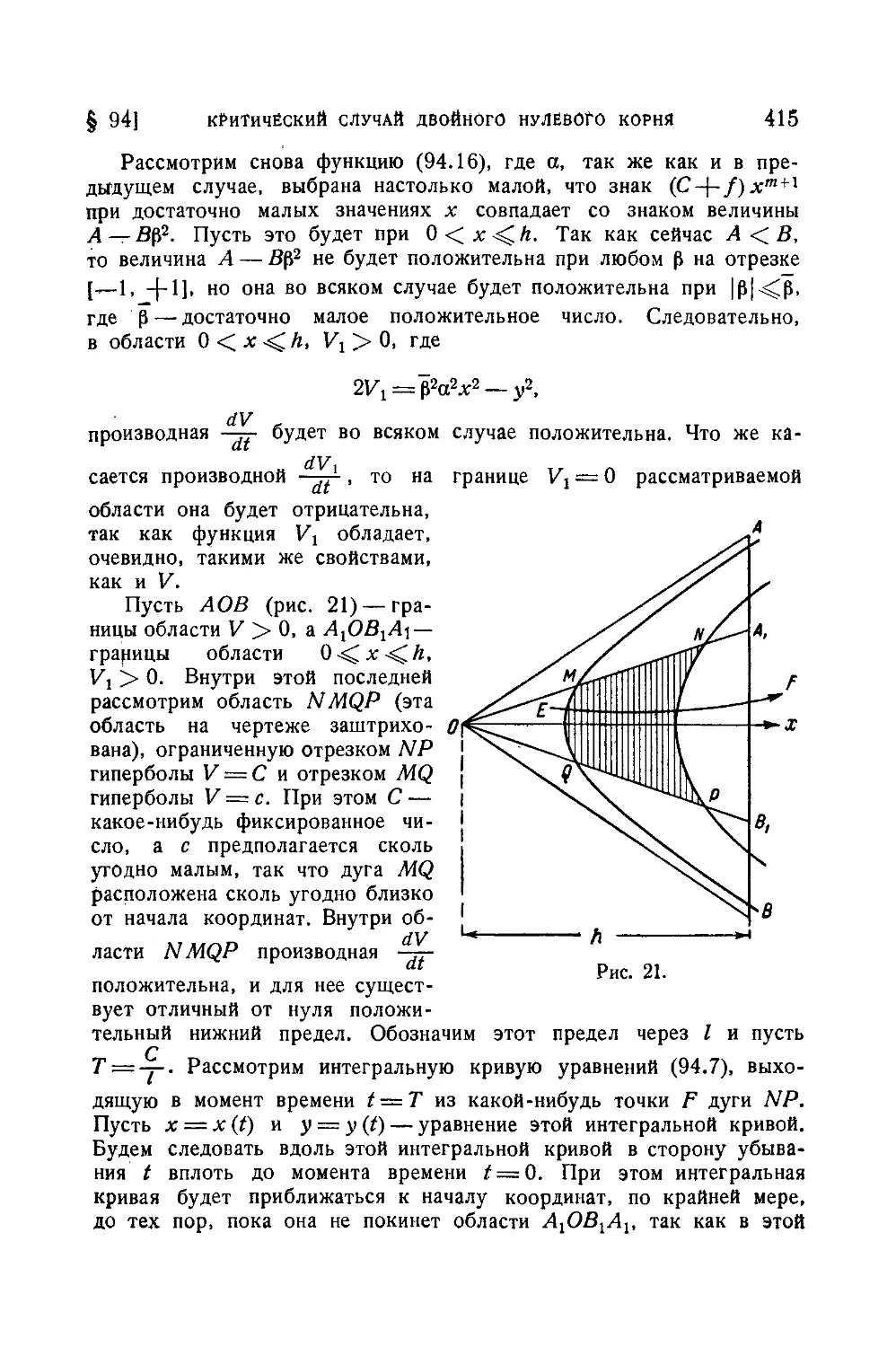
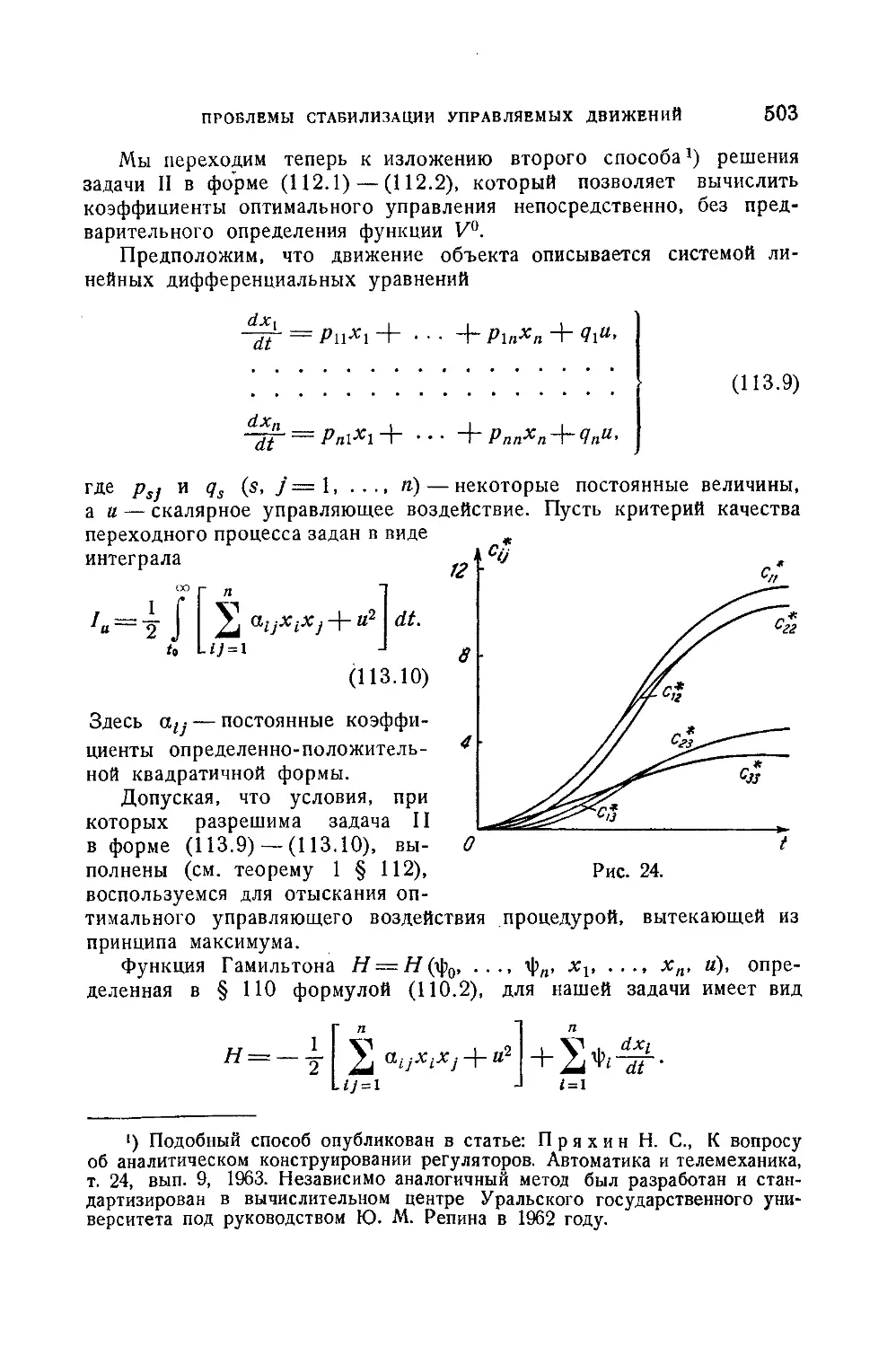
Текст
И.Г.Малкин
ТЕОРИЯ УСТОЙЧИВОСТИ ДВИЖЕНИЯ
Содержание
Предисловие автора 8
Предисловие редактора второго издания 11
Глава I. Основные понятия и определения 13
§ 1. Постановка задачи 13
§ 2. Определение устойчивости 14
§ 3. Дифференциальные уравнения возмущенного движения 17
§ 4. Устойчивость по Ляпунову и некоторые другие определения 20
устойчивости
§ 5. О методах решения задачи устойчивости 23
Глава II. Второй метод Ляпунова для установившихся движений 27
§ 6. Основные определения 27
§ 7. Признаки знакоопределенности и знакопеременности функций 28
§ 8. Геометрическая интерпретация знакоопределенных функций 33
§ 9. Первая теорема Ляпунова об устойчивости движения 34
§ 10. Вторая теорема Ляпунова об устойчивости движения 36
§11. Геометрическая интерпретация предыдущих теорем 38
§ 12. Примеры приложения предыдущих теорем 40
§ 13. Первая теорема Ляпунова о неустойчивости 47
§ 14. Теорема Ляпунова о неустойчивости равновесия, когда силовая 49
функция обращается в минимум
§ 15. Вторая теорема Ляпунова о неустойчивости 51
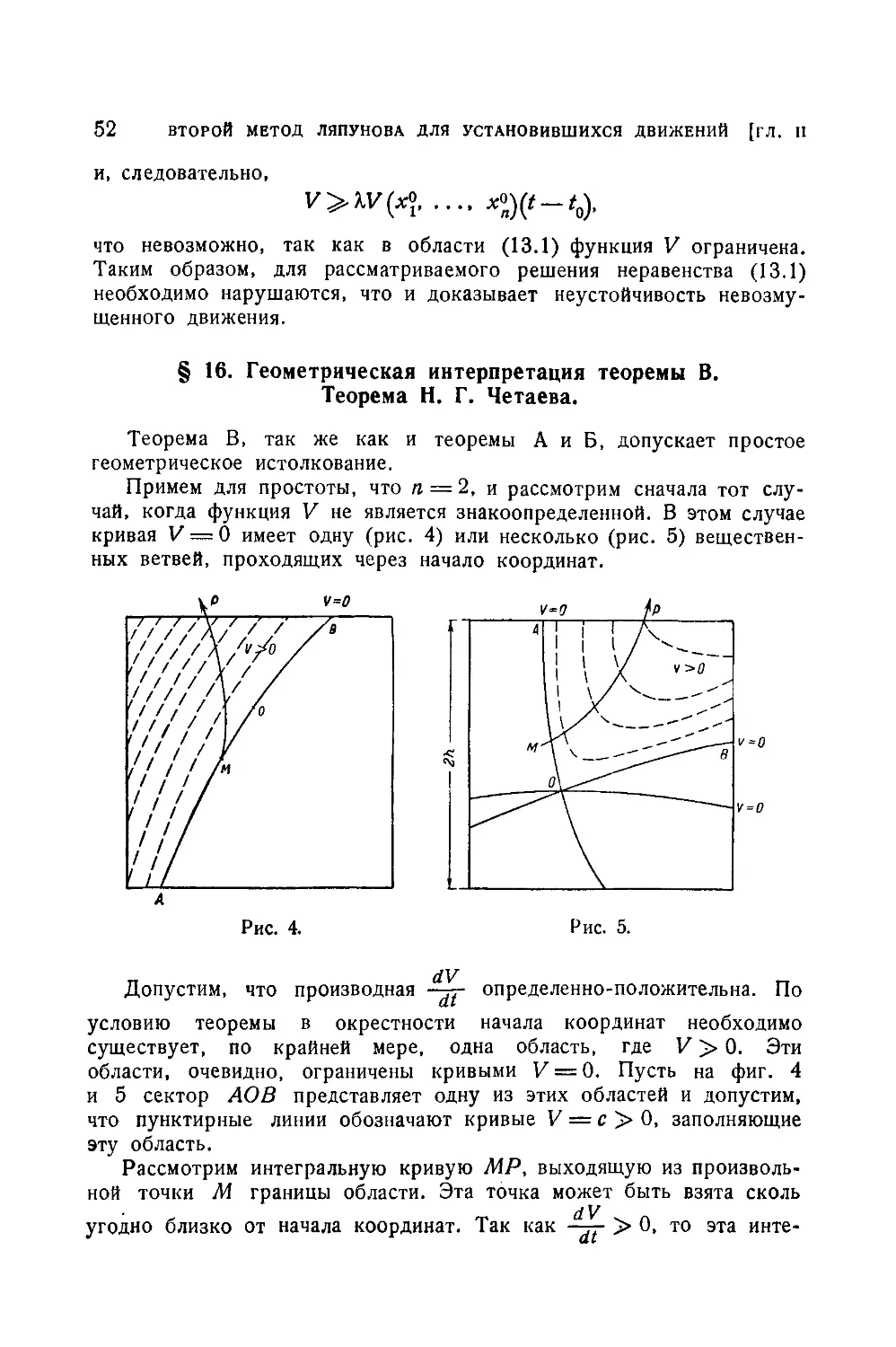
§ 16. Геометрическая интерпретация теоремы В. Теорема Н. Г. Четаева 52
§ 17. Пример приложения теоремы Н. Г. Четаева. Теорема Н. Г. Четаева 54
о неустойчивости равновесия
§ 18. Заключительные замечания 55
Глава III. Критерии устойчивости по первому приближению для 57
установившихся движений
§ 19. Уравнения первого приближения 57
§ 20. Некоторые вспомогательные предложения 62
§ 21. Построение функций Ляпунова для систем линейных уравнений с 67
постоянными коэффициентами
§ 22. Теоремы Ляпунова об устойчивости по первому приближению 71
§ 23. Примеры приложения предыдущих теорем 74
§ 24. Неустойчивость равновесия. Случай канонических систем 76
§ 25. Теорема Гурвица 80
§ 26. Обобщение теорем Ляпунова об устойчивости по первому 81
приближению. Приложение к регулируемым системам
§ 27. Заключительные замечания 89
Глава IV. Исследование критических случаев для установившихся 90
движений
§ 28. Случай одного нулевого корня. Приведение уравнений к 90
специальному виду
§ 29. Исследование задачи для случая системы первого порядка 92
§ 30. Исследование задачи для системы (п+1)-го порядка в частном 93
случае
§ 31. Исследование задачи для системы (п+1)-го порядка в общем 101
случае
§ 32. Примеры 104
§ 33. Особенный случай 108
§ 34. Решение задачи устойчивости в особенном случае 112
§ 35. Случай пары чисто мнимых корней. Приведение уравнений 118
возмущенного движения к специальному виду
§ 36. Системы второго порядка. Первый способ решения задачи 120
§ 37. Системы второго порядка. Второй способ решения задачи 132
§ 38. Системы второго порядка. Третий способ решения задачи 139
§ 39. Вспомогательное предложение 149
§ 40. Исследование системы (п+2)-го порядка в частном случае 153
§ 41. Исследование системы (п+2)-го порядка в общем случае 159
§ 42. Другой способ решения задачи 169
§ 43. Особенный случай 176
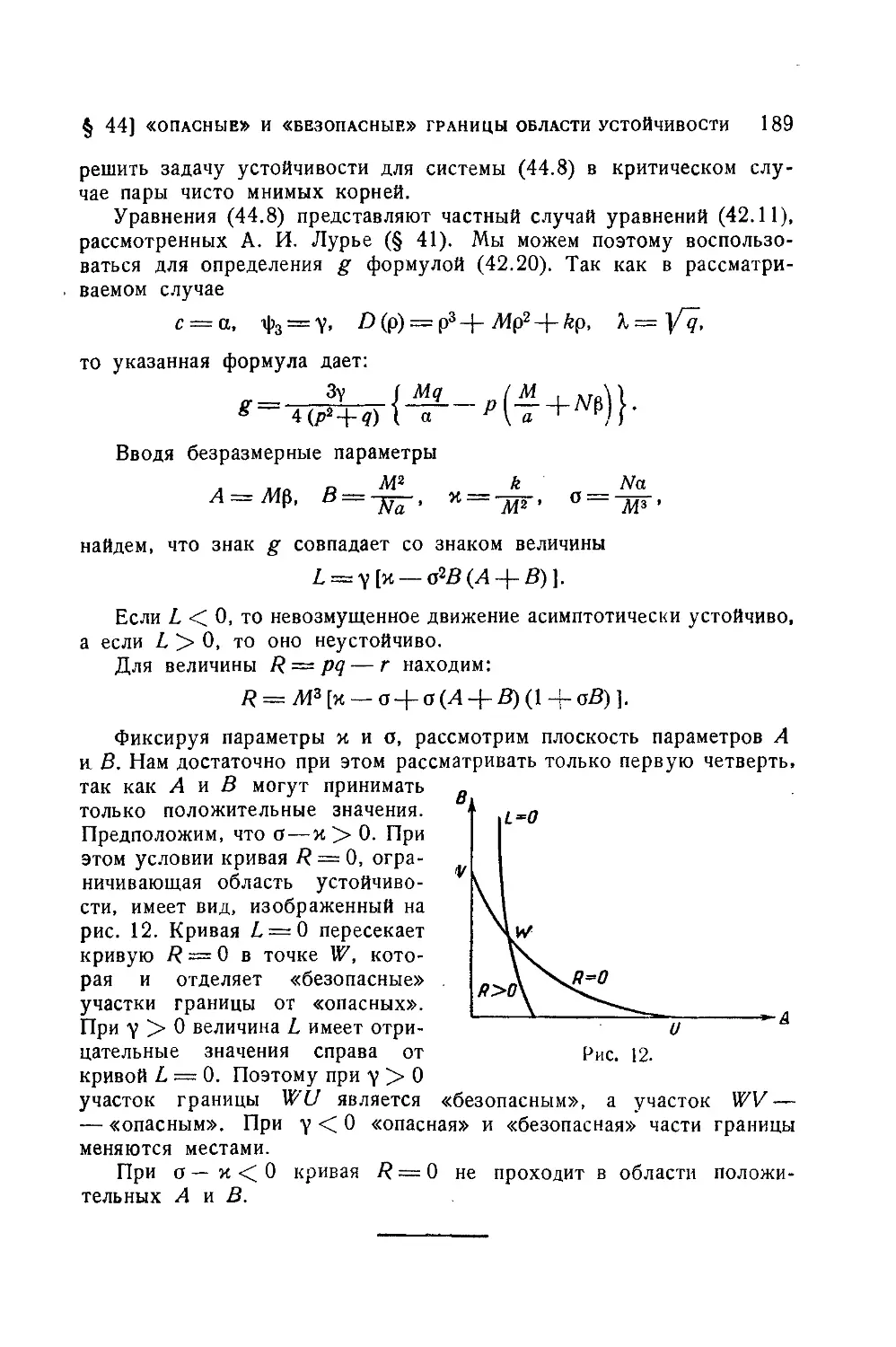
§ 44. «Опасные» и «безопасные» границы области устойчивости 181
Глава V. Устойчивость периодических движений 190
А. Теоремы второго метода для неустановившихся движений
§ 45. Некоторые определения 190
§ 46. Теоремы Ляпунова об устойчивости для неустановившихся 192
движений
§ 47. Теорема Ляпунова о неустойчивости для неустановившихся 196
движении
§ 48. Теорема Н. Г. Четаева 198
Б. Линейные уравнения с периодическими коэффициентами
§ 49. Постановка задачи 199
§ 50. Характеристическое уравнение системы линейных уравнений с 200
периодическими коэффициентами
§ 51. Аналитический вид решений в случае простых корней 203
характеристического уравнения
§ 52. Аналитический вид решений в случае кратных корней 205
характеристического уравнения
§53. Обратное предложение 213
§ 54. Теорема Ляпунова о приводимости линейных уравнений с 215
периодическими коэффициентами
§ 55. Определяющее уравнение приведенной системы. Теорема 220
Ляпунова о корнях характеристических уравнении сопряженных
систем
§ 56. Критерии устойчивости 222
§ 57. Характеристическое уравнение канонических систем 224
§ 58. Вычисление корней характеристического уравнения методом 227
разложения по степеням параметра
§ 59. Приложение к системе второго порядка 229
§ 60. Некоторые технические задачи, приводящиеся к уравнению 236
второго порядка с периодическими коэффициентами, и связанные
с этим вопросы теории
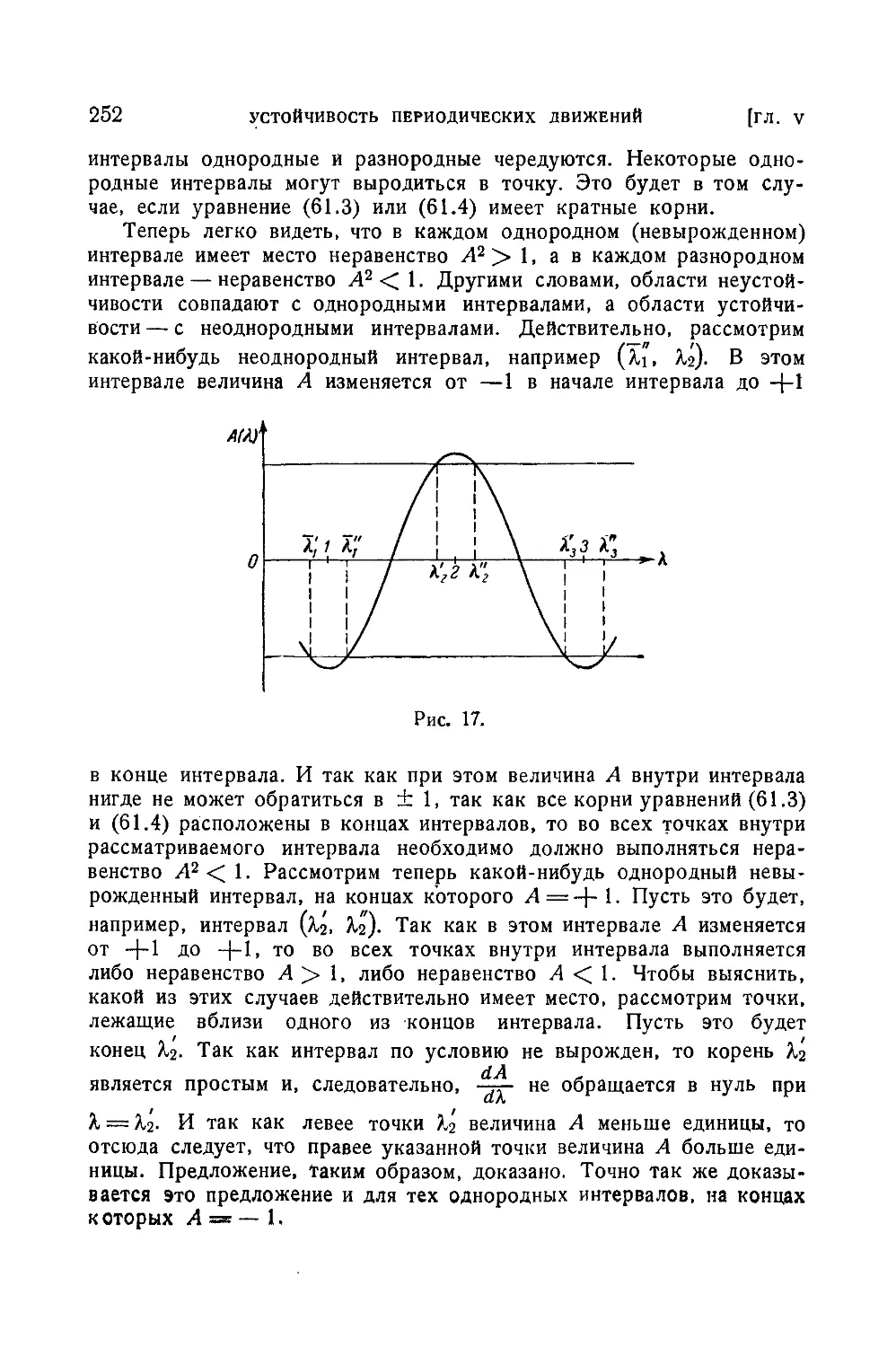
§ 61. Области устойчивости и неустойчивости для уравнений второго 245
порядка
§ 62. Практический способ определения областей устойчивости и 253
неустойчивости для уравнений второго порядка
§ 63. Примеры приложения метода предыдущего параграфа 262
В. Нелинейные уравнения с периодическими коэффициентами
§ 64. Критерии устойчивости по первому приближению 270
§ 65. Критические случаи 273
§ 66. Критический случай, когда характеристическое уравнение имеет 275
один, равный единице корень
§ 67. Критический случай, когда характеристическое уравнение имеет 285
два комплексных корня с модулями, равными единице
§ 68. Устойчивость периодических движений автономных систем 295
Глава VI. Неустановившиеся движения 300
А. Некоторые общие предложения
§ 69. Постановка задачи 300
§ 70. Теорема об устойчивости при постоянно действующих 301
возмущениях
§ 71. Проблема существования функций Ляпунова 305
§ 72. Некоторые свойства установившихся и периодических движений 307
§ 73. Теорема о существовании функций Ляпунова для периодических 310
и установившихся движений в случае асимптотической
устойчивости
§ 74. Основная теорема об устойчивости при постоянно действующих 315
возмущениях для периодических и установившихся движений.
Приложение к вопросу об «опасных» и «безопасных» границах
области устойчивости
§ 75. Условия существования функций Ляпунова для линейных 317
уравнений в случае асимптотической устойчивости
Б. Теория первого приближения
§ 76. Характеристичные числа Ляпунова 325
§ 77. Основные свойства характеристичных чисел 328
§ 78. Характеристичные числа решений линейных дифференциальных 331
уравнений
§ 79. Правильные и неправильные системы 335
§ 80. Устойчивость характеристичных чисел систем линейных 342
дифференциальных уравнений
§ 81. Некоторые признаки устойчивости характеристичных чисел 344
систем линейных дифференциальных уравнений
§ 82. Критерий положительности характеристичных чисел 351
§ 83. Оценка характеристичных чисел методом построения функций 354
Ляпунова
§ 84. Применение метода малого параметра 357
В. Теория устойчивости по первому приближению
§ 85. Теорема об устойчивости по первому приближению 364
§ 86. Некоторые особенности задачи устойчивости по первому 366
приближению для неустановившихся движений
§ 87. Критерий Ляпунова 370
§ 88. Другая группа критериев 374
§ 89. Связь с критерием Ляпунова. Обобщенный критерий 377
Г. Теория критических случаев
§ 90. Постановка задачи. Основные определения 379
§ 91. Первая основная теорема о критических случаях 382
§ 92. Вторая основная теорема о критических случаях 395
§ 93. Случай, когда коэффициенты линейных членов постоянны. 400
Приложение к установившимся и периодическим движениям
§ 94. Критический случай двойного нулевого корня для 409
установившихся движений
§ 95. Критический случай двух пар чисто мнимых корней для 422
установившихся движений
§ 96. Критический случай одного нулевого и пары чисто мнимых 431
корней для установившихся движений
§ 97. Критические случаи периодических движений. Приведение к 437
установившимся движениям
Дополнение I. Об одной задаче теории устойчивости систем 446
автоматического регулирования
§ 98. Постановка задачи 446
§ 99. Исследование системы второго порядка с нелинейностью, 447
зависящей от первой координаты
§ 100. Исследование системы второго порядка с нелинейностью, 450
зависящей от второй координаты
Дополнение II. О существовании функций Ляпунова 452
§ 101. Постановка задачи 452
§ 102. Необходимые и достаточные условия существования функции V 453
Дополнение III. Обобщение теорем второго метода Ляпунова 463
§ 103. Критерии, основанные на функциях Ляпунова со 463
знакопостоянными производными
§ 104. Примеры приложения предыдущих теорем 467
Дополнение IV. Проблемы стабилизации управляемых движений 475
§ 105. Предварительные замечания 475
§ 106. Постановка задачи о стабилизации 476
§ 107. Постановка задачи об оптимальной стабилизации 478
§ 108. Пример задачи о стабилизации 480
§ 109. Второй метод Ляпунова для задач об оптимальной стабилизации 484
§ 110. Замечания ко второму методу Ляпунова в теории стабилизации 489
§111. Решение задачи о стабилизации для уравнений первого 492
приближения
§ 112. Достаточные условия разрешимости задачи о стабилизации для 495
линейных систем
§ 113. Практические способы решения задач об оптимальной 499
стабилизации для линейных систем
§ 114. Теоремы стабилизации по первому приближению 508
Примечания редактора 515
ПРЕДИСЛОВИЕ АВТОРА
За последние годы значительно возрос интерес к теории устой-
устойчивости движения. Созданная в 90-х годах прошлого века гением
А. М. Ляпунова эта теория нашла широкое применение в различных
областях физики и техники. Ее широкому внедрению в практику
способствовали многочисленные исследования главным образом совет-
советских ученых. Появилась настоятельная необходимость дать система-
систематическое изложение теории, применяемых в ней методов, показать
их приложение к решению конкретных практических задач. Этой
цели и служит настоящая книга, как и ранее вышедшая книга
Н. Г. Четаева «Устойчивость движения» A946 г.).
Однако настоящая книга значительно превышает по объему книгу
Н. Г. Четаева, что позволило автору остановиться не только на
основных узловых вопросах теории, но и на некоторых подробностях
отдельных вопросов. Для читателя-прикладника, на которого книга,
в основном, и рассчитана, эти подробности, касающиеся часто мето-
методов вычислений, могут оказаться очень. важными. Вместе с тем
автор сознает, что увеличение объема книги затрудняет ее усвоение,
в особенности для читателя, который впервые будет знакомиться
с теорией устойчивости по этой книге и не обладает большой ма-
математической подготовкой. Чтобы облегчить усвоение книги та-
такому читателю, автор придерживается концентрического метода
изложения.
Первый концентр составляют главы I, II и III. В них излагается
постановка вопроса, основные теоремы второго метода Ляпунова для
установившихся движений и теория устойчивости по первому при-
приближению тоже для установившихся движений. Эти три главы зани-
занимают небольшой объем и охватывают основной круг знаний, необхо-
необходимых для каждого, занимающегося вопросами устойчивости движе-
движения. Изучение этих глав требует знания лишь основных элементов
ПРЕДИСЛОВИЕ АВТОРА 9
теории дифференциальных уравнений и вполне доступно для лиц,
владеющих математикой в объеме программ втузов.
Глава VI — несколько более трудная по содержанию. В ней изла-
излагаются классические критические случаи для установившихся движе-
движений. Еще более трудной для изучения является глава V, в которой
излагается теория устойчивости периодических движений. Изложение
этой теории может быть значительно упрощено, если отказаться от
рассмотрения всех случаев, когда характеристическое уравнение имеет
кратные корни. Однако автор не мог пойти на такое упрощение,
учитывая интересы читателей, желающих более глубоко изучить теорию
устойчивости движения. Аатор учитывал также и то, что теория урав-
уравнений с периодическими коэффициентами (линейных и нелинейных)
имеет очень важноз практическое значение, и счел необходимым дать
подробное и систематическое изложение этой теории, особенно тех ее
частей, которые имеют непосредственное приложение к практике.
Главы IV и V составляют второй концентр. Хотя он и труднее
для изучения, чем первый концентр, он все же доступен читателю,
имеющему математическую подготовку в объеме программы втузов.
Глава VI посвящена общему случаю неустановившихся движений.
Ее изучение требует знания теории дифференциальных уравнений
в объеме, например, «Курса дифференциальных уравнений» В. В. Сте-
Степанова.
Концентрическое ' построение книги отразилось, естественно, на
стиле изложения. В первых главах сравнительно простые вопросы
сопровождаются подробными разъяснениями, в то время как в послед-
последней главе вопросы значительно более сложные излагаются лаконичнее.
Однако автор надеется, что этот недостаток искупается тем, что
книга при таком изложении делается доступной значительно более
широкому кругу читателей.
Как уже указывалось выше, книга рассчитана главным образом
на прикладника. Поэтому практическим приемам решения задач устой-
устойчивости уделяется основное внимание. Все излагаемые методы сопро-
сопровождаются поясняющими примерами. Часть этих примеров взята из те-
текущей технической литературы. Однако автор не ставил себе целью
решение тех или иных технических или физических задач. Его целью
является изложение основных приемов решения задач устойчивости
для того, чтобы дать возможность овладеть этими приемами лицам,
которым приходится решать конкретные физические или технические
10 ПРЕДИСЛОВИЕ АВТОРА
задачи, связанные с вопросами устойчивости. Поэтому приводимые
примеры носят иллюстративный характер. Они преследуют цель пока-
показать, как основные методы, излагаемые в книге, могут быть приме-
применены к решению конкретных задач и как эти методы действительно
применялись отдельными исследователями на практике. Поэтому все
эти задачи, как правило, излагаются значительно короче, чем в ори-
оригинальных статьях, и часто при некоторых упрощающих предположе-
предположениях. Читатель, который пожелает с этими вопросами познакомиться
более подробно, должен обратиться к цитируемой литературе.
В заключение автор выражает глубокую благодарность Н. Г. Че-
таеву и А. И. Лурье, прочитавшим рукопись настоящей работы и
сделавшим ряд ценных замечаний.
И. Малкин
ПРЕДИСЛОВИЕ РЕДАКТОРА ВТОРОГО ИЗДАНИЯ.
Книга И. Г. Малкина «Теория устойчивости движения», первое
издание которой вышло в 1952 году, является ценным научным руко-
руководством, получившим широкое признание. Несмотря на 12 лет, кото-
которые прошли со времени написания книги, эта монография, содержа-
содержащая весьма доступное и в то же время строгое изложение основных
положений теории устойчивости движения, сохраняет важное значе-
значение. Она продолжает пользоваться постоянным спросом у специали-
специалистов и у лиц, начинающих изучение предмета. Это служит веским
основанием для переиздания книги, причем следует также учитывать
большой интерес к основам теории устойчивости движения, вызван-
вызванный развитием новых задач устойчивости и управления.
В настоящем, посмертном издании монографии И. Г. Малкина
сохранен первоначальный текст книги. При редактировании внесены
лишь небольшие изменения, связанные только с необходимостью
устранить отдельные бесспорные неточности. Некоторые ссылки на
литературу заменены более доступными сейчас источниками. Кроме
того, редактор счел целесообразным добавить к тексту монографии
материал, отражающий в известной мере развитие теории устойчи-
устойчивости в годы, прошедшие после выхода в свет первого издания.
Этот ограниченный материал ни в коей мере не может, конечно,
отразить со всей полнотой новые направления исследований и резуль-
результатов. Были выбраны лишь некоторые исследования, относящиеся
главным образом к теории метода функций Ляпунова и имеющие
самое прямое отношение к данной монографии.
Добавления к книге распадаются на четыре основные части.
Первую часть добавлений составляют дополнение 1 и дополнение II,
где даны с небольшими изменениями две важные работы И. Г. Малкина:
«Об одной задаче теории устойчивости систем автоматического регу-
регулирования» и «О существовании функции Ляпунова», опубликованные
в журнале «Прикладная математика и механика» после выхода пер-
первого издания книги. Включение этих работ в настоящее издание обо-
обосновывается тем, что каждая из них находится у истоков двух на-
направлений исследований, которые сыграли существенную роль в раз-
развитии теории устойчивости движения в пятидесятые годы.
Вторую часть добавлений составляет дополнение III, в котором при-
приведены обобщения теорем Ляпунова об асимптотической устойчивости
12 ПРЕДИСЛОВИЕ РЕДАКТОРА ВТОРОГО ИЗДАНИЯ
и неустойчивости на случаи функций со знакопостоянной произ-
производной. Включение этого материала представляется целесообразным по
той причине, что эти теоремы находят применение при исследовании ус-
устойчивости нелинейных систем при больших начальных возмущениях.
Третью часть добавлений составляет дополнение IV, где дан
краткий очерк о приложении методов теории устойчивости движения
к задачам оптимальной стабилизации управляемых систем. Включение
этого материала вызвано следующими обстоятельствами. С одной сто-
стороны, в последнее время несомненно весьма возрос интерес к зада-
задачам оптимального управления, и в частности — к задачам стабилизации
управляемых движений. С другой стороны, широкий круг таких
задач решается методами, которые тесно переплетаются с методами
классической теории устойчивости. Теорию стабилизации управляе-
управляемых движений можно рассматривать как развитие задач устойчивости,
изученных в данной монографии, в приложении к новым проблемам
для управляемых систем. Это определяет тесную связь и преемствен-
преемственность упомянутых проблем с материалом монографии.
В конце книги даны постраничные примечания, которые в весьма
краткой форме упоминают новые результаты и литературу по вопро-
вопросам, затронутым в монографии.
При редактировании книги деликатным моментом был выбор ссылок
на новые работы. В первом издании автор предпочел весьма эконом-
экономный стиль цитат, ограничившись лишь небольшим числом ссылок,
которые он считал совершенно необходимыми. Мы не сочли себя
вправе изменять этот стиль, считая его целесообразным для моно-
монографии подобного характера. В соответствии с этим добавочный
материал также снабжен ссылками на довольно узкий круг работ.
Читатель должен иметь в виду, что при этом многие важные иссле-
исследования остались не упомянутыми. Отбор материала для добавлений,
естественно, неизбежно был ограничен возможностями и интересами
редактора. Только этим обстоятельством следует объяснить большой
удельный вес ссылок на работы свердловских авторов.
В подготовке настоящего издания принял участие коллектив
кафедры механики Уральского госуниверситета им. А. М. Горького,
состоящий из учеников И. Г. Малкина. Особенно большая работа
при подготовке дополнительного материала была проделана сотруд-
сотрудниками кафедры Э. Г. Альбрехтом, А. И. Огурцовым, Ю. С. Оси-
повым, В. Е. Третьяковым. При редактировании мы старались учесть
все известные нам отзывы и замечания по книге. Особенно полезную
службу сослужила острая рецензия Н. П. Еругина'), содержащая
подробную критику книги.
Н. Красовский
') См. Еругин Н. П., И. Г. Малкин «Теория устойчивости движе-
ЛГУ, У
ния», Вестник ЛГУ, № 5, 1953.
ГЛАВА I.
ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ.
§ 1. Постановка задачи.
Теория устойчивости движения занимается исследованием влия-
влияния возмущающих факторов на движение материальной системы.
Под возмущающими факторами понимаются силы, не учитываемые
при описании движения вследствие их малости по сравнению с основ-
основными силами. Эти возмущающие силы обычно неизвестны. Они могут
действовать мгновенно, что сведется к малому изменению начального
состояния материальной системы, т. е. начальных значений координат
и скоростей. Но эти факторы могут действовать и непрерывно, что
будет означать, что составленные дифференциальные уравнения дви-
движения отличаются от истинных, что в них не учтены некоторые
малые поправочные члены.
Хорошо известно, что влияние малых возмущающих факторов
на движение материальной системы будет неодинаковым для различ-
различных движений. На одни движения это влияние незначительно, так
что возмущенное движение мало отличается от невозмущенного.
Напротив, на других движениях влияние возмущений сказывается
весьма значительно, так что возмущенное движение значительно отли-
отличается от невозмущенного, как бы малы ни были возмущающие
силы. Движения первого рода называются устойчивыми, движения
второго рода — неустойчивыми.
Теория устойчивости движения и занимается установлением при-
признаков, позволяющих судить, будет ли рассматриваемое движение
устойчивым или неустойчивым. Так как в действительности возмущаю-
возмущающие факторы всегда неизбежно существуют, то становится понят-
понятным, что задача устойчивости движения приобретает очень важное
теоретическое и практическое значение.
Задачей устойчивости движения занимались многие виднейшие
математики и механики. Основная теорема об устойчивости равно-
равновесия установлена еще Лагранжем. Она служила исходным пунктом
Для исследований Рауса, который установил признаки устойчивости
движения для некоторых частных случаев движений. Задачей устой-
14 ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ [ГЛ. !
чивости занимались также Томсон и Тэт и Н. Е. Жуковский. Все
эти авторы рассматривали весьма частные случаи движений и для
решения задачи применяли нестрогие методы. Первое строгое реше-
решение задачи принадлежит Пуанкаре. Однако результаты Пуанкаре также
носят весьма частный характер.
В 1892 году появилась знаменитая докторская диссертация
А. М. Ляпунова «Общая задача об устойчивости движения»1). В этом
замечательном труде задача об устойчивости движения была впервые
поставлена во всей ее общности и были предложены мощные и вместе
с тем строгие методы ее решения. Эта работа Ляпунова явилась
отправным пунктом всех дальнейших исследований по теории устой-
устойчивости движения.
Выше мы дали весьма схематичное определение устойчивости и
неустойчивости движения. Эти понятия требуют, разумеется, более
точного определения. Различные авторы по-разному определяли эти
понятия и вследствие этого по-разному ставили задачу устойчивости.
Наиболее общая постановка задачи дана Ляпуновым. Эта постановка
оказалась исключительно удачной и наиболее соответствующей нуждам
приложений. Этим и объясняется тот особый интерес, который
проявлен к теории Ляпунова в последние годы, когда современная
техника, в которой приходится иметь дело с огромными скоростями
и широким внедрением автоматики, сделала особо актуальной задачу
об устойчивости движения.
Эта книга посвящена теории устойчивости движения в смысле
Ляпунова. В ней излагаются основные результаты Ляпунова и его по-
последователей.
§ 2. Определение устойчивости.
Понятие об устойчивости движения является непосредственным
обобщением понятия устойчивости равновесия, которое, как известно,
заключается в следующем.
Рассмотрим произвольную динамическую систему с k степенями
свободы, определяемую обобщенными координатами qx, q2, ¦ ¦ ¦, q^.
Допустим, что рассматриваемая система имеет положение равновесия,
определяемое значениями at обобщенных координат, так что уравнения
движения допускают частное решение qL = аг. Выведем систему из
положения равновесия, отклонив ее координаты на величины е(-, и
сообщим ей начальные скорости г'г т. е. рассмотрим движение
системы, определяемое начальными условиями:
= е; (* = 1. 2 к).
') Ляпунов А. М., Общая задача об устойчивости движения, Харь-
Харьков, 1892. 3-е изд., Гостехиздат, 1950. В дальнейшем при изложении тех или
иных результатов А. М. Ляпунова всегда имеется в виду, если противное не
оговорено, эта работа.
§2]
ОПРЕДЕЛЕНИЕ УСТОЙЧИВОСТИ
15
Если для всех такого рода движений отклонения координат
q. — <Х( и скорости будут все время оставаться численно меньшими
сколь угодно малого положительного числа 8 при условии, что
начальные отклонения е,- и начальные скорости е(' численно меньше
достаточно малого положительного числа т|, то равновесие называется
устойчивым. В противном случае равновесие неустойчиво.
Простейшими известными примерами устойчивого и неустойчивого
равновесия являются, соответственно, нижнее и верхнее вертикаль-
вертикальные положения маятника, когда его центр тя-
тяжести не лежит на оси подвеса.
Отметим два основных момента, вытекаю-
вытекающих из определения устойчивости:
1) Об устойчивости или неустойчивости
равновесия судят по характеру тех движений,
которые имеют место вблизи положения равно-
равновесия.
2) Для устойчивости равновесия необхо-
необходимо, чтобы подходящим выбором начальных
отклонений системы от ее положения равнове-
равновесия и начальных скоростей можно было до-
добиться, чтобы эти отклонения и скорости оста-
оставались меньше любого наперед заданного числа.
Так что, например, верхнее вертикальное по-
положение маятника, показанного на рис. 1, будет
неустойчивым, как бы мал ни был угол а,
так как отклонение маятника от положения равновесия не может быть
сделано меньше а, как бы ни были выбраны начальные условия
движения.
Совершенно аналогично устойчивости равновесия определяется по
Ляпунову устойчивость движения.
Рассмотрим произвольную динамическую систему и допустим,
что ее движение может быть описано системой дифференциальных
уравнений, которая может быть приведена к нормальному виду:
Рис. 1.
;~\, 2 га).
B.1)
Здесь ys— некоторые параметры, связанные с движением, как,
например, координаты, скорости или вообще некоторые функции
этих величин.
Рассмотрим какое-нибудь частное движение нашей системы, кото-
которому соответствует некоторое частное решение ys = fs (t) уравне-
уравнений B.1). Мы будем это движение называть невозмущенным
в отличие от других движений нашей системы, которые мы
будем называть возмущенными. Разности значений величин ys в
16 ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ [ГЛ. I
каком-нибудь возмущенном и в невозмущенном движениях будем
называть возмущениями.
Определение. Невозмущенное движение называется устой-
устойчивым по отношению к величинам ys, если для всякого положи-
положительного числа е, как бы мало оно ни было, найдется другое
положительное число т| (е), такое, что для всех возмущенных
движений ys = ys(t), для которых в начальный момент t~t0
выполняются неравенства
I У, Со)-Л Со) К Л. B-2)
будут при всех t > t0 выполняться неравенства
|У,О —ЛС)| <е. B.3)
Невозмущенное движение называется неустойчивым, если оно не
является устойчивым. Таким образом, для неустойчивости движения
достаточно, чтобы существовало какое-нибудь фиксированное число е
и при любом сколь угодно малом т] хотя бы одно возмущенное
движение, для которого выполняются неравенства B.2) и для кото-
которого в некоторый момент времени хотя бы одно из неравенств B.3)
переходит в равенство.
В качестве примера рассмотрим снова обыкновенный маятник,
но исследуем устойчивость не равновесия этого маятника, а какого-
нибудь его движения, определяемого начальными условиями ср(^0)=а,
ф(^0) = 0, где ф — угол отклонения от вертикали, а > 0. Покажем,
что это движение неустойчиво по отношению к ср и ф. Рассмотрим
с этой целью какое-нибудь возмущенное движение, определяемое
начальными условиями <p(?0) = a-f-6, ф(?0) = 0, где б—сколь угодно
малая положительная величина. Как известно, период колебаний
маятника зависит от начальных условий и при начальной скорости,
равной нулю, будет тем больше, чем больше начальная амплитуда.
Поэтому период Т колебаний возмущенного движения будет больше
периода Т колебаний невозмущенного движения. Следовательно,
разность углов <р в обоих движениях, будучи в начальный момент
равной 6, по истечении промежутка времени Т' несколько увели-
увеличится. Это увеличение будет тем меньше, чем меньше 6. Но, как бы
мало ни было 6, по истечении достаточно большого промежутка
времени разность значений ф, постепенно накапливаясь, станет больше,
чем, например, а. Следовательно, невозмущенное движение не-
неустойчиво.
Примером устойчивого движения может служить колебание цикло-
циклоидального маятника. Устойчивость движения в рассматриваемом слу-
случае обусловливается тем, что период колебаний циклоидального маят-
маятника не зависит, как известно, от начальных условий.
§ 3] ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВОЗМУЩЕННОГО ДВИЖЕНИЯ 17
Может случиться, что невозмущенное движение не только устой-
устойчиво, но и что все возмущенные движения, для которых начальные
возмущения достаточно малы, при неограниченно возрастающем t
стремятся асимптотически к невозмущенному. В этом случае мы
будем говорить, что невозмущенное движение устойчиво асимпто-
асимптотически.
§ 3. Дифференциальные уравнения возмущенного движения.
Для исследования устойчивости целесообразно преобразовать
уравнения движения к новым переменным:
*, = У,-Д@ (*=1. 2, .... л). C.1)
Здесь fs(t) — частное решение уравнений B.1), соответствующее не-
невозмущенному движению и, следовательно, xs — возмущения.
Полученные таким образом преобразованные уравнения
называются дифференциальными уравнениями возмущенного дви-
движения. Каждому движению рассматриваемой системы соответствует
частное решение уравнений C.2). В частности, невозмущенному дви-
движению соответствует, очевидно, тривиальное решение х1 = ... =
= хп = 0, которое, следовательно, система C.2) должна иметь.
А для этого необходимо, чтобы функции Xs{t, x1 хп) обраща-
обращались в нуль при хг= ... = хп = 0, что действительно имеет место,
как это непосредственно видно из уравнений C.2).
В переменных xs неравенства B.2) и B.3) принимают соответ-
соответственно вид
¦кД^КЛ C.3)
\xs(t)\ <е, C.4)
и, следовательно, определение устойчивости формулируется следую-
следующим образом.
Невозмущенное движение устойчиво, если для всякого поло-
положительного числа е, как бы мало оно ни было, можно подо-
подобрать другое положительное число т|(е), такое, что для всех
возмущенных движений, для которых в начальный момент
времени t0 выполняются неравенства C.3), при всех t > @
будут выполняться неравенства C.4).
Если невозмущенное движение устойчиво и если число т| можно
выбрать настолько малым, что для всех возмущенных движений,
18 ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ [ГЛ. I
удовлетворяющих неравенствам C.3), будут выполняться условия
lim xs(i) = 0, C.5)
t-+oo
то невозмущенное движение называется устойчивым асимптоти-
асимптотически ').
Рассмотрим несколько примеров на составление уравнений возму-
возмущенного движения.
Пример 1. В качестве первого примера рассмотрим колебания
математического маятника длиной /, описываемые, как известно,
дифференциальным уравнением
-^| = —f slncp, C.6)
где ф — угол отклонения от вертикали. Пусть требуется исследовать
( rf\
устойчивость относительно ф и —п-\ движения, определяемого
начальными условиями ср(О) = а, (—гг| = 0. Соответствующее част-
\ at /о
ное решение уравнения C.6) имеет вид
Ф = /@.
где f(t) — некоторая периодическая функция, которую нам нет необ-
необходимости выписывать явно.
Полагая х = ф — f (f), получим дифференциальное уравнение воз-
возмущенного движения в виде
или, разлагая в ряд по степеням х,
-^- = -j-x cos
Это уравнение может быть, конечно, представлено в виде системы
двух уравнений первого порядка.
Пример 2. Рассмотрим твердое тело, вращающееся вокруг
закрепленной точки по инерции. Дифференциальные уравнения движе-
движения имеют вид
~B)qr =0,
~-
C.8)
') См. примечание в конце книги (стр. 515).
§ 3] ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВОЗМУЩЕННОГО ДВИЖЕНИЯ 19
где р, q, r — проекции вектора мгновенной угловой скорости на
подвижные оси координат, совпадающие с главными осями инерции
тела в закрепленной точке, а А, В, С — моменты инерции относи-
относительно этих осей.
Уравнения C.8) имеют частное решение
р = а = const., q=r = 0 C.9)
и два аналогичных частных решения, соответствующие двум другим
осям координат. Принимая движение C.8) за невозмущенное, положим:
х = р — и, y — q, z — r
и, подставляя в C.8), получим дифференциальные уравнения возму-
возмущенного движения:
= 0,
C.10)
В общем случае дифференциальные уравнения возмущенного дви-
движения содержат явно время t. Но может, однако, случиться, что эти
уравнения не содержат (. Так, например, будет всегда, когда иссле-
исследуется устойчивость относительно координат и скоростей равновесия
какой-нибудь голономной системы со стационарными связями, под-
подверженной действию сил, не зависящих явно от t. В этом случае
уравнения движения B.1) не содержат явно (, и поскольку функ-
функции fs (t) в рассматриваемом случае обращаются в постоянные, то и
уравнения C.2) возмущенного движения также не будут содержать t.
Но уравнения возмущенного движения могут не содержать t и
тогда, когда исследуется устойчивость не равновесия, а движения.
Действительно, поскольку в уравнениях B.1) переменные ys являются,
вообще говоря, не координатами и скоростями, а некоторыми функ-
функциями этих величин, то вполне возможно, что для рассматриваемого
невозмущенного движения они будут постоянными, несмотря на то,
что координаты и скорости изменяются. Если при этом уравнения B.1)
не зависят от t, то и уравнения возмущенного движения также не
будут зависеть от t.
Мы будем в дальнейшем называть невозмущенное движение уста-
установившимся, если соответствующие дифференциальные уравнения воз-
возмущенного движения не содержат явно t. Примером может служить
рассмотренное выше движение C.9) твердого тела вокруг закреплен-
закрепленной точки: соответствующие дифференциальные уравнения возмущен-
возмущенного движения C.10) не содержат явно t.
20 ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ [ГЛ. I
Случай установившихся движений является наиболее простым при
исследовании устойчивости. Вместе с тем к этому случаю приводятся
очень многие практические задачи. Следующим по простоте случаем
будет тот, когда правые части уравнений возмущенного движения
являются по отношению к t периодическими функциями. К такого
рода уравнениям приводятся обычно задачи устойчивости колебатель-
колебательных движений. Примером может служить рассмотренная выше задача
устойчивости колебаний математического маятника. Правая часть урав-
уравнения C.7) периодична относительно t, так как функция f (t)— перио-
периодическая.
§ 4. Устойчивость по Ляпунову и некоторые другие
определения устойчивости.
В данных выше определениях Ляпунова рассматривается устой-
устойчивость невозмущенного движения по отношению к возмущениям
начальных условий. Физически это означает, что рассматривается
устойчивость по отношению к мгновенно действующим возмущениям.
Однако реальная механическая система находится обычно под по-
постоянным воздействием небольших возмущающих сил, учесть которые
при составлении уравнений движения практически невозможно.
Поэтому представляет особый интерес исследование устойчивости
рассматриваемого движения по отношению к таким постоянно дей-
действующим возмущениям. С точки зрения математической это означает,
что необходимо рассматривать возмущения не только начальных
условий, но и самих уравнений движения. Примем следующее опре-
определение устойчивости при постоянно действующих возмущениях ¦).
Наряду с уравнениями движения B.1) рассмотрим дифферен-
дифференциальные уравнения
-^Г = М'. У1 У„)+ад У1 Уп) D.1)
(s=l, 2, .... п),
') См. Дубошин Г. Н., К вопросу об устойчивости движения отно-
относительно постоянно действующих возмущений. Труды ГАИШ, т. XIV,
вып. 1, 1940.
Влияние малых возмущающих сил на устойчивость движения динами-
динамической системы рассмотрена впервые в работе: Ч е т а е в Н. Г., Об устой-
устойчивых траекториях динамики. Учен. зап. Казанского гос. ун-та, кн. 4, вып. 1
(см. также Сборник научных трудов Казанского авиац. ин-та, № 5, 1936).
Этому же вопросу посвящены работы: Артемьев Н. А., Осуществимые
движения. Изв. АН СССР, сер. матем., N° 3, 1939; М а л к и н И. Г., Об устой-
устойчивости при постоянно действующих возмущениях. ПММ, т. VIII, № 3, 1944;
Г о р ш и н С. И., Об устойчивости движения при постоянно действующих
возмущениях. Критические случаи, Известия АН Казахской ССР, № 56,
серия математики и механики, вып. 2; Об устойчивости движения с постоянно
действующими возмущениями, Изв. АН Казахской ССР, № 58, 1948.
С 4] УСТОЙЧИВОСТЬ ПО ЛЯПУНОВУ 21
где Rs(t> У\ Уп)— некоторые неизвестные функции, характери-
характеризующие возмущающие факторы, относительно которых мы можем
сказать только то, что они достаточно малы и удовлетворяют неко-
некоторым общим условиям, обусловливающим существование решений
уравнений D.1) в окрестности рассматриваемого невозмущенного
движения.
Мы будем говорить, что невозмущенное движение ys = fs(t)
(частное решение уравнений B.1)) устойчиво при постоянно дей-
действующих возмущениях, если для всякого положительного числа е,
как бы мало оно ни было, существуют два других положительных
числа %(е) и г\2(е), таких, что всякое решение ys(t) уравнений D.1).
удовлетворяющее при t — t0 неравенствам
удовлетворяет при t > @ неравенствам
каковы бм ни были функции Rs(t, y^ уп), удовлетворяющие
в области t > t0, \ys — fs (f) | < e, неравенствам
I Я
Определенная таким образом устойчивость при постоянно дей-
действующих возмущениях является непосредственным обобщением устой-
устойчивости по Ляпунову и, как было указано выше, имеет наибольшее
практическое значение. Может на первый взгляд показаться, что
этим самым до некоторой степени обесценивается теория устойчи-
устойчивости по Ляпунову. Однако это неверно, ибо, во-первых, методы
Ляпунова пригодны также для исследования устойчивости при по-
постоянно действующих возмущениях и, во-вторых, по крайней мере
в практически наиболее важных случаях, задача об устойчивости
при постоянно действующих возмущениях непосредственно приводится
к задаче об устойчивости по Ляпунову. Ниже (§ 74) будет показано,
что, по крайней мере для установившихся и периодических дви-
движений, достаточным условием устойчивости при постоянно действую-
действующих возмущениях является асимптотическая устойчивость по Ля-
Ляпунову1).
Рассмотрим еще одно возражение, которое иногда приводится при
оценке практической пригодности теории Ляпунова. С этой целью
исследуем простейшую систему, описываемую одним дифференциаль-
дифференциальным уравнением:
42-
D.2)
') См. примечание в конце книги (стр. 516).
22 ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ [ГЛ. I
где а — некоторая постоянная. Для этой системы существует, оче-
очевидно, положение равновесия х = 0. Это равновесие неустойчиво.
В самом деле, общее решение уравнения D.2) имеет вид
D.3)
где х0—начальное значение х (при t — t0).
Решение D.3) дает вещественные значения для функции х как
при ] х01< а, так и при |х0| > а. При этом в обоих случаях
Iim х @ = ± а. D.4)
Отсюда непосредственно следует, что положение равновесия х = 0
неустойчиво, ибо, как бы мало ни было отклонение в начальный
момент, оно в конце концов делается больше некоторого фиксиро-
фиксированного числа (например, -к-j. Но, с другой стороны, если вели-
величина а в рассматриваемой задаче практически мала, так что откло-
отклонение от положения равновесия на величину а не имеет никакого
практического значения, мы должны будем рассматриваемое поло-
положение равновесия считать практически устойчивым. Более того, мы
должны будем считать, что имеет место очень сильная устойчивость,
ибо условие D.4) выполняется при любом х0, как бы велика эта
величина численно ни была. Однако нетрудно видеть, что «практи-
«практическая» устойчивость в рассматриваемом случае обусловлена тем,
что в окрестности неустойчивого положения равновесия х = 0 имеются
два асимптотически устойчивых по Ляпунову положения равновесия
х = + а. Следовательно, в рассматриваемом частном случае задача
о «практической» устойчивости сводится к задаче об устойчивости
по Ляпунову. В общем случае вопрос о «практической» устойчи-
устойчивости в вышеуказанном смысле делается более сложным. Однако,
как будет показано ниже (§ 44), по крайней мере для практически
наиболее важных случаев, задача по-прежнему сводится к исследо-
исследованию устойчивости по Ляпунову.
Все вышеуказанное заставляет считать, что данное Ляпуновым
определение устойчивости имеет особо важное практическое значение.
Вместе с тем последний пример показывает, что для практики важно
не только выяснить, является ли движение устойчивым, но и опре-
определить область допустимых начальных возмущений. Последним
вопросом Ляпунов не занимался, но развитые им методы дают воз-
возможность решать и эту задачу').
') См. примечание к стр. 18 в конце книги (стр. 515).
с 5] О МЕТОДАХ РЕШЕНИЯ ЗАДАЧИ УСТОЙЧИВОСТИ 23
§ 5. О методах решения задачи устойчивости.
Исследование устойчивости не представляет обычно серьезных
трудностей в тех случаях, когда дифференциальные уравнения воз-
возмущенного движения удается проинтегрировать в замкнутой форме.
Но такого рода случаи являются исключительными и на практике
почти не встречаются. Поэтому усилия исследователей были напра-
направлены к тому, чтобы разработать методы решения задачи устойчи-
устойчивости, не прибегая к интегрированию уравнений движения. При этом
предшественники Ляпунова пользовались обычно методом линеари-
линеаризации. Этот метод заключается в следующем.
Разложим правые части уравнений возмущенного движения C.2)
в ряды по степеням xs. Для большинства механических задач такое
разложение возможно. Так как Xs(t, О, ..., 0) = 0, то разложения
не будут содержать свободных членов, и мы можем писать
dXj _ р д. _|_ _i_ n д; _|_ X* (t X X \ E 1)
(s=l, 2 я),
где Xs — совокупность членов выше первого порядка в функциях Хг
И вот, поскольку в задаче устойчивости приходится рассматривать
решения уравнений E.1) при малых начальных значениях величин х^,
естественно ожидать, что характер этих решений определяется сово-
совокупностью членов наинизшего измерения в уравнениях E.1). Другими
словами, естественно ожидать, что для решения задачи устойчивости
достаточно рассмотреть систему линейных уравнений
¦^Г = Л1*1+ ••• +Р,п*« (s=l. 2 я) E.2)
— так называемую систему уравнений первого приближения.
Так решали задачу устойчивости Томсон и Тэт1), Раус2) и
Н. Е. Жуковский3). При этом задача значительно упрощалась, а для
случая установившихся движений разрешалась элементарно, так как
при psj постоянных уравнения E.2) интегрируются в замкнутом виде.
Но такого рода решение задачи является нестрогим и, вообще
говоря, неправильным. Замена нелинейных уравнений E.1) линейными
уравнениями E.2) является, по существу, заменой одной задачи другой,
с которой первая может не иметь ничего общего. Может случиться,
что невозмущенное движение при исследовании лишь первого при-
приближения окажется устойчивым, хотя оно в самом деле неустойчиво,
и наоборот.
') Thomson and Та It, Treatise on Natural Philosophy, т. I, 1879.
2) R о u t h, A Treatise on the Stability of a given State of motion.
3) Жуковский Н. Е., О прочности движения. Учен. зап. Моск. ун-та,
отдел физ.-матем., вып. 4, 1882. См. также: Жуковский Н. Е., Собрание
сочинений, т. 1, Гостехиздат, 1948.
24 ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ [ГЛ. I
Поясним это примерами. Допустим, что дифференциальные урав-
уравнения возмущенного движения имеют вид
^ х3> ?±=х + ау\ E 3)
где а — постоянная. Рассмотрим произвольное решение х = х (t),
y = y{t) этих уравнений и составим производную от выражения
x2(t)-\-y2{t). Так как функции х (t) и y(t) удовлетворяют уравне-
уравнениям E.3), то будем иметь:
{x2(
= a{x*(t) + y4t)). ¦ E.4)
Установив это, допустим сначала, что а > 0. Тогда производная
от функций х2 (t) -j- у2 (t) будет все время положительной, и, следо-
следовательно, эта функция будет с возрастанием t возрастать. При этом
по мере возрастания этой функции ее производная, как это видно
из E.4), будет также возрастать. Отсюда непосредственно вытекает,
что как бы малы ни были начальные значения х (t0) и у (t0), функ-
функция х2 (t) -f- у2 (t) с неограниченным возрастанием t будет возрастать
неограниченно, и, следовательно, невозмущенное движение неустой-
неустойчиво. Напротив, при а < 0 невозмущенное движение будет устойчиво
асимптотически, так как при этом —тт [х2 (t) -\- у2 (t)] < 0, и функция
х2 (t) -j- у2 (t), оставаясь положительной, будет все время убывать,
неограниченно стремясь к нулю.
С другой стороны, отбрасывая в уравнениях E.3) члены третьего
порядка, мы для общего решения полученных таким образом урав-
уравнений первого приближения
dx dy /с гч
будем иметь:
x = x0cost — y0sint \
у =x0sint-+-y0cost,
где х0 и у0—начальные значения (при ^ = 0) величин х и у.
Из E.6) имеем, что
|*1<е, М<е.
если только
Следовательно, в первом приближении невозмущенное движение
устойчиво. Однако устойчивость, как это вытекает из E.6), не будет
асимптотической. В действительности же, как мы видели, невозму-
невозмущенное движение либо асимптотически устойчиво, если а отрица-
отрицательно, либо неустойчиво, если а положительно. Таким образом,
с 5] О МЕТОДАХ РЕШЕНИЯ ЗАДАЧИ УСТОЙЧИВОСТИ 25
в рассматриваемом случае характер певозмущенного движения опре-
определяется членами высших порядков в дифференциальных уравнениях
возмущенного движения.
В качестве второго примера рассмотрим колебания математичь-
ского маятника. За невозмущенное движение примем колебание, опре-
определяемое начальными условиями <р @) = а, <р @) = 0, где ф — угол
отклонения маятника. Дифференциальное уравнение возмущенного
движения, как это мы видели в § 3, имеет вид C.7). Отбрасывая
члены высших порядков, получим уравнение первого приближения:
-jjT = -j-x cos f(t). E.7)
Рассмотрим возмущенное движение, определяемое начальными
условиями х @) = 0, х@) = р. Период возмущенных колебаний отли-
отличается от периода невозмущенных колебаний, и поэтому, как мы
это видели в § 3, настанет такой момент времени, когда разность
значений ф в обоих колебаниях превзойдет некоторую не зависящую
от р величину, как бы мала р ни была. Покажем, однако, что если
эту разность значений ф, т. е. величину х, определять из уравнения
первого приближения E.7), то она при достаточно малой р будет
оставаться меньше любой наперед заданной величины.
В самом деле, подставляя функцию f (f) в уравнение C.6), кото-
которому она удовлетворяет, и дифференцируя полученное тождество
по t, будем иметь:
d2 I df\ ____g_dj_
dt2 \dt)~ I dt C0SJ-
Следовательно, функция х = -~ удовлетворяет уравнению E.7).
Так как при этом функция / (t) удовлетворяет начальным условиям
/@) = а, \-уг) =0. то функция —jr- будет удовлетворять началь-
начальным условиям (-4Л = О, (-/тг) = f-sina. Следовательно, иско-
искомое частное решение уравнения E.7) имеет вид
/р df(t)
х =
g sin a dt
Отсюда, учитывая, что -~ функция ограниченная, убеждаемся,
что величина х будет оставаться меньше любого наперед заданного
числа е, если величина р достаточно мала. Таким образом, и в рас-
рассматриваемом примере первое приближение дает неправильное описа-
описание характера движения.
Можно, однако, привести и такие примеры, когда первое прибли-
приближение действительно решает задачу устойчивости. Отсюда возникает
26 ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ [ГЛ. I
основная задача: установить необходимые и достаточные условия
устойчивости по первому приближению. Эту задачу поставил Ляпунов,
который дал полное ее решение для установившихся и периодических
решений. Ляпунов дал также решение задачи и для широкого класса
неустановившихся движений. Выяснив условия, при которых задача
решается в первом приближении, Ляпунов рассмотрел также некото-
некоторые основные случаи, когда при исследовании устойчивости нельзя
ограничиться рассмотрением первого приближения. Все эти капиталь-
капитальные результаты излагаются ниже.
Для решения поставленных задач Ляпунов разработал специаль-
специальные приемы. Все эти приемы и вообще все способы решения задачи
устойчивости Ляпунов разделяет на две категории. К первой кате-
категории он относит те способы, которые приводятся к непосредствен-
непосредственному рассмотрению возмущенного движения, т. е. к определению
общего или частного решения соответствующих дифференциальных
уравнений. Эти решения приходится обычно искать под видом неко-
некоторых рядов. Совокупность всех способов первой категории Ляпунов
называет первым методом J).
Можно, однако, указать и другие способы решения задачи устой-
устойчивости, которые не требуют нахождения частных или общих реше-
решений уравнений возмущенного движения, а приводятся к отысканию
некоторых функций от t, xv ..., хп, обладающих специальными
свойствами. Примером может служить известная теорема Лагранжа
об устойчивости равновесия, когда силовая функция обращается
в максимум. Здесь устойчивость обеспечивается существованием сило-
силовой функции, обладающей специальными свойствами. Совокупность
всех способов второй категории Ляпунов называет вторым методом.
В основу своего второго метода Ляпунов кладет несколько основ-
основных установленных им теорем. Эти теоремы оказались настолько
эффективными, что при помощи их удалось исключительно просто
разрешить задачу об устойчивости по первому приближению. Вместе
с тем они позволили Ляпунову рассмотреть и некоторые основные
случаи, когда первое приближение задачи не решает и, следова-
следовательно, когда эта задача делается особенно сложной.
Второй метод Ляпунова является и в настоящее время основным
методом решения задачи устойчивости 2).
Изложению основных теорем второго метода Ляпунова и его при-
приложений посвящена следующая глава. При этом для простоты мы
ограничиваемся сначала лишь установившимися движениями. Общий
случай неустановившихся движений рассматривается в главах V и VI.
') См. примечание в конце книги (стр. 517).
2) См. примечание в конце книги (стр. 518).
ГЛАВА И.
ВТОРОЙ МЕТОД ЛЯПУНОВА ДЛЯ УСТАНОВИВШИХСЯ
ДВИЖЕНИЙ.
§ 6. Основные определения.
Мы переходим теперь к изложению основных положений второго
метода Ляпунова исследования устойчивости движения. В этой главе
мы ограничиваемся, однако, рассмотрением только установившихся
движений. Мы будем, следовательно, предполагать, что дифферен-
дифференциальные уравнения возмущенного движения имеют вид
d Xs{Xl хп) 0=1,2 п), F.1)
dt sw ¦
где Xs не зависят явно от t.
В своем исследовании Ляпунов предполагал, что функции Xs
представляют собой степенные ряды, расположенные по степеням
jq xn, сходящиеся в области
|*J<# 0=1, 2 п), F.2)
где Н — некоторая постоянная. Однако все положения второго метода
Ляпунова и все связанные с ними доказательства полностью сохра-
сохраняют силу и при более общих предположениях. Мы заменим поэтому
предположение Ляпунова об аналитичности функций Xs значительно
более общим условием, а именно, мы будем только предполагать,
что функции Xs в области F.2) непрерывны и притом такие, что
уравнения F.1) для каждой системы начальных значений дг° величин х ,
лежащих в области F.2), допускают единственное решение.
Нам придется рассматривать в дальнейшем некоторые функции
V(xv ..., хп) переменных хх хп, определенные в некоторой
окрестности начала координат. Относительно этих функций мы будем
всегда предполагать, что они однозначны, обращаются в нуль при
¦*! = ... = хп = 0 и обладают непрерывными частными производными.
Определение 1. Функция V(хх хп) называется знако-
определенной (определенно-положительной или определенно-
28 ВТОРОЙ МЕТОД ЛЯПУНОВА ДЛЯ УСТАНОВИВШИХСЯ ДВИЖЕНИЙ [ГЛ. II
отрицательной), если она при
\xs\<h, F.3)
где h — достаточно малое положительное число, может при-
принимать значения только одного определенного знака и обра-
обращается в нуль только при х1= ... = хп = 0.
Определение 2. Функция V (хг хп) называется знако-
знакопостоянной (положительной или отрицательной), если она
в области F.3) может принимать значения только одного
определенного знака, но может обращаться в нуль и при
х\+ ...+х\Ф0.
Определение 3. Функция V(х1 хп) называется знако-
знакопеременной, если она не является ни знакоопределенной,
ни знакопостоянной и, следовательно, как бы мало ни было
число h, может принимать в области F.3) как положитель-
положительные, так и отрицательные значения.
Поясним эти определения примерами. Допустим для определен-
определенности, что п = 3. Тогда функции
т/—.Х21 у2_| у4 у— v-2 i Ov v- -1~2х2-4-х2
v —Aj-f- -*2-(- ху v —х\^г 4xxx2-t~ 4х2-\- х3
будут определенно-положительными, и при этом величина h в нера-
неравенствах F.3) может быть взята сколь угодно большой. Функция
V — v-2 I v-2 I v-2 v3
V —Х1-\- л2 I Х3 Х3'
как мы увидим ниже, будет также определенно-положительной, но
теперь уже величина h должна быть взята достаточно малой. Функции
будут обе знакопостоянными .(положительными). Действительно, обе
они могуть принимать кроме положительных еще и нулевые значе-
значения при значениях хх, х2, х3, не равных нулю одновременно (вто-
(вторая— при хх = х2~0 и х3 произвольном). Функции
будут, очевидно, знакопеременными ').
§ 7. Признаки знакоопределенности
и знакопеременности функций.
Как мы увидим ниже, для практического применения второго
метода Ляпунова необходимо знать критерии знакоопределенности и
и знакопеременности функций. К сожалению, общих критериев такого
рода не существует, и задача в общем случае весьма сложна. Однако
') См. примечание в конце книги (стр. 518).
§7]
ПРИЗНАКИ ЗНАКООПРЕДЕЛЕННОСТИ И ЗНАКОПЕРЕМЕННОСТИ 29
в частных случаях, с которыми нам придется иметь дело в дальней-
дальнейшем, эта задача легко разрешается при помощи некоторых простых
критериев, которые мы здесь приводим.
Допустим сначала, что V (хг, ..., хп) представляет однородную
форму т-го порядка. Так как при произвольном X выполняется
тождество
V(Xl lxn) = lmV(xv ..., *„).
то совершенно очевидно, что если форма V является знакоопреде-
ленной, то знакоопределенность будет иметь место во всем про-
пространстве, а не только вблизи начала координат. То же самое будет
справедливо и относительно знакопеременности. При этом очевидно,
что знакоопределенность может иметь место только при т четном.
Следовательно, имеет место следующее предложение.
Лемма 1. Любая форма нечетного порядка есть функция
знакопеременная.
Если т. есть число четное, то форма V может быть как знако-
определенной, так и знакопеременной. Вопрос о том, какой из этих
случаев действительно имеет место, является очень сложным для форм
порядка выше второго, если число независимых переменных больше
двух. Для форм же второго порядка (при любом числе независимых
переменных) эта задача разрешается чрезвычайно просто следующим
образом.
Пусть
п
2V= 2 Са$ХаХ$ G.1)
а, р=1
— квадратичная форма. Тогда, как известно, существует бесчислен-
бесчисленное множество линейных подстановок
У, = °,1*1+ ••• +Й,А E=1-2 п) G.2)
с отличным от нуля определителем, которые преобразуют форму V
к виду
V = A.,y? + a.2^+ ... +\у\. G.3)
Если все коэффициенты hs отличны от нуля и одинакового знака,
то форма V будет знакоопределенной. Действительно, в этом случае
форма V может обратиться в нуль только при у1 = ... =упт=0,
что возможно только при xl= ... = хп = 0, так как определитель
подстановки G.2) отличен от нуля. Если часть коэффициентов ls
равна нулю, а остальные имеют одинаковые знаки, то форма V будет,
очевидно, знакопостоянной. Если же среди коэффициентов Xs имеются
как положительные, так и отрицательные, то форма V будет знако-
знакопеременной.
Число отличных от нуля коэффициентов Xs, а также число перемен
знаков в ряду этих величин не зависит от выбора подстановки G.2).
30 ВТОРОЙ МЕТОД ЛЯПУНОВА ДЛЯ УСТАНОВИВШИХСЯ ДВИЖЕНИЙ [ГЛ. II
Само приведение формы к виду G.3) производится совершенно эле-
элементарными приемами, на которых мы здесь не останавливаемся.
Знакоопределенность или знакопеременность квадратичной формы
можно также установить и не прибегая к вышеуказанному линейному
преобразованию. Имеет место следующая теорема Сильвестра, кото-
которую мы здесь приводим без доказательства.
Теорема Сильвестра. Для того чтобы квадратичная
форма G.1) была определенно-положительной, необходимо и
достаточно, чтобы все главные миноры ее дискриминанта,
т. е. величины
схх, с12, .... с1п
С12' С22 сЧп
С\п' С2л спп
были положительны.
Допустим снова, что V(хх хп) есть форма произвольного
т-го порядка. Рассмотрим произвольную функцию W(хх, ..., хп),
обращающуюся в нуль при хх = ... = хп = 0 и удовлетворяющую
в области F.3) неравенству
\W(xx хп)\<А{\хх\ + ... + \хп\)т, G.4)
где А — некоторая постоянная. Имеет место следующее важное пред-
предложение.
Лемма 2. Если V — знакоопределенная форма т-го порядка,
то функция
U{x{ xn) = V(xx xn) + W(xx, .... хп) G.5)
будет также знакоопределенной того оке знака при любом
выборе функции W(xx xn), удовлетворяющей в области F.3)
неравенству G.4), где А—достаточно малое положительное
число, зависящее исключительно от коэффициентов формы V.
Если V есть форма знакопеременная, то при тех же усло-
условиях функция U будет также знакопе ременной.
Доказательство. Полагая
*, = Р«,- Р =/•*?+ ••• +*«¦
где
а\+ ... +а2 = 1. G.6)
будем иметь:
U(xx, .... xn) = pmV(ax, .... cg+Гфа,, .... ра„).
Допустим сначала, что V есть форма знакоопределенная, напри-
например определенно-положительная. Считая р настолько малым, что вели-
величины xs лежат в области F.3), можем на основании G.4) и G.6)
писать:
\W(pax, .... ра„)|< V{|o,|+ ... +\an\\m<A9V. G.7)
? 7] ПРИЗНАКИ ЗНАКООПРЕДЕЛЕННОСТИ И ЗНАКОПЕРЕМЕННОСТИ 31
Пусть / — нижняя граница величины V (ах a;1), так что
<*„)>'• G.8)
Число I будет обязательно положительным, так как определенно-
положительная форма V (СЦ ап) может принимать на сфере G.6)
только положительные значения. Из G.7) и G.8) вытекает, что если
число А меньше величины , зависящей исключительно от формы V,
пт
то во всех точках области F.3), кроме начала координат, функция U
будет принимать только положительные значения, что и доказывает
первую часть леммы.
Допустим теперь, что V — форма знакопеременная. Тогда на
сфере G.6) она может принимать как положительные, так и отри-
отрицательные значения. Допустим, что У(®[ а'п)~а -^ ^'
а V (а" .... а") = — b < 0. Тогда, считая, что А < —— и А < ——,
будем иметь, что при a^ = a'4. функция U будет положительной,
а при a =a^ функция U будет отрицательной, и это будет спра-
справедливо, как бы мало ни было р. Следовательно, функция U является
знакопеременной.
Таким образом, лемма полиостью доказана.
Лемма 3. Знакоопределенность или знакопеременность
формы сохраняется, если к ней добавить любую форму того же
порядка с достаточно малыми коэффициентами.
Справедливость этой леммы непосредственно вытекает из того
обстоятельства, что всякая форма m-го порядка необходимо удовле-
удовлетворяет неравенству G.4), причем коэффициент А будет сколь угодно
мал, если коэффициенты формы достаточно малы.
Пусть теперь V (xv .... хп) обозначает произвольную функцию,
разлагающуюся в ряд по степеням хх, ..., хп в некоторой окрест-
окрестности начала координат. Допустим, что это разложение начинается
членами некоторого произвольного порядка т, так что мы можем
писать:
V (х, *„) = Vm (*, хп) + К* (*, *„). G.9)
где Vm — форма m-го порядка, а V* (хх хп) — совокупность
членов более высоких порядков. Очевидно, что функцию V* (хх х„)
можно рассматривать, и притом бесчисленным множеством способов,
как форму m-го порядка, коэффициенты которой являются функ-
функциями от ЛГ], .. ., хп, обращающимися в нуль при хх = ... = хп = 0.
Следовательно, если величина п, определяющая область F.3), доста-
достаточно мала, то указанные коэффициенты будут сколь угодно малыми.
Поэтому на основании предыдущего справедлива также следующая
лемма.
32 ВТОРОЙ МЕТОД ЛЯПУНОВА ДЛЯ УСТАНОВИВШИХСЯ ДВИЖЕНИЙ [ГЛ. II
Лемма 4. Если Vm есть форма знакоопределенная, то и
функция G.9) будет знакоопределенной, и если Vт есть форма
знакопеременная, то и функция G.9) будет знакопеременной.
Таким образом, знакоопределенность и знакопеременность анали-
аналитических функций определяются совокупностью членов наинизшего
порядка в разложениях этих функций, за исключением того случая,
когда эта совокупность членов наинизшего порядка представляет
знакопостоянную форму. Так что, например, функция дяух пере-
переменных
V(x, y) = x2-|->'2 + *i>2 + y3
будет знакоопределенной, а функция
V(x, у) = х2 — у2-\-ху2 + у3
— знакопеременной.
Если совокупность членов наинизшего порядка в разложении ана-
аналитической функции представляет собой форму знакопостоянную, то
вопрос о знакоопределенности или знакопеременное™ этой функции
решается, очевидно, членами более высоких порядков. Рассмотрим
в качестве примера следующие четыре функции переменных хну:
V = х2,
V = ,х2 — 1ху2 + У + х4 = (х — у2J + х\
V = х2 — 2ху2 + / + х4 + ху5.
Первая из этих функций представляет собой постоянно-положи-
постоянно-положительную квадратичную форму. Добавляя к ней член третьего
порядка — 2ху2, получим вторую функцию, которая, очевидно, знако-
переменна. Добавляя к полученной функции члены четвертого порядка
у4-)-х4, получим третью функцию, которая уже будет знакоопреде-
знакоопределенной. Наконец, добавляя член шестого порядка ху5, мы получим
четвертую функцию, которая уже снова является знакопеременной.
Действительно, последняя функция на параболе х = у2 принимает
значение у7-|-~.у8> которое при достаточно малом у будет либо поло-
положительным, либо отрицательным, в зависимости от знака у.
Последний пример показывает, что добавлением членов более
высоких порядков можно нарушить знакоопределенность или знако-
знакопеременность функции, если последняя не является формой от всех
переменных.
В заключение отметим, что лемма 4 остается, очевидно, в силе,
если предположение, что функция V* является аналитической с раз-
разложением, начинающимся членами не ниже т-|-1-го порядка, заме-
заменить более общим предположением, что V* обращается в нуль при
¦с. = .. . — хп — 0 и имеет при этом порядок малости более высо-
§ 8]
ГЕОМЕТРИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ
33
кий, чем т, т. е. что V* удовлетворяет в некоторой окрестности
начала координат неравенству
|V (*i хп)\<А{\хх\ + ... + |лг„|Г+а,
где а — положительное число, которое, вообще говоря, может быть
сколь угодно малым. Аналитичность функции V* при этом не требуется.
§ 8. Геометрическая интерпретация знакоопределенных функций.
Рассмотрим для простоты знакоопределенную функцию трех пере-
переменных V (xv х2, х3). Все наши рассуждения останутся, однако,
справедливыми и при п > 3. Допустим также для определенности,
что V — функция положительная. Рассмотрим поверхность
V (xv х2, х3) = с.
(8.1)
где с — положительное число. При с = О в силу знакоопределен-
знакоопределенности V будем иметь хх = х2 = х3 = 0, и, следовательно, поверхность
У = 0 вырождается в точку, в начало координат. Покажем, что
при с достаточно малом поверх-
поверхность (8.1) будет замкнутой и
будет содержать внутри себя на-
начало координат.
С этой целью покажем, что
всякая непрерывная кривая, иду-
идущая из начала координат к ка-
какой-нибудь точке границы обла-
области F.3), непременно пересекает
поверхность (8.1), если только
число с не превосходит некото-
некоторого, зависящего только от h, до-
достаточно малого положительного числа /. В самом деле, пусть / — точ-
точный нижний предел функции V на границе области F.3), так что на
этой границе будем иметь V^-l. Число / будет, очевидно, отличным от
нуля и положительным. Если мы теперь рассмотрим произвольную
непрерывную кривую, выходящую из начала координат к границе
области F.3), и проследим за изменением функции V вдоль этой
кривой, то мы получим, что в начале кривой V обращается в нуль,
а в конце кривой — в некоторую величину, не меньшую чем /. Сле-
Следовательно, в некоторой точке этой кривой V необходимо прини-
принимает значение с, если только с < /, что мы и будем предполагать.
Другими словами, указанная кривая необходимо пересекает поверх-
поверхность (8.1). Таким образом, при достаточно малых значениях с все
поверхности (8.1) будут замкнутыми и окружают начало координат1).
Рис. 2.
') Поверхности V = с могут быть довольно сложной формы. Они не
обязательно гомеоморфны сфере.
34 ВТОРОЙ МЕТОД ЛЯПУНОВА ДЛЯ УСТАНОВИВШИХСЯ ДВИЖЕНИЙ [ГЛ. 11
Если мы теперь будем изменять с от нуля до некоторого доста-
достаточно малого значения, то получим семейство замкнутых, не пересекаю-
пересекающихся между собой (в силу.однозначности V) поверхностей, окружаю-
окружающих начало координат и стягивающихся в эту точку при с = 0 (рис. 2).
§ 9. Первая теорема Ляпунова об устойчивости движения.
Мы переходим теперь к изложению основных теорем второго метода
Ляпунова исследования устойчивости движения. Нам придется при
этом рассматривать одновременно с функциями V(xv .... х„) их
производные по времени, составленные в предположении, что
х, хп являются некоторыми функциями времени, удовлетворяю-
удовлетворяющими дифференциальным уравнениям возмущенного движения F.1).
При таком предположении мы будем для этих производных по вре-
времени иметь:
dt ~~ mJ dxs dt ~ jLd dxs s
и, следовательно, —гг будет также функцией хх хп, обращаю-
обращающейся в нуль при хх — ... — лг„ = О.
Первая теорема Ляпунова об устойчивости, которая в дальнейшем
будет именоваться теоремой А, может быть выражена следующим
образом:
Теорема А. Если для дифференциальных уравнений возму-
возмущенного движения возможно найти знакоопределенную функцию
V (х, хп), полная производная которой по времени, состав-
составленная в силу этих уравнений, есть функция знакопостоянная,
знака, противоположного с у, или тождественно обращается
в нуль, то невозмущенное движение устойчиво.
Доказательство. Не нарушая общности рассуждений, мы
можем предположить, что V есть функция определенно-положитель-
определенно-положительная, так что во всех точках области
Л. (9.1)
за исключением начала координат, V принимает только положитель-
положительные значения. В той же области согласно условию теоремы спра-
справедливо неравенство
(92)
Пусть е — произвольное сколь угодно малое положительное число,
меньшее h. Обозначим через х наибольшую из величин \хх\, ..., \хп\,
т. е. положим
1|х,| \х„\\.
§ 9] ПЕРВАЯ ТЕОРЕМА ЛЯПУНОВА ОБ УСТОЙЧИВОСТИ ДВИЖЕНИЯ 35
и рассмотрим множество всех значений величин хх хп, связан-
связанных соотношением
х = е (9.3)
(т. е. все точки, лежащие на гранях га-мерного куба со стороной 2е,
ребра которого параллельны осям координат и центр которого совпа-
совпадает с началом координат).
Пусть / — точный нижний предел функции V(xlt .... хп) при
условии (9.3), так что
V(x1 *„)>* при х=г. (9.4)
Число I будет, очевидно, положительным, так как V может при-
принимать на множестве (9.1) только положительные значения, и при
этом в силу непрерывности V нижний предел этой функции на мно-
множестве (9.3) есть одно из значений, которые она на этом множестве
принимает.
Рассмотрим теперь произвольное решение xs (t) дифференциальных
уравнений возмущенного движения, начальные значения x°s = xs(t^\
которого лежат в области
К|<Л- (9.5)
Мы будем при этом предполагать, что число т] меньше, чем е, и
что оно настолько мало, что
Такой выбор числа т], очевидно, возможен, так как V — функция
непрерывная и 1/@, ..., 0) = 0.
Подставляя решение xs (t) в функцию V, мы получим функцию
от времени, которая в силу (9.2) будет не возрастающей, по крайней
мере до тех пор, пока величины xs(t) будут оставаться в области (9.1).
Следовательно, при всех t, при которых xs(t) лежат в области (9.1),
будет выполняться неравенство
V (*, @, ....*„ @) < V (*;, ..., х°) < I. (9.6)
Отсюда непосредственно следует, что при всех t > tQ будут выпол-
выполняться неравенства
|*J<e. (9.7)
В самом деле, так как т| < е, то неравенства (9.7) будут выпол-
выполняться в силу непрерывности xs (t), по крайней мере при значе-
значениях t, достаточно близких к t0. И если поэтому эти неравенства
когда-нибудь вообще нарушаются, то должен существовать такой
момент времени t = T, при котором хотя бы одна из величин xs
достигнет численно значения е. Другими словами, должен существо-
существовать такой момент времени t — T, при котором будет выполняться
36 ВТОРОЙ МЕТОД ЛЯПУНОВА ДЛЯ УСТАНОВИВШИХСЯ ДВИЖЕНИЙ [ГЛ. П
условие (9.3), и, следовательно, на основании (9.4)
V(Xl(T), .... хп{Т))>1.
Это, однако, невозможно, так как в силу е < h множество (9.3)
лежит в области (9.1) и, следовательно, при х = г должно выпол-
выполняться неравенство (9.6).
Таким образом, для всех решений дифференциальных уравнений
возмущенного движения, для которых выполняются неравенства (9.5),
будут при всех t > tQ выполняться неравенства (9.7), что и доказы-
доказывает устойчивость невозмущенного движения.
Заметим, что из приведенного доказательства вытекает также и
способ построения по числу е соответствующего числа т\. Для этого,
как видно из предыдущего, необходимо: 1) задавшись числом е,
определить число /(е), являющееся точным нижним пределом функ-
функции V, при условии (9.3); 2) по полученному числу /(е) опреде-
определить т](е) так, чтобы при выполнении (9.5) выполнялось неравенство
у {А *?)<'•
§ 10. Вторая теорема Ляпунова об устойчивости движения.
Рассмотренная в предыдущем параграфе основная теорема Ляпу-
Ляпунова может быть дополнена следующей теоремой, принадлежащей
также Ляпунову.
Теорема Б. Если для дифференциальных уравнений возму-
возмущенного движения возможно найти знакоопределенную функ-
функцию V (xv .... хп), полная производная которой по времени,
составленная в силу этих уравнений, есть функция также
знакоопределенная, знака, противоположного с V, то невозму-
невозмущенное движение устойчиво- асимптотически.
Доказательство. Не нарушая общности рассуждений, мы
можем, так же как и раньше, предположить, что V есть функция
dV
определенно-положительная и, следовательно, —-п—-определенно-
отрицательная, так что в области (9.1) выполняются условия
v>o, 4г<о,
причем знаки равенства возможны только при хх= ... =хп~0.
Пусть е — произвольное положительное число, меньшее h. Так
как в рассматриваемом случае выполняются условия предыдущей
теоремы, то невозмущенное движение во всяком случае устойчиво.
Поэтому найдется такое положительное число ц{г), что для всякого
решения xs{t) уравнений F.1), для которого в начальный момент
времени t = tQ выполняются неравенства
§ 10] ВТОРАЯ ТЕОРЕМА ЛЯПУНОВА ОБ УСТОЙЧИВОСТИ ДВИЖЕНИЯ 37
будут при всех t^>tQ выполняться неравенства
К @1 <е.
Покажем, что при этом будем иметь:
\\mxs{t) = Q, A0.2)
*->со
т. е. что невозмущенное движение устойчиво асимптотически.
В самом деле, так как рассматриваемое решение все время лежит
в области (9.1), то производная по времени функции V [хх (t) xn {t)\
будет по условию теоремы оставаться все время отрицательной, не
обращаясь в нуль ни при каких значениях t. Последнее вытекает
из того обстоятельства, что функции xs{t) не могут обратиться в нуль
одновременно ни при каких значениях t, ибо если бы это имело
место при каком-нибудь значении t — T, то, приняв Т за начальный
момент времени, мы имели бы два разных решения уравнений F.1)
с нулевыми начальными значениями: рассматриваемое xs(t) и три-
тривиальное Х\— ... = хп. Это, однако, невозможно, так как уравне-
уравнения F.1) таковы, что для них при заданных начальных условиях
существует только одно решение.
dV
Итак, производная —тт- остается все время отрицательной. Следо-
Следовательно, функция V [хх (t), .. ., хп (t)\ будет монотонной убывающей
и поэтому она при t—>oo будет необходимо стремиться к некото-
некоторому пределу а, оставаясь все время больше этого предела, так что
все время будем иметь:
V[xx(t), .... *„(/)]> а. A0.3)
Докажем, что а = 0. С этой целью допустим противное: что
а ф 0 и, следовательно, в силу положительности V, а > 0. Так как V
есть функция непрерывная, то из A0.3) вытекает, что
в. (Ю.4)
где а — некоторое положительное число. Но так как —гт- есть функ-
функция определенно-отрицательная, то из A0.4) вытекает, что
где Ь — также положительное число.
Следовательно, при всех t > t0 будет выполняться неравенство
V[Xl{t), .... JCn@] = V[*i(*o) *„('о)]
38 ВТОРОЙ МЕТОД ЛЯПУНОВА ДЛЯ УСТАНОВИВШИХСЯ ДВИЖЕНИЙ [ГЛ. II
что, очевидно, невозможно, так как правая часть этого неравенства
при достаточно больших t делается отрицательной, что противоречит
условию положительности V[xl(t) xn(t)\. Таким образом, мы
приходим к заключению, что
limV[Xl(t), .... xa(f)] = 0.
t->oo
откуда вследствие знакоопределенности V вытекает A0.2), что и
доказывает теорему.
Примечание. Назовем областью асимптотической устой-
устойчивости наибольшую область начальных значений x°s, при которых
для решений уравнений F.1) выполняются условия A0.2). Из пре-
предыдущего доказательства вытекает, что эта область во всяком слу-
случае не меньше области A0.1), где г| —t|(e), причем т](е) строится
по числу е так, как указано в примечании в конце предыдущего
параграфа :).
§ 11. Геометрическая интерпретация предыдущих теорем.
Предыдущие теоремы имеют простое геометрическое истолкование.
Это истолкование не только выясняет основное содержание теорем,
но в последнее время широко используется для решения многих
технических задач2).
Рассмотрим сначала первую теорему Ляпунова. Допустим, что
существует знакоопределенная функция V (хх, х2, x3), для которой
dV
—тг <! 0. Мы предполагаем при этом для простоты, что п = 3. По-
Построим систему поверхностей
V(xv x2, х3) = с, A1.1)
где с — положительный параметр, изменяющийся от нуля до некото-
некоторого достаточно малого значения. Как мы видели в § 8, поверх-
поверхности A1.1) замкнуты, окружают начало координат и стягиваются
в точку при с = 0. При этом если сх < с2, то поверхность V = Cj
целиком заключена внутри поверхности V— с2.
Рассмотрим какую-нибудь интегральную кривую уравнений F.1),
выходящую в начальный момент времени из какой-нибудь точки
окрестности начала координат. Эта интегральная кривая при возра-
возрастающих значениях t никогда не пересечет ни одной из поверхно-
поверхностей A1.1) изнутри наружу. В самом деле, если бы такое пересечение
в какой-нибудь точке имело место, то в этой точке или в окрест-
¦) См. примечание в конце книги (стр. 519).
2) Приводимая ниже геометрическая интерпретация стала нам известна
из бесед с Н. Г. Четаевым и впервые была сформулирована в работе:
М а л к и н И. Г., Проблема существования функций Ляпунова. Изв. Казан-
Казанского физ.-матем. об-ва, т. IV A929—1930), т. V A931).
§ 11]
ГЕОМЕТРИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ
39
ности этой точки функция V[хг{1), x2(t), x3(t)] необходимо имела бы
положительную производную, так как при переходе от какой-нибудь
поверхности A1.1) к другой поверхности этого семейства, охваты-
охватывающей первую, функция V(xv x2, хЛ возрастает. Но это, однако,
dV
невозможно в силу того, что ~тг^^- Таким образом, если какая-
нибудь интегральная кривая в начальный момент времени находилась
внутри какой-нибудь поверхности A1.1), то она и в дальнейшем
будет все время оставаться внутри нее. Но так как при достаточно
малом с поверхности A1.1) ограничи-
ограничивают сколь угодно малую окрестность
начала координат, то отсюда непо-
непосредственно вытекает устойчивость не-
невозмущенного движения.
Легко также геометрически интер-
интерпретировать построение числа г](е) по
числу е. С этой целью рассмотрим наи-
наибольшую поверхность семейства A1.1),
целиком расположенную внутри куба
со стороной 2е. Пусть это будет по-
поверхность V~l (рис. 3)J). Построим
теперь куб со стороной 2т], целиком
расположенный внутри указанной по-
поверхности. Тогда любая интегральная
кривая, начинающаяся внутри этого куба, т. е. такая, для которой
|x^|^ г], будет все время оставаться внутри поверхности V = 1,
а следовательно, и подавно внутри куба со стороной 2е. Мы будем,
таким образом, для каждой такой интегральной кривой иметь \xs\ < e,
т. е. найденная нами величина ц и будет той, которая фигурирует
в условиях устойчивости.
Рис. 3.
Ьсли
есть функция определенно-отрицательная, то каждая
интегральная кривая, выходящая из достаточно малой окрестности
начала координат, будет непременно пересекать каждую из поверх-
поверхностей A1.1) снаружи во внутрь, так как функция V \xx(t), x2(t), x3(t)]
должна непрерывно убывать. Но в таком случае интегральные кривые
должны неограниченно приближаться к началу координат, т. е. не-
невозмущенное движение устойчиво асимптотически.
Таким образом, с точки зрения геометрической второй метод
Ляпунова исследования устойчивости сводится к построению семейства
замкнутых поверхностей, окружающих начало координат и обла-
обладающих тем свойством, что интегральные кривые могут пересекать
') Как легко видеть, I есть точный нижний предел функции V при
условии max { | хх \,\ х21, | х, | } = е.
40 ВТОРОЙ МЕТОД ЛЯПУНОВА ДЛЯ УСТАНОВИВШИХСЯ ДВИЖЕНИЙ [ГЛ. II
каждую из этих поверхностей только снаружи во внутрь. Как только
из каких-нибудь соображений удается установить существование
такого рода семейства поверхностей, то этим самым сразу будет
установлена устойчивость невозмущенного движения.
§ 12. Примеры приложения предыдущих теорем.
Пример 1. Теорема Лагранжа об устойчивости равнове-
равновесия. Простейшим случаем, когда теоремы Ляпунова дают возможность
установить устойчивость невозмущенного движения, будет, очевидно,
тот, когда уравнения F.1) допускают первый интеграл
V (хх х„) = const.,
где V (х1 хп) — знакоопределенная функция. Действительно,
(IV г. , ,,
в этом случае —— = 0, и функция V удовлетворяет условиям тео-
теоремы А, откуда сразу следует устойчивость невозмущенного движе-
движения. С этим случаем мы как раз имеем дело при исследовании
устойчивости равновесия голономной консервативной системы, 'когда
в положении равновесия силовая функция имеет максимум. Действи-
Действительно, пусть qv ..., qn—обобщенные координаты системы, которые
выбраны так, что в положении равновесия они обращаются в нуль.
Допустим, что силовая функция U(<?, qn) имеет в положении
равновесия максимум, который мы, не нарушая общности, можем
положить равным нулю. Тогда U (q^ qn) будет определенно-
отрицательной функцией величин qv ..., qn. Так как невозмущенным
движением в рассматриваемом случае является положение равновесия
ql == . .. —qn = 0, то дифференциальными уравнениями возмущен-
возмущенного движения являются просто уравнения движения, которые мы
можем записать в канонической форме:
dq. дН dp. дН
-jt = ^—. -4r = — ic- ('=1. 2, .... я). A2-1)
dt др. dt dqt v ' ч '
где
H{q, qa, px pn)=:T-U
и pt — обобщенные импульсы. Так как кинетическая энергия Г
является по отношению к переменным ps определенно-положительной
квадратичной формой, а — U — определенно-положительной функцией
переменных qs, то Н является определенно-положительной функцией
переменных ps и qs. Но уравнения A2.1) допускают интеграл энер-
энергии H = h, откуда немедленно вытекает известная теорема Лагранжа
об устойчивости равновесия (по отношению к координатам и скоро-
скоростям), когда силовая функция в положении равновесия имеет максимум.
Пример 2. Устойчивость вращательного движения сна-
снаряда. В предыдущем примере первый интеграл уравнений возмущен-
S 12] ПРИМЕРЫ ПРИЛОЖЕНИЯ ПРЕДЫДУЩИХ ТЕОРЕМ 41
ного движения, который получился из общих теорем механики,
оказался знакоопределенным, что сразу привело к решению задачи.
В некоторых случаях общие теоремы механики дают возможность
получить первые интегралы, которые сами не являются знакоопре-
деленными, но из них удается скомбинировать новый интеграл, уже
являющийся знакоопределенным. Таким путем Н. Г. Четаевуг) удалось
получить решение важной технической задачи об устойчивости вра-
вращательного движения снаряда, к изложению которой мы сейчас
и переходим.
При весьма настильной траектории стрельбы можно приближенно
считать, что центр тяжести снаряда движется прямолинейно и равно-
равномерно. Пусть р — угол, который образует ось снаряда со своей
проекцией на вертикальную плоскость стрельбы, а а — угол между
этой проекцией и касательной к траектории центра тяжести. Эти два
угла, очевидно, вполне определяют положение оси снаряда. Для этих
углов имеют место следующие дифференциальные уравнения, уста-
установленные А. Н. Крыловым2):
Лр -+- Аа2 sin р cos р — Спа cos р = eR sin |5 cos a, )
/lacos|5— 2Лар sin p-j-Crap = е/? sina. j
Здесь С — аксиальный момент инерции снаряда, А—его момент
инерции относительно поперечной оси, проходящей через центр
тяжести, п—постоянная проекция угловой скорости вращения снаряда
на его ось симметрии, е — расстояние между центром тяжести и
центром давления (точкой приложения равнодействующей сил сопро-
сопротивления воздуха) и R — лобовое сопротивление, которое в силу
постоянства скорости центра тяжести снаряда будет также величиной
постоянной.
Уравнения A2.2) допускают частное решение:
a —a = p=p = O,
которому отвечает винтовое движение снаряда вдоль собственной оси
симметрии. Это движение мы примем за невозмущенное. Тогда урав-
уравнения A2.2) можно рассматривать как уравнения возмущенного
движения. Общие теоремы механики дают для этих уравнений два
первых интеграла (интеграл энергии и интеграл момента количества
') Ч е т а е в Н. Г., Устойчивость движения, Гостехиздат, 1946. См. также:
Ч е т а е в Н. Г., Об устойчивости вращательных движений снаряда. ПММ,
т. X, вып. 1, 1946.
2) Крылов А. Н., О вращательном движении продолговатого снаряда
во время полета, Собрание трудов, т. IV, Изд-во АН СССР, 1937. Вывод
дифференциальных уравнений движения снаряда можно найти также в книге:
Лойцянский Л. Г. и Лурье А. И., Курс теоретической механики, т. II,
§ 153, изд. 4-е, Гостехиздат, 1948.
42 ВТОРОЙ МЕТОД ЛЯПУНОВА ДЛЯ УСТАНОВИВШИХСЯ ДВИЖЕНИЙ [ГЛ. II
движения) вида
Fx (а, а, р, р) — -j А ф2 •+ а2 cos2 p) -f- eR (cos а cos p — 1) = const.
A2.3)
и
F2(a, а, р, р) = Л (р sin а — а cos p sin p cos а) +
-f-Сл (cos а cos р — 1) = const. A2.4)
dFl dF2
Действительно, составляя производные ——- и —гг-, в силу урав-
уравнений A2.2) будем иметь:
dFi dFi • , dFi •• , dFi • , dFi 'A
=== (X —j ——' Ct —j р —] ;— Р =
dt da da dp dp
= — ejRasinacosp-)-cosp(ejRsina — Сяр'-f- 2Ларsinp) a —
— Ла2р cos p sin p — eR$ cos a sin p -)-
+ P (eR sinp cos a — Ла2 sin p cos p -4- Cna cos p) ^ 0
и аналогично
Q
это и доказывает, что A2.3) и A2.4) действительно представляют
первые интегралы уравнений A2.2). Каждый из этих интегралов не
является знакоопределенным. Составим из них новый первый интеграл
V=F1 — IF2 = const.,
где к — некоторая постоянная, и подберем эту постоянную таким
образом, чтобы функция V получилась знакоопределенной (относи-
(относительно a, a, p и р). Выясним, при каком условии такой выбор по-
постоянной к возможен. Это и будет условием устойчивости.
Разлагая функцию V в ряд, будем иметь:
V = ~ { Ла? + (Спк — eR) p2 + 2/Uap] +
+ ^ МР2 И" (СпХ — еЮ «2 — 2^paj -4- ..., A2.5)
где ненаписанные члены имеют порядок не ниже третьего. Из этого
разложения сразу видно, что если каждая из квадратичных форм
Ах2-\-(Спк — eR)f±2Akxy A2.6)
будет определенно-положительной, то функция V будет также опре-
определенно-положительной. В самом деле, при выполнении указанных
условий выражение, стоящее в первой скобке разложения A2.5),
будет определенно-положительной квадратичной формой относительно
Л 12] ПРИМЕРЫ ПРИЛОЖЕНИЯ ПРЕДЫДУЩИХ ТЕОРЕМ 43
а и E, а выражение, стоящее во второй скобке, будет такой же
формой относительно а и р. Но тогда совокупность членов второго
порядка в функции V будет определенно-положительной квадратичной
формой всех четырех величин: а, а, E и р, и на основании резуль-
результатов § 7 функция V будет также определенно-положительной.
Таким образом, невозмущенное движение будет устойчиво, если
удастся подобрать такое число к, что обе формы A2.6) будут опре-
определенно-положительными, а для этого необходимо и достаточно,
чтобы выполнялись следующие неравенства:
А > 0, f(l) = Ак2 — Спк -f- eR < 0.
Первое из этих неравенств выполняется. Что же касается вто-
второго, то, поскольку /@)>0, ему можно будет удовлетворить под-
подходящими значениями к тогда и только тогда, когда уравнение
f (к) = 0 будет иметь два вещественных не равных между собой
корня кг и к2. В этом случае можно будет взять любое к, заклю-
заключенное между Х1 и к2.
Итак, для устойчивости достаточно, чтобы уравнение f(k) — Q
имело простые вещественные корни, т. е. чтобы выполнялось условие
—4AeR>0.
Это неравенство дает нижнюю границу угловой скорости враща-
вращательного движения снаряда, при которой его ось будет «следить»
за касательной к траектории центра тяжести. Ниже будет показано,
что при
С2я2 — AAeR < 0
невозмущенное движение будет неустойчиво.
Пример 3. Устойчивость регулируемых систем. Во многих
технических задачах важно, чтобы невозмущенное движение было
асимптотически устойчивым и чтобы эта устойчивость имела место
при любых начальных возмущениях. Так как функция Ляпунова дает
возможность не только установить асимптотическую устойчивость, но
и определить область допустимых начальных возмущений, то есте-
естественно, что второй метод может быть с успехом применен к реше-
решению такого рода технических задач. При этом дело сведется к устано-
установлению условий, при которых в рассматриваемой задаче можно будет
построить функцию V, удовлетворяющую всем условиям теоремы Б2').
Иначе говоря, здесь надо построить функцию V, удовлетворяющую
всем условиям теоремы Б при любых значениях переменных xs и
еще дополнительному условию
п
limV^=oo при 2л2
') См. примечание в конце книги (стр. 519).
44 ВТОРОЙ МЕТОД ЛЯПУНОВА ДЛЯ УСТАНОВИВШИХСЯ ДВИЖЕНИЙ (ГЛ. II
В качестве примера мы приведем здесь исследование А. И. Лурье ')
условий устойчивости одного класса регулируемых систем. Это ис-
исследование послужило отправной точкой для целого ряда других
работ, посвященных тому же вопросу.
Как показал А. И. Лурье, широкий класс регулируемых систем
с одним регулирующим органом может быть описан системой диф-
дифференциальных уравнений вида
dxs . . . . /10
—-f-=—р.л:с + /(о) (s=l, 2 ri),
at й
Здесь г — вещественная положительная постоянная, ps суть п раз-
различных постоянных с положительной вещественной частью, $s — также
постоянные, а /(о)—некоторая функция от о. Относительно этой
функции, являющейся характеристикой сервомотора, предполагается
только, что она является непрерывной, переходящей от отрицатель-
отрицательных значений при о < 0 к положительным при о > 0.
Задача заключается в установлении условий, которым должны
удовлетворять параметры системы (постоянные р5 и (Js), при которых
состояние равновесия jcx = ... = хп = а = 0 асимптотически устой-
устойчиво при любых начальных отклонениях и при любом виде функции
/(а), удовлетворяющей вышеуказанным условиям.
А. И. Лурье рассматривал общий случай, когда постоянные р^
и $s комплексны. Мы, однако, для упрощения изложения ограничимся
здесь рассмотрением лишь того случая, когда все постоянные ps и fis
вещественны. Рассмотрим квадратичную форму
и покажем, что она определенно-положительна. В силу того, что
pft > 0, имеем:
-J
I
0"
и, следовательно,
oo n
/
0 a,p=l
') Лурье А. И., Об устойчивости одного класса регулируемых систем.
ПММ, т. XV, вып. 5, 1951; Лурье А. И., Некоторые нелинейные задачи
теории автоматического регулирования, Гостехиздат, 1951.
§ 12] ПРИМЕРЫ ПРИЛОЖЕНИЯ ПРЕДЫДУЩИХ ТЕОРЕМ 45
Интеграл, стоящий в правой части, может обратиться в нуль
лишь при таких значениях х1 хп, при которых подинтеграль-
ное выражение обращается в нуль. Последнее же, в силу того, что
все ps различны, обращается в нуль только при х1 — ... =л:„ = 0.
Отсюда непосредственно вытекает знакоопределенность формы F.
Установив это, рассмотрим функцию
V(o. хх *„) =
где as и As— произвольные вещественные постоянные, причем все As
положительны. При тех условиях, которые мы наложили на функ-
функцию /(о), величина
ff(a)da
при всех отличных от нуля значениях о положительна и обращается
в нуль при а = 0. Но тогда очевидно, что функция V определенно-
положительна относительно переменных л^, ..., хп, а, что имеет
место при любых значениях этих переменных и при любом выборе
функции /(о), удовлетворяющей указанным для нее условиям. Соста-
Составляя производную от V в силу уравнений A2.7), будем иметь:
a=l a,p=l
n
+ rf(a)-f(o)
откуда, учитывая, что
n
a,p=l
получим:
~4г = 1]ЛаРа*а+ ( ]?
(
а=1 \а=1
Так как г > 0, то полученное выражение будет, очевидно, опре-
определенно-положительным, если коэффициент при /(а) обращается
46 ВТОРОЙ МЕТОД ЛЯПУНОВА ДЛЯ УСТАНОВИВШИХСЯ ДВИЖЕНИЙ [ГЛ. II
в нуль. Однако такое условие является слишком ограничительным,
dV
так как при этом -гг будет определенно-положительным при лю-
любом г > О, а между тем ясно, что если т достаточно велико, то
— получится определенно-положительным, каков бы ни был коэф-
коэффициент при /(о). Для того чтобы получить более общие условия
, dV
знакоопределенности, преобразуем -ц- к следующему виду:
Следовательно, если выполняются условия
p=i
dV
то —гг будет определенно-отрицательной функцией от о, хх хп,
и это будет справедливо при любых значениях указанных переменных.
Для выполнения дополнительного условия
lim V(Xj, .. ., хп, а) = со (x = \xl\, ..., \хп\, а)
*->оо
достаточно в данном случае, чтобы выполнялось предельное соотно-
соотношение
о
f{l)dl = co. A2.9)
Таким образом, мы приходим к следующему предложению: если
можно подобрать п положительных постоянных As таким образом,
чтобы система уравнений A2.8) допускала вещественное решение
для as, и если выполнено условие A2.9), то невозмущенное движе-
движение для системы A2.7) асимптотически устойчиво при любых началь-
начальных возмущениях.
Таким образом, задача нахождения области допустимых значений
параметров регулируемых систем, описываемых уравнениями A2.7),
сведена к алгебраической задаче определения области изменения
коэффициентов системы квадратных уравнений A2.8), при которых
эти уравнения допускают вещественное решение. Мы не останавли-
останавливаемся здесь более подробно на этом вопросе, отсылая читателя
к вышеназванным оригинальным работам, где указанный метод
успешно применен к решению задачи устойчивости для целого ряда
§ 13] ПЕРВАЯ ТЕОРЕМА ЛЯПУНОВА О НЕУСТОЙЧИВОСТИ 47
конкретных систем регулирования. Укажем лишь на одно неравен-
неравенство, непосредственно вытекающее из уравнений A2.8) и выражаю-
выражающее, следовательно, одно из достаточных условий устойчивости,
а именно: разделив уравнения A2.8) на ps и сложив их, получим:
a=l \a=l / a=l
откуда вытекает:
Это и будет интересующее нас неравенство. Ниже мы увидим,
что если /(а) является аналитической функцией, то неравенство A2.9)
выражает необходимое и достаточное условие устойчивостиг).
§ 13. Первая теорема Ляпунова о неустойчивости.
Мы переходим теперь к изложению теорем Ляпунова о неустой-
неустойчивости. Первая из этих теорем, которую мы будем в дальнейшем
называть теоремой В, формулируется следующим образом.
Теорема В. Если для дифференциальных уравнений возму-
возмущенного движения возможно найти функцию V (хх хп),
такую, что ее полная производная по времени —гг> состав-
составленная в силу этих уравнений, есть функция знакоопределен-
ная, а сама функция V не будет знакопостоянной, знака,
противоположного с —тг, то невозмущенное движение не-
неустойчиво.
Доказательство. Пусть
|*5|<А<// A3.1)
dV
— область знакоопределенности функции —гг ¦ Мы будем предпола-
предполагать число h настолько малым, чтобы в области A3.1) выполнялись
все условия для уравнений F.1) возмущенного движения, которые
были оговорены в § 6. Допустим также, для определенности, что —тг
есть функция положительная.
Покажем, что, как бы мало ни было число т), всегда найдется
такая система начальных значений x°s, лежащая в области
| A3.2)
') См. примечание в конце книги (стр. 520).
48 ВТОРОЙ МЕТОД ЛЯПУНОВА ДЛЯ УСТАНОВИВШИХСЯ ДВИЖЕНИЙ [ГЛ. II
что решения xs(t) уравнений F.1) с указанными начальными значе-
значениями выйдут в некоторый момент времени из области A3.1). Этим,
очевидно, и будет доказана неустойчивость движения.
Выберем с этой целью величины x°s таким образом, чтобы выпол-
выполнялись не только неравенства A3.2), но и неравенство
Такой выбор величин x°s возможен, так как по условию функция V
не является знакопостоянной отрицательной и, следовательно, в любой
сколь угодно малой окрестности начала координат она может при-
принимать положительные значения. Рассмотрим теперь решение xs(t)
уравнений F.1) с выбранными таким образом начальными значениями.
Это решение в некоторый момент времени необходимо покинет
область A3.1). В самом деле, допустим противное: пусть величины xs(t)
dV
при всех t > tQ удовлетворяют неравенствам A3.1). Тогда —тт- все
время будет оставаться положительной и, следовательно, V [хх (t), ...
.... xn(t)] будет все время возрастать. Мы можем поэтому написать:
V [*, @ хп Щ > V(jfiv .... *°). A3.3)
Отсюда необходимо получается, что
*(Q = max{|*,(Q| |*„(91}>*. A3.4)
где А, — некоторое положительное число, ибо если бы мы имели
х (t) < X, то при достаточно малом А, неравенство A3.3) не могло бы
выполняться, так как функция V (х^ хп) непрерывна и обра-
обращается в нуль при хг = ... = хп = 0.
Так как —гг есть функция определенно-положительная, то из
неравенства A3.4) вытекает, что для рассматриваемого решения xs(t)
все время выполняется неравенство
dt ^l'
где / — достаточно малое положительное число. Следовательно,
откуда вытекает, что У[х{((), ..., xn(t)\ неограниченно возрастает.
Но это противоречит условию, что решение xs(t) остается в области
A3.1), так как в этой области функция V, будучи непрерывной,
необходимо ограничена. Это и доказывает неустойчивость невозму-
невозмущенного движения.
§ 14] ТЕОРЕМА ЛЯПУНОВА О НЕУСТОЙЧИВОСТИ РАВНОВЕСИЯ 49
§ 14. Теорема Ляпунова о неустойчивости равновесия,
когда силовая функция обращается в минимум.
В качестве первого примера приложения теоремы В рассмот-
рассмотрим вопрос об устойчивости равновесия, когда силовая функция
в положении равновесия имеет не максимум, как в случае Лагранжа,
а минимум.
Рассмотрим консервативную систему с п степенями свободы
и запишем уравнения движения этой системы в канонической форме:
dqs дН dps дН ... ..
dt dps ' dt ' dqs *¦ ' '
(s=l, 2, .... n),
где
qs—обобщенные координаты, ps—обобщенные импульсы, Т — кине-
кинетическая энергия, U — силовая функция. Допустим, что система имеет
положение равновесия, которому соответствуют нулевые значения
координат (а также, очевидно, и импульсов). В этом случае уравне-
уравнения A4.1) будут уравнениями возмущенного движения. Силовую
функцию мы выберем таким образом, чтобы в положении равновесия
она обращалась в нуль. Тогда, разлагая эту функцию в ряд по сте-
степеням qs (полагая, что такое разложение возможно), будем иметь:
где Uj обозначает совокупность членов /-го порядка. При этом, как
известно, т ^ 2. Допустим теперь, что в положении равновесия
силовая функция имеет минимум. Это, очевидно, означает, что U
есть функция определенно-положительная. Тогда на основании резуль-
результатов § 7 форма Uт будет по меньшей мере знакопостоянной поло-
положительной. Мы будем, однако, предполагать, что эта форма является
знакоопределенной, что, как было доказано в § 7, обусловливает
также знакоопределенность функции U.
Кинетическая энергия системы относительно импульсов ps является
квадратичной формой. Коэффициенты этой формы зависят от коор-
координат qs. Обозначая значения этих коэффициентов при ql = ... =¦
= qn = Q через а-, мы можем написать:
где AJqv ..., <7„) — некоторые функции qy ..., qn, обращающиеся
в нуль при qx = . .. = qn = 0. Функция Т по самому своему зна-
значению принимает при р\ -{-...-\- р2п ф 0 только положительные
50 ВТОРОЙ МЕТОД ЛЯПУНОВА ДЛЯ УСТАНОВИВШИХСЯ ДВИЖЕНИЙ [ГЛ. II
значения, каковы бы ни были значения переменных qs. В частности,
это будет также иметь место и при qx = ... = qn = 0. Отсюда
следует, что форма
a|iVaPp A4.2)
будет определенно-положительной.
Рассмотрим теперь функцию
и составим ее полную производную по времени в силу уравнений A4.1).
Будем иметь:
dV VI дН V4 дН
2P 1 4
dt — 2uPs ~др^ 1л 4s dqs
s=l s=l
П дт П
r\ 01
5 = 1 j, a, p=l s = l
или, применяя теорему Эйлера об однородных функциях,
In п i
a, p=l a, p=l \
+ {mt/m + (m + l)t/m+1+...). A4.3)
Выражение, стоящее в первой скобке формулы A4.3), будет
на основании леммы 3 § 7 определенно-положительной функцией
относительно р:, .... рп, так как форма A4.2) определенно-поло-
определенно-положительна, а коэффициенты
обращаются в нуль при qr — . .. =</„ = (), и следовательно, в до-
достаточно малой окрестности начала координат они сколь угодно малы.
Выражение, стоящее во второй скобке формулы A4.3), на основании
леммы 4 § 7 является определенно-положительной функцией перемен-
переменных qx, .... qn, так как форма Um по условию определенно-поло-
определенно-положительна. Следовательно, —— является определенно-положительной
функцией всех 2я переменных qs, ps. С другой стороны, сама функ-
функция V является, очевидно, знакопеременной. Таким образом, V удо-
§ 15] ВТОРАЯ ТЕОРЕМА ЛЯПУНОВА О НЕУСТОЙЧИВОСТИ 51
влетворяет всем условиям теоремы В, и поэтому исследуемое положе-
положение равновесия неустойчиво.
Итак, мы получили следующую теорему, принадлежащую
Ляпунову:
Если в положении равновесия силовая функция имеет мини-
минимум и это определяется совокупностью членов наинизшего
порядка в разложении этой функции, то равновесие неустой-
неустойчиво.
Приведенное доказательство лишь незначительно отличается
от классического доказательства Ляпунова.
§ 15. Вторая теорема Ляпунова о неустойчивости.
Докажем еще одну теорему Ляпунова о неустойчивости.
Теорема Г. Если существует функция V такая, что ее
полная производная по t в силу уравнений возмущенного дви-
движения имеет в области A3.1) вид
*V.=W+W{Xl *„). A5.1)
где X — положительная постоянная, a W или тождественно
обращается в нуль или представляет собой знакопостоянную
функцию, и если в последнем случае функция V не является
знакопостоянной, знака, противоположного с W, то невозму-
невозмущенное движение неустойчиво.
Доказательство. Допустим для определенности, что функ-
функция W положительна. Тогда из A5.1) получаем:
^jf>W- A5.2)
Так же как и при доказательстве теоремы В, выберем начальные
(при t=t^ значения x°s решения xs(t) таким образом, чтобы одно-
одновременно выполнялись неравенства
где т) сколь угодно малое положительное число. Покажем, что это
решение необходимо покидает в некоторый момент времени область
A3.1). Допустим противное: что неравенства A3.1) все время выпол-
выполняются. Тогда все время будет выполняться неравенство A5.2)
и, поскольку V(x°v ..., хо\ положительно, производная -гт- будет все
время оставаться положительной и, следовательно, V[xl (t), .. ., х„(t)]
будет функцией возрастающей. Но тогда из A5.2) находим:
52 ВТОРОЙ МЕТОД ЛЯПУНОВА ДЛЯ УСТАНОВИВШИХСЯ ДВИЖЕНИЙ [ГЛ. II
и, следовательно,
что невозможно, так как в области A3.1) функция V ограничена.
Таким образом, для рассматриваемого решения неравенства A3.1)
необходимо нарушаются, что и доказывает неустойчивость невозму-
невозмущенного движения.
§ 16. Геометрическая интерпретация теоремы В.
Теорема Н. Г. Четаева.
Теорема В, так же как и теоремы А и Б, допускает простое
геометрическое истолкование.
Примем для простоты, что п = 2, и рассмотрим сначала тот слу-
случай, когда функция V не является знакоопределенной. В этом случае
кривая V = 0 имеет одну (рис. 4) или несколько (рис. 5) веществен-
вещественных ветвей, проходящих через начало координат.
Рис. 4.
Рис. 5.
dV
Допустим, что производная —тг определенно-положительна. По
условию теоремы в окрестности начала координат необходимо
существует, по крайней мере, одна область, где V > 0. Эти
области, очевидно, ограничены кривыми У = 0. Пусть на фиг. 4
и 5 сектор АОВ представляет одну из этих областей и допустим,
что пунктирные линии обозначают кривые V = с > 0, заполняющие
эту область.
Рассмотрим интегральную кривую МР, выходящую из произволь-
произвольной точки М границы области. Эта точка может быть взята сколь
dV
угодно близко от начала координат. Так как —гг > 0. то эта инте-
ГЕОМЕТРИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ ТЕОРЕМЫ
53
тральная кривая при возрастании t необходимо входит внутрь области
у > 0 и пересекает кривые семейства V = c в сторону, соответствую-
соответствующую возрастанию с, т. е. удаляясь от границы V = 0. При этом
интегральная кривая все время будет удаляться от начала координат
и в конце концов покинет область A3.1), если только она в неко-
некоторый момент времени не достигнет другой границы области V > 0.
Это, однако, невозможно, так как если бы такое пересечение в какой-
нибудь точке N (рис. 6) имело место, то в этой точке, очевидно,
бЫЛО бы —гг <С Of так как
функция V, изменяясь от по-
положительных значений к ну-
нулевому, необходимо уменьша-
уменьшалась бы.
Таким образом, имеются
интегральные кривые, выходя-
выходящие из точек, сколь угодно
близко расположенных к на-
началу координат, и покидающие
в некоторый момент времени
область A3.1). Отсюда и выте-
вытекает неустойчивость движения.
Мы предположили, что
функция V не является знако-
знакоопределенной. Ничто, однако,
не изменится, если V и Рис. 6.
является знакоопределенной
функцией. В этом случае областью V > 0 будет вся окрестность
начала координат.
Приведенное геометрическое истолкование теоремы В сразу при-
приводит к важному обобщению этой теоремы. Действительно, во всех
предыдущих рассуждениях не играло никакой роли то обстоятель-
dV
ство, что производная —тт- является знакоопределенной. Все преды-
предыдущие рассуждения останутся в силе, если вместо знакоопределен-
dV
ности предположить, что —тт- принимает положительные значения во
всех точках области V > 0. Мы приходим, таким образом, к сле-
следующей теореме, установленной Н. Г. Четаевым J).
Теорема Н. Г. Четаев а. Если для дифференциальных урав-
уравнений возмущенного движения можно найти такую функцию
У(хх хп), что 1) в сколь угодно малой окрестности
') Четаев Н. Г., Одна теорема о неустойчивости, ДАН, т. I, № 9.
1934. См. также монографию: Четаев Н. Г., Устойчивость движения (Гос-
техиздат, 1946), где дана более точная формулировка теоремы.
54 ВТОРОЙ МЕТОД ЛЯПУНОВА ДЛЯ УСТАНОВИВШИХСЯ ДВИЖЕНИЙ {ГЛ. п
начала координат существует область, где V > О, на границе
которой У = 0, и 2) во всех точках области К>0 производ-
dV
ная —тг- принимает положительные значения, то невозмущен-
невозмущенное движение неустойчиво.
Точное аналитическое доказательство теоремы Н. Г. Четаева мы
дадим в главе V, где эта теорема будет изложена в более общей
формулировке.
§ 17. Пример приложения теоремы Н. Г. Четаева.
Теорема Н. Г. Четаева о неустойчивости равновесия.
Согласно теореме Лагранжа положение равновесия системы устой-
устойчиво, если в этом положении силовая функция имеет максимум. На-
Наоборот, согласно теореме Ляпунова положение равновесия будег
неустойчиво, если в этом положении силовая функция имеет минимум,
и этот минимум определяется совокупностью членов наинизшего изме-
измерения в разложении силовой функции.
Исследуем теперь вопрос об устойчивости равновесия, когда
силовая функция в положении равновесия не имеет ни максимума,
ни минимума. Ограничимся при этом рассмотрением того частного
случая, когда силовая функция U является формой какого-нибудь
порядка от, так что
Дифференциальные уравнения возмущенного движения примем,
как и в § 14, в форме A4.1). Рассмотрим функцию
У=—ИЪР1Й1- 07.1)
Так как по условию форма Um при qx — ... = qn = О не имеет
максимума, то эта форма необходимо может принимать положитель-
положительные значения. Отсюда следует, что в окрестности начала координат
пространства 2я переменных qL, p( необходимо существует область,
где
-H = -T + Um>0, A7.2)
причем в этой области Um > 0, так как — Т <Г. 0. Назовем областью С
ту часть области A7.2), в которой выполняется условие
S pai > о-
На основании A7.1) в области С выполняется неравенство V > 0,
§
ЗАКЛЮЧИТЕЛЬНЫЕ ЗАМЕЧАНИЯ
55
а на границе ее, где, очевидно, либо 2 P-fli — 0- ш^о Н = О, функ-
функция V обращается в нуль.
Составим выражение производной —гг. Повторяя выкладки § 14
и принимая во внимание, что—^-=0, найдем:
dV и X1 _ __ i X' I л X1 .. """ар | _ _ t тНП
— mnum.
a, C= 1 a, 0 = 1
Выражение, стоящее в фигурных скобках, как было показано
в § 14, может принимать только положительные или равные нулю
значения. Величина Um, как указывалось выше, может принимать
в области С только положительные значения. Отсюда следует, что
в области С выполняется условие —^- > 0. Таким образом, функ-
функция V удовлетворяет всем условиям теоремы Н. Г. Четаева, откуда
вытекает неустойчивость исследуемого положения равновесия. Следо-
Следовательно, имеет место следующая теорема, установленная Н. Г. Че-
таевым ').
Если в положении равновесия силовая функция не имеет
максимума и эта функция является формой, то равновесие
неустойчиво.
§ 18. Заключительные замечания.
В предыдущих параграфах мы изложили основные теоремы второго
метода Ляпунова. Эти теоремы сводят задачу устойчивости к по-
построению для уравнений возмущенного движения некоторых функций,
обладающих специальными свойствами. Мы будем в дальнейшем эти
функции, удовлетворяющие одной из основных теорем второго ме-
метода, называть функциями Ляпунова.
Мы рассмотрели ряд задач, которые удалось успешно разрешить
при помощи второго метода. В каждой из этих задач было проведено
конкретное построение функции Ляпунова. При этом мы видели, что
это построение в каждом отдельном случае носило специфический
характер, связанный с рассматриваемой конкретной задачей. Общих
правил, позволяющих во всех случаях построить функцию Ляпунова,
не существует. Если бы такие правила существовали, то этим самым
задача устойчивости была бы полностью исчерпана. К сожалению,
мы еще весьма далеки от этого.
') Ч е т а е в Н. Г., К вопросу об обращении теоремы Лагранжа. Сбор-
Сборник научн. трудов Казанск. авиационного ин-та, № 2, 1934.
56 ВТОРОЙ МЕТОД ЛЯПУНОВА ДЛЯ УСТАНОВИВШИХСЯ ДВИЖЕНИЙ [ГЛ. II
Тем не менее, Ляпуновым и его последователями разработаны
некоторые общие приемы и идеи построения функций Ляпунова,
которые с успехом применяются к конкретным задачам. Это позволило
систематически рассмотреть некоторые основные задачи теории устой-
устойчивости при помощи второго метода. К такому систематическому рас-
рассмотрению указанных задач мы сейчас и приступаем. При этом мы
начинаем с основной задачи об установлении необходимых и доста-
достаточных условий устойчивости по первому приближению. Этой задаче
посвящена следующая глава. Как уже указывалось раньше, мы огра-
ограничиваемся сначала установившимися движениями.
ГЛАВА III.
КРИТЕРИИ УСТОЙЧИВОСТИ ПО ПЕРВОМУ ПРИБЛИЖЕНИЮ
ДЛЯ УСТАНОВИВШИХСЯ ДВИЖЕНИЙ.
§ 19. Уравнения первого приближения.
В этой главе мы занимаемся установлением необходимых и до-
достаточных условий устойчивости по первому приближению для того
случая, когда дифференциальные уравнения возмущенного движения
имеют вид
E=1, 2 П).
Здесь psj — постоянные, Xs — не зависящие от t функции пере-
переменных jCj xn, разлагающиеся в области
х|<Я A9.2)
в ряды по степеням этих переменных, причем разложения начинаются
членами не ниже второго порядка.
Рассмотрим уравнения первого приближения
dt
••• Л-PsnXn (s=l. 2 п). A9.3)
Теория интегрирования такого рода уравнений хорошо известна.
Напомним основные положения этой теории ').
Рассмотрим уравнение ге-й степени
D(k) =
—h P\1
Pi\
Pin
Pin
Pa
Pni
A9.4)
') См., например, Степанов В. В., Курс обыкновенных дифферен-
дифференциальных уравнений, Гостехиздат, 1950.
58 КРИТЕРИИ УСТОЙЧИВОСТИ ПО ПЕРВОМУ ПРИБЛИЖЕНИЮ [ГЛ. III
Это уравнение называется характеристическим уравнением,
а определитель D (к) — характеристическим определителем.
Пусть Я,г — какой-нибудь корень этого уравнения. Этому корню от-
отвечает частное решение системы A9.3) вида
xs==AseKit (s=\, 2 я), A9.5)
где As — постоянные, определяемые однородными алгебраическими
уравнениями
pslA,+ ... +(р„ — k,)As + ••• +PsnA« = 0. 09.6)
имеющими в силу D (Xt) — О нетривиальное решение.
Если уравнение A9.4) имеет только простые корни, то, полагая
в A9.5) г=1, 2 п, мы получим п частных решений системы
A9.3). Эти решения будут притом независимы.
Допустим теперь, что Xt является кратным корнем и что кратность
этого корня равна I. Этому корню по-прежнему соответствует реше-
решение A9.5), где As по-прежнему удовлетворяют уравнениям A9.6).
Но в рассматриваемом случае корню Xt будут отвечать еще и другие
частные решения системы A9.3), отличные от A9.5). Эти решения
имеют вид
v f (+\ л'^1? (с 19 п\ /1Q *7\
хs — js \i) с i {s — i, z, .. ., п), ^i у. /)
где fs(t) — некоторые полиномы относительно t. Степень этих поли-
полиномов никогда не превосходит /— 1, но может быть меньше этой
величины. Здесь приходится различать два случая в зависимости от
того, будет ли ранг определителя D (Х^ равен п — 1 или меньше
этой величины.
Допустим сначала, что ранг определителя D(Xl) равен п — 1,
т. е. что хотя бы один из миноров (п— 1)-го порядка1) этого опре-
определителя отличен от нуля. В этом случае система A9.3) имеет
хотя бы одно решение вида A9.7), в котором хотя бы один из поли-
полиномов fs (/) имеет степень /— 1. Заменяя в этом решении полиномы /s (t)
их производными какого-нибудь порядка, мы снова получим решения
системы A9.3). Таким путем получается / решений системы A9.3),
имеющих вид
е ¦
dt A9.8)
') Минором (п — k)-го порядка мы называем определитель, получаю-
получающийся из основного вычеркиванием k строк и колонок.
& 19] УРАВНЕНИЯ ПЕРВОГО ПРИБЛИЖЕНИЯ 59
. Все эти решения независимы. Последнее из них совпадает с A9.5).
Мы будем говорить, что в рассматриваемом случае кратному корню Xt
отвечает одна группа решений.
Допустим теперь, что ранг определителя D(Xt) меньше п—1.
Пусть, например, ранг этого определителя равен п — 2, так что все
миноры (п—1)-го порядка равны нулю, но хотя бы один из мино-
миноров (п — 2)-го порядка отличен от нуля. В этом случае система A9.3)
допускает два частных решения вида A9.7), в которых наивысшие
степени полиномов fs(t) равны, соответственно, р и q, причем
рЦ-q — l—2. Эти решения таковы, что если, исходя из каждого
из них, составлять новые решения путем замены полиномов fs(t) их
производными какого-нибудь порядка, то все полученные таким
образом решения будут независимы.
Пусть
xa = f'se4.\
. lt A9.9)
суть указанные частные решения. Степени полиномов f's (t) не пре-
превосходят р, причем степень хотя бы одного из них достигает этого
значения. Старшая степень полиномов f"s равна q. При этом, как
уже указывалось выше, p-\-q = l — 2.
Заменяя в решениях A9.9) полиномы их последовательными
производными, мы получим две группы решений уравнений A9.3),
состоящих, соответственно, из р-f-l и q-\-\ решений каждая и
имеющих вид
*? = -ДГГеЧ (P=1- 2
Таким образом, и в рассматриваемом случае корню Яг соответ-
соответствует p-\-q-\-2 = l частных решений. Среди этих решений имеются
два (по одному в каждой группе) вида A9.5). Эти решения соот-
соответствуют двум независимым системам чисел As, удовлетворяющим
однородным алгебраическим уравнениям A9.6). Последние действи-
действительно имеют два независимых решения, так как ранг определи-
определителя D (к{) равен п — 2.
В общем случае, когда ранг определителя D(K^) равен n — k,
корню кратности / по-прежнему соответствует / независимых решений,
но эти решения распадаются на k групп, подобных A9.10).
Ранг определителя D(ht) не может быть меньше п — I. В про-
противном случае, как это легко показать, кратность корня %t будет
больше I. Поэтому число групп решений, соответствующих рассматри*
60 КРИТЕРИИ УСТОЙЧИВОСТИ ПО ПЕРВОМУ ПРИБЛИЖЕНИЮ [ГЛ. 111
ваемому корню, не может превосходить числа /, т. е. кратности
корня. Если число групп равно /, то каждая группа будет состоять
из одного решения и все решения будут вида A9.5).
Таким образом, во всех случаях число частных решений уравне-
уравнений A9.3), соответствующих кратному корню, равно кратности этого
корня. Действительное вычисление этих решений приводится к реше-
решению систем линейных алгебраических уравнений. Наиболее простой
способ составления этих уравнений указан Н. Г. Четаевым>).
Рассматривая все корни уравнения A9.4), мы получим п незави-
независимых частных решений уравнений A9.3). Обозначая эти решения
через xsl, xs2 xsn (первый индекс — номер функции, второй
индекс — номер решения), мы получим общее решение уравнений A9.3)
в виде
xs = СЛ, + С2хл + . .. + Cnxsn, A9.11)
где Cl Сп — произвольные постоянные. Эти постоянные опре-
определяются из начальных условий и если начальные значения величин xs
в каком-нибудь решении малы, то и соответствующие значения
постоянных Cj будут также малыми.
Если корень Xi является комплексным, то решения вида A9.5)
или A9.7) будут также комплексными, и так как нас интересуют
только вещественные решения, то необходимо будет их преобразовать
к вещественному виду. Для этого заметим, что так как коэф-
коэффициенты psj являются вещественными, то если дифференциальным
уравнениям A9.3) удовлетворяет какая-нибудь система комплексных
функций, то им удовлетворяют также вещественные и мнимые части
этих функций. Пусть Xt = \i-\- iv. Тогда в решении A9.5) или A9.7)
величины As и fs(t) будут также комплексными. Положим As =
= Ps-\- iQs, fs = (ps-j- i\ips, где постоянные Ps, Qs и функции q>s и tys
будут вещественными. Выделяя в A9.5) и в A9.7) вещественные и
мнимые части, мы получим, что рассматриваемому корню |х —J— tv
отвечают два решения: либо вида
xs = (Pscosvt—Qssm\t)eilt, xs = (Pss\nvt^-Qscosvt)ev-t A9.12)
либо вида
— ipssin v/) e^f, xs = {(fss\nvt-\--^scosyt)ev-t. A9.13)
Эти же самые решения отвечают и корню \а — iv.
Все вышесказанное позволяет легко решить задачу устойчивости
для того случая, когда дифференциальные уравнения возмущенного
движения имеют вид A9.3). Действительно, характер невозмущенного
движения, его устойчивость или неустойчивость, полностью опреде-
определяется корнями характеристического уравнения A9.4).
') Четаев Н. Г., Устойчивость движения, Гостехиздат, 1946.
§ 19) УРАВНЕНИЯ ПЕРВОГО ПРИБЛИЖЕНИЯ 61
Допустим сначала, что все корни характеристического уравнения
имеют отрицательные вещественные части. В этом случае все рас-
рассмотренные выше частные решения независимо от того, имеют ли
они вид A9.5) или A9.7), A9.12) или A9.13), стремятся к нулю
при неограниченном возрастании t. To же самое будет справедливо
и по отношению к общему решению A9.11), каковы бы ни были
постоянные Cj. Кроме того, решения xs(t), отвечающие начальным
условиям | xs (t0) | -^ 1, будут равномерно ограничены при всех
t^-t0. Следовательно, невозмущенное движение устойчиво и притом
асимптотически при любых начальных возмущениях.
Допустим теперь, что среди корней характеристического уравне-
уравнения имеется, по крайней мере, один с положительной вещественной
частью. Этому корню отвечает частное решение, неограниченно воз-
возрастающее при t-*co. Умножая все функции этого решения на
постоянную С, мы снова получим решение, для которого начальные
значения функций xs могут быть сделаны сколь угодно малыми,
если С выбрать достаточно малым. Таким образом, в рассматривае-
рассматриваемом случае система A9.3) имеет решение со сколь угодно малыми
начальными значениями, неограниченно возрастающее при t—>oo, и
следовательно, невозмущенное движение неустойчиво.
Допустим теперь, что характеристическое уравнение, не имея
корней с положительными вещественными частями, имеет корни
с вещественными частями, равными нулю. Это могут быть нулевые
корни или корни чисто мнимые. Каждому нулевому корню отвечают
решения вида
xs = As, A9.14)
если этот корень является простым или даже если он является
кратным, но число групп решений равно кратности корня. В про-
противном случае система A9.3) будет иметь решения вида
*, = /,(*). A9.15)
где fs(t) — полиномы. Для каждой пары чисто мнимых корней
+ v У—1 будут получаться решения вида
xs = Pscosvt — Qssir\vt, xs = Pssinvt-lrQscosvt, A9.16)
если эти корни простые или если они кратные, но число групп
решений, им соответствующих, равно их кратности. Если корни
± v у—1 являются кратными и число групп решений, им соответ-
соответствующих, меньше их кратности, то система A9.3) будет иметь
решения вида
t, A9.17)
где <р, и tyt — полиномы,
62 КРИТЕРИИ УСТОЙЧИВОСТИ ПО ПЕРВОМУ ПРИБЛИЖЕНИЮ [ГЛ. III
Наличие решений вида A9.14) или A9.16) не нарушает устой-
устойчивости, так как все входящие в эти решения функции ограничены.
Правда, при этом устойчивость не будет, очевидно, асимптотической.
Наличие же решений вида A9.15) или A9.17) вызывает, очевидно,
неустойчивость.
Таким образом, для случая, когда уравнения возмущенного дви-
движения имеют вид A9.3), мы приходим к следующим заключениям.
Для того чтобы невозмущенное движение было асимпто-
асимптотически устойчивым, необходимо и достаточно, чтобы все
корни характеристического уравнения имели отрицательные
вещественные части. Если среди корней этого уравнения
имеется хотя бы один с положительной вещественной частью,
то невозмущенное движение неустойчиво. Невозмущенное дви-
движение будет устойчивым, но не асимптотически, когда харак-
характеристическое уравнение, не имея корней с положительными
вещественными частями, имеет корни с вещественными частями,
равными нулю, если эти корни простые или если они крат-
кратные, но число групп решений, им соответствующих, равно их
кратности. Если характеристическое уравнение имеет крат-
кратные корни с нулевыми вещественными частями и если число
групп решений, соответствующих этим корням, меньше их
кратности, то невозмущенное движение неустойчиво.
Таким образом, задача устойчивости для линейных уравнений
с постоянными коэффициентами решается просто. Здесь нет необхо-
необходимости пользоваться вторым методом. Тем не менее мы займемся
построением функций Ляпунова для уравнений A9.3), так как эти
функции будут играть фундаментальную роль в дальнейшем. Нам
придется для этого предварительно доказать некоторые вспомога-
вспомогательные предложения.
§ 20. Некоторые вспомогательные предложения.
Пусть V(x1 хп) — какая-нибудь форма га-го порядка. Рас-
Рассмотрим производную этой формы по времени, составленную в силу
уравнений A9.3), т. е. форму того же порядка:
dV V dv / i i s
s-1
и поставим задачу определить форму V таким образом, чтобы вы-
выполнялось соотношение
п
§ 20] НЕКОТОРЫЕ ВСПОМОГАТЕЛЬНЫЕ ПРЕДЛОЖЕНИЯ 63
где Я, — постоянная. Коэффициенты искомой формы должны удовле-
удовлетворять некоторой системе уравнений, которые мы получим, при-
приравнивая коэффициенты при подобных членах в правой и левой частях
уравнения B0.1). Исследуем подробнее эти уравнения. Для этого
допустим сначала, что т = 1, т. е. положим
V =«!*,+ ...+«»*»• B0.2)
Подставляя B0.2) в B0.1) и приравнивая коэффициенты при
х1 хп, получим следующую систему уравнений, которым должны
удовлетворять коэффициенты а1 ап:
Р\па\~\- Р2па2 + •••
Для того чтобы эта система линейных однородных уравнений
имела решение, отличное от тривиального, необходимо и достаточно,
чтобы определитель этой системы
рп—1 р21 ... рпХ
Р\2 />22 — А- • • • Рп1
Pin Р2п ¦•¦ Рпп — '
обращался в нуль. Таким образом, для того чтобы уравнение B0.1)
могло быть удовлетворено линейной формой, необходимо и доста-
достаточно, чтобы Я, было корнем характеристического уравнения. Каждому
корню этого уравнения отвечает своя форма, и если характеристи-
характеристическое уравнение имеет п различных корней, то мы получим п раз-
различных линейных форм, удовлетворяющих уравнению B0.1).
Допустим теперь, что т. > 1. Обозначим через N число членов
формы /га-го порядка1). Эгих членов будет, очевидно, столько,
Сколько существует различных систем целых неотрицательных чисел
т1% ..., тп, связанных соотношением
/71! —j— /7t 2 —j— ••• '-$- тп = т. B0.3)
Перенумеровав все члены формы V в каком-нибудь порядке,
обозначим через alt a2 aN коэффициенты при этих членах.
Тогда подставляя форму V в уравнение B0.1) и приравнивая коэф-
коэффициенты при подобных членах в правой и левой частях этого урав-
') Число N определяется формулой
64
КРИТЕРИИ УСТОЙЧИВОСТИ ПО ПЕРВОМУ ПРИБЛИЖЕНИЮ [ГЛ. III
нения, мы получим для определения uj систему линейных однород-
однородных уравнений вида
(/=1. 2, ....
B0.4)
где Ац — некоторые постоянные, являющиеся линейными комбина-
комбинациями коэффициентов psg. Так, например, при т — 2 и п = 2
система B0.4) будет иметь вид:
(Pl\
если
=«!¦«?+«8*1*2+«8*2-
Для того чтобы система B0.4) имела решение, отличное от три-
тривиального al = a2= ... =адг = 0, необходимо и достаточно, чтобы
к удовлетворяло уравнению
Ап к
21
12 ... A1N
22 Л, ... A2N
¦ • ¦ ANN A
= 0. B0.5)
Таким образом, для того чтобы уравнению B0.1) можно было
удовлетворить формой т-ro порядка, необходимо и достаточно, чтобы
величина X была корнем алгебраического уравнения ЛЛй степени B0.5).
Между корнями уравнения B0.5) и корнями характеристического
уравнения существует простая зависимость, а именно, имеет место
следующая изящная теорема, принадлежащая Ляпунову.
Теорема 1. Все корни уравнения B0.5) определяются фор-
формулой
1 = т1Х1-\-т212-\- • •¦ +/ип^я' B0.6)
где Xlt Х2' ¦ • • > Х„ — корни характеристического уравнения, а т1,
т2, ..., т„ — любые целые неотрицательные числа, связанные
соотношением
• • .-{-т„ =
B0.7)
Доказательство. Как мы видели выше, каждому корню \]
характеристического уравнения отвечает, по крайней мере, одна ли-
линейная форма, удовлетворяющая уравнению B0.1). Пусть Vj —
§ 20] НЕКОТОРЫЕ ВСПОМОГАТЕЛЬНЫЕ ПРЕДЛОЖЕНИЯ 65
линейная форма, отвечающая корню kj ')> так что
¦ (Psixi + • • • + PSnxn) = ^У] B0.8)
XI
(У=1, 2 я).
Рассмотрим форму т-го порядка
где /Kj, m2 tnn — любые целые неотрицательные числа, связан-
связанные соотношением B0.7). Составляя производную этой функции по
времени в силу уравнений A9.3), будем на основании B0.8) иметь:
?= m№v?... 1С??+ mVtVp ... VZ ^ + ... +
+ maV?V?' ... V^-^f- = (т^ + «2Я.2+ • • • + «„U V'.
Таким образом, форма т-го порядка V удовлетворяет уравнению B0.1)
со значением X, равным величине B0.6). Но для этого, как мы ви-
видели, необходимо, чтобы К было корнем уравнения B0.5). Итак, до-
доказано, что все величины B0.6) являются корнями уравнения B0.5).
Нам остается показать, что величины B0.6) исчерпывают все корни
уравнения B0.5), т. е. что других корней это уравнение не имеет.
Это обстоятельство совершенно очевидно для того случая, когда все
числа B0.6) различны. Действительно, в этом случае формула B0.6)
определяет столько различных корней уравнения B0.5), сколько суще-
существует различных систем целых неотрицательных чисел т{, ..., тп,
связанных соотношением B0.7). Но таких систем существует как раз
N, что равно степени уравнения B0.5).
Допустим теперь, что коэффициенты psq уравнений A9.3) таковы,
что среди чисел B0.6) имеются одинаковые при разных системах зна-
значений т1, ..., тп, связанных соотношением B0.7). Покажем, что и
в этом случае уравнение B0.5) не имеет корней, не содержащихся
в выражении B0.6). Допустим противное, что к = к* является кор-
корнем уравнения B0.5), не содержащимся среди чисел B0.6). Обозначим
через а модуль разности между корнем к* и наиболее близким к нему
числом из системы B0.6). Изменим теперь коэффициенты psa, заме-
заменив их величинами p'sq. Тогда уравнение B0.5) заменится новым урав-
уравнением Dm (к) = 0, и корни нового характеристического уравнения
будут уже другими величинами, которые мы обозначим через к[ к'„-
Если величины psa достаточно мало отличаются от ps(J, то корни
') Между этими формами могут быть одинаковые, если не все числа
различны.
66 КРИТЕРИИ УСТОЙЧИВОСТИ ПО ПЕРВОМУ ПРИБЛИЖЕНИЮ [ГЛ. III
X'v ..., Х„ будут сколь угодно мало отличаться от корней A,j, ..., \п
и корни уравнения Dm(X) — § будут сколь угодно мало отличаться
от корней уравнения B0.5). В частности, уравнение Dm (к) = 0 будет
иметь корень, сколь угодно мало отличающийся от X*. Но pS(J можно
выбрать так, чтобы все числа
m1l[-\-m2l2-Jr •..-{-mnl'n B0.9)
были различны при любых целых неотрицательных ntj, связанных
соотношением B0.7). Тогда все корни уравнения D'm(X) = 0, и в част-
частности тот, который сколь угодно мало отличается от X*, будут на-
находиться среди чисел B0.9). Следовательно, К* сколь угодно мало
отличается от одного из чисел B0.9), которое в свою очередь сколь
угодно мало отличается от соответствующего ему числа из систе-
системы B0.6), что невозможно, так как разность между к* и ближайшим
к нему числом B0.6) равна конечной величине а.
Итак, и в случае, когда среди чисел B0.6) имеются равные, все
корни уравнения B0.5) находятся среди этих чисел. Только в рас-
рассматриваемом случае уравнение B0.5) будет иметь кратные корни.
Таким образом, теорема полностью доказана.
Пусть теперь U(хх, ..., х„) — заданная форма /га-го порядка.
Постараемся определить форму V того же порядка таким образом,
чтобы выполнялось уравнение
*я)-е?-=</. B0.10)
Обозначим, как и прежде, через av .... aN коэффициенты формы V,
а коэффициенты заданной формы U обозначим через Ь:, .... bN. При-
Приравнивая в уравнении B0.10) коэффициенты при подобных членах,
мы получим для определения ах aN уравнения, отличающиеся
от B0.4) только правыми частями, которые теперь будут равны не
величинам kait а величинам bt, так что эти уравнения имеют вид:
АПа\ + А12а2Л- •••+AlNaN~bN B0.11)
(/=1. 2 N).
Определитель этой системы совпадает, очевидно, с Dm @), и если
он отличен от нуля, то уравнения B0.11) будут допускать одно и
только одно решение для аь .. ., aN. В этом случае будет существо-
существовать одна и только одна форма V, удовлетворяющая уравнению B0.10).
Но все корни полинома Dm(h) определяются выражением B0.6), и
мы приходим, таким образом, к следующей теореме.
Теорема 2. Если корни "kj характеристического уравнения
таковы, что выражение B0.6) не обращается в нуль ни при
§ 21] ПОСТРОЕНИЕ ФУНКЦИЙ ЛЯПУНОВА 67
каких целых неотрицательных тх, тп, связанных соот-
соотношением B0.7), то какова бы ни была наперед заданная
форма т-го порядка U (хг, ..., хп), существует одна и только
одна форма того же порядка V{xx xn), удовлетворяющая
уравнению B0.10).
§21. Построение функций Ляпунова для систем
линейных уравнений с постоянными коэффициентами.
Мы переходим теперь к построению функций Ляпунова для си-
систем линейных уравнений
^jf = P,iXi+- ¦ ¦ + Ps«*« (*=1. 2 n) B1.1)
с постоянными коэффициентами.
Допустим сначала, что невозмущенное движение асимптотически
устойчиво. Это, как мы видели, будет тогда и только тогда, когда
все корни kj характеристического уравнения имеют отрицательные
вещественные части. Будет ли при этом существовать функция, удо-
удовлетворяющая всем условиям теоремы Б предыдущей главы? Поло-
Положительный ответ на этот вопрос дается следующей теоремой.
Теорема 1. Если все корни характеристического уравне-
уравнения имеют отрицательные вещественные части, то какова
бы ни была наперед заданная знакоопределенная форма
U{xx xn), существует одна и только одна форма
j, ..., хп) того же порядка, удовлетворяющая уравнению
п
^^U, B1.2)
и эта форма получится обязательно знакоопределенная, знака,
противоположного с U.
Доказательство. Так как вещественные части всех корней Xt
отрицательны, то величина B0.6) не обращается в нуль ни при каких
целых неотрицательных тх, ..., тп, не равных нулю одновременно.
Поэтому на основании теоремы 2 предыдущего параграфа существует
одна и только одна форма V, удовлетворяющая уравнению B1.2).
Остается показать, что если форма U—знакоопределенная, то и
форма V будет также знакоопределенной, знака, противоположного с U.
Допустим для определенности, что форма U определенно-отрица-
определенно-отрицательна. Рассмотрим форму V. Возможны три случая: 1) форма V
может принимать отрицательные значения, 2) форма V — постоянно-
положительная и 3) форма V — определенно-положительная.
Если бы имел место первый случай, то функция V удовлетворяла
бы всем условиям теоремы В и невозмущенное движение было бы
неустойчиво, что противоречит условию.
68 КРИТЕРИИ УСТОЙЧИВОСТИ ПО ПЕРВОМУ ПРИБЛИЖЕНИЮ [ГЛ. Ill
Что касается второго случая, то он вообще невозможен, каковы
бы ни были корни характеристического уравнения. В самом деле,
будем рассматривать величины xs как функции времени, удовлетво-
удовлетворяющие уравнениям B1.1), и выберем их начальные значения x°s таким
образом, чтобы V(x\ x°n) равнялось нулю. Это возможно, так
как форма V по условию — не знакоопределенная, а только знакопо-
знакопостоянная. Но так как производная —гг отрицательна, то функция V
должна уменьшаться и, следовательно, становиться отрицательной, что
противоречит условию ее положительности.
Таким образом, остается только третий случай, что и доказывает
теорему.
Рассмотренная в доказанной теореме функция V удовлетворяет
всем ycjn виям теоремы Б и является, следовательно, функцией Ляпу-
Ляпунова для рассматриваемого случая '). Таким образом, для того чтобы
построить функцию Ляпунова для системы линейных уравнений с по-
постоянными коэффициентами, когда все корпи характеристического
уравнения имеют отрицательные вещественные части, необходимо за-
задаться какой-нибудь знакоопределенной формой произвольного по-
порядка и искать другую форму того же порядка, производная кото-
которой равнялась бы заданной форме. Как мы видели в предыдущем
параграфе, задача сведется к решению системы линейных алгебраических
уравнений. Вычисления при этом будут тем более громоздкими, чем
больше порядок формы. Шэтому если в какой-нибудь задаче имеется
необходимость действительно вычислить коэффициенты формы V, то
в качестве формы U следует взять какую-нибудь знакоопределенную
квадратичную форму, например сумму квадратов величин xs.
Допустим теперь, что среди корней характеристического уравне-
уравнения имеется хотя бы один с положительной вещественной частью.
В этом случ; е невозмущенное движение для уравнений B1.1) неустой-
неустойчиво. Вопрос о существовании и построении функций Ляпунова, т. е.
функций, удовлетворяющих теореме В или теореме Г, решается ни-
нижеследующими теоремами.
Теорема 2. Если среди корней характеристического
уравнения имеется хотя бы один с положительной вещест-
вещественной частью и если эти корни таковы, что величина
14^ +щ\г+... + тпХа B1.3)
не обращается в нуль ни при каких целых неотрицательных
B1.4)
*) См. примечание в конце книги (стр. 520).
§ 21] ПОСТРОЕНИЕ ФУНКЦИЙ ЛЯПУНОВА 69
то, какова бы на была наперед заданная знакоопределенная
форма Uпорядка т, существует одна и только одна форма V
того же порядка, удовлетворяющая уравнению B1.2), и эта
форма наверное не будет знакопостоянной (в частности,
знакоопределенной), знака, противоположного с U.
Доказательство. Пусть U — произвольная знакоопределенная
форма т-го порядка. Допустим для определенности, что эта форма
положительна. На основании теоремы 2 предыдущего параграфа суще-
существует одна и только одна форма V того же порядка, которая удо-
удовлетворяет уравнению B1.2). Нам остается показать, что эта форма
не может быть ни определенно-отрицательной, ни постоянно-отрица-
постоянно-отрицательной. В самом деле, если бы форма V была определенно-отрица-
определенно-отрицательной, то она удовлетворяла бы всем условиям теоремы Б и не-
невозмущенное движение было бы асимптотически устойчиво, что
противоречит условию. С другой стороны, форма V не может быть
постоянно-отрицательной, каковы бы ни были корни характеристиче-
характеристического уравнения. Чтобы в этом убедиться, достаточно, как и при до-
доказательстве предыдущей теоремы, рассмотреть какое-нибудь решение
уравнений B1.1) с начальными значениями, обращающими форму V
в нуль. Для этого решения форма V, возрастая в силу положитель-
ности —гг , необходимо приняла бы положительные значения, что про-
противоречит условию. Таким образом, теорема полностью доказана.
Форма V, фигурирующая в доказанной теореме, представляет собой
функцию Ляпунова, удовлетворяющую всем условиям теоремы В.
Однако доказанная теорема дает возможность построить эту функцию
лишь при некотором добавочном условии о необращении в нуль выра-
выражения B1.3). Это условие может не выполняться, как, например, в слу-
случае, когда характеристическое уравнение имеет, нулевой корень.
В этом случае, каково бы ни было число т, всегда существует ком-
комбинация целых неотрицательных чисел т{, ..., тп, связанных соот-
соотношением B1.4), при которой выражение B1.3) обращается в нуль.
Действительно, если, например, Хх = 0, то достаточно положить
Легко видеть, что в рассматриваемом случае вообще не суще-
существует функции Ляпунова, удовлетворяющей теореме В. В самом
деле, если характеристическое уравнение имеет нулевой корень, то
определитель системы однородных линейных уравнений
Ps\^\ l~ Ps2^2 1~ • • • —Г~ Psn^n ^^
обращается в нуль и эта система имеет решение, отличное от три-
тривиального х1 — ... = хп = 0. Но для этого решения выражение
п
dV _
dt ~
70
КРИТЕРИИ УСТОЙЧИВОСТИ ПО ПЕРВОМУ ПРИБЛИЖЕНИЮ [ГЛ. Ill
обращается в нуль, какова бы ни была функция V, будь то форма
или более сложная функция, и следовательно, это выражение не
является знакоопределенным. Следовательно, в рассматриваемом слу-
случае для уравнений B1.1) не может существовать функции со знако-
определенной производной, что является основным условием, фигури-
фигурирующим в теореме В 1).
Таким образом, для системы линейных уравнений с постоянными
коэффициентами, когда характеристическое уравнение имеет корень
с положительной вещественной частью, не всегда существует функция
Ляпунова, удовлетворяющая теореме В. Однако в этом случае всегда
существует функция Ляпунова, удовлетворяющая теореме Г. Существо-
Существование этой функции и ее вид устанавливаются следующей теоремой.
Теорема 3. Если среди корней характеристического ура-
уравнения системы B1.1) существует хотя бы один с положи-
положительной вещественной частью, то какова бы ни была наперед
заданная знакоопределенная форма U произвольного порядка т,
всегда найдется такая форма V того же порядка и такое
положительное число а, что будет выполняться соотношение
^ = aV-\-U B1.5)
и при этом форма V наверно не будет знакопостоянной,
знака, противоположного с U.
Доказательство. Рассмотрим уравнение
-j[ — 9 P\i
Pin
Рч\
! ^Г Р • • • Р2п
Рп\
Pni
а
т
= 0, B1.6)
где а—положительное число. Корни pj этого уравнения связаны
с корнями Xj характеристического уравнения соотношениями
, а
pt = X, .
f J J m
Поэтому величину а можно выбрать настолько малой, чтобы и
уравнение B1.6) имело, так же как и характеристическое уравнение,
хотя бы один корень с положительной вещественной частью. При
этом, задавшись каким-нибудь т, можно числом а распорядиться,
так, чтобы величина
') См. примечание в конце книги (стр. 520).
§ 22] ТЕОРЕМЫ ЛЯПУНОВА ОБ УСТОЙЧИВОСТИ 71
не обращалась в нуль ни при каких целых неотрицательных тх, ...
..., пгп, равных в сумме т.
Но тогда на основании предыдущей теоремы существует одна и
только одна форма т-го порядка V, удовлетворяющая уравнению
где U — любая наперед заданная знакоопределенная форма m-го по-
порядка. При этом форма V наверно не будет знакопостоянной, знака,
противоположного с U.
Из B1.7), учитывая, что на основании теоремы Эйлера об одно-
однородных функциях
получаем:
п
dV yi dV
~dt Za~&x~s (P
s=l
m
s\x ~Г • • •
dV
oxs
~T Pi
что и доказывает теорему.
Доказанные теоремы дают метод построения функций Ляпунова
для систем линейных уравнений с постоянными коэффициентами,
когда характеристическое уравнение либо имеет все корни с отрица-
отрицательными вещественными частями, либо хотя бы один корень с поло-
положительной вещественной частью. Построение функций Ляпунова для
случая, когда характеристическое уравнение, не имея корней с поло-
положительными вещественными частями, имеет корни с вещественными
частями, равными нулю, мы здесь не рассматриваем, так как нам это
не потребуется для дальнейшего.
Все доказанные в этом параграфе теоремы установлены А. М. Ля-
Ляпуновым.
§ 22. Теоремы Ляпунова об устойчивости
по первому приближению.
Допустим теперь, что дифференциальные уравнения возмущенного
движения имеют вид
• • + PsnXn + *s (*l *n) B2.
=1, 2 Я),
где Xs(xt xn) в области
72 КРИТЕРИИ УСТОЙЧИВОСТИ ПО ПЕРВОМУ ПРИБЛИЖЕНИЮ [ГЛ. Ill
разлагаются в ряды по степеням xv ..., хп, начинающиеся членами
не ниже второго порядка.
Теоремы, установленные в предыдущем параграфе, дают воз-
возможность чрезвычайно просто разрешить основную задачу об уста-
установлении необходимых и достаточных условий, при которых вопрос
об устойчивости для системы B2.1) разрешается рассмотрением лишь
уравнений первого приближения:
¦^Г =/>**!+ ••• +Ps«*n (s=l. 2 я) B2.2)
независимо от того или иного частного выбора функций Xs.
Имеют место следующие основные теоремы, установленные
А. М. Ляпуновым.
Теорема 1. Если все корна характеристического уравне-
уравнения системы первого приближения имеют отрицательные
вещественные части, то невозмущенное движение устойчиво и
притом асимптотически, каковы бы ни были члены высших
порядков в дифференциальных уравнениях возмущенного дви-
движения.
Доказательство. Рассмотрим квадратичную форму V (xv ...
..., хп), определяемую уравнением
.5 = 1
На основании теоремы 2 предыдущего параграфа такая форма V
непременно существует и будет обязательно знакоопределенной поло-
положительной. Составим производную этой формы по времени в силу
полной системы дифференциальных уравнений возмущенного движе-
движения B2.1). Будем иметь:
dV yidF, . , у
j=i s
5 1
Так как разложение функции ^j^tj— начинается членами не
dV s
ниже третьего порядка, то функция —гг- на основании леммы 4 § 7
будет знакоопределенной отрицательной, каковы бы ни были функ-
функции Xs. Следовательно, функция V удовлетворяет всем условиям
теоремы Б и невозмущенное движение асимптотически устойчиво.
Теорема, таким образом, доказана.
Теорема 2. Если среди корней характеристического ура-
уравнения системы первого приближения имеется хотя бы один
§ 22] ТЕОРЕМЫ ЛЯПУНОВА ОБ УСТОЙЧИВОСТИ 73
с положительной вещественной частью, то невозмущенное дви-
движение неустойчиво при любом выборе членов порядка выше
первого в дифференциальных уравнениях возмущенного дви-
окения.
Доказательство. Рассмотрим квадратичную форму
У(хг хп),
определяемую уравнением
s=\
где а — некоторое положительное число. На основании теоремы 3
предыдущего параграфа такая форма V обязательно существует и
эта форма может принимать положительные значения. Составляя
производную этой формы по времени в силу полной системы диффе-
дифференциальных уравнений B2.1), получим:
*L = aV+W(x , *).
dt ' l' n
где
дУ
дх<
s-l
на основании леммы 4 § 7 является функцией определенно-положи-
определенно-положительной при любом выборе функций Xs.
Форма V является, таким образом, функцией Ляпунова, удовле-
удовлетворяющей условиям теоремы Г. Следовательно, невозмущенное дви-
движение при любом выборе функций Xs неустойчиво, и теорема дока-
доказана.
Теоремы 1 и 2 обратимы. Невозмущенное движение будет устой-
устойчиво при любом выборе функций Xs только тогда, когда характери-
характеристическое уравнение первого приближения имеет корни только
с отрицательными вещественными частями и при этом устойчивость
будет асимптотической. В то же время неустойчивость при любом
выборе функций Xs будет иметь место только тогда, когда среди
корней характеристического уравнения имеется хотя бы один с поло-
положительной вещественной частью, а именно: имеет место следующая
теорема Ляпунова, которую мы приводим без доказательства.
Теорема 3. Если характеристическое уравнение системы
первого приближения не имеет корней с положительными
вещественными частями, но имеет корни с вещественными
частями, равными нулю, то члены высших порядков в уравне-
уравнениях возмущенного движения можно выбрать так, чтобы по-
получить по желанию как устойчивость, так и неустойчивосщь.
74 КРИТЕРИИ УСТОЙЧИВОСТИ ПО ПЕРВОМУ ПРИБЛИЖЕНИЮ [ГЛ. III
Как мы видели в § 19, если характеристическое уравнение имеет
часть корней с нулевыми, а остальные с отрицательными веществен-
вещественными частями, то невозмущенное движение в первом приближении
может быть как устойчивым, так и неустойчивым. Теорема 3 пока-
показывает, что какой бы из этих случаев ни имел место, вопрос об
устойчивости решается исключительно членами выше первого порядка
в уравнениях возмущенного движения, так что движение, устойчивое
в первом приближении, может оказаться в действительности неустой-
неустойчивым, и наоборот.
Таким образом, все случаи, которые могут представиться при
исследовании задачи устойчивости, когда уравнения возмущенного
движения имеют вид B2.1), можно разбить на две категории: на слу-
случаи некритические, когда задача решается уравнениями первого
приближения, и случаи критические, когда требуется рассмотрение
членов более высоких порядков. Критические случаи имеют место
тогда и только тогда, когда характеристическое уравнение не имеет
корней с положительными вещественными частями и имеет корни
с вещественными частями, равными нулю. С точки зрения математи-
математической, критические случаи можно рассматривать как исключение.
Но с точки зрения механической эти случаи являются особенно важ-
важными, как в этом легко убедиться из рассматриваемых ниже при-
примеров.
§ 23. Примеры приложения предыдущих теорем.
Рассмотрим несколько примеров приложения теорем предыдущего
параграфа.
Пример 1. Рассмотрим твердое тело, вращающееся по инерции
вокруг неподвижной точки. Если такому телу сообщить в начальный
момент времени вращение вокруг одной из главных осей инерции
в закрепленной точке, то тело и в дальнейшем будет вращаться
вокруг этой оси и притом равномерно. Исследуем устойчивость
этих вращений.
Примем в качестве осей координат главные оси инерции в за-
закрепленной точке, и пусть исследуемое невозмущенное движение
соответствует вращению вокруг оси х. Дифференциальные уравне-
уравнения возмущенного движения составлены нами в § 3 (уравнения C.9))
и имеют вид
B3.1)
§ 23] ПРИМЕРЫ ПРИЛОЖЕНИЯ ПРЕДЫДУЩИХ ТЕОРЕМ 75
Характеристическое уравнение
— р О О
О _о (С~А)ы
о <л-д>»
= 0
системы первого приближения имеет один корень, равный нулю, и
два корня, определяемых формулой
Pi, 2— — w у qb • {J.6.Z)
Если С < А < В или С > А > В, т. е. если вращение происходит
вокруг средней оси инерции, то оба корня B3.2) будут вещественны
и один из них будет обязательно положительным. Следовательно,
невозмущенное движение будет неустойчиво.
Если вращение происходит вокруг малой или большой оси инер-
инерции, так что выполняются неравенства А < В, А < С или А > В,
А^>С, то оба корня B3.2) будут чисто мнимыми. Так как при этом
третий корень равен нулю, то мы имеем дело с критическим случаем
и первое приближение задачи не решает.
Общее исследование случая трех критических корней очень сложно.
Но в рассматриваемом примере задача решается просто.
Уравнения B3.1) имеют, как легко видеть, первый интеграл
В (В — А) у2 ¦+ С (С — A)z2 = const.,
знакоопределенный относительно у и z. Отсюда сразу вытекает
устойчивость по отношению к переменным у и z. Но тогда из пер-
первого интеграла
А (х -г- wJ-f By2 + Cz2 = const.,
которым система B3.1) также обладает1) и который является инте-
интегралом энергии, немедленно вытекает устойчивость и по отношению
к переменной х.
Таким образом, вращение вокруг средней оси инерции неустой-
неустойчиво, а вращения вокруг большой или малой оси инерции устойчивы.
Пример 2. Рассмотрим вопрос об устойчивости вращательных
движений снаряда при настильной траектории стрельбы, которым мы
уже занимались в § 12. Дифференциальные уравнения возмущенного
движения имеют вид A2.2). Отбрасывая члены высших порядков,
') Этот интеграл не может быть принят за функцию Ляпунова, так как
его левая часть не обращается в нуль при лг= у = г=0.
76 КРИТЕРИИ УСТОЙЧИВОСТИ ПО ПЕРВОМУ ПРИБЛИЖЕНИЮ [ГЛ. Ill
получим следующую систему уравнений первого приближения:
Аа-\-Сп§ — eRa — 0. \
Для того чтобы составить характеристическое уравнение без при-
приведения системы B3.3) к нормальному виду, положим в ней
Для нахождения М и N получим систему линейных однородных
уравнений:
— СпкМ -f (Ак2 — eR)N = 0,
(Ак2 — eR)M + CnkN = 0,
и следовательно, искомое характеристическое уравнение имеет вид
C42k2-\-(Ak2 — eRJ = Q.
Все четыре корня этого уравнения даются формулой
. ± Cni±\/~4AeR—C2n*
Al, 2, 3, 4 = 2А "
Следовательно, если выполняется неравенство
4AeR — СЧ2 > О,
то два корня имеют положительную вещественную часть и невозму-
невозмущенное движение неустойчиво. При выполнении неравенства
4 ЛеЯ — С2я2<0 B3.4)
все четыре корня характеристического уравнения будут чисто мни-
мнимые. Мы будем, следовательно, иметь дело с критическим случаем
и для решения задачи необходимо будет рассмотреть и нелинейные
члены в уравнениях A2.2).
Решение задачи устойчивости при четырех критических корнях
очень сложно. Однако в рассматриваемом случае, как мы видели
в § 12, задачу удалось полностью разрешить непосредственным
построением функции Ляпунова. При этом оказалось, что при выпол-
выполнении неравенства B3.4) невозмущенное движение устойчиво.
§ 24. Неустойчивость равновесия.
Случай канонических систем.
В качестве следующего примера вернемся снова к вопросу об
устойчивости равновесия, когда силовая функция в положении равно-
равновесия не обращается в максимум. В предыдущей главе была доказана
неустойчивость равновесия для двух случаев отсутствия максимума:
§ 24J
НЕУСТОЙЧИВОСТЬ РАВНОВЕСИЯ
77
для случая, когда силовая функция в положении равновесия имеет
минимум, который определяется членами наинизшего порядка в раз-
разложении силовой функции, и для случая, когда силовая функция не
имеет ни максимума, ни минимума и является формой.
Мы рассмотрим сейчас случай, когда силовая функция в положе-
положении равновесия не имеет ни максимума, ни минимума, и это опреде-
определяется членами наинизшего порядка в разложении силовой функции,
которое мы будем предполагать начинающимся членами второго
порядка. Этот случай изучен Ляпуновым, доказавшим при этом
неустойчивость равновесия.
Пусть q1 — q2 = ... = qn = О — значения обобщенных координат
в положении равновесия,
2 (р р) % 2
а, р=1 а, р=1
— кинетическая энергия и силовая функция, причем функции
ЛаР (?! дп) и Са3 (qv ..., qn) обращаются в нуль при ql = ... —
— qn — 0, a aap и са|з — постоянные. По предположению квадратич-
квадратичная форма
2 2
а, Р=1
не обращается тождественно в нуль.
Дифференциальные уравнения возмущенного движения возьмем
в форме Лагранжа:
dt
==1, 2 п).
>
Отбрасывая члены высших порядков, получим обычную систему
уравнений малых колебаний:
(/=1, 2 я).
Характеристическое уравнение этой системы первого приближе-
приближения имеет вид
.. аы№ — с,
— с
'1я
аЧУ* — C1\
tft
— С
п\
= 0.
B4.1)
По предположению силовая функция в положении равновесия
9]= ... = qn = 0 не имеет ни максимума, ни минимума. Это зна-
значит, что функция U{qx, .... qn) является знакопеременной. С другой
стороны, мы предположили, что эта знакопеременность определяется
78
КРИТЕРИИ УСТОЙЧИВОСТИ ПО ПЕРВОМУ ПРИБЛИЖЕНИЮ [ГЛ. Ill
членами наинизшего порядка в разложении силовой функции, что
означает, что знакопеременной является уже форма U2. В теории
малых колебаний доказывается, что уравнение B4.1), рассматривае-
рассматриваемое как уравнение относительно X2, имеет только вещественные
корни. В этой же теории доказывается, что если форма U2 является
знакопеременной, то среди этих корней имеются обязательно поло-
положительные. Но тогда уравнение B4.1), рассматриваемое как уравне-
уравнение 2й-го порядка относительно X, также имеет положительные корни,
что и доказывает неустойчивость равновесия.
Для того чтобы равновесие было устойчиво, необходимо, чтобы
все корни №. уравнения B4.1) были отрицательны. Это будет тогда
и только тогда, когда форма U2 является определенно-отрицательной.
Тогда все корни Xj будут чисто мнимыми. Мы будем, следовательно,
иметь дело с критическим случаем. Но равновесие при этом будет
устойчивым на основании теоремы Лагранжа.
Чтобы рассмотреть пример более общего характера, допустим,
что предложена система 2п-го порядка, которая имеет каноническую
форму
dxi дН
dt ду;
-=?¦ = — 4р- (/=1. 2 я),
dt дх, ч "
B4.2)
где Н — произвольная квадратичная форма In переменных л^
Уг Уп-
Уравнения B4.2) можно переписать в виде
хп
nVl + Bi2y2 + ... + В1пУп,
~tff—Cnxl~T~Cl2x2-T~ ••• ТЧА'
"¦У1 Л v A v A v С \) Р \\ Г" ч
(Ц — ЛДЛ1 Л1Ч.Х2 ¦•• ^inxn Wm °2(>2 ••• ^п1Уп'
где
Ч dxi дх< ' Ч дуь дуi ' Ч dyi dxi '
Следовательно, характеристическое уравнение имеет вид
= 0.
B4.3)
§ 24] НЕУСТОЙЧИВОСТЬ РАВНОВЕСИЯ 79
Определитель D (к) можно преобразовать следующим образом:
к ... С
п2
An
J\ in
122
.. . Anl
• • • Ап2
Bn
Вп
Вы
-1)"
СпЛ
Сл
cnl
An
A12
c2n
B2i
B22
B-in
#11 #21
#12 #22
В1п #2я
11 — ^*21
^•12 ^22
°1л ^2/1
- к С12
С22 Ч~ Л •
ся2
^21
^22
...Спп-к А
... Вп1 С
... вп2 с
• • • впП с
...вп1
• • • В „2
¦¦¦Впп
...са1
— к ... Сп2
...спп-
• ¦ Сы Вп
Г R
• ¦ и2л D\2
..Cnn + kBln
..АпХ С„-
• • Ап2 С12
и
и + Л
21
«1
СцЛ-
Сц
Спх
An
А12
кАы
В2Х
в22
— Л t>2]
С22
А2п
с12
С„2
кС12
С22 Н
сп2
A2i
А22
А2п
— А..
. . .
i . . .
¦Я„1
¦ВП2
¦вап
¦СП1
¦ сп2
Ann
Сщ
с2п
спп+к
•си
¦С2п
¦Спп + к
¦АП1
• Ап2
¦Апп
/<
B4.4)
...с„
(сначала делаем строки столбцами, затем меняем местами первые и
последние п строк, после чего меняем местами первые и последние
п колонок). Но так как
то из B4.4) следует, что уравнение B4.3) не меняется при замене к
на—л. Следовательно, уравнение B4.3) содержит только четные
степени к. Поэтому, если оно имеет корни с вещественными частями
отрицательными, то оно будет иметь корни и с положительными ве-
вещественными частями и невозмущенное движение будет неустойчиво.
Следовательно, для того чтобы движение было устойчиво, необхо-
80
КРИТЕРИИ УСТОЙЧИВОСТИ ПО ПЕРВОМУ ПРИБЛИЖЕНИЮ [ГЛ. III
димо, чтобы все корни уравнения B4.3) были чисто мнимыми. Будет
ли при этом действительно иметь место устойчивость, зависит от
членов более высоких порядков в дифференциальных уравнениях воз-
возмущенного движения.
Если форма Н является знакоопределенной, то, учитывая, что
Н — const, является интегралом уравнений B4.2), мы должны будем
заключить на основании теоремы А, что невозмущенное движение
в первом приближении устойчиво. Следовательно, в этом случае все
корни уравнения B4.3) будет обязательно чисто мнимыми. Но урав-
уравнение B4.3) может иметь только чисто мнимые корни и тогда,
когда Н не является знакоопределенной.
§ 25. Теорема Гурвица.
Из предыдущего ясно, что для задачи устойчивости имеет боль-
большое значение вопрос о знаках вещественных частей корней алгебраи-
алгебраических уравнений. В частности, важно знать необходимые и доста-
достаточные условия, при которых все корни уравнения имеют отрица-
отрицательные вещественные части. Эти необходимые и достаточные условия
даются теоремой Гурвица, которую мы приводим здесь без доказа-
доказательства ').
Теорема Г ур вица. Пусть предложено уравнение п-й сте-
степени
О 1 1 | 2 1 * * * I и — 1 I п ^ *
Составим определители
д.-
А =¦
«i
«з
«2/1-1
где at = 0, если 1 >
=
«3
«0
«2
«2/1-2
п.
«0
«2
0
«1
«2/1-3
0
«0
«2Я-4 • •
«1
«3
«5
. 0
. 0
• «л
«0
«2
а4
==
0
«1
«3
а А
') Доказательство теоремы Гурвица можно найти в книге: К у р о ш А. Г.,
Курс высшей алгебры, Гостехиздат, 1946, а также в книге: Ч е т а е в Н. Г.,
Устойчивость движения, Гостехиздат, 1946. В технических приложениях
теории устойчивости движения для проверки отрицательности вещественных
частей корней характеристического уравнения часто используется не теорема
Гурвица, а другие критерии. В частности, в теории автоматического регули-
регулирования, радиотехнике и электронике обычно применяются так называемые
частотные критерии, базирующиеся на понятии передаточной функции
системы (см., например, Попов Е. П., Динамика систем автоматического
регулирования, Гостехиздат, 1954)-
§ 26]
ОБОБЩЕНИЕ ТЕОРЕМ ЛЯПУНОВА
81
Для того чтобы все корни уравнения B5.1) имели отрица-
отрицательные вещественные части, необходимо и достаточно, чтобы
удовлетворялись неравенства
А1 > О, А2 > 0 Дя_! > 0, ап > 0.
Для уравнения третьей степени
а0х3 -f- а-^х2 -f- a2x -f- a3 = 0
имеем условия:
= «^2 — а3а0 > 0, а3
0.
Для уравнения четвертой степени
c3 —J— a2x2 -f- a3
B5.2)
B5.3)
имеем:
или
«1 «0
а4>0
- а4>°-
Из третьего условия на основании четвертого вытекает а3(а1а2 —
— аоаЛ > а^а\ > 0, следовательно, второе условие может быть заме-
заменено неравенством аъ > 0. Таким образом, условия отрицательности
вещественных частей корней уравнения B5.3) имеют вид
«!><). а3>0, а3(а1в2 —e0a3) —e4eJ>0, а4 > 0.
§ 26. Обобщение теорем Ляпунова об устойчивости
по первому приближению. Приложение
к регулируемым системам.
Теоремы Ляпунова об устойчивости и неустойчивости по первому
приближению обобщались различными авторами. Целью этих обоб-
обобщений являлось ослабление условий, налагаемых на функции Xs,
которые Ляпунов, как мы видели, предполагал аналитическими с раз-
разложениями, начинающимися членами не ниже второго порядка. При
этом был предложен ряд довольно сложных доказательств. Так, на-
например, Коттон1) заменил систему дифференциальных уравнений
B2.1) эквивалентной системой интегральных уравнений, которую он
затем интегрировал методом последовательных приближений, приме-
') Cotton E., Sur les solutions asymptotiques des equations different(elles,
Annales sclentifiques de l'Ecole normale superieure, т. 28, 1{Щ.
82 КРИТЕРИИ УСТОЙЧИВОСТИ ПО ПЕРВОМУ ПРИБЛИЖЕНИЮ [ГЛ. III
нив при этом громоздкий метод доказательства сходимости этих
приближений. Аналогичным приемом пользовался Перрон').
Однако метод доказательства, предложенный самим Ляпуновым,
изложенный нами в § 22, показывает без всяких дополнительных
исследований, что указанные теоремы сохраняют силу при значи-
значительно более общих предположениях относительно Xs. А именно,
при доказательстве теоремы 1 § 22 условие, что функции Xs раз-
разлагаются в ряды, начинающиеся членами не ниже второго порядка,
было использовано только для того, чтобы можно было утверждать,
что функция
-^ B6.1)
5=1
является определенно-отрицательной. На основании леммы 2 § 7 для
этого достаточно, чтобы в некоторой окрестности начала координат
выполнялось неравенство
B6.2)
где А — достаточно малая постоянная, а для этого, учитывая линей-
dV
ность функций -г—, достаточно, чтобы функции Xs удовлетворяли
неравенствам
!*,(*„ ...,хл)| <а\\хх\ + ... + \хп\), B6.3)
где а — также достаточно малая постоянная, зависящая исключительно
от коэффициентов формы V.
Таким образом, теорема 1 § 22 остается справедливой, если от
функций Xs потребовать только, чтобы они в некоторой окрестности
начала координат удовлетворяли неравенствам B6.3). Необходимо
также потребовать, чтобы выполнялись общие предположения отно-
относительно дифференциальных уравнений возмущенного движения, сде-
сделанные нами в § 6.
Все сказанное относительно теоремы 1 справедливо также и для
теоремы 2.
Указанные обобщения теорем Ляпунова являются наиболее общими
из известных в литературе. И мы только что видели, как просто
они доказываются при помощи функций Ляпунова. Однако ценность
указанных доказательств заключается не только в их простоте. Глав-
Главная ценность этих доказательств заключается в том, что они дают
') Perron О., Ober Slabilitat und asymptotisches Verhalten der Integrale
yon Differentialgleichungssystemen, Math. Zeit., т. 29, вып. 1, 1928.
§ 26] ОБОБЩЕНИЕ ТЕОРЕМ ЛЯПУНОВА 83
возможность практически вычислить область устойчивости, когда
последняя имеет место.
Действительно, область асимптотической устойчивости в случае
теоремы 1 определяется (см. примечание в конце § 10) областью
знакоопределенности функции B6.1). Что же касается последней, то
она совпадает с областью, где выполняются условия B6.3). Это
может быть все пространство, если, например, функции Xs являются
линейными с достаточно малыми коэффициентами. Если функции Xs
являются аналитическими, начинающимися членами не ниже второго
порядка, то областью выполнимости условий B6.3) будет некоторая
окрестность начала координат, которую нетрудно определить, если
известно число а.
Во всех случаях дело сводится к определению числа а, а по-
поскольку коэффициенты формы V известны, то задача сводится к вы-
вычислению числа А, т. е. числа, при котором функция B6.1) будет
определенно-отрицательной при выполнении неравенства B6.2). По-
Последняя задача элементарна. Действительно, нужно выбрать число А
таким образом, чтобы выполнялось неравенство
А {| хх | + ... -f I ха |}2 < х\ + ... + х\. B6.4)
Поскольку обе части неравенства B6.4) представляют квадратич-
квадратичные формы, это неравенство будет выполняться всюду, если оно
выполняется на сфере единичного радиуса. Таким образом, можно
положить
так как уп есть максимум величины |xj| -f- ... -f- I xn\ на сфере
Вышеуказанный метод определения области устойчивости можно
несколько видоизменить путем другого выбора функции V. Можно,
очевидно, выбрать функцию V таким образом, чтобы удовлетворя-
удовлетворялось уравнение
и
2 (P,i*i + • • • + Psnxn) -щ; = и (*i. ¦ • •. *„).
.5 = 1
где U—любая наперед заданная определенно-отрицательная квадра-
квадратичная форма, а не обязательно сумма отрицательных квадратов.
Тогда неравенство B6.4) заменится неравенством
Л{|*1| + ... + |*в|}2<-*/(*, хп)
и для числа А имеем:
84 КРИТЕРИИ УСТОЙЧИВОСТИ ПО ПЕРВОМУ ПРИБЛИЖЕНИЮ [ГЛ. Ill
где т — наименьшее значение формы — U на сфере единичного ра-
радиуса.
Таким образом, число А получится зависящим от коэффициентов
заданной формы U. Этим можно воспользоваться для расширения
области устойчивости.
Можно, наконец, определить а прямо из условия, что при выпол-
выполнении B6.3) должно выполняться неравенство
\^\~и{Х1 Хп)> B6-5)
.5=1
без перехода через неравенство B6.2).
Приведенные способы определения области устойчивости являются
лишь некоторыми из тех, которые можно рекомендовать. Вообще
здесь следует помнить, что область устойчивости определяется по
правилам § 10, областью, где выполняется неравенство B6.5), и
для определения последней следует воспользоваться любым спосо-
способом, который в каждом отдельном случае окажется наиболее удоб-
удобным.
Практически могут возникнуть следующие три основные задачи,
связанные с определением области устойчивости:
1) заданы уравнения первого приближения (с отрицательными
вещественными частями у корней характеристического уравнения),
заданы нелинейные члены, требуется определить область устойчи-
устойчивости;
2) заданы уравнения первого приближения, задана требуемая
область устойчивости, необходимо определить условия, которым
должны удовлетворять нелинейные члены;
3) задана требуемая область устойчивости, известен характер
нелинейных членов, необходимо определить условия, которым должны
удовлетворять коэффициенты уравнений первого приближения.
Для пояснения всего вышеизложенного рассмотрим одну из задач
этого рода, решенную М. А. Айзерманом').
Допустим, что предложена регулируемая система, описываемая
дифференциальными уравнениями вида
4*j. = PnXl _|_ p12x2 + ... + рихп + / (xk),
- • • • -Г Р'пХп
(/ = 2, 3 п),
где / (xk) — нелинейная функция одного аргумента xk.
') А й з е р м а н М. А., О сходимости процессов автоматического регу-
регулирования после больших начальных отклонений. Автоматика и телемеха-
телемеханика, т. VII, № 2—3, 1946.
§ 26] ОБОБЩЕНИЕ ТЕОРЕМ ЛЯПУНОВА 85
Относительно функции / (хк) предполагается, что при любом хк
кривая / = / (хк) лежит между прямыми f = (а0 — а{) хк и / =
= (ао-\- а2)хк, где at и а2— некоторые постоянные. Предполагается
далее, что для соответствующей линеаризованной системы
аохк,
B6.7)
.. + />/„*„
A=2, 3 п)
характеристическое уравнение имеет корни только с отрицательными
вещественными частями.
Требуется определить такие значения для чисел а1 и а2, при
которых положение равновесия хх = ... = хп = 0 регулируемой
системы асимптотически устойчиво при любых начальных возмуще-
возмущениях.
Мы видим, таким образом, что задача подобна задаче об опре-
определении числа а в неравенствах B6.3). Эту задачу М. А. Айзерман
решает следующим образом.
Пусть V(xv ..., хп) определенно-положительная квадратичная
форма, производная которой в силу линейной системы B6.7) равна
наперед заданной определенно-отрицательной квадратичной форме
U (Xj xn), так что
| Л-|- = У(.1 *„). B6.8)
Тогда квадратичная форма
)хк~ B6.9)
i—I l
будет также определенно-отрицательной, если число |а| достаточно
мало. Пусть —а, и а2 — наименьшее и наибольшее значения а,
при которых форма B6.9) еще определенно-отрицательна. Эти вели-
величины легко определяются простым применением какого-нибудь при-
признака знакоопределенности квадратичных форм. Полученные числа а1
и а2 и являются искомыми. Действительно, если форма B6.9)
является определенно-отрицательной при — at -^ а -^ а2, то функция
86 КРИТЕРИИ УСТОЙЧИВОСТИ ПО ПЕРВОМУ ПРИБЛИЖЕНИЮ (ГЛ. III
будет также определенно-отрицательной, так как кривая f(xk) лежит
между прямыми / = (а0—al)xlt и f = {aQ-\-a{) x k и, следовательно,
при любом хк найдется такое число а, лежащее в интервале (— alt a2),
что будем иметь: f(xk) = (до-(- а)хк.
Пример. Проведем все выкладки на примере автоматического
регулирования числа оборотов силового двигателя, рассмотренном
М. А. Айзерманом. Регулирование осуществляется по схеме, изобра-
изображенной на рис. 7.
+г
Слив
Подвод масла
Н сервомотору
¦*- Слив
Рис. 7.
Обозначим через х отклонение числа оборотов от его значения,
которое нужно поддерживать, считая эту величину положительной,
когда число оборотов растет. Через z обозначим смещение муфты
' измерителя. Эту величину будем считать положительной, если ее
изменение вызвано ростом х. Далее обозначим через s смещение
золотника сервомотора от равновесного положения, считая эту вели-
величину положительной, когда она соответствует росту z. И наконец,
обозначим через у смещение поршня сервомотора, считая эту вели-
§ 26] ОБОБЩЕНИЕ ТЕОРЕМ ЛЯПУНОВА 87
чину положительной, когда смещение поршня сервомотора вызвано
положительным смещением s.
При линейной идеализации имеем следующие уравнения:
уравнение регулируемого объекта: ~гг = — Nax— by;
B6.10)
уравнение сервомотора:
уравнение золотника:
уравнение измерителя:
dy
dt
s
Z
— c3s;
= Cr,Z —
— C-,X.
Здесь a, b, clt c2, c3, d1— положительные постоянные. Что же
касается величины N, то она равна -)-1, если при отсоединенном
регуляторе двигатель устойчиво держит обороты, т. е. обладает
положительным самовыравниванием. Напротив, N =—1, если дви-
двигатель обладает отрицательным самовыравниванием, и, наконец, N = 0,
если двигатель не обладает самовыравниванием.
Мы рассмотрим здесь случай, когда самовыравнивание нелинейно
и характеризуется однозначной нелинейной функцией f(x). Уравне-
Уравнение движения мы получим, заменяя в первом уравнении B6.10) член
— Nax членом / (х). Тогда, исключая s и z, получим следующие
уравнения задачи:
4*. = f(x)-by. M. = cx-dy. B6.11)
где с = схс2сь, d — dxcb.
Мы будем предполагать, что самовыравнивание отрицательно.
В этом случае функция / (х), обращающаяся в нуль при х = 0,
будет обладать в этой точке положительной производной, которую
мы обозначим через а0.
Тогда для системы первого приближения будем иметь:
^- = аох — by, ^L = CX — dy.
Для того чтобы характеристическое уравнение имело корни
с отрицательными вещественными частями, необходимо, чтобы выпол-
выполнялись неравенства
d — ao>O, bc — a0d>0. B6.12)
Мы будем предполагать, что эти условия выполняются.
Для решения задачи положим:
где Ц — некоторая заданная положительная постоянная, и выберем
88 КРИТЕРИИ УСТОЙЧИВОСТИ ПО ПЕРВОМУ ПРИБЛИЖЕНИЮ [ГЛ. III
А, В, С таким образом, чтобы выполнялось уравнение
ig- (аох -Ьу) + ^ (сх - dy) = -M (*2 + у2). B6.13)
Приравнивая в B6.13) коэффициенты при подобных членах, мы
получим следующие уравнения для этих коэффициентов:
а0А 4- сВ = — М,
Отсюда
&B = — M(aoc-\-bd), | B6.14)
где А определяется формулой
A = (bc — a^d) (d — a0)
и является в силу B6.12) величиной положительной.
Рассмотрим теперь форму
— М (** + у2) + ах ^ = (— М + а А) х2 + аВху — Му\
Для того чтобы эта форма была определенно-отрицательной, не-
необходимо и достаточно, чтобы выполнялось неравенство
52а2 + 4Ж (— М + аЛ)< 0.
Это неравенство будет выполняться при всех значениях а, лежа-
лежащих в интервале — а1 < а < а2, где а^ и а2 определяются форму-
формулами
B6-15)
Положим Ж = А, после чего B6.15) примет вид
я1,2 = ^г(+Л* + ТЛ4*2 + ?*2). B6.16)
где
A* = d(d—ao) + c(b + c), В* = — {aoc-\-bd).
Таким образом, если при всех значениях х кривая f — f (х)
лежит между прямыми f = (a0 — а{)х и / = (ао-(- а2) х, где ах и а2
определяются формулами B6.16), то состояние равновесия регули-
регулируемой системы асимптотически устойчиво при любых начальных
возмущениях').
') См. примечание в конце книги (стр. 521).
§ 27] ЗАКЛЮЧИТЕЛЬНЫЕ ЗАМЕЧАНИЯ 89
§ 27. Заключительные замечания.
Итак, все случаи, которые могут представиться при решении
задачи устойчивости, когда уравнения возмущенного движения имеют
вид A9.1), можно подразделить на некритические, когда задача
решается первым приближением, и критические, когда рассмотрение
лишь первого приближения недостаточно. Случаи будут критическими
тогда и только тогда, когда характеристическое уравнение системы
первого приближения, не имея корней с положительными веществен-
вещественными частями, имеет корни с вещественными частями, равными нулю.
С точки зрения математической критические случаи можно рас-
рассматривать как исключительные. Однако с точки зрения механической
эти случаи имеют очень важное значение. Так, во всех примерах,
рассмотренных нами в §§ 23 и 24, устойчивость могла иметь место
только в критических случаях. С другой стороны, для многих механи-
механических систем характеристическое уравнение системы первого прибли-
приближения имеет критические корни в силу самого устройства этих систем.
Такой, например, будет система регулирования, рассмотренная нами
в § 12. Действительно, уравнения возмущенного движения A2.7) этой
системы имеют один характеристический корень, равный нулю.
Таким образом, очень важно иметь методы, позволяющие решать
задачу устойчивости в критических случаях. К сожалению, эта задача
очень сложна и до сих пор нет общих методов ее решения. При
этом задача делается тем сложнее, чем больше число критических
корней. Ляпунов разрешил эту задачу для следующих трех случаев:
1) Характеристическое уравнение имеет один нулевой корень
и п корней с отрицательными вещественными частями.
2) Характеристическое уравнение имеет пару чисто мнимых кор-
корней и п корней с отрицательными вещественными частями.
3) Характеристическое уравнение имеет два нулевых корня, и
система имеет только второй порядок. При этом двойному нулевому
корню соответствует только одна группа решений.
В следующей главе мы рассмотрим первые два случая. Случай
двойного нулевого корня при несколько иных предположениях будет
рассмотрен в главе VI, после того как будут установлены некото-
некоторые общие теоремы теории критических случаев. В этой же главе
будут рассмотрены и критические случаи, когда характеристическое
уравнение имеет две пары чисто мнимых корней и когда оно имеет
один нулевой и пару чисто мнимых корней.
ГЛАВА IV.
ИССЛЕДОВАНИЕ КРИТИЧЕСКИХ СЛУЧАЕВ
ДЛЯ УСТАНОВИВШИХСЯ ДВИЖЕНИЙ.
§ 28. Случай одного нулевого корня.
Приведение уравнений к специальному виду.
Допустим, что система уравнений возмущенного движения есть
система (п -f- 1)-го порядка и имеет вид
5Г цУп + 1 + Ъ(У1 Уп+\) B8.1)
(У=1. 2 л+1).
где qji — постоянные, а функции Yj разлагаются в некоторой окрест-
окрестности начала координат в ряды по степеням величин у,, начинаю-
начинающиеся членами не ниже второго порядка. Мы переходим к рассмо-
рассмотрению критического случая, когда характеристическое уравнение
системы первого приближения
dyi
^ (У=1. 2 п+1) B8.2)
имеет один нулевой корень при остальных п корнях с отрицатель-
отрицательными вещественными частями.
Введем в уравнениях B8.2) вместо одной из переменных у^ пере-
переменную х при помощи подстановки
где ctj — некоторые постоянные. Эти постоянные мы постараемся
выбрать таким образом, чтобы преобразованное уравнение приняло вид
dt
Мы должны, следовательно, иметь тождественно
л+1 л+1
dx Y1 dyJ V1
2a = Z
/=i
§ 28]
СЛУЧАЙ ОДНОГО НУЛЕВОГО КОРНЯ
91
Приравнивая нулю коэффициенты при yk, мы получим следую-
следующую систему линейных однородных алгебраических уравнений:
вв+1 = 0 (А=1, 2 л+1). B8.3)
Так как характеристическое уравнение системы B8.2) имеет нуле-
нулевой корень, то определитель системы B8.3) обращается в нуль и,
следовательно, эта система имеет решение для ajt в котором не все
эти постоянные равны нулю. Допустим для определенности, что
an+i *? 0- Тогда мы можем принять переменную х вместо перемен-
переменной уя+1- Остальные переменные yt сохраним прежние, но будем
обозначать их в дальнейшем через xt. Таким образом, мы преобра-
преобразуем уравнения B8.2) при помощи подстановки
B8.4)
xl — yl A=1, 2
Теперь, обозначая
1
Psk = 4sk — -j— 4s, n+lak'
1
Ps =
«Л+I
4s,
(s. k = l. 2
мы приведем уравнения B8.2) к виду
dx
dt
dxs
dt
¦ = 0,
где ps, psj—постоянные. Характеристическое уравнение этой системы,
имеющее вид
Pn —'
Pix
Рп
Pin
Pin
Pi
Pi
Pnl Pni ••• Pnn—l Pn
0 0 0 — к
распадается на уравнение к = 0 и уравнение
рп — к р12 ... р1п
Рп Рп — л • • • Pin
= 0,
Рт
Рп2
= 0.
B8.5)
Так как характеристическое уравнение инвариантно по отношению
к линейным преобразованиям и в рассматриваемом случае имеет ц
92 ИССЛЕДОВАНИЕ КРИТИЧЕСКИХ СЛУЧАЕВ [ГЛ. IV
корней с отрицательными вещественными частями, то все корни урав-
уравнения B8.5) имеют отрицательные вещественные части.
Если при помощи подстановки B8.4) преобразовать систему B8.1),
то она, очевидно, примет вид
dx ,, , .
dx.
-hPsn^n+PsX + X^X, Xj Хп)
(S=l, 2 й),
B8.6)
где X и Xs— аналитические функции переменных х, хх хп,
разложения которых начинаются членами не ниже второго порядка.
Таковы будут дифференциальные уравнения возмущенного движе-
движения в интересующем нас критическом случае одного нулевого корня
характеристического уравнения. Этот вид дифференциальных уравне-
уравнений будет исходным для дальнейшего исследования.
§ 29. Исследование задачи для случая системы первого порядка.
Мы рассмотрим сначала случай, когда п = 0 и, следовательно,
уравнение возмущенного движения имеет вид
ig- = X (х) = gx™ + gM+1x»+i + • • •. B9.1)
где от !> 2, a g, gm+v ...—некоторые постоянные.
В рассматриваемом частном случае задача устойчивости решается
сразу, а именно: если т является числом четным, то невозмущенное
движение неустойчиво; если же т является числом нечетным, то при
g < 0 невозмущенное движение асимптотически устойчиво, а при
g > 0 оно неустойчиво.
Действительно, если т — число четное, то правая часть уравне-
уравнения B9.1) в некоторой окрестности начала координат принимает
значения одного знака, совпадающего со знаком g. Поэтому если
рассматривать точку, движущуюся по оси х согласно уравнению B9.1),
то скорость этой точки имеет определенное направление, независимо
от того, будет ли точка находиться справа или слева от начала ко-
координат. Следовательно, если при g > 0 движущаяся точка в началь-
начальный момент находится справа от начала координат, а при g < 0 слева
от начала координат, то она будет удаляться от этой точки пока не
выйдет из области знакоопределенности функции X. Следовательно,
невозмущенное движение неустойчиво вне зависимости от знака g.
Если т — число нечетное, то скорость движущейся точки меняет
свое направление при переходе через начало координат. При этом
при g > 0 точка всегда удаляется от начала координат, а при g < О
она, напротив, к нему приближается. Следовательно, в первом случае
§ 30] СИСТЕМА (Я —}— 1)-ГО ПОРЯДКА; ЧАСТНЫЙ СЛУЧАЙ 93
невозмущенное движение неустойчиво, а во втором случае оно устой-
устойчиво и притом асимптотически.
Легко построить функции Ляпунова для рассматриваемой задачи,
а именно, если т—число нечетное, то полагаем:
2
dV
Для —jr имеем:
dV
Обе функции как V, так и —п- знакоопределенны. При этом, если
g > 0, то обе эти функции будут одинакового знака, и V удовле-
удовлетворяет всем условиям теоремы В, откуда мы снова заключаем о не-
dV
устойчивости движения. При g <; 0 V и —гг- имеют противоположные
знаки и, следовательно, функция V удовлетворяет всем условиям
теоремы Б, откуда вытекает асимптотическая устойчивость.
При m четном полагаем просто
V = x.
dV
Тогда —тг будет функцией знакоопределенной, а сама функция V,
каков бы ни был знак g, может принимать значения того же знака, что
и —тг- ¦ Следовательно, как при g > 0, так и при g < 0 V удовлетво-
удовлетворяет всем условиям теоремы В, и невозмущенное движение неустойчиво.
§ 30. Исследование задачи для системы
(я+1)-го порядка в част-ном случае.
Допустим теперь, что п ф 0. Мы будем, однако, сначала пред-
предполагать, что правые части уравнений B8.6) связаны некоторым
ограничительным условием. Это условие заключается в следующем.
Обозначим через Х{0) (х) и X(f (x) соответственно совокупности
всех членов в функциях X и Xs, не содержащих х1 хп, так что
C0.1)
= Х(х, 0 0) = gxm
Xf(x) = X.(Xt о, ..., 0) = gsx +
(s=l. 2 я),
где g, g{m+x\ gs, g(™s+1') — постоянные. Мы будем предполагать, что
1) Х^ (х) не обращается тождественно в нуль,
2) ms ^ гп,
3) все величины ps в уравнениях B8.6) равны нулю.
94 ИССЛЕДОВАНИЕ КРИТИЧЕСКИХ СЛУЧАЕВ [ГЛ. IV
При этих предположениях задача устойчивости решается сразу,
а именно: невозмущенное движение всегда неустойчиво, если т —
число четное. Если т — число нечетное, то при g > 0 невоз-
невозмущенное движение неустойчиво, а при g < 0 оно устойчиво
и притом асимптотически. Другими словами, ответ получается
такой же, как если бы решалась задача устойчивости для одного
уравнения
Таким образом, для решения задачи устойчивости при выполнении
вышеуказанных ограничений можно отбросить все некритические
уравнения, а в критическом уравнении отбросить все члены, содержа-
содержащие некритические переменные, и исследовать полученное таким
образом одно уравнение с одной неизвестной функцией.
Для доказательства высказанных предложений мы постараемся для
уравнений возмущенного движения, которые в рассматриваемом слу-
случае имеют вид
*„) = ?**+...
+ Psn*n + Х'*(*¦ *1 Хп)
(s=l, 2 и),
C0.2)
где функция X' (х, ху, ..., хп) обращается в нуль при хх = ...
... = хп = 0, построить функции Ляпунова, удовлетворяющие усло-
условиям теоремы Б или В. Задача, следовательно, заключается в по-
построении функции V(x, xx, ..., хп), производная которой, состав-
составленная в силу уравнений C0.2), была бы знакоопределенной.
Допустим сначала, что т — число нечетное. Пусть W(xx хп)—
квадратичная форма переменных хг, ..., хп, выбранная согласно
условию
C0.3)
Так как все корни уравнения B8.5) имеют отрицательные веще-
вещественные части, то на основании теоремы 1 § 21 форма W существует
и будет определенно-отрицательной.
Если бы функции Xs не зависели от х, то производная по вре-
времени от формы W, составленная в силу последних п уравнений
системы C0.2), т. е. выражение
п
2 1^- ^Л + • • • + Рзп*п + Xs)- C0.4)
s=l
§ 30] система (й-|- 1)-го порядка; частный случай 95
являлась бы при достаточно малых хх хп определенно-положи-
определенно-положительной функцией относительно xit ..., хп.
С другой стороны, если бы функция X ке зависела от хх хп,
т. е. если бы X' = 0, то производная по времени от функции -^ gx2,
составленная в силу первого уравнения C0.2), равная
gxX = g4^ + ggm+lxm^ + ... + gxX', C0.5)
была бы при х достаточно малом определенно-положительной отно-
относительно х. Поэтому при указанных условиях производная по вре-
времени от функции
Vx = у gx2 + W (*! хп), C0.6)
составленная в силу полной системы уравнений C0.2), была бы
определенно-положительной функцией всех п -f-1 переменных
х, xv ..., хп в некоторой достаточно малой окрестности начала
координат. Эту производную можно было бы представить в виде
я
а, р=1
где / — некоторая функция от х, обращающаяся в нуль при х = 0,
а /аЯ—некоторые функции от хх хп, обращающиеся в нуль
при хх = ... =хп = 0.
Но так как функция X содержит хх, ..., хп, а функции Xs со-
содержат х, то производная от Vx в силу C0.2) не будет определенно-
положительной. В ней появятся члены, нарушающие знакоопределен-
знакоопределенность.
Чтобы выяснить общий вид этих членов, заметим прежде всего,
что выражение C0.7) останется, очевидно, знакоопределеиным, если
функция / содержит не только переменную х, но и переменные
хх хп, а функции /aR содержат не только переменные ху хп,
но и переменную х. Важно только, чтобы функции / и /а„ обраща-
обращались в нуль при х = хх — ... = хп = 0.
Учитывая это обстоятельство, запишем производную от V\ в силу
уравнений C0.2) в виде
„)•
96 ИССЛЕДОВАНИЕ КРИТИЧЕСКИХ СЛУЧАЕВ [ГЛ. IV
где функции / и /„ обращаются в нуль при х = хх — ... = хп = О,
а Р — совокупность всех членов, которые не могут быть включены
ни в выражение
fix, xx хп)хт+\ C0.9)
ни в выражение
п
Рассмотрим подробнее функцию Р. Все члены, входящие в выра-
выражение Р, можно, очевидно, разбить на следующие четыре группы:
на члены, свободные от хх, .. ., хп, на члены, линейные относительно
хх, .... хп, на члены, квадратичные относительно хх, ..., хп, и на
члены, имеющие относительно хх, . .., хп порядок выше второго.
Очевидно, что все члены последней группы можно включить в выра-
выражение C0.10). Нам остается поэтому рассмотреть только первые три
группы членов.
Все члены, свободные от хх хп, содержатся, очевидно,
только в выражении C0.5). Совокупность всех этих членов есть
Первый из них выписан в C0.8) явно, а остальные могут быть вклю-
включены в выражение C0.9). Следовательно, функция Р не содержит
членов, свободных от хг хп.
Члены, линейные относительно хх, ..., хп, входят в выражение
производной C0.8) как через совокупность C0.4), так и через сово-
совокупность C0.5). Если эти члены имеют относительно х порядок, не
меньший т-\-1, то они могут быть, очевидно, включены в выраже-
выражение C0.9). Таким образом, в функции Р содержатся лишь те линей-
линейные относительно хх, .... хп члены, которые имеют относительно х
порядок k, где k = 2 т.
Рассмотрим, наконец, члены, квадратичные относительно хх хп.
Если эти члены имеют общий порядок выше второго, то они могут
быть включены в выражение C0.10) и, следовательно, в функцию Р не
входят. Члены же, квадратичные относительно хг хп и имеющие
только второй порядок, т. е. обладающие постоянными коэффициен-
коэффициентами, содержатся, очевидно, все в выражении
7
и, следовательно, в функцию Р также не входят.
Таким образом, функция Р имеет вид
.. +x"Pn(xl *„), C0.11)
где Pi ixv ..., хп) — некоторые линейные формы от xlt ..., хп.
§ 30] система (п-{-\)-го порядка; частный случай 97
Наличие в выражении производной слагаемого C0.11) нарушает
ее знакоопределенность. Чтобы избавиться от этого слагаемого,
поступим следующим образом.
Добавим к функции V1 член xkQk (xv ..., хп), где Qk — подле-
подлежащая еще определению линейная форма переменных Xj. Другими
словами, рассмотрим вместо Vx функцию
g^\W(X*) + **«(«!...., *„). C0.12)
Член xkQk(x1, ..., хп) внесет в выражение производной два
слагаемых: слагаемое
l хп)Х(х, хх хп) C0.13)
и слагаемое
п
+ • • • + Psn*n + X) -gf • C0.14)
Рассмотрим подробней все члены, входящие в эти слагаемые.
Нас будут при этом интересовать лишь те из этих членов, которые
влияют на знак производной, т. е. члены, не содержащие хх, ..., хп,
члены, линейные относительно хх, ..., хп, и члены, квадратичные
относительно хг, ..., хп.
Члены, свободные от хг хп, содержатся, очевидно, только
в слагаемом C0.14). Совокупность этих членов мы получим, полагая
в этом слагаемом Xj = ... = хп = 0. Следовательно, эта совокуп-
совокупность есть
п
2 ^ C0.15)
Так как по условию ms~^m, то все члены, входящие в C0.15),
имеют порядок не ниже (w-j-ft)-ro и, следовательно, могут быть
включены в выражение C0.9). Таким образом, все новые члены,
свободные от хх, . . ., хп, не влияют на знакоопределенность
производной.
Рассмотрим теперь члены, линейные относительно xv .. ., хп.
Покажем, что все эти члены (входящие в слагаемые C0.13) и C0.14))
имеют относительно х порядок, не меньший k, и притом совокуп-
совокупность всех членов &-го порядка относительно х имеет вид
C0.16)
Действительно, интересующие нас члены содержатся как в сла-
слагаемом C0.13), так и в слагаемом C0.14). Чтобы получить эти члены
98 ИССЛЕДОВАНИЕ КРИТИЧЕСКИХ СЛУЧАЕВ [ГЛ. IV
в слагаемом C0.13), необходимо в функции X взять члены, не со-
содержащие хх хп. Эти члены имеют порядок не ниже т, причем
т^-2. Следовательно, все члены, линейные относительно xv .... хп,
содержащиеся в слагаемом C0.13), имеют порядок относительно х,
не меньший A-f-1.
Обращаясь теперь к слагаемому C0.14), мы видим, что кроме
C0.16) мы получим еще члены интересующего нас вида, если мы
в функциях Xs выделим все члены, линейные относительно хх хп.
Но каждый из этих членов содержит, по крайней мере, первую
степень х, так как все члены в Xs имеют порядок не ниже второго.
Поэтому все члены, линейные относительно хх хп, содержащиеся
в C0.14) и происходящие от функций Xs, имеют порядок относи-
относительно х, не меньший k-\-l.
Итак, все члены, линейные относительно хх хп, которыми
dVi „ dVt
производная—зт5- отличается от производной -jr-, имеют относи-
относительно х порядок не ниже k, причем совокупность всех членов, имею-
имеющих относительно х порядок k, дается выражением C0.16).
Что касается членов, квадратичных относительно хх, .... хп, то
нас могут, интересовать лишь те из них, которые имеют общий по-
порядок, равный двум, так как остальные могут быть включены в выра-
выражение C0.10). Но такого рода членов слагаемое xkQk в выражение
производной не вносит. Действительно, слагаемое C0.13) содержит
члены не ниже третьего порядка, а слагаемое C0.14) имеет множи-
множитель хк, и следовательно, члены, квадратичные относительно хх хп,
будут иметь общий порядок, превышающий два.
Резюмируя вышесказанное, мы приходим к заключению, что про-
производная функция C0.12) может быть представлена в следующем виде:
s=l а, р=1
••• +**-!/>,_!+ **S + x*+i/Vm+ ... +*™pm, C0.17)
где /, /а„— функция такого же типа, как и /, /а„, Рк+1, ¦ ¦ ¦, Рт—
линейные формы от хх, .... хп, вообще говоря, отличные от Яй + ]
Выберем теперь линейную форму Qk таким образом, чтобы выраже-
выражение C0.18) обратилось тождественно в нуль. Это всегда возможно
сделать на основании теоремы 2 § 20, так как все корни уравне-
уравнения B8.5) имеют отрицательные вещественные части.
§ 30] система (я-f- 1)-го порядка; частный случай 99
При такем выборе Qk в выражении C0.17) уничтожится один
из членов, нарушающих его знакоопределенность. При этом другие
члены этого типа, имеющие относительно х меньший порядок, будут
такими же, как и в выражении производной —^-. Мы можем поэтому
последовательно, добавляя к функции Vx члены xQx, x2Q2 xmQm
и подбирая соответствующим образом линейные формы Qt, уничто-
уничтожить в выражении производной все члены, нарушающие ее знако-
знакоопределенность. Другими словами, мы можем линейные формы Qt
выбрать таким образом, чтобы производная от функции
..+xmQm C0.19)
в силу системы C0.2) имела вид
Xn)xaXfi,
a, p=l
где F, Fa$ — некоторые функции от x, xv .. ., xn, обращающиеся
в нуль при х = хх = ... = х„ = 0.
dV
¦ Функция —тг получилась определенно-положительной. Рассмотрим
функцию V. Как было указано выше, квадратичная форма W (хх хп)
определенно-отрицательна. Поэтому если g < 0, то и квадратичная
форма
LWfa, .... хп) C0.20)
п-{-1 переменных х, Xj будет также определенно-отрицательной.
Но тогда определенно-отрицательной будет и функция C0.19), и
она, следовательно, будет удовлетворять всем условиям теоремы Б,
откуда вытекает асимптотическая устойчивость невозмущенного
движения.
Напротив, если g > 0, то квадратичная форма C0.20), а следо-
следовательно, и функция V будет знакопеременной. Функция V будет,
следовательно, удовлетворять всем условиям теоремы В, и невозму-
невозмущенное движение будет неустойчиво.
Допустим теперь, что m есть число четное и покажем, что невоз-
невозмущенное движение независимо от знака g неустойчиво.
В рассматриваемом случае функцию Ляпунова пытаемся искать
в виде
V1 = algx-\-W(x1 xn), C0.21)
где по-прежнему W(xlt ..., хп) обозначает квадратичную форму,
удовлетворяющую уравнению C0.3), а а2 — некоторое положительное
100 ИССЛЕДОВАНИЕ КРИТИЧЕСКИХ СЛУЧАЕВ [ГЛ. IV
число, выбором которого мы распорядимся позже. Функция C0.21),
как и в случае нечетного т, представляет собой сумму функций
Ляпунова, построенных по отдельности для одного первого уравне-
уравнения системы C0.2), если в нем отбросить все члены, содержащие х,,
и для последних п уравнений этой системы, если в них отбросить
все члены, содержащие х.
Производная от C0.21) по времени, составленная в силу полной
системы C0.2), может быть представлена в виде
dVx , dx
f a g
.5 = 1
*=1 a, p=l
где /, /op обращаются в нуль при х = хг = ... = хп = 0, а Я—сово-
Я—совокупность членов, которые не могут быть включены ни в выражение
(a2g2-\-f)xm, C0.23)
ни в выражение C0.10).
Анализируя все члены, входящие в C0.22), мы видим, что те из
них» которые не содержат xv ..., хп, могут быть все включены
в выражение C0.23). То же самое относится и к членам, линейным
относительно xv . .., хп, если они содержат х в степени, не мень-
меньшей т. Члены же вида
где Pt — линейные формы величин х1 хп, должны быть отне-
отнесены к функции Р.
Из членов более высоких порядков относительно Xj нас могут
интересовать квадратичные, имеющие общий порядок, равный двум,
т. е. обладающие постоянными коэффициентами. Все остальные члены,
квадратичные относительно хх, ..., хп, могут быть включены в вы-
выражение C0.10).
В отличие от случая нечетного т. выражение ' содержит ква-
квадратичные относительно Xj члены с постоянными коэффициентами,
отличные от 2 xs- Эти члены содержатся в а2^ —тг, и их совокуп-
совокупность имеет вид
а^*<2>(*1, .... хп), C0.24)
где Х() — квадратичная форма переменных Xj, представляющая собой
совокупность членов второго порядка в разложении функции
Х@, х1 хп).
§ 31] система (я-|-1)-го порядка; общий случай 101
Таким образом, функция Р имеет вид
Рт_1(х1 *„).
Член C0.24), входящий в Р, не нарушит знакоопределенности
производной, если число а2 выбрать настолько малым, чтобы форма
была определенно-положительной. Что же касается остальных членов,
входящих в Р, то их можно уничтожить таким же точно приемом,
какой мы применили в случае нечетного т. Для этого нужно вместо
функции C0.21) рассмотреть функцию
V = a?gx + W (xt хп) + *Q, + ... + xm-iQn_v
где Qlf .... Qm_!—некоторые линейные формы переменных xv ..., хп.
Эти формы можно подобрать таким образом, чтобы производная
от V приняла вид
* C0-25)
*=1 а, р=1
где F и Fa$ — функции такого же вида, как и / и Др.
Если а2 достаточно мало, то производная C0.25) есть функция
определенно-положительная. Сама же функция V, разложение которой
начинается линейными членами, будет, очевидно, знакопеременной.
Функция V удовлетворяет, таким образом, всем условиям теоремы В.
Следовательно, невозмущенное движение неустойчиво.
Таким образом, все утверждения о решении задачи устойчивости
в рассматриваемом случае полностью доказаны.
§ 31. Исследование задачи для системы
(я+1)-го порядка в общем случае.
Мы переходим теперь к рассмотрению общего случая, когда пра-
правые части уравнений возмущенного движения B8.6) не подчинены
никаким ограничительным условиям.
Для решения задачи постараемся преобразовать уравнения возму-
возмущенного движения к такому виду, для которого выполняются огра-
ограничительные условия предыдущего параграфа. С этой целью рассмо-
рассмотрим систему уравнений
fs = PsiXx+...+psnxn + psx + Xs = 0 {s=\, 2,..., и), C1.1)
определяющих переменные xs как функции переменной х. Левые части
этих уравнений обращаются в нуль при х = х1^= ... = х„ = 0.
102
ИССЛЕДОВАНИЕ КРИТИЧЕСКИХ СЛУЧАЕВ
[ГЛ. IV
Функциональный же определитель по переменным хх хп этой
системы уравнений при х = х1 = ... = хп = 0 отличен от нуля.
Действительно,
так как уравнение B8.5) не имеет нулевого корня. Поэтому на
основании известной теоремы существования неявных функций суще-
существует одно и только одно решение системы C1.1), при котором
функции xs обращаются в нуль при х = 0, и эти функции будут
разлагаться в ряды по степеням х, сходящиеся при достаточно малых
значениях этой величины. Пусть
us{x) = A(~})x-\-Afxi-\~ ... C1.2)
будут указанные функции, так что
Л1«1+---+Л»«,. + Л* +*,(•*• «1. ¦••• я„) = 0. C1.3)
Сделаем теперь в уравнениях B8.6) преобразование переменных
*,= ?, + «,(*)• C1.4)
Будем иметь:
или на основании C1.3)
• • • -Ь Psnln + Xs (,
{s— 1, 2 л),
•••.&„).
dt
C1.5)
где
C1.6)
— аналитические функции переменных х, ?,-, разложения которых на-
начинаются членами не ниже второго порядка.
Так как новые переменные обращаются одновременно в нуль тогда
и только тогда, когда обращаются одновременно в нуль старые
. переменные, то задача устойчивости по отношению к одним переменным
§ 31] система (л-(-1)-го порядка; общий случай 103
эквивалентна задаче устойчивости по отношению к другим перемен-
переменным. Мы можем поэтому для решения задачи рассматривать уравне-
уравнения C1.5).
Уравнения C1.5) удовлетворяют второму и третьему ограничи-
ограничительному условиям, введенным в предыдущем параграфе. Действи-
Действительно, коэффициенты при первой степени х в последних п уравне-
уравнениях C1.5) равны нулю, а для функций Хт и Х^ на основа-
основании C1.6) имеем:
Х(о) (х) = Х(х, 0, .... 0) = X (х, и, (*) ип(х)),
*2V) = *,(*. о о) = -^х@>,
откуда непосредственно следует, что разложение функций Х^ начи-
начинается членами, порядок которых не ниже порядка младшего члена
в разложении функции X ¦
Следовательно, если функция А"@) не обращается тождественно
в нуль, то система C1.5) удовлетворяет всем условиям предыдущего
параграфа и для решения задачи устойчивости мы можем восполь-
воспользоваться полученными там результатами. Если же Л"@) = 0, то на
основании C1.7) Х^^О и условия предыдущего параграфа не вы-
выполняются. Этот случай является особенным и требует специального
рассмотрения. Мы этим з.аймемся в § 33. Сейчас мы рассмотрим
неособенный случай.
В этом случае согласно результатам предыдущего параграфа мы
должны рассмотреть лишь первое из уравнений C1.5), отбросить
в нем все члены, зависящие от ?j |л, и решать задачу устойчи-
устойчивости для полученного таким образом уравнения
. C1.8)
Но на основании C1.7) правая часть этого уравнения есть результат
подстановки в правую часть первого из уравнений B8.6) вместо
величин Xj функций C1.2). Следовательно, уравнение C1.8) имеет вид
^=Х(х,а1(х) ип(х)). C1.9)
Задача устойчивости для этого уравнения решается младшим чле-
членом в разложении его правой части. Если степень этого младшего
члена нечетная, а коэффициент при нем отрицателен, то невозмущен-
невозмущенное движение устойчиво и притом асимптотически. Во всех осталь-
остальных случаях оно неустойчиво.
Таким образом, для решения задачи устойчивости в интересую-
интересующем нас случае, когда характеристическое уравнение системы первого
приближения имеет один нулевой корень при остальных корнях
104 ИССЛЕДОВАНИЕ КРИТИЧЕСКИХ СЛУЧАЕВ [ГЛ. IV
с отрицательными вещественными частями, можно руководствоваться
следующим правилом:
Г) приводим уравнения возмущенного движения к виду B8.6);
2) приравниваем нулю правые части некритических уравнений и
решаем относительно Xj полученные таким образом уравнения C1.1);
3) полученными функциями от х заменяем величины Xj в правой
части критического уравнения, и если результат подстановки не об-
обращается тождественно в нуль, то решаем задачу устойчивости для
полученного таким образом одного уравнения с одной неизвестной
функцией C1.9).
Для этого рассматриваем лишь младший член в разложении правой
части уравнения C1.9). Пусть этот член будет gxm. Тогда при т.
нечетном и g < 0 невозмущенное движение устойчиво и притом асим-
асимптотически. В других случаях оно неустойчиво.
§ 32. Примеры.
В предыдущем параграфе мы видели, что для решения задачи
устойчивости в интересующем нас критическом случае необходимо
прежде всего разрешить систему уравнений C1.1) относительно пере-
переменных xs. Для действительного вычисления этого решения будем
искать его в виде рядов
ха (х) = Е^х + Е^х* + ... (s = 1. 2. ..., я) C2.1)
с неопределенными коэффициентами Bs\ Для определения этих коэф-
коэффициентов подставим ряды C2.1) в уравнения C1.1) и приравняем
нулю коэффициенты при различных степенях х. Приравнивая нулю
коэффициенты при первой степени х, мы получим систему уравнений
s = {i <S=1' 2 ») С322)
для определения Bs\ Эти уравнения линейны, обладают отличным от
нуля определителем и дают одно и только $
Точно так же, приравнивая нулю коэффициен
для определения В$ систему уравнений вида
нуля определителем и дают одно и только одно решение для В$\
Точно так же, приравнивая нулю коэффициенты при х1, мы получим
° (s = 1.2 я). C2.3)
где Р^ — некоторые полиномы относительно В^\ Bf\ .... B(j~l\
Уравнения C2.3) дают возможность последовательно определять
коэффициенты В$ по мере возрастания их порядка.
После того как коэффициенты В\^ уже вычислены, необходимо
подставить ряды C2.1) в функцию X вместо xs. Младший член полу-
полученного таким образом ряда относительно х и решает, как мы видели,
задачу устойчивости. Но так как нас интересует лишь младший член
§ 32] примеры 105
указанного ряда, то при действительном проведении вычислений
достаточно в общем случае подсчитать в рядах C2.1) только первые
члены В(^х, которые и определят младший член в функции X. Если,
однако, окажется, что в результате подстановки C2.1) в функцию X
коэффициент при младшем члене благодаря некоторым зависимостям
между коэффициентами функций X и Xs обратится в нуль, то при-
придется в рядах C2.1) учесть и члены Bfx2, а в некоторых случаях
и члены более высоких порядков.
Заметим, что если все величины ps равны нулю, то уравнения C2.2)
дают В\ — В2 — ... = Вп' = 0 и, следовательно, разложение функ-
функций xs (x) начинаются членами не ниже второго порядка. Вообще,
если во всех функциях psx + Xs (x, 0 0) нет членов до k-vo
порядка включительно, но хотя бы в одной из этих функций имеются
члены (&-f-l)-ro порядка, то разложения C2.1) начнутся членами
(&-f- 1)-го порядка.
Рассмотрим несколько примеров.
Пример 1. Исследуем устойчивость регулируемой системы,
описываемой дифференциальными уравнениями
я).
C2.4)
где ps и ps — постоянные, причем ps положительны, а /(о) —некоторая
непрерывная функция, удовлетворяющая условию
а/(а)>0. C2.5)
В § 12 были установлены достаточные условия устойчивости
положения равновесия а = хх = ... = хп = 0 рассматриваемой системы
при любых начальных возмущениях и при любом выборе функции / (о),
удовлетворяющей условию C2.5). При этом было показано, что для
выполнимости этих условий необходимо, чтобы удовлетворялось
неравенство A2.9):
Покажем сейчас!), что если / (а) является аналитической функ-
функцией, разложение которой начинается членами не ниже второго по-
порядка, то условие C2.6) является необходимым для устойчивости.
Более того, если требуется, чтобы равновесие было устойчиво при
достаточно малых начальных возмущениях, то это условие является
также и достаточным.
') Лурье А. И., Об устойчивости одного класса регулируемых систем.
ПММ, т. XV, в«п, 5, 1951.
106 ИССЛЕДОВАНИЕ КРИТИЧЕСКИХ СЛУЧАЕВ [ГЛ. IV
В самом деле, пусть
где т > 2.
Из C2.5) вытекает, что число т является обязательно нечетным
и ат > 0.
Характеристическое уравнение системы первого приближения
имеет п отрицательных корней — ps и один корень, равный нулю.
Эта система первого приближения имеет первый интеграл
Приняв его за новую переменную вместо о, мы приведем уравне-
уравнения C2.4) к виду B8.6):
#-(М+-+*-'М*-Ь-•••-?*•)•
St = — 9sxs + f\x — -^xl— ... — -?- хя].
Здесь
(х) = (Jl + ... +|f - l)/ (*). Xf> (x) = /(*), ps = 0;
следовательно, разложения функций Л^0)(а-) начинаются членами того
же порядка, что и разложение функции Х^ (х). Поэтому мы имеем
дело с частным случаем, рассмотренным в § 30, и в дальнейших
преобразованиях уравнений нет необходимости.
Для того чтобы движение было устойчиво, необходимо., чтобы
младший член в разложении X (х) был нечетного порядка и имел
отрицательный коэффициент. Первое из этих условий выполняется,
а второе приводит к неравенству C2.6).
Пример 2'). Пусть предложена система дифференциальных
уравнений возмущенного движения вида
+ Cn—\)yz — 2tnzx— 2nxy — X (x, y, z),
\i L. V у\ I \\ L_ 9* у*Л ¦¦ — __ \ t ...J v* I \f ( у * I y\
л— ~ , .. K- , -, -2)(y + z — *)= - z + x + Z(^, у, г).
Характеристическое уравнение системы первого приближения имеет
корни—1, —1 и 0. Система уже приведена к виду B8.6). Уело-
') Л я п у н о в А. М., Общая задача об устойчивости движения., Гостех-
издат, 1950.
§ 32] примеры 107
вия § 30 здесь не выполнены, и мы должны поэтому воспользоваться
общим приемом предыдущего параграфа.
Полагая
0, C2.7)
попытаемся удовлетворить этим уравнениям относительно у и z
рядами, расположенными по степеням х. Коэффициенты при первой
степени х будут, очевидно, равны единице, и мы можем написать:
у(х) = х + Л2х2+Л3х3 + .... \
2+Я3*3+ .... I ( }
Подставляя эти ряды в функцию X, получим, что член второго
порядка в ней выпадает, и функция эта примет вид
Х(х, у(х), z(x)) = (n-2m+l)(A2-{-B2)x3 + Cx4-\-Dx5 + ... C2.9)
Следовательно, в рассматриваемом случае необходимо подсчитать
коэффициенты А2 и В2. Для их вычисления приравняем нулю коэф-
коэффициенты при х1 в уравнениях C2.7) после подстановки в них
рядов C2.8). Тогда легко получим, что Л2 = 2, В2 =— 2. Но тогда
в выражении C2.9) обратится в нуль коэффициент при х3 и необхо-
необходимо поэтому вычислить С, а для этого придется вычислить коэф-
коэффициенты Л3 и Вг. Приравнивая нулю в C2.7) коэффициенты при х3,
найдем: Аг — Вг — —6, после чего получим С = 4E/ге — 7п). Если
этот коэффициент отличен от нуля, то невозмущенное движение
неустойчиво, так как разложение функции C2.9) начинается четным
порядком. Допустим, что Ът = In. Тогда, вычисляя А4 и В4, найдем
А4 — — 30, В4 = 30, после чего получим D = 24 (т — п). Этот коэффи-
коэффициент будет отрицательным при тип отрицательных и положитель-
положительным при тип положительных. В первом случае невозмущенное движе-
движение асимптотически устойчиво, а во втором случае оно неустойчиво.
Если т — п = 0, то требуется рассмотреть дальнейшие прибли-
приближения. Однако в этом случае справедливо тождество
2Х = (z— 2у — х) (— у + х+ К) + (У — 2* — 2*) (— г + х + Z).
следовательно, на основании C2.7) X (х, у{х), z(x)) = 0, м имеет
место особенный случай.
Пример 3'). Пусть система уравнений возмущенного движения
имеет вид
-JL = ax2-\- bxy + су> = Х (х, у),
-jjt = — y-f-&x-f-/x2+ mxy-\-ny* = — y-\-kx-\-Y(x, у),
где а, Ь, с, k, I, т., п — постоянные.
') Ляпунов А. М., Общая задача об устойчивости движения, Гос-
техиздат, 1950.
108 ИССЛЕДОВАНИЕ КРИТИЧЕСКИХ СЛУЧАЕВ [ГЛ. IV
Составляя уравнение
— у-\-kx + 1х2-)- тху + пу* = 0, C2.10)
будем иметь:
у (х) = kx +В2х* + Я3х3+ ...
и, подставляя этот ряд в X (х, у), получим:
X(х, у(х)) =
где
Az = (b-\-2ck)B2,
Для того чтобы движение было устойчивым, необходимо, чтобы
выполнялось условие
А2 = а-\- bk-\-ck2 = 0. C2.11)
Допустим, что это условие выполнено. Тогда необходимо рас-
рассмотреть коэффициент А3, для определения которого нужно вычи-
вычислить В2. Вычисляя эту величину, найдем:
C2.12)
Здесь необходимо рассмотреть два случая, в зависимости от того,
будет ли величина В2 равна нулю или нет. Допустим сначала, что В2
не нуль. Тогда если b-\-2ck фО, то невозмущенное движение асим-
асимптотически устойчиво при В2 (Ь -\- 2ck) < 0 и неустойчиво при
B2(b-\-2ck) > 0. Если же b-\-2ck — 0, то необходимо рассмотреть
коэффициент А4. Если с ф 0, то невозмущенное движение неустойчиво.
Если же с = 0, то вследствие допущенных равенств будет а = 0
и b = 0. Следовательно, функция X (х, у) обратится тождественно
в нуль, и мы будем иметь дело с особенным случаем.
Допустим теперь, что В2 = 0. Тогда на основании C2.12) урав-
уравнение C2.10) будет иметь решение y — kx, которое на основа-
основании C2.11) обратит функцию Х(х,у(х)) тождественно в нуль.
Следовательно, опять получится особенный случай.
§ 33. Особенный случай.
Рассмотрим теперь особенный случай. Допустим, следовательно,
что при замене в функции X (х, х1 хп) величин xs функциями
us{x), удовлетворяющими уравнениям C1.3), получится тождественно
нуль. В этом случае при преобразовании уравнений B8.6) при помощи
подстановки C1.4) мы будем иметь в полученных таким образом
уравнениях C1.5) соотношения
0 О)==Аг,(дс. 0 0) = 0 (s=l, 2 я). C3.1)
§ 33] ОСОБЕННЫЙ СЛУЧАЙ 109
Эти соотношения непосредственно вытекают из C1.6).
Но при выполнении соотношений C3.1) уравнения C1.5) имеют
решение
х = с. Ei= ••• =S« = o.
где с — произвольная постоянная. Следовательно, уравнения B8.6)
имеют решение
х = с, xs = us(c). C3.2)
Тривиальное решение х = х1—... = х„ = 0 содержится в семействе
C3.2) и соответствует нулевому значению постоянной с1).
Тривиальному решению соответствует исследуемое невозмущенное
установившееся движение рассматриваемой динамической системы.
Точно так же решению C3.2) соответствуют другие установившиеся
движения рассматриваемой системы. Таким образом, в особенном
случае исследуемое невозмущенное движение принадлежит к семейству
установившихся движений.
Справедливо и обратное. Пусть предложенная динамическая система
описывается уравнениями
¦^¦ = ^(У1 Уп+д ('=1. 2 я+1). C3.3)
где правые части не зависят явно от t, поскольку мы рассматриваем
установившиеся движения. Допустим, что динамическая система имеет
установившееся движение, т. е. что уравнения C3.3) имеют частное
решение yt = at, где at — постоянные. Эти постоянные определяются
системой уравнений
М<4 e»+i) = 0 (/=1,2 я+1). C3.4)
Может случиться, что уравнения C3.4) имеют не изолированное
решение, а целое семейство решений, зависящее от одного произ-
произвольного параметра X, так что эти уравнения удовлетворяются при
yl = ai(k), где at(X) — некоторые функции от к. Следовательно,
рассматриваемая динамическая система имеет однопараметрическое
семейство установившихся движений. Примем одно из движений этого
семейства, соответствующее, например, значению Хо параметра, за
невозмущенное и составим дифференциальные уравнения возмущен-
возмущенного движения. Покажем, что при этом один корень характеристи-
характеристического уравнения будет обязательно равен нулю, и если остальные
корни будут иметь отрицательные вещественные части, то рассма-
рассматриваемый случай будет обязательно особенным.
Мы предполагаем при этом, как во всей этой главе, что урав-
уравнения C3.3) аналитичны в некоторой области и что исследуемое
невозмущенное движение лежит в этой области.
1) См. примечание в конце книги (стр. 521).
no
ИССЛЕДОВАНИЕ КРИТИЧЕСКИХ СЛУЧАЕВ
[ГЛ. IV
Искомые уравнения возмущенного движения получим, преобразуя
C3.3) при помощи подстановки
Таким путем получаем:
== 1Л 2 я
), C3.5)
где Xt — аналитические функции переменных xv .... хп+1, разло-
разложения которых по степеням этих переменных начинаются членами
не ниже второго порядка.
Рассмотрим уравнения
C3.6)
A=1, 2
я+1).
Эти уравнения удовлетворяются при хг = ... = хп+1 = 0. Если
бы в этой точке функциональный определитель системы C3.6)
xn+l)
Яп ¦•¦ Ч\, я+i
Я-22 • • • 42, п + 1
Яп+1,2 • • • Чп + \,п + \
C3.7)
был отличен от нуля, то никакого другого решения в окрестности
начала координат уравнения C3.6) не имели бы. Однако в рассма-
рассматриваемом случае это неверно. Действительно, поскольку дифферен-
дифференциальные уравнения C3.3) имеют решение yl= aiQS), то дифферен-
дифференциальные уравнения C3.5) должны иметь решение xt = ai (Я.) — а,(А,0).
Поэтому уравнения C3.6) должны удовлетворяться при xt =
— at (X) — ai (Xo). Это решение, зависящее от произвольного пара-
параметра, лежит при к, достаточно близком к Я,о> в окрестности начала
координат и переходит в тривиальное при Я = Х0. Итак, решение
х1 = ... =л;п+1 = 0 уравнений C3.6) не является изолированным,
и поэтому определитель C3.7) необходимо равен нулю. Следова-
Следовательно, характеристическое уравнение системы C3.5) имеет, по край-
крайней мере, один нулевой корень.
Допустим, что остальные п корней характеристического уравне-
уравнения отличны от нуля. Преобразуем систему C3.5) к виду B8.6):
dx
-Jf =
(s=l, 2 я).
C3.8)
§ 33]
где уравнение
D(X) =
ОСОБЕННЫЙ СЛУЧАЙ
рп X р12 ... рХп
Рг\ Р22 — X ... р2п
Рп\
Рп1
= 0
111
C3.9)
не имеет нулевого корня. При этом система C3.8) должна иметь
решение xs = fs(X) (s=l, 2, .... п), х = f(X), в которое пере-
переходит решение лг; —аг(Я) — at (Яо) (/=1, 2 п-\-\) системы
C3.5). Здесь все функции /, fs обращаются в нуль при А, = А,0 и
fs(X) = as(X)-as(X0) E=1, 2 п).
Следовательно, уравнения
Х(х, х, *„) = <>.
E=1, 2 П)
должны удовлетворяться решением x — f(X), xs = fs(k), содержа-
содержащим тривиальное решение х = хх = ... = хл = 0.
Но так как П>@)ф0, то последние n уравнений C3.10) могут
быть разрешены относительно xs и дадут xs = us (х), где us — функ-
функции, рассмотренные в § 31. Подставляя эти функции в первое
уравнение C3.10), мы получим одно уравнение для определения х.
Это уравнение должно удовлетворяться при x = f(X), т. е. иметь
бесчисленное множество решений, соответствующих различным зна-
значениям X, что, очевидно, возможно лишь только тогда, когда
X (х, й](х) и„(х)) = 0. Если при этом все корни уравне-
уравнения C3.9) имеют отрицательные вещественные части, то мы будем
иметь особенный случай.
Примером динамической системы, имеющей семейство установив-
установившихся движений, зависящее от произвольного параметра, может
служить твердое тело, вращающееся по инерции вокруг закреплен-
закрепленной точки. Уравнения движения такого тела
где р, q, г —проекции вектора мгновенной угловой скорости на оси
координат, направленные по главным осям инерции в закрепленной
точке, а А, В, С — моменты инерции относительно этих осей, имеют
три семейства решений:
112 ИССЛЕДОВАНИЕ КРИТИЧЕСКИХ СЛУЧАЕВ [ГЛ. IV
зависящих каждое от произвольной постоянной ю. Дифференциальные
уравнения возмущенного движения, когда за невозмущенное движение
принято одно из движений первого семейства, имеют вид B3.1)
C3.11)
Характеристическое уравнение первого приближения действительно
имеет один нулевой корень (см. § 22), и так как в переменных х,
у, z рассматриваемому семейству движений отвечают нулевые значе-
значения переменных у и z, то уравнения C3.11) уже имеют форму C1.5).
Действительно, правые части всех трех уравнений обращаются в нуль
при у — z = 0.
Необходимо, однако, указать, что вещественные части остальных
двух корней характеристического уравнения не могут быть одновре-
одновременно отрицательными, и потому уравнения C3.11) не принадлежат
к типу сейчас рассматриваемых. Напомним, что полное решение
задачи устойчивости для системы C3.11) дано в § 23.
§ 34. Решение задачи устойчивости в особенном случае.
Итак, в особенном случае невозмущенное движение принадлежит
к семейству установившихся движений, которое в переменных х, xs
определяется формулами C3.2), а в переменных х, |4, приводящих
уравнения возмущенного движения к виду C1.5), — формулами
х = с. ?,= ... =|„ = 0. C4.1)
В особенном случае невозмущенное движение всегда устойчиво.
Устойчивость при этом не будет асимптотической. Однако всякое
возмущенное движение, достаточно близкое к невозмущенному, не
стремясь при t->oo к невозмущенному движению, стремится все же
к одному из установившихся движений вышеуказанного семейства.
Другими словами, если пользоваться переменными х, \s, то для всякого
решения x(t), l,s(t) уравнений возмущенного движения, для которого
начальные значения х° и |° достаточно малы, справедливы равенства
lim x(t) — a, lim
где а — некоторая определенная постоянная (зависящая от взятого
возмущенного движения).
Точно такими же свойствами, как и невозмущенное движение,
обладают все движения семейства C4.1), достаточно близкие к не-
невозмущенному.
§ 34] РЕШЕНИЕ ЗАДАЧИ УСТОЙЧИВОСТИ В ОСОБЕННОМ СЛУЧАЕ
113
Это предложение является частным случаем более общей теоремы
Ляпунова, которую мы здесь и приводим 1).
Допустим, что дифференциальные уравнения возмущенного дви-
движения имеют вид
dy.
«. У\ Ук)
I _ ]( 2 k),
= Psi*i
(t,
(s=l, 2
я),
C4.2)
и аналитиче-
аналитичегде Kj, Xs—ограниченные функции t при всех t
ские функции переменных yt, xs в некоторой не зависящей от t
окрестности начала координат, разложения которых по степеням этих
переменных начинаются членами не ниже второго порядка. При этом
имеют место соотношения
0
О,
Yt(t 0 О, у, УЬ) = Х
т. е. функции Y\, Xs обращаются в нуль при равенстве нулю одних
лишь переменных xs.
Коэффициенты psj таковы, что уравнение
Рп ^ Ри • • ¦ Pin
Р21 Р22 А . . . Рчп
Рп\
РпЧ
= 0
C4.3)
имеет корни только с отрицательными вещественными частями.
Уравнения C4.2) допускают частное решение:
У\
У к-
= 0.
C4.4)
определяющее семейство установившихся движений, зависящее от k
произвольных постоянных с1 и содержащее исследуемое невозмущен-
невозмущенное движение. Если Xs и Yi не содержат t и k=l, то система
C4.2) переходит в систему вида C1.5) в особенном случае.
Теорема. Если уравнения возмущенного движения имеют
вид C4.2), то невозмущенное движение устойчиво. При этом
всякое возмущенное движение, достаточно близкое к невозму-
невозмущенному, стремится с неограниченным возрастанием времени
к одному из установившихся движений семейства C4.4).
') См. М а л к и н И. Г., Об устойчивости движения в смысле Ляпунова,
Матем. сб., т. 3, вып. 1, 1938. Теорема Ляпунова обобщена нами в этой
работе, из которой мы заимствуем приводимое здесь доказательство, совер-
совершенно отличающееся от доказательства Ляпунова.
114 ИССЛЕДОВАНИЕ КРИТИЧЕСКИХ СЛУЧАЕВ [ГЛ. IV
Теми же свойствами обладают все движения семейства C4.4),
если только численные значения параметров ct достаточно малы.
Доказательство. Исследуем сначала невозмущенное дви-
движение.
По свойству корней уравнения C4.3) существует определенно-
положительная квадратичная форма V {хх хп) переменных xs,
удовлетворяющая уравнению
Преобразуем вторую группу уравнений C4.2) при помощи под-
подстановки
|, = «"Ч. C4.5)
где а — достаточно малая положительная постоянная. Преобразован-
Преобразованная система примет вид
+ e«<Xs(t, e-«% е~"%п, у, yk) C4.6)
(s=l, 2 п).
Составим полную производную по времени функции V (|t |„)
в силу уравнений C4.6). Будем иметь:
dV _
s=l
Положительную постоянную а можно выбрать настолько малой,
чтобы форма
s = l
была определенно-отрицательной. С другой стороны, так как функ-
функции Xs обращаются в нуль при х1= ... = х„ = О и по отношению
к t они ограничены, то в области
*>0> I6.KP. М<Р ('=1. 2 А; 8=1. 2 я) C4.7)
будет выполняться неравенство
<Р{\1г\+ ,,. +||,| }2. C4.8)
§ 34] РЕШЕНИЕ ЗАДАЧИ УСТОЙЧИВОСТИ В ОСОБЕННОМ СЛУЧАВ 116
если только число р достаточно мало. При этом число р можно
зыбрать настолько малым, чтобы число Р было сколь угодно малым.
Это вытекает из того обстоятельства, что функции Xs не содержат
в своих разложениях членов ниже второго порядка, и поэтому все
члены левой части неравенства C4.8), имея по крайней мере второй
порядок относительно \s, будут иметь общий порядок не ниже
третьего.
Поэтому на основании леммы 2 § 7 число р можно выбрать на-
dV
столько малым, чтобы в области C4.7) функция -гг принимала только
отрицательные значения. Мы будем предполагать, что число р дей-
действительно выбрано указанным образом.
Установив это, рассмотрим произвольное решение ls(t), yt(t)
уравнений возмущенного движения с начальными значениями (при
^ = 0) |°, у®, удовлетворяющими неравенствам
\10,\<Ъ |У?|<Ч E-1,2 п; 1=1, 2 к), C4.9)
где Т1<р.
Для этого решения условия
МОКР. ЫОКР C4.10)
будут выполняться по крайней мере для значений t, близких к началь-
начальному. Пусть t — такой момент времени, для которого условия C4.10)
еще выполняются. Тогда во всем промежутке @, f) выражение —от-
—отбудет отрицательным, и мы можем написать:
\
0
Так как форма V определенно-положительна, то из C4.11) вытекает,
что в рассматриваемом промежутке времени выполняются неравенства
\ls(t)\<A (s=l, 2 я). C4.12)
причем число А можно сделать сколь угодно малым подходящим
выбором величин ?° |°, т. е. если число х\ в неравенствах C4.9)
взять достаточно малым.
Из C4.12) вытекает, что в указанном промежутке времени пере-
переменные xs удовлетворяют неравенствам
\xs(t)\<Ae-ai (s=l, 2 я). C4.13)
Эти неравенства показывают, что для функций К, в указанном
промежутке справедливы оиенки
I «. C4.14)
116 ИССЛЕДОВАНИЕ КРИТИЧЕСКИХ СЛУЧАЕВ [ГЛ. IV
где М — некоторое положительное число, так как эти функции обра-
обращаются в нуль при х^ — ... = хп = 0 и ограничены относительно t.
Следовательно, первая группа уравнений C4.2), из которой вытекает
дает:
C4-15)
= 1, 2
Пусть теперь е — произвольное сколь угодно малое число, кото-
которое мы во всяком случае будем считать меньше р. Выберем число т)
в неравенствах C4.9) таким образом, чтобы число А было меньше е
и чтобы правая часть неравенств C4.15) была также меньше е. Тогда
из C4.12) и C4.15) вытекает, что во всем промежутке времени,
в течение которого выполняются неравенства C4.10), будут также
выполняться неравенства
1?,(9|<е. | У* (О I < е (8=1, 2 я; /=1. 2 к). C4.16)
Но так как ^ < р, то отсюда следует, что неравенства C4.10),
а вместе с ними и неравенства C4.16) выполняются при всех значе-
значениях t. Действительно, если бы условия C4.10), которые в началь-
начальный момент времени выполняются со знаками неравенства, когда-
нибудь нарушились, то в некоторый момент времени хотя бы одна
из величин |У(@|> |lj@| Достигла бы значения р. Это, однако,
невозможно, так как в этот момент времени условия C4.16) еще
оставались бы в силе и, следовательно, все величины ||^@|. |У/@|
были бы меньше е.
Итак, если в начальный момент времени выполняются условия C4.9),
то в дальнейшем все время будут выполняться условия C4.16). Сле-
Следовательно, невозмущенное движение устойчиво по отношению к пере-
переменным |5, уг. Но тогда оно и подавно устойчиво по отношению
к переменным xs, yt.
Покажем теперь, что всякое возмущенное движение, достаточно
близкое к невозмущенному, асимптотически приближается при ^ = оо
к одному из движений семейства C4.4), т. е. что
lim xs(t) — 0, lim yi(t) = ai, C4.17)
t-±oa t-><x>
где al — некоторые постоянные.
§ 34] РЕШЕНИЕ ЗАДАЧИ УСТОЙЧИВОСТИ В ОСОБЕННОМ СЛУЧАЕ 117
Первая группа соотношений C4.17) непосредственно вытекает
из C4.13). Для доказательства второй группы замечаем, что
lim у (/) = уо+ f YiV> *i@. • • •- *«@. Уг(*) yk(t))dt. C4.18)
Интегралы, стоящие в правых частях C4.18), сходятся на осно-
основании оценок C4.14), которые остаются справедливыми, по доказан-
доказанному, при всех значениях t. Отсюда непосредственно следует спра-
справедливость второй группы соотношений C4.17), причем величины сп-
справны правым частям равенств C4.18).
Докажем теперь, что такими же свойствами, как и невозмущен-
невозмущенное движение, обладают все движения семейства C4.4), если только
величины | с( | достаточно малы. С этой целью, приняв какое-нибудь
движение семейства C4.4) за невозмущенное, составим соответствую-
соответствующие дифференциальные уравнения возмущенного движения, положив
в C4.2)
Ui = yt — Ct (/=1. 2 ft),
где ut — новые переменные. Тогда получим:
C4.19)
где Ui, Xs — функции такого же типа, как и Yt, Xs, а величины а^
и с so являются функциями от t и cv ..., ck. По отношению к t
функции а.1 j и csg ограничены, а по отношению к сх, ..., ck они
аналитичны и обращаются в нуль при с1 = ... = ск — 0. По-
Поэтому при I с(. | достаточно малых величины <х„ и psg будут сколь
угодно малы.
Уравнения C4.19) отличаются от уравнений C4.2) только тем,
что в их правых частях добавились новые члены, линейные относи-
относительно ATj. Присутствие этих членов в правых частях первой группы
уравнений C4.19) ничего не меняет в предыдущих рассуждениях,
так как мы в них нигде не пользовались тем обстоятельством, что
разложения функций Yi не содержат линейных членов. Важно было
только, чтобы функции Y[ обращались в ¦ нуль при равенстве нулю
одних лишь переменных xs, что для первой группы уравнений C4.19)
по-прежнему выполняется.
Присутствие новых линейных относительно xs членов во второй
группе уравнений C4.19) также ничего не изменит, если только
dxs
dt
= (Psl
t, XU .
...Xn, И]
A" 1
+ (Psn
+ csn)
t, Xy, .
1*!
х„
...
Xn, Kj,
-г-»*»*».
...,«ft),
118 ИССЛЕДОВАНИЕ КРИТИЧЕСКИХ СЛУЧАЕВ [ГЛ. IV
квадратичная форма
будет по-прежнему определенно-отрицательной, а это действительно
будет иметь место, если только величины | сг"[ достаточно малы, что
мы и будем предполагать.
Таким образом, к уравнениям C4.19) применимы все предыдущие
рассуждения, и следовательно, при достаточно малых | ct | для дви-
движений C4.4) справедливы те же заключения, что и для первоначаль-
первоначального невозмущенного движения х1 = ... = ха = уг = ... = ук = 0.
Таким образом, теорема доказана.
Доказанная теорема полностью исчерпывает исследование особен-
особенного случая, вместе с ним исследование критического случая одного
нулевого корня характеристического уравнения. В следующем пара-
параграфе мы начнем рассмотрение второго критического случая, когда -
характеристическое уравнение имеет пару чисто мнимых корней при
остальных корнях с отрицательными вещественными частями.
§ 35. Случай пары чисто мнимых корней. Приведение уравнений
возмущенного движения к специальному виду.
Рассмотрим систему (ra-f-2)-ro порядка
L п ? —I— —I— П 7 I— 7 (Г ? \ С\Ъ \\
df —4j\6\ ~l ••• 1^ Ч), п+2*п+2 i^ **j \^V •••> *я+2/ ypo.i)
C/=l. 2 я+2),
где Zj — функции переменных Z\ zn+2> аналитические в некото-
некоторой окрестности начала координат, разложения которых по степеням
этих переменных начинаются членами не ниже второго порядка. Мы
будем предполагать, что характеристическое уравнение
—Р ЯП ¦¦¦ 01, я+2
= 0 C5.2)
Яп+2,1 Чп+2,2 ••• Чп + 2,п+2 — Р
системы первого приближения
-jf = 4jl*l + ¦ • • + Я], n+2Z»+2 C5.3)
имеет пару чисто мнимых корней ± Я/ и п корней с отрицательными
вещественными частями.
§ 35] СЛУЧАЙ ПАРЫ ЧИСТО МНИМЫХ КОРНЕЙ 119
Введем в уравнения C5.3) вместо двух каких-нибудь переменных Zj
две новые переменные х и у при помощи подстановки:
где а.] и bj — некоторые постоянные. Мы постараемся эти постоянные
подобрать таким образом, чтобы два уравнения системы C5.3) при-
приняли вид
dx _ kv <*У _ i -
-ж — Ky, -^ — kx.
Мы должны, следовательно, иметь:
л + 2 л+2
]? «у (?,/i*i + • • • + fy, «+2^+2) = — А ]? ?,-?,,
л+2 . я+2
2 *> (9лг1 + • • • +4], n+2Zn+2) = A 2 «;*/•
7=1 У=1
Приравнивая в обеих частях этих равенств коэффициенты при zk,
мы получим для определения uj и bj систему 2л -|- 4 линейных одно-
однородных уравнений:
C5.4)
+ • • • + 7п+2, А+2 — Aflft = 0
(А=1, 2 л+2).
Эту систему легко привести к системе из я—(— 2 уравнений, если
ввести вместо неизвестных а^ и ^ комплексный неизвестные сj=aj-\~ib;-.
Действительно, умножая уравнения второй группы системы C5.4)
на I и складывая с соответствующими уравнениями первой группы,
получим однородную систему из л -\- 2 уравнений
<71Л + <72*С2+ ••• +<7я+2,Л+2 — Мс* = 0 (А = 1. 2, ..., л+2).
Определитель этой системы, равный D (Лг), обращается в нуль, так
как уравнение C5.2) имеет, по условию, корень XL Следовательно,
эта система допускает нетривиальное решение для Cj. Выделяя в нем
вещественные и мнимые части, мы получим решение системы C5.4).
Приняв найденные таким образом переменные х и у вместо двух
каких-нибудь переменных Zj и обозначив остальные переменные Zj
через Xj, мы приведем систему C5.3) к виду
-&- = Ра*\+ +Px + Px + 4y i.s^\, 2 я),
120
ИССЛЕДОВАНИЕ КРИТИЧЕСКИХ СЛУЧАЕВ
[ГЛ. IV
где psj, ps, qs — некоторые постоянные. Если указанную подстановку
сделать в уравнениях C5.1), то они примут вид
их
Я + ^( У. *i хп).
l хп),
Psnxa-\r
(s=l, 2 n),
- У- x\ xa)
где X, Y, Xs — функции такого же вида, как и Zj.
Полученный вид дифференциальных уравнений возмущенного дви-
движения будет исходным для дальнейшего исследования.
Так как характеристическое уравнение любой линейной системы
не изменяется при линейном преобразовании, то характеристическое
уравнение линейной части системы C5.5) должно совпадать с характе-
характеристическим уравнением C5.2). Но характеристическое уравнение
линейной части системы C5.5) распадается на уравнение р2 —|— Я,2 = 0,
Дающее корни ± М, и уравнение
Ри — 9 Р\ч
Pi\ P22
Pin
Pin
= 0.
C5.6)
Рп\ РпЧ ••• Рпп—9
Следовательно, все корни уравнения C5.6) имеют отрицательные
вещественные части.
§ 36. Системы второго порядка. Первый способ решения задачи.
Прежде чем исследовать общий случай, рассмотрим подробно
частный случай, когда п = 0 и когда, следовательно,* дифференциаль-
дифференциальные уравнения возмущенного движения образуют систему второго
порядка вида
у), ±jL =
у),
C6.1)
где X и Y начинаются членами не ниже второго порядка.
В рассматриваемом случае можно не только исследовать характер
невозмущенного движения, но и дать общую картину поведения
интегральных кривых уравнений C6.1) в окрестности начала коор-
координат х).
') Вид интегральных кривых, определяемых уравнениями C6.1), изучил
впервые Пуанкаре. (См. Пуанкаре А., О кривых, определяемых диффе-
дифференциальными уравнениями, Гостехиздат, 1947).
§ 36] СИСТЕМЫ ВТОРОГО ПОРЯДКА. ПЕРВЫЙ СПОСОБ РЕШЕНИЯ 121
С этой целью введем в рассмотрение полярные координаты г и ft
при помощи подстановки
х = г cos ft, у = r sin ft. C6.2)
Уравнения C6.1) примут при этом вид
— = X (г cos ft, г sin ft) cos ft -f- Y (r cos ft, r sin ft) sin ft =
= rR (r, ft),
rift 1
-j7 = Я -I {К (r cos ft, r sin ft) cos ft —
(г, ft).
C6.3)
где R(r, ft), 0(r, ft)— функции переменных гид, разлагающиеся
в ряды по степеням г, сходящиеся при г, достаточно малом, и обра-
обращающиеся в нуль при г = 0. Коэффициенты этих разложений являются
периодическими функциями д периода 2я, причем каждый из них
является простым полиномом относительно cosd и sind и- может
быть поэтому представлен конечной суммой синусов и косинусов
целых кратностей ¦&.
Для получения уравнения интегральных кривых исключим из C6.3)
время t. Будем иметь:
ш=ттв" ==г2/?2 (д)+г3/?3 т + • • • C6-4)
Ряд, стоящий в правой части уравнения C6.4), сходится при г до-
достаточно малом, причем коэффициенты /?2(^)' ^з(^)' ••• также
представляют собой полиномы относительно cosd и sin д.
Уравнение C6.4) имеет тривиальное решение г = 0. Следова-
Следовательно, одной из интегральных кривых является начало координат.
Так как правая часть уравнения C6.4) аналитична в окрестности
начала координат, то через каждую точку этой окрестности на осно-
основании теоремы существования решений дифференциальных уравнений
проходит одна и только одна интегральная кривая. Отсюда следует,
что ни одна интегральная кривая, выходящая из какой-нибудь точки
окрестности начала координат, не пересекает этой точки.
Из аналитичности правой части уравнения C6.4) вытекает также,
что любое решение г = г (¦&, с) этого уравнения, определяемое на-
начальным условием
г@, с) = с, C6.5)
может быть разложено в ряд по степеням с.
г(«, с) = гхф)с + г2(Ъ)с*+ ..., C6.6)
сходящийся, если с достаточно мало. Радиус сходимости этого ряда
зависит от интервала изменения д. Но как бы велик ни был этот
122 ИССЛЕДОВАНИЕ КРИТИЧЕСКИХ СЛУЧАЕВ [ГЛ. IV
интервал, для него всегда найдется такое достаточно малае число у,
что ряд C6.6) будет сходиться при всех |с|-<!у- Мы будем пред-
предполагать число y настолько малым, чтобы ряд C6.6) сходился при
|*|<2
Для вычисления коэффициентов г{ подставим ряд C6.6) в обе
части уравнения C6.4) и приравняем коэффициенты при одинаковых
степенях с. Пусть Ft обозначает коэффициент при с1 в разложении
по степеням с правой части уравнения C6.4) после подстановки
в нее C6.6), так что имеем тождественно:
.. C6.7)
Функции Ft представляют собой, очевидно, полиномы от г2,
г3 гг_1 с коэффициентами, зависящими от R2, R3, .... Rt и
являющимися, следовательно, периодическими функциями Ь периода 2л
(полиномами относительно cosd и sind). В частности, имеем:
F — R г2 F — R r3-i-2R r r
' j — ^2 Г 3 — А3 1 * ^п2 12'
Уравнения, определяющие функции rt, имеют вид
C6.8)
dri О dr2 _i_ п Г2 р *i_p,2
¦^-=Fi (/ = 4, 5, ...).
Кроме того, из C6.5) имеем начальные условии
г,@) = 1. г2@) = г8@) ==...= 0. C6.9)
Следовательно,
0
C6.10)
Таким образом, все функции rt (¦&) последовательно определяются
простыми квадратурами. Для функции г2(Ф) мы имеем квадратуру
периодической функции. Отметим здесь одно общее свойство такого
рода квадратур, которым мы часто будем пользоваться в дальнейшем.
Пусть / (ft) — произвольная непрерывная периодическая функция
какого-нибудь периода ю. Тогда
(fi)r C6.11)
§ 36] СИСТЕМЫ ВТОРОГО ПОРЯДКА. ПЕРВЫЙ СПОСОБ РЕШЕНИЯ 123
где ф (#) — периодическая функция того же периода, a g — постоян-
постоянная, определяемая формулой
со
ь- C6Л2>
Эта формула совершенно очевидна, если /(¦&) разлагается в ряд
Фурье
где g определяется формулой C6.12).
Действительно, в этом случае мы имеем:
В„ Inn
^cos
Отсюда непосредственно вытекает справедливость C6.11) для рас-
рассматриваемого случая. Но и в общем случае эта формула выводится
без всякого труда, на чем мы не будем останавливаться.
Установив это, рассмотрим коэффициент г2. Так как функция, R2
периодическая, то г2 будет либо иметь вид C6.11), либо будет
периодической, если соответствующий коэффициент g обращается
в нуль. Во втором случае функция Rb-\-2R2r2 будет периодической,
и поэтому коэффициент г3 либо будет иметь вид C6.11), либо по-
получится периодическим. Продолжая таким образом дальше, мы видим,
что могут представиться два случая: либо все коэффициенты гг,
как бы велик ни был индекс г, являются периодическими функциями
периода 2л, либо среди этих коэффициентов имеются непериодиче-
непериодические. При этом, если гт является первым непериодическим коэффи-
коэффициентом, то
\ mdu. C6.13)
где ф (§) — периодическая функция периода 2л.
Допустим сначала, что все функции гj являются периодическими.
В этом случае решение C6.6) будет периодическим при всех зна-
значениях с (лежащих в области сходимости ряда). Следовательно,
г Bл, с) — г @, с), и все интегральные кривые, расположенные в до-
достаточно малой окрестности начала координат, замкнуты и окружают
эту точку (рис. 8). Следуя Пуанкаре, начало координат называют
в этом случае центром.
124 ИССЛЕДОВАНИЕ КРИТИЧЕСКИХ СЛУЧАЕВ [ГЛ. IV
Допустим теперь, что не все коэффициенты rt получаются перио-
периодическими. Пусть гт — первый непериодический коэффициент в ряду
г2, г3, .... так что для него справедлива формула C6.13), где
Рис. 8.
а все коэффициенты г2> г3, ..., гт_1 периодичны. Преобразуем урав-
уравнение C6.4) при помощи подстановки
г — (
На основании C6.7) будем иметь:
Р /1
или, принимая во внимание C6.8),
Отсюда находим:
C6.15)
где Rm+n — периодические функции Ф периода 2зт (так как коэффи-
коэффициенты преобразования C6.14) периодичны).
Из полученного уравнения вытекает, что в достаточно малой
do
окрестности начала координат производная -^ сохраняет постоянный
знак, совпадающий со знаком g. Если g < 0, то при Ф —> -f-oo функ-
функция р(д) непрерывно убывает и стремится к нулю. По характеру
§ 36]
СИСТЕМЫ ВТОРОГО ПОРЯДКА. ПЕРВЫЙ СПОСОБ РЕШЕНИЯ
125
подстановки C6.14) то же самое будет иметь место и для радиуса-
вектора г. Следовательно, все интегральные кривые, расположенные
в достаточно малой окрестности начала координат, будут спиралями,
делающими вокруг начала координат бесчисленное множество обо-
оборотов, асимптотически приближаясь к этой точке наподобие лога-
логарифмических спиралей (рис. 9). По терминологии Пуанкаре начало
координат в этом случае называется
фокусом.
То же самое будет, очевидно, иметь
место и при g > 0. Только в этом
случае спирали будут приближаться
к началу координат не при ф->-|-оо,
а при ¦&-> — со.
Обращаемся теперь к вопросу ус-
устойчивости. Очевидно, что в случае
центра невозмущенное движение устой-
устойчиво, так как г, а вместе с ним х и у
будут оставаться сколь угодно малыми,
если они были достаточно малы в на-
начальный момент времени. Устойчивость
при этом не будет асимптотической.
Рассмотрим теперь случай фокуса.
Второе уравнение C6.3) показывает, что
в достаточно малой окрестности начала
координат, когда величина 0 (обращаю-
(обращающаяся в нуль при г — 0) меньше по мо-
dft
дулю величины X, производная —гг будет больше некоторого поло-
положительного числа. Следовательно, с возрастанием t величина Ь будет
также возрастать, причем при ?->оо она будет возрастать неогра-
неограниченно, если только при этом интегральная кривая остается в доста-
достаточно малой окрестности начала координат. Последнее будет как раз
иметь место при g < 0. В этом случае при возрастании 4 интеграль-
интегральные кривые приближаются к началу координат, стремясь к нему
асимптотически при Ф = -j- oo. Следовательно, при g < 0 невозму-
невозмущенное движение асимптотически устойчиво.
При g > 0 интегральные кривые при возрастании •&, а следова-
следовательно, и t, удаляются от начала координат. Любая интегральная
кривая покидает некоторую фиксированную не зависящую от началь-
начальных условий окрестность начала координат, как бы близка от него
ни была точка, из которой она в начальный момент выходит. Мы
имеем, очевидно, полную неустойчивость.
Итак, в случае центра невозмущенное движение устойчиво, но не
асимптотически. В случае фокуса невозмущенное движение асимпто-
асимптотически устойчиво при g < 0 и неустойчиво при g > 0.
Рис. 9.
126 ИССЛЕДОВАНИЕ КРИТИЧЕСКИХ СЛУЧАЕВ [ГЛ. IV
Таким образом, для решения задачи устойчивости в интересую-
интересующем нас случае мы можем поступать следующим образом:
1) Преобразованием C6.2) и исключением t приводим уравнения
возмущенного движения C6.1) к одному уравнению C6.4).
2) Этому уравнению пытаемся удовлетворить рядом
где г2@) = г3@)= ... =0. Подставляя этот ряд в C6.4) и срав-
сравнивая коэффициенты при одинаковых степенях с, мы получим урав-
уравнения, определяющие последовательно все функции rt (Ф) при помощи
квадратур. При этом может оказаться, что либо все коэффициенты г{
являются периодическими, либо среди них имеются непериодические.
В первом случае невозмуц;енное движение будет устойчивым, но
не асимптотически.
Во втором случае первый непериодический коэффициент в ряду
г2, г3 пусть это будет гт, будет необходимо иметь вид C6.13).
Тогда, если g > 0, то невозмущенное движение неустойчиво, а если
g < 0, то оно устойчиво и притом асимптотически.
Определение коэффициентов г1 приводится, как мы видели,
к вычислению квадратур. Последняя задача не представляет никаких
трудностей, так как подинтегральные выражения всегда представляют
собой полиномы относительно cos ft и sin б-. И если мы имеем дело
с тем случаем, когда среди коэффициентов гг имеются непериоди-
непериодические, то мы всегда конечным числом простых действий придем
к решению задачи устойчивости. Правда, вычисления могут оказаться
очень громоздкими, если первый непериодический коэффициент гт
имеет слишком большой индекс. Однако практически такие случаи
встречаются весьма редко.
Гораздо сложнее обстоит дело в случае, когда все коэффициенты rt
оказываются периодическими, т. е. когда начало координат является
центром. В этом случае мы имеем бесчисленное множество условий,
и мы не можем непосредственной проверкой убедиться в их выпол-
выполнимости. Поэтому усилия исследователей были направлены к устано-
установлению некоторых общих признаков, которые позволяли бы, не при-
прибегая к вычислению коэффициентов rf, а непосредственно по виду
уравнений C6.1) судить о том, имеем ли мы дело с центром или
фокусом. В этом направлении достигнуты некоторые успехи. Так,
например, задача полностью разрешена для того случая, когда урав-
уравнения C6.1) не имеют членов выше второго порядка. Однако пол-
полного решения задачи до сих пор не получено. Мы не имеем, однако,
возможности останавливаться подробнее на этом вопросех). Отме-
') Отсылаем интересующихся к книге: Немыцкий В. В. и Степа-
Степанов В. В., Качественная теория дифференциальных уравнений (изд. 2-е, Гос-
техиздат, 1949), в которой дана и библиография вопроса. См. также приме-
примечание в конце книги (стр. 521).
§ 36] СИСТЕМЫ ВТОРОГО ПОРЯДКА. ПЕРВЫЙ СПОСОБ РЕШЕНИЯ 127
тим здесь, однако, одно общее положение, имеющее важное зна-
значение.
Система первого приближения для уравнений C6.1) всегда имеет
первый интеграл вида х2 -\- у2 = const. Может случиться, что си-
система C6.1) с учетом нелинейных членов также имеет первый инте-
интеграл вида
F(x, y) = x2 + y2-\-f(x, у) = const., C6.16)
где / (х, у) — аналитическая в окрестности начала координат функ-
функция от л; и у, разложение которой по степеням этих переменных
начинается членами не ниже третьего порядка. В этом случае начало
координат будет центром. Действительно, интеграл C6.16) пред-
представляет уравнение интегральных кривых в окрестности начала коор-
координат, которые все будут замкнуты, так как функция F(x, у) знако-
определенна.
Ляпунов доказал, что справедливо также обратное предложение:
если начало координат для уравнений C6.1) является центром, то
эти уравнения имеют первый интеграл вида C6.16).
Отметим также.одно важное различие, которое получается в харак-
характере задачи в зависимости от того, имеем ли мы дело с фокусом
или центром.
В выражение функции Ft (fr), определяющей коэффициент rt и
зависящей, как мы видели, от г2, ..., r,-_i> Rlt ..., Rit'входят лишь
те члены правой части уравнения C6.4), которые имеют порядок,
не превышающий /, а эти члены в свою очередь, как это видно из
C6.3), зависят лишь от тех членов уравнений C6.1), которые также
имеют порядок, не превышающий I. Поэтому если гт является пер-
первым непериодическим коэффициентом в ряду г2, г3 то он оста-
останется первым непериодическим коэффициентом, как бы мы ни изме-
изменяли члены выше т-го порядка в уравнениях C6.1). Следовательно,
коэффициент g, знак которого определяет устойчивость или не-
неустойчивость, также не зависит от членов выше т-го порядка в уравне-
уравнениях C6.1). Другими словами, в случае фокуса устойчивость или
неустойчивость определяется конечным числом членов в уравнениях
возмущенного движения. Члены достаточно высокого порядка ника-
никакого значения для задачи не имеют.
Иначе обстоит дело в случае центра. В этом случае, как бы
велико ни было число N, мы можем, очевидно, члены Л/-го порядка
в уравнениях C6.1) изменить таким образом, чтобы функция rN
вышла непериодической и чтобы соответствующий коэффициент g
был по желанию положительным или отрицательным. Следовательно,
в случае центра членами сколь угодно высоких порядков в уравне-
уравнениях возмущенного движения можно распорядиться таким образом,
чтобы получить по желанию как асимптотическую устойчивость,
так и неустойчивость.
128 ИССЛЕДОВАНИЕ КРИТИЧЕСКИХ СЛУЧАЕВ [ГЛ. IV
Из этого следует, что если нам при исследовании уравнений
вида C6.1) удалось каким-нибудь путем убедиться, что изменением
членов сколь угодно высоких порядков можно добиться, чтобы
невозмущенное движение было по желанию асимптотически устойчивым
или неустойчивым, то начало координат является обязательно центром.
Когда начало координат является центром, то ряд C6.6) для г,
представляющий общее решение уравнений C6.1), будет периоди-
периодическим периода 2л. Подставляя это выражение для г в C6.2), мы
получим решение уравнений C6.1), которое также будет периоди-
периодическим по отношению к вспомогательному переменному ф с перио-
периодом 2л. Покажем, что если мы снова перейдем к переменной t и
выразим через нее х и у, то полученные таким путем функции вре-
времени будут тоже периодическими, но период будет зависеть, и при-
притом аналитически, от с.
С этой целью обращаемся ко второму уравнению C6.3), опре-
определяющему Ф как функцию t. Подставляя в него выражение C6.6)
для г, получим:
где 8; ("&) — некоторые периодические функции ft. Полагая, что
и t одновременно обращаются в нуль, получим:
= Л , „Л = /*A+е1(в)с+е2<Ф)с2+¦••)<«>. C6.17)
7 1+9ic+ ¦•• i
, „Л
о 1+9ic+ i
где 8j (б-) — также периодические функции Ь.
Из C6.17) получаем:
—M(d)= J
или, учитывая периодичность функций 8
2с2
C6.18)
где Т — постоянная, определяемая формулой
^Ф)*». C6.19)
Соотношение C6.18) показывает, что при изменении t на постоян-
постоянную величину Т величина Ф изменяется на 2л и, следовательно,
величины л; и у не изменяются. Следовательно, х и у являются
периодическими функциями времени с периодом Т, зависящим ана-
аналитически от с.
§ 36] СИСТЕМЫ ВТОРОГО ПОРЯДКА. ПЕРВЫЙ СПОСОБ РЕШЕНИЯ 129
Полученное таким путем периодическое решение уравнений C6,1)
будет содержать произвольную постоянную с. Эта произвольная
постоянная является, по условию, начальным значением величины г.
Но так как отсчет полярного угла ft выбран таким образом, что он
обращается в нуль при ? —0, то из C6.2) вытекает, что с является
вместе с тем начальным значением величины х. Начальное значение
величины у равно при этом нулю. Таким образом, полученное перио-
периодическое решение уравнений C6.1) характеризуется начальными
условиями
х @) = с, у @) = 0, C6.20)
где произвольная постоянная с подчинена единственному условию,
что она численно достаточно мала.
Полученное периодическое решение, содержащее только одну про-
произвольную постоянную, является частным решением уравнений C6.1).
Но учитывая, что эти уравнения не зависят явно от t, мы можем
получить их общее решение, зависящее от двух произвольных
постоянных, если в указанном периодическом решении мы заме-
заменим t на t-\-h, где h — произвольная постоянная.
Практический способ вычисления вышеуказанного периодического
решения (когда оно существует, т. е. в случае центра) будет ука-
указан в § 38. Сейчас мы рассмотрим примеры решения задачи устой-
устойчивости для уравнений типа C6.1).
Пример 1. Уравнение возмущенного движения имеет вид
) , C6.21)
где a, p, Y — постоянные.
Записав это уравнение в виде системы
~ = -у. ^L = x-№-yxy* + ay\ C6.22)
положим:
х = г cos ft, у — г sin ¦&.
Уравнения C6.22) примут вид
^~ = _ pr2 cos2 ft sin * + (a sin4 ft — y cos ft sin3 ft) r\
i^L = 1 _ p cos3 ft ¦ r + (a sin3 ft cos ft — y cos2 ft sin2 ft) r2.
Исключая t, будем иметь:
% = — p cos2 ft sin ft-r2+(a sin4 ft—Ycosftsln3ft—p2cos5ftsinft)r3-(-...
Этому уравнению стараемся удовлетворить рядом
г = с -f г2с2 -4- г3с3 + . •.
130 ИССЛЕДОВАНИЕ КРИТИЧЕСКИХ СЛУЧАЕВ [ГЛ. IV
при условии г2@) = г3@) = ... =0. Приравнивая коэффициенты
при одинаковых степенях с, получим:
_^2. = _р Cos2 ft sin ft,
-^A = a sin4 ft — (y cos ft sin2 ft + p2 cos5 ft + 2p cos2 ft • r2} sin ft,
откуда
cos3d
—J
о о
Функция г2 вышла периодической. Функция же г3 имеет, очевидно.
вид
где / (ft) — периодическая функция, а g определяется формулой
2л
Следовательно, при a > 0 невозмущенное движение неустойчиво,
а при a < 0 оно устойчиво асимптотически.
Пример 2. Уравнение C6.21) является частным случаем более
общего уравнения
Ы
\2-\
исследованного А. М. Ляпуновым. Здесь п — целое положительное
число, a F — аналитическая функция своих аргументов, не содер-
содержащая членов ниже второго порядка относительно х и -—.
Полагая
х = г cos ft, y== ^- = г sin ft,
олучим:
¦%- = a sin2n+2 ft • r2n+1 — F (r cos ft, r2 sin2 ft) sin ft,
-^-=l-H-asin2"+1ftcosft-r!'1 — i-F(rcosft, r2sin2ft)cosft.
§ 36] СИСТЕМЫ ВТОРОГО ПОРЯДКА. ПЕРВЫЙ СПОСОБ РЕШЕНИЯ 131
Допустим сначала, что а = 0. Тогда, исключая t, получим:
dr F (r cos ft, г2 sin2») . „
*а 1 — Sill tX
1 F (r cos #, г2 sin2 ft) cos ft
= /2(ft)sinft-r2 + /3(ft)sinft-r34- .... C6.23)
где fi (ft) являются, очевидно, полиномами относительно только cos ft.
Ищем решение уравнения C6.23) в виде ряда
при условии г2 @) = г3 @) = . . . = 0. Для коэффициентов rt (ft) полу-
получаем уравнения
-g- = /2 (ft) sin ft, 4J- = I/s (О) + 2/2 (*) r2 (ft)] sin ft
и вообще
(/ = 3, 4, ...), C6.24)
где /^^ft) — полиномы относительно r2, r3, .... rl_v коэффициенты
которых являются полиномами относительно только cos ft.
Функция г2 получается, очевидно, периодической и притом по-
полиномом относительно cos ft. Но тогда такой же будет и функция г3
и все остальные функции rt, в чем убеждаемся методом индукции.
Действительно, если все функции r2, r3 rt_x вышли полиномами
относительно cos ft, то такой же получится и функция Ft (ft), а сле-
следовательно, и функция гI-
Таким образом, при о = 0 мы имеем дело с центром, и невозму-
невозмущенное движение будет устойчиво, но не асимптотически.
Допустим теперь, что а Ф 0. Тогда будем, очевидно, иметь:
где /2(ft), /3(ft) /2л+1 (ft) —те же функции, что и в C6.23). Для
коэффициентов г, получаем теперь
~^ = ^„+1 (*) sin <> + a sin 2»+2 ft,
где F2, F3, .... Fn — те же функции, что и в C6.24). Следова-
Следовательно, коэффициенты rv .... г2п получаются периодическими, а дл«
132 ИССЛЕДОВАНИЕ КРИТИЧЕСКИХ СЛУЧАЕВ [ГЛ. IV
коэффициента г2п+1 будем иметь:
2Л
гщ+i = *Ф + ф (О), g = ? J sin2«+2 d dO.
о
где (рС&) — периодическая функция.
Следовательно, при а < 0 невозмущенное движение асимптоти-
асимптотически устойчиво, а при а > 0 оно неустойчиво.
§ 37. Системы второго порядка. Второй способ
решения задачи.
Изложим второй способ решения задачи устойчивости в инте-
интересующем нас случае, предложенный А. М. Ляпуновым. Этот способ
основан на непосредственном построении для системы C6.1) функ-
функции Ляпунова.
Рассмотрим сначала следующую задачу. Пусть ит(х, у)— задан-
заданная форма m-го порядка переменных х и у. Будем искать другую
форму vm(x, у) того же порядка, производная которой по времени,
составленная в силу линейной части системы C6.1), т. е. уравнений
равнялась бы форме ит. Другими словами, найдем форму vm, удо-
удовлетворяющую уравнению
Задача эта является частным случаем задачи, рассмотренной нами
в общем виде в § 20. Согласно полученным там результатам, посту-
поступаем следующим образом.
Полагая
и приравнивая в C7.2) коэффициенты при подобных членах, мы
получим систему линейных уравнений
Aaai-\-Al^ii-\-...-\-Altm+lam+l=bt (/=1, 2, .... /и+1), C7.3)
определяющих коэффициенты uj. Здесь Л/;- — некоторые постоянные,
которые нам нет необходимости выписывать.
Система C7.3) будет иметь решение и притом единственное, если
определитель этой системы будет отличен от нуля, или, что то же
§ 37]
СИСТЕМЫ ВТОРОГО ПОРЯДКА. ВТОРОЙ СПОСОБ РЕШЕНИЯ
133
самое, если уравнение
Dm (р) =
^i —P
М2
— Р
\, т + 1
2, т + 1
лт+1,2
А
т+1, т+1'
C7.4)
не будет иметь нулевого корня.
Но на основании теоремы 1 § 20 все корни уравнения C7.4)
определяются формулой
р = (mj _ т2) а, C7.5)
где /га, и т2 — любые целые неотрицательные числа (в частности,
нули), связанные соотношением
/и, —\- гп2 == /га.
C7.6)
Если т — число нечетное, то не существует никакой комбинации
для чисел т1 и т2, связанных соотношением C7.6), при которой
величина C7.5) обращалась бы в нуль. Следовательно, при /га не-
нечетном определитель системы C7.3) отличен от нуля, эта система
имеет единственное решение, которое определяет одну и только
одну форму vm, удовлетворяющую уравнению C7.2).
Допустим теперь, что т — число четное. В этом случае мы можем
удовлетворить соотношению C7.6), полагая ml= m2 — ^-. При такой
комбинации, и очевидно, только при такой, выражение C7.5) обра-
обращается в нуль. Следовательно, уравнение C7.4) имеет один и только
один нулевой корень, и определитель системы C7.3) обращается
в нуль. Однако хотя бы один из миноров m-порядка этого опре-
определителя отличен от нуля. Действительно, если бы все указанные
миноры равнялись нулю, то нулевой корень уравнения C7.4) был бы,
по крайней мере, двукратным, так как он обращал бы в нуль
dDm{X)
dX
не только Dm(X), но и
Так как определитель системы C7.3) обращается в нуль, то эта
система, вообще говоря, неразрешима. В этом случае, левые части
уравнений C7.3) связаны между собой линейным соотношением, т. е.
существует такая система чисел Mt,
М
т+1'
из которых хотя бы
одно отлично от нуля, что, умножая соответственно левые части C7.3)
на эти числа и складывая их, мы получим тождественно нуль. Для
того чтобы система C7.3) была разрешима, необходимо, чтобы и ее
правые части были связаны тем же самым линейным соотношением,
т. е. чтобы выполнялось тождество
+мя+1ья+1 =
C7.7)
134 ИССЛЕДОВАНИЕ КРИТИЧЕСКИХ СЛУЧАЕВ [ГЛ. IV
Этого условия будет также и достаточно для разрешимости си-
системы C7.3), так как не все миноры т-ro порядка определителя
Dm@) равны нулю, и поэтому левые части этой системы связаны
только одним линейным соотношением.
Таким образом, при т четном существует тогда и только тогда
форма vm, удовлетворяющая уравнению C7.2), когда коэффициенты
формы ит связаны соотношением C7.7).
В связи с этим при т четном изменим несколько постановку
задачи, а именно: будем искать форму vm таким образом, чтобы
удовлетворялось не уравнение C7.2), а уравнение
т
У, C7.8)
где О — некоторая постоянная, которая должна быть подобрана
таким образом, чтобы это уравнение имело решение.
Система C7.3) перейдет теперь в систему
где kv k2 km+\ — коэффициенты формы
а условие ее разрешимости примет вид
m+l m + 1
2 Mtbt -f- О 2 ktMt = 0. C7.9)
Это уравнение однозначно определяет постоянную О. Для дей-
действительного ее вычисления нет необходимости составлять уравне-
уравнение C7.9). Гораздо проще непосредственно исходить из уравне-
уравнения C7.8). Для этого допустим, что постоянная О и форма vm уже
вычислены. Подставляя их в C7.8), получим тождество, которое,
следовательно, должно удовлетворяться при любых х и у. В част-
частности, оно должно удовлетворяться, если мы положим х = cos ft,
y = sin$. Сделаем действительно в C7.8) указанную замену, по-
помножим полученное тождество на d$ и проинтегрируем в пределах
от 0 до 2л. Тогда, принимая во внимание, что
dvm (cos ft, sin ft) _ ) dvm (x, y) . dvm (x, y) )
_ )
\
дх ' ду
и, следовательно,
2л
/<¦
§ 37] СИСТЕМЫ ВТОРОГО ПОРЯДКА. ВТОРОЙ СПОСОБ РЕШЕНИЯ 135
будем иметь:
2Я
2лО + fttm(cosft, sinft)tf6- = 0. C7.10)
Мы получили таким образом соотношение между постоянной О
и коэффициентами формы ат> которое должно необходимо выпол-
выполняться, если уравнение C7.8) имеет решение, а так как по доказан-
доказанному таких соотношений может быть только одно, то оно необхо-
необходимо совпадает с C7.9).
Формула C7.10) дает возможность сразу определить постоянную О.
Установив это, переходим к нашей задаче. Запишем уравнения
возмущенного движения C6.1) в виде
C7Л1>
где Xk, Yk — совокупности членов k -го порядка в функциях X и Y,
и попытаемся подобрать для них функцию Ляпунова, удовлетворяю-
удовлетворяющую теоремам Б или В, вида
... C7.12)
где fk (x, у) — некоторые формы &-го порядка.
Для этого необходимо формы /3, /4, ... подобрать таким обра-
образом, чтобы производная от V в силу уравнений C7.11) была знако-
определенной.
Для этой производной имеем:
К2+у'з+ •••)- C7ЛЗ>
Полученное выражение начинается членами третьего порядка.
Совокупность этих членов имеет вид
Уй=к(х?±-.уЩ + 2хХ2 + 2yY2. C7.14)
Для членов четвертого порядка имеем:
и вообще совокупность членов т-то порядка в выражении C7.13)
представляется выражением
. У).
136 ИССЛЕДОВАНИЕ КРИТИЧЕСКИХ СЛУЧАЕВ [ГЛ. IV
где Fm(x, у)— форма m-го порядка, зависящая от форм /3, /4, ....
fm-v Эта форма, следовательно, будет известной, если формы /3,
/4, .... /m_i из каких-нибудь условий определены.
Для того чтобы производная —тт- была функцией знакоопределен-
ной, необходимо прежде всего, чтобы она начиналась членами четного
порядка. Поэтому необходимо форму /3 выбрать так, чтобы члены
третьего порядка C7.14) обратились в нуль, т. е. чтобы выполнялось
уравнение
Как было показано выше, такая форма /3 всегда существует и
будет единственной. Выбрав таким образом форму /3, подберем
теперь /4 так, чтобы совокупность членов четвертого порядка в вы-
dV
ражении —гг была формой знакоопределенной, а именно, приравняем
эту совокупность членов форме О4 (х2 -)- у2J. Таким путем для опре-
определения формы /4 получаем уравнение
Так как сейчас речь идет о форме четного порядка, удовлетво-
удовлетворяющей уравнению типа C7.8), то, как было показано выше, для
того чтобы эта форма существовала, необходимо, чтобы О4 была
определенной величиной, а именно, на основании C7.10)
2л
G4 = ~ | /\,(cosd, sinfl)tfd.
о
Допустим, что полученная таким путем величина О4 отлична
от нуля. Тогда производная от функции
имеющая вид
—^- = О4 (х2 -f- у2J -f- члены более высоких порядков,
будет знакоопределенной, знак которой совпадает со знаком О4.
Сама же функция V будет определенно-положительной. Поэтому на
основании теорем Б и В невозмущенное движение будет неустойчиво
при О4 > 0 и асимптотически устойчиво при О4 < 0.
Может, однако, случиться, что величина О4 равна нулю. В этом
случае разложение функции C7.13) начнется членами пятого порядка,
и чтобы эта функция была знакоопределенной, необходимо эти члены
обратить в нуль, а для этого необходимо форму /5 выбрать согласно
§ 37] СИСТЕМЫ ВТОРОГО ПОРЯДКА. ВТОРОЙ СПОСОБ РЕШЕНИЯ 137
уравнению V5 = 0, которое имеет вид C7.2), и так как речь идет
о форме нечетного порядка, то это уравнение однозначно ее опре-
определяет.
Выбрав таким путем /5, ищем /6 из условия, что члены шестого
dV
порядка в выражении —тг обращаются в знакоопределенную форму
О6 (х2 -f- у2K. Таким путем получаем для /6 уравнение
а для О6 величину
2Я
О6 = -L
о
Если О6 =И= 0, то производная от C7.12) будет начинаться чле-
членами О6 (х2 -)- у2K и будет, следовательно, функцией знакоопределен-
ной. Невозмущенное движение будет при этом неустойчиво при О6 > О
и асимптотически устойчиво при О6 < 0.
Если G6 = 0, то необходимо произвести дальнейшие определения
форм fk. Поступая подобно предыдущему, т. е. приравнивая в C7.13)
члены нечетного порядка нулю, а члены четного порядка выражению
Gm (x2 -\- у2) 2 и определяя Gm по формуле
2Я
Fm(cosft, sinft)dft, C7.15)
J
мы можем встретиться с одним из двух возможных случаев: либо
все коэффициенты Gm, как бы велик ни был индекс т, равны нулю,
либо в конце концов мы придем к такому т, что Gm ф 0.
Если мы имеем дело со вторым случаем, то задача устойчивости
решается знаком От, а именно: при От > 0 невозмущенное движение
неустойчиво, а при Gm < 0 оно устойчиво и притом асимптотически.
Допустим теперь, что все коэффициенты От равны нулю. Конечно,
убедиться в этом непосредственным вычислением этих коэффициентов
не представляется возможным, но если каким-нибудь путем нам уда-
удалось установить этот факт, то задача устойчивости разрешается
просто. Действительно, нетрудно убедиться, что в рассматриваемом
случае начало координат является центром. В самом деле, если все
коэффициенты Gm равны нулю, то как бы велико ни было число 2га,
члены Bй—1)-го порядка в уравнениях C7.11) можно изменить
таким образом, чтобы величина О2л получилась отличной от нуля
и имела наперед заданный знак. Это непосредственно вытекает из того
обстоятельства, что в выражение F2n (x, у), определяющее согласно
138 ИССЛЕДОВАНИЕ КРИТИЧЕСКИХ СЛУЧАЕВ [ГЛ. IV
C7.15) О2п, входят члены 2xX2n_l-\-2yY2n_v и подбором Х2п_:
и К2л_! мы можем, очевидно, сделать величину О2п какой угодно.
Следовательно, изменением членов сколь угодно высокого порядка
в уравнениях C7.11) можно добиться, чтобы невозмущенное движе-
движение было по желанию устойчивым или неустойчивым, а это, как было
показано в предыдущем параграфе, является признаком центра.
Итак, если все коэффициенты От равны нулю, то начало коор-
координат является центром и, следовательно, невозмущенное движение
устойчиво, но не асимптотически. При этом общее решение уравне-
уравнений C7.11) является периодическим с периодом, зависящим от на-
начальных условий.
При практическом применении метода можно коэффициенты От
определять либо по формуле C7.15), либо непосредственно применяя
метод, которым эта формула выведена. Для этого, определив в вы-
dV -
ражении —п- члены w-го порядка, приравниваем их Gm(x2-j-y2J,
полагаем в полученном уравнении л; = cos ft, y = sind и интегрируем
в пределах от 0 до 2л. При этом форма fm исключится, и мы можем
сразу не принимать ее в расчет при определении членов m-го по-
dV
рядка в -sr.
Примечание. Пусть G2N — первая из величин Gm(m — 2, 4,
6, ...), которая отлична от нуля. Как мы только что видели,
наивысший порядок членов разложений функций X и Y, определяю-
определяющих эту величину и решающих, таким образом, задачу устойчивости,
есть 2/V—1. Следовательно, наивысший порядок членов, решающих
задачу устойчивости, когда она решается конечным числом членов,
всегда нечетный.
Пример. Рассмотрим систему
dx dy „о
~dt==~y- ~Ш = Х~рх
исследованную в предыдущем параграфе.
Полагая
dV
подберем форму /3 так, чтобы в выражении —гг исчезли члены
третьего порядка. Получим уравнение
з
Делая в нем
/3 = ахх^-\- а2х2у -\- а3ху2-\- а4у3
и приравнивая коэффициенты при подобных членах, получим уравнения
а2 = 0, 2а3 —3ax —2р = 0, За4 — 2а2 — 0, аа=0
§ 38] СИСТЕМЫ ВТбРОГО ПОРЯДКА. ТРЕТИЙ СПОСОБ РЕШЕНИЯ 139
и, следовательно,
Приравнивая члены четвертого порядка выражению О4(лг2
получим для определения /4 уравнение
Чу% °4 (*2 + У2J- C7-16)
Прежде всего определяем постоянную О4. Если она окажется
отличной от нуля, то в определении /4 не будет необходимости и все
вычисления на этом закончатся. Если О4 окажется равной нулю, то
придется определять и /4 и /5 и, может быть, формы более высоких
порядков. Для определения О4 полагаем в C7.16) Ar = cos'&, y = sinft
и интегрируем по Ф в пределах от 0 до 2я. При этом члены
х -~ — у -й- можно не рассматривать, так как они при указанной
операции выпадут. Таким путем получаем:
2л 2Я 2я
О4 = - Г sin4ftdft — - f sin3ftcosutf9-=- I si
0 0 0
Если а < 0, то невозмущенное движение асимптотически устой-
устойчиво, а если а > 0, то оно неустойчиво.
Если а = 0, то, как было показано в предыдущем параграфе,
мы будем иметь случай центра.
§ 38. Системы второго порядка. Третий способ решения задачи.
Рассмотрим еще один способ решения задачи устойчивости для
системы
*?=_Ху + *(*. У). 4?- = и+У(*. у). C8.1)
предложенный также Ляпуновым.
В § 36 было показано, что начало координат для уравнений C8.1)
является либо центром, либо фокусом и что вопрос о том, какой
из этих случаев имеет место, является основным для задачи устой-
устойчивости. Если начало координат является центром, то невозмущенное
движение устойчиво; если оно является фокусом, то устойчивость
или неустойчивость определяется знаком введенной в § 36 постоян-
постоянной g, определяющим направление движения по спиралям, которыми
являются в этом случае интегральные кривые. Далее было пока-
показано, что в случае центра, и только в этом случае, общее решение
140 ИССЛЕДОВАНИЕ КРИТИЧЕСКИХ СЛУЧАЕВ [ГЛ. IV
уравнений C8.1) является периодическим. Поэтому для решения задачи
устойчивости постараемся выяснить, будут ли решения уравне-
уравнений C8.1) периодическими или нет. Если эти решения окажутся пери-
периодическими, то имеет место устойчивость, а если они окажутся не-
непериодическими, то останется еще определить знак постоянной g.
Для выяснения этого вопроса рассмотрим решение х (t), у (t)
уравнений C8.1), определяемое начальными условиями
х @) = с, у @) = 0, C8.2)
где с — достаточно малая произвольная постоянная.
Если начало координат является центром, то это решение будет
периодическим с периодом, определяемым формулой C6.19):
T = ^rV + hlc + h2c'*+ ...)• C8.3)
где Aj, h2, ... — некоторые постоянные, и ряд сходится при с до-
достаточно малом.
Допустим, что мы действительно имеем дело со случаем центра.
Заменим в уравнениях C8.1) переменную t переменной т при помощи
подстановки
C8.4)
Тогда для полученных таким образом уравнений
C8.5)
решение с начальными условиями C8.2) будет периодическим с пе-
периодом 2л.
Уравнения C8.5) содержат аналитически параметр с. Поэтому
любое решение этих уравнений будет, по известной теореме, анали-
аналитическим относительно с. Кроме того, каждое такое решение будет
аналитическим относительно своих начальных значений х° и у0. При-
Применяя это к рассматриваемому периодическому решению, для которого
х° = с, у° = 0, придем к заключению, что это решение будет ана-
аналитическим относительно с.
Следовательно, это решение имеет вид
где ряды, стоящие в правых частях, сходятся при достаточно малом с.
Так как это решение является периодическим с периодом 2л, то все
§ 38] СИСТЕМЫ ВТОРОГО ПОРЯДКА. ТРЕТИЙ СПОСОБ РЕШЕНИЯ 141
функции хт(х), ут(х) являются также периодическими периода 2л.
Кроме того, начальные условия C8.2) дают:
х,@)=1. х2@) = х3@) = ... =У1@) = у2@)= ... =0. C8.7)
Таким образом, если начало координат является центром, то урав-
уравнения C8.5), в которых hi — некоторые определенные постоянные,
имеют решение вида C8.6) с периодическими хт{х), ут(х). Если
окажется, что как бы ни были выбраны постоянные ht, система C8.5)
решения вида C8.6) с периодическими хт (т), ут(х) не имеет, то это
будет свидетельствовать о том, что начало координат является
фокусом.
Подставляя C8.6) в C8.5) и приравнивая коэффициенты при
одинаковых степенях с, мы получим уравнения, которым должны
удовлетворять функции хт и ут. Таким путем прежде всего получаем:
dxt dy,
~ y X
откуда, принимая во внимание начальные условия C8.7), имеем:
После этого получим:
—~ = — у2 — AiSinт-f- у <Y2(cos*, sin*),
dl 1 <38"8>
—jj-L = x2-f- Aj cos т-f jKj (cos *, sin *),
где -Y2(x, у) и K2(jc, у) — совокупность членов второго порядка
в функциях X и Y.
Аналогичные уравнения мы получим и для функций Xk и Yk (k > 2).
Правые части этих уравнений будут содержать постоянные hx,
h2, ..., hk_v Мы выпишем явно лишь те члены, которые содержат
постоянную hk_x. Тогда будем иметь:
dx. dy.
где Pk и Qft — некоторые полиномы относительно х2, у2, хь, уъ
Xjt-v Ук-v коэффициенты которых зависят только от hx, h2 hk_2.
Уравнения C8.8) имеют вид
^=-v + f(x), ^L=u + F(x), C8.10)
где / (т) и F (т) — периодические функции т периода 2л. Задача
состоит в определении периодических решений этих уравнений. Это —
хорошо известная элементарная задача определения вынужденных
142 ИССЛЕДОВАНИЕ КРИТИЧЕСКИХ СЛУЧАЕВ [ГЛ. IV
колебаний линейной системы с одной степенью свободы. В рас-
рассматриваемом случае имеет место резонанс, так как период свободных
колебаний совпадает с периодом возмущающей силы. Поэтому урав-
уравнения C8.10) в общем случае не имеют периодического решения,
и для того чтобы такое решение существовало, необходимо, чтобы
функции / и F удовлетворяли некоторым условиям, которые легко
установить.
Пусть
оо
f = aQ-\-axcosx-\-bxslnx-]- 2 (ancosnx-\-bns\nnx),
со
F = AQ + Al cos т + Bi sin т•+ 2 С<4лсо8ЛТ-[-J3nsin»-t)
— разложения Фурье функций / и F, где, в частности,
2Я 2я
а, = — J / (т) cos xdx, bx = — J / (т) sin т dx,
C8.11)
A1 = — F(x) cos т dx, Bx = —
u
Пусть, далее,
оо
и = c0 + Cj cos т -|- dx sin т -J- 2 (cn COs лт + dn sin ят),
x; = Co -\- Cj cos т -)- Dj sin т -f- 2 (С„ cos ят -+- О„ sin ят)
л = 2
— разложения Фурье искомого периодического решения. Подставляя
эти разложения в C8.10), мы получим CQ —а0, со = — Ао и сле-
следующие уравнения для определения коэффициентов:
ndn = -Cn-\-an, ncn-=Dn~bn,
Эти уравнения дают вполне определенные решения для сп, dn,
Сп. Un при всех я > 1. При я = 1 эти уравнения неразрешимы,
если только не выполняются соотношения
§ 38] СИСТЕМЫ ВТОРОГО ПОРЯДКА. ТРЕТИЙ СПОСОБ РЕШЕНИЯ 143
Если эти соотношения выполняются, то будем иметь:
Dx = a, d1 = р,
С1==а1 — р, cl = a~b1,
где аир — произвольные постоянные. Таким образом, принимая
во внимание C8.11), мы приходим к следующему заключению.
Для того чтобы система C8.10) имела периодическое решение,
необходимо и достаточно, чтобы выполнялись соотношения
Г [/ (т) cos т + F (т) sin т] dx = О,
2я
J [F (т) cos т — / (т) sin т] dx = 0.
C8.12)
Если эти соотношения выполняются, то указанное периодическое
решение имеет вид
C8.13)
где а и р—произвольные постоянные, а и(т), v(x)— периодические
функции периода 2л. Это решение, содержащее две произвольные
постоянные, является общим решением уравнений C8.10).
Если условия C8.12) не выполняются, то уравнения C8.10) не
имеют периодического решения. Членам a1cosx-\-bi sint и A1cosx-\-
?? sin т будут соответствовать частные решения вида
cost,
T cos
x sin x +
и общее решение уравнений C8.10) будет иметь вид
i + Bi
cos t,
C8.14)
где и(т) и г»(т) — периодические функции, а а и р — произвольные
постоянные.
Установив это, допустим, что все функции х2, Уг xk-\* Ук-i
оказались периодическими и что все постоянные hx, й2, .... hk_2
144 ИССЛЕДОВАНИЕ КРИТИЧЕСКИХ СЛУЧАЕВ [ГЛ. IV
известны. Тогда правые части уравнений C8.9), определяющих xk
и yk, будут известными периодическими функциями т. Эти уравнения
будут, таким образом, иметь вид C9.10). Поэтому, для того чтобы
функции хк и yk оказались периодическими, необходимо и доста-
достаточно на основании C8.12), чтобы выполнялись соотношения
2я \
2лйй_! -|- Г (Qk cos т — Рк sin т) dx = О,
C8-15)
о (P*C0ST+Q*SlnT)dT==°' J
Первое из этих соотношений однозначно определяет величину hk_l.
Что же касается второго соотношения, то оно может как выпол-
выполняться, так и не выполняться. Если оно не выполняется, то уравне-
уравнения C8.5) не будут иметь периодических решений, как бы ни были
выбраны постоянные ht. Следовательно, в этом случае начало коор-
координат является фокусом.
Таким образом, для того чтобы начало координат было центром,
необходимо, чтобы второе условие C8.15) выполнялось для любого к.
И если нам каким-нибудь образом удастся установить это обстоя-
обстоятельство, то все функции хк, ук получатся периодическими. Все эти
функции будут вида C8.13) и входящие в каждую из них две про-
произвольные постоянные будут однозначно определяться начальными
условиями хк @) = ук @) = 0. Ряды C8.6) будут при этом, как было
установлено выше, сходиться и действительно представят периоди-
периодическое решение системы C8.1). Начало координат будет в этом
случае центром и невозмущенное движение будет устойчиво.
Допустим, однако, что при вычислении функций хк(х), ук(х) мы
пришли в конце концов к такому значению индекса к, что для
него второе соотношение C8.15) не выполняется, В этом случае,
как мы уже говорили, начало координат является фокусом. Поэтому
для решения задачи устойчивости остается установить знак вели-
величины g, введенной в § 36. Покажем, что
1 Г _1_ й
(г (Р (-ncTj-Л ein-rt/fr ' ' ' /Чй \Р.\
zn j R 2
о
где аг — коэффициент при cost в Рк, а В1 — коэффициент при
sint в Qk.
С этой целью рассмотрим значение величины х при t = T или,
что то же самое, при т = 2я. Мы предполагаем при этом,
что ряд C8.3), определяющий величину Т, обрывается на члене
(k— 1)-го порядка. Общее решение уравнений для хк и ук имеет на
§ 38] СИСТЕМЫ ВТОРОГО ПОРЯДКА. ТРЕТИЙ СПОСОБ РЕШЕНИЯ 145
основании C8.14) вид
= a cos t-j-psint-f-g—
2л
J'
!2л
2яйй_! + J (Qk cos t — Pk sin t),
о
( 2Я
¦ 1 Jo U , Г ,П D
, = asinT—PC0ST-4--JC— { 2яяг,_1 + (Q^cost—Я
2я I B J
taost —
TCOST-f-
2Я
cost +Qft sint) dx
где xk, yk — периодические функции. Для а и р из начальных
условий C8.7) получаем:
и, следовательно,
j 0. C8.17)
Отсюда, учитывая, что все функции х2, у2 ^ft-i- Ук-\ —
периодические, а также учитывая начальные условия C8.7) и соот-
соотношения C8.17), из C8.6)') получим:
2я
C8.18)
Найдем теперь эту же величину, исходя из результатов § 36.
Согласно этим результатам при Ф = 2я на основании C6.6), C6.9)
и C6.13) для величины г, а следовательно, также и для величины
, будем иметь:
••)+ ... C8.19)
В обеих формулах C8.18) и C8.19) с обозначает одну и ту же
величину — значение г и х при ^ = ^ = 0. Сравнение этих формул
показывает, что m — k, так как при t = T полярный угол Ь отли-
отличается от 2я на величину порядка (относительно с) не менее k, и
что g действительно определяется формулой C8.16).
') Так как мы ограничиваемся в подстановке C8.3) только конечным
числом членов, то правые части уравнений C8.5) будут по-прежнему анали-
аналитическими (простыми полиномами) относительно с и ряды C8.6) будут схо-
сходиться на отрезке 0 < т < 2я, если с достаточно мало.
146 ИССЛЕДОВАНИЕ КРИТИЧЕСКИХ СЛУЧАЕВ [ГЛ. IV
Вопрос устойчивости решается знаком величины g. При g > О
невозмущенное движение неустойчиво, а при g < 0 оно устойчиво
асимптотиче^и.
Таким образом, для решения задачи устойчивости мы можем руко-
руководствоваться следующим правилом.
Преобразуя уравнения C8.1) при помощи подстановки C8.4)
к виду C8.5), пытаемся удовлетворить им рядами
где с — произвольная постоянная, a Xj (т), у} (т) — периодические
функции т периода 2л, удовлетворяющие начальным условиям C8.7).
Для определения функций хк, yh получим уравнения вида C8.9).
Эти уравнения будут допускать периодические решения, если выпол-
выполняются условия C8.15). Первое из этих условий однозначно опре-
определяет постоянную /*?_], а второе условие может как выполняться,
так и не выполняться. В первом случае уравнения C8.9) будут
допускать периодическое решение, однозначно определяемое началь-
начальными условиями. И если это будет иметь место для всех значений k,
как бы велико это число ни было, то невозмущенное движение будет
устойчиво, ряды C8.20), а также ряд C8.3) будут сходиться и пред-
представят периодическое решение и период уравнений C8.1).
Если при вычислении функций xk, yk мы придем к такому зна-
значению индекса k, для которого второе условие C8.15) не выпол-
выполняется, то невозмущенное движение будет неустойчиво, если ве-
величина g, определяемая формулой C8.16), будет положительна, и
асимптотически устойчиво, если она будет отрицательна.
Приведенное правило дает очень удобный способ определения
периодических решений уравнений C8.1), когда они. существуют, и
периода этих решений. Сами решения при этом представляются
в очень удобной для практики форме. Эти решения имеют большое
значение в теории нелинейных колебаний1).
Заметим в заключение, что величина Aj всегда получается равной
нулю. Это непосредственно вытекает из C8.16) и C8.8). Можно
доказать, что вообще первая отличная от нуля величина hj имеет
четный индекс.
Пример 1. Рассмотрим снова систему
Полагая
') См., например, М а л к и н И. Г., Некоторые задачи теории нелинейных
колебаний, Гостехиздат, 1956.
§ 38] СИСТЕМЫ ВТОРОГО ПОРЯДКА. ТРЕТИЙ СПОСОБ РЕШЕНИЯ 147
будем иметь:
¦Ц- = (* - Р*2-уху* + ау3) A -
Этой системе пытаемся удовлетворить рядами C8.20). Для коэф-
коэффициентов этих рядов получаем уравнения
dx2_==_ -1" °
dx Л3
Уравнения для х2 и у2 не содержат резонирующих гармоник, и
потому х2 и у2 получаются периодическими. Функции же х3 и у3
не получатся периодическими, так как для них постоянная g на осно-
основании C8.16) имеет вид
2я 2я 2я
— ^
о
^¦ = •^1 sin4Tdt
о
и, следовательно, отлична от нуля. Вопрос устойчивости решается
при этом знаком g, т. е. знаком а.
Пример 2. В качестве второго примера рассмотрим уравнение
(»-*)•
определяющее, как известно, колебания математического маятника
около его нижнего положения равновесия.
В рассматриваемом случае имеет место интеграл энергии
1 — 2 (cos х — 1) = jc2-|- у2 —то- х*-4- ... = const
Т~ЗГ
и следовательно, начало координат х = -^- = 0 является центром.
Равновесие, таким образом, устойчиво, и общее решение уравне-
уравнения C8.21) будет периодическим. Найдем это решение.
Делая
^ i+ ...), C8.22)
получим уравнение
148 ИССЛЕДОВАНИЕ КРИТИЧЕСКИХ СЛУЧАЕВ [ГЛ. IV
которому стараемся удовлетворить рядом
x = ccosx-\-c3x3(x)-\- с5х5(х)-\- •••. C8.23)
где xk (т) — периодические функции т периода 2л, удовлетворяющие
условиям xft@) = 0. При этом ряд C8.22) содержит только четные
степени с, а ряд C8.23) только нечетные степени с, так как урав-
уравнение C8.21) не изменяется при замене х на —х.
Имеем:
d2x3 п, . cos3 т
= — хз— 2«2 cos т + —g— =
( j -^cos3t. C8.24)
Для того чтобы это уравнение имело периодическое решение,
необходимо, чтобы коэффициент при cost обращался в нуль. Таким
образом, получаем:
1
после чего из уравнения C8.24), принимая во внимание начальные
условия, будем иметь:
хз == ~j9JJ cos.t щг cos Зт.
Для х5 имеем уравнение
d?xb . / о. , 11 \ ,1 о 3
-^ = - хъ + [- 2/г4 + -^e J cos т + gelcos Зт ~ 256"cos 5т'
из которого находим:
, _ 11 ¦
~~ 3072 '
= - Sm COS Т ~ 3072 C0S 3T + 2018 C0S 5T-
Этим приближением мы и ограничиваемся. Таким образом, перио-
периодическое решение уравнения C8.21) и его период определяются
формулами:
х = с cos т -)- с3х3 (т) + с5л;5 (т
т) = -J92"cosт ~ 92"cos Зт>
Х C0S Т ~ 3oW C0S Зт + 20Ж C0S
6П4 C0S Т ~ 3oW C0S Зт + 20Ж
§ 39]
ВСПОМОГАТЕЛЬНОЕ ПРЕДЛОЖЕНИЕ
149
Здесь с — начальная амплитуда колебаний. Начальная скорость
равна нулю. Заменяя t на -t-\-a, где а — произвольная постоянная,
получим общее решение уравнения C8.21).
§ 39. Вспомогательное предложение.
Нам понадобится в дальнейшем одно вспомогательное предложе-
предложение, являющееся непосредственным обобщением теоремы 2 § 20.
Пусть их uk суть k заданных форм от-го порядка переменных
хп. Требуется определить условия, при которых суще-
существуют k других форм
щих системе уравнений
vk того же порядка, удовлетворяю-
dvi
</>„*, + ... + psnxn) -g- = qnvl + • • ¦ + qikvk + ut C9.1)
(l=\, 2 k),
где qtj — некоторые постоянные.
Обозначим через pt р„ корни уравнения
Р\\ — Р
Рч\
Р\2
Ргч —
Ри
Pin
а через
Рп\
¦• **
Чи —
Рп2
— корни
и 4l2
¦¦¦ Рпп
уравнения
и ... q2
— Р
*
*
= 0,
C9.2)
= 0.
C9.3)
Имеет место следующее предложение.
Теорема. Если между корнями уравнений C9.2) и C9.3) не
существует никаких соотношений вида
где тх, ...
ношением
\- ... +/к„р„ = иг, C9.4)
тп — целые неотрицательные числа, связанные соот-
соотml-srm2-\- ... -\-тп — т, C9.5)
то существует одна и только одна система форм т-го порядка
vx vk, удовлетворяющих уравнениям C9.1).
Доказательство. Имея в виду применить метод индук-
индукции, рассмотрим сначала случай k = 1. Допустим, следовательно, что
150
ИССЛЕДОВАНИЕ КРИТИЧЕСКИХ СЛУЧАЕВ
[ГЛ. IV
предложено одно уравнение
я
C9.6)
где а — форма т-го порядка. Число и будет, очевидно, в рассматри-
рассматриваемом случае единственным корнем уравнения C9.3). Так как
х
dv
s дх.
¦ = mv.
то уравнение C9.6) можно переписать в виде
Применяя теорему 2 § 20, мы можем утверждать, что это урав-
уравнение имеет решение и притом единственное, если не существует
зависимостей вида
= 0, C9.7)
где тг, ...,/»„ — целые неотрицательные числа, связанные соотно-
соотношением C9.5), а р' — корни уравнения
= 0.
Но,
я
Ргч
Рп\
очевидно,
-Р'
Р22~
имеем:
Рп
я
т
Рп-2
Р' =
-Р'
= Р,-
.. . р
т '
Р\п
Р2п
„П — — — 9
и следовательно, соотношение C9.7) переходит в соотношение
«iPi+ •'•• +'Knpn=-i-(wi+ ••• +««)*=к.
т
откуда и вытекает справедливость нашей теоремы для k = 1.
Рассмотрим теперь случай k > 1. Если мы введем в рассмотрение
формы wu ..., wk, связанные с формами vx vk неособенной
линейной подстановкой
I. 2 k),
§ 39] ВСПОМОГАТЕЛЬНОЕ ПРЕДЛОЖЕНИЕ
то из C9.1) получим для этих форм следующие уравнения:
151
(Psl*l
. . . -f
где «г
2
(/=1. 2 k),
o,tjUj будут также известными формами tn-vo порядка.
Коэффициенты Тц связаны с коэффициентами qtj соотношением
г = a~1qa.
где г—матрица коэффициентов Гц, q — матрица коэффициентов qtj,
а а — матрица коэффициентов а^. Отсюда следует, что уравнение
гп и гп ... г1к
\г— пЕ\ =
Г1\
Г22
гЧк
Гъъ— И
:0
(?—единичная матрица) имеет те же корни, что и уравнение C9.3).
Действительно, имеем:
\г — v.E\==\a-lqa — w.E\=\a-x (q — х.Е)а\==
что и доказывает наше утверждение.
Установив это, допустим, что теорема доказана для системы
с k — 1 неизвестными функциями, и покажем, что она останется
справедливой и для системы с k неизвестными функциями. С этой
целью рассмотрим систему линейных однородных уравнений
Так как определитель этой системы равен нулю, то она имеет
решение, в котором хотя бы одна из величин at отлична от нуля.
Допустим для определенности, что а^О. Тогда, вводя вместо
формы t»i форму w, определяемую равенством
w=^=a1v1-\-a2v2-{- ... -\-akvk,
мы вместо первого уравнения C9.1) получим уравнение
+ • • • + /»,„•*„)-
C9.8)
_ ft
где и, = 2 aiwi — известная форма от-го порядка.
152 ИССЛЕДОВАНИЕ КРИТИЧЕСКИХ СЛУЧАЕВ
Остальные уравнения C9.1) примут вид
[ГЛ. IV
; C9.9)
s=l
U = 2 k),
где Гц—некоторые постоянные, которые нам нет необходимости
выписывать явно.
Уравнение C9.3) для преобразованной системы имеет вид
щ — к О
'22
¦А . . .
О
'2ft
... rkk — -я
= (Щ — X)
rik
= 0,
и так как по доказанному оно инвариантно относительно неособен-
неособенного линейного преобразования, то корнями уравнения
'2ft
rft2
ftft
будут величины щ, ..., ий.
Величина х,, как и остальные корни уравнения C9.3), не свя-
связана, по условию, с величинами pj, .... ря никакими соотношениями
вида C9.4), и поэтому, по доказанному, уравнение C9.8) допускает
одно и только одно решение для w в виде формы га-го порядка.
Подставив это решение в уравнения C9.9), мы получим для определе-
определения v2, ..., vk систему вида C9.1) с k—1 неизвестными функ-
функциями. Эта система, по предположению, допускает одно и только
одно решение для г»2, ..., vk. Переходя к первоначальным перемен-
переменным vl vk, мы получим, таким образом, одно и только одно
решение системы C9.1).
Итак, допустив, что теорема справедлива при k — 1 неизвестных
функциях, мы доказали, что она остается справедливой и при k
неизвестных функциях, и так как она доказана для k = 1, то она
справедлива для всякого k.
Пример. Пусть предложена следующая система:
5=1
dvt
(/=1. 2 k; vo = vll+i =
C9.10)
§ 40]
система (я-)-2)-го порядка; частный случай
153
где их uk — заданные формы произвольного порядка т,
а X — положительное число. Предположим, что все корни уравне-
уравнения C9.2) имеют отрицательные вещественные части. В этом случае
система C9.10) имеет одно и только одно решение для v1 vk
в виде форм /и-го порядка.
Действительно, корни уравнения C9.3), как можно показать,
в рассматриваемом случае будут
± Xt, ± ЗА,/,'
± {k—Z)Xi, ± (k-l)Xt,
если k — число четное, и
0, ± 2X1, ± Ш ±(k
\)Xi,
если k — число нечетное. Очевидно, что в этом случае соотноше-
соотношения C9.4) не могут иметь место ни при каких целых неотрицатель-
неотрицательных т1 тп, не равных нулю одновременно, и потому теорема
применима при любом т.
§ 40. Исследование системы (я -f-2)-ro порядка
в частном случае.
Мы переходим теперь к рассмотрению системы (п -\- 2)-го порядка
при и > 0. Дифференциальные уравнения возмущенного движения,
как мы видели в § 35, имеют вид
dx
~dT
dy
=— Xy -\- X (x, y, xx xn),
= Xx+ Y(x, y, xr xn),
• • • 4 Psnx« +¦ PsX +
dxs
У-
(s=l, 2 n),
причем коэффициенты psj таковы, что уравнение
Pit — Р i°l2 ••• Pin
Рп Р22~-Р ¦ • • Pin
D0.1)
Pn\ Pni
Pnn —
= 0
D0.2)
имеет корни только с отрицательными вещественными частями.
В этом параграфе мы дадим решение задачи устойчивости для
системы D0.1) при некотором частном предположении. Как мы уви-
увидим в следующем параграфе, к этому частному случаю приводится
задача и в общем случае.
154 ИССЛЕДОВАНИЕ КРИТИЧЕСКИХ СЛУЧАЕВ [ГЛ. IV
Обозначим через Х°(х, у), Y°(x, у), ^(л;, у) функции перемен-
переменных х и у, в которые обращаются функции X, Y и Xs, если в них
отбросить все члены, зависящие от хх, .... хп, так что
Х°(х, у) = Х(х, у, 0, .... 0),
Y°(x, y) = Y(x, у, 0 0),
Х°Лх, y) = Xs(x, у, 0 0).
Рассмотрим систему второго порядка
^ . у), ^ = %х+УЦх, у). D0.3)
Решая задачу устойчивости для этой системы, мы встретимся
с одним из двух случаев: с общим случаем, когда задача решается
конечным числом первых членов в разложениях функций Х° и К0
(случай фокуса), и особенным случаем, когда требуется рассмотрение
членов сколь угодно высоких порядков (случай центра). Предполо-
Предположим, что мы имеем дело с первым из этих случаев. Пусть 2N— 1 —
наивысший порядок членов разложений функций Х° и К0, от
которых зависит решение задачи устойчивости для системы D0.3).
Как мы видели (§ 37, примечание), этот порядок всегда нечетный.
Тогда мы будем предполагать, что для уравнений D0.1) выполняются
следующие два условия:
1) все постоянные ps и qs равны нулю;
2) разложения функций X°s начинаются членами не ниже BN—1)-го
порядка.
Покажем, что если эти условия выполняются, то задача устой-
устойчивости для системы (й-|-2)-го порядка D0.1) решается системой
второго порядка D0.3), а именно: если для системы D0.3) получается
неустойчивость, то и для системы D0.1) будет иметь место неустой-
неустойчивость и, наоборот, устойчивость для системы D0.3) обусловливает
устойчивость и для системы D0.1).
Таким образом, при выполнении указанных условий для решения
задачи устойчивости мы попросту отбрасываем все уравнения, соот-
соответствующие некритическим корням, а в уравнениях, соответствующих
критическим корням, отбрасываем все члены, содержащие некрити-
некритические переменные.
Для доказательства справедливости наших предложений поступим
так же, как и в случае одного нулевого корня. Попытаемся по-
построить для уравнений D0.1) функцию Ляпунова в виде суммы функ-
функций Ляпунова, построенных отдельно для системы D0.3) и для системы
последних п уравнений D0.1).
Задача заключается в построении функции V (л;, у, хг хп),
обладающей знакоопределенной производной.
§ 40] система (я + 2)-го порядка; частный случай 155
Как было показано в § 37, функция Ляпунова для системы D0.3)
имеет вид
где fi — формы 1-го порядка переменных х и у. Для производной
этой функции, составленной в силу уравнений D0.3), будем иметь:
_
а+р=2Лг
где <faa(x, у) обращаются в нуль при х = у — 0. Задача устойчи-
устойчивости для системы D0.3) решается при этом знаком О. Невозмущен-
Невозмущенное движение будет неустойчиво при О > 0 и асимптотически устой-
устойчиво при О < 0. Нам нужно показать, что то же самое будет и для
системы D0.1).
Пусть W (xv .... хп)—квадратичная форма переменных xv .... хп,
удовлетворяющая уравнению
Так как все корни уравнения D0.2) имеют отрицательные веще-
вещественные части, то форма W будет определенно-отрицательная.
Рассмотрим функцию
xn) D0.5)
и составим ее производную по t в силу уравнений D0.1). Для этой
производной имеем:
¦1 = [
где функции Л"', к', A"i обращаются в нуль при хг = . . „
и обозначают совокупности тех членов в разложениях X, Y и Xt,
которые зависят от хх хл.
156 ИССЛЕДОВАНИЕ КРИТИЧЕСКИХ СЛУЧАЕВ [ГЛ. IV
Если бы функции X', К', а также функции
ственно в нуль, то производная имела бы вид
Если бы функции X', К', а также функции Х°3 обращались тожде-
тожде*2s+ 2 fijXtXj,
1 l,j = l '
где fij — аналитические функции переменных х, у, хх хп, об-
обращающиеся в нуль при х = у = X] = ... = хп = 0. Эта производ-
производная была бы, очевидно, определенно-положительной функцией я —j- 2
переменных х, у, я,- Но так как вышеуказанные соотношения,
к dV
вообще говоря, не выполняются, то производная —тг не получится
определенно-положительной. Эта производная будет иметь вид
+ 2*»+ S ftjX,Xj + P(x. у, xv ..., х„), D0.6)
5 = 1 (, у = 1
где теперь уже <р содержат и переменные л^, . . ., хп и обращаются
в нуль при x = y = x1=...=xn = 0, а Р — совокупность всех
членов, которые не могут быть отнесены ни к группе
+y2yv+ ^ ФарЯ'У. D0.7)
ни к группе
п
2j fijxixj-
i,j = \
Исследуем подробнее функцию Р. Эта функция не будет содер-
содержать члены ниже третьего порядка, так как единственными членами
второго порядка в выражении —п- будут члены D0.4). Функция Р
не содержит в своем разложении членов, свободных от хх хп,
dV
так как все такие члены в —гг содержатся в выражении
и, следовательно, могут быть включены в группу D0.7).
Из членов, линейных относительно xlt .... хп, в функции Р будут
содержаться лишь такие, порядок которых относительно хну
меньше 2N. Остальные члены этого типа могут быть включены
в группу D0.7). Члены, имеющие относительно хх, . . ., хп второй и
более высокие порядки, могут быть все включены в. D0.7) и поэтому
в Я не содержатся.
§ 40] система (д-|-2)-го порядка; частный случай 157
Таким образом, функция Р имеет вид
Р = Р2(*1 хп, х, y) + P3(xv .... хп, х, у) + •••
ха. х, у), D0.8)
где Pk — формы k-то порядка относительно х и у, коэффициентами
которых являются линейные формы переменных xv .. ., хп.
Наличие в —гг слагаемого Р нарушает ее знакоопределенность.
Нам нужно будет поэтому функцию V изменить таким образом, чтобы
в выражении ее производной не содержалось членов, входящих в Р,
т. е. линейных относительно Xj и имеющих порядок относительно х
и у, меньший 2N. С этой целью введем в функцию V добавочное
слагаемое вида
Qk (*L • • • • Хп, X, у) =
» + г»л+1у*. D0.9)
где 2 <J k <С 2N — 1, a. Vj — линейные формы переменных хх хп.
Исследуем те новые члены, которые внесет это слагаемое в выраже-
выражение-^-. Члены, свободные от хх хп, могут получиться лишь за
счет производных от первых множителей, т. е, за счет функций Xs,
и так как разложения этих функций начинаются членами не ниже
BN—1)-го порядка, то указанные члены будут иметь порядок не
ниже 2N-\-k— 1 ~^-2N -\- 1 и могут быть включены в группу D0.7).
Новые члены, линейные относительно хх, . .., хп, будут иметь отно-
относительно х, у порядок, не меньший k, так как общий порядок чле-
членов, вносимых слагаемым D0.9) в производную, будет, очевидно,
не меньше k-\-\.
Таким образом, производная от функции
V = q>(*. У)+ 1*4*1
будет иметь вид
о*(*'+*>*+
где ф*„, /*. — функции такого же вида, как и фа„, f.., a Р*к,
Р*к+1. ¦¦•' PlN-\ — формы относительно х, у, порядок которых
равен их индексу и коэффициенты которых являются линейными функ-
функциями от Xj хп. Функции Я* P*2n-i отличаются, вообще
говоря, от функций Pk PiN-v Выпишем подробней функ-
функцию P"k. Пусть
158 ИССЛЕДОВАНИЕ КРИТИЧЕСКИХ СЛУЧАЕВ [ГЛ. IV
где at (хх хп) — линейные формы от xv .... хп. Тогда, как
легко видеть, будем иметь:
где
п
А «» «я ^ л-i /-1 )
(/=1, 2 *+1, t»0 = t»ft+2==0).
Выберем теперь функцию D0.9) таким образом, чтобы функция Р*
обратилась в нуль. Для этого придется линейные формы vx vk+1
выбрать так, чтобы выполнялись уравнения
Л = Л =...=/*+! = 0. D0.10)
Эти уравнения имеют как раз тот вид, который мы рассмотрели
с качестве примера в предыдущем параграфе. Мы видели, что в рас-
рассматриваемом нами случае, когда уравнение D0.2) имеет корни только
в отрицательными вещественными частями, уравнения D0.10) имеют
одно и только одно решение для Vj.
Выбрав таким образом функцию D0.9), мы уничтожим в выраже-
dV
нии —-7J- то слагаемое функции Р, которое является формой &-го
порядка относительно х и у, не изменяя при этом тех слагаемых,
которые имеют меньший порядок. Отсюда следует, что, добавляя
к V последовательно слагаемые вида Qk (k — 2, 3 IN— 1), мы
можем последовательно уничтожить в функции Р все члены. Другими
словами, мы можем так подобрать функции Q2, .. ., Q2N-1, каждая
из которых является формой соответствующего порядка относи-
относительно х и у и линейной относительно хх хп, что производная
от функции
У- *1 *П)+ ••• +Q2ff(X, У, *! Хп),
составленная в силу уравнений D0.1), будет иметь вид
а+Р=2ЛГ s=l а, р=1
где Фан и Faa обращаются в нуль при х = у = хх= ... —хп — 0.
dV
Производная-37-будет функцией определенно-положительной. Сама
(XT
функция V имеет вид
§ 41]
система (п-\-2)-то порядка; общий случай
169
где F—аналитическая функция переменных х, у, хх хп, раз-
разложение которой начинается членами не ниже третьего порядка.
Так как форма W определенно-отрицательна, то V будет опре-
определенно-отрицательной функцией всех п-\-2 переменных х, у, xs,
если G < 0, и знакопеременной функцией, если G > 0. Отсюда на
основании теорем Б и В заключаем, что, так же как и для системы
второго порядка D0.3), невозмущенное движение для полной системы
D0.1) будет асимптотически устойчиво при О<0 и неустойчиво при
G > 0. Таким образом, наши утверждения доказаны.
§ 41. Исследование системы (л -(- 2)-го порядка
в общем случае.
В предыдущем параграфе мы рассмотрели систему D0.1) при неко-
некоторых частных предположениях. Чтобы решить задачу в общем слу-
случае, преобразуем эту систему к такому виду, чтобы для нее выпол-
выполнялись ограничения предыдущего параграфа. Для этого необходимо
систему преобразовать так, чтобы она сохранила вид D0.1), но чтобы
разложения правых частей уравнений, соответствующих некрити-
некритическим переменным, после того как в них отбросить все члены, со-
содержащие эти переменные, начинались членами достаточно высокого
порядка.
С этой целью введем в уравнениях D0.1) новые переменные
^ |„ вместо переменных xv ..., хп при помощи подстановки
= xs-vs(x,y) (s=l л),
D1.1)
где vs(x, у) — аналитические функции переменных х и у, обращаю-
обращающиеся в нуль при х = у = 0. Преобразованные уравнения будут
L
L
. у,
. у,
у,
y,
+Psnln
D1.2)
Обозначим через В[°\х, у) совокупность всех членов в функ-
функциях 5,, не зависящих от некритических переменных |lt .... ?„.
160 ИССЛЕДОВАНИЕ КРИТИЧЕСКИХ СЛУЧАЕВ [ГЛ. IV
Будем, очевидно, иметь:
у, v1 vn)-{^[-ly + X(x, у, v, va)] +
} D1.3)
Подберем теперь функции vlt . . ., vn таким образом, чтобы раз-
разложения функций 3?' начинались членами не ниже га-го порядка, где
т — достаточно большое число. Тогда система D1.2) будет иметь
желаемый вид и для решения задачи устойчивости отбросим в пер-
первых двух уравнениях этой системы все члены, содержащие |j, .... |„,
и рассмотрим полученную таким образом систему второго порядка
= -.Xy+X(x. у, vx{x, у) vn(x, у)),
D1.4)
. у, *,(*, у) va(x. у)).
Может случиться, что как бы велико ни было число га, задача
устойчивости для системы D1.4) не решается членами порядка ниже от.
Этот случай будет исключительным, особенным, и мы его рассмот-
рассмотрим в § 43.
Но может, однако, случиться, и это будет общим случаем, что
при т достаточно большом задача устойчивости для системы D1.4)
решается членами не выше га-го порядка (га при этом будет обя-
обязательно нечетным), так что члены порядка выше т на решении
задачи не скажутся. В этом случае задача устойчивости и для исход-
исходной системы (п -f 2)-го порядка D0.1) решается системой второго
порядка D1.4), а именно, если для системы D1.4) имеет место не-
неустойчивость, то и для системы D0.1) имеет место неустойчивость,
и если для системы D1.4) получается асимптотическая устойчивость,
то и для системы D0.1) получится асимптотическая устойчивость.
Действительно, так как по условию задача устойчивости для си-
системы D1.4) решается членами порядка не выше т и разложения
функций D1.3) начинаются членами не ниже /я-го порядка, то си-
система D1.2) удовлетворяет всем ограничениям предыдущего параграфа.
Согласно полученным там результатам система D1.4) полностью
решает задачу устойчивости для системы D1.2) и, следовательно,
для эквивалентной ей системы D0.1).
Остается показать, как определить функции v^(x, у), обращаю-
обращающие в нуль в выражениях D1.3) все члены до порядка га — 1 вклю-
включительно. С этой целью положим:
•ож (jc, у) = <" (х, у) + vf{x, у) + ... E=1.2 п), D1.5)
§ 41] система (д-)-2)-го порядка; общий случай 161
где v^{x, у) — формы &-го порядка переменных хну. Тогда члены
первого порядка в D1.3) будут
= - X (ijiL х -
(s=l, 2 я). D1.6)
а совокупность членов какого-нибудь k-vo порядка имеет вид
(s = l, 2 л). D1.7)
Здесь «(*> (л;, у) — формы й-го порядка, зависящие от форм
ф) и'*-1'.
«У S
Для того чтобы в функциях D1.3) не было членов первого по-
порядка, необходимо линейные формы г»<?> (л;, у) выбрать так, чтобы
удовлетворялись уравнения Н'^ =0, а для того чтобы разложения
функций D1.3) начинались членами не ниже т-го порядка, необхо-
необходимо, чтобы выполнялись уравнения
(s—\, 2 я; k—l, 2 т— 1).
Так как функции и^> зависят только от тех v(J\ для которых
J < й, то уравнения D1.8) дают возможность последовательно опре-
определять формы <&?>, начиная с & = 1, причем для определения ©у
получаются уравнения с известными правыми частями, так как на
основании D1.6) u№ — psx -\-qsy- Всего в рядах D1.5) нужно опре-
определить члены до (т — 1)-го порядка, если мы желаем, чтобы разло-
разложения D1.3) начинались членами не ниже т-го порядка.
Допустим, что все функции v<l\ v^> •y'^ft~1) уже определены.
Тогда для нахождения ©W мы получим уравнения D1.8) с из-
известными правыми частями. Уравнения D1.8) имеют вид уравне-
уравнений C9.1), рассмотренных нами в § 39. Корнями уравнения C9.2)
являются сейчас величины + XI, а корнями уравнения C9.3) —
к^рни рх р„ уравнения D0.2). Соотношение C9.4) принимает
сейчас вид
и так как оно не выполняется ни при каких целых неотрицатель-
неотрицательных «!, т2, то на основании теоремы § 39 система D1.8) имеет
162 ИССЛЕДОВАНИЕ КРИТИЧЕСКИХ СЛУЧАЕВ [ГЛ. IV
решение для v<-*K каков бы ни был индекс k. Это решение нужно
искать в виде форм с неопределенными коэффициентами, для опре-
определения которых получатся линейные неоднородные алгебраические
уравнения.
Выясним теперь, сколько членов нужно определить в рядах D1.5)
при практическом решении задачи. Для этого вспомним, что если
задача устойчивости для системы второго порядка решается членами
не свыше какого-нибудь конечного порядка, то этот порядок всегда
нечетный. В простейшем случае, который на практике и будет наи-
наиболее частым, задача решается членами третьего порядка. Следова-
Следовательно, нужно, чтобы в разложениях D1.3) отсутствовали члены
первого и второго порядков, для чего в функциях vs нужно взять
лишь линейные члены vM (x, у) и члены второго порядка г^2> (х, у).
Определив эти члены, подставим полученные таким образом функ-
функции vs в уравнения D1.4) и решаем для них задачу устойчи-
устойчивости. Если при этом окажется, что задача членами третьего порядка
не решается и требует, следовательно, рассмотрения членов, по
крайней мере, четвертого и пятого порядка, то придется определить
также формы г»*3' и v^K а может быть и формы более высоких по-
порядков, если окажется, что и члены пятого порядка не решают задачи
устойчивости для системы D1.4).
Заметим, наконец, что уравнения D1.4) получаются из первых
двух уравнений D0.1) заменой переменных xs функциями vs(x, у),
а уравнения D1.8) мы получим, если попытаемся найти решение
системы уравнений с частными прозводными
? ^x, у, vlt . ...«„)) =
= Psi°i + • • • + Рзп°п + Ps* + Я*У + Xs С*. У. «i «„)' D1.9)
в виде рядов D1.5). Поэтому все вышесказанное приводит нас
к следующему правилу.
Для того чтобы решить задачу устойчивости для системы D0.1),
составляем систему уравнений с частными производными D1.9),
которой стараемся удовлетворить рядами D1.5). Такие ряды (фор-
(формальные) всегда найдутся и будут единственными. Этими рядами
заменяем величины xs в первых двух уравнениях D0.1), после чего
получим систему второго порядка D1.4). Допустим, что задача
устойчивости для этой системы решается конечным числом членов.
Тогда если для системы D1.4) получается неустойчивость, то
и для системы D0.1) будет иметь_место неустойчивость, а если для
системы D1.4) получится асимптотическая устойчивость, то и для
системы D0.1) будет иметь место асимптотическая устойчивость.
§ 41] система (« + 2)-го порядка; общий случай 163
О количестве членов, которые необходимо взять в рядах D1.5)
для решения задачи устойчивости, мы уже говорили выше *).
Поясним выкладки примерами.
Пример 1. Пусть предложена система:
dx . dy
~dF ~ ~ У ~T~axZ' ~d7~~X
dt ~ Z^~X +-
у, z),
D1.10)
где разложение функции /(х, у, z) начинается членами не ниже
третьего порядка. Составим уравнение с частными производными
которому стараемся удовлетворить рядом
v = vy(x, у) + г>2(х, у) + ...,
где Vj(x, у) — формы у-го порядка. Сначала определим формы
г>1 и г>2- Формы более высоких порядков будем определять лишь
в том случае, если в этом будет необходимость. Для v^ и г>2 имеем
уравнения
dv, . dvt
* дх ' ду 1
dv, . dv2 . о i о dv,
y^xf=^+x+y2ay^
Первое уравнение дает vx = 0, после чего второе уравнение
принимает вид
-уж+х1^ = -ъ+х2+у2- <41Л1)
Полагая
мы получим из D1.11) уравнения
откуда находим, что v2 = x2-j- у2.
') Решение задачи устойчивости в критическом случае пары чисто
мнимых корней, а также в случае одного нулевого корня, когда уравнения
возмущенного движения не аналитичны, дано в работе: В е д р о в В. С, Об
устойчивости движения. Труды ЦАГИ, вып. 327, 1937.
164
ИССЛЕДОВАНИЕ КРИТИЧЕСКИХ СЛУЧАЕВ
[ГЛ. IV
Подставляя теперь в первые два уравнения D1.10) вместо z
величину г> = г>1 + г>2+ ¦••> получим систему второго порядка
dx
х, у),
. У).
D1.12)
где разложения <р и i|) начинаются членами не ниже четвертого по-
порядка. Будем теперь решать задачу устойчивости для системы D1.12).
Здесь лучше всего воспользоваться методом § 37. При этом сразу
видно, что система D1.12) допускает функцию Ляпунова 2V = х2~\-у2,
производная которой, имеющая вид
будет функцией знакоопределенной, если только a =f= 0. Невозмущен-
Невозмущенное движение для системы D1.12), а вместе с ней и для системы D1.10)
будет неустойчиво при а > 0 и асимптотически устойчиво при а < 0.
При а —0 задача устойчивости для системы D1.12) членами
третьего порядка не решается. Однако вычисление форм v3, г>4 и
членов более высоких порядков в разложении функции v излишне,
так как при а —0 первые два уравнения D1.10) не содержат пере-
переменной z. Этот случай, очевидно, принадлежит к числу особенных.
Пример 2. В качестве второго примера рассмотрим одну из
задач устойчивости систем автоматического регулирования, исследо-
исследованную А. И. Лурье!).
Допустим, что дифференциальные уравнения движения системы
(регулируемого объекта, измерительных органов, сервоприводов
и т. д.) имеют вид
D1.13)
а=1
л+2
(i=l, 2
ге+2),
где bla, hr Ja — постоянные, а /(о) — некоторая нелинейная функ-
функция, обращающаяся в нуль при 0 = 0. Рассмотренные нами ранее
в §§ 12 и 26 уравнения систем регулирования являются, очевидно,
частным случаем системы D1.13).
') Лурье А. И., О характере границ области устойчивости регулируе-
регулируемых систем. ПММ, т. XV, вып. 2, 1951.
§ 41]
система (л + 2)-го порядка; общий случай
165
Предположим, что /(о) является аналитической функцией о и
имеет вид
Рассмотрим систему первого приближения
л+2
a=l
A=1, 2 л+2).
Для того чтобы положение равновесия т|г = ... =т)/г+2 = 0
рассматриваемой системы было устойчивым, достаточно, чтобы веще-
вещественные части всех корней уравнения
Д(р) =
—Р
«12
«22 — Р
«1,л+2
«2, л+2
«л + 2, 1 йл+2,2
«л + 2, л+2 Р
= 0 D1.15)
имели отрицательные вещественные части. При этом величина области
устойчивости, как это легко усмотреть из рассуждений § 26, зави-
зависит от величины этих вещественных частей. Если вещественные
части хотя бы некоторых корней уравнения D1.15) численно малы,
то область устойчивости может оказаться слишком малой и с точки
зрения практической исследуемое положение равновесия надо будет
рассматривать как неустойчивое. Как будет показано в § 44, вопрос
о поведении системы в такого рода случаях будет зависеть от того,
будет ли иметь место устойчивость или неустойчивость в предель-
предельном случае, когда указанные вещественные части будут равны нулю.
Таким образом, задача приводится к исследованию критических
случаев. Мы рассмотрим эту задачу для системы D1.13) в предпо-
предположении, что уравнение D1.15) имеет пару чисто мнимых корней
± Xt при остальных корнях с отрицательными вещественными частями.
Допустим, что все корни р[ рл+2 уравнения D1.15) являются
простыми. Рассмотрим линейную подстановку
=1. 2
я+2). D1.16)
где
определяются уравнениями
(/=1, 2 л + 2, s=l, 2 л+2)
и, следовательно,
166
ИССЛЕДОВАНИЕ КРИТИЧЕСКИХ СЛУЧАЕВ
[ГЛ. IV
где Дар — алгебраическое дополнение элемента {5-й строки и а-го
столбца определителя D1.15), а С,— произвольные постоянные. Под-
Подстановка D1.16) преобразует уравнения D1.14) к виду
1' 2 ге
а уравнения D1.13) — к виду
если только постоянные С1 выбраны согласно условиям
л+2
а=1
что мы и будем предполагать. Переменная а примет при этом вид
л+2
а=1
где аа — некоторые постоянные, явное выражение которых мы здесь
не привошм.
Пусть рл+1 = iX, рл+2 = — iX, а остальные корни р^ имеют отри-
отрицательные вещественные части. Тогда, полагая
n+2
==x~iy,
мы приведем уравнения движения к следующему окончательному
виду:
dy -Xx
= ах —
... +апхп,
D1.17)
где а и b — вещественная и мнимая части коэффициента 2ап+1
(коэффициент ап+2 будет, очевидно, комплексно сопряжен с ап+1).
Составляя уравнения
(*=1. 2 п.).
§ 41] система (re -j- 2)-ro порядка; общий случай
пытаемся им удовлетворить рядами
v =
(s=l, 2 п).
167
D1.18)
Для функций x>W получаем уравнения
откуда v№ = 0. Вследствие этого уравнения для
имеют вид
Полагая в этих уравнениях
приравнивая коэффициенты при лгу, х2, у2 и решая полученные
таким образом уравнения, для Ms, Ps, Ns найдем:
2ab9s]'
Имея в виду решать в дальнейшем задачу методом § 36, поло-
положим в форме г»*2' x = r cosu, y = rsiiT&. Тогда, принимая во вни-
внимание значения коэффициентов Ms, Ps, Ns, получим:
vm _ ri ^
где
_ ri
1
cos
sin
D1.19)
Подставляя в первые два уравнения D1.17) вместо xs ряды D1.18),
переходя к полярным координатам и исключая t, получим:
D1.20)
168 ИССЛЕДОВАНИЕ КРИТИЧЕСКИХ СЛУЧАЕВ [ГЛ. IV
где
Я, =.% (a cos ft — b sin ftJ cos ft.
A
2
R4 = -г2- (a cos ft — b sin ftL sin ft cos ft -f-
A2
_j_ JL {2i|>2(acosft — 6 sin ft) (a +p cos 2ft+ y sin 2ft) -f-
+ ijK (a3 cos ft — b sin ftK} cos ft.
Здесь введены обозначения
л л л
a = 2 asas, p = S а,р,, у = 2 «,Y
i 1 i
и, следовательно, на основании D1.19)
a = —к ^ (я2 ~\~ b2) S\,
Р = 2Xa6iJJ52 — -g- (a2 —
Y == Я (а2 — б2) ф252 +
где
л л
D1.21)
2 "
ТЛ. 1 II -^— Ч-Л. I ^
а=1 а=1
Полагая в D1.20)
найдем:
о о
Функция r2(ft) получится, очевидно, периодической. Но тогда то
же самое будет и для функции
9 о
j R2r2dft = j r2dr2 = jr22.
о о
Вследствие этого постоянная g, фигурирующая в соотношении
гз — ?$ + периодическая функция,
определяется формулой
2л
§ 42] ДРУГОЙ СПОСОБ РЕШЕНИЯ ЗАДАЧИ 169
которая дает:
или, принимая во внимание D1.21),
g — да+/г |\$ (_ ab — 2XaSx + 2№S2 — aXSj — -| o
Если теперь входящие сюда величины выразить через коэффи-
коэффициенты исходной системы D1.13) и опустить несущественный поло-
положительный множительтрг- (cfi-^b2), то, как показал А. И. Лурье,
получим:
где D(p) — значение определителя D1.15) при с = 0.
§ 42. Другой способ решения задачи.
Решение задачи устойчивости в критическом случае пары чисто
мнимых корней по методам, изложенным в предыдущих параграфах,
приводит обычно к очень громоздким вычислениям. Уже для системы
второго порядка, если, например, решать задачу приемом § 36,
приводящим обычно к наиболее простым вычислениям, приходится
определять при помощи квадратур коэффициенты rt из уравнений
C6.8), имеющих вид
где F( являются полиномами относительно г2, ..., гг-1. Хотя функ-
функции Fi будут получаться полиномами от cos & и sin ¦&, вычисление
указанных квадратур приводит к громоздким выкладкам, в особен-
особенности ко!да задача устойчивости решается членами порядка выше
третьего, ввиду быстрого усложнения функций Ft по мере возраста-
возрастания /.
Задача значительно усложняется для систем (» + 2)-го порядка.
В этом случае приходится проделывать дополнительные громоздкие
вычисления, связанные с необходимостью действительного определе-
определения форм г//'(л:, у), удовлетворяющих уравнениям D1.8). Для каждого
k эти формы содержат «(А-)-1) коэффициентов, для нахождения
которых мы получим из D1.8) систему из n{k-\~\) линейных не-
неоднородных уравнений. Даже в простейшем случае, когда зада-
задача устойчивости решается членами не выше третьего порядка,
необходимо, как мы видели, определить формы г//' и v'P и,
170 ИССЛЕДОВАНИЕ КРИТИЧЕСКИХ СЛУЧАЕВ [ГЛ. IV
следовательно, решать две системы линейных уравнений, содержащих,
соответственно, 2га и Зга неизвестных.
Определение форм v\' значительно упрощается, если, следуя
Ляпунову, уже в уравнениях D1.9) ввести вместо х и у полярные
координаты г и ¦&, имея в виду решать затем задачу для системы
второго порядка методом § 36. Еще больших упрощений можно
добиться приемом, указанным автором !). Однако, вся задача значи-
значительно упрощается, если ее решать иным приемом 2), к рассмотрению
которого мы сейчас и переходим.
Рассмотрим сначала систему второго порядка. Во всех выше-
вышеизложенных приемах мы приводили уравнения возмущенного движе-
движения к виду C6.1). Мы будем сейчас исходить из другого вида
уравнений возмущенного движения, а именно: мы будем предполагать,
что эти уравнения преобразованы к виду
? . У). % = -&У-\-У(х,у), D2.1)
что всегда может быть выполнено при помощи линейного преобра-
преобразования. Если уравнения, как это часто бывает на практике, были
сразу заданы в виде C6.1), то для приведения их к виду D2.1)
достаточно в качестве новых переменных принять величины x-\-iy
к х — iy.
Если уравнения движения приведены к виду D2.1), то перемен-
переменные хну будут комплексно сопряженными, и поэтому второе из
этих уравнений может быть получено из первого заменой I на — /,
х на у и у на х.
Для решения задачи устойчивости введем в уравнения D2.1)
вместо переменных хну переменные и и v при помощи подста-
подстановки
х^и-^х^Ци, v)-\-xW(u
y = v-\-yW(u, г>) + уC) (и, г>)
где лсМ и у№— некоторые формы у-го порядка, которыми мы по-
• стараемся распорядиться таким образом, чтобы уравнения для и и v
приняли вид
D2.3)
') М а л к и н И. Г., О решении задачи устойчивости в критическом
случае пары чисто мнимых корней. ПММ, т. XV, вып. 2, 1951.
2) М а л к и н И. Г., Об одйом способе решения задачи устойчивости
в критическом случае пары чисто мнимых корней, ПММ, т. XV, выгг. 4,
1951.
§ 42] ДРУГОЙ СПОСОБ РЕШЕНИЯ ЗАДАЧИ 171
Здесь_Л;- и Aj — некоторые подлежащие определению постоянные,
причем Aj комплексно сопряжены с Aj. При таком условии второе
уравнение D2.3) получится из первого заменой i на —I, и на v и
v на и, вследствие чего переменные и и v будут также комплексно
сопряженными.
Подставляя в уравнения D2.1) вместо х и у их выражения D2.2)
и принимая во внимание D2.3), получим:
v+
Приравнивая в обеих частях совокупности членов одинаковых
порядков, получим для нахождения форм xW> и уМ следующие урав-
уравнения:
D2.4)
Здесь Aj при у четном равно нулю и X{J\u, v), YW>(u, v) —
формы у'-го порядка, зависящие от форм Л" и К и постоянных
Аь, для которых Ъ < у. Уравнения D2.4) дают возможность без всяких
вычислений последовательно определять как формы х^ и yW), так и
постоянные Aj.
В самом деле, допустим, что все формы х&\ y(ft) и постоянные
Аь, для которых b<ij, уже определены. Тогда Х^ (и, v) будет
известной формой. Пусть
j P+Q=J
где Лр —известные коэффициенты, а ар? — подлежащие определению.
Тогда, приравнивая в первом уравнении D2.4) коэффициенты при
ufv4, получим, что при у четном коэффициент apq определяется по
172 ИССЛЕДОВАНИЕ КРИТИЧЕСКИХ СЛУЧАЕВ [ГЛ. IV
формуле
pq = Apq. D2.5)
Той же формулой определяются коэффициенты и при нечетном j, за
исключением коэффициента apq, для которого p=-^(j-\-\), ц=-^-{]—1).
Для этого коэффициента получается уравнение
U-\-i). <l = \U—l))- D2.6)
Следовательно, коэффициент apq, для которого p = -j(j~\-l),
q = -y(j—1), остается произвольным. Мы положим его равным
нулю. Вместе с тем уравнение D2.6) однозначно определяет вели-
величину Aj, для которой находим:
1) D2.7)
Точно таким же путем определяются коэффициенты форм уО'>.
Однако ни в вычислении этих коэффициентов, ни в составлении для
них уравнений нет необходимости, так как в силу сопряженности
переменных х, у, а также переменных и и V, мы можем сразу
писать:
yu) = 2 vv.
p+«=j
Таким путем можно подсчитать любое число форм xW> и yU), a
также постоянных Aj. Вычисления нужно производить до тех пор,
пока мы не придем к постоянной Aj с отличной от нуля веще-
вещественной частью. Дело в том, что знаком этой вещественной части и
решается задача устойчивости.
В самом деле, пусть Ak — первая из постоянных Л3, А5
вещественная часть которой отлична от нуля, так что
А3 = 1ВЛ. А5 = 1ВЬ, ..., Ак_2 = iBk_2, Ak = g + iBk, D2.8)
где постоянные Въ, ..., Bk, g вещественны. Покажем, что при
g > 0 невозмущенное движение неустойчиво, а при g < 0 оно устой-
устойчиво асимптотически. Преобразуем с этой целью уравнения D2.3)
при помощи подстановки
и = г (cos Ф-f-isind), v = r (cos ft — / sin &).
Будем иметь:
—^ (cos Ь + / sin Щ + / (cos Ь + i sin *) г -Ц- =
sinд) + Л3
§ 42] ДРУГОЙ СПОСОБ РЕШЕНИЯ ЗАДАЧИ 173
где ненаписанные члены имеют порядок, больший k. При этом мы
предполагаем, что в подстановке D2.2) ряды оборваны на членах
А-го порядка. Выделяя в полученном уравнении вещественные и
мнимые части, найдем:
JL
-\-Вкг*+ ... D2.9)
Все сделанные нами преобразования таковы, что задача устойчи-
устойчивости для исходных уравнений эквивалентна той же задаче для
уравнений D2.9). Что же касается последней задачи, то она, очевидно,
решается знаком величины g. Таким образом, наше предложение
доказано.
Если бы Re (Ak) = 0 при любом k, то это свидетельствовало бы
о том, что задача устойчивости не решается конечным числом чле-
членов. В этом случае начало координат было бы центром, невозмущен-
невозмущенное движение было бы устойчиво, но не асимптотически.
Приведенный способ решения задачи устойчивости требует только
составления уравнения D2.4) для последовательных приближений. Это
может оказаться утомительным, если задача устойчивости решается
членами высоких порядков. Однако такие выкладки приходится делать
при любом способе решения задачи, после чего в других способах
приходится либо вычислять громоздкие квадратуры (метод § 36),
либо разрешать сложные системы линейных алгебраических уравнений
(метод § 37).
Рассмотрим теперь систему (я-)-2)-го порядка. Уравнения возму-
возмущенного движения берем не в форме D0.1), как в предыдущем пара-
параграфе, а в форме
?L
у, хх хп),
D2.10)
¦ • • > хп)'
(s=l, 2, .... я).
Для решения задачи устойчивости мы можем теперь воспользо-
воспользоваться изложенным в предыдущем параграфе методом Ляпунова
и привести систему D2.10) к системе второго порядка. Для этого
нужно будет взять только первые два уравнения D2.10) и заменить
в них величины xs формальными решениями vs(x, у) уравнений
с частными производными D1.9). При этом, вследствие того что урав-
уравнения возмущённого движения взяты в виде D2.10), а не в виде D0.1),
вычисления значительно упрощаются.
174 ИССЛЕДОВАНИЕ КРИТИЧЕСКИХ СЛУЧАЕВ [ГЛ. I
В самом деле, уравнения D1.9) принимают сейчас вид
и вследствие этого уравнения D1.8), определяющие формы vs (x, у),
имеют теперь вид
Если в этих уравнениях положить:
p+q = k p+q = tt
где B(pl— известные, a bp^— подлежащие определению коэффициенты,
то будем иметь:
¦•+[Pss (Р ч) 1Ц bfa +...+ Pjfq + B = о
(s=l, 2 re).
Таким образом, для определения коэффициентов bps] мы получаем
не систему из n(k-\-\) уравнений, как это было бы, если бы мы
пользовались уравнениями D0.1), а А-f-l самостоятельных систем,
состоящих из ге уравнений каждая. Это, разумеется, вносит суще-
существенные упрощения в вычисления. Но этим дело не ограничивается.
Если пользоваться уравнениями в форме D0.1), то определители
систем n(k— 1)-го порядка, определяющих коэффициенты Ь$, будут
разными для форм разных порядков, т. е. они будут зависеть от
индекса k. Если же пользоваться уравнениями D2.10), то придется
все время решать системы одного и того же порядка п, определители
которых отличаются лишь диагональными членами. И если
является решением уравнений
РлС, + .. . + (р„ — /ц) С, + ... + PsnCn + в, = 0. D2.11)
выраженным явно через ц, то для формы vf> любого порядка k
можно сразу писать:
; = 1 p+q-k
Таким образом, для нахождения всех форм vf> достаточно раз-
разрешить лишь одну систему re-го порядка D2.11), т. е. вычислить
§ 42]
определитель
ДРУГОЙ СПОСОБ РЕШЕНИЯ
fi) =
Рп —
Pix
? Рп
р22 — гц
ЗАДАЧИ
Ры
Pin
175
Рп\ Pni •¦• Рпп — ?
и его миноры.
Отметим в заключение, что изложенный сейчас метод можно
видоизменить таким образом, что можно будет сразу исходить из
системы C5.1), не приводя ее предварительно к виду D2.10), т. е.
не выделяя критических корней. Мы не останавливаемся, однако, на
этом вопросе, отсылая интересующихся к уже цитированной работе1).
Пример. Рассмотрим снова уравнение
исследованное уже в § 36. Здесь F — аналитическая функция своих
аргументов, разложение которой не имеет членов ниже второго
порядка относительно х и -?•. Полагая 1-х — l-jr> Ц = х~\-1~,
получим систему
dt
где F* — вещественная функция.
Делая подстановку
будем на основании D2.3) иметь:
-iF4% I).
¦¦¦):
Отсюда сразу видно, что все формы |B), ..., |Bл) получатся
вещественными, а все числа Л3, А5 ^2я-1—чисто мнимыми.
То же самое будет справедливо для форм |(ft) и чисел А% при
') См. сноску2) на стр. 170,
176 ИССЛЕДОВАНИЕ КРИТИЧЕСКИХ СЛУЧАЕВ [ГЛ. IV
любом k, если только а = 0. Поэтому при а = 0 будем иметь
устойчивость, но не асимптотическую.
Допустим, что а =? 0. Тогда уравнение для |B"+D будет:
где F^n+i)— вещественная форма Bre-f-l)-ro порядка. Приравнивая
коэффициент при un+ivn, найдем:
\_4 _ Bв+1Jв ...(д., .,
!л + У — л2я + 1— 22л + 1.Л!
Следовательно, при а > 0 невозмущенное движение неустойчиво,
а при а < 0 оно устойчиво асимптотически.
§ 43. Особенный случай.
Мы переходим теперь к рассмотрению особенного случая. Пусть
*—7т- = — ку-\-Х(х, у, Xi, ..., х„),
at
"(х, у.
=1, 2 п)
D3.1)
суть дифференциальные уравнения возмущенного движения. Следуя
установленному правилу решения задачи устойчивости, составляем
уравнения с частными производными
(-Ху+Х(х, у, v, „„»*? + (**+К(*. y,Vl vn))^ =
= Psivi + • • • + PvFn + Psx + Я*У + xs (x, у, ^ vn). D3.2)
Этим уравнениям можно удовлетворить формальными рядами
vs (х, у) = г>0> (х, у) + vf) (х, у) + ... D3.3)
Ограничившись в этих рядах членами (т — 1)-го порядка, заменим
полученными таким образом целыми рациональными функциями vs(x, у)
величины jcf в первых двух уравнениях D3.1) и рассмотрим систему
§ 43] ОСОБЕННЫЙ СЛУЧАЙ 177
второго порядка:
-JL = — Xy-{-X(x, у, ©,. .... vn),
V, V,, .... V )
Может оказаться, что при т достаточно большом задача устой-
устойчивости для системы D3.4) решается членами не выше от-го по-
порядка. Это будет общий случай, рассмотренный выше. В этом случае
задача устойчивости для системы D3.1) решается системой D3.4).
Но может случиться, что как бы велико ни было число т
и, следовательно, как бы велико ни было число членов, взятых
в рядах D3.3), задача устойчивости для системы D3.4) не решается
членами порядка, не превосходящего т, т. е. что, изменив в этих
уравнениях члены выше т-го порядка, можно получить по желанию
как устойчивость, так и неустойчивость. Этот случай и является
особенным. В особенном случае правило решения задачи устойчивости,
установленное в § 41, неприменимо.
Однако, как мы сейчас покажем, и в особенном случае задача
устойчивости для системы D3.1) эквивалентна задаче устойчивости
для системы второго порядка D3.4). При этом предполагается, что
в уравнениях D3.4) функции vs(x, у) обозначают не конечное число
первых членов в рядах D3.3), а эти ряды целиком. Но тогда, оче-
очевидно, эти уравнения лишь тогда имеют смысл, когда указанные ряды
сходятся. Будут ли эти ряды действительно сходиться?
Вопрос о сходимости рядов D3.3) разрешен А. М. Ляпуновым.
Он показал, что эти ряды могут быть расходящимися. Об этом сви-
свидетельствует уравнение
для которого формальный ряд D3.3) имеет вид
Этот ряд, очевидно, расходится.
Отсюда, однако, не следует, что ряды D3.3) всегда расходятся.
Напротив, Ляпунов показал, что когда мы имеем дело с особенным
случаем, то ряды D3.3) будут обязательно получаться сходящимися.
Это замечательное предложение Ляпунова мы здесь приводим без
доказательства.
На основании предложения Ляпунова уравнения D3.4) будут
вполне определенными. И так как для них задача устойчивости не
решается конечным числом членов, то на основании результатов
§§ 36—38, точка х = у = 0 для уравнений D3.4) будет центром.
Невозмущенное движение для уравнений D3.4) будет при этом
178 ИССЛЕДОВАНИЕ КРИТИЧЕСКИХ СЛУЧАЕВ [ГЛ. IV
устойчивым (не асимптотически), а их общее решение будет перио-
периодическим.
Это периодическое решение может быть представлено в виде
= с cos
D3.5)
где x(i) (т), y(ft> (т.)— периодические функции т периода 2л, обра-
обращающиеся в нуль при т = 0, hj — некоторые вполне определенные
постоянные, ас — произвольная постоянная, являющаяся начальным
значением величины х. Все фигурирующие в D3.5) ряды сходятся
при достаточно малом с.
Аналогичные обстоятельства имеют место в особенном случае и
для полной системы D3.1), а именно: эта система также допускает
периодическое решение, зависящее от одного произвольного постоян-
постоянного *), являющегося начальным значением величины х, и невозмущен-
невозмущенное движение х = у = х1= ... = х„ = 0 для этой системы также
устойчиво. При этом в указанном периодическом решении величины
хну определяются формулами D3.5), а для величин х^ будем
иметь:
xs = vt(x. у) (s=l. 2, .... в). D3.6)
где vs(x, у) — функции D3.3).
Для доказательства заметим прежде всего, что если функции
x^x(t), у — у (t) являются каким-нибудь частным решением уравне-
уравнений D3.4), то функции x = x(t), y = y(t), xs = vs[x(f), у(t)] опре-
определяют частное решение уравнений D3.1). Действительно, подставляя
эти функции в уравнения D3.1), мы на основании D3.2) и D3.4)
убедимся, что они тождественно удовлетворяются. Отсюда непосред-
непосредственно вытекает, что уравнения D3.1) обладают периодическим реше-
решением, определяемым формулами D3.5) и D3.6).
Покажем теперь, что для полной системы D3.1) имеет место
устойчивость. С этой целью введем в этой системе вместо перемен-
переменных х, у, xs переменные р, ф, ls при помощи подстановки
лг=рсо8ф4-р2л;B) (ф)+ ••-.
f-..., D3.7)
У)-
') Заменив в этом решении t на t-\-h, где h — произвольное постоян-
постоянное, мы получим периодическое решение, зависящее от двух произвольных
постоянных.
§ 43) Особенный случай
Тогда первые два уравнения D3.1) примут вид
dx{2)
179
[slnq>+2py<2)(<P)
= /г2<р. ф, у,
D3.8)
где /?i, /?2—аналитические функции переменных р, \х |л, раз-
разложения которых не содержат свободных членов. Коэффициенты этих
разложений являются периодическими функциями ф периода 2л.
Разрешим уравнения D3.8) относительно J ир^. Определитель А
этих линейных относительно указанных величин уравнений имеет вид
2зтфу<2>(ф)]+Р2(-.-)+ ....
откуда вытекает, что величина -г- будет аналитической функцией р,
разложение которой по степеням этой переменной имеет периодиче-
периодические относительно ф коэффициенты. Следовательно, имеем:
D3.9)
где /) и Ф — функции такого же вида, как и Rx, R2, т. е. аналити-
аналитические относительно р и ls, периодические относительно ф и обра-
обращающиеся в нуль при p=r?j= ... =|л = 0.
Последние п уравнений D3.1) после подстановки D3.7) примут
вид
%- = P,iii-b-.-+/'«6» + />,(T)P + S,(p, ф. \х ln), D3.10)
где Ps (ф) — некоторые периодические функции ф периода 2я,
a Es — аналитические функции переменных р, \х \п, разложения
которых начинаются членами не ниже второго порядка. Коэффициенты
этих разложений являются периодическими функциями ф периода 2я.
Периодическое решение D3.5) и D3.6) уравнений D3.1) в пере-
переменных р, ф, |^ принимает, очевидно, вид
р=с> ф = т. g, = 0 (s=I, 2 я). D3.11)
180 ИССЛЕДОВАНИЕ КРИТИЧЕСКИХ СЛУЧАЕВ [ГЛ. IV
Следовательно, уравнения D3.9) и D3.10) имеют частное реше-
решение D3.11), а для этого, очевидно, необходимо, чтобы выполнялись
равенства
Ps(ф) = 0, Rip, ф, 0 0) = 3S(р, ф, 0 0) = 0
0?=1, 2 п).
Но в таком случае система (п-\-1)-го порядка, состоящая из пер-
первого уравнения D3.9) и уравнений D3.10), в которых т является
некоторой неизвестной функцией времени, является частным случаем
систем C4.2), рассмотренных нами в § 34. Согласно результатам
этого параграфа невозмущенное движение р = ?,г == ... = |л = 0
вышеуказанной системы (п-\-\)-то порядка устойчиво. Но тогда по
характеру подстановки D3.7) устойчивым будет и невозмущенное
движение x = y — xl = ... = хп — 0 системы D3.1).
Итак, мы показали, что в особенном случае невозмущенное дви-
движение устойчиво и уравнения возмущенного движения допускают пе-
периодическое решение, определяемое формулами D3.5) и D3.6).
Таким образом, задача устойчивости в особенном случае решается
просто. Но, к сожалению, у нас нет общего приема, который по-
позволил бы нам заранее узнать, что рассматриваемый случай является
особенным. В самом деле, если мы имеем особенный случай, то
сколько бы членов в уравнениях D3.4) мы ни рассмотрели, у нас не
будет уверенности, что, рассмотрев члены еще более высокого по-
порядка, мы не придем к случаю фокуса.
Можно, однако, указать один общий признак, при выполнении
которого можно не сомневаться, что рассматриваемый случай будет
особенным.
Допустим, что уравнения D3.1) допускают первый интеграл вида
x2_|_y2_|_/7(Xi y> Xi *„)== const., D3.12)
где F — аналитическая функция переменных х, у, xs, разложение
которой начинается членами не ниже третьего порядка. Покажем, что
если это выполняется, то рассматриваемый случай будет особенным.
В самом деле, заменив в интеграле D3.12) величины xs рядами
D3.3), которые дают, по крайней мере, формальное решение системы
D3.2), мы получим ряд, который, по крайней мере, формально
является первым интегралом системы D3.4), т. е. все члены ряда
где
Н = х* + у* + F(x, у, «,(*. у) vn(x, у))
уничтожаются. Но в таком случае для системы D3.4), как это выте-
вытекает из рассуждений § 37, точка х = у = 0 является центром, что
и доказывает наше предложение.
§ 44} «ОПАСНЫЕ» И «БЕЗОПАСНЫЕ» ГРАНИЦЫ ОБЛАСТИ УСТОЙЧИВОСТИ 181
А. М. Ляпунов показал, что справедливо и обратное предложение,
т. е. что в особенном случае система D3.1) необходимо имеет пер-
первый интеграл вида D3.12).
А. М. Ляпунов далее показал, что если уравнения D3.1) имеют
первый интеграл вида D3.12), то эти уравнения обладают периодиче-
периодическим решением, определяемым формулами D3.5), D3.6), вне зависи-
зависимости от того, будут ли вещественные части корней уравнения D0.2)
отрицательными или нет. Важно только, чтобы ни один из этих корней
не был вида + ЛШ, где ./V — целое положительное число или нуль.
Указанные периодические решения играют большую роль в теории
нелинейных колебаний. Мы не останавливаемся здесь на этом вопросе,
отсылая читателей к нашей книге1), где он подробно освещен.
§ 44. «Опасные» и «безопасные» границы
области устойчивости.
В заключение этой главы рассмотрим вопрос о так называемых
«опасных» и «безопасных» границах области устойчивости. Этот во-
вопрос непосредственно связан с тем понятием «практической» устой-
устойчивости, о котором мы говорили в § 4.
Пусть
^ = 9siXi + ---+q,«Xn + Xs(*i хп) (s=l,2 п) D4.1)
— дифференциальные уравнения возмущенного движения, где, как и
обычно, разложения функций Xs начинаются членами не ниже вто-
второго порядка. Рассмотрим неравенства
Re(p,)<0 (s=\, 2 я). D4.2)
где р1 р„ — корни характеристического уравнения системы пер-
первого приближения. Эти корни являются функциями некоторых пара-
параметров, характеризующих рассматриваемую динамическую систему.
Если рассматривать пространство этих параметров, то неравенства
D4.2) определяют в этом пространстве некоторую область. Это будет
область устойчивости системы по отношению к исследуемому невоз-
невозмущенному движению, так как при выполнении D4.2) невозмущен-
невозмущенное движение будет асимптотически устойчиво. Напротив, совокуп-
совокупность всех точек пространства параметров, в которых хотя бы один
'из корней ps имеет положительную вещественную часть, определяет
область неустойчивости.
Границей, отделяющей область устойчивости от области неустой-
неустойчивости, является совокупность всех тех точек пространства пара-
параметров, в которых хотя бы одно из неравенств D4.2) переходит
') М а л к и н И. Г., Некоторые задачи теории нелинейных колебаний,
Гостехиздат, 1956.
182 ИССЛЕДОВАНИЕ КРИТИЧЕСКИХ СЛУЧАЕВ [гл. IV
в равенство, т. е. на границе хотя бы некоторые корни о, являются
критическими. При значениях параметров, соответствующих точкам
границы, невозмущенное движение может быть как устойчивым, так
и неустойчивым в зависимости от вида функций Xs.
Допустим, что параметры системы лежат в области устойчивости,
так что вещественные части всех корней р^ отрицательны. Невозму-
Невозмущенное движение будет асимптотически устойчиво. При этом, если
все функции Xs обращаются в нуль, то устойчивость будет иметь
место, каковы бы ни были начальные возмущения. Но если хотя бы
некоторые из функций Xs отличны от нуля, то устойчивость будет
иметь место, вообще говоря, при начальных возмущениях, не превы-
превышающих некоторых пределов. В § 26 мы указали некоторые приемы,
позволяющие оценить эти весьма важные для практики величины. Из
рассуждений этого параграфа легко усмотреть, что если величины
вещественных частей хотя бы некоторых из корней численно малы,
другими словами, если система находится вблизи границы области
устойчивости, то максимальные значения допускаемых начальных воз-
возмущений могут оказаться очень малыми. В справедливости этого мы
сейчас убедимся и из других соображений. Если такое обстоятель-
обстоятельство действительно имеет место, то рассматриваемую систему с точки
зрения практической придется рассматривать как неустойчивую.
Аналогичные обстоятельства могут иметь место и в случае, когда
система находится в области неустойчивости, но очень близко от
границы. В этом случае, несмотря на то, что невозмущенное движе-
движение неустойчиво по Ляпунову, его иногда с точки зрения практиче-
практической можно будет считать устойчивым, вследствие того что макси-
максимальные отклонения системы от невозмущенного движения могут ока-
оказаться очень малыми.
С такого рода практической устойчивостью, несмотря на неустой-
неустойчивость по Ляпунову, мы встретились в § 4 на примере уравнения
dx 2 з
Корень характеристического уравнения первого приближения равен
здесь а2 и, следовательно, положителен. Невозмущенное движение
неустойчиво по Ляпунову. Однако, каково бы ни было начальное
значение величины х, эта величина, как было показано в § 4, с не-
неограниченным возрастанием t стремится либо к -|-а, либо к —а,
т. е. практически к положению равновесия х = 0, если а очень мало.
Напротив, если уравнение движения имеет вид
dx o,i
то корень характеристического уравнения будет отрицателен и невоз-
невозмущенное движение будет асимптотически устойчиво по Ляпунову.
§ 44] «ОПАСНЫЕ» И «БЕЗОПАСНЫЕ» ГРАНИЦЫ ОБЛАСТИ УСТОЙЧИВОСТИ 183
Однако если величина а очень мала, то с точки зрения практиче-
практической это движение нужно будет считать неустойчивым, так как
Пгпх== +со, если начальное значение х численно больше а. В этом
сразу убеждаемся, если заметим, что при \х\ >а справедливо нера-
dx . г,
венство х -д? > 0.
Таким образом, возникает практически важный вопрос о поведе-
поведении динамической системы вблизи границ области устойчивости. Этот
вопрос исследован Н. Н. Баутиным'), который рассматривал лишь
такие участки границы области устойчивости, на которых либо только
один корень, либо только два корня являются критическими, причем
во втором случае предполагается, что оба корня отличны от нуля и,
следовательно, являются чисто мнимыми. В первом случае, когда
имеется один критический корень, он, очевидно, обращается в нуль.
Н. Н. Баутин показал, что в этих случаях поведение динамической
системы вблизи границы области устойчивости определяется их пове-
поведением на самой границе.
В обоих рассматриваемых случаях дифференциальные уравнения
возмущенного движения могут быть представлены в виде
dx
-WT = РЛХ1 + ¦¦¦+ Psn^n + М- (ГлХг + . . • + ГзпХ,
(s = l, 2 га).
Xs
D4.3)
Здесь psa и r5a — некоторые постоянные, причем psa такие, что
¦уравнение
Р\п
D4.4)
Рт
Pni
— Р
= 0
имеет либо один нулевой корень, либо пару чисто мнимых корней
при остальных корнях с отрицательными вещественными частями.
Величина [л является малым параметром, характеризующим степень
близости системы к границе области устойчивости. Этот параметр
предполагается настолько малым, что характеристическое уравнение
— Р Р\2
Pnl +
nn— p
= 0
') Баутин Н. Н., Поведение динамических систем вблизи границ об-
области устойчивости, Гостехиздат, 1950. К рассматриваемому вопросу примы-
примыкает также работа: К у з ь м и н П. А., Замечание о смене устойчивости уста-
установившихся движений, Сборник трудов Казанского авиац. ин-та, № 10, 1939.
184 ИССЛЕДОВАНИЕ КРИТИЧЕСКИХ СЛУЧАЕВ [ГЛ. IV
имеет столько же корней с отрицательными вещественными частями,
как и уравнение D4.4), т. е. либо п — 1, либо п — 2. Остальные
корни этого уравнения могут иметь как отрицательные, так и поло-
положительные вещественные части, т. е. система D4.3) может находиться
как в области устойчивости, так и в области неустойчивости.
Допустим сначала, что на границе рассматриваемая система асим-
асимптотически устойчива. Другими словами, допустим, что невозмущен-
невозмущенное движение для системы
4r = /»»i*i + • • • + />«*« + Х* D4-5)
асимптотически устойчиво. Тогда, как мы видели, будем ли мы иметь
дело с одним нулевым корнем или с парой чисто мнимых корней,
для уравнений D4.5) будет существовать функция Ляпунова, удовле-
удовлетворяющая условиям теоремы Б. Обозначим эту функцию через
V(xv .... хп). Предполагая для определенности, что эта функция
положительная, будем иметь, что выражение
Ps\xx H~ ••• H~ PSnxn ~Ь Xs) -з— D4.6)
,= i
представляет собой функцию определенно отрицательную. Восполь-
Воспользуемся геометрической интерпретацией теоремы Б, данной в § 11.
Рассмотрим систему замкнутых поверхностей V = A. Поверхности
этого семейства, расположенные достаточно близко от начала коор-
координат, пересекаются интегральными кривыми уравнений D4.5) сна-
снаружи во внутрь. Пусть V = A[ и V — й2— две такого рода поверх-
поверхности. При этом первую из этих поверхностей, которую мы пред-
предполагаем расположенной внутри второй (рис. 10), мы можем взять
сколь угодно близкой к началу координат. Напротив, вторую поверх-
поверхность мы можем взять сколь угодно близкой к наибольшей из поверх-
поверхностей семейства, которая еще пересекается интегральными кривыми
уравнений D4.5) во внутрь.
Составим теперь производную от функции V по t в силу уравне-
уравнений D4.3). Будем иметь:
п
4j- = W + ц V (rslXl + ... + rsnxn) ?L. D4.7)
*=i s
Так как функция W является определенно-отрицательной, то для
всех точек, расположенных между поверхностями V = hx и V = k2,
выполняется неравенство W < — /, где / — отличное от нуля поло-
положительное число. Отсюда следует, что во всех этих точках выраже-
выражение D4.7) будет принимать отрицательные значения, если только
число \i достаточно мало. Следовательно, при достаточно малом ц
§ 44] «ОПАСНЫЕ» И «БЕЗОПАСНЫЕ» ГРАНИЦЫ ОБЛАСТИ УСТОЙЧИВОСТИ 185
все поверхности V = h, расположенные между V=hy и V — h2, пере-
пересекаются интегральными кривыми полной системы D4.3) снаружи во
внутрь. И это будет иметь место независимо от того, находится ли
система D4.3) в области неустойчивости или в области устойчивости.
Следовательно, если точка хх хп, изображающая систему D4.3),
попадает в область между поверхностями V = hl и V = h2, то она
будет приближаться к началу координат, по крайней мере, до области,
ограниченной поверхностью V = hx. Эта область, однако, может быть
сделана сколь угодно малой, если ц достаточно мало, т. е. если
система находится достаточно близко от границы области устойчи-
устойчивости. И если даже при этом система находится в области неустой-
неустойчивости, мы можем все же считать, что невозмущенное движение
практически устойчиво, так как возмущения, будучи в начальный
момент очень малыми, хотя и будут нарастать, все же останутся
практически очень малыми (сколь угодно малыми при ц, достаточно
малом). Более того, если начальные возмущения не будут очень
малыми, то они будут уменьшаться, делаясь в конце концов очень
малыми (сколь угодно малыми
при М-, достаточно малом).
И лишь только когда началь-
начальные возмущения достаточно
велики и выходят за область,
ограниченную поверхностью
V = /г2, они могут в дальней-
дальнейшем не уменьшаться.
Если система находится в
области устойчивости, то мо-
можно показать, что функцию V
можно выбрать таким образом,
чтобы не только выражение
D4.6), но и выражение D4.7)
V=Af
Рис. 10.
было определенно-отрицатель-
определенно-отрицательным '). Следовательно, можно положить h1 = 0. Невозмущенное
движение будет асимптотически устойчивым, причем для допускаемых
возмущений будут существовать определенные конечные границы,
не зависящие от \л, т. е. от степени близости системы к границе
области устойчивости.
Таким образом, если на границе области устойчивости система
асимптотически устойчива, то вблизи этой границы устойчивость,
') Построенные нами функции Ляпунова для случая одного нулевого
корня и для случая пары чисто мнимых корней останутся функциями Ляпу-
Ляпунова для системы, которая получится, если, непрерывно меняя коэффициенты
первого приближения, сделать вещественные части всех корней характери-
характеристического уравнения отрицательными. Для этого нужно будет только под-
подходящим образом выбрать независимые переменные.
186
ИССЛЕДОВАНИЕ КРИТИЧЕСКИХ СЛУЧАЕВ
[ГЛ. IV
V=0
если она имеет место, не может перейти в «практическую» неустой-
неустойчивость. Напротив, неустойчивость, если она имеет место, может
рассматриваться с точки зрения практической как устойчивость.
Вышеприведенные геометрические соображения могут быть дока-
доказаны строго аналитически. Мы это сделаем в главе VI, где они полу-
получатся как частный случай более общей теоремы. Там же будет пока-
показано, что все вышеуказанное будет справедливо и в общем случае,
когда на границе области устойчивости имеется любое число крити-
критических корней.
Допустим теперь, что на рассматриваемом участке границы области
устойчивости невозмущекное движение неустойчиво. Тогда как в слу-
случае олного н) левого корня, так и в случае пары чисто мнимых кор-
корней для уравнений D4.5) будет существовать функция Ляпунова
V(Xj, ..., хп), удовлетворяющая условиям теоремы В. Следова-
Следовательно, выражение D4.6) будет по-прежнему знакоопределенным.
Что же касается самой функции V, то она в окрестности начала
координат может принимать значения того же знака, что и D4.6).
Примем для определенности, что
выражение D4.6) определенно-поло-
определенно-положительно, и рассмотрим область,
в которой V>0 (рис. 11). Эта
область ограничена поверхностью
V = 0. Построим в этой области се-
семейство поверхностей V = /z, где
h > 0. Так как производная D4.6)
положительна, то эти поверхности
пересекаются интегральными кри-
кривыми уравнений D4.5) в сторону
возрастания V.
Выделим из семейства V = h
две поверхности V = hx и V = h2,
где hx можно взять сколь угодно
малым, так что поверхность V = hl
сколь угодно близка к поверхно-
поверхности V — Q. Так как функция D4.6)
определенно-положительна, то в области, заключенной между поверх-
поверхностями V — А, и V = й2, она имеет отличный от нуля положитель-
положительный нижний предел '). Но тогда в этой области производная D4.7)
будет также положительной, если только величина (х достаточно
мала. Следовательно, все поверхности V — h, заключенные между
поверхностями V = /Zj и V = й2, пересекаются интегральными кри-
V=0
рис. л.
') Мы рассматриваем, разумеется, во всех наших рассуждениях только
те точки, которые лежат в некоторой окрестности начала координат, в кото-
которой функция V обладает своими свойствами.
§ 44] «ОПАСНЫЕ» И «БЕЗОПАСНЫЕ» ГРАНИЦЫ ОБЛАСТИ УСТОЙЧИВОСТИ 187
выми не только уравнений D4.5), но и уравнений D4.3) в сторону
возрастания V. Поэтому изображающая точка, попав в область
между поверхностями V = hx и V = h2, будет все дальше отбрасы-
отбрасываться от начала координат, пока она не выйдет за пределы поверх-
поверхности V ¦¦= h2, расположенной на конечном расстоянии от начала
координат. Очевидно, мы имеем дело с неустойчивостью, по крайней
мере, с точки зрения практической. В самом деле, если даже не-
невозмущенное движение устойчиво, что будет иметь место, если
система D4.3) находится в области устойчивости, то область допу-
допускаемых начальных возмущений должна быть во всяком случае
настолько малой, чтобы поверхность V=Нг была расположена вне ее.
Что касается последней, то она при (х, достаточно малом, т. е. при
достаточной близости системы к границе области устойчивости,
будет расположена сколь угодно близко к началу координат.
Итак, когда на границе области устойчивости невозмущенное
движение неустойчиво, то если система находится вблизи указанной
границы, безразлично, в области неустойчивости или в области устой-
устойчивости, всегда найдутся очень малые (сколь угодно малые при
достаточной близости к границе) начальные возмущения, которые
будут с течением времени нарастать так, что соответствующее воз-
возмущенное движение будет значительно отличаться от невозмущенного.
Все предыдущие рассуждения показывают, что невозмущенное
движение системы при близости к границе области устойчивости
будет с точки зрения практической устойчивым или неустойчивым,
в зависимости от того, будет ли это движение на самой границе
устойчивым или неустойчивым в смысле Ляпунова.
В связи с этим те границы области устойчивости, на которых
невозмущенное движение устойчиво, называют «безопасными», а те
границы, на которых оно неустойчиво, — «опасными». Нахождение
«опасных» и «безопасных» границ сводится к решению задачи устой-
устойчивости в критических случаях.
Пример. Рассмотрим в качестве примера систему дифферен-
дифференциальных уравнений
описывающих при некоторых упрощающих предположениях движение
самолета с автопилотом. Не останавливаясь на выводе этих уравне-
уравнений 1), укажем лишь значения входящих в эти уравнения величин.
') Его можно найти, например, в работе: Б у тени н Н. В., Автоколеба-
Автоколебания стенда с автопилотом. Труды Ленингр. воен.-возд. акад., т. 3, 1943.
188 ИССЛЕДОВАНИЕ КРИТИЧЕСКИХ СЛУЧАЕВ [ГЛ. IV
Эти значения суть следующие: ф — угол рыскания самолета. г\ — угол
поворота руля, я|) — аргумент сервомотора (например, открытие золот-
золотника), управляющего рулем, F(ty) — характеристика сервомотора. Все
постоянные М, k, N, р, а положительны. При этом М характеризует
естественное демпфирование самолета, N характеризует рулевое
устройство, k характеризует статическую устойчивость самолета,
р — коэффициент искусственного демпфирования, коэффициент
обратной связи.
Характеристику сервомотора примем в виде
Тогда, вводя переменные
мы будем иметь следующие уравнения движения:
dxt _
dt ~
dx2
dt 3>
Av.
— kx2 — Mx3,
Характеристическое уравнение системы первого приближения имеет
вид
Л(Р)=Р3+/>Р2 + ?р+г = 0, D4.9)
где
р = ± + М. q = k+^ + Na$, r^=^- + Na. D4.10)
Для того чтобы это уравнение имело корни с отрицательными
вещественными частями, необходимо и достаточно, чтобы выполня-
выполнялись неравенства B5.2) Гурвица:
р>0, q>0, r>0, R = pq — r>0. D4.11)
Эти неравенства определяют область устойчивости. На границе
этой области хотя бы одно из неравенств D4.11) обращается в равен-
равенство. Из D4.10) видно, что это возможно лишь для последнего из
указанных неравенств. Таким образом, граница области устойчивости
определяется уравнением
R = pq—r = 0. D4.12)
При выполнении этого условия уравнение D4.9) имеет, как легко
видеть, пару чисто мнимых корней ± I Yq- Следовательно, чтобы
выделить «опасные» и «безопасные» участки границы, необходимо
§ 44] «ОПАСНЫЕ» И «БЕЗОПАСНЫЕ» ГРАНИЦЫ ОБЛАСТИ УСТОЙЧИВОСТИ 1 89
решить задачу устойчивости для системы D4.8) в критическом слу-
случае пары чисто мнимых корней.
Уравнения D4.8) представляют частный случай уравнений D2.11),
рассмотренных А. И. Лурье (§ 41). Мы можем поэтому воспользо-
воспользоваться для определения g формулой D2.20). Так как в рассматри-
рассматриваемом случае
то указанная формула дает:
( а \ а.
Вводя безразмерные параметры
a
И — -
Na
найдем, что знак g совпадает со знаком величины
Если L < 0, то невозмущенное движение асимптотически устойчиво,
а если L > 0, то оно неустойчиво.
Для величины R = pq — г находим:
Фиксируя параметры и и о, рассмотрим плоскость параметров А
к В. Нам достаточно при этом рассматривать только первую четверть
так как А и В могут принимать
только положительные значения.
Предположим, что о — и> 0. При
этом условии кривая R — 0, огра-
ограничивающая область устойчиво-
устойчивости, имеет вид, изображенный на
рис. 12. Кривая Z. = 0 пересекает
кривую R = 0 в точке W, кото-
которая и отделяет «безопасные»
участки границы от «опасных».
в
V
При V > 0 величина L имеет отри-
отрицательные значения справа от
кривой L = 0. Поэтому при у > 0
участок границы WU является
— «опасным». При
меняются местами.
При о — к < 0
тельных А и В.
й>0
U
&
Рис. 12.
«безопасным», а участок WV —
у < 0 «опасная» и «безопасная» части границы
кривая /? = 0 не проходит в области положи-
положиГЛАВА V.
УСТОЙЧИВОСТЬ ПЕРИОДИЧЕСКИХ ДВИЖЕНИЙ.
А. ТЕОРЕМЫ ВТОРОГО МЕТОДА ДЛЯ НЕУСТАНОВИВШИХСЯ
ДВИЖЕНИЙ.
§ 45. Некоторые определения.
Периодические движения, изучению которых посвящена настоящая
глава, являются наиболее простым классом неустановившихся движе-
движений. Основным методом исследования устойчивости такого рода
движений будет по-прежнему второй метод Ляпунова. Нам нужно будет
поэтому изложить сначала основные теоремы второго метода Ляпунова
в их общей формулировке, которую они имеют для неустановившихся
движений.
Введем некоторые определения. Рассмотрим функцию V(t, xv ...
..., хп), заданную в области
*>*0>0, |*,|<А, D5.1)
где t0 и h — постоянные. Мы будем предполагать, что функция V
обладает в указанной области непрерывными частными производными
по всем переменным и что она обращается в нуль при хх=.. .=хп=0.
Следуя Ляпунову, будем говорить, что V допускает бесконечно
малый высший предел, если для любого положительного числа Я
можно найти другое положительное число ц, такое, что при всех
значениях t, х1 хп, удовлетворяющих неравенствам
будет выполняться неравенство
\V(t, xv .... *„)
Другими словами, функция V допускает бесконечно малый высший
предел, если она стремится к нулю при 2^s-* 0 равномерно отно-
относительно t. Так, например, функция
..+*„) sin*
§ 45] НЕКОТОРЫЕ ОПРЕДЕЛЕНИЯ 191
допускает бесконечно малый высший предел, а функция
V = sin[t{x1+...+xa)]
такого предела не допускает, несмотря на то, что она ограничена.
Функция V называется знакопостоянной, если при t0 достаточно
большом и h достаточно малом она не может принимать в обла-
области D5.1) значений какого-либо определенного знака.
Таким образом, знакопостоянство для функций, зависящих от t,
определяется так же, как и для функций, не зависящих от t. Несколько
иначе обстоит дело с понятием знакоопределенности, а именно: функ-
функция V{t, xx, .... хп) называется определенно-положительной, если
она в области D5.1) при t0 достаточно большом и h достаточно
малом удовлетворяет неравенству
V it, хг *„) > W (xv .... *„), D5.2)
где W(хх, ..., хп) — не зависящая от t определенно-положительная
функция. Аналогично функция V (t, xx хп) называется опреде-
определенно-отрицательной, если она при тех же условиях удовлетворяет
неравенству
V{t. х, *„)< —И7(ж, хп).
Таким образом, необращение в нуль в области D5.1) не является
достаточным условием знакоопределенности для функций, зависящих
от t, так что, например, функция
несмотря на то, что она обращается в нуль только при хх=.. . =х„=0,
не является знакоопределенной, так как она при фиксированных
хх хп стремится к нулю при ^эо и, следовательно, для нее
не может выполняться неравенство D5,2). Напротив, функции
Vx = B + sin t) 2 xl V2 = (— 2 + sin t) 2 **
s=l s=l
будут знакоопределенными, причем первая из них будет определенно-
положительной, а вторая определенно-отрицательной, так как
(>2 2< %
Легко дать геометрическую интерпретацию знакоопределенных
функций, зависящих от t. С этой целью рассмотрим простран-
пространство переменных хх, ..., хп и построим систему поверхностей
V(t, хх, .. ., хп) = с, рассматривая t как параметр. Пусть с, — какое-
нибудь достаточно малое значение с. Тогда уравнение V=cx представит
при каждом значении t замкнутую поверхность, окружающую начало
координат. Придавая / все возможные для него значения, мы получим
192 УСТОЙЧИВОСТЬ ПЕРИОДИЧЕСКИХ ДВИЖЕНИЙ [ГЛ. V
систему поверхностей, которую мы можем рассматривать как одну
подвижную поверхность. Наряду с ней рассмотрим неподвижную по-
поверхность W (хх xn) = cv Допустим, что V — функция опреде-
определенно-положительная. Легко видеть, что поверхность V = c} при
своем движении все время остается внутри поверхности W = cv Дей-
Действительно, во всех точках, где W принимает значения Cj, функция V
на основании D5.2) принимает значения, большие или равные ср и
следовательно, все эти точки лежат вне поверхности V = с, или на ней.
Если функция V, будучи знакоопределенной, допускает еще
бесконечно малый высший предел, то поверхность V = сх при своем
движении будет все время оставаться вне некоторой достаточно малой
окрестности начала координат. Действительно, если бы указанная
поверхность в какой-нибудь момент времени пересекала сколь угодно
малую окрестность начала координат,-то это означало бы, что при
указанном значении t на этой поверхности имеются точки, для которых
выполняется неравенство
|*,!<Ц. D5.3)
где (.1 — сколь угодно малая положительная постоянная. Но так как V
допускает бесконечно малый высший предел, то она при выполне-
выполнении D5.3) и при любом значении t ^> t0 будет сколь угодно малой,
если только \л достаточно мало и, следовательно, будет меньше, чем сх.
Это и показывает, что все точки поверхности V = сх лежат вне
области D5.3), если ц достаточно мало.
§ 46. Теоремы Ляпунова об устойчивости
для неустановившихся движений.
Мы переходим теперь к изложению основных теорем второго
метода Ляпунова для неустановившихся движений.
Рассмотрим дифференциальные уравнения возмущенного движения
вида
-4?г-= *,(/. *„ .... хп) (s = 1.2 я), D6.1)
где функции Х3 определены в области
*>*» \xs\<H. D6.2)
Мы будем предполагать, что в указанной области функции Ха
являются непрерывными и удовлетворяют некоторым общим условиям,
обеспечивающим существование для уравнений D6.1) единственного
решения, удовлетворяющего заданным начальным условиям.
Первая основная теорема Ляпунова, которую мы в дальнейшем
будем называть теоремой I, может быть сформулирована следующим
образом.
§ 46] ТЕОРЕМЫ ЛЯПУНОВА ОБ УСТОЙЧИВОСТИ 193
Теорема I. Если для дифференциальных уравнений возму-
возмущенного движения D6.1) можно найти знакоопределенную функ-
функцию V(t, xx, .... хп), для которой производная по времени,
составленная в силу этих уравнений, т. е. выражение
dV dV , \л dV v
есть функция знакопостоянная, 'знака, противоположного с V,
или тождественно обращается в нуль, то невозмущенное дви-
движение устойчиво.
Доказательство. Допустим для определенности, что V —
функция положительная. Следовательно, существует такое достаточно
большое число ^0 и такое достаточно малое число h<^.H, что в области
t>t0, |*,|<А D6.4)
выполняется неравенство
V (t, хх хп) > W (*,, ....*„). D6.5)
где W—некоторая не зависящая от t определенно-положительная
функция. Кроме того, в этой же области выражение D6.3) может
принимать только отрицательные или равные нулю значения.
Пусть е — произвольное сколь угодно малое положительное число.
Мы будем предполагать, что во всяком случае е < h. Рассмотрим
совокупность всевозможных значений величин хх хп, связанных
соотношением
|х1| |дгп|}=е> D6.6)
и обозначим через I точный нижний предел функции W при этом
условии. В силу знакоопределенности W число / положительно и
отлично от нуля. В силу D6.5) имеем:
V(t, jcj *„)>' при х = г. D6.7)
Будем теперь рассматривать величины jc, как функции времени,
удовлетворяющие дифференциальным уравнениям возмущенного дви-
движения. Предположим, что начальные значения x°s этих функций при
t^=tQ выбраны согласно неравенствам
|*2|<т|. D6-8)
где ц настолько мало, что
V (*„¦*? <)<L D6-9>
В силу того, что V(t0, 0, .... 0) = 0, такой выбор числа т), оче-
очевидно, возможен. Мы будем предполагать, что число г\ во всяком
случае меньше е. Тогда неравенства
К1<е, D6.10)
194
УСТОЙЧИВОСТЬ ПЕРИОДИЧЕСКИХ ДВИЖЕНИЙ
[гл v
выполняясь в начальный момент времени, будут выполняться, по край-
крайней мере, при t — t0 достаточно малом, так как функции xs{t) изме-
изменяются с течением времени непрерывно. Покажем, что эти неравенства
будут выполняться при всех t ~> tQ. В самом деле, если бы эти нера-
неравенства когда-нибудь нарушились, то должен был бы существовать
такой момент времени t — T, для которого хотя бы одно из этих
неравенств перешло бы в равенство. Другими словами, мы имели бы
х (Г) = max {I Xi (Т) | | *„ (Г) |} = е
и, следовательно, на основании D6.7)
V(T, Xl(T)
D6.11)
С другой стороны, так как е < h, то во всем интервале времени
(t0, T) выполняются неравенства D6.4), а следовательно, во всем
V(to,x,,...,xn)=c
Область \xs\<S
этом интервале —тт-
дает:
V(T,
Это
Xl(T)
x°v
Рис. 13.
что на основании D6.9) проти-
противоречит D6.11). Таким образом,
неравенства D6.10) должны вы-
выполняться при всех t > tQ, от-
откуда и вытекает устойчивость
движения.
Доказанная теорема, так же
как и в случае установившегося
движения, допускает простое гео-
геометрическое истолкование. С этой
целью рассмотрим в пространстве
переменных хх хп область
|jcs|^e (рис. 13). Выберем с настолько малым, чтобы замкнутая по-
поверхность W (хх хп) = с целиком лежала в указанной области.
Рассмотрим, далее, движущуюся поверхность V (t, хх хп) — с.
Как было показано в предыдущем параграфе, эта поверхность все
время лежит внутри поверхности W — c, а следовательно, и подавно
внутри области |х,|<^е. Допустим, что точка (хх хп), движе-
движение которой определяется уравнениями D6.1), в какой-нибудь момент
времени находилась внутри поверхности V —с. Тогда она будет все
время оставаться внутри этой поверхности. Действительно, если бы
она вышла наружу, то в тот момент времени, когда она пересекала бы
dV
указанную поверхность, производная -—— в точке пересечения была бы
§ 46] ТЕОРЕМЫ ЛЯПУНОВА ОБ УСТОЙЧИВОСТИ 195
положительной, что противоречит условию теоремы. Отсюда непо-
непосредственно вытекает, что всякое движение, начавшееся в области
I-kJ^C1!' Целиком расположенной внутри поверхности V (t0, хх, ...
..., хп) = с, будет всегда оставаться в области | xs | ^ е.
Переходим теперь к доказательству второй основной теоремы
Ляпунова, являющейся обобщением теоремы Б. Эту теорему мы будем
в дальнейшем называть теоремой II.
Теорема II. Если при выполнении условий теоремы I про-
производная —гг является знакоопределенной, а сама функция V
допускает бесконечно малый высший предел, то невозмущенное
движение устойчиво асимптотически.
Доказательство. Допустим, что V есть функция опреде-
dV
ленно-положительная и, следовательно, —г, определенно-отрица-
—г, определенно-отрицательная. Таким образом, в области D6.4) будет выполняться не только
неравенство D6.5), но и неравенство
4^<—ИМ*!, .... хп), D6.12)
где Wx—не зависящая от t определенно-положительная функция.
Будем рассматривать величины xs как функции времени, удовле-
удовлетворяющие дифференциальным уравнениям возмущенного движения,
предполагая, что начальные значения x°s = x(tQS этих величин удо-
удовлетворяют неравенствам D6.8). Так как невозмущенное движение во
всяком случае устойчиво, то величину т) можно выбрать настолько
малой, чтобы при всех t > ^0 величины xs оставались в области D6.4).
Тогда на основании D6.12) производная от функции V it, xx(t), ...
..., xn{t)) будет все время отрицательной и, следовательно, эта
функция с неограниченным возрастанием t будет стремиться к неко-¦
торому пределу, оставаясь все время больше этого предела. Пока-
Покажем, что этот предел равен нулю. Допустим противное, что этот
предел равен некоторой положительной величине а, отличной от
нуля. Тогда при всех t > @ будет выполняться неравенство
V{t, x{{t) xn(t))>a. D6.13)
Так как V допускает бесконечно малый высший предел, то из
этого неравенства вытекает, что
*(/) = max {!*!(*)!. ..., |х/г@|}>Я, D6.14)
где X — некоторое достаточно малое положительное число. Действи-
Действительно, если бы такого числа X не существовало, т. е. если бы вели-
величина х (t) была меньше любого сколь угодно малого числа, то и
величина V(t, xx(t) xn{t)), как это следует из определения
196 УСТОЙЧИВОСТЬ ПЕРИОДИЧЕСКИХ ДВИЖЕНИЙ [ГЛ. V
бесконечно малого высшего предела, была бы также сколь угодно
малой, что противоречит D6.13).
Но если при всех t > ^выполняется неравенство D6.14), то D6.12)
показывает, что все время будет также выполняться неравенство
где lt — отличное от нуля положительное число, являющееся точным
нижним пределом функции Wl(xl(t) xn{t)) при условии D6.14).
Следовательно, при всех t~>tu будем иметь:
t
что, очевидно, находится в противоречии с D6.13). Полученное про-
противоречие показывает, что функция V (t, xl(t), ..., xn(t)) с неогра-
неограниченным возрастанием t стремится к нулю. Следовательно, то же
самое будет и для функции W {xx(t), .... xn{f)), откуда непосред-
непосредственно следует
lim xs(t) = 0 (s=l, 2 л).
t ->co
что и доказывает теорему ').
§ 47. Теорема Ляпунова о неустойчивости
для неустановившихся движений.
Переходим теперь к изложению третьей основной теоремы Ляпу,
нова, дающей критерий неустойчивости.
Теорема III. Если существует допускающая бесконечно ма-
малый высший предел функция V (t, xx хп), производная кото-
которой по времени, составленная в силу уравнений возмущенного
движения, есть функция знакоопределенная, а сама функция V
при значениях xs, сколь угодно малых, и при значениях t, сколь
угодно больших, может принимать значения того же знака,
что и производная, то невозмущенное движение неустойчиво.
Доказательство. Примем для определенности, что произ-
производная —тг положительна. Следовательно, в области
t^to>O, |лс,|<й D7.1)
выполняется неравенство
4 ••••*«). D7.2)
') См. примечание в конце книги (стр. 522).
§ 47] ТЕОРЕМА ЛЯПУНОВА О НЕУСТОЙЧИВОСТИ 197
где W (хг хп)—не зависящая от t определенно-положительная
функция.
Пусть т] — произвольное сколь угодно малое положительное число.
Рассмотрим решение xs = xs (t) уравнений возмущенного движения,
для которого начальные значения xds — xs МЛ выбраны согласно
условиям
К| ( ?°
Согласно условиям теоремы такой выбор величин x°s возможен,
как бы мало ни было число т). Покажем, что рассматриваемое реше-
решение обязательно выйдет в некоторый момент времени из области D7.1).
В самом деле, допустим, что это решение все время остается
в области D7.1). Тогда на основании D7.2) производная от функции
V (t, x1 (t), ..., хп (f)) будет во всяком случае положительной, и мы,
следовательно, имеем:
V(t, x1 (t) хп Щ > V(tQ, x\ дев). D7.3)
Так как V допускает бесконечно малый высший предел, то
из D7.3) следует:
{|jc,(f)| |*„(*)|} > Л. D7.4)
где X — достаточно малое положительное число. Но тогда из D7.2)
вытекает, что
dV{t, *,(<), ..., xn(t))
где отличное от нуля положительное число / есть точный нижний
предел функции W(xl(t) xn(t)) ПРИ условии D7.4).
Неравенство D7.5) дает:
t
V(t. xx{t), .... xn(f)) = V(t0. x\
что невозможно, так как функция V, допуская бесконечно малый
высший предел, будет во всяком случае ограниченной.
Из полученного противоречия вытекает, что решение xs = xs (t)
в некоторый момент времени обязательно покинет не зависящую
от начальных значений x°s область D7.1), и так как эти начальные
значения сколь угодно малы, то невозмущенное движение неустойчиво.
Таким образом, теорема доказана.
Функции, удовлетворяющие теоремам I, II или III, мы будем, так
же как и в случае установившихся движений, называть функциями
Ляпунова,
198 УСТОЙЧИВОСТЬ ПЕРИОДИЧЕСКИХ ДВИЖЕНИЙ [ГЛ. V
§ 48. Теорема Н. Г. Четаева.
Доказанная в предыдущем параграфе теорема III, дающая крите-
критерий неустойчивости, обладает одним принципиальным недостатком.
Этот недостаток заключается в том, что функция V должна обладать
определенными свойствами во всей области D7.1). В частности, во
всей этой области производная —jr- должна быть положительной,
что обозначает, что все интегральные кривые, расположенные в об-
области D7.1), должны пересекать поверхности V = c в определенную
сторону. Между тем, для того чтобы обнаружить неустойчивость
движения в тех случаях, когда она действительно имеет место, до-
достаточно обнаружить в сколь угодно малой окрестности начала коор-
координат хотя бы одну неустойчивую интегральную кривую, а для того
чтобы обнаружить такого рода интегральную кривую, достаточно
знать поведение интегральных кривых не во всей области D7.1),
а только в некоторой ее части. В связи с этим необходимо, таким
образом, обобщить теорему Ляпунова, чтобы приходилось рассматри-
рассматривать только некоторые части окрестности начала координат. Такого
рода обобщение было дано Н. Г. Четаевым J).
Назовем областью V > О какую-нибудь область окрестности
1*,|<* D8.1)
начала координат пространства переменных xlt .... хп, ограничен-
ограниченную поверхностью V=0, в которой функция V принимает положи-
положительные значения.
Допустим, что функция V обладает следующими свойствами:
1) При сколь угодно больших значениях t в сколь угодно малой
окрестности начала координат существует область V > 0.
2) В области V > 0 функция V ограничена.
3) В области V > 0 производная -~л-, составленная в силу урав-
уравнений возмущенного движения, принимает положительные значения
и при этом для всех значений t, xlt ..., хп, связанных соотношением
V(t, х, *„)>а,
где а—какое-нибудь положительное число, выполняется неравенство
dt ^L'
где I — также некоторое положительное число, зависящее от а.
Мы можем теперь теорему Н. Г. Четаева сформулировать сле-
следующим образом.
') Ч е та е в Н. Г., Одна теорема о неустойчивости. ДАН, т. I, Ш 9, 1934.
§ 49] ПОСТЛНОЗКА ЗАДАЧИ 199
Теорема. Если для дифференциальных уравнений возму-
возмущенного движения можно найти функцию, удовлетворяющую
условиям 1), 2), 3), то невозмущенное движение неустойчиво.
Доказательство. Зададимся окрестностью D8.1) начала коор-
координат. Согласно условию, если h достаточно мало, то в этой окрест-
окрестности имеется область V > 0. При этом в указанной области при вся-
всяком значении t имеются точки, сколь угодно близкие к началу координат.
Рассмотрим решение xs = xs{t) уравнений возмущенного движе-
движения с начальными значениями x°s = xs(tA выбранными численно
сколь угодно малыми и такими, что
Так как в области V > 0 производная -тг положительна, то функция
V(t, Xi(t), .... xn(t)) будет возрастать и, следовательно, величины
xs (f) будут оставаться в области V > 0, по крайней мере, до тех
пор, пока не нарушаются неравенства D8.1). Покажем, что в неко-
некоторый момент времени неравенства D8.1) действительно нарушаются.
Допустим противное, что неравенства D8.1) никогда не нару-
нарушаются. Следовательно, все время выполняется условие
V(t, Xl(t) xn(t))>V0,
откуда по свойству функции V вытекает, что
dv«,Xl(t),...,Xnm>lt D82)
где / — некоторое отличное от нуля положительное число. Из D8.2)
находим:
что невозможно, так как в области V > 0 функция V ограничена.
Таким образом, в некоторый момент времени решение xs(t) непре-
непременно покинет область D8.1), и так как величины x°s могут быть
взяты сколь угодно малыми, то невозмущенное движение неустойчиво.
Б. ЛИНЕЙНЫЕ УРАВНЕНИЯ С ПЕРИОДИЧЕСКИМИ
КОЭФФИЦИЕНТАМИ.
§ 49. Постановка задачи.
Мы переходим теперь к рассмотрению устойчивости периодических
движений. Мы будем предполагать, что правые части дифференциаль-
дифференциальных уравнений возмущенного движения D6.1) являются по отноше-
отношению к t периодическими функциями некоторого заданного периода w,
200 УСТОЙЧИВОСТЬ ПЕРИОДИЧЕСКИХ ДВИЖЕНИЙ [ГЛ. V
Мы будем, кроме того, предполагать, что эти уравнения могут
быть представлены в виде
(s=l. 2 я),
где psi — непрерывные периодические функции t периода w, а функ-
функции X's в том или ином смысле малы по сравнению с линейными
членами.
Так же как и в случае установившихся движений, нам предстоит
разрешить три следующих вопроса:
1) установить критерии устойчивости и неустойчивости для системы
линейных уравнений первого приближения;
2) установить необходимые и достаточные условия, при которых
задача устойчивости для полной системы D9.1) решается первым
приближением;
3) указать методы решения задачи устойчивости в критических
случаях, когда рассмотрения одного лишь первого приближения недо-
недостаточно.
Мы начинаем с рассмотрения первого вопроса. Для этого нам
придется изложить теорию линейных уравнений с периодическими
коэффициентами. Так как эта теория имеет большое значение в раз-
различных вопросах техники и физики, то мы остановимся на ней по-
подробно.
§ 50. Характеристическое уравнение системы линейных
уравнений с периодическими коэффициентами.
Рассмотрим систему линейных уравнений
-^T = P,i*i+•••+/'«*« E=1, 2, ...,n), E0.1)
где psj — непрерывные периодические функции t периода ©.
Пусть xsj (t) — фундаментальная система решений уравнений E0.1).
Здесь, как и в дальнейшем, первый индекс обозначает номер функ-
функции в каком-нибудь решении, а второй индекс — номер решения.
Если мы во всех функциях xsj(f) какого-нибудь /-го решения заме-
заменим t на t -f- ©, то в силу периодичности коэффициентов psj мы снова
получим решение, так как функции xsj(t-\-u>) будут по-прежнему
удовлетворять уравнениям E0.1), если им удовлетворяли функции xsj(t).
Полученное решение не будет совпадать с первоначальным реше-
решением xsj(t), но как всякое решение уравнений E0.1) оно необходимо
должно являться линейной комбинацией фундаментальной системы
§ 50] ХАРАКТЕРИСТИЧЕСКОЕ УРАВНЕНИЕ СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ 201
решений xSj (/). Следовательно, имеем:
xsj (/ + о) = а1]Хл @ + a2jxs2 (t) + ... + anJxin (t), E0.2)
где «ly, a2j, ..., а„у—некоторые постоянные. Меняя j от 1 до п,
мы получим «2 величин asj.
Составим уравнение
:п —р а 12 ... а1я
= 0. E0.3)
— р
Это уравнение, играющее основную роль в теории линейных
уравнений с периодическими коэффициентами, называется характе-
характеристическим уравнением, соответствующим периоду ©, или,
короче, характеристическим уравнением.
Установим некоторые основные свойства характеристического
уравнения.
1. Характеристическое уравнение не зависит от выбран-
выбранной фундаментальной системы.
Выберем вместо фундаментальной системы xsj другую фундамен-
фундаментальную систему ysj. Для нее будем иметь:
ysj (* + ©) = ClJyA @ + сууЛ @ + ... + cnjysn @, E0.4)
где csJ, вообще говоря, отличны от asj. Покажем, однако, что корни
характеристического уравнения, составленного из коэффициентов csj,
совпадают с корнями уравнения E0.3).
В самом деле, так как величины ysj образуют фундаментальную
систему, то должно быть:
ysj @ = byxsl (t) + b2jxs2 @ + ... + bnJxsn (t) E0.5)
E, j=\, 2 «),
где bsj — некоторые постоянные, причем определитель матрицы {bsj}
отличен от нуля. Обозначим через х (t) матрицу функций xsj (t),
через y(t) — матрицу функций ysj(f) и, соответственно, через а, Ь,
с — матрицы коэффициентов asJ, bsJ, csj. Тогда зависимости E0.2),
E0.4) и E0.5) могут быть представлены следующим образом:
Далее имеем:
у (*-f-«) = х (t + ©) b — х (t) ab = у (t) b~x ab
и, следовательно,
с~Ь~г ab.
202 УСТОЙЧИВОСТЬ ПЕРИОДИЧЕСКИХ ДВИЖЕНИЙ [ГЛ. V
Поэтому, если Е — единичная матрица, то характеристический
определитель из коэффициентов csj может быть представлен следую-
следующим образом:
| с — рЕ\ == |Ь~гаЬ — рЕ |== |b~l (а — рЕ) b | =
= \b~l\- \а —рЕ\ ¦ \Ь\=\а — рЕ\,
что и доказывает наше предложение.
2. Характеристическое уравнение не изменится, если
систему E0.1) подвергнуть неособенному линейному преобра-
преобразованию с периодическими коэффициентами периода ©.
В самом деле, преобразуем уравнения E0.1) при помощи под-
подстановки
У, = ?,i (9*1+ ••• +?м@*я (s=l. 2, .... я), E0.6)
где qsj—непрерывные и дифференцируемые периодические функции t
периода со и притом такие, что определитель \qsj\ отличен от нуля
при всех значениях t на отрезке [0, со].
Подставляя в E0.6) фундаментальную систему xsj(t), мы получим
следующую фундаментальную систему решений преобразованных
уравнений:
Уз] V) = ЯзХ @ XlJ @ + <7*2 @ *2] @ + • • • + Чзп @ *п} (f).
или в матричном обозначении
где ^ — матрица коэффициентов qsj. Отсюда находим, что
и, следовательно, характеристическое уравнение преобразованной
системы совпадает с характеристическим уравнением исходной системы.
Допустим, что рассматриваемая фундаментальная система опреде-
определяется начальными условиями
l(s = A
о (s Ф А
Тогда, полагая в E0.2) ^ = 0, будем иметь:
xsj (со) = ащ, (s, / = 1, 2 П),
§ 51] СЛУЧАЙ ПРОСТЫХ КОРНЕЙ ХАРАКТЕРИСТИЧЕСКОГО УРАВНЕНИЯ 203
и следовательне, характеривтическое уравнение может быть пред-
представлено в следующем виде:
*n С®) — Р хп (ю) • • • х\п (ю)
*21 (<0) ^22 (°>) — Р • • • Х2п (°>)
= 0.
E0.7)
Этим видом характеристического уравнения мы будем часто поль-
пользоваться в дальнейшем.
Воспользуемся им, в частности, для вывода важной формулы,
дающей выражение свободного члена характеристического уравнения.
С этой целью рассмотрим детерминант Вронского
ln
(f)
Xn(f)
Как известно, при любых t0 и t справедливо соотношение
t п
Полагая в этом соотношении ^0 = 0, ^ = со, получим:
со
Д(со) = ехр f
Сравнивая с E0.7), найдем, что если характеристическое уравне-
уравнение представить в виде
E0.8)
то свободный член Ап определяется формулой
0 s=l
§ 51. Аналитический вид решений в случае простых корней
характеристического уравнения.
Система E0.1) не интегрируется в замкнутой форме. Можно,
однако, указать общий аналитический вид ее решений.
Пользуясь каким-нибудь определением логарифмов, рассмотрим
величины
F1.1)
204 УСТОЙЧИВОСТЬ ПЕРИОДИЧЕСКИХ ДВИЖЕНИЙ [ГЛ. V
где pft — корни характеристического уравнения. Эти величины назы-
называются характеристическими показателями системы E0.1).
Покажем, что для каждого корня pft характеристического уравне-
уравнения можно подобрать частное решение уравнений E0.1) вида
*,(Q = eV<P,(O (s=l,2 п.), E1.2)
где ф5 — некоторые периодические функции времени периода со.
Это решение обладает тем свойством, что для него выполняются
соотношения
*,(f + ©) = pft*,(Q. E1.3)
В самом деле, имеем:
*, (* + ©) = еа*( • еа*шср, (* + ©) = р4*а*'Ф, (Q.
Наоборот, если для какого-нибудь решения *s(/) выполняются
соотношения E1.3), то это решение необходимо имеет вид E1.2).
Это непосредственно следует из того, что при выполнении E1.3)
функции xse~uk будут периодическими и, следовательно, функции xs
будут иметь вид E1.2).
Таким образом, задача сводится к определению решения, удо-
удовлетворяющего соотношениям E1.3). Это решение, если оно суще-
существует, должно являться линейной комбинацией фундаментальной
системы. Таким образом, имеем:
*, @ = Р Ai @ + М*2 @ + • • • + Ря*,я @.
где (^ ря — некоторые постоянные. Подставляя E1.3), получим
Sm,/(+)p*2/,((9
i=\ 1=1
и, следовательно, на основании E0.2)
п п
( S jMh*,! @ = Pft S h^sl @-
Приравнивая коэффициенты при л;^ (^), получим, что постоянные
Pj рл удовлетворяют системе линейных однородных уравнений
«nPi+ ••• +(«н —P*)Pi+ ••• +вмРя = 0- E1-4)
Так как pft является корнем характеристического уравнения, то
система E1.4) допускает, по крайней мере, одно решение, отличное
от тривиального $г = ... =Eп = 0. Таким образом, каждому корню
характеристического уравнения отвечает, по крайней мере, одно част-
частное решение дифференциальных уравнений E0.1), имеющее вид E1.2).
Корню pft может отвечать более чем одно решение вида E1.2).
Этих решений будет, очевидно, столько, сколько независимых реше-
§ 52] СЛУЧАЙ КРАТНЫХ КОРНЕЙ ХАРАКТЕРИСТИЧЕСКОГО УРАВНЕНИЯ 205
ний имеет линейная алгебраическая система E1.4). Следовательно,
этих решений будет п — р, если ранг определителя D (pk) равен р.
Ранг указанного определителя может быть меньше чем п — 1 лишь
только в том случае, когда корень pft является кратным. Поэтому
каждому простому корню характеристического уравнения отвечает
одно и только одно решение вида E1.2).
Установив это, допустим сначала, что все корни характеристиче-
характеристического уравнения являются простыми. Тогда каждому такому корню
будет отвечать одно и только одно решение вида E1.2). Рассматри-
Рассматривая все корни характеристического уравнения, мы получим п раз-
различных частных решений уравнений E0.1). Эти решения будут, оче-
очевидно, независимыми и образуют, следовательно, фундаментальную
систему.
§ 52. Аналитический вид решений в случае кратных корней
характеристического уравнения.
Рассмотрим теперь случай, когда характеристическое уравнение
имеет кратные корни. Допустим для определенности, что кратность
корня pft равна |J.. Если этот корень не обращает в нуль, по крайней
мере, одного из миноров (п—1)-го порядка характеристического оп-
определителя, т. е. если ранг этого определителя равен п—1, то, как
мы сейчас покажем, для этого корня может быть построено |J. неза-
независимых частных решений уравнений E0.1) вида
xtl(f) = ea*tPtt(f) (s=l. 2, .... я; /=1. 2 ц). E2.1)
Здесь Psi — полиномы относительно t с периодическими (пе-
(периода со) коэффициентами. При этом степени полиномов Рл не пре-
превосходят ц—1, и степень хотя бы одного из них равна ц—1. Таким
образом, можно написать:
@ + S «Р@ + + *Ф ii-i @ + Ф,ц @.
где фз,- (f) — периодические функции t, причем хотя бы одна из функ-
функций (f>sl не равна тождественно нулю.
Что же касается полиномов Ps2, ..., Psll, то они могут быть
получены из Psl последовательным дифференцированием по t в пред-
предположении, что (pSj являются постоянными. Имеем:
_2I Фя
-3I ф^ @ -f- • ¦ • + Ф5, ц-2.
= фЛ @-
206 ¦ УСТОЙЧИВОСТЬ ПЕРИОДИЧЕСКИХ ДВИЖЕНИЙ [ГЛ. V
Пусть
Р = г*ъ @ +t™-'ф2 (о + ... + t<?m (t) + Фт+1 (t)
— произвольный полином с периодическими коэффициентами фг (t).
Обозначим через —=-г оператор, определяемый соотношением
DP
-ft- = т^-1ф1 @ 4- (« - 1) ^-2Ф2 @4- • ¦ • 4- 2^Фт_1 @ 4- ф™ (О-
Тогда решения E2.1) могут быть записаны в виде
xst(f) = ea* ^'t^' (s=l, 2 n; /=1. 2 |i), E2.2)
где PS = PS\. Мы будем говорить, что решения E2.2) образуют одну,
группу и что в рассматриваемом случае кратному корню отвечает
одна группа решений.
Допустим теперь, что кратный корень рк обращает в нуль все
миноры характеристического определителя до порядка п — р-\-1
включительно, не обращая в нуль хотя бы один из миноров (п — р)-го
порядка, так что ранг характеристического определителя равен я— р.
В этом случае рассматриваемому корню будет по-прежнему соответ-
соответствовать ц решений, но эти решения разбиваются на р самостоятель-
самостоятельных групп. И если мы обозначим через tij число решений в у-й
группе (nl -f- «2 -f- ... -\-np = \i), то решения этой группы имеют вид
(/=1, 2 я,.; s=l, 2, .... я), E2.3)
"si W — * ?)/'-!
где
ф^4- Ф2 4- +ф
1 s — in Ш4^1 ' (л- 2)! '"' /
и Ф(//' — периодические функции t периода со, причем хотя бы одна
из функций ф^Л не обращается тождественно в нуль.
Число р не может, очевидно, превзойти кратности [х рассматри-
рассматриваемого корня, но может этого предела достигать. В последнем слу-
случае каждая группа будет состоять из одного решения. Каждое тако.1
решение будет при этом иметь вид E1.2).
Все эти утверждения можно считать доказанными при (х = 1.
Поэтому, чтобы доказать их в общем случае, мы можем приме-
применить метод индукции, а именно: мы допустим, что все эти утвер-
утверждения справедливы, если кратность корня равна [i—1, и покажем,
что они остаются справедливыми, если эта кратность равна ц.
С этой целью заметим прежде всего, что корню pft соответствует
по доказанному, по крайней мере, одно решение системы E0.1)
§ 52] СЛУЧАЙ КРАТНЫХ КОРНЕЙ ХАРАКТЕРИСТИЧЕСКОГО УРАВНЕНИЯ 207
вида
х, @ = А'ср5 (*) (s=l,2 я), E2.4)
где q>s—периодические функции. Эти функции не могут одновременно
обратиться в нуль ни при каких значениях t. Действительно, если бы
при каком-нибудь значении t = T все функции (fs обратились в нуль,
то, принимая это значение t за начальное, мы имели бы два раз-
различных частных решения уравнений E0.1) с нулевыми начальными
значениями: решение E2.4) и тривиальное решение х{ = ... = хп = 0,
что невозможно.
Перейдем теперь в уравнениях E0.1) от переменных xs к пере-
переменным ys при помощи подстановки
xs = %Ух + &йУг + ¦ • • -\-bsnyn, E2.5)
где bsa — произвольные непрерывные периодические функции t пе-
периода со, подчиненные лишь условию, что подстановка E2.5) не является
особенной, т. е. что определитель
i ф2 • • • Ф«
Ь\п Ь2п ¦ ¦ ¦ bnn
ни при каких значениях t не обращается в нуль. В силу того, что
функции q>s не могут обращаться в нуль одновременно, такой выбор
функций bsa может быть сделан бесчисленным множеством способов.
Преобразованная система примет вид
%¦ = <7,1У1 + <7*2У2 + • • • + Ч,пУ>п (s=l, 2, .... п). E2.6)
где qsa—периодические функции t периода со. Так как система E0.1)
допускает частное решение E2.4), то преобразованная система должна
допускать частное решение
У1 = еа*'. у2= ... =у„ = 0. E2.7)
Подставляя это решение в E2.6), найдем, что все коэффициенты
4i\> <7з1- • • ¦ • Чп\ рэвны нулю, а коэффициент qu равен ak. Следова-
Следовательно, система E2.6) распадается на систему
^ Уп (s = 2, 3, .... я), E2.8)
состоящую из я — 1 уравнений, и на одно уравнение
%- = а*У1 + -712У2 + • • • + ЬпУп- E2.9)
208 УСТОЙЧИВОСТЬ ПЕРИОДИЧЕСКИХ ДВИЖЕНИЙ [ГЛ. V
Уравнения E2.8) образуют самостоятельную систему, определяю-
определяющую п — 1 функций у2 у„. После того как эти функции будут
найдены, мы сумеем найти у1 из уравнения E2.9) при помощи про-
простой квадратуры. В частности, если мы найдем q(q<^.n— 1) линейно
независимых решений у2г (/), ..., ynl(t) (/=1, 2, .... q) уравнений
E2.8), то функции уи (t), y2i(t) ynl (f), где уи определяются
формулами
t
Уи = еа* / е~аь'(qny2i + ... +^ЯУЯ()Л. E2.10)
о
определяют q независимых решений полной системы E2.8) и E2.9).
Присоединяя к ним уже известное решение E2.7), мы получим ^—|—1
решений этой системы, которые будут, очевидно, также независимыми.
Составим характеристическое уравнение полной системы E2.8)
и E2.9). Рассмотрим с этой целью фундаментальную систему реше-
решений y2i(t), уд, (Q уя,(9 (/=1, 2 я-1) уравнений E2.8),
определяемую начальными условиями
0 (s =
Тогда система функций уи (f), yn (t) ynl (t), где уи (t) опре-
определяются формулами E2.10), вместе с решением E2.7) образуют
фундаментальную систему решений системы E2.8) и E2.9) как раз
того вида, который фигурирует в форме E0.7) характеристического
уравнения. Поэтому характеристическое уравнение системы E2.8)
и E2.9) может быть представлено в виде
Pft-P 0 ...0
D(p)= Уп^ , У21.(иOр7'/:Лсо).
У1,л-1(°>) У2,л-1(°>) ••¦ Ул. n-l(°))—P
= (pft—p)D'(p) = 0, E2.11)
где D' (р) — характеристический определитель системы E2.8).
Как было показано в § 50, характеристическое уравнение остается
инвариантным при линейном преобразовании переменных. Поэтому
уравнение E2.11) совпадает с характеристическим уравнением исход-
исходной системы E0.1). Что же касается последнего, то для него pft
является корнем (х-й кратности. Следовательно, из E2.11) вытекает,
что pft является корнем (\i—¦ 1)-й кратности характеристического
уравнения системы E2.8).
Но тогда, по предположению, этому корню отвечает (х—1 част-
частных решений уравнений E2.8), распадающихся на группы вышеука-
вышеуказанного типа. Допустим для определенности, что имеются две такого
§ 521 СЛУЧАЙ КРАТНЫХ КОРНЕЙ ХАРАКТЕРИСТИЧЕСКОГО УРАВНЕНИЯ 209
рода группы. Все наши рассуждения останутся, однако, справедли-
справедливыми при любом числе групп. Пусть первая группа состоит из /
решений
?k (ГТТТ «-+••¦+ tat. ,.l + ust)
(s = 2 га; a= 1, 2 I),
а вторая группа из т решений
E2.12)
(s = 2, .... га; р= 1, 2 /и).
Здесь usj, vsj — периодические функции t и Z-j-m —ц— 1. Как
было указано выше, функции E2.12) и E2.13) вместе с функциями
t
Уia = eak( j е-V (9i2y2a + • • • -Ь ЧиУпа) dt>
dt
E2.14)
(a=l, 2, .... /; p=l, 2 /re)
образуют систему ц—1 независимых решений уравнений E2.8)
и E2.9).
На основании E2.12) и E2.13) подынтегральные выражения
в функциях E2.14) не содержат показательных функций, и мы можем
написать:
— eat[
О
v Г
E2.15)
(a=l, 2 /; р=1, 2 /re),
где я^, Wy — периодические функции периода со.
Пусть ф(?) — произвольная непрерывная периодическая функция
с периодом со. Как мы уже знаем, справедливо соотношение
J* Ф (О Л = й'/Ч-Ф @.
210 УСТОЙЧИВОСТЬ ПЕРИОДИЧЕСКИХ ДВИЖЕНИЙ [ГЛ. V
где ty(t) — некоторая периодическая функция, a g есть постоянная,
определяемая соотношением
j E2.16)
о
и представляющая собой среднее значение функции ф за период.
Интегрируя по частям, легко находим:
t t
о о
откуда вытекает, что если P(t) — полином р-й степени с периодиче-
периодическими коэффициентами
? -^Т)ГФ2@+ • • • +фр@.
то квадратура от него будет полиномом (р ~\- 1)-й степени вида
l E2.17)
= J
о
J
о
где "ф2 ^p+i — некоторые периодические функции, а ^ — посто-
постоянная, определяемая формулой E2.16), т. е. среднее значение коэф-
коэффициента при старшей степени полинома Р (f).
Докажем, что имеет место тождество
t t
ns Г Г nsp
jfpr J P(f)dt- jJLjLdt = A, E2.18)
о о
где А — некоторая постоянная. В самом деле, дифференцируя левую
часть E2.18) по времени и принимая во внимание, что операторы
d Ds ,
—rr и -jrp-, очевидно, переместимы, будем иметь:
it t
Ds Г Г DSP
J P№}
J
0
i
~DF J } j
0 0 ) I 0
откуда и вытекает справедливость E2.18).
Принимая во внимание E2.17) и E2.18), находим, что выраже-
выражения E2.15) могут быть представлены в виде
г)(а-1)
* ^ + U* @J + А"
р=1, 2, .... /к).
§ 52] СЛУЧАЙ КРАТНЫХ КОРНЕЙ ХАРАКТЕРИСТИЧЕСКОГО УРАВНЕНИЯ 211
где А, А* — постоянные, О и Q* — также постоянные, определяемые
формулами
со
о
а (/ в U* суть полиномы с периодическими коэффициентами, при-
причем степень первого не превосходит I—1, а степень второго не
превосходит т — 1. Но так как
то мы можем написать:
(a= 1, 2 /; p= 1, 2 m),
E2.19)
где U и t/* — также полиномы с периодическими коэффициентами,
степени которых не превосходят, соответственно, /—1 и т—1.
Подставляя E2.12), E2.13) и E2.19) в E2.5), мы получим для
системы E0.1) I решений вида
-Jf + Xs (О) (a = 1. 2 0 E2.20)
и т решений вида
где Xs(t) и Xs(f) — некоторые полиномы с периодическими коэффи-
коэффициентами, степени которых не превосходят, соответственно, /—1 и
/те— 1. Вместе с решением E2.4) мы получаем, таким образом, для
рассматриваемого корня I-\-т-\-1 = ц независимых решений си-
системы E0.1).
Допустим сначала, что обе величины О и О* отличны от нуля.
Допустим также для определенности, что 1^-т. Тогда, если мы
к решениям E2.20) присоединим решение E2.4), умножив его пред-
предварительно на О, то получим / —]— 1 решений, составляющих группу.
212 УСТОЙЧИВОСТЬ ПЕРИОДИЧЕСКИХ ДВИЖЕНИЙ [ГЛ. V
Действительно, очевидно, имеем:
<Wq>, @ = Л' -~ (СФ,4 + X, (О) .
а следовательно, решение E2.4), умноженное на О, принадлежит
группе E2.20) и соответствует a = Z-f-l. Что же касается реше-
решений E2.21), то, комбинируя их с т последними решениями E2.20),
мы получим т новых решений:
?
о* Dti_m Xs
(P=l. 2 m),
также образующих группу. В самом деле, степень хотя бы одного
из полиномов, заключенных в скобках, в выражении для xs$ равна
т—1, ибо, если бы все указанные полиномы имели меньшие сте-
степени, то во всяком случае имели бы место тождества
x~sm = Q*xsl — Одг*т = 0 (s=\, 2 п)
и, следовательно, не все решения E2.20) и E2.21) были бы незави-
независимыми, что противоречит условию.
Таким образом, в рассматриваемом случае наше утверждение
о виде решений, отвечающих кратному корню характеристического
уравнения, справедливо.
Допустим теперь, что О = 0, но G* отлично от нуля. В этом
случае степень хотя бы одного из полиномов Xs (() равна / — 1, так
как в противном случае все функции xs[ равнялись бы нулю и, сле-
следовательно, в E2.20) содержалось бы меньше чем / решений. Поэтому
уравнения E2.20) образуют группу нужного нам вида. Присоединяя
решение E2.4), умноженное предварительно на О*, к решениям E2.21),
мы получим еще одну группу. Следовательно, так же как и в пре-
предыдущем случае, мы будем иметь (х решений, разбивающихся на две
группы. Если, наконец, G* также равно нулю, то решения E2.21)
также образуют группу, и решение E2.4) следует рассматривать как
отдельную третью группу, состоящую из одного решения.
Таким образом, во всех случаях наши утверждения об аналитиче-
аналитическом виде решений системы E0.1) можно считать доказанными.
Нам остается еще только показать, что число групп решений,
отвечающих кратному корню, в точности равно р, где п — р — ранг
характеристического определителя для рассматриваемого корня. Это
утверждение легко доказать следующим образом.
Число групп решений, отвечающих рассматриваемому кратному
корню, равно, очевидно, числу независимых решений вида E2.4)
(так как в каждой группе имеется по одному такому решению),
§ 53] ОБРАТНОЕ ПРЕДЛОЖЕНИЕ 213
которыми этот корень обладает, а это число, как мы видели в пре-
предыдущем параграфе, равно числу независимых решений однородной
системы линейных алгебраических уравнений E1.4), т. е. п — р.
Таким образом, все наши утверждения полностью доказаны.
§ 53. Обратное предложение.
Справедливо также обратное предложение. Если для системы E0.1)
удалось найти ц частных решений, разбивающихся на р групп
вида E2.3), то величина pft является корнем характеристического
уравнения, кратность которого не менее (х, причем этот корень обра-
обращает в нуль все миноры характеристического определителя до по-
порядка, по крайней мере, п — р-\-\-
Допустим для определенности, что имеются две такого рода
группы, состоящие, соответственно, из / и т. решений. Все наши
рассуждения останутся, однако, справедливыми при любом числе
групп. Пусть эти решения будут
П/d-l ч ''
Ut E3.1)
где
P? = jrz^r Фи @ + -^щ Ъ* @ + • • • + Ф/, @.
@
и ф18, .... (fls, г|зи, .... tyms — периодические функции периода со. Нам
нужно показать, что величина pft является корнем характеристиче-
характеристического уравнения, кратность которого не менее 1-\-т, и что этот
корень обращает в нуль, по крайней мере, все миноры (п—1)-го
порядка характеристического уравнения.
С этой целью возьмем для составления характеристического урав-
уравнения такую фундаментальную систему решений xsj(t) уравнений E0.1),
которая содержит все решения E3.1). Мы предположим при этом, что
решения E3.1) являются первыми 1-\-т решениями рассматриваемой
фундаментальной системы и примем следующий порядок нумерации:
*,. 1+1 = *%• Xs, l+2 = Х?!т-1 *,,!+„ = Х%
Тогда, принимая во внимание, что для всякого полинома
214
УСТОЙЧИВОСТЬ ПЕРИОДИЧЕСКИХ ДВИЖЕНИЙ
[гл. v
с периодическими периода со коэффициентами ft справедливо оче-
очевидное соотношение
ш<? D1P
' ' ' i ~м
а также, что на основании E1.1)
легко находим:
= Р*«»*Л @
Р* (f __
О)'
* (/ _ 2I *л
Л t+m
,,J+i (О +
—2)!
Сравнивая с E0.2), получим:
../-1
.,'-2
а" —¦
— Pft (/ — 2)!
'1 + 2, 1 + 1 —
= ••• =««. /4-1 = 0,
n, l + l ¦
al,l + 2 = [
+3, 1+2 = fl
1, г+2 =
.ж-\
i+\. i+m
*t, l+m '
"K (m —1)! '
©m~2
1 Pft /jL_2^| ' •
= 0 (s=l, 2, .
•• al+m, l+m-
... /.
q[ Dt"
.. n).
E3.2)
§ 54] ТЕОРЕМА ЛЯПУНОВА О ПРИВОДИМОСТИ ЛИНЕЙНЫХ УРАВНЕНИЙ 215
Следовательно, характеристическое уравнение E0.3) имеет вид
D(p) =
Pft —P °
Pft» pft — p
0
0
и'
о'-2
pft
A—1I p* (/—2)! ' '' Pft P
9 k —9 0
ps<» ps — p
X
X
.jn-\
й/*-2
P* (те—1)! P* (m—2)! ' " '
0
0
. — P
X
X
, l+m + 1 P • • • "лв+l, n
1 + т +1
= (Pft — P)' (Pft — I
, — P
— P
*n, l + m+l
— Р
= 0.
Отсюда непосредственно вытекает, что величина pft является кор-
корнем характеристического уравнения с кратностью, не меньшей 1-\-т.
Кроме того, как это видно из E3.2), все элементы 1-й и (Z —j— 1)-й
колонок характеристического уравнения обращаются в нуль при
p = pft. Следовательно, корень pft обращает в нуль, по крайней мере,
все миноры (п — 1)-го порядка характеристического уравнения.
Таким образом, предложение полностью доказано.
§ 54. Теорема Ляпунова о приводимости линейных
уравнений с периодическими коэффициентами.
А. М. Ляпунов показал, что всякую систему линейных дифферен-
дифференциальных уравнений с периодическими коэффициентами можно пре-
преобразовать при помощи линейной подстановки с периодическими
коэффициентами в систему уравнений с постоянными коэффициентами.
Для выполнения этого преобразования рассмотрим систему линей-
линейных уравнений
216 УСТОЙЧИВОСТЬ ПЕРИОДИЧЕСКИХ ДВИЖЕНИЙ [ГЛ. V
сопряженную с системой E0.1). Если ys(()— какое-нибудь решение
системы E4.1), то линейная форма
У1 @ *i + У2 @ *2+ • • • + У«@ хп E4.2)
переменных xs определяет, как известно, первый интеграл уравне-
уравнений E0.1). Подставляя в эту форму вместо ys(t) какие-нибудь п
независимых частных решений уравнений E4.1), мы получим п неза-
независимых первых интегралов системы E0.1).
Пусть рр р2 рт —корни характеристического уравнения си-
системы E4.1I) и а{, а2, .... ат—соответствующие характеристи-
характеристические показатели. При этом каждый кратный корень мы выписы-
выписываем столько раз, сколько групп решений ему соответствует. Таким
образом, среди чисел р^ могут быть и равные, но каждому из них
соответствует только одна группа решений.
Обозначим через пр число решений в группе, отвечающей корню рр.
При этом, очевидно,
Тогда, как было показано в § 52, система E4.1) имеет га неза-
независимых решений следующего вида:
^
(s=l, 2 га; р = 1, 2, .. ., т),
где ф(р) (t) — периодические функции t периода со. Мы придержи-
придерживаемся при этом следующей системы обозначения решений: верхний
индекс в у^ обозначает номер группы (номер корня), к которой
принадлежит решение, а второй нижний индекс — номер решения
в группе. Положим
f [1 $2 -г- • ¦ • fla
(/>=!. 2 m; J=l, 2 пр). E4.4)
') Обращаем внимание читателя, что в отличие от предыдущих пара-
параграфов через р;- обозначены корни характеристического уравнения системы
E4.1), а не системы E0.1).
54) ТЕОРЕМА ЛЯПУНОВА О ПРИВОДИМОСТИ ЛИНЕЙНЫХ УРАВНЕНИЙ 217
Тогда, подставляя решения E4.3) в E4.2), мы получим следующие п
первых интегралов уравнений E0.1):
const.,
/ л -1
Р \ (пр — 1)!
уЧ»
(Р
t"
(«Р
Р-2
-2)!
1, 2,
.... т).
+ у{,И -
const.,
= const.
E4.5)
Соотношения E4.4) определяют линейную подстановку с период! -
ческими коэффициентами, которая ни при каких значениях t не является
особенной. В самом деле, определитель, составленный из п2 фуш -
ций E4.3), отличен от нуля, так как эти функции образуют фунда-
фундаментальную систему решений линейных уравнений. Но этот опре-
определитель, как легко видеть, отличается никогда не обращающимся
в нуль множителем
е(пха1+пга2+ ... +npap)t
от определителя подстановки E4.4), и следовательно, подстановка
E4.4) не является особенной ни при каких значениях t.
Установив это, преобразуем систему E0.1) при помощи подста-
подстановки E4.4). Учтем, что выражения E4.5) являются первыми инте-
интегралами системы E0.1). Дифференцируя эти интегралы по t и при-
приравнивая производные нулю, легко получим следующие дифферен-
дифференциальные уравнения:
dt
¦ = —Vr
[Р),
dt
dt
=l. 2,
р
т).
E4.6)
Это и будут преобразованные уравнения, обладающие постоянными
коэффициентами. Таким образом, при помощи неособенной линейной
подстановки с периодическими коэффициентами E4.4) система урав-
уравнений E0.1) преобразована в систему уравнений с постоянными
коэффициентами.
Полученная система E4.6) будет иметь комплексные коэффи-
коэффициенты, так как величины а0 будут, вообще говоря, комплексными.
218 УСТОЙЧИВОСТЬ ПЕРИОДИЧЕСКИХ ДВИЖЕНИЙ [ГЛ. V
Поэтому, если мы желаем иметь дело только с вещественными
уравнениями, то необходимы будут дальнейшие преобразования.
Покажем, как это сделать.
Величина ар будет комплексной либо тогда, когда соответствую-
соответствующий корень рр характеристического уравнения является комплексным,
либо когда этот корень является вещественным, но отрицательным.
Рассмотрим сначала первый случай. Допустим, что корень рг является
комплексным. Так как коэффициенты уравнений E0.1) вещественны,
то все комплексные корни характеристического уравнения и все ком-
комплексные решения системы E4.1) распадаются на пары сопряженных.
Пусть рг комплексно сопряжен с р;. Тогда решения системы E4.1),
отвечающие корню рг, т. е. функции yW., будут комплексно сопря-
сопряженными с решениями у$ и, следовательно, nt — га,- и переменные уФ
будут комплексно сопряжены с переменными уФ. Пусть
у@ = Uf + У~\ vf, yf = uf — y
G=1. 2 га),
и примем аФ и х>Ф в качестве новых переменных вместо уФ и уф.
Тогда, выделяя в /-Й и /-Й группах уравнений E4.6) вещественные
и мнимые части, мы получим вместо двух указанных групп, состоящих
из п-i = щ уравнений каждая и обладающих комплексными коэф-
коэффициентами, одну группу, состоящую из 2nt уравнений с веществен-
вещественными коэффициентами следующего вида:
-- = Х^ - ^v{\ -±
С/=2, .... щ).
Допустим теперь, что р(- является отрицательным вещественным
числом. В этом случае, взяв арифметическое значение логарифма,
мы можм писать:
мы можем писать:
где ^—целое число и величина Я.г вещественна. Решения E4.3),
отвечающие корню pt, будут получаться комплексными. Но так как
коэффициенты уравнений E4.1) вещественны, то вещественные части
втих решений будут также являться решениями. Следовательно,
§ 54] ТЕОРЕМА ЛЯПУНОВА О ПРИВОДИМОСТИ ЛИНЕЙНЫХ УРАВНЕНИЙ 219
корню р1 отвечают решения
где
и мы получаем для этого корня дифференциальные уравнения с веще-
вещественными коэффициентами:
dt
E4.9)
С/= 2 nt).
Здесь переменные z(f> отличаются от переменных yV\ опреде-
определяемых формулами E4.4), только тем, что функции ф^>. заменены
функциями tysj .
Таким образом, можно считать доказанным, что систему уравне-
уравнений E0.1) при помощи вещественной неособенной линейной подста-
подстановки можно привести к системе уравнений с постоянными коэффи-
коэффициентами. При этом, если характеристическое уравнение системы E4.1)
не имеет вещественных отрицательных корней, то коэффициенты
подстановки будут периодическими функциями периода а>. Если же
указанное характеристическое уравнение имеет вещественные отрица-
отрицательные корни, то коэффициенты подстановки будут также периоди-
периодическими функциями, но период этих функций будет, вообще, равен 2со.
Это непосредственно вытекает из того обстоятельства, что период
функции E4.8) будет, вообще говоря, 2со, так как этим периодом обла-
обладает множитель
cosB?+l) —+у — lsini
Пусть предложена система линейных уравнений
-^- = ?51*1+ ¦¦¦-\-4snxn (s=1.2 га), E4.10)
где qsj — какие-нибудь непрерывные ограниченные функции t при
всех t^-tQ. Допустим, что эта система может быть преобразована
220 УСТОЙЧИВОСТЬ ПЕРИОДИЧЕСКИХ ДВИЖЕНИЙ [ГЛ. V
в систему линейных уравнений с постоянными коэффициентами при
помощи линейного преобразования
обладающего тем свойством, что его коэффициенты fsj, так же
как и коэффициенты обратного преобразования, являются непрерыв-
непрерывными и ограниченными функциями t при всех t^>t0. В этом случае
систему E4.10) А. М. Ляпунов предложил называть приводимой. Таким
образом, любая линейная система уравнений с непрерывными периоди-
периодическими коэффициентами является приводимой').
§ 55. Определяющее уравнение приведенной системы.
Теорема Ляпунова о корнях характеристических уравнений
сопряженных систем.
Рассмотрим какую-нибудь систему линейных уравнений с постоян-
постоянными коэффициентами:
| I / Ч Г) \ /Г- Г- 4 ч
a iVi~т~ • • • *т ^ Ул \^:~~г ^' и)' (оо. 1)
Составим ее характеристическое уравнение:
ап — X а12 ... аы
а1\ а22 — ^ • • • аЧп
ап\ ап1 ¦¦¦ апп -
= 0. E5.2)
Но система уравнений E5.1) может быть рассматриваема как
частный случай системы уравнений с периодическими коэффициентами
произвольного периода со, и, следовательно, для нее может быть
построено характеристическое уравнение в смысле § 50. Это уравне-
уравнение будет отличаться от уравнения E5.2). Поэтому во избежание
путаницы мы будем в дальнейшем, где эта путаница возможна, назы-
называть уравнение E5.2) определяющим уравнением.
В предыдущем параграфе мы показали, что систему уравнений
с периодическими коэффициентами E0.1) можно неособенной линейной
подстановкой с периодическими коэффициентами преобразовать в си-
систему уравнений с постоянными коэффициентами E4.6). Так как при
таком преобразовании корни характеристического уравнения не изме-
изменяются, то корни характеристического уравнения системы E0.1)
совпадают с корнями характеристического уравнения системы E4.6).
Найдем корни этого последнего уравнения.
') Подробное исследование приводимых систем содержится в работе:
Е р у г и н Н. П., Приводимые системы. Труды матем. ин-та им. В. А. Сте-
клова, т. XIII, 1946.
§ 55] ОПРЕДЕЛЯЮЩЕЕ УРАВНЕНИЕ ПРИВЕДЕННОЙ СИСТЕМЫ 221
С этой целью заметим, что уравнения E4.6) допускают, очевидно,
фундаментальную систему решений, распадающихся на т групп, таких,
что первое решение в какой-нибудь p-R группе имеет вид
P \np — 4'-
z(k) __ z(k) — ,.. = z(k) _ о
(ft=l. 2 /? — 1, />-f 1 m), •
а остальные решения этой группы могут быть получены из первого
последовательным применением оператора -=г? к коэффициентам
прие~а/А Так, например, второе решение указанной группы имеет
вид
2^= О,
р \'1р — ^)-
(k=l, 2 р — 1, р-f 1 /к).
Всего решений в p-R группе будет пр. Таким образом, для каждой
величины — ар получается группа с пр решениями. При этом среди
величин —(Zj, .... —ат могут быть и одинаковые, так как по усло-
условию каждая из величин ар выписывается столько раз, сколько групп
решений соответствует корню pft характеристического уравнения си-
системы E4.1).
Полученные решения системы E4.6) будут как раз такими, какие
фигурируют в предложении, установленном в § 53. Поэтому на осно-
основании этого предложения мы можем утверждать, что величины —ар
являются характеристическими показателями и, следовательно, вели-
величины корнями характеристического уравнения системы E4.6) и
эквивалентной ей системы E0.1). Кроме того, из предложения § 53
вытекает также, что корень — характеристического уравнения си-
системы E0.1) имеет такую же кратность, как и корень pft характери-
характеристического уравнения системы E4.1), и что этим корням в обеих
системах отвечает одинаковое число групп с одинаковым числом
222
УСТОЙЧИВОСТЬ ПЕРИОДИЧЕСКИХ ДВИЖЕНИЙ
[гл: v
решений в каждой rpynfte. Мы приходим, таким образом, к следу-
следующей теореме, установленной А. М. Ляпуновым.
Теорема. Если pft — корень характеристического уравнения
системы линейны к уравнений с периодическими коэффициентами,
то величина — будет корнем характеристического уравнения
сопряженной системы. При этом кратности обоих корней,
числа групп решений, им соответствующие, и числа решений
в соответствующих группах одинаковы.
Рассмотрим теперь определяющее уравнение системы E4.6). Оно,
очевидно, имеет вид
где
D(X) =
j
0
Mi
X 0
— o.p — X
0
...0
...0
... — 1
= 0,
0
0
— o-p — K
Отсюда непосредственно убеждаемся в справедливости следующей
теоремы.
Т е о р е м а. При преобразовании системы линейных уравнений
с периодическими коэффициентами в систему уравнений с по-
постоянными коэффициентами корни определяющего уравнения
преобразованной системы являются характеристическими по-
показателями исходной системы.
§ 56. Критерии устойчивости.
Переходим теперь к вопросу об устойчивости решений линейных
уравнений с периодическими коэффициентами. Из общего вида этих
решений, установленного в § 52, вытекает сразу, что если вещественные
части всех характеристических показателей отрицательны, то все реше-
решения стремятся к нулю при t —> со и, следовательно, имеет место асимпто-
асимптотическая устойчивость. Напротив, если вещественная часть хотя бы
одного характеристического показателя положительна, то система имеет
частные решения, неограниченно возрастающие при t->oo и, следова-
§ 56] КРИТЕРИИ УСТОЙЧИВОСТИ 223
тельно, будет иметь место неустойчивость. Если же вещественные части
некоторых характеристических показателей отрицательны, а остальных
равны нулю, то может иметь место как устойчивость, так и неустой-
неустойчивость, а именно: если характеристические показатели с веществен-
вещественными частями, равными нулю, являются простыми, то соответствующие
им решения будут ограниченными и невозмущенное движение будет
устойчиво, но не асимптотически. То же самое будет справедливо
и в случае кратных характеристических показателей с нулевыми
вещественными частями, если число групп решений, соответствующих
таким показателям, равно их кратности. Но если имеется характеристи-
характеристический показатель с нулевой вещественной частью, кратность которого
превышает число групп решений, ему соответствующих, то рассма-
рассматриваемая система будет иметь решения, содержащие вековые члены.
При этом вековыми членами мы называем члены вида /тф(/), где
(f(t)—ограниченные функции времени. В рассматриваемом случае
невозмущенное движение будет неустойчиво.
Но на основании E1.1) характеристическому показателю с отрица-
отрицательной вещественной частью соответствует корень характеристи-
характеристического уравнения с модулем, меньшим единицы, характеристическому
показателю с положительной вещественной частью соответствует корень
с модулем, большим единицы, и характеристическому показателю
с нулевой вещественной частью отвечает корень с модулем, равным
единице. Поэтому условия устойчивости для линейных уравнений
с периодическими коэффициентами могут быть выражены следующим
образом: если все корни характеристического уравнения имеют модули,
меньшие единицы, то невозмущенное движение устойчиво асимптоти-
асимптотически; если имеется хоть один корень с модулем, большим единицы,
то невозмущенное движение неустойчиво; если модули некоторых
корней меньше единицы, а остальные равны единице, то невозмущен-
невозмущенное движение может быть как устойчивым, так и неустойчивым.
Устойчивость будет иметь место тогда, когда все корни с модулями,
равными единице, будут простыми или когда они являются кратными,
но кратность их равна числу отвечающих им групп решений. Если
кратность хотя бы одного из корней с модулем, равным единице,
превышает число соответствующих ему групп решений, то невозму-
невозмущенное движение неустойчиво.
Пусть
рп+Л1рп-1+...+Лп_1р+Л,, = 0 E6.1)
— характеристическое уравнение рассматриваемой системы. Мы выра-
выразили условия устойчивости через корни этого уравнения. Можно,
однако, выразить эти условия непосредственно через коэффициенты At.
С этой целью произведем в уравнении E6.1) подстановку
E6.2)
224 УСТОЙЧИВОСТЬ ПЕРИОДИЧЕСКИХ ДВИЖЕНИЙ [ГЛ. V
Эта подстановка преобразует круг единичного радиуса с центром
в начале координат плоскости комплексного переменного р в левую
полуплоскость комплексного переменного X. Поэтому условия устой-
устойчивости, выражающиеся в том, что модули всех корней уравне-
уравнения E6.1) не должны превосходить единицы, могут быть выражены
следующим образом: для устойчивости необходимо, чтобы веществен-
вещественные части всех корней уравнения
не были положительными. При этом, если эти вещественные части
все отрицательны, то устойчивость действительно будет иметь место
и притом асимптотическая.
Таким образом, задача, так же как и для случая уравнений
с постоянными коэффициентами, сводится к установлению условий
отрицательности вещественных частей всех корней алгебраического
уравнения. Эти условия даются теоремой Гурвица.
В отличие, однако,. от случая уравнений с постоянными коэффи-
коэффициентами рассматриваемая сейчас задача значительно усложняется тем,
что коэффициенты Aj, кроме коэффициента Ап, который дается фор-
формулой E0.8), неизвестны. Для их определения необходимо знать
какую-нибудь фундаментальную систему решений исследуемых диф-
дифференциальных решений. Но как показывает форма E0.7) характери-
характеристического уравнения, нет необходимости знать эту фундаментальную
систему для всех значений t, а лишь только для одного значения t = о>.
Кроме того, условия устойчивости определяются неравенствами, и
поэтому достаточно знать лишь приближенные значения коэффициентов
характеристического уравнения. Все это позволяет для определения
указанных коэффициентов с успехом пользоваться различными
приближенными приемами интегрирования. В нижеследующих парагра-
параграфах мы подробно останавливаемся на некоторых основных приемах при-
приближенного вычисления корней характеристического уравнения.
§ 57. Характеристическое уравнение канонических систем.
В некоторых случаях по самому виду дифференциальных уравне-
уравнений можно сделать некоторые заключения о корнях характеристиче-
характеристического уравнения. Одним из важнейших случаев такого рода будет
тот, когда рассматриваемая система уравнений имеет канонический вид
dx! дН dy. дН
dt ~~ ду. ' dt ~
(i=l, 2, .... П),
E7.1)
где Н(fv xv .... х„, }>! уп) — квадратичная форма переменных
х±, .... хп, yit ... >• уп, коэффициенты которой являются непрерыв-
§ 57] ХАРАКТЕРИСТИЧЕСКОЕ УРАВНЕНИЕ КАНОНИЧЕСКИХ СИСТЕМ
225
ными периодическими функциями t периода со. Более подробно эта
система может быть записана следующим образом:
dt
dyj_
dt
¦ ZidyidxaXa-^Li-dyTdy^^
a=l a=l
: — 7, -3 з— Xa — 7, -г i— У .
^ дж, <?xa a jU dxt dya ^a
a=l
a=l
E7.1')
Имеет место следующая теорема Ляпунова.
Теорема. Пусть р — корень характеристического уравне-
уравнения системы E7.1). Тогда если р=± 1, то кратность этого
корня будет обязательно четная. Если р=?±1 и этот корень
имеет кратность т и ему отвечает р групп решений, то
величина — будет также корнем характеристического урав-
уравнения и этот корень будет иметь ту же кратность т и
ему будет отвечать то же число р групп решений.
Доказательство. Рассмотрим линейную систему, сопряжен-
сопряженную с E7.1). Эта система имеет вид
dui _ V
dt- ~ Li
a=l
д2Н
dyadxt
a=l
дх„
dt
дуадУ;
a=l
дхадУ1
E7.2)
Пусть p—какой-нибудь корень m-Vi кратности характеристиче-
характеристического уравнения системы E7.1). Допустим сначала, что р=^±1.
На основании теоремы о корнях характеристических уравнений со-
сопряженных систем (§ 55) величина — будет корнем /ге-й кратности
характеристического уравнения системы E7.2). Следовательно, эта
система имеет т независимых решений вида
(a=i-lnp), C/=l, 2 т).
распадающихся на некоторое число групп известного вида. Здесь U'ц
Vu — некоторые полиномы относительно t с периодическими коэф-
коэффициентами.
Но система E7.2), как это сразу видно из ее структуры, пере-
переходит в систему E7.1), если величины ut заменить величинами yt,
а величины vt — величинами — xt. Следовательно, если ut{f), vt(f)
являются решением системы E7.2), то функции х1 = — V((t)>
226 УСТОЙЧИВОСТЬ ПЕРИОДИЧЕСКИХ ДВИЖЕНИЙ [ГЛ. V
yiz?=ai(t) определяют решение системы E7.1). Отсюда непосред-
непосредственно следует, что система E7.1) имеет т независимых частных
решений
xtJ = - e-*>VtJ (t). yu = е-«ии (t)
C/=l. 2 т)
и, следовательно (§ 53), величина —а является характеристическим
показателем, а корнем характеристического уравнения этой си-
системы с кратностью, не меньшей т. Эта кратность, очевидно, не
может быть больше т, так как в противном случае, применяя
только что доказанное предложение к корню —, мы получим, что
вопреки предположению кратность корня р превосходит т.
Из наших рассуждений вытекает также сразу, что корню — со-
соответствует такое же число групп решений и такое же число реше-
решений в каждой группе, как и корню р.
Итак, теорема доказана для каждого корня, отличного от -j-1
или —1. Чтобы полностью доказать теорему, достаточно установить,
что если характеристическое уравнение системы E7.1) имеет корень,
равный -|-1, то кратность такого корня обязательно четная и что
то же самое справедливо и для корня, равного —1. Для этого
прежде всего заметим, что сумма кратностей корней, равных ±1,
будет обязательно четным числом, так как на основании доказанного
сумма кратностей всех корней, отличных от ± 1, будет четной и
порядок 2/1 характеристического уравнения является также четным.
Далее, произведение всех корней характеристического уравнения
равно на основании E0.8) величине
UJ
J
dt.
Но в рассматриваемом случае
у/ д*Н д*Н \_п
ду. дх. дх.
и, следовательно, произведение всех корней характеристического
уравнения равно 1. Но так как произведение всех корней, отличных
от ±1, по доказанному равно 1, то и произведение корней, рав-
равных + 1, тоже равно 1. Следовательно, если характеристическое
уравнение имеет корень, равный —1, то кратность этого корня
будет обязательно четной. Но тогда то же самое будет справедливо
§ 58] ВЫЧИСЛЕНИЕ КОРНЕЙ ХАРАКТЕРИСТИЧЕСКОГО УРАВНЕНИЯ 227
и по отношению к корню, равному +1, если такой корень суще-
существует.
Таким образом, теорема полностью доказана.
Из доказанной теоремы вытекает, что для уравнений вида E7.1)
устойчивость может иметь место лишь только тогда, когда все корни
характеристического уравнения имеют модули, равные единице.
§ 58. Вычисление корней характеристического уравнения
методом разложения по степеням параметра.
Допустим, что коэффициенты системы линейных уравнений с пе-
периодическими коэффициентами
4г = />л*1+ ••• + />,»*« (*=1. 2 я) E8.1)
зависят от р параметров \ilt ..., \ip, по отношению к которым они
голоморфны в области, определяемой неравенствами
||i,|<E, (*=1. 2, .... р), E8.2)
где Ех, . . ., Ер — некоторые постоянные числа. Мы предполагаем
при этом, что период а> от этих параметров не зависит.
Тогда, как известно, в любом решении xs = xs (t, fij цр)
уравнений E8.1), начальные значения которого не зависят от пара-
параметров, функции xs(t, |ij, ..., |ip) будут также голоморфными от-
относительно \iv . . ., \ip в области E8.2). Поэтому, принимая во вни-
внимание форму E0.7) характеристического уравнения, мы приходим
сразу к следующей теореме Ляпунова.
Теорема. Коэффициенты характеристического уравнения
системы E8.1) являются в области E8.2) голоморфными
функциями параметров щ \ip.
Здесь существенным является то обстоятельство, что область
голоморфности коэффициентов характеристического уравнения совпа-
совпадает с областью голоморфности коэффициентов исследуемых диф-
дифференциальных уравнений. В частности, если коэффициенты иссле-
исследуемых уравнений являются целыми функциями параметров, то и
коэффициенты характеристического уравнения являются также целыми
функциями параметров.
Доказанную теорему можно использовать для приближенного
вычисления коэффициентов характеристического уравнения. Покажем,
как это сделать.
Допустим с этой целью, что коэффициенты системы E8.1) за-
зависят только от одного -параметра \i, так что можно написать:
г1 @ -f- \ip«} @+ nVSJ @
228
УСТОЙЧИВОСТЬ ПЕРИОДИЧЕСКИХ ДВИЖЕНИЙ
[гл. v
где qsl (f), р(Ц (t), pfl (t), ... — непрерывные периодические функ-
функции t периода @ и ряды сходятся при | \л | -^ Е.
Рассмотрим фундаментальную систему решений xsj(t, ц) си-
системы E8.1), определяемую начальными условиями
я). E8.3)
E8.4)
. Началь-
E8.5).
Как указывалось выше, мы можем написать:
где ряды при всех значениях ^ сходятся в области
ные условия E8.3) дают:
1= ... =0.
Подставляя ряды E8.4) в уравнения E8.1) и приравнивая коэф-
коэффициенты при одинаковых степенях |i, мы получим для определения
неизвестных функций хЩ, х^Ч, ... следующие системы дифферен-
дифференциальных уравнений:
dxM
sn~nj'
dxA\
aj'
a=l
п k-l
У У л<'
а=1 В=0
(s=l, 2 п).
У всех этих систем линейных неоднородных уравнений одинако-
одинаковая однородная часть. Допустим, что мы можем проинтегрировать
в замкнутой форме однородную систему уравнений
E8.6)
dt
в которую переходит E8.1) при ц = 0.
Тогда уравнения E8.6) дадут возможность последовательно опре-
определять все функции дг'*>, начиная с k = 0. Начальные условия E8.5)
делают их при этом вполне определенными.
Следовательно, решения E8.4) могут быть вычислены с какой
угодно степенью точности. Полагая в этих решениях Ыщ и под-
§ 59] ПРИЛОЖЕНИЕ К СИСТЕМЕ ВТОРОГО ПОРЯДКА 229
ставляя в E0.7), мы получим приближенные значения коэффициентов
характеристического уравнения.
Мы получили, таким образом, способ приближенного вычисления
коэффициентов характеристического уравнения для того частного
случая, когда исследуемые уравнения содержат некоторый параметр [1,
причем при ц = 0 уравнения интегрируются в замкнутой форме.
Мы можем, однако, к этому частному случаю свести и самый общий.
Пусть нам необходимо вычислить коэффициенты характеристиче-
характеристического уравнения заданной системы линейных уравнений
Цг = гл if) х, + ... + гт @ х„ E8.7)
с периодическими коэффициентами, не содержащими никаких пара-
параметров. Заменим систему E8.7) системой
¦^f- = рА (*.,!)*!+...+ Рт (Л ц) *„. E8.8)
где содержащие аналитически параметр ц функции psj(t, ц) выбраны
таким образом, что при ц = 0 система E8.8) интегрируется в зам-
замкнутой форме (обращается, например, в систему с постоянными ко-
коэффициентами), а при |i = [x*, где \i*—некоторое фиксированное
число, лежащее в области сходимости коэффициентов psj(t, \i), она
обращается в заданную систему E8.7), т. е.
Psj(f. \f) = rsj(t) (8, 7=1. 2 Л).
Можно, например, положить:
Полученная таким образом система будет как раз того частного вида,
который мы рассмотрели, и для нее могут быть вычислены коэффи-
коэффициенты характеристического уравнения вышеуказанным приемом.
Положив затем |i = |i*, мы получим коэффициенты характеристиче-
характеристического уравнения заданной системы.
Приведенный прием особенно удобен тогда, когда величина [1*
мала, т. е. когда рассматриваемая система мало отличается от системы,
интегрируемой в замкнутой форме. В этом случае для вычисления
коэффициентов характеристического уравнения можно будет ограни-
ограничиться небольшим числом приближений.
§ 59. Приложение к системе второго порядка.
Мы переходим теперь к подробному рассмотрению системы, опи-
описываемой одним уравнением второго порядка:
230 УСТОЙЧИВОСТЬ ПЕРИОДИЧЕСКИХ ДВИЖЕНИЙ [ГЛ. V
где Q и Р — периодические функции t периода со. Несмотря на част-
частный характер этой системы, к ней приводятся многие важные техни-
технические задачи.
Заменой
у = ехр(— у J Qdt^jx
уравнение E9.1) приводится к виду
= 0, E9.2)
где
р — г 4 ч 2 dt
— также периодическая функция периода со. Мы будем поэтому в даль-
дальнейшем рассматривать только уравнения вида E9.2).
Записав уравнение E9.2) в виде системы
dx_¦ _ , dx' _ _
dt ~ х ' dt ~ рх'
мы видим, что характеристическое уравнение в рассматриваемом слу-
случае имеет вид
Д(р)= Ф(со) ф-(«)-р
где f (f) и <р(/) — два частных решения уравнения E9.2), определяемых
начальными условиями:
@)=1, /'<0) = 0. |
E9-3)
Кроме того, свободный член характеристического уравнения на
основании E0.8) обращается в единицу, и потому характеристическое
уравнение может быть представлено в виде
р2 — 2Лр+1=0, E9.4)
где
Л = у[/(со) + ф'(со)]. E9.5)
Так как произведение корней характеристического уравнения
равно единице, то либо оба корня имеют модули, равные единице,
либо модуль одного из корней больше единицы, а модуль другого
меньше этой величины, а именно: из соотношения
§ 59] ПРИЛОЖЕНИЕ К СИСТЕМЕ ВТОРОГО ПОРЯДКА 231
мы видим, что если А2 < 1, то оба корня будут комплексными и
иметь модули, равные единице, а если Л2 > 1, то оба корня будут
вещественны и один из них будет численно более, а другой численно
менее единицы.
Таким образом, основная задача устойчивости для уравнения E9.2)
сводится к установлению условий, при которых имеет место каждый
из двух возможных случаев: 1) Л2 <С 1 и 2) Л2 > 1.
Некоторые признаки наличия того или другого случая могут быть
получены методом предыдущего параграфа. С этой целью рассмотрим
вместо уравнения E9.2) уравнение
d2y ._. ..
-^ф- — цру, E9.6)
где |i—вспомогательный параметр, и найдем сначала коэффициент Л* (ц)
для этого уравнения. Положив затем ц, = —1, мы получим коэффи-
коэффициент Л для уравнения E9.2). Пусть / (t, ц) и q>(t, ц)—два частных
решения уравнения E9.6), определяемые начальными условиями:
/(О, |i)=l, /'@. И) = 0. 1
ф@, ji) = 0, ф'@, ц) = 1. j
Мы можем написать:
f (t, |x) = /0(t) + цД @ + ц.2Д (t)-\- ..., |
Ф (*. |х) = Фо @ + № @ + Й2Ф2 @ + • • • J E9-8)
Подставляя в E9.6), находим:
• dt2 ~ ' dt3 ~ '
: (я=1. 2,...). E9.9)
Начальные условия E9.8) дают:
/0<0) = 1. /;(О) = о, Фо(О) = о. Ф;@) = 1,
откуда
/о @=1.
t t t t
oo. а о
(я=1. 2, ...).
E9.10)
232 УСТОЙЧИВОСТЬ ПЕРИОДИЧЕСКИХ ДВИЖЕНИЙ [ГЛ. V
Следовательно, на основании E9.5) коэффициент A*(\i) для урав-
уравнения E9.6) имеет вид
со
А* (ц) = 1 + j 21 [/„ (®)+Ф; И !*"• E9-J О
п=1
На основании теоремы предыдущего параграфа ряд E9.11) схо-
сходится при всех значениях |i. Полагая ц = —1, мы получим коэффи-
коэффициент А для уравнения E9.2) в виде сходящегося ряда
п ;]1)«. E9.12)
л=1
Установив это, допустим, что функция p(t) может принимать только
отрицательные или равные нулю значения, не обращаясь в нуль тожде-
тождественно. Тогда все функции fn{t), f'n(t), q>n(t), q'n(t) при п нечетном
будут отрицательны, а при п четном — положительны. Вследствие
этого все члены ряда E9.12) будут положительны, и мы приходим
к следующей теореме Ляпунова.
Теорема. Если в уравнении E9.2) функция р может при-
принимать только отрицательные или равные нулю значения, не
обращаясь в нуль тождественно, то соответствующее этому
уравнению характеристическое уравнение имеет два веще-
вещественных корня, из которых один численно более, а другой
численно менее единицы.
Допустим теперь, что функция р может принимать только поло-
положительные или равные нулю значения, не обращаясь тождественно
в нуль. Будут ли при этом корни характеристического уравнения
иметь модули, равные единице? Этот вопрос естественно возникает,
ибо в случае, когда р постоянно, ответ на него получается положи-
положительный. Однако, как мы увидим ниже, если функция р не обра-
обращается в постоянную, то ответ на указанный вопрос может получиться
отрицательный. Может оказаться, что несмотря на то, что функция р
может принимать только положительные значения, характеристическое
уравнение будет иметь вещественные корни, из которых один более,
а другой менее единицы. Имеет, однако, место следующая теорема,
принадлежащая также Ляпунову.
Теорема. Если функция р может принимать только
положительные или равные нулю значения, не обращаясь в нуль
тождественно, и если при этом выполняется неравенство
E9.13)
то характеристическое уравнение системы E9.2) имеет ком-
комплексные корни, равные по модулю единице.
§ 59]
ПРИЛОЖЕНИЕ К СИСТЕМЕ ВТОРОГО ПОРЯДКА
233
Доказательство. Заметим прежде всего, что при р^-0 все
функции fn и фя, а также их производные f'n и q^ положительны при
всех t ^> 0. Докажем, что при всех t ^- 0 справедливы неравенства
t
>О. E9.14)
Мы можем, очевидно, писать:
с __
откуда, учитывая E9.9), находим:
t
где
dt
-dt.
Если мы докажем, что при t^-Q имеют место неравенства
Fn>0, Ф„>0, E9.15;
то этим самым, очевидно, будет доказано и неравенство E9.14).
Чтобы доказать неравенства E9.15), запишем функции Fn и Фп через
интегралы от их производных. Будем иметь:
где
E9.16)
234
УСТОЙЧИВОСТЬ ПЕРИОДИЧЕСКИХ ДВИЖЕНИЙ
[ГЛ. V
Если функции ип и vn также представить в виде интегралов, то
легко найдем:
t
«„ = / VP (Ф„-2 + tfn-i) + Fn-A dt'
Учитывая, что все функции fn, f'n, <pn, q>'n положительны, мы из
E9.16) и F9.17) найдем, что если при всех ?^>0 имеют место нера-
неравенства Fn_i > О, Ф„_1 > 0, то при тех же значениях t будут иметь
место и неравенства E9.15). Таким образом, неравенства E9.15)
будут доказаны для любого п, если мы их докажем для п = 2. Но
для п. = 2 выражения E9.16) дают:
F2 = 2 J ( J p dt\ + 2/ир; U, Ф2 = 2 J (/,/* 4- 2/0 dt.
о (Vo / J о
Величины F2 и Ф2, очевидно, положительны, и поэтому мы можем
считать неравенства E9.15) доказанными.
Из этих неравенств, полагая ? = о>, находим:
а
1(<й)]]? J Pdt.
о
Заменяя п на 2я, получим:
/2я («) -f- Ф^„ (со) <
(О
_х (со)] ^- J
E9.18)
а заменяя п на 2п~\-1 и обращая знаки неравенств, будем иметь:
Установив это, рассмотрим коэффициент Л, соответствующий
уравнению E9.2), определяемый, как мы видели, рядом E9.12). Если
в этом ряде заменить все четные члены правыми частями нера-
неравенств E9.18), то будем иметь:
§ 59] ПРИЛОЖЕНИЕ К СИСТЕМЕ ВТОРОГО ПОРЯДКА 235
Если же воспользоваться неравенствами E9.19), то получим:
E9.21)
Если теперь функция р удовлетворяет неравенству E9.13), то все
члены, стоящие под знаком суммы в неравенствах E9.20) и E9.21),
будут положительны, и эти неравенства дадут
что и доказывает теорему.
Если р^О, но неравенство E9.13) не выполняется, то, как мы
уже указывали, возможны оба случая: 1) Л2-<1 и 2) Л2 > 1. Для
выяснения, какой из них в каждой конкретной задаче будет иметь
место, требуется более подробное исследование ряда E9.12). В спе-
специальной работе, посвященной этому вопросу, А. М. Ляпунов1)
установил ряд признаков наличия того или другого случая. Этому же
вопросу посвящена работа Н. Е. Жуковского2), в которой дается
обобщение критерия E9.13). Некоторые другие обобщения этого
критерия даны в работах Н. В. Адамова, Н. П. Еругина, Р. С. Гуса-
ровой, В. А. Якубовича, М. Г. Нейгауз и В. Б. Лидского3). Случай,
когда р (t) может менять знак, рассмотрен в большой работе
А. М. Ляпунова4).
>) Ляпунов А. М., Sur une serie dans la theorie des equations differen-
tielles lineaires du second ordre a coefficlentes periodiques. Зап. Акад. наук
по физ.-мат. отделению, 8-я сер., т. XIII, № 2, 1902.
2) Жуковский Н. Е., Условия конечности интегралов уравнения
d2v
—i. -f- /py == 0. Матем. сборник, т. XVI, 1892. См. также: Жуковский Н. Е.,
Собрание сочинений, т. I, Гостехиздат, 1948.
3) Адамов Н. В., О колебаниях интегралов уравнения второго порядка
с периодическими коэффициентами и некоторых условиях устойчивости.
Матем. сборник, т. XLII, вып. 6, 1935.
Е р у г и н Н. П., Обобщение одной теоремы Ляпунова. ПММ, т. XII,
вып. 5, 1948.
Гусарова Р. С, Об ограниченности решения линейного дифферен-
дифференциального уравнения с периодическими коэффициентами. ПММ, т. XIV,
вып. 3, 1950.
Якубович В. А., Об ограниченности решения уравнения у" -\-p(t) у = 0,
p(t-\-e>) = p(t). Докл. Акад. наук СССР, т. LXXIV, № 5, 1950.
Нейгауз М. Г. и Л и д с к и й В. Б., Об ограниченности решений
линейных дифференциальных уравнений с периодическими коэффициентами.
Докл. Акад. наук СССР, т. LXXVII, № 2, 1951.
4) Ляпунов А. М., Об одном вопросе, касающемся линейных диффе-
дифференциальных уравнений второго порядка с периодическими коэффициентами.
Сообщ. Харьк. матем. об-ва, 2-я сер., т. V, №№ 3—4 и 5—6, 1896. См.
также примечание в конце книги (стр. 522).
236 УСТОЙЧИВОСТЬ ПЕРИОДИЧЕСКИХ ДВИЖЕНИЙ [ГЛ. V
§ 60. Некоторые технические задачи, приводящиеся
к уравнению второго порядка с периодическими коэффициентами,
и связанные с этим вопросы теории.
В предыдущем параграфе мы показали, как при помощи искус-
искусственного введения параметра можно найти приближенные значения
корней характеристического уравнения. Однако во многих важных
технических вопросах такого рода параметры содержатся в дифферен-
дифференциальных уравнениях по существу самой задачи, и при этом требуется
определить, будет ли иметь место устойчивость или неустойчивость
не при определенном значении параметра, а при любом его значении.
Чтобы лучше уяснить, какого рода математические проблемы здесь
возникают, рассмотрим некоторые вопросы, приводящиеся к исследо-
исследованию устойчивости решений линейных уравнений с периодическими
коэффициентами. Мы рассматриваем при этом только такие вопросы,
которые приводятся к исследованию одного уравнения второго порядка
вида E9.2).
Пример 1. Маятник с колеблющейся точкой подвеса.
В качестве простейшего примера рассмотрим маятник длиной /, ось
подвеса которого совершает вертикальные гармонические колебания
с малой амплитудой а и частотой ю. Дифференциальное уравнение
движения маятника имеет вид
^/) F0.1)
где ф—угол отклонения от вертикали. Полагая a>t = % и отбрасывая
нелинейные члены, получим:
( ^ ) <60'2>
Так же как и для маятника с неподвижной осью подвеса, верти-
вертикаль является положением равновесия. Но в отличие от случая маят-
маятника с неподвижной осью это положение равновесия может быть как
устойчивым, так и неустойчивым, а именно: в зависимости от значе-
значения @ величина А для уравнения F0.2) может удовлетворять как
неравенству А2 < 1, так и неравенству А2 > 1. Задача заключается
в том, чтобы выделить значения частоты ю, для которых получается
первый из указанных случаев, и те критические значения этой
частоты, для которых получается второй случай. В этом втором
случае будут иметь место поперечные колебания маятника с неогра-
неограниченно возрастающей амплитудой!). Говорят, что в этом случае
имеет место параметрический резонанс.
') В действительности амплитуда колебаний будет оставаться конечной,
так как точное уравнение F0.1) этих колебаний не является линейным.
§60]
НЕКОТОРЫЕ ТЕХНИЧЕСКИЕ ЗАДАЧИ
237
Пример 2. Крутильные колебания коленчатых валов.
Рассмотрим крутильные колебания коленчатых валов силового дви-
двигателя с учетом инерции шатунов и поршней. Дифференциальные
уравнения колебаний составлены Э. ТреффтцомJ). Эти колебания
обстоятельно исследованы Н. Е. Кочиным2). Мы ограничиваемся
здесь рассмотрением случая одноцилиндрового двигателя с махови-
маховиком (рис. 14).
Мы будем считать, что масса маховика достаточно велика, так
что вращение вала можно считать равномерным. Пусть со — угловая
скорость маховика. Обо-
Обозначим через ф угол вра- "~" '
щения кривошипа. Тогда ки-
кинетическая энергия криво-
кривошипа вместе со связанными
с ним движущимися мас-
массами (шатуном и поршнем)
может быть
представлена
в виде
y////t
у////
Рис. 14.
Функцию ./(ф) можно
вычислить, если известны
размеры и распределение
масс кривошипа, шатуна и
поршня. Это будет, оче-
очевидно, периодическая функция ф периода 2я. При приближенном вы-
вычислении принято величину J считать постоянной, равной ее сред-
среднему значению Jo за период. При более точном расчете мы можем
положить:
где F — некоторая периодическая функция периода 2я, a fi—постоян-
fi—постоянная величина, которую мы будем считать малой.
Потенциальная энергия упругих сил, действующих на кривошип,
равна
Пх = -j ciJj2 = -j с (ф — d)ff,
где i|) — угол закручивания, ас — коэффициент жесткости вала при
кручении. Кроме того, на кривошип действует внешний крутящий
•) Trefftz E., Zur Berechnung der Schwlngungen von Kurbelwellen.
Vortrage aus dem Oeblete der Aerodynamik und verw. Oebiete, Berlin, 1930.
2) К о ч и н Н Е., О крутильных колебаниях коленчатых валов. ПММ,
И, вып. 1, 1934.
238 УСТОЙЧИВОСТЬ ПЕРИОДИЧЕСКИХ ДВИЖЕНИЙ [ГЛ. V
момент М (ф) с потенциальной энергией
ф
о
Функция М(ф) будет также периодической. Период этой функ-
функции равен 2л, если двигатель двухтактный, и 4л, если двигатель
четырехтактный, так как в последнем случае рабочий ход поршня
приходится на два оборота вала.
Составляя теперь дифференциальное уравнение Лагранжа, получим:
у(Ф> Ф + 4 -^Г Ф2 == ~ ^ (Ф) - с (Ф - «О- F0.3)
Для упрощения этого уравнения введем вместо обобщенной коор-
координаты ф обобщенную координату q при помощи соотношения
at
Будем иметь:
X
d (at)
Следовательно, уравнение F0.3) может быть переписано в сле-
следующем виде:
•• __ М (ф) с (ф — at) о2 47 (юр
Я~ V7W V7W 2У7Щ d(at) '
Считая угол закручивания ф — со/ малым, примем:
ф
q = Г ]/У(ф)й?ф = (ф — (О/) /-/(«0.
jM (tp) __ At (ю^) с (ф — atf) с (ф — atf)
УУ(Ф) Т VTJaF) ' /У(ф) /У (at) '
после чего получим:
с _ М (at) ю2 dJ (at)
q
,
2УТ(аГ) d(at)
Таким образом, колебания описываются неоднородным линейным
уравнением с периодическими коэффициентами. Поведение его
решений в смысле устойчивости и неустойчивости определяется
§ 60] НЕКОТОРЫЕ ТЕХНИЧЕСКИЕ ЗАДАЧИ
однородным уравнением
239
J(at) ч~ "•
Полагая в этом уравнении со/ = т> окончательно найдем, что
задача сводится к исследованию уравнения второго порядка
F0.4)
где
— периодическая функция периода 2л.
Уравнение F0.4), так же как и уравнение F0.2), содержит пара-
параметр со —угловую скорость вращения вала. И так же как и в случае
ведущая ось
Рис. 15.
маятника, в зависимости от значений со может иметь место параметри-
параметрический резонанс. Задача как раз и заключается в определении крити-
критических значений угловой скорости, т. е. тех значений со, при которых
величина А для уравнения F0.4) будет иметь модуль, больший
единицы.
Пример 3. Колебания в спарниках электровозов1). В ка-
качестве третьего примера рассмотрим колебания, обусловленные пара-
') Мы излагаем здесь эту задачу по книге: Тимошенко С. П., Теория
колебаний в инженерном деле, Гостехиздат, 1931. В этой книге приведена
подробная литература вопроса.
240 УСТОЙЧИВОСТЬ ПЕРИОДИЧЕСКИХ ДВИЖЕНИЙ [ГЛ. V
метрическим резонансом, в электровозах с передачей вращения
спарниками. Гибкость системы между валом мотора и ведущими осями
является переменной, зависящей от положения валов и изменяющейся
периодически с периодом, зависящим от угловой скорости вращения
мотора. Это и дает возможность возникновения параметрического
резонанса.
Рассмотрим простейший пример. Допустим, что крутящий мо-
момент Мт мотора передается на ведущую ось электровоза при помощи
кривошипов О — 1 и (?! — /, спарников 1—1 и 2—2 и кривоши-
кривошипов О — 2 и Oj — 2 (рис. 15). Кривошипы О — 2 и О1 — 2 повер-
повернуты по отношению к кривошипам О — 1 и Ох — 1 на угол -н-.
Обозначим через Дер угол поворота мотора по отношению к веду-
ведущей оси Ох — Oj. Мы можем написать:
Л1г = 9Аф, F0.5)
где 9 — гибкость передачи. Определим эту величину.
Д
Пусть Д^ — угол поворота, вызванный скручиванием конца О А
вала мотора, а А2ф — угол поворота, вызванный сжатием б спарника
1—1. Тогда
Дф = Д1Ф + Л2ф, F0.6)
причем, как это видно из чертежа,
Обозначим через Мт крутящий момент, передаваемый кривоши-
кривошипом О— /:
М'т
где kx — характеристика пружинности конца ОА вала. Далее, если
St — сила, сжимающая спарник 1 — 1, то
»-¦?•
где А — площадь сечения спарника, а Е — модуль упругости его
материала. Но, очевидно,
1 г sin ф
и, следовательно, на основании F0.7)
М'т
§ 60] НЕКОТОРЫЕ ТЕХНИЧЕСКИЕ ЗАДАЧИ 241
где
, _ АЕг2
2 — 2 '
Формулы F0.6), F0.8) и F0.9) дают:
^) F0.10)
Точно так же, обозначая через Mr момент, передаваемый кон-
концом ВО вала, и предполагая, что устройство симметрично относи-
относительно продольной оси электровоза, находим:
Дф=Л1г(т—\~ и * 2 )• F0.11)
Т ' \ kx ' k2 COS2 ф ) V '
Ho
и поэтому формулы F0.10) и F0.11) дают:
2 1
-т— sin2 го cos2ffi + -7—
... k, ko Л а —
где
2.8 , 2 Si8!1 w }
^j &> ^l ^2 ^1^) ^i ^1
Таким образом, обозначая через со угловую скорость вращения
вала (считая приближенно эту скорость постоянной), мы получим
для гибкости системы выражение
a-bcostot 6 2
с — d cos Ш v 7
Заметим, что если бы система не была симметрична относительно
продольной оси, то коэффициенты в формуле F0.11) отличались бы
от коэффициентов в формуле F0.10), и для гибкости получилось бы
выражение вида
fl _ a + bcos2xi)t-{-c cos 4&t ,fin . „.
/> + ?cos2arf + '-cos4<1rf • (ou.io)
Составим теперь дифференциальные уравнения колебаний. Пусть
ф! и ф2 — углы поворота оси мотора и ведущей оси, Jt и J2 — моменты
инерции вращающихся вокруг этих осей масс, Мт и Мг — действую-
действующие на них внешние моменты. Тогда имеем:
F0.14)
242 УСТОЙЧИВОСТЬ ПЕРИОДИЧЕСКИХ ДВИЖЕНИЙ [ГЛ. V
Обозначая через х величину cpj— ср2, из уравнений F0.14) на-
находим:
d2x М„ М.
dt2 Jt
где г|)(со/) в общем случае несимметричной системы определяется
формулой
л 1 h nr\c- 'Jj-.i/ 1_ я r-nrs Лгл-t I \ I
F0.15)
" р 4- Я cos 2w^ 4" r cos 4©< /i/j
Характер колебаний с точки зрения устойчивости определяется
однородной частью уравнения. Эта однородная часть может быть
представлена в виде
-^г + ^гФ(т)* = 0, F0.16)
где положено т = со/.
Мы опять получили линейное уравнение с периодическими коэф-
коэффициентами, содержащее в качестве параметра величину со. При тех
значениях этого параметра, при которых величина А для уравнения
F0.16) будет удовлетворять неравенству Л2 > 1, будет иметь место
параметрический резонанс, т. е. будут возникать колебания с не-
неограниченно возрастающей амплитудой. Это и будут критические
значения угловой скорости. Таким обра-
образом, задача определения критических ско-
скоростей вращения вала сводится к опреде-
определению значений параметра, при которых
с для уравнения F0.16) имеет место не-
неустойчивость.
Пример 4. Параметрический
резонанс в электрическом колеба-
Й тельном контуре.
Рис. 16. Рассмотрим электрический колебатель-
колебательный контур (рис. 16), состоящий из ем-
емкости С, самоиндукции L и сопротивления R. Если через q обозна-
обозначить заряд, то для него, как известно, имеет место дифференциаль-
дифференциальное уравнение
\д = 0. F0.17)
Допустим теперь, что один из параметров системы, например
емкость С, периодически изменяется. Пусть, например,
1 1/,,
-г=-г~ A 4" т cos со/).
Тогда уравнение F0.17) примет вид
Ц 4- Rq 4- -Д- A + т cos Ш) q = 0.
§ 60] НЕКОТОРЫЕ ТЕХНИЧЕСКИЕ ЗАДАЧИ 243
Полагая в этом уравнении
_Л ,
q = xe 2i , t' = (at,
получим:
^ii^^0- F0Л8)
где
Mm
Отсюда видно, что при подходящем выборе частоты со изменения
емкости, несмотря на отсутствие в системе внешних источников тока,
в ней могут возникнуть интенсивные электрические колебания. Этим
можно воспользоваться для устройства генератора электрического
тока, совершенно отличающегося от обычного и основанного на меха-
механическом изменении емкости (или самоиндукции). Такого рода гене-
генератор был впервые осуществлен Л. И. Мандельштамом и Н. Д. Па-
палекси !).
Задача определения необходимой частоты изменения емкости С
сводится к определению параметра и в уравнении F0.18) таким обра-
образом, чтобы решения этого уравнения были неустойчивы, т. е. чтобы
для него величина А удовлетворяла неравенству Л2 > 1.
Во всех рассмотренных примерах задача сводилась к исследова-
исследованию уравнения второго порядка вида
d2x
^ = 0, F0.19)
где p(t) — периодическая функция времени, а X — некоторый пара-
параметр. Необходимо определить те значения параметра к, при которых
для этого уравнения будет иметь место устойчивость или неустойчи-
неустойчивость. Так как условия устойчивости и неустойчивости определяются
неравенствами, то значения X, при которых будет иметь место устой-
устойчивость или неустойчивость, будут, вообще говоря, заполнять неко-
некоторые интервалы. Те интервалы значений X, при которых имеет место
устойчивость, мы будем называть областями устойчивости урав-
уравнения F0.19). Аналогично определяются и области неустойчи-
неустойчивости.
Итак, во всех предыдущих примерах задача сводилась к опре-
определению областей устойчивости и неустойчивости для уравнения вида
F0.19). К этой же задаче приводятся и многочисленные другие важ-
важнейшие вопросы техники, физики и астрономии. Решению этой задачи
•) Для того чтобы амплитуда колебаний в такого рода генераторах оста-
оставалась конечной, необходимо в систему ввести нелинейность.
244 УСТОЙЧИВОСТЬ ПЕРИОДИЧЕСКИХ ДВИЖЕНИЙ [ГЛ. V
посвящены работы А. М. Ляпунова >), в которых получен ряд очень
важных результатов. Некоторые из этих результатов были повторены
О. Хауптом 2). Существенное обобщение результатов А. М. Ляпу-
Ляпунова получено М. Г. Крейном 3), который рассмотрел систему урав-
уравнений второго порядка. Этому же вопросу посвящены также работы
И. М. Рапопорта 4).
Мы рассмотрим подробно указанную задачу при некоторых ча-
частных предположениях, а именно, мы будем предполагать, что функ-
функция р (f) в уравнении F0.19) мало отличается от своего среднего
значения, так что мы можем писать:
где f if)— периодическая функция периода (о, для которой
ff(t)dt = O,
о
а — постоянная, a |i.— постоянная величина, численное значение
которой мало по сравнению с единицей.
При указанном ограничении функция р будет принимать при
всех t значения одного знака, совпадающего со знаком величины а.
На основании первой из теорем, установленных в § 59, для уравне-
уравнения F0.19) всегда имеет место неустойчивость, если ка < 0. Поэтому
нам предстоит исследовать только тот случай, когда Ха > 0. Мы
можем поэтому уравнение F0.19) записать в виде
rl2x
~ + %2{\+\if{t))x = 0. F0.20)
В нижеследующих параграфах мы занимаемся подробным иссле-
исследованием уравнения F0.20). Можно считать с достаточной степенью
точности, что все примеры параметрического резонанса, рассмотрен-
рассмотренные выше, описываются уравнением вида F0.20).
') Liapounoff A., Sur une equation differentielle Hneaire du second
ordre. Comptes Rendus de l'Acad. de sciences. Paris, т. 128, 1899, стр. 910—913.
Liapounoff A., Sur une equation transcendente et les equations diffe-
rentielles Iineaires du second ordre a coefficients perlodiques. Comptes rendus,
Paris, т. 128, 1899, стр. 1085—1088.
2) См. по этому поводу: Коваленко К. Р. и К р е й н М. Г., О -неко-
-некоторых исследованиях А. М. Ляпунова по дифференциальным уравнениям
с периодическими коэффициентами. ДАН, т. LXXV, № 4, 1950.
3) К р е й н М. Г., Обобщение некоторых исследований А. М. Ляпунова
о линейных дифференциальных уравнениях с периодическими коэффициен-
коэффициентами. ДАН, т. LXXIII, № з, 1950.
*) Р а п о п о р т И. М., О линейных дифференциальных уравнениях
с периодическими коэффициентами. ДАН, т. LXXVI, № 6, 1951; Рапо-
Рапопорт И. М., К вопросу об устойчивости колебаний материальной системы.
ДАН, т. LXXVII, № 1, 1951.
§ 61] ОБЛАСТИ УСТОЙЧИВОСТИ И НЕУСТОЙЧИВОСТИ 245
§ 61. Области устойчивости и неустойчивости
для уравнений второго порядка.
Итак, рассмотрим уравнение второго порядка
g* = 0. F1.1)
где /—периодическая функция времени. Для удобства дальнейших
выкладок мы будем предполагать, что период этой функции равен я,
чего, очевидно, всегда можно добиться подходящим выбором единицы
времени. Предположим для общности, что параметр \х входит не
только в качестве множителя перед /, но и что от него зависит
также сама функция /. Мы будем предполагать, что э^а зависимость
является аналитической, так что
/ = /i(Q + |i/2(Q + n78<')+ •••¦ F1-2)
где функции /(- (t) не зависят от ц и являются периодическими
с периодом я и ряд сходится при |ц|<а, где а — некоторая по-
постоянная величина.
Необходимо определить области устойчивости и неустойчивости
для уравнения F1.1) в зависимости от значений параметра X. Будем
изменять этот параметр, придавая ему всевозможные вещественные
значения. При этом достаточно рассматривать только положитель-
положительные значения, так как уравнение F1.1) не изменится при замене X
на —X и, следовательно, распределение интересующих нас областей
будет при X < 0 таким же, как и при X > 0. Областям устойчивости
соответствуют те значения X, при которых коэффициент А для урав-
уравнения F1.1) удовлетворяет неравенству Л2 < 1, а областям неустой-
неустойчивости— те значения, для которых Л2 > 1. Отсюда непосредственно
вытекает, что области устойчивости и неустойчивости разделяются
теми значениями X, для которых выполняются либо уравнение
Л=+1, F1.3)
либо уравнение
Л = — 1. F1.4)
Исследуем подробней эти уравнения. Уравнение F1.1) содержит
параметр Я,2, по отношению к которому оно аналитично (линейно)
при всех значениях, и параметр |а, по отношению к которому оно
аналитично в области |ц|<а. Отсюда на основании теоремы § 58
коэффициент А является целой функцией параметра X2 и аналити-
аналитической функцией параметра ц в области |ц|<а. Для этого коэф-
коэффициента мы имеем:
А = ¦? {
246
УСТОЙЧИВОСТЬ ПЕРИОДИЧЕСКИХ ДВИЖЕНИЙ
[гл. V
где xx{t), x2(t) — два частных решения уравнения F1.1), опреде-
определяемых начальными условиями:
atj @) == 1, Xl@)=,0, I
*а<о) = о. i2@) = i.} FL5)
Эти решения являются целыми функциями к2 и аналитическими
функциями (х в области | [i | <; а. Мы можем поэтому написать:
где ряды сходятся при | [i | < а и являются, кроме того, целыми
функциями параметра X2. Подставляя эти ряды в F1.1) и принимая
во внимание F1.2), получим для определения неизвестных функций
xf\ хС1', ... (/=1, 2) следующие уравнения:
_-
d2xm
F1.6)
(*=1. 2).
Кроме того, начальные условия F1.5) дают:
xf@)=l, *f»@) = 0, *j°>@) = 0,
XU) @) = х{Л @) = xU) @) = хр @) = 0 (У=1,
F1.7)
Уравнения F1.6) вместе с начальными условиями F1.7) одно-
однозначно определяют все функции х[1\ ^h
В частности, имеем:
F1.8)
x(°> — -f sinAi,
и следовательно, для коэффициента Л получаем:
А — cos А,я + -j {х№ (я) + 41* (л)} И- + • • •
Установив это, рассмотрим уравнения F1.3) и F1.4). Из F1.8)
сразу видно, что эти уравнения удовлетворяются при |i, = 0 и к = п,
где п — целое число. При этом при п нечетном удовлетворяется
уравнение F1.4). а при п четном—уравнение F1.3). Поэтому можно
ожидать, что при \х ф 0, но достаточно малом уравнение F1.4)
имеет решение относительно к в окрестности любого целого нечет-
нечетного числа, а уравнение F1.3) имеет решение в окрестности любого
§ 61] ОБЛАСТИ УСТОЙЧИВОСТИ И НЕУСТОЙЧИВОСТИ 247
четного числа, обращающиеся в эти целые числа при (х = 0. Для
выяснения вопроса о существовании этих решений положим в выра-
выражении для Л;
Я, = л+а F1.9)
и приравняем полученное выражение при п нечетном —1, а при п
четном 1. Тогда мы получим следующее уравнение для величины а:
••' =0- F1Л0)
Левая часть этого уравнения является аналитической функцией
величин а и |а, обращающейся в нуль при а = |х = 0. Если бы про-
производная от этой функции по а не обращалась в нуль при а=ц=0,
то на основании теоремы существования неявных функций уравнение
F1.10) при ц, отличном от нуля, но достаточно малом, допускало бы
одно и только одно решение а (|х), обращающееся в нуль при [i = 0.
Однако производная от левой части F1.10) по а обращается при
а = (х=:0 в нуль, и поэтому указанная теорема существования
в рассматриваемом случае неприменима.
Но общая теория неявных функций, определяемых аналитическими
уравнениями1), показывает, что в рассматриваемом случае уравне-
уравнение F1.10) допускает два и только два решения, обращающихся
в нуль при |i, = 0, и эти решения при |х, достаточно малом, являются
аналитическими функциями либо величины ц, либо величины |/"(х.
Эти предложения легко доказать следующим образом.
Выделив в уравнении F1.10) члены, свободные от а, члены, линейные
относительно этой величины, и члены, содержащие эту величину в степени
не ниже второй, мы можем указанное уравнение записать следующим
образом:
-1)п+1-^+/'((г,а)]=0, F1.11)
где ф (ц), г|) (ц), F (ц, а) — аналитические функции своих аргументов, обра-
обращающиеся в нуль при а = [г = 0, & М н N — постоянные. Если постоянная М
равна нулю, что означает, что уравнение F1.10) не содержит членов, сво-
свободных от [г, то это уравнение распадается на два: на уравнение а = 0 и
уравнение
а [(-1) -^ + F ((х, а)] + (г* (N + ф (ц)) = 0.
Последнее уравнение имеет одно и только одно решение для <х(ц),
обращающееся в нуль при (х = 0, так как к нему применима обычная тео-
теорема существования неявных функций. Полученное решение будет при этом
') См. Гурса Е., Курс математического анализа, т. II, глава XVII
355, 356, стр. 241—248, ОНТИ, 1936.
248 УСТОЙЧИВОСТЬ ПЕРИОДИЧЕСКИХ ДВИЖЕНИЙ [ГЛ. V
аналитическим относительно ц. Присоединяя к нему решение <х = 0, мы
получим два и только два решения уравнения F1.10), и эти решения
будут аналитическими относительно ц.
Таким образом, при М = 0 интересующее нас предложение доказано.
Допустим теперь, что М Ф 0. Здесь необходимо рассмотреть три случая:
3) * = -?-.
Допустим сначала, что имеет место случай 1). Тогда, полагая в уравне-
уравнении F1.11)
т
а = ц~р, F1.12)
где р — новая неизвестная, и сокращая на \im, получим:
к- —
2
=0. F1.13)
Это уравнение имеет при ц = 0 два простых корня р =— у(—1)П + 12Л1
и р = Y(—l)n+1 2М- Следовательно, производная -^- для каждого из
этих корней при (х = 0 отлична от нуля. Поэтому на основании обычной
теоремы неявных функций существует при ц, достаточно малом, два и только
два решения уравнения F1.13), из которых одно обращается при ц = 0
в —У(—\)п+12М, а второе в Vl—l)n+1 2Af. Так как функция Ф
аналитична либо относительно W (при т нечетном), либо относительно ц
(при т четном), то и указанные решения будут аналитичны либо относи-
относительно Yn, либо относительно ц. Подставляя эти решения в F1.12), мы
получим два решения уравнения F1.11), обращающиеся в нуль при ^ = 0,
и эти решения будут аналитичны либо относительно У~\[, либо относительно ц.
Допустим теперь, что имеет место случай 2). Положим в уравнении F1.11)
a = [im-*p. F1.14)
Тогда уравнение, определяющее р, будет иметь вид
М + Ф W + р (N + ф fti) ) + ру-2* [(-l)n+1 ^ + F (ft №m-k)] = 0.
Л1
Это уравнение имеет при ц = 0 простой корень р = jt- '). и следо-
следовательно, при [г, отличном от нуля, но достаточно малом, оно допускает одно
') Величина N отлична от нуля, ибо если бы она равнялась нулю, что
означало бы, что k = оо, то мы имели бы случай 1).
§ 61] ОБЛАСТИ УСТОЙЧИВОСТИ И НЕУСТОЙЧИВОСТИ 249
м
и только одно решение для р, обращающееся в j=- при ц = 0. Это реше-
решение будет аналитическим относительно |х, так как таким является само урав-
уравнение. Подставляя это решение в F1.14), мы получим решение уравнения
F1.11), обращающееся в нуль при Ц = 0, и это решение будет аналитиче-
аналитическим относительно ц. Полагая затем в F1.11)
а = |х*р, F1.15)
мы получим для р уравнение
которое имеет одно и только одно решение, обращающееся в —i^
при ц = 0. Подставляя это решение в F1.15), мы получим второе решение
уравнения F1.11), обращающееся в нуль при |х = 0. Это решение будет
также аналитическим относительно ц.
Допустим, наконец, что имеет место случай 3). Положим:
т
О = 1**Р — 1*"*"^
Тогда уравнение, определяющее Р, будет иметь вид
? (р, (г) = М + Ф (|i) + Р {N + ф ((г)) + р2 [(-!)"+' -? + F (|х, ,i*p)] = 0.
F1.16)
Это уравнение при ц = 0 имеет два корня, определяемые квадратным
уравнением
Если это квадратное уравнение имеет простые корни, то уравнение F1.16)
будет при (х = 0 иметь два решения, аналитических относительно ц и обра-
обращающихся, соответственно, при ц = Ов указанные корни квадратного урав-
уравнения. Этим двум решениям уравнения F1.16) соответствуют два решения
уравнения F1.11), также аналитических относительно ц и обращающихся
а нуль при ц = 0.
Но если квадратное уравнение F1.17) имеет два равных корня р = р*,
то вопрос делается несколько сложнее, так как производная -Jr обращается
в нуль при р = р*, (х = 0, и обычная теорема существования для уравне-
уравнения F1.16) неприменима. Для решения вопроса в этом особом случае положим
в уравнении F1.16)
после чего мы получим уравнение для у, которое будет аналитическим отно-
относительно у и ц и которое будет допускать при ц = 0 двойной корень \ = 0.
Следовательно, это уравнение относительно у будет такой же структуры,
как и уравнение F1.11) для а. Прилагая к этому уравнению предыдущие
рассуждения, мы получим два решения для у. если только мы снова не
встретимся со случаем 3), притом с тем его частным видом, который мы
отметили как особенный. В последнем случае для неизвестной у мы должны
будем проделать такую же подстановку, как и с неизвестной р", и получить
250 УСТОЙЧИВОСТЬ ПЕРИОДИЧЕСКИХ ДВИЖЕНИЙ [ГЛ. V
для новой неизвестной, пусть это будет 6, уравнение вида F1.11). Если для
неизвестной 6 не получится особенного случая, то мы получим два решения
для 6, которые дадут два решения для а нужного вида. Если же уравнение
для 6 будет принадлежать к числу особенных, то указанный процесс при-
придется продолжить далее. Если этот процесс окажется конечным, то мы полу-
получим два решения уравнения F1.11) нужного вида. Может, однако, случиться,
что процесс окажется бесконечным. Не останавливаясь на этом исключитель-
исключительном случае, укажем лишь, что в этом случае уравнение F1.11) будет иметь
двойное решение, обращающееся в нуль при |х = 0.
Итак, уравнение F1.11) при ц, достаточно малом, всегда имеет два корня,
обращающихся в нуль при ц = 0. Эти решения будут притом аналитическими
либо относительно Yv1-, либо относительно ц. Легко видеть, что при (х,
достаточно малом, указанное уравнение не имеет других корней, обращаю-
обращающихся в нуль при (х = 0. Действительно, если бы такие корни существовали,
то, переходя к пределу при ц->0, мы получили бы, что уравнение F1.11)
имеет при ц = 0 нулевой корень, кратность которого превышает два.
Подставляя решения для а в F1.9), мы получим решения урав-
уравнений F1.3) и F1.4). Придавая п всевозможные целые значения,
мы получим все решения уравнений F1.3) и F1.4). При этом при п
нечетном мы получим решения уравнения F1.4), а при п четном —
решения уравнения F1.3).
Покажем теперь, что все полученные таким образом решения
уравнений F1.3) и F1.4) являются вещественными. С этой целью
заметим прежде всего, что если X удовлетворяет уравнению F1.3),
то уравнение F1.1) имеет периодическое решение с периодом, равным
периоду коэффициента, т. е. я. Действительно, в этом случае корни
характеристического уравнения равны единице, откуда непосредственно
вытекает существование указанного решения. Если X удовлетворяет
уравнению F1.4), то корни характеристического уравнения будут
равны—1 и, следовательно, будет существовать решение x = (f(t),
удовлетворяющее условию
Функция ,<f(t) будет также периодической, но с периодом 2л.
Установив это, допустим, что к = Х* является корнем уравнения F1.3)
и пусть (f(t)— соответствующее периодическое решение уравне-
уравнения F1.1). Имеем:
Умножим это тождество на ф dt, где ф — величина, комплексно
сопряженная с ф, и проинтегрируем в пределах от 0 до л. Тогда,
интегрируя по частям и принимая во внимание, что в силу перио-
периодичности
§ 61] ОБЛАСТИ УСТОЙЧИВОСТИ И НЕУСТОЙЧИВОСТИ 251
получим:
я _ я
= 0. F1.18)
о
Выражения, стоящие под знаками интегралов, вещественны и поло-
положительны, и следовательно, такими же будут и сами интегралы. Но
тогда тождество F1.18) показывает, что и величина X* будет веще-
вещественной и положительной, и следовательно, величина X* будет веще-
вещественной.
Точно так же доказывается вещественность корней уравнения F1.4).
Разница будет заключаться лишь в том, что теперь в тождестве F1.18)
интегралы будут браться в пределах от 0 до 2я.
Покажем теперь, что все корни уравнений F1.3) и F1.4) будут
при [i, достаточно малом, аналитическими функциями этой величины.
В самом деле, из предыдущего следует, что все корни уравнений F1.3)
и F1.4) являются либо аналитическими функциями величины |/(х,
либо аналитическими функциями величины |д.. Но если хотя бы один
из указанных корней являлся аналитической функцией величины Уц,
то он обязательно был бы комплексным либо при положительных
значениях |а, либо при отрицательных значениях этой величины. Но
мы только что показали, что все корни уравнений F1.3) и F1.4)
являются вещественными, и это будет справедливо вне зависимости
от того, будет ли параметр ц, положительным или отрицательным.
Таким образом, все корни уравнений F1.3) и F1.4) будут аналити-
аналитическими функциями величины |х в некоторой окрестности точки |л, = О,
т. е. они будут разлагаться в ряды по целым положительным степе-
степеням |а, сходящиеся при ]i, достаточно малом.
Будем теперь рассматривать всевозможные значения X и построим
график кривой А (X) (считая ц фиксированным). С этой целью отложим
на оси X все корни уравнений F1-.3) и F1.4). Как мы видели, все
эти корни распадаются на пары, расположенные вблизи целочислен-
целочисленных значений X. Обозначим через Х'п, Хп корни, расположенные вблизи
целого нечетного числа я, и через к'„, Хп— корни, расположенные
вблизи целого четного числа п. Все эти корни разбивают ось к на
интервалы двух типов (рис. 17). Интервалы первого типа ограничены
с обеих сторон корнями одного вида, т. е. такими, которые либо
оба удовлетворяют уравнению F1.3), либо оба удовлетворяют урав-
уравнению F1.4). К такого рода интервалам принадлежат, например,
интервалы (Хи Х\) и (Я-2, Х2). Интервалы первого типа мы будем
называть однородными. Интервалы второго типа, как, например, интер-
интервал (Я,1, А,г), ограничены, с одной стороны, корнем уравнения F1.3),
а с другой стороны — корнем уравнения F1.4). Интервалы такого
вида мы будем называть разнородными. Как видно из чертежа,
252
УСТОЙЧИВОСТЬ ПЕРИОДИЧЕСКИХ ДВИЖЕНИЙ
[гл. v
интервалы однородные и разнородные чередуются. Некоторые одно-
однородные интервалы могут выродиться в точку. Это будет в том слу-
случае, если уравнение F1.3) или F1.4) имеет кратные корни.
Теперь легко видеть, что в каждом однородном (невырожденном)
интервале имеет место неравенство А2 > 1, а в каждом разнородном
интервале — неравенство А2 < 1. Другими словами, области неустой-
неустойчивости совпадают с однородными интервалами, а области устойчи-
устойчивости — с неоднородными интервалами. Действительно, рассмотрим
какой-нибудь неоднородный интервал, например (к", кй). В этом
интервале величина А изменяется от —1 в начале интервала до -f-1
АЩ
Рис. 17.
в конце интервала. И так как при этом величина А внутри интервала
нигде не может обратиться в ± 1, так как все корни уравнений F1.3)
и F1.4) расположены в концах интервалов, то во всех точках внутри
рассматриваемого интервала необходимо должно выполняться нера-
неравенство Л2<1. Рассмотрим теперь какой-нибудь однородный невы-
невырожденный интервал, на концах которого А = -\-1. Пусть это будет,
например, интервал (Я,2, \1). Так как в этом интервале А изменяется
от +1 до -f-1, то во всех точках внутри интервала выполняется
либо неравенство А > 1, либо неравенство А < 1. Чтобы выяснить,
какой из этих случаев действительно имеет место, рассмотрим точки,
лежащие вблизи одного из концов интервала. Пусть это будет
конец ^2- Так как интервал по условию не вырожден, то корень Я,2
dA
является простым и, следовательно, —тт- не обращается в нуль при
Я = Я.2- И так как левее точки %2 величина А меньше единицы, то
отсюда следует, что правее указанной точки величина А больше еди-
единицы. Предложение, таким образом, доказано. Точно так же доказы-
доказывается это предложение и для тех однородных интервалов, на концах
которых А я. — 1.
§ 62] ОПРЕДЕЛЕНИЕ ОБЛАСТИ УСТОЙЧИВОСТИ И НЕУСТОЙЧИВОСТИ 253
Итак, придавая в уравнении F1.1) параметру X всевозможные
значения, мы получим бесконечную последовательность чередующихся
областей устойчивости и неустойчивости. Границами этих областей
являются корни уравнений F1.3) и F1.4), которые делят ось к на
интервалы двух видов: однородные, которые ограничены с обоих
концов либо корнями уравнения F1.3), либо корнями уравнения F1.4),
и разнородные, которые с одной стороны ограничены корнем урав-
уравнения F1.3), а с другой стороны — корнем уравнения F1.4). Области
устойчивости совпадают с неоднородными интервалами, а области
неустойчивости с однородными интервалами. Корни уравнения F1.4)
расположены вблизи целых1) нечетных чисел по два корня вблизи
каждого такого числа, причем при (х = 0 эти корни сливаются и
делаются равными указанному числу2). Корни уравнения F1.3) рас-
располагаются аналогичным образом вблизи целых четных чисел. Все
указанные корни являются при |х, достаточно малом, аналитическими
функциями этой величины.
§ 62. Практический способ определения областей устойчивости
и неустойчивости для уравнения второго порядка.
Из результатов предыдущего параграфа следует, что все области
неустойчивости уравнения F1.1) расположены в окрестности целых
чисел. При этом в окрестности каждого целого числа п расположена
одна область неустойчивости. Эта область при п четном ограничена
корнями уравнения F1.3), а при п нечетном—корнями уравнения F1.4).
При |х = 0 каждая область неустойчивости стягивается в точку.
В настоящем параграфе мы рассматриваем один из приемов практи-
практического определения областей неустойчивости, т. е. корней уравне-
уравнений F1.3) и F1.4).
Допустим, что в уравнении F1.1)
g ю)* = о, F2.1)
где
X является корнем уравнения F1.3) или F1.4). Пусть для опреде-
определенности речь идет о корне, обращающемся при |х = 0 в заданное
') Необходимо иметь в виду, что период функции / в уравнении F1.1)
принят равным я. Если бы этот период равнялся какому-нибудь другому
числу и, то корни уравнений F1.3) и F1.4) располагались бы вблизи чисел
пп
вида , где и — целое число.
о
8) Не следует думать, что каждая такая пара корней непременно раз-
разделяется соответствующим ей целым числом. Может случиться, что оба корня
находятся по одну сторону от указанного числа.
254 УСТОЙЧИВОСТЬ ПЕРИОДИЧЕСКИХ ДВИЖЕНИЙ [ГЛ. V
целое число га. Как мы видели в предыдущем параграфе, при (X,
достаточно малом, указанный корень является аналитической функ-
функцией [i, и мы можем писать:
При сделанном предположении уравнение F2.1), как это уже
указывалось в предыдущем параграфе, имеет периодическое решение
с периодом, равным 2я, если га—число нечетное,- и равным я, если
га — число четное. Будет ли указанное решение также являться ана-
аналитической функцией |х?
Так как коэффициенты уравнения F2.1) являются аналитическими
функциями |а, то всякое решение этого уравнения, начальные значе-
значения которого не зависят от |а, будет аналитическим относительно |х.
То же самое будет справедливо и по отношению к любому решению,
начальные значения которого зависят от ]i, но являются аналитиче-
аналитическими функциями этой величины. Пусть х = х (t) — решение уравне-
уравнения F2.1), определяемое начальными условиями:
лт(О)=1, *@) = 0. F2.3)
Характеристическое уравнение для F2.1) при сделанном предположе-
предположении относительно X имеет двойной корень, равный 1 (при и четном)
или—1 (при га нечетном). Поэтому любое решение уравнения F2.1)
и, в частности, рассматриваемое решение x(f) будет либо периоди-
периодическим, либо вида
*Ю = /ф(/) + ф(/). F2.4)
где (р и ij) — периодические функции времени1). В последнем случае
функция (р также определяет решение уравнения F2.1), которое и
является искомым периодическим решением. Но в силу того, что
начальные условия F2.3) решения F2.4) не зависят от |а, это реше-
решение является аналитическим относительно |а. Поэтому функция <(((),
определяющая искомое периодическое решение, является аналитиче-
аналитической относительно \i.
Итак, мы показали, что в рассматриваемом случае уравнение F2.1)
допускает периодическое решение, аналитическое относительно |х.
Если мы это решение умножим на С (ц), где С (|а) — произвольная
неаналитическая функция ц, то мы получим новое периодическое
решение уравнения F2.1). Отсюда с очевидностью вытекает, что не
всякое периодическое решение уравнения F2.1) является аналитиче-
') Период этих функций равен л, если п — число четное, и 2я, если
п — число нечетное. Вообще в этом параграфе, говоря о периодических
решениях уравнения F2.1), мы будем иметь в виду, не оговаривая это особо,
что речь идет о решениях с периодом я или 2л в зависимости от четности
или нечетности и.
§ 62] ОПРЕДЕЛЕНИЕ ОБЛАСТИ УСТОЙЧИВОСТИ И НЕУСТОЙЧИВОСТИ 255
ским относительно ц. Рассмотрим, однако, аналитическое периоди-
периодическое решение. Пусть это решение имеет вид
х = х0 @ + Vlx1 (f) + ц2х2 (/)+.... F2.5)
где х1 — периодические функции времени, и ряд сходится при доста-
достаточно малом |д,'). Чтобы сделать решение определенным, нужно будет
указать некоторые дополнительные условия, определяющие произволь-
произвольный постоянный множитель, входящий в это решение. Это может
быть сделано следующим образом.
Если решение F2.5) не обращается в нуль при ^ = 0, то, умножив
его на подходящим образом выбранный множитель, мы можем получить
решение, обращающееся при t—О в наперед заданную величину
+... F2.6)
Другими словами, в рассматриваемом случае уравнение F2.1)
допускает периодическое решение вида F2.5), в котором функ-
функции xt (t) удовлетворяют начальным условиям
x,@)=Mt, F2.7)
где Mt — постоянные, удовлетворяющие лишь единственному условию,
что ряд F2.6) сходится. Мы можем поэтому первые N постоянных Mt,
где N—сколь угодно большое число, выбирать совершенно произвольно.
Если решение F2.5) обращается в нуль при /==0, то производная
от него по t при t = 0 будет отличной от нуля, и мы можем потре-
потребовать, чтобы выполнялись начальные условия
^@) = ^. F2.8)
где Nl— произвольные постоянные, для которых ряд
Wo + |iW, + |i2tf2+;.. F2.9)
сходится.
Для того чтобы в каждом конкретном случае выяснить, каким
из начальных условий F2.7) или F2.8) можно удовлетворить, доста-
достаточно определить функцию х0. Если хо(О)фО, то решение F2.5)
при \х, достаточно малом, не будет обращаться в нуль при t — О, и
мы будем иметь начальные условия F2.7). Если же х0 @) = 0, но
х() @) =? 0, то можно удовлетворить условиям F2.8). Если хо(О) =
= хо(О) = О, то, как будет видно ниже из вида xo(t), будем иметь
тождественно х0@ = 0. Этот случай может быть исключен, так как,
разделив, в случае необходимости, решение F2.5) на подходящую
степень ц, мы можем всегда добиться, чтобы оно имело свободный
член.
') Радиус сходимости этого ряда совпадает с радиусом сходимости левой
части уравнения F2.1).
256
УСТОЙЧИВОСТЬ ПЕРИОДИЧЕСКИХ ДВИЖЕНИЙ
[гл.
Условия F2.7) или F2.8) однозначно определяют решение F2.5),
если мы только не имеем дело с тем исключительным случаем, когда
все решения уравнения F2.1) являются периодическими. Этот случай
возможен, так как характеристическое уравнение имеет двукратный
корень, которому могут соответствовать две группы решений (§ 52).
В этом последнем случае, для того чтобы решение F2.5) было вполне
определенным, необходимо задать начальные значения как самого
решения, так и его производной.
Установив это, подставим в уравнение F2.1) вместо Я.2 ряд F2.2),
и постараемся ему удовлетворить формальным рядом вида F2.5)
с периодическими коэффициентами. Из предыдущего следует, что
такой ряд всегда найдется, если только коэффициенты аг в F2.2)
выбраны определенным образом, а именно таким, что ряд F2.2)
удовлетворяет либо уравнению F1.3), либо уравнению F1.4). При
этом можно будет удовлетворить либо начальным условиям F2.7),
либо начальным условиям F2.8), либо тем и другим одновременно.
Рассмотрим те уравнения, которым должны удовлетворять функ-
функции xt(f).
Подставляя в F2.1) ряды F2.2) и F2.5), будем иметь:
/=о
1=0
Приравнивая коэффициенты при одинаковых степенях ц, получим
следующие дифференциальные уравнения:
. 2
г п хо
?L +
и вообще
n2x2 = -
a,) x, -
a,/,) лг0 —
F2.10)
+ n>xk = - («2/,+аг) Xk_x~akxQ+Fk (f. x0 xk_2), F2.11)
xk-2 c периодическими
a
k_l
где Fk — линейные функции от дг0, х1k2
коэффициентами. Эти функции зависят от постоянных alt a2, ..
и не содержат постоянной ak.
Уравнения F2.10) и F2.11) дают возможность последовательно
определять неизвестные функции xk. Однако для того чтобы эти
функции получались периодическими, необходимо, чтобы правые части
указанных уравнений удовлетворяли некоторым условиям. Эти условия
дают возможность определить неизвестные коэффициенты at в выра-
выражении для Я2. Покажем, как это делается.
§ 62] ОПРЕДЕЛЕНИЕ ОБЛАСТИ УСТОЙЧИВОСТИ И НЕУСТОЙЧИВОСТИ 257
Общее решение для х0 имеет вид
х0 = AQ cos nt -f- Bo sin nt.
Оно всегда является периодическим и содержит две произвольные
постоянные AQ и Во. Обращаемся к уравнению, определяющему хх.
Правая часть этого уравнения является периодической функцией t.
Для того чтобы это уравнение допускало периодическое решение,
необходимо и достаточно, чтобы разложение Фурье правой части не
содержало членов с cos nt и sin nt. Найдем коэффициенты при этих
членах.
Так как, по условию, функция fx является периодической с перио-
периодом я, то эта функция разлагается в ряд Фурье по косинусам и
синусам целых (четных) кратностей t. Но тогда функции /, cos nt
и /jSinrei также разлагаются по синусам и косинусам целых (четных,
если ге — четное, и нечетных, если ге — число нечетное) кратностей t,
и мы можем писать:
оо
•tf=2 (amcosmt-\-bmsin mt),
F2.12)
re^jSinre^—2 (cmcosmt-j-dmsinmt),
причем
6 . v
ал = тг. *« = -j.
F2.13)
где р и y — коэффициенты при cos 2re? и sin 2re^ в разложении функ-
функции re2/, l).
Из формул F2.12) и F2.13) сразу находим коэффициенты при
cosre^ и sinre^.B правой части уравнения для хх. Приравнивая эти
коэффициенты нулю, получаем следующие уравнения:
которым должны удовлетворять величины Ао и Во, Для того чтобы эти
уравнения имели решение, отличное от тривиального А0=В0 — 0, необ-
необходимо и достаточно, чтобы величина ах удовлетворяла квадратному
') Разложение Фурье функции /, (t) не содержит свободного члена, так
как, по условию, среднее значение функции / (t) равно нулю. Вследствие
этого члены, содержащие cos nt и slant, в выражениях F2.12) могут по-
появиться лишь за счет членов с cos 2л* и sin 2я* в разложении функции /j (t).
258 устойчивость периодических движений [гл. v
уравнению
Bai
Отсюда находим:
Здесь необходимо рассмотреть два случая в зависимости от того,
будет ли $2-\-у2фО или р2-|--у2 = О- Рассмотрим сначала первый
из указанных случаев. В этом случае уравнение для ах имеет два
простых вещественных корня. Приравняем ctj одному из этих корней.
Так как он является простым, то он не обращает в нуль хотя бы
один из миноров определителя системы F2.14), вследствие чего
только одна из величин Ао и Во может быть выбрана произвольно.
Допустим, что этой величиной является Ао, для чего необходимо,
чтобы она получилась отличной от нуля. Это условие будет, напри-
например, наверняка выполнено, если у Ф 0. При сделанном предположе-
предположении величина хо(О) будет отличной от нуля. Поэтому на основании
вышесказанного мы можем при вычислении функций xt (t) удовлетво-
удовлетворить начальным условиям F2.7). Мы можем, в частности, положить
Ло=1. Тогда уравнения F2.14) дадут для Во определенное зна-
значение.
Выбрав, таким образом, alf Ао и Во, мы будем иметь, что урав-
уравнение для х-у будет допускать периодическое решение. Но тогда и
общее решение этого уравнения, имеющее вид
Xj = Х\ (t) -j- Ax cos nt -f- BY sin nt,
где x\ — частное периодическое решение, а Л, и В, — произвольные
постоянные, будет также периодическим. Величину А1 мы можем
положить равной нулю. Это будет обозначать, что в условиях F2.7)
величина Мх принята равной х\@).
Переходим теперь к вычислению дальнейших приближений. При-
Приравнивая нулю коэффициенты при cosra^ и sin nt в уравнении для х2,
получим систему линейных неоднородных уравнений
где /?2 и q2 — вполне определенные постоянные, представляющие собой
коэффициенты при cos nt и sin nt в выражении nfxx\ + (p-if \-\-t?f ?) х0.
Определитель А этой системы, равный
А = 2 Baj — р) Ао — 2у Во == 8ахА0 = вс^,
отличен от нуля, и потому эта система однозначно определяет вели-
величины а2 и Bv
§ 62] ОПРЕДЕЛЕНИЕ ОБЛАСТИ УСТОЙЧИВОСТИ И НЕУСТОЙЧИВОСТИ 259
После того как а2 и В1 вычислены указанным способом, уравне-
уравнение для х2 будет допускать только периодические решения, и мы
можем написать:
Х2 ~ Х2 (*) + \ C0S Ut + ^2 Sin nt-
где x{t) — некоторая периодическая функция, а А2 и В2— произ-
произвольные постоянные. Постоянную А2, так же как и Аг, можно поло-
положить равной нулю. Что же касается постоянной В2, то она опреде-
определится вместе с постоянной а3 из условия периодичности функции х3.
Действительно, допустим, что постоянные а^ а2, . .., aft_j и
функции х0, Xj xA_i уже определены и что указанные функции
вышли периодическими. При этом мы можем написать:
где x"k_l — некоторая периодическая функция, а Bk_1—оставшаяся
еще неопределенной постоянная, которая должна быть вычислена вместе
с постоянной ak из условия периодичности функции xk. Эти послед-
последние условия мы получим, приравнивая нулю коэффициенты при cosra^
и sinra^ в правой части уравнения для xk. Таким путем мы, как легко
видеть, получим следующие уравнения:
где рк и qk — коэффициенты при cos«^ и sin«^ в выражении
— «2/jXj_j-t- Fk> в котором Fk, являясь, как указывалось выше,
линейной функцией величин х0, хх xft_2 с периодическими коэф-
коэффициентами, будет вполне определенной периодической функцией
времени. Уравнения F2.15) однозначно определяют величины ak и Bk_x.
Мы предположили, что уравнения F2.14) дают для Ао величину,
отличную от нуля. Допустим, что А0 = 0 и, следовательно, В0ф0.
В этом случае хо(О) = О, но х0@)^=0, и поэтому вместо началь-
начальных условий F2.7) будут фигурировать начальные условия F2.8).
В связи с этим в выражениях для xk можно будет отбрасывать члены
с sin nt, и эти выражения будут иметь вид
xk = х* -j- Ak cos nt,
где Ak — произвольные постоянные. Отбрасывание членов Bks\nnt
равносильно предположению, что в начальных условиях F2.8) вели-
величины N4 приняты равными х^@). Постоянная Ak, так же как и
в предыдущем случае, определится вместе с постоянной ak+l из
условия периодичности xk+l.
260 УСТОЙЧИВОСТЬ ПЕРИОДИЧЕСКИХ ДВИЖЕНИЙ [ГЛ. V
Таким образом, в рассматриваемом случае, исходя из какого-
нибудь корня квадратного уравнения для а, мы получим одно и только
одно формальное разложение вида F2.2) для I?, при котором уравне-
уравнение F2.1) допускает формальное периодическое решение вида F2.5),
удовлетворяющее начальным условиям F2.7) или F2.8). Рассмотрев
оба значения для ах, мы получим два различных формальных разло-
разложения для X2 и периодического решения. Но, с другой стороны, по
доказанному, для каждого целого п существует два и только два
значения для "к2, ограничивающие соответствующую область неустой-
неустойчивости и представляемые сходящимися рядами вида F2.2), при ко-
которых уравнение F2.1) допускает периодическое решение вида F2.5),
удовлетворяющее начальным условиям F2.7) или F2.8). Отсюда не-
непосредственно следует, что полученные выше формальные разложения
для Я,2 как раз и представляют искомые границы области неустой-
неустойчивости и, следовательно, сходятся.
Отсюда, однако, не вытекает, что разложения F2.5) для периодического
решения будут также сходиться. Для того чтобы последнее действительно
имело место, необходимо, чтобы ряды F2.6) и F2.9) сходились. Вопрос о том,
будут ли эти условия выполнены при нашем выборе величин M% и N^, тре-
требует еще дальнейшего исследования. Однако, как мы уже отмечали выше,
первые N величин Mk и Nk, где N—сколь угодно большое число, могут
быть выбраны совершенно произвольно и, следовательно, так, как это сде-
сделано выше. Поэтому сумма первых N членов формального ряда F2.5) отли-
отличается от действительного периодического решения на величину порядка
малости (относительно ц) выше N. Мы могли бы, конечно, вести вычисле-
вычисления таким образом, чтобы получить заведомо сходящиеся ряды. Для этого,
например, достаточно было бы в выражениях для х^, вместо того чтобы от-
отбрасывать члены Ак cos nt или Bk sin nt, выбирать постоянные Ak и Bk та-
таким образом, чтобы при &:>1 выполнялись либо условия Jcft(O)=O, либо
условия Xk @) = 0. Однако при этом вычисления значительно усложнятся,
так как каждый лишний член в каком-нибудь приближении значительно
усложняет выражение для последующего приближения. В таком усложнении
вычислений нет никакой необходимости, так как для нашей задачи периоди-
периодическое решение уравнения F2.1) играет лишь вспомогательную роль и его
точное выражение нас не интересует.
Допустим теперь, что p2-j-Y2 —0> что будет иметь место в том
случае, когда разложение функции fx{t) не содержит членов ccos2re?
и sin2«^. В этом случае квадратное уравнение для а{ будет иметь
двойной корень (равный нулю), который обращает в нуль все миноры
определителя системы уравнений F2.14). Эти уравнения не опреде-
определяют поэтому никакой зависимости между Ао и Во. Однако не сле-
следует думать, что Ло и Во могут быть взяты совершенно произвольно.
Эти величины, так же как и в случае \Р-\-у2ф0, вообще говоря,
связаны между собой, но эта зависимость установится при рассмо-
рассмотрении следующих приближений.
В самом деле, рассмотрим уравнение для хх. Правая часть этого
уравнения содержит множитель х0. Поэтому общее решение этого
уравнения, которое согласно выбору а! будет периодическим, имеет
§ 62] ОПРЕДЕЛЕНИЕ ОБЛАСТИ УСТОЙЧИВОСТИ И НЕУСТОЙЧИВОСТИ 261
ВИД
х1 = A-l cos nt + В1 sin nt + Лоф! (t) -\- Во^ (f),
где фх и ajjj — периодические функции, а Ах и В1 — произвольные
постоянные.
Рассмотрим теперь уравнение для х2 и приравняем нулю коэф-
коэффициенты при cosra^ и sinra^ в правой части этого уравнения. По-
Полученные таким образом уравнения будут необходимо однородными
относительно Ло и BQ и не будут содержать At и Bv Эти уравне-
уравнения будут иметь вид
(P-a2)A0 + QB0 = 0, 1
F2Л6)
где Р, Q, R и 5—некоторые определенные постоянные. Действительно,
так как щ = 0, то единственным членом в правой части уравнения
для х2, не содержащим Ао и Во, будет — n2f l(A1 cos nt-\-Bl sin nt),
а этот член по условию не содержит ни cos nt, ни sin nt.
Приравняв нулю определитель уравнений F2.16), мы получим
квадратное уравнение для а. Если это уравнение имеет простые корни,
то для "каждого из них получится вполне определенный ряд для Я,2,
совершенно так же как и в случае ?Р-\-у2ф0. При этом можно
будет положить либо А{ = 0, либо Вг = О в зависимости от того,
какая из величин Ао и Во, определяемая уравнениями F2.16), заве-
заведомо отлична от нуля. Вторая из этих постоянных вместе с а3 опре-
определится из условия периодичности х3. Уравнения для этих постоян-
постоянных получатся линейными и дадут для них вполне определенные
значения. Аналогично вычисляются и дальнейшие приближения. Вычи-
Вычисления при этом будут совершенно такими же, как и в случае
р2_|_.у2=?О. Разница будет заключаться лишь в том, что входя-
входящие в k-e приближение постоянные Ak или Bk будут определяться
из условия периодичности не (k-\-\)-vo, а ф-\-2)-то приближения.
Если окажется, что и уравнение для а2 имеет кратные корни, то
исследование усложняется. Мы не будем здесь рассматривать этих
более сложных случаев в общем виде, так как в каждом отдельном
частном случае их исследование не представит никаких трудностей.
Как бы разнообразны ни были эти частные случаи, мы можем на
основании вышесказанного быть всегда уверенными, что всегда полу-
получатся, по крайней мере, два формальных разложения для интересую-
интересующей нас величины АЛ Можно показать, на чем мы здесь не остана-
останавливаемся, что таких разложений никогда не получится больше двух
и что, следовательно, они и будут искомыми разложениями и будут
сходиться. Может, конечно, случиться, как это вытекает из общей
теории, что оба разложения совпадут. Характер вычислений во всех
случаях мало отличается от рассмотренных выше более простых
случаев и достаточно выясняется на приводимых ниже примерах.
262 УСТОЙЧИВОСТЬ ПЕРИОДИЧЕСКИХ ДВИЖЕНИЙ [ГЛ. V
§ 63. Примеры приложения метода предыдущего параграфа.
Рассмотрим несколько примеров, поясняющих метод предыдущего
параграфа.
Пример 1. Определим первую область неустойчивости (т. е.
соответствующую и = 1) в задаче колебаний спарников электровоза.
Как было показано в § 60, дифференциальное уравнение колебаний
имеет вид
¦^ + ~^(х)х = 0, F3.1)
где
. _ д + Ь cos 2т + с cos 4т Jx-\-J2
* *• ' р -\- q cos 2т -f- г cos 4т JtJ2
Мы будем предполагать, что коэффициенты Ь, с, q, r малы по
сравнению с а и Ь. Тогда, представляя -ф в виде
и вводя обозначения
a Jx-\-Ji. _ Ь Ji-\-J2 _ с Ji+J2
7~TJr~go' J~h7T-gl[l' l~Tj^-
мы можем записать уравнение F3.1) в виде
4f+ifr ij + (aicos 2T+a2cos 4t> •*+
-f (a3cos 2t+ a4cos 4т+ a5cos 6т+ a6cos 8т) ц2 + ...} x = 0, F3.2)
где ay — постоянные, которые могут быть выражены через g-0, gv
g2, g3, g4. В частности, имеем:
go
_ gz gjgo _
tin ' , t*q
2 ^ 3
Для нахождения первой области неустойчивости полагаем в урав-
уравнении F3.2)
J .. F3.3)
и пытаемся ему удовлетворить формальным рядом вида
§ 63] ПРИМЕРЫ ПРИЛОЖЕНИЯ МЕТОДА ПРЕДЫДУЩЕГО ПАРАГРАФА 263
где Ло и Во — постоянные, а ^ — периодические функции т (пе-
(периода 2л). Для хг и х2 получаем следующие уравнения:
- + *i = — («1 cos 2т + а2 cos 4т) х0 — а^ =
= — (т + ai) Ао cos х + (х — «»
2" (al + a2)
(a + a2) ^0 C0S 3t — "J (al — a2) 50 sin 3t
— ^i cos 5т —^ sin 5т,
/ -\-X2 = (flj COS 2t -f- CL2 COS 4Т) X1 —
— (a3 cos 2t -)- o4 cos 4т + a5 cos 6т -f- ле cos 8t)Xj — агх0 —
— ax (aj cos 2t -f- a-2cos 4т) x0 — a2x0.
Для того чтобы функция хх вышла периодической, необходимо
и достаточно, чтобы в правой части уравнения, определяющего эту
функцию, не содержалось членов ни с cost, ни с sin т. Приравнивая
коэффициенты при этих величинах нулю, получим систему линейных
и однородных уравнений для определения Ао и Во, которые в рас-
рассматриваемом случае имеют вид
(?)„ = <>. F3.4)
Приравнивая нулю определитель этой системы, получим для ах два
различных решения:
«•1 = 2" i ai = -у •
Каждое из этих решений дает начало ряду F3.3). Рассматривая
оба эти решения, мы получим два ряда F3.3), которые, по доказан-
доказанному, сходятся и определяют границы области неустойчивости.
Примем сначала а{ = ^-. В этом случае уравнения F3.4) дают
для Во значение, равное нулю. Величину Ао, остающуюся произволь-
произвольной, мы можем согласно общей теории принять равной единице. При
этих предположениях уравнение для хх принимает вид
-1-±Jt-x1= LZ_Lcos3t f cos 5т.
Для общего решения этого уравнения имеем:
хх = Л! cos т + В{ sin т + а' + аа cos Зт + -||- cos 5т. F3.5)
Это решение является периодическим и содержит две произволь-
произвольные постоянные Л1 и Вх. Так как хо(О) = Ло=?0, то согласно
264 УСТОЙЧИВОСТЬ ПЕРИОДИЧЕСКИХ ДВИЖЕНИЙ [ГЛ. V
общей теории мы можем положить А1 — 0. Что же касается постоян-
постоянной Bv то она определится вместе с а2 из условия периодичности х2.
Чтобы получить эти условия, подставим в уравнение для х2 найден-
найденные значения х0, хх и аг и приравняем нулю коэффициенты при cost
и sin т. Таким путем мы должны согласно общей теории получить
два линейных неоднородных уравнения для Вх и а2, из которых они
однозначно определяются. В рассматриваемом случае мы получим:
(а + ДJ а ^[ «
Я О п— ^[
Dl — v, а2— 32 -gQ-r 4 "" 2 •
Таким путем можно найти и дальнейшие приближения, но мы
ограничимся первыми двумя.
Положим теперь а,2 = ~4-- В этом случае из уравнений F3.4) на-
находим: Л0 = 0, Во=\. Так как теперь Л0 = 0, но В0Ф0, то в вы-
выражении F3.5) для ЛГ[ мы не можем полагать Л1 = 0, но можем
положить В1 -= 0. Если теперь найденные значения л:0, х1 и а{ под-
подставить в уравнение для х2, то, приравнивая в нем нулю коэффи-
коэффициенты при cost и sint, мы будем иметь:
(а2-ахJ а] а\ а3
а2 ~ 32 ~Т" 4 96 "^ 2 '
Таким образом, первая область критических значений угловой
скорости со вала определяется неравенствами
Пример 2. Определим вторую область неустойчивости для
колебаний в электрическом контуре с переменной емкостью, рас-
рассмотренных в § 60. Дифференциальное уравнение колебаний имеет
вид
¦Ш + 4Lwc^°- 0 + и cos о * = о. (бз.б)
где
V— 4L- R*C0 •
Мы будем предполагать, что величина (i мала. Чтобы можно было
приложить без всяких изменений правила предыдущего параграфа,
необходимо изменить независимую переменную таким образом, чтобы
период правой части уравнения F3.6) был равен л. Для этого, оче-
очевидно, достаточно положить f = 2т, после чего уравнение F3.6)
§ 63] ПРИМЕРЫ ПРИЛОЖЕНИЯ МЕТОДА ПРЕДЫДУЩЕГО ПАРАГРАФА 265
примет вид
-^ + *2A+HCos2t)x = 0, ф2.7)
где
41 —
Для определения области неустойчивости, расположенной вблизи
Я, = 2, полагаем в уравнении F3.7)
и стараемся удовлетворить ему формальным рядом
Х = Х0-{-[1Х1-\-\12Х2-\- ...
с периодическими (периода я) коэффициентами. При этом
х0 = Ло cos 2т -\- Во sin 2т.
Далее,
¦^L -f 4*, = — 4х0 cos 2т — axxQ =
= — 2 Ло — 2 Ло cos 4т — 2В0 sin 4т — аг (Ао cos 2т -f- Во sin 2т),
?$- + 4х2 = — 4л:, cos 2т — а2х0,
—^- -f- 4лг3 = — 4лг2 cos 2т — а2хх — а2 cos 2т • х0 — а3х0 —
— ахх2 — aj cos 2т • хг.
Приравнивая нулю коэффициенты при cos 2т и sin 2т в уравнении
для хх, находим:
^ = 0, F3.8)
причем величины Ло и Во остаются произвольными. Мы имеем как
раз дело с отмеченным в предыдущем параграфе случаем, когда
введенная там величина |}2-j-Y2 обращается в нуль. Как мы там ука-
указывали, величины Ло и Во будут, вообще говоря, связанными между
собой, но эта связь установится при рассмотрении дальнейших при-
приближений. Вычислим эти приближения. На основании F3.8) имеем:
где Ах и Вх — произвольные постоянные. Так как мы еще не знаем,
какая из величин Ло и Во заведомо отлична от нуля, то мы не
можем пока ни одну из постоянных Ах и Вх принять равной нулю.
Подставив х0 и хх в уравнение для х2, получим:
+ 4*2 = (у - <h) Ло cos 2т - (I + a2) Bo sin 2т -
— 2Л1 cos4т — 2ВХ sin4т — A cos 6т — Щ- sin 6т — 2АХ.
266 УСТОЙЧИВОСТЬ ПЕРИОДИЧЕСКИХ ДВИЖЕНИЙ [ГЛ. V
Условия периодичности дают:
и следовательно, для а2 получаются два различных решения. Имеем,
таким образом, два варианта. При первом варианте
a2 = -g-, Ло=1, ?0 = 0,
а при втором варианте
О2 = —у, Л0 = 0, ?0=1.
Рассмотрим сначала первый вариант. Так как в этом варианте
А0ф0, то мы можем положить в F3.9) величину Аг равной нулю.
После этого получим:
х2 — -к- В, sin 4т + 75fi cos 6т + В2 sin 2т,
где В2—произвольная постоянная. Подставляя найденные прибли-
приближения в уравнение для хг и выписывая условия периодичности этой
функции, получим два линейных неоднородных уравнения для а3
и Вг. Эти уравнения имеют вид
Аналогично подсчитываются и дальнейшие приближения. При
этом в отличие от предыдущего примера, соответствующего случаю
$2-\-у2фО, постоянные Вк, входящие в хк, определяются не из
условия периодичности функций хй+1, а из условия периодичности
функций хк+2.
Рассмотрим теперь второй вариант. В этом случае
xt = -g- sin 4т -)- Al cos 2т,
x2 = к- Ax -f- -g- A1 cos 4t -f- -qg- sin 6т + A2 cos 2т,
и условия периодичности для лг3 дают:
Таким образом, с точностью до величин третьего порядка отно-
относительно (д. вторая область значений частоты со изменения емкости,
при которых уравнение F3.7) имеет неустойчивые решения, опре-
определяется неравенствами
i^^ |^+... F3.10)
§ 63] ПРИМЕРЫ ПРИЛОЖЕНИЯ МЕТОДА ПРЕДЫДУЩЕГО ПАРАГРАФА 267
Из этих неравенств видно, что, для того чтобы указанная область
неустойчивости существовала, необходимо прежде всего, чтобы вы-
выполнялось условие
4L — Я2С0>0.
Мы будем предполагать, что это условие выполняется. Но и при
выполнении этого условия еще нельзя быть уверенным, что в указан-
указанной области в рассматриваемом электрическом контуре действительно
возникнут неустойчивые колебания. Дело в том, что переменная х,
фигурирующая в уравнении F3.7), является вспомогательной. Для
тока q имеем, как мы это видели в § 60, выражение
-?-t
q — e 2L x.
Следовательно, на границах области F3.10), где вещественная
часть характеристических показателей уравнения F3.7) равна нулю,
колебания тока будут затухающими. Если при этом величина -~j-
достаточно мала, а именно меньше наибольшего значения веществен-
вещественной части характеристического показателя уравнения F3.7) в об-
области F3.10), то будет существовать область неустойчивости для
тока <7, расположенная внутри области F3.10). Если это условие
р
относительно -~j- не выполняется, то во всей области F3.10) коле-
колебания тока будут затухающими.
Пример 3. Рассмотрим снова уравнение F3.7) и определим
границы области неустойчивости, расположенной вблизи Я, = 3.
Полагая
х = /40co
будем теперь иметь:
-^. + 9*! = — 9 cos 2т ¦ xo — alXo,
¦ . * -\- 9х2 == — 9 cos 2т • х1 — аг (х1 -f- cos 2т • х0) — а2х0,
¦^f -f- 9л;3 — — 9 cos 2т • х2 — а: (х2 -\- cos 2т ¦ *,) —
— «2 (*i + c°s 2т • л:0) — а3лг0,
.42 у
^± -f- 9х, = - 9 cos 2т • х3 — а, (х3 + cos 2т • х2) —
— а2 (Х2 + cos 2т • хх) — а3 (хг + cos 2т • х0) — а3*0.
Условие периодичности хг дает:
268 УСТОЙЧИВОСТЬ ПЕРИОДИЧЕСКИХ ДВИЖЕНИЙ [ГЛ. V
причем Ао и Во остаются неопределенными. Для хг получаем выра-
выражение
9 9 9 9
* ^cost йsinт4Лo5т + Bsi
где Ау н В1 — произвольные постоянные. Так же как и в предыду-
предыдущем примере, ни одну из этих постоянных мы не можем пока при-
приравнять нулю. Подставляя в уравнение для х2 найденные значения ау
и хх, получим:
9 . c 9D.C 81. _ 81 о _ .
— -у Ax cos 5t — T Bx sin 5t — ж Ao cos 7т — -^ BQ sin 7т +
^пЗт1 F3.11)
и следовательно, условия периодичности х2 имеют вид
Получающееся отсюда решение для а2:
будет опять двухкратным, причем Ло и BQ по-прежнему остаются не-
неопределенными. Из F3.11) находим:
х* = -ж (-ж л° ~ А)cos т —w (-w в°+в>)sin т+
81 81
Aocos7xJr
-f- A2 cos Зт -f- B2 sin Зт,
где Л2 и В2—постоянные, остающиеся пока неопределенными.
Уравнение для х3 после подстановки найденных значений xv x2,
ах и а2 принимает вид
9 /153 . 9 , ,
3 j ^ о Те 1 + г] os т —
"о" i ~ето "о т 1й ~г •-"! Isin х — (аз + тпг I ^о cos
z \ oi^ id / v uiz!
\ г, ¦ о 5103 , ,. 5103 о ¦ г
— а3) Во sin Зт — -JQ240 Л° COS 5t ~ Т0240" °S1" ~
9 9
¦я- Л2 cos 5т— -^ В2 sin 5 т-|-о7 cos 7т+67 sin 7т + ад cos 9т -f- *9 sin 9т,
§ 63] ПРИМЕРЫ ПРИЛОЖЕНИЯ МЕТОДА ПРЕДЫДУЩЕГО ПАРАГРАФА 269
где а7, ад, bv b9 — некоторые вполне определенные коэффициенты,
которые нам нет необходимости выписывать. Следовательно, условия
периодичности х3 имеют вид
Эти условия дают два различных значения для а3, и дальнейшие
вычисления нужно вести в двух вариантах. При первом варианте мы
имеем:
729
О A 0 А1
Теперь уже мы можем положить Лх = Л2 —О и во всех дальнейших
приближениях в выражения для хк не вводить членов с cos3t. При
этих предположениях будем иметь:
1377 9 / 9
* COS Т -(
*з = ~ "8192 COS Т -16 (Ж
+шcos 5т+ж в*sin 5т - жcos 7т - жsin 7т -
— -^- cos 9т — -^ sin 9т + Вг sin Зт,
где S3 — неопределенная постоянная. Подставляя найденные прибли-
приближения в уравнение для х4 и составляя условия периодичности этой
функции, мы получим два линейных неоднородных уравнения для
определения В1 и а4. Получим:
я — п г, —
327 680 "
Если вычисление приближений продолжить, то последовательно
определятся постоянные а5, а6, ... При этом каждая постоянная ак
определится одновременно с постоянной Вк_2 из условий периодич-
периодичности функции xk, которые дадут для этих двух величин разреши-
разрешимую систему линейных неоднородных уравнений.
При втором варианте будем иметь:
а В1 А 0
и все дальнейшие вычисления будут такими же, как и при первом
варианте, с той лишь разницей, что теперь уже нужно будет поло-
положить равными нулю все величины Bk, а величины Ak определять из
условий периодичности функций хк+2. Для величин Ах и а4 мы по-
получим следующие значения:
А -0 а -260953
Л1 —U> а*~ 327 680'
270 УСТОЙЧИВОСТЬ ПЕРИОДИЧЕСКИХ ДВИЖЕНИЙ [ГЛ. V
Таким образом, искомая область неустойчивости определяется
следующими неравенствами:
81 , 72Q , ¦ 236 467
В. НЕЛИНЕЙНЫЕ УРАВНЕНИЯ С ПЕРИОДИЧЕСКИМИ
КОЭФФИЦИЕНТАМИ.
§ 64. Критерии устойчивости по первому приближению.
Мы переходим теперь к рассмотрению устойчивости периоди-
периодических движений, когда в дифференциальных уравнениях возмущен-
возмущенного движения учитываются также и нелинейные члены. Допустим,
что эти уравнения имеют вид
¦^f- = Рлфх^ ...-+¦ psn(f)xn-{-Xs(t, xt хп) F4.1)
(«=1, 2 я),
где psj — непрерывные периодические функции периода и, a Xs —
нелинейные добавки. Первая основная задача, которая здесь воз-
возникает, заключается в установлении необходимых и достаточных
условий устойчивости по первому приближению, т. е. условий, при
которых задача устойчивости для уравнений F4.1) решается урав-
уравнениями первого приближения
^fr=P,i*i+---+Psn*n E=1.2 я). F4.2)
Решению этой задачи и посвящен настоящий параграф. При этом
мы будем предполагать, что нелинейные добавки Xs в уравнениях
F4.1) удовлетворяют следующим общим условиям:
1) Существует область
F4.3)
в которой выполняются неравенства
\*s(t. х, *я)| < А { |*,| + • • • + |*„| }• F4.4)
где А — некоторая постоянная.
2) В области F4.3) функции Xs непрерывны и удовлетворяют
некоторым общим условиям, при которых уравнения F4.1) имеют
единственное решение для всякой системы начальных условий, взятых
в указанной области.
Из F4.4) вытекает, что функции Xs удовлетворяют также обыч-
обычному условию Xs(t, 0, .... 0) = 0.
§ 64] КРИТЕРИИ УСТОЙЧИВОСТИ ПО ПЕРВОМУ ПРИБЛИЖЕНИЮ 271
Хотя мы сейчас рассматриваем устойчивость периодических дви-
движений, мы не будем в этом параграфе предполагать, что функции Xs
по отношению к t являются периодическими, так как все выкладки
этого параграфа остаются справедливыми без этого ограничения.
Докажем теперь следующие теоремы Ляпунова об устойчивости
по первому приближению.
Теорема 1. Если все корни характеристического уравнения
системы первого приближения F4.2) имеют модули, меньшие
единицы, то невозмущенное движение для уравнений F4.1) асим-
асимптотически устойчиво при любом выборе функций Xs, удовле-
удовлетворяющих указанным для них условиям, если только постоян-
постоянная А в неравенствах F4.4) достаточно мала1).
Доказательство. Как было показано в § 54, существует
линейная подстановка
yj = f1x{t)xl+...+fjn(t)xn (у = 1,2 п) F4.5)
с периодическими (периода ю или 2со) коэффициентами, преобразую-
преобразующая систему линейных уравнений F4.2) с периодическими коэффи-
коэффициентами в систему линейных уравнений
п) F4.6)
с постоянными коэффициентами. При этом детерминант преобразо-
преобразования F4.5) не обращается в нуль ни при каких значениях t, вслед-
вследствие чего задача устойчивости по отношению к переменным xs
эквивалентна задаче устойчивости по отношению к переменным ys.
Если преобразование F4.5) применить к уравнениям F4.1), то они
примут вид
Цг = ЯЛУ1 + • • • + W» + У, «• Ух У») F4.7)
(s = l. 2 и),
где Ys — функции такого же вида, как и Xs. В частности, имеем,
что в области, в которую преобразуется область F4.3), выполняются
неравенства
\Y,V. у,. .... уп)\ <В{|у,| + ... + |у„|}. F4.8)
где В — также постоянная, которая будет сколь угодно мала, если
А достаточно мало.
') А. М. Ляпунов предполагал, что функции Xs являются аналитическими
по отношению к х{ хп и их разложения по степеням этих перемен-
переменных начинаются членами не ниже второго порядка. Однако рассуждения
Ляпунова остаются справедливыми и при вышеуказанных общих условиях.
272 УСТОЙЧИВОСТЬ ПЕРИОДИЧЕСКИХ ДВИЖЕНИЙ [ГЛ. V
Согласно § 55 корни определяющего уравнения
qu A, qn ... qXn
Я21 Я22 ^ • • • Я2/1
Яп\ Яп2 ¦¦¦ Чпп —
F4.9)
системы F4.6) являются характеристическими показателями системы
F4.2). Так как, по условию, все корни характеристического уравне-
уравнения системы F4.2) имеют модули, меньшие единицы, то характери-
характеристические показатели этой системы будут иметь отрицательные ве-
вещественные части.
Таким образом, все корни уравнения F4.9) имеют отрицательные
вещественные части. Но тогда существует одна и только одна ква-
квадратичная форма V(y1 уп), удовлетворяющая уравнению
л л
Щ- <ад + ¦ • • + qsnyn) = - 2 У].
4=1 S=l
и эта форма будет обязательно определенно-положительной. Соста-
Составим теперь производную по t от формы V в силу уравнений F4.7).
Будем иметь:
dt XJ *s 1 4j dys '•
5=1 5=1
Эта производная будет определенно-отрицательной при любом вы-
выборе функций Ys, если только величина В в неравенствах F4.8)
будет достаточно малой, т. е. если достаточно малой будет вели-
величина А в неравенствах F4.4). Но при этом условии функция V
удовлетворяет всем условиям теоремы II Ляпунова (§ 46), что и до-
доказывает теорему.
Теорема 2. Если характеристическое уравнение системы
первого приближения F4.2) имеет хотя бы один корень с мо-
модулем, большим единицы, то невозмущенное движение для си-
системы F4.1) будет неустойчиво при любом выборе функций Xs,
удовлетворяющих указанным для них условиям, если только
величина А в неравенствах F4.4) достаточно мала.
Доказательство. Так же как и при доказательстве предыду-
предыдущей теоремы, будем рассматривать вместо системы F4.1) эквива-
эквивалентную ей систему F4.7). В рассматриваемом случае определяющее
уравнение F4.9) имеет, по крайней мере, один корень с положи-
положительной вещественной частью. Вследствие этого (теорема 3 § 21)
можно найти квадратичную форму V {ух уп), удовлетворяющую
§ 65] КРИТИЧЕСКИЕ СЛУЧАИ 273
уравнению
где а—некоторое положительное число, причем форма V может
принимать положительные значения, т. е. существует область, где
V > 0. Производная —п-> составленная в силу уравнений F7.7),
dt
имеет вид
dV
dt
где
x у„). F4.10)
5 = 1 .9=1
есть функция определенно-положительная, каковы бы ни были функ-
функции Ys, если только величина А в неравенствах F4.4) достаточно
мала. Форма V удовлетворяет всем условиям теоремы Н. Г. Четаева
о неустойчивости (§ 48). В самом деле, из F4.10) вытекает, что
dV
в области V > 0 выполняется также неравенство —тг > 0. Кроме того,
как легко видеть, выполняются все остальные условия теоремы
Н. Г. Четаева. Отсюда вытекает справедливость теоремы.
§ 65. Критические случаи.
Из теорем предыдущего параграфа вытекает, что задача устой-
устойчивости для систем вида F4.1) решается уравнениями первого при-
приближения F4.2) во всех случаях, когда характеристическое уравне-
уравнение первого приближения имеет все корни с модулями, меньшими
единицы, либо хотя бы один корень с модулем, большим единицы.
Сомнительными, следовательно, будут те случаи, когда указанное
характеристическое уравнение, не имея корней с модулями, большими
единицы, имеет корни с модулями, равными единице. В этом случае
определяющее уравнение F4.9) системы F4.6), в которую преобра-
преобразуются уравнения F4.2), будет иметь часть корней с отрицательными
вещественными частями и часть корней с вещественными частями,
равными «улю, а именно: корням, равным единице, характеристи-
характеристического уравнения системы F4.2) соответствуют корни, равные нулю,
определяющего уравнения F4.9). Корням же характеристического
уравнения, равным —1, а также комплексным корням с модулями,
равными 1, соответствуют чисто мнимые корни определяющего урав-
уравнения F4.9). Таким образом, если в указанных сомнительных
случаях пользоваться вместо уравнений F4.1) эквивалентными им
274 устойчивость периодических движений [гл. v
уравнениями F4.7), то задача устойчивости в этих случаях будет отли-
отличаться от задачи устойчивости в критических случаях для установив-
установившихся движений только тем, что нелинейные члены Ys будут содержать
явно t. И поскольку в критических случаях для установившихся дви-
движений нелинейными членами можно распорядиться таким образом,
чтобы получить по желанию как устойчивость, так и неустойчивость,
то тем более это будет справедливо и в рассматриваемых сейчас
случаях, так как эти нелинейные члены мы можем, в частности, вы-
выбрать не зависящими от t. Другими словами, если характеристическое
уравнение системы первого приближения F4.2) не имеет корней
с модулями, большими единицы, но имеет корни с модулями, рав-
равными единице, то для решения задачи устойчивости нельзя ограни-
ограничиться первым приближением и необходимо рассмотреть члены более
высоких порядков в уравнениях возмущенного движения. Все такого
рода случаи будут, следовательно, принадлежать к числу критических.
Мы рассмотрим в этой главе два критических случая:
1) когда характеристическое уравнение первого приближения имеет
только один критический корень и этот корень равен единице;
2) когда характеристическое уравнение имеет два критических
корня и эти корни оба комплексны и обладают модулями, равными
единице.
Мы будем пользоваться уравнениями возмущенного движения,
приведенными к виду F4.7). При этом мы вынуждены будем отказаться
от решения задачи при тех весьма общих предположениях относи-
относительно функций Xs, которые были высказаны в предыдущем пара-
параграфе, и подчинить эти функции более ограничительным условиям,
а именно: мы будем предполагать, что функции Xs периодичны от-
относительно t с периодом со и что эти функции разлагаются в ряды
по степеням переменных Xj xn, начинающиеся членами не ниже
второго порядка и сходящиеся в области |х^|<;Я, где Н — неко-
некоторое положительное число.
В первом из указанных критических случаев определяющее урав-
уравнение F4.9) будет иметь один нулевой корень при остальных корнях
с отрицательными вещественными частями. Предполагая, что рас-
рассматриваемая система имеет (ra-f- 1)-й порядок, мы можем уравнения
возмущенного движения привести в этом случае к виду
F5.1)
jj 4 ?1 У1 I ¦ • • I 4 crt У n V~ 4 9*» ~T~ ' c\"' •* »
=l. 2 и).
Во втором критическом случае определяющее уравнение F4.9)
имеет пару чисто мнимых корней вида ± kl, а остальные корни
этого уравнения имеют отрицательные вещественные части. Считая,
§ 66] СЛУЧАЙ ОДНОГО РАВНОГО ЕДИНИЦЕ КОРНЯ 275
что порядок системы равен п -f-2, мы можем уравнения возмущен-
возмущенного движения привести к виду
(t. x, у, yv y2 yn),
x, у, ух, У2. •••» Уп)
пУп+Р*х+Я$У+У$(*- x, у, yx у„)
E=1, 2 И).
F5.2)
В уравнениях F5.1) и F5.2) функции X, Y и Ys будут такого
же вида, как и функции Xs, а величины qsj, ps и qs являются по-
постоянными, причем qsj таковы, что уравнение F4.9) имеет корни
только с отрицательными вещественными частями.
Для того чтобы привести уравнения F4.1) к виду F4.7), а сле-
следовательно, также к виду F5.1) или F5.2), необходимо, конечно,
знать общее решение уравнений F4.2). Мы будем предполагать, что
это решение нам действительно известно и что уравнения задачи уже
приведены к виду F5.1) или F5.2).
В этой главе мы не будем рассматривать уравнений F5.1) и F5.2)
в их общем виде, а ограничимся случаем п = 0. Другими словами,
мы будем предполагать, что в первом критическом случае система
имеет первый порядок и, следовательно, имеется только одно урав-
уравнение возмущенного движения вида
а во втором критическом случае система имеет второй порядок и
состоит, следовательно, из двух уравнений вида
^- = -ky + X(t.x.y). *L = kx+Y(t.x,y).
Общий случай и > 0 будет рассмотрен в следующей главе, где
будут установлены некоторые общие теоремы о критических слу-
случаях. Как мы увидим, исследование случая и > 0 приводится к слу-
случаю и = 0. В следующей главе будут рассмотрены также некоторые
другие критические случаи.
§ 66. Критический случай, когда характеристическое
уравнение имеет один равный единице корень.
Мы переходим к рассмотрению критического случая, когда харак-
характеристическое уравнение первого приближения имеет один равный
единице корень в предположении, что система уравнений возмущен-
возмущенного движения имеет первый порядок. Исследуемое дифференциальное
276 УСТОЙЧИВОСТЬ ПЕРИОДИЧЕСКИХ ДВИЖЕНИЙ [ГЛ. V
уравнение будет иметь вид
где k ^ 2 и ft — периодические функции t периода со.
Если бы коэффициент fk был постоянной величиной, то задача
устойчивости для уравнения F6.1) разрешалась бы чрезвычайно
просто. В самом деле, пусть
fk = g= const. F6.2)
Тогда, если k является числом четным, то правая часть уравне-
уравнения F6.1) будет знакоопределенной функцией и функция V = x
будет удовлетворять всем условиям теоремы III Ляпунова (§ 47) и,
следовательно, невозмущенное движение будет неустойчиво.
При k нечетном знакоопределенным будет выражение
d_
dt
и функция V = -х х1 будет при g < 0 удовлетворять условиям тео-
теоремы II Ляпунова, а при g > 0 —условиям теоремы III. Следовательно,
в первом случае невозмущенное движение асимптотически устойчиво,
а во втором случае оно неустойчиво.
Итак, при выполнении условия F6.2) невозмущенное движение
будет асимптотически устойчиво при k нечетном и g < 0, а при k
нечетном и g > 0, а также при к четном оно неустойчиво. Если
условие F6.2) не выполняется, то для решения задачи устойчивости
необходимо будет подвергнуть уравнение F6.1) некоторому преоб-
преобразованию, целью которого является приведение уравнения к такому
виду, для которого указанное условие выполнялось бы. Это может
быть достигнуто двумя различными способами, вследствие чего мы
имеем два способа решения задачи устойчивости в интересующем нас
случае.
Первый способ решения задачи. Задавшись некоторым
числом N^-k, преобразуем уравнение F6.1) при помощи подстановки
y — x + %(t)xk-lr%+1(t)x'l+1-\- ... +yN(f)xN. F6.3)
где % г|)д, — некоторые периодические, периода со, функции t,
которые мы постараемся выбрать таким образом, чтобы в преобра-
преобразованном уравнении первые N коэффициентов были постоянными.
Преобразованное уравнение должно, следовательно, иметь вид
4f ¦ • • • F6.4)
§ 66] СЛУЧАЙ ОДНОГО РАВНОГО ЕДИНИЦЕ КОРНЯ 277
где ak aN — некоторые постоянные, a f*N+v •••—периоди-
•••—периодические функции t. Для нашей цели, как мы видели, достаточно,
чтобы в уравнении F6.4) был постоянным коэффициент только при
младшей степени х. Однако, как мы сейчас увидим, некоторые из
коэффициентов aj могут оказаться равными нулю, и поэтому вычис-
вычисление этих коэффициентов нужно будет производить до тех пор,
пока мы не придем к первому отличному от нуля коэффициенту.
Если этим коэффициентом будет ат, то для нашей цели достаточно
будет положить N = т.
Подставляя в уравнение F6.4) вместо у его выражение F6.3),
будем иметь:
t
Приравнивая коэффициенты при одинаковых степенях х, получим
следующие уравнения для функций г|)у:
dt
difi _
—— п —— P i'4" 1I1 ih Л
— u-^ i ^ ^t, tA* " * • * t/ — 1/
= A+1 N).
F6.6)
Здесь F[ — полиномы относительно % г|)г-1 с периоди-
периодическими коэффициентами. Эти полиномы зависят от постоянных
ак ai-v н0 не зависят от постоянной аг Из полученных урав-
уравнений функции последовательно определяются одна за другой, но,
для того чтобы эти функции вышли периодическими, необходимо,
чтобы правые части этих уравнений удовлетворяли некоторым усло-
условиям. Эти условия и определяют постоянные аг. Действительно, для
того чтобы функция г|)Л вышла периодической, необходимо и доста-
достаточно, чтобы среднее значение функции ak — fk равнялось нулю.
Это дает:
Таким образом, постоянная ak получилась вполне определенной.
Если она отлична от нуля, то в дальнейших вычислениях нет необ-
необходимости, т. е. мы можем в преобразовании F6.3) положить N = к.
Если же ак = 0, то потребуются дальнейшие вычисления.
278 УСТОЙЧИВОСТЬ ПЕРИОДИЧЕСКИХ ДВИЖЕНИЙ [ГЛ. V
Допустим для определенности, что все постоянные ak aj~i
и все функции %, . .., aj)y г уже вычислены и что последние вышли
периодическими. Тогда функция Fj будет также периодической и
условие периодичности ify однозначно определяет постоянную а, и
дает для нее следующее значение:
Таким путем мы можем вычислить любое число постоянных а;-.
Но для нашей цели, как мы уже говорили, достаточно определить
лишь первую из них, отличную от нуля. Допустим для определен-
определенности, что этой постоянной является ат, так что
«« = ?=? О, ак = ак+1=...=ат.1 = 0. F6.8)
Тогда, полагая в F6.3) N=m, мы приведем уравнение F6.1)
к виду
¦% = gym+--- F6.9)
Преобразование F6.3), очевидно, обладает тем свойством, что
задача устойчивости относительно переменной ^ эквивалентна задаче
устойчивости относительно переменной у. Мы можем поэтому вместо
уравнения F6.1) рассматривать уравнение F6.9). Но для последнего,
как мы видели, задача устойчивости решается сразу, а именно, при
т четном, а также при т нечетном и g положительном невозму-
невозмущенное движение неустойчиво, а при т нечетном и g отрицатель-
отрицательном оно устойчиво и притом асимптотически.
Мы приходим, следовательно, к следующему правилу решения
задачи устойчивости в интересующем нас случае.
Делая в уравнении F6.1) подстановку F6.3), стараемся функции
г|); подобрать таким образом, чтобы они вышли периодическими') и
чтобы уравнение приняло вид F6.4). Для функций г|)г получаются
уравнения F6.6) и постоянные аг однозначно определяются форму-
формулами F6.7). Эти постоянные определяем до тех пор, пока не встре-
встретим отличную от нуля. Пусть ат — первая такая отличная от нуля
постоянная. Тогда при т четном невозмущенное движение всегда не-
неустойчиво, а при т нечетном оно неустойчиво при g > 0 и асим-
асимптотически устойчиво при g < 0.
Сформулированное сейчас правило может быть несколько видо-
видоизменено. К этому видоизменению мы придем, рассматривая задачу
') Для нашей задачи нет, конечно, необходимости, чтобы функции г|з;
были периодическими. Достаточно, чтобы они были ограниченными. Но, как
показывают уравнения F6.5), определяющие эти функции, они будут огра-
ограниченными только тогда, когда они будут периодическими.
§ 66] СЛУЧАЙ ОДНОГО РАВНОГО ЕДИНИЦЕ КОРНЯ 279
нахождения для уравнения F6.1) первого интеграла. Попытаемся
найти для уравнения F6.1) первый интеграл вида
х -f Ф*х* + <Р*-ы**+1 + • • ¦ = const., F6.10)
где Ф1— некоторые периодические функции времени. Необходимо,
следовательно, чтобы выполнялось тождественно условие
r*-i _j_ . . .) (fkx*+ .. .) + ^ xn + ^±i x*+i -f-. . . = 0.
Сравнение с F6.5) показывает, что функции Фг удовлетворяют
уравнениям
-*&- = -г» С66-11)
в которые переходят уравнения F6.6) при а1 = 0. Из уравнений F6.11)
функции Ф; будут получаться, вообще говоря, непериодическими."
Однако, как это следует из F6.8), функции Фк, . . ., Фт_1 совпадут
с функциями % 'Фт-! и получатся периодическими. Что же
касается функции Фт, то, как показывают те же равенства F6.8), она
наверняка получится непериодической, а именно, для нее будем иметь:
фт = — ?* + Ф(*). F6.12)
где Ф@ — некоторая периодическая функция, a g—та же постоян-
постоянная, которая фигурирует в F6.8). Отсюда непосредственно видно,
что при решении задачи устойчивости мы можем руководствоваться
следующим правилом.
Стараемся подобрать для уравнения F6.1) первый интеграл
вида F6.10) с периодическими коэффициентами Фь. Эта попытка не
увенчается в общем случае успехом, так как коэффициенты Ф{ не
получатся, вообще говоря, периодическими. Пусть Фт—первый не-
непериодический коэффициент в ряду Фк, Ф^+г, ¦ ¦ ¦ Этот коэффициент
необходимо будет иметь вид F6.12). Тогда при т четном невозму-
невозмущенное движение всегда неустойчиво, а при т нечетном оно не-
неустойчиво при g > 0 и асимптотически устойчиво при g < 0.
Сформулированное сейчас правило является, очевидно, лишь не-
незначительным видоизменением правила, приведенного выше.
Число т и знак величины g являются, очевидно, некоторыми спе-
специфическими характеристиками дифференциального уравнения F6.1).
Они не могут поэтому зависеть от способа приведения уравнения
F6.1) к виду F6.9), и если это приведение может быть осуществлено
различными приемами, то указанные величины получатся при этом
одинаковыми. Изложенный нами способ приведения обладает извест-
известной неопределенностью, вызванной тем, что функции "ф^, определяе-
определяемые из F6.6) при помощи квадратур, содержат произвольные по-
постоянные. Из вышеизложенного следует, что ни величина т, ни знак
280 УСТОЙЧИВОСТЬ ПЕРИОДИЧЕСКИХ ДВИЖЕНИЙ [ГЛ. V
величины g от этих постоянных не зависят и поэтому они могут
быть выбраны совершенно произвольно.
Мы предполагали, что, вычисляя функции tyt и постоянные а1%
мы придем к такому значению i=m, что величина ат получится
отличной от нуля. Может, однако, случиться, что все величины at,
как бы велик ни был индекс /, получатся равными нулю. В этом
случае предыдущие рассуждения неприменимы. Однако, как мы это
увидим при рассмотрении второго способа решения задачи устой-
устойчивости, в рассматриваемом случае невозмущенное движение будет
устойчиво, но не асимптотически.
- Второй способ решения задачи. Первый способ реше-
решения задачи, как мы видели, связан с вопросом о возможности по-
построения для уравнения F6.1) периодического первого интеграла
вида F6.10). Второй способ, к изложению которого мы сейчас пе-
переходим, связан с возможностью построения для уравнения F6.1)
периодического решения вида
* = с + <р4 (9 с* + ф*+1 @ с*+1 + • • •. F6.13)
где с — произвольная постоянная, a фА, <pft+i. ... — периодические
функции периода со.
Подставляя ряд F6.13) в правую часть уравнения F6.1), будем
иметь:
/*
+ /*+1(c-f-<P*c*
= 2*ВС Ф* Фп-i)'" (** = /*)• F6.14)
где Хп — полиномы относительно <ps, .. ., <pn_i с периодическими
коэффициентами. Отсюда вытекает, что, для того чтобы уравне-
уравнение F6.1) допускало решение вида F6.13), необходимо, чтобы функ-
функции ф(- удовлетворяли уравнениям
^=^((И* <P<-i)- F6.15)
Так как выражения X\ содержат только те из <ру, для которых
J < /, то уравнения F6.15) дают возможность последовательно опре-
определять функции фг. Однако эти функции не будут, вообще говоря,
получаться периодическими. Пусть фт — первая непериодическая
функция в ряду фй, Фа+1, ... Тогда эта функция необходимо имеет
вид
F6.16)
где g — постоянная, а Ф — периодическая функция.
§ 66] СЛУЧАЙ ОДНОГО РАВНОГО ЕДИНИЦЕ КОРНЯ 281
Сделаем теперь в уравнении F6.1) замену переменной
= У + Ф*/ + • • • + Ф^-хУ"-1 + ФтУт - gtym. F6.17)
Будем на основании F6.14) иметь:
или, принимая во внимание F6.15),
Ц «Фу»"») =
--.. F6.18)
где /щ + 1@ — некоторая периодическая функция, а ненаписанные
члены имеют порядок, больший /я-f-l, и периодические коэффи-
коэффициенты. Из F6.18) имеем:
^j- = gym+---> F6.19)
где ненаписанные члены имеют порядок, больший т, и периодические
коэффициенты.
Сделанное преобразование обладает, очевидно, тем свойством,
что задача устойчивости для уравнения F6.1) совпадает с задачей
устойчивости для уравнения F6.19). Но для последнего уравнения
задача устойчивости решается сразу, и мы приходим к следующему
правилу.
Для решения задачи устойчивости для уравнения F6.1) пытаемся
удовлетворить ему решением вида F6.13) с периодическими коэф-
коэффициентами. Эта попытка не увенчается, вообще говоря, успехом,
так как коэффициенты <р; в общем случае не получатся периоди-
периодическими. Пусть фт — первый такой непериодический коэффициент.
Он необходимо будет иметь вид F6.16). Тогда, если т четное или
если т нечетное, но g > 0, то невозмущенное движение неустойчиво,
а если те нечетное и g < 0, то это движение устойчиво и притом
асимптотически.
Так же как и при первом способе решения задачи, функции <рг
содержат постоянные интегрирования, выбором которых мы можем
распорядиться совершенно произвольно. При этом ни величина /га,
ни знак величины g не будут зависеть от выбора этих постоянных.
Мы предположили, что среди функций <рг встречаются непериоди-
непериодические. Может, однако, случиться, что все функции <pi( как бы велико
282 УСТОЙЧИВОСТЬ ПЕРИОДИЧЕСКИХ ДВИЖЕНИЙ [ГЛ. V
ни было t, будут периодическими. Покажем, что в этом случае,
если постоянные интегрирования, входящие в функции ф(-, выбирать
таким образом, чтобы выполнялись условия ф/@) = 0, то ряд F6.13)
будет получаться сходящимся и действительно представит периоди-
периодическое решение уравнения F6.1).
В самом деле, так как правая часть уравнения F6.1) аналитична
относительно х, то решение этого уравнения, определяемое началь-
начальным условием л:@) = с, может быть разложено в ряд по с, сходя-
сходящийся при \с\ < а, где а — достаточно малое положительное число.
Это число может быть выбрано таким образом, чтобы указанный
ряд сходился при всех значениях t на отрезке [0, со]. Пусть
* = с + фй*С* + ф;+1с*+1+ ... F6.20)
— рассматриваемое решение. Из х@) — с вытекает, что ф*@) = 0.
Подставляя F6.20) в F6.1), мы получим для ф* те же уравнения
что и для функций ф?, из которых функции ф* в силу ф*@) = 0
однозначно определяются. Следовательно, если постоянные интегри-
интегрирования, входящие в функции фг, выбрать таким образом, чтобы и
для этих функций выполнялись условия фг@)"=0, то функции ф;
совпадут с функциями ф?, и ряд F6.13), который совпадет с F6.20),
будет также сходиться при достаточно малых значениях с. И это
будет справедливо вне зависимости от того, являются ли функции ф;
периодическими или нет. В рассматриваемом нами случае все эти
функции являются периодическими и, следовательно, ряд F6.13)
представляет периодическое решение уравнения F6.1). Так как оно
содержит произвольную постоянную, то оно является общим реше-
решением уравнения F6.1). Это решение будет, очевидно, устойчивым,
но не асимптотически. Таким образом, если окажется, что все функ-
функции ф;, как бы велик ни был индекс I, являются периодическими,
то невозмущенное движение будет устойчиво,, но не асимптотически.
Разрешая равенство F6.13). относительно с, получим:
с = * + Ф*(О** + Фй+1(О**+1+ .... F6.21)
где фй — периодические функции времени. Соотношение F6.21) опре-
определяет, очевидно, первый интеграл уравнения F6.1). Таким образом,
если все функции ф,- получаются периодическими, то уравнение F6.1)
имеет не только аналитическое периодическое решение, но и анали-
аналитический периодический первый интеграл. Отсюда очевидно, что
если мы для решения задачи устойчивости в рассматриваемом случае
воспользуемся изложенным выше первым методом, то и все функ-
§ 66]
СЛУЧАЙ ОДНОГО РАВНОГО ЕДИНИЦЕ КОРНЯ
283
ции i|)j, фигурирующие в этом методе, выйдут также периодическими.
Справедливо и обратное заключение: если при решении задачи
первым методом все функции г|)г получатся периодическими, то при
решении задачи вторым методом все функции ф; выйдут также
периодическими. В самом деле, если бы не все функции фг вышли
периодическими, то задача устойчивости решалась бы конечным
числом членов в уравнении F6.1) независимо от членов достаточно
высокого порядка, что, очевидно, находится в противоречии с пред-
предположением, что все функции г|)г являются периодическими. Отсюда
непосредственно вытекает, что если при решении задачи устойчивости
первым методом все функции г|), получатся периодическими, то
невозмущенное движение будет устойчиво, но не асимптотически.
Пример 1. Пусть уравнение возмущенного движения имеет вид
¦^-:=asm3*-A:2+Pcos2^-A:4, F6.22)
где аир — постоянные.
Для исследования устойчивости по первому способу полагаем:
и стараемся функции г|)г выбрать таким образом, чтобы они были
периодическими и чтобы уравнение F6.22) приняло вид
т. е. чтобы выполнялось тождество
(asin3/ ¦ x2-fp cos21 ¦ x4) A -f 2^х+ Щх2-{-
d$ 2 #
. .)-f
dt
l
dt
Отсюда находим:
- = «з +
— 2a sin31 ¦ г|>2,
i*i. = a4 + 3a3t2 + а2г|J + 2a2% — p cos2 t — 3asin3/ • %
i
Из условия периодичности
получаем:
2%
находим, что а2 = 0, после чего
284 УСТОЙЧИВОСТЬ ПЕРИОДИЧЕСКИХ ДВИЖЕНИЙ [ГЛ. V
Далее имеем:
Подставляя полученные величины с2, а3 и функции г|J, г|K в урав-
уравнение для г|L, получаем:
J^i = а4 — р cos2t -f a3 (sin71-\- j sin9f) ,
откуда непосредственно следует, что
Таким образом, первый отличный от нуля коэффициент a.t имеет
четный индекс, откуда вытекает, что невозмущенное движение
неустойчиво.
Решим теперь задачу вторым способом. С этой целью пытаемся
удовлетворить уравнению F6.22) решением вида
где с — произвольная постоянная, а фг — периодические функции
времени. Подставляя это решение в F6.22) и приравнивая коэффи-
коэффициенты при одинаковых степенях с, получим:
^-asin;, ^l
dt dt
^- = p cos21-\- a sin31 ¦ ф2+ 2a sin31 ¦ cp3.
Отсюда находим:
Ф2 = — a I cos г о— I.
фз =-J. sin4 f — -^-sin6^,
где ф(^) есть периодическая функция. Таким образом, первая непе-
непериодическая функция ф; имеет четный индекс, откуда вытекает
неустойчивость движения.
Пример 2. В качестве второго примера рассмотрим систему
уравнений второго порядка с постоянными коэффициентами, для
которой характеристическое уравнение имеет пару чисто мнимых
корней ± XI. Эта задача подробно рассматривалась нами в §§ 36—38.
Уравнения возмущенного движения имеют вид
4.
у). ^ = Xx + Y(x,y), F6.23)
§ 67] СЛУЧАЙ ДВУХ КОМПЛЕКСНЫХ КОРНЕЙ 28Б
где X и К — аналитические функции переменных х, у, разложения
которых начинаются членами не ниже второго порядка.
Введением полярных координат
л: = г cos ft, у —г sin ft
система F6.23) приводится к виду
F6.24)
-6 (Л ft),
откуда исключением dt находим:
AL = R(r, ft). , F6.25)
В уравнениях F6.24) и F6.25) функции R, 0 и R будут ана-
аналитическими относительно г, обращающимися в нуль при г — О,
причем разложения R и R начинаются членами не ниже второго
порядка. Коэффициенты в разложениях этих функций являются
полиномами относительно cos ft и sin ft и, следовательно, будут
периодическими функциями ft.
Из второго уравнения F6.24) следует, что при г, достаточно
малом, величина ft является монотонной функцией времени, неогра-
неограниченно возрастающей вместе с последним (если при этом г остается
достаточно малым). Отсюда непосредственно вытекает, что при реше-
решении задачи устойчивости переменная ft может играть роль времени.
Следовательно, задача устойчивости по отношению к переменным х
и у для уравнений F6.23) эквивалентна той же задаче по отноше-
отношению к переменной г для уравнения F6.25). Но последнее уравнение
является, очевидно, частным случаем уравнения F6.1), и мы можем
его исследовать вышеуказанными методами. В частности, мы можем
применить второй метод, что приведет нас, очевидно, к резуль-
результатам § 36.
§ 67. Критический случай,
когда характеристическое уравнение имеет
два комплексных корня с модулями, равными единице.
Мы переходим к рассмотрению случая, когда характеристическое
уравнение первого приближения имеет два комплексных корня
с модулями, равными единице. Как уже указывалось выше, мы
ограничиваемся в этой главе системами второго порядка. Диффе-
286 УСТОЙЧИВОСТЬ ПЕРИОДИЧЕСКИХ ДВИЖЕНИЙ [ГЛ. V
ренциальные уравнения задачи установлены в § 65 и имеют вид
х, у),
F7.1)
х, у),
где X (t, х, у) и Y(t, х, у) — аналитические функции переменных х
и у, разложения которых начинаются членами не ниже второго
порядка и обладают коэффициентами, являющимися периодическими
функциями времени.
Допустим сначала, что функции X и К не зависят от t. Тогда
мы будем иметь критический случай для установившихся движений,
когда определяющее уравнение системы первого приближения имеет
пару чисто мнимых корней ± Х(, и порядок системы равен двум.
Эта задача подробно рассматривалась нами в §§ 36 — 38. В этих
параграфах было показано, что кроме особо исключительных случаев,
которые мы сейчас не будем рассматривать, задача устойчивости
решается конечным числом членов в разложениях правых частей
уравнений возмущенного движения. Допустим для определенности,
что задача устойчивости решается первыми т членами, где т, как
было показано, всегда нечетно, так что можно положить m.~1N—1.
Это значит, что если мы вместо уравнений F7.1), которые по пред-
предположению не зависят от t, рассмотрим уравнения
~df~ — Ъу-\-Х2{х, у)~Ь ... + X2N_\(x,
F7.2)
где X\ и Yk — совокупности членов fe-ro порядка в разложениях
функций X и К, то невозмущенное движение будет устойчивым или
неустойчивым при любом выборе функций ф и \|л если последние
являются аналитическими и их разложения начинаются членами не
ниже 2N-vo порядка. При этом, как было показано в § 37, суще-
существует функция Ляпунова V(x, у) вида
V(x, У) = х2 + у2 + /з(х> у)+ ... +/2/v(x, у), F7.3)
производная которой, составленная в силу уравнений F7.2), имеет
вид
dV
~ = О(х* + у*)»+ ... F7.4)
Здесь fk — формы &-го порядка, не зависящие от ip и ф, О — по-
постоянная и ненаписанные члены имеют порядок, больший 2N. Если
О > 0, то невозмущенное движение неустойчиво, а если О < 0, то
оно устойчиво асимптотически. Это непосредственно вытекает из того
обстоятельства, что V есть функция определенно-положительная,
§ 67] СЛУЧАЙ ДВУХ КОМПЛЕКСНЫХ КОРНЕЙ 287
dV
а —77- есть функция также знакоопределенная, знак которой совпадает
av
со знаком G, каковы бы ни были функции ф и г|), удовлетворяющие
указанным для них условиям.
Из существования для уравнений F7.2) функции Ляпунова F7.3)
можно сделать, однако, более общие выводы. Допустим, что функ-
функции ф и \|) зависят также от t, по отношению к которому они огра-
ограничены, но не обязательно периодичны.
При указанных предположениях выражение F7.4) остается по-
прежнему знакоопределенным; следовательно, V по-прежнему является
функцией Ляпунова, удовлетворяющей всем условиям теоремы II § 46
или теоремы III § 47. Поэтому невозмущенное движение для ура-
уравнений F7.2) будет по-прежнему асимптотическим устойчиво или не-
неустойчиво вне зависимости от функций ф и г|), удовлетворяющих
вышеуказанным условиям. Это непосредственно приводит нас к сле-
следующему заключению.
Допустим, что в уравнениях F7.1) все члены до некоторого
порядка т включительно имеют постоянные коэффициенты, так что
время t входит лишь в те члены, порядок которых превосходит т.
Отбросив в этих уравнениях все члены выше от-го порядка, рассмо-
рассмотрим полученную таким образом систему уравнений с постоянными
коэффициентами. Эта система представляет собой частный случай
системы, рассмотренной в §§ 36—38. Допустим, наконец, что задача
устойчивости для этой системы с постоянными коэффициентами ре-
решается членами порядка не выше т. Тогда если для этой системы
получится неустойчивость, то и для системы F7.1) получится не-
неустойчивость, а если для этой системы получится устойчивость (асим-
(асимптотическая), то и для системы F7.1) будет также иметь место
устойчивость (асимптотическая).
Рассмотрим теперь уравнения F7.1) в общем случае. Из выше-
вышесказанного следует, что если нам удастся при помощи подходящего
преобразования привести уравнения F7.1) к такому виду, в котором t
содержалось бы только в членах достаточно высокого порядка, то
задача сведется к исследованию системы с постоянными коэффициен-
коэффициентами, которую получим, если эти члены высокого порядка, содержа-
содержащие t, попросту отбросим. Что же касается последней задачи, то она
может быть разрешена одним из тех трех приемов, которые были
установлены в главе IV.
Таким образом, задача приводится к разысканию такого преоб-
преобразования переменных х и у в уравнениях F7.1), чтобы преобразо-
преобразованные уравнения сохранили такой же вид, но чтобы в них коэффи-
коэффициенты членов до сколь угодно высокого порядка т были постоянными.
Такое преобразование, как показал Ляпунов, может быть действи-
Ха>
тельно выполнено, если только число иррационально, что мы и
288 УСТОЙЧИВОСТЬ ПЕРИОДИЧЕСКИХ ДВИЖЕНИЙ [ГЛ. V
будем предполагать *). Вычисления Ляпунов располагает таким обра-
образом, что задача устойчивости для преобразованных уравнений ре-
решается одновременно с выполнением самого преобразования. При
этом задача устойчивости решается методом § 36. Однако все вычи-
вычисления значительно упрощаются, если следовать иному методу, пред-
представляющему собой непосредственное развитие метода § 42. К изло-
изложению этого метода мы сейчас и переходим.
Так же как и в § 42, мы будем предполагать, что линейная часть
уравнений возмущенного движения приведена к комплексному кано-
каноническому виду, так что эти уравнения имеют вид
¦?L
х. у)
— iXy -f УР> (t, x. y)+Y<®(t, x, y)
где X(ft) и F(ft) — формы й-го порядка переменных х и у с перио-
периодическими коэффициентами. Если уравнения были заданы в форме F7.1),
то, чтобы перейти к виду F7.5), достаточно будет принять в качестве
новых переменных величины x-\-iy и х — iy. Переменные х и у
будут в уравнениях F7.5) комплексно сопряженными, так что второе
из этих уравнений получится из первого заменой /на — /, х на у
и у на х.
Задавшись теперь числом т, преобразуем уравнения F7.5) при
помощи подстановки
(t, и, v)-4-и^> (t, и, vL- ••• -V-u^Ht, и, v),
¦ , ¦ F7-6)
¦и, и) 4~ ¦ • • -\- ит (t, v, и),
где «W (Л м, v) и и<*> (^, г», и) — формы й-го порядка с периодиче-
периодическими коэффициентами. При этом формы и<*> (t, v, и) комплексно
сопряжены с формами uWtf, и, v) и могут быть, следовательно,
получены из u^k){t, и, v) заменой /на —/, и на v и v на и. От-
Отсюда следует, что переменные и и v являются также комплексно
сопряженными.
Преобразование F7.6) мы постараемся подобрать таким образом,
чтобы в преобразованных уравнениях члены до порядка т имели
постоянные коэффициенты. Эти уравнения должны, следовательно,
иметь вид
(б7-7)
и).
?L= 1Хи +1/B) (и, v) + ... + иШ (я. о) + U.(t. и.
') Относительно этого предположения см. примечание в конце параграфа.
§ 67] СЛУЧАЙ ДВУХ КОМПЛЕКСНЫХ КОРНЕЙ 289
Где U{k)(u, v) и U{k\v, и) — формы k-то порядка с постоянными
коэффициентами, а функции U(t, и, v) и U (t, v, и) имеют порядок,
больший т, и зависят, вообще говоря, от t, по отношению к кото-
которому они периодичны. При этом функции (Jfk)(v, и) и U (t, v, и)
комплексно сопряжены с lfk)(u, v) и U(t, и, v).
Подставляя в первое уравнение F7.5) вместо х и у их выраже-
выражения F7.6) и принимая во внимание F7.7), будем иметь:
г- •••
duW
(t, и+ .... о+ .
Отсюда, приравнивая члены одинаковых порядков, получим для
форм uW(t, и, v) следующие уравнения:
= Гки(к) + F(k) (t, и, v) F7.8)
(k = 2, 3, ..., от).
Здесь /^ — некоторые формы k-vo порядка переменных и, V,
зависящие от тех форм и , U , для которых i < fe. В частности,
Т7^^, u,v) = X^2)(t, и, v). Уравнения F7.8) дают возможность
последовательно определять как формы «<*>, так и формы ?/<*). Пока-
Покажем, как это делать.
Допустим с этой целью, что все и и Lr , для которых t < k,
уже вычислены и коэффициенты форм и<г) вышли при этом периоди-
периодическими. Тогда F будут известными формами й-го порядка с пе-
периодическими коэффициентами. Пусть
где /а„ @ — известные периодические функции времени периода ю.
Положим
ttW(f, и, v)= 2 «ap@«V, t/(ft)(a, о)= 2 ^ap«a#,
где Ла|з — неизвестные постоянные, а иар (^) — неизвестные периоди-
периодические функции времени. Тогда, приравнивая в уравнении для а'*1
290 УСТОЙЧИВОСТЬ ПЕРИОДИЧЕСКИХ ДВИЖЕНИЙ (ГЛ. V
коэффициенты при подобных членах, получим следующие обыкновен-
обыкновенные дифференциальные уравнения:
^ в = /ор-V F7.9)
Нам нужно найти периодическое решение этих уравнений. Здесь
приходится различать два случая в зависимости от того, будет ли
величина а—р—1 равна нулю или нет. Допустим сначала, что
а — р—1—0. Это, очевидно, возможно только при k нечетном.
Пусть /г = 2/г -f- 1. Тогда из а — р — 1=0 следует: а = п -f-1,
Р = п. Уравнение для иар (/) принимает вид
и для того чтобы оно имело периодическое решение, необходимо и
достаточно, чтобы
со
An+i,n = l I fn+bn(t)dt. F7.10)
о
При этом для an+lj „ получаем:
- An+h J-
Входящую сюда постоянную интегрирования выберем по произволу.
Допустим теперь, что а — Р — 1 ф 0. Рассмотрим уравнение
¦^¦ = аф + т|>@. F7Л1)
где а — постоянная, a if(f) — произвольная непрерывная периодиче-
периодическая функция t, периода со. Допустим, что am Ф pnt, где р — целое
число. Тогда уравнение F7.11) имеет частное .решение
I Ш
f*= eat jz~^ J e~a
dt
F7.12)
Это решение является периодическим с периодом со. В самом деле,
из периодичности ty(t) вытекает:
1+а
Г e-at^(t)dt=se f e-aV+^ty(t + G))cit5=e-aa> f
§ 67] СЛУЧАЙ ДВУХ КОМПЛЕКСНЫХ КОРНЕЙ 291
и, следовательно,
„ае>
. ea(t+e>) e-atty(f)dt-\-eaV+ei>
$
J е-"' ф (/) dt + еа «+«» I e~ai ф (О Л =
что и доказывает справедливость нашего утверждения. При этом
из условия относительно а вытекает, что общее решение ф = е°'
однородной части уравнения F7.11) не может быть периодическим
периода ю, и поэтому формула F7.12) дает единственное периодиче-
периодическое решение уравнения F7.11).
Так как по условию число — иррационально и, следовательно,
Л(а+Р— 1) ф ——, то уравнение F7.9) при ct-f-p— 1 #0 имеет
одно и только одно периодическое решение, какова бы ни была
постоянная А^. Мы будем полагать:
Аа$ = 0 (ачьр+1). F7.13)
Выбрав таким образом постоянную Лар, мы получим вполне опре-
определенное решение для иар. Это решение может быть вычислено по
формуле F7.12). На практике, однако, функции /а„ чаще всего бы-
бывают конечными тригонометрическими суммами. В этом случае функ-
функции мар проще всего определять методом неопределенных коэффи-
коэффициентов, так как эти функции также получатся конечными тригоно-
тригонометрическими суммами.
Таким образом, мы можем последовательно определить все формы
UW и ц(Ь)^ гтрИ этом из F7.13) вытекает, что все формы ?/'*' при
k четном будут тождественно равны нулю, а при k нечетном в этих
формах будут отличными от нуля лишь по одному коэффициенту
вида F7.10). Следовательно, преобразованные уравнения будут иметь
292
вид
УСТОЙЧИВОСТЬ ПЕРИОДИЧЕСКИХ ДВИЖЕНИЙ
, v, и),
[гл. v
F7.14)
где положено An+h n = A2n+1, т = 2р-\-\.
Отбрасывая в уравнениях F7.14) члены U и U, мы получим
уравнения с постоянными коэффициентами:
-тг = %lu -f .
V,
U ЧГ
F7.15)
Как было показано выше, задача устойчивости для исходной си-
системы F7.5) решается уравнениями F7.15), если для этих последних
задача устойчивости решается членами не выше Bp-f-1)-порядка.
Задача устойчивости для уравнений F7.15) решается сразу без
каких бы то ни было дополнительных вычислений. Действительно,
уравнения F7.15) имеют как раз вид уравнений D2.3), рассмотрен-
рассмотренных в § 42. И как было показано в этом параграфе, если Ak —
первый из коэффициентов А3, А5 вещественная часть которого
отлична от нуля, то при Re(^4ft)>0 невозмущенное движение не-
неустойчиво, а при Ке(Лй)<0 оно устойчиво асимптотически. Отсюда
следует, что в преобразовании F7.6) можно положить m = k.
Таким образом, мы приходим к следующему правилу для реше-
решения задачи устойчивости в интересующем нас случае.
Делаем в уравнениях F7.5) подстановку
X — U-
-uB)(t, и, г») + иC)(^, и- «) +
t, v,
f, v,
и стараемся формы и<*> подобрать таким образом, чтобы преобразо-
преобразованные уравнения приняли вид F7.15) и чтобы коэффициенты этих
форм вышли периодическими. Такое преобразование всегда найдется,
и при этом коэффициенты Aj получатся вполне определенными. Эти
коэффициенты определяем до тех пор, пока не встретимся с таким,
пусть это будет Ak, —для которого Re(Ak) фО, Тогда при
Ке(Лй)>0 невозмущенное движение неустойчиво, а при Ке(Лй)<0
оно устойчиво асимптотически.
Может случиться, что при любом значении k, как бы велико оно
ни было, Re (Ак) = 0. Этот исключительный случай мы здесь не рас-
рассматриваем.
§ 67] СЛУЧАЙ ДВУХ КОМПЛЕКСНЫХ КОРНЕЙ 293
Пример. Рассмотрим уравнение второго порядка
d2jc i V- u\(dx\z i с-Г* fdxV\
где ф(?) — периодическая функция времени, периода а>, несоизмери-
несоизмеримого с я, обладающая отличным от нуля средним значением, a Z7 —
/ dx\i
аналитическая функция от х и [—тг\ , разложение которой не имеет
членов ниже третьего порядка относительно х и -?-. Коэффициенты
этого разложения являются периодическими функциями t, периода ю.
dx dx
Полагая | = х — i —, ц = х -|- i —тт . получим следующую си-
стему:
где / — вещественная функция.
Делаем далее подстановку
F7.17)
Так как в уравнениях F7.16) нет членов второго порядка, то
можно положить, что и в подстановке F7.17) эти члены отсутст-
отсутствуют. Эту подстановку стараемся подобрать таким образом, чтобы
преобразованные уравнения имели вид F7.15). Из этого условия
находим:
Приравнивая члены третьего порядка, получим:
, и, v), F7.18)
где /C) (/, м, v) — совокупность членов третьего порядка в функции
/(/, и, v). Пусть
иC) — Um @ и3+й21 {t) иЧ -+- м12 @ м©2 + «03т;3.
294 УСТОЙЧИВОСТЬ ПЕРИОДИЧЕСКИХ ДВИЖЕНИЙ [ГЛ. V
Тогда приравнивая в F7.18) коэффициенты при u2v, получим:
где \|)(/) — коэффициент при u2v в f@>(t, и, v).
Для того чтобы это уравнение имело периодическое решение,
необходимо и достаточно, чтобы величина Аг Определялась формулой
со со
О
Так как по условию вещественная часть Аг отлична от нуля,
то в дальнейших вычислениях нет надобности. Невозмущенное дви-
движение будет неустойчиво, если величина
положительна, и асимптотически устойчиво, если эта величина отри-
отрицательна.
Примечание. Мы предположили, что — есть число ирра-
иррациональное. Допустим теперь противное: пусть
да
где р и q— целые числа. Сделаем в уравнениях F7.1) преобразова-
преобразование переменных
коэффициенты которого являются, очевидно, периодическими функ-
функциями периода 2qa. Преобразованные уравнения, как легко видеть,
примут вид
F7.19)
dt
ч).
где S и Т — аналитические функции | и ц, разложения ко-
которых начинаются членами не ниже второго порядка, причем коэф-
коэффициенты разложений являются периодическими функциями пе-
периода 2qa>,
§68] ПЕРИОДИЧЕСКИЕ ДВИЖЕНИЯ АВТОНОМНЫХ СИСТЕМ 295
Определяющее уравнение линейной части системы F7719) имеет
двойной корень, равный нулю. Таким образом, задача сводится
к исследованию критического случая двойного нулевого корня. Этот
случай как для установившихся движений, так и для периодических
движений будет исследован нами в следующей главе.
§ 68. Устойчивость периодических движений
автономных систем.
На практике часто приходится исследовать устойчивость перио-
периодических движений динамических систем, описываемых уравнениями,
не содержащими явно времени. Такого рода случаи всегда принад-
принадлежат к числу критических.
В самом деле, пусть уравнения движения динамической системы
имеют вид
%- = У5(.У1 Уп) (*=1. 2 п), F8.1)
где функции Ys не содержат явно t. Относительно этих функций
мы будем для простоты предполагать, что они аналитичны в неко-
некоторой области пространства О. Допустим, что рассматриваемая
система имеет периодическое движение, так что уравнения F8.1)
имеют в области О частное решение
/s = VAt)> F8.2)
где % (f) — периодические функции, период которых мы обозначим
через со. Принимая движение F8.2) за невозмущенное, составим диф-
дифференциальные уравнения возмущенного движения, т. е. преобразуем
уравнения F8.1) при помощи подстановки
*, = У, — ф,@- F8.3)
Будем иметь:
ТГ = Л1*1 + • • • 4- PSn*n + Xs (t, xt хп) F8.4)
(s=l, 2 п).
где Х3 — аналитические функции переменных хг, .... хп, разложе-
разложения которых начинаются членами не ниже второго порядка. Коэф-
Коэффициенты этих разложений, так же как и коэффициенты psa, являются
периодическими функциями времени, периода ю.
Так как уравнения F8.1) не4 содержат явно t, то, заменяя
в каком-нибудь решении t на t -\- h, где h — произвольная постоянная,
296 УСТОЙЧИВОСТЬ ПЕРИОДИЧЕСКИХ ДВИЖЕНИЙ [ГЛ. V
мы снова получим решение. Таким образом, уравнения F8.1) имеют
решение:
У, = Ф, (*¦+¦*). F8-5)
и следовательно, уравнения F8.4) имеют решение
Так как правые части уравнений F8.1) аналитичны, то функ-
функции (fs(t-\-h) непременно разлагаются в ряд по h, и мы можем
писать:
*, = *Ф, С) + 4 h2% @ + • • • F8.6)
Подставляя это решение в уравнения F8.4), которым оно должно
удовлетворять, и приравнивая коэффициенты при первой степени /г,
получим:
Эти соотношения показывают, что функции ys(t) являются реше-
решением уравнений первого приближения системы F8.4). Но так как
эти функции, очевидно, периодичны, то мы получили, что система
первого приближения уравнений F8.4) имеет периодическое решение.
Отсюда следует, что характеристическое уравнение этой' системы
имеет, по крайней мере, один корень, равный единице. Этот резуль-
результат установлен впервые Пуанкаре.
Допустим, что остальные л— 1 корней характеристического урав-
уравнения системы первого приближения уравнений F8.4) имеют модули,
меньшие единицы. Тогда мы будем как раз иметь дело с критическим
случаем одного корня характеристического уравнения, равного еди-
единице. Как мы знаем, в этом случае задача устойчивости решается
нелинейными членами в уравнениях возмущенного движения F8.4).
Однако в рассматриваемом случае эти нелинейные члены не являются
совершенно произвольными. То обстоятельство, что рассматриваемое
периодическое движение принадлежит семейству F8.5), зависящему
от произвольной постоянной hv накладывает определенные зависи-
зависимости не только на первое приближение уравнений возмущенного
движения, но и на нелинейные части этих уравнений. Эти зависи-
зависимости получаются как раз такими, что для устойчивости движения
достаточно, чтобы остальные п— 1 корней характеристического
уравнения имели модули, меньше единицы. В этом и заключается
теорема, установленная Андроновым и Виттом, которая может
быть сформулирована следующим образом.
Теорема. Периодическое движение динамической системы,
описываемой уравнениями вида F8.1), будет устойчиво, если
§ 68]
ПЕРИОДИЧЕСКИЕ ДВИЖЕНИЯ АВТОНОМНЫХ СИСТЕМ
297
п—1 корней характеристического уравнения первого при-
приближения дифференциальных уравнений возмущенного движе-
движения имеют модули, меньшие единицы.
Доказательство. Итак, допустим, что характеристическое
уравнение системы первого приближения
dxs
dt
PsnXn
F8.7)
имеет п — 1 корней с модулями, меньшими единицы. Один корень
этого уравнения, по доказанному, равен единице. Тогда система F8.4)
при помощи линейного преобразования с периодическими коэффи-
коэффициентами может быть преобразована к виду
dx
dt
Si
t).
F8.8)
(s=l, 2 m).
Здесь m = n—1, asj—постоянные, для которых уравнение
«21
а„
«12
022 —¦
am«
aim
«2m
= 0
F8.9)
имеет корни только с отрицательными вещественными частями, и Ss
и X — функции такого же вида, как и Xs.
Указанное преобразование преобразует периодическое реше-
решение F8.6) уравнений F8.4) в периодическое решение уравнений F8.8),
Это решение будет, очевидно, иметь вид
F8.10)
= а*л@Ч-А*Ф
где г|)(-, г|M( — периодические функции. Линейная часть этого решения
будет являться периодическим решением линейной системы
¦¦•+asmlm.
F8.11)
Но по свойству корней уравнения F8.9) единственным периоди-
периодическим решением системы F8.11) будет
298 УСТОЙЧИВОСТЬ ПЕРИОДИЧЕСКИХ ДВИЖЕНИЙ [ГЛ. V
и поэтому решение F8.10) имеет вид
F8.12)
Установив это, сделаем в уравнениях F8.8) подстановку
F8.13)
Преобразованная система будет, очевидно, иметь вид
du __и
F8.14)
dt
и. Vi vm),
где I) и V — функции такого же типа, как и X и Ss. Все сделан-
сделанные преобразования таковы, что задача устойчивости для уравне-
уравнений F8.1) эквивалентна задаче устойчивости для уравнений F8.14).
Поэтому мы можем рассматривать эти последние уравнения.
Так как уравнения F8.8) имеют частное решение F8.12), то урав-
уравнения F8.14) должны допускать частное решение
u — h, vx — ... —vm = 0,
а для этого, очевидно, необходимо, чтобы функции U и Vs обра-
обращались в нуль при vx = ... =vm~Q. Но в таком случае уравне-
уравнения F8.14) представляют собой частный случай уравнений C4.2),
фигурирующих в теореме, доказанной в § 34. Из последней немед-
немедленно вытекает, что невозмущенное движение устойчиво. Более того,
можно утверждать, что всякое возмущенное движение, достаточно
близкое к невозмущенному, стремится при <->со к одному из дви-
движений семейства F8.5) и что такими же свойствами, как и невоз-
невозмущенное движение, обладает всякое движение указанного семейства,
если только h достаточно мало.
Примечание. Доказанная теорема может быть обобщена').
Допустим, что динамическая система описывается уравнениями
вида
Уп),
') См. М а л к и н И. Г., Об устойчивости периодических движений.
ПММ, т. VIII, вып. 4, 1944; Отроков Н. Ф., К устойчивости периоди-
периодических интегралов. Учен. зап. Горьковского гое. ун-та, вып. 6, 1938.
§ 68} ПЕРИОДИЧЕСКИЕ ДВИЖЕНИЯ АВТОНОМНЫХ СИСТЕМ 299
отличающимися от F8.1) тем, что они могут содержать t, по отно-
отношению к которому они периодичны с периодом ю. Допустим, что
эта система допускает периодическое решение
периода ю, зависящее от k^n произвольных постоянных. Если Ys
не содержат t, то предполагается, что период решения не зависит
от fij. Если исследовать устойчивость какого-нибудь движения семей-
семейства F8.15), то окажется, что характеристическое уравнение системы
первого приближения уравнений возмущенного движения имеет, по
крайней мере, k корней, равных единице. Можно показать, что если
остальные п — k корней этого уравнеиия имеют модули, меньшие
единицы, то невозмущенное движение устойчиво.
ГЛАВА VI.
НЕУСТАНОВИВШИЕСЯ ДВИЖЕНИЯ.
А. НЕКОТОРЫЕ ОБЩИЕ ПРЕДЛОЖЕНИЯ.
§ 69. Постановка задачи.
Мы переходим теперь к рассмотрению общего случая неустано-
неустановившихся движений, т. е. к случаю, когда правые части уравнений
возмущенного движения содержат явно время t, по отношению
к которому они, вообще говоря, не периодичны. Задача при этом
делается значительно сложнее, чем в рассмотренных случаях перио-
периодических и установившихся движений. Однако к этой задаче приво-
приводятся многие важные технические вопросы, в связи с чем за послед-
последние годы она привлекает многих исследователей. В настоящей главе
мы приводим основные результаты, полученные в теории неустано-
неустановившихся движений как самим Ляпуновым, так и в последуюших
исследованиях.
В разделе А этой главы мы рассматриваем некоторые общие
вопросы теории. Сюда относится проблема существования функций
Ляпунова (проблема обращения теорем второго метода), устойчивость
при постоянно действующих возмущениях и связанный с нею вопрос
об опасных и безопасных границах области устойчивости.
В разделе Б рассматривается с точки зрения задачи устойчивости
теория линейных уравнений с зависящими от t коэффициентами,
т. е. теория первого приближения.
В разделе В рассматриваются критерии устойчивости по первому
приближению.
Наконец, в разделе Г рассматривается общая теория критических
случаев. Эта теория затем прилагается к установившимся и периоди-
периодическим движениям. Здесь дается решение задачи устойчивости уста-
установившихся движений в критических случаях двух нулевых корней,
двух пар чисто мнимых корней, одного нулевого и пары чисто мни-
мнимых корней характеристического уравнения. Аналогичные задачи рас-
рассматриваются и для периодических движений.
§ 70] УСТОЙЧИВОСТЬ ПРИ ПОСТОЯННО ДЕЙСТВУЮЩИХ ВОЗМУЩЕНИЯХ 301
§ 70. Теорема об устойчивости при постоянно
действующих возмущениях.
В § 4 мы уже указывали, что большой практический интерес
представляет исследование устойчивости движения не только по отно-
отношению к мгновенным возмущениям, но и по отношению к возмуще-
возмущениям, действие которых не прекращается. С точки зрения математи-
математической устойчивость по отношению к таким постоянно действующим
возмущениям отличается от устойчивости по Ляпунову тем, что
возмущаются не только начальные условия движения, но и самые
дифференциальные уравнения движения.
Рассматривая невозмущенное движение какой-нибудь системы,
составим по обычным правилам дифференциальные уравнения возму-
возмущенного движения. Пусть эти уравнения имеют вид
*^ = Xs{t, xx, .... хп) E=1, 2 п). G0.1)
Относительно правых частей этих уравнений мы будем предполагать,
что они в области
^>0, |*J</f G0.2)
непрерывны и допускают существование единственного решения при
заданных начальных условиях. Разумеется, при этом выполняются
обычные соотношения Xs(t, 0 0) = 0.
Наряду с уравнениями G0.1) рассмотрим уравнения
~jj ЛД(' х\ хп> ~Г Ks (I, Хх, ..., Хп), (IV. О)
где функции Rs характеризуют постоянно действующие возмущаю-
возмущающие факторы. Эти функции Rs также определены в области G0.2),
где они также непрерывны и удовлетворяют условию, что уравне-
уравнения G0.3), так же как и уравнения G0.1), имеют при заданных
начальных условиях единственное решение.
Функции Rs в отличие от функций Xs практически никогда неиз-
неизвестны. Относительно них можно лишь предполагать, что они удо-
удовлетворяют вышеуказанным общим условиям и достаточно малы.
В частности, эти функции не обращаются, вообще говоря, в нуль
при хх = ... =хл = 0. Это объясняется тем, что невозмущенное
движение является частным решением тех дифференциальных уравне-
уравнений, которые не учитывают возмущающих факторов, т. е. уравне-
уравнений G0.1) (если пользоваться переменными хх хп), а не урав-
уравнений G0.3).
Невозмущенное движение хх = ... = хп = 0 будет устойчивым
при постоянно действующих возмущениях, когда величины xs остаются
все время малыми при условии, что они были малыми в начальный
момент времени и что возмущения Rs также малы. Более точное
302 НЕУСТАНОВИВШИЕСЯ ДВИЖЕНИЯ [ГЛ. VI
определение было дано в § 4. Это определение в переменных xs
формулируется следующим образом.
Определение. Невозмущенное движение (тривиальное реше-
решение хх = ... =хп = 0 уравнений G0.1)) называется устойчивым
при постоянно действующих возмущениях, если для всякого
положительного г, как бы мало оно ни было, существуют два
других положительных числа цх{г) и щ(г)> таких, что вся-
всякое решение уравнений G0.3) с начальными значениями x°s
(при t = t0), удовлетворяющими неравенствам
при произвольных Rs, удовлетворяющих в области t~^tOl
|xj<<e, неравенствам
\RsV. *i xn)|<ri2(e),
удовлетворяет при всех t > /0 неравенствам
1*,1<е-
В § 46 была установлена основная теорема второго метода Ляпу-
Ляпунова (теорема II) об асимптотической устойчивости. Согласно этой
теореме невозмущенное движение будет асимптотически устойчиво
в смысле Ляпунова, если для уравнений G0.1) существует функция
Ляпунова V со знакоопределенной производной, допускающая беско-
бесконечно малый высший предел. Оказывается, что если последнее усло-
условие заменить условием, несколько более жестким, что функция V
обладает ограниченными частными производными, то невозмущенное
движение будет устойчиво при постоянно действующих возмущениях.
Покажем, что имеет место следующая теорема 1),
Теорема. Если для дифференциальных уравнений возму-
возмущенного движения G0.1) существует определенно-положитель-
определенно-положительная функция V(t, xv ..., хп), полная производная которой
по времени, составленная в силу этих уравнений, есть функ-
функция определенно-отрицательная, и если в области G0.2)
частные производные -*— ограничены, то невозмущенное дви-
движение устойчиво при постоянно действующих возмущениях.
Доказательство. Согласно условиям теоремы в области G0.2)
выполняются неравенства
V{t, х, *я)>ИМ*1 хп)- G0.4)
+ ЪХ<^() G0-5)
') Малкин И. Г., Об устойчивости при постоянно действующих воз-
возмущениях. ПММ, т. VIII, вып. 3, 1944.
§ 70] УСТОЙЧИВОСТЬ ПРИ ПОСТОЯННО ДЕЙСТВУЮЩИХ ВОЗМУЩЕНИЯХ 303
где W1 и W2—определенно-положительные функции, не зависящие от t.
Кроме того, применяя теорему о среднем значении, мы можем написать:
•*. *¦>-*.(?¦)+-+*.(&)•
где производные вычислены в точке (Qxu .... Qxn) @ < 0 < 1).
_ dV
Так как производные -^— ограничены, то отсюда следует, что для
всякого положительного числа А1р как бы мало оно ни было, можно
найти такое положительное число /z2, что
V(t. х, xn)<h2 при t^t0, \xs\^hu G0.6)
т. е. что функция V допускает бесконечно малый высший предел.
Пусть х — наибольшая из величин \хг\, . . ., \хп\. Обозначим через а
точный нижний предел функции Wi(xl xn) при условии
Н^- х^-г, где е—-произвольное положительное число, меньшее Н.
Имеем, следовательно, на основании G0.4)
V(t, xv .... д:л)>а при t^-t0, д;>е. G0.7)
Пусть / — положительное число, меньшее а. Рассмотрим в про-
пространстве переменных хх, . .., хп подвижную поверхность
V(t, xv ..., хп) —1 = 0. G0.8)
Из G0.6) следует, что для всех точек этой поверхности выпол-
выполняется условие х^>Х, где X — некоторое достаточно малое положи-
положительное число. Кроме того, из G0.7) следует, что во всех точках
этой поверхности выполняется условие д; < е и, следовательно, во
всех этих точках и при всех значениях t^-t0 выполняется неравен-
неравенство G0.5). Мы можем поэтому написать:
IiH_i_V dv
где k2, в силу того что х^-Х, отлично от нуля.
dV
Но тогда в силу ограниченности -г—, можно найти настолько
малое число т]2(е), чтобы при
\Rs(t, xx *я)|<ть(е) G0.9)
выполнялось неравенство
Лт т ж—¦ пт т I
<0. G0.10)
Будем теперь рассматривать величины jCj как функиии вре-
времени, удовлетворяющие уравнениям G0.3) в предположении, что
выполняются неравенства G0.9). Начальные значения д;^ величин д;
304 НЕУСТАНОВИВШИЕСЯ ДВИЖЕНИЯ [ГЛ. VI
(при t~t0) выбираем согласно условиям
K|<4i(e). G0.11)
где положительное число % (е) настолько мало, что выполняются
неравенства
ri1<e, V(t0, *° *о)</ при |*°|<Лг G0.12)
Покажем, что при всех t > t0 будем иметь:
|*,|<«. G0.13)
В самом деле, функции xs не могут перестать удовлетворять
неравенствам G0.13) иначе, как достигнув таких значений, при ко-
которых выполняется неравенство х^-е. Но тогда на основании G0.7)
функция V(t, Xi(f) xn(t)) станет большей, чем /, так как
/ < а. Так как в начальный момент эта функция меньше /, то дол-
должен быть и такой момент времени, при котором эта функция прини-
принимает значение I, переходя от значений, меньших /, к значениям, боль-
большим /. Но тогда в этот момент времени (—тг-| ]>0, что проти-
\ at lv=i
воречит G0.10).
Следовательно, при условиях G0.9) и G0.11) выполняются усло-
условия G0.13), что и требовалось доказать.
Примечание. Покажем, что при условиях теоремы имеет
место своего рода асимптотическая устойчивость.
Выбрав в неравенствах G0.9) число ц2 так, чтобы выполнялось
неравенство G0.10), мы будем в силу непрерывности иметь также и
неравенства
I s=l )v=c
где /j<sCc<^, a /j < /—положительное число, достаточно близкое
к !, С уменьшением щ число /х будет также уменьшаться, и при
г|2=0 это число может быть принято равным нулю. Таким образом,
при всех t > ^0 производная -тт, составленная в силу системы G0.3),
будет принимать отрицательные значения для всех значений переменных,
лежащих в области, определяемой неравенствами /i<^t>(?, xv..., xn)^.l.
Для этой области выполняется неравенство д: > ц, где ц — доста-
достаточно малое положительное число. Вследствие этого мы можем на-
пксать, что в указанной области и при всех значениях t > t0 выпол-
выполняется неравенство
п
dV dV
§ 71] ПРОБЛЕМА СУЩЕСТВОВАНИЯ ФУНКЦИЙ ЛЯПУНОВА 305
где т — отличная от нуля постоянная. Что постоянная т получается
отличной от нуля, несмотря на то, что t изменяется в бесконечном
интервале, вытекает непосредственно из неравенств G0.5), G0.9) и
dV
условия теоремы, что для -*— существуют не зависящие от t верх-
ОХ §
ние пределы.
Из G0.15) вытекает, что точка (х1 хп), находившаяся со-
согласно G0.12) в начальный момент внутри области V < /, попадает
в некоторый момент времени в область V < lv где и будет затем
оставаться. В самом деле, по доказанному выше, точка все время
остается внутри области V < I, и если бы она все время находилась
вне области V < lv то все время выполнялось бы неравенство G0.15),
а отсюда бы следовало неравенство
V(t. xv .... xn) = V(tQ, *° *°)+ J 4^'<
что невозможно, так как левая часть положительна, а правая при
достаточно большом t отрицательна, Таким образом, точка (хх, ..., хп)
непременно попадет в некоторый момент времени в область V < 1Х.
Но попав в эту область, точка (хг, .... хп) будет в ней все время
оставаться, так как \—гг) < 0.
Таким образом, при достаточно малых начальных возмущениях
точка (*i хп) хотя и не будет асимптотически приближаться
к началу координат, но будет отбрасываться в некоторую окрестность
начала координат, которая может быть сделана сколь угодно малой,
если постоянно действующие возмущения достаточно малы.
§ 71. Проблема существования функций Ляпунова.
Таким образом, условия теоремы II второго метода Ляпунова при
некоторых небольших добавочных ограничениях (требование ограни-
ограниченности частных производных вместо условия о бесконечно малом
высшем пределе) обеспечивают не только асимптотическую устойчи-
устойчивость в смысле Ляпунова, но и устойчивость более сильную, а именно,
устойчивость при постоянно действующих возмущениях. Отсюда,
естественно, возникает вопрос, не являются ли условия теоремы II
чрезмерно узкими. Другими словами, возникает вопрос об обрати-
обратимости теоремы П. Этот вопрос представляет интерес не только
в связи с разбираемой сейчас задачей, и он в равной степени отно-
относится как к теореме II, так и к остальным основным теоремам вто-
второго метода. Действительно, если вторым методом пользоваться как
основным для решения задачи устойчивости, т. е. если эту задачу
306 НЕУСТАНОВИВШИЕСЯ ДВИЖЕНИЯ [ГЛ. VI
сводить к попыткам построения функций Ляпунова, то должна быть
уверенность, что такие функции каждый раз действительно существуют.
Поставленная таким образом проблема существования функций
Ляпунова является очень трудной и до сих пор не получила полного
разрешения*). Впервые занимаясь этой задачей, автор2) рассматривал
только установившиеся движения для систем второго порядка. Было
показано, что теорема I Ляпунова необратима, т. е. было показано,
что невозмущенное движение может быть устойчиво и в то же время
может не существовать знакоопределенной функции, для которой
производная в силу уравнений возмущенного движения была бы зна-
знакопостоянной, противоположного знака. При этом речь шла о функциях,
не зависящих от t. Было, однако, показано, что можно всегда найти
функцию другого вида, являющуюся обобщением функций Ляпунова.
Обращением теоремы I занимался также К. П. Персидский3),
который рассматривал произвольные системы уравнений возмущенного
движения. К. П. Персидский показал, что в случае устойчивости для
уравнений возмущенного движения всегда существуют особые функ-
функции, являющиеся обобщением функций Ляпунова.
Обращению теоремы II также посвящено несколько работ. Авто-
Автором была показана4) обратимость этой теоремы для систем второго
порядка с постоянными коэффициентами. Им же были установлены5)
достаточные условия существования функций, удовлетворяющих всем
условиям теоремы II для системы линейных уравнений с переменными
коэффициентами. К. П. Персидский показал6), что эти условия
являются также необходимыми. При этом установлено, что одной
лишь асимптотической устойчивости недостаточно для существования
указанной функции.- Эти результаты, имеющие непосредственную
связь с теорией устойчивости по первому приближению, излагаются
ниже, в § 75.
И. Л. Массера7) подверг детальному анализу теоремы I и II
Ляпунова, а также их различные обобщения. Им было, в частности,
показано, что теорема II обратима для установившихся и периоди-
') См. примечание в конце книги (стр. 523)
2) М а л к и н И. Г., Das Existenzproblem von Liapounoffschen Funktionen.
Изв. Казанского физ.-матем. об-ва, т. IV, 1929—1930.
3) П е р с и д с к и й К. П., Об .одной теореме Ляпунова. ДАН, т. XIV,
№ 9, 1937.
4) М а л к и н И. Г., Проблема существования функций Ляпунова. Изв.
Казанского физ.-матем. об-ва, т. V, 1931.
5) М а л к и н И. Г., Об устойчивости по первому приближению. Сб. науч-
научных трудов Казанского авиац. ин-та, № 3, 1935.
в) Персидский К. П., К теории устойчивости интегралов систем
дифференциальных уравнений. Изв. физ.-матем. об-ва при Казанском гос.
ун-те, т. VIII, 1936—1937.
7) М a s s e r a I. L., On Liapounoff's condition of stability. Annals of Mathe-
Mathematics, т. 50, N° 3, 1949.
§ 72] НЕКОТОРЫЕ СВОЙСТВА УСТАНОВИВШИХСЯ ДВИЖЕНИЙ 307
ческих движений. Показано, более того, что при асимптотической
устойчивости в указанных случаях существует функция V, удовле-
удовлетворяющая не только условиям теоремы II, но и более жестким
условиям теоремы предыдущего параграфа об устойчивости при по-
постоянно действующих возмущениях, т. е. что функция V обладает
ограниченными частными производными. Отсюда вытекает, что уста-
установившиеся и периодические движения резко отличаются в отноше-
отношении обратимости теоремы II от общего случая неустановившихся
движений, для которых, как указано выше, теорема не обратима
даже для линейных уравнений.
Результаты И. Л. Массера относительно установившихся и перио-
периодических движений приводятся в двух следующих параграфах. Эти
результаты, как мы увидим, позволяют установить некоторые важные
общие предложения. Для случая установившихся движений резуль-
результаты И. Л. Массера уточнены Е. А. Барбашиным*).
§ 72. Некоторые свойства установившихся
и периодических движений.
Допустим, что правые части уравнений возмущенного движения
^- — Xs(t, х, х.) (s=l. 2, .... п), G2.1)
dt s ' " i \ /
являются по отношению к t периодическими функциями, периода со.
Мы не исключаем при этом из рассмотрения тот частный случай,
когда Xs совсем не зависят от t. Мы будем предполагать, что
в области t^-0, \xs\^.H функции Xs обладают непрерывными
частными производными первого порядка по переменным xs.
Пусть
— решение системы G2.1), определяемое начальными условиями
Согласно известной теореме о зависимости решений дифферен-
дифференциальных уравнений от начальных условий2) функции Fs будут обла-
обладать непрерывными частными производными первого порядка по
переменным tQ, х\ д;^ для всех значений этих переменных, ле-
лежащих в области |^о|<0, |jcO !<#'<#, и при всех значениях t,
') Б а р б а ш и н Е. А., О существовании гладких решений некоторых
линейных уравнений с частными производными. ДАН, т. XXII, № 3, 1950;
см. также примечание в конце книги (стр. 524)
2) См., например, Степанов В. В., Курс дифференциальных уравнений,
стр. 298, изд. 5-е, Гостехиздат, 1950.
308 НЕУСТАНОВИВШИЕСЯ ДВИЖЕНИЯ [ГЛ. VI
при которых еще выполняются условия |/^|<^/У. Далее, из самого
определения функций Fs вытекает, что для всяких tx и t2 > tx
имеют место тождества
где
*;=¦
G2.2)
В самом деле, точка (хг, . .., хп), выходящая в момент вре-
времени tQ из положения (х®, . . ., х°Л, достигнет в момент t1 положения
(.*,', . .., х'Л и вместе с другой точкой, выходящей в этот же момент
времени tl из этого же положения (х'х х'\ достигнет к моменту
времени t2 положения (х" х"\ так как начальные условия
однозначно определяют движение.
Кроме того, так как уравнения G2.1) не изменяются при замене t
на ^-)-о, то имеют также место тождества
Fs(t ± та,, х* *о, ^ + me>) = Ft(t. де" д:«. t0). G2.3)
где т — произвольное целое число.
Допустим теперь, что невозмущенное движение асимптотически
устойчиво. Тогда в области
G2.4)
где а — достаточно малое положительное число, выполняются пре-
предельные соотношения
lim F (t, x°, ..., х°, 0) = 0. G2.5)
И. Л. Массера показал, что эти соотношения выполняются равно-
равномерно относительно х9., т. е. что для всякого е, как бы мало оно
ни было, можно найти такое не зависящее от х°. число 7"(е), что при
всех ty-T будут выполняться неравенства \Fs(t, л;° х°п, 0I < е.
Чтобы это показать, определим прежде всего число т](е) из условия
\Fs(t, х\ х\, 0)| < в при |*0|<т|(е). G2.6)
Это всегда возможно в силу устойчивости невозмущенного дви-
движения. Далее, допустим противное, что вышеуказанное число Т (е)
не существует. Тогда, как бы велико ни было целое число /и, всегда'
найдется такое tm > ma и такая система начальных значений х®т,
лежащих в области G2.4), что
|^(*.. х°т х°пт, 0I
§ 72] НЕКОТОРЫЕ СВОЙСТВА УСТАНОВИВШИХСЯ ДВИЖЕНИЙ 309
Так как последовательность точек (x°sm) лежит в замкнутой
области G2.4), то в той же области лежит и предельная точка ука-
указанной последовательности. Пусть это будет точка д;*. Для этой
точки выполняются, следовательно, соотношения G2.5), из которых
вытекает, что существует такое достаточно большое целое число N,
что будут иметь место неравенства
\Fs(Nw, х\, .... хщп, 0)|<-iti(e). G2.8)
Но тогда найдутся сколь угодно большие значения т, для кото-
которых будут выполняться неравенства
\x^\ = \Fs(N(o. х\т х°ат. 0)| < л(е). G2.9)
Действительно, в последовательности (x°sm) найдутся точки со сколь
угодно большим значением индекса т, которые будут настолько близки
к предельной точке, что разности Fs(Na, х0-, 0) — F (Л/со, х*., 0)
в силу непрерывности Fs будут меньше -у. Из G2.9) и G2.6) сле-
следует, что при всех t > 0
или, принимая во внимание G2.3) и G2.2),
в>|/%(*. х[Ю хЮ, 0)|=5=|РД^ + Л/(», xW *
Полученные неравенства противоречат G2.7), так как существуют
такие tm, для которых tm > Л/ю. Полученное противоречие и дока-
доказывает справедливость предложения о том, что соотношения G2.5)
выполняются равномерно относительно величин х0..
Покажем теперь, что соотношения
llm Ft(t, x°v ..... х°я, to) = 0 (s=l, 2 и) G2.10)
выполняются также равномерно относительно величин х° и tn, лежа-
S U
щих в области
2| G2.11)
где р — достаточно малое число.
Действительно, имеем в силу G2.2) тождественно
Ft(t. x°,...,xon, to) = Fs(t, х[ х'я. 0),
где величины д;^ определяются из уравнений
310 НЕУСТАНОВИВШИЕСЯ ДВИЖЕНИЯ [ГЛ. VI
Поэтому справедливость интересующего нас сейчас предложения
непосредственно вытекает из уже доказанного предложения о соот-
соотношениях G2.5), если только величину E в G2.11) взять настолько
малой, чтобы величины x's, определяемые уравнениями G2.12), лежали
при всех 0<^0<;g) в области G2.4).
§ 73. Теорема о существовании функций Ляпунова
для периодических н установившихся движений
в случае асимптотической устойчивости.
Мы переходим теперь к доказательству следующей теоремы
И. Л. Массера.
Теорема. Если дифференциальные уравнения возмущенного
движения имеют вид G2.1) и если невозмущенное движение
асимптотически устойчиво, то существует определенно-поло-
определенно-положительная функция V(t, Xj, ..., хп), производная которой -^-,
составленная в силу этих уравнений, есть функция опреде-
определенно-отрицательная. При этом V будет по отношению к t
периодической функцией, периода со, и не будет, в частности,
совсем зависеть от t, если эта величина не содержится явно
в функциях Xs.
Доказательство. Обозначим через ф (t), где t ^> t0 — точный
верхний предел функции
?{*• хг *»• 'о)=2/1('. *? *°. g=S^
S— 1 S—1
по переменным х°- и <0 в области G2.11), так что
F(t. *? *°. *о)<<РЮ пРи К|<Р- 0</0<(о. ^о<^. G3.1)
Функция cp(f) будет, очевидно, положительной. Кроме того,
lim ф(^) = 0. G3.2)
В самом деле, пусть е — сколь угодно малое положительное
число. Выберем Т(е) настолько большим, чтобы при (>Г и всех
значениях х°, и р, лежащих в области G2.11), выполнялось нера-
неравенство
F{t. х\ л*. го)<е, G3.3)
что по доказанному в предыдущем параграфе всегда возможно. Так
как ф (t) является точным нижним пределом непрерывной функции
в замкнутой области, то оно будет одним из значений, которое эта
функция в указанной области принимает. Другими словами, в
§ 73] ТЕОРЕМА О СУЩЕСТВОВАНИИ ФУНКЦИЙ ЛЯПУНОВА 311
области G2.11) существует система чисел х° и tQ, для которой
и, следовательно, на основании G3.3) ф(?)<е при t > Т, что и
доказывает наше утверждение.
Рассмотрим теперь функцию, определяемую равенством
хя, t) = fO[F(x, хх хп, t)\dx. G3.4)
Здесь О (ц) — некоторая функция от г\, определенная при
принимающая при ц > 0 только положительные значения и обращаю-
обращающаяся в нуль вместе со своей производной О' (ц) при ц = 0. Кроме
того, эта функция обладает тем свойством, что интеграл
G3.5)
сходится для любой положительной функции ф*@> удовлетворяющей
неравенству ф* (t) < ф (t), причем сходимость будет равномерной отно-
относительно выбора функции ф*(^). Ниже мы покажем, что такая функ-
функция О (г)) может быть действительно построена.
Покажем прежде всего, что функция V во всех точках области
|*,|<Р. *> 0. G3.6)
действительно существует и непрерывна.
В самом деле, пусть Xj и t лежат в области G3.6), t>/1,
т'=т — /исо^-1 — mco, где m — такое целое число, что 0 <^t —
— ma < со. Тогда на основании G2.3) мы можем написать:
F(x, хх хп, t) — F(x', хг, ..., хп, t—
причем функция ф*(т') при любом t и Xj и области G3.6) удовле-
удовлетворяет на основании G3.1) неравенству ф*(т')^ф(т')- Вводя в G3.4)
вместо переменной интегрирования т переменную х', будем иметь:
со
х„, 0= J О[ф*(т')]йт'. G3.7)
t—
Но согласно выбору функции О интеграл, стоящий в G3.7), схо-
сходится равномерно относительно ф* (т'), т. е. равномерно относи-
относительно Xj и t в области G3.6)* Отсюда вытекает, что в области G3.6)
функция V существует и непрерывна.
312
НЕУСТАНОВИВШИЕСЯ ДВИЖЕНИЯ
[ГЛ. VI
Найдем теперь частные производные от V по t и xs, выполняя
дифференцирование под знаком интеграла. Будем иметь:
дУ
dxs
= f Q'[F{x, xx xn,
dF(x, xi xn, t)
dxs
dx,
¦ = — U\F{f. xx Xn, 01 +
CO
G'[F(x, xx xn. ^fMV'Xj) dx.
G3.8)
Однако, для того чтобы эти выражения действительно предста-
представляли частные производные функции V в области G3.6), необходимо,
чтобы входящие в них интегралы сходились и притом равномерно
для всех значений xs н t в указанной области. Для этого необхо-
необходимо на функцию О наложить еще одно условие, которое может
быть получено следующим образом.
В силу условий, наложенных на правые части уравнений G2.1),
частные производные
dF(t,xl...,x°n,t0)
x°n,t0)
dx°s
dt0
будут существовать и будут непрерывными при всех значениях пере-
переменных в области |.>Л|<;р, 0^^0^ю, to^.t, так как в силу устой-
устойчивости при указанных значениях переменных функции Fs будут
оставаться в области определения функций Xs. Мы можем поэтому
для всякого t назначить для этих производных некоторый положи-
положительный верхний предел M{t). Мы можем при этом предполагать,
что функция М (t) непрерывна и не убывает при возрастании t.
Тогда, если потребовать, чтобы интеграл
f О'[<р* (%)] М (х) dx
G3.9)
сходился при любом выборе функции ф*(т), для которой ф*(т)<
< ф (т), и чтобы сходимость была равномерной относительно ф* (т),
то интегралы, входящие в выражения G3.8), будут равномерно схо-
сходиться в области G3.6). Мы будем предполагать, что функция О(ц)
действительно удовлетворяет указанному условию. Тогда функция V
будет определенной и непрерывной вместе со своими частными про-
производными первого порядка во всех точках области G3.6].
§ 73] ТЕОРЕМА О СУЩЕСТВОВАНИИ ФУНКЦИЙ ЛЯПУНОВА 313
Рассмотрим подробнее свойства функции V. В силу G2.3)
имеем:
оо
., х„, t-\-(?>)= Г G[F (х, хи . .., х„,
t+a
X-i, .... Х„
, *, хп, t)\dx = V{xx хя, f),
t
т. е. функция V является периодической относительно t с перио-
периодом со. Если Xs не содержат явно t, то функция V совсем не будет
зависеть от t. Это непосредственно вытекает из того обстоятельства,
что в этом случае а можно считать произвольным числом.
Функция V положительна во всех точках области G3.6) и обра-
обращается в нуль только при х^= ... = хп — 0. Будучи же по отно-
отношению к t периодической, она необходимо является определенно-
положительной, так как мы можем писать:
где W—определенно-положительная функция, представляющая собой
точный нижний предел функции V{хх хп, f) по переменной t
на отрезке 0^ t -^ а.
Составим производную от V по t в силу уравнений G2.1). Мы
, dV dV r.
будем иметь, что —гг- = —тт-, где V — результат подстановки в функ-
функцию V произвольного решения уравнений G2.1). Но
{ *? Х,
t
так как в силу G2.2)
F Гт F (t х° хп Л F (t х° „о
г |т, r,^f, х1 хп, iy ..., гп{г, xv .... хп,
Следовательно,
т. е. —тт- есть функция определенно-отрицательная.
314
НЕУСТАНОВИВШИЕСЯ ДВИЖЕНИЯ
[ГЛ. VI
Таким образом, функция V удовлетворяет всем условиям теоремы,
и для того чтобы последняя была полностью доказана, необходимо
еще показать, что существует функция О, удовлетворяющая всем
указанным для нее условиям. Необходимо, следовательно, показать,
что существует положительная функция G(tj), определенная для
Г|^0, обращающаяся вместе со своей производной О' (г\) в нуль
при т) = 0 и обладающая тем свойством, что интегралы G3.5) и
G3.9) сходятся при любом выборе функций ф*(т), удовлетворяющих
условию ф* (t) <; ф (t), причем сходимость является равномерной отно-
относительно ф*(х). Фигурирующая в G3.9) величина М (т) является поло-
положительной, неубывающей, непрерывной функцией т, определенной
при всех т^О. Функция О(г\) может быть построена следующим
образом.
Выберем последовательность чисел tn(n=\, 2, 3, .. .) таким
образом, чтобы при t~^tn выполнялось соотношение ф@^—XT'
В силу G3.2) такая последовательность существует. Мы будем при
этом предполагать, что tl'^-\, t„+1 ;>1n-\- 1. Далее строим функ-
функцию r\(t), полагая ц(tn) = —; v\(t) линейна в каждом интервале
между tn и tn+l и т](?) — [-г-)
при
где р—целое число,
Рис. 18.
Рис. 19.
выбранное настолько большим, что ц' (tl — 0) < v[ (t1 -f- 0). Очевидно,
что \imr\(t)= lim /(rj) = 0 и <f>(t)-tC t\(t) при t^tv График функ-
t = co T] -> со
ции y\(t) изображен на рис. 18.
Пусть t(r\)— функция, обратная x\(t). График этой функции пока-
показан на рис. 19. Тогда полагаем:
е-*
M[t\
-dr\.
G3.10)
§ 74] ОСНОВНАЯ ТЕОРЕМА ОБ УСТОЙЧИВОСТИ 315
Функция О (х\), очевидно, положительна при любом ц У> О, и для
нее G @) == О' @) = 0. Далее имеем:
W G3Л1)
При t"^tx справедлива оценка ф* (t) ^ ф (t) -^ ц (t), и, так как
ч) — функция убывающая, t (ф* {t)\ > t [ц (t)] = t. Поэтому, учиты-
учитывая, что М (t) — функция неубывающая, из G3.11) находим:
откуда сразу получается равномерная сходимость интеграла G3.9).
Что же касается интеграла G3.5), то, заменяя в нем нижний предел
числом tv что для вопроса о сходимости не имеет значения, получим
для него выражение
оо Ф* М
h о
для которого справедлива оценка
/
t,
Заменяя во внутреннем интеграле переменную т] переменной
найдем:
Полученный интеграл, очевидно, сходится, так как, по крайней
мере при t^-tv имеем |т]'(^)|<1. Отсюда вытекает равномерная
относительно ф*(?) сходимость интеграла G3.5).
Таким образом, функция V обладает всеми необходимыми свой-
свойствами, и теорема полностью доказана.
§ 74. Основная теорема об устойчивости
при постоянно действующих возмущениях для периодических
и установившихся движений.
Приложение к вопросу об «опасных» и «безопасных»
границах области устойчивости.
Построенная в предыдущем параграфе функции V, будучи перио-
периодической относительно t, не только допускает бесконечно малый
высший предел, но обладает ограниченными частными производными
по переменным х^ хп. Следовательно, эта функция удовлетворяет
316 НЕУСТАНОВИВШИЕСЯ ДВИЖЕНИЯ [ГЛ. VI
всем условиям теоремы § 70. Это приводит сразу к следующей
теореме.
Теорема. Для того чтобы установившееся ила периодиче-
периодическое движение было устойчиво при постоянно действующих воз-
возмущениях, достаточно, чтобы оно было устойчиво асимптоти-
асимптотически в смысле Ляпунова. При этом предполагается, что правые
части уравнений возмущенного движения {без членов, характе-
характеризующих постоянные возмущения) обладают непрерывными
частными производными первого порядка.
Эта теорема показывает, какое важное значение имеет устойчивость
в смысле Ляпунова не только в задачах устойчивости, но и во всякой
другой задаче, когда точные уравнения по тем или иным причинам
приходится заменять приближенными и когда независимое переменное
изменяется в бесконечном интервале. Действительно, по крайней мере
для уравнений с постоянными и периодическими коэффициентами, рас-
рассматриваемое решение приближенных уравнений будет мало отличаться
от решения точных уравнений, если оно асимптотически устойчиво
в смысле Ляпунова.
Рассмотрим частный случай. Допустим, что уравнения возмущен-
возмущенного движения G2.1) имеют вид
dx
-4f~ = Ps\Xl+ ¦¦¦ + Рзпхп + ХЛ*' *1 *„), G4.1)
где Xs—аналитические функции, начинающиеся членами не ниже
второго порядка. Если характеристические показатели первого при-
приближения имеют отрицательные вещественные части, то невозмущенное
движение будет асимптотически устойчиво и, следовательно, устойчиво
при постоянно действующих возмущениях. Этот результат для случая,
когда уравнения G4.1) не содержат явно t, установлен Г. Н. Дубо-
шиным'), а для общего случая периодических коэффициентов —
И. А. Артемьевым2).
В качестве приложения теоремы об устойчивости при постоянно
действующих возмущениях для установившихся и периодических
движений рассмотрим вопрос об «опасных» и «безопасных» границах
области устойчивости, на котором мы уже останавливались в § 44.
Допустим, что уравнения возмущенного движения G2.1) имеют вид
+ XSV> *i xn) G4.2)
E=1, 2, .. ., я),
') Дубошин Г. Н.. К вопросу об устойчивости движения относительно
постоянно действующих возмущений. Труды ГАИШ, т. XIV, вып. 1, 1940.
2) Артемьев И. А., Осуществимые движения. Изв. АН СССР, сер.
матем., № 3, 1939.
§ 75] УСЛОВИЯ СУЩЕСТВОВАНИЯ ФУНКЦИЙ ЛЯПУНОВА 317
где |j, — малый параметр, psj и rSJ- — периодические функции времени,
периода со (в частности, постоянные), a Xs — функции, удовлетворяющие
общим условиям § 72 и имеющие порядок малости выше первого.
Мы будем предполагать, что система первого приближения при
[i = 0 не имеет характеристических показателей с положительной
вещественной частью, но имеет характеристические показатели с веще-
вещественными частями, равными нулю. Таким образом, при ц = 0 система
находится на границе области устойчивости!), а при \х ф 0 она нахо-
находится вблизи этой границы. Величина параметра \х и характеризует
степень близости системы к границе области устойчивости. Мы пред-
предполагаем при этом, что коэффициенты rsj таковы, что система первого
приближения при \х Ф 0 может иметь характеристические показатели
с положительной вещественной частью, так что система может нахо-
находиться в области неустойчивости.
Допустим, что при (X = 0 невозмущенное движение асимптоти-
асимптотически устойчиво в смысле Ляпунова. Тогда оно, по доказанному,
будет устойчиво при постоянно действующих возмущениях. Следо-
Следовательно, при [X, достаточно малом, величины \xs\ будет оставаться
малыми, если они были малы в начальный момент времени. При этом,
как было показано в примечании в § 70, точка (х1 хп) будет
отбрасываться в некоторую окрестность начала координат, которая,
может быть сделана сколь угодно малой при ц, достаточно малом,
т. е. если система находится достаточно близко от границы области
устойчивости.
Таким образом, если пользоваться терминологией § 44, мы можем
сказать, что участки границы области устойчивости, на которых
невозмущенное движение асимптотически устойчиво, являются «без-
«безопасными». При этом не имеет никакого значения, сколько крити-
критических характеристических показателей имеет система первого при-
приближения на границе области устойчивости.
§ 75. Условия существования функций Ляпунова для линейных
уравнений в случае асимптотической устойчивости.
Мы переходим теперь к вопросу об обратимости теоремы II для
уравнений вида
^ •¦¦ +Psn<t)*n (s=\, 2 я), G5.1)
где psj— произвольные непрерывные и ограниченные при t~^> 0 функ-
функции времени. Задача заключается в определении условий, необходи-
необходимых и достаточных, при которых существует допускающая беско-
бесконечно малый высший предел определенно-положительная функция
') Определение границы области устойчивости дано в § 44.
318 НЕУСТАНОВИВШИЕСЯ ДВИЖЕНИЯ [ГЛ. VI
V(t, xv .... хя), производная которой, составленная в силу уравне-
уравнений G5.1), есть функция определенно-отрицательная. Эти. условия
даются двумя нижеследующими теоремами, из которых первая уста-
установлена К. П. Персидским '), а вторая — автором 2).
Обозначим через xl} (t, t0) xnj (t, t0) (j:— 1, 2 n) фун-
фундаментальную систему решений уравнений G5.1), определяемую
начальными условиями:
где to^-0—произвольная постоянная. Эти решения мы рассматриваем
как функции t и t0. Пусть а и Ъ — произвольные положительные
величины. Тогда га2 функций xSJ-(t, а) и ге2 функций xsJ(t, b) обра-
образуют две фундаментальные системы решений уравнений G5.1). Сле-
Следовательно, между ними существуют линейные соотношения
п
xsk(t, a)='2lcakXsa(t, b) (s, k = l, 2 re),
l
где caft—некоторые постоянные. Полагая в этих соотношениях t=b
и принимая во внимание G5.2), находим:
и, следовательно, имеют место следующие тождества:
п
xsk{t, a)=2jc«(f. b)xak(b, a). G5.3)
a=l
Докажем теперь следующие теоремы.
Теорема 1. Если для уравнений G5.1) существует опре-
определенно-положительная функция V (t, хг хп), допускающая
бесконечно малый высший предел, производная которой по вре-
времени, составленная в силу этих уравнений, есть функция
определенно-отрицательная, то при всех t~^s-ton to^>Q выпол-
выполняются неравенства
\xsJ(t, to)\ <?«-<»«-«, G5.4)
где В и а — некоторые не зависящие от t0 положительные
постоянные.
Доказательство. Согласно условиям теоремы существует
такое достаточно малое положительное число h, что в, области
*>0, |xs|<A G5.5)
') См. сноску 6) на стр. 306.
2) М а л к и н И. Г., Об устойчивости по первому приближению. Сб.
научных трудов Казанского авиац. ин-та, № 3, 1935-
§ 75] УСЛОВИЯ СУЩЕСТВОВАНИЯ ФУНКЦИЙ ЛЯПУНОВА 319
выполняются неравенства
V(t, хх *„) > W, (*i *„). G5.6)
u-<,— W2KxV ¦¦¦• xn)> К70-')
где Wx и W2—не зависящие от t определенно-положительные функции.
Так как согласно теореме II невозмущенное движение во всяком
случае устойчиво, то при р, достаточно малом, для любого решения
xs(t, tx) уравнений G5.1), начальные значения x°s = xs(tv *Л кото-
которого связаны соотношением
5=1 .5 = 1 Ч '
будут при всех t^>tx выполняться неравенства \xs\ < h. Здесь tx—¦
произвольное положительное число. Следовательно, для этого реше-
решения все время будет выполняться условие G5.7), из которого выте-
вытекает, что функция V[t, xx(t, tx) xn(t, tx)] будет убывающей,
и можем поэтому для всех t > tx написать неравенство
Wx[xx(t, tx) xa(t. tO\<V[t. xx(t, tx) xn(t, tO]<
< V(tv x\, ..., ^0)</(p). G5.9)
Здесь / есть верхний предел V(ty x°v .. ., д;^) при условии G5.8).
Это число не зависит от tx, так как функция V, допуская беско-
бесконечно малый высший предел, будет во всяком случае ограниченной.
Так как Wx есть функция определенно-положительная, то из G5.9)
вытекает, что при всех t > tx выполняются неравенства
\xs(t, tO\ <C*(p), G5.10)
где С* — некоторая не зависящая от tx постоянная.
Пусть теперь L — произвольная сколь угодно малая постоянная.
Рассмотрим множество значений xs, лежащих в области G5.5) и
удовлетворяющих неравенству V (t, хх, ..., хп) > L. Так как V
допускает бесконечно малый высший предел, то при этом необхо-
необходимо будет л: = тах {l^l \xn\)>X(L), где Я(L) — некоторая
достаточно малая постоянная. Но тогда при этом условии мы будем
также иметь W2(xx, ..., хп) > lx (L), где lx(L) — также некоторая
постоянная. Таким образом, мы можем писать:
dV
-Of<—W2<—lx(L) при V(t, xx, .... xn)>i. G5.11)
320 НЕУСТАНОВИВШИЕСЯ ДВИЖЕНИЯ [ГЛ. VI
Покажем теперь, что если Т = у-, то к моменту времени tx-\-T
мы будем иметь:
V [t, хх it, tx), .... xn(f. tx)] < L. G5.12)
Допустим противное, что это неверно. Тогда на всем отрезке
[tx, tx-\-T] будет выполняться неравенство V^-Z., ибо если бы
неравенство G5.12) выполнялось при каком-нибудь ?1</<?1-f-7\
то оно выполнялось бы и при t = tx-\~T, так как V[t, xx(t, tx),...
..., xn(t, tx)] есть функция убывающая. Но если при всех ^<^<!
-^tx-\-T выполняется V^-L, то на основании G5. 11)
xx(tx + T, tx) xn{tx+T, tx)] =
что невозможно, так как L — число положительное.
Таким образом, при t = tx-\-T выполняется условие G5.12).
Выберем теперь L настолько малым, чтобы из G5.12) вытекало
\х.«- *i)\ <-^-. G5.13)
где Ж—положительное число, меньшее единицы. Это возможно, так
как V допускает бесконечно малый высший предел. При этом число L
не будет зависеть от tv Но тогда и Т= не будет зависеть
от tx. Мы приходим, таким образом, к следующему выводу: для лю-
любого решения xs(t, t{) уравнений G5.1), для начальных значений
которого выполняется условие G5.8), будут при всех t > tx выпол-
выполняться неравенства G5.10) и при t~tx-\-T, где Т — некоторое не
зависящее от tx число, — неравенства G5ЛЗ).
Установив это, положим xs(t, tx) = pxsj(t, tx). Условие G5.8)
при этом, очевидно, выполняется. Тогда из G5.10) и G5.13) нахо-
находим, что при любом tx и t^>tx
1-ЧЛ». мл -ч—~~с (s< J=l> 2 «). G5.14)
где с не зависит от tx, и
!*„(/,-+-Г,. мI<^-- G5.15)
Покажем теперь, что если т—любое целое число-, то
j xsj (tx + mT, tx) | < Mm. G5.16)
Так как эти неравенства во всяком случае выполняются при m = 1,
то нам достаточно показать их справедливость, предположив, что
§ 75] УСЛОВИЯ СУЩЕСТВОВАНИЯ ФУНКЦИЙ ЛЯПУНОВА 321
\xS]\tx-{-(m—1O, tx\\ < Мт~1. Но, сделав такое предположение
и положив в тождествах G5.3) t = mT-\-tv a=-tx, b = (m — l)T-\-t1,
будем иметь:
t{\
j Xaj [tl 4- (m — 1O, tx]\<M- M""=Mm,
a=l
что и доказывает наше предложение.
Рассмотрим теперь произвольные числа t0 > 0 и t > t0. Пусть
mT^it — to = тТ-\~х < (m -f- 1O, где от — целое число. Полагая
в G5.3) a=t0, b = to~{- mT, получим:
п
X?j \t, Tq) ^^ X SQ \t, ?0 —j— /W / ) JC(jy (frQ—j— tit I , ?())l
a=l
и так как t^>to-\-mT, то, применяя G5.14) и G5.16), найдем:
\xsJ(t, to)\<ncMm = ncM T <jf[M T .
j_
Отсюда, полагая ?? = -тг, Мт =е~а, где a > 0, в силу того
что Ж < 1, окончательно найдем, что при всех t0 и t >• t0 выпол-
выполняются неравенства G5.4), что и доказывает теорему.
Теорема 2. Если выполняются неравенства G5.4), то су-
существует определенно-положительная функция V(t, xv ..., хп),
допускающая бесконечно малый высший предел, производная
которой, составленная в силу уравнений G5.1), есть функция
определенно-отрицательная. При этом1), если W(t, xu ..., хп)
есть произвольная определенно-положительная форма какого-
нибудь порядка т, коэффициенты которой являются ограни-
ограниченными и непрерывными функциями времени, то функция V
может быть выбрана в виде формы того же порядка, для
которой
п
dV V4 dV dV
dt /mU dxs si l г ¦ • • ~T~ fsn n)\ fa V > !¦•••! nJ-
G5.17)
') Эта часть теоремы является уточнением формулировки, данной в ра-
работе, цитированной на стр. 318.
322 НЕУСТАНОВИВШИЕСЯ ДВИЖЕНИЯ [ГЛ. VI
Доказательство. Обозначим через xs(t) = F(t, x\, ....
..., х°п, tQ) решение уравнений G5.1) с начальными условиями
x(tr\ = х°. Очевидно, имеем:
о \ U/ о
xs @ = Fs (Л х\ *о, /0) = 2*« ('• '„) Х1- G5-!8)
Пусть W(t, xv .. ., хп) — произвольная форма т-го порядка
переменных jtj, ..., хп, коэффициенты которой являются непрерыв-
непрерывными и ограниченными функциями времени. Рассмотрим форму m-ro
порядка, определяемую равенством
V(t, xx, ..., хп)= '
[x.Fl(x.x1 xn,t), ..., Fn(x. xv .... xn,t)]dx, G5.19)
и покажем, что эта форма удовлетворяет всем условиям теоремы.
В самом деле, коэффициенты формы V представляют собой суммы
членов вида
со
P(f)=ff М<', (т. t) ... Л (т, 0dx, G5.20)
где / (t) — некоторые непрерывные и ограниченные функции t, пред-
представляющие собой линейные комбинации с целочисленными коэффи-
коэффициентами коэффициентов формы W(t, xv ..., хп), a mv ..., тп —
целые неотрицательные числа, для которых т1 -\- т2 -\- ... -\-тп = т.
Из условий G5.4) сразу вытекает, что все интегралы G5.20)
сходятся и, следовательно, форма V действительно существует. Более
того, из этих неравенств сразу вытекает, что все функции G5.20)
ограничены при t^-О. Действительно, имеем:
со со
\P(t)\<Bm \ \f(x)\e-man-Odt<BmM [ е-
_ втм
та '
где М — верхний предел функции /(т). Таким образом, форма V
обладает ограниченными коэффициентами, и, следовательно, допускает
бесконечно малый высший предел.
Форма V, как это непосредственно следует из G5.19), будет
во всяком случае положительной. Покажем, что она является опре-
определенно-положительной.
Обозначим с этой целью через А(т, f) определитель \xsj(x, t)\,
через Ai;(t, f) — его минор, соответствующий элементу xsJ, и рас-
§ 75] УСЛОВИЯ СУЩЕСТВОВАНИЯ ФУНКЦИЙ ЛЯПУНОВА 323
смотрим форму т-го порядка переменных ys:
у, У„)~^22 2А|За(т, ОУр . G5.21)
а = 1 IR-1 )
где к — вещественное число. Из G5.4) следует, что для величин Др„
при т ^г-1 могут быть назначены некоторые, независящие ни от т, ни
от t, постоянные верхние пределы. И так как W есть форма опре-
определенно-положительная, то отсюда следует, что постоянную Я можно
выбрать настолько малой, чтобы форма G5.21) была также опреде-
определенно-положительной. Мы будем предполагать, что X действительно
выбрано согласно этому условию. Следовательно, если в выражение
G5.21) подставим вместо ys любые величины, то оно будет прини-
принимать положительные значения. В частности, если положим:
л
Уз=1&х-ш&> t)Xa = Fs(%, XV ..., Хп, t),
а=1
то будем иметь:
W[x. Ft(x. x, х„, t), .... Fn(x, xv .,., xn, f)]~
SB^ )bx, xv .... xa,f)\
Ho
n n
SApa(T, 0^= 2 Дра(^- O*Pv(T. t)Xy = M?, t)Xa,
P=l P. Y = l
так как
где 6av—символ Кронекера: 6av = 0 при афу и 6aY=l при a = Y-
Следовательно,
, 0 S
a=i
W[x, Рг(х. Jtj хп, f). .... Fn{x, x, хя, О]
— X2A
откуда на основании G5.19) находим:
V(t, дс, хя) > ^q @ 2 х?, G5.22)
где
2
V .s=l t
324 НЕУСТАНОВИВШИЕСЯ ДВИЖЕНИЯ [ГЛ. VI
Далее имеем тождестоенно
( J 2*«(')Лгт==—it-
*=1 ^ / 5=1 /
Применяя теорему о среднем значении, найдем:
i G5-23>
где B PssY—среднее значение функции 2 Pss в интервале (f, со).
Но так как функции pss ограничены, а функция Q (t) положи-
положительна, то из G5.23) следует, что функция Q (t) превосходит при
любом t^O некоторую положительную постоянную а2. Следовательно,
из G5.22) находим:
что показывает, что форма V определенно-положительна.
Остается показать, что выполняется уравнение G5.17). С этой
целью, поступая так же, как и в § 73, обозначим через V (t) функцию,
в которую обратится V для произвольного решения уравнений G5.1),
т. е. результат подстановки в V вместо xs функций G5.18). Тогда
dV d\T
будем иметь —тг ~~jt ¦ Но имеем тождественно (см. § 72, форму-
формулы G2.2))
Fs[t, Ft(t, х\, .... *о„, *„). .... Fa(t,
x°i Х1'
следовательно,
^^ __. Wit F (t x® x® t \ F (t x® x" t W =
= — W ((, xv . . ., xn),
что и доказывает наше предложение.
Справедливость G5.17) может быть, конечно, непосредственно
проверена прямым дифференцированием. Для этого понадобится вос-
воспользоваться легко доказываемыми тождествами
J,; + У paj @ xsa (т, t) = 0. G5.24)
0=1
§ 76] ХАРАКТЕРИСТИЧНЫЕ ЧИСЛА ЛЯПУНОВА 325
Таким образом, теорема полностью доказана.
Теорема 1 и 2 показывают, что необходимым и достаточным
условием существования для уравнений G5.1) функции Ляпунова,
удовлетворяющей всем условиям теоремы II об асимптотической
устойчивости, является выполнение неравенств G5.4). Это более
жесткое требование, чем асимптотическая устойчивость, так как при
выполнении неравенств G5.4) функции xs будут с неограниченным
возрастанием t стремиться к нулю как показательные функции, а между
тем для уравнений с переменными коэффициентами функции xs могут
при t —> oo стремиться к нулю, не удовлетворяя этому условию. Это
легко видеть хотя бы из уравнения
d±__ 1_„
dt ~ \+t x'
для которого общее решение
* —7+7
стремится к нулю как степенная функция. Отсюда следует, что
теорема II А. М. Ляпунова необратима.
Из доказанных теорем вытекает справедливость также и следую-
следующей теоремы.
Теорема 3. Если для уравнений G5.1) существует какая-
нибудь функция Ляпунова, удовлетворяющая всем условиям
теоремы II об асимптотической устойчивости, то для них
существует функция Ляпунова, обладающая такими же свой-
свойствами и представляющая собой форму заданного порядка.
Б. ТЕОРИЯ ПЕРВОГО ПРИБЛИЖЕНИЯ.
§ 76. Характеристичные числа Ляпунова.
В этом разделе мы занимаемся изучением с точки зрения устой-
устойчивости системы линейных уравнений с переменными коэффициентами,
подобно тому как мы это делали для уравнений с постоянными и
периодическими коэффициентами. Задача при этом делается, конечно,
значительно сложнее. Тем не менее и здесь получены некоторые важные
для практики и для теории общие результаты.
Для системы линейных уравнений с переменными коэффициентами
можно подобрать некоторые числа, играющие для них такую же
роль, как корни характеристического уравнения для систем с постоян-
постоянными коэффициентами и характеристические показатели для систем
с периодическими коэффициентами. Это — так называемые характе-
характеристичные числа решений, введенные Ляпуновым. Но прежде чем
рассматривать характеристичные числа решений, дадим определение
характеристичного числа функции.
326 НЕУСТАНОВИВШИЕСЯ ДВИЖЕНИЯ [ГЛ. VI
Мы будем рассматривать вещественные или комплексные функ-
функции / (t) вещественного переменного t, определенные на всей веще-
вещественной полуоси t^O. Для простоты мы будем рассматривать только
непрерывные функции. Функции f (t) могут быть ьак ограниченные,
так и неограниченные. В первом случае для всех t > 0 выполняется
неравенство |/@| <С А гДе -^ — достаточно большое положительное
число, а во втором случае, как бы велико ни было А, найдутся
такие значения t, для которых |/(f)| > А что, очевидно, может
быть записано таким образом: lim \f(t)\ =co.
t->ao
Ограниченную функцию f(t), для которой lim / (/) = 0, будем
называть исчезающей.
Докажем прежде всего следующую лемму.
Лемма. Допустим, что для функции f (t) существуют два
вещественных числа к и [i, таких, что функция f (t) e^ является
неограниченной, а функция f(t)elt—исчезающей. Тогда сущест-
существует вещественное число а, такое, что при любом положитель-
положительном числе е, как бы мало оно на было, функция f(t)e^a+e)t
будет неограниченной, а функция /(^)е(а"?)' — исчезающей,
так что
От |
lim f(t)e(a-e)' O K
Доказательство. Допустим сначала, что в интервале (к, ц)
имеется число а, такое, что функция / (t) eat является ограниченной,
но не исчезающей. Тогда это число а и будет искомым, так как
для него, очевидно, выполняются условия G6.1). Допустим теперь,
что такого числа а не существует. Тогда для всякого числа ^0 в ин-
интервале (к, ц) функции /((:)е1 будет либо неограниченной, либо
исчезающей. При этом очевидно, что число ^0, для которого функ-
функция / (f) е^* является исчезающей, меньше любого к0, при котором
эта функция является неограниченной. Мы можем поэтому в интер-
интервале (к, \i) вставить две последовательности чисел к < к1 < к2 <^3< • • •
и ц > \хг > (i2 > М-з > • • • так> чтобы любое число первой последователь-
последовательности было меньше любого числа второй последовательности, чтобы
разность кп — цп стремилась с возрастанием п к нулю и чтобы при
любом п функция /(t) е%п' была'исчезающей, а функция / (t) e^^ нео-
неограниченной. Полученные последовательности определяют сечение а, не
меньшее ни одного из чисел кп и не большее ни одного из чисел \in.
Это число а и будет искомым. Таким образом, лемма доказана.
Число а, удовлетворяющее условиям G6.1) т. е. условиям, что
функция f(t)e{a+$' при любом сколь угодно малом положительном е
§ 76] ХАРАКТЕРИСТИЧНЫЕ ЧИСЛА ЛЯПУНОВА 327
будет неограниченной, а функция /(?)е(а"~е>' — исчезающей, назы-
называется по Ляпунову характеристичным числом функции f {?).
Если функция / (t) eu является исчезающей при любом X, то мы
будем говорить, что характеристичное число f(t) равно -}-эо. Если же,
напротив, f(t)elt есть функция, неограниченная при любом X, то мы
будем говорить, что характеристичное число f (f) равно — оо. При
этом условии любая функция f (t) имеет конечное или бесконечное
характеристичное число.
Характеристичное число функции / (t) мы будем в дальнейшем
обозначать символом X {/}.
Покажем, что имеем тождественно
1п|//01 G6.2)
В самом деле, пусть X {/} = а, так что при сколь угодно малом
положительном е выполняются условия G6.1). Первое из этих усло-
условий показывает, что существует последовательность tv t2, ... —>оо,
для которой |/ (tn)\e{a+e)tn->oo, так что, начиная с достаточно
большого п, будут во всяком случае выполняться неравенства
1/(^п)К' " ^ !• G6.3)
С другой стороны, из второго условия G6.1) вытекает, что при
всех / > 7\ где Т—достаточно большое число, выполняется
>'<1. G6.4)
Из G6.3) находим:
ln\f(tn)\-\-(a+e)tn>0,
или
^т-а-ш. G6.5)
Точно так же из G6.4) получаем:
In [/@1
t
< —a-fe. G6.6)
Выполнение неравенства G6.6) при любом t > Г и одновремен-
одновременное существование последовательности, для которой выполняется не-
неравенство G6.5), и показывают, что lim " ^ '' == — а, т. е. спра-
ведливость G6.2).
Формула G6.2) дает наиболее простой способ вычисления харак-
характеристичного числа заданной функции. В частности, она показывает,
что если выражение j-\n\f(t)\ стремится к определенному пределу
при t -> со, то этот предел и будет характеристичным числом функции
328 НЕУСТАНОВИВШИЕСЯ ДВИЖЕНИЯ [ГЛ. VI
f (t). Отсюда между прочим ' следует, что характеристичное
число степенной функции при любом показателе степени равно
нулю.
В самом деле, имеем:
.. \atm .. m\nt n
lim —-j—= hm —j— = 0.
Приведем еще несколько примеров, заимствованных у А. М. Ля-
Ляпунова. Имеем:
G6.7)
¦2)
3) X {e±'sin/} =—1,
4) X {t1} =— оо.
В самом деле, имеем:
±1 cos —
lim
t r J -,
= lim ± cos-r = +1,
1 t-*oo L l J
откуда сразу вытекает справедливость первых двух примеров.
Далее,
— \ne±tslnt —
lim = lim [±sin*] = -f-l.
откуда вытекает справедливость третьего примера. Точно так же
легко убеждаемся и в справедливости четвертого примера.
Отметим в заключение, что если характеристичное число функ-
функции положительно, то функция стремится к нулю как показательная
функция. Если же характеристичное число функции отрицательно,
то эта функция будет неограниченной.
§ 77. Основные свойства характеристичных чисел.
Докажем сейчас некоторые основные свойства характеристичных
чисел функций, установленные А. М. Ляпуновым.
Теорема 1. Характеристичное число суммы двух функ-
функций равно наименьшему из характеристичных чисел этих
функций, когда эти числа различны, и не менее их, когда они
равны.
Доказательство. Пусть X = X[f\, \i = X{q>} и допустим
сначала, что К < \х. Тогда для всякого положительного е функция
>'-f фе<х-6>* G7.1)
§ 77] ОСНОВНЫЕ СВОЙСТВА ХАРАКТЕРИСТИЧНЫХ ЧИСЕЛ 829
будет исчезающей, так как исчезающими будут оба слагаемых. На-
Напротив, функция
(^ + ф)«№+е)<=ш/е<*.+е)<_|_(рв(Х+Е)< G7.2)
будет неограниченной при е < \i — к, так как первое слагаемое
будет функцией неограниченной, а второе — исчезающей. Отсюда
следует, что X{f-\-q>}=k.
Допустим теперь, что ^ = ju- Тогда при любом е сумма G7.1)
будет по-прежнему исчезающей, так как исчезающими будут оба сла-
слагаемых этой суммы. Что же касается суммы G7.2), то теперь оба
слагаемых будут неограниченными, вследствие чего сумма может
оказаться исчезающей. Поэтому при X = ц мы можем лишь утвер-
утверждать, что X {/ + ф) ^ к.
Теорема 2. Характеристичное число произведения двух
функций не менее суммы их характеристичных чисел.
Доказательство. Пусть X {/} =Х, X {ср} = ц. Тогда для
всякого положительного е функция
x—e) t
будет исчезающей. Отсюда следует, что X {/ср} ^-X~\-]i, что и требо-
требовалось доказать.
Что характеристичное число произведения может быть больше
суммы характеристичных чисел множителей, легко видеть на следую-
следующем примере. Характеристичное число произведения двух функций
gtsintg-tsint^ равного единице, есть нуль. В то же время характери-
характеристичное число каждого из множителей, как это видно из G6.7),
равно —1, и, следовательно, их сумма равна —2.
Следствие. Сумма характеристичных чисел функций f
и -j не более нуля.
Теорема 3. Для того чтобы сумма характеристичных
чисел функций f и -у равнялась нулю, необходимо и доста-
I
точно, чтобы выражение yln|/(^)| стремилось к определен-
определенному пределу при t->co.
Доказательство. Если по условию lim -т-1п| / (^)| — а, то
на основании G6.2)
X{f)=-a.
что доказывает достаточность высказанного в теореме условия.
330 НЕУСТАНОВИВШИЕСЯ ДВИЖЕНИЯ [ГЛ. VI
Напротив, если X {/} -f- X j -j > = 0, то
11 / (О I ,тг
|== — lim
что показывает, что функции -r-ln|/(tf)| при /->оо имеет опреде-
определенный предел. Этим доказывается необходимость высказанного в тео-
теореме условия.
Теорема 4. Если сумма характеристичных чисел функ-
функций f и -у равна нулю, то характеристичное чцсло произ-
произведения из функции f и какой-либо функции ср равно сумме
характеристичных чисел множителей.
Доказательство. С одной стороны, имеем:
С другой стороны, по условию теоремы
х Ы = х{/ф• у}> х {/Ф} + х{}} = х {/Ф}-х {/},
или
откуда
что и требовалось доказать.
Рассмотрим интеграл
F(t)=ff(t)dt,
где а — произвольная постоянная, если характеристичное число функ-
функции / (() отрицательно или равно нулю, и интеграл
если характеристичное число функции / (t) положительно. При таком
условии о пределах интегрирования имеет место следующая теорема.
Теорема 5. Характеристичное число интеграла не менее
характеристичного числа подынтегральной функции.
Доказательство. Пусть X = X {/}. Тогда при всяком поло-
положительном ц функция fe^-M * будет исчезающей и, следовательно,
ограниченной. Пусть М — верхний предел модуля этой функции.
§ 78] ХАРАКТЕРИСТИЧНЫЕ ЧИСЛА РЕШЕНИЙ ЛИНЕЙНЫХ УРАВНЕНИЙ 331
Допустим сначала, что X > 0. Тогда, полагая ц < X, будем иметь:
со
\F(t)\<M\ e-Q'-^t dt = j^—e-O--4)t,
t
откуда вытекает, что функция F (t) e^-^ f есть исчезающая при лю-
любом е > ц и, следовательно, при любом е, так как ц можно считать
сколь угодно малым. Это показывает, что X [F)^-X.
Пусть теперь X <! 0. Тогда
t
\F{f)\< M Г e-^-^t dt = —^г-е-^-^'Ч-const.,
J Ц — Л
что показывает, что функция F (t) е^~е>' будет исчезающей при лю-
любом е > ц и, следовательно, при любом е. Поэтому и в рассматри-
рассматриваемом случае X {F} ^> X.
§ 78. Характеристичные числа решений линейных
дифференциальных уравнений.
Рассмотрим систему линейных дифференциальных уравнений
%[Г = Р,1*1+ •..+/>,„*„ E=1,2 п), G8.1)
где psj — вещественные, непрерывные и ограниченные функции t,
определенные при всех t~^-0. Пусть Xj (t), .... xn{t) — какое-нибудь
решение уравнений G8.1). Мы будем называть характеристичным
числом рассматриваемого решения наименьшее из характеристичных
чисел функций xs(t). Вообще характеристичным числом какой-нибудь
группы функций /j {f) fk (t) мы будем называть наименьшее из
характеристичных чисел X {/;). Характеристичное число группы
функций Д, .... fk мы будем обозначать символом X {fx, .... fk).
Докажем следующую теорему Ляпунова.
Теорема 1. Всякое решение уравнений G8.1), отличное от
хг= ... = хп = 0, имеет конечное характеристичное число.
Доказательсто. Рассмотрим сначала вещественные решения
уравнений G8.1). Преобразуем эти уравнения при помощи подста-
подстановки
у, = *,«". G8.2)
где X — некоторая постоянная. Преобразованные уравнения будут
иметь вид
У,
332 НЕУСТАНОВИВШИЕСЯ ДВИЖЕНИЯ [ГЛ. VI
Из этих уравнений находим:
п п
AiV yi^ytp _i_xW2+ У (p. + р )у.у =W. G8.3)
s = \ s=l 1фк
Очевидно, что существует такое число Х = ХХ, при котором
форма, стоящая в правой части G8.3), будет определенно-положи-
определенно-положительной, удовлетворяя неравенству
где а — некоторая положительная постоянная.
При Х = Хг будем иметь, что при ?>0 для любого решения
у1 (t) Уд @ выполняется неравенство
2^@>2у5@)«в'. G8.4)
s=l s=l
С другой стороны, существует и такое значение к = 1к2 <.ХЬ
при котором правая часть G8.3) будет формой определенно-отрица-
определенно-отрицательной, удовлетворяя неравенству
При к = Х2 будем иметь:
2 У2, @ < 2 У2, @) в-««. G8.5)
S=l 5=1
Неравенства G8.4) и G8.5) показывают, что для любого нетри-
нетривиального решения уравнений G8.1) все функции G8.2) будут исче-
исчезающими при X = Х2 и хотя бы одна из этих функций будет неогра-
неограниченной при Я, = А,1. Отсюда следует, что характеристичное число
любого нетривиального решения уравнений G8.1) заключено в интер-
интервале (К2, кг), что и доказывает теорему для вещественных решений.
Остается показать справедливость теоремы для комплексных реше-
решений. Для этого достаточно заметить, что всякое комплексное решение
уравнений G8.1) складывается из двух вещественных решений us
и vs. Таким образом, теорема полностью доказана.
Рассмотрим какую-нибудь фундаментальную систему решений
*v@. *у@ *n)<f) (У=Ь 2 »)
уравнений G8.1). Обозначим через Xj характеристичное число реше-
решения xsj. Допустим сначала, что все числа Хх, Х2 Хп различны.
§ 78] ХАРАКТЕРИСТИЧНЫЕ ЧИСЛА РЕШЕНИЙ ЛИНЕЙНЫХ УРАВНЕНИЙ 333
Найдем характеристичное число решения
. G8.6)
являющегося линейной комбинацией с постоянными коэффициентами
каких-нибудь k решений xsi , ..., xsi рассматриваемой фундамен-
фундаментальной системы. Так как все числа Xi , . .., Х{ различны, то на
основании теоремы о характеристичном числе суммы функций харак-
характеристичное число решения G8.6) будет равно наименьшему из чисел
к[ , ..., Xi , т. е. характеристичному числу одного из решений,
входящих в комбинацию. Таким образом, если все числа A,j, . . ., Хп
различны, то характеристичное число любого решения уравнений G8.1)
будет одним из чисел Хх, .... Хп. Имеем, таким образом, теорему:
Теорема 2. Система G8.1) не может иметь более п ре-
решений с различными характеристичными числами.
Допустим теперь, что среди чисел Xv .... Хп имеются равные.
Тогда может оказаться, что при комбинации решений с одинаковыми
характеристичными числами характеристичное число нового решения
окажется больше, чем характеристичные числа решений, входящих в
комбинацию. Если это случится, то полученное новое решение мы
включим в состав фундаментальной системы вместо одного из ком-
комбинируемых решений. Если новая фундаментальная система опять
будет иметь решения, комбинация которых даст решение с характе-
характеристичным числом, большим характеристичных чисел группируемых
решений, то с этой новой системой поступаем так же, как с первой.
Так как число различных характеристичных чисел не превосходит п,
то ясно, что, поступая вышеуказанным способом, мы в конце концов
придем к такой фундаментальной системе, что характеристичное
число решения, скомбинированного из каких угодно решений этой
системы, будет совпадать с характеристичным числом одного из ре-
решений, входящих в комбинацию. Полученная таким образом фунда-
фундаментальная система называется нормальной. Характеристичные
числа Xv .... Хп нормальной системы решений (среди которых могут
быть и равные) называются характеристичными числами системы
дифференциальных уравнений. Характеристичное число любого ре-
решения этих уравнений равно одному из чисел Хх Хп. Действи-
Действительно, каждое такое решение является линейной комбинацией реше-
решений, входящих в нормальную систему.
Из предыдущих рассуждений следует, что если характеристичные
числа какой-нибудь фундаментальной системы решений все различны,
то эта система является нормальной. Имеет также место и следую-
следующая теорема, дающая признак нормальности фундаментальной си-
системы решений.
Теорема 3. Всякая фундаментальная система решений,
для которой сумма характеристичных чисел всех входящих
334 НЕУСТАНОВИВШИЕСЯ ДВИЖЕНИЯ [ГЛ. V!
в нее решений достигает своего высшего предела, есть нор-
нормальная.
В самом деле, если бы рассматриваемая фундаментальная система
не была нормальной, то из некоторых ее решений можно было бы
скомбинировать новые решения с большими характеристичными
числами и, следовательно, получить фундаментальную систему с сум-
суммой характеристичных чисел большей, чем в рассматриваемой, что
противоречит условию.
Допустим, что система уравнений G8.1) подвергнута линейному
преобразованию
У* = asi V) xi + • • • + asn @ xn, xs = bsl @ 3>i + • • • -f- bsn (t) yn,
G8.7)
обладающему следующими свойствами: 1) коэффициенты asj и их
производные ограничены; 2) коэффициенты bSJ- обратного преобразо-
преобразования также ограничены. Преобразования, обладающие этими свой-
свойствами, мы будем называть преобразеваниями Ляпунова, При
таких преобразованиях коэффициенты qSj{f) преобразованной системы
^-=ЧлУ1+ ••• +W». G8.8)
определяемые формулами
а=1 а, |3=1
будут также ограниченными функциями времени.
Теорема 4. Если систему уравнений G8.1) подвергнуть
преобразованию Ляпунова, то группа характеристичных чисел
преобразованной системы будет тождественной с группой
характеристичных чисел первоначальной.
Доказательство. Пусть xs{t) — какое-нибудь решение си-
системы G8.1). Тогда формулы G8.7) определят решенне ys(t) системы
G8.8) из этих формул находим:
так как характеристичные числа ограниченных функций asJ(t) во вся-
всяком случае не менее нуля. С другой стороны, из G8.7) таким же
путем находим:
X{xx(t) xn(t)}>X{yi(t) yn(t)),
так как функции asj (t) также ограничены. Это дает:
X {уг @. .... уп @} = X [хх ф хп @J.
§ 79] ПРАВИЛЬНЫЕ И НЕПРАВИЛЬНЫЕ СИСТЕМЫ 335
Таким образом, каждому решению одной системы соответствует
решение другой системы с таким же точно характеристичным числом.
Отсюда непосредственно следует, что группа характеристичных чисел
одной системы совпадает с группой характеристичных чисел другой
системы, что и доказывает теорему.
Допустим, что коэффициенты ps) уравнений G8.1) являются по-
постоянными. Пусть X—корень характеристического уравнения
этой системы. Если кратность этого корня равна /, то ему отвечает /
независимых решений этой системы вида
xsi @ = е><Psi (О (I = 1, 2, ...,/), G8.10)
где Psl — некоторые полиномы относительно t с постоянными коэф-
коэффициентами. Характеристичное число каждого из решений вида
G8.10) равно — Re (Я). Таким же будет и характеристичное число
решения, являющегося линейной комбинацией решений G8.10). Отсюда
следует, что если решения вида G8.10) построить для каждого корня
характеристического уравнения, то полученная фундаментальная си-
система решений будет нормальной. Кроме того, получаем:
Характеристичные числа системы линейных уравнений
с постоянными коэффициентами равны взятым с об ратными
знаками вещественным частям корней ее характеристиче-
характеристического уравнения.
Если коэффициенты psj системы G8.1) являются периодическими
функциями времени с одним и тем же периодом со, то решения этих
уравнений имеют также вид G8.10) с той лишь разницей, что вели-
величины X будут являться характеристичными показателями системы,
а коэффициенты полиномов Psj будут не постоянными, а периодиче-
периодическими функциями времени, что не влияет на характеристичное число.
Поэтому имеем:
Характеристичными числами системы линейных уравнений
с периодическими коэффициентами являются взятые с обрат-
обратными знаками вещественные части ее характеристических
показателей.
§ 79. Правильные и неправильные системы.
Пусть Xi Хп — характеристичные числа системы линейных
уравнений
Цг = Ра*\ + ¦ • • + Рт*п G9.1)
с непрерывными и ограниченными при t ^- 0 коэффициентами psj.
Докажем следующую теорему Ляпунова.
336 НЕУСТАНОВИВШИЕСЯ ДВИЖЕНИЯ [ГЛ. VI
Теорема 1. Сумма S = X1-{- ... -\-Хп характеристичных
чисел системы G9.1) не превосходит характеристичного числа
функции.
t п.
txpf^Pssdt. G9.2)
О s=l
Доказательство. Пусть xXj xnj(j = 1,2 га)— нор-
нормальная система решений уравнений G9.1) и \xsj\ =A(t) — ее опре-
определитель Вронского. Имеем:
t п
О i = l
Но, применяя к определителю А теоремы о характеристичном числе
суммы и произведения, находим:
что и доказывает теорему.
Доказанная теорема устанавливает верхний предел для суммы ха-
характеристичных чисел системы линейных дифференциальных уравне-
уравнений. Этот предел, действительно, достигается для многих систем. Это,
например, всегда будет иметь место в случае уравнений с постоян-
постоянными коэффициентами. Действительно, при psj постоянных имеем:
^fPssdt U=
X \txp^fPssdt U=_Re(/711+... +¦/>„„) =-(*!+..•+««).
I о |
где at — вещественные части корней характеристического уравнения,
которые, как было показано в предыдущем параграфе, отличаются
лишь знаками от характеристичных чисел.
Можно, однако, привести примеры, когда сумма характеристичных
чисел решений не достигает указанного для них в теореме предела.
Вот один из таких примеров, указанный Ляпуновым. Система урав-
уравнений имеет вид
, , — ^Vl WV4 111 \^V I ± I I
——- = x1sinln(^4- lL-x2C0Sln(^4- О-
Для нее
t
exp J 2 Padt = exp [(/+ 1) [sinIn(f + l)+cos In (t+ 1)] — 1]. G9.3)
§ 79] ПРАВИЛЬНЫЕ И НЕПРАВИЛЬНЫЕ СИСТЕМЫ 837
Характеристичное число этой функции равно —у 2. С другой
стороны, эти уравнения имеют фундаментальную систему решений
u = exp[(f-H)coeln(f+l)].
ai = exp[(f+l)slnln(f+l)],
которая, как нетрудно убедиться, является нормальной. Характери-
Характеристичное число каждого из этих решений равно —1, и следовательно,
их сумма менее характеристичного числа функции G9.3).
Системы линейных уравнений, для которых сумма характеристич-
характеристичных чисел равна характеристичному числу функции G9.2) и для ко-
которой, кроме того, выполняется условие
х ехр(/2р«**\\+х\ехр(-/2Pssat)i =-о. G9-4)
называются, по Ляпунову, правильными.
Система уравнений с постоянными коэффициентами является пра-
правильной, так как для нее дополнительное условие G9.4), очевидно,
также выполняется.
Если правильную систему подвергнуть линейному преобразованию,
удовлетворяющему условиям Ляпунова (§ 78), то преобразованная
система будет также правильной.
В самом деле, как было показано в предыдущем параграфе, при
такого рода преобразовании характеристичные числа и, следовательно,
их сумма не меняются. С другой стороны, если xsj — фундаменталь-
фундаментальная система решений уравнений G9,1), ysj(t) — соответствующая ей
фундаментальная система решений преобразованной системы, D= | as, | —
определитель преобразования, то
Ы=В\*.А- X{\ysj\}^X{\xs}\}, G9.6)
так как по свойству преобразования функция D — ограниченная и
не исчезающая. Применяя теорему Лиувилля, находим:
G9.6)
где Сх и С2—постоянные и qsj—коэффициенты преобразованной
системы. Из G9.5) и G9.6) следует, что характеристичное числа
338 НЕУСТАНОВИВШИЕСЯ ДВИЖЕНИЯ [ГЛ. VI
функции G9.2) также инвариантно относительно рассматриваемого
преобразования, что и показывает, что преобразованная система будет
также правильной.
Из доказанного предложения вытекает, что всякая система, кото-
которая вышеуказанным преобразованием может быть преобразована в
систему уравнений с постоянными коэффициентами, т. е. всякая при-
приводимая (§ 54) система является правильной. В частности, на осно-
основании результатов § 54 имеем такое предложение:
Всякая система линейных уравнений с пе риодическими коэф-
коэффициентами является правильной.
Для общих систем вида G9.1) нет критериев, которые позволяли бы
во всех случаях по виду коэффициентов определить, является ли рас-
рассматриваемая система правильной или нет. Эта задача решена лишь
для уравнений с треугольной матрицей коэффициентов, т. е. для
уравнений вида
^Г = ^Л + • • • + /»„*, (* = 1. 2 я). G9.7)
Для этих уравнений имеет место следующее предложение, уста-
установленное Ляпуновым, которое мы здесь приводим без доказательства:
Для того чтобы система вида G9.7) была правильной, необ-
необходимо и достаточно, чтобы все функции
j pssdt (s=l, 2, .... n)
о
стремились к определенным пределам при t—.>сх>.
Рассмотрим систему
¦^Г + РпУ1-\-РпзУп = °- G9-8)
сопряженную с G9.1). Имеет место следующая теорема, установлен-
установленная О. Перроном !):
Теорема 2. Пусть Х1-СХ2 ... <^„— характеристичные
числа системы G9.1), a jij^[x2^- ... ^\л„—характеристич-
^\л„—характеристичные числа системы G9.8), ей сопряженной. Для того чтобы
система G9.1) была правильной, необходимо и достаточно,
чтобы выполнялись равенства
%s-\-y,s = Q (s=l, 2 п). G9.9)
Доказательство. Докажем сначала достаточность условия.
Допустим, следовательно, что выполняются условия G9.9), и дока-
•) Perron О., Die Ordnungszahlen der Differentialgleichungssysteme.
Mathem. Zeitschrift, т. 31, 1929.
§ 79]
ПРАВИЛЬНЫЕ И НЕПРАВИЛЬНЫЕ СИСТЕМЫ
339
жем, что в этом случае система G9.1) является правильной. Пусть
S = X1-{- ... -f- Хп и S' = (х, 4- ... -\- цп- Применяя к обеим систе-
системам теорему 1, получим:
ехр
S' < X j exp I -
и, следовательно, на основании G9.9)
О < X | ехр
(аН1-
G9.10)
2 / Pss dt\\+x\ exp j - ^ / р„ dt j , G9.11)
причем знак равенства возможен лишь тогда, когда оба соотношения
G9.10) выполняются со знаками равенства. Но по теореме о харак-
характеристичных числах обратных функций
ехр
-US Pss*t
о,
откуда вытекает, что соотношение G9.11) и оба соотношения G9.10)
выполняются со знаками равенства. Следовательно, обе системы G9.1)
и G9.8) являются правильными.
Допустим теперь, что система G9.1) является правильной, и до-
докажем справедливость соотношений G9.9). Рассмотрим с этой целью
какую-нибудь нормальную систему решений х1;- xnj (/—1,
2 п) уравнений G9.1) и пусть А= |х^|—ее определитель
Вронского. Пусть, далее,
ysj = ^f> G9.12)
где Asj — минор элемента xsj определителя А. Покажем, что
-ОГ= — (РиУ1)+ Р2зУ2;+ • • • + РпзУп/) (S. У= 1, 2 П), G9.13)
т. е. что функции ysj образуют фундаментальную систему решений
уравнений G9.8).
Имеем очевидные тождества
2
&~ 1
Л У=1. 2 Я),
где 6(.у — символ Кронекера.
340 НЕУСТАНОВИВШИЕСЯ ДВИЖЕНИЯ [ГЛ. VI
Дифференцируя эти тождества по t и учитывая, что функции xai
удовлетворяют уравнениям G9.1), получим:
Sr0 (W=l. 2 п). G9.14)
а, р=1 а=1
dysi
Отсюда однозначно определяются производные . Чтобы по-
показать, что они совпадают с правыми частями G9.13), достаточно,
очевидно, проверить, что равенства G9.14) выполняются тожде-
dy ¦
ственно, если в них —-У- заменить правыми частями G9.13). Но,
выполняя указанную подстановку, легко убеждаемся, что равен-
равенства G9.14) при этом действительно тождественно выполняются.
Пусть
М-у = ^ {У1/ Ущ\-
Применяя к тождеству
теоремы о характеристичных числах суммы и произведения, получаем
Но, с другой стороны, те же теоремы дают:
или, так как система G9.1) по условию правильная,
и, следовательно,
—V
Отсюда непосредственно вытекает справедливость G9.9). Кроме
того, отсюда находим:
-2, Pssdt ;
следовательно, S' достигает своего верхнего предела. Поэтому реше-
решения G9.12) образуют нормальную систему и величины (х;- действи-
действительно являются характеристичными числами системы G9.8).
Таким образом, теорема полностью доказана.
§ 79]
ПРАВИЛЬНЫЕ И НЕПРАВИЛЬНЫЕ СИСТЕМЫ
341
Допустим, что рассматриваемая система линейных уравнений имеет
каноническую форму
dt
-— -li-— - «-1 2
дН
lx]
*)¦
где H—H(t, х1 хп, уг уп)— квадратичная форма пере-
переменных Xj, yj, коэффициенты которой являются непрерывными огра-
ограниченными функциями времени. Имеет место следующая теорема,
установленная К. П. Персидским*).
Теорема 3. Пусть A,j ^>Х2^ . .. ^-Х2п—характеристичные
числа системы G9.15). Для того чтобы эта система была
правильной, необходимо и достаточно, чтобы выполнялись
соотношения
= 0 (/=1. 2 а).
G9.16)
Доказательство. Система G9.15) более подробно запишется
следующим образом:
dt
dt
dyt dxn
+
д*Н
dyt dy1
¦y«.
x, — ...
dxtdxn
dje, dyt yi ¦
Система, ей сопряженная, есть
~dT
и,—
д2Н
дУпдх1
••• +
G9.17)
дхп
д2Н
ду1 dy
-а,— ... —
dm
dm
дхх dyt
G9.18)
Эта система переходит в систему G9.17) при замене ut на yt и vt
на —xt. Следовательно, если ut{t), vt(t) есть какое-нибудь решение
системы G9.18), то функции xl = — vi(f), yl = ui(t) определяют
') Персидский К. П., О характеристичных числах дифференциальных
уравнений. Изв. АН Казахской ССР, сер. матем. и мех., вып. 1, 1947.
342 НЕУСТАНОВИВШИЕСЯ ДВИЖЕНИЯ [ГЛ. VI
решение системы G9.17). Но оба эти решения обладают, очевидно,
одинаковыми характеристичными числами. Следовательно, группа
характеристичных чисел системы G9.15) совпадает с группой харак-
характеристичных чисел системы, ей сопряженной. Поэтому необходимые и
достаточные условия правильности G9.9) принимают сейчас вид G9.16),
что и доказывает теорему.
Доказанная теорема является, очевидно, обобщением теорем
§§ 24 и 57.
Если система G9.15) не является правильной, то, как показал
Н. Г. Четаев!) и как это вытекает из предыдущих рассуждений,
равенства G9.16) заменяются неравенствами
Отсюда и из G9.16) вытекает, что если система G9.15) вне зави-
зависимости от того, является ли она правильной или нет, обладает поле-
жительными характеристичными числами, то она будет обладать
также и отрицательными характеристичными числами. Следовательно,
справедливо следующее предложение Н. Г. Четаева: для того чтобы
для системы G9.15) имела место устойчивость, необходимо,
чтобы все ее характеристичные числа равнялись нулю. При
этом, как показал Н. Г. Четаев, система G9.15) будет необходимо
приводимой.
§ 80. Устойчивость характеристичных чисел
систем линейных дифференциальных уравнений.
Результаты предыдущих параграфов показывают, что характери-
характеристичные числа систем линейных дифференциальных уравнений с пе-
переменными коэффициентами играют для них такую же роль, как
характеристические показатели для уравнений с периодическими коэф-
коэффициентами и корни характеристического уравнения для уравнений
с постоянными коэффициентами. Эти числа характеризуют порядок
роста решений при t->oo и имеют поэтому основное значение
в вопросах устойчивости. Если все характеристичные числа положи-
положительны, то все решения рассматриваемой системы линейных уравнений
стремятся к нулю при t—>oo и, следовательно, для этих уравнений
имеет место асимптотическая устойчивость. Напротив, если хотя бы
одно из характеристичных чисел отрицательно, то система допускает
неограниченные решения и для нее, следовательно, имеет место
неустойчивость.
Таким образом, при решении задачи устойчивости для линейных
уравнений с переменными коэффициентами необходимо определить
знаки ее характеристичных чисел или, по крайней мере, знак наимень-
') Четаев Н, Г., Устойчивость движения. Гостехиздат, 1946.
§ 80] устойчивость характеристичных чисел 343
шего из них. Эта задача представляет очень большие трудности,
и до сих пор нет достаточно эффективных методов ее решения. Мы
имеем, конечно, в виду те случаи, когда уравнения не разрешаются
в замкнутой форме. С частным случаем этой задачи мы уже встре-
встречались в предыдущей главе, где были показаны некоторые приемы
приближенного определения характеристических показателей уравнений
с периодическими коэффициентами. Наиболее эффективными из этих
методов, хотя и имеющими ограниченную область применения, были
те, в которых так или иначе применялся малый параметр. Сущность
всех этих методов заключается в том, что определение характеристи-
характеристических показателей заданной системы сводят к определению этих
величин для другой системы (например, для системы с постоянными
коэффициентами), которая мало отличается от заданной и для которой
эти величины могут быть определены. При этом используется то
обстоятельство, что малое изменение коэффициентов в случае, когда
эти коэффициенты периодичны, вызывает малое изменение характе-
характеристических показателей.
Это свойство характеристичных чисел уравнений с периодическими
коэффициентами не имеет, вообще говоря, места в общем случае
уравнений с любыми переменными коэффициентами. Можно привести
примеры, когда коэффициенты одной системы уравнений сколь угодно
мало отличаются при всех t ;> 0 от коэффициентов другой системы
уравнений и в то же время характеристичные числа одной системы
отличаются на конечные величины от характеристичных чисел другой,
системы. Таким образом, возникает прежде всего задача о так назы-
называемой устойчивости характеристичных чисел систем линейных
уравнений. Это понятие может быть определено следующим образом.
Пусть предложена система уравнений с переменными коэффи-
коэффициентами
dX A*i-\- ¦•• ~\-Psn*n (*=1. 2 в). (80.1)
одновременно с которой мы будем рассматривать другую систему:
^f = (Psi 4- «P,i) xx + • • • + (Л„ + Ф,„) *„• (80.2)
Коэффициенты psj и ф^. предполагаются ограниченными и непре-
непрерывными при t ^- 0. Пусть %х ;> Я2 ^ ... !> ^„ — характеристичные
числа системы (80.1) и A,i^-А.2^> ... ^Я^ — характеристичные числа
системы (80.2). Примем следующее определение:
Определение. Характеристичные числа %х, Х2 Хп
системы (80.1) называются устойчивыми, если для любого сколь
угодно малого положительного е можно найти такое поло-
положительное число т](е), что характеристичные числа к\
344 НЕУСТАНОВИВШИЕСЯ ДВИЖЕНИЯ [ГЛ. VI
системы (80.2) удовлетворяют неравенствам
U/' — Я/|<е (/=1, 2 ге) (80.3)
при любом выборе функций ф^, удовлетворяющих при f^-Q
неравенствам
О. 7=»1. 2 в). (80.4)
Если характеристичные числа системы (80.1) устойчивы, то нера-
неравенства (80.3) останутся в силе, когда неравенства (80.4) выполняются
не при t^-0, а при f^-T, где Т — сколь угодно большое число.
Это непосредственно вытекает из того, что характеристичные числа
системы уравнений, определяемые поведением ее решений при t—>oo,
зависят лишь от вида коэффициентов "этих уравнений при f^-T.
Отсюда следует, что если характеристичные числа системы (80.1)
устойчивы и если
Ншф =0 (s, j=\, 2, ..,, п), (80.5)
то характеристичные числа системы (80.2) совпадают с характеристич-
характеристичными числами системы (80.1). Действительно, если выполняется (80.5),
то можно выбрать настолько большое Т, чтобы при t^.T. нера-
неравенства (80.4) выполнялись со сколь угодно малым т|. Следовательно,
величина е в неравенствах (80.3) может быть взята сколь угодно
малой, что и доказывает, что k'i=*ki.
§ 81. Некоторые признаки устойчивости характеристичных
чисел систем линейных дифференциальных уравнений *).
Рассмотрим снова систему
^ Л (s=l,2 я) (81.1)
с непрерывными и ограниченными коэффициентами и мало отли-
отличающуюся от нее систему
^*« («-1.8 »). (81.2)
Пусть кх, Х3, .... кп— характеристичные числа системы (81.1)
и %[, А,2, ¦ ¦ •. ^—характеристичные числа системы (81.2). Обозначим,
далее, через x1j, ..., xnj (/=1, 2, ..., re) нормальную систему
решений уравнений (81.1), занумерованную таким образом, что харак-
характеристичное число решения xsj есть kj. Кроме этой системы решений,
') Малкин И. Г., О характеристических числах систем линейных диф-
дифференциальных уравнений. ШМ,М, т. XVI, вуп. 1,, 1962.
§81] НЕКОТОРЫЕ ПРИЗНАКИ УСТОЙЧИВОСТИ ХАРАКТЕРИСТИЧНЫХ ЧИСЕЛ 345
рассмотрим другую фундаментальную систему xsj (t, tQ) решений
уравнений (81.1), определяемую начальными условиями:
xsj(t0, to) = bs]- Fsj — символ Кронекера) (81.3)
(s. /=1. 2 в).
Система решений xsj(t, t0) не будет обязательно нормальной.
Характеристичные числа решений xsj(t, t0) обозначим, соответственно,,
через [ij. При этом каждое из чисел \i} равно одному из чисел Xt.
Допустим, что система (81.1) такова, что при любом положитель-
положительном у выполняются неравенства
l*,;(Uo)|<C«(-^('-4 (81.4)
если t~^>to^-O, и неравенства
|^(ио)|<С^Г^'-'«), (81.5)
если 0^/^/0. Здесь С — некоторая постоянная, зависящая только
от у и не зависящая от t0. Тогда имеет место следующая теорема.
Теорема 1. Если выполняются условия (81.4) и (81.5), то
для всякого положительного е можно найти такое т)(е), что
характеристичные числа %'i системы (81.2) удовлетворяют
неравенствам
l't>h—e (i=l,2 re) (81.6)
при любом выборе функций ф^, удовлетворяющих при f^-0
неравенствам
(81.7)
Доказательство. Г. Замена системы (81.2) интеграль-
интегральными уравнениями. Рассмотрим неоднородную систему
^ O. (81.8)
где fs(f) — некоторые непрерывные функции t. Согласно Коши функции
J xsa((,x)fa(x)dx (81.9)
J
а=1 аа
определяют частное решение этих уравнений. При этом в методе Коши
все постоянные аа принято считать одинаковыми, и если положить
аа — а, то функции (81.9) определяют то решение уравнений (81.8),
для которого все неизвестные обращаются в нуль при t — а. Однако
легко видеть, что функции x's(t) будут удовлетворять уравнениям (81.8)
346 НЕУСТАНОВИВШИЕСЯ ДВИЖЕНИЯ [ГЛ. VI
при любом выборе постоянных аа, причем некоторые из этих постоян-
постоянных можно положить равными бесконечности, если только соответ-
соответствующие интегралы сходятся. В самом деле, непосредственным диф-
дифференцированием, принимая во внимание (81.3), находим:
а=1
J
а=1 аа
= Л@4-S J [Psi@*ta«.T)+... + Рт@*„а(/, т)]/а(т)л =
1
J *1„С Т)/„(Т)Л+ ... +
а=1а
а
Psn (О S J *«« ^ Т> Л W dX =
J PsnX'n>
а=1 а
что и доказывает наше утверждение. Если теперь к решение (81.9)
добавить любое частное решение однородных уравнений (81.1), то
снова получится решение уравнений (81.8).
Установив это, будем рассматривать в уравнениях (81.2) члены,
зависящие от <pj;-, как неоднородную часть уравнений (81.8). Тогда
мы можем утверждать, что решение интегральных уравнений
*,(O = *rt(O + b x™^ т^т' Xl^ xn{x))dx (81.10)
a~laa
(s=l, 2 re),
если оно существует, будет являться решением уравнений (81.2). Здесь
а аа = 0 для тех значений а, для которых Ца^-^А> и аа = 0° ПРИ
Изменяя индекс k от 1 до п, мы получим ге решений уравне-
уравнений (81.2).
2°. Доказательство Существования решений интегральных
уравнений. Пусть е—сколь угодно малое положительное число.
Так как характеристичные числа функций х,к не менее Яй, то
|**(/)|<Л«(-х*+е>'. (81.12)
§ 81] НЕКОТОРЫЕ ПРИЗНАКИ УСТОЙЧИВОСТИ ХАРАКТЕРИСТИЧНЫХ ЧИСЕЛ 347
где А — некоторая постоянная. Покажем, что интегральные уравне-
уравнения (81.10) допускают решение, удовлетворяющее неравенствам
\х,(()\<2Ае(-хь+гУ, (81.13)
если только величина х\ в неравенствах (81.7) достаточно мала.
Будем искать решение уравнений (81.10) методом последователь-
последовательных приближений, полагая
n t
(81.14)
Покажем, прежде всего, что все приближения удовлетворяют не-
неравенствам
№)|
(81.16)
если г| настолько мало, что выполняется неравенство
что мы и будем предполагать.
В самом деле, неравенства (81.15) во всяком случае выпол-
выполняются при т = 0. Допустим, что они выполняются для (т — 1)-го
приближения, и покажем, что они выполняются также и для т-го
приближения.
Пусть a — такой индекс, для которого М-а^-^й и для которого,
следовательно, аа — 0. Тогда, полагая в условиях (81.4) y =-о и при-
принимая во внимание (81.11), будем иметь:
"а
t
2пцАС J
о
2пЧАС
348
НЕУСТАНОВИВШИЕСЯ ДВИЖЕНИЯ
[ГЛ. VI
При том же значении у, считая е настолько малым, что при
кк > ца выполняется неравенство
4-|ie>2e.
из (81.5) получим, что для значений а, для которых ца < %k, спра-
справедливы оценки
t
\xsa(t, x)L (x. *{»
CO
2ni)AC J e("|l«-T)(<
*
Принимая во внимание (81.12), (81.17), (81.18) и (81.16), из (-81.14)
находим:
\х[т)\
'. (81.19)
Оценим теперь величины I лг<[т+1' — Jc'sm' I Пусть
Тогда, применяя к равенствам
J хте (Л т) La (т, *^> - *<«-Ч ^
оценки (81.17) и (81.18), в которых лишь придется заменить 2А на Р,
получим:
|xf+1) —4m)| <^5^«("Х*+е)'==/>в«(-х*+в)'. (81.20)
где на основании (81.16)
Так как на основании (81.15) и (81.12) во всяком случае
§ 81] НЕКОТОРЫЕ ПРИЗНАКИ УСТОЙЧИВОСТИ ХАРАКТЕРИСТИЧНЫХ ЧИСЕЛ 349
то из (81.20) следует, что
Отсюда непосредственно вытекает, что с неограниченным возра-
возрастанием т последовательные приближения равномерно стремятся к не-
некоторым функциям fs(t). Так как все последовательные приближения
удовлетворяют .неравенствам (81.15), то этим же неравенствам удо-
удовлетворяют и функции fs{f). Остается показать, что полученные таким
образом функции fs{t) удовлетворяют уравнениям (81.10). Имеем:
—xim+2>
т+2) _
х | +
e™ + ет+1+ • • .) =
и поэтому
~xsa <*, т) La (т, /, - *<">, ...,/„- xW) dx < §
o=l aa
Правая часть этих неравенств стремится к нулю при т —> оо.
Следовательно,
п t
x\m\
0=1 аа
п t
=iim S rx™{t'x)L*
a = l aa
= lim
m ->o
что и доказывает, что функции fs удовлетворяют уравнениям (81.10).
3°. Оценка характеристичных чисел. Таким образом, мы полу-
получили решение уравнений (81.10), которое является в то же самое
время решением и уравнений (81.2). Как уже указывалось, изменяя
в (81.10) индекс k от 1 до я, мы получим п решений системы (81.2).
Все эти решения образуют фундаментальную систему. Действительно,
при t = 0 полученные решения, как это следует из оценок (81.18),
будут сколь угодно мало отличаться от решений xsk системы (81.1),
если только т| достаточно мало, и следовательно, определитель Врон-
Вронского полученной системы будет при / — 0 сколь угодно мало отли-
отличаться от определителя Вронского ' системы xsj, который заведомо
отличен от нуля.
Обозначим через Я* Я* характеристичные числа полученной
фундаментальной системы решений уравнений (81.1). Из (81.13)
350
вытекает, что
НЕУСТАНОВИВШИЕСЯ ДВИЖЕНИЯ
[ГЛ. VI
Если мы теперь рассмотрим нормальную систему решений уравнений
(81.2), то она будет отличаться от полученной фундаментальной си-
системы тем, что некоторые решения последней заменены другими
решениями с большими характеристичными числами. Следовательно,
характеристичные числа X'v X'2 А/ нормальной системы будут
и подавно удовлетворять неравенствам (81.6).
Таким образом, теорема полностью доказана.
Теорема 2. Если при выполнении условий предыдущей
теоремы система (81.1) является правильной, то ее характер
ристичные числа устойчивы1).
Доказательство. По условию теоремы имеем:
а=1 6
I
j Paadtl.
Далее, на основании теоремы 1 § 79
In t
exp ^ J paa dt • exp
<Z=1 0
Но из (81.7), очевидно, имеем:
X exp
Кроме того, теорема 4 § 77 дает:
I ¦ П t П t
п t ]
^ J фаа dt \.
0 = 1 0 I
0=1 0
а=1 О
Pmdt
0=1 О
n t
а=1 О
так как для правильных систем выполняется условие G9.4). Следо-
Следовательно,
') См. примечание в конце книги (стр. 524).
§82]. КРИТЕРИЙ ПОЛОЖИТЕЛЬНОСТИ ХАРАКТЕРИСТИЧНЫХ ЧИСЕЛ 351
Положим x'i~Xt — e-f-Y»- Из (81.6) вытекает, что Уг^О- По-
Поэтому (81.21) дает Уг^/1(е + 'П) и> следовательно,
Полученные неравенства вместе с (81.6) и доказывают теорему1).
Доказанная сейчас теорема аналогична теореме 2, установленной
Б. Ф. Быловым2).
Рассмотрим частный случай. Допустим, что коэффициенты psj
являются постоянными. Тогда для системы (81.1) условия (81.4) и
(81.5), очевидно, выполняются. И так как система с постоянными
коэффициентами является правильной, то мы приходим к следующей
теореме, установленной К. П. Персидским3).
Теорема 3. Характеристичные числа системы линейных
уравнений с постоянными коэффициентами всегда устойчивы.
Допустим, что коэффициенты psj являются постоянными, а коэф-
коэффициенты cps;- удовлетворяют условиям
Нтф4/==0. (81.22)
Тогда, как об этом было указано в предыдущем параграфе, из
теоремы 3 непосредственно вытекает справедливость также и сле-
следующего предложения:
Теорема 4. Если коэффициенты q>sj являются постоян-
постоянными и выполняются условия (81.22), то характеристичные
числа системы (81.2) совпадают с характеристичными чис-
числами системы (81.1).
Эта теорема, установленная при некоторых ограничениях Пуан-
Пуанкаре4), в общем виде высказана О. Перроном5).
§ 82. Критерий положительности характеристичных чисел.
Допустим, что характеристичные числа системы
*?- = рЛхх+ ... -\-psnxn E=1, 2, .... re) (82.1)
') См. примечание в конце книги (стр. 525).
2) Бы лов Б. Ф., О характеристичных числах решений систем линей-
линейных дифференциальных уравнений. ПММ, т. XIV, вып. 4, 1950.
3) Персидский К. П., О характеристичных числах дифференциаль-
дифференциальных уравнений. Изв. АН Казахской ССР, серия матем. и мех., вып. 1, 1947.
Метод, которым мы доказывали теоремы 1 и 2, имеет много общего с мето-
методом доказательства К. П. Персидского.
4) Р о i n с а г ё A., Sur ies equations lineaires aux differentielles ordlnai-
res et aux differences finies Oeuvres, т. 1, Oauthier Villars, 1928.
6) Perron O., Ober Stabilitat und asymptotisches Verhalten. Atti del
Congresso Intern, dei Mat., 1928.
352 НЕУСТАНОВИВШИЕСЯ ДВИЖЕНИЯ [ГЛ. VI
все положительны. Тогда, если выполняются условия теоремы 1
предыдущего параграфа, характеристичные числа системы
¦1й?- = (Рл + Ф,1)*1+••• + (/»,„ +ф,я)*я (s=1.2 га) (82.2)
будут также положительны, по крайней мере, тогда, когда все вели-
величины |фЛу(О| не превышают некоторого достаточно малого положи-
положительного числа. Знание этого наибольшего предела для функций
|ф^(/)| является, очевидно, для практики наиболее существенным.
Одну из оценок этого предела дает нижеследующая теорема !), в ко-
которой условия теоремы 1 § 81 несколько обобщены, а именно, вместо
условий (81.4) и (81.5) мы будеда предполагать, что для решений
xsj(t, t0) уравнений (82.1), определяемых начальными условиями
х$1 (А)- 'о)== bsj> выполняются неравенства
\xsJ(t, to)\ < Ме-*И-Ы (S, y=i, 2, ..." я), (82.3)
где М~^-\ и а — некоторые не зависящие от t0 положительные
постоянные.
Теорема. Если для уравнений (82.1) выполняются условия
(82.3), то характеристичные числа системы (82.2) будут
положительны при любом выборе функций <pSj(t), удовлетво-
удовлетворяющих при t^-О неравенствам
1 '~' - а (s, /=1, 2 га), (82.4)
где т^п2 — наибольшее кисло членов в каждом из выражений
Jj *sa V. ^) (Ф„,^ +•••¦+ Чтхп). (82.5)
Доказательство. Пусть xs(t)—произвольное решение урав-
уравнений (82.2) с начальными значениями xs@) = Cs, удовлетворяю-
удовлетворяющими неравенствам
|С,|<1 (s=l, 2 я). (82.6)
Рассматривая xs(() как неизвестные, но вполне определенные
функции времени, мы из (82.2) находим, что эти функции необходимо
удовлетворяют интегральным уравнениям
, 0) +
п t
] / Xsa «. т) [ФаЛ (т) + ... + ФаЛ (т)] йх, (82.7)
1 О
/
а = 1 О
') Малкин И. Г., О характеристических числах систем линейных
дифференциальных уравнений. ПММ, т. XVI, вып. 1, 1952.
§ 82] КРИТЕРИЙ ПОЛОЖИТЕЛЬНОСТИ ХАРАКТЕРИСТИЧНЫХ ЧИСЕЛ 353
которые, следовательно, имеют решение ')• Для того чтобы доказать
справедливость теоремы, достаточно, очевидно, показать, что найдется
такое достаточно большое положительное число А и такое доста-
достаточно малое положительное число е, что при всех t > О будут
выполняться условия
. (82.8)
Но, считая А > 1, мы будем на основании (82.6) иметь, что усло-
условия (82.8) выполняются при /==0 со знаками неравенства. Следова-
Следовательно, эти условия будут выполняться, по крайней мере, при t > 0,
достаточно малом. Допустим, что эти условия при некоторых зна-
значениях / нарушаются. Тогда должен существовать такой момент вре-
времени t = T, при котором впервые хотя бы одно из условий (82.8)
выполняется со знаком равенства. Так как при 0 -^ t -^ T условия
(82 8) во всяком случае выполняются, то, полагая е < а, из (82.7)
на основании (82.6) и (82.3) получим:
т
\xs(T)\ < nMe-aT-\-mMAQ J e-o(r-t
о
_ в-<«-в)Г < А (?М
\ A
+ е A в < А Щ е ,
где Q — наибольшее значение, принимаемое функциями |ф^;(^)| на
отрезке [0, Т], am — число членов в выражениях (82.5). Но на
основании (82.4) Q < -^—, и поэтому число е может быть взято
настолько малым, а число А настолько большим, что будет выпол-
выполняться неравенство
пМ . mMQ .
Но тогда мы будем иметь:
\xs(T)\<Ae-*.
что противоречит предположению, что при t — T хотя бы одно из
условий (82.8) будет выполняться со знаком равенства. Таким обра-
образом, условия (82.8) будут выполняться при всех t > 0, что и дока-
доказывает теорему.
Относительно фигурирующей в условиях теоремы величины m
заметим следующее. Эта величина, равная наибольшему числу членов,
входящих в каждое из выражений (82.5), не превосходит га2. Но она
может быть и меньше, чем л2. Так, например, если в правую часть
') В отличие от уравнений (81.10) в уравнениях (82.7) все нижние пре-
пределы интегрирования приняты равными нулю. Вследствие этого отпадает
необходимость в доказательстве существования решения этих уравнений.
354 НЕУСТАНОВИВШИЕСЯ ДВИЖЕНИЯ [ГЛ. VI
каждого из уравнений (82.2) входит только по одному поправочному
члену, т. е. если при каждом значении s только одна из функций
(fsV (fs2 (fsn отлична от нуля, то т ^п. То же самое будет и
в том случае, если при каждом s только одна из функций
xsl(t, t0), . . ., xsn(t, tQ) отлична от нуля. Вообще, если при каждом s
число отличных от нуля функций q>sl, . . ., q>sn не превосходит р^.п,
а число отличных от нуля функций xsl, ..., xsn не превосходит
<7<я, то т < pq.
Рассмотрим частный случай. Допустим, что коэффициенты pSj
являются постоянными. Пусть X — наименьшая из величин Re(—/ij),
Re(—Х2), ¦¦-, Re(—Хп), где kt — корни характеристического урав-
уравнения
\psj-6sjX\=0. (82.9)
Тогда характеристичные числа системы (82.2) будут положи-
положительны при выполнении неравенств
? (82Л0>
В самом деле, в рассматриваемом случае мы можем в условиях
(82.3) положить а — к— т), где ц—сколь угодно малое положи-
положительное число.
§ 83. Оценка характеристичных чисел методом
построения функций Ляпунова.
Рассмотрим снова уравнения (82.1) и (82.2) в предположении, что
коэффициенты psj постоянны. В предыдущем параграфе мы указали
предел для величин |ф5у(О|> ПРИ котором знак наименьшего харак-
характеристичного числа системы (82.2) совпадает со знаком наименьшего
характеристичного числа системы (82.1). При этом мы предполагали,
что указанный знак положителен. Можно указать другой способ
оценки интересующего нас предела, который одинаково применим
как в случае, когда наименьшее характеристичное число рассматри-
рассматриваемых систем положительно, так и в случае, когда это число отри-
отрицательно. Этот способ, предложенный Н. Г. Четаевым, основан на*
построении для уравнений (82.1) функции Ляпунова1).
Допустим сначала, что все корни характеристического уравнения
системы (82.1) имеют отрицательные вещественные части и, следо-
следовательно, ее характеристичные числа положительны. Найдем квадра-
квадратичную форму V (хг хп), удовлетворяющую'уравнению
w (
') Ч е т а е в Н. Г., Устойчивость движения, стр. 194. Гостехиздат, 1946.
§ 83] ОЦЕНКА ХАРАКТЕРИСТИЧНЫХ ЧИСЕЛ 355
где W—некоторая наперед заданная определенно-положительная квад-
квадратичная форма. Форма V при этом получится определенно-отрица-
определенно-отрицательной. Если мы теперь составим производную от V по t в силу
уравнений (82.2), то будем иметь:
dV
dxs ^~! Т
Если функции (psj (t) таковы, что квадратичная форма
я
dV ,
dxs
(83.3)
по-прежнему определенно-положительна, то характеристичные числа
системы (82.2) будут положительны. Форма (83.3) будет определенно-
положительной, если величины |<p5;-(f)| достаточно малы, и практически
никогда не представляет труда определить верхние пределы для
|(p5J,(f)|, при которых знакоопределенность (83.3) сохраняется. Эти
пределы будут зависеть от выбранной формы W, чем можно восполь-
воспользоваться для получения для этих пределов возможно больших зна-
значений.
Допустим теперь, что характеристическое уравнение системы (82.1)
имеет корни с положительными вещественными частями. Тогда, если
равенство
тх^+таЛаЧ- ... +/и„Я,„ = 0, (83.4)
где %i — корни характеристического уравнения, не выполняется ни
при каких целых неотрицательных т1, . .., тп, связанных соотноше-
соотношением щ-\- тп2-\- ¦ ¦ ¦ -f- отл = 2, то форма V, удовлетворяющая урав-
уравнению (83.1), по-прежнему существует, но она не будет ни опреде-
определенно-отрицательной, ни знакопостоянной отрицательной. При этом,
если форма (83.3) определенно-положительна, то наименьшее харак-
характеристичное число системы (82.2) будет отрицательным. Таким обра-
образом, и в рассматриваемом случае предел для \q>sj(t)\, при котором
знаки наименьших характеристичных чисел систем (82.1) и (82.2)
совпадают, определяется из условия знакоопределенности формы (83.3).
Если существует система целых неотрицательных т;, связанных
соотношением щ-{- • • ¦ -f- отл = 2, для которых удовлетворяется
равенство (83.4), то можно построить форму V, удовлетворяющую
уравнению
1 Х„),
где ^ — положительное число, W—определенно-положительная форма,
и при этом форма V может принимать положительные значения. Если
356 НЕУСТАНОВИВШИЕСЯ ДВИЖЕНИЯ [ГЛ. VI
форма (83.3) будет определенно-положительной, то, так же как и
в предыдущем случае, наименьшее характеристичное число системы
(82.2) будет отрицательным.
Пример. Пусть предложена система
^ ^ 2. (83.5)
где cp(f) — непрерывная функция времени. Полагая 2V' = jc^ —J— х\,
получим:
~ = — Хх] — (Я — <р) х\ + (pJCjATj.
Условие знакоопределенности *-^- дает:
4Я (Я, — ф) > ф2
или
|ф|<A/8-2)Я. (83.6)
Если Я > 0, то можно применить оценку предыдущего параграфа.
В рассматриваемом случае
и, следовательно, /И=1, т = 1, и формула (82.10) дает:
Полученный предел несколько выше даваемого формулой (83.6)
и является для рассматриваемого случая наибольшим. В самом деле,
при ф = const > X наименьшее характеристичное число системы (83.5)
отрицательно.
Определение знака наименьшего характеристичного числа при
помощи функций Ляпунова может быть иногда проведено и при psj
переменных. Укажем здесь на один прием, предложенный Н. Г. Че-
таевым ]) и заключающий вышеизложенный как частный случай.
Допустим, что коэффициенты psj в уравнениях (82.1) являются
непрерывными и ограниченными функциями t. Допустим, что корни
уравнения (82.9), которые теперь являются функциями /, ни при каком
t > 0 не связаны соотношением (83.4). Тогда по-прежнему будет суще-
существовать квадратичная форма V (t, xv .... хп), коэффициенты кото-
которой являются функциями времени, удовлетворяющая уравнению (83.1).
Допустим, что коэффициенты psj таковы, что форма
^-+Г(*„ .... хп)
') Четаев Н. Г., О наименьшем характеристичном числе. ПММ, т. IX,
вып. 2, 1945.
§ 84] ПРИМЕНЕНИЕ МЕТОДА МАЛОГО ПАРАМЕТРА 357
будет также определенно-положительной. Тогда, если форма V ока-
окажется определенно-отрицательной, что будет, например, иметь место,
когда при всех достаточно больших значениях t вещественные части
всех корней уравнения (82.9) меньше некоторого отрицательного числа,
то невозмущенное движение для уравнений (82.1) будет устойчиво и,
следовательно, характеристичные числа этих уравнений будут во вся-
всяком случае не менее нуля. Если окажется, что при любом / > Т,
где Т — достаточно большое положительное число, форма V может
принимать положительные значения, и если, кроме того, она допу-
допускает бесконечно малый высший предел, т. е. ее коэффициенты
являются ограниченными, то невозмущенное движение будет неустойчиво.
§ 84. Применение метода малого параметра.
Результаты предыдущих параграфов показывают, что при практи-
практическом определении знака наименьшего характеристичного числа
системы линейных дифференциальных уравнений с переменными коэф-
коэффициентами можно последние в некоторых случаях заменить подхо-
подходящим образом выбранными постоянными. Если при этом отклонения
этих коэффициентов от соответствующих им постоянных не превос-
превосходят некоторых установленных в предыдущих параграфах пределов,
то знак наименьшего характеристичного числа системы с переменными
коэффициентами будет совпадать со знаком наименьшего характери-
характеристичного числа системы с постоянными коэффициентами. Этот прием
не может быть, очевидно, применен в том случае, когда наименьшее
характеристичное число системы с постоянными коэффициентами равно
нулю. То же самое будет и в том случае, когда указанное наимень-
наименьшее характеристичное число будет численно очень мало. В этом слу-
случае верхние пределы для отклонений коэффициентов сравниваемых
систем, даваемые правилами предыдущих параграфов, будут также
очень малыми, вследствие чего метод может потерять всякий практи-
практический интерес. В этом параграфе мы изложим один прием*), кото-
который позволяет для широкого класса систем дать практически при-
пригодные оценки наименьшего характеристичного числа для вышеука-
вышеуказанных критических случаев.
Допустим, что рассматриваемая система имеет вид
E=1, 2 Я),
где ps. — постоянные, <р* —ограниченные и непрерывные при t^-0
функции времени, (х — малый параметр, характеризующий степень
отклонения от системы с постоянными коэффициентами. Мы будем
') См. работу автора, цитированную в сноске на стр. 352.
358 НЕУСТАНОВИВШИЕСЯ ДВИЖЕНИЯ [ГЛ. VI
предполагать, что характеристическое уравнение
системы с постоянными коэффициентами
^ (84.3)
имеет корни с нулевыми вещественными частями и не имеет корней
с положительными вещественными частями. Таким образом, наимень-
наименьшее характеристичное число системы (84.3) равно нулю. Случай, когда
это число отлично от нуля, но очень мало, приводится к рассматри-
рассматриваемому путем отнесения малых Поправочных членов к тем членам
уравнений (82.1), которые имеют множителем |х. Для упрощения даль-
дальнейших выкладок мы предположим, кроме того, что уравнение (84.2)
не имеет кратных корней.
Сущность предлагаемого метода решения задачи состоит в том,
что систему (84.1) при помощи подходящим образом выбранного
линейного преобразования вида
Xl+ ... +/,„*„) (s=l, 2. ...,«), (84.4)
где fsj{t)—некоторые ограниченные и непрерывные при f^-О функ-
функции времени, приводят к виду
+ (х2 (%Л + • • • + *,„*„). (84.5)
Здесь asj — постоянные, a tysj (t) — ограниченные и непрерывные при
t^-О функции времени. Эти функции зависят, вообще говоря, от jx,
относительно которого они аналитичны.
Если теперь в системе (84.5) отбросить члены с переменными
коэффициентами, то может оказаться, что полученная система с по-
постоянными коэффициентами будет иметь наименьшее характеристич-
характеристичное число, отличное от нуля. Это число будет, конечно, иметь
порядок малости (х, но в отличие от системы (84.1) порядок малости
переменных коэффициентов будет не меньше jx2, и поэтому к полу-
полученной системе могут быть применены методы предыдущих парагра-
параграфов ').
') Таким образом, сущность метода заключается в повышении порядка
малости членов с переменными коэффициентами. Этот метод широко исполь-
используется в работах Н. М. Крылова и Н. Н. Боголюбова по нелинейным коле-
колебаниям. Для случая периодических коэффициентов этот прием применялся
Ляпуновым при решении задачи устойчивости в критических случаях (см.
§ 67). При этом Ляпунов рассматривал нелинейные уравнения; малыми явля-
являлись члены, нелинейные относительно xs, и задача сводилась к преобразр-
ванию уравнений к такому виду, чтобы переменные коэффициенты были
у членов сколь угодно высокого порядка.
§ 84] ПРИМЕНЕНИЕ МЕТОДА МАЛОГО ПАРАМЕТРА 359
Чтобы вышеуказанное преобразование действительно могло быть
выполнено, необходимо, чтобы коэффициенты ф*. удовлетворяли сле-
следующим условиям:
1) Существуют такие постоянные asj, что функции
t
j (p*sJdt — asjt (s, y=l, 2 n)
о
ограничены. При этом условии, очевидно, имеем:
t
asJ = lim j- J <p*s.(t)dt.
->co 0
2) Если разность каких-ни')удь двух корней рр и р? уравнения (84.2)
есть чисто мнимое число ib, то функции
J ф*;. cos bt dt, j ф*;. sinbt dt
ограничены.
Условия 1) выполняются для лю5ых периодических и квазиперио-
квазипериодических функций. Для этих .же функций будут выполняться и усло-
условия 2), если только разложения этих функции не содержат «резони-
«резонирующих» гармоник cosW и %'тЫ.
Мы переходим теперь к определению преобразования (84.4). С этой
целью заменим в правой и левой частях уравнений (84.5) величины ys
их значениями (84.4). Тогда, принимая во внимание (84.1), получим:
а=1 \ р=1 / а=1
Приравнивая члены с первой степенью jx, будем иметь:
Pakfsa~1rask~(C*slt (.S, k = l, 2, . . ., Я). (84.6)
<z = l a = l
Мы получили, таким образом, для определения коэффициентов
а2 линейных неоднородных дифференциальных уравнений с постоянными
коэффициентами. Из этих уравнений функции fsk могут быть опре-
определены при помощи квадратур. Необходимо, однако, чтобы эти функ-
функции вышли ограниченными, и мы сейчас покажем, что при сделанных
360 НЕУСТАНОВИВШИЕСЯ ДВИЖЕНИЯ [ГЛ. VI
допущениях постоянными ask можно так распорядиться, чтобы это
обстоятельство действительно имело место.
С этой целью допустим, что система (84.3) при помощи неособен-
неособенного линейного преобразования с постоянными коэффициентами при-
приведена предварительно к каноническому виду. Так как, по предпо-
предположению, уравнение (84.2) не имеет кратных корней, то канонический
вид системы (84.3) будет следующий:
dt
(s=l, 2 я).
Здесь р^ — корни уравнения (84.2). Мы будем предполагать, что
такое преобразование было выполнено с самого начала и будем при-
придерживаться прежнего обозначения переменных. Указанное предвари-
предварительное преобразование не только упрощает выкладки, но и облегчает
значительно вычисление коэффициентов fSJ-, и поэтому его, действи-
действительно целесообразно выполнить.
Уравнения (84.1) имеют теперь вид
^ = РЛ + ^ <<P,i*, + • • • + Ф, А). (84.7)
где функции ф^, являются линейными комбинациями функций ф*.
с постоянными коэффициентами и поэтому удовлетворяют тем же
условиям, что и функции ф*..
Уравнения (84.6) имеют теперь следующий простой вид:
+«,*-<Р,* (s, ft=l. 2. .... я). (84.8)
Для того чтобы эти уравнения имели ограниченное решение,
положим
t
ass = lim j J ф„ dt (s = 1, 2 n)
о
и
ask = 0 (s=? k; s, k=l, 2 я).
Тогда функции fss, определяемые равенствами
согласно условиям, которым удовлетворяют ф^, будут ограничен-
ограниченными. Покажем, что то же самое будет справедливо и по отношению
к функциям fsk (s ф k), если в уравнениях (84.8). которым они удо-
удовлетворяют, надлежащим образом распорядиться постоянными инте-
§ 84] ПРИМЕНЕНИЕ МЕТОДА МАЛОГО ПАРАМЕТРА 361
грирования. Действительно, обозначая
мы можем положить:
t
fsk — — е<1^ (cos Р^+ i sin $skt) j e~ask' (cos $skt — i sin $SJ) ф.й dt,
(84.9)
где а — произвольная постоянная. Эту постоянную мы положим равной
нулю при ask <; 0 и равной оо при ask > 0. Тогда мы будем иметь:
|/,*|<Л1ва**' f e-askf dt = — -^-{\— A*'). (84.10)
если ask < 0, и
I Л» | < Же"**' Г «-«**' Л = —, (84.11)
если ask > 0. Здесь М — верхний предел функций |ф^|. Из (84.10)
и (84.11) вытекает ограниченность функций (84.9) при ask ф 0.
Ограниченность этих функций при ask = 0 непосредственно вытекает
из условия 2), которому удовлетворяют функции <p,ft.
Таким образом, мы действительно можем найти ограниченные
функции fsk, при которых подстановка (84.4) преобразует систему
(84.1) к виду (84.5). При этом входящие в определение функций fsk
произвольные постоянные могут быть выбраны по произволу. При ц,
достаточно малом, определитель подстановки (84.4) превосходит при
любом t > 0 некоторую положительную постоянную, вследствие чего
характеристичные числа системы (84.1) совпадают с характеристич-
характеристичными числами системы (84.5).
Выбрав функции fsk и постоянные ask вышеуказанным образом,
мы приведем систему (84.7) к виду
^ Уп)- (84.12)
Допустим, что наименьшее характеристичное число системы
-^- = (p, + |iajy, (84.13)
с постоянными коэффициентами отлично от нуля. Тогда на основании
теоремы об устойчивости характеристичных чисел систем с постоян-
постоянными коэффициентами величину jx можно всегда выбрать настолько
малой, чтобы знак наименьшего характеристичного числа системы
(84.12) совпадал со знаком наименьшего характеристичного числа
системы (84.13). Оценка верхнего предела для |ц| может быть
362 НЕУСТАНОВИВШИЕСЯ ДВИЖЕНИЯ [ГЛ. VI
сделана по методам предыдущих параграфов. При этом если эту оцен-
оценку делать при помощи функций Ляпунова, то после определения коэф-
коэффициентов fsk можно уже не производить самого преобразования (84.4)
и исходить непосредственно из уравнений (84.7). Действительно,
функцией Ляпунова для системы (84.12) будет выражение
и следовательно, функцией Ляпунова для системы (84.7) будет вы-
выражение
п \2
(84.14)
При этом верхний предел значений ц определится из условия,
что производная от (84.14) в силу уравнений (.84.7) является опре-
определенно-положительной *).
Пример. Пусть предложена система
dx
-jf = М- (— 1 + 2 sin t) xx
= X2
где (j, > 0. Характеристическое уравнение соответствующей системы
с постоянными коэффициентами имеет, с точностью до величин вто-
второго порядка, отрицательные корни —jx и —1. Однако методы пре-
предыдущих параграфов не дают возможности сделать каких-либо заклю-
заключений о знаках характеристичных чисел полной системы (84.15), так
как эти методы дают пределы для модулей переменных коэффициен-
коэффициентов, меньшие модулей корней характеристического уравнения. В рас-
рассматриваемом случае переменный коэффициент 2jxsin^ может вдвое
превосходить модуль корня — (х.
Для системы (84.15) уравнения, определяющие коэффициенты fsk
преобразования (84.4)
имеют вид
у, = 1+|(/i1Jfi + /l22). \ ... .
') См. примечание в конце книги (стр. 527).
§ 84] ПРИМЕНЕНИЕ МЕТОДА МАЛОГО ПАРАМЕТРА 363
Эти уравнения имеют такие ограниченные решения
/„ = 2 cos/. /и = 0,
/12 = 1, /21 = — 1,
причем
и^\ ~==z — 1 > ^22 z===
Подставляя в (84.16) и выполняя преобразование, получим вместо
(84,15) следующую систему:
(84Л7)
где
= х [1 + 2 sin 2^ + цA + 2 cos
i]>12 = i- [1 + 2 cos t-\- \x (— 1 + 4 cos2 * — sin It-f- 2 cos 01.
]>12 = i
ijj22 = -L [— 1 -f- ц (_ 1 -4- 2 sin t ~ 2 cos t)\,
Характеристичные числа системы (84.17) будут положительны,
если величины |А2|т]э^| достаточно малы. Для оценки верхнего пре-
предела этих величин воспользуемся формулой (82.10). В рассматриваемом
случае Х = \х, от = 2иЖ=1. Поэтому, -для того чтобы характе-
характеристичные числа системы (84.17) были положительны, достаточно,
чтобы функции |А2|^у| удовлетворяли неравенствам | [^SJ-1 < -ё1 •
Грубая оценка показывает, что это во всяком случае будет выпол-
выполнено, если \х < -д-.
Примечание. Если коэффициенты tysj в преобразованных урав-
уравнениях (84.5) обладают такими же свойствами, как и коэффициенты ер*.,
то эти уравнения можно подвергнуть такому же преобразованию и
получить новые уравнения, у которых переменные коэффициенты
будут иметь порядок малости \х3. Аналогичным образом можно про-
продолжать и дальше. В частности, если коэффициенты ср*. являются
квазипериодическими функциями, то можно построить любое число
364 НЕУСТАНОВИВШИЕСЯ ДВИЖЕНИЯ {ГЛ. V
приближений и привести уравнения (84.1) к виду
k
а=1
где аН — постоянные. Этот прием использовал И. 3. Штокало !) для
установления критериев устойчивости линейных систем с квазиперио-
квазипериодическими коэффициентами. Однако И. 3. Штокало не устанавливает
пределов для ц и ограничивается доказательством, что при \х, доста-
достаточно малом, невозмущенное движение будет устойчиво, если корни
характеристического уравнения системы с постоянными коэффициентами
k
а=1
имеют отрицательные вещественные части. Более просто и в более
общем виде это предложение доказано Н. П. Еругиным ').
В. ТЕОРИЯ УСТОЙЧИВОСТИ ПО ПЕРВОМУ ПРИБЛИЖЕНИЮ.
§ 85. Теорема об устойчивости по первому приближению.
Мы переходим сейчас к рассмотрению нелинейных уравнений,
зависящих явно от t, и к установлению условий, при которых задача
устойчивости решается совокупностью членов наинизшего порядка
в этих уравнениях. В этом параграфе мы будем рассматривать си-
систему вида
где Х^ — некоторые не зависящие от t формы /и-го порядка )
переменных xv .. ., хп. Функции ср^ зависят также от t. Эти функ-
функции определены в области
t>0, | *,|<//. (85.2)
где они непрерывны и удовлетворяют неравенствам
••• +\хп\}т, (85.3)
') Штокало Иг 3., Критерий устойчивости и неустойчивости решений
линейных дифференциальных уравнений с квазипериодическими коэффициен-
коэффициентами. Матем. сб., т. 19, № 2, 1946.
2) Е р у г и н Н. П., Об асимптотической устойчивости решения некото-
некоторой системы дифференциальных уравнений. ПММ, т. XII, вып. 2, 1948.
§ 85] устойчивость по первому приближению 365
причем А — некоторая постоянная. Кроме того, предполагается, что
уравнения (85.1) допускают в области (85.2) единственное решение
при заданных начальных условиях.
Рассмотрим систему первого приближения
Ч ^ *„> (85.4)
которая, вообще говоря, нелинейна. При каких условиях устойчи-
устойчивость для уравнений (85.4) обусловливает устойчивость для полной
системы (85.1)? Ответ на этот вопрос дается следующей теоремой 1).
Теорема. Если невозмущенное движение для уравнений
(85.4) асимптотически устойчиво, то то же самое будет
справедливо и для уравнений (85.1) при любом выборе функ-
функций <ps, удовлетворяющих неравенствам (85.3), если только
постоянная А достаточно мала.
Доказательство. На основании теоремы § 73 существует опре-
определенно-положительная функция V (jCj, . . ., хп), производная которой,
составленная в силу уравнений (85.4), т. е. выражение
Х<Т\ (85.5)
есть функция определенно-отрицательная. Рассмотрим в пространстве
переменных хх хп семейство поверхностей V — h > 0. При h,
достаточно малом, все эти поверхности замкнуты, окружают начало
координат и пересекаются интегральными кривыми уравнений (85.4)
снаружи во внутрь. Пусть V ~ h* одна из этих поверхностей. Обо-
Обозначим эту поверхность через S. В силу знакоопределенности выра-
выражения (85.5) каждая интегральная кривая системы (84.5) пересекает
поверхность 5 снаружи во внутрь под углом, превосходящим неко-
некоторую положительную величину а.
Соединим радиусами-векторами все точки поверхности 5 с нача-
началом координат и уменьшим все эти радиусы-векторы в k раз. Мы
получим замкнутую поверхность, окружающую начало координат,
подобную поверхности S. Обозначим эту поверхность через Sk. Изме-
Изменяя k от 1 до 0, мы получим семейство такого рода поверхностей2),
стягивающихся при ft = 0 в начало координат.
Пусть А — какая-нибудь точка поверхности S и Ak — соответ-
соответствующая ей точка поверхности Sk. Так как эти поверхности подобны,
то касательные плоскости к ним в точках А и Ak параллельны. С дру-
другой стороны, касательные к интегральным кривым уравнений (85.4)
') М а л к и н И. Г., Теорема об устойчивости по первому приближению.
ДАН СССР, т. LXXVI, № б, 1951.
2) Эти поверхности, вообще говоря, пересекаются между собой.
366 НЕУСТАНОВИВШИЕСЯ ДВИЖЕНИЯ [ГЛ. VI
в точках А и Ak также параллельны, так как в силу однородности
этих уравнений имеем:
dxs
Таким образом, интегральная кривая уравнений (85.4), проходящая
через точку Ak, пересекает поверхность Sk под таким же углом, под
каким интегральная кривая тех же уравнений, проходящая через
точку Л, пересекает поверхность S. Следовательно, так же как и по-
поверхность S, все поверхности Sk пересекаются интегральными кривыми
уравнений (85.4) снаружи во внутрь под углами, превосходящими а.
Рассмотрим теперь полную систему уравнений (85.1). Предположим,
что величина А в неравенствах (85.3) настолько мала, что во всей об-
области (85.2) поле касательных к интегральным кривым уравнений (85.1)
повернуто относительно поля касательных к интегральным кривым
уравнений (85.4) на угол, меньший а. Тогда, очевидно, все интеграль-
интегральные кривые системы (85.1) будут пересекать поверхности Sk снаружи
во внутрь, откуда непосредственно вытекает справедливость теоремы ').
§ 86. Некоторые особенности задачи устойчивости
по первому приближению для неустановившихся движений.
Таким образом, если члены наинизшего порядка в уравнениях воз-
возмущенного движения не зависят явно от t, то для устойчивости не-
невозмущенного движения достаточно, чтобы для первого приближения
имела место асимптотическая устойчивость. Можно показать, что, по
крайней мере, при л=2 справедливо и обратное предложение,
а именно, невозмущенное движение для уравнений (85.1) будет только
тогда устойчиво при любом выборе функций q>s, имеющих порядок
малости выше т, когда для уравнений первого приближения имеет
место асимптотическая устойчивость2).
Значительно сложнее обстоит дело в случае, когда члены наиниз-
наинизшего порядка в уравнениях возмущенного движения также зависят
от t. В этом случае условия асимптотической устойчивости для урав-
уравнений первого приближения недостаточно для обеспечения устойчи-
устойчивости для полной системы уравнений. С другой стороны, это условие
не является необходимым.
Рассмотрим, например, следующую систему уравнений:
^ = ^+ФДг, хх *„)• (86.1)
') См примечание в конце книги (стр. 528).
2) Г м боле;/ это условие будет необходимым, если функции <qs удовле-
удовлетворяю! неравенствам (85.3).
§ 86] НЕКОТОРЫЕ ОСОБЕННОСТИ ЗАДАЧИ УСТОЙЧИВОСТИ 367
К. П. Персидский показал '), что, для того чтобы для этой системы
уравнений имела место устойчивость при любом выборе функций ср^,
удовлетворяющих в области (85.2) условию
|Ф,(*. xv .... *„)|<Л(*? + *1+...+*я2). (86.2)
где А — некоторая постоянная, достаточно, чтобы выполнялись условия
t t т
ехр Г pdt <В, j exp J р (т) dx < В, (86.3)
О 0 0
где В—также постоянная.
В самом деле, полагая
Уз ~ xs ехР (
6
получим:
/ t >
dv l Г \ l Г f
-JJ. = exp — / p dt \(fs\ t, y, exp / p dt yn exp I p dt
4 о 7 о о '
<уда
= с,+ Г exp I— f pdt\(ps\t, yxexp [pdt, ...
0 \ 0 / \ 0
у„ехр fpdt \dt, (86
о
где cs—начальные значения величин ys, а следовательно, также и
величин xs.
Пусть е — произвольно малое положительное число. Мы будем
предполагать, что
< <865>
Выберем г) согласно условию
(86.6)
Тогда, если \cs\ -^т], то при всех ^>0 будут выполняться
неравенства \ys\ < -^-. В самом деле, эти неравенства, выполняясь
в начальный момент, будут выполняться и при t, достаточно малом.
') Персидский К. П., К теории устойчивости интегралов систем диф-
дифференциальных уравнений. Изв. физ.-матем. об-ва при Казанском гос. ун-те,
т. VIII, 1936—1937.
868 НЕУСТАНОВИВШИЕСЯ ДВИЖЕНИЯ [ГЛ. VI
Пусть Т — первый момент времени, при котором хотя бы одна из
величин \ys\, пусть это будет |Уа|, достигает значения -тр. Тогда
из (86.4), (86.2), (86.3), (86.5) и (86.6) получим:
что противоречит условию | yk (Т)[ = -н-. Таким образом, при всех
/>0 будут выполняться неравенства \ys\ <-гг> а следовательно,
и неравенства \xs\ < е, что доказывает устойчивость невозмущенного
движения для уравнений (86.1).
Но условия (86.3) будут выполнены, если положить
,,, 2г3 sin * cos * — 3t2cos2t d , .. , ,, , ..
Р @ =' Г"г"й п = -гг 1п A Ч- ^ cos О-
г ' \-\-P cos21 dt к ' '
При таком выборе функции р уравнения первого приближения
для системы (86.1) имеют общее решение
из которого следует, что невозмущенное движение для первого прибли-
приближения устойчиво, но не асимптотически. В то же время невозмущенное
движение для полной системы (86.1) будет по доказанному устой-
устойчиво при любом выборе функций ср^, удовлетворяющих условиям (86.3).
Рассмотрим теперь систему уравнений •)
(86.7)
(86.8)
dt
где
1 < 2a < 1 -}- -j
Общее решение уравнений первого приближения имеет вид
хх = cxe~at, х2 — с2 ехр [(/-)- 1) sin In (t-\-l)— 2at].
Это решение не только асимптотически устойчиво, но обладает
положительным характеристичным числом. Тем не менее, невоз-
') Perron О., Die Stabilitatsfrage bei Differenttalgleichungen. Mathem.
Zeitschrlft, т. 32, 1930.
§ 86] НЕКОТОРЫЕ ОСОБЕННОСТИ ЗАДАЧИ УСТОЙЧИВОСТИ 369
мущенное движение для полной системы уравнений (86.7) неустой-
неустойчиво. Действительно, это общее решение имеет вид
xl = cxe~at.
х2 = ехр [(*+ 1) sin In {t + 1) — 2at] X
X \e3 + c\ J exp [— (т+ 1) sin In (т + 1)] dx I.
\ о /
Полагая t-\-l — e 2 , где n > 0 — целое число, будем иметь:
еХр [(/_!_ l)sinln(f+l) — 2at] = e- eU-2«x, (i +t) е~я—\ > О
и следующие оценки:
2
—гя
t (I + O e -1
Jexp[—(T+l)sinln(T+ 1)]йт> Г ехр[—(T+l)sinln(T+l)]dT>
0
е -1 (\ + t)e
I e2 dr> J
Поэтому при указанных значениях t второе слагаемое в выраже-
выражении для х2 удовлетворяет неравенству
2 ехр [(f+1) sin In (^+1) — 2at] Jexp [— (т+ l)sin In (т+ 1)] dx >
2
3 — e-n
и, следовательно, на основании (86.8) с неограниченным возраста-
возрастанием t неограниченно возрастает. Первое же слагаемое в выраже-
выражении х2 с неограниченным возрастанием t стремится к нулю. И это
будет справедливо, каковы бы ни были начальные значения сг ф О
и с2 величин хх и х2. Таким образом, при любых начальных значе-
значениях, при которых сг Ф 0, функция х2 будет неограниченной и, сле-
следовательно, невозмущенное движение неустойчиво.
Приведенные примеры показывают, что если уравнения первого
приближения зависят явно от t, то условие асимптотической устой-
устойчивости решений этих уравнений не является ни необходимым, ни
370 НЕУСТАНОВИВШИЕСЯ ДВИЖЕНИЯ [ГЛ. VI
достаточным для устойчивости невозмущенного движения при любом
выборе членов высших- порядков.
Необходимых и достаточных условий устойчивости по первому
приближению неустановившихся движений для общего случая не най-
найдено. Установлен, однако, ряд достаточных критериев, которые мы
ниже и излагаем. Мы будем при этом заниматься только критериями
устойчивости. Критериями неустойчивости по первому приближению
занимался Н. Г. ЧетаевJ).
Мы будем также предполагать, что уравнения первого приближе-
приближения линейны.
§ 87. Критерий Ляпунова.
Рассмотрим уравнения возмущенного движения вида
-^Г ^ р*х* + • • • + Psnxn + Ф5 С *i *п) (87-1)
(s=l, 2 я),
где psj ограничены и непрерывны при t^O, и соответствующую
систему уравнений первого приближения
4г==^1*1+---+^»*»- (87-2)
Первым, установившим достаточные условия устойчивости по пер-
первому приближению для уравнений вида (87.1), был сам А. М. Ляпунов.
При этом Ляпунов предполагал, что функции q>s, ограниченные по
отношению к t, разлагаются в ряды по степеням переменных
х\, . . ., хп, начинающиеся членами не ниже второго порядка. Крите-
Критерий Ляпунова обобщен Э. Коттоном и К. П. Персидским2), наложив-
наложившими на ф5 менее ограничительные условия. Мы докажем теорему
Ляпунова в предположении, что функции q>s удовлетворяют в об-
области
|*,|<Я. *>0 (87.3)
неравенствам
|ф,С *i хп)\<А[\х1\^-...+ \хп\}т, (87.4)
где А и т — положительные числа, из которых второе больше еди-
единицы. Кроме того, предполагается, как обычно, что уравнения (87.1)
допускают в рассматриваемой области единственное решение при
заданных начальных условиях. Наложенные на ср^ ограничения зна-
¦) Четаев Н. Г., Теорема о неустойчивости для правильных систем.
ПММ, т. XII, вып. 5, 1944; Четаев Н. Г., О некоторых вопросах об устой-
устойчивости и неустойчивости для неправильных систем. ПММ, т. XII, вып 5, 1948;
Четаев Н. Г., Устойчивость движения, Гостехиздат, 1946.
2) См. работу, цитированную на стр. 367.
§ 87] КРИТЕРИЙ ЛЯПУНОВА 371
чительно слабее," чем у Э. Коттона, и несколько сильнее, чем
у К. П. Персидского.
Критерий Ляпунова выражается следующей теоремой.
Теорема. Если система уравнений, первого приближения
(87.2) правильная и если все ее характеристичные числа
положительны, то невозмущенное движение для уравнений
(87.1) асимптотически устойчиво при любом выборе функций q>s,
удовлетворяющих в области (87.3) неравенствам (87.4).
Доказательство. Обозначим через xsJ(t) нормальную систему
решений уравнений (87.2), а через kv ..., Хп — ее характеристичные
числа, так что
X {ху, .... xnJ] =lj (J = 1, 2, .. ., п). (87.5)
По условию теоремы все величины А,у- положительны. Обозначим
далее через xsj(t) фундаментальную систему решений уравнений (87.2),
определяемую начальными условиями xsl @) = bSJ- (bsJ — символ Кро-
некера). Тогда, если
А- = tnin {klt .. ., Хп),
то во всяком случае
X\xsj}>\. (87.6)
Пусть Д = \xsj\ —определитель Вронского решений xSJ-, а Д^—
минор этого определителя, соответствующий элементу xsj. Оценим
характеристичное число функций Д^/Д. Применяя теоремы о ха-
характеристичных числах произведения и суммы, получим:
Но, так как система (87.2) —правильная, то
и, следовательно,
X{^r}>-h (87-7>
Из (87.5), (87.6) и (87.7) находим, что при всех t^-О справед-
справедливы оценки
\xsj(t)\<Be{-
д '
372 НЕУСТАНОВИВШИЕСЯ ДВИЖЕНИЯ (ГЛ. VI
где а — сколь угодно малое положительное число, аВ>1 —неко-
—некоторая постоянная (зависящая от а).
Сделаем теперь в уравнениях (87.1) замену переменных
уа = х^вУ*. (87.9)
где у < X. Получим:
% it. «-*y, *-*Уа), (87.10)
причем система первого приближения (87.2) перейдет в систему
Пусть ySj{t)—фундаментальная система решений уравнений (87.11),
определяемая начальными условиями ySj@) = 6SJ; ySj{f) — нормаль-
нормальная система решений этих уравнений, соответствующая системе xs,
уравнений (87.2), D = \ysj\ и Dsj — минор определителя D, соответ-
соответствующий элементу ysj. Тогда, очевидно,
и из (87.8) находим:
Dsj
D
Мы будем предполагать, что а настолько мало, что
Рассмотрим неоднородную систему
-jf = Pslyi+-.- + psnyn + yys + fs @.
где fs—произвольные непрерывные функции времени. Частное реше-
решение этих уравнений, если его искать по методу вариации произволь-
произвольных постоянных Лагранжа, имеет вид
t
J т
Поэтому общее решение этих уравнений определяется равенствами
ys S 2 j J
/ 0
где cs — начальные значения величин ys.
" " Г D
= S ctyai (t) + 2 ysj J ^# /i W. (87.13)
* 1 l 0
§ 87} критерий Ляпунова 373
Установив это, рассмотрим произвольное решение ys(t) уравне-
уравней (87.10) с нача °
мы можем писать:
р
ний (87.10) с начальными условиями ys(t) = y°s- На основании (87.13)
1 = 1
j l 0
e-vlyn(t)]dt. (87.14)
Пусть е — произвольное сколь угодно малое положительное число.
Мы будем при этом предполагать, что оно настолько мало, что
выполняется неравенство
Так как т > 1, то это будет выполняться при всяком е < h, где А
достаточно мало. Выберем теперь т](е) согласно неравенству
<-f <87Лб>
и покажем, что если |у?|^т], то при всех t >0 будет |у5@| < е,
т. е. что невозмущенное движение относительно переменных ys
устойчиво.
В самом деле, пусть t = T — первый момент времени, при кото-
котором хотя бы одна из величин \ys\ достигает значения е. На всем
отрезке [0, Т] на основании (87.4) справедливы оценки
|<Рг(*. e~*y\(t) e-y*yn(t))\ <nmAe-m*Em.
Поэтому, принимая во внимание (87.12), из (87.14) найдем:
\Уз(Т)\ <пВце1-1+а+^>+^ пт+1В2Агте(-^+а+у)' j e(Ve-mv)'dt=
) \ 0
Так как т > 1, то а можно выбрать настолько малой, чтобы
—«Y < 0- Тогда на основании (87.13) показатели степе-
степеней в правых частях полученных неравенств будут отрицательны.
Поэтому указанные неравенства принимают вид
374 НЕУСТАНОВИВШИЕСЯ ДВИЖЕНИЯ [ГЛ. VI
и, следовательно, на основании (87.15) и (87.16)
\У,(П\<г.
что противоречит условию, что хотя бы одна из величин |
равна а.
Таким образом, невозмущенное движение по отношению к пере-
переменным ys устойчиво. Но тогда оно на основании (87.9) будет асим-
асимптотически устойчиво по отношению к переменным xs, что и дока-
доказывает теорему.
Примечание 1. Из устойчивости невозмущенного движения по
отношению ys и равенств (87.9) вытекает, что характеристичное число
функций xs(t) не менее величины у, которая является любым поло-
положительным числом, меньшим наименьшего из характеристичных чисел
системы первого приближения.
Примечание 2. Допустим, что система (87.2) не является
правильной, так что
Ляпунов показал, что доказанная теорема останется в силе, если а
меньше наименьшего характеристического числа системы (87.2).
§ 88. Другая группа критериев.
Мы рассмотрим сейчас три других критерия устойчивости по
первому приближению, отличных от критерия Ляпунова и играющих
важную роль в теории критических случаев. Во всех этих трех кри-
критериях предполагается, что функции ср^, хх хп) в дифферен-
дифференциальных уравнениях возмущенного движения
¦^L = PslXl+---+PsnXn+%V< *1 Хп) (S=l. 2 П)
(88.1)
удовлетворяют в области
г>0, |jtj<tf, (88.2)
неравенствам
\q>5(t, хх, .... хп)\ < А [\хх\ -f .. . 4- |лс„|}, (88.3)
где А — некоторая постоянная.
Первый из указанных критериев выражается следующей тео-
теоремой 1).
') См. Малкин И. Г., Die Stabilitatsfrage bei Differentialglelchungen.
Сб. трудов Казанского авиац. ин-та, № 2, 1934.
§ 88] ДРУГАЯ ГРУППА КРИТЕРИЕВ 375
Теорема 1. Если для уравнений первого приближения
-^А. = Рлхх 4- ... + Psnxn (88.4)
существует функция Ляпунова V(t, хг, .... хп), удовлетворяю-
удовлетворяющая всем условиям теоремы II об асимптотической устойчи-
устойчивости, то невозмущенное движение асимптотически устойчиво
при любом выборе функций qs, удовлетворяющих в области
(88.2) неравенствам (88.3), если только постоянная А доста-
достаточно мала.
Доказательство. Мы воспользуемся для доказательства ре-
результатами § 75. Согласно последним (теорема 3) при выполнении
условий теоремы существует определенно-положительная квадратич-
квадратичная форма V*(t, xx хп) с ограниченными коэффициентами,
производная которой, составленная в силу уравнений (88.4), равна
наперед заданной определенно-отрицательной квадратичной форме.
Мы можем, в частности, положить:
п л
dV , V dV ,
s = l s=\
Составим теперь производную от V по t в силу полной системы
уравнений (88.1). Будем иметь:
п п
it Id xs т 2*i ф* -^7 •
Эта производная, в силу того что коэффициенты формы V огра-
ограничены, будет определенно-отрицательной при любом выборе функ-
функций фг, удовлетворяющих в области (88.2) неравенствам (88.3), если
только постоянная А достаточно мала. Следовательно, форма V
является функцией Ляпунова для полной системы (88.1), удовлетво-
удовлетворяющей всем условиям теоремы II об асимптотической устойчи-
устойчивости. Поэтому невозмущенное движение асимптотически устойчиво,
что и доказывает теорему.
Пусть xSj(t, t0) G=1, 2 п) — фундаментальная система ре-
решений уравнений (88.4), определяемая начальными условиями
(s, 7=1. 2 п).
Тогда имеет место также следующий критерий устойчивости по
первому приближению, установленный К. П. Персидским').
') См. работу, цитированную на стр. 367.
376 НЕУСТАНОВИВШИЕСЯ ДВИЖЕНИЯ [ГЛ. VI
Теорема 2. Если для уравнений первого приближения (88.4)
при любых to^-O и t>t0 выполняются неравенства
\xSJ(t,t0)\<Be-a('-<>\ (88.5)
где В и а — положительные постоянные, не зависящие от t0, то
невозмущенное движение асимптотически устойчиво при любом
выборе функций q>s, удовлетворяющих в области (88.2) неравен-
неравенствам (88.3), если только постоянная А достаточно мала(
Согласно результатам § 75 (теорема 1 и 2) этот критерий, кото-
который может быть доказан и непосредственно, полностью эквивалентен
критерию, даваемому теоремой" 1, и поэтому в отдельном доказа-
доказательстве не нуждается.
Отметим, наконец, еще третий критерий, который также эквива-
эквивалентен первым двум. Этот критерий установлен О. Перроном1) и
выражается следующей теоремой.
Теорема 3. Если уравнения первого приближения (88.4),
обладают тем свойством, что при любых непрерывных и огра-
ограниченных при t^-О функциях f$ система неоднородных урав-
уравнений
^ 0 (88.6)
допускает только ограниченные решения, то невозмущенное
движение асимптотически устойчиво при любом выборе функ-
функций cps, удовлетворяющих в области (88.2) неравенствам (88.3),
если только постоянная А достаточно мала.
Как уже указывалось выше, этот критерий полностью эквивален-
эквивалентен критериям, даваемым теоремами 1 и 2.
Действительно, общее решение уравнений (88.6) имеет вид
п t п
xs = % c,xsj (Л 0) + J ^ xtj {t, t) fj (т) dx,
j = \ 0 j=l
где Cj — произвольные постоянные. Если выполняются условия тео-
теоремы 1, или, что то же самое, неравенства (88.5), то при любом
f^-О будут справедливы оценки
где М — верхний предел функций |/5(?)|. что и доказывает ограни-
ограниченность функций xs. Наоборот, если уравнения (88.6) при любых
ограниченных и непрерывных fs{t) допускают только ограниченные
') См. работу, цитированную на стр. 368.
§ 89] СВЯЗЬ С КРИТЕРИЕМ ЛЯПУНОВА. ОБОБЩЕННЫЙ КРИТЕРИЙ 377
решения, то можно показать>), что выполняются условия теоремы 1,
а следовательно, также и теоремы 2.
Доказанными теоремами выделяется определенный класс линейных
дифференциальных уравнений с переменными коэффициентами. Эти
уравнения обладают тем свойством, что для них одновременно выпол-
выполняются условия всех трех теорем, причем если выполняются условия
хотя бы одной из этих теорем, то выполняются условия и двух дру-
других теорем: Из (88.5) вытекает, что все характеристичные числа этих
уравнений положительны.
Частным случаем такого рода уравнений являются уравнения
с постоянными коэффициентами, если вещественные части всех кор-
корней его характеристического уравнения отрицательны, и уравнения
с периодическими коэффициентами, если их характеристические
показатели также имеют отрицательные вещественные части2).
§ 89. Связь с критерием Ляпунова. Обобщенный критерий.
В предыдущем параграфе установлены три эквивалентных между
собой критерия устойчивости по первому приближению. Естественно,
возникает вопрос, будут ли указанные критерии эквивалентны кри-
критерию Ляпунова или они дают более широкие условия устойчивости по
первому приближению, или, напротив, более узкие условия. Ниже-
Нижеприводимые примеры показывают, что ни одно из этих предположе-
предположений неверно. Может случиться, что для системы первого прибли-
приближения выполняются условия Ляпунова и не выполняются условия
теорем предыдущего параграфа, и наоборот, существуют системы,
для которых выполняются условия указанных теорем и не выпол-
выполняются условия Ляпунова. Чтобы это показать, рассмотрим сначала
систему3)
^f = - B - sin [In (t -f-1)]) xx = pxv
dx2
dt ~Xl X2-
Эта система имеет положительные характеристичные числа, но
она не является правильной, так как выражение
t
1 J pdt = — 2 Н- -i- [sin In (/ -f-1) — cos In (^+ l)]-f
0
i 1-f slnln(f+l) — cosln(f+l)
-, _
') Малкин И. Г., Об устойчивости по первому приближению. Сб.
научных трудов Казанск. авиац. ин-та, № 3, 1935.
2) См. примечание в конце книги (стр. 528).
3) См. работу автора, цитированную в сноске ')•
378 НЕУСТАНОВИВШИЕСЯ ДВИЖЕНИЯ [ГЛ. VI
не стремится ни к какому пределу при t—*¦ уэ, что является (см. § 79)
необходимым и достаточным условием правильности такого рода
систем. Вместе с тем, производная от функции V = -^ (x^ -\- х2Х
составленная в силу этих уравнений, равная
—~TT l^ aul l11 \*- \^ * )\ л \ \^ л.Лп л-g
будет определенно-отрицательной, и следовательно, выполняются
условия теоремы 1, а также и двух других теорем предыдущего
параграфа.
Рассмотрим теперь систему1), состоящую из одного уравнения
dx I—\
-тг = — A -\- 2л cos у t)x = рх.
Так как
t
lim-j р dt = Mm -г \—^—4лсоэ ]/^—4u|/^sin ]/^ +4л] = — Г,
то система правильна и обладает положительным характеристичным
числом, равным единице. Следовательно, выполняются условия кри-
критерия Ляпунова. Вместе с тем легко показать, что для этого урав-
уравнения не выполняются неравенства (88.5) и, следовательно, критерии
предыдущего параграфа. Действительно, в рассматриваемом случае
х (t, t0) = exp [— (t — ^0) — 4л (cos Y t — cos V%) —
Полагая t0 = \2kn -f--g-] и t— Bйл-f-лJ > tQ, где k — целое
число, будем иметь:
xs {t, tQ) = exp [— DАя +1 л) -j + 4л + 4л Bйл + \)] > e^-^.
С неограниченным возрастанием й правая часть этого неравенства
неограниченно возрастает и, следовательно, условия (88.5) не выпол-
выполняются.
Приведем, наконец, еще один критерий устойчивости по первому
приближению, указанный автором2). Этот критерий утверждает, что
невозмущенное движение будет асимптотически устойчиво при любом
') Персидский К. П., К теории устойчивости интегралов систем
дифференциальных уравнений. Изв. физ.-матем. об-ва при Казанск. гос.
ун-те, т. VIII, 1936—1937.
2) М а л к и н И. Г., Об устойчивости движения по первому приближению.
ДАН, т. XVIII, № 3, 1938.
§ 90] ПОСТАНОВКА ЗАДАЧИ. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ 379
выборе функций (ps(t, xv . . ., хп), удовлетворяющих в области (88.2)
условию (87.4), если вместо неравенств (88.5), фигурирующих в тео-
теореме 2 предыдущего параграфа, будут выполняться при всех ta > 0
и t > t0 неравенства
1 SJ \ U/ I ^
где В и а — не зависящие от t0 положительные постоянные,
а 6 — также положительная постоянная, удовлетворяющая неравенству
Р<B/я — 1)а.
Г. ТЕОРИЯ КРИТИЧЕСКИХ СЛУЧАЕВ.
§ 90. Постановка задачи. Основные определения.
В предыдущем разделе установлен ряд теорем, дающих достаточ-
достаточные условия устойчивости по первому приближению. Эти условия,
являясь достаточными, не являются необходимыми, и поэтому при
невыполнении их еще не следует делать заключения, что для решения
задачи устойчивости необходимо исследовать члены более высоких
порядков в уравнениях возмущенного движения. Однако можно ука-
указать такие уравнения, для которых исследование членов более
высоких порядков является безусловно необходимым. Такими будут,
очевидно, уравнения следующего вида:
f ¦ • • +<7«У*+ Yi(t' У\ Ук' xv •••. хп),
dt ~
dxs . . . . , ,
-^- — Pslxl-r ••• ~irPsnXn-±rsiy1-\- ... ~rrskyk-j- ^goj^
(i=l, 2 k; s=l, 2, ..., n).
Здесь Yt и Xs—аналитические функции переменных ylt .... yk,
x: xn, разложения которых начинаются членами не ниже вто-
второго порядка. Коэффициенты этих разложений, а также коэффициенты
Яц< rsj и Psj являются непрерывными и ограниченными функциями
времени. При этом коэффициенты ps) таковы, что для линейной
системы
выполняется какой-нибудь критерий устойчивости по первому
приближению, так что для нелинейной системы, которая получится
из (90.2) путем прибавления нелинейных членов, зависящих только
от х1 хп, будет иметь место асимптотическая устойчивость.
В дальнейшем мы будем предполагать, что для системы (90.2)
380 НЕУСТАНОВИВШИЕСЯ ДВИЖЕНИЯ [ГЛ. VI
выполняются критерии § 88. Это будет необходимо для справедли-
справедливости излагаемых ниже результатов.
Коэффициенты qu, напротив, таковы, что задача устойчивости
для уравнений вида
4т = ЯпУ1 + • • • + qtkyk + Ф, (t, Уг yk), (90.3)
где ф^ — нелинейные добавки, зависящие только от уг ук, не
решается первым приближением. Таким будет, например, случай,
когда коэффициенты q-ц постоянны, а характеристическое уравнение
системы (90.3) имеет корни с вещественными частями, равными нулю,
и не имеет корней с положительными вещественными частями.
Все случаи, для которых задача устойчивости не решается чле-
членами первого порядка, мы будем называть критическими. В настоя-
настоящем разделе мы устанавливаем несколько основных предложений
общего характера о решении задачи устойчивости для критических
случаев и применяем затем эти предложения к некоторым крити'
ческим случаям для установившихся и периодических движений.
Отбросим в системе (и-)-&)-го порядка (90.1) последние п урав-
уравнений, а в первых k уравнениях отбросим все члены, зависящие
от хх, ..., хп, и рассмотрим полученную таким образом систему
k-ro порядка
^ М'. У1- ¦••¦ У». 0 0)
(/=1.-2 ft).
Эту систему мы будем в дальнейшем называть «укороченной».
Допустим, что задачу устойчивости для «укороченной» системы
удалось разрешить. Возникает вопрос: при каких условиях этим
самым решается задача устойчивости и для полной системы (90.1)?
В главе IV, где были рассмотрены два простейших критических
случая для установившихся движений, было показано, что в этих
простых случаях ответ на задачу устойчивости для полной системы
совпадает с ответом на задачу устойчивости для «укороченной»
системы, если последняя решается конечным числом членов и если
выполняются следующие условия: 1) все коэффициенты rsi равны
нулю; 2) разложения функций Xs(t, yv .¦. ., yk, 0, . . ., 0) начинаются
членами достаточно высокого порядка.
Это дало возможность свести решение задачи устойчивости пол-
полной системы к решению задачи для «укороченной» системы (состоя-
(состоящей в рассмотренных случаях из одного или двух уравнений) путем
преобразования полной системы к такому виду, для которого усло-
условия 1) и 2) выполняются. Эти результаты удалось, однако, получить
путем действительного решения задачи устойчивости для «укорочен-
«укороченной» системы и притом вполне определенным методом—построением
§ 90] ПОСТАНОВКА ЗАДАЧИ. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ 381
функций Ляпунова, причем это удалось сделать лишь тольку потому,
что для «укороченной» системы удалось построить функции Ляпу-
Ляпунова очень простого вида, а именно — целые рациональные. Исполь-
Использованные методы дали возможность надеяться, что аналогичные
результаты удастся получить и в других критических случаях, если
для «укороченной» системы удастся построить такие же простые
функции Ляпунова. Таким путем действительно удалось исследовать J)
некоторые критические случаи, не рассмотренные Ляпуновым. Однако
такой метод является очень неудобным и сложным, так как построе-
построение функций Ляпунова представляет иногда непреодолимые трудности,
даже в тех случаях, когда заранее известно решение задачи устой-
устойчивости для «укороченной» системы. Более того, нет вообще
уверенности, что такие простые функции Ляпунова действительно
существуют. Поэтому, естественно, возникает вопрос: всегда ли
вообще задача устойчивости для полной системы при выполнении
условий 1)и 2) решается «укороченной» системой? Можно показать2),
что ответ на поставленный вопрос получается всегда утвердительный,
если задача устойчивости для «укороченной» системы решается
конечным числом членов. Это предложение доказывается в следующем
параграфе. В § 92 показывается, что полная система может быть
всегда преобразована к такому виду, для которого условия 1)
и 2) выполняются. Результатами этих двух параграфов задача
устойчивости для системы (n-{-k)-ro порядка с k критическими
переменными всегда приводится к исследованию системы А-го порядка,
если задача решается конечным числом членов.
Последнее понятие требует уточнения. Рассмотрим произвольную
систему какого-нибудь г-го порядка
*i zr) (90.5)
A=1. 2 r).
определенную в области
*>0, | г, |< H. (90.6)
Здесь Z; —формы 1-го порядка переменных zb ..., zr, коэффи-
коэффициенты которых являются непрерывными и ограниченными функциями
времени, а ер(- обозначают совокупность всех членов порядка выше N.
Мы примем следующие определения.
') Малкин И. Г., Некоторые вопросы теории устойчивости движения
в смысле Ляпунова. Сб. трудов Казанск. авиац. ин-та, № 7, 1937; Камен-
Каменков Г. В., Об устойчивости движения. Сб. трудов Казанск. авиац. ин-та,
№ 9, 1939.
2) Малкин И. Г., Некоторые основные теоремы теории устойчивости
движения в критических случаях. ПММ, т. VI, вып. 6, 1942.
382 НЕУСТАНОВИВШИЕСЯ ДВИЖЕНИЯ [ГЛ. VI
Определение 1. Невозмущенное движение zx = z2= . . .—
= zr — 0 называется устойчивым вне зависимости от вида чле-
членов порядка выше, чем N, если для всякого положительного г,
как бы мало оно ни было, существует такое положительное
число т](е, А), зависящее только от г и А, что для всех решений
уравнений (90.5), начальные значения z°i которых в начальный
момент времени t = 0 выбраны согласно условиям
|*?|<т](е, А),
выполняются при всех t > 0 неравенства
при всяком выборе функций (pt(t, zx zT), удовлетворяющих
в области (90.6) условиям
Ш, г, zt)\<A\\Zl\+ ... + |z,|}"+1. -
где N — некоторая постоянная.
Определение 2. Невозмущенное движение zx = . . . = zr = 0
называется неустойчивым вне зависимости от членов порядка
выше, чем N, если при тех же условиях относительно функций ср;
существует положительное число е(А), зависящее только от А,
что внутри любой сколь угодно малой г\-ок реет нос ти точки
zx== ... = zr = 0 существует, по крайней мере, одна система
величин ах(А, ц), . . ., аг(А, ц), зависящих только от А и г\, что
хотя бы одна из величин \zt\ для решения уравнений (90.5),
определенного начальными условиями
достигает в некоторый момент времени значения г.
§ 91. Первая основная теорема о критических случаях.
Рассмотрим систему дифференциальных уравнений возмущенного
движения (п -\- k)-ro порядка следующего вида:
\+ ••• +PsnXn + Xs(t' У\ Ук- Х1 Хп)
(г=1, 2, .... k; s=\, 2, ..., п).
(91.1)
Здесь Уi и Xs— ряды по степеням переменных yv ..., -yk,
xv ..., х,г, сходящиеся в области
(91,2)
§ 91] ПЕРВАЯ ОСНОВНАЯ ТЕОРЕМА О КРИТИЧЕСКИХ СЛУЧАЯХ 383
и начинающиеся членами не ниже второго порядка. Коэффициенты
этих рядов, а также коэффициенты q^, rtj и psj суть ограниченные
и непрерывные функции времени. Коэффициенты psj таковы, что для
системы линейных уравнений (90.2) выполняются критерии устойчи-
устойчивости по первому приближению, установленные в § 88. Мы можем,
следовательно, предположить, что существует определенно-положи-
определенно-положительная квадратичная форма V(t, x1 хп) переменных xv .... х„,
коэффициенты которой являются ограниченными функциями времени,
для которой
.5 = 1 S=l
Для самой же формы V в силу ее знакоопределенности мы можем
писать
п
V(t, xx, .... .*:„)> а2 2 х\. (91.4)
5 = 1
где а—вещественная постоянная.
Рассмотрим далее «укороченную» систему
dyi , |^ _i у' ,, р. п\
= y°i(t. у, уk) (91.5)
(г=1, 2, .... k)
и докажем следующую теорему.
Теорема. Допустим, что невозмущенное движение ух=. . . =
= yk = Q для «укороченной» системы устойчиво или асимпто-
асимптотически устойчиво, или неустойчиво вне зависимости от чле-
членов порядка выше, чем N. Тогда, если разложения функций
Xs{t, уг yk, 0 0) начинаются членами порядка не ниже
N -\~ 1, то и невозмущённое движение уг = . . . = yk = хх =...=.-
= хп = 0 для полной системы (91.1) соответственно устой-
устойчиво, асимптотически устойчиво или неустойчиво !).
Доказательство. 1°. Для упрощения доказательства2) мы
сделаем относительно уравнений (91.1) некоторые дополнительные
ограничения. Мы предположим, прежде всего, что все коэффициенты г-^
- •. ') См. примечание в конце книги (стр. 529).
2) Это упрощение сделано В. Н. Постниковым (Постников В. Н.,
К теории устойчивости движения в критических случаях. Диссертация, 1942).
Он же исправил и неточность в формулировке теоремы, данной в работе
автора (см. сноску 2) на стр. 381), где вместо условия, что разложения функ-
функций Xs(t, уь ..., Уи, 0, ..., 0) начинаются членами не ниже (Л^-)-1)-го
порядка, указывалось, что это разложение должно начинаться членами
не ниже Л^-го порядка.
384 НЕУСТАНОВИВШИЕСЯ ДВИЖЕНИЯ [ГЛ. VI
равны нулю. Это ограничение не существенно, и его легко добиться
простым преобразованием переменных. Второе ограничение заклю-
заключается в следующем.
Так как коэффициенты qtj ограничены, то мы можем писать:
(91.6)
где Ъ — некоторая вещественная постоянная. Мы будем предполагать,
что эта постоянная настолько мала, что квадратичная форма
п
— ^x2s-\-2Nb2V (91.7)
5=1
определенно-отрицательна. Как мы увидим ниже, во всех тех слу-
случаях, для которых мы будем применять теорему, это ограничение
будет выполняться.
При этом ограничении, мы можем писать неравенство
dV * *
п
^1, (91.8)
где а — вещественная постоянная, справедливое при любых значениях
/^0, у1 и xs. Действительно, в силу (91.3) и (91.6) левая часть
этого неравенства не превосходит формы (91.7), которая, по усло-
условию, определенно-отрицательна.
Сделаем теперь преобразование переменных !)
(91.9)
Тогда первая группа уравнений (91.1) примет вид
^ = Г?(/, У1 У*)+г"ад у, у„, |х 1п) (91.10)
(/=1. 2 ft).
где функции Чг/ в силу сделанного предположения, что все коэф-
коэффициенты Гц равны нулю, удовлетворяют тождествам
?,(<¦ 0 0. \х |я) = 0 «=1,2 к). (91.11)
') См. примечание в конце книги (стр. 529).
§ 91] ПЕРВАЯ ОСНОВНАЯ ТЕОРЕМА О КРИТИЧЕСКИХ СЛУЧАЯХ 385
Для второй группы уравнений (91.1) имеем:
s(t> УI У*. hrN
или, принимая во внимание, что разложения функций Xs(t, yv ...,
ук, 0 0) начинаются членами не ниже (/V-J- 1)-го порядка,
п
2 У* ^iiVi + ¦¦¦ + ЯНгУк
%-=Ps&+ ••• +Psnin-ms— 72 ь
t. У! У*. lt ln)> (91-12)
где функции 3S также удовлетворяют тождествам
Ss(/, 0 О, |х ?„) = ° (s=l, 2 л). (91.13)
2°. Пусть е < Н — произвольное положительное число. Обозначим
через | наибольшую из величин ||J, а через /(е) — некоторое отлич-
отличное от нуля положительное число, меньшее точного нижнего предела
формы V при условии #>|^е. В силу (91.4) такое число /(е)
существует. Итак,
VV.li ln)>l(e)>0 при Я>?>е. (91.14)
Рассмотрим теперь множество всевозможных значений переменных
|j \п, связанных соотношением
V(f, |t ln) = l{&). (91.15)
Для этого множества выполняется, очевидно, неравенство ||5| <е.
Кроме того, так как коэффициенты формы V ограничены, то будет
также выполняться условие
я
2 ll>^^) ПРИ V(t, \х 1п) = 1(г), (91.16)
где ^-2(е) — достаточно положительное число.
Установив это, вычислим производную от функции V (t, |j ln)
по времени в силу уравнений (91.12) при условии (91.15). Будем
иметь:
(dV_) _ | dV_
• • * П^ Fsnbn iybs * = 1
386 НЕУСТАНОВИВШИЕСЯ ДВИЖЕНИЯ (гл. VI
Но на основании (91.8) и (91.16)
dV „ ,. .. . . \\
i ln)\ ¦ (91-17)
\v=i
Поэтому, принимая во внимание тождества (91.13), мы видим, что
всегда найдется такое положительное число h (е) (зависящее только
от е). что при всех значениях величин \yt\, удовлетворяющих нера-
неравенствам |У/|^А(е), выражение (91.17) будет отрицательным. Мы
будем предполагать, что во всяком случае А(е)<е. Таким образом,
Уг|<А(е)<е> (91Л8)
Построенные в этом пункте области и поверхности, их ограни-
ограничивающие:
= Я.2(е). у = А@, V(t, |, lj =
yj| \yk\),
для наглядности дальнейших рассуждений полезно изобразить схема-
схематически так, как это сделано на рис. 20. Здесь вертикальная ось
изображает ^-мерное многообразие точек, где х1 = ... =хл = 0,
У[ — любые, а горизонтальная ось — л-мерное многообразие, где
уг~ ... :=Уй = О, xs — любые.
Подчеркнем следующее важное обстоятельство. Поверхность
V(t, 1г |я) = ;(е) охватывает многообразие хх = ... =хл = 0,
которое, таким образом, оказывается внутри полости, ограниченной
этой поверхностью. Поверхности V(t, \lt ..., |я) —/(е), у = к(г)
в совокупности ограничивают некоторые замкнутые полости. Вслед-
Вследствие неравенства (91.18) интегральные кривые xs(t), yt{t) систе-
системы (91.1) пересекают при этом поверхность V (t, |j ?„) = /(е)
внутрь, т. е. в сторону убывания функции V. При этом число А(е)
будем считать столь малым, что область у <; А (е), V {t, l,x \п) ^ 1{г)
лежит в области | xs | < е.
3°. Допустим сначала, что для «укороченной» системы невозму-
невозмущенное движение устойчиво. Покажем, что тогда и для полной си-
системы невозмущенное движение будет также устойчиво. Заменим
с этой целью в уравнениях (91.10) величины |5 произвольными функ-
функциями времени, удовлетворяющими при всех / ^- 0 неравенствам
|У<Я (s=l, 2 я). (91.19)
Тогда получим систему уравнений
). (91.20)
§ 91]
ПЕРВАЯ ОСНОВНАЯ ТЕОРЕМА О КРИТИЧЕСКИХ СЛУЧАЯХ
387
где Yf® — формы /-го порядка переменных ух yk, представляю-
щие собой совокупности членов Z-го порядки в разложениях функ-
функций ку»(/, у, ук) и
В силу (91.11), очевидно, имеем:
... +\yk\}
N+1
(91.21)
где А — некоторая постоянная, зависящая, очевидно, только от струк-
структуры уравнений (91.10) и не зависящая от того или иного частного
Рис. 20.
выбора функций \s. Согласно условию об устойчивости для «укоро-
«укороченной» системы вне зависимости от членов порядка выше ./V суще-
существует положительная постоянная Ьх (h (e), А), такая, что все решения
уравнений (91.20), удовлетворяющие в начальный момент / —0
условиям
|у?|<6,(А(е). А) (91.22)
будут при всех /> 0 удовлетворять условиям
|У|@| <А(е). (91.23)
При этом постоянная 6i будет зависеть только от А(е) и, сле-
следовательно, в конечном счете только от е, т. е. Ь1 = 6j (e),
388 НЕУСТАНОВИВШИЕСЯ ДВИЖЕНИЯ [ГЛ. VI
Допустим теперь, что в уравнениях (91.10) величины ^ заме-
заменены функциями времени, удовлетворяющими неравенствам (91.19) не
при всех значениях /, а только при значениях /, не превосходящих
некоторого числа Т. Тогда все решения уравнений (91.20), удовлетво-
удовлетворяющие начальным условиям (91.22), будут удовлетворять неравен-
неравенствам (91.23), по крайней мере, при всех значениях /, лежащих на
отрезке [0, Т].
В самом деле, пусть %s = fs(f) будут указанные функции. Заме-
Заменим в уравнениях (91.10) величины \s функциями \s — ys{t), опреде-
определенными следующим образом:
Ф,(') = /,Ю при 0<*<7\
(fs (t) = ф5 (Г) = const при t > Т.
Тогда уравнения (91.10) примут вид
?h. = Kf) + .. . + ПОЛ0 + К {*• Ух У*)- (91-24)
причем
Так как функции фл(/) удовлетворяют условиям (91.19) при всех
t^-0, то для всех решений уравнений (91.24), для которых спра-
справедливо (91.22), будет при всех />0 выполняться (91.23). Но реше-
решения уравнений (91.24) на отрезке [0, Т] совпадают с решениями
уравнений (91.20), и мы, следовательно, приходим к следующему
выводу: если в уравнениях (91.10) заменить все величины ^ произ-
произвольными функциями времени, удовлетворяющими на отрезке [0, Т]
условию (91.19), то все решения полученной таким образом системы
уравнений, удовлетворяющие начальным условиям (91.22), будут на
отрезке [0, Т] удовлетворять неравенствам (91.23). Если условия
(91.19) выполняются при всех t ^>0, то и неравенства (91.23) будут
выполняться при всех />- 0.
Рассмотрим теперь произвольное решение |j {f) ?л@>
yj(/) yn(t) уравнений (91.10) и (91.12), для которого в началь-
начальный момент t = 0 выполняются условия
s\ |У?|<*Г (s=l.2 я;/=1, 2. .... ft). (91.25)
Мы будем при этом предполагать, что
T|<oi(e) (91.26)
и что постоянная т) настолько мала, что выполняется неравенство
V{0. Щ |°)<*(е). (91.27)
§ 91] ПЕРВАЯ ОСНОВНАЯ ТЕОРЕМА О КРИТИЧЕСКИХ СЛУЧАЯХ 389
Покажем, что все функции |Д/) и yt(t) будут при всех />0
удовлетворять неравенствам
1б,(О|<е. (91.28)
М*)|<е. (91.29)
Рассмотрим сначала функции \s. Для этих функций условия (91.28),
выполняясь при t = 0, будут выполняться при /, достаточно малом.
Пусть Т—первый момент времени, для которого |=тах{||1|, .. .
'. .., Цл|}=е. Тогда на основании (91.14) будем иметь:
V[T, 6,(Г) 1„(Т)]>1(г).
Отсюда на основании (91.27) заключаем, что в интервале (О, Т)
должен существовать такой момент времени / = Т'', что одновре-
одновременно будут выполняться условия
w\ -г^° при * = т'- (91.30)
Но во всем интервале @, Т), несомненно, выполняется условие
(91.19). Следовательно, на основании предыдущего во всем этом
интервале будут выполняться неравенства (91.23), так как число т)
выбрано согласно (91.26), а функции уг(/) будут, очевидно, одним
из решений уравнений (91.20), которые получатся из (91.10), если
в последних величины h,s заменить рассматриваемыми сейчас функ-
функциями |5(/). Поэтому на основании (91.18) во всем интервале @, Т)
будет выполняться неравенство
что противоречит (91.30).
Таким образом, приходим к заключению, что неравенства (91.28)
будут выполняться при всех t > 0. Но тогда при всех t > 0 будут
выполняться и неравенства (91.23), а следовательно, и подавно не-
неравенства (91.29), так как /г(е)<е. Следовательно, невозмущенное
движение устойчиво по отношению к переменным |lf ..., |я, ух yk.
Таким образом установлен следующий факт. Траектория xs{t),
yt(t) системы (91.1), начавшаяся в любой точке N(xs(t0), yt{t^)
в области |уг(/0)|^тЬ |ij|^Tl- He покидает область, ограниченную
поверхностями
у = А(е), V{t, I, &„) = /(е)
(см. рис. 20). При этом величины \s(t) при всех t^>t0 не прево-
превосходят Н и, следовательно, использование в рассуждениях преобра-
преобразования (91.9) является законным. Итак, пока доказана лишь услов-
условная устойчивость решения xs — 0, yt = 0 относительно возмущений
xs(t$, yi (t0) из области V (t0, |i y<i (e). Поэтому для
390 НЕУСТАНОВИВШИЕСЯ ДВИЖЕНИЯ [ГЛ. VI
завершения доказательства первого утверждения теоремы следует еще
показать, что из такой условной устойчивости в данном случае выте-
вытекает устойчивость движения xs = 0, yi = 0 при любых малых возму-
возмущениях xs(t0), i>i(t0) из полной окрестности1) точки х5 = 0, уг = 0.
Сделаем это. Вернемся снова к записи уравнений возмущенного
движения в форме (91.1). Рассмотрим поверхности
V(t, Xl, .... xn) = S.
Это — цилиндрические поверхности в пространстве {х^, yt}, охва-
охватывающие многообразие хх = ... = хп = 0 (см. рис. 20). Рассма-
Рассматриваемые поверхности перемещаются со временем, но для любого
S > 0 можно указать два числа juij (S) и n2(S)(|i,j < ц2) таких,, что
при всех / поверхность V(t, Xj xn) — S лежит между поверх-
поверхностями х = ^E), х—Иг(?) (х = тах(|х1| |хя|)> причем
lim|х2 = lim [Xj = 0 при S -*¦ 0. Это обстоятельство является следствием
того, что квадратичная форма V определенно положительна и допу-
допускает бесконечно малый высший предел.
Теперь можно выбрать достаточно малое положительное число 5 (е),
которое удовлетворяет следующим трем условиям:
1) число ц2[5(е)]<е;
2) при 5<^5(е) поверхности V(t, хг xn) = S пересекаются
с поверхностью 2^ —^2(е) (а следовательно, и с поверхностью
V (t, |j, .. ., |„) = / (е)) при
Ы<*1(е): (а)
3) на поверхностях V{t, xv .... xn) = S при 5-^5(е) и при
условии
5С5 *>
выполняется неравенство
dt ^ '
где —тт производная функции V в силу уравнений (91 Л).
Действительно, первбе и второе условия удовлетворяются при
малом S(г) потому, что при 5—>0 поверхности V(t, x1 xn) = S
равномерно стягиваются к многообразию Xj — ... = хп — 0. Третьему
условию можно удовлетворить по свойствам функций Xs(t, yv ...
.... yk, xv ..., xn) в уравнениях (91.1). В самом деле, разложе-
') На это существенное обстоятельство обратил внимание Н. П. Еругин.
См. его рецензию о книге И. Г. Малкина «Теория устойчивости движения»
В Вестнице ЛГУ № 5, J953r
§ 91] ПЕРВАЯ ОСНОВНАЯ ТЕОРЕМА О КРИТИЧЕСКИХ СЛУЧАЯХ 391
ние функции Xs(t, ух ук, 0 0) начинается членами по-
порядка не ниже (Л^-f-1), поэтому при условии (р) и при достаточно
где постоянная a > 0 сколь угодно мала, если величины xs доста-
достаточно малы. Из условия (у) обычными приемами выводится неравен-
неравенство —тг < 0, на чем мы останавливаться не будем.
Итак, пусть выбрано число 5(е)>0, удовлетворяющее указан-
указанным условиям 1), 2) и 3). Выберем число ц > 0 так, чтобы помимо
условий (91.26) и (91.27) это число еще удовлетворяло следующему
требованию: область |jCj|-^/r) должна лежать внутри поверхности
V(t, xv ..., xn) = S(e), т. е. должно быть V(t, xt хп) < 5(е)
при |xs|<;ti.
Покажем, что при условиях |хД/0)|^т], ly^o)!^1! выполня-
выполняются неравенства |хД0|<е> |У;@|<е для всех t^>t0. В самом
деле, выше уже показано, что указанные неравенства выполняются,
если начальное возмущение лежит в области V(t, \x, .... ?„)^/(е).
Пусть теперь начальное возмущение этому условию не удовлетво-
удовлетворяет. По выбору числа т) и по предыдущим построениям в таком
случае заключаем, что точка xs (t0), yt (t0) (назовем ее Q) лежит
в области, ограниченной поверхностями .-
V(t, xv .... *„) = 5(е) (при V<S(fi)),
V(t, $г и = Цг) (при V
dV
(см. рис. 20). Вследствие неравенства —тг < 0 траектория xs(t),
yt{t) при t^-tQ может покинуть эту область лишь через поверх-
поверхность V(t, ?1( ..., ?л) = /(е). Следовательно, либо траектория xs(t),
yt (f) все время остается в указанной области и тогда по построе-
построению ее все время |л^(/)|<е, |уД0|<е (и, более того, xs(t)->0,
yi(t)-->0), либо, начиная с какого-то момента, траектория xs(t),
у lit) попадает в область V{t, \v ..., |л)-^/(е) и при этом обя-
обязательно при \yl\<ibl(z). Но в таком случае уже по доказанному
выше траектория xs{t), yt(t) в дальнейшем все время остается в
области y^.h(e), V(t,lx, .... |л)^/(е), причем также выполняются
неравенства |xs(?)|< e, |.V/(/)|< е. Тем самым устанавливается устой-
устойчивость решения ^ = 0, у; = 0и завершается доказательство первого
пункта теоремы.
4°. Допустим теперь, что для «укороченной» системы получается
асимптотическая устойчивость. Покажем, что невозмущенное движе-
движение для полной системы будет также асимптотически устойчиво.
Рассмотрим с этой целью произвольное решение |Д/), yt(t) урав-
уравнений (91.10) и (91.12) с начальными значениями, удовлетворяющими
392 НЕУСТАНОВИВШИЕСЯ ДВИЖЕНИЯ [гЛ. VI
неравенствам
1Й| 1?1
где число т) достаточно мало. На основании доказанного тривиальное
решение |t = ... = |„ = У\ = ¦ ¦ ¦ = Ук = 0 устойчиво, и поэтому
функции ^(/) будут во всяком случае удовлетворять неравенствам
(91.19) при всех f>0. Но тогда согласно условию все решения
уравнений (91.20), которые получим, если в уравнениях (91.10) за-
заменим все величины ls функциями ls(t), будут удовлетворять ус-
условиям
если только начальные значения этих решений численно достаточно
малы.-Но одним из этих решений будут, очевидно, функции yt(t).
Следовательно, если число ц выбрано достаточно малым, то все
функции уi{t) при неограниченном возрастании / будут стремиться
к нулю. Покажем, что то же самое будет и для функции \s(t).
Рассмотрим произвольное сколь угодно малое положительное
число I и покажем, что всегда найдется такой момент времени,
начиная с которого будет все время выполняться неравенство
V[t, hit) lnit)]<l, (91.31)
т. е. что
WmV[t, hit) ?„(91 = 0. (91.32)
/->-оо
С этой целью заменим в уравнениях (91.12) величины yt функ-
функциями у,: it) и найдем выражение полной производной по времени от
формы V it, \i, . >. i 1„) в силу полученных таким образом уравне-
уравнений
2
%- = Pslll + • • • + Psnln - Nls— ТЩ Ь
*. yxit) ykif), &„..., у, (91.33)
одним из решений которых будут функции ^(/). Будем иметь:
-%+1тЬ(*ь+¦¦¦+'•*•-
§ 91] ПЕРВАЯ ОСНОВНАЯ ТЕОРЕМА О КРИТИЧЕСКИХ СЛУЧАЯХ 393
Рассмотрим совокупность значений переменных |s, удовлетворяю-
удовлетворяющих неравенствам
V(t. U !„)>/, |&,|<Я. (91.34)
Для этой совокупности будет выполняться условие
<2&
где № — некоторое положительное число. Поэтому на основании
(91.8) находим, что при условии (91.34) будет выполняться также
условие
п
^Щ,Ц. МО, •••• У*@. lv ¦¦¦• U-
С другой стороны, функции ys(t) стремятся к нулю при t->co.
Поэтому на основании (91.13) всегда найдется такой момент времени
/==7\ что будет выполняться условие
(91.35)
для всех решений уравнений (91.33) и, в частности, для \s = \s(f).
Отсюда следует, что если для какого-нибудь решения уравнений
(91.33) будет выполняться неравенство (91.31) в какой-нибудь мо-
момент времени / = Г'>7\ то это неравенство будет для него выпол-
выполняться при всех t > V'. Допустим, что такого момента времени для
решения l,s (/) не существует, т. е. что при всех / > Т будет
Так как при этом ЦДО!^^ т0 из
t+т .
V[t, l,(t) ln(f)] = V[T, Ы7) |„(Л1+J ^f
т
будем на основании (91.35) иметь:
„212
V\t, l^t). .... ln(t)]<V[T, ЫТ), .... 1(Г)]**
-у-Т).
Однако последнее неравенство не может выполняться при всех
/ > Т, так как форма V положительна. Таким образом, приходим
к заключению, что всегда наступит такой момент времени, начиная
с которого будет выполняться неравенство (91.31). Это, однако,
эквивалентно (91.32), откуда в силу (91.4) находим:
=l, 2 п).
394 НЕУСТАНОВИВШИЕСЯ ДВИЖЕНИЯ [ГЛ. VI
Следовательно, невозмущенное движение для полной системы
асимптотически устойчиво относительно переменных ls и yt.
Теперь, как и выше, для завершения доказательства достаточно
показать, что невозмущенное движение xs—0, У( = 0 асимптоти-
асимптотически устойчиво не только относительно возмущений xs(t0), у? (^0),
стесненных условиями |?s(^o)|<T)> н0 и относительно любых доста-
достаточно малых начальных возмущений xs(t0), у^ (^о)- Это доказатель-
доказательство, однако, в точности повторяет те рассуждения, которые были
приведены выше при доказательстве первого пункта теоремы. По-
Поэтому здесь на этом рассуждении останавливаться не будем.
5°. Допустим, наконец, что для «укороченной» системы имеет
место неустойчивость, и покажем, что то же самое будет справед-
справедливо и для пояной системы.
Рассмотрим снова систему (91.20), которая получается из системы
(91.10) заменой величин ^ произвольными функциями времени, удо-
удовлетворяющими при всех t^O неравенствам (91.19). По условию
найдется число е > 0 такое, что как бы мало ни было число т|,
существует система величин Pj (т)) РаОт)» Для которых |Р;|^т|,
и при этом для решения уравнений (91.20) с начальными условиями
уО = р. будет в некоторый момент времени t — Т выполняться ус-
условие
.... \ук(Т)\] =А(е), (91.36)
где h (е) — величина, фигурирующая в (91.18).
При этом величины рг зависят тольчо от ц и не зависят от
выбора функций |5, лишь бы они удовлетворяли неравенствам
(91.19).
Рассмотрим теперь полную систему уравнений (91.1) и допустим,
что вопреки утверждению невозмущенное движение устойчиво. Тогда
существует такое число т), что для всех решений этих уравнений,
для которых начальные значения удовлетворяют неравенствам
|У?|<т|. KK1!- (91.37)
будут при всех / > 0 выполняться неравенства
|У/|<А(е)<е, |*,|<А(е)<е. (91.38)
Из всех этих решений выделим какое-нибудь одно yt (t), xs (t), для
которого y°i = (>i> x°s==as' где as — некоторые постоянные, выбран-
выбранные настолько малыми, чтобы для переменных c,s, определяемых
преобразованием (91.9), в начальный момент времени выполнялось
неравенство
V@, ?»,.... &°)</(е). (91.39)
§ 92] ВТОРАЯ ОСНОВНАЯ ТЕОРЕМА О КРИТИЧЕСКИХ СЛУЧАЯХ 395
Тогда из (91.18) вытекает, что при всех f>0 переменные |5
для рассматриваемого решения будут удовлетворять неравенству
V[t. !,(/), .... ln{t)\<U
из которого на основании (91.14) вытекает, что |^(^)|<е и, сле-
следовательно, при / ^ 0 будут во всяком случае выполняться усло-
условия (91.19)
Будем теперь считать, что уравнения (91.20) получились из (91.10)
заменой величин ^ функциями \s(t), соответствующими рассматри-
рассматриваемому решению. Тогда решение этих уравнений с начальными
условиями у°.=:$. даст как раз функции y{(t), во всяком случае
до тех пор, пока |у,(/)| ^Л(е). Но для этого решения выполнено
условие (91.36), так как функции l,s(t) удовлетворяют, по доказан-
доказанному, (91.19). Это, однако, противоречит (91.38). Полученное про-
противоречие и доказывает неустойчивость невозмущенного движения.
Таким образом, теорема полностью доказана.
§ 92. Вторая основная теорема о критических случаях.
Рассмотрим теперь систему уравнений возмущенного движения
вида
dy.
-jj- = Y( (t, yv .... yk, Xj xn),
dxs
dt
t, у, yk, xx xn)
(i= 1, 2 k; s— 1, 2 л),
(92.1)
где Yt и Xs— ряды по степеням переменных уг yk, xv .. ., xn,
начинающиеся членами не ниже второго порядка и сходящиеся
в области (91.2). Коэффициенты этих разложений, а также коэффи-
коэффициенты psj и rSj являются непрерывными и ограниченными функ-
функциями t. При этом, как и в предыдущем параграфе, предполагается,
что для системы линейных уравнений
X
=l,2 п) (92.2)
выполняются условия устойчивости по первому приближению, уста-
установленные в § 88.
Для возможности применения к уравнениям (92.1) теоремы пре-
предыдущего параграфа необходимо, очевидно, привести эти уравнения
к такому виду, для которого разложения функций
396
неустановившиеся движения
[гл. vl
начинались бы членами достаточно высокого порядка. С этой целью
положим:
x* = ls+«s(t' У1. •••• Ук) («=1. 2 я). (92.3)
где us—целые рациональные функции переменных yv ..., yk, коэф-
коэффициенты которых являются ограниченными функциями времени.
Тогда уравнения (92.1) примут вид
dt
где
yv
yk.
ук,
(92.4)
При этом имеем:
(*. yt Ук> 0 0)
(=1
-+- ••• +ЛА +
yi у*. «1 «„) —
1' ••- У*. «1 «»)• 02.5)
Задача заключается, следовательно, в таком выборе функций
tts(t, уг ук) чтобы разложения выражений (92.5) начинались
членами достаточно высокого порядка. Рассмотрим для этого систему
уравнений с частными производными
i
к, «1 ип) (96.6)
(s=l, 2 п)
и попытаемся удовлетворить этим уравнениям формальными рядами
вида
••• (92-7)
§ 92] ВТОРАЯ ОСНОВНАЯ ТЕОРЕМА О КРИТИЧЕСКИХ СЛУЧАЯХ 397
где иEт> — формы т-го порядка переменных ух yk с ограничен-
ограниченными коэффициентами. Подставляя эти ряды в (92.6), приравнивая
члены первого порядка и учитывая, что разложения функций Y\ на-
начинаются членами не ниже второго порядка, найдем:
Аналогично приравнивая члены /м-го порядка, получим:
ди{т)
Am)+ +
W n T){t- Уi У,) (92-9)
(ж = 2. 3, ...).
где Us—некоторые формы /я-го порядка переменных yl yk,
зависящие от тех и</\ для которых j < т. Если все формы и'у> при
j < т уже вычислены и вышли с ограниченными коэффициентами, то
формы t/im) будут известными и будут также обладать ограничен-
ограниченными коэффициентами.
Уравнения (92.8) и (92.9) служат для последовательного опреде-
определения форм и^ш). Если мы вычислим все эти формы до какого-нибудь
заданного порядка N включительно, то, положив в подста-
подстановке (92.3)
(!> +и
мы приведем уравнения (92.1) к виду (92.4), для которого разложе-
разложение функций Es (/, ух, .. ., yk, 0, ..., 0) начинается членами не ниже
(Л/-)-1)-го порядка. Уравнения (92.4) будут, следовательно, иметь
нужный вид.
Переходим к вопросу о вычислении форм и^т\ Полагая
будем, очевидно, иметь:
(s=l, 2 n), (92.10)
где С^ m^ будут известными функциями времени, если формы
и'1', кB), .... и^т-1) уже вычислены. Эти коэффициенты будут притом
ограниченными функциями времени, если такими вышли коэффициенты
форм «A) а^"). Но при т1 -(-... + та= 1 каждая из функ-
функций С^»'"" т"\ совпадающая, как это следует из (92.8), с одним из
398 НЕУСТАНОВИВШИЕСЯ ДВИЖЕНИЯ [ГЛ. VI
коэффициентов rsl, будет известной и ограниченной. Отсюда следует,
что из уравнений (92.8) и (92.9) можно последовательно определять
формы u,W нужного вида, если только уравнения
(92.11)
допускают ограниченные решения при любом выборе ограниченных
и непрерывных функций fs{t). Но так как для уравнений (92,2)
выполняются критерии § 88, то, как было показано в этом параграфе
(критерий О. Перрона), все решения уравнений (92.11) ограничены.
Таким образом, существует бесчисленное множество разложений (92.7)
с ограниченными коэффициентами, формально удовлетворяющими
уравнениям (92.6). Для нашей цели пригодно любое из этих разло-
разложений. И так как нам нужно лишь конечное число членов в этих
разложениях, то вопрос о их сходимости не представляет для нас
интереса.
Итак, допустим, что в качестве функций as в преобразовании (92.3)
взяты первые N членов разложений (92.7). Отбросим в правых частях
первой группы уравнений (92.4) все члены, содержащие |j |я,
и рассмотрим полученную таким образом «укороченную» систему
= Щ* Ух У*) = У7('' У1 У*- «1 «») 02.12)
(/=1. 2 АО-
Допустим, что число N выбрано настолько большим, что невозму-
невозмущенное движение у1 = ... = yk = Q системы (92.12) устойчиво либо
асимптотически устойчиво, либо неустойчиво при любом выборе чле-
членов порядка выше, чем ЛЛ Тогда на основании теоремы предыдущего
параграфа невозмущенное движение для системы (92.4) будет соот-
соответственно устойчиво, асимптотически устойчиво или неустойчиво. То
же самое будет справедливо и для исходной системы (92.1), так как
по свойству преобразования (92.3) устойчивость по отношению к пере-
переменным yt и |4 равносильна устойчивости по отношению к перемен-
переменным yt и xs.
Так как
Щ- Ух у*)=к/С- vv •••¦ у*- "i »»)•
то полученный результат приводит к следующей теореме:
Теорема. Допустим, что дифференциальные уравнения
возмущенного движения имеют вид (92.1). Составим систему
уравнений с частными производными (92.6), которой всегда
можно удовлетворить формальными рядами вида
«,=S 41 "¦
§ 92] ВТОРАЯ ОСНОВНАЯ ТЕОРЕМА О КРИТИЧЕСКИХ СЛУЧАЯХ 399
с ограниченными коэффициентами. Подставим эти ряды
вместо величин xs в первую группу уравнений системы (92.1),
после чего они примут вид (92.12), где К? — формальные ряды,
расположенные по степеням yv ..., yk с ограниченными коэф-
коэффициентами.
Тогда, если невозмущенное движение ух = ... =yft = 0 для
системы (92.12)z) устойчиво или асимптотически устойчиво,
или неустойчиво, и это определяется произвольным, но конеч-
конечным числом N первых членов, вне зависимости от членов более
высокого порядка системы (92.12), то невозмущенное движе-
движение ух = ... = yk = хх = ... = хп = О для системы (92.1) соот-
соответственно устойчиво, асимптотически устойчиво или не-
неустойчиво.
При практическом применении теоремы необходимо задаться
числом N. Очевидно, что увеличение числа N не изменит в уравне-
уравнениях (92.12) членов порядка, не превосходящего первоначального
значения N. Поэтому при выполнении вычислений следует сначала
положить N = I, a затем если в этом будет необходимость, это число
увеличивать. При этом само собой разумеется, что общее решение
линейной системы (92.2) предполагается известным, что соответствует
существу задачи. Тогда решение уравнений (92.10) приведется
к квадратурам.
Примечание. Допустим, что в уравнениях (92.1) все коэф-
коэффициенты rsj равны нулю и что разложение функций Xs (t, yv ...
.. ., yk, 0 0) начинается членами p-ro (р > 1) порядка. Тогда, как
легко видеть, можно считать, что разложение функций us(t, yv ..., ук)
начинается членами также р-го порядка. Допустим, что наинизший
порядок членов, зависящих от хх, .... хп, в разложениях функций
Yt(t, yv .... yk, xx х„) есть q, а наинизший порядок этих
членов относительно хх хп есть r^.q. Тогда очевидно, что
в «укороченной» системе уравнений (92.12), которая решает задачу
устойчивости, влияние второй группы уравнений (92.1) скажется лишь
на членах порядка, не ниже чем q—г-\-рг. Поэтому, если задача
устойчивости для «укороченной» системы решается членами порядка,
не выше чем N, то вторая группа уравнений не будет иметь влияния
на ответ и может быть отброшена, если выполняется условие
p>N+1~9 + r . (92.13)
Отсюда следует, что когда правые части первой группы уравне-
уравнений (91.1) не содержат линейных членов, то основная теорема преды-
') То есть тех уравнений, которые получатся из уравнений (92.12), если
в последних взять произвольно большое, но конечное число членов.
400 НЕУСТАНОВИВШИЕСЯ ДВИЖЕНИЯ [ГЛ. VI
дущерв параграфа #етанется в силе, если наименьший порядок р
членов разложений функций Xs(t, ух yk, 0 0) удовлетворяет
не условию р^> N-\- 1, а условию (92.13), которое может оказаться
значительно слабее.
§ 93. Случай, когда коэффициенты линейных членов постоянны.
Приложение к установившимся и периодическим движениям.
Мы предполагали в предыдущем параграфе, что разложения пра-
правых частей первой группы уравнений (92.1) не содержат линейных
членов. Однако многие критические случаи приводятся к исследова-
исследованию систем вида
dyt
dxs _ ,
dt ~~ Psl l ~*~ ш '
t, ух yk, xv .... х„)
(/=1, 2, .... k; s=l, 2 n),
(93.1)
отличающихся от (92.1) наличием в первой группе уравнений линей-
линейных относительно yt членов. Наличие этих членов не препятствует
применению теоремы § 91, так как эти члены содержатся в уравне-
уравнениях (91.1), к которым эта теорема относится. Однако эти члены
мешают привести систему (92.1) к виду (91.1), т. е. уничтожить во
второй группе уравнений этой системы все не зависящие от xt х„
члены до достаточного высокого порядка.
Действительно, поступая так же, как в предыдущем параграфе,
т. е. делая замену переменных
*('¦ У\ У*) =
и стараясь подобрать функции us так, чтобы уничтожить вышеука-
вышеуказанные мешающие члены, мы придем вместо уравнений с частными
производными (92.6) к уравнениям
yk>Ul
У\ h- U\
§ 93] СЛУЧАЙ, КОГДА КОЭФФИЦИЕНТЫ ЛИНЕЙНЫХ ЧЛЕНОВ ПОСТОЯННЫ 401
Тогда уравнения, определяющие формы и№\ примут вместо (92.9)
более сложный вид
да<т) ^
„Г jr i!- У. Уи) (93.4)
(s=l, 2 и).
Вопрос о возможности удовлетворения уравнениям (93.4) формами
с ограниченными коэффициентами представляет в общем случае боль-
большие трудности. Но если такие формы существуют и уравнениям (93.3)
можно, следовательно, удовлетворить формальными рядами
— (93-5)
(s=l, 2 п)
с ограниченными коэффициентами, то все результаты предыдущего
параграфа сохраняют силу. В этом случае задача устойчивости будет
решаться первой группой уравнений (93.1), в которых величины xs
должны быть заменены функциями us, т. е. формальными рядами (93.5).
Таким образом, вопрос о применимости к уравнениям (93.1) основ-
основной теоремы предыдущего параграфа сводится к выяснению возмож-
возможности удовлетворения уравнениям (93.3) формальными рядами с огра-
ограниченными коэффициентами, или, что то же самое, к вопросу о суще-
существовании форм с ограниченными коэффициентами, удовлетворяющих
уравнениям вида (93.4). Этот вопрос легко разрешается в случае,
когда все коэффициенты qtj и rsj являются постоянными. К этому
важному случаю, охватывающему все критические случаи устано-
установившихся и периодических движений, мы сейчас и переходим.
Полагая m — n-\-k, рассмотрим систему т-то порядка
Г = в1*1+ -\-aJz-\-Z(f. zx zm) (93.6)
(/=1. 2 m),
где ujs — постоянные, а коэффициенты разложений Zj, начинающихся
членами не ниже второго порядка, являются непрерывными и огра-
ограниченными функциями времени. Допустим, что характеристическое
уравнение
I a]s — bjJK | = 0 (93.7)
имеет п корней с отрицательными вещественными частями и k корней
с вещественными частями, равными нулю. Если, в частности, функ-
функции Zj не зависят явно от t, то мы будем иметь самый общий кри-
критический случай установившихся движений, а если Z, являются
402
НЕУСТАНОВИВШИЕСЯ ДВИЖЕНИЯ
(ГЛ. VI
периодическими функциями t, то мы получим самый общий случай
периодических движений.
При помощи неособенного линейного преобразования с постоян-
постоянными коэффициентами мы можем вместо переменных zx, . . ., zm
ввести переменные yv
yk,
хп таким образом, чтобы
линейная часть уравнений (93.6) приняла вид
= 1, 2 k; s — 1, 2 п).
(93.8)
Здесь коэффициенты qtj и psj таковы, что вещественные части
всех корней уравнения п-то порядка
Ри
Р22 —
Pin
Р2я
= 0
(93.9)
отрицательны,
порядка
Рп\ Рп2 ¦¦¦ Рпп — 9
а вещественные части всех корней уравнения k-то
Ян — ^ Яп ¦ ¦ • Я\к
Я%\ 422 — ^ ¦¦¦ Я2к
= 0
(93.10)
равны нулю. Совокупность n-\-k корней уравнения (93.7) и опре-
определяет все корни уравнений (93.9), (93.10). При этом в случае не-
необходимости указанное преобразование может быть выбрано таким
образом, чтобы уравнения (93.8) имели канонический вид
dt
dy.
dxs
~dT
= 2, 3,
= 2, 3
k), (93.11)
n). (93.12)
Здесь Aj, ..., Xk — корни уравнения (93.10), apt, .... р„ — корни
уравнения (93.9). При этом корни %t и ps могут быть как простыми,
так и кратными. Каждому кратному корню может отвечать как одна,
так и несколько групп решений (в смысле § 19) уравнений (93.8).
Все величины at и $s являются постоянными, среди которых некото-
некоторые могут быть равны нулю, а именно: если общее число групп реше-
решений, соответствующих всем корням ht и р5, равно р, то р—2
постоянных а,- и р^ равны нулю, так как каждая такая группа имеет
§ 93] СЛУЧАЙ, КОГДА КОЭФФИЦИЕНТЫ ЛИНЕЙНЫХ ЧЛЕНОВ ПОСТОЯННЫ 403
одно уравнение, содержащее только ту переменную, которая фигури-
фигурирует в леаой части уравнения. Каждая отличная от нуля постоян-
постоянная at может быть сделана какой угодно, в частности, сколь угодно
малой. Действительно, сделав дополнительное преобразование
у[ = yv у'2 = А1Уг у'г = АхА2уг у; = Л, ... Ak_xyk,
где At — произвольные постоянные, мы приведем уравнения (93.11)
к виду
в котором постоянные а', имеют значения a't = Al_lal, и если какая-
нибудь а. ф 0, то а', подбором коэффициента Л;-1 может быть сде-
сделана равной наперед заданной отличной от нуля величине. То же
самое можно, конечно, сделать и с постоянными рг
Если указанному линейному преобразованию подвергнуть нелиней-
нелинейные уравнения (93.6), то они примут вид (93.1), в котором все коэф-
коэффициенты qtj, pSJ- и rsJ являются постоянными. Так как при этом все
корни уравнения (93.9) имеют отрицательные вещественные части,
то для коэффициентов pSJ- выполняются условия теоремы предыду-
предыдущего параграфа. Эта теорема может быть, следовательно, применена
к рассматриваемой сейчас системе, если только существуют формы и^">
с ограниченными коэффициентами, удовлетворяющие уравнениям
вида (93.4).
Покажем, что такие формы действительно существуют. С этой
целью будем предполагать, что линейная часть уравнений (93.1) при-
приведена к виду (93.11), (93.12). Тогда уравнения (93.4) будут иметь
следующий вид:
ди[т) yi ди\т)
1=1
ди(т)
(s = 2 п; Ol = 0).
Следовательно, если формы й^т> вычислять последовательно в по-
порядке возрастания индекса s, то для каждой такой формы получится
уравнение вида
ди(т) ^
~d7~~r^J~dy~K"iyi~r™iyi-i)~iJsuV'~r'-"s{.'-'yv ••••Ун) (93-13)
E=1, 2, .... т; ^==0),
404 НЕУСТАНОВИВШИЕСЯ ДВИЖЕНИЯ [ГЛ. VI
где форма ?/<.т) будет известной, если формы и[т\ .... и(™) и все
формы «W, для которых / < т, уже вычислены. Допустим, что все
указанные формы действительно вычислены и вышли с ограничен-
ограниченными коэффициентами. Тогда коэффициенты формы f/j"' будут также
ограниченными. Положим:
(т) VI ц(т ,
И =2^i !
Тогда, если коэффициенты л(т1' "" т*) вычислять в определенном
порядке, то для каждого такого коэффициента получится уравнение
вида
dt ~~
-=(Ps-miK- ••• -»Л)ЛГ' Я#+В1т1 "*)@. (93.14)
где В^' т*^ — линейные функции от уже вычисленных коэффи-
коэффициентов с ограниченными коэффициентами. При этом нужно при-
придерживаться следующего порядка вычисления коэффициентов. Сначала
нужно вычислить коэффициент As''"' . После этого нужно вычи-
вычислить все коэффициенты, для которых mk_1-\- mk= т, в порядке
возрастания тк_1, затем те, для которых mk_2=l, mk_l-\- mk =
= т — 1, также в порядке возрастания mk_l и т. д.
Допустим, что все уже вычисленные коэффициенты получились
ограниченными. Тогда функция ?(m' mb)(f) в уравнении (93.14)
будет ограниченной и из этого уравнения находим частное решение
==е(Р*-Я1Л-•••-"•**•*)' Г e-(Ps-mi%r ¦¦¦-mkh)tBflv ¦¦- mk)dt, (93.15)
о
которое также получится ограниченным. Действительно, пусть
а^<0 — вещественная часть корня ps. Тогда, учитывая, что веще-
вещественные части всех величин Xt равны нулю, и обозначая через
C(mv...,mtt) верхний предел функции [?(mi m*)(9]' будем иметь:
о
as s
что и доказывает предложение.
§ 93] СЛУЧАЙ, КОГДА КОЭФФИЦИЕНТЫ ЛИНЕЙНЫХ ЧЛЕНОВ ПОСТОЯННЫ 405
Если теперь учесть, что вещественная часть величины
р^—ot^j— . .-. —Tftkhk отрицательна, то мы придем к заключению,
что не только решение (93.15), но и все решения уравнения (93.14)
получатся ограниченными.
Таким образом, если все формы «W н^"-1) получились
с ограниченными коэффициентами, то существует бесчисленное мно-
множество форм и<-™К удовлетворяющих уравнению (93.4) и обладаю-
обладающих ограниченными коэффициентами. Но так как формы U^K для
которых, очевидно, имеем:
известны и обладают ограниченными (постоянными) коэффициентами,
то из вышесказанного следует, что существует бесчисленное множество
разложений, формально удовлетворяющих уравнениям (93.3). Следо-.
вательно, в рассматриваемом случае теорема предыдущего параграфа
имеет силу, и мы приходим к следующей теореме.
Теорема 1. Допустим, что в уравнениях (93.1) коэффи-
коэффициенты qtj, psj и rsj постоянны, причем уравнение (93.9) имеет
корни только с отрицательными вещественными частями,
а вещественные части всех корней уравнения (93.10) равны
нулю. Тогда существует бесчисленное множество разложений
(93.5) с ограниченными коэффициент а ми,фо рмально удовлетво-
удовлетворяющих системе уравнений с частными производными (93.3).
Выбрае какое-нибудь одно из этих разложений, подставим его
вместо величин xs в первую группу уравнений (93.1) и рас-
рассмотрим полученную таким образом «укороченную» систему
^- = ЧпУх¦+¦¦¦+ ЧпУи + YiV' Ух У*. «1 «») (93-16)
(/=1.2 k).
Если невозмущенное движение Уу=... — у k = Q «укороченной»
системы устойчиво или асимптотически устойчиво, или не-
неустойчиво, и это определяется конечным числом членов в этих
уравнениях, то и невозмущенное движение хх = ... — хп = ух =
= ... = yk = Q для системы (93.1) соответственно устойчиво
или асимптотически устойчиво, или неустойчиво.
Допустим, что мы имеем дело со случаем периодических движе-
движений, т. е. что функции Yt и Xs в уравнениях (93.1) по отношению
к t периодичны с некоторым периодом и. Применяя доказанную
теорему, приведем задачу к исследованию системы А-го порядка.
Однако такое приведение будет, вообще говоря, иметь смысл лишь
в том случае, если система (93.16) также будет обладать периоди-
406 НЕУСТАНОВИВШИЕСЯ ДВИЖЕНИЯ [ГЛ. VI
ческими коэффициентами, ибо система из я-f-A уравнений с перио-
периодическими коэффициентами может оказаться для исследования более
простой, чем система из k уравнений с непериодическими коэф-
коэффициентами.
Система (93.16) будет, очевидно, обладать периодическими коэф-
коэффициентами, если такими коэффициентами обладают формальные
разложения (93.5). Покажем, что действительно существует система
разложений вида (93.5) с периодическими коэффициентами, формально
удовлетворяющих уравнениям (93.3), и что такая система будет
единственной.
Для этого, очевидно, достаточно показать, что если коэффициент
By*1 т*) в уравнении (93.14) является периодической функцией
времени периода а>, то это уравнение допускает одно и только одно
периодическое решение для Ау1^ т*) с тем же периодом. Но урав-
уравнение (93.14) имеет частное решение
где для краткости положено
а = ps - mfa - ... - mklk, f (t) = ?(m> m*) (t).
Это решение, как было показано в § 67, является периодическим
с периодом и. Остальные решения уравнения (93.14) не будут перио-
периодическими, так как общее решение однородной части этого уравне-
уравнения не периодично.
Из вышесказанного вытекает справедливость следующей теоремы.
Теорема 2. Если при выполнении условий теоремы 1 коэф-
коэффициенты разложений функций Yt и Xs являются периоди-
периодическими функциями времени с периодом и, то существует одна
и только одна система разложений (93.5), формально удовле-
удовлетворяющих уравнениям (93.3) и обладающих периодическими ко-
коэффициентами с тем же периодом. Подставляя эта разложе-
разложения вместо величин xs в первую группу уравнений (93.1), мы
получим «укороченную» систему (93.16) также с периодическими
коэффициентами. Задача устойчивости для системы (93.1)
эквивалентна той же задаче для «укороченной» системы, если
последняя задача решается конечным числом членов.
Допустим, наконец, что правые части уравнений (93.1) не зависят
совсем от времени. Тогда, как легко видеть, существует одна и
только одна система разложений (93.5) с постоянными коэффициен-
коэффициентами, удовлетворяющих формально уравнениям (93.3), которые вслед-
§ 93] СЛУЧАЙ, КОГДА КОЭФФИЦИЕНТЫ ЛИНЕЙНЫХ ЧЛЕНОВ ПОСТОЯННЫ 407
ствие этого принимают вид
ft
= Ps\u\ + • • • -f ^лмя + Гз\У\ + • • • 4-
+ *,(У1 у*. «!..... ия). (93.17)
Действительно, если величина ?(mi' ¦"¦ m*) в уравнении (93.14)
является постоянной, то это уравнение имеет единственное постоянное
решение
B{mv..., mk)
k)
тЛ __ "s
9s — miKi — ... — rnk^k
Мы приходим, таким образом, к следующей теореме.
Теорема 3. Если при выполнении условий теоремы 1 правые
части уравнений (93.1) не зависят явно от времени, то суще-
существует одна и только одна система разложений
«,=«№ у*)+й№ **)+••¦•
формально удовлетворяющих уравнениям (93.17). Если этими
разложениями заменить величины xs в первой группе уравне-
уравнений (93.1), то получится «укороченная» система уравнений
(93.16), также не зависящих от времени. Задача устойчивости
для системы (93.1) эквивалентна задаче устойчивости для
«укороченной» системы, если последняя задача решается ко-
конечным числом членов.
При доказательстве основной теоремы § 91 мы сделали относи-
относительно коэффициентов qi} ограничение, что модули коэффициентов
квадратичной формы
k
2у/(?пУ1+----Ь?йУ*) (93.18)
достаточно малы. Покажем, что при подходящем выборе перемен-
переменных yt во всех рассмотренных в настоящем параграфе случаях ука-
указанное ограничение действительно выполняется, так что теоремы 1,
2 и 3 можно будет считать полностью доказанными.
Мы будем для этого предполагать, что линейная часть первой
группы уравнений (93.1) имеет вид (93.11), который придется, однако,
привести к вещественной форме, так как коэффициенты q{j в уравне-
уравнениях (91.1) предполагались вещественными.
Коэффициенты <х(- в уравнениях (93.11) можно предполагать веще-
вещественными, так как, по доказанному, каждый такой коэффициент,
отличный от нуля, может быть сделан совершенно произвольным,
408
НЕУСТАНОВИВШИЕСЯ ДВИЖЕНИЯ
[ГЛ. VI
Что же касается коэффициентов Я,г, являющихся корнями уравне-
уравнения (93.10), то они могут либо равняться нулю, либо быть чисто
мнимыми. Допустим для определенности, что уравнение (93.10) имеет
нулевой корень р-Л кратности. Пусть А,1 = А,2= ... —^ — 0. Тогда
первые р уравнений (93.11) не нуждаются в дальнейших преобразова-
преобразованиях и имеют вид
р). (93.19)
Остальные k — р уравнений (93.11), соответствующие чисто мнимым
корням, требуют дальнейших преобразований. Пусть ± XI— какая-
нибудь пара чисто мнимых корней уравнения (93.10) q-ft кратности.
Пусть у у и у. у —соответствующие этим корням
переменные у,-, так что соответствующие этим корням уравнения (93.11)
имеют вид
dym
dt
dt
¦ = XtyM.
• = — AiyW,
dt
dt
7-1)
@=2, 3 q),
(93.20)
где yg — соответствующие рассматриваемым уравнениям постоянные сс(,
причем мы считаем, что эти постоянные в уравнениях для у'а» и
для у^ имеют одинаковые значения, что не нарушает общности.
Вводя вместо переменных у(°) и у(а) переменные ах, .. .
при помощи подстановки
<) y@) = e<r- tva (о=1. 2
u
q,
vq
. Я).
мы заменим 2q уравнений (93.20) с мнимыми коэффициентами 1q
уравнениями
du, . dan
If
Ж
~df
dv,
dt
¦ = — kva-\-yaua-i,
(a'==2, 3 q)
(93.21)
с вещественными коэффициентами.
Аналогичным образом мы поступаем со всеми остальными чисто
мнимыми корнями. Таким образом, линейная часть первой группы
системы (93.1) состоит из уравнений (93.19) и одной или нескольких
групп уравнений вида (93.21). Соответственно с этим квадратичная
§ 94]
КРИТИЧЕСКИЙ СЛУЧАЙ ДВОЙНОГО НУЛЕВОГО КОРНЯ
40Э
форма (93.18) будет складываться из квадратичной формы
S2
и из одной или нескольких квадратичных форм вида
q
0=2
Но коэффициенты всех этих форм можно считать численно сколь
угодно малыми, так как такими, по доказанному выше, можно считать
величины а. и уа. ¦
Таким образом, вышеуказанное ограничение для коэффициентов ql}
в рассматриваемых сейчас случаях действительно выполняется, и мы
можем поэтому теоремы 1, 2 и 3 считать полностью доказанными.
На этом мы заканчиваем изложение общей теории критических
случаев. В оставшейся части этой главы мы, используя полученные
результаты, исследуем ряд критических случаев для установившихся
и периодических движений. Мы рассматриваем установившиеся дви-
движения, когда характеристическое уравнение первого приближения
имеет пару нулевых корней, когда оно имеет две пары чисто мнимых
корней и когда оно имеет один нулевой и пару чисто мнимых корней.
Аналогичные случаи рассматриваются и для периодических движений.
§ 94. Критический случай двойного нулевого корня
для установившихся движений.
Рассмотрим систему (re-f- 2)-ro порядка с постоянными коэф-
коэффициентами, для которой характеристическое уравнение первого при-
приближения имеет п корней с отрицательными вещественными частями
и два корня, равных нулю. Подходящим выбором переменных система
может быть приведена к виду
~f =
у,
У>
¦ хп)>
хп)
E=1, 2,
П.),
(94.1)
где коэффициенты psj таковы, что характеристическое уравнение
Р\2 ¦¦• Рт
(94.2)
Р21
Pal
Р22~Р
Рп2
Р2п
Рпп-9
= 0
410
НЕУСТАНОВИВШИЕСЯ ДВИЖЕНИЯ
[гл. VI
имеет корни только с отрицательными вещественными частями, а оба
корня характеристического уравнения
Яп — ^ Ч\1
=0
(94.3)
равны нулю. Л', Y vl Xs — сходящиеся в некоторой окрестности
начала координат ряды, расположенные по степеням переменных х, у,
jcj, .... хп, начинающиеся членами не ниже второго порядка.
Наряду с системой (94.1) рассмотрим систему второго порядка
~ = qnx-\-q12y-\-X(x, у, av .... и„),
(x, у, их ип),
(94.4)
где us(x, у) — формальные решения уравнений с частными произ-
производными (93.17). Обозначим соответственно через Х(т)(х, у) и
Y (х, у) совокупности членов m-го порядка в правых частях урав-
уравнений (94.4) и заменим эти уравнения следующими:
dx
x, у),
x, у).
(94.5)
Здесь N — достаточно большое целое число, а ф(/, х, у) и
х, у) — аналитические функции переменных х и у, которые при
всех t ^> 0 удовлетворяют неравенствам
\<f(t,x,y)\<A{\x\
(94-6)
где А — положительная постоянная. Тогда на основании теоремы 3
предыдущего параграфа, если невозмущенное движение х = у = 0
для системы (94.5) устойчиво или асимптотически устойчиво, или
неустойчиво при любом выборе функций ф и г]), удовлетворяющих
условиям (94.6), то это же самое будет справедливо и для невозму-
невозмущенного движения х — у = Хх— ...=хп — 0 полной системы (94.1).
Таким образом, задача сводится к исследованию системы (94.5).
Мы будем предполагать, что переменные х и у выбраны таким
образом, что линейная часть уравнений (94.5) имеет каноническую
форму. Здесь приходится рассматривать два случая. В первом случае
двойной нулевой корень не обращает в нуль хотя бы один из мино-
§ 94] КРИТИЧЕСКИЙ СЛУЧАЙ ДВОЙНОГО НУЛЕВОГО КОРНЯ 411
ров (ra-(-l)-ro порядка характеристического определителя исходной
системы уравнений возмущенного движения, или, что то же самое,
этому корню отвечает одна группа решений первого приближения
этой системы. В этом случае, если линейная часть уравнений (94.5)
имеет каноническую форму, то будем иметь qn = q12 = q22 — О,
q2l =1 и, следовательно, эта линейная часть имеет вид
— = 0 ^-==х
Вторым случаем будет тот, когда двойному нулевому корню
отвечают две группы решений уравнений первого приближения.
В этом случае все коэффициенты qn, q12, q2l, q22 равны нулю и
уравнения (94.5) имеют вид
. У).
(94.7)
i?L= К(га> (х, у)+ • • • + У (*. У) +W. *. У)
где т ^ 2.
Первый из указанных случаев для системы второго порядка под-
подробно рассмотрен А. М. Ляпуновым1). Для систем произвольного
порядка этот случай исследован Г. В. Каменковым2). Второй случай
как для систем второго порядка, так и для систем произвольного
порядка рассмотрен автором 3) и другим методом — Г. В. Каменко-
Каменковым. Мы ограничимся здесь рассмотрением второго случая. Этот
случай является особенно важным, так как к нему приводятся наи-
наиболее интересные для практики другие критические случаи, когда
характеристическое уравнение имеет чисто мнимые корни. В этом
мы убедимся в двух следующих параграфах.
Итак, мы будем рассматривать задачу устойчивости- для системы
(94.7). Рассмотрим две формы (т-{- 1)-го порядка Р(х, у) и G(x, у),
определяемые равенствами
Р (х, у) = хХ(т) (х, у) + уК(т) (х, у), 1
Q(x, y) = xY(m){x, у) — уХ{т)(х, у). ( ( 4' "*
Эти формы будут играть важную роль в дальнейшем исследо-
исследовании. Если форма G(x, у) не является знакоопределенной, то
') Ляпунов А. М., Исследование одного из особенных случаев задачи
об устойчивости движения. Матем. сб., т. XVII, вып. 2, 1893. Работа пере-
переиздана во втором и третьем A950 г.) изданиях книги: Ляпунов А. М.,
Общая задача об устойчивости движения.
2) К а м е н к о в Г. В., Об устойчивости движения. Сб. трудов Казан-
Казанского авиац. ин-та, № 9, 1939.
3) М а л к и н И. Г., Некоторые вопросы теории устойчивости движения
В смысле Ляпунова. Сб. трудов Казанского авиац. ин-та, Д; 7, 1937.
412 НЕУСТАНОВИВШИЕСЯ ДВИЖЕНИЯ [ГЛ. VI
уравнение
0{х, у) = 0 (94.9)
определяет одну или несколько прямых, проходящих через начало
координат.
Угловой коэффициент k каждой такой прямой определяется, оче-
очевидно, уравнением
K(m)(l. k) — kX{m\\, k) = 0. (94.10)
Число этих прямых не превосходит т -f-1.
Мы будем различать четыре случая.
1°. Форма О не является знакоопределенной, и на всех пря-
прямых (94.9) форма Р может принимать только отрицательные значе-
значения (за исключением, конечно, начала координат).
2°. Форма G не является знакоопределенной, и хотя бы на одной
прямой (94.9) форма Р может принимать положительные значения.
3°. Форма О знакоопределенна, и величина
2я
1 Г Р (cos ft, sin ft)
K — 2n J G (cos ft, sin ft)m 194.11)
0
отлична от нуля.
4°. Форма G знакоопределенна, и величина (94.11) равна нулю.
Мы исследуем каждый из этих случаев по отдельности.
Случай 1°. Рассмотрим систему однородных уравнений
— = ХК '(х, у), -?-=У (х, у). (94.12)
В рассматриваемом случае уравнение (94.9) имеет вещественные
решения. Каждая определяемая этим решением прямая является
интегральной кривой уравнений (94.12). Действительно, согласно
определению формы О на каждой такой прямой имеем тождественно
Тождество (94.13) показывает также, что каждая проходящая
через начало координат интегральная кривая необходимо касается
одной из прямых (94.9).
По условию, на каждой прямой (94.9) форма Р, представляющая
собой, очевидно, для уравнений (94.12) производную по времени от
выражения -^ (х2 -f- у2), принимает только отрицательные значения.
Следовательно, движение по этим прямым, являющимся, как уже
указывалось, интегральными кривыми уравнений (94.12), направлено
к началу координат. Отсюда в силу непрерывности поля скоростей
для уравнений (94.12) и того обстоятельства, что каждая интеграль-
§ 94] КРИТИЧЕСКИЙ СЛУЧАЙ ДВОЙНОГО НУЛЕВОГО КОРНЯ 413
ная кривдя этих уравнений, проходящая через начало координат,
касается одной из прямых (94.9), непосредственно вытекает, что все
интегральные кривые уравнений (94.12) проходят через начало коор-
координат и движение по ним направлено к этой точке. Следовательно,
невозмущенное движение для уравнений (94.12) асимптотически устой-
устойчиво. Но тогда на основании общей теоремы § 85 невозмущенное
движение для уравнений (94.7) будет также асимптотически устой-
устойчиво при любом выборе функций (f(t, х, у) и г|)(/, х, у), удовле-
удовлетворяющих условиям (94.6).
Итак, в случае 1° невозмущенное движение асимптотически
устойчиво.
Случай 2°. Допустим теперь, что уравнение (94.9) имеет по-
прежнему вещественные решения, но хотя бы на одной из прямых,
определяемых этим уравнением, форма Р может принимать положи-
положительные значения. Не нарушая общности рассуждений, мы можем
считать, что этой прямой является ось х. Действительно, этого
всегда можно добиться простым поворотом осей координат. Но если
уравнение (94.9) имеет решение у = 0, то форма К(т) должна обра-
обращаться в нуль при у — 0. Мы можем, следовательно, писать:
у^ = Вухт-1+В2у2хт^+ ... +Вт_1Ут-1х + Втут. (94.14)
Для формы Х^т' имеем:
Х^ = Ахт + Ахухт-1+ ... +Ат_хут-1х + Атут, (94.15)
причем коэффициент А необходимо отличен от нуля, так как при
у = 0 форма Р может принимать положительные значения. Кроме
того, при т нечетном он должен быть положительным, а при т чет-
четном он может быть как положительным, так и отрицательным. Но
в последнем случае замена в дифференциальных уравнениях х на — х
изменяет знак коэффициента А на обратный. Поэтому, не нарушая
общности рассуждений, мы можем предполагать, что коэффициент
А > 0 положителен.
Имея в виду доказать неустойчивость невозмущенного Движения,
мы постараемся в рассматриваемом случае построить для уравне-
уравнений (94.7) функцию, удовлетворяющую условиям теоремы о не-
неустойчивости Н. Г. Четаева (§ 48).
Рассмотрим с этой целью функцию
2K = cc2jc2 — у2, (94.16)
где а2 — некоторая положительная постоянная, и составим полную
производную от этой функции по времени в силу уравнений (94.7).
Будем иметь:
где ненаписанные члены имеют порядок, не меньший т -\- 2.
414 НЕУСТАНОВИВШИЕСЯ ДВИЖЕНИЯ [ГЛ. VI
Функция V принимает положительные значения при у = 0. То же
самое будет иметь место и по отношению к функции —тр, если
численные значения х предполагать достаточно малыми и в случае
четкого m х > .0. Это непосредственно следует из того, что Лг(т)
имеет вид (94.15), и коэффициент А положителен. Следовательно,
вблизи начала координат существует область, содержащая внутри
себя ось х, где одновременно V > 0 и —тт- > 0.
Установив это, допустим сначала, что А > В. Покажем, что
в этом случае постоянную а можно выбрать настолько малой, чтобы
область V > 0 была заключена внутри области —ут- > 0.
В самом деле, функция V может принимать положительные зна-
значения только при условии у — рал;, где р — произвольная величина,
dV
лежащая на отрезке [—1, -f-1]. Но, заменяя в выражении —п- вели-
величину 'у через fax и принимая во внимание (94.14) и (94.15), будем
иметь:
где
С-=,{А — Вр2) а2 -+- (А !Р - ЗД а3 + ...
a / — аналитическая функция х, обращающаяся в нуль при х = 0.
Отсюда следует, что при достаточно малом х знак величины
(C-\-f)xm+1 совпадает со знаком величины С (по крайней мере,
при х > 0). Что же касается знака величины С, то постоянную а
можно выбрать настолько малой по абсолютному значению, чтобы
знак С совпадал со знаком величины А — Бр2. Но так как А > В
и А > 0, то величина А — Вр2 будет положительной при всех зна-
значениях величины р на отрезке [—1, -|-1].
Таким образом, в достаточно малой окрестности начала коорди-
dV
нат существует область V > 0, заключенная внутри области —гт- > 0.
Следовательно, функция V удовлетворяет всем условиям теоремы
о неустойчивости Н. Г. Четаева и невозмущенное движение не-
неустойчиво.
Допустим теперь, что А < В. В этом случае на границе области
V > 0 производная —зт- будет отрицательной, и, следовательно, функ-
функция V не будет удовлетворять условиям теоремы Н. Г. Четаева.
Тем не менее, невозмущенное движение будет также неустойчиво,
что может быть доказано следующим образом,
94]
КРИТИЧЕСКИЙ СЛУЧАЙ ДВОЙНОГО НУЛЕВОГО КОРНЯ
415
Рассмотрим снова функцию (94.16), где а, так же как и в пре-
предыдущем случае, выбрана настолько малой, что знак (С-(-/)д;ш+1
при достаточно малых значениях х совпадает со знаком величины
А — В$Р. Пусть это будет при 0<л;<:/г. Так как сейчас А < В,
то величина А — Вр2 не будет положительна при любом р на отрезке
[—1, -f-1 ], но она во всяком случае будет положительна при |р|<1р,
где р — достаточно малое положительное число. Следовательно,
в области 0 < х <; h, Vx > 0, где
2V"! = р2а2х2 — у2,
dV
производная —тт- будет во всяком случае положительна. Что же ка-
то на границе V1 — 0 рассматриваемой
сается производной
dt
области она будет отрицательна,
так как функция V\ обладает,
очевидно, такими же свойствами,
как и V.
Пусть АОВ (рис. 21) — гра-
границы области V > 0, a AfiBxA\ —
границы области 0 <; х <! h,
Vj > 0. Внутри этой последней
рассмотрим область NMQP (эта
область на чертеже заштрихо- 0\
вана), ограниченную отрезком NP
гиперболы V = C и отрезком MQ
гиперболы V = с. При этом С —
какое-нибудь фиксированное чи-
число, а с предполагается сколь
угодно малым, так что дуга MQ
расположена сколь угодно близко
от начала координат. Внутри об-
области NMQP производная —гг-
положительна, и для нее сущест-
существует отличный от нуля положи-
положительный нижний предел. Обозначим этот предел через / и пусть
Q
T = -j-. Рассмотрим интегральную кривую уравнений (94.7), выхо-
выходящую в момент времени t = T из какой-нибудь точки F дуги NP.
Пусть х = х (t) и у = у (t) — уравнение этой интегральной кривой.
Будем следовать вдоль этой интегральной кривой в сторону убыва-
убывания t вплоть до момента времени ? = 0. При этом интегральная
кривая будет приближаться к началу координат, по крайней мере,
до тех пор, пока она не покинет области AlOBlAv так как в этой
Рис. 21.
416 НЕУСТАНОВИВШИЕСЯ ДВИЖЕНИЯ [ГЛ. VI
области —зт- > 0. Но если бы указанная интегральная кривая в какой-
нибудь момент времени 0^т<Г покинула область Л1ОД1Л1, что
она могла бы сделать лишь только через границы ON или ОР, то
в ьтот момент времени одновременно выполнялись бы условия Vt = 0,
—з/^-О, что невозможно, так как на отрезках ОАХ и О^.произ-
dVi
водная —ф отрицательна.
Таким образом, на всем отрезке времени от Г до 0 рассматри-
рассматриваемая интегральная кривая будет оставаться внутри области NOPN.
Допустим, что при / = 0 она будет проходить через точку Е. Пока-
Покажем, что точка Е непременно находится внутри области OMQO.
Для этого, очевидно, достаточно показать, что при убывании t от Т
до 0 рассматриваемая интегральная кривая пересекает в какой-нибудь
момент времени дугу MQ. Допустим противное, что интегральная
кривая при всех 0 <С t ^ T находится внутри области A1QNP. Тогда
будем иметь:
г
V [х @), у @)] = V[x (Г), у (Г)] - J 4?- dt <
о
< V [х (Г), у (Т)] — 1Т = С — С = 0,
что невозможно, так как по предположению точка х @), у @) нахо-
находится в области MQNP и, следовательно, V[x@), y@)]>c>0.
Таким образом, точка Е находится внутри области OMQ. Рас-
Рассмотрим теперь интегральную кривую, выходящую в момент вре-
времени t = 0 из точки Е. Это, очевидно, будет та же самая интеграль-
интегральная кривая х (t), у (t). К моменту времени t = Г эта кривая достигнет
точки F, находящейся на определенном расстоянии от начала коор-
координат. Но так как при этом точка Е находится сколь угодно близко
от начала координат, то невозмущенное движение неустойчиво:).
Допустим, наконец, что А—В. Рассмотрим функцию
2V = х4 — у2
и область
0<л:</г, V>0. (94.17)
Все значения переменных, лежащих в этой области, удовлетворяют
соотношению у = fix2, где р — произвольная величина, лежащая на
отрезке [—1, -f-1]. Составим производную от V по времени в силу
уравнений (94.7) и заменим в ней величину у через рх2. Тогда,
:) Построенные нами функции Vi и V2 удовлетворяют другой теореме
Н. Г. Четаева о неустойчивости.
§ 94] КРИТИЧЕСКИЙ СЛУЧАЙ ДВОЙНОГО НУЛЕВОГО КОРНЯ 417
принимая во внимание (94.14) и (94.15), получим:
где р — коэффициент при хт+1 в форме Х{т+1\ а/—аналитическая
функция переменной х, обращающаяся в нуль при х = 0.
Коэффициент р можно предполагать сколь угодно малым. В самом
деле, если в уравнениях (94.7) переменную у заменить переменной г\
при помощи подстановки ц~оу, где о — постоянная, то в фор-
формах Х^т) и К(т) коэффициенты Л и Б не изменятся, а в форме х^т+1)
коэффициент при хт+1 умножится на а. Следовательно, выбрав о
достаточно малой, можно всегда добиться, чтобы этот коэффициент
был численно сколь угодно малым.
Так как Л > 0, В = А и р численно мало, то вблизи начала
координат величина —тг будет принимать положительные зна-
L at Jj,=Pjt:2
чения (при х > 0, если т — четное) при всех значениях р, лежащих
на отрезке [—1, -f-1]. Следовательно, при h, достаточно малой,
во всей области (94.17) производная —тт- принимает положительные
значения и функция V удовлетворяет всем условиям теоремы Н. Г. Че-
таева. Отсюда вытекает, что невозмущенное движение неустойчиво.
Итак, в случае 2° невозмущенное движение неустойчиво. При
этом очевидно, что это будет справедливо при любом выборе функ-
функций ф(/, х, у) и ty(t, х, у), удовлетворяющих условиям (94.6).
Случай 3°. Допустим теперь, что О есть форма знакоопреде-
ленная и величина X, определяемая равенством (94.11), отлична от
нуля. Вводя полярные координаты
преобразуем систему (94.7) к следующему виду:
t, О. г),
(У4.1Й)
(cos
dt
где Pk и Gk — периодические функции й, периода 2я (формы отно-
относительно cosu и sinu), a R(t, Ь, г) и Q(t, й, г) при всех значениях
(^.0 и & удовлетворяют условиям
\R(t, Ъ, r)\<BrN+\ \Q(t, Ъ, r)\<BrN, (94.19)
где В — некоторая постоянная.
418 НЕУСТАНОВИВШИЕСЯ ДВИЖЕНИЯ [ГЛ. VI
Из (94.11) следует, что функция ip(ft), определяемая равенством
кг
\
являющаяся вследствие знакоопределенности G непрерывной, будет
периодической периода 2я. Такой же, следовательно, будет и функция
(94.21)
которая к тому же никогда не обращается в нуль.. Вследствие этого
функция [ф(Ф)] будет также непрерывной. Из (94.20) находим:
j, /P(cos»,8ln»)_ Л
rfd V G (cos ft, sin ¦&) / \ K
Введем теперь вместо переменной г переменную р при помощи
подстановки
' (94.23)
Из отмеченных свойств функции ф(й) вытекает, что задача устой-
устойчивости по отношению к переменной г равносильна той же задаче
по отношению к переменной р. Уравнения (94.18) на основании (94.22)
примут вид
•|?- = XG (cos ft, sin ft) Ф-1 (ft) pm -f
+ /?*(^ ft, p),
+ е*(г, ft, p),
где Pa (ft) и Qk (ft) — периодические функции ft, периода 2я, а функ-
функции /?* и 0* при всех значениях t^>>0 и ft удовлетворяют неравен-
неравенствам
| R* (t, ft, р) | < Ср"+». 19* (t, ft, p) |< Cp'V, (94.25)
где С — некоторая постоянная.
Так как G (cos ft, sin ft) никогда не обращается в нуль, то из пер-
первого уравнения (94.24) сразу вытекает, что невозмущенное движение
при ХО < 0 асимптотически устойчиво, а при XG > 0 неустойчиво,
и это будет иметь место при любом выборе функций R* -и 0*, удо-
удовлетворяющих условиям (94.25) и, следовательно, при любом выборе
функций (f(t, х, у) и г])(?, х, у), удовлетворяющих условиям (94.6).
Итак, в случае 3° невозмущенное движение будет асимптотически
устойчиво при XG < 0 и неустойчиво при XG > 0.
§ 94] КРИТИЧЕСКИЙ СЛУЧАЙ ДВОЙНОГО НУЛЕВОГО КОРНЯ 419
Случай 4. Допустим, наконец, что G есть форма знакоопреде-
ленная и величина X, определяемая формулой (94.11), равна нулю.
Поступая, как и в предыдущем случае, т. е. вводя полярные коор-
координаты и затем переменную р при помощи подстановки (94.23), мы
получим уравнения (94.24), которые сейчас примут вид
(94.26)
-^ = G(cosu, sinfl^m-1(u)pm~1-r-Qm(*)Pm+ ¦•¦
... -\-QN-i(Q)pN-1-\-Q*(t, *, p).
Отсюда, исключая dt, находим:
g iV о, р), (94.27)
где Rk {&) — периодические функции $ с периодом 2я, а Ф имеет
порядок малости не ниже N-\~2 — т и является функцией такого же
типа, как и R* и 9*.
Если в уравнении (94.27) отбросить член Ф, то оно будет отли-
отличаться от уравнения F6.1), подробно изученного в § 66, только тем,
что независимой переменной является не время, а полярный угол Ф.
Мы можем поэтому применить к уравнению (94.27) все рассужде-
рассуждения § 66. Поступая по указанному в этом параграфе второму спо-
способу решения задачи, попытаемся удовлетворить уравнению (94.27)
решением вида
(94.28)
где с — произвольная постоянная, a <pk — некоторые периодические
функции 4, периода 2л. Подставляя (94.28) в (94.27) и приравнивая
коэффициенты при одинаковых степенях с, мы получим для опреде-
определения фд, уравнения вида
Jj*- = Fk(fi) (k = 2, 3, ...), (94.29)
где Fk (u) — некоторые полиномы с периодическими коэффициентами
(если А<Л/-(-1 — т) от q>2, ..., фА_г. Уравнения (94.29) дают
возможность последовательно определять коэффициенты q>k при по-
помощи квадратур. Однако кроме особо исключительных случаев,
которые мы здесь не будем рассматривать, коэффициенты фА не будут
получаться периодическими при любом k. Пусть ф(- — первый непе-
непериодический коэффициент в ряду q>2, ф3, ... Этот коэффициент
будет иметь вид
>). (94.30)
420 НЕУСТАНОВИВШИЕСЯ ДВИЖЕНИЯ [ГЛ. VI
где g— некоторая постоянная, а \|зг (¦&)— периодическая функция.
Введем теперь в уравнение (94.27) вместо переменной р переменную z
при помощи подстановки
Тогда, считая, что N > 1-\- т — 1, мы получим, как это было
показано в § 66, следующее уравнение:
¦?¦=**'+¦•••
где ненаписанные члены имеют порядок, не меньший 1-\-\. При этом
очевидно, что задача устойчивости по отношению к переменной z
эквивалентна той же задаче по отношению к переменной р.
Для производной —тг на основании (94.26) имеем:
Отсюда непосредственно вытекает, что при gO > 0 невозмущен-
невозмущенное движение неустойчиво, а при gQ < 0 оно устойчиво асимпто-
асимптотически, причем этот результат будет справедлив при любом выборе
функций (f(t, х, у), \|з(Л х, у), удовлетворяющих условиям (94.6).
Это и дает решение задачи устойчивости в случае 4°.
Полученные результаты могут быть сведены в следующую теорему.
Теорема. Допустим, что предложена система (п-\-2)-го
порядка дифференциальных уравнений возмущенного движения,
для которых характеристическое уравнение первого прибли-
приближения имеет п корней с отрицательными вещественными ча-
частями и двойной нулевой корень, которому соответствуют
две группы решений уравнений первого приближения. Подхо-
Подходящим выбором переменных эту систему можно представить
в следующем виде:
dxs
dt
^L — у йУ —у
dt ~ ' dt
= Ps\x\ + • • • + Psnxn 4- Psx
(94.31)
где X, Y, Xs— аналитические функции переменных х, у,
Xj xn, разложения которых начинаются членами не ниже
второго порядка, а коэффициенты psj таковы, что уравне-
уравнение (94.2) имеет корни только с отрицательными веществен-
вещественными частями.
Составляя систему уравнений с частными производными
<^и ди .
Un) =
-\-Xs(X, у, UX Я„),
§ 94] КРИТИЧЕСКИЙ СЛУЧАЙ ДВОЙНОГО НУЛЕВОГО КОРНЯ 421
попытаемся удовлетворить ей формально выражениями us (x, у),
являющимися рядами по степеням х и у, не имеющими сво-
свободных членов. Такие ряды всегда найдутся и будут един-
единственными. Этими рядами заменяем величины xs в первых
двух уравнениях (94.31), после чего они примут вид
(94.32)
где ХA) и К(;) — формы 1-го порядка переменных х и у. Далее
составляем формы Р(х, у) и G(x, у) по формулам (94.8).
Тогда:
1) Если форма G не является знакоопределенной и форма Р
на всех прямых, определяемых уравнением (94.9), может при-
принимать только отрицательные значения, то невозмущенное
движение асимптотически устойчиво.
2) Если форма G не является знакоопределенной и хотя бы
на одной из прямых, определяемых уравнением (94.9), форма Р
может принимать положительные значения, то невозмущен-
невозмущенное движение неустойчиво.
3) Если форма G является знакоопределенной и величина X,
определяемая формулой (94.11), отлична от нуля, то невоз-
невозмущенное движение асимптотически устойчиво при XG < 0 и
неустойчиво при XG > О.
4) Если форма G является знакоопределенной и X = О, то
для решения задачи устойчивости поступаем следующим об ра-
разом.
Вводим в уравнения (94.32) вместо переменных х и у пере-
переменные р и $ при помощи подстановки х —pcp(u)cosu, y =
= pcp(u)sinu, где ф — периодическая с периодом 2я функция й,
определяемая формулой (94.21), в которой гр (#) определяется
формулой (94,20). У равнения (94.32) примут вид
(94.33)
где Pk и Qk — периодические функции й, периода
Из (94.33), исключая t, находим уравнение
где Rk—периодические функции периода In. Этому уравнению
пытаемся удовлетворить решением вида (94.28), в котором
422 неустановившиеся движения [гл. vr
с—произвольная постоянная, а ф4 — периодические функции
периода 2л. Для определения (fk получаем уравнения (94.29),
из которых эти функции последовательно определяются при
помои\и квадратур. Функции q>k лишь только в особо исклю-
исключительных случаях будут все получаться периодическими.
Оставляя в стороне этот случай, допустим, что фг является
первой непериодической функцией в ряду ф2, ф3, ... Эта функ-
функция будет необходимо иметь вид (94.30). Тогда, если gG > 0,
то невозмущенное движение неустойчиво, а при gG < 0 оно
устойчиво асимптотически.
Доказанная теорема охватывает все случаи, кроме тех, при кото-
которых форма G не является знакоопределенной, а форма Р обращается
в нуль на некоторых прямых, определяемых уравнением (94.9), но
ни на одной из этих прямых она не может принимать положительных
значений. В этих случаях, так же как и в случае 4°, задача не ре-
решается формами Лг(ш) и Y(m) в уравнениях (94.32), а требует рас-
рассмотрения членов более высоких порядков. На этих случаях мы здесь
не останавливаемся !).
§ 95. Критический случай двух пар чисто мнимых
корней для установившихся движений 2).
Рассмотрим систему («4-4)-го порядка с постоянными коэффи-
коэффициентами, для которой характеристическое уравнение первого при-
приближения имеет две пары чисто мнимых корней ±ХХ1 к ± X2i и
и корней с отрицательными вещественными частями. Мы будем пред-
предполагать, что отношение —¦ иррационально. Подходящим выбором
переменных эту систему можно представить в виде
—-?г- — ХЛх,-\-Xj(xv yv x2, y2, гг, ..., zn),
*2' Уа> zi zn).
+ Zs{xv yv x2, y2, zt zn)
(j=\, 2; s=\, 2 «),
где коэффициенты psl таковы, что уравнение
') См. примечание в конце книги (стр. 530).
2) М а л к и н И. Г., Решение некоторых критических случаев задачи
устойчивости движения. Прикл. матем. и мех., т. XV, вып. 5, 1951.
§ 95] КРИТИЧЕСКИЙ СЛУЧАЙ ДВУХ ПАР ЧИСТО МНИМЫХ КОРНЕЙ
423
имеет корни только с отрицательными вещественными частями. Функ-
Функции Xj, Yj, Zs, как обычно, предполагаются аналитическими с раз-
разложениями, начинающимися членами не ниже второго порядка.
Наряду с системой (95.1) рассмотрим «укороченную» систему
dt
';(*1- У1' X2> У2- Ul>
V^+^^l- У1' X2- У2' Л
(У — I, ¦i),
un)
(95.2)
где us(xx, yx, x2, y2) — ряды по степеням переменных xx, yx, x2, y2,
не имеющие свободных членов и представляющие формальные реше-
решения уравнений с частными производными:
Уа- "i
л- х*< л- «1-
••• »«)] =
Psn"n
х2, у2, их и„)
ге).
(s=l, 2
Пусть v?ym), Kjrm)—формы m-ro порядка переменных xv yv
х2, у2, представляющие, соответственно, члены m-го порядка в пра-
правых частях уравнений ((95.2). Рассмотрим систему
Уу
G=1, 2),
(95'3)
где Л/ — сколь угодно большое целое число, а ср;- и т|)у- — зависящие
от ^ аналитические функции переменных xv yx, х2, у2, удовлетво-
удовлетворяющие при всех <>0 в некоторой окрестности начала координат
условиям
xx, yx, x2, y2)\<A{\xx\ + \yx\ + \x2\ + \y2\f+\ I
j
где А — некоторая постоянная. Если невозмущенное движение хх =
= ух = х2 = у2 = 0 для системы (95.3) будет устойчиво или асимпто-
асимптотически устойчиво, или неустойчиво при любом выборе функций
424
НЕУСТАНОВИВШИЕСЯ ДВИЖЕНИЯ
[ГЛ. VI
Фу и яру, то согласно § 93 невозмущенное движение хх = ух — х2 =
= у2 = zx — ... —zn = Q для системы (95.1) будет также соответ-
соответственно, устойчиво или асимптотически устойчиво, или неустойчиво.
Таким ббразом, задача сводится к исследованию системы (95.3).
Заметим прежде всего, что переменные Xj и у у являются ком-
комплексно сопряженными. Поэтому вторая группа уравнений (95.3> мо-
может быть получена из первой заменой / на — t, Xj на уу-, у у на Xj. Этим
обстоятельством мы неоднократно будем пользоваться в дальнейшем.
Введем теперь в уравнения (95.3) вместо переменных хх, ух,
х2, Уъ переменные uv vx, u2, v2 при помощи подстановки
vv a2. v2),
vv uv v2)
G=1.2)
(95.5)
где
vv m2
v vv u2, i>2)—некоторые подлежа-
подлежащие определению формы т-го порядка переменных uv vv u2, v2.
Эти формы мы постараемся подобрать та1гим образом, чтобы преоб-
преобразованные уравнения приняли вид
fe=1
1
(ЛГ-1)
dVj
~dl
v U2,
v v2,
t, UX, Vv U2, V2),
v uv v2)
(J=l. 2).
(95.6)
Здесь функции Фу и Ч^ начинаются членами не ниже (jV-|-l)-ro
порядка (число N предполагаем нечетным), (Уут> (их, vx, u2, v2) и
U] (vx, ux, v2, и2) — формы /га-го порядка переменных их, vx, «2> ^г-
Черта над буквой обозначает комплексную сопряженность, так что
формы ?/ym)(flj, ир v2, u2) получаются из ?/'/" (их, vx, u2, v2) заме-
заменой I на — /, Uj на Vj и г/у на иу-, т. е. если
Uf\uv vv u2, v2) = 2 ^f" m2> "" ni
(У=1, 2; /raj + m2-f n1-f«2
то
p «p ©2. и2) = 2 <
(У = 1, 2; OTj -f /и2
(95.7)
(95.8)
)~ я2 = in).
§ 95] КРИТИЧЕСКИЙ СЛУЧАЙ ДВУХ ПАР ЧИСТО МНИМЫХ КОРНЕЙ 425
Формы ?/у"\ кроме того, таковы, что
Л(Л т" "'• ) = 0, если {пх — n2f + (и, — m2 — IJ Ф 0; j
Л2т" тг' "" ) = 0, если (/га, — /га2J + (щ — п2 — IJ =? о, j
так что из всех коэффициентов А\' m2' "'' " отличными от нуля
являются лишь те, для. которых одновременно пх = п2 и т1 — т2 = 1.
а из коэффициентов А2 " "*2' "'' " отличными от нуля будут лишь те,
для которых одновременно т1 = от2, й1 — л2 — 1 = 0.
Мы сейчас покажем, что эти условия могут быть удовлетворены
и что они определяют как формы и(.т>, г>(.т\ так и коэффициенты
Л'/™1' т*' "" , причем все эти величины определяются крайне про-
простыми вычислениями, так как для каждого коэффициента форм
u(m)t v(m) и для каждого коэффициента A'f1" Ш2' "" > получится линей-
линейное алгебраическое уравнение с одной неизвестной.
Заметим прежде всего, что, как показывают уравнения (95.6),
вторая группа этих уравнений должна получиться (по крайней мере,
с точностью до членов N-ro порядка) из первой группы заменой i
на —г, Uj на Vj, Vj на Uj, т. е. переменные Uj и Vj должны полу-
получиться комплексно сопряженными. Так как такими же свойствами
обладают и исходные уравнения (95.3), то должно быть v^{uv vv
uv v2) = u^ {vv и,, v2, м2), т. е. если
M(;m) == 2 ^f" тъ "" )u'"lv^u^vn22 (95.10)
(y=l, 2; mx -f- m2 -\- n{ -j-n2 = /ra),
то
G=1, 2; m1+m2 +
Если при выполнении этих условий удастся подобрать преобразо-
преобразование (95.5) так, чтобы первая группа уравнений (95.6) имела тре-
требуемый вид, то требуемый вид будет иметь также и вторая группа
этих уравнений. '
Заменяя в первой группе уравнений (95.3) Xj и у;- их выраже-
выражениями (95.5) и принимая во внимание (95.6), получим:
Р=2 а=1
(/=1.2). (95.12)
426 НЕУСТАНОВИВШИЕСЯ ДВИЖЕНИЯ [ГЛ. VI
Задавшись произвольным числом т < N, приравняем в обеих
частях полученных уравнений коэффициенты при u™>vpu^v%2, где
Щ~\- т^-\-п1-\-п2= т. Тогда, принимая во внимание (95.7), (95.8),
(95.10) и (95.11), мы получим для определения коэффициентов
в(т„ т2, «„ п2) следующие уравнения:
[(т, - т2) I, + (пх -п2) Х2 — Xj] fif" т* "'¦ > +
/1 т " щ) {™ Ш2:"" >. (95.13)
где а = 0 при т четном и а=1 при т нечетном.
Здесь Су1' Ш2'"'" — целые рациональные функции от тех коэф-
коэффициентов A(sm" '"ъ "'¦ щ) и B{sm" ть Пь ) (и комплексно сопряженные
с ними величин), для которых /их —|— т2-\-п1-\-п2 < т. Допустим,
что все эти коэффициенты уже определены и, следовательно', вели-
величины С(/"" т2'"") известны. Тогда будем различать два случая. Пер-
Первым из них будет тот, когда при 7=1 одновременно выполняются
условия тх — т2-\-\, nl = n2, а при /=2 — условия ml = m2,
ге1 = й2~т~1- Этот случай возможен лишь при т нечетном. В первом
случае коэффициент при fi(/"" m" "" > в уравнении (95.13) обращается
в нуль, и мы получим вполне определенное значение для Ау1' Шг' "" .
А] — Су-
Коэффициент B^j" m""" ) остается произвольным, и мы его можем
положить равным нулю.
Во втором случае вышеуказанные условия относительно индексов
не выполняются. В этом случае коэффициент при В^т" тъ "" "г) в урав-
уравнении (95.13) не обращается в нуль, так как, по условию, отноше-
отношение XJX2 является числом иррациональным. Мы можем тогда положить
д{ть т2, пи п2) п о(т„ т%, пи л2) . j_ :_
л! ~и' — (/Bt-m^
Если теперь учесть, что при т = \ коэффициенты Cym"m*'"" >
являются известными величинами, то из вышесказанного вытекает,
что мы можем действительно определить преобразование (95.5), при-
приводящее систему (95.3) к виду (95.6), причем для коэффициентов
форм Uy)(uv %>i, u2, v2) будут выполняться условия (95.9). Само
определение преобразования, как мы сейчас видели, чрезвычайно
просто и сводится к составлению уравнений (95.13), что требует
лишь развертывания левых и правых частей уравнений (95.12).
§ 95] КРИТИЧЕСКИЙ СЛУЧАЙ ДВУХ ПАР ЧИСТО МНИМЫХ КОРНЕЙ
427
Рассмотрим подробнее преобразованные уравнения. Очевидно,
прежде всего, что функции Фу и Wj удовлетворяют при всех t ^> О
и при значениях Иу и Vj, достаточно малых, неравенствам
Фу(?, Mj, Vv U2,
^Vjit, uv vu u2,
где В—некоторое положительное число.
Положим теперь
«У = ру (cos fry -f-* sin fry), Vj = py (cos fry — /sin fly) (95.15)
G=1. 2),
где pj, p2, ¦O'j и fl2—новые переменные. Тогда, принимая во внима-
внимание (95.7), (95.8) и (95.9), легко найдем, что уравнения (95.6) при-
примут вид
dp 4 dfti
j-mt-i-mi-ni
Pl P2
-f
If
lPj dt ~
y=l, 2;
Полагая
„(nil,
s1+«2 = 3, 5 TV).
2. "i.
__ Jm д(.
и выделяя вещественные и мнимые части, получим две группы урав-
уравнений
7=1. 2; mv
1p2m H
4-л, + л2 = 3, 5 TV)
Pi-
(95.16)
Здесь функции Rj, 0y, очевидно, таковы, что при всех t^>0, при
всех значениях ftj, ¦О'г и при достаточно малых значениях pj и р2
выполняются неравенства
\Rj(t, *„ #2, Pl> p2)| <C{|Pl| + |p
(95.17)
где С — положительная постоянная.
428 НЕУСТАНОВИВШИЕСЯ ДВИЖЕНИЯ [ГЛ. VI
Если невозмущенное движение рх = р2 = 0 для уравнений (95.16),
в которых ¦&! и $2 рассматриваются как произвольные функции вре-
времени, устойчиво, асимптотически устойчиво или неустойчиво при
любом выборе функций Rj, удовлетворяющих условиям (95.17), то
по характеру преобразования (95.15) то же самое будет иметь место
и для невозмущенного движения хх = ух = х2 = у2 — 0 уравнений (95.3)
при любом выборе функций фу и яру, удовлетворяющих условиям (95.4).
Справедливо, очевидно, и обратное соотношение между системами (95.3)
и (95.16). Поэтому задача сводится к исследованию на устойчивость
системы второго порядка (95.16).
Обращаясь к последней, замечаем, что она представляет некото-
некоторый частный случай задачи, рассмотренной в предыдущем параграфе,
и для решения ее мы можем воспользоваться полученными в этом
параграфе результатами. Запишем с этой целью уравнения (95.16)
в виде
+ Rj(t, % flv,, Pl, p2) (95.18)
C/=l'. 2),
где т ]> 3 (т — нечетное), а /?у' — формы k-то порядка перемен-
переменных pj и р2. При этом, принимая во внимание (95.9), мы можем
писать:
_2Pr2p?+ ¦ ¦ • -Г-Я1Р2РГ1.
где As и Bs — некоторые постоянные.
Составляя далее формы/э(р1, р2) и G (pv p2) (§ 94), будем иметь:
P(Pv P2) = M) M)
о Oh. P2)=p1Mm)-p2Mm) =
= Р1Р2 [(*1 --Aa) рГ14- (S3 ~ Лт_2) рГ 3pl+ ¦ • •+ (Bm - Ax) pa-1].
В рассматриваемом случае G никогда не будет знакоопределен-
ной. При этом уравнение G = 0 выполняется для осей координат
pt = р2 =г 0 и прямых, определяемых уравнением
— Ai)$-l = Q. (95.19)
На осях координат pt = 0 и р2 = 0 форма Р принимает соответ-
соответственно значения Втр2п+1 и Атр™+1- Поэтому на основании теоремы
§ 95] КРИТИЧЕСКИЙ СЛУЧАЙ ДВУХ ПАР ЧИСТО МНИМЫХ КОРНЕЙ 429
предыдущего параграфа невозмущенное движение будет неустойчиво,
если хотя бы одна из величин Ат, Вт положительна. Если Ат -^ О
и Вт <^ 0, то невозмущенное движение будет неустойчиво, если
хотя бы на одной из вещественных прямых, определяемых уравне-
уравнением (95.19), форма Р может принимать положительные значения.
Напротив, если на каждой такой вещественной прямой форма Р мо-
может принимать только отрицательные значения и если при этом
Ат < 0, Вт < 0, то невозмущенное движение устойчиво асимптоти-
асимптотически. Если форма Р обращается в нуль либо при pj = 0 (т. е.
Вт = 0), либо при ?2 = О (Т- е- Ат — ®)< либ° на одной из прямых
(95.19) и если при этом ни на одной из прямых (95.19) или осях
координат она не может принимать положительных значений, то
решение задачи требует рассмотрения в уравнениях (95.18) членов
порядков более высоких, чем т. На этих исключительных случаях
мы здесь не останавливаемся.
В тех случаях, которые мы сейчас рассмотрели, задача решается
членами наинизшего порядка в уравнениях (95.18). Следовательно,
коэффициенты Ау1' т*'п" нужно вычислять до тех пор, пока мы
не придем к некоторому порядку т, для которого не все вели-
величины Re (Л {m|> тъ л""г)) равны нулю при /rex —|— т2-\-п1-\- п2= т. Мо-
Может случиться, что все величины Re (Л у m""h ') обращаются в нуль,
как бы велико ни было число ml-\-m2-\-nl-\-n2. Этот исключи-
исключительный случай, при котором задача устойчивости вообще не ре-
решается конечным числом членов, как и все другие аналогичные слу-
случаи, здесь не рассматривается.
Таким образом, мы получили решение задачи устойчивости для
рассматриваемого критического случая, когда характеристическое
уравнение первого приближения имеет две пары чисто мнимых кор-
корней !).
Пример. Пусть предложена система четвертого порядка
d2x | j2 t\ (dx\2 (dy\4 / dx\3
X \2 I dv \2~\ . . I rfv\3
где а и b — постоянные, а / и F — аналитические функции своих
dx dv
аргументов, разложения которых по степеням х, у, —п-, -±г
1) Этот критический случай рассмотрен впервые в работе Г. В. Камен-
Каменкова, цитированной на стр. 411, который также приводит задачу к случаю
двух нулевых корней. Однако предложенный Г. В. Каменковым метод реше-
решения задачи требует проведения большого числа предварительных преобразо-
преобразований, каждое из которых приводит к очень громоздким вычислениям.
430
НЕУСТАНОВИВШИЕСЯ ДВИЖЕНИЯ
[ГЛ. VI
начинаются членами не ниже третьего порядка. Полагая
_ l dx — l dx
xi~—x~ х ~W У1 — х~т-х dt •
i dy ,1 dy
Х^^-^Ж У* = У+^ИГ
приведем данную систему к виду
dx + /ф1 Oi, yv х2, у2) + 4тг (У\ — xxf.
dt
dx2
#—**
х2,
у2,
¦sr (Уя — хг?'
(95.20)
где ф] и ф2— вещественные аналитические функции своих аргумен-
аргументов, разложения которых начинаются членами не ниже третьего по-
порядка. Делаем далее подстановку (95.5), в которой можно поло-
положить и№ — 1№ = 0, так как правые части уравнений (95.20) не со-
содержат членов второго порядка. Таким образом, полагаем:
v vv u2,v2)+
U =1.2).
где
f
" "" >
(У=1, 2; OTi
Подстановку (95.21) подбираем таким образом, чтобы уравнения
приняли вид (95.6) с соблюдением условий (95.9), так что можно
положить:
(95.23)
¦2Щи2
где a,, a2, Pj, p2 — подлежащие определению постоянные и ненапи-
ненаписанные члены имеют порядок не ниже четвертого.
§ 96] ОДИН НУЛЕВОЙ И ПАРА ЧИСТО МНИМЫХ КОРНЕЙ 431
Подставляя в первое уравнение (95.20) вместо xv yx, х2, у2 их
du/ dvi
значения из (95.21), заменяя при этом производные —тг, —гг их вы-
выражениями (95.23) и приравнивая члены третьего порядка, получим:
duf> ди® <Ц3) «Ц3>
3
?- (vx - в,)». (95.24)
где ер® — совокупность членов третьего порядка в функции q^. При-
Приравнивая в обеих частях (95.24) коэффициенты при u\vx и иги^2,
учитывая при этом (95.22), найдем:
о,+Bа - a) Bf- *> °>0) = аМ2< !> 0> 0)+tai+?$?-.
рх + (/A, -f to — to) М1' °'!> Х) = /А,5?'0> *'1( + lbv
или
Здесь «j и 6Х — вещественные числа, представляющие собой коэф-
коэффициенты при u2lv1 и uxu2v2 в функции cpj^j, vv ur vX Аналогич-
Аналогичным образом находим:
где а2 и ^—коэффициенты при и^2 и и1и2ю1 в функции q^Mj, vv u2, юХ
Делая теперь подстановку (95.15), окончательно найдем:
rfp, ЗаЯ3 о |
| ф2 _ 3to3 о |
dt ~ 8ш pi ~г" ' ' "' dt ~ 8Я р2 "Г • ¦ • •
где ненаписанные члены имеют порядок не ниже четвертого. Отсюда
сразу следует, что если хотя бы один из коэффициентов а или b
положителен, то невозмущенное движение неустойчиво. Если же оба
коэффициента отрицательны, то невозмущенное движение устойчиво
и притом асимптотически.
§ 96. Критический случай одного нулевого и пары чисто
мнимых корней для установившихся движений1).
Рассмотрим теперь систему (п-\-Ъ)-то порядка с постоянными
коэффициентами, для которой характеристическое уравнение первого
') См. М а л к и н И. Г., Решение некоторых критических случаев задачи
устойчивости движения. ПММ, т. XV, вып. 5, 1951.
Эта задача также впервые рассматривалась Г. В. Каменковым. Пред-
Предлагаемый ниже метод отличается от метода Г. В. Каменкова и приводит
К значительно более простым вычислениям-
432
НЕУСТАНОВИВШИЕСЯ ДВИЖЕНИЯ
[ГЛ. VI
приближения имеет один нулевой корень, два чисто мнимых корня + 1к
и п корней с отрицательными вещественными частями.
Подходящим выбором переменных рассматриваемые уравнения
могут быть представлены в следующем виде:
dx ,,, ч
-f- Xx (x, xx, yx, zx zn),
i+^i(Jf. xv yx, zx zn),
dxx
~dT
dy,
dt
~т~ Zs(x, xx, yx, zx, ..., zn)
(s=l, 2, .... n),
где разложения функций X, Xv Yx, Zs начинаются членами не ниже
второго порядка, а коэффициенты psj таковы, что уравнение
имеет корни только с отрицательными вещественными частями.
Пользуясь методом § 93, мы можем привести задачу к исследо-
исследованию системы третьего порядка вида
dx уф
dt l!
x, x
i. yi). i
(96.1)
dy,
x
x
(k\
[k)
\k)
v Vl)+ ... +C(x, xv
, xx, yx),
где X(k\ X[k) и Y\k) — формы й-го порядка переменных х, хх, у,
а ф, ф, и ф! — зависящие от t аналитические функции переменных х
х\> У\~ удовлетворяющие при всех Г^-0 в окрестности начала коор-
координат неравенствам
|Ф(Л х, хх, ух)\
|ф1(Л х, *!. yOl
1ЛГ+1
(96.2)
При этом переменные хх и ух являются комплексно сопряженными,
так что третье уравнение (96.1) может быть получено из второго
§ 96]
ОДИН НУЛЕВОЙ И ПАРА ЧИСТО МНИМЫХ КОРНЕЙ
433
заменой I на —I, хх на ух и у, на xv Первое уравнение (96.1) при
такой замене не изменяется.
Преобразуем теперь уравнения (96.1) при помощи подстановки
л; = и Н-и<2> (и, uv г>!)+ ••• + «(лт)(«. uv vx),
и,,
(96.3)
где и'*), и'.*', гК*> — подлежащие определению формы й-ro порядка
новых переменных и, Hj, vv Эти формы мы постараемся подобрать
таким образом, чтобы преобразованные уравнения приняли вид
№),
. «1.
«1.
я.
, И,
1, «0 + ...
(я.
(96.4)
i. «0 +
Здесь t/ ', t/j , ?Д '—-формы й-го порядка переменных и, их, vx,
причем формы U\ получаются из и[ заменой / на — i, ux на vx
и vx на их. Кроме того, формы U и i/[ таковы, что если ввести
обозначения
(96.5)
то для коэффициентов А
соотношения
j^n, га„ га2)
.(я, т„ т2)
«(я, т„ яг2)
должны выполняться
: 0 при
тх
т2,
= 0 при тхФтг-\-\.
(96.6)
Покажем, что формы «<Ч
в преобразовании (96.3)
можно действительно выбрать так, чтобы для уравнений (96.4) выпол-
выполнялись указанные условия. Положим с этой целью
<*>== 2 я1я>'В11т1)вявГ1«Г
2 я1
(96.7)
Так как второе уравнение (96.4) должно перейти в третье (по
крайней мере, с точностью до величин N-ro порядка) при замене /
434 НЕУСТАНОВИВШИЕСЯ ДВИЖЕНИЯ
на —/, иг на vl и vx на их, то должно быть:
[ГЛ. VI
, + m2 =~ *)¦ (96.8)
При таком выборе форм ©<*> третье уравнение (96f.4) будет нужного
вида, если только этим свойством будут обладать и первые два урав-
уравнения. Остается, таким образом, определить формы и'й> и «<*>. Под-
Подставим с этой целью в первые два уравнения (96.1) вместо х, xv yx
их выражения (96.3). Тогда, принимая во внимание (96.4), получим:
а=2
а=2
N
а=2
.... «1+ •
(96.9)
а=2
Задавшись каким-нибудь числом k < N, приравняем в обеих
частях полученных уравнений коэффициенты при «"apivj"», где
п-\- Щ-\- Щ = к. Будем на основании (96.6) и (96.7) иметь:
А(п, т» тг)^_ (Wi _ т^ ав(п, т„ т2) == tfn, mu )
Здесь c("'m"m2), C("'m" ma) — целые рациональные функции от тех
Ato,<h.rtt Ар1ы.\ д(а «..*)_ д|й *..«*) и КОМПлексно сопряженных
с ними величин, для которых p-\-q\-\-q2<.k. Допустим, что все
указанные величины уже вычислены и, следовательно, величины
с(п, т„ m,)f С(я, т„ т2) извесТНЫ Тогда при mj _t m2 мы можем
положить:
j^n, т„ т,) __ q ?(л, т„ т2) I ^(л, т„ т2)
а при тх = от2 получим, что
„ т2) __ q{ji, т„ т,)
§ 96] ОДИН НУЛЕВОЙ И ПАРА ЧИСТО МНИМЫХ КОРНЕЙ 435
а коэффициент $"'т" остается произвольным. Мы можем положить
его равным нулю или любой другой величине. Далее, при т1фт2 +1
мы можем положить:
Wn, я»,, пг2)
Л», «1„ «J п rin, mi, mi) 1
Л1 —U, DX — (mi_m2_1)a.
Если тх = т2 + 1, то
.(я, m,, m2l /-•("> mi> "*!>
а коэффициент М"' т" т^ может быть выбран совершенно произвольно.
Так как при п-\-тх + т2=2 величины С{п' т" тг) и С\п' т"тг)
известны, то отсюда следует, что действительно существует преобра-
преобразование (96.3), обладающее всеми указанными для него свойствами.
При этом легко видеть, что все коэффициенты А1-"' т" т2) будут веще-
вещественными. Действительно, первое уравнение (96.1) не изменяется
при замене i на —I, хх на ух и уг на xv Так как для преобразова-
преобразования (96.3) выполняется (96.8), то первое уравнение (96.4) не изме-
изменится при замене I на —/, щ на vl w vx на их. Но так как
j^n, т„ т2) __ q при щфт^ то перВое уравнение (96.4) не меняется
при замене их на vx и vx на их. Следовательно, это уравнение не
меняется при замене / па — /, откуда и вытекает вещественность
юэффициентов Л("'т>' т*\ Определение преобразования (96.3) при-
одится, как мы видим, к весьма простым вычислениям, сводящимся
развертыванию правых и левых частей уравнений (96.9).
Допустим, что указанное преобразование выполнено. Тогда функ-
1я U (t, и, их, vx) в уравнениях (96.4) будет, очевидно, удовлетво-
1ть неравенству
\U(t. и, иг, «r,)| <-S{|«H-|ei|-hl<'i|}'V+1- (96.10)
г В—положительная постоянная. Таким же точно неравенствам
1ут удовлетворять и функции Ux и Vx. Положим теперь:
их = р (cos ft +1 sin ¦&), vx = p (cos ¦& — i sin ¦&). (96.11)
Тогда получим:
N
du V /i(". m, m) n 2m , Ir(, rt> -<d\
N-l
а
~d
n+2m=l
N-1
A
dt
Я + 2я1=1
436
НЕУСТАНОВИВШИЕСЯ ДВИЖЕНИЯ
[ГЛ. VI
или, выделяя вещественные и мнимые части и учитывая, что коэф-
коэффициенты Л("' т' т) вещественны, получим два уравненр:
N
_
я+2т=2
ЛГ-1
Р. «)
(96.12)
и уравнение
Здесь
ЛГ—1
b(n, m+i, »)яу»_|_в(Л Ь. р, и).
(я, т + 1, т) г> / «(я, т + 1, т)\
^^ ¦ ¦ — 1т(л! ' ' ),
/,(t, *. p, я)|<С{|р| + |а|Г+1.
и функции R, Ut при достаточно малых р и и и при всех значе-
значениях ¦& и t'^-О удовлетворяют условиям
(96.13)
где С — положительная постоянная.
Аналогичному условию удовлетворяет и функция 0(?, ¦&, р).
Если невозмущенное движение и = р = 0 для уравнений (96.12),
в которых й рассматривается как произвольная функция времени,
будет устойчиво или асимптотически устойчиво, или неустойчиво при
любом выборе функций Ut, R, удовлетворяющих условиям (96.13),
то невозмущенное движение х = х1 = у1 = 0 для системы (96.1)
будет, соответственно, устойчиво или асимптотически устойчиво, или
неустойчиво при любом выборе функций ср (t, x, xv y{), cpj (t, x, xv y{),
^i(t, x, xv уО, удовлетворяющих условиям (96.2). Но тогда такие же
обстоятельства будут иметь место и для невозмущенного движения
х =
= ух = zx—
=zn==0 исходной системы.
n
Таким образом, задача сводится к исследованию на устойчивость
системы (96.12). Последняя задача является частным случаем задачи,
рассмотренной в § 94, и для ее решения мы запишем уравнения
(96:12) в виде
-g-={/.*> (а,
О, а. р).
*. «. Р).
(96.14)
§ 97] КРИТИЧЕСКИЕ СЛУЧАИ ПЕРИОДИЧЕСКИХ ДВИЖЕНИЙ 437
где k ^> 2 и U^\ Rw — формы 1-го порядка переменных и и р. При
этом в силу (96.12) формы U^ содержат только четные степени р,
а формы /?('* — только нечетные степени р. Так что мы можем,
в частности, писать:
Отсюда следует, что
О (и, p) = uRm—pU(*k) = pG'(u, p),
где О' (и, р)—форма fe-ro порядка переменных и и р. Следовательно,
форма О не является знакоопределенной. Невозмущенное движение
будет неустойчиво, если существует хотя бы одна вещественная
прямая О (и, о) —0, на которой Р(и, р) может принимать положи-
положительные значения, и асимптотически устойчиво, если на всех веще-
вещественных прямых О = 0 форма Р может принимать только отрица-
отрицательные значения. Все это будет справедливо при любом выборе
функций Ut и R, и число N можно будет положить равным k.
Случаи, когда ни на одной из вещественных прямых, определяе-
определяемых уравнением 0 = 0, форма Р не может принимать положитель-
положительных значений, но на некоторых из них может обращаться в нуль,
мы здесь не рассматриваем. Мы не рассматриваем также и тех исклю-
исключительных случаев, когда все формы LT , R , как бы велико ни
было число k, обращаются тождественно в нуль, что будет иметь
место тогда, когда все величины А т' и аУ1' т+ ' равны нулю.
В этих случаях задача устойчивости не решается, очевидно, конеч-
конечным числом членов в уравнениях возмущенного движения.
§ 97. Критические случаи периодических движений.
Приведение к установившимся движениям').
Мы переходим к исследованию критических случаев периодиче-
периодических движений. Допустим, что предложена система (я-)-&)-го порядка
с периодическими коэффициентами, для которой уравнения первого
приближения имеют п характеристических показателей с отрицатель-
отрицательными вещественными частями и k характеристических показателей
с вещественными частями, равными нулю. Мы будем предполагать,
что переменные выбраны таким образом, что первое приближение имеет
постоянные коэффициенты и в нем разделены критические и некри-
некритические переменные. Таким образом, уравнения возмущенного
') М а л к и н И. Г., Решение некоторых критических случаев задачи
устойчивости движения. ПММ, т. XV, вып. 5, 1951.
438 НЕУСТАНОВИВШИЕСЯ ДВИЖЕНИЯ [ГЛ. VI
движения имеют вид
dt
yk. *„ ..лхп),
dx
s
(97.1)
+ X,(t. У! у„, Xl Хп)
G=1, 2 k; s=l, 2 n).
Здесь Yj и Xs — аналитические функции переменных yt и xs,
разложения которых начинаются членами не ниже второго порядка.
Эти функции зависят также от t, по отношению к которому они
периодичны с периодом со. Коэффициенты q^, psl и rsi являются
постоянными, причем уравнение
имеет корни только с отрицательными вещественными частями, а вйе
корни уравнения
\Ч» — Ъ»\=° (97-2)
имеют вещественные части, равные нулю.
Согласно теореме 2 § 93 ответ на задачу устойчивости для си-
системы (97.1) совпадает с ответом на ту же задачу для системы &-го
порядка
У1 Ук- "i «„). (97.3)
где us {t, уi yk) — ряды по степеням ylf . . ., yh с периодиче-
периодическими коэффициентами, являющиеся формальными решениями уравне-
уравнений с частными производными (93.3). Это будет, однако, справедливо
лишь в том случае, когда задача устойчивости для системы (97.3)
решается конечным числом членов.
Мы будем предполагать, что переменные yt выбраны таким обра-
образом, что линейная часть уравнений (97.3) имеет каноническую форму,
так что
а остальные коэффициенты qtj равны нулю. Здесь "kt — корни урав-
уравнения (97.2), которые, как уже указывалось, имеют вещественные
части, равные нулю, а щ — некоторые постоянные. Все эти постоян-
постоянные равны нулю, если уравнение (97.2) не имеет кратных корней.
Но если указанное уравнение имеет кратные корни, то некоторые
из этих постоянных могут быть отличными от нуля и эти отличные
от нуля величины щ можно предполагать произвольными. Обозначим,
§ 97] КРИТИЧЕСКИЕ СЛУЧАИ ПЕРИОДИЧЕСКИХ ДВИЖЕНИЙ 439
далее, через Yf (t, yx yk) формы с периодическими коэффи-
коэффициентами, представляющими собой члены &-го порядка в разложе-
разложениях правых частей уравнений (97.3). Тогда, обозначая через N
достаточно большое целое число, рассмотрим систему
^ , yi> ..., п) (97.4)
A=1, 2 k; ao = O),
совпадающую до членов TV-го порядка с системой (97.3). Если невоз-
невозмущенное движение для системы (97.4) будет устойчиво или асим-
асимптотически устойчиво, или неустойчиво при любом выборе функций фг,
удовлетворяющих при всех t ^> 0 в некоторой окрестности начала
координат неравенствам
|ф,С Ух У»)К>ЧЫ-г- ••• +Ы}"+1. (97.5)
где А — некоторая постоянная, то и невозмущенное движение для
системы (97.1) будет, соответственно, устойчиво или асимптотически
устойчиво, или неустойчиво.
Для решения задачи устойчивости для системы (97.4) мы восполь-
воспользуемся методом, который мы уже применяли в §§ 66 и 67 при реше-
решении частных случаев рассматриваемой сейчас задачи. Этот метод
заключается в преобразовании уравнений (97.4) к такому виду, чтобы
в нем члены до порядка N имели постоянные коэффициенты. Тогда
задача сведется к уже рассмотренной задаче критических случаев
установившихся движений.
Мы сейчас покажем, что указанное преобразование действительно
может быть выполнено, если между корнями Я,г и периодом со не
существует никаких соотношений вида
(/=1, 2 k),
где ть ..., mk — произвольные целые положительные числа (неко-
(некоторые из них могут равняться нулю), связанные соотношением
ml-\- ... -}-Аий-^ЛЛ Мы будем предполагать, что это условие выпол-
выполнено и будем искать интересующее нас преобразование в виде
} ' 2 *'(*) '«22 ¦ • • я** (97.6)
=1, 2 k;
(f) — некотор фу р
дом оз. Мы постараемся подобрать эти функции таким образом, чтобы
где а\ '' '"' (f) — некоторые периодические функции t с перио-
периоб
440 НЕУСТАНОВИВШИЕСЯ ДВИЖЕНИЯ [ГЛ. VI
преобразованные уравнения приняли вид
ВД ux uk) (97.7)
A=1, 2,..., k; 2<m,+ ... +mft<7V),
где a| '' "" —постоянные, а f/; — зависящие от t аналитические
функции переменных их, ..., uk, разложения которых начинаются
членами не ниже (TV-j-l)-ro порядка. Эти функции, очевидно, удо-
удовлетворяют соотношениям вида (97.5).
Пусть и\ (t, «J uk) обозначает совокупность членов /га-го
порядка в подстановке (97.6). Допустим, что все и[р, для которых
s < т, и все oW, для которых j < I, уже вычислены согласно выше-
вышеуказанным условиям. Тогда, подставляя в уравнения (97.4) вместо у,
их выражения (97.6), заменяя при этом производные -Ц±- их выра-
выражениями (97.7) и приравнивая члены т-то порядка в левых и правых
частях полученных таким образом уравнений, мы найдем для опре-
определения форм и(т> следующие уравнения:
+ ^m) (<,«, «*) (97.8)
(/—1, 2 ^; тх-\- ... -\-тк = т; ао = О).
Здесь U\m) обозначает известные формы tn-го порядка перемен-
переменных uv . .., uk, коэффициенты которых являются периодическими
функциями t, периода со.
Приравнивая в уравнениях (97.8) подобные члены, мы получим
для определения коэффициентов л(тг ••¦• mft)(?) систему линейных
неоднородных дифференциальных уравнений. При этом, если эти
коэффициенты вычислять в определенном порядке (см. § 93, урав-
уравнения (93.13)), то для каждого из них получится уравнение вида
dA(mi mk)
L
-L—
__a(mi. •••• mft)-f-5(mi т*)@, (97.9)
где в(т1'•••• т*) являются линейными функциями уже вычисленных
величин л("г ••••"*) с периодическими коэффициентами.
§ 97] КРИТИЧЕСКИЕ СЛУЧАИ ПЕРИОДИЧЕСКИХ ДВИЖЕНИЙ 441
Допустим, что все входящие в fi(mi'"•'mft) величины Ж"'1' ••'"*)
уже вычислены и вышли периодическими. Тогда B(mt' "¦• ть) будут
известными периодическими функциями времени и уравнение (97.9)
даст возможность вычислить коэффициент Л(т'' "" ть).
Для того чтобы этот коэффициент получился периодическим,
необходимо, вообще говоря, подобрать постоянную aV''"' ть). Мы
положим
a(mi mft) =1. J S<mi m*>dt при mjXj+ ... + mkkk — ki = 0.
о
При таком и только таком выборе постоянной a('ni m*) урав-
уравнение (97.9) при т1Х1-\- ... -\-mkXk — ^,= 0 будет иметь перио-
периодическое решение, определяемое, очевидно, формулой
k)
~ ffi(mi mk)dt.
Входящую сюда постоянную интегрирования можно выбрать по про-
произволу. При т1Х1-{- ... -{-mkXk — Kt Ф 0 уравнение (97.9) имеет
периодическое решение при любом выборе постоянной д(т1'¦¦¦¦ mft),
С целью упрощения (весьма существенного) получаемых после пре-
преобразования уравнений (97.7) мы будем полагать:
a(mv-mk) = 0 при m^jH- ...,+ mk\ —1^0. (97.10)
При таком выборе постоянной a[mi ть) уравнение (97.9), как
было показано в § 67, имеет периодическое решение
(
1 — еаь .
о
, (97.11)
где для краткости положено:
Так как по условию а никогда не равняется ± — Y—Ь то
знаменатель в решении (97.11) всегда отличен от нуля и это решение
действительно существует. Благодаря тому же условию однородная
часть уравнения не имеет периодического решения с периодом,
соизмеримым с со, вследствие чего уравнение (97.9) кроме решения
(97.11) не имеет других периодических решений.
442 НЕУСТАНОВИВШИЕСЯ ДВИЖЕНИЯ [ГЛ. VI
Таким путем можно последовательно определить коэффициенты
Ау1^'"' ть> преобразования и одновременно с ними коэффициенты
aji m*' преобразованных уравнений. Если теперь учесть, что
каждая из величин Xt либо равна нулю, либо является чисто мнимой
и что в последнем случае какая-нибудь из величин Xj равна — Xt,
то мы придем к заключению, что, по крайней мере, при нечетном т
некоторые из величин тхХх -(-...-)- mkXk — Xt равны нулю. Следо-
Следовательно, не все постоянные д(т1'•¦¦•"**) равны нулю, если только
не рассматривать тот особо исключительный случай, когда все
интегралы
00
imi mk)dt.
как бы велико ни было т, равны нулю. Исключая из рассмотрения
указанный случай, как и все другие случаи, при которых задача
устойчивости не решается конечным числом членов, мы приведем
любой критический случай для периодических движений к аналогич-
аналогичному случаю для установившихся движений.
В частности, мы имеем возможность решить задачу устойчивости
для критических случаев одного нулевого корня и пары чисто мни-
мнимых корней и двух пар чисто мнимых корней. Заметим, что в этих
случаях в силу (97.10) уравнения (97.7) будут уже иметь вид, при
котором задача устойчивости решается сразу, т. е. вид (95.6)
в случае двух пар чисто мнимых корней и вид (96.4) в случае
одного нулевого и пары чисто мнимых корней.
Пример. Пусть предложена система третьего порядка
dfi
с одним нулевым и парой чисто мнимых корней ± Xt. Здесь / и
F—аналитические функции переменных х, -гг, у, разложения кото-
которых по степеням этих переменных начинаются членами не ниже третьего
¦ * Ах
порядка, причем функция / содержит только четные степени —гг.
Коэффициенты этих разложений, так же как и коэффициент cp(f),
являются периодическими функциями t, периода со.
Полагая
i dx ]' ^х
x x У хЧ
§ 97] КРИТИЧЕСКИЕ СЛУЧАИ ПЕРИОДИЧЕСКИХ ДВИЖЕНИЙ
приведем рассматриваемую систему к виду
, — л:,)
443
dt
dt
. У
—4
8
Делаем, далее, подстановку (97.6):
у — v -\- г>C> (t, ux, vx, v
. uv vv
где
(97.12)
(97.13)
(m1 -\~m2-\-n = k).
Мы не вводим в подстановку членов второго порядка, так как
эти члены отсутствуют в уравнениях (97.12). Кроме того, мы учиты-
учитываем, что переменные хг и ух являются комплексно сопряженными,
и делаем поэтому такими же переменные и1 и vx.
Стараемся подобрать преобразование (97.13) таким образом, чтобы
преобразованные уравнения приняли вид (97.7). В рассматриваемом
случае, учитывая (97.10), мы должны получить:
dv
dt
du,
~~dT
dv.
= av3-\-f>vu1v1-\-
(97.14)
444
НЕУСТАНОВИВШИЕСЯ ДВИЖЕНИЯ
[ГЛ. VI
Подставляя (97.13) и (97.14) в первые два уравнения (97.12) и
приравнивая члены третьего порядка, получим:
= F<3> U,
-и,)
ди
— и, — И
(97.15)
где /C) и FC> — совокупность членов третьего порядка в / и F.
Если в первом из этих уравнений приравнять коэффициент при v3,
то получим:
@,0,3)
= F<3)(', 0,0, 1),
и условие периодичности Л@> °' 3) дает:
t, 0, 0, \)dt.
(97.16)
Приравнивая во втором уравнении (97.15) коэффициенты при и^у1
и игхр, будем иметь:
djp, 1, о) i з
ai"i ^77 = — "
где г()(/) и 4*40—некоторые вещественные функции t, представляющие
собой коэффициенты при u*v1 и игхР в /^3) it, '^~ ', — ' —!^-, г;).
Отсюда находим:
га
о
Коэффициент р мы не подсчитываем, так как он нам не потребуется.
Полагая теперь:
§ 97] КРИТИЧЕСКИЕ' СЛУЧАИ ПЕРИОДИЧЕСКИХ ДВИЖЕНИЙ 445
мы получим из (97.14) следующую решающую задачу систему вто-
второго порядка с двумя нулевыми корнями:
Здесь
&/ (97Л7)
Для форм Р и О имеем:
P(v, p) = at p
О (г/, /?) = ор[(а — р) р2 — aw2].
Уравнение О = 0 дает две прямые v = О, р = 0 и две прямые,
определяемые уравнением
аи2 — (а — р)р2 = 0, (97.18)
если только а (а — р) > 0. Отсюда находим, чго невозмущенное
движение будет неустойчиво, если хотя бы одна из величин а или а
положительна. Если a < 0 и а < О, то, невозмущенное движение
будет асимптотически устойчиво, если уравнение (97.18) не имеет
вещественных решений, т. е. если a (a — р) < 0. Но то же самое
будет и в том случае, когда прямые (97.18) являются вещественными.
Действительно, при условии (97.18) имеем:
и следовательно, если а < 0, то на обеих прямых (97.18) форма Р
отрицательна. Итак, принимая во внимание (97.16) и (97.17), находим,
что невозмущенное движение будет асимптотически устойчиво, если
обе величины
со
Fi3)(t, 0, 0, \)dt
отрицательны и неустойчиво, если хотя бы одна из них положи-
положительна. Если одна из этих величин отрицательна, а другая равна
нулю, то требуется рассмотреть члены более высокого порядка
в уравнениях (97.14).
ДОПОЛНЕНИЕ I.
ОБ ОДНОЙ ЗАДАЧЕ ТЕОРИИ УСТОЙЧИВОСТИ
СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ.
§ 98. Постановка задачи.
В 1949 году М. А. Айзерманом1) была поставлена следующая
задача об устойчивости систем автоматического регулирования с од-
одним нелинейным органом.
Допустим, что поведение системы автоматического регулирования
описывается дифференциальными уравнениями вида
(98Л>
где asj—постоянные. Наряду с системой (98.1) рассмотрим линей-
линейную систему
dx, . . , .
-^=anX[+ ... +alaxn-\-hxk,
Ц± = aslx: + . . . + asnxa (s = 2 п)
и допустим, что все корни ее характеристического уравнения имеют
отрицательные вещественные части при всех значениях h, лежащих
в интервале
а < h < p.. (98.2)
Требуется узнать, будет ли при любом выборе однозначной и
непрерывной функции / (хк), обращающейся в нуль при хк = 0 и
удовлетворяющей при всех значениях хк ф 0 неравенствам
') А й з е р м а н М. А., Об одной проблеме, касающейся устойчивости
«в большом» динамических систем, Успехи матем. наук, т. IV, вып. 4, 1949.
OB УСТОЙЧИВОСТИ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ 447
состояние равновесия xl= ... —хп = 0 системы (98.1) асимпто-
асимптотически устойчивым при любых начальных возмущениях.
Указанная задача для систем второго порядка была досконально
изучена в 1950 году Н. П. Еругиным1), который в рассмотренных
им случаях дал положительный ответ на вопрос М. А. Айзермана.
Его работы опирались на качественные методы исследования траек-
траекторий на плоскости переменных {xlt x2]. Эти исследования при-
привлекли внимание многих математиков к данной проблеме и к другим
задачам устойчивости в целом.
В 1952 году, уже после выхода первого издания настоящей
монографии, И. Г. Малкиным была выполнена работа2), в которой
также изучалась проблема М. А. Айзермана для систем второго
порядка. Это исследование опиралось на второй метод Ляпунова.
При этом автор нашел весьма простое доказательство, построив
функцию Ляпунова в виде суммы квадратичной формы и интеграла
с переменным верхним пределом. Такой метод впервые был пред-
предложен в работе А. И. Лурье и В. Н. Постникова3). Статья
И. Г. Малкина, где "этот метод был развит для данной задачи, по-
послужила толчком для ряда работ, посвященных исследованию нели-
нелинейных проблем устойчивости в целом на базе функций Ляпунова.
Содержанием настоящего Дополнения I является упомянутая
работа И. Г. Малкина с небольшими изменениями.
§ 99. Исследование системы второго порядка
с нелинейностью, зависящей от первой координаты.
Рассмотрим сначала систему второго порядка
i? =/(*) +«у. % = Ьх + су. (99.1)
Характеристическое уравнение соответствующей линейной системы
имеет вид
р2 —
') Е р у г и н Н. П., О некоторых вопросах устойчивости движения и
качественной теории дифференциальных уравнений. ПММ, т. XIV, вып. 5,
1950; Качественное исследование интегральных кривых дифференциальных
уравнений. ПММ, т. XIV, вып. 6, 1950.
2) М а л к и н И. Г., Об одной задаче теории устойчивости систем авто-
автоматического регулирования. ПММ, т. XVI, вып. 3, 1952.
3) Л у р ь е А. И., П о с т н и к о в В. Н., К теории устойчивости регули-
регулируемых систем. ПММ, т. VIII, вып. 3, 1944.
448 ДОПОЛНЕНИЕ I
Корни этого уравнения будут иметь отрицательные вещественные
части при всех значениях h, удовлетворяющих условиям
A-f c<0, he — ab > 0.
Поэтому, полагая / (х) = xh (x) (х ф 0), будем по условию задачи
иметь:
h (х) 4- с < 0, h(x)c — ab>0 (x ф 0). (99.2)
Мы будем, кроме того, предполагать, что при \х\ > ?, где
| — достаточно большое число, выполняется неравенство
h ( y\ г nh ^> p (I v I "¦>» %\ ('QQ /V>
IV I л I О 1*1/ ^^ С I л ^s* C.J, IC/C/.OI
где е — положительное число, которое может быть сколь угодно
малым.
Рассмотрим функцию
х
2V = 2с Г / (х) dx 4- (с2 — а*) х2 — 2асху + а2у2 ==
о
х
==2 Г[h(x)c — ab] x dx -f- (ex — ayf.
На основании (99.2) эта функция определенно-положительна.
Составляя производную этой функции по / в силу уравнений (99.1),
найдем:
/71/
~F = — abcx* + Ф (х) 4- (с2 — ab) х/ (х).
Полученное выражение, обращаясь в нуль при х — 0, при х Ф 0
может принимать только отрицательные значения при любом выборе
функции f(x), удовлетворяющей условию (99.2). Действительно, при
условии (99.2) и при х ф 0 будем иметь:
~ = (h 4- с) (ch — ab) x2 < 0, (99.4)
что и доказывает наше утверждение.
Таким образом, при любом выборе функции f(x), удовлетворяю-
удовлетворяющей условию (99.2), V будет являться для уравнений (99.1) функ-
функцией Ляпунова. Отсюда немедленно вытекает устойчивость равнове-
равновесия х = v = 0. Легко видеть, что при этом устойчивость будет
dV
асимптотической, несмотря на то, что функция —п- является не знако-
at
dV
определенной, а только знакопостоянной. Действительно, —jj- обра-
обращается в нуль только при х — 0 и, следовательно, интегральные
OB УСТОЙЧИВОСТИ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ 449
кривые во всех точках, не лежащих на оси у, пересекают семейство
замкнутых кривых V — const снаружи внутрь. Но то же самое будет,
очевидно, иметь место и в точках, лежащих на оси у, так как при
х = 0, как это следует из уравнений (99.1), ~ягФ®- Разница будет
лишь в том, что на оси у интегральные кривые, входя внутрь кри-
кривых V = const, будут при этом их касаться*).
Итак, при любом выборе функции f(x), удовлетворяющей усло-
условию (99.2), равновесие х = у = 0 асимптотически устойчиво. И это
будет иметь место, каковы бы ни были начальные значения вели-
величин хну, так как, учитывая (99.3), можно показать, что кривые
V(x, y) = c при любом с замкнуты. Это можно также показать и
не обращаясь к геометрической интерпретации2).
Достаточно рассмотреть лишь случаи, когда в уравнениях (99.1)
а Ф О, так как при а = О асимптотическая устойчивость движения
х = у — 0 в целом при условиях (99.2), (99.3) проверяется непо-
непосредственно последовательным интегрированием уравнений (99.1).
Действительно, при \х\ > | мы можем на основании (99.3) писать
(знак плюс перед | берется при х > | и знак минус — при х < —|):
±1 х
IV = 2 J [h (х) с — ab] х dx -f- 2 J \h (x) с — ab\ x dx +
о ±1
-f- (ex — ayf > 2e (x2 — |2) + {ex — ayJ. (99.5)
Пусть x(t), y(f) — произвольное решение уравнений (99.1).
На основании (99.4)
V(х(t), у (t))<Vo = V(х (t0), у(t0)).
Но так как при достаточно больших х выполняется (99.5), то отсюда
следует, что при всех t J> t0 рассматриваемое решение остается вну-
внутри круга достаточно большого радиуса с центром в начале коорди-
координат. Но тогда это решение с неограниченным возрастанием t либо
стремится к какому-нибудь периодическому решению х* (t), у* (t),
либо к единственной особой точке х = у — 0. Но первый из этих
случаев невозможен. Действительно, функция V (х* (t), у* (t)) отлична
от постоянной, так как в силу (99.4) ее производная может обра-
обратиться тождественно в нуль только, если ;t*(f)^O, а последнее
невозможно, если в уравнениях (99.1) величина а ф 0. Но если
функция V(х*(t), у*(t)) отлична от постоянной, то, будучи периоди-
периодической, она вопреки (99.4) не может обладать знакопостоянной
') См. Дополнение III.
2) См. также примечание к стр. 38.
450 ДОПОЛНЕНИЕ I
производной. Таким образом, система (99.1) не имеет периодических
решений и, следовательно, решение х (t), у (/) при t -> о? стремится
к нулю. Поэтому для уравнений (99.1) ответ на вопрос, поставлен-
поставленный М. А. Айзерманом, всегда получается утвердительный.
§ 100. Исследование системы второго порядка
с нелинейностью, зависящей от второй координаты.
Рассмотрим теперь систему
4 ^ A00.1)
Характеристическое уравнение соответствующей линейной системы
имеет теперь вид
р2 — (а +
Следовательно, для того чтобы корни этого уравнения имели
отрицательные вещественные части, необходимо и достаточно, чтобы
выполнялись неравенства
а-\-с<0, ac — bh>0.
Полагая / (у) = yh (у), будем иметь
ас — bh(y)>0. A00.2)
Кроме того, предположим, что при достаточно больших значе-
значениях \у\ выполняется неравенство ас— bh (у) > е.
В частности, если ? = 0, то функция f(y) ничем не ограничена.
Но при ? = 0, как это следует из A00.2), должно быть а < 0, с < 0
и непосредственное интегрирование системы A00.1) показывает, что
равновесие асимптотически устойчиво при любом начальном возму-
возмущении и при любом выборе функции /(у).
Допустим, что b Ф 0, и рассмотрим функцию
у
2V = — 2bjf (у) dy -f b2x2 — labxy -f (a +• с) ау2зз
:2J[ac—bh (у)] ydy-\- (bx — ayf.
На основании A00.2) функция V определенно-положительна.
Составляя ее производную в силу уравнений A00.1), получим:
(IV
—— = ас (a -f- с) у2 — b (a -j- с) у/ (у).
ОБ УСТОЙЧИВОСТИ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ 451
Полагая /(у) — hy, где h = h(y) удовлетворяет условию A00.2),
получим:
^- = (а + с)(ас — bh)f<0 при уфО.
Отсюда, так же как и в предыдущем параграфе, заключаем, что
если в уравнениях A00.1) функция удовлетворяет условию A00.2),
то равновесие будет асимптотически устойчиво при любом начальном
возмущении.
Итак, для системы A00.1) ответ на вопрос М. А. Айзермана тоже
получается всегда утвердительный.
Во всех наших рассуждениях не исключалась возможность, что
кривая z — f(x) касается при лг = О одной из прямых z = ах и
z = fix. В этом случае характеристическое уравнение будет иметь
корни с вещественной частью, равной нулю. Следовательно, линеа-
линеаризованная система будет находиться на границе области устойчи-
устойчивости. Так как при этом нелинейная система будет по доказанному
устойчива, то по Н. Н. Баутину эта граница всегда является «безо-
«безопасной» *).
В заключение заметим, что предположение о дифференцируемое™
функции / (х) не делалось и, следовательно, кривая z = f(x) может
не иметь в начале координат определенной касательной.
') См. § 44.
ДОПОЛНЕНИЕ II.
О СУЩЕСТВОВАНИИ ФУНКЦИЙ ЛЯПУНОВА.
§ 101. Постановка задачи.
В §§ 71—73, 75 настоящей книги рассматривалась проблема
обращения теоремы Ляпунова об асимптотической устойчивости. Ниже
приводится с небольшими изменениями содержание статьи И. Г. Мал-
кина «К вопросу об обратимости теоремы Ляпунова об асимптоти-
асимптотической устойчивости», опубликованной после выхода в свет первого
издания настоящей монографии. В этой статье установлены необхо-
необходимые и достаточные условия существования функции Ляпунова
в общем случае неустановившихся движений.
Рассмотрим систему дифференциальных уравнений возмущенного
движения
*?±. = Xs{t, х, хп) (Xs(t, 0, .... 0) = 0; s=l я).
A01.1)
определенную в области
п
^>0, аг<Я2, х=2 *2. A01.2)
s = l
где Н—положительная постоянная. Согласно теореме II Ляпунова
(стр. 189) невозмущенное движение хг= ... =хп = 0 будет асимп-
асимптотически устойчиво, если существует определенно-положительная
функция V(t, xx хп), полная производная которой по времени,
составленная в силу уравнений A01.1), есть функция определенно-
отрицательная и если при этом функция V допускает бесконечно
малый высший предел. Возникает вопрос об обратимости этой тео-
теоремы, т. е. вопрос о существовании функции V, удовлетворяющей
всем указанным условиям, всякий раз, когда невозмущенное движе-
движение асимптотически устойчиво 1). В общем случае теорема Ляпунова
об асимптотической устойчивости не обратима. Этот вопрос исследо-
') См. стр. ЗЩ
О СУЩЕСТВОВАНИИ ФУНКЦИЙ ЛЯПУНОВА 453
ван в § 75 для случая, когда функции Xs линейны относительно
хх, хп и по отношению к t непрерывны и ограничены, причем
для такого рода систем установлены необходимые и достаточные усло-
условия существования функций V, удовлетворяющих всем условиям тео-
теоремы Ляпунова.
Здесь мы будем рассматривать нелинейные уравнения A01.1),
правые части которых в области A01.2) непрерывны и допускают
непрерывные и ограниченные частные производные по xv .... хп.
§ 102. Необходимые и достаточные условия
существования функции V.
Рассмотрим решение xs — Fs(t, х® х°п, tA уравнений A01.1)
с начальными условиями Fs (^0, х®, ..., х°п, tA = x°s. Если невозму-
невозмущенное движение асимптотически устойчиво, то найдется такое доста-
достаточно малое положительное число 6, что при всех начальных значе-
значениях, лежащих в области
, A02.1)
будут выполняться соотношения
Hm FJt, x° ifi <) = 0. A02.2)
Мы сейчас покажем, что для того, чтобы для уравнений A01.1)
существовала функция V, удовлетворяющая всем условиям теоремы
Ляпунова об асимптотической устойчивости, необходимо и достаточно,
чтобы соотношения A02.2) выполнялись равномерно относительно х°,
и t0. Мы докажем, следовательно, что имеют место две следующие
теоремы.
Теорема 1. Если существует такое положительное число 6,
что соотношения A02.2) выполняются равномерно относи*
тельно х^, .... х°п, tQ, лежащих в области A02.1), то суще-
существует допускающая бехконечно малый высший предел опре-
определенно-положительная фунщияУ (t, хх хп), полная произ-
производная которой по времени, составленная в силу уравнений
A01.1), есть функция определенно-отрицательная.
Доказательство. Заметим прежде всего, что при выполнении
условий теоремы невозмущенное движение будет равномерно устой-
устойчивым. Другими словами, для всякого положительного числа е можно
найти не зависящее от t0 положительное число т](е) такое, что при
всех t~^-tQ будут выполняться условия F < е2, коль скоро х° <! ц2.
Здесь введено обозначение
F ('. *? 4. *о) = S F\ (t, x\ х°а, t0). A02.3)
454 ДОПОЛНЕНИЕ II
В самом деле, полагая tj < 6, мы на основании условий теоремы
найдем такое число Т (г), зависящее только от е, что при всех
t^tu-\-T будет выполняться неравенство F < е2. Будем теперь счи-
считать г| настолько малым, чтобы это неравенство выполнялось также
в течение конечного промежутка времени (t0, to-\-T). Это возможно
в силу теоремы о непрерывной зависимости решений от начальных
условий (решение Fs сравниваем с тривиальным решением хх= . ..
. .. = хп = 0). При этом, как это вытекает из доказательства ука-
указанной теоремы, число т] определяется исключительно числом Т(е)
и верхними пределами функций \XS\ и их постоянных Липшица по
переменным Xj в области to<g^.t < tQ-\- T, х4^.г2. Полученное таким
образом число tj будет удовлетворять всем требуемым условиям. Из
сказанного следует, что если число 6 в неравенствах A02.1) доста-
достаточно мало, то функция F будет при всех t > t0 во всяком случае
оставаться в области х^.Н2. Мы будем в дальнейшем предполагать,
что число 6 удовлетворяет указанному условию.
Покажем теперь, что для функции F при всех т > 0 выполняется
неравенство *)
F (t0 + т. *?...., xl, fQ) < Ф (т), A02.4)
где ф (т) — некоторая положительная непрерывная функция, для кото-
которой Птф(т) = 0 при т->оо. С этой целью рассмотрим какую-нибудь
убывающую и сходящуюся к нулю бесконечную последовательность
положительных чисел elt е2, . • •, е„, .. . По условию теоремы для
всякого числа е, этой последовательности найдется число Tt (e^) такое,
что при всех т > Tt будет выполняться неравенство F(^0 + t, x°v ...
.... х°п, tQ\ < ег и это число Т( не будет зависеть от x°s, tQ. Последо-
Последовательность Tt будет, очевидно, расходящейся, и мы можем при этом
предполагать, что Т1+1 > Ть. Рассмотрим теперь произвольную моно-
монотонно убывающую функцию ф (т), для которой фG'/+1)==
= е/(/=1, 2, . . .). Если мы при этом предположим, что в интер-
интервале @, 7^) справедливо неравенство /7<ф(т), что, очевидно, воз-
возможно, так как при всех значениях аргументов F ^ Н2, то построен-
построенная таким образом функция ф (т) будет удовлетворять всем требуемым
условиям.
Рассмотрим теперь частные производные —^- и . Так как
dxs dt0
по доказанному при всех t ^-10 и всех значениях x°s, лежащих в обла-
области A02.1), функции Fs остаются в области A01.2), то эти частные
производные при указанных значениях аргументов существуют и не-
') См. аналогичное рассуждение в § 73 на стр. 314,
О СУЩЕСТВОВАНИИ ФУНКЦИЙ ЛЯПУНОВА 455
прерывны. Покажем, что при т > 0 справедливы неравенства
Х'Х° *"'*°) <Ае" = М(%).
A02.5)
= М(х),
dx°s
где А и X— не зависящие от х0,, t0 положительные числа. С этой
целью рассмотрим уравнения в вариациях для системы A01.1):
*Ь = Рлих + ... + р|А (Psj = Щ) ¦ (Ю2.6)
При этом в производных psj величины xs заменены функциями Fs.
Пусть us-(t, (Л и u*s(t, (Л — решения этой системы, определяемые
начальными условиями:
usj (t0, t0) = bsJ (bsj — символ Кронекера),
«•,('<>• 'o) = -^('o- A *°»> (Ю2.7)
Тогда, как известно, имеем тождественно
С/Л л ^"Q
Полагая в уравнениях A02.6) vs — use~ki, будем иметь
dvs _ . _,
eft У si 1 \ • • " 1^ rsn п s •
откуда
S, ] = l
Правая часть этого выражения при достаточно большом положи-
положительном X будет формой определенно-отрицательной, так как, по
определению, в области A01.2) частные производные функций Xs
ограничены. Полагая, что X удовлетворяет указанному условию, полу-
получим при t > ^о
и, следовательно,
п п
Ль^ о /rf\ ¦ \ь^ 9 / 1 \ 1> ^/ / ^
^71 ^й 1^1 <^ /, ^« ( г \ Д*Л *' — fo',
J=l «=1 S ^ '
Применяя эти неравенства к решениям usj и и* и учитывая, что
на основании A02.7) для модулей начальных значений этих решений
458 ДОПОЛНЕНИЕ II
могут быть назначены некоторые не зависящие от x°s, tQ верхние пре-
пред/7 dF.
делы, находим, что частные производные ——, —*¦, а следовательно,
dF dF
также и частные производные —^-, удовлетворяют неравенствам
dxj dtQ
вида A02.5).
Как показал И. Л. Массера '), для всякой пары положительных
функций М (т]) и фСп), определенных при всех т]^-0, из которых
первая возрастающая, а вторая стремится к нулю при ц -> оо, можно
построить функцию О(т]), удовлетворяющую следующим условиям.
1. Функция О(ц) — положительная возрастающая функция, опре-
определенная при всех Ti ^- 0 и обладающая непрерывной возрастающей
(очевидно, положительной) производной О' (г\).
2. О@) = 0. О'@) = 0.
3. Имеют место неравенства
оо оо
J О [ф (т)] dx < оо, J О' [Ф (т)] М (т) dx < оо. A02.8)
о
Принимая, что ф (т]) и М Сп) — функции, фигурирующие в не-
неравенствах A02.4) и (Ш2. 5), положим
V(t, х, *») = / O[F(x, х, хп, t)\dx~
t
CO
= J Q[F(t + x, xx *„. t)\dx A02.9)
о
и покажем, что функция V удовлетворяет всем условиям теоремы.
Заметим прежде всего, что в области
A02.10)
на основании A02.4) справедливы при всех т>0 неравенства
так как О (ti) — функция возрастающая. Отсюда на основании A02.8)
вытекает, что интеграл, фигурирующий в выражения V, сходится и
притом равномерно в области A02.10). Следовательно, в этой обла-
области функция V существует и непрерывна по всем своим аргументам.
Дифференцируя далее выражение V формально под знаком интеграла,
') См. выше стр. 314—315.
О СУЩЕСТВОВАНИИ ФУНКЦИЙ ЛЯПУНОВА
457
будем иметь:
~дх~-
J
,Xl xn,t)
х
, X! ха,
A02.11)
f О' [Р(г,хг хп. 01
Но на основании A02.4) и A02.5) в области A02.10) при всех
т > t имеем:
'[F(т, *„.... х„.
< **?•• *»
(т, ДГь ..., хп, t)
,[ф(т_
dt
так как функция G' (tj) также возрастающая. Поэтому интегралы,
входящие в A02.11), сходятся в области A02.1,0) абсолютно и равно-
равномерно. Следовательно, выражения A02.11) представляют в области
A02.10) непрерывные и ограниченные функции, которые действи-
действительно являются частными производными функции V. Итак, функ^
ция V обладает в области A02.10) непрерывными и ограниченными ча-
частными производными первого порядка. Но это условие является более
сильным, чем существование бесконечно малого высшего предела.
Покажем теперь, что функция V определенно-положительна.
С этой целью положим
a=^7=zVxl+ •••
где L — верхний предел величин \XS\ в области A01.2). Из A02.9)
имеем:
а
V>
о
Но
, хп.
A02.12)
/
.... Xn, f), ...
Fn(r\, xv .,., xn, f))dt\
458
ДОПОЛНЕНИЕ II
и, следовательно, в интервале 0 -< т -< а справедлива оценка
Я I Я
*i х„, f)-x,)*
s=l
s=l
откуда
и из A02.12) получаем:
Правая часть этого неравенства представляет собой не завися-
зависящую от t определенно-положительную функцию. Следовательно,
V есть определенно-положительная функция.
dV
Составим теперь выражение для полной производной —п- в силу
дифференциальных уравнений A01.1). Будем, очевидно, иметь:
dV
dt
dV*
dt
где V* означает результат замены в выражении V величин xs. функ-
функциями Fs (t, х°\ x°n, ^o)- Имеем
°i x°a.t0),....Fa(t, x°x
t, x\ x°n, to)}dx.
x°
° x°n, to)} = — G {
x\
откуда
~dT==~dT~ — (J
Следовательно, —гг есть функция определенно-отрицательная.
Таким образом, V удовлетворяет всем нужным условиям, что и
доказывает теорему.
Теорема 2. Если для системы уравнений A01.1) суще-
существует допускающая бесконечно малый высший предел опре-
определенно-положительная функция V(t, xl хп), полная про-
производная которой по времени, составленная в силу этих
уравнений, есть функция определенно-отрицательная, то
существует такое достаточно малое число 6 > 0, что решения
Xf = Fl!(tt, Xi xl, t0) удовлетворяют соотношениям A02-2)
О СУЩЕСТВОВАНИИ ФУНКЦИЙ ЛЯПУНОВА 459
равномерно относительно величин x°s, t0, лежащих в области
A02.1I).
Доказательство. Согласно условию теоремы существует
допускающая бесконечно малый высший предел функция V такая,
что в области f^-О, х^Н2 выполняются неравенства
V(t. xx xn)>Wl(x1 xn), A02.13)
4йг=тг+2 *?¦*.<-*»<*> *•>• <10214>
.5 = 1
где Wx и W2— не зависящие от / определенно-положительные
функции.
Пусть С > 0 — точный нижний предел функции Wx при условии
х = Н2. Тогда на основании A02.13) имеем:
V(t, х, *„)>С при х = Н2, t>0. A02.15)
Так как V допускает бесконечно малый высший предел, то най-
найдется такое положительное число 6, что будет справедливо нера-
неравенство
V(t. хх хп)<С при х<№, *>0. A02.16)
Покажем, что 6 и является искомым числом, фигурирующим
в теореме. С этой целью рассмотрим произвольное положительное
число е < 6 и обозначим через с > 0 точный нижний предел функ-
функции Wx при условии Н2^> х^-е2. На основании A02.13) будем
иметь:
V{t, xx *„)>с при /^>лг>е2, f>0. A02.17)
Далее выберем настолько малое положительное число а < е,
чтобы выполнялось условие
V{t, xv .... хп)<с при лг<а2, *>0 A02.18)
и обозначим через / > 0 точный нижний предел функции W2 при
условии Н2^. х^-а2. Таким образом, на основании A02.14)
4jr< — I при W2>jc>a2. ^>0. A02.19)
Рассмотрим теперь произвольное решение xs == Fs (t. xl, ...
..., х°п, tQ] уравнения A01.1), начальные значения которого x°s и tQ
лежат в области, определенной неравенствами A02.1).
') К. П. Персидский доказал, что при выполнении условий теоремы реше-
решения стремятся к нулю равномерно относительно t0, а И. Л. Массера — что
при тех же условиях решения стремятся к нулю равномерно относительно x°s.
460 ДОПОЛНЕНИЕ II
Покажем прежде всего, что при всех t > t0 справедливо нера-
неравенство
¦ F < Я2.
В самом деле, функция V*(t) = V(t, Fv .... Fn) на основании
A02.14) монотонно убывает и при t = t0 на основании A02.1) и
A02.16) V*(f)<C.C. Следовательно, то же самое неравенство спра-
справедливо и при всех t > t0. Но тогда при всех t > tQ будет спра-
справедливо неравенство F < Я2, ибо если бы в какой-нибудь момент
времени это неравенство нарушилось, то для этого момента на осно-
основании A02.15) мы имели бы V*(t)>C.
Обозначим теперь через Т (е) зависящее только от е положи-
положительное число, определяемое равенством
и покажем, что в интервале (t0, tQ-\-T) найдется такой момент вре-
времени t — tx, для которого
В самом деле, рассмотрим следующее равенство:
??t. A02.20)
J
и
Если бы во всем интервале (?0, to-\-T) было справедливо нера-
неравенство !/*(?)> с и, следовательно, на основании A02.18) также и
неравенство F>a2, то из A02.20) на основании A02.16) и A02.19)
мы получили бы
V* C
что противоречит условию. Таким образом, в интервале (/0, tQ~\-T)
найдется такой момент времени, для которого V*(?)<c. Так как
V* (() — функция убывающая, то это неравенство будет справедливо
при всех значениях
Но тогда при всех f^-to-{-T будет на основании A02.17)
выполняться неравенство х < е2, что и доказывает теорему, так как
число е можно взять сколь угодно малым.
Приведенное доказательство может быть проиллюстрировано гео-
геометрически (рис. 22).
При рассмотрении рисунка необходимо учесть, что уравнение
Wj (хг jkJ = k2 при k, достаточно малом, представляет собой
О СУЩЕСТВОВАНИИ ФУНКЦИЙ ЛЯПУНОВА
461
замкнутую поверхность, окружающую начало координат. Точно
так же и уравнение V{t, xv .... xn)^=k2 представляет собой в про-
пространстве переменных хх хп замкнутую поверхность, окружаю-
окружающую начало координат, но изменяющуюся с течением времени. При
этом при всех ?>0 поверхность V = k2 в силу A02.13) лежит
внутри поверхности Wx = k2 и остается вне некоторой окрестности
начала координат, так как V допускает бесконечно малый высший
предел.
Поверхность W1= С лежит внутри сферы х = Н2 и имеет с нею
по крайней мере одну общую точку на (рисунке эта поверхность
не показана). То же самое можно сказать и относительно поверх-
поверхности Wx = с и сферы х = е2.
Примечание. Для справедливости теоремы 2 нет, очевидно,
необходимости, чтобы функции X s допускали частные производные.
Достаточно, чтобы эти функции были непрерывными и такими,
чтобы была обеспечена единствен-
единственность решений для уравнений A01.1).
Впрочем, последнее условие также
не существенно.
При доказательстве теоремы 1
мы видели, что при выполнении
условий этой теоремы функция V
будет не только допускать беско-
бесконечно малый высший предел, но и
обладать ограниченными частными
dV „
производными -г—. Поэтому, при-
принимая во внимание теорему 2, убе-
убеждаемся в справедливости следую-
следующей теоремы.
Теорема 3. Если для урав-
уравнений A01.1) существует опре-
определенно-положительная функция V, допускающая бесконечно
малый высший предел, производная которой по времени, со-
составленная в силу этих уравнений, есть функция определенно-
отрицательная, то для этих уравнений существует функ-
функция V**, обладающая такими же свойствами и для которой
dV*
Рис. 22.
частные производные
oxs
в некоторой окрестности начала
s
координат и при всех t > 0 ограничены х).
') Это утверждение было усилено в работах Я. Курцвейля (Об обра-
обращении второй теоремы Ляпунова об устойчивости движения, Чехосл. матем.
журнал, 1956, т. 6 (81), № 2, стр. 217—259, № 4, стр. 455—484) и И. Мас-
сера (Contributions to stability theory, Annals of Mathematics, 1956, т. 64,
вып. 1, стр. 182—206), которые показали, что в случае равномерной асимпто-
462 ДОПОЛНЕНИЕ II
Наряду с уравнениями A01.1) рассмотрим систему
*?з. = Х,Ц,хх xn) + Rs(t,Xl Л)- 002-21)
Здесь функции Rs описывают постоянно действующие возмущаю-
возмущающие факторы. Эти функции определены в области A01.2), где они
непрерывны и таковы, что для уравнений A02.21) обеспечены условия
единственности решений.
При этом функции Rs в отличие от функций Xs не обращаются,
вообще говоря, в нуль при хх = ... = хп — 0.
В § 70 мы доказали, что если для уравнений A01.1) существует
определенно-положительная функция V, производная которой по вре-
времени, составленная в силу этих уравнений, есть функция определенно-
определенному
отрицательная, и если частные производные -^— этой функции
ОХ §
в области A01.2) ограничены, то v тривиальное решение хх— ...
... = хп = 0 устойчиво при постоянно действующих возмущениях.
Отсюда на основании теорем 1 и 3 мы приходим к следующему
результату').
Теорема 4. Если тривиальное решение лг, = ... =лг„ = О
системы A01.1) асимптотически устойчиво в смысле Ляпунова
и если при этом соотношения A02.2) выполняются равно-
равномерно относительно x°s и t0, лежащих в области A02.1), то
это решение устойчиво при постоянно действующих воз-
возмущениях.
тической устойчивости существует сколь угодно гладкая функция Ляпунова,
если предполагать лишь, что" правые части уравнения A01.1) непрерывны,
д V
но не требовать существования производных -г—. Кроме того, Я. Курцвей-
лем было показано, что поверхности V = с гомеоморфны сфере. Последний
результат уточняет геометрическую интерпретацию теоремы Ляпунова об
асимптотической устойчивости.
') Аналогичная теорема сформулирована в работе С. И. Горшина
(Об устойчивости движения с постоянно действующими возмущениями,
Изв. АН Казахской ССР, № 58, 1948). Доказательство С. И. Горшина суще-
существенно отличается от приведенного здесь, где теорема 4 оказывается след-
следствием теоремы 1 о существовании функции Ляпунова.
ДОПОЛНЕНИЕ III.
ОБОБЩЕНИЕ ТЕОРЕМ ВТОРОГО МЕТОДА ЛЯПУНОВА.
§ 103. Критерии, основанные на функциях Ляпунова
со знакопостоянными производными.
Критерии асимптотической устойчивости, приведенные в § 10
(теорема Б) и в § 46 (теорема II), опираются на функции Ляпу-
dV
нова V, производные которых —гг- в силу уравнений возмущенного
движения являются функциями знакоопределенными. В приложениях,
особенно при исследовании устойчивости в большом и в целом
нелинейных систем, иногда удается построить определенно-положи-
dV
тельную функцию V, производная которой —гг- является лишь
функцией знакопостоянной отрицательной, но не определенно-отри-
определенно-отрицательной. Именно с этим случаем мы встретились в Дополнении I.
В то же время попытки построить функцию Ляпунова V с опреде-
определенно-отрицательной производной приводят к серьезным трудностям.
Поэтому возникает необходимость сформулировать общий критерий,
который указывал бы условия, обеспечивающие асимптотическую
устойчивость невозмущенного движения при наличии лишь функции
Ляпунова со знакопостоянной производной. В последнее время был
предложен ряд таких критериев. По-видимому, наиболее ранними
из них были теоремы, доказанные для систем уравнений, правые
части которых не зависят явно от времени*). Без существенных
изменений эти критерии обобщаются на периодические по времени
системы. Позднее были доказаны аналогичные критерии для общего
случая нестационарных систем с использованием, однако, двух и
более функций Ляпунова2).
') Б а р б а ш и н Е. А., К р а с о в с к и й Н. Н., Об устойчивости дви-
движения в целом, ДАН, т. 86, вып. 3, 1952; Тузов А. П., Вопросы устойчи-
устойчивости для одной системы регулирования, Вестник ЛГУ, вып. 2, 1955.
2) Матросов В. М., Об устойчивости движения. ПММ, т. XXVI,
§ьщ. §, 1962. '
464 ДОПОЛНЕНИЕ HI
Приведем здесь одну теорему об асимптотической устойчивости
в форме, близкой к той, которая предложена в работе Е. А. Барба-
шина и Н. Н. Красовского').
Рассмотрим систему уравнений возмущенного движения
?jf- = Xa{Xl *„). (s=\, 2 п) A03.1)
где правые части Xs определенны, непрерывны и удовлетворяют
условиям единственности решений в области
\xs\<H (Н = const, или # = оо). A03.2)
Как и раньше, предполагаем, что Xs@, ..., 0) = 0.
Пусть V(x1 хп)—некоторая функция Ляпунова, имеющая
dV
знакопостоянную отрицательную производную —гг в силу уравне-
уравнений A03.1). Обозначим через М множество тех точек xs из области
\xs\ < Н, где —зт-:=0. При этом, однако, не будем включать точку
dV
Xi= ... =хп = 0, где всегда —- = 0. Тогда можно сформули-
сформулировать следующий критерий асимптотической устойчивости.
Теорема Д. Если для дифференциальных уравнений воз-
возмущенного движения A03.1) можно найти определенно'поло-
определенно'положительную в области A03.2) функцию V такую, что ее
производная —гг удовлетворяет в этой области условиям:
dV
1) ЧГ<° вне М'<
2) 4г^° на М-
где М — многообразие точек \xs], не содержащее целых дви-
движений xs(t) системы при 0 < t < oo, то невозмущенное движе-
движение асимптотически устойчиво.
Доказательство. Устойчивость невозмущенного движения
следует из теоремы А (§ 9). Значит, для всякого 0 < е < Н най-
найдется такое г] (е) > 0, что любое возмущенное движение xs (t) си-
системы A03.1),. выходящее в момент времени t = tu из области
|*ЛА))| ^ТЬ будет удовлетворять условию
|*,(9|<е. A03.3)
при всех t^-t0. Покажем, что эта устойчивость является асимпто-
асимптотической, т. е.
?) —0 при ?—>-оо.
См. первую работу в сноске на стр. 463.
ОБОБЩЕНИЕ ТЕОРЕМ ВТОРОГО МЕТОДА, ЛЯПУНОВА 465
Так как 4гг<0- т0
at
<V((')(t)) при t>t0
и функция V{xx(t) xn{t)) как невозрастающая и неотрицатель-
неотрицательная функция времени имеет определенный предел Vo при ?->оо,
причем
V(Xl(t) *„(*)) >V0 при t^t0. A03.4)
Допустим, что У0Ф0. Из ограниченности области A03.3) выте-
вытекает, что найдется последовательность точек jsW = xs(tQ-\-kx\
(k — kv k2, ...; t = const > 0), которая сходится к точке q с коорди-
координатами Xj х*п, лежащей в области A03.3). Вследствие непрерыв-
непрерывности функции V должно выполняться равенство V(x* -О— ^о-
Рассмотрим теперь движения x^f (t) и x^i* (t), выходящие при
t = tQ соответственно из1 точек q и x^i). Так как по условию тео-
теоремы движение xlf (t) при ^0 <^ t < oo не может лежать целиком
на многообразии М, то должны существовать такие интервалы вре-
dV
мени, когда —зт- < 0 вдоль этого движения. Значит, можно указать
момент времени Т > tQ, в который выполняется условие
Так как последовательность x&i> сходится к точке q, то вслед-
вследствие непрерывной зависимости решений от начальных данных можно
записать неравенство
max {| 4* G1) - xfi) (T)\ | xf (Т) — х^ (Т) |} < 6
при всех kt^>NF), каково бы ни было наперед заданное число
6 > 0. Следовательно,
lim V (*<*,> (Г) *<**> (Т)) < Vl при kt -> оо. A03.Б)
Вследствие независимости функций Xs от времени справедливы
равенства
поэтому условие A03.5) можно записать таким образом:
при ft,->oo.
Это неравенство противоречит A03.4), поэтому наше допущение
Уо ф 0 неверно. Следовательно, \/0 = 0, т. е.
lV^^)— 0 при
466 ДОПОЛНЕНИЕ III
и
\imxs(f) = 0 при t—>oo.
Примечание. Если многообразие М есть поверхность, за-
заданная уравнением
F(x1 хп) — 0, A03.6)
то условие
s=\
в области A03.3) является достаточным для отсутствия целых дви-
движений на М.
Действительно, если в некоторый момент t = tx траектория xs (t),
выходящая из области | хs (t0) | <; ц, попадает на поверхность A03.6),
то сразу при t > tt она должна покинуть эту поверхность, так как
dF(Xl{t) xn(t))\ vi dF
) =Ь
Заметим теперь, что если в случае Я = оо к условиям доказав-
ной теоремы добавить требование, чтобы функция V {хх хп)
удовлетворяла условию1)
liml/(x1 хп) = оо при л;->оо, A03.7)
где х = max {\хг\, .... \хп\], то получится критерий асимптоти-
асимптотической устойчивости в целом.
В самом деле, рассмотрим возмущенное движение xs(t) си-
системы A03.1), выходящее в момент времени t0 из произвольной
точки пространства [хх хп]. Условие A03.7) обеспечивает
ограниченность области
V(*i xj<y(^(y xn(tQ)),
в которой будет оставаться движение xs (f) при всех t0 -^ t < схэ.
Повторяя, далее, рассуждения, приведенные в доказательстве тео-
теоремы, убеждаемся в том, что асимптотическая устойчивость имеет
место при любых начальных возмущениях. Таким образом, при
указанном дополнительном условии мы действительно имеем дело
с устойчивостью в целом.
Мы рассмотрели теорему, обобщающую теорему Ляпунова
об асимптотической устойчивости. Можно сформулировать также
критерий неустойчивости, который является обобщением соответ-
соответствующей теоремы Ляпунова (теорема В § 13).
') См. примечание к стр. 68.
ОБОБЩЕНИЕ ТЕОРЕМ ВТОРОГО МЕТОДА ЛЯПУНОВА 467
Теорема Е. Если для дифференциальных уравнений возму-
возмущенного движения A03.1) можно найти функцию V (хх хп)
такую, что ее производная —п- удовлетворяет условиям:
dV
1) -^г>0 вне М;
2) -^- = 0 на М,
где М — многообразие точек {xs}, не содержащее целых дви-
движений при 0 < t < сю, и если при этом можно указать точки,
лежащие в произвольной окрестности начала координат,
такие, что в них V > 0, то невозмущенное движение не-
неустойчиво.
Доказательство этой теоремы1) приводить не будем.
§ 104. Примеры приложения предыдущих теорем.
В качестве первого примера, когда функция V удовлетворяет
всем условиям теоремы Д и условию A03.7), можно привести функ-
функции Ляпунова, построенные в Дополнении I при решении задачи
М. А. Айзермана для систем (99.1) и A00.1).
В самом деле, рассмотрим, например, функцию
X
IV = 2 Г [с/ (х) — abx] dx + (сх — ayf (а ф 0).
о
Ее производная по времени в силу (99.1) равна
dV
При условиях, наложенных на функцию f (х) в § 98, имеем:
dV
=^ < 0 при х Ф 0,
dV
-57- = 0 при х = 0.
Многообразием М, о котором шла речь в теореме Д, является
в данном случае ось у без точки х — у = 0. Так как при х = 0, у=?0
-?- = ау Ф 0, то это многообразие не содержит целых движений,
кроме л; = у = 0. Нетрудно,' далее, заметить, что условие (99.2)
•)Красовский Н. Н., Некоторые задачи об устойчивости движе-
движения, Физматгиз, 1959.
468 ДОПОЛНЕНИЕ III
обеспечивает определенную положительность функции V и выполне-
выполнение условия
П
при max {\х\, |у|} ->оо.
Таким образом, устойчивость невозмущенного движения си-
системы (99.1) в целом действительно следует в данном случае из тео-
теорем § 103.
Приведем еще один пример приложения теорем Д и Е из преды-
предыдущего параграфа.
Рассмотрим голономную консервативную механическую систему
с п степенями свободы, подверженную дополнительно управляющему
воздействию и описываемую следующими уравнениями Лагранжа:
dt V да, / да, да,
Здесь qt — обобщенные координаты; Т — кинетическая, П — потен-
потенциальная энергия; и—скаляр, который характеризует величину
управляющего воздействия; Ь^ъ ..., qn) — функции, определяющие
направление силы и. Функции Т, П и bt заданы. Закон регулирова-
регулирования u—u(qv .... qn; q[ q'\ является искомым.
Пусть при и = 0 система A04.1) обладает положением равнове-
равновесия qt — 0 (/ = 1 п). Равновесие консервативной механической
системы не может быть асимптотически устойчивым по Ляпунову,
так как эти системы допускают интеграл энергии. Задача состоит
в таком выборе управления и (q, q'), при котором положение равно-
равновесия становится асимптотически устойчивым. Упрочнение равновесия
до асимптотической устойчивости выбором и назовем стабилизацией
системы. Систему будем называть стабилизируемой, если возможна
ее стабилизация1).
Рассмотрим уравнения первого приближения системы A04.1)
в окрестности точки qt = 0, q'{ — 0:
dt
Здесь
,0 \
j, bi — постоянные).
') См. дополнение IV, § 106.
ОБОБЩЕНИЕ ТЕОРЕМ ВТОРОГО МЕТОДА ЛЯПУНОВА 469
Будем говорить, что управление
и = и» (д. д') = 2 (^ + г]д'\ A04.3)
I = 1
(р° = const, r° = const),
найденное для уравнений A04.2), стабилизирует систему A04.1) по
первому приближению, если равновесие q. = q'. = 0 A=1 ri)
системы A04.1) асимптотически устойчиво при u = u°-\-\i(q, q'),
каковы бы ни были высшие нелинейные члены Т — Т°, П — П°,
\i = u — и0.
Запишем уравнения A04.2) в нормальных координатах1):
A04)
где вектор {е;} связан с вектором {&<} неособым линейным преобра-
преобразованием; x2i-.\ — новые координаты, x2i — скорости.
Рассмотрим сначала случай, когда все числа Xt в уравнениях
A04.4) положительны. Тогда при и = 0 невозмущенное движение
xs = 6 системы A04.4) устойчиво, но не асимптотически. Предпо-
Предположим, что все Х( различны и все числа е° не равны нулю.
Тогда систему A04.4) можно стабилизировать до асимптотической
устойчивости диссипативной силой2)
х по
e\u = — -^V (/=1. .... я), A04.5)
где R° — знакоположительная функция Релея
Действительно, функция
qn; q\
равная полной энергии системы, является в этом случае определенно
положительной. Ее производная —г— в силу системы A04.4) при и
') Ч е т а е в Н. Г., Устойчивость движения, Гостехиздат, 1955, стр. 97—99.
2) См. П о ж а р и ц к и й Г. К., Об асимптотической устойчивости равно-
равновесий и стационарных движений механических систем с частичной диссипа-
диссипацией. ПММ, т. XXVIII вып. 3. 1964.
470 ДОПОЛНЕНИЕ III
из A04.3) удовлетворяет равенству
dV _ /"V о
dt —~\2aeix2i
A04.7)
и является функцией знакопостоянной отрицательной. Покажем, что
поверхность
dV
где —^- = 0, не содержит целых движений xs(f) системы A04.4),
отличных от xs — 0. Действительно, если бы это было не так, то
выполнялись бы п равенств:
A04.8)
(k
и, в частности, при некотором t = f система A04.8) имела бы не
тривиальное решение X2l (t*). Но это невозможно, так как при наших
предположениях (e°=t0, К.фХ.; 1ф]\ /=1, ..., n; j—\ я)
определитель
л Л
Л-1 0
е
Л-1 0
е
Л-1 0
?=0.
Итак, в данном случае выполнены все условия теоремы Д. Тем
самым доказана асимптотическая устойчивость движения xs = 0 си-
системы A04.4) при воздействии и, определенном равенством A04.5).
Из теоремы Ляпунова об устойчивости по первому приближению за-
заключаем, что управляющее воздействие и вида
, дЯ
Ър = —
u4l
A04.9)
ОБОБЩЕНИЕ ТЕОРЕМ ВТОРОГО МЕТОДА ЛЯПУНОВА 471
стабилизирует до асимптотической устойчивости нелинейную си-
систему A04.1).
Предположим теперь, что невозмущенное движение xs = 0 си-
системы A04.4) при и^О неустойчиво и, следовательно, среди чисел Х1
есть отрицательные. Предположим при этом, что в одном из урав-
уравнений A04.4), где kk < 0, имеем е^ = 0. Тогда, очевидно, движение
xs = 0 системы A04.1) нельзя сделать асимптотически устойчивым,
как бы ни выбирать воздействие и в форме
«(*! *«) = ViJfi+ ¦•¦ +У„*в. A04.10)
Действительно, система первого приближения A04.4) при выборе и
в виде A04.9) всегда будет иметь среди своих собственных чисел
Pi- •••• Ргл п0 крайней мере одно положительное число p*=\k.
Отсюда по теореме Ляпунова о неустойчивости по первому прибли-
приближению заключаем, что движение qs==q's=^0 системы A04.1) при и
A04.10) неустойчиво. Следовательно, в этом случае стабилизация
системы A04.1) по первому приближению невозможна.
Подчас удается, налагая на систему A04.1) сверх и дополнитель-
дополнительные гироскопические силы, изменить систему A04.4) первого при-
приближения так, что движение xs = 0 этой системы становится устой-
устойчивым (неасимптотически), и при этом для новой системы первого
приближения будут выполняться достаточные условия, при которых
возможно упрочнение системы до асимптотической устойчивости вы-
выбором воздействия и вида A04.5). Эти условия указаны теоремой 1
§ П2.
Гироскопические силы Q,- описываются в линейном приближе-
приближении Qi кососимметрической матрицей {g* }(g« =— gi \ ^g0 . — по-
постоянные),
Поэтому уравнения A04.4) после наложения гироскопических сил
принимают вид
A=1 п.).
Ограничимся в дальнейшем случаями, когда среди собственных
чисел Xt нет нулей.
Вопрос о том, каким образом вычисляются гироскопические силы,
обладающие указанными свойствами, а также вывод эффективных кри-
критериев, при которых это вычисление возможно, здесь рассматривать
472
ДОПОЛНЕНИЕ HI
не будем. Отметим лишь следующее. Согласно общей теории ука-
указанная математическая задача будет решена, если будет дайдена косо-
симметрическая матрица {§"?,¦ К описывающая в линейном приближении
гироскопические силы, такая, что при добавлении в уравнения A04.2)
членов g^g', система первого приближения будет удовлетворять усло-
условиям общего положения1). Это можно сделать в широком классе
случаев.
Простым примером такой ситуации является маятник с двумя степенями
свободы (?, г)) в окрестности верхнего неустойчивого положения равновесия,
управляемый моментом и, воздействующим
на координату <р (рис. 23).
Гироскопический эффект, возникаю-
возникающий при быстром вращении маховичка т,
делает систему устойчивой. Пусть система
уравнений первого приближения A04.1) за-
записана в данном случае в виде
= Х2,
= х\ — <
A04.12)
' где величины хи х% изображают коорди-
координаты | и г|; величины х2, xt — скорости |'
к ц', а величина <в пропорциональна скоро-
скорости вращения маховичка т вокруг стер-
жия /t.
Рис. 23. Легко проверить, что в данном случае
выполняются условия теоремы 1 § 112.
В самом деле, матрица IF в данном случае имеет вид
О 0 —ш О
О —«в 0 —2о»-(-и
0 1 0 1—ш2
1 о 1 —со2 О
и ранг ее равен 4.
Итак, мы рассматриваем случаи, когда система A04.4) неустой-
неустойчива и ее, а следовательно, и исходную систему A04.1) нельзя ста-
стабилизировать выбором управления и в виде A04.9). Однако после
наложения на A04.1) гироскопических сил Qt получаем систему
dt
(Ю4.13)
A=1
«).
') См. Дополнение IV, § 112-
ОБОБЩЕНИЕ ТЕОРЕМ ВТОРОГО МЕТОДА ЛЯПУНОВА 473
для которой система первого приближения A04.10) приобретает
свойство стабилизируемое™.
Оказывается в таких случаях система A04.4) приобретает обя-
обязательно еще одно важное свойство: поверхность
не может при этом содержать целиком движений xs (t) (s = 1 2я)
системы A04.10), отличных от xs=0 (s—\, ..., 2п). Такое же
свойство приобретает система A04.1): поверхность
системы A04.1) не может при этом содержать целиком движений
{qs(t), q's(t)) системы A04.13), отличных от ql{t) = q'i{t) = Q*).
Здесь мы примем это утверждение без доказательства.
Теперь можно доказать следующее интересное свойство системы
A04.13) в рассматриваемом случае.
Теорема 1. Пусть консервативная система A04.1) в пер-
первом приближении A04.2) неустойчива и не стабилизируема
воздействием и. Предположим, что при наложении подходящих
гироскопических сил система A04.2) переходит в устойчивую
и стабилизируемую систему A04.11). Тогда система A04.13)
стабилизируется по первому приближению силой A04.3)
в классе сил общей природы. При этом, однако, система
A04.13) не только не может быть стабилизирована дисси-
пативной силой A04.9) но, напротив, диссипативная сила
A04.9) с частичной диссипацией обязательно разрушает устой-
устойчивость, которой обладает система A04.13) при м = 0.
Примечание. Теорема 1 утверждает, следовательно, что дис-
диссипативная сила и A04.9) с частичной диссипацией обязательно раз-
разрушает устойчивость системы A04.13), если только гироскопическая
устойчивая система может быть упрочнена по первому приближению
до асимптотической устойчивости силой A04.3) общей природы.
Доказательство теоремы 1. Итак, следует показать, что
диссипативная сила A04.9) обязательно разрушает устойчивость
положения равновесия ^ = 0 системы A04.13), если только при
наложении гироскопических сил Q; неустойчивая система A04.1)
') Крас овс кий Н. Н., Об одном свойстве гироскопической стабили-
стабилизируемое™ управляемой консервативной механической системы. Изв.
АН СССР, Техническая кибернетика, № 5, 1964.
474 ДОПОЛНЕНИЕ HI
переходит s стабилизируемую по первому приближению систе-
систему A04.13). Покажем это.
Функция V = H(q, q') вида A04.6), где Н — полная энергия си-
системы A04.1), в рассматриваемом случае является знакопеременной.
dV
Ее производная —гг- вдоль движений системы A04.12) при управле-
управлении и A04.9) удовлетворяет равенству
dV
Следовательно, величина —тг является знакоотрицательной функцией
и может обращаться тождественно в нуль лишь при R(g(t), g'(t)) = 0,
Но, как только что отмечено, не существует движения [q^t), q^it)),
отличного от положения равновесия и такого, что на нем /? = 0,
Следовательно, движений lqt(t), q't(jt)\, отличных от ql — 0, q', = 0
dV
(i=l, ..., п), на которых-^т-^0, нет. Это означает, что функ-
функция V удовлетворяет в данном случае всем условиям теоремы о не-
неустойчивости. Следовательно, неустойчивость положения равновесия
системы A04.13) установлена.
В заключение отметим, что этот результат для управляемых
механических систем тесно связан с результатами Н. Г. Четаева •)
о влиянии диссипативных сил на устойчивость равновесий механи-
механических систем.
') См. монографию, упомянутую в сноске на стр. 342.
ДОПОЛНЕНИЕ IV.
ПРОБЛЕМЫ СТАБИЛИЗАЦИИ УПРАВЛЯЕМЫХ ДВИЖЕНИЙ.
§ 105. Предварительные замечания.
В последнее время получила большое развитие теория оптималь-.
ных процессов в управляемых динамических системах. Этой теории
посвящен ряд фундаментальных монографий, появившихся в последние
годы J). Среди проблем оптимального управления занимает важное
место задачи о стабилизации заданного движения. Это — задача о по-
построении регулирующих воздействий, которые обеспечивают устой-
устойчивое осуществление желаемого движения при наилучшем возможном
качестве переходного процесса. Задача об оптимальной стабилизации
тесно смыкается с общей задачей об устойчивости движения, соста-
составляющей предмет настоящей монографии. Она является дальнейшим
развитием проблемы устойчивости в приложении к теории управляе-
управляемых систем. Методы исследования проблем оптимальной стабилизации
переплетаются с классическими методами теории устойчивости Ляпу-
Ляпунова. В частности, метод динамического программирования, один
из основных в задачах оптимального управления 2), является по су-
существу объединением методов вариационного исчисления с методом
функций Ляпунова.
В монографиях по теории оптимальных процессов, посвященных
весьма общим аспектам этой теории, указанное обстоятельство не
выдвигается, естественно, на первый план и не рассматривается спе-
специально с позиций теории устойчивости Ляпунова. В то же время
развитие проблем оптимального управления и методов их реше-
решения определило некоторые новые направления исследований по
устойчивости регулируемых движений. Эти исследования тесно связаны
') Понтрягин Л. С, Болтянский В. Г., ГамкрелидзеР. В.,
Мищенко Е. Ф., Математическая теория оптимальных процессов, М., Физ-
матгиз, 1961; Беллман Р., Гликсберг И., Гросс О., Некоторые
вопросы математической теории процессов управления, М., Изд-во иностр.
лит-ры, 1962; Ф е л ь д б а у м А. А., Основы теории оптимальных автомати-
автоматических систем, М., Физматгиз, 1963.
2) См. монографию Бевдмана и др., упомянутую в сноске ').
476 ДОПОЛНЕНИЕ IV
с материалом настоящей монографии. По указанным причинам
мы сочли целесообразным дать настоящее приложение к книге
И. Г. Малкина.
Это приложение содержит краткий очерк некоторых проблем
стабилизации управляемых движений и методов их решения. При
этом выбран лишь тот материал, который имеет прямое отношение
к содержанию монографии. Автор приложения старался в меру воз-
возможности согласовать характер изложения с основным текстом
книги.
В основу материала настоящего приложения легли исследования,
выполненные в последние годы и имеющие своим источником про-
проблему аналитического конструирования регуляторов, поставленную
А. М. Летовым 1).
§ 106. Постановка задачи о стабилизации.
Рассмотрим некоторую управляемую динамическую систему и до-
допустим, что ее движение может быть описано системой дифферен-
дифференциальных уравнений, которая может быть приведена к нормальному
виду
•^- = М'. л у„. «1 «V) 006.1)
(в=1 Я).
Здесь, как и в уравнениях B.1), переменные ys—это некоторые
параметры, связанные с движением, например координаты, скорости
и т. д. Уравнения A06.1) отличаются от уравнений B.1) тем, что
здесь фигурируют величины v1 vr, которые описывают упра-
управляющие воздействия, приложенные к рассматриваемому объекту.
Такие воздействия не исключались, конечно, и выше всюду в тексте
книги при изучении движений, описываемых уравнениями B.1). Функ-
Функции Vj\f) могли входить неявно в правые части уравнений B.1) и
в правые части вытекающих из них уравнений возмущенного движе-
движения C.2). Однако сейчас эти переменные Vj фигурируют явно и
играют центральную роль во всем дальнейшем изложении.
Предположим, что нас интересует какое-либо частное движение
нашей системы, порождаемое управляющими воздействиями Vj = pj(t)
(j= I, ... г). Этому движению соответствует некоторое частное
решение ys = fs(t) (s = 1 n) уравнений A06.1) (при Vj = Pj{t)).
Как и выше, будем это движение называть невозмущенным. "Наряду
с невозмущенным движением [fs(t)} будем рассматривать возмущен-
возмущенные движения {ys(t)\. Предполагается, что возмущенные движения ys(t)
') Летов А. М., Аналитическое конструирование регуляторов. Авто-
Автоматика и телемеханика, т. XXI, № 4, 5, 6, 1960; т. XXII, № 4, 1961; т. ХХШ,
п, 1962.
ПРОБЛЕМЫ СТАБИЛИЗАЦИИ УПРАВЛЯЕМЫХ ДВИЖЕНИЙ 477
также описываются уравнениями A06.1) но уже при значениях Vj(t),
отличных, вообще говоря, от величин Pj(t). Отклонения Vj(t)—Pj(f)
переменных Vj от Pj(t) обусловливают здесь специфические особен-
особенности задачи об устойчивости движения ys = fs(t). Проблема стаби-
стабилизации невозмущенного движения ys = fs (t), собственно, и состоит
в таком выборе величин h.Vj = Vj—Pj(t), при которых движение
ys = fs(t) оказывается устойчивым.
Для исследования проблем стабилизации целесообразно составить
уравнения возмущенного движения управляемой системы, перейдя
к новым переменным
х, = У, — /ЛЪ Uj = Vj~Pj(t) A06.2)
(s=l п; j=\ г),
где, следовательно, xs— возмущения движений, и}-—отклонения
управляющих воздействий от величин Pj(t).
Полученные таким образом преобразованные уравнения
—~=Xs{t, хх, ..., хп; uv ..., ит) =
= Ys(t, *! + /! Xn + fn> Ul+P\ "r+Pr) —
-УЛ*- h /„; Pi Pr) (Ю6.3)
(s=l n)
мы и будем рассматривать в дальнейшем.
Теперь можно сформулировать задачу о стабилизации.
Задача I (о стабилизации). Требуется найти такие упра-
управляющие воздействия ux(t, xv ..., хп) ur(t, x1 хп),
которые обеспечивают асимптотическую устойчивость невоз-
невозмущенного движения xs = 0 в силу уравнений A06.3) (при
«; = «?('¦*! хп))-
Реальной основой для сформулированной задачи I является сле-
следующая ситуация. Предполагается, что в ходе регулирования можно
измерять текущие значения всех координат xs(t) (s = 1, .... п). На
основе этого измерения управляющее устройство должно выраба-
вырабатывать воздействия tij(t, xx(l), .... xn(f)) (J= I, .... г) на объект.
Эти воздействия должны обеспечивать асимптотическую устойчивость
заданного невозмущенного движения xs = 0.
По смыслу величин xs и Uj A06.2) предполагается, что функции
Uj(t, хх д:л), определение которых составляет задачу I, должны
удовлетворять равенствам
uj(t, 0 0) = 0 (J=\ г). A06.4)
478 ДОПОЛНЕНИЕ IV
Будем предполагать, что функции Uj(t, хх хп) должны быть
определены и непрерывны в области
*>0, \xs\<H, E=1 п), A06.5)
где заданы функции Xs, являющиеся правыми частями уравнений
A06.3). Кроме того, примем, что функции Xs и Uj удовлетворяют
условиям, которые обеспечивают существование и единственность
решений xs при любых начальных условиях t0, xs (t0) из области
A06.5). Мы будем исследовать задачу о стабилизации, предполагая, что
функции Uj(t, xl хп) не стеснены никакими дополнительными
неравенствами, т. е. предполагается, что в A06.3) переменные ttj
могут принимать любые, сколь угодно большие значения. В соответ-
соответствии с этим считаем, что функции Ха определены при t и xs
из области A06.5) для всех значений — оо<«у < -|-оо (у— 1 г).
Задача о стабилизации сформулирована нами для случая асимпто-
асимптотической устойчивости. Наряду с этой задачей можно изучать задачу
о стабилизации, которая содержит более слабое требование лишь
устойчивости заданного движения xs = 0. Однако здесь мы ограни-
ограничимся только более грубой проблемой о стабилизации управляемой
системы до асимптотической устойчивости.
§ 107. Постановка задачи об оптимальной стабилизации.
Прикладные задачи о стабилизации наряду с требованием асимп-
асимптотической устойчивости заданного движения xs = 0 содержат обычно
пожелания о наилучшем возможном качестве переходного процесса,
т. е. пожелания о наилучшем (с какой-либо точки зрения) качестве
возмущенного движения xs(t) в процессе его приближения к состоя-
состоянию л;^ = 0 при t-+co. При этом обычно высказывается также по-
пожелание о наименьшей возможной затрате ресурсов (энергии, импуль-
импульсов и т. д.), расходуемых на формирование управляющих воздействий
Uj(t, хх хп). Такие пожелания часто можно выразить в виде
условия минимальности некоторого интеграла
оо
/=J ©(*.*,[*] xn[t\, ux\t\ ur[t])dt. A07.1)
и
Здесь <a{t, xx хп, их иг)— неотрицательная функция,
определенная в области A06.5). Символом Uj[t] будем обозначать
величины управляющих воздействий Uj[t] = Uj(t, xx[t\ xn[t])
(в функции только от времени), которые реализуются в системе A06.3)
при Uj = Uj(t, хх, ..., хп). При этом символы xs[t] обозначают
как раз те движения системы A06.3), которые порождаются упра-
управлением Uj [t] = Uj (t, xx [t] xn [t]). Иногда, чтобы подчеркнуть,
ПРОБЛЕМЫ СТАБИЛИЗАЦИИ УПРАВЛЯЕМЫХ ДВИЖЕНИЙ 479
что движение xs [t] порождается некоторым фиксированным управле-
управлением и. = u*j (t, x1 хп), будем снабжать символы xs [t] и м;- [t\
индексом *, т. е. будем писать x*s [t] и и* [t].
Вопрос о выборе функции со, определяющей оценку качества /
A07.1) процесса xs{t), здесь подробно обсуждать не будем. То или
иное решение этого вопроса определяется в каждом случае кон-
конкретными особенностями рассматриваемой прикладной задачи. Заме-
Заметим лишь, что обычно при выборе функции со ведущие роли играют
следующие три мотива.
1. Условие минимума интеграла A07.1) должно обеспечивать до-
достаточно быстрое затухание движений xs [t].
2. Величина интеграла / должна удовлетворительно оценивать
ресурсы, затрачиваемые на формирование управляющих воздей-
воздействий Uj[t].
3. Функция со должна быть такой, чтобы решение задачи не ока-
оказалось чрезмерно трудным и чтобы по возможности это решение
можно было получить в замкнутой форме.
В частности, условиям 1 — 3 во многих случаях удовлетвори-
удовлетворительно отвечает функция a>(t, хх хп\ uv ..., иг), выбранная
в виде определенно положительной квадратичной формы
п г
@= 2_ а/;*/*/+ . 2j VijuiUj- A07.2)
Задачу о стабилизации системы A06.3) при условии минимума
какого-либо критерия качества / A07.1) будем называть задачей об
оптимальной стабилизации. Следовательно, эта проблема формули-
формулируется так: -
Задача II (об оптимальной стабилизации). Пусть выбран
критерий качества процесса xs(f) в виде интеграла A07.1).
Требуется найти такие управляющие воздействия и°М,
хх х\ u^(t, xx х\ которые обеспечивают
асимптотическую устойчивость невозмущенного движения
xs—0 в силу уравнений A06.3) (при u. = u°.(t, xv ..., х\ \.
При этом каковы бы ни были другие управляющие воздействия
u*,(t, xv ..., х\ решающие задачу I, должно выполняться
неравенство
*, x\[t) x°nM; u°[t] а»
ОО
< J со (г, x\[t\ x\[t\\ u\]t\ u)[t))dt A07.3)
480 ДОПОЛНЕНИЕ IV
для всех начальных условий t0, xs(t0) из области
A07.4)
Здесь положительная постоянная ц или задана заранее по усло-
условиям задачи, или эта величина имеет тот же смысл, что и вели-
величина ц в постановке задачи об устойчивости (см. стр. 16).
В частности, если речь идет о задаче об оптимальной стабили-
стабилизации в целом, то условие A07.3) должно выполняться для всех
начальных возмущений xs(t0), как бы велики они ни были.
Функции u°j(t, xv .... х\ (У=1 /¦), разрешающие за-
задачу II, будем называть оптимальным управлением.
Задача II об оптимальной стабилизации предъявляет к функ-
функциям и°. больше требований, чем задача I к разрешающим ее функ-
функциям Uj. Однако исследование и решение задачи II облегчаются тем
обстоятельством, что эта проблема, как правило, имеет единст-
единственное решение ifi, (t, xx х\. Напротив, выбор функций
Uj(t, х{, ..., хп), решающих задачу I, обычно содержит большой
произвол. По этой причине часто оказывается целесообразным такой
путь решения задачи I.
Для исключения произвола в выборе функций Uj(t, хх, .,-, хп)
вводят в условия этой задачи вспомогательное условие A07.3) ми-
минимума некоторого интеграла / A07.1), хотя может быть исходная
проблема стабилизации никаких явных условий оптимальности не
содержит. Тем самым исходная задача I превращается во вспомога-
вспомогательную задачу И. При этом, естественно, функция со в A07.1)
должна выбираться так, чтобы решение вспомогательной задачи II
было возможно более простым. При решении сложных проблем
стабилизации вспомогательные задачи II могут также вводиться лишь
на отдельных этапах (см. сноску на стр, 492).
Материал настоящего приложения посвящен исследованию задач I
и II методами, опирающимися на основные идеи классической теории
устойчивости движения.
§ 108. Пример задачи о стабилизации.
В качестве примера рассмотрим задачу о переводе точки, нахо-
находящейся под действием центральной силы F, с некоторой эллипти-
эллиптической траектории на круговую орбиту, достаточно близкую к "эллип-
"эллиптической. Эту задачу можно сформулировать как проблему стаби-
стабилизации невозмущенного движения, соответствующего заданной
орбите.
Будем полагать, что движение точки управляется реактивной
силой R; тогда масса точки т является величиной переменной и ее
ПРОБЛЕМЫ СТАБИЛИЗАЦИИ УПРАВЛЯЕМЫХ ДВИЖЕНИЙ 481
движение будет описываться известным уравнением Мещерского1)
где m{t) = mo-\-ml{t), mo = const, ^
v — скорость точки, а — скорость частицы dm1 в момент t~\-dt
после ее отделения от точки, так что с = а — v есть относительная
скорость отделяющейся частицы.
Если вектор реактивной силы R во все время движения точки
остается в плоскости первоначальной траектории, то движение точки
будет плоским и оно вполне будет определяться изменением ее по-
полярных координат г и <р.
Дифференциальные уравнения, описывающие изменение г и <р,
можно получить, если спроектировать векторное уравнение A08.1)
на направление радиуса движущейся точки и перпендикулярное
х. нему направление. Известно2), что проекции вектора ускорения
w = -^г на указанные направления вычисляются по формулам
wr = г — гф2, Wy = 2гф + гф.
Тогда можно записать два дифференциальных уравнения, каждое
из которых есть уравнение второго порядка относительно г и ср:
т (г — r(f) = F-\-Rr m—±-f-!-=rRm,
где
а сг и сф — проекции относительной скорости отделяющейся частицы
на направление радиуса и поперечное направление, соответственно.
Разделив оба уравнения на т (t) и полагая, что сила F есть
сила всемирного тяготения, окончательно получим:
din» * A08-2)
Здесь ц = /М, f — постоянная всемирного тяготения, М — масса
притягивающего тела, которую мы считаем большой по сравнению
с m и поэтому принимаем ее неподвижной.
') Мещерский И. В., Работы по механике тел переменной массы,
Гостехиздат, 1949.
2) Суслов Г. К., Теоретическая механика, Гостехиздат, 1946.
482
ДОПОЛНЕНИЕ IV
Предположим теперь, что задана некоторая круговая орбита
радиуса г0 и достаточно близкая к круговой эллиптическая траекто-
траектория, по которой точка движется под действием только силы притяже-
притяжения, пока реактивная сила отсутствует. Примем движение точки по
круговой орбите за невозмущенное. Требуется определить закон из-
изменения массы, следуя которому движение точки могло бы с тече-
течением времени неограниченно приблизиться к движению по круговой
орбите.
Обозначая гос<р —-г,— = и, г = ylf г = у2 и вводя новую коор-
координату уг = г2(р, запишем уравнения A08.2) в нормальной форме:
dt
П Ух
A08.3)
Полагая величины |сг|и|с,р[ постоянными во все время движения,
т. е. считая, что выброс массы производится ориентированно отно-
1 С
сительно системы координат, связанной с точкой, имеем b = —— =
Vo
k
= — = const. Невозмущенное движение нашей точки определится,
Г° /
очевидно, соотношениями ух = г0, у2 — 0> Уз == У №го> которые
представляют собой частное решение системы A08.3) при и^О,
соответствующее движению по круговой орбите.
Положим х1 = у1 — г0, х2 = у2> ^^"^Уг—Ywo и> подставляя
в A08.3), получим дифференциальные уравнения возмущенного дви-
движения:
dt
dx2
dx3
где обозначено а = ^- • P ==
ro
х2,
A08.4)
'o3
а функции /2 и /3 раскла-
раскладываются в некоторой окрестности точки хх = х2 = хг = 0 в ряды
по степеням xv x2, х3, начинающиеся членами не ниже второго
порядка.
Итак, задачу, поставленную в начале параграфа, можно сформу-
сформулировать следующим образом: найти функцию и = и (xt, x2, х3),
ПРОБЛЕМЫ СТАБИЛИЗАЦИИ УПРАВЛЯЕМЫХ ДВИЖЕНИЙ 483
обращающуюся в нуль при хх — х2 = х3 = 0 и такую, чтобы три-
тривиальное решение системы A08.4) было асимптотически устойчивым
при достаточно малых начальных возмущениях xt (t0) — xi0 (/=1,
2, 3). Эти возмущения определяются в момент @ включения упра-
управляющего воздействия. Таким образом, получаем задачу I (о стаби-
стабилизации). Очевидно, что решение этой задачи не является един-
единственным.
Допустим, что к переходному процессу и управляющему воз-
воздействию и предъявлены некоторые требования. Например, требуется,
чтобы переходный процесс, характеризующийся значениями x1(t),
х2 (t), x3 (t) при t > t0, затухал достаточно быстро, и одновременно
желательно, чтобы количество переменной массы, израсходованной
на управление, было бы при этом не слишком велико. Для этого
надо среди всех управляющих воздействий, решающих задачу I (до-
(допустимых управлений), определить такое управление а°(хх, х2, х^) —
оптимальное управление, — которое минимизирует некоторую цену
качества, определяемую изложенными выше требованиями. Таким
образом, получим задачу II (об оптимальной стабилизации).
Для нашего примера целесообразным критерием качества был бы
интеграл
(Mi Va Va+Ylel)^ (Ю8.5)
to
где fx1, [i2, Мз—некоторые положительные константы, а у — -.—j—•
lc<plr0
В самом деле, интеграл
характеризует известным образом качество переходного процесса,
оценивая малость величин xs(t), а интеграл
оо оо
/L2)= f y\u\dt = ~ fj*lg™ in
J r' ' J dt
t U
J J m0
to U
определяет запас переменной массы mi в начальный момент упра-
управления t0. Итак, переход на круговую орбиту можно осуществить
за счет минимальных управляющих ресурсов и вместе с тем при
хорошем качестве переходного процесса, если удастся найти опти-
оптимальное управление и0, для которого
/цо (Хю, Хго, -КЗО) < /« (ЛГИ), *2
при любых хю A= 1» 2, 3) и для всех и, решающих задачу I.
484 ДОПОЛНЕНИЕ IV
Однако два обстоятельства вынуждают отказаться от критерия
A08.5), несмотря на всю его целесообразность.
Во-первых, неаналитичность подынтегральной функций приводит
к трудоемким вычислениям при определении оптимального управляю-
управляющего воздействия, а в замкнутой форме найти решение вряд ли
возможно. Во-вторых, по той же причине структура алгоритма упра-
управления получается весьма сложной, а потому технически трудно
осуществимой.
Учитывая указанные обстоятельства, можно предложить вместо
A08.5) в качестве критерия оптимальности интеграл
. (Ю8.6)
который несущественно отличается от A08.5) лишь в части, харак-
характеризующей расход переменной массы, но зато позволяет найти опти-
оптимальное управление в замкнутой форме и простое по своей структуре.
Решение этой задачи будет приведено после изложения общей
теории (см. § 113).
§ 109. Второй метод Ляпунова для задач об оптимальной
стабилизации.
В этом параграфе мы изложим основную теорему второго метода
Ляпунова исследования проблем оптимальной стабилизации. Эта тео-
теорема является модификацией теоремы II Ляпунова (см. стр. 195),
причем учитываются соображения метода динамического программи-
программирования Р. Беллмана*).
Рассмотрим дифференциальные уравнения возмущенного движения
^- = Xs(t;xx хп; и, ur) (s=l я), A09.1)
где функции Х$ определены в области
A09.2)
и удовлетворяют в этой области всем условиям, перечисленным
в § 106.
Как и в теореме II, нам придется рассматривать функции Ляпу-
Ляпунова V(t, xv . . ., хп), определенно-положительные в области A09.2).
Существенную роль будет играть одно выражение, которое мы обо-
') См. его монографию, упомянутую в сноске на стр. 475.
ПРОБЛЕМЫ СТАБИЛИЗАЦИИ УПРАВЛЯЕМЫХ ДВИЖЕНИЙ 485
значим символом S[V; t; х1 хп; их иг]:
B[V; t; хх хп; и, иг) =
п
1 = 1
-+-©<?; xx хп\ «! иг). A09.3)
Здесь со — функция, определяющая показатель A07.1) качества
регулирования.
Очевидно, если при некотором выборе функции V (t, хг хп)
и функций uj = u".{t; xv .. ., х^ (j = 1 г) в области A09.2)
выполняется равенство
В [V; t; xt хп; а\ и*] = 0, A09.4)
dV
то это означает, что производная —тт- функции V в силу уравне-
уравнений A06.3) при u. = u*.{t, xv .... хЛ удовлетворяет в этой области
равенству
dV
-?!. = — ©(*.*!,..., хп). A09.5)
Основная теорема об оптимальной стабилизации, которую мы
в дальнейшем будем называть теоремой IV, может быть сформули-
сформулирована следующим образом.
Теорема IV. Если для дифференциальных уравнений воз-
возмущенного движения A09.1) можно найти допускающую беско-
бесконечно малый высший предел определенно положительную функ-
функцию V°(t, х1 хЛ и функции u°j(t; xt хЛ, удовлетво-
удовлетворяющие в области A09.2) условиям:
1) функция
является определенно положительной;
2) справедливо равенство
B[V°;t;Xl xn;u0(t,Xl xn). ...
...,e»(f. xv .... *я)] = 0; A09.6)
3) каковы бы ни были числа Uj, справедливо неравенство
BIV°; t; хх хп\ ах, .... иг]>0, A09.7)
486 ДОПОЛНЕНИЕ IV
то функции a0, (t, xv .... х\ разрешают задачу II об опти-
оптимальной стабилизации. При этом выполняется равенство
(*. *?м х°п it); u\m
оо
= min f
Xl(t0) xn(t0)). A09.8)
Примечание. Как отмечено выше в книге (см. стр. 38, 195),
функции V, удовлетворяющие условиям теорем Ляпунова об асимпто-
асимптотической устойчивости, не только устанавливают сам факт устойчи-
устойчивости, но и позволяют оценить область
|*,('о)|<Л <*=1 «) A09.9)
тех начальных возмущений xs(t0), для которых выполняются нера-
неравенства
\xs(()\<H (t^to,s=l re) A09.10)
и предельное соотношение
limxs(t) = 0 при *->оо. A09.11)
При u. = u°.(t, Xj х\ в уравнениях A09.1) функция V0
удовлетворяет условиям теоремы II об асимптотической устойчивости.
Число т], определяющее область A09.9), в соответствии с изложен-
изложенным в § 10 может быть, следовательно, найдено из соотношения
sup{V°(t,x1 xn) при К|<т)}<
<inf {V°(/, xv .... хп) при max(|jci| \xn\) = h], A09.12)
где я — некоторое положительное число, меньшее чем Н (t^to^-O).
Будем считать число h фиксированным.
Утверждение теоремы IV, выражаемое неравенством A09.8), надо
понимать в следующем смысле: при и. — и°.(t, xx х\ интеграл
A07.1) достигает наименьшего значения для всех начальных
условий xs(@) (@^-0) из области A09.9), где число т) выбрано
в соответствии с неравенством A09.12).
Доказательство теоремы. При u. = u°.(t, хг , х )
функция V0 удовлетворяет всем условиям теоремы II. Ее производ-
производило
ная —зт- в силу уравнений A09.1) (при и, = и°Л определяется
равенством
-Ж = -«>('.*1 Х»'а° И°) A09ЛЗ>
ПРОБЛЕМЫ СТАБИЛИЗАЦИИ УПРАВЛЯЕМЫХ ДВИЖЕНИЙ 487
и, следовательно, является функцией определенно-отрицательной.
Поэтому воздействия и° (t, x^ хЛ обеспечивают асимптотиче-
асимптотическую устойчивость невозмущенного движения xs = 0 и выполнение
предельного соотношения A09.11) для всех начальных условий x(t0)
из области A09.9), A09.12).
Теперь для доказательства теоремы достаточно проверить спра-
справедливость соотношения A09.8). Сделаем это. Движения x°s[t] при
условии A09.9), A09.12) удовлетворяют неравенству | x°s [t]\^.h < Н.
Следовательно, вдоль таких движений при всех t^-t0 выполняется
равенство A09.6) или, иначе говоря, равенство A09.13). Кроме того,
вследствие асимптотической устойчивости выполняется предельное
соотношение
UmV°(t, x°[t], .... x°n[t]) = 0 при *->oo. A09.14)
Интегрируя равенство A09.13) вдоль движения x°[t] в пределах
от / = /0 до i = co и учитывая A09.14), получим:
СО
= f m(t, *°[fl x°a[t]\ и\Щ, .... u°[t])dt. A09.15)
С другой стороны, пусть и*М, х1 х\ ..., u*(t, xv ..., хЛ —
какие-либо функции, также решающие задачу о стабилизации движе-
движения xs = 0 для начальных возмущений из области A09.9). Примем
сначала, что соответствующие движения л;* [t] не выходят при t^-t0
из области |jcs|-^A. Тогда в процессе движения x*s [t] все время
будет выполняться A09.7), или, иначе говоря, будет выполняться
неравенство
^-> —q(/, x'tlt] x'n[f\). A09.16)
dV°
Здесь —тг производная функции V0 вдоль движения х*$ Щ. Инте-
Интегрируя неравенство A09.16) от t — tQ до /=оо и снова учитывая
предельное соотношение
HmV°(*. x\[t\ *;[/]) = 0 при ^->оо, A09.17)
получим:
: /©(*. x\it] xma[ty, u\\t] u;it])dt. (Ю9.18)
488 ДОПОЛНЕНИЕ IV
Аналогичное неравенство получается и в том случае, когда дви-
движение x"s [t] на время покидает область
|jcJ<A (s=l и). A09.19)
Действительно, в последнем случае имеет место следующая ситуа-
ситуация. Пусть т > f0 — момент времени, когда движение jc* [t] в послед-
последний раз вошло в область A09.19) и уже при t^-x не покидает эту
область. Тогда с этого момента вдоль движения x*s [t] все время
выполняется условие A09.16). Интегрируя это неравенство от t = x
до t = oo и учитывая опять предельное соотношение A09.17), получим:
V°(t, x\[x\ *>])<
u"r[f\)dt. A09.20)
т
Но по выбору xs(t^) из области A09.9), A09.12) справедливо
неравенство
V°(P, *,(/„).-.... *„(/„)) <V0(t. хЦх) хЦх]), A09.21)
а вследствие неотрицательности функции о имеем:
х\ Щ *; И; а\ Щ, ...,«; Щ) dt <
. A09.22)
J
Из A09.20)—A09.22) снова следует справедливость неравенства
A09.18). Соотношения A09.15) и A09.18) доказывают A09.8). Тем
самым теорема IV полностью доказана.
Примечание. В условиях теоремы IV предполагается, что
величины Uj в уравнениях A09.1) являются функциями от t и xs(t).
Однако анализ доказательства этой теоремы показывает, что соотно-
соотношение A09.8) справедливо и в том случае, когда в A09.8) Uj=Uj[t]
представляют собой любые функции времени Uj = Uj (t), обеспечи-
обеспечивающие предельное соотношение limx^] —0 при t-+oo. Действи-
Действительно, в этом доказательстве по существу нигде не использовалось
предположение, что функция и", [t] имеет форму и", [t] = и* (t, x\[t\
х*п [t]\ а не просто является явной функцией только от времени (.
Следовательно, теорема IV устанавливает оптимальность управления
и0, = и° (t, x1 хЛ как по отношению к управляющим воздей-
воздействиям вида Uj=u.]{t, X\ хп), так и по отношению к упра-
управляющим воздействиям Uj = и,-(t) для всех начальных возмущений
из области A09.9), A09.12),
ПРОБЛЕМЫ СТАБИЛИЗАЦИИ УПРАВЛЯЕМЫХ ДВИЖЕНИЙ 489
§ 110. Замечания ко второму методу Ляпунова
в теории стабилизации.
Итак, для решения задачи II об оптимальной стабилизации сле-
следует попытаться найти функции V0 и и° удовлетворяющие условиям
теоремы IV. При этом необходимо обеспечить выполнение равенства
A09.6), которое является уравнением в частных производных отно-
относительно искомой функции V0. Уравнение A09.6) надо разрешить
с учетом дополнительного условия A09.7). В результате получается
достаточно трудная задача. Однако, как и в случае общей задачи
об устойчивости движения, где также проблема эффективного по-
построения функций Ляпунова весьма нелегка, можно указать неко-
некоторые типы уравнений A09.1), для которых функция V0 строится
в замкнутой форме. Отыскание этих типов уравнений и построение
соответствующих функций V0 облегчаются известными результатами
теории устойчивости движения. В частности, для линейных систем,
как и в обычных задачах устойчивости, полезным аппаратом иссле-
исследования являются функции V0 в виде квадратичных форм.
Функции V°(t, xl хп), удовлетворяющие условиям тео-
теоремы IV, будем называть оптимальными функциями Ляпунова,
отвечающими соответствующей задаче II об оптимальной стабилизации.
Теорема IV может обобщаться в различных направлениях. Если
речь идет о проблеме оптимальной стабилизации в целом (см. стр. 480),
то в формулировке теоремы IV достаточно потребовать выпол-
выполнения соотношений A09.6), A09.7) при всех xs (—оо < xs < -j-oo,
s=l и) и добавить условия, обеспечивающие устойчивость
движения д^ —0 в целом. Эти условия указаны в примечании
к стр. 38. Поэтому мы не будем приводить здесь соответствующую
полную формулировку теоремы IV в этом случае. Теорема IV также
сохраняет свою силу и в тех случаях, когда управляющие воздей-
воздействия стеснены дополнительными неравенствами (например, |и^|<^ 1).
В таких случаях следует лишь потребовать, чтобы функция V0 удо-
удовлетворяла неравенству A09.7) при всех значениях и;-, стесненных
заданными ограничениями. Можно, наконец, ослабить условия опре-
определенной положительности функции m(t, xv ..., хп; uv ..., и\,
заменив его условием знакоположительности при дополнительных
ограничениях в духе критерия асимптотической устойчивости, данного
в приложении III. Изменения, которые при этом следует внести
в формулировку теоремы IV, очевидны, и мы на них здесь не оста-
останавливаемся.
В теореме IV естественно предполагается, что функция
Vй((, хь . . ., хп) имеет в области A09.2) непрерывные частные произ-
dV> dV° . N „
водные —Т7-, -r?— (s=l, .... re). Для задач оптимального упра-
490 ДОПОЛНЕНИЕ IV
вления, однако, интересны случаи, когда это предположение не выпол-
выполняется при отдельных значениях t и xs, заполняющих, может быть,
некоторые поверхности. Критерий оптимальности, подобный тео-
теореме IV, но работающий с применением таких не гладких функций
V°(t, xx, .... хп), разработан В. Г. Болтянским1).
В заключение этого параграфа сделаем еще несколько кратких
замечаний о связи теоремы IV с общими методами вариационного
исчисления и, в частности, с известными методами математической
теории оптимальных процессов.
Критерий оптимальности воздействий и0., который выражается
равенством A09.6) и неравенством A09.7), соответствует известному
методу в вариационном исчислении, опирающемуся на теорию рас-
распространения возмущений2). Здесь, однако, в отличие от наиболее
распространенной формы необходимых условий экстремальности,
критерий приведен в форме достаточных условий минимума интеграла
A07.1). При этом условия теоремы IV одновременно обеспечивают
выполнение предельного соотношения iim xs (t) = 0 при t-+oo. Такая
формулировка соответствует характеру основных теорем второго
метода Ляпунова исследования устойчивости движения. Поэтому она
и выбрана нами здесь. Естественным результатом отмеченной связи
теоремы IV с методами классического вариационного исчисления
является тот факт, что соотношение A09.6) имеет форму уравнения
в частных производных вида известного уравнения Гамильтона—Якоби.
Фундаментальным методом исследования задач об оптимальном
управлении является метод, основанный на принципе максимума
Л. С. Понтрягина3). В теории оптимальных процессов, развитой
Л. С. Понтрягиным и его сотрудниками В. Г. Болтянским, Р. В. Гам-
крелидзе и Е. Ф. Мищенко, оптимальное управление и;- ищется
в виде функции только от времени и, = и0, (t) (отдельно для каждых
фиксированных начальных условий xs (t0)).
Для задачи, аналогичной задаче II, но состоящей в определении
управления и . в форме и, = и0, {t), принцип максимума утверждает,
что на оптимальном движении х° [t] системы A09.1), порожденном
управлением и0, (t), обязательно выполняется условие
Н[%® %+1 @; t. *?М х°п [fl; «ои«] >
п
) Ч>я+1@; Ь *?Ю х°я[П; «х иг]. (пол)
') Болтянский В. Г., Достаточные условия оптимальности и обо-
обоснование метода динамического программирования. Изв. АН СССР, серия
математическая, т. XXVIII, № 3, 1964.
2) См., например, монографию: Гельфанд И. М., Фомин СВ.,
Вариационное исчисление, М., Физматгиз, 1961.
3) См. монографию Л. С. Понтрягина и др., упомянутую в сноске на
стр. 475.
ПРОБЛЕМЫ СТАБИЛИЗАЦИИ УПРАВЛЯЕМЫХ ДВИЖЕНИЙ 491
каковы бы ни были числа их иг. Здесь величина Н определена
равенством
#№о Уп+\> *> xv .... хп; ut иг] =
п
= ^Ei^iXt(t, xv .... хп; их
а величины tipt (() являются некоторым частным решением системы
" дХ,
dt
A10.3)
где Хо — & и А'л+1^=1. При этом на оптимальном движении x°s[t]
величина Н остается постоянной, т. е.
H[%(t) %+l(f): t; x\[t] *»[fl;e?@ «?@]=0
при f^>tQ. A10.4)
Связь принципа максимума с теоремой IV определяется следующим
обстоятельством: можно проверить, что при выполнении условий
теоремы IV на движении х° [t], порожденном оптимальным упра-
управлением и0. [?] = и°.(t, x°[t] x°n [t]\ справедливы равенства
dV°(t, x\[t] x°n[t])
Но в таком случае понятно, что равенство A10.4) и условие
A10.1) имеют тот же смысл, что и равенство A09.6) и неравен-
неравенство A09.7), соответственно. Подчеркнем, однако, еще раз, что
принцип максимума указывает необходимые условия оптималь-
оптимальности управления u. — u°,(f), в то время как теорема IV дает доста-
достаточные условия для оптимального управления Uj в форме и. =
= «° (*' *1 Хп)- '
Заметим, наконец, что в случае установившихся движений xs = 0,
т. е. в случаях, когда функции Xs и со не зависят явно от времени,
оптимальную функцию Ляпунова V0 и оптимальное управление и0, также
следует искать в виде функций, не зависящих явно от времени, т. е.
«5
фу
5 =
;492 дополнение iv
§ 111. Решение задачи о стабилизации
для уравнений первого приближения.
Для задач I и II о стабилизации, как и для общей проблемы
устойчивости, может быть развита теория исследования этих задач
по первому приближению. Здесь можно указать случаи, когда реше-
решение проблемы определяется линейным приближением, а также кри-
критические случаи, когда возможность разрешения проблемы и сами
искомые воздействия Uj(t, xv . . ., хп) определяются членами высшего
порядка малости в уравнениях A09.1) возмущенного движения.
В настоящем приложении мы ограничимся лишь одним резуль-
результатом, относящимся к этой теории. Именно, мы рассмотрим случай,
когда задача I для нелинейной системы решается исходя из ее линей-
линейного Приближения. Имеются работы1), в которых можно найти
более подробное изложение теории стабилизации по первому при-
приближению.
Примем, что дифференциальные уравнения возмущенного движе-
движения имеют вид
+ ад *i хп> «1 «г) AП-1)
(s=l и).
Здесь psj, qsj — ограниченные и непрерывные функции времени,
в частности psj, qsj — постоянные; Rs — функции, разлагающиеся
в области
*>0, \xs\<H (s=l и) A11.2)
в ряды по степеням переменных xs и us с ограниченными коэффи-
коэффициентами, причем разложения начинаются членами не ниже второго
порядка.
Мы переходим теперь к исследованию задач о стабилизации для
уравнений первого приближения
lH — rsl-~l Г • • • I fsn^
(*=1 «)¦
¦) Альбрехт Э. Г., Об оптимальной стабилизации нелинейных систем,
ПММ, т. XXV, вып. 5, 1961; К теории аналитического конструирования регу-
регуляторов, Труды Межвузовской конференции по прикладной теории устойчиво-
устойчивости движения и аналитической механике, Изд. КАИ, Казань, 1962; Зубов В. И.,
К теории аналитического построения регуляторов. Автоматика и телемеха-
телемеханика, т. XXIV, № 8, 1963; Гальперин Е. А., Красовский Н. Н.,
О стабилизации установившихся движений нелинейных управляемых систем,
ПММ, т. XXVII, вып. 6, 1963; Красовский Н. Н., Осипов Ю. С,
О стабилизации движений управляемого объекта с запаздыванием в системе
регулирования. Изв. АН СССР, Техническая кибернетика № 6, 1963.
ПРОБЛЕМЫ СТАБИЛИЗАЦИИ УПРАВЛЯЕМЫХ ДВИЖЕНИЙ 493
Исследование начнем с задачи II об оптимальной стабилизации,
причем в качестве критерия качества A07.1) выберем интеграл
'-;
/1 Г
где квадратичные формы 2 auxixt и 2 $uuiai предполагаются
», ] = i i, / = i
определенно-положительными.
Оптимальную функцию Ляпунова V°(t, xt хп), которая
удовлетворяла бы условиям теоремы IV, следует здесь искать в виде
квадратичной формы
я
V°(t, xr *„)= S c,j{f)XiXj. A11.5)
Составим выражение B[V°; t; xx xn; uv ..., ur] A09.3):
B[V°; t; JCj xn; uv .... ur] =
n [ n т \
При к. = u°.(t, xv ..., хЛ величина В должна иметь минимум
и обращаться при этом в нуль. Поэтому, приравнивая правую
часть A11.6) к нулю, получим первое уравнение для V0 и и0.. Диф-
Дифференцируя правую часть A11.6) по Uj (у'=1 г) и приравни-
приравнивая результаты к нулю, получим еще г уравнений для определения V0
и и0.. Эти уравнения имеют вид
f
(У=1 я).
Уравнения A11.7) можно разрешить относительно и0., так как
т
вследствие определенной положительности формы 2 Р^и<«/
494
детерминант
ДОПОЛНЕНИЕ IV
Pll Pl2 • • • Plr
Р21 Р22 • • ¦ Ргг
Prl Pr2 • ¦ • Р/т
отличен от нуля.
Определим из уравнений A11.7) величины
A11.8)
„о L
k=\ »=i
dV<>
A11.9)
С/=1 г).
Здесь &kj — алгебраическое дополнение элемента k-й строки и
у'-й колонки в A11.8). Внося значения и0. A11.9) в равенство
BYV°; t; хх хл; и° и°1 = 0, получаем уравнение для опре-
определения функции V0:
л /я \
г=1
Подставляя в A11.10) выражения
дУ<>
dt
~ jU dt X>XJ'
__ О
и приравнивая к нулю коэффициенты при произведениях xtXj, полу-
получим уравнения для определения величин ctj(t):
dt
_ у
а/; = 0 A11.11)
ПРОБЛЕМЫ СТАБИЛИЗАЦИИ УПРАВЛЯЕМЫХ ДВИЖЕНИЙ 495
Если удастся найти ограниченное частное решение ctj(f) уравне-
уравнения A11.11) такое, что форма A11.5) окажется определенно-поло-
определенно-положительной, то согласно теореме IV задача будет решена. При этом
оптимальные управляющие воздействия имеют вид A11.9) и являются,
следовательно, линейными функциями от координат xs.
В частности, в случае установившегося движения х^ = 0, когда
Psi> Я si — постоянные величины и коэффициенты atj, -fr^ — тоже
постоянные числа, форму V0 следует искать в виде
V= 2 еих^ A11.12)
i,j=\ ' J
где Сц = const. Тогда дифференциальные уравнения A11.11) пре-
превращаются в алгебраические уравнения*)
, У=1, .... и; сц —
Итак, решение задачи II сводится в данном случае к разрешению
уравнений (Г11.11). При этом возникает проблема о существовании
ограниченного частного решения ctj{t), обеспечивающего определен-
определенную положительность формы V0 A11.5).
§ 112. Достаточные условия разрешимости задачи
о стабилизации для линейных систем.
Мы переходим теперь к изложению достаточных условий, при
которых может быть решена задача II об оптимальной стабилизации
для линейной управляемой системы
(s=l, .... re)
при условии минимума интеграла
Л л г \
J] щ, (t) xt (*) Xj (t) + J] p/y (/) щ (t) uj (t) dt, A12.2)
/1 T
где формы 2 <fy (f) xt (f) Xj (f) и 2 $t/ai @ м; @> как и выше,
предполагаются определенно-положительными.
') См. работы в сноске на стр. 476.
496
ДОПОЛНЕНИЕ IV
Согласно § 111 для существования решения этой задачи доста-
достаточно, чтобы уравнения A11.11) имели ограниченные решения ctj{t)
такие, что форма
V°(t, Xl хп)= 2 cls{t)xiXj A12.3)
является определенно-положительной.
Как и в общей задаче об устойчивости, будем различать случаи
установившегося движения xs = 0, когда величины pl}-, qtj, atj и $ц
будем полагать постоянными, и общие случаи неустановившегося
движения xs — 0, когда ptj{f), qt](t), a^it), $ij(t)— переменные
функции времени t.
Обсудим сначала случай установившегося невозмущенного дви-
движения xs = 0. Оптимальная функция Ляпунова V0 A12.3) ищется
в этом случае в виде квадратичной формы
A12.4)
с постоянными коэффициентами с^. Дифференциальные уравне-
уравнения A11.11) для Сц обращаются в систему алгебраических уравне-
уравнений A11.13). Управляющие воздействия и°,(Ху ..., х\ имеют при
этом вид
a°(xv .... *я) = ^^+ ... +vnjxn, A12.5)
где v
'si'
постоянные.
В обсуждаемом случае важную роль играет матрица W, построен-
построенная следующим образом:
W={Q, PQ
A12.6)
Здесь Q — матрица {qsj} (s=l, ..., и; 7=1, .... г), Р — ма-
матрица {psj} (s= I, • ¦ -. и; _/=: 1, .. ., и). В частности, если система
A12.1) управляется лишь одним воздействием u = uv то матрица Q
превращается в вектор-столбец
~Яи
Яи
ПРОБЛЕМЫ СТАБИЛИЗАЦИИ УПРАВЛЯЕМЫХ ДВИЖЕНИЙ
матрицы P*Q также обращаются в векторы-столбцы .
497
Ри Рп
Pi\ P22
Ры
Pin
Яп
W,
2ft+ 1
_ Pn\ Pn2 ¦¦¦ Pan - _<7nl_
и матрица W оказывается и X и-матрицей
w =
да,
да,
"In
да.
'22
Ш,
В общем случае матрица 11^ имеет п строк и и X г столбцов.
Оказывается, что возможность решения задачи II об оптимальной
стабилизации системы A12.1) при условии минимума величины A12.2)
определяется свойствами матрицы №. В частности, достаточные
условия разрешимости задачи даются следующей теоремой.
Теорема 1. Пусть ранг матрицы W равен п. Тогда
справедливы следующие заключения:
1. Задача II для системы A12.1) при условии минимума
величины A12.2) имеет решение, причем существуют квадра-
квадратичная форма V°(Xi, ..., хп) A12.4) и управляющие воз-
воздействия u°.(xv ..., х\ вида A12.5), удовлетворяющие всем
условиям теоремы IV.
2. Управляющие воздействия иа.(хх х\ A12.5), опре-
определяемые оптимальной функцией Ляпунова V'°(x1, ..., хп)
A12.4) в соответствии с равенствами A11.19), являются
единственным решением задачи.
Мы не будем приводить здесь доказательство первого утвержде-
утверждения теоремы 1. Это доказательство можно найти в работах Р. Е. Кал-
мана, Я. Курцвейля и Ф. М. Кирилловой1). Проверим здесь лишь
справедливость второго утверждения.
') Калкан Р. Е., Об общей теории систем управления, Труды I кон-
конгресса ИФАК, т. I, Изд. АН СССР, 1961; Contributions to the theory of
optimal control Sumposium Internacional de Ecnacipnes Differenciales Ordina-
rias, Publ. por La Univ. Nac. Automa de Mexico у La Soci^ded. Matem.
Mexicana, 1961; Курцвейль Я., К аналитическому конструированию
регуляторов. Автоматика и телемеханика, т. XXII, №6, 1961; Кирил-
Кириллова Ф. М., К задаче об аналитическом конструировании регуляторов
ПММ, т. XXV, вып. 3, 1961.
498 ДОПОЛНЕНИЕ IV
Итак, пусть в соответствии с пунктом 1 теоремы функция V0
вида A12.4) является оптимальной функцией Ляпунова м в сово-
совокупности с функциями и°.(х1 хл) вида A12.5) удовлетво-
удовлетворяет всем условиям теоремы IV. Но при известной функции
V°(xv .... хп) управляющие воздействия и0.(х1 хЛ опреде-
определяются единственным образом из условий A11.7) минимума выраже-
выражения B{V°; хг хп; и{, .... ur] no Uj. Если выбрать какие-либо
непрерывные управляющие воздействия и*.(хх хЛфи0.(xv ..., х\
в некоторой, пусть даже очень малой области S изменения величин xs,
то в этой области выражение BjV°; хх хп; и* и*] будет
положительным. Но тогда согласно рассуждениям на стр. 488
интеграл
Л л
^ atJx]
г
Л
^ atJx] [t] x) [t] + S P/;«; W и) Щ at
to \l,j = l l,j = X J
будет больше, чем величина 1^° (л:* Г^о] ^pol) ДЛЯ всех дви*
жений x*s[t], проходящих через область 5 при t%-t0. Это означает,
что управление a*. (xv ..., х\ не является оптимальным. Тем самым
доказана единственность оптимального управления и0. (xv ...,.x\
найденного по функции V0 (хх хп) из уравнений A11.19).
Матрицы вида PkQ были рассмотрены в связи с задачами об опти-
оптимальном регулировании Р. В. Гамкрелидзе1). В частности, условие
независимости векторов Q, PQ, . . ., Рп~ Q в случае, когда линейная
система A12.1) управляется одним воздействием и — и^ было названо
им «условием общего положения». Это условие играет важную роль
в теории линейных управляемых систем. Позднее свойства матрицы W
в связи с проблемами управления были изучены во многих работах2).
Перейдем теперь к обсуждению случаев неустановившегося не-
невозмущенного движения х^ = 0. В этих случаях разрешимость задачи II
об оптимальной стабилизации связана со свойствами матрицы W (t),
которая имеет следующий вид:
W(f)=[Ll(O ?„(/)}. A12.7)
Здесь Lk(f) — матрицы, определенные рекуррентными соотноше-
соотношениями
Ц it) = Q @ Lk+l {t) = ^%Д -Р @ Lk it), A12.8)
') См. монографию Л. С. Понтрягина и др. в сноске на стр. 475.
2) См., например, работы в сноске на стр. 492.
ПРОБЛЕМЫ СТАБИЛИЗАЦИИ УПРАВЛЯЕМЫХ ДВИЖЕНИЙ 499
причем, естественно, предполагается, что элементы psk (f) и qs] (/)
матриц P{t) и Q(t) имеют все производные, необходимые для по-
построения матрицы W (t).
Достаточные условия разрешимости задачи II для системы A12.1)
при условии минимума величины A12.2) даются следующей тео-
теоремой.
Теорема 2. Пусть функции psk(t) и qsj(t) имеют при t^-0
равномерно непрерывные и ограниченные производные до
(п—\)-го порядка включительно, и пусть существует число
т > 0, удовлетворяющее следующему условию:
На любом отрезке ^<^<^ + т найдется точка d* (f)
такая, что в матрице W({)¦*) можно выделить п линейно
независимых векторов-столбцов
w(ln)(ф») — \wsik(Щ {k~\ га; s—\ п)
причем квадратичная форма
п I п \
/. h /„)= 2 21 да,/Л«*@)»,/,(*• @ Vy 012.9)
определенно-положительна.
Тогда справедливы следующие заключения:
1. Задача II для системы A12.1) при условии минимума
величины A12.2) имеет решение, причем существуют квадра-
квадратичная форма V°(t, xv ..., хп) A12.3) и управляющие воздей-
воздействия
ifij(t. xv .... jg = viy (*)*,+ ... +vn.(t)xn, A12.10)
удовлетворяющие всем условиям теоремы IV.
2. Управляющие воздействия u°,(t, xv ..., х\ A12.10), опре-
определяемые оптимальной функцией Ляпунова V°(t, xit ..., д;л)
A12.3) в соответствии с равенствами A11.19), являются
единственным решением задачи.
Справедливость теоремы 2 мы также примем без доказательства.
Это доказательство можно найти в работе Н. Н. Красовского').
§ 113. Практические способы решения задач
об оптимальной стабилизации для линейных систем.
Теоремы, сформулированные в предыдущем параграфе, указывают
достаточные условия, при выполнении которых разрешима задача II
об оптимальной стабилизации системы A12.1) при условии минимума
') К р а с о в с к и й Н. Н., О стабилизации неустойчивых движений до-
дополнительными силами при неполной обратной связи. ПММ, т. XXVII,
вып. 4, 196а
500 ДОПОЛНЕНИЕ IV
показателя качества A12.2) процесса xs(t) (s=\ п). Следова-
Следовательно, при этих условиях уравнения A11.13) (или уравнений A11.11)),
определяющие оптимальную функцию Ляпунова V0, имеют решения Сц
(или ctj(t)), обладающие всеми нужными свойствами.
Решение уравнений A11.11) может представить серьезные труд-
трудности, а решение уравнений A11.13) обычно не вызывает принци-
принципиальных затруднений, однако и в этом случае практический счет
может оказаться весьма громоздким.
Предполагая в дальнейшем, что величины pkl, qik, a/;- и рг;-,
фигурирующие в A12.1) и A12.2), не зависят от времени, изложим
два возможных способа решения задачи об оптимальной стабили-
стабилизации.
Первый способ основан на таком свойстве искомых решений ct,
уравнений, A11.13): если задача II в форме A12.1)—A12.2) имеет
решение, то величины с(;-, удовлетворяющие уравнениям A11.13) и
определяющие оптимальную функцию Ляпунова
V°(*i xa) = i%^cltxlx), A13.1)
суть числа I
си = \\тс"ч(г) при t->-{-oo A13.2)
(/. 7=1 «).
где с*. (f) — частное решение системы дифференциальных уравнений
ft, s-\
отвечающее начальным условиям
c*y@) = 0 (/. 7=1. ... и). A13.4)
(Уравнения A13.3) получаются из уравнений вида A11.11), в кото-
которых t заменяется на — t.)
Упомянутое свойство подсказывает метод вычисления величин с,;-.
Для этой цели следует найти решение с* (t) уравнений A13.3) —
A13.4) при достаточно больших значениях t = t. Вследствие соот-
соотношений A13.2) можно принять
с.. = с*;.(т) (/. 7=1 »)•'
Таким образом,, коэффициенты оптимальной функции Ляпунова
могут быть вычислены сколь угодно точно, если т достаточно ве-
ПРОБЛЕМЫ СТАБИЛИЗАЦИИ УПРАВЛЯЕМЫХ ДВИЖЕНИЙ 501
лико. Для практических вычислений, легко поддающихся стандарти-
стандартизации, удобно пользоваться вычислительными устройствами и,
в частности, аналоговыми машинами.
Доказательство предельных соотношений A13.2) и подробное
описание рассмотренного способа вычисления величин c{j с исполь-
использованием электронных моделей можно найти в работе Ю. М. Репина
и В. Е. Третьякова1).
После вычисления величин ctj управляющие воздействия опреде-
определяются без труда по формулам A11.9).
Пример 1. В качестве иллюстрации изложенного способа рассмотрим
решение задачи о стабилизации математического маятника в верхнем, не-
неустойчивом положении равновесия моментом, приложенным к нему на оси
подвеса. Этот момент вырабатывается исполнительным механизмом, который
является интегрирующим звеном. Исполнительный механизм в свою очередь
подвержен некоторому управляющему воздействию и.
Выбирая соответствующим образом масштабы времени, координат и
усилий, запишем уравнения возмущенного движения в нормальной форме:
dx2 .,_ .. , .. dx3
dt 2> dt —-"""I г~з> dt ¦
где Xi = ф — угол отклонения маятника от вертикали, х2 = ср, х3 — момент,
приложенный к маятнику.
Составим уравнения первого приближения:
dxt _ dx2 _ , dXi
Для этой системы рассмотрим задачу II об оптимальной стабилизации, вы-
выбрав следующий критерий качества:
со
'« = / И (О + х\ @ + 4 <<> + (О] dt. A13.6)
Проверим достаточное условие разрешимости задачи (см. теорему 1
§ 112). С этой целью вычислим матрицу W= {Q, PQ, P2Q}-
В нашем случае
и поэтому
Ранг матрицы W равен порядку системы A13.5). Следовательно, рас-
рассматриваемая задача имеет решение. Уравнения A11.13) для определения
') Репин Ю. М., Т р е т ь я к о в В. Е., Решение задачи об аналитиче-
аналитическом конструировании регуляторов на электронных моделирующих устрой-
устройствах. Автоматика и телемеханика, т. 24, вып. 6, 1963.
502
ДОПОЛНЕНИЕ IV
коэффициентов формы A13.1) принимают следующий вид:
С
f 12
— С13 + 1 = 0,
—4+1=0,
«22 — С13С23 =
«22
С22
13С23
A13.7)
Пусть Cjj — искомое решение системы уравнений A13.7), для которого
квадратичная форма A13.1) является определенно-положительной.
Согласно A13.2)
ctj = lira c'j (t) (i, j =1,2,3) при t -> + oo,
где Cij(t) — решение системы дифференциальных уравнений
dc*n (Q
dt
dc*2i (t)
dt
di
A13.3)
4@+4@-4@-4@'
= 4 @+4 @—4 @ ¦ 4 (o>
dt
,(O
dt
соответствующее начальным условиям
(/, у = 1,2,3).
На рис. 24 приведены графики переходных кривых для уравнений A13.8),
вычисленные на цифровой вычислительной машине. Значения сц (i, _/= 1, 2, 3)
получаются такими:
с,, = 11,1333, с12 = 10,1333,
с22= 10,1333, с,3= 4,6116,
с33= 3,1974, с23= 4,6116.
Искомое оптимальное управление и0 находится по формуле A11.9):
1 dV°
°
D,6116*! + 4,6116л-2 + 3,1974*3).
Из примера, в частности, видно, что для определения оптимального упра-
управляющего воздействия знание всех коэффициентов оптимальной функции Ля-
Ляпунова не обязательно.
ПРОБЛЕМЫ СТАБИЛИЗАЦИИ УПРАВЛЯЕМЫХ ДВИЖЕНИЙ
603
Мы переходим теперь к изложению второго способаг) решения
задачи II в форме A12.1) — A12.2), который позволяет вычислить
коэффициенты оптимального управления непосредственно, без пред-
предварительного определения функции V0.
Предположим, что движение объекта описывается системой ли-
линейных дифференциальных уравнений
dxl
dxn
dt
А
A13.9)
где psj и qs (s, j=\, .... п) — некоторые постоянные величины,
а« — скалярное управляющее воздействие. Пусть критерий качества
переходного процесса задан в виде
интеграла
dt.
A13.10)
Здесь atj — постоянные коэффи-
коэффициенты определенно-положитель-
определенно-положительной квадратичной формы.
Допуская, что условия, при
которых разрешима задача II
в форме A13.9) —A13.10), вы-
выполнены (см. теорему 1 § 112),
воспользуемся для отыскания оп-
оптимального управляющего воздействия процедурой, вытекающей из
принципа максимума.
Функция Гамильтона H = H(ty0 ipn, xlt .... хп, и), опре-
определенная в § ПО формулой (ПО.2), для нашей задачи имеет вид
Рис.24.
') Подобный способ опубликован в статье: П р я х и н Н. С, К вопросу
об аналитическом конструировании регуляторов. Автоматика и телемеханика,
т. 24, вып. 9, 1963. Независимо аналогичный метод был разработан и стан-
стандартизирован в вычислительном центре Уральского государственного уни-
университета под руководством Ю. М. Репина в 1962 году.
504
ДОПОЛНЕНИЕ IV
Оптимальное управление в каждый момент времени должно фор-
формироваться так, чтобы максимизировалась величина Н или, что то же
самое, минимизировалась величина В (см. § 109)
дН дВ
Поэтому, приравнивая производную -т— или -^ нулю, находим
-т
структуру оптимального управления
V A13.11)
Составим, далее, канонически сопряженные уравнения' A09.1) и
A10.3):
dx. дН d^. дН
1, . . ., п),
dt
1?
dt
dxt
которые в нашем случае после подстановки вместо и функции м°
из формулы A13.11) примут вид
dx.
A13.12)
dxn
• • Л-ЧпЧ
PniAn-
Эту систему уравнений, решающих задачу об оптимальной стабили-
стабилизации, можно получить также, используя классический вариационный
метод Эйлера — Лагранжа. Именно таким путем она была получена
впервые А. М. Летовым*).
Построим характеристический определитель для системы A13.12):
Р— IE Qx
а р* j
где обозначено P={psJ}, Ql={qs-qj}, P*={pjs}, a = {аи}
Б= {Ъц}. Известно, что построенный определитель обладает свой-
свойством D(—k) — D(X), т. е. характеристический полином содержит
только четные степени к. Тогда уравнение D(A,) = 0 наряду с каж-
') Л е т о в А. М., Аналитическое конструирование регуляторов, Автома-
Автоматика и телемеханика, т. 21, вып. 4, 1960.
. ПРОБЛЕМЫ СТАБИЛИЗАЦИИ УПРАВЛЯЕМЫХ ДВИЖЕНИЙ 505
дым корнем, имеющим отрицательную действительную часть, будет
обладать соответствующим корнем с положительной действительной
частью. Следовательно, характеристический многочлен может быть
выражен в виде произведения двух полиномов га-й степени
причем корни полинома rfj(A,) расположены в левой полуплоскости,
а корни многочлена d2(V) —в правой.
Обратим теперь внимание на следующее обстоятельство. Движе-
Движение, определяемое уравнениями A13.9), в которые вместо и подста-
подставлено оптимальное управление u°(Xi хп), являющееся согласно
результатам § 111 линейной функцией координат xs(s=\, .... п),
совпадает с движением, получающимся в силу системы уравнений
в которых вектор гр= [tyv .... ipn} вычислен на оптимальных траек-
траекториях x°s(t) (s = 1 п).
Но по условиям задачи оптимальное управляющее воздействие
должно быть таким, чтобы тривиальное решение системы
^ .... хп), A13.13)
где
Я=[Я\ Яп\>
было асимптотически устойчивым, следовательно, характеристический
многочлен, составленный для A13.13), обязан иметь все корни
с отрицательной действительной частью и этот многочлен должен
тождественно совпадать с (—l)"rfj(A,) в силу отмеченного выше
обстоятельства.
Полагая H° = v1x1-j- ... -\-vnxn и подставляя его в таком виде
в уравнения A13.13), приравниваем характеристический полином
многочлену (—l)"dj(A,):
A13.14)
Если многочлен dx (X) нам известен, то, сравнивая в тождестве
A13.14) коэффициенты при одинаковых степенях ^, получим систему
уравнений для определения коэффициентов оптимального управления.
Нетрудно убедиться в том, что эта система алгебраических уравне-
уравнений всегда будет линейной.
БОб ДОПОЛНЕНИЕ IV
Таким образом, вопрос об отыскании оптимального управления
сводится по существу к вопросу о разложении полинома степени 2п
на два указанных выше множителя rfx (Я,) и d2{X). Как только много-
многочлен rf, (X) становится известным, коэффициенты оптимального упра-
управления находятся сразу же из решения линейной системы алгебраи-
алгебраических уравнений.
Проиллюстрируем изложенный метод, решив в линейном прибли-
приближении задачу, сформулированную в примере § 108.
Пример 2. Отбрасывая нелинейные члены в уравнениях A08.4), полу-
получим систему первого приближения
dt *' dt
Полагаем для простоты выкладок ц, = [х2 = |*3 = у = у» так что
оэ
/«= у J И (о+А @+4 (о+«2@] dt. A13.16)
и
Канонически сопряженная система A13.12) имеет для нашего примера
вид
Раскрывая характеристический определитель этой системы, получим
D (Л) = (Л2 — 1) [(Я2 — аJ —
Многочлен D (X) нетрудно в нашем случае представить в виде произведе-
произведения полиномов dx (Я) и d2 (к):
D (л) = (Л3 + «i>-2 + л2Я + a3) (^-3 — atl2 + агХ — а3).
Здесь Я3 -|- ахк2 -\- а2Я -\- а3 — dl (Я). Коэффициенты аь а2, а3 определяются
формулами:
а, = А
Легко проверить, что уравнение
имеет все корни с отрицательной действительной частью. Полагая и0 --
-\-v2x2-\-\3x3 и составляя тождество A13.14), имеем:
— Я 1 О
a -(- bvt bv2 — Я, |3 -f- 6v3
v, v? v3 — Я
= — Я3 — а(Я2 — агЯ — а3.
ПРОБЛЕМЫ СТАБИЛИЗАЦИИ УПРАВЛЯЕМЫХ ДВИЖЕНИЙ 607
Отсюда, сравнивая коэффициенты при одинаковых степенях Я, получаем
систему линейных уравнений относительно V], v2, v3:
— 6v2 — v3 = п\, — 6V[ — Pv2 = a2 -\- a, — Pvi -}~ av3 = a3.
Решая эту систему, находим коэффициенты оптимального управления:
6а (а2 -|- а) — |
v,=
Д
Ь(а3-\-аа1)~
А
v3 =.-—'
A13.17)
А
где А = р2 — аб2.
Учитывая, что а = —-^г, Р = V „ ° , b = ~, k=-^~ (см. § 108),
г г f с
0 0 0 ф
и D -+- k?)
имеем А = д——. Если с Ф 0, то А не обращается в нуль ни при
го
каких г0 и является конечным числом. Следовательно, задача об оптималь-
оптимальной стабилизации для нашего примера имеет решение при любых г0 и
Заметим, кстати, что условие А ф 0 совпадает с достаточным условием
разрешимости задачи из теоремы 1 § 112. Это условие для нашего примера
оказывается невыполненным, если сф = 0, что соответствует выбросу массы
только в радиальном направлении. Можно показать, что в этом случае за-
задача II в форме A13.15) — A13.16) решения не имеет.
В самом деле, если сф = 0, то система уравнений A08.2) имеет первый
интеграл у3 = г\ = у. = const, где постоянная х определяется начальными
условиями, которым соответствует движение точки по исходной эллиптиче-
эллиптической орбите. В невозмущенном движении у3 = У^цга (см. § 108). Вообще
говоря, К(хго ф х, так как г0 по условиям задачи — произвольно; число,
связанное только предположением о достаточной близости эллиптической
траектории к круговой орбите радиуса г0. Следовательно, в процессе упра-
управления уз (t) должно меняться от величины х до величины Vs-ir^, но у3 из-
леняться вообще не может, так как при с =0 в силу уравнений A08.2)
J? =0 во все время переходного процесса. Таким образом, условие с^фО
является в рассмотренной задаче необходимым условием осуществления
перехода точки с эллиптической траектории на круговую орбиту заданного
радиуса.
Заметим, что решение первого примера, рассмотренного в этом пара-
параграфе, можно также получить из формул A13.17), если принять а = р = 1,
6 = 0, так как системы уравнений A13.5) и A13.15) в этом случае совпадают.
В заключение можно сказать, что оба изложенных способа ре-
решения задачи II об оптимальной стабилизации для линейных систем
A12.1) при условии минимума показателя качества A12.2) процесса
xs(t) (s=l га) позволяют с успехом использовать современные
508 ДОПОЛНЕНИЕ IV
вычислительные устройства1). Однако второй метод, в отличие от
первого, иногда может привести к решению задачи в замкнутой
форме и для такого случая надобность в применении вычислитель-
вычислительных машин отпадает. Но первый способ является более универсаль-
универсальным и он значительно проще по своей вычислительной схеме.
Отметим еще, что задаче о вычислении параметров оптимального
управления посвящена интересная работа А. И. Лурье2).
§ 114. Теоремы о стабилизации по первому приближению.
Мы переходим теперь к рассмотрению нелинейных уравнений
+ Rs(t, xl хп; их ur) (s=l п), A14.1)
описывающих возмущенные движения xs(t) управляемой системы
в окрестности заданного движения xs — 0. Будем предполагать, как
обычно, что функции Rs определены в области
*>0, |*J'<# (s=l n), A14.2)
где они непрерывны и удовлетворяют неравенствам
|ЯД*. *i хп; й! иг)|<
<Л{|*,| + ... +|хл| + |Й1|+ ... + |я,|}, A14.3)
причем А — некоторая постоянная.
Наряду с уравнениями A14.1) рассмотрим систему первого при-
приближения
dx
-of- = Psixi + ¦ • • + PSnxn + ЧлЩ. + • • • + ч*,щ (П4.4)
E=1 П).
При каких условиях возможность стабилизации системы A14.1)
вытекает из решения проблемы в первом приближении? Исследование
этого вопроса составляет предмет теории стабилизации системы A14.1)
по линейному приближению. Мы ограничимся здесь лишь достаточ-
достаточными условиями, при которых ответ на заданный вопрос является
положительным. Эти результаты являются следствием достаточных
условий разрешимости задач II для системы A14.4) при условии мини-
') Стандартные программы для решения задач изложенными способами
имеются, например, в вычислительном центре Уральского государственного
университета.
2) Лурье А. И., Минимальный квадратичный критерий качества регу-
регулируемой системы. Изв. АН СССР, Техническая кибернетика, № 4, 1933.
ПРОБЛЕМЫ СТАБИЛИЗАЦИИ УПРАВЛЯЕМЫХ ДВИЖЕНИЙ 509
мума интеграла
данных в теоремах 1 и 2 § 112, и следствием общих теорем об
асимптотической устойчивости по первому приближению, приведен-
приведенных в §§ 22, 85.
Рассмотрим сначала случай установившегося невозмущенного дви-
движения xs = 0, когда величины psj и qsj в уравнениях A14.1) явля-
являются постоянными и функции Rs не зависят явно от времени.
Тогда справедливо следующее утверждение.
Теорема 1. Если ранг матрицы
W={Q, PQ Я"*?} A14.6)
равен п, то задача I о стабилизации системы A14.1) решается
исходя из линейного приближения A14.4) при любом выборе
функций Rs, удовлетворяющих неравенствам A14.3), если
только постоянная А достаточно мала. Управляющие воз-
воздействия Uj(xv ..., хп) можно выбрать в форме линейных
функций
uj(x1 xJ = vyx1-{- ... -\-vnjxn, A14.7)
где Vy — постоянные.
Доказательство. Выберем как-нибудь определенно положи-
положительные квадратичные формы
Л Г
2_ a-tjXiXj и ]? hjuiuj
с постоянными a(jf- и р^. Согласно теореме 1 § 112, если ранг ИР
равен п, то для системы A14.4) можно решить задачу II об оптималь-
оптимальной стабилизации при условии минимума интеграла A14.5). При этом
получатся оптимальные стабилизирующие воздействия и°.(хх, ..., хп),
описываемые линейными функциями
-»(*,. .... xn) = vx.xl+ ...+vnjxn. A14.8)
При u.~uu.(xlt ..., х\ линейная система, описываемая уравне-
уравнениями
будет асимптотически устойчивой.
510
ДОПОЛНЕНИЕ IV
Выберем для нелинейной системы A14.1) в качестве управляю-
управляющих воздействий и;- величины a°.(xv ..., х\ A14.8). Подставив
и . = u°.(xv ..., х\ в уравнения A14.1), получим нелинейные урав-
уравнения возмущенного движения
dt
Psaxn
(s=l, .... я),
где функции
вследствие A14.3) удовлетворяют неравенству
(s = 1 п),
где
: А A -f- v), v = max 2 I Vn l> У =
*„)
A14.10)
....*„)
A14.11)
A14.12)
Уравнения A14.9) составляют для системы уравнений A14.10)
систему первого приближения.
Характеристическое уравнение
—Я, ...
= 0 A14.13)
асимптотически устойчивой системы A14.9) имеет все корни Xt
с отрицательными действительными частями. Отсюда по теореме 1
§ 22 заключаем, что невозмущенное движение д;^ = 0 системы A14.10)
при условии A14.12) асимптотически устойчиво, если только по-
постоянная А достаточно мала. Тем самым теорема 1 полностью до-
доказана.
Перейдем теперь к случаю неустановившегося невозмущенного
движения xs = 0, когда величины psi и qsj в уравнениях A14.4)
предполагаются переменными функциями времени. Теорема о стаби-
стабилизации по первому приближению в этом случае может быть сфор-
сформулирована следующим образом.
где
ПРОБЛЕМЫ СТАБИЛИЗАЦИИ УПРАВЛЯЕМЫХ ДВИЖЕНИЙ 511
Теорема 2. Составим матрицу
= {Ll(f) Ln(t)},
(k = 1 га— 1).
Пусть функции psi{t) и qsj(t) имеют при t^t0 равномерно
непрерывные и ограниченные производные до (п — \)-го порядка
включительно. Если при каждом t~^>t0 в матрице W(t) можно
выделить га линейно независимых векторов-столбцов w (9
(&=1 га) таких, что квадратичная форма1)
ф(*. h *»)= 2 B «ч(9«•**,(*) )/*/, (П4.14)
ft, ]=\ \S=1 " > I
является определенно положительной, то задача I о стабили-
стабилизации системы {МАЛ) решается исходя из линейного приближе-
приближения A14.4) при любом выборе функций Rs, удовлетворяющих
неравенствам A14.3), если только постоянная А достаточно
мала. Управляющие воздействия Uj(t, xlt ..., хп) можно вы-
выбрать в форме линейных функций
и jit, xx *e) = v,y(9*i+ ••¦ +vnj(t)xn, A14.15)
где Vij{t) — непрерывные и ограниченные функции времени L
Доказательство. Выберем как-нибудь определенно-положи-
определенно-положительные функции
л л
2 (lij^XiXj и 2 Р/у(9 «*«/• A14.16)
При условиях доказываемой теоремы выполняются предположе-
предположения теоремы 2 § 112. Поэтому для системы A14.4) можно решить
задачу II об оптимальной стабилизации при условии минимума интег-
интеграла A14.5). При этом получатся оптимальные стабилизирующие
воздействия u°j(t, xv .... х\ вида
и»(Л х1 *„) = *1;(9*!+ ... +vni(9*n. (П4.17)
где v(;-(9 — ограниченные и непрерывные функции времени.
') Условие определенной положительности формы Ф(^, lt /„) озна-
означает, что линейная независимость выбранных векторов tit k> в известно!»
смысле равномерна по t^-t0 и углы между этими векторами не могут ста-
становиться произвольно малыми.
512 ДОПОЛНЕНИЕ IV
Подставляя u. — tfitt, xi х\ в уравнения A14.17), получим
линейную систему с переменными коэффициентами
-§-= Psi @ *i + ••• +psa(t)xa +
-{-qsl(t)a°(t. Xj хл)+ ... -\-qsr(t)u°r(t, x1 хп) A14.18)
(s = 1 п.).
По построению управляющих воздействий и0, (t, хг х\ не-
невозмущенное движение х^ = 0 системы A14.18) асимптотически устой-
устойчиво. Более того, для системы A14.18) можно указать допускающую
бесконечно малый высший предел определенно-положительную функцию
Ляпунова V (t, xv ..., х„), имеющую определенно отрицательную
dV
производную —уг в силу уравнений A14.18). В качестве такой функ-
функции V можно выбрать оптимальную функцию Ляпунова У0 (t, xv ..., х„),
существование которой обеспечивается теоремой 2 из § 112.
Выберем теперь в нелинейной системе A14.1) в качестве упра-
управляющих воздействий и} величины u°,(t, xv ..., хЛ A14.17). Под-
Подставив u. = u°j(t, х,, ..., х\ в уравнения A14.1), получим нелиней-
нелинейные уравнения возмущенного движения:
dxs . , .
A14.19)
E=1, .... я).
Здесь функции
=**,('• Х1 Хп' а\{*' Х1 Хп) »%*• Х1 *„))
удовлетворяют неравенству
|ф,С *i *яI<Л,{|*1Ц- •¦• +|*я|}. AН.20)
где
v = max I ^j | vtj |, j = 1, ..., r; t ^> (
Невозмущенное движение xs — Q системы A14.19) асимтотически
устойчиво вследствие теоремы I из § 88, если только постоянная А
достаточно мала. В самом деле, для системы первого приближения.
A14.18) существует функция Ляпунова V°(t, xx, .... х„), удовлет-
ПРОБЛЕМЫ СТАБИЛИЗАЦИИ УПРАВЛЯЕМЫХ ДВИЖЕНИЙ 513
воряющая теореме II об асимптотической устойчивости, и имеет место
оценка A14.20). Отсюда следует справедливость теоремы 2.
Итак, мы указали достаточные условия разрешимости задачи I
о стабилизации нелинейной системы A14.1) по первому приближе-
приближению A14.2).
Вопрос о решении задачи II об оптимальной стабилизации си-
системы A14.1) по первому приближению решается аналогичным об-
образом. Мы приведем здесь лишь формулировку результатов. Дока-
Доказательство этих результатов можно найти в работах Э. Г. Альбрехта
и В. И. Зубова1).
Рассмотрим снова систему уравнений A14.1), где будем предпо-
предполагать, что функции Rs разлагаются в области A14.2) в ряды по
степеням xs и Uj с коэффициентами, являющимися непрерывными и
ограниченными функциями времени t. Предполагаем, как всегда, что
эти разложения начинаются с членов, порядок которых не ниже
второго.
Для системы A14.1) рассмотрим задачу II об оптимальной стаби-
стабилизации при условии минимума интеграла
оо
/= fv>(t. x,(t) *„(*), «,@ ur(t))dt, A14.21)
где функция @ также предполагается аналитической функцией вели-
величин xs и Uj, т. е. разлагается в ряд по степеням этих величин с не-
непрерывными и ограниченными коэффициентами.
По смыслу задачи об оптимальной стабилизации функцию со
целесообразно выбирать в виде определенно-положительной функции
от xs и н;-. Поэтому можно предполагать, что разложение функции ю
в ряд начинается с четных степеней xs и Uj. В соответствии с этим
обсудим случаи, когда функция со имеет разложение
<«>(*. *1 Хп\ UX Ur) =
оо
= 2@<*>tf, *, хп; и, и,), A14.22)
где <#' — формы переменных xs и Uj. При этом полагаем, что пер-
первый член со'2) разложения A14.22) является определенно-положитель-
определенно-положительной функцией вида
л г
(й<2) = ^ 2j t aU*txJ + . S_ i hj*i*i. A14.23)
') См. сноски на стр. 492.
514 ДОПОЛНЕНИЕ IV
т. е. формы
л г
и 2
предполагаются определенно-положительными.
Допустим, что система уравнений первого приближения удовле-
удовлетворяет условиям теоремы 1 (стр. 497) в случае установившегося
невозмущенного движения xs = О, или условиям теоремы 2 в случае
неустановившегося движения д^ = 0 (стр. 499). Тогда согласно тео-
теоремам 1 и 2 § 112 задача II об оптимальной стабилизации линейных
систем A14.4) при условиях минимума интеграла A14.5) от квадра-
квадратичных форм A14.22) имеет решение вида
Оказывается, что в таких случаях задача II об оптимальной ста-
стабилизации нелинейной системы A14.1) при условии минимума инте-
интеграла A14.21) с функцией со общего вида A14.22) также имеет реше-
решение. При этом оптимальное управление u°(t, х1 х\ такой
задачи представляется в виде рядов
«2 ('. *, *„) S
«2 ('. *, *„)= S/f^ *, ха) A14.25)
г),
которые сходятся при всех достаточно малых значениях xs.
Здесь яФр, хг ..., хЛ представляют собой линейные формы
совпадающие с оптимальным управлением A14.24), решающим за-
задачу A14.1), A14.21) в первом приближении. Коэффициенты форм
uW(t, xv ..., х\ при k%2 определяются из некоторых систем
линейных уравнений. В случае постоянных psj, qsj, aLJ, $tj эти ура-
уравнения оказываются алгебраическими. В общем случае переменных
pSj(f), qSj{t), a.ij(t), $y(t) эти уравнения являются обыкновенными
дифференциальными уравнениями. Область сходимости рядов A14.25)
определяется коэффициентами и свойствами линейной системы A14.18).
ПРИМЕЧАНИЯ РЕДАКТОРА.
К стр. 18. Большое число исследований было посвящено в по-
последнее время задачам об асимптотической устойчивости, где область
начальных возмущений xs (t0), для которых должно выполняться усло-
условие C.5), нельзя считать малой. Такие задачи изучены, например,
в работах: Еругин Н. П., Качественное исследование интеграль-
интегральных кривых системы дифференциальных уравнений. ПММ, т. 14,
вып. 5, 1950; О некоторых вопросах теории устойчивости движения
и качественной теории дифференциальных уравнений. ПММ, т. 14,
вып. 6, 1950; Лурье А. И., Некоторые нелинейные задачи теории
автоматического регулирования, Гостехиздат, 1951; Малкин И. Г.,
Об устойчивости систем автоматического регулирования. ПММ, т. 16,
вып. 4, 1952; Барбашин Е. А., Об устойчивости решения одного
нелинейного уравнения третьего порядка. ПММ, т. 16, вып. 5, 1952;
Лето в А. М., Устойчивость нелинейных систем автоматического
регулирования, Гостехиздат, 1955; Зубов В. И., Методы А. М. Ля-
Ляпунова и их применение, Изд. ЛГУ, 1957; Плисе В. А., Некоторые
проблемы теории устойчивости движения в целом. Изд. ЛГУ, 1958;
Айзерман М. А., Гантмахер Ф. Р., Абсолютная устойчивость
регулируемых систем, Изд. АН СССР, 1963.
В подобных случаях приобретает особенное значение оценка
области C.3) тех начальных возмущений xs(t0), Для которых выпол-
выполняется предельное соотношение C.5). В соответствии с этим оказы-
оказывается полезным дополнить определение асимптотической устойчивости
следующим образом.
(а) Пусть G — некоторая, наперед заданная область из-
изменения переменных xs, в которой по условиям задачи могут лежать
значения xs (t0) начальных возмущений. Тогда невозмущенное движе-
движение х,. = 0 называется асимптотически устойчивым в большом,
если это движение устойчиво и если условие C.5) выполняется для
всех xs(t0) из области О.
В частности, область О может быть определена неравенствами
где N — заданное число.
516 ПРИМЕЧАНИЯ РЕДАКТОРА
Если в изучаемой реальной системе начальные возмущения xs(t0)
могут оказаться весьма большими и их трудно или нецелесообразно
заранее оценивать каким-либо числом N, то оказывается полезным
следующее определение.
(Р) Невозмущенное движение называется асимптотически
устойчивым в целом, если это движение устойчиво и если
условие C.5) выполняется для любых начальных возмуще-
возмущений xs(t0), как бы велики они ни были.
Отметим еще, что свойство устойчивости, выражаемое неравен-
неравенствами C.3) и C.4), не следует, вообще говоря, из условия C.5)
даже в случае, когда в уравнениях C.2) функции Xs не зависят явно
от времени t. Именно, можно построить пример, когда условие C.5)
выполняется для всех начальных возмущений xs(t0), но невозмущен-
невозмущенное движение xs = 0 неустойчиво. Подобная ситуация рассмотрена,
например, в работе: Красовский Н. Н., Об устойчивости ре-
решений системы двух дифференциальных уравнений. ПММ, т. 17,
вып. 6, 1953.
К стр. 21. Приведенное определение устойчивости при постоянно
действующих возмущениях является наиболее употребительным.
В исследованиях, однако, встречались некоторые модификации этого
определения, учитывающие дополнительные обстоятельства. Данное
определение требует малости возмущений Rs в каждый момент вре- /
мени t. Однако возможны случаи, когда возмущения Rs в отдельные
моменты достигают немалой величины, оставаясь значительную часть
времени достаточно мальши. В таких случаях может оказаться по-
полезным следующее определение.
(у) Невозмущенное движение ys = fs(t) устойчиво при по-
постоянно действующих возмущениях малых в среднем (на ин-
интервале Т), если для всякого положительного числа е, как бы
мало оно ни было, существуют два других положительных
числа щ(е) и r]2(e) таких, что всякое решение ys(t) уравнений
D.1), удовлетворяющее при t = t0 неравенствам
удовлетворяет при t>t0 неравенствам
каковы бы ни были функции Rs(t, yx уп), удовлетворяю-
удовлетворяющие при t > t0 для всех постоянных as = ys — fs(t), |сц|<е
неравенствам
t + T
ПРИМЕЧАНИЯ РЕДАКТОРА 517
Здесь Т — положительное число, выбранное в меру большим для
того, чтобы в изучаемой системе отдельные всплески возмущений
Rs(t, yi(t) Уя(^)) компенсировались в среднем малостью их
на большей части интервала (t, t-\-T). Задача об устойчивости при
возмущениях, малых в среднем, изучалась, например, И. Вркочем
(Интегральная устойчивость, Чехослов. матем. журнал, т. 9, № 1,
1959) и В. Е. Гермаидзе и Н. Н. Красовским (Об устойчивости
при постоянно действующих возмущениях, ПММ, т. 21, вып. 6, 1957).
Были исследованы также аналогичные задачи об устойчивости
при малых запаздываниях воздействий и сигналов в системах, опи-
описываемых уравнениями вида B.1) и уравнениями с запаздывающим
аргументом (см., например, работу. Репин Ю. М., Об устойчивости
решений уравнений с запаздывающим аргументом. ПММ, т. 21,
вып. 2, 1957).
Е. А. Барбашиным была поставлена и исследована задача об
осуществлении программного движения ys — fs(t) при импульсных
возмущениях (см. работы: О построении периодических движений.
ПММ, т. 25, вып. 2, 1961; Программное регулирование систем со
случайными параметрами. ПММ, т. 25, вып. 5, 1961).
Были изучены некоторые задачи об устойчивости при случайных
возмущениях Rs с известными вероятностными характеристиками
(см., например, работы: Кац И. Я., Красовский Н. Н., Об
устойчивости систем со случайными параметрами. ПММ, т. 24,
вып. 5, 1960; Хасьминский Р. 3., Об устойчивости траекторий
марковских процессов. ПММ, т. 26, вып. 6, 1962).
Это перечисление ни в коей мере не претендует на полноту. Из
весьма большого числа исследований, посвященных рассматриваемым
вопросам, мы ограничились лишь упоминанием отдельных работ.
Все упомянутые задачи обладают общим свойством, отмеченным
выше в монографии для основного определения устойчивости при
постоянно действующих возмущениях Rs, а именно справедливы
следующие утверждения:
1) В практически интересных случаях эти задачи приводятся
к проблеме устойчивости по Ляпунову.
2) Асимптотическая устойчивость движения xs = 0 является до-
достаточным условием его устойчивости при постоянно действующих
возмущениях описанных типов (по крайней мере для установившихся
и периодических невозмущенных движений).
3) Для исследования новых задач устойчивости при различных
возмущениях Rs пригодны классические методы теории Ляпунова,
модернизированные в соответствии с особенностями этих задач.
К стр. 26. Первый метод А. М. Ляпунова позволил ему полу-
получить ряд весьма глубоких и важных результатов. В качестве при-
примера отметим изящную теорию условной устойчивости, развитую
518 ПРИМЕЧАНИЯ РЕДАКТОРА
А. М. Ляпуновым в работе «Общая задача об устойчивости движения»
(Гостехиздат, 1950) на основе первого метода. Эти результаты послу-
послужили источником глубоких исследований более поздних авторов по
теории дифференциальных уравнений и, в частности, по устойчивости
движения и по проблемам теории нелинейных колебаний. Одно из
достоинств данного метода состоит в том, что он работает в наибо-
наиболее тонких случаях и позволяет не только указать качественную
картину изучаемого явления, но и построить явный вид исследуемых
решений xs{f).
В настоящей монографии основной упор делается на второй метод
Ляпунова. Поэтому результаты теории устойчивости, связанные
с первым методом, затрагиваются лишь частично.
К стр. 26. В связи с новыми задачами об устойчивости нелиней-
нелинейных систем и в связи с проблемами стабилизации управляемых дви-
движений в последние годы (начиная приблизительно с 1950 года) ин-
интерес ко второму методу Ляпунова весьма возрос. Исследование
принципиальных математических проблем, относящихся к этому методу,
а также исследование вопросов эффективного построения функций
Ляпунова для прикладных задач, начатые впервые в нашей стране,
были развиты в эти годы в большом числе серьезных работ совет-
советских и иностранных специалистов. При этом всестороннем исследо-
исследовании были установлены универсальность и эффективность второго
метода Ляпунова для широкого круга проблем, включая, например,
задачи об устойчивости в целом нелинейных систем автоматического
регулирования, задачи об устойчивости систем с запаздываниями
воздействий во времени, задачи об устойчивости стохастических си-
систем и т. д. Выяснилось также, что метод функций Ляпунова может
быть использован для решения проблем синтеза оптимальных упра-
управляемых систем с обратной связью, так как он тесно переплетается
с методами динамического программирования в теории оптимальных
процессов (см. приложение IV).
К стр. 28. Данные определения свойств знакоопределенности и
знакопостоянства функций V описывают поведение этих функций
лишь в малой окрестности F.3) невозмущенного движения х^ = 0.
Этого достаточно для исследования вопросов об устойчивости, не-
неустойчивости или об асимптотической устойчивости при достаточно
малых начальных возмущениях xs(t0). При исследовании вторым ме-
методом Ляпунова задачи об асимптотической устойчивости в большом
(см. выше примечание к стр. 18) приходится рассматривать поведе-
поведение функций V в достаточно большой области О изменения перемен-
переменных xs, а в случае задачи об устойчивости в целом следует рассма-
рассматривать V при всех значениях xs. Поэтому в таких случаях опреде-
определение свойства знакопостоянства или знакоопределенности должно
ПРИМЕЧАНИЯ РЕДАКТОРА 619
сопровождаться указанием или оценкой той. области изменения xs,
в которой выполняется соответствующее свойство.
К стр. 38. Теорема Б может быть обобщена на случаи асимпто-
асимптотической устойчивости в большом и в целом (см. примечание
к стр. 18). Это обобщение достигается за счет введения в форму-
формулировку теоремы оценок, характеризующих область асимптотической
устойчивости. Таким путем получаются следующие критерии асим-
асимптотической устойчивости.
Теорема Bt. Если для дифференциальных уравнений воз-
возмущенного движения возможно найти функцию V (х^ хп),
знакоопределенную в области
\xs\KQ, A0.5)
полная производная которой по времени, составленная в силу
этих уравнений, есть функция, также знакоопределенная
в этой области, знака, противоположного с V, причем вы-
выполняется неравенство MN < mQ, то невозмущенное движение
асимптотически устойчиво в большом относительно началь-
начальных возмущений xs(t0) из области
Здесь символ mQ означает точный нижний предел функции
|V(Xi, ..., хп)\ при условии л; —Q (х — тах(|х1 \ |*л|))»
символ MN означает точный верхний предел функции | V (хг хп) \
при x = N. Предполагается, естественно, что /V < Q.
Читателю, внимательно разобравшему доказательство теоремы Б,
смысл неравенства MN < mQ в формулировке теоремы Б± должен
быть ясен, и он сможет сам провести доказательство теоремы Bj
по тому же плану, по которому проведено выше доказательство
теоремы Б. Достаточный критерий устойчивости в целом формули-
формулируется следующим образом.
Теорема Б2. Если для дифференциальных уравнений воз-
возмущенного движения возможно найти определенно-положи-
определенно-положительную функцию V(x1 xn), полная производная по вре-
времени которой, составленная в силу этих уравнений, есть
при всех xs функция определенно-отрицательная, и если при
этом
то невозмущенное движение асимптотически устойчиво в целом.
Смысл последнего условия Нт\/ = оо состоит в следующем: при
этом условии для любого числа N можно подобрать число Q > N,
удовлетворяющее неравенству MN < /Kq. Но тогда справедливость
520 ПРИМЕЧАНИЯ РЕДАКТОРА
теоремы Б2 выводится из теоремы Bj. Важность этого условия для
задач устойчивости в целом была отмечена Н. П. Еругиным (см.
работу: Об одной задаче теории устойчивости систем автоматиче-
автоматического регулирования. ПММ, т. XVI, вып. 5, 1952) и Е. А. Бар-
башиным (см. работу: Барбашин Е. А., Красовский Н. Н.,
Об устойчивости движения в целом. ДАН СССР, т. 86, вып. 3,
1952).
К стр. 47. Дополнительное условие A2.9) не является стесни-
стеснительным, так как всегда можно предполагать, что характеристики / (а)
реальных систем этому условию удовлетворяют. Кроме того, следует
иметь в виду, что теорема Б2 является достаточным критерием
устойчивости. Поэтому дополнительное условие A2.9) является в по-
подобных случаях достаточным, но отнюдь не необходимым условием
устойчивости в целом. Детальный анализ рассмотренной в этом па-
параграфе задачи А. И. Лурье, учитывающий многие исследования
этой проблемы, выполненные в последнее время, содержится в книге
М. А. Айзермана и Ф. Р. Гантмахера, упомянутой выше в приме-
примечании к стр. 18. Отметим еще, что исследование данной задачи
А. И. Лурье занимает большое место в монографии А. М. Летова,
посвященной нелинейным регулируемым системам (см. также приме-
примечание к стр. 18).
К стр. 68. Функция V удовлетворяет, естественно, и дополни-
дополнительному условию
фигурирующему в теореме Б2 (см. примечание к стр. 38), указы-
указывающей достаточные условия устойчивости в целом. Отметим,
кстати, что для линейных систем асимптотическая устойчивость в
целом является очевидным следствием асимптотической устойчивости
относительно начальных возмущений xs(t) из малой окрестности
невозмущенного движения xs = 0.
К стр. 70. Необходимые и достаточные! условия существования
функции V(xv .... хп), удовлетворяющей условиям теоремы В в
предположении неустойчивости установившегося движения xs = 0,
заключаются в следующем: достаточно малая окрестность |х^|<т]
точки xs = 0 не должна содержать целиком движений xs(t)(—оо <
< t < оо), отличных от невозмущенного движения xs = 0. Доказа-
Доказательство этого утверждения можно найти в книге: Красов-
Красовский Н. Н., Некоторые задачи теории устойчивости движения,
Физматгиз, 1959, стр. 43. В рассмотренном в данном параграфе
примере указанное условие не выполняется, так как в любой ок-
ПРИМЕЧАНИЯ РЕДАКТОРА 521
рестности точки xs — 0 содержатся положения равновесия xs = cs,
отличные от этой точки.
К стр. 89. При применении более гибкого способа построения
функции Ляпунова V(x, у), включающей, помимо квадратичных
членов, слагаемые вида
для задач, подобных рассматриваемой здесь, получаются более общие
достаточные условия устойчивости в целом, весьма близкие к необ-
необходимым условиям (см. дополнение I). Однако такой метод пост-
построения функций Ляпунова V, естественно, выходит за рамки класси-
классической теории устойчивости движения по первому приближению, рас-
рассматриваемой в этой главе.
К стр. 109. В этом случае система B8.6) допускает голоморф-
голоморфный интеграл — семейство инвариантных поверхностей
x = f{xv х2 хп, с), /@, 0 0) = 0,
на каждой из которых имеется особая точка х = с, xs = us(c),
s=l, 2, ..., га (см. Ляпунов А. М.., Общая задача об устой-
устойчивости движения, Гостехиздат, 1950). Расположение траекторий си-
системы B8.6) при га = 2 на произвольной поверхности х = f {xv x2, с)
для достаточно малого с в окрестности точки х = с, xs=us(c),
s=l, 2 выяснено в работе Б. Н. Скачкова (Вестник ЛГУ, № 8,
1954).
К стр. 126. Проблема центра и фокуса до последнего времени
продолжает оставаться одной из основных задач качественной и
аналитической теорий обыкновенных дифференциальных уравнений.
Например, отметим следующий результат. Если в системе C6.1)
X и Y—многочлены от х и у фиксированной степени, то для нее
число условий центра конечно (Альмухамедов М. И. Изв. физ.-
матем. общества, C), 8, Казань, 1936—1937; 9, 1937). Эти усло-
условия найдены в явном виде для случаев: a) ,Y = 0, Y—многочлен от
х и у третьей или пятой степени (Кук лес И. С. ДАН СССР, т. 42,
№ 4 и 5, 1944); б) X и Y — однородные многочлены от х и у
второй степени (Сибирский К. С. Изв. АН СССР, сер. матем.,
№ 11, 1963); в) А' и Y — однородные многочлены от х и у третьей
степени (Сахарников Н. А. ПММ, т. 14, вып. 6, 1950; Мал-
Малки н К. Е. Волжский матем. сб., вып. 2, 1964).
Для системы C6.1) в общем случае разработаны новые варианты
записи условий центра и новые способы составления таких условий
522 ПРИМЕЧАНИЯ РЕДАКТОРА
(Кук л ее И. С, Ну ров Т. Н. Изв. высш. учебн. заведений, Ма-
Математика, № 6, 1963; Альмухамедов М. И. Уч. зан. Казанск.
пед. ин-та, вып. 10, 1955; Малкин К. Е. Уч. зап. Рязанск. пед.
ин-та, т. 24, 1960). Полностью решен вопрос о существовании про-
проходящей через начало координат оси симметрии поля направлений
(Сибирский К. С. ДАН СССР, т. 151, № 3, 1963).
К стр. 196. Теорема II, так же как и аналогичная теорема Б
в стационарном случае, может быть обобщена на случаи асимпто-
асимптотической устойчивости в большом и в целом. Таким путем полу-
получается, например, следующий критерий устойчивости в целом. Будем
говорить, что функция V(t, jtj, . . ., хп) является определенно-поло-
определенно-положительной и допускает высший предел в целом, если можно ука-
указать две непрерывные функции w(xv .... хп), W(хг хп) та-
таw(xv xn)^CV(t. xv .... xn)^CW(xl xn),
причем функция w(xv ..., xn) определенно-положительна, кроме
того,
Hmw(x1 х„) = оо (х = тах(\х1\ \хп\))
JOoo
W@, .... 0) = 0.
Справедливо утверждение.
Теорема II1. Если можно указать функцию V {t, хх хп),
которая била бы определенно положительной и допускала бы
dV
высший предел в целом, причем ее производная —гг в силу
уравнений возмущенного движения была бы функцией опреде-
определенно-отрицательной, при всех значениях xs, то невозмущен-
невозмущенное движение xs — 0 асимптотически устойчиво в целом.
На доказательстве этой теоремы останавливаться не будем, так
как оно проводится по тому же плану, что и доказательство тео-
теоремы II с небольшими дополнениями, связанными с особенностями
постановки задачи об устойчивости в целом. Эти особенности под-
подчеркнуты выше в примечаниях к стр. 18 и 38.
К стр. 235. В последнее время уравнение E9.2), так же как и
более общие случаи линейных канонических систем с периодическими
коэффициентами, было подвергнуто дальнейшему подробному изуче-
изучению. При этом были получены новые интересные результаты.
Теории периодических систем посвящен обзорный доклад
В. М. Старжинского и В. А. Якубовича на II Всесоюзном съезде
по теоретической и прикладной механике в Москве 27. I — 3. II
ПРИМЕЧАНИЯ РЕДАКТОРА 623
1964 г. (Сборник трудов II Всесоюзного съезда по теоретической
и прикладной механике, Изд. АН СССР, 1965).
К стр. 306. За время, прошедшее после выхода в свет первого
издания настоящей монографии, проблема существования функций
Ляпунова V(t, хх хп), удовлетворяющих условиям теорем I, II
и III, послужила предметом весьма большого числа исследований.
Основной вывод, который следует из результатов этих работ, таков:
Характер поведения возмущенных движений, определенный
той или иной функцией V из классических теорем второго
метода Ляпунова, является не только необходимым, но и
достаточным условием существования такой функции.
При этом выяснилось, что свойства гладкости функций V могут
быть намного выше, чем гладкость правых частей соответствующих
уравнений возмущенного движения.
В частности, вопрос об обратимости теоремы II с достаточной
полнотой был решен в работе И. Г. Малкина «К вопросу об обра-
обратимости теоремы Ляпунова об асимптотической устойчивости», кото-
которая составляет содержание дополнения II, приведенного в настоящем
издании этой монографии. Более подробно с проблемами существо-
существования функций Ляпунова и методами исследования этих проблем чи-
читатель может ознакомиться также по работам: Барбашин Е. А.,
Метод сечений в теории динамических систем, Матем. сб., т. 29,
вып. 2, 1951; Барбашин Е. А., Красовский Н. Н., Об устой-
устойчивости движения в целом. ДАН СССР, т. 86, вып. 3, 1952; О су-
существовании функции Ляпунова в случае асимптотической устойчи-
устойчивости в целом. ПММ, т. 18, вып. 3, 1954; Massera J. L., On
Liapounolfs condition of stability. Annals of Mathematics, т. 50, № 3,
1949. Contributiono to stability theory. Annalo of Math., v. 64,
№ 1, 1956; Курцвейль Я., К обращению первой теоремы
Ляпунова об устойчивости движения. Чехосл. матем. журнал,
т. 5 (80), 1955; Об обращении второй теоремы Ляпунова об
устойчивости движения. Чехосл. матем. журнал, т. 6 (81), № 2,
1956; Курцвейль Я., Вркоч И., Об обращении теоремы Ля-
Ляпунова об устойчивости и теоремы Персидского о равномерной
устойчивости. Чехосл. матем. журнал, т. 7 (82), № 2, 1957;
Зубов В. И., К теории второго метода А. М. Ляпунова. ДАН
СССР, т. 99, вып. 3, 1954; Вопросы теории второго метода
Ляпунова, построение общего решения в области асимптотической
устойчивости. ПММ, т. 19, вып. 6, 1955; К теории второго метода
А. М. Ляпунова. ДАН СССР, т. 100, вып. 5, 1955; Методы А. М. Ля-
Ляпунова и их применение, Изд-во ЛГУ, 1957; Вркоч И., Обраще-
Обращение теоремы Четаева. Чехосл. матем. журнал, т. 5 (80), 1955;
Joshizawa Т., On the stability of solutions of a system of diffe-
differential equations. Memoirs of the Colledge of science. Univ. of Kyoto,
524 ПРИМЕЧАНИЯ РЕДАКТОРА
XXIX, № 1, ser. A, math, 1955; Красовский Н. Н., Некоторые
задачи теории устойчивости движения, Физматгиз, 1959.
Подчеркнем, что здесь упомянута лишь небольшая часть работ из
обширной библиографии вопроса.
Отметим еще два обстоятельства, связанные с задачами о сущест-
существовании функций Ляпунова.
1. Решение этих проблем в положительном смысле позволило
продвинуть теорию устойчивости движений при постоянно действую-
действующих возмущениях. Это объясняется тем, что наличие функции Ляпу-
Ляпунова позволяет обычно доказать сохранение соответствующих свойств
при малых добавках к уравнениям возмущенного движения (см., на-
например, материал на стр. 461—462 настоящей монографии). Таким
образом, параллельно с теорией существования функций Ляпунова в
последние годы существенно развилась теория устойчивости при посто-
постоянно действующих возмущениях (см. также примечание к стр. 21).
2. Методы, использованные в большинстве работ о существова-
существовании функций Ляпунова, позволяют решить вопрос лишь в принципе.
Однако эти методы, как правило, мало полезны для эффективного
построения функций Ляпунова в конкретных прикладных задачах.
К стр. 307. Вопрос об обратимости теорем А. М. Ляпунова и
Н. Г. Четаева о неустойчивости решается следующим образом.
Функция V(t, xv ..., хп), удовлетворяющая условиям теоремы
Н. Г. Четаева, существует во всех случаях неустойчивости (см. упо-
упомянутую работу И. Вркоча и монографию Н. Н. Красовского).
Теорема Ляпунова о неустойчивости (теорема В) обратима не
всегда, как это уже отмечалось выше на стр. 70 (см. также примеча-
примечание к этой странице). Необходимые и достаточные условия сущест-
существования функции V({, хх, ..., х„), которая удовлетворяет условиям
теоремы III, таковы:
Функция V из теоремы III существует тогда и только тогда,
когда выполнены условия: 1) невозмущенное движение л^ = 0 не-
неустойчиво; 2) существует число е > 0 такое, что каково бы ни было
число т] < е, можно указать число T(ti) > 0 так, что x(f) > e в не-
некоторый момент времени \t* — ?0|<7\ если только е> x(to)^r\.
Здесь х = тах(|х1|, ..., \хп\).
В частности, в случае установившегося движения xs = 0, когда
правые части уравнений возмущенного движения не зависят явно
от t, условие 2) означает, что е—окрестность точки х^ = 0 не
содержит целиком движений xs (t) (— оо < t < оо), кроме самой
точки Л"^ = 0. Доказательство приведенных утверждений можно найти
в цитированной монографии Н. Н. Красовского.
К стр. 350. После 1952 года были построены весьма интерес-
интересные примеры, показывающие, что характеристичные числа правиль-
ПРИМЕЧАНИЯ РЕДАКТОРА 525
ных систем могут оказаться неустойчивыми (см. работы: Виног-
Виноград Р. Э. ПММ, т. 17, вып. 6, 1953; ДАН СССР, т. 103, № 4,
1955). Были найдены условия устойчивости характеристичных чисел
(см. работы: Виноград Р. Э. ДАН СССР, т. 119, № 4, 1958;
Бы лов Б. Ф. Мат. сборник, т. 48, № 1, 1959). Отметим, в част-
частности, один тонкий результат (Богданов Ю. С, О существовании
аппроксимирующей последовательности для правильной линейной диф-
дифференциальной системы. Успехи матем. наук, т. XV, вып. 1, 1960),
относящийся к вопросу об устойчивости характеристичных чисел
правильных систем.
Пусть р — вещественная (п X ге)-матрица, заданная, кусочно-
непрерывная и ограниченная для вещественного аргумента t ^ 0,
k— 1, 2, 3, . . .; т означает k или отсутствие индекса; Т — без-
безгранично возрастающая последовательность положительных чисел /4;
pk — матрица-функция, совпадающая с р на интервале [0, tk) и пе-
периодически продолженная вне его; Sm — система линейных диффе-
дифференциальных уравнений —тт- = ртх; Хт — совокупность расположен-
расположенных в порядке возрастания характеристичных чисел нормальной системы
решений Sm, рассматриваемая как вектор. Последовательность Т назо-
назовем аппроксимирующей, если Xk—>K при &-*-оо.
К. П. Персидский (см. работу, цитированную в сноске на
стр. 341) высказал следующее утверждение: если S—правильная
система, то любая последовательность Т является аппроксимирую-
аппроксимирующей. Впоследствии Р. Э. Виноград (Успехи матем. наук, т. IX,
вып. 2, 1954) на примере ряда систем двух уравнений показал не-
несостоятельность этого утверждения. Оказалось, что для правильных
(более того, периодических) систем, рассмотренных Р. Э. Виногра-
Виноградом, существуют Т, которые не являются аппроксимирующими.
Н. П. Еругин поставил вопрос: можно ли для любой правильной
системы 5 указать по крайней мере одну аппроксимирующую по-
последовательность Т. Оказалось, что: 1) существуют правильные
системы, для которых ни одна последовательность Т не
является аппроксимирующей; 2) любая правильная двумерная
система S ортогональной подстановкой переменных, коэф-
коэффициенты которой зависят только от аргумента системы
и верхней грани модулей элементов р, может быть преоб-
преобразована к виду, при котором аппроксимирующая последо-
последовательность Т заведомо существует.
К стр. 351. Доказанная теорема допускает уточнение, которое
проведено в работе: Богданов Ю. С, Замечание к § 81 моно-
графиии И. Г. Малкина «Теория устойчивости движения», Гостех-
теориздат, 1952. ПММ, т. 20, вып. 3, 1956.
Ниже эта работа приводится целиком.
526 ПРИМЕЧАНИЯ РЕДАКТОРА
Рассмотрим систему однородных линейных дифференциальных
уравнений
Xi = Pux\+ ••• -\-Pnixn ('=1 ") A)
с коэффициентами Pij = Pij{t), заданными, непрерывными и огра-
ограниченными для t^-О. Если хп, ..., xin, i=\, ..., п — фунда-
фундаментальная система решений A) с характеристичными числами реше-
решений (J,j, . . ., (i/,, то всегда
M-i —I— ¦•• -hJ*;+llm/(^n + /»22+ ••• ~+-Pnn)di<0. B)
Система A) правильна тогда и только тогда, если можно указать
такую фундаментальную систему решений ее, для которой в B) имеет
место знак равенства. Если такая фундаментальная система решений
существует, то она необходимо нормальная согласно Ляпунову.
Пусть X (t, x)^(xij(t, х))— матрица, которая при фиксирован-
фиксированном т представляет собой фундаментальную систему решений A),
нормированную для t = x{X{x, x) = I), a \it означает характеристич-
характеристичное число решения A) xn(t, 0) xin (t, 0).
Определение. Назовем A) системой А, если по любому
положительному у можно указать постоянное CY, не зависящее ни
от t, ни от х, такое, что
C?exp[(Y —|i,)(f—т)] @<т</), C)
(t, т) |< j ^ ехр [(y + ^ (t f)] @<t< т). C/)
Именно такие системы рассматриваются в одном из раз-
разделов (§ 81) книги И. Г. Малкина. В указанном разделе доказы-
доказывается, что если система A) удовлетворяет условию C) и правильна,
то ее характеристичные числа устойчивы. Нетрудно убедиться, что
верно следующее предложение. Системы А всегда правильны (след-
(следствие: характеристичные числа любой, системы А устойчивы).
Доказательство. Из известных свойств фундаментальных
систем решений следует, что X (t, т) — Х~х (т, Q)X(t, 0). Поэтому
X~\t, x) = X(x, t), X'l(t, 0) = *(<). t). Далее,
п
| \\.pttdt — —hm ilnldet*-1^, 0)| =
= — Hm iln |det^(O, t)\.
lim |
ПРИМЕЧАНИЯ РЕДАКТОРА 527
но |detA"(O. 0|<С"л!ехр(лу + ц1+ •" +^ (cMl C') при t==0'
х = t). Поэтому
— Hm (^"Mnl det АГ(О, /)|)> — ny — цг— ... — (х„ при *->oo
Число у — произвольное, значит,
lim 4" I У, Piidt = — lTm 1 In | det A" @. *)|> — ft— . . .. — Ц„.
Таким образом, для фундаментальной системы решений системы A)
t
щ + ... 4-Aя+11п|7 f (A1 + P22+ ••• +/»„„) Л >0. D)
f-»oo J
Сопоставляя D) с соотношением B), верным для любой фунда-
фундаментальной системы решений A), приходим к заключению, что D)
должно быть равенством, а это и доказывает правильность системы
A) — произвольной системы А (фундаментальная система решений A),
нормированная в точке ? = 0, попутно оказалась нормальной).
Замечание 1. Условия C) можно сформулировать, не предпо-
предполагая (X; характеристичными числами системы A), но лишь некото-
некоторыми постоянными, не зависящими ни от у, ни от т. Однако из
проведенных рассуждений ясно, что ничем другим как характери-
характеристичными числами системы A) \it быть не могут.
Замечание 2. Если A) — система А, то нормальной будет
любая фундаментальная система решений A), нормированная в какой-
нибудь точке t — x, поэтому, например, из цх > ц2 > .. . . > \in сле-
следует, что /?/у==0 для / < J (t, J — 1, .... «).
К стр. 362. После 1952 года в теории характеристичных чисел
Ляпунова получен ряд новых результатов.
Проведены глубокие исследования зависимости характеристичных
чисел системы линейных дифференциальных уравнений с периодиче-
периодическими и почти периодическими коэффициентами от параметров, вхо-
входящих в коэффициенты. Получены разложения характеристичных
чисел в ряды по степеням параметра, найдены оценки снизу радиуса
сходимости таких рядов, позволяющие эффективно оценивать погреш-
.ность, возникающую при замене указанных рядов частными суммами.
Все эти вопросы подробно освещены в монографии: Еругин Н. П.,
Линейные системы обыкновенных дифференциальных уравнений
с периодическими и квазипериодическими коэффициентами, Изд.
АН БССР, Минск, 1963.
Опубликованы оценки характеристичных чисел, найденные в свое
время Н. Г- Четаевым (ПММ, т. 24. вып. 1, I960") как для систем
528 ПРИМЕЧАНИЯ РЕДАКТОРА
общего вида, так и для систем, коэффициенты которых имеют огра-
ограниченное колебание. Указаны и другие эффективные оценки характе-
характеристичных чисел (Горбунов А. Д. Вестник МГУ, № 2, 1956).
Открыта новая характеристика системы — центральный показатель,
управляющий скачками характеристичных чисел, и указаны способы
вычисления этой характеристики для ряда систем (Виноград Р. Э.
Матем. сб., т. 42, № 2, 1957).
Доказано, что данную систему уравнений всегда можно заменить
системой с кусочно постоянными коэффициентами, причем характе-
характеристичные числа обеих систем будут совпадать (Богданов Ю. С.
Матем. сб., т. 41, № 1, 1957). Предпринята попытка распространить
теорию характеристичных чисел на нелинейные системы (Богда-
(Богданов Ю. С. ДАН СССР, т. 158, № 1, 1964).
К стр. 366. Приведенные геометрические соображения указывают
путь для обоснованного аналитического доказательства теоремы,
которое, строго говоря, должно дополнить эти соображения. Это
подробное доказательство, однако, помимо технических деталей не
содержит интересных новых моментов и здесь не приводится. Кроме
того, следует иметь в виду, что возможно и другое доказательство
теоремы, исходя непосредственно из существования в рассматриваемом
случае функции Ляпунова V, удовлетворяющей оценке (см. моно-
монографию: Красовский Н. Н., Некоторые задачи теории устойчи-
устойчивости движения, Физматгиз, 1959)
/ л \ v+m-1
dV
v-1
dV
(c3 > 0, c4 > 0 — постоянные).
Доказательство теоремы с помощью такой функции V проводится
стандартным путем.
К стр. 377. Как отмечено выше, критерии устойчивости по
линейному приближению, даваемые теоремами 1—3, означают сле-
следующее. Если в случае неустановившегося движения xs = 0 в линей-
линейном приближении движение х^ = 0 асимптотически устойчиво и если
при этом возмущенные движения xs(t, t0) линейного приближения (88.4)
удовлетворяют оценке (88.5), характерной для асимптотической устой-
устойчивости линейных систем с постоянными параметрами, то имеет место
асимптотическая устойчивость и полной нелинейной системы (88.1)
при условиях (88.3). В такой форме этот критерий обобщается на
ПРИМЕЧАНИЯ РЕДАКТОРА 629
задачи устойчивости по первому приближению и в тех случаях, когда
первое приближение не является линейным, но когда в правых частях
уравнений первого приближения стоят однородные формы от xs
произвольного порядка т>1 с переменными по времени t, непре-
непрерывными и ограниченными коэффициентами (см. монографию Н. Н. Кра-
совского в примечании к стр. 306).
Отметим еще, что выяснился следующий любопытный факт: линей-
линейность системы (88.4) не является существенной для справедливости
утверждения, подобного теореме 2. Именно, если для некоторых
уравнений
d
dt
где Xs— произвольные нелинейные функции, удовлетворяющие усло-
условиям Липшица, выполняется оценка (88.5), то невозмущенное движе-
движение х^ = 0 асимптотически устойчиво в силу уравнений
^ t, xv ..., хп)
при любом выборе функций ф^, удовлетворяющих неравенству (88.3),
если только постоянная А достаточно мала.
Это утверждение доказано в работе: Барбашин Е. А., Скал-
Скалки на М. А., К вопросу об устойчивости по первому приближению.
ПММ, т. 19, вып. 5, 1955.
К стр. 383. Сформулированная теорема известна под названием
«принципа сведения». Этот принцип, введенный фактически А. М. Ля-
Ляпуновым и лежащий в основе его метода исследования критических
случаев, играет постоянно центральную роль при изучении этих слу-
случаев, фигурируя в той или иной форме почти во всех работах,
посвященных им. В процессе использования принцип сведения под-
подвергся усовершенствованию в соответствии с рассматриваемыми кон-
конкретными задачами. Заметим, в частности, что в последнее время
этот принцип получил весьма существенное развитие в работах
В. А. Плисса (см., например, работы: Плисе В. А., О принципе
сведения в теории устойчивости движения. ДАН СССР, т. 164, № 5,
1964; О принципе сведения в теории устойчивости движения. Изв.
АН СССР, Математика, т. XXVIII, № 6, 1964).
К стр. 384. Это преобразование можно использовать лишь при
условии, что г Ф 0. В самом деле, при г —0, но xs Ф 0 величины ^
становились бы бесконечно большими. В соответствии с этим ниже,
если не сделано дополнительных оговорок, следует иметь в виду,
что новые переменные ls используются при рассмотрении траекто-
траектории xs(t), yt(t) системы (91.1) лишь в такой области изменения xs, yt,
гДе 1Ы *^Н- Здесь Н— некоторая положительная постоянная. Область
530 ПРИМЕЧАНИЯ РЕДАКТОРА
в пространстве {xs, yt), где \\s\ < Н, будем обозначать символом О.
Область G охватывает многообразие х1 = ... =хл = 0, у\-\- ...
... -)- у\ ф 0, сжимаясь в точку при приближении к началу координат.
К стр. 422. Задача, рассмотренная в этом параграфе, для системы
второго порядка решалась также методами качественной теории диф-
дифференциальных уравнений на плоскости.
Для системы
L
у), ^-=
выяснены возможные топологические типы расположения траекторий
[в окрестности точки @, 0) встречается 10 различных типов] и пол-
полностью решена задача их различения с точностью до проблемы раз-
различения центра и фокуса (Хаимов Н. Б., Уч. зап. Сталинабад.
пед. ин-та, т. II, 1952; Андреев А. Ф. Вестник ЛГУ, № 8, 1955).
Последняя проблема решена для случая, когда X и Y являются од-
однородными многочленами от х и у третьей степени (Андреев А. Ф.
ПММ, т. 17, вып. 3, 1953).
Для произвольной системы второго порядка с аналитическими
в точке @, 0) правыми частями
?L = X(x.y
^r = Y(х, у) (X@, 0)= К@, 0) = 0)
разработан алгоритм, позволяющий конечным числом операций,
во-первых, выяснить, является ли точка @, 0) особой точкой 1-й
группы (имеются ли траектории, примыкающие к этой точке с опре-
определенными касательными) или 2-й группы (центр или фокус); во-вто-
во-вторых, в случае, когда точка @, 0) принадлежит к 1-й группе, выяснить
расположение траекторий в ее окрестности (исключая некоторые
особые подслучаи) (К у к л е с И. С. Труды 3-го Всесоюзн. матем.
съезда, М., АН СССР, т. III, 1958; Андреев А. Ф. Вестник ЛГУ,
№ 1, 1962), причем найдены оценки для упомянутого выше числа
операций (Кук л ее И. С, Груз Д. М. Изв. АН Уз.ССР, № 1,
1958; Андреев А. Ф., Дифференциальные уравнения, т. 1, № 9,
1965).
ОГЛАВЛЕНИЕ.
Предисловие автора 8
Предисловие редактора второго издания 11
Глава I. Основные понятия и определения 13
§ 1. Постановка задачи 13
§ 2. Определение устойчивости 14
§ 3. Дифференциальные уравнения возмущенного движения .... 17
§ 4. Устойчивость по Ляпунову и некоторые другие определения
устойчивости 20
§ 5. О методах решения задачи устойчивости 23
Глава П. Второй метод Ляпунова для установившихся движе-
движений 27
§ 6. Основные определения 27
§ 7. Признаки знакоопределенности и знакопеременности функций 28
§ 8. Геометрическая интерпретация знакоопределенных функций . 33
§ 9. Первая теорема Ляпунова об устойчивости движения .... 34
§ 10. Вторая теорема Ляпунова об устойчивости движения .... 36
§ 11. Геометрическая интерпретация предыдущих теорем 38
§ 12. Примеры приложения предыдущих теорем 40
§ 13. Первая теорема Ляпунова о неустойчивости 47
§ 14. Теорема Ляпунова о неустойчивости равновесия, когда сило-
силовая функция обращается в минимум 49
§ 15. Вторая теорема Ляпунова о неустойчивости 51
§ 16. Геометрическая интерпретация теоремы В. Теорема Н. Г. Че-
таева 52
§ 17. Пример приложения теоремы Н. Г. Четаева. Теорема Н. Г. Че-
таева о неустойчивости равновесия 54
§ 18. Заключительные замечания 55
Глава 111. Критерии устойчивости по первому приближению для
установившихся движений 57
§ 19. Уравнения первого приближения 57
§ 20. Некоторые вспомогательные предложения 62
§ 21. Построение функций Ляпунова для систем линейных уравне-
уравнений с постоянными коэффициентами 67
§ 22. Теоремы Ляпунова об устойчивости по первому приближению 71
§ 23. Примеры приложения предыдущих теорем 74
§ 24. Неустойчивость равновесия. Случай канонических систем . . 76
4 ОГЛАВЛЕНИЕ
§ 25. Теорема Гурвица 80
§ 26. Обобщение теорем Ляпунова об устойчивости по первому
приближению. Приложение к регулируемым системам .... 81
§ 27. Заключительные замечания 89
Глава IV. Исследование критических случаев для установившихся
движений 90
§ 28. Случай одного нулевого корня. Приведение уравнений к спе-
специальному виду 90
§ 29. Исследование задачи для случая системы первого порядка . . 92
§ 30. Исследование задачи для системы (п-{-1)-го порядка в част-
частном случае 93
§ 31. Исследование задачи для системы (п-\-1)-го порядка в общем
случае 101
§ 32. Примеры 104
§ 33. Особенный случай 108
§ 34. Решение задачи устойчивости в особенном случае 112
§ 35. Случай пары чисто мнимых корней. Приведение уравнений
возмущенного движения к специальному виду 118
§ 36. Системы второго порядка. Первый способ решения задачи . . 120
§ 37. Системы второго порядка. Второй способ решения задачи . . 132
§ 38. Системы второго порядка. Третий способ решения задачи . . 139
§ 39. Вспомогательное предложение 149
§ 40. Исследование системы (я-|-2)-го порядка в частном случае 153
§ 41. Исследование системы (я-|-2)-го порядка в общем случае . . 159
§ 42. Другой способ решения задачи 169
§ 43. Особенный случай 176
§ 44. «Опасные» и «безопасные» границы области устойчивости . . 181
Глава V. Устойчивость периодических движений 190
А. Теоремы второго метода для неустановившихся
движений.
§ 45. Некоторые определения 190
§ 46. Теоремы Ляпунова об устойчивости для неустановившихся
движений 192
§ 47. Теорема Ляпунова о неустойчивости для неустановившихся
движений 196
§ 48. Теорема Н. Г. Четаева 198
Б. Линейные уравнения с периодическими
коэффициентами.
§ 49. Постановка задачи 199
§ 50. Характеристическое уравнение системы линейных уравнений
с периодическими коэффициентами 200
§ 51. Аналитический вид решений в случае простых корней харак-
характеристического уравнения 203
§ 52. Аналитический вид решений в случае кратных корней харак-
характеристического уравнения 205
§ 53. Обратное предложение 213
§ 54. Теорема Ляпунова о приводимости линейных уравнений с пе-
периодическими коэффициентами 215
ОГЛАВЛЕНИЕ 5
§ 55. Определяющее уравнение приведенной системы. Теорема Ля-
Ляпунова о корнях характеристических уравнений сопряженных
систем 220
§ 56. Критерии устойчивости 222
§ 57. Характеристическое уравнение канонических систем 224
§ 58. Вычисление корней характеристического уравнения методом
разложения по степеням параметра 227
§ 59. Приложение к системе второго порядка 229
§ 60. Некоторые технические задачи, приводящиеся к уравнению
второго порядка с периодическими коэффициентами, и связан-
связанные с этим вопросы теории 236
§ 61. Области устойчивости и неустойчивости для уравнений второ-
второго порядка 245
§ 62. Практический способ определения областей устойчивости и
неустойчивости для уравнений второго порядка 253
§ 63. Примеры приложения метода предыдущего параграфа .... 262
В. Нелинейные уравнения с периодическими
коэффициентами.
§ 64. Критерии устойчивости по первому приближению 270
§ 65. Критические случаи 273
§ 66. Критический случай, когда характеристическое уравнение
имеет один, равный единице корень 275
§ 67. Критический случай, когда характеристическое уравнение
имеет два комплексных корня с модулями, равными единице 285
§ 68. Устойчивость периодических движений автономных систем 295
Глава VI. Неустановившиеся движения 300
А. Некоторые общие предложения.
§ 69. Постановка задачи 300
§ 70. Теорема об устойчивости при постоянно действующих возму-
возмущениях 301
§ 71. Проблема существования функций Ляпунова 305
§ 72- Некоторые свойства установившихся и периодических движе-
движений 307
§ 73. Теорема о существовании функций Ляпунова для периодиче-
периодических и установившихся движений в случае асимптотической
устойчивости 310
§ 74. Основная теорема об устойчивости при постоянно действую-
действующих возмущениях для периодических и установившихся дви-
движений. Приложение к вопросу об «опасных» и «безопасных»
границах области устойчивости 315
§ 75. Условия существования функций Ляпунова для линейных
уравнений в случае асимптотической устойчивости 317
Б. Теория первого приближения.
§ 76. Характеристичные числа Ляпунова 325
§ 77. Основные свойства характеристичных чисел 328
§ 78. Характеристичные числа решений линейных дифференциаль-
дифференциальных уравнений 331
§ 79. Правильные и неправильные системы . 335
6 ОГЛАВЛЕНИЕ
§ 80. Устойчивость характеристичных чисел систем линейных диф-
дифференциальных уравнений 342
§ 81. Некоторые признаки устойчивости характеристичных чисел
систем линейных дифференциальных уравнений 344
§ 82. Критерий положительности характеристичных чисел 351
§ 83. Оценка характеристичных чисел методом построения функций
Ляпунова 354
§ 84. Применение метода малого параметра 357
В. Теория устойчивости по первому приближению
§ 85. Теорема об устойчивости по первому приближению 364
§ 86. Некоторые особенности задачи устойчивости по первому при-
приближению для неустановившихся движений 366
§ 87. Критерий Ляпунова 370
§ 88. Другая группа критериев 374
§ 89. Связь с критерием Ляпунова. Обобщенный критерий .... 377
Г. Теория критических случаев.
§ 90. Постановка задачи. Основные определения 379
§ 91. Первая основная теорема о критических случаях ...... 382
§ 92. Вторая основная теорема о критических случаях 395
§ 93. Случай, когда коэффициенты линейных членов постоянны. При-
Приложение к установившимся и периодическим движениям . . 400
§ 94. Критический случай двойного нулевого корня для устано-
установившихся движений 409
§ 95. Критический случай двух пар чисто мнимых корней для
установившихся движений 422
§ 96. Критический случай одного нулевого и пары чисто мнимых
корней для установившихся движений 431
§ 97. Критические случаи периодических движений. Приведение
к установившимся движениям 437
Дополнение!. Об одной задаче теории устойчивости систем
автоматического регулирования 446
§ 98. Постановка задачи 446
§ 99. Исследование системы второго порядка с нелинейностью,
зависящей от первой координаты 447
§ 100. Исследование системы второго порядка с нелинейностью, за-
зависящей от второй координаты 450
Дополнение П. О существовании функций Ляпунова 452
§ 101. Постановка задачи 452
§ 102. Необходимые и достаточные условия существования функ-
функции '/ 453
Дополнение III. Обобщение теорем второго метода Ляпунова 463
§ 103. Критерии, основанные на функциях Ляпунова со знакопосто-
знакопостоянными производными 463
§ 104. Примеры приложения предыдущих теорем 467
ОГЛАВЛЕНИЕ 7
Дополнение IV. Проблемы стабилизации управляемых дви-
движений 475
§ 105. Предварительные замечания 475
§ 106. Постановка задачи о стабилизации 476
§ 107. Постановка задачи об оптимальной стабилизации 478
§ 108. Пример задачи о стабилизации 480
§ 109. Второй метод Ляпунова для задач об оптимальной стабили-
стабилизации 484
§110. Замечания ко второму методу Ляпунова в теории стабили-
стабилизации 489
§ 111. Решение задачи о стабилизации для уравнений первого при-
приближения 492
§ 112. Достаточные условия разрешимости задачи о стабилизации
для линейных систем 495
§ 113. Практические способы решения задач об оптимальной стаби-
стабилизации для линейных систем 499
§ 114. Теоремы стабилизации по первому приближению 508
Примечания редактора 515